Автор: Мелков Г.А. Гуревич А.Г
Теги: электромагнетизм электромагнитное поле электродинамика теория максвелла физика магнитные явления
ISBN: 5-02-014366-9
Год: 1994
Текст
ББК 22.336
Г95
УДК 537.871
ГУРЕВИЧ А. Г., МЕЛКОВ Г. А. Магнитные колебания и волны.— М.:
Физматлит, 1994.—464 с—ISBN 5-02-014366-9
Излагаются физические представления и основы теории ферромагнитного
и антиферромагнитного резонансов и спиновых волн; основы электродинамики
гиротропных сред и принципы построения ферритовых СВЧ устройств.
Рассматриваются нелинейные явления, в частности, параметрическое
возбуждение спиновых волн; взаимодействие колебаний и волн намагниченности
с упругими волнами и носителями заряда; процессы релаксации.
Для научных работников, инженеров-разработчиков магнитных материалов
и приборов, аспирантов и студентов.
Табл. 17. Ил. 240. Библиогр. 466 назв.
Рецензент
доктор физико-математических наук профессор Г. В. Скроцкий
ФБ СП6ГТУ
НИ III III
0000071514
1604050000-0)3
Г КБ-40-41-92 ГАГ. Гуревич, Г. А. Мелков, 199 4
053(02)-94 _ „.,_=_^/
ISBN 5-02-014366-9 „-^i- *""v\
*
'Л
M^ojiUL
ОГЛАВЛЕНИЕ
Предисловие 6
Глава 1. Намагниченный до насыщения изотропный ферромагнетик 9
§ 1.1. Ферромагнетизм 9
§ 1.2. Уравнение движения намагниченности 16
§ 1.3. Высокочастотная магнитная восприимчивость 18
§ 1.4. Учет диссипации 25
§ 1.5. Однородные колебания намагниченности малого эллипсоида 31
Глава 2. Анизотропный ферромагнетик 40
§ 2.1. Уравнение Ландау — Лифшица 40
§ 2.2. Магнитная кристаллографическая анизотропия 47
§ 2.3. Ферромагнитный резонанс в монокристаллах 53
§ 2.4. Ферромагнитный резонанс в поликристаллах 63
Глава 3. Антнферромагнетики и ферриты 69
§ 3.1. Антиферромагнетизм и ферримагнетизм 69
§ 3.2. Антиферромагнитный резонанс 77
§ 3.3. Магнитные колебания в ферримагнетиках 90
Глава 4. Основы электродинамики гиротропных сред 103
§4.1. Уравнения и граничные условия 103
§ 4.2. Однородные плоские волны 108
§ 4.3. Невзаимность 117
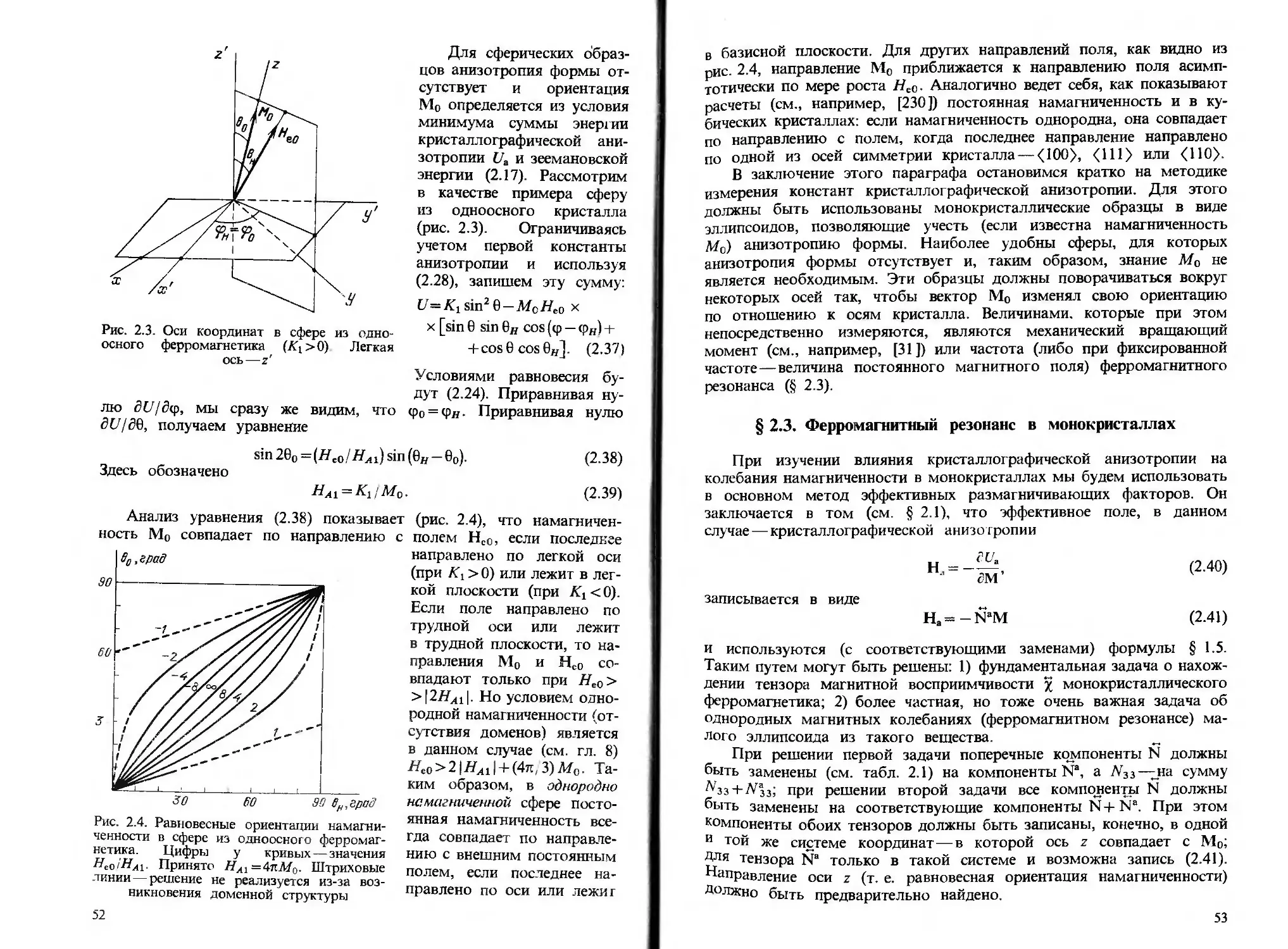
§4.4. Энергетические соотношения 119
§4.5. Метод возмущений 122
Глава 5. Волноводы и резонаторы с гнротропными средами.
Феррнтовые СВЧ устройства 129
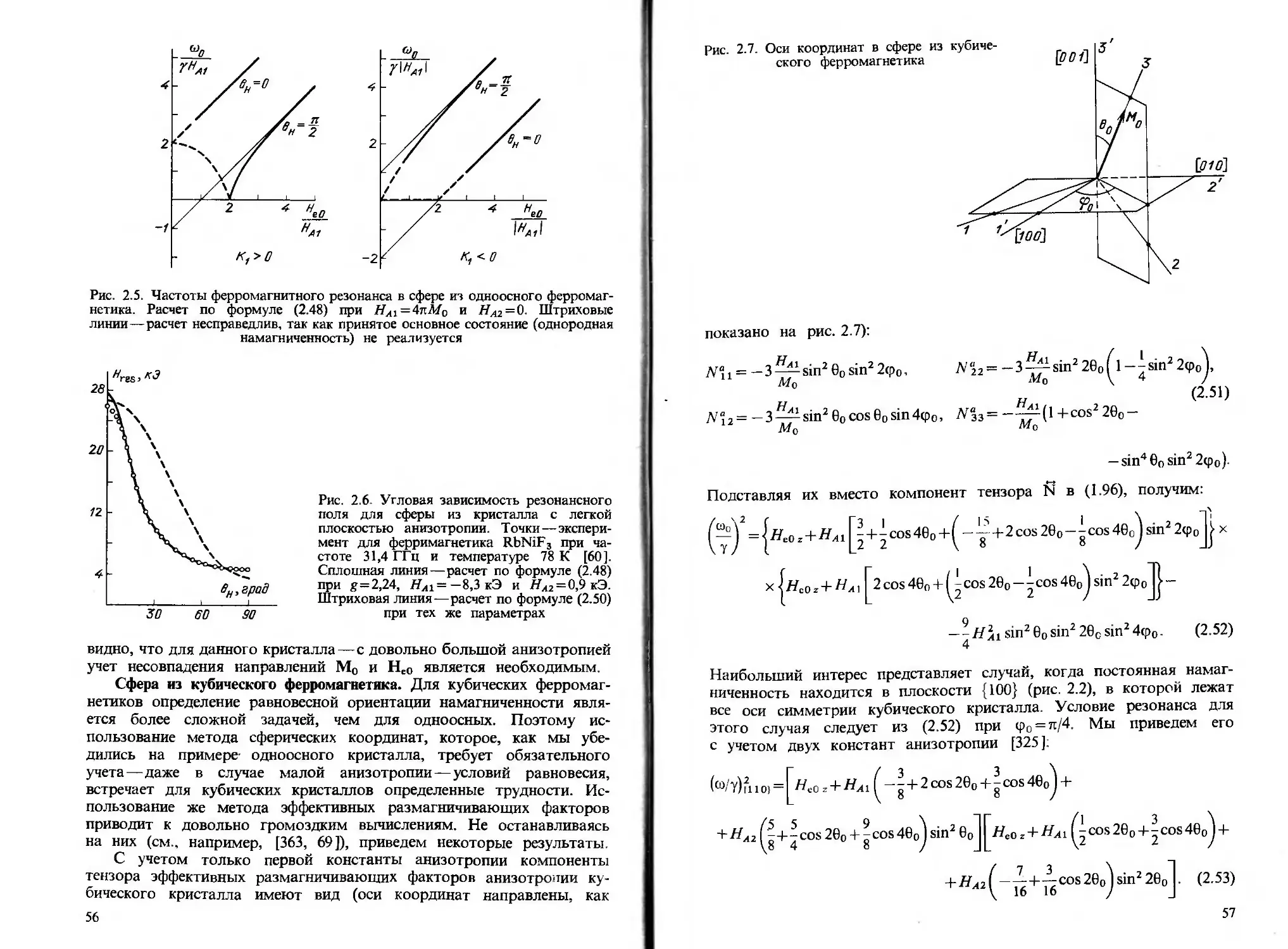
§5.1. Волновод с продольно-намагниченной средой 129
§ 5.2. Волновод с поперечно-намагниченным ферритом 135
§ 5.3. Резонаторы с гиротропными средами 144
§ 5.4. Волноводные сочленения с ферритовыми образцами 151
Глава 6. Магнитостатическяе волны и колебания 161
§6.1. Магнитостатическое приближение 161
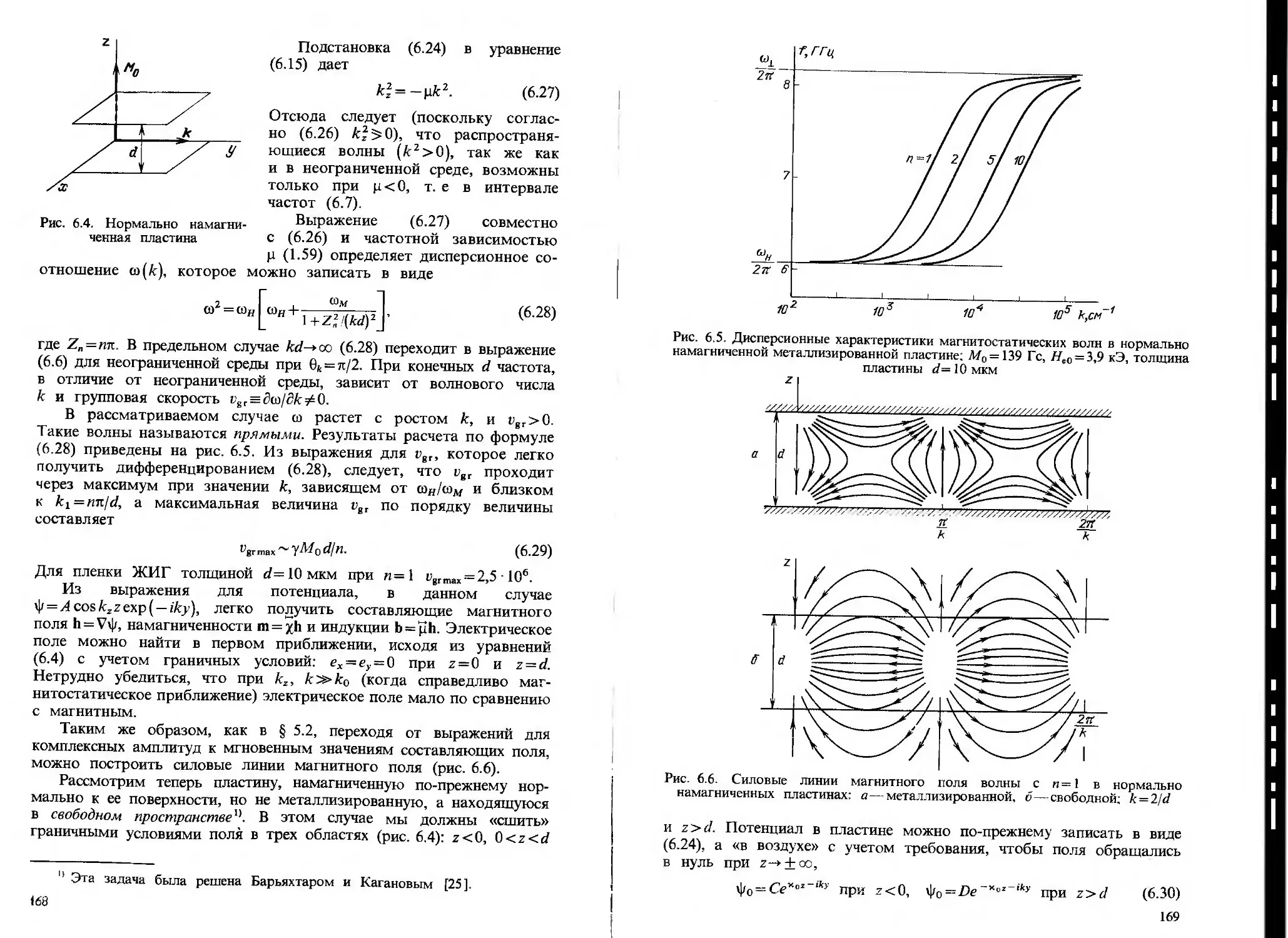
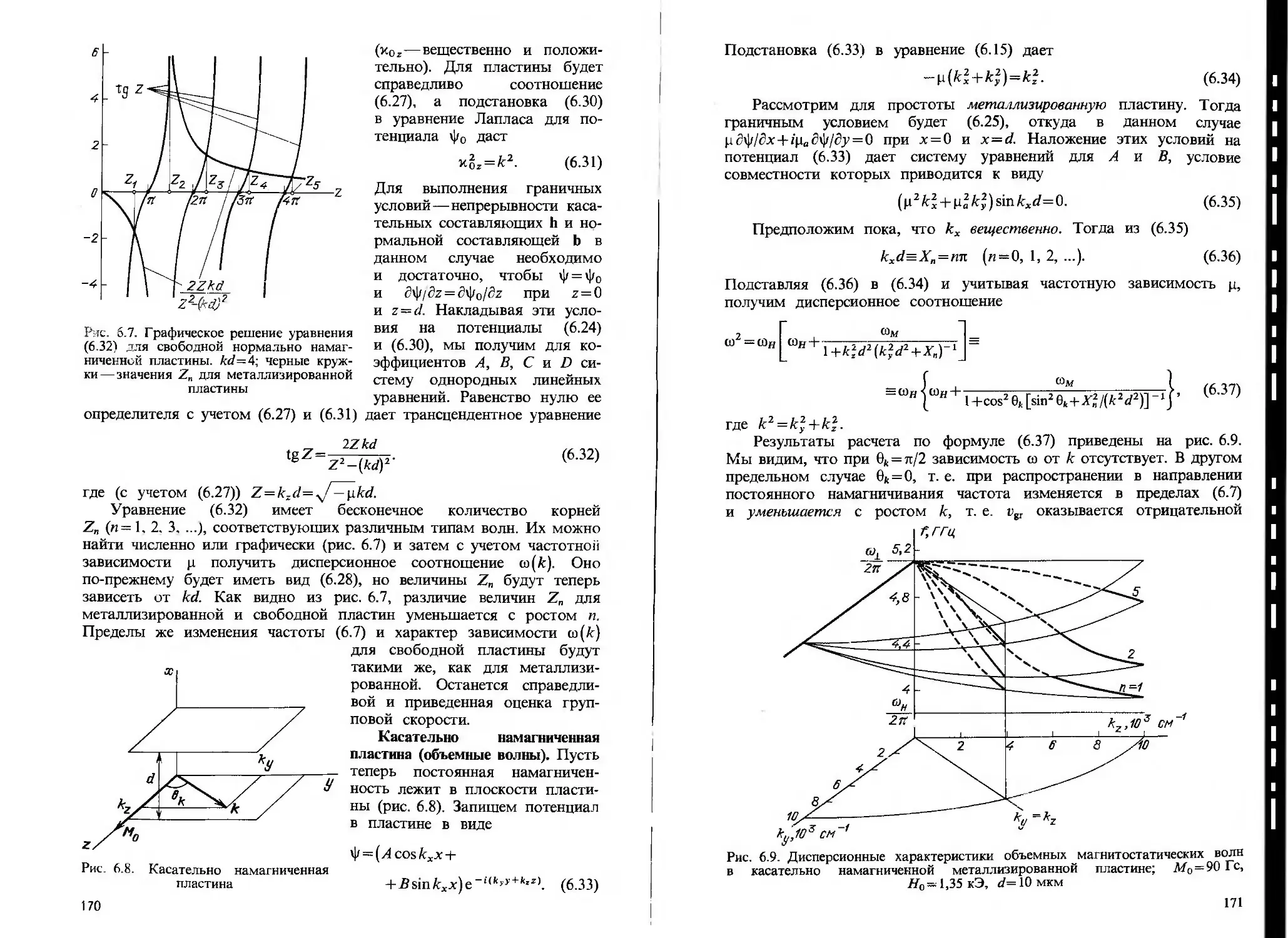
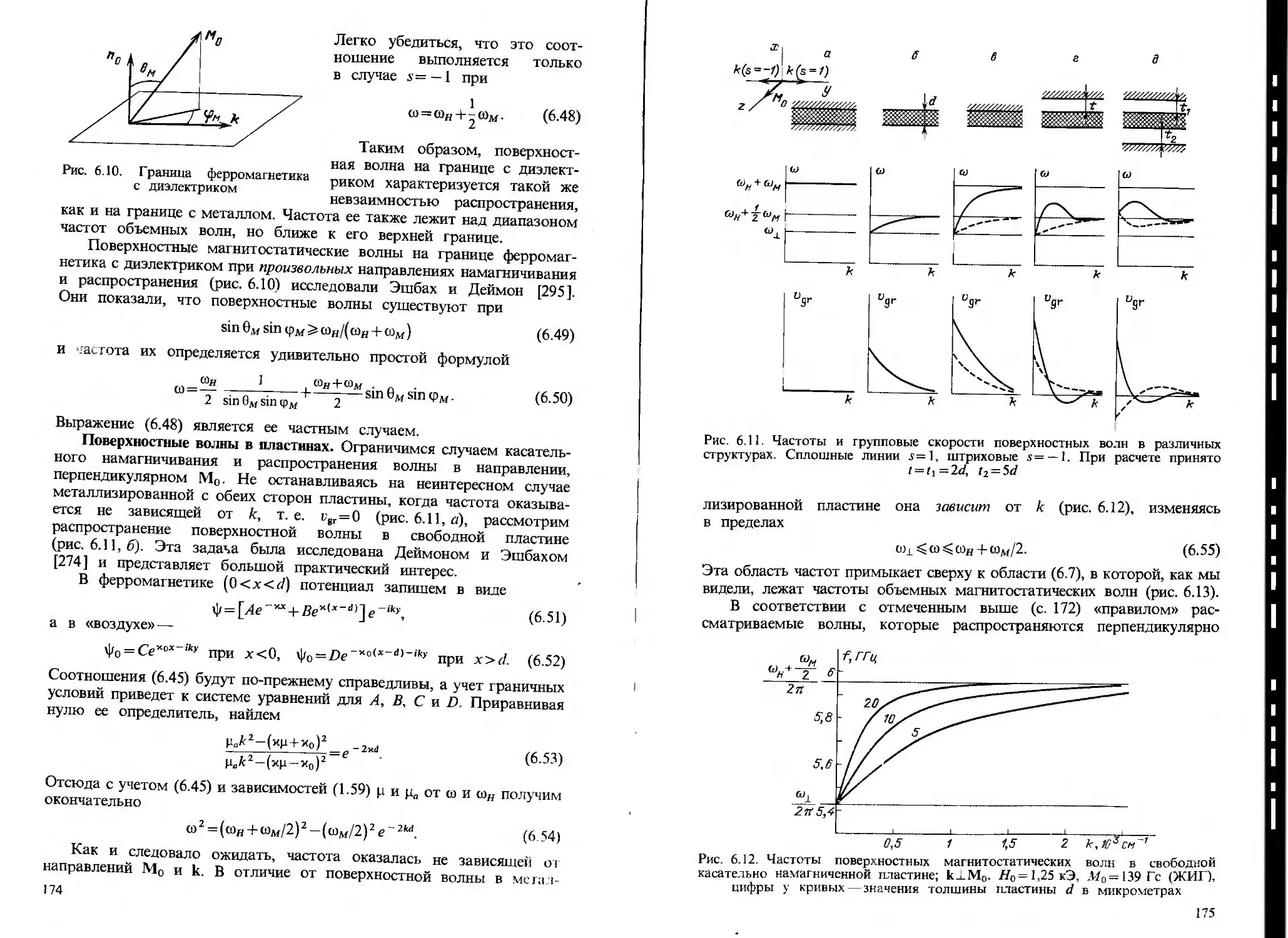
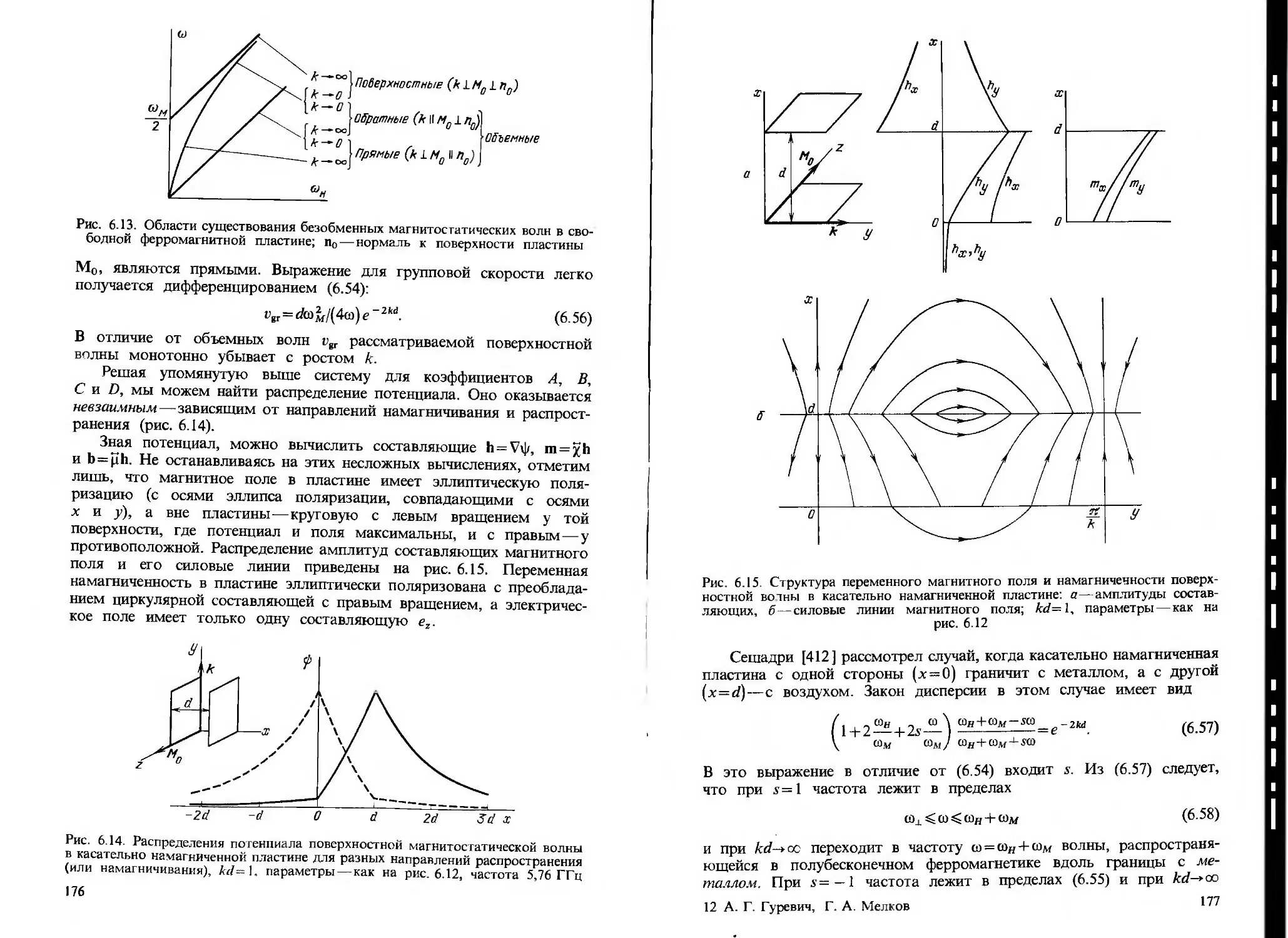
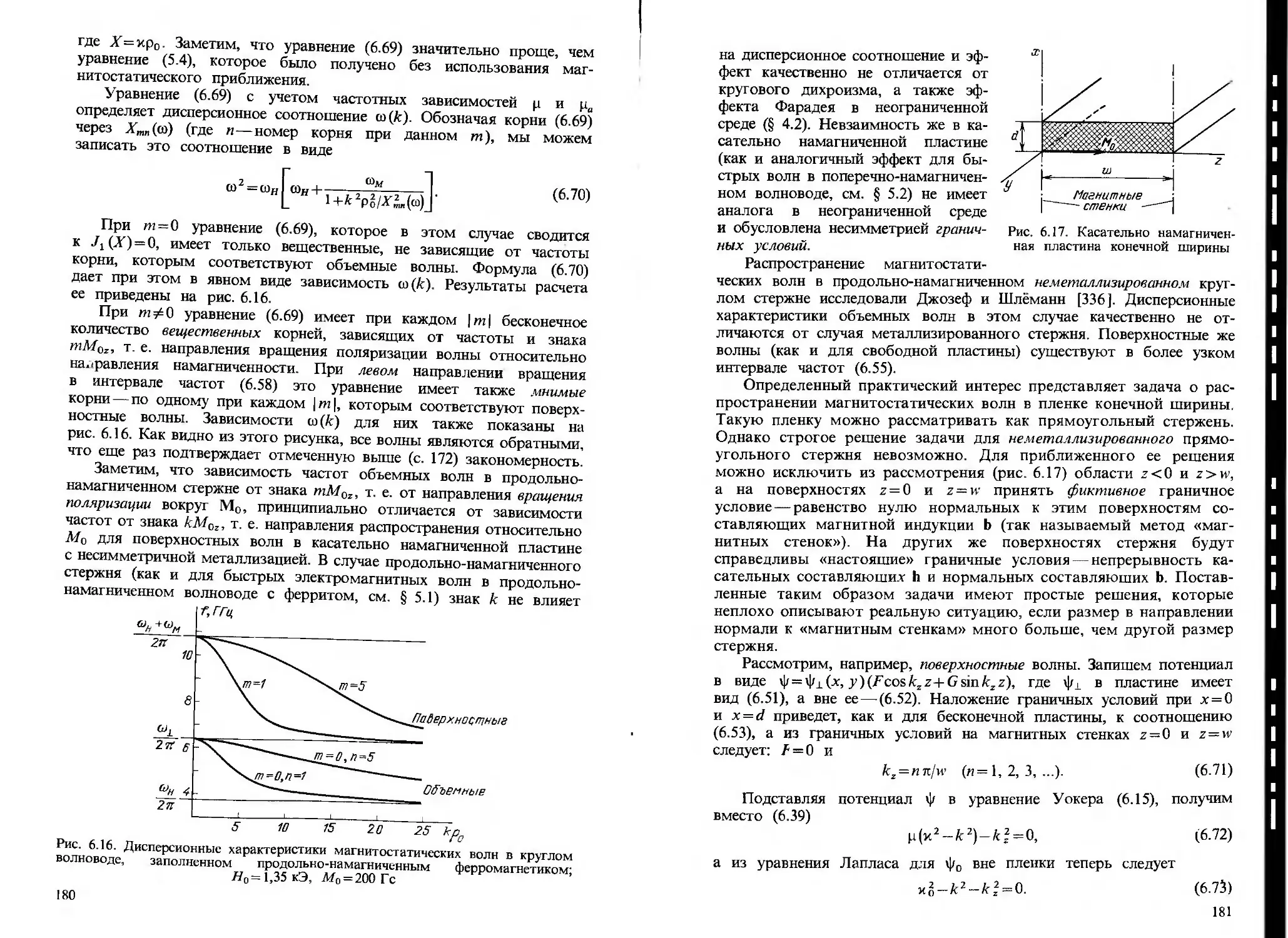
§ 6-.2. Магнитостатическяе волны в пластинах и стержнях 167
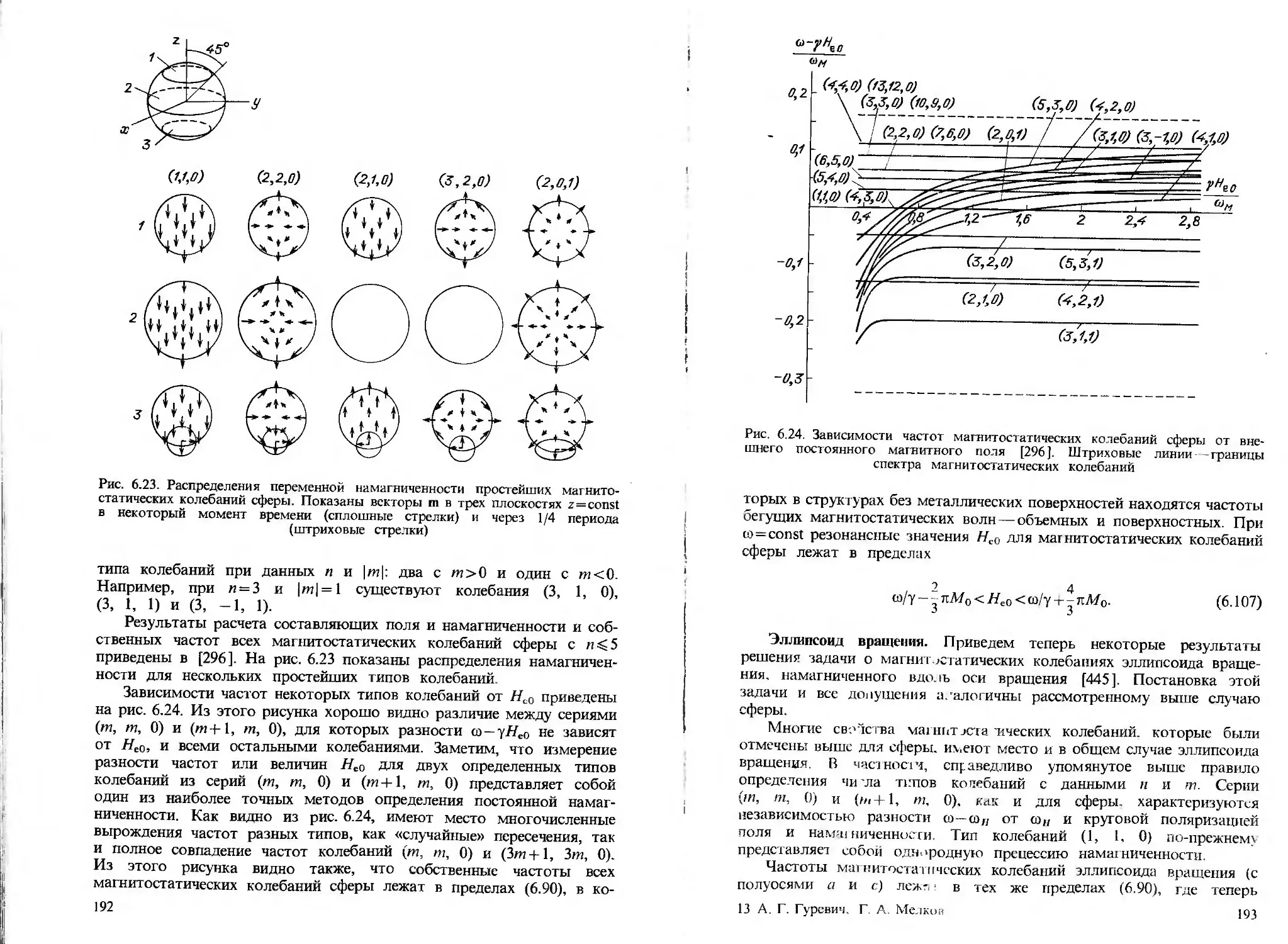
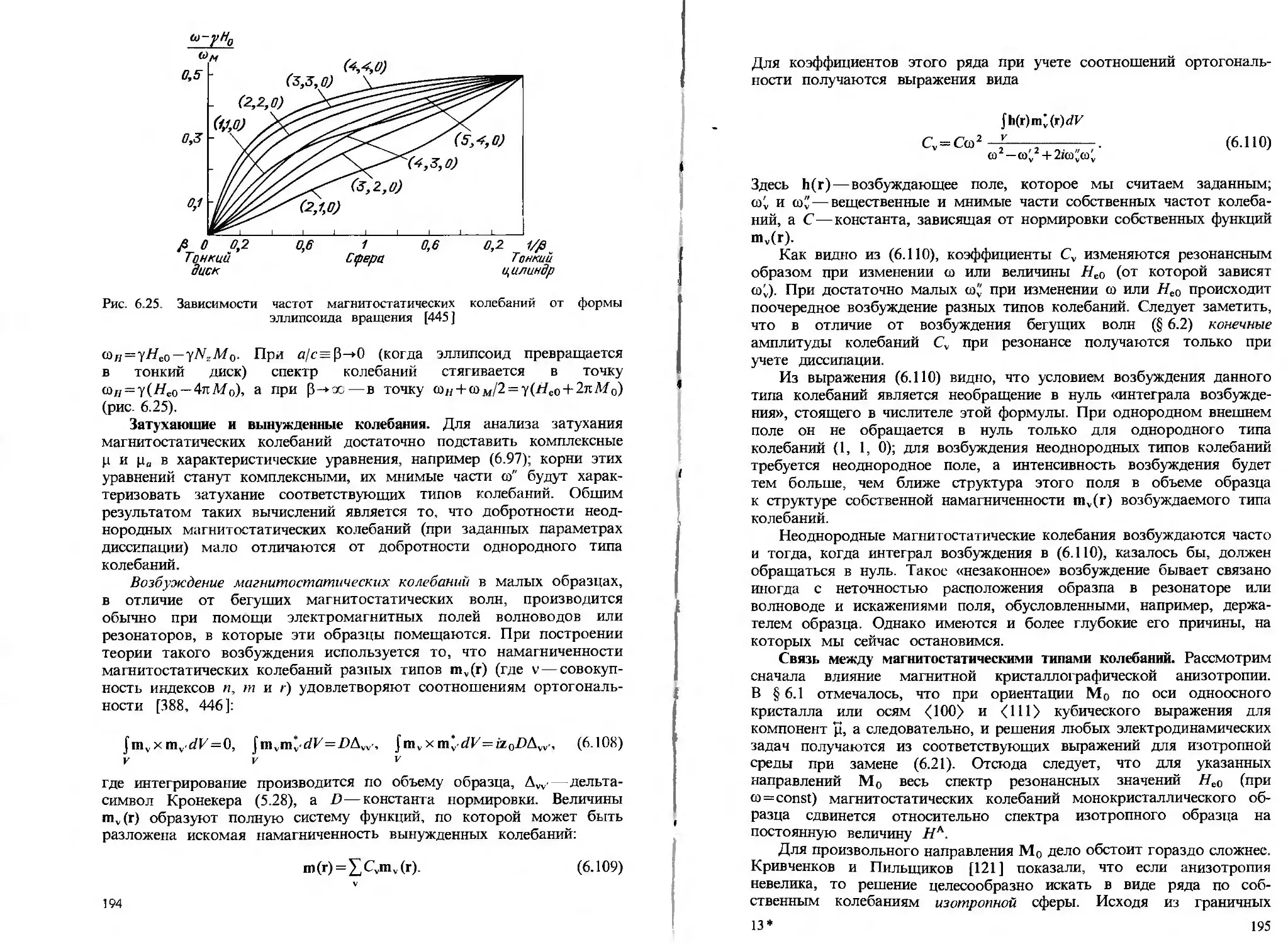
§ 6.3. Магнитостатическяе колебания 187
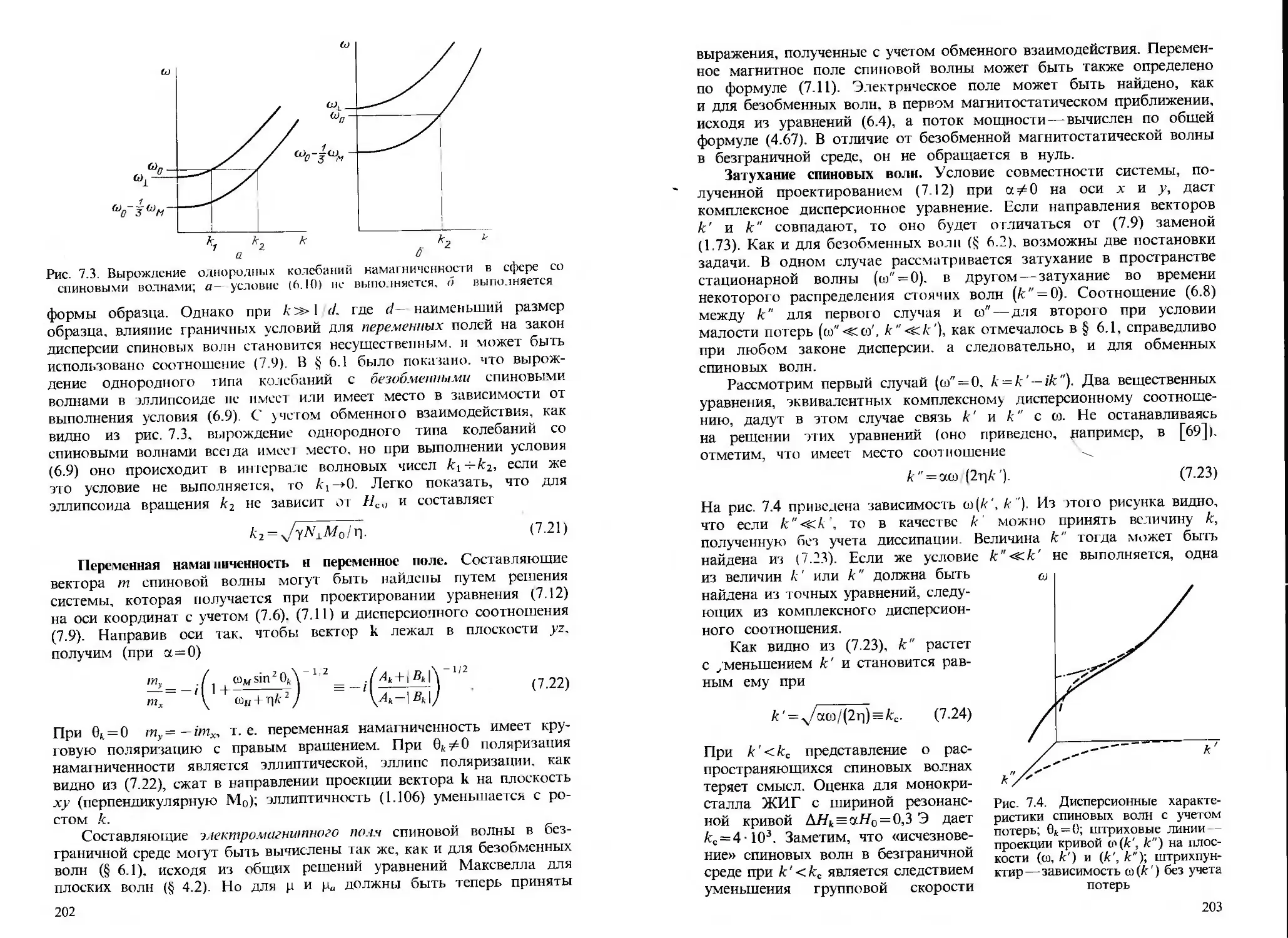
Глава 7. Спиновые иолны 198
§7.1. Спиноиые волны в неограниченном ферромагнетике 198
§ 7.2. Спиновые волны в ограниченных телах 205
§ 7.3. Магноны 221
§ 7.4. Микроскопическая теория спиновых волн 229
Г л а в а 8. Колебания и волны намагниченности при палнчин домеиои 240
§8.1. Магнитные домены 240
§ 8.2. Колебания доменных стенок 244
§ 8.3. Ферромагнитный резонанс при наличии доменной структуры 248
Глава 9. Нелинейные колебания памагниченности 258
§9.1. Ферромагнитный резонанс в сильных переменных полях 258
§ 9.2. Умножение и преобразование частоты 265
Глава 10. Параметрическое иозбуждение магнитных колебаний и иолн .... 273
§ 10.1. Нелинейная связь колебаний и волн намагниченности 273
§ 10.2. Пороги параметрического возбуждения при поперечной накачке .... 278
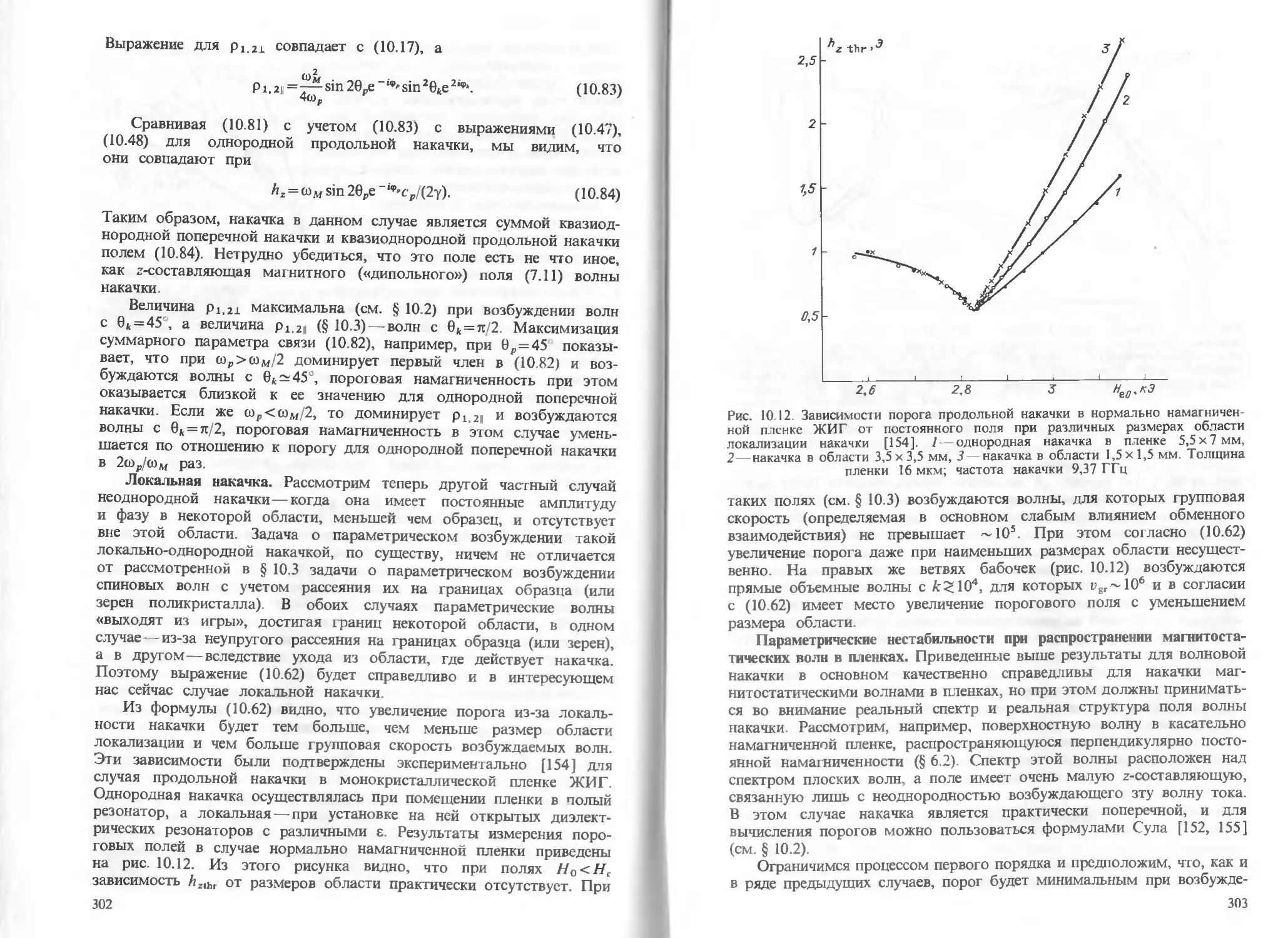
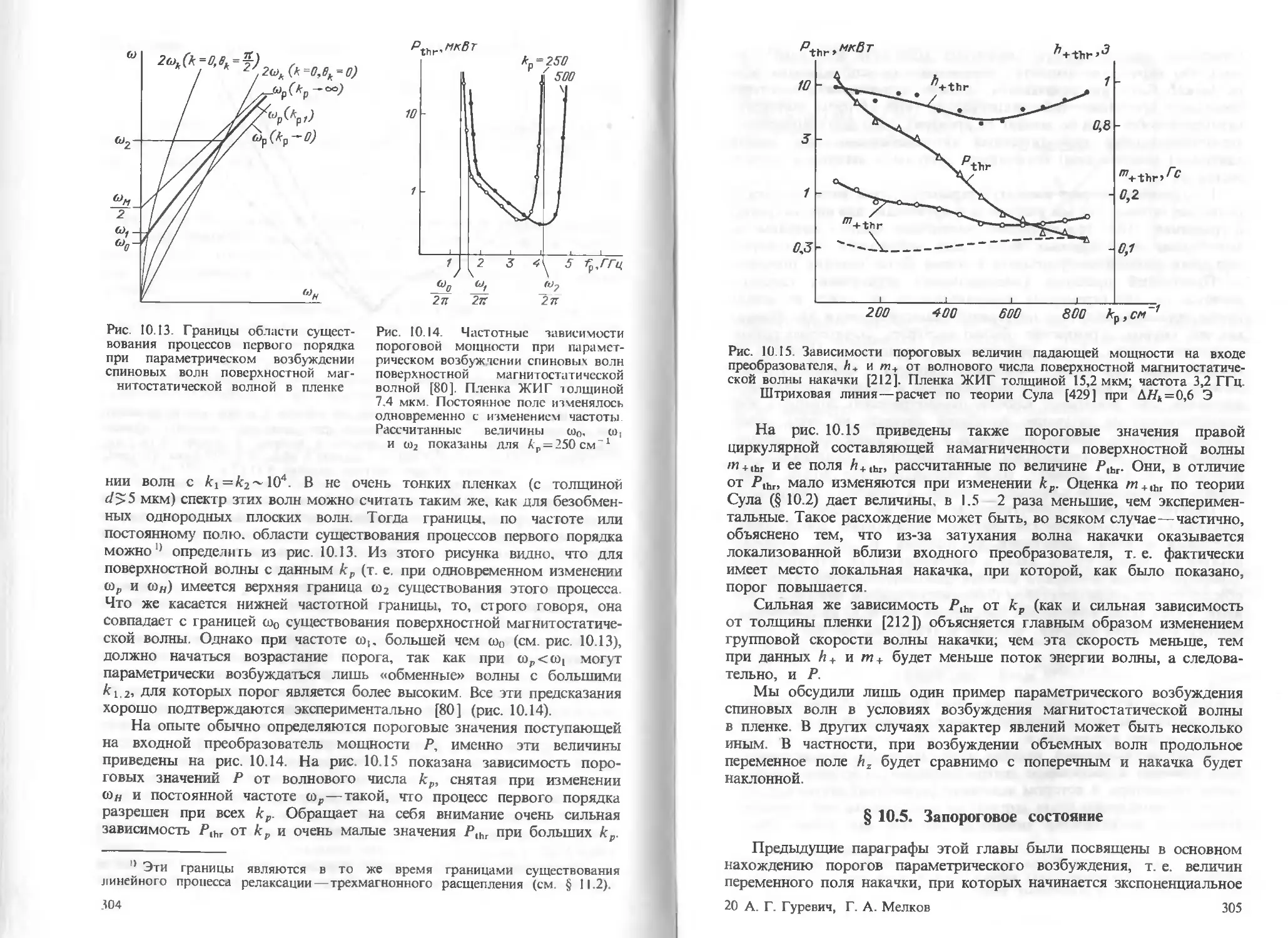
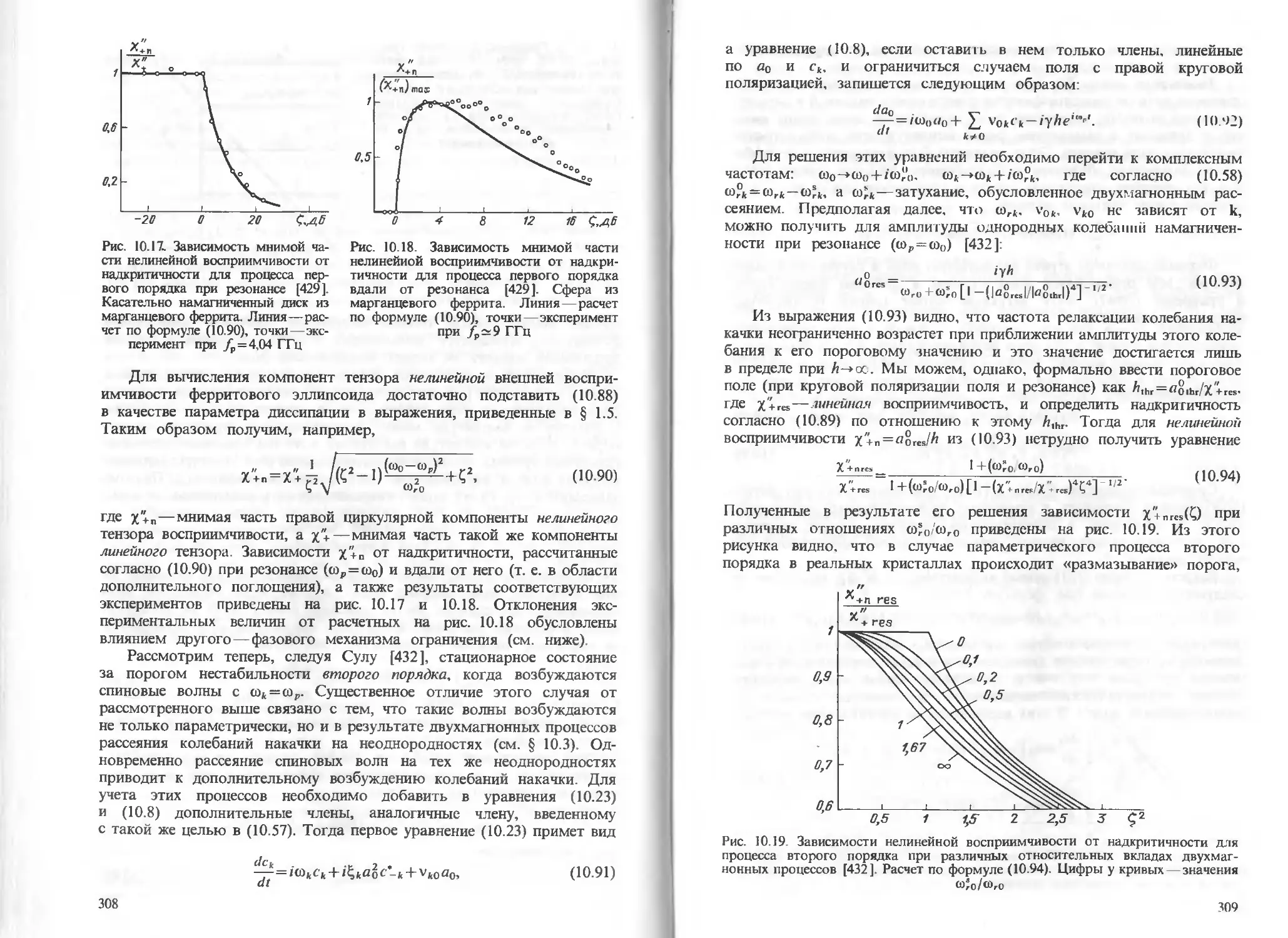
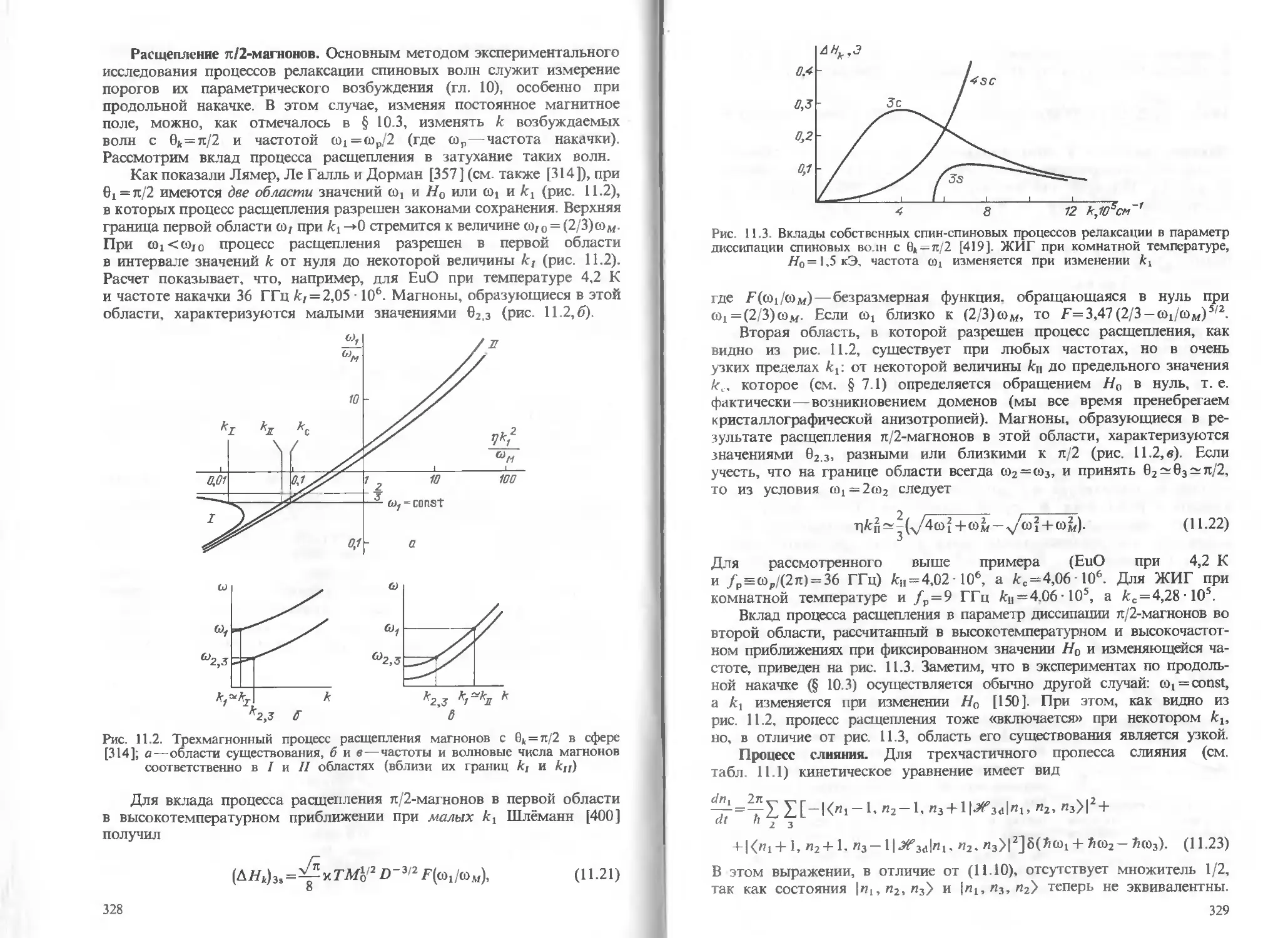
§ 10.3. Продольная и наклонная накачка 285
§ 10.4. Нестабильность неоднородных колебаний и неоднородная накачка 294
§ 10.5. Запороговое состояние 305
Глава 11. Спин-спиноиая релаксация 318
§11.1. Процессы релаксации в магнитоупорядоченных веществах 318
§ 11.2. Собственные процессы спин-спиновой релаксации 324
§ 11.3. Двухмагнонные процессы 338
Глава 12. Магнитоупругаи свизь 352
§ 12.1. Упругие свойства н магнитоупругое взаимодействие 352
§ 12.2. Влияние упругих напряжений на ферромагнитный резонанс 359
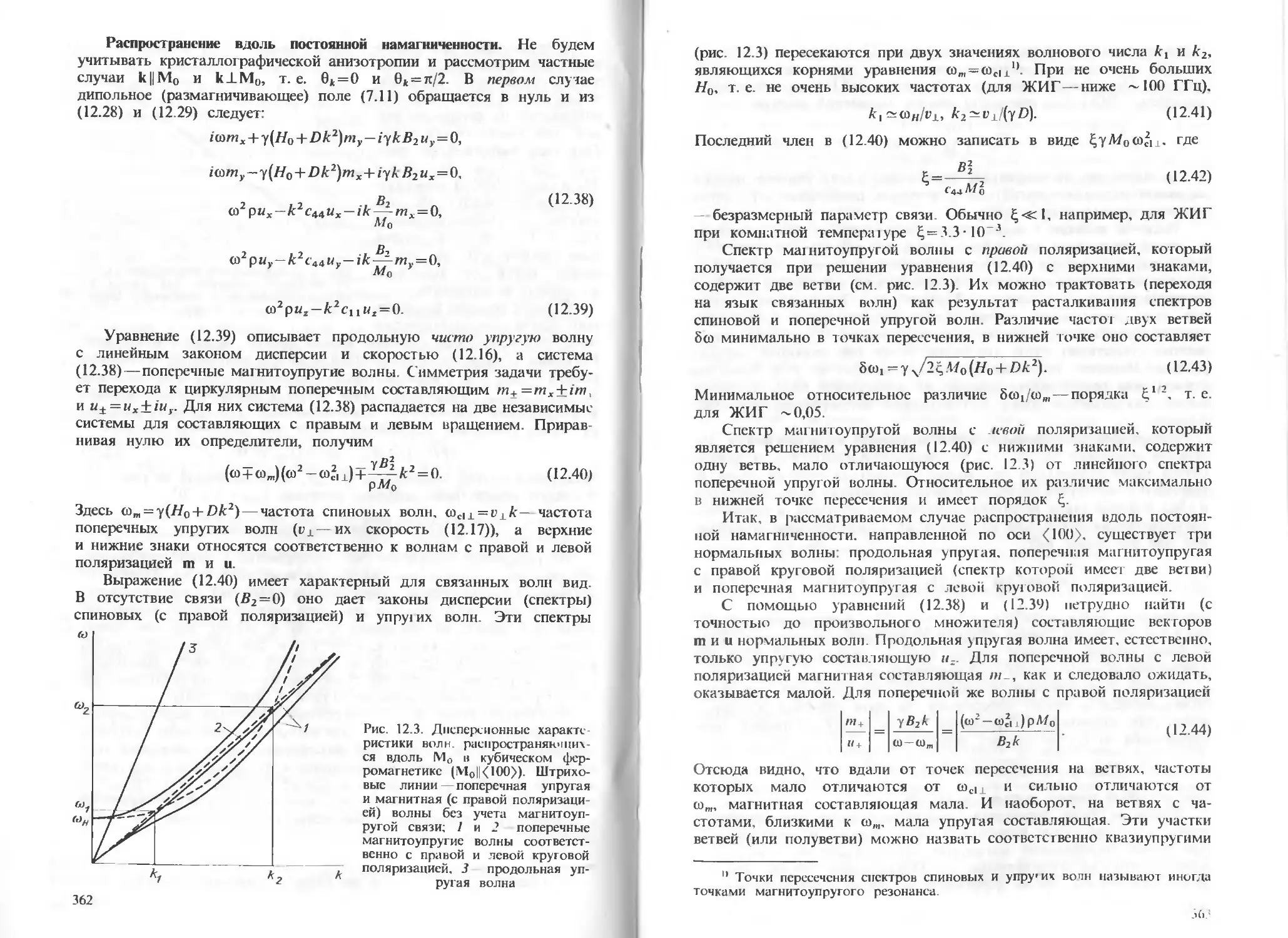
§ 12.3. Магнитоупругие волны 361
§ 12.4. Параметрическое возбуждение магнитоупругих волн 369
§ 12.5. Спин-решеточная релаксация 375
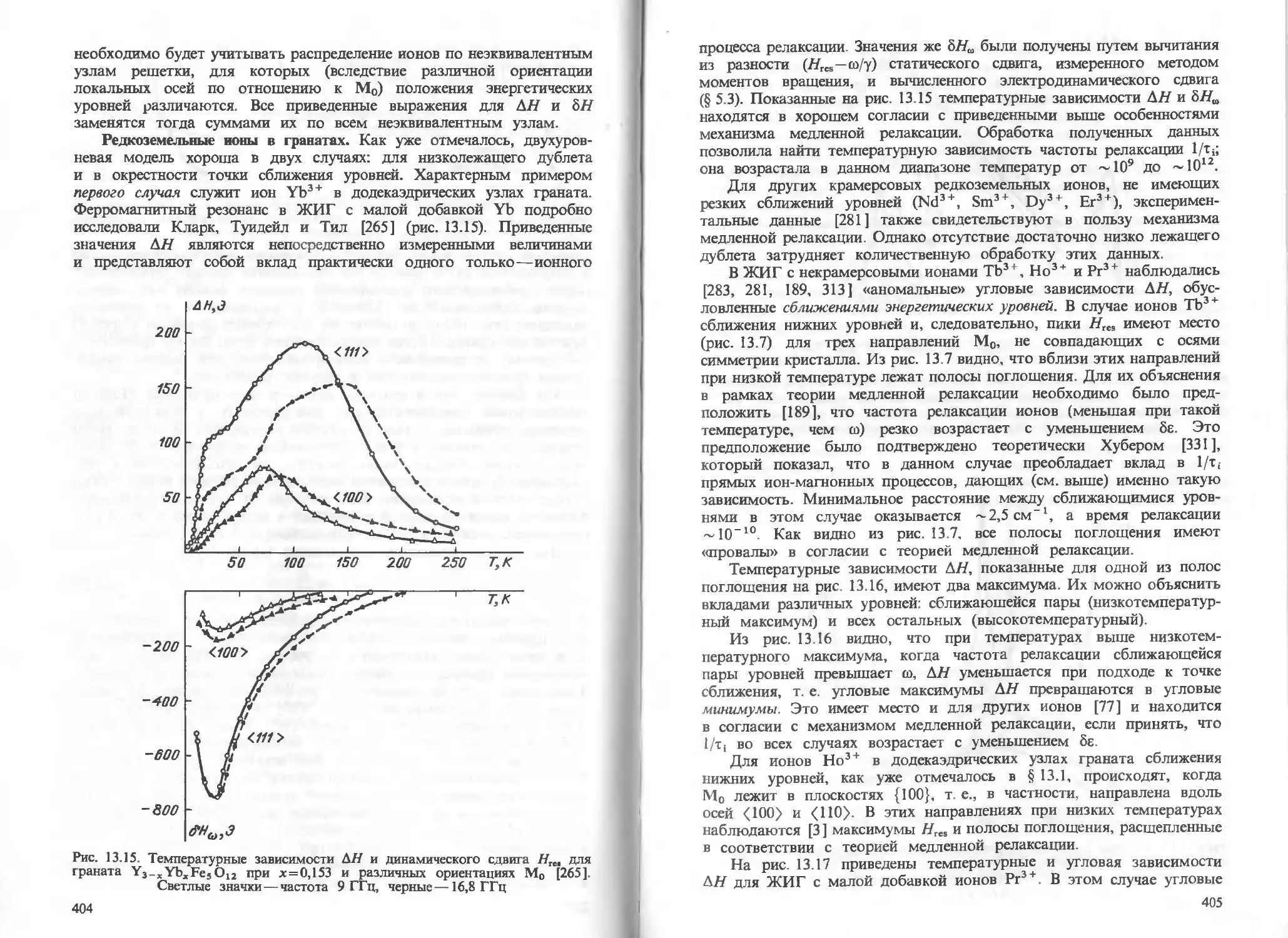
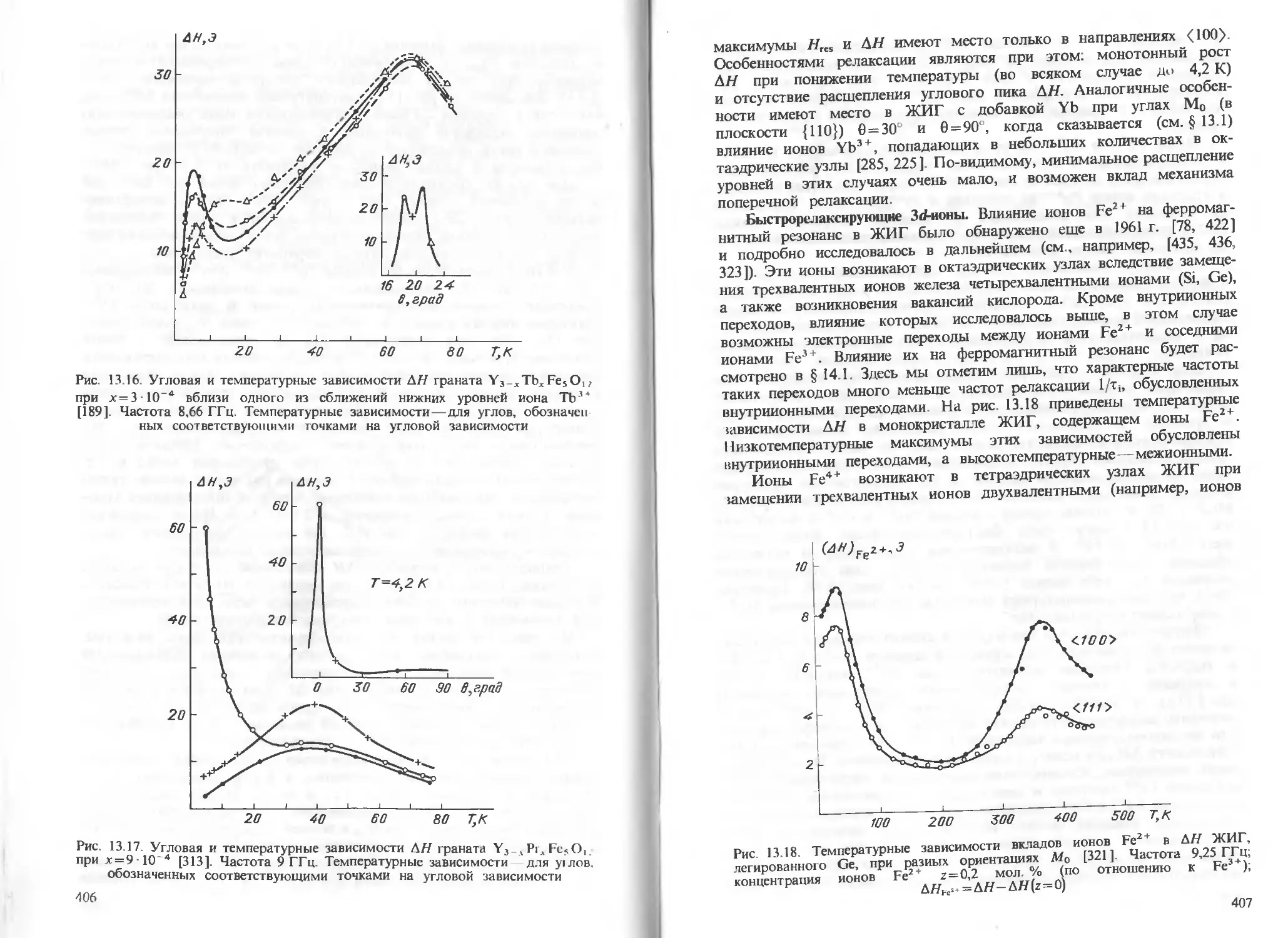
Глава 13. Ионная анизотропия и релаксация 381
§ 13.1. Анизотропия, вызванная ионами с сильной спин-орбитальной
связью 381
§ 13.2. Ионные процессы релаксации 393
4
Глава 14. Взаимодействие магнитных колебаний и волн с носителями
зарида 410
§ 14.1. Влияние носителей заряда в полупроводниках 410
§ 14.2. Ферромагнитный резонанс и спиновые волны в металлах 422
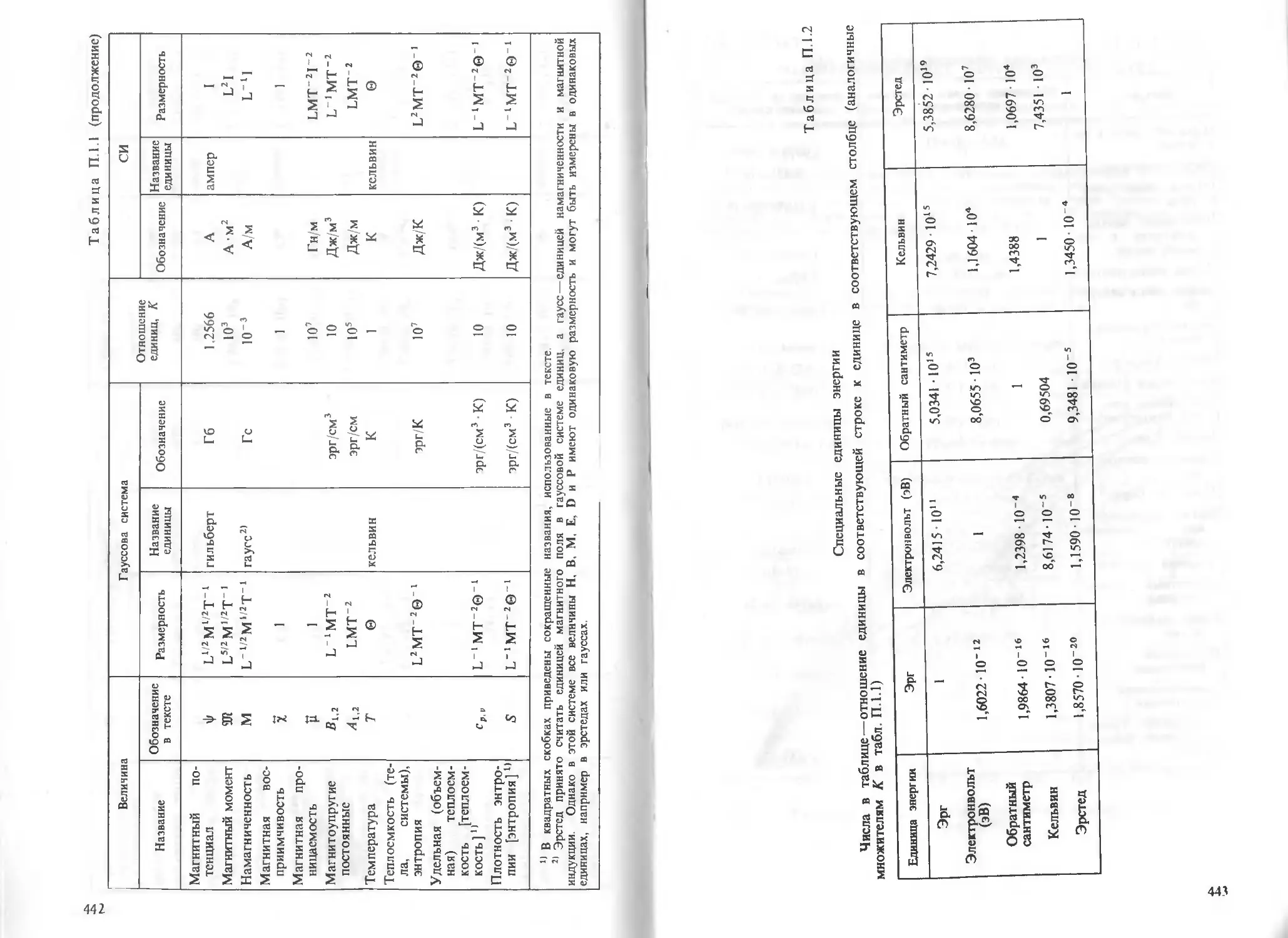
Приложение 1. Единицы и константы 438
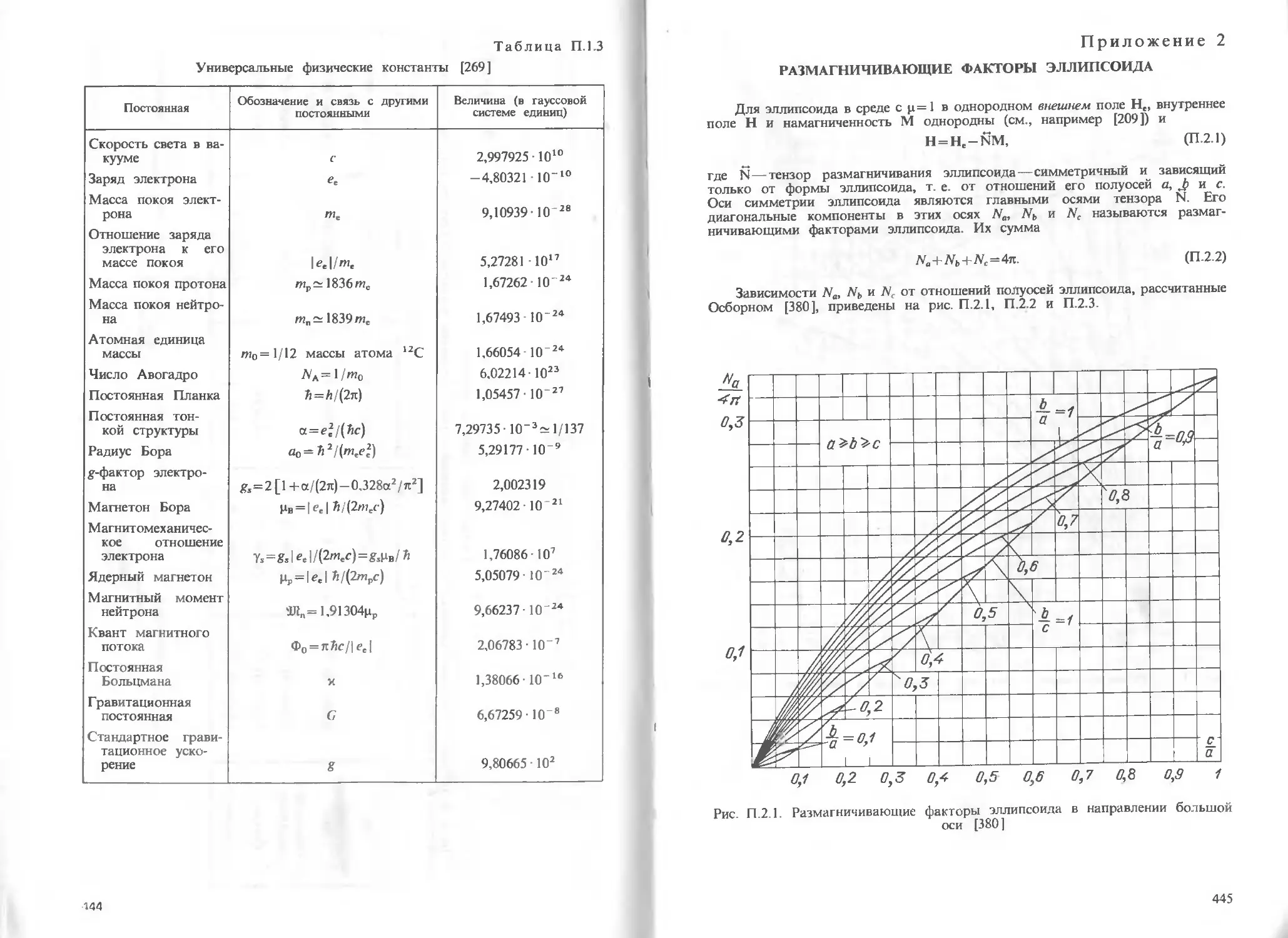
Приложение 2. Размагничивающие факторы эллипсоида 445
Список литературы 448
Указатель к списку литературы 460
ПРЕДИСЛОВИЕ
В этой книге рассматриваются электромагнитные колебания
и волны в магнитоупорядоченных веществах: ферро-, антиферро-
и ферримагнетиках. Сюда входят такие вопросы, как ферромагнитный
и антиферромагнитный резонансы, спиновые волны, в частности, их
параметрическое возбуждение, процессы в волноводах и резонаторах,
содержащих намагниченные ферриты. Рассмотрение ведется в
основном в рамках классической теории с использованием уравнений
электродинамики и уравнения движения намагниченности.
К магнитному упорядочению приводит, как известно, обменное
взаимодействие, природа которого является квантовой, т. е. не может
быть понята на основе классических представлений. Но наличие
)того взаимодействия не препятствует, а наоборот, приводит к
возможности классического рассмотрения динамических процессов, в
частности, колебаний и воли и магнитоупорядоченных веществах.
Квантовый подход необходим лишь при описании процессов
релаксации, определяющих затухание исследуемых колебаний или волн.
Колебания и волны в магнитоупорядоченных средах представляют
интерес по крайней мере с трех точек зрения:
1) как часть фундаментальной проблемы взаимодействия
электромагнитного поля с веществом, находящимся в постоянном
магнитном поле, т. е. проблемы магнитного резонанса;
2) как эффективный способ исследования магнитоупорядоченных
веществ, в частности, магнитных материалов, используемых в технике;
3) как основа для создания магнитных устройств диапазона СВЧ;
разработкой и производством таких устройств занимается целая
отрасль электронной промышленности, перед которой возникают все
новые задачи в связи с освоением новых диапазонов частот и
расширением функциональных возможностей аппаратуры.
Со времени обнаружения ферромагнитного (1946 г.) и
антиферромагнитного (1952 г.) резонансов исследованию колебаний и волн
в магнитоупорядоченных веществах было посвящено огромное количество
оригинальных работ и ряд монографий [66, 204, 159, 417, 128, 15. 162. 69,
145. 423]. Эта книга отличается от предыдущих монографий, во-первых,
более широким охватом вопросов, входящих в рассматриваемую
проблему, и, во-вторых -от многих из них—доступностью для широкого
круга читателей. Она может служить учебным пособием для всех
изучающих данную область как физиков, так и инженеров-разработчиков
магнитных материалов или приборов. В то же время она может выполнять
функции справочной монографии для тех, к i о уже с этой областью знаком.
6
Предполагается, что читатель изучал математику, физику твердого
тела, электродинамику и радиотехнику в объеме курсов университетов
или технических вузов, однако мог изрядно забыть эти дисциплины.
Поэтому все необходимые для понимания излагаемых вопросов
сведения кратко напоминаются. Прежде всего это относится к
основным представлениям физики магнитных явлений, которым
посвящены § 1.1, 2.2, 3.1. 8.1 и 12.1.
Задача этой книги — не только изложить некоторые результаты,
но и научить их получать. Поэтому большинство выводов дается
с такой степенью подробности, чтобы читатель, обладающий
указанной выше подготовкой, мог их воспроизвести. В тех случаях, когда
выполнить это было невозможно из-за громоздкости или сложности
математического аппарата, результаты приводятся без попыток дать
«сокращенный вывод».
В книге не описывается техника эксперимента, ибо авторы
согласны с Блаттом [28] в том, что «экспериментальную технику
нельзя выучить по книгам, она должна быть освоена в лаборатории».
Экспериментальные результаты приводятся, как правило, только в тех
случаях, когда они сушественно дополняют существующие теории
i или противоречат им. Исключения сделаны лишь для небольшого
числа экспериментов, вошедших в «золотой фонд» данной области
физики. Тем не менее эксперимент незримо присутствует в книге,
определяя выбор задач и характер изложения. Книга написана
экспериментаторами и в первую очередь для экспериментаторов.
Однако авторы питают надежду, что и теоретикам, в особенности
начинающим, она сможет оказаться полезной.
При отборе рассматриваемых вопросов мы старались
руководствоваться следующими критериями: фундаментальность,
поучительность и актуальность. И когда эти критерии вступали в противоречие,
принимались решения, которые не могли не быть субъективными.
Однако некоторые вопросы, даже удовлетворяющие всем упомянутым
критериям, оказались не затронутыми. К числу их относятся спиновые
волны в антиферромагнетиках, их параметрическое возбуждение,
взаимодействие спиновых волн с электромагнитным полем более
высокой частоты (светом), связь электронных магнитных колебаний
с ядерной магнитной системой. Следовало бы обсудить вопрос
о взаимоотношении нестационарных динамических процессов, таких
как движение доменов и доменных стенок, распространение ударных
волн и солитонов (которые сами по себе находятся за рамками
этой книги), с рассматриваемыми в ней колебательными процессами.
Но благими намерениями вымощена дорога... в данном случае
к безграничному росту объема книги и срока ее написания.
Два замечания методического характера. Первое: изложение
ведется с нарастающей сложностью, с многочисленными ссылками
, на предыдущие главы. Поэтому (кроме случаев, когда к книге
обращаются за конкретными справками) рекомендуется читать ее
последовательно, уделяя, конечно, меньше внимания тем вопросам,
которые в данный момент читателя меньше интересуют, но не
пропуская их совсем. И второе: в книге не приводится специально
7
сформулированных задач. Однако читателю настоятельно
рекомендуется проводить подробные выводы формул, оценки и сравнение
различных результатов. Слова «нетрудно убедиться», «можно
показать» и т. п. следует рассматривать как предлагаемые задачи.
В книге используется гауссова система единиц, наилучшим образом
соответствующая главной цели книги — выяснению физической
сущности рассматриваемых явлений. В ряде случаев, как это принято
в докладах и дискуссиях, размерности числовых величин (в этой
системе) опускаются.
Список литературы включает все источники, на которые в тексте
имеются ссылки. При этом авторы не стремились ни к полноте,
ни к утверждению приоритетов. Исходя из этого, мы избегали
ссылок на труднодоступные издания и из работ на данную тему
обычно выбирали позднейшую, если она — более подробная и ясная.
Однако в список литературы включен ряд старых (но не устаревших)
работ, которые явились важными этапами в формировании
современных взглядов на обсуждаемые вопросы. В него включен также ряд
работ, в основном новых, на которые прямых ссылок в тексте нет,
но с которыми полезно ознакомиться при изучении затронутых
в книге вопросов. Для того чтобы список литературы можно было
использовать и независимо от текста, приведен тематический указатель
к нему.
Авторы сожалеют, что они не в состоянии перечислить всех,
кто в процессе нашей работы над этой книгой своими замечаниями
и советами способствовал ее улучшению. Мы глубоко благодарны им.
В заключение мы хотим отметить, что все содержание книги
является результатом совместной работы обоих авторов и они вместе
несут ответственность за все возможные ошибки и упущения. Тем
читателям, кто возьмет на себя труд сообщить нам о них, мы
будем очень признательны.
Глава 1
НАМАГНИЧЕННЫЙ ДО НАСЫЩЕНИЯ
ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
§ 1.1. Ферромагнетизм
Задачей этой книги является изучение динамических магнитных
процессов — колебаний и волн намагниченности в магнитоупорядочен-
ных веществах. Но прежде чем перейти к рассмотрению этих
процессов, мы напомним основные представления теории
ферромагнетизма".
Все вещества делятся на диамагнетики и парамагнетики. Последние
содержат элементарные магнитные моменты, которые ориентируются
внешним магнитным полем, вследствие чего возникает
намагниченность в направлении этого поля. Однако в некоторых парамагнетиках
ориентация (упорядочение) элементарных магнитных моментов может
происходить спонтанно, в отсутствие внешнего поля. К ним относятся,
в частности, ферромагнетики, в которых упорядочение заключается
в параллельной ориентации всех элементарных моментов, приводящей
к возникновению большой спонтанной намагниченности; им будет
уделено в этой книге наибольшее внимание.
Необходимо сразу же подчеркнуть два обстоятельства. Во-первых,
магнитному упорядочению препятствует тепловое движение.
Вследствие этого спонтанное упорядочение близко к идеальному только
при очень низких температурах. А при некоторой температуре,
температуре Кюри 7с, тепловое движение полностью разрушает
дальний магнитный порядок, и (в отсутствие внешнего магнитного
поля) происходит фазовый переход в неупорядоченное состояние.
Во-вторых, направления, по которым происходит спонтанная
ориентация магнитных моментов ферромагнетика, в отсутствие
внешнего магнитного поля и в слабых полях обычно не являются
одинаковыми во всем объеме образцов; образцы распадаются на
области — домены, внутри которых эти направления приблизительно
одинаковы, но сушественно изменяются от одного домена к другому.
В результате намагниченность, усредненная по большому числу
доменов, оказывается значительно меньшей, чем спонтанная
намагниченность в каждом домене, и часто (в отсутствие внешнего
магнитного поля) обрашается в нуль.
Элементарные магнитные моменты. Моменты, об упорядочении
ориентации которых шла речь — это собственные (спиновые) и ор-
" Для краткого изучения (или повторения) основ теории ферромагнетизма
можно рекомендовать руководства [31, 1131, а для более углубленного — [49,
201, 122, 187].
ч
битальные магнитные моменты электронов. Поскольку моменты
электронов внутренних, замкнутых оболочек атомов компенсируют
друг друга, вклад в парамагнетизм и ферромагнетизм могут вносить
лишь электроны незаполненных, в частности, 3d- и 4/-оболочек,
а также электроны внешних .s-оболочек, участвующие в
электропроводности. При этом проявляются существенные особенности различных
классов веществ. В ионных кристаллах1' элементарными магнитными
моментами могут считаться, вообще говоря, суммарные (спиновые
плюс орбитальные) моменты ионов. Однако орбитальные моменты
некоторых Зб?-ионов либо равны нулю, либо «заморожены» (см.
§ 13.1). В этих случаях элементарными магнитными моментами
могут считаться спиновые моменты ионов.
Магнитные моменты в диэлектриках и полупроводниках можно
считать локализованными в узлах кристаллической решетки. В
металлах моменты 3d- или 4/-электронов локализованы лишь частично,
в большей мере — в 4/-металлах; существенный вклад вносит также
делокализованная плотность магнитного момента электронов
проводимости.
Будем сначала рассматривать локализованные элементарные
магнитные моменты как классические магнитные диполи. Такой диполь,
находящийся в точке / и имеющий магнитный момент 9И/, создает
в точке f магнитное поле [196]
Пг г/г
где г ff—радиус-вектор, соединяющий точки / и /'. Если в точке
/' расположен другой диполь с моментом 9И/', то на него действует
момент сил
Т = 9И/,хН, (1.2)
а энергия взаимодействия этих двух диполей
Е/г = -<ГСГН = - тг'гг)1*г'гг) + Щ™г (L3)
Такая—классическая — трактовка элементарных магнитных моментов
позволяет найти энергию магнитного взаимодействия всех моментов
образца
^м={Х Ie/r, (1.4)
/ r*f
однако, как мы увидим, не может объяснить причину магнитного
упорядочения.
Приступая к выяснению этой причины, отметим прежде всего,
что элементарные магнитные моменты являются микроскопическими
объектами, подчиняющимися законам квантовой механики. Эти
моменты, как и другие динамические переменные, квантовая механика
" Говоря об ионных кристаллах, мы не исключаем некоторо! о вклада
ковалентности в их химическую связь.
10
(см., например, [132]) рассматривает как операторы, в данном
случае—векторные, действующие на соответствующие волновые
функции. Величинами, которые могут быть получены в результате
измерений, являются собственные значения этих операторов.
Собственные значения оператора проекции момента количества
движения (или механического момента) на некоторую ось (z),
выбираемую за ось квантования, представляют собой дискретные
величины, ближайшие из которых различаются на h. Их принято
измерять в единицах h, тогда, например, для спинового момента
{5г}=5, 5-1, ...,(-S), (1.5)
где фигурные скобки обозначают собственные значения стоящего
в них оператора, a 5—спиновое квантовое число (спин) данной
частицы, которое может быть полуцелым или целым. Для электрона
5=1/2 и {&}=±Г2. Для иона Fe3+ спин 5=5 2 и {5г} = 5 2, 3/2,
1/2, (-1/2), ( — 3/2), ( — 5/2). Аналогичным образом квантуются и
проекции Lz орбитального момента, но значения орбитального квантового
числа L могут быть только целыми.
Проекции оператора момента количества движения на две другие
оси х и у не имеют определенных собственных значений в том
представлении, в котором осью квантования является ось z. а
собственные значения квадрата длины вектора, например, спинового
момента (в единицах Ъ2)
{|S|2} = 5(5+1). (1.6)
Полный механический момент / является геометрической суммой
спинового и орбитального моментов:
J = S + L. (1.7)
Собственные значения его проекции J. квантуются аналогично (1.5),
а квантовое число J (при заданных квантовых числах 5 и L) может
принимать значения
У=(5+£), (S + L-l), ..., \S-L\ (1.8)
в зависимости от взаимной ориентации векторов S и L.
Магнитные моменты — спиновый 9Ws, орбитальный 9Лх, и полный
9И пропорциональны соответствуюшим механическим моментам.
Магнитные моменты, в отличие от механических, принято измерять
в абсолютных единицах. Тогда, например, для спиновых моментов
Ws=-ystiS, (1.9)
а магнитомеханическое отношение
Ys=^- (1-Ю)
2тес
Здесь ее- -заряд электрона. тс — его масса покоя, с — скорость света,
a gs — фактор спектроскопического расщепления (или g-фактор), для
которого квантовая электродинамика дает значение
gs = 2[l+x'(2Tc)-0,328a2,/7r]. (1.11)
11
где а = е?/(йс)=; 1/137. Знак минус в выражении (1.9) связан с тем,
что для электронов направления магнитных и механических моментов
противоположны, а магнитомеханическое отношение мы будем всегда
считать положительной величиной.
Соотношения, аналогичные (1.9) и (1.10), могут быть записаны
и для орбитальных моментов, но для них д.= 1. Можно такие же
соотношения записать и для полных моментов:
Л—уй1—^1*1; (1.12)
входящий в (1.12) g-фактор будет зависеть от квантовых чисел S,
L к J. Например, принимая gs — 2,
3 S(S+l)-L(L+l)
К— 1 -—■■— П 13}
ё 2 27(7+1) ( '
Из (1.9) и аналогичных выражений для 50lt и 501 следует, что
магнитные моменты квантуются так же, как и механические. В
частности, собственные значения проекции 50J на ось квантования
{501г} = уЙ7, yh{J+\),...,{-ybJ). (1.14)
Соседние собственные значения 501г различаются на
5SW2 = Y/j=guB, (1.15)
где
Ив=^ (1.16)
2тсс
— магнетон Бора.
Парамагнетизм. В отсутствие внешнего магнитного поля состояния
с различными {501г} вырождены, т. е. им соответствуют одинаковые
энергии. При наложении внешнего магнитного поля Н появляется
потенциальная энергия магнитного момента в этом поле (зеемановская
энергия)
ez=-2RH, (1.17)
и вырождение состояний с различными проекциями момента на
направление поля Н снимается—возникают (27+1) эквидистантных
энергетических уровня с интервалами
бЕ = уйЯ=яцв#. (1.18)
Между соседними уровнями могут происходить переходы с
поглощением квантов йсо электромагнитного поля (a = 2nf—круговая частота
поля). Это явление носит название электронного парамагнитного
резонанса (ЭПР)". Условие его (йсо = 8е) с учетом (1.10) и (1.6) имеет вид
и=7Яе^. (1.19)
2т. с
Аналогичные переходы могут происходить между уровнями,
отличающимися проекциями ядерного магнитного момента,—ядерный магнитный
резонанс (ЯМР).
12
Различие населенностей
уровней с разными {50JZ} приводит
к появлению среднего магнитного
момента, направленного по полю
Н. Вычисление методами
статистической физики (см., например,
[187, 16]) приводит к следующему
выражению для намагниченности
(среднего магнитного момента
единицы объема) парамагнетика:
-***(0)- (1'20)
где намагниченность насыщения
M° = yhJN, (1.21)
N—число магнитных моментов в единице объема, и—постоянная
Больцмана, а
— функция Бриллюэна. Графики этой функции приведены на рис. 1.1.
При х-юо, т. е. в очень сильных полях или при очень низких
температурах, Bj{x)-*\, все магнитные моменты в этом случае
«выстраиваются» по полю. При малых х, разлагая функцию Bj(x)
в ряд по степеням х и ограничиваясь первым членом ряда, получаем
М=%Н. (1-23)
Парамагнитная восприимчивость х оказывается обратно
пропорциональной температуре и может быть записана в виде
Х = С/Т, (1.24)
где
C=-J(J+l)(yh)2N/yi. (1.25)
Выражение (1.24) представляет собой закон Кюри, а величина С
называется постоянной Кюри.
Теория Вейсса. В ферромагнетиках большая намагниченность,
близкая к сумме всех элементарных моментов, наблюдается, в отличие
от «обычных» парамагнетиков, при не очень низких температурах
и в слабых магнитных полях. Причину этого объяснили в 1928 г.
Френкель и Гейзенберг на основе созданной незадолго до этого
квантовой механики. Однако формальное описание ферромагнетизма
было дано еще в 1907 г. Вейссом. Он предположил, что на магнитные
моменты ферромагнетика действует кроме внепнего поля Н большое
внутреннее («молекулярное») поле
НЛ = ЛМ. (1.26)
Вj Се)
Рис. 1.1. Функции Бриллюэна [187]
13
NxT
Заменяя в (1.20) Н на (#+#л),
получим
M=M°Bj
Nx.T
{Н+ЛМ)
(1.27)
Рис. 1.2. Графическое решение
уравнения (1.27) для спонтанной
намагниченности
Решая уравнение (1.27)
графически при Н=0 (рис. 1.2), мы
можем убедиться, что при условии
Т<ТС, где
7с = ЛС, (1.28)
а С определяется выражением (1.25),
это уравнение имеет решение МФО.
Температура 7с—это температура
Кюри, а намагниченность М
представляет собой спонтанную намагниченность ферромагнетика.
При Т> Тс спонтанная намагниченность обращается в нуль
и аргумент функции Бриллюэна в (1.27) становится малым. Тогда,
используя разложение этой функции в ряд, получим восприимчивость
(1.29)
Это выражение представляет собой закон Кюри—Вейсса (рис. 1.3).
Обменное взаимодействие. Магнитное взаимодействие
элементарных магнитных моментов, энергия которого определяется выражением
(1.4), не может явиться причиной возникновения спонтанной
намагниченности обычных ферромагнетиков с температурами Кюри порядка
десятков и сотен Кельвинов. Действительно, обусловленное этим
взаимодействием внутреннее магнитное поле не превышает (см. § 1.5)
величины 4пМ, т. е. постоянная Л не может быть больше 4я, в то
время как оценка Л согласно (1.28) дает для таких ферромагнетиков
величины ~ 103 (т. е. молекулярные поля ~106). Этот вывод следует
и из сравнения отнесенной к одному атому энергии теплового
движения, разрушающего ферромагнитное упорядочение (х7с), с
энергией (1.3) магнитного взаимодействия двух соседних диполей, которая
Х=С/{Т-Тс).
Рис. 1.3. Температурные
зависимости обратной восприимчивости.
/ — парамагнетик (закон Кюри),
2—ферромагнетик (закон Кюри -
Вейсса), 3 антиферромагнетик,
4 — ферри магнетик
1А
составляет ~цв/«3~Ю-17 (а~3-Ю-8— расстояние между соседними
моментами).
В то же время энергия электростатического (кулоновского)
взаимодействия двух электронов на таком же расстоянии составляет
ее/а~10~п, так что даже небольшой (~0,01) части этой энергии
достаточно для обеспечения реальных температур Кюри
ферромагнетиков. Из квантовой механики [132] известно, что вид волновых
функций двух электронов определяется взаимной ориентацией их
спинов и, следовательно, от этой ориентации зависит средняя энергия
их кулоновского взаимодействия. Зависящая от спинов часть энергии
кулоновского взаимодействия электронов носит название обменной
энергии. Эта энергия и является причиной магнитного упорядочения.
В ферромагнетиках она минимизируется при параллельной ориентации
всех спиновых моментов. Именно в этом заключается объяснение
природы ферромагнетизма Френкелем и Гейзенбергом.
Как показал^ Дирак, оператор обменной энергии двух частиц со
спинами Si и §2 может быть представлен в виде
#ex=-2/12(r12)SiS2. (1.30)
Величина hi —обменный интеграл — быстро убывает при увеличении
расстояния Г\г между частицами. Во многих феррома! иетиках (а
также антиферро- и ферримагнетиках) элементарные магнитные
моменты находятся на таких больших расстояниях друг от друга, что
прямое обменное взаимодействие, о котором шла речь выше, не
может быть ответственным за магнитное упорядочение. В этих
случаях «работают» различные механизмы косвенного обменного
взаимодействия, в которых участвуют и другие частицы. В ионных
кристаллах основную роль играет обменное взаимодействие спинов
катионов через расположенные между ними анионы. В металлах
большую роль играет взаимодействие через электроны
проводимости — взаимодействие Рудермана—Киттеля — Касуйя — Иосиды
(РККИ). Во всех этих случаях оператор энергии обменного
взаимодействия может быть, во всяком случае приближенно, представлен
в . дираковской форме (1.30).
Гейзенберговская модель. Система спиновых моментов,
расположенных в узлах кристаллической решетки и связанных обменным
взаимодействием, гамильтониан которого имеет вид (1.30), носит
название гейзенберговской модели ферромагнетика. Обобщая эту
модель, следует включить в рассмотрение, кроме обменного, и
другие— более слабые взаимодействия, в первую очередь—магнитное
(диполь-дипольное) и взаимодействие (зеемановское) с внешним
магнитным полем.
Основными допущениями, принятыми в гейзенберговской модели,
являются полная локализация моментов в узлах решетки и отсутствие
орбитальных моментов. Первое допущение довольно хорошо
выполняется для ферромагнитных диэлектриков и полупроводников и
хуже—для магнитоупорядоченных металлов. Для них часто
используется зонная модель (см., например, [116]). Второе допущение
выполняется тем лучше, чем сильнее «заморожены» орбитальные
15
моменты. Если они заморожены почти полностью, то сравнительно
небольшое их влияние можно учесть в рамках обобщенной
гейзенберговской модели, полагая, во-первых, что величина магнитомеха-
нического отношения у (в зеемановском члене гамильтониана этой
модели) отличается от его значения ys для спиновых моментов, и,
во-вторых, вводя в гамильтониан дополнительные члены,
описывающие магнитную кристаллографическую анизотропию (см. § 2.2).
В другом случае—для соединений редкоземельных элементов, когда
орбитальные моменты не заморожены, гейзенберговская модель тоже
может быть использована, но с заменой спиновых моментов S на
полные моменты J.
Некоторые другие вопросы теории ферромагнетизма будут
затронуты в дальнейшем по мере необходимости.
§ 1.2. Уравнение движения намагниченности
Для описания интересующих нас динамических процессов в
ферромагнетиках может быть использована континуальная модель". При
этом мы отвлекаемся от микроскопической картины ферромагнетика,
а в качестве величины, характеризующей его состояние, используем
намагниченность
М=£ЯИ/(ДК), (1.31)
где £9И—суммарный магнитный момент малого, но
макроскопического объема А К Вектор М входит в уравнения макроскопической
электродинамики (см. гл. 4) и, в частности, в соотношение
В = Н + 4яМ, (1.32)
где Н и В—соответственно магнитное поле и магнитная индукция.
При использовании континуальной модели для описания поведения
ферромагнетика может быть применена классическая (не квантовая)
теория. Обменное взаимодействие, природа которого, как было
отмечено в предыдущем параграфе, является квантовой, при этом
должно постулироваться. В случае однородной намагниченности (или
при достаточно медленном изменении вектора М в пространстве)
для его учета достаточно «молекулярного» поля Вейсса (1.26).
При классическом описании процессов в ферромагнетике уравнения
макроскопической электродинамики должны быть дополнены
материальными соотношениями, отражающими специфическую для данного
вещества связь между векторами Н и В или Н и М. В качестве
такого соотношения целесообразно использовать уравнение движения
намагниченности. Поскольку природа ферромагнетизма является
квантовой, в рамках классической теории это уравнение должно быть
постулировано. Уравнение движения намагниченности было впервые
записано в 1935 г. Ландау и Лифшицем [130]; для некоторых
случаев оно было в дальнейшем обосновано квантовомеханически
Эта модель использовалась и в теории Вейсса (§ 1.1).
«б
(см.,например, [113]). Мы рассмотрим это уравнение в достаточно
общем виде в § 2.1, а сейчас приведем «вывод» его (в рамках
классической теории он не может быть строгим) для случая
однородных колебаний намагниченности изотропного ферромагнетика.
Будем рассматривать ферромагнетик как набор классических
волчков (в этом прежде всего и заключается нестрогость «вывода»)
с моментом количества движения J и магнитным моментом 2R.
Уравнение движения волчка (твердого тела, закрепленного в одной
точке) с учетом (1.2) запишется в виде [131]
й — =9ИхН (1.33)
(так как J измеряется в единицах h, а 9И—в абсолютных единицах).
Исключая J из (1.33) и (1.12) и умножая полученное уравнение на
число N магнитных моментов в единице объема, мы придем
к уравнению движения намагниченности М = А^9И:
^ = -7МхН. (1.34)
Заметим, что это уравнение справедливо лишь для гипотетической
среды «без потерь», в которой при изменении намагниченности не
происходит диссипации магнитной энергии. Учет диссипации будет
проведен в § 1.4.
При «выводе» уравнения (1.34) мы не принимали во внимание
обменного взаимодействия. Но легко видеть, что молекулярное поле
(1.26), если мы добавим его к полю Н, не войдет в это уравнение.
Что же касается дополнительного поля, учитывающего увеличение
энергии обменного взаимодействия в случае неоднородной
намагниченности, то оно, как мы увидим в дальнейшем, войдет в уравнение
движения. Таким образом, уравнение (1.34) справедливо лишь при
достаточно медленном изменении М в пространстве.
Сделаем еще одно замечание, касающееся уравнения (1.34).
Входящая в него величина у является характеристикой коллективного
движения магнитных моментов ферромагнетика. Значение ее в
уравнении (1.34), вообще говоря, не совпадает со значением у для тех
же магнитных ионов ни в свободном состоянии, ни в парамагнитных
кристаллах. В рамках классической континуальной теории величина
у должна рассматриваться как феноменологическая постоянная,
значение которой находится из эксперимента. Отличие величины у от ее
спинового значения (1.10) связано с вкладом орбитальных моментов.
Поэтому в тех случаях, когда магнитные ионы ферромагнетика не
имеют орбитальных моментов (находятся в ^-состоянии) или их
орбитальные моменты сильно «заморожены», g-фактор,
соответствующий величине у в уравнении (1.34), оказывается близким к 2.
Это имеет место, в частности, для ферромагнетиков CdCr2Se4 и ЕиО
и для ферримагнетиков (ферритов), в которых магнитными ионами
являются только ионы Fe3+, например, для иттриевого феррита со
структурой граната Y3FesOi2 (ЖИГ) или литиевого феррита
Lio,sFe2,5 04 со структурой шпинели.
2 А. Г. Гуревич, Г. А. Мелков 17
Интересно, что вклад орбитальных моментов, который приводит
к меньшим чем 2 значениям ^-фактора свободного иона, а также
вызывает уменьшение ^-фактора (#'), определяемого из наблюдений
гиромагнитных эффектов, например, Барнета или Эйнштейна—де
Гааза (см. [113]), дает большие чем 2 величины g-фактора в уравнении
(1.34). Это различие объяснили Киттель [113] и Ван Флек [443].
Полученное ими соотношение g—2 = 2— g' неплохо подтверждается
для металлов (§ 14.2), в неметаллических ферро- и ферримагнетиках
величины g—2, как правило, превышают 2—g' (см., например, [113]).
Важным свойством уравнения (1.34) является то, что оно
обеспечивает сохранение длины вектора М. Действительно, умножая обе
части (1.34) скалярно на М, получим
^-М2 = 0. (1.35)
ct
Если рассматривать М как вектор, один конец которого закреплен,
то вследствие (1.35) другой конец будет двигаться по сфере. Такое
движение называют прецессией намагниченности. При наличии
цилиндрической симметрии конец вектора М будет описывать окружность
(круговая прецессия), в других случаях его траектория будет более
сложной.
§ 1.3. Высокочастотная магнитная восприимчивость
Приступая к решению уравнения движения намагниченности,
рассмотрим прежде всего задачу о колебаниях намагниченности
в некоторой точке намагниченного до насыщения ферромагнетика
под воздействием переменного магнитного поля в этой точке.
В результате ее решения будет найдена высокочастотная магнитная
восприимчивость ферромагнетика, в этом параграфе — в
идеализированном случае отсутствия потерь.
Представим магнитное поле и намагниченность, входящие в
уравнение движения (1.34), в виде сумм постоянных и переменных
составляюших:
H = H0 + »U, М = М0 + пи. (1.36)
Предположим, что
Л^«:Я0, m^<zMo. (I.37)
Условие равновесия. Подставим суммы (1.36) в уравнение (1.34)
и, принимая во внимание условия (1.37), используем метод
последовательных приближений. В нулевом приближении, оставляя
только постоянные составляющие, получим
МохНо = 0. (1.38)
Это соотношение определяет равновесную ориентапию вектора Мо;
в рассматриваемом случае изотропного ферромагнетика она совпадает
с направлением постоянного магнитного поля Но. Длина же вектора
Мо уравнением (1.38) не определяется; в рамках излагаемой в этой
18
книге теории магнитных колебаний и волн она должна
рассматриваться как известная величина.
Линеаризация и решение уравнения движения намагниченности.
В первом приближении, пренебрегая произведениями малых
переменных величин и учитывая условие (1.38). получим
спи
а
+ упк хН0=-уМ0х»и. (1.39)
Это уравнение, в отличие от (1.34), является линейным относительно
переменных величин lu и пи, получение его из (1.34) называется
линеаризацией уравнения движения.
Будем решать уравнение (1.39) для случая гармонической
зависимости lu от времени. В силу линейности уравнения и пи будет
гармонической функцией времени. Используя метод комплексных
амплитуд (см., например, [64]), введем комплексные переменные
величины
rii = mexp(/cor), h = h exp (ко/), (1-40)
действительными частями которых являются реальные
величины пи и 1и. Комплексные величины m и h в (1.40) — это
комплексные амплитуды векторов пи и lu; их проекции на оси
координат являются комплексными амплитудами соответствующих
проекций этих векторов. Для комплексных амплитуд справедливо
следующее уравнение, совпадающее по форме (кроме первого
члена) с (1.39):
7'сшп + утхН0= -yM0xh. (1-41)
Спроектируем это уравнение на оси декартовой системы
координат, в которой ось z совпадает с направлением векторов М0 и Н0:
г'со тх + у Н0 ту = уМ0 hy,
— у Н0 тх + /со т,. = - уМ о hx, (1-42)
tomz = 0.
Решая систему (1.42), получим
mx = xK + iXahy,
ту=-iXaK + xK' С1-43)
mz = 0,
уМст„ уМ0сй
х=—2—ъ Хв=——1- С1-44)
Здесь введено обозначение
сон = уЯ0. (1.45)
Выражения (1.43), (1.44), полученные Полдером [389], можно
записать в тензорной форме:
m = xh> (l-46)
2* 19
где магнитная восприимчивость %—тензор второго ранга (см.,
например, [119]) следующего вида:
(1.47)
Х =
X iXo О
-'Ха X О
0 0 0
Эти выражения могут быть записаны и в векторной форме
m=xhi+«h1xGm, (1.48)
где bi=x0hx+yohy=h—z0hz—поперечная (по отношению к оси
z) составляющая комплексной амплитуды переменного магнитного
поля, а
Gm=z0x„ (1.49)
—магнитный вектор гирации.
Особенности тензора восприимчивости. Переходя к обсуждению
полученного решения, отметим прежде всего, что продольная
составляющая переменного магнитного поля в данном случае
(намагниченного до насыщения ферромагнетика) не вызывает переменной
намагниченности. Поперечные же составляющие hx и hy вызывают
намагниченности, не только параллельные этим составляющим, но
и перпендикулярные им, причем сдвинутые по фазе соответственно
на — я/2 и я/2, о чем говорят множители г и —/в (1.47). В результате
тензор % оказывается несимметричным—с антисимметричными
компонентами i%a и — i%a- Такое свойство среды называется гиротропией.
Как мы увидим в § 4.2, оно приводит, в частности, к повороту
поляризации линейно поляризованной волны, распространяющейся
в этой среде в направлении, параллельном или антипараллельном
постоянной намагниченности—эффекту Фарадея.
Здесь необходимо сделать два замечания. Во-первых,
несимметричным тензором при наличии постоянного магнитного поля или
постоянной намагниченности становится и электрическая
восприимчивость й (а следовательно, и электрическая проницаемость ё)
некоторых сред. К ним принадлежат все парамагнетики и
ферромагнетики. Несимметрия е приводит в этих средах к эффекту Фарадея
(см., например, [134]), который наблюдается обычно в оптическом
диапазоне. К средам, в которых несимметрия ё и, следовательно,
эффект Фарадея наблюдается в диапазоне СВЧ, принадлежат
газоразрядная [11] и твердотельная [191, 199] плазмы в магнитном поле.
Во-вторых, существует и другая причина возникновения гирот-
ропии, т. е. несимметрии тензора ё. Она заключается [209, 134, 199]
в отсутствии у среды центра инверсии, т. е. в структурной
неэквивалентности противоположных направлений. Такая гиротропия (ее
называют иногда естественной, в отличие от индуцированной
магнитным полем) проявляется лишь при неоднородности переменного
поля, в частности, для бегущих волн и приводит к повороту
поляризации этих волн, который в первом приближении
пропорционален волновому числу к. Этот эффект носит название оптической
->с\
активности. Существенное отличие такого вида гиротропии от гирот-
ропии, вызванной постоянным магнитным полем, заключается в том,
что знаки антисимметричных компонент (в фиксированной системе
координат!) изменяются на обратные при замене к на —к, в то
время как знаки (и величины) антисимметричных компонент в (1.47)
не зависят от к и определяются, как видно из (1.44), постоянной
намагниченностью. Мы в дальнейшем оптической активностью
интересоваться не будем и под термином гиротропия будем понимать
гиротропию, вызванную постоянным магнитным полем или
постоянной намагниченностью. При этом, конечно, нас будет больше всего
интересовать гиротропия (ее можно назвать магнитной),
обусловленная антисимметричными компонентами тензора % Для ферро-
и ферримагнетиков в диапазоне СВЧ, а также в далеком инфракрасном
диапазоне она существенно преобладает над гиротропией, обуслов-
тенной несимметрией тензора ё.
Второй особенностью полученного решения является резонансная
зависимость компонент тензора восприимчивости от частоты
переменного поля со и величины постоянного поля Н0. В рассматриваемом
нами пока идеализированном случае — без учета диссипации эти
компоненты неограниченно возрастают при
ю = сон = уЯ0. (1.50)
Зависимости % и %„ от (о и Н0 показаны на рис. 1.4.
Резонансная зависимость компонент тензора высокочастотной
магнитной восприимчивости ферромагнетика от со и #0 является
причиной ферромагнитного резонанса, т. е. явления резонансного
поглощения энергии электромагнитного поля ферромагнетиком. Это
явление было предсказано еще в 1912 г. Аркадьевым [10] на базе
классических представлений. В 1923 г. Дорфман [287] показал его
возможность с квантовой точки зрения, но, конечно, без учета
спиновой природы ферромагнетизма (спин электрона бьш открыт
только в 1925 г.). Первая теория ферромагнитного резонанса,
основанная на правильном понимании природы ферромагнетизма, была
развита Ландау и Лифшицем в 1935 г. [130]. Экспериментально
'■■ 1.4. Зависимости компонент тензора восприимчивости от частоты со и
постоянного магнитного поля Н0
21
ферромагнитный резонанс был открыт в 1946 г. Гриффитсом [312]
и независимо Завойским [87]".
Важный вклад в теорию ферромагнитного резонанса внес Киттель
[348], он показал, что частота, при которой происходит поглощение
энергии образцом (т. е. частота ферромагнитного резонанса), не
определяется соотношением (1.50) и существенно зависит от формы
образца. Эту зависимость мы исследуем в § 1.5.
Третьей особенностью полученного решения (1.43) является то.
что резонанс имеет место только при наличии составляющей
h с круговой поляризацией и правым (относительно направления
М0, т. е. оси z) вращением. Чтобы убедиться в этом, перейдем
к циркулярным составляющим векторов m и h и циркулярным
компонентам тензора х-
Циркулярные компоненты восприимчивости. Циркулярные
поперечные составляющие вектора m определяются следующим образом:
m+=mx + imy, m-=mx — imy\ (1-51)
аналогично определяются циркулярные составляющие и других
векторов. Легко показать, что справедливы следующие соотношения:
m+=x±h±, (1.52)
где
Х±=Х±Ха=——■ (1-53)
Таким образом, составляющая поля /г+ вызывает только
составляющую намагниченности /ит, а составляющая /г_ вызывает
только гп-. Иными словами, в новых переменных h + , /z_, hz и т + ,
гп-, mz тензор восприимчивости стал диагональным, с компонентами
Х + , Х- и 0.
Как видно из (1.53), только компонента х + изменяется
резонансным образом—имеет полюс при условии (1.50). Зависимости
Х+ и Х- от #о приведены на рис. 1.5.
Покажем теперь, что если вектор, например, m имеет только
составляющую w + , то этот вектор является вектором с круговой
поляризацией и правым вращением. По условию т~=0; отсюда
согласно (1.51) следует
my=—imx. (1.54)
Пусть, например, х-составляющая реального вектора пи имеет вид
m~.x = m0cosv)t, т. е. ее комплексная амплитуда тх = т0. Тогда согласно
(1.54) комплексная амплитуда j-составляющей my=—im0, т. е.
реальная ^-составляющая m^y = Re[ — W20exp(«cof)]=m0sincof. Из выражений
для т^х и т„у следует, что поперечный вектор пи вращается
с круговой частотой со в плоскости ху, проходя по кратчайшему
мягн JLL tL Завоискии обнаружил резонансное поглощение электро-
u7rT^^Lэнергии в парамагнетике (электронный парамагнитный резонанс)
что явилось открытием магнитного резонанса в твердом теле
22
О)
—~—^
V4
\ +
f ио
пути от положительного
направления оси х к положительному
направлению оси у, т. е. (в правой системе
координат) вращается против
часовой стрелки, если смотреть со
стороны положительного направления
оси -. Это и соответствует по
определению круговой поляризации
вектора пи с правым вращением
относительно оси z". Аналогично
легко убедиться, что наличие только
составляющей т- говорит о
круговой поляризации пи с вращением
в обратном направлении—левым
вращением. При этом my = imx.
Нетрудно убедиться, что произвольно
поляризованный поперечный вектор
может быть представлен в виде суммы двух векторов с круговой
поляризацией — с правым и левым вращением.
Высокочастотная магнитная проницаемость. Комплексная
амплитуда переменной составляющей вектора магнитной индукции
Ь = Ь + 4лт. (1.55)
Подставляя (1.46) в (1.55), получим
b = ph,
где тензор высокочастотной магнитной проницаемости
р=1+4лх
Учитывая (1.47) и (1.44), запишем
Рис. 1.5. Зависимости
циркулярных компонент тензора
восприимчивости от Н0
2)
ц=1+4лх:
"'На И
0 0
С0„(ю„+юм)-ю2.
2 2
Юн—со
Ц0 = 4пх0 =
2 2 *
сон—от
Здесь введено обозначение
(1.56)
(1-57)
(1.58)
(1.59)
(1.60)
сом = 74лМ0.
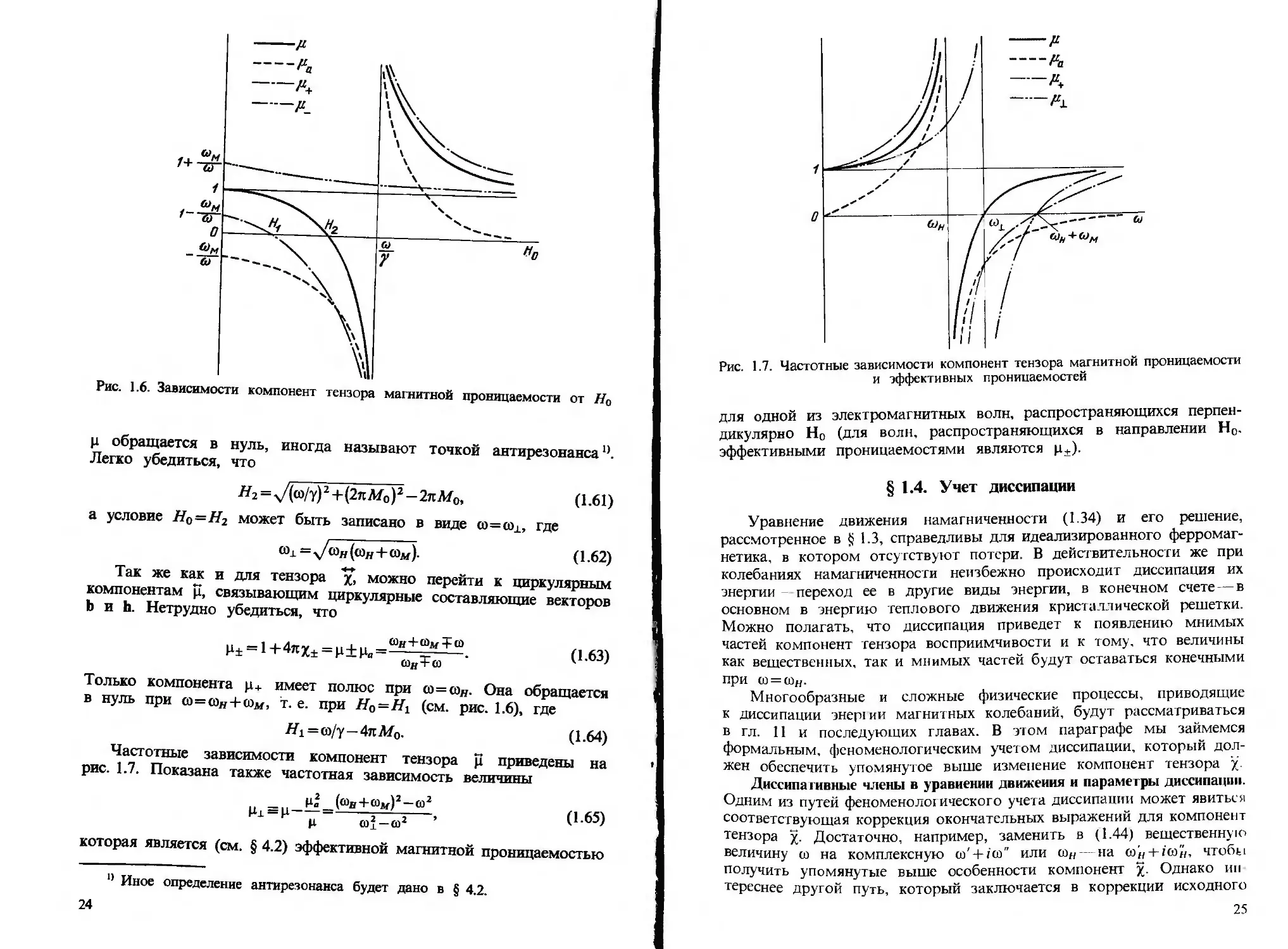
Зависимости ц и ц0 от Н0 приведены на рис. 1.6. Из этого
рисунка видно, в частности, что ц обращается в нуль при Н0 — Н2
и отрицательна в области полей от Н2 до со/у. Точку, где
' Этому определению правого вращения вектора относительно
некоторого направления эквивалентно следующее: конец вектора движется как
головка правого винта при поступательном перемещении винта в данном
направлении.
Здесь I—единичный тензор—диагональный, со всеми компонентами,
равными 1 (очень часто вместо Т пишут просто 1).
23
Рис. 1.6. Зависимости компонент тензора магнитной проницаемости от Н0
ц обращается в нуль, иногда называют точкой антирезонанса,}.
Легко убедиться, что
«2=v/(co/y)2+(2яМ0)2 -2яМ0, (1.61)
а условие Н0=Н2 может быть записано в виде со=сох, где
«х = у/(Он(сзн+(Ом)- (1.62)
Так же как и для тензора Y> можно перейти к циркулярным
компонентам Ц, связывающим циркулярные составляющие векторов
b и h. Нетрудно убедиться, что
ц± = 1+4ях± = ц+ц0 =
шя+ш
(1.63)
Только компонента ц+ имеет полюс при co=cow. Она обращается
в нуль при (о=(ои+(Ом, т. е. при #0=#i (см. рис. 1.6), где
#1=ю/у-4яМ0.
(1.64)
п^^Т0!^16 зависимости компонент тензора ц приведены на
рис. 1.7. Показана также частотная зависимость величины
И coi-ш2 '
(1.65)
которая является (см. §4.2) эффективной магнитной проницаемостью
" Иное определение антирезонанса будет дано в § 4.2.
24
Рис. 1.7. Частотные зависимости компонент тензора магнитной проницаемости
и эффективных проницаемостей
для одной из электромагнитных волн, распространяющихся
перпендикулярно Н0 (для волн, распространяющихся в направлении Н0.
эффективными проницаемостями являются ц±).
§ 1.4. Учет диссипации
Уравнение движения намагниченности (1.34) и его решение,
рассмотренное в § 1.3, справедливы для идеализированного
ферромагнетика, в котором отсутствуют потери. В действительности же при
колебаниях намагниченности неизбежно происходит диссипация их
энергии - переход ее в другие виды энергии, в конечном счете — в
основном в энергию теплового движения кристаллической решетки.
Можно полагать, что диссипация приведет к появлению мнимых
частей компонент тензора восприимчивости и к тому, что величины
как вещественных, так и мнимых частей будут оставаться конечными
при со = шн.
Многообразные и сложные физические процессы, приводящие
к диссипации энер1ии магнитных колебаний, будут рассматриваться
в гл. 11 и последующих главах. В этом параграфе мы займемся
формальным, феноменологическим учетом диссипации, который
должен обеспечить упомянутое выше изменение компонент тензора х'-
Диссипа i ивные члены в уравнении движения и параметры диссипации.
Одним из путей феноменологического учета диссипации может явиться
соответствующая коррекция окончательных выражений для компонент
тензора %. Достаточно, например, заменить в (1.44) вещественную
величину со на комплексную ш' + гш" или сон — на сон + 'СОн, чтобы
получить упомянутые выше особенности компонент %■ Однако ип
тереснее другой путь, который заключается в коррекции исходного
25
уравнения движения. При этом основной член ъ правой части (1.34)
можно оставить без изменения и добавить другой — сравнительно
малый член, учитывающий диссипацию энергии. Именно такой путь
был использован Ландау и Лифшицем [130]. Предложенное ими
уравнение движения (для случая изотропного ферромагнетика, который
рассматривается в данной главе) имеет вид
Ё=_уМхН-^Мх(МхН), (1.66)
ot м
где X—параметр диссипации0.
Если в диссипативном члене уравнения (1.66) заменить приближенно
(используя уравнение без диссипативного члена) МхНна —y~1dM/dt
и вместо X ввести параметр <х = Х/М, то мы придем к уравнению
которое было предложено Гильбертом. Диссипативный член этого
уравнения можно было бы записать, предполагая, что на
намагниченность, кроме поля Н, действует эффективное поле «сил трения»,
пропорциональное скорости изменения М. Нетрудно убедиться, что
при замене
у->у/(1+а2), Х->аМ/(1+а2) (1.68)
уравнение (1.66) уже не приближенно, а точно переходит в (1.67).
В § 1.2 отмечалось, что уравнение движения (1.34) обеспечивает
выполнение условия (1.35). Поскольку диссипативные члены как
в (1.66), так и в (1.68) перпендикулярны М, то оба эти уравнения
также обеспечивают выполнение условия сохранения длины вектора
М. Как мы увидим в гл. 11, длина вектора М сохраняется при
некоторых диссипативных процессах и не сохраняется при других.
Уравнения (1.66) и (1.67), строго говоря, пригодны только для
описания диссипации, определяемой первой группой процессов.
В качестве уравнения движения, допускающего изменения длины
вектора М, часто используется так называемое модифицированное
уравнение Блоха (или уравнение Блоха — Бломбергена)
^ = -уМхН-сог(М-ХоН). (1.69)
Здесь Хо = М0/Н0—статическая восприимчивость, а сог=1/тг = у//г —
частота релаксации (тг—время релаксации, а Яг—параметр
релаксации, имеющий, как и X в (1.66), размерность магнитного поля).
Диссипативный член в (1.69) пропорционален отличию реального
мгновенного значения намагниченности от того значения ее, которое
установилось бы, если бы было «заморожено» мгновенное значение
поля Н.
'• В некоторых более поздних работах под «параметром диссипации
Ландау—Лифшица» понимается величина Х1=уХ.
26
Следует подчеркнуть, что уравнения (1.66), (1.67) и (1.69)
различаются, во-первых, формой диссипативного члена и, во-вторых,
размерностью параметра диссипации. Второе различие связано лишь
с традицией; в каждом из этих уравнений можно было бы перейти
к параметру диссипации с любой размерностью.
Было много попыток (см., например, [185, 258]) использовать для
ферромагнетиков уравнения движения с большим числом параметров
диссипации. Использовалось, в частности, уравнение Блоха [250]
с двумя временами релаксации — продольным и поперечным, которое
применяют обычно в теории парамагнитного резонанса (см., например,
[6]). Однако сложные и многообразные процессы диссипации в
ферромагнетиках нельзя строго описать при помощи уравнений движения ни
с одним, ни с двумя параметрами диссипации (если не считать, конечно,
эти параметры зависящими от многих величин). Для приближенного же
их описания, особенно при небольшой диссипации, обычно оказывается
пригодным любое из приведенных выше уравнений.
Линеаризация уравнений движения. Используя, как в § 1.3, метод
последовательных приближений, мы убеждаемся прежде всего, что
условие равновесия (1.38), как и следовало ожидать, остается
справедливым. Для комплексных амплитуд переменных составляющих из
(1.67) следует уравнение
itom + ymxHoH mxM0= -yM0xh. (1.70)
М0
Линеаризация уравнения (1.66) дает
уХ
icom+ymxHo-l-—m=-yM0xh + y>.h, (1-71)
Хо
а линеаризированное уравнение, получающееся из (1.69), совпадает
с (1.71) при сог = уХ/хо- -Ясно, что уравнения (1.70) и (1.71), как
и уравнения (1.67) и (1.66), из которых они получены, эквивалентны
при перенормировке (1.68) или—при малой диссипации — при условии
Х = аМ0.
Таким образом, в случае малых переменных величин (когда
справедливы линеаризированные уравнения) и одновременно малой
диссипации все три уравнения движения эквивалентны и входящие
в них параметры диссипации связаны соотношениями
а = Х/Мо = сог/сон = Яг///0. (1-72)
Компоненты тензора восприимчивости. Компоненты ?С с
учетом диссипации могут быть найдены, если спроектировать
линеаризированное уравнение (1.70) или (1.71) на оси координат
и решить, как и в § 1.3, полученную систему уравнений для
составляющих вектора т. Однако в случае уравнения (1.70) в этом
даже нет необходимости, так как это уравнение (с учетом условия
равновесия (1.38)) отличается от уравнения без диссипации (1.41)
лишь заменой
сон-+сон + гасо, ' (1-73)
27
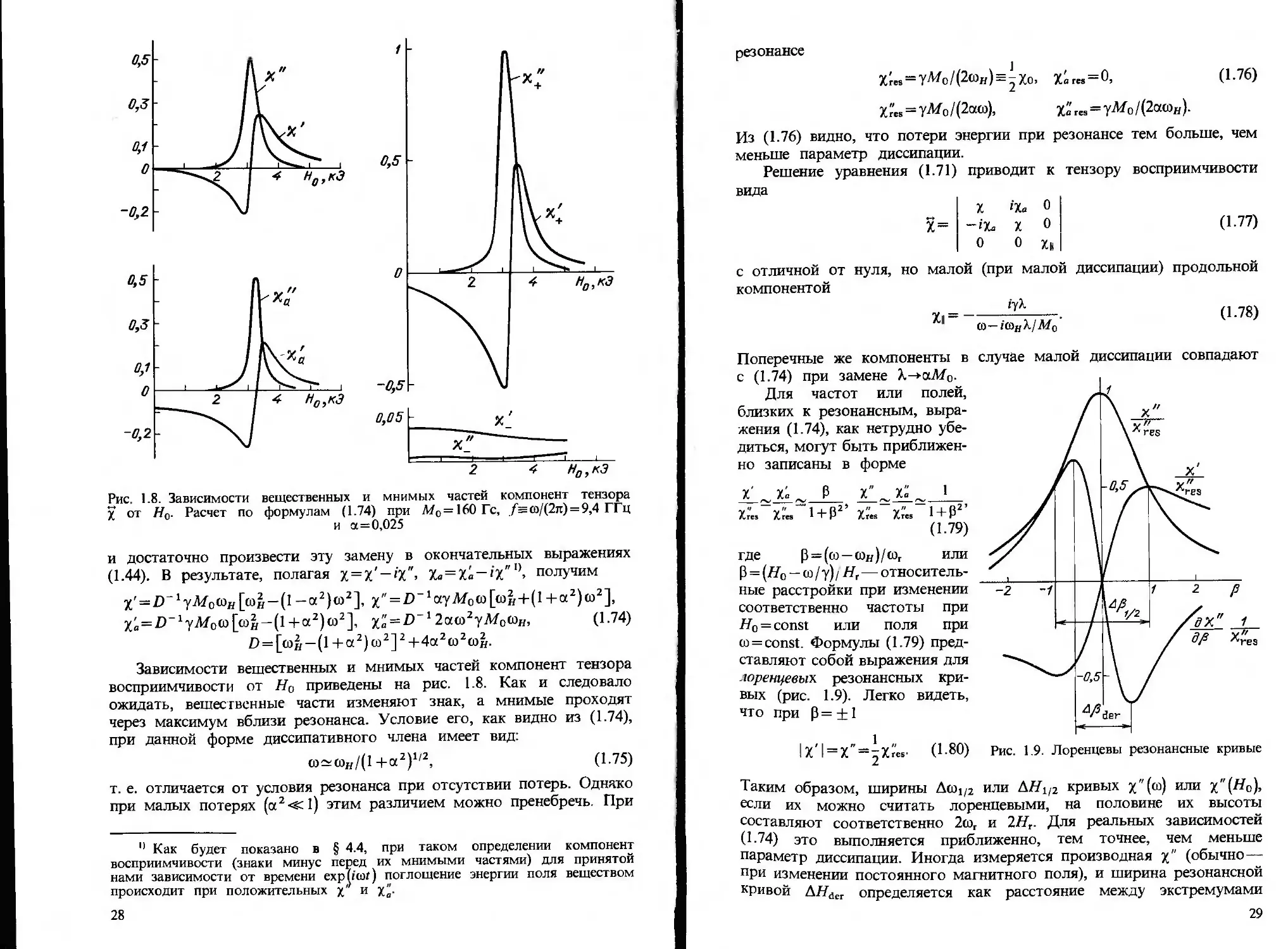
Рис. 1.8. Зависимости вещественных и мнимых частей компонент тензора
X от Н0. Расчет по формулам (1.74) при М0=160Гс, f=(aj(2n) = 9,4 ГГц
и а=0,025
и достаточно произвести эту замену в окончательных выражениях
(1.44). В результате, полагая Х = Х'-'Х"> Хв = Хо-'Х"0> получим
Х' = /)-1уЛ/0сон[ю^-(1-а2)со2], х" = С"1ауМ0со[ю^+(1+а2)со2],
Х^Д-^Л/оСоСш^-О+и2)©2], х« = ^"12асо2уМ0сон, (1.74)
D = [to2/-(l+a2)co2]2+4a2to2to2,.
Зависимости вещественных и мнимых частей компонент тензора
восприимчивости от #0 приведены на рис. 1.8. Как и следовало
ожидать, вещественные части изменяют знак, а мнимые проходят
через максимум вблизи резонанса. Условие его, как видно из (1.74),
при данной форме диссипативного члена имеет вид:
co^cWfl+a2)1'2, (1.75)
т. е. отличается от условия резонанса при отсутствии потерь. Однако
при малых потерях (a2-«l) этим различием можно пренебречь. При
" Как будет показано в § 4.4, при таком определении компонент
восприимчивости (знаки минус перед их мнимыми частями) для принятой
нами зависимости от времени expfirai) поглощение энергии поля веществом
происходит при положительных % и %"„■
28
резонансе
X«s = Y^o/(2co„)=.-Xo, X'a
= 0, (1.76)
Xer» = y-^o/(2atoH).
Х;'в = уМ0/(2асо),
Из (1.76) видно, что потери энергии при резонансе тем больше, чем
меньше параметр диссипации.
Решение уравнения (1.71) приводит к тензору восприимчивости
вида
X iTU 0
Х = -«Х- X 0 (1.77)
о о хв
с отличной от нуля, но малой (при малой диссипации) продольной
компонентой
iyX
Xir
a—i(oHk/M0'
(1.78)
Поперечные же компоненты в случае малой диссипации совпадают
с (1.74) при замене \-кхМ0.
Для частот или полей,
близких к резонансным,
выражения (1.74), как нетрудно
убедиться, могут быть
приближенно записаны в форме
Р
г_
Хге
К, а
Хге
1
1 + Р2' x'L x'L i + P2'
(1.79)
где р = (со —toH)/tor или
Р = (Н0 — со / у) i
H,—относительные расстройки при изменении
соответственно частоты при
Нъ — const или поля при
со = const. Формулы (1.79)
представляют собой выражения для
лоренцевых резонансных
кривых (рис. 1.9). Легко видеть,
что при Р= + 1
1Х'1 = Х"
1
(1.80) Рис. 1.9. Лоренцевы резонансные кривые
Таким образом, ширины Асо1/2 или АН1/2 кривых х"(ю) или Х'(^М>
если их можно считать лоренцевыми, на половине их высоты
составляют соответственно 2сог и 2НГ. Для реальных зависимостей
(1.74) это выполняется приближенно, тем точнее, чем меньше
параметр диссипации. Иногда измеряется производная %" (обычно—
при изменении постоянного магнитного поля), и ширина резонансной
кривой ДЯаег определяется как расстояние между экстремумами
29
этой производной. Для лоренцевых кривых, как легко убедиться.
А/У1.2 = Ч/ЗД//11СГ. (1.81)
Различные параметры диссипации в силу существующих между
ними соотношений (при малой диссипации (1 "2 и по-ранюму зависят
от со и Н0. Действительные зависимости их от -них величин
определяются физическими процессами, приводящими к диссипации
энергии магнитных колебаний и волн, и будут исследоиагься в гл.
II —14. Здесь мы отметим, что эти параметры могут рассматриваться
как постоянные лишь приближенно в некоторых пределах изменения
со или Н0. Предпочтение при этом следует отдавать тому параметру,
изменение которого будет наименьшим.
Из (1.72) и (1.76) следует важное соотношение
2НгХ'^=М0. (1.82)
Интегрируя х" и х" в (1-74) при посюянном параметре диссипации,
можно убедиться, что
jх" dH0 - Jх: dH„ - i f х" tkas- JxHa<ko = CM„.
о о '/о Ь
где С—постоянный множитель порядка 1. Эти соопюшеппя осчаются
справедливыми и при ос—>0. Отсюда с учетом того, чт пя лоренцевых
кривых (1.79) С=л 2, следует
limx'' = limx;; = -TcM(16(W0-M'Y), (1.83)
Ot-0 7L-0 ~
где о{х) —дельта-функция Дирака (см., например, [132, 81]). которая
определяется следующим образом:
8(.\) = 0 при хФО. (1.84)
J 5(х)dx = 1, если точка л=0 находится в интервале л, — л_2.
Циркулярные компоненты тензора восприимчивости с учетом
/диссипации
Х==Х + Х,= Iм:. ■ (1-85)
FV-личины xV и X" ведут себя вблизи резонанса (см. рис. 1.8)
подобно вещественным и мнимым частям х и Х<и н0 в Два раза
больше их по абсолютной величине; х'- и Х- остаются малыми
При ВСС.Х О) И Н0.
Компоненты тензора проницаемости. Компоненты и с учеюм
диссипации легко получить из приведенных выражений для компонент
Х- Точка антнрезонанса теперь может быть определена как точка,
в которой вдали от резонанса. ц' = 0. При малой диссипации условие
антирезонанса мало отличается от приведенного в § 1.3. а
и.',',,,-27((о.оз„|[1+г1)„ (2ю„)]. (1.86)
30
Если вблизи резонанса потери энергии тем больше, чем меньше
параметр диссипации, то в точке антирезонанса, как и вообще вдали
от резонанса, потери увеличиваются с увеличением параметра
диссипации.
Заметим, что в ферро- и ферримагнетиках с малыми потерями
компоненты тензора высокочастотной магнитной проницаемости
достигают весьма больших величин. Например, для монокристаллов
ЖИГ при частоте 9 ГГп а~5 10~5 (т.е. #г~0,15 Э) и ц^бООО.
§ 1.5. Однородные колебания намагниченности
малого эллипсоида
В предыдущих параграфах мы вычисляли магнитную
восприимчивое ib ферромагнетика, которая связывает переменную
намагниченность в некоторой точке с переменными магнитным полем в этой
же точке—внутренним переменным полем. Однако это поле обычно
нельзя считать заданным, оно в свою очередь зависит от переменной
намагниченности, причем не только в данной точке, а во всей
рассматриваемой системе. Не является заданным и внутреннее
постоянное поле—оно зависит от распределения постоянной
намагниченности в системе. Заданными можно считать, например, потоки
высокочастотной мощности, которые поступают на вход
рассматриваемых систем, а для постоянных полей — величины токов или
размеры и параметры постоянных магнитов. Внутренние поля и
намагниченности как переменные,так и постоянные, должны быть найдены
путем решения соответствующих граничных задач. При этом должны
быть использованы уравнения Максвелла—для переменных
составляющих, уравнения магнитостатики — для постоянных составляющих
и граничные условия. В качестве материальных соотношений для
переменных составляющих могут быть использованы найденные выше
выражения для компонент тензора х (или Р), в которых под полем
Н0 следует понимать внутреннее постоянное поле, найденное в
результате решения упомянутой выше магнитостатической задачи.
Ясно, что решение таких граничных задач представляет большие
математические трудное!и и может быть доведено до конца в
ограниченном числе случаев. Некоторые из них будут рассмотрены в гл.
5 и 6. Однако уже сейчас целесообразно остановиться на самой
простой из таких граничных задач — об однородных магнитных
колебаниях малого ферромагнитного эллипсоида. Решение ее позволит
нам интерпретировать эксперименты по ферромагнитному резонансу,
15 которых, как правило, используются малые образцы.
Малость размеров образцов следует при этом понимать в двух
смыслах. Малость их по сравнению с другими размерами системы
лает возможность рассматривать в качестве заданных величин внешние
магнитные поля — постоянное и переменное, которые можно
определить как поля в том месте, где находится образец, но в его
отсутствие. Малость же размеров образца по сравнению с длиной
электромагнитной волны дает возможность для переменных
составляющих использовать квазистатическое (или магнитостатическое, см.
31
§ 6.1) приближение, т. е. для определения комплексных амплитуд
этих составляющих использовать уравнения магнитостатики.
Если при этом образец является эллипсоидом, то можно
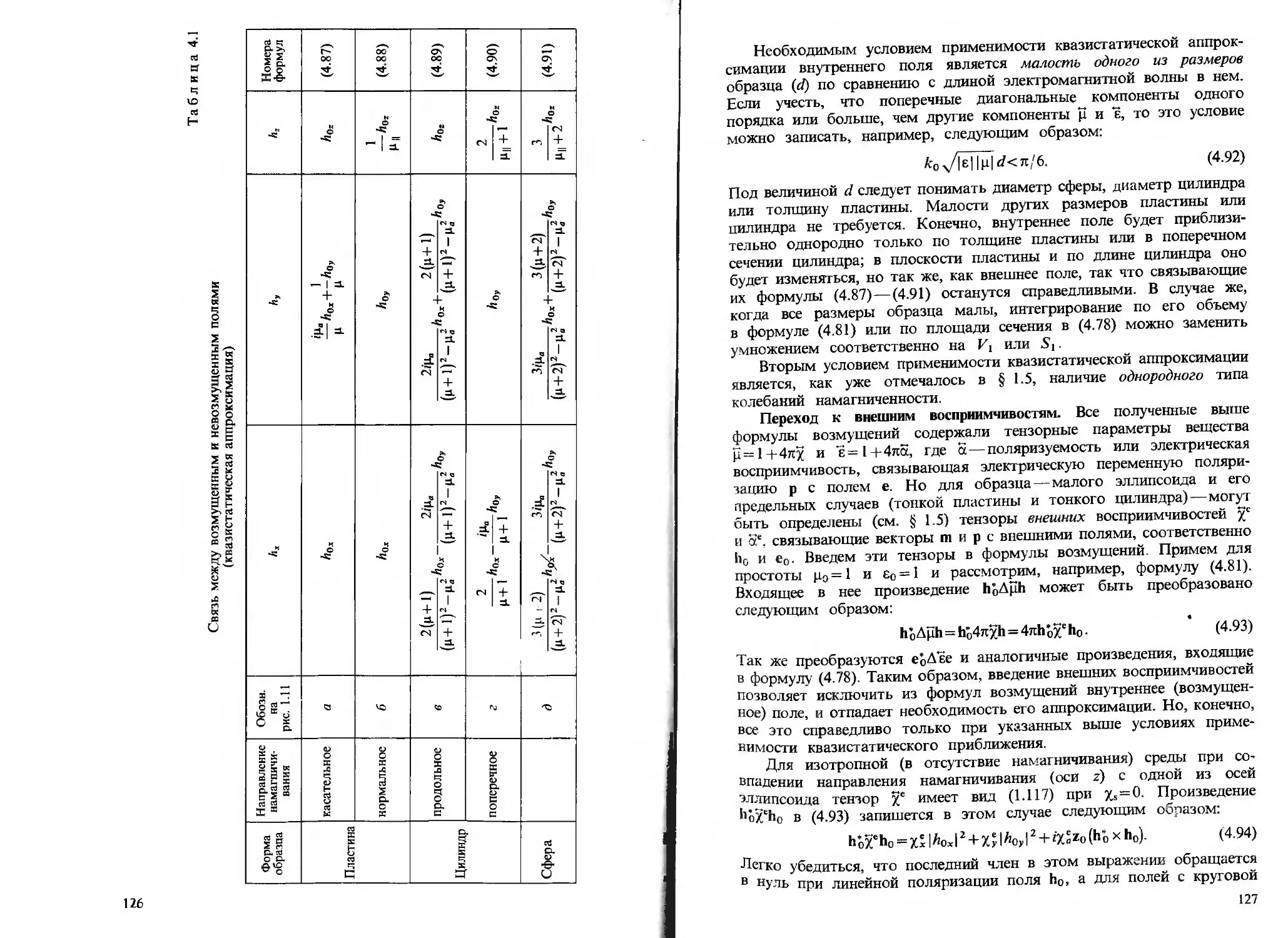
применить известный (см., например, [209]) результат магнитостатики:
внутреннее магнитное поле в эллипсоиде, помещенном в однородное
внешнее поле Не, однородно и составляет
Н = Нс-Км = Не+Нм, (1.87)
где М—намагниченность (которая тоже однородна), 55—тензор
размагничивания (или размагничивающих факторов), а Нм=— 55м—
размагничивающее поле.
Тензор N — симметричный и становится диагональным в системе
координат, оси которой совпадают с осями эллипсоида. Его
диагональные компоненты в этой системе Nx, Ny, Nz называются
размагничивающими факторами. Они зависят только от формы
(отношений осей) эллипсоида; сумма их"
Nx + Ny + Nz = 4n. (1.88)
Подставляя в (1.87) поля и намагниченность в виде сумм
постоянных и переменных составляющих, мы получим для постоянных
Н0 = Не0-ЙМ0, (1.89)
а для комплексных амплитуд переменных составляющих
h = he-55m. (1.90)
Остановимся подробнее на условиях применимости соотношения
(1.90). Одно из них, так же как и для (1.89), заключается в том, что образец
должен быть эллипсоидом. Вторым условием является малость размеров
образца по сравнению с длиной электромагнитной волны в веществе. Это
условие часто выполняется для слабопроводящих ферромагнетиков, так
как ферромагнитный резонанс является очень сильным эффектом, и для
его наблюдения (а иногда и использования) достаточно малых образцов.
Однако для металлов глубина проникновения электромагнитного поля
в вещество (толщина скин-слоя) становится очень малой (порядка Ю-4 см
на сверхвысоких частотах), и для образцов больших размеров (1.90) теряет
смысл2'. Третьим условием применимости этого соотношения является
наличие однородных колебаний намагниченности; как мы увидим в § 6.3,
в малом ферромагнитном эллипсоиде могут существовать и неоднородные
колебания, для которых соотношение (1.90) не имеет смысла.
Условие равновесия (1.38) с учетом (1.89) запишется так:
Мох(НеО-55мо) = 0, (1.91)
а линеаризированное уравнение движения (1.70) с учетом (1.90)
" Иногда эту сумму нормируют к 1; тогда множитель 4л переходит
в (1.87). Графики размагничивающих факторов эллипсоида приведены в
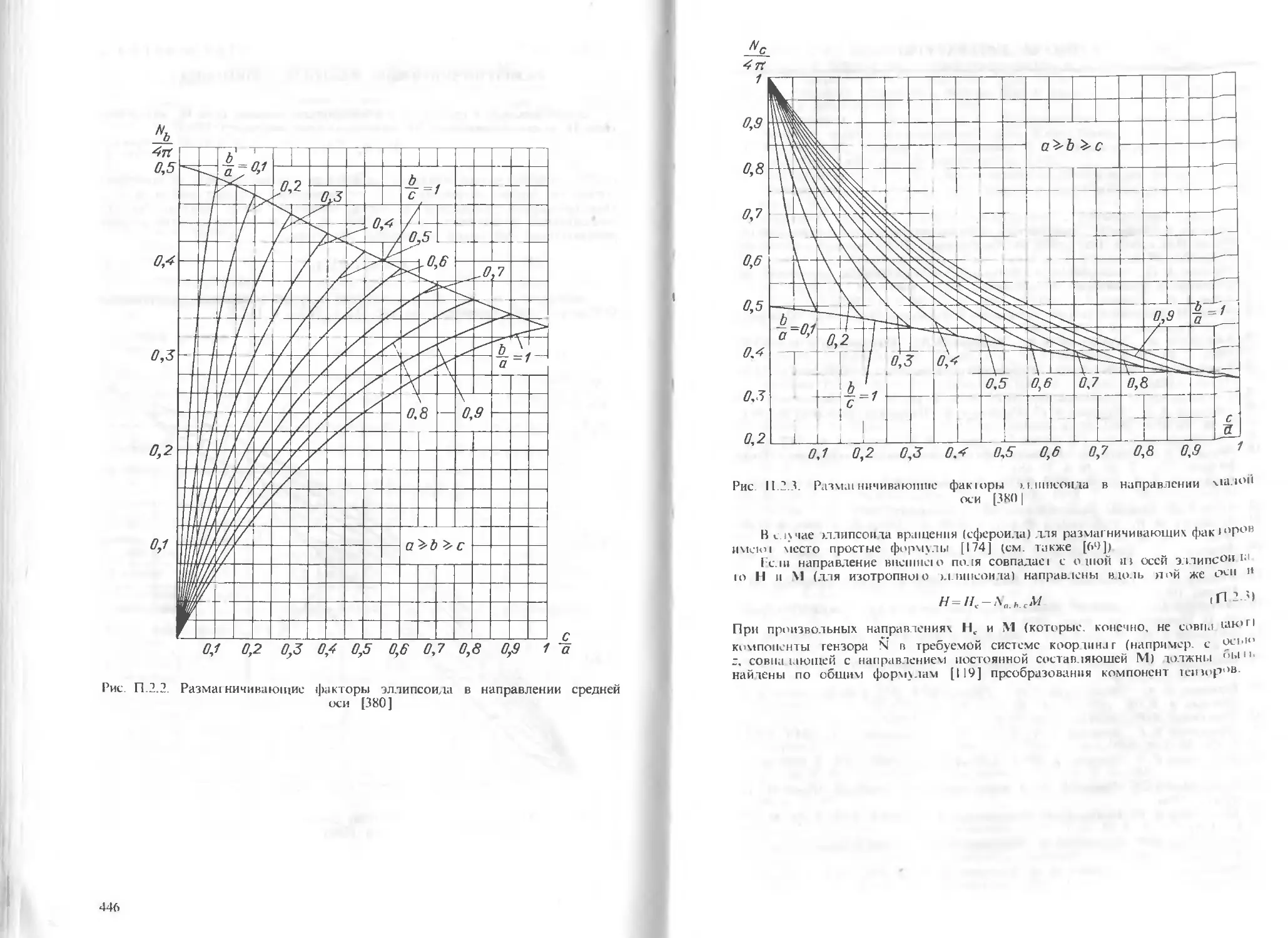
Приложении 2.
21 Особенности ферромагнитного резонанса в металлах будут рассмотрены
в (j 14.2.
32
примет вид
кот+утхН0 + у(Ат)хМ0 +
Н тхМ0 =
М0
-YM0xhc, (1.92)
где внутреннее постоянное поле Н0
определяется согласно (1.89).
Выражения (1.91) и (1.92) (с учетом (1.89))
содержат внешние поля Не0 и he,
которые можно считать заданными.
Собственные колебания. Изучение
любых колебательных систем
целесообразно начинать с задачи о
собственных колебаниях, т. е.
свободных (в отсутствие вынуждающей
силы) и незатухающих (в отсутствие
диссипации). Поэтому положим
сначала в уравнении (1.92) he = 0 и а = 0:
Рис. 1.10. Оси координат при
рассмотрении колебаний
намагниченности эллипсоида
itom+Ym х (Не0-Км0) +Y(>5m) х Мо = 0.
(1.93)
Спроектируем (1.93) на оси системы координат (рис. 1.10),
в которой ось z совпадает с направлением Н0 и М0. Пусть в этих
осях (не совпадающих, вообще говоря, с осями х', у', z' эллипсоида)
тензор 55 имеет вид
55=
Nn N12 N13
N12 N22 N23
N13 N23 N33
(1.94)
С использованием (см., например, [119]) правила умножения тензора
на вектор получим
(ко + y^i 2М0) тх + y (Яе0г - Ni3M0 + N22M 0) ту = 0,
(1.95)
-y{HcO:-N33Mo + N11Mo)mx + (i(o-yN12Mo)my = 0.
Равенство нулю определителя системы (1.95) даст формулу для
собственной частоты:
cog = (toH + ^iiY^o)K + ^22Y^o)-^i2Y2^o, (1-96)
где в соответствии с (1.45) (uH = yH0 = l{He0z-N33M0). Очевидно, что
при частотах, близких к собственной частоте со0, будет происходить
сильное поглощение энергии электромагнитного поля. Поэтому
именно частота со0, а не частота сон, при которой имеют место полюсы
компонент тензора восприимчивости вещества, является частотой
ферромагнитного резонанса в малом эллипсоиде. Подчеркнем, что
вычисление ш0 по формуле (1.96) требует предварительного решения
статической задачи об определении равновесной ориентации
намагниченности (с которой мы совместили ось z) при заданной ориентации
постоянного поля. Для этого может быть использовано условие (1.91).
3 А. Г. Гуревич, Г. А. Мелков 33
a fr В г д
Рис. 1.11. Предельные и частный случаи эллипсоида
Если внешнее постоянное поле направлено по одной из осей
эллипсоида, то постоянная намагниченность (и, следовательно, ось
г) будет также совпадать с этой осью. Тензор N станет
диагональным—с компонентами Nx, TV,, и Nz, и выражение (1.96) перейдет в
v>2o = y2[He0 + (Nx-Nz)Mo][He0 + {Ny-Nz)M0]. (1.97)
Формула (1.97) была получена Киттелем [348].
Предельными случаями эллипсоида являются бесконечно тонкий
диск (или пластинка, так как форма ее при этом уже несущественна)
и бесконечно тонкий цилиндр («иголочка»), а частным случаем —
сфера. Эти случаи показаны на рис. 1.11, а значения
размагничивающих факторов и собственных частот для них приведены в табл. 1.1.
Таблица 1.1
Частота ферромагнитного резонанса в малых образцах
Образец
Бесконечно
тонкая
пластина
Бесконечно
тонкий
цилиндр
Сфера
Направление
намагниченности
Касательное
Нормальное
Продольное
Поперечное
значение на
рис.
1.11
а
б
в
г
д
Размагничивающие
факторы
N,
0
0
2л
2л
4л
Т
Ny
4л
0
2л
0
4л
Т
N„
0
4л
0
2л
4л
Т
Собственные частоты
( —) =Яе0(Яе0+4лМ0)
^у/ (1.98)
—= Яе0-4лМ0 (1.99)
У
—= Яе0 + 2лМ0 (1.100)
Y
(—) =#е0(Яе0-2лМ0)
\У/ (1.101)
— = Яе0 (1.102)
У
В случае сферы выражение для частоты ферромагнитного
резонанса имеет наиболее простой вид и, самое главное, в него не входит
постоянная намагниченность. Прежде всего поэтому сферические
образцы наиболее часто используются в экспериментальных работах
34
по ферромагнитному резонансу в слабопроводящих веществах". Для
сферы уравнение (1.92) принимает вид (ср. с (1.70))
icom + ymxHeoH mxM0= -M0xhe, (1.103)
влияния постоянного и переменного размагничивающих полей
компенсируют друг друга, и движение намагниченности происходит как
бы во внешних полях Не0 и he. Ясно, что из (1.103) следует формула
(1.102).
Заметим, что величины N1U N12 и N12 в формуле (1.96) или
Nx и Ny в (1.97) представляют сооой размагничивающие факторы
для переменного, a N33 или Nz—для постоянного магнитных полей.
Это обстоятельство является существенным в двух случаях: при
использовании указанных формул для приближенного расчета
ферромагнитного резонанса в металлических образцах (см. § 14.2) и—для
слабопроводящих образцов—когда в силу особенностей возбуждения
переменное магнитное поле существует не во всем их объеме.
Примером является возбуждение поля в большом образце,
находящемся вне резонатора, через отверстие в его стенке. Конечно, и в этом
случае формулы (1.96) или (1.97) применимы лишь приближенно,
так как переменное поле в действительности неоднородно.
Исследуем теперь поляризацию собственных колебаний
намагниченности малого эллипсоида. Из уравнений (1.95)
ivy/y+N12M0 H0+NUM0
тх H0 + N22M0 ia>/y-Nl2M0
или с учетом (1.96)
(1.104)
Я04-АГПМ0_
\jH0 + N22M0
где £, = N12i(N22 + HoiM0), а Н0—внутреннее постоянное поле. Из
(1.104а) видно, что переменная намагниченность имеет эллиптичегт.--, -j
поляризацию с осями эллипса поляризации, не совпадающими с осями
х и у (так как разность фаз тх и ту не равна л/2).
В «киттелевском» случае, когда Не0 направлено по одной из
осей эллипсоида и N12 = 0,
ту_ . jHc0+(Nx-Nz)
«х V He0 + (Ny-Nz)
и оси эллипса поляризации совпадают с осями х и ; Большой
осью является ось х, если Ny > Nx (т. е. ось а эллипсоида ь направлении
х больше, чем ось Ъ в направлении у), и Hao6oir;i. Если же а = Ь,
т- е. эллипсоид является эллипсоидом вращения (сфероидом1*, то
Некоторую роль играет и то, что гферы малых размеров правильной
формы и с гладкой поверхностью м'';ут быть очень просто изготовлены,
например, методом обкатки сжатым воздухом [62].
3*
Iw>>l = lwxl и поляризация является круговой. В случае афЪ поляризация
приближается к круговой при Не0-юо, т. е. с ростом частоты.
Поляризацию колебаний удобно характеризовать параметром,
который можно назвать эллиптичностью:
3=1-^!!, (1.Ю6)
HraaJ
где |wmax| и |mmin| — большая и малая оси эллипса поляризации.
В киттелевском случае они совпадают с \тх\ и \ту\. И если,
например, Ny>Nx (т. е. а>Ь), то
N —N
Ny-N, + He0/M0
Затухание свободных колебаний. Примем в уравнении (1.92)
по-прежнему he = 0, но а#0. Тогда, как легко убедиться (поскольку
Н0||М0), это уравнение будет отличаться от (1.93) лишь заменой
(1.73). Проведя указанную замену в выражении (1.96), получим
tog-to2 (l+a2) + 2i'aroto1=0. (1.108)
Здесь to0 — частота собственных колебаний (1.96), а
(Oi = wH+^{N11 + N12)yM0. (1.109)
Комплексному уравнению (1.108) можно удовлетворить, если
принять to = co' + i'co", величина со' представляет собой частоту, а со" —
коэффициент затухания свободных колебаний. Подставляя со = to'+ ко"
в (1.108), найдем
Н2=(т4й-(^[^-л^2+л'"
у2 Ml, (1.110)
со" = ^\ (1.111)
1+ог
Как видно из (1.110), наличие диссипации, кроме затухания колебаний,
привело к некоторому изменению их собственной частоты, которое,
однако, при малой диссипации является величиной второго порядка
малости.
Затухание в колебательных системах часто характеризуется
добротностью, которая определяется следующим образом:
е=— или е=—, (1.П2)
где W—энергия, запасенная в системе, а Р—мощность потерь;
нетрудно убедиться, что оба определения равносильны. В нашем
случае в первом приближении (при малой диссипации)
Со=^. (1.113)
36
Эту величину можно назвать собственной добротностью, так как
она учитывает потери энергии только в самом ферромагнитном
образце.
Выражения (1.110), (1.111) и (1.113) становятся особенно простыми
для эллипсоида вращения (вокруг оси z), когда N12 = 0 и Nn=N21.
В этом случае tOi = to0 и
бо = 1/(2«), (1.114)
причем это выражение справедливо в рассматриваемом случае при
произвольной диссипации.
Вынужденные колебания. Положим в уравнении (192) he^0 и а^0.
В силу линейности этого уравнения его решение будет иметь вид
m = xehe, (1.115)
где Xе—тензор внешней восприимчивости малого эллипсоида,
связывающий комплексные амплитуды переменной намагниченности и
внешнего переменного поля. Эта восприимчивость принципиально
отличается от восприимчивости вещества х> которая была определена
соотношением (1.46). Тензор Xе возникает в результате решения
уравнения (1.92), полученного в рамках магнитостатического
приближения, и поэтому имеет смысл в тех же рамках. Более того,
он введен для определенного, а именно однородного типа колебаний
намагниченности в образце определенной формы—эллипсоиде. Тензор
же *х представляет собой восприимчивость вещества, ему «нет дела»
до того, выполняются или нет условия применимости
квазистатического приближения и какой тип колебаний имеет место0. Можно
ожидать, что полюса хе (без учета диссипации) или максимумы
мнимых частей его компонент (при ее учете) будут близки к найденным
выше собственным частотам колебаний намагниченности эллипсоида,
в то время как полюса тензора х имеют место при ю = сон.
Компоненты тензора 'yf, считая тензор х известным, можно
найти, казалось бы, очень простым путем—исключая внутреннее
поле h из тензорных выражений (1.46) и (1.90):
где (Xе)"1 и (х)-1 — обратные тензоры [119]. Заметим, что, следуя
Аркадьеву (см., например, [174]), величину (N)-1 можно назвать
«восприимчивостью формы», тогда согласно (1.116) обратная величина
«восприимчивости тела» (эллипсоида) равна сумме обратных величин
восприимчивостей вещества и формы.
Однако вычисление компонент Xе по формуле (1.116) оказывается
Довольно громоздким, и проще непосредственно решить уравнение
" Некоторая зависимость г от типа колебании (и от формы образца^
все же имеет место в силу того, что от этих Ф*^" ^^«^Г^
1см., например, § 11.3) величина параметра диссипации. Кроме того, тензор
X, конечно, существенно зависит от формы образца через величину и ори
ентацию внутреннего постоянного поля Н0.
37
(1.92). Приведем результат такого решения при а = 0:
X's-iXl Xl О
О 0 0
(1.117)
Зй^Д-'уМоСо,.^, xca = D~lyM0a, (1.118)
сйх = шн + уЛ'22Мо, (uy = (On + yN11M0. a>s=-yN12Mo, (1-П9)
Z) = tOo —со2, соо = со^со,, —со2 (1.120)
(со0 — собственная частота (1.96)).
Для учсча диссипации достаточно в (1.119) произвести замену
(1.73). Приведем значения вещественных и мнимых частей компонент
тензора хс ПРИ резонансе, когда Юо = со2(1+о!2):
2C0| 2OC0C0!
(Xl);cs = 0, № = %^, (1.121)
2QMBCCI!
Гу'Г =0 fyeV = —
(X«)res u, \Xah™ 2ami-
Для эллипсоида вращения вокруг оси г выражения для компонент
Xе существенно упрощаются. В этом случае
(хГ)^=о. {x%)'LMx%sHxl)'L=~o=xZ. (1.122)
Как мы увидим ниже (§5.3 и 5.4), взаимодействие малого
ферромагнитного эллипсоида с электромагнитным полем определяется
внешней восприимчивостью х*. Из измерений характеристик
электромагнитных систем, содержащих малый эллипсоид, можно найти
резонансные зависимости (Хх.у)" и (Хя)" от частоты или от внешнего
постоянного поля. Представляет интерес связать ширины этих
резонансных кривых с параметрами диссипации.
Нетрудно убедиться, что при малой диссипации (а«1) ширина
резонансной кривой при изменении поля АН1), определенная на
половине максимального (резонансного) значения (ХхУ- (Ху)" или
(Ха)", составляет (с учетом (1.72) и (1.112))
2аю0 2шгсо0 2#гЮо 2Xm0 cog
Д/7 = = = = = . (l.lZj)
У 7<% ш„ уМ0 ydjQo
Ширина кривой при изменении частоты
Дш = 2асо1. (1-124)
Для эллипсоида вращения вокруг оси z, в частности, для сферы,
как уже отмечалось выше, со, = со0 и Асо = у АН.
" Заметим, что в [66. 69] АН обозначало полуширит- резонансной кривой
38
Выражения (1.123). если считать какой-либо параметр диссипации
постоянным, дают формально зависимость АН от со, Н0, М0 и формы
эллипсоида (поскольку размагничивающие факторы входят в сон и со!).
Однако от всех этих величин могут зависеть и параметры диссипации,
и эти зависимости могут быть найдены лишь из эксперимента или
микроскопических теорий процессов, приводящих к диссипации
энергии. Поэтому действительные зависимости АН от со, Н0, М0 и формы
эллипсоида в рамках рассматриваемой феноменологической теории
не могут быть найдены.
Для высококачественных монокристаллов ЖИГ параметр
диссипации а, во всяком случае в сантиметровом диапазоне, слабо
зависит от частоты и составляет, как уже отмечалось выше. ~5-10~5.
Тогда согласно (1.114) добротность для эллипсоида вращения,
например, для сферы, тоже приблизительно постоянна и имеет порядок
104, а ширина кривой АН растет с частотой и при /=со, 2п~9 ГГц
составляет ~0,3 Э.
Из выражений (1.122) и (1.123) следует, что для эллипсоида
вращения имеет место важное соотношение
Д//Х«,= -1Л.. (1.125)
аналогичное соотношению (1.82) для тензора восприимчивости
вещества. Для произвольного эллипсоида в этом соотношении появится
множитель порядка 1.
Выражения для компонент тензора %с (которые нетр\дно получить,
например, производя замену (1.73) в (1.118) — (1.120)), позволяют
найти поляризацию вынужденных однородных колебаний
намагниченности в малом ферромащишом эллипсоиде. Из соображений
симметрии ясно, что поляризация является круговой только в гом
случае, когда внешнее поле имеет круговую поляризацию, а образец
является эллипсоидом вращения вокруг оси :. Однако если образец
представляет собой эллипсоид вращения (в частности, сферу), а
диссипация мала (а«1), то при ферромагнитном резонансе поляризация
переменной намагниченности мало отличается от круговой даже при
линейной поляризации внешнего поля.
Глава 2
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
§ 2.1. Уравнение Ландау—Лифшица
В этой главе будут рассмотрены однородные магнитные колебания
анизотропного ферромагнетика. Анизотропия—это зависимость
свойств вещества (или тела) от углов между направлениями, в которых
прикладываются внешние поля, и некоторыми выделенными
направлениями, которые задаются, например, структурой вещества или
формой тела. Следует заметить, что отдельные виды анизотропии
уже фигурировали в гл. 1. Во-первых, выделялось направление
постоянной намагниченности М0, и магнитная восприимчивость
ферромагнетика становилась тензором (1.47). Такой вид анизотропии, как
уже отмечалось в § 1.3, носит название гиротропии. Во-вторых,
в § 1.5, рассматривая ферромагнитный резонанс в малом эллипсоиде,
мы видели, что условие резонанса и компоненты тензора внешней
восприимчивости образца зависят от ориентации М0 относительно
осей эллипсоида. Такая анизотропия может быть названа анизотропией
формы образца. Однако на протяжении всей гл. 1 предполагалось,
что исследуемое вещество (ферромагнетик) в отсутствие постоянной
намагниченности является изотропным, т. е. в нем нет каких-либо
выделенных направлений.
В действительности ферромагнетики обычно представляют собой
кристаллы, и им присуща магнитная кристаллографическая
анизотропия; для нее выделенными направлениями являются оси
кристаллической решетки и все характеристики (в том числе компоненты
тензора %) зависят от углов, которые образуют М0, а также
переменное поле h с этими осями.
В реальных ферромагнетиках имеется также магнитоупругая
анизотропия, причиной которой является магнитоупругое
взаимодействие (см. гл. 12), а выделенные направления задаются механическими
напряжениями. Существуют, хотя играют обычно меньшую роль,
и другие виды анизотропии, связанные, например, с электрическими
полями, градиентами температуры и пр. Задачей этой главы является
рассмотрение общих методов учета влияния анизотропии на
ферромагнитный резонанс и применение их к случаю магнитной
кристаллографической анизотропии.
При классическом описании ферромагнитного резонанса различные
виды взаимодействия, приводящие к анизотропии, могут быть учтены
путем введения соответствующих членов внутренней (при температуре
Г=0) или свободной (при Г>0) энергии ферромагнетика. Не
интересуясь пока явлениями на граничных поверхностях (которые
40
проявляются для ферромагнитных тел малых размеров), мы будем
иметь дело только с объемными плотностями внутренней энергии
Ui и свободной энергии Uf. Они связаны между собой соотношением
(см., например, [133]):
Uf=Ui-TS, (2.1)
где S—объемная плотность энтропии1'. При записи величин Ut или
U/, зависящих от углов между вектором намагниченности и
выделенными направлениями, принимаются во внимание в первую очередь
требования симметрии; константы же, входящие в эти выражения,
могут быть найдены из микроскопических теорий или из эксперимента.
При этом член (— TS) обычно в явном виде не выписывается,
а «размазывается» по всему выражению для Uf', тогда входящая
в это выражение намагниченность и все константы становятся
функциями температуры2).
Обобщение уравнения движения намагниченности. Уравнение
движения намагниченности анизотропного ферромагнетика было впервые
записано Ландау и Лифшицем в 1935 г. [130]. Строгий вывод его
в рамках классической теории невозможен, и цель приводимых ниже
рассуждений состоит в том, чтобы показать, что это уравнение
является разумным обобщением уравнения движения намагниченности
для изотропного ферромагнетика (1.34) (которое, впрочем, тоже не
может быть выведено строго в рамках классической теории).
Пренебрежем сначала диссипацией и заметим, что уравнение
(1.34) можно переписать следующим образом3':
^ = уМх^, (2.2)
dt ' ёМ к '
где
C/mag=-MH (2.3)
— «энергия» (т. е. в соответствии со сделанными выше замечаниями —
плотность энергии или свободной энергии) намагниченности в
магнитном поле Н. Напомним, что условие, определяющее равновесную
ориентацию вектора намагниченности, для изотропного
ферромагнетика имеет вид (1.38), т. е. с учетом (2.3)
Мх^=0. (2.4)
дМ
" Слова «объемная плотность» мы будем в дальнейшем опускать, т. с^
называть величины U„ Uf к S соответственно внутренней энергией, свободной
энергией и штропией.
2) Индексы * и / часто будут опускаться, так что U будет представлять
собой объемную плотность внутренней (при Г=0) или свободной (при Г>0)
энергии. Для краткости мы будем обычно называть эту величину просто
энергией.
31 Производная скаляра по вектору—это вектор, составляющие которого —
производные скаляра по соответствующим составляющим вектора. В данном
случае SU/dM = x0dU/dMx+y0BU!eMy+z0dUI6Mz> где х0, у0 и z0—единичные
векторы.
41
Рассмотрим теперь равновесие анизотропного ферромагнетика.
Необходимым условием его (см., например, [131]) является
стационарность энергии, т. е. равенство нулю ее вариации:
b$U(M)dV=0. (2.5)
При этом следует принять во внимание условие (1.35) постоянства
длины вектора М, которое, как мы видели, выполняется для
изотропного ферромагнетика, во всяком случае в отсутствие
диссипации. Это постоянство является результатом сильного обменного
взаимодействия, и поскольку все взаимодействия, приводящие к
анизотропии, слабее обменного, есть основания полагать, что (1.35)
будет справедливо и для анизотропного феррома! нетика. Как известно
из вариационного исчисления (см, например, [127]), условие
стационарности интеграла \U(M)dl' мри дополнительном условии
М2 = const имеет вид
ш{и+хм2)=ш+2Ш=°<
(2.6J
где X — произвольный множитель Лафанжа. Из (2.6) следует, что
Мх— = о
6М
(2.7)
Если намагниченность неоднородна, то вариационная произиодная
[127]
■и
>(гм1£Хр
(2.8)
Сравнивая (2.7) с (2.4), мы видим, что в условии равновесия
"^mag/^M заменилась на величину 6U/8M (в которую dUnwg/3M
вхолит как одно из слагаемых). Естественно предположить, что
такую же замену можно произвести в уравнении движения. Тогда,
обозначая
НсГ =
— у Л
си
j(dM/cx„)
мы приходим к уравнению Ландау — Лифшица
ем
-YMxHef + R,
(2.9)
(2.10)
где R—диссипативный член, формы записи которого (для изотопного
X™a)MrMaTPMCb в § ы- у™е ^"= ™'>
MoxHcfO = 0. (2П)
и ур^г„:тип;нГетчлвгв уравнении (L67) останется без —
(\\ -у rvr
— =-vMxH,r+-Mx-
'' М и ■
(2.12)
42
В диссипативных членах, входящих в (1.66) и (1.69), следует,
по-видимому, замени ib H на НсГ.
Для анизотропного ферромагнетика параметр у и g-фактор,
.вязанный с ним соотношением (1.12). счедует считать, вообще
творя, тензорными величинами. Заме!им, что при интерпреiации
результатов измерения парамагнитного резонанса (см., например,
[6]) вся анизотропия учитывается обычно при помощи тензорного
^-фактора. Имеются экспериментальные данные [316].
свидетельствующие о том. что для ферромагнетиков в некоторых случаях — при
большой анизотропии учет тензорного характера g-фактора наряду
с членами энер!ии, ошегствепными за анизотропию, является
необходимым. Однако вопрос об уравнении движения намагниченности,
которое следует использовать в этом случае, не вполне ясен. И так
как поправка, возникающая в результате учета анизотропии g-фактора,
оказывается малой, мы в дальнейшем будем всегда считать величину
у в уравнении движения скалярной и учитывать всю анизотропию
при помощи соответствующих членов энергии U.
Члены энергии. В рассма i риваемом случае анизотропного
ферромагнетика
I'^U^ + U^+U,, (2.13)
где Ип — обменная энерши. {/„,.,,, магнитная энергия, a L,. энергия
анизотропии.
Обменная эиершя. ио очником которой, как отмечалось fj 1.1,
является электростатическое по своей природе обменное
взаимодействие, может быть преде швлена в виде
U„=UA+Uq. (2.14)
где
иА=-^АМ2 (2.15)
— однородная, a Uq—неоднородная ее части. Эффективным полем,
которое со!ласно (2.9) соответствует энергии Ь\, является
«молекулярное поле» (1.26). Для ферромагнетика это поле не входит в уравнение
лвижения, во всяком случае в основной его член и в диссипативные
члены в форме Гильберта или Ландау — Лифшица. Неоднородная
часть Uq, которая характеризует возрастание обменной энергии при
неоднородной намагниченности, вообще говоря, входит в уравнение
движения. Но мы пока рассматриваем однородные магнитные
колебания и можем ее не учитывать.
Магнитная мерги.ч может быть представлена в виде
{„..:=£,+ £.,. (2.16)
1де 1У — 3et лановская энергия —эиершя взаимодействия намашичен-
ности с внешним полем Н,., а I ц -внутренняя магнитная энергия,
источником которой (см. <j 1 !) является vni нитное (дип<>ль-дипольное)
4-
взаимодействие магнитных моментов образца. Зеемановскую энергию
можно записать аналогично (2.3):
£/z=-MHe. (2.17)
В случае малого ферромагнитного эллипсоида (§ 1.5) эффективным
полем диполь-дипрльного взаимодействия должно быть
размагничивающее поле (—NM). Легко убедиться с учетом симметрии тензора-
N, что в этом случае
UM=!-MNM. (2.18)
Величина £/„ учитывает все виды анизотропии. Конкретные выражения
для нее в случае магнитной кристаллографической анизотропии будут
приведены в § 2.2.
Линеаризации уравнения Ландау—Лифшица. Подставим в
уравнение (2.12) М = М0 + техр(/юО и
Hcf = Hcf о+hef exp (tof)+h exp (to/). (2.19)
При этом мы выделили из переменного эффективного поля заданное
переменное поле h, в то время как заданное постоянное поле осталось
включенным в Н-го- Следует подчеркнуть, что поле h может представлять
собой как внутреннее, так и внешнее поле в зависимости от того,
какая задача решается—об определении восприимчивости вещества
X или об определении внешнего тензора восприимчивости %'. Принимая
во внимание условие равновесия (2.11) и считая переменные величины
малыми, получим линейное уравнение для комплексных амплитуд
Kom + ymxHrfo + YMoxhefH mxM0 = —yM0xh. (2.20)
Покажем прежде всего, что результаты, полученные в § 1.5, могут
быть найдены и с помощью развитого в данном параграфе формализма.
Будем считать заданными внешние поля—постоянное Не0 и переменное
he, а ферромагнетик, как и в § 1.5,—изотропным. Тогда энергия U
будет суммой зеемановской энергии (2.17) и энергии размагничивающего
поля (2.18). Применяя формулу (2.9) (для рассматриваемых однородных
колебаний^ играет роль лишь первый ее член), находим Hefo=He0— NM0
и hef= —Nm. Подставляя эти величины в (2.20), мы получим уравнение
(1.92), из которого была выведена вся теория однородного
ферромагнитного резонанса в малом эллипсоиде.
Методы расчета ферромагнитного резонанса в анизотропном
ферромагнетике. Один из них—метод эффективных размагничивающих
факторов, который был предложен Киттелем [348] и разработан
Макдональдом [363], заключается в следующем. Выражения для
эффективных полей мы пытаемся представить аналогично
размагничивающему полю в виде
Hcf=-NefM, (2.21)
вводя таким образом тензор эффективных размагничивающих
факторов. В § 2.3 будет показано, что такое представление оказывается
44
возможным в случае малых колебаний (т«М), если ось z направить
по равновесной намагниченности М0. Если эффективные поля
записаны в виде (2.21), то задача об учете анизотропии, по существу,
решена, так как могут быть использованы формулыи§ 1.5. В них
следует лишь произвести^ замену компонент тензора N на
соответствующие компоненты Nef или суммы N + N'f—в зависимости от
постановки задачи, согласно табл. 2.1.
Таблица 2.1
Замена компонент тензоров при использовании формул § 1.5
для учета анизотропии (ось 3 совпадает с направлением М0)
Компоненты
тензора N
NtJ(iJ=\,2)
N
зз
заменяются на
при вычислении х
анизотропного
ферромагнетика
N-
Nl3 + N&
при вычислении %'
эллипсоида из
анизотропного ферромагнетика
N„+N1
N31 + N«3
Другой метод учета влияния анизотропии на ферромагнитный
резонанс, который можно назвать методом сферических координат,
предложили Смит и Бельерс [416] и Су л, обобщение его на случай
наличия диссипации было проведено Скроцким и Курбатовым [185].
Этот метод основан на переходе от переменных Мх,
Му и Мг к переменным 6, ср и М (рис. 2.1); если длина вектора
М сохраняется, то достаточно двух переменных 6 и ср. Полярная
ось (ось z на рис. 2.1) при использовании этого метода может не
совпадать с направлением М0.
Получим прежде всего уравнение движения намагниченности
в новых переменных. Для и ого в проекциях, например, уравнения
(2.12) (обеспечивающего постоянство М) перейдем от Мх, Му,
Мг к переменным 6, ср. Предположим,
что намагниченность однородна, так
что в выражении для эффективного
поля (2.9) можно ограничиться первым
членом. Тогда полученные три
уравнения, как нетрудно убедиться, будут
тождественно удовлетворяться, если
будут справедливы следующие два
уравнения (мы запишем их для случая
малой диссипации, т.е. а2«1):
у с U яу с U
а
Гф
М sin G гф М ("6
7 с U ху с U
(2.22)
сt M sin G ев М sin 2 G сц>
Если бы мы исходили из
уравнения движения (1.69) с диссипативным
Рис. 2.1. Декартовы и
сферические координаты
намагниченности
45
членом, не обеспечивающим сохранения М, то два уравнения совпали
бы с (2.22) при замене сог->асоя и добавилось бы третье уравнение
Рассмотрим теперь случай малых отклонений М от равновесного
вектора М0, который характеризуется углами 60 и ф0. Эти углы
могуть быть найдены из условий равновесия
Щ _/зи\
.геЛ=е — ~\^1 =°>
6о.9 = 9о \Сф/е=е0,9=ср0
которые эквивалентны условию (2.11) (необходимо, конечно, убедиться,
что найденные углы 60 и ф0 соответствуют именно минимуму
энергии). Разложим dU/дв и dU/dq> в (2.22) по степеням малых
величин 50.=6—60 и 6ф.= ф —ф0, учтем условия (2.24) и отбросим
члены со степенями 66. и 6ф„ выше первой. Тогда, предполагая
колебания гармоническими (66.= 66 exp (tor), 6ф.= 5ф ехр (Ш)), получим
для комплексных амплитуд 86 и 6ф линейные уравнения
\MBsmeo ^ М0 J \MBsmeo ™ M0 ^J
\M0sm60 ^ M0sm2e0 *y \M0sme0 M0sm260 ^J
Здесь обозначено
V^Ve=e0,9=9o ** V5<P/e=e0,P=90 * ^<Р/е=е0,9=Ф,
Равенство нулю определителя системы (2.25) при а=0 даст
выражение для собственной частоты ферромагнитного резонанса
ш-м^Ыи*и~-иЫт> (2-26)
известное как формула Смита—Сула.
При учете диссипации частота свободных колебаний становится
комплексной, ее вещественная часть в первом приближении (а2«1)
дается выражением (2.26), а мнимая часть
2М0\ sin2G0 "у
Зеемановская энергия (2.17), которая является одним из членов
энергии U, в сферических координатах запишется следующим образом:
Uz=~ MHC [cos 6 cos 6H + sin 6 sin 6Я cos (ф - фя)], (2.28)
где 6;/ и фя—углы вектора Не; аналогичным образом—с заменой
Не на И может быть записана полная магнитная энергия (2.3).
При рассмотрении вынужденных колебаний мы должны включить
в энергию члены, содержащие заданное переменное поле
h_—внутреннее или внешнее, в зависимости от постановки задачи. Энергия
Uh намагниченности в этом поле будет иметь вид, аналогичный
(2.28). Мы сохраним обозначение U для энергии без этого члена,
так что полная энергия Ui = U+Uh. Если мы теперь проделаем те
же операции, как и при выводе уравнений (2.25), но заменив U на
Ui, то придем к двум уравнениям, левые части которых будут
такими же, как в (2.25), а в правых частях появятся члены
соответственно
уЛsin6Лsin(ф0 — фЛ) и — y/z[ctg60sin6,,cos(ф0 — Ф*)—cos6fc], (2.29)
где И — комплексная амплитуда длины вектора h_, а 6Л и фЛ—его углы.
Метод сферических координат приводит обычно к более
компактным вычислениям, чем метод эффективных размагничивающих
факторов. Однако при его использовании следует очень аккуратно
учитывать условие равновесия" и стараться не направлять ось z по
М0 (когда sin60 = 0). При использовании же метода эффективных
размагничивающих факторов ось z должна обязательно совпадать
с направлением равновесной намагниченности. В остальном же оба
метода совершенно эквивалентны, так как базируются на одном
и том же уравнении движения намагниченности.
§ 2.2. Магнитная кристаллографическая анизотропия
В этом и следующих параграфах данной главы мы остановимся
на наиболее важном виде анизотропии ферромагнетиков — магнитной
кристаллографической анизотропии.
Природа магнитной кристаллографической анизотропии. Как
отмечалось в § 1.1, обменное взаимодействие между спиновыми
моментами (в отсутствие орбитальных) изотропно. Поэтому причинами
возникновения кристаллографической анизотропии могут явиться либо
другие виды взаимодействия спиновых моментов, либо наличие
орбитальных моментов, связанных со спиновыми моментами спин-
орбитальным взаимодействием.
Одним из источников кристаллографической анизотропии маг-
нитоупорядоченных кристаллов является магнитное (диполь-диполь-
ное) взаимодействие элементарных магнитных моментов (см. § 1.1).
В интересующем нас случае намагниченного до насыщения
ферромагнетика, когда величины и ориентации всех моментов одинаковы,
энергия магнитного взаимодействия пары моментов 9И согласно (1.3)
составит
sfr= -^(cos2Qfr-^= -c(cos*Qfr-?j, (2-30>
В частности, нельзя, считая отклонение М0 от направления Нс0 малым,
просто принять 60 = 6Н; возникающая при этом ошибка может быть того
же порядка, как и сам эффект анизотропии.
47
где Qff—угол между 9И и г/г. Если магнитные моменты
расположены в пространстве упорядоченно, образуя решетку, то величина
UM, являющаяся суммой выражений (2.30), должна, вообще говоря,
зависеть от ориентации моментов по отношению к осям этой
решетки. Однако для кубических кристаллов Uu изотропна, а для
других — некубических ферромагнетиков ее вклад в энергию
кристаллографической анизотропии оказывается очень малым.
Другим источником кристаллографической аники ропии
ферромагнетиков является анизотропия обменного взаимодействия, которая
возникает при наличии орбитальных моментов и является следствием
спин-орбитального взаимодействия. Возникновение ее (в случае
прямого обмена) можно пояснить следующим образом [343]. В силу
спин-орбитального взаимодействия попорот спинов относительно
решетки приводит к некоторому изменению формы электронных
оболочек атомов. Следовательно, изменяется энергия обменного
взаимодействия, которая является частью кулоновской энергии
взаимодействия этих оболочек. В случае косвенного обмена механизм
появления анизотропии обменного взаимодействия является более
сложным, но по-прежнему основную роль в нем играет спин-
орбитальное взаимодействие.
Если обменное взаимодействие становится анизотропным, то
его энергию (в случае однородной намагниченности) следует
записать в виде
иА=-1-МЛМ, (2.31)
где Л — тензор обменного взаимодействия, заменивший скалярную
обменную константу в (2.15). Однако принято обменную энергию
по-прежнему считать изотропной, а зависящую от углов между
М и осями кристалла часть энергии (2.31) относить к энергии
анизотропии.
Оба рассмотренных выше источника анизотропии, несмотря на
их разную физическую природу, объединяет то, что в основе их
лежат парные взаимодействия магнитных моментов. Фигурирующая
в (2.30) угловая зависимость представляет собой (см., например,
[123]) первый член разложения произвольной угловой зависимости
в ряд по «естес!ионным» для данной задачи функциям -полиномам
Лежандра [127] or cos0. Это дало основание Ван-Флеку ввести как
формальный источник анизотропии псевдодипольное взаимодействие
с угловой зависимостью, как в (2.30), но с другим коэффициентом
С. При попытке описать при помощи такого взаимодействия реальные
величины анизотропии ферромагнетиков значения С оказываются
обычно на 2—3 порядка ббльшими, чем в (2.30). Существенный
вклад в найденные таким образом величины коэффициента С может
вносить анизотропия обменного взаимодействия.
Совершенно иным, с первого взгляда, является одшпюнный
источник кристаллографической анизотропии [458, 343]. В этом
случае зависящая от углов (между намагниченностью и осями
кристалла) свободная энергия возникает не в результате суммирования
4s
энергий парных взаимодействий, а в результате суммирования энергий
индивидуальных ионов, но, конечно, не без учета их взаимодействий.
Характеристикой иона служит его энергетический спектр, т. е. набор
разрешенных уровней энергии. Для ионов справедливо больцмановское
распределение по энергиям, и плотность свободной энергии (в случае
ионов одного сорта) может быть вычислена по формуле (см. [133])
Uin„=-y.T\n
■'ion
м"£е-е'1ЫГ) .
■ J'=l
(2.32)
Здесь е7-—энергетические уровни иона, а N—концентрация ионов.
Как видно из (2.32), источником анизотропии являются теперь
угловые зависимости энергетических уровней ионов.
Расчеты одноионных вкладов в магнитную кристаллографическую
анизотропию ионных кристаллов, как ферро- так и ферримагнитных,
дают величины, близкие к экспериментальным.
Следует подчеркнуть, что как в случае анизотропии обменного
взаимодействия, так и для одноионного механизма причиной
кристаллографической магнитной анизотропии является спин-орбитальное (а
также внутриионное спин-спиновое) взаимодействие. Обменное
взаимодействие (которое при наличии спин-орбитальной связи
обязательно является анизотропным) существенно влияет на расщепление
энергетических уровней, определяя совместно со спин-орбитальным
взаимодействием их угловые зависимости. Отсюда следует, что
анизотропное обменное взаимодействие и одноионная анизотропия
являются не независимыми механизмами, а моделями, или теориями,
отражающими в той или иной мере реальные ситуации.
Феноменологическое описание кристаллографической анизотропии.
Независимо от природы магнитной кристаллографической
анизотропии можно записать, как предложил Акулов, выражения для ее
свободной энергии в виде степенных рядов по проекциям М на оси
кристалла (или по тригонометрическим функциям углов вектора
М относительно этих осей). Такие выражения должны быть
совместимы с симметрией данного кристалла, т. е. оставаться
инвариантными при всех операциях, входящих в его группу симметрии.
Коэффициенты в этих рядах называются константами анизотропии.
В разложениях энергии анизотропии по проекциям
намагниченности могут присутствовать только члены с четными степенями.
Причина этого заключается в том, что намагниченность, являющаяся
аксиальным вектором (см., например, [198]), изменяет знак при
обращении знака времени, в то время как энергия кристалла должна
быть инвариантна относительно такой операции.
Для кристаллов ромбической сингонии (с тремя взаимно
перпендикулярными осями второго порядка)
C/a = AT(11>af + ЛГ^2)а2+члены более высоких порядков, (2.33)
где <Xj = Mj/M(j=l, 2, 3)—косинусы углов вектора JV1 с указанными
осями. При записи (2.33) учтено, что ai+a2 + 0C3=l, и поэтому
один из членов К^а] опущен.
4 А. Г. Гуревич, Г. А. Мелков 49
Для так называемых одноосных ферромагнетиков — тригональной,
тетрагональной и гексагональной сиш оний (имеющих одну— главную
ось соответственно третьего, четвертого и шестого порядка) — в
первом прибтижении можно пренебречь анизотропией в
перпендикулярной этой оси (базисной) плоское i и и записать
c/a = tf1sin26 + A:2sin4e+A'3sin60+..., (2.34)
где 6—угол между вектором М и главной осью. При учетз
анизотропии в базисной плоскости (которая обычно невелика) для
тетрагональных кристаллов в (2.34) войдет член A"2sin46cos4ip. а для
тритональных и гексагональных — член К'3 sin6 6 cos 6ф, 1де ф — угол
п базисной плоскости.
Для кубических кристаллов энергию анизотропии обычно
записывают в виде, предложенном Акуловым:
Ua = Kl(a21a.l + a%aj + aja.l) + K2ai21ai22al+ .... (2.35)
где о,-—косинусы углов между М и осями четвертого порядка, т. е.
(см. рис. 2.2) направлениями [100], [010] и [001]. Перный член
в (2.35) может быть заменен на величину К\ (а4 + а4 + а4),
отличающуюся от первого члена в (2.35) (при К\ = —-К.А лишь
несущественным постоянным слагаемым. Если от направляющих косинусов
о,- перейти к углам 0 и ф в сферической системе координат, то
(2.35) примет вид
L,a = -^1(sin22e + sin46sin22V) I ~Ar2sin20sin226sin22V+... (2.36)
В энергию магнитной кристаллографической анизотропии обычно
включают зависящие от углов части упругой и магнитоупрутой
энергий (см. § 12.1), связанные со спонтанными (магнитострикциоп-
ными) деформациями, которые возникают в ферромагнетике
вследствие его намагничивания. Поскольку вид выражений (2.34) и (2.35)
определяется только симметрией кристалла, они остаются
справедливыми и для этой суммарной энергии, изменяются
(перенормируются) лишь величины констант анизотропии. Измерения анизотропии
«статическими» методами, т. с. при медленном (по сравнению с
временем установления равновесных упругих деформаций) изменении
направления намагниченности, дают именно такие - перенормированные
константы. При быстрых же изменениях намагниченности, например,
при ферромагнитном резонансе, деформации «не поспеваю!» за этими
изменениями, и колебания нама! ниченности происходят в «застывшей»
решетке. Поэтому величины констанг анизотропии, найденные из
резонансных измерений, отличаются, вообще говоря, от их статических
значений. ?'oi вопрос будет рассматриваться в гл. 12.
Равновесные ориентации намагниченности. Как уже неоднократно
отмечалось, исследованию малых магнитных колебаний должн"
предшествовать определение равновесной ориентации намаишчеп-
Hociii. Мы остановимся сейчас кратко на этой задаче. Если н,-
учшывать никаких других видов \[nni\ (ЮО)
шергии, кроме онергии
кристаллографической анизотропии, то
равновесные направления
намагниченности •' удут определяться из
условия минимума этой энергии.
1акие направления называются
осями легкого намагничивания или
просто легкими осями.
Направления же, в которых £/.,
максимальна,— это оси трудного
намагничивания (трудные оси).
Рассмотрим сначала
одноосные кристаллы и о: раничимся
в (2.34) первой коне кипой Kt.
Тогда, если А", >0, то легкой осью
будет ось анизотропии (8 = 0); ес-
.ти К1<0, то ось будет трудной, а плоскость 6=я/2—легкой. Учет
анизотропии в базисной плоскости приведет, конечно, к тому, что в
этой плоскости выделится некоторое число «легчайших» направлений.
Для кубических кристаллов также ограничимся сначала учетом
первой константы Кх. Если А",>0, то как нетрудно убедиться,
ле1кими будут (рис. 2.2) направления <100>п. Трудными осями будут
в этом случае направления <111> (6 = 54 44'). При Л\<0 оси <111>
будут легкими, а <100> - трудными. При К2¥=0 трудные и легкие
Рис. 2.2. Оси и плоскости симметрии
в кубическом кристалле
4
направления останутся такими же, если
В действительности для нахождения равновесной ориентации
намагниченности необходимо, кроме энергии кристаллографической
анизотропии, учитывать шергию (2.17) во внешнем магнитном поле,
внутреннюю магнитную эпер! ию (2.18) и- при наличии внешних
упругих напряжений еще и ма! нитоупругую и упругую энергии.
При этом можно идти по двум (совершенно эквивалентным) путям:
минимизировать суммарную энергию или использовать условие
(2.11).
Заметим, что однородная намагниченность всего образца отнюдь
не является всегда равновесным состоянием; в отсутствие внешнего
поля или в слабых полях образцы (не очень малых размеров)
распадаются на домены (см. ит. X). В данной главе мы будем
предполагать, что внешнее поле достаточно велико, чтобы образцы
были намагничены до насыщения. И так как мы будем рассматривать
образцы эллипсоидальной формы, то намагниченность их будет
однородна, п задача будет заключаться в определении ориентации
этой намагниченности.
< > обозначает одно из эквивалентных направлений, например- /
одно из направлений [100]. [010] и [001]. Хиалогично '
"J эквивалентных плоскостей, например,
№10) и (001).
00>
обозначает одн)
{100J одну из плоскостей (100)
4 *
Ч
Для сферических
образцов анизотропия формы
отсутствует и ориентация
Мо определяется из условия
минимума суммы энергии
кристаллографической
анизотропии U„ и зеемановской
энергии (2.17). Рассмотрим
в качестве примера сферу
из одноосного кристалла
(рис. 2.3). Ограничиваясь
учетом первой константы
анизотропии и используя
(2.28), запишем эту сумму:
U=KiSin2Q-M0He0 х
Рис. 2.3. Оси координат в сфере из одно- х [sin 6 sin 6Я cos (Ф - Фн) +
осного ферромагнетика (К1>0) Легкая +cos6cos0ff]. (2.37)
ось—z'
Условиями равновесия
будут (2.24). Приравнивая
нулю dU/d(p, мы сразу же видим, что ф0 = Фя- Приравнивая нулю
dU/dQ, получаем уравнение
sin 260 = (Hc0IHA1) sin (6Я - 0О)
Здесь обозначено
HAl = KliMD.
Анализ уравнения (2.38) показывает
ность М0 совпадает по направлению с
\в0,ерад
SO Вн,град
Рис. 2.4. Равновесные ориентации
намагниченности в сфере из одноосного
ферромагнетика. Цифры у кривых—значения
Нсо 1НАу. Принято НА1=4лМ0. Штриховые
линии—решение не реализуется из-за
возникновения доменной структуры
52
(2.38)
(2.39)
(рис. 2.4), что намагничен-
полем Не0, если последнее
направлено по легкой оси
(при К у > 0) или лежит в
легкой плоскости (при Ky < 0).
Если поле направлено по
трудной оси или лежит
в трудной плоскости, то
направления М0 и Не0
совпадают только при Не0>
>\2НА1\. Но условием
однородной намагниченности
(отсутствия доменов) является
в данном случае (см. гл. 8)
Не0>2\НА1\ + (4п,3)М0.
Таким образом, в однородно
не магниченной сфере
постоянная намагниченность
всегда совпадает по
направлению с внешним постоянным
полем, если последнее
направлено по оси или лежи г
в базисной плоскости. Для других направлений поля, как видно из
рис. 2.4, направление М0 приближается к направлению поля
асимптотически по мере роста Не0. Аналогично ведет себя, как показывают
расчеты (см., например, [230]) постоянная намагниченность и в
кубических кристаллах: если намагниченность однородна, она совпадает
по направлению с полем, когда последнее направление направлено
по одной из осей симметрии кристалла — <100>, <111> или <110>.
В заключение этого параграфа остановимся кратко на методике
измерения констант кристаллографической анизотропии. Для этого
должны быть использованы монокристаллические образцы в виде
эллипсоидов, позволяющие учесть (если известна намагниченность
Мо) анизотропию формы. Наиболее удобны сферы, для которых
анизотропия формы отсутствует и, таким образом, знание М0 не
является необходимым. Эти образцы должны поворачиваться вокруг
некоторых осей так, чтобы вектор М0 изменял свою ориентацию
по отношению к осям кристалла. Величинами, которые при этом
непосредственно измеряются, являются механический вращающий
момент (см., например, [31]) или частота (либо при фиксированной
частоте — величина постоянного магнитного поля) ферромагнитного
резонанса (§ 2.3).
§ 2.3. Ферромагнитный резонанс в монокристаллах
При изучении влияния кристаллографической анизотропии на
колебания намагниченности в монокристаллах мы будем использовать
в основном метод эффективных размагничивающих факторов. Он
заключается в том (см. § 2.1), что эффективное поле, в данном
случае — кристаллографической анизотропии
Н, = -^, (2.40)
записывается в виде
Ha=-NaM (2.41)
и используются (с соответствующими заменами) формулы § 1.5.
Таким путем могут быть решены: 1) фундаментальная задача о
нахождении тензора магнитной восприимчивости % монокристаллического
ферромагнетика; 2) более частная, но тоже очень важная задача об
однородных магнитных колебаниях (ферромагнитном резонансе)
малого эллипсоида из такого вещества. ^
При решении первой задачи поперечные компоненты N должны
быть заменены (см. табл. 2.1) на компоненты Na, a Nzi—jia. сумму
^зз + N33; при решении второй задачи все компоненты N должны
быть заменены на соответствующие компоненты N+Na. При этом
компоненты обоих тензоров должны быть записаны, конечно, в одной
и той же системе координат—в которой ось z совпадает с М0;
ДЛЯ тензора Na только в такой системе и возможна запись (2.41).
направление оси z (т. е. равновесная ориентация намагниченности)
Должно быть предварительно найдено.
53
Остановимся сначала на первой из упомянутых задач и приведем
следующие из (1.117) общие выражения для компонент тензора
магнитной проницаемости анизотропного ферромагнетика, которые
понадобятся нам в дальнейшем:
Vx Vs + Wa О
ц,-г'цй Цу О
О 0 1
(2.42)
, , Юм<*> юмю5 юмю
ю2-ю2 cog-co2 Юо-ю2
Здесь (D0 имеет вид (1.120), а величины аХш у, s, если не учитывать
диссипации,^определяются выражениями (1.П9) с заменой поперечных
компонент N на поперечные компоненты Na и N33 — на N33 + N%3.
Для учета диссипации достаточно провести замену величины
сон (входящей в ах и ау) иа со^Ч-гасо.
Решение второй задачи мы рассмотрим более подробно для
двух частных случаев — одноосного и кубического ферромагнетика.
Сфера из одноосного ферромагнетика. Пренебрежем анизотропией
в базисной плоскости и ограничимся сначала учетом только первой
константы анизотропии в (2.34). Тогда
иг = К, sin2 е0 = *,(1 - Mi-I Ml), (2.44)
где ось z' совпадает с осью анизотропии кристалла. Записывая
составляющие эффективного поля согласно (2.40) в координатах х,
у', z' (см. рис. 2.3) и переходя затем к системе х, у, z (в которой
ось z направлена по М0, а ось х совпадает с х'), мы получим,
как легко убедиться.
2Н
Яа х = 0, Яа у = — (М. соь 60 - М, sin Go) sin G0,
Ma (2.45)
Яаг =—-(Mzcoseo-M}.sineo)cos0o,
где НА1 определено согласно (2.39). Выражения (2.45) имеют вид
(2.41). В случае малых колебаний (MXt у«Mz ~ M 0) Яа можно
представить (см., например, [69]) в виде (2.41) и при учете высших
членов в (2.34). В частности, с учетом первых двух членов
N\y=N\2 = Q, iVa22=-^isin2e0+^(2sin2e0-3sin4e0),
Mo M0 (246)
N%3 = ~± cos2 e0 -^ (cos2 Go - cos4 60),
Mr, Mr,
где, аналогично (2.39),
НА2 = К2;М0. (2.47)
Получим теперь выражение для собственной частоты однородных
колебаний намагниченности (частоты ферромагнитного резонанса) в
сфере из одноосного ферромагнетика. Для этого мы должны согласно
54
табл. 2.1 подставить в формулу (1.96) суммы компонент тензора
55 и компонент (2.46) тензора эффективных размагничивающих факторов
анизотропии. Однако для сферы все компоненты 51 равны и сократятся, и
(ио/7)2 = [Д'сог + 2ЯА1со8 2е0+4ЯА28т2ео(1+2со8 2ео)][Яео2+
+ 2Ял1со82е0-2ЯА28т22е0], (2.48)
где He0z = He0cos(QH—60), а 6Я и 60—углы, которые образуют
соответственно векторы Не0 и М0 с осью анизотропии. Угол 60 при заданном
GH должен быть найден в результате решения задачи о равновесной
ориентации намагниченности, которая рассматривалась в § 2.2.
Заметим, что важной особенностью сферических образцов, которая
является следствием изотропии их тензора N, является то, что все
выражения для компонент тензора %е отличаются от соответствующих
выражений для компонент % только заменой в последних Я02 на
He0z. Поэтому выражение (2.48), если заменить в нем Яе0г на Я0г,
даст резонансную частоту тензора х анизотропного ферромагнетика.
Покажем теперь (для простоты—при учете только Ki), что
такое же выражение для частоты ферромагнитного резонанса в сфере
из одноосного ферромагнетика можно получить и методом
сферических координат. Энергия U, входящая в формулу Смита—Сула (2.26),
будет являться суммой зеемановской энергии и энергии анизотропии
(внутреннюю магнитную энергию для сферы не нужно учитывать,
так как она изотропна). Учитывая условие равновесия ф0 = Фн>
получим согласно (2.26):
№) =[Яе0со5(ео-е„) + 2ЯЛ1со82е0]Яе0^. (2.49)
Используя второе условие равновесия (2.38), нетрудно показать, что
sin 6н ,п л \ 2//л 1 1 „
—-?=Cos(e0-e„)+--^cos2e0,
Sill D0 ПеО
т. е. что выражение (2.49) совпадает с (2.48), если положить в нем
Я,42 = 0. Отсюда видно (на это уже обращалось внимание выше),
что недопустимо, даже в случае малой анизотропии, когда углы
6о и QH мало различаются, пренебрегать их различием в (2.49).
Однако в (2.48) в случае малой анизотропии можно принять
6о = 6я. И если при этом пренебречь членами второго порядка малости
относительно НА1/Нс0 и НА2/Не0, то это выражение примет вид
j^Hc0 + HA1(^+^cos2eH\ + HA2(-l-+cos2QH-hos4%\ (2.50)
На рис. 2.5 приведены результаты расчета условий
ферромагнитного резонанса в сфере из одноосного кристалла для двух направлений
постоянного поля. Угловые зависимости Яе0 при со = const,
рассчитанные как в предположении совпадения направлений М0 и Не0,
так и с учетом истинной равновесной ориентации М0, а также
Результаты эксперимента показаны на рис. 2.6. Из этого рисунка
55
4
2
-1
Рис. 2.5. Частоты ферромагнитного резонанса в сфере из одноосного
ферромагнетика. Расчет по формуле (2.48) при HAi=4nM0 и НА2=0. Штриховые
линии—расчет несправедлив, так как принятое основное состояние (однородная
намагниченность) не реализуется
Рис. 2.6. Угловая зависимость резонансного
поля для сферы из кристалла с легкой
плоскостью анизотропии.
Точки—эксперимент для ферримагнетика RbNiF3 при
частоте 31,4 ГГц и температуре 78 К [60].
Сплошная линия—расчет по формуле (2.48)
при g=2,24, Я,и=-8,ЗкЭ и ЯЛ2=0,9кЭ.
Штриховая линия—расчет по формуле (2.50)
при тех же параметрах
видно, что для данного кристалла—с довольно большой анизотропией
учет несовпадения направлений М0 и Не0 является необходимым.
Сфера из кубического ферромагнетика. Для кубических
ферромагнетиков определение равновесной ориентации намагниченности
является более сложной задачей, чем для одноосных. Поэтому
использование метода сферических координат, которое, как мы
убедились на примере- одноосного кристалла, требует обязательного
учета—даже в случае малой анизотропии — условий равновесия,
встречает для кубических кристаллов определенные трудности.
Использование же метода эффективных размагничивающих факторов
приводит к довольно громоздким вычислениям. Не останавливаясь
на них (см., например, [363, 69]), приведем некоторые результаты.
С учетом только первой константы анизотропии компоненты
тензора эффективных размагничивающих факторов анизотропии
кубического кристалла имеют вид (оси координат направлены, как
56
к,>0
^<0
"res > *Э
3D 60 90
Рис. 2.7. Оси координат в сфере из
кубического ферромагнетика
показано на рис. 2.7):
Nc.=_з^И«ш12е0ап22фо. JV"22=-3^sin22e0(l-^sin22(po),
Mr. М° \ /
н (2-51)
Nc. з — sin2e0cose0sin4cpo, iVfl33=-^7i(l+cos22eo-
-sin460sin22(p0)-
Подставляя их вместо компонент тензора N в (1.96), получим:
IcOz + HaI
xIhc0z + H
!+lCOs4e0+('-y+2cos2eo-^cos4e0jsin22cpo j
Во + У
2cos460+ -cos20o--cos40o sin22cp
„}-
--#;,! sin2 0O sin2 20c sin2 4cp0- (2.52)
4
Наибольший интерес представляет случай, когда постоянная
намагниченность находится в плоскости {100} (рис. 2.2), в которой лежат
все оси симметрии кубического кристалла. Условие резонанса для
этого случая следует из (2.52) при ср0 = гс/4. Мы приведем его
с учетом двух констант анизотропии [325]:
(ю/у)21Ю} =
+ HMl+lcos
Нмг + НлА -§+2cos260 + -cos4e0) +
rA1(icos20o+^cos40o) +
260 + - cos 460 J sin2 60 \\не0 z + Нл
+ HA2( --^+—cos 20o J sin2 20o .
(2.53)
57
Следующие из (2.53) выражения для частных случаев, когда
М0 совпадает по направлению с осями симметрии, приведены
в табл. 2.2. В этой таблице даны значения ви и Не0г заменено на
Нс0, поскольку для осей симметрии кубического кристалла (так же
как для оси и базисной плоскости в одноосном кристалле) направления
М0 и Но совпадают, если только поле Нс0 достаточно велико,
чтобы в образце отсутствовали домены. Заметим, что отличие
структуры формулы (2.56) от первых двух формул в табл. 2.2 связано
с тем, что в направлениях <100> и <111> (как и в направлении
оси одноосного кристалла) находятся экстремумы энергии
анизотропии, а направление <110> является точкой седла поверхности
С/а (6, ф).
Направление
<100>
<111>
<по>
Та
Частоты ферромагнитного резонанса в сфере
из кубического кристалла
е„
0
54 44'
90
блица 2.2
(а/у
Нс0 + 2НМ
4 4
НсО— -НА1— ~На2
(Я«0-2ЯХ1)(".,.+ Им + l-HA2 j
(2-54)
(2.55)
1/2
(2.56)
В случае малой анизотропии формулу (2.53) можно записать
следующим образом:
ш/у = //„.,, + HAlF, (6„) + НА2 F2 (6Я), (2.57)
где функции Fx и F2 имеют вид (рис. 2.8)
/"i(e)=—^+^cos26+^cos4e, (2.58)
16 4 16
F2(Q)=-1+—cos26+—cos46-—cos60. (2.59)
w 64 128 64 128 v '
На рис. 2.9 показаны результаты расчета угловой зависимости
резонансного поля по формулам (2.57), (2.58) (без учета К2). На этом
же графике приведены экспериментальные результаты для ЖИГ.
Очень хорошее совпадение экспериментальных и расчетных данных
(при подобранной величине АГЖ) говорит о том, что в данном
случае—малой анизотропии и достаточно высокой частоты—нет
необходимости в учете ни второй константы анизотропии, ни различия
углов 60 и QH. Конечно, в других случаях учет этих факторов, как
и для одноосных кристаллов, может стать необходимым.
Из (2.52) легко получить выражение для резонансной частоты
и в том случае, когда М0 лежит в плоскости {100}, т. е. когда
Фо = 0 или фо = тг/2 (либо 60 = л/2). Угловая зависимость резонансного
58
ffres ~ Ы/У
Рис. 2.8. Функции, характеризу- Рис. 2.9. Угловая зависимость резонанс-
ющие анизотропию кубического ного поля в сфере из кубического кри-
ферромагнетика сталла с /fi<0, вн—угол между
#е0 и осью <100> в плоскости {ПО}.
Сплошная кривая—расчет по формуле
(2.57) при Ял2=0; точки—эксперимент
для сферы ЖИГ при частоте 9,3 ГГц
и комнатной температуре [73]
поля при ш = const для этого случая без учета К2 и различия углов
60 и 6Д показана на рис. 2.10. Из рис. 2.9 и 2.10 видно, что в обеих
плоскостях имеются направления, в которых #е0 = ю/у. При
практическом использовании сфер из монокристаллов ферритов
целесообразно ориентировать их таким образом, чтобы М0 совпадало с этими
направлениями; тогда резонансное поле не будет зависеть от Кх и,
следовательно, от температуры1'.
Представляет интерес и случай, когда направление М0 лежит
в плоскости {111} 2>- Можно убедиться, переходя от углов
60 и ф0 в формуле (2.52) к углу \|/0, который образует вектор М0,
лежащий в плоскости {111}, с некоторым направлением, например,
<110>, что в этом случае в первом приближении при HA1<s:He0
и НЛ2 = 0 плоскость {111} «является изотропной», т. е. резонансная
частота отличается от уНе0 на не зависящую от угла \|/0 величину.
Ясно, что эта величина составляет —уНА1. Во втором приближении
по HAlIHt0 вследствие влияния размагничивающего фактора N\2,
т. е. последнего члена в (2.52), возникает анизотропия резонансной
'' Такие направления приобрели курьезное название «тепловых осей».
2) Случай, когда М0 лежит в произвольной плоскости кубического
кристалла, рассмотрели Яковлев и Бурдин (см. [217]).
59
Рис. 2.10. Угловая зависимость
резонансного поля в сфере из
кубического ферромагнетика
с АГ, <0. <рн— угол между
Яе0 и осью <100> в плоскости
[ 100}. Расчет по формуле (2.52)
при 60=п/2 и HA1<s:HcQ
30 <р„,град
частоты. Кубическая ось третьего порядка < 111 > является при этом
осью шестого порядка для зависимости со0 от v]/0. Такая же
анизотропия возникает и вследствие влияния второй константы
анизотропии, и выражение для резонансной частоты сферы из
кубического кристалла для случая, когда М0 лежит в плоскости
{111}, принимает вид (при HA2<zHA1<s:Hc0)
Y 2 18 2 Нс0 \ 2 Нс0 36 /
Одновременный учет нескольких видов анизотропии. Рассмотренные
примеры относились к случаю, когда образец представлял собой сферу
и принималась во внимание кристаллографическая анизотропия какого-
либо одного вида — одноосная или кубическая. Однако часто мы
встречаемся с необходимостью учета одновременно анизотропии формы
(для несферических образцов) и одного или нескольких видов анизотропии
вещества. Характерным примером являются монокристаллические пленки
ЖИГ, выращенные эпитаксиально на диа- или парамагнитных подложках.
Наряду с кубической анизотропией в этих пленках всегда в той или иной
степени присутствует «ростовая» анизотропия, обычно — одноосная
с осью, совпадающей с нормалью к плоскости пленки.
Оба рассмотренных метода—эффективных размагничивающих
факторов и сферических координат могут быть использованы для
одновременного учета нескольких видов анизотропии. В первом
случае компоненты результирующего тензора эффективных
размагничивающих факторов являются суммами компонент эффективных
размагничивающих факторов всех учитываемых видов анизотропии;
во втором случае энергия U в формулах (2.26) и (2.27) является
суммой зеемановской энергии, внутренней магнитной энергии и
энергий всех видов анизотропии (при нахождении тензора % внутренняя
магнитная энергия не учитывается). Необходимо подчеркнуть, что
из аддитивности энергий и размагничивающих факторов, соответст-
60
вующих различным видам анизотропии, не следует аддитивности их
вкладов в резонансную частоту, что видно из формул (1.96) или
(2.26). Такая аддитивность имеет место лишь приближенно в случае
малых вкладов анизотропии.
Из сказанного ясно, что вычисление компонент тензоров % или
Xе и резонансных частот или полей при одновременном учете
нескольких видов анизотропии не представляет (кроме, конечно,
нахождения основного состояния) каких-либо принципиальных
трудностей, но приводит иногда к довольно громоздким вычислениям
в связи с необходимостью записи компонент всех эффективных
размагничивающих факторов в одной и той же системе координат.
Мы ограничимся одним простым примером.
Найдем условие ферромагнитного резонанса в тонкой пленке из
кубического ферромагнетика, намагниченной нормально либо
касательно к ее плоскости, которая совпадает, например, с плоскостью
{ПО}. Ограничимся учетом только первой константы кубической
анизотропии К1г но примем во внимание одноосную ростовую
анизотропию с константой К" и осью, совпадающей с нормалью
к плоскости пленки.
В случае нормального намагничивания в осях координат,
показанных на рис. 2.11, размагничивающие факторы формы (считая пленку
бесконечно тонкой): Nu=N22 = Nl2=0, N33 = 4n. Для получения
размагничивающих факторов кубической анизотропии следует положить
Фо = п/4 и 60=п/2 в (2.51):
№ц = -ЪНм1М0, N%2=N\2 = 0, N\3=-HAl/M0,
а размагничивающие факторы одноосной анизотропии получатся,
если принять 60 = 0 в (2.46):
Nun=Nii = Nh = 0, N»33=-2HAJM0,
где обозначено НАи = К\/М0. Подставляя суммы этих
размагничивающих факторов вместо соответствующих компонент N в формулу
<1Ю>
itf„
k«a
<f10>
knn
<100>
Рис. 2.11. Оси координат при нормальном и касательном намагничивании
пленки из кубического монокристалла. п0—нормаль к плоскости пленки
61
(1.96), получим частоту ферромагнитного резонанса в нормально
намагниченной пленке. Запишем приближенное выражение для нее
в случае малой кубической анизотропии (НЛ1<з:Не0)
(й0/у = Не0-4пМ0 + 2НЛи--НЛ1.
(2.61)
При касательном намагничивании (под углом 0О к оси <100>
в осях координат, показанных на рис. 2.11) размагничивающие
факторы формы: Лг11=4я, N22 = N12 = N33=0. Для получения
размагничивающих факторов кубической анизотропии достаточно положить
Фо = я/4 в выражениях (2.51). Размагничивающие факторы одноосной
анизотропии в данном случае: NU11 = -2HAJM0, N42 = Nul2 = N33 = 0.
Выражение для резонансной частоты, которое получается при
подстановке суммы этих размагничивающих факторов в (1.96), мы
приведем тоже для случая малой кубической анизотропии:
«о /Y=у/(Н,о - 4пМ0 + 2HAu)Ht0 + HA1F1 (6), (2.62)
где Fj(0) имеет вид (2.58). Если Нс0 и М0 направлены по оси
<110>, то в (2.62) fi=—.
Измерение констант анизотропии. Снятие угловых зависимостей
резонансного поля или частоты ферромагнитного резонанса в
монокристаллических образпах является самым распространенным и
наиболее точным методом изучения кристаллографической анизотропии
ферро- или ферримагнетиков. Из этих зависимостей могут быть,
вообще говоря, найдены ^-фактор, константы различных видов
анизотропии и — при использовании несферических
образцов—постоянная намагниченность М0. В случае слабопроводящих веществ для
таких измерений чаще всего ис-
юо zoo зоо т,к пользуются сферы. Если, в
частности, имеет место только
кубическая анизотропия и для ее
описания достаточно двух констант,
то эти константы и ^-фактор
могут быть найдены из измерений
резонансного поля при со = const
для трех приведенных в табл. 2.2
направлений Не0. Найденные
таким методом температурные
зависимости Кг и К2 для ЖИГ
приведены на рис. 2.12.
В случае пленки, выращенной
так, что ее плоскость является
плоскостью {ПО}, первая и вто-
Рис. 2.12. Температурные зависимо- рая константы кубической анизот-
V"n=™^Z™ZUi£- P™ МОТ бь- определены
магнитного резонанса в сфере при таким же образом при касатель-
частоте ~9 ГГц ном намагничивании. Измерение
62
!
резонансного поля также и при нормальном намагничивании в
отсутствие одноосной анизотропии дает возможность найти А/о- При
наличии такой анизотропии—с осью, совпадающей с нормалью
к плоскости пленки,—может быть определена, как видно из формул
(2.61) и (2.62), лишь величина М0-К\/(2пМ0).
Величины констант анизотропии, найденные из измерений
ферромагнитного резонанса, вообще говоря, не должны совпадать с их
значениями, полученными из статических измерений. Одной из причин
этого, как уже указывалось в § 2.2, является различие вкладов
магнитострикционных деформаций (см. подробнее § 12.2). Другая
причина—различный вклад быстрорелаксирующих ионов—будет
рассмотрена в § 13.2. Однако для ферритов с небольшой анизотропией,
используемых в технике СВЧ, в частности, для ЖИГ оба упомянутых
вклада невелики и результаты измерения констант анизотропии
методом ферромагнитного резонанса обычно мало отличаются от
результатов статических измерений.
§ 2.4. Ферромагнитный резонанс в поликристаллах
Поликристаллические материалы представляют собой конгломераты
маленьких монокристаллов (кристаллитов или зерен) различной формы
с размерами порядка Ю-5—Ю-3 см. Между ними находятся поры
различной формы, занимающие часто значительную долю всего объема.
Обычно кристаллографические оси зерен ориентированы произвольным
образом, отсутствует какая-либо преимущественная ориентация и их
геометрических осей. Лишь в том случае, когда при изготовлении
поликристаллических образцов принимаются специальные меры,
например прессование или термообработка проводятся в магнитном
поле, равномерность углового распределения кристаллографических
или геометрических осей зерен нарушается. Такой, текстурованный
поликристалл приближается по свойствам к монокристаллу.
Мы будем рассматривать только нетекстурованные
поликристаллы, представляющие собой в среднем изотропную среду. Для такой
среды (см. [69]) любой тензорный параметр, в частности магнитная
восприимчивость, имеет в самом общем случае следующий вид:
Х =
X
-Ча
0
%,
X
0
0
0
л.
(2.63)
Таким образом, высокочастотные свойства поликристаллического
ферромагнетика могут быть описаны с помощью трех величин: %,
Ха и Х||- В достаточно сильных постоянных магнитных полях, когда
имеет место однородная постоянная намагниченность, компонента
Хц (см. § 1.4) равна нулю или имеет малую величину и для описания
высокочастотных свойств поликристалла достаточно двух величин
X и ха. Однако поликристалл является сложной системой, и
зависимости его х и Ха от частоты и постоянного поля отличаются от
таковых для идеализированной изотропной среды, которая
рассматривалась в гл. 1.
63
Приближение независимых зерен. Еще на заре исследований
ферромагнитного резонанса Ван Флек [443] предложил рассматривать
поликристалл как набор независимых (невзаимодействующих) зерен
условия ферромагнитного резонанса в которых определяются только
ориентацией их кристаллографических осей. Возможность такого
рассмотрения основывается на двух предположениях: пренебрегается
связью между колебаниями намагниченности соседних зерен и
пренебрегается влиянием формы зерен и пор. Системой, для которой эти
предположения выполняются строго, является набор
монокристаллических сфер, расположенных в немагнитной среде далеко друг от
друга. Однако допустим, что имеет место условие
|Ял|»4яЛ/0, (2.64)
где Нл—некоторое поле анизотропии, например НА1, если
последующие константы анизотропии не превышают по величине первую.
Тогда оба упомянутых предположения приближенно выполняются
и модель независимых зерен может быть применена к расчету
ферромагнитного резонанса в поликристаллах.
Для расчета зависимостей % и Ъ, поликристалла от ю м //„ на
модели независимых зерен мы должны были бы записать выражения
для компонент тензора %' каждого зерна, а затем усреднить их
с учетом распределения зерен по ориентациям — равномерного в случае
нетекстурованного поликристалла. Такой расчет, особенно при учете
конечной ширины (Д//)0 резонансной кривой каждого зерна
представляет большие трудности. Шлёманн [397] принял (ДЯ)о = 0 и
ограничился вычислением мнимых частей х и %а. Тогда, предполагая
равномерное распределение зерен по ориентациям их
кристаллографических осей и пренебрегая влиянием формы зерен, с учетом
(1.84), получим
л
2 2*
Х"(со, Н0) = Ха{<й, #0)=^р J" j" б[Я0-tfrt>, e, Ф)]sinQdQdip. (2.65)
е=-2ф=о
Здесь #res(co, 9, ф) —резонансное значение Н0 при данных со, 9 и ф.
•Заметим,^ что, заменяя в (2.65) Я0 на Яс0, мы получим выражение
для (х ) или (xl)" поликристаллической сферы.
Интеграл в (2.65) пропорционален функции распределения w(H0)
зерен по значениям резонансною поля, и при его вычислении можно
использовать общие свойства таких функций, в частности, то, что
функция w(H0) имеет разрывы («ступеньки») в точках экстремумов
и пики (логарифмические особенности) в точках седла функции
Н0 (0, ф). В случае кубического кристалла с учетом только первой
константы анизотропии при К^О (см. рис. 2.9) функция w(H0)
отлична от нуля в интервале полей Я0 (или для сферы- Яе0) от
#mjn = co/Y--|//,4i| до tfniax = cu/Y + 2|//,4i| и имеет пик при поле
1 ,
"-<й/у--\НЛ1\, являющемся, как уже отмечалось, точкой седла
64
"Ч.
^
ч4;
1
«J
«J
■^
-Q
%
■О
<S
<s
«ъ
со
>§■
к"
-****
t
|1
И
Si К*!«»//»
и
11
JI \
// а
/' \
тГ vv
7 ^^
/ *^-»«_^
/{ ^^Ч н°~ы/у
1 1 1 1 1 ^— ' Я1
-2
HAf\~0,35a/y
Рис. 2.13. Резонансные кривые сферы из кубического поликристалла с Ki<0
в приближении независимых зерен [397]. Штриховые линии—при (ДН)о=0,
сплошные—с учетом конечной величины (Д#)0 (где ДН0—ширина резонансной
кривой монокристалла)
поверхности Н0 (0, ф). Полевые зависимости %" для этого случая
приведены на рис. 2.13.
Учет конечной величины (ДД)0 приводит к сглаживанию этих
зависимостей. Однако и в этом случае рез'онансные кривые
поликристалла, полученные на модели независимых зерен, сильно
отличаются по форме от резонансных кривых для изотропной среды
или монокристаллов: они несимметричны, имеют уступы на обоих
склонах, а при большой анизотропии—два максимума. Как видно
из рис. 2.13, АН поликристалла (при достаточно малой (Д#)0)
составляет в приближении независимых зерен
{LH\^2\KAIM0, (2.66)
а сдвиг максимума
(бЯ^аД^/Мо. (2.67)
Условием применимости модели независимых зерен является
(2.64). И действительно, резонансные кривые, близкие по форме
к показанным на рис. 2.13, наблюдались в ферритах с очень большой
анизотропией, а также вблизи точек компенсации (см. § 3.2). Для
5 А. Г. Гуревич, Г. А. Мелков
65
большинства же поликристаллических ферромагнетиков и ферритов
условие (2.64) не выполняется; экспериментальные резонансные кривые
не имеют в этом случае характерной формы (рис. 2.13), а их ширина
оказывается значительно меньшей, чем (2.66).
Приближение сильно связанных зерен. Основной причиной
несоответствия модели независимых зерен реальным поликристаллам
является то, что магнитные колебания зерен в действительности связаны
между собой переменными размагничивающими полями (которые
зависят от переменных намагниченностей обоих взаимодействующих
зерен). Это приводит к «дипольному сужению» кривой
ферромагнитного резонанса в поликристалле, в результате чего в выражении
(2.66) появляется множитель
U>~l^il/(47iM0), (2.68)
который много меньше 1 для применяемых в технике СВЧ ферритов
с малой анизотропией. Для таких веществ, когда имеет место
неравенство, обратное (2.64), более подходящей является модель сильно
связанных зерен. При этом поликристалл рассматривается как
однородная среда, на которую накладывается неоднородное эффективное поле,
моделирующее наличие зерен с различной ориентацией осей. Это
поле приводит к связи между рассматриваемым однородным типом
колебаний образца и другими типами колебаний. В результате
происходит передача им энергии рассматриваемого типа колебаний
и, следовательно, расширение его резонансной кривой. Такие процессы
будут подробно исследованы в § 11.3. Теория их в случае поликристалла
приводит к значениям АН, которые по порядку величины совпадают
с результатом умножения (2.66) на множитель (2.68).
Влияние пористости. Очень существенной причиной расширения
резонансных кривых в поликристаллических образцах являются поры
(а также включения других фаз). Именно пористостью объясняется
то, что поликристаллические образцы ЖИГ имеют обычно ширину
резонансной кривой ~ 50 Э, существенно превышающую вклад
анизотропии. Для учета влияния пор могут быть использованы обе
упомянутые выше модели: независимых, в данном случае уже не
зерен, а областей, и возмущающего поля, которое приводит к связи
различных типов колебаний. Для грубой оценки с помощью первой
модели можно принять, что ширина кривой будет порядка
усредненного по образцу размагничивающего поля пор:
(АН)р^4пМ0р, (2.69)
где пористость p=Vp/V0, Vp—суммарный объем пор, a V0 — объем
всего образца. Проведенный Шлёманном расчет на модели
сферической полости в центре образца привел к выражению, отличающемуся
от (2.69) множителем ~1,5, и сдвигу максимума резонансной кривой
4-7Г
{ЪН\^~М0р. (2.70)
На рис. 2.14 приведена зависимость АН от р для большого
числа образцов ЖИГ. Из этого рисунка видно, что, несмотря на
66
разброс точек,
обусловленный различием размеров
и формы пор,
экспериментальные данные находятся
в довольно хорошем
соответствии с результатами
расчета на модели
независимых областей.
В действительности
колебания намагниченности
в отдельных областях
ферромагнитного образца
нельзя считать независимыми;
связь между ними,
обусловленная магнитными (ди-
поль-дипольными) силами,
оказывается настолько
сильной, что следует говорить
о различных типах
колебаний всего неоднородного
образца. Это убедительно
продемонстрировали Геш-
винд и Клогстон [308],
наблюдавшие
ферромагнитный резонанс в образцах из
монокристаллов ферритов,
форма которых существенно
поле было поэтому сильно неоднородным (рис. 2.15). Например,
в случае полусферы, намагниченной касательно к ее плоской
поверхности, неоднородность внутреннего постоянного поля составляет
— пМ0, и модель независимых областей дает резонансную кривую
нелоренпевой формы и приблизительно такой ширины (~200 Э для
ЖИГ). В действительности же резонансная кривая для этого образца
почти не отличалась от кривой для сферы.
Тем не менее расчет вклада гористости в АН поликристалла,
проведенный на модели независимых областей, дает, как мы видели,
неплохое совпадение с экспериментом. Интересно, что результаты
этого расчета совпадают по порядку величины с результатами расчета
в приближении сильно связанных областей (см. § 11.3). Причина
этого совпадения заключается в том, что в случае пор в множителе,
аналогичном (2.68), учитывающем дипольное сужение, как в числителе,
так и в знаменателе будут находиться величины порядка пМ0-
Из рис. 2.14 видно, каких больших значений даже для феррита
с не очень большой намагниченностью может достигать вклад
пористости в ширину резонансных кривых поликристаллических
образцов. Лишь в очень плотных (р^.1%) образцах этот вклад
удается сделать малым. И если при этом приняты меры к уменьшению
5* 67
(AH)0+47tMoP
OfP
Рис. 2.14. Зависимость АН сфер из
поликристалла ЖИГ от пористости [74].
Различные кружки—экспериментальные значения
для образцов, изготовленных в различных
условиях. Частота 9 ГГц
отличалась от эллипсоида и внутреннее
8,6 Г, Г ГЦ
Рис. 2.15. Резонансные кривые: для образцов различной формы из
монокристалла ЖИГ [308]. Частота 24 ГГц, диаметр ~ 0,25 мм
анизотропии и «собственной» ширины кривой монокристалла то
для поликристаллических образцов ЖИГ могут быть получены
значения ЛЯ~1 Э [386]. ^ч-чсны
В заключение заметим, что источниками расширения резонансных
кривых как в поликристаллах, так и в монокристаллических образцах
могут явиться шероховатости поверхности образцов и неоднородные
механические напряжения (§ 11.3).
Глава 3
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИТЫ
§ 3.1. Антиферромагнетизм и ферримагнетизм
До сих пор мы изучали колебания намагниченности в
ферромагнетиках; задачей этой главы является рассмотрение магнитных
колебаний в веществах с другими видами магнитного упорядочения—
антиферромагнетиках и ферримагнетиках.
Антиферромагнетики—это вещества, в которых
упорядочение элементарных магнитных моментов носит такой характер,
что спонтанный (возникающий в отсутствие внешнего
магнитного поля) магнитный момент элементарной ячейки и,
следовательно, любой макроскопической области равен нулю или имеет
небольшую, по сравнению с суммой элементарных моментов,
величину. Замечание о возможном небольшом моменте связано
с тем, что сушествует класс веществ — так называемые слабые
ферромагнетики, которые обладают таким моментом и которые
тем не менее следует относить к антиферромагнетикам. В простых
случаях элементарная магнитная ячейка антиферромагнетиков
содержит равные числа одинаковых моментов, направленных в
противоположные стороны. Статическая восприимчивость
антиферромагнетиков мала и (в монокристаллах) сильно анизотропна (см.
рис. 1.3).
В ферримагнетиках характер магнитного упорядочения такой
же, как в антиферромагнетиках. Но момент элементарной ячейки
(а в отсутствие доменов — и всего образца) имеет большую
величину — меньшую, чем сумма элементарных моментов, но
Сравнимую с ней. В простейшем случае в элементарную ячейку
входят моменты, направленные в противоположные стороны;
количества их или величины (или и то, и другое) неодинаковы.
Магнитные восприимчивости ферримагнетиков, как статическая (см.
рис. 1.3), так и динамическая (§ 3.3), достигают больших величин.
Таким образом, ферримагнетики, наряду с ферромагнетиками
и в отличие от антиферромагнетиков, являются сильно-магнитными
веществами.
Выше некоторой температуры Гк—температуры Нееля1' в
антиферромагнетиках и ферримагнетиках (как в
ферромагнетиках выше температуры Кюри Гс) магнитный порядок
разрушается.
" В случае ферримагнетиков температуру упорядочения называют также
температурой Кюри.
69
Магнитные структуры. Идея антиферромагнитного упорядочения
элементарных магнитных моментов вещества была выдвинута
независимо Неелем и Ландау [129]. Неель предположил
существование «шахматной» структуры, в которой каждый момент имеет
в качестве всех ближайших соседей моменты, направленные в
противоположную сторону. Ландау предложил модель
антиферромагнетика, в которой чередуются слои моментов, направленных
в противоположные стороны. До работ по магнитной
нейтронографии антиферромагнетиков наличие той или иной
антиферромагнитной структуры оставалось гипотезой, выдвигаемой для
объяснения их магнитных свойств. Эти работы (см., например, [32])
доказали реальность существования антиферромагнитного
упорядочения и позволили определить магнитные структуры многих
веществ. При этом оказалось, что встречаются оба вида
антиферромагнитного упорядочения—«по Неелю» и «по Ландау» и,
конечно, более сложные структуры.
Выяснилось [293], что в кристалле MnF2 обладающие магнитным
моментом ионы Мп2+ образуют объемно-центрированную
тетрагональную решетку (рис. 3.1) и их моменты направлены вдоль оси
четвертого порядка, причем моменты ионов, находящихся в вершинах
и в центре ячейки, антипараллельны. Таким образом, осуществляется
«шахматное» упорядочение. Такое же упорядочение имеет место
и в тетрагональном антиферромагнетике NiF2 (см. рис. 3.1), но
моменты ионов Ni2+ лежат в базисной (перпендикулярной оси
четвертого порядка) плоскости. Моменты ионов, находящихся в
вершинах и в центре ячейки, в этом случае образуют угол, несколько
отличающийся от п. Поэтому антиферромагнетик NiF2 имеет
небольшой спонтанный момент и принадлежит к упомянутым выше слабым
ферромагнетикам.
Примером антиферромагнетиков со «слоистым» упорядочением
является кубический (с небольшими григональными искажениями ниже
точки Нееля) кристалл МпО (рис. 3.2), в котором ионы Мп2 +
образуют гранецентрированную решетку. Для этого
антиферромагнетика, в отличие от показанных на рис. 3.1, магнитное упорядочение
приводит к удвоению линейных размеров элементарной магнитной
ячейки по сравнению с кристаллографической (или кристаллохимиче-
ской) ячейкой.
Рис. 3.1. Магнитные структуры тетрагональных антиферромагнетиков [293].
Черные кружки—ионы Мп2+ и Ni2 + , светлые— ионы F~. Небольшая
неколлинеарность моментов ионов Ni2+ не показана
70
Рис. 3.2. Mai нитная структура анти- Рис. 3.3. Магнитные структуры триго-
ферромагнетика МпО [248]. Черные нальных антиферромагнетиков [271].
кружки—ионы Мп2 + , светлые—ионы Черные кружки—ионы Сг3+ и Fe3+,
О . Магнитные моменты лежат анионы не показаны. Магнитные мо-
в плоское 1ях {111}. Небольшое сжатие менты в a-Fe203 при Т>Тм слегка
по оси < 111 > (в магнитоупорядочен- неколлинеарны
ном состоянии) не показано
На рис. 3.3 приведены магнитные структуры шригональных
антиферромагнетиков. Для одного из них—гематита a-Fe203 " при
температуре Тм = 250 К (в точке Морина) происходит фазовый
переход—изменение направления магнитных моментов; в области
температур TM<T<TN a-Fe203 является слабым ферромагнетиком.
Слабым ферромагнетиком во всей области магнитного упорядочения
является, как показали Боровик-Романов и Орлова [34], тригональный
антиферромагнетик МпС03.
Высокие температуры Гц для многих антиферромагнетиков и фер-
римагнетиков, сравнимые с температурами Тс для ферромагнетиков,
говорят о том, что за магнитное упорядочение в антиферромагнетиках
и ферримагнетиках также ответственно обменное взаимодействие. То
обстоятельство, что оно в данном случае стимулирует
антипараллельную ориентацию спинов, заставляет полагать, что обменный интеграл
в (1.30) теперь отрицателен. Так же как и в ферромагнетиках,
обменное взаимодействие в антиферромагнетиках и ферримагнетиках
является обычно в значительной степени косвенным. В
неметаллических пеществах, к которым принадлежат все упомянутые выше
антиферромагнетики, основным механизмом обменного
взаимодействия является косвенный обмен с участием анионов (см., например,
[227]).
Подрешетки. Перейдем теперь к континуальному описанию ан-
тиферро- и ферримагнетиков. В основе его лежит подрешеточная
модель Нееля [375]: элементарные магнитные моменты, находящиеся
" Окись железа имеет и другую — кубическую модификацию y-Fe203,
которая является ферримагнетиком.
71
в эквивалентных узлах кристаллической решетки и одинаково
направленные, объединяются в магнитные подрешетки и вводятся их
намагниченности
Щ=~1<^/Х (31)
где <S9lj/>—квантовомеханические средние значения элементарных
магнитных моментов, входящих в каждую подрешетку, а
суммирование производится по всем таким моментам, находящимся в малом
объеме б К. Намагниченность вещества
М=£М,, (3.2)
J
Заметим, что возможность применения подрешеточной модели
априори не очевидна. Она подтверждается прежде всего совпадением
с опытом многочисленных результатов, полученных на основе этой
модели. К ним относятся спектры антиферромагнитного и ферримаг-
нитного резонансов, которые будут рассмотрены ниже.
Число подрешеток должно быть равно числу магнитных ионов
в примитивной" элементарной магнитной ячейке. Оно может быть
очень велико, например, 20 для ферримагнетика ЖИГ (§ 3.3). Однако
при описании многих свойств антиферро- и ферримагнетиков некоторые
подрешетки могут быть объединены. Могут быть объединены в одну
подрешетку все магнитные моменты, направленные одинаково, либо
все моменты, хотя и направленные антипараллельно, но занимающие
одинаковые кристаллографические позиции. В результате такого
объединения часто «остаются» лишь две подрешетки. Ясно, что для
антиферромагнетиков, в примитивную магнитную ячейку которых
входят два магнитных иона, двухподрешеточная модель является
строгой, а для более сложных магнитных структур—приближенной.
Уравнения движения. Континуальная теория антиферро- и
ферримагнетиков строится аналогично континуальной теории
ферромагнетиков (§ 2.1). Исходным является выражение для плотности энергии
U, как функции всех векторов Mj. Естественно предположить, что
для этих векторов будут справедливы уравнения Ландау—Лифшица
d-^=-yjMjxHe{j+Rj, (3.3)
где Yj—магнитомеханические отношения, вообще говоря, различные
для разных подрешеток, а эффективные поля, действующие на
подрешетки, могут быть определены с помощью выражений,
аналогичных (2.9). Диссипативные члены могут быть записаны в одной из
форм, обсуждавшихся в § 1.4. Наиболее удобной является форма
Гильберта (как в (1.67), но с заменой а-юс; и M->Mj), в которую
не входят эффективные поля.
" Примитивной (см., например, [16]) называется элементарная ячейка
наименьшего объема.
72
Виды энергии. Энергия обменного взаимодействия, как и в случае
ферромагнетика, может быть представлена в виде суммы однородной
и неоднородной частей. Однородную часть для вещества с п подрешет-
ками можно записать в виде
U*=-\t t VM,Mr, (3.4)
где Лу—константы обменного взаимодействия между у-й и /-Й
подрешетками и (при j=j") внутри подрешеток. Эти константы мы
считаем скалярными, включая, как и в случае ферромагнетика,
анизотропную (обычно небольшую) часть обменной энергии в энергию
анизотропии. Эффективное поле однородной части обменного
взаимодействия, действующее на у'-ю подрешетку,
Нл;= t Ajj.My. (3.5)
Если Ajj->0, то соответствующее обменное взаимодействие носит
ферромагнитный характер, если Л# <0,— оно является
антиферромагнитным. Величины Ajj- могут иметь разные знаки, но
очевидно, что в антиферромагнетиках и ферримагнетиках по
крайней мере одна из этих констант должна быть отрицательной.
Эффективные поля, описывающие обменные взаимодействия между
подрешетками, войдут в уравнения движения (3.3), и это
обстоятельство, как мы увидим, окажет существенное влияние на спектры
и характер магнитных колебаний в антиферромагнетиках и
ферримагнетиках.
Энергия магнитной кристаллографической анизотропии Ua
антиферро- и ферримагнетиков должна быть записана в виде ряда по
степеням составляющих Mix_y<z 0=1, 2, ..., и), допускаемого
симметрией данной кристаллической решетки. Эффективные поля
анизотропии, действующие на каждую подрешетку, могут быть определены
дифференцированием 1/а по соответствующему Mj. Отметим три
важных обстоятельства. Во-первых, при записи энергии анизотропии
веществ с несколькими подрешетками часто делается предположение
об аддитивности энергий анизотропии подрешеток, т. е. из упомянутых
рядов исключаются «перекрестные» члены, содержащие произведения
составляющих намагниченностей разных подрешеток. Ясно, что это
справедливо лишь в предположении одноионного источника
анизотропии (§ 2.2). Во-вторых, в случае антиферромагнетиков роль
кристаллографической анизотропии оказывается, как мы увидим, гораздо
более важной, чем для ферромагнетиков. В-третьих, в некоторых
кристаллах в энергии Ua появляются члены, которые минимизируются
при углах между векторами Mj, отличающихся от тех углов
(например, л), при которых минимизируется обменная энергия. Это,
как показал Дзялошинский [85], является причиной упоминавшегося
выше слабого ферромагнетизма.
Зеемановская энергия запишется, как и для ферромагнетика,
в виде (2.17), где М—суммарная намагниченность (3.2).
73
г
Так как магнитные подрешетки «перемешаны» («вставлены друг
в друга») на микроскопическом уровне, внутренняя магнитная энергия
UM, являющаяся результатом дальнодействующих дипольных
взаимодействий, зависит только от суммарной намагниченности М,
а эффективные размагничивающие поля, действующие на все
подрешетки, одинаковы. В частности, для эллипсоида справедливы
выражения (2.18) и (1.87).
Основные состояния. Рассмотрению магнитных колебаний в ан-
тиферро- и ферримагнетиках должно предшествовать отыскание
равновесных (основных) состояний, т. е. определение длин и
ориентации всех векторов Mj0 в зависимости от величины и направления
постоянного поля Не0 и от температуры Т. При Т=0 длины векторов
Mj0 постоянны и в рамках классической континуальной теории
должны считаться известными; задача об основном состоянии
заключается в нахождении их ориентации, т. е. углов 6,0 и pj0. При
решении этой задачи можно, как и в случае ферромагнетиков (§ 2.1),
идти по двум путям; приравнивать нулю производные энергии U по
углам 0j- и <pj или использовать выражения
MjcxHeW = 0, (3.6)
которые следуют из уравнений движения (3.3).
Примеры решения задач об основных состояниях антиферро-
и ферримагнетиков (при Г=0) будут приведены в § 3.2 и 3.3. Здесь
мы остановимся кратко лишь на явлении слабого ферромагнетизма
[32, 198, 372]. Как уже отмечалось, причиной его являются члены
энергии, имеющие ту же природу, что и «обычные» члены энергии
анизотропии (см. § 2.2), но в отличие от них минимизирующиеся
при некоторых углах между векторами М,-, отличающихся от тех,
при которых минимизируется обменная энергия. Такие члены
допускаются симметрией не всех кристаллов". Если ограничиться
членами второго порядка по составляющим М,-, то оказывается, что
в двухподрешеточном антиферромагнетике такие члены могут быть
двух типов:
C/D=-Dz0(M1xM2), (3.7)
Ur=-F(MlxM2y-M2xMly). (3.8)
К членам (3.7) может привести анизотропное обменное взаимодействие
(§ 2.2) между элементарными моментами, входящими в разные
подрешетки. Причиной же возникновения членов (3.8), как показал
Мория [372], является одноионная анизотропия.
Член (3.7) является единственно возможным в тригональных
кристаллах, им определяется слабый ферромагнетизм в a-Fe203
и МпС03. Член (3.8) возможен в некоторых тетрагональных
кристаллах, им обусловлен слабый ферромагнетизм в NiF2.
Легко убедиться, что оба члена, UD и UF, минимизируются при
угле л/2 между Мх и М2, но член UF «требует», кроме того, чтобы
'' Этот вопрос подробно исследовал Туров [198] (см. также [69]).
74
векторы Мх и М2 были определенным образом (а именно, под
углами +я/4 и —я/4 к оси х) направлены по отношению к осям
кристалла. Минимизация суммарной энергии, включающей UD или
UF и обменную энергию Uex, приводит к небольшой (так как
£/сх з> C/D, C/F) спонтанной неколлинеарности Mj и М2—отклонению
угла между ними от п.
При Т>0 уравнения движения, формула для Hefj- и выражения
для различных членов U остаются в силе, но под Mj0 следует
понимать термодинамические средние величины намагниченностеи
подрешеток при данной температуре. Длины этих векторов будут
зависеть от температуры и поля, и для отыскания основного
состояния нужны дополнительные условия. Можно, например,
предположить, что зависимости Mj0 от HefJ0 и Т будут аналогичны
(1.20):
«»~»1ъ(*Щ?} (19)
где M^ = yjhJjNj—намагниченность>й подрешетки при Т=0, а Bj—
функция Бриллюэна (1.22). Тогда совместное решение уравнений
(3.9), выражений, связывающих эффективные поля Hef;0 c Що>
и условий равновесия позволяет, в принципе, найти равновесные
намагниченности М,0 (их длины и ориентации) при заданных Нео и Г.
Эта задача может быть просто решена лишь для температур,
очень близких к температуре Нееля TN или превышающих ее. Тогда
все MJ0 малы и можно, во-первых, пренебречь влиянием
размагничивающих полей (а также анизотропии) и, во-вторых, ограничиться
первым членом в разложениях функций В3 по их аргументам.
Рассмотрим, например, антиферромагнетик или ферримагнетик с
двумя подрешетками. Эффективные поля в этом случае будут включать
поле Не0 и обменные поля (3.5):
НеП0=Н0 + ЛпМ10+Л12М20,
НеГ20 = Н0 + Л12М10 + Л22М20.
Из условий равновесия (3.6) следует коллинеарность векторов Н0,
М10 и М20, а выражения (3.9) приведут к системе линейных уравнений
для М10 и М20.
Приравнивая нулю определитель этой системы, можно найти
температуру Нееля. Для антиферромагнетика с двумя идентичными
подрешетками, обозначая An=A22s—Л; и Л12=—Л, получим
rN = C(A-Ai), (3.11)
где постоянная С имеет такой же вид, как постоянная Кюри в (1.25),
но величины /, у и N относятся к одной (любой, поскольку они
идентичны) подрешетке. Для ферримагнетика в предположении |ЛП|,
|Л22|«:|Л12| = Л
Гк^УоСгЛ, (3.12)
где d и С2 относятся к двум подрешеткам.
75
Решая упомянутую систему при Н0фО, мы можем найти
статическую парамагнитную восприимчивость Хо (при T>TN). В случае
антиферромагнетика с идентичными подрешетками
1С 2С
*°=г+С(л-л,г^: <3-13>
Выражение (3.13) представляет собой закон Кюри—Вейсса с
отрицательной парамагнитной температурой Кюри Тр. В случае
ферримагнетика зависимость (Хо)1 от Т оказывается нелинейной, закон
Кюри—Вейсса выполняется лишь асимптотически (см. рис. 1.3).
Малые колебания. Линеаризируем уравнения движения (3.3), для
чего представим намагниченности и эффективные поля в виде сумм
постоянных и переменных составляющих, подставим эти суммы
в уравнения (3.3) и учтем малость переменных составляющих по
сравнению с постоянными. Тогда в нулевом приближении получим
условия (3.6), а в первом—систему п (где п—число подрешеток)
линейных уравнений для комплексных амплитуд т/.
(3.14)
Здесь hefj-—комплексные амплитуды переменных эффективных полей
(без поля, которое мы считаем заданным), a h—комплексная
амплитуда заданного переменного поля. Уравнения (3.14) являются
связанными, потому что каждое hefj зависит, вообще говоря, от
всех тк (к=\, 2, ..., и).
К решению системы (3.14) сводится рассмотрение магнитных
колебаний в антиферромагнетиках и ферримагнетиках, которому
будут посвящены § 3.2 и 3.3. Здесь мы ограничимся некоторыми
общими замечаниями.
Приравнивая нулю определитель системы Ъп скалярных уравнений,
полученных проектированием уравнений (3.14) на оси координат, мы
придем к характеристическому уравнению для частот свободных
колебаний. Если положить все а,-=0, то решения этого уравнения
дадут вещественные собственные частоты. Как мы убедимся в
дальнейшем, это уравнение будет иметь всегда п положительных корней,
соответствующих собственным колебаниям рассматриваемой системы
с п степенями свободы.
При h^O система неоднородных линейных уравнений, полученная
в результате проектирования (3.14), будет иметь однозначные решения
т;, соответствующие амплитудам вынужденных колебаний. Все
проекции т,- будут, конечно, линейно зависеть от проекций h, и суммарную
переменную намагниченность можно будет представить в виде
л
£ П1;=п1=хп, (3.15)
где х—тензор высокочастотной магнитной восприимчивости антифер-
ро- или ферримагнетика. Причем, если переменные размагничивающие
76
поля (в случае образца—эллипсоида) включены в hefj-, то поле
h является внешним полем, а тензор х> как и для ферромагнетика
(см. § 1.5),—внешним тензором восприимчивости эллипсоида. Если
же размагничивающие поля не включать в hef j, то h будет внутренним
магнитным полем, а тензор х—тензором восприимчивости вещества.
Для антиферромагнетиков (в не очень сильных постоянных полях)
различие между этими тензорами не будет большим. Но в
ферримагнетиках оно будет, вообще говоря, столь же существенным,
как и в ферромагнетиках.
§ 3.2. Антиферромагнитный резонанс
Антиферромагнитный резонанс теоретически впервые рассмотрели
Киттель [349] и Нагамия [373], а экспериментально обнаружили
в СиС12-2Н20 Уббинк и др. [442]. С тех пор было выполнено
огромное количество работ, посвященных исследованию
антиферромагнитного резонанса в кристаллах с различными магнитными
структурами. Изложение даже самых важных результатов этих работ
выходит далеко за рамки данной книги. Задача этого параграфа
заключается в том, чтобы проиллюстрировать применение к
антиферромагнетикам континуальной теории магнитных колебаний в
веществах с несколькими подрешетками, и выявить основные
особенности этих колебаний. Поэтому мы ограничимся наиболее простым
случаем антиферромагнетика с двумя идентичными подрешетками
и одноосной анизотропией.
Как отмечалось в § 3.1, должны быть учтены, вообще говоря,
следующие виды энергии: обменная С/ех, зеемановская Uz, анизотропии
Ua и размагничивающих полей UM- Примем следующие допущения:
1) предположим, что С/а складывается из энергий анизотропии
подрешеток, и записывая их в виде, аналогичном (?.34), ограничимся
учетом только первой константы К^ = К, а анизотропией в базисной
(перпендикулярной главной оси) плоскости пренебрежем;
2) пренебрежем различием длин векторов намагниченностей
подрешеток, т. е. (см. § 3.1) рассмотрим случай Т=0;
3) не будем учитывать размагничивающих полей.
Поскольку эффективные поля обменных взаимодействий внутри
подрешеток не входят в уравнения движения, учтем лишь энергию
обменного взаимодействия между подрешетками, обозначая Л12=— Л. Тогда
C/=AM1M2-H(M1+M2)+A:(sin2e1+sin2e2), (3.16)
где 0! и 02 — углы, которые образуют векторы Mi и М2 с осью
анизотропии. Поскольку Mi и М2 однородны,
H*i.2= -5ST AM2il+H+-^«o(Mi.2Zo), (3.17)
оМ1-2 М0
где М°—длина векторов Мх и М2, a z0—единичный вектор,
направленный по оси анизотропии.
Антиферромагнетик с легкой осью анизотропии: основные состояния.
Рассмотрим сначала случай АГ>0, когда ось анизотропии является
77
2 О
MtOlAf2 0 SH
72 О
М10 М0
у 4 ~ъТ~и
72 О
Рис. 3.4. Основные состояния двухподрешеточного антиферромагнетика с
легкой осью анизотропии (К>0)
легкой осью. Из соображений симметрии ясно, что равновесные
векторы Mj о и М2 о и вектор Н0 лежат в одной плоскости,
проходящей через ось анизотропии—ось z, образуя с этой осью
углы соответственно 6Ь 02 и Од". Для нахождения углов
Gi и 02 следует (см. § 3.1) приравнять нулю производные U по
этим углам или учесть условия (3.6). Оба пути приведут к следующим
необходимым условиям равновесия:
A(M0)2sin(e1,2-e2,j)-H0M0sin(eH-e1.2)-t-/i:sine1,2cosej.2=o, (з.18>
где М°—длина векторов М10 и М20- Найдя углы, удовлетворяющие
этим условиям, мы должны затем выяснить, при каких их значениях
энергия является минимальной.
Ограничимся рассмотрением двух частных случаев: когда поле
Н0 направлено по оси анизотропии (Н0II z0) и когда оно
перпендикулярно этой оси (H0lz0). Симметрия допускает в указанных
случаях основные состояния, показанные на рис. 3.4, и из условий
(3.18) следует
(3.19)
(3.20)
со8вц=Яо/(2Я£-ЯД
sine± = H0/(2HE + HA).
Здесь использованы обозначения
НЕ=АМ°, НА = К/М°.
(3.21)
Сравнивая величины энергии (3.16) в различных состояниях,
можно убедиться, что они являются минимальными в пределах
изменения Н0, которые приведены в табл. 3.1. Из этой таблицы
видно, что в случае Н0 || z0 в слабых полях имеет место
антипараллельное состояние +0ц; при увеличении Я0 скачком происходит
переход в состояние +1ц. Этот переход, являющийся фазовым
переходом 1-го рода, называют «опрокидыванием» подрешеток (spin-
flop). Заметим, что в узком интервале полей HCi<H0<HC2 (см.
" Мы опускаем индексы 0 у равновесных углов в10 и 02о.
78
табл. 3.1) оба состояния +0ц и +1ц оказываются устойчивыми. Это
приводит (см., например, [23]) к образованию доменных структур,
в которых сосуществуют два состояния, и к гистерезису. При
дальнейшем увеличении Н0 угол между векторами Mj 0 и М2 0
уменьшается, и при Н0 = НЕ« происходит «захлопывание» подрешеток —
переход в состояние 2ц. В отличие от «опрокидывания» этот
переход обычно носит характер фазового перехода второго рода [133].
Таблица 3.1
Основные состояния и собственные частоты
двухподрешеточного антиферромагнетика с легкой осью
анизотропии (К/М =НЛ>0) при Т=0
Направление
поля
Состояния
(рис. 3.4)
+0
Hol|z0
Антипараллельное
Неколлине-
арное
(опрокинутое)
Параллельное
(захлопнутое)
Пределы изменения
поля
= ^НА(2НЕ+НА)
JHA(2HE-HA) =
= На <Н0< Нщ =
= 2НЕ-НА
Не и < #о
H0J_z0
Собственные частоты"
ш±
= НС2±Н0
У
(3.24)
[«112=0]
(3.25)
«in
—=н0+нА,
У
|_~=я°-я*|| J
(3.26)
+ 1х
Неколлине-
арное
22х
Параллельное
(захлопнутое)
Н0<НЕ1 =
= 2НЕ+НА
нЕ±<н0
(~J=H0(HB-HA), (3.29)
[(^)2 = (^о-2Я£)(Я0-Н£1)1
" В квадратных скобках—частоты колебаний, которые не возбуждаются
однородным переменным магнитным полем.
В случае H0±z0 по мере увеличения Н0 угол между М! 0 и М2 0
постепенно уменьшается, и при Н0 = НЕ± происходит переход из
состояния +li в состояние +2j..
79
Рис. 3.5. Статические
намагниченности и восприимчивости
антиферромагнетика с легкой осью
анизотропии при поле Н0, параллельном
(индексы ||) и перпендикулярном
(индексы i) оси. Масштаб по оси
абсцисс искажен, чтобы сделать
заметными малые интервалы
Нсг — НС1 и НЕ1 — НЬи
JJ! [
Для обеих рассмотренных ориентации Н0 во всех состояниях
суммарная намагниченность М0 = М10 + М2о параллельна Н0, и может
быть введена скалярная восприимчивость %о = М0/Н0. Зависимости
М0 и Хо от Я0 показаны на рис. 3.5. Из этого рисунка видно, что
при малых полях имеет место резкая анизотропия Хо-
Для большинства антиферромагнетиков HA<s:HE. В этом случае
шириной интервала полей #cl-=-#C2 и различием НЕ-\ и НЕ± можно
пренебречь и использовать приближенные выражения
НС1^НС2~НС = ^2НЕНА, Я£,|~Я£1^2Я£. (3.22)
Принимая во внимание соотношение (3.1), мы получим для
антиферромагнетиков с температурами Нееля порядка 100 К и полями
анизотропии Ял~10—100 Э следующие величины характерных полей:
Я£~106Э и ЯС~Ю4—105Э.
Колебания в антипараллельном состоянии. Теперь можно перейти
к исследованию магнитных колебаний. Для этого нужно
спроектировать линеаризированные уравнения движения (3.14) на оси координат
с учетом выражений (3.17) для эффективных полей. Для
антипараллельного состояния +0ц (рис. 3.4), проектируя (3.14) на ось z, получим
Wiz = wi2r = 0; проекции на оси х и у дадут систему четырех уравнений
для т1х, т1у, т2х и т2у. После перехода к циркулярным переменным
для пар переменных т1+, т2+ и wx_, m2- получатся независимые
системы (соответственно с верхними и нижними знаками)
[±<u-iato-y(H0+HE + HA)~]m1±-yHEm2± = -yM°h±,
(3 23)
yHEm1±+[±a-iaxu-y(H0-HE-HA)]m2±=yM°h±.
Для того чтобы найти собственные частоты колебаний, приравняем
нулю определители систем (3.23) при а = 0. В результате получим
две частоты со+ и со_, выражения для которых (3.24) приведены
80
2М
в табл. 3.1. Зависимости
этих частот от Я0 показаны
на рис. 3.6. При Яо = 0
co+=co_sco0. Частоты со0
оказываются обычно
довольно высокими;
например, для Сг203 /о= 165 ГГц.
Для выяснения
характера собственных колебаний
можно рассуждать (см.
§ 1.3) следующим образом.
Для колебания с частотой
со+ определитель системы
(3.23) с нижними знаками
не обращается в нуль.
Следовательно, эта система
имеет при со = ю+ только
тривиальное решение
w1_=w2_=0. Это означает,
что miy=—imix и т2у =
= — imix, T- е. имеет место
круговая прецессия векторов
Mj и М2 с правым
вращением. Таким же образом
стотой ю- представляет собой круговую прецессию с левым
вращением.
Подставляя значения частот со+ или со- в любое из уравнений
(3.23) (при а = 0 и &±=0), мы можем найти отношения переменных
намагниченностей подрешеток: при HA<zHE
т2±/т1± = -(1+Нс1НЕ), (3.30)
так что результирующая переменная намагниченность оказывается
малой. Характер движения намагниченностей подрешеток в состоянии
+0ц показан на рис. 3.7.
Чтобы найти затухание свободных колебаний, следует приравнять
нулю определитель системы (3.23) при /i±=0 и а/0. В первом
приближении (а«:1) получим прежние выражения (3.24) для со± и (при
#л«Я£)
ю'^асо'±Я£/Яс. (3.31)
Сравнивая (3.31) с соотношением ш"^асо' для ферромагнетика, мы
видим, что при одинаковых величинах а затухание колебаний в
антиферромагнетике будет значительно ббльшим. Однако параметры
диссипации а для них могут существенно различаться.
Переходя к рассмотрению вынужденных колебаний, отметим
прежде всего, что наибольший интерес представляет суммарная
переменная намагниченность m = mi + m2, которой определяются
все наблюдаемые эффекты при антиферромагнитном резонансе.
6 А. Г. Гуревич, Г. А. Мелков 81
НС1 НС2 НЕ\\ НЕ1 Н0
Рис. 3.6. Собственные частоты однородных
колебаний в антиферромагнетике с легкой
осью анизотропии. Индексы || и 1 и
искажение масштаба—такие же, как на рис. 3.5.
Штриховые линии — частоты колебаний
с m=m1 + m2=0
легко убедиться, что колебание с ча-
Рис. 3.7. Предания векторов намагниченностей подрешеток
антиферромагнетика с легкой осью анизотропии в антипараллельном основном
состоянии; а- ветвь с частотой ш+, б—с частотой со_. Различие Im^ и |т2|
утрировано
Решая систему (3.23), получим в случае малой диссипации
(а«с 1) и Нл<е:НЕ
т±=т1±+тг±~
2у2 М°НА
(со + — со) (со _ — со)+2iacoy Я
h±=X±h±, (3.32)
где со+ и со_—собственные частоты (3.24), а х+ и Х-—
Циркулярные компоненты (см. § 1.3) тензора %. При резонансе (со = со+
или со = со_)
(х"±)гс* = уМ°Нл1(аа>±НЕ) = уК/(<ш±НЕ).
(3.33)
Эта величина отличается от резонансной циркулярной
восприимчивости ферромагнетика (см. § 1.4) при сравнимых собственных
частотах и близких ос малым множителем НЛ/НЕ.
Ширину резонансной кривой можно определить, как и для
ферромагнетиков, как разность частот или полей, при которых
Х" = г(х"Ц- При ос«:1 и НА<^НЕ
У У Нст
(3.34)
Колебания в неколлинеарном состоянии. В состоянии +1ц (см.
рис. 3.4)
M10 = (zoCose||-y0sine||)Af0, M2o = (zocose„+y0sine )M°. (3.35)
Проектируя (3.14) при а = 0 и h = 0 с учетом (3.17) и (3.35) на оси
координат, получим систему шести уравнений для составляющих
искюров nij и m2. Для того чтобы получить две независимые
системы (соошетствующие двум типам колебаний), теперь необходимо
32
Рис. 3.8. Прецессия векторов
намагниченностей
подрешеток антиферромагнетика
с легкой осью анизотропии
в неколлинеарном основном
состоянии 1ц. Цифрами
обозначены положения
концов векторов Mj, М2 и
М = М!+М2 в одинаковые
последовательные моменты
времени
^^ У
X
перейти к составляющим векторов m = irii-|-m2 и l = m1 — m2IJ. Первая
система свяжет переменные тх, ту и 1г, а вторая -mz, /х и 1У.
Равенство нулю определителя первой системы даст выражение (3.25)
(в табл. 3.1) для собственной частоты со,. Зависимость ее от
Но показана на рис. 3.6. Приравнивая нулю определитель второй
системы, получим со2 = 0.
Характер собственных колебаний в состоянии +1 ц можно выяснить
тем же способом, который был использован выше. Для первого
типа колебаний вторая система (для переменных тг, 1Х, 1У) имеет
только нулевые решения, поэтому для него
fnix = m2x, wily = w2j„ mlz=-m2z (3.36)
(см. рис. 3.8). Для второго типа колебаний mx = my = mz = 0. Этот тип
колебаний представляет собой бесконечно медленное вращение
векторов М, и М2 вокруг оси z. Такое движение происходит без
изменения энергии системы, поэтому собственная частота его равна
нулю. Конечно, в действительности различные неучтенные нами
факторы, в частности, анизотропия в базисной плоскости, приведут
к отличию со2 от нуля, однако эта частота будет все же оставаться
низкой2'.
Из характера прецессии вектора М (рис. 3.8) ясно, что первый
тип колебаний будет возбуждаться поперечным (относительно
направления Н0) переменным полем. Второй же тип колебаний вообще
не будет возбуждаться однородным переменным полем. Таким
" Вектор 1 представляет собой комплексную амплитуду переменной
составляющей вектора L=M,—М2, который называют вектором
антиферромагнетизма.
2) Такие колебания с частотами, обращающимися в идеальном случае
в нуль (а реально—с низкими по сравнению с другими частотами системы),
называются мягкими модами. Появление мягкой моды в данном случае
связано с тем, что основное состояние (для которого векторы Mt 0 и М2 0
направлены некоторым определенным образом, например, лежат в плоскости
vz, как на рис. 3.4) «нарушает» симметрию энергии системы (являющуюся
при Н01| z0 цилиндрической). Общее утверждение, что в случае нарушения
основным состоянием симметрии энергии системы возникает мягкая мода,
представляет собой теорему Голдстоуна (см., например, [109])
Z
1 т
но
^10
Mio+"zo
М20/
6*
83
образом, тензор х Ддя опрокинутого состояния + 1ц будет иметь
такой же вид (1.47), как и для антипараллельного состояния.
Компоненты этого тензора легко найти, решая систему уравнений
для тх, ту и /z при h^O и а^О. Ясно, что они будут проходить
через резонанс при частоте coi.
Для захлопнутого состояния +2\ решение системы (3.14) дает
два типа колебаний с частотами, приведенными в табл. 3.1. Однако
для второго типа колебаний ш = 0, т. е. он не может быть возбужден
однородным переменным полем. Первый же тип колебаний совпадает
(см. § 2.3) с колебаниями в одноосном ферромагнетике с
намагниченностью 2М° и константой анизотропии К.
Колебания в поперечном постоянном поле. Для основного состояния
+ 1_l (см. рис. 3.4), поступая таким же образом, как и для состояния
+ 1ц, получим две независимые системы уравнений: для тх, mz,
ly и для lx, /z, ту (#о направлено по оси у), которые соответствуют
двум типам собственных колебаний. Равенство нулю определителей
указанных систем дает выражения для собственных частот этих
колебаний, которые приведены в табл. 3.1. Зависимости их от
Н0 показаны на рис. 3.6. Поскольку для первого типа колебаний
ту = 0, он будет возбуждаться поперечным (относительно Н0)
переменным полем. Для второго типа колебаний mx = mz = 0, и он возбуждается
продольным (параллельным Н0) переменным полем. Таким образом,
ieraop х имеет в данном случае вид
Х =
Хп
0
-1Ха
0
Х22
0
iXa
0
Хзз
(3.37)
причем Mi является резонансной частотой поперечных компонент
Хп. Хзз и Хо. а со2 —продольной компоненты 1гг- При Н0 = НЕ1
первый тип колебаний переходит в «ферромагнитный» тип колебаний
в параллельном основном состоянии +2±. Частота его совпадает
с собственной частотой для одноосного ферромагнетика (§ 2.3) при
соответствующей ориентации Н0.
Для произвольной ориентации Н0 относительно оси анизотропии
приведем лишь зависимости частот колебаний от Я0 (рис. 3.9).
Зная эти зависимости, можно рассчитать в приближении
независимых зерен (см. § 2.4) спектры резонансного поглощения в
поликристаллическом антиферромагнетике. Причем ввиду малости (при
Н0 <s НЕ) суммарной намагниченности М0 это приближение
выполняется хорошо. Из рис. 3.9 следует, что в поликристаллических
антиферромагнетиках будут наблюдаться очень широкие полосы
поглощения как по полю (при со = const), так и по частоте (при
Но = const).
Антиферромагнетики с легкой плоскостью анизотропии. Перейдем
теперь к случаю К<0, когда легкие направления векторов М! и М?
лежат в базисной плоскости. Мы приведем для этого случая лишь
основные результаты, способ их получения (см., например, [69]) не
отличается от использованного выше.
R4
Рис. 3.9. Частоты колебаний антиферромагнетика с легкой осью анизотропии
при различных углах между Н0 и осью анизотропии [299]. Сплошные
и штриховые линии—два типа колебаний. Принято НА<е:НЕ, и малый интервал
попей НС2 — НС\ (в отличие от рис. 3.6) не показан
При Л^<0 для обеих ориентации поля: H0||z0 и H0-Lz0 могут
существовать два основных состояния — неколлинеарные ~Ь| и ~1±
и параллельные (захлопнутые) ~2ц и ~2± (рис. 3.10 и табл. 3.2). Для
равновесных углов в неколлинеарных состояниях имеют место
выражения
cosQ}l=H0l(2HE-HA),
simp± = Ho/(2HE),
(3.38)
(3.39)
где НЕ и НА по-прежнему определяются согласно (3.21), но теперь
НЛ<0. Сравнивая рис. 3.10 с рис. 3.4, мы видим, что состояния ~1ц,
но "ю У
Рис. 3.10. Основные состояния двухподрешеточного антиферромагнетика с
легкой плоскостью анизотропии (А^<0)
85
Таблица 3.2
Основные состояния и собственные частоты
двухподрешеточного антиферромагнетика с легкой плоскостью
анизотропии (К11М°шНА<0) при 7"= О
Направление
поля
Н0 II г0
Состояния
(см. рис. 3.10)
"111
неколлинеарное
H0±z„
параллельное
(захлопнутое)
Пределы изменения
поля
Н0<2НЕ + \НА\
Собственные частоты
Совпадают с (3.25)
2"с + \Нл\<Н0
li
неколлинеарное
"2Х
параллельное
(захлопнутое)
Ио<2Не
Совпадают с (3.26)
2НЕ<Н0
(3.41)
Совпадают с (3.29)
~2ц и ~2Х совпадают с состояниями соответственно +1ц, +2ц и +2±.
Поэтому выражения для собственных частот во всех перечисленных
состояниях при К<0 будут такими же, как приведенные в табл. 3.1
для соответствующих состояний при К>0. Различие, однако,
заключается в знаке НА. Поэтому фактическая зависимость tOi для
состояния ~1ц от Н0 (рис. 3.11) будет отличаться от такой
зависимости для опрокинутого состояния +1ц, приближенно (при
| НА | <к//£) она будет совпадать с зависимостью cot (Н0) для состояния
+ lj. (рис. 3.6).
у/2Н \н.
с'"д|
ы12
ЫП2 >^
/
/
/
/
Щ "о
Рис. 3.11. Частоты
колебаний антиферромагне гика
с легкой плоскостью
анизотропии при Ho'lzo (индексы
) и H0lz0 (индексы J_).
Штриховая тиния —
колебания с т = 0, штрих-пунк-
тир~ при небольшом
отличии угла между Н0 и г0 от
я'2. Принято НА<е:НЕ (в
отличие от рис. 3.6)
Рис. 3.12. Прецессия
векторов намагниченностей под-
решеток
антиферромагнетика с легкой плоскостью
анизотропии в постоянном
поле, лежащем в легкой
плоскости (основное состояние
~1±); а—колебание с
частотой coib б—с частотой
ш±2 (рис. 3.11). Цифры—как
на рис. 3.8
Существенно новым в случае К<0 будет состояние ~1± при
поле Н0, лежащем в легкой плоскости. Выражения для собственных
частот в этом состоянии приведены в табл. 3.2, а зависимости их
от Н0 показаны на рис. 3.11. Характер движения векторов
намагниченности для этих типов колебаний показан на рис. 3.12. Для
первого типа колебаний не обращаются в нуль тх, тг и /,,, и он
возбуждается переменным полем, поперечным относительна поля
Н0 (направленного по оси у). Второй тип колебаний, для которого
не обращаются в нуль lx, L и ту, возбуждается продольным
(параллельным Н0) переменным полем.
Как видно из рис. 3.12 и 3.6, частоты со2 в (различных) состояниях
+ 1Х и ~1Х фактически—из-за различия знаков НА—мало отличаются
друг от друга. Поведение же частоты со, в состоянии ~1± (при А^<0)
не имеет аналога в случае К>0. При #о->0 частота coi —>0, т.е. ее
зависимость от Н0 является бесщелевой. Эта интересная особенность
данного типа колебаний связана с тем, чго для него (см рис. 3.121
угол между векторами Mi и \12 не изменяется при их движении.
Антиферромагнитный резонанс в этом случае может наблюдаться при
низких частотах и в слабых постоянных магнитных полях.
Другой особенностью спектра магнитных колебаний
антиферромагнетика при Н0. лежащем в лг| кой тоскости анизотропии.
87
является пересечение его ветвей, т. е. вырождение двух типов
колебаний при Н0=?НС (см. рис. 3.11). Заметим, что даже при небольших
отклонениях Н0 от легкой плоскости это вырождение снимается—
ветви спектра начинают «расталкиваться».
Анизотропия в базисной плоскости сушесшсшю повлияет лишь
на первый («бесщелевой») тип колебаний при К<() и H0±z0. Она
приведет к появлению щели в спектре этой) типа колебаний (т. е.
к конечной величине to t при Я0 -»0), зависящей от азимутального
угла Н0. Следует заметить, что анизотропия в базисной плоскости
является не единственной причиной появления такой щели, источником
ее может явиться также магнитоупругое взаимодействие (гл. 12).
Слабые ферромагнетики. Остановимся теперь на некоторых
особенностях магнитных колебаний в антиферромагнетиках со слабым
ферромагнетизмом. Ограничимся рассмотрением антиферромагнетика
с легкой плоскостью анизотропии при поле Н0, лежащем в этой
плоскости. Наличие члена энергии (3.7) не приведет к качественному
изменению основного состояния ~1± (рис. 3.10), но теперь
sm<p±=(H0 + HD)/(2HE), (3.42)
где HD = DM°. Член энергии (3.8), в отличие от (3.7), не инвариантен
относительно поворотов вокруг оси z и поэтому не только
стимулирует определенную взаимную ориентацию М! и М2, но и является
одновременно источником анизотропии в базисной плоскости. Если
для простоты направить Н0 по оси у, то основное состояние будет
качественно таким же, как на рис. 3.10, и в выражении (3.42) HD
заменится на HF = FM°.
Исследование магнитных колебаний может быть проведено теперь
по той же схеме, которая была неоднократно использована выше.
Мы приведем лишь некоторые результаты. Для собственной частоты
первого типа колебаний в случае инварианта (3.7) при малом ф±
получается выражение
(ю1/у)2 = Я0(Я0 + Яв). (3.43)
В случае же инварианта (3.8) при том же условии
(со1/у)2 = (Я0 + Я,)(Я0 + 4Яг). (3.44)
Сравнивая выражения (3.43) и (3.44) с (3.30), мы видим, что наличие
слабого ферромагнетизма привело к существенному изменению
спектра бесщелевого (в его отсутствие) типа колебаний при малых полях
Я0. Причем в случае инварианта (3.7) этот тип колебаний остался
бесщелевым, а в случае инварианта (3.8) в спектре появилась шель.
Мы рассмотрели антиферромагнитный резонанс в простом
частном случае одноосного двухподрешеточного антиферромагнетика
при температуре Г=0 без учета влияния формы образца (а также
его размеров). Рассмотрение более сложных случаев выходит за
рамки этой книги, и мы ограничимся несколькими краткими
замечаниями. Во-первых, все приведенные результаты справедливы, строго
говоря, только для сферических образцов с ишметрами, малыми
по сравнению с длиной электромагнитной волны. Учет влияния
88
формы образца—малого эллипсоида может быть проведен в маг-
нитостатическом приближении так же, как для ферромагнетика (§ 1.5).
Но поскольку намагниченности антиферромагнетика, как постоянная
так и переменная, малы при И0«НЕ, то при таких полях влияние
формы образца на антиферромагнитный резонанс является малым.
Требование малости размеров образца по сравнению с длиной
электромагнитной волны, которое является условием применимости
магнитостатического приближения, при экспериментальном
исследовании антиферромагнитного резонанса часто бывает трудно выполнить.
Второе замечание относится к влиянию температуры. При Т>0
величины намагниченностей подрешеток М10 и М20 отличаются от
Af°(T=0) и, вообще говоря, друг от друга. Если эти величины
найдены, то рассмотренная выше теория антиферромагнитного
резонанса остается почти без изменения; необходимо лишь для
параметров у, НА, НЕ принять их значения при данной температуре и учесть
различие величин М10 и М10. Приведем в качестве примера
выражение для собственных частот в антипараллельном состоянии
+0ц, полученное при таком учете (в случае НА«НЕ) [300]:
^ = JlHAHE + Hi Р2/4 ± Я0 (1 - р/2). (3.45)
где НА и НЕ определяются согласно (3.21), но с заменой М° на
jMl0M10, a p = A(Af10-Af2o)/tf0sWXoi- Заметим, что у и ЯЕ
почти не зависят от температуры, так что фактические температурные
зависимости частот антиферромагнитного резонанса определяются
зависимостями от Т величин Хоц и НА.
Последнее замечание касается антиферромагнитного резонанса
в веществах с более сложными магнитными структурами. В § 3.1
отмечалось, что число подрешеток п, необходимое для полного
описания свойств антиферромагнетика, должно быть равно числу
магнитных ионов в примитивной магнитной ячейке, а число типов
колебаний в каждом основном состоянии равно числу подрешеток.
Однако во многих случаях подрешетки объединяют, часто — в две
группы с магнитными моментами, направленными в противоположные
стороны. Рассматривая каждую такую группу как подрешетку, мы
можем воспользоваться рассмотренной выше «двухподрешеточнои»
теорией. Она дает, обычно с достаточной точностью, спектры двух
типов колебаний с наименьшими частотами, но остальные п — 2
типов колебаний при этом теряются.
В заключение отметим особенности антиферромагнитного
резонанса по сравнению с ферромагнитным.
1) Для антиферромагнетиков характерно наличие нескольких
основных состояний в зависимости от величины постоянного магнитного
поля; в каждом состоянии возможно несколько типов магнитных
колебаний.
2) Магнитная кристаллографическая анизотропия играет большую
роль, чем в ферромагнетиках; характер ее существенно влияет на
вид спектров; вклады анизотропии в частоты колебаний, как правило,
89
определяются средними геометрическими полей анизотропии и
больших обменных полей.
3) Спектры антиферромагнитного резонанса, как правило,
характеризуются шелью: бесщелевой (в первом приближении) является
лишь одна из ветвей при Н0, лежащем и легкой плоскости
анизотропии; спектры содержат ветви, частоты которых как
увеличиваются, так и уменьшаются с ростом Н0.
4) Компоненты тензора восприимчивости антиферромагнетиков
в не очень сильных постоянных полях малы.
Заметим, что последнее обстоятельство не исключает возможности
использования антиферромагнетиков в коротковолновой части
диапазона СВЧ; малость компонент тензора восприимчивости может
быть скомпенсирована «большими» (по сравнению с длиной
электромагнитной волны) размерами устройств.
§ 3.3. Магнитные колебания в ферримагнетиках
В этом параграфе будут рассмотрены однородные магнитные
колебания в ферримагнетиках или ферритах", которые, как и
антиферромагнетики, имеют несколько подрешеток, но обладают
большой спонтанной намагниченностью. Теория ферромагнитного
резонанса, развитая в гл. 1 и 2, как мы увидим, применима с некоторыми
ограничениями к одному из типов колебаний в ферримагнетиках,
который и используется на практике. Доказательство этого положения
и выявление указанных ограничений и особенностей магнитных
колебаний в ферримагнетиках представляет собой цель данного
параграфа.
Кристаллические структуры. Большинство ферримагнетиков
представляет собой ионные кристаллы. Основой их кристаллических
структур является решетка анионов. Катионы обычно размещаются
в пространствах (пустотах) между ними. Занятые катионами пустоты
называются катионными позициями или узлами. Такие позиции
различаются числом Л' ближайших соседей — анионов. Если N=4,
то эти анионы образуют более или менее правильный тетраэдр
и узлы называются тетраэдрическими. При N=6 узлы называются
октаэдрическими, при N=8—додекаэдрическими. Как правило,
кристаллические структуры ферримагнетиков содержат катионные узлы
с двумя или тремя разными N. При этом одинаковые ионы могут
находиться в разных узлах, а по одинаковым узлам могут быть
распределены — случайным образом или упорядоченно—разные ионы.
Наиболее широкое применение в технике и при физических
исследованиях нашли кислородные ферримагнетики с двумя
кубическими структурами — типа шпинели и типа граната, и некоторыми
гексагональными.
11 Ферриты в узком смысле слова—это соединения состава MFe204, где
М—двухвалентный металл. Однако термин «ферриты» часто используют
в гораздо более широком смысле, понимая под ними любые неметаллические
ферри- (а иногда и ферро-) магнетики.
90
Структуру типа шпинели (минерала MgAl204) имеют ферриты
MFe2+04, где М—двухвалентный ион, например, Ni, Co, Fe, Mn,
Mg или комбинация одно- и трехвалентных ионов, например,
Lio,5 Feo,5- Ионы Fe3+ могут замещаться другими трехвалентными
ионами — Сг, А1.
Анионы в структуре шпинели (см. подробнее [123, 217]) образуют
плотно-упакованную кубическую решетку, в которой имеются пустоты
двух типов—тетраэдрические и октаэдрические. Число занятых тет-
раэдрических пустот, т. е. тетраэдрических (А) узлов, в два раза
меньше, чем октаэдрических (В). В результате образуется довольно
сложная структура кубической сингонии, в элементарную ячейку
которой (куб с ребром—для кислородных шпинелей—8,5 А) входит
8 формульных единиц MFe204. Локальная симметрия окружения
катиона в тетраэдрических узлах—кубическая, а в октаэдрических—
кубическая с тригональными искажениями, причем имеется 4
неэквивалентных типа октаэдрических узлов, отличающихся друг от друга
направлениями локальных осей третьего порядка.
Распределение катионов по узлам в ферритах со структурой
шпинели обычно записывают в виде (M^Fe,^) [M^Fej+j, ]04, где
в круглые скобки заключены ионы в тетраэдрических узлах, а в
квадратные— в октаэдрических. Если у=\, то шпинель называется
нормальной, если у = 0 — полностью обращенной. Все ферримагнитные
кислородные шпинели—частично или полностью обращенные1'.
Структуру типа граната (минерала Ca3Al2Si3012) имеют
ферримагнетики R3Fe5 + 012, где R—трехвалентный ион иттрия или
редкоземельных элементов от Sm до Lu. Ферримагнетик Y3Fe5012—
иттриевый феррит или железоиттриевый гранат (ЖИГ) обладает
наиболее узкой линией ферромагнитного резонанса из известных
в настоящее время веществ.
Структура граната, относящаяся к кубической сингонии, является
очень сложной (см., например, [123, 217]); в элементарную ячейку—
куб с ребром более 12 А (12,376 А для ЖИГ) входит 8 формульных
единиц. Примитивная ячейка имеет в два раза меньший объем,
содержит 48 анионов и 20 ионов Fe3 + . В структуре граната имеются
катионные узлы трех типов: тетраэдрические, октаэдрические и до-
декаэдрические. Локальная симметрия окружения катионов в
тетраэдрических узлах—тетрагональная. Как и в шпинели, имеется 4
неэквивалентных типа октаэдрических узлов с тригональной локальной
симметрией. Локальная симметрия додекаэдрических узлов является
орторомбической, имеется 6 неэквивалентных типов таких узлов,
различающихся направлениями локальных осей.
Распределение ионов по узлам в ЖИГ имеет вид
(Y3}(Fe3) [Fe2]012, где фигурные скобки обозначают додекаэдричес-
кие узлы, а круглые и квадратные, как и раньше,—тетраэдрические
и октаэдрические.
11 Структуру нормальной шпинели имеют ферромагнетики МСг2Х4, где
X = S, Se, a M = Cd, Hg. Нормальные кислородные шпинели (M=Zn, Cd) —
антиферромагнетики.
91
К сильно анизотропным гексагональным ферримагнетикам
принадлежат соединения составов M'Fe12019, M'2M2Fe12022 и др., где
М'—крупные двухвалетные ионы: Ва, Sr, Pb, a М—перечисленные
выше двухвалентные ионы. Размеры их элементарных ячеек в
направлении главной оси достигают ~ 50 А при поперечных размерах ~ 5 А.
Магнитное упорядочение. Наиболее сильным косвенным обменным
взаимодействием является взаимодействие между катионами,
находящимися в октаэдрических и тетраэдрических узлах; оно носит
антиферромагнитный характер и приводит к антипараллельной
ориентации моментов этих ионов.
Число подрешеток, необходимое для полного описания свойств
ферримагнетиков. как уже отмечалось, равно числу магнитных ионов
в примитивной магнитной ячейке (которая для этих кристаллов
совпадает с кристаллографической). Однако, как и для
антиферромагнетиков, магнитные колебания с наинизшими частотами (и,
как мы увидим, с наибольшей интенсивностью) могут быть описаны
на основе моделей с гораздо меньшим числом подрешеток, во
многих случаях—только двумя. Так, для ЖИГ 12 ионов Fe3 +
в тетраэдрических и 8 таких ионов в октаэдрических узлах могут
быть объединены в две подрешетки с антипараллельными намаг-
ниченностями.
Особенностью ферримагнетиков является неидентичность
подрешеток. Причем их статические намагниченности могут различным
образом зависеть от состава и температуры. При некоторых составах
или температурах суммарная намагниченность £Mj-o = 0. Такие со-
j
ставы или температуры называются магнитными точками
компенсации. Поскольку магнитомеханические отношения уу тоже
различаются, механические точки компенсации, в которых £М;О/у;=0, не
J
совпадают с магнитными.
Основные состояния двухподрешеточного ферримагнетика. Вдали
от точек компенсации изучение ферримагнетиков, в отличие от
антиферромагнетиков, можно в первом приближении проводить,
пренебрегая кристаллографической анизотропией. Следуя Шлёманну
[398], рассмотрим в таком приближении основные состояния
двухподрешеточного ферримагнетика0. Плотность его энергии
запишется в виде
С/=-^Л11М?-^Л22М22-Л12М1М2-Н0(М1+М2), (3.46)
где Лп, Л22 и Л12—константы обменного взаимодействия внутри
подрешеток и между подрешетками. Ограничиваясь случаем Г=0,
будем длины векторов Mt и М2 считать заданными. Равновесные
значения углов Gt и 62 (рис. 3.13) могут быть найдены из условий
минимума энергии (3.46).
" Впервые эта задача, но в другой—микроскопической трактовке была
решена Тябликовым (см. [201 ]).
92
Приравнивая нулю
производные от (3.46) по Gt и 62,
находим, что либо
sin61 = sin62=0, либо
cos6j =
~2W0AAf10
(3.47)
cos 6, =■
2Н0ЛМ20
где обозначено Л = — Л12,
a #±=A(Afl0±Af20)> причем
всегда
Af10sinei=-M20sine2. (3.48)
Можно убедиться, что
минимумы энергии (3.46) в
зависимости от величины Я0
имеют место при значениях
углов 0! и 62, приведенных
в табл. 3.3. Зависимости
равновесных углов 01О и 620 от
Рис. 3.13. Полевые зависимости
равновесных углов намагниченностей
подрешеток, суммарной постоянной намагни-
Н0 показаны на рис. 3.13. ченности и статической восприимчивости
- - -> ™n„vnnmv.mpTniiHnrn Летжмагнетика.
двухподрешеточного ферримагнетика.
Расчет при М10 = \,5М2о
В обычных ферритах Л~103
и, следовательно, первое
обменное поле Н_~105Э, второе обменное поле Н+ превышает его
в несколько раз.
Таблица 3.3
Основные состояния изотропного
двухподрешеточного ферримагнетика при Г=0
Состояние
Антипараллельное
Неколлинеарное
Параллельное
(захлопнутое)
Пределы изменения
н_<н0<н+
н,<н0
Равновесные значения
углов 6, и 62
(рис. 3.13)
е10=о, е20=п
Формулы (3.47)
е10=о, е20=о
Как следует из (3.48), постоянная намагниченность М0 = М10 + М20
во всех состояниях параллельна Н0. Зависимости М0 и %0 от Я0
показаны на рис. 3.13.
Нахождение основных состояний при Г>0, как и в случае
антиферомагнетиков, требует учета температурных зависимостей М10
и М20. При разном характере этих зависимостей, а именно, если
большая (при Г=0) намагниченность убывает с ростом температуры
быстрее, могут возникнуть точки компенсации по температуре.
93
20 Uf * I
Рис. 3.14. Фазовые диаграммы двухподрешеточного ферримагнетика при
отсутствии (о и в) и при наличии (б к г) точки компенсации по температуре
(схематически); а и б—без учета анизотропии [263], в и г—с учетом первой
константы анизотропии кубического кристалла при Н0, направленном по легкой
оси < 111 > [5, 91]
Характерным примером являются редкоземельные гранаты (см.,
например, [123, 459]), в которых намагниченность додекаэдрической
подрешетки спадает с температурой быстрее, чем намагниченность
«объединенной» подрешетки железа. Расчетные фазовые диаграммы
(области существования различных основных со'стояний)
двухподрешеточного ферримагнетика при наличии и в отсутствие точек
компенсации по температуре показаны на рис. 3.14.
Колебания в антипараллельном состоянии. Не будем пока
учитывать размагничивающих полей и кристаллографической
анизотропии. Тогда
НеП,2 = Н0-ЛМ2л.
(3.49)
Проектируя уравнения (3.14) с учетом (3.49) на оси координат
и переходя к циркулярным переменным, получим
[±ю-у1(Я0+ЛМ20)-т1ю]т1±-у1ЛМ10т2±=-у1М10Л,
у2ЛМ20т1± + [±(0_У2(яо-ЛМ10) + /а2со]т2±=У2М20/1±.
(3.50)
Приравнивая нулю
определитель этой системы при ai,2=0
и Л± = 0, мы получим уравнение
для собственных частот:
со2 + со [Л(у2 М! 0 - Yt M2о) -
-(Yi+Y2)#0]-
-у1у2[Л(М10-М20)-Я0]Я0 =
= 0. (3.51)
V,v2
<Г' /
Рис. 3.15. Частоты однородных
колебаний ферримагнетика в
антипараллельном основном состоянии [309]
Знаки + в этом уравнении
соответствуют двум типам колебаний.
При исследовании его эти знаки
удобно заменить на +: корни
уравнения после такой замены
дадут частоту первого типа
колебаний (со+) и частоту второго
с обратным знаком ( — со_).
Нетрудно убедиться, что это будет уравнение гипербол в плоскости
(со, Я0), проходящих через начало координат и точку (0, Я_) [309].
Вид их (рис. 3.15) зависит от знака разности (Yi—у2); при У!=у2
гипербола вырождается в пару параллельных прямых. Физический
смысл имеют, конечно, только отрезки гипербол в пределах
0<Яо<Я_, в которых существует антипараллельное основное
состояние. Поскольку собственные частоты колебаний должны быть
положительными, отрезки с со>0 дают частоты со+, а отрезки
с со<0 — величины ( — со_). Как видно из рис. 3.15, частота со+ растет
с ростом Я0 в общем случае (у^у2) не по линейному закону,
а со_ имеет при Яо = 0 большую величину и уменьшается с ростом
Я0. При Я0~Я_/2 происходит вырождение двух типов колебаний
Приведем приближенные выражения для частот со+ и ц>- при
Я0«Я_ , которые получил Уонгснесс [448 ]:
М10-М20
<В+ =: ——: ——;—л0 = ус(Н0,
+ M10h\-M2ohi
(3.52)
со.
*A(Y2M10-YlM20)- Miohi_Mioh2 Я0 = ш£-уеГЯ0. (3.53)
Заметим, что величина yef представляет собой отношение суммарного
магнитного момента к суммарному механическому.
Нетрудно убедиться таким же образом, как и в случае
антиферромагнетиков (§ 3.2), что первый тип колебаний—с-частотой со+
представляет собой (рис. 3.16) правую круговую прецессию, а второй—
левую. Отношения амплитуд намагниченностей подрешеток (при
Н0«Н_)
(3.54)
ml+!m2+^—MloIM2o>
mi_/m2_~-Yi/y2.
(3.55)
95
Рис. 3.16. Прецессия намаг-
ниченностей подрешеток
ферримагнетика в
антипараллельном основном
состоянии; а—ферромагнитный,
б—обменный типы
колебаний. Малое (при
IYj— Уг^Уь Уг) различие
амплитуд nti- и т2- не
показано
Соотношение (3.54) означает,
что векторы М1 и М2, прецес-
сируя, остаются все время
антипараллельными; при этом не
совершается работы против
обменных сил, вследствие чего
обменная константа не входич
в выражение для частоты со+.
Для второго типа колебаний
такая антипараллельность не
имеет места, и собственная
частота его со_ существенно
зависит от обменной
константы. Этот тип колебаний
называют часто обменным, а
первый — ферромагнитным.
Из (3.52) следует, что
частота со+ стремится к нулю
при подходе к магнитной точке
компенсации и к
бесконечности— при подходе к
механической точке компенсации.
Частота же со_, которая при
небольших Н0 лежит обычно
в инфракрасном диапазоне, при
подходе к точкам компенсации,
как следует из (3.53), уменьшается. Хотя выражения (3.52) и (3.53)
справедливы (приближенно) только при условии Н0«Н_=Л(М10 —
-М20), т. е. вдали от точек компенсации, указанные тенденции
подтверждаются экспериментально (рис. 3.17 и 3.18). Теория магнитных
колебаний в ферримагнетике вблизи точек компенсации, как и теория
колебаний в антиферромагнетиках, может быть построена лишь
с учетом анизотропии (см., например, работу Гешвинда и Уокера [309]).
Рис. 3.17. Эффективный g-фактор и
эффективное поле анизотропии граната
Y3Fe5-xGa^012 с точками компенсации
по составу [177]. Точки—эксперимент
(при частоте 9,1 ГГц и температуре
77 К); gt —g-фактор тетраэдрической
подрешетки, рассчитанный в
предположении, что g-фактор октаэдрической
подрешетки g2 не зависит от х
9о
АН,Э i I
700 I
\
500
500
100
100 200 | 400 500 Т,К
ТУ
Рис. 3.18. Эффективный g-фактор и АН граната Gd3Fe5012 с точками
компенсации по температуре [394]. Частота 9,5 ГГц, значения АН—для
HolKlll)
Колебания в неколлннеарном состоянии. Теперь
M1,2o = (20cose1.2-|-y0sine1-2)Af1-2o, (3.56)
где углы 6, и 62 определяются выражениями (3.47). Проектируя
уравнения движения при а1-2 = 0 и h = 0 на оси координат с учетом
(3.49) и (3.56), мы получим систему шести однородных уравнений
для составляющих векторов ml и т2. Ограничимся для простоты
частным случаем у1=у2. Тогда из упомянутой системы получаются
следующие весьма простые уравнения для составляющих вектора
m = m j + m 2:
i(umx + yHomy = 0,
~y Homx+i(omy = 0, (3.57)
/comz = 0.
Из них следует, что в данном случае возможны два типа колебаний;
для одного w7 = 0,
со^уЯо (3-58)
и my=—imx. Для другого со2 = 0 и tnx = my = 0. Частоты этих
колебаний приведены на рис. 3.19. Заметим, что появления колебания
с нулевой частотой (мягкой моды) можно было ожидать в данном
случае, так как осноиное состояние (не обладающее цилиндрической
симметрией) нарушае - цилиндрическую симметрию энергии системы
(см. примечание на с. 83).
Уравнения (3.57) и выражение (3.58) совпадают с
соответствующими выражениями для ферромагнетика (§ 1.3). Таким образом,
в неколлияеарном состоянии, так же как в антипараллельном, имеется
7 А. Г. Гурснич, Г. А. Мелков 97
ферромагнитный тип колебаний
с правой круговой прецессией
вектора суммарной намагниченности
и такой же частотой, как для
ферромагнетика.
С помощью исходной системы
уравнений для составляющих ш,
и ш2 можно исследовать характер
движения векторов М, и М2 для
обоих типов колебаний. Для второго
(мягкой моды) это будет,
естественно, прецессия (бесконечно
медленная) обоих векторов вокруг оси z.
Для первого (ферромагнитного) типа
колебаний концы векторов Мх и М2
будут двигаться по эллипсам
(рис. 3.20); однако проекции этих
эллипсов на плоскость ху представляют собой окружности. Можно
убедиться, что угол между векторами Mj и М2 не изменяется при
их движении; это ясно и из того, что константа обменного
взаимодействия не входит в выражение для частоты данного типа
колебаний. Легко убедиться, что и в захлопнутом основном состоянии
(табл. 3.3) один из типов колебаний будет совпадать с колебаниями
ферромагнетика с суммарной намагниченностью.
Рис. 3.19. Частоты колебаний
двухподрешеточного ферримагне-
тика при Yi=Y2- Штриховые
линии— частоты колебаний с ш=0
Рис. 3.20. Прецессия намаг-
ниченностей подрешеток
ферримагнетика в неколли-
неарном основном
состоянии для ферромагнитного
типа колебаний (с частотой
toj на рис. 3.19)
98
Затухание колебаний. Ограничимся антипараллельным основным
состоянием. Тогда для учета затухания необходимо приравнять нулю
определитель системы (3.50) при oti.2^0. Предположим, что а1 и а2
меньше или порядка 1 и ограничимся случаем малых постоянных
полей при достаточном удалении от точек компенсации, т. е. примем,
что Н0«Н_ и (для первого типа колебаний) co'+/Yi2«#_. Тогда
для этого типа колебаний
со'+=Уег#0/(1+ас2,), (3.59)
со+=а,.гсо', (3.60)
где Yef выражается согласно (3.52), а
a*f=—тг~,—тг~1—• (3-61)
М10/у1-М20/у2
Как видно из (3.61), эффективный параметр диссипации содержит
вклады обеих подрешеток и стремится к бесконечности при подходе
к механической точке компенсации. Но, конечно, здесь можно говорить
только о тенденции, так как вблизи точек компенсации проведенный
расчет несправедлив. Аналогичным образом может быть рассмотрено
затухание и второго типа колебаний. При Н0«Н. и ali2«l для
него получается соотношение, аналогичное (3.60), но с несколько
иной величиной эффективного параметра диссипации.
Вынужденные колебания. Решая систему (3.50) с верхними знаками
при тех же допущениях, что и выше (Я0«Я_ и aJi2 меньше или
порядка 1), но при наличии переменного поля с правой круговой
поляризацией, найдем m+=mt + +m2+=x+h+, где
со+— co+iaefa>
Здесь co+^Yef^o—собственная частота первого (ферромагнитного)
типа колебаний. Полученный результат является чрезвычайно важным.
Выражение (3.62) совпадает с выражением для х+ ферромагнетика
(которое получается при замене (1.73) в (1-53)), если перейти в нем
от намагниченности М0 к результирующей намагниченности
ферримагнетика в данном состоянии М10 — М20, а от величин уиаких
эффективным значениям.
Из (3.62) с учетом (3.52) и (3.61) следует, что
АЯ=2соа'М1о/у'+а*М"/Уг. (3.63)
М10~М20
Как видно из (3.63), ширина резонансной кривой ферримагнетика по
полю возрастает при подходе к магнитной точке компенсации. Заметим,
что такое возрастание, как и возрастание acf и ширины кривой по
частоте Aco = 2aefco при подходе к механической точке компенсации,
не связано с появлением какого-то дополнительного механизма
релаксации, а представляет собой чисто феноменологический эффект.
Если величины Yi и Уг мало различаются, и точки компенсации —
магнитная и механическая — близки друг к другу, то эксперимент
7*
99
дает возрастание величин ЛЯ и Дсо при подходе к области, где
лежат точки компенсации (см. рис. 3.18). Однако если g -факторы
подрешеток сильно различаются и точки компенсации далеко отстоят
друг от друга, то большие величины эффективного g -фактора могут
иметь место (в механической точке компенсации) при сравнительно
небольших АН. Этот эффект наблюдался 1358] в гранате
Eu3Fe5-xGax012.
Решая систему (3.50) с нижними знаками при //0«Я_ и ос1>2«1,
мы получим, что восприимчивость Х- по отношению к полю с левой
круговой поляризацией пропорциональна (Yi—Уг)2> т-е- стремится
к нулю при уменьшении различия g -факторов подрешеток. Заметим,
что это следует и из соотношения (3.55).
Произвольное поперечное (по отношению к Н0) переменное поле
может быть разложено на два поля с круговой поляризацией
и разными направлениями вращения. Каждое из них будет возбуждать
переменную намагниченность с круговой поляризацией и
соответствующим направлением вращения. И поскольку собственные частоты
го+ и со_ везде, кроме узкой области вблизи Н0^Н_/2, сильно
отличаются друг от друга, составляющие т+ и т_ практически не
будут возбуждаться одновременно.
Учет влияния кристаллографической анизотропии на магнитные
колебания ферримагнетиков не представляет принципиальных
трудностей—необходимо только добавить в выражение для энергии (3.46)
члены, описывающие тот или иной вид анизотропии. При этом
часто, как и для антиферромагнетиков, считают, что энергия
анизотропии С/а складывается из энергий анизотропии подрешеток. Учет
энергии анизотропии необходим вблизи точек компенсации, где эта
энергия оказывается большей, чем зеемановская. и определяет, как
и в антиферромагнетиках, основные состояния и характер колебаний.
Вдали же от точек компенсации учет энергии анизотропии, если
она невелика, приводит, как и в ферромагнетиках, лишь к небольшим,
зависящим от углов поправкам.
В наиболее важном случае ферромагнитного типа
колебаний в антипараллельном основном состоянии при Н0«Н_ для
ферримагнетика с любым видом анизотропии получаются такие
же выражения для частот колебаний и компонент тензора
восприимчивости, как и для ферромагнетика, но входящие в них
константы анизотропии представляют собой некоторые
эффективные величины. При аддитивности энергий анизотропии подрешеток
эти эффективные величины представляют собой просто суммы
соответствующих констант анизотропии для подрешеток.
Эффективные же значения полей анизотропии являются частными от
деления эффективных констант анизотропии на статическую
намагниченность (М10 — М20) и возрастают при подходе к точке
компенсации (см. рис. 3.17).
Таким образом, для первого типа колебаний в слабых постоянных
полях и вдали от точек компенсации двухподрешеточный ферримаг-
нетик эквивалентен ферромагнетику с эффективными параметрами.
Это важное положение справедливо при произвольном числе под-
100
решеток, в том числе и с неколлинеарными намагниченностями, но
непременно с большой суммарной постоянной намагниченностью
обменной природы. Как показал Туров [198], в этом случае всегда
существует один тип колебаний, для которого весь «пучок» намаг-
ниченностей (в слабых постоянных полях) прецессирует как одно
целое, для этого типа колебаний и имеет место указанная
эквивалентность.
До сих пор при рассмотрении ферримагнетиков мы не принимали
во внимание размагничивающих полей. Поэтому полученные
величины х+ их- представляют собой компоненты восприимчивости
вещества по отношению к внутреннему переменному полю. В § 1.5
было показано, что для малых эллипсоидальных образцов может
быть введена восприимчивость %е — по отношению к внешнему
переменному полю. Переход от восприимчивости х к
восприимчивости хс представляет собой магнитостатическую задачу, решение
которой справедливо для любой среды. Отсюда следует, что все
выражения для собственных частот и компонент тензора х*е, которые
были приведены в гл. 1 и 2, будут справедливы и для ферримаг-
нитных образцов с эффективными параметрами при условиях,
неоднократно перечислявшихся выше (ферромагнитный тип
колебаний, малость #0 по сравнению с Я_, составы и температуры
вдали от точек компенсации).
Рассмотренная теория магнитных колебаний в ферримагнетиках
так же, как и теория антиферромагнитного резонанса (§ 3.2),
справедлива и при температуре Г>0, если для всех параметров принять
их значения при данной температуре. В частности, под М10 и М20
следует понимать равновесные намагниченности подрешеток, которые
определятся в результате решения задачи об основном состоянии.
При 7>0 не только направления, но и величины этих векторов
зависят от Я0. Для низкочастотного (ферромагнитного) типа
колебаний в слабых постоянных полях и вдали от точек компенсации
параметрами, температурные зависимости которых практически
должны быть учтены, являются намагниченность М0, эффективные
константы анизотропии и эффективный параметр диссипации.
Ферримагнешки являются единственным классом магнитных
материалов, широко применяемым в настоящее время в технике СВЧ.
То обстоятельство, что они при указанных выше условиях (которые
на практике обычно выполняются) ведут себя как ферромагнетики,
позволяет «забыть» об их феррима гни гной природе и применять
к ним все резулыаты сравнительно прости теории ферромагнитного
резонанса.
Однако необходимо иметь в виду и особенности магнитных
колебаний в ферримагнетиках.
I) Кроме ферромагнитного типа колебаний, в них существует
еше я — 1 (где п — число подрешеток) обменных типов колебаний.
собственные частоты которых при малых Я0 лежат обычно в
инфракрасном диапазоне. Соответствующие им максимумы поглощения
электромагнитной энергии обнаружены в редкоземельных гранатах
[414].
101
2) В сильных постоянных полях Н0—порядка //_зЛ(М10 — М20)
частоты двух типов колебаний (в случае двух подрешеток) становятся
сравнимыми друг с другом и обе зависят от обменной константы.
3) Вблизи точек компенсации частоты двух типов колебаний
сближаются и даже в слабых постоянных полях зависят от обменной
константы; магнитная анизотропия оказывает при этом весьма
существенное влияние на характер и частоты колебаний.
4) При постоянных полях, лежащих между Н_=А(М10 — М20)
и H+=A(Ml0 + M2Q), основное состояние ферримагнетика является
неколлинеарным. При этом, наряду с ферромагнитным типом
колебаний, для которого ферримагнетик (в рассмотренном выше смысле)
эквивалентен ферромагнетику, существует другой тип колебаний,
являющийся мягкой модой.
Глава 4
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
§ 4.1. Уравнения и граничные условия
В предыдущих главах основное внимание уделялось поведению
ферро-, антиферро- или ферримагнетиков в заданном переменном
магнитном поле. Однако, как уже подчеркивалось в § 1.5, переменное
магнитное поле, действующее на вещество, обычно нельзя считать
заданным. Заданными являются поля или потоки энергии в некоторых,
как правило, удаленных от ферромагнитных образцов частях
рассматриваемых систем. И для того чтобы описать поведение таких
систем, т. е. найти как поля в них, так и намагниченности, необходимо
кроме уравнения движения намагниченности использовать уравнения
электромагнитного поля и граничные условия на поверхностях раздела
различных сред.
Одна из таких задач — самая простая—рассматривалась в § 1.5;
исследуемая система представляла собой малый ферромагнитный
эллипсоид в свободном пространстве. Заданным являлось внешнее
переменное поле, т. е. поле в том месте, где находится образец,
но в его отсутствие. В этом случае как для постоянных полей,
так и для комплексных амплитуд переменных полей были
справедливы уравнения магнитостатики. И при дополнительном
предположении об однородности переменной намагниченности мы
воспользовались известным решением этих уравнений для эллипсоида
в однородном внешнем поле. В общем случае уравнения
магнитостатики неприменимы и необходимо использовать полные
уравнения Максвелла.
Задачей данной главы является рассмотрение особенностей этих
уравнений, некоторых путей их решения и ряда фундаментальных
следствий из них для интересующего нас случая гиротропных сред.
Под гиротропными средами в этой и двух следующих главах мы
будем понимать среды, в которых компоненты (1 и 1, в том числе
и антисимметричные, зависят от ю, Н0 и М0 и не зависят от
волнового вектора к. В гл. 7 мы учтем зависимость компонент ц от
к—пространственную дисперсию, но только тот ее вид, при котором
антисимметричные компоненты р. не изменяются при замене к на
—к. Это даст нам возможность исследовать неоднородные колебания
и волны в намагниченных ферро- и ферримагнетиках Среды же,
обладающие «естественной» гиротропией (оптической активностью)
останутся за пределами нашего рассмотрения.
103
Уравнения Максвелла (см., например, [196, 134]) записываются
следующим образом:
rotE+- — =0, divB = ().
с dt
(4.1)
rotH--—= —J, dM) = 4n/f,
с St с
где Е и D—векторы соответственно макроскопического электрического
поля и электрической индукции, Н и В — макроскопического
магнитного поля и магнитной индукции, J и R— плотности свободного
тока и свободного заряда. Входящие в (4.1) величины Е, D,
В и Н являются, как известно, усредненными в пространстве и во
времени значениями, соответственно следующих величин: Ега,
Ет+4лР, Нт и Нт —4лМ, где Ет и Нт — напряженности
микроскопических электрического и магнитного полей, Р — электрическая
поляризация, а М—намагниченность. Из третьего и четвертого
уравнений (4.1) следует уравнение сохранения электрическою заряда
divJ+ ^=0. (4.2)
dt
Граничные условия, т. е. соотношения, которым удовлетворяют
векторы электромагнитного поля в двух средах на поверхности их
раздела, являются следствиями уравнений Максвелла. Если ввести
единичный вектор нормали к граничной поверхности п0, направленный
из 1-й среды во 2-ю, то эти условия будут иметь вид
4я
Ej xn0 —E2 xno = 0, HiXn0 —Н2хп0 = —I,
(4.3)
D1n0-D2n0 = 4nr|, B1n0-B2n0=0,
где т) и I—поверхностные плотности заряда и тока; они равны
нулю для реальных сред, так что в действительности касательные
составляющие Е и Н и нормальные составляющие D и В непрерывны
на границе раздела. Однако величины г) и I вводятся при рассмотрении
в первом приближении границы диэлектрика с металлом. В этом
случае можно считать, что поле в металле отсутствует, а поле
в диэлектрике на границе с металлом удовлетворяет условиям
4л
Ejxn^O, H!xn0 = —I,
(4.4)
D1n0 = 4jr^, B1no = 0.
Материальные соотношения. Для того чтобы получить полную
систему уравнений электродинамики, к уравнениям (4.1) необходимо
добавить материальные соотношения [209, 196, 134, 199], которые
отражают конкретные свойства веществ и могут быть получены из
теорий, описывающих эти свойства, или из эксперимента. Поскольку
104
плотность заряда связана с плотностью тока уравнением (4.2),
достаточно дополнить уравнения (4.1) соотношениями, связывающими
векторы D, В и J с векторами Е и Н. Заметим, что разделение
задачи нахождения материальных соотношений и задачи
интегрирования уравнений Максвелла возможно не всегда (см., например, § 14.2).
Но в случае намагниченных до насыщения слабопроводящих ферро-
или ферримагнетиков оно возможно. Мы уже использовали это
обстоятельство, решая задачу об определении восприимчивости % без
учета уравнений поля (§ 1.3).
Уравнения для комплексных амплитуд. Нас интересует случай,
когда магнитное поле является суммой постоянного (или медленно
меняющегося) и быстропеременного полей. Примем, что и
электрическое поле, а следовательно, все входящие в (4.1) величины
представляют собой такие суммы. Предположим, что переменные
составляющие входящих в (4.1) величин h_, e^, b^, d^,
j, и р^ достаточно малы, чтобы все соотношения между ними
можно было считать линейными, а заданные («возбуждающие») поля
и токи изменяются во времени по гармоническому закону. Тогда
все переменные величины будут изменяться по такому же закону,
и мы сможем использовать метод комплексных амплитуд (см. § 1.3).
Подставив суммы постоянных и переменных составляющих в
уравнения (4.1), получим две независимые системы: одну—для постоянных
составляющих и другую—для комплексных амплитуд переменных
величин". Первая, в свою очередь, распадается на две независимые
системы уравнений: магнитостатики
4л
rotH0 = — J0, divBo = 0 (4.5)
с
и электростатики. Вторая система будет иметь вид (к0 = (и/с)
rote + /7c0b = 0, (4.6)
divb = 0, (4.7)
4л
rot h — //с0 d = — j, (4.8)
с
divd = 4np. (4.9)
Заметим, что теперь для величин, зависящих от времени по
гармоническому закону, уравнение (4.7) является следствием (4.6),
а (4.9)—следствием (4.8) и уравнения сохранения заряда divj + ;'(op = 0.
Граничные условия для переменных составляющих будут такими же,
как (4.3) или (4.4).
Остановимся на материальных соотношениях для переменных
величин. Примем, пренебрегая слабыми «смешанными» эффектами,
что d зависит только от е, a b—только от h. Тогда для малых
В дальнейшем мы будем опускать слова «комплексная амплитуда»,
подразумевая, как и в предыдущих главах, под всеми переменными величинами
их комплексные амплитуды.
105
амплитуд
d = ede, (4.10)
b = ph, (4.11)
где ed—диэлектрическая проницаемость, a jl — магнитная
проницаемость. Плотность тока можно записать в виде
j = ae+j„. (4.12)
где a—тензор высокочастотной удельной проводимости. Величина
jCT представляет собой плотность стороннего тока, который обусловлен
полями, не рассматриваемыми в данной задаче, и должен считаться
заданным.
Используя (4.10)—(4.12), исключим из уравнений Максвелла (4.6)—
(4.9) векторы d, b и j:
rote + /7c0jlh = 0, (4.13)
div(]lh) = 0, (4.14)
.i « 4я .
roth-//c0ee = -—JcT, (4.15)
div(ee) = 4npCT. (4.16)
Здесь обозначено pCT = (;/co)divjCT и
e = ed-/ — о. (4.17)
со
Тензор е в отличие от ed будем называть электрической
проницаемостью. Заметим, что из (4.13) и (4.15) нетрудно исключить е или
h и получить дифференциальные уравнения второго порядка для
каждого из этих векторов.
Введем теперь обозначения для компонент тензора р (аналогичные
обозначения можно ввести и для компонент "е). Представим ц в виде
суммы симметричного Дс и антисимметричного цас тензоров (см.,
например, [119]). Компоненты цс обозначим
(Hc)ps = (Hc)sp = Hps = Hps-'HPS (A s=l, 2, 3 = х, у, z), (4.18)
а компоненты цас—
(^c)Ps=-{^c)Sp^iP-ap>. = i{[i.'apS-iP-'opS) (р, s=l, 2, 3; рфз), (4.19)
где все величины \i'ps, uj;,, \i'aps и p.'^ps—вещественные:
целесообразность введения именно таких обозначений будет ясна из
§ 4.4. Три компоненты ц„12, ц„2з и uo3i тензора цас можно
считать проекциями вектора 4л Gm, где Gm— введенный в § 1.3
магнитный вектор тирании. Тогда
b=]lch + /4nhxGm. (4.20)
Тензор £ можно представить также в виде суммы эрмитова цэ
нтиэрмитоеа цаэ тензоров с компонентами"
(m)ps = HPS + 'Vops, {Vb,)ps = Kp,-iK*- (4.21)
" Соотношения (4.21) и представляют собой определения таких тензоров.
106
Все компоненты тензоров fi и е являются функциями частоты,
параметров вещества (постоянной намагниченности, констант
анизотропии и пр.), а также величин и направлений постоянных полей
Н0 и Е0; для интересующих нас магнитоупорядоченных сред влиянием
Е0 обычно можно пренебречь.
Бигиротропная среда. Рассмотрим среду, изотропную в отсутствие
постоянного намагничивания. В этом случае единственное выделенное
направление—это направление М0; совместим его с осью z. Тогда
тензоры ц и "е будут иметь следующий вид:
И =
V-
Фа
0
Фа
и
0
0
0
и
, е =
е
-'Ч,
0
'Ч,
е
0
0
0
е.
(4.22)
Для поликристаллических ферритов в СВЧ диапазоне е можно
считать скалярной величиной. Для видимого света и при еще более
высоких частотах ц даже для ферромагнетиков мало отличается от
1. Тем не менее мы рассматриваем среду, одновременно имеющую
Ц и е вида (4.22), так как антисимметричные компоненты ц
и е могут оказаться одного порядка, например, для ферритов — в
инфракрасном диапазоне, а для сильно проводящих ферромагнитных
полупроводников—и в диапазоне СВЧ.
Итак, рассмотрим некоторые особенности уравнений
электродинамики для сред с параметрами (4.22) в случае jCT = 0. Исключая
из проекций уравнений Максвелла (4.13) и (4.15) поперечные
(относительно М0) составляющие векторов е и h, получим для
продольных составляющих следующие уравнения:
vi+7 h+kl*lVii) е*+к°^ I т+т ) к h*=°>
в
У1+^+*8.1Ц,)^М,(?+^)^.^
(4.23)
где
Е Ц
(4.24)
а Vj_ — оператор Гамильтона («набла») в плоскости ху:
S д „. д2 82
Из (4.23) видно, что для гиротропных сред (с еаФ0 или ufl^0)
поля, поперечно-электрические относительно направления
намагничивания (с ez = 0 и Лг/0) и поперечно-магнитные относительно того же
направления (с hz = 0 и егФ0), могут существовать только в случае
д/дг = 0. Что же касается полей ТЕМ (с ez = hz = 0), то их существование
Уравнениями (4.23) не запрещено.
107
Из (4.23) можно исключить ez или hz и получить линейные
дифференциальные уравнения if(ez) = 0 и if(/;z) = 0, где
S£—дифференциальный оператор четвертого порядка [66]. Таким же
уравнениям удовлетворяют и поперечные компоненты е и h. Можно
ввести скалярную функцию (потенциал) \|/ [66], которая также
удовлетворяет уравнению if (\|/) = 0 и через которую все составляющие
полей е и h выражаются при помощи операций дифференцирования.
Однако решение уравнения четвертого порядка для этой функции
может быть проведено лишь для весьма ограниченного класса задач.
Гармоническая зависимость от z. Положение существенно
упрощается в частном (но важном) случае, когда зависимость полей и,
следовательно, функции \|/ от координаты z (в направлении постоянной
намагниченности) является гармонической: \|/ = Z(z)xl/±(x, у), где
Z(z) = exp( + //czz), cos kzz, sin kzz или их линейные комбинации. Этот
случай включает и поля, не зависящие от z (kz = 0). В случае
гармонической зависимости от z (когда д2/dz2=—k2) оператор
if является произведением двух операторов второго порядка [66]:
if = (Vi + x?)(Vi + Ki). (4.25)
Здесь у,1 и и2—корни квадратного уравнения
\ к4-рк2 + ? = 0, (4.26)
где
р = {£ц\1±+£±\1„)к2.-{е11/£ + р.,1/[1)к2,
(4.27)
Я = в}\1гехцхЦ+^^ И-2е||Ц (l+E-^)k20k2.
Таким образом, в случае гармонической зависимости от z имеются
две волны, для которых функция \|/± удовлетворяет уравнениям
Гельмгольца
Vi^+xL\K = 0. (4.28)
Собственные значения щ и и2 определяют зависимости полей от
поперечных координат. Найдя решения уравнений (4.28), мы можем
затем вычислить все составляющие е и h. Этот путь решения граничных
электродинамических задач для сред с тензорными параметрами вида
(4.22) при гармонической зависимости (или отсутствии зависимости)
от z рассмотрен в [66]. В гл. 5 будут приведены примеры его применения.
§ 4.2. Однородные плоские волны
В этом параграфе мы остановимся на самой простой задаче
электродинамики—о распространении однородных плоских волн"
в безграничном пространстве. При этом мы ограничимся случаем
" Однородные волны -это такие, для которых поля зависят только от
одной координаты, вдоль координатных линий которой происходит
распространение. Для плоских волн такая координата—декартова, т.е. волновые
фронты — плоскости.
108
изотропной (в отсутствие постоянного намагничивания) среды — с
параметрами (4.22).
Для однородной плоской волны комплексные амплитуды векторов
электромагнитного поля запишутся следующим образом:
e = e0exp(-/kr), h = h0exp(-/kr), (4.29)
где е0 и h„ - постоянные величины, а к—волновой вектор.
Подставляя (4.29) в уравнения Максвелла (4.13) и (4.15) при jCT = 0,
получим
кхе-коцп = 0, kxh + k01e = 0. (4.30)
Проектируя уравнения (4.30) на оси координат с учетом (4.22)
и приравнивая нулю определитель полученной системы однородных
линейных уравнений для составляющих е и h, можно найти
дисперсионное соотношение, связывающее частоту со с величиной и
направлением волнового вектора к. Это соотношение можно получить
и более простым путем, используя (поскольку в данном случае
зависимость от z гармоническая) методику, изложенную в конце
предыдущего параграфа. Фигурирующие в ней величины имеют
и данном случае следующий смысл: x~ksmQk, kz = kcosQk, где
i)k — угол между вектором к и направлением постоянного
намагничивания— осью z. Подставляя эти величины в (4.26) и (4.27),
получим дисперсионное соотношение
k*fsm2Qk cos2 бД/sin2 6,, cos26A
kt\ в,, б Д Hi И /
+ е±цх = 0, (4.31)
где £± и цх определяются согласно (4.24). Квадратное относительно
к2 уравнение (4.31) имеет два корня, соответствующих двум нормальным
волнам, которые могут распространяться в данном направлении.
Решения уравнения (4.31) в общем случае среды с параметрами
(4.22) и произвольного направления распространения не могут быть
представлены в виде
k2 = k2Qzct[ief, (4.32)
где Eef зависело бы только от компонент *£, a nef—только от
компонент ц. Однако такая запись возможна, если либо электрическая,
либо магнитная проницаемость скалярна. В частности, при скалярной
е из (4.31) следует
к2 = к20еце{(Вк) =
.^дс2 + 5Ц12е»(ц±/ц,-1)± y/sin4fcx/H|.-l)2+4cos2e*^2M2 (433)
2(sin2ek/H, + cos26t/H)
Запись (4.32) возможна, как мы увидим, и при тензорных 1 и ц,
но для некоторых направлений распространения.
109
Если справедливо (4.33), то, как легко убедиться.
v2 (4.34)
к"=~к0(\ее{\\це{\-г'е{^{+е'^:{)112
у/2
(формулы Аркадьева). При этом eef = Erf —/е^, M-ef = Hef — Ща
и к = к —ik"; тогда (для используемой нами зависимости от времени
ехр(/соф волна, распространяющаяся в положительном направлении,
затухает при положительном к".
Нас интересуют среды со скалярной е = е' —г'е". Рассмотрим два
предельных случая. Если е" = 0, г' = г (идеальный диэлектрик), то
к> = Ьф(\»е[\ + ц'е[у>2, (4.35)
к" = Ьф(\Ы-»«У12- (4-36)
В другом предельном случае хорошо проводящего металла можно
принять е' = 0 и согласно (4.17) е" = 4яа/со. Тогда из (4.34) следует
*' = *0 ^(|Цег|-Цег)1/2 = У^/81. (4-37)
\ СО
к"=к0 ^(|Цег| + ц;'г)1/2 = У^/б„ (4.38)
V со
где
к0\]2па JiTtaa
—глубина прониковения электромагнитного поля в металл с ц=1
(или толщина скин-слоя в нем). Заметим, что, как видно из (4.37)
и (4.38), с учетом магнитных потерь в металле к'фк".
Если же величина е" конечна, но мала (е"«;е'), то, считая для
простоты (при оценках) Uef = 0, получим к''~k0s/s.''\i'ef и
6sl=^_ /fls_L_ /Z. (4.40)
к" к0Е"\]ц'сГ 2na\J ц;г
Продольное намагничивание. В случае 0* = О, т. е. среды,
намагниченной в направлении распространения, решения уравнения (4.31)
будут иметь вид
k±=k0y/{B±ea)fa±\i~). (4.41)
Верхние и нижние знаки в (4.41) соответствуют двум нормальным
волнам. Для выяснения структуры полей этих волн спроектируем
уравнения (4.30) при 0* = О на оси координат и перейдем, как этого
110
требует симметрия задачи, к циркулярным составляющим (см. § 1.3)
векторов е и h:
ке ±±iko(\i±na)h±=0,
-kh,±iko(E±eu)e±=0, (4.42)
e: = hz = 0.
Легко убедиться, что верхние и нижние знаки в системе (4.42)
соответствуют верхним и нижним знакам в (4.41). Таким же методом,
как в § 1.3 и 3.2, можно показать, что для волны с верхними знаками
поперечные (так как е. = /7. = 0) поля е и h будут иметь круговую
поляризацию с правым вращением, а для волны с нижними знаками—с
левым вращением относительно положительного направления оси z.
Подставляя (4.41) в (4.42), получим
t'w/i± = +/v/(u±kiH)/(E±Ea)3+/i;±. (4.43)
Величину С,± можно назвать волновым импедансом"
продольно-намагниченной среды для воли с правой или левой круговой поляризацией.
Легко убедиться, что для обеих волн
lx=exlhr=-eylhx. (4.43а)
Из (4.41) и (4.43) следует, что в случае продольного намагничивания
могут быть введены эффективные параметры среды eef ±=e + efl
и uef± = u + ufl.
При распространении в продольно-намагниченной среде волн
с круговой поляризацией комплексные амплитуды полей будут
изменяться согласно (4.29), а поляризация их будет оставаться
неизменной. Неизменность структуры поля при распространении
и является определением нормальных волн. Любая другая волна
в данной системе может быть представлена в виде суммы нормальных
волн; вследствие различия их постоянных распространения
суммирование их после прохождения некоторого пути даст волну со
структурой поля, отличной от структуры поля «на входе».
Рассмотрим, например, случай, когда при z = 0 имеет место волна
с линейной поляризацией, т. е. е = е0х0. Ее можно разложить на две
нормальные волны с комплексными амплитудами
е+ = -<'о(хо-'Уо), е-=-е0(х0 + /'Уо)- (4-44)
Постоянные распространения этих волн k±=k'± — ik"± будут
различаться, и при z = /
е+=-е0(х0-/у0)ехр (-/&'+/) ехр(-/с+/),
, (4-45)
е_=-е0(хо + /Уо)ехр(-//с'_/)ехр(-А''1/).
" Волновой импеданс (как и поверхностный импеданс, см. § 14.2) можно
определить и по-другому [199] —как отношение соответствующих поперечных
составляющих электрического поля е и магнитной индукции Ь.
111
Нетрудно убедиться, что поле суммарной волны е = е++е_ при z = l
будет иметь эллиптическую поляризацию и большая ось эллипса
поляризации будет составлять с направлением линейной поляризации
при z = 0, т. е. в данном случае—с осью х, угол
Э=-(*'+-*'-)/.
(4.46)
Эта формула будет справедлива и тогда, когда волна при 2=0
имеет произвольную эллиптическую поляризацию, угол 9 в этом
случае представляет собой угол поворота большой оси эллипса
поляризации на отрезке длиной /. Если определить эллиптичность
аналогично (1.106), то при 2=0 Э=1, а при 2=/
3=l-emin/emax = ch"
к"+ -к".
(4.47)
Поворот поляризации волны" в продольно-намагниченной гиро-
тропной среде—это эффект Фарадея. Как видно из (4.46) и (4.41),
он обусловлен антисимметричными компонентами тензоров 1 и р.
При изменении направления распространения волны на обратное
в формуле (4.46) одновременно меняются местами к'+ и £'_,
а / заменяется на (—t), так что величина и знак 9 остаются
неизменными. Изменение же направления намагничивания на обратное
приводит к тому, что изменяются знаки efl и ц„, и знак 9 изменяется
на обратный.
Остановимся теперь подробнее на распространении
электромагнитных волн в продольно-намагниченном слабопроводящем ферро-
или ферримагнетике. Рассмотрим два случая, один из которых
реализуется в диапазоне СВЧ, а другой—в оптике. В первом случае
е можно считать скалярной величиной, не зависящей от частоты,
а для компонент £ принять выражения, полученные в предыдущих
главах. Предположим, что изотропный ферромагнетик намагничен
до насыщения, и не будем сначала учитывать диссипации. Тогда
для ц + цй будет справедливо выражение (1.63). Подставляя его
в (4.41), получим дисперсионное соотношение
К + со)(—-П-сом = 0,
(4.48)
где верхний знак соответствует волне с правым, а нижний—с левым
вращением. Зависимости со от к для этих волн показаны на рис.
4.1. Из этого рисунка видно, что для волны с левым вращением
(ее можно назвать обыкновенной) зависимость со (к) (закон дисперсии
волны) мало отличается от той, которая имела бы место при не
зависящей от частоты скалярной магнитной проницаемости. Для
волны же с правым вращением эта зависимость содержит две ветви;
для одной со неограниченно растет с ростом к, приближаясь (как
Здесь и в дальнейшем термин «поворот поляризации» используется
вместо традиционного «вращение плоскости поляризации».
112
вк-о
Рис. 4.1. Дисперсионные характеристики электромагнитных волн в
неограниченном намагниченном до насыщения непроводящем ферромагнетике (без учета
диссипации)
и для волны с левым вращением) к ск/у/е. Для другой ветви
частота с ростом к стремится к постоянной величине сон. Фазовая
скорость i>ph = co//c и групповая скорость vSI = B(n/Bk для этой ветви
при больших к становятся очень малыми.
Как видно из рис. 4.! (построенного без учета диссипации),
волны с правым вращением не существует в интервале частот от
сон до (еон + сом), в котором (см. рис. 1.7) эффективная проницаемость
(ц+Ца)<0. При со = const ему соответствует интервал постоянных
полей от со/7 Д° (ю/7 — 4лМ0). Наличие диссипации приводит к тому,
что волна с правым вращением может существовать в этих интервалах,
но сильно затухает {к">к').
В другом случае, который реализуется на оптических частотах,
со:»сон, сом, и из выражений (1.74) следует в первом приближении
(пренебрегая членами второго и более высоких порядков по еон/со
и сом/со и полагая а<зс1)
ц'^1, u^-coM/co, ц"~асом/со, ц^О. (4.49)
В этом случае уже нельзя считать 1 скалярной, величина е^ может
быть даже больше, чем \i'a. Но обычно можно считать z'a, e"<sce'.
Тогда из (4.46) и (4.41) с учетом (4.49) следует
9 = —I -OMyfE' + Ea—pz
(4.50)
Первый член в скобках в (4.50) соответствует «магнитному»
(определяемому ца) фарадееву вращению, которое в рассмотренном
приближении не зависит от частоты. Для обычных ферритов (е'-15,
Afo~ 200 Гс) оно составляет ~40 град/см. Второй член дает
«электрическое» вращение, которое может очень сильно зависеть от частоты,
8 А. Г. Гуревич, Г. А. Мелков ИЗ
так как е'0 сильно—резонансным образом изменяется при переходе
через линии поглощения вещества".
В случае продольного намагничивания сравнительно легко
решаются задачи об отражении и прохождении волн через плоские
поверхности раздела сред, перпендикулярные направлению
распространения, а также о прохождении через слои гиротропных сред.
Волны с круговой поляризацией, являющиеся нормальными волнами,
проходят и отражаются от таких поверхностей раздела без изменения
поляризации. Для определения же амплитуд и поляризаций
отраженной и проходящей волн при произвольной поляризации падающей
волны достаточно разложить эту волну на две нормальные,
рассмотреть их прохождение и снова сложить. В результате такого
рассмотрения оказывается, в частности, что при падении волны
с линейной поляризацией из изотропной среды на границу раздела
с гиротропной большая ось эллипса поляризации отраженной волны
повернута относительно направления поляризации падающей волны.
Это явление носит название магнитооптического полярного эффекта
Керра и имеет место только при наличии диссипации в гиротропной
среде. Другим важным результатом является осциллирующая
зависимость угла поворота поляризации волны, прошедшей через гирот-
ропный слой, от толщины слоя [69].
Поперечное намагничивание. В этом случае (0t = n/2) дисперсионное
уравнение (4.31) имеет решения
А-,=А-(1Ч гГи~. (4.51)
к2 = ки% ц ех. (4.52)
где е± и ц± определяются согласно (4.24). Система шести уравнений —
проекций (4.30) распадается на две независимые системы: первую
kez -k0\xhx- i к „ \iahy = 0,
-;u„/;4 + u/)v = 0. (4.53)
А-„Е e-—khx = 0
и вторую, которая получается in нее при замене e<±h и *е<=* — ц.
Легко убедиться, что (4.51) является условием совместности первой
системы, а (4.52)—второй.
Таким образом, для одной из нормальных волн - с
дисперсионным соотношением (4.51)—не равны нулю ег, hx и hy, согласно
второму уравнению (4.53) для )гой волны обращается в нуль Ьу.
Итак, для нее (рис. 4.2) векторы е и b являются поперечными
(относительно направления распространения), линейно поляризованы
" В некоторых работах по исследованию распространения волн
оптического диапазона в магнитоупорядоченных средах высказывалось утверждение,
что все наблюдаемые при этом эффекты можно описать (в рамках
используемой в этой книге формы уравнений Максвелла) при помощи только
компонент "е, считая ц=1. Из всего предыдущего совершенно ясно, что
такое утверждение лишено оснований. Критика его содержится в работах
Кринчика и др., например, в [122] (см. также [199]).
114
Рис. 4.2. Векторы электромагнитного поля нормальных волн в поперечно-
намагниченной бигиротропной среде
и перпендикулярны друг другу. Вектор же h не является поперечным
(относительно этого направления) и эллиптически поляризован
в плоскости, перпендикулярной М0. Для второй нормальной волны —
с дисперсионным соотношением (4.52)—не обращается в нуль hz,
ех и еу, поперечными и линейно поляризованными (см. рис. 4.2)
являются векторы h и d.
В случае поперечного намагничивания могут быть тоже введены
волновые импедансы — отношения поперечных (относительно
направления распространения) составляющих е и h нормальных волн. Для
первой волны, как следует из (4.53) и (4.51),
(4.54)
^=ejhx = j\ijev
а для второй
bs-eJh^y/^/Ej
(4.55)
Из выражений для А12 и С,1<2 видно, что при поперечном
намагничивании эффективными проницаемостями являются: для первой
нормальной волны ц± и е,, а для второй—ц и ех.
Если мы возбудим в поперечно-намагниченной среде волну со
структурой поля (поляризацией), отличающейся от структуры полей
нормальных волн, то ее поляризация будет преобразовываться по
мере распространения [69]. Следует подчеркнуть, что преобразование
поляризации в данном случае—поперечного намагничивания (эффект
Коттона — Мутона), в отличие от эффекта Фарадея, не зависит от
направления постоянного намагничивания (так как ца и еа входят
в (4.51) и (4.52) только в квадратах) и происходит в обратном
направлении при изменении на обратное направления распространения
волны.
Рассмотрим теперь конкретный вид дисперсионных соотношений
для случая поперечно-намагниченного ферромагнетика в диапазоне
СВЧ. При этом, как уже отмечалось, е можно считать скалярной
и не зависящей от частоты. Предположим, что ферромагнетик
намагничен до насыщения. Тогда ц,= 1 и, согласно (4.51) и (4.52),
'ci=^ovellx и k2 = k0yfe. Распространение второй волны (ее в этом
случае можно назвать обыкновенной) происходит, как в немагнитном
диэлектрике. Для получения закона дисперсии первой—необыкновен-
8* П5
ной волны подставим, пренебрегая диссипацией, (1.65) в выражение
для к^. В результате получим
K-ffl2)(j^-l)-fflbO. (4.56)
Зависимость а (к), вытекающая из (4.56), показана на рис. 4.1. Как
видно из этого рисунка, для необыкновенной волны дисперсионная
характеристика содержит две ветви. Одна из них с ростом к
асимптотически сближается с дисперсионной характеристикой для
обыкновенной волны, а для другой — частота стремится к постоянной
величине ю±.
Из рис. 4.1 видно также, что необыкновенной волны (в
пренебрежении диссипацией) не существует в интервале частот от ю± до
(ан + а>м), в котором (см. рис. 1.7) эффективная проницаемость для
этой волны и±<0. Ему соответствует «запрещенный» интервал полей
от Н2 (см. формулу (1.61)) до (ю/у—АпМ0). С учетом диссипации
необыкновенная волна существует, но сильно затухает в этих
интервалах.
На нижней границе «запрещенного» интервала частот (см. рис.
1.7) ц±-»сс, а на верхней обращается в нуль, т. е. эти границы
являются соответственно точками резонанса и антирезонанса
эффективной проницаемости. Это имело место и в рассмотренном выше
случае продольного намагничивания, причем точки резонанса
эффективных проницаемостей в этих двух случаях различаются, а точки
антирезонанса, как это видно из рис. 1.7, совпадают. Нетрудно
показать, используя выражение (4.33), что частота антирезонанса
(определяемая условием цсг = 0) не зависит от направления
распространения волны и составляет всегда
<йаге5 = юн + юм. (457)
\ ■■■''/
При наличии диссипации точки резонанса и антирезопанса могут
быть определены как точки, в которых соответственно цёг максимальна
и Uef = 0 (при малом не',). В случае малой диссипации их положения
будут, конечно, мало отличаться от найденных без учета диссипации.
Легко убедиться, что в точке антирезонанса и вблизи точки резонанса
(где uef = 0) k' = k". Но если вблизи резонанса величины к' я к"
приблизительно пропорциональны оГш, то в точке антирезонанса
они пропорциональны а1'2 (ас—параметр диссипации).
В заключение заметим, что выражения (4.48) и (4.56) можно
трактовать как дисперсионные уравнения для двух связанных волн.
Дисперсионные соотношения для первых—магнитных или спиновых
волн (без связи со вторыми) получаются, если приравнять нулю
первые скобки в этих выражениях. Как будет показано в § 6.1,
дисперсионные соотношения для этих волн можно получить и
непосредственно, пренебрегая членом /fc0*ee в уравнениях Максвелла.
Дисперсионные соотношения для вторых — электромагнитных волн
(в среде с ц=1) получаются в результате приравнивания нулю
шорых скобок в (4.4.S) и (4.56). Последние члены в этих уравнениях
описывают связь между волнами. Она приводит, как видно из рис.
4.1, к «расталкиванию» дисперсионных кривых спиновых и
электромагнитных волн в широкой области значений ю и к. Для рассматриваемой
задачи о волнах в неограниченной среде такая трактовка — «на языке
связанных волн» — не дает ничего нового. Однако для более сложных
задач трактовка на языке связанных волн (или связанных колебаний
при рассмотрении процессов в ограниченных телах) может оказаться
полезной.
§ 4.3. Невзаимность
Наличие антисимметричных компонент тензоров £ или "е,
обусловленных постоянным магнитным полем или постоянной
намагниченностью, приводит к тому, что в системах, содержащих такие
среды, наблюдается ряд явлений, характеризуемых общим термином
невзаимность. Этот термин возник потому, что для таких систем
несправедлива широко используемая в электро- и радиотехнике
теорема взаимности. К невзаимным явлениям относятся различие
постоянных распространения волн с круговой поляризацией с правым
и левым вращением (относительно направления постоянного поля),
а также поворот поляризации линейно поляризованной волны (эффект
Фарадея) при продольном намагничивании. Эти эффекты были
рассмотрены в § 4.2 для случая неограниченной среды. Аналогичные
явления, как мы увидим в гл. 5, наблюдаются и в волноводах,
содержащих среды с несимметричными £ и *е. В гл. 5 и 6 будут
изучены и другие невзаимные эффекты, которые проявляются только
и системах, содержащих границы раздела.
Задачей данного параграфа является рассмотрение
некоторых общих соотношений, которые могут быть использованы при
анализе невзаимных явлений. Важнейшим из них является лемма
Лоренца.
Лемма Лоренца. Выведем эту лемму для общего случая сред
с произвольными несимметричными тензорами ц и 1. Рассмотрим
два переменных электромагнитных поля с одной и той же частотой
и комплексными амплитудами еь ht и е2, h2, возбуждаемых
сторонними токами jCT] и jCT2 в одной и той же системе,
характеризуемой величинами £ и *е. которые произвольным образом
зависят от координат; система может содержать поверхности раздела,
в том числе и металлические поверхности. Запишем для полей
с индексами 1 и 2 уравнения Максвелла (4.13) и (4.15), умножим
их скалярно соответственно на h2, e2, ( — hi) и ( —е^ и сложим все
полученные равенства. В результате найдем
div(ei xh2 —e2xhi)-i-2i/co(h2,jlh1—Ь^Ьг —e^e^eile^^
= 4n/c(jCTle2-jCT2e1). (4.58)
Представим £ и 1 в виде сумм симметричных и антисимметричных
тензоров (см. § 4.1). Легко убедиться, что
ЬГДсЬ2=Ь211с111, h,'jlach2=-h2yach1;
117
аналогичные соотношения имеют место для тензоров *ес и *£„,..
С учетом этих соотношений (4.58) примет вид [65]
— div(eixh2-e2xhi)+—(h2Machi-e2eacei)=jcrie2 j^ei. (4.59)
Выражение (4.59) и представляет собой лемму Лоренпа. обобщенную
на случай гиротропных сред.
Интегральные соотношения. Интегрируя лемм> (4.59) по
некоторому объему V и используя теорему Гаусса [119], получим
— J(exh2-e2xh,)nn«K'+— J (b1'[iachl-e^£acel)dV=
4л s 2п уа
= Jjcxie2^-}jCT2ei^, (4.60)
Vi Vi
где 5*—поверхность, ограничивающая объем V, п0—единичный вектор
внешней нормали к этой поверхности, Уа—часть объема V, заполненная
гиротропными средами, a V\ и Уг—части объема V. в которых
находятся соответственно токи jCTl и jCT2- Выражение (4.60) представляет
собой интегральную формулировку обобщенной леммы Лоренца.
Выбор объема V определяется характером задачи. При
исследовании антенн выбирается бесконечно большой объем, включающий
передающую и приемную антенны. Тогда поверхностный интеграл
и (4.60) обращается в нуль: и если £ и 1 всех сред симметричны,
го из (4.60) следует одна из формулировок теоремы взаимности:
iiai*2dV=fj„2eidV. (4.61)
При исследовании волноводиых устройств целесообразно в
качестве V выбрать объем, ограниченный стенками волновода (или, см.
рис. 5.30, сочленениями нескольких волноводов) и поперечными
сечениями волноводов. Источники, возбуждающие поля еь h, и е2,
h2, находятся в этом случае вне объема V, и правая часть (4.60)
равна нулю. Поверхностный интеграл по металлическим стенкам
(которые считаются идеально проводящими) обращается в нуль,
и (4.60) принимает вид
Tzl. I(eiPxh2p-e2pxhlp)n0pc?5=
Hh2Vachl-e2l.acei)dv=jat (4.62)
4,1 „-1 С
ICO
где p —номер полноводного плеча, Sp -его поперечное сечение
^-единичный вектор нормали' к этому с Гению'
d ei.2p и п1>2р—поля на нем. '
свойстТи'путиТ К0Т0РЫХ/^0- называются нееэаимиы.ни. Их
свойства и пути реализации будут рассматриваться в гл 5 Зяег*.
мы ограничимся некоторыми общими замечаниями Величине 7
кроме тривиального случая ра, = вас = 0, может обратить™ пупь
118
по двум причинам. Первая связана со структурой полей 1 и 2 в месте
расположения гкротропного вещества. Рассмотрим для определенности
случай магнитной гиротропии (еас = 0). Тогда, как следует из (4.20),
uachi =i4nh1 xGm, где Gm — вектор гирации. С учетом этого
Ja = 2ю f Gra (h, х h2) dV. (4.63)
va
Ясно, что Ja = 0, если комплексные амплитуды ht и h2 параллельны.
Это может иметь место при расположении гиротропного образца
в области линейной поляризации магнитного поля волновода. Во-
вторых, из-за симметрии устройства интегралы по разным частям
объема V могут скомпенсировать друг друга. Характерный пример
этого — ферритовая пластина, симметрично расположенная в
прямоугольном волноводе и намагниченная перпендикулярно его широкой
стенке (§ 5.2). Необходимо подчеркнуть, что невзаимность устройства
в указанном интегральном смысле не исключает того, что структуры
полей при поступлении энергии из разных плеч будут существенно
различаться.
Вернемся к общему случаю Ja=£0. Мы неоднократно убеждались
в том, что антисимметричные компоненты х и Ц всегда содержат
множитель М0 и, следовательно, изменяют знаки при изменении
направления намагниченности на обратное. Отсюда следует, что вектор
гирации Gm всегда параллелен М0 (см., например, формулу (1.50)).
Поэтому при изменении знака М0 величина (4.63) изменяет знак.
Подчеркнем еще раз, что необходимым условием появления
антисимметричных компонент (I и 1, не зависящих линейно от
волнового вектора к (т. е. не изменяющих знак при замене к на
—к и не обращающихся в нуль при к-*0), является наличие
постоянного поля или постоянной намагниченности. Это находится
в соответствии с обобщенным принципом симметрии кинетических
коэффициентов (принципом Онсагера, см., например, [134, 199]),
который может быть записан в виде [199]
ups(co, k, В0) = ц5р(ю, -к, -В0), (4.64)
где В0 = Н0+4лМ0—постоянная магнитная индукция.
Наличие сред, обладающих тензорами £ или 1 с такими
антисимметричными компонентами, является по определению
условием создания невзаимных систем. Таким образом, наличие постоянного
магнитного поля или постоянной намагниченности служит
необходимым (но, как отмечалось выше, не достаточным) условием
создания невзаимных устройств.
§ 4.4. Энергетические соотношения
Рассмотренная в предыдущем параграфе лемма Лоренца
представляет собой пример квадратичных соотношений электродинамики.
Другим важным примером служат энергетические соотношения,
связывающие приращения или потери оперши и потоки энергии
119
электромагнитного поля. Такие соотношения для общего случая сред
с тензорными ц и *е будут получены в этом параграфе. Поскольку
мы все время интересуемся стационарными процессами, при которых
все линейные величины изменяются во времени по гармоническому
закону, мы так же, как и в § 4.3, рассмотрим квадратичные
соотношения для комплексных амплитуд.
Отметим прежде всего, что если а^=а0 cos (сог + ф0)
и b^=b0cos(ш + щ) и если согласно методу комплексных амплитуд
введены комплексные величины а = а0ехр[/(сог4-фа)]=аехр(/сог)
и £> = £>оехР['(юг + Фь)] = 6ехр(/(о?), вещественными частями которых
являются величины а^ и Ь^, то, как легко показать, среднее за
период колебаний значение произведения этих величин
1
aj^ = j" a^ dt = ~Re(ab') = -Re(a'b),
0 2 2
где а = а0е\р (г'ф„) и b = b0exp(iq>h)—комплексные амплитуды величин
а~ и Ь^. Соотношения, аналогичные приведенному, будут иметь
место и для векторных величин, причем как для скалярного, так
и для векторного их произведения.
Уравнение баланса энергии. Умножим уравнение Максвелла (4.13)
скалярно на h*, а уравнение, комплексно-сопряженное с (4.15), на
(—е). Сложив полученные выражения, найдем
f- div (е + h*)+^ (ь/Дп - eeV) + ej 'T = 0. (4.65)
4я 4я
Равенство нулю вещественной части (4.65) можно записать в виде
divn+P+PCT = 0, (4.66)
n = ^Re(exh*), (4.67)
со , «_ <->
Р=-—Im(h'uh-eeV), (4.68)
071
PCT = iRe(ej*T). (4.69)
Величина П представляет собой среднее значение вектора Пойнтинга —
плотности потока электромагнитной энергии, а величина Рст—среднее
значение мощности потерь (в единице объема) сторонних токов.
Тогда ясно, что величина Р является плотностью потерь
электромагнитной энергии в веществе, а соотношение (4.66) представляет собой
уравнение баланса энергии переменного электромагнитного поля (в
дифференциальной форме). Это соотношение с учетом (4.17) и (4.12)
можно записать в виде
divn + Pra + Pe = 0, (4.70)
где Рт = — co/(8n)Im(h*(xh)—плотность магнитных потерь,
a Pe=l/2Re(ej*) — плотность полных электрических потерь,
обусловленных как омическим, так и сторонним токами.
120
Интегрируя (4.66) по некоторому объему V, получим
\Iln0dS+lPdV+lPcrdV, (4.71)
S V V
где S—поверхность, ограничивающая этот объем, а п0—единичный
вектор внешней нормали к ней. Соотношение (4.71) представляет
собой уравнение баланса энергии поля в объеме V или теорему
Пойнтинга для случая стационарного переменного поля.
Потери энергии. Остановимся более подробно на величине (4.68),
представляющей собой потери энергии электромагнитного поля в
веществе, усредненные за период колебаний и отнесенные к 1 с и 1 см3.
В § 4.1 отмечалось, что тензоры ц и е можно представить в виде
сумм эрмитовых и антиэрмитовых тензоров. Легко показать, что
эрмитовы тензоры не дают вклада в Р, а вклад антиэрмитовых
может быть представлен следующим образом:
Р=^1т(пр*зП*+её*эе*). (4.72)
071
Итак, потери энергии в среде определяются антиэрмитовыми частями
ц и ё, т. е. мнимыми частями их симметричных компонент и
вещественными частями антисимметричных".
Рассмотрим, например, изотропный (в отсутствие постоянного
намагничивания) ферромагнетик с магнитной проницаемостью (4.22)
и скалярной электрической проницаемостью е = е' —/е".
Для него
ie" О О
О ie" О
О 0 ге"
Комплексные амплитуды составляющих векторов h и е с произвольной
поляризацией можно записать- в виде hp = h'p+ih'p, ep = e'p + iep, где
р = х, у, z. Тогда, как нетрудно убедиться,
^=^-[^"(1^12+1М2)+и;;|Лг|2 + 2ц»(А^-^;')]+~е"|е|2. (4.73)
071 «571
Для сред с тензорной е (например, плазмы в магнитном поле,
в том числе твердотельной, или ферромагнетиков в оптических
диапазонах) электрические потери запишутся аналогично магнитным
потерям в (4.73).
Из выражения (4.73) видно, что диссипация энергии связана для
полей любой поляризации с положительными значениями \х", ц"| и е"
(если знаки перед ними выбраны, как в (4.18)). В отношении ц2 (и
£а) такого заключения сделать нельзя, так как величина (h'yh'Z — h'xhy)
(и аналогичная—для составляющих е) может иметь разные знаки
в зависимости от поляризации поля. При круговой поляризации
поперечного (относительно направления намагничивания) поля с пра-
По этой причине и было введено i перед антисимметричными
компонентами ц в (4.19).
V
-Л
0
Л
1Ц"
0
0
0
«и
121
вым вращением (hy = — ihx) эта величина положительна, а для поля
с круговой поляризацией и левым вращением (hy = ihx) отрицательна.
Для поля с линейной поляризацией (hy=Chx, где С—вещественная
величина) она обращается в нуль. Таким образом, одни и те же
величины Ца в Eg вносят для полей с круговой поляризацией либо
положительные потери, либо «отрицательные потери» (т. е. приводят
к уменьшению потерь, обусловленных другими компонентами ц и е),
в зависимости от направления вращения поляризации. Для полей
с линейной поляризацией антисимметричные компоненты Цо и е'а не
участвуют в диссипации энергии стационарного переменного поля.
Для пассивной среды (не содержащей сторонних источников
энергии) при любой поляризации поля должно быть Р>0. Отсюда
вытекают следующие ограничения на значения антиэрмитовых частей
компонент тензора ц:
ц">0, м'|>0, |цй|<и" (4.74)
и аналогичные — на значения компонент е. Знаки же Цо и е„ могут
бь;ть, вообще говоря, любыми. Они зависят, как и знаки \i'a и е'ш
от направления намагничивания.
§ 4.5. Метод возмущений
Трудности, возникающие при строгом решении граничных
электродинамических задач, существенно возрастают при переходе от
сред со скалярными ц и е к гиротропным средам. Поэтому для
таких сред особенно большое значение приобретают приближенные
методы решения граничных задач. Наиболее простым и
универсальным из них является метод возмущений. Исследуемая система
рассматривается при этом как результат малого изменения
(возмущения) другой — более простой, невозмущенной системы, для
которой решение задачи известно. В нашем случае невозмущенной
системой будет всегда система, не содержащая гиротропных сред.
Возмущением же может являться либо малое изменение параметров
среды, в частности появление малых антисимметричных компонент
тензоров ц и е (в произвольных объемах), либо существенное
изменение параметров, но в малых объемах. Второй вариант является
с практической точки зрения более интересным, и ему будет уделено
основное внимание.
Метод возмущений оказывается наиболее эффективным при
вычислении величин, которые являются функционалами электромагнитных
полей и представляют непосредственный интерес. К ним относятся
собственные частоты резонаторов и постоянные распространения
в волноводах. Формулы для этих величин могут быть выведены из
довольно общих квадратичных соотношений, которые мы сейчас
получим.
Леммы возмущений. Рассмотрим две системы: невозмущенную—со
скалярными параметрами Цо и Ео и возмущенную — с тензорными
параметрами и и е. Пусть в первой системе имеет место
электромагнитное поле с комплексными амплитудами h0 и е0 и с частотой
122
юо, а во второй—поле h, e с частотой со. Предположим, что
сторонние токи отсутствуют в обеих системах. Тогда, записав для
возмущенной системы уравнения (4.13) и (4.15), а для
невозмущенной—уравнения, комплексно-сопряженные с ними, умножив их на
соответствующие векторы и сложив полученные выражения, подобно
тому как при выводе формул (4.58) или (4.65), получим (при
вещественных Цо и Ео)
div(exh8+e<? xh)+ -(cohguh — со0Ьц0Ь8+сое8ее — сооеЕОе8) = 0.
(4.75)
Это соотношение можно назвать леммой возмущений. Таким же
образом, но исходя из уравнений (4.13) и (4.15) для обеих систем,
можно получить вторую лемму, отличающуюся от (4.75) заменой
h<?-►ho и eS-f— e0.
Гиротропное возмущение волновода. Рассмотрим бесконечный
волновод с сечением So (рис. 4.3). В невозмущенном состоянии он
заполнен средой с параметрами цо и Ео и в нем имеется поле
бегущей волны ео=е8ехр( — //с,ол)> ho=li8exp( —&потт), где ось г\
направлена вдоль оси волновода. Собственные функции невозмущенного
волновода е8 и ho (см., например, [64]) и постоянная распространения
к^о предполагаются известными. Возмущение заключается в том,
что внутрь волновода вводится бесконечный цилиндр с сечением
Si и параметрами ц и е. В возмущенном состоянии имеет место
поле е = е°ехр( — г&„г|), h = h°exp( — г'^т]), постоянная распространения
к^ подлежит определению.
Подставляя поля е0, h0 и е, h в лемму (4.75) и принимая во
внимание, что в данном случае со = соо, получим после некоторых
преобразований
div±(e°xh8, + e8,xh°)-i(*1]-All0)(eJxh8l+e8lxhyi|0 +
im (4.76)
+-(ho"Aph°+eo*Aeeo)=0.
Здесь индексом ± обозначены поперечные (относительно оси
волновода) составляющие собственных. функций; ц0—единичный вектор
в направлении оси волновода; div±—двумерная дивергенция в
плоскости его поперечного сечения; ДЦ = Д— ц0 и Де=е — е0. Интегрируя
(4.76) по поперечному сечению волновода и принимая во внимание
граничные условия—равенство нуля касательных составляющих
£о и е° на кривой, ограничивающей это сечение, получим формулу
для приращения постоянной
распространения
J(h8*Aph°+e8*Aee°)<AS
С J(e£xh8l+e8lxh2)4odS
*° (4.77)
Эта формула, как и лемма
возмущении (4.75), является строгой. Но входящие
Рис. 4.3. Гиротропное
возмущение волновода
123
в нее возмущенные собственные функции е° и h° неизвестны. Если
площадь сечения Si мала по сравнению с 50, то в знаменателе
(4.77) можно заменить неизвестные функции е? и h° известными
hoi- Тогда, принимая во внимание формулу теории волноводов
(см., например, [64])
Ь8х = (1/Со)ЛоХе8±,
где Со—волновое сопротивление невозмущенного волновода, найдем'>
^-fc^aA J(h8*Aph0 + e8-Aee°) dS, (4.78)
2c/V0 Sj
где
^0=J|e8xl2^5 (4.79)
So
—константа нормировки собственных функций волновода (она должна
быть выбрана такой же, как для функций под интегралом в (4.78)).
Гиротропное возмущение резонатора. Получим теперь формулу,
связывающую собственную частоту со полого резонатора с малым
гиротропным образцом (рис. 4.4) с частотой со0 того же резонатора
без образца. Пусть поле е0, h0 в (4.75) представляет собой поле
одного из типов собственных колебаний невозмущенного резонатора,
а е, h—поле «того же» (т. е. переходящего в него при ^i->0) типа
колебаний резонатора с образцом. Интегрируя (4.75) по объему
резонатора и учитывая граничные условия, получим
f(ir0Aph+e0AeeWF
ш-ш0_ yt '
со „ . . "
J(h0uoh+e0eoe)rfF
Уо
(4.80)
Аналогично случаю волновода в знаменателе (4.80) можно
(если Vi« V0) заменить возмущенные поля невозмущенными.
Тогда [165]
Ш0_Ш= -Ч5Г J(h*oAph+e*0Aee)JF, (4.81)
где
со 2W0Vi
W0=$E0\e0\2dV=$ii0\b0\2dV (4.82)
— умноженная на 8л энергия поля в резонаторе.
В формулы возмущений входят под интегралами величины типа
h0Aph и аналогичные для электрических полей. Запишем их через
составляющие полей в частном случае среды с параметрами (4.22).
Например,
h*0Auh = Auhoihj. + in0z0(h*oj. x Ьх)+Дц,Л'0Л» (4.83)
11 Формулы (4.78) и (4.81) были получены Никольским [166, 165].
124
где Ац=ц—Цо, АЦ||=Цц—ц0. ось z направлена,
как всегда, вдоль М0. а индексы ± обозначают
теперь составляющие, пфпендикулярные этой оси.
С учетом диссипации, т. е. при наличии
антиэрмитовых частей тензоров ji и ё правые
части (4.78) и (4.81) будут комплексными. Таким
образом, эти формулы позволяют найти как
приращения вещественных частей, так и мнимые
части к^ и со, т. е. затухание волны в волноводе рис 4.4. Гиротропное
и мнимую часть собственной частоты резона- возмущение полого
тора, связанную соотношением (1.112) с его резонатора
добротностью.
Квазистатическая аппроксимация. Возмущенные поля в формулах
(4.78) и (4.81) при сколь угодно малых размерах образцов существенно
отличаются от невозмущенных, и при использовании этих формул
их приходится как-то аппроксимировать. Наиболее простой является
квазистатическая аппроксимация. Она заключается в том, что связь
между возмущенным полем в образце и невозмущенным полем (в
тех же точках волновода или резонатора при отсутствии образца)
принимается такой же, как между статическим полем в образце
той же формы и внешним однородным статическим полем.
Именно такая аппроксимация принималась в § 1.5; там
отмечалось, что магнитостатическая задача о связи внутреннего и
внешнего полей имеет простое решение (1.90), если образец является
эллипсоидом, расположенным в немагнитной среде (и0=1)- Исключая
из (1.90) и соотношения
п + 4ят = рп (4.84)
внутреннее поле h, мы нашли § 1.5 связь намагниченности m с
внешним полем. Теперь же нас интересует связь h с этим полем (которое
здесь обозначено h0). Исключая m из (1.90) и (4.84), находим
h-Tho, (4.85)
где (при ц0=1)
Т=Л+1йдр) (4.86)
Если же ц0/1, то в (4.86) Ар заменится на Др/ц0- Решение
электростатической задачи о связи возмущенного поля е с
невозмущенным е0 будет аналогичным с заменой в (4.86) Ар на Аё.
Компоненты тензора Т нетрудно найти согласно (4.86), используя
общие правила тензорной алгебры [119].
Рассмотрим среду с параметрами (4.22) и примем для простоты,
что ось z (направление постоянного намагничивания) совпадает
с одной из осей эллипсоида, а ц0 = 1. Соотношения между
составляющими полей h и h0, полученные при этих предположениях для
образцов различной формы, приведены в табл. 4.1. Аналогичные
выражения для электрического поля получаются при замене компонент
й соответствующими компонентами ё.
125
ев
Я
К
ч
ю
са
Н
ч
о
и
= ?
5 s
СО
о
>i са
2 h
со
и
о 5
4i
IS
и
Номера
формул
N
"С
-а
,
з: ~*.
О я
w о.
<1>
Направлени
намагничивания
II
&&
e<g
f^1
00
■*
>»^
о
-s:
*.
о
-S
— 1 з.
+
Н
О
•«;
в i
•3-1 л
и
о
-к
а
и
о
в
л
CJ
г-
Св
О
ев
W
S
К
,5
Е
^-s
00
00
тГ
^mS
о
-s:
-1*
О
-s:
н
о
-с
чг
О
о
X
л
5
s
о.
о
к
^-ч
OS
ОО
■*
*~^
О
-s:
*».
о
-s:
•—'
+
a.
CN
М Q
=Х
|
IS
-^-
+
a.
к
о
-с
4
CN
мч
a.
1
+
ss
О
-s:
л.
Д
м а
3.
1
+
о
-s:
, .
"*
+
=1.
CN
М Q
=1.
1
м
■^~-
+
=1
ев
Ш
О
В
о
ч
о
о.
с
1
|
s
Я
о4
ON
тГ
"w*
N
О
•«;
CN
■—'
+
з7
О
о
-s:
"~ 1 i
1
и
с
1 *—
CN +
I 3.
г\)
CJ
О
в
(Г
о
С
CJ
С
О
с
о\
■*
Ч_^
N
О
-s:
го
CN
+
з7
as
О
-s:
CN
+
a.
c*i
мв
3.
I
м
'tN^
+
3.
H
о
-s:
а
.з.
c*5
М Q
1
+
3.
ss
О
-С
•=l
ГО
IS Q
3.
1
CN
+
3.
^-^
ч
гч
—
-;
Г^,
<ч а
3.
1
М
^"^
+
=1
'О
ев
О.
о
•е-
о
U6
Необходимым условием применимости квазистатическои
аппроксимации внутреннего поля является малость одного из размеров
образца (d) по сравнению с длиной электромагнитной волны в нем.
Если учесть, что поперечные диагональные компоненты одного
порядка или больше, чем другие компоненты р и в, то это условие
можно записать, например, следующим образом:
koy/\^\v\d<n!6. (4-92)
Под величиной d следует понимать диаметр сферы, диаметр цилиндра
или толщину пластины. Малости других размеров пластины или
цилиндра не требуется. Конечно, внутреннее поле будет
приблизительно однородно только по толщине пластины или в поперечном
сечении цилиндра; в плоскости пластины и по длине цилиндра оно
будет изменяться, но так же, как внешнее поле, так что связывающие
их формулы (4.87) —(4.91) останутся справедливыми. В случае же,
когда все размеры образца малы, интегрирование по его объему
в формуле (4.81) или по площади сечения в (4.78) можно заменить
умножением соответственно на Vi или S^
Вторым условием применимости квазистатической аппроксимации
является, как уже отмечалось в § 1.5, наличие однородного типа
колебаний намагниченности.
Переход к внешним восприимчивостям. Все полученные выше
формулы возмущений содержали тензорные параметры вещества
П=1+4ях и E=l+47iS, где 5—поляризуемость или электрическая
восприимчивость, связывающая электрическую переменную
поляризацию р с полем е. Но для образца —малого эллипсоида и его
предельных случаев (тонкой пластины и тонкого цилиндра)—могут
быть определены (см. § 1.5) тензоры внешних восприимчивостеи %
и ае связывающие векторы тирс внешними полями, соответственно
h0 и е0. Введем эти тензоры в формулы возмущений. Примем для
простоты iio=l и е0=1 и рассмотрим, например, формулу (4.81).
Входящее в нее произведение h0Aph может быть преобразовано
следующим образом:
h0Aph = h*047ixh = 47ih0Xeh0. ' (4-93)
Так же преобразуются е'0Аее и аналогичные произведения, входящие
в формулу (4.78). Таким образом, введение внешних восприимчивостеи
позволяет исключить из формул возмущений внутреннее
(возмущенное) поле и отпадает необходимость его аппроксимации. Но, конечно,
все это справедливо только при указанных выше условиях
применимости квазистатического приближения.
Для изотропной (в отсутствие намагничивания) среды при
совпадении направления намагничивания (оси z) с одной из осей
эллипсоида тензор Г имеет вид (1.117) при ь = 0. Произведение
hoXeh0 в (4.93) запишется в этом случае следующим образом:
hbXeho = Xil^l2 + x?l4l2 + ^zo(h*oxh0). (4-94)
Легко убедиться, что последний член в этом выражении обращается
в нуль при линейной поляризации поля h0, а для полей с круговой
поляризацией веществен и имеет разные знаки при разных
направлениях вращения поляризации.
Резонатор со стенками из реального металла. Метод возмущений
может быть применен для приближенного решения задачи о влиянии
стенок из неидеального, в частности ферромагнитного металла, на
параметры электромагнитных систем. Рассмотрим, например, полый
резонатор, часть St поверхности которого представляет собой границу
с металлом, обладающим большой, но конечной проводимостью.
Остальную часть поверхности резонатора для простоты будем считать
идеально проводящей. Тогда, интегрируя лемму (4.75) по объему
резонатора (не содержащему в данном случае гиротропного образца),
но учитывая, что на Si касательная составляющая электрического
поля не равна нулю, и пренебрегая различием со и со0 везде, кроме
разности (со —со0), мы придем к формуле возмущений, полученной
Слэтером [186],
са-Шо со'-Юо i к е. .
-= -н = \(exh')n0dS, (4.95)
где W0 определяется выражением (4.82), п0—единичный вектор
внешней нормали к поверхности резонатора, а е и h—вообще
говоря, возмущенные поля1}. Однако в качестве h может быть
принято невозмущенное, касательное к поверхности поле
h0 в резонаторе с идеально проводящими стенками. Касательная
составляющая электрического поля ет, которая входит в (4.95), точнее,
связь ее с h0 может быть найдена из рассмотрения волны,
распространяющейся в стенке от поверхности резонатора. Заметим, что
для неферромагнитного хорошо (но не идеально) проводящего металла
такое рассмотрение приводит к граничному условию Леонтовича
(см., например, [134]):
e,/*o=^(l+i)*o6i, (4.96)
где &0 = со/с, а 5г — глубина проникновения поля в металл с ц=1,
для которой справедлива формула (4.39). Случай ферромагнитного
металла будет рассмотрен в § 14.2.
" Вещественная часть интеграла в (4.95) есть не что иное, как умноженный
на 8тг/с поток мощности через поверхность 5Х, что находится в соответствии
с определением добротности (1.113).
Глава 5
ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ
СРЕДАМИ. ФЕРРИТОВЫЕ СВЧ УСТРОЙСТВА
§ 5.1. Волновод с продольно-намагниченной средой
В этой главе будут исследованы электромагнитные волны в
волноводах и колебания в резонаторах, содержащих гиротропные среды.
При этом мы ограничимся средами с параметрами (4.22) и во
многих случаях будем считать е скалярной величиной. Будут также
рассмотрены кратко принципы построения ферритовых устройств,
основанных на использовании таких волн и колебаний.
В первых двух параграфах этой главы мы будем иметь дело
с регулярными волноводами, заполненными целиком или частично
гиротропной средой. Прежде всего остановимся на случае продольно-
намагниченной среды — когда направление намагничивания совпадает
с осью волновода.
Произвольный волновод, заполненный продольно-намагниченной
средой. Рассмотрим полый металлический волновод произвольного
сечения с идеально проводящими стенками, заполненный средой
с параметрами (4.22), которая намагничена в направлении оси
волновода — оси z. Пусть волна распространяется в положительном
направлении этой оси. Тогда для продольных составляющих поля
будут справедливы уравнения, получающиеся из (4.23) при замене
6/dz-* — ikz. Из этих уравнений следует, что если hz = 0, то и ег = 0,
и наоборот. Таким образом, типы волн в волноводе с продольно-
намагниченной гиротропной средой не являются волнами ТЕ и ТМ.
Однако они переходят в волны ТЕ и ТМ при цо->0 и ео->0 и могут
классифицироваться как волны квази-ТЕ и квази-ТМ. Кроме того,
они становятся волнами ТЕ или ТМ, когда kz->0, т. е. при отсечке.
Уравнения (4.23) в этом случае совпадают с уравнениями (см.,
например. [64]) для изотропной среды с параметрами ёц и ц± (волны
ТМ) или Ei и Цу (волны ТЕ). Можно показать [66], что для случая
магнитно-гиротропной среды — с ео = 0, в частности, для ферритов
в диапазоне СВЧ, граничные условия при отсечке тоже совпадают
с граничными условиями для изотропной среды. И тогда, аналогично
волноводу с изотропной средой, справедливы следующие выражения
Для предельных длин волн:
^cTM = (^cTm)o\/E^-L> ^cTE = (^cTe)oV Ф|| > (5-1)
1ле (\™,те)о—предельные длины волн пустого волновода.
Для определения к2 и структуры поля в волноводе с продольно-
намагниченной средой можно использовать метод скалярных функций,
9 А. Г. Гуревич, Г. А. Мелков 129
Рис. 5.1. Круглый волновод,
заполненный продольно-намагниченной
гиромагнитной средой
упомянутый в § 4.1". Поскольку
зависимость от z является в данном
случае гармонической, функции
v]/±1 2 удовлетворяют уравнению
(4.28), а величины х12 являются
корнями уравнения (4.26).
Как показано в [66], поля,
определяемые функциями v]/±1 и v]/±2 по
отдельности, не удовлетворяют
граничным условиям. Им могут
удовлетворить лишь некоторые линейные
комбинации этих полей, которые
и являются нормальными волнами
рассматриваемого волновода. Найти
поля и постоянные распространения для этих волн удается строго
лишь в весьма ограниченном числе случаев, в том числе для круглого
волновода, заполненного гиротропной средой.
Круглый волновод. Рассмотрим круглую трубу (рис. 5.1) с идеально
проводящими стенками, заполненную средой с Ц вида (4.22) и
скалярной е; направление намагничивания (ось z) совпадает с осью
волновода. Частным решением уравнения (4.28) в цилиндрической
системе координат (рис. 5.1). конечным при р = 0, является (см.,
например, [163])
\|/±=Уж(хр)е|"'\ (5.2)
где Jm — функция Бесселя, а т = 0, ±1, +2... Скалярную функцию,
соответствующую нормальной волне, следует записать в виде
*l>± = {Al>\,Ll+A2^12)e-ik>z = [AlJm(xlP)+A2Jm(x2pj]eiim*-k*z). (5.3)
Подставляя (5.3) в граничные условия для функции \|/± [66] на
окружности р = ро, получим систему двух линейных однородных
уравнений для At и А2. Равенство нулю ее определителя даст
трансцендентное уравнение
(5.4)
Л.2 =
*1,2
■^(*1,2Ро) U-gtn к\
■ЛЛ^.гРо) ИРо И1.2'
где J'm — производная Jm по аргументу. Это уравнение независимо
получили Кейлс [340], Гинцбург [58] и Сул и Уокер [192]. Решая
его совместно с выражениями для величин щ и х2— корней
биквадратного уравнения (4.26), можно найти эти величины и
постоянную распространения kz.
Отметим прежде всего, что kz входит в (5.4) и в коэффициенты
(4.27) уравнения (4.26) только в квадрате. Поэтому знак kz, т. е.
направление распространения волны, не влияет на величину \kz\.
Величины же д„ и т входят в (5.4) в первых степенях, причем
' Более подробно этот метод рассмотрен в [66].
130
в виде произведения \iam. Поскольку знак ц0 определяется
направлением М0, а знак т обозначает направление вращения поляризации
волны (правое при т<0 и левое при т>0), то знак \iam говорит о
направлении вращения поляризапии относительно направления
намагничивания. Волны с правым и левым вращением относительно этого
направления имеют разные постоянные распространения kz+ и кг-.
Это различие приводит, как и в неограниченной среде (§ 4.2),
к повороту большей оси эллипса поляризации — эффекту Фарадея.
Однако формула (4.46) заменяется при этом (см., например, [192]) на
э=1(*;+-л;_)//м. (5.5)
Заметим, что роль вектора, о поляризации которого идет речь,
в случае волновода играет некоторый вектор, лежащий в плоскости
поперечного сечения и жестко связанный со структурой поля в этом
сечении; его можно назвать вектором поляризации волны.
Подробный анализ решений уравнения (5.4) совместно с (4.26)
проведен в [192]. В случае й0<к1 может быть применен метод
возмущений (§ 4.5).
Круглый волновод с гиротропным стержнем. Круглый волновод,
целиком заполненный ферритом, с практической точки зрения обладает
существенными недостатками: низкой «добротностью» (отношение
угла поворота поляризации к потерям) и трудностью согласования
с пустым волноводом. Эти недостатки могут быть уменьшены при
частичном заполнении волновода ферритом (рис. 5.2).
Задача о регулярном круглом волноводе с круглым коаксиальным
стержнем из гиротропного вещества, намагниченного вдоль оси
волновода, как и рассмотренная выше задача о целиком заполненном
круглом волноводе, может быть решена строго. Поле в феррите (p<Lpx)
должно быть представлено в виде суммы двух полей, соответствующих
У-i и к2. Поле в изотропной среде с параметрами £0 и ц0= 1, т. е. в
области p>pi, будет суммой полей ТЕ и ТМ, каждое из которых
содержит теперь как функции Бесселя Jm(v.0p), так и функции Неймана
Nm(x0p), поскольку точка р = 0, в которой Nm-*oo, не принадлежит
этой области. Таким образом, в выражения для составляющих поля
войдут 6 произвольных постоянных. Граничные условия,
заключающиеся в равенстве нулю е. и е, при
Р=Ро и непрерывности ez, еф,
hz и /1ф при р=рь дадут систему
6 однородных линейных уравнений
для этих постоянных. Равенство
нулю ее определителя приведет
к трансцендентному уравнению,
связывающему величины kz, x1; х2 и х0>
которое должно решаться совместно
с выражениями для Xi 2—корнями
(4.26) и соотношением . рис. 5.2. Круглый волновод с
продольно-намагниченным гиромаг-
y.o — koBo—kj. (5.6) нитным стержнем
Рис. 5.3. Поворот поляризации в круглом
волноводе с ферритовым стержнем [159].
9i—угол поворота на длине 1 см,
к0 = 2л/\о—волновое число в свободном
пространстве. Сплошные линии—точный
расчет, штриховые—расчет в слабоги-
ротропном приближении, штрихпунк-
тир— по формуле (5.7); цо = 0,5, Ц=1>
РоАо=0,3
Не останавливаясь на
громоздких вычислениях, к которым
приводит решение этой задачи
[66, 159], заметим лишь, что
в упомянутое трансцендентное
уравнение, как и в (5.4), войдут
к\ и произведение \iam.
Поэтому свойства круглого
волновода со стержнем
качественно не отличаются от
упомянутых выше свойств волновода,
заполненного ферритом. В
частности, по-прежнему будет
справедлива формула (5.5).
Если pi/p0<Kl, то для
расчета постоянных
распространения, а следовательно, и угла
поворота поляризации может
быть применена формула
возмущений (4.78) с
квазистатической аппроксимацией
возмущенного поля (табл. 4.1).
Такой расчет для
представляющей наибольший интерес волны квази-ТЕц дает [66, 69]
1 W (м+02-цо2
(5.7)
Оценка предела применимости этого метода по формуле (4.92) при
е=10 приводит к значению pi/po<0,05.
Для расчета круглого волновода с ферритовым стержнем
можно использовать и другой вариант метода возмущений, когда
в качестве невозмущенной системы принимается волновод со
стержнем того же радиуса, с теми же е и ц, но с цо = 0,
а параметром малости является отношение \хв/ц (слабогиротропное
приближение).
На рис. 5.3 приведены результаты расчетов угла поворота
поляризации волны квази-ТЕц в круглом волноводе с ферритовым
стержнем всеми упомянутыми методами. Из этого рисунка видно,
что метод возмущений с квазистатической аппроксимацией
возмущенного поля в согласии с приведенной оценкой справедлив лишь при
очень малых pi/p0. Расчет же в слабогиротропном приближении
при ц0 = 0,5 дает еще неплохое согласие с результатом строгого
расчета.
Описание на языке связанных волн. Поворот поляризации в
круглом волноводе можно трактовать и как результат постепенной
перекачки энергии из линейно поляризованной волны квази-ТЕи
в аналогичную волну квази-ТЕц, но обладающую картиной полей,
повернутой на 90° вокруг оси волновода относительно картины
132
Рис. 5.4. Основные типы нормальных волн в плоском диэлектрическом
волноводе
полей первой волны. Эти волны, которые являлись нормальными
в пустом волноводе, в волноводе с продольно-намагниченной средой
становятся связанными. Такой подход справедлив и в случае
квадратного волновода, где продольно-намагниченная среда приводит
к связи нормальных волн пустого волновода TE0i и TEi0.
Описание на языке связанных волн особенно целесообразно
использовать при небольших отличиях волн квази-ТЕ от волн ТЕ
изотропного волновода, что имеет место при малом радиусе гирот-
ропного стержня или малых величинах ц0 или е0.
Последний случай реализуется в оптике. Рассмотрим, например,
плоский оптический волновод (рис. 5.4), представляющий собой
трехслойный диэлектрик с диэлектрической проницаемостью среднего
слоя E2>e1i3". При отсутствии гиротропных сред нормальными
волнами в таком волноводе (см., например, [4]) являются волны
ТЕ и ТМ; конфигурации их полей в случае основных волн TEi
и ТМ! показаны схематически на рис. 5.4. Если один из слоев
волновода является гиротропным, то волны квази-ТЕ и квази-ТМ
становятся связанными. И если на входе возбуждается одна из
них, то по мере распространения ее энергия перекачивается в другую
волну. Конечно, этот процесс можно трактовать и на языке
нормальных волн в волноводе с гиротропнои средой, которые
являются комбинациями волн квази-ТЕ и квази-ТМ. Они не
преобразуются одна в другую, но имеют разные величины kz,
вследствие чего поляризация суммарной волны преобразуется при
распространении.
Фарадеевскне ферритовые устройства. Как уже отмечалось,
направление поворота поляризации волны в продольно-намагниченной
гиротропнои среде или в волноводе, содержащем такую среду, не
зависит от направления распространения волны и изменяется на
обратное при изменении направления постоянного намагничивания.
Это свойство, являющееся проявлением невзаимности (см. § 4.3),
используется в СВЧ ферритовых устройствах поляризационного или
" Практически он представляет собой обычно тонкую пленку со слоем
е2 на подложке со слоем г1<г2; третьим слоем является воздух.
133
Рис. 5.5. Фарадеевский циркулятор
фарадеевского типа, которые впервые подробно исследовал Хоган
[328] (см. [128, 159]).
Рассмотрим прежде всего фарадеевский циркулятор, показанный
схематически на рис. 5.5. Он представляет собой отрезок круглого
волновода с ферритовым образцом и двумя парами ортогональных
друг другу входных и выходных плеч — прямоугольных волноводов.
Ферритовый образец находится в продольном магнитном поле
Не0 и осуществляет поворот поляризации волны ТЕИ в круглом
волноводе на угол 9 = я/4. На такой же угол повернуты друг
относительно друга пары прямоугольных волноводов. В результате
этого, как легко видеть, волна, поступающая, например, из плеча
/ (рис. 5.5), проходит в плечо 2. а волна из плеча 3— в плечо 4.
Поскольку знак угла S не изменяется при изменении направления
распространения, волна из плеча 2 проходит в плечо 3, а из плеча
4—в плечо /. Устройство, обладающее такими свойствами, называется
циркулятором и на схемах обозначается, как показано на рис. 5.5.
При изменении знака Не0 направление циркуляции заменяется на
обратное.
Если к плечам 3 и 4 присоединить согласованные нагрузки, то
циркулятор превращается в вентиль, осуществляющий развязку
генератора (в плече /) от нагрузки (в плече 2). Если к плечу
/ циркулятора присоединить передатчик, к плечу 2—антенну, а к плечу
3 — приемник, то такое устройство будет выполнять функции
автоматического антенного переключателя (дуплексера). Фарадеевский
циркулятор и его частные случаи — вентиль, дуплексер обладают
обычно следующими параметрами: прямые потери <0,5 дБ, обратные
потери (развязка) 25—30 дБ, правда, в неширокой полосе частот —
порядка 10%. Изменение — плавное или дискретное — магнитного поля
в устройстве, показанном на рис. 5.5 (или аналогичном другой
конструкции), позволяет осуществить амплитудный модулятор или
переключатель. При этом могут быть достигнуты [159] частоты
134
модуляции до ~ 10 Мгц при сравнительно малых величинах
управляющих магнитных полей.
Круглый волновод с продольно-намагниченным ферритовым
образцом может быть использован и для создания
регулируемого фазовращателя или фазового модулятора. При этом
используется волна с круговой поляризацией, фазовая постоянная
которой k'z изменяется при изменении магнитного поля. Все
рассмотренные фарадеевские устройства могут быть реализованы
и на основе упомянутого выше квадратного волновода, так как
я в нем, подобно круглому волноводу, могут распространяться
две связанные волны с взаимно ортогональными линейными
поляризациями.
Для создания управляемых ферритовых устройств может быть
использован и волновод с продольно-намагниченной средой, в котором
может распространяться только одна волна. Примером таких
устройств является взаимный фазовращатель Реджиа — Спенсера (см.,
например, [159]), который представляет собой отрезок прямоугольного
волновода с расположенным на его оси продольно-намагниченным
ферритовым стержнем.
§ 5.2. Волновод с поперечно-намагниченным ферритом
Перейдем к исследованию распространения волн в волноводах,
содержащих гиротропную среду, намагниченную в поперечном по
отношению к оси волновода направлении.
Волны ТЕ „0 в прямоугольном волноводе, заполненном гиротропной
средой. Остановимся прежде всего на задаче о регулярном
прямоугольном волноводе, который целиком заполнен средой с параметрами
(4.22), намагниченной перпендикулярно его широким стенкам (рис. 5.6).
Рассмотрим простейшие типы волн, для которых поля не зависят
от координаты г. В этом случае, как видно из (4.23), могут
(отвлекаясь от граничных условий) существовать волны с е, = 0 или
hz = 0. Действительно, подставляя поля е = е0ехр( — ikyy)
и h = h0exp( — ikyy) в уравнении Максвелла (4.13) и (4.15) и проектируя
их на оси координат, получим в этом случае (djdz = 0), как и для
неограниченной поперечно-намагниченной среды (ср. с (4.53)), две
независимые системы":
ку ех — к0 \ihx — ik0 ц0 hy = 0,
i-^-iko^ahx + koiihy^O; (5.8)
ex
dh.
ex
и другую—для составляющих /?., ех и еу. Система (5.8) описывает
волны ТЕ„0, а вторая система—волны ТМ„0 (индексы и и 0 указывают на
" В (5.8) и в дальнейшем мы опускаем индексы 0 у (зависящих в данном
случае только от х) компонент векторов е0 и h0.
135
число вариаций поля по осям х и
z). Однако волны ТМ„0 в данном
случае не могут существовать в
силу граничных условий; для них
ех и еу обращаются в нуль на
стенках z = 0 и z = b, а
следовательно, и везде, так как d/cz = 0.
Для волн ТЕп0, исключая из
системы (5.8) hx и hy, получим
Рис. 5.6. Прямоугольный волновод,
заполненный
поперечно-намагниченной гиротропной средой
/Ре
dx
(5.9)
где
Xx = £oE|ikL — к2. (5.10)
Решение уравнения (5.9), удовлетворяющее граничным условиям ez = 0
при х = 0 и х = а, имеет вид
(5.11)
ez = Asiay.xx, у.х = пк/а. и=1, 2, 3, ...
Из (5.10) и (5.11) постоянная распространения
^ = Ул2е,|^-(яп/а)2. (5.12)
Таким образом, в прямоугольном волноводе, заполненном
поперечно-намагниченной гиротропной средой, могут распространяться
волны ТЕп0 с такой же структурой электрического поля, как и в случае
изотропной среды. Не отличается, как легко убедиться, от случая
изотропной среды и распределение магнитной индукции. Однако
структура магнитного поля будет существенно иной (рис. 5.7). Она
изменяется при изменении направления распространения или
направления намагничивания и остается неизменной при одновременном
изменении этих направлений. В этом проявляется (см. § 4.3)
невзаимность данной системы.
Рис. 5.7. Силовые линии магнитного поля вотчы TF „ г™
волновода, заполненном поперечно-намагниченным Лерритох, ^™°У™**™
ленни распространения- к-9- ,, — г> Q- ,, -п лым ^ РР ом' Д-'Я дьух
направления, ь-У, ц-ь,У, ц„ = 0,6, длина волны в свободном
136
пространстве Х0=^/2а
Волновод с поперечно-намагниченной
ферритовой пластиной. Переходя к
исследованию волноводов, частично
заполненных поперечно-намагниченной
гиротропной средой, остановимся на
простом случае прямоугольного волновода
с ферритовой пластиной, параллельной
его узкой стенке (рис. 5.8). Снова
ограничимся рассмотрением полей, для
которых d/dz = 0. В феррите имеет место
уравнение (5.9), а вне его
d е. 2 _г) ,г i->\ Рис. 5.8. Прямоугольный вол-
dx2 £z~ P-iJj новод с
поперечно-намагниченной ферритовой пластиной
x2x0 = k2-k2. (5.14)
Решения уравнений (5.9) и (5.13),
удовлетворяющие граничным условиям при х = 0 и х = а, можно записать
следующим образом (рис. 5.8):
ez = Asinxx0x при 0<x<g,
ez=Csmy.x(x—g) + Dcosy.x(x—g) при g<x<g + d, (5.15)
ez = BsinKx0(a — x) при g + d<x<a.
Четыре условия непрерывности е, и hy при x—g и x=g + d дадут
систему уравнений для коэффициентов А, В, С и D. Приравнивая
нулю ее определитель, получим уравнение для постоянной
распространения ку [66 ]:
pK0ctgnxd(tgxx0g+tgnx0l)-(p2 + q2){gyix0gtgy.x0l+yix0 +
+ K*otf(igKvo£-tgKxo/) = 0,
P = v-x,Vi- tf = Ha M WO» l=a-g-d. (5.16)
Уравнение (5.16) содержит произведение \ааку Следовательно,
корни его—постоянные распространения \ку | и \ку \, а также
структуры полей в волноводе будут различными для разных
направлений намагничивания или распространения. При одновременном
изменении обоих направлений они останутся прежними. К такому
же изменению постоянных распространения, как и изменение знака
ку или ц0, приводит и замена g&l. При g=l, как видно из (5.16),
\ку \ = \к~ \. Положив в (5.16) /с,. = 0, мы получим уравнение для
предельных величин (частот или—при заданной частоте—размеров
волновода). В это уравнение ца войдет только в квадрате, т. е.
предельные величины не зависят от направления намагничивания.
Структура поля в волноводе с поперечно-намагниченной
гиротропной пластиной, как видно из (5.14), носит разный характер в
зависимости от того, имеет ли место неравенство k2>k\ или обратное ему.
3 первом случае зависимость полей вне феррита от д: описывается
гиперболическими функциями, во втором—тригонометрическими.
Структура поля внутри феррита согласно (5.10) существенно
зависит от величины д±. При Цх<0, т. е. в интервале частот
137
Рис. 5.9. Распределение
электрического поля в прямоугольном волноводе,
частично заполненном ферритом,
в случае щ<0 для двух направлений
распространения (сплошные и
штриховые линии)
(о±<(о<(ом + сои (см. рис. 1.7),
зависимость полей в феррите от
х описывается гиперболическими
функциями. В случае
безграничной поперечно-намагниченной
среды (§ 4.2) при Uj.<0
распространение волн было бы
невозможно. В волноводе с поперечно-
намагниченной пластиной волна
в этом случае может
распространяться, однако поле ее будет
«выталкиваться» из тех областей,
в которых оно сильно
взаимодействует с ферритом, т. е. из
областей с поляризацией
магнитного поля, близкой к правой круговой. Вследствие этого поля для
разных направлений распространения будут «прижиматься» к
противоположным поверхностям пластины (рис. 5.9). Это является одним
из проявлений эффекта невзаимного смещения поля, который, вообще
говоря, заключается в зависимости структуры электромагнитного
поля от направления распространения волн или направления
намагничивания.
При 0<Uj_<l (т.е. co>coH + cow) выталкивание полей из областей
правой круговой поляризации магнитного поля тоже имеет место,
но не так ярко выражено, как при д±<0. Если же Ui>l, т.е.
ю<(о±, то как для прямой, так и для обратной волны имеет место
концентрация электромагнитного поля в феррите. Эффект невзаимного
смещения поля в этом случае уменьшается, хотя и не исчезает
полностью.
Уравнения для постоянной распространения и структуры поля
волн с d/dz = 0 в прямоугольном волноводе могут быть получены
при любом числе поперечно-намагниченных гиротропных пластин,
параллельных узким стенкам волновода [66, 128]. На рис. 5.10
показаны структуры поля в волноводе для интересного случая двух
пластин одинаковой толщины, симметрично расположенных в
волноводе и намагниченных одинаково или в противоположных
направлениях. В первом случае (это ясно и из симметрийных соображений)
Рис. 5.10. Распределение электрического поля в волноводах с вач™Чно ня«-,г
ничейными ферритовыми пластинами. Сплошные и штриТовые^ГГ-ра^ньш
направления распространения
138
&к„в, град
Рис. 5.11. Зависимость невзаимной разности постоянных распространения от
толщины и положения поперечно-намагниченной пластины в прямоугольном
волноводе (рис. 5.8). Штриховые линии—расчет методом возмущений с
квазистатической аппроксимацией поля, сплошные — точный расчет [72]; е = 9, ц=0,9,
ц„=0,5, Х0= 1,39а; цифры у кривых—значения d/a
постоянные распространения \ку\ не различаются для разных
направлений распространения или намагничивания, несмотря на то,
что структуры поля различны. Во втором случае \ку\ и структура
поля зависят от направления распространения и направлений
намагничивания.
В случае очень тонкой пластины, т. е. d<£a (см. рис. 5.8), для
расчета ку может быть использован метод возмущений с
квазистатической аппроксимацией внутреннего поля (§ 4.5). Зависимости
8ку = \ку | — \ку | от положения пластины, вычисленные этим методом,
приведены, наряду с результатами точного расчета [66], на рис. 5.11.
Как видно из этого рисунка, расчет методом возмущений справедлив
лишь для очень тонких пластин (d<0,02a). В случае двух тонких
пластин вызванные ими приращения постоянной распространения
приближенно можно считать аддитивными; для противоположно
намагниченных симметрично расположенных пластин (см. рис. 5.10)
величина Ьку удваивается, а в случае одинакового намагничивания—
обращается в нуль. Для пластин произвольной толщины аддитивность
не имеет места, но и здесь в случае противоположного намагничивания
&ку увеличивается по сравнению с одной пластиной, а в случае
одинакового—обращается в нуль.
Высшие типы волн. Остановимся теперь кратко на волнах
в прямоугольном волноводе с поперечно-намагниченным ферритом,
139
для которых поля зависят от обеих поперечных координат х и z.
Нормальные волны в этом случае представляют собой суперпозиции
парциальных волн с двумя значениями у.х и не являются волнами
ТЕ и ТМ, а имеют все 6 составляющих поля [159, 413] (см. также
[128]).
В случае волновода, целиком заполненного ферритом, при Kl<0
могут распространяться, как следует из (5.12), только высшие типы
волн. Зависимости полей от х при этом могут описываться как
гиперболическими функциями (ил—мнимые), так и
тригонометрическими. В первом случае поля «прижимаются» к одной из боковых
стенок волновода — разных для разных направлений распространения
или намагничивания.
При частичном заполнении волновода поперечно-намагниченной
средой с цх<0 наряду с волнами, прижатыми к металлическим
поверхностям, которые можно назвать волнами феррит-металл,
возникают высшие (с д/dz^O) волны феррит-диэлектрик, поля которых
концентрируются вблизи границ феррита и диэлектрика (воздуха).
При ц±>0 поля высших типов волн внутри феррита описываются
тригонометрическими функциями, а вне его—гиперболическими. Такие
типы волн иногда называют ферритовыми.
Полосковый н коаксиальный волноводы. Рассмотрим сначала
плоскопараллельный волновод, образованный двумя бесконечными
параллельными металлическими плоскостями. Такой волновод,
конечно, не может быть реализован, но он допускает строгий анализ
как при продольном, так и при поперечном намагничивании
заполняющей его гиротропной среды. В случае намагничивания
в направлении, перпендикулярном металлическим плоскостям, можно
воспользоваться результатами, полученными выше для
прямоугольного волновода, при а-юэ. В частности, в плоскопараллельном
волноводе с ферритовой пластиной при и±<0 могут иметь место
поверхностные волны со структурой полей, аналогичной показанной
на рис. 5.9.
Полосковый волновод (рис. 5.12) не может быть строго рассчитан
даже в случае изотропной среды, а тем более при наличии феррита.
Простейшим приближением при его анализе является замена его
плоскопараллельным. Это же относится и к коаксиальному волноводу
(или коаксиальной линии, рис. 5.13). Например, в коаксиальной линии
с радиально намагниченным ферритовым образцом (рис. 5.13, 6) могут
существовать поверхностные волны, прижатые при разных
направлениях распространения к противоположным боковым поверхностям
образца. Постоянная распространения одной из них может быть
существенно изменена размещением
вблизи соответствующей поверхности
диэлектрика (рис. 5.13, в). Такой способ
применяется для создания кевзаимных
устройств на коаксиальном волноводе;
как ясно из соображений симметрии,
Рис. 5.12. Полосковый волно- без размещения диэлектрика с одной
пол с гиротропной средой стороны ферритовой пластины в этом
140
Z
Кн.
еа
х
i".
ВО
Рис. 5.13. Коаксиальные волноводы и их плоскопараллельные аналоги
случае не может быть достигнуто различие постоянных
распространения для прямой и обратной волн.
Учет потерь в феррите. В этом случае электрическая проницаемость
е феррита и компоненты тензора Ц, а следовательно, и дисперсионные
уравнения, например (5.16), становятся комплексными. Для
интересующих нас стационарных волн частота вещественна и решениями
комплексных дисперсионных уравнений являются комплексные
постоянные распространения ky — k'y—ik'y. Величина к'у представляет собой
коэффициент затухания (декремент) волны.
Если мнимые части ц, ц0 и е малы по сравнению с вещественными,
то при нахождении к'у ими можно пренебречь, а для вычисления
к'у воспользоваться приближенной формулой
дк'
дк'
ек
у де дц дца
(5.17)
В области ферромагнитного резонанса, где величины ц" и и„ одного
порядка или больше, чем ц' и ц„, эта формула, конечно, неприменима,
и необходимо находить комплексные корни дисперсионных уравнений.
Результаты такого расчета [72] (см. также [66, 69]) приведены на
рис. 5.14. Как видно из этого рисунка, при определенном положении
пластины, близком к точке круговой поляризации магнитного поля,
имеет место сильная зависимость затухания от направления
намагничивания. Это явление—невзаимного поглощения широко
используется для создания ферритовых СВЧ приборов. Интересно заметить,
что максимальное поглощение (рис. 5.14) имеет место при величине
141
к и а, град
3 /Le,/r3
5 Не0,кЭ
Рис. 5.14. Вещественная и мнимая части постоянной распространения при
различных положениях поперечно-намагниченной ферритовой пластины в
волноводе [72]; d= 0,02с; цифры у кривых—значения g-a\ частота 9,4 ГГц.
М0=170Гс, юг=2-109с-1, £ = 9. Величины р и ц„ рассчитаны согласно (1.74)
внешнего постоянного поля, совпадающей с полем ферромагнитного
резонанса, найденным по формуле (1.97) для эллипсоида с теми же
отношениями размеров и так же намагниченного, как пластина, для
которой проводился расчет.
Приборы на основе волноводов с поперечно-намагниченным
ферритом. Такие приборы могут выполнять все функции, которые
выполняют рассмотренные в предыдущем параграфе фарадеевские
устройства. При этом в большинстве случаев, не уступая последним по
параметрам, они имеют более простые конструкции.
Рассмотрим сначала вентили. Один из них—резонансный вентиль—
использует явление невзаимного поглощения в волноводе с поперечно-
намагниченным ферритовым образцом. Такой вентиль может быть
создан на основе любого волновода, в котором имеются точки
с круговой поляризацией магнитного поля, например прямоугольного
волновода или коаксиального (см. рис. 5.13, в), частично заполненного
диэлектриком. Конструкция
резонансного вентиля на прямоугольном волноводе
показана схематически на рис. 5.15.
Назначение диэлектрической пластины
в данном случае—повысить
концентрацию поля в феррите. Лучшие
резонансные вентили сантиметрового
диапазона в полосе частот ~20% имеют
Рис. 5.15. Резонансный вентиль прямые потери 0,2—0,3 дБ и вентильное
142
Поглощающая /глас/пина
Рис. 5.16. Вентиль,
использующий эффект «смещения поля»
отношение—отношение обратных
потерь к прямым — более 100.
Коаксиальный и полосковый
волноводы (с волной квази-ТЕМ) являются
весьма широкополосными, и для
создания широкополосных вентилей
необходимо лишь обеспечить выполнение
условия ферромагнитного резонанса во
всей полосе частот. Этого можно
добиться, например, применением
постоянных магнитов с сильно
неоднородным полем. Полоса таких вентилей может превышать октаву при
прямых потерях 0,2—0,4 дБ и вентильном отношении ~50.
Конструкция вентиля «со смещением поля» на прямоугольном
волноводе показана схематически на рис. 5.16. Размеры и положение
ферритовой пластины и величина постоянного магнитного поля
выбираются такими, чтобы в месте расположения поглотителя
электрическое поле прямой волны было равно нулю. Выше
отмечалось, что «выталкивание» одной из волн из феррита наиболее
эффективно происходит при ц±<0, выполнение этого неравенства
является условием хорошей работы вентиля со смещением поля.
Ширина полосы частот вентилей со смещением поля ограничена
зависимостью структуры поля в волноводе от частоты и оказывается
меньшей, чем для резонансных вентилей. Прямые потери составляют
0,1—0,3 дБ, обратные достигают 30 дБ.
Явление невзаимного смещения поля может быть использовано
для создания и других невзаимных устройств, например, вентилей
и циркуляторов на полосковых волноводах, которые получили
название приборов с поверхностной или краевой волной [41].
Остановимся кратко на ферритовых фазовращателях с поперечно-
намагниченным ферритом. Простейшим невзаимным фазовращателем
такого типа является рассмотренный выше прямоугольный волновод
с ферритовой пластиной, расположенной вблизи плоскости круговой
поляризации магнитного поля. В этом случае постоянное магнитное
поле сильно отличается от резонансного—меньше или иногда больше
его. Тогда величины k"y оказываются достаточно малыми при
необходимых значениях невзаимной разности постоянных
распространения Ыс'у. Взаимный фазовращатель реализуется при расположении
ферритовой пластины в центре волновода или при использовании
двух симметрично расположенных пластин, намагниченных в одном
направлении (см. рис. 5.10).
На рис. 5.17 приведена конструкция «тороидального» невзаимного
фазовращателя с поперечно-намагниченным ферритом. Вследствие того,
что ферритовый образец представляет собой в этом случае замкнутый
магнитопровод, управление его намагниченностью, а следовательно,
" Поля большие резонансных («зарезонансные»), используются при низких
частотах с целью устранения так называемых начальных потерь, обусловленных
естественным ферромагнитным резонансом (§ о.з).
143
Управляющий
ток
Рис. 5.17. Ферритовый фазовращатель
с магнитной памятью. Стрелками
показано одно из двух направлений
намагниченности ферритового тороида
фазовым сдвигом может
осуществляться с помощью
небольшого тока (порядка 1 А),
протекающего по проволоке.
Такой фазовращатель обычно
используется в качестве
прибора с «магнитной памятью» —
он может управляться
микросекундными импульсами тока.
Фазовые сдвиги тороидального
фазовращателя могут быть
рассчитаны на модели,
представляющей собой отрезок
волновода с двумя противоположно намагниченными пластинами (см.
рис. 5.10). Типичные параметры «тороидальных» фазовращателей:
полоса частот 10%, потери (при фазовом сдвиге 360°) 0,5—1 дБ.
§ 5.3. Резонаторы с гиротропными средами
Перейдем теперь ко второй фундаментальной задаче
электродинамики систем с гиротропными средами—задаче о колебаниях
электромагнитного резонатора, заполненного целиком или частично такой средой.
Собственные колебания. Рассмотрим полый резонатор, ограниченный
металлическими стенками и содержащий среду, тензорные параметры
которой ё и р являются функциями координат. Пренебрежем
диссипацией энергии, т. е. будем считать тензоры ё и р эрмитовыми
(§ 4.1), а проводимость стенок резонатора—бесконечно большой.
Комплексные амплитуды е„ И4*п„ поля собственных колебаний
резонатора должны удовлетворять уравнениям Максвелла (4.13)
и (4.15) при jCT = 0 и граничным условиям (4.4). Таким образом:
rotev = — |ihv, rothv= —eev
с с
evxno = 0, nophv = 0 на S,
(5.18)
(5.19)
где n0 — единичный вектор нормали к поверхности резонатора 5.
Каждой паре функций hv и ev соответствует собственная частота
cov, индекс v имеет смысл номера типа колебаний.
Если ё и р являются симметричными тензорами (в частности,
скалярами), компоненты которых при отсутствии диссипации
вещественны, то ev и hv удовлетворяют уравнениям (5.18) с вещественными
коэффициентами и могут быть приняты вещественными. Им
соответствуют колебания, представляющие собой стоячие волны. Если
же тензоры ё или р имеют антисимметричные компоненты, мнимые
в отсутствие диссипации, то собственные функции будут
комплексными. Это означает, что поле собственных колебаний в резонаторе
с гиротропной средой в общем случае не является полем стоячих
волн. Однако собственные частоты, как и следовало ожидать,
оказываются вещественными [66].
144
Вынужденные колебания.
Рассмотрим возбуждение в полом резонаторе
гармонических колебаний с частотой
со, заданными (сторонними) токами jCT,
зарядами рст, намагниченностью тст и
внешними полями, имеющими на
отверстиях резонатора St (рис. 5.18)
касательную составляющую
электрического поля Ест и нормальную
составляющую магнитной индукции Вст.
Уравнения Максвелла и граничные условия Рис- 5.18. Возбуждение колеба-
_ ' нии в резонаторе
запишутся следующим образом: ^
rote+i7c0ph = — /4п/с0тст, (5.20)
div(ph)=-4ndivmCT, (5.21)
4тг
roth— ik0ee=—jCT, (5.22)
с
div(ee) = 4npCT, (5.23)
n0x(exn0) = ECT. n0ph = £CT на Su
n0x(exn0) = 0, n0ph = 0 на 50-S,.
Комплексные амплитуды е и h поля вынужденных колебаний
можно искать в виде [66]
ас со
е= X svev-Vi]/e; h= V Ж vhv —V\|/ft, (5.25)
v=1 v=l
где ev и hv—введенные выше собственные функции резонатора,
а коэффициенты <fv, Жv и градиентные функции V\|/e и Vi]/;, подлежат
определению.
Коэффициенты <fv и Ж^ можно найти, используя соотношения
ортогональности и нормировки [66]:
J ellV\\it.clV= j h;pViMP=0, (5-26)
J e;eev-rfK= J h*vphv.rfF=Avv., (5.27)
где дельта-символ Кронекера
Avv = {i ПРИ V:V; (5-28)
[0 при v#v .
Умножим первое выражение (5.25) скалярно на ё и затем на
е„, а второе—на р и h„, проинтегрируем по объему резонатора
и учтем соотношения (5.26) и (5.27). В результате найдем
<fv=|e*veerfF, Жv= J h*vphrfF. (5.29)
10 А. Г. Гуревич, Г. А. Мелков 145
Умножая (5.20) скалярно на h'v, а (5.22)—на ej, и интегрируя по
объему резонатора, получим после преобразований, в ходе которых
используются формулы (5.29) и граничные условия и учитывается,
что тензоры рис эрмитовы:
£v=(- /co/v+covFv - /cocov (7v)/(co I - со2), (5.30)
^v = (cov/v + /coFv + co2Gv)/(co2-co2), (5.31)
где
/v = 4n|eIjCTrfF, (5.32)
Gv = 4n$hlm„dV, (5.33)
Fv = с | (h> ECT)n0 dS. (5.34)
So
Если потери в среде невелики (ц"«;|я', |Ло<Цв и т- Д-). то учет
их приближенно может быть произведен путем замены в (5.30)
и (5.31)
av->a'v+i(u'C=a'v+ia'J(2Qv), (5.35)
где Qv—добротность резонатора для v-ro типа колебаний,
обусловленная потерями в среде.
Волноводные резонаторы. Волноводный резонатор
представляет собой отрезок волновода, ограниченный двумя торцевыми —
перпендикулярными оси волновода металлическими плоскостями.
На этих плоскостях касательные составляющие суммарного
электрического поля падающих и отраженных волн должны обращаться
в нуль. Ясно, что это условие для одного типа волны может
быть выполнено только в случае взаимности структуры
электрического поля этой волны, т. е. независимости ее от
направления распространения. В этом случае, если постоянная
распространения тоже взаимна, то условие для собственных частот резонатора
имеет вид:
к(а) = пр/1; р=1, 2, 3 (5.36)
где к(а>) — постоянная распространения в волноводе, а
/—длина резонатора. В общем же случае граничные условия на
торцевых стенках волноводного резонатора могут быть удовлетворены
лишь «при участии» бесконечного числа нормальных волн
волновода, образующих в результате поле собственного колебания
в резонаторе.
Рассмотрим примеры волноводных резонаторов с гиротропными
средами, для которых распределение электрического поля взаимно
и собственные колебания можно рассчитать строго, используя
соответствующие решения волноводных задач. Один из них — это
прямоугольный резонатор, заполненный гиротропной средой, который можно
рассматривать как отрезок прямоугольного волновода (см. рис. 5.6)
146
длиной /. Как было показано в § 5.2, в таком
волноводе существуют волны ТЕя0, для
которых распределение электрического поля и
постоянная распространения взаимны. Используя
уравнения (5.36) и (5.12), можно получить урав-
HiK
£л
12 3 ""vo
Рис. 5.19. Зависимость собственных частот
прямоугольного резонатора, заполненного
поперечно-намагниченным ферритом
(сплошные линии), от величины постоянного
магнитного поля. Штриховые
линии—невозмущенные частоты резонатора (cov0) и
феррита (сох); шм=0,5юу0
нение для собственной частоты резонатора cov [128]:
2Ро
со
WvO.
сод(сод+сом)-сОу
(сон+сом)2-со?
Рис. 5.20.
Цилиндрический резонатор с
продольно -
намагниченным ферритовым
стержнем
(5.37)
где covo = (с/ч/ен)%/(ил/а)2 + (рп/[)2 — собственная частота
прямоугольного резонатора, заполненного изотропной средой с той же
проницаемостью б и и ц=1. Зависимость cov от сон приведена на рис. 5.19.
Она напоминает график Вина для собственных частот связанных
колебаний [158]. Таким образом, резонатор с ферритом можно
трактовать как колебательную систему, состоящую из двух
взаимодействующих подсистем: резонатора и феррита.
Строго может быть решена задача о колебаниях еще одного
волноводного резонатора—цилиндрического, представляющего собой
отрезок круглого волновода с продольно-намагниченным ферритом
(рис. 5.20). Для такого волновода (см. § 5.1) структура электрического
поля и постоянная распространения взаимны, и для расчета
резонатора, как и в предыдущем примере, может быть использовано
уравнение (5.36). Зависимость собственных частот от постоянного
магнитного поля будет содержать в этом случае не две, как
в предыдущем примере, а четыре ветви. Это объясняется тем, что
право- и левополяризационные волны в круглом волноводе имеют
разные постоянные распространения, а следовательно, колебания
резонатора с зависимостями от азимутального угла ехр( — гср)
и ехр(/ср)— разные собственные частоты. Интересно отметить, что
расталкивание ветвей больше для колебания с ехр (— icp), т. е. с правым
(относительно направления постоянного намагничивания) вращением;
ю* 147
в этом случае (на языке связанных колебаний) резонатор сильнее
взаимодействует с ферритом.
Обобщение метода связанных колебаний. В рассмотренных выше
примерах резонатор с ферритом можно было трактовать как
связанную систему электродинамических колебаний резонатора с
колебаниями намагниченности феррита. Покажем теперь, следуя Олду [231],
что такая трактовка возможна в весьма общем случае. Перепишем
уравнения для собственных колебаний (5.18), опустив индекс v, в виде,
подобном (5.20) и (5.22):
rote + //r0h=-/A-04nm, roth-/'A-0ee = 0. (5.38)
Эти уравнения можно рассматривать как уравнения вынужденных
колебаний резонатора с изотропной средой, возбуждаемых
намагниченностью т. Совместно с уравнением движения
намагниченности под действием поля h (1.41) они представляют собой
систему уравнений, описывающих связанные колебания резонатора
и феррита.
С учетом (5.25) уравнение (1.41) примет вид
гсот+утхН0 + уМ0хУ\]/,,= -уМох£,#'Х. (5.39)
V
Выражение (5.31) в данном случае, когда /V = FV = 0, с учетом (5.33)
запишется
Жv = -^4 f KmdV, (5.40)
|де интегрирование проводится по объему ферритового образца.
Итак, система уравнений (5.38), (1.41) свелась к системе (5.39),
(5.40). В ней hv и cov—собственные функции и частоты резонатора
с изотропной средой, а со — искомая частота связанных колебаний
такого резонатора и ферритового образца. Его намагниченность
m может быть в свою очередь представлена в виде бесконечной
суммы собственных функций. Если размеры образца достаточно
малы (по сравнению с длиной волны в среде с той же е), то эти
собственные функции являются магнитостатическими типами
колебаний, которые будут исследованы в § 6.3.
Бесконечная система уравнений (5.39) и (5.40) является строгой,
но найти ее точные решения затруднительно. Приближенные решения
можно получить, ограничиваясь учетом конечного числа собственных
типов колебаний резонатора и образца, наиболее сильно
взаимодействующих друг с другом.
Ферритовые резонаторы. Наряду с полыми резонаторами широкое
применение в технике СВЧ получили открытые диэлектрические
резонаторы [94], которые представляют собой свободные (неметал-
лизированные) диэлектрические образцы с е:»1. Изложенная выше
теория связанных колебаний применима и к открытым резонаторам,
состоящим из диэлектрических и ферритовых образцов. Однако
наибольший интерес представляют открытые резонаторы,
образование
ные самими ферритовыми образцами. Связанные колебания феррита
и открытого диэлектрического резонатора, которым является сам
ферритовый образец, называются магнитодинамическими колебаниями.
Во всех экспериментальных исследованиях ферромагнитного резонанса
в слабопроводящих веществах наблюдаются именно такие колебания.
Рассмотрение ферромагнитного резонанса в § 1.5, при котором это
обстоятельство игнорировалось, приближенно справедливо только
для малых образцов — с размерами много меньшими, чем ясДсОу/е)
(что, конечно, отмечалось в § 1.5).
Частота магнитодинамических колебаний ферритовой сферы была
рассчитана методом связанных колебаний—с помощью системы
(5.39), (5.40) [94]. При этом учитывались только однородные колебания
намагниченности и два сильно взаимодействующих с ними нижних
вырожденных типа колебаний диэлектрической сферы, частоты
которых (см., например, [94]) при е»1 сй1=яс/(Лх/е), где R—радиус
сферы. Учет только этих типов колебаний допустим при частотах,
далеких от частот других — высших типов колебаний, в частности,
при частотах, меньших или порядка coi. He останавливаясь на
вычислениях, приведем выражение для резонансной величины внешнего
поля магнитодинамических колебаний ферритовой сферы
со 4 со
//гс„ = - + -г4яМ0^—
(5.41)
Как видно из этого выражения, «обычное» условие ферромагнитного
резонанса в сфере #res = co/y справедливо лишь приближенно (хотя
и с хорошей точностью) при co<k:cui. Результаты расчета по формуле
(5.41) для конкретного случая довольно большой ферритовой сферы,
а также экспериментальные данные приведены на рис. 5.21.
Г,ГГц
Рис. 5.21. Спектр колебаний сферы ЖИГ
[393]. Диаметр сферы 2Л=3,72 мм.
Сплошные линии—теоретическая зависимость
(5.41), точки—эксперимент, штриховая
линия— «киттелевская» частота однородного
резонанса при Л->0
Z
>>"е0
£
2*0 ,
1
i
2R
^■ч
1
•
Рис. 5.22. Малая ферри-
товая сфера в
цилиндрическом резонаторе
149
Для низких частот или малых сфер (co<s:coi) из (5.41) приближенно
следует
#rcs = (и/у) + (4/я4)4я М0 е (ко R)2. (5.42)
Заметим, что влияние размеров образца на частоту ферромагнитного
резонанса (точнее—магнитодинамических колебаний) может быть учтено
и по-другому — путем решения уравнений Максвелла методом
последовательных приближений (см. § 6.1). Таким метолом Хард [332] получил
Яге8 = (со/у)+^4лЛ/0(Е + 5)(А'0/?)2. (5.43)
При е»1 это выражение отличается от (5.42) лишь множителем,
близким к 1. В отличие от (5.42) оно верно при произвольных е,
но, так же как (5.42), только для малых сфер. Формула же (5.41)
свободна от этого ограничения, но справедлива только при е»1.
Расчет методом возмущений. Если объем ферритового образца
много меньше объема полого резонатора V0, то для нахождения
собственных частот и добротностей резонатора может быть
использован метод возмущений с квазистатической аппроксимацией
внутреннего поля (§ 4.5). Приведем пример применения этого
метода"—рассмотрим цилиндрический резонатор (рис. 5.22) с типом
колебаний ТЕ„шр и малой ферритовой сферой на его оси. Если
сфера намагничена в направлении оси резонатора, то в качестве
невозмущенных колебаний следует принять колебания с круговой
поляризацией (т. е. с полем, бегущим по азимуту), потому что они
останутся собственными колебаниями и при наличии намагниченного
ферритового образца. Для таких колебаний составляющие
невозмущенного (внешнего) поля можно записать следующим образом [64]:
Ar = x2Z\|/x, h1=(dZ/dz)S7)\il, e = k0Zz0 х V\|/x.
Здесь Z=sin/crz, \|/х=У|т|(хр)ехр(гтф), kz = np/l, a y.R0—и-й корень
уравнения J[mi(xRo) = 0. Используя формулу (4.81) и таблицу 4.1,
получим, например, для колебаний ТЕ1И
со—шп я3
-=-SA~
ш lR2o
л Yp±H„-I 2ng е-] . 2ng
— I rCosz— sin2 —
kJJ H±P„ + 2 / £ + 2 /
(5.44)
где знаки + соответствуют ш = + 1, т. е. правому и левому вращению
поляризации. Заметим, что если сфера будет намагничена
перпендикулярно оси резонатора (собственными колебаниями —
невозмущенным и возмущенным—в этом случае являются колебания с линейной
поляризацией), то \х±\хв в (5.44) заменится на ц .
Использование резонатора с ферритом при измерениях. Полые
резонаторы с малыми ферритовыми образцами могут быть
использованы, как предложил Никольский [166] (см. также [69]), для
измерения компонент тензора р и е ферритов. В случае
поликристаллических ферритов независимых комплексных параметров
' Ряд других примеров рассмотрен в [66,69].
150
будет четыре: ц, ца, щ и е, и для их определения необходимо
измерить изменения резонансной частоты и добротности резонатора
при помещении в него образца в четырех независимых опытах.
Например, в рассмотренном выше случае сферы в цилиндрическом
резонаторе с колебанием ТЕИ1 (рис. 5.22) при g = l/2 и продольном
и поперечном намагничивании будут найдены вещественные и мнимые
части ц, ца и цц. Для определения е достаточно провести измерения
при g=0, либо при том же положении сферы, как и для остальных
опытов, но при постоянном поле, много большем резонансного.
Резонаторы с малыми ферритовыми образцами используются
и для измерения параметров ферромагнитного
резонанса—резонансного поля и ширины линии с целью, например, изучения
кристаллографической анизотропии (§ 2.3) или процессов релаксации (гл. 11 —
14). В этом случае вторым членом (с Ае) под интегралом в (4.81)
обычно можно пренебречь либо потому что он мал, либо потому
что измеряется приращение частоты по отношению не к частоте
пустого резонатора, а к частоте резонатора с образцом вдали от
резонанса. Первый член (с Ар) в формуле (4.81) может быть
преобразован с учетом соотношения (4.93), и эта формула примет вид
со—со0 2л
у,
KrKdV. (5.45)
Приращение частоты связано теперь с компонентами внешнего тензора
восприимчивости.
Рассмотрим случай, когда образец находится в области линейно
поляризованного внешнего переменного магнитного поля
(направленного, например, по оси х), а размер образца настолько мал, что
зто поле в объеме образца можно считать не зависящим от
координат. Тогда из (5.45) после учета соотношения (4.82) и разделения
вещественной и мнимой частей получатся следующие формулы для
приращений резонансной частоты и добротности резонатора:
to>=-2mo0ci(VJV0)xl'. 8(l/Q) = 4nct(VJV0)Xi \ (5.46)
гДе X*—диагональная компонента тензора х*%
a = (V0\h0\2V\\h0\2dV, (5.47)
Vt—объем образца, a V0 — объем резонатора. Множитель а легко
может быть рассчитан для резонаторов простой формы. При помещении
образца в пучность магнитного поля прямоугольного резонатора
с волной ТЕп0 а = 2; для других резонаторов выпуклой формы а~2.
§ 5.4. Волноводные сочленения с ферритовыми образцами
В этом параграфе мы рассмотрим задачи о ферритовых образцах
в волноводах и волноводных сочленениях. Простейшей задачей такого
типа является задача о ферритовом эллипсоиде в регулярном
волноводе [68] (см. также [69]).
151
Ферритовый эллипсоид в волноводе; метод самосогласованного
поля. Постановка задачи заключается в следующем: в регулярном
волноводе находится эллипсоид с параметрами р и е, задана
амплитуда падающей на него волны, требуется найти
электромагнитное поле в волноводе вдали от эллипсоида. Метод возмущений
в том его варианте (§ 4.5), когда в качестве внешнего поля,
действующего на образец, принимается заданное поле волновода, не
дает корректного решения этой задачи. Для того чтобы получить
такое решение, нужно учесть «обратную реакцию» образца, т. е.
предположить, что его намагниченность определяется
самосогласованным полем, являющимся суммой заданного поля падающей волны
h0 и поля излучения образца в волновод пи. Если образец представляет
собой эллипсоид и выполняется условие (4.92) применимости
квазистатического приближения, то намагниченность (которая
предполагается однородной)
m=xe(ho+h„), (5.48)
где хе — внешняя восприимчивость эллипсоида (§ 1.5), а шачения
полей берутся в точке, где находится центр образца. Поле излучения,
т. е. поле, возбуждаемое в волноводе намагниченностью образца,
можно записать в виде
h„ = rwm, (5.49)
где w—некоторый тензор, зависящий от формы и размеров волновода
и образца, расположения образца в волноводе и частоты. Для
вычисления коэффициентов прохождения и отражения достаточно
исключить намагниченность из выражений (5.48) и (5.49), найдя
таким образом связь h„ и h0.
Поле излучения, вообще говоря, может быть представлено в виде
суммы нормальных волн и ближних (нераспространяющихся) полей
волновода. Но если в волноводе распространяется волна только
одного типа, то можно учесть только эту волну: учет быстроза-
тухающих ближних полей в выражении (5.48), справедливом для
случая однородного поля, не имеет смысла.
Предположим для
определенности, что образец находится на
оси прямоугольного волновода
(рис. 5.23), в котором может
распространяться только волна ТЕю-
Поперечная составляющая
магнитного поля этой волны с
единичной амплитудой
Л0 х = sin (юг /а) ехр (—ikyy). (5.50)
Явный вид выражения (5.49) мо-
'у жет быть найден в результате
Рис. 5.23. Намагниченный феррито- Решения задачи о возбуждении
вый эллипсоид в прямоугольном вол- волновода заданной намагничен-
новоде ностью [64]. Не приводя этого
152
решения, запишем сразу выражение для поперечной составляющей
магнитного поля в интересующем нас случае расположения малого
ферритового образца на оси волновода:
Кх= -iwmxsin(nx/a)exp(+ikyy), (5.51)
где
w=4nF1A:J,/S)
(5.52)
S—площадь поперечного сечения волновода, a V1—объем образца.
Подставляя (5.50) и (5.51) при х — а\2 и ^ = 0 в проекцию (5.48) на
ось х, находим тх и затем поле излучения
h„x =
1+z'wx
: sin (nx/a) ехр (+ iky у),
(5.53)
где хе—поперечная диагональная компонента тензора %е.
Коэффициент отражения, отнесенный к сечению волновода, в
котором находится центр образца,
а коэффициент прохождения, отнесенный к тому же сечению,
(5.54)
£> =
M.y=0)+Mz=°)_ 1
Ло*(.у = и) 1+iwx''
Отношение мощности, поглощенной образцом, к
падающей волны
T=l-\r\2-\D\2.
При ферромагнитном резонансе (хс'^0, хе"==Х"ю)
-Я „ 1 2?
г =
J res
1 + <7
£>г,
1+?'
Т"° (i+?)2'
где
? = wx"es = 4nF1/cyx;'es/S.
(5.55)
мощности
(5.56)
(5.57)
(5.58)
Величину q можно назвать коэффициентом связи ферритового
резонатора с волноводом. Зависимости Гги, Z)res и Ties от
q приведены на рис. 5.24. Из этого рисунка видно, что при
Рис. 5.24. Зависимость
коэффициентов отражения Г„, и
прохождения Drcs и относительной
поглощенной мощности ТТСВ в
прямоугольном волноводе с
ферритовым эллипсоидом на
его оси от коэффициента связи
Рис. 5.25. Ферритовый эллипсоид в
закороченном прямоугольном волноводе
увеличении коэффициента
связи, т. е. увеличении
объема образца или сужении
его резонансной кривой
|Гге8|-1, Й^Ои Г-0.
Результаты
аналогичного расчета для образца,
расположенного в произвольной
точке прямоугольного
волновода, приведены в [30].
При расположении образца
в точке правой круговой
поляризации магнитного поля
Гге8 = 0, a Du
при
увеличении q стремятся соответственно к 1 и к нулю. Полное
поглощение (Гге8=1, Z)res = 0) имеет место в этом случае при q=\.
Эллипсоид в закороченном волноводе. В этом случае (рис. 5.25)
внешнее поле h0 в выражении (5.48) представляет собой сумму поля
падающей волны и поля волны, отраженной от плоскости короткого
замыкания y=—d. С учетом граничных условий на этой плоскости
h0x(x=a/2, y = 0) = 2coskyd. (5.59)
Поле излучения Ия будет являться суммой полей первичной волны,
возбужденной намагниченностью образца, и волны, отраженной от
короткого замыкания. Проделав такие же вычисления, как для
бесконечного волновода, мы получим, что коэффициент отражения
при резонансе, отнесенный к сечению волновода, где находится
образец, при kyd=nn (и = 0, 1, 2, ...)
rtes = (l-2q)/(l+2q). (5.60)
Эта величина обращается в нуль при q—l/2 и стремится к —1 при
увеличении размера образца или сужении его резонансной кривой.
Связь скрещенных волноводов. Перейдем теперь к несколько
более сложной задаче о ферритовом эллипсоиде, расположенном
в отверстии, которое соединяет два волновода, причем в отсутствие
эллипсоида связь между волноводами отсутствует. Рассмотрим
для определенности два скрещенных прямоугольных волновода
(рис. 5.26) с отверстием в середине широких стенок и ферритовым
эллипсоидом в центре отверстия. Предположим, что в объеме
образца магнитное поле однородно и является суммой полей волн
ТЕ10 в обоих волноводах у их общей стенки в отсутствие отверстия.
Конечно, это предположение не выполняется точно, но оно дает
возможность просто решить задачу; сложный учет действительной
конфигурации поля в отверстии не изменит качественных
результатов решения.
В данном случае на основании (5.48) можно записать (см. рис. 5.26)
mx = %e{hoxi.+Kxi) + i%l(hoy2+Ky2),
my=-i%l(h0xl+huxl) + %e(h0y2 + huy2).
154
(5.61)
ПвоЬ
-Wi
Рис. 5.26. Ферритовый
эллипсоид, связывающий два
скрещенных волновода
Здесь h0xl и h0y2—заданные поля
падающих волн соответственно в первом и
втором волноводах в точке, где находится
центр образца, а Аях1 и hBy2—поля
излучения в этих волноводах в той же точке.
12
0,1 0,2 0,5 1
Рис. 5.27. Зависимость
коэффициента прохождения в закороченных
скрещенных прямоугольных
волноводах от коэффициента связи
Поступая далее аналогично исследованному выше случаю одного
волновода, легко найти все интересующие нас характеристики
рассматриваемого волноводного сочленения. Например, для случая
эллипсоида, связывающего два скрещенных закороченных волновода,
выражение для резонансного коэффициента прохождения при
расположении эллипсоида на одинаковом расстоянии d от плоскостей
короткого замыкания в обоих волноводах имеет вид [68]:
DTa,=
Щ cos2 kyde-M>"
l+4qcoskyde-ik'd'
(5.62)
Зависимость Dres от q в этом случае приведена на рис. 5.27. Теперь
с увеличением параметра связи |Z)res|-»l, т.е. ферритовый образец
достаточно больших размеров или с достаточно узкой резонансной
кривой переизлучает почти всю мощность во второй волновод.
Ферритовые фильтры. С использованием ферритовых образцов
в волноводах могут быть созданы СВЧ фильтры [94],
перестраиваемые в широких пределах путем изменения внешнего постоянного
магнитного поля.
Образец в бесконечном волноводе обладает свойствами полосно-
запирающего фильтра с центральной частотой, равной резонансной
частоте образца. Если он, как в рассмотренном выше примере,
расположен на оси прямоугольного волновода, то такой фильтр
реализуется (см. рис. 5.24) при 0»1, причем он является отражающим,
так как при q ->со поглощение в образце отсутствует, а |Гги|-»1.
Поглощающий полосно-запирающий фильтр можно осуществить,
поместив образец в точке круговой поляризации магнитного поля.
Поскольку феррит взаимодействует только с той волной, для которой
155
2,3
Рис. 5.28. Ферритовый
фильтр-цирку лятор
те0 эта поляризация—правая, такой фильтр
является невзаимным. При подаче мощности
на одно из его плеч он обладает амплитудно-
частотной характеристикой полосно-запира-
ющего фильтра, а энергия из другого плеча
проходит без отражения и поглощения.
Максимальное поглощение в этом случае имеет
место, как уже отмечалось, при q=l.
Рассмотренные выше сочленения двух
закороченных волноводов с ферритовым
образцом в отверстии связи представляют собой
полосно-пропускающие фильтры. Как видно из
рис. 5.27, малые потери в них при резонансе,
т. е. в центре полосы пропускания,
достигаются при <?:»1. Если же образец разместить
в точке круговой поляризации магнитного
поля, то минимальные потери (как и
максимальное поглощение в полосно-запирающем
фильтре) будут иметь место при д=1.
Невзаимность, проявляющаяся при расположении образца в точке
круговой поляризации магнитного поля, позволяет реализовать
фильтр-цирку лятор, показанный на рис. 5.28. Пусть мощность
подается в плечо 1 этого устройства. В точке расположения образца
магнитное поле падающей волны имеет правую круговую поляризацию
(как всегда, относительно направления Не0)- Образец возбуждает
волну в верхнем (на рис. 5.28) волноводе, распространяющуюся только
в том направлении—к плечу 2, для которого магнитное поле имеет
в точке расположения образца тоже правое вращение. Отраженной
волны в плече 1 не будет, а при q~\ не будет и прохождения энергии
в плечо 4. Легко убедиться, что мощность из плеча 2 будет проходить
в плечо 3, из плеча 3— в плечо 4, а из плеча 4—в плечо 1, т. е.
рассматриваемое устройство является циркулятором. В то же время
оно обладает свойствами полосно-пропускающего фильтра, который
может перестраиваться при помощи изменения внешнего постоянного
магнитного поля.
Для создания ферритовых фильтров используются, кроме
прямоугольных, и другие волноводы (см., например, [94]). Широкое
распространение получили коаксиальные фильтры с витковыми элементами
связи (рис. 5.29). Плоскости входного и выходного витков
перпендикулярны, и передача мощности со входа фильтра на выход возможна
лишь в результате переизлучения энергии ферритовым образцом,
обычно—сферой. Из-за того, что коаксиальный волновод и витки
характеризуются малой частотной зависимостью параметров,
перестройка таких фильтров возможна в широких пределах—до
нескольких октав. Их рабочие частоты лежат в очень широком диапазоне—
приблизительно 0,1—20 ГГц.
Потери ферритовых полосно-пропускающих фильтров на
центральной частоте полосы пропускания составляют в случае одного
ферритового образца 0,5—1 дБ, а ширина этой полосы—обычно
156
'ео
Ферритобая
сфера
/ zp=0
Рис. 5.29. Коаксиальный ферритовый фильтр
несколько десятков мегагерц. Для увеличения избирательности, т. е.
приближения формы амплитудно-частотной характеристики фильтра
к прямоугольной,
используются фильтры с двумя, тремя
и более ферритовыми
образцами [94].
Матрица рассеяния.
Перейдем к исследованию некоторых
общих свойств волноводных
сочленений, содержащих фер-
ритовые образцы. Применим В,
для этого метод анализа,
основанный на использовании
матрицы рассеяния [128].
На рис. 5.30 изображено
волноводное сочленение
с и плечами. В каждом из них
могут иметься падающие и отраженные от сочленения волны, поля
которых можно записать в виде
Рис. 5.30. Многоплечевое волноводное
сочленение
е„+=Лр<Уре-
--ВрЖр&к->*>
(5.63)
..р =АрЖре-к->*', К
где Sp и ^fp—собственные функции волноводов (см. § 4.5),
являющихся плечами сочленения.
Предполагая линейность сочленения, можно записать:
В,
= 15
pqAq
или в матричной форме:
где \\А\\
II В\\ = 11511 Ml
(5.64)
(5.65)
Ар и Вр, а || 5||
и ||В||— матрицы-столбцы, образованные амплитудами
квадратная матрица рассеяния
Ц5|| =
Si.
^2n
(5.66)
157
величина Spp представляет собой коэффициент отражения от р-то
плеча при отсутствии падающих волн во всех остальных плечах,
т. е. при отсутствии в этих плечах источников и несогласованных
нагрузок, a Spq—коэффициент прохождения из д-то плеча в р-е
(а не наоборот!) при отсутствии падающих волн во всех плечах,
кроме д-то.
Для сочленения без потерь матрица ||S|| унитарна,}, а для
взаимного (см. § 4.3) сочленения—симметрична (SPt=Sqp). Для
невзаимного сочленения
8SptsStp-Spq*0. (5.67)
Для вычисления невзаимной разности коэффициентов прохождения
&Spq воспользуемся соотношением (4.62). Представим в нем поля
с индексами (1) и (2) в виде сумм полей падающих и отраженных
волн, учтем (5.63) и предположим, что для процесса (1) падающая
волна имеется только в плече /, а для процесса (2)—только в плече
т. Тогда из (4.62) получим
bSlm=\j0l{A^A^). (5.68)
Таким образом, условием несимметрии матрицы рассеяния, т. е.
невзаимности сочленения является неравенство нулю интеграла Ja.
Свойства невзаимных сочленений. Начнем с простейшего—двух-
плечевого сочленения, многие частные случаи которого
рассматривались выше. В отсутствие потерь в силу условия унитарности
матрица рассеяния такого сочленения должна иметь вид:
1|5|| =
y/l-a2e'" ae'b***
-ае'(Р+ф) ^/l-a^e^l
(5.69)
где а, а, Р и ф—произвольные (а<1) действительные числа.
Как видно из (5.69), двухплечевое сочленение без потерь может
быть невзаимным, но модули коэффициентов прохождения
5*21 и 5*12 всегда одинаковы. Это означает, что такое сочленение не
может быть вентилем, оно может быть лишь невзаимным
фазовращателем. Матрица идеального вентиля (51i = S'i2 = 522 = 0, 15*211 = 1)
неунитарна, и устройство, обладающее такой матрицей, может быть
реализовано только при наличии потерь. Из (5.69) следует еще один
интересный вывод: поскольку |5ц| = |522|, согласование произвольного
двухплечевого сочленения без потерь со стороны одного плеча
приводит к согласованию и со стороны другого.
Перейдем к анализу трехплечевых сочленений. Нетрудно
убедиться, воспользовавшись унитарностью матрицы ||S||, что никакое
взаимное трехплечевое сочленение без потерь не может быть со-
комплексно-сопряженная с II 511 (с элементами И* Т^Л> • 1$»*—матрица,
матрица (диагональная сЭлементамиMf™$.{S)"=S^ а IIЛ|-единичная
158
гласовано одновременно со стороны всех трех плеч. Для невзаимного
трехплечевого сочленения без потерь это может быть выполнено,
и такое сочленение представляет собой идеальный циркулятор.
Докажем эту важную теорему [128].
Пусть трехплечевое сочленение без потерь согласовано со стороны
всех плеч, т. е.
(5.70)
(5.71)
Si 1 — S22 — 5зз — 0.
Тогда из условия унитарности матрицы Ц5|| следует
5з15з2 = 0, 52i523 = 0, 5i25i3 = 0,
|512|2 + |532|2 = |521|2 + |5з1|2 = |513|2 + |52з12=1.
Для того чтобы выполнить первое из равенств (5.71), положим,
например, 53i=0. Из остальных равенств тогда следует, что
5ц = 512 = 522 = 52з = 5з1=53з=0, а |513| = |521| = |532| = 1. Матрица
с такими элементами представляет собой матрицу рассеяния
идеального циркулятора с направлением циркуляции 1^>2-*3-*1. Если
же положить S32 = 0, то получится матрица циркулятора с
противоположным направлением циркуляции. При изменении направления
циркуляции все невзаимные разности 8Spt изменят знак. Для этого,
как следует из (5.68) и (4.62), необходимо, чтобы изменился знак
рас, что, в свою очередь, произойдет при изменении направления
постоянного намагничивания на обратное. Итак, если трехплечевое
сочленение без потерь согласовано со стороны всех пчеч, то оно
является идеальным циркулятором, а направление циркуляции
определяется направлением намагничивания.
Циркуляторы могут быть созданы с четырьмя и более плечами.
Но в этом случае невзаимности и полного согласования недостаточно
для того, чтобы данное сочленение являлось циркулятором. Требуется
еще наличие определенных фазовых сдвигов между коэффициентами
прохождения в разные плечи [128].
Y-циркуляторы. Симметричные трехплечевые—так называемые
Y-циркуляторы созданы на основе различных волноводов и широко
используются в технике СВЧ. Принцип работы Y-циркулятора на
прямоугольном волноводе (рис. 5.31) можно пояснить следующим
образом. Находящийся в нем ферритовый цилиндр напоминает
ферритовый стержень в цилиндрическом ре- И. , ферри„обьш
зонаторе (см. рис. 5.20). Силовые линии Г цилиндр
электромагнитного поля в нем для не за- ^
висящего от z типа колебаний ТМ110
изображены на рис. 5.32. Как отмечалось
в § 5.3, поле в таком резонаторе является
суммой полей колебаний с правым и левым
вращением поляризации или волн, бегущих
по азимуту в противоположных
направлениях. Для изотропного стержня (рис. 5.32, а)
длины этих волн равны друг другу,
вследствие чего максимум поля будет находиться Рис. 5.31. Y-пиркулятор
159
цилипиу
Рис. 5.32. Структура электрического и магнитного полей вблизи ферритового
цилиндра Y-циркулятора в случае ц„=0 (о) и ц„#0 (б). Римскими цифрами
показано положение плеч
в точке, противоположной центру сечения входного плеча /.
Поступающая из него мощность будет при этом делиться поровну между
плечами // и III. В случае же намагниченного ферритового стержня
длины волн, бегущих по азимуту в противоположных направлениях,
будут различаться, и максимум поля будет смещаться к одному из
плеч II и III, а минимум—к другому. Выбором параметров устройства
(размеров и величины постоянного магнитного поля) можно добиться,
чтобы максимум и минимум поля совпали, соответственно, с центрами
сечений плеч /7 и /// (см. рис. 5.32, б); тогда мощность из плеча
/ будет проходить в плечо II, а плечо III окажется развязанным.
Приведенные выше рассуждения могут быть распространены на
Y-циркуляторы, использующие другие волноводы [2], поскольку из-за
большой величины е ферритов основная часть энергии концентрируется
в ферритовых образцах и конфигурация окружения не играет особенно
существенной роли.
В связи с тем, что Y-пиркулятор, как ясно из качественного
его рассмотрения, является, по существу, резонансным устройством,
полоса его рабочих частот, если не принять специальных мер,
оказывается небольшой. Для ее увеличения можно использовать
ферритовые образцы с сильно неоднородным внутренним магнитным
полем, например, треугольные призмы. В настоящее время полоса
частот Y-циркуляторов достигает ~30%, а в отдельных случаях
и больше, прямые потери составляют менее 0,5 дБ, развязки—более
20 дБ [2, 404].
Глава 6
МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ И КОЛЕБАНИЯ
§ 6.1. Магнитостатическое приближение
В § 4.2 было показано, что в спектре однородных плоских волн 1
в неограниченном ферромагнетике возникают «медленные» ветви—с
малыми фазовой и групповой скоростями и сильной зависимостью
их от постоянного магнитного поля. Подобные ветви имеются
и в спектрах волн в волноводах, содержащих ферро- или ферримаг-
нетики. Как мы убедились в предыдущей главе, решение граничных
задач для систем с гиротропными средами встречает большие
трудности, которые особенно возрастают в областях сильной
дисперсии р, где и существуют медленные волны.
С другой стороны, для таких волн
/с:» Ar0 s со/с. (6.1)
Это позволяет использовать при их анализе метод последовательных
приближений. В нулевом приближении, учитывая неравенство (6.1),
мы пренебрегаем в уравнении Максвелла (4.15) членом ik0ee. Тогда
это уравнение и уравнение (4.14) совпадут по форме с уравнениями
магнитостатики (4.5). Для интересующих нас задач jCT = 0 и эти
уравнения запишутся так:
roth = 0, (6.2)
div(ph)=0. (6.3)
В результате решения этих уравнений с учетом граничных условий
на всех поверхностях раздела сред могут быть найдены h и m = 5Ch,
а также дисперсионные соотношения со(к) для нормальных волн,
собственные частоты резонаторов и т. п. Затем — в первом
приближении по к0/к из уравнений Максвелла (4.13) и (4.16) может быть
найдено электрическое поле е. При рст = 0 и скалярной е эти уравнения
примут вид
rot е = - ik0 р h, div е = 0. (6.4)
Во втором приближении — с использованием полного уравнения (4.15)
могут быть найдены поправки к величинам h и т, дисперсионным
соотношениям и собственным частотам. Волны и колебания, для
которых этот метод последовательных приближений «работает»,
называют обычно магнитостатическими волнами и колебаниями.
Указанное нулевое приближение использовалось в § 1.5 и затем
в некоторой мере — в § 4.5 и гл. 5. При этом рассматривались
11 А. Г. Гуревич, Г. А. Мелков 161
только образцы, представляющие собой эллипсоид (или его предельные
случаи), и было сделано дополнительное предположение об
однородности переменной намагниченности. Это дало возможность
воспользоваться известным решением магнитостатической задачи для
эллипсоида. Теперь нам придется (на этапе нулевого приближения)
решать уравнения Mai нитостатики для других граничных условий
и без предположения об однородности колебаний.
Заметим, что с увеличением к начинает сказываться обменное
взаимодействие. Но в некотором интервале значений /- (он будет
определен ниже) его влиянием еще можно пренебречь. Такие волны
следует называть безобменными магнитостатическими. Но часто их
называют просто магнитостатическими, а магнитостатические с учетом
обмена — спиновыми, хотя и те и другие являются и спиновыми,
и магнитостатическими, и наоборот, чем больше к, тем лучше
применимо магнитостатическое приближение.
Безобменные магнитостатические волны в неограниченной среде.
Рассмотрим сначала такие волны, как предельный случай волн,
исследованных в § 4.2. Если выполняется неравенство (6.1), то
в нулевом приближении в (4.31) можно сохранить только первый
член. Тогда при скалярной е
ц/ц р = - ctg2 9* = - кЦ(к2х + ку) (6.5)
(Qk—угол между к и М0). При ц =1 (ферромагнетик, намагниченный
до насыщения) и в отсутствие потерь из (6.5) с учетом (1.59) следует
co2 = coH(coH + coMsin29k). (6.6)
Из этой формулы видно, что со зависит от направления
распространения и лежит в интервале
юн^ю^ю±гУсОн(юн + юм), (6.7)
в котором ц<0. От волнового же числа к частота не зависит, т. е.
групповая скорость vgr = d(o/dk=0.
Структуру полей рассматриваемых однородных плоских
безобменных магнитостатических волн легко найти, используя обшие результаты,
полученные в § 4.2. В частности, при 9fc = 0 поля h и е—поперечные,
с круговой поляризацией и правым вращением. При 0к = я/2 поле
е параллельно М0, a h параллельно направлению распространения.
Легко убедиться, что в обоих случаях (а также и при промежуточных
значениях вк) средний поток мощности (§ 4.4) равен нулю. Это
коррелирует с тем, что vgr = 0, поскольку скорость переноса энергии
(в отсутствие потерь) совпадает с групповой скоростью.
Затухание рассматриваемых волн (т. е. величина к") оказывается
бесконечно большим при любом конечном параметре диссипации
среды. Это ясно из того, что между к" для стационарной волны
(при со"=0) и величиной со" для затухающих колебаний (при к" = 0)
существует при любом законе дисперсии, но при условии малости
потерь в веществе соотношение
a" = vgrk", (6.8)
162
а величина со" отличается от частоты релаксации сог (§ 1.4) лишь
множителем порядка 1.
Казалось бы, рассмотрение таких волн не имеет смысла. В
действительности существуют три причины, которые приводят к конечной
групповой скорости и «разумным» величинам потока энергии и
затухания магнитостатических волн: неточность магнитостатического
приближения, влияние обменного взаимодействия и влияние граничных
условий (§ 6.2). Однако воздействие их на выражение для спектра
(6.6) в некоторых пределах изменения к оказывается несущественным,
и это выражение может быть использовано при исследовании ряда
важных вопросов.
Одним из них является вырождение (совпадение частот)
однородных колебаний намагниченности и длинноволновых (безобменных)
магнитостатических волн, которое представляет интерес при изучении
процессов релаксации (§ 11.3). Сравнивая (6.6) с формулой (1.97)
для собственной частоты со0 однородных колебаний эллипсоида
в «киттелевском» случае, мы видим, что со0 может либо находиться
в интервале (6.7), либо лежать выше его верхней границы. Условием
того, чтобы со0 лежала в этом интервале, т. е. имело место
вырождение, как легко убедиться, является
Ht0>(N, + NxNyINs)M0, (6.9)
где #со — внешнее поле, a NXyy,z — размагничивающие факторы
образца. Это условие не может быть выполнено в предельном случае
бесконечно тонкого цилиндра, намагниченного вдоль его оси (когда
JVz = 0), и всегда выполняется для нормально намагниченной
бесконечно тонкой пластины (пленки); в последнем случае со0 совпадает
с нижней границей интервала (6.7). В случае сферы условие (6.9)
принимает вид
-)
со0>=сом. (6.10)
Уравнение Уокера. Получим теперь уравнения, которые могут
быть использованы при решении в магнитостатическом приближении
более сложных, граничных задач. Согласно (6.2) можно ввести
магнитостатический потенциал v[/, так что
h = Vv[/. (6.П)
Подставляя (6.11) в (6.3), получим уравнение
div(pVv[/) = 0, (6.12)
которое можно назвать обобщенным уравнением Уокера. Для того
чтобы записать граничные условия, введем локальную систему
координат %, г], С, с осью С,, совпадающей с нормалью к поверхности
S раздела двух сред. Потенциалы в этих средах обозначим v^ и »|'2-
Тогда из общих условий (4.3) следует
*£«*£, £?! = ?!, (PiVvMHUWc на 5. (6.13)
5Е, St, cr\ сг)
12* 163
Покажем прежде всего, что из уравнения (6.12) могут
быть получены выражения (6.5) и (6.6). Для однородной плоской
волны комплексная амплитуда потенциала v[/ = v[/0exp( — /kr) =
= v[/0exp( — ikxx—iky у— ikzz), где v[/0—постоянная величина. Подставляя
ty в (6.12), получим
k(pk)=0. (6.14)
Для р вида (4.22) из (6.14) непосредственно следует соотношение
(6.5), следствием которого при цц = 1 является (6.6). В этом случае
уравнение (6.12) примет вид (в котором оно было первоначально
записано Уокером [445])
'£4 г2\|Л г2(|/
Для монокриспалла, намагниченного до насыщения в направлении
оси z, с магнитной проницаемостью вида (2.42) уравнение (6.12)
запишется следующим образом:
г2(|/ г2х> а2х> е2^
°х Су* дхду 8z
^^г+2^^х:+^г=0- (6.16)
Здесь цх, цу и |J.S имеют вид (2.43), а входящие в них величины
сох, со,, и ifls выражаются согласно (1.119) с заменой (см. § 2.3)
величин Nu, jy22 и дг12 на соответствующие компоненты тензора
анизотропии Na, а УУ3з—на сумму Л'зз-^А'зз- Отметим, что
антисимметричная компонента ца не вошла в (6.15) и (6.16); однако
она войдет в граничные условия (6.13).
Спектр магнитостатических волн в монокристалле. Для однородной
плоской волны, когда v[/ = v[/0exp(—fkr), из (6.16) следует
цх cos2 ф,( + |J.}, sin2 cpk + |J.S sin 2cpk + ctg2 6k = 0, (6.17)
где б* и (pt — углы вектора к в системе координат, в которой ось
z совпадает с направлением М0.мВ этой же системе должны быть
записаны и компоненты тензора N°. Подставляя в (6.17) выражения
(2.43) и решая полученное уравнение относительно со, найдем
со2 = юхюу-ю2 + юм
2(rax + coJ,J+-(coJ[-coJ,)cos2<pt+co1sin2<pt
sin29k. (6.18)
Рассмотрим сначала одноосный кристалл. Предположим что
направления М0 и Н0 совпадают, пренебрежем анизотропией в
базисной плоскости и ограничимся учетом только первой константы
анизотропии Тогда, заменяя в (1.119) в соответствии с табл. 2.1
^у (г,7-1, 2) на Nfj, а величину 7V33 (входящую в со„) на N^+N%,
и подставляя в (1.119) после указанной замены выражения (2 4)
при //„2 = 0, получим согласно (6.18)
Ну)2 = {Н0 + 2НЛ1со&2д0)(Ц0+2НА1со&2%) +
+ 4rcM0[#o + #41(3cos2e0-l-sin2e0cos29k)]sin2ek. (619)
164
Z
Л СЭ"7
\&
"^.А
V
/ /^
^У
Г / 'у
Здесь Hai-KJMo, 60 — угол,
который образуют векторы
Н0 и М0 с осью анизотропии,
а Вк и фк — углы вектора
к (рис. 6.1).
Для кубического кристалла
предположим снова, Что
направления М0 и Но совпадают,
ограничимся учетом первой константы
анизотропии и рассмотрим
важный частный случай, когда
М0 лежит в плоскости {ПО}.
Тогда таким же образом, как для
одноосного кристалла, но под- Рис- 6L Магнитостатическая волна
,, ,,V,. ,, ,,, в одноосном кристалле. Ось анизот-
ставляя в (1.119) выражения (2.51) ропии—z'
при (ро = л/4, получим
(-J = \н0 + НЛ1(~+2ая2В0+^ая«о\ х
х #0 + #,4i(2-cos2eo+-cos4eo] +4пМ0\н0 + НАА -—+-cos260 +
-I—- cos 460 -I-1 cos 260 H—- cos 460 I cos 2cpk > sin2 6k. (6.20)
16 \1б 4 16 J JJ
Здесь б0 — угол, который образуют векторы Н0 и М0 с направлением
<100>, а 6к и фк (рис. 6.2) — углы вектора к. Из рис. 6.3 видно, что
зависимость со от (рк отсутствует, когда М0 направлено по осям
<100> или <1П>, и максимальна, когда Мо||<110>.
Сравнивая выражения (6.19) и (6.20) с (6.6), мы видим, что если
постоянная намагниченность направлена по оси анизотропии
одноосного кристалла или осям <Ю0> или <1П> кубического, то выражения
для частоты магнитостатических волн совпадают с выражением для
Рис. 6.2.
Магнитостатическая волна в кубическом
кристалле
165
Г, ГГц
90 в0, а рад
Рис. 6.3. Зависимости
частоты магнитостатических волн
в кубическом кристалле от
направления М0 при разных
направлениях
распространения; G0—угол между М0 и
осью <100> в плоскости
{ПО}. Л/0=139Гс, Ki =
= 6 103 (ЖИГ при
комнатной температуре), Н0 =
= 2,5 кЭ
am
этой частоты в изотропной среде при замене
Яо-#0 + #А,
(6.21)
где НА = 2НЛ1 для одноосного кристалла и оси <100> в кубическом
4
и (при учете только первой константы анизотропии) НА =—НА1
для оси <111>. Такие же совпадения имели место (см. § 2.3) и в случае
однородных колебаний намагниченности. Они являются проявлениями
общего положения (см. [69]), которое заключается в том, гчто для
данных направлений намагничивания (и только для них) решения
любых электродинамических задач в одноосном или кубическом
кристалле получаются при указанной замене из соответствующих
решений для изотропной среды. Напомним (см. § 2.3), что эти
направления являются направлениями экстремумов угловой
зависимости энергии анизотропии.
Пределы применимости магнитостатического приближения. В
качестве критерия для оценки нижнего (по к) предела применимости
рассматриваемого нулевого магнитостатического приближения можно
принять следующее условие: отличие частоты (6.6) от точного ее
значения, найденного с использованием полных уравнений Максвелла,
не должно превышать некоторой заданной величины 8ю. В качестве
6ю для веществ с узкой резонансной кривой можно принять ширину
резонансной кривой у АН. Тогда сравнивая (6.6), например, при бк = 0
с (4.48), получим
к > kmin = k0y/l yj4nM0 /АН. (6.22)
Для ЖИГ (ДЯ-0.5Э) в десятисантиметровом диапазоне
*п„п-ои см . Для веществ со значительно большими АН, например
поликристаллических ферритов, необходимо, конечно, задаваться
меньшими, чем уАН, значениями бсо.
Оценка (6.22) может быть использована и в случае колебаний
намагниченности в ограниченных образцах (§ 6.3). Под kmin тогда
166
следует понимать величину 2я/4пах> где dmM для неоднородных
колебаний — расстояние, на котором их фаза изменяется на 2л, а для
однородных—размер образца.
В § 7.1 будет показано, что учет обменного взаимодействия
приводит к увеличению частот магнитных волн в ферромагнетике на
величины порядка yDk2, где D—постоянная неоднородного обмена. Из
условия, чтобы yDk2 не превосходила некоторой заданной величины,
например, для монокристаллов — у АН, следует оценка верхнего предела
применимости безобменного магнитостатического приближения:
к<ктЛХ = ^/АН1Б. (6.23)
Для ЖИГ £> = 5,2 1(Г9 и кпах = 6-103 см-1. Таким образом, имеется
некоторый интервал значений к (для ЖИГ приблизительно 102—
104 см-1), в котором для расчета частот магнитных колебаний и волн
с хорошей точностью может быть использовано безобменное нулевое
магнитостатическое приближение—без поправки второго приближения
(первое приближение, необходимое для нахождения электрического
поля, не оказывает влияния на спектры колебаний и волн).
§ 6.2. Магнитостатические волны в пластинах и стержнях
В этом параграфе мы будем исследовать безобменные
магнитостатические волны в системах, в которых имеются границы
ферромагнетика с диэлектриком и металлом.
Нормально намагниченная пластина. Рассмотрим сначала пластину
из изотропного ферромагнетика, ограниченную двумя параллельными
металлическими поверхностями и намагниченную до насыщения
в направлении нормали к этим поверхностям (рис. 6.4). Пусть
направление распространения совпадает с осью у, а зависимость
полей от координаты х отсутствует. Тогда решение уравнения (6.15)
в пластине может быть записано в виде"
ty = (Acoskzz + Bsinkzz)e-iky. (6.24)
При идеальной проводимости металла граничные условия на
поверхностях пластины заключаются в равенстве нулю нормальной
составляющей магнитной индукции:
(pV\l/)no = 0. (6.25)
В данном случае из (6.25) следует d\\rjdz = 0 при z = 0 и z = d.
Накладывая эти условия на решение (6.24), получаем В=0 и
kM = m/d (и = 0, 1, 2, ...). (6.26)
Различным значениям п соответствуют разные типы волн; п
представляет собой число стоячих полуволн потенциала (а следовательно,
и составляющих поля), укладывающихся на толщине пластины.
" Здесь и в дальнейшем мы опускаем индекс (в данном случае у)
у составляющей к в направлении распространения волны.
167
Подстановка (6.24) в уравнение
(6.15) дает
к2=-
-\ik2.
(6.27)
Рис. 6.4. Нормально
намагниченная пластина
Отсюда следует (поскольку
согласно (6.26) кг^О), что
распространяющиеся волны (к2>0), так же как
и в неограниченной среде, возможны
только при ц<0, т. е в интервале
частот (6.7).
Выражение (6.27) совместно
с (6.26) и частотной зависимостью
|j. (1.59) определяет дисперсионное
соотношение (о(к), которое можно записать в виде
ю2 = юн
юн +
\+Zl!(kd)2
(6.28)
где Zn = nK. В предельном случае kd-юо (6.28) переходит в выражение
(6.6) для неограниченной среды при Qk = n/2. При конечных d частота,
в отличие от неограниченной среды, зависит от волнового числа
к и групповая скорость vgr = daldk^0.
В рассматриваемом случае со растет с ростом к, и vBT>0.
Такие волны называются прямыми. Результаты расчета по формуле
(6.28) приведены на рис. 6.5. Из выражения для vgr, которое легко
получить дифференцированием (6.28), следует, что vgr проходит
через максимум при значении к, зависящем от шн/юм и близком
к ki=nn/d, а максимальная величина vgT по порядку величины
составляет
Vgrma^yMod/n. (6.29)
Для пленки ЖИГ толщиной </=10мкм при п=\ i;grmax = 2,5 ■ 106.
Из выражения для потенциала, в данном случае
ty = Acoskzzexp( — iky), легко получить составляющие магнитного
поля h = Vv[/, намагниченности m=xh и индукции b = ph. Электрическое
поле можно найти в первом приближении, исходя из уравнений
(6.4) с учетом граничных условий: ех = еу = 0 при z = 0 и z = d.
Нетрудно убедиться, что при kz, k^>k0 (когда справедливо маг-
нитостатическое приближение) электрическое поле мало по сравнению
с магнитным.
Таким же образом, как в § 5.2, переходя от выражений для
комплексных амплитуд к мгновенным значениям составляющих поля,
можно построить силовые линии магнитного поля (рис. 6.6).
Рассмотрим теперь пластину, намагниченную по-прежнему
нормально к ее поверхности, но не металлизированную, а находящуюся
в свободном пространстве^. В этом случае мы должны «сшить»
граничными условиями поля в трех областях (рис. 6.4): z<0, 0<z<d
" Эта задача была решена Барьяхтаром и Кагановым [25].
«68
ах
271 в
7
ын
гж в
Г, ГГц
i
П=1/
I I
21
5/
i
10/
10'
№"■
10"
105 к,см i
Рис. 6.5. Дисперсионные характеристики магнитостатических волн в нормально
намагниченной металлизированной пластине; Л/0 = 139 Гс, #е0 = 3,9 кЭ, толщина
пластины d= 10 мкм
z
'//////////////////////////////У/,////////////////////////////Л
Рис. 6.6. Силовые линии магнитного поля волны с п=\ в нормально
намагниченных пластинах: о—металлизированной, б—свободной; k=2/d
и z>d. Потенциал в пластине можно по-прежнему записать в виде
(6.24), а «в воздухе» с учетом требования, чтобы поля обращались
в нуль при z-*±co,
ty0=.--Ce*°*-iky при z<0, ty0=De~K°'-iky при z>d (6.30)
169
Рис. -5.7. Графическое решение уравнения
(6.32) для свободной нормально
намагниченной пластины. kd=4; черные
кружки—значения Z„ для металлизированной
пластины
определителя с учетом (6.27) и (6.31)
(к0г—вещественно и
положительно). Для пластины будет
справедливо соотношение
(6.27), а подстановка (6.30)
в уравнение Лапласа для
потенциала v[/0 даст
v.lz = k2. (6.31)
Для выполнения граничных
условий—непрерывности
касательных составляющих h и
нормальной составляющей b в
данном случае необходимо
и достаточно, чтобы v[/ = v[/0
и B\\i/Bz = B\\i0/dz при z = 0
и z = d. Накладывая эти
условия на потенциалы (6.24)
и (6.30), мы получим для
коэффициентов А, В, С и D
систему однородных линейных
уравнений. Равенство нулю ее
дает трансцендентное уравнение
tgZ=
2Zkd
Z2-(kd)2
(6.32)
где (с учетом (6.27)) Z=kzd=^J-\ikd.
Уравнение (6.32) имеет бесконечное количество корней
Z„ (п— 1, 2. 3, ...), соответствующих различным типам волн. Их можно
найти численно или графически (рис. 6.7) и затем с учетом частотной
зависимости |j. получить дисперсионное соотношение а (к). Оно
по-прежнему будет иметь вид (6.28), но величины Z„ будут теперь
зависеть от kd. Как видно из рис. 6.7, различие величин Z„ для
металлизированной и свободной пластин уменьшается с ростом п.
Пределы же изменения частоты (6.7) и характер зависимости со(&)
для свободной пластины будут
такими же, как для
металлизированной. Останется
справедливой и приведенная оценка
групповой скорости.
Касательно намагниченная
пластина (объемные волны). Пусть
теперь постоянная
намагниченность лежит в плоскости
пластины (рис. 6.8). Запишем потенциал
в пластине в виде
Рис. 6.8.
170
Касательно намагниченная
пластина
ty = (Acoskxx +
+Bsinkxx)e~i(k'y+k'z).
(6.33)
Подстановка (6.33) в уравнение (6.15) дает
-V{kl + k2y) = k2z.
(6.34)
Рассмотрим для простоты металлизированную пластину. Тогда
граничным условием будет (6.25), откуда в данном случае
H<3v[//cbc+/uad\\i/dy = 0 при х = 0 и x=d. Наложение этих условий на
потенциал (6.33) дает систему уравнений для А и В, условие
совместности которых приводится к виду
(n2kl + y.2k2)smkxd=0. (6.35)
Предположим пока, что кх вещественно. Тогда из (6.35)
kxd=Xn = nn (и = 0, 1, 2, ...). (6.36)
Подставляя (6.36) в (6.34) и учитывая частотную зависимость ц,
получим дисперсионное соотношение
СО'
= сон сон+-
\+k2d2(k2d2+X„Y
2ЮН<
мм
СЮн+ 1 +cos2 G, [sin2 ek+X2J(k2d2j] -
(6.37)
где к2=к2 + к2.
Результаты расчета по формуле (6.37) приведены на рис. 6.9.
Мы видим, что при вк = п/2 зависимость со от к отсутствует. В другом
предельном случае 6Л = 0, т. е. при распространении в направлении
постоянного намагничивания частота изменяется в пределах (6.7)
и уменьшается с ростом к, т. е. t)gr оказывается отрицательной
Г, Г Гц
hz,103 см i
Рис. 6.9. Дисперсионные характеристики объемных магнитостатических волн
в касательно намагниченной металлизированной пластине; Мо = 90 Гс,
#0=1,35 кЭ, </=10мкм
171
величиной. Это означает, что вектор групповой скорости1' vgr = ско/йк
в данном случае антипараллелен вектору к и вектору фазовой
скорости vph = (co/ft2)k. Такие волны называются обратными.
Напомним, что в случае нормального намагничивания волны являлись
прямыми. Как мы увидим в дальнейшем, безобменные магнитоста-
тические волны всегда являются прямыми при к±М0 и обратными
при к || Мо.
В общем случае 6к^0, я/2 зависимость и от к является также
убывающей (рис. 6.9), но групповая скорость составляет с фазовой
скоростью угол, не равный ни нулю, ни п. Это является следствием
анизотропии в плоскости yz, обусловленной постоянным намагничиванием
в направлении оси z. Направление vph обычно бывает фиксировано
возбуждающими проводниками (см. ниже), а направление vgr зависит
от направления постоянного поля, его величины и частоты со.
Мы не будем приводить решения задачи об аналогичных
(объемных) волнах в свободной (неметаллизированной) касательно
намагниченной пластине, отсылая читателя к подробной работе Дэймона
и Эшбаха [274]. Заметим лишь, что пределы изменения частоты
и характер ее зависимости от ку и kz остаются такими же, как
для металлизированной пластины (рис. 6.9). Формула (6.37) будет
тоже справедлива, но величины Х„ будут зависеть от ку и к,.
Поверхностные волны. До сих пор мы рассматривали только
такие решения уравнения (6.15), для которых зависимость \J/ в
ферромагнетике от координаты К, в направлении нормали к поверхности
пластины описывалась тригонометрическими функциями. Волны,
которым соответствуют такие решения, называются объемными. Однако
могут существовать решения, для которых kf<0, т. е. зависимость
v[/ от координаты С, описывается гиперболическими функциями не
только вне ферромагнетика, но и внутри него. Соответствующие
этим решениям волны носят название поверхностных.
Для поверхностных волн имеет смысл задача о распространении
волны вдоль одной границы полубесконечного ферромагнетика с
полубесконечным диэлектриком или металлом. Рассмотрим частный
случай касательного намагничивания и распространения волны под
прямым углом к М0 — по оси у (ось х перпендикулярна граничной
поверхности). Исследуем сначала распространение поверхностной
волны вдоль границы с металлом, который будем считать идеально
проводящим. Потенциал запишем в виде v|/ = /4exp(—их—ifcv), где
у. вещественно и положительно (исходя из условия, чтобы v|/->0 при
х->оо), а
k=sk\k\. (6.38)
Здесь sk = +1 при распространении в положительном и sk = — 1 — в
отрицательном направлении оси у2).
Определение производной скаляра по вектору см. с. 41.
Записать к в виде (6.38), конечно, можно было бы и в случае объемных
г™™ Н° В ЭТ0М не возникало необходимости, так как дисперсионные
соотношения не зависели от направления распространения
172
Подставляя потенциал v|/ в уравнение (6.15) (которое в
рассматриваемом случае сводится к уравнению Лапласа), получим
ф2-к2) = 0. (6.39)
Граничное условие (6.25) дает
цх = ц„А;. (6.40)
Из (6.39) следует, что либо
х = |*|, (6.41)
либо ц = 0. Однако вторая возможность не представляет интереса,
так как при этом согласно (6.40) к=0.
Как нетрудно убедиться, выражение (1.59) для ца изменит знак,
если постоянная намагниченность будет направлена не в
положительном (как предполагалось при выводе (1.59)), а в отрицательном
направлении оси z. Поэтому можно записать
^ = &Лм, (6-42)
где Да определяется согласно (1.59), a sM=l при M0 = z0M0 и sM—— 1
при М0=— г0М0. Подставляя (6.38) и (6.42) в (6.40) и учитывая
(6.41), получим
VlHa = SMSk = S. (6.43)
Из (1.53) или рис. 1.6 видно, что отношение ц/(да никогда не
обращается в 1 и равно (—1) при ю = сон + юм. Таким образом, частота
поверхностной безобменной магнитостатической волны,
распространяющейся вдоль границы ферромагнетика с металлом, не зависит от
к и лежит выше диапазона (6.7), в котором находятся частоты таких
волн в неограниченном ферромагнетике и частоты объемных волн
в пластине. Направление же распространения определяется условием
s=—l. Нетрудно убедиться, что оно эквивалентно условию
k/|fc|=n0xM0/A/0, (6.44)
где п0 — единичный вектор нормали к граничной поверхности,
направленный в ферромагнетик.
Рассмотрим теперь распространение поверхностной волны вдоль
границы с диэлектриком («воздухом»). В ферромагнетике (х>0)
потенциал запишется по-прежнему и будет справедливо соотношение
(6.39). В воздухе же (х<0) v|/0 = Cexp(K0x—iky), где к0 вещественно
и положительно. Подстановка v|/0 в уравнение Лапласа даст у.\ = к2.
Таким образом,
x0 = x = |fc|. (6.45)
Из граничных условий (6.13) при х = 0 следует, что A — Cyl
x0 + nx = nafc (6.46)
или с учетом (6.45), (6.38) и (6.42)
(l + v№a = sMsk = s. (6.47)
173
Рис. 6.10.
Граница ферромагнетика
с диэлектриком
Легко убедиться, что это
соотношение выполняется только
в случае s= — 1 при
со = сон+-юм. (6.48)
Таким образом,
поверхностная волна на границе с
диэлектриком характеризуется такой же
невзаимностью распространения,
как и на границе с металлом. Частота ее также лежит над диапазоном
частот объемных волн, но ближе к его верхней границе.
Поверхностные магнитостатические волны на границе
ферромагнетика с диэлектриком при произвольных направлениях намагничивания
и распространения (рис. 6.10) исследовали Эшбах и Деймон [295].
Они показали, что поверхностные волны существуют при
sineMsincpM2scoH/(coH + coM) (6.49)
и частота их определяется удивительно простой формулой
сон
сон+сом . .
Н —sineMsmcpM.
(6.50)
2 sin бм sin фм
Выражение (6.48) является ее частным случаем.
Поверхностные волны в пластинах. Ограничимся случаем
касательного намагничивания и распространения волны в направлении,
перпендикулярном М0. Не останавливаясь на неинтересном случае
металлизированной с обеих сторон пластины, когда частота
оказывается не зависящей от к, т.е. fgr = 0 (рис. 6.11, а), рассмотрим
распространение поверхностной волны в свободной пластине
(рис. 6.11, б). Эта задача была исследована Деймоном и Эшбахом
[274] и представляет большой практический интерес.
В ферромагнетике (0<x<d) потенциал запишем в виде
\]/ = [>le--*x+fle*,*-d,]e-'*>, (6.51)
а в «воздухе»—
ty0 = Ce*BX-iky при х<0, il/0 = ArX0(*-d)-''k> при x>d. (6.52)
Соотношения (6.45) будут по-прежнему справедливы, а учет граничных
условий приведет к системе уравнений для А, В, С и D. Приравнивая
нулю ее определитель, найдем
^2-(иЦ + И0)2 _„-2xd «„ч
Vak 2-(ХЦ-И0Г
Отсюда с учетом (6.45) и зависимостей (1.59) ц и ц0 от со и соя получим
окончательно
со2 = (шн + сом/2)2-(сом/2)2е-2М. (6.54)
Как и следовало ожидать, частота оказалась не зависящей от
направлений М0 и к. В отличие от поверхностной волны в мсгал-
174
k(s = -f)' k(s = t)
*> > :
fniu+Tbl
Рис. 6.11. Частоты и групповые скорости поверхностных волн в различных
структурах. Сплошные линии s=\, штриховые s= — 1. При расчете принято
t = ti-2d, t2 = Sd
лизированнои пластине она зависит от к (рис. 6.12), изменяясь
в пределах
ш±<ю<сон + юм/2. (6.55)
Эта область частот примыкает сверху к области (6.7), в которой, как мы
видели, лежат частоты объемных магнитостатических волн (рис. 6.13).
В соответствии с отмеченным выше (с. 172) «правилом»
рассматриваемые волны, которые распространяются перпендикулярно
2я
5,8
5,6
ых
2tt5,4
Л ГГц
20
10/
5^-"^""^
.._ 1 1 1 ! I
0,5 1 1,5 2 к,№3см~'
Рис. 6.12. Частоты поверхностных магнитостатических волн в свободной
касательно намагниченной пластине; k_L.M0. #0=1,25кЭ, Л/0=139Гс (ЖИГ),
цифры у кривых — значения толшины пластины d в микрометрах
175
Поверхностные (kLM0inB)
Обратные (к II м01 п0)
Прямые (к i Н0 II п0)
Объемные
Рис. 6.13. Области существования безобменных магнитостатических волн в
свободной ферромагнитной пластине; п0—нормаль к поверхности пластины
М0, являются прямыми. Выражение для групповой скорости легко
получается дифференцированием (6.54):
«„ = *&/(4ш)е-2М. (6.56)
В отличие от объемных волн t)gr рассматриваемой поверхностной
волны монотонно убывает с ростом к.
Решая упомянутую выше систему для коэффициентов А, В,
С и D, мы можем найти распределение потенциала. Оно оказывается
невзаимным—зависящим от направлений намагничивания и
распространения (рис. 6.14).
Зная потенциал, можно вычислить составляющие h = V\J/, m = xh
и b = ph. He останавливаясь на этих несложных вычислениях, отметим
лишь, что магнитное поле в пластине имеет эллиптическую
поляризацию (с осями эллипса поляризации, совпадающими с осями
х и у), а вне пластины—круговую с левым вращением у той
поверхности, где потенциал и поля максимальны, и с правым — у
противоположной. Распределение амплитуд составляющих магнитного
поля и его силовые линии приведены на рис. 6.15. Переменная
намагниченность в пластине эллиптически поляризована с
преобладанием циркулярной составляющей с правым вращением, а
электрическое поле имеет только одну составляющую ez.
3d х
Рис. 6.14. Распределения потенциала поверхностной магнитостатической волны
в касательно намагниченной пластине для разных направлений распространения
(или намагничивания), Ы=1. параметры—как на рис 6 12 частота 5 76 ГГц
176
/
/
1,
d
V
1
/
,z
/
* У
А
0
\
//
/ (
\hx->hy
Рис. 6.15. Структура переменного магнитного поля и намагниченности
поверхностной во1ны в касательно намагниченной пластине: а—амплитуды
составляющих, б—силовые линии магнитного поля; kd=l, параметры—как на
рис. 6.12
Сешадри [412] рассмотрел случай, когда касательно намагниченная
пластина с одной стороны (л:=0) граничит с металлом, а с другой
(x=d)—с воздухом. Закон дисперсии в этом случае имеет вид
1+2 I-2.S-
Юм
ЙН + %-М_ 2Ы
(6.57)
В это выражение в отличие от (6.54) входит s. Из (6.57) следует,
что при 5=1 частота лежит в пределах
со^со^юн + сод/ (6.58)
и при kd-*cc переходит в частоту ю = юн + сом волны,
распространяющейся в полубесконечном ферромагнетике вдоль границы с
металлом. При s= — 1 частота лежит в пределах (6.55) и при Ы->оо
12 А. Г. Гуревич, Г. А. Мелков
177
переходит в частоту (6.48) волны, распространяющейся в
полубесконечном ферромагнетике вдоль границы с диэлектриком. Зависимости ю(к)
при разных s показаны на рис. 6.11, в.
Дисперсионные характеристики поверхностных волн были
рассчитаны и для ряда более сложных структур, показанных на рис. 6.11.
Для волн в структуре рис. 6.11, г, которые исследовал Бонжианни
[254], дисперсионное уравнение имеет вид
Л +2^+2,-^) °»+;°--"")П+**0 = е-аЫ. (6.59)
\ сом (ом/ (oM+((oH+sa)(l-thkt)
Интересной особенностью этой структуры, как и структуры рис. 6.11, д
[466], является немонотонная (при s=l) зависимость а (к): волна
является прямой при малых к и обратной—при больших.
Были исследованы объемные и поверхностные волны и в ряде
других структур, в частности, содержащих два ферромагнитных слоя
[223]. Варьируя параметры структур: толщины слоев, величины М0,
во многих случаях удалось приблизиться в более или менее широком
диапазоне частот к необходимым для конкретных применений
дисперсионным характеристикам, например, с постоянной i>gr—для
широкополосных линий задержки, или с линейной зависимостью vgr от
со—для систем сжатия импульсов [221].
Магнитостатические волны в волноводах с ограниченным
поперечным сечением. До сих пор мы рассматривали плоские системы,
неограниченные в двух измерениях: в направлении распространения
волны и в другом, перпендикулярном ему направлении. Реальные
системы, конечно, всегда ограничены во всех измерениях. Но не
выходя пока за рамки задачи о регулярных волноводах, мы
рассмотрим распространение магнитостатических волн в системах,
имеющих ограниченное поперечное сечение.
Существование медленных электромагнитных волн в
волноводах со сколь угодно малым поперечным сечением,
содержащих ферромагнетик, продемонстрировал теоретически еще в
1956 г. Сейдел [413]; он исходил при этом из полных
уравнений Максвелла. Задача о распространении медленных волн,
рассматриваемых с самого начала как магнитостатические, решается
очень просто для случая прямоугольного поперечно-паматнпчетюто
металлизированного стержня, т. е. полого прямоугольного
волновода, целиком заполненного поперечно-намагниченным
ферромагнетиком [233].
Магнитостатический потенциал в данном случае (см. рис. 5.6)
можно записать в виде
v|/ = (Ах cos kxx+Bx sin kxx)(Az cos kzz + Bz sin kzz)e ~iky. (6.60)
Подстановка его в уравнение Уокера (6.15) дает
-\i(k2x + k2) = kl (6 61)
Ич граничных условий (6.25) при z = 0 и z = b следует
д„ = 0, kz = mn/b (w=l, 2, 3, ...). (6.62)
178
Что же касается граничных условий при х — 0 и х=а, то, как
нетрудно убедиться, имеются две возможности удовлетворить им:
1)
2)
В,
ч/а (и=1, 2, 3, ...);
Bx = iAx, kx = ixx, v.x=sp.akj\i.
(6.63)
(6.64)
Первая возможность соответствует объемным волнам. Для них
из (6.61)—(6.63) с учетом частотной зависимости ц следует
со = сон
%+-
мм
1+
(rnn/b)2
{rm/a)2+k2-i
(6.65)
Вторая возможность приводит к волнам, которые можно назвать
полуповерхностными—с гиперболической зависимостью \j/ or ,v и
тригонометрической— от z. Соотношение (6.61) для таких волн с учетом
(6.64) принимает вид: к\—— у.±к2. Отсюда с учетом (1.651 следует
дисперсионное соотношение
со2 = (сон + сом)
сон +
им
\+(ггт)2{кЬ)2
(6.66
Дисперсионные соотношения для обоих классов волн являются
взаимными. Распределения же потенциала и, следовательно, структуры
полей, как видно из (6.63) и (6.64), невзаимны. Как объемные, так
и полуповерхностные волны являются прямыми, как этого и следовало
ожидать, поскольку к±М0.
Второй задачей о распространении магнитостатических волн в
волноводах с ограниченным поперечным сечением, которая может быть
решена строго, является задача о продольно-намагниченном круглом
стержне. В этом случае необходимо использовать цилиндрические координаты
р. ф, z (см. рис. 5.1). в которых уравнение (6.12) будет иметь вид
/с2\|/ I <Ц> 1 г2\]Л г2(|/ л
\ср р др р сф / cz
(6.67)
Для металлизированного стержня" граничным условием будет (6.25)
или в данном случае (рис. 5.1)
cvj/ 1 Л|/
Ц—+ 'Ца-~- = 0 при р = р0.
6'р р Сф
(6.68)
Решение уравнения (6.67) следует записать в виде, аналогичном (5.2):
vl/= Ут(кр)ехр(г>иф — ikz\ где Jm — функция Бесселя, а/л = 0, ±1. ±2 ...
Подстановка v[/ в уравнение (6.67) дает соотношение /г2=— ци2, а из
граничного условия (6.68) следует
JJX)'
(6.69)
" Это та же задача, что и в § 5.1, но теперь мы решаем ее
в магнитостатическом приближении.
12я
179
где Х=у.р0. Заметим, что уравнение (6.69) значительно проще, чем
уравнение (5.4), которое было получено без использования маг-
нитостатического приближения.
Уравнение (6.69) с учетом частотных зависимостей ц и ца
определяет дисперсионное соотношение ю(/с). Обозначая корни (6.69)
через Хт„(<о) (где п—номер корня при данном т), мы можем
записать это соотношение в виде
ю
! = юн юн +
юм
1+*2рЗ/*2.Ц
>_■
(6.70)
При ж = 0 уравнение (6.69), которое в этом случае сводится
к Jx (X) = 0, имеет только вещественные, не зависящие от частоты
корни, которым соответствуют объемные волны. Формула (6.70)
дает при этом в явном виде зависимость а (к). Результаты расчета
ее приведены на рис. 6.16.
При тфО уравнение (6.69) имеет при каждом \т\ бесконечное
количество вещественных корней, зависящих от частоты и знака
mM0z, т. е. направления вращения поляризации волны относительно
направления намагниченности. При левом направлении вращения
в интервале частот (6.58) это уравнение имеет также мнимые
корни — по одному при каждом \т\, которым соответствуют
поверхностные волны. Зависимости а (к) для них также показаны на
рис. 6.16. Как видно из этого рисунка, все волны являются обратными,
что еще раз подтверждает отмеченную выше (с. 172) закономерность.
Заметим, что зависимость частот объемных волн в продольно-
намагниченном стержне от знака mM0z, т. е. от направления вращения
поляризации вокруг М0, принципиально отличается от зависимости
частот от знака kM0z, т. е. направления распространения относительно
М0 для поверхностных волн в касательно намагниченной пластине
с несимметричной металлизацией. В случае продольно-намагниченного
стержня (как и для быстрых электромагнитных волн в продольно-
намагниченном волноводе с ферритом, см. § 5.1) знак к не влияет
\ЛГГц
Поверхностные
OffbBMhblE
ГолновочеДИС^СИ°ННЫе хаРактеРистики магнитостатических волн в круглом
волноводе, заполненном продольно-намагниченным ферромагнетиков
Я0=1,35кЭ, Л/0 = 200Гс
180
Магнитные ^.
■ стенки •—"|
Рис. 6.17. Касательно
намагниченная пластина конечной ширины
на дисперсионное соотношение и
эффект качественно не отличается от
кругового дихроизма, а также
эффекта Фарадея в неограниченной
среде (§ 4.2). Невзаимность же в
касательно намагниченной пластине
(как и аналогичный эффект для
быстрых волн в
поперечно-намагниченном волноводе, см. § 5.2) не имеет
аналога в неограниченной среде
и обусловлена несимметрией
граничных условий.
Распространение
магнитостатических волн в продольно-намагниченном неметаллизированном
круглом стержне исследовали Джозеф и Шлёманн [336]. Дисперсионные
характеристики объемных волн в этом случае качественно не
отличаются от случая металлизированного стержня. Поверхностные же
волны (как и для свободной пластины) существуют в более узком
интервале частот (6.55).
Определенный практический интерес представляет задача о
распространении магнитостатических волн в пленке конечной ширины.
Такую пленку можно рассматривать как прямоугольный стержень.
Однако строгое решение задачи для неметаллизированного
прямоугольного стержня невозможно. Для приближенного ее решения
можно исключить из рассмотрения (рис. 6.17) области z<0 и z>w,
а на поверхностях z = 0 и z = w принять фиктивное граничное
условие — равенство нулю нормальных к этим поверхностям
составляющих магнитной индукции b (так называемый метод
«магнитных стенок»). На других же поверхностях стержня будут
справедливы «настояшие» граничные условия — непрерывность
касательных составляющие h и нормальных составляюших Ь.
Поставленные таким образом задачи имеют простые решения, которые
неплохо описывают реальную ситуацию, если размер в направлении
нормали к «магнитным стенкам» много больше, чем другой размер
стержня.
Рассмотрим, например, поверхностные волны. Запишем потенциал
в виде vl/ = v|/x(x, y)(Fcoskzz+Gsinkzz), где v|/± в пластине имеет
вид (6.51), а вне ее — (6.52). Наложение граничных условий при х = 0
и x = d приведет, как и для бесконечной пластины, к соотношению
(6.53), а из граничных условий на магнитных стенках z = 0 и z = w
следует: / = 0 и
kz = nn/w (и= 1,2,3,...)- (6-71)
Подставляя потенциал v[/ в уравнение Уокера (6.15), получим
вместо (6.39)
ц(х2-А;2)-/с2=0, (6.72)
а из уравнения Лапласа для v[/0 вне пленки теперь следует
и2, ■ "
-2-k2~kt = 0.
(6.73)
181
Выражения (6.53) и (6.71) — (6.73) с учетом зависимостей ц и ц0 от
ш и (он определяют приближенный закон дисперсии ш(ши, к) для
пластины конечной ширины. Как видно из (6.72) и (6.78), отличие
от случая бесконечной пластины существенно лишь при малых kw.
Рассмотренный приближенный метод учета конечной ширины
пленки может быть применен и для более сложных структур. Для
структуры рис. 6.11, г подробный анализ закона дисперсии и сравнение
с экспериментом провели О'Киффе и Паттерсон [377]. При этом
был выявлен ряд интересных особенностей, обусловленных конечной
шириной, в частности, существование объемных волн в некоторой
области частот ниже <Bj_.
Поток энергии. Электрическое поле магнитостатических волн
может быть найдено в первом приближении, исходя из уравнений
(6.4). Зная его, можно найти (см. § 4.4) среднее значение вектора
Пойнтинга П и, интегрируя составляющую этого вектора в
направлении переноса энергии по всему поперечному сечению структуры,
вычислить мощность, переносимую волной. Направление переноса
энергии, как и для других волновых процессов, совпадает с
направлением групповой скороси vgr.
Рассмотрим простой случай, когда направления vph и vgr, а
следовательно, и потока энергии совпадают. Тогда поток энергии, отнесенный
к единице ширины структуры (в направлении ^ на рис. 6.18),
Л®=1 fnj&Qdb
(6.74)
где интегрирование производится по толщине каждого слоя структуры,
а суммирование—по всем слоям, как ферромагнитным, так и
диэлектрическим. Для волн, распространяющихся вдоль г) и не
зависящих от £, из (6.4) следует
ее,= ~(к0/к)Ь^.
Тогда, поскольку /^ = 0,
С t0
(6.75)
(6.76)
В качестве простого примера запишем поток энергии маг-
нитостатической волны в
нормально намагниченной
металлизированной пластине (через единицу ее
ширины):
d
у 16пк
Pl=\n.dz = ^-I
(6.77)
Приведем также выражение для потока
/£ энергии поверхностной волны в
свободной пленке, которое получается
Рис. 6.18. Планарная структура в результате суммирования потоков
182
в трех областях: ферромагнитной пластине и двух диэлектрических
полупространствах:
D _wd (со2-со?)(сон + сом/2-ю)(сон + со)ь2
1—о i 1 2~. 2\1 "хтах- (О. /б)
Здесь hxm!iX—значение нормальной составляющей магнитного поля
в пластине у той ее поверхности, где поле максимально. Заметим,
что для обратных волн потоки энергии в разных слоях структуры
могут иметь противоположные знаки, но суммарный поток будет
всегда в направлении групповой скорости.
Потери. Затухание магнитостатических волн может быть вызвано
следующими причинами: магнитными потерями, учитываемыми
(см. § 4.4) антиэрмитовыми частями компонент тензора Д;
электрическими потерями, учитываемыми мнимыми частями е ферромагнетика
и диэлектриков; потерями в металлических экранах, обусловленными
их конечной проводимостью; излучением в окружающее пространство
(если структура не экранирована полностью); возбуждением
рассматриваемой волной других типов волн и колебаний, в том числе упругих.
Первый источник является, как показывают оценки и эксперимент,
наиболее важным. При его учете мы можем исходить из тех же
дисперсионных соотношений, которые были получены и исследовались выше, но
при этом должны считать в них тензор р неэрмитовым, т. е. величины
ц и \iB—комплексными. Если же зависимости ц и \iB от ю и а>н уже
введены в дисперсионное соотношение и оно имеет вид F(a>, шн, к) = 0
(как, например, (6.28), (6.37) и (6.54)), то для учета потерь достаточно
произвести замену (1.73). Для стационарных волн ш остается
вещественной величиной и решение полученных комплексных уравнений дает
комплексные значения k=k' — ik". Если потери малы (к"<§:к' и ое<к1),
то можно /-"(со, Юя + госсо, k' — ik") разложить в ряд по приращениям
гаю и (—ik") и ограничиться линейными членами этого ряда. Тогда
учитывая, что F(a>, coH, k') — 0, a dFjdk'(dF/dw)~1 = vgr, получим
*' = «^. (6.79)
Важной характеристикой волны является величина ют, которая
характеризует затухание, отнесенное ко времени передачи сигнала
или энергии. Переходя в множителе exp [i(ot—i(k' — ik")y] для
стационарной волны (со" = 0) к системе координат, движущейся
с групповой скоростью в направлении распространения, т. е. производя
замену у-^Ух+v^t, мы видим, что в новой системе волна затухает
во времени по закону ехр( — штг), где
шт = ^Д"- (6-80)
Как видно из сравнения (6.80) с (6.8), величина шт совпадает (при
том же законе дисперсии) с декрементом колебаний ш" (при к" = 0).
Из (6.80) и (6.79) следует, что
шт = ошэ^—. (6.81)
183
Для поверхностной волны в свободной пленке при М01к из
(6.81) и (6.54) следует
шт = ое(шя + шм/2). (6.82)
Возбуждение и прием. Для возбуждения магнитостатических волн
в пленках (мы ограничимся рассмотрением этого случая) обычно
используются тонкие металлические проводники, располагаемые на
поверхности пленки или вблизи нее. Простейшим возбуждающим
элементом или преобразователем является (см. рис. 6.19, а)
одиночный прямолинейный проводник. Вследствие (6.1) волновой фронт
возбуждаемой волны почти параллелен проводнику, т. е. вектор
к перпендикулярен ему. Величина же А: в случае одиночного
достаточно тонкого (см. ниже) проводника может изменяться
в широких пределах и определяется значениями М0, со, сои и
поперечными размерами структуры в соответствии с законом дисперсии
возбуждаемой волны.
Для волн с взаимной структурой поля амплитуды волн,
распространяющихся в обе стороны от преобразователя, одинаковы.
При невзаимной структуре поля более интенсивно возбуждается
волна, распространяющаяся в том направлении, для которого ее
поле максимально у той поверхности пленки, где находится
преобразователь.
При изучении возбуждения волн в любых системах первым
приближением является задача об их возбуждении заданными
источниками, в данном случае — заданными токами в возбуждающих
проводниках. Такие задачи в различной постановке и разными
методами решались в работах [307, 291, 104]. Наиболее важным
результатом этих работ является то, что составляющие поля
возбуждаемой волны с некоторым к пропорциональны фурье-гармонике
возбуждающего тока с этим к.
В действительности, конечно, токи в возбуждающих проводниках
не являются заданными и должны быть найдены, наряду с
амплитудами возбуждаемых волн, при заданной, например, падающей
ill
aff веде
Рис. 6.19. Преобразователи, используемые для возбуждения и приема
магнитостатических волн в пленках. Микрополосковые: а — одиночный,
б—синфазная решетка, в — меандр. Копланарные: г — симметричный, д —
несимметричный, е—щелевой
184
мощности в волноводе, «питающем» преобразователь. Такие
самосогласованные (учитывающие «обратное» влияние возбуждаемых волн
на возбуждающие токи) теории возбуждения магнитостатических волн
в пленках разработали для разных случаев Вугальтер и Махалин
[54], Гилинский и Щеглов [57, 214] и др.
Сравнительно простой задачей, которая может быть использована
как исходная при рассмотрении ряда более сложных случаев, является
задача о возбуждении магнитостатических волн линейным током,
текущим по поверхности пленки. Результаты решения таких задач
можно представить в виде
Лс(гь $)=С/АР(Т1, & (6-83)
где /г{(г], £) — нормальная составляющая (см. рис. 6.18;
предполагается, что c/cq = 0) магнитного поля возбуждаемой волны, А?(г],
Ъ) — та же составляющая, но нормированная, т. е. собственная функция
магнитного поля волны; /—комплексная амплитуда линейного тока,
а С—комплексная величина, которая и находится в результате
решения задачи. Для волн (поверхностных) с невзаимной структурой
поля величины С+ и С~ будут различными для волн,
распространяющихся в разные стороны. Зная h.(r\, £,), мы можем найти для
этих волн потоки мощности Pi и Pf. Ясно, что они будут
пропорциональны \1\2, и можно записать
Pi = Pt+Pi=l- Rtr,6\I\2 + \ Яи*Ж- = \ /?.rad|/|2, (6.84)
определив таким образом погонные (отнесенные к единице длины
преобразователей) сопротивления излучения—для волн,
распространяющихся в обе стороны, и суммарное.
Рассмотрим теперь преобразователь, состоящий из N параллельных
линейных проводников с токами /,- = |/,-1 ехр (/фу) (./=1, 2, ...). Поле
волны, возбуждаемой этим преобразователем,
Лс=£ C\Ij\ei{'f'+kl')hf = Ah9. (6.85)
где lj—расстояние от у'-го проводника до некоторой фиксированной
точки. В частном случае одинаковых и синфазных токов, находящихся
на равных расстояниях 8/ друг от друга, из (6.85) следует
,4 = Csin(-A:5/7v) / sin(\k&l) = CFN. (6.861
Аналогичное выражение легко получить и для противофазного
преобразователя — когда фазы соседних токов отличаются на к.
Зависимости множителей Fy от ко! для этих двух случаев приведены
на рис. 6.20. Обращаясь к рис. 6.19. vibi видим, что преобразователь
б может приближенно рассматриваться как синфазный, а
преобразователи в, г и д — как противофазные.
Выражение (6.86) можно использовать и для выяснения
зависимости интенсивности возбуждения m ширины h одиночного возбуждаю-
185
47t kffl
Рис. 6.20. Зависимости «решеточных» множителей FN от кЫ для синфазного
(сплошные линии) и противофазного (штриховые) преобразователей
щего проводника (до сих пор мы считали Ь = 0) в предположении
однородного распределения тока по его ширине. Рассматривая этот
проводник как предел N синфазных токов I/N, находящихся на расстояниях
b/N друг от друга, при jV-юс, получим C(b) = C(b = 0)Fb, где
Fb = sin[^kb
■kb
(6.87)
Из (6.87) видно, что с увеличением Ъ интенсивность возбуждения
падает и этот спад становится существенным при b>nl{2k). Например,
для возбуждения волн с &=103 ширина проводника не должна быть
больше ~20 мкм. Приведенная оценка остается приближенно
справедливой, несмотря на то, что распределение тока по ширине проводника
существенно отличается от однородного.
Для расчета возбуждения и приема магнитостатических волн,
т. е. вычисления мощностей, поступающих в плечи сочленения
(восьмиполюсника), образованного возбуждающим и приемным
преобразователями, при заданной падающей мощности в одном из плеч
необходимо найти распределение тока по длине возбуждающего
преобразователя. Для этого может быть использован аппарат теории
линий передачи с потерями (см., например, [12]). Из четырех
погонных параметров Ru Lu Gy и Сь характеризующих такую
линию, проводимостью утечки Gi можно в данном случае пренебречь,
а емкость Q считать равной погонной емкости линии с размерами
преобразователя в отсутствие пленки. Величина /?t складывается из
рассмотренного выше сопротивления излучения и омического
сопротивления преобразователя, обычно небольшого. Наибольшую
трудность представляет определение индуктивности Lt; предположение,
что она равна погонной индуктивности линии с размерами преоб-
186
разователя без учета возбуждения магнитостатической волны,
является, конечно, очень грубым.
Для приемного преобразователя, как показали Вугальтер и Гилин-
ский [51 ], также может быть использована теория линий с потерями,
но с учетом распределенной ЭДС в приемном преобразователе,
которая пропорциональна амплитуде падающей на этот
преобразователь волны, а следовательно, амплитуде тока в возбуждающем
преобразователе. При этом, конечно, должно быть учтено затухание
при распространении волны между преобразователями.
Особенности магнитостатических волн. Перечислим теперь
характерные черты когерентных бегущих спиновых (магнитостатических)
волн в ферритовых пленках.
1) Широкий диапазон частот (~1—50 ГГц), ограниченный сверху
увеличением постоянного магнитного поля Н0, а
снизу—возникновением в малых полях Н0 доменной структуры.
2) Возможность перестройки частоты в широких пределах
изменением Н0.
3) Не зависящий от частоты диапазон волновых чисел (~10—
104 см-1).
4) Малая групповая скорость.
5) Возможность управления законом дисперсии простыми
средствами, в частности, выбором типа волны и толшин слоев
структуры.
6) Сравнительно небольшие потери при распространении.
7) Простые конструкции преобразователей.
Перечисленные особенности приводят к широким
возможностям применения магнитостатических волн в ферритовых
пленках для создания СВЧ устройств: линий задержки — с заданным
законом дисперсии или управляемых, фильтров, генераторов или
усилителей с использованием полупроводниковых активных
элементов (см., например, [220, 334]), а также нелинейных устройств
(см. § 10.5).
В заключение заметим, что при к> 104 см ' или малых толщинах
пленок (меньше ~3 мкм) должно учитываться обменное
взаимодействие, которым мы пока пренебрегали. Этот учет будет проведен
в § 7.2.
§ 6.3. Магнитостатические колебания
В ферро- (или ферри-) магнитных телах конечных размеров
имеют место колебания намагниченности с дискретными собственными
частотами. В этом параграфе мы исследуем такие колебания в рамках
магнитостатического приближения.
Один из типов колебаний намагниченности—однородные колеоания
в эллипсоиде — был подробно исследован в магнитоста отческом
приближении в § 1.5 и при менее жестких предположениях (маг-
нитодинамические колебания) для частного случая сферы в s > ч.
Неоднородные колебания наблюдались, как стало ясно biiol/i>. ictb.v .,
еще в ранних опытах по ферромагнитному резонансу в wu.
'«7
дополнительных максимумов поглощения, накладывавшихся на
основную резонансную кривую, обусловленную однородным
типом колебаний. Уайт и Солт [453] впервые отчетливо
разрешили эти дополнительные максимумы и дали их качественное
объяснение. Теория магнитостатических колебаний была разработана Уо-
кером [445] для случая эллипсоида вращения. Ниже мы приведем
результаты этой теории, но сначала рассмотрим более простые
примеры.
Цилиндр между металлическими плоскостями. В § 5.3 отмечалось,
что зная дисперсионное соотношение для волновода, можно в
некоторых случаях найти собственные частоты «волноводного»
резонатора, представляющего собой отрезок такого волновода,
ограниченный двумя металлическими плоскостями, перпендикулярными его
оси. Необходимым условием для этого является (см. § 5.3)
независимость структуры электрического поля в плоскости поперечного
сечения волновода от направления распространения. Это условие
выполняется, в частности, для продольно-намагниченного
металлизированного круглого стержня (§ 6.2). Собственные частоты
резонатора, образованного из такого волновода (рис. 6.21), определяются
условием (5.36) и дисперсионным соотношением (6.70). Подставляя
(5.36) в (6.70), получим
ш =ш,
шн+-
Шм
1 +
;tV
a-LNV /
Ро
(6.88)
Здесь ^„„(ш) — корни трансцендентного уравнения (6.69). Из формулы
(6.88) видно, что собственные частоты зависят от отношения
размеров резонатора и трех целых чисел от, п и р, определяющих
тип колебаний. Пределы, в которых лежат собственные частоты,
будут, конечно, такими же, как для баущих волн — объемных
и поверхностных:
шн<ю<шн+шм. (6.89)
Заметим, что для цилиндра с неметаллизированной боковой
поверхностью эти пределы были бы более узкими:
z
шя<ю<сон + шм/2. (6.90)
ь/*„
гр
: .а
Ро
Металлические
^поверхности
/
Рис. 6.21. Цилиндрический
ферромагнитный резонатор
188
Составляющие магнитного поля
h = V\|/, намагниченности т = %\\ и
индукции b = jlh могут быть вычислены
для каждого типа колебаний. При
этом для потенциала должно быть
принято выражение
^ = Jm(xp)e-im"coskzz (6.91)
(где kz = np/l), обеспечивающее
выполнение граничных условий на
торцевых плоскостях. Заметим, что
наложение на потенциал (6.91) граничных условий на боковой
поверхности позволяет получить выражение (6.88) и без использования
каких-либо результатов для бегущих волн.
Сфера. Магнитостатические колебания в сфере представляют
большой практический интерес, потому что сферические образцы обычно
используются при исследовании ферромагнитного резонанса, а также
применяются в ряде ферритовых СВЧ устройств. Магнитостатические
колебания в сфере могут быть получены как частный случай решенной
Уокером [445] задачи об эллипсоиде вращения. Но возникающие при
этом математические трудности делают более целесообразным
независимое решение задачи для сферы. Мы остановимся на некоторых
результатах этого решения, которое провели Флетчер и Белл [296].
Рассмотрим сферу радиуса R (рис. 6.22) из изотропного
непроводящего ферромагнетика, намагниченную до насыщения и
находящуюся в свободном пространстве. Исследование ее собственных
магнитостатических колебаний сводится к отысканию решений уравнения
(6.15) для потенциала \|/ внутри сферы и уравнения Лапласа для
потенциала \|/0 вне ее, удовлетворяющих граничным условиям на
поверхности сферы. Эти условия заключаются в непрерывности
касательных к поверхности составляющих h и нормальных
составляющих b и приводят к следующим требованиям:
v]/ = vJ/o, (PVi]/)r0 = ^ при r=R, (6.92)
где г0—единичный вектор, направленный по радиусу. Необходимость
наложения граничных условий заставляет искать решение в системе
координат, в которой поверхность сферы является координатной поверхностью.
Простейшей такой системой является сферическая (г, 6, ср); решение
уравнения Лапласа в ней, стремящееся к нулю при г-» ос, имеет вид [163]:
vJ,0 = r-(''+1,/'i,m|(cose)e_im,>. (6-93>
где Р1™1—присоединенные полиномы Лежандра первого рода, п =
= 1, 2, 3, ..., от = 0, +1, ±2, ..., ±п.
К сожалению, решения уравнения (6.15) в сферической системе
координат не могут быть получены.
Поэтому в [296] были введены более
сложные координаты £, г), <р, связанные с
декартовыми координатами х, у, z
следующим образом:
х = у/ц—1 Ryjt,2— 1 sin г) cos ф,
y=J\a-\ ,R,/£2-lsinr|sin(p, (6.94)
z = J(vL-\)l\iRl,cosr\.
В этих координатах решение уравнения
(6.15), конечное при г = 0, имеет вид
vj/ = /'i,'"1 (^) /'[Г1 (cos л) е-"im<p, (6.95)
189
Рис. 6.22. Намагниченная
сфера
а поверхность сферы является координатной поверхностью £, = с,в, где
^ = VW(M-1). (6.96)
Подстановка (6.93) и (6.95) в граничные условия (6.92) приводит
[296] (см. также [69]) к уравнению
^Щ^+п+1+^т = 0, (6.97)
где штрих обозначает дифференцирование по аргументу. Это
уравнение с учетом частотных зависимостей ц и ця определяет собственные
частоты магнитостатических колебаний сферы.
Как и следовало ожидать, собственные частоты не зависят от
R: они зависят от величин Я0 и М0 (входящих в ц и ц„) и от
трех целых чисел — индексов колебаний: и, т и третьего индекса г.
который характеризует номер корня уравнения (6.97) при данных // и т.
По традиции [445] число г определяется таким образом, чтобы
порядковый номер корня был г+1 при т>0 и г при ш<0; тогда число
корней при данных пит равно rmax+l при т>0 и rmas при т^О.
Анализ уравнения (6.97) показывает, что гта% равно целой части
числа (п — \т\)'2. Положительным и отрицательным т согласно (6.93)
и (6.95) соответствуют разные направления изменения фазы потенциала
(а следовательно, и намагниченности) при изменении угла ф.
Исходя из (6.95) и (6.93), для каждого типа колебаний могут
быть определены составляющие поля h = V\|/ и намагниченности
m = xh. Положительным и отрицательным т будут соответствовать
правое и левое направления вращения поляризации колебания, т. е.
всей структуры h и т. Локальная поляризация h и т может быть
при этом и круговой (см. ниже), и эллиптической, причем различной
в разных точках сферы.
Рассмотрим сначала колебания с п = \т\. Тогда (6.97) сведется
к весьма простому уравнению
т \т\ + \
»+п»'= -гг- (б-98)
\т\ \т\
Легко убедиться, принимая во внимание (1.59), что это уравнение
удовлетворяется только при т>0 и имеет при каждом т по
одному корню
т \ т — 1
<йт,т,о = сзн+- -wM = yHe0+- -<вм. (6.99)
2т +1 А 2т+\
Потенциал (6.95) в этом случае примет вид
^=рте-'т*Щх-1у)т, (6.100)
/~2 J
где р = у/х +у , а составляющие намагниченности
mx = imy = (x-iy)m~1 = pm~1e~iim~Li". (6.101)
Как видно из (6.101), намагниченность имеет во всех точках сферы
круговую поляризацию с правым вращением, амплитуда ее растет
19С
при удалении от оси z, а фаза изменяется по закону волны, бегущей
по азимуту с угловой скоростью ч>/(т— 1).
При п = т-—\ переменная намагниченность, как видно из (6.101),
не -зависит от координат, а частота согласно (6.99) равна уЯе0.
Этот тип колебаний (1, 1, 0) представляет собой однородную
прецессию намагниченности, которая подробно рассматривалась
в § 1.5.
Для другой серии колебаний {п — \т\ + 1) из (6.97) следует
Ц + г-тИ«.= п~- (6.102)
\т\ \т\
Это уравнение, как и (6.98), удовлетворяется только при т>0
и имеет при каждом т один корень
tn 1 tyi — 3
и„н.м.о = Шй+г—— а>м=гуЯе0 + - -—-шм. (6.103)
Ъп + 5 3 2т + 5
Потенциал и составляющие нама1 ниченности для этой серии
отличаются от (6.100) и (6.101) дополнительным множителем г, т. е.
амплитуда намагниченности равна нулю в экваториальной плоскости
и растет при удалении от нее. Поляризация намагниченности, как
и для серии (т, т, 0), является во всех точках сферы круговой.
Из формул (6.99) и (6.103) видно, что разности со —уЯе0 для
обеих рассмотренных серий пропорциональны М0 и не зависят от
Яе0. Распределения же потенциала и намагниченности для них не
зависят ни от Яс0, ни от М0. Эти особенности, как и круговая
поляризация h и т, имеют место только для колебаний (т, т, 0)
и (т+1, пи 0).
Собственные частоты и структуры поля сравнительно легко могут
быть рассчитаны и для колебаний с т = 0. В этом случае (6.97)
переходит в уравнение
ЪяР&я)1Рп(Чк)=-{п+1), (6.Ю4)
где P„(£,R) — полиномы Лежандра [163]. Если и=1, то уравнение
(6.104) не имеет решения. При п — 2 Р2{£) = {Ъ11г—\)'12 и (6.104) имеет
корень ^|=1/5, откуда
ш1о.1=% шн+тшм • (6.105)
Составляющие т для колебания (2, 0, 1)
тх = %х + 1ХаУ, iny = %y-ix„x. (.6.1061
Намагниченность теперь имеет эллиптическую поляризацию и зависши
от Яе0 и М0. Эти особенности имеют место и для последующих
колебаний серии {п, 0, г). В соответствии с отмеченным выше общим
свойством уравнения (6.97) величина »так. равная в данном случае чнс.л
корней, составляет: rmax = l для и = 3, rmax = 2 для и = 4 и п — 5 л т. i.
Во всех других случаях, кроме трех рассмотренных сери;!,
возможны колебания с т>0 и т<0, причем как ми ним v.м "с ."р1
Рис. 6.23. Распределения переменной намагниченности простейших магнито-
статических колебаний сферы. Показаны векторы m в трех плоскостях г=const
в некоторый момент времени (сплошные стрелки) и через 1/4 периода
(штриховые стрелки)
типа колебаний при данных п и |то|: два с то>0 и один с то<0.
Например, при и = 3 и |то| = 1 существуют колебания (3, 1, 0),
(3, 1, 1) и (3, -1, 1).
Результаты расчета составляющих поля и намагниченности и
собственных частот всех магнитостатических колебаний сферы с и^5
приведены в [296]. На рис. 6.23 показаны распределения
намагниченности для нескольких простейших типов колебаний.
Зависимости частот некоторых типов колебаний от Нс0 приведены
на рис. 6.24. Из этого рисунка хорошо видно различие между сериями
(то, то, 0) и (т+1, т, 0), для которых разности ю—у#е0 не зависят
от Не0, и всеми остальными колебаниями. Заметим, что измерение
разности частот или величин Нс0 для двух определенных типов
колебаний из серий (то, то, 0) и (т+1, то, 0) представляет собой
один из наиболее точных методов определения постоянной
намагниченности. Как видно из рис. 6.24, имеют место многочисленные
вырождения частот разных типов, как «случайные» пересечения, так
и полное совпадение частот колебаний (то, то, 0) и (Зто+1, Ът, 0).
Из этого рисунка видно также, что собственные частоты всех
магнитостатических колебаний сферы лежат в пределах (6.90), в ко-
192
°-Г"во
Рис. 6.24. Зависимости частот магнитостатических колебаний сферы от
внешнего постоянного магнитного поля [296]. Штриховые линии -границы
спектра магнитостатических колебаний
торых в структурах без металлических поверхностей находятся частоты
бегущих магнитостатических волн — объемных и поверхностных. При
со = const резонансные значения Нс0 для магнитостатических колебаний
сферы лежат в пределах
2 4
(а/у~~кМ0<Нео<(й/у-г-пМ0. (6.107)
Эллипсоид вращения. Приведем теперь некоторые результаты
решения задачи о магнитостатических колебаниях эллипсоида
вращения, намагниченного вдоль оси вращения [445]. Постановка этой
задачи и все допущения аналогичны рассмотренному выше случаю
сферы.
Многие св-.^Чства магнит jcra кческих колебаний, которые были
отмечены выше для сферы. и\,еют место и в общем случае эллипсоида
вращения. В частносп, справедливо упомянутое выше правило
определения чи\па типов колебаний с данными п и т. Серии
(т, т, 0) и (н,+ \, то, 0), как и для сферы, характеризуются
независимостью разности со—шя от шн и круговой поляризацией
поля и намч! ниченности. Тип колебаний (1, 1, 0) по-прежнему
представляет собой однородную прецессию намагниченности.
Частоты магнитостатических колебаний эллипсоида вращения (с
полуосями а и с) лежг,; в тех же пределах (6.90), где теперь
13 А. Г. Гуревич, Г. А. Мелков 193
Рис. 6.25. Зависимости частот магнитостатических колебаний от формы
эллипсоида вращения [445]
mH = yHe0 — yNzM0. При я/с^р->0 (когда эллипсоид превращается
в тонкий диск) спектр колебаний стягивается в точку
шя = у(Яе0 — 4лМ0), а при |3->х—в точку шн + шм/2 = у(Яе0 + 2п:Л/0)
(рис. 6.25).
Затухающие и вынужденные колебания. Для анализа затухания
магнитостатических колебаний достаточно подставить комплексные
ц и \ia в характеристические уравнения, например (6.97); корни этих
уравнений станут комплексными, их мнимые части ш" будут
характеризовать затухание соответствующих типов колебаний. Общим
результатом таких вычислений является то, что добротности
неоднородных магнитостатических колебаний (при заданных параметрах
диссипации) мало отличаются от добротности однородного типа
колебаний.
Возбуждение магнитостатических колебаний в малых образцах,
в отличие от бегущих магнитостатических волн, производится
обычно при помощи электромагнитных полей волноводов или
резонаторов, в которые эти образцы помещаются. При построении
теории такого возбуждения используется то, что намагниченности
магнитостатических колебаний разных типов mv(r) (где v —
совокупность индексов и, т и г) удовлетворяют соотношениям
ортогональности [388, 446]:
|mvxmv.uf|/=0, |mvm*-ufl/=DAvv-, |mvxm*uf|/=/z0Z)Avv., (6.108)
V V V
где интегрирование производится по объему образца, Avv—дельта-
символ Кронекера (5.28), a D—константа нормировки. Величины
mv(r) образуют полную систему функций, по которой может быть
разложена искомая намагниченность вынужденных колебаний:
m(r) = ICvmv(r). (6.109)
194
Для коэффициентов этого ряда при учете соотношений
ортогональности получаются выражения вида
$h(r)m'v(r)dV
Cv=Cco2-f ; . (6.110)
со2-с<2 + 2коХ
Здесь h(r) — возбуждающее поле, которое мы считаем заданным;
a>v и ш" — вещественные и мнимые части собственных частот
колебаний, а С—константа, зависящая от нормировки собственных функций
mv(r).
Как видно из (6.110), коэффициенты Cv изменяются резонансным
образом при изменении ш или величины Не0 (от которой зависят
a>v). При достаточно малых ш" при изменении ш или Не0 происходит
поочередное возбуждение разных типов колебаний. Следует заметить,
что в отличие от возбуждения бегущих волн (§ 6.2) конечные
амплитуды колебаний Cv при резонансе получаются только при
учете диссипации.
Из выражения (6.110) видно, что условием возбуждения данного
типа колебаний является необращение в нуль «интеграла
возбуждения», стоящего в числителе этой формулы. При однородном внешнем
поле он не обращается в нуль только для однородного типа
колебаний (1, 1, 0); для возбуждения неоднородных типов колебаний
требуется неоднородное поле, а интенсивность возбуждения будет
тем больше, чем ближе структура этого поля в объеме образца
к структуре собственной намагниченности mv(r) возбуждаемого типа
колебаний.
Неоднородные магнитостатические колебания возбуждаются часто
и тогда, когда интеграл возбуждения в (6.110), казалось бы, должен
обращаться в нуль. Такое «незаконное» возбуждение бывает связано
иногда с неточностью расположения образпа в резонаторе или
волноводе и искажениями поля, обусловленными, например,
держателем образца. Однако имеются и более глубокие его причины, на
которых мы сейчас остановимся.
Связь между магнитостатическими типами колебаний. Рассмотрим
сначала влияние магнитной кристаллографической анизотропии.
В § 6.1 отмечалось, что при ориентации М0 по оси одноосного
кристалла или осям <100> и <111> кубического выражения для
компонент р, а следовательно, и решения любых электродинамических
задач получаются из соответствующих выражений для изотропной
среды при замене (6.21). Отсюда следует, что для указанных
направлений М0 весь спектр резонансных значений #е0 (при
ш = const) магнитостатических колебаний монокристаллического
образца сдвинется относительно спектра изотропного образца на
постоянную величину НА.
Для произвольного направления М0 дело обстоит гораздо сложнее.
Кривченков и Пильщиков [121] показали, что если анизотропия
невелика, то решение целесообразно искать в виде ряда по
собственным колебаниям изотропной сферы. Исходя из граничных
13* 195
условий, может быть получена система уравнений для коэффициентов
этого ряда, а условие совместности ее приводит к уравнению для
собственных частот. При этом оказывается, что собственные колебания
анизотропной сферы получаются в результате суммирования
колебаний изотропной сферы со значениями п одинаковой четности (четными
либо нечетными) и значениями т также одинаковой четности (не
обязательно такой же, как для и). В этих рядах какие-то члены
всегда являются преобладающими, остальные вносят вклады,
уменьшающиеся по мере уменьшения анизотропии, так что собственные
колебания анизотропных образцов переходят при уменьшении
анизотропии в соответствующие типы колебаний изотропных.
Если перейти с языка собственных (нормальных) колебаний на
язык связанных колебаний, то можно считать, что магнитная
кристаллографическая анизотропия приводит к связи различных типов
колебаний, которые были независимыми в изотропном образце. Связь
существует только между колебаниями определенной (см. выше)
четности, уменьшается с уменьшением анизотропии и отсутствует
(для кубического кристалла) при ориентации М0 по осям <100> или
<111>. Связь приводит, вообще говоря, к сдвигу резонансной частоты
рассматриваемого типа колебаний и к возбуждению, наряду с ним,
всех связанных с ним типов. Однако в кристаллах с малой
анизотропией связь проявляется только в «расталкивании» кривых
ю(#е0) (рис. 6.26) вблизи точек вырождения двух типов колебаний.
Рассмотренная выше теория магнитостатических колебаний (в
изотропном ферромагнетике) была развита [445] только для
эллипсоида вращения, намагниченного вдоль его оси, т. е. для случая,
когда система обладает цилиндрической симметрией относительно
направления М0. Для произвольного эллипсоида или эллипсоида
вращения, но намагниченного не по оси вращения, ситуация
оказывается аналогичной той, которая имеет место для анизотропной сферы,
где также (кроме случаев намагничивания по осям <100> и <Ш»
отсутствует цилиндрическая симметрия. Любые «геометрические»
0,5
0,4
0,3
0,2
0.1
1 2 3
I'nc b-2(\ '«Расталкивание» частот связанных магнитостатических колебании
сферы [298]
I 6
/У.
еО
4пМп
искажения такой симметрии, в том числе макроскопические дефекты
образца—поры, трещины и пр., на языке связанных колебаний
можно тоже трактовать как факторы, приводящие к связи колебаний
разных типов. Это является второй причиной упомянутого выше
«незаконного» возбуждения магнитостатических типов колебаний.
Третьей причиной являются конечные размеры образца. В § 5.3
отмечалось, что учет «запаздывающих» членов в уравнениях
Максвелла для однородного типа колебаний небольшой сферы дает
поправку (5.43) к резонансному полю. Аналогичные поправки были
вычислены [388] и для неоднородных магнитостатических типов
колебаний. Оказалось, что они уменьшаются с увеличением чисел
пит, чего, конечно, и следовало ожидать, так как с увеличением
числа вариаций поля в образце облегчается выполнение условия
(6.22) применимости магнитостатического приближения. Влияние
отбрасываемых в магнитостатическом приближении членов на структуру
собственных колебаний на языке связанных колебаний может
трактоваться как появление связи между магнитостатическими типами
колебаний. Как показал Сюй Янь-шен [194], связанными в этом
случае оказываются типы колебаний, для которых п имеют
одинаковую четность, а т одинаковы.
В заключение заметим, что согласно теории Уокера [445]
неоднородные магнитостатические колебания возникают из-за того,
что компоненты тензора магнитной проницаемости имеют вид (1.59),
что в свою очередь справедливо для любых (изотропных) вешеств,
намагниченных постоянным полем. В частности, неоднородные
магнитостатические колебания должны иметь место и в парамагнетиках,
но диапазон их существования (6.90) является в этом случае узким,
и поэтому для их разрешения необходимы малые АН. Однако ни
конкретный вид (1.59) выражений для компонент тензора ft, ни даже
наличие постоянной намагниченности не являются необходимыми
условиями возникновения неоднородных магнитостатических
колебаний. Они наблюдались, в частности, в одноосном антиферромагнетике
[241] (см. также [69]) в антипараллельном основном состоянии (§ 3.2),
когда постоянная намагниченность равна нулю.
Глава 7
СПИНОВЫЕ ВОЛНЫ
§ 7.1. Спиновые волны в неограниченном ферромагнетике
В предыдущей главе рассматривались волны намагниченности
в ферромагнетике в таком интервале волновых чисел, когда можно
было использовать магнитостатическое приближение и в то же
время не учитывать обменного взаимодействия. Теперь мы перейдем
к изучению волн с большими волновыми числами. Для них
магнитостатическое приближение будет еще лучше применимо, но
злизния обменного взаимодействия нельзя будет не учитывать.
Такие волны принято называть спиновыми волнами, хотя, как уже
отмечалось, этот термин можно отнести и к волнам, исследованным
в гл. 6.
В первом параграфе гл. 7 мы рассмотрим спиновые волны
в неограниченном, однородном, намагниченном до насыщения
ферромагнетике. Используя по-прежнему континуальную модель, мы
будем считать ферромагнетик средой, характеризуемой
намагниченностью М(г, t). Теория спиновых волн в такой среде будет отличаться
от теории, рассмотренной в предыдущей главе, прежде всего тем,
что в уравнение движения намагниченности войдет эффективное поле
обменного взаимодействия.
Энергия и эффективное поле обменного взаимодействия. Энергия
обменного взаимодействия в ферромагнетике может быть
представлена в виде суммы (2.14) однородного члена 11л и неоднородного
Uq, который представляет собой увеличение энергии обменного
взаимодействия вследствие непараллельности соседних магнитных
моментов, т. е. при континуальном рассмотрении — зависимости М от
координат. Величина 11л имеет вид (2.31), a Ug можно представить
в виде [15 ]
Zp=ls=l VXP VX"
где qps—компоненты некоторого тензора q. Вычисляя по формуле
(2.9) эффективное поле обменного взаимодействия, получим
На = НА+Ня=ЛМ+ X I <?PS^-. (7.2)
p=ls=l CXpPX,
Для изотропного ферромагнетика Л и q становятся скалярами,
НЛ принимает вид (1.26), а
H,=?V2M. (7.3)
198
Намагниченность М представляет собой сумму постоянной
составляющей М0 и переменной составляющей с комплексной
амплитудой т. Мы будем рассматривать в этой главе намагниченный
до насыщения ферромагнетик, в котором М0 не изменяется быстро
в пространстве (кроме, конечно, границ образца). Тогда эффективное
поле Нв имеет только переменную составляющую; ее комплексная
амплитуда для изотропного ферромагнетика
he = ?V2m. (7.4)
Используются также величины D и г\, связанные с q следующим
образом:
П = у/) = уМо<7. (7.5)
Все эти величины называют постоянными (или константами)
неоднородного обмена или константами обменной жесткости.
Закон дисперсии. Дисперсионное соотношение для спиновых волн
можно получит^ двумя способами. Первый основывается на
выражении (6.5), которое справедливо независимо от того, учитывается
или нет обменное взаимодействие. От обменного взаимодействия
зависит только вид \i (рассматривая намагниченный до насыщения
ферромагнетик, мы считаем цц = 1). Для того чтобы его найти,
необходимо решить уравнение движения намагниченности, например
(2.20), с учетом (для изотропного ферромагнетика) эффективного
поля (7.4).
Рассмотрим плоскую волну: m = m0exp(—/kr), h = h0exp( —гкг). Для
нее из (7.4) следует
hq=-qk2m. (7.6)
Легко видеть, что уравнение движения (2.20) с этим полем отличается
от уравнения (1.70) без него заменой
ш„-со„-ыУс2. (7.7)
Поэтому, не решая заново уравнения движения, можно произвести
такую замену в окончательных выражениях для компонент Ц,
приведенных в § 1.3 или 1.4. В частности, из (1.59)
(сон + т]А:2)(сон + Г1А:2-1-сом)-со2 ш>м „ _.
^ 1 ;—Ггй 2 ' V-a='i ;—Г2Т2 2- у'-°>
(сод + rifc ■')''—ю (сод + г)*:'') — a/
Для учета диссипации достаточно в этих выражениях произвести
замену (1.73). Величины ц и ц„ зависят теперь не только от частоты,
но и от волнового вектора к. Такая зависимость носит название
пространственной дисперсииХ). Для изотропного ферромагнетика
компоненты Ц зависят только от к2, в общем случае они зависели бы
и от направления вектора к относительно осей анизотропии.
Подставляя (7.8) в (6.5) при иц = 1, получим закон дисперсии спиновых волн
Другим видом пространственной дисперсии является линейная
зависимость антисимметричных компонент "е от к, приводящая к упоминавшемуся
выше (с. 20) явлению оптической активности.
199
в изотропном ферромагнетике
о2 = (а>я + t\k2) (соя + цк2 + сом sin2 вк) =
= (ш„ + лЛ2)(шн + лЛ2+^^) = .1г-|А12. (7-9)
Ak = wH + r\k2+-cuMsin2Bk, \Bk\=j<aMsm2ek. (7.10)
Второй путь вывода закона дисперсии (7.9) использовали Херринг
и Киттель [326], получившие его на континуальной модели0. При
этом сначала находится связь внутреннего магнитного поля с
намагниченностью, которая определяется магнитостатическими уравнениями
(6.2) и (6.3). Для плоских волн из этих уравнений, как нетрудно
убедиться, следует
Ьм=-4т;к(тк)Д2. (7.11)
Это поле подставляется затем в уравнение движения (2.20), которое
в данном случае будет иметь вид
/com +(сон + /оссо) m x z0 -t-—-z0 х \+~т-г0 х hM = 0, (7.12)
у ' 4л 4л
где z0—единичный вектор, направленный вдоль М0. Уравнение (7.12)
с учетом (7.6) и (7.11) представляет собой однородное уравнение для
намагниченности т. Проектируя его при ое = 0 на оси х и у и
приравнивая нулю определитель получающейся системы, мы приходим к
соотношению (7.9). Таким образом, второй способ его получения
отличается от первого последовательностью учета уравнений
электродинамики (в магнитос!этическом приближении) и уравнения движения.
Анализ закона дисперсии. Зависимости co(fc) при cow = const показаны
на рис. 7.1. При увеличении постоянного магнитного поля весь спектр
смещается в большие частоты. При больших к, когда r)^2^>co/(,
сом, закон дисперсии спиновых волн приближается к квадратичному,
полученному еще в 1930 г. Блохом [249]
ш = л&2. (7-13)
Если же сам <<он+ Г|/с2. то
o)~^fcscow + r)^2+-tt>Msin26k. (7.14)
Фазовая скоршть спиновой волны vph = mik, как видно из рис. 7.1,
проходит через минимум при некотором, зависящем от Qk значении
k = ki. В частности, при 6^ = 0
(в точке минимума со 2coH).
" На микроскопической модели Гейзенберга дисперсионное соотношение,
являющееся обобщением (7 9), получили ранее Холстейн и Примаков [329]
(см § 7.4).
200
Г, ГГц
КЮ5см '
Рис. 7.1. Закон дисперсии спиновых
волн в изотропном
ферромагнетике; А/0 = 139Гс (ЖИГ при
комнатной температуре), #0 = 1 кЭ
Н„,кЭ
КЮ6'см '
Рис. 7.2. Дисперсионные
характеристики спиновых волн в
изотропном ферромагнетике при со=const;
А/0=139 Гс, /=ю/(2л) = 9 ГГц
Групповая скорость
д(о , 1
^=-^ = 2г[к(сйн + цк2+-(йм5т2вк)т'1 = 2цк^. (7.16)
Множитель £ представляет собой отношение приближенного значения
частоты (7.14) к точному и при достаточно больших со мало
отличается от 1.
Соотношение (7.9) можно также записать в виде
цк2 = (оНс(вк)-сйн,
(7.17)
где
Юяс(е*) = У#ос(6*)= /co2 + QcoMsin2eJ -UMsin2efc. (7.18)
Зависимости к от Н0 = (он/у при со = const показаны на рис. 7.2. Из
этого рисунка, как и из выражения (7.17), видно, что
распространяющиеся (с к2>0) спиновые волны с данной частотой могут
существовать лишь при магнитных полях, не превышающих величины
#0с(64). При вк = 0 она оказывается наибольшей и составляет
#о с (6* = 0) = со/у. (7.19)
Наибольшее значение к (при со=const) достигается также при 6^ = 0:
кпиа = у/(й/т\- (7-20)
Для ЖИГ при частоте 9 ГГц к -8-Ю5
т- ч х1^ "-так — ° lw -
ьольшои интерес представляет вопрос о вырождении спиновых
волн и однородного типа колебаний. Ответ на него требует учета
201
а В
Рис. 7.3. Вырождение однородных колебаний намагниченное™ в сфере со
спиновыми волнами; а— условие (6.10) не выполняется. г7 выполняется
формы образца. Однако при к:»1 d. где d— наименьший размер
образца, влияние граничных условий для переменных полей на закон
дисперсии спиновых волн становится несущественным, и может быть
использовано соотношение (7.9). В § 6.1 было показано, что
вырождение однородного типа колебаний с безобменпыми спиновыми
волнами в эллипсоиде не имеет или имеет место в зависимости от
выполнения условия (6.9). С у четом обменного взаимодействия, как
видно из рис. 7.3, вырождение однородного типа колебаний со
спиновыми волнами всида имеет место, но при выполнении условия
(6.9) оно происходит в интервале волновых чисел ку-¥к2, если же
это условие не выполняется, то А^-^О. Легко показать, что для
эллипсоида вращения к2 не зависит от Нс„ и составляет
l<2 = s/yNxMolr).
(7.21)
Переменная нама! ниченность н переменное поле. Составляющие
вектора т спиновой волны могут быть найдены путем решения
системы, которая получается при проектировании уравнения (7.12)
на оси координат с учетом (7.6). (7.11) и дисперсионного соотношения
(7.9). Направив оси так, чтобы вектор к лежал в плоскости yz.
получим (при а = 0)
■1.2 /л , п> ,\ -1/2
ту_ .1 coMsin20,
к>н + лА"
Л + |Д»1
Ак-\Вк\
(7.22)
При Qk = 0 ту = — imx, т. е. переменная намагниченность имеет
круговую поляризацию с правым вращением. При 0^0 поляризация
намагниченности является эллиптической, эллипс поляризации, как
видно из (7.22), сжат в направлении проекции вектора к на плоскость
ху (перпендикулярную М0); эллиптичность (1.106) уменьшается с
ростом к.
Составляющие электромагнитного поля спиновой волны в
безграничной среде могут быть вычислены так же, как и для безобменных
волн (§ 6.1). исходя из общих решений уравнений Максвелла для
плоских волн (§ 4.2). Но для [I и р, должны быть теперь приняты
202
выражения, полученные с учетом обменного взаимодействия.
Переменное магнитное поле спиновой волны может быть также определено
по формуле (7.11). Электрическое поле может быть найдено, как
и для безобменных волн, в первом магнитостатическом приближении,
исходя из уравнений (6.4), а поток мощности — вычислен по общей
формуле (4.67). В отличие от безобменной магнитостатической волны
в безграничной среде, он не обращается в нуль.
Затухание спиновых волн. Условие совместности системы,
полученной проектированием (7.12) при а^0 на оси х и у, даст
комплексное дисперсионное уравнение. Если направления векторов
к' и к" совпадают, то оно будет отличаться от (7.9) заменой
(1.73). Как и для безобменных воли (§ 6.2), возможны две постановки
задачи. В одном случае рассматривается затухание в пространстве
стационарной волны (со" = 0). в другом — затухание во времени
некоторого распределения стоячих волн (к" = 0). Соотношение (6.8)
между к" для первого случая и со" — для второго при условии
малости потерь (co"<s:co', к "«с/с'), как отмечалось в § 6.1, справедливо
при любом законе дисперсии, а следовательно, и для обменных
спиновых волн.
Рассмотрим первый случай (со" = 0, k = k' — ik"). Два вещественных
уравнения, эквивалентных комплексному дисперсионному
соотношению, дадут в этом случае связь к' и к" с со. Не останавливаясь
на решении этих уравнений (оно приведено, например, в [69]).
отметим, что имеет место соотношение ^
/с" = асо (2-пАг'). (7.23)
На рис. 7.4 приведена зависимость to (A-', A-"). Из этого рисунка видно,
что если к"<$:к', то в качестве к' можно принять величину к,
полученную без учета диссипации. Величина к" тогда может быть
найдена из (7.23). Если же условие k"<s:k' не выполняется, одна
из величин к' или к" должна быть
найдена из точных уравнений,
следующих из комплексного
дисперсионного соотношения.
Как видно из (7.23), к" растет
с уменьшением к' и становится
равным ему при
к' = ^/аы1{2ц) = кс. (7.24)
При к'<кс представление о
распространяющихся спиновых волнах
теряет смысл. Оценка для
монокристалла ЖИГ с шириной
резонансной кривой АНк = аН0 = 0,3 Э дает
А:с = 4-103. Заметим, что
«исчезновение» спиновых волн в безграничной
среде при к'<кс является следствием
уменьшения групповой скорости
Рис. 7.4. Дисперсионные
характеристики спиновых волн с учетом
потерь; 9t=0; штриховые линии -
проекции кривой и>(к', к") на
плоскости (со, к') и (к1, к"); штрихпун-
ктир—зависимость <о(к') без учета
потерь
203
и устраняется при учете граничных условий, так что
рассмотренные в § 6.2 волны с малыми к' в пластинах и стержнях сохраняют
смысл.
Примем теперь ю = ю'-Ию", к" = 0. В этом случае при cx<s:l
всегда ю"-«сй' и комплексное дисперсионное уравнение можно решать
в первом приближении, полагая ю' таким же, как в отсутствие
потерь. Тогда, как легко убедиться,
ю" = асо'£, (7.25)
где ^ имеет тот же смысл, что в (7.16).
При рассмотрении затухающих спиновых волн часто вводят
величины: длину пробега
4=1/(2/:") (7.26)
и время жизни спиновой волны
т*=1/(2ш"). (7.27)
Они характеризуют затухание соответственно в пространстве и во
времени квадрата амплитуды волны. Приведенные названия этих
величин имеют прямой смысл для квазичастиц, соответствующих
спиновым волнам,— магнонов (§ 7.3).
Анизотропный ферромагнетик. При рассмотрении спиновых волн
в анизотропном ферромагнетике — монокристалле—мы не будем
учитывать диссипации; в случае малых потерь величины к" и ю"
можно будет оценить по формулам (7.23) и (7.25). Не будем
учитывать также анизотропии неоднородного обмена, т. е.
по-прежнему будем считать q скалярной величиной и использовать
выражение (7.4).
Подставим эффективное поле (7.4) в линеаризированное
уравнение движения анизотропного ферромагнетика, которое, как
отмечалось в § 2.3, получается из уравнения (1.92) путем замены
в нем поперечных компонент тензора N на соответствующие
компоненты Na, а величины N33 (входящей в Я0)—на сумму
Л^з+^зз- Полученное уравнение будет отличаться от аналогичного
уравнения в безобменном приближении заменой (7.7). Поэтому
дисперсионные соотношения для обменных спиновых волн в
монокристаллах могут быть найдены путем этой замены, в частности,
в (6.19) и (6.20).
Приведем в качестве примера дисперсионное соотношение
(со/у)2 = (Н0 + Н А + Dk 2) (Н0 + Н А+Dk 2 + 4яМ0 sin 2 в»), (7.28)
которое справедливо: при НА = 2К1/М0 — когда намагниченность
М0 направлена по оси одноосного кристалла или по оси <100>
4
кубического кристалла, и при НА=—-К1/М0 — когда М0
направлена по оси <111> кубического кристалла (при учете только первой
константы анизотропии).
204
§ 7.2. Спиновые волны в ограниченных телах
В этом параграфе будет исследовано влияние неоднородности
параметров среды, в первую очередь—границ раздела между
различными средами на распространение спиновых волн. Так же
как в § 6.2, задача будет заключаться в совместном решении
уравнения движения намагниченности и уравнений электродинамики
с учетом граничных условий. С еще большим основанием (для
неметаллических ферромагнетиков) можно будет использовать маг-
нитостатическое приближение. Но, во-первых, в уравнение движения
надо будет теперь ввести эффективное поле обменного
взаимодействия (7.4), а, во-вторых, к электродинамическим граничным
условиям (4.3) или (6.13) добавить дополнительные граничные условия,
накладываемые на намагниченность. Этими условиями мы и
займемся прежде всего.
Дополнительные граничные условия. Необходимость их введения
формально следует из того, что учет обменного взаимодействия
приводит к появлению в уравнении движения производных переменной
намагниченности m по координатам. Вследствие этого повышается
порядок дифференциальных уравнений, которые получаются при
совместном решении уравнения движения и уравнений
электродинамики; общие решения этих уравнений содержат теперь большее число
постоянных, и электродинамических граничных условий становится
недостаточно для их определения.
Физическая причина, которая требует введения дополнительных
граничных условий для т, заключается в том, что на магнитные
моменты вблизи поверхности раздела сред действую* поля,
отличающиеся от таковых внутри тела. И если мы не рютим детально
исследовать колебания намагниченности в этих полях, то должны
(считая слой, в ко юром они существуют, достаточно тонким) учесть
их воздействие на колебания намагниченности внутри ферромагнетика
при помощи некоторых граничных условий.
Дополнительные граничные условия могут быть получены из
уравнений движения намагниченности подобно тому, как
электродинамические граничные условия (§ 4.1) следуют из уравнений
Максвелла. Будем считать, как и в § 7.1, обменное
взаимодействие изотропным. Тогда уравнение (2.12) можно будет записать
в виде
—+MxHt(1+#xV2M+MxHs = 0. (7.29)
У (I
Здесь qV2M—неоднородная часть (7.3) эффективного поля обменного
взаимодействия; НеГ1 включает все остальные поля, сравнительно
медленно изменяющиеся в пространстве: внешнее магнитное поле,
размагничивающее поле, эффективные поля анизотропии и
эффективное поле, учитывающее диссипацию; Hs представляет собой
эффективное поле поверхностной анизотропии, существующее лишь в тонком
поверхностном слое и учитывающее особые условия, в которых
находятся магнитные моменты в этом слое
205
Рис. 7.5. Граница ферромагнетика (£<0)
с немагнитной средой
Поверхностная
анизотропия может быть как
одноосной—с легкой либо трудной
осью, перпендикулярной
поверхности, так и однонаправ-
кнной—когда два
противоположных направления нормали
к поверхности неэквивалентны.
Возможен и более сложный ее
характер, когда легкой
является коническая поверхность
с осью — нормалью к
поверхности раздела. Примем для
определенности, что
поверхностная анизотропия—одноосная. Тогда, ограничиваясь первой
константой, запишем согласно (2.44) ее энергию в виде
^-(^/Л/^ММпо)2, (7.30)
где п0 — единичный вектор внешней (по отношению к ферромагнетику)
нормали к поверхности (рис. 7.5). С помощью формулы (2.9) находим
Hs = (2*r1/Wg)(Mn0)no. (7.31)
Рассмотрим границу ферромагнетика с немагнитной средой
и проинтегрируем (7.29) по объему V диска (рис. 7.5) толщиной
2d, «разрезанного» граничной поверхностью S; величина d больше,
чем толщина ds поверхностного слоя (в котором К\/0), но
все же мала. Тогда первые два члена (7.29) дадут пренебрежимо
малые вклады, и результат интегрирования с учетом (7.31) можно
будет представить в виде
Ii+I2 = 0,
l^^qMx^MdV, L2=2$(Kl/M$}(Mn0)Mxn0dV.
(7.32)
Преобразуя интеграл l! в поверхностный, учитывая малость d и считая
площадь диска а тоже малой, получим1'
ll = —aqMx
ВМ
(7.33)
где д/дп означает производную по направлению внешней нормали
п0. Интеграл Ij, с учетом малости а примет вид
12 = ст J 2(KilM §)(M х и0)(МпоК, (7.34)
о
где £—координата в направлении п0. Его можно записать:
l2 = 2aKs/(M20)(Mxn0)(Mvi0), (7.34а)
" Ьилее подробный вывод приведен в [69].
2.06
определив таким ооразом константу поверхностной анизотропии Ks.
Если М не зависит от С,, то
о
Подстановка (7.33) и (7.34а) в (7.32) дает искомое граничное
условие:
</Мх^ + ^%поМ)п0хМ = 0. (7.35)
en Mi
Оно накладывается на вектор М в ферромагнетике вблизи его
границы, но, строго говоря, вне тонкого поверхностного слоя. Этот
слой, таким образом, исключается из рассмотрения, а его свойства
учитываются параметром Ks.
В интересующем нас случае малых колебаний намагниченности при
М0 = const (т. е. в отсутствие доменов), подставляя М = М0 + техр(/со<)
в (7.35) и приравнивая нулю сумму линейных по т членов, получим
граничное условие для комплексной амплитуды m
z0 х -—h^ [(n0m)n0 x z0+(n0z0)n0 x m] = 0, (7.36)
где z0 — единичный вектор в направлении М0, а
£, = 2Ksl(qM$) {131)
— параметр (с размерностью см-1), характеризующий отношение
энергии поверхностной анизотропии к неоднородной обменной энергии.
Его называют параметром закрепления (магнитных моментов на
поверхности). Он может быть положительным или отрицательным
в зависимости от знака Ks, т. е. от тогб, является нормаль
к поверхности легкой или трудной осью поверхностной анизотропии.
Предельные случаи ^ = 0 и ^=оо называют соответственно отсутствием
закрепления и полным закреплением. Эти предельные случаи
рассмотрели соответственно Амент и Радо [226] и Киттель [351]:
общий случай исследовали Радо и Уиртмен [392] и Каганов [95].
Проектируя (7.36) на оси координат, показанные на рис. 7.5 (ось
у касательна к граничной поверхности), найдем условия, которые
записал Суху [193]:
—+^и1,со82в = 0, ^-Km,cos2G = 0, (7.38)
дп дп
где 9 — угол между М0 и нормалью к поверхности. В случае
нормального намагничивания (6 = 0)
^+^., = 0, (7.39)
СП
а при касательном намагничивании (0 = л/2)
сп ^ дп
(7.40)
207
В предельном случае £ = 0 (отсутствие закрепления) имеет место
граничное условие Амента—Радо
а при полном закреплении (кроме случая касательного
намагничивания)—условие Киттеля
ш=0. (7.42)
Заметим, что относительные величины первого и второго членов
в (7.38), а следовательно, и возможность приближенного использования
того или другого предельного случая (Амента—Радо или Киттеля)
зависят не только от величины параметра вещества £, но и от
скорости изменения переменной намагниченности в направлении
нормали к поверхности, т. е. в случае волнового процесса—от величины
составляющей к± волнового вектора в этом направлении. При конечном
^ граничное условие будет приближаться к условию Киттеля с
уменьшением к± и к условию Амента—Радо—с увеличением кх.
Стоячие спиновые волны в пленке (спин-волновой резоьанс).
Перейдем к рассмотрению спиновых волн в плоскопараллельной
ферромагнитной пластине. Остановимся сначала на частном случае,
когда составляющая волнового вектора в плоскости пластины Агц =0,
т. е. рассмотрим однородные в этой плоскости (но неоднородные
по толщине) колебания намагниченности. Возможность возбуждения
таких колебаний (стоячих спиновых волн) однородным переменным
магнитным полем предсказал Киттель [351] и экспериментально
подтвердили Сиви и Танненвальд [411]. Это явление получило
название спин-волнового резонанса.
Рассмотрим сначала собственные колебания—в отсутствие
затухания и возбуждающего поля. Задача будет заключаться в отыскании
совместных решений уравнения движения намагниченности и
уравнений магнитостатики, удовлетворяющих электродинамическим и
рассмотренным выше дополнительным граничным условиям на
поверхностях ферромагнитной пластины. Уравнение движения будет по-
прежнему иметь вид (7.12), a h, запишется согласно (7.4). При
решении этой задачи, как и при рассмотрении волн в безграничной
среде (§ 7.1), можно идти по двум путям, различающимся
последовательностью учета уравнения движения и уравнений
магнитостатики. Воспользуемся вторым путем, т. е. найдем прежде всего связь
магнитного поля с намагниченностью, вытекающую из уравнений
магнитостатики и электродинамических граничных условий.
Выражение (7.11) для поля Ьм будет справедливо и в
рассматриваемом случае стоячих волн. Вектор к при этом направлен по
нормали к плоскости пластины и, таким образом,
Ъм = - 47ГПо (mn0). (7.43)
Для собственных колебаний это поле является полным переменным
магнитным полем. Снаружи пластины оно равно нулю, а внутри
208
не имеет касательных составляющих. Таким образом, первое
электродинамическое граничное условие выполняется. Выполнение второго
также обеспечивается выражением (7.43). Поле hM должно быть
подставлено в уравнение (7.12) и найдены решения этого уравнения,
удовлетворяющие дополнительным граничным условиям.
Рассмотрим нормально намагниченную пластину (рис. 6.4). Поле
hM в этом случае обращается в нуль. Цилиндрическая симметрия
системы делает целесообразным использование циркулярных
составляющих т± (см. § 1.3). Условие существования ненулевых решений
уравнения (7.12) в этих составляющих при сх = 0 и hM = 0 дает
выражение для собственных частот
<о±=±(сон + Г|А:22). (7-44)
Поскольку частота по определению положительна, колебания с левым
вращением (с частотой со_) возможны только при мнимых и
достаточно больших по модулю значениях kz. Для колебаний с правым
вращением и вещественных kz частота со+ совпадает с частотой
спиновых волн (7.9), распространяющихся в безграничной среде
в направлении М0.
Пусть параметр закрепления с, имеет различные значения на
разных сторонах пластины (что, в частности, всегда имеет место
для пленок на подложках). Тогда дополнительные граничные условия
согласно (7.39) запишутся следующим образом:
дт±
—-—\-c,im±=0 при 2 = 0,
(7.45)
——|-Ч2>"±=0 при z = d.
Решения, удовлетворяющие этим условиям, можно искать в виде
т±=А± coskzz + B± sin kzz. (7.46)_^
Подставляя (7.46) в условия (7.45), мы получаем уравнение для kz.
cxgkzd=k\-^\\. had
Остановимся на частном случае ^i = !U = ^- Уравнение, в которое
при этом перейдет (7.47), эквивалентно двум более простым:
ctg(<p/2) = <p/(!jrf), (7.48)
-tg(<p/2) = <p/(!#), (7.49)
где y = kzd. При £>0 эти уравнения имеют только вещественные
корни и, следовательно, возможны только правополяризованные
колебания. Графическое нахождение корней в этом случае
иллюстрирует рис. 7.6. Обозначая корни в порядке их возрастания kz„
(н=1, 2, 3, ...) и учитывая, что в данном случае (йн = уНе0—(йм,
получим из (7.44)
a„h = Ht0-4nM0 + Dkln. (7.50)
14 А. Г. Гуревич, Г. А. Мелков 209
При £=оо (полное закрепление)
kIn = nn/d, а при cj = 0 (отсутствие
закрепления) к„ = (п— l)n/d;
последнее выражение, как видно из рис. 7.6,
приближенно справедливо и для
промежуточных значений cj при
достаточно больших п.
Нетрудно убедиться, что корням
(7.48), т. е. нечетным п,
соответствуют зависимости m+(z),
симметричные относительно середины
пластины (z = d/2), а корням (7.49), т. е.
четным и—антисимметричные.
Зависимости w+(z) показаны на
рис. 7.7. Из этого рисунка видно,
в частности, что решение с п=\
Рис. 7.6. Графическое решение ура- при Ej = 0 представляет собой одно-
внений (7.48) и (7.49); |rf=4; цифры родное колебание намагниченности;
у точек пересечения-значения п частота его (1.101) следует из (7.50).
При cj^O однородного колебания не существует.
При tj<0 уравнения (7.48) и (7.49) имеют, кроме вещественных,
по одному мнимому корню k. = iy.t. Этим решениям соответствуют
колебания с гиперболической зависимостью m+{z)—гиперболические
или поверхностные типы колебаний (рис. 7.7). Поведение вещественных
и мнимых корней при изменении параметра cj иллюстрирует рис. 7.8.
Как видно из этого рисунка, величины у. (при d= const) неограниченно
'
'l \ 4
\ Дл
\ у* \
1хк \
У\ \ \
v \ v
i \ 4
» \ *
i I i
\
i
i
i
i
S.
1
1
! 7s
6У\
у 9
У £*
! Р
Y i U^ctsz-
> \ ' Г \
\ \ \ \ 1
1 \ \ \ »
V \ \ \ *
4 \ ч \ Ч'
\4П\ \6ix\ \ 8п а>
\ v \ v \
\ v \ » \
\ ' 1 * \
i 1
i 1
i I
i |
п=1
л=3
/1=4
FWfWMVkA
Рис. 7.7. Распределения переменной намагниченности стоячих спиновых волн
в нормально намагниченной пленке при симметричных граничных условиях
(^i = ^2 = ^)- Колебания с и=1 и и=2 при £<0—гиперболические
210
kzd
_--'
, **
—-—-"""^ .--''"
_^"
.-'"" п=1
/
/
-16 -12 -8 -4 / /
/ /
Поверхностные // 4
колебания г\/ /
\/у
У в
/У
/У
У 12
\ 4 8 12 16 20 §d
Однородное колебание
Рис. 7.8. Зависимости корней уравнений (7.48) (сплошные линии) и (7.49)
(штриховые) от параметра закрепления [178]
растут с увеличением |tj|. При этом, как видно из (7.44), частоты
поверхностных типов колебаний уменьшаются и обращаются в нуль
при Dx2 = Hc0 — 4nM0. При еще больших у. (или меньших Яе0)
собственным типом колебаний становится намагниченность с левым
направлением вращения [210].
Остановимся теперь, следуя работе Корчагина, Хлебопроса и
Чистякова [117]. на другом частном случае Z,i=— £j2s£, т.е.
антисимметричных граничных условий. В этом
случае из (7.47) следует, что независимо
от величины Ь, имеет место kz = rm\d. Это
хорошо видно и из рис. 7.9. Такие
граничные условия могут быть реализованы
[455] путем нанесения на пленку
(толщиной d с намагниченностью М0) тонких—с
толщинами dy_2 *g.d— слоев с намагничен-
ностями М01>М0 и Мо2<М0.
Перейдем к рассмотрению
вынужденных колебаний. Их намагниченность будем
искать в виде ряда
т+ = X Ow+„
(7.51)
по намагниченностям собственных
колебаний (7.46). Они ортогональны и
могут быть нормированы, например, так,
чтобы
jA\n + B\n=\,
(7.52)
14"
Рис. 7.9. Распределения
переменной намагниченности
стоячих спиновьпСвотгн-в
нормально намагниченной
пленке при
антисимметричных граничных условиях
211
где А+„ и В+„—коэффициенты в (7.46) для и-го типа колебаний.
Для коэффициентов Сп справедлива формул? (6.110). Из нее видно
прежде всего, что рассматриваемые колебания будут наиболее
эффективно возбуждаться переменным магнитным полем h, лежащим
в плоскости пленки и имеющим круговую поляризацию с правым
(для правополяризованных колебаний) вращением.
Если поле h однородно, его можно вынести из-под интеграла
в (6.110); интеграл
W„ = [m+ndz,
(7.53)
который появится тогда в числителе этой формулы, представляет
собой собственный магнитный момент для и-го колебания (отнесенный
к единице площади пленки).
Как видно из рис. 7.7 и 7.9, 5Ш+П обращается в нуль для всех
четных и. Таким образом, как для симметричных, так и для
антисимметричных (но не произвольных!) граничных условий только
колебания с нечетными и возбуждаются однородным полем.
Ограничимся теперь случаем ^! = ^2 = ^>0. Подставим в (7.53)
выражение (7.46) и учтем соотношения (7.48) и (7.52). Тогда для
нечетных и (т. е. симметричных типов колебаний) найдем
т+п = к^(1+к?Л2)-1'2 (7.54)
(для несимметричных 5Ш+П = 0). Из (7.54) видно, что величина Ш+„,
а следовательно, интенсивность возбуждения являются наибольшими
при tj=oo и стремятся к нулю при 4~*0 (это следует и из рис. 7.7).
^ппг л
I
I
1
I
/2 = 3
16
18
20 Не0,кЗ
Рис. 7.10. Спектр спин-волнового резонанса в нормально намагниченной пленке
кобальта [434]. Частота 8,8 ГГц, толщина пленки 0,294 мкм
При изменении частоты или постоянного поля будут резонансным
образом изменяться коэффициенты при собственных функциях с
различными и, т. е. будут поочередно возбуждаться различные типы
колебаний (рис. 7.10). Для того чтобы эти типы колебаний были
различимы, например при изменении Нс0, должно, как нетрудно
показать, выполняться условие
4(n+l)Dn2ld2^AH.
(7.55)
212
Из этого выражения видно, что для наблюдения спин-волнового
резонанса необходимы тонкие пленки.
Величиной, которая регистрируется в опытах по спин-волновому
резонансу, является переменный магнитный момент пленки *)Я. Если
условие (7.55) выполняется, т. е. при каждом Нс0 возбуждается только
один тип колебаний, то
<m = SCnlm+ndz = SC„mm (7.56)
о
где 5ШП—нормированный собственный момент (7.53), a S—площадь
пленки (или части ее, связанной с электромагнитным полем). При
резонансе (со = со^) с учетом (6.110) и (7.54)
|да|»-^К1+^)Г*+- (757)
В частности, при полном закреплении (Ej = oo, kxn = nn/d) |$Ш|гмоои2.
В случае касательно намагниченной пленки (рис. 6.8) поле (7.43)
не обращается в нуль. Подставляя его в уравнение движения (7.12)
и проектируя это уравнение на оси х и у, мы получим из условия
совместности уравнений для тх и ту соотношение
to2 = (со„ + т)Л:^) (ш„ + т)А:^ + шм), (7.58)
которое не отличается от дисперсионного соотношения (7.9) при
0к = я/2. При фиксированной частоте уравнение (7.58) имеет два корня
kxl_2. Можно убедиться, что один из них fc2i>0 при coxuj.
и отрицателен при co<cojj в первом случае колебание представляет
собой стоячую волну с тригонометрической зависимостью от д. во
втором— зависимость от х является гиперболической. Второй корень
к\2 всегда отрицателен [178].
Решения уравнения движения в данном случае можно искать
в виде, аналогичном (7.46). Но при произвольном параметре
закрепления tj колебание с одним значением кх (в выражения тх и ту для
него войдут две постоянные) не сможет удовлетворить четырем (на
двух сторонах пленки) дополнительным граничным условиям (7.40).
Только в случае £j = 0, когда для тх и ту имеют место одинаковые
условия (7.41), им удовлетворяют по отдельности парциальные
колебания с кх1 и кх2.
Не останавливаясь подробно на спин-волновом резонансе при
касательном намагничивании (см., например, [178]), отметим лишь, что
при реальных толщинах и параметрах пленок амплитуда парциального
колебания с кх2 быстро убывает при удалении от поверхности. Это
колебание играет существенную роль в обеспечении выполнения
граничных условий, но влияние его на частоты собственных колебаний
оказывается несущественным. Уравнение же для кх1 в этом случае
оказывается возможным привести к виду, аналогичному (7.48), но
с эффективным — зависящим от частоты параметром закрепления £,cf.
При низких частотах £cf-+0. а при высоких £jcf->cj'2 [178].
Экспериментальному исследованию спин-волнового резонанса
было посвящено огромное количество раоот (см. [178, 303]). Сначала
213
использовались металлические пленки (см., например, [411, 434, 455,
117]); их проводимость при этом мало сказывалась, так как толщина
пленки d была меньше, чем толщина скин-слоя 6. В дальнейшем,
когда были получены высококачественные неметаллические магнитные
пленки, исследования спин-волнового резонанса были выполнены и на
них [409. 465].
В большинстве ранних работ наблюдались отклонения от
приведенных выше теоретических зависимостей, причиной которых
являлось несовершенство пленок, в частности, непостоянство М0 по
всей их толщине [275] (а не только в тонком поверхностном слое,
что учитывается граничными условиями). Когда же были приняты
необходимые меры для получения однородных пленок, предсказания
теории начали хорошо выполняться [238, 237]. Спин-волновой
резонанс стал одним из методов исследования магнитных пленок
и прежде всего — измерения постоянной неоднородного обмена D.
Для этого особенно удобным оказался рассмотренный выше случай
антисимметричных граничных условий (£i=— £,г)> для которого
D может быть найдено из измеренного спектра независимо от
величины ^i [117].
Спиновые волны, распространяющиеся в плоскости пленки. При
рассмотрении таких волн (с &ц/0), как мы увидим, возникает
трудность, аналогичная той, с которой мы уже встретились в случае
Лц=0 при касательном намагничивании — парциальные волны по
отдельности не могут удовлетворить всем граничным условиям.
Имеется, однако, исключение — нормально намагниченная
металлизированная пластина при отсутствии закрепления (£ = 0) на обеих ее
поверхностях. Хотя экспериментальная реализация этого случая,
по-видимому, затруднительна, рассмотрение его полезно, так как
позволит выявить ряд особенностей, которые встретятся и в более
сложных случаях.
Рассматривая в § 6.2 нормально намагниченную
металлизированную пластину в безобменном приближении, мы видели, что потенциал
i|/ = cosA:zzexp(—/t,,j) при выполнении соотношения (6.26) обеспечивает
выполнение электродинамических граничных условий. Вычисляя
составляющие поля h = Vi|/ и намагниченности m = 5th, мы убеждаемся,
что дополнительные граничные условия (7.41) тоже выполняются.
Таким образом, волна с этим потенциалом является нормальной
волной и при учете обменного взаимодействия. Подставляя k2 = ky+k2
в (7.9), мы находим дисперсионное соотношение для нее
со2 = (ш„ + цк\ + цк2) LH + г, Л2 + г,к2у + Г^т), (7-59)
где согласно (6.26) kz = nn/d, а и = 0, 1, 2, ... характеризует номер
ветви спектра. При г)-»0 (7.59) переходит в (6.28), а при rf-+oo—в
дисперсионное соотношение (7.9) для спиновых волн в безграничной
среде при вк = п/2. При ку-+0 частоты (7.59) переходят в частоты
(7.50) стоячих спиновых волн при £ = 0. Зависимости w(ky),
вычисленные по формуле (7.59), приведены на рис. 7.11.
214
Г, ГГц
14
12
10
8
b
f,rru.
d=0,1 мкм 1
У
-
- у
" / S
1/''
I —I
ЛГ
ющ
10s k,CM '
Рис. 7.11. Дисперсионные характеристики спиновых волн в нормально
намагниченных металлизированных пленках при £=0. Расчет по формуле (7.59);
цифры у кривых значения п. Штриховые линии—без учета обмена, по
формуле (6.28); М0=139Гс (ЖИГ), Hv„ = \9 кЭ
В других случаях решения уравнений магнитостатики и уравнения
движения, удовлетворяющие электродинамическим и дополнительным
граничным условиям и соответствующие распространяющимся вдоль
пластины волнам, носят значительно более сложный характер. Для
отыскания этих решений, как и в случае безграничной среды (§ 7.1)
и пленки при /с н= 0, возможны два пути, отличающиеся
последовательное 1 ыо учета уравнений и граничных условий
магнитостатики и уравнения движения намагниченности.
Первый путь, который использовали Ганн [55] и затем Филиппов
[207, 208], Де Вэймс и Вольфрам [279, 460, 461] и многие другие,
заключается в том, что сначала учитывается связь переменной
намагниченности m с магнитным полем h. вытекающая из уравнения
движения. Эта связь характеризуется тензором х. компоненты
которого (см. § 7.1) зависят теперь не только от частоты, но и от
волнового вектора к. Затем ищутся решения уравнений
электродинамики (в магнитостатическом приближении), удовлетворяющие как
электродинамическим, так и дополнительным граничным условиям.
Второй путь, который разработали для случая пленок Вендик,
Чарторижский и Калиникос [45, 104], отличается от первого тем, что
сначала находится связь размагничивающего поля hM с намагниченностью,
вытекающая из уравнений магнитостатики и электродинамических
граничных условий, а затем ищутся решения уравнения движения,
удовлетворяющие дополнительным граничным условиям.
Остановимся несколько подробнее на основных этапах решения
задачи обоими методами. При этом для определенности рассмотрим
нормально намагниченную пластину. Направим оси координат, как
215
на рис. 6.4, и предположим, что зависимость от х отсутствует.
Тогда, идя по первому пути, мы должны найти, с учетом выражения
(7.8) для и, решения уравнения Уокера (6.15), удовлетворяющие
электродинамическим граничным условиям и граничным условиям
(7.39). Выражения для потенциала «в воздухе» (в случае свободной
пластины) можно по-прежнему записать в виде (6.30). Что же
касается потенциала в пластине, то, как легко убедиться, выражение
(6.24) не может обеспечить (кроме рассмотренного выше частного
случая) одновременного выполнения всех граничных условий. Тем
не менее, имея в виду парциальные волны, подставим (6.24) в уравнение
Уокера и учтем выражение (7.8), в котором в данном случае (д/дх = 0)
к2=ку+к*. Тогда мы получим выражение, совпадающее с (7.59),
но, конечно, теперь кгфпп/(1.
Выражение (7.59) при фиксированных ю и ку представляет собой
бикубическое уравнение для к. и имеет корни кгр (/7=1, 2, 3). Им
соответствуют парциальные волны, потенциалы которых v|/p получатся
при подстановке корней кгр((о) в (6.24). Суперпозиция этих волн
может удовлетворить всем граничным условиям и явиться, таким
образом, нормальной волной исследуемой системы. Действительно,
для металлизированной пластины имеется шесть постоянных и шесть
граничных условий: по одному электродинамическому и двум
дополнительным на каждой поверхности пластины. Для свободной
пластины добавляются две постоянные—в выражениях для
потенциала в воздухе—и два электродинамических граничных условия.
Приравнивая нулю определитель полученной таким образом системы
шести или восьми уравнений, мы придем к уравнению, связываюшему
ку и ю, т. е. дисперсионному соотношению для нормальных волн.
Идя по второму пути, мы сначала находим связь между
намагниченностью m (которая на этом этапе рассматривается как
заданная) и полем hM, которое совместно с m должно удовлетворять
магнитостатическим уравнениям и электродинамическим граничным
условиям. Следует отметить, что поле hM не является, вообще
говоря, полным магнитным полем h (которое связано с m
соотношением m = xh), а представляет собой, как и поле (7.11), эффективное
поле, соответствующее внутренней магнитной энергии (см. § 2.1),
или размагничивающее поле (в широком смысле этого термина).
Но пока мы рассматриваем задачу о нормальных волнах (в отсутствие
вынуждающего поля), hM является единственным переменным
магнитным полем в уравнении движения.
Поле hM должно быть затем подставлено в уравнение движения
намагниченности. Кроме него, в это уравнение войдут эффективное
поле обменного взаимодействия, эффективные поля анизотропии,
а при рассмотрении задачи о возбуждении спиновых волн сторонним
полем hCT—и это поле. Кроме hCT, все остальные переменные поля
в уравнении движения будут записаны как функции намагниченности
m(z, j) = m(z)exp( — ikyy). Необходимо найти решения такого уравнения,
удовлетворяющие дополнительным граничным условиям.
Неизвестные функции mx(z) и my(z) оказывается целесообразным
[45] искать в виде рядов по решениям m}xy(z) уравнения движения
216
без поля hM, удовлетворяющим тем же дополнительным граничным
условиям, что и искомая намагниченность. В рассматриваемом случае
нормального намагничивания целесообразно, конечно, перейти к их
циркулярным составляющим mj±(z). Собственные функции nij±{z)
представляют собой не что иное, как решения рассмотренной выше
задачи о нераспространяющихся колебаниях (стоячих спиновых волнах)
в нормально намагниченной пленке, ибо, как уже отмечалось выше,
в этом случае поле hM отсутствует.
После подстановки в уравнение движения разложений m±(z) по
функциям mj±(z) мы приходим к бесконечной системе линейных
уравнений для коэффициентов в этих разложениях. Условие
совместности ее дает дисперсионное уравнение F(a>, ky) = 0, корни которого
(й„(ку) соответствуют различным ветвям спектра.
Оба пути, основные этапы которых были кратко рассмотрены
выше, конечно, эквивалентны, так как исходят из одних и тех же
уравнений и граничных условий и оба приводят к расчетам, которые
обычно осуществимы лишь численными методами с помощью ЭВМ.
Не имея возможности вникать здесь в детали этих расчетов, приведем
для иллюстрации некоторые их результаты.
На рис. 7.12 приведены дисперсионные кривые для нормально
намагниченной свободной пленки при двух крайних значениях параметра
Рис. 7.12. Дисперсионные характеристики и распределения переменной
намагниченности спиновых волн в нормально намагниченной пленке [460]. Толщина
пленки ^/=0,61 мкм, ЖИГ; цифры у кривых—значения и
217
закрепления. Показаны также
зависимости переменной
намагниченности т+ от координаты
в направлении нормали к
пленке. При увеличении ку частоты
всех ветвей возрастают, так же
как и в простом случае,
рассмотренном выше (рис. 7.11).
Но, конечно, теперь
дисперсионные характеристики являются
более сложными. Одно из
усложнений заключается в том,
что пересечение ветвей на
рис. 7.11 заменяется теперь
«расталкиванием» некоторых
ветвей. Сравнение между собой
рис. 7.12, а и б показывает, что
характер дополнительных
граничных условий сильно влияет
на распределения
намагниченности; при малых ку они
оказываются довольно близкими к
показанным на рис. 7.7
распределениям для спин-волнового резонанса (ку = 0) при соответствующих ^.
Для каждой ветви спектра в каждой ее точке могут быть оценены
вклады в энергию волны обменного и магнитного взаимодействий. И
если один из этих вкладов преобладает, данная ветвь может быть
названа обменно-доминантной (или, кратко, обменной), либо
магнитно-доминантной (магнитной). Так, например, при малых ку (рис. 7.12)
магнитной будет ветвь с и=1 при £=0, а обменными—все остальные ветви.
На рис. 7.13 показаны дисперсионные характеристики спиновых
волн в касательно намагниченной пленке. Значения со„ при к =0
представляют собой частоты спин-волнового резонанса. При
распространении волн перпендикулярно М0 с увеличением к = ку частоты
всех ветвей растут и для ветвей одинаковой четности имеет место
«расталкивание». При учете потерь в точках сближения
расталкивающихся ветвей возникают пики к" [63].
При распространении параллельно М0 зависимости соп от к\\=к:
(рис. 7.13) являются немонотонными. При малых к- преобладает
влияние магнитного взаимодействия (т. е. электродинамических
граничных условий), которое, как и для безобменных волн при таком
направлении распространения (§ 6.2), приводит к уменьшению
соп с ростом kz (волны являются обратными), а затем начинает
преобладать обменное взаимодействие и частоты со„ растут.
Сравнение результатов точных расчетов дисперсионных соотношений
для спиновых волн в пленках с результатами § 6.2 показывает, что
последние приближенно справедливы при достаточно малых величинах
к и и достаточно больших d. Это не является совсем очевидным, так
как дополнительные граничные условия, которые в § 6.2 не учитывачись
218
10z fO5 10* Н,см '
Рис. 7.13. Дисперсионные характеристики
спиновых волн в касательно
намагниченной пленке при разных направлениях
распространения (схематически).
Сплошные линии—к±М0. штриховые—к || М0;
cfelMKM, ЖИГ, Я0=1,25кЭ
(и которые невозможно учесть без одновременного учета обмена),
всегда накладываются на намагниченность. И действительно,
дополнительные граничные условия всегда существенно влияют на
распределение намагниченности вблизи границ ферромагнетика. Но с уменьшением
fc|i и увеличением d относительный объем этих областей уменьшается,
и влияние их на дисперсионные соотношения становится малым.
Спин-волновые волноводы. До сих пор мы все время считали, что
намагниченность и поле зависят только от одной из поперечных (по
отношению к направлению распространения) координат, а именно от
координаты в направлении нормали к поверхности пленки. Зависимость
от второй поперечной координаты (в случае нормального
намагничивания— от х) необходимо учитывать для пленок конечной ширины w (см.
рис. 6.17). При этом к граничным условиям на поверхностях z = 0 и z = d
добавляются граничные условия на боковых поверхностях х = 0 и x = w
(при 0<z<d). Учет их даже в безобменном приближении (§ 6.2) приводит,
кроме случая полностью металлизированной пленки, к существенным
трудностям. Тем более они будут велики при наличии обмена. Однако
если размер и- достаточно велик, то приближенно можно заменить (при
нормальном намагничивании) к* па к\ t кх и, отвлекаясь от реальных
граничных условий, принять для кх аналогично (6.71) разрешенные
«квантованные» значения кх = пхп/н-. В результате каждая ветвь спектра
расщепится на бесконечное число близких (при больших и-) ветвей.
Подобное расщепление имело бы место и при точном решении задачи.
Другим примером системы с ограниченным поперечным сечением
ферромагнетика является продольно-намагниченный круглый цилиндр,
который в безобменном приближении рассматривался в § 6.2. Строгое
решение этой задачи с учетом обмена пока отсутствует. Но если
радиус цилиндра р0 достаточно велик (р0з>1 мкм для ЖИГ), чтобы
можно было пренебречь вкладом обменного взаимодействия,
обусловленным вариацией намагниченности по радиусу, то вклад этого
взаимодействия, связанный с вариацией по г, можно учесть путем
замены сон-»ейн + г]А-? в формуле (6.70). При больших kz (когда
и необходим учет обмена) эту формулу можно упростить, и после
указанной замены она примет вид [297 ]:
ы~юн + Г1/сг2+ -(амХ1П/(к;Ро)2- (7-60)
Спиновые колебания в образцах конечных размеров. Пусть теперь
образец будет ограничен во всех трех измерениях. Спектр спин-
волновых колебаний в нем, как и спектр безобменных (уокеровских)
колебаний, рассмотренных в § 6.3, должен представлять собой
бесконечное дискретное множество собственных частот. Строгое
отыскание этих частот с учетом обмена и всех граничных условий на
всех поверхностях образца представляет собой очень сложную задачу,
не решенную до настоящего времени. Однако некоторые соображения
относительно спектров таких колебаний могут быть высказаны.
Рассмотрим, например, нормально намагниченную прямоугольную
пленку конечной длины /. Предположим, что для бесконечно длинной
пленки такой же ширины известен закон дисперсии а(ку). Конечно,
219
решение в виде стоячей волны с одним значением ку не сможет
удовлетворить всем электродинамическим и дополнительным
граничным условиям на поверхностях у=0 и у=1. Но если длина пленки
/ достаточно велика, это обстоятельство можно игнорировать и учесть,
что для ку будет иметь место некоторое условие «квантования»,
например, ку=пуп/1. Тогда разрешенные значения ку обозначат на
всех ветвях дисперсионных характеристик и>„(ку) дискретные точки,
являющиеся собственными частотами образца. Интервалы между
соседними частотами будут тем больше, чем меньше /.
Спиновые волны в неоднородном постоянном поле. Вторым
представляющим интерес случаем спиновых волн в неоднородных системах
является неоднородность параметров ферромагнетика, обусловленная
неоднородностью внутреннего постоянного поля Н0. При этом в
уравнении движения коэффициент у m становится функцией координат.
Если изменение Н0 является достаточно медленным, то можно считать,
что в такой среде с медленно меняющимися параметрами
распространяется «обычная» спиновая волна, но ее волновой вектор к
непрерывно изменяется в пространстве. Его величина в данной точке
определяется значением Н0 в этой же точке в соответствии с законом
дисперсии (7.9). Условием медленного изменения поля Н0 является
\VH0\^kH0. (7.61)
Наибольший интерес представляет случай, когда на некоторых
поверхностях поле Н0 имеет такую величину Н%, что значение к,
найденное с помощью (7.9), обращается в нуль. Например, для волны
с 6* = 0 #о=ю/у. Тогда условие (7.61) не выполняется, и вблизи этой
поверхности необходимо искать решение уравнения движения с
переменными коэффициентами. По одну сторону от упомянутой поверхности
на достаточном от нее удалении это решение будет переходить
в волну с медленно меняющимся к, а по другую—в колебание
с амплитудой, экспоненциально убывающей в направлении градиента
Я0. Это дает основание, по аналогии с квантово-механическими
задачами о движении частиц вблизи потенциальных барьеров [132],
назвать рассматриваемые поверхности поверхностями поворота.
Остановимся кратко" на наиболее простой—одномерной задаче,
которая была решена Шлёманном и Джозефом [401, 407]. Рассмотрим
безграничный ферромагнетик в поле Н0, направленном по оси
z и монотонно изменяющемся при изменении z (рис. 7.14); плоскость
z=z0 является поверхностью поворота. Собственной модой
намагниченности в этом случае будет колебание с круговой поляризацией,
и мы можем ожидать, что мгновенное значение т~.+ будет зависеть
от z приблизительно так, как показано на рис. 7.14. При этом
вблизи плоскости z=z0 возникает не обращающийся в нуль
собственный магнитный момент. И если в этой области будет приложено
однородное переменное магнитное поле, то оно «зацепится» за этот
момент и возбудит волну т+ с переменным к, распространяющуюся
вправо от точки поворота.
" Подробный расчет приведен в [69].
220
Неоднородное внутреннее поле,
необходимое для такого возбуждения,
может быть реализовано, например,
в ферро- (или ферри-) магнитном
цилиндре, помещенном в однородное
внешнее поле //е0, параллельное его оси.
Аналогичную задачу, но для
нормально намагниченного диска
теоретически и экспериментально исследовал
Эшбах [294]. В этом случае поле
#о неоднородно по радиусу и
поверхности поворота представляют собой
цилиндрические поверхности; спиновые
волны распространяются по радиусам
к центру диска.
В дальнейшем Моргенталлер и Стэ-
нсил подробно исследовали
распространение спиновых волн в тонких
пленках в неоднородных постоянных полях.
В этом случае для получения
неоднородного Н0 внешнее поле Не0
должно быть неоднородным. Эти
исследования показали, в частности [425], что
волны могут распространяться и вдоль упомянутых выше поверхностей
поворота.
Особый интерес представляет случай, когда поверхность поворота
является замкнутой и ограничивает некоторую область («магнитную
яму»), ь которой к2>0. Тогда в этой области могут существовать
спин-волновые колебания, а снаружи намагниченность быстро убывает
по экспоненциальному закону при удалении от границы области —
поверхности поворота. Такой спин-волновой «резонатор» может быть
реализован, например, в нормально намагниченной пленке путем
уменьшения внешнего поля в некоторой небольшой ее области [105].
Особенность колебаний в таком резонаторе (как и волн, бегущих
вдоль поверхностей поворота) заключается в том, что отсутствуют
вклады в их затухание диссипативных процессов (см. § 11.3),
обусловленных рассеянием на различных неоднородностях, неизбежно
существующих на реальных поверхностях раздела сред.
В заключение подчеркнем, что в этом параграфе распространение
спиновых волн в ограниченных телах и неоднородных средах
рассматривалось с макроскопической точки зрения. Микроскопический
подход к этим проблемам развит, в частности, в работах [206, 278].
Рис. 7.14. Возбуждение
спиновой волны у поверхности
поворота
§ 7.3. Магноны
Высокочастотные процессы в ферромагнетике трактовались нами
все время как колебания или волны намагниченности в непрерывной
среде. Рассмотренная выше теория таких процессов была классической
(не квантовой). Она не могла не быть феноменологической, так как,
221
оставаясь в рамках классических представлений, нельзя выяснить
природу взаимодействий в ферромагнетике. В следующем параграфе
мы рассмотрим спиновые волны в ферромагнетике, исходя из
микроскопической модели и используя, естественно, методы квантовой
механики. Но предварительно, основываясь на принципе корпускуляр-
но-волнового дуализма, мы переведем на квантовый язык («прокван-
туем») полученные выше результаты. Этот принцип—один из
фундаментальных принципов физики—заключается в том, что любые
колебания или волны можно рассматривать также как скопления
или потоки частиц, энергия которых пропорциональна частоте
колебаний, а импульс—волновому вектору. В соответствии с этим
принципом возбуждения в твердом теле—механические, магнитные и др.
можно рассматривать либо как колебательные процессы в среде,
либо как кьашчастицы (см., например, [81]). В случае механических
колебаний такими квазичастицами являются фононы [16].
Квантование магнитных колебаний и спиновых волн. Из сказанного
ясно, что можно «проквантовать» и магнитные колебания и волны,
т. е. сопоставить им некоторые квазичастицы. Энергия каждой из них
е=йсо, (7.62)
где со—частота магнитных колебаний или волн, а импульс
р=йк, (7.63)
где к—волновой вектор магнитной (спиновой) волны. Такие
квазичастицы носят название магнонов". Зависимость со (к) дает в то же
время закон дисперсии г(р) магнонов.
Для однородных колебаний намагниченности импульс магнонов
р=0, а энергия е=йсо0, где со0—частота однородного
ферромагнитного резонанса. В другом крайнем случае больших к, когда
приближенно справедливо (7.13),
Е^ху?2 jh. (7.64)
Сравнивая это выражение с соотношением между кинетической
энергией и импульсом нерелятивистской частицы, мы видим, что
магнон при достаточно больших к может рассматриваться как
свободная частица с массой
™тав=й/(2п)- (7.65)
Для ЖИГ wmag=5,7-10~27—приблизительно в 6 раз больше массы
покоя электрона. Избыток энергии магнона е = йсо над величиной (7.64)
может трактоваться как его потенциальная энергия в магнитных полях —
внешнем и размагничивающем, эффективных полях анизотропии и пр.
Числа магнонов. Колебательная энергия магнитоупорядоченного
тела XV на корпускулярном языке представляет собой сумму энергий
" Для квазичастиц—корпускулярных аналогов спиновых волн в
ферромагнетике Вонсовский [48] первоначально ввел термин—ферромагноны (маг-
нонами ранее [175] были названы элементарные возбуждения в
парамагнетиках). Однако в дальнейшем термин «магноны» стали относить к
квазичастицам—аналогам спиновых волн во всех веществах
222
всех существующих в нем магнонов. Эту сумму условно можно
разбить на две:
W^=£nvEv+5]nkE». (7.66)
v к
Здесь п„—числа магнонов, соответствующих различным типам
колебаний, в том числе—и однородному, для которых существенно влияние
граничных условий; nk — числа колебаний с быстрыми вариациями
в пространстве, для которых влияние граничных условий для
переменных полей на спектр несущественно и которые можно
рассматривать как однородные плоские спиновые волны (§ 7.1).
Для того чтобы сохранить дискретность спектра, которая
предполагалась при записи (7.66), и в то же время избавиться от
необходимости сложного учета граничных условий, во второй сумме
в (7.66) можно заменить реальные граничные условия (конечно,
только для переменных величин) периодическими граничными условиями
Борна—фон Кармана (см., например, [16]). При этом все переменные
величины считаются периодическими функциями координат с
периодами 1и 12 и /3. Для плоской волны отсюда следует, что допустимыми
значениями проекций волнового вектора к являются
kx = 2nql/ll, ky^lnqjili, kz = 2nq3/l3, (7.67)
где qlt q2 и q} целые числа. Пока используется континуальная
модель, значения >гих чисел не ограничены.
Запись энергии в виде (7.66) предполагает, что взаимодействие
между различными типами колебаний отсутствует, т. е. «газ» магнонов
является идеальным. Пока мы рассматриваем малые колебания (т. е.
находимся в рамках линейной теории) и не учитываем диссипации,
это предположение выполняется.
Найдем теперь связь между числами магнонов и амплитудами
составляющих век юра переменной намагниченности. Для этого
следует приравнять классическую высокочастотную магнитную энергию
разных типов колебаний величинам nv/zcov или rtk/zcofc. Рассмотрим
сначала однородный тип колебаний малого эллипсоида. Его энергия
состоит из зеемановской энергии (2.17), внутренней магнитной энергии
(2.18) и энергии анизотропии. Последнюю мы можем формально
включить в энергию (2.18), считая, что в этом выражении N=Nf+Na,
где Nr — тензор размагничивающих факторов формы (см. § 1.5, где
он обозначен N), а N°—тензор эффективных размагничивающих
факторов анизотропии (§ 2.1). Выделим
колебательные—пропорциональные квадратам переменных составляющих т~.х и т~у члены
энергии и учтем соотношение
Мж ^M0-(mix+m iy)j(2 M0), (7.68)
которое вытекает в случае малых колебаний (т,ч.«М„) из условия
сохранения длины вектора М. Тогда мы придем к следующему
выражению для плотности энергии:
U= ^-(ml, + mlt)+±ml<(Xx-Nz) + \m~>{Ny-N:). (7.69)
2т о 2 2
223
Приравняв его величине и=п0Ыо, где со0—частота (1.96) однородного
типа колебаний, a n0 = n0/V—плотность числа соответствующих ему
магнонов (V—объем образца), можно найти связь п0 с амплитудами
переменных составляющих намагниченности. Она оказывается очень
простой, если образец представляет собой эллипсоид вращения,
намагниченный вдоль оси вращения, а ось анизотропии одноосного
кристалла или одна из осей < 111 > или <100> кубического совпадает
с этой осью. Тогда прецессия намагниченности является круговой
с амплитудой w0 = N/wlJt+wi> и, как легко убедиться,
n0 = m%/(2yhM0). (7.70)
Для спиновых волн в выражение для плотности энергии U
необходимо включить неоднородную часть обменной энергии и энергию
объемных размагничивающих полей hM, но не нужно включать энергию
поверхностных размагничивающих полей. Результат снова оказывается
простым, когда прецессия намагниченности—круговая, т. е. для
спиновых волн с 6к = 0. В этом случае число магнонов в единице объема
nk = nk/V=mk2/(2yhM0), (7.71)
где mk = Jmlkx + mlky.
Выражения (7.70) и (7.71) приближенно справедливы и для
однородных колебаний в произвольном эллипсоиде, если #0»47гМ0,
и для спиновых волн, распространяющихся в произвольном
направлении при условии #0 + £>fc2»47rM0sin26k, когда прецессия
намагниченности близка к круговой. Если же эти условия не выполняются,
то (7.70) и (7.71) справедливы лишь по порядку величин.
С учетом (7.70) и (7.71) из (7.68) можно получить важное
соотношение
М0-Мг = пуп, (7.72)
где п = п0 + пк—число магнонов однородной прецессии и спиновых
волн в единице объема. Это означает, что каждый магнон однородной
прецессии или (и) спиновых волн уменьшает г-проекцию
намагниченности на величину уЛгг#цв, где цв—магнетон Бора (см. § 1.1).
Для неоднородных длинноволновых (уокеровских) колебаний имеет
смысл говорить лишь о числах магнонов во всем образце. Их можно
найти, приравнивая колебательную энергию образца при данном
типе колебаний величине tivycov. В случае круговой прецессии (с
амплитудой mv(r))
^ = {2yhM0)-l\ml{T)dV. (7.73)
v
Если в образце существуют однородная прецессия, уокеровские типы
колебаний и коротковолновые спиновые волны, то полное изменение
2-проекции магнитного момента образца
M0V-SSKz = nyh, (7.74)
где n= Vn0 + Y,nv+У~£пк—полное число магнонов в образце.
v к
224
Для всех неоднородных типов колебаний (как уокеровских, так
и спиновых волн) поперечные составляющие магнитного момента
5Ш всего образца обращаются в нуль. Тогда, вычисляя
5Ш2 = 5Ш2+5Ш2+5Ш2 с учетом (7.74) и (7.00) и принимая во внимание,
что для малых колебаний nyh«М0У, получим
2К = М0К-(п-и0К)уЛ. (7.75)
Таким образом, длину вектора 5Ш уменьшают все магноны, кроме
магнонов однородной прецессии. Соотношение (7.74) справедливо
в общем случае только для образца в целом. Но если уокеровские
типы колебаний отсутствуют, то аналогичное соотношение может
быть записано для любой области, размеры которой значительно
превышают длины спиновых волн.
Таким образом, числа магнонов пропорциональны квадратам
амплитуд переменной намагниченности аналогично тому, как в квантовой
механике вероятности обнаружения частиц (при большом их
количестве—их числа) пропорциональны квадрату модуля волновой функции \|/.
Это дает основание предположить, что уравнение движения
намагниченности должно быть аналогично уравнению Шредингера [132].
Действительно, нетрудно убедиться, что в случае круговой прецессии уравнение
для амплитуды прецессии (безотносительно к рассматриваемому в этом
параграфе квантованию спиновых волн) совпадает по форме с
уравнением Шредингера для частицы с массой (7.65) и потенциальной
энергией yhH0. Эту аналогию впервые отметил Шлёманн. Цукерник
[211] показал, что она имеет место и в случае некруговой
прецессии.
Учет диссипации. По определению е и р—всегда вещественные
величины. Наличие диссипации приводит к тому, что время жизни
магнонов и длина их пробега становятся конечными. Как следует
из (7.70), (7.71) и (7.73), среднее время жизни магнонов тк равно
времени релаксации квадрата амплитуды соответствующих колебаний
или волн, т. е. (для спиновых волн) совпадает с введенной выше
величиной (7.27). Средняя длина пробега магнонов 1к в случае
спиновых волн совпадает с (7.26). Для колебаний, как однородных,
так и неоднородных, время жизни магнонов по-прежнему определяется
выражением (7.27), а длина пробега равна нулю.
Уменьшение чисел магнонов в соответствии с их конечным
временем жизни происходит в результате различных элементарных
процессов столкновений магнонов друг с другом и с иными частицами.
Вследствие этого число магнонов при свободных затухающих
колебаниях уменьшается, стремясь к равновесному тепловому уровню (см.
ниже). При стационарных вынужденных колебаниях постоянство
чисел магнонов поддерживается процессами их рождения, например,
за счет уничтожения фотонов возбуждающего электромагнитного
поля.
Статистика магнонов. Как следует из (7.72), магнитный момент
одного магнона
m=— Zoyfi=— Zo£Hb. (7-76)
15 А. Г. Гурсвич, Г. А. Мелков
225
где z0 — единичный вектор в направлении постоянной намагниченности.
Магноны представляют собой элементарные возбуждения электронной
магнитной системы. Поэтому можно считать, что магнитомеханическое
отношение для них будет таким же, как для электронов. Тогда с учетом
(7.76) механический момент магнона в единицах h будет
s = z0. (7.77)
Таким образом, магнон является частицей с собственным
механическим мгментом (спином), равным 1.
Частицы с нулевым или целым спином подчиняются, как известно
[133], статистике Бозе—Эйнштейна. Число таких частиц (бозонов)
в каждом состоянии не ограничено. Функция их распределения по
энергиям, т. е. среднее число частиц в состоянии с энергией е в случае,
когда число частиц в системе не фиксировано (что имеет место
для магнонов),
й = (ее",т-1)-1. (7.78)
Тепловые магноны и их вклады в термодинамические величины.
До сих пор мы все время интересовались когерентными магнитными
колебаниями и волнами. Им соответствуют магноны. которые тоже
можно назвать когерентными. Обычно это магноны одного какого-то
типа, например, однородной прецессии — в опытах по
ферромагнитному резонансу или бегущей спиновой волны с некоторым к—при
возбуждении магнитостатических волн (§ 6.2). Энергия таких магнонов
(если ограничиться линейными процессами) равна Лео, где со—частота
возбуждающего поля. Числа же их могут быть велики. Таким
образом, распределение когерентных магнонов в к-пространстве
характеризуется небольшим числом точек, часто — одной точкой.
Ясно, что такое распределение неравновесно и поддерживается только
путем непрерывного «пополнения» магнонами, рождаемыми,
например, электромагнитным полем.
В отличие от таких неравновесных когерентных магнонов, в маг-
нитоупорядоченном веществе при любой температуре Т>0 (а с учетом
квантовомеханических нулевых колебаний—и при Г=0) имеются
некогерентные (тепловые) магноны, находящиеся в термодинамическом
равновесии с другими квазичастицами, в первую очередь с фононами.
Распределение тепловых магнонов по энергиям и в к-пространстве
определяется законом дисперсии магнонов и их статистикой и зависит
от температуры и магнитного поля. В отличие от распределения
неравновесных магнонов, оно является весьма широким, особенно
при высоких температурах.
Тепловые магноны существенно влияют на термодинамические
характеристики магнитоупорядоченных веществ, в частности на
температурные зависимости их намагниченности и теплоемкости.
Рассмотрим эти зависимости для изотропного ферромагнетика.
Для вычисления намагниченности М(Т) воспользуемся формулой
(7.72), где теперь Мо = М(0) — намагниченность при отс\ ictihh
магнонов, т.е. при Г=0, MZ = M{T) — искомая намагничение ть при
температуре Г, а и — число всех равновесных (тепловых) магнонов
226
в единице объема при этой температуре. Если пренебречь
несущественным в данном случае вкладом магнонов с энергиями Ev (первая
сумма в (7.66)), а при вычислении вклада магнонов с ек перейти
от суммирования по состояниям в k-пространстве к интегрированию,
то число магнонов п определится следующим образом:
fndk, (7.79)
где V—объем (в координатном пространстве), й—среднее число
магнонов в каждом состоянии (7.78), а /—плотность состояний (т. е.
разрешенных значений к) в к-пространстве.
Примем периодические граничные условия; тогда согласно (7.67)
разрешенные значения к образуют решетку с постоянными 2п/1р
(/>=1, 2, 3), и плотность состояний
/= У/(2п)3, (7.80)
где V=lll2h — объем параллелепипеда периодичности, который при
вычислении величин, отнесенных к единице объема вещества
(намагниченности, теплоемкости), можно принять равным 1 см3. В качестве
закона дисперсии примем для простоты квадратичный закон (7.13).
Это не исказит существенно результата (кроме веществ с очень
большой намагниченностью), так как мы будем интегрировать по
всему k-пространству и наибольший вклад дадут состояния с
большими к. Тогда, подставляя (7.78) и (7.80) в (7.79) и выполняя
интегрирование по углам вк и q>k вектора к, получим
М(0)-М(7>^
k2dk
о е -1
(7.81)
Вычисление интеграла в (7.81) (см. [346] или [69]) приводит
к окончательному выражению:
М(0)-М(Г) = 5,863-10-2ул('^у/2Г3'2 = 5,157-10-5г1~3/2Г3/2. (7.82)
Оно представляет собой знаменитый закон трех вторых, который
впервые получил (на микроскопической модели) Блох [249].
Использование выражения (7.82) является одним из способов
определения константы неоднородного обмена rj. На рис. 7.15
приведены экспериментальные зависимости М(Т) для ферромагнетиков
ЕиО и CdCr2Se4 и ферримагнетика ЖИГ и прямые, соответствующие
закону трех вторых. Мы видим, что для ЖИГ этот закон выполняется
лишь при очень низких температурах. В этом нет ничего удивительного,
так как спектр спиновых волн в ЖИГ содержит 20 ветвей (§ 3.3), и
пренебрежение всеми ими, кроме нижней, «ферромагнитной» ветви,
допустимо лишь при самых низких температурах. Однако прямая, к которой
стремятся точки для ЖИГ при низких температурах, соответствует
значению ri = 0,092, найденному более точным способом (см. § 12.4).
15* 227
\М(0)-М(Г),Гс
s'luO
0,001
Рис. 7.15. Температурные зависимости намагниченности. Точки—эксперимент:
для ЕиО [179], CdCr2Se4 [426] и ЖИГ [93]. Прямые, соответствующие
3
закону (7.82), пересекают ось ординат в точках (—4,288— lgr]); они проведены:
для ЕиО и ЖИГ—согласно полученным другими методами [383, 360]
значениям т), для CdCr2Se4—через экспериментальные точки
Для ЕиО закон трех вторых выполняется плохо,
поскольку при такой большой намагниченности пренебрежение диполь-
ным членом coMsin26k в спектре спиновых волн становится
недопустимым.
Для ферромагнетика CdCr2Se4 с намагниченностью в 5 раз
меньшей, чем у ЕиО, указанное обстоятельство является уже не
столь существенным, и как видно из рис. 7.15, закон трех вторых
хорошо выполняется в широком интервале температур. Найденную
исходя из него величину г] = 5,9-10_3 можно принять в качестве
константы неоднородного обмена для этого вещества.
Вклад магнонов в теплоемкость ферромагнетика определяется
следующим образом:
Cvm~BT
friEdk.
(7.83)
При законе дисперсии (7.13) вычисление по этой, формуле дает
с„т = 0,113х5/2(Йг))-3/2Г3/2 = 0,74п-3'2Г3/2. (7.84)
22S
Если отделить магнонный вклад в с„ от фононного (учитывая, что
последний пропорционален Г3 [16]), то измерение cv(T) тоже может
быть использовано для определения величины rj. Для ЖИГ таким
образом получено (см. [112]) г]~0,1.
§ 7.4. Микроскопическая теория спиновых волн
До сих пор мы рассматривали ферромагнетик как сплошную
среду, которая характеризовалась плотностью магнитного момента
(намагниченностью), являющейся непрерывной функцией координат.
Однако магнитоупорядоченные вещества, как все твердые тела,
построены из дискретных микроскопических объектов—атомов, ионов,
электронов проводимости. Мы должны теперь выяснить влияние их
микроскопической структуры на магнитные колебания и волны. Ясно,
что классическое описание—на основе уравнения Ландау—Лифшица
теперь не годится, и мы должны использовать микроскопические
модели и квантово-механические методы их рассмотрения.
Постановка задачи. Будем использовать гейзенберговскую модель
ферромагнетика (§ 1.1), которая представляет собой систему
локализованных спиновых моментов, расположенных в узлах магнитной решетки
и связанных обменными взаимодействиями. Как будет показано ниже,
микроскопическое рассмотрение необходимо в случае коротковолновых
возбуждений—когда к становится сравнимым с 1/а, где а—расстояние
между ближайшими магнитными атомами или ионами. Для таких
нозбуждений влияние границ раздела между средами обычно несущест-
ненно; поэтому мы будем рассматривать в этом параграфе только
безграничный ферромагнетик. Не будем учитывать и анизотропии.
Спиновые волны в ферромагнетике были впервые получены
теоретически на гейзенберговской модели Блохом [249] с учетом
только обменпою взаимодействия. Учет энергии спинов во внешнем
магнитном поле и магнитного (диполь-дипольного) их взаимодействия
провели Холстейн и Примаков [329]. Мы будем следовать в основном
работе [329], но для простоты сначала не будем учитывать диполь-
дипольного взаимодействия. Тогда в оператор энергии—гамильтониан
(который при квантово-механическом рассмотрении является исходным
пунктом теории) войдут операторы энергии обменного и зееманов-
ского взаимодействий. Первый будет являться суммой выражений
(1.30). Второй мы запишем по аналогии с классическим выражением
(2.3). Учтем также, что в гейзенберговской модели оператор проекции
намагниченности на ось z (направленную по полю Н0)
у I
где V—объем образца, а суммирование проводится по всем спинам
в этом объеме. Таким образом, гамильтониан будет иметь вид
jf = Y^5^o-II//rS/Sr. (7.86)
/ / /'
i.T*T)
229
Здесь
&f&r = §}Sf. + §jS'r + SfS}.,
a Sf\y/-Z — операторы проекций спиновых механических моментов (как
всегда, в единицах п), находящихся в узлах/и/' решетки. Операторы
Sf*/? удовлетворяют (см., например, [132]) коммутационным
соотношениям:
[§},§',.] = &„■$} (7.87)
и двум другим, которые получаются из (7.87) при циклической
замене индексов х, у и г; квадратные скобки обозначают коммутаторы
стоящих в них операторов: [a,b] = ab—ba, а А{{—дельта-символ
Кронекера (5.28).
Задача заключается в том, чтобы привести гамильтониан
(7.86) к виду
jf'-l/o+I'inbM (7.88)
к
(диагонализировать его), где пк—оператор, собственные значения
которого являются целыми числами, а суммирование проводится по
всем разрешенным значениям к. Тогда U0 будет энергией основного
состояния, Ек(к)—энергией элементарного возбуждения (магнона)
с волновым вектором к, а пк—оператором числа магнонов. Такое
преобразование было проведено (для более общего гамильтониана—с
включением энергии диполь-дипольного взаимодействия) в [329]
путем последовательных переходов от одних операторов к другим —
знаменитых преобразований Холстейна — Примакова.
Переход к операторам рождения и уничтожения спиновых
отклонений—первое преобразование Холстейна — Примакова. Прежде всего
перейдем от операторов §} и S} к их циклическим комбинациям
Sf = Sf±iS}. (7.89)
Операторы 5/, 5/ и Sf связаны условием сохранения длины вектора
Sf. Поэтому целесообразно выразить их через два независимых
оператора. Потребуем, чтобы эти операторы а} и df удовлетворяли
коммутационным соотношениям
[af, <5Л = Д/Г, [df, аг] = 0. [а;, «/.] = 0 (7.90)
и чтобы
Sf=-S+a +
faf.
(7.91)
Тогда, как можно убедиться.
v-^-pp,, tj.^.^.py (,921
нош^нияГаоп^' И *'• Удовлетв°РЯ1°Щие коммутационным соот-
»Г™ п^ ЯВЛЯЮТСЯ (СМ- НаПР"меР- М операторами соот-
в к,«янола W, н униишпжени, частиц, подчиняющихся ст.писти-
Знппнеина-бозонов Действуя на волновые функции
в представлении вторичного квантования (когда эти функции
представляют собой совокупности чисел частиц в различных состояниях),
оператор а} увеличивает на 1 число частиц в состоянии / (не влияя
на числа частиц в других состояниях), а оператор а{ уменьшает
это число на 1. Оператор
d}afSnf (7.93)
является оператором числа частиц в состоянии / Его собственные
значения представляют собой числа частиц в этом состоянии.
В нашем случае /—это номер узла, и из (7.91) следует, что
«частицы», операторами рождения и уничтожения которых являются
df и df, представляют собой спиновые отклонения на узле /:
рождение одной такой «частицы» увеличивает на 1 величину Sf,
т. е. уменьшает на yh магнитный момент на этом узле. Состояние
всего ферромагнетика в представлении вторичного квантования
характеризуется теперь числами спиновых отклонений на всех узлах.
Операторные соотношения (7.92) сложны. Поэтому разложим
входящие в них радикалы в ряды и ограничимся первыми членами
этих рядов, т. е. вместо (7.92) положим
Sf-^JlSdf, SJ^JlSa}. (7.94)
Эта замена является, с первого взгляда, очень грубой, особенно
при малых 5. Основное предположение теории
Холстейна—Примакова состоит в том, что она все же допустима при достаточно
низких температурах, когда средние значения чисел частиц
nf«l. (7.95)
Собственные значения Sf не могут превышать величины S;
поэтому числа спиновых отклонений
иг<25. (7.96)
Это условие отличает спиновые отклонения от обычных бозе-частиц,
для которых числа частиц не ограничены. Оно выделяет из всего
пространства чисел отклонений разрешенную или «физическую»
область. Выполнение условия (7.96) обеспечивается точными
соотношениями (7.92). Замена их приближенными соотношениями (7.94)
снимает это ограничение.
Введем теперь, пользуясь формулами (7.89), (7.94) и (7.91), новые
операторы df и ds в гамильтониан (7.86). С учетом соотношений
(7.90) получим
& = и0 + #г + Я*, (7-97)
где (везде f^f)
U0=~yfiSNH0-S2YYlfr, (7.98)
/ r
.^2 = 7////oI«/ df + 2SYllff(6fьг-й}ar ). (7.99)
/ If
•** = -I L ///■ d/ ufdf-.df . (7 100)
Суммирование здесь, как и в (7.86), проводится по всем узлам
решетки в рассматриваемом объеме, а. N в (7.98)—число этих узлов.
При низких температурах, когда справедливо (7.95),
гамильтонианом Jr4 можно пренебречь с не меньшим основанием, чем высшими
членами в разложениях радикалов (7.92) в ряды. Однако квадратичный
гамильтониан (7.99) не имеет еще требуемого диагонального вида
(7.88). Это означает, что спиновые отклонения, локализованные на
узлах решетки, не являются элементарными возбуждениями
ферромагнетика. Ими должны быть, как и в рассмотренной выше
континуальной теории, коллективизированные возбуждения—спиновые волны.
Переход к операторам рождения и уничтожения спиновых волн—
второе преобразование Холстейна—Примакова. Для «коллективизации»
спиновых отклонений необходимо перейти от координатного
пространства (в котором в точках тг находятся спины) к пространству
волновых чисел—импульсному или k-пространству, т. е. осуществить
фурье-преобразование операторов а} и af:
у/*/ у/Л/
Решетке с узлами тг в координатном пространстве можно
сопоставить в k-пространстве (см., например, [16]) обратную решетку
с узлами к„, так что
e'k"r/=l. (7.102)
Вследствие этого волновые векторы в (7.101) определяются лишь
с точностью до прибавления векторов к„. Чтобы устранить эту
неоднозначность, следует ограничиться одной элементарной ячейкой
обратной решетки. В качестве нее обычно выбирают элементарную
ячейку Вигнера — Зейца [16], которую называют первой зоной Брил-
люэна. Например, в случае простой кубической решетки в
координатном пространстве с постоянной решетки а первая зона Брил-
люэна представляет собой куб с ребром 2к/а.
Примем, как и в § 7.3, в качестве объема ферромагнетика
параллелепипед с ребрами h, h, hc периодическими граничными условиями
на его гранях. Тогда разрешенные этими условиями значения к будут
определяться согласно (7.68), но теперь—для дискретной решетки
числа иь п2 и п3 и, следовательно, величины к будут ограничены первой
зоной Бриллюэна. Можно показать [16], что число разрешенных
значений к в этой зоне равно числу N узлов в параллелепипеде
периодичности и что имеют место следующие соотношения:
/V-'Xeitft/-v'=A/r5A(r/-rr),
к (7.103)
ЛГ-1^е,*_ь'),' = Дц. = Д(к-к').
/
Символ Кронекера А (см. (5.28)) в этих соотношениях можно
определить также следующим образом:
, . Jl при х = 0,
А(х) = <г. ' (7.104)
v > [0 при х#0.
232
В дальнейшем объем параллелепипеда периодичности мы будем
принимать равным 1, и N будет числом спинов в 1 см3. Для
решетки с одним спином в кубической элементарной ячейке (с
ребром a) N=a~3.
Как легко убедиться с учетом (7.102). преобразования, обратные
(7.101), имеют вид
«/=-S=Xe-ikr/«,+ , о/=4=2Укг'ак. (7.105)
yfNk y/Nk
Операторы ак+ и йк удовлетворяют таким же коммутационным
соотношениям (с заменой в (7.90) / на к), как и операторы а} и af.
Следовательно, их также можно считать операторами рождения
и уничтожения некоторых бозе-частиц. Но эти частицы (или, точнее,
квазичастицы) уже не локализованы в узлах решетки спинов, а
коллективизированы— «размазаны» по всей решетке. Оператор
пк = акак (7.106)
является оператором числа таких квазичастиц. Его собственные
значения пк = 0, 1, 2, ... — это числа их в состоянии с волновым
вектором к.
Подставляя (7.105) в (7.99), получим (см., например, [69])
^2 = уЛЯ0Хи» + 25Х«к1(1 -е'к"К, (7.107)
к к g
где тв=тг—rf, а интеграл обмена Iff- теперь обозначен 1е;
суммирование по к производится по всем разрешенным значениям
волнового вектора в пределах первой зоны Бриллюэна, а
суммирование по g—по всем узлам решетки, кроме одного—«отсчетного».
Полученное выражение (7.107) в сумме с (7.98) имеет искомый вид
(7.88), где
Ек = уЛЯ0 + 25Х(1-е'кг")/в. (7.108)
в
Таким образом, перейдя к операторам ак и ак, мы привели
приближенно гамильтониан гейзенберговской модели ферромагнетика
к диагональному виду. Иными словами, эти операторы являются
приближенно операторами рождения и уничтожения элементарных
возбуждений в такой модели—спиновых волн или магнонов.
С помощью (7.105) нетрудно выразить проекции спинового
оператора S и все зависящие от них величины через операторы ак и ак.
В частности, подставляя (7.105) в (7.91) и суммируя затем по/, получим
ZS'^-SN+ZAb, (7.109)
/ к
откуда непосредственно следует (7.72). Соотношение (7.74) может
быть получено [417] аналогичным образом.
Анализ закона дисперсии. Дисперсионное соотношение (7.108),
найденное путем диагонализации гамильтониана (7.86), следует срав-
233
7<L
ksy
№
Те?
-rt
T^
*K.
fr
3'j.
#
~W
\X/
wT
в \.
"IT
IzT.
k*
& 3k
Рис. 7.16. Ферромагнитные решетки спинов: а—простая кубическая, б—гра-
нецентрированная кубическая. Цифры без штриха — ближайшие соседи
нейтрального спина, цифры со штрихом—вторая координационная сфера
нить с классическим выражением (7.9) при 6*=0, так как именно
для этого направления не сказывается диполь-дипольное
взаимодействие. В обоих случаях энергия магнона является суммой зееманов-
ского члена уШ0 и обменного члена, различие заключается в виде
этого последнего. Теперь в него входят микроскопические параметры
5 и 1д и зависимость от к является более сложной, она определяется
реальной структурой ферромагнетика.
Обменные интегралы 1д быстро убывают при увеличении
расстояния гд между спинами. Поэтому при вычислении суммы в (7.108)
можно в первом приближении ограничиться ближайшими соседями.
Рассмотрим сначала простую кубическую решетку спинов (рис. 7.16, а)
с постоянной решетки а. Вычисление суммы в (7.108) по шести
ближайшим соседям дает в этом случае
ek = yhH0 + 45/! (3 - cos kxa - cos куа - cos kza),
(7.110)
где Ix — обменный интеграл, который предполагается не зависящим
от направления г„. В качестве второго примера рассмотрим гранецен-
трированную кубическую решетку (рис. 7.16,6), в которой число
ближайших соседей Z= 12. В этом случае, как легко убедиться,
ек = уЛЯ0 + 45Л Гб-cos^^-cos^^.
(ky+kz)a
-cos^ у ''—cos
У2
(*,-*.)« _cos(ktMf_cosfc
У2 У2 У2
J~2 J'
(7.111)
где я-
2j4
■по-прежнему расстояние между ближайшими соседями.
В длинноволновом пределе (ка«\\оба выражения (7.110) и (7.111)
переходят в
Ek = yhH0 + X-ZSha2k2, (7.112)
что совпадает с дисперсионным соотношением для непрерывной
среды при
r\ = X-ZSha2lh. (7.113)
Аналогичные соотношения нетрудно получить и с учетом большего
числа соседей. Например, с учетом соседей, следующих за ближайшими
(второй координационной сферы), для простой кубической решетки
r\ = 2s(h+UAa2lh, (7.114)
а для гранецентрированной
r\ = 4SU1+I2)a2lh, (7.115)
где /t и /2—интегралы обмена соответственно с ближайшими
соседями и со спинами второй координационной сферы.
Выражения (7.113)—(7.115) могут быть использованы для
определения величины г). Если же значения обменных интегралов
неизвестны, то для оценки этой важной величины (в приближении
ближайших соседей) можно использовать соотношения
ц = ~АМ0уа2, (7.116)
6
*-1тшЛ (71,7>
Они вытекают из (1.28), (1.25) и выражения
Л=ГГ^' (7Л18>
(ybyN
которое получается, если приравнять обменную часть (7.98)
феноменологическому выражению для обменной энергии (2.15). Заметим,
что соотношение (7.116) может быть представлено в виде
D=l-HAa2, (7.119)
о
где Ял—«молекулярное» поле (1.26).
Рассмотрим примеры применения полученных выражений. В
ферромагнетике ЕиО со структурой типа NaCl и постоянной решетки
aiat = 5,14lA [157] ионы Еи2+ (5=7/2) образуют кубическую гранецен-
трированную решетку с расстоянием между ближайшими соседями
a = fliat/\/2- Для этого кристалла из опытов по дифракции нейтронов
[383] были найдены /i=0,606x и /2 = 0,119х; по формуле (7.115)
находим т]= 1,75 ■ Ю-3. Эта величина согласуется с температурной
235
Рис. 7.17. Дисперсионные
характеристики спиновых волн в
ферромагнетике с простой кубической
решеткой для разных направлений
к без учета диполь-дипольного
взаимодействия (или при 6ц = 0) в
приближении ближайших соседей.
Расчет по формуле (7.110). Штриховая
линия —континуальная теория
(§7.1)
зависимостью намагниченности (рис. 7.15). Оценка же по формуле
(7.117) (Гс = 69,5 К [157]) лает величину 1,34-10~3.
Для ферромагнетика C"dCr2Se4 величины обменных интегралов
неизвестны. Для оценки по формуле (7.117) примем в качестве
а среднее расстояние между ионами Сг3+, которое легко найти,
если принять во внимание, что в кубическую элементарную ячейку
этого кристалла с постоянной решетки яы=10,75А [157] входят 16
ионов Сг3 + . Учитывая, что Гс-=130 К, а 5=3/2, получим т] = 6,2-10~3.
Величина же, найденная из закона трех вторых для намагниченности
(§7.3), составила 5,9 10~3. Такое хорошее совпадение является,
конечно, случайным, но из обоих приведенных примеров следует,
что оценка величины г\ для ферромагнетиков по формуле (7.117)
возможна. При попытке использовать эту формулу для ферримаг-
нетиков возникают трудности, связанные прежде всего с
невозможностью сколько-нибудь строгого определения величины а.
Итак, при ка «: 1 результаты микроскопической и континуальной
теорий спиновых волн совпадают. Когда же условие ка «: 1 перестает
выполняться, расхождение между ними становится существенным.
Согласно континуальной теории (и микроскопической—в предельном
случае ка -»0) дисперсионное соотношение изотропно (т. е. сок зависит
только от \к\), если, конечно, не учитывается диполь-дипольное
взаимодействие и магнитная кристаллографическая анизотропия.
Микроскопическая же теория при больших ка, как это видно, например,
из рис. 7.17, дает и без учета указанных взаимодействий зависимость
(£>к от направления вектора к по отношению к осям решетки спинов.
Кроме того, если для континуальной модели значения к и ак не
ограничены, то для дискретной величина к определяется однозначно
лишь в пределах первой зоны Бриллюэна. а сок не превышает
величин порядка AZSIJft, т.е. ~ 1014—1015.
Учет диполь-дипольного взаимодействия. Добавим теперь к
гамильтониану (7.86) оператор энергии диполь-дипольного взаимодействия,
который можно записать по аналогии с классическими выражениями
(1.4) и (1.3), заменив в них ЧЯ-^yTiS. После перехода к операторам
а} и af и затем к ак и ак такой суммарный гамильтониан будет
236
<т>
т/2 nSf
содержать, кроме членов нулевого, второго и четвертого порядка,
еще члены третьего порядка по операторам ак и ак. Квадратичная
же часть его будет иметь вид (см., например, [346])
*2 = * I Uk# ак + \{Вкака_к + Вкак+ а ±к)\ (7.120)
Л,=шн+2 | £/f(l-eft'.)+i coMsin2Gt, (7.121)
8
Bk=l-«>Msm2eke'2*. (7.122)
Здесь сом=у4яА/°, где M°=NyhS—намагниченность насыщения, а вк
и Ф*—углы вектора к в сферической системе координат с осью,
совпадающей с направлением намагничивания. Как видно из (7.120), с учетом
диполь-дипольного взаимодействия переход к операторам ак и ак
еще не приводит (если только 6к^0) гамильтониан к диагональному
виду (7.88), т. е. эти операторы не являются операторами рождения
и уничтожения элементарных возбуждений—спиновых волн. Необходим
переход к некоторым другим операторам ск и ск, в которых
квадратичная часть гамильтониана приобретет диагональный вид.
Не останавливаясь подробно на этом переходе—третьем
преобразовании Холстейна—Примакова [329] (см. также [346, 15, 69]),
приведем основной результат:
zk-TijAl-\Bk\\ (7.123)
Сравнивая это выражение с классическим дисперсионным
соотношением (7.9), мы видим, что учет дискретности структуры
ферромагнетика (переход от континуальной к
микроскопической—гейзенберговской модели) затронул лишь обменный член. Диполь-дипольное
взаимодействие, в отличие от обменного, является дальнодейст-
вующим, и микроскопическое—квантовое его рассмотрение дает
такой же результат, как и классическое—континуальное.
Если 6к=0, то Вк=0, т. е. для спиновых волн, распространяющихся
вдоль направления намагничивания, диполь-дипольное взаимодействие
не сказывается. Если же 6к^0, но |2?к| <zAk, то допустимо приближение
гк^ЬАк, которое является микроскопическим обобщением
приближенного соотношения (7.14). В этом случае операторы ск и ск мало
отличаются от операторов ак и ак, и последние можно приближенно
считать операторами рождения и уничтожения магнонов. Поляризация
намагниченности спиновой волны при этом приближается к круговой,
и приближенно справедливо простое соотношение (7.71). Для обычных
ферро- и ферримагнетиков |2?к|/к~0,1 К. Поэтому для тепловых
магнонов, энергии которых в основном порядка Y.T, рассматриваемое
приближение справедливо, кроме случая очень низких температур.
Для когерентных же спиновых волн с волновыми числами к ^ 10б
оно выполняется лишь при очень высоких частотах.
Учет магнитной кристаллографической анизотропии, основным
источником которой является спин-орбитальное взаимодействие, в рам-
237
ках гейзенберговской модели (имеюшей дело только со спиновыми
моментами) возможен лишь феноменологическим путем [201]. При
не очень больших к можно просто заменить в выражениях для
спектров спиновых волн, полученных в континуальной теории с учетом
кристаллографической магнитной анизотропии, например, в (7.28),
«классический» обменный член Dk2 на его микроскопический «аналог».
При больших к. приближающихся к границам нерпой зоны Бриллюэна,
такой учет анизотропии, как и учет диполь-дипольпого взаимодействия,
становится несущественным. Главную роль в дисперсионном
соотношении играет в эгом случае обменный член, который приводит, как
мы видели (см. рис. 7.17). к сильной зависимости энергии магнонов
от направления век юра к по о i ношению к осям машптной решетки.
Влияние дискретности структуры на гермодинамику ферромагнетика.
Результаты pacneia машинных вкладов в термодинамические
характеристики ферромагнетика зависят от грех факторов: статистики,
которой подчиняются магноны: облаем и k-прострапства. по которой
производится суммирование состояний, и закона дисперсии. Посмотрим,
как изменится влияние этих факторов при переходе от континуальной
модели к дискретной. Mai ноны в дискретной 1ет'иенберговской
модели, как и в континуальной, приближенно являются (первый фактор)
бозе-частицами. Суммирование по состояниям (второй фактор) должно
теперь проводиться только в пределах первой зоны Бриллюэна.
Однако при достаточно низких температурах магнонов с большими
к мало, и обычно шисфпрование, например, в (7.79) и (7.83), можно
по-прежнему проводин, но псему k-пространству. Существенное влияние
на результаты расчети оказывает тогда лишь третий фактор.
Пренебрежем, как и u <j 7.3, влиянием постоянного магнитного
поля и диполь-дипольпш о взаимодействия, рассмотрим для
определенности простую кубическую решетку и ограничимся учетом в ней
ближайших соседей Тшда дисперсионное соотношение будет иметь
вид (7.110) без первою члена. Вычисление намагниченности с учетом
этого соотношения дает (см., например. [346])
M(0)-M(r) = Ci2Ti2 + C52T5Z + C,2T72 + ... (7.124)
Коэффициент С, 2 оказывайся таким же, как в (7.82), а в последующие
входит постоянная решетки а: во второй степени в С52, в четвертой —
в С7/2 и т. д. Оценка показывает, что все эти члены малы при
температурах ниже приблизительно Тс/2.
Взаимодействие магнонов. Теперь следует остановиться на вопросе
о принципиальных ограничениях рассмотренной в этом параграфе
теории Холстейна — Примакова. Как уже отмечалось, основными ее
допущениями являются:
1) возможность замены радикалов в (7.92) на их разложения в ряды:
2) возможность пренебречь всеми высшими членами (со степенями
выше второй по операторам а} и df) в гамильтониане: к ним
относятся как члены (7.100) и члены третьего порядка, которые
появляются при учете диполь-дипольного взаимодействия, так и
члены, возникающие в результате сохранения более высоких степеней
в разложениях ратикалов.
238
Второе допущение представляется обоснованным при достаточно
низких температурах. Отбрасываемые высшие члены описывают
столкновения магнонов; при низких температурах, когда средние
значения чисел магнонов малы, столкновения маловероятны, и их
влиянием на спектр можно пренебречь.
Первое допущение вызывает серьезные сомнения. Как уже
отмечалось, замена радикалов на ряды ликвидирует «автоматическое»
ограничение числа спиновых отклонений nf на одном узле, и его
приходится специально вводить при построении более точных теорий.
Вопрос о справедливости теории Холстейна— Примакова и в связи с этим
вообще о правомерности представления о Mai нонах как об
элементарных возбуждениях ферромагнетика подверг а тся всестороннему
изучению (см., например, [346, 15, 201]). Первый фундамешальный вклад
в выяснение этого вопроса был внесен Дайсоном [289]. Он показал,
что учет свойств спиновых опера юров Sf. приводящих к ограничению
чисел «у, эквивалентен введению некоторого дополнительного —
кинематического взаимодействия магнонов. которое носит характер
отталкивания. Однако практически оно может не приниматься во
внимание при низких температурах — вплоть до ~ Тс/2.
Отбрасываемые в теории Холстейна — Примакова высшие члены
гамильтониана приводят согласно Дайсону к динамическому
взаимодействию магнонов. которое носит характер притяжения. Оно дает
поправку к спскфу. более существенную, чем кинематическое
взаимодействие, но тже малую при низких температурах. Эта поправка
приводит, в частости, к дополнительному члену в зависимости
М(Т), пропорциональному Г4 [290]. При 7~<7~с'2 этим членом
также можно препеоречь.
Таким образом, магноны Холстейна - Примакова— бозе-частицы
с законом дисперсии (7.123) не являются, строю говоря,
элементарными возбуждениями т'псиберговскою ферромагнетика, но могут
приближенно счикпься шкоиыми при сравнительно низких уровнях
возбуждения спиновой системы, т. е. для равновесных (тепловых)
магнонов — при достаточно низких температурах.
При более высоких уровнях возбуждения (для тепловых
магнонов— при высоких температурах) элементарные возбуждения
ферромагнетика по спектру и сташетике существенно отличаются от
рассмотренных выше ма1Нонов. Однако их можно по-прежнему
называть магнонами или спиновыми волнами. Более мощные
теоретические метлы: метод функций Грина, примененный к
ферромагнетикам Боюлюбовым и Тябликовым [201]. днафаммная
техника Вакса, Ларкина и Пикина [39, 40] и др. позволяют iiaiiiH
дисперсионные соотношения для таких элемеш арных возбуждений
и вычислить их вклады в термодинамические величины в широком
диапазоне температур. Единственным условием справедливости
представления о квазичастииах - mui нонах являемся cooiношение
ctT\>2rc/i. (7.125>
которое означает, чю время жизни м;м нона толжно оьпь больше
периода колебаний, coo i вет ст иу кщкм о »чо ч.илоте.
239
Глава 8
КОЛЕБАНИЯ И ВОЛНЫ НАМАГНИЧЕННОСТИ
ПРИ НАЛИЧИИ ДОМЕНОВ
§ 8.1. Магнитные домены
До сих пор мы все время предполагали, что основное состояние
ферро- или ферримагнитного образца, около которого происходят
колебания намагниченности, есть однородная намагниченность всего
образца. Однако такое состояние является равновесным лишь при достаточно
большой величине внешнего магнитного поля или (при любых полях) в
случае весьма малых образцов. При меньших полях равновесным
состоянием образца не очень малых размеров будет неоднородная
намагниченность. При этом обычно образец разбивается на небольшие, но
макроскопические области—с наименьшим размером порядка 1 мкм—
магнитные домены. Намагниченность в них почти однородна, но
в разных доменах различно направлена. Переход от одного направления
к другому совершается . плавно, но в основном в пограничном
слое—доменной стенке, толщина которой обычно мала по сравнению
с размерами доменов. В этой главе мы будем исследовать колебания
и волны намагниченности в таких разбитых на домены образцах.
Причина образования домеиов. В этом параграфе мы рассмотрим
кратко основные физические представления, связанные с
ферромагнитными доменами (подробнее см. [22, 23], а также [49, 122]).
Предположим сначала, что внешнее магнитное поле отсутствует,
а образец—монокристалл. Энергия его (см. § 2.1) состоит из
обменной энергии, энергии кристаллографической анизотропии,
упругой и магнитоупругой энергии (которые будут рассматриваться
в гл. 12) и магнитной энергии, связанной с размагничивающими
полями. Равновесное
распределение намагниченности в образце
должно соответствовать
минимуму суммы всех этих видов
энергии. Такое распределение не
обязательно будет однородным, так
как при этом большой величины
достигала бы магнитная энергия.
При возникновении же доменов,
намагниченных в
противоположных направлениях, она
существенно уменьшается. Например,
х можно показать, что для образца
Рис 8.1. Пластина со слоистой до- (пластины), разбитого на домены-
менной структурой слои (рис. 8.1), магнитная энер-
240
гия, отнесенная к единице поверхности образпа, по порядку величины
составляет
WM^MU, (8.1)
где М0 — намагниченность доменов, a d—их толщина. Эта энергия
уменьшается при уменьшении d, т. е. увеличении числа доменов.
Однако при этом возрастают виды энергии, связанные с доменными
границами. В результате в образце устанавливается равновесная
доменная структура с определенной толщиной доменов,
соответствующая минимуму суммы всех видов энергии.
Доменные стенки. Выясним прежде всего, что представляет собой
граница между доменами. На достаточном удалении от нее направления
намагниченностей Mt и М2 в соседних доменах совпадают с легкими
осями. Энергия анизотропии была бы минимальной, если бы поворот
намагниченности от М, к М2 совершался скачком. Но при этом
была бы велика обменная энергия. Она тем меньше, чем более плавно
совершается поворот намагниченности. Магнитная же энергия
минимальна, если этот поворот происходит в плоскости границы, при этом
не возникает дополнительных размагничивающих полей, связанных с
изменением нормальной составляющей намагниченности. Часто именно
такой случай соответствует минимуму полной энергии, доменная
стенка при этом называется блоховской. В тонких касательно намагниченных
пленках блоховская стенка может оказаться невыгодной из-за сильного
возрастания магнитной энергии вследствие выхода векторов
намагниченности из плоскости пленки. В этом случае реализуется неелевская
доменная стенка, в которой поворот намагниченности совершается
в плоскости, перпендикулярной границе между доменами.
Закон изменения угла поворота намагниченности 6 (рис. 8.2) в
блоховской стенке определяется компромиссом между энергией
анизотропии и обменной энергией и может быть найден в результате решения
вариационной задачи о минимизации их суммы. Такая задача была
впервые решена Ландау и Лифшицем [130] (см. также [134]) для случая
одноосного кристалла с легкой осью. Полученный закон имеет вид
cosG= -th(yjК, j{qMl)x) =
= -th(nx/b), (8.2)
где Kl—первая константа анизотропии,
a q—постоянная неоднородного обмена
(§ 7.1). Величину
b^nMoy/g/Ki
(8.3)
можно назвать толщиной стенки, она
представляет собой расстояние, на
котором совершается в основном (на ~75%)
поворот намагниченности. Для найденного
закона (8.2) обменная энергия и энергия
анизотропии оказываются равными,
и суммарная энергия доменной стенки,
16 А. Г. Гуревич, Г. А. Мелков
Рис. 8.2. Поворот векторов
намагниченности в
блоховской доменной стенке
241
отнесенная к единице ее площади,
W„ = 2nMoyfqK1 = 2bK1. (8.4)
Аналогичные расчеты были проведены и для кубического
кристалла (см., например, [122]), при этом для толщины и энергии стенки
получились величины такого же порядка, как (8.3) и (8.4), в которых
К1—теперь абсолютная величина первой константы анизотропии
кубического кристалла. Для ЖИГ при комнатной температуре
(l*! | = 5,5-103) 6 = 5-КГ5 см, a Ww=0,5 эрг/см2.
Доменные структуры. В отличие от толщины стенок, форма и
размеры доменов существенно зависят от формы и размеров образца.
Рассмотрим, например, плоскопараллельную пластину толщиной /,
поверхности которой перпендикулярны легкой оси, и предположим, что
домены представляют собой слои, параллельные этой оси (рис. 8.1). Тогда
энергия кристалла будет состоять из магнитной энергии (8.1) и энергии
доменных стенок. Отнесем ее тоже к единице поверхности образца:
W'v=WJId. (8.5)
Минимизация суммы энергий (8.1) и (8.5) дает
d=JwjW0. (8.6)
Домены-слои, параллельные осям легкого намагничивания
(рис. 8.1), реализуются, как правило, в объеме образцов. Вблизи их
поверхностей обычно имеют место более сложные структуры.
Простейшая поверхностная доменная структура показана на рис. 8.3. В этом
случае для одноосного кристалла толщина доменов d определяется
компромиссом между энергией границ (8.5) и энергией анизотропии
в поверхностных замыкающих доменах-призмах
Это приводит к толщине доменов
(8.7)
d=j2WvljK1. (8.8)
Такая структура, предсказанная Ландау и Лифшицем [130],
реализуется в одноосных кристаллах в определенном интервале значений
/. При малых / (в тонких пленках) более выгодна простая структура,
приведенная на рис. 8.1, а при больших / возникают более сложные
у\^у\^у\^у\^.у^./\—т- поверхностные структуры [49].
[]||| Структура, показанная на рис. 83,
может возникать и в кубических
кристаллах. Если при этом К1 > 0, то
fl | I | I ^ направления намагниченности в за-
{ | t I т мыкающих призмах тоже являются
легкими и энергия анизотропии не
-*- -^ участвует в определении размера до-
^ДААА A. w менов. Он определяется тогда ком-
Рис. 8.3. Слоистая доменная промиссом между энергией границ
структура с замыкающими до- и магнитоупругои энергией. В случае
менами [130] К, < 0 роль играет по-прежнему энер-
242
гия анизотропии, и для размера доменов по порядку величины
справедлива формула (8.8). Для ЖИГ J~10_2x/7.
В реальных кристаллах доменные структуры, похожие на
поверхностные, возникают и внутри образцов на различных неоднородностях:
пустотах, границах между зернами поликристаллов и др. Кроме
того, на этих неоднородностях домены искривляются и доменная
структура становится серпантинной или лабиринтной [23, 122].
Как видно из формул (8.6) и (8.8), размер доменов d
пропорционален yfl, и достаточно малый образец—с /</0 во всех трех
измерениях—не будет разбиваться на домены. При малых размерах
образца можно использовать формулу (8.6), из которой следует
l0^WJMl. (8.9)
Более точные расчеты, проведенные Кондорским и др. (см., например,
[23, 35]), показывают, что оценка (8.9) справедлива по порядку
величины. Для ЖИГ /0~10~5см.
Доменные структуры при наличии магнитного поля. При наложении
внешнего магнитного поля Не в энергии образца появляется дополнительный
член—зеемановская энергия (2.17). Равновесное состояние при этом
достигается при наличии некоторой средней намагниченности образца
М в направлении, близком к направлению внешнего поля (часто—
совпадающем с ним). Переход в новое равновесное состояние может
происходить двумя путями [23, 122]: 1) путем перемещения доменных
стенок, ведущего к росту тех доменов, в которых намагниченность составляет
острый угол с полем Ц. (процессы смещения); 2) путем поворотов векторов
М0 в доменах (процессы вращения). Процессы смещения преобладают при
малых полях и практически заканчиваются с исчезновением основной
доменной структуры, когда в образце могут оставаться лишь отдельные
локальные домены. Процессы вращения в общем случае начинаются тоже
при малых полях и продолжаются после
исчезновения (в результате процессов смещения)
доменной структуры, заканчиваясь, когда
намагниченность будет направлена по внешнему полю.
Такой ход процессов намагничивания
иногда усложняется качественным преобразова-
структуры при некоторых
Не. Например, в пленках
одноосной анизотропией
с легкой осью,
направленной перпендикулярно поверхности пленки,
в некотором интервале значений поля,
приложенного перпендикулярно этой
поверхности, слоистая (полосовая) доменная структура
трансформируется в изолированные
цилиндрические домены (ЦМД). Процесс разбиения
полосового домена на ЦМД по мере
увеличения внешнего магнитного поля иллюстрирует
рис. 8.4. ЦМД существуют в интервале
магнитных полей от Ят!п до Ятах [23, 122].
16* 243
нием доменной
значениях поля
с большой
(KJ{2nM20)>l)
в
© © i
Рис. 8.4. Преобразование
полосового домена (а)
в цилиндрические (г) при
увеличении магнитного
поля [167].
Заштрихованы домены,
намагниченные против поля
Минимальное поле называется полем эллиптической неустойчивости,
а максимальное—полем коллапса; при Н > Ятм основным состоянием
является однородная намагниченность. Радиус ЦМД, как и значения
полей Hmin и Нтлх, зависит от толщины пленки и характеристической
длины вещества
lx=WJ{4nMl). (8.10)
Минимальный радиус реализуется в пленках толщиной 1^Ъ,Ъ1Х
и составляет rmin = 2lx. Характеристическая длина 1Х в редкоземельных
ферритах со структурой граната составляет обычно несколько десятых,
а в гексагональных ферритах, например бариевом,— несколько сотых
микрометра.
Наиболее интересным свойством изолированных ЦМД является
возможность генерации, разрушения и передвижения отдельного
домена независимо от всех других [23, 167]. Это создает возможность
осуществления запоминающих устройств для ЭВМ, в которых наличие
или отсутствие ЦМД в определенном месте пленки соответствует
1 биту информации.
§ 8.2. Колебания доменных стенок
Перейдем теперь к изучению процессов в образцах с доменной
структурой, происходящих под воздействием переменного магнитного
поля. Если частота поля много меньше всех собственных частот
ферромагнитного образца, то перемагничивание его происходит
квазистатически—магнитное состояние образца в данный момент
определяется величиной поля в этот момент (но, конечно, с учетом
магнитной предыстории образца). Это состояние характеризуется при
малых амплитудах переменного поля начальной магнитной
восприимчивостью, а при больших—статической петлей гистерезиса. Потери
в этом случае (в непроводящих магнитных веществах)
пропорциональны площади статической петли гистерезиса и частоте.
При увеличении частоты переменного магнитного поля начинает
сказываться сначала инерционность процессов смещения доменных
границ, а затем—инерционность процессов вращения, обусловленная
ферромагнитным резонансом. Эти явления будут рассмотрены
соответственно в данном и следующем параграфах.
Уравнение движения доменной границы. Рассмотрим движение
доменной стенки под действием переменного магнитного поля.
Постоянное поле может отсутствовать либо иметь величину и
направление, при котором еще сохраняется доменная структура. Переменное
же поле для того, чтобы осуществлялись процессы смещения, не
должно образовывать равных углов с намагниченностями соседних
доменов.
Смещение доменной стенки происходит в результате поворотов
векторов намагниченности. Поэтому теоретическое рассмотрение этого
процесса должно основываться на решении уравнения движения
намагниченности. Учет диссипации при этом необходим, так как
иначе скорость движения стенки оказалась бы бесконечно большой.
244
Можно использовать, например, уравнение (1.66). Эффективное поле,
входящее в него, должно включать внешнее магнитное поле,
эффективные поля анизотропии и обменного взаимодействия и
размагничивающее поле, вызванное изменением намагниченности в
стенке. Такой расчет был проведен впервые Ландау и Лифшицем [130]
для случая одноосного кристалла с доменной структурой, показанной
на рис. 8.3. При этом предполагалось, что поле приложено
параллельно намагниченностям доменов, а влияние замыкающих доменов-
призм не учитывалось. Оказалось [130], что уравнение движения
намагниченности в пограничном слое между доменами имеет решение,
зависящее от координаты х в направлении нормали к границе
(рис. 8.2) и от времени в комбинации x—vt, где
v = M0H/p. (8.11)
Это решение соответствует смещению доменной стенки (без ее
деформации) со скоростью v. В выражении (8.11)
р=хч/|*11Мул/оГ1. (812>
где X—параметр диссипации в уравнении движения (1.66), К1 —
константа анизотропии, a q—постоянная неоднородного обмена
(§ 7.1).
Выражение (8.11) можно записать в виде
р? = М0Я (8.13)
at
и считать уравнением движения границы. Левая часть его—это
«сила трения», а правая—сила, вызывающая смещение границы.
Как показали в дальнейшем Беккер [240] и Дёринг [288],
в уравнение движения границы необходимо ввести упругую силу
и инерционный член. Тогда это уравнение примет вид
и будет совпадать по форме с уравнением гармонического осцил!
лятора.
d2x
Появление в уравнении (8.14) инерционного члена w„-—j- связано
с кинетической энергией движущейся границы. Оказывается [240]
(см. также [69 ]), что
m-^y2b, (8.15)
где b—толщина доменной стенки (8.3). Формула (8.15) по порядку
величины справедлива и для кубических кристаллов. Для ЖИГ
(см.§8.1) Л^5-НГ5см и «7ж = 0,5-НГ1Ог/см2.
Наличие в уравнении (8.14) упругой силы к,х обусловлено тем,
что в реальном кристалле доменная стенка занимает (в отсутствие
переменного поля) некоторое равновесное положение — находится
в «потенциальной яме», при отклонении ее от этого положения
245
возникает упругая сила. Коэффициент упругости £ можно связать
со статической начальной восприимчивостью0 хтч = М0/Н0, где
М0—средняя намагниченность в малом постоянном магнитном поле
Н0. Она возникает в результате смещения соседних доменных границ
в противоположные стороны на расстояние х:
M0 = 2xMJd, (8.16)
где d—толщина доменов. Из (8.14) в статическом случае
х=М0ВД. (8.17)
Из (8.16) и (8.17) следует, что
S=2M20/(xm4d). (8.18)
Высокочастотная восприимчивость. Решая уравнение (8.14) в случае
гармонического переменного поля //=/zexp(/co/) и переходя затем
от х к переменной намагниченности m^=mexp(i(ut) согласно (8.16),
получим выражение для высокочастотной восприимчивости,
обусловленной колебаниями доменных границ:
т (. со2 . 1 ш V1 ,„ ,.ч
h \ cogw e„fW
Здесь собственная частота
to0w = V£/^, (8.20)
а добротность
Cw = x/UUP- (8-21)
При <2„>1 зависимость %ц от ш (см-. например, [174]) носит
резонансный характер, при £?„<1—релаксационный (рис. 8.5).
Из (8.20) с учетом (8.15), (8.18), (8.3), (8.8) и (8.4) следует
Юо* = уЛ/Г№1/8'1,4(ХнаЧ)-1/2. <8-22)
Это выражение может быть использовано для оценки величины co0w.
При этом под / для монокристаллов следует понимать размер
образца, а для поликристаллов — размер зерен (обычно 10~3—10~4).
Тогда, например, для поликристаллического ЖИГ (хНач~Ю) получим
/0w = to0„/(2n)~25—45 МГц. а для поликристаллического кобальтового
феррита (Хнач~0,3) /Ои^200—350 МГц. Для монокристаллов значения
/0„ будут в несколько раз большими.
Для ширины резонансной кривой Ato0u=ro0„,gw из (8.20) и (8.21)
с учетом (8.12), (8.15) и (8.3) следует простое выражение
Дю0„ = луХ. (8.23)
Однако оценка величины параметра диссипации X встречает трудности.
Эксперименты по ферромагнитному резонансу, из коюрых может
" Эту ветчину не слетует путать со скиической восприимчивостью
намагниченного до насыщения ферро- п.!и ферримагнетика у_о = Мо'Н0.
246
'~ х"
i
х' J
м
; \
/ 1
/
/ '
__,^
aow
а
\
\
\
\
\
ч-~
X
со
Ь>т,Я,
Omvv>
Рис. 8.5. Магнитные спектры, обусловленные колебаниями границ доменов
[174]. а—резонансный (g„,=5), б—релаксационный (Q„=0,2)
быть найдена эта величина, проводятся, как правило, при более
высоких частотах, а частотная зависимость X может быть сильной.
Используя значение X, найденное Голтом [306], из измерений скорости
движения доменной стенки в монокристалле железо-никелевого
феррита получим A/0w = 35 МГц. Оценка же резонансной частоты для
этого вещества (поликристаллического) дает /Ош=280МГц. Таким
образом, в данном случае (как и в большинстве других) оценка
приводит к С>1, так что частотная зависимость Хц должна носить
резонансный характер.
Экспериментальные зависимости вещественной и мнимой частей
магнитной проницаемости ц от частоты в отсутствие постоянного
магнитного поля—магнитные спектры монокристаллического феррита
приведены на рис. 8.6. Эти зависимости, безусловно, связаны с
колебаниями доменных стенок, так как собственные частоты процессов
вращения, т. е. частоты «естественного» ферромагнитного резонанса
в этом феррите с очень большой анизотропией, должны быть
значительно более высокими (см. § 8.3). Экспериментальные значения
(рис. 8.6) /Ow=360 МГц и Д/0„ = 25 МГц находятся в разумном
соответствии с приведенными оценками.
В отличие от этого, в магнитных спектрах поликристаллов
никогда не наблюдаются узкие области резонансного изменения
ц' и ц", обусловленные
колебаниями доменных стенок.
Основной причиной этого
является разброс форм,
размеров и ориентации доменов
в поликристаллических
образцах. Область резонанса
доменных стенок для них часто
сливается с областью
изменения магнитной
проницаемости, вызванного
ферромагнитным резонансом в доменах
(§ 8.3).
250
300
350
400
Ъ»Гц
Рис. 8.6. Магнитный спектр
монокристаллического кобальтового феррита
[170]
247
§ 8.3. Ферромагнитный резонанс
при наличии доменной структуры
Если бы переменные намагниченности в разных доменах не были
связаны между собой, то собственными колебаниями были бы
независимые колебания намагниченности в этих доменах. Однако, как мы
убедимся, переменные намагниченности в соседних доменах сильно
связаны, и собственными частотами являются частоты связи. Аналогичное
положение имело место в антиферро- и ферримагнетиках (гл. 3), где
собственными колебаниями являлись не колебания отдельных подре-
шеток, а связанные колебания всей системы, в каждом из которых
участвовали все подрешетки. Отличие (конечно, весьма существенное)
ненасыщенного ферромагнетика от антиферромагнетика заключается
в том, что в антиферромагнетике (и ферримагнетике) подрешетки
«перемешаны» на микроскопическом уровне, вследствие чего связь
между ними осуществляется в основном обменным взаимодействием;
домены же представляют собой макроскопические образования, и связь
между ними обусловлена в основном размагничивающими полями,
которые возникают вследствие скачков намагниченности на границах
доменов. В этом параграфе мм рассмотрим такие связанные колебания.
При этом доменные стенки мы будем считать бесконечно тонкими.
Уравнения движения намагниченности в различных группах
доменов имеют такой же вид (3.3), как уравнения движения намаг-
ниченностей подрешеток. Но теперь j—номер группы доменов,
a Mj — их намагниченность. Средняя намагниченность образца
М = 1г,;М,., (8.24)
j
где 1j=^/X'/j—относительный объем j-Pi группы доменов. Эф-
1
фективное поле, действующее на М^, аналогично (2.9) запишется
в виде:
\ ги 1 „ ^
■ш
(8.25)
где U—плотность энергии, отнесенная к единице объема всего
разбитого на домены образца, с чем и связано появление в (8.25)
множителей 1/tj ^. В U должны войти все виды энергии
ферромагнетика, в том числе обусловленные наличием доменной структуры.
К ним относятся энергия доменных стенок и магнитная энергия,
связанная с размагничивающими полями доменов.
Размагничивающие поля. Поскольку мы рассматриваем доменную
стенку как бесконечно тонкую границу между доменами, то из
условия непрерывности нормальной составляющей магнитной
индукции на этой границе следует, что
Н1п0-Н2п0=-4п(М1п0-М2пс), (8.26)
248
где индексы 1 и 2 соответствуют двум соседним доменам, а
п0—единичный вектор нормали к границе. Так как внешнее поле не имеет
особенностей на границе доменов (или вообще отсутствует), то должно
возникнуть размагничивающее поле, испытывающее на границе такой скачок.
В случае доменов, представляющих собой бесконечные
плоскопараллельные слои одинаковой толщины, размагничивающие поля,
удовлетворяющие условию (8.26), направлены перпендикулярно
границам и составляют
#м1.2=+2л(Л/1и-Л/2п), (8.27)
где М1Лп — проекции намагниченностей доменов на нормаль к границе.
Энергия этих полей
UMw^\HMl.2\2=^(Mln-M2n)2. (8.28)
Для более сложных доменных структур размагничивающие поля
могут быть найдены в результате решения соответствующих маг-
нитостатических задач [47, 338].
Строгий расчет магнитных колебаний в ненасыщенных образцах
с доменной структурой возможен лишь при некоторых простых
предположениях об этой структуре. Такой расчет впервые провел
Нагамия [374] для случая диска из тетрагонального кристалла. Для
эллипсоида вращения из магнитно-одноосного кристалла он был
проведен Смитом и Бельерсом [416], а для сферы из кубического
кристалла — Артманом [230]. В этих работах предполагалась
простейшая и не зависящая от постоянного магнитного поля доменная
структура, представляющая собой тонкие плоскопараллельные слои
одинаковой толщины. Доменные l-ichkii считались при этом
бесконечно тонкими, неподвижными, и энергия их не учитывалась''.
Заметим, что доменная структура сохраняется при наложении
постоянного магнитного поля, если оно (рис. 8.7) образует одинаковые
углы с намагниченностями обеих групп доменов: угол же,
образованный полем с границами доменов, может быть любым. Намагничивание
* в этом случае происходит путем поворотов векторов намагниченности
по направлению к полю (процесс вращения).
Эллипсоид из одноосного ферромагнетика [416]. Пусть легкая ось
анизотропии (К1>0) совпадает с одной из осей эллипсоида, а
постоянное поле направлено перпендикулярно ей (см. рис. 8.7). Тогда
показанная на этом рисунке слоистая доменная структура «лласно
приведенному выше условию будет сохраняться при увеличении
магнитного поля, а направления равновесных намагниченностей
доменов будут приближаться к направлению поля, пока при некоторой
его величине Hs доменная структура не исчезнет. Переменное
" В более поздних работах, например. [47, 181, 182] удатось отказаться
от некоторых из указанных ограничений: была учтена энергия доменных
стенок и их подвижность, исследован случай доменных структур с
изменяющимися под действием внешнего поля параметрами. Однако во всех работах
Рассматривались лишь простейшие доменные структуры—с
плоскопараллельными доменами, а также с ЦМД.
249
Рис. 8.7. Доменная структура и направления полей, принятые при расчете
условий резонанса в эллипсоиде из одноосного ферромагнетика
магнитное поле hexpOco/) пусть лежит в плоскости, перпендикулярной
оси анизотропии (рис. 8.7).
Учтем следующие виды энергии: зеемаповскую Uz, анизотропии
£/а и два вида внутренней магнитной Jiiepi ии: обусловленную
размагничивающими полями поверхности эллипсоида UM m и
обусловленную скачками намагниченности на границах доменов UMw.
Поскольку домены имеют равные толшины (п., =г]2=1/2), то полная
зеемановская энергия, включающая и энергию в переменном поле,
согласно (2.17) и (8.24) запишется
и,=-
К + чьин^ + ьу»').
(8.29)
Энергию анизотропии, отнесенную, как и другие виды энергии,
к единице объема образца, согласно (2.44) можно записать в виде
I М\,
, ~2"л7Г
Предположим, что толщина доменов много меньше размеров
образца. Тогда при вычислении С'м ,л неоднородностью
намагниченности можно пренебречь и записать согласно (2.18)
t/a=A'l I
2 М
D-
(8.30)
Vu -,„ = '- (NM + КУМ* + Nz Л/r),
(8.31)
где Мху-.- составляющие средней намагниченности М = -(М! + М2),
a ^x.y.z размагничивающие факторы образца. Для UMw будет
справедливо выражение (8.28). где М1а„ = М1 2у.
Для решения уравнений движения намагниченностей доменов Мь2
(которые, как уже отмечалось, имеют вид (3.3)) воспользуемся, следуя
работе [416], методом сферических координат (§ 2.1). Исходные уравнения,
аналошчные уравнениям (2.22) без учета диссипации, будут иметь вид
'"0i.2_ 2у ГС <>^_ 2у П>
Ct
г 1С 0, , и ф, 2
Л/0sin0,.2 #>,.,' it М0япй1ЛРЪ^2-
полярные и азимутальные углы векторов М, 2.
(8.32)
Прежде всего необходимо найти равновесные значения углов
(01.2)0 и (ф1.2)о- Для этого можно использовать условия равновесия,
являющиеся обобщением условий (2.24) (энергия при этом не включает
зеемановской энергии в переменном поле). Ограничимся для простоты
случаем фн = тс/2 (см. рис. 8.7); как уже отмечалось. 0н = я/2 для
того, чтобы не было смещения доменных границ. Тогда из
соображений симметрии
(«Pi)o = Mo = n/2, (е1)о=л-(92)0 = е0. (8.33)
Угол 0О находится из условия I—-) =0 или 1 — 1 =0:
sine0 = #(:o/tfs при Яс0<Я8,
0о = я/2 при Яе0^й5,
(8.34)
где Hs = 2HAl+NyM0, а НЛ1 = К1/М0- Таким образом, как мы
и предполагали, с увеличением Яе0 направления векторов
М10 и М20 приближаются к направлению поля и совпадают с ним
при Ht0^Hs.
Затем необходимо линеаризировать уравнения (8.32). Для этого,
приняв 0i.2 = (0i.2)o + 50i.2exp(KOf), Ф1.2 = (ф1.2)о + 5ф1.2ехр(нй/),
разложим производные в (8.32) в ряды по переменным составляющим
углов, ограничимся их первыми членами и учтем условия
равновесия. В полученных таким образом четырех линейных уравнениях
для комплексных амплитуд 601-2 и бфх.г перейдем к новым
переменным
8в±=-(8в1±892). 5ф±=-(6ф1 + 5ф2).
(8.35)
Для них получатся две независимые системы уравнений,
соответствующие двум типам нормальных колебаний:
2(f/ee+f/e1eJ6e+-^(o6V+=o) (g36)
/^ю50+ +2({/„+ £05Ф+ =Шо5гпе0со5ф„,
2(£/„- С/о.о.) 86" -^швф" = АМ°cos 0o sin Ч>*-
^ео8в-+2(£/^-£/ф1ф1)8ф-=0.
(8.37)
Здесь t/ee=t/e,e, = £4v U^=UVl<f=UMl, a C/e,„, и т. д.- вторые
производные энергии по соответствующим углам при их равновесных
значениях; ^ = (A/o/Y)sin0o, а Ф„-угол, который образует переменное
поле h (рис. 8.7) с границами доменов.
Колебания первого типа (система (8.36)) возбуждаются
составляющей переменного поля, перпендикулярной постоянному полю,
а колебания второго типа (система (8.37))-составляющеи,
параллельной ему. Собственные частоты этих колебании ео± и со,,
получаются из условий равенства нулю определителей систем (8.36)
251
Рис. 8.8. Частоты ферромагнитного
резонанса в сфере из одноосного
кристалла (А!>0) при наличии доменной
структуры, -показанной на рис. 8.7
[416]. Постоянное поле
перпендикулярно оси анизотропии и границам
доменов, НА1=(4п/3)М0
и (8.37):
{^j = (2HAl+4nM0){2HAl + NxM0)-
(2HAI+NxM0)[2HAl+(Nx + Ny)M0] ц2
(2HAl+NyM0)2
(^J = 2HAl(2HAl+NyM0)- 2Нл1
НеО,
2HAi+NyM0
НеО-
(8.38)
(8.39)
На рис. 8.8 показаны зависимости ю± и Шц от Не0, вычисленные
по формулам (8.38) и (8.39) для случая сферы. Из этого рисунка
видно, что наличие доменной структуры приводит, во-первых, к тому,
что частота колебания, возбуждаемого поперечным (относительно
направления постоянного поля) переменным полем, ни при каких
Яе0 не обращается в нуль. Во-вторых, появляется тип колебаний
с частотой соц, который возбуждается переменным полем,
параллельным постоянному. Частоты юх и а>ц в отсутствие постоянного
магнитного поля — частоты «естественного ферромагнитного
резонанса» оказываются конечными и различными.
В более общем случае, когда угол между постоянным полем
и доменными границами Фн^О, л/2, возбуждаются оба нормальных
типа колебаний, но, конечно, с разными амплитудами, при любой
ориентации h относительно Нс0. Собственные частоты этих колебаний
лежат всегда между найденными выше частотами а>± и а>ц, совпадая
с ними при #ео=0 и Hc0 = Hs [47]. Если доменная структура
оиаичается от рассматривавшейся до сих пор слоистой структуры,
но по-прежнему является регулярной, то в изложенной выше теории
изменится лишь выражение для магнитной энергии, связанной со
скачками намагниченности на границах доменов [338].
Кубический кристалл. Колебания намагниченности в ненасыщенных
образцах из кубического монокристалла тоже могут быть рассмотрены
сравнительно просто в тех случаях, когда реализуется регулярная
слоистая доменная структура. Одна из таких задач была решена
в [230] для случая сферического образца с учетом только первой
константы анизотропии. Постоянное поле Нс0 было приложено
в направлении <П0>- При этом слоистая структура с доменами
равной толщины сохраняется в поле #с0^0 как при К1>0, так
и при ЛГ, <0. При Ki>0 равновесные намагниченности доменов.
252
[О Of]
[ooi]
[010]
[010]
Kf>0
Рис. 8.9. Доменные структуры, ушитые при расчете условий резонанса
в сфере из кубического ферромагнетика [230]
направленные при He0 = 0 по легким осям <1(Ю> и <010> (рис. 8.9),
с ростом Нс0 приближаются к направлению поля, находясь в
плоскости {001}. При Ki<0 они лежат в плоскости {ПО}.
Вычисление собственных частот колебаний в этом случае
аналогично расчету для одноосного кристалла, но энергия анизотропии
записывается теперь согласно (2.36). Вычисления показывают, что
и в случае кубического кристалла имеют место два нормальных
типа колебаний. Один из них (с частотой ы±) возбуждается
переменным полем, перпендикулярным постоянному, а другой (с частотой
Юц)—полем, параллельным постоянному полю. Зависимости частот
ш± и соц от Яс0 показаны на рис. 8.10.
До сих пор в этом параграфе мы считали доменные стенки
неподвижными. Более строгий подход к исследованию магнитных
колебаний в ненасыщенных образцах заключается в одновременном
расмотрении колебаний намагниченности в доменах и колебаний
и
ГНА,
- (о±
Ch
1
К,>0
1 1
Н*0
«Л,
16 V
12
7'l"/,l
К4<0
■ 8 12
Рис. 8.10. Частоты ферромагнитного резонанса в сфере из кубического
кристалла с доменными структурами, показанными на рис. 8.9 [230]. Постоянное
эле направлено по оси <110>, ЯЛ1=(4л/3)М0 при А:,>0 и \НЛ1\=-М0 при
Ki<0. Штриховые линии —границы области существования принятой при
расчете доменной структуры
253
*>/rKA
№z/\v\L*
24
го
w
12
0,5
ы4 "зь>г '
16 24
а
16 ., 20
»ео/КА
Рис. 8. II. Результаты экспериментального исследования ферромагнитного
резонанса в сфере ЖИГ [148]; а зависимость резонансной частоты от
постоянного поля, линии расчет согласно [230] (см. рис. 8.Ю), ючки —
эксперимент; о — кривые резонансного поглощения при различных часютах,
\D\—модуль коэффициента прохождения через резонатор с исследуемой сферой
доменных границ [47]. При этом имеют место три нормальных
колебания''; их частоты наиболее сильно отличаются от частот колебаний
в доменах (рассмотренных в этом параграфе) и частот колебаний
доменных границ (§ 8.2) при сближении этих невозмущенных частот.
Остановимся теперь на вопросе об интенсивности и форме линий
ферромагнитного резонансного поглощения в образцах с доменной
структурой [111, 403]. Для этого необходимо решить уравнения
движения нама1ниченностей доменов, например, уравнения (8.36)
и (8.37), и затем найти тензор восприимчивости ненасыщенного
образца хс. который определяется следующим образом:
m = xchc,
(8.40)
где m—переменная составляющая средней намашиченности образца
(8.24), a hc— внешнее переменное поле. Конечно, введенный таким
образом тензор хе имеет смысл лишь при условии малости толщины
доменов по сравнению как с размерами ооразца. так и с длиной
волны. Тензор х'с, в отличие от тензора восприимчивости
намагниченного до насыщения ферромагнетика, в общем случае имеет
все 9 компонент, каждая из которых проходит через резонанс на
всех собственных частотах разбитого на домены образца (трех
частотах—в рассмотренных выше случаях).
Не приводя решения_ уравнений (8.36) и (8.37) [111], отметим
лишь, что компоненты хе совпадают по порядку величин с
компонентами тензора восприимчивости насыщенного образца с такими
" На языке связанных колебаний -учитывается связь между колебаниями
намагниченностей доменов и колебаниями доменных границ.
254
40
X
ю4 ю6 т ю8 ж 1°ю f>r4
-* =—■—■—*--«—— *-
Рис. 8.12. Магнитный спектр поликристаллического никелевого феррита [369].
Комнатная температура; / колебания границ доменов, //—естественный
ферромагнитный резонанс
же значениями М0 и параметра диссипации, а форма и ширина
резонансных кривых гоже не отличаются от таковых в насыщенных
образцах. Это иллюстрирует рис. 8.11. Однако это относи гея только
к интервалам полей, в которых доменная структура является
регулярной. Сложная, нере]улярная доменная структура приведет к
существенному «неоднородному уширснию» и искажению формы
резонансных кривых. Нерегулярность доменной структуры является причиной
того, что область «естественного» ферромагнитного резонанса в
поликристаллах является обычно очень широкой (см., например рис. 8.12)
и иногда частично перекрывается с областью существования колебаний
доменных степок [369].
Границы области естественного ферромагнитного резонанса в
поликристаллах можно оценить, используя формулы (8.38) и (8.39).
Величины coj. и соц при Яс0 = 0, как видно из этих формул, зависят
от размагничивающих факторов Nx и А\ череп поликристалла.
Предполагая произвольными их форму и ориентацию, получим
выражения
<отт = 2уНЛ1. coin„ = Y(2^i + 4nA/„), (8.41)
известные как формулы Полдера- Смита [390]. Особенно большой
интерес представляет величина сотах, которая является граничной
частотой так называемых начальных потерь в ферритах; при частотах,
меньших ытах, при малых //,.0. когда еще сохраняется доменная
структура, имеют место большие величины и", которые препятствуют
применению данною феррита в устройствах, работающих при малых
постоянных полях.
Неоднородные тины прецессии. В образцах с доменной структурой
могут, конечно, иметь место не только рассмотренные выше
однородные (в каждой группе доменов) магнитные колебания, по и
неоднородные типы колебаний и спиновые волны. Строгий их анализ
должен основываться на совместном решении уравнений движения ьама1-
ниченности (3.3) для всех ipynn доменов и уравнений электродинамики
255
при соответствующих граничных условиях как на поверхности образца,
так и на границах доменов—при условии, что толщины доменных
стенок достаточно малы по сравнению с размерами доменов Даже
при указанном допущении и для простых, рассмотренных выше
доменных структур решение такой задачи приводит к сложным
интегродифференциальным уравнениям [24]. Сравнительно простое
приближенное решение возможно, если длина волны неоднородного
колебания значительно больше размера доменов. Тогда собственные
частоты и поля колебаний могут быть найдены [ПО] таким же
образом, как для намагниченного до насыщения ферромагнетика
(§ 6.3), но принимая в качестве магнитной восприимчивости вещества
усредненную по доменам восприимчивость %. Как и для
рассмотренных выше однородных колебаний, в области существования
доменной структуры все неоднородные типы прецессии образца
разделяются на два типа. Одни возбуждаются поперечным
относительно Не0 переменным полем; в полях, больших поля насыщения
#s, они переходят в обычные уокеровские типы прецессии
намагниченного до насыщения образца. Другие, возбуждаемые переменным
продольным полем, не имеют аналогов в области насыщения.
Спиновые волны. Строгое рассмотрение спиновых волп при
наличии доменной структуры сопряжено с большими трудностями.
Различные приближенные подходы возможны при выполнении какого-
либо из неравенств:
\)2nlk»d,b, 2) 2n/k~d»h. 3) 2n/k«d»b. (8.42)
Здесь к—волновое число, d— ширина доменов, а Ь—толщина
доменных стенок.
В первом случае, как и при рассмотрении магнитостатических
типов прецессии, можно использовать усредненный тензор
восприимчивости х- Поскольку размер доменов (§ 8.1) J~ 1 мкм и,
следовательно, /с«105, обменное взаимодействие в этом случае для многих
веществ, в частности для ЖИГ, может не приниматься во внимание,
так что волны будут безобменными магнитостатическими волнами.
Во втором случае можно по-прежнему не учитывать энергии
доменных стенок, считая их бесконечно тонкими границами областей
с разными направлениями намагниченности. Однако введение
усредненного тензора % теперь недопустимо, и необходимо искать решения
магнитостатической задачи для каждого домена и связывать эти
решения при помощи условий на границах доменов. Рассмотрим,
например, безобменные магнитостатические волны в пластине с
одноосной анизотропией с легкой осью, перпендикулярной ее
поверхности. Предположим, что в пластине (см. рис. 8.1) имеет место
простая слоистая доменная структура. Потенциал внутри и-го домена
(ср. с (6.60)) будем искать в виде
\\i п=(А2 cos kzz + Bzsmkzz)(Axncoskxnx+ Bx„smkx„x)e~iky. (8.43)
Значения At, Bz и kz во всех доменах приняты одинаковыми, чтобы
можно было выполнить граничные условия на границах доменов.
В выражениях для потенциала вне пластины множители, зависящие
256
от х и у, должны остаться такими же, как в (8.43), чтобы могли
быть выполнены граничные условия на поверхностях пластины,
а множитель, зависящий от z, заменится на Сехр( —xl0z) при z>a
и £>exp(xz0z) при z<0. Величина кг определится граничными
условиями на поверхностях пластины: для нее будет справедливо уравнение,
отличающееся от (6.32) заменой d-*l. Подстановка же потенциала
(8.43) и потенциала вне пластины соответственно в уравнение Уокера
и уравнение Лапласа даст соотношения
к2=-ц{к2п+к2), x2z0 = (kL + k2). (8.44)
Отсюда видно, в частности, что все кхп должны быть одинаковы,
так что индекс п у кх„ можно опустить.
Рассмотрим теперь простейшие типы волн, для которых
потенциалы во всех доменах, намагниченных в одинаковом направлении,
одинаковы. Тогда достаточно учесть условия на границе одного
домена с соседним. Нетрудно убедиться [261], что эти условия,
аналогично рассмотренному в § 6.2 случаю касательно намагниченной
пластины, выполняются, если выполняется либо соотношение (6.36)
(но теперь d—толщина домена!), либо равенство y.kx + \iak2=Q.
В первом случае имеют место волны с тригонометрической
зависимостью полей от х, т. е. объемные. Во втором случае, как было
показано в § 6.2. к2<0, т. е. имеет место волна с гиперболической
зависимостью от .v — поверхностная волна, распространяющаяся вдоль
доменных границ [161, 83].
Если условие 2n/k»b не выполняется, то доменную стенку
нельзя считать бесконечно тонкой границей, и рассмотренное выше
решение теряет смысл. При достаточно больших к, т. е. в третьем
случае (8.42), можно, игнорируя вообще доменные стенки, считать,
что в каждом домене распространяются плоские спиновые волны,
закон дисперсии которых — такой же. как в безграничной среде.
Такое приближение «хорошо работает», в частности, при исследовании
параметрического возбуждения спиновых волн (гл. 10) в образцах
с доменной структурой [136. 172].
Глава 9
НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ
§ 9.1. Ферромагнитный резонанс в сильных переменных полях
Во всех предыдущих главах мы имели дело с линейными
соотношениями между переменными составляющими поля и
намагниченности, которые получались при решении линеаризированных
уравнений движения намагниченности, например, (1.70), (2.20). Однако
исходное уравнение движения, уравнение Ландау—Лифшица (2.12),
является нелинейным, линеаризированные уравнения и следующие из
них линейные соотношения между амплитудами поля и
намагниченности приближенно справедливы только при малых их величинах.
При больших амплитудах поля и намагниченности линейная связь
между ними нарушается, и возникает ряд новых, нелинейных эффектов,
в частности, детектирование колебаний, умножение и преобразование
частоты. Рассмотрению этих явлений посвящена данная глава.
Точное решение уравнения движения. Решение уравнения Ландау—
Лифшица при произвольной амплитуде переменного поля возможно
лишь в ограниченном числе случаев. Самым простым из них является
прецессия намагниченности под действием переменного магнитного
поля с круговой поляризацией, которая была исследована Скроцким
и Алимовым [183]. Как мы увидим, характер нелинейной прецессии
существенно зависит от вида диссипативного члена в уравнении
движения. Рассмотрим сначала решение уравнения (1.69) с дис-
сипативным членом в форме Блоха—Бломбергена.
Положим в уравнении (169)
Н = Н0+!и, (9.1)
где H0 = z0#0 — внутреннее постоянное поле, a ru—поперечное
переменное поле с круговой поляризацией и правым вращением. Теперь,
при рассмотрении нелинейных процессов, нам придется отказаться
от метода комплексных амплитуд в той его форме, которая
использовалась во всех предыдущих главах, и иметь дело с
мгновенными значениями переменных величин. Тогда
lK=/i0(x0cosart+y0sinart). (9.2)
Из соображений симметрии следует, что переменная
намагниченность будет лежать в плоскости ху и иметь круговую поляризацию
с правым вращением, но может быть сдвинута по фазе относительно
поля h,. а постоянная намагниченность будет направлена по оси
г. по не будет, как в линейном случае, равна равновесной намаг-
/Ь8
7
0,5
х"
л+ res
Л
V
sat
Рис. 9.1. Зависимости Мг и нелинейной восприимчивости при резонансе от
амплитуды переменного поля, найденные путем решения уравнений движения
намагниченности с диссипативными членами в форме Блоха—Бломбергена
(кривые В) и Гильберта (кривые G). В первом случае Л5а, = сог/у. во втором
Лм,=аш/у; в обоих случаях А8Ы=;-ДЯ. где Д#—ширина линейной резонансной
кривой
ниченности М0. Таким образом, решение уравнения (1.69) можно
искать в виде
M = w0[x0cos(a>/ + <p) + yoSin(ra,' + <p)]+ZoAfz. (9-3)
Подставляя (9.1)—(9.3) в проекции уравнения (1.69) на оси координат,
мы получим три уравнения, из которых можно найти три неизвестные
величины т0, ф и М:. а затем и комплексную нелинейную циркулярную
восприимчивость которую можно определить следующим образом:
Хч„ = /"<><'TV (9.4)
Приведем найденные таким образом выражения для М- и мнимой
части х + п при резонансе (w = yH0)'
MZTC^M0{l+y2h20l^)-1, x'-™ = (7;Wr)A/rfe. (9.5)
Нелинейная восприимчивость не является, как в предельном
(линейном) случае малых амплитуд, посюянной величиной, а уменьшается
с ростом амплитуды переменного поля, причем пропорционально
уменьшению А/-гс> (рис. 9 1).
Решение уравнения движения (1.67) с днесииашвным членом
в форме Гильберта (когда длина вектора М сохраняется) приводит
к качественно друг им результатам [183] (рис. 9.1):
Х+..го = ПР" Ло-^-хсоу.
ч т.-or/ эко (96)
М, rcs = 0, у.'; „ м = Мп Л„ при Л„ > это/у.
м,
\ 7* КГ /
Мы рассмотрели решения уравнений движения
намагниченности (1.69) и (1.67) лля бел р.ншчной срелы. Эш решении будут
17* 259
справедливы, первое — приближенно, а второе—строго, и для
сферы, если h0 будет внешним полем. Действительно, уравнение
движения, описывающее однородные колебания намагниченности
малого изотропного эллипсоида в постоянном Нс0 и переменном
hc^ внешних полях, с диссипативным членом в форме Гильберта
имеет вид
ЯМ •- ft с М
— =-7Mx(Ht0 + hc.-NM)+-Mx —. (9.7)
ct М it
В случае сферы N—скаляр, и размагничивающее поле NM выпадает
из уравнения; тогда уравнение (9.7) совпадает при замене внешних
полей на внутренние с уравнением (1.67)".
Существенное различие поведения переменной намагниченности
в сильных переменных полях при разных формах диссипативного
члена, казалось бы, дает возможность отдать предпочтение той
или иной форме его на основе экспериментального исследования
ферромагнитного резонанса в сфере в сильном переменном поле.
Однако это осуществить не удается, так как при амплитудах поля,
значительно меньших, чем асо/у, возникают другие нелинейные
процессы — обусловленные параметрическим возбуждением спиновых
волн (гл. 10). Они ограничивают дальнейший рост амплитуды
переменной намагниченности и не дают проявиться рассмотренным
выше особенностям.
Строгое решение нелинейного уравнения движения
намагниченности возможно и для эллипсоида вращения (сфероида), находящегося
в постоянном поле (которое направлено вдоль оси вращения)
и переменном поле с круговой поляризацией. Решение и в этом
случае можно искать в виде (9.3). Подставляя его в уравнение (9.7),
можно найти все неизвестные величины т0, ср и Мг. Собственная
частота будет в этом случае иметь вид
o>on = y[Hc0+(NL-Nz)M:], (9.8)
где NL и Nz — размагничивающие факторы сфероида (см. § 1.5).
Выражение (9.8) отличается от формулы для собственной частоты
малых (линейных) колебаний заменой постоянной намагниченности
М0 на величину Mz, которая уменьшается согласно (7.68) или (9.6)
с ростом гп0. Поэтому собственная частота будет теперь зависеть
от амплитуды прецессии т0, а именно согласно (9.8) будет расти
с ростом т0 для сплющенного сфероида—диска (когда NZ>N±)
и уменьшаться—для вытянутого (когда NZ<NL). В свою очередь,
амплитуда т0 зависит резонансным образом (при заданг )й частоте
переменного поля со) от собственной частоты со0п. Такая взг имосвязан-
ность может привести к нестабильности колебаний.
Действительно, пусть, например, в случае диска при co>to0n
амплитуда т0 случайно несколько увеличится. Тогда Л/, уменьшится,
" Это обстоятельство отмечалось в $ 1.5 для линеаризованных уравнений,
но, как мы видим, имеет место и в общем случае.
260
Иг
L
*0>\г
Рис. 9.2. Решения уравнения движения намагниченности сфероида (N2 — N±>0)
при различных амплитудах переменного поля (схематически). Стрелками
показано направление изменения постоянного магнитного поля
а со0п возрастет и приблизится, таким образом, к со. Это приведет
к дальнейшему росту т0 и т. д., пока собственная (резонансная)
частота не совпадет с частотой to.
Как показали Скропкий и Алимов, решившие строго эту задачу
[184], в некотором интервале значений со и Не0 упомянутая
нестабильность приводит к неоднозначной зависимости ш0 и Mz от со или
#е0 (Рис- 9.2). Неоднозначность возникает, когда амплитуда
переменного поля с круговой поляризацией превышает некоторую критическую
величину. В случае NZ>N± она составляет
(9.9)
где ДЯ=2асо/у, a -y\ = 2(Nz-Nl)M0IAH. Для сферы г) = 0 и /гсг-+со,
т. е. неоднозначность не имеет места. В предельном случае тонкого
диска (Nz — iV±~4n) критическое поле минимально:
(9.10)
_,(ДЯГ
"сг min — п г '
2 j4nM0
Для монокристалла ЖИГ (АН = 0,5 Э) hcimia = 0,004 Э, т. е. в -50 раз
меньше, чем поле АН/2, при котором, как мы видели, происходит
насыщение ферромагнитного резонанса в сфере.
261
Упомянутая выше неустойчивость имеет место, как нетрудно
убедиться, на средней ветви зависимости Мг или т0 от со (рис. 9.2)
или Не0, а верхняя и нижняя ветви являются устойчивыми. В результате
резонансные кривые (зависимости поглощенной мощности от со или
#е0) оказываются резко-нелоренцевыми и имеет место гистерезис.
В электродинамических системах, содержащих такие, несферические,
образцы, при достаточно больших уровнях мощности могут возникать
автоколебания [262, 451], гармонические или релаксационные.
Рассмотренные явления наблюдал впервые в ферритовых дисках
Вейсс [451]. Андерсон и Сул [229] объяснили их" на основе
приближенного решения уравнения движения; полученная ими
величина й„ отличается от точного результата (9.10) лишь множителем,
близким к 1.
Очевидно, что такая нестабильность и все связанные с ней
явления могут быть обусловлены не только анизотропией формы,
но и любой анизотропией, например, кристаллографической [310],
приводящей к зависимости собственной частоты от амплитуды
колебаний. К такой зависимости может привести и изменение констант
анизотропии при изменении температуры, которое происходит
вследствие нагрева образца переменным полем [273].
Детектирование магнитных колебаний. Итак, большие,
приближающиеся к М0 амплитуды переменной намагниченности в ферро- или
ферримагнетиках практически недостижимы из-за возникновения
рассмотренных выше нестабильностей, а также, причем в любых
образцах, в том числе и в изотропных сферах,— из-за
параметрического возбуждения спиновых волн (гл. 10). Однако и при величинах
переменного поля меньших, чем пороговые значения для указанных
процессов, нелинейность движения намагниченности приводит к ряду
легко наблюдаемых эффектов. Одним из них является уменьшение
постоянной составляющей М. при колебаниях намагниченности, т. е.
детектирование этих колебаний.
При малых амплитудах поля (йо^асо/у) из (9.6) следует
5Мгге5 = Л/0-А/гге5^У*/, (9.11)
2crcir
а из (9.5) — при соотношении (1.72) между параметрами диссипации—в
два раза большая величина 6Л/гге5. Ясно, что это различие (оно
видно и из рис. 9.1) связано с сохранением в одном случае
и с несохранением в другом длины вектора М.
Изменение постоянной намагниченности Мг может быть
обнаружено (рис. 9.3) различными способами. Один из них [253]
заключается в регистрации ЭДС, которая наводится в катушке,
расположенной вблизи ферритозого образца. Другой способ [335]
основан на обнаружении магнитострикционной деформации образца
с помощью пьезоэффекта в сегнетоэлектрическом образце, скреплен-
спин-^тао^^Т ЯВШЮС- ПСРВЫМ Шагт' на "У™ к созДанию теории
волн ™™ ™ щ 6кЛЪИО"ек' т- е- параметрического возбуждения спиновых
262
\ К усилителю
Пьезоэлектрик
К усилителю
Рис. 9.3. Фсрритовые детекторы: а—индукционный [253], б—Mai нитострик-
ционный [335]
ном с ферритовым. Применение таких ферритовых детекторов
ограничивается тем, что их чувствительность оказывается значительно
меньшей, чем у полупроводниковых детекторов. Однако важным
преимуществом ферритового детектора является его большая
стойкость при больших мощностях, в условиях радиации, при
многократных изменениях температуры и пр., связанная с тем, что
используемый в нем эффект является объемным.
Приближенные методы исследования нелинейных колебаний
намагниченности. Один из таких методов основан на использовании условия
сохранения длины вектора намагниченности
М\ + М] + М\ = М\.
(9.12)
Рассмотрим случай сравнительно малых колебаний, когда
амплитуды Мх и Му значительно меньше равновесной намагниченности
М0. Тогда, во-первых, из (9.12) следует
MS*M0-—(M2x+M2t).
2М0
(9.13)
Во-вторых, малость Мх, Му и М0 — М. по сравнению с М0 позволяет
использовать метод последовательных приближений и находить
Мх и Му в первом приближении с помощью линейной теории.
Тогда для изотропного ферромагнетика
М, = Re К е <ю0 = Re [(Х^ +' ХА) *'"']•
(9.14)
Входящие сюда величины hx и hy представляют собой комплексные
амплитуды переменного магнитного поля: внутреннего, если
X и ia—компоненты тензора восприимчивости вещества, или
внешнего—если это компоненты внешнего тензора восприимчивости
образца. При произвольной поляризации поля можно принять
hx = hx0, *, = *,„*", (9-15)
261
где hx0 и hy0—вещественные величины. Подставляя (9.15) в (9.14)
и в аналогичное выражение для Му, а затем используя (9.13), получим
Мг = М0 + Шг+Мг2, (9.16)
m2=-^[(\x\2 + \Xa\2)(h2xo + h^)-4Sinq>(x'%'o + %''x^hx0hyOl (9.17)
MZ2=-^{(x'2-X''2-Xo2 + X'o2)[h2xoCos2at + h2yoCos2(M + <pj\ +
+2(xY-X'oX:)[b20sin2m+hl0sm2(m+<p)]}. (9.18)
В выражение (9.18) гармонические функции с частотой 2(0 входят
линейно; поэтому теперь—после того, как это выражение
получено,—можно воспользоваться методом комплексных амплитуд. Тогда для
комплексной амплитуды составляющей Мг2 получится следующее выражение:
м"=~(х2-х.№+а,2)- (9л9>
Если для х и Ха принять выражения, которые получаются из (1.44)
при замене (1.73), то формула (9.19) приобретет еще более простой вид
mz2=-yMh2x+h2y). (9.20)
Величина 8Мг описывает эффект детектирования, который был
кратко рассмотрен выше, а величина Мг2 — эффект удвоения частоты,
который будет рассматриваться в следующем параграфе. Как видно
из (9.17), детектирование имеет место при любой поляризации
переменного поля. При круговой его поляризации с правым вращением
выражение (9.17) при резонансе совпадает с выражением (9.11),
которое справедливо при тех же условиях, что и (9.17): сохранение
длины вектора намагниченности и малость амплитуды переменной
намагниченности по сравнению с М0.
Рассмотренный приближенный метод, основанный на условии
сохранения длины вектора намагниченности, имеет существенные
недостатки. Не говоря о том, что это условие выполняется не для
всех видов диссипативного члена в уравнении движения (а реально,
как будет показано в гл. 11, не для всех процессов релаксации),
с его помощью можно найти нелинейные слагаемые только
продольной составляющей намагниченности Мг. Более универсальным
является другой вариант метода последовательных приближений [67],
к изложению которого мы переходим. Будем искать решение
уравнения движения намагниченности в виде
М = М0+М(1, + М(2) + ... (9.21)
и предположим, что |Мо|»|М(1)|»|М(2,|... Ограничимся
рассмотрением однородных колебаний намагниченности. Тогда эффективное
поле, входящее в уравнение движения намагниченности (см. § 2.1),
Hef=H0+Iu-NM, (9.22)
264
где Н0 и h„—заданные магнитные поля (|h_ \<slHq), а N—суммарный
тензор размагничивающих факторов формы и анизотропии.
Подставим (9.21) и (9.22) в уравнение движения (2.10) с диссипатив-
ным членом, например, в форме Блоха — Бломбергена; такое
уравнение, (1.69), было записано для случая N=0, теперь мы должны
заменить в нем Н на Hef как в основном, так и в диссипативном членах. В
нулевом приближении, пренебрегая всеми М(1), М(2), ... и lu, получим
условие равновесной ориентации намагниченности (1.91). В первом
приближении, сохраняя члены первого порядка по М(1) nh. и
учитывая условие равновесия, получим линеаризированное уравнение
ИМИ) „
——+уМ(1) х (Н0 -NM0) - уМ0 х NM(1) + юг (1 + x0N) M(1) =
= -YM0xh..+corXolu, (9.23)
где Хо = М0/|Н0—NM0|. Во втором приближении, сохраняя члены
второго порядка малости и учитывая условие равновесия и уравнение
(9.23), получим уравнение для определения М(2). Продолжая этот
процесс, мы убедимся, что намагниченность и-го порядка (и>2)
удовлетворяет рекуррентному (содержащему намагниченности более
низких порядков) уравнению
й М(л) " -
—— + у £ M№>xH(enf-*, + cor(l+XoN)M('', = 0. (9.24)
"' *=о
Входящие в него величины НИ-*' имеют следующий вид:
Hg^Ho-NMo, H(c}) = h.-NM(1), HS>=-NM№> (/c>2). (9.25)
Рассмотренный метод последовательных приближений может быть
применен как для исследования колебаний намагниченности
эллипсоида (тогда h_ — внешнее поле), так и для вычисления переменной
намагниченности при заданном внутреннем переменном поле. Если
в последнем случае вещество изотропно, то во всех выражениях
(9.25), кроме первого, следует- принять 5? = 0. Тогда уравнения (9.24)
упростятся:
ЯМ'"'
^-+уМ(п) х Н0 + согМ(п)= -уМ1"-1' х h^, (9.26)
ct
где Н0 = Не0 — 5?М0—внутреннее постоянное поле. Намагниченность
М(п) выражается теперь не через все намагниченности более низкого
порядка, а только через М0 и М1"-1'. Ясно (см. с. 260), что уравнения
(9.26) будут справедливы в случае сферы, если h„ считать внешним
переменным полем, а Н0 заменить на внешнее постоянное поле Не0-
§ 9.2. Умножение и преобразование частоты
В этом параграфе рассмотренные выше методы приближенного
анализа нелинейных колебаний намагниченности будут применены
к исследованию нелинейных эффектов, которые заключаются
265
V У
Рис. 9.4. Положение вектора намагниченности в последовательные моменты
времени
в появлении составляющих намагниченности с частотами, отличными
от частот внешних переменных полей.
Удвоение частоты. Как следует, например, из (9.19), составляющая
намагниченности с удвоенной частотой не возникает (в рассмотренном
случае цилиндрической симметрии тензора х) ПРИ круговой
поляризации поля h. Поляризация переменной намагниченности в этом
случае тоже является круговой, т. е. конец вектора М движется по
окружности в плоскости, перпендикулярной М0, и переменных
составляющих Mz с любой частотой, а Мх и Му—с частотой, отличной
от частоты поля, не возникает.
Если же система не имеет цилиндрической симметрии или поле—
круговой поляризации, то вследствие сохранения (точного или
приближенного) длины вектора М при колебаниях с достаточно большой
(строго говоря, с любой конечной) амплитудой будет возникать
переменная составляющая намагниченности с частотой 2со. Это
иллюстрирует рис. 9.4. Заметим, что оси х и у на этом рисунке направлены
таким образом, что составляющая намагниченности тх максимальна,
а составляющая ту минимальна. Из рис. 9.4 видно, что составляющая
Mz колеблется с частотой 2со, и амплитуда этих колебаний
mz2 =* | mlo - т20 |/(4M 0),
(9.27)
где тх0 и ту0—амплитуды (не комплексные) составляющих Мх и Му.
Нетрудно убедиться, что это соотношение эквивалентно выражению
(9.19). Из (9.27) следует, что эффективность удвоения частоты
определяется различием величин wx0 и т^. Его можно
характеризовать параметром Э (1.106), который можно по-прежнему называть
эллиптичностью, хотя конеп вектора М теперь (при больших
амплитудах колебаний) движется не по эллипсу, а по более сложной —
неплоской кривой (рис. 9.4). С учетом (1.106) выражение (9.27) можно
записать в виде
mz2 = mx03/(4M0). (9.28)
В случае ферритового образца с цилиндрической симметрией
небольшая эллиптичность переменной намагниченности будет возникать
266
при некруговой поляризации внешнего переменного поля.
Эллиптичность максимальна в случае линейной его поляризации и при резонансе,
как можно убедиться с помощью выражения (1.122), составляет
Э„к2а. (9.29)
Тогда согласно (9.28) и (1.122)
mz2m=y2M0h20l(8aa2), (9.30)
где Л о—амплитуда внешнего поля с линейной поляризацией.
Существенно большая эллиптичность прецессии намагниченности
имеет место в образцах с неравными друг другу поперечными
размагничивающими факторами. Ясно, что наибольшей она будет
в касательно намагниченном тонком диске, когда разность Ny—Nx
достигает максимально возможной величины 4л. При малой
диссипации (а<зс1) эллиптичность слабо зависит от поляризации поля
и при резонансе равна эллиптичности свободных колебаний (1.105),
т. е. в данном случае
Э = 4пМо1(Нм+4пМ0). (9.31)
Вычисляя тх0 при резонансе согласно (1.122) с учетом (1.97) и (1.109)
и подставляя полученную величину и (9.31) в формулу (9.28), найдем
»'z2res= г„ /„ , , ,. и"0- (9-32)
Для монокристаллов ЖИГ {АН ^0,5 Э) величина (9.32) в
трехсантиметровом диапнюне более чем на три порядка превышает (9.30).
Еще большего увеличения эллиптичности можно добиться, если
кроме анизотропии формы использовать кристаллографическую
анизотропию. Наиболее выгодным случаем будет касательно
намагниченный диск из монокристалла с легкой лоскостью анизотропии,
совпадающей с плоскостью диска [235]. Тогда (см. § 2.3) в выражении
(9.31) 4пМ0 заменится на (4лЛ/04-2Ях1). Для гексагональных ферритов
величина 2НЛ1 достигает 30 кЭ, и эллиптичность становится близкой
к 1 даже при сравнительно высоких частотах.
Эллиптичность намагниченности в случае линейной поляризации
поля увеличивается при расстройке частоты относительно условия
ферромагнитного резонанса. Особенно это существенно для
эллипсоида вращения, в частности, сферы, когда, как мы видели,
эллиптичность при резонансе очень мала. Сравнительно большие значения
эллиптичности достигаются и при магнитодинамическом резонансе
в больших ферритовых образцах (§ 5.3).
Как видно, например, из (9.28) или (9.32), удвоение частоты
является квадратичным эффектом. Поэтому эффективность его
(которую можно определить как отношение выходной мощности Рг на
частоте 2со к входной Pi на частоте со) повышается с ростом Pt.
Практически достижимые значения ее ограничиваются либо тепловым
режимом устройства, либо параметрическим возбуждением спиновых
волн (см. гл. 10).
267
Уже в первых конструкциях ферритовых удвоителей
частоты были получены весьма высокие эффективности. Выходная
импульсная мощность в удвоителе Мэлчора, Эйрса и Вертэне-
на [368] на частоте 18 ГГц достигала 8 кВт при входной
мощности 32 кВт. По-видимому, при этом имел место магнитодина-
мический резонанс. В дальнейшем эффективность ферритового
удвоителя частоты с использованием магнитодинамического
резонанса была доведена до — 2 дБ при выходной мощности 2 кВт
[144]. Выходная мощность 50 Вт была получена при удвоенной
частоте 140 ГГц [234].
Гармоники поперечной намагниченности. Применим теперь к
исследованию нелинейных колебаний намагниченности метод
последовательных приближений, основанный на решении рекуррентных
уравнений (9.23)—(9.26). Ограничиваясь случаем изотропного
ферромагнетика, рассмотрим во втором приближении колебания, происходящие
под воздействием заданного внутреннего поля. Тогда мы сможем
использовать сравнительно простое уравнение (9.26). Проектируя его
на оси координат, получим при и = 2
°-^- + уМ™Н0 + согЛ42> = -yMy»h„z
8M[2t
(9.33)
Bt
8М[2)
-yA^'Ho+cM/J^yM4*....
8t
+ <ьгМ™ = -y{M^h^-M^h^x). (9.34)
Составляющие намагниченности первого порядка, стоящие в правых
частях этих уравнений, можно считать известными. Величина
Л/г2) в уравнении (9.34)—это та самая продольная составляющая
намагниченности второго порядка, которая подробно рассматривалась
выше.
Система (9.33) определяет поперечные составляющие
намагниченности второго порядка М(2). Они возникают, как видно из
(9.33), только в том случае, когда переменное поле, кроме
поперечных составляющих (необходимых для возбуждения
намагниченности первого порядка М(1)), содержит продольную
составляющую h^z. Рассмотрим случай, когда эта составляющая, как
и поперечные, изменяется с частотой со, т. е. имеется одно
переменное поле, образующее с постоянным полем угол, не равный
0 или я/2. Тогда поскольку в правых частях уравнений (9.33)
находятся произведения изменяющихся с частотой со величин
Мх\у и h^z, решения этих уравнений Л/12' и М(у2) будут содержать
составляющие с частотой 2со. Выражения для них в комплексной
форме (A/'2)),2 = Re[mJCi),2exp(2/cur)]) имеют вид
_ y2M0hz[(2a2+y2H2)hx.y±3iwyH0hy,x'\
т*.>2- 2(у2Я?-ш2+2/шшг)(г2Яё-4ш2+4/(ошг)' ^ " '
268
Как видно из (9.35), величины тх_у2 при заданной частоте
переменного поля проходят через резонанс при двух значениях
постоянного поля:
#01=co/Y, Н02 = 2(й1у. (9.36)
Если бы мы рассматривали задачу о нелинейных колебаниях при
заданном внешнем поле и с учетом кристаллографической анизотропии,
т. е. решали уравнение (9.24). то резонансные условия (9.36) заменились
бы на более общие:
co0 = w, ы„ = 2со. (9.37)
где ы0(Н0, М0, N)—собственная частота малых колебаний в данном
образце — частота ферромагнитного резонанса. Максимумы величин
тх_У2, как видно из (9.35), при обоих резонансах одинаковы и,
например, при линейной поляризации переменного поля (Л,=0)
составляют
-my2 = imx2 = -—-hzhx. (9.38)
Сравнивая (9.38) с выражением (9.30) для амплитуды второй
гармоники продольной составляющей намашиченносчи в изотропном
образце с цилиндрической симметрией, мы видим, что в этом
случае (при hx и hz одного порядка) величины вторых гармоник
продольной и поперечных составляющих оказываются приблизительно
одинаковыми. Но, как было показано выше, при наличии анизотропии
величины тг2 существенно возрастают по сравнению с (9.30).
Можно показать, решая уравнение второго порядка (9.24) с N^0.
что для поперечных составляющих такого существенного увеличения
не будет. И, казалось бы. использовать поперечные составляющие
"V>2 в устройствах для удвоения частоты не имеет смысла.
Однако эти составляющие в отличие от mz2 имеют максимумы
и при со0 = 2со. в частности, для изотропной сферы достаточно
малого диаметра, при Не0 — 2щу. При таких полях спектр спиновых
волн будет лежать выше частоты ш и процессы параметрического
возбуждения спиновых волн низких порядков (гл. 10) окажутся
невозможными. Поэтому для удвоителей частоты, использующих
вторые гармоники поперечных сос1авляюших намагниченности, при
условии со0 = 2сй удается «добраться» до больших величин входной
мощности и, следовательно, получить большие эффективности
удвоения— сравнимые с эффективностями удвоителей, использующих
mz2. Например, в одном из таких удвоителей [153] была достигнута
эффективность — 5 дБ.
При со0 = 2со возникает интересный, хотя и слабый нелинейный
эффект [84], который по аналогии с нелинейной опекой (см,
например, [29 ]) можно назвать овухквантовым по г мщением Он
заключается в появлении при поле, удовлетворяющем этом} vc ;овшр.
максимума поглощаемой образцом мощности. Качественно он iipeyi
ставляется очевидным: на образование второй гарм' пики поперечной
2;,9
намагниченности, имеющей при указанном условии максимум,
требуется энергия. Но в рамках рассмотренных до сих пор приближений —
до второго включительно—этот эффект отсутствует, так как
поглощение энергии поля, имеющего частоту со, определяется амплитудой
первой гармоники намагниченности, которая находится в первом,
линейном, приближении и максимума при co0 = 2cu не имеет.
Нелинейный вклад в эту амплитуду может быть найден лишь в следующем,
третьем, приближении. Он проходит через резонанс при со0 = 2со, что
и приводит к максимуму поглощения при этом условии. Отношение
величины этого максимума к максимуму поглощения при
ферромагнитном резонансе (при со0 = ю). конечно, зависит от входной мощности
Pi, для монокристалла ЖИГ при Р, = 15 Bi >ro отношение составляет
приблизительно —60 дБ [84].
С помощью цепочки уравнений (9.24) или (9.26) может быть,
в принципе, найдена амплитуда любой гармоники намагниченности.
Не останавливаясь на этих вычислениях, отметим лишь, что
поперечные составляющие и-й гармоники имеют всегда п максимумов — при
полях, определяемых условиями сй0 = &со (к= 1, 2, 3, ..., и).
Интенсивности их уменьшаются с увеличением п как (h0/H0)n. Практически
удалось реализовать [415] утроение частоты с эффективностью
— 24 дБ при входной импульсной мощности 32 кВт.
Преобразование частоты. Если на ферритовый образец будут
одновременно действовать несколько переменных полей с частотами
(йь оъ, —, то наряду с рассмотренными выше нелинейными эффектами
детектирования и умножения частоты следует ожидать появления
составляющих намагниченности с комбинационными частотами
и1а>1+и2ьъ±-.- (и1,2.з... = 0, li 2, ...).
Ограничимся случаем двух полей h, и h2 с частотами
соответственно СО) и ю2 и будем использовать метод последовательных
приближений, изложенный в конце §9.1. Намагниченность первого
порядка М'" представляет собой решение линейного уравнения (9.23)
и поэтому будет являться суммой поперечных намагниченностей
М1,1' и М21( с частотами со, и со2, вызванных соответственно
поперечными составляющими полей h, и h2. Намагниченность второго
порядка М(2) удовлетворяет уравнениям (9.24) или (9.26) при и = 2,
линейным относительно неизвестной М(2), но нелинейным
относительно М^'г и hli2. Ясно, что М(2) будет содержать комбинационные
гармоники, в данном случае—с частотами (coj + ow) и |cOi —со2|. Эти
гармоники ответственны за эффекты преобразования частоты, которые
нас сейчас интересуют. При их исследовании мы будем для простоты
использовать уравнения (9.33) и (9.34); комбинационные гармоники
продольной составляющей М™, как и в случае удвоения частоты,
могут быть найдены и из условия сохранения длины вектора М.
Возможны, вообще говоря, три частных случая: 1) оба переменных
поля — поперечные по отношению к направлению постоянной
намагниченности, оси z; 2) одно поле поперечное (h1zo = 0), а другое
продольное (h2xzo = 0); 3) оба поля продольные. Однако в последнем
случае М(1), а следовательно, и М(2) будут равны нулю; так что
необходимо рассмотреть только первые два случая.
Z70
Если оба переменных поля поперечные (Л1г = Л2г = 0)1), то, как
следует из (9.33), М™ = М{у) = 0, а величина М(22) может быть найдена
из (9.34) или (9.13). Остановимся сначала на случае круговой
поляризации обоих полей:
A^JC = /ii0cosco1t-t-/!20cosco2r,
/i^=(±)i/i1oSinco1r+(±)2/!20smco2t, (9.39)
где знаки ( + ), и (±)2 соответствуют правому или левому вращению
каждого поля и являются независимыми. Вычисляя в этом случае
A/LVy = Re [wJC,,,1exp(?co10 + wJC,y2exp(?cu2r)] и подставляя их в (9.13),
получим
Мг-М0^М(г2)=-^-|х1±|2Л2о-щ1Х2±12Л1о-
-^H-Xi±X'2±(±)x"i±x;±)co8K(±)co2)'+
+ (х"1±Х2±(±)Х1хХг±)яп(юД±)сог)0. (9-40)
где Xi.2± = Zi.2±Xai.2 (верхние знаки—при правом, а нижние—при
левом вращении), а знаки ( + ) имеют следующий смысл: ( + ) при
разных направлениях вращения обоих полей и (—) при одинаковых.
Из выражения (9.40) видно прежде всего, что эффекты детектирования
в рассматриваемом приближении аддитивны, а эффект удвоения
частоты отсутствует, как этого и можно было ожидать при круговой
поляризации обоих полей. Переменные члены в (9.40) соответствуют
эффекту преобразования частоты, причем разностная частота
возникает при одинаковых направлениях вращения обоих полей, а
суммарная—при разных.
Приведем вытекаюшее из (9.40) выражение для комплексной
амплитуды намагниченности разностной частоты:
Wz_ = --i-Xi±X?±M2- (9-41)
Мнимые части восприимчивостей %i+ и %2+ достигают больших
значений при ферромагнитном резонансе на частотах соответственно
со, и со2. И если эти частоты близки (!«!—со2|<сог), то условие
разонанса может приближенно выполняться одновременно на обеих
частотах. Тогда, как легко убедиться, амплитуда намагниченности
разностной частоты при правой круговой поляризации обоих полей
tMlh.^h,.. (9-42>
mz-ra——г~ "юп20
В случае же одинаковой линейной ™>?П£^ °^* ПОЛеЙ'
который наиболее интересен с практической точки зрения,
..2
т
fMo. h (9.43)
:-г—Г«10й20- ч
'> Этот случай впервые рассмотрел Пиппин [387].
271
Перейдем теперь ко второму частному случаю, когда одно
переменное поле—поперечное, а другое—продольное. В этом случае
для исследования эффекта преобразования частоты необходимо искать
решение системы (9.33). Не останавливаясь на этом решении [66],
заметим, что рассматриваемая задача является обобщением
исследованной выше задачи об удвоении частоты под воздействием
поперечного и продольного полей с одинаковой частотой. Аналогично
приведенному частному случаю намагниченности суммарной и
разностной частоты имеют теперь максимумы при двух значениях
постоянного поля: соответствующего резонансу на частоте поперечного
переменного поля cOj (Н0=(й11у) и при резонансе на суммарной
(Я0=(со1 + со2)/у) или разностной (Я0 = |сй,-со2|/у) частотах.
В случае выделения разностной частоты возможно осуществление
резонанса только на частоте со,. Приведем выражение для комплексной
амплитуды гармоники намагниченности разностной частоты для этого
случая, предполагая, что |со1-со2|«сон,
mx-=im,-=- ^AtA2. (9.44)
4юню, * v '
Сравнивая (9.44) с (9.42), легко видеть, что из-за выполнения двух
резонансных условий эффективность преобразования частоты в случае
двух поперечных полей существенно превышает эффективность
преобразования при одном поперечном и одном продольном полях.
Конструкции макетов ферритовых преобразователей частоты с
выделением разностной частоты (см., например. [160]) похожи на
рассмотренные в § 9.1 конструкции ферритовых детекторов, но
включают обычно резонансную систему, настроенную на эту частоту.
Ее можно осуществить, включая катушку (рис. 9.3, а) в
колебательный контур или выбирая размеры сегнетоэлектрического образца
(рис. 9.3, б). Несмотря на все «ухищрения», эффективность ферритовых
преобразователей частоты при малых амплитудах одного из полей
оказывается значительно меньшей, чем полупроводниковых приборов.
Однако ферритовые преобразователи частоты, как и ферритовые
детекторы, обладают некоторыми преимуществами (см. § 9.1),
связанными с тем, что используемый в них нелинейный эффект является
объемным.
Глава 10
ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ
МАГНИТНЫХ КОЛЕБАНИЙ И ВОЛН
§ 10.1. Нелинейная связь колебаний и волн намагниченности
В гл. 9 мы изучали нелинейные явления, которые происходят
в ферромагнитных образцах при наличии какого-либо одного, например,
однородного типа колебаний намагниченности. Однако в таких образпах
возможны различные типы колебаний и волн, подробно исследованные
в линейном приближении в предыдущих главах. В этом приближении
они независимы. Нелинейность уравнения движения намагниченности
приводит к связи этих колебаний и волн и вызывает ряд новых
нелинейных явлений. Важнейшим из них является параметрическое
возбуждение одних типов колебаний или волн под воздействием
других, когда амплитуды последних превосходят некоторые пороговые
значения. Изучению таких явлений и будет посвящена данная глава.
Нелинейные явления, обусловленные, как потом стало ясно,
параметрическим возбуждением спиновых волн, были впервые
обнаружены в опытах Бломбергена и Дэймона [252] и Бломбергена
и Уанга [253] по исследованию ферромагнитного резонанса в сильных
переменных полях. В этих опытах измерялись независимо мнимая
часть диагональной компоненты тензора высокочастотной
восприимчивости %" и изменение постоянной намагниченности Mz (эффект
детектирования). Согласно (9.5) или (9.6) существенное уменьшение
-(О,
0,5
30 h,3
Рис. 10.1. Экспериментальные
зависимости Мг и х" ПРИ ферромагнитном
резонансе от амплитуды переменного
поля [253]. Сфера из монокристалла
никелевого феррита. Частота -~9 ГГц,
температура 300 К
18 А. Г. Гуревич, Г. А. Мелков
3 Не0,кЭ
Рис. 10.2. Резонансные кривые при
различных уровнях мощности [253].
Условия—как на рис. 10.1
273
обеих этих величин при резонансе должно было наступать (см. рис. 9.1) при
амплитудах переменного поля h порядка полуширины резонансной кривой.
В действительности (рис. 10.1) заметный спад Mz происходил именно при
таких полях, величина же %"cs начинала быстро уменьшаться при
существенно меньших значениях h. Кроме того, возникал дополнительный
максимум х" при постоянных магнитных полях, меньших, чем резонансное
(рис. 10.2). В дальнейшем было выяснено, что дополнительное поглощение
наступает, когда амплитуда h превышает некоторую, пороговую, величину
[395]. Оба эти эффекта не могут быть объяснены в рамках нелинейной
теории однородных колебаний намагниченности, изложенной в гл. 9.
Объяснение этих «аномальных» явлений дали Андерсон и Сул [229]
на основе представления о нестабильности некоторых групп спиновых
волн, наступающей под воздействием однородной прецессии
намагниченности. Спиновые волны с очень малыми—равновесными (или
«тепловыми») амплитудами всегда существуют (см. § 7.3) в магнито-
упорядоченных веществах. Вследствие нелинейности спиновой системы
они оказываются связанными с однородной прецессией и при
определенных условиях могут получать от нее энергию. Когда амплитуда
однородной прецессии достигает порогового значения, эта энергия
компенсирует потери спиновых волн и возникает их нестабильность—
экспоненциальный рост их амплитуд. Этот рост, как всегда в реальных
системах, ограничивается другими вступающими в игру нелинейными
процессами. Теория такой нестабильности (параметрического
возбуждения спиновых волн) была создана Сулом [428, 429]. Поскольку
переменная намагниченность, как и возбуждающее ее переменное поле,
перпендикулярны постоянной намагниченности, это явление получило
название параметрического возбуждения при поперечной накачке.
В дальнейшем Шлёманн, Грин и Милано [405] обнаружили
предсказанное несколько ранее Шлёманном пороговое поглощение
электромагнитной энергии ферритом, находящимся в переменном
магнитном поле, параллельном постоянному. Это явление также
обусловлено нестабильностью спиновых волн или параметрическим их
возбуждением, но под воздействием не переменной намагниченности,
а непосредственно переменного магнитного поля ". Оно получило название
параметрического возбуждения при продольной (или параллельной) накачке.
Параметрическое возбуждение спиновых волн имеет место и в ск-ч
тиферромагнетиках и обладает в этом случае рядом интересных
особенностей (см., например, [168, 176, 362]). Однако мы ограничимся
рассмотрением теории параметрического возбуждения в
ферромагнетиках. Она дает, как мы убедимся, объяснение всех основных
явлений, наблюдаемых при параметрическом возбуждении спиновых
волн и в ферримагнетиках—ферритах, поскольку в используемых
обычно диапазонах частот и полей эти явления происходят при
участии только нижних, «ферромагнитных» (см. § 3.3), ветвей
колебаний и волн в ферримагнетиках.
" Еще раньше Каганов и Цукерник [101 ] показали, что в продольном
переменном поле может происходить поглощение электромагнитной энергии
феррома гнетиком.
274
Уравнения для амплитуд спиновых волн. Приступая к изучению
теории параметрического возбуждения спиновых волн в
ферромагнетике, обратимся к уравнению движения намагниченности (2.10).
Опустим в нем диссипативный член; затухание будет учтено позднее.
Эффективное поле, входящее в это уравнение,
Hef=H0+h,+hM+Hex, (10.1)
где Н0 и h^—заданные постоянное (внутреннее) и переменное
(внешнее) поля; hM— эффективное поле диполь-дипольного
взаимодействия («размагничивающее» поле), кроме его постоянной
составляющей, которая вошла i» Н0; Н,.., — эффективное поле обменного
взаимодействия.
Решение уравнения движения будем искать в виде
M = z0M0 + m.(r, 0 (10.2)
и предположим, что переменная составляющая m^(r, t)«M0.
Разложим ее в ряд Фурье
nUr,0=Imk(/K"", (10.3)
к
где суммирование ведется по всем разрешенным значениям к.
Заметим, что nu(r, t) — вещественная величина, а коэффициенты
mk(t) комплексны, поэтому mk(?) = m*k(/). Член ряда (10.3) с к = 0 —
это однородное колебание намагниченности, а все остальные
члены — однородные плоские волны с волновыми векторами к. Эти
волны, не удовлетворяющие граничным условиям на поверхностях
образцов, не являются собственными функциями задачи. Лишь
при k>kmi„, где kmin значительно превышает обратные размеры
образца, влияние граничных условий становится несущественным,
и однородные плоские волны могут рассматриваться как
собственные функции. Основное допущение теорий Сула [429] и Шлё-
манна [405] заключается в использовании, тем не менее, разложений
(10.3)1). Что же касается однородного колебания, т.е. члена ряда
с к = 0, то влиянием граничных условий для него, конечно,
пренебречь нельзя. Для случая образца — малого эллипсоида оно
может^быть учтено при помощи однородного размагничивающего
поля Nm (см. § 1.5), которое войдет в hM. Для плоских волн
(к^О) члены эффективного поля диполь-дипольного взаимодействия
будут иметь вид (7.11).
Подставляя (10.3) и (10.1) с учетом всех высказанных соображений
в уравнение (2.10), находя его проекции на оси х и у и приравнивая
коэффициенты при одинаковых гармониках в левых и правых частях,
мы получим для каждого к пару дифференциальных уравнений.
В них, однако, кроме ткх и wkv, войдет и составляющая mkz. Для
'> При этом «остаются за бортом» рассмотренные в гл. 6 магнитостатичес-
кие волны и неоднородные колебания; их параметрическое возбуждение будет
исследоваться в § 10.4.
18*
275
ее исключения, поскольку мы предположили, что m^(r, t)«Mc,
можно воспользоваться соотношением (9.13). Из него следует
mkz=—— Y,[m(k-kl)xmklX+m(k-kl)ymkiy]. (10.4)
Затем, следуя Сулу [429], от ткх и тку перейдем к новым переменным
ak = (mkx+imky)/M0, atk=(m*kx-imtky)/M0 = (mkx-imky)/M0.
(10.5)
В соответствии с рассмотренными в § 7.3 соотношениями между
намагниченностями спиновых волн и числами магнонов эти числа
(в единице объема) связаны с переменными ак следующим образом:
2уЬ\ак\\
Выражение (10.4) в новых переменных принимает простой вид
ткх=--М^а1!,а\к,-к)- (Ю.7)
Рассмотрим случай эллипсоида вращения (Nx = Ny = N±). Тогда
для переменных (10.5), если ограничиться членами до третьего
порядка малости, получатся следующие дифференциальные уравнения
[429]: при к = 0, т. е. для амплитуды однородного колебания —
уравнение
-i'-3T = t0o«o-Y(A~«+/A~,)—^ £ а-к(акк\ + а'-кк±)-^+
at i кф0 к
8п
к *■ k*0 k, \K I К J
4 k*0 k, K
где k±=kx+iky, a &0 = ти + уМ±М0—собственная частота однородного
колебания; при кФО, а строго говоря, при k>kmin—уравнение
-i-£ = {Ak+yh^z)ak + Bka'-k- '
fOukj.ktx, , юм v //.,•/ \ki' ,
-^r-rrLa-^ak-ki-— I ak-ki(aklk\1_ + a-kik1±)—+
1 K k, "^ k,*0 Kl
ы k, k,
^II*10*1eI1+*,-lkU(*2-2kk1)+c»M^rF-
k, ka l_
f^l-T I 5>4<W*,-*^ (10-9)
4 J ч k.^O k2 *1
towlfei
2 A:
276
и второе, присоединенное уравнение—комплексно-сопряженное с
полученным из (10.9) при замене к-»(—к). Величины Ак и Вк в (10.9)
определяются выражениями (7.10) и (7.122).
В линейном приближении уравнения (10.9) и присоединенное
описывают связанные колебания двух гармонических «осцилляторов»
ак и а"-к. Для перехода к нормальным их колебаниям следует
использовать классический аналог упоминавшегося в § 7.4 третьего
преобразования Холстейна — Примакова. Это означает, что от
переменных ак и а*-к нужно перейти к новым переменным ск и с*-*,
для которых линейные части уравнений (без члена yh^zak) будут
иметь диагональный вид:
dck dc'-k . ,.nim
— = ко*сь —= -ткс'-к. (10.10)
Новые переменные связаны со старыми соотношениями (см.,
например, [15, 145])
ak = ukck+vkc'-k, a'-k = v'kck + ukc'-k, (Ю.11)
ик=—у/Ак1<йк+и vk= -у/Ак/(йк-1е21^,
V2 V2 (10.12)
(pk = arctg(kylkx).
Здесь со*—частота (7.9) спиновых волн с волновым вектором к.
Уравнение (10.8) в линейной приближении сводится к
-i^ = cooeo+Y(A~« + tt-,)- (10.13)
Его решение соответствует вынужденным однородным колебаниям
намагниченности под действием заданного переменного поля. Решения
линейных уравнений (10.10), которые можно представить в виде
ск = с°ке1^, с--к = с0-ке-^', (10.14)
соответствуют спиновым волнам с амплитудами ск и сЧ-к и волновыми
векторами к и —к. Таким образом, в линейном приближении
однородная прецессия и спиновые волны представляют собой, как
и следовало ожидать, независимые типы колебаний; однородная
прецессия возбуждается поперечным переменным полем, а спиновые
волны существуют «сами по себе» с весьма малыми равновесными
(тепловыми) амплитудами. Нелинейные члены уравнений (10.8) и (10.9)
описывают связь спиновых волн друг с другом и с однородной
прецессией намагниченности, а также (член с И^г в (10.9)) с
продольным переменным полем.
Заметим, что различные члены классического уравнения (10.9)
для амплитуд спиновых волн аналогичны соответствующим членам
квантово-механических уравнений движения для операторов рождения
и уничтожения спиновых волн, которые в свою очередь получаются
(см., например, [15]) из записанного в этих операторах гамильтониана
(§ 7.4). Поскольку параметрическое возбуждение спиновых волн можно
277
и целесообразно описывать на классическом языке, мы не будем
останавливаться подробно на указанной аналогии. Отметим лишь,
что линейные члены (10.9) аналогичны линейным членам операторного
уравнения движения, которые соответствуют квадратичным членам
гамильтониана (7.120). Третье и четвертое слагаемые в правой части
(10.9), содержащие члены второго порядка по ак и с_ь соответствуют
членам третьего порядка в гамильтониане; на квантовом языке эти
члены описывают процессы слияния двух магнонов в один или
расщепления одного магнона на два. Члены третьего порядка в (10.9)
соответствуют в гамильтониане членам четвертого порядка по
операторам рождения и уничтожения магнонов.
§ 10.2. Пороги параметрического возбуждения
при поперечной накачке
Рассмотрим случай, когда А^2 = 0, т. е. переменное магнитное
поле перпендикулярно постоянной намагниченности. Это поле (мы
предполагаем его однородным), как видно из (10.8) и (10.9),
непосредственно возбуждает лишь однородную переменную
намагниченность с амплитудой а0, которая является в данном случае
накачкой.
Нестабильности первого и второго порядков^ Мы интересуемся
пока только порогами параметрического возбуждения спиновых волн
или спиновых нестабильностей. Поэтому в уравнении (10.9) амплитуды
всех спиновых волн можем считать малыми по сравнению с а0,
а для с0 использовать линейное уравнение (10.13). Тогда, считая
пока, что поле h_ с частотой сор имеет правую круговую поляризацию,
т.е. что h„x + ih^.y = h+ exp(icopr), и учитывая потери путем замены
cD0-*cuo + 'Wr0, получим из (10.13)
с0= — e'Vscge'V. (10.15)
В уравнениях (10.9) и присоединенном сохраним члены до второго
порядка включительно по с0. Переходя затем к переменным
ск и с'-к с помощью преобразований (10.11), получим (без учета
затухания спиновых волн) уравнение
^ = /(cot+rt|c0|2)rt + /(p,c0 + ^^)c*-t (10.16)
и присоединенное, отличающееся от (10.16) заменой к-*{ — к) и
комплексным сопряжением. Здесь
р* = р_к=-^(со* + ы„ + г,А'2)ып2е*е'<\ (10.17)
4ы*
^k=^_k = ^-((ok + Ah)(r]k2 + mMcOS2Qk~(oM^], (10.18)
Tk=^\2Ak(cos26k + ^^-\sm26ky^Sm'6k\. (10.19)
278
Сравнивая (10.16) с (10.10), мы видим, что связь однородных
колебаний со спиновыми волнами привела, во-первых, к нелинейному
сдвигу собственной частоты спиновых волн:
&* = со* + Гк|с0|2. (10.20)
Во-вторых, спиновые волны с равными по величине и противоположно
направленными волновыми векторами оказались связанными друг
с другом, причем в коэффициент связи вошли зависящие от времени
величины а0 и Со-
Как известно из теории колебаний (см., например, [158]), наличие
зависящей от времени связи между двумя осцилляторами может
привести к передаче им энергии от источника, вызывающего
модуляцию связи. Эта передача происходит наиболее эффективно, если
выполняется условие"
псор = ш1 + сй2, (10.21)
где cut и со2—собственные частоты осцилляторов, а сор—частота
изменения связи, или частота накачки. При достаточно большой—
превышающей некоторую пороговую величину—амплитуде
модуляции параметра связи передаваемая осцилляторам энергия
компенсирует их потери энергии, и колебания этих осцилляторов начинают
экспоненциально нарастать во времени — возникает их
параметрическая нестабильность. При этом сумма фаз нарастающих колебаний
оказывается жестко связанной с фазой накачки. Величина и в (10.21)—
это порядок процесса параметрического возбуждения или порядок
нестабильности. В нашем случае связанными «осцилляторами»
являются спиновые волны с волновыми векторами к и (—к), а
источником связи между ними—однородная прецессия намагниченности.
При этом имеет место вырождение (со1=со2), поскольку &* = &_*.
Из уравнения (10.16) и присоединенного видно, что к нарастанию
величин ск и с*-к, т. е. к нестабильности могут привести лишь те
члены уравнений, которые изменяются во времени с частотой (Ьк;
остальные члены при исследовании порогов нестабильности можно
отбросить. Как следует из (10.19), частота 5>к мало отличается от
со*, и мы этим различием пренебрежем. Тогда, как видно из (10.15)
и (10.14), член ipka0c*-k в (10.16) будет изменяться с частотой
(сор—со*), и его следует принимать во внимание при сор~2соь членом
/^tGoC*_t в этом случае можно пренебречь. И наоборот, этот член,
изменяющийся с частотой (2сор—со*), следует учитывать (а член
ipka0c*-k отбросить) при сор=сол.
Итак, при со* = сор/2 уравнение (10.16) и присоединенное сведутся
к системе
~=mkck+ipka0c'-k, -^■=-mkc*-k-ip'ka'0ck, (10.22)
at at
" На корпускулярном языке условие (10.21) означает сохранение энергии
при элементарном процессе превращения и квазичастиц накачки в пару
квазичастиц, соответствующих колебаниям осцилляторов.
а при cD^cDp—к системе
-^=iv>kck + i%kalc\k, -^=-imkc'-k-i^kal'ck. (10.23)
at at
В соответствии с (10.21) первая система описывает нестабильность
(параметрическое возбуждение) спиновых волн первого порядка, а
вторая—второго.
Решение системы (10.22) можно искать в виде
ск = с°ке^\ с'-к = сЧ?ке-%\ (10.24)
где амплитуды ск и с°*к — медленно меняющиеся функции времени:
с*° = с?о<?1', с*к = с%0еи. (Ю.25)
ск0 и с^к0—постоянные, а X — вещественная величина. Условием
нарастания амплитуд (т. е. нестабильности спиновых волн) будет Х>0.
Примем теперь во внимание затухание спиновых волн путем
замены в уравнениях (10.22) ы*-юй* + /а>гк и подставим в эти уравнения
выражения (10.24) с учетом (10.25). Мы получим тогда систему двух
однородных линейных алгебраических уравнений для ск0 и с°**о- Из
равенства нулю ее определителя следует
(Х + сйг*)2+ со*-^ )=a°02pkpl (10.26)
Пороговая амплитуда однородной прецессии определится из условия
Х = 0:
eS«*i=V«»?* + K/2-cD»)2/lP*l- (10.27)
Выражение (10.27) дает пороговую величину с 8 Для нестабильности
спиновых волн с данными ык и к. Для нахождения реальной
величины порога необходимо минимизировать выражение (10.27). Из
этого выражения видно, что порог будет наименьшим, т. е.
нестабильность возникает сначала, как и ожидалось, для спиновых волн
с сок = сйр/2. Таким образом, с учетом (10.17)
eg^-min Ы=.тш j , уАЯ'Ю- . 1. (10.28)
Минимизация должна проводиться по всем допустимым значениям
к или 0* (связанным условием ык(к, 0t) = cop/2); азимутальный угол
спиновых волн фк остается пока (для образца — эллипсоида вращения
из изотропного ферромагнетика и круговой поляризации переменного
поля) неопределенным. Если можно пренебречь зависимостью АНк
от к и Qk, то как видно из (10.28), амплитуда накачки Со№г1
оказывается минимальной для спиновых волн с углами Qk, несколько
меньшими (из-за члена г\кг), чем 45°. Необходимо, конечно, чтобы
такие волны имелись при данных сор и юн (рис. 10.3).
Для нестабильности второго порядка, поступая аналогичным
образом, но исходя из системы (10.23) и полагая вместо (10.24)
c* = r?e"V, c*-4 = c°\e-'V, (10.29)
280
(V, ("о)2 С'>з (но)<
Рис. 10.3. Дисперсионные характеристика спиновых волн при различных
значениях постоянного поля (схематически): (H0)i <(Нп)1<{Н0)г<{Н0)л. Штриховые
линии—0*=45 . Точки спиновые волны, которые становятся нестабильными
в процессе параметрического возбуждения первого порядка при поперечной
накачке
получим при cot = cop
а% .ы2 =min K/yAM2IU)}. (Ю.ЗО)
где i,k определяется выражением (10.18). Без учета зависимости АНк
от к и 0* величина a°lhr2 оказывается в данном случае минимальной
для волн с 0* = О.
Параметры связи |р*| и E,t, как видно из (10.17) и (10.18),
порядка сом, а для хороших монокристаллов ферритов, которые
обычно используются при экспериментальном исследовании
параметрического возбуждения спиновых волн, уАНк<$аам. Поэтому
пороговые значения намагниченности для нестабильности первого порядка
много меньше, чем для нестабильности второго порядка.
Для реализации порогов (10.28) и (10.30) необходимо, чтобы
частоты Шр/2 в первом случае или сор во втором лежали (см.,
например, рис. 10.3) выше нижней границы сон спектра спиновых
волн (7.9). Для образца — эллипсоида отсюда следует, что для
нестабильности первого порядка внешнее поле
H.0«apl{2y) + NZM0, (10.31)
а для нестабильности второго порядка
He0<uply + NZM0. (10.32)
Пороговые поля нестабильности первого порядка. Перейдем теперь
от пороговых амплитуд намагниченности к пороговым величинам
внешнего переменного поля (с правой круговой поляризацией).
Подставляя в (10.28) величину «8 из (10.15) и учитывая (10.17),
получим
, . Г 2(o,,fc),t4/Wo+K-q>o)2 | ,imi\
hihri=mm{ „„. г^мГ (10.33)
281
О),
о,
"к
v«-
«<)„
р
2
/
/ ' 1
^ ' / .
"^ / / 1
"^ S / 1
--'У''
^s / '
_-"^ •
s
^'
-шт **
а * 5 к В *
Рис. 10.4. Взаимное расположение спгктра спиновых волн, частоты однородных
колебаний соп и частоты поперечной накачки сор для сферы (схематически):
а—условие (10.35) хорошо выполняется, 6—это условие едва только
выполнено, в—условие (10.35) не выполняется. Сплошные линии — при резонансе
(He0 = HTta) на частоте шГ. штриховые—при Нс0<Нга
Из этого выражения видно, что пороговое поле минимально,
когда частота накачки совпадает с собственной частотой со0
однородных колебаний намагниченности образца, т. е. когда
(10.34)
Легко убедиться с помощью выражений (1.97) и (7.9), что это
равенство в случае эллипсоида вращения может быть выполнено
только при условии
ыр<ыиЛ L!(2n) = (£>np. (10.35)
Для сферы ыпр = 2ым/3 и, в частности, для сферы ЖИГ при
комнатной температуре /пр = сопр/(2я) = 3,27 ГГц. Заметим, что в случае
сферы (сяр совпадает с частотой, при которой ы0 переходит через
верхнюю границу безобменного спектра спиновых волн (§ 6.1).
Если условие (10.35) будет едва только выполнено (рис. 10.4),
то угол 6* будет мал и, как видно из (10.33), пороговое поле (как
и пороговая величина я°) будет велико. При понижении частоты
угол вк будет возрастать (рис. 10.4) и пороговое поле будет
уменьшаться, достигая при 6t~45° величин порядка"
ИЛг1г„~АНкАН0 (пМп). (10.36)
Нестабильными при этом будут спиновые волны с малыми к,
в рамках рассматриваемой теории Сула с А: = 0. В монокристаллах
ЖИГ, для которых при частотах, удовлетворяющих условию (10.35)
и комнатной температуре, можно принять ДЯо = 0,3 Э и ДЯЬ = 0,15 Э,
величина hlhrlrcs составляет ~10~4Э. При дальнейшем понижении
частоты wp (по-прежнему равной а>0) будут возбуждаться спиновые
волны с 0Ь близким к 45°, но со все большими к. Порог для них
в действительности будет несколько возрастать из-за увеличения АНк.
При высоких частотах, не удовлетворяющих неравенству (10.35)
(рис. 10.4. в), когда условие cDt = a>p/2 не может быть выполнено при
" В этой формуле, как и везде в данной книге, в отличие от работ
Сула [428, 429], а также от [69], АН0, как и АНк,—полная ширина
резонансной кривой.
282
1
0,8
0,6
0,4
0,2
0,2 0,4 0,6 0,8 1
Рис. 10.5. Зависимость порогового поля нерезонансной нее1аби.1ьности первого
порядка от постоянного поля для сферы [429]
резонансе (юр = ы0)^ минимизация выражения (10.33), проведенная
Сулом, показала, что наименьшее пороговое поле имеет место
в постоянном поле H0 = H0rni„, меньшем чем резонансное (рис. 10.5).
Нестабильными при этом становятся спиновые волны с/с=0и 6к~45°
Величины порогового переменного поля и значения Яе0т!п зависят
от формы образца и отношения ыр/ым- Для сфер значения He0min,
как видно из рис. 10.5, лежат в пределах (0.5-^0,9) а>р/у.
Для оценки величины /7,hri примем ыи~шр^1,5ын-
и ыр—соо = 0,25юр, что приблизительно соответствует сфере ЖИГ при
комнатной температуре и частоте ~5 ГГц. Тогда по формуле (10.33)
или из рис. 10.5 /7,Ьг1=0,2Д#к. Если принять по-прежнему АНк = 0,\5 Э,
то /7thr 1 = 0,03 Э. Таким образом, в этом нере юнансном случае
пороговые значения поля (но не намагниченности!) оказываются
значительно большими, чем при с)р=ы0- Однако такие значения
тоже легко достигаю 1ся экспериментально, причем не только для
монокристаллов, но и для поликристаллических ферритов с АНк,
измеряемымыми десятками эрстед.
Слева от минимума Лц,Г1 на рис. 10.5 нестабильными становятся
спиновые волны с углами Qk. по-прежнему близкими к 45 (но
с большими к), определяемыми формулой (7.17), а справа от
минимумов — волны с к^0 и углами, меньшими чем 45 . Следует
подчеркнуть, что все это получено в результате минимизации
выражения (10.33) при постоянном АНк. Учет конкретных зависимостей
АНк(к, Qk) может изменить результаты, особенно в области полей
между #0с(45 ) (где лежат минимумы на рис. 10.5) и ЯОс(90').
В этой области полей частоты ыр/2 вырождены с широкой областью
спектра спиновых волн, включающей и малые к, для которых
величины АНк могут быть (см. гл. 11) существенно меньшими, чем
283
для больших к, в результате чего будут параметрически возбуждаться
спиновые волны с малыми к и 6*>45 ".
Нестабильность спиновых волн первого порядка при сор^сх>0 Сул
[429] назвал дополнительным (subsidiary) поглощением, а при сх>р = а>о —
совпадением дополнительного поглощения с основным (main)
резонансом. Широкий максимум поглощения, который наблюдали Бломберген
и Уанг (рис. 10.2) при постоянных полях, меньших чем резонансное,
представлял собой именно такое дополнительное поглощение. Оно
является основным фактором, ограничивающим динамический
диапазон ферритовых СВЧ устройств (гл. 5), которые работают при
постоянных магнитных полях, меньших резонансного.
Насыщение ферромагнитного резонанса. Если условие (10.35) не
выполняется, то в игру вступает параметрический процесс второго
порядка. Его пороговая намагниченность определяется выражением
(10.30), а пороговое поле с учетом (10.15)
Alhr 2 = min { v/w^O,2,, + (сор-ш0) 2]/(y2U}• (10.37)
Минимальная величина поля (10.37) достигается при резонансе
(cDp = {£>o) и для той пары спиновых волн, для которой параметр
связи i,k максимален. Как видно из (10.18), это имеет место для
пары волн с 6* = 0 и Qk = n. Для сферы
Л,иг2=уАЯ0ч/ДЯЛ4яМ0). (10.38)
Оценка по этой формуле для ЖИГ в трехсантиметровом диапазоне
при комнатной температуре (АНо^АНк^0,3 Э) дает /7lhr2 = 2-10_3Э.
Эта величина на порядок больше, чем пороговое поле для
нестабильности первого порядка при резонансе, и на порядок меньше, чем
для нестабильности первого порядка вне резонанса (дополнительного
поглощения). Заметим, что именно этим процессом было вызвано
уменьшение резонансной восприимчивости («насыщение основного
резонанса») в опытах Бломбергена и Уанга (рис. 10.2), в которых
условие (10.35) не выполнялось.
Влияние поляризации поля накачки. Все приведенные выше
выражения для пороговых амплитуд поля накачки были получены для
правой круговой поляризации этого поля и эллипсоида вращения.
Такое поле возбуждает правую циркулярную составляющую
переменной намагниченности, которая и приводит к параметрическому
возбуждению спиновых волн. При эллиптической, в частности,
линейной поляризации поля накачки или при ЫХФИУ намагниченность
будет иметь циркулярные составляющие как с правым, так и с левым
вращением. Однако если частота поля равна или близка к частоте
ферромагнитного резонанса, то, как отмечалось в § 1.5, составляющая
намагниченности с правым вращением будет преобладать. В этом
случае для процессов как первого, так и второго порядка формулы
для пороговых амплитуд поля с линейной поляризацией будут
" Экспериментальная зависимость Л,Ьг1(Яс0) будет приведена на рис 10.9
284
отличаться от (10.36) и (10.38) лишь множителем 2. Например, для
процессов второго порядка
Л1Ьг2.т = АЯ0ч/ДЯк/(4пМо). (10.39)
Для нерезонансного процесса первого порядка (дополнительного
поглощения) левой циркулярной составляющей намагниченности
априори пренебрегать нельзя. Рассмотрим случай линейной поляризации
поля накачки, когда
h ~х+ih ~y = he1'"- cos copt
((ph = aTctg(h~y/h~x)—угол между направлением поля и осью х). В этом
случае решением уравнения (10.13) будет
а0 = а0+е'ш''+аое-''ш'', (10.40)
где
«0*=^-^ (10.41)
(т+=Моа$ и т~=МоаЪ — амплитуды циркулярных составляющих
намагниченности соответственно с правым и левым вращением).
Подставляя (10.40) в (10.8) и сохраняя члены, линейные по
а о и ао, получим (полагая й* = 10*) вместо (10.22) уравнения
^ =mkck + i(pkaS +rtaE*)eia"c*k (10.42)
at
и присоединенное. Здесь
1 шм
2 со.
inn = min<-
(7
(aH + r\k2-(^\s\n2Qke-3i^. (10.43)
Пороговое условие находится так же, как в случае круговой
поляризации. Пороговая амплитуда линейно поляризованного поля
оказывается наименьшей для волн с ф* = ф* и при со* = со,,/2 составляет
2co,,cortK-cog) |
|ушм sin 2 Gt [шР/2+шо (шя+лА2)] J
Сравнивая (10.44) с выражением (10.33), мы видим, что отношение
hailhJhttal мало отличается от 2, т. е. влияние составляющей
намагниченности с левой круговой поляризацией даже для нерезонансного
процесса невелико. Однако случай линейно поляризованного поля накачки
интересен тем, что в нем возбуждаются спиновые волны с определенным
значением азимутального угла. Заметим, что при круговой поляризации
поля накачки определенные значения углов срк возбуждаемых спиновых
волн возникнут лишь при учете анизотропии ферромагнетика (в § 10.3
это будет продемонстрировано на примере продольной накачки).
§ 10.3. Продольная и наклонная накачка
Перейдем к исследованию параметрического возбуждения
спиновых волн под воздействием переменного магнитного поля,
имеющего продольную (параллельную постоянной намагниченности)
составляющую.
285
Продольная накачка. Предположим сначала, что переменное
магнитное поле имеет только продольную составляющую h^z. Тогда
переменная намагниченность в линейном приближении отсутствует,
а уравнения (10.9) и присоединенное, если опустить в них члены,
которые не могут привести к нестабильности, и перейти согласно
(10.11) к переменным ск и с*ь примут следующий вид [406]:
dck . i Вк . dc*-k . . . Bl ...
—- = i(okck + iyh„z — c'-k, —7-=-i(okc*-k-iyh~z — ck, (10.45)
at (ok at (ok
где Вк определяется выражением (7.122). Из (10.45) видно, что
продольная составляющая переменного магнитного поля
непосредственно приводит к связи «осцилляторов» ск и с*-к, если Вк¥=0.
Величина Вк, пропорциональная coMsin26t, возникает вследствие
магнитного (диполь-дипольного) взаимодействия и связана, как видно
из выражения (7.22), с эллиптичностью спиновой волны.
Необходимость эллиптичности (некруговой поляризации)
намагниченности спиновых волн для их параметрического возбуждения
при продольной накачке легко понять, если вспомнить (§ 9.2), что
при такой поляризации возникает продольная составляющая
намагниченности с частотой 2со*. Она взаимодействует с продольным
полем накачки, имеющим ту же частоту, в результате чего и
происходит передача энергии спиновым волнам.
Запишем продольное поле в виде
h^^-h^e'^ + e-™'') (10.46)
и подставим его и выражения для ск и c*_t (10.14) в уравнения
(10.45). Предположим, что частота переменного поля top близка
к 2сок, и сохраним в уравнениях (10.45), как и при решении уравнений
(10.22) и (10.23). лишь «резонансные» члены — изменяющиеся с
частотой, близкой к ак. Тогда первое уравнение (10.45) (второе мы
не выписываем) примет вид
^ = ткск + 1Ук112е^си, (10.47)
at
где параметр связи
VkJ-^ = l^Lsin2Qke2i4 (1048)
2 coi 4 со»
Сравнивая (10.47) с первым уравнением (10.22), которое тоже
справедливо при top~2cot, мы видим, что они различаются только
заменой ркао на Vkhz. Поэтому, не решая уравнений (10.47) и
присоединенного, мы можем провести указанную замену прямо в пороговых
формулах (10.27) или (10.28). Итак, для спиновых волн с со4 = сор/2
(для которых порог будет наименьшим)
\\Vk\\ jcoMsmJeJ
286
Н„<Н,
Рис. 10.6. Взаимное расположение спектра спиновых волн и частоты
продольной накачки. Точки—спиновые волны, которые становятся нестабильными
Если считать параметр диссипации спиновых волн независимым
от к и 6*, то, как видно из (10.49), порог будет минимален для
спиновых волн с углами Qk, наиболее близкими к л/2, т. е. (при
заданной их частоте со* = сор/2)—с наименьшими к. В области малых
магнитных полей, когда top/2 лежит выше верхней границы
безобменного спектра спиновых волн (рис. 10.6, а), будут возбуждаться
волны с 6ц = л/2. Их волновое число, как следует, например, из
(7.17), определяется соотношением
Dk2 = Hc-H0, (10.50)
где величина #с = #0с(л/2) выражается согласно (7.18) и представляет
собой внутреннее постоянное поле, при котором спиновые волны
с 6к = л/2 и частотой <ак имеют к=0. В нашем случае tok = top/2, и
Яс= 1(^\2 + (2пМ0)2-2пМс
(10.51)
При уменьшении внутреннего постоянного поля Н0 волновые
числа параметрически возбуждаемых спиновых волн" возрастают
и при #о = 0 достигают наибольшей возможной при данной частоте
накачки величины. Для ЖИГ при комнатной температуре эта величина
составляет ~5-105 при частоте накачки сор = 9 ГГц и ~106 при
шр=36 ГГц. Что же касается азимутальных углов параметрических
спиновых волн, то в рассматриваемом пока случае изотропного
ферромагнетика все их значения равновероятны, т. е. возбуждается
весь «веер» волн с волновыми векторами к и —к, лежашими
в плоскости 6* = я/2.
Если же поле Н0 будет больше Нс (рис. 10.6, в), то минимальный
порог будет достигаться, как следует из условия cot = top/2 с учетом
(10.49), для спиновых волн с к = 0 и
К/2)г-ю&
сомшн
sin26k=-
(10.52)
При увеличении Н0 угол дк будет уменьшаться, а пороговое
поле—расти, пока при Я0 = сор/(2у) оно не обратится в бесконечность.
" В дальнейшем для краткости мы будем называть их параметрическими.
287
При больших полях процесс параметрического возбуждения спиновых
волн первого порядка при продольной накачке невозможен.
Измерение порогов. Экспериментальное исследование
параметрического возбуждения спиновых волн, особенно при продольной накачке,
широко используется для определения параметра диссипации спиновых
волн. При этом образцы (для ферритов обычно—сферы или пленки,
а для металлов—пленки или проволоки) помещаются в полые
резонаторы. Непосредственно измеряется зависимость порогового
значения падающей на резонатор мощности Р от постоянного
магнитного поля. Для перехода к пороговым значениям амплитуды
переменного поля в случае отражательного резонатора может быть
использовано соотношение
2_8тга J*
<oV0 \+q
h\=—-Q0-^P. (10.53)
Здесь hx—амплитуда переменного поля в той точке, где находится
образец, У о—объем резонатора, q = QcJQo, Co и QCB—соответственно
собственная добротность резонатора (с образцом) и добротность
связи, а а определяется формулой (5.47).
До порога образец (находящийся в продольном
переменном поле) практически не поглощает электромагнитной
энергии. За порогом поглощение быстро увеличивается,
собственная добротность резонатора уменьшается и вследствие этого
изменяется (увеличивается или уменьшается в зависимости от
первоначальной величины q) коэффициент отражения от
резонатора. Измерения проводятся обычно в импульсном режиме, и
порог индицируется по появлению характерного «скола» на
импульсе отраженной от резонатора (или прошедшей через него)
мощности (рис. 10.7). Он появляется тогда, когда нарастающие
во времени амплитуды нестабильных спиновых волн достигают
такой величины, что идущая на их возбуждение мощность снижает
заметным образом добротность резонатора. Такой «скол» возникает
сначала в конце импульса и сдвигается к его началу по мере
увеличения hz. Поэтому измеренная величина Azthr будет тем
меньше, чем больше длительность импульса т. Для нахождения
истинного порога следует величину т выбрать достаточно большой
или провести измерения при разных т и экстраполировать
результаты на т-*оо[405].
Измеренная таким образом зависимость
Azthr от внешнего постоянного поля Нс0
приведена на рис. 10.8. Такие кривые получили
название «бабочек». Минимумы их находятся
t_ обычно при поле Htc=Hc+NzM0, при котором
(в рамках рассмотренной теории) возбуждаются
Рис. 10.7. Форма им- спиновые волны с к = 0 и 6к = я/2. На левых
пульса отраженной от ветвях «бабочек» возбуждаются волны с 0* = я/2
вь^НаТо°6рашцомРРИил^ и *>0- Увеличение Ко* при уменьшении Яе0)
прошедшей через него т- е- ПРИ увеличении к на этих ветвях (см. рис.
мощности при hz>hxth, 10.8), объясняется зависимостью АНк от к. Рост
288
же Azlhr с увеличением Нс0 на
правых ветвях в рамках
рассмотренной теории связан с влиянием
множителя (sin20k)_I в формуле
(10.49).
Зная Azlhr, можно с помощью
(10.49) найти параметры
диссипации спиновых волн а>гк или
АНк, а значения волнового числа
к (на левых ветвях бабочек)
определяются с помощью (10.50).
Полученные таким образом
зависимости АНк(к) будут подробно
обсуждаться в §11.2.
Кристаллографическая
анизотропия. До сих пор мы
рассматривали параметрическое возбуждение
спиновых волн в изотропном
ферромагнетике. В экспериментальных
же работах по исследованию этого
явления и в устройствах,
использующих его (см. § 10.5),
применяются чаще всего
монокристаллические образцы. Учет влияния
кристаллографической анизотропии на
параметрическое возбуждение
спиновых волн мы проведем на
примере продольной накачки; в этом
случае определяющим фактором
является эллиптичность намагни-
еО'
Рис. 10.8. Экспериментальная
зависимость порогового поля от внешнего
постоянного поля [405] и
рассчитанные значения к и 64 параметрических
спиновых волн при продольной
накачке. Сфера ЖИГ при комнатной
температуре, частота накачки 9.4 ГГц
ченности спиновых волн, на которую существенно влияет анизотропия.
Для учета кристаллографической анизотропии ее эффективное
поле должно быть включено в уравнение движения намагниченности,
из которого затем рассмотренным выше путем получатся уравнения
для амплитуд ск и с*-к. В частном случае кубического кристалла,
намагниченного в плоскости {ПО}, это приведет к замене в уравнении
(10.47) Vk на Kt + ywa/(4o)J, где
ы^уЛ/о^п-^Ь),
(10.54)
а Ni! и N$2 — эффективные размагничивающие факторы анизотропии
кубического кристалла (2.51) при ф0 = 45°. Пороговое поле продольной
накачки в этом случае
AZIhr=min
гАЯ,
}
(10.55)
1^1 шм sin 2 Gfc e2,,,ik + С0а |
Минимальный порог имеет место при постоянной намагниченности,
направленной вдоль оси <П0), когда вклад анизотропии в
эллиптичность спиновых волн максимален.
■9 А. Г. Гуревич, Г. А. Мелков 289
Заметим, что теперь порог зависит от обоих углов вектора к.
При ^!<0 он минимален при 8* = я/2 и ф* = л/2, Зя/2, т.е.
возбуждаются спиновые волны, распространяющиеся по оси <1Ю).
При ^!>0 возбуждаются спиновые волны с 8* = я/2 и ф* = 0, я,
распространяющиеся по оси <100>. В обоих случаях [171]
ftz,h,<iio>= "' .АНк. (10.56)
(йм + Зу\НЛ1\
Таким образом, анизотропия ферромагнетика приводит (как и
линейная поляризация поля поперечной накачки) к появлению
преимущественных направлений распространения параметрических спиновых волн
(см. также [236]).
Влияние неоднородностей. Мы все время считали ферромагнетик
идеальным кристаллом. Однако в реальных образцах всегда имеются
неоднородности: поры, включения других фаз, дефекты поверхности,
в поликристаллах—границы зерен. Они приводят к двухмагнонным
процессам — рассеянию магнитных колебаний и волн на неоднород-
ностях с образованием колебаний или волн с той же частотой, но
с другими к. Особенности таких процессов и их вклады в линейное
(происходящее при сколь угодно малых амплитудах) затухание
магнитных колебаний и волн будут рассмотрены в § 11.3. Здесь мы
остановимся кратко на влиянии этих процессов на порог
параметрического возбуждения при продольной накачке, которое исследовали
Захаров и Львов [89] (см. также [145]).
Для учета влияния двухмагнонных процессов при продольной
накачке следует добавить описывающие эти процессы члены в
уравнения (10.45). Тогда первое из этих уравнений примет вид
-^=tofcCfc + X) v«,c*.+2/A ~«^*с-». (10.57)
Суммирование здесь ведется по всем вырожденным (со* =сок) спиновым
волнам, а величины v^ —коэффициенты двухмагнонного рассеяния
зависят от характера неоднородностей и волновых векторов к и kt.
Аналогичные уравнения могут быть записаны для всех амплитуд ск .
Заметим, что к описанию влияния неоднородностей (как и к
решению ряда рассмотренных выше задач) возможны два подхода: связанных
мод и нормальных мод. В первом случае мы считаем, что внешнее
воздействие непосредственно возбуждает волну с волновым вектором
к, а связь между этой волной и вырожденными с ней волнами
приводит к возбуждению последних. Это вызывает увеличение затухания
первичных волн—их параметр диссипации (который был равен coj* без
учета двухмагнонных процессов) становится
au = a>8k + m:*. (10.58)
Для со** справедливо следующее выражение [405]:
c^ = nX|vMi|25(coti-cut), (10.59)
где 5(cot]— tok)—дельта-функция Дирака (1.84).
290
При втором подходе, нормальных мод, мы переходим (например,
в уравнениях (10.57)) от переменных ск, ск , скг и т. д. к новым,
нормальным переменным, в которых эти уравнения (в линейном
приближении, т.е. без членов с h^z) перестают быть связанными —
диагонализуются"). Новым переменным соответствуют нормальные
моды, которые не являются плоскими волнами, их частоты лежат
в некоторых полосах, расположенных вблизи частот, которые
определяются законом дисперсии в отсутствие неоднородностей. Частоты
релаксации новых, нормальных мод не равны (со^ + соиО, а
близки к со?*.
Нахождение пороговой амплитуды Azthr при наличии
неоднородностей, основанное на решении бесконечной системы уравнений
(10.57), представляет собой весьма сложную задачу. Мы приведем
лишь качественные соображения (используя при этом оба упомянутых
подхода) и некоторые результаты [89].
Прежде всего ясно, что порог не будет определяться такими
же выражениями, как в отсутствие неоднородностей, но с заменой
cort на (tojfc + curit), поскольку (на языке нормальных мод) накачка
связывает между собой некоторую пару таких мод, частоты релаксации
которых, как отмечалось, не равны (со^ + со^). Может даже показаться
(такие утверждения встречались в ранних работах), что
неоднородности вообще не будут влиять на величину порога, поскольку
частоты релаксации нормальных мод близки к а°к. Однако это не
так; в рамках подхода связанных мод двухмагнонные процессы
приводят к хаотизапии фаз возбуждаемых волн, они перестают
удовлетворять оптимальным соотношениям при параметрическом
возбуждении (см., например [145], а также § 10.5), вследствие чего
связь их с накачкой уменьшается и порог возрастает. Используя
же подход нормальных мод, можно ослабление связи с накачкой,
обусловленное неоднородностями, объяснить тем, что эти моды не
являются плоскими волнами, возникающая при их взаимодействии
составляющая М: с частотой 2tot = cop не является, как при
взаимодействии двух плоских волн с к и (—к), однородной, и взаимодействие
ее с однородным полем накачки уменьшается.
В случае, когда неоднородности хаотически распределены по
объему образца и их размеры малы по сравнению с k~l
параметрических спиновых волн, в [89] было получено: при со^^со?*
Az,hr=^U,U-^ln(o,42^)
(10.60)
а при со**:» со?*
2со„
А* = ^>Х. (Ю.61)
ушм
" Эта операция аналогична рассмотренному в § 10.1 переходу от
переменных ак и а'-к к нормальным (в отсутствие неоднородностей!) переменным
ск и с'-к, но гораздо сложнее, поскольку число связанных переменных теперь
бесконечно, а неоднородности носят хаотический характер.
19*
291
В другом интересном случае, когда рассеяние происходит только
на поверхности образца и размер его d^>\/k [145],
A2Ihr = ^ч/Ю2+М2. (10.62)
Величина и>% в этом случае пропорциональна отношению длины
пробега спиновых волн 1к (7.26) к размеру образца и может быть
записана с учетом (6.8) следующим образом:
cu'rk=£,{lkld)(u?k = £,vgT/d, (10.63)
где £—множитель порядка 1 (£=я при 4/f/«;l и £=я/2 при /*/</:» 1).
Из выражений (10.62), (10.63) видно, что увеличение порога
вследствие рассматриваемого эффекта тем больше, чем больше групповая
скорость спиновых волн. Этот эффект можно трактовать как результат
выноса энергии из пространства взаимодействия: спиновые волны
рассеиваются на границах образца, не успевая нарасти достаточным
образом под воздействием накачки. Аналогичные эффекты,
обусловленные влиянием неоднородностей и, в частности, рассеянием спиновых
волн на границах образца, имеют место и в случае поперечной накачки.
В поликристаллах роль размера d играет размер зерен, с его
уменьшением согласно (10.62), (10.63) Azlhr возрастает. Это широко
используется для повышения максимальной рабочей мощности ферритовых
устройств (см., например, [247]). В высококачественных
монокристаллических образцах при комнатной температуре обычно (о^<*:юйь
и поверхностные неоднородности практически не влияют на порог.
Это влияние проявляется лишь при низких температурах для образцов
малых размеров, когда длина пробега 1к становится сравнимой с ^[151].
Наклонная накачка. До сих пор мы исследовали параметрическое
возбуждение спиновых волн либо при поперечной (й- = 0), либо при
продольной (А = Аг) накачке. Однако переменное поле накачки может
иметь продольную и поперечные составляющие. В этом случае
пороговая его амплитуда будет определяться одновременным
воздействием на спиновые волны как переменной намагниченности,
вызванной поперечными составляющими поля, так и продольной
составляющей поля. Рассмотрим, например, случай произвольно
ориентированного линейно поляризованного поля:
А„ х = A sin Qh cos cp,, cos apt, A..,. = A sin Qh sin фЛ cos a>pt,
h^7 = hcosQhcoswpt (10.64)
и ограничимся процессами первого порядка в идеальном кристалле.
Тогда уравнения для амплитуд спиновых волн ск и с-к будут
содержать нелинейные члены, входящие как в уравнение (10.42), так
и в (10.45). С учетом (10.64)
-j- ±i(ukck + i(VkhcosQh + pka$+rZao*)em''ctk. (10.65)
где
. 1 у Л sin G^""*
ао = Т т '
292
Л*Ы-1»5
0,< 0,8 1,2 1,6 2 2,4 Нг0,кЭ
Рис. 10.9. Зависимости порогового поля для процессов первого порядка от
Ht0 при разных углах между h и Н«0 [217]. Сфера ЖИГ, намагниченная
по оси <100>; частота накачки 9,3 ГГц
Находя пороговое поле из уравнения (10.65) и присоединенного
таким же путем, как в предыдущих задачах, получим согласно
Яковлеву [216]
йшг 1=min < —- AHk sin 26t cos Qh+
К L
+ cooK + nfr2) + co;/2s.n2et sine<T4 (Ю.66)
ыЦ-Шо J J
При этом, как и для линейно поляризованной поперечной накачки
(§ 10.2), было принято фЛ = фЛ, поскольку в этом случае порог
оказывается наименьшим. Легко видеть, что при 0Л = О выражение
(10.66) совпадает с (10.49), а при 6л = п/2 —с (10.44).
Минимизация (10.66) по 6* и к позволяет найти величину /?lhri и
значения к и 6* возбуждаемых волн. При Н0<ЯС будут возбуждаться
волны с большими к, и их полярные углы будут иметь зависящие
от 6fc значения 6tl, лежащие между 90 (6Л = 0) и -45 (6Л = 90°). При
Я0>Я0с(е*1) будут возбуждаться волны с к = 0 и углами, которые,
как и в случае продольной накачки, будут определяться формулой
(10.52). Что же касается промежуточной области полей Hc<H0<H0c(Qkl).
то в ней характеристики параметрических волн и величины порога
могут быть найдены (как и в предельном случае поперечной накачки,
см. § 10.2) только с учетом конкретной зависимости АНк от к и 9*.
Экспериментальные зависимости A,hri от постоянного поля при
наклонной накачке приведены на рис. 10.9. Заметим, что с помощью
наклонной накачки можно измерить параметр диссипации спиновых
волн с углами Qk, лежащими в пределах ~45°-^90 .
Параметрическое возбуждение при наличии доменной структуры.
Как мы видели в гл. 8, спектр собственных колебаний при наличии
293
доменов удается рассчитать лишь для некоторых простых структур,
например, для плоскопараллельных слоев. Но даже для таких структур
при анализе параметрического возбуждения спиновых волн приходится
делать дополнительные допущения. Основное из них — взаимодействие
между спиновыми волнами в разных доменах отсутствует, т. е.
параметрическое возбуждение их в каждом домене происходит
независимо. Не принимаются также во внимание (как и в гл. 8)
процессы в доменных стенках и, как и во всем предыдущем
рассмотрении спин-волновых нестабильностей, спиновые волны в
доменах считаются однородными плоскими волнами. Последнее
предположение применимо, если волновые числа возбуждаемых волн
много больше обратных размеров доменов.
При указанных допущениях для вычисления порогов
параметрического возбуждения спиновых волн может быть использован путь,
аналогичный примененному выше для намагниченных до насыщения
образцов. Необходимо лишь, во-первых, учесть размагничивающие поля в
доменах, и, во-вторых, принять во внимание ориентацию поля накачки
относительно направлений намагниченности разных доменов. Кроме
того, на параметрическое возбуждение спиновых волн в образцах с
доменной структурой будет влиять то обстоятельство, что в них имеется
несколько типов колебаний намагниченности, в частности (см. § 8.3), при
наличии двух групп доменов—колебаний с частотами сох и соц.
При увеличении поля накачки спиновые нестабильности будут
возникать сначала в тех доменах, для которых величина полярного
угла накачки 6Л (а при учете анизотропии — и азимутального угла
Фь) обеспечит более низкий порог. Какие углы окажутся более
«выгодными», т. е. в каких доменах раньше возникнет нестабильность,
будет зависеть, главным образом, от соотношения частоты накачки
и собственных частот ыхи Юц. Для процессов первого порядка вдали
от резонансов (ыр#Ыц и ыр#со±) наименьший порог, как это следует
из формулы (10.66). будет в доменах, для которых накачка продольная
(6Л=0) или близка к ней, а вблизи резонансов—в доменах, для
которых накачка поперечная.
Наиболее полное теоретическое и экспериментальное исследование
параметрического возбуждения при наличии доменной структуры было
проведено Пилыциковым, Лебедевой и Седлецкой [136, 172] для того
же случая, для которого (см. § 8.3) наиболее подробно были изучены
линейные колебания намагниченности, а именно для сферы из кубического
кристалла, намагничиваемой вдоль оси <110>. Не приводя довольно
громоздких пороговых формул, полученных в [172], и
экспериментальных данных [136], отметим лишь, что они полностью
подтверждают те качественные соображения, которые были высказаны выше.
§ 10.4. Нестабильность неоднородных колебаний
и неоднородная накачка
В предыдущих параграфах этой главы мы считали, что
параметрически возбуждаемые моды представляют собой однородные плоские
волны, а намагниченность или переменное поле накачки являются
294
однородными. В этом параграфе мы откажемся от указанных
предположений.
Выше уже неоднократно отмечалось, что первое из этих
предположений, являющееся основным допущением теорий Сула и Шлё-
манна, перестает быть справедливым, когда минимизация пороговых
полей в рамках этих теорий приводит к значениям волнового числа
порядка или меньше обратных размеров образца. В этом случае
в качестве возбуждаемых мод следует принять собственные колебания
образца. Если пренебречь вкладом обменного взаимодействия в спектр
эжх колебаний и в то же время ограничиться магнитостатическим
приближением, то такими собственными колебаниями для образцов —
эллипсоидов вращения будут рассмотренные в § 6.3 неоднородные
магнитостатические (уокеровские) колебания.
Параметрическое возбуждение магнитостатических колебаний.
В этом случае мы должны заменить разложение (10.3) разложением
намагниченности по собственным магнитостатическим колебаниям
образца mv(r):
m~M= Yl[avmv(') + av*m*(r)], (10.67)
V
где av—зависящие от времени комплексные амплитуды. Эффективное
поле, входящее в уравнение Ландау—Лифшица, будет включать теперь
постоянное поле Н0 и переменное магнитное поле h^; обменного
взаимодействия мы не учитываем, анизотропией для простоты
пренебрежем. Переменное поле можно представить в виде
h^=he^+X(avhv+av*h;), (10.68)
V
где he^—заданное внешнее поле, а составляющие поля собственных
колебаний согласно (1.42) запишутся так:
Avx = —— (coHmvx-icovwvy), hvy = —-(i(ovmvx+<uHmvy). (10.69)
Подставляя (10.67) и (10.68) с учетом (10.69), а также Н0 в уравнение
Ландау—Лифшица и учитывая условия ортогональности магнитостатических
колебаний (6.108), получим дифференциальные уравнения для амплитуд
flv, аналогичные уравнениям (10.9) и (10.8) для амплитуд ак и а~к.
Рассмотрим случай продольной накачки, когда все амплитуды
av до порога малы. Тогда для них, опуская члены высших порядков
и члены, которые не могут привести к нестабильности, можно
получить уравнения [406]
^ = /covav+byAz(eto'r+e-i<0'')I^v«;-. (10.70)
Здесь hz — комплексная амплитуда продольного поля h„z, а интеграл
перекрытия колебаний v и v'
Xvv.=-)-Jnunv dV, (10.71)
295
где интегрирование производится по объему образца, a D—константа
нормировки в (6.108).
Как и в § 10.2 и 10.3, сохраним в уравнениях (10.70) только те
члены, которые изменяются с частотой cov и могут поэтому привести
к нестабильности, для них соу + соу' = сор- Нестабильность будет
определяться тем членом (т. е. той парой колебаний Vx и v2),
для которого порог окажется минимальным. Запишем уравнения
(10.70) для этой пары, учтем потери путем замены
(0v-*(av + i(0rv = (0v + iAHv/(2y) и таким же образом, как в § 10.3, получим
hzlta = rmnyhHViLHvJ\k12\2}. (10.72)
Оказывается, что для сферы Х12#0, если индексы пит колебаний
(см. §6.3) удовлетворяют следующим «правилам отбора» [162]:
tii=n2, т1 = —т2. (10.73)
Отсюда видно, что возможна вырожденная нестабильность (coVi=coVj)
колебаний с т = 0, например, колебаний типа (2, 0, 1). Для него
намагниченность имеет эллиптическую (не круговую) поляризацию,
что и является необходимым условием параметрического возбуждения
при продольной накачке. Используя для вычисления
^■(2.0.1X2.0.1) выражение (6.106), можно получить [162]
йг1Ьг=1,25(со>м)ЛЯ<2.о.1>. (Ю.74)
Невырожденная нестабильность согласно (10.73) возможна,
например, для пары колебаний (3, 1, 0) и (3, —1, 0). В этом случае [277]
Лг1Нг=1,14(ы>м)ч/АЯ(з.1.о)АЯ(з.-1.о,. (10.75)
Выражения (10.74) и (10.75) представляют собой наименьшие
пороговые поля при продольной накачке магнитостатических колебаний.
Сравнивая их с (10.49), мы видим, что при одинаковых параметрах
диссипации пороги для магнитостатических колебаний несколько
выше, чем для однородных плоских спиновых волн.
При поперечной накачке правила отбора оказываются иными.
Для процесса первого порядка в случае сферы согласно Моносову
[162]
п\=пг, wi = l— т2. (10.76)
Заметим, что второе из этих условий выражает равенство суммы
азимутальных индексов возбуждаемых колебаний азимутальному
индексу колебания накачки (1, 1, 0). Из (10.76) видно, что вырожденное
возбуждение при поперечной накачке невозможно. Наименьший порог
в этом случае имеет пара колебаний (2, 0, 1) и (2, 1, 0). Но и для
нее порог оказывается значительно выше, чем для плоских спиновых
волн при тех же сор и Н0.
Параметрическое возбуждение магнитостатических волн.
Рассмотренный выше путь может быть использован и для исследования
параметрического возбуждения безобменных магнитостатических волн
(§ 6.2) в образцах (стержнях, пластинах), которые при этом считаются
296
бесконечно протяженными. Такая задача была впервые решена
Шлёманном и Джозефом [406] для случая продольной накачки волн
в продольно-намагниченном круглом цилиндре. Приведем некоторые
результаты этой работы. Правила отбора, обеспечивающие
необращение в нуль интегралов перекрытия Х12 (которые имеют такой
же смысл, как в (10.70)), в данном случае оказываются следующими:
kzi=-kz2, т1=-т2, (10.77)
где fczi,2—волновые числа волн, распространяющихся вдоль оси
цилиндра (в противоположных, как видно из (10.77), направлениях),
а га1-2— индексы, характеризующие зависимость от азимутального
угла. Для волн с т = 0 возможен вырожденный случай—возбуждение
двух волн одинакового типа (и, 0); частоты их одинаковы, так как
при т = 0 (см. § 6.2) невзаимность отсутствует. Пороговое поле для
этого случая оказывается наименьшим и может быть представлено
следующим образом:
*„„, = , "ff" гАЯи0. (10.78)
Интересно, что (10.78) совпадает (при АН„0 = АНк) с выражением
(10.49) для порогового поля при возбуждении однородных плоских
волн в области Н0>НС, в чем легко убедиться, если учесть (10.52).
Остановимся теперь на параметрическом возбуждении при
продольной накачке безобменных магнитостатических волн в пластинах;
в линейном приближении эти волны были подробно рассмотрены
в § 6.2. Как и для цилиндра, нестабильными становятся пары волн,
распространяющихся в плоскости пластины в противоположных
направлениях. В случае нормально намагниченной пластины [43],
когда возбуждаются прямые объемные волны, возможна вырожденная
нестабильность, и в этом случае по-прежнему справедливо выражение
(10.78). При касательном намагничивании это же имеет место для
обратных объемных волн, которые распространяются в направлении
намагничивания [44, 156].
Для поверхностных волн, распространяющихся в касательно
намагниченной пластине перпендикулярно направлению
намагничивания, пороговое поле при продольной накачке может быть приближенно
записано в виде [156]
*«■■■,* , *"' , Мк. (Ю.79)
2V(uh+com/2)2-K/2)2
При шр 2 = Ш1 (т.е. для волн с к-*0) это выражение совпадает
с (10.78), а при Ыр/2 = сон+ым/2 (для волн с к-*со) hzttiT-*cc; для
промежуточных значений к порог параметрического возбуждения
поверхностных волн выше, чем объемных с той же частотой. Причина
этого заключается в том, что для поверхностных волн (см. § 6.2)
распределение намагниченности невзаимно, для волн параметрически
возбуждаемой пары намагниченности «прижимаются» к разным
плоскостям пластины, причем тем сильнее, чем больше к, вследствие
297
чего интеграл перекрытия оказывается меньшим, чем для объемных
волн, и уменьшается с ростом к.
Не останавливаясь подробно на возбуждении магнитостатических
волн в пластинах при поперечной накачке [141], заметим лишь, что
пороговые поля в этом случае оказываются обычно большими, чем
при продольной накачке, и в отличие от нее неограниченно возрастают
не только при fc-юо, но и при к-*0.
Теперь мы можем вернуться к вопросу о том, что же
действительно возбуждается в тех областях, где из теорий, имеющих
дело с однородными плоскими спиновыми волнами, следует
возбуждение волн с к = 0. При поперечной накачке, как мы видели,
магнитостатические типы колебаний (это справедливо и для
магнитостатических волн) имеют более высокие пороги, чем однородные
плоские спиновые волны с волновыми векторами k»\jd (для которых
теории Сула и Шлёманна справедливы), но не настолько большими,
чтобы для них сказывалось увеличение АНк с ростом к (гл. 11).
Такие спиновые волны—с к~ 104—и возбуждаются в этом случае.
В случае продольной накачки пороги при равных АНк, как мы
видели, приблизительно одинаковы для магнитос i а гических колебаний
и волн с fc~104. Однако для первых они обычно оказываются
несколько большими из-за влияния на АНк поверхностных неоднород-
ностей, радиационного затухания (т. е. потерь на излучение
электромагнитных волн) и др. Таким образом, как для поперечной, так
и для продольной накачки при Н0 > Нс обычно возбуждаются спиновые
волны с А:—10*, для которых влияние граничных условий на спектр
уже несушественно, а влиянием обменного взаимодействия еще
можно пренебречь [455]. Величины порогов для них хорошо
совпадают с результатами теорий Сула и Шлёманна для волн с ЬО.
Возбуждение волн в пленках с учетом обмена. При изучении
параметрических нестабильностей в тонких пленках (для ЖИГ—с
толщиной порядка или меньше 1 мкм) необходимо учитывать
обменное взаимодействие. Теорию параметрического возбуждения
спиновых волн в таких пленках разработали Лукомский и Кузько [141]
и Вендик, Калиникос и Чарторижский [43, 44]. Наиболее интересным
эффектом, который имеет место в этом случае, является поочередное
(при изменении постоянного поля или частоты) параметрическое
возбуждение волн на разных ветвях спектра.
Рассмотрим, например (рис. 10.10), случай продольной накачки
в касательно намагниченной пленке [106]. Как уже отмечалось,
пороги являются более низкими для объемных волн,
распространяющихся в направлении постоянного намагничивания. Их спектр
приведен на рис. 10.10, а (см. также рис. 7.13). На всех его ветвях
пороги уменьшаются при уменьшении кг, так как при этом возрастает
эллиптичность намагниченности. При достаточно больших постоянных
полях Яе0 частота сор/2 лежит ниже «дна» спектра, и параметрического
возбуждения первого порядка не происходит. По мере уменьшения
Нс0 весь спектр опускается (конечно, несколько деформируясь), при
некоторой величине Нс0 = Н1 его нижняя ветвь касается линии юр/2
и начинается параметрическое возбуждение волн этой ветви. При
298
Рис. 10.10. Спектр спиновых волн (схематически) и экспериментальная
зависимость порогового поля продольной накачки от постоянного поля [106]
в касательно намагниченной пленке ЖИГ толщиной 0,5 мкм. Стрелками
показано перемещение «пороговой точки» при уменьшении Нс0; участки
спектра, на которых происходит параметрическое возбуждение спиновых волн,
выделены жирными линиями
дальнейшем уменьшении #с0 точка со „/2 перемещается по нижней
ветви спектра и пороговое поле уменьшается (рис. 10.10, б). При
некотором поле Н2 порог оказывается меньшим на близко
расположенной ветви с п = 2 и пороговая точка перескакивает на эту
ветвь, затем движется по ней влево и т. д. По мере увеличения
п частотные интервалы между ветвями спектра (см. § 7.2) возрастают,
и, как видно из рис. 10.10, наблюдаются участки зависимости
ПньгШео), разделенные промежутками, в которых величина A2thr
превышает максимально достижимое в данном эксперименте поле.
Рис. 10.10 соответствует толщине пленки d= 0,5 мкм, при увеличении
d ветви спектра сближаются и кривая hzlhr(He0) переходит в
монотонную левую ветвь бабочки (см. рис. 10.8).
Ферритовый параметрический усилитель. Мы до сих пор
интересовались параметрическим возбуждением магнитных волн или
колебаний, которое происходило в результате регенерации — компенсации
их потерь энергией, поступающей от накачки. Но очевидно, что
299
накачка может привести и к усилению колебаний, возбуждаемых
какими-либо внешними источниками. Такие—параметрические
усилители диапазона СВЧ созданы с использованием нелинейности
различных сред: полупроводников, потока электронов и др. Сул [430]
(см. также [431]) предложил использовать нелинейность спиновой
системы ферромагнетика (или феррита). В зависимости от типа
регенерируемых колебаний существуют три режима работы фер-
ритового параметрического усилителя: 1) магнитостатический режим,
при котором оба колебания являются собственными магнитостатиче-
скими типами колебаний или волн образца; 2) э гектромагнитный
режим, при котором происходит регенерация двух собственных
колебаний резонатора с находящимся в нем ферритом; 3)
полустатический режим, когда одним из регенерируемых колебаний является
собственное колебание резонатора, а другим — ферритового образца.
Мощность накачки параметрических усилителей определяется в
основном коэффициентом заполнения q ферритом резонатора. Для
магнитостатического усилителя резонатором является сам ферритовый
образец и 9— 1, для электромагнитного—q«. 1. Поэтому минимальная
мощность накачки требуется для работы магнитостатического
ферритового усилителя, максимальная—для электромагнитного. Однако
магнитостатический усилитель обладает недостатком, связанным с
параметрическим возбуждением плоских спиновых волн, порог которого,
как мы видели, обычно ниже порога возбуждения магнитостатических
типов колебаний. Энергия этих волн в результате упоминавшихся
(§ 10.3) двухмагнонных процессов релаксации частично преобразуемся
в энергию длинноволновых колебаний, связанных с выходной цепью
усилителя, и воспринимается как шум.
Впервые ферритовый усилитель реализовал Вейсс [450]. Это был
усилитель электромагнитного типа, для него требовалась мощность
накачки 20 кВт (конечно, при этом накачка могла быть только
импульсной). Магнитостатический усилитель был осуществлен
Дейтоном [277]. В нем использовались типы колебаний: (3, 1, 0) —
сигнальный и (3, —1, 1)—холостой в сфере ЖИГ; собственные
частоты их составляли соответственно 4560 и 4620 МГц. Сфера
помещалась в резонатор, настроенный на частоту накачки 9180 МГц,
и связывалась с входным (и в то же время—выходным) коаксиальным
волноводом при помощи петельки. Полоса этого усилителя составляла
100 кГц при мощности накачки 450 мВт, а коэффициент усиления на
центральной частоте—20 дБ. В результате параметрического
возбуждения спиновых волн коэффициент шума усилителя превышал 10 дБ.
Проведенные в дальнейшем исследования с целью использования
в ферритбвых усилителях бегущих волн [438], а также применения
открытых диэлектрических резонаторов [94] не привели к заметным
качественным улучшениям—в настоящее время ферритовый
параметрический усилитель по большинству параметров уступает другим
усилителям СВЧ, например, транзисторным и полупроводниковым
параметрическим.
Волновая накачка. При всем многообразии рассмотренных выше
вариантов параметрического возбуждения магнитных колебаний и волн
300
одно условие все время выполнялось —
накачка была однородной по
амплитуде и фазе. Теперь настало время
рассмотреть параметрическое
возбуждение под действием неоднородной
накачки. В общей постановке эта задача
очень сложна, и целесообразно
исследовать два частных случая: накачки
бегущей волной с постоянной амплитудой
и локально-однородной накачки.
Остановимся сначала на первом
случае. Пусть накачкой служит
однородная незатухающая плоская волна
с частотой Юр и волновым вектором
кр. Предположим, что параметрически
возбуждаемыми модами являются (как
в § 10.2 и 10.3) тоже однородные
плоские волны с частотами ы1-2, волновыми
векторами ki-2 и нормальными
переменными сil2 = Ci.2exp(to12r). Для волны накачки ср = сР'ехр(/сйрГ).
Ограничимся рассмотрением процессов первого порядка. Тогда
для того, чтобы под действием волны накачки возникла нелинейная
связь некоторой пары волн, ведущая к их нестабильности, необходимо,
чтобы кроме условия временного синхронизма (10.21) (на
корпускулярном языке—условия сохранения энергии) выполнялось
условие
k, + k2=k„. (10.80)
Его называют условием пространственного синхронизма, на
корпускулярном языке это — условие сохранения квазиимпульса. В пределе
кр-»0 это условие переходит в условие к2=—кь которое, как мы
видели, имеет место при процессах параметрического возбуждения
однородной накачкой. Условия (10.21) и (10.80) ограничивают область
значений сор и кр, в которой возможен процесс первого порядка.
Причем, как всегда, на границах этой области процесс является
вырожденным (Ы1=ы2 = ык). Ограничения, накладываемые условием
(10.21) при и=1, иллюстрирует рис. 10.11.
Для переменных Ci и с2 параметрической пары волн в
рассматриваемом случае из (10.9) таким же образом, как при выводе
уравнений (10.16), можно получить систему
ас 1. . * ас 2 *.** /iaoi\
—- = JC0iCi+/Pi,2Cp(T2, —-=-HD2C2-jpi.2CpCi. (10.81)
at at
Здесь pii2 — параметр связи, являющийся функцией ын, и>м и частот,
а также волновых векторов всех трех взаимодействующих волн.
В случае fcp«fci.2, когда можно считать, что kt~— k2sk, т.е.
0!~я —e2 = 6i и (p!~H + (p2s(pb параметр связи имеет следующий вид:
Pl.2 = Pl.21 + Pl.2l|- (10.82)
301
2*>*(Ь-<0
Рис. 10.11. Область
существования (заштрихована) процессов
первого порядка при
параметрическом возбуждении
спиновых волн однородной плоской
спиновой волной с небольшим
/ср («безобменной»)
Выражение для p1-2i совпадает с (10.17), а
Pi 211 =—втгО-е^т^е2'". (10.83)
4(0,,
Сравнивая (10.81) с учетом (10.83) с выражениями (10.47),
(10.48) для однородной продольной накачки, мы видим, что
они совпадают при
А, = а>мяп2ере-,*Ср/(2у). (10.84)
Таким образом, накачка в данном случае является суммой
квазиоднородной поперечной накачки и квазиоднородной продольной накачки
полем (10.84). Нетрудно убедиться, что это поле есть не что иное,
как z-составляющая магнитного («дипольного») поля (7.11) волны
накачки.
Величина pi,2± максимальна (см. § 10.2) при возбуждении волн
с 6k = 45r, а величина р1-2ц (§ 10.3) — волн с 6к = я/2. Максимизация
суммарного параметра связи (10.82), например, при 0Р = 45
показывает, что при (ор>(ом/2 доминирует первый член в (10.82) и
возбуждаются волны с 6*^45°, пороговая намагниченность при этом
оказывается близкой к ее значению для однородной поперечной
накачки. Если же сор<сом/2, то доминирует pli2n и возбуждаются
волны с вк = п/2, пороговая намагниченность в этом случае
уменьшается по отношению к порогу для однородной поперечной накачки
в 2юр/сом раз.
Локальная накачка. Рассмотрим теперь другой частный случай
неоднородной накачки—когда она имеет постоянные амплитуду
и фазу в некоторой области, меньшей чем образец, и отсутствует
вне этой области. Задача о параметрическом возбуждении такой
локально-однородной накачкой, по существу, ничем не отличается
от рассмотренной в § 10.3 задачи о параметрическом возбуждении
спиновых волн с учетом рассеяния их на границах образца (или
зерен поликристалла). В обоих случаях параметрические волны
«выходят из игры», достигая границ некоторой области, в одном
случае—из-за неупругого рассеяния на границах образца (или зерен),
а в другом—вследствие ухода из области, где действует накачка.
Поэтому выражение (10.62) будет справедливо и в интересующем
нас сейчас случае локальной накачки.
Из формулы (10.62) видно, что увеличение порога из-за
локальности накачки будет тем больше, чем меньше размер области
локализации и чем больше групповая скорость возбуждаемых волн.
Эти зависимости были подтверждены экспериментально [154] для
случая продольной накачки в монокристаллической пленке ЖИГ.
Однородная накачка осуществлялась при помещении пленки в полый
резонатор, а локальная—при установке на ней открытых
диэлектрических резонаторов с различными е. Результаты измерения
пороговых полей в случае нормально намагниченной пленки приведены
на рис. 10.12. Из этого рисунка видно, что при полях Н0<НС
зависимость Azthr от размеров области практически отсутствует. При
302
2,5
2
1,5
1
0,5
2,6 2,8 J Нг0.кЭ
Рис. 10.12. Зависимости порога продольной накачки в нормально
намагниченной пленке ЖИГ от постоянного поля при различных размерах области
локализации накачки [154]. 1 — однородная накачка в пленке 5,5x7 мм,
2—накачка в области 3,5x3,5 мм, 3—накачка в области 1,5x1,5 мм. Толщина
пленки 16 мкм; частота накачки 9,37 ГГц
таких полях (см. § 10.3) возбуждаются волны, для которых групповая
скорость (определяемая в основном слабым влиянием обменного
взаимодействия) не превышает ~105. При этом согласно (10.62)
увеличение порога даже при наименьших размерах области
несущественно. На правых же ветвях бабочек (рис. 10.12) возбуждаются
прямые объемные волны с fc<104, для которых vgr~\Q6 и в согласии
с (10.62) имеет место увеличение порогового поля с уменьшением
размера области.
Параметрические нестабильности при распространении магнитоста-
тических волн в пленках. Приведенные выше результаты для волновой
накачки в основном качественно справедливы для накачки маг-
нитостатическими волнами в пленках, но при этом должны
приниматься во внимание реальный спектр и реальная структура поля волны
накачки. Рассмотрим, например, поверхностную волну в касательно
намагниченной пленке, распространяющуюся перпендикулярно
постоянной намагниченности (§ 6.2). Спектр этой волны расположен над
спектром плоских волн, а поле имеет очень малую z-составляющую,
связанную лишь с неоднородностью возбуждающего зту волну тока.
В этом случае накачка является практически поперечной, и для
вычисления порогов можно пользоваться формулами Сула [152, 155]
(см. § 10.2).
Ограничимся процессом первого порядка и предположим, что, как и
в ряде предыдущих случаев, порог будет минимальным при возбужде-
303
^thr>5
_1 I I I L.
2o,k(k=0,ffk = f)
2wk(h=0,Bk~0)
-Ь>р(*р~°°)
ыр(*рг)
cip(kp-O)
РПг.нкВг
10 -
Рис. I0.13. Границы области
существования процессов первого порядка
при параметрическом возбуждении
спиновых волн поверхностной маг-
нитостатической волной в пленке
Рис. I0.14. Частотные зависимости
пороговой мощности при
параметрическом возбуж!снии спиновых волн
поверхностной магнитостати ческой
волной [80]. Пленка ЖИГ толщиной
7,4 мкм. Постоянное поле изменялось
одновременно с изменением частоты.
Рассчитанные величины w0. Wi
и ы2 показаны для Ар = 250см-1
нии волн с /c!=/c2~104. В не очень тонких пленках (с толщиной
d>5 мкм) спектр этих волн можно считать таким же, как для
безобменных однородных плоских волн. Тогда границы, по частоте или
постоянному полю, области существования процессов первого порядка
можно" определить из рис. 10.13. Из этого рисунка видно, что для
поверхностной волны с данным кр (т. е. при одновременном изменении
Юр и Юн) имеется верхняя граница ю2 существования этого процесса.
Что же касается нижней частотной границы, то, строго говоря, она
совпадает с границей ю0 существования поверхностной магнитостатиче-
ской волны. Однако при частоте ю,. большей чем ю0 (см. рис. 10.13),
должно начаться возрастание порога, так как при юр<ю, могут
параметрически возбуждаться лишь «обменные» волны с большими
к 12-, Для которых порог является более высоким. Все эти предсказания
хорошо подтверждаются экспериментально [80] (рис. 10.14).
На опыте обычно определяются пороговые значения поступающей
на входной преобразователь мощности Р, именно эти величины
приведены на рис. 10.14. На рис. 10.15 показана зависимость
пороговых значений Р от волнового числа кр, снятая при изменении
юн и постоянной частоте юр—такой, что процесс первого порядка
разрешен при всех кр. Обращает на себя внимание очень сильная
зависимость PlhT от кр и очень малые значения Plhr при больших кр.
" Эти границы являются в то же время границами существования
линейного процесса релаксации—трехмагнонного расщепления (см. § 11.2).
304
Р±Ьг,мкВт
200
400
600
800 Ар, см
Рис. 10.15. Зависимости пороговых величин падающей мощности на входе
преобразователя. А* и т+ от волнового числа поверхностной магнитостатиче-
ской волны накачки [212]. Пленка ЖИГ толщиной 15,2 мкм; частота 3,2 ГГц.
Штриховая линия—расчет по теории Сула [429] при Д#»=0,6 Э
На рис. 10.15 приведены также пороговые значения правой
циркулярной составляющей намагниченности поверхностной волны
/и + ,ьг и ее поля /z+thr, рассчитанные по величине РЛ[. Они, в отличие
от Plhl, мало изменяются при изменении кр. Оценка w+thr по теории
Сула (§ 10.2) дает величины, в 1.5 2 раза меньшие, чем
экспериментальные. Такое расхождение может быть, во всяком случае—частично,
объяснено тем, что из-за затухания волна накачки оказывается
локализованной вблизи входного преобразователя, т. е. фактически
имеет место локальная накачка, при которой, как было показано,
порог повышается.
Сильная же зависимость Plhr от кр (как и сильная зависимость
от толщины пленки [212]) объясняется главным образом изменением
групповой скорости волны накачки; чем эта скорость меньше, тем
при данных И+ и ш+ будет меньше поток энергии волны, а
следовательно, и Р.
Мы обсудили лишь один пример параметрического возбуждения
спиновых волн в условиях возбуждения магнитостатической волны
в пленке. В других случаях характер явлений может быть несколько
иным. В частности, при возбуждении объемных волн продольное
переменное поле hz будет сравнимо с поперечным и накачка будет
наклонной.
§ 10.5. Запороговое состояние
Предыдущие параграфы этой главы были посвящены в основном
нахождению порогов параметрического возбуждения, т. е. величин
переменного поля накачки, при которых начинается экспоненциальное
20 А. Г. Гуревич, Г. А. Мелков 305
нарастание (нестабильность) магнитных колебаний или волн", hu
ясно, что нарастание амплитуд параметрически возбуждаемых волн
не может быть неограниченным, должно существовать некоторое
предельное состояние, либо стационарное (при котором амплитуды
параметрических волн не зависят от времени), либо нестационарное —
характеризующееся периодическими автоколебаниями или
непериодическим (хаотическим) блужданием системы в некоторой области
состояний [433 ].
Неограниченный рост амплитуд параметрических волн за порогом
получался потому, что мы учитывали в уравнениях для них, например,
в уравнениях (10.9) только низшие нелинейные члены—линейные по
амплитудам возбуждаемых волн. Для нахождения запорогового
состояния необходимо учитывать и члены более высоких порядков.
Простейшей причиной («механизмом») ограничения амплитуд
является то, что переменная намагниченность не может во всяком
случае превысить величину постоянной намагниченности М0. Однако,
как мы увидим, ограничение обычно наступает значительно раньше
вследствие других, более эффективных механизмов. Известно по
крайней мере три таких механизма: обратного влияния
параметрических волн на накачку, фазовый механизм и механизм нелинейного
затухания. Они учитывают влияние параметрических спиновых волн
соответственно на затухание колебаний накачки, на связь между
параметрическими волнами и накачкой и на затухание самих
параметрических волн. Мы рассмотрим эти механизмы, ограничиваясь, как
и в § 10.2 и 10.3, случаем, когда параметрические волны можно
считать однородными плоскими волнами, а накачку—однородной.
Обратное влияние параметрических волн на накачку. Энергия,
передаваемая параметрическим волнам, представляет собой
дополнительный источник диссипации для накачки. В случае поперечной
накачки это можно учесть, введя в выражение (10.15) для амплитуды
однородной намагниченности накачки дополнительное затухание со*0,
обусловленное взаимодействием с параметрическими спиновыми
волнами. Учтем также воздействие параметрических волн на собственную
частоту колебаний накачки, заменив в (10.15) со0 на со0:
а°о=- ff ^ kV (Ю.85)
С ростом амплитуд параметрических волн величина coJo увеличивается,
рост амплитуды намагниченности накачки замедляется и, как мы
увидим, может прекратиться.
В случае продольной накачки рост амплитуд параметрических
волн приводит к увеличению потерь (снижению собственной
добротности) резонатора, в котором находится ферритовый образец, и из-за
этого—к замедлению роста амплитуды поля накачки при увеличении
подаваемой на резонатор мощности. Но так как объем образца
" В дальнейшем мы будем для краткости говорить о параметрически
возбужденных (параметрических) волнах, подразумевая при этом как волны,
гак и колебания в ограниченных телах.
306
Рис. 10.16. Графическое решение
уравнения (10.85) [429]. 1—левая часть
этого уравнения, 2—его правые части
при амплитудах поля hl<h2<h3<ht.
Сплошные линии—аппроксимация
(10.86), штриховая (при А4)—Для
действительной зависимости coJ0 от
а о (схематически)
/
<
h3~hXbr
V4
hz /\
h1 /
/
у1
^%2
\4\
к\ к\
WL-WI
'3.4
-fhf
обычно много меньше объема резонатора, снижение добротности
резонатора оказывается небольшим, и этот механизм в случае
продольной накачки не играет существенной роли.
Возвращаясь к поперечной накачке, рассмотрим сначала процесс
первого порядка [429]. В этом случае нарастание нестабильных спиновых
волн начинается с очень низкого—равновесного (теплового) уровня,
и поэтому их амплитуды можно считать малыми вплоть до самого
порога. Если же амплитуда накачки а о хотя бы ненамного превысит
пороговый уровень, начнется экспоненциальный рост амплитуд
параметрических волн и, как следствие этого, резкое увеличение со*0- Поэтому
зависимость со*0 от а% можно аппроксимировать следующим образом:
0 при а% <a8.hr,
со
гО
Ч
со при a8>flothr-
(10.86)
Тогда уравнение (10.85) можно решать графически, как показано на
рис. 10.16. Из этого рисунка видно, что по мере увеличения поля
h амплитуда а% сначала растет линейно, пока h и аЧ не достигнут
своих пороговых значений. Затем рост амплитуды а% прекращается,
ее пороговое значение «замораживается». Итак,
\yh/((u0-<up + i<ur0) при h<hlbr,
при h>hlbl,
„ОМ
(10.87)
где aothr определяется согласно (10.28), а Л,Ьг—в результате
подстановки этой величины в (10.87).
Из соотношений (10.85) и (10.87) следует (если пренебречь
различием с50 и со0) выражение для эффективного параметра
диссипации в запороговой области
coro+cor*o = 4/(C2-l)K-toP)2 + C2tor2o,
где надкритичность
Z = h/hlbr.
20"
(10.88)
(10.89)
307
/
0,6
0,1
X"
-
i
о
1
-20
О
20
Слб
1
0,5
^+п
\^+п) таге
°г
о/
""о
_ о" о
S. "о
1
в
12
16 $,АВ
Рис. 10.17. Зависимость мнимой
части нелинейной восприимчивости от
надкритичности для процесса
первого порядка при резонансе [429].
Касательно намагниченный диск из
марганцевого феррита.
Линия—расчет по формуле (10.90),
точки—эксперимент при _/j,=4,04 ГГц
Рис. 10.18. Зависимость мнимой части
нелинейной восприимчивости от
надкритичности для процесса первого порядка
вдали от резонанса [429]. Сфера из
марганцевого феррита. Линия—расчет
по формуле (10.90), точки—эксперимент
при /р^9 ГГц
Для вычисления компонент тензора нелинейной внешней
восприимчивости ферритового эллипсоида достаточно подставить (10.88)
в качестве параметра диссипации в выражения, приведенные в § 1.5.
Таким образом получим, например,
«■..-rt^P-o^S^-
(10.90)
где х+п—мнимая часть правой циркулярной компоненты нелинейного
тензора восприимчивости, а х +—мнимая часть такой же компоненты
линейного тензора. Зависимости х+п от надкритичности, рассчитанные
согласно (10.90) при резонансе (сор = со0) и вдали от него (т. е. в области
дополнительного поглощения), а также результаты соответствующих
экспериментов приведены на рис. 10.17 и 10.18. Отклонения
экспериментальных величин от расчетных на рис. 10.18 обусловлены
влиянием другого—фазового механизма ограничения (см. ниже).
Рассмотрим теперь, следуя Сулу [432], стационарное состояние
за порогом нестабильности второго порядка, когда возбуждаются
спиновые волны с сок = сор. Существенное отличие этого случая от
рассмотренного выше связано с тем, что такие волны возбуждаются
не только параметрически, но и в результате двухмагнонных процессов
рассеяния колебаний накачки на неоднородностях (см. § 10.3).
Одновременно рассеяние спиновых волн на тех же неоднородностях
приводит к дополнительному возбуждению колебаний накачки. Для
учета этих процессов необходимо добавить в уравнения (10.23)
и (10.8) дополнительные члены, аналогичные члену, введенному
с такой же целью в (10.57). Тогда первое уравнение (10.23) примет вид
dt
= i(ukck + iZ,kaoc'-k + vk0a0,
(10.91)
308
а уравнение (10.8), если оставить в нем только члены, линейные
по а0 и ск, и ограничиться случаем поля с правой круговой
поляризацией, запишется следующим образом:
da0 ^ ,
—=/ш„«о+ 2, v0kck-iyhe"'
(10.42)
Для решения этих уравнений необходимо перейти к комплексным
частотам: t0o-»to0 + ito"0. to*-»tok + /'coft, где согласно (10.58)
(й?к = (йГк — Иг*, а со^—затухание, обусловленное двухмагнонным
рассеянием. Предполагая далее, что u>rk. v0k, vk0 не зависят от к,
можно получить для амплитуды однородных колебаний
намагниченности при резонансе (сор = со0) [432]:
iyh
п° —
"Ores — "
o»,o+e>;o[i-(ie8»№8dJ)*]-"2" (10'93)
Из выражения (10.93) видно, что частота релаксации колебания
накачки неограниченно возрастет при приближении амплитуды этого
колебания к его пороговому значению и это значение достигается лишь
в пределе при й-»оо. Мы можем, однако, формально ввести пороговое
поле (при круговой поляризации поля и резонансе) как AIhr=floihr/X+reS-
где x'+res—линейная восприимчивость, и определить надкритичность
согласно (10.89) по отношению к этому /zlhr. Тогда для нелинейной
восприимчивости x+n = flores/A из (10.93) нетрудно получить уравнение
I+(c^0,cor0)
(10.94)
х"+» i +Ko/cor0)[i-(x"-,»/x"*n.)4e4]""*'
Полученные в результате его решения зависимости x+n res (О ПРИ
различных отношениях coj0/toro приведены на рис. 10.19. Из этого
рисунка видно, что в случае параметрического процесса второго
порядка в реальных кристаллах происходит «размазывание» порога,
Рис. 10.19. Зависимости нелинейной восприимчивости от надкритичности для
процесса второго порядка при различных относительных вкладах
двухмагнонных процессов [432]. Расчет по формуле (10.94). Цифры у кривых—значения
309
тем более сильное, чем больше относительный вклад двухмагнонных
процессов в диссипацию.
Фазовый механизм. По мере увеличения амплитуд параметрических
спиновых волн изменяются фазовые сдвиги между накачкой и
параметрическими волнами, вследствие этого ослабляется связь между ними,
что и приводит к замедлению роста амплитуд этих волн с ростом
амплитуды поля накачки. Этот механизм был предложен и подробно
изучен Захаровым, Львовым и Старобинцем [90] (см. также [145]).
Для его описания достаточно учесть в уравнениях для ск и с*-к
следующие члены третьего порядка:
2«'X:r**.c*c*.c*. + 'Z'S'**,c-*c*.c-*,- (10.95)
*i *■
Фазовый механизм играет наибольшую роль в случае продольной
накачки. Мы ограничимся этим случаем и добавим члены (10.95)
в уравнение (10.47). Учтя затухание путем замены (йк-кйк + 1(йгк,
придем к уравнениям
i+fDrt-i/cBt-^ c°k-iPkc°Jk = 0 (10.96)
и присоединенному, в которых
&k = (ok + 2^Tkki\c°ki\2, (10.97)
Л^.^+IWJ.cV (10-98)
*.
Сравнивая уравнение (10.96) с (10.47), мы видим, что учет членов
(10.95) привел, во-первых, к изменению (перенормировке) собственных
частот, и, во-вторых, к перенормировке накачки—замене величины
hz Vk (которую можно назвать внешней накачкой) эффективной или
полной накачкой Рк.
Введем согласно [90] новые переменные пк и tyk, определив их
следующим образом (см. формулу (10.6)):
с1с\ = \с1\е^\с\\е1^ = \с1\2е1№^-^ = 2{уЪ1М0)пке{^ (10.99)
(при параметрическом возбуждении спиновых волн всегда |ck| = |c_k|).
Величина пк характеризует интенсивность параметрических волн с
волновыми векторами к и — к и представляет собой число
соответствующих параметрических магнонов, a tyk является суммой фаз
параметрических волн". В этих переменных из (10.96) можно получить
l-^=nk[-(urk + lm(PUi^)l
(10.100)
2 dt 2 у '
Разность их фаз остается неопределенной. Таким образом,
параметрические спиновые волны не являются полностью когерентными (это
справедливо и в случае поперечной накачки).
310
С помощью (10.100) можно показать [90, 124], что в стационарном
состоянии за порогом возбуждения (т. е. при пкф0) существуют лишь
волны, обладающие минимальным порогом параметрического
возбуждения, для которых, в частности (см. § 10.3), й>к=<йр/2. В простейшем
случае постоянства полной накачки Рк (10.98) для всех параметрически
возбужденных спиновых волн, что вполне оправданно при возбуждении
узкого по волновому вектору пакета волн, это утверждение допускает
простую интерпретацию. Действительно, из (10.100) следует, что при
dnk/dt=dtyk/dt=0 для всех возбужденных волн (пкф0) суммарная
накачка должна удовлетворять условию
1Л12 = <ог2*+((5*-юр/2)2. (Ю.101)
Если теперь возбуждены волны с юк = сор/2, то, согласно (10.101)
и в силу предположения о постоянстве полной накачки, для всех
возбужденных волн \Рк\ = <ятк. Этого достаточно для возбуждения
волн с с5к = Юр/2, но меньше, чем требуется условием (10.101) для
возбуждения волн с ®кф<йр/2. Поэтому для них пк = 0. Аналогично
и полярный угол вк возбуждающихся волн после порога возбуждения,
по крайней мере вблизи порога, остается равным своему значению
при пороге; для изотропного ферромагнетика согласно § 10.3 8к = я/2.
С учетом сказанного решение системы (10.100) для стационарного
состояния имеет вид [88] (см. также [145]):
(l-itlM0)N=y/(hI V)2-w2k/S,
sin viz» = arkj{hz V), cos \|/* = - SN/(hz V).
(10.102)
(10.103)
Здесь величина N характеризует суммарную интенсивность
параметрических спиновых волн, она равна полному числу параметрических
магнонов в единице объема: N=Y^nk;
1,
S=i(coM/cop)2[4/co^ + co^-(47i-7Vz)YMo], (10.104)
r=|Fk(efc = 7r/2)| = ycoM/(2cop). (10.105)
Из (10.103) видно, что сумма фаз параметрических волн
\)/к (отсчитываемая от фазы поля накачки) в момент порога (hzV=wrk)
составляет л/2. По мере увеличения надкритичности, т. е. с ростом
hz, это фазовое соотношение, обеспечивающее оптимальную передачу
энергии параметрическим волнам,
нарушается, угол tyk растет и при
Az-»oo стремится к л (рис. 10.20).
С помощью соотношений (10.7),
(10.11), (10.99), (10.102)—(10.105)
можно вычислить изменяющуюся с
частотой накачки сор z-составляющую
однородной намагниченности т2(сор).
Именно ее возникновением
обусловлено поглощение продольной накач- рис. ю.20. Фазовые соотношения
ки в феррите. Это вычисление дает при продольной накачке
311
1,5
1
0,5
1*1
I/O
[*/
/о
u""~
/ о \
/ о о \
/о о \
° \
ч ^
ч
ч
1 1
^
г.
ч
■ч
J
*;„
v^z n/mnx
х"
Az n
i
Рис. 10.21. Зависимости вещественной
и мнимой частей нелинейной
восприимчивости при продольной накачке
от надкритичности [88]. Штриховые
линии — расчет по формулам (10.106);
сплошные—с учетом возбуждения
(см. ниже) второй группы спиновых
волн, начало его обозначено стрелкой.
Точки—эксперимент для сферы ЖИГ
при /р = 9,4ГГц и Н0 = НС-100 Э
(Но||<100»
Ю 15 $.Аб
Wz(top) = %zn/iz, где xIn = Xz„
продольной накачке,
-iXzn — нелинейная восприимчивость при
М0 V1
Xzn
У
t;2-i
Х- у |S| ^ •
(10.106)
Полученные выражения, как видно, например, из рис. 10.21, при не
очень больших надкритичностях (£,< 10) находятся в хорошем согласии
с экспериментом, что свидетельствам о преобладающей роли фазового
механизма при продольной накачке.
Фазовый механизм «работает» и при поперечной накачке. Для
процесса первого порядка при резонансе его вклад невелик [90],
а для нерезонансного (см. рис. 10.18), а также для процесса второго
порядка может быть существенным.
Нелинейное затухание. Этот механизм ограничения обусловлен
зависимостью параметра диссипации параметрических спиновых волн
от их амплитуд; до сих пор мы этой зависимостью пренебрегали,
считая величины wrk постоянными. В обшем же случае
(urk = (ark0 + aiN+a2N2 +
«i. a2.
(10.107)
— некоторые
где N—число параметрических магнонов, а
постоянные коэффициенты.
Наиболее ярким примером нелинейного вклада в <агк является
вклад элементарных процессов слияния (рис. 10.22, а) двух
параметрических магнонов, который исследовали Готтлиб и Сул [311J. Ясно,
что этот вклад будет положителен и пропорционален числу
параметрических магнонов jV. Условия сохранения энергии и импульса
ю1+со1' = со2, k!+k,' = k2 выполняются при полях Н0<Н3св, где
^3^(80 = ^(6,,)-—(v/4to^ + (o^sin46)[-4/co^ + (o|fsin4efc). (10.108)
Здесь вк—полярный угол параметрических спиновых волн (6* = л/2
в случае продольной накачки), а Нс(вк) определяется согласно (7.18).
312
Л
'к,- "2
3s
'*г
*2 h. *з к1
в
Ь*5
Рис. 10.22. Элементарные трехмагнонные процессы: а—нелинейного слияния,
б слияния с тепловым магноном, в—расщепления
Нелинейные вклады в ыгк могут вносить и трехмагнонные
процессы с участием одного параметрического магнона (см. рис. 10.22):
слияния параметрического магнона с тепловым и расщепления. Их
вклады становятся зависящими от числа параметрических магнонов
вследствие того, то числа тепловых магнонов начинают (при больших
числах параметрических магнонов) отличаться от равновесных.
Очевидно, что нелинейный вклад таких процессов слияния (рис. 10.22, 6)
отрицателен, поскольку при больших числах релаксирующих магнонов
обедняется «резервуар» магнонов к2. Как показали Львов и Фалькович
[146] (см. также [145]), этот вклад в случае продольной накачки
в сфере существует лишь при поле Н0<Н3с, где
//3с=Л^ш„-1Шм). (10.109)
Нелинейный вклад процесса расщепления (рис. 10.22, в) оказывается
положительным и пропорциональным (как и нелинейные вклады
процессов слияния) числу параметрических магнонов [146]. Процессы
расщепления разрешены также в ограниченных областях значений
параметров, в частности, в случае продольной накачки в сфере — при
поле Н0, меньшем чем
H3t = Hc~U^fwh-l^+<oh\ (ЮЛЮ)
Возможны, конечно, и нелинейные четырехмагнонные процессы, но
их роль в ограничении амплитуд параметрических волн оказывается
несущественной.
В случае продольной накачки, как уже отмечалось, механизм
обратного влияния параметрических волн на накачку неэффективен.
Поэтому мы рассмотрим для этого случая совместное влияние двух
других механизмов: фазового и нелинейного затухания. Для этого
в уравнениях (10.100) положим a^^w^o + aiN. Расчет нелинейной
восприимчивости может быть проведен аналогично рассмотренному
выше случаю ai=0. Результаты его приведены на рис. 10.23. Из
этого рисунка видно, что положительное нелинейное затухание, не
влияя на величину максимума %z'n(C). приводит к сдвигу его в сторону
больших надкритичностей. Отрицательное же нелинейное затухание
приводит к жесткому возбуждению спиновых волн — при увеличении
313
0,25
0,25
Рис. 10.23. Зависимости
мнимой части нелинейной
восприимчивости при продольной
накачке от надкритичности с
учетом нелинейного затухания
[90]. Цифры у
кривых—значения (согц — а>гю)/а>гю. Стрелками
показаны направления
изменения восприимчивости
амплитуды накачки в точке £=1 происходит скачкообразное
возбуждение спиновых волн с конечной амплитудой, а при ее уменьшении
параметрические волны существуют и при С<1-
Как видно из рис. 10.23, при малых надкритичностях включение
положительного нелинейного затухания приводит к уменьшению,
а отрицательного к увеличению Хг'п- Результаты измерения
зависимости Xzn(Ho) при небольшой надкритичности приведены на
рис. 10.24. Как видно из этого рисунка, экспериментальные результаты
находятся в согласии с приведенными соображениями—величины
полей, при которых происходят резкие изменения x'L, мало
отличаются от значений, рассчитанных по формулам (10.108)—(10.110).
0,1
0,П6
ом
47tXzn
у
*»s н
I ■
'
/
^
S
Н3сп Н5с
, I , I ,
200
400
600
»о,э
Рис. 10.24. Полевая зависимость мнимой части нелинейной восприимчивости
при продольной накачке [150]. Сфера ЖИГ, Но||<100>,/„=9,37 ГГц, комнатная
температура, £=1дБ. Hs=2\HAl\; Я'3сп, Я'3с, #3s—расчет по формулам
(10.108)—(10.110) с добавкой Hs
314
Устойчивость запорогового состояния. Отметим прежде всего, что
следует различать внешнюю устойчивость— по отношению к рождению
других групп параметрических спиновых волн, и внутреннюю - по
отношению к малым изменениям амплитуд и фаз первичной группы.
В случае продольной накачки первичной является группа спиновых
волн с 6)1 = 6!= тс/2, амплитуда и фаза которой определяются
выражениями (10.102) и (10.103). Это запороговое состояние будет устойчиво
по отношению к возбуждению другой группы спиновых волн с 6* = 62
(внешняя устойчивость) до тех пор, пока согласно (10.101) полная
накачка (10.98) для новой группы не достигнет величины ark.
Используя это условие, для изотропного ферромагнетика было
получено [90], что внешняя устойчивость сохраняется до
надкритичности £ = 3,5; при таком значении £ возникает вторая группа спиновых
волн, по-прежнему с й>к = сор/2, но с 6к = 62 —50 . Эксперименты [125]
свидетельствуют о пороговом возникновении второй группы
параметрических спиновых волн с 62=45-=-50 , но при больших, чем указанная
выше, величинах надкритичности — порядка 10-^20. Расхождение
может быть связано с зависимостью сог* от вк, которая при расчете
игнорировалась. С дальнейшим ростом надкритичности будут
возбуждаться все новые группы спиновых волн на поверхности й>* = сор/2
в к-пространстве.
Внутренняя устойчивость запорогового состояния —по
отношению к изменениям амплитуды и фазы первичных параметрических
волн (10.102), (10.103) — может быть исследована с помощью
уравнения (10.96) при малых отклонениях ос амплитуд спиновых волн
от стационарного состояния. Если с течением времени а убывает —
состояние устойчиво, если нет — неустойчиво. Конкретный анализ
внутренней устойчивости системы параметрических спиновых волн
при продольной накачке был проведен для кубического
ферромагнетика [90], его результаты для однородных по образцу отклонений
у. представлены на рис. 10.25.
В случае внутренней неустойчивости амплитуды и фазы спиновых
волн совершают коллективные колебания вокруг стационарных
значений (10.102), (10.103), эти колебания проявляются в виде автоколебаний
продольной намагниченности. Как видно из рис. 10.25, при продольной
накачке трехсантиметрового диапазона в сфере ЖИГ при комнатной
Рис. 10.25. Области устойчивости по
отношению к возникновению однородных
коллективных колебаний в кубическом
ферромагнетике при продольной накачке
[90]; N2 = NZ + &\HU\IM0, где при
Мо11<100> £ = 9, а при М0||<т> £=-8.
В областях / и /// внутренняя
устойчивость, в области //—неустойчивость.
Точки—сфера ЖИГ при комнатной
температуре и /р = 9 ГГц
3
I \ Ж
1 1
«Ур
\М0\\<100>
\ ж
' 1
-8Л
-4П
■fit
315
температуре внутренняя устойчивость по отношению к однородным
коллективным колебаниям не имеет места при Н0||<111> и имеет
место при Но||<100>; в последнем случае возможны лишь
неоднородные колебания, которые менее интенсивны. Это находится в согласии
с тем экспериментальным фактом, что при указанных условиях
сильные автоколебания наблюдаются при Но II < 111 > и не наблюдаются
при Но||<100>.
Частоты коллективных колебаний лежат в пределах от десятков
килогерц до десятков мегагерц и сильно зависят (как и форма
колебаний) от надкритичности. При малых надкритичностях форма
их часто мало отличается от синусоидальной, при больших —
колебания становятся резко негармоническими, а при очень больших —
часто носят шумовой характер [162].
Проблему устойчивости стационарного запорогового состояния
параметрически возбужденной спиновой системы мы рассмотрели
для случая продольной накачки, для которого этот вопрос наиболее
детально исследован [90]. Однако подобные явления, в частности
автоколебания наблюдаются и при поперечной накачке (см., например,
[162]).
Нелинейные ферритовые устройства СВЧ. Остановимся теперь
кратко на вопросе о практическом значении рассмотренных в этой
главе нелинейных явлений. Как уже указывалось выше, необходимость
изучения этих явлений связана прежде всего с тем, что они
ограничивают динамические диапазоны линейных ферритовых
устройств. Было отмечено также, что измерение порогов
параметрического возбуждения, особенно при продольной накачке, является
методом определения параметра диссипации спиновых волн.
Запороговые явления, которые исследовались в этом параграфе,
нашли применение для создания нелинейных ферритовых устройств,
используемых (хотя в значительно меньшем объеме, чем линейные)
в технике СВЧ. Одним из таких устройств является ограничитель
мощности, т. е. устройство (нелинейный четырехполюсник), выходная
мощность которого остается приблизительно постоянной в некотором
диапазоне входных мощностей. Такие устройства используются,
например, для защиты входных цепей приемников от перегрузок.
Для создания ограничителя мощности можно использовать
нерезонансное параметрическое возбуждение первого порядка как при
поперечной, так и при продольной накачке в ферритовом образце,
помещенном в волновод или резонатор. До порога поглощение
энергии ферритом мало, так как постоянное магнитное поле сильно
отличается от резонансного. За порогом поглощение существенно
возрастает вследствие параметрического возбуждения спиновых волн.
Меньшими уровнями пороговой входной мощности обладают
ограничители, использующие переизлучение мощности ферритовым
образцом при ферромагнитном резонансе в «ортогональный»
(развязанный в отсутствие образца или вдали от резонанса) канал.
Такое устройство до порога представляет собой ферритовый фильтр
(см. § 5.4). Его работа в качестве ограничителя основана на
рассмотренном выше «замораживании» амплитуды однородного ко-
316
1*АВ
Рис. 10.26. Конструкция (схематически) и характеристики подавителя слабых
сигналов, использующего поверхностную магнитостатическую волну [222].
1—пленка ЖИГ толщиной 26,6 мкм, 2—подложка из гадолиний-галлиевого
граната (ГГГ), 3—подложка из АЬОз, 4—металлизация, #0=425 Э;
лебания накачки за порогом. Если при этом используется
параметрическое возбуждение первого порядка, то пороговая входная
мощность такого фильтра-ограничителя составляет единицы микроватт,
а динамический диапазон—20-^40 дБ. Однако параметрический
процесс первого порядка при резонансе или при возбуждении маг-
нитостатической волны (см., например, рис. 10.14) возможен лишь
при достаточно низких частотах, для ЖИГ—ниже 3-н5 ГГц. На
более высоких частотах для создания фильтров-ограничителей
приходится использовать процессы второго порядка. При этом пороговые
мощности существенно возрастают.
В § 5.4 отмечалось, что наряду с полосно-пропускающими фер-
ритовыми фильтрами могут быть осуществлены полосно-заграж-
дающие, простейшим вариантом которых является просто отрезок
волновода с ферритовым образцом в условиях ферромагнитного
резонанса. В широком динамическом диапазоне такое устройство
является подавителем слабых сигналов: потери сильного сигнала —
превышающего порог параметрического возбуждения — уменьшаются
с ростом его мощности вследствие того, что амплитуда однородной
намагниченности за порогом «замораживается». Порог является,
конечно, более низким, а замораживание—более эффективным для
процессов первого порядка.
Полоса частот ферритового подавителя слабых сигналов (или
шумоподавителя, как его иногда называют) может быть существенно
расширена при использовании не ферромагнитного резонансного
поглощения, а возбуждения магнитостатических волн в пленке (§ 6.2).
Используется обычно поверхностная волна и нестабильность первого
порядка. Подавитель слабых сигналов такого типа был предложен
Эдемом [222]; конструкция и характеристики его приведены на
рис. 10.26.
317
Глава 11
СПИН-СПИНОВАЯ РЕЛАКСАЦИЯ
§ 11.1. Процессы релаксации
в магнитоупорядоченных веществах
Диссипация энергии магнитных колебаний и волн учитывалась
в предыдущих главах лишь феноменологически. Теперь мы переходим
к изучению тех физических процессов процессов релаксации,
которыми она определяется. Этому будет посвящена данная глава,
а также в значительной мере главы 12, 13 и 14.
Процессами релаксации принято называть те процессы, которые
приближают систему к состоянию термодинамическою равновесия.
Если силы, которые вывели ее из такого состояния, прекратили
затем свое действие, то процессы релаксации будут приводить систему
в это состояние. Нас интересует случай, когда неравновесное состояние
системы заключается в наличии в ней колебаний какого-то одного
или нескольких типов с амплитудами, превышающими равновесный
уровень. Тогда после прекращения действия внешних сил, возбудивших
эти колебания, энергия, которая была передана ими системе, будет
перераспределяться между всеми собственными типами ее колебаний,
и их амплитуды достигнут (строго говоря, через бесконечное время)
величин, соответствующих термодинамическому равновесию.
Процессы релаксации будут определять в этом случае скорость убывания
неравновесных амплитуд колебаний.
Если же система находится под воздействием внешних сил,
непрерывно возбуждающих какие-либо типы собственных колебаний,
то несмотря на наличие процессов релаксации, термодинамическое
равновесие, конечно, не будет достигаться. Система будет находиться
в стационарном неравновесном состоянии, в котором амплитуды
возбуждаемых внешними силами колебаний, а также
других—наиболее сильно с ними связанных, будут значительно превышать
равновесные уровни. Процессы релаксации осуществляют в этом
случае непрерывный отток энергии от возбуждаемых внешними
силами колебаний. Ими определяются диссипативные характеристики
системы при вынужденных колебаниях—антиэрмитовы части
компонент тензора восприимчивости (§ 4.4).
Заметим, что диссипативные свойства системы, определяемые
процессами релаксации, тесно связаны с флуктуациями, которые
имеют место в ней при термодинамическом равновесии. Эта связь
первоначально была установлена Найквистом для электрических цепей:
Каллен и Уэлтон сформулировали флуктуационно-диссипационную
теорему, согласно которой (см., например, [134]) средний квадрат
318
флуктуации .повой величины (например, намагниченности)
пропорционален антиэрмитовой части соответствующей (в данном случае
магнитной) восприимчивости.
Виды процессов релаксации в ферромагнетике. Системой, которая
нас интересует, является магнитная система магнитоупорядоченного
вещества. Ее собственные колебания — это исследованные выше
однородные и неоднородные магнитные колебания и спиновые волны,
которым на корпускулярном языке соответствуют магноны.
Возбуждение этих колебаний и воли электромагнитным полем происходит
в результате элементарных процессов уничтожения фотонов и
рождения магнонов. Некоторые процессы релаксации приводят к
перераспределению энер1 ии внутри магнитной системы, т. е. к возбуждению
за счет первичных (возбужденных полем) колебаний системы других
типов ее колебаний. Такие процессы принято называть спин-спиновыми.
Спин-спиновые процессы релаксации подразделяются на
собственные— которые происходят и в идеальных кристаллах и процессы,
обусловленные неоднородны пиши (дефектами), которые можно
трактовать как рассеяние ма1нонов на дефектах.
Магнитная система Mai нитоупорядоченного кристалла не
изолирована, а связана с другими системами: решеткой, свободными
носителями заряда, ядерной магнитной системой. Поэтому существуют
процессы релаксации, которые обеспечивают передачу энергии из
магнитной системы в другие. В конечном счете энергия передается
обычно в решетку, приводя к ее пафеванию (на корпускулярном
языке — к рождению фононов), и поскольку образец всегда находится
в тепловом контакте с окружающими телами (термостатом)—к
передаче тепла в термостат. Все такие процессы, обеспечивающие
вытекание энергии из магнитной системы, называют часто спин-
решеточными, подразделяя их на прямые спин-решеточные процессы,
при которых происходит уничтожение магнонов и рождение фононов,
и косвенные—когда энергия передается из магнитной системы в
решетку через другие системы.
Понятия спин-спиновой и спин-решеточной релаксации были
введены сначала в теории парамагнитной релаксации [6]. Для
магнитоупорядоченных веществ, в которых собственные типы
колебаний являются коллективными, эти понятия существенно отличаются
от таковых в парамагнетиках. В частности, в парамагнетиках
релаксация продольной (относительно направления постоянного
магнитного поля) составляющей намагниченности обычно определяется
процессами спин-решеточной релаксации и является значительно более
медленной, чем релаксация поперечных составляющих, обусловленная
спин-спиновыми процессами. В магнитоупорядоченных веществах
скорости релаксации продольных и поперечных составляющих
намагниченности оказываются обычно одного порядка и определяются
как спин-спиновыми, так и спин-решеточными процессами [228].
Рассмотрим теперь, как происходит в результате действия процессов
релаксации перетекание энергии между системами ферромагнетика в
стационарном режиме. Пусть, например, электромагнитное поле
возбуждает некоторый тип колебаний, для определенности—однородный
319
Электромагнитное
поле
родности
к
*=0
к*0
Магнитная
система
Носители
заряда
Ионы
с сильной
спин-
орбитальной
связью
Решетка
Окружаю -
щие тела
(.^термостату^)
Рис. 11.1. Потоки энергии между системами магнитоупорядоченного вещества
(с k=0), а образец, кроме магнитной системы и решетки, содержит
свободные носители заряда и ионы с сильной спин-орбитальной
связью. Потоки энергии, которые возникают в этом случае внутри
магнитной системы и между системами, показаны на рис. 11.1.
Методы теоретического исследования релаксации. Процессы
релаксации в магнитоупорядоченных веществах впервые теоретически
исследовал Ахиезер [224]. С тех пор теории таких процессов было
посвящено огромное количество работ (см. монографии и обзоры
[319, 417, 346, 15, 69]). При этом наиболее широко использовались
два метода: связанных уравнений движения и вероятностей переходов.
Метод связанных уравнений движения основан на том, что
процессы релаксации обусловлены взаимодействием различных типов
колебаний. Это могут быть колебания магнитной системы—если
рассматриваются процессы спин-спиновой релаксации, или колебания
магнитной системы и решетки—в случае спин-решеточной релаксации.
В нулевом приближении уравнения движения для различных типов
колебаний не связаны, и их решения дают соответствующие
собственные колебания. Учет в следующих приближениях различных
взаимодействий приводит к тому, что уравнения становятся
связанными. В результате происходит передача энергии от одних типов
колебаний к другим, т. е. протекают процессы релаксации. Заметим,
что метод связанных уравнений движения использовался в гл. 10
для изучения параметрического возбуждения спиновых волн.
Метод вероятностей переходов основан на том, что процессы
релаксации представляют собой переходы системы из одного
состояния в другое, и мы можем применить для вычисления скоростей
этих переходов квантово-механическую нестационарную теорию
возмущений (см., например, [81]). Этот метод дает (что было проверено
во многих случаях) такие же результаты, как и метод связанных
уравнений движения.
Для анализа процессов релаксации в дальнейшем были применены
и более мощные теоретические методы, в частности, метод функций
320
Грина [201], метод Кубо [126] и другие. Мы будем использовать
только метод вероятностей переходов, как наиболее наглядный.
Остановимся на некоторых чертах этого метода.
Метод вероятностей переходов (или кинетических уравнений). Кван-
тово-механическая нестационарная теория возмущений в случае
возмущения, не зависящего от времени, дает число переходов в единицу
времени из состояния / в состояние т
25(е,-ет), (11.1)
где (т\Жр\1у—матричный элемент оператора энергии возмущения
Жр для перехода между состояниями / и т; е, и е„,—собственные
значения энергии системы в этих состояниях, а 5 (х)—дельта-функция
Дирака (1.84).
При рассмотрении процессов релаксации методом вероятностей
переходов следует перейти к представлению вторичного квантования
(§ 7.4), в котором состояния системы характеризуются числами
квазичастиц—элементарных возбуждений системы, а переходы из одного
состояния в другое заключаются в изменении этих чисел. В этом
представлении оператор энергии магнитной системы можно записать в виде
Ж=и0 + Ж2 + Жр, (11.2)
где Жг—квадратичный гамильтониан, который для случая
гейзенберговской модели подробно рассматривался в § 7.4, а Жр для этой
модели — сумма членов более высокого порядка, чем квадратичные
по операторам рождения и уничтожения спиновых волн ак+ и ак.
В идеальном кристалле оператор Жр (см., например. [346, 15])
имеет следующий вид":
■^Ш^.зэ^аз A(k1-k2-k3) +
1 2 3
+ 1111*1.234а.Й2+аз+Й4+А(к1-к2-кз-к4)+
12 3 4
+ 1111Ч>12.34Й1й2<5з+«4+Д(к1+к2-кз-к4) +
12 3 4
+члены более высоких порядков+ э. с. (11.3)
Здесь 4Y23, 4V234, ^12.34, •••—некоторые комплексные величины,
А(х)—дельта-символ (7.104); э. с. обозначает члены, эрмитово-со-
пряженные со всеми записанными, причем оператором, сопряженным
с ак, является ак и наоборот, а порядок следования операторов
при сопряжении изменяется на обратный. Подчеркнем, что появление
дельта-символов во всех членах гамильтониана (11.3) обусловлено
идеальностью—строгой периодичностью кристалла.
Каждый член гамильтониана (11.3) вносит вклад только
в один матричный элемент <т\Жр\1У, соответствующий переходу
" Здесь и в дальнейшем индексы 1, 2, 3, ... обозначают ки к2, к3, ...
21 А. Г. Гуревич, Г. А. Мелков 321
2л
Щт=-
<т\Жр\0
из состояния / в состояние т; при этом переходе увеличиваются
на 1 числа квазичастиц, операторы рождения которых входят
в данный член, и уменьшаются на 1 числа квазичастиц, операторы
уничтожения которых входят в него. Например, член с аха2а3
дает матричный элемент перехода, при котором число nt уменьшается,
а числа п2 и п3 увеличиваются на 1. Этот матричный элемент
имеет следующий вид [81]:
<«!-l, и2+1, п3+1\Жр\пи п2, п3} =
= Jnl{n2+l){n3 + l)4>l.23A(kl-k2-k3). (11.4)
Член гамильтониана, эрмитово-сопряженный с рассмотренным, даст
матричный элемент
<«1+1, «2-1, П3-\\Жр\П1, П2, П3} =
= ч/("1 + 1)"2«з,1'*1.2зА(к1-к2-кз). (11.5)
Член гамильтониана с ахС/2а3а£ даст матричный элемент
<«1-1, «2-1- Из+1, ПА.+ \\Жр\п1, П2, И3, ПЛ} =
= ^п1п2(п3+1){пл+\)Ч112_злА(к1+к2-к3-кл). (11.6)
Использование нестационарной теории возмущений в
представлении вторичного квантования дает обоснование возможности сведения
процессов релаксации в магнитной системе магнитоупорядоченных
веществ к элементарным процессам рождения и уничтожения маг-
нонов. Каждому члену гамильтониана возмущений Жр (и,
следовательно, относящемуся к нему матричному элементу) соответствует
определенный элементарный процесс, а эрмитово-сопряженному с ним
члену—элементарный процесс, обратный по отношению к данному.
Так, например, члену гамильтониана аха2 а3 и матричному элементу
(11.4) соответствует элементарный процесс расщепления одного маг-
нона на два, а члену гамильтониана a3a2at—элементарный процесс
слияния двух магнонов в один. Члену гамильтониана aia2a3a£
и матричному элементу (11.6) соответствует элементарный процесс
рассеяния, при котором два магнона уничтожаются и два рождаются.
Все эти элементарные процессы рассматривались уже в гл. 10 (см.,
например, рис. 10.22).
Наличие дельта-функции в формуле (11.1) приводит к сохранению
энергии, а наличие дельта-символов в (11.3) или (11.4)—(11.6)—к
сохранению импульса при каждом элементарном процессе. Причем,
в отличие от сохранения энергии, сохранение импульса является
следствием идеальности кристалла и не имеет места (при каждом
элементарном процессе) для таких возмущений, которые эту
идеальность нарушают.
При изучении процессов релаксации нас прежде всего интересуют
скорости изменения чисел квазичастиц какого-то одного сорта—с
заданными ех и kl5 обусловленные элементарными процессами
определенного типа. Для того чтобы найти их, следует просуммировать
322
вероятности (11.1) элементарных процессов такого типа по всем
допустимым значениям k2,k3... всех других участвующих в этих
процессах квазичастиц. При этом необходимо учитывать как прямые
элементарные процессы, при которых интересующие нас квазичастицы
уничтожаются, так и обратные, при которых они рождаются. Тогда
получаются выражения такого вида:
^i=TlI-t-|<w'l^pl/'>|2+l<w"l^|/">|2]6(e'-e'»)' (11Л)
at ъ 2 3
где /' и т' обозначают соответственно начальное и конечное состояния
для прямых процессов, а /" и т" для обратных. Выражение (11.7)
носит название кинетического уравнения для числа и15 а его правую
часть называют суммой или (если от суммирования по значениям
k2,k3, ... перейти к интегрированию по соответствующим к-простран-
ствам) интегралом столкновений.
Наличие дельта-функции в (11.7) и дельта-символов в выражениях
для матричных элементов ограничивает области k-пространств, по
которым фактически (после исключения дельта-функций и дельта-
символов) будет производиться интегрирование. Так, например, в случае
трехчастичных процессов наличие одного скалярного и одного
векторного условий приводит к тому, что интегрирование будет
производиться по некоторой поверхности в одном из пространств к2 или к3.
В правую часть уравнения (11.7) войдут не только nls но и числа
п2,п3, ... других квазичастиц. Эти числа, в свою очередь, зависят от
скоростей всех процессов, в которых участвуют соответствующие
квазичастицы; для них также могут быть записаны кинетические
уравнения, содержащие в правых частях суммы интегралов
столкновений для процессов различных типов. Мы приходим, таким образом,
к цепочке все усложняющихся связанных кинетических уравнений.
Задача существенно упрощается, если предположить, что все
числа п2,п3,..., кроме пх, мало отличаются от их равновесных
значений п2, п3, ...". Величины п2, п3, ... (как и равновесное значение
«i) могут быть легко найдены при данной температуре, если известна
статистика квазичастиц. Магноны, как отмечалось в § 7.3 и 7.4,
являются, во всяком случае приближенно, бозе-частицами, и для
равновесных значений их чисел справедливо выражение (7.78). Теперь
кинетическое уравнение (11.7) будет содержи гь только одну
неизвестную величину их. Как мы убедимся в дальнейшем на ряде примеров,
его можно будет представить в виде
^-=-2сог1(и,-й1), (11.8)
at
где сог1 не зависит от И]. Величина 2cori представляет собой частоту
релаксации числа квазичастиц их к равновесному значению
" Это предположение, как уже отмечалось в § 10.5, справедливо лишь
при малых числах релаксирующих магнонов, оно выполняется в теории
линейного затухания, которая рассматривается в этой главе.
21*
323
п, в результате протекания элементарных процессов рассматриваемого
типа. Обратную величину xri = l/(2corl) можно назвать временем
релаксации для процессов этого типа. Поскольку числа магнонов
(§ 7.3) пропорциональны квадратам амплитуд переменной
намагниченности, частотой релаксации этих амплитуд будет являться
величина сог1. Она представляет собой вклад рассмотренного при
ее вычислении процесса в феноменологический параметр диссипации
сог (§ 1.4). Причем в рамках метода вероятностей переходов,
являющегося методом возмущений, вклады различных процессов
аддитивны.
Эксперимент непосредственно дает лишь суммарный параметр
диссипации сог. Заключение о вкладах в него тех или иных процессов
можно сделать, сравнивая температурные и иные зависимости этого
параметра с теоретическими, а его величину—с теоретическими
оценками. Это является обычно нелегкой задачей, так как в маг-
нитоупорядоченных веществах вклады различных процессов
релаксации, как правило, бывают сравнимы по величине. Тогда ее решение
оказывается возможным только после проведения специальных
экспериментов, при которых стимулируются те или иные процессы
релаксации.
§ 11.2. Собственные процессы спин-спиновой релаксации
Перейдем теперь к рассмотрению собственных (происходящих
и в идеальном кристалле) процессов спин-спиновой релаксации
магнитных колебаний и волн в ферромагнетике. Эти процессы
обусловлены элементарными процессами с участием трех, четырех
и более магнонов. Вероятности таких процессов, вообще говоря,
тем больше, чем меньшее число частиц в них участвует. Однако
трехмагнонные процессы не могут быть вызваны самым сильным —
обменным взаимодействием, так как для них число магнонов и,
следовательно, согласно (7.72) величина М, не сохраняются; оператор
же энергии обменного взаимодействия коммутирует с оператором
Мг, и среднее его значение Мг должно сохраняться при процессах,
обусловленных этим взаимодействием. Обменное взаимодействие не
может также явиться причиной четырехмагнонных процессов слияния
и расщепления. Лишь четырехмагнонный процесс рассеяния, при
котором число магнонов сохраняется, может быть обусловлен этим
взаимодействием. Интенсивность его может оказаться сравнимой
с интенсивностью трехмагнонных процессов, вызванных, например,
диполь-дипольным взаимодействием.
Трехмагнонные процессы релаксации впервые были теоретически
исследованы Ахиезером в уже упоминавшейся работе [224]. Затем
их изучали Каганов и Цукерник [99], Ахиезер, Барьяхтар и Пелет-
минский (см. [15]), Спаркс, Лудон и Киттель [419], Шлёманн [400]
и многие другие.
Как показано в [224], входящая в выражения (11.4) и (11.5)
амплитуда 4,li23, обусловленная диполь-дипольным взаимодействием,
в длинноволновом приближении {ka<sz.\, где а—постоянная решетки)
324
и без учета третьего преобразования Холстейна — Примакова (§ 7.4)
имеет следующий вид:
4,i,23=-^v/A/o/(2J/)(7/i);)'2(sin2e2e-'^ + sin2e3e-i*3), (Ц.9)
где V—объем образца (который в дальнейшем сократится),
a 62,3 и ф2.з—углы векторов к2 и к3.
Следует различать два вида трехмагнонных процессов релаксации:
процесс расщепления и процесс слияния. В основе их (см. табл. 11.1)
лежат одни и те же элементарные процессы. Но для процесса расщепления
прямыми элементарными процессами (ведущими к уменьшению числа
магнонов, релаксация которых рассматривается) являются процессы
расщепления, а обратными—элементарные процессы слияния. Для
процесса же слияния, наоборот, прямыми элементарными процессами
являются процессы слияния, а обратными—процессы расщепления. Это
различие после суммирования по к2 и к3 приведет, как мы увидим, к
разным областям существования обоих процессов и разным зависимостям
их вкладов в параметр диссипации от частоты и волнового числа к\.
Таблица 11.1
Элементарные процессы, лежащие в основе трехмагнонных процессов
релаксации
Процесс
релаксации
Расщепления
Слияния
Элементарные процессы
прямые
Skz
><5
^^
уЛ, *з
обратные
^^
/*г
—<"'
N^2
Жирными стрелками обозначены магноны, релаксация которых рассматривается.
Процесс расщепления. Для него скорость изменения числа
интересующих нас магнонов, обусловленная как прямыми, так и
обратными элементарными процессами, запишется согласно (11.7)
следующим образом:
^=Y ^1П-К"1-1. "2+1, Из+ЦЛ*3*|И1. "2, «3>|2 +
+ |<И1 + 1, Иа-1, пъ-\\ЖЗЛ\пи пг, и3>|2]8(Лсо1-Лсо2-Лсо3); (11.10)
множитель 1/2 перед суммой введен потому, что одинаковые в
действительности состояния \щ, п2, и3> и |«i, и3, и2> при суммировании
325
будут считаться дважды. Входящие в (11.10) матричные элементы
будут иметь вид, подобный (11.4) и (11.5), но с заменой ЧЧгз на
сумму ОРигз + ЧЧ.згХ поскольку вклады в эти матричные элементы
вносят члены гамильтониана uid2a3 и йуа3а2—для прямых
процессов или аъагаХ и а2а3а?—для обратных. И так как Ч,1,2з = Ч,1,зг.
кинетическое уравнение для процесса расщепления (11.10) запишется
следующим образом:
^L=-flIl*1.23|2[«l("2+«3+l)-«2«3]A(k1-k2-k3)X
xS^COj— ЙС02 — П(й3). (НИ)
Примем теперь, что числа п2 и п3 не отличаются от их
равновесных значений п2 и п3. Выражение (11.11) будет справедливо
и при п1=п1, но тогда, конечно, dnt/dt=0. Учитывая это, мы
убеждаемся, что (1111) можно записать в виде (11.8), и частота
релаксации
с°п=^Ц|,1'1.2з12(«2 + йз+1)А(к1-к2-кз)8(Йсо1-Йсо2-Йсоз)-(П.12)
"23
Наличие в этом выражении множителя A(ki— k2 — к3) означает, что,
поскольку кх задано, к3 однозначно связано с к2. Следовательно,
суммирование должно фактически проводиться по значениям одного
из этих векторов, например, по к2, а соотношение k3 = kx—к2 должно
учитываться при записи Ч^.гз и дельта-функции.
От суммирования по значениям к2 можно перейти к
интегрированию по к2-пространству так же, как при вычислении намагниченности
в § 7.3. Тогда, принимая во внимание следующее свойство дельта-
функции (С—постоянная величина) [81]:
8(Сх) = (1/С)8(х), (1МЗ)
получим
п 2п
{t0rl)3s=(2^J J J 1,р1.2з|2(«2 + «з + 1)б(со1-со2-соз)х
к2 е2=о р2=о
xkjsmQ2dk2dQ2d(p2, (11.14)
где 62 и ф2—углы вектора к2, а пределы интегрирования по
к2 определяются законами сохранения энергии и импульса.
Наличие дельта-функции в (11.14) приводит к тому, что
интегрирование проводится фактически по некоторой поверхности в к2-простран-
стве. При вычислениях обычно оказывается целесообразным от дельта-
функции разности частот перейти к дельта-функции одной из координат
в к2-пространстве, например, 62, используя формулу [81 ]
8[/(*)-/(*о)] =
дх
-1
6(*-*о), (11.15)
326
а затем исключить интегрирование по этой координате с помощью
соотношения:
\ f{x)b(x—x0)dx=f(x0), если х1<х0<х2. (11.16)
xi
Вычисления по формулам типа (11.14), вообще говоря, требуют
применения ЭВМ, приближенные аналитические выражения удается
получить лишь в некоторых частных случаях. При этом часто
используется высокотемпературное приближение, когда
хГ» Л©!, Лсо2. Йсо3- (П-17)
В этом приближении й2.з-к77(Йсо2>3) и (11.14) для процесса
расщепления, обусловленного диполь-дипольным взаимодействием, с
учетом (11.9) принимает вид
п 2п
(ЛЯ^^У^со^ | | Ы2(И1_И2)
2ы" ' 2 -г *, Г Г Г |sin2e2e-,'»2+sin2e3e-i'"|2
*, е2=о фг = о
хб^ — со2 — (d3)klsmQ2dk2dB2d(p2. (11.18)
Для процесса расщепления заданная частота coi является наибольшей,
и условие (11.17) сводится к хГ^Йсох, что для диапазона СВЧ
выполняется даже при температуре жидкого гелия.
Иногда используется высокочастотное приближение
coj, со2, со3, — » сом = у4лА/0. (1119)
Оно позволяет пренебречь третьим преобразованием Хольштейна —
Примакова (что уже было сделано при записи (11.18), а также
принять для спектра спиновых волн приближенное выражение (7.14)
или даже более грубое соотношение со = сон + г1^2.
Остановимся на некоторых частных случаях. Для однородной
прецессии (fc1=0, co1sco0) из условий сохранения импульса и энергии
к3 = — к2 и со3 = ю2 — <*>0/2. Последнее соотношение может быть
выполнено только в том случае, когда со0/2 лежит выше нижней границы
спектра спиновых волн. Условием этого для эллипсоида вращения,
как легко убедиться, является
co0<2y^j.M0, (11.20)
где N±— размагничивающий фактор в направлении, перпендикулярном
оси вращения. Для сферы со0<(2/3)сом, что совпадает с условием
(6.10) перехода со0 через верхнюю границу безобменного спектра
спиновых волн.
Простое выражение для вклада процесса расщепления в параметр
диссипации однородной прецессии в сфере может быть получено
(при некоторых дополнительных допущениях) лишь в высокочастотном
приближении (11.19). Поскольку это приближение плохо совместимо
с условием (11.20), такое выражение [69] может быть использовано
лишь для грубых оценок. Для ЖИГ при комнатной температуре
л частоте 2,5 Ггц эта оценка дает (ДЯ)35~0,03 Э.
327
Расщепление я/2-магнонов. Основным методом экспериментального
исследования процессов релаксации спиновых волн служит измерение
порогов их параметрического возбуждения (гл. 10), особенно при
продольной накачке. В этом случае, изменяя постоянное магнитное
поле, можно, как отмечалось в § 10.3, изменять к возбуждаемых
волн с 6* = л/2 и частотой со!=сор/2 (где сор—частота накачки).
Рассмотрим вклад процесса расщепления в затухание таких волн.
Как показали Лямер, Ле Галль и Дорман [357] (см. также [314]), при
6i = rc/2 имеются две области значений C0i и Н0 или coi и кх (рис. 11.2),
в которых процесс расщепления разрешен законами сохранения. Верхняя
граница первой области со, при к^ -*0 стремится к величине со/0 = (2/3)сом.
При co!<coi0 процесс расщепления разрешен в первой области
в интервале значений к от нуля до некоторой величины kt (рис. 11.2).
Расчет показывает, что, например, для ЕиО при температуре 4,2 К
и частоте накачки 36 ГГц £, = 2,05 ■ 106. Магноны, образующиеся в этой
области, характеризуются малыми значениями 62,з (рис. 11.2,6).
Рис. 11.2. Трехмагнонный процесс расщепления магнонов с 6* = я/2 в сфере
[314]; а—области существования, б и в—частоты и волновые числа магнонов
соответственно в / и // областях (вблизи их границ к, и кц)
Для вклада процесса расщепления я/2-магнонов в первой области
в высокотемпературном приближении при малых kt Шлёманн [400]
получил
{АН^и^кТМУ2 D-3* Ffalau), (11.21)
328
лнк,з
4 8 12 к,Г05см
Рис. 11.3. Вклады собственных спин-спиновых процессов релаксации в параметр
диссипации спиновых во.ш с 6* = я/2 [419]. ЖИГ при комнатной температуре,
/70=1,5кЭ, частота Wi изменяется при изменении kt
где F(coi/coM)—безразмерная функция, обращающаяся в нуль при
со1=(2/3)сом. Если СО! близко к (2/3) сом, то F= 3,47 (2/3 -coi/coM)5/2.
Вторая область, в которой разрешен процесс расщепления, как
видно из рис. 11.2, существует при любых частотах, но в очень
узких пределах кх: от некоторой величины кц до предельного значения
/fc, которое (см. §7.1) определяется обращением Н0 в нуль, т.е.
фактически — возникновением доменов (мы все время пренебрегаем
кристаллографической анизотропией). Магноны, образующиеся в
результате расщепления я/2-магнонов в этой области, характеризуются
значениями 623, разными или близкими к я/2 (рис. 11.2, в). Если
учесть, что на границе области всегда со2 = со3, и принять 62~63^л/2,
то из условия со1=2со2 следует
Tlk^iy/Aai+ah-y/al+ajt)- 01-22)
Для рассмотренного выше примера (ЕиО при 4,2 К
и /р = оу(2я) = 36 ГГц) А:,, = 4,02-106, а А:с=4,06-106. Для ЖИГ при
комнатной температуре и /р = 9 ГГц £ц =4.06-10s, a fcc = 4,28-105.
Вклад процесса расщепления в параметр диссипации я/2-магнонов во
второй области, рассчитанный в высокотемпературном и
высокочастотном приближениях при фиксированном значении И0 и изменяющейся
частоте, приведен на рис. 11.3. Заметим, что в экспериментах по
продольной накачке (§ 10.3) осуществляется обычно другой случай: cox = const,
а А, изменяется при изменении Н0 [150]. При этом, как видно из
рис. 11.2, процесс расщепления тоже «включается» при некотором ки
но, в отличие от рис. 11.3, область его существования является узкой.
Процесс слияния. Для трехчастичного пропесса слияния (см.
табл. 11.1) кинетическое уравнение имеет вид
~ = ЧЪ П-10Ч-1. "2-1, П3 + \\ЖЪй\Пх, «2, «3>|2 +
+ K"i + 1, «2 + 1- из- 11-^заК. «2. Из>|2]8(Л(°1 + Йсо2- Тио3). (11.23)
В этом выражении, в отличие от (11.10), отсутствует множитель 1/2,
так как состояния \п1,п2,п3у и |иь п3, и2> теперь не эквивалентны.
329
Записывая матричные элемешы в (11.23) аналогично (11.4) и (11.5)
и заменяя числа п2 и п3 их равновесными значениями, получим
(сог1)зс=^Ц|,1'з..21г(Й2-йз)А(к1+к2-кз)8(Йсй1+Йсо2-Йсоз). (П.24)
"23
Наличие Д-индекса в этом выражении, как и в (11.11), приводит
к тому, что суммирование фактически проводится только по значениям
к2 или к3. Переходя так же, как и в случае расщепления, к
интегрированию, например, по к2-просгранству, получим
п 2л
Ki)3c = ^r^ 14*3.1212(й2-й3) 8 (coj+coa-eojjx
*2 6, = 0 ф2 = 0
xklsmB2dk2dQ2d(p2, (П-25)
где пределы интегрирования по к2 определяются законами сохранения.
Для процесса, обусловленного диполь-дипольным взаимодействием,
Чзл2 имеет вид, аналогичный (11.9).
В высокотемпературном приближении (11.17), как и для процесса
расщепления, частота релаксации (сог1)3с оказывается
пропорциональной температуре. Однако для процесса слияния условия
справедливости этого приближения становятся очень жесткими, так
как теперь со3 всегда больше, а со2 также может быть больше,
чем coi, и выполнение условия (11.17) для рассматриваемых магнонов
отнюдь не гарантирует его выполнения для всех магнонов,
участвующих в релаксации. В другом предельном случае—низких
температур—зависимость (сог1)3с от Т будет экспоненциальной, в то
время как для процесса расщепления в этом предельном случае
(corl)3s не зависит от Т (рис. 11.4). Такое различие объясняется
тем, что для процесса слияния необходимы тепловые магноны
с со2 и к2, число которых убывает с
понижением температуры.
Условия сохранения энергии и импульса
для процесса слияния не могут выполняться
при ki = 0, так что для однородной прецессии
этот процесс релаксации «не работает». Не
работает он и при малых к\, когда для
выполнения законов сохранения
кг и к3 должны быть большими; вследствие
же дискретности структуры ферромагнетика
их величины (см. § 7.4) ограничены
размерами первой зоны Бриллюэна. Рассмотрим
Рис. 11.4. Температурные Д™ определенности простую кубическую ре-
зависимости вкладов шетку и, поскольку к2 и к3 велики, пренеб-
трехмагнонных процессов режем в выражении (7.110) для
со2 и со3 зеемановскими членами. Тогда,
учитывая, что со!«:со23, и принимая во
внимание соотношение (7.113), получим из
расщепления (3s) и ели
яния (Зс) в параметр
диссипации спиновых волн
(схема шчески)
330
законов сохранения
<u1~(2r)l'a)(klxsmk2xa + klysink2ya+k1:sink2-a), (11.26)
где я — постоянная решетки. Отсюда видно, что при данном
coi процесс слияния «включается» при некотором конечном kl=klm,„.
Для оценки примем, что kix = ki, a kiy — klz = 0. Тогда
Л1пйп = ю1о/(2л). (П-27)
Для других направлений kt, а также для других решеток в этом
выражении появится множитель порядка 1. Для ЖИГ
(рассматриваемого как ферромагнетик с постоянной решетки, равной среднему
расстоянию между ионами железа) при /,=4,5 ГГц A.lmin= 1.5 ■ К)4.
Эта величина близка к минимальному к волн, возбуждаемых при
продольной накачке (§ 10.3). Однако для веществ с меньшими
значениями ц, например ЕиО. и при более высоких частотах величины
klmin будут значительно большими.
Вклад процесса слияния в параметр диссипации спиновых волн
был рассчитан в 1419] в высокотемпературном и высокочастотном
приближениях. Оказалось, что при б^л/2 и малых (но. конечно,
превосходящих kimi„) величинах ki
{AHk)3c = 2((atl)3Jy = nyAf0nTk1l{2Dfa1). (11.28)
Оценка по этой формуле для сферы ЖИГ при комнатной температуре,
частоте накачки 9 ГГц и /С] = 105 дает (АНк)3с = 0,2 Э.
Для произвольных kt угловой множитель в (11.9) был заменен
[419] постоянной величиной, выбранной таким образом, чтобы
получить (11.28) при малых /с,. Результат такого расчета приведен
на рис. 11.3.
Все трехмагнонные процессы релаксации приводят к изменению
полного числа магнонов и поэтому согласно (7.72) могут участвовать
в релаксации М,. Согласно (7.75) при трехмагнонных процессах
происходит изменение и длины вектора М. и строго говоря, при
наличии таких процессов использование уравнений движения (1.66)
или (1.67) с диссипативными членами, обеспечивающими сохранение
|М|, недопустимо. Однако при малых амплитудах колебаний и малой
диссипации различные формы записи диссипативного члена
приблизительно эквивалентны, и при этих условиях уравнения (1.66) и (1.67)
обычно используются и в тех случаях, когда трехмагнонные процессы
вносят вклад в диссипацию.
Четырехмагионный обменный процесс рассеяния. Кинетическое
уравнение для четырехчастичных процессов рассеяния с учетом (11.6)
будет имегь вид
^i = ¥ilII|lP12.3i + *12.43 + 4'21.34 + 4'21.43|2[(«1+l)(«2+l)«3«4-
dl h 2 2 з 4
-и1и2(и3+1)(й4+1)]А(к1 + к2-к3-к4)8(Йсо1 + Ло)2-Лш3- Йсо4). (11.29)
Множитель 1/2 перед суммой, как и в (11.10), введен потому,
что одинаковые состояния \пг. п2, п3, и4> и |и,, «,, п4, н3> при
суммировании учитываются дважды. Принимая для п2, «з и пл их
равновесные значения, мы убеждаемся, что и в данном случае
кинетическое уравнение приобретает вид (11.8) и с учетом (11.13)
К1)4к=Г^1Ц|1'|2[''2(йэ+Й«+1)-ЙзЙ4]х
1" 2 3 4
xA(ki+k2—k3—k4)6(t0i+co2— w3—w4), (11.30)
где Ч^Ч'.^ + Ч'^з + Ч^^ + Ч^.дз.
Наличие Д-символа в (11.30) позволяет исключить суммирование
по одному из волновых векторов, например, по к4. Переходя затем
к интегрированию по к2- и к3-пространствам, получим
V2h2 С С
Kl)4,c=^ [Й2(Йз+Й4+1)-ЙзЯ4]|Ч'|2Х
kjk> хб^+Юг-сОз-со^кгЛз. (11.31)
В высокотемпературном приближении (11.17) для бозе-частид
«статистический» множитель в (11.31) принимает вид
Й2(йз+Й4+1)-й3Й4 = (кГ/й)2со1/(ю2а>зС04) (11.32)
и параметр диссипации оказывается пропорциональным Т2. Но, как
и для трехчастичного процесса слияния, условия йсо1«*:х7' отнюдь
недостаточно для того, чтобы было справедливо это приближение.
Для длинноволновых магнонов (ka<s:l) в высокочастотном
приближении, когда для всех магнонов можно принять co = coH + T)fc2,
согласно [99] (см. также [346])
|T|=JD(Y/!)2/(Mo^(k1k2+k3k4). (11.33)
Можно убедиться, что в этом приближении с учетом законов
сохранения энергии и импульса k1k2 = k3k4, и
|¥| = 2£>(7Й)2/(МоИ^2С08ф12, (11.34)
где ф12—угол между к2 и заданным вектором кх. После подстановки
(11.34) в (11.31) величина к2 может быть вынесена за знаки интегралов.
И хотя множителем к\ не будет исчерпываться зависимость (corl)4SC
от ки его наличие приведет к сильному возрастанию вклада
рассматриваемого четырехмагнонного процесса с ростом fct. Этот
вклад стремится к нулю при ki-*Q.
Вклад процесса четырехмагнонного обменного рассеяния в
затухание спиновых волн был впервые рассчитан Дайсоном [289] для
низких температур (нТ^ТкаС) и бесщелевого спектра спиновых волн
т. е. в отсутствие внешнего постоянного поля и без учета диполь-
дипольного взаимодействия. Этот вклад оказался пропорциональным
к\Т*12. Для более высоких температур
им, <*T<z.vlTc (11.35)
(где Тс—температура Кюри) Кащеев и Кривоглаз [108], приняв
такой же бесщелевой спектр, получили, что
(^i)^ = Afaik\T2Fu (11-36)
ззг
где А — постоянная величина,
F^hripta^KT)], (11.37)
а Е,—множитель порядка 1. Четырехмагнонный процесс релаксации
при наличии внешнего поля исследовали еще в 1958 г. Каганов
и Цукерник [99]. но выражения для параметра диссипации волны
с данными со, и А, в этой работе приведено не было ". Такое
выражение получили (без учета диполь-дипольного взаимодействия)
Вакс, Ларкин и Пикин [40] и Уонг [447]. Для интервала температур
(11.35) оно может быть представлено в виде
(ДЯ,)4,С= J^-(^)V2, (11.38)
v ' 48тг3 7 \M0DJ
где F2 — множитель, зависящий от со,. А-, и Т. В [40] было приведено
приближенное выражение для него, совпадающее (при £, = 2) с (11.37),
но справедливое и при наличии внешнего поля. Вычисление F2 [7]
по формулам, полученным в [447], показало, что при заданной
частоте to, и yDk2< 0,1 со, множитель F2 мало зависит mfc, и близок
к (11.37) при £ = 2. При больших А, он возрастает и зависимость
(Д#к)45с от к1 становится более сильной, чем квадратичная.
Множитель F2 растет также с ростом Т, вследствие чего температурная
»ависимость {АНк)Лвс является более сильной, чем Т2.
Рассмотренный четырехмагнонный процесс играет большую роль
и релаксации вторичных магнонов (с к2 и к3 для трехмагнонного
расщепления, с к3— для слияния и с к3 и к4—для четырехмагнонного
рассеяния), а также магнонов следующих «поколений», т. е. в
растекании энергии неравновесных магнонов по спин-волновому спектру.
Ниже мы увидим, что роль четырехма! ионного процесса рассеяния
может быть велика и на первом этапе релаксации.
Собственные процессы при ki->0. Из рассмотренных выше
процессов релаксации только процесс трехмагнонного расщепления при
достаточно низких частотах (для я/2-магнонов — при ш<(2/3)сом) дает
вклад, не исчезающий при /с,->0. В то же время как ширина линии
однородного резонанса Д//0, гак и параметр диссипации спиновых
волн, экстраполированный к А;х = 0 (Д//*_0)> не могут быть
обусловлены только влиянием неоднородностеи, а должны существовать
собственные (присущие идеальному кристаллу) процессы,
«работающие» при A-J-+0 и любых частотах. Первая попытка решения этой
проблемы была сделана Касуйя и Ле Кроу [345]. Они учли, что
условия сохранения энергии и импульса могут выполняться и при
А-!-*0 для трехмагнонных процессов слияния, но при условии, что
второй и третий магноны принадлежат верхним (обменным) ветвям
спин-волнового спектра ферримагнетика. Оценка вклада такого
процесса, проведенная в работе Колоколова. Львова и Черепанова [115]
на основе рассчитанного ими [114] реального спектра спиновых
волн в 20-подрешеточном ферримагнетике, каким является ЖИГ,
'» Как и для трехмагнонных процессов, в [99] вычислялась лишь скорость
релаксации, усредненная по всему равновесному распределению спиновых волн.
333
показала, что этот процесс может дать существенную часть
наблюдаемых величин АН0 и АНк^0. Заметим, что возможны и другие
трехчастичные процессы, вклады которых не исчезают при /г-»0 —
процессы слияния магнонов с фоионими верхних (оптических) ветвей1'.
Все эти процессы слияния с участием магнонов или фононов
оптических ветвей называют процессами типа Касуйя —Ле Кроу.
Некоторую роль в релаксации ма1нонов с к = 0 могут играть
и четырехмагнонные процессы слияния и расщепления, обусловленные
диполь-дипольным взаимодействием [15]. Однако величины их
вкладов, по-видимому, меньше, чем упомянутых выше процессов.
Сравнение с экспериментом. Большинство экспериментальных
работ, ставивших своей целью исследование собственных процессов
релаксации, было выпоанено на монокристаллах ЖИГ. обладающих
наиболее узкой резонансной кривой из всех известных в настоящее
время магнитоупорядоченных веществ. Сравнение результатов этих
работ с теорией осложняется, конечно, тем обстоятельством, что
ЖИГ является ферримагнетиком, в то время как большинство
теоретических работ и, в частности, все упоминавшиеся выше, кроме
[345, 115], используют ферромагнитную модель.
Остановимся прежде всего на ширине линии однородного
ферромагнитного резонанса. Ее минимальные значения в монокристаллах
ЖИГ составляют 0,2 — 0,3 Э. Вклад собственных процессов в эти
величины пока неясен, вряд ли он превышает 0,1 Э. Этот вклад
должен возрастать, когда при понижении частоты происходит
«включение» процесса трехмагнонного расщепления, обусловленное переходом
со0/2 через нижнюю границу спектра спиновых волн. Однако
экспериментального подтверждения этого пока не получено, потому
что в сферах (с которыми проводились эксперименты) одновременно
с переходом со0/2 через нижнюю границу спектра спиновых волн
со0 переходит через верхнюю границу безобменного спектра. Вследствие
этого полностью или частично «выключаются» (см. § 11.3) двухмаг-
нонные процессы релаксации, что маскирует включение процесса
трехмагнонпою расщепления.
В тех случаях, когда такого совпадения нет. вклад трехмагнонных
процессов удается обнаружить. Например, частоты cos поверхностных
магнитостатических волн (§ 6.2) всегда лежат выше верхней границы
безобменного спектра (6.6) спиновых воли в «безграничной среде»
(т. е. волн с такими к, для которых влияние граничных условий
уже несущественно). Величина же cos/2, как следует из (6.54) и (6.6),
лежит внутри этого спектра лишь в некотором интервале
частот, положение которого зависит от волнового числа A"s
магнитостатической волны. На рис. 11.5 приведены частотные
зависимости параметра диссипации AHS поверхностной
магнитостатической волны. Положения «горбов» AHS на этом рисунке
соответствуют расчетным границам области, в которой ioJ2 находится
в безобменном спектре спиновых волн. Оценка вклада трехмагнонного
' Они относятся к процессам спин-решеточной релаксации и будут
рассмотрены в гл. 12.
334
4"в,Э
0,8
0.6
0,4
0.Z
к =200 50D
в*°« °>о*-<
2 4 6 8 Гь,ГГц
Рис. 11.5. Частотные зависимости параметра диссипации поверхностной
магнитостатической волны в касательно намагниченной пленке ЖИГ [80].
Толщина пленки 7,2 мкм. Точки—эксперимент, штриховые линии—расчет
вклада трехмагнонного процесса расщепления
А"к-е,Э
расщепления в этом случае [80] дает величины, согласующиеся
с экспериментом.
Двухмагнонные процессы, как отмечалось в § 10.3, оказывают
меньшее влияние на порог параметрического возбуждения спиновых
волн при продольной накачке, чем на релаксацию линейных колебаний.
Поэтому на частотных зависимостях АНк_0, полученных из измерений
порога параметрического возбуждения в сферах, можно наблюдать
подъемы, вызванные включением
трехмагнонного процесса
расщепления. Таким включением
обусловлен излом кривой при
со=(2/3)сом на рис. 11.6. Значения
же Д//*_0 при со>(2/3)сом могут
быть обусловлены
упоминавшимися выше трехбозонными
процессами Касуйя—Ле Кроу; в
пользу этого свидетельствуют
температурные зависимости АНк^0,
которые оказываются близкими
к линейным при достаточно
высоких температурах (см. [417]).
При кфО вклады в параметр
диссипации спиновых волн и,
в частности, волн с вк = п[2,
возбуждаемых параметрически при
продольной накачке, будут вно-
< 6 Г,ГГц
ТУ "о
Рис. 11.6. Частотная зависимость
параметра диссипации спиновых волн
с к->0 и 6*=я/2, полученная методом
параметрического возбуждения при
продольной накачке [417]. Сфера
ЖИГ, комнатная температура
335
сить рассмотренные выше трехмагнонные дипольные процессы Зс
и 3s и четырехмагнонный обменный процесс 4sc. Для сравнения
с предсказаниями теории необходимо выделить вклады этих процессов
из экспериментальной зависимости АИк(к), которая (см. § 10.3)
получается из измерений порогового поля при продольной накачке.
Это было выполнено [7] при допущении, что вклад процессов,
определяющих Д/Д_0, от к не зависит и, таким образом, величина
(Д//* —Д/4_о) представляет собой суммарный вклад процессов Зс,
3 s и 4sc. Такое допущение представляется правдоподобным для
процессов типа Касуйя—Ле Кроу с участием фононов или магнонов
с большими волновыми числами. Для разделения же вкладов трех-
и четырехмагнонных процессов было использовано различие их
теоретических температурных зависимостей. При этом в качестве
величины Л/0, входящей в формулы для вкладов этих процессов,
принималась экспериментальная величина М0(Т). Заметим, что такое
предположение делается всегда при рассмотрении температурных
зависимостей динамических характеристик магнитоупорядоченных
веществ: резонансных частот, спектров спиновых волн.
На рис. 11.7 приведены зависимости от к найденных таким
образом экспериментальных вкладов трех- и четырехмагнонных
процессов в параметр диссипации спиновых волн с Вк = я 2 и величин
этих вкладов, рассчитанных соответственно согласно [419] и по
формуле (11.38). Из этого рисунка видно прежде всего, что вклад
четырехмагнонного обменного рассеяния является весьма
существенным при комнатной температуре и больших к. Вклад трехмагнонных
10s, эта величина находится
в хорошем согласии с
выражением (11.22) для
границы второй области
существования процесса
расщепления (первая область в
данном случае отсутствует). Из
рис. 11.7 видно, что имеется
довольно хорошее
количественное согласие расчетных
вкладов трех- и
четырехмагнонных процессов с
экспериментом (без каких-либо
подгоночных
коэффициентов). Оно свидетельствует
о том, что многочисленные
предположения, сделанные
при расчете этих вкладов,
удовлетворительно
выполняются для ЖИГ в условиях
данного эксперимента.
Положение существенно
изменяется для таких
кристаллов, также с малыми
ЗЗо
процессов резко возрастает при Л = 8,9-
; Зс+3s +4sc +йнк _^п
2 4 6 8 10 к,Ю5См''
Рис. М.7. Вклады различных процессов
релаксации в параметр диссипации спиновых
волн с О* = 71,2 [7]. Сфера ЖИГ, частота
накачки 35,5 ГГц, комнатная температура.
Точки — эксперимент (метолом продольной
накачки, § 10.3), сплошные
линии—результат разделения вкладов, штриховые линии —
расчет этих вкладов
АНк, как CdCr2Se4 или EuO. С одной стороны, они являются
ферромагнетиками, так что рассмотренная выше теория собственных
процессов спин-спиновой релаксации в гейзенберговском
ферромагнетике должна быть лучше к ним применима, чем к ферримагнетику
ЖИГ. Но, с другой стороны, их параметры М0 и D (см. табл.
11.2) очень сильно, особенно для EuO, отличаются от таковых для
ЖИГ, и допущения, которые более или менее хорошо выполнялись
для ЖИГ (и были сделаны «с оглядкой на него»), становятся теперь
неприемлемыми. Формулы, которые использовались для ЖИГ, в
частности (11.38), пригодны теперь лишь для самых грубых оценок.
Таблица 11.2
Параметры некоторых ферро- и ферромагнетиков с малыми АНк
4пМ0
Вещество (при 4,2 К), ГС,К D, Э-см2 (дя»^о„;„.э
Гс
Y3Fe5012 2470 560 5,17-10~9 0,2(/р=36ГГц)
CdCr2Se4 4450 130 3.3-КГ10 0,6(/„=9ГГц)
EuO 24000 69,5 1,0-1<Г10 0,75(/„=36ГГц)
Из них следует, что вклады трехмагнонных дипольных процессов
будут для этих веществ значительно (для EuO—приблизительно
в 10* раз) больше, чем для ЖИГ. Эти вклады можно обнаружить
и при температуре жидкого гелия [8, 314]. Вклад же
четырехмагнонного рассеяния возрастет, как видно из (11.38), в меньшей степени
(в 25 раз для EuO), при низких температурах он будет пренебрежимо
мал по сравнению с вкладами трехмагнонных процессов.
Для таких веществ целесообразно провести численные расчеты
на ЭВМ непосредственно по исходным формулам (11.14), (11.25)
5г
eh
Рис. 11.8. Вклады трехмагнонных
процессов релаксации в АНк спиновых
волн, возбуждаемых параметрически
при продольной иакачке в EuO [314].
Частота накачки 36 ГГц, температура
4,2 К. Точки—эксперимент для двух
направлений М0, штриховые линии—
расчет без учета
кристаллографической анизотропии, но с учетом
анизотропии спектра спиновых волн
(§ 7.4) для М0 и к, направленных по
разным осям <100>
• в<1О0>
о
• о
• о
• о
•
о
• о
>
J /Зс
"*С^ / k,tffGCM'f
113 4 5
22 А. Г. Гуревич, Г. А. Мелков
337
и (11.31). При этом можно отказаться как от высокотемпературного,
так и высокочастотного приближения, использовать точные
дисперсионные соотношения, полученные с учетом магнитной структуры
данного вещества (§ 7.4), и выражение для амплитуды Ч\,2э. найденное
[400] с учетом третьего преобразования Холстейна — Примакова. На
рис. 11.8 приведены результаты такого расчета и экспериментальная
зависимость АНк(к) для ЕиО. Из этого рисунка видно, что процесс
расщепления в согласии с рис. 11.2 существует в двух областях
значений к, а процесс слияния включается при конечном значении
к, согласующемся с приведенной выше оценкой. Суммарный расчетный
вклад этих процессов довольно хорошо отражает экспериментальную
зависимость АНк(к). Открытым, как и для ЖИГ, остается пока
вопрос о возможных вкладах других процессов, которые не исчезают
при fc->0, но могут зависеть от к.
§ 11.3. Двухмагнонные процессы
Собственные процессы спин-спиновой релаксации, рассмотренные
в предыдущем параграфе, либо совсем не вносят вкладов в ширину
линии однородного ферромагнитного резонанса АН0 (процессы Зс
и 4sc). либо их вклады малы — порядка 0,1 Э (процесс 3s при низких
частотах, процесс Касуйя—Ле Кроу в ферримагнетиках). Как будет
показано в гл. 12, вклад прямых процессов спин-решеточной
релаксации в Д//0 весьма мал. В то же время минимальные значения
ширины линии, которые наблюдались в ранних экспериментах по
ферромагнитному резонансу в ферритах и металлах (в 40-х и начале
50-х годов), составляли десятки или даже сотни эрстед. И сейчас
такие величины часто имеют место для поликристаллов и даже
монокристаллов некоторых веществ. Кроме того, все собственные
процессы, как мы видели, приводят к возрастающим температурным
зависимостям Д//0, а экспериментальные величины часто
уменьшаются с ростом температуры или имеют температурные максимумы.
Эти противоречия были отмечены еше в начале исследования
ферромагнитного резонанса и привели к постановке проблемы
ферромагнитной релаксации. Эта проблема была в основном решена
в конце 50-х—начале 60-х годов. Стало ясно, что большие величины
и «аномальные» температурные зависимости АН0 обусловлены двумя
несобственными каналами релаксации (см. рис. 11.1):
1) спин-спиновая релаксация, вызванная неоднородностями,
2) косвенная спин-решеточная (а в некоторых случаях и спин-
спиновая) релаксация, вызванная ионами с сильной спин-орбитальной
связью или электронами проводимости.
В этом параграфе мы рассмотрим первый из упомянутых каналов.
Неоднородностями, которые приводят к его появлению, являются,
как будет показано ниже, любые нарушения периодичности кристалла.
Наибольшую роль играют следующие виды неоднородностей:
а) неоднородности состава (или химические неоднородности),
в частности, нарушения порядка в расположении магнитных ионов
в узлах решетки;
338
\
б) вариации направлений осей кристалла—поликристалличность,
блочность монокристаллов;
в) неоднородные упругие напряжения, в частности, вызванные
дислокациями;
г) «геометрические» неоднородности — поры, шероховатости
поверхности.
Методы учета влияния неоднородностей. В § 2.4 отмечалось, что
расширение резонансных кривых в поликристаллах можно попытаться
объяснить разбросом резонансных частот (или резонансных полей)
зерен вследствие разной ориентации их кристаллических осей. Такой
подход к магнитному резонансу в неоднородных средах получил
название приближения независимых областей. В этом приближении
расширение резонансных кривых является результатом не какого-то
дополнительного механизма диссипации, а просто различия условий
резонанса в разных точках образца.
Приближение независимых областей хорошо применимо в случае
достаточно крупных неоднородностей при парамагнитном или
антиферромагнитном резонансе. Для ферромагнитного резонанса оно
и при крупных неоднородностях обычно неприменимо, так как
магнитное (диполь-дипольное) взаимодействие осуществляет в этом
случае сильную связь между колебаниями различных областей. Для
поликристалла условием его применимости является неравенство
(2.64), которое обычно не выполняется.
Наличие сильной связи, обусловленной обменным или магнитным
взаимодействием (в зависимости от размера неоднородностей) между
колебаниями намагниченности в различных точках образца, приводит
к тому, что колебания в этих точках нельзя рассматривать как
независимые даже в нулевом приближении, а следует говорить
о собственных типах колебаний всего неоднородного образца.
Вследствие нерегулярности (случайного характера) тех неоднородностей.
которыми мы сейчас интересуемся, задача определения полей и
собственных частот колебаний неоднородного образца может
рассматриваться лишь статистически. Следует ожидать, что собственные
частоты колебаний неоднородного образца будут группироваться
около частот колебаний однородного, и каждая такая группа (рис.
11.9) будет представлять собой практически непрерывное
распределение частот. Переменное
поле будет возбуждать
всю эту группу
собственных колебаний, и
резонансная кривая уширится
на величину порядка
ширины упомянутой
области частот. Заметим,
что при такой трактовке
влияния
неоднородностей на языке собствен- рис ц 9 Часть спектра магнитных колебаний
ных или нормальных ко- ферромагнитного образца: / — однородного,
лебаний — это влияние, 2—содержащего неоднородности
22* 339
с*
ез
II
II
как и в приближении независимых областей, не связано с появлением
какого-то нового механизма диссипации. Но, в отличие от
приближения независимых областей, расширение и сдвиг резонансной кривой
объясняются теперь распределением собственных частот не разных
областей образца, а разных типов колебаний всего образца.
Сложность задачи о собственных магнитных колебаниях
неоднородных образцов приводит к тому, что ферромагнитный резонанс
в таких образцах обычно трактуется на языке не собственных,
а связанных колебаний. Ими в данном случае являются собственные
(невозмущенные) колебания образца без неоднородностей.
Неоднородности, рассматриваемые как возмущение, приводят теперь к связи
этих колебаний, что вызывает перекачку энергии из рассматриваемого
типа колебаний в другие, т. е. к диссипации, а также к сдвигу
резонансных частот. Интересно, что при такой трактовке, в отличие
от трактовки на языке нормальных колебаний, неоднородности
вызывают появление нового процесса релаксации. Таким образом,
различие между диссипативными и недиссипативными механизмами
расширения резонансных кривых в данном случае—сильно связанной
системы является условным.
В классической теории рассмотрение на языке связанных колебаний
заключается в решении уравнений движения намагниченности для
различных типов колебаний однородного образца, которые становятся
связанными благодаря наличию неоднородностей. Это и есть
упоминавшийся в § 11.1 метод связанных уравнений движения.
В квантовой теории этот метод также применим, но уравнения
движения должны быть квантовыми (см., например, [81]). Однако
в этом случае может быть применен и метод вероятностей переходов
(§ 11.1). Возмущением, вызывающим переход энергии от одних типов
колебаний к другим, будет являться оператор энергии, связанной
с неоднородностями. Наиболее вероятными являются процессы с
участием наименьшего числа частиц. Ими в данном случае будут
двухмагнонные процессы. В идеальном (бесконечном, строго
периодическом) кристалле эти процессы не могут происходить из-за
наличия в матричных элементах возмущений множителей A(ki— k2);
иными словами, двухмагнонные процессы в идеальном кристалле
запрещены законом сохранения квазиимпульса. В кристалле же,
содержащем неоднородности, как мы убедимся, эти процессы имеют
конечную вероятность. Такие процессы можно назвать процессами
рассеяния магнонов на неоднородностях. В случае, когда исходный
тип колебаний представляет собой однородную прецессию, их часто
называют 0—Л-процессами.
Общая теория двухмагнонных процессов. Рассмотрим методом
вероятностей переходов релаксацию магнонов с волновым вектором
ки обусловленную неоднородностями. Воспользуемся
гейзенберговской моделью и предположим, что возмущение можно описать
некоторым эффективным полем Нп(гу), так что энергия возмущения
будет трактоваться как зеемановская энергия спинов в этом поле.
Примем для простоты, что поле Нп направлено по оси z
(определяемой равновесной ориентацией магнитных моментов); тогда опе-
340
ратор энергии возмущения запишется согласно (7.86) следующим
образом:
ЖП^уН £ S=Hn{rf), (11.39)
где N—число спинов в образце. Перейдем согласно (7.91) к
операторам рождения и уничтожения спиновых отклонений а} и af,
а от них, с использованием формул (7.105),—к операторам ак и ак.
Одновременно разложим по пространственным фурье-гармоникам
поле И „(if). То1да билинейная по операторам ак и ак часть
гамильтониана (11.39) примет вид
^пг=уй i4=ieik,rj^-pie"'M/^+4=ie'k"r'Hb <n-4°)
где
Hk = ~ £ Hn(rf)e '""" (11.41)
s/Nf=i
— амплитуда к„-й гармоники поля //„, а суммирования в (11.40)
(кроме первого) ведутся по всем разрешенным значениям (см. § 7.4)
в первой зоне Бриллюэна.
Поскольку возмущение уже учтено при помощи эффективного
поля, теперь можно считать кристалл идеальным, для которого
справедливы соотношения (7.103). С учетом их гамильтониан (11.40)
примет вид
^„2 = ^=1 I £Нка1 а1А(к2-к1+кп). (11.42)
С помощью формул (7.103) можно также получить важное
соотношение
Матричные элементы оператора Жп1- которые входят в
кинетическое уравнение (11.7), запишутся для прямых переходов — с
уничтожением магнона к, и рождением магнона к2 следующим
образом [81]:
<и1-1,й2 + 1|^п2|й1,й2> = ч/й1(«2 + 1)Ч'1,2, (11.44)
а для обратных — аналогично с заменой 1^2. Здесь
*1.г=-^1^А(к2-к1+кп)=^//(к1-к2). (11.45)
Jut Jn
Кинетическое уравнение будет теперь иметь вид
~ = ^I|4'..2|2(«2-«l)6(^1-^C02). (11.46)
dt ъ к2
341
Примем, как обычно, что п2 = пг- И так как магноны с kt и к2
вырождены, то Hi=h2. Тогда согласно (11.8) частота релаксации,
обусловленная рассматриваемыми двухмагнонными процессами,
«Vi-Jll^fSfffl.-fflJ. (П.47)
Из (11.46) или (11.47) видно, что при элементарных двухмагнонных
процессах энергия сохраняется. Сохранение же импульса при каждом
элементарном процессе не имеет места; импульс Л (к!— к2) передается
кристаллу в целом.
Переходя, как и в § 7.4 и 11.2, от суммирования по
значениям к 2 к интегрированию по к2-пространству, получим с
учетом (11.45)
АНк= ^i = -^ Гя^.^бК-ш,)*! sinG2 dk2 сВг d<p2. (11.48)
у (2л)2 N J
Хаотические неоднородности. Предположим сначала, что амплитуды
гармоник Я* эффективного поля неоднородностей не зависят от к,
т. е. неоднородность является хаотической («белым шумом»). Тогда
из (11.43) следует, что
#г=4х #„>/)=#£ (11-49)
(Яр— среднеквадратичное эффективное поле неоднородности). Считая
среду изотропной, примем, что спектр спиновых волн не зависит
от (р; интегрирование по <р2 в (11.48) тогда даст просто множитель
2 я. Избавляясь затем от интегрирования по к2, получим (опуская
индекс у 02)
AHk = la3Hl f feV kjsinQdQ. (11.50)
Здесь a=3y/VjN — среднее расстояние между ближайшими
спинами, kd(Q) определяется из условия вырождения (ок(кй, 6) = t0i-
а бтах (рис. 11.10) либо равно я/2, либо находится из условия
(йк(к = 0, етах) = со1.
Рассмотрим, например, релаксацию однородного типа колебаний
эллипсоида вращения, т. е. примем А:, =0 и al=a0 = a)H + N±M0. Для
простоты примем приближенное выражение (7.14) для спектра
спиновых волн. Тогда вычисление по формуле (11.50) даст
AH0 = (2n)-l'2a3Mhl2D Ъ'21,Н2Р. (11.51)
Здесь It—численный множитель, зависимость которого от N±
приведена на рис. 11.11 (нижняя кривая), для сферы /г = 0,217. Оценка
по формуле (11.51) для сферы ЖИГ показывает, что для получения
ощутимого вклада неоднородностей в ДЯ0 (~ 1 Э) в рассматриваемом
случае хаотической неоднородности необходимы очень большие поля
р
342
Нр (~105 Э).
coz
Й ~*
в1 2у
вм
/
Рис. 11.10. Пути ИН1С1 рирования (показаны жирными линиями) при вычислении
вклада двухмагнонного процесса в ЬЯк\ а, б—хаотические неоднородности
е. г -крупные неоднородности (в этом случае принято /ri=0)
С учетом (7.119) формулу
(11.51) можно записать, опуская
множитель порядка 1, в виде
ДЯп~Я„
Я„
у/нЩАпМ~0)
(11.52)
Величину ДЯ0 можно
трактовать как результат
неоднородного уширения
резонансной линии, которое по
порядку величины составляет
Нр, и ее «последующего» <>б-
Сфера
Рис. 11.11. Множитель It(N±, Н01(4пМп))
в выражении (11.51) [267]. Цифры у
кривых—значения Я0/(4яМ0)
пенного сужения. Если для
Нр принять приведенную
выше оценку, то коэффициент
обменного сужения £„ буде1 для ЖИГ порядка Ю-4.
Кр>пные неоднородности. Рассмотрим теперь другой случай, когда
амплшуды гармоник Нк имеют заметную величину лишь в узкой
об иипш значений к. Примем, например, что
Нк = <
С при к<к,= 1/1,
0 при к>ки
(11.53)
343
где /—характерный размер неоднородности. С помощью формулы
(11.43) (переходя в ее правой части к интегрированию по к-
пространству) нетрудно связать величину С со среднеквадратичным
эффективным полем неоднородностей:
С2 = 6к2(1/а)3Н2р. (11.54)
Рассматривая по-прежнему релаксацию однородных колебаний
намагниченности эллипсоида вращения, подставим (11.53) с учетом (11.54)
в формулу (11.48) и исключим интегрирование по углу 02. Тогда,
принимая снова для спектра спиновых волн выражение (7.14), получим
*/
3 /ъНг С к2
&H=--^\-^-dk, (11.55)
2 Mo J cosGd
о
где полярный угол вырожденных с однородной прецессией спиновых
волн 0d определяется условием ак(к,6d) = to0, из которого следует
cosed= /^+ ?!*!. (11.56)
Если характерный размер неоднородности / достаточно велик,
чтобы область, где Я*#0, была значительно меньше всей области
вырожденных значений к (рис. 11.10. г), то вторым членом под
корнем в (11.56) можно пренебречь, и
АЯ= ^ = "' (11.57)
2jW0cosedo 2M0y/NJ(4n)
В этом случае для получения таких же вкладов в АН требуются
значительно меньшие величины эффективного поля неоднородностей,
чем в случае хаотических неоднородностей. Например, для получения
в сфере ЖИГ ДЯ= 1 Э необходимо теперь ЯР~10Э.
Формулу (11.57), опуская множитель порядка 1, можно записать
в виде, аналогичным (11.52):
АЯ-Яр-^-^Я^р, (11.58)
где £djp—коэффициент дипольного сужения, который в частном случае
неоднородных полей анизотропии (поликристалл) был уже введен в § 2.4.
При выводе формулы (11.57) были сделаны, кроме принятия
модели (11.53), два предположения: замена спектра спиновых волн
приближенным спектром (7.14) и предположение, что kl<s:kraax (см.
рис. 11.10), которое дало возможность пренебречь вкладом обменного
взаимодействия в спектр. Не делая первого из этих предположений,
Шлёманн [396] получил для случая сферы", когда cos 0dO= 1/^/3,
ДЯ=-^Я^/2 (coo/сом), (П.59)
2м о
'' Аналогичное выражение для эллипсоида вращения получили Гешвинд
и Клогстон [308 ].
344
Рис II 12. Множитесь в выражении
для ДЯ0, учитывающий плотность
вырожденных состояний при
рассеянии млгнонов однородной прецессии
на крупных неоднородностях.
Сплошная линия —/2 в формуле (11.59),
штриховая — с учетом обменного
члена в спектре спиновых волн [396]
51
_
_
г2
' 11
/г
1
1
1
1
1
/
\\
\\
\\
>х
где (йо = уНе0—частота однородных колебаний, а график ^(©о/юм)
приведен на рис. 11.12. Выражение (11.59) отличается от (11.57)
наличием множителя /2. Как видно из рис 11 12, он
стремится к бесконечности, когда частота релаксирующего типа колебаний,
в данном случае — однородной прецессии — подходит к верхней границе
йезооменного спектра спиновых волн. Появление такой сингулярности
связано с тем, что плотность вырожденных состояний стремится
при этом к бесконечности. Важно подчеркнуть, что это имеет место
только при следующих условиях: пренебрежение обменным членом
в спектре спиновых волн, неучет диссипации спиновых волн и
пренебрежение влиянием неоднородностей на их спектр-
Учет хотя бы одного из этих факторов сглаживает сингулярность,
как показано на рис. 11.12. Влияние первого фактора должно быть тем
меньше, т. е. величина (АЯ)ПЫХ в точке перехода со0 через верхнюю
границу безобменного спектра—тем больше, чем крупнее неоднородность.
И действительно, в [396] было показано, что с учетом обменного
взаимодействия (АЯ)П1ах пропорциональна 1'а Влияние второго и
третьего факторов было исслеповано [402] на модели, учитывающей не
только первичные 0 — /г-процессы, но и вторичные (А— к )-процессы
рассеяния образующихся спиновых волн на тех же неоднородностях.
Беспорядок в распределении ионов по узлам. Переходя к изучению
влияния конкретных видов неоднородностей, рассмотрим сначала
беспорядок в распределении магнитных ионов по узлам решетки.
Этот случай был исследован в работе Клогстона, Сула, Уокера
и Андерсона [267], которая явилась первой подробной теоретической
работой по двчхмагнонным процессам релаксации". В ней был
использован метод связанных уравнений движения. Но, как показал
Каллен [258], такие же результаты могут быть получены и методом
вероятностей переходов в предельном случае хаотической
неоднородности. Полученное в [267] выражение для вклада данного процесса
в параметр диссипации однородных колебаний эллипсоида вращения
можно записать в виде (11.51). Но поскольку в [267] был использован
не приближенный (7.14), а точный спектр спиновых волн, множитель
" Идею таких процессов выдвинул Касуйя [344].
345
/, оказался зависящим и от отношения Нс0/(4кМ0). Графики
/i (N±, He0/4nMо) приведены на рис. 11.11.
Беспорядок в распределении магнитных ионов по узлам решетки
обычно имеет место в ферритах со структурой обращенной шпинели
(§ 3.3), например, в никелевом и марганцевом ферритах. В то время,
когда выполнялась работа [267], минимальные величины АН для
монокристаллов этих ферритов составляли ~40 Э. В работе было
сделано предположение, что неоднородность представляет собой
вариацию псевдодипольного взаимодействия (см. § 2.2). Если бы
вся магнитная кристаллографическая анизотропия, например,
никелевого феррита была обусловлена этим взаимодействием, то его
эффективное поле (а в случае полного беспорядка в распределении
ионов по узлам — и его среднеквадратичная вариация Нр), было бы
порядка 105 Э, что давало бы указанную величину АН. Таким
образом, создалось впечатление, что беспорядок в распределении
ионов по узлам вносит основной вклад в ширину линии в ферритах
с обращенной структурой шпинели, а теория, учитывающая псев-
додипольное взаимодействие, правильно этот вклад описывает.
Однако полученные в дальнейшем экспериментальные результаты
опровергли эти выводы. Во-первых, по мере улучшения качества
монокристаллов ферритов со структурой шпинели в них были
получены значительно меньшие величины АН, например 1, 2 Э
в никелевом феррите [218]. Во-вторых, выяснилось (см. § 2.2), что
анизотропия ферритов имеет в основном внутриионное («одноионное»)
происхождение. Это заставило Каллена и Питтелли [259], а затем
Хааза и Каллена [318] провести расчеты АН, считая возмущением
вариацию от иона к иону внутриионного спин-орбитального
взаимодействия в случаях соответственно невырожденного и
вырожденного нижнего энергетического уровня иона в кристаллическом поле
(см. § 13.1). Первый случай имеет место для ионов Fe2+ и Ni2+
в октаэдрических узлах шпинели, а второй—для ионов Со2+ в этих
узлах.
Полученные в [259, 318] выражения можно представить в виде
(11.51). В случае невырожденного нижнего уровня [259] эффективное
поле Нр оказалось пропорциональным с(\ — c)(GA — GB)2, где
с и (1-е)—относительные концентрации двух сортов ионов,
беспорядочно распределенных по октаэдрическим узлам, a GA и GB—их
константы спин-орбитального взаимодействия. Оценка для ионов
A—Fe2+ и ионов В—Fe3+ (с GB = 0) при с=1/2 дает #Р = 2-105Э
и ДЯ~10Э, что значительно меньше величин АН в ферритах,
содержащих, даже в меньших количествах, ионы Fe2 + . Для иона Ni2 +
спин-орбитальное взаимодействие является более слабым, и, таким
образом, экспериментальные результаты для никелевого феррита [218]
не противоречат явно теории [259]. Однако выделить вклад ионного
беспорядка в АН в этом случае, как и в предыдущем, не удается.
В случае вырожденного нижнего уровня (ионы Со2+ в
октаэдрических узлах) вклад ионного беспорядка в АН оказался большим,
чем для ионов Fe2 + —20 —30 Э на 1% Со [318]. Но и эти величины
значительно меньше экспериментальных значений АН в ферритах,
346
содержащих ионы Со2+, а их угловые и температурные зависимости
существенно различаются. Причина, как и в случае ионов Fe2 + ,
заключается в том, что механизм рассеяния магнонов на неоднород-
ностях — ионном беспорядке маскируется другим — тоже
обусловленным этими ионами, но более сильным механизмом ионной релаксации,
который будет рассматриваться в гл. 13.
Вариации полей анизотропии в поликристаллах. Модель независимых
областей, в данном случае—зерен, применима к магнитным колебаниям
в поликристаллах лишь при условии (2.64), которое выполняется для
веществ с очень большой анизотропией или вблизи точек компенсации
ферримагнетиков. Если же это условие не выполняется, то происходит
дипольное сужение и применима рассматриваемая в этом параграфе
теория рассеяния магнонов на неоднородностях. Ими в поликристаллах
являются вариации направлений кристаллографических осей (т. е.
эффективного поля анизотропии) и поры, а в некоторых случаях—также
включения других фаз и неоднородные упругие напряжения.
Мы остановимся сначала на наиболее типичном для поликристаллов
(хотя и не всегда дающем наибольший вклад) рассеянии на вариациях
направлений осей. Характерным размером неоднородности является при
этом средний размер зерен, который обычно не бывает меньше единиц
микрометров, так что наибольшие значения kt (рис. 11.10) всегда
существенно меньше, чем предельные величины ктм вырожденных
спиновых волн. Поэтому к поликристаллам, как правило, применимы
рассмотренный выше второй предельный случай и, в частности, формула
(11.57). В нетекстурованных поликристаллах, когда все направления
кристаллических осей зерен равновероятны, в качестве Нр в этой формуле
следует принять среднеквадратичную величину эффективного поля
анизотропии Яа. Для кубического кристалла с учетом только первой
константы анизотропии Я2 = (16/21)Я21 [396], где HAl = K-JM0. Тогда
оценка по формуле (11.59) для ЖИГ при комнатной температуре дает
(ДЯ)а~10 Э, что не противоречит эксперименту (подробнее см. ниже).
Формулы (11.57) или (11.59) могут быть использованы для
вычисления вкладов в АН и других неоднородных эффективных
полей, например, обусловленных механическими напряжениями,
которые возникают вблизи дислокаций0.
Поры в поликристаллах. Перейдем теперь к рассмотрению
«геометрических» неоднородностей, к которым относятся поры между зернами
поликристаллов, трещины и шероховатости поверхности образцов.
В § 2.4 отмечалось, что оценка вкладов таких неоднородностей на
основе модели независимых областей дает значения А Я, по порядку
величин совпадающие с экспериментальными. Однако это совпадение
свидетельствует не об адэкватности модели, а о том, что коэффициент
дипольного сужения в данном случае имеет порядок 1.
Расчет вклада геометрических неоднородностей в ЛЯ методом
вероятностей переходов был проведен в уже упоминавшейся работе
[419]. При этом была использована та же модель сферической
'• Расчет для этого случая провели Барьяхтар, Савченко и Тарасенко [26].
347
полости, что и при расчете методом независимых областей (§ 2.4).
Энергия размагничивающего поля полости была выражена через
операторы а£ и ак, найденная таким образом амплитуда рассеяния
4V* подставлена в формулу (11.47), и после расчета, аналогичного
тому, который был проведен при выводе (11.57), получено выражение
/•а о! 4п vp л it G(6do) ,.,,„,
(Д Н)р=— тг АпМо —S~ ■ (11.60)
у 9 V0 cosGd0
где Кр = (4'3)я/?р — объем полости, У0 — объем образца, угол
0dO определяется согласно (11.57), а
G(Gon) = (3cos2ed0-l)2. (1161)
При этом были сделаны такие же допущения, как и при выводе
(11.57): замена спектра спиновых волн приближенным (7.14) и
пренебрежение вкладом обменного взаимодействия, т. е. вторым членом
под корнем в (11.56). Отказ от первого из этих допущений привел
бы, как и в случае вариации полей анизотропии, к появлению
сингулярности при переходе частоты однородного резонанса через
верхнюю границу безобменного спектра спиновых волн при изменении
(о или М0 (с этим допущением, т. е. в высокочастотном приближении,
сингулярность возникает только при Nz -* 0), а отказ о i второго - к
сглаживанию этой сингулярности.
Выражение (11.60) справедливо и при наличии в образце
некоторого количества сферических пор. При этом Ур—суммарный обьем
пор, а отношение Vv Vo=P— пористость. Формула (11.60).
учитывающая дипо.тьное сужение, отличается от оценочной формулы (2.69),
не учитывающей его, коэффициен i ом порядка 1 и множителями
(11.61) и (cosOdo'i-1- Второй из них учитывает плотность вырожденных
состояний и присутствует (в высокочастотном приближении) во всех
формулах для крупных неоднородностей. Множи!ель же (11.61)
обусловлен конкретной сферической формой полости. Так как
реальные поры в поликрис iаллах отнюдь не являются сферическими,
определяемое этим множителем поведение (А//)р не должно иметь
(и, как мы \ видим, не имеет) места в действительности.
Экспериментальном) исследованию процессов релаксации в
поликрис 1ал.чичесьих ферритах было посвящено очень много paooi
(например, [257. "4 386, 107]). При этом почти всем да. начиная с работы
Баффлера [257], наблюдался предсказываемый теорией дв>хма1Ноиных
процессов максимум АН при переходе частоты релаксируюшею типа
колебаний через верхнюю границу безобменно! о спектра спиновых
волн. Для разделения вкладов пор (Д#)р и вариаций поля аниютроппи
(Д//)„ в ширину реюнансной кривой поликристаллов можно либо
использовать их разную зависимость от температуры, либо (чю.
конечно, белее надежно) варьировать по оiдельности величины
H\i и /), стремясь к тому, чтобы при вариации каждою из эшх
параметров вклад фугого не изменялся и, по возможности быт
мал На рис. 11.13 приведены результаты, которые получили таким
мопсом Касаткин.1. Яковлев, Мацкевич и Берестовая [Ю7| И:
34,-
\ЛН,Э
НА1-45Э
**>*§*>*
2П 2п
12
&г
ан.э
ю г,ггц
2 | 4
2Л
А ГГц
Рис 11.13. Частотные зависимости Д// в поликристаллических ферритах [107 J:
а- преобладает вклад анизотропии (пористость р<0.003), цифры у кривых
значения IH^I; б—преобладает вклад пористости (|//41|~2Э). цифры
v кривых—значения р
этого рисунка видно, что частотные зависимости АН. когда до
минирует вклад анизотропии (рис. 11.13,о), качественно соответствуют
рассмотренной выше теории рассеяния на крупных неоднородностях
Частотные же зависимости АН при малой анизотропии, когда
доминирует вклад пор (рис. 11.13,6), совершенно не соответствую!
теории двухмагнонного рассеяния на крупных неоднородностях.
в точке перехода со0 через верхнюю границу безобменного спектра
имеет место не максимум, а минимум: значения АН слева от него
не ниже, чем справа; с ростом частоты имеет место значительное
увеличение АН. Что же касается пропорциональности (Д//)Р
намагниченности и пористости (которая получается и при испольювании
метода независимых областей), то она, как уже отмечалось в § 2.4.
хорошо подтверждается всеми экспериментами.
Шероховатоеiи поверхности. В высококачественных мопокристал-
лических образцах среди неоднородностей, вызывающих двухмагнон-
ные процессы релаксации, на первый план выступают шероховатости
поверхности. Их влияние впервые четко установили экспериментально
Ле Кроу, Спенсер и Портер [359]. Оно очень существенно: при
шлифовке поверхности сфер из монокристаллов ЖИГ абрашвным
порошком со средним размером зерна ~ 10 мкм величины АН
возрастают на порядок по сравнению со значениями (~0,3 Э) для
очень хорошо полированных сфер. Рассмотренная выше теория
рассеяния магнонов на геометрических неоднородностях была развита
[419] именно с целью учета влияния поверхностных неоднородностей.
При этом было сделано допущение, что они приставляют собой
полусферические ямки полностью покрывающие поверхность образца
и вносящие тем не менее аддитивные вклады в АН. Амплитуда
рассеяния 4Vk при переходе oi внутренних сферических полостей
349
к поверхностным полусферам с тем же радиусом Ri должна быть
согласно [419] уменьшена в 2 раза для учета уменьшения
эффективности центра рассеяния и еще в 2 раза—из-за уменьшения его
объема. Число же полусфер легко определяется из условия полного
покрытия ими поверхности. Тогда вместо (11.60) получим
9 Д0 cos6d0
(11.62)
Зависимости (AH)S от М0 и от размера образца R0 имеют ясный
физический смысл и хорошо подтверждаются экспериментально
(рис. 11.14 и 11.15). Величины (A//)s возрастают с увеличением
размера зерна абразива, с помощью которого производится обработка
поверхности (рис. 11.15), так что имеется некоторое соответствие
между этим размером и величиной Ri в (11.62). Однако вследствие
грубости принятой модели эта формула, как и (11.60). не дает
частотной зависимости, в то время как экспериментальные величины
(Д#)5 и (Д#)р растут с ростом частоты.
Учет точного спектра спиновых волн приводит, как отмечалось
выше, к тому, что при переходе частоты релаксирующего колебания
через верхнюю границу безобменного спектра должны наблюдаться
максимумы АН,. Однако для монокристаллических образцов с
шероховатой поверхностью эти максимумы не обнаруживаются
экспериментально. Причиной этого, как и для рассмотренного выше
вклада пористости в
поликристаллах, может явиться широкий
спектр пространственных гармо- оц .
ник неоднородности, обусловлен- / • |!
ный их весьма неправильной фор- ^ - / / аХ ^
I
i
14
12
10
8
6
4
2
ДН,Э
120мкм
'
-
60
/40 .
//20
^10
4
j
200 300 400 М0,Гс
Рис. 11.14. Зависимости вклада
шероховатостей поверхности в АН
монокристаллических сфер от
намагниченности [75]. Зависимости снимались
при изменении температуры; АН,—
разность значений АН для грубо
обработанных и хорошо полированных
сфер
350
f/fi0,»"~f
Рис. 11.15. Записимости АН сфер
ЖИГ от их радиуса R0 и обработки
поверхности. Жирные
линии—эксперимент при частоте ~9 ГГц и
комнатной температуре; цифры у
кривых—значения среднего размера
зерна абразива при окончательной
обработке сфер. Подъем кривых при
больших R0 связан с возбуждением
неоднородных типов колебаний
(cv.. § 6.3)
мой; вырождение с безобменной частью спектра спиновых волн не
играет тогда существенной роли.
Вклад поверхностных неоднородиостей в параметр диссипации
пропорционален отношению поверхности образца к его объему.
В случае сферы это приводит к множитечю (Ro)'1 в (11.62). Для
тонких пленок вклад поверхностных неоднородиостей становится
большим. Только благодаря высокому качеству поверхности эпитак-
сиальных пленок ЖИГ. выращенных на очень хорошо обработанных
подложках, удается получить достаточно малые значения параметра
диссипации в таких пленках (§ 6.2).
В заключение сделаем несколько замечаний, касающихся двухмаг-
нонных процессов релаксации. Эти процессы играют значительную
роль и на «последующих» стадиях релаксации, обеспечивая растекание
энергии по всей области спин-волнового спектра, вырожденной
с первичным релаксирующим колебанием.
Наличие верхних (обменных) ветвей спектра спиновых волн в фер-
рииагнепшках не должно сущее 1венно повлиять на двухмагнонные
процессы в них, так как с колебаниями или волнами, релаксация
которых нас интересует, обычно вырождена только нижняя («фер-
poMai нитная») ветвь. В антиферромагнетиках частоты однородных
колебаний обычно вырождены со спиновыми волнами, и двухмагнонные
процессы релаксации играют существенную роль (см., например, [361]).
Очень узкие линии антиферромагнитного резонанса наблюдались
именно в том случае [355], когда вырождение не имело места.
Двухмагнонные процессы, как было показано в § 10.3, не вносят
аддитивного вклада в эффективный параметр диссипации АНк, но
оказывают существенное влияние на параметрическое возбуждение
спиновых волн. Для процессов первого порядка они приводят
к возрастанию порога, а в случае процессов второго порядка — к его
размазыванию (§ 10.2).
Двухмагнонные процессы, для которых полное число магнонов
сохраняется, не вносят в первом приближении — без учета диполь-
дипольного взаимодействия (см., например, [7.74]) вклада в релаксацию
z-проекции намагниченности. Однако 0—^-процессы участвуют в
релаксации длины вектора М, которая в том же приближении определяется
(§ 7.3) числом всех магнонов, кроме магнонов однородной прецессии.
И наконец, заметим, что иногда к двухмагнонным процессам
относят и «рассеяние магнонов на флуктуациях намагниченности»,
амплитуды которых и характерные размеры возрастают (см.,
например, [147]) при подходе к точкам фазовых переходов второго
рода, в частности к точке Кюри ферромагнетиков. Существенное
увеличение АН всех магнитоупорядоченных веществ при приближении
к точкам Кюри или Нееля часто объясняют вкладом этого рассеяния.
Однако такая трактовка не вполне корректна. Флуктуации, в том
числе и критические (вблизи точек фазового перехода второго рода),
присущи и идеальным кристаллам. Поэтому влияние их на релаксацию
магнитных колебаний и волн следует трактовать как воздействие
флуктуации на собственные процессы релаксации, которые (без учета
флуктуации) рассматривались в §11.2.
351
Глава 12
МАГНИТОУПРУГАЯ СВЯЗЬ
§ 12.1. Упругие свойства и магнитоупругое взаимодействие
До сих пор мы считали магнитную систему изолированной
и лишь упоминали в гл. 2 и 11 о ее связи с другими системами
магнитоупорядоченного вещества. Приступая теперь к изучению
влияния этих систем на магнитные колебания и волны, мы рассмотрим
в данной главе влияние кристаллической решетки. Приведем прежде
всего некоторые соотношения из теории упругости (см., например,
[135]). которые понадобятся нам в дальнейшем.
Деформации и напряжения. Как и при изучении динамики магнитной
системы, будем рассматривать сначала кристаллическую решетку как
непрерывную среду. Тогда ее упругое состояние будет описываться
иектором смещений точек тела относительно их равновесных положений
u(r) = r-r0 (12.1.
и тензором деформаций ё(г) с компонентами
где р, q=\, 2. 3. Тензор 7 симметричен и может быть приведен
к главным осям, в которых он будет иметь только диагональные
компоненты. Они представляют собой относительные удлинения
в направлениях соответствующих осей, а их сумма равна
относительному изменению объема малого элемента тела.
Сила, действующая на элемент объема, является, вообще говоря,
суммой упругой силы dfcl и объемной силы dfvoi. Первая представляет
собой равнодействующую сил, приложенных к поверхности данного
элемента и обусловленных воздействием на него соседних элементов.
Сила же </fvol является результатом воздействия внешних полей
гравитационного и (если элемент объема содержит электрические
заряды или электрические либо магнитные диполи) электромагнитного.
Эта сита нас интересовать не будет. Упругая сила, отнесенная
к единице объема, может быть представлена в виде
/-,= I 7Г- (123)
где стр, - компоненты симметричного тензора напряжений с (г).
Напряжения могут быть вызваны внешними силами на поверхности
352
тела 5. Связь этих сил с напряжениями определяется граничными
условиями [135]
з
Z n0qopq = Ftp на S, (12.4)
«=i
где п0— единичный вектор внешней нормали к поверхности тела,
a Fc—внешняя сила, отнесенная к единице этой поверхности.
В частном случае однородного растяжения или сжатия в направлении
единичного вектора р
ор,= +РрР,о. (12.5)
Такая однородная деформация реализуется, например, при сжатии
стержня (или диска), тогда величина а представляет собой давление
на его торцевые поверхности.
Плотность свободной энергии упругодеформированного тела
z p=i«=i
Здесь apq зависит от epq, и с учетом этого оказывается [135], что
dUcl
(12.7)
се
В случае малых упругих деформаций справедлив закон Гуна:
з з
°рв= X X см1те,т, (12.8)
1=1 171=1
где cpqlm— компоненты тензора (четвертого ранга) модулей упругости.
Из симметрии тензоров ~е и S следует, что число независимых
компонент Ср,|„ в общем случае равно 21. Оно уменьшается для
кристаллов всех сингоний, кроме триклинной. Для кубических
кристаллов остается 3 независимых компоненты; в осях координат,
совпадающих с осями <100>:
В случае же изотропной среды
fll-fi2 = 2c44 (12.10)
и имеется лишь 2 независимых компоненты. Условие (12.10)
приближенно выполняется и для некоторых кубических кристаллов.
Например, для ЖИГ при комнатной температуре Сц = 2,69-1012, ci2 =
= 1,077-1012, £-44 = 7.64-10й и, таким образом, 2c44/(cii-Ci2) = 0,947.
С учетом закона Гука выражение для упругой энергии (12.6)
в случае кубического кристалла в осях координат, совпадающих
с осями <100>, принимает вид
^ci=^cii(elx+e^/ + elz) + ci2(exxeyy + eyye:z+exxez:)+
+ 2c^(eiy+e% + exz). (12.11)
23 А. Г. Гурсвич, Г. А. Мелков 353
Работа внешних сил при упругой деформации тела (отнесенная
к единице объема) в упомянутом выше частном случае однородного
сжатия может быть записана в виде [49]
tfb=XX°P,R.<w О2-12)
Р Я
Упругие волны и колебания. Уравнение движения упругой среды
(без учета объемной силы и диссипации) имеет вид
P^ = fc, (12-13)
где р—плотность. Диссипация энергии может быть учтена либо
добавлением в уравнение диссипативного члена («силы трения»),
пропорционального ( — cu/dt), либо одним из способов, аналогичных
использованным в предыдущих главах для учета затухания магнитных
колебаний и волн. Уравнение (12.13) можно, принимая во внимание
(12.3), (12.8) и (12.2). привести к виду
Решение этого уравнения для случая однородных плоских волн,
когда u = u°exp(uof—/qr), показывает [135], что существуют три
нормальные волны с законами дисперсии
w = Vjq, (12.15)
где Vj 0=1. 2> 3) — скорости этих волн. Для изотропной среды,
а также кубического кристалла в случае, когда волновой вектор
q параллелен оси <1СЮ>. одна из нормальных волн является
продольной (щ || q) со скоростью
vi=vl = s/cn/p, (12.16)
а две другие—поперечными (u2.3-Lq) со скоростями
v2 = v3 = v1=y/cZJp- (12.17)
В монокристалле ЖИГ (р = 5,17) величины этих скоростей (при
комнатной температуре): v =7,209-105, v± = 3,843 • 105.
Плотность потока энергии упругих волн (вектор Умова) [202]
Пе| = рш2|м|2у||а. (12.18)
Упругие волны в системах, содержащих границы раздела сред
(волноводах), и колебания в ограниченных телах необходимо искать
как решения уравнения движения (12.13) с учетом граничных условий.
Для свободной поверхности S упругой среды они заключаются
в равенстве нулю сил (12.4) на этой поверхности:
Х>о,стРв = 0 на 5- (12.19)
«
В случае закрепленной поверхности на ней обращаются в нуль
упругие смешения и. Волны в системах, содержащих поверхности
354
раздела, параллельные направлению распространения,— волноводах
не являются и в указанных выше случаях (изотропной среды
и кубического кристалла при q||<100» чисто продольными или чисто
поперечными.
В системах, ограниченных в направлении распространения волны,
например в пластинах, могут возникать (подобно стоячим спиновым
волнам в ферромагншных пластинах, см. § 7.2) упругие стоячие
волны, т. е. колебания, собственные частоты которых определяются
толщиной пластины и граничными условиями. Например, в случае
свободной пластины в соответствии с условием (12.19) собственные
частоты
uVl. =илг±. (I.
(12.20)
где d—толщина пластины, а и=1. 2. 3,...
Отыскание собственных частот упругих колебаний тел даже
простой формы, ограниченных со всех строи, представляет большие
трудности. Д;:я изотропной сферы со свободной поверхностью
существуют (см.. например, [137]) чист поперечные (относительно
радиуса) Ттш и смешанные Smnr колебания. Индексы т, и и г
обозначают числа вариаций соответственно по азимутальному углу, полярному
углу и радиусу. Однако от т собственные частоты не завися!,
и этот индекс можно отбросить. Приведем значения собственных
uicTOT некоторых типов колебаний в сфере ЖИГ:
/г21 =3.0810 -105</. /s,, = 3,2588 ■ 105/4 ./s0, =6.0674- W5/d,
ie d диаметр сферы (в сантиметрах). Тип колебаний
/'2i соответствует поворотам «верхней» и «нижней» полусфер в
противоположных направлениях; при колебаниях S2\ сфера сплющивается
и вытягивается вдоль некоторого направления, a .V01 является
радиалыю-симметричнон («дышашей») модой.
Квашоиание \иругих волн дает квазичаешцы фонопы с энергией
е = йсо и квазиимпульсом p = //q. Каждой нормальной волне
соответствует свои copi фононов.
Рассмотрение ynpyi их волн в
дискретной криста ллической решетке
[16. 113] приводит. аилло1Ичио
спиновым волнам в дискретной
магнитной решетке (§ 7.4), к тому, что
законы дисперсии (12.15) заменяются
более сложными (рис. 12.1). Кроме
трех акуешческих ветвей, законы
дисперсии которых переходят при
ац <§: 1 (и - постоянная решет ки)
в (12.15). возникает 3(/г—1) новых -
оптических ветвей, где п- число
ионов в примитивной ячейке, частоты
этих ветвей не стремятся к нулю
при q -»0.
Границ а
зоны
бриллюэна
23*
Рис. 12.1. Спекф упругих воли
в дискретной решетке
(схематически). Шфичовля .пиши спектр
н непрерывной среле
355
Магнитоупругая энергия. Одной из причин связи магнитной
и упругой систем в магнитоупорядоченном веществе является
зависимость обменного взаимодействия от расстояний между магнитными
ионами. Другой причиной служит зависимость от этих расстояний
магнитного (диполь-дипольного) взаимодействия. И, наконец,
причиной, обычно—наиболее существенной, магнитоупругой связи
является спин-орбитальное взаимодействие. Как отмечалось в § 2.2,
это взаимодействие является наиболее важной причиной и магнитной
кристаллографической анизотропии. Так же, как для нее (§ 2.2),
отвлекаясь от природы магнитоупругой связи, можно записать
феноменологические выражения для магнитоупругой энергии Umet.
В частном случае кубического кристалла, если, как и при записи
(12.11), направить оси координат вдоль осей <Ш0>, а обменное
взаимодействие считать изотропным [100],
u^~2lMUPP+^iI I MpMqepq +
М° р М° р я(р*я)
М° р ч K«*i) 6х* 0Xl М° р Лй</
где р, q, 1=1, 2, 3. Две первые суммы в (12.21) обусловлены
релятивистским взаимодействием, две вторые — обменным. В
выражении (12.21) оставлены слагаемые, линейные по компонентам "е и
квадратичные" по составляющим М. Для изотропной среды в этом
выражении следует положить By = Вг. Для ЖИГ при комнатной
температуре релятивистские магнитоупругие постоянные [195]:
J?! =3,48-10е, #2 = 6,96-106.
Магнитострикция. Наличие магнитоупругой энергии Lmci привод /
прежде всего к изменению равновесного упругого состояния магнито-
упорядоченного вещества, т. е. к появлению спонтанных — вызванных
намагниченностью деформаций ё°. Это явление носит название
магнитострикции. Ограничимся случаем намагниченного до насыщения
ферромагнетика. Тогда для нахождения деформаций ?° необходимо
минимизировать сумму энергий £/,., и Umcl.
Рассмотрим кубический кристалл и пренебрежем обменным
вкладом в магнитоупругую энергию. Тогда (см., например, [122])
относительные магнитострикционные удлинения (или сжатия) в
направлениях осей <100> и <Ш> при намагничивании ферромагнетика
вдоль соответствующих осей оказываются равными
(5///)<100> = X100=-?51/(cu-cl2), (Ц1)<т>^^т = ~ Вг с**. (12.22)
Величины Х10о и ^1П называются константами ма1ниюстрикиии
кубического ферромагнетика. Для ЖИГ при комнатной температуре
они составляют: Х10о= -1,4-10~6, ХИ1 =-2,4-10-fi.
Членов, линейных по составляющим М, не может быть (§ 2.2).
356
В случае поликристалла (нетекстурованного), зерна которого
являются кубическими кристалликами с константами Х100 и ХцЬ
усредненная константа магнитострикции [188]
2 3
^poiy=7 ^1оо+т ^-ш- (12.23)
Подставляя равновесные деформации epq в выражение для
магнитоупругой энергии Umcu получим [122], что часть этой энергии,
зависящая от направления намагниченности, будет иметь вид
U2,«=K?mM*l+oiloil+oiloil). (12.24)
где а1>21з = МЯ(>12/Мо—косинусы углов вектора М с осями <Ш0>, а
Сц— Си 2 Си,
Энергия (12.24) добавляется к энергии магнитной
кристаллографической анизотропии (2.35). Это приводит к изменению (перенормировке)
первой константы анизотропии, которая становится теперь суммой
•^1 и Kimti.
Если бы мы учли в Umti члены более высоких (четвертого
и т. д.) порядков по составляющим М, то аналогичным образом
перенормировались бы и следующие константы анизотропии.
Необходимо подчеркнуть, что такая перенормировка, основанная на
нахождении равновесных магнитострикционных деформаций,
справедлива лишь в статическом случае или—приближенно—в
квазистатическом, т. е. при изменениях намагниченности, медленных по сравнению
с временем установления упругого равновесия.
При наличии внешних механических сил (статических или
достаточно медленно изменяющихся во времени) равновесные деформации
могут быть найдены путем минимизации суммы Ucl+Uli+Umcu где
энергия U\\, обусловленная внешними силами, определяется согласно
(12.12). Подставив найденные таким образом компоненты равновесного
тензора деформаций ё° в выражение для энергии (Uti + Umcl), мы
получим, что эта энергия, кроме члена (12.24), будет содержать часть
Vе0, зависящую от внешних сил. В частном случае однородного
сжатия образца из кубического кристалла согласно [122, 188]
t/e0=-|<T[X100(afp?+aiPt+cxip|) +
+2X111(a1a2p1p2+a2a3p2p3+a1a3p1p3)], (12.26)
где, как и в (12.5), рр(/>=1, 2, 3)—косинусы углов, которые
направление сжатия образует с осями <100>.
Уравнения движения. Перейдем теперь к рассмотрению динамики
ферромагнетика с учетом магнитоупругой связи. Мы должны исходить
при этом из уравнения движения намагниченности и механического
уравнения движения, которые теперь оказываются связанными. Для
получения этих уравнений необходимо добавить в уравнение Ландау —
Лифшица эффективное поле магнитоупругого взаимодействия НгаС|,
357
а в механическое уравнение (12.13)—силу fmei, определяемую этим
взаимодействием. Для нахождения Hmci можно использовать общую
формулу (2.9). Сила же fmei определится согласно (12.3); в это
выражение войдут теперь компоненты тензора напряжений 5meb
обусловленного магнитоупругим взаимодействием, которые, в свою
очередь, могут быть найдены из соотношений
(amci)pe = -r^, (12.27)
дем
аналогичных (12.7).
Рассмотрим, как и раньше, кубический кристалл, намагниченный
в направлении <100>, т. е. будем использовать выражение для
магнитоупругой энергии (12.21). Булем учитывать в этом выражении
только релятивистские члены, ограничиваясь, таким образом, случаем
не очень быстрых вариаций М в пространстве. Предположим для
простоты, что выполняется условие упругой изотропии (12.10) и
обменное взаимодействие (см. § 7.1) является изотропным. Тогда
указанным выше путем мы получим следующие уравнения движения
(без учета диссипации):
(12.28)
-yMzHtf+yB2
диг ЗиЛ
дх cz у
д_
^ = c44V2wx + (r44 +■ с12) — divu +
Ml дх +М
ЩуШхму)+имхм^,
° "у п2 д
P-^T=c44V w,, + (c44 + c12) — divu-t- (12.29)
Я, дМ2 В2
3 у(МуМг)+-^(МуМх) ,
о \_oz ох
Ml ду М,
о2иг 7 g
Р -^г=С44^мг + (с44 + с12) — divu +
Bt дМ: В2 Y д , д 1
Поле Hef, составляющие которого входя- в (12.28), включает в себя
внешние магнитные поля —постоянное и переменное, дипольное
(размагничивающее) поле Нм и эффективное поле анизотропии Н„.
358
Мы не записали третью проекцию уравнения Ландау—Лифшица (с
dMz/dt), предположив, что длина вектора М сохраняется и для
определения Mz (в случае Mx-y*s:Mz) может быть использовано
соотношение (9.13).
§ 12.2. Влияние упругих напряжений
на ферромагнитный резонанс
Переходя к исследованию магнитных колебаний и волн с учетом
магнитоупругой связи, остановимся прежде всего на задаче об
однородных колебаниях намагниченности ферромагнетика при наличии
статических упругих напряжений—спонтанных (магнитострикционных)
или вызванных внешними механическими силами.
Однородная переменная намагниченность не входит в механические
уравнения движения (12.29) (точно так же, как однородные смещения
ux,y.z не входят в уравнгния движения намагниченности). Таким
образом, упругие колебания происходят независимо от однородных
магнитных колебаний. Однако, как видно из уравнений (12.28), упругие
деформации оказывают воздействие на магнитные колебания, в том числе
и однородные. Рассмотрим сначала случай статических
магнитострикционных деформаций, обусловленных постоянной намагниченностью.
Влияние магнитострикционных деформаций. Рассмотрим эллипсоид
из кубического монокристалла, намагниченный вдоль одной из
главных осей эллипсоида и, конечно, вдоль оси <100> кристалла
(так как только для этого случая были записаны уравнения движения).
Находя (см. § 12.1) равновесные магнитострикционные деформации
и", и подставляя их в уравнения для комплексных амплитуд тх,у,
являющиеся следствием линеаризированных уравнений (12.28), мы
убедимся, что статические магнитострикционные деформации приводят
к появлению эффективного поля
"■«■ = „ ,2Д! ,- (12-30>
M0(Cll~Cl2)
Резонасная частота, например, в случае сферы запишется:
<Оо = у(яе0+^ + Яте1). (1231)
Как видно из этого выражения, при Яе0 -* 0 и Kt -»0 (если бы при
этом не возникли домены) частота со0 -»уНтс1. Поэтому величину
уНте1 называют магнитоупругой щелью.
Поле (12.30) не совпадает с добавочным статическим полем
анизотропии Я°е1, которое рассматривалось в § 12.1; для данного
направления намагничивания согласно (12.25)
**-=^=iM-^-^V"---ir-- (1232)
М0 М0\сп—с12 2с44/ M0c*4
Для изотропной сферы Я£,е|, конечно, обращается в нуль, а НтЛ¥=0.
Различие величин Я£,е! и Hmtl обусловлено тем, как это отметили
359
Туров и Шавров [239], что в случае, который мы сейчас
рассматриваем, намагниченность прецессирует в неподвижной упругой среде
(«застывшей» кристаллической решетке), деформированной постоянной
намагниченностью, в то время как в статическом случае (который
рассматривался в предыдущем параграфе) деформации среды успевали
следовать за поворотами вектора М.
Для ЖИГ при комнатной температуре #£,„1 = 0,4 Э, а #те| = 0,5 Э,
т. е. в данном случае обе магнитоупругие «поправки» малы и
незаконное использование статических констант анизотропии при расчетах
ферромагнитного резонанса или, наоборот, использование значений
этих констант, найденных из резонансных измерений, в расчетах
статической анизотропии не вносит существенных ошибок.
Влияние внешнего давления. Переходя к рассмотрению влияния
внешних постоянных упругих напряжений на магнитные колебания,
ограничимся снова однородными колебаниями малого эллипсоида
из кубического кристалла и остановимся на важном случае
однородного сжатия в направлении одной из главных осей эллипсоида.
Подставляя в уравнение Ландау—Лифшица эффективное поле маг-
нитоупругого взаимодействия, найденное исходя из энергии (12.26),
можно получить следующее выражение для резонансной частоты
однородно сжатого эллипсоида (с постоянной намагниченностью,
направленной по оси z):
(^oly)2 = \_He0z + (Nix+Nall +Wl-N33-N33-N°33)M0] x
x[Hc0z + (N22 + Nh + N°22-N33-№33-№33)M0]-
-(Ni2 + N\2 + m2)2Ml (12.33)
Здесь Npq—размагничивающие факторы формы (компоненты тензора
N), Npq—эффективные размагничивающие факторы анизотропии,
a Npq—эффективные размагничивающие факторы магнитоупругого
взаимодействия. Для них из (12.26) следует
Л^=-Зо [(Я.юо-Я.111) Аи+ >■!„] P,pf/Afg, (12.34)
где с—давление (как и в (12.5)), Х100 и Х1П определяются согласно
(12.22), а Ар,—дельта-символ Кронекера (5.28).
Рассмотрим некоторые частные случаи. Если постоянное поле
и внешнее давление (т. е. вектор р) направлены по одной и той
же оси <100>, совпадающей с осью вращения сфероида, то
намагниченность М0 будет направлена по той же оси и, как следует из
(12.33), (12.34) и (2.54),
<uoly = Ht0 + (N1-Nz)M0 + 2K1/M0 + 3a\100IM0. (12.35)
Если же Н0 и р параллельны оси <111>, совпадающей с осью
врашения сфероида, то
fOoly = H,0 + (N1-NM)Mo~K1IMo + 3a%lll/M0. (12.36)
Выражения (12.35) и (12.36) могут быть использованы при измерениях
констант магнитострикции кубического кристалла Х100 и А.1П.
360
Нетрудно получить
выражение для резонансной
частоты и в случае, когда М0 лежит
в плоскости {ПО}, а давление
направлено по
перпендикулярной этой плоскости оси <110>.
При этом частота будет
зависеть от угла 0 между
М0 и осью <100> и в
выражение для нее войдут обе
константы магнитострикции
^■100 и ХП1. В этом случае,
сняв зависимость ш0 от 0,
можно найти эти константы
из одного эксперимента.
Строгое решение
аналогичной задачи для поликристал-
(**r~)e,3
Рис. 12.2. Зависимость резонансного поля
от внешнего давления для сферы из
поликристаллического никелевого
феррита [118]
лического эллипсоида, конечно, весьма сложно. Будем считать
приближенно поликристалл изотропной средой с константой
магнитострикции Хро!у и воспользуемся формулой (12.34), положив
Х10о=^Х111=Хро,у. Тогда для случая сферы и давления, приложенного
в направлении постоянного намагничивания (т. е. р||М0), получим
из (12.33) изменение резонансного поля под действием давления
(5Яге8)с = tfr£S -ш/у = ЗХр^о/Л/о. (12.37)
Экспериментальная зависимость (8#rcs)0 от а приведена на рис. 12.2.
Из этого опыта была получена величина A.poiy = 2,4- 10s.
§ 12.3. Магнитоупругие волны
В предыдущем параграфе было исследовано влияние статических
деформаций на однородные колебания намагниченности. Теперь мы
перейдем к рассмотрению неоднородных колебаний намагниченности
и упругих смещений, которые при учете магнитоупругого
взаимодействия, как видно из уравнений (12.28) и (12.29), связаны между
собой. Эта связь проявляется, в частности, для однородных плоских
волн в ферромагнетике, которые перестают быть чисто спиновыми
и чисто упругими, а становятся связанными — магнитоупругими. На
зто впервые обратили внимание Туров и Ирхин [200].
Рассмотрим снова упруго-изотропный кубический ферромагнетик,
намагниченный вдоль оси <100>, для которого справедливы уравнения
движения (12.28) и (12.29). Для нахождения закона дисперсии маг-
нитоупругих волн следует линеаризировать эти уравнения и подставить
в них Mx,y = m°tyexp(i(ot-ikT) и ux,yiZ = ux,.y,zexp(i(ut—ikr). Тогда для
амплитуд тХшУ и и*.,,^ получится система однородных линейных
алгебраических уравнений, условие совместности которых даст закон
дисперсии.
0 Индексы 0 у этих величин мы будем в дальнейшем опускать.
361
Распространение вдоль постоянной намагниченности. Не будем
учитывать кристаллографической анизотропии и рассмотрим частные
случаи к||М0 и к±М0, т.е. 6*=0 и Gt = 7t/2. В первом случае
дипольное (размагничивающее) поле (7.11) обращается в нуль и из
(12.28) и (12.29) следует:
iwmx + у(Н0 + D к2) ту—i укВ2 иу = О,
i<amy—y(Ho + Dk2)mx+iykB2ux = 0,
■h.
Mo
<£>2pux—k2C44Ux — ik — mx = 0,
<u2puy—k2C44Uy—ik—my = 0,
M0
(12.38)
co2p«2—A:2cmm2 = 0.
(12.39)
Уравнение (12.39) описывает продольную чисто упругую волну
с линейным законом дисперсии и скоростью (12.16), а система
(12.38)—поперечные магнитоупругие волны. Симметрия задачи
требует перехода к циркулярным поперечным составляющим m±=mx + im,
и u±=ux + iuy. Для них система (12.38) распадается на две независимые
системы для составляющих с правым и левым вращением.
Приравнивая нулю их определители, получим
рМ0
(12.40)
Здесь u>m = y(H0 + Dk2)— частота спиновых волн, u>cll = v1k— частота
поперечных упругих волн (uj, —их скорость (12.17)), а верхние
и нижние знаки относятся соответственно к волнам с правой и левой
поляризацией m и и.
Выражение (12.40) имеет характерный для связанных волн вид.
В отсутствие связи (B2 = 0) оно дает законы дисперсии (спектры)
спиновых (с правой поляризацией) и ynpyinx волн. Эти спектры
Рис. 12.3. Дисперсионные
характеристики волн,
распространяющихся вдоль М0 и кубическом
ферромагнетике (Мо||<100>).
Штриховые линии—поперечная упругая
и магнитная (с правой
поляризацией) волны без учета магнитоуп-
ругой связи; / и 2 поперечные
магнитоупругие волны
соответственно с правой и левой круговой
поляризацией. 3 продольная
упругая волна
362
(рис. 12.3) пересекаются при двух значениях волнового числа kt и к2,
являющихся корнями уравнения «„^cOen". При не очень больших
Н0, т.е. не очень высоких частотах (для ЖИГ—ниже ~ 100 ГГц).
*i=«W»jl, k2^vJ{yD). (12.41)
Последний член в (12.40) можно записать в виде £уЛ/0(о21х. где
^-~ (12-42)
сллМо
— безразмерный параметр связи. Обычно cj<s:l, например, для ЖИГ
при комнатной темпера1уре £=3.3-10~3.
Спектр Mai нитоупругой волны с правой поляризацией, который
получается при решении уравнения (12.40) с верхними знаками,
содержит две ветви (см. рис. 12.3). Их можно трактовать (переходя
на язык связанных волн) как результат расталкивания спектров
спиновой и поперечной упругой волн. Различие часто! двух ветвей
5(0 минимально в точках пересечения, в нижней точке оно составляет
5<o,=Yv/2qM0(//o + £>*2). (12.43)
Минимальное относительное различие бо^/со,,, — порядка с12, т. е.
для ЖИГ -0,05.
Спектр магнитоупругой волны с .и-вой поляризацией, который
является решением уравнения (12.40) с нижними знаками, содержит
одну ветвь, мало отличающуюся (рис. 12.3) от линейного спектра
поперечной упругой волны. Относительное их различие максимально
в нижней точке пересечения и имеет порядок Ъ,.
Итак, в рассматриваемом случае распространения вдоль
постоянной намагниченности, направленной по оси <10()>, существует три
нормальных волны: продольная упругая, поперечная магнитоупругая
с правой круговой поляризацией (спектр которой имеет две ветви)
и поперечная магнитоупругая с левом круговой поляризацией.
С помощью уравнений (12.38) и (12.39) нетрудно найти (с
точностью до произвольного множитеая) составляющие векторов
m и и нормальных волн. Продольная >пругая волна имеет, естественно,
только упругую составляющую и.. Для поперечной волны с левой
поляризацией магнитная составляющая /н_, как и следовало ожидать,
оказывается малой. Для поперечной же волны с правой поляризацией
т +
" +
=
уВ2к
со-сот
=
(ш--ш2и)рЛ/0
В2к
(12.44)
Отсюда видно, что вдали от точек пересечения на вегвях, частоты
которых мало отличаются от сос1± и сильно отличаются от
со„„ магнитная составляющая мала. И наоборот, на ветвях с
частотами, близкими к со„„ мала упругая составляющая. Эти участки
ветвей (или полуветви) можно назвать соответственно квазиупругими
" Точки пересечения спектров спиновых и упру их вопн называют иногда
точками магнитоупругого резонанса.
и квазимагнитными (или квазиспиновыми). Поскольку т и и имеют
разную размерность, непосредственное их сравнение не имеет
смысла. Но можно показать, используя (12.18) и аналогичное
выражение [408] для плотности потока магнитной энергии
nm=\^-m\yv, (12.45)
2 М0
что на квазиупругих полуветвях преобладает поток упругой энергии,
на квазимагнитных—магнитной, а в точках пересечения эти потоки
делаются равными друг другу.
Различие величин А: нормальных магнитоупругих волн с правым
и левым вращением при одной и той же частоте (см. рис. 12.3)
приводит, так же как и в случае электромагнитных волн (§ 4.2),
к повороту поляризации волны с эллиптической, в частности линейной
поляризацией, т. е. к эффекту Фарадея [46]. Наибольший интерес
при этом представляет случай, когда частота волны существенно
меньше частоты «! (в нижней точке пересечения). Тогда при данной
частоте существуют лишь две волны и обе они являются
квазиупругими. Различие их волновых чисел мало, т. е. угол поворота
поляризации сравнительно невелик, но и затухание мало, и эффект
хорошо наблюдается [366]. Его называют акустическим эффектом
Фарадея.
Распространение перпендикулярно постоянной намагниченности.
Используя уравнения (12.28), (12.29), можно получить, что в данном
случае также существуют три волны: продольная упругая волна, не
связанная с магнитной системой; поперечная упругая волна с вектором
и±Мо, которая также не связана с магнитной системой, и поперечная
магнитоупругая волна, для которой и||М0. Дисперсионное
соотношение для нее имеет вид
[<b2-<bJ](<b2-<bS±)—^<ви*2 = 0, (12.46)
рМ0
где теперь com = [(wH + Dk2)(v)H + Dk2 + v)M]112 — частота спиновой
волны с 0|, = 7t/2. Волну, спектр которой определяется уравнением (12.46),
с точки зрения акустика можно назвать необыкновенной, а две
другие нормальные волны — обыкновенными.
Спектр, определенный уравнением (12.46), содержит две ветви,
сближающиеся в точках пересечения спектров спиновой и упругой
волн. Для минимального различия частот ветвей в нижней точке
пересечения из (12.46) следует выражение
5со1=уч/^Л/о[(Я0 + £)А:2)(Я0 + /)А:2+4лМо]|/2. (12.47)
Эта величина одного порядка с (12.43).
Вдали от точек пересечения полуветви спектра магнитоупругой
волны и в этом случае являются квазимагнитными и квазиупругими,
для первых преобладают магнитные составляющие тх и т„ а для
вторых—упругая составляющая uz. Предположим теперь, что «на
входе» некоторого участка ферромагнетика будет иметься поперечная
364
волна с к±М0 и поляризацией, отличающейся от поляризаций
рассмотренных нормальных волн, т. е. с вектором и, направленным
под некоторым углом к М0. Тогда по мере распространения
поляризация волны будет преобразовываться аналогично
рассмотренному в § 4.2 преобразованию поляризации электромагнитной волны
в поперечно-(относительно вектора к) намагниченной среде.
При произвольных направлениях М0 (относительно осей
кубического кристалла) и к (относительно М0) ситуация оказывается более
сложной, а анализ ее—громоздким. Приведем лишь некоторые
качественные результаты [137, 138, 399]. Спектры магнитоупругих
волн в общем случае зависят не только от В2, но и от В^,
независимость от Ву имеет место лишь в том случае, когда оба
направления, М0 и к, совпадают с осями <100>. При 6fc^0, л/2,
а также при 6* = 0. л/2, но при М0, не параллельном осям <100>,
или <1Ю>, в частности, и при М0||<111>, возникает связь с магнитной
системой и продольной упругой волны.
Затухание. Для учета потерь при распространении магнитоупругих
волн, как и в случае спиновых волн, следует ввести в уравнения
движения или непосредственно в дисперсионные соотношения
феноменологические параметры диссипации. Однако теперь мы должны
ввести раздельно параметры, учитывающие потери в магнитной
и упругой системах, например, путем замены ©„-no^-l-iioU,
и соеи.-»соёц+«'со"и.. Тогда при к||М0 получим, опуская индекс
-L У Well. И ШТрИХИ у <Л'т И COgi,
„ 2cDd(cD-CDm)cD;', + (G>2-Wel)t0^
10 = ;г 1 J—r~j л (ПАК)
2co(lu-COm) + (cD't-CD*,)
Отсюда видно, что магнитные и упругие потери вносят аддитивные
вклады в со". Вблизи точек пересечения (<£>^(£>m = (£>ct)
со'ЦК+со;',), (12.49)
а вдали от них на квазимагнитных полуветвях со"~оС, а на
квазиупругих со"=;со^. Очевидно, что такое же положение будет
иметь место и в случае к±М0. Постоянная затухания (декремент)
магнитоупругой волны к" может быть затем найдена по формуле (6.8).
Следует подчеркнуть, что все это справедливо только в случае
малых потерь, когда выполняются неравенства со"«:со' и k"<s:k'.
При больших потерях зависимости со'(А:', к") и со" (А:', Аг") можно
найти лишь путем решения комплексных дисперсионных уравнений,
как это было для чисто-спиновых волн показано в § 7.1. При этом
оказывается, что «расталкивание» ветвей зависимости to'(Л')
происходит лишь при потерях, не превышающих некоторой величины.
При больших потерях оно заменяется пересечением ветвей".
" Эта универсальная закономерность будет продемонстрирована в § 14.2
на другом примере — электромагнитных волн в металлическом
ферромагнетике.
365
Рис. 12.4. Возбуждение
квазиупругих колебаний
в пластине однородной
намагниченностью [137]
Возбуждение. Магнитоупругие волны
могут быть возбуждены как магнитным
путем—когда непосредственно возбуждается
переменная намагниченность, так и
упругим— когда непосредственно возбуждается
упругое смещение.
Упругое возбуждение магнитоупругой
волны в ферромагнитном образце может быть
осуществлено, например, с помощью
пьезоэлектрического преобразователя — пластины
кварца, приклеенной к поверхности образца
и возбуждающей в нем линейно
поляризованное упругое смещение с частотой
подведенного к преобразователю электрического
напряжения. Такой же преобразователь может
быть использован и для «приема» волны.
Магнитное возбуждение магнитоупругих волн, строго говоря,
всегда имеет место при возбуждении волн в намагниченных ферро-
или ферримагнитных пленках тонкими проводниками (§ 6.2). Но
поскольку при этом волновые числа не превышают обычно ~ 103
при частотах ~ 1 ГГц, возбуждаются волны на квазимагнитной
полуветви достаточно далеко от точки пересечения, и упругой
составляющей этих волн, как и влиянием магнитоупругой связи на
спектр, можно пренебречь, как мы и поступали в § 6.2. Другим
вариантом магнитного возбуждения магнитоупругих волн является
возбуждение их однородной намагниченностью, которое становится
возможным благодаря наличию граничной поверхности образца.
Рассмотрим в качестве примера, следуя Ле Кроу и Комстоку [137],
возбуждение магнитоупругих колебаний в тонкой нормально
намагниченной ферромагнитной пластине, находящейся в однородном
переменном магнитном поле (рис. 12.4). Это поле возбуждает в образце
однородную переменную намагниченность, ее правую циркулярную
составляющую т+ будем считать заданной. Ограничимся рассмотрением
колебаний, не зависящих от поперечных координат х и у, а зависимость
от z будем считать достаточно медленной, чтобы обменным вкладом
в спектр можно было пренебречь. Тогда правая циркулярная
составляющая упругого смещения будет удовлетворять уравнению
co2pM++L4+—1^-1^ = 0, (12.50)
которое нетрудно получить из системы (12.28), (12.29), переходя
к циркулярным переменным и исключая т + .
Уравнение (12.50) не содержит сторонней однородной
намагниченности, она «вступает в игру» только через граничные условия
на поверхностях пластины. Если эти поверхности не закреплены, то
граничным условием будет (12.19), т.е. в данном случае
Gxz = Gyz = Gzz=:Q при z = 0, d. (12.51)
В напряжения ар, вносят вклады упругая и магнитоупругая энергии.
366
-т+=0 при z = 0, d.
(12.52)
Используя выражения (12.11) и (12.21) для этих энергий и соотношения
(12.7) и (12.27), можно показать, что из (12.51) в данном случае
следует неоднородное граничное условие
\с I yBl "И"' I Bzi
|_ М0((0 — coH)J dz М0
Таким образом, задача свелась к решению однородного линейного
дифференциального уравнения для упругого смещения с неоднородным
граничным условием. В этом ее отличие от задачи о возбуждении
стоячих спиновых волн в пластине однородным переменным полем
(§ 7.2), где уравнение было неоднородным (в него входило заданное
переменное магнитное поле), а граничные условия—однородными.
Не останавливаясь на решении уравнения (12.50) [137], отметим
лишь, что «+ оказывается суммой однородной сдвиговой деформации
и бесконечного числа резонансных членов, соответствующих
собственным квазиупругим колебаниям пластины с нечетными числами
полуволн, укладывающихся на ее толщине. Такая пластина может
быть использована как преобразователь, возбуждающий поперечную
упругую волну с круговой поляризацией в стержне из какого-либо
немагнитного кристалла. Заметим, что для возбуждения поперечной
упругой волны с линейной поляризацией может быть аналогичным
образом использована касательно намагниченная пластина.
Магнитоупругие волны в неоднородном постоянном поле. Мы до
сих пор, рассматривая магнитоупругие волны, считали внутреннее
постоянное магнитное поле в пределах образца однородным.
Неоднородность его приводит к ряду новых явлений, одним из которых
является преобразование магнитоупругих волн из квазимагнитных
в квазиупругие и обратно. Рассмотрим, например, волну с правой
круговой поляризацией в случае к||М0 и обратимся к рис. 12.5, на
котором спектр этой волны, определяемый уравнением (12.40),
построен в координатах Н0{к) при со = const. Если поле Н0 зависит
от координаты (в данном случае z) в направлении распространения,
к, /бГ к t-1 *-о
а ^ S
Рис. 12.5. Магнитоупругая волна в неоднородном постоянном поле; а—
зависимость Я0 (к) для волны с правой круговой поляризацией,
распространяющейся вдоль М0 (ср. с рис. 7.2), б—зависимость Н0 от координаты
в направлении распространения
367
то характер волны при ее распространении будет изменяться. Можно
полагать, что если зависимость H0(z) будет достаточно плавной,
а именно если будет выполняться условие (7.61), то волна будет
все время «находиться» на одной и той же ветви спектра. И если
точка zl (см. рис. 12.5), соответствующая максимальному сближению
ветвей магнитоупругого спектра, будет лежать внутри проходимого
волной пути, то при проходе этой точки волна из квазиупругой
почти полностью превратится в квазимагнитную или наоборот. Если
же градиент поля велик, так что неравенство (7.61) не выполняется,
то будет происходить частичное возбуждение волны на другой ветви
и вследствие этого — неполное преобразование характера волны. Эти
качественные соображения подтверждаются теорией, которую
разработали Шлёманн и Джозеф [401, 407, 408]. Заметим, что высказывая
эти соображения, мы пользовались языком нормальных волн; на
языке связанных волн они бы звучали следующим образом: при
проходе точки пересечения спектров спиновой и упругой волн спиновая
волна частично превращается в упругую (или наоборот), причем
тем в большей степени, чем меньше градиент Н0, т. е. чем длиннее
путь, на котором происходит взаимодействие волн.
Неоднородное внутреннее постоянное поле имеет место, в
частности, в цилиндрическом ферромагнитном образце, помещенном в
однородное внешнее поле Нс0, параллельное его оси. Этот случай уже
упоминался в § 7.2. При определенных значениях Яе0 в цилиндре
возникают «поверхности поворота» (г = г0 на рис. 12.5). Если цилиндр находится
но внешнем однородном поперечном переменном поле, то вблизи
)тих поверхностей, как было показано в § 7.2, возбуждается спиновая
волна, распространяющаяся в направлении убывания внутреннего поля
//о, т. е. к ближнему торцу цилиндра. Но на некотором расстоянии
от поверхности поворота будет расположена «поверхность пересечения»
спектров спиновых и упругих волн (r=rt на рис. 12.5). Проходя эту
поверхность, спиновая (точнее—квазиспиновая) волна
преобразовывается, как указывалось выше, в квазиупругую. Она распространяется
к торцу стержня, отражается от него и т. д. Таким образом, описанный
двухстадийный процесс (сначала возбуждается квазиспиновая волна,
затем она превращается в квазиупругую) может рассматриваться как
вариант магнитного возбуждения квазиупругих, а практически — почти
чисто упругих волн в ферро- или ферримагнитных кристаллах.
Аналогичное преобразование происходит при проходе магнитоупру-
гой волной поверхности пересечения спектров в неоднородном
постоянном поле и в случае к±М0. Этот случай (о чем тоже упоминалось
в § 7.2) может быть реализован в нормально намагниченном диске
при распространении волн в радиальном направлении [294].
Обе упомянутые «геометрии» могут быть использованы для
создания магнитоупругих управляемых линий задержки. Изменение
времени задержки в таких линиях при изменении внешнего поля
Яе0 происходит в основном потому, что изменяется путь, проходимый
волной на квазимагнитной полуветви, на которой, как видно,
например, из рис. 12.3, групповая скорость значительно меньше, чем
на кпазиупругой. Исследованию таких устройств было уделено
5t>8
большое внимание в 60-е годы (см., например, [213]), но затем
этот вопрос утратил актуальность в связи с разработкой пленочных
линий задержки, использующих магнитостатические волны (§ 6.2).
§ 12.4. Параметрическое возбуждение магнитоупругих волн
В этом параграфе мы рассмотрим влияние магнитоупругого
взаимодействия на процессы параметрического возбуждения, которые
без учета этого взаимодействия подробно исследовались в гл. 10.
При этом возникают задачи двух типов: 1) об учете того
обстоятельства, что параметрически возбуждаемые волны в
действительности являются не чисто магнитными, а магнитоупругими, и 2) о
параметрическом возбуждении, обусловленном магнитоупругим
взаимодействием. Остановимся сначала на задачах первого типа и
рассмотрим в качестве примера параметрическое возбуждение
магнитоупругих волн при продольной магнитной накачке.
Продольная накачка магнитоупругих волн. Поскольку накачкой
в данном случае является продольное магнитное поле hz,
непосредственно взаимодействующее с намагниченностью, следует ожидать,
что учет магнитоупругого взаимодействия приведет к увеличению
порога. Это становится особенно очевидным, если перейти на язык
связанных волн: параметрически возбуждаемые магнитные (спиновые)
волны линейно возбуждают связанные с ними упругие волны,
вследствие чего увеличивается их затухание и возрастает порог. Ясно, что
31 о возрастание становится особенно существенным при приближении
к точкам пересечения спектров магнитных и упругих волн.
Наличие двух ветвей магнитоупругих волн приводит, как видно
из рис. 12.6, к тому, что законы сохранения при продольной накачке:
Рис. 12.6. Продольная накачка магнито- Рис. 12.7. Перемещение вырожден-
упругих волн. Жирные линии- ветви ной пары магнитоупругих волн,
спектра волн, распространяющихся пер- возбуждаемых при продольной на-
пендикулярно М0; /', / и 2, 2' вырож- качке, по спектру при уменьшении
денные, 3, 3' и 4, 4' — невырожденные частоты накачки. Штриховые ли-
потенциально нестабильные пары волн нии — спектры магнитных и
упругих волн без учета
магнитоупругого взаимодействия
24 А. Г. Гуревич, Г. А. Мелков
369
(0,+(й2 = с0р и к,+к2 = 0, могут выполняться как в вырожденном
(со1=(о2), так и в невырожденном случаях. Обычно реализуется
вырожденный случай, для которого порог является более низким.
Обратимся теперь к рис. 12.7 и предположим, что при неизменном
поле //о частота накачки уменьшается. Если сор/2 существенно
превышает частоту со, пересечения спектров спиновых и упругих
волн, отличие от рассмотренного в § 10.3 параметрического
возбуждения спиновых волн будет несущественным — будут возбуждаться
вырожденные квазимагнитные волны с 6* = л/2 и противоположно
направленными к. По мере приближения сор/2 к со, упругая
составляющая uz этих волн увеличивается и hzth, возрастает. При а>р/2^и>1
произойдет перескок пороговой точки на другую ветвь магнитоупругих
волн, и при дальнейшем уменьшении сор порог будет уменьшаться,
приближаясь по мере удаления от точки пересечения к его чисто
магнитной величине. При сор/2<сон параметрическое возбуждение без
учета магнитоупругой связи невозможно, с учетом ее могут
возбуждаться волны на квазиупругой ветви, но, конечно, с высоким
порогом. Возрастание (пик) /izthr вследствие магнитоупругой связи
при переходе сор/2 через точку пересечения со, было обнаружено
Тернером [441 ] и затем исследовано теоретически Моргенталером
[370].
Ограничимся случаем, для которого справедлива система (12.28),
(12.29). Для распространяющихся по оси х волн с составляющими
Мх, Му, uz и поля накачки /;.coscop/ из этой системы следует
~= -l(0H-yD^--2 + yh2cos(upt\My,
дму ( „ с2 \ ., Suz
-z~ = [(HH + (HM-yD-rit + yhzcos(i,pt)Mx + yB2-—,
ct у ex* J Sx
(12.53)
Вгих_ d2u2 B2 BMX
~dtT~°^'dxT + W0~dx~
В отличие от § 10.3 мы не будем переходить к нормальным
переменным (в § 10.3 с* и с'-к), в данном случае такой переход
сложен. Будем непосредственно искать решения системы (12.53),
соответствующие двум параметрически возбуждаемым волнам с
частотой со = сор/2 и волновыми векторами к и —к:
A/x., = Re[f»iltx.,e,fr-bE> + m_lkjt.,effr-+bt>],
«J = Re[Mjtee''(M,-*x) + H-*_-e'"(''"+''x)].
Подставляя (12.54) в уравнения (12.53) и учитывая потери так
же, как и в § 12.3, т. е. заменяя coms [(vyH + yDk2){(aH+yDk2+(i)M)]1'2 -»
->com + ico^ и соС| = л/с44/р -»coCi + i'tOti, получим систему шести
алгебраических уравнений для переменных ткху, m*-kXiy, ukz и u*-kz.
Равенство нулю ее определителя даст уравнение для пороговой
величины hz. Действительно, если бы мы искали, как в § 10.2,
нарастающие решения, содержащие множитель ехр(А./), то при
370
заданной величине hz равенство нулю определителя системы дало
бы уравнение для X, а при заданной X.—уравнение для hz. Для
нахождения порога следует принять Х=0, что мы и сделали, записав
решение в виде (12.54). Выражение для пороговой величины
hz оказывается следующим [370]:
= mm
fl6 [(ro^i-co^/4)cowco^,+(ro^-ro^/4)coei4i,iJ2 | (12 55)
{у2[у^2В1/(рМ0)-юм(юе21-со^4)]2 + 4со2мю>:'2'"
Здесь min означает, что из величин Лг|Ьг на двух ветвях (рис. 12.7)
должна бы к. выбрана меньшая; когда они становятся равными,
происходи! \помянутый выше перескок с одной ветви на другую.
Анализ выражения (12.55) показывает, что при cop/2>coj. вдали
от точки пересечения спектров (см. рис. 12.7) величины hzthI
действительно наименьшие на квазимагнитных полуветвях и практически не
отличаются от значений, найденных в § 10.3. Порог возбуждения
волн на нижней квазиупругой полуветви (при сор/г-^сох)
'' y2BlQcl
(12.56)
где Qci = tOei/(2coe,)—упругая добротность. Заметим, что (12.56), как
и общая формула (12.55), предполагает возбуждение волн с 6* = л/2.
Однако при сор/2<сон порог оказывается наименьшим для воли
(квазиупругих) с малыми 6* [337] и выражение (12.56) дает лишь
порядок величины /izlhr.
Рассмотрим теперь подробно поведение порога вблизи точки
пересечения спектров. В этом случае из (12.55) следует
• /2ш"ли , 0ш2-ю2/4
со.2. \
'е|УШм/'
(12.57)
Второе слагаемое в этом выражении всегда положительно, т. е.
магнитоупругое взаимодействие, как и предполагалось, всегда
приводит к увеличению порога. Результаты расчета hzlhr по формуле
(12.57) в зависимости от Н0 при cop=const для обеих ветвей приведены
на рис. 12.8. Как видно из этого рисунка, пересечение кривых, т. е.
наибольшая величина порога, имеет место при поле //0 = Яреак,
Рис. 12.8. Пороговые
значения продольного поля
накачки вблизи точки
пересечения спектров магнитных
и упругих волн. Расчет по
формуле (12.57)
24*
"peak Н1
'zthr
371
Рис. 12.9.
Экспериментальная зависимость порогового
поля продольной накачки от
постоянного поля [378 ].
Сфера из монокристалла
ЖИГ; частота 23,2 ГГц,
температура 194 К, Мо||<100>
15 у/Н-Нп.Э1/г
несколько меньшем, чем поле Н0 = Н1, при котором при частоте
Юр/2 происходит пересечение ^ спектров. Из условий com = coe| = cop/2
следует, что Н\ = Нс-Dm^(4ui). где Нс определяется согласно (7.18).
Из (12.57) могут быть полугены [370] следующие выражения:
для высоты магнитоупругого пика (см. рис. 12.8)
v\Qc\2 шмУ'
его ширины на половине высоты
nDHt
V 1ШМ
Pk+YW,/roMj
и смещения его относительно точки пересечения спектров
(12.58)
(12.59)
"\ "peak —
yAWt6.,(AW0)^k / to
2шм(Яс-Я,)
I+-
УНх
(12.60)
Экспериментальная зависимость Л,|Ьг от постоянного поля
представлена на рис. 12.9. Используя такую зависимость, можно с
помощью приведенных формул найти величины В2, Qel и D (или vL).
Мы рассмотрели подробно случай, когда Мо||<100>. В других
случаях, в частности, при М0||<111>, когда, как отмечалось в § 12.3,
имеет место связь магнитных волн не только с поперечными, но
также и с продольными упругими волнами, на зависимостях h.tbr от
Н0 наблюдаются два магнитоупругих («тёрнеровских») пичка.
Заметим, что при поперечной накачке (рассмотренной без учета
магнитоупругой связи в § 10.2) тоже фактически возбуждаются
372
магнитоупругие волны. Влияние этого обстоятельства на величину
порогов существенно, конечно, лишь вблизи точек пересечения
спектров. Однако магнитоупругая связь позволяет и при поперечной
магнитной накачке возбудить волны на нижней квазиупругой
полуветви—с частотой Шр/2<ын. Такое во Суждение было осуществлено
[439 ] в сфере из монокристалла . i ексаферрита при /р = 1,32 ГГц;
пороговое поле составило ~ 10 Э.
Параметрическое возбуждение, обусловленное нелинейной
магнитоупругой связью. Перейдем теперь к другому случаю
воздействия магнитоупругой связи на параметрическое возбуждение,
когда эта связь является причиной нелинейности, приводящей
к параметрическому возбуждению тех или иных волн (или
колебаний). Эти волны могут быть как магнитоупругими, так и чисто
магнитными или чисто упругими, если в линейном приближении
магнитоупругая связь отсутствует. Второй случай представляет
наибольший интерес, особенно если при этом оказывается
невозможным параметрическое возбуждение, обусловленное чисто
магнитной нелинейностью.
Этому требованию удовлетворяет задача о параметрическом
возбуждении магнитных (спиновых) и продольных упругих волн,
распространяющихся в направлении М0 (совпадающем с осью <100»,
под воздействием поперечной накачки—однородной прецессии
намагниченности. Из уравнений (12.28) и (12.29) в этом случае с учетом
малости Мх и Му по сравнению с М. и в предположении упругой
и магнитной изотропии следует система уравнений
--=-^H-yD-2-2—-JMy,
д^Мн-уП^-2^)мх, (12-61)
d2uz д2и. В, ?,,., ,,2\
Величины Мх и Му в уравнениях (12.61) содержат как
составляющие однородной намагниченности накачки, так и составляющие
намагниченности возбуждаемой магнитной волны с волновым
вектором к. Второй возбуждаемой волной является продольная упругая
волна с волновым вектором ( — к), поскольку накачка является
однородной. Таким образом, в случае накачки с правой круговой
поляризацией
МХ = М0 а% cos сор / + Re [ткхе' <-.'-**>],
My = M0a%sm(Dpt+Re[mkyei^,-kz)'\, (12.62)
м:: = Re[w_jke''(ю''+'Iг,].
Подставляя выражения (12.62) в систему (12.61), получим при
условии со1+(й2 = Шр независимые эквивалентные системы для ткх„,
и*-к и т*кх^у, и-к, в которые войдет амплитуда накачки я'.
Учитывая потери путем замены со, -*(0l+iyAHkj2 и m2^m2+im2/{2Qei)
373
и приравнивая нулю, как и при выводе
(12.55), определитель любой из этих
систем, найдем пороговое значение
а°0 [232]
1 1сиМ0АНк
Рис. 12.10. Параметрическое
возбуждение невырожденных
магнитной и упругой волн при
однородной накачке
«^--/^РадГ5- (12-63)
Как и следовало ожидать,
пороговая амплитуда накачки оказалась
пропорциональной корню из произведения
параметров диссипации АНк и l/Qtl.
Оба эти параметра уменьшаются при
уменьшении к, но особенно резко l/6ei
вследствие уменьшения частоты со2.
Поэтому наиболее низкие пороги
должны наблюдаться при таких значениях
Юр и Н0, при которых (рис. 12.10) £->0
и (о1~(ор. Однако при малых к
приближение однородных плоских волн неприменимо, возбуждаются
в действительности собственные магнитные и упругие колебания
образца, и задача должна решаться с учетом характера этих колебаний
при конкретной форме образца. Для тонкой нормально намагниченной
пластины [37, 137] порог оказывается наиболее низким и по порядку
величины совпадает с (12.63), когда возбуждаются магнитостатическж-
волны (§ 6.2) и упругие колебания с малым числом вариаций пи
толщине пластины (§12.1). В случае сферы будут возбуждаться
магнитостатические колебания (§ 6.3) и низшие упругие колебания
сферы (§12.1), а пороговая амплитуда однородной прецессии по-
прежнему будет порядка (12.63).
В случае достаточно высоких частот накачки, когда магнитное
параметрическое возбуждение первого порядка при резонансе (см.
§ 10.2) невозможно, целесообразно сравнить найденный порог (12.63)
с порогом для магнитного процесса второго порядка (10.30). Оценка
показывает, что, например, для ЖИГ отношение o8ihr2/°oihrmei может
превысить 10, однако при условии, чтобы иеличина Q& не снижалась
внешней механической нагрузкой образна. Именно при этом условии
магнитоупругое параметрическое возбуждение упругих колебаний
сферы наблюдали Спенсер и Ле Кроу [420]. Это явление получило
название магнитоакустического резонанса (MAP).
В качестве накачки при магнитоупругом параметрическом
возбуждении могут выступать и спиновые волны, возбуждаемые
параметрически при продольной [162] или поперечной [333] накачке. Этот
процесс был назван вторичным MAP. Как показали Лукомский
и Кузько [141 ], он разрешен законами сохранения только при малых
кр, для ЖИГ—порядка 103-=-104.
Упругая накачка. До сих пор мы рассматривали магнитоупругое
параметрическое возбуждение квазиупругих волн или колебаний при
накачке квазимагнитными волнами или колебаниями. Но возможен
и обратный процесс, при котором в качестве накачки выступает
374
квазиупругая волна. Рассмотрим снова случай Мо||<100>, для
которого справедливы уравнения (12.28) и (12.29). Пусть накачкой
является продольная упругая волна, распространяющаяся вдоль оси
z в направлении М0, а возбуждаются магнитоупругие волны с
волновыми векторами kL и к2, лежащими в плоскости xz. Предположим,
что А,,2»А:р, так что к^к1х^ — к2х = к. Уравнения (12.28) в этом
случае примут вид
dMv ( nI, 2yB, СиЛ
ч \ М0 дг)
где M. = Mpcos(c0pf—kpz)—заданная величина.
Из (12.64) видно, что упругая волна накачки
продольному магнитному полю
h:c,= ——- —^= -^-kpupsm((opt-kpz). (12.65)
Поскольку Ар мало, можно игнорировать волновой характер этого
поля и, считая возбуждаемые волны чисто магнитными, восполь-
юваться для нахождения его пороговой величины формулой (10.49).
Тогда, как легко убедиться, пороговое значение амплитуды упругой
волны накачки
4тгуВ,
где v\\—скорость упругой волны (12.16).
Оценка пороговой величины потока упругой энергии по формуле
(12.18) дает в этом случае для ЖИГ ~ 0,1 Вт см2, что не противоречит
эксперименту [367]. Такого же порядка оказывается порог и в случае
накачки магнитных (строго говоря, квазимагнитных) волн поперечной
упругой волной. При возбуждении же упругой и магнитной или двух
упругих волн пороги оказываются значительно более высокими [140].
§ 12.5. Спин-решеточная релаксация
Как уже отмечалось в § 11.1, энергия магнитных колебаний
и волн передается в конечном счете в основном кристаллической
решетке, и осуществляющие эту передачу процессы могут быть
прямыми и косвенными. Косвенные процессы — происходящие с
участием других систем будут рассмотрены в гл. 13 и 14, в этом
параграфе мы остановимся на прямых процессах спин-решеточной
релаксапии. Источником их является магнитоупругое взаимодействие,
а именно, как мы увидим, те члены его энергии, которые являлись
(§ 12.4) источником параметрического возбуждения. Но если в случае
параметрического возбуждения генерировались когерентные колебания
или волны и было целесообразно классическое рассмотрение, то
375
(12.64)
эквивалентна
в теории процессов релаксации, носящих микроскопический,
статистический характер, целесообразно использовать (см. гл. 11) квантово-
механические методы.
Микроскопический подход. В § 7.4 при рассмотрении
микроскопической теории спиновых волн была использована гейзенберговская
модель— решетка спиновых магнитных моментов, связанных обменным
и магнитным взаимодействиями. На основе этой модели можно
построить теорию процессов спин-решеточной релаксации, учитывающую два
упомянутых в §12.1 источника магнитоупругой энергии: обменный
и диполь-дипольный. Это было осуществлено Ахиезером в
неоднократно упоминавшейся выше работе [224]. Входящая в гейзенберговский
гамильтониан величина rf (оператор радиуса-вектора спина в узле /)
должна быть для этого представлена аналогично (12.1) в виде
r/ = f/0 + u/, (12.67)
где операторы f/0 соответствуют равновесным положениям спиновых
моментов. Затем следует разложить гамильтониан в ряд по
операторам смещений й^ и ограничиться нулевым и первым членами
этого ряда. Используя затем представление вторичного квантования,
т. е. переходя от операторов спиновых отклонений, как в § 7.4,
к операторам ак и ак+ , а от uf—к операторам рождения и уничтожения
фононов b\ и 6Я+ , мы приведем гамильтониан к виду
Ж=Ж0 + ^тс12+Жтс13+ ... , (12.68.
где Ж о— не возмущенный колебаниями решетки гейзенберговский
гамильтониан (который использовался в § 7.4, а также в § 11.2).
а остальные члены описывают магнитоупругую связь. Они содержат
операторы bq и hq в первой степени, а операторы о* и ак+—в
возрастающих степенях: Jfmei2 — в первой, Жтец — во второй и т. д.
Однако основной источник магнитоупругой
связи—спин-орбитальное взаимодействие не может быть исследовано на i ейзенберговской
модели, которая не содержит орбитальных моментов. Современное
состояние микроскопической теории этого взаимодействия не дает
возможности надежно учесть его вклад в магнитоупругую связь.
Остается единственная возможность построить квантовую теорию,
основываясь на феноменологических выражениях для магнитоупругой
энергии, например (12.21). Этот путь предложили Абрахаме и Киттель
[219] и осуществили Каганов и Цуксрник [100].
Феноменологическая теория. Выразим соответственно через я*,
а£ и Sq, Sq+ входящие в (12.21) и рассматриваемые теперь как
операторы составляющие М и и. Согласно [15]
где р —плотность, V— объем образца, p0qj (/= 1, 2, 3)—единичный
вектор поляризации фононов, соответствующий направлению вектора
и для каждой из трех нормальных упругих волн с данным волновым
вектором q, а сощ — частбты этих волн.
376
Рассмотрим случай изотропной среды, т. е. положим в (12.21)
Bt = В2 = В. Тогда, используя (12.69) и соотношения, связывающие
проекции М с операторами я* и йу (§ 7.4), получим, ограничиваясь
членами, линейными по bqJ и £+-, гамильтониан вида (12.68), где
^me.2=ILL(4V4Jdk£i + 3. c.)A(k-q), (12.70)
J" к ч
^'mei3=IIII[(4,fclll2.wflfcl42^+3. c.)A(k,+k2-q) +
J ki кг ч
+ (^2.,АА+А^- + э. с.)Д(к1-к2-Ч)]. (12.71)
Здесь, как и в § 7.4, э. с. обозначает величину, эрмитово-сопряженную
с приведенной, Д—дельта-символ Кронекера (7.104), а выражения
для амплитуд Ч^,,;, Ч**^.,; и Ч**,,*^-, полученные в [100], приведены,
например, в [69 ].
Элементарные процессы. Аналогично случаю изолированной
магнитной системы (§ 11.2) отдельные члены в (12.70) и (12.71) соответствуют
шементарным процессам с рождением или уничтожением магнонов и
фононов. Для них, как видно из (12.70) и (12.71), выполняются (в иде-
лльном кристалле!) условия сохранения импульса. В первом
приближении теории возмущений выполняются и условия сохранения энергии.
Билинейный гамильтониан (12.70) описывает элементарные
двухчастичные процессы превращения магнона в фонон и обратно. После
диагонализации его совместно с квадратичными гамильтонианами
упругой и магнитной систем получаются новые квазичастицы, которые
соответствуют магнитоупругим волнам, исследованным на
континуальной модели в § 12.3. Трехчастичный гамильтониан (12.71)
описывает рассмотренное в § 12.4 параметрическое возбуждение,
обусловленное магнитоупругой связью, а также спин-решеточную релаксацию.
Членам с амплитудами Ч** k ^ соответствуют элементарные процессы
слияния двух магнонов с образованием фонона, а эрмитово-со-
пряженным с ними членам—процессы расщепления фонона на два
магнона. Членам с амплитудами Ч^ *2<^ соответствуют элементарные
процессы расщепления магнона на магнон и фонон, а эрмитово-
сопряженным с ними —процессы слияния магнона с фононом. Эти
процессы были названы черепковскими по аналогии с эффектом
Черенкова—Вавилова (см., например, [134]) —излучением света при
торможении электронов в среде. В данном случае магноны являются
аналогами электронов, а фононы —света, и условие существования
эффекта Черенкова — Вавилова (скорость электронов больше скорости
света в среде) переходит в неравенство
vmsr>vqj, (12.72)
где L'mgr—групповая скорость спиновых волн, a vqJ—скорость упругих
волн. Как видно из рис. 12.3, это условие может быть выполнено
при достаточно больших А:.
Процессы слияния магнонов в фонон и расщепления фонона на
магноны, при которых изменяется число магнонов, могут быть (как
377
и процессы с изменением числа магнонов в § 11.2) обусловлены
только релятивистскими взаимодействиями. Черенковские же
процессы, при которых число магнонов не изменяется, могут быть вызваны
как релятивистскими, так и обменными взаимодействиями. Отношение
вкладов этих взаимодействий в амплитуду Ч\ * ^ при к1~к2 = к
составляет [100]
{Vk„tl„)a/{4>tl wU~M0Dk2/B. (12.73)
Оценка показывает, что для ЖИГ эти вклады становятся одного
порядка при А~106, при меньших к преобладает вклад релятивистских
взаимодействий, в первую очередь—спин-орбитального,
ответственных за магнитоупругую постоянную В.
Черенковские процессы расщепления магнона на магнон и фонон
лежат в основе исследованного в § 12.4 параметрического возбуждения
магнитных и упругих колебаний под действием магнитной накачки
(MAP), а процесс расщепления фонона на два магнона—в основе
параметрического возбуждения магнитных колебаний или волн при
упругой накачке.
Процессы релаксации. Рассмотренные трехчастичные элементарные
процессы лежат в основе трех процессов спин-решеточной релаксации,
приведенных в табл. 12.1. То обстоятельство, что теперь трехчастичные
процессы могут быть обусловлены и обменным взаимодействием,
делает ненужным (в отличие от чисто магнонных процессов, § 11.2)
рассмотрение четырехчастичных процессов, поскольку их вероятности
всегда будут меньше, чем процессов с участием трех частиц.
Таблица 12.1
Процессы прямой спин-решеточной релаксации
(рассматривается релаксация магнонов с кО
Процесс
Слияния магнонов
Черенковские
Расщепления
Слияния
Амплитуда
Ъ,*,.4
ъ,.ы
^**2.*|в/
Элементарные процессы
Прямые
^
^t
ХЛ.
■*
Обратные
к* ^
*N^
Для расчета частот релаксации упомянутых процессов,
обусловленных магнон-фононными элементарными процессами, полностью
применима рассмотренная в гл. 11 теория, основанная на вычислении
378
вероятностей переходов в первом приближении теории возмущений.
Не останавливаясь на этих вычислениях (см. [100], а также [15,
319, 346]), приведем лишь некоторые результаты. Оказывается, что
вклад рассмотренных спин-решеточных процессов в диссипацию
колебаний намагниченности, в том числе однородных, а также
спиновых волн с к < 105, которые возбуждаются в результате
двухмагнонных процессов (§ 11.3) или параметрически, пренебрежимо
мал. Эти процессы становятся все более эффективными по мере
увеличения к,}. И в тех веществах, в которых не играют заметной
роли процессы косвенной спин-решеточной релаксации (см. гл. 13
и 14), рассматриваемые процессы прямой спин-решеточной релаксации
передают в конечном счете в решетку энергию магнитных колебаний
или волн, предварительно «размазанную» по k-пространству спин-
спиновыми процессами.
В случае однородных магнитных колебаний или волн с
небольшими к в совершенных кристаллах ферритов, таких как ЖИГ,
возникает трудность при объяснении самого первого этапа
упомянутого размазывания, определяющего в основном наблюдаемую
ширину резонансных кривых — порядка 0,3 Э для ЖИГ. Эта
трудность уже обсуждалась в § 11.2; при этом отмечалось, что
существенный вклад в ширину кривой однородного резонанса Д//0,
а также в минимальные величины Д//* при параметрическом
возбуждении спиновых волн могут давать процессы, впервые
упомянутые Касуйя и Ле Кроу [345]. Это — процессы трехбозонного
слияния, отличающиеся от исследованных в § 11.2 и данном
параграфе тем, что, во-первых, принимаются во внимание
«верхние»— «оптические» ветви спектра магнонов (в ферримагнетиках)
или фононов, а во-вторых, учитывается, что локальная симметрия
окружения ионов в кубических кристаллах может быть более
низкой и величины локальных констант анизотропии и магнито-
упругого взаимодействия — значительно большими, чем величины
их, усредненные по всему кристаллу. При этих двух условиях, как
показано в [345] (см. также [115]), возможны трехб'озонные
процессы релаксации магнонов с А: = 0 или малыми /с, дающие
заметные вклады в параметры диссипации этих магнонов. Они
могут быть двух типов: слияния магнона с магноном обменной
ветви и слияния магнона с оптическим фононом с образованием — в
обоих случаях — магнона. Процессы первого типа упоминались
в § 11.2, второго — должны быть рассмотрены в данном параграфе.
Заметим, что магнон-фононные черенковские процессы слияния,
в том числе и процесс Касуйя — Ле Кроу второго типа, приводят
к передаче энергии не из магнитной системы в решетку, а из
решетки в магнитную систему. Однако они ведут к уничтожению
рассматриваемых нами магнонов и, таким образом, вносят вклад
в их параметр диссипации. На последующих стадиях релаксации
" Поэтому для усредненных по всему k-пространству значений частот
релаксации этих процессов были получены [100, 224] довольно большие
величины—порядка 107.
?79
**2
k,g
Рис. 12.11. Спектры магнонов (сплошные линии) и фононов (штриховые)
в ферримагнетике и реализация условий сохранения для спин-решеточного
процесса Касуйя- -Ле Кроу (одна из возможностей)
энергия, конечно, будет передана в решетку другими процессами.
Выполнение законов сохранения энергии и импульса при спин-
решеточном (второго типа) процессе Касуйя—Ле Кроу иллюстрирует
рис. 12.11. Как видно из этого рисунка, такие процессы, вообще
говоря, возможны с участием фононов не только оптической, но
и акустической ветви, рождающиеся магноны тоже могут
принадлежать как верхним (обменным), так и нижним ветвям.
Оценки показывают, что вклады магнон-фононных процессов
Касуйя — Ле Кроу, как и магнон-магнонных, рассмотренных в § 11.2.
могут быть, в частности, для ЖИГ порядка 0,1 Э, т. е. составлять
заметную, если не преобладающую, часть параметра диссипации.
Глава 13
ИОННАЯ АНИЗОТРОПИЯ И РЕЛАКСАЦИЯ
§ 13.1. Анизотропия, вызванная ионами
с сильной спин-орбитальной связью
В этой главе мы рассмотрим влияние на ферромагнитный
резонанс ионов с сильной спин-орбитальной связью. Как уже
отмечалось в §11.1, они приводят к появлению весьма
эффективного процесса релаксации, который мы для краткости
будем называть ионным процессом. Эти ионы являются также
источником кристаллографической анизотропии, которая
проявляется как при ферромагнитном резонансе, так и при более медленных
процессах.
К ионам, влияние которых будет исследоваться в этой главе,
принадлежат все «магнитные» ионы (т. е. ионы с недостроенными
Id- или 4/-оболочками) кроме тех. которые либо вообще не имеют
орбитального момента (находятся в S-состоянии), либо имеют
в кристалле «замороженный» орбитальный момент. Последнее
означает, что в основном состоянии в данном кристаллическом
поле равно нулю среднее значение </-2> проекции орбитального
момента на ось квантования (совпадающую в ферромагнетике
с направлением М0), т. е. что нижним энергетическим уровнем
иона является орбитальный синглет. В S-состоянии находятся ионы
Mn2 + , Fe3 + , Eu2 + , Gd3 + , а характерным примером иона с
замороженным орбитальным моментом является ион Сг3+ в окта-
эдрическом окружении. Ионы с равным нулю или замороженным
орбитальным моментом, прежде всего ионы Fe3 + , являются
основными магнитными ионами во всех используемых в диапазоне
СВЧ магнитных материалах. Ионы с сильной спин-орбитальной
связью могут появиться в этих материалах либо из-за
недостаточной чистоты сырья, либо вследствие изменения по тем или иным
причинам валентности основных ионов, а также могут быть
добавлены специально, например, для повышения порога
параметрического возбуждения спиновых волн.
Остановимся прежде всего на структуре энергетических спектров
ионов переходных и редкоземельных элементов в магнитоупорядочен-
ных веществах, в частности ионов с сильной спин-орбитальной
связью. Этими спектрами в соответствии с одноионнои теорией
анизотропии (§ 2.2) определяются вклады таких ионов в
кристаллографическую анизотропию.
Энергетические уровни ионов. Электронные механический J
и магнитный 501 моменты ионов с недостроенными 3d- или
381
4/-оболочками являются (см., например, [132]) векторными
суммами соответственно механических и магнитных моментов —
орбитальных и спиновых — всех электронов этих оболочек. Причем
взаимодействие электронов носит в этом случае такой характер
(связь Рассела — Саундерса или L — S-связь), что целесообразно
сначала суммировать все спиновые (§„) и все орбитальные (1„)
моменты электронов 3d- или 4/-оболочки: £s„ = S, £!„ = £,, а затем
- - - - * л л
уже складывать S и L:S + L = J.
Как уже отмечалось в § 1.1, собственные значения проекций
S и L (измеренные в единицах Л) на ось квантования принимают
значения 5, (5—1) (-S) и L,- (L—\), ...,( —L), где целое или
полу целое число S и целое (или нуль) число L—соответственно
спиновое и орбитальное квантовые числа иона. Собственные
значения полного момента J могут иметь величины J, (J— 1), ...
..., (—J), а квантовое число J—величины (S + L), (S + L— 1), ...
...,\S-L\.
Величины квантовых чисел S и L ионов в основном состоянии
определяются эмпирическими правилами Хунда [132].
Энергетические уровни свободных ионов без учета релятивистских спин-
орбитально!о и внутриионного спин-спинового взаимодействий"
зависят только от этих чисел и вырождены с кратностью (2S+l)x
x(2L+l). ("пин-орбита.ibttoe взаимодействие приводит к расщеп-
1ению их \i.\ уровни (м\.п,1иплеты) с разными значениями J.
вырожденные с крат нос ilk> (2./+1). При этом нижним является
уровень с J=\L — S\, гели оболочка заполнена менее чем
наполовину, и с J=L + S, если она заполнена более чем наполовину.
Значения S, L и J свободных 3d- и 4/:ионов в основном состоянии
приведены в табл. 13.1 и 13.2.
Наложение внешних no.icit приводит к дальнейшему снятию
вырождения состояний (расщеплению энергетических уровней) ионов.
Внешнее магнитное поле, как уже отмечалось в § 1.1, приводит
к расщеплению каждого мультиплета с данным J на (2./+1)
эквидисташных уровня с интервалами (1.18). Внешнее электрическое
поле тоже приводит к снятию вырождения этих мультиплетов,
полному или частичному, в зависимости от симметрии поля и
величины J. Поле орторомбической или еще более низкой симметрии
расщепляет мультиплет полностью, если J целое (т. е. число 3d-
илн 4/-электроиов — четное), или на (./+1/2) крамерсовых дублетов —
если ./ полуцелое. Электрические поля более высокой симметрии
приводят к частичному снятию вырождения мультиплетов. Например,
поле кубической симметрии совсем не расщепляет мультиплеты при
J<2, пятикратно вырожденный уровень с ./=2 расщепляется им на
дублет и триплет, семикратно вырожденный уровень с У=3— на
сииглет и два триплета [1].
1 В млмгсГписм мы часто для краткости будем творить о спин-
|>рбита.1мкш взиимотейетвнп. имея в виду оба эти взаимоценсгвия.
я
S
к
ю
я
3
и
ю
О (~
х о
о о
О. и
es
g§
is
sg
a °
jq pa
я
4
о
ю
о
л
ра
о
г-
я
я
о
и
о
и
~. «ч ~, С •"
<*:Г™ЙО
оо — г-1 "=»■ ■*,
— ™ _ С? S
Г«1 ^ **ч
с
2
и
чОГ^ rJ rj- Q
'й-^йсо
it гч м о Q
U
"S"^
СЧ — гОП Ц,
«ч _. CJ "
—™ —*^ ^^ /*\
5 Б
я о
со я
я
о
2 г- 5.
S я р
■з 5 u
? II*
т S'S я
О t £ Я
Н Я Я Я п
о яю 5 о
S ВО.ОЮ
УиОСО
£
1
s
о
я
pa
О
я
и
о
ш
о
I
D
СЭ <Ч ЧО ОО *«ч
— 1Л
<0
3
-а
С
5
00 **"> **"> ^ ^*ч
jmmO^
J
я
О
1С
о
1
V<NVO<t"-
<s — vi rj-132
я р
Я X
СО ь
■ <*> Lr
1
о. е.
S ь -
I
(и - J«
Т ^ s *
•*• я « ?
О Н- £ я
с= Я S Я t-^
s с aOio
p-UOEO
383
В кристалле магнитные ионы находятся под воздействием
электростатического взаимодействия с соседними ионами. Часть
его, зависящая от взаимной ориентации спиновых моментов,
называется обменным взаимодействием. Это взаимодействие можно
описывать при помощи эффективного, так называемого
молекулярного поля (§ 1.1). Оно приводит к такому же по характеру
расщеплению уровней иона, как и внешнее .магнитное поле.
Остальную же часть электростатического взаимодействия с
соседними ионами обычно описывают при помощи кристаллического
поля, которое имеет такую же симметрию, как локальное окружение
иона, и приводит к соответствующему этой симметрии расщеплению
уровней.
Рассматривая воздействие различных факторов на
энергетические уровни ионов, следует начинать с наиболее сильных
воздействий, переходя последовательно ко все более слабым.
Эта последовательность оказывается различной для 3d- и
4/-ИОНОВ. Для Зй?-ионов незаполненная электронная оболочка
является внешней, и кристаллическое поле представляет собой
наиболее сильный фактор; затем идет обменное
взаимодействие и уже затем — спин-орбитальная связь. При этом
следует различать два случая — сильного и промежуточного
кристаллического поля [1]. В первом случае энергия Зй?-электронов
в кристаллическом поле превышает энергию их
взаимодействия, приводящего к формированию суммарных моментов L и S
иона. Этот случай реализуется сравнительно редко, и мы не будем
на нем останавливаться. В случае промежуточного
кристаллического поля энергия Зг/-электронов в кристаллическом поле меньше
энергии их взаимодействия и энергетический спектр (как и для
свободных ионов с рассел-саундерсовской связью) определяется
в первую очередь величинами L и 5. Но как уже отмечалось
выше, воздействие кристаллического поля для Зй?-ионов является
более сильным, чем спин-орбитальное взаимодействие, приводящее
к формированию полного момента J, и энергетический спектр
иона определяется воздействием этого поля на орбитальные муль-
типлеты.
Симметрия кристаллического поля соответствует симметрии
локального окружения иона. Однако во всех случаях
наибольшей величиной обладает кубическая составляющая этого
поля. Поэтому при рассмотрении mepi стических уровней ионов
целесообразно сначала выяснить их структуру в кубическом
кристаллическом поле, а затем учесть как вочмушение
воздействия тригональных, тетрагональных или орт ромбических
искажений.
В табл. 13.3 показано расщепление орбитальных мультиплетов
с L = 2 и L = 3 на триплеты, дублеты и синглеты кристаллическим
полем кубической симметрии. В октаэдрических узлах шпинели
и граната (§ 3.3) кристаллическое поле имеет кроме кубической
небольшую тригональную составляющую, приводящую к
расщеплению триплетов на синглет и дублет.
384
Таблица 13.3
Расщепление орбитальных мультиплетов кубическим кристаллическим полем
Орбт ильный
момент
2
3
Кратность
вырождения
до
расщепления
5
7
Числа
3*/-электронов
1 ИЛИ 6
4 или 9
3 или 8
2 или 7
Примеры ионов
Fe2+, Co3+
Cr2+, Mn3+, Fe4"
Сг3+, Ni2 +
Сг4+, Со2 +
Кратности вырождения после
расщепления (в порядке
возрастания энергии)
Октаэдриче-
ское
окружение
3; 2
2; 3
1; 3; 3
3; 3; 1
Тетраэдриче-
ское
окружение
2; 3
3; 2
3; 3; 1
1; 3; 3
В качестве примера на рис. 13.1 показано «последовательное»
расщепление нижнего орбитального мультиплета 5D ионов Сг2 + , Мп3 +
или Fe4+ (конфигурации dA) в октаэдрическом узле. Кубическая
составляющая кристаллического поля приводит, согласно табл. 13.3,
к расщеплению терма 5D на дублет и триплет. Следующее по силе
обменное взаимодействие приводит к снятию вырождения по спину;
все пять нижних эквидистантных уровней остаются дублетами. И
наконец, самое слабое в рассматриваемом случае—спин-орбитальное
взаимодействие расщепляет эти дублеты. Существенно, что это
расщепление оказывается зависящим от направления вектора Мо
относительно осей кристалла. Причина этой зависимости заключается в том,
что поворот вектора Мо приводит в силу обменного взаимодействия
Свободный
ион
*3
«2
Куби-
/
*1
"Z
*2
<:
-<с
Триво-
-С
Обмен- Спин.
(без"спин- состав-^ 7осТа7-+аЛ^мо °^та'
ообиталь- ляюшая JL^.7.^ 6зЛЧ.м° + /">ное
ново
взаимодействия)
Кристалл и ческа е
поле
ляюш,ая
действие
взаимодействие
Рис. 13.1. Энергетические уровни ионов с конфигурацией cl* в октаэдрических
узлах, х 3, х 2 и х 1 обозначают кратность орбитального вырождения
25 А. Г. Гуревич, Г. А. Мелков 385
<tfO>
Рис. 13.2. Расщепление нижнего
дублета ионов d* или d6 в октаэдрических
узлах спин-орбитальным
взаимодействием [327] (штриховые линии)
и с учетом возмущений [315]
(сплошные)
к повороту спинового момента
иона S; вследствие
спин-орбитальной связи поворачивается и
орбитальный момент L, что
приводит к изменению энергии в
кристаллическом поле. Как показано
в [376, 327], угловые зависимости
нижних уровней Ei.2 в этом случае
(рис. 13.1) в первом приближении
имеют вид
El.2=±- 1--
2\_ '
'(sin2 26 +
+ sin40sin22(p) , (13.1)
" 1/2
) •
где 8 — максимальное расстояние
между уровнями (рис. 13.2),
а 0 и ф—углы вектора М0 (полярная ось совпадает с осью <100».
Для 4/-ионов незаполненная электронная оболочка «глубоко
запрятана», экранирована от соседних ионов 5s- и 5/>-оболочками.
и поэтому воздействие кристаллического поля является слабым.
Наиболее сильным в этом случае оказывается спин-орбитальное
взаимодействие, объединяющее моменты L и S в полный момент
J. Мультиплеты, соответствующие различным J, расщепляются (так
же как орбитальные мультиплеты в. случае Зй?-ионов) кристаллическим
и обменным полями. На рис. 13.3 показано такое расщепление для
случая, когда обменное взаимодействие является слабым по сравнению
с расщеплением в кристаллическом поле. Расстояния между уровнями,
на которые расщепился, в частности, нижний дублет, оказываются
Свободный
ион
(без спин-
орбитального
взаимодействия)
Спин-
орбитальное
взаимодействие
Кубическая +
составляющая
Орто-
ромби-
ческая
составляющая
'-30см
Кристаллическое поле
Обменное
+
взаимодействие
РИС'Г4541' и™™460™6 УР°ВНИ ИОНа Yb3+ B лодекаэдрических узлах граната
1454]. Величины интервалов -для ЖИГ с малой добавкой иттербия
386
при этом зависящими от ориентации
вектора М0. Для редкоземельных
ионов с большими спиновыми
моментами, таких как ТЪ3 + , Но3 + ,
реализуется другая ситуация, когда
расщепления в обменном и
кристаллическом полях оказываются одного
порядка. В этом случае могут иметь
место пересечения уровней при
некоторых ориентациях М0. Различные
не учтенные пока взаимодействия
приводят к тому, что эти
пересечения заменяются сближениями (near-
crossings) уровней (рис. 13.4).
Одноионная теория анизотропии
ферромагнитного резонанса.
Рассмотрим влияние интересующих нас
ионов на условие ферромагнитного
резонанса". Свободная энергия ионов
при термодинамическом равновесии
может быть определена по формуле,
являющейся обобщением (2.32):
t/i«n =
200
100
-100
-200
J0
60 SO 8,ерад
= -иГ1п
IZ Nh £ ехр (- ЕьДхГ)) .
I v j
Рис. 13.4. Угловые зависимости
уровней иона ТЪ3+ в одном ич
неэквивалентных додекаэдрических
узлов [286]. Расчет проведен,
исходя из экспериментальных данных
по ферромагнитному резонансу
в ЖИГ с малой добавкой тербия.
G угол между М0 и осью <100>
в плоскости {110}
(13.2)
Здесь индекс / характеризует сорт
иона, v—кристаллографически неэквивалентные узлы решетки, a j—
энергетические уровни данного иона в данном узле. Имея в виду,
что при малых концентрациях ионов (именно этот случай нас
интересует) вклады разных ионов и ионов в разных узлах в
анизотропию аддитивны, мы будем исследовать их по отдельности и
использовать формулу (2.32).
Для получения условия ферромагнитного резонанса следует
подставить в формулу (2.26) в качестве U сумму свободной энергии
ионов (2.32), зеемановской энергии Uz во внешнем поле и, вообще
говоря, энергии в размагничивающих полях UM. Но ограничиваясь
для простоты случаем сферы, мы можем энергию UM (не зависящую
в этом случае от направления вектора М) опустить. Для энергии
Uz справедливо выражение (2.28). и поскольку мы здесь рассматриваем
случай малой концентрации ионов, углы 0 и ф в этом выражении
можно считать совпадающими (в случае сферы и без учета собственной
анизотропии основной магнитной системы) с углами 0Н и фн.
Ограничимся учетом только двух нижних уровней ионов. Это
будет хорошим приближением при достаточно низких температурах,
" Пока—без учета динамического вклада в анизотропию (§ 13.2).
25* 187
а без жесткого ограничения температуры—в двух важных частных
случаях;
а) низколежащего дублета, расщепленного спин-орбитальным (для
Зй?-ионов, рис. 13.1) или обменным (для 4/-ионов, рис. 13.3)
взаимодействием;
б) в области резкого сближения двух нижних уровней (см.,
например, рис. 13.4).
При учете только двух нижних уровней из (2.32) легко получить
(опуская несущественное постоянное слагаемое)
Uion = Ne0-NxT In сп[5е/(2хГ)], (13.3)
где £0 = (1/2)(e1+e2), a 8е = е2 —Et; средняя энергия е0 и расщепление
8е являются в общем случае функциями углов 6 и ср. Подставим
сумму (13.3), и зеемановской энергии (2.28) в формулу (2.26) и,
принимая во внимание, что концентрация ионов мала, пренебрежем
членами второго порядка по TV. Тогда после простых преобразований
придем к следующему выражению [315]:
где индексами G и ср, как и в (2.26), обозначены частные производные
по соответствующим углам вектора М0 (совпадающим в нашем
случае с заданными углами Не0).
Сближающиеся уровни. Рассмотрим сначала случай расщепления
нижнего орбитального дублета спин-орбитальным взаимодействием
и примем, что М0 лежит в плоскости {ПО}. Тогда, как видно из
рис. 13.2, в направлении <111> имеет место пересечение уровней
(вырождение). В действительности вырождение снимается различными
не учтенными взаимодействиями, и происходит сближение уровней.
Для феноменологического учета этого обстоятельства выражение
(13.1) можно скорректировать следующим образом [315]:
Ei.2=±(8/2) l-^(sin22e + sin4esin22cp) + S2 , (13.5)
где £ = (5E)min/8, a (8E)min—минимальное расстояние между уровнями
(см. рис. 13.2). Тогда расчет по формуле (13.4) даст, в частности,
6Я<М1> = ^-1Ъ^. (13.6)
<! м> М0Ъ, 2хГ y '
Угловая зависимость ЪН, рассчитанная по формуле (13.4) с учетом
(13.5), показана на рис. 13.5. Как видно из этого рисунка, при
соответствующем подборе значений 8, Ь, и N расчетная зависимость
хорошо согласуется с экспериментом, проведенным для монокристалла
CdCr2Se4, подвергнутого отжигу в вакууме. При этом возникали
вакансии Se, стимулирующие образование ионов Сг2+ (в стехиомет-
388
Рис. 13.5. Угловая зависимость
6Я=Я„,—ш/т, обусловленная ионами
Сг2+. Линия—расчет при Af0=350 Гс
и подобранных значениях: 8/х=20 К,
£=0,3, #=1,3 1019.
Точки—эксперимент для сферы CdCr2Se4,
подвергнутой отжигу в вакууме [71 ]. Частота
9,1 ГГц, температура 4,2 К
\#Н,Э
рическом CdCr2Se4 все ионы хрома—трехвалентные, находятся
в октаэдрических узлах и согласно табл. 13.3 имеют нижний
орбитальный синглет, т. е. «замороженный» орбитальный момент).
Следует отметить, что при (8E)min-*0 величина пика ЪН в точке
пересечения уровней остается конечной:
(бя<->>-°4£г (13-7)
В качестве второго примера рассмотрим несимметричное
сближение двух уровней (рис. 13.6) и, в отличие от предыдущего случая,
будем интересоваться только областью углов вблизи сближения.
В этой области пересекающиеся уровни можно аппроксимировать
прямыми Ei.2=/>i,20, а возмущение, приводящее к их расталкиванию,
учесть, записав уравнение
(Е-^1е)(Е-р2в)-^(бе)2л1п=0.
(13.8)
Для вычисления ЪН воспользуемся формулой (13.4) и предположим
(поскольку расчет носит все равно оценочный характер), что члены
с производными по углу ф вносят такой же вклад, как и члены
с производными по 9, так что их учет сводится просто к удвоению
величины ЪН. Тогда получим, что
в точке сближения (при 9=0)
(13.9)
2Л/0(8е)га1„ 2хГ "
Нетрудно убедиться, что
выражения (13.9) и (13.6) совпадают,
если, как в первом примере,
Рг=-Р\=Ъ1у/2.
«Гигантские» пики #„, в
точках сближения нижних
энергетических уровней примесных ионов,
в частности тербия, объяснил
Киттель [353 ]. Приведенные
Рис. 13.6. Несимметричное сближение
уровней
389
в [353] выражения для ЪН представляют собой предельные случаи
(13.9) при (8е)т!п«хГ и (8E)min»x7'.
Экспериментальные результаты. Впервые влияние ионов с сильной
спин-орбитальной связью на ферромагнитный резонанс обнаружили
и исследовали Диллон и Нильсен [284] для случая примесных
редкоземельных ионов в монокристаллах ЖИГ.
На рис. 13.7 приведены экспериментальные угловые зависимости
Hres для ЖИГ с малой добавкой ТЬ3 + . Мы видим, что из трех
угловых максимумов Hns, обусловленных ионами ТЪ3+, два—при
0 = 36° и 0 = 78°—вызваны сближениями нижних уровней, показанных
на рис. 13.4 (третий максимум—при 0=19°—обусловлен сближением
уровней в других неэквивалентных узлах). Сравним величины
максимумов на рис. 13.7 (~200Э) с оценкой по формуле (13.9).
lores'*3
Jff
" 30 60 до в, град
РИС" l3'7k m™°B,ble завис™ости #„. и Д# граната Yj^TbJe.O,, пси
*=4 10 (по шихте) [313]. Частота 8,9 ГГц, температура 4Л К Р
390
Концентрацию ионов (пренебрегая различием ее в загружаемой
в тигель шихте и в полученном кристалле) легко определить,
учитывая, что ребро элементарной кубической ячейки ЖИГ,
включающей 8 формульных единиц, составляет 12,5 А. При этом, однако,
необходимо принять во внимание, что только 1/3 ионов находится
в тех неэквивалентных позициях (двух из шести), которым
соответствует рис. 13.4. Для намагниченности М0 при столь малой
концентрации ионов ТЬ3+ может быть принято ее значение для чистого
ЖИГ (195 Гс при 4,2 К). Величины (pi~p2) (~120и) и (5E)min(~5x)
могут быть определены из рис. 13.4. Тогда по формуле (13.9) находим
5Я=250Э.
Учет связи между направлениями локальных осей в шести
неэквивалентных додекаэдрических узлах граната и направлениями
кубических осей кристалла позволил Хуберу [330] объяснить
«странные» положения угловых максимумов #res, обусловленных ионами
ТЬ3 + . Оказалось, что направления М0, при которых имеют место
эти максимумы и, следовательно, сближения уровней, образуют один
и тот же угол (71е) с одной из локальных осей.
Кроме ТЪ3 + , мощные острые пики Hres, связанные с резкими
сближениями нижних уровней, были обнаружены [284] для некрамер-
совых (см. табл. 13.2) ионов: Рг3 + —в направлениях <100> и Но3+ —
в плоскостях {100}. Вклады других ионов: Nd3 + , Sm3 + , Dy3 + , Er3 +
и Yb3+ были также сильными, но (кроме Yb3+, см. ниже) не
наблюдалось острых пиков HTes. Для иона Еи3 + , имеющего в основном
состоянии J=0 (табл. 13.2), существенного вклада в анизотропию,
как и следовало ожидать, обнаружено не было. И наконец, для
иона Yb3 + , кроме сравнительно гладких угловых зависимостей Hies,
которые находятся в согласии со структурой его энергетических
уровней в додекаэдрических узлах, наблюдались слабые, но острые
«аномальные» пики Hies. Как было установлено в дальнейшем [285],
они обусловлены проникновением ионов Yb3+ в октаэдрические узлы.
Одноионная теория магнитной кристаллографической анизотропии
применима, в принципе, и для объяснения «гигантской» анизотропии
редкоземельных гранатов (например, ТЬзРе5012, HosFesO^)- Однако
в этом случае положение осложняется по сравнению с рассмотренным
выше случаем малых добавок редкоземельных ионов к ЖИГ.
в частности, необходимостью учета существенного различия между
направлениями М0 и Не0.
Переходя к рассмотрению влияния Ъй-ионов, заметим, что для
случая монокристаллов ЖИГ наибольший интерес представляют
ионы Fe2+ и Fe4 + , которые могут в небольших количествах возникать
вместо ионов Fe3+ при росте кристаллов. Ионы Fe2+ образуются
вследствие попадания в кристалл ионов Si4+ или Pt4 + или образования
вакансий кислорода, а ионы Fe4+—вследствие вхождения в кристалл
ионов РЬ2 + . Аналогичные причины могут приводить к появлению
ионов Fe2+ и Fe4+ и других ионов с сильной спин-орбитальной
связью, например, Мп3+ в ферритах со структурой шпинели. Зй?-ионы
с сильной спин-орбитальной связью, например Со2 + , могут специально
вводиться с целью изменения анизотропии или повышения порога
391
параметрического возбуждения спиновых волн, а также появляться
как малая примесь в исходном сырье. В большинстве случаев эти
ионы не имеют резких сближений нижних уровней, и наиболее
интересными результатами их влияния являются низкотемпературные
максимумы ширины резонансной кривой, которые будут
рассматриваться в следующем параграфе.
Однако в некоторых случаях сближения энергетических уровней
Зй?-ионов являются достаточно резкими, чтобы проявились и
«аномалии» угловых зависимостей Яги. Один такой пример—ионов Сг2 +
в октаэдрических узлах ферромагнетика CdCr2Se4—был уже
рассмотрен выше (рис. 13.5). В этом кристалле и аналогичных
ферромагнетиках CdCr2S4 и HgCr2Se4 могут возникать, например, при
легировании серебром, и ионы Сг4+ [17]. Эти ионы с конфигурацией
d2 и L=3 (см. табл. 13.1) имеют в октаэдрическом кубическом
окружении нижний орбитальный триплет, который слабым тригональ-
ным полем расщепляется на дублет и нижележащий синглет.
Эксперимент (рис. 13.8) дает в этом случае пики Яге, в направлениях
200
150
100
50
о"
-50
-100*
100
ВО
20*
О
30 ВО 30 120 150 180 в,г рад
Рис. 13.8. Угловые зависимости 8#=ff„s—со/у и АН ферромагнетика
Cd1_:cAgICr2Se4 при х=0,015: в исходном состоянии (кривые /), после отжига
в вакууме (кривые 2) и после последующего отжига в атмосфере Se
(кривые 3) [18]. Частота 9,1 ГГц, температура 4,2 К
392
<ГН.Э
180 в,арад
an,j
<100> и <1Ю>. Можно предположить, что после спин-орбитального
расщепления дублета в этих направлениях имеют место сближения
нижнего уровня дублета с синглетным уровнем.
Проведенное выше рассмотрение анизотропии, обусловленной
ионами с сильной спин-орбитальной связью, основывалось на одном
важном допущении: времена релаксации населенностей уровней ионов
предполагались много меньшими, чем период колебаний при
ферромагнитном резонансе. Это позволило использовать равновесную
формулу (13.2). Полученная анизотропия не зависит от частоты
и совпадает с измеренной в статическом режиме, например, методом
моментов вращения. Это дает основание называть ее статической,
хотя она проявляется и при таком существенно динамическом
явлении, как ферромагнитный резонанс. Указанное допущение будет
снято в следующем параграфе.
§ 13.2. Ионные процессы релаксации
Ионы с сильной спин-орбитальной связью, вклад которых в
статическую магнитную анизотропию рассматривался в предыдущем
параграфе, имеют обычно малые времена релаксации населенностей
их энергетических уровней, т. е. быстро передают энергию
кристаллической решетке (а в некоторых случаях, как мы увидим, и основной
магнитной системе). В то же время эти быстрорелаксирующие ионы,
связанные обменным взаимодействием с магнитной системой, могут
переходить в возбужденные состояния под действием ее колебаний —
магнонов. Таким образом возникает эффективный канал косвенной
спин-решеточной (а в случае передачи энергии ионами в магнитную
систему—и спин-спиновой) релаксации, который для краткости мы
называем ионным.
Вклад ионного процесса релаксации в ширину линии
ферромагнитного резонанса наблюдался, как теперь ясно, еще в начале
50-х годов (см., например, [463], быстрорелаксируюшими ионами
были в этом случае ионы Fe2+). Однако понят этот процесс
был лишь после того, как Диллон и Нильсен [283] и Спенсер,
Ле Кроу и Клогстон [421] обнаружили низкотемпературные
максимумы АЯ в монокристаллах ЖИГ, обусловленные примесными
редкоземельными ионами. Для объяснения их Киттель, Де Жанн
и Портис [352, 276] создали теорию, которая получила название
теории быстрой релаксации. Согласно этой теории максимумы
АЯ имеют место при таких температурах, при которых частота
релаксации ионов 1/т, становится равной бе/й, где 5е—расстояние
между нижними уровнями иона.
Однако вскоре выяснилось, что предсказания теории быстрой
релаксации обычно не согласуются с экспериментом. Кроме того,
величины 1/х, вряд ли могут быть так велики, как требует эта
теория при тех низких температурах, при которых лежат максимумы
АЯ Скорее они близки при таких температурах к частоте колебаний
со. Исходя из этого, Тил и Туидэйл [437] и Диллон [281]
предположили, что основной вклад в ширину резонансной линии
393
в ЖИГ с редкоземельными примесями при низких температурах
вносит другой механизм ионной релаксации, который был назван
механизмом медленной релаксации. Для него максимумы Д# лежат
при таких температурах, при которых 1/т, = со.
Поперечная релаксация. Механизм быстрой релаксации является
частным случаем поперечной релаксации, при которой возбуждение
быстрорелаксирующих ионов осуществляется путем прямых переходов
между уровнями ионов с поглощением магнонов. На рис. 13.9
показаны различные случаи такого возбуждения. Случай в, когда
йсо«8е, а ширина уровней 2й/Т(~8е, соответствует механизму
быстрой релаксации.
Для описания быстрой релаксации в [352] была использована
макроскопическая модель, в которой обе системы — основная
магнитная и ионная — рассматривались как подрешетки (§ 3.3) с на-
магниченностями соответственно М^ и М2 = ЛГ5Ш (N—концентрация,
а 5ГО — магнитный момент быстрорелаксирующих ионов). Пренебрегая
собственной диссипацией первой подрешетки и всеми видами
анизотропии и считая, что обменное взаимодействие между под-
решетками, как и в случае ферритов, является антиферромагнитным,
можно записать (см. § 1.4 и 3.3) уравнения движения для свободных
колебаний:
^i=-YlM1x(H0-AM2),
-^= -у2М2 xfHo-AMJ-^Ma х [М2 x^-AMj]
(13.10)
(параметр диссипации Х2 может быть сколь угодно большим).
■72Ш222Ш21
<fe
Ifico
,\SSSSSSSS\£5SS
a
гъ
i\
±-r'+-f'^
ffe
^^m^
Ъы
Рис. 13.9. Различные случаи поперечной ионной релаксации: а—вероятность
перехода весьма мала, б— резонансная релаксация, в—быстрая релаксация
394
Линеаризируя уравнения (13.10), проектируя их на оси координат
и переходя к циклическим переменным т1± и т2±, мы можем из
условия совместности системы для wl+ и т2+ найти комплексную
собственную частоту со = со' + ко". С учетом того, что АМ10»Н0,
получим в интересующем нас случае малой концентрации
быстрорелаксирующих ионов
2со" 2у,М20 юл П111Л
АЯ = = ТГ~ 1 , 2 2 Н0- (13.11)
у, у2Мю l+co|xf
Здесь (оЕ^Ау2М10, а величина т( определена следующим образом:
1/т(=Л(М10/М20)уД2.
Как отмечалось в § 3.3, систему редкоземельных ионов в до-
декаэдрических узлах гранатов даже при больших концентрациях
можно считать под решеткой только при низких температурах. Тем
более нуждается в обосновании рассмотренная выше «подрешеточная»
теория в случае малых концентраций. Таким обоснованием служит
микроскопический расчет, проведенный [276] для высоких температур
(когда co£Tj«l). Он дал выражение, совпадающее с тем, в которое
переходит (13.11) в этом случае в предположении, что в (13.11)
т,- есть не что иное, как время релаксации населенностей уровней
ионов, а М20 = ЛГ9ЭТ, где 9JI—магнитный момент иона. Ионную
систему можно рассматривать как ансамбль парамагнитных ионов
в эффективном поле ЛМю- Тогда (см. § 1.1)
M20=N<mx>=NmBj№^\ (13.12)
где Вj—функция Бриллюэна с У=9Л/(йу2). Оценка показывает, что
при тех температурах, при которых лежат обычно максимумы АЯ,
аргумент этой функции больше 1, и, следовательно,
M20 = N{4mzy~NW.
Заметим, что в обоих упомянутых расчетах быстрой
релаксации— континуальном и микроскопическом обменное
взаимодействие считалось изотропным, а орбитально-решеточное
взаимодействие (которое описывается при помощи кристаллического поля)
не принималось во внимание. При этих допущениях постоянные
составляющие Mt и ЯЯ параллельны и переменное эффективное
поле Ami, действующее на ионы (поперечное по отношению к Мю),
является поперечным и относительно 9И0- Именно это дает
основание считать механизм быстрой релаксации частным случаем
поперечной релаксации.
Более общая теория поперечной релаксации, охватывающая
все показанные на рис. 13.9 частные случаи, была разработана
Ван Флеком [444]. Она основывается на рассмотрении двух
связанных систем; первая характеризуется намагниченностью Mi,
для которой справедливо уравнение Ландау — Лифшица; вторая
представляет собой ансамбль ионов, который характеризуется
своими энергетическими уровнями. В результате, считая обменное
взаимодействие изотропным и принимая во внимание только два
395
нижних уровня, разделенных интервалом 8е, было (для случая
сферы) получено
5H+]-iAH=c0~( , ' „ + 7 -)н01Ъ~, (13.13)
где с0 — отношение механических моментов подсистем, ионной и
основной магнитной, при Г->0. Не выписывая вещественной и мнимой
частей (13.13), заметим лишь, что в предельном случае быстрой
релаксации (со«8е/Й; т[~1~Ье/Ь) из (13.13) следует выражение для
ДЯ, которое переходит в (13.11), если заменить th[8£/(2x7)] на
Bj[4DlAMi0/(xT)]sBj[fiJ(i3E/(xT)] или (с учетом того, что в данном
случае 8е=йсо£) на Bj [JSe/(y.T)]; при достаточно низких температурах
обе функции мало отличаются от 1. Отношение 8Я/ДЯ в той
области температур и частот, где выполняются приведенные выше
условия быстрой релаксации, оказывается малым.
Таким образом, механизм быстрой релаксации обладает
следующими особенностями:
а) ширина резонансной кривой ДЯ остается конечной при Г->0
и имеет максимум при 1/т; = 8е/Л, положение его не зависит явно
от частоты со, может сказываться лишь частотная зависимость т(;
б) величина максимума АЯ растет с увеличением со;
в) динамический сдвиг резонансного поля 8Я мал.
В случае резонансной релаксации (со=;8е/Л; т_1«8е/й)
максимальные значения ДЯ могут быть значительно ббльшими, чем в случае
быстрой релаксации, но они, конечно, резко уменьшаются при
отклонении со от резонансной частоты.
Медленная (продольная) релаксация. В этом случае механизм
передачи энергии от магнитной системы быстрорелаксирующим
ионам основан на модуляпии энергетических уровней ионов
колебаниями магнитной системы. Рассмотрим его сначала качественно
(рис. 13.10). Пусть расстояние 8е
между двумя уровнями ионов
модулируется с частотой со. При
этом будут изменяться с той же
частотой равновесные
населенности уровней и будут все время
происходить переходы между
уровнями, направленные на
восстановление непрерывно
нарушающегося равновесия. Среднее
уменьшение энергии ансамбля
ионов в результате таких
переходов составляет энергию U\,
передаваемую ионами решетке.
В стационарном режиме эта
энергия компенсируется энергией,
которая затрачивается магнитной
системой на модуляцию уровней
ионов.
А
А
Ч*
К
ш
v
Рис. 13.10. Переходы между уровнями
иона при их модуляции: а — без
запаздывания, б—при наличии
запаздывания
396
Предположим сначала, что переходы происходят без запаздывания
по отношению к изменению 8е (рис. 13.10, а), т. е. с нижнего уровня
на верхний во время уменьшения 8е и наоборот. Очевидно, что
при этом U1=0. Если же переходы происходят с запаздыванием,
т. е. ионная подсистема имеет конечное время релаксации Ti, to,
как видно из рис. 13.10, б, U^ (а следовательно, и энергия,
передаваемая ионам магнитной системой) будет конечной и положительной.
Однако при очень большом запаздывании (ti-юо) переходы «не
будут успевать происходить» и снова будет t7t=0. Можно полагать,
что максимальная передача энергии имеет место, когда частота
релаксации 1/tj равна частоте модуляции со.
Рассмотренный механизм похож на дебаевский механизм
электрических потерь [82] и на механизм релаксации в парамагнетиках
[260, 61 ]. Его механической моделью могут служить колебания
маятника в вязкой среде. В ферро- и ферримагнетиках аналогичные
механизмы (но с ббльшими временами релаксации и поэтому
проявляющиеся при более низких частотах) лежат в основе различных
явлений магнитного последействия (см., например, [123]). Для случая
электронных переходов между ионами Fe2+ и Fe3+ в ферритах (см.
§ 14.1) такой механизм предложили Вейн и Ван дер Хейде [456]
и—применительно к ферромагнитному резонансу—Егер, Голт и Мер-
ритт ([463]). Теория его была разработана Клогстоном [266]. Она
полностью применима и к интересующему нас сейчас процессу
медленной релаксации, обусловленному внутриионными переходами.
Теория Клогстона. Рассмотрим две связанные системы: магнитную
и ионную. Первая характеризуется вектором М, для которого
справедливо уравнение Ландау—Лифшица. Вторая состоит из N
ионов, характеризующихся энергетическими уровнями е; и их населен-
ностями Nj, так что £7Vj=JV. В силу связи между системами
(которая в этой теории не конкретизируется) уровни Ej изменяются
с частотой колебаний магнитной системы со. С этой же частотой
изменяются равновесные населенности NjX, которые определяются
мгновенными значениями е,-. Мгновенные населенности Nj тоже
изменяются с частотой со, но вследствие запаздывания, о котором
шла речь выше, не совпадают с Ni0B. Основным предположением
теории является:
dt Tj
(13.14)
т. е. что мгновенные населенности релаксируют к равновесным
с общим для всех уровней временем релаксации х{.
Предполагая, что колебания намагниченности и обусловленную
ими модуляпию величин е,, Njx и Nj можно считать малыми,
подставим Njoo=(Nj<z)o+>ijX,exp(i<ot) и Nj = (Nj)0+njexp(iat) в (13.14)
и найдем
"'=W-b+!tfee,e- (13Л5)
397
Ограничимся случаем однородных
магнитных колебаний и пренебрежем
всеми видами анизотропии, кроме
обусловленной ионной системой.
Свободную энергию запишем в виде
U= -MH+£ NjEj-SiT, (13.16)
}
где первый член в правой части
представляет собой свободную энергию
магнитной системы, включающую
(см. §2.1) и энтропийный член
(поскольку М—намагниченность при
данной температуре), а два
последующих—свободную энергию ионной
системы. Подчеркнем, что для свободной
энергии ионной системы теперь нельзя использовать формулу (13.2),
так как она справедлива лишь при термодинамическом равновесии.
Линеаризированное уравнение движения для собственных
колебаний магнитной системы:
кшп= — ушхНеГ0 — уМ0хп,,г, (13.17)
где Hef0 и hef-—соответственно постоянная составляющая и
комплексная амплитуда переменной составляющей эффективного поля
Рис. 13.11. Координаты в
теории Клогстона
Н =-(^\
(13.18)
Чрезвычайно существенно, что дифференцирование в (13.18)
производится при постоянных населенностях. Действительно, правая часть
(13.17) представляет собой момент сил, действующих на систему,
для его вычисления необходимо брать частные производные энергии
по углам (т. е. по составляющим М), а соответствующие населенности
являются просто множителями.
В рассматриваемой теории используется декартова система
координат с осью z, направленной вдоль М0 (рис. 13.11). Переменные
составляющие намагниченности в этой системе: тх = М05в
и ту=М0&ф. Здесь 86=0—0О, а 6ф = бф5т0, где бф = ф —ф0; 6 и ф—
углы вектора М, а 90 и ф0 — вектора М0 в сферической системе
координат. Составляющие эффективного поля.
\дМх)н,-
const Afoy J^«'
' дв'
Я
(13.19)
эти нясе^н J" опРе^яются выражением (13.15) Разложим
о1внове™ой хоИ' а ТЖС пР°ИЗВ°ДНЫе dEj/d6 И дЕ№ в Р^1 ок°л°
равновесной точки (0О, фо)> подставим их в проекции уравнения
398
(13.17) и сохраним члены не выше первого порядка малости. Условие
совместности полученной таким образом системы даст комплексную
частоту колебаний со = ю' + ко". В случае малой концентрации ионов,
пренебрегая произведениями членов, содержащих концентрацию
NJa> или ее производные, получим
s(8We)e+(8fl)e,
ЬН=2а"/у={11М0)РП,
у\ дв дв дф сф/
П-
(13.20)
(13.21)
(13.22)
(13.23)
1 +ш2т,2
(все производные берутся в равновесной точке 0О, Фо).
Из полученных выражений видно, что зависимость ДЯ от частоты
определяется релаксационным множителем П; ДЯ стремится к нулю
при оя,->0 и coTj-юс и максимальна при соТ|=1 (рис. 13.12). Этот
множитель отличается от релаксационного множителя в выражении
(13.11) для быстрой поперечной релаксации заменой со£ на частоту
колебаний ю.
Выражение (13.20) можно привести к виду
8Я=
2М0
2 ■> 1
СО Tf 1 ^
1+а2х?~2М~оу
= 8ЯШ + (6Я)0. (13.24)
При cotj->0 первое слагаемое в (13.24) 8Яш->0 и, следовательно,
(8Я)о представляет собой статический сдвиг резонансного поля,
обусловленный ионной подсистемой. Он должен совпасть и, как мы
убедимся ниже на примере двухуровневой системы, действительно
совпадает с вычисленным в § 13.1. Величина же (бЯщ)^ в (13.20)
стремится к нулю при cuTj-»oo и, следовательно, второе слагаемое
в этом выражении (ЬН)Х
представляет собой сдвиг
резонансного поля в условиях, когда
населенности «совсем не
успевают» релаксировать к быстро
изменяющимся равновесным
значениям; эту величину,
согласно [260], можно назвать
адиабатическим сдвигом
резонансного поля. Интересно, что
величины (8Я)о и (8#)ro
получаются в результате двукратного рис 1312 Частотные зависимости АН
дифференцирования равновес- и динамических сдвигов резонансного
ной энергии ионов ^NjwEj по поля при медленной релаксации
399
углам, причем первое дифференцирование (связанное с вычислением
эффективного поля) производится в обоих случаях при NJo0= const.
Второе же производится при NJa0 = const, если переходов не
происходит, т. е. при вычислении (ЪН)Х, или с учетом зависимостей
равновесных населенностей от углов—если переходы происходят
безынерционно — при вычислении (8#)0.
Из (13.24), (13.20) и (13.21) следуют характерные для медленной
релаксации соотношения
8Яш = со2т?(5Яш)го = -^сот,ДЯ. (13.25)
Теория Армаи-Бутрон. Дальнейшее развитие теории медленной
релаксации было проведено Арман-Бутрон [322]. В этой работе
в качестве причины, приводящей к связи колебаний магнитной
системы и ионов, рассматривалось обменное взаимодействие. Его
энергию (ограничиваясь однородными колебаниями) можно,
аналогично (2.31), записать в виде
иа=-тяКм=-ммКтщ (13.26)
где Ш—магнитный момент иона, Л—тензор анизотропного
обменного взаимодействия, а Лт—тензор, транспонированный по
отношению к Л (так что Лтр5 = Л1р). Тогда эффективное поле, действующее
на магнитную систему,
HctM = n0 + NATm. (13.27)
В аналогичном выражении для поля, действующего на ионы, внешним
полем можно пренебречь. Тогда
ед = ЗДо+те'ш' = ЛГ-1х0ЛМ0 + Лп1х~Лте'ш', (13.28)
где %0—статическая восприимчивость ионной подсистемы, а %^—ее
восприимчивость по отношению к переменному полю.
Подстановка (13.27) и (13.28) в линеаризированное уравнение
движения магнитной системы (без учета ее собственной анизотропии
и диссипации) дает
;(co/Y)m + mxHo+mx^oMo + Mox1^m = 0, (13.29)
где введены тензоры £о = ЛтХоЛ и ^=Лтх~Л. Спроектируем (13.29)
на оси х и у (ось z, как всегда, совпадает с М0) и приравняем
нулю определитель полученной системы. Тогда, считая концентрацию
ионов TV достаточно малой, найдем
6H=H0-tf/y = -Mt^o„+{M0/2){^„ + ^„-^.x, + ^yx), (13.30)
ДЯ=2ш7у = Л/0(51« + £„ + е~ „-?-*,)■ (13-31)
В рассмотренной теории существенным является предположение
об анизотропии обменного взаимодействия. Оно обеспечивает
непараллельность векторов 5ГО0 и Мо, вследствие чего переменное эффективное
поле, действующее на ионы, имеет продольную (по отношению
к ЧИ0) составляющую. А это, в свою очередь, является условием
400
того, что переменная намагниченность m приводит уже в линейном
приближении к модуляции уровней ионов, что является необходимым
условием механизма медленной (или продольной) релаксации.
Заметим, что причиной появления продольного переменного поля,
действующего на ионы, может явиться также кристаллическое поле
(см. § 2.2 и 13.1), которое при наличии спин-орбитальной связи и при
изотропном обмене приводит к различию направлений Ш0 и М0.
В работе [322] допущение (13.14) было заменено следующим:
dJh= -{Nj-NJa) £ -L + £ iNr-Nrn)±. (13.32)
at Г+1*>Г Y+i ХП
Первый член в правой части (13.32) представляет собой число ионов,
уходящих в единицу времени с рассматриваемого уровня, а второй
является суммой чисел ионов, приходящих на данный уровень со
всех других.
Заметим, что при исследовании в § 11.2, 11.3 и 12.5 процессов
релаксации магнонов мы не учитывали «обратных» членов,
аналогичных второму члену в правой части (13.32), считая, что числа всех
квазичастиц, кроме первичных (релаксация которых рассматривалась),
не отличаются от равновесных. Это допущение не выполняется
иногда и при релаксации квазичастиц, а именно в двух случаях:
когда концентрация первичных квазичастиц становится достаточно
большой (как при нелинейном затухании, см. § 10.5) или когда
некоторая область спектра вторичных (рождающихся при данном
процессе) квазичастиц переполняется в результате какого-либо другого
процесса. В рассматриваемом же в данном параграфе случае ионов
внешнее воздействие—колебания магнитной подсистемы—приводит
к модуляции всех уровней ионов, и поэтому отличиями их
населенностей от равновесных пренебрегать нельзя.
Случай двух энергетических уровней. В этом случае, когда
Nl + N2=Nlco+N2<B==N, для Ni и N2 из (13.32) следуют уравнения
(13.14) с одинаковой частотой релаксации
т^-тйЧтй1. (13.33)
Равновесное распределение ионов по уровням можно считать
больцмановским [133]:
^1,2ГО=е(-«^+^хТ), (13.34)
где, как и в § 13.1, eli2=e0 + 8e/2, а ц—химический потенциал.
Определяя его из условия Nlx + N2ai=N, получим
^1.2»=ЛГ[1+етчя",71"1. (13.35)
Подставляя е1>2 и Nli2oo в (13.22), находим
'-ИМ Ш>"£г
Вычисление же по формуле (13.24) величины (8Я)0 (с учетом того,
что d/^=(sin_19)S/S<p) дает выражение (13.4).
26 А. Г. Гуревич, Г. А- Мелков 401
0,65
Рис. 13.13. Температурная
зависимость множителя Р в случае двух
уровней
Как отмечалось выше, частотная
зависимость АН определяется в
случае медленной релаксации
множителем Q в (13.21). Температурная
же зависимость определяется как
этим множителем (поскольку tj
зависит от Т), так и множителем Р.
Как мы увидим, зависимость х-, от
Т является обычно монотонно
убывающей, и множитель Q имеет
максимум при той температуре Гп, при
которой coTi(7,)=l. Выражение
(13.36), как функция температуры,
имеет максимум при у.ТР = 0,658г
(рис. 13.13). Результирующая
функция АЩТ) может иметь один мак-
от того, насколько различаются
согласно (13.24),
симум или два в зависимости
температуры Тп и ТР. Динамический же сдвиг б#,
имеет один температурный минимум, лежащий вблизи ТР.
Итак, основные особенности механизма медленной (продольной)
ионной релаксации:
а) АН стремится к нулю при Т-*0 и имеет два (часто
сливающихся) температурных максимума, один из них, обусловленный
множителем Q, сдвигается в сторону более высоких температур
с увеличением частоты;
б) величина максимума АН слабо зависит от частоты, сказывается
лишь смещение друг относительно друга максимумов Q и Р;
в) угловые зависимости АН имеют минимумы, когда д(де)/дв
и д(8е)/ё<р обращаются в нуль, в частности, в точках сближения
уровней ионов;
г) динамический сдвиг резонансноУо поля всегда отрицателен,
отношение его абсолютной величины к АН пропорционально частоте.
Релаксация населенностей уровней ионов. Процессы релаксации насе-
ленностей энергетических уровней ионов, которыми определяются
величины Tj, аналогичны процессам релаксации в парамагнетиках [6, 1 ].
Однако «спин-спиновая» (т. е. в данном случае—ион-ионная) релаксация
не играет здесь, в отличие от парамагнетиков, существенной роли, так
как взаимодействие ионов между собой гораздо слабее их
взаимодействия с магнитной системой и решеткой. На характер процессов
релаксации ионов влияет то, что обменное расщепление уровней в данном
случае (см. § 13.1) гораздо больше, чем расщепление во внешнем поле
в случае парамагнетиков. И, наконец, наряду с процессами релаксацчи
с участием фононов (их можно назвать ион-фононными) могут идти
аналогичные им процессы с участием магнонов (ион-магнонные),
исследованные теоретически Буишвили [36] и Хубером [331].
Как ион-фононные, так и ион-магнонные процессы с участием более
чем двух квазичастиц, по-видимому, несущественны. Одночастичные—
так называемые прямые процессы (рис. 13.14) заключаются в испускании
или поглощении фонона или магнона с переходом иона с одного
402
У ~РД
^e"EkSSklfShZ
^е=е*2-е*/
Т
Рис. 13.14. Элементарные процессы релаксации ионов и температурные
зависимости их вкладов в частоту релаксации (схематически). 1—прямые
процессы, 2—рамановские, 3—орбаховские
уровня на другой. К двухчастичным процессам относятся рамановский
и орбаховский [379] (рис. 13.14). Рамановский процесс представляет
собой комбинационное (рамановское) рассеяние фонона или магнона
на ионе. Орбаховский не отличается от рамановского по конечному
результату (рис. 13.14), но состоит из двух прямых процессов и требует
наличия еще одного—более высокого уровня иона. Все эти процессы—
собственные, не связанные с неоднородностями, при каждом
элементарном процессе сохраняются и энергия, и импульс.
Как фононы, так и магноны являются бозе-частицами. Поэтому
температурные зависимости для ион-фононных и ион-магнонных
процессов одинакового типа не должны различаться. В то же время
величины их вкладов в 1/ti и зависимости, например, от бе могут
быть разными. Следует также заметить, что ион-фононные и ион-
магнонные процессы релаксации населенностей уровней ионов играют
разные роли в релаксации всей системы. В случае ион-фононных
процессов механизм ионной релаксации в целом является (см. § 11.1)
спин-решеточным, а в случае ион-магнонных—спин-спиновым.
Для прямых процессов, как показал Орбах [379],
Ti = T0th^. (13.37)
В случае прямого ион-фононного процесса наиболее существенным
возмущением является орбитально-решеточное взаимодействие,
т; в этом случае уменьшается с ростом бе. Для прямого ион-
магнонного процесса основным возмущением является обменное.
Зависимости tj от бе оказываются при этом различными для разных
ионов [331]. Например, для ионов Yb3+ в додекаэдрических узлах
ЖИГ ti уменьшается, а для ионов ТЬ3+ в тех же узлах вблизи
точек сближения уровней—растет с увеличением бе.
Для рамановского процесса т; приблизительно пропорционально
Т~п для некрамерсовых (с четным числом 4/-электронов) и Т~9 для
крамерсовых ионов; для орбаховского процесса Tj уменьшается с
ростом температуры по экспоненциальному закону [379]. Таким образом
(см. рис. 13.14), вклады прямых процессов преобладают при низких,
а рамановского и орбаховского—при высоких температурах.
Перейдем теперь к обсуждению результатов экспериментального
исследования ионного процесса релаксации. Как и в § 13.1, при этом
26*
403
необходимо будет учитывать распределение ионов по неэквивалентным
узлам решетки, для которых (вследствие различной ориентации
локальных осей по отношению к М0) положения энергетических
уровней различаются. Все приведенные выражения для АН и 8Н
заменятся тогда суммами их по всем неэквивалентным узлам.
Редкоземельные ионы в гранатах. Как уже отмечалось,
двухуровневая модель хороша в двух случаях: для низколежащего дублета
и в окрестности точки сближения уровней. Характерным примером
первого случая служит ион Yb3+ в додекаэдрических узлах граната.
Ферромагнитный резонанс в ЖИГ с малой добавкой Yb подробно
исследовали Кларк, Туидейл и Тил [265] (рис. 13.15). Приведенные
значения АН являются непосредственно измеренными величинами
и представляют собой вклад практически одного только—ионного
200
150
100
50
АН,Э
S**>\<111>
J '' \\
J* t \ \
'( '' \\
s s^. \ \
t ^^к \ \
i /ууЧч \\
#/У Х*>^ Х^
50 100 150 200 250 Т,К
-200
-400 -
-600 -
-800 -
Рис. 13.15. Температурные зависимости АН и динамического сдвига Нп, для
граната Ys-jYb^FejO^ при х=0,153 и различных ориентациях М0 [265].
Светлые значки—частота 9 ГГц, черные—16,8 ГГц
404
I
процесса релаксации. Значения же 6#ш были получены путем вычитания
из разности (#res—со/у) статического сдвига, измеренного методом
моментов вращения, и вычисленного электродинамического сдвига
(§ 5.3). Показанные на рис. 13.15 температурные зависимости АН и 6#ш
находятся в хорошем согласии с приведенными выше особенностями
механизма медленной релаксации. Обработка полученных данных
позволила найти температурную зависимость частоты релаксации 1/т;;
она возрастала в данном диапазоне температур от ~109 до ~1012.
Для других крамерсовых редкоземельных ионов, не имеющих
резких сближений уровней (Nd3+, Sm3 + , Dy3 + , Er3+),
экспериментальные данные [281] также свидетельствуют в пользу механизма
медленной релаксации. Однако отсутствие достаточно низко лежащего
дублета затрудняет количественную обработку этих данных.
В ЖИГ с некрамерсовыми ионами ТЬ3 + , Но3+ и Рг3+ наблюдались
[283, 281, 189, 313] «аномальные» угловые зависимости АН,
обусловленные сближениями энергетических уровней. В случае ионов ТЬ3 +
сближения нижних уровьей и, следовательно, пики HTes имеют место
(рис. 13.7) для трех направлений М0, не совпадающих с осями
симметрии кристалла. Из рис. 13.7 видно, что вблизи этих направлений
при низкой температуре лежат полосы поглощения. Для их объяснения
в рамках теории медленной релаксации необходимо было
предположить [189], что частота релаксации ионов (меньшая при такой
температуре, чем со) резко возрастает с уменьшением бе. Это
предположение было подтверждено теоретически Хубером [331],
который показал, что в данном случае преобладает вклад в 1/т,-
прямых ион-магнонных процессов, дающих (см. выше) именно такую
зависимость. Минимальное расстояние между сближающимися
уровнями в этом случае оказывается ~-2,5 см-1, а время релаксации
~Ю-10. Как видно из рис. 13.7, все полосы поглощения имеют
«провалы» в согласии с теорией медленной релаксации.
Температурные зависимости АН, показанные для одной из полос
поглощения на рис. 13.16, имеют два максимума. Их можно объяснить
вкладами различных уровней: сближаюшейся пары
(низкотемпературный максимум) и всех остальных (высокотемпературный).
Из рис. 13.16 видно, что при температурах выше
низкотемпературного максимума, когда частота релаксации сближающейся
пары уровней превышает со, АН уменьшается при подходе к точке
сближения, т. е. угловые максимумы АН превращаются в угловые
минимумы. Это имеет место и для других ионов [77] и находится
в согласии с механизмом медленной релаксации, если принять, что
1/Т| во всех случаях возрастает с уменьшением бе.
Для ионов Но3+ в додекаэдрических узлах граната сближения
нижних уровней, как уже отмечалось в § 13.1, происходят, когда
М0 лежит в плоскостях {100}, т. е., в частности, направлена вдоль
осей <100> и <110>. В этих направлениях при низких температурах
наблюдаются [3 ] максимумы #res и полосы поглощения, расщепленные
в соответствии с теорией медленной релаксации.
На рис. 13.17 приведены температурные и угловая зависимости
АН для ЖИГ с малой добавкой ионов Рг3 + . В этом случае угловые
405
so
20
ю
йн,э
J^%
16 20 24
В, град
20
40
ВО
ВО
Т. К
Рис. 13.16. Угловая и температурные зависимости АН граната Ys-jTb^FesO,,
при х=ЗЮ~* вблизи одного из сближений нижних уровней иона ТЬ-14
[189]. Частота 8,66 ГГц. Температурные зависимости—для углов,
обозначенных соответствующими точками на угловой зависимости
60
40
20
&Н,Э
60
40
20
АН,Э
■ I
:
-
■
-' \
V.
1
Т=4,2 К
"г— ' i i
О SO 60 90 в, град
80 Т,К
Рис. 13.17. Угловая и температурные зависимости АН граната У3_дРгд Fc50,.
при * = 9-1СГ4 [313]. Частота 9 ГГц. Температурные зависимости — для у1лов,
обозначенных соответствующими точками на угловой зависимости
-106
максимумы Hrcs и ДЯ имеют место только в направлениях <100>.
Особенностями релаксации являются при этом: монотонный рост
ДЯ при понижении температуры (во всяком случае до 4,2 К)
и отсутствие расщепления углового пика ДЯ. Аналогичные
особенности имеют место в ЖИГ с добавкой Yb при углах М0 (в
плоскости {110}) G = 30D и 6 = 90°, когда сказывается (см. § 13.1)
влияние ионов Yb3 + , попадающих в небольших количествах в ок-
таэдрические узлы [285, 225 ]. По-видимому, минимальное расщепление
уровней в этих случаях очень мало, и возможен вклад механизма
поперечной релаксации.
Быстрорелаксирующие 34-ионы. Влияние ионов Fe2+ на
ферромагнитный резонанс в ЖИГ было обнаружено еще в 1961 г. [78, 422]
и подробно исследовалось в дальнейшем (см., например, [435, 436,
323]). Эти ионы возникают в октаэдрических узлах вследствие
замещения трехвалентных ионов железа четырехвалентными ионами (Si, Ge),
а также возникновения вакансий кислорода. Кроме внутриионных
переходов, влияние которых исследовалось выше, в этом случае
возможны электронные переходы между ионами Fe2+ и соседними
ионами Fe3 + . Влияние их на ферромагнитный резонанс будет
рассмотрено в § 14.1. Здесь мы отметим лишь, что характерные частоты
таких переходов много меньше частот релаксации 1/х„ обусловленных
внутриионными переходами. На рис. 13.18 приведены температурные
«внешности ДЯ в монокристалле ЖИГ, содержащем ионы Fe2+.
Низкотемпературные максимумы этих зависимостей обусловлены
ннутриионными переходами, а высокотемпературные—межионными.
Ионы Fe4+ возникают в тетраэдрических узлах ЖИГ при
тмещении трехвалентных ионов двухвалентными (например, ионов
(J*)Fez+,3
<100>
500 Т,К
Рис. 13.18. Температурные ™"£™j£^^iXj^7^
легированного Geприр РДЗиьа ориентаииях М„ q [3 J^^ r ^
концентрация ионов he ^ 1^дя_ДН(г=0)
407
Y3+ ионами Са2+) и приводят [436] к появлению температурных
максимумов АН, похожих на низкотемпературные максимумы,
обусловленные ионами Fe2 + . Это связано с тем, что ионы Fe2 +
в октаэдрическом окружении и ионы Fe4+ в тетраэдрическом имеют
(см. табл. 13.3) одинаковый характер расщепления энергетических
уровней.
Ионы Fe2 + и Fe4+ могут в небольших количествах возникать
в монокристаллах и эпитаксиальных пленках ЖИГ, выращиваемых
без специальных добавок из очень чистого сырья вследствие попадания
в кристалл ионов РЬ2+ из расплава и Pt4+ из тигля. Уменьшение
их количеств или компенсация их влияния, например, влияния
Pt4+—путем небольшой добавки Са2 + , является необходимым
условием получения малых величин АН.
В качестве специальных добавок быстрорелаксирующих З^-ионов
в ЖИГ исследовались ионы Мп [317] и Со[427]. При интерпретации
результатов этих работ возникают большие трудности, связанные
с переменной валентностью ионов Мп и Со, возможностью вхождения
их в различные узлы и стимуляцией ими изменений валентности
ионов Fe.
Еще в 1959 г. Уайт [452] предположил, что в ферритах со
структурой шпинели может иметь место вклад 3«/-ионов в
анизотропию и релаксацию, аналогичный вкладу редкоземельных ионов
в гранатах. В дальнейшем стало ясно, что в шпинелях, как
и в гранатах, в большинстве случаев работает механизм медленной
ионной релаксации. Однако упомянутые выше трудности
интерпретации в полной мере возникают и для ферритов со структурой
шпинели. Наибольшее внимание было уделено марганцевому ферриту
MnIFe2-y04, в котором наряду с ионами Мп2+ и Fe3+ в 5-состоянии
(см. табл. 13.1) могут быть быстрорелаксирующие ионы, прежде
всего — Мп3+ и Fe2+ в октаэдрических узлах [123]. В различных
образцах этого феррита наблюдались либо один температурный
максимум АН, либо наряду с ним —второй (рис. 13.19). Оказалось
[264], что низкотемпературный максимум обусловлен ионами Мп3 + .
а высокотемпературный—Fe2 + .
Интересным объектом для изучения ионных процессов релаксации
являются ферромагнетики со структурой шпинели: CdCr2S4, CdCr2Se4
и HgCr2Se4. Основные магнитные ионы Сг3+ находятся в них
в состоянии с «хорошо замороженным» орбитальным моментом
(см. § 13.1), а быстрорелаксирующие ионы Сг2+ и Сг4+ могут
возникать вследствие образования анионных или катионных вакансий
или же соответствующих замещений. На рис. 13.8 приведены угловые
зависимости АН для одного из этих ферромагнетиков. На них имеют
место максимумы, обусловленные сближениями энергетических
уровней ионов Сг4+ (которые возникли при росте кристаллов,
легированных ионами Ag+) и Сг2+ (возникших при отжиге в вакууме вследствие
образования вакансий селена). Преобладающим механизмом
релаксации является в этом случае, по-видимому, все же медленная
релаксация, несмотря на отсутствие характерных для нее угловых
минимумов АН в точках сближения уровней, а также температурных
408
i i i i 1 1 1——
too 200 зоо <оо т,к
Рис. 13.19. Температурные зависимости АН двух ферритов MnxFe2-x04 [264].
Частота 9,3 ГГц, М01| < 111 >
максимумов АН. Для другого кристалла той же группы HgCr2Se4
обе эти особенности наблюдались [215].
Мы рассмотрели ряд примеров проявления ионной релаксации
в неметаллических ферро- и ферримагнетиках. Из них следует, что
этот процесс является распространенным и во многих случаях—
преобладающим, особенно при низких температурах. Ионный процесс
вносит существенные вклады в релаксацию магнитных колебаний
и волн и в антиферромагнетиках (см., например, [410]), и в маг-
нитоупорядоченных металлах (§ 14.2).
В основе ионного процесса релаксации лежат переходы между
энергетическими уровнями индивидуальных ионов. Отсюда следует,
что вклады ионной релаксации не должны существенно зависеть от
волнового числа к магнонов.
Глава 14
ВЗАИМОДЕЙСТВИЕ МАГНИТНЫХ КОЛЕБАНИЙ И ВОЛН
С НОСИТЕЛЯМИ ЗАРЯДА
§ 14.1. Влияние носителей заряда в полупроводниках
До сих пор, исследуя колебания и волны в магнитоупорядоченных
средах, мы не учитывали электропроводности, т. е. считали эти
среды идеальными диэлектриками. В действительности они являются
полупроводниками или металлами. Правда, ферриты, которые
используются при исследовании магнитных колебаний и в технике
СВЧ, обычно являются полупроводниками с настолько малой
проводимостью, что влияние носителей заряда оказывается
несущественным. Но для некоторых ферритов (см., например, [123]) — с большей
проводимостью — влиянием ее на магнитные колебания пренебрегать
уже нельзя. Кроме того, существуют «магнитные полупроводники»
[157] — вещества, в которых магнитное упорядочение сочетается
с электрическими параметрами (подвижность носителей и др.).
близкими по величине к параметрам таких «настоящих»
полупроводников, как Si или GaAs. К ним принадлежат упоминавшиеся выше
ЕиО и CdCr2Se4. И, наконец, имеются металлические ферро- и
антиферромагнетики, в которых носители заряда оказывают весьма
существенное влияние на динамические магнитные явления.
Теоретическое рассмотрение магнитных колебаний и волн в
проводящих средах должно основываться на совместном решении
уравнений Максвелла, уравнений движения намагниченности и уравнений
движения носителей. Характер решений и особенности происходящих
явлений определяются в первую очередь соотношением между
размерами исследуемой системы и глубиной проникновения
электромагнитного поля в среду (или толщиной скин-слоя) 1//<г" = 6 (§4.2).
В этом параграфе мы уделим основное внимание предельному
случаю 8>х/, где d—характерный размер образца: для сферы —
диаметр, для пластины (пленки)—толщина. Этот случай реализуется
для сферических образцов из обычных СВЧ ферритов и для тонких
пленок из материалов с гораздо большей проводимостью, даже
металлических.
Вклад проводимости в затухание магнитных колебаний. Для
колебаний намагниченности в случае 8 » d наиболее важным эффектом
является вклад электрических потерь в затухание [70, 365]. Мы
рассмотрим его на примере однородных колебаний в малой
ферромагнитной сфере [70]. При этом можно будет испочьзовать метод
последовательных приближений; нулевым приближением будут
колебания намагниченности в непроводящем образце, электрическое попе
первого приближения будет индуцироваться такой намагниченное п,ю;
410
джоулевы потери токов, вызванных этим полем, будут вносить вклад
в затухание колебаний.
Ограничимся рассмотрением однородных колебаний вблизи
ферромагнитного резонанса при достаточно малой Д//. Тогда
|m|»|he|(he—внешнее поле), поляризация переменной
намагниченности m близка к круговой:
m=w(x0-iy0), (14.1)
а переменная магнитная индукция
b = h + 4jim = hc т + 4лт~ — m. (14.2)
3 3
Для вычисления электрического поля et следует воспользоваться
уравнениями (6.4), подставив в первое из них индукцию в нулевом
приближении (14.2)". Результат такого вычисления, которое провели
Пистолькорс и Сюй Яныпен [173], можно представить в виде
el=~k0[(-x0Jtiy0)z+t0(x-iy)]in. (14.3)
Интересно, что поле ех, индуцированное переменной магнитной
индукцией при ферромагнитном резонансе, при достаточно малой
АН и не очень малых размерах образца оказывается значительно
большим, чем внешнее поле /гс, а следовательно, и электрическое
поле в резонаторе или волноводе, где находится образец. Пусть,
например, R = 0,5 мм, М0=139Гс и ДЯ=0,5 Э. Тогда при
Хо = 2п/к0 = 3 см с учетом соотношения m^M0hc/AH (§1.5) получим,
что поле на поверхности сферы elmax= 100 Ле. Полый резонатор
с такой сферой будет иметь при ферромагнитном резонансе, согласно
(5.46) с учетом (1.125), добротность Q~5. И, как легко убедиться,
поле е1тах составит 10 кВ/см при мощности, поглощенной в
резонаторе, всего ~ 1 Вт.
Мощность электрических потерь, обусловленных полем el5
согласно (4.72)
Ра = ^[\ег\ЧУ, (14.4)
v
где V— объем сферы. Эта мощность черпается из энергии магнитных
колебаний и вносит в их параметр диссипации вклад
ЛЯ„ = Л,/(у^, (I4-5)
где W—энергия рассматриваемого однородного типа колебаний.
Согласно (7.70)
W=am2l(2yM0). (14.6)
" Найдя е„ можно затем из другого уравнения Максвелла найти поправки
второго приближения к m и частоте колебаний, т. е. получить формулу (5.43).
411
Выполняя
интегрирование в (14.4) с учетом
(14.3) и принимая во
внимание (14.5) и (14.6),
получим окончательно
АНа =
= ^Е"4тгМо(А-оЯ)2. (14-7)
Как и следовало
ожидать, вклад
проводимости в ширину линии
ферромагнитного резонанса
оказался размерным —
пропорциональным R2".
Для стехиометрических
монокристаллов
ферритов и поликрисгалличес-
ких СВЧ ферритовых материалов, например, для ЖИГ при комнатной
температуре е"<0,01. Для сфер из таких материалов с R<1 мм
величины АНа пренебрежимо малы (<0,02 Э). Однако они становятся
существенными для ферритов с большей проводимостью, например,
содержащих ионы Fe2 + . Вследствие полупроводникового характера
проводимости эти величины быстро возрастают с повышением
температуры (см., например, рис. 14.1).
Формулы, подобные (14.7), для образцов другой формы получил
Марышко [365]. Зависимости АНа от е", М0, со и характерного
размера (например, для пленки—ее толщины) и порядок величины
остаются при этом такими же, как в (14.7). Аналогичные расчеты
могут быть проведены и для неоднородных типов колебаний и
спиновых волн. Но ясно, что величины АНП окажутся в этих случаях
гораздо меньшими, так как роль размера 27? в (14.7) будет играть
длина волны 2п/к или—для неоднородных колебаний - расстояние,
на котором фаза намагниченности изменяется на 2л.
Вклад межионных электронных переходов. В ряде ферритов
преобладающим механизмом электропроводности является
прыжковый или перескоковый механизм, называемый также механизмом
обмена валентностями или механизмом Вервея (см., например, [123]).
В таких веществах наряду с основными ионами переходных элементов
имеются в том или ином количестве ионы тех же элементов с другой
валентностью: Fe2 + , Fe4 + , Mn3+—в ферритах, Сг2+ и Сг4+—в
халкогенидных шпинелях. Эти иновалентные ионы являются обычно
быстрорелаксирующими; в предыдущей главе мы подробно
рассмотрели их вклады в анизотропию и диссипацию энергии магнитных
колебаний. При этом мы игнорировали возможность электронных
11 Заметим, что (14.7) представляет собой удвоенную мнимую часть
выражения, которое получается при подстановке е=е' —/е" в формулу (5.43).
АН.Э
100 200 300 400 Т,К
Рис. 14.1. Температурные зависимости Д// сфер
из монокристалла феррита Nio.75Fe2.25O4
[4631. Частота 24 ГГц. Цифры у кривых-
диаметры сфер в мм. Сплошные линии—
М0||<1П>, штриховая-Мо]|<100>
412
переходов между ними и соседними ионами—с основной
валентностью. Такие переходы, связанные с преодолением некоторых
(обычно — небольших, порядка 0,1 эВ) энергетических барьеров,
происходят под действием тепловых колебаний. При наложении
электрического поля появляется преимущественное их направление, и
возникает электрический ток. Если электрическое поле является быстро-
переменным, начинает сказываться инерционность переходов и
возникают электрические потери. Максимум их имеет место, когда
частота переменного поля со оказывается равной частоте релаксации
1/те, связанной с этими переходами.
Преимущественные направления термоактивированных
электронных переходов могут возникать и вследствие изменений
направления намагниченности. К межионным переходам полностью
применима изложенная в § 13.2 теория (которая и была создана
Клогстоном именно для этого случая). Необходимо лишь под
уровнями е^ понимать теперь уровни не индивидуальных ионов,
а комплексов, различающихся пребыванием лишнего электрона (как
в случае Fe2+) или отсутствием электрона (в случае Fe4+) на разных
ионах. Различие энергий б,- обусловлено при этом различием углов,
образованных постоянной намагниченностью с локальными осями
ионов, так что число уровней должно быть равно числу кристалло-
i рафически неэквивалентных узлов, которые могут занимать
рассматриваемые ионы.
Ионы Fe2+ предпочитают октаэдрические узлы [123]. В структурах
шпинели и граната имеется 4 неэквивалентных октаэдрических узла,
итя которых оси тригональных искажений (см. § 3.3) направлены
ндоль четырех осей <111> кристалла. Исходя из этого, Клогстон
рассмотрел модель с четырьмя уровнями. В результате расчета по
формуле (13.21) для этой модели оказалось, что АН максимальна
при Мо||<100> и минимальна при М0||<111>. Как видно из рис. 13.18,
такая анизотропия имеет место для высокотемпературного максимума
АН в ЖИГ с добавкой Ge. Что же касается экспериментальных
данных для никель-железного феррита, с которыми сравнивал свой
расчет Клогстон, то там (рис. 14.1) анизотропия АН имеет обратный
знак. В дальнейшем стало ясно, что противоречия здесь нет, так
как температурный максимум для этого феррита обусловлен внутри-
ионными переходами.
При достаточно низкой температуре межионные переходы не
будут успевать происходить за время, «имеющееся в распоряжении»
экспериментаторов. Это является одной из причин наведенной
анизотропии в ферритах [123]. Если же (при более высоких температурах)
те становится сравнимым с временами, используемыми при
экспериментах, то при изменении внешних параметров, например,
величины магнитного поля, могут наблюдаться нестационарные
явления, объединяемые понятием магнитного последействия. При еще
более высоких температурах электронные переходы могут явиться
причиной магнитной вязкости—запаздывания и потерь энергии при
импульсном или периодическом перемагничивании. Заметим, что
электронные переходы между ионами могут происходить и под
413
Рис. 14.2. Характерные времена различных процессов и области, в которых
эти процессы проявляются в разных явлениях (схематически). Штрихпунктирная
линия соответствует эксперименту рис. 14.1
воздействием света, что приводит к интересным фотомагнитным
явлениям, в частности, к наведенной светом магнитной анизотропии.
Эти явления были особенно подробно исследованы для случая ЖИГ
с добавкой Si [282].
К наведенной магнитной анизотропии, а при более высоких
температурах — магни i ному последействию могут приводить и
процессы диффузии атомов или ионов в решетке. Поскольку эти процессы
характеризуются значительно большими временами релаксации, то
все обусловленные ими явления смещены по отношению к таким
же явлениям, вызванным электронными переходами, в область более
высоких температур. Положение различных явлений, обусловленных
всеми упомянутыми процессами, на шкалах времени и температуры
иллюстрирует рис. 14.2.
Взаимодействие магнитных волн с носителями. Перейдем теперь
к рассмотрению влияния носителей заряда на распространение
в магнитоупорядоченных веществах магнитных (спиновых) волн.
Исследуя в гл. 6 и 7 эти волны, мы исходили из уравнений
Максвелла и уравнения движения намагниченности, определяющего
магнитную проницаемость среды. При рассмотрении в гл. 12
магнитоупругих волн дополнительно учитывались механические
уравнения движения упругодеформируемой среды. Электрическая же
проницаемость среды е при этом считалась скалярной, вещественной
и не зависящей от частоты. Теперь, при учете электропроводности
среды, электрическая проницаемость будет комплексной величиной,
зависящей от частоты (вообще говоря, и от волнового вектора),
а при наличии постоянной намагниченности станет тензором с
комплексными компонентами. Материальными уравнениями для
нахождения ее должны явиться уравнения движения носителей заряда.
В общем случае вследствие распределения носителей по скоростям,
обусловленного их тепловым движением, роль уравнений движения
414
выполняет кинетическое уравнение Больцмана (см., например, [16])
для функции распределения f(\, г, t) (v—скорость носителей). Эта
функция представляет собой число носителей в элементе фазового
пространства d\dr, отнесенное к объему этого элемента. Зная функцию
/, можно вычислить все характеризующие носителей величины,
в частности их концентрацию
N(t,t) = $f(y,r,t)a\ (14.8)
и среднюю скорость
v(r, r)=ijv/(v, r, i)ds. (14.9)
При наличии носителей разных типов (например, электронов
и дырок) такие вычисления должны быть проведены для каждого
типа. Затем может быть определена плотность тока
J = Xe0sWsvs, (14.10)
S
где eos—заряд носителей, а суммирование проводится по всем типам
носителей. Если справедлив закон Ома J=5E, то можно найти
проводимость 6 и для гармонических процессов—электрическую
проницаемость (4.17); диэлектрическую проницаемость ё„ в
рассматриваемом диапазоне частот можно считать постоянной скалярной величиной.
Для интересующей нас задачи о взаимодействии магнитных волн
с носителями заряда можно использовать так называемое
гидродинамическое приближение, в котором носители каждого типа полностью
характеризуются следующими параметрами: концентрация N, средняя
скорость v° и средняя частота столкновений 1/т [11]. Уравнение
движения в этом приближении запишется в виде
^+(vV)v = ^(E+-vxB) + ^---, (14.11)
где ms—масса носителя, а Р—давление. Это уравнение может быть
получено из кинетического уравнения для функции распределения.
Однако его можно рассматривать как уравнение Ньютона для
носителей в элементе объема, движущемся со средней скоростью v.
Левая часть (14.11) есть полная производная d\/dt, а члены в правой
части представляют: лоренцеву силу, силу, обусловленную градиенюм
давления, и «силу трения», вызванную столкновениями. Уравнения
(14.11) должны быть записаны для носителей всех типов. Мы
ограничимся случаем, когда имеются носители одного типа, для
определенности—электроны.
Входящие в (14.11) величины являются суммами
постоянных и переменных составляющих. Считая последние малыми и
изменяющимися по гармоническому закону, получим для их
комплексных емплитуд линеаризованное уравнение. Если пренебречь
членом с градиентом давления и считать постоянную составляющую
" В дальнейшем средняя скорость будет обозначаться просто v.
415
vo
ъ
,b
'у
Рис. 14.3. Частные случаи распространения волн в среде с дрейфующими
носителями
скорости v0 не зависящей от координат, то это уравнение будет
иметь вид
icov+(v0V)v=-—(e+-v0xb+-vxB0)--. (14.12)
/ие с с ' т
(Здесь и далее v—переменная составляющая скорости носителей.)
Рассмотрим решения уравнения (14.12) для плоской волны в двух
частных случаях (рис. 14.3): волны, распространяющейся в направлении
постоянного намагничивания (к||В0) и перпендикулярно этому
направлению (k-LBo). В обоих случаях заданную дрейфовую скорость
носителей v0 будем считать параллельной к.
В первом случае (k||v0||B0), проектируя (14.12) на оси х и у (ось
z, как всегда, совпадает с В0) и переходя к циркулярным переменным,
получим
v±L
i со +1 юв — ikv0 Н— I =
т.
4e±±'-v0b± V
(14.13)
где <uB = \ee\B0/(intc). Для того чтобы исключить из этого уравнения
Ь±, можно воспользоваться уравнением Максвелла (4.6), из которого
в данном случае следует: b±= ±i(ck/a)e+.
Линеаризация (14.10) в случае носителей одного типа —
электронов—дает
j=-\ec\{N0\ + nv0). (14.14)
Пренебрежем вторым членом в этом выражении. Тогда, переходя
к циркулярным составляющим, получим
j±=-\et\N0v±=u±e±, (14.15)
где о±—циркулярные компоненты тензора проводимости. Записывая
их с учетом (14.13) и (14.15) и переходя к тензору электрической
проницаемости (4.17), найдем окончательно
-2 l-(fc/co)i>0
=
Earn со — kv0 + aB — г/т'
(14.16)
416
Здесь
l4nNoel
те
(14.17)
— плазменная (ленгмюровская) частота [11]. С носителями будут
сильно взаимодействовать волны, имеющие медленные—спиновые
ветви (§ 4.2). В данном частном случае такой волной будет волна
с правой круговой поляризацией (верхние знаки в (14.16)).
Во втором частном случае (k||v0-LB0) медленную ветвь имеет
(§ 4.2) волна с е, направленным по оси г. Для нее, поступая
аналогично предыдущему случаю (теперь Ьх=(ск/а>)ег), получим
Е -Ed_^ '-(fc/Фо (ИЛ8)
1 со со—kv0— 1/т
Итак, в обоих случаях соответствующие компоненты тензора
3? являются комплексными величинами и зависят от частоты
(в первом случае также от постоянного магнитного поля) и от
волнового числа. Распространение электромагнитных волн в таких
средах (газоразрядной плазме, полупроводниках, металлах)—так
называемых электрокинетических волн подробно исследовано (см.,
например, [11]). Волны с круговой поляризацией, распространяющиеся
в направлении В0, получили название спиральных волн (геликонов),
а линейно поляризованные, распространяющиеся перпендикулярно
В0,— циклотронных волн.
Одним из самых интересных результатов приведенного расчета
является уменьшение электрических потерь вследствие дрейфа
носителей. В первом случае, разделяя вещественную и мнимую части
(14.16), получим
е;=-, , : :?..._!• (14-19)
cog \-(kj(o)v0
сот (со—Аг„±сов)2+ 1/х2'
выражение для е" во втором случае будет отличаться от (14.19)
только отсутствием члена +сов. Отсюда видно, что с ростом
to электрические потери уменьшаются и при v0 = G>/k = vph наступает
полная их компенсация. Механизм компенсации заключается в данном
случае в том, что лоренцева сила ee/(wec)v0xb вызывает
высокочастотный ток, антипараллельный электрическому полю е.
При t;0>uPh потери становятся отрицательными (е"<0). И если
их абсолютная величина превысит потери, обусловленные другими
источниками (например, магнитные потери в среде с р.¥=1), то волны
в такой среде будут усиливаться. Ясно, что энергия при этом будет
черпаться из источника, поддерживающего постоянную дрейфовую
скорость, либо носители будут тормозиться.
Нетрудно убедиться, что компенсация электрических потерь
дрейфом носителей будет иметь место и при произвольном остром угле
между v0 и к, член kv0/a> в (14.16), (14.18) и (14.19) заменится на
kv0/co, а условие компенсации примет вид
kv0>co. (14.20)
27 А. Г. Гуревич, Г. А. Мелков
417
Заметим, что условие (14.20) является весьма обшим. Оно
совпадает, в частности, с условием черепковского излучения [134]
электромагнитных волн электронами, движущимися в диэлектрике.
Дисперсионные соотношения для волн в магнитоупорядоченной
проводящей среде можно получить в результате совместного решения
уравнений Максвелла, уравнений движения носителей (или
кинетических уравнений) и уравнения движения намагниченности. Должны
быть, конечно, учтены и граничные условия на поверхностях раздела
сред. Для волн в полупроводниках (но не в металлах, см. § 14.2)
все характерные размеры среды, в частности средняя длина свободного
пробега носителей, меньше длины волны. При этом условии можно
искать удовлетворяющие граничным условиям решения уравнений
Максвелла при ё и р, найденных предварительно, исходя из
соответствующих уравнений движения.
Для неограниченной среды могут быть использованы соотношения,
приведенные в §4.2, например, (4.41) — при распространении волн
в направлении постоянной намагниченности и (4.51)—при
распространении перпендикулярно этому направлению. В первом случае для
e + e0se± следует принять выражение (14.16), а во втором для
е —выражение (14.18). При отсутствии потерь анализ получающихся
таким образом дисперсионных соотношений не представляет больших
трудностей. Эти соотношения можно трактовать (на языке связанных
волн) как результат взаимодействия магнитных волн -в среде
с данной р и не зависящей от частоты скалярной е—и
электрокинетических волн — в среде с данной е и и = 1. Так же как и в случае
магнитоупругих волн (§ 12.3), вдали от точек пересечения
дисперсионных характеристик магнитных и электрокинетических волн спектр
смешанных волн будет состоять из ветвей, мало отличающихся от
соответствующих невзаимодействующих волн. Вблизи же точек
пересечения будет происходить «расталкивание» этих ветвей.
Явления существенно усложняются при учете потерь.
Дисперсионные уравнения для смешанных волн становятся комплексными.
В случае стационарных волн (со вещественно) решениями их являются
комплексные волновые числа k = k' — ik". При наличии дрейфа
носителей, как мы видели, величины е + или е" становятся (при выполнении
условия (14.20)) отрицательными. Это может привести к
отрицательным к", т. е. к усилению рассматриваемых смешанных волн.
На достаточном удалении от точек пересечения спектров
магнитных (спиновых) и электрокинетических волн можно говорить об
усилении спиновых волн дрейфующими носителями. Возможность
такого усиления впервые продемонстрировали теоретически Ахиезер,
Барьяхтар и Пелетминский [14] (см. также [15]) на модели пучка
электронов, пронизывающего неограниченный ферромагнетик. Для
того чтобы усиление имело место, скорость пучка v0, согласно
(14.26), должна быть во всяком случае больше минимальной фазовой
скорости спиновых волн (рис. 14.4), которая, как следует из (7.9),
составляет vphmin = у/т\(я и достигается при Аг, =,/10/11. Для ЖИГ
в сантиметровом диапазоне А:1~5-105 и ь"р1)т1п~ Ш3. Такие скорости
418
Рис. 14.4. Дисперсионные
характеристики спиновых волн в
неограниченной среде и поверхностных
безобменных волн в пластине при
двух значениях ее толщины d
(схематически). Прямая /
соответствует uphmin в неограниченной среде,
прямая 2—некоторой скорости
дрейфа; 6coi и 6со2—полосы
частот, в которых при этой скорости
дрейфа возможно (без учета
магнитных потере усиление
безобменных волн в пластинах с
толщинами, соответственно dt и d2
пучка, конечно, легко достижимы в вакууме, но использованная
модель — пучка, пронизывающего ферромагнетик,— нереализуема.
Усиление спиновых волн дрейфующими носителями в
неограниченном ферромагнитном полупроводнике исследовали Махмудов и
Барьяхтар [149]. Проведенный в дальнейшем детальный анализ [272]
дисперсионного соотношения для этого случая с учетом магнитных
потерь показал, что полная их компенсация требует таких параметров
(АЯ~0,3 Э, t;o~106). которые в настоящее время вряд ли могут
быть получены в одном веществе.
Большое внимание в последнее время было поэтому уделено
задаче об усилении потоком носителей волн в составных структурах,
состоящих из сопрокасающихся слоев «хорошего» слабопроводящего
ферромагнетика (или феррита) и «хорошего» немагнитного
полупроводника. Рассмотрение этой задачи заключается в отыскании
решений уравнений Максвелла для всех сред: феррита—с тензорной
р и скалярной е, полупроводника -с ц=1 и рассмотренной выше
Ё и граничащих с ними диэлектриков. Эти решения должны
удовлетворять граничным условиям на всех поверхностях раздела.
Разумным упрощением может явиться лишь предположение /-+со,
где /—толщина слоя полупроводника.
Подробный анализ такой задачи для случая поверхностной
магнитостатической волны (§ 6.2) в ферритовой пленке при k||v0±B0
провели Бини, Милланта и Рубино [246]. Оказалось, что если не
учитывать магнитных потерь, то усиление с ростом частоты
действительно начинается при v0/vpb=\ (при k = k2 на рис. 14.4)
и возрастает по мере роста этого отношения в пределах существования
поверхностной волны. При достаточно малой толщине ферритовой
пленки d и большой скорости г0 полоса частот 8го, в которой имеет
место усиление, может быть (см. рис. 14.4) довольно большой.
С ростом проводимости полупроводника усиление сначала растет,
а затем проходит через максимум и уменьшается. Это находится
в качественном согласии с (14.19), поскольку о обратно
пропорциональна т.
Наличие магнитных потерь в феррите сужает полосу частот,
в которой происходит усиление: со стороны низких частот—из-за
того, что усиление начинается теперь при v0/vph>l, а со стороны
27* 419
etra,6/MM
Рис. 14.5. Расчетные частотные зависимости коэффициента усиления
поверхностных магнитостатических волн в структуре феррит-полупроводник [246];
с/=3,6мкм; А=оо; и0 = 3-107; Я0 = 553Э; М0=139Гс, £,= 17 (ЖИГ), цифры
у кривых—значения Д//к; е=17,7; о = 191 Ом-1 см-1
высоких—потому, что при данном АНк обусловленный магнитными
потерями вклад в к" резко растет с ростом к' вследствие уменьшения
групповой скорости. Эти соображения подтверждаются результатами
численного расчета, приведенными на рис. 14.5.
Усиление магнитных волн дрейфующими носителями
экспериментально пока достоверно не обнаружено. Основными причинами
)того являются: для однородных магнитных полупроводников, как
уже отмечалось,— трудность совмещения в одном веществе
необходимых параметров; для структур феррит—полупроводник — узкая
полоса частот, критичность величины о; в случае пучка электронов —
трудность реализации пучка, пролетающего близко к поверхности
феррита.
Заметим, что рассмотренное явление усиления стационарной
бегущей волны (описываемое отрицательным к" при вещественной
со) называют часто конвективной неустойчивостью. В отличие от
нее абсолютная неустойчивость заключается в нарастании амплитуд
поля во времени и описывается отрицательной мнимой частью
частоты со".
Обменное взаимодействие носителей с магнитной системой.
Рассмотрим теперь, следуя Турову [197], взаимодействие носителей
с магнитной системой ферромагнетика с более общей точки зрения.
Носители будем характеризовать их моментом количества движения
(импульсом) р и спином s (в единицах й), которые, конечно, должны
рассматриваться как операторы (собственные значения оператора
s составляют +1/2). Магнитную систему будем характеризовать
намагниченностью М. Тогда оператор энергии (гамильтониан)
взаимодействия носителей с магнитной системой (отнесенный к одному
носителю) запишется в виде [197]
Ж = - 2ц в Ар - 2u„Hs - 2 (// М0) Ms,
(14.21)
420
где \iB = \ee\h/(2mec)—магнетон Бора, А—векторный потенциал
электромагнитного поля, а /—обменный интеграл, характеризующий
в рамках s-d- (или s-f-)обменной модели Шубина—Вонсовского [49]
энергию обменного взаимодействия носителей с магнитной системой.
Все рассмотренные выше эффекты взаимодействия магнитных
колебаний и волн с носителями проистекают из первого члена
(14.21). Сейчас мы остановимся кратко на явлениях, которые
определяются двумя другими членами, т. е. взаимодействием магнитной
системы со спинами носителей. В качестве носителей мы будем
рассматривать электроны проводимости; дырки в полупроводниках
слабее взаимодействуют с магнитной системой.
Энергия взаимодействия электронов проводимости с магнитной
системой может быть записана следующим образом (V—объем
образца):
£/= £ Гф*(г, s)#ty{i,s)dV, (14.22)
s=±l/2K
где i|/(r, s)—волновая функция электронов проводимости, а Ж—
гамильтониан (14.21). Если подставить его в (14.22) и от i|/*
и i|/ перейти к 8qs и Sqs—операторам рождения и уничтожения
электронов с импульсом p = Aq, а от М (§ 7.4) — к операторам
рождения и уничтожения магнонов с? и ск, то в выражении для
U появятся члены различных порядков, содержащие произведения
операторов 6qs, B„s, ск и ск.
Самые низшие, квадратичные члены, содержащие произведения
операторов 6qs и £„„ дают поправку к энергии носителей,
обусловленную их взаимодействием с магнитной системой. Члены третьего,
четвертого и более высоких порядков по операторам Ь£„ bqs, ск
и ск соответствуют элементарным процессам рождения и уничтожения
электронов (с данными q и i) и магнонов. Эти элементарные
процессы лежат в основе процессов релаксации магнонов,
обусловленных их взаимодействием с носителями. Ясно, что при таких
низкоэнергетических процессах электроны «совсем» уничтожаться или
рождаться не могут, а лишь изменяют свои q и s, так что операторы
bqS и Sqs входят парами SqsSq.s..
Заметим далее, что s-d-обменное взаимодействие, подобно
обменному взаимодействию внутри магнитной системы (§ 11.2), может
вызвать лишь процессы с сохранением полного спина
взаимодействующих квазичастиц. И так как это взаимодействие является самым
сильным, то наибольшие вклады в параметр диссипации магнонов
будут вносить именно такие процессы. Поскольку при уничтожении
одного магнона (см. § 7.3) спин магнитной системы возрастает на
1, то, как легко убедиться, наинизшими (а следовательно, наиболее
вероятными) процессами с сохранением полного спина будут процессы,
показанные на рис. 14.6. Вообще говоря, процессы с участием
меньшего числа частиц более вероятны. Но в данном случае переворот
спина электрона проводимости при тройном процессе связан с
возрастанием его энергии на величину, которая может превышать
энергию релаксирующих магнонов. Тогда тройной процесс будет
421
Прямые Обратные Рис. 14.6. Элементарные процессы
с сохранением полного спина,
лежащие в основе: а—трехчастичных
процессов слияния, 6—четырехча-
стичных процессов рассеяния.
Прямые линии—магноны,
волнистые - электроны проводимости;
вертикальные стрелки обозначают
их спины
v4 /К
запрещен (в первом приближении теории возмущений), и основной
вклад в параметр диссипации магнонов будет вносить четырехчастич-
ный процесс рассеяния магнонов на электронах [143].
§ 14.2. Ферромагнитный резонанс и спиновые волны в металлах
В этом параграфе будут рассмотрены магнитные колебания
и волны в средах с большой проводимостью—металлах. При этом
мы ограничимся ферромагнитными металлами. К ним принадлежат
переходные металлы группы железа (Fe, Co и Ni), ряд редкоземельных
металлов (Gd, Dy, Но, Ег) и многие сплавы. Магнитные колебания
и волны в металлах представляют как принципиальный интерес—для
изучения взаимодействия магнитной системы с носителями
электрического заряда, так и прикладной—как средство измерения
характеристик ферромагнитных металлов. Не исключается и практическое
применение ферромагнитных металлов в диапазоне СВЧ и оптике.
В металлах (см., например, [16, 139]) электроны наружных
оболочек атомов коллективизированы и образуют электронную
«жидкость» с плотностью (числом электронов в 1 см3) и~1022. В эту
«жидкость» погружена решетка из положительных ионов, наличие
которой (как и в полупроводниках) приводит к тому, что
энергетический спектр электронов состоит из чередующихся разрешенных
и запрещенных зон. Вследствие принципа Паули (запрещающего
нахождение в каждом состоянии более двух электронов с
противоположными спинами) все нижние зоны заполнены, а верхняя—зона
проводимости заполнена частично. Граница заполненной и
незаполненной частей этой зоны при Т=0 (в согласии со статистикой
Ферми—Дирака [16, 133]) является резкой, а с повышением
температуры размывается. Граничная (при Т = 0) энергия ef называется
энергией Ферми. Она зависит, вообще говоря, сложным образом от
направления импульса, поверхность e = ef в пространстве импульсов
называется поверхностью Ферми [139]. В изотропном случае эта
поверхность — сфера с радиусом — фермиевским импульсом
>-н:
422
I В магнитоупорядоченных металлах положительными ионами,
погруженными в электронную жидкость, являются ионы элементов
с недостроенными внутренними 3d- или 4/-оболочками. Следует
прежде всего отметить, что прямое обменное взаимодействие
моментов этих ионов не может обеспечить магнитного упорядочения,
и большую роль играет косвенное обменное взаимодействие, главным
образом через коллективизированные электроны
проводимости—взаимодействие Рудермана — Киттеля — Касуйи - Иосиды (РККИ).
Необходимо различать случаи 3d- и 4/:мегаллов. В последних магнитные
моменты ионов в хорошем приближении можно считать
локализованными, а в Зг/-металлах имеет место значи тельная делокализация
Зс/-электронов и их гибридизация с электронами проводимости. При
теоретическом исследовании магнитно-упорядоченных металлов
широко используется упоминавшаяся уже в § 14.1 s-d- или ^-/-обменная
модель Шубина— Вонсовского [49]. Она является сочетанием
гейзенберговской решетки локализованных магнитных моментов 3d-
или 4/-ионов и делокализованной электронной жидкости, связанных
между собой обменным взаимодействием. Ясно, что эта модель
гораздо лучше применима к 4/-металлам.
Вследствие большой проводимости металлов электромагнитные
волны в них затухают на очень малых расстояниях. В диапазоне
СВЧ глубина проникновения поля в металл (или толщина скин-слоя
5) составляет единицы или даже доли микрометра. Это обстоятельство
I определяет наиболее существенные отличия магнитных колебаний
и волн в металлах от случая сред с небольшой проводимостью.
Проводимость металла можно в первом приближении игнорировать
при рассмотрении магнитных колебаний или волн в нем, только
если размер образца (в направлении распространения волны) </<ё:6.
как, например, для стоячих спиновых волн в тонких пленках (§ 7.2).
Второй особенностью магнитных колебаний и волн в металлах,
которая тоже обусловлена большой плотностью электронов
проводимости, является значительный вклад процессов релаксации с
участием этих электронов в затухание колебаний.
Пленочная модель. Ферромагнитный резонанс в металлах (и,
вообще, ферромагнитный резонанс) впервые наблюдал Гриффите [312].
Результаты, полученные в [312] для тонких пленок Fe. Ni и Со.
намагниченных касательно к их поверхности, были сначала совершенно
непонятны: кажущийся g-фактор (найденный из отношения часто 1Ы
к постоянному магнитному полю) оказался в несколько раз больше
2. Киттель [347] объяснил эту «аномалию» влиянием переменного
размагничивающего поля (см. § 1.5) и покупал, ни резонансная
частота в этом случае определяется формулой (1.98)''. Вскоре стало
ясно, что резонансная частота и для массивных металлических образцов,
намагниченных касательно к их поверхности, близка к
ю = а±=у[Н0(Н0 + 4т1М0)У'\ (14.?Ч)
" Обобщив эту идею на случай произвольного эллипсоида. Киггси.
вывел [448] знаменитую формулу (1.97).
Рис. 14.7. Оси координат для
металла (г'>0), намагниченного под
произвольным углом к его
поверхности
х хг но теперь, конечно, Н0фНс0.
Выражение (14.23) следует из формулы
(1.97), если принять, что для
переменных полей размагничивающие
факторы—такие же, как для тонкой
пленки—скин-слоя, а для
постоянных— такие же, как для зсего
образца. Это предположение и
характеризует пленочную модель
ферромагнитного резонанса в массивных
металлических образцах.
Обобщим формулу (14.23) на
случай, когда постоянная
намагниченность составляет произвольный
угол G с нормалью к поверхности
металла. В осях х', у', z (рис. 14.7)
все компоненты тензора размагничивающих факторов для переменных
полей равны нулю, кроме Nyy = 4n. Переходя по правилам
преобразования компонент тензора (см., например, [119]) к осям х, у, z
и используя формулу (1.97), получим
(Go/Y)2 = #o(//0 + 4nA/0sm2e). (14.24)
При 9 = л/2 отсюда следует (14.23), в другом предельном случае 6 = 0, т. е.
для металла, намагниченного нормально к его поверхности, а=а>н = уН0.
При выводе выражения (14.24) предполагалось, что на всей
находящейся в переменном поле поверхности металла направление
М0 составляет один и тот же угол с поверхностью. Это осуществляется
для образцов с плоской поверхностью и для цилиндрического образца,
намагниченного вдоль его оси. Если же указанное условие не
выполняется (как, например, для металлической сферы), то пленочную
модель можно использовать для расчета условия резонанса и ширины
линии в приближении независимых областей. Аналогично расчету
в случае поликристалла (§ 2.4), для металлического образца без
учета собственной диссипации
Х"(со, Н0)=^М0 \6[H0-Hrcs((o)]dS\ (14.25)
S
где 5—поверхность образца. В случае сферы поле //res не зависит
от азимутального угла ф и определяется формулой (14.24). Расчет
по формуле (14.25) приводит в данном случае к кривой резонансного
поглощения, показанной на рис. 14.8 штриховой линией. Ширина ее
(на половине высоты)
f
1,
(^о^ш^^уУ+^м^^^щ^ц^^ (142б)
ниГл^иис^ГнГпоГеТ И3-За бОЛЬШОГ° ™°РоДного ущире-
424
I
4А Н,п.кЭ
Рис. 14.8. Кривые ферромагнитнся о резонансного поглощения в металлической
сфере согласно пленочной модели. Штриховая линия—без учета собственной
ширины кривой (формула (14.25) при ш/у=8яЛ/0); сплошная —с учетом ее
(схематически)
Теория, не учитывающая обменного взаимодействия. Пленочная
модель, основанная на предположении об однородной переменной
намагниченности в поверхностном слое, является грубой. В
действительности в металлическом образце с размерами, превышающими
толщину скин-слоя 5, возбуждаются волны, которые, быстро затухая,
распространяются в глубь металла. Теория ферромагнитного
резонанса в металлах должна основываться на рассмотрении этих волн.
Если проводимость металла достаточно велика, так что 5<ё:А,0 (где
Хо—длина волны вне металла), то можно считать, что
распространение и затухание волн в металле происходит по направлению
нормали к поверхности. И если радиусы кривизны поверхности
много больше 5, то эти волны можно считать плоскими.
Не учитывая магнитоплазменных и магнитооптических эффектов
[139] (влияние которых в интересующем нас диапазоне частот обычно
несущественно) и пренебрегая кристаллографической анизотропией
электрических свойств, мы будем электрическую проницаемость
металла (4.17) считать скалярной величиной. Для интересующих нас
металлов проводимость а настолько велика, что вещественной частью
е (т. е. токами смещения в уравнениях Максвелла) можно пренебречь.
Таким образом, мы примем е= — /е" = — /4ла/со. Для компонент
тензора р, пренебрегая влиянием кристаллографической анизотропии,
примем: без учета магнитной диссипации—выражения (1.59), а с
учетом ее—выражения, которые получаются из (1.59) при замене (1.73).
В случае скалярной е (см. § 4.2) для любого направления
намагничивания могут быть введены эффективные скалярные
магнитные проницаемости, различные для двух нормальных волн. При
нормальном (по отношению к поверхности металла) намагничивании
такими волнами являются волны с круговой поляризацией,
и Цеп,2 = И±Иа- При касательном намагничивании нормальными
425
волнами являются две волны с различными линейными поляризациями
векторов е и Ь, в этом случае (iCfi=lIx и Vet 2—1- Волновое число
А- и волновой импеданс С, нормальных волн в металле выражаются
через вещественные величины ixefL и |i£f«, первая из них согласно
(4.37) определяет фазовую скорость, а вторая согласно (4.38) —
затухание".
Конечным результатом теории ферромагнитного резонанса в
металле (так же как и в диэлектрике), допускающим экспериментальную
проверку, должно явиться выяснение того, как изменяются в области
резонанса параметры электромагнитных систем, содержащих
исследуемые образцы. Для резонатора такими параметрами являются
резонансная частота и добротность, а для волновода — коэффициенты
отражения и прохождения. Если такая задача будет решена, то
измеряя эти параметры, например, в зависимости от величины
постоянного магнитного поля, мы сможем найти характеристики
исследуемого металла.
Существенное влияние на упомянутые параметры систем в области
ферромагнитного резонанса будут оказывать те нормальные волны
в металле, для которых \ief будет испытывать резонансное изменение.
В случае нормального намагничивания это будет волна с правым
вращением, а при касательном намагничивании — «необыкновенная»
волна с Hef = ni. Резонанс для них (не учитывая пока обменного
взаимодействия) будет иметь место (см. рис. 1.7) при со = сон в случае
нормального и co = coj. — в случае касательного намагничивания. Это
те самые частоты, которые дает пленочная модель. Отсюда, впрочем,
не следует, что другие—нерезонансньге нормальные волны можно
игнорировать при точном решении рассматриваемой задачи.
Это решение, в принципе, заключается в отыскании полей внутри
электромагнитной системы (резонатора или волновода) и в
ферромагнитных образцах (которые представляют собой часть стенок
этой системы или помещаются внутрь ее), связанных обычными (мы
не учитываем пока обменного взаимодействия!) электродинамическими
граничными условиями. При этом должны рассматриваться как
известные такие величины, которые действительно можно считать
заданными, например мощность падающей волны в волноводе,
подводящем энергию к системе. Очевидно, что строгое решение
поставленной таким образом задачи явилось бы чрезвычайно
сложным. Поэтому приходится использовать метод последовательных
приближений. В качестве нулевою приближения можно принять
магнитное поле h(0) в рассматриваемой системе у поверхности
металлического образца при бесконечной его проводимости. Затем,
используя граничные условия на поверхности металла, можно найти
магнитные и электрические поля обеих нормальных волн в металле.
Электрические поля этих волн (поскольку е скалярна) касательны
426
к поверхности, и их сумма у
поверхности дает касательную
составляющую электрического поля первого
приближения eU). Зная же поля h<0)
и е(1), можно лайти все
характеристики рассматриваемой системы.
Заметим, что можно учесть влияние их
на величину поля h(0), что делает
задачу самосогласованной и
позволяет существенно повысить точность
решения.
Рассмотрим для определенности
полый резонатор, часть поверхности
которого представляет собой ферромагнитный металл. Для
вычисления обусловленных им изменений резонансной частоты и
добротности резонатора может быть использована формула возмущений
Слэтера (4.95). Ее можно преобразовать, если ввести импеданс-
поверхности C,s, определив его следующим образом:
(n0xe)h* = Cshh*.
Рис. 14.9. Оси координат для
металла О'>0), намагниченного
касательно к его поверхности
(14.27)
Если, как это чаще всего бывает, h имеет линейную поляризацию
и, следовательно, h* параллельно h, то, как легко убедиться, импеданс
^s есть отношение еТ к Л, где ех—проекция е на направление,
перпендикулярное векторам п0 и h. С учетом (14.27) формула (4.95)
примет вид (опуская штрих у вещественной части частоты)
Ш —(Оо
ш0
-И
2Q
2co0^oJ
|Ь("»|2аК.
(14.28)
Остановимся, следуя в основном работе Юнга и Улинга [464],
на случае касательного намагничивания. Пусть поле h(0) будет
направлено (рис. 14.9) под углом ф к М0- Нормальными волнами
в металле будут: волна с составляющими hix, 1цу и f1:, для которой
ki=k0yJe\iL, a £,i=eiz/hlx = s/\iL/E, и волна с составляющими h2z и е2х,
для которой k2=k0^/e и t,2 = \J 1/E- Из граничных условий —
непрерывности hx и hz на поверхности St следует, что /?1д.( г = 0) = Л(О) sincp.
h2z(y = 0) = h(0icostp. Подст;м1.1ЯЯ h(0) и электрическое поле
e(1' = x0^2/'(0)cos9 + z0^1/7(0)sin(p в формулу (4.95), получим
-ш0 1 K-(x/Li1sin29 + cos29)
Н'г—= -
ш0
2ш0 И-'о^/ё
I
Л'0»2^.
(14.29)
С экспериментальной точки зрения больший интерес представляет
не полный вклад (14.29) ферромагнитной стенки в комплексную
частоту резонатора, а изменение этой величины либо при замене
обычной стенки на ферромагнитную, либо при переходе от значения
Н0 вдали от резонанса (где для обеих волн можно считать |ief=0
427
120
к значению его вблизи резонанса.
Чтобы найти это изменение,
следует вычесть из (14.29) такое же
выражение, но с \i± = 1 и, вообще
говоря, другой электрической
проницаемостью е0. Тогда, учитывая,
что е= — /'4яст/а>, а е0= —/4ла0/со,
ш-шо i/l _ 1 \_
=w ^ [sin2{p('V^-v/^I)+
4W,
+ cos29(/-l)] +
'I
-.?0
Рис. 14.10. Полевые зависимости
Ни и (it для касательно
намагниченного образца супермаллоя [251 ].
Точки—эксперимент; линии—расчет при
подобранных значениях параметров
+(Мо(1-0} h^2dS. (14.30)
нъ0'*э Здесь ц1Л и \x1L определяются
выражениями (4.37) и (4.38), 5j —
формулой (4.39), a (5i)0 — этой же
формулой, но с заменой
проводимости а ферромагнетика
вблизи резонанса проводимостью ст„
обычной стенки или
ферромагнетика вдали от резонанса.
Итак, измеряя сдвиг собственной частоты резонатора с
ферромагнитным образцом и изменение его добротности, например,
в зависимости от Н0, можно найти величины ц1Л и |1ц,- На рис. 14.10
показаны результаты определения этих величин в работе Бломбергена
[251 ] — одной из первых работ по ферромагнитному резонансу
в металлах.
Случай нормального намагничивания может быть рассмотрен
аналогичным образом [464]. При этом нормальными волнами будут
волны с круговой поляризацией, и в случае линейной поляризации
поля h(0) их амплитуды у поверхности будут равны (1/2)/г<0).
Вычисляя затем е(1) = е++е_ и используя формулу возмущений
(4.95), придем к выражениям, аналогичным (14.29) или (14.30).
Вблизи резонанса вкладом волны с левым вращением можно
пренебречь, и
з—ш0 1
N— =
ш0 2Q
h^2dS,
(14.31)
где ji+j.Hti + H.I+Oi' + Mft a \i+L = \»+Ha\-{\i" + \i'fr
Оценка вклада обменного взаимодействия. Неоднородность
намагниченности в поверхностном слое металла требует учета
неоднородного обменного взаимодействия. Как отметили еще в 1950 г Киттель
428
и Херринг [354], это должно привести к расширению резонансной
кривой на величину
AHcx~D/82 (14.32)
и к уменьшению резонансного поля такого же порядка. Обосновать
это можно следующим образом: затухающую на расстоянии 5 волну
намагниченности можно разложить в интеграл Фурье по
незатухающим спиновым волнам с ft ~ 1/5; их резонансные поля будут
представлять собой некоторое распределение, сдвиг максимума
которого и ширина будут порядка Dk2-^D/b2.
Однако входящая в (14.32) величина 5 зависит от магнитной
проницаемости, а следовательно, от ширины резонансной кривой,
в которую вносит вклад и обменное взаимодействие. Получающаяся
таким образом самосогласованная цепочка соотношений позволяет,
как показали Ахиезер, Барьяхтар и Каганов (см. [197]), оценить
величину АНех. Проведем такую оценку. Согласно (4.38)
6 = &ilJv^i. (14-33)
Вблизи резонанса можно принять
KfR^(Hcf)reS- (14.34)
В свою очередь
06)™.= р47гЛ/0/(ЛЯо + Д#сх), (14.35)
где АН0— вклад всех других источников расширения линии, кроме
обменного, а р— множитель порядка 1. Нетрудно убедиться, что
в случае касательного намагничивания Р = (сон + соЛ<)/1 coH+-coM I,
а в случае нормального р = 2.
Из соотношений (14.32) — (14.35) следует
AH„(AH0 + AHcx) = $D4nMol82. (14.36)
В частности, если А//ех:»Д#о, то
АН„^8о 1 УР£,4лМ0 = (2л/с)ч/2р/)Моасо. (14.37)
Поскольку а и М0 уменьшаются с повышением температуры,
обменный вклад в ширину резонансной линии проявляется при
низких температурах.
В проведенной опенке, как и во всех предыдущих рассуждениях,
предполагалось, что скин-эффект является нормальным, что имеет
место (см., например, [139]), когда средняя длина свободного пробега
электронов /с<5. При этом а не зависит от толщины скин-слоя и для
металлов в диапазоне СВЧ мало отличается от статической
проводимости. В случае же аномального скин-эффекта, когда /е>5
и часть электронов (тем большая, чем больше /е/8) выходит из
скин-слоя до столкновения, а в выражении для глубины проникновения
поля в металл заменяется [139] на
aef = va6//c. (14.38)
429
Здесь (в отсутствие магнитного поля) v~5, a a—проводимость при
более низких частотах. С учетом этого вместо (14.36) получим
(Д*вГ(д//0 + дЯ„) = Ё*^. (14.39)
Теперь при Д//„:»А//0
Конечная величина АНСХ в отсутствие магнитной диссипации
и монотонный рост ее с уменьшением 5 свидетельствуют о том.
что диссипация энергии магнитных колебаний и волн в этом случае
осуществляется электронами проводимости.
Строгая теория, учитывающая обменное взаимодействие. Путь
построения этой теории - такой же, как и рассмотренной выше
теории, не учитывающей обменного взаимодействия. Но теперь мы
должны использовать выражения для компонент тензора Ц, найденные
с учетом этого взаимодействия, например, полученные из (7.8) при
замене (1.73). Подставляя эти выражения в формулы (4.41) или
(4.51). мы получим уравнения для А2: квадратные в случае 6 = 0
(для каждого направления вращения) и кубическое при 6 = л/2 для
необыкновенной волны; для обыкновенной, по-прежнему, А2 = А"оЕ.
Таким образом, в обоих случаях (а также и при произвольном
направлении намагничивания) будут не две, как без учета обмена,
а «все четыре» нормальные волны.
Дисперсионные характеристики этих волн исследовал Паттон
[385]. Оказалось, что для двух нормальных волн имеет место правое
вращение вектора переменной намагниченности ш (по терминологии
работы [385] это ларморовы ветви), для двух других — левое
(антиларморовы ве1ви). Из каждой пары волн с одинаковыми
направлениями вращения одна волна — «электромагнитная» (Е)
с большой фазовой скоростью и сравнительно малым влиянием
обмена, а другая - «спиновая» (S). Ларморовы спиновые (S + ) ветви
при больших к' переходят в «обычные», сравнительно слабо
затухающие спиновые волны, а антиларморовы (S_) характеризуются
очень большим затуханием.
При величинах параметра диссипации, превышающих некоторые
критические значения (например, для пермаллоя при а>ас = 0,013),
ветви Е+ и S+ не пересекаются и сохраняют свой характер во всей
области значений к (рис. 14.11); проекции же их на плоскость (со. А')
пересекаются. При малой диссипации эти ветви расталкиваются
и переходят друг в друга. Это обстоятельство представляет собой
общую закономерность для всех видов смешанных (связанных) волн.
Оно. как отмечалось в § 12.3, имеет место и для магнитоупругих волн.
Амплитуды магнитных полей всех четырех нормальных волн
в металле могут быть выражены через амплитуду магнитного поля
у поверхности с помощью четырех граничных условий: двух
электродинамических и двух дополнительных (§ 7.2). С использованием
430
компонент тензора %
(записанных, конечно, с учетом
обмена) дополнительные
условия, как и
электродинамические, дадут
уравнения для амплитуд
составляющих магнитного поля
нормальных волн.
Дальнейшие вычисления могут
быть проведены по той же
схеме, как и без учета
обмена. Сначала с
использованием выражений для
волновых импедансов
нормальных волн находятся их
электрические поля и их сумма
у поверхности е(1). Затем
можно вычислить импеданс
поверхности, определяемый
согласно (14.27), либо (в
случае образца в
резонаторе) непосредственно
воспользоваться формулой
возмущений (4.95).
Как и в безобменном приближении, рассмотрим более подробно
резонанс при касательном намагничивании. Ограничимся при этом для
простоты случаем h(0,_LH0, т. е. ф = ти/2 на рис. 14.9. Тогда обыкновенная
волна (с (ief=l) возбуждаться не будет, и поле в металле будет суммой
трех волн с ej=z0ej2: одной «электромагнитной» и двух «спиновых».
Их комплексные волновые числа kj будут определяться кубическим
уравнением для к2, которое получится при подстановке в (4.51)
выражения для \ix с учетом диссипации и обмена Волновые импедансы
этих волн, представляющие собой отношения е^ к hjx, в
рассматриваемом случае хорошо проводящего металла будут иметь вид
C,j = ickj/{4na). (14.41)
Такую задачу при дополнительных граничных условиях (7.41)
(отсутствии закрепления) решили Амент и Радо [226]. Полученное ими
выражение для импеданса поверхности в низкочастотном пределе, когда
со/сом <sc 1, toH/coM«:l, p/coM«;l (14.42)
(где р = уу/D4nM0/8i). может быть записано в виде
Г =- с (\ лУ^К-чУ+'^+^'+'И"2 (14 43)
s 4л стб, ш„—ш2/шм+1'осо+(1 +i)p
Для металлов, в которых обычно исследуется ферромагнитный резонанс
(см. табл. 14.1), условия (14.42) выполняются (и, следовательно,
выражение (14.43) приближенно справедливо) во всем сантиметровом диапазоне.
431
Рис. 14.11. Дисперсионные характеристики
нормальных волн в металле в случае 0ц = л/2
при касательном намагничивании [385];
#0=1135 Э, а = 0,03, остальные
параметры— для пермаллоя (близкие к приведенным
в табл. 14.1). Штриховые линии — проекции
кривых S+ и Е+ на плоскость А-'А"
Таблица 14.1
Параметры ферромагнитных металлов
Металл
Fe
Fe97 Si3
Ni77Fe23
Ni
Co
Гс, К
1043
631
1904
Примечания. 1.
пературе.
4пЛ/0, Гс
21580
20148
11000
6084
17900
о, Ом ' • см '
1,03 10'
1,46 10'
1.6 10'
g
2,088
а
0,0023
0,027
D, Эсм2
2,2-10"»
2,5 10-»
3,1 10"»
Звачения всех параметров (кроме Тс)—при комнатной тем-
2. Используемые во многих работах по ферромагнитному резовансу в металлах
обменная постоянвая А и параметр диссипации «Ландау—Лифшица» X, связаны
следующим образом с
величинами, приведенными в таблице: A = DM0/2, >.,=уаЛ/0-
Из (14.43) видно, что при а=0 и р=0, т. е. без учета магнитной
диссипации и обмена, резонансная частота (при которой Cs-*00)
югея = \/к>нС0м, что является низкочастотным пределом формулы
(14.23). Учет диссипации (афО, р = 0), как следует из (14.43), приводит
к конечной вещественной величине импеданса при резонансе и
конечной ширине резонансной кривой. Если определить ее по точкам,
где (Cs)' = (l/2)(Cs)res. то она составит 2аа>, т. е. совпадет с «обычной»
АН, определяемой по спаду в 2 раза величины %". Это совпадение
обусловлено тем, что в случае металла, когда е можно считать
чисто мнимой величиной, квадрат импеданса поверхности (с учетом
только одной из двух нормальных волн)
CsZ = K0/(4rca)|^f (14.44)
и, следовательно, (Cs)' = (G>/a)Xef- Сдвш же резонансного поля
относительно его значения ео2/(усом) без диссипации оказывается второго
порядка малости по а.
Если же р¥=0 (и не мало по сравнению с асо), то, как видно
из (14.43), сдвиг резонансного поля 5//ги и ширина резонансной
кривой оказываются одного порядка. Определяя их так же, как при
р = 0—соответственно по максимуму и по спаду в 2 раза величины
(£s)' и полагая для простоты а = 0, можно получить, что
(5tfrcs)ex= -0,78 у/МлЛ/о/б,, (14.45)
а ширина резонансной кривой
Д Яех = 1,26 ^/МкМо/Ь,. (14.46)
Полученная выше оценка (14.37) находится в очень хорошем согласии
с этой величиной (в низкочастотном пределе Р = 2).
В дальнейшем Каганов и Юй Лу [95, 102] показали, что на
ферромагнитный резонанс в металле существенное влияние оказывают
величина параметра закрепления \ (см. § 7.2): величины |(5//гея)ех|
и АНех возрастают с увеличением £. Эта зависимость была
подтверждена численными расчетами Фрайта и Макфадена [304] и получена
теоретически Фрайтовой [305] (рис. 14.12).
432
Случай нормального
намагничивания может быть
рассмотрен аналогичным образом.
Нормальными волнами в этом
случае являются две волны
с правой и две с левой
круговой поляризацией. Такая
задача была решена при £=0
В. Л. Гуревичем [79]. В
низкочастотном приближении
(14.42) было получено
выражение для £s, отличающееся от
(14.43) заменой ю2/а>м на со.
Выражения (14.45) и (14.46)
оказываются справедливыми
и при нормальном
намагничивании.
Ферромагнитный резонанс
в условиях аномального скин-
эффекта был впервые
исследован в [79]—для
нормального намагничивания, а затем
для касательного — в [27]. Для
случая, когда обменный вклад
в ширину резонансной линии
преобладает, в [79] было получено выражение для АЯСХ, отличающееся
от оценки (14.40) лишь множителем порядка единицы.
Итак, влияние обменного взаимодействия (совместно с
проводимостью) на ферромагнитный резонанс в металлах характеризуется
тем, что его вклады в ширину линии и сдвиг резонансного поля—
одного порядка и не исчезают в отсутствие магнитной диссипации.
Экспериментальные результаты. Как уже отмечалось, (5//„„)„
и ДЯех слабо зависят от частоты. Вклад же магнитной диссипации
в АН в случае, когда а не зависит от со (что, как мы увидим,
обычно имеет место), растет пропорционально со. Таким образом,
выгодными условиями для наблюдения обменного вклада являются
низкие частоты и, конечно, низкие температуры, так как проводимость
металлов растет с понижением температуры; необходимы также
высококачественные образцы для уменьшения вклада неоднородностей
в АН0. Именно при низких частотах (но комнатной температуре)
обменный вклад в ширину линии ферромагнитного резонанса в
металлах обнаружили Радо и Уиртмен [392].
Оценка с использованием формулы (14.46) и данных табл. 14.1
показывает, что при комнатной температуре граничная частота, при которой
магнитный и обменный вклады в диссипацию становятся равными,
составляет для железа ~ 300 ГТц, а для никеля ~ 1 ГГц. Таким образом,
для этих металлов в сантиметровом диапазоне и длинноволновой части
миллиметрового диапазона реализуются предельные случаи, когда
преобладает либо один, либо другой вклад. Обменный вклад преобладает
Рис. 14.12. Расчетные полевые
зависимости импеданса поверхности металла
в случае касательного намагничивания
при двух значениях параметра
закрепления 4 [305]. Сплошные линии t,=0,
штриховые—4—1- Частота 11,5 ГГц; все
параметры—для железа при комнатной
температуре (табл. 14.1)
28 А. Г. Гуревич, Г. А. Мелков
433
7-00
500
300
100
20 ВО 100 140 Т,ГГц
Рис. 14.13. Частотные зависимости ширины резонансных кривых [304, 243].
Комнатная температура. Значения ширины кривых—между экстремумами
производной
также для пермаллоя и кремнистого железа. На рис. 14.13 приведены
частотные зависимости ширины линии для упомянутых металлов. Из
этого рисунка видно, что для Ni зависимость АН (со) действительно
близка к линейной, а для остальных металлов—к корневой. Тем не
менее обработка экспериментальных данных с использованием строгой
теории позволяет выделить, например, для Fe, малый магнитный
вклад АН0 и определить параметр а.
Антирезонанс. Для точного нахождения параметра магнитной
диссипации, когда вклад его в ширину линии ферромагнитного
резонанса мал по сравнению с обменным вкладом, может быть
использовано измерение ширины линии ферромагнитного
антирезонанса. Явление антирезонанса (см. § 4.2) заключается в обращении
в нуль вещественной части соответствующей эффективной
проницаемости, причем в отличие от резонанса (когда ii'Cf тоже обращается
в нуль) Цег имеет не максимальное, а минимальное значение. Условие
антирезонанса не зависит от направления намагничивания и имеет
вид (4.57). Отсюда видно, что антирезонанс может наблюдаться
лишь при ео>еом. например, для Fe на частоте /5 60 ГГц.
Можно показать, что в первом приближении при малой диссипации
для любого направления намагничивания в точке антирезонанса
(Hef)arcs = aai/U).M. (14.47)
Ширину линии антирезонанса (ЛЯ) я res можно определить как
расстояние между точками, в которых Ue'f = 2(|ief)ares. Легко убедиться,
что независимо от направления намагничивания в первом приближении
ДЯагю совпадает с шириной линии ферромагнитного резонанса 2аю/у.
Выражения (4.57) и (14.47) получены без учета обменного
взаимодействия. Но вблизи антирезонанса величины глубины проникновения поля
в металл, согласно (4.38), становятся большими, и в учете этого
взаимодействия нет необходимости. Таким образом, измерение параметров
электромагнитной системы, содержащей металлический образец, вблизи
антирезонанса позволяет независимо определить величину а. Эти
параметры, например, добротность полого резонатора с металлическим
434
образцом, как и вблизи резонанса,
определяются импедансом
поверхности металла. Его вычисление может
быть проведено по рассмотренной
выше схеме, но без учета обмена
[98] (см. также [97]).
Антирезонансный минимум
поглощения наблюдал впервые Егер
[462] (рис. 14.14). Совместные
измерения ширины линии резонанса и
антирезонанса были использованы [302]
для определения параметра
диссипации и параметра закрепления £.
Совместные же измерения полей
резонанса и антирезонанса были
использованы для точного определения g-фак-
тора [301 ] и намагниченности [391 ].
Увеличение глубины проникновения 5 вблизи антирезонанса приводит
к резкому возрастанию мощности, «просачивающейся» через пластинку
из ферромагнитного металла. Этот эффект предсказал Каганов (см. [96])
и обнаружили Гейнрих и Мещеряков [56]. Они наблюдали просачивание
через металлическую пленку толщиной ~10мкм при антирезонансе
с ослаблением 80 дБ, в то время как вдали от антирезонанса ослабление
в этом случае должно было составлять более 160 дБ.
Для пленки с толщиной d, сравнимой с глубиной проникновения
поля в металл, расчет как просачивающейся мощности, так и
импеданса поверхности (определяющего отражение от нее) требует учета
граничных условий на обеих поверхностях пленки. Этот расчет
следует проводить, вообще говоря, с учетом обменного
взаимодействия, т. е. принимать во внимание все четыре нормальные волны
(для каждого направления распространения) и как
электродинамические, так и дополнительные граничные условия. На рис. 14.15
Рис. 14.14. Полевая зависимость
I^lr супермаллоя [462]. Частота
23,9 ГГц
(0„
1,5 ы"
р„. mis Расчетные полевые зависимости вещественной части импеданса
Рис. 14.15. Расчетные »"-'с»ыс * d _и касательном намагничивании
поверхности пленок разной толщины\ й при к щ4кд/08?) = 5 ■ ИГ5;
и симметричном возбуждении [280]; ш=1,5 шм, a-iu , ицчпт0ох,
и симмоу кривых—значения rf/6,
28'
435
приведены результаты расчета, которые провели Де Вэймс и Вольфрам
[280] для случая касательного намагничивания и симметричного
возбуждения пленки (при одинаковых Л<0) с обеих ее сторон). Из
этого рисунка видно, что при уменьшении толщины пленки влияние
параметра закрепления £ становится все более сильным. В случае
полного закрепления (£=оо) на характерную для полубесконечного
металла зависимость ^s(H0) накладываются острые пики,
обусловленные «пространственным квантованием» — возбуждением стоячих
спиновых волн. При £=0 эти стоячие волны не возбуждаются (см.
§ 7.2).
Процессы магнитной релаксации. Измерения параметра магнитной
диссипации а. ферромагнитных металлов показали, что этот параметр
практически не зависит от частоты. Температурные его зависимости
в достаточно совершенных образцах оказываются, как правило,
слабыми. Обсудим вопрос о том, какими процессами релаксации
определяется этот параметр.
Все процессы, исследованные в гл. 11, 12 и 13, конечно, могут
протекать и в металлах. Кроме того, могут идти— и в металлах
быть весьма эффективными—процессы с участием электронов
проводимости, рассмотренные в конце § 14.1. Вклады собственных
процессов магнонной релаксации (§ 11.2) в АН в металлах должны
быть такого же порядка, как в диэлектриках или полупроводниках.
Как мы видели, это доли или, в крайнем случае, единицы эрстед.
В то же время приведенным в табл. 14.1 (для весьма совершенных
образцов) значениям а соответствуют (при частоте ~ 10 ГГц) величины
АН порядка нескольких десятков или сотен эрстед. Таким образом,
вклад собственных магнонных процессов не может играть в металлах
существенной роли. Несобственные двухмагнонные процессы,
обусловленные «геометрическими» неоднородностями (§11.3), в металлах
вследствие их большой намагниченности очень эффективны и приводят
к резкому увеличению АН в недостаточно совершенных образцах,
например в образцах с недостаточно хорошо полированной
поверхностью. Существенными могут быть также вклады двухмагнонных
процессов, обусловленных неоднородными полями анизотропии (в
поликристаллах), если только анизотропия не является, как в
пермаллоях, очень малой, или обусловленных неоднородными упругими
напряжениями (в плохо отожженных образцах). Если же, как во
всех хороших работах по ферромагнитному резонансу в металлах,
качеству образцов уделялось должное внимание, вклад двухмагнонных
процессов является небольшим. Ионные процессы релаксации (гл.
13), обусловленные быстрорелаксирующими ионами (основного
элемента, образующего данный металл, или примесными), могут играть
и в металлах существенную роль, особенно при низких температурах.
Возможно, что ими определяется резкий рост АН в Ni при низких
температурах и большие величины АН в Со [244]. Сравнительно
большие и слабо зависящие от частоты и температуры значения
параметра а во всех ферромагнитных металлах должны быть
обусловлены характерными для веществ с большим числом носителей
з;| ряда электрон-магнонными процессами релаксации.
436
В § 14.1 отмечалось, что наиболее вероятными из этих процессов
являются, вообще говоря, тройные и четверные процессы,
обусловленные л-^-(или «-/)-обменным взаимодействием. Однако тройные
процессы (см. § 14.1) разрешены лишь при энергии магнонов,
превышающей величину W-обменного расщепления электронных зон.
В металлах эта величина —порядка 1 эВ и основным процессом
электрон-магнонной релаксации СВЧ магнонов является четверной
процесс, происходящий без переворота спина электрона. Расчет
вероятности такого процесса провели Лутовинов и Рейзер [143]
и получили для частоты релаксации выражение, которое можно
записать в виде
Юг = j — -7Г^1пТ~- (14.48)
yjrc ти- ipxiinMoP xi (1449)
Згс ш ffik\
r = 64^W
где S—спин магнитных ионов, р?—фермиевский импульс электрона,
а со и к—частота и волновое число релаксирующих магнонов.
В случае ферромагнитного резонанса в массивных металлических
образцах (с толщиной d»8) величина к"1—порядка толщины
скин-слоя 5, зависящей, в свою очередь, от АН. С учетом этого,
предполагая, что рассматриваемый вклад в АН является
преобладающим, нетрудно получить таким же образом, как при выводе
выражения (14.37),
д „ Jin toft2 /РхГ4гсЛ/0с, V.T
л"~-^ 7 / In—.
cySpl V bD tim
Ширина линии оказалась пропорциональной частоте и слабо (с
учетом температурных зависимостей Л/о и а) зависящей от Т, что,
как мы видели, находится в согласии с экспериментом. Оценки по
формуле (14.49) дают величины, тоже находящиеся в согласии
с экспериментальными данными.
В заключение отметим, что в металлах, конечно, могут
существовать спиновые волны с параллельными поверхности
составляющими волнового вектора, сравнимыми с составляющими,
перпендикулярными поверхности (вещественные и мнимые части которых
порядка 5-1). Они не возбуждаются при линейном ферромагнитном
резонансе в металлических образцах, расположенных в резонаторах
или волноводах, поскольку длина волны вне металла А.о»6. Однако
такие спиновые волны (точнее—пары их) могут возбуждаться
параметрически под воздействием полей с амплитудами, превышающими
пороговые. Такое возбуждение наблюдалось в пленках [270, 242]
и проволоках [120].
Приложение 1
ЕДИНИЦЫ И КОНСТАНТЫ
В книге используется гауссова система единиц (СГС). Соотношения между
единицами этой системы и СИ дань, в табл. П. 1.1. В „ей приведены за
небольшими исключениями, только те величины, которые встречаются в тексте
ь физике твердого тела энергия частиц и квазичастиц измеряется часто
в специальных единицах, которые определяются следующим образом
алов ^=Тв"в0""""_ЭНерГИЯ kel V электР°на- прошедшего разность потенци-
„„„ °6PamHhllJ сттиметр квант энергии 2 n ft с/А. электромагнитного
излучения С ДЛИНОЙ ВОЛНЫ Х=1 СМ. "JJiyic
Келвин—средняя mspim v.T. приходящаяся на две степени свободы
идеального газа при темпсрат\рс Т=\ К
г„„ Эрстед-величина уЬН^\ыН тссман'овосого расщепления уровней
энергии при g-факторе (электронного с ia) ,и=2.0023 в магнитном поле Н=1 Э
п ^кп"? о ЭТ4'Х еДИНИ" в -?рг;14 " «отношения их между собой приведены
1 ка7=4,1868 10 эР™Я" осиос""° ,спловая- измеряется также в калориях;
Универсальные физические константы, коюрые могут понадобиться при
проведении расчетов по icmuiiik .ишноп книги, приведены (в гауссовой
системе единиц) в табл. П. 1.3. v гауссовой
Таблица П.1.1 (продолжение)
Величина
Название
Плотность
(объемная) энергии
[энергия]1'
Мощность
Плотность
(поверхностная)
потока энергии
(вектор Умова—
Пойнтинга)
Упругие
деформации
Упругие
напряжения
Модули
упругости
Количество
электричества
(заряд)
Плотность
(объемная) заряда
Напряженность
электрического
поля
[электрическое поле]1'
Обозначение
в тексте
и
Р
П
е
ст
С pslm
е
Р
Е
Гауссова система
Размерность
L"'MT"2
L2MT"3
МТ"3
1
L-'MT"2
L3/2Mt/2T-i
L-3/2Ml/2T-l
L-l/2Ml/2T-l
Название
единицы
2)
Обозначение
эрг/см3
эрг/с
)pi (CM2 с)
дин/см2
Отношение
единиц, К
10
107
103
1
10
2,9979-10'
2,9979-103
3,3356-Ю"5
СИ
Обозначение
Дж/м3
Вт
Вт/м2
Па
Кл
Кл/м3
В/м
Название
единицы
ватт
паскаль
кулон
Размерность
L-'MT-2
L2MT"3
МТ"3
1
L-'MT"2
TI
L~3T1
LMT"3r'
Электрический
потенциал,
напряжение, ЭДС
Емкость
Электрический ди-
польный момент
Поляризация
Электрическая
проницаемость
Электрическая
индукция
(смещение)
Сила тока [ток]"
Электрическое
сопротивление
Удельное
сопротивление
Электрическая
проводимость
Удельная
проводимость
[проводимость]''
Магнитная
индукция
Магнитный поток
Индуктивность
Напряженность
магнитного поля
[магнитное поле]'
С
Р
Р
1
D
/
R
Р
G
о
В
L
Н
Ll/2Ml,2T-t
L
L5,2M1/2T-1
L-1/2M1/2T-1
1
L-t/2Ml/2T-l
L3/2Ml,2T-2
L_1T
T
LT-'
T"'
L"1/2M"2T"'
L3/2M1/2T-!
L
L-"2M"2T-'
сантиметр
2)
2)
гаусс 2)
максвелл
сантиметр
эрстед 2)
см
Гс
Мкс
см
Э
3,3356-Ю"3
8,9876-10й
2,9979-10"
2,9979 105
8,9876-109
2,9979-105
2,9979-109
1,1126-Ю"12
1,1126-Ю-10
8,9876-10"
8,9876-10'
10*
108
10»
1,2566-Ю"2
В
Ф
Кл -м
Кл/м2
Ф/м
Кл/м2
А
Ом
Ом-м
См
См/м
Тл
Вб
Гн
А/м
вольт
фарад
ампер
ом
сименс
тесла
вебер
генри
L2MT"3I"1
L"2M"'T4I2
LTI
L"2TI
L"3M"'T*I2
L"2TI
I
L:MT"3I"2
L3MT"3I"2
L"2M'1T3I2
L-3M-iT3i2
MT"2I"'
L2MT-2I"'
L2MT"2I"2
L-'I
-с
Величина
Название
Магнитный
потенциал
Магнитный момент
Намагниченность
Магнитная
восприимчивость
Магнитная
проницаемость
Магнитоупругие
постоянные
Температура
Теплоемкость
(тела, системы),
энтропия
Удельная
(объемная)
теплоемкость
[теплоемкость ]''
Плотность
энтропии [энтропия]1'
11 В квадратных
21 Эрстед принятс
индукции. Однако в
единицах, например
Обозначение
в тексте
Ф
ОТ
м
X
£
*1.2
Т
Ср, v
S
Гауссова система
Размерность
Ц/2м1/2Т-1
L5/2MI/2T-I
L-mMwT-i
1
1
L-'MT"2
LMT"2
0
l^mt-2©-1
L-'MT"2©"1
L-'MT"2©"1
Название
единицы
гильберт
гаугс21
кельвин
Обозначение
Гб
Гс
эрг/см3
эрг/см
к
эрг/К
эрг/(см3 ■ К)
эрг/(см3 ■ К)
Отношение
единиц, К
1,2566
103
10~3
1
107
10
105
1
107
10
10
Таблица П.1.1
(продолжение)
СИ
Обозначение
А
А-м2
А/м
Гн/м
Дж/м3
Дж/м
К
Дж/К
Дж/(м3 • К)
Дж/(мэ ■ К)
Название
единицы
ампер
кельвин
Размерность
I
L2I
L-Ч
1
LMT"2r2
L-'MT"2
LMT"2
0
L2MT-2©-'
L-'MT"2©-'
L-'MT"2©-1
скобках приведены сокращенные названия, использованные в тексте.
з считать единицей магнитного поля в гауссовой системе единиц, а гаусс — единицей намагниченности и магнитной
этой системе все величины Н, В, М, Е, D и Р имеют одинаковую размерность и могут быть измерены в одинаковых
i эрстедах или гауссах.
Таблица П.1.2
Специальные единицы энергии
Числа в таблице-отношение единицы в соответствующей строке к единице в соответствующем столбце (аналогичные
Единица энергии
Эрг
Электронвольт
(эВ)
Обратный
сантиметр
Кельвин
Эрстед
Эрг
1
1,6022-Ю-12
1,9864-Ю-16
1,3807-Ю-16
1,8570-Ю-20
Электронвольт (эВ)
6,2415-10"
1
1,2398-Ю-"
8,6174-Ю-5
1,1590-КГ8
Обратный сантиметр
5,0341-1015
8,0655 • 10э
1
0,69504
9,3481 -Ю-5
Кельвин
7,2429-1015
1,1604-10*
1,4388
1
1,3450-10-*
Эрстед
5,3852-10"
8,6280-107
1,0697 10*
7,4351 ■ 10э
1
Таблица П.1.3
Универсальные физические константы [269]
Постоянная
Скорость света в
вакууме
Заряд электрона
Масса покоя
электрона
Отношение заряда
электрона к его
массе покоя
Масса покоя протона
Масса покоя
нейтрона
Атомная единица
массы
Число Авогадро
Постоянная Планка
Постоянная
тонкой структуры
Радиус Бора
g-фактор
электрона
Магнетон Бора
Магнитомеханичес-
кое отношение
электрона
Ядерный магнетон
Магнитный момент
нейтрона
Квант магнитного
потока
Постоянная
Больцмана
Гравитационная
постоянная
Стандартное
гравитационное
ускорение
Обозначение и связь с другими
постоянными
с
ес
тс
\ее\/т.
wp~1836me
m„~1839mc
m0=l/12 массы атома 12С
NA=\/m0
b=h/(2n)
a = e2j(Jtc)
а0=й2/(т,ес2)
&=2[1+а/(2л)-0,328а2/тг2]
Ив = |«'«|Й/(2|Яег)
ys=gs\ec\/(2mec)=gs\iB/ Ъ
Hp = \ec\h/(2mvc)
дап=1,91304цр
Ф0 = пЬс/\ес\
У.
G
g
Величина (в гауссовой
системе единиц)
2,997925 • Ю10
-4,80321-10"10
9,10939-Ю'28
5,27281 1017
1,67262-10 ~24
1,67493-10 "24
1,66054-Ю-24
6,02214-1023
1,05457-10" "
7,29735-10_3~ 1/137
5,29177-10"9
2,002319
9,27402-10" 21
1,76086 107
5,05079-Ю-24
9,66237-Ю-24
2,06783 Ю-7
1,38066-10-16
6,67259 Ю-8
9,80665 102
144
Приложение 2
РАЗМАГНИЧИВАЮЩИЕ ФАКТОРЫ ЭЛЛИПСОИДА
Для эллипсоида в среде с ц=1 в однородном внешнем поле Не, внутреннее
поле Н и намагниченность М однородны (см., например [209]) и
H = HC-NM, (П.2.1)
где N—тензор размагничивания эллипсоида—симметричный и зависящий
только от формы эллипсоида, т. е. от отношений его полуосей a, J> и с.
Оси симметрии эллипсоида являются главными осями тензора N. Его
диагональные компоненты в этих осях Л^, Nb и Ne называются
размагничивающими факторами эллипсоида. Их сумма
Na + Nb+Nc = 4n. (П.2.2)
Зависимости Na, Nb и Nc от отношений полуосей эллипсоида, рассчитанные
Осборном [380], приведены на рис. П.2.1, П.2.2 и П.2.3.
Рис. П.2.1. Размагничивающие факторы эллипсоида в направлении большой
оси [380]
445
4lX
UjD
0,4
0,3
0,2
01
U,l
T
/
b
a
1
1-
lit
Tj
/
/'//
//
Ш
IIII
ж
Hi
%
k
>/
i\
/ /
/
//
//
//
^
/
/
i
i
4'
/
'{-,
1
V
/
/
7
A
/
//
;/;
//
/
'
0,2
/
/
f
/
f t
/
1
/
ф.3
t
o,<
у
—
\
'\ s
1
4=>
*
5
-0,6
и, о
\
—
\
-0,7
\
0,9
a^-b^c
a
r^
Л
— 1
—
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 ~a
Рис. П.2.2. Размагничивающие факторы эллипсоида в направлении средней
оси [380]
Nr
4п
1
0,9
0,8
0,7
0,6
0,5
0.-+
0,3
0,2
V
у
^N
Vtv
0,2
i
i
b \
C~
o,l
1
4. I
'
0,4
o,t
a-i'C
0,6
-
f С
OJ
-
0,1
0,9
/
s
b _
a
-.1
с
0,1 0,2 0,3 0.4 0,5 0,6 0,7 0,8 0,9 1
Рис II.2.1. P.n\iai ннчиваюшне факюры >. i.niiieoina в направлении \ла.юи
оси [ЗМ)|
В с. in чае ).тлипсота вращения (сфероида) для размагничивающих фак'°ров
нмеки место простые форч\лы [174] (см. также [64])
Гели направление внешнею поля совпадас! с о шой ut осей эдлипсои ia
ю Н и М (для изотропною и.шисоита) направлены в н>ль пой же <>-" "
H=H.-Sa.hcM
,П^>
При произвольных направлениях Нс и М (которые, конечно, не совиа uik>n
компоненты гензора N в требуемой системе коортннаг (например, с ос'.ю
г, совна ыюшей с направлением постоянной составляющей М) толжны "н"'
найтены по общим форм\лам [119] преобразования компонент тепюр,)В-
СПИСОК ЛИТЕРАТУРЫ
1. Абрагам А., Блини Б. Электронный парамагнижый резонанс переходных
ионов: Пер. с англ./Пот ред. С. А. Альтшулера и Г. В. Скроикого. М.: Мир.
1972. Т. 1; Т. 2.
2. Абрамов В. П.. Дмитриев В. 4.. Шелухин С. А. Невзаимные устройства на
ферритовых резонаторах. М.. Радио и связь, 1989.
3. Агеев А. Н., Гуревич А. Г./'ФТТ. 1969. Т. II. № X. С. 2122.
4. Адаме М. Введение в теорию отических волноводов: Пер. с атл. Под ред.
И. Н. Сисакяна. М.: Мир. 1984.
5. Алексеев В. В., Дргжитт В. В.. Писарев В. В.. Шкарубский В. В. ФТТ.
1987. Т. 29. № 4. С. 1048.
6. Ачьтшулер С. А.. Козырев Б. М. Электронный парамагнитный резонанс. М.:
Наука, 1972.
7. Анисимов А. Н.. Гуревич А. Г. ) ФТТ. 1976. Т. 18. № 1. С. 38.
8. Анисичов А. Н., Шукшров А. С, Гуревич А. Г., Эииряи Л. М '/ЖЭТФ. 1983
Т. 84. № 4. С. 1407.
9. Антиферромагнетизм: Сб. статей'Под ред. С. В. Вонсовского. М.: ИЛ, 1956.
10. Аркадьев В. К.//Журнал Русского физико-химического общества. Отд.
физики. 1912. Т. 44. № 4. С. 165.
П. Арцимович Л. А.. Сагдеев Р. 3. Физика плазмы для физиков. М.: Атомиздат,
1979.
12. Асеев Б. П. Основы радиотехники. М.: Связьиздат, 1947.
13. Аусленоер М. И., Самохвалов А. А.. Со ши Н. И.. Шумилов И. Ю //ЖЭТФ.
1988. Т. 94. № 12. С. 223.
14. Ахиезер А. И.. Барьяхтар В. Г., Пелетминский С. В I, ЖЭТФ. 1963. Т. 45.
№ 2. С. 337.
15. Ахиезер А. И., Барьяхтар В. Г., Пеаетмииекий С. В. Спиновые волны. М.
Наука, 1967.
16. Ашкрофт И.. Мермии И. Физика твердого тела: Пер. с англ./Под ред.
М. И. Каганова. М.: Мир, 1979. Т. 1; Т. 2.
17. Байрамов А. И.. Гуревич А. Г., Карпович В. И.//ФТТ. 1976. Т. 18. № 3.
С. 687.
18. Байраиов А. И., Гуревич А. Г., ЭмиряиЛ. М., Парфенова Н. Н.//ФТТ. 1977.
Т. 19. № 9. С. 1668.
19. Барышев Д. А., Вашковский А. В.. Гречушкин К. В., Стачъмахов А. В.\\
Письма в ЖТФ. 1990. Т. 16. № 3. С. 5.
20. Барьяхтар В. Г.//ЖЭТФ. 1984. Т. 87. № 4. С. 1501.
21. Барьяхтар В. Г., Богданов А. Н.. Телепа В. Т.. Ябгонский Д. А.//ФТТ 1984.
Т. 26. № 2. С. 389.
22. Барьяхтар В. Г., Богданов А. И., Яблонский Д. А.//УФН. 1988. Т. 156. № 1.
С. 47.
23. Барьяхтар В. Г., Иванов Б. А. В мире магнитных доменов, Киев: Наук,
думка, 1986.
24. Барьяхтар В. Г. Иванов Б. А.. Сукстанский А. Л.//ФТТ. 1979. Т. 21. № 12.
С. 3003.
25. Барьяхтар В. Г., Каганов М. И. Неоднородный резонанс и спиновые волны
В [204]. С. 266.
26. Барьяхтар В. Г, Савченко М. А.. Тарасепко В. Й.„ЖЭТФ. 1968. Т. 34. № 5.
С. 1603.
448
27. Бланк А. Я.. Каганов М. И. /у ЖЭТФ. 1965. Т. 49. №3. С. 807.
28. Блатш Ф. Физика электронной проводимости в твердых телах: Пер. с англ.
Г. Л. Краско и Р. А. Суриса. М.: Мир, 1971.
29. Бломберген Н. Нелинейная оптика: Пер. с англ./Под ред. С. А. Ахманова
и Р. В. Хохлова. М.: Мир, 1961.
30. Бокринська О. Я.. Bynmecuepi В. С, Кисляковський А. В. Феромагштний
резонанс у техтщ сантиметрових хвиль. КиТв: Техшка. 1966.
31. Боровик Е. С. Милънер А. С.. Еременко В. В. Лекции по магнетизму.
Харьков: Изд. Харьковского университета, 1972.
32. Боровик-Романов А. С. Антиферромагнетизм//Итоги науки.
Физико-математические науки. 4. Антиферромагнетизм и ферриты 'Под ред. Я. Г. Дорф-
мана. М.: Изд. АН СССР, 1962. С. 7.
33. Боровик-Романов А. С. Антиферромагнетики с анизотропией типа легкая
плоскость//Проблемы магнетизма. М.: Наука, 1972. С. 47.
34. Боровик-Романов А. С. Орлова М. П.//ЖЭТФ. 1956. Т. 31. №4. С. 579.
35. Браун У. Ф. Микромагнетизм: Пер. с англ. А. Г. Гуревича. М.: Наука, 1979.
36. БуишвилиЛ.Л.Ц ФТТ. 1961. Т. 3. № 12. С. 3706.
37. Бурков В. Д., Вашковский А. В., Ки гъдишев В. Н.ЦРадиотехн. и электрон.
1970. Т. 15. № 4. С. 764.
38. Бурлак Г. П., Гримальский В. В.. Коцаренко Н. Я./, ЖТФ. 1989. Т. 59. № 8.
С. 32.
39. Вакс В. Г., ЛаркинА.И.. Пиши С. А.//ЖЭТФ. 1967. Т. 53. № 1. С. 281.
40. Вакс В. Г., Ларкин А. И., Пикин С. А. /У ЖЭТФ. 1967. Т. 53. № 3. С. 1089.
41. Ватерский М. В., Абрамов В. П., Казанцев В. И. Конструирование
ферритовых развязывающих приборов СВЧ. М.: Радио и связь, 1982.
42. Вашковский А. В., Стальмахов А. В., Шахназарян Д. Г.//Изв. вузов СССР.
Сер. Физика, 1988. Т. 31. № 11. С. 67.
43. Вендик О Г., Калиникос Б. А., Чарторижский Д. М.//ФТТ. 1974. Т. 16. № 9.
С. 2757.
44. Вендик О. Г., Калиникос Б. А., Чарторижский Д. Н.Ц ФТТ. 1977. Т. 19.
№ 2. С. 387.
45. Вендик О. Г.. Чарторижский Д. Я.//ФТТ. 1970. Т. 12. № 5. С. 1538.
46. Власов К Б.. Пшмухаметов Б. А".//ЖЭТФ. 1959. Т. 37. № 3. С. 745.
47. Власов К. Б., Оноприенко Л. ГЦФММ. 1963. Т. 15. № 1. С. 45.
48. Вонсовский С. В.' ЖЭТФ. 1948. Т. 18. № 2. С. 219.
49. Вонсовский С. В. Магнетизм. М.: Наука, 1971.
50. Вугальтер Г. А.ЦЖ1Ф. 1989. Т. 59. № 8. С. 92.
51. Вугальтер Г. А., Гитнский И. А. ЖТФ. 1985. Т. 55. № 11. С. 2250.
52. Вугальтер Г. А., Гилинский И. А. Изв. вузов СССР. Сер. Радиофизика.
1989. Т. 32. № 10. С. 1187.
53. Вугальтер Г. А.. Гусев Б. Н., Гуревич А. Г.. Чивилева О. А. Ц ЖТФ. 1986.
Т. 56. № 1. С. 149.
54. Вугальтер Г. А., Махалип В. Н.ЦЖТФ. 1985. Т. 55. №3. С. 497.
55. Гаин В. В./, ФТТ. 1966. Т. 8. № 11. С. 3167.
56. Гейнрих Б., Мещеряков Б. Ф.//Письма в ЖЭТФ. 1969. Т. 9. № 11. С. 618
57. Гилинский И. А., Щегюв И. М.ЦЖТФ. 1985. Т. 55. № 12. С. 2323.
58. Гинибург M.A./IJXAU СССР. 1954. Т. 95. № 3. С. 489.
59. Гииибург М.А.ЦЖЭТФ. 1958. Т. 34. № 6. С. 1635.
60. Головенчиц Е. И.. Санина В. А.. Гуревич А. ГЦ ФТТ. 1968. Т. 10. №10.
С. 2956.
61. Гортер К. Парамагнитная релаксация: Пер. с англ./Под ред. С. А.
Альтшулера и В. М. Козырева. М.: ИЛ, 1949.
62. Гублер И. E./i Приборы и техн. экспер. 1960. № 5. С. 145.
63. Гуляев Ю. В., Бугаев А. С, Зилъберман П. £.//Письма в ЖЭТФ. 1979. Т. 30.
№ 9. С. 600.
64. Гуревич А. Г. Полые резонаторы и волноводы. М.: Сов. радио, 1952.
65. Гуревич А. Г. Ц Радиотехн. и электрон. 1957. Т. 2. № 8. С. 960.
66. Гуревич А. Г. Ферриты на сверхвысоких частотах. М.: Физматгиз. 1960.
67. Гуревич А. Г. Нелинейные процессы в ферритах в полях СВЧ. В [204].
С. 285.
68. Гуревич А. Г.//Радиотехн. и электрон. 1963. Т. 8. № 5. С. 780.
29 А. Г. Гуревич, Г. А. Мелков
449
69. Гуревич А. Г. Магнитный резонанс в ферритах и антиферромагнетиках.
М.: Наука, 1973.
70. Гуревич А. Г.; ФТТ. 1974. Т. 16. № 6. С. 1784.
71. Гуревич А. Г., Байрамов А. И., Эмирян Л. М. и др. Ферромагнитный
резонанс и механизмы проводимости в легированном магнитном
полупроводнике CdCr2Se4 "Магнитные полупроводниковые шпинели типа
CdCr2Se4. Кишинев: Штиинца, 1978. С. 30.
72. Гуревич А. Г., Богомаз М. А. // Радиотехн. и электрон. 1958. Т. 3. №9.
С. 1133.
73. Гуревич А. Г., Гублер И. Е.Ц ФТТ. 1959. Т. 1. № 12. С. 1847
74. Гуревич А. Г., Гублер И. Е., Сафантьевский А. П.ЦФТТ. 1959. Т. 1. № 12.
С. 1862.
75. Гуревич А. Г., Гублер И. Е., Титова А. Г.,, ФТТ. 1961. Т. 3. № 1. С. 19.
76. Гуревич А. Г., Драбкин Г. М., Лазебник И. М. и др.//ФТТ. 1968. Т. 10.
№ 2. С. 647.
77. Гуревич А. Г., Мэн Счнь-чжень, Старобинец С. С.//ФТТ. 1963. Т. 5. № 3.
С. 740.
78. Гуревич А. Г., Сафантьевский А. П., Соловьев В. И.. Шер Е. С.//Изв. АН
СССР. Сер. физич. 1961. Т. 25. № 11. С. 1361.
79. Гуревич В. Л.//ЖЭТФ. 1957. Т. 23. № 6. С. 1497.
80. Гусев Б. Н., Гуревич А. Г., Анисимов А. Н. и др./, ФТТ. 1986. Т. 28. № 10.
С. 2969.
81. Давыдов А. С. Квантовая механика. М.: Наука, 1973.
82. Дебай П., Закк Г. Теория электрических свойств молекул: Пер. с нем./ Под
ред. Л. Э. Гуревича. Л. М.: Гл. ред. общетсхн. лит, 1936.
83. ДедухЛ. М., Кабанов Ю. П., Никитенко В. И./, ЖЭТФ. 1990. Т. 97. № 2.
С. 570.
84. Дерюгин И. А., Запорожец В. В., Мелков Г. А.//Письма в ЖЭТФ. 1967.
Т. 5. № 10. С. 352.
85. Дзялошинский И. £./7 ЖЭТФ. 1957. Т. 32. № 6. С. 1547.
86. Еременко В. В., Криворучко В. Н., Лавриненко Н. М., Яблонский Д. А.//
ФТТ. 1988. Т. 30. № 12. С. 3605.
87. Завойский Е. К.ЦЖЭТФ. 1947. Т. 17. № 10. С. 883.
88. Зауткин В. В., Захаров В. Е., Львов В. С. и др./, ЖЭТФ. 1972. Т. 62. № 5.
С. 1782.
89. Захаров В. Е., Львов В. С.//ФТТ. 1972. Т. 14. № 10. С. 2913.
90. Захаров В. Е.. Львов В. С, Старобинец С. Г.//УФН. 1974. Т. 114. № 4. С. 609.
91. Звездин А. К.. Матвеев В. М. '/ЖЭТФ. 1972. Т. 62. № 1. С. 260.
92. Зилъбершн П. Е., Гогубева Н. С, Темирнзев А. Г.//ЖЭТФ. 1990. Т. 97.
№ 2. С. 634.
93. Зотов Т. Д.. Сукровцева М.М.,, ФТТ. 1969. Т. 11. № 3. С. 649.
94. И 1ъченко М. Е., МехковГ.А., Мирских Г. А.. Твердотельные СВЧ
фильтры. Киев: Техника, 1977.
95. Каганов М. И. Ц ЖЭТФ. 1960. Т. 39. № 1. С. 158.
96. Каганов М. И. // Письма в ЖЭТФ. 1969. Т. 10. № 7. С. 336.
97. Каганов М. И. Свойст ва ферромагнетика вблизи антирезонанса. //
Проблемы магнетизма. М.: Наука, 1972. С. 118.
98. Каганов М. И.. Пааш Г. ЖЭТФ. 1976. Т. 70. № 3. С. 1112.
99. Каганов М. И.. Цуксрник В. М.//ЖЭТФ. 1958. Т. 34. № 6. С. 1610.
100. Каганов М. И.. Цукерник В. М. ЖЭТФ. 1959. Т. 36. № 1. С. 224.
101. Каганов М. И.. Цукерник В. М., ЖЭТФ. 1959. Т. 37. № 9. С. 824.
102. Каганов М. И.. Юй Лу. Изв. АН СССР. Сер. физич. 1961. Т. 25. № 11.
С. 1375.
103. Каюков Г. Т., Филимонов Ю. А., Изв. вузов СССР. Сер. Физика. 1989.
Т. 32. № 1. С. 5.
104. Камншкос Б. А. Изв. вузов СССР. Сер. Физика. 1981. Т. 24. № 8. С. 42.
105. Катникос Б. А., Ковшиков Н. Г.. Кожусъ Н. В.//Тез. докл. VIII Всееоюз.
школы-семинара «Новые магнитные материалы для микроэлектроники».
Донецк. 1982. С. 319.
106. Катникос Б. А., Ковшиков Н. Г.. Кажусь Н. В. ФТТ. 1985. Т 27. №9.
С. 2794.
450
107. Касаткина Т. С, Яковлев Ю. М.. Мацкевич С. Л., Берестовая И. К ФТТ.
1983. Т. 25. № 6. С. 1734.
108. КашеевВ.Н., Кривоглаз М. А.//ФТТ. 1961. Т. 3. № 5. С. 1541.
109. КиржницД. А.//УФН. 1978. Т. 125. № 1. С. 169.
ПО. Киров С. А., Пиаыциков А. И., Сырьев Н. Е.//ФТТ. 1974. Т. 16. №10
С. 3051.
111. КировС. А., Пильщиков А. И./, ФТТ. 1977. Т. 19. № 1. С. 141.
112. Киттелъ Ч. Квантовая теория твердых тел: Пер. с англ. А. А. Гусев.!.
М.: Наука, 1967.
113. Киттелъ Ч. Введение в физику твердого тела: Пер. с англ. А. А. Гусева
М.: Наука, 1978.
114. Колоколов И. В.. Львов В. С, Черепанов В. Б /, ЖЭТФ. 1983. Т. 84. № 3.
С. 1043.
115. Колоколов И. В., Львов В. С, Черепанов В. Б , ЖЭТФ. 1984. Т. 86. № 5.
С. 1946.
116. Кондорский Е. И. Зонная теория магнетизма. М.: Изд. МГУ, 1976. Ч. 1;
1977. Ч. 2.
117. Корчагин Е. А., Хлебопрос Р. Г., Чистяков Н. С/, ФТТ. 1972. Т. 14. № 7.
С. 2121.
118. Котюков Ю. Н. Изв. вузов СССР. Сер. Физика. 1965. №4. С. 82.
119. Кочин Н. Е. Векторное исчисление и начала тензорного исчисления. М.:
Изд. АН СССР, 1961.
120. Краус Л., Анисимов А. //., Гуревич А. Г., Атлас чан А. В. Письма
в ЖЭТФ. 1983. Т. 37. № 2. С. 100.
121. Кривченков В. Д.. Пильщиков А. И. /, ЖЭТФ. 1962. Т. 43. №2. С. 573.
122. Кринчик Г. С. Физика магнитных явлений. М.: Изд. МГУ, 1976.
123. Крупичка С. Физика ферритов и родственных им магнитных окислов:
Пер. с нем. 'Под ред. А. С. Пахомова. М.: Мир. 1976. Т. 1; Т. 2.
124. Круценко И. В.. Львов В. С, Мелков Г. А.ЦЖЭТФ. 1978. Т. 75. №3
С. 1114.
125. Круценко И. В., МехковГ.А. ФТТ. 1979. Т. 21. № 1. С. 271.
126. Кубо Р. Некоторые вопросы статистическо-механической теории
необратимых процессов/ Термодинамика необратимых процессов Пот ред.
Д. Н. Зубарева. М.: ИЛ, 1962. С. 345.
127. Курант Р.. Гхиьаерт Д. Методы математической физики: Пер. с нем.
Ю.Рабиновича и 3. Либина. М.: ГИТТЛ, 1951. Т. 1.
128. Лаке Б.. Баттон К. Сверхвысокочастогные ферриты и ферримагнегики:
Пер. с англ. Пот ре i. А. Г. Гуревича. М.: Мир. 1965.
129. Ландау Л. Д. Возможное объяснение зависимости восприимчивости от
поля при низких температурах/у Ландау Л. Д. Собрание трудов: в 2 г. Пот
ред. Е. М. Лифшииа. М.: Наука, 1969. Т. 1. С. 97.
130. Ландау Л. Д., Лифшнц Е. М. К теории дисперсии магнитной
проницаемости ферромагнитных тел'/Ландау Л. Д. Собрание трудов, в 2 т. Под
ред. Е. М. Лифшииа. М.: Наука, 1969. Т. I. С. 128.
131. Ландау Л. Д.. Лнфшххц Е. М. Теоретическая физика. В 10 г. Г I Механика
4-е изд. М.: На>ка, 1988.
132. Ландау Л. Д.. Лифшиц Е. М. Теоретическая физика. В 10 г. "I. III.
Квантовая механика. Нерелягивистская теория 4-е и i.t. М.: Наука. 1989.
133. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. В 10 т. I V.
Статистическая физика. 3-е из i. M.: Наука. 1976
134. Ландау Л. Д.. Лифшиц Е. W. Теоретическая фишка. В II) г. 1. VIII
Электродинамика епчошных сред. 2-е изд. М.: Наука, 1982.
135. Ландау Л. Д.. Лифхииц Е. М. Теоретическая фишка. В 10 г. Т VII. Теория
упругости. 4-е и»л. М.: Наука, 1987.
136. Лебедева Е. В.. Пи ihu/иков А. И . Сен н-нка.ч Н С. ЖЭТФ. 11>77 Т. 72.
№ 2. С. 667.
137. ЛеКроу Р.. Ко.испюк Р. Магнитоупрутие вмимоаействия в
ферромагнитных шэ.тектриках Физическая акустика. Г. III. Ч. В. Динамика
решетки Под ред. У. Мэзона: Пер. i аш.т. М.: Мир, 1968. С 156.
138. Леманов В. В. Мапштоупругие взаимодействия, Физика магнитных ти-
хтекфиков. Л.. Наука. 1974. С. 284.
29*
45|
139. Лифшиц И. М., Азбель М. #., Каганов М. И. Электронная теория металлов.
М.: Наука, 1971.
140. Лукомский В. /7.,/ФТТ. 1967. Т. 9. № 2. С. 607.
141. ЛукпжкийВ. П., Кузъко А. В.ЦФТТ. 1969. Т. 11. № 5. С. 1297.
142. Лутовииов В. С. Мелков Г. А., Тараненко А. Ю., Черепанов В. Б. /у ЖЭТФ.
1989. Т. 95. № 2. С. 760.
143. Лутовинов В. С, Рейзер М. /О.//ЖЭТФ. 1979. Т. 77. №2. С. 707.
144. Луценко А. Л.. Мелков Г. А.ЦРадиотехн. и электрон. 1973. Т. 18. № П.
С'. 2284.
145. Львов В. С. Нелинейные спиновые волны. М.: Наука, 1987.
146. Львов В. С, Фалькович Г. £.//ЖЭТФ. 1982. Т. 82. № 5. С. 1562.
147. МаШ. Современная теория критических явлений: Пер. с англ./Под ред.
Н. Н. Боголюбова и В. К. Федянина. М.: Мир, 1982.
148. Матйлова А. А., Богданова Л. П.//ФТТ. 1964. Т. 6. №9. С. 2703.
149. Махмудов 3. 3., Барьяхтар В. Г.//ФТТ. 1965. Т. 7. № 7. С. 2082.
150. Мелков Г. А.//ЖЭТФ. 1971. Т. 61. № 1. С. 373.
151. Мелков Г. А.//ЖЭТФ. 1976. Т. 70. № 4. С. 1324.
152. Маков Г. А. IIФТТ. 1988. Т. 30. № 8. С. 2533.
153. Маков Г. А., Луценко А. Л.//Радиотехн. и электрон. 1973. Т. 18. №2.
С. 350.
154. Межов Г. А., Шолом С. В.//ФТТ. 1987. Т. 29. № П. С. 3257.
155. Мелков Г. А.. Шолом С. В.//ЖЭТФ. 1989. Т. 96. № 2. С. 712.
156. Мелков Г. А., Шолом С. В.ЦЖТФ. 1990. Т. 60. № 8. С. 118.
157. Метфессель 3., Маттис Д. Магнитные полупроводники: Пер. с англ./Под
ред. С. В. Вонсовского. М.: Мир, 1972.
158. Мигулин В. В., Медведев В. И., Mvcme гь Е. Р., Парыгин В. М. Основы
теории колебаний. М.: Наука. 1978.
I ~>9. Микаэлян А. Л. Теория и применение ферритов на сверхвысоких частотах.
М.: Госэнергоиздат, 1963.
160. Микаэлян А. Л., Антоньящ В. Я.//Радиотехн. и электрон. 1960. Т. 5.
№ 1. С. 90.
161. Михайловская Л. В., Богомаз И. В.ЦФТТ. 1977. Т. 19. № 8. С. 1245.
162. Моносов Я. А. Нелинейный ферромагнитный резонанс. М.: Наука, 1971.
163. Морс Ф. М., Фешбах Г. Методы теоретической физики: Пер. с англ./Под
ред. С. П. Аллилуева, Н. С. Кошлякова, А. Д. Мышкиса. А. Г.
Свешникова. М.: ИЛ 1958. Т. 1; 1960. Т. 2.
164. Нелинейные свойства ферритов в полях СВЧ: Сб. статей: Пер. с англ./Под
ред. А. Л. Микаэляна. М.: ИЛ, 1963.
165. Никольский В. В. Ц Радиотехн. и электрон. 1956. Т. 1. № 4. С. 447; № 5.
С. 638.
166. Никольский В. В. IIРадиотехн. и электрон. 1957. Т. 2. № 2. С. 157.
167. О'Делл Т. Магнитные домены высокой подвижности: Пер. с англ./Под
ред. В. И. Ожогина. М.: Мир, 1978.
168. Ожогии В. И. //ЖЭТФ. 1970. Т. 58. № 6. С. 2079.
169. Ожогип В. И., Фарзетдинова Р. М.. Михайлов А. С.//ЖЭТФ. 1990. Т. 97.
№ 3. С. 863.
170. Перекалина Т. М., Аскочинский А. А., Санников Д. Г. //ЖЭТФ. 1961. Т. 40.
№ 2. С. 441.
171. Петраковский Г. Л.//Изв. вузов СССР. Сер. Физика. 1962. №6. С. 29.
172. Пильщиков А. И.//ЖЭТФ. 1974. Т. 66. №2. С. 679.
173. Пистолькорс А. А., Сюй Янь-шен. //Радиотехн. и электрон. 1960. Т. 5.
№ 1. С. 3.
174. Поливанов К. М. Ферромагнетики: Основы теории технического
применения. М.—Л.: Госэнергоиздат, 1957.
175. Померанчук И. Я.//ЖЭТФ. 1941. Т.П. №2—3. С. 226.
176. Прозорова Л. А., Боровик-Романов А. С.}/Письма в ЖЭТФ. 1969. Т. 10.
№ 7. С. 316.
177. Рубинштейн Б. Е., Титова А. Г., Лаповок Б. Л. П ФТТ. 1965. Т. 7. №6.
С. 1639.
178. Са шнский Н. М., ЕрухимовМ.Ш. Физические свойства и применение
магнитных пленок Новосибирск: Наука, Сиб. отд., 1975.
452
179. Самохвалов А. А., Морозов Ю. Н и др. Ц ФТТ. 1970. Т. 12. № 10. С. 2865.
180. Сена Л. А. Единицы физических величин и их размерности. М.:
Наука, 1988.
181. Сигаг М. А.ЦЖТФ. 1989. Т. 59. № 10. С. 137.
182. СигалМ.А., Костенко В. И. Ц ФТТ. 1980. Т. 22. № 1. С. 117.
183. СкроцкийГ. В., Алимов Ю. Я.//ЖЭТФ. 1958. Т. 35. № 12. С. 1481.
184 Скроцкий Г. В., Алимов Ю. Я.//ЖЭТФ. 1959. Т. 36. №4. С. 1267.
185. Скроикий Г. В., Курбатов Л. В. Феноменологическая теория
ферромагнитного резонанса. В [204]. С. 25.
186. Слэтер Дж. Электроника сверхвысоких частот: Пер. с англ.//Под ред.
С. Д. Гвоздовера. М.: Сов. радио, 1948.
187. Смарт Дж. Эффективное поле в теории магнетизма: Пер. с англ./Под
ред. С. В. Тябликова. М.: Мир, 1968.
188. Смит Я., ВеипХ. Ферриты: Пер. с англ./Под ред. Ю. П. Ирхина
и И. Е. Старцевой. М.: ИЛ, 1962.
189. Соловьев В. И., Гуревич А. Г.//ФТТ. 1965. Т. 7. № 6. С. 1761.
№. Сорокин В. Г., Богун П. В., Кандыба П. Е.ЦЖТФ. 1986. Т. 56. №12.
С. 2377.
191. Сшил М., Вюралъ Б. Взаимодействие волн в плазме твердого тела: Пер.
с англ. И. С. Веселовского. М.: Атомиздат, 1973.
192. Су л Г., Уокер Л. Вопросы волноводного распространения
электромагнитных волн в гиротропных средах: Пер. с англ., Под ред. Г. Мириманова.
М.: ИЛ, 1955.
193. Суху Р. Магнитные тонкие пленки: Пер. с англ./Под ред. Р. В. Телеснина.
М.: Мир, 1967.
194. Сюй Янь-шен./'Радиотехн. и электрон. 1960. Т. 5. № 12. С. 1951.
195. Таблицы физических величин/Под ред. И. К. Кикоина. М.: Энергоатомиз-
дат, 1987.
196. Тамм И. Е. Основы теории электричества. М.: Наука, 1989.
197. Туров Е. А. Особенности ферромагнитного резонанса в металлах. В [204].
С. 170.
198. Туров Е. А. Физические свойства магнитоупорядоченных кристаллов. М.:
Изд. АН СССР, 1963.
199. Туров Е. А. Материальные уравнения электродинамики. М.: Наука, 1983.
200. Туров Е. А., ИрхинЮ.П.ЦФЫЫ. 1956. Т. 3. № I. С. 15.
201. Тябликов С. В. Методы квантовой теории магнетизма. М.: Наука, 1975.
202. Федоров Ф. И. Теория упругих волн в кристаллах. М.: Наука, 1965.
203. Ферриты в нелинейных сверхвысокочастотны\ устройствах: Сб. статей:
Пер. с англ./Под ред. А. Г. Гуревича. М.: ИЛ. 1961.
204. Ферромагнитный резонанс//Под ред. С. В. Вонсовского. М.: Физматгиз,
1961.
205. Ферромагнитный резонанс и поведение ферромагнетиков в переменных
магнитных полях: Сб. статей: Пер. с англ./Под ред. С. В. Вонсовского. М.:
ИЛ, 1952.
206. Филиппов Б. Н. I/ЖЭТФ. 1968- Т. 55. №1. С. 208.
207. Фигиппов Б. Н.//ФММ. 1971. Т. 32. № 5. С. 911.
208. Филиппов Б. Н., Титяков И. Г.//ФММ. 1973. Т. 35. № 1. С. 28.
209. Френкель Я. И. Электродинамика Л.—М.: ОНТИ, 1935, Т. 2.
210. Хлебопрос Р. Г.. Михайловская Л. В.ЦФТТ. 1970. Т. 12. №8. С. 2476.
211. Цукерник В. M.I ФТТ. 1968. Т. 10. №4. С. 1006.
212. Чивилева О. А., Гуревич А. Г.. Анисимов А. Н. и др.//ФТТ. 1987.
Т. 29. № 6. С. 1774.
213. Штраусе В. Магнитоупругие свойства иттриевого
феррита-граната//Физическая акустика. Т. IV. Ч. Б. Применения физической акустики в
квантовой физике и физике твердого тела/Под ред. У. Мэзона: Пер. с англ. М.:
Мир, 1970. С. 247.
214. Щеглов И. М., Гилинский И. А., Сорокин В. Г.//ЖТФ. 1987. Т. 57. №5.
С. 943.
215. Эмирян Л.М.. Гуревич А. Г., Шукюров А. С, Бержанский В. Н.//ФТТ.
1981. Т. 23. № 10. С. 2916.
'16. Яховл Ю М. "ФТТ. 1968. Т. 10. №8 С. 2431.
?3
217. Яковлев Ю. М., Генделев С Ш. Монокристаллы ферритов в
радиоэлектронике. М.: Сов. радио, 1975.
218. Яковлев Ю. М.. Рубальская Э. В., Годес Л. Г. и др.//ФТТ. 1971. Т. 13. № 4.
С. 1151.
219. Abrahams Е., Kittel С Ц Phys. Rev. 1952 V. 88. №5. P. 1200.
220. AdamJ.D./iPToc. IEEE. 1988. V. 76. №2. P. 159.
221. Adam J. D.. Collins J.H.//Proc. IEEE. 1976. V. 64. №5. P. 794.
222. Adam J. D.. Stitzer S. TV.//Appl. Phys. Lett. 1980. V. 36. №6. P. 485.
223. Adkins L. R., Glass H. L.//J. Appl. Phys. 1982. V. 53. №12. P. 8928.
224. Akhieser A.//S. Phys. USSR. 1946. V. 10. №3. P. 217.
225. Alben R.S./1 Phys. Rev. 1968. V. 167. №2. P. 249.
226. Ament W. S., Rado G. Г.//Phys. Rev. 1955. V. 97. №6. P. 1558.
227. Anderson P. W. Exchange in insulators: superexchange and double exchange. In
[364]. V. 1. P. 25.
228. Anderson P. W./1 Phys. Rev. 1952. V. 88. №5. P. 1214.
229. Anderson P. W., Suhl tf.//Phys. Rev. 1955. V. 100. № 6. P. 1788.
230. Artman J. O.jI Phys. Rev. 1957. V. 105. № 1. P. 62.
231. Auld B. A.//}. Appl. Phys. 1963. V. 34. №6. P. 1629.
232. Auld B. A. )l J. Appl. Phys. 1965. V. 36. №3. Pt. 1. P. 689.
233. Auld B. A.. Mechta К. В.//J. Appl. Phys. 1967. V. 38. №10. P. 4081.
234. Ayres W.P.'IIRE Trans. 1959. V. MTT—7. №1. P. 62.
235. Body /.//IRE Trans. 1962. V. MTT—10. №1. P. 55.
236. Body I., Schlomann Е.Ц}. Appl. Phys. 1962. V. 33. №3. P. 1377.
237. Bailey G.C., Vittoria С F./, Phys. Rev. Lett. 1972. V. 28. №2. P. 100.
238. Bajorek СИ., Wills С W.//J. Appl. Phys. 1971. V. 42. №11. P. 4324.
239. Bar'yakhtar V.G.. Turov E. A. Magnetoelastic excitation. In [423]. Pt. 2.
P. 333.
240. Becker R.i13. Phys. Rad. 1951. V. 12. №3. P. 332 (Перевод в [205]).
241. Beeman D. E.//J. Appl. Phys. 1966. V. 37. №3. P. 1136.
242. Berteaud A. J.. Pascard Н.Ц J. Appl. Phys. 1966. V. 37. №5. P. 2035.
243. Bhagat S. M.. Hirst L. L., Anderson J. R.//J. Appl. Phys. 1966. V. 37. № 1.
P. 194.
244. Bhagat S. M., Lubit: P. '/Phys. Rev. 1974. V. B10. №1. P. 179.
245. BiniM., Filletti P. L., Millanta L.. Rubino N./jJ. Appl. Phys. 1978. V. 49.
№ 6. P. 3554.
246. BiniM.. Millanta L.. Rubino /V.//IEEE Trans. 1978. V. MAG 14. № 5. P. 811.
247. Blankenship A. C. Huntt R. L. "J. Appl. Phys. 1966. V. 37. № 3. P. 1066.
248. Blech I. A., Averhach B. L./'Phys. Rev. 1966. V. 142. № 2. P. 287.
249. Bloch F./l Zs. f. Phys. 1930. Bd61. №3 4. S. 206.
250. Bloch F./l Phys. Rev. 1946. V. 70. №7—8. P. 460.
251. Bloembergen N. // Phys. Rev. 1950. V. 78. № 5. P. 572.
252. Bloembergen N, Damon R. tt.//Phys. Rev. 1952. V. 85. №4. P. 699.
253. Bloembergen N.. Wang S. /, Phys. Rev. 1954. V. 93. №1. P. 72 (Перевод
в [203]).
254. Bongianni W. L. /, J. Appl. Phys. 1972. V. 43. №6. P. 2541.
255. Borovik-Romanov A. S., Kreines N. M. Light scattering from spin waves. In
[423]. PU. P. 81
256. Bucholtz F.. Webb DC. Ymmg CIV. J. Appl. Phys. 1984. V. 56. №6.
P. 1859.
257. Buffler С R./l J. Appl. Phys. 1959. V. 30. №4 Suppl. P. I72S (Перевод
в [203]).
258. Callen H. В. i J. Pins. Chem. Sol. 1958. V. 4. №4. P. 256.
259. Callen H. В., Pittel'li F.,,Ph\s. Rev. 1960. V. 119. №5. P. 1523.
260. Casimir H.B.G.. du Pre F. k. Physica. 1938. V. 5. №6. P. 507.
261. Cliarap S. H.. Annum JO. I. \ppl. Phys. 1978. V. 49. №3. P. 1585
262. Chen M.. Patton С £.. Srinwasaii С Zhang У. Т. IEEE Trans. 1989.
V. MAG-25. № 5. P 3485.
263. Chirk A. F.. Callen E. J. Appl. Phvs 1968. V. 39. № 13. P. 5972.
264. Clarke В. Н. J. Phys. Chem. Fol 1966. V. 27. № 2. P. 353.
^65. Clarke B. H.. Twcedale K.. Ъ de R. W. Phvs. Rev. 1965. V. 139. №6\
P А1УЗЗ.
266. Clogston A.M. Ц Bell System. Tech. J. 1955. V. 34. №4. P. 739.
267. Clogston A. M.. Suhl H.. Walker L. R.. Anderson P. W.//}. Phys. Chem. Sol.
1956. V. 1. № 3. P. 129 (Перевод в [203]).
268. Cochran J. F. Heinrich В., Dewar G.//Canad J. Phys. 1977. V. 55. № 9. P. 787.
269. Cohen E. R., Taylor B. N. //Physics Today. 1988. V. 41. №8. Pt. 2. P. BG9.
270. Comly J. В.. Jones R. V. J. Appl. Phys. 1965. V. 36. № 3. Pt. 2. P. 1201.
271. Corliss L. M., Hastings J. M., Nathans R., Shirane G.j/3. Appl. Phys. 1965.
V. 36. № 3. Pt. 2. P. 1099.
272. Coutinho M. D. Filho. Miranda L. С M.. Rezcnde S. M./1 Phys. Stat. Sol. (b).
1973. V. 57. № 1. P. 85.
273. Damon R. W./l Phys. Stat. Sol. 1965. V. 8. №2. P. K89.
274. Damon R. W.. Eshbach J. R.//J. Phys. Chem. Sol. 1961. V. 19. № 3/4. P. 308.
275. Davies J. T. "J. Appl. Phys. 1964. V. 35. №3. Pt. 2. P. 804
276. De Gennes P. G.. Kittel C, Portis A. M./IPhys. Rev. 1959. V. 116. № 2. P. 323.
277. Denton R.T.II J. Appl. Phys. 1961. V. 32. №3 Suppl. P. 300S (Перевод
в [164]).
278. De Wames R. E., Wolfram T // Phys. Rev. 1969. V. 185. №2. P. 720.
279. De Wames R. E., Wolfram T./'J. Appl. Phys. 1970. V. 41. №3. P. 987.
280. De Wames R. E.. Wolfram T./'Jap. J. Appl. Phys. 1974. V. 13. № 1. P. 68.
281. Dillon J.F.Jr., Phys. Rev. 1962. V. 127. №5. P. 1495.
282. Dillon J. F. Jr., Gyorgy E. M.. Remeiku J. P.Hi. Appl. Phys. 1970. V. 41. № 3.
P. 1211.
283. Dillon J.F.Jr., Nielsen J.W.IIPhys. Rev. Letl. 1959. V. 3. №1. P. 30
(Перевод в [203]).
284. Dillon J.F.Jr., Nielsen J. И'.//Phys. Rev. 1960. V. 120. №1. P. 105.
285. Dillon J.F.Jr.. Remeika J. P.. Walker L. R./l J. Appl. Phys. 1967. V. 38.
№ 5. P. 2235.
286. Dillon J.F.Jr., Walker L.R./IPhys. Rev. 1961. V. 124. №5. P. 1401.
m.Dorfmann J Zs Г. Phys. 1923. Bd 17. №2. S 98.
288. Doring W.I'Zs. Г. Naturforsch. 1948. Bd 3a. №7. S. 373 (Перевод в [205]).
289. Dyson F.J Phys. Rev. 1956. V. 102. №5. P. 1217 (Перевод в сб.-
Проблемы современной физики. М.: ИЛ, 1958. № 2. С. 101).
290. Dyson F. J , Phys. Rev. 1956. V. 102. № 5. P. 1230 (Перевод в сб.:
Проблемы современной физики. М.: ИЛ, 1958. № 2. С. 129).
291. Emtage P. R./,J. Appl. Phys. 1978. V. 49. № 8. P. 4475.
292. Epstein P. S. II Rev. Mod. Phys. 1956. V. 28. № 1. P. 3 (Перевод в УФН.
1958. Т. 65. № 2. С. 283).
293. Erickson R. ,4./, Phys. Rev. 1953. V. 90. № 5. P. 779 (Перевод в [9]).
294. Eshbach J. R./l J. Appl. Phys. 1963. V. 34. № 4. Pt. 2. P. 1298.
295. Eshbach J. R.. Damon R. W. ' Phys. Rev. 1960. V. 118. № 5. P. 1208.
296. Fletcher P. C, Bell R. О.ЦЗ. Appl. Phys. 1959. V. 30. № 5. P. 687 (Перевод
в [203]).
297. Fletcher P. C, Kittel С ЦPhys. Rev. 1960. V. 120. № 6. P. 2004.
298. Fletcher P. C. Solt I. Н.Ц J. Appl. Phys. 1959. V. 30. № 4 Suppl. P. 181S
(Перевод в [203]).
299. FonerS.I/i. Phys. Rad. 1959. V. 20. № 2- 3 P. 336.
300. Foner S. Antilerromagnetic and ferrimagnetic resonanse. In [364]. V. 1. P. 383.
301. FraitZ./l Czech. J. Phys. 1977. V. B27. № 2. P. 185.
302. Frail Z., Fraitova £>.//J. Magnet, and Magn. Mater. 1980. V. 15—18. Pt. 2.
P. 1081.
303. Frait Z., Fraitova D. Spin-wave resonance in metals. In [423]. Pt. 2. P. 1.
304. Frait Z., Mac Faden H. I/ Phys. Rev. 1965. V. 139. № 4A. P. A1173.
305. Fraitova D. 11 Phys. Stat. Sol. (b). 1983. V. 120. № 1. P. 341; 1983. V. 120.
№ 2. P. 659; 1984. V 124. № 2. P. 587.
306. GaltJ.K.HBe\\ System Tech. J. 1954. V. 33. № 5. P. 1023.
307. Ganguly A. K.. Webb D. СI' IEEE Trans. 1975. V. MTT-23. № 12. P. 998.
308. GeschwindS.. Clogston A. M.//Phvs. Rev. 1957. V. 108. № 1. P. 49.
309. Geschwiiul ^ Walker L. R./i J. Appl. PBys. 1959. V. 30. № 4 Suppl. P. 163S.
310. Gottlieb P J. Appl. Phys. 1960. V. 31. № 11. P. 2059.
311. Gottlieb P.. Suhl H. // J. Appl. Phys. 1962. V. 33. №4. P. 1508.
312. Griffiths J. H. E/l Nature. 1946. V. 158. № 4019. P. 670 (Перевод в [205]).
455
313. Gurevich А. С, Ageev A. N.. /dinger M. /.//J. Appl. Phys. 1970. V. 41. № 3.
P. 1295.
314. Gurevich A. C, Anisimov A. N.. Samokhvalov A. A., Solin N. 1.Ц Acta Phys.
Polonica. 1985. V. A68. № 3. P. 467.
315. Gurevich A. G., Karpovich V. I., Rubalskaya E. V. et al.//Phys. Stat. Sol. (b).
1975. V. 69. № 2. P. 731.
316. Gurevich A. G., Sanina V. A., Golovenchits E. I., Starobinets S. S. //J. Appl.
Phys. 1969. V. 40. № 3. P. 1512.
317. Gyorgy E. M., Le Craw R. C, Slurge M. D.//3. Appl. Phys. 1966. V. 37. № 3.
P. 1303.
318. Haas С W., Callen H. B. // Phys. Rev. 1961. V. 122. № 1. P. 59.
319. Haas C. W., Callen H. B. Ferromagnetic relaxation and resonance line widths.
In [364]. V. 1. P. 449.
320. Handbuch der Physik. Bd XVIH/2, Ferromagnetismus. - Springer Verl., 1966.
321. Hansen P., TolksdorfW., Schuldt G.//J. Appl. Phys. 1972. V. 43. №11.
P. 4740.
322. Hartmann-Boutran F./IJ. Appl. Phys. 1964. V. 35. № 3. Pt. 2. P. 889.
323. Hartwick T. S., Smit J.ЦЗ. Appl. Phys. 1969. V. 40. № 10. P. 3995.
324. Hatfield W. В.. Auld В. А.Ц]. Appl. Phys. 1963. V. 34. № 10. P. 2941.
325. Healy D. W.//Phys. Rev. 1952. V. 86. № 6. P. 1009.
326. Herring C, Kittel С // Phys. Rev. 1951. V. 81. № 5. P. 869 (Перевод в сб.:
Проблемы современной физики. М.: ИЛ, 1958. № 5. С. 6).
327. HoekstraB., van Stopele R. P., Voermans А. В./1 Phys. Rev. 1972. V. B6.
№ 7. P. 2762.
328. HoganC. L.//Bell System Techn. J. 1952. V. 31. № 1. P. 1.
329. HolsteinT.. Primakoff H. I/Phys. Rev. 1940. V. 58. № 12. P. 1098.
330. Huber D. L.//J. Appl. Phys. 1965. V. 36. № 3. Pt. 2. P. 1005.
331. Huber D. L.//So\. St. Com. 1966. V. 4. № 9. P. 435.
332. HurdR. A./I Canad. J. Phys. 1958. V. 36. № 8. P. 1072.
333. IkolaR. J. Hi. Appl. Phys. 1965. V. 36. № 10. P. 3260.
334. Ishak W. SJ/Proc. IEEE. 1988. V. 76. № 2. P. 171.
335. Jaffe D., Cacheris J. C. Karayianis NJ/Ptoc. IRE. 1958. V. 46. № 3. P. 594
(Перевод в [203]).
336. Joseph R. I.. Schlomann Е.ЦЗ. Appl. Phys. 1961. V. 32. № 6. P. 1001.
337. Joseph R. I.. Schlomann Е.Ц J. Appl. Phys. 1970. V. 41. № 6. P. 2513.
338. KaczerJ., Murtinova L./l Phys. St. Sol. (a). 1974. V. 23. № 1. P. 79.
339. Kaganov M. I.. Chubukov A. V. Spin waves in magnetic dielectrics. Current
status of the theory. In [423]. Pt. 1. P. 1.
340. Kales M. L.//J. Appl. Phys. 1953. V. 24. № 5. P. 604.
341. Kales M. L., Chait H. M., Sakiotis N. G. // J. Appl. Phys. 1953. V. 24. №6.
P. 816; № 12. P. 1529.
342. Kalinikos B. A., Kovshikov N. G., Slavin A. TV.//Phys. Rev. B. 1990. V. 42.
№ 13. P. 8659.
343. Kanamori J. Anisotropy and magnetostriction of ferromagnetic and
antiferromagnetic materials. In [364]. V. 1. P. 127.
344. Kasuya 7".//Progr. Theor. Phys. 1954. V. 12. № 6. P. 802.
345. Kasuya Т., Le Craw R. C.//Phys. Rev. Lett. 1961. V. 6. № 5. P. 223.
346. Keffer F. Spin waves. In [320]. P. 1.
347. Kittel C.I/Phys. Rev. 1947. V. 71. № 4. P. 270 (Перевод в [205]).
348. Kittel С./IPhys. Rev. 1948. V. 73. № 2. P. 155 (Перевод в [205]).
349. Kittel С. 11 Phys. Rev. 1951. V. 82. № 4. P. 565 (Перевод в [205]).
350. Kittel С. 11 Phys. Rev. 1958. V. 110. № 4. P. 836.
351. Kittel С11 Phys. Rev. 1958. V. 110. № 6. P. 1295 (Перевод в [203]).
352. Kittel С. 11 Phys. Rev. 1959. V. 115. № 6. P. 1587.
353. Kittel С I/Phys. Rev. 1960. V. 117. № 3. P. 681.
354. Kittel C. Herring С //Phys. Rev. 1950. V. 77. № 5. P. 725.
355. KotthausJ. P.. Jaccarino V.//Phys. Rev. Lett. 1972. V. 28. N° 25. P. 1649.
356. Kurkin M. I., TurovE.A. Nuclear spin excitations. In [423]. Pt. 2. P. 381.
357. Lamaire В., Le Gall H., Dormann J. L.//Sol. St. Com. 1967. V. 5. № 6. P. 499.
358. Le Craw R. C, Remeika J. P., Matthews Н.ЦЗ. Appl. Phys. 1965. V. 36. № 3.
Pt. 2 P. 901.
456
359. Le Craw R. C, Spencer E. С, Porter С S. // Phys. Rev. 1958. V. 110. №6.
P. 1311 (Перевод в [203]).
360. Le Craw R. С. Walker L. R.//3. Appl. Phys. 1961. V. 32. № 3 Suppl. P. 167S.
361. Loudon R.. Pincus P. 11 Phys. Rev. 1963. V. 132. № 2. P. 673.
362. L'rov V. S.. Prozorova L. A. Spin waves above the threshold of parametric
excitation. In [423]. Pt. 1. P. 233.
163. Macdonald J. R.I I Proc. Phys. Soc. 1951. V. 64. Pt. II. № 383A. P. 968
(Перевод в [205]).
364. Magnetizm. A Treatise on Modern Theory and Materials / Ed. G. T. Rado
and H. Suhl. N. Y.: Academic Press, 1963. V. 1, V. 3; 1965. V. 2A; 1966.
V. 2B, V. 4.
365. Marvsko M.I I Phys. Stat. Sol. (a). 1975. V. 28. № 2. P. K159.
366. Matthews 4.. Le Craw R. С /1 Phys. Rev. Lett. 1962. V. 8. № 10. P. 397.
367. Matthews H.. Morgenthaler F. RJ/Phys. Rev. Lett. 1964. V. 13. № 21. P. 614.
368. Melchor L.J., Ayre.s W. P.. Varlanian P. tf.//Proc. IRE. 1957. V. 45. № 5.
P. 643 (Перевод в [203]).
369. Miles P. A.. Westphal W. В.. ron Hippel A. 11 Rev. Mod. Phys. 1957. V. 29.
N° 3. P. 279 (Перевод в сб.: Диэлектрическая спектроскопия /Под ред.
Г. А. Смоленского. М.: ИЛ. I960. С. 21).
370. Morgenthaler F. R. //J. Appl. Phys. 1963. V. 34. № 4. Pt. 2. P. 1289.
371. Morgenthaler F. Я.//Ргос. IEEE. 1988. V. 76. № 2. P. 138.
372. Morija T. Week ferromaenetism. In [364]. V. 1. P. 86.
373. NagamivaT.i Proer. Theor. Phys. 1951. V. 6. № 3. P. 342, 380.
374. Nagamiva T. Proer. Theor. Phys. 1953. V. 10. № 1. P. 72.
375. NeelLJ \xvcl. de'phys. 1948. V. 3. № 2. P. 137 (Перевод в [9]).
376. Novak P. , Czech, 3. Plivs. 1971. V. B21. № 11. P. 1198.
377. O'Keeffe T. W.. Patterson R. W.//3. Appl. Phys. 1978. V. 49. N° 9. P. 4886.
378. Olson F. A • 3. Appl. Phys. 1963. V. 34. № 4. Pt. 2. P. 1281.
379. Orbach R. Proc. Roy. Soc. 1961. V. A264. № 1319. P. 458.
380. OsbornJ.A.1 Phvs. Rev. 1945. V. 67. № 11 — 12. P. 351.
381. ParekhJ.P., Tulm H. S.//1EEE Trans. 1980. V. MAG-16. № 5. P. 1165.
382. ParekhJ.P.. Tmin H. S-Ц IEEE Trans. 1984. V. MAG-20. № 5. P. 1249.
m. Passell L.. Dietrich O. W.. Als Nilsen J. // Phys. Rev. 1976. V. B14. №11.
P. 4897.
384. Patton С E.I 1 Phys. Rev. 1969. V. 179. № 2. P. 352.
385. Patton С. Е.Ц Czech. J. Phys. 1976. V. B26. № 8. P. 925.
386. Patton С E., Van Hook H. J. // J. Appl. Phys. 1972. V. 43. № 6. P. 2872.
387. Pippin J. Е.Ц Proc. IRE. 1956. V. 44. № 8. P 1053 (Перевод в [203]).
388. Plumier R. // Physica. 1962. V. 28. № 4. P. 423.
389. Polder D.И PhWos. Mag. 1949. V. 40. № 300. P. 99 (Перевод в [205]).
390. Polder D.. Smit J. II Rev. Mod. Phys. 1953. V. 25. № 1. P. 89.
391. Pust L., Frail Z.//S0I. St. Com. 1983. V. 45. № 2. P. 103.
392. RadoG. Т.. WeertmanJ. R./li. Phys. Chem. Sol. 1959. V. 11. № 3/4. P. 315.
393. Roberts R. W., Auld В. A.. Schell R. R.//}. Appl. Phys. 1962. V. 33. № 3 Suppl.
P. 1267.
394. Rodrigue G. Т.. Meyer H.. Jones R. V.//3. Appl. Phys. 1960. V. 31. № 5 Suppl.
P. 376S.
395. Sakiotis N. G., Chait H. N.. Kales M. L.//IRE Trans. 1956. V. AP—4. № 2.
P. 111.
396. Schlomanr, E.jli. Phys. Chem. Sol. 1958. V. 6. № 2 3. P. 242.
397. Schlomann Е.ЦЗ. Phys. Chem. Sol. 1958. V. 6. № 2—3. P. 257.
398. Schlomann E. Ferrimagnetic resonance in the compensation region // Sol. St.
Phys. in Electron, and Telecom. Academic Press, 1960. V. 3. P. 322.
399. Schlomann E.//S. Appl. Phys. 1960. V. 31. № 9. P. 1647.
400. Schlomann E. 11 Phys. Rev. 1961. V. 121. № 5. P. 1312.
401. Schlomann E.//3. Appl. Phys. 1964. V. 35. № 1. P. 159.
402. Schlomann E.// Phys. Rev. 1969. V. 182. № 2. P. 632.
403. Schlomann Е.ЦЗ. Appl. Phys. 1970. V. 41. № 1. P. 204.
404. Schlomann E.I I Proc. IEEE. 1988 V. 76. № 2. P. 188.
405. Schlomoim E., Green J. J., Milano I/.//J. Appl. Phys. I960. V. 31. № 5 Suppl.
P. 386S (Перевод в [164]).
457
406. Schlomann E.. Joseph R. I. J. *Vppl. Phys. 1961. V. 32. № 6. P 1006 (Псревол
в [164]).
407. Schlomann E.. Joseph R. /.//J. Appl. Phys. 1964. V. 35. № I. P. 167.
408. Schlomann E., Joseph R. I. /J. Appl. Phys. 1964. V. 35. № 8. P. 2382; 1965.
V. 36. № 3. Pt. 1. P. 875.
409. Schwab P. K.. Tachiki M.. Evcreii G. E. Phys. Rev. 1974 V 310. №1.
P. 165.
410 ScarleC. W.. Wang S. T. J. \ppl. Phvs. 1968. V. 39. № 2. Pi. 2. P. 1025.
411. Seavey M. H. Jr., TannenwaUl I'. E Phys. Rev. Lett. 1958. V. I. № 5 P 168
(Перевод в [203]).
412. Seshadri S. R. Proc. IEEE. 1970. V. 58. № 3. P. 506.
413 SeidelH., Bell Svstem. Tech. J. 1957. V. 36. №2. P. 409.
414. Sievers A. J.. Tinkham M. Phys. Rev. 1963. V. 129. № 5. P. 1W5.
415. Skamal E. N.. Medina M. 4 J. Appl. Phys. 1959. V. 30. № 4 Suppl. P. IMS
(Перевод в [203]).
416 Smit J.. Bi-ljers H. G." Philips Res. Rep. 1955. V. 10. №2. P. 113
417. Sparks M. Ferromagnetic relaxation theory. McGraw-Hill Book ( o.. 1964.
418. Sparks M. Phys. Rev. 1967. V. 160. № 2. P. 364.
419. Sparks XI.. London R.. Kittel С Phys. Rev. 1961. V. 122. № 3 P 791
420. Spencer E. G.. Le Craw R. С J. Appl. Phys. 1959. V. 30. № 4 Suppl P. I49S
(Перевод в [203]).
421. Spencer E.G.. Le Craw R. C. Clogston 4. M Phys Rev. Lett. 1959 V 3.
№ I. P. 32 (Перевод в [203]).
422. Spencer E.G.. le Gran- R. С Linares R. С. Phys. Re\ 1961 V 123. №6.
P. 1937.
423. Spin waves and magnetic excitations. Ed. A. S. Borovik-Romunov and
S. K. Sinha. Amsierdam: North-Holland. 1988. Pt. I. 2.
424. Srinhasan G.. Patton С E.. Eniiiige P. E. 3. Appl. Phvs 1987. V 61. № 6 P. 2318
425 Standi D. D.. Wargenthaler F. R. .1 Appl. Phys. 1983. V. 54. № 1 P 1613
+26. StaussG. H.. Rubinstein M.. Fcinleih ./., Diiight K... Menvuk V J Appl. Phvs
1968. V 39. № 2. P. 667.
427. Sturge M. D.. Grorgr E. M.. Le Gra» R. C, Remeika J. P. Phys Rev 1964
V. 180. № 2. P. 413.
t28. Suhl II Proc. IRE. 1956. V. 44. № 10. P. 1270.
429. Suhl H }. Phys. Chem. Sol. 1957. V 1. № 4. P. 209 (Перевод в [203]).
430 Snhl H. J. Appl. Phys. 1957. V. 28. №11. P 1225 (Перевод в [203]).
431 Suhl H. J. \ppl. Phys. 1958. V. 29. № 3. P. 416 (Перевод в [203 J).
432. Suhl H. 3. Appl. Phys. 1959. V. 30. № 12. P. 1961.
433. Suhl H.. Zhang X. Y.1 J Appl. Phys. 1988. V. 63. № 8. Pt. 2B P 4147
434. Tarmeimald P. E.. Weber R. // Phys. Rev. 1961. V. 121 №3 P. 715.
435. Tchernev D. I. i. Appl. Phys. 1967. V. 38. № 3. P. 1046.
436. Tchernet D. I .! Appl. Phys. 1968. V 39 № 2 Pt. 1. P 826.
437. Те ale R W., Twecdule К I Phys. Lett. 1962. V. I. № 7. P. 298.
438. Tien P. K.. Suhl H. Proc. IRE. 1958. V. 46. № 4. P. 700.
439. Tokheim R. E., Winslaw D. K... 4uld B. A. J. Appl. Ph>s 1964. V 3* № 3
Pt. 2. P. 1010.
440. TsaiC.S.. Young D. I Appl Phvs. Leu. 1989. V. 54. №3. P 196
441 Turner E. H. Phvs. Rev. Lett. 1960. V 5. № 3. P. 100.
442. Ubbink J.. PoulisJ.A., Gerritsen H. J. Gorier С J. Physica 1952. V 18.
№ 6 7. P. 361.
443. Van VleckJ. H , Physica. 1951. V. 17. № 3 4. P 234 (Перевод в [205])
444. Van 1 leek J H.I J. Appl. Phys 1964. V. 35 № 3. Pt. 2. P. 882.
445. Walker L. R. Phys. Rev. 1957. V. 105. №2. P. 340 (Перевот n [203]).
446. Walker L. R. Spin waves and other magnetic modes In [364] V I P. 299.
447. Wang J. Shv-Yih.i Phys. Rev. 1972. V. B6. №5. I» 1908.
448 Wang.sncss R. K./I Phys. Rev. 1953. V. 91. №5. P. 1085.
449. Wangsness R. К.'iPhys. Rev. 1954. V. 95. №2. P. 339.
451». Weiss M T Phys. Rev. 1957. V. 107. № 1. P 317 (Перевод в [203]).
451 H'ciiiM. T Phys. Rev. Lett. 1958. V. 1. № 7. P 239 (Перевод н [203]).
452. White R L. Phys. Rev. Lett. 1959. V. 2. № II. P. 465.
I" White R L.. Salt I. H./i Phys. Rev. 1956. V. 104. № IP. 56 (Перево i в [203]).
i W
454 Wkkersheim K. A. Phys. Rev 1961. V. 122. №5. P. 1376.
455. Wizen P. E., KooiC.F.. Shanabarger M. R.. Rossing T. D. I'/ Phys. Rev. Lett.
1962. V. 9. № 5. P. 206.
456. Wijn H. P. У.. Van der Heide H. A Rev. Mod. Phys. 1953. V. 25. № 1 P. 98.
457 Wither W D . Booth J G.. Paiton С £.. Srhmasan G.. Cross R. W. ' J. Appl.
Phys. 1988. V. 64. № 10. Pt. 2. P. 5477.
458. Wolf \\ P. Phvs. Rev. 1957. V. 108. № 5. P. 1152.
459 Woll W P. Ferrimaenetism Reports on Progr. in Phys. 1961. V. 24. P. 212.
460 Wolfram Т.. De Wames R. E. Phvs. Rev. Lett. 1971. V. 26. №23.
P. 1445.
461 Wolfram Т.. De Wames R. E. Sol. Si. Com. 1971. V. 9. №2. P. 171.
462 Yager W 4 Phvb. Rev. 1949. V. 75. № 2. P. 316.
461 Yager W A., bait J. k.. Mem,, I R Phvs. Rev. 1955. V. 99. № 4. P. 1203.
464. Young./. A . Uehling H. A Phys. Rev. 1954. V. 94. № 3. P. 544.
465. YuJ. Т.. Turk R. A.. Wi<-en P. E Phys. Rev. B. 1975. V. II. № 1. P. 420
466 Yukawa Т.. YumadaJ.. *L Ikenaue J. ч Japan. J. Appl. Phys. 1977.
V. 16. № 12. P. 2187.
УКАЗАТЕЛЬ К СПИСКУ ЛИТЕРАТУРЫ"
A. Учебники и монографии общего характера
АЛ. Магнетизм и магнитный резонанс
6, 15, 23, 31, 35. 49, 66, 69, 116, 122, 123, 128, 145, 157, 162, 174,
178, 187, 193. 198, 201, 204, 217, 320, 346, 364, 417. 423.
А.2. Ферритовые СВЧ устройства
2, 30, 41, 94, 128. 159.
А.З. Математика, физика, радиотехника
4, 11, 12, 16, 28, 29, 64, 81, 82, 112, 113, 119. 127, 131 135, 139.
147, 158, 163, 180, 186, 191, 195, 196, 199, 202. 209.
Б. Сборники статей
205, 9, 203, 164.
См. также тематические выпуски журналов:
Ргос. IRE. 1956. V. 44. № 2
Circuits, Systems and Signal Ргос. 1985. V. 4. № 1—2
Proc. IEEE. 1988. V. 76. № 2
Изв. вузов СССР, сер. физика. 1988. Т. 31. № 11.
B. Статьи и монографии по узким вопросам
I. Магнетизм: основные состояния, термодинамика и пр.
1.1. Общие вопросы, ферромагнетизм
227, 343, 39, 426. 179.
1.2. Антиферромагнетики
129, 293, 34, 85, 32, 372, 271, 248, 33, 21.
1.3. Ферримагнетики
375, 398, 459, 263, 93, 91, 5.
II. Однородные колебания намагниченности (гл. I, 2. 3)
11.1. Ферромагнитный резонанс: теория
287. 130. 347, 348, 389, 443, 363, 416,^ 325, 230, 332, 397, 185.
11.2. Ферромагнитный резонанс: ■эксперимент21
10, 312, 87, 325, 74, 73, 62, 75, 60, 316, 218, 386.
11.3. Антиферромагнитный резонанс
373, 442, 349, 299. 300. 355, 86.
11.4. Особенности резонанса в ферримагнетиках
448. 449, 309, 299, 398, 394, 414. 300. 177. 358.
' В разделах А.1, А.2 и А.З указателя номера (по списку шгсратуры)
приведены в алфавитном порядке, а в остальных разделах в хронологическом.
-' См. также разделы V.2, VII.2. V1I.3, IX. X.l. X.2.
460
III. Электродинамика и СВЧ устройства (гл. 4, 5)
III. 1. Основы электродинамики гиротропных сред
389, 292, 165, 65, 166, 59.
IfI.2. Волноводы с ферритом и устройства на их основе
328, 340, 341, 58, 192, 413, 72.
Ш.З. Резонаторы и элементы связи
332, 393, 68, 231, 404, 2.
IV. Неоднородные колебания и спиновые волны (гл. 6, 7)
IV. 1. Магнитостатические (безобменные) волны
295, 274, 336, 233, 412, 254, 307, 221, 466, 291, 377, 222, 381, 223,
382, 57, 54, 51, 53, 190, 214. 220, 42, 334, 38, 50, 52, 19.
IV.2. Неоднородные магнитостатические колебания
453, 445, 296, 298, 173, 194, 121, 388, 446, 241, 402, ПО, 161, 261, 181.
IV.3. Спиновые волны (в неограниченной среде)
249. 329, 326, 289, 290, 360, 346. 39, 40. 211, 114.
IV.4. Спиновые волны в ограниченных телах
226, 351, 411, 392, 95, 295, 297, 25, 434, 455, 294, 275, 401, 407, 55,
206, 278, 45, 210, 279, 207. 238, 460, 461, 117, 237, 208, 409, 465, 63,
104. 105, 425, 303.
V. Колебания и волны в ненасыщенном ферромагнетике (гл. 8)
V.I. Колебания границ доменов
130, 240, 288, 306, 369, 170, 47, 22.
V.2. Резонанс и спиновые волны при наличии доменов
130, 374, 390, 416, 230, 369, 47, 148, 403, ПО, 338, 172, 111, 136, 161.
261, 24, 182, 181, 83.
VI. Нелинейные явления (гл. 9, 10)
V1.1. Одномодовые нелинейные процессы (преобразование частоты и др.)
229, 387, 368, 183, 335, 451, 184, 234, 415. 160, 310, 67, 234, 273, 84,
144, 153, 382, 262.
V1.2. Параметрическое возбуждение магнитных колебаний и волн: пороги
252, 253, 229, 395, 428, 429, 430, 450, 431, 438, 101, 405, 406, 277,
171, 236, 393, 247, 216, 141, 176, 168, 89, 43, 90, 172, 151, 44, 136,
120, 106, 80, 154, 212, 152, 155, 156.
VI.3. Параметрическое возбуждение: запороговое состояние
252, 253, 429, 432, 311, 150, 88, 90, 124, 125, 222, 146, 362, 457, 142, 92.
VI.4. Ударные волны, солитоны, эхо, хаос1'
324, 256, 433, 342.
VII. Спин-спиновая релаксация (гл. 11)
VII. 1. Общие вопросы релаксации, феноменология, обзоры
130, 260, 250, 61, 228, 258. 185, 126, 319. 417, 346, 20.
VII.2. Собственные процессы
224, 289, 99, 108, 345, 400, 419, 40, 357, 447, 7, 8, 115, 314, 80.
VII.3. Двухмагнонные процессы
344. 267, 308, 258, 359, 396, 397, 259, 75, 318, 361, 26, 402, 384, 355, 386, 107.
VIII. Магнитоупругое взаимодействие (гл. 12)
VIII. 1. Магнитоупругая связь, магнитоупругие волны
200, 350, 46, 399, 366. 294, 401, 407, 118, 408, 137. 213, 138, 239.
VIII.2. Магнитоупругие нелинейные явления
420, 441, 370, 378, 367, 439, 232, 333, 140, 141, 37, 337.
VIII.3. Спин-решеточная релаксация
224, 219, 100, 345.
■> По этим вопросам, не затронутым в тексте, приведены лишь отдельные
461
IX. Анизотропия и релаксация, обусловленные быстрорелаксируюшими ионами
(гл. 13)
266, 276, 283, 352, 421, 452, 284, 353, 36, 78, 286, 379, 422, 454, 281,
437, 77, 322, 444, 189, 265, 330, 264, 317, 331, 285. 435, 225, 436, 3,
427, 323, 313, 376, 321, 327, 315, 17, 18, 71, 215, 8, 169.
X. Взаимодействие с носителями заряда (гл. 14)
Х.1. Полупроводники
456, 266, 463, 388, 14, 149, 410, 323, 272, 70, 365, 245, 246, 13. 103.
Х.2. Металлы
312, 347, 462, 251, 354, 219, 464, 226, 79, 392, 102, 197, 27, 270, 304,
242, 243, 56, 96, 97, 244, 280, 98, 385, 268, 301, 143, 302, 120, 391, 305, 303.
XI. Взаимодействия со светом, ядерными моментами, нейтронами"
76, 282, 424, 383, 255, 356, 457.
" По этим вопросам, не затронутым в тексте, приведены лишь отдельные
работы.
\
Alexander Gurevich and Gennadiy Melkov
MAGNETIC OSCILLATIONS AND WAVES
Moscow, Nauka. Main Editorial Board for Literature on Physics
and Mathematics, 1994, pp. 464
Readership: Scientists, electronic engineers and students.
Summary: The book is a review and a manual on dynamics of magnetically
ordered substances, their properties and applications at microwave and optical
frequencies. It differs considerably from existing monographs on this subject: it
coveres a wider class of problems including many recent achievements and is
aimed at a broader range of readers. All the calculations are given with details
necessary to reproduce them.
Contents: Theory of ferromagnetic and antiferromagnetic resonances in isotropic
and anisotropic substances. Principles of gyrotropic-media electrodynamics and
their applications to main classes of fcrrite microwave and optical devices. Theory
and applications of magnetostatic waves in thin magnetic films. Theory of spin
waves. Nonlinear processes in ferromagnets at microwave frequencies, parametric
excitation of spin waves. Magnetoelastic waves. Relaxation processes: intrinsic
' ones and processes caused by impurities, fast-relaxing ions and charge carriers.
The peculiarities of ferromagnetic resonance in metals.
The authors: Professor Alexander Gurevich is a head researcher in the
A. F. loffe Physico-Technical Institute in Leningrad, author of approx. 150
scientific papers and monographs. His monograph «Ferrites at Microwave
Frequencies» was the first one on this suject. In 1988 he won a USSR State Prize.
Professor of the Kiev State University Gennadiy Melkov has published more
than 100 scientific papers and monographs on properties and applications of
ferrites at microwave frequencies.