wixioiM
Н. А. ВИРЧЕНКО, И. И. ЛЯШКО, К. И. ШВЕЦОВ
ГРАФИКИ
ФУНКЦИЙ
СПРАВОЧНИК
Под редакцией
академика АН УССР
И. И. ЛЯШКО
Перевод с украинского
КИЕВ
«НАУКОВА ДУМКА»
1979
УДК 51(08)
Графики функций t Справочник/Вирченко Н. А*, Ляшко И. И.,
Швецов К. И. — Киев : Наук, думка, 1979. — 320 е.
Справочник содержит основные сведения о функциях и методах
построения графиков функций, в частности сведения о построении
графиков функций элементарными способами и с помощью производ-
ной. Впервые в литературе систематизированы сведения о построении
графиков не только в декартовой, но ив полярной системе координат,
Рассматриваются основные принципы теории геометрического изобра-
жения функций.
Рассчитан на инженеров, преподавателей и учащихся средних
школ, а также на поступающих в высшие учебные заведения*
Ил. 501,
Рецензенты Н. И. Шкилъ, Т, В, Колесник
Редакция справочной литературы
1702050000
(С) Издательство «Наукова думка», 1979
ПРЕДИСЛОВИЕ
При исследовании различных явлений и процессов природы, ре*
шении технических задач, изучении математики сплошь и рядом встре-
чаются примеры изменения одной величины в зависимости от измене-
ния другой — так называемой функциональной зависимости. Понятие
функциональной зависимости — одно из важнейших понятий совре-
менной математики, оно «как ни одно другое, воплощает в себе
диалектические черты современного математического мышления; именно
оно приучает мыслить величины в их живой изменчивости, а не
в искусственно препарированной неподвижности, в их взаимной связи
и обусловленности, а не в искусственном отрыве их друг от друга»*.
Существуют различные способы задания функций: аналитический,
табличный, словесный, а также графический. Иногда график является
единственно возможным способом задания функции. Он широко исполь-
зуется в технике, лежит в основе работы многих самопишущих авто-
матических приборбв. Однако несмотря на значительное распростра-
нение этого способа, справочной литературы, достаточно полно осве-
щающей вопросы исследования функций и построения графиков
разнообразнейших функций, причем с привлечением методов высшей
математики, пока неоправданно мало. Например, в популярных по-
собиях И. П. Гурского «Функции и построение графиков», И. X. Си-
вашинского «Элементарные функции и графики», Н. Н. Шунды
«Функции и их графики» (на украинском языке) в основном изло-
жены методы построения графиков с помощью средств элементарной
математики. Определенное место графикам функций отведено во мно-
гих пособиях для поступающих в вузы, но и здесь изложение мате-
риала ограничивается школьным курсом математики.
Настоящий справочник представляет собой попытку системати-
зировать основные сведения о функциях и методах построения гра-
фиков функций, в частности о построении графиков элементарными
способами и с помощью производной. Основное внимание уделено
следующим вопросам: исследованию функций, методам построения
графиков функций, преобразованию графиков. Кроме того, подробно
анализируются построение графиков функций, заданных неявно и в
параметрическом виде, построение графиков в полярных координатах
и другие вопросы, недостаточно освещенные в литературе.
* Хинчин, А Я. Педагогические статьи. — М.: Изд-вэ Акад. пед. наук РСФСР.
1963, с. 68.
3
Справочник состоит из двух частей. В первой изложены основ-
ные сведения р функциях, их свойствах, построении графикой функ-
ций элементарными способами. Вторая часть посвящена построению
графиков функций с помощью производной. Приведено свыше 500
графиков. Рассмотрены примеры построения графиков повышенной
сложности, графиков некоторых важных кривых (спираль Архимеда,
улитка Паскаля, астроида, циклоида и др.). В справочнике исполь-
зован материал из опубликованной справочной литературы, пособий,
статей, посвященных этой теме.
Настоящее издание является переводом с украинского (В1рчен-
ко Н. О., Ляшко I. I., Швецов К. I. Графши функщй. Довщник.—
К.: Наук, думка, 1977). В нем исправлены ошибки и неточности,
замеченные в издании на украинском языке, в частности уточнены
некоторые обозначения, термины и формулировки.
Авторы
ЧАСТЬ I
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
ЭЛЕМЕНТАРНЫМИ СПОСОБАМИ
РАЗДЕЛ 1
ОСНОВНЫЕ СВЕДЕНИЯ О ЧИСЛЕ, ПЕРЕМЕННОЙ ВЕЛИЧИНЕ
И ФУНКЦИИ
§ 1. Число. Переменная величина. Функция
Множество действительных чисел
Совокупность бесконечных десятичных дробей (положительных
и отрицательных) и число 0 образуют множество действительных
чисел (числовой континуум) /?. Это множество состоит из двух частей
(подмножеств): подмножества рациональных чисел (чисел целых и
дробных, как положительных, так и отрицательных, а также числа 0)
и подмножества иррациональных чисел.
Каждое рациональное число может быть изображено в виде
отношения ± — , где р и q — натуральные числа 1, 2, ...» п, ... ,
при этом оно представляет собой периодическую десятичную дробь.
Иррациональное число представляет собой непериодическую десятич-
ную дробь. Например, ~ — 0,333 ... , 5 = —рациональные числам
<5	1
л = 3,14159 ... , У2 = 1,4142 ... — иррациональные числа.
Основные свойства множества действительных
чисел
1.	Множество упорядочено, т. е. любые два числа а и b этого
множества' либо равны, либо одно из них больше другого. Упорядо-
ченность обозначают так:
а < b (а меньше Ь),
а^Ь (а не больше Ь),
а > b (а больше Ь),
а^Ь (а не меньше Ь).
2.	Множество плотно, т. е. между любыми двумя сколь угодно
близкими действительными числами а и b содержится бесконечное
множество промежуточных действительных чисел (как рациональных,
так и иррациональных).
5
3.	Множество непрерывно. Это означает, что любое дедекиндово
сечение определяет единственное действительное число а, которое
отделяет числа класса А от чисел класса В, само же а является
или наибольшим числом в классе А (и тогда в классе В нет наимень-
шего числа), или наименьшим числом в классе В (и тогда в классе А
нет наибольшего числа)*
Дедекиндовым сечением множества D называется разбитие всех
действительных чисел на два класса: нижний класс А и верхний
класс В, причем так, что каждое действительное число содержится
лишь в одном классе и произвольное число из нижнего класса А
меньше произвольного числа из верхнего класса В.
Действительные числа удобно изображать точками числовой оси.
Числовая ось — бесконечная прямая, на которой выбраны начальная
точка О, некоторое направление, которое считается Положительным,
и масштаб (отрезок, являющийся единицей измерения длины). Каж-
дому действительному числу ставится в соответствие одна и только
одна точка числовой оси. Числу 0 отвечает точка О. Если число х
положительное, то его изображают точкой Р, лежащей справа от
точки О на расстоянии ОР = х; если же число х отрицательное, то
его изображают точкой Q, лежащей слева от точки О на расстоянии
QQ — ~—х (рис. 1). Справедливо и обратное утверждение: каждая
точка числовой оси является изображением одного и только одногд
Q	О	Р
------------Н-| -4.1 1-1- м I | 1-1Ч--1 |------------
Рис, 1, Числовая ось: О начальная точка}, точки Р и Q лежат
на оси.
действительного числа. Следовательно, между всеми действительными
числами и всеми точками числовой оси существует взаимно однознач-
ное соответствие. Для практических целей отметим следующее утвер-
ждение: каждое иррациональное число с произвольной степенью
точности можно изобразить с помощью рациональных чисел.
Действительные числа делят на две группы: действительные
алгебраические числа (действительные корни алгебраических урав-
нений с целочисленными коэффициентами) и действительные транс-
цендентные числа (остальные действительные числа).
Любую конечную или бесконечную совокупность действительных
чисел называют числовым множеством. Множества обозначают про-
писными буквами латинского алфавита: X, Y, Z, .. а числа, им
принадлежащие, — строчными буквами: х, у, г, .. . Например, х £ X
(х принадлежит X). Если же элемент х не принадлежит X, то это
записывают так: х С X.
Рассмотрим два множества А и В. Если каждый элемент мно-
жества X является одновременно и элементом множества В, то гово-
рят, что множество А является подмножеством множества В, и за-
писывают: Лез В, или BzdA. Если же А сз В и В сз Л, то говорят,
что множества А и В равны, и записывают так: А — В. Множество,
которое не содержит ни одного элемента, называют пустым мно-
жеством и обозначают так: 0.
Простейшие действия надмножествами — объеди-
нение (сумма), пересечение (произведение), разность.
Пусть заданы два множества А и В.
6
'Объединением (суммой) множеств А и В называют множество С,
которое содержит все элементы множеств Л и В и не содержит ни-
каких других элементов (обозначают: С = A (J В).
Пересечением (произведением) множеств А и В называют мно-
жество D, которое содержит все сбщие элементы множеств А и В
и не содержит никаких других элементов (обозначают: D A f| В).
Разностью множеств А и В называют множество F, состоящее
из всех тех элементов множества А, которые не принадлежат мно-
жеству В, и не содержащее никаких других элементов (записывают:
F — А\В).
Среди числовых множеств отметим следующие:
ограниченный замкнутый промежуток (сегмент, отрезок) X =* [а;
6] — множество X содержит все числа х, для которых выполняется
неравенство а х -С Ь\ на числовой оси эта совокупность чисел об-
разует отрезок ab, включающий его концевые точки (рис. 2, а);
ограниченный открытый промежуток (интервал) Х*=]а', Ь[ —
множество X содержит все числа х, для которых выполняется не-
равенство а < х < Ь\ на числовой прямой эта совокупность чисел
образует отрезок ab без его концевых точек (рис. 2, б);
а [а;Ь]
а
ь
f, ]а;Ь[
S
Рис. 2. Числовая ось! а «=• сегмент [а; £]; б — интервал ]а; Ь[.
неограниченные полуоткрытые (или полузамкнутые) промежутки
[а; и ]а; б]—множество X, содержащее все числа, для которых
выполняются неравенства ц < х < b и а < х^Ь. Соответствующий
отрезок на числовой оси включает левый конец и не включает пра-
вый— в первом случае; включает правый конец и не включает
левый — во втором.
Пблубесконечные промежутки:
р; оо —множество X, для элементов которого х > Ь\
[6; сю[ — множество X, для элементов которого х^Ь\
]—оо; а —множество X, для элементов которого х < а\
]—оо; а —множество X, для элементов которого х<а.
На числовой оси эти множества изображают всеми точками соответ-
ствующей бесконечной полупрямой.
Множество всех действительных чисел (всю числовую ось) на-
зывают промежутком и обозначают ]—оо, оо[.
Пусть а — произвольное число, ^-окрестностью точки а назы-
вают произвольный открытый интервал вида ]а — 6; а + 6[, иначе:
6-окрестность точки а — это множество всех точек х, для которых
выполняется условие | х—а | < 6, где 6 — некоторое положительное
число (рис. 3). Окрестность точки х а — это произвольное мно-
жество, которое содержит некоторую 6-окрестность этой точки.
Абсолютной величиной или модулем действительного числа а
(обозначается | а |, читается «модуль а») называется неотрицательное
число, для которого выполняются
I а\ —
а,
—а,
О,
условия:
если а > О,
если а < О,
если а = 0.
7
Основные свойства абсолютных величин:

Если | а |	0, то а = О,
1И1-1И1
1И-Ш
ab
а
~Ь
<|а + &|<|а|+|6|,
<|a-fr|<|a|+|6|,
= {у-|(*¥=0).
Если | а | < А и | b | < В, то | а + b | < А + В и | ab | АВ.
-------------4---------(------1-----)--
О а-б х=а а+6
Рис. 3. 8-окрестность точки а.
Рассмотрим непустое множество X. Верхней гранью множества X
называется произвольное числоМ такое, что для ух С X выполняется
неравенство
х< М.
Нижней гранью множества X называется число т такое, что
для ух € X справедливо неравенство
х>> tn.
Множества, имеющие верхнюю грань, называются ограниченными
сверху. Множества, имеющие нижнюю грань, называются ограничен-
ными снизу. Множества, ограниченные и сверху и снизу, называются
ограниченными. Наименьшее из чисел М называется точной верхней,
а наибольшее из чисел tn — точной нижней гранью множества.
Если М*— точная верхняя грань множества X (Л4* sup X —
= sup {х}), то при произвольном сколь угодно малом числе 8 > О
всегда найдется хотя бы одно число х0 € X такое, что х0 > Л4* — е.
Если т* — точная нижняя грань множества X (tn* = inf X =t
inf {х}), то для произвольного сколь угодно малого числа 8 > О
всегда найдется хотя бы одно число х0 € X такое, что х0 < tn* + е.
Если множество X ограничено сверху (снизу), то оно имеет и точ-
ную верхнюю (нижнюю) грань, т. е. любое ограниченное множество
имеет и точную верхнюю и точную нижнюю грани.
Постоянные и переменные величины
В природе и в производственных процессах одни величины изме-
няются, т. е. изменяются их численные значения, а другие не изме-
няются. Например, при равномерном движении время и расстояние
изменяются, а скорость остается постоянной; при нагреваний газа
в герметически закрытом сосуде давление и температура газа изме-
няются, а масса и объем его не меняются.
8
Переменной величиной называется величина, которая может при-
нимать разные численные значения в данном процессе. Величина,
численные значения которой в данном процессе не меняются, назы-
вается постоянной. Величины, которые сохраняют значение при любых
условиях, называются абсолютными постоянными, например л ~
3,141...
Характер изменения величин очень разнообразен. Одни могут
принимать только целые положительные значения, другие — неогра-
ниченные отрицательные значения и т. д. Различают дискретные пере-
менные, которые могут принимать конечное или бесконечное мно-
жество изолированных численных значений, и непрерывные перемен-
ные, которые, приняв два значения: х а и х = Ь, принимают также
(неважно, в каком порядке) и все промежуточные значения а < х < Ь.
Множество значений, которые может принимать рассматриваемая
величина х, называется областью изменения переменной х или об-
ластью значений х. Переменная величина называется возрастающей,
если каждое ее последующее значение больше предыдущего. Пере-
менная величина называется убывающей, если каждое последующее
ее значение меньше предыдущего. Возрастающие и убывающие пере-
менные величины называются монотонными. Переменная величина
ограничена, если* область ее изменения — ограниченное множество.
Понятие функции
У
Рис. 4. Область определения
функции у = f (х) — отрезок
[а; Ь] и область значений
функции — отрезок [с; d).
При изучении и исследовании разнообразных явлений природы,
решении технических задач приходится рассматривать не столько
переменные величины, взятые отдельно, сколько связь между ними,
зависимость одной величины от другой.
В природе не существует переменных ве-
личин, которые изменялись бы изолиро-
ванно, без связи с другими физическими
величинами. Например, пройденный путь
можно рассматривать как величину, ко-
торая изменяется в зависимости от изме-
нения времени, т. е. пройденный путь
является функцией времени. Расстояние,
на которое летит пушечный снаряд, и точ-
ность попадания зависят от массы сна-
ряда, угла возвышения дула пушки, на-
чальной скорости снаряда, направления
и силы ветра и многих других факторов.
Абстрагируясь от этих конкретных при-
меров зависимостей между конкретными
величинами, в математике ввели понятие функциональной зависи-
мости или функции.
Рассмотрим два множества: X и У, элементами которых могут
быть любые объекты, и допустим, что каждому элементу х множе-
ства X по некоторому закону поставлен в соответствие один элемент
множества У, который обозначим у — f (х). Тогда f называется функ-
цией * из X в У (или отображением множества X в У). Таким обра-
зом, если задано отображение f множества X в множество У, то
* Термин «функция» ввел Лейбниц (1692 г.), а обозначение / (х)
принадлежит Эйлеру.
9
говорят, что на множестве X определена функция /, которая прини-
мает значения у = f (х) из множества У. Множество X называю^
областью определения функции, а множество f (X) — множеством
значений функции /. Очевидно, что f (X) сз У. Переменную величину
х называют независимой переменной или аргументом. Равенство
у — f (х) означает, что, применив к значению аргумента х закон £
найдем соответствующее этому значению х значение функции у (рис. 4),
Например, равенство у = х3 + 5 определяет у как функцию х пря
всех значениях х [X — ]—оо; оо[], т. е. определяет закон, по кото-
рому любому действительному значению х поставлено в соответствие
значение функции у, т. е. в этом случае символ f означает следую-
щие операции: возвести значение х в куб и к результату прибавить 5г
Способы задания функции
г Задать функцию означает установить правило (закон), с помощью
которого по данным значениям независимой переменной находим соот-
ветствующие им значения функции. Рассмотрим некоторые способы
задания функции.
Табличный способ. При этом способе в определенном порядке
выписываются ряд значений независимой переменной xlt х2, ...» хп
и соответствующие им значения функции уь yit ... , уп. Таковы,;
например, таблицы логарифмов, таблицы значений тригонометрических
функций и т. д. Табличный способ задания функции очень распро-
странен в технике, естествознании и т. п. Численные результаты по-
следовательных наблюдений какого-либо процесса или явления выпи-
сывают в виде таблицы. Например, результаты измерений темпера-
туры воздуха на метеорологической станции за один день оформляют-
ся так:
/, ч 1	23	456789 10
71, °C —1 —2 —2,5 —2 —0,5 1 3 3,4 3,6 3,9
Эта запись определяет температуру Т как функцию времени ti Т =««
^/(0.
Преимущества табличного способа задания функции состоят в
том, что он дает возможность определить те или другие конкретные
значения функции сразу, без дополнительных измерений или вычис-
лений. Недостатки: определяет функцию не полностью, а лишь для
некоторых значений аргумента, не дает наглядного изображения
характера изменения функции с изменением аргумента.
Графический споссб. Графиком функции у = f (х) называется
множество всех точек плоскости, координаты которых удовлетво- ’
ряют данному уравнению. Графиком функции могут быть некоторая
кривая, в частности и прямая, множество отдельных точек на плос-
кости и т. д.
Графический способ задания функции не дает возможности точно -
определить численные значения аргумента. Однако он имеет большое:
преимущество перед другими способами — наглядность.
В технике и физике часто пользуются графическим способом
задания функции, причем иногда график бывает единственно доступ-
ным для этого способом, например при пользовании самопишущими
приборами, которые автоматически записывают изменение одной гели-
чины в зависимости от изменения другой (барограф, термограф и др.).
10
Аналитический споссб. По этому способу функция задается ана-
литически, с помощью формулы. Такой способ дает возможность по
каждому численному значению аргумента х найти соответствующее
ему численное значение функции у точно или с некоторой точностью.
При аналитическом способе функция может быть задана и не-
сколькими разными формулами. Например, функция
Цх) =
COS X,
1,
1
X ’
если —л < х < О,
если 0 < х < 1,
если
1 < х < 2,
задана в области определения [—л; 2] с помощью трех формул.
Если зависимость между х и у задана формулой, разрешенной
относительно у, т. е. имеет вид у — f (х), то говорят, что функция
от х задана в явном виде, например
у = бх — 2, у = х21пх.
Если же значения х и у связаны некоторым уравнением вида F (х, у)=?
= 0, т. е. формула не разрешена относительно у, то говорят, что
функция у — f (х) задана неявно, например, уравнение
х2 4- у? — г2 = О
неявно определяет две функции! у = ± г2 — х2.
Заметим, что не любую неявно заданную функцию можно пред*
ставить в явном виде: у = f (х). Наоборот, любую явную функцию
У = f (*) можно всегда представить и в виде неявной: у — f (х) = 0.
Укажем еще одну разновидность аналитического задания функ-
ции, когда и аргумент х и функция у являются функциями третьей
величины — параметра /:
*=ф(0,
у = t (0.
где t принимает значения на множестве Т. Здесь каждому числен-
ному значению tQ параметра t из области его изменения Т ставятся
в соответствие численные значения’ х0 = ф (/0) и z/0 = Ф (U величин
х и у. Это соответствие определяет у как функцию от х (или х как
функцию от у). Такое задание функциональной зависимости назы-
вается параметрическим.
Если рассматривать значения х и у как координаты точки на
координатной плоскости хОу, то каждому значению t будет соответ-
ствовать определенная точка плоскссти. Если / изменяется от if до /2,
то точка на плоскости описывает некоторую кривую. Если же исклю-
чить параметр t из уравнений, то получим функцию, заданную в яв-
ном виде: у = f (х). Параметрическое задание кривых широко при-
меняется в механике, в некоторых теоретических исследованиях по
геометрии и т. д.
Аналитический способ является самым распространенным спосо-
бом задания функции. Это основной способ задания функции в мате-
матическом анализе. Компактность, возможность вычисления значения
функции при произвольном значении аргумента из области определе-
ния, возможность применения к данной функции аппарата математи-
ческого анализа — основные преимущества аналитического способа
11
задания функции. Недостатки: недостаточная наглядность, необходим
мость выполнения иногда очень громоздких вычислений.
Словесный способ. Этот способ состоит в том, что функциональ-
ная зависимость выражается словами.
Пример 1. Функция Е (х)— «целая часть числа х». Вообще
через Е (х) = [х] обозначают наибольшее из целых чисел, которые
не превышают х. Иными словами, если х = п + г, где п — целое
число (может быть и отрицательным) и 0< г < 1, то [х] = п. Функ-
ция Е (х) = [х] постоянна на промежутке [n; n-f- 1[. На этом про-
межутке [х] = п. (Е — начальная буква французского слова entier,
которое означает «целый», Читается функция у = Е (х) так: «игрек
равен антье от икс»),
Е (2, 3) = 2, Е (-л)	—4.
Пример 2. Функция Дирихле определяется так:
у (г) == Р’ если х'~ рациональное,
А '	(0, если х — иррациональное.
Эта функция определена на множестве всех действительных чисел.
Аналитическое выражение этой функции было найдено, но оно на-
столько сложно, что не имеет практического применения. Словесный
способ дает краткое и четкое ее определение.
Пример 3. у — {х}. Так обозначают функцию, которая назы-
вается дробной частью числа х. Точнее:
У= {х)=х— И,
где [х] — целая часть х. Эта функция определена для всех х. Если
х — произвольное, то, изобразив его в виде х = п + г (п = [х]), где
п — целое число и 0 < г < 1, получим {х} = п + г — п— г. На-
пример:
{0} = 0, {1} = {2} = • • • = {/г} = 0,
{1,37} = 0,37, {—1,3} = —1,3 + 2 = 0,7.
Пример 4. Функция Римана задается так:
{1	т
— , если х — —-, где m и п — взаимно простые числа,
0, если х — иррациональное.
Здесь функция задана описанием закона соответствия между х и f(x).
П p-и м е р 5. Такими же являются так называемые арифметичес-’
кие функции, т. е. функции натурального аргумента, которые прини-,
мают только натуральные значения, например п\ = 1 «2«3... п, или
функция т (п), которая изображает число делителей числа л, напри-
мер т (16) = 5, т(12) = 6. Еще пример: функция ф (п), которая по-
казывает, сколько в ряду натуральных чисел 1, 2, 3, ... , п есть
чисел, взаимно простых с и, например ф (12) = 4, ф(16) = 8.
Полуграфический спссоб. Здесь значения функции представляют-
ся в виде отрезков, а значения аргумента — в виде чисел, простав-
ленных на концах отрезков, указывающих значения функции. Так,
например, на дощечке термометра есть шкала с равными делениями,
у которых проставлены числа. Эти числа являются значениями аргу-
мента (температуры). Они стоят на том месте, которое определяет
графическое удлинение столбца ртути (значения функции) в связи с ее
объемным расширением в результате температурных изменений.
12
§ 2. Классификация функций
Обратные функции
Рис. 5. у = х2.
Функция у = f (х) называется обратимой, если она принимает
каждое свое значение один раз.
Пусть f—отображение множества Е на множество М. Если
для любого элемента у из множества М существует единственный
элемент х = g (у) множества Е, для которого f (х) = у, то отобра-
жение f называется обратимым. Отображение, обратное к у, обозна-
чают f~x и называют обратной функцией. Функция у — f (х) при
этом называется прямой функцией.
Областью определения обратной функ-
ции является множество значений функ-
ции f, а множество значений Д’1 является
областью определения функции f.
Функции у = f (х) и х = /~х (у) назы-
ваются взаимно обратными.
Например:
/(х) = 1(х=#°),
Для того чтобы некоторая функция имела
обратную, необходимо и достаточно, чтобы
разным значениям аргумента из области ее
определения соответствовали разные значе-
ния функции. Следовательно, чтобы доказать, что некоторая функция
необратимая, достаточно указать какие-либо два значения аргумента
Xi =# х2, для которых f (Хх) = f (х2).
Например, функция / (х) = х2 (рис. 5), х£ ]—оо; оо[, обратной
не имеет, так как двум разным точкам: — 3 6 ]—оо; оо[ и 3 С ]—001
оо[ она ставит в соответствие одну точку: 9— /(—3) = f (3). Функ-
ция же у = f (х) = х2, х 6 [0; оо[, имеет обратную х = У у, так как
каждым двум разным точкам xt #= х2 из [0; оо[ она ставит в соот-
ветствие две разные точки: у± = х2, у2 = х2. Действительно, уг—y2=z
2	2	12
\ ~ *2 =	~	+ х*> * °‘
По графику прямой функции у = f (х) достаточно просто опреде-
лить, имеет ли эта функция обратную. Если какая-либо прямая, па-
раллельная оси Ох, пересекает график прямой функции не более чем
в одной точке, то обратная функция х =	(у) существует. Если же
хотя бы одна из таких прямых пересекает график прямой функции
в двух или большем числе точек, то обратная функция не существует.
Если прямая функция у = / (х) строго монотонна на множестве х,
то обратная функция х = f”1 (у) существует и строго монотонна, на
множестве Y.
13
^Сложные функции	'	|
Пусть даны две функции: у — f (z), определенная на множестве^
Z, и z?=g(x), определенная на множестве X. Если g(X)crZ, то^
на множестве X можно определить функцию, которая каждому?
х С X поставит в соответствие g (х) = z С Z. Тогда на множестве ।
X определена функция у = f [g (х)] = /у (х). Эта функция назы- 1
вается сложной функцией х или суперпозицией (наложением) функ- |
ций f и g.
Областью определения сложной функции у — f (х)] является '
либо вся область определения функции г — g (х), либо та ее часть,
в которой определены значения г, не выходящие из области опреде- ,
ления f (г).
Пример 1. Пусть r/ = sinz, где г = х3. Функция у —sin г :
определена на всей числовой оси, функция г — х3 также определена ~
на всей числовой оси. Суперпозиция этих функций у — sin х3 являет- ;
ся сложной функцией х, определенной в ]—оо; оо[.
Пример 2. у=У\ — x?(z/ = yfz, z = 4—х2). Функция у —
== /z определена при z >> О, т. е. при 4 — х2 О (| х |	2), хотя
функция z = 4 — х? определена при всех значениях х. Область опре-
деления функции = у 4 — х2: [—2; 2].
При рассмотрении сложных функций следует иметь в виду облас-
ти определения составляющих функций. Например, из функций у =
= arccos г и z — 3 + х4 нельзя образовать сложную функцию. Дей-
ствительно, выражение у = arccos (3 + х4) не задает сложную функ- .
цию х, так как функция у = arccos z определена на [—1; 1], а зна-
чения функции z = 3 + х4 при любом х не принадлежат отрезку
[—1; 1].
Можно рассматривать суперпозиции не только двух, но и любого
конечного числа функций.
Элементарные функции
Основными элементарными функциями называются следующие:
степенная функция у-х*, где
показательная функция у = ах, где а > 0, а =/= 1;
логарифмическая функция у — loga х, где а > 0, а #= 1;
тригонометрические функции: у = sinx, у — cos х, */= tg х,
У = ctgx;
обратные тригонометрические функции: r/ = arcsinx, #=arccos х,
у = arctg х, у = arcctg х.
Элементарными функциями являются основные элементарные
функции и те, которые можно образовать из них с помощью конеч-
ного числа операций (сложение, вычитание, умножение, деление) и
суперпозиции, например
у = У1	3 sin3 х,
1о& х 4- 3 у^х 4- 3 tg х
у 102*+2x4-4
Назовем некрторые классы элементарных функций.
14
Целая рациональная функция, или многочлен
0 = <V" + «М"'1 + • • ♦ + «я»
где п—целое неотрицательное число (степень многочлена), св,
«1, . • • , ап — постоянные числа {коэффициенты).
Дробно-рацио на льна я функция, которая является отношением
двух целых рациональных функций:
QqX” +	-|----f- ап
 boxm + Z,xXm-i+...+ 6m>
4х3 — 2х2 + 5	х
-y=~27+t	=
например
Целые рациональные и дробно-рациональные функции образуют
класс рациональных функций.
Иррациональная функция — это та, которая изображается с по*
мощью суперпозиций рациональных функций и степенных функций
с рациональными нецелыми показателями, например:
Зх2 + /х2 - 1
+6х —4
у = Ух+\.
Рациональные и иррациональные функции образуют класс алгеб-
раических функций. Алгебраическая функция — произвольная функ-
ция у = f (х), которая удовлетворяет уравнению
4 (х) уп + Aj, (х) у"-1 Н--4- An_f (х) у + Ап (х) = О,
где п — целое положительное число, Ао (х),	(х), ... ,	(х),
Ап (*) — целые рациональные функции от х, Ао (х) #= 0.
Пример 3.	= у^х? + 1 — алгебраическая функция, так как
она удовлетворяет уравнению у3 — х? — 1 = 0.
Пример 4. Функция, определенная уравнением уъ + у — х3 =
= 0, является алгебраической, но эта функция не есть явной алгеб-
раической, так как алгебраические уравнения пятой степени и выше,
как известно из высшей алгебры, вообще говоря, не разрешимы в
радикалах. В этом случае имеем неявную алгебраическую функцию.
Элементарные функции, которые не являются алгебраическими,
называются трансцендентными, например: у — cos х, у — 2х, у =
= logs
Таким образом, все элементарные функции делятся на алгеб-
раические и трансцендентные.
Однозначные и многозначные функции
Если каждому элементу х множества X по некоторому закону
поставлен в соответствие не один, а несколько или даже бесконе-
чное число элементов у из множества У, то функцию называют
многозначной. Так, у = ±^х — двузначная функция (часто вместо
этой двузначной функции рассматривают отдельно две однозначные
функции: t/=-|-|/x и у = —V~x — ветви двузначной функции); t/=»
= Arcsinx — многозначная функция и др.
15
Замечание. Хотя теперь в анализе не рассматривают многой
значные функции, пока не будем исключать их из рассмотрения/;
учитывая существующую техническую литературу.	’
Ограниченные и неограниченные функции
Функция /, определенная на множестве X, называется ограни-
ченной на множестве Xj сз X, если f (х*), т. е. множество ее зна-
чений на множестве Xf, ограничено, т. е. если существуют постоян-
ные т и М такие, что для всех значений х из Xj выполняется
неравенство
m < / (х) < 7И.
В противном случае функция называется неограниченной.
Число /и0 = inf {/(х)} называется точной нижней гранью функ-
ции f (х) на множестве Х{, а число Мо = sup {/ (х)} —точной верх*
ней гранью функции f (х) на множестве Хр
Разность Мо — mQ называется колебанием функции на множе-
стве
Пример 5. f (х) = sin х ограничена на всей числовой оси, так
как для произвольного х выполняется условие | sin х | < 1.
Пример 6. f (х) = ах ограничена снизу, так как для любого
х выполняется неравенство
О < ах
Пример 7. f (х) == tg х ограничена на
на этом отрезке | tgx|^ 1, а также на любом отрезке
—^- < а < о <	. Однако эта функция не ограничена на
1 л л Г
на ]~; ~2|/
Функция f (х) называется ограниченной в точке х0, если она
ограничена в некоторой окрестности точки х0. Для ограниченности
функции у = f (х). на [а; необходимо и достаточно, чтобы она
была ограничена в любой ючке отрезка.
, так как
a; b}t если
Монотонные функции
Функция f (х) называется возрастающей на множестве X, если
для произвольных Х£, х2 из X при Xi < х2 выполняется неравенство
f (xi) < f (хг), т. е- большему значению аргумента соответствует
большее значение функции.
Функция f (х) называется убывающей на множестве X, если для
произвольных Xf, х2 из X при Xf < х2 выполняется неравенство
f (*i) > f (*2), т. е- большему значению аргумента соответствует
меньшее значение функции. Возрастающие и убывающие функции
называют строго монотонными.
Если для любых Xf и х2 из множества X таких, что х± < х2,
справедливо неравенство f (xj) < f (х2) (/ (хх) f (х2)), то функцию
16
f (х) называют неубывающей (невозрастающей) на множестве X.
Невозрастающие и неубывающие функции называют монотонными.
Функция f (х) называется кусочно-монотонной на некотором множе-
стве X, если множество X можно разбить на конечное число под-
множеств так, что на каждом из них функция является монотонной.
Сумма двух возрастающих (убывающих) функций является функ-
цией возрастающей (убывающей).
Произведение двух положительных возрастающих (убывающих)
функций является функцией возрастающей (убывающей).
Если функция у f (х) возрастающая, то функция — f (х) убы-
вающая, и наоборот.
Если функция у = f (х) возрастающая (/ (х) #= 0), то функция
1
убывающая, и наоборот.
Если функция у = f (х) строго монотонна, то обратная функция
x^f-^ty) однозначна, строго монотонна.
Если функция х f (/) возрастает на [а; 0], а функция у ;=
F (х) возрастает на [/ (a); f (0)], то функция y~F [/(/)] возра-
стает на [ос; 0].
Если функция х :=/(/) убывает на [а; 0], а функция z/s=F(x)
убывает на [f (0); f (а)], то функция у = F [/(/)] возрастает на
[a; 0J.
Если функция х = f (/) возрастает на [ос; 0], а функция yt=
= F (х) убывает на [f (0); f(a)]t то функция у s= F [f (/)] убывает на
[а; 0].
Пусть ср (х), ф (х) и f (х) — монотонно возрастающие функции;
тогда, если ф (х)< f (х) < ф (х), то ф [ф (х)] < f [f (х)] < ф [ф (х)].
Заметим, что немонотонная функция у f (х) (—оо < х < оо)
может иметь обратную функцию, если уравнение у^= f (х) при каж-
дом фиксированном у £ ]—оо; оо[ имеет единственное решение.
Все основные элементарные функции являются функциями моно-
тонными или во всей области своего определения, или в отдельных
ее частях.
Четные и нечетные функции
Числовое множество X называется симметричным, если для про-
извольного х 6 X число —х С X, например множество целых чисел,
отрезок [—а; а], интервалы ]—а; а[ и ]—оо? оо[ и другие мно-
жества, симметричные относительно начала координат.*
Функция /, определенная на симметричном множестве X, назы-
вается четной, если для ух С X выполняется равенство
f(-x)~=f(x),
например у г= х2, у = cos х, у s=. | х |, у = f (| х |).
Функция f, определенная на симметричном множестве х, на-
зывается нечетной, если для ух С X выполняется равенство
f (—X) = —f (х),
например у = х3, у = tg х, у =	.
17
Основные свойства четных и нечетных функций
1.	Алгебраическая сумма двух четных (нечетных) функций есть
функция четная (нечетная).
2.	Произведение двух четных (нечетных) функций есть функция
четная; произведение четной и нечетной функций есть функция не-
четная.
3.	Если y^f(x)t х*= ср (0 — нечетные функции, то сложная
функция у — f [ф (0] — нечетная.
4.	Если у ;= f (х) — четная функция, а х = ф (0 — нечетная, то
функция у — f [ф (0] — четная; если ф (х) — четная функция, то и
функция / [ф (х)] — четная.
5.	Если у± — f (х) — четная функция, причем f (х)	0, то и функ-
ция -г-— — четная.
f (х)
И для четных, и для нечетных функций выполняется равенство
\f(x)\ = \f(-x)\.
Из определения четной и нечетной функций следует, что нет
смысла говорить о четности или нечетности функции, определенной
на несимметричном множестве. Условие симметричности области опре-
деления функции является необходимым для того, чтобы функция
могла быть четной или нечетной. Однако оно не является достаточ-
ным. Например, области определения функций // = х + 3 и у^=Зх
симметричны (вся числовая ось), но эти функции не являются ни чет-
ными, ни нечетными. Функции, которые не есть ни четными, ни не-
четными, называются функциями общего вида. Заметим, что произ-
вольную функцию /(х), определенную на симметричном множестве,
можно изобразить в виде суммы четной и нечетной функций:
f (х) _ /(*) + /(-*)	/(*)-/ (-х)
2*2’
где первое слагаемое — четная функция, а второе — нечетная, причем
такое изображение единственное.
ex _l е~х ех_е~х
Пример 8. ех -----1--. Здесь функция общего
вида ех, определенная на интервале ] — оо; оо [, представлена в виде
суммы четной и нечетной функций.
Периодические функции
Пусть / определена на множестве X. Если существует со =# О та-
кое, что для у х С X числа х + со и х — со также принадлежат мно-
жеству Хи / (х + со) — / (х) (/ (х — со) — / (х)), то функцию f назы-
вают периодической с периодом со.
Пример 9. Функции sin хи cos х имеют период 2пл, где п С Z.
Пример 10. Функции tg х и ctg х имеют период пл, где п £ Z.
Если периодическая функция имеет период со, то она имеет бес-
конечное множество периодов: 2со, Зсо,..., —со, —2со, —Зсо,... Наи-
меньший из положительных периодов (если он существует) называет-
ся основным периодом периодической функции. Следовательно, если
периодическая функция имеет основной период соо, то любой другой
18
ее период кратен шо. Следует иметь в виду, что наименьшего поло-
жительного периода функция может и не иметь. Например, для фун-
кции f (х) = 3 любое действительное число является периодом, а на-
именьшего положительного среди действительных чисел нет. Вообще
функция f (х) — const является периодической, так как имеет одно и
то же постоянное значение при произвольном значении аргумента, т. е.
при любом действительном значении а #= 0 f (х -f- а) ?= f (х). Таким
образом, любое число а являете?. периодом этой функции, т. е. функ-
ция не имеет основного периода.
Функция f (х) называется антипериод ической, если
/(х + со)^= — / (х) (со#=0),
в этом случае f (х) является периодической с периодом 2со. Действи-
тельно,
f (х + 2(d) = f (х + О) + со) — f (х + о>) = — (—f (х)) J= f (x).
Из определения периодичности следует, что сумма и произведе-
ние двух функций с одним и тем же периодом со являются функция-
ми с периодом со. Заметим при этом, что если число со было наимень-
шим положительным периодом двух заданных функций, то после их
сложения или умножения со может перестать быть наименьшим из по-
ложительных периодов.
Пример 11. Функции (х) = 3 sin х + 2 и f2 (х) ;= 2 — 3 sin х
имеют наименьший период 2л, а их сумма fi (х) + /2 W — 4* наимень-
шего периода йе имеет.
Пример 12. Функции (х) sin х + 1 и ср2 (х) — 1 — sin X
имеют наименьший период 2л, а для произведения epf (х) • ср2 (*) *=*
9	1 4- cos 2х
s= cos2 х——-------- наименьшим положительным периодом есть
число л.
Если f (х) — периодическая функция с периодом со, то функция
у (х) = f (ах) также периодическая с периодом т, где т *= ~ , а —
произвольное действительное число (а #= 0), и точки х и ах принад-
лежат области определения f (х).
Если / (х) — периодическая функция с периодом со, то функция
f (ax-\~b), где а > 0, также периодическая с периодом .
Если при всех х и некотором со выполняется равенство
/(x + <0)=-L(<o^O))
/ \л)
то функция f (х) периодическая с периодом 2со.
Если функция -и = ср (х) — периодическая, то и сложная функция
у— / [<р (х)]— периодическая, причем периоды этих функций совпа-
дают, если функция у ~ f (и) строго монотонна. Если же у — f (и)
не строго монотонна, то период функции у = f [ср (х)] может быть
меньше периода функции н^=ср(х).
Если для функции f (х) (— оо < х < оо) выполняется равенство
f (х + (0) — kf (X),
где k и о — положительные посточнныг, то f (х) = axtp (х), где а —
постоянная, а ср (х) — периодическая функция с периодом со.
19
_ Период алгебраической суммы периодических функций равен наи-
меньшему кратному периодов всех слагаемых (за исключением перио-
дов тех подобных членов, сумма которых после приведения равна
нулю). В частности, периоды функций
v п	т
sin bi* + S Ck C0S X
i=l	k=l
И
n	m
f (x) — yj сц tg bi X 4- yj Ck ctg dk X,
(=1	fe=i
где a;, Ck — действительные, отличные от нуля числа, a bi, dk € Nt
вычисляются соответственно по формулам
_ _______________2л______________
а2,..., ап, clt с2. ст)
И
л
со = тг7-------------------------------------------:.
D (aj,	аП> ^1» c2f’t Ст)
Если же bit dk — рациональные числа имеют вид соответственно Ь,;
s= , dk =	, то периоды приведенных функций вычисляются по
формулам
^ 2nK(qif q2,..., qn> Ч, Ч>-,Чп)
D(Pi, Рп, Ч> 'г,-, 'т)
и
(0	<k>***> Ргь Ч* sm)
D(Pi, Р2,-, Рп, Ч, r2,..., rm) •
Для установления непериодичности функции достаточно показать,
что она непериодически повторяет какое-либо свойство рассматри-
ваемой функции.
Приведем некоторые примеры периодических функций.
Пример 13. f (х) s= {х} s= х — [х]. Эта функция имеет период
со=1. Действительно, f (х + 1) s= {х + 1} = х + 1 — [х + 1 ], но[х +
+ 1] = [х] + 1, тогда {х+ 1} = х+ 1 — [х] — 1 = х — [х] = {х} для
произвольного X.
Пример 14. Для функции Дирихле
. П> если х — рациональное,
(О, если х — иррациональное,
произвольное рациональное число г является периодом. Действитель-
но,
.	_ Н, если х — рациональное,
X (х -f- г) — J
(О, если х — иррациональное;
так как г — рациональное, то' сумма х + г — рациональное число,
как сумма двух рациональных чисел; с другой стороны, х+г—ир-
рациональное, как сумма иррационального и рационального чисел.
Следовательно,
X (х + г) = X (х).
20
§ 3. Предел функции. Непрерывность функции
Предел числовой последовательности
Пусть функция f (х) определена на множестве N {1,2, 3,...,п,...}
всех натуральных чисел. Такая функция называется бесконечной чис-
ловой последовательностью. Если обозначить f (п) через хп, то чис-
ловую последовательность можно записать в виде {хп} или в развер-
нутом виде Л'1, х2,..., 'хп,...
Последовательность считается заданной, если известен закон ее
образования, т. е. правило, по которому можно определить любой
член последовательности.
Число а называется пределом числовой последовательности, если
для ye > Og/V (е) такое, что для всех значений хп, у которых номер
п> N (е), выполняется неравенство | хп — а | < е. Символическая
запись:
lim хп = а или хп -> а (п оо).
л->«>
ч-
0
Рис. 6. Геометрический смысл предела последовательности {хл
Геометрический смысл предела последова-
тельности. Если последовательность _{хл} имеет предел а, то все
члены этой последовательности начиная с номера п j= N + 1 попадают
в е-окрестность точки а (рис. 6).
Числовая последовательность, имеющая предел, называется сходя-
щейся, а последовательность, не имеющая предела,—расходящейся.
Необходимое и достаточное условие суще-
ствования' предела последовательности (крите-
рий Коши). Для того чтобы последовательность {хп} имела предел,
необходимо и достаточно, чтобы для ye > Одх^ такое, что произволь-
ные два члена последовательности, стоящие после xN, отличались
друг от друга на число, меньшее е:
Iхп-!гР — хп 1 < 8 Для всех п> N при ур > 0.
Основные теоремы о пределах последовательности
1.	Последовательность может иметь только один предел.
2.	Последовательность, имеющая конечный предел, ограниченна;
последовательность, имеющая бесконечный предел, не ограниченна.
3.	Монотонная ограниченная последовательность имеет конечный
предел; если эта последовательность монотонно возрастает, то
lim хл>» хп\ если она монотонно убывает, то Нтхл<хл.
И-»-оо	П-+оо
4.	Монотонная неограниченная последовательность имеет беско-
нечный предел; если эта последовательность монотонно возрастает,
то lim хп — + 00; если она монотонно убывает, то limxn —— оо.
Л1-+- оо	п-¥ 00
21
Пример 1. Доказать, что последовательность х„ s= —имеет
/14-1
предел, равный 1.
Надо доказать, что для Vе > Оэ^(е) такое, что для y/i > М
выполняется неравенство
Выберем любое е > 0. Поскольку
I*. -	-1 |=|^-i | < в,
то для отыскания N достаточно решить неравенство —; < в. Имеем
п 4~ 1
п>±-1.
е
Следовательно, если номер N больше --— 1, то неравенство | хп -*
— 1 | < е выполняется. В качестве W можно взять наибольшее целое
число из чисел------1 : NЕ I--------11 . Этим доказано,что lim х/г^1.
®	/	П->00
Примера. Пользуясь критерием Коши, доказать расходи-
мость последовательности
хп;= 1 4~—(п—1, 2,...).
Пусть е — произвольное число из Jo; . Поскольку
.	1	,__1	. f 1 Р
I Хп^-Р */11" Ц- 1 “Г nJr2^r * ’ * п 4- р п + р’
а при р = п | хп_|_р — хп | > у > 8 для всех п, то заданная после-
довательность расходящаяся.
Предел функции
Рис. 7. Геометрический смысл
предела функции lim f (х) = Ъ.
х-+а
Пусть функция у — f (х) опреде-
лена в некоторой окрестности точки а.
Функция у — f (х) стремится к пре- •
делу b при х -> а, если для V8 >0
36 (е) > 0 такое, что для всех х, от-
личных от а, для которых | х — а | <6,
выполняется неравенство | f (х) — b | <
< е. Это записывают так: lim f (х) =
х-+а
Геометрически: поскольку из | х — а | <
< 6=> | f (х)— b | < е, то это означает,
что для всех точек х, удаленных от
точки а не далее чем на д', точки гра-
фика у = / (х) лежат внутри полосы
шириной 2е, ограниченной прямыми
у = b — 8 и у = Ь е (рис. 7).
II
Признаки существования предела
Функция f (х) имеет предел b при х=а, если при произволь-
ной последовательности значений х (хь х2, »в» , хл, j • •)» принадле-
жащей области определения функции и имеющей пределом число а,
последовательность соответствующих значений функции f (хх),
f (*2), • • • , f(xn), .. * имеет предел Ь.
2. Критерий Коши. Для того чтобы функция f (х) имела
конечный предел при х — а, необходимо и достаточно, чтобы для
Ve > О3 6 (е) > 0 такое, что для любых х^ и х2 из области опреде-
ления функции и при |хх — а | < 6, j х2 — а | <6 выполнялось уело-
вие | f (xj — f (х2)| < е.
Односторонние пределы функции. Число b называется правым пре-
делом 'функции f (х) в точке а, если для Ve > О Я 6 > 0 такое, что для
всех х, для которых выполняются неравенства а *< х а + 6, имеет
место неравенство | f (х) — b | < е. Правый предел функции f (х)
в точке а обозначают lim/(x) или
х->а-\-0
Число b называется левым пределом функций f (х) в точке а,
если для Ve > О Э6 > 0 такое, что для врех X, для которых выполня-
ются неравенства а — б < х < а, будет | f (х) b | <6* Левый предел
функции f (х) в точке а обозначают lim / (х) или f (а —0)*
0
Для того чтобы число b было пределом функции f (х) при
х -> а, необходимо и достаточно, чтобы левый и правый пределы
f (а + 0) и f (а — 0) существовали и равнялись Ь<
Функция f (X) имеет предел 4- оо при х -> а, если, какое бы
большое ни было положительное число М, существует такое число
6 > 0, что для всех значений х, для которых выполняется неравен-
ство | х — а | <6, f (х) > ЛЕ
Функция f (х) имеет предел —оо при х-> оо, ес^и, какое бы
большое ни было отрицательное число -*• М, существует такое число
6 > 0, что для всех значений х, для которых выполняется неравен-
ство | х — а | <6, f (х) < —М.
Функция f (х) имеет предел оо при х -> а, если, какое бы боль-
шое ни было положительное число М, существует такое число 6 > 0, что
для всех значений х, для которых выполняется неравенство |х — а\ < 6,
Функция f (х) имеет предел о при х->4-оо, если существует
такое 8 > 0, что для всех х > W, где N — сколь угодно большое положи-
тельное число, | f (х) — Ь \ <8.
Функция f (х) имеет предел b при х->— оо, если существует
такое 8 > 0, что для всех х < —W, где W— сколь угодно большое
положительное число, | f (х) — b | <8.
Функция / (х) имеет предел b при х-> оо, если существует такое
е > 0, что для всех | х| > W, где N — сколь угодно большое поло-
жительное число, | / (х) — b | <8*
Теоремы о пределах
1.	Предел постоянной величины равен этой величине:
lim а = а.
2.	Предел алгебраической суммы конечного числа функций, име-
ющих конечные пределы, равен алгебраической сумме пределов этих
23
фуйкций:
lim [Л (x) ± f2 (x) ± ... ± fn (x)] = lim ft (x) ± lim f2 (x) ±
x-+a	x-t-a	x-+a
± ... ± lim fn (x).
x-+a
3.	Предел произведения конечного числа функций равен произве-
дению пределов этих функций, если существуют конечные пределы
сомножителей:
lim [Л (х) • /2 (х)... fn (x)J = lim fj (х) • lim f2 (x) . , t lim fn (x).
x-+a	x-+a	x-+a	x-*a
4.	Предел частного двух функций равен частному пределов этих
функций, если предел делителя отличен от нуля и пределы делимого
и делителя существуют:
lim f (х)
lim (If) —	----- (lim ф (х) =£ 0),
х^а ф(х) lim ф (X) х-*а
х-+а
5.	Если функция f (х) удовлетворяет неравенству
Ф(х </(х)<ф(х)
и если lim ф (х) = b и lim ф (х) = Ь, то lim f(x) = b.
х-+а	х-+а	х-+а
6.	Монотонная функция -непрерывного аргумента имеет предел
(конечный или бесконечный) при любом значении аргумента х (ко-
нечном или бесконечном); монотонная ограниченная функция имеет
конечный предел при любом значении аргумента х.
Некоторые важные пределы. 1 im= 1, где х —
х->0 X
длина дуги или угол в радианах;
[ ' 1 V
число е: lim ( 1 +	== е = 2,71828 . . . (иррациональное число);
Х-+ оо \ х J
число С: lim 11 + 4 + 4 + • • • + --lnn) = C= 0,5772...
fl-к» '	*	°	П	/
(постоянная Эйлера).
Символ Ландау. Для двух функций f (х) и g (х) > О,
определенных в области D, символ
f (х) = 0(£(х))
означает, что существует такая постоянная К > 0, что
| f (х) К Kg (х) для V х 6 D.
Классификация бесконечно малых функций
Если lim f (х) = 0, то функция f (х) называется бесконечно ма-
X^-Xq
лой при х -> х0.
Если lim f (х) == b, то всегда можно записать f (х) = b + а (хи),
где а(х) — бесконечно малая при х х0 функция.
24
Пусть а (х) и р (х) — бесконечно малые функции при х -» х0.
а)	Если lim ^44 = L (L = const, L ^Сг), то функции а (х) и р (х)
х->х„Р(х)
называют бесконечно малыми одного порядка малости и записывают
а=Оф), 0 = О(а).
Пусть а (х) и 0 (х) — бесконечно малые функции при х -> х0, k —
фиксированное положительное число. Если а (х) и 0* (х) — беско-
нечно малые функции одного порядка, то а (х) называется беско-
нечно малой порядка k относительно бесконечно малой 0 (х).
б)	Если lim = 0, то функцию а (х) называют бесконечно
x-^xq Р (х)
малой высшего порядка малости, чем Р(х), и записывают
а = о (Р);
функцию Р (х) в этом случае называют бесконечно малой низшего
порядка малости, чем а (х).
в)	Если lim = 1, т. е. а (х) —- 0 (х) = о (а), то функции
Р (*)
а (х) и -Р (х) называют эквивалентными бесконечно малыми и запи-
сывают
а 0.
.	а (х)
г) Если предел отношения-д—г при х-> х0 не существует, то
Р W
функции а(х) и р (х) называют несравнимыми.
При отыскании предела отношения двух бесконечно малых фун-
кций каждая из них может быть заменена эквивалентной ей беско-
нечно малой.
Пример 3. Дано функцию / (х) =	+ 4. Пользуясь опреде-
лением предела функции, доказать, что
lim f (х) = 3.
х—> 5
Надо доказать, что для V8 > 0Н6 (е) > 0 такое, что из | х — 5| <
< 6=>| f (х) — 3 | <е. Рассмотрим выражение
|/х + 4-3| =
_ |х-5|
I Ух + 4 +3|
Так как | У х + 4 -1- 3 |	3 при всех х из области определения фун-
кции [— 4;оо[, то | ]Лх 4 — 3 | < Х| з1	• Поэтому для всех х,
для которых | х — 5 | <38, справедливо неравенство
|/х + 4 — 3 | < е.
Положим 6 = Зе. Будем иметь lim ]Лх + 4 = 3.
х->5
2S
' ' П р и м е р 4. Найти предел
х-2 X3 — 8
Здесь числитель и знаменатель в точке х = 2 имеют, предел,
равный нулю. Применить теорему о пределе частного нельзя. Раз-
лагаем числитель и знаменатель на множители:
х2 4- 2х — 8 = (х — 2) (х + 4), х3 — 8 = (х - 2) (х2 4- 2х 4- 4).
После сокращения на х — 2 получим выражение
х2 + 2x + 4
и, применив теорему о пределе частного, найдем
lim —* + 4	= А = _1,
-л^2Х3 + 2х + 4	12	2
Заметим, что сокращение дроби на х — 2 было законным, так как прц
отыскании предела функции в точке х = 2 значение ее в точке х= i
не принимает участия, а потому мы на 0 не сокращали.
Пример 5. Найти предел
lim +
оо 5х3 4- х — 8
В данном случае теорему о пределе частного непосредственно
применить нельзя, так как ни делимое, ни делитель не имеют ко-
нечного предела при х->4-°°« Преобразуем дробь, разделив ее чис-
литель и знаменатель на х3. Получим
4 + 1_А
lim	«	«
V-+- оо 5х3 4~ % — 8	Х~* оо . 1	8
5+^-^
Так как при х -> оо
£
х
°> 4 -* °* 4 -* °> 4 -* °-
X3 X* X3
то, применив теорему о пределе суммы, убеждаемся, что числитель
имеет предел, равный 4, а знаменатель имеет предел 5. По теореме
о пределе частного имеем
Um 4х3 + 2х2 — 5 _ 4
х->оо 5х3 4-х —8	5
Пример 6. Найти предел
lim х(]/х?+ 1 — х).
а)	Пусть x -> + оо. Теорему о пределе суммы непосредственно
применить нельзя так как выражение в скобках есть разность двух
26
бесконечно малых величин, о которой без специального исследование
ничего конкретного сказать нельзя. Умножим и разделим функцию
на выражение, сопряженное о 1 — х, т. е. на Ух? + 1 + xt
lim х (/ИТГ - х) = lim '*(№+'~
Х-++*	х+4-оо	угх2_|_1^_х
так как lim -4=0,
Х-юо х?
б)	Пусть х -> — оо. Выражение, стоящее в скобках, имеет в этом
случае положительное значение и неограниченно возрастает по аб*
солютной величине; множитель х, стоящий перед скобкой, такжб
неограниченйб возрастает по абсолютной величине, но сохраняет
отрицательное значение. А потому все выражение х (Ух2 + 1 — *)
при х -> неограниченно возрастает по абсолютной величине,
сохраняя Отрицательное значение, и
lim х (Ух? 4- 1 — х) == — оо,
Х-+ —оо
Пример 7. Найти предел
limtg * — s*n *.
Z-+0 X3
X
Так как sin х х и 1 — cos х = 2 sin2 — , то
lim tg х ~ sin х = lim sinx([ -cqsx) = lim sinx(l —cosx) x
x3	x-+0 X3COSX x+o	X3
X2
Пример 8. Доказать, что функция
f(x)=
cos — , если 0 < х < оо,
X
х cos — , если — оо < х < О,
имеет левый предел в точке 0 и не имеет в ней. правого предела.
И
Рассмотрим две последовательности значений, сходящиеся к нулю
_ 1 ~ 2 ;
Хп ~ 2пп И Хп~ л(4п + 1) ‘
Тогда f (хп) — cos 2пп = 1, f (хп) = cos	= о.	%
Следовательно, lim / (хп) = 1, a lim f(xn) = 0. Но хп -> + 0, хп -> -J-01
ОО	ОО
тогда правый предел не существует. Выражение xcos-i- прих.->—О
является произведением бесконечно малой функции х на ограничен-,
ную функцию cos—, тогда lim х—?— = 0. Отсюда и следует, что/
х	*-►—о cos х	7 ’	;
lim f (x) ~ lim x cos — = 0.
0	x->—О X	*
Непрерывность функции
Функция у = f (х) называется непрерывной в точке х = а, если
число а принадлежит области определения функции, предел lim f (х) ‘
х-+а
существует и равен значению функции в точке х= а:
lim f (х) = f (а),
х-+а
т. е. если функция f (х) определена при х=а и для Ve > 0 Н6=6 (е, а) > О
такое, что при всех х, для которых | х — а [ <6, выполняется нера-
венство
J / (х) — /(a) J < е.
Определение непрерывной функ- \
ции можно дать с помощью поня-А
тия приращений. Приращением ap-Ji
гумента х в точке хэ называется'»
разность	ж
Дх = х — х0.	Я
Приращением функции f (х) в точ- >
ке х0 называется разность
Рис. 8. Приращение аргумента и при-	Д/ С^о) — f W — f
ращение функции.
Приращения аргумента и функции
по знаку могут быть и положительными, и отрицательными (рис. 8). i
Функция / (х), определенная в окрестности точки а, называется |
непрерывной в точке х = а, если	|
lim Д / (а) = О,	I
Дл->0	|
т. е. функция f (х) называется непрерывной в точке а, если беско- :
нечно малому приращению аргумента соответствует бесконечно ма-
лое приращение функции.
Критерий непрерывности. Для того чтобы функиця
f (х), определенная в некоторой окрестности точки а, включая и
точку а, была непрерывной в точке а, необходимо и достаточно,
чтобы для любой последовательности точек хп (п = 1, 2, ...), взятых
из этой окрестности, сходящейся к точке а, последовательность
f (п = 1, 2, ...) сходилась к f (а).
Функция, непрерывная в каждой точке некоторого множества X,
называется непрерывной на этом множестве X.
Если выполняется равенство
f (а— 0) = / (a) (f (а + 0) = f (а)),
то говорят, что функция f (х) непрерывна слева (справа) в точке
х = а. Для непрерывности функции в точке х = а необходимо и до-
статочно, чтобы выполнялось условие
f(a-O) = f(a + O) = f(a),
В тех точках а, которые находятся внутри или на границе области
определения функции и в которых она неопределенна либо значение
f (а) не совпадает со значением предела lim f (х), либо lim f (x) не cy-
x-+a
ществует, функция имеет разрыв.
Различают точки разрыва первого рода.и точки разрыва второго
рода. Точки разрыва первого рода — это точки, в которых сущест-
вуют конечные односторонние пределы
f (а — 0) = lim f (х) и f (а + 0) = lim f (х).
0	х->а+0
Если а — точка разрыва первого рода функции f (х) и правый пре-
дел функции f (х) в точке а не равен левому пределу этой функции,
то абсолютную величину разности правого и левого пределов функции
f (х) в точке а называют скачком функции в точке а. Точки разрыва
второго рода — это точки разрыва функции f (х), в которых не су-
ществует хотя бы один из пределов или этот предел бесконечен*
Устранимая точка — это точка разрыва функции ffx), когда
limf(x) существует: f (а — 0) = / (a-f-0), но при х=а функция
или не задана, или имеет значение
f(a) + lim f(x).
Х-*й
Если хотя бы один из пределов f (а— 0) или / (а + 0) равен оо,
то точка х = а называется точкой бесконечного разрыва.
Теорема о непрерывности монотонной функции*
Если множество значений монотонно возрастающей (убывающей) функ-
ции f (х), которые она принимает, когда х изменяется на множестве X,
находится в некотором множестве Y и заполняет его сплошь, то функ-
ция f (х) в X непрерывна.
Из теорем о пределах функций следует
теорема об арифметических операциях над
непрерывными функциями. Если функции f (х) и g (х)
непрерывны в точке а, то в этой точке непрерывны и функции
f (х)
f(x)±g(x), f (x)-g(x), ‘—TR (при g(a)^Q). Из этой и предыду-
& \х)
щей теорем следует
29
теорема о непрерывности элементарных функ-
ций. Любая элементарная функция непрерывна в области своего 4
определения.
Теорема о суперпозиции непрерывных функций, ?
Пусть функция ф (у) определена на множестве У, а функция f (ж) —
на множестве X, причем значения последней функции не выходят
за пределы У, когда X изменяется в X. Если f (х) непрерывна
в точке х = а £ X, а ф (у) непрерывна в соответствующей точке yQ~
= f (а) 6 У» то и сложная функция ф (/ (х)) непрерывна в точке х = а<
Пример 9. Задана функция
Их) = /Г+6.	.	,
Доказать, что в точке х = 3 функция непрерывна,
В точке х = 3 функция определена! / (х) = 3. Выберем Ve > 0.
Рассмотрим разность f (х) -* f (3) = У X + 6 — 3 и оценим ее по ;
модулю. При б > 0 для значений х, для которых выполняется нера-
венство | х — 31 <6, выполняется также и неравенство	'
| х 4- 6 — 3 | «
l*Z3|
I х 4“ 6 4" 3 {
|х —3| б*
Пусть б = Зе, тогда при всех значениях х, для которых | х — 31 < Зе,
выполняется неравенство I’j/x + G — з|<е, Непрерывность функции
при х = 3 доказана.
Пример 10. Доказать непрерывность функции
f (х) = 5х2 — Зх + 2
при любом х.
Пусть х0 — произвольная точка числовой оси, Найдем lim f (x)i
Х~+Хц
lim f (x) = lim (5x2 — 3x + 2) = 5Xg — 3x0 + 2.
Далее вычисляем значение функции в точке х0:
f (*э) — 5х0 — Зх0 4- 2.
Сравнивая полученные результаты, видим, что
lim f(x) =4 (х0).
х^х0
Следовательно, функция f (х) непрерывна в точке хэ по определению .
непрерывности. Так как точка х0 — произвольная точка числовой оси,
то функция f (х) непрерывна для всех значений х.
Пример 11. Доказать, что функция	<
f (х) = cos х
непрерывна при любом х.
Из
| А/ (х0) | = | cos (х0 + Ах) — cos х0
о . Ах .
2 sin -g- sin
<2
. х
Sin у
< 2
Ax I . . .
Т| = |Ax|
«ледуег равенство
lim Д/ (х0) =» 0.
Этим доказана непрерывность функции f (х) = cos х в произвольной
фиксированной точке х0 € ]—00; <» [, а следовательно, и на всей
числовой оси,
Пример 12. Исследовать на непрерывность функцию
(х2 — 4) 3* + arctg х « cos х 4~ 4х
sin3 х	*
Каждое слагаемое в числителе при всех значениях х является
непрерывной функцией как произведение непрерывных функций. Сумма
Трех непрерывных функций также непрерывная функция. Знаменатель
содержит функцию, непрерывную при всех значениях х, кроме Х=
(п £ 2). Следовательно, рассматриваемая функция непрерывна при
всех значениях х, кроме х лп, где она не определена.
Призер 13. Исбледобать на непрерывность функцию
f (х) = cos loga 2х (0 < х < оо).
Имеем суперпозицию функций. Положим tt = Iogd2x. Так как
логарифмическая функция и** loga2x непрерывна на J 0; оо[, а функ-
ция cosh непрерывна на ] —оо; оо [, то по теореме о непрерывности
суперпозиции функций функция f (х) = cos loga 2х непрерывна на
] 0; оо [.
Пример 14. Исследовать на непрерывность функцию
у (2x3 + 5), если —оо < х< 1,
f W —	5 4Xj если 1 < х < 3,
х —5, если 3<х<оо*
Область определения функции: ] —оо; оо (. На интервалах
] —оо; 1 [, ] 1; 3 [, ] 3; оо [ функция непрерывна. Разрывы могуТ
быть только в точках х = 1, х = 3.
Вычислим односторонние пределы функции в точке х= 1|
/(1-0)= lim 1(2х2 + 5) = 1,
х->1—О I
f(14-0)= lim (5 — 4х) = L
1-J-0
Значение функции в точке х = 1 определяется первым аналитическим
выражением, т. е.
 /(1)=1(2+5)= 1.
Так как / (1 — 0) = / (1 4~ 0) = / (1) = 1, то в точке х = 1 заданная
функция непрерывна.
Рассмотрим / (х) в точке х = 3:
/(3 — 0)= lim (5 — 4х) = —7,
х—>-3—О
f(3 4-0)= lim (х — 5) = —2,
X-+3-J-0
/(3.-0) #=/(3 4-0).
31
Функция в точке х — 3 имеет разрыв первого рода. Скачок функции,
в точке разрыва: f (3 + 0) — / (3 — 0) = —2 — (—7) = 5.
"Пример 15. Исследовать на непрерывность функцию
f (X) = COS2 — '
Пусть хп = (п 6 Ю* Тогда хп 0 при п -> оо, a cos? —	1
2	~	'
Если хп = —(ng#), то	при п->оо,
при м —> оо. Следовательно, предел iimcosS— не
Х-+-0 X
су-
При п->оо.
a cos2 0
Хп
Шествует, х == 0 — точка разрыва второго рода.
Основные свойства непрерывных функций на отрезка^
1. Первая теорема Вейерштрасса. Непрерывная функ- *.
ция на отрезке [а; 6] ограничена на этом отрезке*
2* Вторая теорема Вейерштрасса* Если функция ;
f (х) непрерывна на отрезке [а; 6], то среди ее значений на этом ч
отрезке существуют» наименьшее и наибольшее.
3. Первая теорема Больцано — Коши. Если функ-
ция f (х) непрерывна на отрезке [а; Ь] и если значения этой функции
на концах этого отрезка противоположны по знаку, то существует
по меньшей мере одна точка с а\ b [, значение функции в которой
равно нулю: f (с) = О*
4. Вторая теорема Больцано —Коши. Если функ-
ция f (х) непрерывна на отрезке [а; и если f (а) f (b), то для <
произвольного числа А, находящегося между числами f (а) и f (b), <
существует по меньшей мере одна точка с С ] а; И такая, что f(c) — А*
РАЗДЕЛ 2
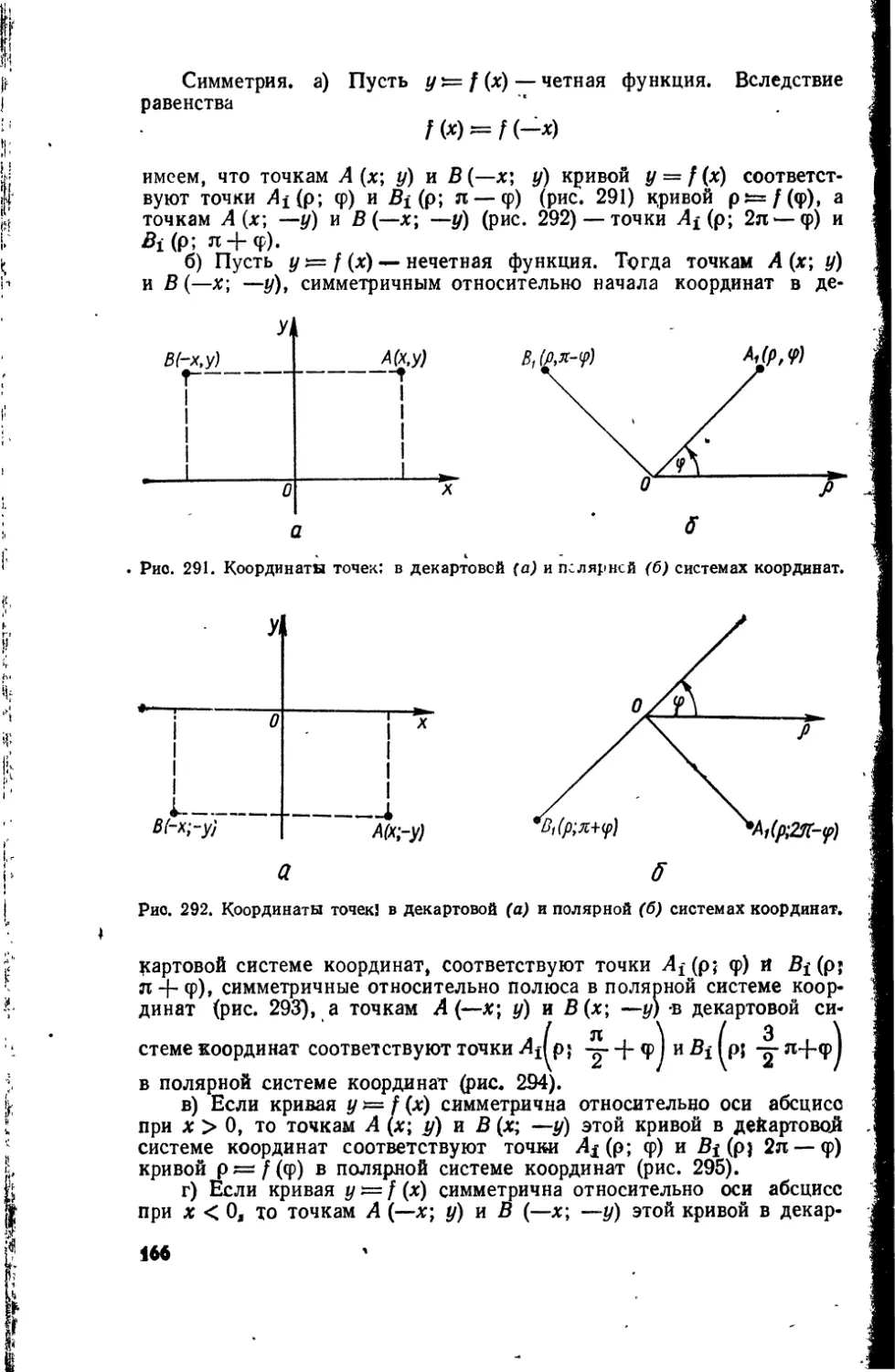
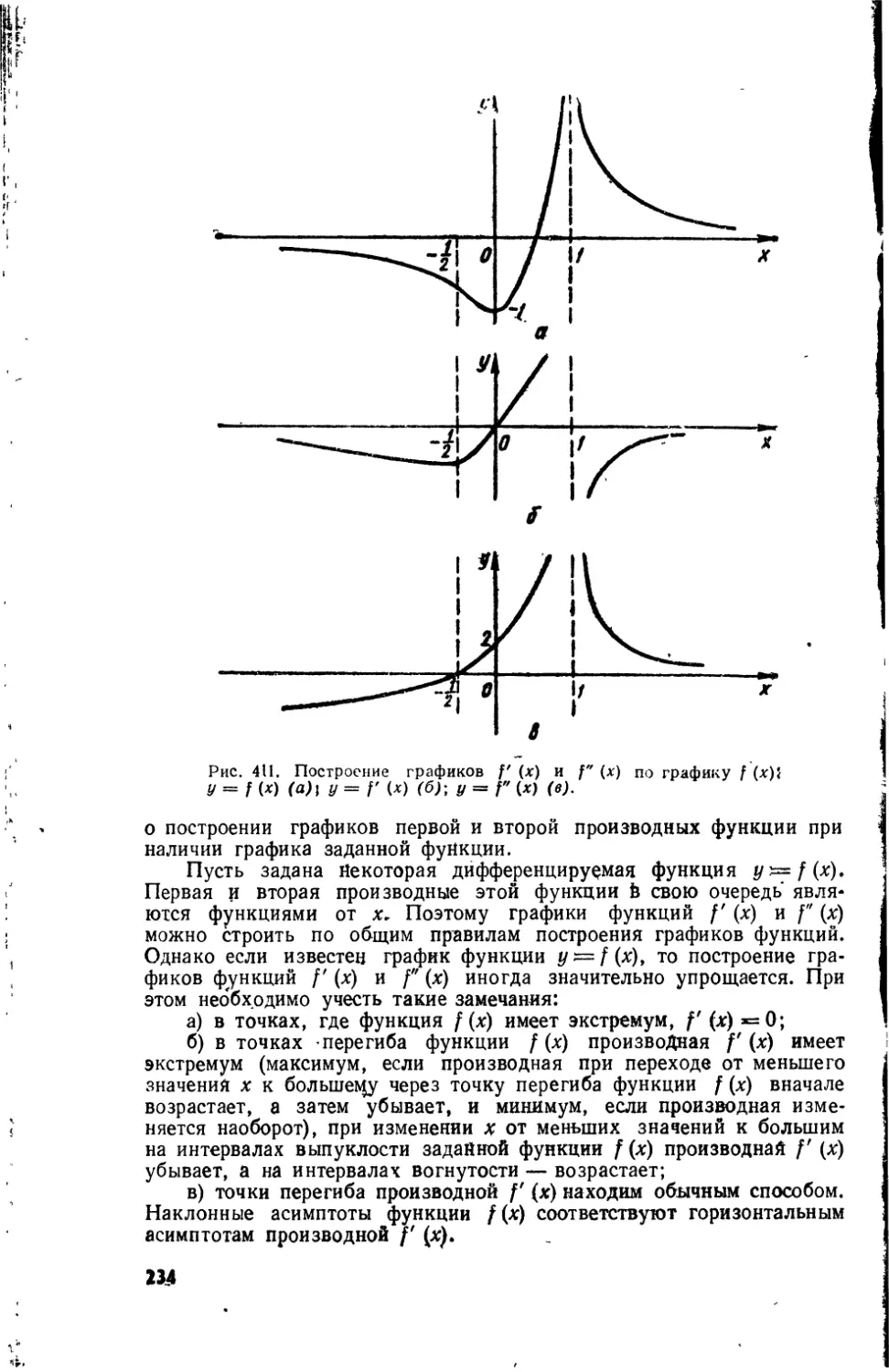
ИССЛЕДОВАНИЕ ФУНКЦИЙ ДЛЯ ПОСТРОЕНИЯ ГРАФИКА
§ 1. Системы координат
Декартова система координат
Плоскость, на которой задана система координат, называется
координатной плоскостью. Декартова, или прямоугольная, система
координат определяется линейной единицей измерения и двумя вза-
имно перпендикулярными числовыми осями. Точка пересечения осей
называется началом координат, а оси — координатными осями.
Одна из них называется осью абсцисс,, а другая — осью ординат*
Оси координат соответственно обозначаются Ох и Оу.
С каждой точкой Р плоскости, в которой выбрана система коор-
динат, можно связать два числа, которые получаем следующим обра-
зом. Опускаем из точки Р перпендикуляры на оси координат. Пусть
32
Рх — основание перпендикуляра на оси абсцисс, а Ру — основание
перпендикуляра на оси ординат. Точке Рх на числовой прямой, како-
вой является ось абсцисс, соответствует действительное число х,
точке Ру на оси ординат соответствует также действительное число у.
Эти числа называются координатами точки Р:х — абсциссой, ay—
ординатой (рис. 9). Каждую пару действительных чисел можно рас-
сматривать как координаты некоторой точки на плоскости. Чтобы
построить точку по ее координатам х0 и yQ,' надо отложить числа
и Ув соответственно на оси абсцисс и оси ординат, а затем из этих
точек провести перпендикуляры к соответствующим осям. Точка
пересечения перпендикуляров и есть искомой.
Координаты точек плоскости записывают в такой последователь-
ности — сначала абсцисса, затем ордината: Р (х0; у0). Если на плос-
Ун л				Р(х;у)
ГУ		
		-
0		
Рис. 9. Координаты точки Р на плос-
кости хОу.
X п	I
0 Ш	V ff
Рис. 10. Квадранты 7, 77, 777, IV
координатной плоскости хОу.
кости выбрана система координат, то между ее точками, и множеством
пар действительных чисел существует взаимно однозначное соот-
ветствие.
Координатные оси разбивают всю плоскость на четыре части,
которые имеют название квадрантов. Каждый из квадрантов явля-
ется прямым углом с вершиной в начале координат. Квадранты нуме-
руют так, как показано на рис. 10. В каждом квадранте знаки коор-
динат точек не изменяются. Эти знаки такие: в. I квадранте — (+; +),
во II - (-; +), в III - (—; —), в IV — (+; -)<
Полярная система координат
Полярные координаты точки на плоскости — это два чис;ла, кото-
рые определяют положение этой точки.относительно некоторой фикси-
рованной точки О (полюса) и некоторого фиксированного луча Ор
(полярной оси). Первая координата р точки М (р; ср) — полярный
радиус — определяет расстояние точки от полюса: ОМ = р; вторая
координата ср — полярный угол — угол, на который надо повернуть
ось Ор в положительном или отрицательном направлении до совпа-
дения с лучом ОМ (рис« 11). Полярный угол считается положитель-
ным при отсчете от полярной оси против часовой стрелки и отрица-
тельным — при отсчете в противоположную сторону.
Если в полярной системе координат условимся длину полярного
радиуса считать неотрицательной (0< р < оо) и полярный угол брать
2 8-413
33
в интервале 0<ф < 2л, то этим устанавливается взаимно однознач-
ное соответствие между точками плоскости и полярными координа-
тами (р; ф), за исключением полюса, который конкретного полярного
угла не имеет. Это соответствие удобно иметь в виду при решении
задач на построение отдельных точек на плоскости, определение рас-
стояния между двумя точками, деление отрезка в заданном отноше-
нии и др*
При исследовании функций и построении их графиков часто
полярный радиус принимает отрицательные значения, а полярный угол
принимает значения, большие 2л или отрицательные. Например,
2	V 3
в функции р » sin 2ф при ф = — л полярный радиус р =----------*»
в функции р = 2ф угол может принимать произвольные значения*
Во многих задачах приходится
рассматривать значения полярного
угла ф и полярного радиуса р от
—оо до 4~оо. Отрицательные зна-
Рис. 12. Построение точки в поляр-
ной системе координат.
Рис. 11. Полярные координаты
точки Af.
чения ф откладывают от полярной оси по часовой стрелке, а отри-
цательные значения р — на продолжении луча OQ с другой стороны
от прлюса* Тогда значения ф между 0 и 2л или между —л и +л
называют главными. В этом случае произвольная пара координат (р; ф)
определяет на плоскости только одну точку, а одной точке плоскости
соответствует множество пар чисел. Действительно, при изменении ф
от —оо до + оо луч может бесконечное число раз занимать одно
и то же положение, например луч OQ при ф — а, а + 2л, а + 4л,
. . * , а + 2kл, ,. f , где k — целое положительное или отрицательное
число, занимает одно и то же положение (рис. 12)* Точка на луче
с полярным радиусом р = а может быть определена одной из пар
координат
(а; а), (а; а + 2л), *.. , (а; а + 26л), *.»
Это следует иметь в виду и при построении графиков функций,
заданных в полярной системе координат.
Переход от декартовых координат к полярным и наоборот выпол-
няется по формулам
X = р COS ф,
У = р sin ф
и	_______
р =	+ у2,
Ф = Arctg = Arcsin ~ (х =# 0),
34
где х, у—декартовы координаты произвольной точки М (х; у),
а р, ф — ее полярные координаты. Здесь декартова система коорди-
нат выбрана так, что ее начало О совпадает с полюсом полярной
системы, а ось абсцисс Ох — с полярной осью.
Преобразования декартовой системы координат
Известно, что положение точки на плоскости определяется двумя
координатами относительно некоторой системы координат. Коорди-
наты точки изменятся, если выберем другую систему координат.
Задача преобразования координат и заключается в том, чтобы, зная
координат, определить ее коор-
координаты точки в одной системе
динаты в другой системе.
Перенос начала координат. При
этом преобразовании изменяется
начало системы координат, а на-
правление осей и масштаб остают-
ся неизменными. Пусть имеем две
системы координат с разными нача-
лами О и Of и одинаковым направ-
лением осей (рис. 13). Обозначим
через а и & координатй нового на-
чала Of в старой системе коорди-
нат и через х, у и х', у' — коор-
динаты произвольной точки М со-
ответственно в старой и новой си-
стеме. Тогда старые координаты х
и у произвольной точки М через ее
новые хг и у' выразятся формулами
Я У'
Рис. 13. Перенос начала координат.
х= а + х',

где ОА = a, OB = х, АВ = х', АО± — bt ВМ = у, В'М — у' (см.
рис. 13), а новые координаты точки через ее старые — формулами
х' = х — а,
у' = у —£•
Поворот координатных осей. При этом преобразовании начало
координат и масштаб ье изменяются, но оси поворачиваются на один
и тот же угол.
Пусть М — точка на плоскости с координатами х и у в старой
системе координат (рис. 14) и пусть новая ось Ох' образует со ста-
рой осью Ох (так же, как и ось Оу' с осью Оу) угол а. Угол пово-
рота отсчитывается в направлении, противоположном движению часо-
вой стрелки. Координаты точки М в новой системе координат
обозначим через х' и у'.
Старые координаты произвольной точки М через ее новые коор-
динаты при повороте осей на угол а выразятся формулами
х = х' cos а — у' sin а,
у = х' sin а + У' cos а-
2*
35
Здесь О А = х, OB = х't AM —у, МВ = у’. Новые координаты
точки М через старые выразятся так:
Xх — х cos а + у sin а,
у' = х sin а + У cos а.
Общий случай (перенос начала и поворот осей координат). Объе-
диняя формулы переноса начала координат и формулы поворота осей
координат, получаем формулы общего преобразования координат,
которое включает как частные случаи параллельный перенос (при
а = 0) и поворот осей (при а — b — 0):
х — х' cos а —4/' sin а + а,
у = х' sin а + / cos а -|- Ь.
Заметим, что эти формулы — линейные относительно х' и у', т. е.
имеют общий*вид:
х — Ах' + By' + £»
у = А±х' + В±у' 4- С±.
Новые координаты х', у' выразятся через старые х, у так:
х' = (х — a) cos a -f- (у — b) sin а,
у' = — (х — a) sin а + (у — b) cos а.
Эти формулы также линейны относительно х, у.
§ 2. Исследование функции
в декартовой системе координат
Область определения функции
При табличном способе задания функции к области ее опреде-
ления относятся^ все значения х, указанные в таблице. При этом для
промежуточного’ значения х, которого нет в таблице, функция может
быть и не определена. Следует заметить, что при табличном способе
задания функция может быть задана и для всех значений х, которые
36
находятся между двумя крайними числами в таблице. При этом дол-
жен быть указан способ определения для произвольных промежуточ-
ных значений х (чаще всего таким способом является линейное интер-
полирование).
При графическом способе задания функции область определения
очевидна из графика, а при словесном — из словесного определения
данной функции.
При аналитическом способе задания функции область определе-
ния функции находят как множество всех значений х, при которых
формула, определяющая функцию, имеет смысл. Часто такую область
определения функции называют естественной. Дополнительные усло-
вия могу г уменьшить естественную область определения функции.
Областью определения функции может быть множество отдель-
ных точек. Так, например, функция f (х) = V—(х — 1)? областью
определения имеет только одну точку х= 1. При аналитическом спо-
собе задания функции может случиться, что выражение для-функции
содержит дробь, знаменатель которой превращается в нуль при
определенном .значении х, или корни четной степени из отрицатель-
ного выражения и др. Чтобы найти область определения функции
в таких случаях, надо отбросить все значения х, для которых зна-
менатели дробей, входящих в выражение для функции, превращаются
в нуль, и все значения х, для которых подкоренные выражения
четной степени отрицательны. Заметим, что при исследовании области
определения функции не рекомендуется осуществлять преобразования
в формуле, которой задана функция.
Рассмотрим некоторые примеры на отыскание области определе-
ния функции.
Пример!.
Выражение 4 — х? принимает действительные значения, если
4 —х2>0, т. е. если | х |< 2. Но при х= ±2 знаменатель дроби
равен нулю, дробь теряет смысл, а потому значения +2 не могут
входить в область определения функции. Функция определена только
при | х| <2. Область определения: ] —2; 2 [.
Пример 2.
г/ х	. 4х
/ (х) = arcsin .
Область определения функции у = arcsin х есть совокупность
значений |х|< 1. В данном примере отыскание области определения
сводится к решению неравенства
I—1<1-
|2 + хПь. >
Имеем
Г 4х < 2 + х,
( —2 — х < 4х,
-22	Г 2
откуда х , х > —=-. Область определения: —j=- ;
о	О	[ О
2_]
3 ]
37


Пример 3.
f (х) = 3 + ]/ lg cos x. *
Функция имеет смысл, если подкоренное выражение существует
и неотрицательно: Igcosx^O, отсюда cosx^> 1; но cosx не может
быть большим единицы, следовательно, возможен только случай
cos х — 1, тогда х — 2kn (k 6 Z). Область определения заданной функ-
ции — множество точек х = 2kn (k £ Z).
П р и ме р 4.
f W = logs log« logs X.
Чтобы функция f (х) была определена, должно выполняться
неравенство
log4 log5 х > О,
отсюда log5 х > 1 и х > 5. Область определения: ] 5; оо [.
Пример 5.
;«=4+загс51п"-Гд7=.
*	у х —2
Заданная функция определена, если одновременно выполняются
следующие неравенства:
я ¥= 0, —1 < х < 1 и х > 2.
Неравенства — 1 х 1 и х > 2 несовместимы, потому функция
не определена ни при каком х.
Пример 6. Функция f (х) определена на отрезке [0; 1]. Найти
область определения функций: a) f (4л2); б) /(tgx).
а)	Введем вспомогательный аргумент t = 4х2. Тогда функция
/ (4х2) — f (/) определена, если	т. е. 0<4х2<1, отсюда
---< х < • Область определения функции f (4х3): £--------; -i- j •
б)	Введем вспомогательный аргумент f = tgx. Тогда функция
f (tg *) = f (0 определена, если 0 < t < 1, т. е. 0 < tgx < 1, отсюда
kn х — + kn (k С Z), Область определения функции f (tg х): kn <
< х <	+ kn (k С Z).
Область значений функции. График ограниченной функции
Область значений функции Е (/) — это множество значений функ-
ции, которые она принимает при всех значениях аргумента из области
определения ее (см. рис. 4). Область значений функции может состоять
из отдельных точек, одной точки, одного или нескольких интервалов
и т. д. Очевидно, что для ограниченной функции область ее значений
не может быть неограниченным множеством, а для неограниченной
функции — ограниченным. Например, для неограниченной функции
у = х4 область значений функции — [0; оо [, а для ограниченной
функции у —cosx сбласгь значений — отрезок [—1; 1].
38
При табличном и графическом способах задания функции области
з тений очевидны. Для отыскания области значений функции, задан-
ной аналитически: у = f (х), надо найти все значения у, при которых
уравнение f (х) = у имеет действительные решения.
Если общее решение уравнения f (х) = у можно записать в виде
х = F (у), то для отыскания области значений функции f надо найти
мужество тех у, для которых выражение F (у) имеет смысл.
Если функция задана на нескольких интервалах и по-разному
на каждом из них, то исследуют значения такой функции на каж-
дом интервале.
Иногда для отыскания области значений функции удобно при-
менить другой способ, а именно вычислить lim f(x). Этот способ
Х->+ ОО
часто применяют, когда рассматриваемая функция является дробно-
линейной.
Во многих случаях найти область значений функции нелегко.
Тогда выполняют возможные исследования функции, строят график,
а после этого область значений функции становится очевидной.
Если известна область значений функции, то легко указать воз-
можные наибольшее и наименьшее значения, которые принимает эта
функция.
График ограниченной функции (| f (х) |< М) находится в полосе
между прямыми, параллельными оси абсцисс, проведенными на рас-
стоянии М от нее.
График функции, ограниченной снизу (/(х) >/и), расположен
выше прямой, параллельной б£и абсцисс, проведенной на расстоянии tn
от нее.
График функции, ограниченной сверху (f (х) < М), расположен
ниже прямой, проведенной параллельно оси абсцисс на расстоянии М.
Так, например, график функции у = sin х находится между прямыми
у = —1 и t/= 1, так как | sin х| < 1. Функция у = ах ограничена
снизу (ах > 0), и ее график находится над осью абсцисс. Функция
У = —х2 ограничена сверху ~ х2 < 0 j , и ее график лежит под
осью абсцисс.
Рассмотрим некоторые примеры на отыскание области значений
функции.
Пример 7. Найти область значений функции
х2 — 1
у ~ х2 — 3 •
Решив это равенство относительно х, получим
Х= + /Е/.
~ Г у— 1
ОI сюда следует, что действительным значениям х соответствуют
только те значения у, для которых ——- 0. Решив это неравен-
У' *
ство, получим у < — и у> 1, т. е. областью значений функции
О
39
является — оо; — I (J ] 1; оо [. Выданном случае функция не огра-
ничена сверху, так как область значений содержит интервал ]1; оо(,
и не ограничена снизу,- так как область значений содержит
1 1 1
J °°; з]’
Пример 8. Найти область значений функции
у = х2 — 4х + 7-	-
Преобразуем квадратный трехчлен х2 — 4х + 7, выделив из него
полный квадрат:
!/=(х-2)2+3.
Выражение {х — 2)2 принимает все неотрицательные значения, а потому
областью значений заданной функции является множество #>3.
Эта функция не ограничена сверху.
Пример 9. Найти область значений функции
3
у ~ 1 — хг 
Решив это равенство относительно х, получим
Область значений функции у определяем из соотношения
^-3>0 (!/¥=0).
У
Область значений функции: ] —оо; 0 [ (J [3; оо [. Область опре-
деления функции: ]—оо; —1 [ (J ]—h 4U]U'°°[- Чтобы найти
область значений функции на каждом из интервалов области опреде-
ления функции, учтем, что для х, для которых х2 < 1, функция
отрицательна, а для х, для которых х2 < 1, функция положительна.
Интервалу ]—Г, 1[ области определения функции соответствует
[+3; оо [ области значений функции. Если у < 0, а х =	,
то Vt/ 6 ]—оо; 0[ будут соответствовать два значения х. Интервалам
]—оо; —1 [ и ] 1; оо [ области определения функции будет соответ-
ствовать интервал ]—оо; 0[ области значений функции.
Пример 10. Найти область значений функции
Для отыскания области, значений заданной функции решаем
X “1	J-Г	У + 1
равенство у =	। относительно х. Получаем х =	—- • Отсюда
40
у . Область значений функции: J — оо; — (J 00 |_* Поль-
зуясь другим способом, находим
lim у — lim = _L .
х->±со	х~* ± со 2х 1	2
 Область значений:
Значения у = -i надо исключить из области значений функции.
1 f II [ 1 • Г
т[и|у; “Г
Четность и нечетность функции.
Особенности графика четной и нечетной функций
Четность или нечетность функции проверяем, исходя из опреде-
ления четной и нечетной функций (см. § 2 разд. 1).
П р и м е р 11.
f (х) =	4 — х2.
Функция определена на множестве |х| <:2, симметричном отно-
сительно начала координат, и
7 (-х) = /4-(-х)2 = ]/4^2 = f (х) для Vx € [-2; 2J.
Следовательно, / (х) = ]/ 4 — х2 — четная функция.
Пр и м е р 12.
f (X) = logo (х 4-	1 + х2) (а #= 1, а > 0).
Функция определена на множестве ]—оо; оо [, симметричном
относительно начала координат, и
f (— X) — loga (—X + V 14-Х2) = loga ——^==== =
= —loga (х + V 1 + X2) = — f (X),
т. е. выполняется равенство f (—х) = — f (х) для Vx С ] —00; оо [.
Функция нечетная.
П р и м е р 13.
/(x) = logax.
Функция4 определена на несимметричном множестве ] 0; оо [*
Следовательно, из определения четности и нечетности функций делаем
вывод, что данная функция не может быть ни четной, ни нечетной.
График четной функции — кривая, для которой ось Оу является
осью симметрии. График нечетной функции—кривая, для которой
начало координат является центром симметрии.
Эти особенности графиков четной и нечетной функций позволяют'
сократить процесс построения графиков таких функций,_а именно:
достаточно начертить график функции в той части области опреде-
ления, которая соответствует положительным значениям аргумента,
41
а затем продолжить этот график симметрично относительно оси Оу,
если функция четная, и симметрично относительно начала координат,
если функция нечетная (рис. 15).
Пример 14. Продолжить функцию
f (х) = 4х5 + х1 — 6 sin х, х > О,
на всю числовую ось так, чтобы получить нечетную функцию.
Пус гь х < 0. Тогда
7 (—х) = 4 (—х)5 + (—х)2 — 6 sin (—х) = —4 х5 + х2 + 6 sin х.
Рис. 15. Графики четной (а) и нечетной (б) функций.
Так как надо получить нечетную функцию, то будем требовать,
• чтобы при х < 0 выполнялось равенство
/ W = —/ (—X),
т. е.
f (х) = —/ (—х) = —(—4х5 + х2 + 6 sin х) = 4х5 — х2 — 6 sin х.
Следовательно, искомая функция будет иметь вид
(4х5 + х2 — 6 sin х, если х > 0,
'	— 14х5 — х2 — 6 sin х, если х < 0.
Виды симметрии. График обратной функции
Симметрия графика функции у — f (х) относительно вертикальной
о?и х = х0. График функции у — f (х) симметричен относительно
вертикальной оси х = хэ, если
f («0 - X) = f (Хэ + X)
42
для всех х из области определения функции f (х). В частности, гра-
фик четной функции симметричен относительно оси ординат (х0 = 0).
Пример 15. Определить, относительно какой вертикальной оси
симметричен график функции
у = ах2 + Ьх + с.
Из условия симметрии имеем
—2axxQ — bx = 2axxQ + Ьх.
„	b	b
Отсюда х0 = —	, т. е. х = —	— ось симметрии.
Пример 16. Определить вертикальную ось симметрии графика
функции
1 4.	1
У № + (1—X)?'
Записываем условие симметрии!
1	,	1	=	1	, I
(х0 — х)2 "r (1 — х, + х)2 (хэ + х)2	(1 — х3— х)4 •
Отсюда, считая, что знаменатели не равны нулю, имеем
х0 [(1 — 2х0)2 +2(1— 2х0) (ху — х2) + (х2 - х2)2]=э
= (1-Хо) (*о-х2)2.
(Ху — X") Ху = 1 — Ху,
Ху — X2 2ху (1 — 2х0) = 0,
(Ху — х2)0 х0 (1 — 2х)2 = 0,
1 •
х° - т •
„ 1
Следовательно, х = -% — ось симметрии.
Пример 17. Определить вертикальную ось симметрии графика
функции	*
у = а + Ь cos х.
Записываем условие симметрии:
а + b cos (х0 — х) = а + b cos (х0 + *)>
cos х0 cos х + sin Xq sin x ~ cos Xq cos x — sin Xq sin X.
Отсюда получаем
Sin Xq = 0, Xq — kit (k £ Z),
следовательно, x — kre (k 6 Z) — оси симметрии.
Симметрия графика функции у = f (х) относительно точки
(хс; .У»,)* Точка М (хс; г/0) является центром симметрии графика функ*
43
цпи у = f (х), если для всех х, принадлежащих области ее определения,
выполняется тождество
у о == у [/ (х0 — х) + f (х0 + X)]. .
В частности, график нечетной функции симметричен. относительно
начала координат 0(0; 0).
Пример 18. Определить центры симметрии графиков функций:
а) у = ах + Ь\ б) у =	; в) у = ах3 + Ьх* + ex-}- d.
а)	Записываем условие симметрии:
2у0 = а (х0 — х) + b + а (х0 + х) + Ь.
Отсюда ,уп=ах0 + &, где х0 — произвольное. Точка М (х0; ах0+&)—
центр симметрии графика функции у = ах 4- Ь.
б)	Из условия симметрии
___ах0 + 6 — ах * ах0 + & + ах
*	сх0 + d — сх ‘ сх0 + d 4- сх
получаем
2t/0 [(с*о + d)2 — с2*2! = 2 (ахо + ь) (схо + Ф ~ 2асх*.
Приравниваем коэффициенты при одинаковых степенях х:
х21 — 2yQc2 = — 2ас,
х° I 2yQ (cxQ + d)2 = 2 (ах0 + b) (сх0 + d).
а	d k / d а\
Отсюда находим, что у0 = — , хп =------, т. е. точка М[----— —
с	с	\ с ’ с /
.	,	ах + b
центр симметрии графика функции у = д •
в) Условие симметрии:	_
2у0 == а (х0 — х)3 + b (х0 — х)2 + с (х0 — х) + d 4-
+ а (х0 + х)3 + b (х0 + х)2 + с (х0 + х) + d,
отсюда
у0 = ахр + ЗаХрХ2 + Ьх2 + Ьх2 + сх0 + d.
Приравнивая коэффициенты при одинаковых степенях х, находим
х0 = — ~ г Уо— ахо +	-J- сх0 4” d.
Точка М ; ахр4~ Ьх% + сх0 4-	— центр симметрии графика
функции у = ах3 4- Ьх2 + сх 4- d.
При исследовании функций надо иметь в виду следующие поло-
жения.
1.	Если график функции у = f (х) (—оо < х < оо) симметричен
относительно двух вертикальных осей х— а и х = Ь (Ь > а), то функ-
ция f (х) — периодическая, ее период 2Ь — 2а.
44
2.	Если график функции y—f(x) (—00 < х < оо) симметричен
относительно двух точек A (a; t/0) и В (Z?; t/J (b > а), то функцию
f (х) можно изобразить в виде суммы линейной функции и некоторой
периодической функции с периодом 2Ь — 2а. В частности, если
yQ = ylt то функция f (х) — периодическая.
3.	Если график функции у = f (х) (—оо-< х < оо) симметричен
относительно точки Л (a; t/0) и прямой x — b (Ь=£а), то функция
f (х) — периодическая с периодом 4Ь — 4а.
График обратной функции. Если независимую переменную у в об-
ратной функции х — f~x (у) откладывать по оси Оу, а значения функ-
ции х = f~l (у)— по оси Ох, то гра-
фик обратной функции будет совпа-
дать с графиком прямой функции
У = f W-
Гис. 17. Графики функции у = 2х —-1
X _1_ 1
(/) и обратной ей у =	— (<?); ось
симметрии у = х (2).
Рис. 16. Построение точек двух
взаимно обратных функций.
Обозначим независимую переменную в обратной функции буквой х,
а обратную функцию — буквой у, т. е. вместо функции х = f"1 (у)
будем рассматривать функцию у = ср (х). Заметим, что обратная функ-
ция z/ = cp(x), когда х пробегает точки множества Y, и функция х=*
= Г1 (У)> когда у £ У, те же, так как у них одинаковые область опре-
деления и закон соответствия.
Чтобы построить график обратной функции t/ = (p(x), надо гра-
фик прямой функции у = f (х) симметрично отобразить относительно
биссектрисы первого и третьего координатных углов.
Действительно, допустим, что при х == а, у — f (а) = b точка
М (а; Ь) принадлежит графику прямой функции, а точка М' (Ь\ а) —
графику обратной функции, так как а — ср (Ь). Имеем (рис. 16)
A ON'M' = A ONM, отсюда ^N'OM' = /_NOM и ОМ' — ОМ,
тогда биссектриса OR координатного угла является биссектрисой
/_МЭМ', и так как А МОМ' равнобедренный, биссектриса OR явля-
ется осью симметрии Д МОМ'. Следовательно, каждой точке М на
графике прямой функции соответствует точка М' на графике обратной
функции, симметричном .относительно биссектрисы первого и третьего
координатных углов’ графику прямой функции.
Пример 19. Найти функцию, обратную функции у=2х—1,
и построить ее график.
45
Находим из заданного уравнения х:
Х-У±1
Х 2 •
Заменяя в этом равенстве х на у, а у на х, получаем
Графики заданной функции и обратной ей показаны на рис. 17.
Замечание. График обратной функции можно построить еще
так: сначала построить график функции у = f (—х) (симметричным
отображением относительно оси Оу), затем этот график повернуть на
90° относительно начала координат по часовой стрелке.
Периодичность функции. График периодической функции
Установление факта периодичности функции существенно облег-
чает ее изучение и построение графика: периодическую функцию
можно исследовать в пределах одного периода. Для построения гра-
фика периодической функции с периодом со достаточно построить
график этой функции на интервале ] х; х+со[, а затем полученный
график периодически продолжить. Периодическим продолжением задан-
ной функции f (х) с периодом со, определенной на некотором отрезке
[а; Ь] или на интервале ] о; Ь[, называется построение такой перио-
дической функции F (х) с периодом со, которая совпадает с заданной
функцией f (х) на [о; Ь] или на ] а; b [.
Рассмотрим некоторые примеры на установление периодичности
функции.
П р и м е р 20.
f (х) = sin 4х.
Существует ли такое со =/= 0, чтобы для всех действительных х
(область определения заданной функции — вся числовая ось) выпол-
нялось условие sin 4’ (х + со) = sin 4х?
Имеем
sin 4 (х + со) — sin 4х — 0,
или
2 cos (4х 4- 2со) sin 2со = 0,
что может выполняться при sin 2со — 0; тогда 2со = kit (k £ Z). Сле-
довательно, такие значения со существуют, функция является перио-
и	и	U	Л
дическои, наименьший положительный ее период .
Пример 21.
Y
f(x)= 1-tgy.
Функция периодическая с периодом со = 2л, так как
l-tgy= l-tg^y + 4= 1 — tgy (х+2л).
46
Пример 22.
f W = 1 + tg у + cos j .
имеет период сох = 6л, так как
1	X
Функция cos —
cos ~ — COS ( ~ + 2л ) = COS (Х + 6л).
о \ о /	3
Функция tg-^- имеет период со2 = 5л, так как
э
. X I I Х ,	\	11/. гч
. tg -5 = tg ^-5 + ftj = tg -5- (X + 5л).
Период заданной функции / (х) — наименьшее кратное чисел 6я и 5л,
т. е. со = 30л.
Пример 23,
f (х) = a sin (ах + 0) (а^ 0),
где а, а, 0 — постоянные числа.
Эту функцию часто называют гармоникой. Покажем, что она
2л
периодическая и ее периодом является со = — , т. е. для всех х вы-
/	2л\
полняется равенство f х -]-I = f (х). Действительно,
a sin (ах + 0) = a sin [{ах + 0) + 2л] = a sin а (х + — j + 0J ;
2л	.	/
 можно доказать, что число — является и наименьшим положитель*
а
ным периодом.
Пример 24. Докажем, что функция
f (х) = sin х2
непериодическая.
Допустим обратное: пусть существует такое число со =# 0, что
при всех значениях х справедливо равенство sin х2 = sin (х + со)2.
Положив х = 0, будем иметь 0 = sin со2. Но тогда со2 = пл (п С Z),
следовательно, со = Упп. Подставив это значение со в равенство
sin х2 = sin (х + со)2, получим
sin х2 = sin (х + Vпп)2 = sin (я2 + 2х ]/пл + ля)*
Пусть
, 26л — пл . л „
X — , —- , где k g Z,
2 у пп
тогда
2х ]Л пл -р- пл #= 26л
и, следовательно,
sin х2 #= sin (х2 + 2х )Лпл + пл),
47
Пришли к противоречию. Это и доказывает, что f (х) = sin х2 — не-
периодическая функция.
П р и м е р 25.
f (х) = cos4 х + sin4 х.
Имеем
f (х) = cos4 х + sin4 х = (sin2 x + cos2 x}2 — 2 sin2 x cos2 x ==
.	1	. 9 л , -v i / «	л \	3	.	1	.	/ .	, Л \
= 1------ sin2 2x = 1 — — (1 — cos 4x) = — 4- sin 4x 4- — L
2	4	4	4	\	2 /
~	2л л
Отсюда co = —- = — t
4	2
Замечание. Используя свойства периодических функций
(см. с. 19), можно в примерах 20—23 сразу записать 'периоды за-
данных функций.
Пример 26. Продолжить функцию
/ (х) = 3х, 0<х<4,
четным способом на отрезок [—4; 0], а затем периодически продол-
жить полученную функцию на всю ось с периодом со = 8.
Продолжим функцию f(x) = 3x четным способом на отрезок
[—4; 0], при этом должно выполняться условие
Дх) = /(-х) = 3*.
Четное продолжение будет иметь вид:
(3*, 0<*<4,
' w { 3”*, — 4<х<0.
Так как функция имеет период со = 8, то для всех %, дня которых
выполняется условие
8k < х < 8k + 4,
имеем
/ (х, = f (х — 8fc).
Так как 0<:х — 8k < 4, то f (х) = f (х — 8k) = 3x~8k. Аналогично
находим, чго при 8& —4<х<8£
f (х) = f (х - 8k) = 3-<x~8k\
Следовательно,
f, у _ ( 3*~8/г, если 8k < х < 8k + 4,
' ' ~ I 38/г“\ если Еk — 4 < х с 8k.
Нули и знаки функции
Нулем функции называется то действительное значение х, при
котором значение функции равно нулю.
Геометрический смысл понятия нулей функ-
ции. Нули функции — это абсциссы точек, в которых график функ-
ции пересекает ось Ох или касается ее. При переходе через эти
точки функция может менять знак (рис. 18). Заметим, что функция
48
может менять знак и при переходе через точку разрыва. Есйи гра-
фик только касается оси Ох, то в точке касания функция знака не
меняет*
Для того чтобы найти нули функции f (х), надо решить уравне-
ние f (х) — 0. Действительные корни этого уравнения и есть нулями
функции у = f (х). Допустим, что решениями уравнения f (х) = 0
являются хь х2, Х3,	, хл, т. е. нулями функции y=f(x) явля-
ются xlt х2, х3, 4 4 , хп. Они разбивают область определения функ-
ции /(х) на части, причем на каждой из этих частей функция опре-
делена и не превращается в нуль.
Интервалы, где функция не имеет ни нулей, ни точек разрыва,
т. е. знак функции не меняется, называют интервалами знакопо-
стоянства.
Чтобы определить знак функ-
ции для всех точек интервала зна-
копостоянства, достаточно опреде-
лить знак функции в произволь-
ной точке этого интервала (проще
всего вычислить значение функции
в какой-либо конкретной точке).
Если область определения функции
состоит из нескольких интервалов
знакопостоянства, то исследование
знаков функции проводится отдель-
Рис. 18. Нули функции у= f (х): хь
х2, xs, х4. На интервалах ]х,; xf[,
]*з; х4[ функция отрицательна, на ин-
тервале ]х2; х3[ —положительна.
но на каждом интервале.
Пример 27. Найти интервалы знакопостоянства функции
1 v 1 х— 4
Область определения этой функции: ]— оо; 4 [(J] 4; оо[4 Опре-
делим точки, где’ функция превращается в нуль. Для этого прирав-
няем нулю числитель:
х2-5х + 6 = 0,
откуда х± = 2, х2 — 3. Исследование знаков функции будем прово-
дить на таких интервалах:	- v
]_ оо; 2[, ]2; 3[, ] 3; 4[, ]4; оо[.
В каждЪм из этих интервалов берем по конкретной точке. Напри-
мер, рассмотрим в каждом интервале соответственно точки
Исследуем знаки в этих точках. Получим соответственно следующие
знаки в каждом из интервалов:
«—», «+», «—», «+».
Нули функции: х=2, х=3. Интервалы знакопостоянства:
]—оо; 2(, ]2; 3[, ]3; 4[, ]4; оо[.
49
Пример 28. Исследовать знаки функции
/х2 —2—/3 + 2х
/З^х- 1
Функция определена при выполнении условий
х2 — 2>0, 3 + 2х>0, 3 —х>0,
У 3 _ х — 1 =£ 0.
О	_ I	_
— ; — У2 , [У2; 2[, ]2; 3]. Ищем нули
Область определения:
функции. Для этого приравняем числитель нулю:
-2 — /з+ 2х = 0, х2 — 2 = 3 + 2х,
х2 —2х —5 = 0, Хх=1 —j/б, х2=1+Уб.
Следовательно, нулями функции являются точки 1 — ]/б, 1 + ]/б5
из них лишь цервая входит в область определения функции. Учи-
тывая это, область определения функции разбиваем на следующие
промежутки:
[—	1-/б[, ]1 - Уб; - /2], {/2; 2[, ]2; 3].
Исследуем знаки функции в этих промежутках, не вычисляя ее зна-
чений в конкретных точках. Для этого преобразуем формулу, кото-
рой задана функция:
С,'Л /х2-2- /з+"2х _ /х2 — 2- Уз + 2х „
/ (х) — г. . . —	—	...—	X ~
Уз — х — 1	|/ 3-х- 1
/^2 + /3~+2^ . 	Уз~=~х+ 1	=
/З-х+1	]/х2-2+ Уз~+2х
_____Уз^х+ 1-	. х2 — 2 — (3 + 2х) = х2 —-2х — 5
“ У х2 - 2 + У 3 + 2х ’	3 —х—1	~	2-х
х /3^+1
Ух2 — 2+ Уз + 2х '•
Второй сомножитель в этом произведении в области определения
функции положителен, а знак первого сомножителя исследуем.
Имеем
в [—у: 1 —/6 «+»
» ]1- Уб; — /2} «—»
•	» [У2; 2[	«—»
» ]2; 3]	«4~»
50
Монотонность функции
Монотонность функции — одна из важных характеристик функ-
ции. При исследовании функции надо уметь находить интервалы ее
монотонности. Чтобы найти эти интервалы, можно воспользоваться
таким утверждением: если функция строго монотонна на [a; Ь]> то
она каждое свое значение принимает только при одном значении х.
При элементарном исследовании функций на монотонность поль-
зуются преимущественно определением монотонности и основными
свойствами (см. с. 16).
Пусть из уравнения f (х) =у имеем несколько однозначных вы-
ражений х через у.
х = Ф1 (у), х = ф2 (у), . . . , х = фл (у)>
Если х С ]ц; Ь[, то каждому значению f (х) = у соответствует только
одно значение х из ]а; Ь[, а именно ф; (у) (i ~ 1, 2, ; <. , /г). Чтобы
найти все интервалы монотонности/надо определить все интервалы,
которые являются областями определения функций фх (у), ... , фЛ (#)♦
Если функция монотонна на отрезке [а; д], то
а)	когда она положительна и возрастает, ее график отклоняется
от оси Ох с возрастанием х;
б)	когда она положительна и убывает, ее график приближается
к оси Ох с возрастанием х;	<
в)	когда она отрицательна и убывает, ее график отклоняется от
оси Ох (вниз) с возрастанием х;
г)	когда она отрицательна и возрастает, ее график приближается
к оси Ох с возрастанием х.
Пример 29. Исследовать на монотонность функцию
f (X) = X3 + X.
-Функция определена для всех точек числовой оси. "Возьмем на
числовой оси произвольные точки Xj и х2. Пусть х2 > хх. Рассмотрим
разность
f М — f (Xj) = (X. — Xi) (Х1 + XjX2 + х2 + I).
Второй множитель при любых действительных значениях хх и х2 по-
ложителен. Действительно'
i	\2 о
Хх + ХХХ2 + Xj + 1 = ^Хх +	+ -4“
Так как х2 — хх > 0, то f (х2) — f (х£) > 0, т. е. f (х2) > f (хх), а это
означает, что функция f (х) возрастает во всей области своего опре-
деления.
Пример 30. Исследовать на монотонность функцию
f (х) = (х2 +’6х + 11) 1п(х? + 6х+ 11).
Пусть х2 + 6х + 11 = t. Функция у = t In t при t > 1 является
произведением двух возрастающих положительных функций (см. с. 17)
и потому возрастает. Функция t = х2 + 6х + 11 = (х + З)2 + 2 воз-
растает при х > —3 и убывает при х < —3. Поэтому (см. с. 17)
данная функция возрастает при х > —3 й убывает при х < —3.
Пример 31. Исследовать на монотонность функцию
х —3
y~x + 3’
51
Область определения данной функции: ]—оо; —3[ |J ]—3; оо[.
Представим х через у:
3(t/+0
Каждому значению у из области значений соответствует одно зна-
чение х из области определения функции. Функция монотонна на
каждом интервале ]—оо; —3[ и ]—3; оо[. Далее с помощью сравне-
ния значений функции в двух точках каждого интервала устанавли-
ваем, убывает или возрастает функция на соответствующем интер-
вале. Возьмем на первом интервале х = —4 и х = —5, значения
функции в этих точках будут: у = 7 и у = 41 Следовательно, на ин-
тервале ]—оо; —3[ функция возрастает. Аналогично, на втором
интервале возьмем х — 4 и х — 5, соответствующие значения функции
будут: -у- и Функция возрастает и на интервале ]—3; оо[.
Выпуклость функции
Рассмотрим функцию /(*), определенную на отрезке [а; 6].
Функция на этом отрезке выпуклая, если выполняется неравенство
для всех Xi и х2 € [л; 6] (рис. 19, а). Функция на отрезке [а;
вогнутая, если выполняется неравенство
fM + f(x2)>f
Ml + *2^
\ 2 }
для всех Xi и х2 € [а; &] (рис. 19, б).
Некоторые свойства выпуклых функций
1.	Произведение выпуклой (вогнутой) функции на положительное
постоянное число является выпуклой (вогнутой) функцией.
2.	Произведение выпуклой (вогнутой) функции на отрицательное
постоянное число является вогнутой (выпуклой) функцией.
52
3.	Сумма двух выпуклых функций является выпуклой функцией.
4.	Если f (х) — вогнутая и возрастающая функция, а х = ср (0—
вогнутая, то и сложная функция f (ср (0) является вогнутой.
5.	Если f (х) — вогнутая и убывающая функция, а х = q? (Z) —
выпуклая, то сложная функция f (ср (0) является вогнутой.
6.	Если f (х) — выпуклая и возрастающая функция, а х = ср (/) —
выпуклая, то и сложная функция f (ср (0) является выпуклой.
7.	Если f (х) — выпуклая и убывающая функция, а х = ср (0 —
вогнутая, то функция f (ср (0) является выпуклой.,
8.	Если у = f (х) и y = g(x)— взаимно обратные функции (в со-
ответствующих промежутках), то:
а)	если функция j (х) — вогнутая и возрастающая, то
g (х) является выпуклой и возрастающей;
б)	если функция f (х) — выпуклая и убывающая, то
g (х) является вогнутой и убывающей;
в)	если функция f (х) — выпуклая и убывающая, то
g (х) является выпуклой и убывающей.
9.	Вогнутая функция f (х) на [а; &], -отличная от постоянной, не
может принимать наибольшего значения внутри этого отрезка.
10.	Если функции f (х) и ср (х) — положительные и выпуклые, то
для того чтобы функция у = т-т-г была выпуклой, надо, чтобы
/ W
одна из этих функций была возрастающей, а другая — убывающей.
f (х)
11.	Если функция у= — выпуклая, а функция f (х) — от-
рицательная, выпуклая и возрастающая, то функция ср (х) является
положительной, вогнутой и возрастающей.
/ (х)
12.	Если функция // = -——'— вогнутая, а / (х) и ср (х) — вы-
Ф (х)
пуклые и отрицательные, то одна из рассматриваемых функции яв-
ляется возрастающей, а другая — убывающей.	।
13.	Если функция f (х)—выпуклая, то функция является
вогнутой (/ (х) =# 0).
14.	Если функция f (х) — положительная и выпуклая, то функ- -
функция
функция
функция
ция у = f (х) является выпуклой (п — натуральное число).
15.	Если функция y=\f(x)]n — выпуклая (п—натуральное
число), то функция f (х) является положительной и вогнутой. -
16.	Если функции f (х) и ф (х) — положительные, возрастающие,
вогнутые, то функция у = f (х) • ф (х) является положительной, воз-
растающей, вогнутой.
17.	Если функции f (х) и ф (х)— положительные, убывающие,
вогнутые, ю функция у ~ f (х) • ф (х) является положительной, во-
гнутой.
18.	Если функции f (х) и ф (х) — отрицательные, возрастающие,
выпуклые, то функция у = f (х) • ф (х) является положительной, во-
гнутой.
19.	Если функции f (х) и ф (х) — отрицательные, убывающие,
выпуклые, то функция у — f (х) • ф (х) является положительной, во-
гнутой.
20.	Если функция f (х) — положительная, убывающая, выпуклая,
а функция ф (х) — положительная, возрастающая, выпуклая, то функ-
ция у = f (х) • ф (х) является положительной^ выпуклой.
53
21.	Если функция f (х) — отрицательная, возрастающая, вогну-
тая, а функция ср (х) — отрицательная, убывающая, вогнутая, то
функция у = f (х) • ф (х) является положительной, выпуклой.
22.	Если функция /,(х) — положительная, возрастающая, выпук-'
лая, а функция ф (х) — отрицательная, возрастающая, вогнутая, то
функция у = f (х) • ф (х) является отрицательной, вогнутой.
23.	Если функция f (х) — положительная, убывающая, выпуклая,
а функция ф (х) — отрицательная, убывающая, вогнутая, то функция
у = f (х) • ф (х) является отрицательной, вогнутой.
24.	Если функция f (х) — положительная, возрастающая, вогну-
тая, а функция ф (х)—отрицательная, возрастающая, выпуклая, то
функция у = f (х) • ф (х) является отрицательной, выпуклой.
25.	Если функция / (х) — положительная, убывающая, вогнутая,
а функция ф (х) — отрицательная, возрастающая, выпуклая, то функ-
ция у = f (х) • ф (х) является отрицательной, выпуклой.
Применение этих свойств упрощает исследование функций на
выпуклость.
Пример 32. Исследовать на выпуклость функцию
f « = lg (-х2 + 5х-6).
Корни квадратного трехчлена: 2 и 3. Поэтому —х2 + 5х —6 > О
на интервале ]2; 3[, и функция / (х) = 1g (—х2 + 5х — 6) определена
на ]2; 3[. Функция 1 = —х2 + 5х—6 выпуклая. Функция f (х) =
= lg t возрастающая и выпуклая. Следовательно, и функция f (х) ==
= 1g (—*2 + 5х — 6) является выпуклой.
Исследовать кривую на выпуклость просто и удобно с помощью
методов высшей математики (к этим исследованиям вернемся ниже).
С помощью методов элементарной математики исследуют функцию
на выпуклость таким образом: определяют знак величины 4
в области определения функции. Если знак в области определения
изменяется, то область раскладывают на части, где выражение зна-
копостоянно. Если величина D положительная на рассматриваемом
интервале, то функция на этом интервале вогнутая, если же вели-
чина D отрицательная, то функция выпуклая.
П р"й м е р 33. Исследовать на выпуклость функцию
f (х) = ах2 + Ьх + с.
Рассматриваем выражение
[/	!	2
+
। 1 I “F" ^2 1 fl |2i2	12	1 2 J
+ &  2-----t + £j = а Y 1 + *2---2*	-- х1х2	2"Х2у “
О /	к П
= у (Х1 — хг) •
Из. последнего очевидно, что при а < 0 функция выпуклая, а ппи
а > 0 — вогнутая.
54
Пример 34. Для функции
f (х) = ах3 + Ьх2 + сх + d
О = (хг — х2)2 а (*! + х2) +	.
Следовательно,
D > 0, если	(х, + х2),
zS	ОIX
D < 0, если	~ (X! + х2).
п	<
На интервале —оо; —функция выпуклая, а на интервале
J	оа l
1 ь г
— — ; оо —вогнутая.
Точка графика, в которой изменяется направление выпуклости,
называется точкой перегиба. Касательная к кривой в точке перегиба
пересекает график, если она существует.
Характерные точки графика функции
К характерным точкам графика относятся:
точки пересечения графика с координатными осями;
предельные значения функции, т. е. ее значения на границе об-
ласти определения;
точки, в которых функция принимает экстремальные значения;
точки перегиба и др.
Рассмотрим коротко, как находят эти точки.
Точки пересечения графика с координатными
осями.
а)	С осью Оу: х — 0, у = f (0).
б)	С осью Ох: у = 0, а из уравнения f (х) = 0 находят х.
П р и м е р 35.
У logs (х + 8) — 1.
Точки пересечения с осью ординат:
х^О; у (0) = log2 (0 + 8) — 1 Iog2 8 - 1 — 3 —	2.
Имеем одну точку пересечения графика с осью Оу: (0; 2). Точки пе-
ресечения с осью Ох:
log2(x'+ 8) — 1 z=0, log2 (х + 8)	1,
x + 8j=2, х	—6.
Следовательно, график пересекает ось Ох в одной точке (—6; 0).
Предельные значения функции. Если область опре-
деления функции — отрезок, то предельные значения функции вы-
числяем, подставив в выражение для функции предельные значения
аргумента.
55
Если область определения функции — открытый промежуток, то
находят предел функции, если он существует, когда аргумент стре-
мится к предельному значению:
lim f (х),
х-*а
где а — абсцисса открытого конца промежутка. Этот предел может
быть конечным, а может случиться, что функция-стремится к беско-
нечности определенного знака.
На графике разный характер поведения функции у конца интер-
вала, где она определена, выражается так. Если в точке а функция
имеет бесконечный предел, то график функции прилегает к верти-
кальной прямой х*= а; при приближении х к а график неограниченно
отклоняется от оси Ох вверх или вниз в зависимости от знака
функции.
Если в точке а, не принадлежащей области определения, функ-
ция имеет конечный предел у0, то график функции при приближении
х к а приближается к точке плоскости с координатами (а; //0). Этот
факт будем изображать на графике с помощью стрелки на том конце
кривой графика, который лежит в точке с координатами (a; yQ).
Если предел (конечный или бесконечный) функции на конце
промежутка не существует, то построить график функции у этой
точки невозможно.
Пример 36. Исследовать предельные значения функции
- . Область определения функции: ]—- оо; 1[ (J ]1; оо[. Вычисляем
1 —
lim f (х) lim -------— == — оо,
X-»—<»	— оо 1  X
lim f (x) lim 1—== 2,
X-> 1	X-t-1 1 x
1 —
lim f (x) lim ---------—-{-co.
X->-|-co	X->4~oo	1 - X
П p и м e p 37.
f (x) = ]/ X — 1 - 2.
Область определения функции: [1; oo[.
Предельные значения функции:
lim Vх — 1 — 2 = оо,
со
f(l)=/T=l-2 = -2.
Точки экстремума. Для нахождения наибольшего (наи-
меньшего) значения функции иногда удобно преобразовать аналити-
ческое выражение, с помощью которого задана функция, так, чтобы
было легко определить наибольшее (наименьшее) ее значение, или же
воспользоваться замечаниями, что:
среднее арифметическое двух (или больше) положительных вели-
чин не меньше среднего геометрического этих величин;
56
сумма двух переменных положительных величин наименьшая, если
эти величины равны (при условии, что произведение их является
постоянной величиной).
Максимум функции — это ее значение в той точке, в которой
оно является наибольшим в любой достаточно малой окрестности
этой точки.
Минимум функции — это значение функции в той ее точке, в ко-
торой оно является наименьшим в любой достаточно малой окрест-
ности этой точки.
Максимум (минимум) функции означает, чю функция имеет' наи-
большее (наименьшее) значение сравнительно с ее значениями в до-
статочно близких соседних точках с обеих сторон.
Подробнее этот .вопрос рассмотрен в ч. II.
Пример 38. Найти точки экстремума функции
у^~^.,
4(х—1)	
Находим х:
4ху — 4у^=х2 — 6х + 9,
x2^(6 + 4z/)x + 4t/ + 9z=0,
х1( 2 = 3 4- 2у ± 2	+
В точках экстремума должно быть хх *= х2, а следовательно,
у2 + 2х/ = О,
откуда
£/1 = 0. Уг = ~ 2.
Соответствующие им значения аргумента:
-	!== 3, а?2 -— ~~ 1 •
Точки экстремума: (3; 0) и (—1; —2).
Асимптоты графика функции
При исследовании Характера поведения функции большое значе-
ние имеют исследование поведения f (х) при неограниченном возрас-
тании (по абсолютной величине) аргумента х, а также исследование
случаев неограниченного возрастания абсолютной величины значений
f (х) в конечной части области определения. Геометрически эти ис-
следования приводят к понятию асимптоты графика.
Прямая у;=1гх-\-Ь называется асимптотой кривой у f (х),
если расстояние от точки Р (х; f (х)), лежащей на кривой, до этой
прямой стремится к нулю при х->+ °° (х->— оо) (рис. 20).
,Различают горизонтальные, вертикальные и наклонные асимп-
тоты.
Кривая у f (х) имеет горизонтальную асимптоту у~Ь, если су-
ществует конечный предел функции f (х) прих->-роо (х~>—оо)
и этот предел равен Ь, т. е.
lim f(x)*=b или lim f(x) — b.
X—У--|-оо	— оо
57
Кривая y~f(x} имеет вертикальную асимптоту xt=^a, если при
х -> а, х а — 0, х -> а + 0 / (х) -> оо (/ (х) -> —оо). Для отыскания
вертикальных асимптот надо найти те значения аргумента, вблизи
которых f (х) неограниченно возрастает по абсолютной величине. Есди
такими значениями аргумента окажутся alt а2, ... , ап, то уравне-
ния вертикальных асимптот будут иметь вид
х= а±, х — а2, ... , х — ап.
Кривая у= f (х) имеет наклонную асимптоту y^=kx-\-b в том
и только в том случае, если существуют конечные пределы
k = lim
X
b == lim [f (x) — kx]
Х-юо
(надо отдельно рассматривать случаи х—>-|~°° и х->—оо). Наклон-
ная асимптота — правая, если график приближается к ней при х->
->-|-оо, левая, если график приближается к ней при х->—оо; дву-
сторонняя, если график приближается к ней как
при х —>—оо, так и при x-h 4-00. Заметим, что .
асимптота кривой у (х) может пересекаться^1	У,
с этой кривой как в конечном, так и в бесконеч- ,
ном множестве точек.	——/
Рис. 20. Прямая АВ — асимп-
тота кривой у — f (х).
Рис. 21. Двусторонняя асимпгота кри- ,
вой у — У л3 + 2.
Чтобы сделать вывод об интервалах, на которых кривая распо-
ложена над асимптотой или под ней, надо рассмотреть разность
® ‘ ^крив ^асимпт*
На тех интервалах, где б > О, кривая находится над асимптотой,
а на тех, где 6 < 0, — под ней.
Пример 39. Найти асимптоты кривой
Имеем
у = ^х3 + 2.
fe = lim Пт	- 1,
Х-»-+оо X	i со X
58
bt=3 lim (# — kx) = lim (Ух34-2 —x)x=
Х->+оо	X-h+oo
= lim ........<*3 + *)^L.-------= o.
*-±~ у(хз^.2)2.+'хУх3 + 2 + х2.
Кривая у = Ух3 + 2 имеет двустороннюю наклонную асимптоту у
= х (рис. 21).
Пример 40. Найти асимптоты
кривой
3
у ~ хг _ 4 •
Находим горизонтальные асимп-
тоты:
lim -т^-г = 0-
Хч-±оо X2 ~ 4
Горизонтальная асимптота одна: у ~ 0
(ось Ох). Для определения верти-
кальных асимптот находим те значе-
ния х, в окрестности которых f (х) s=
3
= х?---4 неогРаниченно возрастает
по абсолютной величине. Такими зна-
чениями являются х = ±2. Сле-
довательно, вертикальными асимп-
тотами являются прямые х — —2 и
х == 2 (рис. 22).
Пример 41. Найти асимптоты
кривой
у = х + 2 In х.
Имеем
Рис. 22. Эскиз графика у =*
«=	" * х — ±2 — вертикаль-
ные асимптоты; у = 0 — горизон-
Рис. 23. График у = x + 2 In x
не имеет правой асимптоты.
k == lim —
X-j.-1-оо X
lim
2 In х'
X
b = lira (y — kx) — lim 21nx=oo.
График данной функции правой наклонной асимптоты не имеет. Так
как при х->0 + 0 z/ -> — оо, то кривая имеет вертикальную асимптоту
х = 0 (ось Оу) (рис. 23).
Порядок исследования функции '
и схема построения ее графика
Рекомендуем следующий порядок исследования функции и по-
строения ее графика:
1)	область определения функции;
59
2)	область значений функции;	*
3)	четность и нечетность функции, периодичность;
4)	характер 1ые ючки графика, монотонность и выпуклость
_ функции;
5)	асимптоты графика;
6)	построение графика функции.
Сделаем некоторые замечания относительно этой схемы.
При построении графиков многих функций нет надобности про-
водить полное исследование функции по этой схеме, некоторые пункты
можно опустить. Это касается в первую очередь графиков основных
элементарных функций, хорошо изученных в теоретическом курсе ма-
тематики средней школы, а также графиков некоторых простейших
элементарных функций.
Построение графика функции - удобно выполнять параллельно
с исследованием функций. Чтобы эскиз графика функции в больших
па размерам интервалах ее области определения, в которых нет осо-
бенностей этой функции, был болеё точным, надо взять несколько
точек и вычислить значения функции в них.
РАЗ ДЕЛ 3
ГРАФИКИ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИИ
§ 1.	Степенная функция
*
Степенной функцией называется функция у = ха, где a — любое
действительное число. Природа такой функции существенно зависит от
арифметической природы числа а. Если а — число рациональное, то
функция у — ха — алгебраическая; если же a — число иррациональ-
ное, то функция у = х* — трансцендентная.
Степенная функция с натуральным показателем
Пусть a = т, где т — натуральное число. Область определения
функции: ]—оо; оо [. Если х->+оо, то функция неограниченно
возрастает. Действительно, какое бы большое число N мы ни взяли,
при х > N будет выполняться неравенство хт > N,
Если т — четное число, то функция у — хт — четная и ее график
симметричен относительно оси ординат; если т—нечетное число, то
функция у^= хт — нечетная и ее график симметричен относи-
тельно начала координат. Пусть т = 2л. Тогда
•	f (—х) = (—х)2" = x2n = f (х).
Если т = 2л 4» 1, то
f (—х) = (—х)2п+1 = — х2'1+1 = — f (х).
На [0; оо [ функция монотонно возрастает от.О до оо. Действи-
тельно, если 0 < xt < х2, то у (х2) — у (xj = х£* — х™ — (х2 — xj X
X (х?—1 +	+ • • • + я?-1) > 0- Функция у — хт при т == 2л
60
на ] — оо; 0 [ монотонно убывает от + оо до 0, а при т = 2п + 1
монотонно возрастает от — со до 0.
Функция у = хт при т > 1 для х Е ] 0; оо { вогнутая. Действи-
тельно, при *1 ф х2 выполняется неравенство
. /Х1 + Х2\ f (Xt) + f (*2)
Ц 2	2
Справедливость этого неравенства доказывается методом полной мате-
матической индукции.
При т = 2 неравенство выполняется. Действительно, если т = 2f
то
(Х1 +	2 х*+х]+2х1ха x'J-J-х“ + х* + х^ х|+ х%
\ -2 -/ =	4 С 4	“ “2
Допустим, что неравенство справедливо для т== k:
V	К	Х1 + *2
Умножив обе части последнего неравенства на —~—-, получим
/	.	\Л+1	I <Л+Х I YkY I Y
/Х1 + х2] X1 х2 ~г *i*2 + *i*2
\	2	/	<	4
*1 "Г *2	+ *1	+ *2	*1 Т *2
4	:	“ ~Г~2
Следовательно, мы доказали, что если неравенство‘справедливо для
т = k, то оно справедливо и для m = &+ 1. Этим самым начальное
неравенство доказано.
Функция у — х'п для х 6] — оо [ при т — 2п вогнутая, а при
т — 2п + 1 — выпуклая.
61
График функции у — хт проходит через точки (0; 0), (1; 1).
При т = 2 график функции называется квадратной параболой
(см. рис. 5), при tn = 3 — кубической параболой, при т = 4, 5, .. .—
параболой соответствующей степени.
Заметим, что функция у = ах, где а — любое действительное
число, задает прямо пропорциональную зависимость между величи-
нами хну. Графиком прямо пропорциональной зависимости является
прямая, проходящая через начало координат. График функции у—ах
проходит в I и III квадрантах, если а > 0 (рис. 24), или во II и
квадрантах, если а < 0 (рис. 25).
Степенная функция с целым отрицательным показателем
Пусть а = —г, где г — натуральное число. Область определения
функции у =	: ] — оо; 0 [ (J ] 0; + оо [. При г четном функция у=
= ~ — четная и ее график симметричен относительно оси Оу, при г
натуральное число. туральное число.
ж	1
нечетном функция у = ~ нечетная и ее график симметричен относи-
тельно начала координат. Действительно,
f (—*) = (_хуп = ^-п== f (*)•
= (_х)2«+1 = ~ хЗпП = ~/ (*)•
Функция на интервале ] 0; +©о [ убывает от + оо до 0.
Это следует из того, что функция у — хг для х € ] 0; оо [ возрастает
62
I	T Г	1	1 \
от 0 до + оо если Xi < х2, то хх < х2, а следовательно, — > — )
\	.	хх х2 / *
Учитывая четность или нечетность при соответствующих г (четных
При хС]0; оо [ функция у = — вогнутая. Это очевидно из не-
равенств
{Xi + Х2\Г *1 + *2
\ 2 I <	2	’
2
63
Для г£] —оо; 0[ функция у = — при четном г вогнутая, а при
нечетном г — выпуклая.
График функции не пересекает координатных осей и проходит ?
через точку (I; 1).
Горизонтальная асимптота: у = 0. Действительно,
Вертикальная асимптота: х = 0, так как в окрестности точки
х = 0 функция у = ~ неограниченно возрастает по абсолютной'ве-
личине.
64
Заметим, что функция у = — , где k — любое действительное
число, задает обратно пропорциональную зависимость между вели-
чинами х и у. График ее-—гипербола, причем при k > 0 ветви ги-
перболы расположены в I и III квадрантах; если же k < 0, то ветви
гиперболы расположены во II и IV квадрантах (рис. 34, 35).
Рис. 34. Обратно пропорциональная за-
висимость у = —• , k > 0.
Рис. 35. Обратно пропорциональная
' k
зависимость у — — , k < 0.
X
Степенная функция с рациональным показателем
Рассмотрим функцию у — ха, где а = г — рациональное число.
а)	Пусть г == ^-, где т — натуральное число. Допустим^ что
т — нечетное число. Из графика функции у = х2л+1 (см. рис. 28)
видно, что каждому значению у С] — 00; оо [ соответствует одно и
только одно значение x=2Zl+jA/. Следовательно, при нечетном т
функция у = хт имеет обратную функцию х — ^у, определенную
при всех у. Обозначив аргумент функции через х, а значение функ-
ции— через у, получим у = ”^х— обратную функцию, график ко-
торой образуем из графика функции у = хт е помощью симметричного
отображения относительно биссектрисы первого и третьего коорди-
натных углов (рис. 36).
Пусть теперь т — четное число. Рассмотрим график функции
# = ^/х. Каждому положительному значению у соответствуют сле-
дующие два значения х‘. х — ”Уу и х — —”¥у- Следовательно, при
четном т функция, обратная функции у = хт, двузначна. Однако
если рассматривать функцию у = хт только на промежутке [0; + оо [,
на котором она возрастает, то каждому значению у будет соответст-
вовать только-одно значение х — у (х > 0); функция у = хт на
промежутке [0; + оо [ имеет однозначную обратную функцию х =
3 8-413	$5
= ty^yi определенную на промежутке [0; оо [. Далее под ^х, где
т — четное число, будем понимать неотрицательное значение корня.
График функции у —Ух (рис. 37) получается с помощью симмет-
ричного отображения относительно биссектрисы первого и третьего
координатных углов графика функции у = хт.
Рис. 36. Степенная функция с положительным рациональным показа-
телем у = х т , т ® нечетное.
б)	Пусть г = —, где р и ^—натуральные и взаимно простые
Г . '	.	9	_ Я/—
числа. График функции у— у х$ зависит от чисел р и q.
Рис. 37. Степенная функция с по-
ложительным ( рациональным по-
казателем у — х т а т «= четное.
Рассмотрим несколько случаев.
Первый случай: р — четное
число, q—нечетное. 'Функция у —
= определена на интервале ] —оо;
q .-   _
оо [. Функция четная: у (______—
Q г—
— ухР, ее график симметричен от-
носительно оси Оу. На [0; оо [ функ-
ция монотонно возрастает от 0 до
+ оо. Для всех х у — у хр 0, сле-
довательно, график функции располо-
жен над осью абсцисс, проходит через
точки (0; 0) и (1; 1). Функция у —
= у хр на [0 j до [ выпуклая при
66
О < -2- < 1 и вогнутая при ~- > 1. При условии 0 < ~- < 1 график
функции на ] 0; 1 [ лежит выше биссектрисы у — х, а на ] 1; оо [ —
ниже; если же ~ > 1, то на ] 0; 1 [ график , функции расположен
ниже биссектрисы у = х, а на ] 1; оо [—выше (рис. 38).
Рис. 38. Степенная функция с пэлэжительчыи рациональным показателем ’
Р
у = х Я , р — четное, q — нечетное; — < 1 (а); — > 1 (б).
Второй случай: р и q — нечетные числа. Функция у =
q г—	q . — 
— у определена на ] — оо; оо [. Функция нечетная: у/___________Х)р ~
<7 г—
— — у хр, ее график симметричен относительно начала координат.
3*
67
Функция монотонно возрастает от —оо до + оо на ] — оо; оо [.
График функции проходит через точки (0; 0) и (1; 1). Функция у =
Q г——	О
— у хр на [0*> 00 I выпуклая при 0 < ~ <_ 1 и вогнутая при
~ > 1 (рис. 39).
Третий случай: р — нечетное число, q — четное. Функция
У = frx? — (*Р) q определена на [0; оо [, монотонно возрастает на
а	б
Рис. 40. Степенная функция с положительным рациональным показателем у =*
Р
«=Н, р нечетное, q — четное; < 1 (а)\	> 1 (б).
Р
[0; оо [ от 0 до + оо. Для х £ [0; оо { у = х q 0, следовательно,
р
график функции расположен над осью абсцисс. Функция y—xq на
[0; оо [ выпуклая при 0 < < 1 и вогнутая при -^ > 1. График
функции проходи! через точки (0; 0) и (1; 1) (рис. 40).
в) Пусть г = —— , где р и q — натуральные и взаимно простые
числа. Степенную функцию с отрицательным рациональным показа-
телем запишем в виде
68
Рис. 41. Степенная функция с отрицательным рациональным показателем
Рис. 42. Степенная функция с отрицательным рациональным показателем
Р
У = * q > Р>
q — нечетные; — > 0.
69
Первый случай: р — четное число, q — нечетное. Область
определения функции: ] — <*>; О [[J ] 0; оо [. Функция четная, ее гра-
фик симметричен относительно оси ординат. На ] 0; оо [ функция
__ р_	р_
у = х q убывающая, так как функция у = xq на этом промежутке
возрастающая (см. рис. 38). Для х G ] 0; оо [ у = х q > 0, следо-
Рис. 43. Степенная функция с отри-
цательным рациональным показателем
_______Р_
У = х Я , р нечетное, q — четное;
п	'
вательно, график функции лежит
над осью абсцисс. Гр£фик функции
проходит через точку (1; 1). Го-
ризонтальная асимптота: у = 0
(рис. 41).
Второй случай: р и q —
нечетные числа. Область определе-
ния функции: ] — оо; 0 [ (J ] 0; оо [.
Функция нечетная, ее график сим-
метричен относительно начала коор-
динат. Функция убывающая. Гори-
зонтальная асимптота: у = 0. Вер-
тикальная асимптота: х = 0 (рис.42).
Третий случай: р — не-
четное число, q — четное. Область
определения функции: ] 0; оо [.
Функция убывающая на ] 0; оо[.
Горизонтальная асимптота: у = 0.
Вертикальная асимптота: х = О
(рис. 43).
Степенная функция
с иррациональным
показателем
Степенью положительного чис-
ла х с иррациональным показате-
лем а называется предел, к кото-
рому стремится последовательность
рациональных степеней этого чис-
ла, если последовательность пока-
зателей стремится к а, т. е.
ха= lim хгп.
гп^
Будем считать в случае иррационального а > 0, что функция
1/ = ха определена на ]0; оо[4 Функция возрастает на ]0; оо[ от О
до + оо4 Для всех х С [0; оо [ у = ха >> 0, следовательно, график
функции лежит над осью абсцисс. Функция вогнутая при а > 1
и выпуклая при 0 < а < L График функции проходит через начало
координат и точку (1; 1) (рис. 44).
График функции у = х~а, где а — иррациональное число, при-
веден на рис. 45.
70
Рис. 44. Степенная функция с положительным иррациональным пока-
зателем у = ха, а — положительное иррациональное число: а < 1 (а)\
а > 1 (б).
§ 2. Показательная
функция
У
Показательная функция имеет
вид
У = аж,
где а > 0 и а =/= 1. Эта функция
принадлежит к трансцендентным
функциям. Область определения
функции: ]— оо; оо[. Область зна-
чений функции: 0 < у < оо, график
лежит над осью абсцисс.
Если х = 0, то i/ = a°, т. е.
график пересекает ось ординат
в точке (0; 1).
При а > 1 функция у = ах мо-
нотонно возрастает, а при а < 1
монотонно убывает. Действитель-
но, вычислим значения функции
в точках Xt и х2 (х2 > хх):
f (Xi) = ах‘, f (x2) = aXt,
далее рассмотрим разность
Рис. 45. Степенная функция с отри-
цательным иррациональным показа-
телем у =
0х* — aX1 = aXi (ax*~X1 — 1)
и определим ее знак. Так как aXl всегда больше нуля, знак произ-
ведения зависит от знака второго сомножителя.
Если х2 — xt > 0, то aXi~~Xi > 1 при а > 1 и aX2~Xl < 1 при
а < 1. Поэтому
f — f (хх) > 0 при а > 1,
f (*2) — f (хх) < 0 при а < 1,
т. е. f (х2) > f (хх) при а > 1 и f (х2) < f (хх) при а < 1, если
Х2 > хх.
71
Если х->+оо, то а* -► + оо при а > 1 и ах -* 0 при а < 1.
Если х — оо, то ах -+ 0 при а > 1 и ах -► + оо при а < 1. Ось
абсцисс — асимптота графика функции, причем кривая приближается
асимптотически к оси Ох.
Для исследования выпуклости графика определим знак разности
Н*1)+Нх2)
Рис. 46. Показательная функция у = ах: а > 1 (а)\ а < 1 (б)
Рис. 47. Показательная функция у == а < 1 (а); а > 1 (б).
а именно:
I	*LX?
L 2 - a 2 )
2
ах' + ах*
2
>0<
Следовательно, график функции вогнутый.
Заметим, что графики функций ах и а~х симметричны относи-
тельно оси ординат.
Примеры показательных функций приведены на рис. 46—49.
72
§ 3. Логарифмическая
функция
Логарифмическая функция имеет
вид
У = lcgax,
где а > 0, а =# 1. Область определе-
ния функции: ]0; оо[. Если а > 1,
то логарифмическая функция поло-
жительна при х > 1, отрицательна
при 0 < х < 1 и равна нулю при х = 1.
Если 0 < а < 1, то логарифмичес-
кая функция положительна при 0 <
<х< 1, отрицательна при х> 1 и
равна нулю при х— 1. При а > 1
функция монотонно возрастает от — оо
до + оопри а < 1 монотонно убы-
вает от + оо до — оо, причем тем
медленнее, чем больше | In а |. Если
а > 1, то
lim logflx = + оо,
X-*- оо
lim loga х — — оо.
х~* 0-{-0
Если a < 1, то
lim logax = — oo,
lim logax = + oo.
X+C+O
Рис. 49. Показательная функции
у = ах- а —2 (l)-t а = е (2); а =
=10(3); о=^-(«); а = ^-(5){
nprf* a > 1 функция у = logaX выпук-
лая, при a < 1 — вогнутая. График
функции проходит через точку (Г, 0)
и приближается асимптотически к оси
ординат. Заметим, что так как лога-
рифмическая функция у = logaX ЯВЛЯ-
ется обратной показательной функции
у = ах, то ее график симметричен графику показательной функции (при
одном и том же основании) относительно биссектрисы первого и тре-
тьего координатных углов.
Примеры логарифмических функций приведены на рис. 50, 5L
§ 4. Тригонометрические функции
К ним принадлежат функции
у = sin X, у = COS X, у = tg х, у = ctg X.
Функция у =sin х. Область определения функции: ]— оо; оо[*
Область значений функции: [—1; 1]. Функция нечетная, периоди-
ческая с периодом 2л. Точки пересечения с осью абсцисс: х =
= nn(n£Z), эти точки являются и точками перегиба графика крн-
73
Рис. 50. Логарифмическая функция: у — log2 х (а)\ у — log j х (б).
Рис. 51. Логарифмическая функция у *= loga х, а > 0; а = 10
(I); а = е (2); а = ~ (3)-а = ~ (4).

Л
вой. Функция на 0;-у возрастает от 0 до 1, на тр ; — л|
j & L	J. * I
13 Г
убывает от 1 до —1, на -^-л; 2л возрастает от —1 до 0. Функ-
ция на [0; л] выпуклая, а на ]л; 2л[ вогнутая.
График функции у = sin х представлен на рис. 52. Кривую у =»
= sin х называют синусоидой.
Функция у — cos х. Область определения функции! ]—оо; оо[<
Область значений функции: [—1; 1]. Функция четная, периодиче-
л
ская с периодом 2л* Точки пересечения с осью абсцисс: — (2п +
-|- 1) (n £ Z), эти точки являются и точками перегиба, Функция на
Рис. 54. Тригонометрическая функция Рис. 55. Тригонометрическая функ*
у = tg х.	цня у = ctg х.
]л; 2л [ возрастает от —1 дэ I.
1л 3 Г	[3
I— ; -g-л вогнутая, на у л|
]0; л[ убывает от 1 до —1, на
-	L л 1
Функция на 10; -g-1 выпуклая, на
2л j выпуклая.
График функции изображен на рис. 53. Кривую у — с.озх назы-
вают косинусоидой.
Функция у z= tgx. Область определения функции — множество
всех действительных чисел, кроме х = ~ + kn (k $ Z)t Область зна-
чений функции; ]— оо; оо[4 Функция нечетная, периодическая с пе-
риодом л* Точки пересечения с осью абсцисс; х = kn (k £ Z), эти же
точки — точки перегиба. Функция иа j— ~возрастает от
-	L л Г
Функция вогнутая на 0; g- , выпуклая — на
— оо До -Jf оо.
Jjt I	/ I \
—2 ; 0 . Вертикальные асимптоты: х == I k 4- -% I л (k £ Z).
График функции у = tg х изображен на рис. 54* Кривая у =
= tg х называется тангенсоидой
75
Ф у н к ци я‘// = ctg х. Область определения функции—множество
всех действительных чисел, кроме х = kn (k Z). Область значений
функции: ]— оо; оо[. Функция нечетная, периодическая с перио-
дом л. Точки пересечения с осью абсцисс: х = + у j л (& € Z),
эти же точки — точки перегиба. Функция на ]0; л[ убывает от
+ оо до — оо. На j(); функция вогнутая, на	—выпук-
лая. Вертикальные асимптоты: х — kn (k Z).
График функции у = ctg х представлен на рис. 55. Кривую
у = ctg х называют котангенсоидой*
§ 5. Обратные тригонометрические функции
Простейшие обратные тригонометрические функции следующие:
у = arcsin х, у — arccos х, t/ = arctgx, у = arcctg х. Заметим, что
функции у = sin х ну = Arcsin х, у = cos х и у — Arccos х, у = tg х и
# = Arctgx, r/^=ctgx и у = Arcctg х являются попарно взаимно
обратными.
Для построения графиков обратных тригонометрических функций
используют свойства графиков взаимно обратных функций (см. § 2
разд. 2). Построение осуществляют так: соответствующий график
прямой тригонометрической функции зеркально отображают относи-
тельно биссектрисы первого и третьего координатных углов.
Кратко рассмотрим свойства и графики обратных тригономет-
рических функций.
Арксинус у — Arcsin х. Функция у — Arcsin х определена для
| х |	1, многозначна. Рассматривают одну ветвь этой функции,
Г л Л 1
соответствующую у С — -у »	• Это значение у называют глав-
ным значением Arcsin х и обозначают arcsin х. Другие значения
у = Arcsin х выражаются через главное его значение формулой
Arc sin х = arcsin х + 2£л (k С Z),
Следовательно, область определения функции у = arcsin х : [—1; 1];
область значений: — -у ; ~ . Функция у = arcsin х — нечетная,
на [—1; 1] монотонно возрастает от до -2-. График функции
проходит через точку (0; 0). Эта точка является и точкой перегиба
графика. На [—1; 0] функция выпуклая, на ]0; 1[ —вогнутая.
Графики функций у — Arcsin х и у == arcsin х приведены соответ-
ственно на рис. 56 и 57.
Арккосинус у — Arccosх. Функция у = Arccos'xопределена
для |х|< 1, многозначна. Ветвь этой функции, соответствующую
л], называют главным значением Arccosх и обозначают
у — arccos х. Другие значения у = Arccos х выражаются через глав-
ное его значение формулой
Arccos х = 2&л — arccos х (k £ Z).
76
Область определения функции i/ = arccos х: [—1; 1]. Область зна-
чений функции t/= arccos х: [0; л]. На [—1; 1] функция # = arccos х
монотонно убывает от л до 0. Для функции у = arccos х выполня-
ется равенство
*	'	arccos (~х) = л — arccos х.,
(л \
0; I, кото-
рая одновременно является и точкой перегиба, и центром симметрии
кривой. На [—1; 0] функция t/= arccos х вогнутая, на ]0; 1[ —
выпуклая.
Графики функций у = Arccosх и у — arccosх приведены соответ-
ственно на рис. 58 и 59.
Рис. 56. Обратная тригономет-
рическая функция #=Arcsinx.
Арктангенс //= Arctg х.
Функция у — Arctg х определена
для — оо < х < + оо, многознач-
на. Значение функции у— Arctgх,
Рис. 57. Обратная тригономет-
рическая функция £/=arcsin х.
Jn л
—2" ’ 2г называют главным значением
Arctg х и обозначают у= arctg х. Другие значения у = Arctgх выра-
жаются через главное его значение формулой
Arctg х — arctg х + kn (k C Z)-
Область определения функции у = arctgx: ]—оо; оо[. Область зна-
чений функции* у — arctg х: j— у ;	. Функция у — arctg х не-
четная. Функция (/ = arctgх на ]— оо; оо[ монотонно возрастает
от до ~ ^значения ± у не - достигаются j . График функции
у = arctg х проходит через точку (0; 0), которая одновременно явля-
ется и точкой перегиба, и центром симметрии кривой. На ]— оо; 0]
П
функция у — arctg х вогнутая, на ]0; оо [ —выпуклая. Горизонталь-
ные
асимптоты для
у = Arctg х: у = ± (2k 4-1) у (k = 0, ±1,
± 2, ...).
Графики функций у= Arctgx и t/ =
= arctg х приведены соответственно на
рис. 60 и 61.
Рис. 59. Обратная тригономет-
рическая функция ^=arccos х.
Рис. 58. Обратная тригономет-
рическая функция ^=Arccos х.
Рис. 61. Обратная тригонометричес-
кая функция у = arctg х.
Арккотангенс // =
== Arcctgx. Функция у — Arcctgx
определена для—оо<х<4-оо,
многозначна. Значение функции у =
= Arcctgx, соответствующее
у С ]0; nf, называют главным зна-
чением Arcctgx и обозначают у —
=arcctg х. Все другие значения у =
= Arcctg х выражаются через глав-
ное его значение формулой
Arcctgx = arcctgx + kn (k C Z)-
Рис. 62. Обратная тригонометричес-
кая функция у — Arcctg х.
Область определения функции у =
= arcctgx: ] — оо; оо[. Область
значений функции у — arcctg х: ]0;
л[. Функция у = arcctg х— функ-
ция общего вида. Выполняется ра-
венство
* arcctg (—х) = л — arcctg х.
Функция У — arcctg х монотонно
убывает от л до 0 на [—оо; оо[
(значения л и 0 не достигают-
ся). График функции у = arcctg х
Рис. 63. Обратная тригонометричес-
кая функция у — arcctg х.
проходит через точку 10; I, которая одновременно является и
точкой перегиба, и центром симметрии кривой. На ]— оо; 0[ функ-
ция у = arcctg х выпуклая, на ]0; оо[ — вогнутая. Горизонтальные
асимптоты для у — Arcctg х: у — ± kit (k = 0, 1,2, ...).
Графики функций у = Arcctg х и у = arcctg х приведены соот-
ветственно на рис. 62 и 63.
РАЗДЕЛ 4
ДЕЙСТВИЯ С ГРАФИКАМИ. ПРЕОБРАЗОВАНИЯ ГРАФИКОВ
В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ
§ 1. Арифметические действия с графиками
Сложение и вычитание графиков
Общий метод построения графиков суммы и разности двух функ-
ций заключается в том, что предварительно строят два графика для
обеих функций, а затем складывают или вычитают ординаты этих
кривых при одних и тех же значениях х (удобно — в характерных
точках). По полученным точкам строят искомый график и выполняют
проверку в нескольких контрольных точках.
В отдельных случаях построение графиков суммы и разности
функций можно выполнять так.
79
Если надо построить график суммы двух функций, то строят
вначале график одной, более простой, функции, затем к нему при-
страивают график второй функции, ординаты которого откладывают
от соответствующих точек первого графика.
Если надо постройть график разности двух функций, то строят
сначала график функции-уменьшаемого, а затем от него откладывают
ординаты функции-вычитаемого, взятые с противоположным знаком.
Иногда удобно начертить график5 функции-вычитаемого с противопо-
ложным знаком и ординаты обеих кривых (функции-уменьшаемого
и функции-вычитаемого с противоположным знаком) сложить.
Рис. 64. у — х — sin х (1)\ У — х (2)\ у == — sin х (3).
Замечание. Представленный метод построения графика алгеб-
раической суммы конечного числа_ функций удобно применять в более
простых случаях. Если же функции-слагаемые имеют более сложную
природу, то следует выполнять исследование и построение графика
функции по схеме § 2 разд. 2, а еще лучше — с помощью методов
высшей математики (см. ч. II).
Пример 1. Построить график функции
у = х — sin х.
Имеем две функции: у (х)=х и у (х) ==• — sin х. Строим график функ-
ции I/ == х, затем от цего (а не от оси абсцисс) откладываем ор-
динаты второй функции. Поскольку |sinx|<l, то целесообразно
провести две вспомогательные прямые: у = х + 1 и у — х — 1. В точ-
ках, где sinx = 0 (т. е. при х=&л, k С Z), у — xt а это значит,
чго соответствующие точки графика заданной функции лежат на
3°
прямой у — х. В тех точках, где sin х = 1 I т. е. при х = — 4- 2&л,
k £ у — х— 1, а это значит, что соответствующие точки графика
заданной функции лежат на прямой у—х—1. В точках, где
sin х = — 1 (х =---- + 2£л, k С , у = х + 1, а это означает, что
соответствующие точки лежат на прямой у = х + 1. Следовательно,
на прямых у = х— 1 и у = х + 1 лежат вершины синусоиды (рис. 64).
Пример 2. Построить график функции
, 1
y=*+T-
Строим графики функций-сла-
гаемых у = и у = х. Затем
складываем ординаты кривых при
одинаковых значениях х. Возьмем
значения х =	, 1,2, 3, .. . Скла-
дывая ординаты обоих графиков
для каждого из этих значений х,
получаем точки Л, В, С, D. Со-
единив их плавной линией, полу-
чим одну ветвь графика функции
(при х > 0). Заметив, что функция
нечетная и график ее симметричен
относительно начала координат,
строим вторую ветвь графика за-
данной функции (при х<0).
График функции у = х + —
представлен на -рис. 65.
Пример
у = х (3).
3. Построить график функции
у — sin х + cos х.
Заданную функцию рассматриваем как сумму двух функций:
у = sin х, у — cos х.
Проведем исследование и построение графика функции по схеме § 2
разд. 2.
Область определения функции-суммы: общая часть областей опре-
деления функций-слагаемых, в данном случае ]—оо; оо[. Область
значений функции-суммы: [—1; 1]. Функция периодическая с пе-
риодом 2л. Характерные точки графика функции-суммы: точки пере-
сечения с осью абсцисс л; 0 jл; 0^ ; точка пересечения
с осью ординат (0; 1); предельные значения функции равны 1;
Л1 ; 1^2^ — точка максимума заданной функции, Л2 л;
81
Рис. 68. у — л* -j- Эх (a)i у =х’ =* Зх (6).
82
Рис. 70. у — arctg х -|- 2х.
83
точка минимума заданной
функции. На
3 П I
-—л; 2л
4	1
возрастает, на
интервалах О; —
функция монотонно
1 л . 3 Г
— > т л — моно-
J 4	4 [
13 I
0; — л функ-.
13	7 Г
ция выпуклая, на I— л; — л —
17 '
вогнутая, на|—л; 2л
— выпук-
лая.
График функции у sin х +
4- cos х представлен на рис. 66.
Примеры построения графиков
суммы и разности функций пред-
ставлены на рис. 67—76.
Рис. 73. у = х2 — л*
Рис. 76. у — cos X.
Умножение и деление графиков
Если заданы графики функций yr s= fx (х) и z/2 — /2 (х), то можно
построить «по точкам» график функции у = У1 (х) У% (х) или у *=
— (Уъ 0)» Заметим, что если при сложении (вычитании) гра-
У2 (X)
фиков можно пользоваться циркулем для сложения ординат, то при
умножении (делении) надо предварительно выразить отрезки (орди-
наты) числами и лишь затем умножить (разделить) эти числа с уче-
том их знаков. Деление графиков можно привести к умножению:
Л5
Заметим, что произведение или частное двух функций лучше
исследовать и строить их график по схеме § 2 разд. 2. Иногда произ-
ведение или частное двух функций можно упростить, и построение
графика упрощенной функции значительно облегчается.
Указанный метод построения графиков произведения или част-
ного функций нерационален и используется крайне редко. Такие
графики лучше всего строить с помощью методов высшей математики
(см. ч. II).
Пример 4. Построить график функции
у х sin х.
Строим графики функций у~х, y^=sinx (рис. 77). Умножение
этих графиков упрощается благодаря тому, что функция у sin х
периодически принимает значения 0, 1, —1. При x=ikTi(k£Z)
sin№=0 и 1/~xsinx —0, т. е. соответствующая точка графика
функции у s= х sin х находится на оси абсцисс. При х —
4- 2kn (k = 0, 1, 2, ...) sin + 2kn) =i 1, a у + 26л, т. e.
соответствующая точка графика функции у s= х sin х лежит на прямой
у s= х. При х s=----+ 26л (6	0, 4, 2, ...) sin --4- 26л j =
—1, следовательно; соответствующая точка графика функции у^
= х sin х лежит на прямой у = —х.
Поскольку заданная функция у = х sin х четная, то указанное
построение производим только для правой части графика, левую
часть графика (для х < 0) строим симметрично правой относительно
оси ординат.
График функции y = xsinx представлен на рис. 77.
86
Пример 5. Построить график функции
у е~ xsin х.
Строим графики функций у^=е~х и у — sinх. Поскольку
sinx = 0 при x — kn (fee Z), график функции у ?= е~х sin х проходит
через точки (fen; 0) (fe 6 Z), Кроме того, следует иметь в виду, что
при х = -у + 2fen (fe € Z) sinx= 1 и график функции у^= е"х sinх
(k £ Z) sinx^=—1 и график функции у г= е~х sin х касается графика
функции у = —е~~х снизу. Следовательно, график функции у
— е~х sin х располагается между графиками функций у х= ё~х и у^
t= —е~~х и периодически (со 2л) касается их.
График функции представлен на рйс. 78.
Пример 6. Построить график функции
Строим графики функций у = In х, у ~ ~ . График функции
у — — пересекает ось абсцисс в точке (1; 0). Умножим ординаты
87

*
графиков у = 1пх и t/ = у при х — е 2,72 ... , х s= 4. Учитывая
предельные значения функции
lim lim — ос
х-+04~0	х-4-0+0 х
lim у= lim —* = О,
х
.	.	In х
строим график функции y=i —
(рис. 79).
Пример 7. Построить гра-
фик функции
х
У ~~ 2х
Строим графики функций у —
= х, yt= 2х. Далее делим ордина-
ты графика функции у == х на орди-
наты графика у = 2х при одинако-
вых значениях абсцисс. При этом учитываем, что если х->+оо, то
у = 2х возрастает быстрее, чем у = х, а поэтому у -> 0 при х -> 4-°°»
т. е. ось абсцисс — асимптота графика. Заметим, что точки (0; 0),
(1 \ /	1 \	х
1; -£-1> 12; -^-1 принадлежат графику функции у = —.
График функции = представлен на рис. 80.
2х
Примеры построения графиков произведения и частного функций
приведены на рис. 81—87.
90
§ 2. Простейшие преобразования графиков
Преобразования, не изменяющие масштаба
Приведем здесь преобразования симметрии, обусловленные осо-
бенностями графиков четных и нечетных функций, а именно:
график функции у = —f (х) симметричен графику функции у *=*
= f (х) относительно оси абсцисс (рис. 88);
график функции у = f (—х) симметричен графику функции
yz=f(x) относительно оси ординат (см. рис. 15, а);
график функции у = —/(—х) симметричен графику функции
у = f (х) относительно начала координат (см. рис. 15, б).
Параллельный перенос (сдвиг) вдоль оси	г .
абсцисс. График функции	/
</=/(* + «) /
получаем из графика функции у — f (х)	/
с помощью параллельного переноса (сдви-	у
га) последнего вдоль оси Ох на | а | единиц
масштаба в направлении, имеющем знак,	/—
противоположный знаку числа а. Это вы- г	________
полняется так: строим известный график	0	х
функции у = / (х). Далее ось ординат па- 2-----
раллельно переносим вдоль оси абсцисс на
| а | единиц масштаба в направлении, имею-	<
щем знак числа а. Эго и есть окончательная	\
ось ординат. Например, для построения	\
графика функции у — f (х + 2) вспомога-	\
тельную ось ординат графика функции у —	»
= f (х) переносим параллельно вдоль оси
абсцисс на две единицы масштаба вправо. Рис. 88. у = f (х) (1)\ у =э
Для построения графика функции у =	= — И*) (2)-
= / (х — 2) вспомогательную ось ординат
графика функции у = f (х) переносим параллельно вдоль оси абсцисс
на две единицы масштаба влево.
Пример 1. Построить график функции
z/=(x —З)2.
Строим график функции у = х2. Далее ось ординат переносим
параллельно вдоль оси абсцисс на три единицы масштаба влево,
как показано на рис. 89.
Параллельный перенос (сдвиг) вдоль оси ординат. График функ-
ции у f (х) + b получаем из графика функции у = f (х) с помощью
параллельного переноса (сдвига) последнего вдоль оси Оу на |b |
единиц масштаба в направлении, имеющем знак числа Ь. Этот пере-
нос выполняется так; строим известный график функции у = f (х).
Далее ось абсцисс переносим параллельно вдоль оси ординат на | b |
единиц масштаба в направлении, имеющем знак, противоположный
знаку числа Ь. Это и есть окончательная ось абсцисс. Например,
для построения графика функции у = f (х) + 4 вспомогательную ось
абсцисс графика функции у = f (х) опускаем вдоль оси ординат на
четыре единицы. Для построения графика функции у — f (х) — 4
91
вспомогательную ось абсцисс графика функции у = / (х) поднимаем
вдоль оси ординат на четыре единицы вверх.
Пример 2. Построить график функции
у = х2 + 3.
Строим график функции у = х2. Далее ось обсцисс опускаем
вдоль оси ординат на три единицы, как показано на рис.- 90.
Преобразования, изменяющие масштаб
Растяжение или сжатие по оси абсцисс. График'функции
У = f<kx)
получаем из графика функции y~f(x) с помощью сжатия по оси
абсцисс исходного графика пропорционально коэффициенту k при
аргументе (если k > 1, то график сжимается в k раз, а если
0 < k < 1, то график растягивается в -i- раз^ . Если k < 0, то
можно сначала построить график функции у = f (| k | х), а затем
отобразить его симметрично относительно оси Оу.
Сжатие или растяжение графика функции по оси абсцисс осу-
ществляется так: строим график функции у = f (х), далее при k > 1
уменьшаем абсциссы точек этого графика в k раз, при 0 < k < 1
увеличиваем абсциссы точек в раз, оставляя при этом ординаты
без изменения.
Пример 3. Построить график функции
у == sin 2х.
Строим график функции y = sinx, далее сжимаем график по
оси абсцисс в два раза (здесь & = 2 > 1), т. е. уменьшаем абсциссы
точек графика в два раза, оставив ординаты без изменения (рис. 91).
Заметим, что период функции у — sin 2х равен л. Сжатие удобно
проводить в характерных точках графика функции у s= sin х.
П
Примеры построения графиков функций с помощью сжатия или
растяжения приведены на рис. 92—98.
Растяжение или сжатие по оси ординат. График функции
рис. 91. у = sin
получаем из графика функции y^f(x) с помощью растяжения
этого графика по оси ординат пропорционально коэффициенту т
при функции (если т > 1, то график растягивается в т раз, если
О < т < 1, то график сжимается в — раз]. Если т < 0, то можно
93
94
сначала построить график функции у s= [ tn | f (х), а затем отобразить
его симметрично относительно оси Ох.
Растяжение или сжатие графика функции по оси ординат выпол-
няется так: строим график функции yt=f (х), далее при т > 1 уве-
личиваем ординаты точек этого графика в т раз, при 0 < т < 1
уменьшаем ординаты точек в — раз, оставляя при этом абсциссы
Пример 4. Построить график функции
Строим график функции у — sin х, далее осуществляем сжатие
.	/	1 Л
графика по оси ординат в три раза (здесь т ?= — < 1 |, т. е. умень-
\	о /
шаем ординаты точек графика в три раза, оставляя абсциссы без
изменения (рис. 99). Сжатие удобно проводить в характерных точках
графика функции у sin х.
95
Построение графика функции у ;= mf (kx + а) + b. Этот график
строят, применяя в определенной последовательности описанные
выше преобразования.
Сначала строим график функции z/s=/(x + a), далее строим
график функции y = f(kx-\-a) (заметим, что при этом преобразова-
нии на k умножается только х}. Затем строим график функции
yt=mf(kx-[-a). Наконец, получаем график функции
у = mf (kx + а) + b.
Рис. 100. у = Ух (а); у = ЗУ 2х (б); у = 3 У—2х (в); у=3 У—2(х±2) —
- 0,7 (г).
Можно эти преобразования выполнять в другом порядке: сначала
построить график функции y~f(kx), .затем перенести его вправо
(или влево) на , поднять (или опустить) на — и, наконец, рас-
тянуть (или сжать) в т раз. В зависимости от знаков k и т при-
дется, возможно, отображать график симметрично относительно оси
Оу или оси Ох.
Заметим, что рассмотренные преобразования можно выполнять
в любом порядке, но величины, на которые график переносится вдоль
осей, зависят от порядка преобразований.
Пример 5. Построить график функции
0 = 3/—2 (Х+2) —0,7.
96
Строим график функции г/^=]Лх(рис. 100). Далее последова-
тельно преобразуем график функции y — V х, а именно: увеличив
в 3 ]Л2 раза ординаты точек графика функции у=У%, оставив
неизменными их абсциссы, построим график функции z/ = 3 ]/2х; с по-
мощью симметричного отображения относительно оси Оу строим
график функции i/i== 3 ]/—2х;, затем выполняем параллельный пере-
нос полученного графика на' две единицы масштаба влево, т. е.
вспомогательную ось ординат графика функции у^= 3 ]/—2х пере-
носим параллельно вдоль оси абсцисс
на две единицы масштаба вправо, нако-
нец, выполняем параллельный перенос
последнего графика на 0,7 единицы мас-
штаба вдоль оси ординат вниз, т. е. вспо-
могательную ось абсцисс графика под-
нимаем вдоль оси ординат на 0,7 единицы
масштаба вверх.	________-*•
График функции у i= 3 У—2 (х+2)—
— 0,7 приведен на рис. 100.
Пример 6. Построить график
функции
у s= 8х — 2х2.
Записываем заданную функцию в виде
^^-2[(х-2)2-4].
Рис. 101. у = х2 (!)• у = (Х_*
— 2)2 (2); ^ = 2[(х—2)2-ч
~ 4] (3); у = 8х — 2хг =
= -2 [(х —2)8—-4] (4).
Очевидно, что график функции у ±=
= — 2 [(х —2)2 — 4] получим из графика
параболы у х2, выполнив последова-
тельно ( такие преобразования: парал-
лельный перенос вдоль оси абсцисс на
две единицы масштаба вправо; параллель-
ный перенос вдоль оси ординат на четыре
единицы масштаба вниз; растяжение по
оси ординат в два раза; симметричное
отображение относительно оси абсцисс.
График функции у = 8х— 2х2 приведен на рис. 101.
Пример 7. Построить график ^функции
у ;= sin2 х.
Записываем заданную функцию в виде
1	п.1*
у — — 2-cos2x + y.
Очевидно, что график функции у cos 2х + -~ получим из гра-
фика функции у = cos х, выполнив последовательно такие преобра-
зования: сжатие по оси абсцисс в два раза; сжатие по оси ординат
в два раза; симметричное отображение относительно оси абсцисс;
параллельный перенос вдоль оси ординат вверх на единицы
масшгаба.
4 8-413
97
График функции #;=sin2x представлен на рис. 102.
Примеры построения графиков функций с помощью рассмотрев’
ных преобразований приведены на рис. 103—113.
Рис. 103. у == -i- cos 2x (1)\ У*=~2
(2)i у = cos2 x (3).
з	1
Рис. 104. у аж —- (!)• у = cos 4х
4	4
(2); У e sin* х 4- cos* х = -i- cos 4x±
+ 7- (3).
It
98
4*
99
Построение графиков функций,
аналитическое выражение которых содержит знак модуля
Построение графика функции ys=/(|x|). Для построения этого
графика нужно построить график функции у — f (х) для х^>0,‘
а затем отобразить построенную кривую симметрично относительно
оси ординат. Эти две части (построенная и отображенная) дадут
в совокупности график функции t/ = f(|x|) (рис. 114).
Пример 8. Построить график функции
£/ S= sin | X |.
Строим график функции у sin х для х>.0, а затем этот гра-
фик зеркально отображаем относительно оси Оу. Получаем график
заданной функции (рис. 115).
100
Рис. 113. у — arcsin (х — 1)
(О; У = arcsin 2 (х — 1) (2);
у = —arcsin 2 (х — 1) (3).
Рис. 114. y=f(x) (1); у = f (I х |)
101
Пример 9. Построить гргфик функции
у =
График функции у^=2х при х>Ои его зеркальное отображение
относительно оси Оу дадут в совокупности график заданной функции
(рис. 116).
Пример 10. Построить гра-
фик функции
у arcsin J х — 1 |.
Сначала строим график функ-
ции у = arcsin х для	От-
ображаем построенный график для
х>0 симметрично относителы о
оси ординат. Далее выполняем
параллельный перенос вдоль сси
абсцисс на единицу масштаба впраго.
График функции t/ =
= arcsin | х—1 | представлен на
рис. 117.
Примеры построения графиков
функций, со;ержащих модуль аргу-
мента, приведены на рис. 118—121.
Построение графика функции
у >= |./ (х) |. Для построения гра-
фика функций у | f (х) | надо
---------------------------------$	х
Рис. 119. // = /ПИ.
построить график функции у = f (х), далее оставить без изменения
все части построенного графика, которые лежат выше оси абсцисс,
а части, расположенные ниже ее, отобразить симметрично относи-
тельно этой оси (рис. 122).
102
Пример 11. Построить график функции
Р=|Х2-1|.
Строим график функции у — х2—1 на ]—оо; оо]. На интервале
]—1; 1[ функция у — х2—1<0 (кривая расположена под осью
абсцисс). Эту часть графика функции
у х2 — 1 симметрично отображаем
относительно оси абсцисс, а осталь-
ную его часть оставляем без измене-
ния (рис. 123).
Пример 12. Построить график
функции
У= I logo х|, а > 1.
Строим график функции у — loga х.
На интервале ]0; 1[ функция у^
Рис. 120. у = log8 I х |.
= loga х < 0 (кривая расположена под осью абсцисс). Эту часть
графика функции у — loga х симметрично отображаем относительно
оси абсцисс, а остальную оставляем без изменения (рис. 124).
Построение графика функции у s= | f (| х |) |. Для построения
графика функции у = | f (| х |)| надо
у = f (|х|), далее оставить без изме-
нения все части построенного гра-
фика, которые лежат выше оси абс-
цисс, а части, расположенные ниже
ее, отобразить симметрично относи-
тельно этой оси.
Пример 13. Построить график
функции
i/=|log2|x||.
Строим график функции у~
= 1°&21 х I- Затем строим график мо-
построить график функции
дуля этой функции и получаем график заданной функции у =
S= I log2 I х 11 (рис. 125).
Пример 14. Построить график функции

Построение графика выполняем в три этапа: строим график
функции у ?=|х|, выполняем его параллельный перенос вддль оси
ординат на одну единицу масштаба вниз, часть графика, располо-
103
Рис. 124. у — | loga х |, а > 1.
Рис. 125. # = | log/| х ||.
Рис. 126. у = || х | — 1 |.
104
женную под осью абсцисс, симметрично отображаем относительно
этой оси (рис. 126).
Примеры построения графиков функций рассмотренного вида
приведены на рис. 127, 128. •
рис. 128. у — | logs (| х | — 1) |.
Пример 15. Построить график функции

Строим график функции У — \х— 1 |, затем симметрично отобра-
жаем его относительно оси абсцисс (рис. 129).
Примеры построения графиков
функций, содержащих модули,
приведены на рис. 130—134.
Замечание. При построе-
нии графиков функций, являющих-
ся суммой, произведением, частным
функций или более сложной функ-
цией, из которых одна или не-
сколько содержат знак модуля,
находят область определения функ-
ции, раскрывают знак модуля на
тех промежутках, где выражения
с модулем не меняют знака, и, на-
конец, строят график функции,
заданной на разных промежутках
разными формулами.
Пример 16. Построить гра-
фик функции
4/Н*+2|+|Зх+1
| + |x-y|-Sx + 2.
Область определения функции: ]—оо; оо[. Решаем уравнения
х + 2	0, х~ —2,
Зх4-1=0, х = -|,
о
1®?
Рис. 130. 1^1 = I log, (I x |-1)|.
tM
1
Рассмотрим промежутки ]—оо; —2],
]т ’ °°[ ’ ЭТИХ пРомежУтках функции г/==х+2, у = Зх + 1,
1
у^х—— не меняют знака.
*	2
При х £ ]—оо; — 2] у = — х — 2 — Зх — 1 — х + у — Зх + 2 =
Риг. 133. у = -у (| sin х | — sin х).
Рис. 134. у = cos х + I cos х |.
при х £ —2;
= -бх+з1;
-4- У = х + 2-Зх-1-х + ~-Зх + 2 =
и J	Z
при X € I— у ; у I у = X + 2 + Зх + 1 — х + у
-Зх+2= 5-i;
I—2" ’» 001 */ = х+ 2 + Зх+1+* —2— Зх + 2
при х С
= 2x + 4-
График заданной функции приведен на рис. 351, б.
107
РАЗДЕЛ S
ГРАФИКИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
§ 1. Построение графиков сложных функций
Рассмотрим сложную функцию
У—f [ф (я)].
Здесь функция у зависит от аргумента х не непосредственно, а через
Промежуточную функцию ср (х). Обозначив ср (х) через и, получим
Рис. 135. Геометрическое построение
Рис. 136. Построение графика слож-
ной функции с помощью линейки и
циркуля; у = f(x) (1)-, у = ср (х) (2).
Часто промежуточную функ-
цию и = ср (х) называют внутрен-
ней, а функцию у *= f (и) — внеш-
ней.
Графики сложных функций
можно строить, учитывая резуль-
таты общего исследования функции
(см. § 2 разд. 2) и используя свой-
ства функций у — f.(u) и и ф (х).
При этом надо иметь в виду, что
выражение f [ф (х)] будет иметь
смысл для тех значений х, для
которых имеет смысл выражение
Ф (х), и принимать такие значения
и, для которых определено выра-
жение f (и).
При построении графиков слож-
ных функций следует учитывать
основные свойства четных и нечет-
ных функций, периодических функ-
ций, монотонных функций (см. § 2
разд. 1). Надо также найти зна-
чения сложной функции на концах
интервалов монотонности или уста-
новить, как ведет себя функция
в окрестноспгэтих точек, если они
(или одна из них) не принадлежат
области определения.
Приведем другой способ по-
строения графика сложной функции
0:=/[ф(х)] (рис. 135). Обозначим через 4, Alt А2, А3, А4 соответ-
ственно точки (х; 0), (х; ф (х)), (ф(х); ф (х)), (ф(х); f (ф (х))),
(х; Н<р(х))).
Построение выполняем в таком порядке:-строим графики- функ-
ций y — f(x) и £/;=ф(х); проводим биссектрису первого и третьего
координатных углов (i/z=x); проводим через точку А прямую, парал-
лельную оси Оу, до пересечения с графиком функции у — ф (х)
(получаем точку 4J; проводим через точку 4X прямую, параллель-
ную оси Ох, до пересечения с биссектрисой (получаем точку А2);
- проводим через точку А2 прямую, параллельную оси Оу, до пересе-
чения с графиком у = f (х) (получаем точку 43); проводим через
108
точку А3 прямую, параллельную оси Ох, до пересечения с продол-
жением отрезка АА}. Полученная в пересечении точка А4 (х; f (<р (х)))
и будет точкой графика функции у = f [<р (х)]. Аналогично строятся
и остальные точки графика.
Пользуясь линейкой и циркулем, можно этот способ упростить.
Через точку Р (х; 0) проводим перпендикуляр до пересечения с гра-
фиком у = (р (х)\ Получаем точку Q, причем PQ^=y(x). Далее, на
оси абсцисс берем точку Т с абсциссой ОТ ;= PQ. Проведя через
точку Т перпендикуляр до пересечения с графиком у == /(х) в точке
S, получим TS = /(x). Проектируя затем точку S на перпендику-
ляр, проведенный через точку Р, получаем точку М (х; f(<p(x)))
(рис. 136).
Замечание. График функции у = f (ср(х)] можно построить
еще и так: строим график функции ц = ф(х), а затем, учитывая
значения ординат этой функции
и основные ' свойства функции
у = f (и), выполняем построение
графика заданной функции*.
Пример 1. Построить график
функции
у = е"~х* (кривая Гаусса).
Записываем данную функцию
через промежуточный аргумент и:
у — е~и, TJ& и — х2. Исследуем
функцию у — е~х^ по схеме § 2
разд. 2. Область определения функ-
ции: ]—оо; оо[. Область значений
функции: ]0; 1]. Функция четная,
поскольку внутренняя функция
и = х2 — четная. Поэтому достаточ-
но построить график функции для
Рис. 138. Другой способ построения
графика функции у = е~х2; у = е~х
.(1)\ У = х* (2).
х^О. Функция у — е~и — убывающая на ]0; оо[, а функция н = х2
на ]0; оо [ возрастает, следовательно, сложная функция у = е~х*
на ]0; оо[ убывающая. Функция у = е~и вогнутая и убывающая,
а функция и = х2 — вогнутая и возрастающая. Функция у = е~х —
♦ Более детально о построении графиков сложных функций вида у —
= U У — у = logQ f fx), у — sin f (x), у — arcsin f (x) и т. п. см. в
книге: ШундаН. М. ФункцЦта ix графши.—К.: Рад. школа, 1976.
109
убывающая на [0; оо[. График функции проходит через точку(0; 1).
Предельные значения функции на концах интервала ]—оо; оо[ равны
нулю. Горизонтальная асимптота: у = 0.
График функции представлен на рис. 137.
Теперь выполним построение графика функции У — ё~х* другим
способом. Для примера представим построение произвольной точки
Л42 графика функции у = е~х\ Возь-
мем точку Р2 (2; 0); проведем перпенди-
куляр до пересечения с графиком у = х2,
получим точку Q2 (2; 4). Отложим на оси
абсцисс от начала координат отрезок
P2Q2,получим точку Т2. Через точку Т2
проведем перпендикуляр к оси абсцисс
до пересечения с кривой у = е~х, полу-
чим точку S2. Далее, через точку S2 про-
ведем прямую, параллельную оси абс-
цисс, до пересечения с прямой P2Q2t по-
лучим точку М2. Аналогично строим
еще несколько точек графика функции
y — e~xi (рис. 138).
Примеры построения графиков слож-
ных функций приведены на рис. 139—
144.
Пример 2. Построить график функции
у = 2C0S х.
Область определения функции: ]—оо; +оо[. Область значений
функции:
-i- ; 2 . Функция периодическая с периодом 2л. Функция
Рис. 140. у — е^х.
410
на интервалах
4г- ; 0 и л; л] возрастающая, на J0; л[ —
L J 2 L
убывающая;
График функции представлен на рис. 145.
Примеры построения графиков
сложных функций приведены на
рис. 146—149.
Рис. 142. у = е1/*8.
Рис. 144. у == el-~x\
Ш
Пример 3. Дан график функции у f (х) (рис. 150). Построить
график функции y — [f(x)]2.
Строим график функции у х2. Заметим, что точки At Bf С, D
и Е графика функции у^= f (х) будут принадлежать и графику функ-.
ции у = [f(x)]2, поскольку в этих,точках
заданная функция у = f (х) равна 0 или 1.
Пример 4. Построить график функ-
ции
У= In (1 + х2).
Область определения функции: ]—оо;
9о[. Область значений функции: [0; оо[.
функция четная. Функция монотонно
возрастает при | х | оо:
4
Ул
2
Рис. 145. д = 2COS х.
х
о
7
Рис. 146. у « 2*& х.
lim In (1 4-х2) = 4-оо.
Х=±оо
Трафик^функции у = In (1 + х2)
Представлен на рис. 151.
Пример 5. Построить график
функции
у = In cos х 4- cos х.
Рис. 147. у == 2s^n х.
Область определения функции:--------— 4~ 2&л; — 4~ 2£лI. Об-
ласть значений функции: ]^оо; 1]. Функция четная. Функция пе-
риодическая с периодом 2л. Для х С jo; функция убывающая
как сумма двух убывающих функций. Для х£----------; ~4 график
|12
функции выпуклый. Наибольшего значения (у^= 1) функция дости-
гает при Х5=0. Вертикальная асимптота: х>=-^--
График функции у = In cos х + cos х представлен на рис. 152.
Рис. 150. Построение графика у =
= [/ (х)]2 по Данному графику у =•
•=/(х): у = х« (1)-, у = Цх) (2)}
V=lf W]2 (3).
113
Примеры построения графиков сложных функций приведены на
рис. 153—164.
Пример 6. Построить график функции
. 1
у = arcsin — .
х
Область определения функции: ^~-|<1,или]—оо;—1] Ц [1; оо[.
Л	9	1	.1 Я . Л	/	« \	Л
Область значении функции. I —— ; "2"г пРичем —0 —-’
л
1/(1) = >2”. Функция нечетная. Функция монотонно убывает в обл.асти
_ «ее	,	1 ~ х
Рис. 155. у — In ~— .
14-х
определения. Заметим, что lim 1/^=0.
«>
Горизонтальная асимптота: t/= 0.
График функции у — arcsin представ-
лен на рис. 165.
Пример 7. Построить график функ-
ции
у — arccos (cos х).
Функция периодическая с периодом 2л,
четная. Область значений функции: [0; л].
Имеем cos у — cos х, откуда у = х + 2£л
или у^=—х + 2^л (k £ Z). Записываем
функцию на [0; 2л] так:
х,
—х + 2л,
если 0 < х < л,
если л < х < 2л.
Учитывая периодичность, строим график
заданной функции (рис. 166).
Рис. 156. у = х2 4-	4- 3 (Г)\ у == log, х (2)- log, (х2 4- 2х 4- 3) (3).
114
Рис. 159. д — In (1 -f- ех).	Рис. 160. у = In (arctg к).
115
Рис. 162. £/=VrlgCOSX.
Рис. 161. у — 1g tg X.
Примеры построения графиков сложных функций приведены на
рис. 167—182.
Пример 8. Построить график функции
у *= sin (sin х).
Облаолъ определения: ]—оо; оо[. Область значений функции:
[—sin 1; sin 1]. Функция периодическая с периодом 2л, нечетная.
116
Функция возрастает и убывает там, где возрастает и убывает функ-
ция sinx. Нули функции: х — kn (k £ Z).
Fmax — sin 1 при x = ~- + 2&л,
3
sin 1 при	+
t17
Рис. 169. у = arccfg-i- ,
Рис. 171. у = arccos х2.
118
Рис. 175. у = arctg (tg x).
tw
Рис. 182. у = arcsln ах, а > 1.
Рис. 183. у = sin (sin х).
120
График функции у — sin (sin х) представлен на рис. 183.
Пример 9. Построить график функции
у = sin (arcsin х).
Область определения функции: [—1; 1].
В пределах области определения функции
sin (arcsin х) = х.
График функции x/=sin (arcsin х)
представлен на рис. 184.
Примеры построения графиков
сложных функций приведены на
рис. 185—187.
Рис. 187. у — tg (arcctgx) = -i. Я
у = ctg (arcfg *) = “-•
Рис. 186. у — sin (arccos х) = V1 — хг
и у = cos (arcsin х) = /1 — хг.
Пример 10. Построить график функции у — -г по графику
/ W
функции г/ = / (х).
Исследование функции у = выполняем по схеме, представ-
/ W
ленной в § 2 разд. 2, причем существенно используем свойства функ-
ции у^=/(х).
Функция у =  определена для тех значений х, для которых
/(х)=/=0. Нули функции у f (х)—это точки разрыва функции
121
у =	- Обозначим их через хи х2, ... , хп. Прямые х = Х1,
х = х2, ..., х = хп — вертикальные асимптоты графика функции
У~ f '
Учитывая область значений функции y=f (х), определяем область
ч л.	1
значений функции у =	•
/
Если функция у = f (х) четная, то и функция у	четная.
Если функция у — f (х) нечетная, то и функция у —	нечетная.
Если функция у = f (х) периодическая с периодом со, то и функ-
1
ция у— ... периодическая с периодом со.
I \х)
На интервалах возрастания функции у — f (х) функция у —
- убывающая, на интервалах убывания функции y = f(x)
I (х)	1
функция у =
Если функция
функция 1/ = -^
Наклонные асимптоты графика функции у	определяем
/ Iх)
по формулам § 2 разд. 2.
Замечание/ Для построения графика функции у = у до"
по графику функции у = f (х) можно использовать преобразование
инверсии относительно оси абсцисс для графика функции у — f (х).
Рассмотрим некоторые примеры.
П р и м е р 11. Построить график функции
1
’ /х
А 1
Выполняем исследование функции у = —— , используя свойства
/х
возрастающая.
у = f (х) на некотором интервале выпуклая, то
на этом интервале вогнутая.
3/^
функции у = у X.
Функция у = равна нулю только при х = 0. Следовательно,
область определения функции у = --: ]—оо; 0[ (J ]0; + ©о[. Пря-
/х
мая х — 0 — вертикальная асимптота графика функции у^—!—.
1
Предельные значения функции у — — : на интервале ]— оо; 0[
соответственно 0 и — оо; на интервале ]0; оо[ соответственно + оо и 0.
Ш
Функция у = Ух нечетная, следовательно, и функция J/ = -JL
|/ж
нечетная, ее график симметричен относительно начала координат.
Поскольку на интервале ]0; + 00[ функция у— Ух возрастает,
то функция у = на этом интервале убывает* На интервале
10; оо[ функция у = Ух выпуклая, а функция у=— на этом
3/i
интервале вогнутая.
3 1
Рис. 188. у = Vic (1)\ у = — (2).
з
Vx
График функции у —представлен на рис. 188.
У х
Пример 12. Построить график функции
у = sec х.
v	1
Учитывая, что sec х — — - , проводим исследование функции
у — sec х, существенно используя свойства функции у — cos х.
Поскольку нули функции i/ = cosx: х=~(2п-{-1) (n£Z)t
то функция y=’secx определена при всех х, кроме х=-~ (2n+ 1)
ИЗ
(п С 2). Прямые х = у (2п+ 1) (n € Z) являются вертикальны-
ми асимптотами графика функции y = secx.
Нулевых значений функция у = sec х не принимает, ее график
не пересекает ось абсцисс. Область значений функции i/ = cosx:
[— 1; 1], следовательно, при всех допустимых значениях х| secx |:> 1.
Функция t/ = cosx четная, следовательно, и- функция t/ = secx
четная* Функция у = cos х периодическая с периодом 2л, следова-
тельно, и функция у = sec х периодическая с периодом 2л.
На -g-; л функция у = cos х убывает от 0 до —1, а функция
1л Г	. _
y — secx на 1у ; л| возрастает от —оо до —1. Функция y — cosx
L л Г 1 L
на 0; -g-l выпуклая, следовательно, функция t/=secx на этом
интервале вогнутая. На у; л функция y=cosx вогнутая, сле-
довательно, функция у = sec х выпуклая на у ; л *
График функции # = secx представлен на рис. 189.
Примеры построения графиков функций приведены на
рис. 190—202*
Построение графика функции у = с помощью циркуля
и линейки приведено на рис* 203.
124
Рис. 192. у = cosec х.
125
Рис. 195. У -------:.
arcsin х
126
127
§ 2. Графики алгебраических функций
В этом параграфе рассмотрены графики целых рациональных
функций (многочленов), дробно-рациональных, иррациональных
и. трансцендентных функций. Бесспорно, построение их графиков
можно осуществлять общим способом построения графиков сложных
функций (cMi § 1 разд. 5), выполняя соответствующие действия и
преобразования графиков (см\ разд. 4). Выделим наиболее важные
и распространенные группы этих функций и рассмотрим особенности
построения их графиков.
128
Графики целых рациональных функций
Целая рациональная функция, или многочлен,— это функция вида
у = аохп + а1хп~1 + • • • + ап—1Х + ап,
где п — целое неотрицательное число; а0, s, ап — действительные
постоянные числа.
Линейная функция. Простейшей целой рациональной'функцией
является линейная функция (при n = 1). Запишем ее в виде
Рис. 204. Линейная функция у = ах д; а > 0, Ъ > 0 (а); а < 0, Ъ > 0
(б); а > 0, Ь < 0 (в)\ а < 0, b < 0 (г).
•График линейной функции — прямая линия. Функция . монотонно
возрастает при а > 0, монотонно убывает при а < 0, постоянна
л	{ b \
при а = 0. Точки пересечения с координатными осями: I-------; 01
и (0; b)t
Различные виды графика у = ах + b в зависимости от знаков
а и b представлены на рис. 204.
Другие примеры графиков линейных функций приведены на
рис* 205, 206.
Квадратная функция (квадратный трехчлен). Общий вид квад**
ратного трехчлена
у = ах2 + Ьх + с,
где с — любые действительные числа.
5 8-413
129
График квадратного трехчлена—парабола с вертикальной осью
симметрии: х = —- ~ (рис. 207).
Представим два способа построения графиков квадратного трех-
члена: выделение полного квадрата и применение соответствующих
преобразований графиков, рассмотренных в разд. 4, для построения
графика; построение графика на основе исследования квадратного
трехчлена.
Рис. 205. у = ах b. b — 0: у = 2х Рис. 2С6. у — ах	Ь, а = у = 2
(/); b * 0: у = 2х — 3 (2).	(1), у = -3 (2).
Пер вый способ. Будем считать, что а Ф 0. Преобразуем
правую часть функции:
I 2 , b \ | I 2 , п ь , ь2 ь2\ ,
^ = 4 * +Т*) + С=а(Х + 2хГа+4^-4а^) + с =
[[	. Ь\2	Ь2	, 	(	, ь \2	ь2 .
[\	1 2а/	4а2]	\	1 2а/	4а 1
I , b
— А * + 7Г-
\ 1 2а
Ь2 — 4ас
4а
Следовательно,
__ & ~ 4 ас
4а
Отсюда очевидно, что
130
график квадратного трехчлена у = ах2 + Ьх + с получим из парабо:
лы у = х2 с помощью последовательного выполнения таких преобра-
"	ь
зований: параллельного переноса вдоль оси абсцисс влево на --
единиц масштаба; растяжения (сжатия) по оси ординат в |а| раз;
| Ь2 — 4ас|
параллельного переноса вдоль оси ординат на I———[единиц
масштаба в направлении, знак которого противоположен знаку
Ь2 — 4<7С
4а
Заметим, что если а = 1 (у = х2 + рх + q), то построение гра-
фика значительно упрощается (не надо выполнять растяжение гра-
фика).
Второй способ. Область определения функции у = ах2 +
+ Ьх +	]— 00; 00[• График функции у = ах2 + Ьх + с симметричен
„	Ь	( Ь Ь2 — 4ас\
относительно прямой х = —	. Точка 1 —	;--------- — точка
г	2а	\ 2а 4а /
экстремума функции (одновременно и вершина параболы), причем
если а > 0, то в этой точке минимум; если а < 0, то максимум.
1 ь Г
При а>0 функция на I—оо;——| монотонно убывает, а на
1 b , Г	.
— 2^; + оо монотонно возрастает, на ]—оо; оо[ кривая вогнутая.
При а<0 функция на J—оо;—монотонно возрастает, а на
—	+ оо монотонно убывает, на ]—оо-; оо[ кривая выпуклая.
Точки пересечения с осью абсцисс:	-------; 0J, с осью
ординат: (0; с).
Заметим, что значение коэффициента влияет на форму графика
функции у = ах2 + Ьх + с, а именно: ветви параболы у = ах2 + Ьх + с
теги круче, чем больше | а |.
Примеры построения графиков квадратных функций приведены
на рис. 208.
Кубическая функция (многочлен третьей степени). Общий вид
многочлена третьей степени
. У = ах* + Ьх2 + сх + </,
где а =£ 0, b, с, d — любые действительные числа.
а)	Если а = 1, Ь = с = d — О, то многочлен имеет вид
У = х\
Эта функция уже изучена нами (см. § 1 разд. 3).
6)	Если а=1, с = k 0, /> = d = О, то функция у = ах3 -f-
+ Ьх2 + сх + d имеет вид
у = X* + kx.
Область определения функции: ]—оо; оо[. Функция нечетная.
5*	131
Если k > 0, то график функции проходит через точку (0; 0)«
Поскольку функции у = х3 и у = kx возрастающие (при k > 0), то
функция у— х3kx возрастающая, экстремума нет.
Функция вогнутая при х£ ]0; оо[.
Заметим, что сложение линейной функции с любой функцией не
влияет на выпуклость (вогнутость) графика. Точка (0; 0) — точка
перегиба графика функции. Очевидно, что график функции у = х3 +
4- kx (при k > 0) круче, чем график функции у — х3 (рис. 209).
Если k < 0> то график функции у = х3 + kx проходит через
точки (0; 0),(]/—£;0),	£;0). Функция при х£ I— оо;
Рис. 209. Кубические функции;
у = х* (1) \ у = ха + х (2),
возрастает, а при х 6
убывает. Функция имеет максимум при х =
Утах
-у у — yl и минимум при х = у y-l*/min = y у — — .
График функции у = х3 + kx (k < 0) представлен на рис. 210.
В) График функции
у = X3 + kx + Ь
получим из графика у = х3 + kx с помощью параллельного переноса
вдоль оси ординат на | b | единиц масштаба в направлении, знак
которого совпадает со знаком числа Ь.
г) Для построения графика функции
у = х3 + Ьх2 + сх + d
выполняем преобразование параллельного переноса начала координат:
, b
У = У'»
132
После преобразования функция принимает вид
у = х' -|"
Следовательно, график функции у == х3.+ bx2 + cx + d имеет такой же
вид, как и график функции у = х3 + kx + b, только центр его сим-
„	b
метрии передвинут по оси абсцисс на ——.
д) Построение графика у = ах3 + Ьх2 + сх + d сводится к по-
строению графика функции вида
у = х3 + kx + b.
Действительно, запишем функцию у = ах3 + bx2 + сх + d так:
(о  b л . с d ।
х3 Ч— х2 4— х-]— .
а 1 а а)
Далее, строим график функции t/ = x3 + -^-x2 + ~x + ~, а растя-
нув последний по оси ординат в а
раз, получим искомый график. Гра-
фик функции у = ах3 + bx2 + сх + d
называют кубической параболой.
Отметим, что поведение функции
у — ах3 + bx2 + сх + d зависит от зна-
ков а и А = Зас— Ь2. Если А^>0
(рис. 211), то функция монотонно воз-
растает при а > 0 и монотонно убы-
вает при а < 0. Если А < 0, то функ-
ция имеет один максимум и один ми-
Рис. 210. у = х* + kx, k < о.
нимум:
' b + /-Д	26s — ЭаЬс — (бас — 26?) /—Д’
„ За ’	27а?
И
6 — /—Д .	263 — 9а6с + (бас — 26?) /—А
За а+	27а?
Точки пересечения с осью Ох определяются действительными кор-
нями уравнения ах3 + bx2 + сх + d — 0. Их может быть от одной до
Рис. 211. Кубическая функция у = ах* 4- Ьхг + сх 4~ d: Д > 0; а < 0 (а):
Д == 0, а > 0 (б)\ Д < 0, а > 0 (в).
133
трех. Точка перегиба (эта точка является одновременно и центром
b . 2b*-$abc , Л
симметрии кривой): £ I — — , —---------Н а) •
Биквадратная функция. Функция вида у = ох4 + Ьх2 + с (а #= 0)
называется биквадратной.
Исследование и построение графика биквадратной функции про-
водят по общей схеме (см. § 2 разд. 2).
Рис. 212. Биквадратная
функция у = х4 + х2.
Иногда можно строить график биквадратной функции с помощью
соответствующих действий и преобразования графиков функций
у = х4, у = х2. Действительно, поскольку
/»2 /д2	л \
у = ах1 + Ьх* + с = — xi + у х2) + с =
то очевидно, что график функции у — ах4 + 6х2 + г можно получить
из графика функции у = х4 + х2 или из графика функции у = х4— х2
с помощью растяжения по обеим координатным осям и параллельно-
го переноса вдоль оси ординат на | с | единиц масштаба.
График функции # = х4 + х3 является суммой графиков функций
у = х4 и у = х2 (рис. 212).
График функции у = х4 — х2 представлен на рис. 213.
Многочлен я-й степени у = аохп +	+ • • • + 0ц—1* + ап>
График — кривая n-го порядка, параболического типа.
а)	Если п — нечетное, то у непрерывно меняется при а0 > 0 от
— оо до 4~оо, а при а0 < 0 — от +°° Д° —°°- Кривая может пере-
секать ось абсцисс (или касаться ее) от 1 до п раз. Экстремумов
эта функция не имеет или имеет их четное число (от 2 до п — 1),
причем максимумы и минимумы чередуются. Точек перегиба — нечет-
ное число (от 1 до п — 2).
134
б)	Если п — четное, то у непрерывно меняется при а0 > 0 от
-|-оо до 4~оо, а при а0 < О GT —00 Д° ~°°- Кривая или не пере-
секает ось абсцисс или пересекает ее (или касается ее) от 1 до п
раз. Функция имеет нечетное число экстремумов (от 1 до п—1),
причем максимумы и минимумы чередуются. Точек перегиба
— четное число (от 0 до п — 2). Асимптот эти кривые не имеют
(рис. 214). Заметим, что исследование и построение графика много-
члена n-й степени целесообразно проводить, пользуясь методами
высшей математики.
Пример 1. Построить график функции
У= х2 + *+ 1.
Преобразуем функцию, выделив полный квадрат:
/	1 \? з
0 = x2 + x+1 = ^ + 2J +2_.
Строим график функции у = х2, затем выполняем следующие пре-
образования графика функции у = х2: параллельный перенос вдоль
оси абсцисс на единицы масштаба влево (вспомогательную ось
ординат переносим параллельно ,вдоль оси абсцисс на -у единицы
масштаба вправо); параллельный перенос вдоль' оси ординат на
3	к	(
— единицы масштаба вверх (вспомогательную ось абсцисс опускаем
3	к
вдоль оси ординат на — единицы масштаба I ♦
График функции приведен на рис. 215.
Пример 2. Построить график функции
у = —2х2 — х 4- 6.
Построим график на основе исследования квадратного трехчлена.
3
Область определения функции: ]— оо; оо[. Нули функции: -% , —2.
График кривой пересекает ось ординат в точке (0; 6). Вершина пара-
135
49\ rr
-g- I. Поскольку
максимум. Функция на
49	11.
до-g-, а на I—-J-; +°
а = —2 < 0, то в
1 Г
---МОНОТОННО
4 I
/	1 . 49\
точке I—— ; -g-1 —
монотонно убывает от
возрастает от —оо
49
— до —оо. Кривая
о
.	гх	1
выпуклая в области определения. Ось симметрии: х ---------.
График функции представлен на
рис. 216.
Пример 3. Построить график
функции
Рис. 216. у = — 2х2— хН-6.	Рис. 217. у = х* — Зх2 + 2.
Выполняем преобразование параллельного переноса начала коор-
динат:
х = х' + 2,
У = У' -2.
Будем иметь
у' = х'г — 1х'.
Следовательно, построение графика заданной функции свелось к по-
строению графика функции у' — х'3— 7х' в системе координат
х'ОгУ' (см. рис. 210). В данном случае k = —7 < 0, следовательно,
график функции у' = х'3—- 7х' проходит через точки^0; 0), (]/7; О);
(—	О). Функция при х С
оо I возрастает, при х' Е
убывает. Функция имеет
максимум при х'
'max
и минимум при
136
Пример 4. Построить график функции
*/=(! + *) (5 —X).
Выполнив умножение в правой части выражения, получим квад- •
ратный трехчлен	,
у=^Х2 + 4х + ^
Однако в данном случае нет нужды в этом, проще исследовать функ*
цию в заданном виде. Нули функции: хг = — 1, х2 = 5. Точки пере-
сечения кривой с осью абсцисс: (—1; 0) и (5; 0). Ось параболы:
xi + х2 _ —1 + 5 _ 9
х------2	2
Точка (2; 9) — вершина параболы. Точка пе-
ресечения с осью ординат: х = 0; у = 5.
График функции у — (1 + х) (5 — х)
представлен на рис. 218.
Пример 5. Построить график функции
у = х4 - 2х2 + 2.
Область определения функции: ]—оо;
оо[. Функция четная, ее график симметри-
чен относительно оси ординат. Записав
функцию в виде
у == х4 — 2х2 + 2 = (х2 — I)2 + 1,
видим, что при х = ±1 функция имеет ми-
нимум (ymin = 1). Поскольку у = (X2 — I)2 4-
+ 1>1, то график кривой располагается
не ниже прямой у= 1. Функция имеет м$к-
Рис. 218. ^ = (1 + л) (5—
-х).
симум при х = 0 (t/max = 2). При х 6 ]—оо; — 1 [ (J ] 0; 1 [ функция
убывает, а при х С ]—1; О [(JJ И + °°[ возрастает.
График функции у=х4 —2х2+2 представлен на рис. 219.
Примеры построения графиков многочленов приведены на
рис. 220—222v
Функция вида у = (ах2 + Ьх + с)п, где п — целое положитель-
ное число» Если квадратный трехчлен ах2 + Ьх + с имеет равные
действительные корни, то функцию у = (ах2 + Ьх + с)п записыва-
ем так:	4
у = ап (х — a)2/J,
где а — корень трехчлена. Построение графика этой функции осу-
ществляем с помощью преобразования графика степенной функции
у = х2п (см. § 2 разд. 4).
Если квадратный трехчлен ах2 + Ьх + с имеет действительные
различные корни а и Р, то функцию у = (ах2 + Ьх Ц- С)п записыва-
ем так:
У = ап (х — а)п (х — Р)л.
137
Рис. 220. у~2-}-х(1); у —
= 1 -х2 (2); у = (1 - л2) X
X (2 4-х) (3).
Рис. 221. у = 1 4-
-Ы —X» |.
138
Построение графика этой функции сводится к построению графиков
функций
у = ап (х — а)л и у = (х — 0)л
и их умножению.
Если квадратный трехчлен ах2 +	+ с имеет комплексные кор-
ни, то график функции у = (ах2 + Ьх + с)п строим как график
сложной функции (см. § 1 разд. 5).
Примеры построения графиков функций приведены на рис. 223,
224.
Графики дробно-рациональных функций
Дробно-линейная функция — это функция вида
ах + b
сх + d
(ad — be #= 0),
где числитель и знаменатель — линейные функции.
Разделив числитель на знаменатель, получим
а , tc — ad
У = ~7+—,--------ТГ
X + —1
Теперь очевидно, что график дробно-линейной функции можно полу-
чить из графика функции у = — с помощью следующих преобразо-
Х	к	\d I
вании: параллельного переноса вдоль оси абсцисс на у единиц
d
масштаба в направлении, знак которого противоположен знаку —;
, . tc — ad
растяжения по оси ординат пропорционально коэффициенту —;
параллельного переноса вдоль оси ординат на | ~ J единиц масш-
.	а
таба в направлении, знак которого совпадает со знаком — .
Замечание. График любой др об но-линей ной функции можно
строить и способом непосредственного исследования функции по схеме
§ 2 разд. 2.
График дробно-линейной функции—равносторонняя гипербола
с асимптотами, параллельными осям координат:
х =
d а
-----и у — —
с	у с
Примеры построения графиков дробно-л инейных функций приве-
дены на рис. 225, 226.
139
Дробно-рациональная функция. Рассмотрим дробную рациональ-
ную функцию
=	+ а^-1 + ... дп_1Х + ап = Р (х)
Ьцхт	4- • • • 4“	4- Q (я) ’
у которой числитель и знаменатель — многочлены соответственно п-й
Р (х)
и m-й степени. Пусть дробь 7^-4 — правильная (п < tn). Известно,
х (х)
что любую несократимую рациональную дробь можно представить,
и притом единственным образом, в виде суммы конечного числа эле-
ментарных дробей, вид которых определяется разложением знамена-
теля дроби Q (х) в произведение действительных сомножителей:
£ (Х)	f___^2__L . . . _L
QW~ (x — kj”1'	(x-k^^ ~т~х — ki
4-----bi----1-----bl—
(x-As)m’ (x-ks)ms
BjX 4~ Cf	. t
(x?+ />!* +ft)11*
, MjX + Nj ,
Lm
Г1+ +ттггЛ
^u. x 4~ C a
Hi 1 P-t I
X2- + P1X + Я1
M.tx+\
’ + + PfX + qtx ’
140
если
Q (*) = а« (х —	... (х — ks)ms (х? 4- pix +
+ «/i)14 (X2 + ptx +
где ki, ...» k$— корни многочлена Q (х), имеющие соответственно
кратности mi, .. . , mSi а трехчлены соответствуют парам сопряжен-
ных комплексных корней Q (х) кратностей jn, ...» р/. Дроби вида
А А Вх + С Вх + С
х —.k * (х — k)m ’ х2 + рх + q 9 (х2 + рх + q)^
называют элементарными рациональ-
ными дробями соответственно перво-
го, второго, третьего и четвертого ти-
па. Тут Л, В, С, k — действительные
числа; тир — натуральные числа,
т, р > 1; трехчлен с действительны-
ми коэффициентами х? + рх + q имеет
мнимые корни.
Очевидно, что график дробно-ра-
циональной функции можно получить
как сумму графиков элементарных
дробей.
График функции у —
(m—\t 2, .. .) получаем
фика функции (т — 1, !
носа последнего вдоль оси абсцисс на | k | единиц масштаба вправо.
Трафик функции вида

' (х — k)m
из гра-
2, ...) с помощью параллельного пере-
1
У х2 + рх + q
легко построить, если в знаменателе выделить полный квадрат
а затем осуществить соответствующие преобразования графика функ-
ции ~ . Построение графика функции
_ Вх+С"
У ~ х^ + рх + q
сводится к построению произведения графиков двух функций:
у = Вх + С И у — -5—т—!--;-.
у 1 у x2 + px + q
141
Замечание. Построение графиков функций
Р (х) lax-}- Ь\п
’ где
Р W1"
V (ax2bxс)п ' V LQWJ *
где п — натуральное число, можно выполнять по общей схеме иссле-
дования функции и построения графика (см. § 2 разд. 2); в некото-
рых конкретных примерах с успехом можно осуществлять построение
xt__4
Рис. 227. Дробно-рациональная функция у — ~2 __ 2х — 3 '
графика, выполняя соответствующие преобразования графика (см.
разд. 4); наилучший способ дают методы высшей математики
(см. ч. II).
Пример 6. Построить график функции
х2 — 4
У -х« — 2х -3‘
Выделив целую часть, будем иметь
* 2х — 1
У 1 + х» — 2х — 3 '
2х —— 1
Дробь _ 2х — 3 из°бразим в виде суммы элементарных дробей:
2х-— 1 = _5	1____3	1
х2 — 2х — 3 “ 4 х — 3 + 4 х + Г
142
Строим графики функций
°	1’ У 4 (х — 3) ’ У 4(х+ 1) ’
после сложения этих графиков получаем график заданной функции
(рис. 227).
143
Примеры построения графиков дробно-рациональных функций при-
ведены на рис. 228—238.
144
145
Рис. 236. у
Рис’ 237‘
Графики иррациональных функций
Рассмотрим некоторые простейшие случаи.
Функция вида J=± У ах + Ъ. График функции у — ± У ах-\-Ь
легко получить из графика функции у = У х с помощью соответ-
ствующих преобразований (см. разд. 4).
График функции у = ±Уах + b — парабола, ее ось — ось абс-
цисс, вершина: л(—— ; О), параметр: р = (рис. 239).
Функция вида у=±Уах2 &х + с. Исследование и построе-
ние графика функции проводим по схеме § 2 разд. 2.
Вид графика функции у — ± У ах2 -j- Ьх + с (рис. 240) зависит
от знаков а и 6 s= 4ас — Ь2, Если а < 0, 6 < 0, то график — эллипс,
если а > 0, 6^0, то график—гипербола; оси: t/ = 0, х-— — ;
вершины:
«46
При а < 0 и 6 > О кривая не существует в области действитель-
ных значений х.
Замечание. Графики функций
, . , . .	/ax + fiW ГР(х)]р/’
^(ах‘ + Ьх+С)р/^ = '^	’
где р и q — взаимно простые числа, проще строить с помощью ме-
тодов высшей математики (см ч. II).
Пример 7. Построить график функции
у х — 2 — 1.
Строим график функции у~У к, затем параллельно переносим
график вдоль оси абсцисс на две единицы масштаба вправо и опу-
скаем на одну единицу масштаба (рис. 241).
Пример 8. Построить график функции
у V—x2. + х + 2.
Построим сначала график квадратного трехлена
I 1 \-	9
У — —х? + х + 2 = — (х — у) +-^-.
Очевидно, что функция у г=	—х? + х + 2 определена на отрезке
[1 1	3
—1’ *2| 0НЗ В03Растает от 0 До -g-, з на
[1 Г	з
~; 2 убывает от — до 0 (рис. 242).
Примеры построения графиков иррациональных функций приве-
дены на рис. 243—247.
Графики трансцендентных функций
Графики простейших трансцендентных функций (показательных,
логарифмических, тригонометрических, обратных тригонометрических)
рассмотрены в разд. 3 (§ 2—5), более сложных — в этом разделе
(§ О-
Исследование и построение графиков более сложных трансцен-
дентных функций можно производить по схеме § 2 разд. 2, а еще
лучше — с помощью методов высшей математики (см. ч. II).
Здесь представлены примеры графиков еще некоторых трансцен-
дентных функций.
у г= sinn х, у = cosn х, у ;= tgn х, у ctgn х, где п — целое по-
ложительное число (см. рис. 105, 106, рис. 248—250).
y = sin±p/<7x, у = cos±p^ х, у — tg±p/<7 х, у — ctg±p/<7x, где р
и q— взаимно простые числа (рис. 251—263).
Гиперболические функции. Гиперболический синуа
(shx) определяется формулой
147
Рис. 240. у — ±V ах2 + bx с\ а < 0, 8 <0 (а); а > 0. 8 > 0 (б); а > 0, 8 < 0 (в).
>. ____________
_ "г
о Гл*
ч---У
Рис. 241. у ® Vx — 2 — 1.
- Рис. 242. у = ^х* 4- х 4- 2 (а); у = хг 4- х 4- 2 (б).
149
149
rf
Ik
i
f
J
f
£
• *
Рис. 249. у = tg8 x (1); у = tg x (2); у = ig* x (3).
150
Уь
Рис. 255. у = sin*/* х.
Рис. 258. у = cos’/» х.
Рис. 257. у — ig!• х,

Рио. 263. у = tg“Vi х.
рис. 264. Гиперболический косинус
//=chx (1)\ гиперболический синус
у = sh х (2)л
152
Область определения: ]—оо; оо[. Область значений; ]—оо; оо[. функ-
ция нечетная4. Точка (0; 0) — центр симметрии и одновременно точка
перегиба графика функции. Асимптот нет.
График функции у = sh х строится по графикам функций у^=е*
и у = е~х (рис. 264).
Гиперболический, косинус (ch х) определяется фор-
мулой
Область определения: ]—оо; оо[*
Область значений: [1, оо[. Функция
четная. Минимум в точке (0; 1).
Асимптот нет.
График функции у г= ch х пред-
ставлен на рис. 264.
Гиперболический тан-
генс (th х) опреде ляется фор-
мулой
рХ_ р—х
y^=thx=}—
Область определения:. ]— оо; оо[.
Область значений: ]—1; 1[. Функ-
ция нечетная. Точка (0; 0) — центр
симметрии и одновременно точка
перегиба графика функции. Гори-
зонтальные асимптоты:
График функции у th х пред-
ставлен на рис. 265.
Гиперболический ко-
тангенс (cth х) определяется
формулой
cth х — ,т—
th*
Рис. 265. Гиперболический тангенс
ех — в х *'
Область определения: ]-oo;0](J]0;
оо[. Область значений: ]—оо;
—HUH; 00[• Функция нечетная.
Горизонтальные асимптоты:	Вертикальная асимптота:
График функции представлен на рис. 266.
Гиперболический секанс (sch х)
и *	2
sch х — -г— — —-—— .
ch х ех + е х
График функции приведен на рис. 266.
Гиперболический косеканс (cschх)
,	1	2
CSCh *:=—;= ---— .
sh х ех — е х
График функции приведен на рис. 266.
153
Обратные гиперболические функции (ареа-функции) — это функции
вида
t/ — Arshx (ареа^синус),	если	x = sh$,
у = Arch х (ареа-коси нус),	если	х — ch у,
у = Arth х (ареа-тангенс).,	если	х — th у,
у — Arcth х (ареа-котангенс),	если	х = cth у.
Рис. ^68. Ареа-косинус у = Arch х.
= Arth х.
Эти функции можно выразить и через логарифм:
Arsh х In (х + V & + 0,
Archx^= ±ln (x+ Yx* — 1), x> U
Arth x== 4" In J—— , I x I < 1,
Arcth x — — ln !' » I x l > !•
2 x—1 ’ ‘
Графики обратных гиперболических функций можно получить из
соответствующих графиков гиперболических функций с помощью
симметричного отображения последних относительно биссектрисы
Z хОу.
154
Ареа-синус у — Arshx. Область определения: ]—оо; оо[.
Область значений функции: ]—оо; оо[. Функция нечетная. Точка
(0; о) — центр симметрии (и одновременно точка перегиба), графика
функции. Асимптот график не имеет.
График ареа-синуса представлен на рис. 267.
Аре a-к оси нус t/^=Archx. Область определения: [I;. оо[.
Область значений функции: ]—оо; оо[. Кривая симметрична относи-
тельно оси абсцисс. В точке А(1; 0) кривая касается вертикальной
прямой х^= 1, далее значения функции по абсолютной величине воз-
растают.
График ареа-косинуса представлен на рис. 268.
Аре а-т ангенс у Arth х. Область определения: ]—1; 1[.
Область значений функции: ]—-оо; оо[. Функция нечетная. Точка
(0; 0) — центр симметрии (и одновременно точка перегиба) графика
функции. Вертикальные асимптоты: xi=±l.
График функции представлен на рис. 269.
А р е a-к о т а н г е н с у = Arc th х. Область определения: ] — оо;
— ЦЩН 00[• Область значений функции: ]—оо; оо[. Функция не-
четная. При х С ]—оо, —1[ функция монотонно убывает от 0 до
—оо, при х£ ]1; оо[-г-убывает от оо до 0. Точек% перегиба нет.
Вертикальные асимптоты: х=±1. Горизонтальная асимптота: у = 0.
График ареа-котангенса представлен на рис. 270.
РАЗДЕЛ 6
ГРАФИКИ ПАРАМЕТРИЧЕСКИ ЗАДАННЫХ ФУНКЦИИ
§ 1. Исследование параметрически заданных функций
Пусть функция задана параметрически:
где t — параметр*	t <
В этом случае исследование и построение графика функции про-
водятся так, как для функции, заданной уравнением
Сначала строят графики» функций х^=ф(/) и у^= ф (/) соответственно
в системах координат tOx и 10у. Учитывая графическое изображение
функций х — <р (ty и у = ф (/), исследуют функцию у у (х) по схеме
§ 2 разд. 2. Отметим некоторые особенности графика функции (*):
он симметричен относительно оси ординат, если при замене пере-
менной t на —t не меняется значение у, а х переходит в —х; график
функции симметричен относительно оси абсцисс* если при замене
переменной t на —t не'меняется значение х, а у переходит в —у\
период функции определяется по периодам функций х^=ф'(/) и у —
5=ф(/); для нахождения точек пересечения графика функции (*) с
осью ординат надо найти те значения при которых х = 0 (решаем
уравнение ф(7)х=0)„ и соответствующее значение 1/х=ф(/); для на-
хождения точек пересечения графика функции (*) с осью абсцисс
надо найти те значения t, при которых */~0 (решаем уравнение
155
ф(/) —0), и соответствующее значение х^=ф(/); иногда целесооб-
разно определять точки пересечения графика с биссектрисами коор-
динатных углов у~х и у^=—х, для чего решают соответственно
уравнения
Ч5 (О = ф (0 и Ч (0 = — ф (0.
значения функций х = ф (/), г/ —ф(/) ПРИ найденных t и дадут коор-
динаты искомых точек.
У
Рис. 271. Параметри-
чески заданная функ-
ция х = t2, у
§ 2. Примеры построения графиков
параметрически заданных функций
Пример 1. Построить график функции	j
X = /2,
у = /3.	;
Покажем на этом примере, как иногда (в простейших случаях) >
можно строить графики параметрически заданных функций по точ- *
кам. Составим таблицу значений:	J
/0123—1—2—3	'
х 0	1	4	9	1	4	9	1
0	1	8 27	—1	—8	—27
Построив найденные точки (х; у), полу-
чим искомую кривую (рис. 271).	j
Пример 2. Построить график функции
х—1 — t,
Исследование и построение графика пара- >
метрически заданной функции сводим к иссле-
дованию и построению графика функции, за- •
данной в явном виде у^=у(х).
В системе координат Юх строим график i
функции х=1— t (рис. 272, а), а в системе
координат Юу — график функции у — 1—Я ;
(рис. 272, б). Теперь проводим исследование 1
функции у — у (х). Область определения (см.
рис. 272, а): ]—оо; оо[. Область значений :
(см. рис. 272, б): J—оо; 1[. Поскольку у (—/) —
= у(0, то —0, т. е. х=1,— ось симметрии.
Предельные значения функции: lim	—оо.
Точки пересечения с осями координат:
а)	с осью ординат. Решаем уравнение х = 0, т. е. 1—/ = 0,
откуда / = 1. Вычисляем значение функции у~\— fl при 1,
получаем у — 0. Следовательно, график функции у^у(х) пересекает
ось ординат в точке 0(0; 0);
б)	с осью абсцисс. Решаем уравнение у — 0, т. е. 1 — fl — О,
получаем /—±1, соответственно хх —О, х2 = 2. Точки пересечения
графика функции у = у (х) с осью абсцисс: О (0; 0), С (2; 0).
156
Точки пересечения с биссектрисами координатных углов:
а)	с биссектрисой у^=х. Решаем уравнение 1 — /2г=1—/, от-
куда /1 = 0, /2— !• Следовательно, график функции у^=у(х) пере-
секает биссектрису у = х в точках £)(1; 1) и 0(0; 0);
б)	с биссектрисой у^=—х. Решаем уравнение 1 — /2^=—(1 — /),
иди + — 2 = 0, откуда — — 2, i2— 1. Следовательно, с бис-
сектрисой у = —х график функции у = у (х) пересекается в точках
0(0; 0) и £ (3; —3).
Рис. 272.	1 - / (a); y=l—t2 (б); х = 1 — t, у =±= 1 - /2 (в).
Рис. 273. х =	— 2/ (a); y = t* + 2t (6)-t х = V- — 2t, у = /2 + 2t (в).
График асимптот не имеет.
Теперь выполняем построение графика функции у?=у(х): про-
водим прямую у?= 1 (график функции у — у(х) располагается ниже
этой прямой), далее обозначим точки пересечения графика функции
У = У (х) с осями координат и биссектрисами координатных углов:
О, С, D, Е.
График функции х = 1 — /, у — 1 — /2 представлен на рис. 272, в.
Пример 3. Построить график функции
х = /2 — 2/,
У = + 2/.
В системе координат Юх и Юу строим соответственно графики
функций *)=/? —2/ (рис. 273, a), y^=t2.-j-2t (рис. 273, б).
157
Учитывая графическое изображение функций х^= t2— 2t и у~
= /2 + 2t, исследуем функцию у^=у(х). Область определения (см.
рис. 273, а): ]—1; оо[. Область значений (см. рис. 273, б): ]—1; оо[.
Следовательно, график функции у = у (х) расположен выше прямой
у ——1 и справа от прямой х =—1. Предельное значение функции:
lim # =
Точки пересечения с осями координат:
а)	с осью ординат. Решаем уравнение х=/2— 2t = 0, откуда
= 0, /2 = 2. Вычислив соответствующие значения у, получим точки
пересечения графика с осью Оу*. (0; 0) и (0; 8);
б)	с осью абсцисс; Решаем уравнение z/ = Z24-2/ = 0, откуда
= 0, /2 = —2. Вычислив соответствующие значения у, получим
точки пересечения графика с осью Ох: (0; 0) и (8; 0).
Точки пересечения с биссектрисами координатных углов:
а)	с биссектрисой у — х. Решаем уравнение /2 4- 2/ = /2 — 2/,
откуда t — 0. Вычислив значения х и у при t = 0, получим точку
пересечения графика с биссектрисой у — х: (0; 0);
б)	с биссектрисой .у = —х график пересекается также в точке
(0; 0).
Проводим прямые х — —1, у — —1, у — х, у — —х. Обозначаем
точки (0; 0), (0; 8), (8; 0).
График функции х=/2— 2/, у = t2 + 2t представлен на
рис. 273, в.
Пример 4. Построить график функции
t
у~ в—
t2	t
Строим графики функций х = у—j и у = j (рис. 274, а, б).
Исследуем функцию у — у (х). Область определения: ]—оо;
—00 Ь Область значений: ]—оо; оо[.
График проходит через точку (0; 0).
Точки пересечения с биссектрисами: с у^=х — (0; 0) и (—1;
—1); с у »=—х — (0; 0).
о	'	1 /	4 Ч	I
Вертикальная асимптота: х= — |при / = —1 х^=—% > у—
s= оо). Горизонтальная асимптота: у ~ 0. Наклонная асимптота: 'у —
х _ 3
~2	4 *
Действительно,
t
158
Г 1	1 i3 1
b~ lim (у — kx) — limH----i—‘5'7---fl
f-и L‘-—1	z »—ij
_ lim П - О П 0 + 0 + <1	3
-2(1 - 0(1 +0
4 •
Строим графики функций x=tel, y^=te~t.
Исследуем функцию y — y(x). Область определения: ]—е-1; оо[.
Область значений функции: ]—оо; е-1[. Предельное значение функ-
ции: lim у — 0.
Х-+ оо
График проходит через точку (0; 0). График функции симмет-
ричен относительно прямой х-]-у^=0.
159
График представлен на рис. 275.
Пример 6. Построить кардиоиду
х = 2а cos t — a cos 2/,
у = 2а sin't — a sin 2t.
Строим графики функций х ;= 2а cos t — a cos 2/ и у^= 2а sin t—
— a sin 2t.
Исследуем функцию у*=у(х). Область определения функции:
[—За; а]. Область значений функции: [—2а; 2а]. График функции
симметричен относительно оси абсцисс'. Поскольку функции х~
2а cos t — a cos 2tt у s= 2а sin t — a sin 2t периодические с периодом
2л, то и функция у^=у(х) периодическая с периодом 2л. Предель-
ные значения функции у^=у(х) на концах отрезка [0; 2л] равны
нулю.
График представлен на рис. 276.
Пример 7. Построить циклоиду
xz=a(t— sin f)t
у^=а(1—cos/).
Строим графики функций х ?= a (t — sin t), у=а(\ — cos /)•
Исследуем функцию ys=y(x). Область определения: ]—оо; оо[.
Область значений: [0; 2а]. Функция периодическая с периодом 2л.
График функции симметричен относительно оси ординат.
Точки пересечения с осями координат; с осью абсцисс: (0; 0),
(0; 2ла), (0; 4ла), . .. ; с осью ординат: (0; 0).
График циклоиды представлен на рис. 277.
Пример 8. Построить астроиду
х х= a cos3 t,
у s= a sin3 t
Строим графики функций х=а cos31 (см. рис. 105) и у = a sin3 t
(см. рис. 106).
160
Исследуем функцию у^= у(х). Область определения функции:
[—а; а]. Область значений функции: [—а; а]. График функция сим-
метричен относительно координатных осей. Функция периодическая
с периодом 2л.
Точки пересечения с осями координат:
с осью абсцисс: (а; 0), (—а; 0);
с осью ординат: (0; а), (0; —а).
График астроиды представлен на рис. 278.
Рис. 277. X = a (t — sin /), у = а (1 — cos t) (циклоида).
Пример 9. Построить график функции
х 1= t3 — Зя,
/у — /3 — 6 arctg t.
Рис. 278. х = a cos* у = a sin* t
(астроида).
которых	i/z=oo. График
Строим графики функций х^=
:= t3— Зл (см. рис. 26) и у
= t3 -— 6 arctg t (рис. 279).
Исследуем функцию у^= у (х).
Область определения функции:
]—оо; ©о[. Область значений функ-
ции: ]—оо ; оо[.
Точки пересечения графика
функции с осями координат:
с осью абсцисс: точки Д,
В и С;
с осью ординат: (0; Зл —
— 6 arctg Зл).
График функции вертикальных
асимптот не имеет, поскольку не
существует таких значений t, при
функции имеет наклонные асимптоты. Действительно,
h	У 1- Р —6 arctg/
lim lim —--------------
x-+—co x	ж t —— 3 л
b*= lim (y— kx) lim (/3 — 6 arctg t — t3 + 3л)	6л.
Следовательно, ' прямая у х + 6л — асимптота. Если х + оо
(/ -> 4~оо), то k — 1 и й;=0 и вторая асимптота: у х.
График функции х>= t3 — Зл, у = i3 — 6 arctg t представлен на
рис. 280.
Пример 10. Построить график функции
х s= a (sh t — t), у^=а (ch t — 1).
6	8-413

Рис. 281. у = a (sh t — t) (а)* х = a (ch /- 1) (б); х =** a (sh $ « /ъ у = а (ch Z —
*-1)(вЛ«>0.	f
162
тов лист).
Рис. 284. х = у « (/ +
t > 0.
6*
163
у — '2t + e~~2t (б); х = i е у —	+ e~7t (в).


(2
Рис. 286. х = t + е~* (а);
Строим графики функций x*=a(sh/—-1) (рис. 281, а) и yr=
*=a(cht — 1) (рис. 281, б).
Исследуем функцию у*=у(х). Область определения: ]—со; оо[.
Область значений: [0; оо[. График функции симметричен относительно
• оси ординат. График функции проходит через точку (0; 0).
График функции х s= a (sh t — /), у a (ch t — 1) представлен
на рис. 281, в.
Примеры графиков параметрически заданных функций приведены
иа рис. 282—290.
'164
РАЗДЕЛ 7
ГРАФИКИ ФУНКЦИЙ В ПОЛЯРНОЙ СИСТЕМЕ
КООРДИНАТ .
$ 1. Исследование функций в полярной
системе координат
Общий вид функции, заданной уравнением в полярных коорди-
натах, такой:
p = f(q>)> ~~	' -
а в неявном виде!
F(p, ф)—0.
Функцию р ±= f (ср) можно исследовать в полярной системе координат
пу^ем сравнения ее с функцией в декартовой системе координат
= f (х), которую получаем из первой, меняя в ней р на у, а ф на х.
Тогда естественно, что исследование функции р / (ф) можно вы-
полнять по схеме исследования функции у f (х) (см. § 2 разд. 2).
Отметим некоторые особенности графика функции р г» f (ф) (срав-
нивая его с графиком соответствующей функции y^=f(x)). Область
определения а^х^Ь функции y~ f(x) соответствует [области оп-
ределения а < ф < b функции р ;= f (ф). Особым точкам Х£, х%, ...
функции у f (х) соответствуют особые точки ф£ Xff фа s= х2, ...
функции р •= / (ф).
Н5
Симметрия, а) Пусть y^=f(x)— четная функция. Вследствие
равенства
f(x)^f(-x)
имеем, что точкам А (х; у) и В (—х; у) кривой у = f(x) соответст-
вуют точки Af (р; ср) и Bi (р; л — ф) (рис. 291) кривой р5=/(ф), а
точкам А (х; —у) и В(—х; —у) (рис. 292) — точки Л$ (р; 2л— ф) и
£i(p; л + ф).
б)	Пусть у := f (х) — нечетная функция. Тогда точкам А (х; у)
и В (—х; —у), симметричным относительно начала координат в де-
. Рис. 291. Координаты точек: в декартовой (а) и пслярнсй (б) системах координат.
Рис. 292. Координаты точек! в декартовой (а) и полярной (б) системах координат.
Картовой системе координат, соответствуют точки Л^ (р; ф) й Bi (р;
л + ф), симметричные относительно полюса в полярной системе коор-
динат (рис. 293), а точкам Л(—х; у) и В(х; — у) -в декартовой си-
- [ л . \ п /	3 , \
стеме координат соответствуют точки ЛЛ р; -g- + Ф I и I pj -% л+ф I
в полярной системе координат (рис. 294).
в)	Если кривая y*= f(x) симметрична относительно оси абсцисс
при х > 0, то точкам Л (х; у) и В (х; —у) этой кривой в дейартовой
системе координат соответствуют точки Л$ (р; ф) и В± (р| 2л — ф)
кривой Р—/(ф) в полярной системе координат (рис. 295).
г)	Если кривая у 5= f (х) симметрична относительно оси абсцисс
при х < 0, то точкам Л (-—х; у) и В (—х; — у) этой кривой в декар-
166
товой системе координат соответствуют точки I р; + ф) и
Bt (р; у я ““ ф) (P«c- 296)-
Период функции у — f (г) такой же,- как и период функции р s=*
t= f (ф) Отсюда следует, что достаточно построить график функции
Рис. 294. Координаты точек; в декартовой (а) и полярной (б) системах
координат.
Рис. 295. координаты точек: в декартовой (а) и полярной (б) системах
координат.
167
р*=/(ф) в секторе с углом у вершины, равным периоду, а затем о
помощью постепенного поворота на углы, кратные периоду, строим
искомый график.
Если функция у f (х) ограничена (М < f (х) < 2V), то, как из-
вестно, ее график располагается между прямыми у s== М и у ?= N.
Для соответствующей функции р f (<р) справедливо неравенство
2И < f (ср) < А, и график функции р — f (ср) располагается в кольце,
внутренний радиус которого равен М, а внешний — N. *
Если функция у f (х) имеет экстремум при х s= х0, то функция
р^=/(ф) имеет экстремум при ф = <р0- Если функция y^=f(x) убы-
вает в некотором промежутке, то в полярной системе координат для
функции р^= / (ф) при движении по часовой стрелке значение
Риг. 296. Координаты точек: в де-
картовой (а) и полярной (б) систе-
мах координат.
= — + 2&л, 'где k — некоторое
радиуса уменьшается, а при дви-
жении против часовой стрелки —
увеличивается. х
Горизонтальная асимптота у
— с кривой у = / (х) в декартовой
системе координат переходит в
асимптотическую окружность р
в полярной системе координат.
В частности, если с = 0, то окруж-
ность вырождается в точку.
Вертикальная асимптота х = b
кривой у^= f (х) в декартовой си-
стеме координат переходит в общем
случае в луч*ф = b в полярной си-
стеме координат. В частности, если
6 = 0, то асимптота х = 0 перехо-
дит - в полярной системе коорди-
нат в полярную ось; если b =
целое число, то асимптота х = Ь
переходит в вертикальный луч ф = ~ + 2&л.
Наклонная асимптота у = ах-\-Ь кривой y = f(x) в декартовой
системе координат переходит в спираль Архимеда р = дф + b в по-
лярной системе координат. В частности, асимптота у = ах кривой
у = f (х) переходит в спираль Архимеда р = дф.
Замечание. Для построения графика функции р *= f (ф) при
значениях ф, соответствующих таким значениям х, при которых
/ (х) < 0, достаточно построить график функции i/ = | J(x)|. Затем
по этому графику строят кривую в полярной системе координат и
поворачивают ее вокруг полюса* на угол л. Получают кривую, соот-
ветствующую отрицательным значениям функции р^=/(ф). Следова-
тельно, построение кривой р^/(ф) надо вначале выполнить для ф,
соответствующих значениям х, при которых f (х) > 0, а затем строить
кривую Р^/(ф) для ф, соответствующих значениям х, при которых
f W < о.
168
$ 2. Построение графиков функций
в полярной системе координат
Построение графика функции
р = / (ф)
осуществляют так: а) строят для функции р *= f (ср) соответствую-
щую функцию y~f(x); б) исследуют функцию Р“/(ф), сравнивая
ее с соответствующей функцией yt=f(x), по схеме § 2 разд. 2,
учитывая отмеченные выше особенности графика функции р f (ф);
в) выполняют построение графика функции р “ / (ф) по графику
функции y^=f(x).
Примеры построения графиков функций
Пример 1. Построить график функции
pt= аср (спираль Архимеда), а > 0.
Проиллюстрируем на этом при-
мере, как иногда (в простейших слу-
чаях) графики функций, заданных в по-
лярных координатах, строят по точкам.
Составим таблицу значений для
Ф > 0, придавая ф значения через
л
промежутки, например —:
Рис. 297. р = (спираль Архи-
меда).
п л л 3	53	7_9	5	11 о
ф о	—	— Л Л “Г Л -X- Л - Л 2л Л -тг Л т-лЗЯ
424	424	424
р 0 0,8а 1,6а 2,5а 3,1а 3,9а 4,7а 5,5а 6,3а 7,1а 7,9а 8,7а 9,5а
Значения р в таблице приведены приближенно.
Построив точки в плоскости координат и соединив их плавной
линией, получим график функции для ф > 0. Из уравнения р)=аф
очевидно, что область определения функции: ]—оо; оо[. При 0<ф<оо
имеем: 0 < р < + °°- Если —оо < ф < 0, то —оо < р < 0. Следо-
вательно, спираль Архимеда состоит из двух ветвей, расположенных
симметрично относительно прямой, проходящей через полюс перпен-
дикулярно к полярной оси.
График функции рх=аф представлен на рис. 297. Основной ли-
нией изображена ветвь при ф > 0, вспомогательной — при ф 0.
Замечание. Уравнение р — аф 4- является также спиралью
Архимеда. Действительно, если повернем полярную ось на угол
— —- ~ , то получим уравнение р — аО.
Пример 2. Построить график функции
р*=3зт2ф (четырехлепестковая роза р^=аз1п2ф при а^=3).
Сначала строим график функции y*=3sin2x (см. рис. 91), рас-
тянутый предварительно по оси ординат в три раза.
ли
Исследуем функцию р >= 3 sin 2ф, сравнивая ее с функцией у »
s= 3 sin 2х. Функция у 3 sin 2х определена для Vx, следовательно,
функция р ж 3 sin 2ф также определена для Уф. Функция у s= 3 sin 2х
нечетная, следовательно, кривая р 3 sin 2ф симметрична относи-
тельно полюса. Поскольку функция у — 3sin 2х периодическая
с периодом л, то и функция р 3 sin 2ф периодическая с перио-
дом %. Функция у 3 sin 2х ограничена (| 3 sin 2х | < 3), следова-
тельно, функция р 3 sin 2ф также ограничена (J 3 sin 2ф | < 3).
Функция gtej 3sin 2х на |0; л] имеет максимум при ~ (Утах—
3
м=3) й минимум при х^= ~ л (i/min *= —3). Соответственно, функция
о . л	л	3
р & 3 sin 2ф имеет экстремальные значения при ф ~ и ф — л,
эти значения равны 3 и — 3.
]л Г П з
О’’ "J U л; л
возраста io-
щая, при х $
ii убывающая; соответственно»
функция р ж» 3 sin 2ф возрастающая при ф С
и убывающая при ф С -г I тг U hr i -т-л • Кривая # *= 3 sin 2х
J *	* L А	1
асимптот не имеет, не имеет их -и кривая р ж= 3 sin 2ф. Следовательно,
кривая р )=Е 3 Sin 2ф располагается в круге радиусом 3 с центром
в полюсе.
Учитывая симметрию кривой , р s= 3 sin 2ф относительно полюса
и ее периодичность, строим кривую p^=3sin2(p для 0<ф<~-,
Это построение выполняем так: сначала строим точку экстремума
Лх I 3; -3-1 и точки, для которых р )= 0: 42 (0; 0), А310; -у I; после
этого строим точки Вх р; — , В21 р; -3- л •
Заметим, что значения р для точек Bf и В2 получим из графика
функции у 3 sin 2х, взяв соответствующую ординату кривой для
я	3	„
точек x:=*-q- и х s= — л. Аналогично строим точки Cf и С2. Про-
о	о
’ ведя через эти точки линию, получим график функции р 3 sin 2ф
для 0 < ф < (рис. 298, а). Учитывая симметрию кривой относи-
эх
тельно полюса, строим кривую р г= 3 sin 2ф для — тр < Ф < 0
(рис. 298, б). Наконец, с помощью поворота на угол л вокруг полюса
получаем график функции р s= 3 sin 2ф (рис. 298, в).
Пример 3. Построить график функции
р s= a cos 2ф (четырехлепестковая роза).
17Q
Воспользовавшись формулой
cos 2ф *= sin I у + 2ф
Приведем заданную функцию к виду
Рис. 298. р = 3 sin 2<р (четырехлепестковая роза).
Очевидно, что график функции р я= a sin ^у + 2ф j получим из гра-
л
поворота на угол у
фика функции р г= a sin 2ф о помощью
(рис. 299).
Пример 4. Построить график	Z \
функции	I )
ре=а!§ф.	\	/
Строим график функции у *= a tg #	Л
(см. рис. 54), растянутый по оси ординар ( ЗЖ. " J
в а раз.	/	----У
Исследуем функцию р a tg ф. Об-	/	\
ласть определения функции^ все значе-	/ Q \
ния ф, кроме ф^у (2п+1), где п % Z.
Область значений функции! ]-*ooj оо [»
Поскольку функция y&atgx нечетная, рцс, 29^ р а 90s 2<р (четы*
то график функции р a tg ф симметри- ре&лепесткЪаая роза),
чен относительно полюса. Функция р*=з
a tg ф периодическая с периодом л.
Учтя симметрию и периодичность функции р ж a tg ф, достаточно
I л Г
Построить график функции для ф € у I • Поскольку функция у=*
]л . л Г
—о" } "о” > то надо Учесть> что ПРИ
Z И I
171
построении графика функции р ж a 1g ф при изменении ф по часовой
стрелке значение р уменьшается.
График функции р s= a tg <р проходит через точку (0; 0).
Вертикальные асимптоты графика функции у t= a tg х: х s=
у (2п + 1) (п 6 Z); соответственно, асимптоты графика функции
р;=д^ф:ф:=~- (2л + 1) (л С Z). Наклонных асимптот график
функции у *= a tg х не имеет, следовательно, не имеет их и график
функции р a tg ф. С помощью поворота графика функции р :=
л \	.
у I на угол л получим график функции р^=
Рис. 300. р = a tg <р-
1 л \
*= a tg <р I для у < ф < л I.
График функции рг=а^ф представлен
на рис, 300.
Пример 5. Построить график функции
р^^, или 1пр~аф (логарифмическая
спираль), а > 0.
Строим график функции у = е“х (рис. 301).
Исследуем функцию р^Л Область
определения функции: ] —оо, оо [. Область зна-
чений функции: ] 0; оо [. Функция у s= еах
возрастающая на ]—оо; оо [. Тогда при изме-
нении ф от —оо до оо против часовой стрелки
значение р s= увеличивается. Кривая In р =
< л
аф пересекает полярную ось приф^=Лу
(k ^Z). Поскольку горизонтальной асимптотой
кривой у ;= является прямая у s= 0, то для
функции р?=еа<р соответственно будем иметь
асимптотическую точку р j= 0.
График логарифмической спирали р представлен на рис. 302.
Пример 6. Построить график функции
_ а
У cos Зф
а > 0.
Строим график функции у *=	(рис. 303).
У cos Зх	’
Исследуем функцию р ;=	. Функция определена для всех
ф (2л + 1) (л С Область значений функции: [а; оо [. Функ-
2
ция периодическая с периодом ~ л. Минимум р s= а при ф 0, фх=
о
*= ± Vя* Асимптоты функции: ф*=± ± ~ , фх= ± ~, Ф — ± л, ...
о	о	2	о
in
График функции р s= ! - представлен на рис. 304.
у cos Зср
Примеры построения графиков некоторых функций в полярной
системе координат приведены на рис. 305—308.
Пример 7. Построить график функции
р я= Ь + a cos ф, 0 < а < Ь, р 0.
Рие. 301. у = а > 0. Рис. 302. р = (логарифмическая
спираль), а > 0.
Строим график функции i/s= 6 + a cos х (рис. 309).
Исследуем функцию р s= b + a cos ф. Поскольку область опре-
деления функции у = b + a cos х: ] —оо; оо [, функция р ;= b + a cos ф
определена для ¥ф. Область значений ф, при которых р^0, опре-
/ b х
деляется неравенством | ф |< а, где а := arccos j. При ф :=±а
173
174
получаем точки пересечения графика функции р j» b + a cos ф с по*
лярной осью и полупрямой ]— оо; 0 [. Поскольку функция l/t=6 +
+ acos х для | х |< а ограничена: —Ь < у < b + а, то и функция
р i= b 4- a cos ф при J ф | < а ограничена: 0 < р < b + а.
Функция у х= b + a cos х периодическая с периодом 2л. Функции
р Ь + a cos ф также периодическая с периодом 2л. При построении
графика функции р b -f- a cos ф ее периодичность не используетея,
потому что нам надо построить график только для р^О. Функция
Рис. 306. р = a sin 3<р (трех-
лепестковая роза).
Рис. 307. р == q, cos 3<р (трех*
лепестковая роза).
с/Ь + a cos х на отрезке | х | < а имеет максимум в точке х *= О
и !/тах*= а + 6. На ] —а; 0 [ функция у возрастающая, на ]0; а[—
убывающая. Следовательно, функция р ;= b + a cos ф Имеет макси-
мум при ф 5= 0. На ]—а; 0[ прй движении по часовой стрелке значе-
ние р уменьшается, на ] 0; а [ — увеличивается. Поскольку график
функции у &+ acos х пересекает ось абсцисс в точках (—а; 0)
и (а; 0), то график функции р b + a cos ф пересекает полярную
ось в точках (—а; 0) и (а; 0). Поскольку график функции уг=&4*
4- acos х пересекает ось ординат в точке (0; а + Ь), то график функ-
ции р=6 + а cos Ф пересекает полярную ось в точке [0; arccosl — А 11.
\	\ а / /
График функции р =е b + acos ф представлен на рис. 310.
Пример 8. Построить график функции
р = а (1 + b cos ф) (улитка Паскалй), a > 0, &	1.
Строим график функции у^=а (1 4-6 cos х) (рис. 31ia а).
Рис. 310. р = ft -f- a cos ср; b > a (a); а^Ь (б); Ь < а (в).
Рис 311. у = а (1 4- b cos х) (а); р — а (1 + b cos ср) (улитка Паскаля) (6)t
а = 1, 6=2.
176
Исследуем функцию р = а (1 + b cos ф). Функция р ?= а (1 +
4-^созф) определена для ¥ф. График функции р ;= а (1-J-& cos ф)
симметричен относительно полярной оси.
Функция периодическая с периодом 2л. Основной промежуток:
[—л; л], на концах этого промежутка рг=а(1 —Ь) и pj=a(l +&).
Для ф€[—л; л] функция ограничена: а(1—Ц<р<а(1-|-&).
Экстремум функции при ф^=0 (pmax *= а (1 + Ъ)), на [—л; 0] при
движении по часовой стрелке р уменьшается, а на [0; л] —^увели-
чивается. График функции р у= а (1 + b cos ф) пересекает полярную
/	2 \	(	2	\
ось в точках 10;	—	— л)	и I 0;	— л I •
\	3 /	ч	3 /
График функции pt=a(14*
+ b cos ф) (при а 1 и b s=s 2) пред-
ставлен на рис. 311, б.
Рис. 313. р — ...  -Г	Ь, л = 2Й
r cos <р
b = 1 (конхоида).
Пример 9. Построить график функции
р == —— ± b (конхоида).
r COS ф
Строим график функции	+& (рис. 312).
Исследуем функцию р^=^~ + &. Будем рассматривать функ-
цию и = —----h 6, как и функцию р = —------1- Ь, на [~л; л]. Функ-
*	cos х	СОЗф
а	я
ция о *=-----1- b на [—л; л] определена при —л < ф < — ту ,
*	cos ф	z
~ < ф < л. Область значений функции р г=*
-= —----U:l- оо; оо Г. Функция р — ——\-Ь имеет наибольшее
cos ф ~ J	L	cos ф
значение' р := b — а при <р = —л, затем р убывает от Ь — а до —<х>
на —л; —1; при ср 0 р s= а + Ь, на I — ~ ; ОI р убывает от -|-оо
L	J	L z J
I- Л I	, ,	, I Л I
0; — I р возрастает от а о до 4~°°, на I 'Tf ’> я
р возрастает от —оо до b — а и при ср s= л имеет наименьшее значе-
ние р s= b — а. Асимптоты: <р j= — — , ср	. Заметим, что для
различных а и b конхоида имеет различный вид. График конхоиды
представлен на риё. 313.
Преобразования графиков в полярной системе координат
В полярной системе координат так же, как и в декаруовой, по
графику функции р s= f (<р) можно построить график функййи
Р = mf (<р + а) + Ь.
Это построение сводится к простым геометрическим преобразованиям
графика функции р j= f (ср) согласно перечисленным ниже свойствам.
Основные свойства графиков функций
в полярной системе координат
1.	График функции р^—/(ср) симметричен графику функции
р s= f (<р) относительно полюса.
2.	График функции ps=f(—<р) симметричен графику функции
р s= f (ср) относительно полярной оси.
3.	График функции р ~ mf (ср), т > 0, — это растянутцй или
сжатый вдоль полярной оси в т раз график функции р *= f (<р).
4.	График функции р х= f (tp + а) — это график, полученный из
графика функции р 5= f (ср) с помощью поворота последнего на угол а,
5.	График функции р f (<р) + b — это график функции р s=* /(ср),
параллельно перенесенный вдоль полярной оси на величину Ь.
Пример 10. Построить график функции
а
р j= —2—^ а < о.
л
Сначала строим кривую р^®=— (гиперболическую спираль) при
а > 0 (рис. 314). Полюс является асимптотической точкой кривой,
прямая, параллельная полярной оси и отстоящая от нее на расстоя-
ние, равное а,— асимптота кривой, причем приближение к асимптоте
при возрастании ср происходит против часовой стрелки. При возрас-
тании (р от 0 до оо точка спирали пробегает асимптотический учас-
ток кривой и, пересекая полярную ось, устремляется к полюсу,
делая вокруг него бесчисленное множество витков, расстояние Между
которыми быстро убывает.
График функции р^= —-— получим из графика функции ps=;
Ф-Т
178
179
a > 0.
s=s— с помощью поворота по-
эт
следнего на угол — против
часовой стрелки (рис. 315).
Пример 11. Построить
график функции
р = а(1 + tg q>).
График функции р j= tg ф
параллельно переносим Htf еди-
ницу вдоль полярной оси. За-
тем растягиваем (или сжимаем)
в а раз график функции р~
*= 1 + tg ф.
График функции р = а (1 +
4- tg ф) представлен на рис. 316.
Примеры построения гра-
фиков некоторых функций в по-
лярной системе координат при-
ведены на рис. 317—319.
РАЗДЕЛ 8
ГРАФИКИ НЕЯВНО ЗАДАННЫХ ФУНКЦИЙ
§ 1. Исследование неявно заданных функций
Рассмотрим функцию, заданную неявно уравнением
F(x, i/)^0.
В зависимости от того, какой является функция F (х, у) — алгеб-
раической или трансцендентной,— кривые, представленные уравне-
нием F (х, //)*=(), делятся на алгебраические и трансцендентные.
Если F (х, у) можно разложить на множители ф$ (х, у), ф2 (х, у),
..., фл (х, у), то данному уравнению соответствует система кривых
<Р1 (*. У) = 0. Фа (X, у) В= о.фл (х, у) = 0.
Укажем на некоторые особенности и преобразование графика
кривой
Г (х, e/)z=0.
Если уравнение кривой F (х, у) s= 0 не меняется при замене
х на —х, то кривая симметрична относительно оси ординат.
Если уравнение кривой F (х, у) s= 0 не меняется при замене
у на —у, то кривая симметрична относительно оси абсцисс.
Если уравнение кривой F (х, z/)j=O не меняется при одновремен-
ной замене х на —х и у на —у, то кривая симметрична относительно
начала координат.
Если уравнение кривой F (х, у) не меняется при замене у на х,
а х на у9 то кривая симметрична относительно биссектрисы у ~ х.
180
График кривой F(x + a, у) = 0 получают из графика кривой
F (х, у) 5=0 с помощью параллельного переноса последнего вдоль
оси абсцисс на | а | единиц масштаба в направлении, имеющем знак,
противоположный знаку а.
График кривой г (х, у + Ь) получают из графика кривой
F (х, у) г= 0 с помощью параллельного переноса последнего вдоль
оси ординат на I b | единиц масштаба в направлении, имеющем знак,
противоположный знаку Ь.
График кривой	получают из графика кривой
F (х, у) 0 с помощью растяжения (сжатия) последнего в р раз по
оси абсцисс.
График кривой F ^х, —j 0 получают из графика кривой
F (х, у) — 0 с помощью растяжения (сжатия) последнего в q раз по
оси ординат.
С помощью указанных преобразований можно получить из гра-
фика кривой F (х, у) 0 график кривой F + а,	&j х= 0.
Точки пересечения кривой F (х, Ос осями координат. Точки
пересечения с осью абсцисс — это решения системы уравнений
F (х, 0)	0,
F (х, у)	0.
Точки пересечения с осью ординат — это решения системы уравнений
F(0, !/) = 0,
F (х, у) 0.
Заметим, что для более точного построения графика кривой
F (х, у) иногда полезно найти отдельные точки этой кривой, не ле-
жащие на координатных осях. Такие дополнительные точки целе-
сообразно искать как точки пересечения кривой с прямыми у — kx
при различных значениях k.
Если уравнения кривой F (х, у) 0 можно преобразовать к виду
Ф1 (X, у) Фг (х, у) + Ч»! (х, у) Ара (х, у) = 0,
то координаты точек пересечения, кривых
Ф1^=0, ( Фх = 0, Гф2^=0, f ф2 = о»
Ф1^=0; 1ф2^=0;	—О*» I 'Фг — 0
удовлетворяют уравнению начальной кривой и, следовательно, при-
надлежат ей.
Асимптоты кривой F (х, у) — 0. Для нахождения горизонтальных
асимптот кривой F (х, у) = 0 приравнивают нулю коэффициент при
высшей степени х, входящей в уравнение; причем если этот коэффи-
циент— постоянная величина, то горизонтальных асимптот нет.
Для нахождения вертикальных асимптот кривой F (х, у) j= 0 при-
равнивают нулю коэффициент при высшей степени у, входящей
в уравнение этой кривой.
181
Для нахождения наклонных асимптот кривой F (х, у)^=0 надо
в уравнении кривой заменить у на kx + Ъ* приравнять нулю коэф-
фициенты пр» двух высших степенях х и полученную систему решить
относительно k и Ь.
П р и м> е р 1. Кривая х2у% + у4 —- 16х2	0 имеет две горизон-
тальные асимптоты.
Действительно, переписываем уравнение в виде
(у? — 16) хЗ + у4 = 0.
Приравниваем нулю коэффициент при х?!
у2 ~ 16 = 0,
откуда у 4 з= 0 и г/ 4 *= 0 — горизонтальные асимптоты рассмат-
риваемой кривой.
Пример 2. Кривая ЗуЪ — ху% — Зх2у з= 0 имеет одну верти-
кальную асимптоту.
Действительно, переписываем уравнение в виде
(3 **• х) уЗ бхЗу *= 0,
откуда 3 — хх=5 0	вертикальная асимптота, Кстати, эта кривая
будет иметь и горизонтальную асимптоту у *= 0.
Пример 3. Кривая х3 + у2 Зх2 = 0 имеет наклонную асимп-
тоту»
Действительно, заменяем в уравнении кривой у на kx + bi
х2 + (kx + b)2 — Зх? 0,
•	(1 +№)x2- + 3(bk2 — 1)х2— 3bkx — 3x3 = О,
Решаем систему
Г 1 +	0,
I Ь№ — 1	0,
откуда k j=s —1, b з= 1. Следовательно* у « —х -|- 1 — наклонная
асимптота рассматриваемой кривой.
§ 2. Построение графиков неявно заданных функций
Будем рассматривать случаи, когда неявно заданный функций
приводятся к функциям, заданным в явном виде.
Пример 1. Исследовать и построить график кривой
х4 + 2у? — х? — у4 = 0.
Для нахождения области определения неявно заданной функций
решаем заданное уравнение относительно у. Получаем
У = ± Г1 + х* — х? + 1 и ± У1 — хЗ + 7 ,
т. е.л имеем две ветви кривой. В области определения обеих ветвей
должно выполняться неравенство
х4 — х? + 1 > 0, или (хЗ — 1)3 4- х? > 0,
182
справедливое для Vx. Для точек второй ветви необходимо, чтобы
х4 — х2 + 1 <: 1, или х? — 1 < 0, что возможно лишь при условии
|Х|<1.
Следовательно, область определения первой ветви:«5—оо; оо [,
область определения второй ветви: [—1; 1].
Кривая симметрична относительно осей координат. Горизонталь-
ных и вертикальных асимптот она не имеет, поскольку коэффициенты
при высших степенях х и у в уравнении постоянные. Находим
наклонные асимптоты. Имеем
х4 _ (kx + 5)4 _	+ 2 (kx + 6)? = 0.
Приравниваем нулю коэффициенты при х4, х3 и получаем
р4 — 1 х* 0f
14k3bt= 0,
откуда k = ± 1, 6 = 0.
Следовательно, прямые у — х и у	—х — наклонные асимптоты
рассматриваемой кривой.
Рассмотрим несколько дополнительных точек кривой. Для этого
решим систему уравнений
Г х4 + 2у2 — х2 —• $4 =
\yt=kx
при различных значениях kt
*1,2 = 0;
X?
1—26*
1 - 64 ’
Эскиз графика представлен на рис, 320.
Пример 2. Построить -график функции
г/2 х3 + 1.
Решаем уравнение относительно yt
у*= ± lA? + i.
Функция определена при х>»—1. Кривая симметрична относительно
оси абсцисс. Кривая асимптот не имеет.
Для построения графика верхней ветви кривой записываем функ-
цию х3 + 1 с помощью промежуточного аргумента ti
У^=У t > ?«“Х3+1.
По графикам этих функций строим график верхней ветви кри-
вой, а отобразив последнюю Относительно оси абсцисс, получим
график и нижней,ветви кривой (рис. 321).
Пример 3. Построить график функции
уЗ = Qx2 — хЗл
183
Решаем уравнение относительно yi
у — у4 6х? — х3.
Область определения функции: ] —оо; оо [. Вертикальных и го-
ризонтальных асимптот нет. Наклонная асимптота: x + t/^=2.
Записываем функцию с помощью промежуточного аргумента /:
/ = 6х3 — х3.
По их графикам строим гра-
фик заданной функции (рис. 322).
Пример 4. Построить гра-
фик функции
л4 + у4 8= X? + у*.
Кривая симметрична относи-
тельно осей координат, относи-
тельно биссектрис у я= х и у ?== —х.
Следовательно, можно рассматри-
вать восьмую часть плоскости, т. е.
0<х<1/. При этих условиях ре-
шаем заданное уравнение относи-
тельно у\
Корни взяты со знаком плюс. Очевидно, достаточно ограничиться
рассмотрением х< 1, так как если х > 1, то "j/"+ х? — х4 < -i-,
у < 1, что противоречит условию x<iz/, или у принимает комплекс-
ные значения.
184
Очевидно,
у   _1 L у2   у4 .— _2_ f х2	-i- ,
2“ 4 ^х'	2	\	2/^2
поэтому	-к- + У V достигает наибольшего значения при
1	1 п- 1 Г	I .	1 \?
В интервале Iй»
убывает от до 0. Функция
х^=
= значение выражения I х?-----I
1	1
убывает от -~ до — , а функция у
Л	4
Рис. 323. х4 + у4 = х* 4- у*.
Рис. 324. у = х + cos х (1); у~\~
4- cos у — х = 0 (2).
возрастает
1
X от ——
/2
ОТ
до
г убывает
от
1
до
При дальнейшем возрастании
1 \2 1
значение / х2 —— г возрастает от 0 до поэтому
1 1
~2 До а у убывает от
до 1.
График функции х4 + у4 х2 + представлен на рис. 323.
Пример 5. Построить график функции
Z
1
у + cos у — х s= 0.
Заметим, что из этого уравнения нельзя выразить у как явную
функцию от х. Но учитывая, что графики функций F (х, у) =0
и Г (У> х) ~ 0 симметричны относительно прямой у г= х, строим гра-
фик заданной функции как кривую, симметричную графику кривой
х + cos х — у = 0. Из последнего уравнения легко выразить у явно
через х: у х + cos х.
График функции у + cos у — х — 0 представлен на рис. 324?*
185
Примеры построения графиков
ведены на рис. 325—345.
неявно заданных функций при-
Рис. 326. у2 = х9 — х.
Рис. 328. у2 = х2 (х — 1) (О — изоли-
рованная точка).
tM
Рис. 331. (у — Х2)2 =
= х6.
Рис. 332. Зху* == л* — 2.
187
188
18»
$ 3. Исследование кривых,'
заданных алгебраическим уравнением второй степени
Рассмотрим детальнее кривые, заданные уравнением второй
степени.
Общее уравнение второй степени с двумя переменными имеет вид
Ах% + 2Вху + Ctfl + 2Dx + 2Еу + F = 0,	(1)
где А, В, С, D, Е и F заданные, причем по крайней мере один
из коэффициентов А, В, С отличен от нуля. При А == С и В = О
это уравнение определяет окружность/ Например, рассмотрим кри-
вую, заданную уравнением
х? + у% — 4х 4- 4у + 2	0.
Запишем данное уравнение в виде
(х — 2)2- — 4 + (у + 2)2. — 4 + 2 — 0,
или
(х — 2)? + (у + 2)? = 6.
Это, а следовательно, и заданное уравнения определяют окружность
с центром в точке (2; *-2) и радиусом У 6.
В общем случае с помощью параллельного переноса и поворота
координат уравнение (1) можно привести к простейшему виду и по-
лучить каноническое уравнение эллипса, гиперболы, параболы или
пару уравнений первой степени. Действительно, выполним парал-
лельный перенос координат по формулам
хз=х' + а, y = y'+bt
190
где х' и у' **• переменные координаты новой системы, а и коор-
динаты начала новой системы. Подставляя значения х и у в уравне-
ние (1), получаем
Ах'* + 2Вх’у’ + Су'* + 2 (Аа + Bb + D) х' + 2 (Ba 4- СЬ 4- В) / +
4- Аа2 + 2Bab + Cb2 + 2Da + 2ЕЬ 4- D = 0.	(2)
Выберем а и b так, чтобы члены при х' и у' равнялись нулю, т. е.
Aa + Bb + D^O, Ва + СЬ + £ == 0.	(3)
Тогда при условии, что детерминант системы (3) АС — В2 =£ 0,
уравнение (2) принимает вид
Ах'* 4- 2Вх'у' + Су'* + (Аа2 4- 2ВаЬ 4- СЬ2 4- 2D а 4- 2ЕЬ 4- £)=0. (4)
Обозначая
Аа2 4- 2ВаЬ 4- СЬ2 4- 2Da 4- 2ЕЬ 4- D kt
уравнение (4) перепишем в виде
Ах'2 4- 2Вх'у' 4- Су2 4- k = 0.	(5)
Изучая уравнение (5), следует иметь в виду два случая.
Первый случай: & = 0. Уравнение (5) принимает вид
Ах,г + 2Вх’у' + Су,г = 0.	‘	(6)
Если А ;= С = 0; В #= 0 (учитывая, что АС В? 0), то уравне-
ние (5) будет иметь вид 2Вх'у’ й= 0. Отсюда х' = 0, у' *= 0. Следо-
вательно, имеем две прямые (новые оси координат), пересекающиеся
в точке (0; 0).
Один из коэффициентов А или С отличен от нуля (например,
А =£ 0). Умножив уравнение (6) на Л, получим
А2*'2 + 2АВх'у’ + АСу'* 0.
Это уравнение перепишем так:
(Ах' 4- By')2 4- (АС — В2) у'* j= 0.	(7)
При АС — В? > 0 уравнение (7) изображает точку (0; 0), при
АС — В2. <0 — две пересекающиеся прямые: Ах' + By’ х=»
>= ± V АС — В“у'.
Следовательно, при k *=. 0 уравнение (5) вырождается в две пря-
мые или точку *.
Второй случай: k #= 0. Для исследования уравнения (5)
выполним поворот осей координат х'Оу’ на угол а. Заменив х’ Й y,J
в уравнении (5) по формулам
х’ = х' cos а — If' sin а,
у' = x' sin а 4" У' c°s а,
• Окружность и эллипс могут быть действительными или мнимыми.
191
Г	1
*	.
получим
4“ 2BjXz -|“ Cjj/' -|- k s= 0,	(8) t 
где
Лх == A cos2 а + 2В cos а sin а 4 С sin2 а.
Bi s= (С — Л) sin а cos а + В (cos^ а — sin2 а),
Ci — A sin2 а — 2В cos а sin а + С cos2 а.
Выберем а так, чтобы Bjs=O, т. е.
(С — Л) sin а cos а + В (cos2 а — sin2 а) «= 0, -
или
q____________________д
—g— sin 2а 4- В cos 2а s= 0.
Отсюда
о о*
tg2a=j^.	(9)
/1 - V»
Рассмотрим кривую, соответствующую уравнению (1) в случае,
если АС — В2 *= 0.
Пусть Л и С одновременно отличны от нуля (Л =£ 0, С =/= 0).
Умножим уравнение (1) на Л:
Л2х2 + 2АВху + ЛСуЗ + 2ADx + 2АЕу 4- AF ев 0.
Принимая во внимание, что АС — В2 = 0, это ypaeneipie можно
записать так:
(Лх 4- By 4- X)2 + 2 (AD — АЛ) х 4- 2 (ЛВ — АВ) у 4-
4. (Д£ __ х2) = 0,	(10)
где % — произвольный параметр.’
Выберем новую систему координат так, чтобы прямая Лх 4е
4- By 4- А — 0 была осью абсцисс, а прямая 2 (AD — АЛ) х 4 2 (АС—
— АВ) у 4- ЛВ — № s= 0 — осью ординат. Из условия перпендикуляр-
ности этих прямых можем записать
2 (AD — АЛ) Л 4- 2 (АЕ — 1В)В^= 0,
откуда
Л2И _ АВЕ
Л — Д2 + £2	*
* Условие (9) дает бесконечное множество значений а, но существенно различ-
ных поворотов — четыре. Действительно, если а0 является углом одного из поворо-
тов, то из уравнения (9) следует, что 2а=2а0-}-тс6 (k — целое число). Следовательно,
. гс ,	к
а — «0 + ~2 т- е- или а — ао, или а = ао + ~2 » или а ~ ао + или а =
. 3
== а0 4- — гс, Есе другие значения а дают те же положения новой системы коор-
динат. При А = С ' г — неограниченная величина и 2а = ±	, т. е. а =
А G	2»
я	2S
= ±	. При Л = С и В = 0 отношение—--------- неопределенное, а уравнение (4)
4	А — G
является уравнением окружности.
192
Подставив % в уравнение, получим
(Ax+By + W+m(Bx — А//) + п^=0,	(11)
где т и п определяются через коэффициенты уравнения (1).
Первый случай: т j=0. Уравнение (11J принимает вид
(Ax+Bi/ + Z)2 + nx=0.	(12)
При п > 0 уравнение (12) изображает мнимое геометрическое
место точек, при п^=0 оно вырождается в прямую Ах-]-Ву + 'к= О,
а при п < 0, т. е. т=—/2,— в параллельные прямые Ах-\-Ву-\-
Л — I = 0, Ах -J- By -|- X = 0.
Второй случай: т #= 0. Пусть — *=р. Тогда уравнение (11)
принимает вид
(Ах++X)2 +/и (Вх— Ai/ + p)j=O. - (13)
Выберем новую систему координат: в качестве оси абсцисс х' при-
мем прямую Ax + Bi/ + Xt=0, в качестве оси ординат у'—прямую
Вх— Ау + р = 0. В новой системе координат формулы преобразова-
ния будут иметь вид
.	, Вх — Ау + р	Лх-ЬВу + А, 
X != ±	, у ± 1	. 	«
/л? + в?	/Лх? + В?
а уравнение (13) —
(Л? + В2) у'г + т (Л? + В?)? / = 0,
ИЛИ
,г , т ,
у ~ ± /л? + В? Х 
Получаем уравнение параболы, в котором знак перед А24-В2
берем тождественным знаку т.
Пример 1. Исследовать кривую, заданную уравнением
х2 + 4^2 —2х+1 ^=0.
Вводим новые координаты:
х?=х' + а, у*=у' + Ъ,
по лучаем
4.- 4^'2 + (2а — 2) х' + Sby' + а? — 2а + 1 даО.	(*)
Приравнивая нулю коэффициенты при первых степенях х* и у',
имеем
2а — 2*=0, 6^0,
откуда as=la 6j==0. Подставив значения а и Ъ в уравнение (*),
получим
х'8 + 4/’ j=0.
Это уравнение изображает точку (0; 0) в системе координат х'О^у'.
В системе координат хОу это будет точка (НО).
7	8-413	1*1
Пример 2i Исследовать кривую, заданную уравнением
х? — ху + уЪ + 2х — Ay z= 0.
Выполнив параллельный перенос координат, получим заданное
уравнение в виде
+ (**)
По формуле
следовательно,
л
4 •
Выполнив преобразование координат в уравнении (♦♦) по фор-
мулам
''Пг+’1'
получим
+	—4s=0, или х7‘ + 3у72 = 8.
Следовательно, заданное уравнение является уравнением эллипса
в системе координат х'С^у'.
Пример 3. Исследовать кривую, заданную уравнением
х? — бху + 90? — Зх + 24// = 0.
Для данного уравнения имеем
4=1, В = — 3, С = 9, АС — В? = 0.
Заданное уравнение можно переписать в виде
(х — 3// + 1)? — X? — 21 (х — Зу) — 8х + 24у = 0,
или
(х — Зу + 1)? — (21 + 8) х.+ <61 + 24) у — 1? = 0.
Выбирая прямую х — Зу + 1 = 0 в качестве оси абсцисс, а пря-
мую — (21 + 8) х + (61 + 24) у — 1? = 0 в качестве оси ординат, из
условия перпендикулярности прямых записываем
-*• (21 + 8) — <61 + 24)3	0,
откуда 1 = —4. Подставляя значение 1 в преобразованное уравнение,
получаем
(х—30 — 4)2—16=0.
Это уравнение вырождается в две прямые:
X—30 —8 = 0, х —30 = 0,
1*4
Пример 4. Исследовать кривую, заданную уравнением
xl — 4ху + 4уЪ — Зх 4- 5у ** 1 = 0.
Для данного уравнения
Л^1, В = —2, 0 = 4, ЛС — ^ = 0,
Запишем это -уравнение в виде
(х *~2у +	(2Х + 8) х + (4% + 5) у — I ₽ 0.
Выбираем реи координат, как указано выше; из условия их перпен-
дикулярности будем иметь
«** (2% + 8)	2 (4Х + 5) = О,
откуда Х=—	. Подставив значение К В преобразованное уравнение,
получим
(** - Ц)' * Б) (2х + So) “ °'
Вводим новую систему координат! В качестве оси абсцисс выбираем
13
прямую х -* 2у «ь 0, 6 качестве оси ординат прямую 2х 4-
	269 Л о ч	х
4- у — «доф = 0. В этой системе преобразованное уравнение имеет вид
и изображает параболу,
Пример 5. Исследовать кривую, заданную уравнением
хЪ	icy 4- у Ъ	Л
Заданное уравнение имеет вид (5)
Ах$ + 2Вху 4-Су?4-%«0а
гдеЛ = С=1, 2B^<*>lt
Для того чтобы избавиться of коэффициента при xyt надо вы-
полнить поворот осей координат На угол а & I
х=у^(х'^УЪ
у = у=г (X' + у').
Получим
|х'5 + |^-агх=0,
х'? + Зу'$ « 2а5»
7*
J9S
Переписав последнее уравнение в виДе^2- +	= видим, что
это — уравнение эллипса в системе координат х'О^у' с полуосями
а V 2 и —2—. .
Пример 6. Исследовать кривую, заданную уравнением
16*2 — 9р2 — 64х — 54i/ — 161 = 0.
Выполним параллельный перенос координат:
х = х' + а,
~	У=у’ + Ь,
где (а; Ь) — координаты начала новой системы. Они определяются
из системы уравнений
16а —64 = 0,
—96 — 27 = 0.
Решив эту систему уравнений, получим а = 4, 6 = —3. Вычислив
значение Л по формуле
Аа2 + 2Bab + Cb2 + 2Da + 2£6 + F = X
при А 16, В = 0, С = — 9, £> = —32, £ = —27, F= —161,
а = 4, Ь = —3, получим X ч= —80.
Заданное уравнение в новой системе координат имеет вид
16х'2 — 9//'? — 80 = 0,
или
5	80
9
Следовательно, заданное уравнение изображает гиперболу с по-
луосями У5 , j/" = -у Уб в новой системе координат.
Пример -7. Исследовать кривую, заданную уравнением
ху+Уз«;?+6х-4Уз^+5Уз = 0.
Выполняем параллельный перенос координат. Заданное уравнение
будет иметь вид
х'у' + У-3/? + 193 У3 = 0 (а = 16 Уз; Ь = —6).
Теперь выполним поворот координат на угол а:
ls2e_W-
Отсюда 2a = 30°, a = 15°. Заданное уравнение принимает вид
С,У« + 193 У з”= о.
196
Коэффициент Ct находим из равенства
Лх + Ci ~ А 4“ Ct Ci — V 3.
Окончательно будем иметь
-	/2 + 193 = 0.
Следовательно, заданное уравнение в области действительной
переменной смысла не имеет.
Замечание. Об окружности, эллипсе, гиперболе, параболе
см. в ч. II.
§ 4. Графики неявных функций,
аналитическое выражение которых содержит знак
модуля
Пример 1. Построить множество ючек
I *1 + I У\ = 1.
Функция четная относительно координатных осей. А поэтому
достаточно рассмотреть функцию только в I квадранте, т. е. npit
х > 0 и у 0. Поскольку при этом | х | = х и | у | = у, заданная
функция принимает вид
х + У=\, или у=*\—х.
Следовательно, строим график пря-
мой у—1—х. Графику заданной
функции принадлежит лишь отре-
зок прямой у — 1 — х, который ле-
жит в I квадранте. Учитывая сим-
метрию графика заданной функции,
строим график функции во II—IV
квадрантах.
Множество точек | х | + | у | = 1
представлено на рис. 346.
Множества точек | х | — | у |=1
и I У I — I х | = 1 приведены на
рис. 347.
Пример 2. Построить множество точек
Рис. 346. |х|-ы 1/1 »1.
11*1-1 Л
Дайное уравнение эквивалентно двум уравнениям:
|х| —1,| = 1 и|у| — |х| = 1.
Сдедовательно, искомый график является объединением двух графи-
ков, представленных на рис. 347. Он приведен на рис. 348.
Пример 3. Построить множество точек
|,-2|=|*+1|.
W
Переходим к новой системе координат:
У' = У — 2, х' = х+1.
Тогда уравнение принимает вид
'	]у' j = |*' I-
Пример 4» Построить множество точек
р-М0|=*+1*1-
Уравнение не имеет свойства четности относительно переменных.
Рассматриваем это уравнение в каждом квадраНТе- отдельно.
В I квадранте уравнение принимает вид
Следовательно, графиком функции
в пределах I квадранта является
биссектриса первого координатного
угла.
Во II квадранте | у | = у,
| х | — —х. Окончательно: у = О,
а это отрицательная полуось абс-
цисс.
В III квадранте уравнение име-
ет вид у — у — х — х, а это уже
тождество, которое означает, что
любая точка III квадранта принад-
лежит множеству точек, удовлетво-
ряющих заданному уравнению.
В IV квадранте уравнение име-
ет вид х = 0, а это отрицательная
рис. 350. г/+|у|=х-|-|х|.
полуось ордигаг.
Множество точек у + | у | = х + | х [ представлено на рис. 350.
Примеры построения графиков неявных функций, аналитическое
выражение которых содержит знак модуля, приведены на рис. 351—358.
Рис. 351. |х-2 14-1 1/4-11 =1 (а); у^ | л; Ч-2 |+ I Зх + 1 |+
— Зх 4- 2 (б).	11
199
Рис. Збв. у = |^| COS X.
§ 5. Примеры построения графиков
неявно заданных функций, которые удобно строить
в полярной системе координат
Пример 1. Построить график функции
(xi + у?)3 =в 4a2x2i/2.
. Переходим к полярной системе координат:
х — р cos <р,
у = р sin <р.
200
Рис. 357. |у — 1 | ч- 1г/4-1| +
4- 2 | х | = 4.
Рис. 358. II х|4- IP~3 | — з I ^1.
Уравнение принимает вид р- ® a2 sin^ 2<р, откуда
р = ± a sin 2<р.
Графиком обеих функций является четырехлепестковая роза
(см. рис. 298).
Пример 2. Построить график функции
(х? + у?) (х? — у2) = 4х2у?.
График функции симметричен относительно биссектрис у = х,
у — —х, а следовательно, и относительно начала координат.
Переходим к полярной системе координат
х — р cos ф,
У = р sin ф.
Уравнение* принимает вид р- = tg2 2ф, откуда р = ± tg 2ф.
График функции и его построение приведены на рис. 305.
Пример 3. Построить графите функции
(х? + у2) х = а2у.
Перейдя к полярной системе координат, получим такое урав-
нение:
р2 s= a2 tg ф,
откуда
р — ± a /tg^p.
Графики функции представлены на рис. 359, 360.
201
Графики функций
№ + У-)2	№ — У2)* или Р — ± оУ cos 2<р
(лемниската рернулли), и р? -f- ср? 100 приведены соответственно
на риб. 361, 362*
Замечание. Более полное исследование и построение гра*
фика неявно заданной функции целесообразнее проводить, используя
производные (см. ч. II). Однако во многих случаях, как мы убеди*
лись выше, можно достаточно легко * построить график кривой F (л^
у) Sas 0, Йе прибегая к элементам дифференциального исчисления.
Рис. 360. р=±а V tg <р,- (х* х «
«= а2у.
Рио. 361. (л2 + ^2)8 == а2 (х2 — у2),
или р ± а V cos 2<р (лемниската
Бернулли).
Рис. 362. р2 + <Р8 = 100.
202
РАЗДЕЛ 9
ГРАФИКИ БОЛЕЕ СЛОЖНЫХ ФУНКЦИИ
§ 1. Построение графиков функций,
заданных несколькими аналитическими выражениями
В каждом из приведенных ниже примеров будем рассматривать
одну функцию, но она для разных промежутков из области ее опре-
деления задана разными формулами.
Пример 1. Построить график функции
Область определения функции: J—оо; оо[.
Если х^О, то график функции является частью параболы y=i
s= х2, при х < 0 функция изображается лучом прямой у =? — х. Следо-
вательно, график заданной функции состоит из луча прямой у ;= —х
и части параболы 1/=?х? (рис. 363).
Пример 2. Построить график функции
У —
sinx, если —Л<<х<0,
2,	если 0 < х< 1,
I'	i
-----; , если 1 < х < 4.
х — 1
Область определения функции: [—л; 4]. График функции со*
Стоит из части синусоиды у s= sin х на [л; 0], прямой у — 2 на ] 0;
1]/и части ветви гиперболы у^= на ]1; 4] (рис. 364).
Л *
203
Пример 3. Построить график функций
—2, если х > О,
у , если х =< О,
—х3, если х < 0.
У —
График функции состоит из части кубической параболы, одной изо-
лированной точки и полупрямой (рис. 365).
Пример 4. Построить график функции
(х, если х =/= 2,
у^= <
(5, если х = 2.
Рис. 367
У = sign х =
х > 0,
хО,
х < О,
График функции состоит из всех
точек прямой х, кроме точки
(2; 2). Точка 4(2; 5) — изолирован-
ная точка графика функции (рис. 366).
Стрелки на графике показывают, что
точка (2; 2) не принадлежит графику.
Пример 5. Построить график
функции
1, если х > 0,
у «= sign х =
0, если хх=0,
—1, если х < 0.
График функции представлен на рис. 367. Он состоит из двух
полупрямых и точки (0; 0). Стрелки на графике показывают, что
точки (0; 1) и (0; —1)„не принадлежат графику.
Пример 6. Построить график функции
^fesign(tgx).
204
Область определения функции— все значения я, кроме +
+ пп (п 6 Z). Функция периодическая с периодом со л. Функция
ограничена. Из ограниченности функции следует, 4fo график не
имеет вертикальных асимптот; из периодичности функции следует,
что он не имеет горизонтальных и наклонных асимптот.
График функции представлен на рис. 368. На рис. 369 приведен
график функции у =: sign (sin лх).
Рис. 368. у « sign (tg л).
Замечание. Построение графика функции у sign (f (х))
по графику функции у =s f (х) осуществляется так: строим графики
функций	и ——1 соответственно на промежутках, на кото-
рых график функции у =: f (х) лежит в верхней и нижней полуплос-
костях. Точки пересечения графика
функции y=if (х) оставляем без
изменений.
При построении графика функ-
ции у 5= / (sign х) учитываем,, что
। f (1) при х > О,
4 f (sign *) *= | / (0) при х *= 0,
I f (— 1) при x < 0,
при этом значения —1, 0, 1 долж-
ны входить в область определения
функции.
§ 2. Построение графиков функций,
заданных некоторым рекуррентным соотношением
Пример 1. Построить график функции у f (х), х £ R, если
/ (х+ 1) = 2/(х) и f (х)^=х(1 —х) для 0<х< 1.
Для натурального п имеем
f(x + n) — 2f (х + п — 1) = 22/ (х + п-2)— ... =2"/ (х),
т. е.
f (х + п) х= 2nf (х) для п £ Z.
205
Поскольку f (х) ИС X (1—х) для 0<х<1Лто, ПОЛОЖИВ 1X 4- п{
получим
|(0*к2Л(* —П)(п+1 —О, п</<п+1,
f (х)^2П(*/~ л)(п+ 1— х), Л<Х</Л+1, nfZ.
Отсюда имеем
♦ • ♦ I 1 L * М * < I < ’ *
2-1(х+ 1)(-х), М<х<0,
х(1 — х),	0<х< 1,
2(х — 1) (2 — х),	1 < Х< 2;
f 22(х —2)(3 — х), 2<д:<3,
f(x)== 28(х-3)(4~-х), 3<х<4,
Теперь строим график функции (рис. 370).
4 х
Рис. 370. у = f (х) (х £ jR), если f (х + 1) = 2/ (х) и f (х) = х (1 — х)
для 0 < х< 1.
Пример 2. Построить график функции
У=Ч(х), х 6 R,
f (х 4- л)*= f W + sin X И f (х) i== 0 для 0 < X < я.
Имеем
/ (х 4- л) = / (х) 4- sin х,
f (х 4- 2л) =* f (х 4- л) 4- sin (х 4- л) да f (х) 4~ sin х — sin х / (х) ~
f (х 4" Зя) да f (х + 2л) 4- sin (х 4" 2л) да f (х) 4" sin х,
f (х + 4л) sa f (х + Зя) 4" sin (х + Зл) f (х) 4- sin х — sin х f (х),
f (х), если п — четное,
f (х) 4- sin х, если п — нечетное.
Заменив в равенстве f (х) f (х + л) — sin х х на х — л, получим
/(х — л) = / (х) 4~'Sin х. Далее, рассуждая, как и выше, получаем
равенство (*) для целых отрицательных значений л. Пусть х +
206
4- лл 5= t. Тогда, если 0<х<л, то пи< t <* (л 4*1) л (л £ Z) и
f (х) =5 0. Следовательно,
{0, если п — четное,
sinx, если п— нечетное, лл<(<
(л -р 1) я (л Z).
Теперь строим график функции (рис. 371).
У>Г~
РЙС. 371. д = f (х) (х € R), если f (х + тс) = f (х) 4- sin х И f U) =» 0
ДЛЯ 0 < X < ТС.
§ 3. Построение графиков функций вида
У = !/(*)!
Пусть график функции y^=f(x) построен (рис. 372). Построение
графика функции
[/(*)]
207

а)	проводят прямые у п (п С Z) и рассматривают одну из полос,
образованных прямыми у =: п и у = п + Ь
б)	точки пересечения прямых у=п, y^ti-^i с графиком функ-
ции у ;= f (х) будут принадлежать графику функции у = f [(*)], по-
скольку их ординаты целые числа; другие точки графика у =: [/ (х)]
в рассматриваемой полосе получим как
проекцию части графика y^=f(x)t
которая лежит в этой полосе, на пря-
мую у п, поскольку любая точка М
этой части графика функции у = f (х)
имеет такую ординату у0, что п <
<Уо < л+ b т. е. [i/o] — п;
в) в каждой другой полосе, где
есть точки графика функции у*= f (х),
построение проводится аналогично.
Примеры построения графиков
Функц ий вида у = [/ (х)] представлены
на рис. 373—381.
§ 4. Построение графиков функций вида у = /(pd)
Пусть график функции y=if(x) построен (рис. 382). Построение
графика функции
выполняют в таком порядке:
а)	проводят прямые х s= п (п С Z) и рассматривают одну из полос,
образованную прямыми х^п, x^=n+ 1;
б)	точки пересечения графика функции у *= f (х) с этими прямыми
209
принадлежат графику функции yt= f ([х]), поскольку их абсциссы —
целые числа; другие точки графика функции t/ = /([x]) в рассматри-
ваемой полосе получим как проекцию части графика функции у^=
s= f (х), которая находится в этой полосе, на прямую у f (п), по-
скольку любая точка N этой части графика имеет такую абсциссу
х0, что
п < х0 < п 4-1, т. е. [х0] =; п;
в) в Каждой другой полосе, где есть точки графика функции
y^=f (х), построение производится аналогично.
Примеры построения графиков функций вида y^=f ([х]) приве-
дены нз рис. 383—390.
21Э
211
§ 5.	Построение графиков функций вида у — {/(*)}
Поскольку {f (х)} ;= f (х)— [f (х)], то построение графика функ-
ции 'у {f (х) } сводят к построению графика разности графиков
Функций у—f(x) и у = [f (х)].
Практически построение графика функций yt={f(x)} по задан-
ному графику функции у>= f (х) выполняют так:
а)	проводят прямые у з= п (п 6 Z);
б)	в точках пересечения этих прямых с графиком функции у=*
*= f (х) проводят прямые, параллельные оси ординат. Значения функ-
ции	попадают в образованные прямоугольники. Части
графика функции y — f (х), которые попали в эти прямоугольники
и располагаются в верхней полуплоскости, опускают вниз на рас-
стояние п. Части графика, которые попали в прямоугольники и рас-
полагаются в нижней полуплоскости, переносят вверх на расстояние
Iп I + 1 •
Примеры построения графиков функций вида у= {/(х)} приве-
дены на рис. 391—394.
Рис. 391. у = [л].
Рис. 392. у = х2 (1)\у = {х2} (2).
ИЗ
$ 6. Построение графиков функций вида у = /({л?})
Заметим, что функция i/x=if({x}) периодическая с периодом
О)- 1 и на [0; 1]
Отсюда следует способ построения графика функции y^f({x})\
а)	строят график функции f(x) на [0j Ц;
б)	продолжают этот график, учитывая свойство периодичносхи
функции y*=f ({*}).
Примеры построения графиков функций вида y=zf({x}) приве-
дены на рис. 395—399.
ЧАСТЬ II
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИИ
С ПОМОЩЬЮ ПРОИЗВОДНОЙ
РАЗДЕЛ I
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ, ИХ ПРИМЕНЕНИЙ
К ПОСТРОЕНИЮ ГРАФИКОВ ФУНКЦИЙ
§ 1. Производная функции одной переменной,
Свойства производной.
Производные основных функций
Пусть функция у = f(x) определена в некоторой окрестности
точки х0 и пусть х — точка из этой окрестности, причем х =/= х0.
Рассмотрим отношение
f(x)-f(x0)
х — хл ’
если существует конечный предел этого отношения при х -* х0, то его
называют производной функции f (х) в точке х0 и записывают-
f (х0) = lira
• * U*	у	у»
X-+XQ л	л0
или, введя обозначение Дх = х — xOji
г (х0) =а lim f (х° + Ах)----------lim
'	х-*х„	Дх	д*-»о Дх
(1)
Производной функции / (х) в точке х0 называется предел отноше-
ния приращения функции A# в точке х0 к приращению аргумента Дх,
когда последний произвольным образом стремится к нулю.
Обозначения производной:
f У', Ух (Лагранж),
- I-£(Лейбниц)*
Dy, Df (Коши).
ИЛИ у |Ж'=О.
производная
Конкретное значение производной при х = а обозначают f' (а)
В каждой точке хл в которой предел (1) существует,
du ,
-т-^f W является мерой скорости изменения у ОТНОСИ-
СЬ
214
тельно х. Операция нахождения производной функции f (х) называ-
ется дифференцированием этой функции.
Геометрический смысл производной. Производ-
ная f' (х) функции f (х) в точке х является угловым коэффициентом
касательной, проведенной к кривой у f (х) в точке с абсциссой xi
Г (*) — tg
где а — угол между осью Ох и касательной к кривой в данной ее
точке, отсчитываемый от положительного направления оси Ох против
часовой стрелки (рис. 400).’
Если функция
у = f (*)
имеет производную в точке х*=х0, т. е. если существует предел (1),
то говорят, что при данном значении х~х0 функция дифференци-
руема. Если функция дифференцируема в каждой точке некоторого
отрезка [а; 6] или интервала ]а; &[, то говорят, что она дифферен-
цируема на отрезке [а; Ь] или на интервале ]а; &[.
Если функция y^f(x) дифференцируема в некоторой точке
х^=х0, то она в этой точке непрерывна.
Рис. 400. Геометрический смысл про-
изводной функции; f (х) = tg а.
Рио. 401. Геометрический смысл про-
изводной функции справа и слева.
Если производная при данном значении х Xf . не существует,
то в соответствующей точке графика функции или не существует
касательной, или эта касательная образует с осью Ох угол 90°.
Например, производная функции f (х) ~ ]/х f' (х)	в точке
2/х
х^0 принимает бесконечное значение, не существует. Не имеет
предела (1) функция f (х) =xsin~ при х*=0.
Если для данного значения х = а предел (1) не существует, но
существуют пределы слева и справа, то их называют соответственно
производной слева и производной справа»
Геометрический смысл односторонних произ-
водных f (а — 0) s= tg Of, (а + 0) =? tg а2 (рис. 401). Кривая
имеет излом в точке х ==? а. Например, функция f (х)	| х | в точке
х==0 fимеет такие односторонние производные: f (0 — 0) = — 1,
215
Правила дифференцирования
1.	Производная постоянной равна нулю:
с' = 0.
i.	Постоянный множитель можно выносить за знак производной
(си)' =* си'.
3.	Производная алгебраической суммы конечного числа диффе-
ренцируемых функций «равна соответствующей сумме производных
этих функций:
(Uf ± «2 ± • " • ± ипУ *= и/ ± ^2 ± • V ± Un.
4.	Производная произведения двух дифференцируемых функций
равна сумме произведений производной первой функции на вторую
функцию и первой функции на производную второй функции:
(UU)' = u'v + uv'.
5.	Производная дроби двух дифференцируемых функций равна
дроби, знаменателем которой является квадрат знаменателя данной
дроби, а числителем — разность между произведением знаменателя на
производную числителя и произведением числителя на производную
знаменателя:
I и V u'v — uv'
\v / v%
6.	Если для функции f(x) существует обратная функция и
в точке x^=Xq функция f(x) имеет конечную и отличную от нуля
производную f' (х0), то для обратной функции х = g (у) в соответ-
ствующей точке i/0 =х f (х0) также существует производная, равная
7ч^’т,е’
g,(y*)=rw'
7.	Если функция и =»< ср (х) имеет в некоторой точке х производ-
ную ф' (х), а функция у =5 F (и) имеет при соответствующем значе-
нии и производную Ци =* F' (и), то сложная функция у *= г [ф (*)]
в данной точке х также имеет производную
И» = Fu (и) Ф' (х),
или»
Ух =
т.	е. производная сложной функции равна произведению производной
данной функции по промежуточному аргументу и на производную
промежуточного аргумента по х.
8. Дифференцирование функции, заданной неявно, выполняется
по формуле
9. Дифференцирование функции, заданной параметрически:
р = Ф (0,
316
где	выполняется так. Будем считать, что функция х?=*
= ф (/) имеет обратную функцию t = фх (х) и функции х = ф (0
и у = ф (/) дифференцируемы на отрезке [f0; /j]. Тогда
Ух <р' (0 •
или
xt
Производные основных функций
у = с У = Ха	у' = 0 у1 = ах"*"1, а £ R
y=Vx	У 2/х
у = в* у — ах	у' *= 6х у* = ах In а
у*= 1пх	у1 *= — X
y — loga*	t logqe = 1 и	х xlna
у = sin х у — C.QS X	p' = -llge уг — COS X у’ = — sin х
y = tg*	У =c-^ = sec?x
у == ctg X	у' =	Дп” = — cosec? х *	sin? X
у = arcsin х	Р'"/Т2гг? , 1
у =s arccos х	У	/1-х?
У — arctg х	у ~ 1 4- х?
у = arcctg х	у “ гт^ , 1
у = arcsec х	V х У х2 — 1
у =arccosec х		1 V	х/х2— 1
у = sh х	у' = ch х
JM7
y = ch ж
t/=thx
у =» cth х
у =* Arsh х
у =: Arch х
у *= Arth x
у =* Arcth x
У=*хх
у' = sh х
,_____1_
~~ ch2 х
, 1
sh2 х
, 1
у = -7--' —-
/1 + X2
у ух2 — !
, 1
У 1 — х2
, 1
У X2 — 1
у' =^х*(1 + In х)
Производная производной данной функции f (х) называется про-
изводной второго порядка или второй производной.
Производной п-го порядка функции f (х) называют производную
производной (и —* 1)-го порядка. Производные высших порядков
обозначают так:
или
f (*),	.... Д>(Х).....
или >
d2y	d3y	d\y dny
dx2* ’ dx3-' dx* ' *“1 dxn 1
Чтобы найти производную высшего порядка, надо найти произ-
водные всех предыдущих порядков.
Производную /г-то порядка произведения двух функций вычис-
ляем по формуле Лейбница:
(U0(n) uv(n) + у u'v(n~i) +	u"p(n-«) 4-... 4.
т п(п— 1)...(л— m + l)	।	.
4-----------и(тМп т) + • • • 4- u(n)vt
4	ml	* i я
или
п
s=< У
т=о
Производные высших порядков простейших функций
у^хт	у(п)	1)(т — 2)... (т — n+1) xtn'~n9
Если т — целое и п > т, то у(п) s= О
У -In х	(-!)"-! (я-1)1 -~
218
У =* loga X
у 5= ekx
yt=^ax
У ;= a^x
у z= sin x
у cos x
yi= sin kx
У z=£ cos kx
y^ishx
y=tchx
ym =: (—1)«-1	-V1. -L
y	J In a xn
y[n) knekx
yln) = (In a)n a*
у(л) =x (k In
z - . ( , nn\
£(")=; sin (* + -2")
I . nj*\
у{П) — COS lx 4- — I
y(n) ^=z kn sin ^x + -yj
у(П) kn COS [kx +
{shx, n — четное,
ch x, n — нечетное
{chx, n — четное,
sh x, n — нечетное
§ 2.	Дифференциал функции одной переменной
Пусть функция у f (х) дифференцируема в некотором проме-
жутке Xl
f' (х) sx lim
дх->0 &х*
т. е.
или
Ау /' (х) Дх + аДх,
Лу — f' (х) Дх-f-o (Дх), f(x)^0,
где a -> 0 при Дх -> 0, f (х) Дх — бесконечно малая первого порядка
относительно Дх; аДх^=о(Дх). Главная часть приращения функции
f' (х) Дх, линейная относительна приращения аргумента, называется
дифференциалом функции и обозначается символом
dy^= df (х)^= f (х) dxt
потому что \x=idx.
Функция y^=f(x} имеет в точке х дифференциал тогда и только
тогда, когда она имеет в этой точке (первую^ производную. Диффе-
ренциал функции характеризуется двумя основными свойствами: он
является линейной однородной функцией приращения Дх аргумента,
а также отличается от приращения функции на величину, которая
при Дх->0 является бесконечно малой велиинной порядка более
высокого, чем Дх.
Геометрический смысл дифференциала-. Диффе-
ренциал функции / (х), ’соответствующий данным значениям х и Дх,
219
равен приращению ординаты касательной к кривой у =* f(x) в дан-
ной точке х (рис. 402).
Поскольку дифференциал dy отличается от производной у Л только
множителем dx, то по таблице производных для элементарных функ-
ций легко составить таблицу дифференциалов для них. Например:
у = ха, dy =
у s= axf dy ax Ina dx
Н T. Д.
Основные свойства дифференциалов:
d (си) cdut
Рис. 402. Геометрический смысл диф-
ференциала функции.
d (Ui ± и2 ± • • • ±un) >= dui ±
± du2 ± • • • ± dun,
d (uv) =? vdu + adv,
J u\ vdu —udv
d ( — r=--------x------.
\ v J	vfc
Инвариантность формы диффе-
ренциала первого порядка заклю-
чается в том, что его форма не за-
висит от того, является ли аргу-
мент функции независимой пере-
менной или функцией ’Другого
аргумента.
Дифференциалы используются
для приближенных вычислений:
/ (х 4- Дх) — f (х) « f (х) Дх,
или
f (х 4- Дх) « f (х) 4- Г (х) Дх;
для оценки погрешности:
бу = I Ух I 6х,	.
где 6х — максимальная абсолютная погрешность величины х: | Дх |<
< бх; ду — максимальная абсолютная погрешность у.
Дифференциалы высших порядков определяются индуктивна,
Дифференциалом, второго порядка или вторым дифференциалом функ-
ции у = f (х) в некоторой *точке называется дифференциал в этой
точке ее (первого) дифференциала
d*y = d (dy) = f" (х) (dx)? = f* (х) dx?.
Дифференциалом я-го порядка функции у = / (х) называется первый
дифференциал дифференциала (п— 1)-го порядка
dny = d (dn~*y)~ f(n) (x) dx<
Формула Лейбница имеет вид
dn (uv) =
Z==0
220
Для дифференциалов второго и высших порядков нарушается
инвариантность формы.
§ 3.	Основные теоремы
дифференциального исчисления
Рис. 403. Геометрический смысл тео*
ремы Ферма.
Теорема Ферма. Пусть функция у = f (х) определена
в некотором промежутке, имеет во внутренней толке х = с этого
промежутка наибольшее или наименьшее значение и имеет в точке с
конечную производную; тогда эта
производная равна нулю: /' (с) =0.
Геометрический смысл
теоремы. В точках А и В гра-
фика функции, удовлетворяющей
условию теоремы, касательная па-
раллельна оси Ох (рис. 403).
Теорема Ролля. Пусть
функция у = f(x) определена и не-
прерывна на отрезке [а; Ь] и су-
ществует конечная производная
/' (х) по крайней мере в открытом
промежутке ]а; b[ nf(d) = f(b)-t
тогда между а и b найдется по
крайней мере одна такая точка
с (а < с < Ь), в которой производ-
ная функции равна нулю: f (с) = 0.
Геометрический смысл
теоремы. Если крайние ординаты
кривой у = f (х) равны, то на кривой найдется точка, в которой
касательная к этой кривой параллельна оси Ох (рис. 404).
Рис. 404. Геометрический смысл теоремы Ролля.
Теорема Лагранжа (о среднем значении). Пусть функция
*/=/(х) определена и непрерывна на отрезке [а; &] и существует
конечная производная /' (х) по крайней мере в открытом промежутке
Ja; b[; тогда внутри [a; &] найдется по крайней мере одна такая
точка с (а <^,с <Ь), для которой выполняется равенство
Ь — а	}
(2)
Геометрический смысл теоремы. На дуге АВ кривой
у = f (х) всегда найдется по крайней мере одна точка С, в которой
касательная параллельна хорде АВ (рис. 405). Формулу (2) называют
формулой Лагранжа или формулой конечных приращений. Ее можно
переписать в виде
Д f (Xq) = Г (?) где с = х0 + ОДх, 0 < 0 < 1,
Рис. 405. Геометрический смысл тео-
ремы Лагранжа.
©ели применить формулу (2) к [х0;
х0 + Дх] при Дх > 0. Эта формула
дает точное^ выражение приращения
функции при любом конечном при-
ращении Дх аргумента.
Теорема Коши (обобщен-
ная теорема о среднем значении).
Пусть функции у — f (х) и у —
— g(x) непрерывны на отрезке [а;
&], дифференцируемы по крайней
мере в открытом промежутке ]а;
ЭД, (х) =/= 0 в la; ЭД, тогда внутри
[а; Ь] найдется такая то^ка с,
в которой
f(b)—f(a) Г (с)	,
S (Ь) — g (a) g' (с) •	' '
Формулу (3) называют формулой Коши. Г еометрический
смысл теоремы. Угловой коэффициент касательной к кривой
в точке С, заданной параметрически: х = g(t), у — f (/) (см. рис. 405),
где точка А соответствует значению параметра t = а, а точка В —
значению t = bt выражается формулой
7(6)-На) Г (с)
8 g (ь) — g (a) g' (с) ‘
Формула Тейлора. Пусть функция f (х) на отрезке [а; 6]
непрерывна и имеет непрерывные производные до («+ 1)-го порядка
включительно; тогда выполняется равенство (формула Тейлора)
+ (6-а)л+1‘
/*•	I Г1 “ | 1 /•
О < 0 < 1.	(4)
222
Последнее слагаемое называют остаточным членом в форме Лаг-
ранжа:
d — С—LA*' (Ь — ар+х.
(«4-1)! а)
Если а — постоянная, а b — переменная величины, то вместо b
пишут х:
/(х) = /(а) + ЦР(х-а)+...+^^(х-а)« +
+ Гх>|7^~а)''и’ |=а+0(*-а)> 0<0 < 1.	(б)
(П “j~ 1/*
Из выражения (5) при а = 0 получают формулу Маклорена:
,и = Н0) + Щ>+... + £М1. + ^)^.
Остаточный член в форме Коши имеет вид
Rn = !!2i®(« -Ей»-.),
или (при £ = а + 0 (х — а), 0 < 0 < 1)
Rn = /(П+1)[а+0(-у—Д)! (] _ Qyi (Х _ а)Л+1.
п\
Остаточный член в форме Шлемильха — Роша
Rn = f^^(x-^+i-P(x^a)P, р>0.
§ 4.	Исследование функции
с помощью производных
Условие постоянства функции. Теорема*!. Пусть функция
f(x) непрерывна на отрезке [а; Ь] и/имеет производную f' (х)
по крайней мере в интервале ]а; &[. Для того чтобы данная функ-
ция f (х) была постоянной на отрезке [а; 6], необходимо и доста-
точно выполнение условия /' (х) = 0 во всех точках интервала ]а; Ь[.
Условие монотонности функции. Теорема 2. Для того чтобы
функция / (х), имеющая конечную или бесконечную производную,
в каждой точке отрезка [а; 6] была возрастающей (убывающей),
необходимо и достаточно выполнение условий: f' (х)^>Ю (/' (х)<<0);
f (х) ЙО ни на каком отрезке, входящем в состав отрезка (о; Ь].
Геометрический смысл т е о р е м ы. Если на отрезке [а;
функция f (х) возрастает, то касательная к кривой у f (ж) в каж-
дой точке на этом отрезке образует с осью Ох острый угол ф или
(в отдельных точках) горизонтальна; тангенс этого угла неотрица-
телен (/' (х) =; tg ср >> 0) (рис. 406); если функция f (х) убывает
на отрезке [а; 6], то угол наклона касательной тупой или (в отделу
ных точках) касательная горизонтальна. Тангенс этого угЛа неполо'*
жителей. Следовательно, по знаку производной функции можно
определить, возрастает или убывает функция.
Для определения интервалов строгого возрастания (строгого
убывания) функции надо решить неравенство
f'W>0	(/'W<0).
Кроме того, надо рассмотреть, как размещены в этих интервалах •
точки, в которых f (х) равна -нулю, а именно: не заполняют ли они
•сплошь какую-нибудь часть интервала, в котором рассматриваем
функцию.
Рис. 406. Функции: возрастающая (а); убывающая (б).
Пример 1. Определить интервалы возрастания и убывания
функции
f . . Зх?
Прежде всего находим область определения функции. Функция
существует при всех значениях х, кроме xs=—2 и хг=2/ т. е.
область ее определения: ]—оо; — 2[ J ]—2; 2[ J ]2; °°[« Находим
производную функции
о2х(4 — х«) + х«.2х__, 8х
'	(4_Х2)2	(4-х?)Г
Знаменатель последней дроби положителен при всех значениях х
(кроме х= ±2). Дробь положительна при х > 0. Данная функция
возрастает на ]0; 2[ J ]2; <х>[. Дробь отрицательна при х < 0. Сле-
довательно, данная функция убывает на ]—оо; —2[ J 1—2; 0[.
Производная равна нулю при х s= 0. В этой точке функция перехо-
дит от убывания к возрастанию.
Пример 2. Найти интервалы возрастания и убывания функции
/(х);=4х$ + х.
«4
Находим производную:
f'(x)=^Sx+ 1.
Чтобы найти интервалы возрастания функции, решаем неравенство
получаем
8 *
Следовательно, данная функция возрастает в инлервале
---5"* 001 • Решив неравенство
о I
£
8
.	1 1Г
находим, что данная функция убывает в интервале —оо| — -j-1 >
Максимум и минимум функции
Пусть функция у f (х) определена в некоторой окрестности
точки х^=х9. -
Функция y^=f(x) имеет максимум в точке х х0, $сли суще-
ствует такая 6-окрестность точки х0, что при — 6 < х < х0 4* 8
выполняется неравенство
т. е, значение функции в этой точке ^больше, чем ее значение во _
всех других точках, достаточно близких к х0.
Функция y*=f(x) имеет минимум в точке х^=х0, если сущест-
вует такая 6-окрестность течки х0, что при — 6 < я < х0 + 6
выпблняется неравенство
т. е. значение функции в этой точке меньше, чем ее значение во
всех других точках, достаточно близких к х0.
Если в некоторой точке функция имеет максимум или минимум,
то говорят, что в этой точке функция имеет экстремум, а значение
функции в этой точке называют экстремальным. Функция, опреде-
ленная на отрезке, может достигать экстремума лишь во внутренние
точках этого отрезка; максимум (минимум) не обязательно является
наибольшим (наименьшим) значением функции в области определения
функции: вне рассматриваемой окрестности точки функция Может
принимать большие (меньшие) значения, чем в этой точке; функций
может иметь несколько максимумов и минимумов в области своего
определения.
Необходимое условие существования экстремума функции. Если
функция y~f(x) в точке	имеет экстремум, то ее производ-
ная в этой точке или равна нулю, или не существует^
8 8-413
225
Точки, в которых производная равна нулю или не существует,
но функция при этом сохраняет непрерывность, называются крити-
ческими точками функции. Следовательно, функция может иметь
экстремум только в критической точке, но ие всякая критическая
точка является точкой экстремума. Например, для функции у = х3
точка х^=0 является критической, так как производная у' Зх2
равна нулю в этой точке, но ни максимума, ни минимума в этой
точке функция не имеет (см. рис. 26). Производная функции у^
х при х = 0 бесконечна, т. е. точка х — 0 является критичес-
кой, но в этой точке функция не имеет экстремума. При х < О
у < 0, при х > 0 у > 0, а при хг= 0 у s= 0 (см. рис. 36).
Достаточные условия существования экстремума функции. Если
функция у s= f (х) непрерывна в интервале ]а; b[t содержащем кри-
тическую точку х0, дифференцируема во всех точках этого интер-
вала, за исключением, может быть, точки х0, и если производи г я
этой функции f (х) меняет знак при переходе х через критическую
точку х0, то функция у = f (х) имеет экстремум при х = х0. При
этом если знак производной меняется с «+» на «—», то при Х“х0
функция имеет максимум, а если знак производной меняется с «—»
на «+», то при xs=x0 функция имеет минимум. Если же при пере-
ходе через критическую точку первая производная функции не меняет
знака, то экстремума нет.
Исследование функции на экстремум
с помощью первой производной
Правило для исследования функции на экстре-
мум с помощью первой производной:
1)	находят первую производную /' (х);
2)	находят критические точки функции, для чего решают урав-
нение f' (х) ь= 0;
3)	определят действительные его корни, а также те точки,
в которых производная не существует.
Пусть критическими точками являются точки хь х2, .. ., хп,
которые находятся в интервале Ja; b[.
Размещают все критические точки в порядке возрастания их
абсцисс в интервале ]а; &[:
а < хх < х2 < • • • < хп < Ь.
В каждом из интервалов Ja; xt[, ]хх; х2[, ... , ]х/г; х^+1[, ..., ]хп; Ь\
выбирают произвольную точку и устанавливают в этой точке знак
первой производной.
Рассматривают знаки ff (х) в двух соседних интервалах, после-
довательно переходя слева направо от первого интервала до послед-
него. Если, например, производная f' (х) меняет знак с «—» на «-р>,
то функция имеет минимум в данной критической точке. Если же
в двух соседних интервалах производная f' (х) не меняет знака, то
экстремума в рассматриваемой критической точке нет.
Вычисляют значения функции в точках, где она достигает
экстремума (экстремальные значения функции).
Ход графика функции, имеющей экстремум, в окрестности кри-
тической точки показан на рис. 407.
226
Пример 3. Исследовать на экстремум функцию
f (х) — 2х3 — Зх? + 1.
Находим производную
/' (х)	6х? — 6х s= 6х (х — 1).
Решаем уравнение f' (х) ~ 0, т. е. уравнение
6х(х — 1) = 0,
и получаем критические точки
хх — О, х2 1.
Исследуем знак производной в окрестности каждой из критических
точек. Рассматриваем интервалы ]—оо; 0[, JO; 1{, J1; 4-оо[. Выби-
раем внутри каждого из этих интервалов произвольную точку и опре-
деляем в этой точке знак первой производной.
В первом интервале берем точку во втором—точку ~ f
в третьем — точку 2. Соответственно имеем
Г (-1) > О,
г(1)<0«
Г (2) > о.
В критической точке х s= 0 функция имеет максимум, в критической
точке х s= 1 ** минимум.
Вычисляем экстремальные значения функции:
/(0)^=1.
8*
217
Исследование функции на экстремум
с помощью втброй производной
Если производная функции y^=f(x) равна нулю при x = Xf,
а вторая производная при этом значении аргумента не равна нулю,
то функция у = f (х) при х=!Х1 имеет максимум, если f (х) < О,
и минимум, если (х) > 0.
П p-а в и л о д л я и сс л е д о в а н и я ф у н к ци и на экстре-
му м'с п о мощью второй производной:
1) находят первую производную функции f (х). Решая уравнение
/'(х) = 0, находят действительные корни, которые и определяют
критические точки;
2) находят вторую производную. Исследуют в каждой крити-
ческой точке знак второй производной. Если в критической точке
х =ж xi вторая производная Г (*i) < то в этой точке функция f (х)
имеет максимум, если же f (хх) >0, то в точке Xf функция f (х)
имеет минимум. Если вторая производная равна нулю или не суще-
ствует, то исследование функции на экстремум надо производить
с помощью первой производной.
Пример 4. Исследовать на экстремум функцию
/(х) = х3 — 3x3 — 9х + 2.
Находим первую производную
Г (х) = ЗхЗ —6х —9.
Решаем уравнение f' (х) *= 0:	*
3x3 — 6х — 9 = 0,
хЗ —2х —3 = 0,
Xi х= — 1, х2 5= 3.
Так как производная существует при любом х, критическими будут'
ТОЧКИ Xi = —1 и х2*=3.
Находим вторую производную:
f (х)^=6х — 6.
-Определяем знак второй производной в каждой критической .точке:
I" (—1) < 0, функция при Xf = —1 имеет максимум; f (3) > 0, функ-
ция при х2=3 имеет минимум, причем
/max = /Н) =?, fm[n « f (3) « -23.
Исследование функции на экстремум
с помощью формулы Тейлор^
Если в некоторой точке х = х0 f' (х0) = 0 и /* (х0) = 0, то
можно производить исследование функции на экстремум в этой точке
с помощью производных высших порядков. При этом используется
лемма о сохранении знака: если функция y;=f(x) непре-
рывна и отлична от нуля в точке* х0, то она отлична от нуля
И имеет знак, совпадающий со знаком f (х0), и в некоторой окрест-
ности точки X#
22S
Пусть функция у г= f (х) при х *= х0 имеет производные до л*го
порядка включительно и
Г (х0) *= Г W *=•••:= f (*0) « 0, а /(«) (х0) * О
и /СЛ) (х) при х^=ха непрерывна. Тогда при п нечетном функция
у -= f (х) в точке х0 не имеет экстремума, а при п четном имеет
максимум, если /(Л) (х0) < 0, и минимум, если f<n\(xQ) >
Отсюда следует правило для исследования функции на экстремум
с помощью производных высших порядков.
Пример 5. Исследовать на экстремум функцию
f(x)s=5x4.
Находим производные:
Г (х) s= 20х3, f (х)	60х2,	(х) = 120х, /(IV) (х)	120.
В критической точке х s= 0 /' (0) s=s f” (0) =	(0) s= 0, a (0)
^=0, причем f(IV) (0) = 120 > 0. Следовательно, в точке xj=O функ-
ция имеет минимум.
Пример 6. Исследовать на экстремум функцию
/(х)^=2х5-+1.
Находим производные:
f(x) —Юх4, Г(х) = 40х8, Ги) —120х«,
f(IV) (х) =х 240х, /(V) (х) 5= 240 ^ 0.
Следовательно, экстремума в точке х=*0 функция не имеет.
Наибольшее и наименьшее значения функции на отрезке
Если функция у==:/(х) определена и непрерывна на отрезке
[а; д], то на этом отрезке всегда найдутся точки, в которых она
принимает наибольшее и наименьшее значения. Эти значения функ-
ция принимает или в критических точках, или на концах отрезка
[а; 6].
Правило. Чтобы определить наибольшее (наименьшее) значе-
ние функции на отрезке, надо:
1)	определить критические точки функции;
2)	вычислить значения функции в критических точках и на кон-
цах отрезка;
3)	выбрать из полученных значений функции наибольшее (наи-
меньшее) значение функции на отрезке [а; Ь].
Следует обратить внимание на важный частный случай. Если
точка Xf — единственная точка экстремума функции f (х) на отрезке
[а; Ь], то f (хх) — наибольшее значение функции f (х) на этом
отрезке, если f (хх) — максимум, и f (xj) — наименьшее значение
функции f(x) на отрезке [а; &], если /(xj—минимум функции.
Пример 7. Найти наибольшее и наименьшее значения функции
f (х) ₽= х* — 5х4 + 5х3 + 1
на отрезке [—1; 2].
Находим критические точки, принадлежащие данному отрезку.
Первая производная
(х)^=5х4 —20х3+15х?,
211
откуда
х? (х? — 4х + 3) = 0;
корни этого уравнения: хх:=0,	х2=*1,	х3^=3; точка х —
^3€|г~1;2^
Значения функции в критических точках х*=0 и х^= 1 и на
концах отрезка [—I; 2];
/<0>=1, /(1) = 2,
f (-I)^-IO, f (2)^-7.
Следовательно, на данном отрезке наибольшее значение функции
Ux = Hl) = 2,
наименьшее значение
Выпуклость кривой. Точки перегиба
Пусть y^=f(x) — дифференцируемая функция. Кривая y~f{x)
называется выпуклой (вогнутой) в точке х^=х0, если существует
такая окрестность точки х^=х0, 50 всех точках которой кривая
у = f (х) расположена под. (над) касательной к этой кривой в точке
М(х0; f(x0)). Если кривая выпуклая (вогнутая) во всех точках
некоторого интервала, те она* называется выпуклой (вогнутой) на этом
интервале (рис. 408).
Рис. 409. Точки перегиба
кривой.
Достаточные условия, при которых кривая#:=
^=/(х) выпуклая или вогнутая. Если во всех Точках
интервала ]а;	/" (х) < 0 (/" (х) > 0)г то. кривая y^f(x) на этом
интервале выпуклая (вогнутая).
Течкой перегиба непрерывной кривой' называется точка, при
переходе через которую кривая меняет выпуклость на вогнутость
или наоборот. В этой точке касательная к кривой пересекает кри-
вую (рис* 409).
Достаточные условия, при которых данная
точка кривой является точкой перегиба. Пусть
кривая определена уравнением yt=f(x). Если f(a) = 0 или Г (а)
не существует и при переходе через значение xs=a /"(х) меняет
знак, то точка кривой с абсциссой х=*а является точкой перегиба.
Правило для нахождения точек перегиба и исследования гра-
фика функции на выпуклость и вогнутость:
па
1)	находят вторую производную
2)	решают уравнение	а также определяют те значе-
ния х, при которых f (х) не существует;
3)	исследуют знак второй производной /*<(*) в окрестности каж-
дого корня уравнения f" (х) и тех точек, в которых f” (х) не суще-
ствует. flycib xs=Xf является одной из таких точек. Определяют
знак fn(x) при х < х± и при х > ,хх. Если знак второй производной
меняется, то точка М (хх; f (хх>) является точкой перегиба данной
кривой. Если же знак второй производной f' (х) не меняется, то
точка М (х^ f-(xx)) не является точкой перегиба. В точках, в кото-
рых fn\x) ><), кривая вогнутая, а в точках, в которых Г (г) < О,
кривая выпуклая.
Пример 8. Найти точку перегиба и исследовать на выпуклость
и вогнутость график кривой, заданной уравнением
*	у?=е х .
Находим первую и вторую производные:
ц	i
y'r=2e '*8х~2# у"*=2ё *8x~4 (2х-3 — 3).
, х*=0, но при
Вторая производная у"=*0 при х*=
х =; 0 функция н$ определена.
Исследуем знаки второй производной окрестности корней
Х1 *= |/ у И хг =« —	-j-: для X < |Лу у" > о, для х >
-у ун < 0. Знак второй производной изменился, следователь-
но, точка
является точкой перегиба.
у” < 0,^ля х >
следова-
тельно,
и точка х5х=
является точкой перегиба.
На
интервалах — оо; •*•
кривая эыпук-
лая, на
интервалах
]•- W »[• b Vi[
кривая вогнутая.
§ 5.	Построение графиков функций
с помощью производных
Исследование функций с помощью производных и построение их
графиков производят по такой схеме.
1.	Находят область определения функции <(см.	2 разд. 2 ч. I),
устанавливают при этом точки разрыва, их характер и интервалы
непрерывности функции.
£31
2.	Исследуют функцию на четность или нечетность, на перио-
дичность, определяют точки пересечения кривой с осями координат,
интервалы зна непостоянства (см. § 2 разд. 2 ч. 1).
3.	Находят точки экстремума функции и вычисляют значения |
функции в этих точках, устанавливают интервалы монотонности 1
функций (см. § 4 разд. 1 ч. II).	]
4.	Находят точки перегиба графика функции и исследуют график *
функции на выпуклость или вогнутость (см. § 4 разд. 1 ч. II).
5.	Находят асимптоты графика функции (см. § 2 разд. 2 ч. I). .
6.	Строят график функции. Для большей точности эскиза гра-
фика можно рекомендовать построить еще и отдельные точки гра- ।
фика, придав конкретные значения независимой переменной и on ре- 1
делив соответствующие значения функции.	1
Желательно выполнять чертеж графика наряду с исследованием 1
функции, иногда удобнее вначале построить на координатной пло-
скости асимптоты, точки экстремума, точки перегиба графика
фуйкции.
Если функция окажется четной (нечетной) или периодической,
то следует учесть особенности графиков таких функций.
Пример. Исследовать функпию

” х — 2
и построить ее график.
Область определения функции: ]—оо; 2| (J 1 2; оо|. Точка х-
=: 2 — точка разрыва второго рода. Функция общего вида, неперио-
дическая. Точки пересечения с осями координат: (—1; 0), ^0; —
На интервале ]—оо; 2[ функция отрицательная, на интервале
J2; оо [ — положи тельная.
Находим точки экстремума и определяем интервалы монотон-
ности функции.
Первая' производная
2(х+1)(х-2) -(х+1)Г (х+ 1) (х — б)
' W —	(х-2)?	~	(х~2)3	
Для нахождения критических точек решаем уравнение f (х) ?= 0,
т. е. (х+1)(х —5)^=0, откуда	1, х2 —5 (х=*2 —точка, 4
в которой производная не существует, но это значение мы не рас- :
сматриваем, так как х = 2 не принадлежит области определения *
функции). Критические точки xr j= — 1, х2^=5 и точка х>=2 делят \
область определения функции на такие интервалы: J—оо; —1[,
J—1; 2[, ]2; 5[, ]5; oof. В каждом из этих интервалов производная
сохраняет соответственно знак «+»> «—>» «—», «+>•
Следовательно, на интервалах ]— оо; —1[ Q [ 5; оо| функция |
возрастает, а на 1—1; 2[ J 12; 5[ убывает.	1
При 1 функция имеет максимум: //тах>=0. При х=д5
функция имеет минимум: ymin j== 12.
Находим точки перегиба графика кривой и исследуем кривую
на выпуклость и вогнутость»	’
i
- - ’	j
i
Вторая производная
. ч Гх? — 4х—51'
f	(x - 2)5“J -
(2х — 4)(х — 2)? — (х? — 4х — 5)2(х — 2) _	18
“	(х — 2)*	(х— 2)3 ‘
Точек перегиба нет.
Асимптоты. Вертикальные асимптоты найдем, приравнивая зна-
менатель нулю:
х — 2 0, х 2.
Вертикальная асимптота одна,
ее уравнение
хг= 2.
Для нахождения горизонталь-
ных асимптот определяем
lim /(х);=
Х-^±оо
, и» <1±Д!_±оо;
Х-* ± сю X —2
а это означает, что горизонталь-
ных асимптот нет.
Наклонные асимптоты:
А»= lim ;
x-+i °° X
b s= lim
Л->±сю
lim
Х->±оо
Г(х-Ь- 1)S
[ х — 2
Нт ^±4 = 4.
Следовательно, у — х + 4 — наклонная асимптота.
Полученные сведения наносим на рисунок и получаем эскиз
кривой (рис. 410).
$ 6. Построение графиков функций /' (х) и f" (х)
по графику функции fix')
Во многих прикладных науках, например в теории машин и меха-
низмов (при построении плана-диаграммы ускорений по плану ско-
ростей и т. п.), часто возникает необходимость решения задачи
233
о построении графиков первой и второй производных функции при
наличии графика заданной функции.
Пусть задана Некоторая дифференцируемая функция t/i==/(x).
Первая и вторая производные этой функции fe свою очередь явля-
ются функциями от х. Поэтому графики функций f' (х) и f" (х)
можно строить по общим правилам построения графиков функций.
Однако если известен график функции у>= f (х), то построение гра-
фиков функций /' (х) и /" (х) иногда значительно упрощается. При
этом необходимо учесть такие замечания:
а)	в точках, где функция f (х) имеет экстремум, f (х) =0;
б)	в точках перегиба функции f (х) производная f' (х) имеет
экстремум (максимум, если производная при переходе от меньшего
значения х к большему через точку перегиба функции f (х) вначале
возрастает, а затем убывает, и минимум, если производная изме-
няется наоборот), при изменении х от меньших значений к большим
на интервалах выпуклости заданной функции f (х) производная f' (х)
убывает, а на интервалах вогнутости — возрастает;
в)	точки перегиба производной f (х) находим обычным способом.
Наклонные асимптоты функции /(х) соответствуют горизонтальным
асимптотам производной /' (х).
234
Замечание. Эти соображения используем и при построении
графика второй производной /" (х), причем следует погнить, что рель
основного играет график первой производной /' (х).
Пример. Построить график функции
_ 2х — 1
У~ (х— 1)«
и графики ее производных у', у".
2х______________1
а)	у=-------T-rj-. Область определения! ]—оо; 1 [(J] 1; оо[.
Прямая х — 1 — вертикальная асимптота. Точка (0; —1) — точка
(1	8 \
—;--------g-1 — точка перегиба. Кривая прохо-
-о°; ~4[ кри- <
дит через точки (0; —1) и ~ ; О
~ ; 1 [ J J 1; оо —вогнутая.
вая выпуклая, для х €
—2х
б)	t/z —	_ из • Область определения! ]— оо; 1[|J]1; оо[.
I) -
(1	8 \
-----------------------------------------------2 ’ — 27/ — точка
минимума. Для х£ ]1; оо[ у' < 0, на этом же промежутке кривая
выпуклая.
ч и 2 (2х -|- 1) TZ
в)	у -------ттг*- Кривая проходит через точки
(X 1)
и (0; 2). Для х 6 ] — 00; 1 [ (J ] 1J 00 [кривая вогнутая.
Графики функций у =	, у' = — и / = fffnT
\Л	*) “	\Л	1)	\Л 1 /
приведены на рис. 41L
о
§ 7. Правило Лолиталя
Иногда при исследовании функции для построения графика при-
ходится иметь дело с неопределенностями вида
~	; 0 • оо; оо — оо; 0°; 100; оо^
О оо	.
Во многих случаях раскрытие неопределенности выполняется
0 помощью правил Лопиталя.
Неопределенность вида -у. Пусть функции f (х) и ф(х) опреде-
лены в интервале ]а; Ь[, конечном или бесконечном.
Раскрыть неопределенность вида ——это значит найти предел
Пт
х->а-}-0 ф (х)
235
при условии, что lim f (х) lim ф (х) s== 0 и ф (х) =£ О для ух£ ] а\
Af-^e-J-O x-*-a-}-0
с [, где а < с < Ь9 или найти предел
lim
х-*&—О Ф W
при условии, что lim f (х) =? lim ф (х)	0 и ф (х) У= О для ух £ ] с;
х-+Ь—0	х-+Ь—0
Ь[, где а< с < Ь.
Действительно, имеем «неопределенность», поскольку предел,
о котором здесь идет речь, может существовать и может не сущест-
вовать, а если и существует, то его значение неизвестно.	'
Теорема 1 (первое правило Лопиталя). Пусть функции f (х)	’
и ф (х) дифференцируемы в интервале ]а; 6[.	*
Если lim f (х) =х lim ф(х)*=0, ф'(х)	0 для ух а;	!
хч-а-|-0	х-ч-а-|-0	'	{
(х)	
С1[, а < Ct < b\ существует предел lim -L2-L, конечный или бес- ?
х-а+о ф' (х)	Г
конечный, то Hm 1^). a=g lim £./*)
х-*а+0 ф (X) х-н^-О ф (х)
Если limf(x)=s lim ф(х);=0, ф' (х) 0 для ух€]с2*
х->&—о	хч-6—о
-SJ
а < с. < Ь; существует предел lim	конечный или бесконеч-
х^й-Оф (х)
ный,
то lim ДЙг
х->й—о Ф W
lim -Ш
х->&—о ф W
Следствие. Пусть функции f (х) и ф (х) дифференцируемы
в интервалах 1ха — 6; х0[ и ] х0; х04-6[, где 6 > 0.
Если lim f (х) = lim ф (х)	0, ф' (х) ± 0 для ух£]х0 —6;
х->хв	х-+х0
Г (х)
х0 [0 ] х0; х0 + 6[; существует предел lim 1	\ , конечный или
х-+ха ф \х)
к	«	1- f W V Г(х)
бесконечный, то lim --	=? lim
х+х0 Ф (*) х-х0 ф (*)
Неопределенность вида —.
Теорема 2 (второе правило Лопиталя). Пусть функции f(x)
и ф (х) дифференцируемы в интервале ]а; Ь[, конечном или беско-
нечном.
Если lim f (х)« оо, Нтф(х)!=оо, ф' (*)	0 для ух €]а;
f' (х)
q[, а < Ci < b; существует предел lim Ц-Y 7 , конечный или бес-
х-ч-а-ро ф W
конечный, то lim ?= lim .
х->а-Ь0 Ф (*) х+а+0 Ф W
236
,1
Если lim / (х) = со, lim q> (х) s= оо, <р' (х)	0 для ух €] са; Ъ [,
х->д—О	х-*-Ь—О
/' (х)
a < с2 < Ь; существует предел lim  Д <==; Л, конечный или беско-
х-*Ь^-0 Ф W ~
„ V f (х)	.. f'(х)
нечныи, то lim =g hm - Д \,
^д_оФ(*) х-^оФ (*)
Следствие. Пусть функции f (х) и ф(х) дифференцируемы
в интервалах ]хв — 6; х0[ и ] х0; х0 + 6 f, где о > 0.
Если lim f (х) г= оо, lim ф (х) ;= оо, ф' (л)	0 для у* €1 *о — в;
Х-*Х9	Х-+Хо
(х)
х0 [ UI х<н х0 + 6[; существует предел lim -77-7, конечный или
х-*хвФ W
бесконечный, то lim — s= lim .
х-*х9 Ф (*)	х-*х9 Ф* (*)
Этими следствиями на практике пользуются чаще всего.
Неопределенность вида 0 • оо с помощью преобразования
/ (х) • <р (х)
/(*)
1/ф (X)
U
приводится к неопределенности вида
Неопределенность вида оо — со с помощью преобразования
1_______
, / ч / ч ф(Х) f(x)
f(x)-4 (х)
1	/(•«) ’ Ф(х)
О
приводится к неопределенности вида -g-.
Неопределенности вида 0°, I00, оо°. Использовав равенство
f (х)т(х)	1п^х>
и учтя непрерывность ^показательной функции, будем иметь
lim Ср(х) In /(х)
lim /(х^(дг)х=г-+о+0
х-*-д4-0
или
lim <р(х) In /(х)
lim f(x)^-ex^b~0
х-*&—О
Следовательно, неопределенности этих видов приводятся к неопре-
деленности вида 0 • оо, которая в свою очередь приводится к неопре-
деленности вида -Q-.
2Э7
Пример 1. Найти предел
еах_е-гаж
1Г ГЛ —	.
In (1 + х)
Имеем lim f (х) s= lim (е^ — е 2ах) = 1 — 1=<0, Итф(х)=:
х->0	х-+0	х->0
*= lim In (1-f-х) ==; In 1 s= 0. В любой окрестности точки х —0, не
содержащей точки х^=—1, существуют f' (х), ф' (х), причем
ф'« = пЬ*0<х>_1)-
i -f X
Существует предел отношения производных
.. f (х)	,. аеах 4- 2аг~2ах
lim --Д-  =* hm — 'ii —----
хчоФ W х-0 V0 4-*)
За.
Правило Лопиталя применима^ имеем
еы__е-2аХ аеах + 2ае~2ах
х™о 1п(1 +*) х™о 1/а+х)
Пример 2. Найти предел
г [ 1 ! \
lim -т------------------------г I а
1ПХ х— [}•
Имеем неопределенность вида оо — оо. Приведем ее к неопреде-
0
ленности вида -у, а затем применим правило Лопиталя:
.. { 1	1 \	х— 1 — In х
lim -------------- k= lim —---—-----s=
Х-+1 \ Inx х—1/	(х—1)1пх
.. х—1 р 1	1
ч  =т 1 im —:-;---г i= hm  -7-Т--	.
J_ x+ixlnx4-x—1	х-+{1пх + %	2
Пример 3. Найти предел
lim (tgx)c-g*
тс	♦
Воспользуемся тождеством
(fg X)ctg х __ gctg x in tg X,
Ho
Jim ctgxlntgx» lim --n*gX ==?0,
тс	к	X
2~°
238
откуда
lim (tg x)cfg * fc= e* ₽ 1.
0
Замечание.
Если отношение производных
Г (*)
ф' (х)
опять
яв-
ляется неопределенностью, то правило Лопиталя применяют по-
вторно, пока не избавятся от неопределенности или не обнаружат,
что нужные пределы не существуют.
§ 8. Приближенное вычисление корней уравнения
’Рассмотрим уравнение
Если это уравнение — алгебраическое, причем степени не выше чет-
вертой, то вообще существуют формулы для нахождения корней
этого уравнения. Для уравнений выше четвертой степени в общем
случае таких формул не существует.
Рассмотрим некоторые методы приближенного вычисления кор-
ней уравнения
f(x)x=0.
Метод хорд
Пусть задано уравнение f(x)^=O, где/(х)— непрерывная дважды
дифференцируемая функция на Ja; &].
Выделим на [а; Ь] отрезок [хх; xj] такой, что внутри этого
отрезка функция монотонна, а на концах его значения функции Дх)
имеют разные знаки. Пусть f (хх) <0, f (х2) > 0 (рис. 412). Поскольку
функция y=tf(x) непрерывна на (xj; x2J, то ее график пересечет
ось абсцисс в какой-то одной точке между хх и х2.
Рис. 412. Метод f X 9 f > 0 fty
239
1 '*
Проведем хорду АВ, которая соединит концы кривой
с абсциссами Хх и х2. Абсцисса щ точки пересечения этой хорды
с осью абсцисс является приближенным значением корня уравнения
f(x)=sO:
Xiffa) —W(*l)
Для получения более точного значения корня определяем"? (at).
Если f (flx) < то повторяем предыдущий процесс, применяя по-
следнюю формулу к отрезку [х$; #xL Повторяя этот процесс
построения точек несколько раз, будем, очевидно, получать более
Метод касательных (способ Ньютона]
Пусть опять f (хх) <0, f (х2) > 0, причем на [xt; х2] первая
производная не меняет свой знак. Тогда в интервале ]хх; есть
один корень уравнения f (х) = 0. Допустим, что и вторая производ-
ная сохраняет свой знак на [xj; х2], т. е. кривая или выпуклая, или
вогнутая на [хх; х2].
Проведем касательную к кривой в точке В (рис. 413, а). Абсцисса
а± точки пересечения касательной с осью абсцисс’является прибли-
женным значением корня:
1 а~Т7Я’
Проводя касательную в точке Вх(аь аналогично находим
более точное значение корня а2 (рис. 413, б). Повторив этот процесс
несколько раз, сможем вычислить. приближенное значение корня
с любой необходимой точностью.
Заметим, что касательную надо проводить в том конце дуги,
в котором знаки' функции и ее второй производной совпадают. Это
замечание справедливо и для случая, когда /х (х) <
Если касательная проведена в левом конце интервала, то для
а± справедлива такая формула:
а—х- t^L
Если внутри интервала ]хх; х2[ есть точка перегиба С, то спо-
соб касательных может дать-приближенное значение корня, которое
лежит вне интервала ]х±\ х2[ (рис. 413, в).
Заметим, что на практике часто применяют комбинированный
метод, который заключается в поочередном применении метода каса-
240
тельных и метода хорд. Применяя на [хх; х2] одновременно метод
хорд и метод касательных, получаем две точки: а± и .а*,^лежащие
по разные стороны от искомого корн£ а, так как f (а2) и f (ах) имеют
разные знаки. Теперь уже на [а^; а*] применяют метод хорд и метод
касательных. Получаем еще два числа: а2 и а^, которые еще ближе
к значению корня. Продолжаем этот процесс до тех пор, пока раз-
ность между найденными приближенными значениями не станет
меньше допустимой.
Пример. Найти действительный корень уравнения
/ (х) — х3 4- Зх — 2х2 — 5 =ж О
с точностью до 10~4.
Сначала убеждаемся, что уравнение имеет лишь один действи-
тельный корень. Это следует из того, что производная f' (х) ₽= Зх2 +
4-3 — 4х > 0. Из условий / (1) = —3 <0 и f (2) =* 1 > 0 делаем
вывод, что данное уравнение имеет единственный положительный
корень, который находится в интервале J1; 2[.
а)	Методом хорд получим
1 • 1 —2 . (—3)	7
1—(—3)	4	,75>
Но f (ах) *= f (1,75) = —0,5156 <0, a f (2) *=s 1 > 0, следовательно,
1,75 < а2 < 2.
Применим еще раз метод хорд к отрезку [1,75; 2]:
 _ 1,75. 1 -2 . (-0,5156)
------2-(-0,5156)-------1 -8350-
Проверяем: /(1,8350) = —0,05059 < 0, следовательно, 1,835 <
< а3 < 2. Уменьшим интервал. Действительно, f (1,9) = 0,339 > 0,
следовательно, 1,835 < а3 < 1,9.
Применим еще* раз метод хорд к отрезку [1,835; 1,9]:
а3= 1,8434.
Далее, а4= 1,8437, а5= 1,8438; но /(1,8437) < 0, a f (1,8438) > 0,
следовательно, корень а5 ж 1,8438 и будет искомым приближенным
корнем заданного уравнения.
б)	Методом касательных результат можно получить быстрее.
Применим этот метод.*
Поскольку /(2)=1 >0 и f (х)=6х — 4>0 на [1; 2], а пер-
вая производная /' (х) также сохраняет свой знак на (If 2], то ме- < “
тод касательных можно применить.
Имеем
f (х) = Зх2 — 4х 4- 3, f' (2) = 7,
01=^2 —у =; 1,857,
Следовательно, а9 дает уже нужную точность.
241
РАЗДЕЛ 2
ПОСТРОЕНИЕ ГРАФИКОВ ВСЕХ ВИДОВ ФУНКЦИЙ
Исследование функций' с помощью производных и построение
их графиков будем производить ио схеме § 5 разд. 1 ч. 1Г. В отдель-
ных случаях будем производить дополнительные исследования. Заме-
тим, что исследование иногда будет упрощаться, а порядок исследо-
вания — нарушаться.
§ 1. Примеры построения графиков функций
вида у =/(х) в декартовой системе координат
Пример I. Построить график, целой рациональной функции
ах*+Зх?-5. *
Область определения функции: ]—ао; oof. Функция непрерывна
при всех х С] — оо; оо[. Функция четная.
График функции симметричен относительно оси ординат, пере-
секает ось ординат в точке (0; —5), ось абсцисс в точках
(—	о)и(|/^/4 + 1; О') . Интервалы знакопостоянства
]+ 1; оо [ функция положитель-
на j — оо;
на, на l-V’/4 + l; УТ? -f- — отрицательна.
Определяем критические точки. Первая производная
у' 1= 6хб — 12х3’+ €*•
Решаем уравнение у' ;= 0, т. е. уравнение
х^бх4 — 12х2-Н)>=0. ’
Имеем хх;=Д *2—1, *з ——1- При переходе через точки х2 = 1
и	—Ь производная не меняет-знакам точки х2^=1; *з~—1
не являются точками экстремума данной функции. При переходе через
точку хх = О функция меняет знак с «—» на «+», следовательно,
в точке Xi=?O функция достигает минимума —причем при
— оо < х < 0 функция убывающая, при 0 < х < + оо — возрастаю-
щая.
Находим вторую производную
у" — ЗОх4 - Збх?+ б;
Приравниваем ее нулюг
у" х= ЗОх4 — Збх? + б =( О,
1‘	1	1 тл
откуда Xi=x—1, х2=ч------7=^ > *3 — • z—1 > х4^=1. При переходе
242
через эти точки вторая производная меняет знак, следовательно,
точками перегиба графика функции являются точки
Б4 \	/1
-уГ”М’Ч/Г
P4(i; -4).
График функции выпуклый при х£ |—1;
вогнутый при х 6 J — оо; —-1
1
/5
Асимптот нет.
График функции t/^=x6—-
— Зх4 + Зх? 5 представлен на
рис. 414.
Пример 2. Построить гра-
фик функции
х — 3
У^=- ------' .
/44-х?
Область определения: ]—оо;
оо[. Функция непрерывна при всех
х£ ] —оо; оо [. Точки пересечения
с осями координат: (3; 0) и (0;
—3/2). Первая производная
, Зх+4
У s=--- 1	1
/(4 4-х2)3' ,
Определяем критические
Зх+4
— = 0, откуда х
/(4 4-х?)3
точки: решаем уравнение у' s= 0, т. е.
4	4
=* — V ПРИ х < “ V у' < 0 (функция
о	о
убывает), при х > —— у' > 0 (функция возрастает). Следовательно,
о
4
при х=х — у функция имеет минимум #т-ш~—*1,8. Вторая произ-
водная	1
3 /(4 + х2)8 — (3x4- 4) 4 (4 4- х2) 2 2х
и"—---------------------------f____________—
у	(4 4- х)3
_ 3 (4 4-х2) — Зх (Зх 4-4) _ _е х24-2х-2 _	(х4~ 1)2-3 _
V(4 -4- х2)в-	/(4 4- х2)5.	/(4 4- х?)£
_ е(х4-1-/3)(х4-14-/3)
=* — 0------,
/(4 4-х2)?
/_=0,
*1==-(1+/3). ^=/T—1.
243
- * ' ' ' 
При х < — (I + /3) tf < 0, при — (1 + /3) < х < /3 — 1 if > О,
при х > j/T— 1 tf < 0. Следовательно, при х < -(1_+/3)
и х > ]/з — 1 график функции выпуклый, при — (1 + }^3) < х,<
<	— 1 —вогнутый. Точки перегиба:
Pi(—2,73; —1,7), Pt (0,73; —1,6).
Находим асимптоты:
1-	v х —3	, t
lim у= lim	+ 1.
Г-*±<Ю Х->±СО у 4
Рве. 415.	.
У4 4-*2
Горизонтальные асимптоты; у*=19 У*= — 1. Вертикальных и наклон-
ных асимптот нет.	'
х__з
График функции у =:	представлен на рис. 415.
Пример 3. Построить график функции
3/~	3/--ГТ
{/—/х—/*+ 1.
Область определения функции: ]—оо; оо[. Функция непрерывна
при всех х£ ] — оо; 4-оо[. Точка пересечения с осями координат
(0; -1).
Определяем критические точки. Первая производная
___£	___2_
,	1	3	1 / । з
У ~^~3Х у(х+ 0	,
[«. 2	— 2.1
х" 3_(х+1)“3
s= 0, откуда х? =! (х + 1)а,
2 •
Х=:
Производная не существует в точках х===—1, х~0. Следовательно,
244
1	I
критическими точками являются точки Xjs=—1, х2 =—g-, х3*=0.
Так как/(--i—0^ < 0, а у' (—Т0 В точке xt=±
1	2
— — “o’ функция имеет минимум ymin*=-з^тт^-1,6. При пере-
2 ’	/2
ходе через точки х=гО, х=—1 производная функции не меняет
знака:
/(-1-0)<0,	/ (—1 + 0) < 0,
/(0 + 0) > 0,	-
/(0 — 0) >0,
Находим точки перегиба:
б 5 1
«ка  	|8м9  
(х+1) 3 -х 3
/
5
+ |(х+0 3-|
Вторая производная в точках х — —1, х^=0 не существует. При
—1 < х < 0 / > 0 (кривая вогнутая), при — оо < х < —1 и 0 <
< х < + оо / < 0 (кривая выпуклая). Следовательно, точками
перегиба являются точки Рх(—1; —1), Р2 (0; —1).
Определяем асимптоты. Вертикальных асимптот нет.
3 г~ 3 г '	»
.	,.	/х— /х+ 1
П lim —--------------!— =s
Х-+-±оо	X
.. (Ух —Ух + 1-](Ух?+Ух(х+1) + У(*+1)з)
lim -------7з   О      о" ' ' , —7------ *=*
*±~ Д/д2 + /х(х+1) + /(х+1)?)
^±- X (Ух? + Ух (X + 1) + У(Х + D?)
Ьг= lim (Ух-— У + 0 = О,
Л->± СО
Наклонных асимптот нет. Прямая у = 0 — горизонтальная асимптота,
3 •	3 ———~
График функции у>=/х— y^x-J-l представлен на рис. 416.
Ш
Пример 4. Построить график функции
_ I 1 + X |а/*
у~ /Г •
Функция определена, непрерывна и положительна при всех х>0.
Первая производная у' удовлетворяет неравенствам:
у'	+х)‘/‘(2х-1)
<0, если х < i ,
> 0, если х > у ,
Рис. 417.,=11±^Л.
следовательно, функция убывает при 0 < х < -у , возрастает ври х>
1	J	3	—>
>	, а при -^*=“2“ имеет минимум, равный —	« 2,60. Поско-
льку
г/" = -|-х_1/г (14-х)-’/» > о, о < х < +оо,
то график функции вогнутый.
Из равенства
lim ^^=4-оо.
следует, что xj=O — вертикальная асимптота при х -> -|-0. Имеется
наклонная асимптота у — kx + bt где
k i= Итп —	1
х
з
&₽= lim (*/ —x) = -=>,
л->4-00	£
, 3
т. е. у *= х + -у — наклонная асимптота.
I J _1_ х |3/2
График функции у^=----------— приведен на рис. 417,
\х	*
Пример 5. Построить график функции
1
у *= х2е х .
Область определения функции! ]—:оо; 0[(J ]0; оо[. Функция не-
прерывна на каждом из интервалов ]—оо; 0[, ]0; оо[. Точка х = 0 —
точка разрыва. С координатными осями график функции не пересе-
кается.
Вертикальная асимптота х *= 0, так как
1
Нт х2ех ?= 4-оо.
х-^-04-0
Наклонных асимптот нет,
Находим критические то4ки. Первая производная
X 1 . i
— х2ех	(2х— 1).
I
Решаем уравнение у' ₽= О, т. е. ех (2х—1)*=0, откуда х^
1
— критическая точка.
При х > -i- у' > а при х < -i- у1 < 0. Следовательно, в точке
I *	е2
с абсциссой функция достигает минимума	к, 1,87.
Вторая производная
„ л х 2 к t х 1	—• 2х4“ 1) . л
у" — 2г ---ек +ех	5----—- > 0.
у	х	х2	х2
Точек перегиба нет. Для	]—со; 0{ [J ]0; 4”°°1 график функции
вогнутый.
График функции у^х2ех представлен на рис. 418.
Пример 6. Построить график функции
ех
у = 16 — •
247
Область определения функции: ]—оо; —4[ J ]—4; 4[ [J ]4; оо[. Функ-
ция непрерывна на каждом из интервалов j—оо; —4[, ]—4; 4[, ]4; оо[т
Вертикальные асимптоты:	—4, xj=4. Наклонных асимптот
нет.	z
Точка пересечения графика с осями координат ^0;
Первая производная
, е* (16 —х2) + ех2х х16 —х2 + 2х
у ~~	(16 —х2)2 ~е (16 — X2)2 '
Рис. 418. у s= хЧ * .
Определяем критические точки:
/ —0, х2 —2х — 16= 0,
хЬ2«=1 ±/17 « 1 ±4,12,
у' (1-/17 — 0) <0,
/ (1-/17 4-0) > 0.
В точке с абсциссой х==1—/17
функция имеет минимум
е-з,12
Ут1п8= 16 —3,12? ~
«	°’044 -ЛПЛ6
16-9,73“0,006,
у' (1 4- /17 - 0) > 0,
В точке с абсциссой хя= 1 4-/17 функция имеет максимум
,	е’+/1?	eS'В * * * 12	16 a
‘'max“16 — (14-/17)? ~ 16 — 5,12? ~	’
Вторая производная
, _ [e* (16 - x? 4- 2x) 4- ex (2 - 2x)] (16 - x2)?
y ~	(16—x2)4	-r
e» (16 —x? 4-2x) 2 (.16 — x2) 2x _	ex	'
+	(16 —x2)4	—(16 — х?)3Ц	*-4-^.4-
4-2 —2x) (16 —x2)4-4x(16 —x?4-2x)].
Уравнение у*я=0, т. e, x4 — 4X3 — 26x?	64x 4-288 — 0, действи-
тельных корней не имеет. Точек перегиба нет. Для х € ]—оо; —4[ Q
UJ4; 4- оо[ график функции выпуклый, а для х £ ]—4; 4[ — вогнутый.
График функции	представлен на рис. 419.
Пример 7. Построить график функции
у яе= 'V1 —	•
248
Область определения функции: J—оо; оо[. функция чётная, так
как /(—x)s=f(x), кривая симметрична относительно Оси Оу; /(0) =
= 0. Функция непрерывна для ]—<*>; оо[.
Так как lim /(*)=» 1, у*= 1 — асимптота»
Исследуем монотонность функции, находим точки экстремума:
при х = 0 производная не существует. Других критических точек
нет. При х<0 f (х) <0, а при х >0 /' (х) > 0. Следовательно, при
х = 0 функция имеет минимум, причем /min (0) — 0.
Функция при х < 0 убывает, а при х > 0 возрастает!
г (.г). (^-0 + 0 + 2^)^^
(1-е-Л’)Т
При х = 0 f” (х) не существует. При всех х, кроме х » 0, fn (х) < О,
Кривая выпуклая для х £ ]—qq; 0[ J ]0; 00[• Точек перегиба нет.
График функции у —	1 —представлей на рис. 420.
Пример 8. Построить график функции
1Й
Область определения функции: J—1,; Q[ ,(J JO; оо(. Функция по-
ложительна и непрерывна в этой области. Рассмотрим
1
•lim (1 +#)* s=-|-oo,
х-+—l-J-0
следовательно, х =—1—вертикальная асимптота;
—	JL lim — .1п(х+1)
lim(l+x)x=e, lim (1 + х)х = ех~*00 *	= е°=1,
X—>-0	X—»--}-оо
следовательно, у^\ — горизонтальная асимптота.
Первая производная
г ^. _41п(1+х)^-(1+х)1п(1 + х)
' W	X2 (1 + X)
--1п(ЛГ-Ь1)
Здесь е х >0, х* (1 + х) > 0.
Покажем, далее, что ср (х)«
*= [*— (1 + х) (1 + *)] < 0 при всех
х из области определения. Действи-
тельно,
ф' (х) =.' [х — (4 + х) In (1 + х)]'
==-l-JLn.(l+x)-l±? =
= —In (1 +х) > О на ]—1; 0[.
Следовательно, на этом интервале ф (х) возрастает. Отсюда, посколь-
ку ф(0) = 0, и следует, что ф(х) <0 на ]—I ; 0{. Аналогично, из
условий ф' (х) < 0 на ]0; +оо[ и ф (0) ж= 0 следует, что ф (х) < 0
при х > 0. Следовательно, f' (х) < 0 и функция убывает во -всей-
области определения, экстремума нет.
Исследуем график функции на выпуклость и точки перегиба:
_ 2 0 + *)*1п 0 + *) - (2х + Зх2)
' У ) ~	X3 (1 + х)2
Очевидно, что
[2 (1 + х)2 In (1 + х) — (2х+ Зх2)]' s= —4ф (х).
Учитывая, что ф (х) < 0, имеем
ф (х) ;= [2 (1 + х)2 In (Г + х) — (2х + Зх2)]' > 0.
Но ф (0) t= 0, тогда ф (х) < 0 на ]—1; 0[ и ф (х) > 0 при х > 0.
Следовательно, f" (х) > 0 при всех х=£ 0. Кривая выпуклая, не имеет
точек перегиба.
График функции #*=(1 +х)х лредставлен на рис. 4gb
Пример 9. Построить график функции
J
1— хг
__ в1 Х
1 +*«•
2*0
Функция определена и непрерывна для х£]—оо; — 1[ Q ]— 1;
0[ U ]0; П U П; °°[- В точках х^= ±1 функция имеет разрыв второго
рода, поскольку
lim
е1— Л
1—0 1 4х х2
lim г-:—р
.-14-0 1 +
lim
х->1—0
Функция четная.
График функции симметричен
относительно оси ординат.
Так как
lim v^=4-oof
х->-14-о
lim i/^+oo,
x->l—0
to x s= —1, x = 1 — вертикальные
асимптоты; у = 0 — горизонталь-
ная асимптота.
Первая производная
1
у' 2х3е1—
9-х?
(1 + X2)2 (1 ~ х2)* *
Критические тачки: х = ±Уз, х—0. Исследуем знак первой произ-
водной при переходе через эти точки. При —оо < х < —/3, 0 <
<х<1, 1<х<]/3 1/'>0 — функция возрастает. При—]/3 < х <
< —1, —1 < х < 0, ]Лз < х < +оо у' < 0 — функция убывает.
Так как первая производная меняет знак, то в точке х^=0
функция имеет минимум i/min = e; в точках х := ± ]/3 — максимум
Вторая производная
" — о (3 — х®р 4г х2 (1 — х2) (9 х2 4~ 7х4 — х6)
У У	(1 —X2)4 (1 + х2)2	•
При |х| < 1 у" > 0, ПрИХ=)Л1>1 у" > 0, при Хг=]/3 у’ <0j
У" W +0 при х -> 4-оо.
Следовательно,, на каждом из интервалов ]1; ]/з[, ]]/3; 4-°°1»
а в силу четности функций и на каждой из интервалов ]—оо;
—]/3f, ]—У 3;—1[: есть по крайней мере по одной точке пере-
гиба,
2 Я
1
el—**
График функции у » -q—представлен на рис. 422.
Пример 10. Построить график функции
Область определения: ]—оо; —1] (J [1; оо[, для xQ ]—оо; —1] (J
ОН; оо[ функция непрерывна и положительна. Функция четная.
Так как
lim у = lim 2^^-^“== 1,
Х->± оо
то у^= 1 — горизонтальная асимптота. Других асимптот нет.
Первая производная
у' = 2V^+i-V~i 1п 2 / х _ 2L_'l в
\/х?+1 /ха—1/
Точки х*=* ± 1 — критические. При х < —1 у' > 0— функция воз-
растает. При х > 1 у' < 0 — функция убывает.
lim ух= lim 2^х2+1—^л2—1	2*^,
х-И-f-O X-+-1-J-0
lim #s= lim	s= 2^.
0	x-»-—1«*0

В точке №=—1 левосторонний максимум, а в точке х==1— право-
сторонний максимум.
Вторая производная
[1	1	/1	9	\2
-т==— -Т=== + Х?1п2177== —77== +
/х2+1	/х2 —1	\/х2+1	/х2—1/
, „/ 1 1 \]
_1_ I	- _ ,,	| |
\/(Х2-1)3	/(х2 + 1)3/J‘
Г 1 1
Очевидно, что
1_______1	, lni2 Г 1___________1
/хГП	+ * П% 1/хГ+Т /хГ=П
»/__!____________1 ’
\У(х2 — I)3 У(х3+1)3
. X2_______________________X2 1
+ У(х? — I)3 У(х2 + 1)а]’
т. е.
у" > у Г 7^2_____l+ ,-=£^-2=11п2 > О
1У(^+о* V (*’ — o3J
в области определения функции. Кривая вогнута. Точек перегиба
нет.	____
График функции у	представлен на рис. 423.
Пример 11. Построить гра-
фик функции
У^= loga(l — х2).
Функция определена и непре-
рывна на ]—1; 1[. Прямые x^=L
и х^=—1—вертикальные асимп-
тоты. Функция четная, ее график
симметричен относительно оси ор-
динат. График функции проходит	____
через точку (0; 0). При —1 < х < 1 Рис 423 у ==	- /TTZT'i.
Исследуем функцию на экстремум:
у (1- х2)1п2
Точки х- 0, 1, —1 — критические, но точки ±1 не принадлежат
области определения функции. Исследуем поведение первой произ-
водной при переходе лишь через точку х^=0. Имеем у' (0 — 0) > 0,
у' (0 + 0) < 0; в точке х s= 0 функция имеет максимум r/max f (0)	0.
Для х£ ]—Г, 0[ функция возрастает, для х£ ]0; If —убывает.
Вторая производная
2 ((1 — х2) —2х • х]_	2(1+х2)
У " 1п2	(1-х2)2	~ (1— х2)21п2’,
3S3
у” <0 для ух£ ]—Г, 1[, точек перегиба нет, график функции вы-
пуклый.
График функции у = log2 (1 — х2) представлен на рис. 424.
Пример 12. Построить график функции
У —х + In (х2 — 1).
Функция определена и непрерывна на ]—оо; —1[ (J ]1; оо[. Вер-
тикальные асимптоты: хг=±1.
Находим точки пересечения с координатными осями:
у^=0, х+1п(х2— 1) = 0, (х2— 1) —
решаем последнее уравнение графически или с помощью одного из
методов приближенных вычислений корней. Получаем х« 1,12. Ось '
ординат график функции не пересекает. -
Исследуем функцию на экстремум:
г 1 ,	1 о х2 + 2х — 1
9 ~ + ж* — 1 2х ~ X* — 1	’
X? —1 #=0, х2 + 2х— 1=0,
Х1>2 = -1 ± /2,
Xj j== —1 + У 2 не входит в область опре-
деления функции. Точка х*= —-1 — V2 —
критическая; у' (—1 — ]/ 2 + 0) <0,
у' (—1 — ]/2—0) > 0, в точке х*=—1 —
— ]/2 функция имеет максимум #max «
«—0,7. Для х £ ]—оо; — 1 — уЛ2[ функция возрастает, для х£
£ ]—1 — ]Л2; —1[ — убывает.
Вторая производная	>
„	(2х + 2)(хЗ-1)-2х(х2-2х-'Т)_ (фх?+1
9	(х? — 1)?	~ 2(х2 — ,1)2 <
Функция выпуклая во всей области определения. Точек перегиба нет,
График функции у = х+In (х? — I) представлен на рис. 425.
Пример 13. Построить график функции
у t=sinx+ sin2x.
Область определения функции: ] —оо; оо [. Функция непрерывна
при всех хС ]—оо; оо [. Функция нечетная. График функции сим-
метричен относительно начала координат.
Функция периодическая с периодом 2л; так как период фу.нк-
2л
ции sinx равен 2л, а период функции sin 2х равен у х= л, то период
суммы равен наименьшему кратному периодов слагаемых. ‘
Исследуем функцию на периоде [0; 2л}. Найдем точки пересе-
чения графика с осью Ох:
sin х + 2 sin x * cos xs= О,
sinx(l + 2co'sx) s= 0,
154
sinxs=O, х^=лп, n 6 2,
1	2
1 + 2cosx = 0, cosxr=—x—±л + 2лп, n £ Z.
2,	О
В промежутке [0; 2л] график функции пересекает ось Ох в точках
2	4
х —О, ^~у	—	х^=2л.
Первая производная
у' — cos х + 2 cos 2х.
i
Находим критические точки:
у' cos х + 2 cos 2х i= 0,
cos х + 2 cos2 х — 2 sin2 х ?= 0,
4. cos2 х + cos x — 2^0,
—1 ± 1/Г+32 — 1 ± V 33
Cosk2_--------g----__-----------,
—1 + /33	—1 — /33
cos X := -, COS X —---------3----- ,
о	о
*1, 2 = ± arccos
± arccos 0,6 + 2лп, Z,
*3, 4х= ±arcccrs|
-f- 2лп + arccos (—0, 8) + 2лл, п £ Z,
Поскольку вторая производная
у" —sin х — 4 sin 2х ?= —sin х (1 + 8 cos х)
ш
при х )= jq arccos 0,6, x xs 2л — arccos (—0,8) отрицательна,
то при этих значениях x функция достигает максимума: */i~l,76,
у9 0,45. Аналогично при х х2 *= arccos (—0,8), х ~ х4 а= 2л —
— arccos0,6 ^>0 —функция достигает минимума:	0,45,
у, 1,76.
Интервалы выпуклости кривой: J 0; arccos 0,6 [, J arccos0,6;
2 Г	1	4 Г
— л I , J л; 2л — arccos (—0,8) [, 2л — arccos (—0,8; -х- л •
з l	J	з l
12	Г	1 4
Интервалы вогнутости кривой: -х- л; arccos (—0,8) ♦ I-х- л;
j з	L	J з
2л — arccos 0,6 , ] 2л — arccos 0,6; 2л [. При переходе через точки
2	4	.
л, х^=л, х±= —л, хх=2л вторая производная меняет знак.
3	3
/2	\	/ 4	\
Следовательно, точки Р± I -х- л; 0 I, Р2 (л; 0), Р31 л; 01, Р4 (2л$ 0)
\ 3	/	\ 3	/
являются точками перегиба.
График функции у s= sin х + sin 2х представлен на рис. 426.
Пример 14. Построить график функции
у j= tg х + sin х.
Рис. 426. у = sin х 4- sin 2х.
Функция определена и непре-
рывна для всех значений х, кроме
х s= у + пя (П е Z).
Функция нечетная, периодическая
с периодом 2л. Поэтому достаточно
построить график на [0; л].
Прямые х —	+ пл (п £ Z) —
вертикальные асимптоты графика.
Исследуем функцию на экстремум
, / .	1	.	1 + cos3 X
У (*)	—5—F cos	——rs— .
v ' COS2 X	COS2 X
При х»=л производная равна нулю, точка х*=л — критическая.
На интервалах ^О; у [♦* ] у * я [ и ]я; уя[	^ледова-
(Зт \
х у I функция не имеет экстремума.
Исследуем график на точки перегиба:
При я 5= 0 и хг=л вторая производная равна нулю, причем, как
легко убедиться, справа и слева в, достаточно малых окрестностях
этих точек имеет разные знаки. Следовательно, точки (0; 0) и (л; 0)
являются точками перегиба графика функции.
График функции у ?= tg х + sin х представлен на рис. 427.
Пример 15. Построить график функции
у s= sin4 х + cos4 х.
Область определения функции: J— оо; оо [. Функция непрерывна
на ] -г-оо; оо [. Функция четная; график ее симметричен относительно
оси ординат. Функция периодическая с периодом © *=	•
sin4 х + cos4 х s= (sin? x + cos2 x)? — 2 sin? x cos2 x »
*	2л л „	,
откуда.© j= у . Поэтому достаточно построить график на
[л 1
0; — I. График функции расположен над осью абсцисс: ух=з
sin4 х + cos4 х > 0 при ух С
Первая производная
у' ;= 4 sin3 х cos х — 4 cos3 х sin х —4 sin>x cos х X
X (cos2 х — sin? х) s= —2 sin 2x cos 2x == —sin 4x.
эт I
0; ~ I, проходит через точку (0; 1).
Ищем критические точки: у' — sin 4х s= 0, откуда х^= ~ (fc £ Z).
Рассмотрим xj=^ при ^х=0, 1, 2.
9 8-413.
257
Определим характер экстремума с помощью второй производной
уи х= —4 cos 4х,
у" (0) = —4 < 0, при хх= 0 функция достигает максимума */max — 1,
^-^j==4>0, при x»s функция достигает минимума */min —
1	»/ лс । л л	Д' .
Т ’	\2~/	ПРИ Х 9=2 ~2~ ФУНКЦИЯ Достигает максимума
^max ~ 1 ’
Точки перегиба:
Ит-°)<°> Ит + °)>0-
р"(4л-°)> о, И4л + о) < 0.
\ О	/	\ о	/
График функции на j 0; ~ выпуклый, на j 5
]3 л Г
“o’я; — выпуклый.
о ~ L
График функции у j= sin4 х + cos4 х представлен
Пример 16. Построить график функции
3 Г
-Q- Л I — вогну-
о I
на рис. 428.
у х= arcsin
1—х?
1 + хГ
f___^2
Область определения функции: — 1 < . . -2 < 1, т. е. х £ ]—оо;
I X-
оо [. Функция четная, ось симметрии графика — ось ординат. Функ-
ция непрерывна в области определения. Точки пересечения графика
с осями координат: у^= 0 при х^= ± 1, при х = 01,57.
/(х) > 0 при —1 < х < 1,
/ (х) < 0 при х < — 1 и х > 1. •
258
Исследуем наличие асимптот:
arcsin ? ,
fe = lim -------!±l' = 0,
х
.	..	. 1— х$ я
6=1ипarcsin ^ = -2-.
Jt
Следовательно, у ~ — -у — горизонтальная асимптота. График функ-
ции расположен над асимптотой.
f (х)~	|х| 1 +xi '
При х > 0 f (г) < 0 — функция монотонно убывает на интервале
] 0; оо [. При х < 0 /' (х) > 0 — функция монотонно возрастает на
интервале ]—оо; 0|.
Производная не существует в точке Исследуем поведе-
ние производной в окрестности этой точки:
/ х 2 \ Л .. х
11тп [ —:—- ——51 ;= —2 lim -—г	2,
Я-^0 \ I X ( 1 + х2/	х-^01 XI	**
( х 2 \ Л
lim I . а | =-г —2.
**+0\	1*1 1+ *1-/
Следовательно, первая производ-
ная в точке х 5= б имеет разрыв
первого рода, причем при переходе
через эту точку производная меня-
ет знак с «-(-» на «—». Поскольку
функция в этой точке непрерывна,
то она имеет максимум в этой
точке: утак₽=~.
Вторая производная у* t=s
— (1 4,^)2 на интервале ] 0; +<ю [
у">0 — график функции вогнутый;
- 4х
У— "^*.2)2 на Интервале
Рио. 429. д « arcsin -Лл .
J — оо; 0 [ if > 0 — график функции
также вогнутый. Точек перегиба нет.
График функции у s== arcsin
1 —X2
1-Ма
представлен на рис.
429.
Пример 17. Построить график функции
. * —3
carets
9*
259
Область определения функции: J —оо; оо f. Функция непрерывна
в области определения. Нули функции: ys=0 при xs=3, при х»=0
у «= arctg	t= arctg (—0,75)« —0,64.
Первая производная
,	1 х* + 4 _ (х _ 3) 2х _	— х2 + 6х + 4
У в , , /х- 3	(*? + <)*	& + 4)» + (X - 3)? •
у1 ж= 0, X2 —6х —4 — 0, Xj 2 t= 3 ± У13,
х£м=3+ /Т3«6,7, xas=3 — /Тз«—0,7:
Исследуем знак у’ (х). Знаменатель всегда положителен. Тогда
у' < 0 при х < 3 — /13 — функция убывающая; у' > 0 при х > 3—
— ]/ТЗ —функция возрастающая. В точке хж=3— ]/13 функция
имеет минимум; у' > 0 при х < 3 + ]/13 — функция возрастающая;
у1 < 0 при х > 3 + У ТЗ— функция убывающая. В точке х *= 3 4-]/ 13
функция имеет максимум.
Вычисляем вторую производную:
(—2х + 6) (х4 + 9х2 — 6х + 25) + (х2 — 6х — 4) (4х* + 18х—6) _
V *	(х4 + 9х2 —6х+25)2
2 (х5 — 9Х4 + 19х3 — 51х2 — 61х + 87)
**	(х*-|-9х? —6x4-25)?
У *=, 0, х? — 9х* 4- 16х® — 51х« — 61х 4- 87 *= О,
Х£«0,5, х2як—1,5, х8«9,5.
л
а)	При переходе через точку х як 0,5, у&*— кривая меняет
вогнутость на выпуклость. Точка ^0,5; ——точка перегиба.
б)	При переходе через точку х« —1,5, у ~ —0,2л кривая меняет
выпуклость на вогнутость. Точка (—1,5; —0,2л) — точка перегиба.
в)	В точке (9,5; 0,022л) кривая меняет выпуклость на вогну-
тость, следовательно, эта точка является точкой перегиба.
Асимптоты.
lim arctg-77? ?= 0,
х2+4
следовательно, ^я=0 — горизонтальная асимптота графика функции.
Вертикальных и наклонных асимптот нет.
График функции у *= arctg
х —3
х2 + 4
представлен на рис.
430.
Пример 18. Построить график функции
у*» In х —arctgх.
Область определения функции: J 0; оо (. Функция непрерывна
в области определения. При х +0 имеем
lim (In х — arctg х) s=i —оо.
лм-|-0	'	*
Следовательно, кривая имеет вертикальную асимптоту XssrO.
Исследуем функцию на экстремум:
Очевидно, что у' > 0 при х > 0. Функция возрастает во всей области
своего определения. Функция не имеет экстремума.	♦
Точки перегиба.
„.	1 . 2х	__ —х4 + 2х3 — 2х2 — 1
У X2 + (1 + X2)2 ~ X2 (1 + X2)2
но
ф(х)^=— х4+2х3 — 2х2 — 1;=— [(х2+ I)2 — 2Х3] <: 0
во всей области определения, т. е. кривая выпуклая на ] 0; оо [.
Точек перегиба нет.
261
Точки пересечения кривой с осью Oxi
In х — arctg х j= 0, In x — arctg x,
откуда xx3,7.
Кик функции i/x=lnx — arctg x представлен на рис. 431.
iepw построения графиков функций приведены на
рис. 432—441.
Рис. 433. у«= (1 4-л2)е*.
Рве. 435. у
Sy-......
хг 4-1
Рив ^*"2тет
ж
ш
§ 2. Построение графиков
параметрически заданных функций
В разд. 6 ч. I были рассмотрены исследование и построение
графиков функций, заданных параметрическими уравнениями
хж=<р(0,
методами элементарной математики. В этом параграфе представлены
дополнения к исследованию и построению графиков таких функций.
Исследование параметрически заданных функций
с помощью производных
Симметрия. Если ф (0 — четная, а ф (0 — нечетная функции, то
кривая симметрична относительно оси абсцисс.
Если ф (0 — нечетная, а ф (0 — четная функции, то кривая сим-
метрична относительно оси ординат.
Если ф (0 и ф (0 — нечетные функции, то кривая симметрична
относительно начала координат.
Заметим, что это достаточные признаки, но не необходимые.
Точки пересечения с осями координат. Из уравнения ф (0 s= О
находим значения /, которые определяют точки пересечения кривой
с осью абсцисс.
Из уравнения ф (0 ;== 0 находим значения /, которые определяют
точки пересечения кривой с осью ординат.
Особые точки. Точка (х0; у0) кривой
х = Ф(0.
{/ = ф(0
называется особой, если при t = tQ
*0=ф(О. г/«!=Ф(и> Ф' (Q = °*
Другие точки кривой, в которых хоть одна из производных ф'(0,
или ф' (0 не равна нулю, называются неособыми точками. В любой
неособой точке (х0; у9) уравнение касательной имеет вид
У — У о =	(* — xj, если ф' (<0) * О,
ф V0/
х — х9 — ^-777 (у — у0), если V + О-
т V0/
Определение точек кривой, в которых касательные параллельны
осям ксордииат.
а)	Чтобы касательная к кривой была параллельна оси абсцисс,
как известно, должно выполняться условие
Ух — Ь,
т. е. значения i, соответствующие таким точкам, ищем из уравнения
у/₽=0, если х} ^0.
б)	Значения t, соответствующие точкам, в которых касательная
к кривой параллельна оси ординат, ищем из уравнения
х/ J» 0, если р/ 0.
Точки перегиба. Значения /, соответствующие точкам перегиба,
кривой, определяем из уравнения
х/у/ — у{х? 7=. 0, если х/ 0.
Определение двойных точек кривой. В двойной точке (хх; ух)
кривой пересекаются две ветви кривой, имеющие различные каса-
тельные. Отсюда следует, что должны существовать два различных
значения и t2 параметра t такие, что
(*1«Ф(<1)«=Ф(У,
Решаем эту систему и проверяем, имеют ли угловые коэффициенты
касательных к кривой при найденных значениях параметра /, т. е.
Ф' (G) Ф' (У	С
дроби и > разные значения. Если да, то кривая имеет
Ф Vi) Ф (*а)
двойную точку.
Определение точек возврата. В точке возврата должны выпол-
няться равенства
<р' (0 ~ 0 и ф’ (0 ж= 0 (х?^' - yfx? * 0),
г. е. в этой точке угловой коэффициент касательной неопределенный.
Асимптоты кривой. Кривая имеет вертикальную асимптоту х *= а,
если одновременно выполняются равенства
Итф (0 оо,.
lim <p (/) а.
Кривая имеет горизонтальную асимптоту у Ь, если одновременно
выполняются равенства
Нт<р(0*=аоо,
/-►/1
1Ш1ф(0х=Ь.
Для определения наклонных асимптот у = kx + b надо найти такое
значение параметра, при котором х« оо и у оо. Если такое
значение t найдено, то k и b определяем по формулам
Л»=Пт2^,
м. Ф (О
д*=Иш(ф(0 —йф(0], , .
причем пределы, стоящие в правых частях этих формул, существуют.
Ш
Примеры построения графиков параметрически заданных
функций
Пример L Построить график функции
Р
хг= 1 •
7_ /(1 — *2)
У /2 ft •
Область определения функции: [0; 1 [. (Действительно, значение
Ж / ПРИ любом t является положительным числом, меньшим
единицы, следовательно, кривая расположена между прямыми x*=0
и 1). Область значений функции: ] —оо; оо [.
Так как x(t) — четная, а у (t)— нечетная функции, то кривая
симметрична относительно оси абсцисс.
Точки пересечения с осями координат. При / ^=0 х*=0 и
следовательно, кривая проходит через точку (0; 0), р*=0 и при
t 1, следовательно, кривая проходит через точку ; 0j •
Находим первые производные:
,	2/
х‘ ** (I? +1)? ’
,	—	,	1 4t _ t*
Vi (Й 4-1)^ *
При fs= ± у —2 +существуют две точки А и В, в которых
касательная параллельна оси абсцисс, причем при 0 < х < —, у > .0
&у	1	Ру
< 0 — кривая выпуклая, а при у<х<1, у>0	® — кри-
вая вогнутая.
Проверяем, имеет ли кривая двойную точку:
Р	Р
Г1	г2
2t
4+i 4+*’
4+i	4+i
Решив эту систему, находим два разных значения 1 и	—1,
для которых соответствующие значения х одинаковы и соответствую-
щие значения у также одинаковы. Следовательно, точка	; 0j —
двойная точка кривой. Находим угловые коэффициенты и k2
касательных к ветвям кривой, которые пересекаются в этой точке:
Л V1)	X
266
Асимптоты.
/2
lim х (/) — lim -%-.' := 1,
/-»• CO	*
..	...	..	/(1 — t2)
limу (t) «= hm —7^-;-)  z= oo.
t-+eo	/->oo i *
Кривая имеет вертикальную асимптоту. Наклонных асимптот нет.
График функции представлен на рис. 442.
Пример 2. Построить график
функции
х = 2/—/?,
yt=z 3t — t3.
ft
Рис. 442. х = —-р у=>
/ (1 -П
Область определения"функции: ] —оо;
1]. Область значений функции: ]—оо;
©о [. Функции x(t) и y(i) непрерывные
При —оо < t < ОО.
Находим первую производную:
dy_ 3 1 —/3
dx~~ 2 1 — t •
При if х= — 1 (xf s«= —3) s= 0, а при /2 s=s
s= 1 (xo 1) lim ~	3. Следовательно.
Ml dx
dy
при —oo < x < —3	< 0, т. e. функция
убывает, а при — 3 < x < 1 (—1 < t < 1)
> 0 — функция возрастает. При x ?= —3
функция имеет минимум ymin —2,
^max 2»
Вычисляем вторую производную:
d?y _ 3 (1— t3)3
dx* “ 4 (1 — O3 *
d/*u
При —oo < x < 1	>0 — кривая вогнута. Точка (1; 2) — точка
перегиба.
Так как
а при x s= 1 —. максимум
lim x (/) ;= —oo,
->±00
lim ?(>>?“,
lim Гт=±0°’
->± 00 X
то асимптот нет»
1ЬТ
График функции хх= 2/ — /а, у '*= 31 — t3 представлен на рис. 443.
Пример 3. Построить график функции
а
X з= —“я", .
cos8 t •
{/t=atg3 t (a > 0).
Область определения функции: ]—оо; —a] (J [а; оо [. Область
значений функции: ] —оо; оо [. Функция х (0 — четная, у (0 — нечет- /
ная, следовательно, график функции у = у(х) симметричен относи-
тельно оси абсцисс. Для 0 < t < график функции у s= у (х) сим- ?
метричен относительно оси ординат.	<
Находим первую производную:
sin /	> 0 при 0 < / < ~	'
b	dx ’ dx н	2 *
i
Функция у*&у(х) .возрастает при 0 < / < у , причем х->+оо, -
у—>-|-оо.	j
Вторая производная
d2y__________________________ 1 cos6 t
dx%~~.3a sin t ’
§ > 0 при 0 < f < £ ,
-r
1	следовательно, кривая у (x) вогнута при 0 < t < у .
Ж
i' ’	/	j
k.	.	1
х' (/) — О,
, ' ' л ИЛИ
у (0«о,
Проверим наличие точек возврата:
х' (0 = —За cos~4 sin t О,
,-(0зЗ<.18.^-0,
отсюда /z=0, л, причем в этих точках х^у* — у"х” 0. Следова-
тельно, точки (а; 0), (—а; 0) — точки возврата. t
Асимптоты.
a	•
---- ;= 4-00,
cos81	’	’
lim х (0 —
х + ~~~о	t-+
Нт у (0 —
lim
f-0
lim atg3/:=4-oo.
Вертикальных асимптот нет. Проверяем наличие наклонных асимптот:
. г У (0 г atg3/
& = lim	lim	—-—^=1,
*	лХ(0 <	« л а
*	** 2	“* 2 COS8 t
\ lim (tg8/-------“rJ — — 00 •
TC \ b COS3 //
= lim (у (0 — х (01 = а
Наклонных асимптот нет.
Г рафик функции х *= ~з^ » У *= о tg8 t (а > 0) см. на рис. 290, б.
Пример 4. Построить график функции
/а
i
Область определения функции: J—©о; —~
U [4; ©о [.
Первая производная
dy
dy^dt	<а+1
dx dx~~ t{t — 2) (/+ I)2 ’
dt
; о U
y’x > 0 при —oo<x<0 (при 0</< 1) — функция возрастает.
2
Если 1 </<2, то 4<х < 4-оо,	< 4-оо, ух > 0 — функция
«5
2И
/	2 \
также возрастает. При 2< t < 4-00 (0 < х< 4, 0 < у <0—
функция убывающая. При —оо < t < —1 ^—00 < х < ——, —©о <
< У < 0) Ух <0 — функция убывающая.
Вторая производная
&у d (dy\ _ 2 (f — I)3 (/3+ 3t + 1),
dxi^ dx\dx) ~ /3 (* — 2)8 G + О3 ’
при	—3,22 (x (tj) «0,17), t2 1 (y (/f) «0,37). Вторая
производная у" > 0 при — 1 < i < t± и у* < 0 при /f < t < 0. Сле-
довательно, точка Pf(—0,17; 0,37) — точка перегиба графика функ-
ции у = у(х).
При 0< t< 1 (—00 < х<0) ухх > 0 — кривая вогнутая; при
1 < /<2(4<х < +<x>)y”)ix < 0— кривая выпуклая; при 2</<
< 4-оа (0 < х< 4) ухх > 0 — кривая вогнутая.
Так как
lim х (t) *= ioo,
f-*-± 0®
lim у (0 = 0,
lim x(0=-|-
/-«14-0	2 ’
lim x(0=l,
/-+—1—0	*
lim HO’=*+<*>»
/->-14-0
lim HO — *”'00,
/-*-—1—0
To 0 —горизонтальная асимптота графика функции yt=y(x)‘>
X *= ~— вертикальная асимптота графика функции у ж= у (х).
Проверим, есть ли наклонные асимптоты:
t
Г—1
f^ihnp______12LV-3.
LlV»— 1	2t—l)	4'
х 3
у « -г--— наклонная асимптота.
2	4
/2	t
График функций х» j—।, У*=~р—[ см* на рис. 274, в.
ПО
Пример 5. Построить график функции
х ж t + е"**;
у «= 214“ е~2*.
Область определения функции! [1; оо Область значений функ>
ции: [1; со
a)	х' (/) *= 1 — х' (/)	0 при t *** 0;
х" (t) хз е~\ х!' (t) > 0 при всех /.
б)	у’ (/) х= 2 (1 — e~2i), у' (0 =0 при i 0}
/ (/) j=z 4е“2/, у" (/) > 0 при всех t
Имеем	при ? = 0min *= 1 при /г=0.
При — ОО < t < О (1 < х < +оо, 1 < у < J-oo) у’х >0 — фушсция
у;={/(х) возрастающая. Прй 0 < t < -f-oo (1 < % < -Цю, 1<м
< +00) Ух > 0 — функция у 3» у (х) возрастающая.
Вторая производная
При t < 0 ухх > 0 — кривая вогнутая, рри I > 0 ухх < 0 — кривая
выпуклая. При /~>+оо прямая у^2х является наклонной асимптб*
той графика функции ух=у(х).
График функции х- t + е~*, у m 21 + см. на рис. 286.
§ 3. Построение графиков неявно заданных функций
В разд. 8 ч. I были рассмотрены исследование и построение гра-
фиков функций F (х, у)^=0 с помощью методов элементарной мате-
матики. В этом, параграфе дано некоторое дополнение к исследованию
и построению графиков таких функций.
Особые точки кривой F(x, у)д=0. Точка М (х0; у^ кривой
F (х, у) х= 0 называется особой точкой, если ее координаты одновре-
менно удовлетворяют таким трем уравнениям:
F (*о. Ke)s0,
Fx(x,, уй)=0,
Угловой коэффициент касательной к кривой в особой точке
Ik	) неопределенный.
\	* у/
Пусть в особой точке М (х0; yQ) производные второго порядке
рхх, Fxy> Fyy не равны одновременно нулю, тогда точка М (х0; у0)
271
является двойной точкой кривой, причем форма кривой у ее двойной
точки характеризуется значением
Д д= FXy (х0; у^ — Fxx (х0; yj) Fyy (х^ #0),
а именно: а) при Д > 0 кривая имеет узловую точку (рис. 444);
б) при Д<0 М (х0; у 0) — изолированная точка (рис. 445); в) при
Рис. 445. Особая
(изолированная)
точка М кривой
F (х, у) « 0.
Рис. 444. Особая (узловая)
точка М кривой F (х, у)=
® 0.
Рис. 446. Точка М ~ точка
возврата первого рода кривой
F (х, у) == 0.
д х=0 точка М (х0; у0) может быть точкой возврата первого (рис. 446)
или второго (рис. 447) рода или изолированной точкой, или точкой
самокасания (рис. 448).
М
Рис. 447. Точка М — точка воз-
врата второго рода кривой
F (х, у) = 0.
Рис. 448. Точка О — точка
самокасания кривой F (х, у)~
== 0.
Наличие двойной точки в начале координат у алгебраической
кривой определяют так: в приведенном уравнении такой кривой
не должно быть свободного члена и членов с первыми степенями
переменных.
Заметим, что уравнение касательных к кривым в особой точке,
которая совпадает с точкой (0; 0), можно получить, если приравнять
нулю группу членов наиболее низкой степени. Если особая точка
не совпадает с началом координат, то уравнение касательных к кри-
вым в этой точке можно получить, если принять особую точку нача-
т
лом новой системы и приравнять (в полученном после преобразова-
ний уравнении) нулю группу членов самой низкой степени.
Точки экстремума кривой F (х, у) = 0. Для определения крити-
ческих точек кривой, заданной уравнениями F (х, y);=Q, заметим,
что угловой коэффициент касательной в произвольной точке такой
кривой
Чтобы определить на кривой точку, в которой касательная парал-
лельна оси абсцисс, надо решить систему
рх(х, У) —О,
Р(х, у)=0.
Пусть xt и yi — корни этой системы, причем F (xf, уд =h 0, тогда
точка М (х$; уд является для кривой
точкой максимума z/max, если Fxx (xit j/x) Fy(xit уд > 0;
точкой минимума если Fxx (Xf, уд Fy (х£, уд < 0.
Чтобы определить на кривой точку, в которой касательная парал-
лельна оси ординат, надо решить систему
Fy(x, </)=0,
F (х, у)-0.
Если Xf и yi — корни этой системы, причем Fx (xj, уд 0, то
’точка М является для кривой
точкой максимума хтах, если Fyy(xi, уд Рх fa, уд >0;
точкой минимума xmin, если Fyy (х*, уд Рх (*i, Уд < 0-
Точки перегиба кривой F (х, у) — 0. Если уравнение F (х, у) = 0
нельзя решить относительно у, то найти точки перегиба кривой
в общем виде трудно. Иногда можно использовать такое свойство:
точки перегиба алгебраической кривой F (х, //)—0 должны нахо-
диться в точках пересечения этой кривой с ее гессианой. Так назы-
вают вспомогательную кривую, уравнение которой
Fxxpiy ~ ^xyFxFy + Fyypx = °-
Замечание. Иногда удобно исследовать и строить график
неявно заданной функции, записав уравнение кривой в параметри-
ческом виде.
Пример 1. Построить график кривой
х4 — У4 — х? + 2у2- *= 0.
Кривая симметрична относительно координатных осей.
Критические точки:
Fx 4х3 — 2х,
Fy = -4y» + 4y.
273
Координаты точек, в которых касательные параллельны осиабсцисе,
найдем, решив систему
(F (х, у) Е X* — у* — х? + 2у? s=O,
Ifx{x, У)^№ — 2х₽0.
Имеем (0; ± V 2),	; ±	? ±'У , (0; 0).
Гхх-12х?-2,
Fyy~-I2y*+ +
В точке Мо (0; / 2) будет ^тах, поскольку (F^Fy)^ > 0,
_____________________________________	»=О
I V~2 i/2 + V 3| ,
а в точках MI 2I±-^- ; I/ ——I будет ymin, поскольку
VxxFy)	у/ < °-
х=± Т_____
.-V+
Координаты точек, в которых касательные параллельны оси ординат,
найдем, решив систему
(^ = -4у’ + 4у₽0,
If = x* — у* — х? + 2//?-0.
Получим (±1; 0), (0; 0). В точке Ях(Г, 0) будет	поскольку
(FyyFx)x=\ > 0, а н точке Л2(—1; 0) будет xroin, поскольку
у=0
(FyyFx)x=—\ < 0.
#=о
Особые точки:
Fx = 4х3 — 2x^=0,
Fy = — 4i/3 + 4у == 0,
F = х4 — у4 — х2 + 2#2 - 0.
Точка (0; 0) — единственная особая точка. Так как As= F\y— Fxx X
X Fyy > 0 в этой точке, то точка (0; 0) — узловая особая точка;
х? — 2х/2 = 0,
т. е.	__ __
х — У2у и х + У2у^=О — две касательные.
Другие исследования этой кривой см. в разд. 8 ч. I.
График кривой х4 — у4 — х2 +	== 0 см. на рис. 320.
Пример 2. Построить график кривой
j= х3 — у3.

Запишем уравнение кривой в параметрическом виде. Пусть
у txt тогда х?/?х? — х3 — /зх3, отсюда
х>==и~1.
причем / =/= 0. Функции х (/) — i — / и у (/)	--/? определены на
] —оо; 0 [ (J J 0; оо [. Функция у х= у (х) определена на ] —оо; оо [.
Кривая симметрична относительно прямой х + у — 0. Действи-
тельно, пусть х — у^=т, х-\-у — п, тогда из уравнения кривой
будем иметь (п? — /п2)2	12п?/п + 4/п3. Из последнего очевидно! что
график кривой симметричен относительно оси лх=О.
Первая производная
(1+2/3)
dx 2 + /»
При /»— У 2«—1,26 (х « 1,89, У^— 2,38) производная
du ~	3 /“ 1
не существует; ^^=0 при /s= — 1/	—0,79 (х^2,38; р»
1,89);	< 0 при —оо < t < —1/"2 — функция убывает; > О
лх	ох
при
— функция возрастает; ^<0при — у
< t < 0 —функция убывает; ~ > 0 при 0 < I < -f-оо — функция
возрастает.
Вторая производная
d*y	2/3(/* + 7/3+1)
dx* (2 + /з)з	v Г л
d?u
^ = 0при
1,90 (x^ 2,18; p«—4,14)
и при
-0,53 (х» 4,14; у^— 2,18).
(Ру
dxl
8| / 7 + 3 V 5
• I/ '—-----------кривая выпуклая|
V
d*y
dx*
при
< t < —2 — кривая во гнутая j
d*y
dx*
при
< t < 0— кривая вогнутая;.
27S
Й < ° при ~V 2 < t < - |
7-3/5
кривая выпуклая;
d^jj
< 0 при О < t < 00 — кривая выпуклая.
Точки перегиба: Pt (2,18; -4,14), Р2 (1,89; —2,38), Р3 (4,14; —2,18).
График кривой представлен на рис. 449.
Пример 3. Построить график кривой
ch? х — ch? у — 1 z= 0.
Кривая симметрична относительно координатных осей. При х>0,
у > 0 кривая будет иметь уравнение
sh х s= ch у,
откуда х х= In (ch у + V 1 + ch2 у).
Асимптоты:	________
* = lim lim Infchy+Zl+chM^),
b я= lim [x (у) — у] e= lim [in (ch у + /1 + ch? у) — у] я= 0,
p-*4-®o	<;-*+«»
x у — наклонная асимптота.
274
Первая производная ,
^8=*	Shi/
dy /14-ch?y*
dx л л
-т- > 0 при у > 0 — функция возрастает?
dx
< О при у < 0 — функция убывает;
1
в точке 1п(1 + /2); <М
функция имеет минимум.
Вторая производная
dtx 2 ch у
dy$	£ *
(Ц-сМу)2
d^x
Ха > О при у > 0.
График кривой представлен на
рис. 450.
§ 4. Построение графиков функций
в полярной системе координат
Исследование и построение графиков функций в полярной
системе координат были рассмотрены в разд. 7 ч. I. Здесь представ-
лено некоторое дополнение к исследованию и построению графиков
в полярной системе координат с существенным использованием аппа-
рата дифференциального исчисления.
Рассмотрим функцию вида
P~f (ф)> —°0 < ф < оо.
Условимся отрицательные значения р откладывать в направлении
ф + л, т. е. в направлении, противоположном направлению, которое
определяется углом ф.
Если р х= f (ф) — ограничена, т. е. значение | р | < а, то вся кри-
вая находится внутри круга р ;= а.
Если /(—ф) = / (ф), то кривая симметрична относительно поляр-
ной оси; если f (л — ф)^=/(ф), то кривая симметрична относительно
перпендикуляра к полярной оси (в полюсе); если / (л + ф) *=7 (ф),
то кривая симметрична относительно полюса.
Исследование функции р = f (ф) на экстремум производится
обычным способом: если f' (ф) =0, Ф—Фх, то: / (Ф1) является ртах,
если /' (ф) при переходе ф через значение фх меняет. знак с «+»
на «—> или Г(фх) <0; f (фх) является pmin, если /'(ф) при пере-
ходе ф через значение фх меняет знак с «—» на «+» или f" (фх) > 0.
211
Касательные к кривой в точках ртах и pmin перпендикулярны
к радиусу-вектору точки касания. Для того чтобы найти на кривой
р₽:/(ф) точки, в которых касательная перпендикулярна к поляр-
ной оси, надо в формуле tg р, =-Ц- (рис. 451) положить	+
Р
+ 7^- — ф. Значения ф, найденные из этого уравнения, и определяют
искомые точки.
Если кривая имеет точки перегиба, то соответствующие значе-
ния ф должны быть корнями нечетной кратности уравнения
р? + 2р'2 — р'р*»= 0.
Рис. 452. Асимптота кривой р «
— Р (?) 5 Р — cos	.
Уравнение асимптоты в полярной системе координат:
Р cos (ф — Y) *
где V —угол, образованный перпендикуляром, опущенным на асимп-
тоту из полюса, с полярной осью; р — длина этого перпендикуляра
(рис. 452). Для нахождения Y исследуют по уравнению заданной
кривой, существует ли такое значение ф ф$, для которого соот-
ветствующее значение р*=оо. Если такое значение ф найдено, то
кривая имеет бесконечную ветвь. Ищут
г Р*
р*= hm .
Если этот предел существует, то бесконечная ветвь имеет асимптоту.
Если предел не существует, то бесконечная ветвь кривой не имеет
асимптоты (является параболической ветвью кривой). Если р > 0,
то асимптота находится справа от радиуса-вектора, который прости-
рается в бесконечность, если р < 0 — то слева.
Пример 1. Построить график функции
___________________________ а
Р COS? ф •
278
Кривая имеет бесконечные ветви. Кривая симметрична относи-
тельно полярной оси и перпендикулярна к ней (в Полюсе). Функция
периодическая с периодом (о *= 2л.
Исследуем функцию на экстремум:
, 2а sin <р , Л • л
л хзв-л—х p t=0, sin ф О*
r dos3 ф
откуда ф£^0, ф2*=л,
Имеем
р' (0 — 0) < 0, р' (0 + 0) > 0, при ф ж* 0 pmin ;= а,
р' (л — 0) < 0, р' (л + 0) > 0, при ф л pmin а.
Находим точки, в которых касательная к кривой параллельна
полярной оси.
В формуле tg р s= -Д- положим р s= kn — ф, получим
Р
tg (kn — ф)*= 4- ctg ф, откуда tg2 ф ~ ;
f	2	2
последнее уравнение не имеет действительных корней.
Находим точки, в которых касательная к кривой перпендику-
лярна к полярной оси. В формуле tg р = ~ положим р = kn +
. л	, Л , л ’ \	1 '
+ —----Ф, получим уравнение tg ял + -------ф) = ctg р, откуда
2	у 2 у 2	.
Ф1 = 0, ф2 = л. В точках (а; 0) и (а; л) кривая перпендикулярна
к полярной оси.
279
Для нахождения точек перегиба решаем уравнение
р? + 2р'2 — р'р" 0, имеем cos ф *= ±
т. е. на [0; 2л] определены значения ф для четырех точек перегиба.
*	Т-Т	П
Асимптоты. При ф== у р = оо, следовательно, возможна асимп-
тота, но
а
р = lim . “	— оо [
п sin 2<р
следовательно, асимптоты нет.
График функции р «= —- представлен на рис. 453.
Пример 2. Построить график функции
th ф Л .
P =	а>°> Ф>1‘
Функция при ф > 1 непрерывна,
lim р (ф) = + оо,
<р-И4-о
т. е. ф « 1 — асимптота,
lim р (ф) == б,
dp _ Г_______1__________th ф ]
Жр ~ а [ch? ф • (ф — 1) (ф — 1)а] *
dp
< 0 при ф > 1 — функция убывающая?
Эскиз графика см. на рис. 319, б.
Примерз. Построить график функции
р— 1
Ф же arccos --а->.
Р-
Областьопределения функции: j -	| <
=Ч<5 <Р <
lim <р (р) = lim ’
,.xl±12+.
.. у ч	Р - 1
1«м*| м\ ini *<*• Ittn оглглс !__
р — 1
arccos £—- *= л.
Р?
, ,	. р— 1 я я
lim <jp(p)i=	lim	arccos £—т-=»-х-;	-я-.
Р-Н- Р-+“ р? 2	2
м»
Первая производная
^2 = 0 при р =? 2, причем ~ < 0 при —	< р < 2, ^2 > О
dp r r r dp г	2	ар
при р > 2, следовательно, при р=<2 функция имеет минимум ^<ps=»
^arccos4-K В точке р » ~ * t' - производная не существует,
4 /	2
в ней функция равна я (максимальное значение).
Эскиз графика функции показан на рис. 454.
РАЗДЕЛ 3
НЕКОТОРЫЕ ВАЖНЫЕ КРИВЫЕ
§ 1. Кривые второго порядка *
Окружность с центром в точке С и радиусом /? — это геометри-
ческое место точек плоскости, удаленных от точки С на расстояние
/?. Уравнение окружности:
где С (а; Ь) — центр окружности, /? —радиус (рис. 455).
В полярной системе координат уравнение окружности с центром
в полюсе имеет вид
Эллипс — геометрическое место точек, для которых сумма рас-
стояний от двух заданных точек (фокусов) является величиной по-
* Порядок кривой определяется степенно уравнения кривой.
Ж
стоянной (2а) (рис. 456, а), каждое из этих расстояний (фокальный
радиус-вектор) равно:
— ех, г2 *= MF2 х= а + ех, Г£-^г2^=2а.	11
ЛВ —большая ось (2а); CD —малая ось (2Ь)\ А, В, С, D — вер-
шины; О — центр; Fj, F2— фокусы (точки, лежащие на большой оси
по обе стороны от центра на расстоянии а*— 6? от него);
—фокальный параметр (половина хорды, проведенной через фокус
Ь- с
параллельно малой оси), р ; е = — < 1 — эксцентриситет.
Рис. 456. Эллипс (определение).
Каноническое уравнение эллипса (если оси координат совпадают
6 осями эллипса):
Параметрическое уравнение эллипса:
х a cos t,
у s= b sin t (0 < t < 2л).
Уравнение эллипса в полярных координатах:
____________________________р
Р 1 4- е cos <р *
если полюс находится в фокусе, то полярная ось направлена от фо-
куса к ближайшей вершине.
Директрисы — прямые, параллельные малой оси и расположен-
ные на расстоянии от нее (рис. 456, б). Для любой точки
М(х\ у) эллипса
Диаметры — хорды, проходящие через центр эллипса; они де-
лятся в центре поцолам. Геометрическое место середин хорд, парад-
дельных одному из диаметров эллипса, является диаметром еопря»
женным с заданным (рис. 456, в). Если kf и k2 — угловые коэффД
циенты сопряженных диаметров, то kjkz ——
а*
Касательная к эллипсу в точке М (xj ух) имеет уравнение
а» + fc? ь
Прямая Ах + By + С == 0 касается эллипса при условии
Л2а? + В2&? — С? = 0.
Радиус кривизны в точке
М (-М 4fo) (рис. 457)
2	2	3
«“•!И(;? + Ег) =
3
01'2) 2 Р
ab	sin8 <р ’
где ф — угол между касательной
и ради усом-вектором точки ка-
сания.
Площадь эллипса S 5= nab. Площадь сектора BQM ж? у arccos —.
Площадь сегмента MBN =< ab arccos Д — ху.
а
Гипербола — геометрическое место точек, для каждой из которых
разность расстояний для двух заданных точек (фокусов) является
величиной постоянной (2а). Точки, для которых rj — r2 s= 2а, при-
надлежат одной ветви гиперболы (на рис. 458, а — левой); точки,
для которых — fl ?= 2а — второй ее ветви (правой). Каждое из
этих расстояний (фокальный радиус-вектор) выражается формулой
ms i (ex — a), r2 *= ± (ex + a),
где верхний знак — для точек правой ветви, нижний — для левой|
АВ — действительная ось (2а)] А, В — вершины; О — центр; Fj, Fa—
фокусы (точки, лежащие на действительной оси по обе стороны от
центра на расстоянии с (большем, чем а) от него); CD — мнимая ось
у .	Q
(2b>=s2 у А — о?); р — фокальный параметр, р »= — ; е — > 1 -•
эксцентриситет.
Каноническое уравнение гиперболы (если ось Ох совпадает
с действительной осью гиперболы):
х- ifi
=,1>
из
Параметрическое уравнение гиперболы:
х =? a ch tt
у s=bsht9
или
х s= a sec t,
У — btg t.
Уравнение гиперболы в полярных координатах:
р — г~Г'с-----;
1 + е cos <р
Рис. 458. Гипербола (определение).
если полюс находится в фокусе, то полярная ось направлена от фо-
куса к ближайшей вершине. Последнее уравнение определяет лишь
Одну ветвь гиперболы.
Директрисы — прямые, расположенные на расстоянии	от
центра и перпендикулярные к действительной оси (рис. 458, б).
Касательная к гиперболе в точке М (хх; ух):
XXi УУ1_
Прямая Ах + By + С *= 0 касается гиперболы, если
А№ - В2№ « (Д
184
ь
Уравнение асимптот: у ± — х.
Сопряженные гиперболы (рис. 459)
и £_х1=1
а? Ы Ы а»
имеют общие асимптоты. Действительная ось каждой из них совпа-
дает с мнимой осью и наоборот.
Диаметры — хорды гиперболы и ее сопряженной, проходящие
через общий центр гипербол; они делятся в центре пополам. Два
диаметра с угловыми коэффициентами kt и k% называются сопряжен-
. . №
ными, если =
Радиус кривизны R гиперболы
в точке М (хх; yi)
Рис. 459. Сопряженные гиперболы.
7?==аад
Р
ab Sin3 ф ’
где ф — угол между касательной и радиусом-вектором точки каса-
ния. В вершинах А и В (см. рис. 458, a) R^=	•
Площадь сегмента AMN (рис. 458, в)
ху — ab In	m ху — ab Arch .
Равносторонняя гипербола — гипербола, оси которой равны: а а= b
(рис. 458, г). Уравнение равносторонней гиперболы: х2— у2~а2.
Асимптоты такой гиперболы взаимно перпендикулярны. Если осями
координат выбрать асимптоты, то уравнение равносторонней гипер-
.	.	а*
болы будет иметь вид ху ж» .
Парабола — геометрическое место точек М (х; у), равноудален-
ных от данной точки (фокуса) и от данной прямой (директрисы):
MF*=MK*=x + -^,
MF — фокальный радиус-вектор точек параболы; Ох — ось параболы;
(р
точка, лежащая на оси иа расстоянии у
от вершины j ;	— директриса ^прямая, проходящая на расстоя-
р	\
вин от вершины по другую сторону от фокуса 1; р — фокальный
параметр (рис. 460, а). Эксцентриситет параболы равен единице.
Каноническое уравнение параболы:
у* s= 2pxt
вершина параболы находится в начале координат, ось Ох совпадает
ф ее осью, парабола повернута вершиной влево.
Уравнение в полярных координатах:
Рис. 460. Парабола.
полюс находится в фокусе, полярная ось направлена от фокуса
к вершине.
Уравнение параболы с вертикальной осью (рис. 460, б):
у s= ах? + Ьх + с,
1
при этом параметр параболы р ;=	. Если а > 0, то парабола по-
I а I
вернута вершиной вниз, если а < 0, — то вершиной вверх; коорди-
b 4ас — 6?	„
наты вершины: х0 ~ , Уо^= —. Диаметр — прямая, па-
286
раллельная оси параболы. Диаметр делит пополам хорды, параллель-
ные касательной, проведенной в конце диаметра. Уравнение диа-
метра!
Где k — угловой коэффициент этих хорд (рис. 460, &).
Касательная к параболе (рис. 460, д) в точке М (xj; yji
УУ1 *= Р (х + xj.
Прямая у =? kx + b касается параболы при условии р s= 2b k.
Радиус кривизны параболы в точке М (xi; уг)1
з
П _,(р + 2^1)2 Р '
Ур	sin3 <р'
В вершине О радиус кривизны /?;= р.
Площадь сегмента параболы *= у $pqnm <Рис* *)•
§ 2.	Кривые третьего порядка
Декартов лист. Декартовым листом (рис. 461) называется кривая
третьего порядка, уравнение которой в декартовой системе коорди«
нат имеет вид
х3 + у3 — Заху ==х 0.
Параметрическое уравнение:
3at
х=яг+в‘
3at2.
У~~ 1 + t3’
В полярной системе координат (О—
полюс; Ох — полярная ось) уравнение
кривой имеет вид
За cos ср sin ф
Р cos3 ф + sin3 ф *
Рис. 461. Декартов лист х9 у9
— Заху = О.
Кривая симметрична относительно биссектрисы у^=х. Начало коорл
динат (0; 0) — узловая точка с касательными — осями координат.
В I квадранте кривая имеет петлю, пересекающуюся с прямой у*=%
в точке л(|а; -у aj- Точки петли, в которых касательные парал-
лельны координатным осям, имеют координаты
Ml (а^2; а У4) и М2 (а р4; а ^2).
287
Л л За Л	- За <
О А ?=	. Радиус кривизны в начале координат Я s= — . Асимптота
3
х + у + а 0. Площадь петли = — а2; площадь между кривой
3
и асимптотой S2 s= у а2.
Циссоида Диокла. Геометрическое место точек М, для которых
0M—PQ (Р— произвольная точка начальной окружности с диамет-
ром а) (рис. 462) называется циссоидой Диокла (Диоклеса).
Уравнение кривой в декартовой си-
стеме координат:
2
* а—х
Уравнение кривой в полярной си-
стеме координат (О — полюс; Ох — по-
лярная ось):
2а sin2 ф
р !=--------- .
г COS ф
Параметрическое уравнение кривой:
а
/2+Г
 а
X =
U2 — --
у а—х
Кривая симметрична относительно оси абсцисс. Начало коорди-
нат — точка возврата первого рода.
Асимптота: х ;= 2а. *
Площадь между кривой и асимптотой Ss=3na2. Объем тела, по*
лученного вращением полосы между циссоидой и ее асимптотой
вокруг асимптоты, 4
V *= 2л2а3.
Если из вершины параболы у^=2рх опустить перпендикуляры на
касательные к параболе, то геометрическое место оснований этих
Перпендикуляров является циссоидой: 1
2	X3
Замечание. Из циссоид — кривых третьего порядка — назовем
трисектрису Лояшама (рис. 463)—геометрическое место точек Р пере-
сечения касательных к окружности радиуса а,.проведенных в точках
С и В этой окружности, если эти точки являются концами дуг
АВ = <о и АС = со, где со — любой центральный угол, а точка А —
фиксированная.
28t
Полярное уравнение трисектрисы:
_ а
Р cos 3<р *
ее уравнение в декартовой системе координат:
(л \ /	1	\	4
х + Т) 12/2 —Т *? I + o'ах* — °-
О / \	о	/	У
Заметим, что с помощью преобразования инверсии из трисек-
трисы можно получить трехлепестковую розу	Зф (см. рис. 307),
Строфоида — это геометрическое
место точек и М2, которые лежат
на произвольных лучах, проходящих
через точку А, и для которых РЛ4Х =
s= РМ2 — ОР(Р — произвольная точка
оси ординат) (рис. 464).
Рис. 463. Трисектриса Лоншама р = Рис. 464. Строфоида уг =
= -А-. '
cos 3<p	'•а — X'
Уравнение в декартовой системе координат:
в параметрической форме:
_ /2-1
х—а& +1 ’
./? —1
y^attrri’
в полярной системе координат (О — полюс; Ох — полярная ось):
cos 2ф
р == — а-----.
cos ф
Кривая симметрична относительно оси абсцисс. Начало координат
(0; 0) — узловая точка (касательные у = ± х). Радиус кривизны
в узловой точке R — а ]/2.
10 8-413
289
Асимптота: х = а.
Площадь петли — 2а2-------у- , площадь между кривой и асимп-
па2
тотой S2 = 2а2 + -g" .
Верзиера Аньези. На отрезке ОС = а (рис. 465) как на диа-
метре построим окружность. Продлим полухорду BD до точки М,
определяемой из пропорции
ВМ : BD = ОС : ОВ,
геометрическое место точек М является верзиерой.
Уравнение кривой в декартовой системе координат:
_ а3
У~ а? + х? •	1
Рис. 465. Верзиера Аньези у =
— д3
~ а2 4- х* '
Параметрическое уравнение
кривой:
х = t,
_ а3
у~ t2 +а2.’
Кривая симметрична относи-
тельно оси ординат. Максимум
С(0;а), радиус кривизны в нем:
m	I а За\ .. {—а За>
Точки перегиба: М± ; -j-j >	» Ту ’ наклон КРИВОИ
/	з тЛз
в точке перегиба: tg ф =	—з— •
о
Площадь между кривой и асимптотой S = па2. Объем тела, об-
разованного вращением верзиеры вокруг асимптоты, равен удвоенному
объему Vt тела вращения начального круга вокруг той же оси:
2 ’
.. _ п2а3
Псевдоверзиера — кривая, которую можно получить из верзиеры,
удвоив все ординаты последней. Ее уравнение:
__ 2а3
у~х? + а?’
Приведем еще некоторые примеры важных кривых третьего по-
рядка.
290
Офиурида — кривая, определяемая как подера* параболы отно*
сительно какой-либо точки, лежащей на касательной в вершине этой
параболы (рис. 466); ее уравнение:
X (Х2 + у2) *= у (су — Ьх).
Если в уравнении офиуриды принять 6 = 0, то
циссоиды.
Трисектриса Маклорена — кривая, кото-
рую определяют как подеру параболы относи-
тельно такой точки ее оси, которая удалена от
директрисы на расстояние, равное расстоянию -
директрисы от фокуса (рис. 467); ее уравнение
в декартовой системе координат:
(х — За) (х? + у2) + 4а30,
в полярной системе координат:
получим уравнение
Рис. 466. Офиурида
х (х2 + £«) ® У {су —
— Ьх).
Из последнего уравнения следует, что трисек-
трису Маклорена можно получить в резуль-
Ф
тате инверсии розы р a cos относительно
о
полюса.
Кубика Чирнгаузена — кривая, для которой парабола является
подерой (рис. 468). Если уравнение параболы представить в виде
у2 2рх + р2, то уравнение кубики Чирнгаузена в декартовой си-
стеме координат будет иметь вид
2(2р + х)3 = 27р(х2 + р2),
Рис. 467. Трисектриса Маклорена
(х - За) {х2 + у*) + 4а3 = 0.
Рис. 468. К убйка Чирнгаузена
2 {2р	х)* =< 97р (х2 4- уг).
а в полярной системе координат:
о ЭТ ф
р cos3 ——L
о
р_
2 *
* Подерой данной кривой К относительно любой точки плоскости называется
новая кривая, которая является геометрическим местом оснований перпендикуля-
ров, опущенных из этой точки на касательные к заданной кривой.
10*
291
Заметим, что кубика Чирнгаузена является огибающей отраженных
от параболы световых лучей, перпендикулярных к ее оси, т. е. ката-
каустикой параболы.
§ 3. Кривые четвертого и высших порядков
Конхоида Никомеда. Конхоидой данной кривой называется кри-
вая, которую можно получить при увеличении или уменьшении ра-
диуса-вектора каждой точки данной кривой на постоянный отрезок /.
Если уравнение кривой в полярных координатах: р^=/(ф), то
уравнение ее конхоиды: р = / (ср) ± /.
Рио. 469. Конхоида Никомеда (х а)2 (х2	у2) 1гхг ~ 0.
Конхоида Никомеда — конхоида прямой линии, т. е. геометриче-
ское место точек 7И, для которых ОМ — ОР ± I (внешняя ветвь для
«-}-», внутренняя ветвь для «—») (рис. 469).
Уравнение в декартовой системе координат:
(х — а)? (х2. + у2) — /Ы 0;	Л
в параметрической форме:
х а + I cos <р,
yt= a tg ф + I sin ф;
в полярных координатах:
Р ~~ COS ф
Для внешней ветви: асимптота х — ал вершина +/; 0), точки
перегиба В и С. Площадь между ветвью и асимптотой оо.
292
Для внутренней ветви: асимптота х*=а, вершина D (а —1\ 0),
точка (0; 0) — двойная точка, характер которой зависит от величин
а и /: а) I < а — изолированная точка (рис. 469, а), кривая имеет
еще две точки перегиба: Е и F; б) при / > а — узловая точка
(рис. 469, б), кривая имеет максимум и минимум при х^=а — j^al2;
в) при lt=a — точка возврата (рис. 469, в).
Улитку Паскаля можно определить как конхоиду окружности
ОМ = ОР ± I (полюс лежит на окружности) (рис. 470).
Уравнение кривой в прямоугольной декартовой системе коор-
динат:
(х2 + у2. — ах)2 I2 (х2 + у2);
Рис. 470. Улитка Паскаля (х2+ Уг — ах)2 — Р (*2 + У*)-
в параметрической форме:
х~а cos2 ср + Z cos ф,
у — a sin ф cos ф + sin ф;
в полярной системе (О — полюс; Ох — полярная ось):
р =; a cos ф + I
(а — диаметр окружности). Вершины 4, В (а ± Z; 0). Вид кривой за-
висит от величин а и Z.
Кривая имеет четыре экстремума, если а > Z; два экстремума,
если а < I: С, D, F (cos ф s= *	4~	, Точки перегиба G,
\	4а /
(2д?	/2\
cos ф	— I, если а < I <2а. Начало координат — двой-
ка/ /
ная точка: изолированная при а < I, узловая при а > Z, точка воз-
врата при а I.
Площадь, описываемая полярным радиусом улитки при полном
обороте,
293
При наличии петли имеет место равенство
5 *=	*“*2>
где
si = (у а? + j Ф1 + у I /а? — /2 (ф! = arccos у |
S2t= /у а? 4- М <ра —у i у а2 _ /? /ф2 _ arccos 2Л (
здесь Sj — площадь, ограниченная внешней петлей; S2—площадь одной
внутренней петли.
Рис. 471. Эпициклоида х — (А -} а) cos ? — а cos g т) » # = (А a) sin <р »
— a sin	; т == 3 (а)\ т =	(б).
Циклоидальные кривые. Пусть некоторая кривая катится без
скольжения по другой кривой. При этом любая точка, неизменно
связанная с первой кривой, описывает новую линию. Среди кривых,
образованных таким способом, выделяют кривые, являющиеся -траек-
ториями точки, неизменно связанной с окружностью, которая катится
без скольжения по второй окружности. Полученные при этом линий
называют циклоидальными. Циклоидальные кривые могут быть как
алгебраическими, так и трансцендентными. Рассмотрим некоторые
примеры алгебраических циклоидальных кривых.
Эпициклоида — кривая, описываемая точкой окружности, которая
катится без скольжения по другой окружности извне (рис. 471).
В параметрической форме уравнение эпициклоиды имеет вид
/ л । \	/ А -|- а \
х	(А + a) cos <р — a cos I —— ф j ?
у	(А + a) sin ф — a sin I —— ф J f
»4
где А — радиус неподвижной окружности; а —радиус подвижной
окружности; ф / СОх.
Вид кривой зависит от отношения — т, В частности, при
т = 1 имеем кардиоиду (см. ниже). При этом т эпициклоида со-
стоит из т ветвей, которые обходят неподвижный круг. Точки воз-
(2& л	\
р — Л, ф	—- (&	0, 1, ... , т — 1)1
(2л /	1 \'
р ;= А + 2а, Ф — — I k + — j ।. При
дробном т ветви перекрещиваются, подвижная точка М, описав ко-
нечное число ветвей, возвращается в начальное положение. Если
т — иррациональное, то число ветвей бесконечно, точка М в началь-
ное положение не возвращается.
tz	«	« г	8 (Л ”1“ а)
Кривая имеет иг ветвей, длина одной ветви	—-1
если т—целое, то длина всей кривой L=? 8 (Л-}-«)•
Площадь сектора Л1В1Л2Л1

лаЗ
Радиус кривизны
в вершинах
4а (А+а)~.~ Лер
2а + А 2а ’
4а (Л + а)
2а + Л *
Натуральное уравнение обычной эпициклоиды:
а* Й
4а (Л ± а) г	4а (Л ± а)	с
где а =; 	, Q—- ; b ----------- ; г — радиус кривизны; о — длина
Л х	Л
дуги, которую отсчитывают от одной из начальных точек.
Последнее уравнение выражает такое кинематическое свойство
эпициклоиды: если дуга обычной эпициклоиды перекатывается «без
скольжения по прямой, то центр кривизны точки касания двигается
по эллипсу: центр эллипса лежит в той точке прямой, через которую
перекатывается вершина эпициклоиды.
Гипоциклоида — кривая, описываемая точкой окружности, кото-
рая катится без скольжения по другой окружности внутри нее
(рис. 472). Уравнение гипоциклоиды, координаты вершин и точек
возврата, формулы длины дуги, площади и радиуса кривизны — те
же, что и для эпициклоиды с заменой «-]-» на «—»; ’число точек воз-
врата такое же, как и у эпициклоиды.
Удлиненные и укороченные эпи- и гипоциклоиды (их называют
также эпи- и гипотрохоидами) (рис. 473, 474) — это кривые, образо-
295
ванные тэчкой, лежащей снаружи или внутри окружности, которая
перекатьвается без скольжения по другой окружности снаружи или
внутри ее.
Уравнение в параметрической форме имеет вид
/ л । \	1 (А Н” \
X s= (Д + а) cos ф — cos ------ф J ,
/Я1	\	*	л . /А а \
z/ — (Д + a) sin ср — Ха sin I —— ф I,
где А — радиус неподвижной окружности; а — радиус движущейся
окружности, причем в случае гипоциклоиды «4-а» в уравнении заме-
Рис. 472. Гипоциклоида: т — 3 (а)-, т = 4 (6).
няется на «—а»; к^=СМ (для удлиненной Х> 1, для укороченной
X < 1). При А>=2а(к — любое число) гипоциклоида превращается
в эллипс с полуосями а (1 + X) и а(1— X). При А^= а получаем
улитку Паскаля:
х — а (2 cos ф — X cos 2ф),
у — а (2 sin ф — X sin 2ф).
Кардиоида, Кардиоиду можно определить как эпициклоиду, у ко-
торой диаметры подвижнойи неподвижной окружностей равны (/n=l)
(рис. 475).
Уравнение кардиоиды в прямоугольной декартовой системе коор-
динат:
(х2 + у2)2 — 2ах (х2 + У2) — а2У2,
в параметрической форме:
х^=а cos ф (1 + cos <р),
у — a sin ф (1 + cos ф),
в полярных координатах:
р ==: а (1 + cos ф).
296
’Ч J?
Рис. 473. Эпитрохоида: X > 1, а > 0 (а)\ к < 1, а > 0 (б).
Рис. 474. Гипотрохоида} X > 1, а
< 0 (а); X < 1, а < 0 (б).
Рис. 475. Кардиоида х =
= a cos <р (1 4- cos <р), у =
= a sin <р (1 -j- cos ?)•
297
Начало координат — точка возврата. Вершина А (2а; 0).	Я
(I \	/ з з 1/3 \ Я
cos<p^= — i—С, Z)l —а; ±——а). я
3	9
Площадь кардиоиды S == — ла2, длина всей кардиоиды L = 8а. 1
Кривая Штейнера. Кривую Штейнера можно определить как ги- 3
поциклоиду, у которой радиус подвижной окружности в три раза Д
меньше радиуса неподвижной окружности, т. е. т — -i-(рис. 476).	|
Параметрическое уравнение кривой:	1
n t у 2t	1
х ?= 2а cos — + a cos -5- ,	1
О	О	я
'	. f . 2/	I
у~ 2а sin —— a sin	j
В декартовой системе координат уравнение кривой имеет вид
(х2	1/2)2 Sax (Зу2 — х2) + 18а? (х? + у2) — 27а4 — 0.
Отметим интересное свойство касательных к кривой Штейнера: точка 1
пересечения'взаимно перпендикулярных касательных к кривой Штей- |
нера лежит на окружности, вписанной в эту |
кривую.	!
Кривая Штейнера интересна и формами |
своих подер. Уравнение подеры кривой
Штейнера относительно точки S (Ь; 0) имеет J
вид	;
(х? + у*)* + [(а + За) у* + (Ь - а) х2] х*= О, 
или
р — 4а cos3- ф — (Ь + За) cos Ф,
Рис. 477. Подера кривой
Штейнера относительно
начала координат.
откуда:
а)	при Ь = 0 получаем трехлепестко-
вую розу — подеру кривой Штейнера отно-
сительно начала координат (рис. 477);
при Ь— а имеем
р = —4а cos ф sin? ф
— прямой двулистник — подера кривой Штейнера относительно точки
S (рис. 478);
б)	при &;=—а имеем
р t= 2а cos ф cos 2ф
— прямой трилистник — подера кривой Штейнера относительно
точки Sf (рис. 479);
в)	при Ь*= — За имеем
р s= 4а cos3 ф
т
— однолистник — подера кривой Штейнера относительно точки Sa
(рис. 480).
Астроида — частный случай гипоциклоиды при m — — (рис. 481).
Уравнение кривой;
(х? + у2 _ ^2)3 + 27R2x*y = 0.
Это алгебраическая кривая 6-го
Рис. 478. Прямой Дву-
листник.
Рис. 479. Прямой три-
листник.
Рис. 480. Однолистник.
Параметрическое уравнение:
D 3 t
х— R cos3 -7-,
4 *
y=R sin3 у.
Исключая t, получаем распространенный вид уравнения астроидьн
?/з+ у*/3 — ^2/з.
Кривая Кассини (ее часто называют свалом Кассини, хотя на
самом деле она не всегда овальная) — геометрическое место точек
299
М, для которых произведение MFj. MF2 расстояний от концов дан-
ного отрезка F^^Zc равно квадрату данного отрезка (рис. 482):
MFt . MF2 — а2.
Точки Flf F2 называются фокусами; прямая FtF2 — ось кривой Кас-
сини; середина О отрезка F±F2 — центр.
Уравнение кривой в декартовой системе координат:
(х2 + у2) — 2с2 (х2 — у2) := а4 — с4
(О — начало координат; F2F± — ось абсцисс);
Рис. 482. Кривая Кассини: а>с /2 (а);
с < а < cV2 (б)\ а < с (в).
в полярной системе (О — полюс; Ох — полярная ось):
р4 — 2с2р2 cos 2ф + с4 — а4 ;= О,
или	_____________
р2 ;= с2 cos 2tp ± а4 — с4 sin2 2ф,
или	_____________________
р2 z= с2 cos 2ф ± j/c4 cos2 2ф + (а4 — с4).
Двойной знак берем, если а < с. В противном случае берем только
знак «+».
Кривая Кассини симметрична относительно Ох и Оу, следова-
тельно, и относительно точки О, Форма кривой зависит от отношения
а к с:
а) при а > с У2 имеем эллипсоподобный овал (рис. 482, а).
В данном случае точки пересечения с осью Ox: А, С(± Vя2 + с2; 0),
точки пересечения с осью Оу: В, D (0; ± ф^а2 —с2);
300
к -
б) если а = с 1/2, то также имеем эллипсоподобный овал; в этом
случае А, С(±с]/3; 0), Bt D (0; ±с); в точках В и D кривизна
равна нулю;	_
в) прис < а < с ]/2 им^ем овал (рис. 482, б), точки пересечения
с осями Ох и Оу те же, что и в предыдущем случае; максимумы и
минимумы: В, D (0; +с), £, G, Д’,	j/"- - 2с °  \ ±	*» че’
тыре точки перегиба: Р, £, М, Л^±	—:	y(m+n)]’
а4 — с4 1 Г а* — с*
где п^=—3^2—, т у ——; при а^=с имеем лемнискату (см.
ниже); при а < с имеем два овала (рис. 482, в). Точки пересечения
с осью Ох*. А, С (± ]/а2 + с2; 0) и Р, Q ( + ]/с2 — а2; 0); максимумы
(- /”	_ q4	Д2 \
± у —± 2с)- Радиус кривизны
2а2р3
Я д^+ Зр4 ’ где р "" Pawc-BeKT0P-
Лемниската Бернулли. Лемниската — геометрическое место точек,
для которых произведение расстояний от концов данного отрезка
F1F2^=2c равно с2, т. е. это частный случай овала Кассини, когда
а = с (рис. 483).
Прямая FtF2 — ось лемнискаты.
Уравнение лемнискаты:
(х2 + у2)2	2с2 (х2 — у2).
Начало координат О — середина
отрезка FtF2\ ось Ох направлена
по F2Fp
Уравнение лемнискаты в поляр-
ной системе (О—полюс; Ох —’поляр-
ная ось):
р? 2с2 cos 2ср,
где угол ср изменяется в промежутках
Рис. 483. Лемниската Вернул пи.
л л I [Зл 5л
~Т : т| и JT; т •
Параметрическое изображение:.

r-t—l3
у—с/2^ (i (—00 < t < оо),
t связано с ф соотношением
<р).
Лемниската имеет две оси симметрии: прямые FtF2 (Ох) и Oyt
Точка О — узловая точка с касательными у^=±х, эта же точка —
точка перегиба. Точки пересечения кривой с осью Ох: Л, С (±aj/2; 0),
301
максимумы и минимумы: Е, G, К, L | ±	; ±	, поляр-
jt	2с2
ный угол в этих точках <р = ± — . Радиус кривизны 7? — — .
/ зх \
Площадь каждой петли лемнискаты: 2S -г-	г2.
Рис. 484. Каппа р = a ctg <р.
Если из центра О равносторон-
ней гиперболы с вершинами Л*,
А2 опустить перпендикуляры на ее
касательные, то геометрическое место
оснований этих перпендикуляров бу-
дет лемнискатой с теми же верши-
нами.
Приведем еще некоторые при-
меры важных кривых четвертого и
высших порядков.
Каппа — геометрическое место
точек касания касательных, прове-
денных из начала координат к окружности радиусом ак центр кото-
рого перемещается по оси абсцисс (рис. 484).
Уравнение каппы в полярной системе координат
p = actgq>,
в декартовой системе координат:
(х2 + у2) у2 s= а2х2.
Заметим, что каппа входит в семей-
ство кривых, уравнение которых
р a ctg
и которые называются узлами. Все
эти кривые имеют в точке (0; 0) узло-
вую точку и асимптоты, параллель-
ные координатным осям. К семейству
узлов, в частности, принадлежат стро-
фоида, для которой k === —, и «ветря-
ная мельница» — кривая, для которой
k ~ 2 (рис. 485).
Синусоидальные спирали — семейство
в полярной системе координат
Рис. 485. КРивая «ветряная мель-
ница» р = ctg 2<р.
кривых, уравнение которых
p/n __ ат sin /Пф или рт S= ат COS Шф.
При рациональном т эти кривые являются алгебраическими кривыми
того или Другого порядка в зависимости от значения /и, в частности:
при	р — a cos ф — окружность, при т^=—1	cos —
прямая, при m 2 р a2 cos 2ф — лемниската Бернулли, при т j==
л2	1
г= —2 р2 *= ^^ф — равносторонняя гипербола, при т —
302
9 Ф	1	2а
р j== a cos2 ---кардиоида, при т ~ — у р — j~qicos у парабо-
ла и т. д.
«Розы», или кривые Гвидо Гранди,— семейство кривых, полярное
уравнение которых имеет вид
р a sin &ф или р х= a cos &ф,
где а и k — постоянные, которые будем считать положительными
числами.
Рис. 486. Кривые Гвидо Гранди («роЕЫ»).’ р = a sin Аср, р = a cos £<?.
Если k — целое число, то «роза» состоит из k лепестков при k
нечетном и из 2k лепестков при k четном; если	1) — ра-
циональное число, то «роза» состоит из т лепестков, если тип —
нечетные, и из 2m лепестков, если одно из этих чисел — четнсе, при-
чем следующий лепесток частично покрывает предыдущий (рис. 486).
Площадь одного лепестка «розы» находим по формуле
7С
т
„	1 f 2 . ла?
О
«Колоски» — кривые, уравнение которых имеет вид
а	а
Р — ——т— ИЛИ р --------г- *
sin пф	cos kq>
где k — любое рациональное число.
Эти кривые можно образовать из «роз», если выполнить преоб-
разование инверсии относительно окружности радиусом а.
Если k — целое и нечетное, то кривые ps=-r~— состоят из k
r sin kq
конгруэнтных гиперболических веток; если k — целое и четное, то
число ветвей составляет 2k.
Примеры «колосков»:
__ а
Р cos Зф
а
Ф
cos|
трисектриса Лоншама,
трисектриса Маклорена.
ЗОЭ
Кривые Ламе. Уравнение кривых Ламе:
где т — любое рациональное число, а постоянные а и b — положи-
тельные числа.
— > 1, р, я— нечетные (в)\ — < 1, р —четное, q — нечетное (г);
Q	Q
£- < 1, р — нечетное, q — четное (д)\ —< 1, Р, q — нечетные (е).
q	Q
Параболические кривые: у^=схт, где т^=—> 0. Пример —па-
рабола Нейля: y^=ax3/2t а > 0 (см. рис. 40).
Гиперболические кривые: yt=ax~mt m — ~>0.
§ 4. Трансцендентные кривые
Трансцендентная кривая — это кривая, уравнение которой в де-
картовой системе координат не является алгебраическим (в других
системах координат может быть алгебраическим).
Приведем примеры некоторых важных трансцендентных кривых. -
Спираль Архимеда — кривая, которая описывается точкой, дви-
жущейся с постоянной скоростью и вдоль луча, который < вращается
вокруг полюса О с постоянной угловой скоростью со (рис. 488).
304
Кинематические понятия, входящие в определение, можно исклю-
чит ь, если заменить их условием, чтобы расстояние р — ОМ было про-
порционально углу поворота ф луча, вращающегося вокруг точки О,
Повороту луча из любою положения на данный угол соответствует
одно и то же приращение расстоя-
ния р. В частности, полному обороту
соответствует одно и то же смеще-
ние	(рис. 488, б). Отрезок а
называется шагом спирали Архимеда.
Данному шагу а соответствуют
две спирали Архимеда, которые раз-
личаются направлением вращения лу-
ча. При вращении против часовой
стрелки получаем правую спираль
(рис. 488, б, основная линия), при вра-
щении по часовой стрелке — левую
(рис, 488, б, вспомогательная линия).
Правую и левую спирали
две ветви кривой, которую
и проходя через точку О.
Полярное уравнение:
одного шага можно рассматривать как
описывает точка М, пробегая весь луч
р s= kq,
где & —параметр спирали Архимеда; k = ~ — смешение точки М
2л
вдоль луча при повороте последнего на угол 1 рад.
Положительным значениям ф соответствует правая ветвь; отри-
цательным значениям — левая.
Площадь Sn, ограниченная n-й ветвью спирали и отрезком ОАп,
выражается формулой
S _ПЗ-(П-1)3	П3_(„_,)3
3 ла	sn,,
где Sn, — площадь круга радиусом ОАп.
305
Площадь n-ro кольца спирали Архимеда
— S/i s= 6nSi,
где S], = 4- ядЗ — площадь нулевого кольца.
О
Длина дуги ОМ:
k
/=4[<plAp2+1+ln <<р-ь v <рэ-ь о]
1 Г /рЧТ2 , ., p + Zp^+T2]
= у I Р L-£-£J--F k In I—!—1—£-!- I
1	2/
[tg a sec a + Ь (tg a + sec a)],	-> 0
при больших ф, где a — острый угол между касательной МТ и по-
лярным радиусом ОМ. Радиус кривизны
(р2 + 62)3/2 _ . (Ф2 + 1)3/2 _ ь (tg2a + 1)3/2
Л~~ р« + 2fe? ~	<р? + 2 sec?a4-l "
ь
В точке (0; 0) 7?0 = у.
Гиперболическая спираль. В полярных координатах гиперболи-
ческая спираль имеет уравнение
а
• р~ ф 
Кривая состоит из двух ветвей, симметрично расположенных отно-
сительно перпендикуляра к полярной оси (в полюсе) (рис. 489). Для
каждой ветви прямая у — а является асимптотой и начало координат
О — асимптотическая точка.
а21 \	1 \	1- о сЛ
Площадь сектора МгОМ2 : S ±= -1-------------1 ; нт о — —.
2 \фх ф2'	<р2-+оо ^ф
л /1/ 1	т2\3
Радиус кривизны rt=
306
Рис. 490. Конхоида гиперболической Рис. 491. Спираль Гали-
Рис. 493. Спираль Ферма р =>
= а
Рис. 494. Параболическая
спираль р = a /cp-f-
Сравнивая уравнения спирали
Рис. 495, Логарифмическая
спираль р = рае^.
Архимеда и гиперболической спи-
рали, замечаем, что каждую из них можно получить из другой с
помощью превращения инверсии относительно полюса.
Конхоида гиперболической спирали — обобщенная гиперболичес-
кая спираль, уравнение ее:
Р =	+ I, / > о (рис. 490).
Примеры других спиралей.
307
Спираль Галилея р = аф?—/, /^0. При /^=0 р=аф2(рис. 491).
Р==^5 <РИС- 492)-
Спираль
Спираль Ферма р = а ]Лф (рис. 493). Характерная особенность
этой спирали: по мере удаления от полюса расстояние между вет-
вями неограниченно уменьшается, у спирали Архимеда это расстояние
остается постоянным, у логарифмической спирали — неограниченно
возрастает.
Параболическая спираль р а Уф + /, I > 0 (рис. 494).
Логарифмическая спираль — кривая, которая пересекает все лучи,
выходящие из одной точки О, под одним и тем же углом а (рис. 495).
Уравнение кривой в полярных координатах:
p = poeft'f>,
где k — параметр (^k s= ; q — коэффициент роста) .
Цепная линия — линия, по которой провисает однородная нерас-
тяжимая нить, закрепленная в двух точках (рис. 496). В зависимости
1	*
у — a ch — —
а
от положения точек, в кото-
рых закрепляются концы нити,
и от длины нити дуга провиса-
ния принимает различный вид.
Самая низкая точка цепной ли-
нии называется ее вершиной.
Если ось ординат направить
вертикально вверх, а вершину
взять началом координат, то
цепная линия изобразится так:
У = ^[а + е-*!а)-а,
где а — параметр цепной линии.
Если же начало координат
взять в точке О, лежащей ниже
вершины цепной линии на рас-
стоянии, а, то получим более
простое уравнение:
Прямая х'х (см. рис. 496), параллельная касательной в вершине
и расположенная ниже этой вершины на расстоянии а, называется
директрисой цепной линии. Длина s дуги ДМ цепной линии равна
проекции MMi ординаты РМ на касательную МТ:
s = ДМ == ММ± = ~ (ех/а — е~х/а) ;= a sh — .
2 v	1 а
Справедливо такое соотношение:
s2 4- а? = у2,
где у = РМ.
308
Проекция A4W ординаты МР цепной линии на нормаль имеет
постоянную длину:	<
MN s= О А = а.
Радиус кривизны
(X _____________________________х\
еа +е ~“=ach2 —.
1	/	а
Натуральное уравнение цепной линии имеет вид
Кинематический смысл: если цепная
линия катится без скольжения по
прямой, то центр кривизны точки ка-
сания описывает парабдлу.
Площадь криволинейной трапеции
ОАМР равна площади прямоугольни-
ка со сторонами a, s:
Рис. 497. Трактриса х—Arch ±
± У а2 - у*.
S as a2sh — .
а
Трактриса — кривая, для которой
длина отрезка касательной от точки
касания М до точки пересечения с данной прямой Р — постоянная
величина (рис. 497). Если к одному концу нерастяжимой нити данной,
длины (а) прикреплена материальная точка (М), а второй конец.(Р)
двигается по прямой (Ох), то эта точка (М) опишет трактрису.
Точка А трактрисы, наиболее удаленная от направляющей,
называется вершиной трактрисы.
Уравнение трактрисы:
х— a Arch ~ ± У а2 — у2	a In -а	+ У а2 — у\
Параметрическое уравнение:
х=х a cos ср + a In tg-~ , i/^=asin9.
Натуральное уравнение:
У R2
s —aln I/
та2
Асимптота кривой — ось абсцисс, точка А (а \ 0) — точка возврата
(с вертикальной касательной).
Кривая симметрична относительно оси ординат.
Площадь, ограниченная трактрисой и ее асимптотой, определя-
ется по формуле
оо	ТС
с	С ,	С . a cos2 ф ,	лаЗ
о —	\ ydx	\	a Sin ф —:-1 б/ф =;	-х-	.
J	J	sin ф v 2
— оо	О
Объем тела, полученного вращением трактрисы вокруг ее асимп-
тоты, определяется по формуле
309
00
♦	С 9 J	f 2 • 2 а C0S Ф 2 о
V s= л \ и2 dx = л | a2 sin2 ср —:—— ср ~ — ла3.
J *	J	sin <р	3
—-©о	О
Площадь поверхности тела вращения, полученного вращением
трактрисы относительно ее асимптоты, определяется по формуле
7С
_ л С . a cos ср . А „
Р ₽= 4л i a sin ф —:—- аф г= 4ла?.
J Y Sin ф т
7С
~2*
Радиус кривизны в произвольной точке трактрисы
# a ctg ф.
Циклоида—кривая, которую описывает точка, закрепленная
в плоскости круга, когда этот круг катится без скольжения по
прямой линии (рис. 498).
Если точка лежит на окружности круга, который катится без
скольжения по прямой, то образуется обычная циклоида, или просто
циклоида (рис. 498, а); если точка находится вне круга, то образо-
ванная циклоида называется удлиненной (рис. 498, б), а если внутри
круга, то укороченной (рис. 498, в).
Уравнение циклоиды в параметрической форме:
х a (i — sin /), у =t а (1 — cos 0,
где а —радиус круга;
В декартовых координатах уравнение циклоиды:
х + VУ (2а — у) ==: a Arccos	.
Кривая периодическая; период (базис циклоиды) 00х^=2ла.
Точки возврата: О, 0^, 02, ••• > (2л£а; 0); вершины: Aj, А2, •••.
[(2fc + 1) ла; 2а]. Удлиненные и укороченные циклоиды точек воз-
врата не имеют. Длина ОМ : L = 8a sin? ~ ; длина одной арки ци-
клоиды Lqa 0 = 8а; площадь одной арки OAiOiO : 5 Зла2. Радиус
t
кривизны r 4а sin— в вершинах гл=:4а.
Эволюта циклоиды — такая же циклоида (на рис. 498 изобра-
жена вспомогательной линией).
Для удлиненных и укороченных циклоид уравнение в парамет-
рической форме:
Xf= a (t — X sin О,
у = а (1 + % cos /),
где а —радиус круга; 1 — ^МСгВ;	(для удлиненной ци-
клоиды Х = 1, для укороченной X < 1).
Кривые периодические: период 00х=^2ла; максимумы: Aj, А2,
• ••, [(2& + 1) ла; (1 +%) а]; минимумы: Во, Bj, В2.......[2kna;
(1 —X) а]. Для удлиненной циклоиды узловые точки DOf Dit D2i ...,
t2kna; a [1 — 1/"X? — /2)1 где tQ — наименьший положительный
310
Рис. 498. Циклоида х = a (t — sin t),	= а (1 — cos /).
корень уравнения f = lsint Для укороченной циклоиды точки пе-
региба Ер Е2, ... , [a (arccos 1 — X]/1—X2); а (1 — X2)]. Длина
одного цикла L=ta J 1 + X2 — 2Z cos tdt,
о
Площадь, заштрихованная на рисунке:
$ = ла2 (2 +Л2).
о	п (I + V —2Xcos/)3/2
Радиус кривизныR = а-------X(cos Д)------
(1 + *)2
мума гА — —а -—'» в точках минимума г в — а----------.
Натуральное уравнение обычной циклоиды (в пределах одной
арки):
R2 4- ($ — 4а)2 = (4а)2 (0 < s < 2nd),
; в точках макси-
(1-М2
где R — радиус кривизны.
Кинематическое свойство обычной циклоиды.
Натуральное уравнение выражает свойство: если обычная циклоида
катится (без скольжения) по прямой, то центр кривизны точки каса-
ния движется по окружности. Радиус последней в четыре раза
311
больше радиуса начального круга, а центр лежит в той точке прямой,
через которую прокатывается вершина циклоиды.
Тавтохронное свойство циклоиды. Материальная
точка, движущаяся под действием силы тяготения по обычной ци-
клоиде ADB (рис. 499), достигает самого низкого положения D за
Рис. 499.	Тавтохронное свойство	Рис. 500. Эвольвента окружности
циклоиды.	х — k (cos а-}-а sin а), у = k (sin а—«
*- а cos а).
промежуток времени /5=л у ~ , где а — радиус круга, g— ус-
корение силы тяготения. Этот промежуток не зависит от начального
положения точки. Поэтому период Т колебания циклоидального маят-
ника (Т = 4/) не зависит от его амплитуды. Нить циклоидального
маятника закрепляется в начальной точке К Другой циклоиды АКВ,
которая является эволютой циклоиды ADB.
Брахистохрона точки, которая перемещается под действием силы
тяготения в среде, сопротивлением которой можно пренебречь, из
данной точки А в расположенную ниже точку В, не расположенную
на одной вертикали с А, является обычной циклоидой.
Замечание. Если по прямой линии катится без скольжения
эллипс, гипербола или парабола, то полученные при этом кривые
называются кривыми Штурма.
Развертка (эвольвента) окружности. Эвольвента окружности —
кривая, описываемая концом натянутой нити, которая разматывается
с окружности (АВ=:ВМ) (рис. 500). Одна окружность -имеет беско-
нечное число эвольвент (соответствующих различным положениям
начальной точки). Основание перпендикуляра, опущенного из центра
О на касательную МТ эвольвенты, описывает спираль Архимеда.
Полярное уравнение эвольвенты окружности:
]/р2 — fe?	k
ф г -----------arccos — ,
т k	ср
где полюс О — центр данной окружности, полярная ось Ох направ-
лена по начальному радиусу OB, k— радиус окружности.
Уравнение эвольвенты окружности в параметрической форме
имеет вид
x*= k (cos а + а sin а), у k (sin а — а cos а),
где а==21В0х.
312
Натуральное уравнение эвольвенты окружности: R*=z2ks. ~
Кинематическое свойство. Если дуга эвольвенты ок-
ружности перекатывается без скольжения по прямой, то центр кри-
визны L, соответствующий точке касания, движется по параболе
с параметром k.
к	те
. Рис. 501. Клотоида	cos dt, у = а /те sin — dt.
6	6
Клотоида — кривая, для которой радиус кривизны обратно про-
порционален длине дуги:
а2
г ---------------------------------
s
Уравнение клотоиды в параметрической форме:
те	t
.л— Г	-л/2	f . nt2 ,
х =: а у л I cos -у dt, у а у л j sin -у dt,
6	о
где	s~OM (рис. 501). Клотоида симметрична относи-
а у я
тельно начала координат.
Кривая имеет две асимптотические точки:
л la]/'л	а ]/ л \	Dl а У я а л \
—2~]’ В\-----------2-)’
Начало координат — точка перегиба кривой.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютная величина действительного
числа 7
Абсцисса 32
Аргумент функции 10
Ареа-косинус 154, 155
Ареа.котангенс 154, 155
Ареа-синус 154, 155
Ареа-тангенс 154, 155
Ареа-функции 154
Асимптота 57, 265, 278
—	вертикальная 58
—	горизонтальная 57
—	наклонная 58
Астроида 160, 16(, 299
Величина дискретная 9
—	непрерывная 9
—	переменная 9
—	постоянная 9
Верзиера Аньези 290
Ветвь многозначной функции ф
Вогнутость функции 52, 53. 230
Выпуклость функции 52, 53, 230
Вычитание графиков 79, 80
Гессиана кривой 273
Гипербола 283, 284
Гиперболический косеканс 153
— косинус 153
— котангенс 153
— секанс 153
— синус 147, 152, 153
— тангенс 153
Гипотрохоида 295, 297
Гипоциклоида 295
Грань множества 8
---- верхняя 8
— нижняя 8
---- точная верхняя 8
----— нижняя 8
График функции алгебраической 128
---- в декартовой системе координат
242
----в полярной системе координат
169, 277
----дробно-линейной 139	*
— — дробно-рациональной 140
---- заданной несколькими аналитиче-
скими выражениями 203—205
•---заданной параметрически 155—
165 ,
----заданной рекуррентными соотно-
шениями 205—207
— — иррациональной 146, 147
---- монотонной 51
---- нечетной 41
— — неявно заданной 180, 271
— — обратной 45
---ограниченной 39
---периодической 46
---сложной 108, 109	.
---трансцендентной 147
--- целой рациональной 129	'ж
~ — элементарной 108
Действительное число 5	Л
Декартов лист 163, 287	.д
Декартова система координат 32
Деление графиков 85	Я
Дифференциал 219	Я
Др’обная часть числа 12, 20	*Я
Знак функции 48, 49
Значение функции наибольшее 229	’ Я
---наименьшее 229	Я
Интервал замкнутый 7	ж
— знакопостоянства функции 49	, W
— монотонности функции 51, 224	,
— открытый 7	j
Иррациональные числа 5	J
Исследование функции в декартовой f
системе координат 36—60
--- в полярной системе координат JI
165—168? 277, 278	- J
---неявно заданной 180—182	ж
— — параметрически заданной 155, 156, Я
264, 265	Я
---с помощью производных 223—231 Я
Каппа 302	. Я
Кардиоида 160, 296	Я
Квадрант 33
Клотоида 313	Ж
Конхоида 292	Я
— Никомеда 177, 292	Ж
Координатная плоскость 32	Я
Координатные оси 32	Я
Косеканс 125	Ж
Косинус 75	W
Косинусоида 75	Д
Котангенс 76	- Jw
Котангенсоида 76	ж
Кривая алгебраическая 180	Ж
—	«ветряная мельница» 302	Ж
—	Гаусса 109	®
—	«узел» 302	Д|
Кривые Гвидо Гранди («розы») 303 гЯ
— гиперболические 304	'Ж
—	Кассини 299	Я
—	«колоски» 303	is
—	Ламе 304	Л
—	параболические 304	Ж
—	трансцендентные 304—313	Д
—	Штейнера 298
Кубика Чирнгаузена 291	Я
314
Лемниската Бернулли 202, 301, 302
Максимум функции 57, 225
Метод касательных 240
— хорд 239
Минимум функции 57, 225
Монотонность функции 16, 17, 51
Нули функции 48
Область значений функции 38, 39
— определения функции 36, 37
Обратно пропорциональная зависимость
65
Однолистник 299
Ордината 33
Ось абсцисс 32
—	ординат 32
Отрезок 7
Офиурида 291
Парабола 285
—	Нейля 68, 304
Перенос начала координат 35
Период 18, 19
Периодичность функции 18—20, 46
Поворот координатных осей 35, 36
Подера кривой 291
Полярная система координат 33, 34
Полярные координаты 33, 34
Правила дифференцирования 215—217
Преобразование графиков 79, 80, 91-*
96, 178
Предел функции 22—24
—	числовой последовательности 21
Предельные функции 55
Приращение аргумента 28
—	функции 28
Продолжение функции 46
Производная функции 214
— — заданной параметрически 216, 217
--- неявной 216
--- обратной 216
---сложной 216
Прямо пропорциональная зависимость
62
Прямой двулистник 298
—	трилистник 298
Псевдоверзиера 290
Равносторонняя гипербола 285, 303
Раскрытие неопределенностей 235—239
Рациональные числа 5
Сегмент 7
Секанс 123, 124
Символ Ландау 24
Симметрия графика функции 42, 166, 264
Синус 73—75
Синусоида 74
Синусоидальные спирали 302
Сложение графиков 79, 80
Сопряженные гиперболы 285’
Спираль Архимеда 169, 304—306
—	- Галилея 308
гиперболическая 178, 179, 306
—	логарифмическая 308
—	параболическая 308
—	Ферма 308
Способ задания функции 10
-------- — аналитический 11
--------------графический 11
—	*7 параметрический 11
•--полуграфический 12
*	* — Ф> словесный 12
-г — & табличный 10
Строфоида 289
Таблица производных 217, 218
Тангенс 75
Тангенсоида 75
Точка возврата 265, 272
— двойная 265, 272
— изолированная 272
— особая 264, 271
— перегиба 230, 265, 273, 278
— пересечения с координатными осями
55, 264
—	разрыва 29
—	самокасания 272
—	узловая 272
—	устранимая 29
Трактриса 309, 310
Трисектриса Лоншама 288, 303
—	Маклорена 291, 303
Улитка Паскаля 176, 293, 294
Умножение графиков 85, 86
Условие монотонности функции 223
—	постоянства функции 223
Формула Коши 222
—	Лейбница 218, 220
—	Маклорена 223
—	Тейлора 222
Функции взаимно обратные 13
—	гиперболические 147, 153
—	обратные гиперболические 154, 155
«=• обратные тригонометрические 76—79
—	тригонометрические 73—76
—	элементарные 14, 15
Функция 9
—	алгебраическая 15
антье 12
—	биквадратная 134
—	возрастающая 16
—	Дирихле 12
—	дробно-линейная 139
—	дробно-рациональная 15, 140
—	иррациональная 15, 146
—	квадратная 129—131
—	кубическая 131—134
—	линейная 129
—	логарифмическая 73
—	многозначная 15
—	монотонная 17
—	* неограниченная 16
—	непрерывная 28
—	неубывающая 17
—	нечетная 17
—	обратная 13
—	ограниченная 16
—	однозначная 15
—	показательная 71, 72
—	рациональная 15, 129
—	Римана 12
—	сложная 14
—	степенная 14, 60—71
—	трансцендентная 15
—	убывающая 16
—	четная 17
Характерные точки графика 55, 56
Цепная линия 308,309
Циклоида 160, 310
Циссоида Диокла 288
Эвольвента окружности 312
Экстремум функции 56, 225, 226, 273,
277
Эллипс 281—283
Эпитрохоида 295, 296
Эпициклоида 294, 295
СОДЕРЖАНИЕ
Предисловие................................................ 3
ЧАСТЬ I
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
ЭЛЕМЕНТАРНЫМИ СПОСОБАМИ
РАЗДЕЛ 1
ОСНОВНЫЕ СВЕДЕНИЯ О ЧИСЛЕ, ПЕРЕМЕННОЙ ВЕЛИЧИНЕ
И ФУНКЦИИ............................................ . * «	5
§ 1.	Число. Переменная величина. Функция............... 5
Множество действительных чисел..................... 5
Основные свойства множества действительных чисел ( 5 )
Постоянные и переменные величины................... 8
Понятие функции.................................... 9
Способы задания функции........................... 10
Табличный способ (10 ). Графический способ (10 ). Аналитичес-
кий способ (11 ). Словесный способ (12 ). Полуграфический
способ (12 )
§ 2.	Классификация функций............................. 13
Обратные функции.................................. 13
Сложные функции . ...	•........................ 14
Элементарные функции................'	•........... 14
Однозначные и многозначные функции................ 15
Ограниченные и неограниченные функции............. 16
Монотонные функции..................•............. 16
Четные и нечетные функции......................... 17
Основные свойства четных и нечетных функций (18 )
Периодические функции............................. 18
§ 3.	Предел функции. Непрерывность	функции............. 21
Предел числовой последовательности	.	.	•.......... 21
Основные теоремы о пределах последовательности (21 )
Предел функции.................................... 22
Признаки существования предела (23 ). Односторонние пре-
делы функции (23 ). Теоремы о пределах (23 ). Классифика-
ция бесконечно малых функций (24 )
Непрерывность функции ............................ 28
Основные свойства непрерывных функций на отрезке (32 )
316
РАЗДЕЛ 2
ИССЛЕДОВАНИЕ ФУНКЦИЙ ДЛЯ ПОСТРОЕНИЯ ГРАФИКА . 32
§ 1.	Системы координат...................................................... 32
Декартова система координат..................; * 32
Полярная система координат.............................................. 33
Преобразования декартовой системы координат ....	35
Перенос начала координат (35). Поворот координатных
осей (35). Общий случай (перенос начала и поворот осей
координат) (36)
§ 2.	Исследование функции в декартовой системе координат 36
Область определения функции............................................. 36
Область значений функции. График ограниченной
функции................................................................  38
Четность и нечетность функции. Особенности графика
четной и нечетной функций............................................... 41
Виды симметрии. График обратной функции................................. 42
Симметрия графика функции у = f (х) относительно верти-
кальной оси х = х0 (42). Симметрия графика функции у = f (л)
относительно точки (х0; у0) (43). График обратной функ-
ции (45)
Периодичность функции. График периодической функ-
ции .........'.......................................................... 46
Нули и знаки функции.................................................... 48
Монотонность функции.................................................... 51
Выпуклость функции...................................................... 52
Некоторые свойства выпуклых функций (52)
Характерные точкц графика функции....................................... 55
Асимптоты графика функции............................................... 57
Порядок исследования функции и схема построения ее
графика................................................................. 59
РАЗДЕЛ 3
ГРАФИКИ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ ..... 60
§ 1.	Степенная функция...................................................... 60
Степенная функция с натуральным показателем ....	60
Степенная функция с целым отрицательным показате-
. лем.................................................................... 62
Степенная функция с рациональным показателем ...	65
Степенная функция с иррациональным показателем ...	70
§	2.	Показательная функция.................................................. 71
§	3.	Логарифмическая функция. 73
§	4.	Тригонометрические функции................... 73
§	5.	Обратные тригонометрические функции. 76
РАЗДЕЛ 4
ДЕЙСТВИЯ С ГРАФИКАМИ. ПРЕОБРАЗОВАНИЯ ГРАФИКОВ
В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ...................................................79
§ 1.	Арифметические действия с графиками.................................... 79
* Сложение и вычитание графиков.......................................... 79
Умножение и деление графиков....................•	85
§ 2.	Простейшие преобразования графиков..................................... 91
Э17
Преобразования, не изменяющие масштаба............ 91
Параллельный перенос (сдвиг) вдоль оси абсцисс (91). Парал-
лельный перенос (сдвиг) вдоль оси ординар (91)
Преобразования, изменяющие масштаб................ 92
Растяжение или сжатие по оси абсцисс (92). Растяжение или
сжатие по оси ординат (93). Построение графика функции
у = tnf (kx 4- а) 4- b (96)
Построение’графиков функций, аналитическое выраже-
ние которых содержит знак модуля..................100
Построение графика функции у = f (| х |) (100). Построение
графика функции у = | f (х) | (102). Построение графика
функции у = | f (|lx | ) | (103)
РАЗДЕЛ 5
ГРАФИКИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ . . , • . » , , , . 108
§ 1.	Построение графиков сложных функций.............. . 108
§ 2.	Графики алгебраических функций ...................128
Графики целых рациональных функций................129
Линейная функция (129). Квадратная функция (квадратный
трехчлен) (129). Кубическая функция (многочлен третьей
степени) (131). Биквадратная функция (134). Многочлен м-й
степени у — аохп 4- atxn—' 4- ... 4- an—1Х 4- ап (134). Функ-
ция вида у = (ах2 4- Ьх 4~ с)п, где п — целое положительное
число (137)
Графики дробно-рациональных функций ....... 139
Дробно-линейная функция (139). Дробно-рациональная функ-
ция (140)
Графики иррациональных функций ....	♦ . . , . 146
Функция вида у = ± Vax 4~ Ь 046). Функция вида у —
— ± /ах24- Ьх 4- с (146)
Графики трансцендентных функций...................147
# = sinrtx, ^/= cos# х, у — tgn х, у — ctg« х (147). у —
= sin-P/<?x, у = q-QS-P/Q х, у — tg — P/У х, y=ctg±P/Q х(147).
Гиперболические функции (147). Обратные гиперболические
функции (154)
РАЗДЕЛ 6
ГРАФИКИ ПАРАМЕТРИЧЕСКИ ЗАДАННЫХ ФУНКЦИЙ ... 155
§ 1.	Исследование параметрически ‘заданных функций . . . 155
§ 2. Примеры построения графиков параметрически задан-
ных функций........................................156
РАЗДЕЛ 7
ГРАФИКИ ФУНКЦИЙ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ 165
§ 1.	Исследование функций в полярной системе координат . 165
§ 2. Построение графиков функций в полярной системе
координат .... •.................................  169
Примеры построения графиков функций................169
Преобразования графиков в полярной системе коорди-
нат ............................,..................178
Основные свойства графиков функций в полярной системе ко-
ординат (178)
318
РАЗДЕЛ 8
ГРАФИКИ НЕЯВНО ЗАДАННЫХ ФУНКЦИЙ.............................180
§ 1.	Исследование неявно заданных функций................180
§ 2.	Построение графиков неявно заданных функций .... 182
§ 3.	Исследование кривых, заданных алгебраическим урав-
нением второй степени...............................190
§ 4.	Графики неявных функций, аналитическое выражение
которых содержит знак модуля........................197
§ 5.	Примеры построения графиков неявно заданных функ-
ций, которые удобно строить в полярной системе коор-
динат ..................................... ».•««•«.	200
РАЗДЕЛ 9
ГРАФИКИ БОЛЕЕ СЛОЖНЫХ ФУНКЦИЙ ........ 203
§ 1.	Построение графиков функций, заданных несколькими
аналитическими выражениями..........................203
§ 2.	Построение графиков функций, заданных некоторым
рекуррентным соотношением...........................205
§ 3.	Построение	графиков функций	вида	у^= [f (х)]	....	207
§ 4.	Построение	графиков функций	вида	y^=f([x])	....	209
§ 5.	Построение	графиков функций	вида	y= {f (x)}	...»	212
§ 6.	Построение	графиков функций	вида	#*=/({*})	. • • •	213
ЧАСТЫ1
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ С ПОМОЩЬЮ
ПРОИЗВОДНОЙ
РАЗДЕЛ 1
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ, ИХ ПРИМЕНЕНИЕ
К ПОСТРОЕНИЮ ГРАФИКОВ ФУНКЦИЙ........................  .	214
§ 1.	Производная функции одной переменной. Свойства про-
изводной. Производные основных функций...............214
Правила дифференцирования (216). Производные основных
функций (217). Прозводные высших порядков простейших
функций (218)
§ 2.	Дифференциал функции одной переменной...........219
§ 3.	Основные теоремы дифференциального исчисления ... 221
§ 4.	Исследование функции с помощью производных .... 223
Максимум и минимум функции.......................225
Исследование функции на экстремум с помощью первой
производной......................................226
Исследование функции на экстремум с помощью второй
производной .....................................228
Исследование функции на экстремум с помощью фор- .
мулы Тейлора.....................................228
Наибольшее и наименьшее значения функции на отрезке 229
Выпуклость кривой. Точки перегиба................230
, § 5. Построение графиков функций $ помощью производ-
ных ......................... ♦	. . i * ........ ♦ 231
В19
§ 6.	Построение графиков функций /' (х) и f' (х) по графику
функции /(х).......................-...........
§ 7.	Правило Лопиталя.........................
§ 8.	Приближенное вычисление корней уравнения.....
Метод хорд....................................
Метод касательных (способ Ньютона)............
РАЗДЕЛ 2
ПОСТРОЕНИЕ ГРАФИКОВ ВСЕХ ВИДОВ ФУНКЦИЙ . . . .
233 £
2351
239 J
239Т
240}
$
24^
§ 1.	Примеры построения графиков функций вида yt=f(x) i'.
в декартовой системе координат......................... 242|;\
§ 2.	Построение графиков параметрически заданных функ- |
ций...............................•...................... 264(у
Исследование параметрически заданных функций с по- И
мощью производных. . •.............................. 264 у
Примеры построения графиков параметрически задан- /
ных функций......................................... 266L
§ 3.	Построение графиков неявно заданных функций . . . 271К
§ 4.	Построение графиков функций в полярной системе
координат ....	............................. 277 у
раздел з
НЕКОТОРЫЕ ВАЖНЫЕ КРИВЫЕ..................................
§ 1.	Кривые второго порядка..........................
§ 2.	Кривые третьего порядка.........................
§ 3.	Кривые четвертого и высших порядков.............
§ 4.	Трансцендентные кривые............•.............
Предметный указатель	......................
281 '
287 F.
292 к
304^
314
£
НИНА АФАНАСЬЕВНА ВИРЧЕНКО
ИВАН ИВАНОВИЧ ЛЯШКО
КОНСТАНТИН ИВАНОВИЧ ШВЕЦОВ
ГРАФИКИ ФУНКЦИЙ
СПРАВОЧНИК
Редактор Р. И. Гусячая
Оформление художника В. Г. Самсонове
Худ9жественный редактор И. П Антонюк
Технический редактор Б. М. Кричегская
Корректоры М. Т Кравчук, Р С. Коган
Информ, бланк № 2949.
Сдано в набор 09.10.78. Подп. в печ. 28.02.79. БФ 00577. Формат 84x108/32. Бумаг
типогр. № 3 Лит гари. Выс. печ. Усл печ л 16,8 Уч -изд л. 17,08 Тирам
90000 экз Заказ 8-413. Цена 1 руб
Издательство «Наукова думка» 252601, Киев, ГСП, Репина, 3
Книжная фабрика им. М. В. Фрунзе Республиканского производственного объеди-
нения «Полиграфкйига» Госкомиздата УССР, Харьков, Донец-Захаржевская, 6/8.
1руБ.