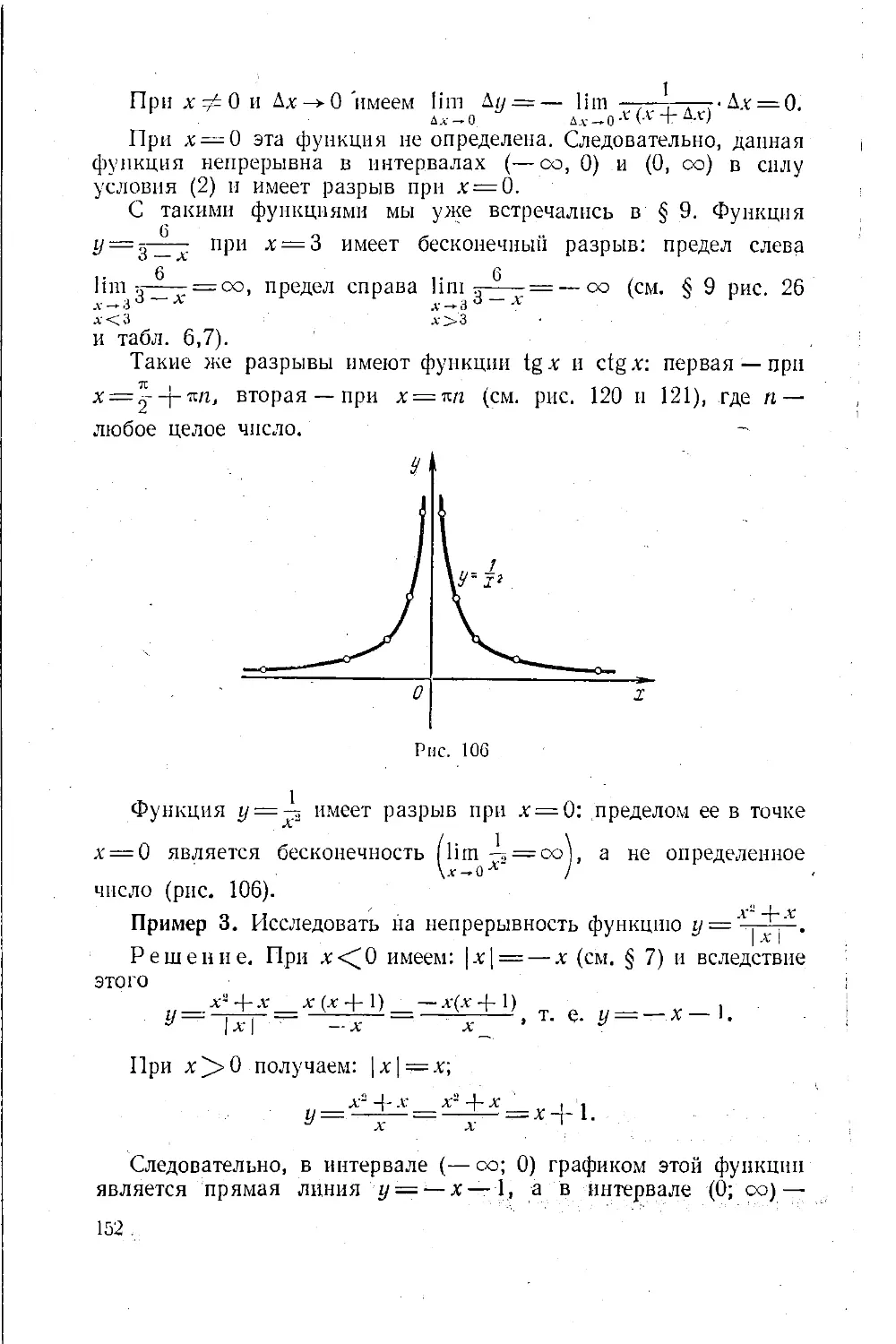
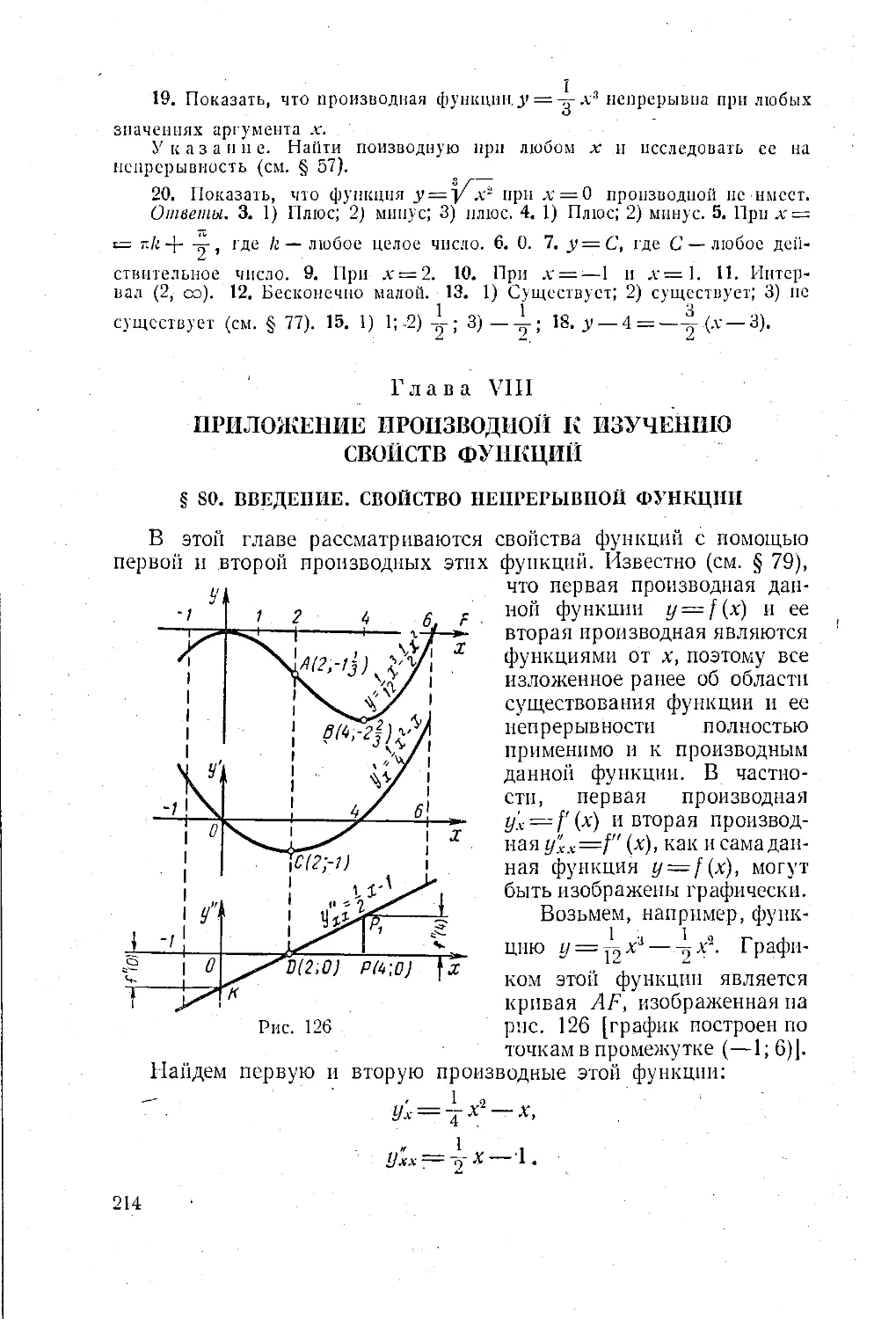
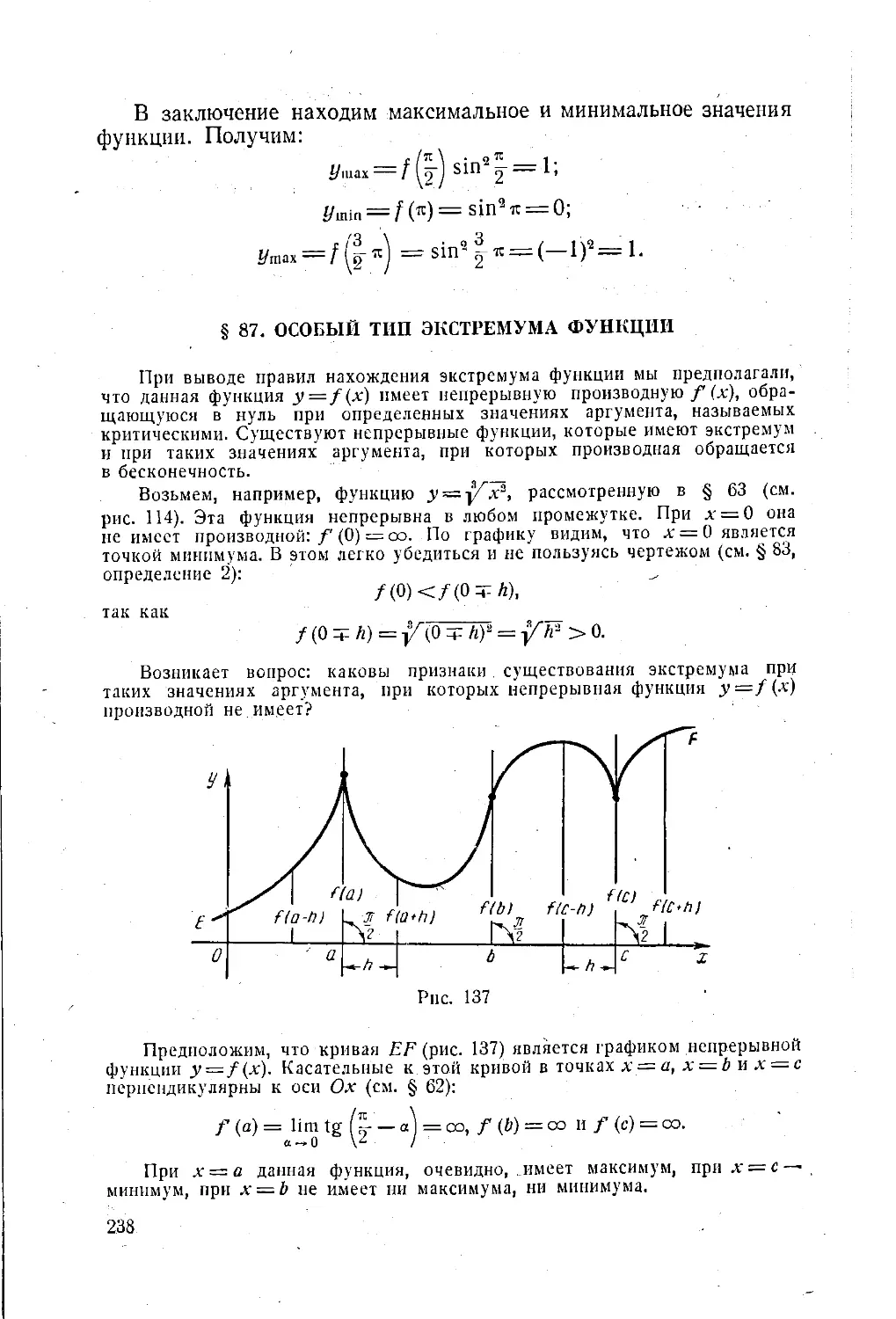
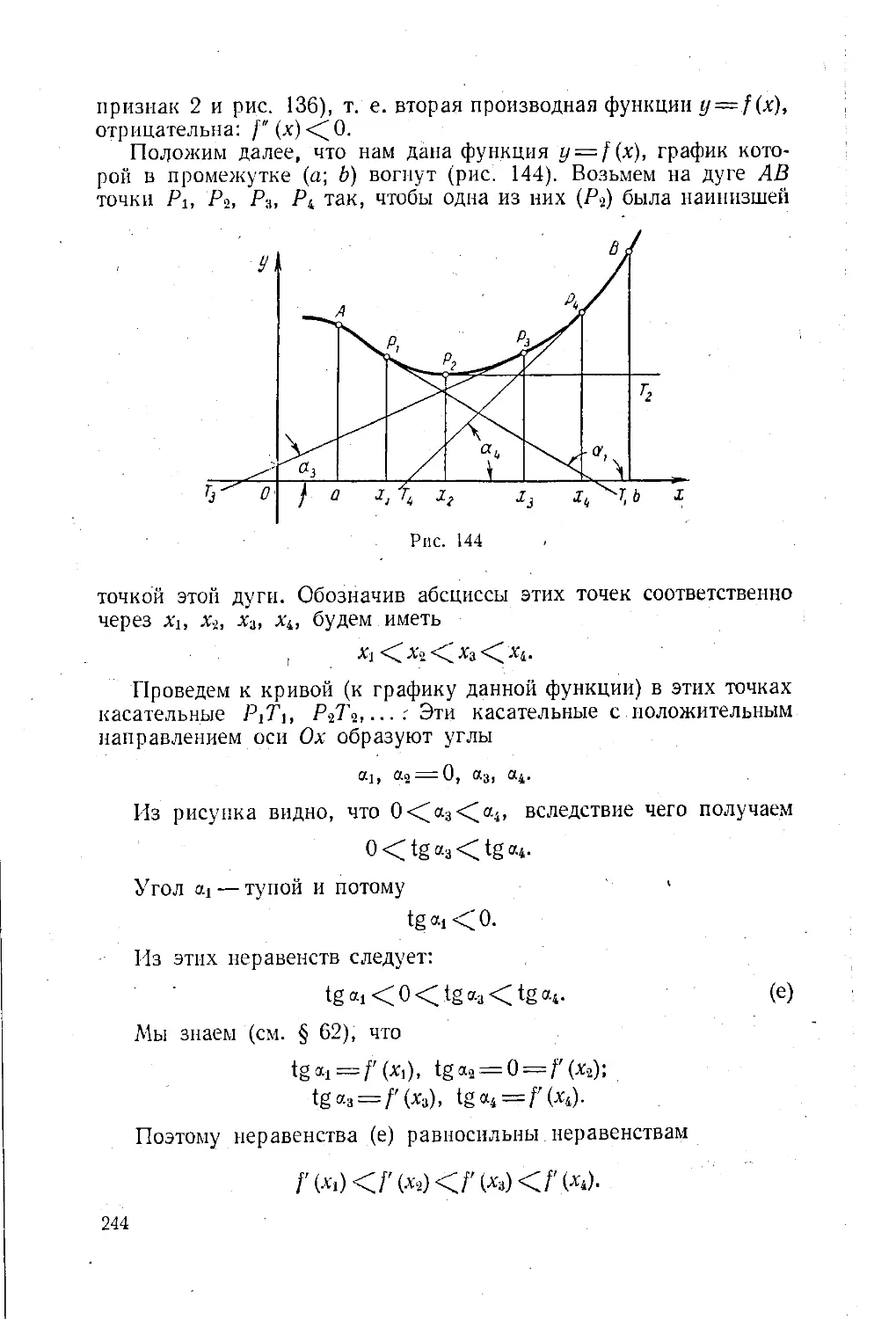
Текст
П. Е. А Г А Ч Е В
КУРС ВЫСШЕЙ
МАТЕМАТИКИ
ДЛЯ ЗАОЧНЫХ ТЕХНИКУМОВ
Допущено Министерством высшего и среднего
специального образования СССР в качестве
учебного пособия для заочных техникумов
ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА» МОСКВА — 1970
517
А23
Агачев П. Е.
А23 Курс высшей математики (для заочных
техникумов). Учеб, пособие для заочных
техникумов. М., «Высш, школа», 1970.
544 с. с илл.
В книге изложен в элементарной
форме курс высшей математики для уча-
щихся заочных техникумов и для зани-
мающихся самообразованием. Каждая те-
ма сопровождается задачами, упражне-
ниями и заданиями для самостоятельной
проработки, составленными применитель-
но к условиям заочного обучения и само-
образования. Значительная часть упраж-
нений и задач снабжена методическими
указаниями.
2-2-3
517
419-69
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Данный курс «Высшей математики для учащихся заочных
техникумов» составлен в соответствии с программой, утвержден-
ной Управлением средних специальных учебных заведений Ми-
нистерства высшего образования СССР в 1959 г. В основную часть
его сверх этой программы включены следующие темы: «Функцио-
нальная зависимость и способы ее выражения»; «Параметрические
уравнения кривых»; «Дифференцирование неявных функций»; «Осо-
бый тип экстремума функций»; «Кривизна кривой».
Первая тема введена с целью повторения материала, изучен-
ного на I курсе техникума, расширения, углубления и закреп-
ления учащимися основных понятий, подготовки на конкретных
примерах к пониманию и надлежащему усвоению теоретических
основ аналитической геометрии и анализа бесконечно малых ве-
личин. Вторая, третья и пятая темы даны с учетом требований
общетехнических и специальных дисциплин. Четвертая тема поз-
волит изучить более полно вопрос об экстремуме функции.
Некоторые главы (гл. Ill, VI, VII, VIII и X) начинаются с
.«Введения». Это объясняется тем, что при заочном обучении
сущность такой дисциплины, как математика, раскрывается лишь
по мере ее изучения и дать исчерпывающие методические указа-
ния в начале курса не представляется возможным. Введение под-
готавливает к изучению данной, и последующих глав, дает ука-
зания, какие вопросы из пройденного курса следует повторить,
чтобы успешно усвоить последующий теоретический материал.
Каждая глава завершается вопросами для самопроверки, пре-
имущественно теоретического характера. Практические вопросы
предлагаются лишь в меру необходимости проверки учащимися
степени понимания и усвоения темы.
Теория изложена возможно проще, с постепенным нараста-
нием трудности. К усвоению каждой новой темы учащийся под-
водится предшествующими задачами и упражнениями.
Степень трудности примеров, упражнений и задач также воз-
растает постепенно. Значительная часть их снабжена указаниями,
а некоторые — полным решением с пояснениями (такие задачи и
упражнения отмечены звездочкой).
1* з
Дополнительный материал дан в книге более мелким шрифтом.
Сравнительно большое количество рисунков объясняется стрем-
лением к. наибольшей конкретности и наглядности изложения.
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
В соответствии с программой, утвержденной 21 апреля 1968 г.,
настоящее издание книги дополнено следующими вновь написан-
ными темами: «Длина окружности»; «Площадь круга»; «Сумма
членов бесконечно убывающей геометрической прогрессии»; «Наи-
большее и наименьшее значение функции на данном отрезке» и
«Задачи на наибольшее и наименьшее значение функции».
В связи с изменением программы заново написана глава
XII — «Дифференциальные уравнения».
Сверх программы включены в книгу глава XIII — «Ряды» и
глава XIV — «Ряды Фурье».
Прежний текст исправлен и переработан. Исправлена также
нумерация формул. Сделаны многочисленные сокращения, исправ-
ления, дополнения и перестановки в теоретической части курса.
Кроме того, исправлены многочисленные опечатки и ошибки
в условиях задач и в ответах к ним. В этой работе неоценимую
помощь оказали своими замечаниями читатели книги — учащиеся-
заочники и лица, занимающиеся самообразованием. Считаю своим
приятным долгом выразить всем им мою искреннюю и глубокую
благодарность.
Автор
Поворотным пунктом в математика
была декартова переменная величина.
Благодаря этому в математику вошли
движение и диалектика.
Ф. ЭНГЕЛЬС
«Диалектика природы».
ВВЕДЕНИЕ
Предлагаемый курс высшей математики является продолже-
нием «Элементарной математики», изученной в школе и техникуме.
Возникла высшая математика в XVI—XVII вв. , когда быстрый
рост промышленности и международной торговли, а также бурное
развитие естественных наук и техники поставили перед матема-
тикой задачи, потребовавшие для их решения новых методов и
нового подхода к изучению взаимной связи величии.
Курс состоит из трех частей. О первой части — «Аналитичес-
кой геометрии» — вы уже имеете представление: числовая ось,
оси координат и координаты точки на плоскости — это понятия,
на которых основывается аналитическая геометрия. Кроме того,
вы умеете графически изображать зависимость между двумя ве-
личинами, связанными одним уравнением. Вспомните, как вы-
ражаются уравнениями прямо пропорциональная зависимость
(y = kx) и обратно пропорциональная зависимость (у—-^ между
двумя величинами х и у_ и как они изображаются на чертеже;
вспомните, как строятся графики функций:
r/ = sinx, y — cosx, y = tgx, у = а\ y — \ogax.
Во всех этих случаях хну рассматривались как величины
переменные и оказывалось, что каждому уравнению соответствует
на плоскости определенная линия как геометрическое место точек,
координаты которых удовлетворяют этому уравнению.
В чем же существо аналитической геометрии и чем она вами1
мается? На этот вопрос можно ответить следующее: сущность
аналитической геометрии заключается в том, что она, устанавли-
вая соответствие между точкой и парой чисел, называемых ее
координатами, и между линией и уравнением, связывающим коор-
динаты точек этой линии, дает возможность определить положение,
форму, размеры и свойства геометрических образов при помощи
алгебры.
По своему содержанию первая часть данного курса есть начало
науки, созданной под названием «Аналитическая геометрия» зна-
5
менитым французским философом и математиком Рене Декартом
(1596—1650).
Вторую и третью части, озаглавленные соответственно «Диффе-
ренциальное и интегральное исчисление» можно, объединить тер-
мином «анализ бесконечно малых величин». Эта наука возникла
в непосредственной связи с аналитической геометрией на основе
потребностей физики, астрономии, мореплавания, военного дела
и строительной техники; ее роль и значение в разрешении науч-
ных, технических и хозяйственных вопросов увеличиваются с
каждым годом.
Главная заслуга в создании анализа бесконечно малых вели-
чин принадлежит великому английскому математику, физику и
астроному Исааку Ньютону (1643—1727) и немецкому философу
и математику Готфриду Лейбницу (1646—1716)). Дать ясное поня-
тие о содержании и методах анализа бесконечно малых величин
сейчас невозможно, можно лишь заметить, что, установив понятия
«бесконечно малая величина», «производная» и «интеграл», анализ
бесконечно малых величин дал возможность легко и просто решать
такие задачи, как проведение касательной к любой кривой, вы-
числение площади фигур, ограниченных любыми кривыми линиями,
нахождение закона изменения скорости по данному закону этого
движения и обратно, вычисление величины давления жидкости
на стенки сосуда и т. д.
Некоторые учащиеся считают, что изучать математику, осо-
бенно высшую, — дело трудное, требующее особых способностей.
Это мнение справедливо лишь постольку, поскольку изучение
математики вообще и высшей в частности требует систематиче-
ской работы. Чтобы понять и усвоить содержание новой темы,
надо иметь ясные и отчетливые понятия по предшествующему
материалу и уровень математического развития, соответствую-
щий проработанному курсу, а также уметь пользоваться вычис-
лительными приемами, практиковавшимися ранее. Это доступно
каждому, и мнение, чго успешное изучение высшей математики
требует каких-то особых способностей, в корне неверно. Любой
учащийся, успешно усвоивший элементарную математику и при-
учивший себя к систематической и самостоятельной работе, долж-
ным образом усвоит предлагаемый курс высшей математики и
научился прилагать ее к решению практических вопросов.
В.ам предстоит изучить этот курс самостоятельно, по книге.
Как же наиболее плодотворно работать с математической кни-
гой? Ответ заключается в следующем.
1. Изучать математику по книге нужно не спеша, системати-
чески, изо дня в день. Перерывы в работе затрудняют понима-
ние и усвоение нового материала потому, что в силу естествен-
ного свойства человеческой памяти часть усвоенного ранее за-
бывается. Если учащийся двигается вперед поспешно, не проду-
мывая и не усваивая пройденное, он перестает понимать мате-
li
риал и напрасно теряет время. Вдумчивая же систематическая
работа повышает степень понимания и, следовательно, качество
усвоения, новые темы усваиваются тем легче, чем больше мате-
риала уже проработано.
2. Перед тем как изучать новую главу, следует прочитать
введение (если оно имеется) и восстановить в памяти все необ-
ходимое для понимания и усвоения содержащегося в этой главе
материала.
3. Каждый параграф надо изучать в таком порядке:
а) внимательно, не торопясь прочитать содержание; если
оно не совсем понятно, повторить пройденный материал, на ко-
тором базируется новая тема, и вновь прочитать параграф.
В некоторых случаях для уяснения существа вопроса полезно ра-
зобрать последующий пример;
б) параллельно с чтением текста построить в черновой тет-
ради чертеж и проделать все приведенные вычисления;
в) конспективно записать в тетрадь содержание параграфа,
не пользуясь книгой и черновиком;
г) основательно продумать решение примеров и задач, при-
веденных в конце параграфа;
д) самостоятельно перерешать задачи и примеры, служащие
практическим приложением к теории, изложенной в параграфе.
Если задачи решаются без больших затруднений, можно перейти
к. изучению следующей темы.
Основное требование при изучении теории — ясное понима-
ние. То, что не понято, не может быть усвоено. Механическое
заучивание ничего не дает, да и трудно запомнить то, чего не по-
нимаешь. Хорошо же понятые выводы легко запоминаются и
при надобности быстро восстанавливаются в памяти.
Изучая элементарную математику в школе и техникуме, вы
затрачивали на решение примеров и задач значительно больше
времени, чем на изучение теории. Решение задач имеет не менее
важное значение и в высшей математике: на задачах вы будете
учиться применять теорию к практическим вопросам, что очень
важно, так как теория без практики, знания без умения прила-
гать их к делу никакой ценности не представляют. Обдумыва-
ние и решение задач приучает активно, творчески мыслить, что
необходимо хорошему работнику любой профессии.
В процессе решения примеров и задач будут закрепляться
приемы вычислительной техники, без чего невозможно успешное
продвижение вперед ни в теории, ни в решении практических
вопросов. Наконец, степень умения решать задачи явится само-
контролем: если по данному разделу курса задачи решаются без
больших затруднений, это свидетельствует, что теоретический
материал усвоен вполне удовлетворительно; трудности, возника-
ющие при решении задач, — признак того, что материал плохо
усвоен и его следует повторить.
7
В книге много упражнений и задач; значительная часть их
снабжена методическими указаниями. Ряд задач имеет полное
решение с подробными пояснениями. Назначение таких указа-
ний— подготовка к самостоятельному решению сходных задач и
упражнений. Подобные указания необходимы самостоятельно
изучающим математическую дисциплину, но пользоваться ими
следует осторожно и сознательно. Приучайтесь после разбора
примеров в конце параграфа самостоятельно решать примеры и
задачи, не пользуясь указаниями. Одна самостоятельно решен-
ная задача приносит больше пользы, чем десять, решенных по
подсказке.
В заключение хотелось бы предупредить о следующем. Неко-
торые учащиеся, прочитав условие задачи, начинают рыться в
книге и в записях в поисках нужных формул. Это свидетель-
ствует о том, что материал усвоен плохо. Основные форму-
лы— это рабочий инструмент, и их надо запомнить. Учащийся,
приступающий к решению задачи, должен направить внимание
и усилия не на поиски формул (инструментов), а на то, как и
в какой последовательности применить их в данном конкретном
случае.
ЧА СТЬ ПЕРВАЯ
ОСНОВЫ АНАЛИТИЧЕСКОЙ
ГЕОМЕТРИИ НА ПЛОСКОСТИ
Глава I
МЕТОД КООРДИНАТ
§ 1. КООРДИНАТЫ ТОЧЕК НА ПРЯМОЙ
Аналитическая геометрия занимается изучением свойств гео-
метрических образов (линий, фигур) при помощи особого мето-
да— метода координат, сущность которого заключается в том,
что положение точек определяется при помощи чисел. В этом
параграфе рассматривается простейшая задача аналитической гео-
метрии— определение положения точки на прямой при помощи
числа.
Возьмем произвольную прямую (рис.1). По этой прямой воз-
можно перемещение в двух направлениях: вправо и влево. На-
N в 0 А М
—О---1—I—О—I—I—I—I—I—I—I—I—н-о 1— -------------
, е,
Рис. 1
правление вправо (показано стрелкой) будем считать положи-
тельным, а обратное (справа налево) — отрицательным. Такая на-
правленная прямая называется осью. Возьмем на оси произволь-
ную точку О и будем считать ее начальной точкой. Примем далее
некоторый отрезок г за единицу длины. Совокупность направ-
ленной прямой (оси), начальной точки О и указанной единицы
длины (масштаба) называется системой координат на прямой.
Установленная нами система координат дает возможность опреде-
лить положение любой точки, взятой на оси, одним числом.
Пусть на оси отмечены точки А и В. Положение точки А оп-
ределится одним числом ——= Ц-6, показывающим, во-первых,
сколько раз отрезок е, принятый за единицу, содержится в от-
резке длиной О А, во-вторых, в каком направлении (-)-) от иа-
9
чальной точки находится точка А. Точно так же одним числом
определится-и положение точки В: —— = —4.
Аналогично, любой точке М, расположенной вправо от началь-
ной точки О, будет соответствовать некоторое число х, опреде-
ляемое по форму ле х — , и любой точке N, расположенной влево
от точки О, — число Xi— 0N'
’ 1 е
Прямая Ох называется осью' координат, точка О — началом
координат, а число, определяющее точки на оси,—координатой
этой точки. Координату точки принято записывать в скобках у
названия точки справа. Так, например, запись В (—4) означает,
что координатой точки В является число :—4.
Очевидно, любому действительному числу на оси координат
будет соответствовать одна точка и, наоборот, положение любой
точки определится одним числом, называемым координатой этой
точки. Следовательно, на прямой устанавливается однозначное
соответствие между числом и точкой и наоборот.
Пример. Построить точки А (з и В (—4,5).
-8 -4 ~2 0 2 4 Ь
-4-1 Г1"' 1 1 ' ' 1? ' ' '
ВН.5)
Рис. 2
Решение. Возьмем ось координат (Ох), приняв какой-ни-
будь отрезок е за единицу масштаба (рис. 2). Положение точки А
определим, отложив отрезок, равный 3 у единицы масштаба,
вправо от начала координат, а точку В найдем, отложив отре-
зок, равный 4,5 единицы масштаба, влево от начала координат.
§ 2. НАПРАВЛЕННЫЙ ОТРЕЗОК. РАССТОЯНИЕ МЕЖДУ ДВУМЯ
ТОЧКАМИ НА ПРЯМОЙ ЛИНИИ
1. В элементарной геометрии отрезки прямой линии сравни-
ваются только по длине и не делается различия между нача-
лом отрезка и концом его. Поэтому отрезок, ограниченный точ-
ками В и С, а также длина его могут обозначаться ВС или СВ.
При этом очевидно:
ВС = СВ.
В аналитической геометрии принято указывать начало и конец
отрезка. Стргзок, ограниченный точками В и С (рис. 3), назы-
10
вается направленным, если одна из ограничивающих точек прини-
мается за его начало, а другая — за конец.
Направленный отрезок принято обозначать двумя буквами
с чертой над ними, ставя первой букву, которой помечено начало
отрезка. Следовательно, ВС будет обозначать направленный отре-
зок, началом которого является точ-
ка В, а СВ — отрезок, началом ко- , ,________,
торого является точка С. О в с I
Направленному отрезку ВС со- ,
ответствует перемещение от точки В Рис'
до точки С, а отрезку СВ — переме-
щение от точки С до точки В. Эти перемещения, очевидно, будут
равны по абсолютной величине, но противоположны по знаку.
Следовательно,
ВС = — СВ. (1)
2. Координата любой точки, взятой на оси координат, яв-
ляется относительным числом, соответствующим направленному
отрезку, началом которого следует считать начало координат,
концом — данную точку. Это число и есть величина направленного
отрезка. Так, на рис. 2 ОЛ = 4“Зу, ОВ = — 4,5. В этих прп-
0 А/Х,) в(12)
X,—J 1
В(Хг} О А1х,)
А(Х,) В(х2) О
j-----т, ~
Рис. 4
мерах начальной точкой направленных
отрезков служит начало координат (точ-
ка 0).
Выведем формулу для определения
величины направленного отрезка АВ, на-
чало которого (точка Л) не совпадает с
началом координат, по данным координа-
там точек Л и В.
На рис. 4 представлены три различных
случая взаимного расположения точек Л,
О и В. Во всех этих случаях координата
начальной точки Л обозначена через л'(
и координата конечной точки — через хг.
Следовательно, дано: ОА — xt, ОВ — х3, требуется найти величину
направленного отрезка АВ.
Рассмотрим 1-й случай. Из рис. 4 видно: OA-j-AB = OB или
АВ = ОВ — О А. Подставив вместо О В и О А соответствующие им
числа, получим
АВ = .y> —
Теперь рассмотрим 2-й случай. Из рис. 4 видно, что АВ =
— АО-^-ОВ', но по формуле (1) имеем АО — — ОА, значит
АВ ---- — ОЛ + ОВ - ОВ — ОА = х2 — х,.
11
3-й случай приводит к равенству
АВВО = АО или АВ=АО-ВО;
приняв во внимание формулу (1), получим
А0 = — О А — — хр, ВО —— 0В = —х2.
Подставив в предыдущее равенство вместо АО и ВО их зна-
чения, получим
АВ = —— (—х2) =—Х1Д-х2 = х2 — Xi.
Как видим, во всех этих случаях
AB^Xt-Xi . (2)
Следовательно, величина направленного отрезка АВ равна раз-
ности координат его конца х2 и начала Эта величина будет
положительной, если направление отрезка совпадает с положи-
тельным направлением оси координат, и отрицательной, если его
направление противоположно положительному направлению этой
оси.
Расстояние между двумя точками равно длине отрезка, огра-
ниченного этими точками. Длина отрезка — всегда положительная
величина. Следовательно, при любом возможном расположении
точек A (xj) и В (х2) на оси координат расстояние d между ними
будет определяться по формуле
d = АВ = \х.2 — %! | , (2а)
где запись | х.2 — xt1 означает абсолютную величину разности коор-
динат конца и начала направленного оi резка АВ.
Пример 1. Даны точки: А (7); В (—2); С (Д-4); D (—7).
Вычислить: 1) АВ; 2) ВС; 3) CD; 4) BD.
Решение. По формуле (2) найдем:
1) ЛВ = х2— Xi — хв — хА =—2 — 7 = —9;
2) ВС — х2 — Л] — хс — Хц = 4 — (—2) = 6;
3) CD = xd-xc = — 7 —4 = —11;
4) BD = xD — хв = —7 — (—2) = 2 — 7 = —5.
Пример 2. По данным предыдущей задачи найти расстояния
между точками: 1) А и С; 2) В и D; 3) С и В.
Решение. По формуле (2а) получим:
1) d2 = АС — | хг — Xi | = | хс — хА | = | 4 — 7 | =) — 3 | = 3;
2) d. = BD = \xd — xb\ = \—7-(—2) | = | —7 Д-21 = 5,
3) а2 — СВ — \хв — хс| = | — 2—4| = |—6| = 6.
12
§ 3. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ.
КООРДИНАТЫ ТОЧКИ НА ПЛОСКОСТИ
Возьмем на плоскости две взаимно перпендикулярные оси
координат: Ох и Оу (рис. 5). На первой из них (обычно горизон-
тальной) за положительное примем направление слева направо,
на второй (вертикальной) — снизу вверх (показаны стрелками).
Затем примем какой-либо отрезок е за единицу масштаба; жела-
тельно общего для обеих осей.
Определенные так две взаимно перпендикулярные оси коорди-
нат образуют прямоугольную систему координат на плоскости,
впервые введенную французским философом и математиком Рене
Декартом (1596—1650). Горизонтальная ось Ох называется осью
абсцисс, вертикальная Оу — осью ординат.. Осями координат пло-
скость разбивается на четыре части, называемые четвертями.
Нумеруются они в направлении, обратном движению часовой
стрелки, начиная с той части плоскости, которая ограничивается
положительными полуосями Ох и Оу (см. рис. 5).
Посмотрим теперь, как может быть определено положение
точки относительно осей, координат. Положим, что на плоскости
во второй четверти отмечена точка А (рис. 6). Опустив из этой
точки перпендикуляры AAt и АА3 на оси координат, получаем
направленные отрезки ОД и ОА$, которым будут соответствовав
два относительных числа:
О А, —5г г- О А, 4г .
Ха = —£ —----==—о; 1)л=—-=- = А.
е е < ул е е
Для точки В, расположенной в четвертой четверти, аналогич-
ным построением найдем-.
ОВ, 6,5г с ОВ„ —4,5г . _
*в = —L = — = 6,5; ув — —= = —— = —4,5.
г г ’ J г г
13
Очевидно, что в какой бы из четырех четвертей ни находи-
лась точка, ей будет соответствовать пара чисел х и у. Эти числа,
определяющие положение точки относительно осей координат,
называются координатами данной точки. Первое из них (х), явля-
ющееся величиной направленного отрезка от начала координат
до проекции данной точки на ось абсцисс, называется абсциссой
точки, второе (у), величина направленного отрезка от начала
С(-У;У) с2
ь.
у
ми, у)
Г,! Д
О
-2
-2
-у-
Ш-2,5,-6)^—
-6
е‘! 1
-----------ЬЕ(5,-3)
координат до проекции точки на ось
Оу, — ординатой точки. Координаты
точки принято записывать в скобках
рядом с буквой, которой обозначена
эта точка, ставя на первое место
абсциссу (рис. 7). Ординаты точек,
расположенных на оси Ох, очевидно,
будут равны нулю, точно так же
нулю будет равна абсцисса любой
точки оси Оу (рис. 8).
Мы видим, что положение любой
точки плоскости относительно осей
Рис. 7 координат определяется парой чисел,
называемых координатами этой точ-
ки. При этом, очевидно, любой данной точке соответствует един-
ственная пара чисел — ее координаты, и обратно, любой данной
паре чисел х и у, принятой за координаты точки, соответствует
точка на плоскости и притом единственная. Примем, например,
6 -4
У
2 Ч
2 4 1
х = —6; у =—3. Построив на осях координат отрезки (рис. 9)
Л- = Ши1=—6, у = = —3
и проведя через точки Mi и М$ перпендикуляры к осям Ох и Оу,
найдем точку М, в которой эти перпендикуляры пересекаются.
Так как две прямые могут пересекаться только в одной точке,
то точка М будет единственной, соответствующей числам —6, —3.
Следовательно, каждой паре чисел (х, у) на плоскости соот-
ветствует единственная точка, и обратно, положение любой точки
14
определяется одной вполне определенной парой чисел, называемых
ее координатами.
Пример. Построить точки: 1) А (6; —5); 2) В (4; 0); 3) С (0; —2).
Решение (рис. 10). 1) Возьмем на
оси Ох отрезок OAt, равный 6 единицам
масштаба, и через точку А, проведем
перпендикуляр к оси Ох, а затем на
оси Оу построим отрезок ОА?, рав-
ный —5 единицам масштаба, и через '
точку Ач проведем перпендикуляр к оси
Оу. Точка пересечения этих перпенди-
куляров А (6; —5) и будет искомой.
2) У точки В ордината равна нулю,
следовательно, она находится на оси
Ох на расстоянии ОВ от начала коор-
динат, равном 4.
3) У точки С абсцисса равна нулю, следовательно, она нахо-
дится на оси Оу и является концом направленного отрезка ОС.
Задача. Даны точки А (хА; уА) и В (хв; ув). Найти величины
проекций направленного отрезка АВ на оси координат.
Решение. Построив проекции точек А и В на оси коорди-
(рис. 11), получаем направленные отрезки А\В2 и Л2В2, пер-
из которых является проекцией АВ на ось Ох, второй — его
проекцией на ось Оу. Но мы знаем [см.
формулу (2)], что
-6
-k
-?
у.
о
-?
- 4
-6
6
4
2
г 4 si
А
С(О;-2) 1
-Ал--------4
А(6;-5)
Рис. 10
н ат
вый
А1В1 = х^ — Xt = xI} — Ха- -
Аналогично, для направленного от-
резка оси Оу будем Иметь
—1/в— ул.
Обозначив проекции АВ на оси Ох
Оу соответственно символами прЛАВ
пру.ДВ, получим:
прЛ АВ = хл — хА;
пру АВ = ув —уА.
II
II
§ 4. РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ ПА ПЛОСКОСТИ
В § 2 мы доказали, что расстояние между двумя точками А
и В, взятыми на оси Ох, определяется по формуле
d = AB — \x.2 — %] |,
где Xi и х-2 являются соответственно абсциссами точек А и В
15
(рис. 12). Расстояние между двумя точками С и D оси Оу опре-
делится, очевидно, по аналогичной формуле
di = CD = | y-i — yi |,
где у2 и у-i являются ординатами точек С и D.
Теперь решим такую задачу. Даны две точки: А (хй уА и
В (хс, у2); найти расстояние между этими точками.
Рис. 13
-р т-у,;
хз
Рис. 12
Построив проекции точек Л и В на оси координат, получим
(рис. 13): __ ___
OAi =xjj = ур,
0В1 = х-2; ОВ2 = у.2.
Через точку А параллельно оси Ох проведем прямую до пере-
сечения с прямой В>В в точке С. Получим прямоугольный тре-
угольник АВС, из которого по теореме Пифагора найдем
d'2 = АВ2 = АС2ВС2,
или
d=--AB--=V АС^г ВС.
Но мы знаем:
АС = AjB.i = | х2 — х21,
СВ = А2В-2 = | у2 — у\ |.
Подставим в предыдущее равенство вместо АС и СВ их най-
денные значения, получим
d = V(x.> — X,)- +((/1 — уА'2 . (3)
Итак, расстояние между двумя точками равно корню квадрат-
ному из суммы квадратов разностей одноименных координат этих
точек.
Замечание 1. При выводе формулы (3) точка А была взята
во второй четверти, точка В — в первой. Легко убедиться, что
16
эта формула будет справедлива и тогда, когда точки А и В рас-
полагаются в других четвертях.
Замечание 2. Так как
(х2 — Xt)2 = (Xi — х,)2
и
(№ —= —^)а.
то формула (3) будет равносильна формуле
d = /(X — х3)2 -]- — у.2)2.'
В частном случае, полагая х2 = 0 и т/2 = 0, получим формулу
для расстояния точки М (x; ijt) от начала координат:
или
rf = /(x-0)2 + (//1-0)a,
d = Vxf + y't
Эту формулу можно было получить непосредственно из чер-
тежа (рис. 14), применив теорему Пифагора к прямоугольному
треугольнику OKKi-
d = OK = VOK' + KiK* = /хЬЫ-
Пример 1. Найти расстояние отточ-
ки А (—3; — /7) до начала координат.
Решение. По формуле (За) найдем
d = = V (-3)2 + (-V7)2 =
= /9-}-7 — 4.
(За)
Пример 2. Найти расстояние между точками В(—2; —4) и
С(3; -1).
Решение. По формуле (3), приняв xt =—2, у\=—4,
х2 = 3, у> =— 1, получим
d = У(х2 -х)2 + (у,-yrf -У[3 - (-2)Г4 [-1 -(-4)Г —
= У(3 42)24-(-1-Н)‘2=Уз4.
Пример 3. Найти абсциссу точки, находящейся от начала
координат на расстоянии 5' единиц масштаба, если ордината ее
равна —3 единицы масштаба.
Решение. Обозначим искомую точку буквой /<, а координаты
ее — соответственно через хк и ук. Нам дано: Ук ——3, ОК —
= d — 5. Требуется найти хк. Известно [см. формулу (За)], что
расстояние от начала координат до точки К (хк\ ук) определяется
по формуле.
\ d=VxK-\-y‘1K.
17
Подставив в эту формулу вместо d и ук их данные значения,
получаем уравнение
5 = 1 хА-- -(—3)у
из которого находим:
х?<4-9 = 25; xj< = 16;
(хх)1,2 = ±4 ИЛИ (хх)! = 4; (ху<)2 = —4.
Задача, как видим, имеет два решения. Это значит, что на
данном расстоянии от начала координат имеются две точки с орди-
У
О
-4 у'
к/-2-
К'Н;-зГ-4-
ж-л
Рис. 15
правые части. Получаем
натой, равной —3 (рис. 15).
Пример 4. На оси абсцисс найти точ-
ку, равноудаленную от данных точек
А (—5; 4) и В (7; 8):
Решение. Найти точку — это значит
определить ее координаты. В данном слу-
чае искомая точка (обозначим ее через М)
должна лежать на оси Ох. Нам уже из-
вестно, что ордината любой точки оси Ох
равна нулю, следовательно, ум — 0. Ос-
тается неизвестной абсцисса этой точки (х^). В условии задачи
нам дано: AM = ВМ — d. По формуле (3) имеем:
d = AM = У(хм — хАГ + (ум-уАГ = (0—4)"’;
d = ВМ = у (хА1 - xtf 4- (1/Л1 - yrf = К(хм - 7)2 + (0—8)2.
Левые части последних двух равенств равны между собой,
следовательно, должны быть равны и ~
уравнение с одним неизвестным хЛ1:
V (Ли 4~5)'2 -j-16 = ]/\хм—7)а —j— 64.
Решаем это иррациональное
уравнение:
хм 4" 1 0хА1 4~ 25 4- 16 ==
= хм — 14хА| 4- 49 4- ^4;
24x^ = 49 4-64 — 25— 16 = 72;
хА1 = 3.
Итак, искомой точкой будет
Л1(3; 0).
В заключение рассмотрим гра-
фическое решение этой задачи.
Из элементарной геометрии известно, что любая точка, равноуда-
ленная от концов отрезка, лежит на перпендикуляре к этому
отрезку, проведенном через его середину. Отсюда следует, что гра-
фическое решение данной задачи (рис. 16) сводится к нахожде-
нию точки пересечения перпендикуляра к отрезку АВ в его сере-
дине с осью Ох.
18
§ 5. ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ
Рассмотрим задачу определения координат точки, делящеи
в данном отношении отрезок, ограниченный любыми двумя точ-
ками, взятыми на плоскости.
Задача может быть сформулирована следующим образом: дан
отрезок АВ координатами своего начала А(хь щ) и конца
В %)• Найти координаты хп ц
и г/о такой точки с, которая де-
лила бы этот отрезок в данном
отношении, т. е. чтобы
АС_,
СВ~ К'
где X — любое положительное чи-
сло*.
Положим, что точка С (х0; Уд)
(рис. 17) делит отрезок АВ так,
АС , „
что Проведем параллель-
но оси Оу отрезки AAj, CCi и Е
порциональных отрезках получим
Тогда по теореме о про-
А1С1_АС_
СД СВ~
У TiCt , ..
х- или с^=х-
Приняв во внимание, что
одинаково (слева направо) и
один и тот же знак, получим
отрезки Д]С1 и CtBl направлены
соответствующие им числа имеют
TliCi Л2С1 - AiCi у
----- = - = А ИЛИ •-----------А.
СА ClBl CLBL
Но мы знаем [см. формулу (2)], что
Л1С] — %о — хг, CiBi— Х-2 — Хд.
Внесем эти значения A)Ci и CjBi в предыдущее равенство:
Получилось уравнение с одним неизвестным. Решаем это урав-
нение:
Хо — Xi = Хх> — Ххо; Хо “J— Xxq = Xj -ф- Хх2;
(1 —X) Хо = Х| -j— XXgJ
получаем
v __xi + Хх3
Хп ;—; —г— .
* X—греческая буква; читается «лямбда».
19
Для определения у0 проведем параллельно оси Ох отрезки АЕ
и CD и, применив ту же теорему о пропорциональных отрезках
к сторонам угла АВЕ, получим
Отрезки ED и DB направлены одинаково (на чертеже снизу
вверх), поэтому очевидно:
Но, как мы уже знаем,
ED = ур — уЕ - Ус — Уа = Ул — УА
DB = yB —уо = уг — уй;
подставив найденные значения Е и В в предыдущее равенство,
получаем уравнение с одним неизвестным (у0):
У % У о
Решив это уравнение, получим:
Следовательно, координаты точки С (х0; у0), делящей отрезок АВ
АС ,
в отношении = Л, определяются по формулам:
_ А'1 + ^Х2. . ,, _ V, + Ъ’’
— 1 X > — 1 + X
(4)
где л-], iji являются координатами' начальной точки А, а и
у-2 — координатами конечной точки В отрезка АВ.
В случае, когда точкой С отрезок АВ делится пополам, полу-
чим
при этом.формулы (4) примут вид:
Следовательно, координаты середины отрезка равны средним
арифметическим координат его начала и конца.
Пример 1. Даны точки А (—4; —2) и В (6; 8). Найти: 1) коор-
АС 9
динаты точки С, делящей отрезок АВ в отношении =
2) координаты точки D, делящей этот отрезок в отношении
BD 2
UA 3 •
20
Решение. Определяем искомые координаты по формулам (4):
(рис. 18).
Пример 2. Даны точки А(—3; 1) и В(3; 3). Найти: 1) коор-
динаты точки С, ’делящей
отрезок АВ пополам; 2) координаты
точки D, если известно, что точка В
является серединой отрезка AD.
Рис. 18 Рис. 19
Решение. По формулам (4а) находим:
+ -3+'3__ З'д+А’в 1+3
лс_—-----_ — _0, ус = —— = ^ = ‘2.
2) По формулам (4а), выражающим координаты середины
отрезка в зависимости от координат его концов, имеем:
Подставив в эти формулы координаты точек <4 и В, полу-
чаем уравнения:
3~ 3 + xd. g 1 + -+
Решив указанные уравнения, найдем:
Хо — 9', уо = 5 (рис. 19).
21
Пример 3. Даны вершины треугольника: A (xt\ yt), B(xAyt),
С (х3; y-j). Найти центр тяжести этого треугольника.
Р/ешение. Из физики известно, что центром тяжести тре-
угольника является точка пересечения его медиан. В элемен-
X
воспользовавшись тем, что
находим:
тарной геометрии доказывается,
что точкой пересечения медиан
любая медиана делится на две
части в отношении 2:1, считая
эти части от вершины угла. Сле-
довательно, задача решается по
следующему плану:
1) находим координаты середи-
ны одной из сторон треугольника;
2) зная координаты концов
одной медианы (на рис. 20 взята
медиана АК~), определяем коор-
динаты . (х0; т/0) центра тяжести,
"Ж^Т^2’ ио Ф°РмУлам <4а)
по формулам
(4) получаем:
2“^’ Ух
2
V 1 О Л'з ~Ь Х'з
А'д + Чс_ 1 + 2 Г1+
1+2 — 3
. . 31 + 2 2 уЖзч+зч
~ 1 + А — 1+2 ~~ 3
Следовательно, координаты центра тяжести треугольника
равны средним арифметическим одноименных координат его
вершин:
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Что называется направленным отрезком прямой?
2. Если буквами К и М помечены две точки оси координат, то чем
будут отличаться друг от друга отрезки КМ и .МА'?
3. При соблюдении предыдущих условий! чему будут равны отношения:
1^-2)^?
км мк
4. На оси координат взяты точки А(—5), В (—1), С (5). Вычислить отно-
,, СА СА AS ' АВ АС АС CS я, СВ
шепни: I) =, 2) 757s; 3) ---; 4) — • 5) ==; 6) 7-7; 7) =;8) 77.
ВС ВС' ! ВС ВС' ' ВС ВС' АВ АВ
99
5. При каком условии будут справедливы равенства:
Лй= Л5. ДВ = _ А50
’ "ВС ВС' ~ ВС вс
Указание. На последующие вопросы отвечать, не пользуясь чер-
тежом.
6. Как расположена относительно оси Ох прямая, проходящая через
точки А (4; —3) и В (—5; —3)?
7. Как расположена относительно оси Оу прямая, проходящая через
точки С (—4; —2) и D (—4; 5)?
8. Если отрезок, ограниченный точками (7; а) и (7; 0), равен 4, то: 1) че-
му будет равно а; 2) чему будет равен отрезок, ограниченный точками
(7; а) и (7; —ai?
9. Как расположена прямая, проходящая через точки D (а; Ь) и Е (а; с),
относительно: 1) оси Ох; 2) оси Оу (а, Ъ и с — любые действительные
числа, отличные от нуля)?
10. Каково будет взаимное расположение двух прямых, если первая
пз них проходит через точки Л (а; Ь) и В (с; Ь), а вторая — через точки
С (d; е) и D (d; Л)?
11. Даны точки: Е (0; — 3), F (2; — 2), /<(4; —7), М (4, 2), Д7(—1;3),
L (—2; 0). Не пользуясь чертежом, выделить точки, которые лежат внутри
четырехугольника с вершинами в точках Д(—2; 4), 5(6; 4), С(—2; —3)
и D (6; —3).
12. При каких значениях а расстояние от начала координат до точки
К (а; 3) будет равно 5?
13. Чему равно Ь, если расстояние точки М (—7; Ь) от начала коорди-
нат равно 25?
14. При каких значениях у расстояние между точками А (—1; 2) и
В (3; у) будет равно 5?
15. При каких значениях х и у отрезок, ограниченный точками А (—1;у)
АВ 1
С (.г; 8), разделится точкой В (—2; 4) в отношении у-.-. =
L$\~j Z
и
Ответы- 4. 1) --Д; 2) 4; 3) 4; 4) т; 5) 4; 6) 4; 7) ~4; 8) 4.
О О О О О О £ £
6. Под осью Ох. 7. Влево от оси Оу. 8. 1) 4; 2) 2а. 9.1) Перпендикулярна оси Ох;
2) параллельна оси Оу. 10. Взаимно перпендикулярны. 11. Л4 (4; 2), ЛГ(—I; 3)
и F (2; —2). 12. а = щ 4 [составить уравнение с. неизвестным а, воспользо-
вавшись формулой (За)]. 13. = 14. У1=—1, = 5. 15. х = 2, у~
— 2 [воспользоваться формулами (3)].
Глава IL
ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И СПОСОБЫ
ЕЕ ВЫРАЖЕНИЯ
§ 6. ВЕЛИЧИНЫ ПЕРЕМЕННЫЕ И ПОСТОЯННЫЕ
В физике и математике вам встречались уже самые разнооб-
разные величины: в.физике— удельный вес, атмосферное давле-
ние, температура, скорость движения, ускорение и т.д.; в мате-
матике — длина, площадь, объем, угол и т. д.
При изучении процессов, связанных с теми или иными вели-
чинами, обращалось внимание также на то, что при заданных
23
условиях одни величины сохраняют значение неизменным, другие
же, изменяясь, принимают различные числовые значения. По этому
признаку различают величины постоянные и переменные.
Переменной называется такая величина, которая при задан-
ных условиях может принимать различные числовые значения. Так,
в равномерном движении переменными величинами будут время и
пройденный путь, в равноускоренном — скорость, путь и время.
Величина называется постоянной, если она при заданных
условиях сохраняет свое значение неизменным. В предыдущих при-
мерах постоянными величинами являются скорость и ускорение.
Как видно, одна и та же величина (в данном случае — скорость)
в одной задаче может быть переменной и в другой — постоянной,
при этом как скорость в равномерном движении, так и ускорение
в равноускоренном движении сохраняют свои значения неизмен-
ными лишь в условиях данной частной задачи.
Имеются, однако, величины, сохраняющие значение неизмен-
ным при любых возможных случаях. Такие величины принято
называть абсолютно постоянными. Как пример абсолютно постоян-
ных величин можно привести отношение длины окружности к
длине диаметра (число л), сумму внутренних углов прямолиней-
ного треугольника, скорость света в пустоте (300 000 км/сек).
Величины, сохраняющие значение неизменным лишь в условиях дан-
ной частной задачи, часто называют параметрами. .
Постоянные величины обычно обозначают первыми буквами
латинского алфавита (a, b, с, d), переменные — последними
(/, и, X, у, Z).
§ 7. АБСОЛЮТНАЯ ВЕЛИЧИНА ОТНОСИТЕЛЬНОГО ЧИСЛА. .
ДОПУСТИМОЕ ЗНАЧЕНИЕ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ
1. Абсолютной величиной положительного числа а или нуля
называется само это число. Если а — число отрицательное, то его
абсолютной величиной называется число а, взятое с противополож-
ным знаком.
Абсолютную величину относительного числа принято обозна-
чать, помещая его между двумя вертикальными черточками. Так,
. |а [ = а, если a5s0;
| а | — — а, если а <Г 0 *;
|6| = 6; I — 6| = 6; 101 =0.
Согласно определению уравнение |х|= 8 должно иметь два
корня: л'1 = —8, х2 = 8, что легко проверить. Подставляя в урав-
* Если 0, то, очевидно, (—а)>0.
24
нение вместо х последовательно числа — 8 и 8, получаем:
| — 81 = 8, или 8 = 8;
181 = 8, или 8 = 8.
Из алгебры известно, что в неравенстве х<(8 значения х мо-
гут быть лишь меньше 8.
Из неравенства | х | <( 8 следует, что х может принимать лю-
бые числовые значения, заключающиеся между числами —8 и 8,
т. е. удовлетворяющие условию —8 <^х <^8.
Тогда из записи | х | -С 8 (символ читается «меньше или
равно») следует, что х может принимать любые значения, начиная
от числа —8 и кончая числом 8. Кратко это можно записать в
следующем виде:
— 8'<-V-c8.
Примечание. Абсолютная величина отрицательного числа
тем больше, чем меньше это отрицательное число, и обратно.
Например,
— 6< —4, а |-6|>| — 4|.
2. В предыдущем параграфе было сказано, что переменной
называется такая величина, которая при заданном условии может
принимать различные числовые значения. Значит ли это, что пе-
ременная величина х при любых условиях _______
может принимать любые числовые значения?
Для выяснения разберем следующие примеры. / \Л
1. Из точки окружности, радиус которой /
равен 7?, проводится хорда. Какие значения 4 ( “дДя
может принимать длина этой хорды при всех /
возможных ее положениях? \\ у
При заданном условии переменной ве-
личиной (обозначим ее через х) является дли- Рис. 21
на хорды. Здесь х может принимать лишь
такие числовые значения, которые удовлетворяют условию
О ДД'С 2/?, т. е. большие нуля и непревышающие/шсла 2Д (рис. 2Г).
2. Основание треугольника АС — b, его вершина В перемеща-
ется по прямой КМ, параллельной основанию треугольника и на-
ходящейся от него на расстоянии h. При таком преобразовании
треугольника какие значения могут принимать: 1) любой из уг-
лов при основании? 2) любая из боковых сторон?
Очевидно, что при данных условиях:
1) любой из внутренних углов а и [3 при основании (рис. 22)
может принимать лишь такие значения, которые заключаются между
0° и 180°, т. е. удовлетворяют условиям:
0°<а<180°; 0<^< 180°;
25 1
2) длина каждой из боковых сторон АВ и ВС может принимать
значения, удовлетворяющие условиям
/1=^ЛВ<^оо; /1ь<БС<^оо.
3. При соблюдении условий предыдущей задачи какие зна-
чения могут принимать: 1) синус угла при основании треуголь-
ника? 2) косинус этого угла?
А С
Рис. 22
Из тригонометрии известно, что: 1) в первой четверти синус
угла возрастает от 0 до 1, во второй убывает от 1 до 0, сле-
довательно, синус угла при основании треугольника может при-
нимать лишь такие значения, которые удовлетворяют условиям
0<^sina<4, 0<^ sin 1; 2) косинус угла в первой четверти
убывает от 1 до 0, во второй — от 0 до —1, значит для данной
задачи косинус угла при основании треугольника может при-
нимать значения, удовлетворяющие условиям:
— 1 <С cos a <С 1; —l<COSp<l.
4. Какие значения может принимать sinx, когда угол изме-
няется от 0° до 360°?
Из тригонометрии известно, что при любых значениях угла х
абсолютная величина sinx не может быть больше единицы, т. е.
| sinx| 1. Значит sinx может принимать только такие значения,
которые удовлетворяют условиям
—l^sinx^l.
Из рассмотренных примеров видно, что значения, принимае-
мые переменной величиной, в каждом отдельном случае зависят
от конкретных условий.
Числовые значения, которые данная переменная величина может
принимать при данных условиях, принято называть допусти-
мыми значениями этой величины.
§ 8. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
-Понятие о функциональной зависимости между переменными
величинами уже усвоено вами из алгебры и тригонометрии.
Известны также и основные способы выражения функциональной
зависимости, или проще функции: табличный, графический и
аналитический. '
26
Примером на задание функции с помощью таблицы служат
хорошо 'известные таблицы тригонометрических функций, лога-
рифмов чисел и логарифмов тригонометрических функций, по
каждой из которых по данному значению одной вели-
чины быстро, без вычислительной работы, находится соот-
ветствующее значение другой (например, по данному
значению угла а находится sin а). Много таблиц, в которых
приводятся соответствующие значения двух переменных величин,
зависящих друг от друга, можно встретить в технических спра-
вочниках (например, таблица зависимости температуры кипения
воды — /°C и давления — Р, атм).
Графическим способом задания функции являются известные
вам графики температуры и атмосферного давления. Этот способ
применяется преимущественно при возможности использования
самопишущих приборов (графики температуры . и атмосферного
давления, вычерчиваемые термографом и барографом, графики-
осциллограммы колебательных явлений, записываемые осцил-
лографом).
Аналитический способ задания функции особенно
важен в математике. Заключается он в том, что зависимость
между переменными величинами выражается уравнением или
формулой. В качестве примеров можно привести следующие
уравнения.
Пример 1. y — kx (уравнение, выражающее зависимость между
двумя прямо пропорциональными величинами х и у).
Пример 2. у = — (уравнение, связывающее обратно пропор-
циональные величины х и у).
Пример 3. у = ах2 Ьх с (полином второй степени).
Пример 4. г/= sinx (уравнение, связывающее угол х с его
синусом у). .
Во всех этих случаях изменение х вызывает изменение у, и
любому допустимому значению переменной х соответствует одно
определенное значение у.
Определение. Переменная величина у называется функцией
переменной величины х, если каждому допустимому значению х
соответствует определенное значение у. При этом переменная
величина х называется независимой переменной, или аргументом,
а переменная у, изменяющаяся в зависимости от изменения х, —
зависимой переменной, или функцией х.
В примерах 1—4 зависимость между переменными величинами
х и у выражалась уравнением, разрешенным относительно функ-
ции, но бывает и так, что уравнение, связывающее функцию у и
аргумент х, не разрешено относительно у. Рассмотрим такую задачу.
Пример 5. Выразить аналитически зависимость между коор-
динатами любой точки плоскости, находящейся от начала коор-
динат на расстоянии 5 единиц масштаба.
27
Решение. Обозначив координаты произвольной точки,
удовлетворяющей условию задачи, через х и у, по формуле
будем иметь
Возвысив обе части этого равенства в квадрат, получим х2ф-
-фу- — 25 — уравнение, не разрешенное относительно функции
(у рассматриваем как функцию от х).
Решив это уравнение относительно функции, найдем
z/ = rk/25^A
Как видим, в этом случае каждому допустимому значению
независимой переменной х соответствуют два значения функции:
если х = 3, то
У! = У 25 — 3- ----- 4; у> = — /25 — 9 - — 4;
если х =— 4, то
у1==У25 — (—4У = 3- у.2 = —]/25- 16 = —3.
Пример 6. Возьмем уравнение tgy = x. Рассматривая угол у
как функцию от х и решив это уравнение относительно функции,
получим
у — кп arc tg х,
где п — любое целое число.
Это значит, что всякому действительному значению х соот-
ветствует бесконечное множество значений функции у. Например,
при х—1 (давая п последовательно значения 0, 1, 2, 3, ...
.... —1, —2, —3) получаем:
Функция называется однозначной, если
значению аргумента соответствует одно
каждому допустимому
определенное значение
функции (примеры 1—4). Если каждому допустимому значению
аргумента соответствуют два и более значений, то функция
называется многозначной (двузначной, трехзначной и т. д., при-
меры 5—6).
Выше мы видели, что связь между функцией и аргументом
может быть выражена уравнением, разрешенным относительно
функции (примеры 1—4), и уравнением, не разрешенным относи-
тельно функции (примеры 5—6). В зависимости от этого функции
разделяются на явные и неявные.
28
Явной называется такая функция, которая задается уравне-
нием, разрешенным относительно функции. Явными функциями,
например, будут
у= 2х'3-ф Зх — 5, r/ = arcsinx; у = Vax1 Ьх с.
Функция называется неявной, если она задается уравнением,
не разрешенным относительно этой функции. Таковы, например,
функции
ах-\-Ьу=с, 4х2 -ф-у1 = 12; у1 = 8х.
Для определения значения функции у, заданной в неявном
виде (при данном значении аргумента х), надо предварительно
представить ее в явном виде. Получим:
У=; у = ± /12 —4х2; у = ± 2 /2х.
Разберем некоторые вопросы о допустимых значениях аргу-
мента.
1. Какие значения аргумента следует считать допустимыми
для любой данной функции? Для любой данной функции следует
считать допустимыми такие значения аргумента, при которых
значения функции будут выражаться действительными числами.
2. Какие значения может принимать независимая переменная
х в уравнении T/ = log5x? Из алгебры известно, что отрицатель-
ные числа при положительном основании логарифма не имеют,
а нуль не имеет логарифма ни при каком основании. Следова-
тельно, в данном случае допустимыми значениями аргумента
х будут числа, удовлетворяющие условиям
3. Дана функция у = ^ , где а — любое действительное число,
отличное от нуля. Какие значения может принимать аргумент х?
Для этой функции допустимыми значениями аргумента являются
все действительные числа, за исключением нуля, так как при
х = 0 дробь y теряет смысл — на нуль делить нельзя*.
4. Дана функция y = V4— х1. Какие значения может при-
нимать независимая переменная х? В этом случае- допустимыми
значениями х являются числа, по абсолютной величине не превы-
шающие числа 2, так как при значениях х, по абсолютной вели-
чине больших 2, значения у оказываются мнимыми.
* Известно, что из равенства у= — следует, что х • у = а. Еслих = 0,
то при любом у(—со<_у<со) произведение х-_у равно нулю, а нс числу а.
Следовательно, не существует такого значения у, при котором х = 0.
29
§ 9. ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ФУНКЦИОНАЛЬНОЙ
ЗАВИСИМОСТИ, ВЫРАЖЕННОЙ АНАЛИТИЧЕСКИ
Изучая алгебру и тригонометрию, вы уже занимались пост-
роением графиков функций, задаваемых уравнением, разрешенным
относительно функции (явных функций). Здесь мы ставим задачей
определить геометрический смысл любого уравнения с двумя не-
известными, когда эти неизвестные рассматриваются как перемен-
ные величины, "связанные между собой данным уравнением.
Разберем несколько примеров, начиная с известных ранее.
Пример 1. Построить график линейной функции у — 2х—1.
Составим таблицу значений аргумента и функции (табл. 1),
давая аргументу х последовательно значения —5, —4, —3,
—2, .... 5, 6, ... и определяя соответствующие значения у.
Таблица 1
А' —5 —4 —3 —2 —1 0 1 2 3 4 5 6
У —11 —9 —7 —5 —3 —1 1 3 5 .7 9 11
Нетрудно понять, что в этой таблице помещена очень малая
часть пар значений аргумента и функции (всего 12): во-первых,
аргументу х можно давать еще множество целых положительных
и отрицательных значений, во-вторых, можно себе представить,
как будет увеличиваться число пар значений аргумента и функ-
ции, если х изменять так, чтобы каждое последующее значение
отличалось от предыдущего на очень малую дробь (например,
на 0,00001, 0,000001, 0,0000001 и т. д.).
Если на каждую пару значений хну смотреть как на коор-
динаты точек, то окажется, что одному уравнению с двумя пере-
менными на плоскости соответствует бесчисленное множество
точек. Посмотрим, как эти точки располагаются на плоскости.
Построим сначала точки (—5; —-11), (—4; —9), ..., (6; 11)
(на рис. 23 показаны кружками). Мы видим, что они распола-
гаются на плоскости не в случайном порядке, а по прямой
линии.
Попробуем дальше изменять х так, чтобы разность двух
соседних значений была меньше 1. Пусть, например, х принимает
значения
. в .1.1 з 1
-1 у, -1 -2-, -1Т, -т, -у ... и т. д.
Вычислив соответствующие значения у, находим пары чисел
(координат точек), приведенные в табл. 2.
30
таблице, располагаются на той же прямой (на рис. 23 они пока-
заны крестиками). Точно так же
можно показать, что любая точ-
ка, координатами которой яв-
ляется пара чисел, удовлетво-
ряющих данному уравнению, будет
лежать на этой прямой.
Значит данному уравнению
первой степени с двумя перемен-
ными на плоскости соответствует
прямая линия как геометри-
ческое место точек, координаты
которых удовлетворяют этому
уравнению. Эта прямая называ-
ется графиком данной функции
у=Чх—1.
Известно, что графиком поли-
нома первой степени y = kx-\-b
при любых значениях параметров
k и b является прямая линия,
поэтому функция у = Лх-|- b назы-
вается линейной.
Пример 2. Построить график
функции второй степени у =
= ту- X2 — 3 X.
Давая аргументу х последовательно значения —3, •—2, —1,
О, 1, 2, ... и вычислив соответствующие значения у, получим
следующую таблицу пар чисел, удовлетворяющих данному урав-
нению (табл. 3).
Таблиц а 3
Л* — 3 — 2 —1 0 1 2 3 4 5 6 7 8 9
У 13 — 13 2 8 Зд 0 1 [О - — 4 -4 — 4 9 1 “ 2 0 4 8 4
31
Таблица 4
X 1 2 1 2 Ч- 4 з 1 8 2-
у 1 5- 8 1 со [ ос со |со 7 - СО |со 7
Строим точки (—2; 8), f—1; 3^ и т, д. (на рис. 24 пока-
заны кружками). Как видим, в расположении этих точек тоже
есть закономерность, но не такая, как в первом примере. Соста-
вим еще дополнительную таблицу, да-
вая х дробные значения (табл. 4).
гг ! 1 1 5\ / 1 1 3)
Построив точки I— 1 gI, l-g; — 1 gj
и т. д. на том же чертеже (они пока-
заны крестиками) и соединив все точки
плавной линией, получим кривую ли-
нию, называемую параболой.
Пример 3. Построить график функции
х1 -р 4т/2 = 16. .
Этим уравнением у задается как не-
явная функция х. Решив уравнение от-
носительно у, получаем явную функцию
z/=±iVi6
Здесь наименьшим допустимым значением аргумента будет
чцсло —4, наибольшим Ц~4, так как при значениях х, ио абсо-
лютной величине больших 4, значения у делаются мнимыми.
Каждому допустимому значению х соответствуют два значения у.
Следовательно, у является двузначной функцией от х.
Таблица 5
X — — 4 — 3 — 2. —1 0 1 2 3 4
У = 0 Ци Щрз 1 + -2)'П5 ±2 0
У^ щ 1,3 щ1,9 11 1,7
32
Принимая последовательно х равным —4, —3, —2, —1, О,
1, .... 4, находим:
У, = ± | К16-(- 4)* = 0; у,.з = ± /16 -(-Зу2 = ± 1 /7
и т. д. (табл. 5).
Строим точки (—4; 0), (—3; -1/7^, (—3; —
]/3), (—2; —/3) и т. д. и, соединив их плавной кривой, полу-
чаем кривую линию, называе-
мую эллипсом (рис. 25).
Пример 4. Построить график
функции Зу— ху — 6 = 0.
Решив данное уравнение от-
носительно у, получаем
6
В данном случае допустимы-
ми значениями аргумента явля- Рис. 25
ются все действительные числа,
6
за исключением числа 3, так как при х = 3 дробь ~5 теряет
о — о
смысл — на нуль делить нельзя.
При значениях х, удовлетворяющих неравенству 3 — х^>0
или х</3, у, очевидно, будет принимать положительные значе-
ния, а при значениях его, больших числа 3, значения у будут
отрицательны.
Таблица 6
X = — 5 — 4 — 3 — 2 —1 0 1 2 2 — 2 4 ц — 3
У — 2 4 6 7 1 4 4 2 3 6 12 24 48 —* со
Составим сначала таблицу значений аргумента и функции при
значениях х, меньших 3, например при х —— 5, х = — 4, ...
(табл. 6):
_ 6 __ 3
— з - (— 5) ~ 4 ’
6 6
^ = 3-(-4) = Т И Т- Д-
Как видно из таблицы, при значениях х, приближающихся
к числу. 3. значения у быстро возрастают. Построив точки
2 П. В. Агачев
33
Таблица 7
х = 10 9 8 7 6 5 4 34 3 1 — 3
У = 6 7 —1 -4 -4 — 2 — 3 — б — 12 — 24 — 48 -* оо
(—5; -^j, —4; yj........^2у; 12J и соединив их плавной кри-
вой, получим одну ветвь графика данной функции (рис. 26).
При значениях х, больших 3, получим значения, приведенные
в табл. 7. Плавная кривая,
соединяющая точки (10; —yj, (9;
—1), ..., —12^, является вто-
рой ветвью графика этой функции.
Мы получили кривую линию,
являющуюся геометрическим местом
точек, координаты которых удов-
летворяют уравнению Зу— ху—6=0.
Такая линия называется гипер-
болой.
Вывод. Одно уравнение с двумя
переменными величинами х и у имеет
бесконечное множество решений. Если
каждую пару значений х и у рас-
сматривать как координаты точки,
то оказывается, что уравнению с
двумя переменными на плоскости со-
ответствует бесчисленное множество
точек, геометрическим местом кото-
рых является линия. Следовательно,
одному уравнению, связывающему пе-
ременные координаты х и у, на плоскости соответствует линия,
положение и вид которой вполне определяются данным уравнением.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Какая величина называется переменной?
2. Какая величина называется постоянной?
3. Какими величинами являются координаты данной точки?
4. Точка перемещается по прямой, перпендикулярной к оси Ох. Какой
величиной будет: 1) абсцисса этой точки; 2) ордината этой точки?
5. Какими величинами являются координаты точки, перемещающейся по
какой-нибудь кривой?
6. Две вершины треугольника совпадают с концами диаметра данной
окружности, а третья вершина перемещается по полуокружности. Какими
34
величинами будут: 1) внутренние углы; 2) стороны; 3) высота; 4) периметр;
5) сумма внутренних углов этого треугольника?
7. Между какими числами содержатся все допустимые значения х и у,
если точка А (х; у) может занимать любое положение внутри окружности,
проведенной из начала координат радиусом, равным 4 единицам масштаба?
8. Две стороны треугольника соответственно равны а и b (а>Ь). Какие
значения может принимать длина х третьей стороны, когда противополож-
ный угол, изменяясь, принимает все допустимые значения?
9. Гипотенуза прямоугольного треугольника равна с. Какие значения
может принимать катет а, если противолежащий угол, изменяясь, принимает
все допустимые значения?
10. Зависимость между переменными величинами х и у задана уравне-
нием Зх— 2у 4-5 = 0. Выразить: 1) у как явную функцию х; 2) х как явную
функцию У-
11. Дано уравнение: Зх2 — 4у2—12 = 0. Решить это уравнение: 1) отно-
сительно х; 2) относительно у.
12. Какой геометрический образ соответствует на плоскости одному
уравнению, связывающему две переменные х и у?
13. Какой геометрический образ соответствует уравнению y = kx-\-b,
где k и b — любые действительные числа?
14. Дана функция ^ = ]/ а2 — ха. Какие значения может принимать аргу-
мент х?
15. Зависимость между переменными х и у выражена уравнением
4х24-9у2 = 36. Какие значения могут принимать переменные х и _у?
16. Какие значения могут принимать переменные величины х и у, свя-
занные уравнением х2 4-у3 — а; 1) при а = 36; 2) при а = 0; 3) при а =
= —16?
17. Переменные величины х и у связаны уравнением у3—х4~9 = 0.
1) Сколько действительных значений у соответствует любому допустимому
значению х; 2) Сколько значений х соответствует данному значению у?
Ответы. 7. — 4<х<4; —4<jf<4. 8. а — b <Z х <Z а-\- b. 9. 0<а<с.
О о к о
10. 1)Л,= 'х4-^; 2) х = 4^-4< 11. 1) хм = + =У3^4-9;
L Z 0,0 О
2) yIi2 = ±у'Зх3—12. 12. Какая-нибудь линия. 13. Прямая линия.
14. |x|sge. 15. —З^х^З; —2sgy>sg2. 16. 1) —6^v=g6; —6sgxsg6;
2) х = 0, _v = 0; 3) сумма квадратов действительных чисел не может быть
отрицательным числом; ни при каких действительных х и у это уравнение
не удовлетворяется. 17. 1) Два значения; 2) одно значение.
Глава III
ПРЯМАЯ ЛИНИЯ
§ 10. ВВЕДЕНИЕ
В предыдущей главе на опыте построения графиков функций
по их аналитическим выражениям мы убедились, что уравнению
с двумя переменными (х и у} на плоскости соответствует линия
как геометрическое место точек, координаты которых удовлетво-
ряют этому уравнению. При этом было установлено, что каждому
виду уравнения с двумя переменными соответствует свой особый
2* 35
вид линии (например, графиком функции первой степени является
прямая линия; графиком функции второй степени — кривая линия,
называемая параболой, см. рис. 226—231; графиком третьей
степени — кривая линия, называемая кубической параболой, см.
рис. 232—235). В данной и следующей главах рассматривается
обратная задача, а именно составление уравнений линий по изве-
стным их геометрическим свойствам. Начнем с прямой линии,
свойства которой нам хорошо известны.
Для успешной проработки этой главы необходимо следующее.
1. Иметь ясное представление о тождестве и уравнении, о рав-
носильности уравнений, знать способы решения системы уравне-
ний первой степени с двумя неизвестными и иметь хорошие на-
выки в тождественных преобразованиях алгебраических выражений.
2. Из курса геометрии знать свойства сторон, углов, диаго-
налей параллелограмма и ромба; свойства высот треугольника
и биссектрисы внутреннего его угла; свойство перпендикуляров
к сторонам треугольника в их серединах; признаки подобия тре-
угольников; метрические соотношения в прямоугольном треуголь-
нике.
3. По тригонометрии знать решение прямоугольных треуголь-
ников, знаки тригонометрических функций в разных четвертях,
формулы приведения тригонометрических функций углов любой
четверти к тригонометрическим функциям положительного острого
угла, формулы сложения, численные значения тригонометричес-
ких функций углов в 0, 30, 45, 60, 90°.
То, что забыто, необходимо повторить.
Параллельно с проработкой теоретического материала вы бу-
дете учиться решать задачи (так, на прямую линию даны за-
дачи 54—147). К решению задач любого типа следует приступать
только после того, как хорошо усвоен соответствующий теорети-
ческий материал и продуманы решения примеров, приведенных в
конце параграфа. Часть задач снабжена (в конце задачника) ука-
заниями. Приучайтесь пользоваться этими указаниями только для
проверки самостоятельно выполненных решений.
Независимо от имеющихся в учебнике рисунков решение задач
начинайте с построения четкого чертежа, соответствующего усло-
вию. Это облегчит понимание и повысит качество усвоения. Боль-
шинство задач (54—107) несложно. Решение их сводится к созна-
тельному применению вывода какого-нибудь параграфа учебника
и грамотным вычислениям. Затем следуют задачи более сложные
(108—147), решение которых складывается из решения двух —
четырех простых задач, расположенных в определенной последо-
вательности. В таких случаях решение задачи следует начинать
с составления плана, т. е. с уяснения и установления того, в
какой последовательности располагать те простые задачи, из кото-
рых составляется данная сложная задача. Образцы составления
таких планов приводятся в § 23.
36
§ tt. УРАВНЕНИЕ ПРЯМОЙ С УГЛОВЫМ КОЭФФИЦИЕНТОМ
Мы знаем, что через данную точку под данным углом к дан-
ной прямой можно провести только одну прямую линию. Следо-
вательно, положение прямой линии относительно осей координат
можно определить: 1) углом, образуемым этой прямой с одной из
осей координат, и 2) положением какой-нибудь точки ее на плос-
кости координат. В частности, положение прямой будет вполне
определенно, если будут известны:
1) угол а, образованный этой прямой
(рис. 27) с положительным направле-
нием оси Ох, и 2) отрезок ОВ = Ь,
отсекаемый ею от оси Оу.
Выведем уравнение этой прямой
АВ, т. е. установим функциональную
зависимость между координатами лю-
бой точки этой прямой. Возьмем на
ней произвольную точку М. Так как Рис. 27
точка М может быть взята на этой
прямой где угодно, координаты ее, очевидно, будут величинами
переменными. Обозначим их через х и у. Из точки М на ось Ох
опустим перпендикуляр МК. и через точку В проведем прямую
ВС параллельно оси Ох.
Из треугольника ВСМ, в котором Z СВМ= Z, О АВ =а, полу-
чим СМ = ВС tg а. Из чертежа видно, что
ВС = ОК = Х-, СМ = КМ-КС = КМ-ОВ = У~Ь,
следовательно, предыдущее равенство можно переписать в таком
виде:
у — Z> = xtga.
Приняв tga = £ и перенеся свободный член вправо, получим
у = , (1)
где х и у являются текущими координатами (координатами про-
извольной точки прямой).
Уравнение прямой линии с угловым коэффициентом (1) содер-
жит параметры k и Ь. Первый из них, A = tga, где а является
углом между положительным направлением оси Ох и прямой,
называется угловым коэффициентом', второй, Ь — ОВ, — отрезком
на оси Оу, или начальной ординатой прямой.
Примечание. Под углом между положительным направле-
нием оси Ох и данной прямой следует понимать угол, на кото- ,
рый нужно повернуть положительную полуось абсцисс против часо-
31
вой стрелки до совпадения с данной прямой. Для прямых АВ,
ABi, ABi (рис. 28) такими углами соответственно будут а, а(,
а2. Этот
угол, очевидно,
с
может принимать значения от 0° до 180°,
a k = tg а — любые числовые значения,
как положительные, так и отрица-
тельные.
Пример 1. Построить прямые линии:
1) = + 2)// = -|х-2.
Решение. 1) Уравнение прямой
угловым коэффициентом имеет вид
y=kx-\-b. В данном случае £=tga= ^;
b = 3. Следовательно, эта прямая про-
ходит через точку В (0; 3), образуя
с положительным направлением оси Ох угол а, тангенс которого
3 I 3
равен = Ер4- Отсюда вытекает следующий способ построения
(рис. 29): строим точку В (0; 3), проводим через нее вспомога-
тельную полупрямую параллельно оси Ох в положительном на-
правлении и откладываем на ней отрезок BD = 4 единицам мас-
штаба. В точке D восставляем к от-
резку BD перпендикуляр и на нем
в положительном направлении от-
кладываем DE = 3 единицам масш-
таба. Прямая, проходящая через В и
Е, и будет искомой.
2) В этом случае будем иметь:
k — — у = i-|, tg a < 0, следова-
тельно, a — тупой угол, Ь — — 2.
Через точку В проводим полу-
прямую (в отрицательном направ-
лении) параллельно оси Ох и от-
кладываем на ней В1ЕЕ = — 3. В точке Di к отрезку BtDi вос-
ставляем перпендикуляр и на нем берем DiEi = 2.
Прямая, проходящая через точки Bi и Eit будет искомой.
Примечание. Эту прямую можно построить, приняв k =
2 __2
= — Предлагается выполнить построение самостоя-
тельно.
Пример 2. Проходит ли прямая у —У 2 - х-|-3 через точки А
(0; 3), В (У2; 5), С (—/8; —1), D (1; 4)?
Решение. В уравнении прямой х и у являются текущими
координатами, т. е. координатами любой ее точки. Поэтому на
данной прямой могут лежать лишь такие точки, координаты кото-
рых удовлетворяют ее уравнению, т. е. обращают его в тождество.
38
Подставив в данное уравнение координаты точки А, получим
3 = V 2 • 0 3; 3 = 3 — тождество. Следовательно, прямая про -
ходит через точку Л (0; 3). Аналогично , 5 = 1^25-=5 ,
т. е. через точку В(]/^2; 5) прямая проходит . Через точку
С(—V8; —1) данная прямая тоже проходит, потому что —1=
= уг2-(—J-z8) -1- 3; —1= — 4—1-3; —1= — 1. Через точку D
(Г, 4) прямая не проходит, так 4 ^К2-1 + 3.
Пример 3. При каких значениях параметров k и b прямая
y==kx-\-b пройдет через точки А {2; 7) и В{—4; —2)?
Решение. Координаты любой точки прямой удовлетворяют
уравнению этой прямой; прямая должна пройти через точки А
и В. Подставляя в уравнение (1) вместо х и у последовательно
координаты двух данных точек, получаем два уравнения с неиз-
вестными k и Ь:
1) 7=А-2-у&-, 2) —2=А •(—4)-|-Ь
пли
1) 2& + 6 = 7; 2) 4£ —6=2.
з
Решив эту систему уравнений, найдем: k = -^-, b = 4. Следо-
3
вательно, через данные точки пройдет прямая у = ^-х-{- 4.
§ 12. ЧАСТНЫЕ СЛУЧАИ УРАВНЕНИЯ ПРЯМОЙ
С УГЛОВЫМ КОЭФФИЦИЕНТОМ
В уравнении (1) параметры k и b в зависимости от положе-
ния прямой относительно осей координат могут принимать раз-
личные числовые значения, в частности, каждый из них может
быть равен нулю.
1. Предположим, что 6 = 0; & = tga 0. По-видимому, в этом
случае прямая пройдет через начало координат (рис. 30) и урав-
нение (1) примет вид ,
--------- у 1
У=Лх (2)
--------- о *
{уравнение прямой, проходящей через начало -—♦ г
координат). '''у х
Указание. См. решение задачи 58. I :
2. Предположим теперь, что A = tga = O; Рис.30
6 0. Если £ = tga = O, то а = 0. Это зна-
чит, что прямая образует с осью Ох угол 0°, т. е. параллельна ей
(рис. 31). Уравнение (1) в этом случае принимает вид y — 0-xA^b,
или ________
z/=6 (3)
{уравнение прямой, параллельной оси Ох).
39
Уравнение (3) легко запомнить. Оно является аналитическим
выражением утверждения, что все точки прямой имеют одну и ту
же ординату, равную Ь.
3. Может быть Ь~0 н k = tga — O. При этих условиях полу-
чится прямая: 1) проходящая через начало координат (так как
Ь — 0) и 2) образующая с осью
Ох угол 0° (так как а = 0).
Такой прямой, очевидно, будет
сама ось Ох. Уравнение (1) при
этом пр имет вид у = kx -f- b —
= 0 • х0 = 0, или
y = 0 (4)
{уравнение оси Ох).
§ 13. УРАВНЕНИЕ ПРЯМОЙ, ПАРАЛЛЕЛЬНОЙ ОСИ Оу
На рис. 32 дана прямая АК, параллельная оси Оу и нахо-
дящаяся от нее на расстоянии ОА — а. У всех точек этой пря-
мой одна и та же абсцисса, равная а. Следовательно, уравнением
этой прямой будет
х — а (5)
(уравнение прямой, параллельной
оси Оу).
Если прямая совпадает с
равны нулю и ее уравнение
осью Оу, то абсциссы всех
будет иметь вид
ее точек
л- = 0 (6)
(уравнение оси Оу).
Пример 1. Построить фигуру, ограниченную линиями: 1) х — 0;
2) г/ = 0; 3) х = 5; 4) у — 3.
40
Решение. Первой стороной этой фигуры является ось Оу (6),
второй — ось Ох (4). Третья сторона параллельна оси Оу (5); для
нее ОА ~а = 5. Четвертая сторона направлена параллельно оси
Ох; для нее ОВ — Ь = 3 (рис. 33).
Пример 2. Построить фигуру, ог-
раниченную линиями:
1) х —0; 2) у=0; 3) х = —7;
4) У = — 5.
Решение. Первые две сторо-
ны совпадают с осями координат.
Третья сторона параллельна оси
Оу; для нее ОА = а = — 7. Четвер-
тая сторона параллельна оси Ох;
ОВ = Ь =— 5 (рис. 34).
§ 14. УРАВНЕНИЕ ПРЯМОЙ В ОТРЕЗКАХ
прямой линии на плоскости можно определить
нею
Положение
отрезками, отсекаемыми этой прямой на осях координат, так как
в этом случае будет известно положение двух ее точек.
Предположим, нам дано: ОА — а, ОВ — b. Требуется вывести
уравнение прямой АВ (рис. 35), т. е. установить функциональ-
зависимость между координатами любой точки этой прямой.
Возьмем на ней произвольную точку
М (х; у). Построив координаты этой точки
OMt=x, MiM — y, получим два прямо-
угольных треугольника: ОАВ и /ИМ44.
По лемме о свойстве прямой, параллель-
ной стороне треугольника (М}М || ОВ),
утверждаем: А ОЛВсе А А4М44. Из по-
добия этих треугольников получается про-
MtM MiA п
порция Мн-=-„4-. Приняв во внимание,
(JD U А *
MiA — OA — OMi — a — х, ОА = а, полу-
что 441/14 = у, ОВ = Ь,
чаем -у — а ах . Это уравнение преобразуем, разделив числитель
правой части на ее знаменатель у = 1 — у и перенеся члены с те-
кущими координатами влево:
(7)
получаем уравнение прямой в отрезках. В этом уравнении х и у —
текущие координаты, а и b — отрезки, отсекаемые прямой на
осях координат.
41
ные стороны должны
порцию, беря все отр
При выводе уравнения (7) было взято а^>0 и b^>Q (рис. 36).
Можно показать, что такой же вид будет иметь уравнение пря-
мой и в случаях, когда а^>0, Ь<^0; а<^0, Ь^>0; а<(0, Ь<^0.
Мы рассмотрим только случай, когда
а<А) и b<^Q.
Предположим, что прямая АВ распо-
лагается на плоскости так, как это пока-
зано на рис. 36. Возьмем на ней произ-
вольную точку М (х; у) и построим ее
координаты MtM — у<^0, OMi — х0.
Получим подобные треугольники О АВ и
MjAM. В этих треугольниках сходствен-
быть пропорциональны. Составляем про-
зки положительно направленными:
ММ,___AM,
ВО — АО '
Нам известно, что А В = — В А (см. § 2), следовательно, преды-
дущую пропорцию можно переписать в виде
— Муи — М~,А AljM М,А
---А=- —----= или
— OB — ОА OB ОА
Приняв во внимание, что ЛЦМ — у, ОВ — b', ОА = а; MiA =
= ОА—ОМ — а—х, получим:
у а — х ' у . х
b а ’ Ъ а ’
или
Получили уже известное нам уравнение. Отсюда можно сде-
лать такое заключение: при любом положении прямой, не парал-
лельной оси координат и не проходящей через 'начало координат,
уравнение ее может быть представлено в виде
Х_\У___1
а "г b '
где хи у — текущие координаты, а и b — любые действительные
числа, отличные от нуля.
Пример. Построить прямые:
nf+з—1;
•Решение. 1) Уравнение прямой в отрезках имеет вид
а 1 Ь
42
В нашем примере на месте а стоит число 6, на месте b —
число 5. Значит а = 6; д = 5 (рис. 37).
X V
2) Уравнение ------^- = 1 можно переписать в следующем
виде: ^+^7^=1- Сопоставляя
видим: а = 10, Ь = — 6 (см.
рис. 37).
3) Данное уравнение можно
представить в виде у = 1,
откуда следует: а = —4; Ь = 7
(рис. 37).
4) Переписав уравнение в
х , v .
виде г7§ + ±^==1’ находим
а = — 8, Ь — — 3 (см. рис. 37).
это уравнение с уравнением (7),
§ 15. ОБЩЕЕ УРАВНЕНИЕ ПРЯМОЙ
В § 12—15, рассмотрев все возможные случаи положения прямой
линии относительно осей координат, мы получили следующие
виды ее уравнения:
1) х = а (5), если прямая параллельна оси Оу,
2) у = Ь (3), если прямая параллельна оси Ох\
3) х = 0 (6), если прямая совпадает с осью Оу,
4) г/ = 0 (4), если прямая совпадает с осью Ох;
5) у = £х (2), если прямая проходит через начало координат,
образуя с положительным направлением оси
абсцисс любой острый или тупой угол;
43
6) y = kx-rb (1) 1 если прямая не параллельна ни одной из
х j у______1/711 осей К00РДинат и 11е проходит через начало
+ ~ь~ 1 J координат.
Все эти уравнения являются уравнениями первой степени.
Следовательно, мы вправе утверждать, что прямой линии (при
всех ее возможных положениях на координатной плоскости} соот-
ветствует уравнение первой степени относительно текущих коор-
динат х и у.
Докажем теперь обратное: всякому уравнению первой степени
относительно текущих координат на плоскости соответствует
прямая линия.
Возьмем общее уравнение первой степени с двумя неизвест-
ными
Ах-\- By С — 0. (8)
Из алгебры известно, что: 1) перенося любой член уравнения
из одной части в другую с обратным знаком и 2) умножив или
разделив обе части его на какое-нибудь число, отличное от нуля,
мы получаем уравнение, равносильное данному, т. е. такое, ко-
торое удовлетворяется теми же значениями неизвестных, что и
данное уравнение. Следовательно, если в уравнении (8) А, ВиС
числа, отличные от нуля, то после переноса любого ею члена
вправо с обратным знаком и деления на какой-нибудь из коэффи-
циентов А, В, С всех его членов получится уравнение, равно-
сильное данному (8).
Выполним это преобразование двумя способами:
1-й способ
Ах -f- By -ф- С = 0;
Ву = — Ах — С;
А С
У~ В х В'
Приняв
А , С ,
~B=k' ~В=Ь’
получаем
у — kx -j- b.
(1)
2-й способ
Лх-|” Ву-\-С = 0;
Ах-\- Ву= — С\
Ах ! By __ ..
— С"1"—С ’
Ах By
~А . В _ .
С "Г С ~ 1 ’
А В
А В
Приняв
С С .
~А=а'-В=Ь' .
получаем
44
Уравнения (1) и (7) равносильны данному уравнению (8). Выше
было доказано, что эти уравнения являются уравнениями прямой.
Следовательно, уравнению Ах By -f-С = 0, если считать х и у
текущими, координатами точки на плоскости, соответствует,
прямая линия.
Рассмотрим частные случаи этого уравнения, когда один из
коэффициентов А, В, С или два из них одновременно обращаются
в нуль.
1-й случай: Л = 0; В Ф 0; С —0. В этом случае получаем:
Q-x-\-ByA~C = G', ВуфС = 0\ Ву = — С\
у=-сГ1=ь, (3)
т. е. уравнение прямой, параллельной оси Ох.
2-й случай. В = 0; А Ф 0; С ф 0. В данном случае уравне-
ние (8) приводится к виду
Лх-)-0-г/ + С=0; Лх4~С=0,- Ах=— С;
х — — ~=а. Следовательно, Лх-4-С = 0 является уравнением
прямой, параллельной оси Оу (5).
3-й случай. А Ф 0; ВФ0; С = 0. Уравнение (8) принимает
вид
Ax^-By=0', Ву =—Ах\ у = — jx—kx\
отсюда следует, что АхфВу = д является уравнением прямой,
проходящей через начало координат (2).
4-й случай. 4 = 0; В Ф 0; С = 0. При таких значениях
коэффициентов А, В и С уравнение (8) принимает вид Лх-ф0
—0 = 0; Лх = 0; х = 0. Следовательно, Ах —0 является уравне-
нием оси Оу (6).
5-й случай. Л=0; В ф 0; С = 0. Получается: O-x-f-Bz/4*
-р-0 = 0; Ву = 0 или у = 0 — уравнение оси Ох (4).
Мы видим, что уравнения (1) — (7) являются иной формой,
или частными случаями уравнения (8). Поэтому уравнение
Ах-^Ву^-С = 0 (8)
называется общим уравнением прямой или уравнением прямой в
общем виде.
§ 16. ПОСТРОЕНИЕ ПРЯМОЙ ПО ЕЕ УРАВНЕНИЮ,
ДАННОМУ В ОБЩЕМ ВИДЕ
Прямая линия, данная уравнением вида (8), может быть по-
строена тремя способами.
1-й способ. Приводим данное уравнение к виду уравнения
с угловым коэффициентом (см. § 15) и строим прямую уже из-
вестным нам способом.
45
2-й способ. Приводим данное уравнение к виду уравнения
в отрезках (7) и строим прямую по отрезкам, отсекаемым ею на
осях координат.
3-й способ. Чтобы построить прямую линию, достаточно
знать любые две ее точки. Например, если прямая не проходит
через начало координат и не параллельна оси координат, то она
пересекает каждую из них в определенной точке. Ордината у
точки, в которой прямая пересекает ось Ох, должна быть равна
нулю. Полагая в данном уравнении у —О, найдем абсциссу точки
пересечения прямой с осью Ох, т. е. а (отрезок на оси Ох).
Абсцисса точки пересечения прямой с осью Оу должна быть равна
нулю. Положив в данном случае х = 0, найдем отрезок Ь, отсе-
каемый прямой на оси Оу.
Пример. Построить прямую 4х — Зу — 12 = 0.
Решение. 1) Найдем точку пересечения прямой с осью Ох.
Ордината любой точки этой оси равна нулю. Подставив в данное
уравнение вместо у нуль, найдем: 4х — 3-0—12 = 0; х = 3. Сле-
довательно, эта прямая пересекает ось Ох в точке (3; 0); отрезок
на этой оси а = 3.
2) Абсцисса любой точки оси Оу должна быть равна нулю.
Подставив в уравнение прямой вместо х нуль, получим 4-0 —
— Зу — 12 = 0; Зу = —12; у — — 4. Прямая пересекает ось Оу
в точке (0; —4) (см. рис. 37).
§ 17. УРАВНЕНИЕ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДАННУЮ ТОЧКУ
В ДАННОМ НАПРАВЛЕНИИ
Положим, нам даны точка В (xb yj, принадлежащая прямой
АВ (рис. 38), и угол а0, образуемый этой прямой с положи-
тельным направлением оси Ох. Требуется составить по этим данным
уравнение прямой АВ. Выполним это двумя способами.
1-й способ. Берем на прямой произвольную точку М (х; у).
Координаты точек В и М на чертеже изобразятся отрезками:
OBi — Xt, BiB = yh 0Mi = x, MiM = y. Через точку В проводим
отрезок ВМ.2 параллельно оси Ох. Получим Z, М2ВМ = Z BiAB—
= а0. Из прямоугольного треугольника М2ВМ имеем
М2М = ВМ2 tg «о, (а)
но так как
M2M = MtM—MiM2 — y — BtB — y — yb
BM2 — В^М^ — OMi — OBi — x — x1;
то равенство (а) можно переписать в виде
у — yi = ka (х — Xi)
, где 7к’о = tg а0; (9)
4Q
это и будет уравнением прямой, проходящей через данную точку
B(xi; z/i) в данном направлении (под данным углом а0 к оси Ох).
Следует помнить, что в уравнении (9) xt и у2 как координаты
данной точки являются величинами постоянными, а х и у как
координаты произвольной точки прямой — величинами перемен-
ными.
2-й способ (предварительно надо основательно продумать
указания к решению задач 77 и 79).
Уравнение прямой, проходящей через данную точку В(ху, yt)
под данным углом к оси Ох, можно получить, рассуждая сле-
дующим образом. Уравнение любой прямой, образующей с поло-
жительным направлением оси Ох угол а0, не равный , может
быть представлено в виде (§ II)
z/^=AoX-|-&, (б)
где
Ao-=-tgao.
В уравнении (б) b остается неопределенным. Таких прямых
на плоскости можно провести сколько угодно (рис. 39), и уравнения
их будут отличаться друг от друга
только численными значениями на-
чальной ординаты (ОС = b, OCi = bt,
OC<i = bi и т. д.). Из совокупности
прямых, уравнения которых имеют
вид у — !гЛх-\-Ь, требуется выделить
ту, которая проходит через точку
В (xf, г/1), т. е. найти такое значение
Ь, при котором прямая прошла бы
через точку В. Мы знаем, что пря-
мая проходит через данную точку,
если координаты ее удовлетворяют
уравнению этой прямой. Подставив Рис. 39
в уравнение у — kt>x -|- b вместо теку-
щих координат х и у координаты данной точки В, получаем ра-
венство #! = В этом равенстве нам известны и yt.
Следовательно, оно является уравнением с одним неизвестным Ь.
Решив его, найдем b=yt — koXt. Итак, приняв b — yi — Aoxi, мы
из прямых, определяемых уравнением у — Аох-|-6, отберем ту,
которая проходит через данную точку В (xf, z/i). После подста-
новки получим
или
y = kax^-yl — A0Xi
у — У1—ка(х — Xj),
(9)
т. е. известное уже нам уравнение прямой, проходящей через
данную точку В (xj; yt) в данном направлении.
47
Решен не. Уравнение любой прямой, проходящей через данную
точку, имеет вид
У — yi = k(x — xi).
В данном случае
У — 4 — А(х-|-3)-,
1) Л = tg [arctg (— 4)] = — у! У — 4 = — (xJ-3);
3*4-2*/+ 1 = 0,-
2) A=tgO=O’, у —4 — 0 -(х +3)-,
У~ 4 = 0; */ = 4;
3) очевидно, всякая прямая, образую-
щая с осью Ох прямой угол, параллельна
оси Оу. Уравнение такой прямой имеет
вид х = а. В данном случае будем иметь
х =— 3 [см. формулу (5)].
Во втором и третьем случаях следо-
вало сразу писать ответы: */ = 4; х — — 3
[см. уравнения (3), (4) и рис. 41].
§ 19. УРАВНЕНИЕ ПРЯМОЙ , ПРОХОДЯЩЕЙ ЧЕРЕЗ
ДВЕ ДАННЫЕ ТОЧКИ
Тогда Z. В^АВ= Z. +СД=а,
Даны точки A (хр, yi) и В(ху, yi). Составить уравнение прямой
АВ, проходящей через эти точки (рис. 42).
На рисунке координаты данных точек изобразятся отрезками
OAt — X!; AiA = yr, 0В! = х2; BiB = y->. Уравнение любой прямой ,
проходящей через данную точку
А (хь ух), имеет вид
У~У1= k (х — Х1). (10)
При любом k прямая, опреде-
ляемая уравнением (10), пройдет
через точку А (хр, yi). Нам остается
найти такое значение k, при кото-
ром она прошла бы и через точку
В (хр у^.
Проведем через точку А от-
резок ABi параллельно оси Сх.
тангенс которого в уравнении (10)
обозначен буквой k. Из прямоугольного треугольника АВВ* находим
h______ja а._В2В_BiB BiB2_BlB — AlA y2 —yt
ё AB2~ AlBl ~OB1-OAl ~x8-x/
Итак, прямая, проходящая через точку А (хр yt), пройдет
также и через течку В (х2; у>), когда
1 a—(И)
лд I '
49
Примечание. Формула (11) выражает угловой коэффициент
прямой через координаты двух ее точек. При этом безразлично,
какая из этих двух точек берется за первую, так как
k—Л'3 ~ -ft = я—я
Xs — Xt XL — Х3
Подставив в уравнение (10) вместо k найденное его значение,
получим
У-У^ = ^~(Х~Х^
Остается придать этому уравнению более простой и легче за-
поминаемый вид. С этой целью разделим обе части на у.2 — гц;
получим _____________
У-Л - х — хЦ
Ун ~ У1 — Xi ‘ v ’
Это и есть уравнение прямой, проходящей через две данные
точки А (%ь у А и В (х2; у2).
Другой способ вывода уравнения (12). Уравнение пучка
прямых с центром в данной точке А (хр, z/i) имеет вид
y — yi = k(x — Xi). (10)
Из этого пучка прямых (см. рис. 41) требуется выделить ту,
которая проходит через точку В (х%; у2), т. е. найти такое значе-
ние k, при котором прямая, проходящая через точку А, прошла
бы также и через точку В.
Мы знаем, что если прямая проходит через данную точку, то
координаты этой точки удовлетворяют уравнению данной прямой.
На этом основании, подставив в уравнение (10) вместо текущих
координат х и у координаты точки В, получим равенство
У1 — yi = k(xs — xi),
в котором неизвестным является только k. Решив уравнение от-
носительно k, получим
* = (11)
Теперь, чтобы получить искомое уравнение, остается в урав-
нение (10) вместо k ввести найденное его значение. Получим
У-У^^~^(х~хд,
Ло — Л1
или
У~ У! _ X — Xi
Уз - У1 х2 — Х1 *
50
Пример. Написать уравнение прямой, проходящей через точку
А (—4; 3) и образующей с положительным направлением оси Ох
угол arctg у.
Р е ш е н и е. Из тригонометрии известно, что arctg х — это угол,
тангенс которого равен х. Следовательно, в данном случае ka —
, / , 1 \ 1
— tg arctg =-9, и искомое уравнение мы найдем, подставив
в уравнение (9) вместо Xi и r/j их известные значения. Получим:
у-3 = |[х-(— 4)], 2z/ —6 = х4-4, х-2НЮ = 0.
§ 18. УРАВНЕНИЕ ПУЧКА ПРЯМЫХ С ЦЕНТРОМ
В ДАННОЙ ТОЧКЕ
Через данную точку А (хг, yt) можно провести бесчисленное
множество прямых (рис. 40). Совокупность прямых, связанных
одной тонкой, через которую они проходят, принято называть
пучком прямых с центром в данной точке. Положение отдельных
прямых этого пучка будет
отличаться только угла-
ми их наклона к оси
Ох (ой, а.2, aa, ...), а уравне-
ния — угловыми коэффи-
циентами : ki — tg at, ^2 —
= tga.,, At=tga3, ...и т. д.
Вследствие этого у равнение
любой из них будет иметь
вид
у — у\==-k (х — х^) , (10)
где k в зависимости от направления прямой может принимать
всевозможные числовые значения, заключающиеся между —оо
и оо.
Уравнение (10) принято называть уравнением пучка прямых
с центром в данной точке (xg yt). В частном случае, когда прямая,
проходящая через данную точку А (хр, yt), образует с положи-
тельным направлением оси Ох угол а = 90°, уравнение ее будет
иметь вид
x = xj = a. (5)
Пример. Написать уравнение прямой, проходящей через точку
А (—3; 4) и образующей с положительным направлением оси Ох
углы: 1) arctg2) 0°; 3) 90°.
48
Примечание. Если точки A (хк z/i) и В (х2; уА лежат на
прямой, параллельной оси Ох (когда yi — y-i), или на прямой,
параллельной оси Оу (когда Xi = x,>), то уравнения их соответст-
венно будут
у=у1==Ь, (3)
x = xi — a. (5)
Пример. Написать уравнение прямой, проходящей через две
точки А (—5; 3), В (3; —3), и результат проверить.
Решение. Уравнение прямой, проходящей через точки, имеет
вид (12). Применительно к нашему случаю оно может быть напи-
сано в двух видах:
. У-УА х~хл . б) У-Ув = Х~ХВ
У В — ХВ ~~ ХА ’ Уа — у В ХА ~ хв
Оба вида равноправны и дают искомый результат. Мы прове-
дем вычисления, располагая координаты данных точек, как ука-
зано в уравнении (а):
у — 3 х — (— 5). — У + 3 х + 5.
— 3 — 3— 3 + 5 ’ 6 7 ~8
— 4Z/-L 12 = 3x4-15;
3x4-4z/4“3 = 0 — уравнение прямой АВ.
Проверка. Точки А (—5; 3) и В (3; —3) должны лежать
на прямой АВ, поэтому их координаты должны обращать ее
уравнение в тождество. Подставляем в уравнение 3x-|-4z/-1-3 = 0
координаты точки А: 3(—5) —4 - 3 —3 = 0; —15 4-12 4-3 = 0;
0 = 0; получаем тождество. Сделаем то же самое с координатами
точки В: 3-34-4(—3) 4-3 = 0; 9 — 12-]—3 = 0; 0 = 0; опять по-
лучаем тождество. Следовательно, в наших вычислениях ошибок
не было. Уравнение найдено правильно.
§ 20. УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ
Даны две прямые своими уравнениями. Требуется найти угол
между ними.
Прямые AD и CD при своем пересечении образуют четыре
попарно равных угла: ADC— BiDB = <р; CDB1 = ADB—
= <Pi (рис. 43). Зачастую при решении задач из двух разных по
величине углов ® и cpi требуется вычислить один определенный,
т. е. или <р, или <f>i.
Выведем в первую очередь формулу для нахождения угла ®.
Примем: /ОЛО = аь Z ОСО = а2. Далее, обозначив tga1 = >fe*1,
tga2 = A2, OBi — bt, OBi = bi, получим:
y — kiX-{-bi — уравнение прямой AD;
y — k>x^-bi—-уравнение прямой CD.
51
Итак, нашей задачей является определение угла <р, образу-
емого прямыми y — ^x-^bt и у.2 — k<j,x ф- Ь.2. Из рис. 43 видно,
что угол а.2 является внешним углом треугольника ACD, а углы
aj и <р — его внутренними углами, не смежными с углом а2. По
свойству внешнего угла треугольника по-
лучаем равенство ср-j-a, =a2 или <p=a2—a,,
откуда будет следовать tgcp — tg (a2 —- a,).
Развернув правую часть этого равенства
по формуле тангенса разности двух углов,
найдем
, ' 4../ \ tg a„ — tgaj k.>—1г,
tg? = (g («, - а,) =
Итак,
При выводе формулы для тангенса угла <pi воспользуемся тем,
что углы ср и cpj смежные, а потому —|— <р = 180° или cpj = 180°—
— <р, откуда получим
tg cpi = tg (180° — ср) = — tg <р
или [см. равенство (а)]
I kr> ~~~ k.
Следовательно,
I kt ~
^ = г+м?
(б)
В формулах (а) и (б) в числителе правой части вычитаемым
берется угловой коэффициент той из сторон угла, которая своим
вращением вокруг вершины угла против часовой стрелки до
совпадения с другой стороной описывает определяемый угол.
Это дает нам возможность заменить формулы (а) и (б) одной
формулой
tg? =
fe3 — А,
1 4" ^1^2
(13)
где k[ и ki являются угловыми коэффициентами прямых, обра-
зующих угол ср, причем k\ является угловым коэффициентом той
из этих прямых, вращением которой против часовой стрелки до
совпадения с другой прямой описывается искомый угол.
Пример 1. Найти внутренние углы треугольника, сторонами
которого являются прямые у— ухф-4; у—Чх — 4‘, у = 0.
52
Составить уравнения сторон ромба, если острый угол его <f =
= 2 arctg
133. Даны уравнения сторон треугольника: 5х— Зу—15 = 0,
хД-5//— 3 = 0, Зх-)-у + 5 = 0. Написать уравнения прямых,
проходящих через вершины этого треугольника параллельно
противоположным сторонам.
134. Даны уравнения двух сторон параллелограмма х— у—
— 1=0, х—2y — Q и точка пересечения его диагоналей (3; —1).
Написать уравнения двух других сторон.
135. Вычислить координаты вершин ромба, если известны:
уравнения двух его сторон 2х— 5у—1=0, 2х — 5у — 34 = 0 и
уравнение одной диагонали х-\-Зу — 6 = 0.
136. Даны координаты середин сторон треугольника: К (1; 2),
' £(7; 4), Л4(3; —4). Написать уравнения сторон.
137. В параллелограмме ABCD даны: уравнение стороны АВ
Зх-1-4у—12 = 0, уравнение стороны AD 5х—12г/ — 6 = 0 и
середина стороны ВС точка Л1 (— 2; . Написать уравнения
двух других сторон.
138*. Дана прямая Зх — 4у— 6 = 0 и точка А (2; 3). Найти
точку Ai, симметричную точке А относительно данной прямой.
139*. Луч света, выйдя из точки Л (2; 3), отражается от оси
Ох и попадает в точку В (5; 8). Найти уравнения луча падающего
и отраженного.
140. Луч света, выйдя из точки Л4 (1; 5), отражается от пря-
мой у — х и попадает в точку В (5; 9). Составить уравнения
луча падающего и отраженного.
Геометрические места точек (к.§ 24)
141. Составить уравнение геометрического места точек, равно-
удаленных от точек А (4; 2), В (8; 6).
142. Составить уравнение геометрического места точек, равно-
удаленных от начала координат и точки А (а; 2а).
143. Составить уравнение геометрического места точек, зная,
что расстояния их от точки А (8; 0) в два раза больше их рас-
стояний от точки В (2; 0).
144. Составить уравнение геометрического места точек, равно-
удаленных от точки В (0; 2) и оси Ох, и построить график.
145*. Найти уравнение геометрического места точек, сумма
квадратов расстояний которых от двух данных точек Л (0; 4) и
В (0; —4) — величина постоянная, равная 64.
146. Составить уравнение геометрического места точек, раз-
ность квадратов расстояний которых от начала координат и от
точки В (а; —За) — величина постоянная, равная 4а2.
147. Написать уравнение геометрического места точек, равно-
удаленных от прямой z/ = 2 и точки В (0; 4).
408
Решение. Строим этот треугольник АВС по уравнениям его'
сторон (рис. 44). Первому уравнению соответствует сторона АВ,
второму — сторона ВС и третьему — сторона АС.
1) Угол cpi образуется вращением
совой стрелки прямой АВ до совпа-
дения с прямой ВС. Поэтому в фор-
муле (13) при вычислении этого утла
берем=-у,/г2 = 2; получаем
вокруг точки В против ча-
Рис. 44
По таблице тригонометрических
функций находим <р| = 36°52'.
2) <ра является углом наклона прямой АВ
тельно, tg = = 0,5; по таблице получаем
где а — угол наклона прямой ВС к оси Ох.
Мы знаем, что tgoi = 2; по таблице на-
ходим а = 63'26'. Значит <р3= 180° —
— а = 180° — 63°26' = 116°34'.
Проверка, cpj —|— <р3 = 36°52'-|-
+ 26°34'+ 116°34'= 180°.
Пример 2. Найти острый угол, об-
разуемый прямыми у=~х-]-4; у =
к оси Ох, следовa-
О, = 26°34'.
3) ср3 = 180° —
Найдем сначала '
• а,
угол
а.
вычислении этого угла следует принять
Решение. Искомым углом (рис. 45)
является угол ср. В формуле (13) при
тогда
откуда найдем = 45°.
bi = kAC =—k^ — knc — у;
§ 21. УСЛОВИЯ ПАРАЛЛЕЛЬНОСТИ И ПЕРПЕНДИКУЛЯРНОСТИ
ДВУХ ПРЯМЫХ
1. Если прямые y = k\X-4~bt и у = Ь.гх-\-Ьг параллельны между
собой (рис. 46), то углы наклона их к оси Ох будут равны, как
соответственные углы при параллельных прямых, т. е. О4 = ос.2.
53
Равные углы, очевидно, имеют и равные тангенсы:
tga1 = tga.2, или ki=kt.
Мы доказали, что если две прямые параллельны, то угловые
коэффициенты их равны между собой. Докажем теперь обратное:
если угловые коэффициенты двух прямых равны между собой, то
эти прямые параллельны.
В самом деле, если Л1 = &2, то tgaj = tga2 или aj = a.2. Сле-
довательно, для того чтобы две прямые были параллельны
между собой, необходимо и достаточно, чтобы их угловые коэф-
фициенты были равны. Отсюда следует, что условием параллель-
ности двух прямых у = kpc bi и у — k2x -ф- Ь2 является равенство
их угловых коэффициентов:
fr=68|. (14)
2. Если две прямые y = kiX-\-bi и у = кгх-\- Z>2 взаимно пер-
пендикулярны (рис. 47), то
а2 = 90°4~аГ> (а)
tga2 = tg(90°4-a1) = —ctgaj —-L,
т. e. tga2 = -^L- или
ki = ~^ ’ (15)
так как tga2 = #2, tgai = ^.
Обратно, если зависимость между угловыми коэффициентами
k2 и k2 двух прямых выражается равенством (15), то
tg a2 = — = — ctg a, — tg (90° Д- aj),
т. e. tga2 = tg(90°4-aj),
откуда
a2 = 90° aj. (a)
Следовательно, две прямые взаимно перпендикулярны, если их
угловые коэффициенты обратны по абсолютной величине и про-
тивоположны по знаку.
54
2
Пример 1. Дана прямая у = —^х-]-4. Составить уравнение
прямой, проходящей через точку А (—4; 1) параллельно данной
прямой.
Решение. Уравнение любой прямой, проходящей через точ-
ку А (—4; 1), имеет вид
У~~ 1=^(хД-4).
Из этого пучка прямых требуется
выделить ту, которая параллельна
2
данной прямой у —— ^-хЦ-4. Мы
знаем, что если прямые параллельны
между собой,то угловые коэффициен-
ты их равны. Следовательно, /г =
—
~ 3’
Уравнение искомой прямой: у—1=—у(хД~4); Зу — 3 =
= — 2х— 8; 2хЗу-ф- 5 — 0 (рис. 48).
Пример 2. Написать уравнение прямой, проходящей через
точку В (2; —4) и перпендикулярной к прямой 2х — 5уД-10 = 0.
Решение. Уравнение лю-
бой прямой, проходящей через
точку В (2; —4), имеет вид
Рис. 49
у + 4 = Цх-2). (б)
Из этого пучка прямых
предлагается отобрать ту, ко-
торая перпендикулярна к дан-
ной прямой 2х — 5г/—10 = 0.
Мы знаем, что угловые коэффи-
циенты двух взаимно перпенди-
кулярных прямых обратны по
абсолютной величине и проти-
воположны по знаку. Для определения углового коэффициента
прямой ВС (рис. 49) будем иметь равенство
^вс
1
kAc'
Решив уравнение прямой АС относительно у, найдем: 5у =
2 2
== 2х 10; у = ^хА-2; ^c = -g-. Следовательно,
h 115
5
55
Подставив найденное значение knc в уравнение (б) вместо k,
5
получим у 4-4 =— (х — 2) или 5х Ц- 2у — 2 = 0 — уравнение
прямой, проходящей через точку (2; —4) перпендикулярно пря-
мой 2х — Ъу 4- 10 — 0.
Пример 3. Какова должна быть зависимость между коэффи-
циентами A], Bi, А.2 и Во в уравнениях прямых: AjX BtyA~ Ct — 0
и Д2х4~ Сг — 0, чтобы эти прямые были параллельны между
собой?
Решение. Мы знаем, что две прямые будут параллельны
между собой, если их угловые коэффициенты равны: k2 = k.2.
Решив данные уравнения относительно у, получим:
А, С, А2 С.,
У^-в-^-вг у=~в;х-в\а
где —= = ki. Следовательно, две данные прямые будут
параллельны между собой, если
( jAq -Al _ А%
~в~1~ — в? или в?-в?
Это условие можно сформулировать так: две прямые, данные
общими уравнениями, будут параллельны тогда, когда коэффи-
циенты при текущих координатах в их уравнениях будут про-
порциональны.
§ 22. ПЕРЕСЕЧЕНИЕ ДВУХ ПРЯМЫХ
Рассмотрим такую задачу: даны две прямые своими уравне-
ниями: 1) А,х 4- Вщ 4- Ci = 0; 2) А2х —|— В2уА- Найти
координаты точки их пересечения.
Нам известно, что координаты любой точки прямой удовлет-
воряют уравнению этой прямой. Так как точка пересечения двух
прямых является их общей точкой, то координаты ее должны
удовлетворять уравнениям обеих прямых, т. е. должны быть их
общими корнями.
Отсюда вывод: чтобы найти координаты точки пересечения
двух прямых, надо решить совместно их уравнения.
Пример 1. Найти точку пересечения прямых
2*4-3//— 12 = 0; х — у— 1=0.
Решение. Здесь удобнее применить способ подстановки.
Из второго уравнения находим х = у-}-1. Подставив в первое
уравнение вместо х его выражение через у, получим
2(//4- 1)-гЗд- 12 = 0; 5у- 10 = 0; i/ = 2.
56
Далее определяем х, подставив в уравнение х — у А- 1 вместо у
его значение. Получаем
х = 2+1=3.
Следовательно, эти прямые пересекаются в точке (3; 2) (рис. 50).
Пример 2. Найти точку пересечения прямых
2х — Зу — 6 = 0; 4х — бу Д- 21 =0.
Решение. В данном случае коэффициенты при текущих коор-
2 i ,.
динатах в уравнениях прямых пропорциональны: —^=—g. ^ле"
довательно, эти прямые параллельны, а потому общей точки не
имеют (рис. 51).
§ 23. СОСТАВЛЕНИЕ.ПЛАНА РЕШЕНИЯ ЗАДАЧИ
Пример 1. Найти расстояние от точки С (3; —4) до прямой
Зх - 4у + 25 = 0.
Строим точку С (3; —4), прямую АВ по ее уравнению и пер-
пендикуляр СМ из точки С на пря-
мую АВ (рис. 52). Очевидно, иско-
мым расстоянием является длина от-
резка СМ.
Приступаем к анализу этой слож-
ной задачи, т. е. к разложению ее
на простые задачи (см. последний
абзац § 10), отвечая на ряд последо-
вательных вопросов, идя от искомого
(неизвестного) к данным (известным).
1) Что надо знать для нахожде-
ния длины отрезка СА4? Надо знать
координаты точки М.
2) Чем характерна точка М для прямых АВ и СМ? Точка М
является их общей точкой (точкой пересечения).
3) Что надо знать, чтобы найти координаты точки пересече-
ния двух прямых? Надо иметь уравнения этих прямых.
57
4) Даны ли эти уравнения в условиях задачи? Не дано уравне-
ние перпендикуляра СМ.
5) Уравнением какого вида можно воспользоваться для сос-
тавления уравнения прямой СЛ4? Уравнением прямой, проходя-
щей через данную точку в данном направлении.
6) Как найти угловой коэффициент этой прямой? Воспользо-
вавшись условием перпендикулярности двух прямых.
Решение, очевидно, должно идти в обратном порядке, т. е.
от известного к неизвестному.
План решения:
1) Найти угловой коэффициент перпендикуляра СМ;
2) Составить уравнение этого перпендикуляра;
3) Найти координаты точки пересечения прямых АВ и СМ;
4) Найти длину отрезка СМ.
Решение. 1) Представив уравнение данной прямой в виде
3 25
У = -^х-\--^, находим из условия перпендикулярности угловой
коэффициент прямой СМ. Получаем
, 1 1 4
.,.,4 • .
2) Составляем уравнение прямой СМ:
г/ + 4 = -|(х-3); 4х-|-3^ = 0.
3) Решаем систему уравнений Зх — 4z/-p25 — 0; 4х -(- Зу — 0
способом подстановки. Получим:
у = — 4-х; Зх — 4^—4 х^ -У 25 = 0;
Зх-Ь^хД- 25 = 0; уХ-(-25=.О; х = хж = —3;
4 4
У/л = — -^Хм —---з (~ 3) = 4.
4) Вычисляем длину перпендикуляра. Получаем
d = СМ = V(хс - х.42 + (Ус - W -1 (3 + 3)44-4 - 4)*= 10.
Как видим, решение сложной задачи составилось из решения
четырех простых задач.
Пример 2. Даны уравнения двух сторон параллелограмма
х — 2у-(-8 = 0; х у — 7=0 и точка пересечения его диагона-
лей М (—2; 6). Составить уравнения двух других сторон.
Строим точку М (—2; 6) и стороны параллелограмма по их
уравнениям (рис. 53). Основываясь на теоремах о свойствах сто-
рон и диагоналей параллелограмма, путем такого же анализа, ка-
кой предшествовал составлению плана в первом примере, полу-
чаем следующий план решения:
58
1) Найти координаты точки пересечения (на рис. 53 обозна-
чена буквой А) двух данных прямых;
2) Найти координаты вершины С, лежащей против вершины А,
пользуясь формулами деления отрезка пополам;
3) Составить уравнения сторон ВС и CD, воспользовавшись
условием параллельности двух
прямых.
Решение. 1) Решаем сов-
местно уравнения х — 2д-(-8=
= 0; х-\-у — 7 = 0. Получаем:
х —хд = 2; у—ул—5.
2) Находим координаты точ-
ки С, решив уравнения
______Хс + ХА. ,, З’с+З'а
Хм —_2 » £, /И 2 *
в которых неизвестными яв-
ляются хс и ус. Получаем: хс —
= —6; ус~7.
3) Составляем уравнения сторон ВС и
фициентами этих прямых будут kDc = kAD-
Получаем:
CD. Угловыми коэф-
- 2; kcD=kAS=—1.
х — 2у -j- 20 = 0 — уравнение ВС:
х у — 1=0 — уравнение CD.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Чем определяется положение прямой на плоскости, когда уравнение
се дается а виде у= Ьх Ь7
2. Какие числовые значения могут принимать в уравнении у — kx-\- b
параметры k и Ь?
3. Чем определяется положение прямой на плоскости, когда уравнение
х . у ...
се дается в виде---1?
а о
4. При каком численном значении параметра b прямая, данная уравне-
нием вида y — kx-^-b, пройдет через начало координат?
5. При каком значении параметра А эта прямая будет параллельна
оси 0x7
6. Можно ли уравнению прямой, проходящей через начало координат,
придать вид ^--|-у=1?
1- Как располагается относительно1 осей координат прямая Ar-f-C=O?
8. Можно ли из уравнения Эх — 2у—15 = 0 найти х и у7 Сколько
таких решений?
Y* V
91 Сколько- решений имеет уравнение — -(-< = [?
- 2
10. При каком значении b прямая у= x-j-б пройдет через точку
(—6; 8)?
59
11. При каких значениях коэффициентов А и В прямая Ах By — 14 = 0
пройдет через точки (4; 2) и (10; —2)?
12. Две прямые, параллельные осям координат, проходят через точку'
(—5; 4). Написать уравнения этих прямых.
13. При каком значении а прямая 4- = 1 пройдет через точку (6; 4)?
14. Основанием равностороннего треугольника является отрезок па
оси Ох. Чему будут равны угловые коэффициенты боковых сторон этого
треугольника?
15. Прямая линия проходит через точки (5; 4); (—6; 4). Написать уравне-
ние этой прямой, не пользуясь уравнением (12).
16. Прямая линия проходит через точки (—7; 4) и (—7; 199). Написать
уравнение этой прямой.
17. Не решая системы уравнений и не пользуясь чертежом, определить,
пересекаются или не пересекаются данные прямые:
2 1
1) у = ±х-}-4;у = - — %4-175;
2) у = 1,375% + 100; у = — 1 х - 73;
3) 2% - 5у + 17 = 0; 5х + 2у - 41 = 0;
4) 2% + Зу - 25 = 0; 4% + бу - 17 = 0.
18. Какой геометрический образ соответствует системе двух уравнений:
1) 96% - 37 у — 64 = 0; 5% + 2у - 41 = 0:
2) у - 75% + 99 = 0; 2у = 150% + 183 = 0.
19. При каком значении коэффициента k прямые y — kx-j-З и 2% — 5_у-|-
4-8=0 будут параллельны?
3
20. При каком значении коэффициента А прямые у = --%-]- 4 и Д%4-
4~8_у—17=0 будут перпендикулярны?
21. При каком значении а уравнения
%4-Зу —12 = 0; £-4-^ = 1.
За 1 а
будут равносильны?
Ответы: 10. При Ь= 12. 11. Л = 2, В = 3. 13. При а — 7. 14. kL=y~3,
k,=— КЗ. 18. 1) Точка; 2) пара параллельных прямых, 20. При Д = 4^-.
21. При а = 4.
Глава IV
КРИВЫЕ ВТОРОГО ПОРЯДКА
§ 24. ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК
Одной из основных задач аналитической геометрии является
следующая: дана линия как геометрическое место точек, обла-
дающих каким-нибудь известным свойством. Выразить уравнением
(аналитически) зависимость между координатами точек этой линии,
или, как говорят, составить уравнение этой линии.
О линии как геометрическом месте точек уже была речь в § 9,
а уравнения геометрических мест точек и составление таких
60
уравнений (прямых линий) известны из гл. III. В данной главе
займемся составлением уравнений кривых линий, рассматривая
их как геометрическое место точек, обладающих одним и тем же
свойством, и изучением этих кривых по их уравнениям.
Пример 1. Составить уравнение окружности с центром в начале
координат, если радиус равен 5.
Решение. Вспомним определение окружности: окружностью
называется геометрическое место то-
чек, одинаково удаленных от одной
точки, называемой центром. Этим оп-
ределением выражается свойство, об-
щее для всех точек окружности.
Возьмем на окружности (рис. 54)
произвольные точки В (хв уг), С (х2; у.2),
D(x3; у3) и Е (х4; z/4) и соединим их
с центром. Согласно свойству, прису-
щему всем точкам окружности,
0B=0C = 0D = 0E = 5. (а)
Пользуясь формулой для определения расстояния точки от
начала координат, равенства (а) можно представить в следующем
виде: _____ ______
/*1 + ^=5; Ух$ + у-2 =5;
г_____ г------------ (б)
+ = Ух1 + у1=5.
Очевидно, такого же вида равенство получится и для коорди-
нат любой точки окружности. Поэтому, обозначив через х и у
Если . же точка М
координаты любой точки окружности,
равенства (б) можно заменить одним
уравнением ___________
]/\'2 + //4 = 5. (в)
Это уравнение аналитически выражает
геометрическое свойство, общее для всех
точек окружности; ему должны удовлет-
ворять координаты всех точек окружно-
сти данного радиуса. Координаты же
точек, не лежащих на окружности, удов-
летворять этому уравнению не будут.
В самом деле, если точка Р (хр\ ур)
находится внутри окружности (рис. 55),
то ОР<^5 или kGtp-j-ур<^5.
(хт; ут) находится вне окружности, то
ОЛ4>5 ИЛИ Ухт-^Ут >5.
Итак, уравнению (в) удовлетворяют только координаты точек
окружности, радиус которой равен. 5, и притом любых. Поэтому
61“
уравнение
yV+F=5
называется уравнением окружности с центром в начале коорди-
нат. Возведением обеих частей равенства в квадрат ему можно
придать рациональный вид
x24-t/2=25.
Из рассуждений, приведенных выше, должно быть ясно, что
для составления уравнения линии, все точки которой обладают
одним и тем же свойством,
нет нужды рассматривать много точек.
В рассмотренном примере для этой
цели достаточно было взять одну
любую точку окружности, например
точку А (х, у), и мы получили бы
уравнение (в). Убедимся в этом на
следующем примере.
Пример 2. Составить уравнение
геометрического места точек, равно-
удаленных от оси Ох и от данной
точки В (0; 4).
Решение. Пусть М (х; у) яв-
ляется произвольной точкой иско-
места точек (рис. 56). Тогда, согласно
мого геометрического
условию задачи, должно быть справедливо равенство MiM — ВМ,
где МгМ = у, ВМ = ]/(х — О)2 + (у — 4)2.
Заменив М^М и ВМ их значениями, будем иметь уравнение
г/ = У(х-0)24-(у-4)2.
Возводя обе части этого уравнения в квадрат, получим
г/2 = х2 + г/2-8(/+16; 8(/ = х2+16
или
Можно легко убедиться в том, что любая точка, координаты
которой удовлетворяют этому уравнению, находится на равных
расстояниях от оси Ох и от данной точки В.
Возьмем, например, точку А с абсциссой, равной —6. Полу-
чим:
AiA =у(—6)2 + 2 = 4у + 2 = 6,5;
АВ = ]/(— 6— О)2 4- (6,5-4)2" = /42^5 = 6,5.
Следовательно, геометрическим местом точек, удовлетворяющих
условию нашей задачи, является парабола (см. § 9, пример 2).
02
Пример 3. Составить уравнение геометрического места точек,
разность квадратов расстояний которых от данных точек А (—2; 0)
и В (2; 6) постоянна и равна 4.
Решение. Пусть точка М (х, у)
(рис. 57) является одной из точек, принад-
лежащих искомому геометрическому месту.
Тогда
AM2 — BM'2 = 4.
Приняв во внимание, что
А М = V (х + 2)24-(// —О)2;
ВМ = ]/(х —2)s + (// —6)3,
получим:
(У(х + 2Г + (У-О)2)2 - (V (х-2)3 + (у-6)Ч2 = 4;
х2 -ф- 4х 4 4~ у'2— х24-4х — 4 — y2+12z/ — 36 = 4;
8x4-12// — 40 = 0
или
2х-|- Зг/ — 10 = 0.
Искомое геометрическое место точек есть прямая линия 2x4-
4-3//—10 = 0. Легко доказать, что эта прямая перпендикулярна
отрезку, соединяющему точки А и В.
§ 25. ОКРУЖНОСТЬ И ЕЕ УРАВНЕНИЕ В НОРМАЛЬНОМ ВИДЕ
Положение окружности относительно осей
вполне определено, если даны координаты ее
радиуса.
Положим, что центр окружности находится
а радиус ее равен г
координат будет
центра и длина
в точке С (а, Ь),
этой окружности
(рис. 58). Возьмем на
произвольную точку К (х; у). Тогда, со-
гласно определению окружности, должно
быть справедливо равенство СК = г, где
бы на данной окружности ни находи-
лась точка К-
По формуле (3) § 4 получаем
СК =-- К(х-а)‘2 + (у-6)2.
Заменив в этом равенстве СК его
значением, получим
У(х — а)'2 4- (у — Ь)'2 = г.
Мы вывели уравнение, устанавливающее связь между коорди-
натами х й «/. любой точки окружности. Возведя обе части этого
63
уравнения в квадрат, получим
(х-о)2 + (у-6)2 = г2
(1)
—уравнение окружности в нормальном виде.
В уравнении (1) а, b и г будут параметрами, ахи у — вели-
чинами переменными — текущими координатами. Так как каждой
точке окружности будет соответствовать одна пара значений х
и у, то, очевидно, это уравнение будет иметь бесчисленное мно-
жество решений. Рассмотрим три частных случая.
1. Центр окружности находится на оси Ох. В этом случае
b = Q, и уравнение (1) примет вид (рис. 59, а)
(х — а)2 у2 — г2. (а)
2. Центром окружности является точка, лежащая на оси Оу.
В таком случае нулю будет равна абсцисса центра: а = 0 (рис. 59, б),
и уравнение (1) примет вид
х* + (у-Ь)* = Л (б)
3. Центром окружности служит начало координат (см. рис. 54).
При этом условии а = 0 и 6 = 0, и мы получим
E+ZE3 (2)
— уравнение окружности с центром в начале координат.
64
Зная координаты центра (а; Ь) и радиус г окружности, можно
написать уравнение этой окружности, и наоборот, имея уравне-
ние вида (1), можно найти а, Ь, и г и построить эту окружность.
Пример 1. Построить окружность
(х+3)3 + (у-2)3=16.
Решение. Сравнивая данное уравнение с нормальным урав-
нением окружности (1), видим, что —а = 3, —6 =—2, г3 =16,
откуда получаем: а — — 3, 6 = 2, г = lz16 = 4. Далее строим
центр С(—3; 2) и радиусом, равным 4, описываем окружность
(рис. 59, в).
Пример 2. Построить окружность
х2 + (у-6)3 = 9.
В этом случае a = G, b = 6, г = фЛ9 =3 (см. рис. 59, в).
Пример 3. Построить окружность
(х + 5)2 + у2=16.
Это уравнение можно переписать в таком виде:
к- (-5)Г+(у- О)3 =16,
следовательно, а = —5, 6 = 0, г = 4 (рис. 59, г).
Пример 4. Составить уравнение окружности, зная, что центр
ее находится в точке С(1; —2) и радиус равен 3 единицам мас-
штаба.
Решение. Подставив в уравнение (1) вместо а, 6 и г их
значения, будем иметь
(х-1)34-[у-(-2)]3 = 3\
или
(х-1)3 + (у-|-2)3 = 9.
Мы получили уравнение данной окружности в нормальном
виде. Этому уравнению можно придать другой вид, раскрыв скобки
и перенеся все члены в левую часть. Получим
А-2_2л- + 1-Н3 + 4у + 4 = 9,
или
x3-|-z/3-2x4-4//-4 = 0.
Пример 5. Составить уравнение окружности, зная, что точки
—5; 2 у) и В(1; —1) являются концами одного из ее диа-
метров.
План решения:
1) Находим длину радиуса по формуле (3) § 4;
2) Определяем координаты центра по формулам (4а) § 5;
3 П. Е. Дгачеа
65
3) Пишем уравнение окружности.
Решение. 1) г = уV (хА — {уА —УвТ =
=4 5-1)2+[24- <- d]M/36+4 =
о 1
3) Подставив найденные значения а, b и г в уравнение (1),
получаем
, I 0X2 I / 3? 193
(x+2)2 + [y-Tj =-j6-.
Преобразуем это уравнение, раскрыв скобки, приведя к общему
знаменателю и перенеся все члены в левую часть:
„ . . , . , о 3 ,9 193
х2 + 4х + 4 + у.__у + _==_.
3 193 9 ,
получим
2х‘- -г 2у* + 8х - Зу — 15 = 0.
Указание. Прежде чем перейти к проработке следующего
параграфа, следует решить задачи 149—152.
§ 26. УРАВНЕНИЕ ОКРУЖНОСТИ КАК ЧАСТНЫЙ ВИД
ОБЩЕГО УРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ
С ДВУМЯ ПЕРЕМЕННЫМИ
После раскрытия скобок, перенесения члена г2 влево и рас-
положения всех членов по убывающим степеням х и у (см. реше-
ние примера 4 в предыдущем параграфе) уравнение (1) принимает
вид
*2 + У9 — 2ах — 2Ьуа?Ьг— г3 —0.
Приняв
—2а = т, —2Ь — п, а2-\-Ь2 — г^ — р,
получим уравнение окружности в общем виде
х1 + + тх -ф- пу 4- р = 0 . (3)
66
Если коэффициенты т, п и р (все или по крайней мере один
из них) — числа дробные (см. пример 5 в § 25), то после приве-
дения к общему знаменателю это уравнение примет вид
Лх24- Ay'1 A-Dx А-Еу A-F = С) . (За)
Это уравнение, как и уравнение (3), является частным случаем
общего уравнения второй степени с двумя переменными
Ах* 4- Вху Су* 4-0*4- Еу-\- F = Q,
когда коэффициенты при квадратах х и у равны между собой
(С = Л) и отсутствует член, содержащий произведение ху (В = 0).
Следовательно, любой данной окружности (при любых числен-
ных значениях а, Ь и г) соответствует такое уравнение второй
степени с текущими координатами х и у, в котором коэффи-
циенты при х* и у* равны и отсутствует член, содержащий про-
изведение координат (ху).
Обратно, геометрическое место точек, определяемое уравне-
нием (3) или (За), является окружностью.
Чтобы убедиться в этом, рассмотрим примеры. Положим, нам
дано уравнение
х* 4- — 2х 4- 4у — 4 = 0,
в котором т = — 2, п = 4, р = — 4. Переписываем это уравне-
ние, собирая в одну группу члены, содержащие х, а в другую —
члены, содержащие у, и перенося свободный член вправо:
(*3-2х)4-(г/а + 4г/) = 4.
Затем первую группу дополняем до полного квадрата разно-
сти двух количеств, прибавив 1у) = I2, вторую — до полного
/ 4 v
квадрата суммы, прибавляя (у) = 22; к правой части прибав-
ляем 124-23. Получается уравнение, равносильное данному:
х2 - 2 1 • х 4- 12 4- у* 4- 2 - 2 • у 4- 22 = 4 4~ I2 -}- 2а,
или
(х-1)24-(//4-2)2 = 9.
Это уравнение [сравните его с уравнением (1)] является
уравнением окружности с центром в точке (1; —2) и с радиусом
г = |/9=3. Следовательно, данному уравнению х2-}- у* — 2х 4~
4- 4у — 4 = 0 соответствует окружность.
Возьмем другой пример. Пусть нам дано уравнение
2х2 4- 2щ 4- 8х — Зу — 15 = О,
где Л=2, 0 = 8, Е = — 3, Е = —15.
3’
67
Разделим все члены этого уравнения на коэффициент А = 2.
Получится уравнение
——^ = 0.
Это уравнение преобразуем так же, как это было сделано
в предыдущем примере:
+ +
(xs + 2.2.x + 2*) + [z7-2.1 • у+(|)2] = § + 22 + ^У;
Получили уравнение окружности с центром в точке (—2; 4)
и радиусом г = — ]/ 193. Следовательно, данное уравнение выра-
жает окружность.
Допустим теперь, что нам дано такое уравнение:
х3 -J- у2 — 6х Д- 8у -j- 25 — 0.
Преобразуем его так же, как это мы делали выше:
(х3 - 6х) + (у1 Д- 8//) = — 25;
(х3-2.3-х + 33) + (//3 + 2.4-г/ + 43) = -25 + 32 + 43;
получим
(х-3)3 + (у + 4)3 = 0.
Сумма квадратов двух действительных чисел (х — 3) и (//-)-4)
может быть равна нулю лишь тогда, когда каждое из них равно
нулю, т. е. х-3 = 0 и //-|-4 = 0, откуда х = 3, у — — 4. Сле-
довательно, данному уравнению на плоскости соответствует
только одна точка М (3; —4).
Может случиться и так, что уравнению вида (1) никакого
геометрического образа соответствовать не будет. Возьмем, напри-
мер, уравнение
х3 4“ У* — 4х — 6д/ —29 = 0.
В результате преобразований оно примет вид
(х — 2)3 Д-(у — З)3 = —16.
Сумма квадратов чисел (х — 2) и (у— 3) ни при каких дей-
ствительных значениях х и у не может быть меньше нуля. Сле-
довательно, это уравнение никакого геометрического образа не
выражает.
Указание. На окружность даны задачи 149 — 172; рекомен-
дуется иллюстрировать их решение чертежами. Звездочками отме-
чены номера задач, к которььм даны подробные указания.
68
§ 27. ЭЛЛИПС. ВЫЧЕРЧИВАНИЕ ЭЛЛИПСА НЕПРЕРЫВНЫМ
ДВИЖЕНИЕМ. УРАВНЕНИЕ ЭЛЛИПСА
Эллипсом называется геометрическое место точек, сумма рас-
стояний которых от двух данных точек, называемых фокусами,
является величиной постоянной.
На основании этого определения эллипс можно вычертить
непрерывным движением при помощи нерастяжимой нити. Берем
на плоскости две произвольные точки Fi и (рис. 60) и закреп-
ляем в этих точках кнопками концы нити длиной / так, чтобы
длина I была больше расстояния между фокусами Fi и Ft. Затем,
натянув нить острием карандаша, перемещаем его по бумаге,
следя за тем, чтобы нить все время оставалась натянутой. Острие
карандаша опишет замкнутую кривую линию, для точек М, Mi,
М3, ... которой будут справедливы равенства
FjM + /W = FtM, + FtMt = F,M2 + F,M, = ...=l.
Займемся теперь выводом уравнения эллипса. Предположим,
что фокусами его являются точки Fi и F> (рис. 61). Примем
прямую, проходящую через фокусы, за ось абсцисс, а за начало
координат возьмем середину отрезка F>F\. Расстояние между
фокусами обозначим через 2с (FiFl = 2c). Следовательно, коорди-
натами фокусов будут (—с; 0) и (с; 0). Пусть М (х; у) будет
произвольной точкой эллипса; тогда, согласно определению,
сумма расстояний точки М от фокусов должна быть величиной
постоянной независимо от того, где на кривой находится эта
точка. Обозначив постоянную величину через 2а, будем иметь
равенство
FiM + F<iM = 2a,
определяющее геометрическое свойство любой точки эллипса.
Очевидно, FiM -ф- FM ф> F2Ft, или 2йф>2с, откуда следует;
й^>с;
й3ф>с'2; а3 — саф>0.
69
'Выразим длины отрезков FiM и Е'М через координаты их кон-
цов. Найдем:
FiM = V (х — с}1 + (у — О)2 =•• У х2 — 2сх + с2 + у1\
F.M = /[х-(-с)]2 + (//-0)2 = /x24-2Cx4-c2 + z/2.
Подставив в равенство FiM 4~ F-.M = 2а вместо FiM и РгМ
их значения, получим уравнение
Ух2 — 2сх 4~ с2 4- + У*1 + 2сх 4- с2 Ц- У1 = 2а.
Этим уравнением будут связаны координаты х и у любой
точки эллипса, следовательно, оно является уравнением эллипса.
Упростим уравнение, освободившись от радикалов. Для этого
перенесем один из радикалов вправо и обе части преобразован-
ного уравнения возвысим в квадрат:
(Ух2 4~ 2сх 4* с2 + уУ" — (2а — Ух2 — 2сх 4~ с2 -|- z/2)2;
х2 4- 2сх 4~ с2 4~ У1 = 4а2 — 4а Ух2 — 2сх 4- с2 4~ у2 4~
4~ х2 — 2сх 4- с2 4- У1-
Уединяем радикал и приводим подобные члены:
4а Ух2 — 2сх 4- с2 4- у2 = 4а2 4-х2 — 2сх 4- с2 4~ у2 —
-(х24-2сх4-с24-г/2);
4а У~У — 2сх 4- с2 4- у2 — 4а2 — 4сх.
После сокращения на 4 получаем
а Ух2 — 2сх 4* с2 4- У2 — а2 — сх.
Возводим в квадрат повторно и делаем приведение подобных
членов:
(а У х2 — 2сх 4- с2 4- уУ = (а2 — сх)2;
а2 (х2 — 2сх 4- с2 4- у2) — а^ — 2а2сх 4- с2х2;
а2х2 — 2а2сх Д- а2с2 4~ a V — °4 — 2а2сх 4- с2х2;
а2х2 4- а2с2 4- а2у2 = а4 4~ с2х2.
Переносим члены, содержащие текущие координаты хну,
влево, свободные члены — вправо. Получаем
а2х2 — с2х2 4- а 2у2 = а* — а2с2,
или
(а2 — с2) х2 4- а2у2 = а2 (а2 — с2). (а)
Выше было показано, что а2 — с24>0. Следовательно, У а2 — с2
будет числом действительным. Обозначив этот корень через Ь,
получим
У а2 — с2 — Ь, или а2 — с2 — Ь2.
70
Заменив в уравнении (а) разность а9 — с9 ее значением tr,
найдем
Ьгх1 -|- а2//9 = а963.
Разделив все члены этого уравнения на а3/?9, получим
й2л2 , а2У а2Ь2
а2Ь2 ~1~ а2Ь2 а2Ь2 ’
(4)
Это и есть каноническое (нормальное) уравнение эллипса.
В нем х и у — текущие координаты точки эллипса, а и b —
параметры, связанные с половиной расстояния между фокусами
равенством
а9 — с* = Ь? . (4а)
—
Отрезки FtM и F^M (расстояния точки М эллипса от его
фокусов) принято называть фокальными радиусами этой точки.
§ 28. ИССЛЕДОВАНИЕ ФОРМЬ'1 ЭЛЛИПСА ПО ЕГО УРАВНЕНИЮ
Решим уравнение (4) относительно у.
У1 х2. у_й3-х2.
Ь2 а2' Ь2 а2 '
= — yl,i = ±b~Vai — xi.
(а)
Как видим, у является двузначной функцией х; при этом каж-
дому допустимому значению абсцис-
сы х соответствуют два таких значе-
ния ординаты у, которые равны по
абсолютной величине и противопо-
ложны по знаку. Это значит, что лю-
бой точке К (хк‘, Ук) эллипса, распо-
ложенной над осью Ox(yK^>Q),
соответствует точка /С (ху —уф),
расположенная под осью Ох и нахо-
дящаяся от нее на таком же рас-
стоянии, что и точка К (рис. 62).
Следовательно, эллипс симметричен
относительно оси Ох.
При х = 0 имеем yi^ = ± — ]/ra‘i — Qi — ±b. Значит эллипс
(4) пересекает ось Оу в точках В (0; Ь) и Bi (0; — b).
Когда абсцисса х возрастает от 0 до а, абсолютная величина
ординаты у убывает и при х = а обращается в нуль: =
71
— ^.--Ya4, — a2 = 0. Следовательно, эллипс пересекает ось Ох
в точке А (а; 0).
При значениях абсциссы х, превышающих по абсолютной
величине число а, в уравнении (а) под знаком квадратного корня
получаются отрицательные числа и вследствие этого значения у
становятся мнимыми. Значит, абсцисса х может принимать лишь
такие значения, которые удовлетворяют условиям
|x|sSa, или —
т. е. эллипс всеми своими точками укладывается внутри полосы,
ограниченной прямыми х — а, х = — а.
Решив уравнение (4) относительно х, получим
Х1.2 = ± у — у1. (б)
Из уравнения (б) видно, чго ордината у может принимать
только такие значения, которые удовлетворяют условиям
и что каждому допустимому значению ее (у) соответствуют два
значения абсциссы х, равные по абсолютной величине, но противо-
положные по знаку. Так, например, точкам К(х/<; уА), А (а; 0)
и Ki (хк-, — ук) соответствуют
точки К' (—хА; ук), Л1 (—а; 0)
и Ki (—ху — Ук) (рис. 63). Сле-
довательно, эллипс симметричен
относительно оси Оу и всеми
своими точками располагается
внутри полосы, ограниченной
прямыми у — Ь, у — — Ь.
Раз эллипс симметричен от-
носительно осей Ох и Оу, то он
будет симметричен и относитель-
но начала координат, т. е. любой
точке К (хА; Ук) будет соответствовать точка KJ (—хк\ —ук).
Это значит, что любая хорда эллипса, проходящая через точку
О (0; 0), делится ею пополам. Точку, обладающую таким свой-
ством, принято называть центром кривой, а хорду, проходящую
через нее, — диаметром кривой. Следовательно, центром эллипса
(4) является начало координат.
Точки А (а; 0), А, (—а; 0), В (0; Ь) и Bt (0; —b) называются
вершинами эллипса. Отрезок AtA = 2a называется большой осью
эллипса, а отрезок В^В = 2Ь— его малой осью.
Полуоси эллипса О А —а, ОВ = Ь и полуфокусное расстояние
OFt = c (рис. 64) связаны формулой (4а); из этой формулы следует
а°- = Ь* -[ с\
(46)
72
т. е. большая полуось а эллипса может быть рассматриваема
как гипотенуза такого прямоугольного треугольника, катетами
Рис. 64
Рис. 65
эллипса делается отрезок BjB = 2b, формула (46) принимает вид
№ = + (4в)
Пример 1. Построить вершины и фокусы эллипса, если даны
малая полуось b и полуфокусное расстояние с.
Решение. Положим, нам дано CD = b, КМ = с (см. рис. 64).
По этим данным строим вершины В(0; b), Bj (0; —b) и фокусы
Fi (с; 0) и В>(—с\ 0). По формуле (4а) большая полуось должна
быть равна гипотенузе прямоугольного треугольника ВОС. На
оси Ох по обе стороны от начала координат делаем засечки
радиусом, равным BFi — a: найдем вершины А и At.
Пример 2. Составить каноническое уравнение эллипса, зная,
что полуфокусное расстояние его равно 2, большая полуось
равна 4.
Решение. Каноническое уравнение эллипса имеет вид
где а и b являются его полуосями. Нам дано: а = 4, с = 2.
Зная а и с, легко найти квадрат малой полуоси (№) по формуле
(4а). Получаем
К = а- — 42 — 2! = 12,
следовательно, искомым уравнением будет
или Зх34у‘л = 48.
73
Пример 3. Составить каноническое уравнение эллипса, зная,
что он проходит через точку (2; ф^б), а большая полуось его
равна 4.
Решение. Уравнение эллипса имеет вид
-+^ = 1
а2 ь-
В данном случае нам известно, что а —4. Требуется найти №.
По условию, точка (2; —j/б) должна лежать на эллипсе
и поэтому ее координаты должны удовлетворять искомому урав-
нению. Подставив в уравнение (4) вместо текущих координат
координаты данной точки, получим:
?1 + ЬГЗ=1; А+»=1;
а- 1 Ь- 16 1 Ъ- '
§ 29. ЭКСЦЕНТРИСИТЕТ ЭЛЛИПСА. СВЯЗЬ МЕЖДУ ЭЛЛИПСОМ
П ОКРУЖНОСТЬЮ
Эксцентриситетом эллипса называется отношение расстояния
между фокусами 2с к длине его большой оси 2а. Это отношение
равно так как c<Za> то> очевидно, ~<^1- Из формулы
или с = У"а2 — №. Обозначив величину
эксцентриситета эллипса буквой е,
получим
(5)
а а
(4а) следует с2 = а- — &2,
Из формулы (5) видно, что 0<^
при этом с увеличением
длины малой полуоси b (при данной
длине большой полуоси а) разность
№ — № уменьшается и вследствие
этого уменьшается и эксцентриситет
е, приближаясь к нулю; при умень-
шении b эксцентриситет, наоборот,
увеличивается, приближаясь к еди-
нице. Следовательно, по величине
эксцентриситета можно судить о форме эллипса: чем больше экс-
центриситет, тем более вытянут эллипс.
На рис. 66 сплошной линией изображен эллипс = Ь
а пунктирной ^4--^= 1.
74
У обоих эллипсов а9 = 25, а = 5. У первого эллипса
6.=9; (,=3.
а 5 5’
у второго
tA 1С и л /25^Лб 3
Ь!= 16, о = 4; е=-—=-----= —.
’ 5 э
Как видим, у более сжатого эллипса эксцентриситет больше,
чем у менее сжатого.
В частном случае, когда Ь = а, уравнение (4) принимает вид
5 + 5 = ’’ или + = (2)
но мы знаем, что уравнение (2) является уравнением окружности
с центром в начале координат и с радиусом, равным а. Значит,
окружность можно рассматривать как частный случай эллипса,
когда полуоси его равны между собой и эксцентриситет равен
нулю:
__per —а3___ 0 _п
Пример 1. Найти вершины, фокусы и эксцентриситет эллипса
19ха+ 16г/9 —9 = 0.
Решение. 1) Приводим данное уравнение к каноническому
виду. Для этого переносим свободный член вправо и делим все
члены на свободный член:
9х9+ 16у9 = 9; ^Ц-+Е = 1.
2) Делим числитель и знаменатель первой дроби на 9, вто-
рой — на 16:
16
получаем
Сопоставив это уравнение с уравнением (4), находим:
.=£=jL_ El
а 1 4 *
75
Следовательно, вершинами этого эллипса будут точки А_(1; 0),
Л|(—1; 0), В (о-, Bi ^0; — фокусами — Ft ; о),
Ft 0У Эксцентриситет будет равен
Пример 2, Составить уравнение эллипса, зная, что сумма его
4
полуосей равна 8, а эксцентриситет равен .
Р е ш е н и е. Уравнение эллипса имеет вид
^ + £=1.
а- 1 Ь-
Полуоси эллипса нам не даны. Для нахождения двух неизвест-
ных надо иметь два уравнения, связывающих эти неизвестные.
Одно из таких уравнений нам дано в условии задачи:
а—|—6 = 8.
Второе уравнение найдем, заменив в формуле (5) е данным
его значением. Получим
у а- —ь-4
а 5
Затем решаем систему уравнений:
| а -ф- Ь = 8,
| 5 \ (Г — Ь^—4а.
Получим а = 5, Ь = 3.
Следовательно, искомым уравнением будет
§5+^ = 1 или 9а:2 —25г/2 — 225 = 0.
„ г I о О 1^«2 — Fs 'I''" 25 — 9 4
Проверка: 5-ф3 — о; е =-----------= —g------= .
Указание. На эллипс приведены задачи 173—191. К зада-
чам, у номеров которых поставлены звездочки, в конце книги
даны подробные указания.
§ 30. ГИПЕРБОЛА. УРАВНЕНИЕ ГИПЕРБОЛЫ
Гиперболой называется геометрическое место точек, разность
расстояний которых от двух данных точек, называемых фокусами,
является величиной постоянной.
Пусть М (х; у) является произвольной точкой гиперболы,
фокусы которой расположены в точках Ft, F> (рис. 67). Обозна-
чив расстояние между фокусами через 2с, а постоянную разность
76
расстояний любой точки от фокусов — через 2а, согласно опреде-
лению гиперболы будем иметь
FiM — F1M = 2a,
где а — число положительное.
Если бы точка М (х; у) была взята так, как это показано на
рис. 68, то, очевидно, получилось бы следующее равенство;
FiM — FiM = 2a,
или
F^M — FiM = — 2а.
Объединив эти равенства общей записью, получим
F.>M — FtM — ± 2а. (а)
Из геометрии известно, что любая сторона треугольника больше
разности двух других его сторон. На основании этой теоремы
утверждаем:
/4F, > РгМ — FiM
или
2с^>2а,
откуда будет следовать:
с^>а; с9^>а3; с2 — а2^>0.
Примем, как и в случае эллипса, за ось Ох прямую, про-
ходящую через фокусы и Ft, за ось Оу — прямую, перпенди-
кулярную к оси Ох и проходящую через середину отрезка
FzFi = 2c (см. рис. 67,68). Тогда координатами фокусов Ft и
будут соответственно (с; 0) н (—с; 0).
Выразим длины отрезков F%M и FtM через координаты их
концов по формуле расстояния между двумя точками:
FtM = У|х - (- с)]2 + (у - 0)~ = У(х + с)2 -V
или
FiM = ]/х'2 ф- 2сх ф- с2 -ф- у2,
FiM — У (х — с)2 4- (у — О)’2 —V'x2 — 2сх -ф с2 ф- у2.
77
Заменив в равенстве (a) F^M и FiM их значениями, получим
уравнение
+ + + — Ух2-2сх + с2-гу2 - ± 2а.
Этому уравнению будут удовлетворять координаты всех точек
гиперболы, следовательно, оно является уравнением гиперболы.
Остается упростить уравнение, освободившись от радикалов. Для
этого один из радикалов переносим вправо и обе части получен-
ного уравнения возводим в квадрат:
(/х2 + 2сх + с2 + уУ = (± 2а + Кх2 - 2сх 4~ с2 4-
х2 4- 2сх с2 у2 — 4а2 ± 4а ]'Лх- — 2сх Д- с2 4~ f/2 +
4- х2 — 2сх 4- с2 4- у2.
Получилось уравнение с одним радикалом. Уединяем радикал,
перенося все рациональные члены влево, и приводим подобные
члены:
х2 -J- 2сх 4~ с2 4~ У2 — 4а2 — х2 4~ 2сх — с2 — у2 =
— ± 4а У х2 — 2сх 4- с2 4- у2',
4сх — 4а2 — ± 4а Ух2 — 2сх 4- с2 4- у2.
Сокращаем на 4 и повторно возводим в квадрат обе части
уравнения: _________________
сх — а2 — ± а Ух2 — 2сх 4- с2 -j- у2',
(сх — а2)2 = (± аУх2 — 2сх 4- с2 4- У2}2',
с2х2 — 2а2сх а4 = а2 (х2 — 2сх 4~ £2 +
с2х2 — 2а2сх 4- а4 = а2х2 — 2а2сх 4- а2 с2 4- а2 у2-,
с2х2 4~ а4 = а2х2 4- а2 с2 4~ а2 У2-
Переносим члены, содержащие текущие координаты, влево,
свободные члены — вправо. Получаем
с2х2 — а2х2 — а2у2 — а2с2 — а1,
или
(с2 — а2) х2 — а2у2 = а2 (с2 - а2).
Выше было показано, что
с2 — а2>0;
это значит, что Ус2— а2 будет числом действительным. Примем
У с2 — а2 = Ь, откуда
с2 — а2 — Ь2 . (6а)
Приняв во внимание равенство (6а), предыдущее уравнение
можно переписать в следующем виде:
Ь2х2 — а2у2 = а2Ь2,
78
откуда, разделив все
в простейшем виде:
члены на (did1-, получим уравнение гиперболы
£ _ _____
а2 6а
(6)
где х и у —текущие координаты точек гиперболы, а и Ь — пара-
, 2с
метры, связанные с полуфокусным расстоянием =
формулой (6а).
§31. ИССЛЕДОВАНИЕ ФОРМЫ ГИПЕРБОЛЫ ПО ЕЕ УРАВНЕНИЮ
Решим уравнение (6) относительно у:
У“ _ .V2 , t __ 1 i g л. о ___ Ь / q q.
р- — !> ^(х —а); у — —
Получаем
У1)2 = ± —а3.
(а)
Из уравнения (а) следует:
1) ординаты ум действительны лишь при таких значениях
абсциссы х, которые удов-
летворяют условию х'2 а3, Ун
или | х 12= а. Следователь-
но, гипербола (6) всеми
своими точками распола-
гается вне полосы, огра-
ниченной прямыми Х = й,
х=— а (рис. 69);
2) каждому допустимо-
му значению абсциссы х
соответствуют два значения
ординаты у, равные по аб-
Рис. 69
солютной величине и про-
тивоположные по знаку.
Это значит, что произвольной точке гиперболы К (хк уд) соответ-
5
ствует точка /G(xi; —уд). Например, при х — ^а найдем
т. е. точке D^a\ | бу соответствует точка А й; —Сле^
довательно, гипербола (6) симметрична относительно оси Ох.
79
Выразим из уравнения (6) абсциссу х как явную функцию
ординаты у. —
^=-£+1; х2=Й(^ + ^);
а- Ь~ 1 ’ а- Ь~ 1 7 Ь' 1 7
л-1.2 = ±^-'1/ У'Ч-^1- (б)
Уравнение (б) показывает, что на гиперболе любой точке
K(xv, yi) соответствует точка КА—хг, щ). Так, например, точке
Z? ( | cz; будет соответствовать точка —~а; Следова-
тельно, гипербола (6) будет симметрична также и относительно
оси Оу.
Раз гипербола симметрична относительно осей Ох и Оу, то
она будет симметрична и относительно начала координат, т. е.
точке К (xv, yi) будет соответствовать точка /<3(—xv, —уф.
При х — Оса из уравнения (а) находим
£/1,2 = ± Ь~ /(± а)1 — а- = О,
значит, гипербола (6) пересекает ось Ох в точках А (а; 0)
и Л| (— а; 0).
При возрастающих значениях абсциссы х, удовлетворяющих
условию х>Щ подкоренное выражение в уравнении (а) будет
увеличиваться и вследствие этого абсолютные значения ординаты
тоже будут возрастать.
Наконец, из того же уравнения видно, что при х->со орди-
наты yY ±оо. Приходим к . заключению, что правая часть
гиперболы имеет вид, изображенный на рис. 69, а так как гипер-
бола симметрична относительно оси Оу, то левая ее часть будет
зеркальным отражением правой части. Мы видим, что гипербола
состоит из двух частей: правой ветви, простирающейся
неограниченно вправо, и левой ветви, симметричной правой
относительно оси бу.
Точки А (а; 0) и Ai (—а; 0), в которых гипербола пересекается
с осью Ох, называются вершинами гиперболы, а отрезок А}А = 2а —
ее действительной осью. В полосе, ограниченной прямыми х = а
и х ——а, как было показано выше, точек гиперболы нет, следо-
вательно, гипербола (6) с осью Оу общих точек не имеет. Отрезок,
ограниченный точками В (0; Ь) и Bi (0; — b), равный 2Ь, называется
мнимой осью этой гиперболы, а точка 0(0; 0) пересечения осей
симметрии (Ох и Оу) — ее центром. Отрезки, соединяющие точку
гиперболы с ее фокусами, называются фокальными радиусами
этой точки.
При выводе уравнения (6) фокусы были взяты на оси Ох.
Если бы за фокусы гиперболы приняли точки F\ (0; с) и Fj (0; —с),
лежащие на оси Оу, и за действительную ось — отрезок SjB = 2b, 80
80
то уравнение гиперболы получило бы вид
1, или
(7)
Гиперболы
х9 у2____________. х9 _уа______________ .
о9 ~ й9 — 1 ’ а2~Ь2^~[
принято называть сопряженными. На рис. 70 гипербола ~—Ур~ 1
X9 V9
изображена сплошной линией, а гипербола —1—пунк-
тиром.
Пример 1. Написать уравнение
гиперболы, вершины которой нахо-
дятся в точках А (3; 0), и Aj (—3; 0),
а полуфокусное расстояние равно 5.
Решение. Вершины гиперболы
находятся на оси Ох. Следовательно,
ось Ох является ее действительной
осью и уравнение имеет вид
a2 b2 '
F F
Из условия задачи известно, что а = 3, с = —’—‘ = 5. Для
нахождения мнимой полуоси b в формулу (6а) вместо а и с под-
ставляем их значения, получаем:
5- —3'2 = ^; й3=16; Ь = Ь
х9 .у9 , х9 у” ,
Д 4а Н ИЛИ у [д-1.
Пример 2. Составить уравнение гиперболы, зная, что фокусы
ее находятся в точках F\ (0; 5), Fi (0; —5) и действительная ось
равна 8.
Решение. Фокусы находятся на оси Оу. Действительной
осью является отрезок на оси Оу. Уравнение имеет вид
_ 1
а2 Ь2
Нам дано: с —5, Ь — — Для нахождения мнимой полу-
оси в формулу (6а) вместо с и b подставляем их значения; полу-
чаем:
52 — а'3 —42; а* = 5*— 43; а = 3;
9 1б— к
81
§ 32. ПОСТРОЕНИЕ ФОКУСОВ ГИПЕРБОЛЫ ПО ДАННЫМ ПОЛУОСЯМ.
ЭКСЦЕНТРИСИТЕТ ГИПЕРБОЛЫ
Зависимость между полуосями гиперболы и полуфокусным
расстоянием выражается формулой
с2 — а2 = £г или с2 = а'- -ф 1г.
Из последней формулы видно, что с может быть определено как ги-
потенуза прямоугольного треугольника, катеты которого равны а и Ь.
На рис. 71 О А —а, ОВ — b, /_АОВ = 90°, следовательно, АВ=с,
откуда следует, что для построения фо-
кусов Fi и F? нужно отложить на оси
Ох по обе стороны от начала коорди-
нат отрезки, равные гипотенузе прямо-
угольного треугольника, катетами кото-
рого являются полуоси гиперболы.
Эксцентриситетом гиперболы назы-
вается отношение расстояния между
фокусами 2с к длине действительной оси
2а. Обозначив эксцентриситет гипербо-
лы буквой е, получим
У дроби ~ числитель с больше знаменателя а. Следовательно,
эксцентриситет гиперболы будет больше единицы.
Из формулы (6а) имеем с—Уа’А-Ь'. Заменив в равенстве (а)
с его выражением через поуоси гиперболы, найдем
(8)
Из формулы видно, что с уменьшением длины мнимой полуоси
b при постоянной длине действительной полуоси а эксцентриситет
гиперболы убывает, приближаясь к единице.
Пример 1. Дана гипербола 2х2 — Зф=12. Найти эксцентри-
ситет этой гиперболы.
Решение. Известно, что
а '
Следовательно, для вычисления эксцентриситета данной ги-
перболы надо предварительно найти ее полуоси. Приводим дан-
ное уравнение к простейшему виду:
2х’-Зг'=|2; ф-ф=1; 7-5 = 1.
82
Сопоставив это уравнение с уравнением (6), находим:
а9 = 6; а — У~6; 69 = 4; 6 = 2.
По формуле (8) получаем
_ /6 + 4 _ /10 _ /5 _ J_ 1/Тн
а /6 /6 /3 ' 3
Пример 2. Написать каноническое уравнение гиперболы, зная,
5
что мнимая полуось 6 = 2, эксцентриситет е = у.
Решение. Уравнение гиперболы имеет вид
Чтобы написать уравнение гиперболы, удовлетворяющей
условиям данной задачи, надо знать ее полуоси. Мнимая полуось нам
дана. Следовательно, задача сводится к составлению и решению
уравнения с одним неизвестным а.
Известно, что — (8). Подставив в эту формулу
вместо е и 6 их значения, найдем:
5 =/^ + 2; 25 25а9 = 9а936;
3 а ’ 9 а- 9 1
16а9 = 36; а9 = ^- = 2,25; -^ — ^ = 1.
4 ’ 2,2э 4
§ 33. АСИМПТОТЫ ГИПЕРБОЛЫ
В § 31 мы видели, что гипербола состоит из двух ветвей,
одна из которых неограниченно простирается вправо (при х^>а),
другая — влево (при х<^ — а). Чтобы
получить ясное представление о харак- 'Х м
тере изменения кривой, когда описы- /) м
вающая ее точка Л4 (х; у) уходит в бес- \\' Ь>'—~~я /
конечность, возьмем прямоугольник со \\ /
сторонами 2а и 26, расположенными от i \ / /
осей координат Ох и Оу на расстоя- --------АгМ/ХЛ?—I *
ниях, соответственно равных а и 6 п / \ /й+J х
(рис. 72). /I/ \ \
Построив диагонали этого прямо-
угольника и неограниченно их про- // ' ' ’
должив, получим две прямые, прохо- // 'Х
дящие через начало координат. Одна Рис. 72
из них, проходящая через верши-
ны О (а; 6) и Е (—а; —6), будет иметь своим уравнением
(а)
83
другая выразится уравнением
У—~ ~х. (б)
Возьмем на прямой у — ^х и на верхней части правой
ветви гиперболы ]/х2 — а1] точки К и М, имеющие одну
и ту же абсциссу, и сравним их ординаты. Обозначив ординату
точки К, взятой на прямой, через уп и ординату точки гипер-
болы М — через уг, получим:
РК=уп=^х; PM=yt = ±Vx*~=&;
МК =^yn~y[ = ^x — ~Vx1 — ai = ~{x — Vxi —
Чтобы уверенно судить о том, как изменяется (увеличивается
или уменьшается) длина отрезка МК, когда абсцисса х возрастает
и ордината РК удаляется от оси Оу, преобразуем правую часть
последнего равенства, умножив и разделив ее на x-j-pCx2 — а2:
мк=yn-yt=-- • =
U U а х-^ух3-^
__ Ь х2 — (х2 — а2) _ ъ
а . х -j- У'л2 — а2 а х -f- У Xs — а2 ’
Получим
Числитель правой части равенства — величина постоянная.
При х->оо знаменатель неограниченно возрастает. Следовательно,
по мере увеличения х дробь убывает и при стремлении х->оо
стремится к нулю. Отсюда следует МК — уп—у, -* О или ус-*уп,
когда х->оо. Значит, точка М, удаляясь по гиперболе в бесконеч-
ность, неограниченно близко подходит к прямой у = ^х.
Прямая линия, к которой как угодно близко приближается
переменная точка М, удаляясь по кривой линии в бесконечность,
называется асимптотой этой кривой. Следовательно, прямая
у = ~х является асимптотой верхней части правой ветви ги-
перболы
= (6)
Вследствие симметричности гиперболы и прямых (а) и (б) отно-
сительно оси Ох асимптотой нижней части этой ветви будет пря-
мая у —— ~ х. Гипербола (6) и прямые (а) и (б) симметричны
84
также и относительно оси Оу, следовательно, эти прямые будут
асимптотами и левой ветви гиперболы.
V2 V2
Итак, гипербола — р = 1 имеет две асимптоты:
, Ь
± — X
а
(9)
Ранее, в § 31, было замечено, что все точки гиперболы рас-
положены вне полосы, ограниченной прямыми х = а и х = — а.
Теперь мы имеем основание утверждать, что гипербола всеми
своими точками располагается внутри вертикальных углов, обра-
зуемых ее асимптотами, и вне полосы, ограниченной прямыми
х = — а и х = а. Проведенные в данном параграфе исследования
приводят нас к следующей схеме построения гиперболы (от руки)
по данному ее уравнению:
1) найти полуоси а и b и построить точки А (а; 0), ЛД—а; 0),
В(0; Ь) и ВДО; — 6);
2) построить прямоугольник со сторонами, проходящими че-
рез эти точки параллельно осям координат, и асимптоты ги-
перболы;
3) начертить ветви гиперболы как кривые, проходящие через
точки А (а; 0) и Ai (—а; 0) и приближающиеся к асимптотам
по мере удаления от начала ко-
ординат.
Примечание. Две сопря-
женные гиперболы
имеют одни и те же асимп-
тоты.
Пример 1. Построить ги-
перболы: 1) 4№ — 9у! — 36 = 0;
2) 4х2 —9у2 4-36 = 0.
Решение. 1) Разделив все
члены этих уравнений на абсо-
лютную величину их свободных членов, получим:
хг v2 V2
1) 9 — т- 1 =0 илп т
Г2 V2 г2
2) '9 — д+’=° ИЛИ -д-
сравнивая эти уравнения с уравнениями (6) и (7), видим: а2 = 9,
а = 3, 6'2 = 4, 6 = 2.
Строим точки (рис. 73); А (3, 0), Ai (—3; 0), В (0; 2) и
Bi (0; -2).
85
2) Через эти точки проводим прямые, параллельные осям
координат, и строим асимптоты
у — ± ~ х (а = 3, b — 2).
3) Вычерчиваем ветви гиперболы, учитывая свойства асимптот.
На рис. 73 гипербола^—~ = —1 изображена пунктиром.
Пример 2. Составить каноническое уравнение гиперболы, зная,
что расстояние между ее фокусами равно 4113 и асимптотами
являются прямые:
, 2
Решение. Чтобы написать искомое уравнение, надо знать
полуоси гиперболы а и Ь. Они нам не даны. Решение задачи
сводится к составлению и решению системы двух уравнений
2с
с неизвестными а и Ь. Из условия задачи известно, что с = -^ —
_4J_13_2 j/13; но мы знаем также, что с = ]/аа + Ь-. Соединив
знаком равенства правые части этих равенств, получим уравнение
-|- Ь? = 2 V13, или а- + А = 52.
Сопоставление уравнения асимптот (9) с уравнением у =
= ± д Х приводит ко второму уравнению с этими неизвестными
А —2
а 3 •
В результате совместного решения этих уравнений найдем:
а = 6, 6 = 4. Искомое уравнение будет иметь вид
— 1
36 16 ‘
§ 34. РАВНОСТОРОННЯЯ ГИПЕРБОЛА
Гипербола называется равносторонней, если мнимая полуось
ее равна действительной полуоси, т. е. если Ь — а (рис. 74, а).
Очевидно, уравнение равносторонней гиперболы явится част-
ным случаем уравнения
х3 V3 , ,
-т — ^=1 ПРИ Ь = а
и будет иметь вид
g-5=1, или р-г/* = а2 (10)
86
Асимптотами равносторонней гиперболы будут служить пря-
мые у = ±- х [см. формулу (9)] или у — ±х. Угловые коэф-
фициенты прямых у~х и у = — х соответственно равны ^ = 1,
ki = —1. С положительным направлением оси Ох первая из них
образует угол он = arctg 1 = 45°, вторая — угол а2=180° — а,—
—135°. Следовательно, асимптоты равносторонней гиперболы
взаимно перпендикулярны и являются биссектрисами координат-
ных углов. Полуфокусное расстояние такой гиперболы опреде-
ляется по формуле (6а):
с1 = а2-ф-а2 = 2о3; с = ]/2а- = аУ2.
Следовательно, фокусами равносторонней гиперболы (10) будут
точки Л (а /2; 0) и К2(— а/2; 0).
Пример. Составить каноническое уравнение равносторонней
гиперболы, зная, что она проходит через точку (—Pl 5; —1^6).
Решение. Каноническое уравнение равносторонней гипер-
болы имеет вид
х2-у2 = а2. (10)
В этом уравнении имеется только один параметр а. Следует
его определить так, чтобы кривая (10) прошла через данную
точку. Мы знаем, что линия проходит через точку в случае,
когда координаты точки удовлетворяют уравнению этой линии.
Получаем:
(—/15)2-(—Кб)2 = а9; 6?= 15 —6 = 9;
87
§ 35. УРАВНЕНИЕ РАВНОСТОРОННЕЙ ГИПЕРБОЛЫ, ОТНЕСЕННОЙ
К АСИМПТОТАМ. ВЫЧЕРЧИВАНИЕ ГИПЕРБОЛЫ
НЕПРЕРЫВНЫМ ДВИЖЕНИЕМ
Составим уравнение равносторонней гиперболы, приняв за
оси координат ее асимптоты. Для этого повернем рис. 74, а
против часовой стрелки на 45°. Тогда асимптота CL(y —— х)
примет горизонтальное положение, асимптота DE(y=x) напра-
вится вертикально и гипербола расположится так, как это ука-
зано на рис. 74, б.
Выведем уравнение этой гиперболы, приняв за оси координат
ее взаимно перпендикулярные асимптоты CL и DE. Определим
в первую очередь координаты
фокусов Fi и F-2 относительно но-
вой системы координат (рис. 75).
В § 34 было найдено, что с = а 1/2.
Из прямоугольного треугольника
OPFi найдем:
xFi — OP — OFi cos 45° —
= a 1/2 • = a;
yFl — PEi — OP— a,
следовательно, координатами фо-
куса Fi будут числа (а; а). Фо-
кус Е> симметричен фокусу Д
относительно начала координат, вследствие этого его координа-
тами будут числа (—а; —а).
Возьмем на гиперболе произвольную точку М (х; у). Тогда,
согласно определению гиперболы (см. § 30),
РгМ — FiM = ± 2а, (а)
где
F>M = /[х — (— а)]- 4- [у — (— а)]'2 — 1'/Н-г у1 Д- 2ах --2ау Mia1',
FiM = V (х — а}'14- [у — а)- = j/x2 4~ У'1 — 2.ах — 2ау 4- 2а’2.
Подставив в равенство (а) вместо FiM и FiM их выражения
получим уравнение
1 х2 -Д if Д- 2ах Д- 2ау 4- 2d1 — Дх2 4 - У2 — 2ах — 2ау Д- 2а’2 — ±2а.
Остается упростить это уравнение, освободившись от ради-
калов. Для этого второй радикал перенесем вправо и обе части
88
полученного уравнения возведем в квадрат:
(/ x'2 -j- yi 4- 2дх 4- Чау 2а'2)9 =
= (]/ х24- if — %ах — Ъщ/ + 2а2 zb 2а)9;
г* + f + Чах 4- Чау 4- 2а2 = х2 4~ уг — Чах — Чау 4- 2а2 ±
zb 4а ]/ л2 -р if — Чах — Чау 4~ 2а2 -4 4а'3.
Это уравнение после переноса всех рациональных членов
влево и приведения подобных членов примет вид
4ах ~4 4ау — 4а'2 = zb 4а4 42 4- if — 2а.у — Чау 4- 2а2,
или
4а (х -4 У — а) = ± 4а]/ .4 -4 У9 — 2ах — Чау -4 2а'2.
Далее сократим обе части на 4а и возведем повторно в
квадрат:
(х 4~ у — а)'2 = (zb ]f х'2 Д- у2 — Чах — Чау 4- 2а2)9;
х1 4- if + «9 + 2-ту — Чах — Чау = .4 4~ if — Чах — Чау -4 2а'2.
После приведения подобных членов это уравнение примет
вид
2ху=а>, или ху = ~.
of
Положив для краткости -y — k, получим xy = k, следова-
тельно, уравнение равносторонней гиперболы относительно асим-
птот имеет вид
xy = k , или
(Н)
Это уравнение известно из курса алгебры как аналитическое
выражение обратно пропорциональной зависимости.
Пример. Написать уравнение равносторонней гиперболы,
отнесенной к асимптотам, зная, что она проходит через точку
(/13-43; /13-3).
Решение. Рассуждаем так же, как при решении примера
в конце § 34:
1) xy = k\
2) (/134-3) (/13 — 3) = k; \3~9 = k или А = 4;
3) ху = 4.
Гиперболу, как и эллипс (см. § 27), можно построить непрерывным
движением.
Пусть требуется построить гиперболу по данному фокусному расстоя-
нию F-\Pt=.'2c и данной действительной оси AiA = 2a. Берем линейку дли-
ной I и прикрепляем один конец в фокусе /Ь штифтом так, чтобы она
89
могла вращаться вокруг него (рис. 76). В другом конце линейки М прикре-
пляем нерастяжимую нить MM=l — 2а (на рисунке показана пунктиром).
Прикрепив другой конец нити к фокусу Flt натягиваем ее острием каран-
даша /< (рис. 77), прижимая карандаш к линейке (нить показана пунктиром).
При вращении линейки вокруг F2 острие карандаша L опишет правую ветвь
гиперболы, так как при любых возможных положениях линейки будет спра-
ведливо равенство FSL — L\L — 2а, так как FSL = I — ML, FiL — I — 2а — ML.
Так же построим и левую ветвь гиперболы, прикрепив конец линейки
в фокусе Ft, а конец нити в фокусе FL
§ 36. ПАРАБОЛА II ЕЕ ПРОСТЕЙШЕЕ УРАВНЕНИЕ
Параболой называется геометрическое место точек, равноот-
стоящих от данной
точки, называемой фокусом, и данной пря-
мой, называемой директрисой параболы.
Из определения параболы следует,
что A, Ai, А^, ..., АП будут точками
параболы (рис. 78), директрисой которой
является данная прямая CD и фоку-
сом — данная точка F, если будут спра-
ведливы равенства
АК — AF-, AiKi = AiF-,
АчКг — A%F', ... АпКп = AnF.
Параболу, как и другие кривые второго ио-
рядка (см. § 27 и 35), можно построить непре-
рывным движением. На рис. 79 F— фокус,
MN — директриса параболы, /. — линейка, при-
крепленная вдоль директрисы. Нерастяжимая
нить длиной, равной катету АС треугольника
АВС, одним концом прикреплена в фокусе па-
раболы, а другим — в вершине А треугольника.
Если карандашом К натянуть нить, прижав ее
к треугольнику, то при скольжении треугольника
по линейке острие карандаша опишет параболу, потому что для любого
положения D острия карандаша будет справедливо равенство CD = DF
(нить на рис. 79 показана пунктиром).
90
Положим, что прямая РТ является директрисой параболы,
точка F — ее фокусом (рис. 80). Через фокус F проведем пря-
мую FK перпендикулярно к директрисе РТ и примем эту прямую
за ось Ох. За начало координат
О возьмем середину перпендику-
ляра FK, опущенного из фоку-
са на директрису. Тогда ось Оу
Ту. '
------
Рис. 80
будет, очевидно, параллельна директрисе РТ. Обозначим KF = p,
тогда KO = OF = P/., координаты фокуса будут 0^ и уравне-
ние директрисы будет иметь вид
%— 2 .
Пусть М (х; у) является произвольной точкой параболы. Сое-
диним эту точку с фокусом F и опустим из нее перпендику-
ляр ME на директрису РТ. Точка Е имеет координаты —у; у).
Согласно определению параболы получим равенство
FM = ЕМ.
Выразим длины отрезков FM и ЕМ через координаты их
концов. Получим:
FM = + ;
ЕМ = К Mi = КО + OMV = х 4- .
После замены FM и ЕМ их найденными выражениями равен-
ство FM — EM примет вид
Получили уравнение параболы, т. е. такое уравнение, кото-
рым устанавливается связь между текущими координатами (х и у)
91
и параметром (р) параболы. Остаётся упростить уравнение,
сделав некоторые алгебраические преобразования. Возводим обе
части в квадрат:
( ]/X2 - рх 4-+ у2) = (х 4- ;
х2 - рх 4- f 4- у- = х2 4- рх 4- ,
откуда после приведения
Рис. 81
иметь вид
подобных членов получаем простейшее
или каноническое уравнение параболы
у1 = 2рх , (12)
где хи у — текущие координаты, ар —
параметр (расстояние от фокуса до ди-
ректрисы).
При выводе уравнения (12) за ось
Ох была принята прямая, проведенная
через фокус перпендикулярно дирек-
трисе. При взаимном расположении ди-
ректрисы РТ и фокуса F, показанных
на рис. 81, целесообразнее за ось Ох принять прямую, прове-
денную через середину отрезка FK параллельно директрисе РТ,
а за ось Оу —прямую, перпендикулярную директрисе и прохо-
дящую через фокус F. В этом случае уравнение параболы будет
х2 = 2ру
(13)
Вывод этого уравнения такой же, как и уравнения (12). Предла-
гается выполнить эту работу самостоятельно.
§ 37. ИССЛЕДОВАНИЕ ФОРМЫ ПАРАЕОЛЫ ПО ЕЕ УРАВНЕНИЮ
Из уравнения (12)
цшо х. Получаем
выражаем ординату у как явную функ-
у = ± /2рх.
Из этого уравнения можно заключить следующее.
1. Допустимыми будут лишь такие значения абсциссы х, кото-
рые удовлетворяют условиям
О < х < оо,
следовательно, эта парабола всеми своими точками располагается
вправо от оси Оу.
92
2. Каждому допустимому значению абсциссы х соответствуют
два значения ординаты у, равные по абсолютной величине и
противоположные по знаку. В частности, при х = Р- найдем
z/i.2 = ±V2px = ±]f 2рР> =±У р' = ± р.
Как видим, точке pj соответствует точка —р)
(рис. 82), отсюда делаем вывод: парабола (12) симметрична отно-
сительно оси Ох.
3. При х=0 ордината z/i,2—±V<2p-0 =
= 0. Следовательно, парабола проходит
через начало координат. Эта точка (0; 0)
называется вершиной параболы.
4. При возрастании абсциссы х от 0
до оо абсолютные значения ординаты у
возрастают от 0 до со. В результате этого
исследования приходим к заключению, что
парабола yi = 2px располагается на пло-
скости так, как это показано на рис. 82.
Отрезок FM, соединяющий точку М(х; у)
с фокусом F, называется радиусом-векто-
ром этой точки параболы, ось Ох — осью
симметрии параболы.
Примечание. При построении параболы с вершиной в на-
чале координат и симметричной относительно координатной оси,
если это надо сделать быстро и от руки, следует в качестве
обязательных точек строить концы ее хорды,
перпендикулярной к оси симметрии и про-
ходящей через фокус параболы. В случае па-
раболы (12) такими точками будут
А р}’ А‘ (у: — р)-
Мы рассмотрели случай, когда дирек-
трисой служит прямая х = — и парабола
располагается вправо от оси Оу.
Если за директрису такой параболы при-
нять прямую х = ~ (рис. 83), то фокусом
ее будет точка F^— — oj и парабола расположится влево от осп
Оу. Очевидно, абсциссы всех точек этой параболы будут удовлет-
ворять условию
0.
(а)
93
В этом случае уравнение параболы будет иметь вид
у* =— 2рх. (12а)
Парабола (13) симметрична относительно оси Оу, имеет своим
фокусом точку f(o-, и директрисой — прямую у = —она
расположена над осью Ох, а потому ординаты всех ее точек
удовлетворяют условию у^О (рис. 84); концами хорды, перпен-
дикулярной к оси симметрии и проходящей через фокус, являются
точки л(р-, и Л1(— р; у).
Если за директрису такой параболы принять прямую у = у,
то фокусом ее будет точка (0; —у). В этом случае парабола
располагается под осью Ох (рис. 85) и ее уравнение имеет вид
х2 — — 2ру. (13а)
Очевидно, ординаты всех точек этой параболы удовлетворяют
условию
(б)
Пример 1. Составить уравнение параболы с вершиной в начале
координат и построить ее от руки, зная, что она симметрична
относительно оси Ох и проходит через точку (—2; —КЮ-
Решение. Абсцисса этой точки отрицательна. Следовательно
(см. условие (а)], уравнение параболы имеет вид
if = — 2рх. (12а)
Координаты данной точки должны удовлетворять искомому урав-
нению. Находим:
(— К8)а = — 2р(— 2); 8 = 4р; р = 2; — £ = —1.
Подставив в (12а) вместо р его значение, получим
У* = — 4х.
Фокус этой параболы будет в точке (—1; 0).
94
Концами хорды, проходящей через фокус перпендикулярно к
оси симметрии, будут точки А(—1; 2) и ИД—1; —2). Строим вер-
шину параболы (0; 0), фокус F(—1; 0), точки А и Ai и проводим
плавную кривую, учитывая свойства параболы
трисой будет прямая х—1.
Пример 2. Парабола с вершиной в начале
координат симметрична относительности оси
Оу. Составить уравнение этой параболы, зная,
что она проходит через точку (2 ]/3; —1,5).
Р еше н и е. Ордината данной точки отри-
цательна. Следовательно [см. условие (б)],
уравнение искомой параболы имеет вид
х2 =—2 ру. (13а)
(рис. 86). Дирек-
Рис. 86
Подставив в это уравнение вместо текущих координат коор-
динаты данной точки, находим:
(2 ]/з)2 = — 2р (—1,5); 12 = 3р; д=4.
Заменив в уравнении (13а) параметр р его значением, получаем
х2 = — 8у.
Директрисой этой параболы (рис. 87) является прямая
Фокус будет находиться в точке, абсцисса которой нуль, а
ордината —~ = — -^ = — 2. Концами хорды, проходящей через
фокус перпендикулярно к оси, будут точки А (4; — 2) и
Ai (—4; —2). Строим вершину параболы, фокус (0; —2), точки А,
Ai и через эти точки (С, А и Л1) проводим плавную кривую,
учитывая свойства параболы.
Пример 3. Построить параболу, симметричную относительно
прямой, параллельной оси Оу, зная, что вершиной ее является
точка С (2;—4) и директрисой — прямая у = — 6.
Решение. Построим вершину параболы (рис. 88) и проведем
через нее ось (CD\\Oy). Нам известно, что директриса параболы
95
и ее фокус располагаются по разные стороны от вершины и на
расстояниях, равных у. В данном случае у =— 4 — (—6) = 2.
Следовательно, фокусом параболы будет точка F (2; —2), так как
-4 + ^ =-4 + 2 = -2.
Концами хорды, перпендикулярной оси и проходящей через
фокус, будут точки А (6; —2) и Л] (—2; —2). Построив эти
точки, проводим плавную кривую так же, как указано в преды-
дущем примере.
§ 38. ПАРАБОЛА у = ах2 -ф Ъх с
Поставим задачу: составить уравнение параболы, симметричной
относительно прямой, параллельной оси Оу, зная положение ее
вершины С (а; р) и параметр р.
Согласно условию задачи осью симметрии этой параболы будет
прямая СЕ (рис. 89), параллельная оси Оу и проходящая через
вершину С (а; р), директрисой —
прямая DT, параллельная оси Ох,
находящаяся от фокуса на рас-
стоянии р и от вершины С — на
расстоянии у (см. § 37). Фокусом
этой параболы явится точка
F (а; р -)- , директрисой — пря-
мая у~ р --- у.
Положим, что М (х; у) яв-
ляется произвольной точкой этой
параболы. Тогда, согласно опре-
делению параболы (см. § 36), рас-
стояние этой точки от директрисы (длина отрезка Л12Л4) должно
быть равно ее расстоянию от фокуса. Получаем равенство
M^M = FM. (а)
Из чертежа видно, что
= MiM - = у - DiD = у — (р — = у - р +1.
Выражаем FM по формуле расстояния между двумя точками;
получаем:
FM. — У (л'Л1 — Xf)1 -ф- (ум — yf)- = J/ (х — а)2 —|— у — ^р -ф- yjj =
= |/(х-а)2-ф-Р)-£[2.
96
Заменив в равенстве (а) М«_М и FM их выражениями, полу-
чаем уравнение параболы, соответствующей данным условиям:
У-? + ^=}Л (х-а)‘2 + [(У-₽Г--у2.
Остается упростить это уравнение. Возведем обе его части в
квадрат:
[(У - 3) +1]2 = (/(*- а)2 + [(У - 3) - Ч J7;
[(У - 3) + у]2 = - “)2 + [(У - 3) - т]3 •
Г РI2
Переносим член I(у — Р) — у| влево:
[(у ~ 3) + у] — [(У — ?) — f ] = (X — а)2.
Левую часть последнего уравнения разлагаем на множители
по формуле разности квадратов:
— (у — 3 — j)] = (х — а)2.
Раскрыв в левой части круглые скобки и выполнив надлежа-
щие преобразования, найдем:
(у ~ 3 + у 4“ У — 3 — S’) ' (у ~ 3 4~ у — У 4~ 3 + 4) = ~ я^’
(2y-2?)[f+ ^ = (х-а)2;
2р (у — р) = (х — а)9;
У—3 = ^(Х —а)9;
у=тР(х~а)2 + 3 • О4)
Это уравнение и будет искомым. В нем х и у являются те-
кущими координатами, р — параметром параболы, а и [3 — коор-
динатами ее вершины.
Уравнению (14) можно придать другой вид, раскрыв скобки.
Получим:
У == ~ 2ях + я2) + Р ’’
У — щ х9 —- х 4- 4- 9.
J 2р /? 1 2р 1 1
4 П. Е. Агачев
97
Приняв в последнем уравнении
1 1 о
2р = а' ~^ = Ь> 2/, + ₽ = С>
получим _________________
у = ах* -J- Ьх 4- с .
(б)
(14а)
Уравнение (14) было выведено в предположении, что фокус .
параболы находится выше директрисы. Если фокус параболы по-
местить ниже директрисы, то ее уравнение при тех же данных
примет вид
у^-й>(х_а)2+р’ (14б)
или
у = ах* -4 Ьх 4- с,
где
а = — .'-<0; Ь = ~-, с= — “-4-р.
2р р 1 2р 1 г
Следовательно, уравнение (14а) является общим видом урав-
нений парабол, симметричных относительно прямой, параллель-
ной оси Оу.
Таким же путем можно вывести и уравнение параболы, сим-
метричной относительно прямой, параллельной оси Ох. Это урав-
нение имеет вид
*=^(у-₽)‘2+а (15)
где р -- параметр параболы, а и р —координаты ее вершины.
После раскрытия скобок это уравнение приводится к виду
х — ay*4~ by 4- с ,
(15а)
где
1 , в а2 ,
а = 27/’ Ь = ~р’ С = 27+а-
Очевидно, что уравнения (12), (12а) и (13а) являются частными
видами уравнений (14а) и (15а). Так, например, уравнение (14а)
при 6 = 0 и с = 0 принимает вид у = ах*, а так как а = ~ , то
1 V
У = ‘2рх‘1 или х* = 2ру.
Пример 1. Вершиной параболы является точка С (4; 2), пара-
метр р = 2. Составить уравнение этой, параболы, если ее ось
параллельна: 1) оси Оу, 2) оси Ох.
Решение. 1) Искомое уравнение имеет вид (14). Подставив
в это уравнение вместо р, о. и р их данные значения, получаем
*/ = 2~2 (х ~ 4)24~2, или у~-^х* — 2х4~6 .
98
2) Искомое уравнение имеет вид (15). Заменив в этом уравне-
нии р, а и р их данными значениями, находим
x = 2T2(z/ —2)24-4, или х=^у‘ — I/-J-5.
Пример 2. Построить параболу
У = ^Х1 — 4. (г)
Решение. Это уравнение приводится к виду (14). Получаем
у=1(х2-4х-32) = |(х2-4х + 4-36),
т. е.
У = 2^4^ - 2)3“4 у-
Следовательно, р = 4, а = 2, р = — 4 у, ордината фокуса
pF=P-|-y =— 4y-j~2 =— 2у, вершиной параболы является
точка С (2; —4,5), фокусом — /7 (2; —2,5), концами хорды, пер-
пендикулярной к оси симметрии и проходящей через фокус, будут
точки А (6; —2,5) и Aj (—2; —2,5). Нам уже известно положе-
ние трех точек параболы (рис. 90). Как дополнительные, реко-
мендуется брать точки пересече-
ния данной параболы с осями
координат. При х = 0 находим <
у — у-О2 — у-0 — 4 = — 4. При
у = 0 получаем:
уХ2 — у х — 4 = 0;
х2 — 4х — 32 = 0; Xi, 2 = 2 ± 6.
Следовательно, с осями координат
кается в точках D (0; — 4), Е (8; 0), Ei (— 4; 0).
Учитывая свойства параболы (см. § 37), через эти шесть точек
проводим плавную кривую, которая и будет параболой, заданной
уравнением (г).
Пример 3. Построить параболу х = у (у-}-2)24-3.
Решение. Из сопоставления данного уравнения с уравне-.
пнем (15) следует: ^ = у; у = 2, а = 3, ф = — 2; абсцисса фо-
куса xf = a-|-^- = 34-24-5, ордината уР = Ъ =—2. Следова-
тельно, точка С (3; — 2) — вершина параболы, F (5; — 2) — ее
Рис. 90
данная парабола пересе-
4*
99
фокус; концами хорды, перпендикулярной к оси симметрии у~—2
и проходящей через
фокус параболы, являются точки А (5; 2) и
Л) (5; — 6). Нам уже известно поло-
жение трех точек параболы. Для боль-
шей,точности найдем еще одну точку:
при у = 6 имеем х = -|-(6-|-2)24-3= 11.
Следовательно, точка В (11; 6) при-
надлежит параболе. Строим точки С,
А, А] В и, учитывая свойства пара-
болы, проводим через эти точки плав-
ную кривую (рис. 91).
Пример 4. Построить параболу «/ =
— 6 2•
уравнение в результате тождественных
Решение. Данное
преобразований принимает следующий вид:
у = — (х- — 6х 3) = — (я2 — 6х 4- З2 — 9 -f- 3),
т. е.
— 2Т3И — 3)’+ 1.
Сопоставляя это уравнение с уравнением (146), находим: р = 3;
а—3; р = 1; в этом случае фокус находится ниже вершины пара-
болы: ул=р — у =1 — 1,5 = — 0,5..
Следовательно, точка С (3; 1)—вершина параболы, F (3; —0,5)—
ее фокус; концами хорды у~ — 0,5 являются точки
и (0; —0,5). Находим точки пере-
сечения с осью Ох; при у = 0 имеем:
= 0; х2 — 6х + 3 = 0
л-, о = 3 ± у 9 — 3 3 ± 2,5. Следова-
тельно, данная парабола с осью Ох пе-
ресекается в точках
D(3 + J/6; 0), Di(3-K6; 0).
А (6; —0,5)
Возьмем еще одну точку: при х =— 3
находим у=— 5;
Е (—3; —5). Через эти точки проводим плавную кривую, которая
и будет параболой, соответствующей данному уравнению (рис. 92).
Пример 5. Написать уравнение параболы, симметричной отно-
сительно прямой, параллельной оси Оу, зная, что она проходит
через точки А (—2; 6), В (0; —4), С (4; 0).
Решение. В уравнении (14а) параболы, симметричной отно-
сительно прямой, параллельной оси Оу, имеется три параметра;
100
a, b и с. Следует определить их так, чтобы парабола прошла
через три данные точки. Известно, что линия проходит лишь через
те точки, координаты которых обращают в тождество уравнение
этой линии. Следовательно, кривая (14а) пройдет через точки А,
В и С только при таких значениях а, b и с, при которых будут
справедливы равенства:
1) 6 = а(—2)24-6(—2) + с;
2) —4 = а-0‘24-6-0Ч-с;
3) 0 = а • 4'2• 4-|-с.
Получается система уравнений с тремя неизвестными а, b и
с, решив которую, найдем: а=\,Ь = — 3, с=— 4. Следовательно,
искомым уравнением будет z/ = x'2— Зх-1- 4.
§ 39. ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ КРИВЫХ
1. Иногда целесообразно аналитически представлять кривую линию двумя
уравнениями, в которых текущие координаты х и у выражаются через третью
переменную, называемую параметром.
Если параметр обозначить через t, то параметрические уравнения кривой
запишутся в следующем виде:
х=/(0*.
у = (16).
Особенно часто применяется такой способ задания кривой в механике,
где помимо формы кривой (траектории движения материальной точки) нужно
знать, как меняется положение точки с течением времени, т. е. иметь фор-
мулы, выражающие текущие координаты движущейся точки в зависимости
от времени.
В механике за параметр t обычно принимается время, и уравнения (16)
дают возможность определить положение движущейся точки в любой момент.
Имея параметрические уравнения кривой, можно написать ее обычное
уравнение (в декартовых координатах), для чего достаточно из двух данных
уравнений исключить параметр t.
Пример. Координаты движущейся точки в зависимости от времени t
выражаются уравнениями
х = 2<, у = — 2/3 4- 8/ 5.
1) Найти положение движущейся точки в момент, когда / = 2 единицам
времени.
2) Выразить уравнение траектории движения этой точки в декартовых
координатах.
Р е щ е и и с. 1) Подставляем в уравнения, которые даны в условии,
вместо t ею значение t = 2. Получаем: х = 2 2 = 4, у> = — 4 22 + 8 • 2 4*5=
= 5. Следовательно, в момент 1 = 2 движущаяся точка будет занимать по-
ложение, определяемое координатами (4; 5).
2) Решаем первое уравнение относительно t и подставляем во второе
уравнение вместо t его выражение через х. Получаем:
, = _,.(*у + 8.| + 5,
ИЛИ
у = — х2-|-4x4-5.
* Такая запись означает, что х и > являются функциями от t.
101
2. Параметрические уравнения окружности. Возьмем окружность с
центром в начале координат
(х; у) является произвольной
и радиусом, равным г (рис. 93). Положим, М
точкой этой окружности. Обозначим угол между
подвижным радиусом ОМ и положительным
направлением оси Ох через ср. Очевидно, с из-
менением ср будут изменяться и текущие ко-
ординаты х и у. Следовательно, х и у могут
быть рассматриваемы как функции перемен-
ного угла ср.
• Из треугольника ОМХМ находим:
х = г cos <р,
(17)
у = г sin <р,
где <р — переменный параметр.
Мы получили параметрические уравнения
окружности. Очевидно, при изменении <р от
0° до 360° точка М описывает всю окруж-
ность. Как было замечено выше, от двух па-
раметрических уравнений кривой можно пе-
рейти к одному уравнению, связывающему текущие координаты х и у. В дан-
ном случае это преобразование может быть выполнено в следующем порядке.
Из уравнений (17) находим:
или
X . у
cos ср = — • Sin ср = — •
7 г ’ ‘ г ’
f x\a . f у\а 2 । . . . х2 . у2 .
= COS2 ср + sin2 ср;
X2 + у2 — г3.
Получилось уже известное нам уравнение окружности с центром в на-
чале координат.
3. Параметрические уравнения эллипса. Возьмем две концентрические
окружности с центром в начале координат и с радиусами а и Ь (рис. 94).
Произвольный луч, проведенный из начала
координат, пересечет эти окружности в точ-
ках С и D. Проведем из точки С прямую,
параллельную оси Ох, а из точки D — пря-
мую, параллельную оси Оу, и пометим точку
их пересечения буквой М.
Очевидно, с изменением угла между на-
правлением луча OD и положительным на-
правлением оси Ох положение точки М будет
меняться и вследствие этого будут изменяться
ее координаты. Обозначив этот угол через ср,
текущие координаты точки М — через х и у,
получим:
х —- OD cos ср = a cos ср;
у = ОХЛ4 = CiC = ОС sin ср = 6 sin ср.
Следовательно, в зависимости от величины угла ср координаты точки М
выражаются уравнениями
х = a cos ср;
у — b sin ср.
Докажем, что эти два уравнения выражают эллипс. Исключим из этих
уравнений переменный параметр ср. Разделив первое из них на а, второе —
102
на b, найдем:
Возведя обе части каждого из этих уравнений в квадрат и сложив, по-
лучим:
т. е. уже известное уравнение эллипса.
Следовательно, параметрически эллипс выражается уравнениями:
( х = a cos о,
I у = Ь sin о,
(18)
где а и Ь — полуоси эллипса, <о — переменный параметр, изменяющийся от
0° до 360°.
Замечание. На основании изложенной" теории выполняется построе-
ние эллипса по точкам, когда даются его оси Ча и ЧЬ.
§ 40. КРИВЫЕ ВТОРОГО ПОРЯДКА КАК КОНИЧЕСКИЕ СЕЧЕНИЯ
1. Степень уравнения линии относительно текущих координат
х и у называется порядком этой линии. Согласно этому опреде-
лению прямую линию можно назвать линией первого порядка,
так как она аналитически выражается уравнением первой степе-
ни. Как мы видели, окружность, эллипс, гипербола и парабола
выражаются уравнениями второй степени, поэтому они называ-
ются кривыми второго порядка.
Вид уравнения линии зависит не только от свойств этой линии,
но и от ее положения относительно осей координат. Так, напри-
мер, нам известно несколько видов уравнения окружности одно-
го и того же радиуса (см. § 25) и четыре вида уравнения пара-
болы с одним и тем же параметром (см. § 36—38). Нам известны
простейшие уравнения эллипса и гиперболы. Если бы мы измени-
ли положение осей координат, то для этих кривых получили бы
другие, более сложные, уравнения, но тоже второй степени..
2. Положим, нам дана фигура, образованная прямыми АА, и
ВС, пересекающимися в некоторой точке S (рис. 95). Если вра-
щать фигуру вокруг одной из этих прямых (на чертеже вокруг
ЛЛ|), то любая точка другой прямой (ВС) опишет окружность,
а вся она — поверхность прямого кругового конуса, состоящую
из двух полостей, простирающихся бесконечно по обе стороны
от точки S. При этом прямая ВС будет называться образующей
103
поверхности прямого кругового конуса, пли (для краткости) кру-
гового конуса, или просто конуса, прямая AAi—осью конуса,
точка S — его вершиной.
Эллипс, гипербола и парабола были открыты древнегречески-
ми математиками. Уже за 2200 лет до нашего времени была раз-
работана и теория этих кривых. Изучали эти кривые приемами
элементарной геометрии как плоские конические сечения, т. е.
как линии пересечения поверхности прямого круглого конуса с
плоскостями, не проходящими через вершину конуса.
Посмотрим, при каких положениях секущей плоскости -полу-
чается каждая из кривых второго порядка.
Рис. 95
плоскость
этом случае
Секущая
95, а). В
Р перпендикулярна
в сечении, очевидно,
(рис.
ружиость — частный случай эллипса при Ь — а.
к оси конуса
получится ок-
2. Секущая плоскость Q не перпендикулярна к оси конуса, но
пересекает все его образующие. Можно доказать, что вытянутая
овальная линия, получающаяся в сечении, будет эллипсом.
3. Секущая плоскость R (рис. 95, б) параллельна одной из
образующих (на чертеже R\\BC). В этом случае в сечении полу-
чается кривая, состоящая из одной бесконечной ветви. Эта кри-
вая будет параболой.
4. Секущая плоскость Т (рис. 96) пересекает обе плоскости
конуса. В сечении получается кривая, состоящая из двух беско-
нечных ветвей. Эта кривая будет гиперболой.
Следовательно, все кривые второго порядка являются линия-
ми пересечения поверхности прямого круглого конуса с плоскос-
тями и поэтому их называют коническими сечениями.
104
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Какие кривые линии называются коническими сечениями и почему?
2. Какая кривая линия называется эллипсом?
3. Как построить фокусы гиперболы по данным ее полуосям?
4. Что называется, эксцентриситетом гиперболы?
5. Как изменяется форма, эллипса, когда эксцентриситет его, увеличи-
ваясь, приближается к единице?
6. Что называется параболой?
7. Какая, из кривых второго порядка имеет асимптоты?
8. Как называется гипербола, мнимая полуось которой равняется дейст-
вительной полуоси?
9. Какой вид будет иметь уравнение равносторонней гиперболы, если
за оси координат принять ее асимптоты?
10. Какая зависимость существует между полуосями и полуфокусным
расстоянием: 1) эллипса; 2) гиперболы?
11. Чему равен угол между асимптотами равносторонней гиперболы?
12. Написать уравнения асимптот гиперболы:
П 2)х»-^ = й’;, 3).vy = 6.
13. Какой вид имеет уравнение окружности с центром в любой точке
осп Ох?.
14. Какой вид имеет уравнение гиперболы, действительной осью которой
является отрезок на осп Оу?
15. Какой вид имеет уравнение любой параболы, симметричной относи-
тельно прямой, параллельной осп Оу?
16. Фокусом параболы с вершиной в начале координат служит точка
^0; . Написать уравнение директрисы этой параболы й найти абсциссы
тех ее точек, ординаты которых равны ординате фокуса.
17. Какая линия соответствует уравнению вида
Ах3 + Ау2 + Dx + Еу 4- F = 0?
18. Дано уравнение Ах2 Су2 = F(A > 0 и F>0). Какой знак должен
иметь коэффициент С, чтобы уравнение выражало: 1) эллипс; 2) гиперболу?
19. Сколько точек эллипса, не лежащих на концах одной из его осей,
необходимо знать, чтобы составить его уравнение?
20. Как находятся точки пересечения кривой с осями координат?
21. Даны окружность x34-5’3 = 4 и точки А (—3; 0), В(—1; )/з),
С (—/2; 1), О(У‘2; — /2); Е (— 2; 1), F(—1,5; 1). Выдел ить: 1) точки, кото-
рые лежат на этой окружности; 2) внутри окружности; 3) вне окружности.
22. Какой геометрический образ соответствует уравнению:
1) xs +У = 8; 2) А 4-у2 = 0?
23. Какой геометрический образ соответствует уравнению:
1) .v- — у2 = а2; 2) х3 — у2 = 0; 3).vy = 6?
24. Чем будут отличаться друг от друга окружности:
1) (л-- 3)а 4-(у - 2)а = 16 и (х 4- 1 )3 4- (у - 5)3 = 16;
2) (х - З)2 4- (у 4- 4)2 = 49 и (х - З)3 4- (у 4- 4)2 = 25?
Ответы. 12. 1) у = ±. х; 2) у = ± х; 3) х = 0, у = 0. 16. у = — — t
р и —р. 18. 1) С > 0; 2) С<0. 19. Две точки. 21. 1) В(—1; }'3) и
£>(|/2; —/2); 2) С(-/2; 1) и F(—1,5; 1); 3) Д(—3; 0) и Е (— 2; 1).
22. 1) Окружность; 2) точка (0; 0). 23. Гипербола; 2) пара прямых х4~У = 0;
х — у = 0; 3) гипербола. 24. 1) Положением относительно осей координат;
2) величиной радиусов.
ЧАСТЬ ВТОРАЯ
ЭЛЕМЕНТЫ
ДИФФЕРЕНЦИАЛЬНОГО
ИСЧИСЛЕНИЯ
Глава V
ТЕОРИЯ ПРЕДЕЛОВ
§ 41. АБСОЛЮТНАЯ ВЕЛИЧИНА И СВЯЗАННЫЕ
С НЕИ СООТНОШЕНИЯ
Об абсолютной величине относительного числа уже говори-
лось в § 7; это понятие неоднократно встречалось также в гл II,
III и IV. В данном параграфе рассмотрим некоторые свойства
абсолютных величин алгебраических выражений.
1-е свойство. Абсолютная величина алгебраической суммы
равна или меньше суммы абсолютных величин слагаемых.
Пусть нам даны алгебраические суммы:
1) 5 4- 3 + 6 + 2; 2) — 5-3-6-2; 3) 5-34-6 — 2;
4) —54-3-6-2.
Вычислим абсолютную величину каждой из этих сумм:
1) |54-34-64-2|==| 16 | = 16;
2) | — 5 —3 —6 — 2| = |—16| = 16; I
3) 15-34-6 —2| = |6| = 6; ( }
4) Г—5-4-3 —6 —2| = |—10| = 10. J
Сумма абсолютных величин слагаемых этих алгебраических
сумм соответственно будут равны:
1) |5|4-|3|4-|6|4-|2| = 54-34-64-2=16; .
2) |_5|4-|-3| + |-6|4-|-2| = 54-34-64-2=16;
3) |5|4-|-3|4-|6|4-|-2| = 54-34-64-2=16;
4) |-5|4-|ЗЦ-|-614-1-21 = 54-34-64-2= 16.
Сопоставляя (I) и (II), видим;
1)
2)
3)
4)
5Ч_34_64-2| = |5(4-|3[4-|6]-Ы 2|;
-5-з-6-2| = |-5|4-1-3|4-|-6|-Ы-2|;
5-34-6-2|<|5|4-|-3| + |6|4-|-2|;
-5 4-3-6-2|<|-5|4-|3|4-|-6|4-|-2|.
106
Из данных примеров следует; что абсолютная величина алгеб-
раической суммы равна сумме абсолютных величин слагаемых, когда
все слагаемые имеют одинаковые знаки (примеры 1 и 2), и меньше
этой суммы, когда знаки у слагаемых различны (примеры 3 и 4).
Следовательно, при любых значениях a, b, с, d (больших или
меньших нуля) будет справедлива запись
\a + b + c-\-d\^\a\ + \b\ + \c\ + \d\.
2-е свойство. Абсолютная величина произведения равна
произведению абсолютных величин сомножителей.
Например,
15-(— 3) -21 = I — 30 | = 30;
|5-| — 3|[2| = 5 3-2 = 30;
|5 • ( — 3) • 2 | = |5 | • | — 3 | | 2
Очевидно, при любых значениях a, b, с, d (больших или
меньших нуля) будет справедливо равенство
. | abed | = | а | • | b | • | с | • | d |.
3-е свойство. Абсолютная величина частного равна част-
ному абсолютных величин делимого и делителя.
Возьмем, например, (—18): 9. Абсолютная величина частного
будет равна
|(-18):9К|^| = |-2| = 2.
Частное абсолютных величин делимого и делителя будет равно
|-18|:|9| = Ь^1 = ^ = 2,
откуда
I ~18 Г— I—181
I 9 |- |9| •
Очевидно, что при любых а и b будет справедливо равенство
ИI — ।
I ь |~Iь|•
§ 42. БЕСКОНЕЧНО МАЛАЯ ВЕЛИЧИНА
Известно (см. § 6), что переменной называется такая величина,
которая в течение данного процесса принимает различные значе-
ния, то последовательно убывая и возрастая (например, угол
отклонения часового маятника от вертикали), то все время убы-
вая (например, количество воды в открытом сосуде в сухом и
теплом помещении), то возрастая (время).
107
В пауке, именующейся анализом бесконечно малых величин,
к изучению которой мы приступаем, исключительно важное зна-
чение имеют переменные величины, изменяющиеся так, что по
абсолютной величине они становятся и в дальнейшем остаются
меньше любого наперед за-
данного положительного чис-
ла, как бы мало это число
ни было. Переменные величи-
ны, обладающие таким свой-
ством, принято называть
бесконечно малыми. Позна-
комимся с характером изме-
нения этих переменных ве-
личин на примерах.
Пример 1. Возьмем пе-
ременную ординату точки
М (х, у), перемещающейся по
вправо от оси Оу (рис. 97). (Эта
в § 35.)
я 1
равносторонней гиперболе У= —
гипербола рассматривалась нами
Положим, что абсцисса ее последовательно принимает зна-
чения
х= 1; 2; 3; 4; 5;
и;
тогда ордината последовательно будет принимать значения
1 1 1 1 1 1
у~ 1 - 3 : 4 ’ 5 ’ •" : 7Г:
По мере увеличения х (удаления точки от оси Оу вправо)
ордината у убывает, приближаясь к нулю. При х, неограниченно
возрастающем, ордината ///убывая, становится и в дальнейшем
остается меньше любого наперед заданного положительного числа,
как бы мало оно ни было. Положим, таким наперед заданным
числом является е * = 0,0001. Уже при х= 10001 получим] у \ =
~ юооТ^ е‘ ПРИ значениях х/> 10 001 значения у, очевидно, будут
убывать, оставаясь меньше заданного числа е.
Допустим теперь, что точка АД (х; у), перемещаясь по этой
гиперболе, удаляется от оси Оу влево. Тогда переменная орди-
ната у последовательно будет принимать значения
_____1^ _J_ __1_ . __1_
1 : 2 ’ 3 ’ ’ п : •" : 2н : •
При неограниченном удалении точки Mt (х; у) от оси Оу влево
абсолютная величина у делается меньше и в дальнейшем остается
* е— буква греческого алфавита, называется «эпсилон»,.
108
меньше любого наперед заданного числа е, как бы ни было мало
это число. Следовательно, ордината у точки М является вели-
чиной бесконечно малой при неограниченном увеличении абсолют-
ного значения х.
Пример 2. Возьмем маятник (рис. 98), отклоним его от поло-
жения равновесия АВ на некоторый угол о и отпустим. Под
действием силы тяжести маятник М начнет
колебаться. Угол отклонения маятника от по- //К
ложения равновесия АВ в одну сторону (напри- / \
мер, вправо) будем считать положительным, / \
в другую (влево) — отрицательным. Угол в этом / \
процессе становится то положительным, то от- / \
рицательным. Так как вследствие сопротивле-
ния воздуха и трения размах колебаний будет " д'"
непрерывно уменьшаться, неизбежно наступит Т
момент, начиная с которого абсолютная вели- Рис. 98
чина угла <о станет и в дальнейшем будет оста-
ваться меньше любого наперед заданного положительного числа е,
как бы мало оно ни было, т. е. такой момент, начиная с кото-
рого будет удовлетворяться неравенство
I ? I < £•
Следовательно, в рассмотренном нами процессе угол <р является
величиной бесконечно малой.
Пример 3.. Из физики известно, что Солнце притягивает всякое
небесное тело с силой, равной Д, где k — постоянная величина,
г—расстояние между центрами Солнца и небесного тела (закон
. всемирного тяготения). Допустим, что этим не-
,/ бесным телом является комета, появляющаяся
г/ в пределах солнечной системы только один
// раз. Такая комета огибает Солнце и уходит за
у пределы солнечной системы (рис. 99). По мере
ее удаления от Солнца у дроби ~, выражаю-
щей силу притяжения, при постоянном числи-
Рис. 99 теле знаменатель возрастает и вследствие этого
сила притяжения убывает. При г -> со дробь
k „ ,
р- становится и в дальнейшем остается меньше любого наперед
заданного положительного числа, как бы мало оно ни было. Сле-
довательно, сила, с которой Солнце притягивает комету, удаляю-
щуюся от него в бесконечное мировое пространство, является ве-
личиной бесконечно малой.
Определение. Переменная величина х называется бесконечно
малой, если в процессе своего изменения она по абсолютной вели-
чине становится и в дальнейшем остается меньше любого наперед
109
заданного положительного числа е, как бы мало это число ни было.
Согласно приведенному определению бесконечно малая величина —
величина переменная, поэтому нельзя смешивать очень малое
число с бесконечно малой величиной.
Нуль — единственное число, условно рассматриваемое как бес-
конечно малая величина в силу того, что |0| = 0<^е, где е—
сколь угодно малое положительное число.
Задача 1. Показать, что переменная величина х ——при не-
ограниченном увеличении п является величиной бесконечно малой.
Решение. Давая п последовательно значения: п=1; 2;
3; ...; п; , получим ряд последовательных значений х:
_ 1 1 1 .1.1
х— 2; -22; 23; ...; 2100; ...; 2„; ...
Какое бы малое положительное число е мы ни взяли, в этом
ряду значений х найдется такое число, абсолютная величина кото-
рого будет меньше е. Положим, например, мы приняли е —0,0001.
Уже при п=14 получим
I-J.
| С11
При п — 15, 16,
= ПЙ84<-0,0001, ИЛИ I X I < е.
7, ... будем иметь
1
'21й
1
’210
1 1
32768 ^30000
1 1
65536 60000
1 I е
217 < 13 И
соответственно:
ИЛИ
или | х К ,
Т. д. .
Отсюда видно, что абсолютная величина | х | переменной вели-
чины х становится и в дальнейшем остается меньше сколь угодно
е
У’
...). Следо-
малого положительного числа [е, у,
вательно, эта переменная величина (х =— ± при п неограниченно
возрастающем) является величиной бесконечно малой.
,, L 100
Задача 2. Показать, что переменная величина у — — при не-
ограниченном возрастании х является величиной бесконечно малой.
Решение. Известно, что при постоянном числителе и возра-
стающем знаменателе величина дроби убывает. При неограничен-
ном возрастании х величина у может сделаться и в дальнейшем
оставаться меньше любого наперед заданного числа е, как бы
мало оно ни было. Например, если мы примем е = 0,00001, то
при № 10000001 будем иметь
l»l=I«Sn<0-00001-
110
Следовательно, при х, неограниченно возрастающем, перемен-
ная величина у есть величина бесконечно малая.
Задача 3. Доказать, что синус бесконечно малого угла есть
величина бесконечно малая.
Доказательство. Возьмем окружность радиуса г (рис. 100).
Обозначив радианную меру угла АОМ через х, длину дуги AM —
через /, будем иметь:
l = rx, sinx = -y-. (а)
Очевидно, что половина NM хорды MMt
меньше половины дуги ММ1г т> е.
NM < гх.
Разделив обе части этого неравенства на
г, получим
NM
(б)
rx NM
—, или —
Г ’ У
X.
Приняв во внимание, что левая часть неравенства (б) является
правой частью равенства, (а), получим ^при 0<^х<;у)
sinx<^x.
По условию, х — величина бесконечно малая, т. е. такая пере-
менная величина, которая в процессе своего изменения становится
и в дальнейшем остается по абсолютной величине меньше любого
наперед заданного сколь угодно малого положительного числа е.
А так как | sinx | х |, то, безусловно, | sinх| <^е. Следовательно,
синус бесконечно малого угла есть величина бесконечно малая.
§ 43. БЕСКОНЕЧНО БОЛЬШАЯ ВЕЛИЧИНА
Допустим, что точка М перемещается по оси Ох вправо от
начала координат. При этом ее абсцисса х будет возрастать и
притом так, что неизбежно наступит момент, когда она станет
и в дальнейшем будет оставаться больше любого наперед задан-
ного положительного числа N, как бы велико это число ни было.
В этом случае говорят, что переменная величина х является по-
ложительной бесконечно большой величиной и стремится к -j-oo.
Пусть теперь точка М перемещается по той же оси влево от
начала координат. При этом абсцисса этой точки х будет прини-
мать отрицательные значения, возрастающие по абсолютной вели-
чине. Как бы велико ни было произвольное и наперед нами взятое
положительное число N, наступит момент, когда абсолютная вели-
чина переменной абсциссы | х | станет и в дальнейшем будет оста-
ваться больше числа N. В этом случае говорят,, что переменная
Ш
величина х является отрицательной бесконечно большой величи-
ной и стремится к — оо.
В обоих этих случаях переменная величина х изменяется так,
что абсолютная величина ее становится и в дальнейшем остается
больше любого наперед заданного положительного числа, как бы
велико это число ни было. Такие переменные величины принято
- называть бесконечно большими.
Определение. Переменная величина х называется бесконечно
большой, если она в процессе своего изменения по абсолютной вели-
чине становится и в дальнейшем остается больше любого наперед
заданного положительного числа, как бы велико это число ни
было.
Следует знать и помнить, что термином «бесконечно большая
величина» определяется характер изменения переменной величины
и что бесконечность не есть число. Всякое число, каким бы боль-
шим оно ни было, конечно.
Пример 1. Положим, что точка М (х, у) перемещается по ветви
равносторонней гиперболы ху=1 (см. рис. 97), расположенной
в первой четверти, неограниченно приближаясь к оси Оу. Рас-
смотрим, как при таком перемещении точки М изменяется ее
переменная ордината у. При таком перемещении точки М, оче-
видно, л'->0. При х = 0,5; 0,1; 0,02; 0,004; ... получим ряд по-
следовательных значений у — 2; 10; 50; 250; ...
По мере приближения точки к оси Оу (х->0) переменная
ордината у возрастает и притом так, что, как бы велико ни было
наперед заданное положительное число N, неизбежно наступает
момент, когда абсолютная величина у становится и в дальнейшем
остается больше этого числа. Допустим, нами было взято N —
= 1000. Тогда при любых значениях х, начиная с х = , по-
лучим
1У| = ||| = п= = 1001: \У\>К-
Tool
Следовательно, при х-»0 ордината гиперболы ху= Гявляется
величиной бесконечно большой.
Пример 2. Рассмотрим изменение переменной величины у =
— — > когда х неограниченно возрастает.
При х = 0; 1; 2; 3; 4; ... получим следующий ряд последо-
вательных значений у.
__3 _9_ __27 _81_ 243
2 ; 4 ; 8 : 1б: “32 ’ •••
Члены этого ряда быстро возрастают по абсолютной вели-
чине. Как бы велико ни было наперед заданное положительное
число N, найдется такое значение х, при котором абсолютное
112
значение х станет, а затем при дальнейшем увеличении х и оста-
нется больше этого числа.
Положим, мы взяли N= 1000. Уже при х = 18 получаем
Г^62Т4Г>1470>Л/’
следовательно, при х->со переменная величина
- величиной бесконечно большой.
Пример 3. Возьмем переменную величину y = ctgx и рассмо-
трим ее изменение при х->0
(рис. 101).
Допустим, что r= 1. Из три-
гонометрии известно, что
, BF BF „г.
y = ctgx = —=-j- = BF.
является
По мере приближения угла х
к нулю конец линии котангенса
(точка F) все дальше и дальше
будет удаляться от точки В и
y = ctgx=BF будет неограниченно возрастать. Как бы велико
ни было наперед заданное положительное число N, найдется
такое значение угла х, близкое к нулю, котангенс которого ста-
нет и в дальнейшем останется больше- этого числа.
Следовательно, прих->0 ctgx является величиной бесконечно
большой.
§ 44. СВЯЗЬ МЕЖДУ БЕСКОНЕЧНО МАЛОЙ И БЕСКОНЕЧНО
БОЛЬШОЙ ВЕЛИЧИНАМИ
Между бесконечно малой и бесконечно большой величинами
существует тесная связь, которая определяется следующим:
1. Если х — величина бесконечно большая, то обратная ей вели-
чина y будет величиной бесконечно малой.
2. Если х — величина бесконечно малая, то обратная ей вели-
чина у будет величиной бесконечно большой.
Поясним справедливость этих утверждений на примерах.
Пример 1. Положим, что х — величина бесконечно большая.
Тогда, согласно определению § 43, она в процессе своего изменения
по абсолютной величине становится и в дальнейшем остается
больше любого наперед заданного положительного числа, как бы
велико это число ни было. При |х| = 10; 100; 1000; ... -> со
последовательно будет принимать значения
0,1; 0,01; 0,001; ... ->0.
113
Как видим, абсолютные значения у неограниченно убывают,
приближаясь к нулю. Следовательно, —, когда х — величина бес-
конечно большая, является величиной бесконечно малой.
Пример 2. Положим теперь, что х — величина бесконечно
малая. Тогда, согласно определению § 42, абсолютная величина х
будет убывать, неограниченно приближаясь к нулю.
При |х| — 0,1; 0,01; 0,001; ...->0 последовательно будет
принимать значения
10; 100; 1000; ... ->со.
Как видим, в процессе своего изменения по абсолютной ве-
личине может стать и в дальнейшем оставаться больше любого
положительного числа, как бы это число велико ни было. Следо-
1 ,
вательно, —, когда х — величина бесконечно малая, является
величиной бесконечно большой.
§ 45. ОГРАНИЧЕННАЯ ПЕРЕМЕННАЯ ВЕЛИЧИНА
Переменная величина у называется ограниченной, если при усло-
виях данного вопроса ее абсолютная величина | у | остается меньше
некоторого положительного числа N, т. е. | у | N. Уясним смысл
этого определения на примерах.
Пример 1. Рассмотрим переменную величину у = sinx. Из три-
гонометрии известно, что при любом х
--1 ЗШХгС 1.
Отсюда видно, что sinx — величина ограниченная, так как,
приняв за N любое число больше единицы, например 1,1, будем
иметь
•| z/| = | sinx К 1,1.
А"2 V3
Пример 2. Возьмем эллипс ^-|-р-=1. Очевидно, фокальный
радиус FiM точки М (см. рис. 60), описывающей этот эллипс,
будет ограниченной переменной, так как FtM -ф- F>M — 2а и FiM =
= 2а— К>М<^2а, где 2а — данное положительное число.
Пример 3. Вернемся к примеру 2 из § 7. По условиям этого
примера, ограниченными переменными являются углы аир (см.
рис. 24), так как, в какой бы'точке на прямой КМ ни находи-
лась вершина В треугольника, будут справедливы неравенства;
а <180°; р<180°.
114
§ 46. ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ
В этой главе нами уже рассмотрены два особых вида измене-
ния переменной величины: переменная величина х в процессе
изменения убывает по абсолютной величине, неограниченно при-
ближаясь к нулю, и переменная величина неограниченно возра-
стает по абсолютной величине.
В данном и последующих параграфах изучим третий, особый
вид изменения переменной величины, служащий основой высшей
математики и имеющий первостепенное значение во многих обла-
стях науки и техники. Познакомимся с ним на примерах.
Пример 1. Положим, нам дана убывающая геометрическая
прогрессия:
11111
2 ’ 22 ’ 23 ’ 24.2га ’ • • *
Обозначив сумму первых п членов прогрессии через Sn, будем
иметь
Первый член этой прогрессии ai = y> знаменатель q = у. Из
алгебры известно, что по данному первому члену щ и знамена-
телю q сумма п первых членов геометрической прогрессии нахо-
дится по формуле
о _в1(1-^)
Подставив в эту формулу вместо щ и q их значения, получим
Ifi-Jlfl
Sn = —-----или S„=l— (а)
Заметим тут же, что при любом п (сколько бы слагаемых ни
было взято) эта сумма остается меньше единицы.
Обозначив через Si, S2, S3, ... суммы одного, двух, трех
и т. д. членов, найдем:
Si==l-4 = 4; — 4 =
с___1___L___L.
г>3 - 23 — 8 ’
15 <г _31. О_63.
16’ г>5 32’ 64’ •••
Замечаем, что с увеличением п сумма Sn все более и более
приближается к единице. Из формулы (а) получаем:
5П 1 = —2^; | Sn 1|=1 2" | или । И = 25>
115
Положим теперь, что /г->оо. Тогда становится величиной
бесконечно малой (см. задачу 1, § 42). Это значит, что перемен-
ная величина S„ в процессе своего изменения неограниченно при-
ближается к постоянной величине — единице. В таких случаях
говорят, что постоянная величина (в данном случае единица)
является пределом переменной величины Sn и записывают это так:
lim Sn = 1 *.
п —► со
Эта запись читается: «предел переменной величины Sn при п,
стремящемся к бесконечности, равен единице».
Пример 2. Рассмотрим изменение переменной величины
х =---J— при /->оо.
Придадим этой формуле другой вид, разделив члены числи-
теля на знаменатель. Получим
х = (б)
По условию вопроса, t последовательно может принимать зна-
чения:
t= 10; 100; 1000; 10000; 100000; ...; 10";
при этом соответствующие значения х будут:
, 1 .1 ,1
Х~ а+ю; а' 100’ Й ‘ 1000’
, 1 , 1
10000’ ••• ’ 10й’. ••• •
Замечаем, что чем больше t, тем ближе значения переменной
величины х подходят к постоянной величине а. Из равенства (б)
имеем
1
х — а — —.
При /->оо правая часть этого равенства является величиной
бесконечно малой (см. пример 1, § 42). Это значит, что перемен-
ная величина х неограниченно приближается к постоянной вели-
чине а, т. е.
lim х — а.
X f -* со
Разбор этих примеров приводит нас к следующему определе-
нию понятия предела переменной величины.
* lim — сокращенная запись латинского слова «.limes», что означает,
^предел». .
116
Постоянная величина а называется пределом, переменной вели-
чины х, если разность между ними является величиной бесконечно
малой, т. е.
- limx = a, если х — а —я, (1)
где а — бесконечно малая величина. Разность между бесконечно
малой величиной и нулем, очевидно, равна самой бесконечно
малой величине: а — 0 = а. 'Следовательно, пределом бесконечно
малой величины является нуль. Из равенства (1) следует
х — а-^-а
(2)
т. е. переменная величина х, имеющая своим пределом постоянную
величину а, равняется своему пределу а плюс бесконечно малая
величина.
Примечание 1. Всякая переменная величина, имеющая
предел, является ограниченной переменной.
Примечание 2. Бесконечно большая величина х предела
не имеет, тем не менее вместо записи х->оо в дальнейшем часто
будем писать limx=co, помня при этом, что символ оо никакого
числа не выражает.
Примечание 3. Пределом постоянной величины а является
сама эта постоянная величина: lima = a.
Пример 3. Показать, что числовая последовательность
0,1; 0,11; 0,111; ...; 0,11 ... 1
» единиц
1
имеет своим пределом число у.
Решение. Обозначив члены этой последовательности соот-
ветственно через аь а?,, а2, ..., ап, ..., получим:
а1 = 0,1; а2 = 0,11; «3 = 0,111; ...; а„==0,11 ... 1.
п единиц
Требуется доказать, что при п -> со разность ап — у является
величиной бесконечно малой. Имеем
п депяток
1_Л11 .1 1
ап э — и,и ... 1 -g — 9.10« ,
п единиц
ПЛИ
1 _ 1
ап 9 — 9 10" ‘
Из этого равенства
переменной величиной
видно, что при п -> со разность между
ап и постоянной величиной у есть вели-
П7
чина бесконечно малая. Следовательно (см. определение), число
~ является пределом данной числовой,последовательности.
Пример 4. Показать, что при х->со предел переменной вели-
чины у ——_р3л^— равен 2.
Решение. Находим разность между переменной величиной у
и числом 2:
„ 2х2 4- 6х 4- 1 о 2-v- + 6.v + 1 - 2 (х- + Зх)
У~2 = —^+зг—2 =----------------Р+аГ--------'
Получаем
У — 2=: х3^-3х '
При х->со знаменатель дроби в правой части последнего
равенства — величина бесконечно большая, вследствие чего (см.
§ 44) дробь Л.2][.;->v будет величиной бесконечно малой. Разность
между переменной величиной у и постоянной величиной 2 — вели-
чина бесконечно малая. Следовательно, число 2 является преде-
лом у при х->оо, т. е.
limy —2.
§ 47. ОСНОВНЫЕ СВОЙСТВА БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИН
Первое свойство. Алгебраическая сумма конечного числа
бесконечно малых величин есть также бесконечно малая величина.
Докажем, что если а и р —бесконечно малые величины, то
бесконечно малой величиной будет и их алгебраическая сумма
а-(-р, т. е. докажем, что в процессе приближения переменных
а и р к нулю неизбежно наступит момент, начиная с которого
будет справедливо неравенство
1а + ₽1<£, (а)
где е — сколь угодно малое положительное число.
Доказательство. Так как а и р— бесконечно малые
величины, то независимо от характера изменения каждой из них
неизбежно наступит момент, начиная с которого будут удовлетво-
ряться неравенства (см. решение задачи 1, § 42):
Ы<т;
1М<Ь
Сложив эти неравенства, получим
и+т<-|-+Ь \
или
н+то
118
Нам известно (см. § 41, первое свойство), что абсолютная
величина алгебраической суммы не превышает суммы абсолютных
величин слагаемых. Следовательно,
1*-М1^И + 1₽1О.
или .
1“ е. -
т. е. в процессе приближения переменных а и р к нулю насту-
пит момент, начиная скоторого будет удовлетворяться условие (а).
Следовательно, алгебраическая сумма двух бесконечно малых
величин есть величина бесконечно малая. Таким же путем можно
доказать справедливость этого свойства для трех, четырех и т. д.
бесконечно малых величин.
Уясним себе смысл этого свойства бесконечно малых величин
на примере. Положим, что бесконечно малые величины а и 3
в процессе приближения к нулю последовательно принимают зна-
чения:
а = 0,1; 0,01; 0,001; 0,0001; ... ->0;
В = — 0,12; —0,012; —0,0012; —0,00012; ... ->0.
Тогда их алгебраическая сумма последовательно будет при-
нимать значения:
а-рр = —0,02; —0,002; —0, 0002; —0,00002; ...
Как видим, эта сумма —тоже величина бесконечно малая,
так как среди ее значений найдется такое, начиная с которого
будет удовлетворяться неравенство. | а —|— р | <^ е, где е — любое
сколь угодно малое положительное число.
Примечание. Доказанное свойство бесконечно малых вели-
чин не может быть распространено на случай, когда число сла-
гаемых неограниченно велико. Позднее (в гл. XI) мы увидим,
что пределом суммы бесконечного множества бесконечно малых
величин может оказаться число, отличное от нуля.
Пример 1. Показать, что при х->оо переменная величина'
5*'” —— jc
ц = -Ц-j-- является величиной бесконечно малой.
5-v,v
Решение. Разделим числитель почленно на знаменатель:
* _ 5х х
У ~ 5хх 5хх *
После сокращения получим
1 1 1 , / 1 \
У = х—5^> или y =
При х-*оо правая часть этого равенства является алгебраи-
ческой суммой бесконечно малых величин и —поэтому на
119
основании доказанной теоремы (1-е свойство бесконечно малых
величин) утверждаем, что у— величина бесконечно малая.
Второе свойство. П роизведение ограниченной переменной
величины на бесконечно малую величину есть величина бесконечно
малая.
Положим, что х — ограниченная переменная величина, а —
величина бесконечно малая. Нам нужно доказать, что ха—вели-
чина бесконечно малая.
Доказательство. Мы знаем, что это произведение будет
бесконечно малой величиной, если в процессе изменения пере-
менных х и а наступит момент, начиная с которого будет спра-
ведливо неравенство
| га-| < е ,
где е — произвольно взятое сколь угодно малое положительное
число.
По условию, х — ограниченная величина. Это означает, что
ее абсолютная, величина |х| будет оставаться меньше некоторого
положительного числа. Пусть таким числом будет N, тогда
И<лл
Переменная - а — величина бесконечно малая. Это значит, что
ее абсолютная величина |а|, начиная с некоторого момента, ста-
новится и в дальнейшем остается меньше любого сколь угодно
малого положительного числа. Какое бы малое положительное
число е мы ни взяли, в процессе приближения к нулю неизбежно
наступит момент, начиная с которого будет удовлетворяться
неравенство
Умножив | х|.< N на | а | <Д-Д, получим
l*|-.lal<77‘A или 1*Ыа1<е-
Но мы знаем (см. § 41, второе свойство), что
|x|-|a| = jxa|, . ; .
следовательно,
|ха |<^е,
откуда следует, что ха — величина бесконечно малая. '
Следствие 1. Произведение постоянной величины на беско-
нечно малую величину есть величина бесконечно малая.
Это положение является следствием из доказанного положе-
ния потому, что любая постоянная величина является величиной
ограниченной.
Примечание. Из сказанного следует, что частное от деле-
ния постоянной величины а на бесконечно большую величину х
120
z a 1 1
есть величина бесконечно малая, так как — = а-~, где — при
X X X
х -> со — величина бесконечно малая (см. § 44).
Следствие 2. Прдизведение нескольких бесконечно малых
величин есть величина бесконечно малая.
Любая бесконечно малая величина есть величина ограничен-
ная. Поэтому произведение а-p, где а и р— бесконечно малые
величины, есть величина бесконечно малая.
Точно так же бесконечно малой величиной будет и произве-
дение я • Э • = (я • 9) где -(— третья бесконечно малая величина,
и т. д.
Следствие 3. Целая положительная степень бесконечно
малой ееличины есть величина бесконечно малая.
Это вытекает из 2-го следствия, так как при п целом и поло-
жительном
ап = а а • а •... а.
п раз
Пример 2. Показать, что при х-*оо переменная величина
1000 „ ,
у =----является величиной бесконечно малои.
J х
Решение. Представляем правую часть данного равенства
в виде произведения двух сомножителей:
у=1000~.
1000 — величина постоянная, дробь при х->оо— величина
бесконечно малая. Мы знаем (см. следствие из второго свойства),
что произведение постоянной величины на бесконечно малую есть
, . 1000
величина бесконечно малая, следовательно, у=—-- при х->со—
величина бесконечно малая.
Пример 3. Показать, что при х->0 переменная у = 500.С
является бесконечно малой.
Решение. При х -> 0 квадрат его (х2) — величина бесконечно
малая (3-е следствие из второго свойства). Произведение постоян-
ной величины (500) на бесконечно малую х2 — величина беско-
нечно малая. Следовательно, при х->0 переменная у является
величиной бесконечно малой.
Пример 4. Показать, что при х-->0 переменная величина
у = 6х2 -|- сх, где а, b и с — постоянные величины, является
бесконечно малой.
Решение. Основываясь на следствиях из второго свойства,
утверждаем, что ах3, Ьх'! и сх — величины бесконечно малые.
Значит, у является алгебраической суммой трех бесконечно малых
величин. Первое свойство бесконечно малых величин утверждает,
что такая сумма является величиной бесконечно малой. Следова-
тельно, у —величина бесконечно малая.
121
Пример 5. Доказать, что при х->оо переменная величина
За-’ — 17.V — 19 _
у =-----—--------величина бесконечно малая.
Доказательство. Разделив числитель почленно на зна-
менатель, получим
3 17 19 „ 1 1 1
у —------5-— —г, или у = 3-----17 • ——19•-т.
", X X- Хл й X X- X'1
п ' * 1 1 1 й
При х -> оо дроби —, — и — будут величинами бесконечно
малыми. Тогда в силу следствия из второго свойства слагаемые
3 • Д-, 17 •-i- и 19также будут, бесконечно малыми величинами.
X X X1
Значит, у является алгебраической суммой бесконечно малых вели-
чин, откуда следует, что у — величина бесконечно малая.
§ 48. ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ
Теорема 1. Предел алгебраической суммы конечного числа пере-
менных величин, имеющих пределы, равен алгебраической сумме
пределов слагаемых..
Доказательство. Пусть пределами переменных величин
х, у и 2 будут-числа а, b и с, т. е.
limx —a; limy = &; lim2 = c.
Тогда, согласно определению предела переменной величины
[см. § 46, формула (2)], получим:
х — а-\-щ у=Ьz = c-^-i,
где а, р и у — бесконечно малые величины.
Взяв алгебраическую сумму (х — у 4~ г) этих переменных вели-
чин, получим
х — у -L 2 = (а + а) — (b + Р) 4- (с + 7),
или
х — у 4- 2 = (а — b -4 с) -Н (а — р 4- 7).
Перенося член (а —fe-j-с) влево, получаем
(х — у 4- 2) — (а — b 4-с) — а — р 4- 7.
В этом равенстве (х — у 4- z) — величина переменная, (а — Ь-\~
4- с) — постоянная, а алгебраическая сумма (a —p-j-7) (в силу
первого свойства бесконечно малых величин) — величина беско-
нечно малая. Значит разность между переменной величиной
(х — у4~г) и постоянной величиной . (а — Ь-]-с) является вели-
чиной бесконечно малой. Следовательно, постоянная величина
(а — Ь-\- с) является пределом переменной величины (х — у + г)>
т. е. .
lim (х — у 2) = а — b 4~ с.
122
Приняв во внимание, что а = lim х, b — lim у, с — lim 2, получаем
lim (х — у-\- z) — limx— limу-[- lim z. (3)
Теорема доказана для трех переменных величин. Таким же
путем можно доказать справедливость этой теоремы и для любого
данного числа переменных величин.
Пример 1. Найти предел алгебраической суммы
х3 — х9 + 2х5 при х->0.
Решение. По доказанной теореме получим
lim (х3 — х9 + 2х -ф- 5) = lim х3 — lim х9 lim 2х Ц- lim 5.
х-»0 х —О х —О х-* О х - П
В силу следствий из свойств бесконечно малых величин
limx3 = 0; limx9 = 0; lim2x = 0,
х -» О х -> О X -> О
следовательно,
lim(x3 — х9-]-2хЦ-5) = 5. '
х —О
Теорема 2. Предел произведения конечного числа переменных
величин, имеющих пределы, равен произведению пределов этих
переменных.
Ограничимся доказательством этой теоремы только для
двух переменных. Положим, такими переменными являются х
и у. Пусть
limx = a, limz/ = &;
согласно определению предела переменной величины [см. § 46,
формула (2)], получим:
х = а-|-а, t/=&4“P>
где аи^ — бесконечно малые величины. Перемножив эти равен-
ства, находим
ху = (а -ф- а) (Ь 4" р) = ай -ф- ар 4~ Ьа ар,
или
ху = ab 4- (ар 4~ Ьа. 4- ар).
Перепишем это равенство, перенося член ab влево:
ху — а& = (аР-[-&а4-ар).
В этом равенстве ху—переменная величина, ab — постоянная,
а каждое слагаемое правой части — величина бесконечно малая
(см. следствие из второго свойства и третье свойство бесконечно
малых величин), вследствие чего бесконечно малой величиной
будет и сумма, заключенная в скобки (см. § 47, первое свойство).
123
Оказалось, что разность между переменной величиной ху и постоян-
ной величиной ab — величина бесконечно малая. Следовательно,
lim xy = ab,
или
lim ху — lim х lim у, (4)
Теперь эту теорему можно легко доказать для любого числа
переменных величин, имеющих пределы. Например, при трех
переменных сомножителях х, у иг это доказательство сведется
к следующей записи:
liinxi/г — lim (ху) • lim z= limx- lim у - lim г.
Следствие 1. Предел произведения постоянной величины на
переменную величину равен произведению постоянной величины на
предел переменной величины, т. е. постоянный множитель можно
вынести за знак предела.
Положим, а — постоянная величина, х — переменная величина,
имеющая предел. Тогда, по доказанной теореме, получим
lim ах = lim a- lim х — а •limx, (5)
так как lim а — а.
Следствие 2. Предел целой положительной степени пере-
менной величины, имеющей предел, равен той же степени предела
этой переменной.
Положим, х—переменная величина, имеющая предел, а
п — целое положительное число. Тогда
хп — х-х-х- ... х;
п раз
limхп— limх-limх-limх ... limx,
пли
lim хп — (limx)'1. (6)
Пример 2. Найти предел произведения
(ах Ь) (ах — Ь) (сх -(- d) (сх — d) при х 1.
Решение. Применив теорему 2 и первое следствие из нее,
получим
lim [(ах-|- Ь) (ах — Ь) (сх 4- d) (сх — d) =
X -> 1
— lim (ax-r-b) • lim (ax — b) • lim (ex 4- d) • lim (ex — d) =
Л’-* I Л'-* I x— 1 Л—1
— ('alimx4-• (a limx — b'j • (c limx4-d^ • limx — dj =
= (a • 1 4- b) (a • 1 — b) (с-1 4-d) (c-1 — d) = (a2 - b°) (c- - cP).
Пример 3. Найти lim (x3— 2x2 4" 12x 4-7).
Л'-*• — 1
124 ' .
Решение. Основываясь на теореме 1, пишем
lim (х3— 2х'212x-f~?) = 1|т — lim 2х'24~ lim 12х-|-7.
X— 1 .V—*—1 л- 1 л-—1
Далее применяем следствия из теоремы 2. Получаем
lim (х3 — 2х'212хД-7) — (lim xj3 — 2^ lim хуД-12 lim +7=
= (—I)3 — 2(—1)'2+ 12-(—1)4-7 =—1 -2-124-7 = —8. .
Как видим, нахождение предела данного рационального алгеб-
раического выражения х3 — 2х’24-12х-47 свелось к определению
его значения при х = — 1, т. е.
lim(x3 —2х'2^ 12х-47) = (—I)3 —2(—1)2+12-(—1)4-7. '
X • - 1
.Пример 4. Доказать, что пределом апофемы правильного впи-
санного n-угольника, когда число его сторон п неограниченно
возрастает, является радиус R.
Решение. Положим, что хорда ЛДЛ1 (см. рис. 100) является
одной из сторон n-угольника. Тогда ОМ = О A — R, 0N=g,„
М,0Л4 = —, /Д0М = х = —.
Из прямоугольного треугольника N0M имеем
ON = ОМ cos х или gn = R cos .
Это равенство справедливо при любом п, оно будет справед-
ливо и при п->оо, т. е.
180°
lim gn= lim 7?cos---.
n co n — co ,г
К правой части этого равенства применимо следствие 1 из
теоремы 2. Получаем
1- п 1- 180°
lim gn = R lim cos—.
n оэ n — co n
180- Л .. 180° . _
Так как ——>0, когда rt->oo, то lim cos— = 1. Следова-
П _ n- co n
тельно,
lim £„ = /?• 1 =R.
n-+ co
Теорема 3. Предел частного двух переменных величин, имею-
щих пределы, равен частному пределов делимого и делителя, если
предел делителя не равен нулю.
Доказательство. Пусть х и у — переменные величины.
Положим,
limx = «, lim £/ = 6, b^Q.
125
Тогда будем иметь: x = a-j-a, у = Ь-{-$, где а и р-—беско-
нечно малые величины;
X а 4- а
й + Г
Вычтем из обеих частей этого равенства Получим
х а а л а
У 1) й + Р Ъ ‘
Приведя правую часть этого равенства к общему знаменателю,
будем иметь
х а _____ ab Ьа — аЬ — аЗ___Ьа — аЗ
У- (& + ₽)& — У + ’
или
Дробь ПРИ любом Ь, отличном от нуля,—величина
ограниченная. Множитель Ьх— а$— величина бесконечно малая
(см. § 47, первое свойство и следствие из второго свойства).
Следовательно, правая часть этого равенства — величина беско-
нечно малая (см. § 47, второе свойство). Оказалось, что разность
между переменной величиной -- и постоянной величиной у—
величина бесконечно малая (см. решение примера 4 в конце § 46).
Это значит (согласно определению предела переменной вели-
чины), что
1пп-- = у, или 11Гп7 = — (7)
при условии lim у — Ь 4-0.
3Л-2 _ g
Пример 5. Найти lim 5л. 2'.
Решение. Прежде чем применять теорему о пределе част-
ного (дроби), необходимо убедиться в том, что предел знамена-
теля не равен нулю. Находим:
lim (5x4-2)= lim 5x-|-2 = 51im х4-2 = 5-(—2)-|-2 = —8.
Х--2 х-^-1 х —2
Следовательно, теорема 3 применима. Получаем
, lim (3.v2— 8) 3/ lim лЛ2 — 8
.. Зл- — 8 х — — 2 v __ \х — — 2 J_______
A._J—2 зх + 2 lim (5х -|- 2) 5 lim х -р 2
_ 3 (—2)2 - 8 _ 4 _ ’ ~*1 *-
— 5 • (—2) + 2 ~ — 8 — 2 '
Этот же результат мы могли бы получить проще. Заменив
в данном алгебраическом выражении переменную х ее пределом
126
(приняв х = —2), найдем
.. Зх2 — 8 _ 3 • (—2)3 — 8
5x4-2 ~ 5.(-2) 4-2
I
2 •
Пример 6. Найти lim ~где с —постоянная величина.
3 4Х — d
Решение. Находим предел делителя:
lim (4х-3) =4.|-3 = 3 —3 = 0.
з 4
Пределом делителя является нуль. Следовательно, теорема
о пределе частного неприменима (на нуль делить нельзя). Так
как
lim (4х— 3) = 0,
з
3
то 4х— 3 при х-+ 4—величина бесконечно малая. Тогда вели-
чина, ей обратная, 4л?—3 будет величиной бесконечно большой
(см. § 44, п. 1). Приняв это во внимание, получим
lim . с „ = lim с- ?=с- lim^—5—^ = с • 00 = 00.
з 4л- - 3 3 4х — 3 3 4х — 3
Л“*Т х~*-4
Пример 7. Найти lim * -Зд7.
х — ах а~
Решение. Находим предел делителя:
lim (х9— a9) = (limxV— а9 = а9 —а9 = 0.
х -* а \х а )
Теорему о пределе частного применить нельзя. Заметим, что
при х-±а делимое — величина ограниченная:
Hm TrzS = lim (х + 3а)--т^—г= lim (x-|-3a)-lim ---- -.
х -I-а л “ х—*• а л а х-* а х-а( а
При х-+а разность х9— а9 —величина бесконечно малая,
а поэтому будет величиной бесконечно большой. Получаем
lim-4^=-^,= lim (х-|-За) • lim-г-!—; = 4а-оо = оо.
х_^ 1 > х^аХ1_а*
Замечание. Из разбора примеров 6 и 7 видно, что частное
от деления ограниченной величины на бесконечно малую вели-
чину является величиной бесконечно большой.
127
Теорема 4. Предел корня целой положительной степени из
переменной величины, имеющий предел, равен корню той же сте-
пени из предела этой переменной.
Доказательство. Пусть х — переменная величина, имеющая предел,
п /
а п — целое положительное число. Обозначив у х через у, будем иметь
н >-
у х —у. Очевидно, у будет величиной переменной. Возведя обе части ра-
венства в n-ю степень, получим
х=уп.
Нам известно (следствие второе из теоремы 2), что
limy'’ — (limy)" или (limy)" — limy'1,
откуда
tl г---------------- п.------ п,----------------
у (limy)4 = у limуп или limy = у limу'1.
Заменив в этом равенстве у и уп нх значениями, получим
Z- tl г
х — у Unix. (8)
Пример 8. Найти lim (Ух 2/х — 5).
Решение.
lim (Ух -4- 2-Ух — 5) = Hm /J + 2 1im у*—5 =
= /Т1пГх-|-,2уПййГх —5 = КТб + 2/1б —5 = 3.
«я -* 16 х -* 16
Пример 9. Найти lim 1/х‘2 * — х 4- 7
х - 2 1
Решение.
liin Ух1 — х4- 7 = /Tim (х2 — х7) =
= У 2^—2/7 = /9=3.
, Указание, Прежде чем приступить к проработке следую-
щего параграфа, рекомендуется решить примеры 259—265.
§ 49. ПОНЯТИЕ О ПРЕДЕЛЕ ФУНКЦИИ.
НЕКОТОРЫЕ ПРИЕМЫ НАХОЖДЕНИЯ ПРЕДЕЛОВ ФУНКЦИИ
1. Очевидно, вопрос о пределе функции у может иметь смысл
лишь в том случае, если указывается предел, к которому стре-
мится аргумент х. Зададимся целью уяснить себе смысл утвер-
ждения, что пределом функции у при х->а (а — какое-либо число)
является число Ь.
Возьмем какую-нибудь последовательность значений аргу-
мента х:
Xi, Xi, х3, Xt..х„, (а)
128
стремящуюся к числу а, т. е. когда lim хп — а. Таких последо-
.V -* оэ
вательностей можно выбрать сколько угодно. Всякой последова-
тельности (а) будет соответствовать последовательность значений
самой функции у.
Уи Уъ Уя, У1, Уп, ... (б)
Если любая такая последовательность (б) имеет предел и этот
предел равен числу Ь, то число b называется пределом функции у
при х-*а и это записывается так: lim y — b. Поясним на при-
х -♦ а
мере.
Пусть нам дана функция // = ,v9-J-2. Проследим ход измене-
ния этой функции при х->-1. Положим, что аргумент х прини-
мает последовательность значений:
«/=1,1; 1,01; 1,001; ... -> 1,
стремящуюся к 1, убывая. Тогда функция //= х - —2 последова-
тельно будет принимать значения
у = 3,21; 3,0201; 3,002001; ...->3. (в)
Отсюда следует
lim у = lim (х2 -ф- 2) = 3.
Возьмем далее последовательность значений х, стремящуюся к I,
возрастая (х<4):
л-= 0,9; 0,99; 0,999; ...->1.
Тогда данная функция последовательно будет принимать сле-
дующие значения:
у =2,81; 2,9801; 2,9979; ...^3. (г)
Очевидно, что
limy= 1 im (х2 -|- 2) = 3.
Следовательно,
lim у— lim у = 3.
Последовательности (г) и (в) имеют один и тот же предел,
значит функция y = xn'-\-2 при х->1 имеет предел, равный
числу 3.
Определение. Функция у при х-+а имеет своим пределом
число Ь, если для любой последовательности значений аргумента х,
б П. Е. Агачеа 129
стремящейся к числу а, соответствующие последовательности зна-
чений функции у имеют один и тот же предел, равный Ь.
2. Рассмотрим нахождение пределов функций в тех случаях,
когда непосредственное применение теорем о пределах не при-
водит к. определенным результатам.
Пример 1. Найти предел функции у — х'3— 20х2—17х-|-Зпри
х-> сю.
Решение. При х-»-оо три слагаемых этой алгебраической
суммы (х3, —20х2, —17х) пределов не имеют. Следовательно,
в данном случае теорему о пределе алгебраической суммы непо-
средственно применить нельзя.
Преобразуем данное выражение, вынося х3 за скобки:
lim у — lim (х3— 20х2— 17х-{—3) =
По теореме о пределе произведения находим
Приняв во внимание, что члены — —, —-2, при х->сю
будут бесконечно малыми величинами, получаем
lim г/ = (сю)3(1—0 — 0-|-0) = оо.
х -*• со
Пример 2. Дана кривая у — хг — 5х2— 4. Найти предел пере-
менной ординаты у, когда абсцисса х-> — оо.
Решение. При х->— сю два первых слагаемых (х4, —5х2)
предела иметь не будут. Непосредственно применить теорему
о пределе алгебраической суммы нельзя. Выносим х4 за скобки:
lim у= lim (х4— 5х2Ц-4) = lim |х4[1— 4 + ^
X— — СО х-*—со X —— ooL \ X X
Применяем теорему о пределе произведения. Получаем
Пример 3. Найти предел переменной ординаты у кривой
у— |х:!— 2х2, когда абсцисса х-> — сю.
Решение. Имеем
lim у— lim f-^-x3 — 2х2''} = lim Гх3^-'-------'ll =
Л‘-> — со х — оо V / х~* — оо L V'4 -Г /J
/ I ? \ 1
= 7 lim хР- lim Н--------(—сю);| =— сю.
\х->—со ] — х ! d
130
П 1 ГЛ « . 6д’“ + 5
Пример 4. Наити предел функции y — когда х->оэ.
Решение. Если непосредственно применить теорему о пре-
деле частного, то получится
- ,im (6х2 + 5)
1. , . 6.V- 4-5 X со
lim у — lim = ——...
х _ со .V -, со Зл;- + 2 ' 'Зл + 2)
Запись — никакого числа не выражает. Следовательно, в слу-
чае, когда делимое и делитель являются бесконечно большими
величинами, непосредственное применение теоремы о пределе
частного определенного результата не дает. В таких случаях
нахождение предела частного ведется в следующем порядке:
делимое и делитель делят на наивысшую степень аргумента в
знаменателе (в данном случае на ха):
6л2 4-5 _ 5
6л- 4- 5 _ х2 _ +
3,^ + 2-^2-3+2-
xJ х'
В результате преобразования под знаком предела получается
дробь, числитель и знаменатель которой при х-> оо — величины
ограниченные. Процесс нахождения предела записывается так:
lim
Л-*СО
6х2 4-5___
За2 + 2 —
'—Л
6+ lim £
х -* оо Л*
3+ lim Д
х со X"
64-0
34-0
Результат можно подтвердить способом, рассмотренным в п. 1
данного параграфа. ( Деля числитель на знаменатель, получаем
ОН 4- 5
За2 4- 2 — “Г За2 4- 2
Пусть аргумент х принимает такую последовательность зна-
чений:
10, 100, 1000, ... ->оо;
тогда функция (у) последовательно будет принимать значения
2 J- 2 - — 2 ____!__:
302’ 30002’ 3000002’ ’ ‘' ’
неограниченно приближающиеся к числу 2.
Пример 5. Найти
5*
131
Решение. При х->оо числитель и знаменатель — бесконечно
большие величины. Применяем прием, разобранный в предыду-
щем примере:
xi - Зх2 + 5 ,.
lim —'—= lim
2л“ + 7
Зл- + 5
3 , 5
х--------------
v 1 V-J
lim -
V с с
При х->-оо числитель дроби, стоящей под знаком предела,—
величина бесконечно большая:
знаменатель — ограниченная
величина:
lim
2,
поэтому дробь
X x л
—-------> oo, следовательно,
lira
С СО
lim
7
х'1
Пример 6. Найти
.. 3.V2
lim
4л1 - 7 •
Решен ие. Числитель и
знаком предела,—бесконечно
знаменатель дроби, стоящей под
большие величины:
lim t = lim
4x‘ — 7
lini 7э+ ,ira J
7
4— lim Д
уггу о
4-0
Пример 7. Найти
lim
7 5х + 2
3 • 5Л — 4 •
3 , 5
7
3
7
Решение. При х->оо члены дроби — величины бесконечно
большие. Поэтому предварительно числитель и знаменатель по-
членно делим на 5*. Получаем
lim g —v = lim
о • 5* — 4
с —> m к —ь гс
д
5х _ ?+ 0 o 1
4 —'3 — 0— 3
132
Из примеров видно, что отношение двух бесконечно больших
величин может оказаться: 1) величиной бесконечно большой (при-
мер 5), 2) величиной ограниченной, имеющей своим пределом любое
число, отличное от нуля (примеры 4 и 7), и 3) величиной беско-
нечно малой (пример 6)*.
Для успешной проработки последующих разделов анализа
бесконечно малых величин особенно важно умение находить пре-
дел отношения (частного) двух бесконечно малых величин, т. е.
таких функций, пределы которых равны нулю. Ознакомимся
с приемом нахождения пределов таких отношений на примерах.
Пример 8. Дана функция у =
Найти предел этой функции, когда х->0.
Решение. К этому примеру теорему
посредственно применить нельзя, так как
нулю: lim (ах1 -ф-х) = а• О3-ф-0 = 0.
-V - о >
Нельзя также воспользоваться замечанием, сделанным в § 48
после 7-го примера, так как предел делимого тоже равен нулю:
lim (х2-|-ах) —0. Получается выражение вида не имеющее
х-0 и
смысла**. В таких случаях применяется следующий прием.
1. Разлагаем числитель и знаменатель дроби, стоящий под
знаком предела, на множители:
lim у= lim
X - О х - О
2. Сокращаем числитель и знаменатель на их общий множи-
тель (в данном случае на х), полагая, что этот множитель не
равен нулю и только стремится к нему (в данном случае х О,
х->0). Получаем
где а — любое число.
о пределе частного ие-
предел делителя равен
= lim
lim у = lim —.
х-.п Х^оах+Л
3. Применяем теорему о пределе частного и находим
lim (x-f-a)
, • х —• о 0 -4- а
1 ни у — т—---j—г, = —тг-гл = а-
x_q l,nl (ах + 1) а ’ 0 + 1
* В связи с этим отношение двух бесконечно больших величин называют
неопределенностью вида Ц, а процесс нахождения предела такого отноше-
ния — раскрытием неопределенности.
** Из равенства ~ = х следует, что Ьх=а. Если в этом равенстве при-
нять я = 0 и b = 0, то получится равенство 0-.v = 0, справедливое при лю-
бом х. Следовательно, дробь ~ при .л = 0 и & = 0 не имеет смысла, ибо
обозначает любое число.
133
Пример 9. Найти lim----------.
Решение. Если непосредственно применить теорему о пре-
деле частного, то получается
(х2 — 6х + 9)|х=з Зх2 — 6 • 3 + 9 О
(х— 3Г|л = 3 3— 3 О
Записи никакого определенного числа не соответствует.
1. Разлагаем на множители числитель дроби, стоящей под
знаком предела:
. х- — 6л' + 9 ,. (х — З)2
11ГП ---у—тг = 11111
х > 3 ~~ х > 3 л 6
2. Сокращаем полученную дробь на х— 3, полагая, что х—
— 3 Ф 0, или х^Зи только х—>3. Получаем
.. л'3 — Gx 4- 9 ,. (,v — З)2 1- /
lira-------Р— == lira = lira (x — 3).
л->з х — а А._з х — а х —> з
3. Находим предел, пользуясь первой теоремой о пределах:
lira ~~ 6*.+ 9 z= lira (х — 3) = 3 — 3 = 0.
Л-->3 Х~3 л--
3x4-15
Л-2 4- 10х 4- 25 •
Пример 10. Найти lira
х —— 5
Решение. При х-> —5 числитель и знаменатель дроби,
стоящей под знаком предела, — величины бесконечно малые. Тео-
рему о пределе частного без предварительных преобразований
применить нельзя. Выполняя последовательно преобразования,
указанные в примерах 8 и 9, находим
lira
Л'—* —5
Зл'4- 15
Л-2 4- 10х 4- 25
lim
х-* —5
3(х4-5)_
(Л-+ 5)2
lira —^-5 = 00,
Л,_5х-Ь3
В результате разбора примеров 8—10 приходим к следующим
заключениям:
1. Если знаменатель дроби бесконечно малая величина, то
дробь может иметь конечный предел лишь тогда, когда и числи-
тель— величина бесконечно малая. Последнее условие является
ЛГ 1
необходимым, но недостаточным. Пример: lira -^ = lim—= оо.
х — ох х — о х
2. Отношение двух бесконечно малых величин может оказаться'.
1) величиной ограниченной, имеющей своим пределом любое число,
отличное от нуля (пример 8); 2) величиной бесконечно малой (при-
мер 9) и 3) величиной бесконечно большой (пример 10) *.
2
* В связи с этим выражение вида —, где г —> 0 и у —> 0 (2 и у — бсско-
т °
нечпо малые величины), называют неопреоеленностыо вида .
134
Пример 11. Найти lim 7—t — у2_ jj.
Решение. При х->1 имеем: х—1-> 0; х3 — 1->0; 1
——: —► ОО И -S-J—Г —> со .
X — 1 Л- — 1
Как видим, теоремы о пределах непосредственно неприменимы,
так как получается неопределенность вида со—со. Преобразуем
выражение, заключенное в скобки, 'приведя к общему знамеиа-
Разлагаем знаменатель на множители, сокращаем дробь на
общий для числителя и знаменателя множитель и, применив тео-
ремы о пределах, находим
.. / 1 2 \ .. .г-1 1
lim -----;----—г = lim -—г------------fv= lim —r-j- =
_ 1 _ 1 _ 1
lim (x 1) 1 -|- 1 2 '
x -* 1
Указание. Рекомендуется разобрать решение примера 277
и решить примеры 278—283.
§ 50. ВЫЧИСЛЕНИЕ ДЛИНЫ ОКРУЖНОСТИ
Чтобы измерить длину отрезка прямой линии, мы сравниваем
его с другим отрезком прямой, принятым за единицу длины.
Таким способом невозможно изме-
рить длину окружности, так как
никакую ее часть нельзя совместить
с отрезком прямой. Поэтому длину
окружности определяют при помо-
щи теории пределов, пользуясь
свойствами правильных вписанных
и описанных многоугольников.
Теорема 1. Периметры правиль-
ных многоугольников, вписанных
в окружность и ’ описанных около
нее, стремятся к одному и тому
же пределу, когда число их сто-
рон п неограниченно возрастает.
Доказательство. Из гео-
метрии известно, что правильные
многоугольники с одинаковым числом сторон подобны и пери-
метры их относятся как апофемы. Возьмем окружность радиуса R
(рис. 102), впишем в эту окружность и опишем около нее пра-
125
вильные «-угольники (на рисунке « = 8). Обозначив периметры
вписанного и описанного n-угольников соответственно через рп
и Рп, будем иметь
Рп ОА PnR
Рп ОК Рп gn
где ОА — R — апофема описанного «-угольника, OK=gn — апо-
фема вписанного «-угольника. Эта пропорция справедлива при
любом «; она будет справедлива и при «->со, т. е.
lim Рп
lim— = lim—, или -п~ "—в>
П-*<Х>ёп 11П1 Рп п
п-><л
так как (см. решение примера 4 в § 48) lim gn — R.
lim Pn
Следовательно, "Д”-----= 1, т. е. lim Рп~ Ит р„. (а)
11111 Рп п-гоз п-юз
Определение. За длину окружности принимается общий
предел периметров правильных многоугольников, вписанных в эту
окружность и описанных около нее, когда число их сторон неогра-
ниченно возрастает.
Теорема 2. Отношение длины любой окружности к длине ее
диаметра — величина постоянная.
Доказательство. Положим, что R и г — радиусы двух
окружностей, С и с — длины этих окружностей, а Рп и рп — пе-
риметры правильных вписанных «-угольников. Тогда (см. начало
доказательства теоремы 1)
Рп Г'
Эта пропорция справедлива при любом «; она будет справед-
лива и при «-> со, т. е.
lim — = lim 7
п-,соРп\ п-.а.Г
Пт Рп п
или
/i—> со
(б)
так как R и г—постоянные величины. Согласно определению,
lim Рп — С и lim рп = с-
п-> сс п -> со
Поэтому равенство (б) равносильно равенству
С R С 2R
с г’ с 2г
Переставив в последней пропорции средние члены, получаем
С^_ е
2R~~2r’
136
т. е. отношение длины окружности к длине ее диаметра величина
постоянная, не зависящая от длины радиуса. Эта постоянная ве-
личина обозначается греческой буквой тс (читается «пи»). Итак,
Q
2^ = тс, откуда С = 2тс/?, или C = ~d, где d— диаметр окружно-
сти. Следовательно, вычисление длины окружности сводится к
вычислению числа тс. Это число несоизмеримо с единицей и может
быть вычислено только приближенно, но с какой угодно точ-
ностью.
Возьмем двойное неравенство
Рп<С<Рп, (в)
где С — длина окружности радиуса R, а рп и Рп — периметры
правильных вписанных и описанных n-угольников (см. рис. 102).
Из равнобедренных треугольников ЛОВ и Л^/?! находим:
^ХОВ = — £АОК = — -,
п ’ п ’
1 d on * 180“ , , D . 180"
ап = АВ = 2/? sin —; bn = AtBj = 2R tg — ;
on 180°
pn = nan = 2Rn sin —;
180“
Pn = nbn = 2Rn^.\
После замены pn и Pn их выражениями (г) неравенства (в)
принимают вид
. 180“ 180’
2Rn s ш — < С < 2Rn tg —.
Разделив все члены этого двойного неравенства на положи-
тельную постоянную величину 2R, получаем:1
. 180“ . С . 180’ . 180“ , 180’ , ч
п Sin------------------, ИЛИ П S1O ----' О < П tg-----, (д)
п I 2R & п ’ п ь п ’ ' '
.. . 180’ . 180’*
при этом lim п tg — = lim«sin— .
tl — от П п -* со п
Следовательно, число тс является общим пределом последова-
. 180" , 180’ ~
тельностеи nstn— и п tg—, когда п—*оо. Основываясь па
п ° п ’
неравенствах (д), это число можно вычислить с какой угодно
г> о sin 180“ t 180"
точностью. В табл, о приведены значения п —-— и ntg-^-,
* Из равенств (г) и (а) следует: Urn IRn tg—— = lim 2/?л sin-----------------------------•
п -> oo 11 п-*са
.. , 180° . . 180°
Игл л tg-------= itni п sm-----------.
п -> СО Л п -*• СО Л
137
вычисленные с помощью пятизначных тригонометрических таблиц.
Уже при п = 60 находим л = 3,14 с точностью, достаточной для
практических целей, а при п = 540 получаем его более точное
значение л = 3,1416, которым вполне можно довольствоваться и
в случаях, требующих особой точности.
Таблица 8
п 180° п . 180' п sin н С t 180й П (Д ь п 180е . 180° П til П SIR п п
30 6- 3,1359 7С 3,1530 - 0,0171
60 3“ 3,1404 Л 3,1446 0,0042
180 г 3,1410 К 3,1428 0,0016
360 30' 3,1412 • к 3,1416 0,0004
540 20’ 3,1415 7Z 3,1416 0,0001
§ 51. ВЫЧИСЛЕНИЕ ПЛОЩАДИ КРУГА
Определение. Площадь круга является пределом площади
правильного вписанного п-угольника, когда число его сторон п не-
ограниченно возрастает.
Теорема. Площадь круга равна половине произведения длины,
окружности на радиус.
Доказательство. Известно, что площадь правильного
многоугольника равна половине произведения периметра на апо-
фему. Очевидно, эта теорема применима и к. правильному впи-
санному «-угольнику (см. рис. 102). Обозначив его площадь
через Sn, будем иметь..
о __Рп * Sn
& п ? з
где р,периметр этого-л-уголышка, g„ — его апофема. Согласно
определению,
<SKp=lim s„ = lim
п -> со п -» со
ИЛИ
£кР = у lim рп lim gH. (а)
Нам уже известно: lim рп = С, где С — длина окружности (см. § 50);
lim gn = R (см. пример 4 в § 48). Подставив в равенство (а)
п -»се
вместо пределов их значения, получаем
$К1> = у • с • R = 4 • 2л/? • R, или 5Кр = л/?1.
138
После замены R через -%, где d —диаметр круга, эта формула
принимает вид (более удобный для практических целен)
о ___ / d V- q ___тар
*Лкр — \"ч / * Т* ^кр — •
§ 52. СУММА ЧЛЕНОВ БЕСКОНЕЧНО УБЫВАЮЩЕЙ
ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ
Определение 1. Геометрическая прогрессия называется убы-
вающей, если ее знаменатель по абсолютной величине меньше еди-
ницы (| g | <Ч).
Определение 2. Убывающая геометрическая прогрессия на-
зывается бесконечно убывающей, если число ее членов бесконечно
велико.
Так, например, числовые последовательности:
. 2 4 8 16 32
1' ’ 3 ’ Т ’ 27 ’ 81 ’ 243 ’ • • •
представляют собой бесконечно убывающие геометрические про-
грессии, знаменатели которых соответственно равны: 1) q = -^-,
2) q =— Так как знаменатель любой бесконечно убывающей
геометрической прогрессии по абсолютной величине меньше еди-
ницы, то с увеличением номера п абсолютная величина ап все
время убывает неограниченно:
I «11 > I a-i | > | аЛ | > ... > |ял_11 > Ы > K+i I > ...
и поэтому всегда можно найти такое значение п, начиная с кото-
рого будет удовлетворяться неравенство
I | <'С £»
где е — сколь угодно малое наперед заданное положительное число
(см. определение в § 42). Это значит (см. § 46), что
lim ап = 0.
11 -* со
Сумма Sn первых п членов убывающей геометрической про-
грессии находится по формуле (см. пример 1 § 46)
О ___ в-п<1
\-q
Суммой членов бесконечно убывающей геометрической прогрессии
называется предел суммы первых п членов ее, когда п неограни-
139
ченно возрастает. Обозначив этот предел буквой S и учитывая,
что а1 и — постоянные величины, получаем
S= lim S„= \im а'т~-пЯ= lim =
n-оэ " 1-? л-»оэ\1~9 1-?/
= 7^------lim -=^, т. е. S = ~—— г-^— lim а (а)
1-9 !-9 !-9n-.raa«- V ’
Так как lim ая = 0, то S = t-^—, т. е. сумма членов бесконечно
убывающей геометрической прогрессии равна первому члену, делен-
ному на разность между единицей и знаменателем прогрессии.
Применив эту формулу к двум бесконечно убывающим прогрес-
сиям, приведенным в начале параграфа, найдем:
1)3 = -Ц-=3; =
3 1 Д 2/ .
Пользуясь этой формулой, можно установить правило для
обращения бесконечной периодической дроби в простую. Рассмот-
рим примеры.
Пример 1. Обратить периодическую дробь 0,555 ... в простую.
Решение. Здесь периодом является число 5; период начи-
нается тотчас после запятой. Такие десятичные дроби называются
чистыми периодическими. Часто период пишут в скобках: 0,555...
. . .=0, (5). Эту дробь можно представить в виде бесконечно
убывающей геометрической прогрессии:
0,555 • • • = 10 + Уоо + 1000 + ioooo + • • >
у которой первый член а1 = 0,5; знаменатель с/= 0,05 : 0,5 = 0,1.
По формуле (а) получим
с а, 0,5 __________ 5
d 1 — 0,1 "Э'
Пример 2. Обратить периодическую дробь 0,243243243 ... в про-
стую.
Решение. Здесь периодом является трехзначное число 243:
0 (243)—-243 -I__—_____|__——______L
и, 1000 -7- J 000 000 Т ! ООО 000 0001’
at — 0,243; <7 = 0,001. По формуле (а) находим
0 (243)— °’243 — 243-9
Из этих примеров видно, что чистая периодическая дробь
равна такой простой дроби, числителем которой является триод,
а знаменателем — число, изображаемое столькими девятками,
сколько цифр имеется в периоде. ।
140
Пример 3. Обратить в простые дроби следующие периодические
дроби: 1) 0,2454545 ..., 2) 0,13363636 ... .
Решение. В этих примерах период начинается не тотчас
после запятой. Такие бесконечные десятичные дроби называются
смешанными периодическими.
1) В изображении данной дроби до периода после запятой
одна, цифра (2). Чтобы можно было воспользоваться правилом,
установленным для чистой периодической дроби, умножаем эту
дробь на 10', перенося запятую вправо через одну цифру, и делим
на 101, чтобы не изменилась величина дроби. Получаем
0 2(45)=—=2—-10 =—
ю z99 ПО*
2) В этом случае после занятой до периода две цифры (1 и 2),
Умножаем данную дробь на 10‘2, переносим запятую вправо через
две цифры, и делим на 10J. Получаем
, °’W6) = ^=l<-100 = ^.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какая величина называется бесконечно малой?
2. Какой величиной будет х, если в процессе своего изменения он после-
довательно принимает значения:
х = 0,1; 0,01; 0,001; ...; 0,00 ... 01 при /г —со?
п нулей
3. Сформулируйте первое свойство бесконечно малых величин.
4. Переменные величины к и у в процессе изменения последовательно
принимают значения:
.г = 0,2; 0,02; 0,002; ..., 0,00 ... 02;
п пулей
_£.£]_ ]_
У — 2*’2s’’232"'
Какой величиной будет при п —> со: 1) сумма х-|-.у; 2) разность х— у?
5. Какой величиной является дробь 1) 0 jOOOOOOOl’, 2) ?
6. а, р и у — бесконечно малые величины. Какой величиной является’.
1) а+р-7; 2) яР/(?
7. с — величина постоянная, х — бесконечно малая. Какой величиной
будет: 1) сх-, 2) сх2; 3) ca.t; 4) ’
8. с,, с}, с3 — постоянные величины; а, р и у.— бесконечно малые. Какой-
величиной будет: 1) сщ + с2Р + с3т; 2) —-f-e^p-f- Vm?
ci
9. Какая переменная величина называется ограниченной?
10. Можно ли считать любое данное число величиной ограниченной.’
Если можно, то почему?
11. Какая переменная величина называется бесконечно большой’.
141
12. Какой величиной является у — 2х —1, когда: 1) х —»со; 2) х —«--j-;
3) х — 2? -
13. z— величина ограниченная, х— бесконечно малая. Какой величиной
будет: 1) 2Х, 2) -у; 3) -|?
14. Сформулируйте зависимость между бесконечно малой и бесконечно
большой величинами.
15. Какой величиной будет 2~Л' при х —»оэ?
16. lim у — Д Какой величиной будет разность у—Ь?
17. Переменная величина х в процессе своего изменения последовательно
принимает значения:
л = 1,9; 1,99; 1,999; ...; 1,99 ... 9.
п девяток
Какое число будет пределом этой переменной величины при п —► со?
18. at, а2, а3.. а,, —бесконечно малые величины, п — любое число
натурального ряда. Найти:
1) lim (а,“а + аз + + “л);
2) lim (о, а2 • аа ... ап).
19. е1( е2, е3 — величины постоянные, liinx = a, limу= l>, limz — с. Найти:
1) lim (cLx — с»у); 2) lim (^у- -|-с.з3); 3) lim (с, Vх + с» у~У + z'j.
Л' с
20. с — величина постоянная. -Найти: 1) lim сх; 2) lim —• 3) lim —:
л-со Л--.0 С ’ л-0* ’
4) lim —; 5) lim •
х—► ОО Л‘ —t со
21. При каком условии дробь, знаменатель которой величина бесконечно
малая, может иметь конечный предел? Является ли это условие необходимым
и достаточным или только необходимым, но недостаточным?
Ответы. 12. 1) Бесконечно большой; 2) бесконечно малой; 3) ограни-
ченной. 15. Бесконечно малой. 18. 1) 0; 2) 0. 19. 1) acl — bc2; 2) й-'с, Д с3с3;
3) с, У а е2 уД 4-с3]//' с. 20. 1) со; 2) 0; 3) со; 4) со; 5) 0. 21. При усло-
вии, что числитель — величина бесконечно малая. Это условие необходимо,
по недостаточно.
Г л а в а VI
ПРОИЗВОДНАЯ ФУНКЦИИ
§ 53. ВВЕДЕНИЕ
Дифференциальное исчисление является одним из основных
разделов обширной области высшей математики, называемой ана-
лизом бесконечно малых величин, или, кратко, анализом. Главная
заслуга в открытии дифференциального исчисления, как уже было ;
сказано, принадлежит английскому математику, физику и астро-
ному Исааку Ньютону (1643—1727) и немецкому философу и мате-
матику Готфриду Лейбницу (1646—1716).
Ньютон сделал свое открытие, работая в области механики.
Основной задачей, приведшей его к этому открытию, была задача
142
о нахождении, закона изменения скорости любого движения ио
данному закону (уравнению) этого движения.
Лейбниц подошел к открытию дифференциального исчисления
в поисках общего метода построения касательной к любой кри-
вой, заданной своим уравнением.
Обе задачи, как будет видно из последующих параграфов,
сводятся к одной и той же математической операции — отысканию
предела отношения двух бесконечно малых величин и тесно свя-
заны между собой. Эта связь обусловлена тем, что скорость дви-
жущейся точки направлена по касательной к ее траектории, поэтому
определение скорости снаряда на его траектории, скорости любой
планеты на ее орбите пли любой точки всякого механизма сво-
дится к определению направления касательной к кривой.
В вашем учебном плане первым учебным предметом, базирую-
щимся на высшей математике вообще и на дифференциальном
исчислении в частности, явится теоретическая механика — наука
о движении и силах, его вызывающих, которая в свою очередь
служит основой ряда специальных технических наук. Эти науки
настолько пронизаны математикой, что их часто называют при-
кладной математикой. Поэтому знание основ дифференциального
исчисления — одного из самых существенных разделов высшей
математики — для техника необходимо.
Теория пределов (гл. V) является вводной частью дифферен-
циального исчисления, а аналитическая геометрия — основой изу-
чаемых в данном курсе разделов высшей математики, поэтому,
приступая к изучению данной главы, необходимо знать предшест-
вующий материал. •
§ 54. СИМВОЛИКА ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ.
ЧАСТНОЕ ЗНАЧЕНИЕ ФУНКЦИИ
1. Тот факт, что переменная величина у является функцией
переменной величины х, кратко символически записывают так:
(/ = /(*) (а)
Эта запись читается так: «игрек есть функция от икс» или
«игрек равен эф от икс». Здесь буква f играет ту. же роль, что
буквы 1g, sin, cos, tg и т. д. в записях ig х, sinx, cosx, tgx
и т. д., но каждой из записей 1gх, sinx и т. д. соответствует
одна вполне определенная функция, а записью /(х) может быть
обозначена любая функция от х.
Запись (а) применяется и тогда, когда дается функция, выра-
женная определенной конкретной формулой. Пусть, например,
нам дана задача, в процессе решения которой много раз упоми-
нается функция
х1 * * * * * * * - Зх9 + 5
У —-------------•
2х — 5 |/ х + 4
143
Чтобы при каждом упоминании такой функции не повторять
громоздкой записи правой части, условились такие уравнения
записывать кратко: у — f(x), приняв
х1 — Зх2 + 5 г , ,
----777^7 =/(*)•
2х — 5 У х + 4
Если одновременно рассматривается несколько различных функ-
ций от одной и той же переменной (например, х), то, чтобы их
не смешивать, употребляют символы: /(х), ср (х), Е(х), Ф(х), ...
Например, если такими функциями являются
«“3*+s«+i;
Л 1 А с/
то можно кратко записать: y = f(x), z = <p(x), u = E(x) и, разу-
меется, в дальнейшем иметь в виду, что
Нх) = §т?т; W = 3x2 + 5x+1; F(X) = —+^Л5+-.
Итак, символы f (х), <р(х), F (х), Ф (х), fi (х),... обозначают различ-
ные функции от одного и того же аргумента х, а символы /(х),
/(/), /(z), ... обозначают одну и ту же функцию от различных
аргументов. Например, если
Зх2 + 1 з/2 -pi з/ + 1
xJ 4- 8 ’ z2 4-8 У' + 8
то можно писать сокращенно: y — f(x), v = f(f), u — f(y).
Пример 1. Дано:
f (х) = х9 — 5x-f-4; ш(х) = х2 —Зх —4.
Найти: 1) /(х)4-5х — 4; 2) <р (х) — х94~4; 3) /(х) -ф- ср (х).
Решение.
1) f (х) Д- 5х — 4 = (х9 — 5х ф- 4) 5х — 4 = х9;
2) <р (х) — х9 4- 4 = (х9 — Зх — 4) — х2 4~ 4 = — Зх;
3) /(х)4-<р(х) = (х2 —5х4-4)4-(х9-Зх —4) = 2х2 —8х. '
Пример 2. Дан(>:
/ (х) = cos х 4-sin х; ср(х)_ cosx — sinx.
Найти: 1) /(x).cp W; 2) [/«- [т«; 3)
Решение.
1) / (х) • ср (х) = (cos х 4- sin х) (cos х — sin х) = cos9 х — sin2 x =
= cos2x (по формуле косинуса двойного угла);
144
2) [f Wl2 — [? (x)]2 = (cos x4~ sinx)2 — (cosx— sinx)2 = cos2xJ-
4-2 sinx cosx 4- sin2x — cos'-x 4~2 sinx cos x — sin2x = 4sinxcosx=
= 2sin2x (по формуле для синуса двойного угла);
-| / <? (х) -] Г cos х — sin x' Г (cos х — sin х) (cos х 4- sin х)
' У f (х) г cos х sin х У (cos х 4“ sin х)3
__1 Г cos3 х — sin3 х _ cos 2x
У (cos X 4- sin X)2 COS X 4- sinx"
Указание. Решить пример 293.
2. Частные значения функции. Числовое значение функции,
соответствующее данному значению аргумента, называется част-
ным значением этой функции.
Например, при х = 1; 2; а", b частными значениями функции
У = х* будут: tji= I3 = 1; у, = 23 = 8; уЛ = ащ tji = b'.
Если некоторая функция обозначена символом fix), то частное
ее значение при х = а запишется так: /(а). Символ /(а) следует
понимать в том смысле, что для нахождения частного значения
функции при х = а надо в выражение этой функции вместо х
подставить число а. Например, если
/(х)=х2 — хД-З, то f(a) = cP — аД-3, / (2) = 23 — 2-L 3 = 5,
/(|/'а) = (К а)2— Ка-\-3 = а—
Пример 3. Дана функция f (х) = tg х -|- ctg х. Найти частные
значения этой функции при Х = *4;
Решение..
1)7(»=1ёН< = ^4-Гз=1/з:
2) f(j) = tgj + ctg5-=l + 1=2;
3) =tg^4-ctgJ = r3 + -$ = i/3.
\O JOO о о
Пример 4. Даны функции
f (х) = х2 -4 Зх; <? (х) = х2 — Зх.
Найти: 1) f(a)4~®(a); 2) f(3) —<р(3); 3) f(a-\-b) — y(a-i-b).
Решение.
1) f (а) + ф (а) = (а2 4- За) 4~ (а<2 — За) = 2а2;
2) /(3) — ср(3) = (334-3-3) — (З2—3-3) = 18;
3) f (а 4- Ь) - ф (а 4- Ь) = [(а + 6)2 4- 3 (а 4- 6)] -
- [ (а 4-6)2 - 3 (а 4-&)] = (а + &)2-4 3 (а + &) - (а +1>)2 4-
-4 3(а -f- &) = 6 (а 4- Ь).
Пример 5. Дана функция /(х) = х24~2. Найти:
В lim/(x4-/0-/(x); 2 [im/(х 4-Л)—/(х —
Л-кО а Л-0 г'
145
Решение.
1) lim (х= lim + - — (-И + 2) _
7 Л-,0 Л Л~0 h
,. Xs 4- 2/ix + Л-’ + 2 - .v2 — 2 ,. 2/ix + /г2
= lim —!------2—_г------------— hm —~Р~.
Л-»0 “ Л-.0 "
Теорему о пределе частного непосредственно применять нельзя,
, п г О
так как при /г —> (J получается дробь вида
Преобразовав выражение, стоящее под знаком предела (см. § 52,
примеры 8—10), находим
lim f(x + h) —f (л) ЛЦ2л + /') । jm (2X ft) — 2x.
>i-0 11 Л-0 " h-,0
2) lin / <-V + /.> - / (A- ; n| <.V + /.)- + 2 - (« - 1.У-2 =
Л-» ,l h-c h
- lim ~r = 4x.
Л-.0 11
§ 55. ОБЛАСТЬ СУЩЕСТВОВАНИЯ ФУНКЦИИ
В § 8 (см. ответы на вопросы 1—4) и в § 28, 31, 37 было
установлено, что для всякой функции y = f(x) аргумент х имеет
свою совокупность допустимых значений. Такую совокупность
допустимых значений . аргумента принято называть областью
существования функции (или областью определения функции).
Наиболее часто область существования функции представляет
собой пли интервал, или отрезок.
0
а
Рис. 103
Интервалом называется совокупность всех действительных
чисел х, удовлетворяющих условиям а<^х<^Ь. Интервал принято
кратко обозначать (а, Ь).
Отрезком называется совокупность всех действительных чисел х,
удовлетворяющих условиям а^х^Ь. Отрезок кратко обозначают
символом [а; Ь].
Общим наименованием для отрезка или интервала служит
термин «промежуток».
Следовательно, промежуток — это либо отрезок, либо интервал.
На числовой оси промежутку соответствует отрезок ab (рис. 103)
с включением в него концевых точек (отрезок) или без включения
их (интервал). При рассмотрении бесконечных промежутков упо-
146
требляются аналогичные обозначения, например: (—оо; оо)—
множество всех действительных чисел, (а; -ф- оо) — множество всех
действительных чисел, удовлетворяющих условию х^>а, и т. д.
Пример 1. Определить область существования функции-
у = х34-2х2 — 3x-j-4.
Решение. В данном случае любому действительному значе-
нию аргумента будет соответствовать определенное действительное
значение функции. Следовательно, эта функция существует (опре-
делена) при любом конечном значении х, т. е. — оо <^х<Ъо.
Пример 2. Определить область существования функции у = ~.
Решение. При х = 0 получим Такого числа не сущест-
вует. На графике этой функции (см. рис. 97) нет точки с абсцис-
сой, равной нулю. Любому действительному значению х, отлич-
ному от нуля, соответствует определенное действительное значе-
ние у. Следовательно, эта функция существует в интервалах
(— оо; 0) и (0; оо).
Пример 3. Указать область существования функции
У = 1/9 —х3.
Решение. При значениях аргумента х, превышающих по
абсолютной величине число 3, под знаком квадратного корня
получаются числа отрицательные. Следовательно, областью суще-
ствования будет отрезок [—3; 3].
§ 56. ПРИРАЩЕНИЕ ФУНКЦИИ
Если переменная величина в процессе своего изменения пере-
ходит от данного значения к другому, то первое значение назы-
вается начальным значением этой переменной величины, второе —
новым, или наращенным, значением.
Разность между новым (наращенным) и начальным значением
называется приращением переменной величины.
Приращение переменной величины х принято обозначать сим-
волом Дх (читается «дельта икс»). Приращение переменной вели-
чины у обозначается символом Ду (читается «дельта игрек»).
Если новым (наращенным) значением аргумента является хь
а начальное его значение было равно х (х какое-либо определен-
ное число), то xt — х —Дх, откуда следует Х1=х4~Д*- Это
равенство можно выразить так: наращенное (новое) значение аргу-
мента равно его начальному значению плюс приращение.
Пусть нам дана функция y = f(x). Когда аргумент от началь-
ного значения х переходит к наращенному значению Х1 = х4*Дх',
эта функция от значения y = f(x), соответствующего начальному
значению аргумента, переходит к новому (наращенному) значению:
У1~ у4-д'/ = /(-^+М-
147
Разность
&y=yi — y=f(x-]-&X) — f(x) (1)
называется приращением данной функции.
Пример 1. Дана функция y — f(x) — х\ Найти приращение
этой функции, когда аргумент от значения, равного числу 2,.
переходит к значению, равному числу 2,1.
Решение. В данном случае начальным значением аргумента
явится число 2, наращенным значением — число 2,1, приращение
будет равно 2,1—2 — 0,1. При этих данных начальное значение
функции, очевидно, будет равно у — f(2) = 22 = 4, наращенное
значение: уД- Дг/= /(20,1) = / (2,1) = 2,12 = 4,41.
Приращение функции найдется как разность двух значений.
Получим Дг/ = /(2,1) —/(2) = 4,41— 4 = 0,41.
Пример 2. Найти приращение функции г/ = /(х) = -, когда
аргумент от значения, равного 4, переходит к значению, равному
числу 5.
Решение. В данном случае начальным значением аргумента
является число 4, наращенным — число 5, приращение — число
5 — 4 = 1.
Находим:
уН-Д// = /(х + Дх) = /(4+1) = /(5)=^ = 0,8;
у==/(х) = И4) = |=1;
Дг/==/(хДх) —/(х) = 0,8 — 1 = — 0,2.
Как видим, приращение функции может быть как положитель-
ным числом (пример 1), так и отрицательным (пример 2).
Порядок вычисления приращения функции
, (/ = /(/).
1-й шаг. Даем аргументу х приращение Дх и находим нара-
щенное значение функции
г/4-Дг/ = /(хН-Дх).
2-й шаг. Вычитаем из наращенного значения функции ее началь-
ное значение и находим приращение функции
Дг/^^х-^Дх) — /(х).
Рассмотрим, как геометрически изображается при-
ращение аргумента и функции. Положим, что кривая
линия CD (рис. 104) является графиком функции
г/ = /(х). (а)
Тогда любое допустимое значение аргумента х можно будет
рассматривать как абсциссу некоторой точки этой кривой, а соот-
ветствующее значение функции — как ординату этой точки.
148
Возьмем за начальное значение абсциссы отрезок OAt — x.
Этому значению абсциссы будет соответствовать значение ординаты:
Придав абсциссе х приращение AiBi — Ax, получим наращен-
ное значение абсциссы:
ОВ1 = О At + AiBt = х-\-Ьх.
Тогда наращенное значениефунк-
ции будет равно
В1В = //+Дг/ = /(х4-Дх). (б)
Из точки А проведем прямую ДВ>,
параллельную оси Ох. Из рисунка
видно, что BiB — BiB — BtBi =
— BtB — А\А. Приняв во внимание
равенства (а) и (б), получим
В2В=/(х4- Дх) — /(х), или BJB=lXy.
Следовательно, геометрически приращение аргумента изобра-
жается приращением абсциссы точки графика функции, а прираще-
ние функции — приращением ординаты этой точки.
§ 57. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Определение 1. Функция у — [(х) называется непрерывной
при х = х, (или в точке Х| *), если’. 1) эта функция существует
(определена') при x = Xt и 2) приращение этой функции в точке
Xi стремится к нулю, когда приращение Axj аргумента стремится
к нулю (оставаясь меньше или больше нуля), т. е.
lim Ayl = 0, (2)
A.V(—О
или, что то же самое,
lim [/(xi —Axi) — /(xi)] = 0. (2а)
Геометрически непрерывность функции при х — х\ можно пояс-
нить следующим образом. Положим, что кривая линия DE
(рис. 105) является графиком функции у = [(х) и пусть ОД( —хь
Тогда ____
AiBt = Axi и В2В = Д^.
* В дальнейшем выражение «в точке .ер следует понимать в смысле:
«в точке, абсцисса которой равна х^. »
140
Проведем хорду АВ. Обозначив длину хорды через d, по теореме
Пифагора будем иметь
d = -ф- Дг/i.
Если при ДХ)->0 и Дг/1->0, то независимо от их знаков
(Дх^О, Дг/i^O)
d = ]/’(Дл-1)2 + (Дг/1)'2 -»0.
Это значит, что точка В, перемещаясь по кривой, как указано
на рисунке, неограниченно приближается к точке А и что
при х — xt график этой функции разрыва не имеет.
Условие непрерывности (2) можно представить в другой
форме.
Из равенства (2а), применив к его левой части теорему о пре-
деле алгебраической суммы, получаем:
lim /(Xi-ф ДХ]) — limf(x1) = 0; lim f (xi + AxJ = lim /(xi),
Ax,-. О ДЛ1-.0 Дл-1-.О Дл-1-.О
t. e.
lim f(xl-]-^Xl) = f(x1),
ДЛЦ-.0
так как f (x,) (при данном Xi) — величина постоянная. Если в этом-
равенстве примем Х1-|-ДХ1 = х, то при Дх1->0 будем иметь
lim/(х) = /(х1)*. (26)
Итак, из равенства (2а) вытекает равенство (26). Обратно,
легко показать, что из равенства (26) следует равенство (2а).
* Очевидно, равенство (26) предполагает, что: 1) частное значение/CvJ
функции f (x) имеет определенное численное значение; 2). предел
при х —. лу существует и 3) этот предел равен/(xj.
150
Следовательно, условие непрерывности (2) можно заменить усло-
вием (26) и определение 1 заменить ему равносильным.
Определение 2. Функция y = f(x) называется непрерывной
в точке Xi, если предел этой функции при x->Xi равен значению
функции При X = Xt.
На рис. 105 при Ахх -»0 имеем: 1) BjBI4jC1<o-*/(xi-|-
Д-Дх1)->/(х1); 2) ЛА = /(х1).
Геометрически условие (26) означает, что
lim BrB—AjA и lim BiB = AiA*,
Х<-Г1 -V>Vl
т. e. величина ординаты точки Xj является общим пределом вели-
' чин ординат точек кривой, стремящихся к точке Xi слева и справа.
Определение 3. Функция y = f(x) называется непрерывной
в интервале (а, Ь), если она непрерывна при любых значениях
аргумента х, заключающихся между числами а и Ь.
Непрерывная функция графически изображается непрерывной
линией, т. е. такой линией, которая может быть вычерчена непре-
рывным движением карандаша (см. § 27,35).
Пример 1. Исследовать на непрерывность функцию y=logox,
а^> 1.
Решение. Областью существования этой функции является
интервал (0; сю). Находим выражение приращения функции при
любом х из этого интервала:
A// = loga(x-}-Дх),
Ду = loga (х-(-Дх) — log„x = log3—или A// = logJl-(-^.
Если Дх—>0, то 1 —^-->1, Ду-> log3l =0, т. е. Д//->0 при
любом х, когда Дх->0. Из формулы (2) следует, что данная
функция непрерывна в интервале (0; со).
Определение 4. Если при х = хц нарушается непрерывность
функции, то говорят, что функция у = [(х) в точке Xj имеет
разрыв, и называют эту точку точкой разрыва функции.
Пример 2. Доказать, что функция у = —— непрерывна при
любых значениях х, кроме х = 0.
Решение. Находим выражение приращения этой функции
при любом х. Получаем
. х + Дх + 1 х + 1 1 . -
Д'/ = । л------— =------—г-г-г ’Дх-
х Дх х х (х + Дх)
® Пределы вида: 1) lim /(х) п 2) lim f (х) — соответственно называ-
х -* а ха
х<.а х > а
ются: 1) предел слева и 2) предел справа.
151
При х Ф 0 и Дх —> О имеем lim Ьу =— lim. *, . • Дх = 0.
Дл-0 Av-ол' <-v । &х>
При х —0 эта функция не определена. Следовательно, данная
функция непрерывна в интервалах (—со, 0) и (0, оо) в силу
условия (2) и имеет разрыв при х = 0.
С такими функциями мы уже встречались в § 9. Функция
y — при х = 3 имеет бесконечный разрыв: предел слева
lim — оо, предел справа lim — = — оо (см. § 9 рис. 26
х 3 ’З — х —* 3 *
л<3 л>3
и табл. 6,7).
Такие же разрывы имеют функции tgx и ctg х: первая — при
х=^-\-т, вторая — при х = л/г (см. рис. 120 и 121), где п —
= оо , а не определенное
Функция У — ^ имеет разрыв при x — Q: пределом ее в точке
х —0 является бесконечность Aim Д
число (рис. 106).
Пример 3. Исследовать на непрерывность функцию у = Х\ ^'г.
Решение. При х<^0 имеем: |х] = — х (см. § 7) и вследствие
этого
X2 4- X X (х 4- 1) — Х(Х 4- 1) 1
у =- - - -L—1—- — —4—1—, т. е. у — — х — 1.
J | х | — х А‘ _ J
При х^>0 получаем: | х | = х;
Следовательно, в интервале (— оо; 0) графиком этой функции
является прямая линия у = — х— 1, а в интервале (0; со)—
152 .
прямая у = х-ф1 (рис. 107). Пределом этой функции, когда х->0
слева (возрастая), является число —1:
lim у — lim (— х — 1) = — 1,
,г->0 х->0
х<0
а когда х стремится к нулю справа (убывая) — число -ф1:
lim у = lim (x-j-1) = + 1.
л*-* 0 х-*0
х>0
Следовательно, в точке х = 0 данная функция не определена
и имеет разрыв (конечный*): d =
= 1 — (— 1) = 2. Очевидно, эта функ-
ция непрерывна в интервалах (— со, 0)
и (0, сю).
Равенству (26), выражающему ус-
ловие непрерывности функции f(x)
в точке хь можно придать другую
форму, приняв во внимание, что
Xi =.- lim х. Получим
x-*xt
lim f(x)=f( lim ). (3)
Это равенство кратко словами можно выразить так: предел
непрерывной функции равен функции от предела аргумента.
Пример 4. Функция y~\ogax непрерывна (см. пример 1)
в интервале (0; со), а потому
lim log^x—logj lim x^log^xj,
f-.Vl \*--4 J !
где X| — любое положительное число.
Пример 5. Функция у = —(— непрерывна (см. пример 2)
в интервалах (—со; 0) и (0; со), а потому при любом а, не рав-
ном нулю,
.. .г+1 JL"V'+1 «+1
1™ Л = lint .V =—-
х -* а
Пример 6. Функция у = sinx непрерывна (см. задачу 307)
в любом интервале (— со; со), а потому При любом действитель-
ном а
lim sinx = sin (lim х) = sin а.
~ ' x ft. \x -» a j
Указание. Предлагается разобрать решение примера 305 и
решить задачи 306 — 310.
* Конечный разрыв принято называть разрывом первого рода, бесконеч-
ный разрыв—разрывом второго рода.
153
§ 58. СКОРОСТЬ ДВИЖЕНИЯ В ДАННЫЙ МОМЕНТ
1. Равномерное движение и его скорость. Движение точки
называется равномерным, если она в равные промежутки времени
проходит равные расстояния. Путь, пройденный равномерно
движущейся точкой за единицу времени, называется скоростью
этого движения.
Из физики известно, что при равномерном движении пройден-
ный путь s выражается уравнением первой степени (линейной
функцией) от времени /, т. е. уравнением вида
8 = [)/Д80, (а)
где v — скорость движения;
So — путь, пройденный к моменту 1 = 0.
Возьмем некоторый момент времени t. Путь, пройденный
точкой к моменту t, очевидно, определится по формуле (а).
Дадим времени t произвольное приращение Д/. Тогда путь
зДДз, пройденный точкой к моменту /ДД/, найдем, подставив
в (а) вместо t его наращенное значение /ДДЛ Получим
s Дз = v (t —|- Д/) Д- 5ц. (б)
Вычитая из равенства (б) равенство (а), найдем путь, пройден-
ный точкой за промежуток времени от момента t до момента
/ ДД/. Он будет равен
з Д Дз — s — [ц (/ Д Д/) Д s0] — (vt Д so) = vt Д 1>Д/ Д s0 — vt — sa,
или
As = v&t.
Разделив .обе части этого равенства на Д/, получим
Это значит, что скорость v равномерного движения, опре-
деляемого уравнением (а), есть отношение приращения Дз пути
за произвольный промежуток времени М к величине этого про-
межутка.
2. Равноускоренное движение и его скорость. Из физики
известно, что закон падения материальной точки в пустоте выра-
жается формулой
5 = (г)
где g— ускорение силы тяжести, равное (приближенно) 9,8^^;
t — время;
s — путь, пройденный за время t.
154
Материальная точка, движущаяся по этому закону, в равные
промежутки времени будет проходить неравные пути. Так, за
первую секунду она пройдет Si = 4 gP =~ g • Г2 = g\ за вто-
1 ,» 1 1 о» 1 “ 3
РУЮ Si = ^gP — -g = -g.^.^^g = -g.
Следовательно, скорость движения будет изменяться с изме-
нением времени /. Возникает вопрос, как определить скорость
такого движения в какой-нибудь данный момент t.
Будем рассуждать следующим образом: примем за начало
отсчета пути точку О (рис. 108) и возьмем два момента времени:
t и /-|-ДЛ Положим, что в момент t движущаяся точка заняла
положение Р, а в момент t Д/ — положение Pi. _<->£
По формуле (г) найдем
OP==s = ^gf\
Подставив в эту формулу вместо t его наращенное
значение /—|—Д/, получим:
OPi =Si = s -I- As = ±g (f 4- Д/)2;
= | g [(/ + W - И = j g & Ы + (Д/)*],
или
Дя = 4 g (2^ + Д/) • Д/.
Рис. 108
Определим отношение приращения As пути s за промежуток
времени от момента t до момента к величине этого про-
межутка: /-|-Д/ — t = M. Получим
д5 +
пли
Й=4£(2/ + Д/).
Как мы видели выше [см. формулу (в)], в случае равномер-
As
ного движения отношение является величиной постоянной,
at
выражающей скорость движения в любой момент. В данном
случае это отношение — величина переменная, зависящая от t и
от Д/. При неизменном (постоянном) М величина этого отноше-
ния в разные моменты времени будет иметь разные значения.
155
Например, при Д/ = 0,2 сек, 1 = \ сек получим
^ = ^(8 + °,2) = 4,U;
при этом же значении А/, по при / — 5 сек, получим
Й = Т^(10 + 0,2) = 5,1 g.
Поэтому в случае неравномерного движения отношение может
выражать лишь среднюю скорость (уср) движения за промежуток
времени Д/, т. е. ту скорость, двигаясь с которой равномерно,
некоторая точка за промежуток времени Д/ прошла бы тот же
путь As, как и данная точка, движущаяся неравномерно, п эти
точки, выйдя в момент t из положения Р (см. рис. 108), пришли
бы одновременно в момент Z —j—Д/ в положение Rt, расходясь
в промежуточные моменты. Чем меньше Д/ и, следовательно, чем
меньше As, тем меньше расхождение между средним и истинным
движениями и тем ближе средняя скорость
= = + 4 Д/ (Д)
подходит к некоторой величине, постоянной при данном t.
Например, при / = 4 и Д/, последовательно принимающем
значения: Д/= 0,2; 0,02; 0,002; ...; 0,0 ... 02, по формуле (д)
п нулей
будем получать
t’cp = ^ = 4>1^; 4’01£; 4-001^ 4,00 ... 01g.
п—I пулей
Отсюда видно, что по мере уменьшения промежутка Д/ сред-
няя скорость приближается к постоянной величине 4 g. При
п->оо и М -> 0 разность между переменной величиной и
постоянной величиной 4 g
д с
g--4g = 0,00 ... 01g
п нулей
является величиной бесконечно малой. Следовательно [см. (1)
в § 46],
р= lim uc„ = 4g —.
при Л/О С₽ S
, . Z • I
Отсюда видно, что скорость и движения в данный момент t
есть предел средней скорости (д) за промежуток времени от
156
момента t до момента когда А/->0. Итак, найдем, что
a = Iimt7cp = lim = lim (gt -4- 4-g • Д/^ = gt4- О,
или
v = gt.
I .
3. При любом "движении пройденный путь s является функцией
от времени t. Положим, что закон прямолинейного движения
материальной точки выражается уравнением
« = ДО,
где /(/) —какая-нибудь непрерывная функция от t. Определим
скорость этого движения в данный момент t.
За время t точка пройдет путь s = /(/), а за время /-|-Д/
она пройдет путь, равный
s, = s -j- As — f (t A/).
Вычитая из последнего равенства предыдущее, найдем путь,
пройденный за промежуток времени от момента t до момента.
t -J- А/. Получим
Sj — s = (s-j-As) — $ = /(^4-Д/) —/(/),
или /
As = /(/-[- А/) -/(/).
Найдем отношение пути As, пройденного за промежуток вре-
мени А/, к величине этого промежутка, т. е. среднюю скорость
движения за промежуток времени от момента t до момента
Vcp — st — At
Предел средней скорости при А/ -> 0 представляет собой ско-
рость в момент t:
v — lim аср
1• As 1 •
= lim = = Itm
AZ —0 П£ AZ-0
At
Итак, скорость прямолинейного движения в момент, t есть
предел средней скорости за промежуток времени от момента t
до момента t , когда А/->0.
Пример 1. Закон движения дан формулой
s = /34~2/, (е)
где / выражено в секундах, a s —в метрах.
Найти среднюю скорость движения за промежуток времени
от момента t = 2 сек до момента / = (2 4-сек при: а) Д/= 1 сек-,
б) А/ = 0,1 сек.
157
Решение. К моменту / — 2 сек. точка пройдет путь, равный
s = /'2-|-2/ = 2'24-2-2 = 8 м. (ж)
Путь, пройденный к моменту (2-|-Д/)се«, найдем, подставив
в равенство (е) вместо t его значение 2 -4 Ы. Получим
s 4- As = (2 А/)2 + 2 (2 А/) = 4 4- 4 • А/ (А/)2 4- 4 + 2А/ =
= 8 4- 6AZ + (АД2,
или
s4-As = 8 4-6A/4-(A/)2. (и)
Вычитая из (и) равенство (ж), получим величину пути, прой-
денного за промежуток времени (24-^0 — 2 —А/ сек\
Д5 = 6-Д/-|-(Д/)2.
Найдем среднюю скорость движения за промежуток Д/т
As (6 + Д£ЬД/ g , д
При Д/=1 сек = (64- 1)=7
при А/ —0,1 сек уср = (6 4- 0,1) = 6,1
Пример 2. Дано уравнение движения точки
3 = (к)
где t выражено в секундах, a s —в метрах. Найти скорость
движения точки в момент t — A.
Решение. При t — 4 по формуле (к) имеем
s = |-42 = 8. '
При Z = 4 4” получим
8-4Д8^1(4+до2=|[1б+8-дтт
или
8 4-As = 8 4-4Д/4-у (А/)2.
Из этих равенств найдем
As = [8 4- 4AZ 4- (А/)2] - 8 = ^4 4- у • А/) А/,
откуда
Находим скорость в момент / — 4 сек. Получаем
t> = limucp = lim(44-4-A/) = 4
Д/->0 д/-^о\ z i сек
158
§ 59. ПРОИЗВОДНАЯ ФУНКЦИИ. ОБЩИЙ МЕТОД
НАХОЖДЕНИЯ ПРОИЗВОДНОЙ
Из предыдущего параграфа мы знаем, что решение любой
задачи на определение скорости неравномерного движения по
данному уравнению этого движения
приводит к нахождению предела вида
lim
Дд_ Нт /(< + Д/)-/(0
Предел этого вида играет весьма важную роль во многих
областях науки и техники, поэтому в анализе бесконечно малых
величин ему дано специальное название «производная функции».
Определение. Производной данной функции y = f(x) при
данном значении аргумента х называется предел отношения при-
ращения Ду этой функции к приращению Дх аргумента, когда
приращение аргумента стремится к нулю.
На основании этого определения, например, можно сказать,
что скорость движения в данный момент t есть производная от
пути s по времени t.
Г1роизводную функции y = f(x) принято обозначать следующими
символами:
у'х (читается «игрек штрих по икс»);
f (х) (читается «эф штрих от икс»);
у' (читается «игрек штрих»).
Пользуясь этими обозначениями, можно написать
п, \ 1- Ду г /(х+Дх)—/(х)
Ух — f (x) = lim lim J ’
Д*-*0аЛ Д.у-^О
Аналогично, если s = <p(/), то
I. Да ф (t 4- Д/f) — со (t)
</(/) = hm lim ’ ' -,—
д/^од/-*о Ц£
(4)
si
Для того чтобы функция y = f(x) при данном значении аргу-
мента х имела производную y’v = lim необходимо, чтобы бес-
ах _0 XX
конечно малому Дх соответствовало бесконечно малое приращение
Ьу функции у, т. е. чтобы при Дх->0 и Ду->0 (см. § 49). Отсюда
следует, что функция y = f(x) имеет производную лишь при
таких значениях аргумента х, при которых она непрерывна *
(см. § 57).
* Это условие необходимо, но недостаточно. Вопрос будет рассмотрен
подробно в § 63.
159
Процесс нахождения производной называется дифференцирова-
нием, поэтому фраза «продифференцировать функцию» равно-
сильна фразе «найти производную функции».
Из определения производной вытекает общее правило
дифференцирования любой функции, приведенное в табл. 9.
Таблица 9
Данная функция Х=/(л)
1-11 шаг Аргументу д- дастся приращение Дл и находится новое | (наращенное) значение функции: 3’+д3’ = /(л' + 4л') | 3’ + ^У = (х + Длф
2-й шаг Находится приращение ф У + &У (-V + ^х) У—/(х) ункции: \ У ~Ь д3’= (х -р Дл)5 у = хг
Ду=/(х4- Дх) — У(х') Ху = (х Дл)а — ха = = (2х Дх) Хх
З-й ш а г Находится отношение прт ипю аргумента: д3’ __ /(х + Дх) — /(х) Д.у Дх ращения функции к прираще- Ду_ (2х-|-Дд-) Хх_ Ду Ду “ " I
4-й шаг Находится производная пия приращения функции к приращение аргумента стре , .. Ду I у = lim х- = л д^-оД-v 1 = цп1 < (-у+ дл-) —/(х) Дх —0 Дх зункции, т. е. предел отпоше- 'i приращению аргумента, когда мптся к нулю: 1 . ,. Ху V =11111 — = х Дл-оД-v = lim (2л-4- Дх) = 2.у A*-»0 Итак, у'л = 2х
Производная у'х = j'(x) данной функции y = f(x) при любом
допустимом значении аргумента х является новой функцией от х,
полученной (произведенной) из данной функции. Так, например,
мы из функции у — х1 (см. табл. 9) производим функцию г/х = 2х.
Значение производной функции y — f{x) при данном численном
значении аргумента х называется частным значением производной.
Например, частными значениями производной функции у — f(x) =
= xi при х —— 3 и при х = 4 будут
/'(-3) -2 •( 3) =-6, /’(4) =2-4 — 8.
.160
Пример 1. Найти производную функции у=х'1 — х при х = 2.
Решение. При х = 2 будем иметь у = 22— 2 — 2. Дальше
поведем дифференцирование по общему правилу:
1-й шаг. у 4- Дг/ = (2 4- Дх)'2 — (2 -+- Дх).
2-й шаг. Ьу = (у-+-Ьу) — г/=={(2 4-Дх),~ (2Д-Дх)] — 2 =
= 4 Ц- 4Дх 4- (Дх)2 - 2 - Дх — 2 = ЗДх + (Дх)2 = (3 4- Дх) • Дх.
„ „ Av (3 -+- Дх) Дх о . .
- 3-и ш а г. - = -Д--.2— = 3 4~ Дх.
Дх Дх 1
4-й шаг. у'х= lim — = lim (3-\-^х) — 3.
1.Х —0 ах Дх-0
Пример 2. Найти производную функции у = \ —х'\
Решение. В данном случае нам предлагается найти произ-
водную данной функции при любом значении аргумента х. По
общему правилу дифференцирования получим:
1-й шаг. у 4* Ду = 1 — (х-'|-Дх)’'.
2-й шаг. Ду=(у4-Ду) — у—П — (*4-дх)31 — (1 — х%) = 1 —
— (х 4- Дх)3 — 1 + х3 = хя — [хя 4- Зх2 • Дх 4- Зх (Дх)2 4- (Дх)3] =
= — [Зх2 -4 Зх • Дх 4- (Дх)2] • Дх.
3-й шаг. g = - + 3-v • • дх= - [Зх2 + ЗхДх +
+ (Дх)2].
4-й шаг. у'х = Нт -^- = — lim [Зх24~3х-Дх4~(Дх)2].
дл_ОдХ Дж— О
Разумея под х любое данное число и применив теоремы о пре-
делах, будем иметь
ух =— lim [Зх24-Зх• Дх-[-(Дх)2] = —[Зх24~3х- lim Дхф-
Дх -> О Дх ->0
4- ( lim Дх)2] = — (Зх2 4- Зх • 0 4- О)2 = —Зх2.
Дж-0
Пример 3. Дано уравнение движения материальной точки
s = 8/-/2
(за единицу времени принята секунда, за единицу длины — метр).
Найти: а) скорость в момент 4 б) момент времени, когда ско-
рость точки будет равна нулю; в) скорость в момент / = 3 сек.
Решение. Мы знаем, что скоростью движения в данный
момент называется производная от пути s по времени t.
а) По общему правилу дифференцирования найдем:
1-й шаг. з-фД$==8(/4-Д/) — 44-Д42==8/4-8Д/ —/2 —
— 2Ш — (Д/)2.
2-й шаг. Дх=(s-J-As) — s = [8^ 4_ ЗД/—/2 — 2/Д/— (Д/)2] —
— (8/ — Г2) = 8Д/ — 2Ш — (Д^)2 - (8 — 2/ — М) • Д/.
О « As (8 — 2t — At)-At 0 o, ..
3-и шаг. vcp = rt ='-------м—-— = 8 — 2t — ДЛ
4-й шаг. v = lim оср = lim (8 — 2f— Д/) = 8 — 2t.
xt-o
6 П. E. Агачев 161
Итак, скорость точки в любой момент t определится по формуле
у = (8 —2/)--.
v ' сек
б) В искомый момент t скорость должна быть равна нулю.
Для определения / получим уравнение 8—2t = 0, откуда t — ^ сек.
в) При t — З сек получим
• ц = (8-2-3)—= 2 —.
v 7 сек сек
§ 60. ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
В § 58 и 59 было доказано, что если зависимость между прой-
денным путем s и временем t выражается уравнением
то скорость движения в момент t определяется по формуле
.. As .. At) —/(t)
v = s(= lim lim ——.
дг—оа£ дг-о а£
Всякое уравнение вида y = f(x) независимо от физического
смысла переменных х и у выражает процесс изменения перемен-
ной величины у (функции) в зависимости от изменения перемен-
ной х (аргумента). Поэтому все сказанное выше о нахождении
закона изменения скорости по данному закону движения приме-
нимо к скорости изменения любой функции y = f(x) по отноше-
нию к аргументу х. Рассмотрим примеры.
Пример 1. Когда маховое колесо вращается вокруг оси, то,
очевидно, угол поворота ср * является функцией от времени t, т. е.
Если за промежуток времени от момента t до момента /Д-Д/
маховое колесо повернулось на угол
—/(0.
то отношение приращения Дер угла ср к приращению Д/ времени t
можно будет назвать средней угловой скоростью вращения за
промежуток Д/. Обозначив угловую скорость вращения через ш**,
получим
_A?_/(t + At)-/(t)
“ср — At
* Угол поворота во вращательном движении обычно выражается в ради-
анной мере.
** Буква греческого алфавита, называется «омега».
162
Тогда угловая скорость <о в момент t определится как предел
средней угловой скорости за промежуток времени от момента t
до момента t-\-M при Д£->0, т. е. как производная угла пово-
рота <р по времени t:
ш= lim <оср = lim =
Д/->0 Д/-0
lim/(Z + А<) -/(/)
Задача 1. Маховик, задерживаемый тормозом, за t сек пово-
рачивается на угол <p — 8t — 0,5Л 1) Определить угловую ско-
рость: а) в момент /; б) в момент t — З сек. 2) Найти момент,
когда прекратится вращение.
Решение. Найдем производную данной функции по общему
правилу дифференцирования:
1-й шаг. -J-Д? = 8 (^-|-Д/) — 0,5 (t Д£)2.
2-й шаг. Д-р = 8 (/4“ — 0,5 (Z Ц-Д/)а — (8/— 0,5/!) = (8 — /—
— 0,5Д^)Д/.
п „ п Дш (8 —1~0,5AZ)Ai 0 , Л
3-ишаг. — 1----------г?—— = 8—-t—0,5ДЛ
At At
4-й ш а г. <?i — lim т~= lim (8 — t — 0,5Д/) — 8 — t.
д/—о
1) Согласно определению будем иметь:
а) ш = <р^ = (8 —
б) при t = 3 получим
. ш = (8-3) = 5^.
х • гене
2) Вращение прекратится в момент, когда ш = 8 — t = 0, откуда
найдем: 8 — / = 0, t — 8 сек.
Пример 2. Из физики известно, что количество теплоты, необ-
ходимое для нагревания 1 г вещества на 1°, называется удельной
теплоемкостью этого вещества. Опытами установлено, что удель-
ная теплоемкость — величина переменная, изменяющаяся с изме-
нением температуры. Это значит, что количество теплоты Q, кото-
рое необходимо сообщить 1 г вещества, чтобы повысить его тем-
пературу от 0° до t°, не пропорционально температуре. Поэтому
в формуле Q = f(t), выражающей зависимость между температу-
рой t и количеством теплоты Q, /(/) не является линейной функ-
цией t.
Если температуре t дадим приращение Д£, то Q получит при-
ращение, равное Д<2 = /(/Д^) —/(0-
Отношение
Д<? ./(^+Д0-/(0
At At ’ . *а>
выражающее среднюю скорость изменения количества теплоты при
изменении температуры от t° до называется средней
удельной теплоемкостью данного вещества в интервале (t; Z-j-Д/),
6* 163
а удельной теплоемкостью при температуре t называется предел
средней удельной теплоемкости (а), когда Д/—>0.
Обозначив удельную теплоемкость при данной температуре /°
через с, получим
г —о — lim Д(?— НтЯ' + д0-/(0
с — У/— нт -д7= нт ---------т----.
д/-.о д/-о ас
Задача 2. Количество Q теплоты (в малых калориях), полу-
чаемое 1 г некоторого вещества при нагревании его от 0° до /°,
определяется по формуле
Q = 0,1054/4-0,000002/*.
Найти удельную теплоемкость этого вещества при /=100°.
Решение. Как мы установили выше, удельной теплоемко-
стью вещества при данной температуре называется
-
д/ —о
Следуя общему правилу дифференцирования (см. § 59), найдем
с =--q; = 0,1054 4-0,000004/.
При /—100° получим
Сюо = 0,1054 4- 0,000004 - 100 = 0,1058.
Пример 3. При нагревании тела температура его Т изменяется
в зависимости от времени /, т. е. Т является функцией от /:
Если обозначим повышение температуры за промежуток вре-
мени от момента t до момента /-|-Д/ через ДТ, то получим
дт=/(/4-д/)— /(/).
Тогда отношение
АГ /(Z-4-др—/(/)
м м
будет средней скоростью изменения температуры за промежуток
времени от момента / до момента а предел этого отноше-
ния при Д/ -> 0, т. е.
.. ДГ ,. f(t + Д/)-f(t)
Tt - lim = — lim ——I—-—
Д/-.0 Д/-+0
явится выражением скорости изменения температуры Т в момент/.
Задача 3. Закон изменения температуры Т тела в зависимости
от времени / выражается формулой
Т = 0,5/2.
С какой скоростью нагревается это тело в момент / = 4/сс«?
164
\t
Решение. Находим производную этой функции по общему
правилу дифференцирования, приняв t — 4:
1-й шаг. Т-|-АТ = 0,5(4 +А/)*.
2-й шаг. А 7'= 0,5 (4 + А/)-’ —0,5-4-= 0,5 (8-НА/). А/.
о “ А Т 0,5 (8 -I- AZ) • л е /о । л л
3-и шаг. ---= 0,5 (84-А/).
4-й шаг. Игл [0,5 (8 -ф- А/)] = 0,5 (8 0) = 4.
Следовательно, в момент t = 4 сек, данное тело нагревается со
скоростью 4° в секунду.
§ 61. КАСАТЕЛЬНАЯ И НАКЛОН КРИВОЙ
В элементарной геометрии касательная к окружности опре-
деляется как прямая линия, имеющая с окружностью только
одну общую точку.
Такое определение нельзя принять как общее определение
касательной ко всякой кривой. Возьмем, например, кривую у =
4
=. , (рис. 109). Как видим, касательная АВ к этой кривой
1 -4- Д'"'
в точке А имеет с ней не одну, а две общие точки А и В. С дру-
гой стороны, прямая АС, которую за касательную принять нельзя,
имеет с кривой только одну общую точку А.
Чтобы определить касательную к кривой y = f(x) (рис. ПО)
в точке А, возьмем на этой кривой точки В и С, расположен-
ные по разные стороны от точки А, и проведем касательные АВ
и АС. Если эти точки, перемещаясь по кривой, будут прибли-
жаться к точке А, то секущие последовательно будут занимать
положения: APj,' АР.г,... и А1\, А7\,... Когда точки В и С
будут стремиться к совпадению с точкой А (при Дх->0), то се-
кущие АВ и АС, вращаясь вокруг точки Л, будут стремиться
занять предельное положение АТ. Эта прямая (ЛГ) называется
касательной к кривой у = ](х) в точке А.
Определение. Касательной к кривой y = f\x) в данной
точке А называется общее предельное положение секущих АВ и
165
АС, когда точки В и С, перемещаясь по этой кривой, неограни-
ченно приближаются к точке А справа и слева.
Как же построить касательную к кривой в данной на ней
точке A (xi, /л)? Из аналитической геометрии известно, что для
построения любой прямой достаточно знать ее уравнение. Следо-
вательно, задача сводится к составлению уравнения такой прямой,
которая в данной точке касается кривой. Мы знаем, что урав-
нение прямой, проходящей через точку A (xi, уд, имеет вид
У — yi = k(x— xi),
где k — угловой коэффициент, значение которого изменяется с из-
менением направления прямой. Следовательно, для построения
касательной к кривой y = f(x) в данной на ней точке М (х^ уд
необходимо и достаточно найти угловой коэффициент k. Этот воп-
рос рассматривается в следующем параграфе.
§ 62. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Пусть кривая EF (рис. 111) является графиком непрерывной
функции y — f(x). Возьмем на этой кривой точку А (х; у). Получим
ОXj = х, AiA — y~f(x).
Дадим абсциссе х приращение Дх^ДВь Тогда наращенному
значению абсциссы, равному
OBi = ОAi AiBi == х —|- Дх,
166
будет соответствовать наращенное значение ординаты, равное
В1В = г/4-Дг/ = /(х4-Дх). (а)
Из точки А проведем прямую АВ2, параллельную оси Ох, и
секущую АВ. Получим прямоугольник AiAB2B) и прямоугольный
треугольник АВВ2. Очевидно,
АВ2 =\4jBi = Дх
и
BlB2 = AiA—y = f(x) (б)
как противоположные стороны
прямоугольника А2АВ2В2.
Вычитая из равенства (а) ра-
венство (б), найдем
BiB — BiB2 =
= /(х4-Дх)— f(x) = by,
или
В2В = ку.
Рис. 111
Обозначив угол между секущей АВ и положительным направ-
лением оси Ох через [3, получим
^В2АВ= ^А1КА = $.
Тогда из прямоугольного треугольника В2АВ будем иметь
tgZBMB = ?g,
или
tgp=K- (5)
Равенство (5) показывает, что с геометрической точки зрения
отношение приращения Д// функции у к приращению Дх аргу-
мента х является тангенсом угла наклона к оси Ох секущей,
проходящей через точки А (х; у) и В(х-|-Дх; у-$-Ду).
При Дх—>0 точка В, перемещаясь по кривой, будет неогра-
ниченно приближаться к неподвижной точке А (х; у), секущая АВ,
поворачиваясь около точки А, будет стремиться занять предель-
ное положение, а именно положение касательной AM. При этом,
очевидно, угол р будет стремиться к углу а, образуемому каса-
тельной AM с положительным направлением оси Ох. Получим
lim р = а и lim tg[3 = tga. (в)
Д^->0 Дл;->0
С другой стороны, из равенства (5) будет следовать
lim tg 8 = lim , или lim tg 8 = ух. (г)
Дл‘—>0 Дл?->0 Дх->0
167
Левые части равенств (в) и (г) равны между собой, следова-
тельно, должны быть равны и правые части, т. е.
= или y'x = k , (6)
где k — угловой коэффициент касательной AM к графику функ-
ции y = f(x) в точке А (х; у).
Итак, производная функции y = f(x) при данном значении
аргумента х — х\ равна угловому коэффициенту касательной, про-
веденной к графику этой функции в точке, абсцисса которой
равна Xi.
Угловой коэффициент касательной к кривой в данной на ней
точке Д(хь уд) принято называть подъемом кривой в этой точке,
или наклоном кривой относительно оси Ох. Поэтому, можно ска-
зать, что геометрически произ-
водная выражает наклон кривой
в данной точке.
Пример 1. Дана кривая у —
=4 х2 — 2х. Найти наклон этой
кривой в точке, абсцисса кото-
рой равна: 1) 0; 2) 6; 3) 8.
Решение. Согласно опре-
делению, наклон кривой в данной
точке определяется по формуле
Рис. 112 k=y'x=f'(x).
Найдем производную данной функции по методу, указанному
в § 59:
1-й ш а г. г/-|-Дг/ = -^-(х-|-Дх)2 — 2(хф-Дх).
2-й ш а г. Дг/ = (х -ф- Дх)2 — 2 (х -ф- Дх) — х2 — 2xj =
= 4- х2 -ф-4- х Дх -ф- (Дх2) — 2х — 2Дх — 4 х2 -ф- 2х;
после преобразования получим
Дг/ = (у х -ф- 2- Дх — 2) • Дх.
3-й шаг. ^ = уХф-уДх —2.
4-й ш а г. у'х = f (х) — lim (4' х 4- Дх — 2^) — 4 х — 2.
Дл-o\z 4 ‘ 1
В данном случае наклон (k) кривой в точке с абсциссой х
(рис. 112) определится по формуле
k = уХ — 2;
168
1) при х== 0 получим
£ ==/'(0) ==у • 0 — 2 = —2 == tg ац
2) при х = 6 получим
/г=/'(6)=у-6 —2 = 1 ==tga2;
3) при х = 8 получим
k = f' (8) = 1.8 — 2 = 2 = tga3.
Пример 2. Дана кривая у = — х24~4. Провести к этой кривой
касательную в точке, абсцисса которой равна —1.
Решение. В § 61 было указано, что для построения каса-
тельной к кривой в данной точке
надо предварительно составить ее
уравнение. Абсцисса точки каса-
ния нам дана. Найдем ординату
этой точки
у = —х24~4 = —(—1)24"4 = 3
при х = — 1.
Уравнение любой прямой, про-
ходящей через точку А (—1; 3),
имеет вид
у — 3 = А(хД-1). (д) Рис. ИЗ
Для того чтобы эта прямая была касательной, необходимо
и достаточно, чтобы
A = y}Jx=_i=f'(—1).
Найдем производную данной функции:
1-й шаг. уЬу = — (хА-Дх)2-}-4.
2-й ш а г. Ду = — (х Дх)2 -}- 4 — (— х2 4) — — х2 — 2хДх —
— (Дх)24-}-х2 — 4;
в результате преобразования получим
Ду = — (2х -ф- Дх) Дх.
3-й шаг. (2х ‘= — (2х Дх).
4-й шаг. ух= lim lim [—(2х-}-Дх)] = —2х.
Дл-0
Итак, при любом х угловой коэффициент касательной опре-
делится по формуле k = — 2х.
При х =— 1 получим k = —2(—1) = 2. Следовательно, угло-
вой коэффициент k касательной к данной кривой в точке (—1; 3)
169
будет равен 2. Заменим в уравнении (д) k найденным его значе-
нием 2. Получим уравнение касательной в точке А (рис. 113)
У — 3 = 2(x-f- 1),
или
У — 2x4-5.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Что означает запись y=f(xft
2. Какой геометрический образ соответствует любому уравнению вида
y=f(x)">
3. Можно ли вычислить As, зная только,'что yt = 3, если s = 4Z3?
4. Дана функция у — х~. Можно ли вычислить Ду, если известно только,
что Дх = 2?
5. Уравнение с одним неизвестным записано в следующем виде: f(x) — 0.
Как показать, что: 1) число 3 является корнем этого уравнения; 2) число 5
не является корнем этого уравнения?
6. Сформулируйте условие непрерывности функции при данном значе-
нии аргумента.
7. Сформулируйте условие непрерывности функции в данном проме-
жутке.
8. Какой величиной является в случае равномерного движения отноше-
ние приращения As пути s за любой промежуток времени к величине этого
промежутка?
,
9. Как называется отношение в случае неравномерного движения,
если yt является промежутком времени от момента < = 5 сек до момента
t — 8 сек>
10. Как определится скорость неравномерного движения в данный мо-
мент t, если закон движения выражен формулой s =/(£)?
И. Если переменные величины х и у, каждая из которых имеет опре-
деленный физический смысл, связаны уравнением y=f(x), то как назы-
Ду □
вается отношение уД при данном значении аргумента х?
12. При условии предыдущего вопроса как определяется скорость изме-
нения функции при данном значении аргумента?
13. Что называется производной функции у = /(х)?
14. Дать определение касательной линии к кривой у = f(x) в данной
на ней точке.
15. Что называется наклоном прямой у — kxb к оси Ох?
16. Что называется наклоном кривой у=/(х) в данной точке?
17. Какой геометрический смысл имеет производная функции у =f(x)
при данном значении аргумента'х?
18. Какой линией изображается график непрерывной функции?
19. Можно ли начертить непрерывным движением (не отрывая каран-
2
даш от бумаги) кривую: 1) у = ха; 2) ху — 3; 3) у — ех; 4) У — ~
Ответы-
3. Можно, так как в данном случае As не зависит от t (см. § 58).
4. Нельзя, так как в этом случае Уу зависит не только от Дх, по и от х.
5. 1) /(х) = 0; 2) /(5) т^О. 7, 8 и 9 (в § 57). 11. Средняя скорость измене-
ния функции в промежутке (х; х.Д-Дх). 12 (в § 60). 19. 1) можно; 2) нельзя,
так как эта функция имеет разрыв в точке х = 0; 3) можно; 4) нельзя:
функция имеет разрыв при х — 2.
170
Глава VII
ОСНОВНЫЕ ФОРМУЛЫ И ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
§ 63. ВВЕДЕНИЕ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ,
ИМЕЮЩЕЙ ПРОИЗВОДНУЮ
Нахождение производной по общему правилу, данному в § 59,
в большинстве случаев приводит к громоздким вычислениям и
отнимает много времени. Существуют правила и специальные
формулы, значительно упрощающие процесс нахождения произ-
водной. В данной главе рассматривается вывод указанных фор-
мул и применение их к дифференцированию функций.
Теорема. Если функция у = [(х) при данном значении аргу-
мента х имеет производную, то при этом значении аргумента
данная функция непрерывна.
Доказательство. Положим, что при х = а (а — данное
число) функция y — f(x) имеет производную
При Дх->0 отношение^, очевидно, — величина переменная,
f (а) — величина постоянная как предел этого отношения. Со-
гласно определению предела имеем
g_f(a)=a, (0
где а — бесконечно малая величина при Дх->0.
Решив уравнение (а) относительно Ду, получим
Ду = f' (а) Дх а • Дх.
В этом равенстве (при Дх->0) слагаемые /'(а)-Дх и а-Дх—
бесконечно малые (см. § 47, второе свойство и следствия из него).
Мы знаем (см. § 47, первое свойство), что сумма двух бесконечно
'малых величин — величина бесконечно малая. Следовательно,
1 iгл Ду = 1 im [/'(а) • Дх Д-а • Дх] = О,
Дх-*0 Д.к-^0
т. е. при Дх->0 и Ду->0. Это значит, что при данном значении
аргумента х функция непрерывна (см. § 57). Обратное предполо-
жение не всегда верно, так как существуют функции, непрерыв-
ные при данном значении аргумента, но при этом не имеющие
производной.
Возьмем, например, функцию у~f(х) = {Ех‘1. При х = 0,
следуя общему правилу дифференцирования функции, получаем
Z/M(0) = ^0* = 0;
171
1 - и ш а г. у-.-Ь y=J(O -I X =4^ •
2-й шаг. ^y — f (0 -ф Дх)—/(0) —j/(AxV—О,
или г
Дг/ = (Дх)3;
из этого равенства видно, что при Дх->0 и Дг/->0 как при Дх<^0,
так и при Дхф>0. Это значит (см. § 57), что при х = 0 данная
функция непрерывна.
Ду /(0 + Дх)-/(0) = (Дх)3
Дх Дх Дх
у'х = lim ~у~= lim -37== =
Дх —О Дх —о -(/ Дх
3-й шаг.
4-й шаг.
Производная функции при данном значении аргумента, если
она существует, есть определенное число. Полученный же резуль-
тат показывает, что в данном слу-
чае такого числа не существует.
Следовательно, функция у —
= -jZx\ непрерывная при х=;0,
при этом значении аргумента
производной не имеет. График
этой функции дан на рис. 114.
На практике преимуществен-
но встречаются такие непрерыв-
ные функции, которые имеют про-
изводные при любых допустимых
значениях аргумента, поэтому в
последующем при . доказательстве
правил и выводе формул дифференцирования будем полагать, что
все рассматриваемые функции имеют производную при рассматри-
ваемом (данном) значении аргумента х.
§ 64. ПРОИЗВОДНАЯ ПОСТОЯННОЙ ВЕЛИЧИНЫ
Пусть y = f(x) является такой функцией, которая при всех
зачеииях
Отсюда
аргумента имеет одно и то же значение, равное числу с.
У I <
или
= f (х) = с,
У — с-
Из аналитической геометрии из-
вестно, что графиком такой функции
является прямая линия, параллель-
ная оси Ох (рис. 115). Ордината лю-
бой точки этой прямой (при любом х)
Рйс. 115
172
равна числу с. Найдем производную этой функции, следуя об-
щему правилу дифференцирования, данному в §59:
1-й шаг. у-\- Ду = /(х-|-Дх);
так как f (х -|- Дх) = / (х) = с, то
У + дУ = с.
2-й шаг. ^у = (у ф-д//) — у = с — с = 0,
или
Л/ = 0-
4-й шаг. y'r= lim -£-= lim 0 = 0.
Следовательно, ух = 0,
или
с;=о . (1)
Это выражение можно сформулировать так: производная по-
стоянной величины равна нулю.
§ 65. ПРОИЗВОДНАЯ ФУНКЦИИ у — х
Найдем производную этой функции по общему правилу диф-
ференцирования:
1-й шаг. у-]-Ду = хД-дх.
2-й шаг. Ду = (?/ + Д//) — у =
= х + Дх — х = Дх.
4-й шаг. у'х = lim^~= lim 1=1.
Итак,
Ул = (х);= 1,
или _______
хх = 1 . (2)
Эта формула читается так: производная аргумента по самому
аргументу равна единице.
Данный вывод легко подтвердить геометрически. Из аналити-
ческой геометрии известно, что графиком функции у = х является
прямая линия, проходящая через начало координат и образую-
щая с положительным направлением оси'Ох угол 45°. Вследствие
этого (рис. 116) при любом х и произвольном Дх получим Д;/ =
= Дх, откуда
^ = 1; уж = lim ^=1
Дх J дЛ_0 Дх
173
§ 66. ПРОИЗВОДНАЯ АЛГЕБРАИЧЕСКОЙ СУММЫ ФУНКЦИЙ
Положим, нам дано у —и — v-\-w, где u = f(x), п = <р(х),
w — F(x). Требуется найти у'х = (и— иЦ-ш)*-
Следуя общему правилу дифференцирования (см. § 59), най-
дем у'х.
1-й шаг. Дадим аргументу х приращение Дх. Тогда нара-
щенному значению х-(~Да аргумента х будут соответствовать
наращенные значения иД-Д«, пЦ-Дц, шД-Дда функций и, v, w.
Наращенным значениям этих функций будет соответствовать на-
ращенное значение у. Получим
у-\- ^у—(и -j- Ьи) — (у-)-+ (да + Д®) = « + Д« — v —
—Дада+Ада-
2-й шаг. Ду - (у 4- Ду)— у = («-)-Ди — v — Да -j- w -j- Дда)—’
— (и — n-j-да), '
или
Ly = ku — Да-|~Ада.
3-й шаг. М’ Ди — До -|- Да/ Ди До । Дго
Дх Дх Дх Дх Г Дх’
4-й шаг. Ух = lim lim Дх-*0 /Ди \Дх До , Да»' Дх д_£
На основании первой теоремы о пределах последнее равен-
ство можно переписать в следующем виде:
,. Ди ,. До ... Ди/
ух= lim -------lim —н lim -г-.
Дх —О Дх-0 Дх—0
В этом равенстве каждое из отношений, стоящих под знаком
предела, является отношением приращения функции к прираще-
нию аргумента. На основании определения производной получим
У* = 11т дТ- 11т дт+ 11т -rx^-Ux~Vx^Wx’
Дх-0 аА Дх-ОаА Дх-0
следовательно,
или
Ухя= (u — V + да); = и'х —• vx + да;,
(и — v -|- да); = их — v'x да;.
(3)
Это правило формулируется так: производная алгебраической
суммы функции равна алгебраической сумме производных этих
функций.
Пример. Найти производную функции у = х4-Ю.
Решение. Применив последовательно формулы (1), (2) и (3),
получим
у;=(х4-1О)л=х; + 1ол=1+о=1.
174
§ 67. ПРОИЗВОДНАЯ ПРОИЗВЕДЕНИЯ ДВУХ ФУНКЦИЙ
Даны функции: u — i> = <p(x). Требуется найти производ-
ную функции y — f(x) • ср (х), или, короче, у== uv.
Поведем нахождение производной по общему правилу.
1-й шаг. Дадим аргументу х приращение Дх. Тогда нара-
щенному значению x-f-Дх аргумента х будут соответствовать
наращенные значения функций и и о: u-f-Aa и ц-ф-Дщ Подста-
вив в равенство y=uv вместо и и у их наращенные значения,
получим
у -ф- Дг/ = (и Ди) (у 4- &v) = uv v Ьи и &v &и bv.
2-й шаг. ку = (у-\- ку) — у — (uv Д- v Ди -\-и Ди -ф- Ди • Ди)—
.— uv = vДи-фи Ди -ф- Ди- Ди.
Q Й m а г -°A“ + “to + 4“'
о-И Ш d 1 . "7— ----~.
Дх Дх ’
ИЛИ
Ду Да . Да , 4 Да
&=идт + идт + ДыдГ-
4-й шаг. у'х = lim т^= lim-lv^ -ф- и Ди .
Дх-0Д* . Дх-о\ М
Применив к правой части этого равенства теорему о пределе
алгебраической суммы функций, найдем
у'х = lim lim lim Ди^.
Дх-0 Дх 1 Дх-0 Дх-0 ^х
Нам было дано: и —f(x), и = ср (х). Очевидно, что и и v от Дх не
зависят и при Дх->0 сохраняют свои значения неизменными.
Рассматривая и и v как постоянные величины, по теореме о пре-
деле произведения двух функций и ее следствию (см. § 48) полу-
чаем
уф = и-Нт ^-4-u-lim 4^4- lim Ди- lim
Дх-0Дл‘ ' Дх-0 Дх 1 Дх-0 Дх-0Дл'
Под и и v мы разумеем функции, имеющие производные,
поэтому
нт д7 = «х; bm ту. = щ;
lim Ди = 0 (см. § 63).
A.v->0
Следовательно,
yx = v lim ^Д-u lim ^-ф- lim Ди-lim =
Дх —0 ал Дх—0 л Дх —0 Дх — 0
— vux 4- uvx -ф- О • v'x.
175
Итак,
у'х — (uv)'x — vu'x + uv'x,
или __________________
(uv)x — vux~\~uv‘x . (4)
Это правило формулируется так: производная произведения
двух функций равна сумме произведений второй функции на про-
изводную первой и первой функции на производную второй функции.
Пример 1, Найти производную функции у = (х-\- 12) (х — 7).
Решение, По формуле (4) найдем
Ух = (х - 7) (х + 12). -Н (х + 12) (х - 7)..
Далее последовательно применяем формулы (3), (2), (1):
у'х = - 7) (хх Ч- 12.) + (х + 12) (хх - 7Д =
= (х-7)(1Ч-0) + (хЧ-12)(1-0).
Получаем
^ = [(х+ 12) (х — 7)]. —х - 7 + х+ 12 = 2х ф- 5;
у'х — 2х -1- 5.
Рассмотрим частный случай: произведение постоян-
ной вел и чины на фу и к ц н ю.
1, Пусть нам дана функция у = си, где с — постоянная вели-
чина, и = /(х), имеющая производную. Требуется найти ух =
= (си)'х.
По формуле (4) найдем
у'х = (си)х = и • с 'х сих-
Нам известно, что сх = 0, откуда
ух — (си)х и • 0.
Итак, ____________
(си)'х = сих . (5)
Следовательно, производная произведения постоянной величины
на функцию равна произведению постоянной величины на произ-
водную этой функции.
2. Производная функции у = — , где и = /(х); с — постоянная
„ , 1
величина. Данную функцию можно переписать так: у= — и.
В этом равенстве сомножитель — величина постоянная. По
формуле (5) получим
176
или
(6)
Пример 2. Найти производную функции у — 5х.
Решение. По формуле (5) найдем
у'х = (5х)1- - - 5 • х'х — 5 • 1 5.
Пример 3. Найти производную функции у = (5х -ф- 6) (Зх — 11).
Решение. В первую очередь применим формулу (4)
ух = (Зх — 11) (5х + 6); 4- (5х + 6) (Зх - 11 )'х.
Далее, по формулам (3), (2), (1) и (5) найдем:
ух = (Зх - 11) (5x4 6'с) 4- (5х + 6) (3x;v - 1П) =
= (3х — 11) (5-14- 0)4- (5x4-6) (3-1—0) =
= 15х-554-15х4-18 = 30х —37;
= [(5х-4 6) (Зх - 11 )]* = ЗОх — 37.
§ 68. ПОНЯТИЕ ФУНКЦИИ ОТ ФУНКЦИИ.
ПРОИЗВОДНАЯ ФУНКЦИИ ОТ ФУНКЦИИ
1. Возьмем логарифмические функции
y = lgx,
z/ = lg(3x2 + 5x+ 4).
В первом из этих уравнений под знаком логарифма находится
аргумент х, во втором — функция от аргумента х, В первом
случае мы имеем функцию (логарифм) от аргумента х, во вто-
ром— функцию (логарифм) от функции. Такие функции принято
называть функциями от функции, или сложными функциями.
Обозначив функцию 3x2-|-5x-L-4 через и, получим
у = 1g и, где и = Зх2 4- 5х 4- 4.
Рассмотрим еще три примера. 1) Положим, нам дана триго-
нометрическая функция
у = sin (wf -4 а).
В этом случае мы под знаком синуса имеем функцию от вре-
мени /, следовательно, у является функцией от функции otf-4a-
Обозначив эту функцию через и, получим
y = sin«, где « = ю/4-а.
177
2) . Возьмем показательные функции:
у = ах, где а > 0 и а # 1;
у = а1^х+\ где а^>0 и а^\.
В первом уравнении показателем степени является аргумент х,
во втором — функция от х: 2]/x-j-3. Следовательно, функция
у = а2уГх +3 есть функция от функции
у~ а’1, где и = 2 Ух 4~ 3.
3) Рассмотрим степенные функции: у — хп, где п — любое дей-
ствительное число; у — (ах11 -f- Ьх 4- с)п, где п — любое действи-
тельное число.
В первом уравнении основанием является аргумент х, во вто-
ром—функция от аргумента х, т. е. у = ип, где
и — <? (х) = ах14- Ьх с.
2. Предположим, что
y — f(u), где и = <р(х).
Допустим, что при данном х и при соответствующем значении и функ-
ции y=f(u) и и = <р(х) имеют производные у'и и их. Дадим аргументу х
приращение &х; тогда функция и получит приращение Ди, а функция у —
приращение Ду». При этом (см. § 63)
Ди —- 0, когда Дх —< 0. (а)
Возьмем тождество
Уу _ Ду Ди
Дх Ди Дх'
Очевидно, предел левой части этого тождества равен пределу правой
части. Применив к правой части теорему о пределе произведения, получим
Ду Ду Ди lim -f- = lim -У-• lim -т—, Дх —0дХ Дх — 0 Дх—одх
или [см. (а)] Ду Ду Ди lim = lim -У- • lim -г—, Дх —оДх Ди —0 Дц Дх —оД^
Нам известно (см. § 59), что
1 &У
lim -г~=Ух,
дх-оДх Jx'
Ду . Ди ,
1шт -х-=у Inn — = и
ди-од« “ ,дх-одх х
Следовательно, если у=/(и), где u = tp(x), то
Ух=Уи’их-
(б)
Формулы (7), (8), (10) —(22), следующие ниже, являются частными слу-
чаями этой формулы (б).
178
§ 69. ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ -
1. Дана функция у = ип, где u — имеющая производную,
а п— любое целое положительное число. Требуется найти
Ух = (ип)’х.
Предположим сначала, что у=и*. Производную этой функ-
ции можно найти по формуле (4). Получим
у'х = (и-)'х = (ии)’х = и (и)'х -ф- ии'х — ии'х ф- иих = 2ии'х,
или
{и°)'х — 2ии'х. (а)
Возьмем теперь функцию у = и\ Эта функция может быть
переписана в следующем виде:
у —и1-и.
Применив 'формулу (4) и приняв во внимание равенство (а),
найдем
у’х = (и и)'х = и (и2)х + и" (и)х — и • 2ии'х ф- U'U'x = 2U'UX ф- и2и'х,
или
(и3)’х = 3u2u'x. (б)
Положим далее, что у=и1. Дифференцируя, как это делалось
в двух предыдущих случаях, и приняв во внимание равенство (б),
найдем
ух = (или)'х = и (а3)х ф- и* • (и)'х = и 3tru'x ф- и'и'х =
— Зи^и'х-]-и:1и'х = 4и‘'и'х.
Если мы продолжим дифференцирование, давая показателю
степени последовательно значения 5, 6, 7,..., то получим;
(и:')'х ~ {и'и)’х — и • 4U*UX -|- и'и'х = Su'u'x",
(ueyx = Qu<>~lUx = &U^Ux‘,
(иух = 7и’~'и'х = 7ие'и'х,
(Us)'x = 8u‘i^iUx = 8u7Ux‘,
Отсюда видно, что производная степенной функции у = ип,
где u = f(x), находится по формуле
(u'l')’x — nun~iu'x . (7)
При и = х будем иметь:
у = Хп', у'х—(хп)’х==ПХп~1Хх — ПХп~1 -1, '
ИЛИ _________________
(Хп)’х = пхп-1 . (7а)
179
Формулы (7) и (7а) были выведены нами в предположении,
что п — целое положительное число. Эти формулы справедливы
при любом действительном п, что будет доказано позднее (§ 73).
.-4
Пример 1. Найти, производную функции: 1) у — х"‘\ 2) у =
3) У=~\ 4)у=2х3.
Решение. 1) По формуле (7а) находим
t/; = (x7); = 7x7-1 = 7x°.
2) Эту функцию можно переписать в виде произведения
постоянной величины на функцию. Получим у = --хг. Далее, по
формуле (5) и (7а) получим
Ух = = 4 у • 4х3 = х\
В подобных случаях' решение следует записывать короче
по формуле (6):
/х4\’ (х4); 4х3
=-т=^3.
3) Из алгебры известно: ~==ах~\ Применив формулы (5)
и (7а), получим
ух = (ах-3)!- = а • (лг3); = а • (— 3) х^1 = — .
/ IV * 2
4) у'х— (Дх3]х — 2-у*3 — у-1'3'
Пример 2. Найти производную функции у — ^-х3—2х2-|-Зх—7.
Решение. Применив последовательно формулы (3), (5), (1)
и (7а), получим
у; = (4 X3 - 2х2 + Зх - 7Y | • (х% - 2 (х2), + 3 (хД - 7Х =
= ^-Зх2-2-2х4-3-1 —0=.х2 —4х 4-3.
Указание. Чтобы хорошо овладеть техникой дифференци-
рования по формулам, необходимо знать правила действий над
степенями с любым показателем и иметь твердые навыки в их
применении.
Прежде чем приступить к разбору примера 3, рекомендуется
проделать упражнения 328—356.
Пример 3. Найти производную функции у == (ах4 4- Ь)9.
Решение. В данном случае у является функцией от функ-
ции и—ах14-Ь, т. е. у —и1, где и — axi4-9.
180
Дифференцируем по формуле (7). Получаем
= 9u'r= 9 (ах1-ф Л)4 • (ах4-ф/7)'v =
= 9 (ах1 -j- Ь)я • а 4.У = Збах1 (ах1 -ф- й)8.
Пример 4. Найти производную функции
. , y = Y(axi~'[-by.
Решение. Переписываем данную функцию, заменив радикал
дробным показателем:
4_
у=|/ (ах’^Ь)'1 = (ах1 -ф- Ь)5.
4
Получаем у = и\ где и = ах1 -ф-Ь. Дифференцируем по фор-
мулам (7) и (5):
( 4 £ _ 1 4 _ -L
ух = \иг,}х = -^ иъ -их = -^(ах1 -ф-Ь) 5 • (ах1 -ф-Ь)'х =
— А. 1 .4^ = 21^.
5 |/ a.v4 Ь у ах* у Ь
Производная функции у = У и, где u — f(x). Диффе-
ренцируя эту функцию по формуле (7), найдем
Пример 5. Найти производную функции
^==(2/х-уЗ)(3/х-2).
' Решение. По формулам (4) и (5) получим
у( = [(2 Vx + 3) (3 Yx - 2)]; = (3J/х - 2) (2 /х ф- 3)'х -ф-
-г (2 Yx 4- з) (3 Ух - 2); = (3 Ух_ - 2) [2 (/х); 4~0] +
+ (2Vx+3)[3(/xK- 0].
181
Далее применим формулу (8а). Получим
^ = (3/х-2)-2.—^- + (2]/х+3).3.—=
2. |/ х 2 у х
_2(зу'х—2) , 3(2J/T + 3)_12/x+5
— 2/х 2/х 2рТ ‘
Пример 6. Найти производную функции у — ^Зх21.
Решение. Здесь мы имеем функцию от функции и — Зх-Л- 1.
Дифференцирование ведем по формуле (8). Кратко запишем ре-
шение так:
, (Зх2 4-1 )х бх Зх
а 2/Зх24-1 2/Зх2+1 /Зха+1
Указание. Рекомендуется самостоятельно решить примеры
357—366.
§ 70. ПРОИЗВОДНАЯ ЧАСТНОГО ДВУХ ФУНКЦИИ
1. Пусть нам даны функции u—f(x) и у = <р(х), имеющие
производные их и vx при данном значении х.
Возьмем функцию У — -~ и найдем ее производную у'х = (^ ,
предполагая, что ц = <р(х)^0. При дифференцировании этой
функции примем во внимание, что
и 1 .
— — U- — = uv \
v V
По формуле (5) получим
у'х = = №~'УХ = v~l ‘ и'х + и (v (а)
По формуле (7) найдем (см. решение примера 4, § 69)
1 V
(^д=(— i)u'1_1-y;=—(б)
Заменив в равенстве (a) Д|Ч)1- его значением из равенства (б),
получим
Итак,
(9)
Это правило можно сформулировать так: производная част-
ного (дроби) двух функций равна дроби, знаменателем которой
182
является квадрат делителя, а числителем — разность между про-
изведением делителя (знаменателя) на производную делимого
(числителя) и произведением делимого (числителя) на производ-
ную делителя (знаменателя).
Пример 1. Найти производную функции t/— 2х— 1 '
Решение. Эта функция не имеет производной лишь при
2х—1=0 или при х = Дифференцируя по формуле (9),
найдем
(2х - 1) (2х ф- 1/ - (2х + 1) (2х - 1);
Vх = '' (2х — I)* 2 =
_ (2х — 1) 2 — (2х + 1) • 2 _ 4х — 2 — 4х — 2 _ -4
— (2х—l)s (2х—I)3 * (2.v—1)-'
Пример 2. Найти производную функции
У ах2-Ь
у— ,-------.
J У ах2 4- b
Решение. По формуле (9) получим
. У ах2 ф- b (V ах2 — b)x — |/ ах2 — b (У ах2 ф- b)x
Ух ~ (У^ё+ь)*
Производные — b)x и (Vах1 ф- Ь)'х найдем по фор-
муле (8), получим
У ах2 — Ь----,
2 /ах2 ф- й
У ах2 4- b г______
. _ 2 у ах2 •- Ь
Ух ах2 4- b
,/---гт-1 2ах —5---й ^ах
У ах2 4- Ь --, ---у ах- — Ь -----,
__ 2У ах2-Ь________________2/ax34~^ _
ах2 4- b
ах У ах2-(-Ь ах У ах2— b ах (ах2 ф- Ь) — ах (ах2 — Ь)
У ах'1 — b У ах2 4- b ____ У ах2 — b У ах2 4- b
ах2 -(-Ь ах2 ф- Ъ
2abx
Уa2xi — b2 2abx
ах2 ф- b (ах2 ф- Ь) Уа2х'‘ — Ь2
Указания; 1. Прежде чем приступить к изучению следую-
щего параграфа, надо усвоить технику дифференцирования част-
ного двух функций, решая упражнения 367—374, 379—382.
2. Чтобы обеспечить усвоение теории, изложенной в § 71, 72,
77, и овладеть техникой дифференцирования тригонометрических
и обратных тригонометрических функций, необходимо повторить
из курса тригонометрии следующие темы:
1) радианная мера угла;
183
2) формулы приведения тригонометрических функций углов
любой четверти к функциям острого положительного угла;
3) формулы сложения: sin(a±p), cos(a±p), tg (a ± p);
4) формулы двойного угла и половины угла;
5) формулы преобразования сумм и разностей тригонометри-
ческих функций в произведение;
6) обратные тригонометрические функции.
§ 71. ПРЕДЕЛ ОТНОШЕНИЯ КОГДА .V — О
Мы уже доказали (см. § 42, задача 3), что при х->0 и
sinx->0. Известно также (см. § 49), что отношение двух беско-
нечно малых величин не, всегда имеет предел. Докажем, что
sin .г п
отношение при х->0 имеет предел и что этот предел равен
единице.
Пусть нам дана окружность радиуса /? (рис. 117). Возьмем
сектор А41ОЛ4 и проведем хорду А4А4]. Прямая ОК, перпендику-
Рис. 117
лярная хорде А4А41, ‘разде-
лит пополам эту хорду, стя-
гиваемую ею дугу ММ] и
центральный угол ЛДОА4. По-
лучим:
MtK = NM,
А4jА = AM,
Z MiOA = Z AOM.
Проведя к данной окруж-
ности касательные МТГ и МТ,
получим прямоугольные тре-
угольники ОМгТ и ОМТ,
имеющие по равному катету (OA4i = OAt) и равному острому углу
(Z MtOA — Z АОМ). Такие треугольники равны между собой.
14з равенства этих треугольников будет следовать
МХТ — МТ.
Из рисунка видно, что
MiM < MtAM < MtT + МТ,
или
2NM<2 АМ<^2МТ.
Разделив части этого двойного неравенства на 2R, получим
2NM ^2^ AM '2МТ
184
или
NM AM ^ МТ
R R R •
Из тригонометрии известно, что отношение — радианная
А
мера угла ЛОМ. Обозначив ее через х, из прямоугольных тре-
угольников ONM. и ОМТ получим:
NM . МТ .
-^- = sinx; —=tgx.
„ NM ... ДЛ1 ^МТ
Следовательно, двойное неравенство —5—можно
А А А
переписать так:
sin x<x<Hgx,
или
В этих неравенствах sinx^>0, так как х — острый угол. Из
алгебры известно, что смысл неравенства не меняется, когда части
его делятся на одно и то же положительное число. Поэтому, раз-
делив части этого двойного неравенства на sinx, получим
sin х х sin х
sin х sin х cos х sin х
или
1 ’V 1
1 sin х cos х ‘
Если возьмем величины, обратные тем, которые входят в по-
следнее двойное неравенство, то получим неравенства противо-
положного смысла*, а именно:
1 sin х cos х
или
, . sin
1 > ------> COS X.
ГЧ sin X „ „
Jto значит, что величина отношения —— не может быть больше
1 и меньше, чем cosx. Вследствие этого lim не может быть
Х — П Х
больше 1 и меньше, чем limcosx=l. Следовательно,
х-0
,. sin х
lim------— 1
х — О х
*
2
1
и
£
2 •
(Ю)
185
То, что отношение —когда х->0, видно также из
табл. 10.
Таблица 10
£ = 0.17453 13 £ 0,08727 3b Л ^0,03491 ТВ -°'0'745 -* 0
sin х 0,17365 0,08716 0,03490 0,01745 — 0
sin х X 0,9949 0,9987 0,9997 1 ... — 1
Формула (10) читается так: предел отношения синуса беско-
нечно, малого угла к самому углу, выраженному в радианной мере,
равен единице.
Указание. Прежде чем приступить к проработке следующего
параграфа, необходимо основательно продумать решение ниже-
следующих примеров (1—4) и решить задачи 391 —401.
Пример 1. Найти lim S1^x, где k — данное число.
Решение. Мы знаем, что произведение постоянной величины
на бесконечно малую величину х — величина бесконечно малая,
т. е. kx^-О, когда х->0. Это значит, что в данном случае мы
имеем предел отношения синуса бесконечно малого угла к самому
углу. По формуле (10) находим
lim
л-0
sin kx
kx
. Ьи
Sin -g-
Пример 2. Найти lim .
Ди.-о
Решение. Чтобы под знаком предела иметь отношение синуса
угла ~ к этому углу, предварительно умножим числитель и зна-
1 п
менатель на у. Получим
. Ди
sin -g-
1 . Ди
,. Ts,nT
lim —т——
ди —о Д“
— lim •
Дио 2
2
.Ди .Ди
SII1T 1 ,. sinT
~ 2 д„™ Ди •
, 2 2
186
Очевидно, -у -> 0, когда
Д«->0. Применив формулу (10), на-
ходим
. ки . Ди
- sin -у sm у . ,
lim —т— — lim 1=7,-.
дг/_о Au 2 дя-,0 Ди 2 2
2.......
. , . . . Да
cos (z -ф Да) sin у
Пример 3. Найти lim----------т-------—.
дз —о Д2
Решение. Переписываем в виде предела произведения и при-
меняем теорему о пределе произведения двух функций:
cos (z + Да) sin у sin у
' lim ----—г-------lim cos(z-l-Az) —r-2- ~
Л.--.П м Дз-о L -
. kz .. .kz
Sin у Sin у
= lim cos (z-[-Az) • lim —r-A- =cos (z -ф-O) - lim —r—.
Дз —0 Дз->0 Лг Дз-»0 Дг
Умножаем числитель и знаменатель дроби, стоящей под знаком
1 гт
предела, на у. Получаем
. . . , . да . I . kz
COS (z kz) Sin -S- =- Sin -7-
lim-------r—-----=cosz-lim—j-------~
Дз-0 аг Дг-0 1 д7
3
. Дг . kz
I Sin у | Sin у J ।
= cos z • lim o- —г2-=cos z • -y • lim —;— =cos z • 1 =-5- cos z.
дз-»о3 3 Д2-0 3 3
3 3
. Ди
sin у
Пример 4. Найти lim =— при условии, что u = f(x) имеет
дх -»о Лх
производную их.
Решение. Так как при данном значении х существует иХу
то Ди->0, когда Л.с-»0 (см. § 63). Нам известно, что формула
(10) применима непосредственно лишь в том случае, когда под
знаком предела берется отношение синуса угла к этому углу.
Умножив числитель и знаменатель дроби, стоящей под знаком
предела, на уА«, получим
. ки
sin-y
. Ди 1
lim "ДУ
Дх->0
lim
Дх
£
2
д™0
. Ди
sin-y
• Ди
Sin у • у ки
П
кх • у ки
. ки
, Sin у
= lim
Дх ->0
1 . ки
2 S,n Т • Д“
Ди .
у. Ах
2
lim
д« -»• о
Ап
Т
Ди 1
• lim — = 75-
дх-.о^-*- 2
, . 1 ,
1 • их = у их .
187
§ 72. ДИФФЕРЕНЦИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
На рис. 118—121 изображены графики тригонометрических
функций: у = мпх (рис. 118); y — cosx (рис. 119); z/ = tgx
(рис. 120), у — ctgx (рис. 121).
Функции y = sinx и y — cosx. графически изображаются не-
прерывными кривыми линиями. Область их существования (— оо;
оо). При любых значениях аргумента эти функции имеют произ-
водную.
Функция y = tgx претерпевает разрыв при х — у (2п,-ф- 1),
а функция у = ctgx — при х~т. При этих значениях аргумента
данные функции теряют смысл.
В этом параграфе рассмотрим дифференцирование тригоно-
метрических функций, причем всюду под./(х) будем разуметь
функцию, имеющую производную (см. § 63, теорема).
1. Производная функции y = sinu, где и = /(х).
Проведем дифференцирование по общему правилу.
1-й шаг. Если аргументу х придадим приращение Дх, то функ-
ция и=[(х) получит приращение Ди:
и -ф- Ди = f (х -ф- Дх).
Наращенному значению этой функции будет соответствовать
наращенное значение функции у — sin и:
у -ф- Ду = sin (и -ф- Ди).
2-й шаг. Ду = (у -ф- Ду) — у — sin (и ф- Ди)— sin и.
Правую часть этого равенства преобразуем в произведение
по формуле sin а — sin [3 = 2 cos —sin-Фф2-. Получим
. u 4- Au + u • и Xu — и ,, t , Xu\ . Xu
Ду=2со§——2“^—sin—!—----------= 2cos (u-f-g-lsiny..
3-й шаг.
4-й шаг.
. Au"
л л \ Sln T
Ух — lim lim 2 cos [и -ф- .
Дл'~ U Да —О1 \ 2 / аА J
Применив затем теорему о пределе произведения и учитывая
при этом, что Ди->0, когда Дх->0, получим
. Хи
sin
у'х = 2 lim cos (u 4- -~\ • lim — =
у ди-о \ 2 1 Да-0 Ьх
. Хи . Хи
/ 0\ Sln“2‘ SlnT
= 2 cos (иф-тг) lim —т— = 2 cosulim -т—.
\ Дл-0 ЬХ Дл-0
188
Рис. 121
. Ди
Sln ?’ 1
Умножив числитель и знаменатель дроби —на -^-Дц (см.
решение примера 4 § 71), получим
. Ди 1 .
sin &и
ух~2 cos и • lim —=-------=
Ал —О — Ди•Дх
. Ди , / . Ди \
, Sin -н- • Ди , / Sin -у \
„ ,. 1 2 г, I ,. 2 Ди |
= 2с““.'“07тг-7Г== 0S“'T*-"H“'E/ =
2 Л 2 . /
.Ди
5111 -7Г Л ...
2 Ди ,
= cosu-lim—;— hm -r- = cosu-1 -ux = cosu-ux.
Ди-О Дл-Оах
2
Следовательно, yx = cosu-u'x,
или _________________
(sin и) х = cos и • и'х , (11)
т. е. производная синуса функции равна произведению косинуса
этой функции на ее производную.
В частном случае при и — х найдем
(sinx)* = cosx-x*,
или просто '
(sin хух — cosx
(На)
Пример 1. Найти производную функции у —1^2 sinx-)-1
Решение. В данном случае у — квадратный корень из функ-
ции u —2sinx-[- 1.
По формулам (8) и (Па) находим
(2 sin х 1) х
2 У 2 sin х 4- 1
2 (sin х) 'х cos х
2 У 2 sin х -|- 1 1^2 sin х 4~ 1
2. Производная функции у = cos и, где и — f(x). Тре-
буется найти ух = (cos и) х.
Из тригонометрии известно, что cos и = sin —и^. Поэтому
данную функцию можно переписать в следующем виде:
4 t/ = costz = sin (у — и\.
190
Эту функцию Можно дифференцировать ио формуле (11). По-
лучим
z/.v = (cos и)'х = ^sin =cos^- — —uj =
= sin и- (0 — ux) = — sinu-u'x.
Итак, y'x = — sinu-u'x,
или
(cos U) x = — sin U • u'x
(12)
Эта формула читается так: производная косинуса функции равна
произведению синуса этой функции на ее производную, взятому с
обратным знаком.
В частном случае при и = х получим
(cos х)'х = — sin х • х’х,
или
(cosx)i =— sinx . (12а)
Пример 2. Дана функция y = cos[2x —
Найти: 1) Г(х); 2) /'(0); 3)
Решение. Здесь мы имеем косинус функции и = 2х —
По формуле (12) найдем
/6 = /'(*) = [cos (2х — £)], = — sin^2x — (2х~ £)* =
- sinfex— -^-2 =— 2sinf2x— -4.
\ 61 \ 6 j
Следовательно, 1) f (x) — — 2 sin [2x — ; 2) f (0) =
— — 2sin(2-0— = — 2 sin f—~-^ = — 2 • (— sin = 2sin ~ =
\ b / \ 6 / \ 6 J 6
24=1; 3) /,(|iK) = -2sin(24^-|) = -2sin4^-|) =
= - 2sin ~ = — 2-— /2.
3. Производная функции z/ = tgw, где u = f(x).
Дифференцируем как частное двух функций, переписав: у =
= tg и = . Получим
, _ /sin и\ _ cos и. (sin и)'х — sin а • (cos и)'х ~
У* ( х ^COS и]х cos3 и 4 "
Но мы знаем, что
(sin и)’х = cos и u'x", (cos и) х = — sin и и'х.
191
Получим
cos a - cos и • u'x — sin и (— sin u) u’x
yx = (tgu)’x =-----------------------------------=
cos2 и ux + sin2 u • u'x (cos2 и + sin2 u) u'x ux
cos2 и cos2 и
cos1' и
n u'x
Следовательно, г/Л — ——,
cos- и
или
u’
(tg u)'x — —j— - sec2 и • ux
\ ь /л cosj u Л
(13)
т. e. производная тангенса функции равна производной этой функ-
ции, деленной на квадрат косинуса этой функции.
В частном случае при и==х получим
или
(tg х)'х — —Д = sec2 х
v ь /Л cos2 х
(13а)
4. Производная функции z/ = ctgw, где u — f(x).
Дифференцирование ведем так же, как и в случае функции
у — tgu. Получаем
sin и (cos и)'х — cos и (sin и)’х
sina и
sin и (—• sin и и'х") — cos и (cos и и'х}
sin2 и
— sin2 и и'х — cos2 и их (sin2 и 4- cos2 и) и'х
sin2 и sin2 и ’
. i 1 х , /cos a\f
Wx = (ctg U)x=^(-T~}_
ux
(ctg u)x = — = — cosec2 и ux
(14)
t. e. производная котангенса функции равняется минус частное
от деления производной этой функции на квадрат ее синуса.
_ При и — х будем иметь (ctg х) х —— s-^x<
или
(14а)
(ctg х) v = — г-Д— = — cosec9 х
V Ь ' Sin-А"
Пример 3. Найти производную функции y — s\nlx — cos9x.
Решение.'В данном случае мы имеем разность квадратов
синуса и косинуса аргумента х. Дифференцируем по формулам
192
(3), (7), (На), (12а). Получаем
у'х = (siП2 X— COS2 х) ‘х = [(sin х)2]« — [(cos x)2['v =
= 2 (sin x)2-1 (sin x) 'x — 2 (cosx)2-1 (cos x)'x =
= 2 sin x cos x — 2 cos x (— sinx) — sin 2x -4- sin 2x = 2 sin 2x.
Пример можно решить проще, предварительно преобразовав
правую часть в.одночлен:
y = sin2x— cos2 х — — (cos2x— sin2x) = — cos2x.
Тогда по формуле (12) получится
£/.;. = (sin2X — COS2X).v = (—COS 2x) x = — (cos 2x) х —
— — (—sin2x) (2x) x = 2 sin 2x.
Пример 4, Найти производную функции z/ = tg3^x.
Решение. Здесь дается третья степень тангенса функции
и = kx.
Применяя последовательно формулы (7) и (13), получим
у'х = [(tg kxf\'x = 3 tg2 kx (tg kx)x =
» (kx)' a k 3k tg9 kx
— 3 tg2 kx • ---3-7- = 3 tg3 kx —3-r- =-------,
° . cos9 kx ° COS- kx cos- kx
Указание. Прежде чем приступить к изучению § 73—75,
необходимо повторить из курса алгебры следующие темы: пока-
зательная функция и ее свойства; логарифмическая функция и
ее свойства; правила логарифмирования; десятичные логарифмы
и их свойства,
§ 73. ЧИСЛО е. НАТУРАЛЬНЫЕ ЛОГАРИФМЫ. ПЕРЕХОД
ОТ НАТУРАЛЬНЫХ ЛОГАРИФМОВ К ДЕСЯТИЧНЫМ И ОБРАТНО
1. В более полных курсах высшей математики доказывается,
что функция г = (1 —— j при п->оэ имеет предел, выражаю-
щийся иррациональным числом (бесконечной и непериодической
дробью). Этот предел принято обозначать буквой! е. Записывается
это так:
/ 1 \п f 1
limz = lim 1 — =е, или lim 1-[— =е.
Я —* ОО П СО \ Ч п -* ОО \ П 1
Чтобы убедиться в том, что при п->оо данная функция имеет
предел, и найти приближенное значение этого предела, возьмем
таблицу значений этой функции при возрастающих значениях п
(табл. 11), вычисленную с точностью до 0,0001 (все значения г
взяты с недостатком).
7 П. Е. Агачев
193
Таблица 11
п 5 10 100 1000 10 000 100 000 —* со
/ 1 \'г г = 1 + - \ н 1 2,4883 2,5937 2,7048 2,7169 2,7181 2,7182 —> е
Из таблицы видно, что при /г 10 000. в ряду
тыре первых знака (2,718) остаются неизменными,
будет приближенным значением числа е.
Итак,
значений 2 че-
Число 2,718 и
(15)
Число е имеет важное значение в математике и в технических
пауках. Оно принято за основание логарифмов, называемых на-
туральными. Натуральный логарифм числа N, т. е. log^JV, при-
нято обозначать символом InJV.
2. Из алгебры известно, что логарифмом числа при данном
основании называется показатель степени, в которую надо воз-
высить это основание, чтобы получить данное число, т. е. если
a' = N, то
logaA' = x.
Из этого определения видно, что за основание логарифмов
положительных чисел может быть взято любое положительное
число, не равное единице, или иначе: можно составить таблицу
логарифмов при любом а, большем нуля и не равном единице.
Обычно для практических вычислений пользуются таблицами
логарифмов, взятых при основании 10. В высшей математике,
в вопросах теоретических, преимущественно применяются на-
туральные логарифмы.
Зная натуральный логарифм числа, можно вычислить его де-
сятичный логарифм и обратно. Пусть нам известно, что
1пМ = р, т. е. logejV — р.
Тогда, согласно определению логарифма, будем иметь N = ep.
Возьмем от обеих частей этого равенства логарифмы, приняв за
основание число 10. Получим
log10Af =ploglue*,
или (после замены р его значением)
lg/V = In jV 1g (а)
* В дальнейшем IgA'означает десятичный логарифм числа N, \пЫ озна-
чает натуральный логарифм числа N.
194
где lge = lg2,718 = 0,4343. Это число называется модулем пере-
хода от натуральных логарифмов к десятичным. Итак, по данному
натуральному логарифму (In Л7) числа N его десятичный логарифм
находится по формуле • .
lg N = In N- 0,4343. (16)
Из равенства (а) следует:
lnAMge = lg/V;' 1пХ = дД
& & ]g е 1
ПЛИ
In N = lg N •,
где
Следовательно, по данному десятичному логарифму числа его
натуральный логарифм находится по следующей формуле:
In W = 1g ЛИ 2,303, (16а)
где -т-5—=2,303 — модуль перехода от десятичных логарифмов к
натуральным.
Пример. Найти: a) In 3,246; б) In 0,348.
Решение.
a) In 3,246 = 1g 3,246--Д- = 0,5113-2,303^1,18;
б) In 0,348= lg0,348.-^=l,5416.2,303 = (— 1 +0,5416) X
X 2,303 = —0,4584 2,303 = —1,056.
§ 74. ДИФФЕРЕНЦИРОВАНИЕ ЛОГАРИФМИЧЕСКИХ ФУНКЦИИ
Из алгебры известно, что отрицательные числа логарифма не
имеют, поэтому логарифмическая функция y = log^«, где « =
— f(x) (a'J>0, niXl), существует лишь при таких значениях
аргумента х, при которых f(x)^>0.
Производная функции y = \ogau, где u = f(x), находится по
формуле
Ух = (log„ и)х = — • loga е,
или
и'
(loga«); = — -log„e. (17)
Докажем справедливость этой формулы, пользуясь об!цим пра-
вилом дифференцирования (см. § 59);
7* 195
1-й шаг. у 4~ ^У = loga(u +Д«)‘.
2-й шаг. ^у — logfl (и Ди) — logau, или (так как разность
логарифмов равна логарифму дроби)
^ = 108.4^= +
/. , Ди\
„ - Ду °^а \ "г” и ] 1 , /. . Ди\
3-ишаг. =)•
Правую часть этого равенства можно преобразовать, умножив
на дробь т. е. на 1. Получим
-^=——102
Дх Дх Ди 1 °а\ и J’
ПЛИ
Ду Ди 1 , . Ди\
дГ Тх ' 1й \Ч и]'
. „ . , ,. Ду ,. Г Ди 1 , „ /. , Ди\1
4-и шаг. ^=hm^=2im [^.^loge(14-—)].
Применив к правой части этого равенства теорему о пределе
произведения двух функций и учитывая при этом (см. § 63), что
Ди -> 0, когда Дх -> 0, будем иметь
у1=Н1т ^-lim |^loga (1+^)1,
дл-0аА iu^0LZi“ \ и /J
или
и’ = и'х lim IЧ log (1 -ф- —}].
д.^0 1-Ди \ «Л
т-r Ди 1 1 п к п
Положим, — — —, тогда -г- = — /г^-сю при Ди-^-0:
’и и ’ Д и и ’ 1
у'х = и'х lim 14 loga (1 + Д1 = и'х lim I-J- • п loga (1 + 4
h-^ooL. и \ 1 л /w.ooL^ \ и,
или (после потенцирования) -
loga (1+Я1-
К правой части этого равенства можно применить формулу (5)
из § 48, так как множитель — при и->оо сохраняет свое зна-
чение неизменным. Получаем
или
и' г ! 1
^=T/ilmJ,og41+ «/!•
196
В § 57 было показано [равенство (3) и -пример 4], что предел
логарифма переменной величины равен логарифму предела этой
величины. Применив эту формулу к данному случаю, находим
Г / 1VI
+ 1’
или [в силу формулы (15) § 73]
//.v = (loga«).; = -^logae. (17)
В случае, когда а =10, эта формула принимает вид
и'х
Ух = (login и)х = — logio е,
или
(1g и)'х = 1g е (18)
где 1g е = 0,4343. При и — х формула или (17) примет вид (loga х)1- = ^logae
откуда (loga x)’v = 7 logae (lgx); = ^lge (17a) (18a)
Если в формуле (17) за основание примем число е, то получим
(loge«); = loge е,
или
(19)
так как
logc е = In е = 1.
Подставив в формулу (19) вместо функции и аргумент х,
получим
(1ПХ)х = ^,
197
или
/I v 1
(In х)^ = —
(19а)
Формула (19) читается так: производная натурального лога-
рифма функции u — f(x) равна частному от деления производной
функции на эту функцию.
Из сопоставления последних формул видно, что производная
натурального логарифма функции имеет значительно более прос-
той вид, чем производная логарифма этой функции при любом
другом основании.
Пример 1. Найти производную функции 4/= Inх —f-1gх —|—3.
Решение. Применив формулы (3), (1), (19а) и (18а), найдем
. /1 V । /1 v ! л 1 I 1 1 I 0,4343 1,4343
^ = (lnx)^4-(lgx)^ + 0 = - + -1ge = -4--^—- =
Л Л, -V Л Л
Пример 2. Найти производную функции г/= In (х‘2 —|-2х —J-3).
Решение. В данном случае мы имеем натуральный логарифм
функции и = х1 2х -ф- 3.
По формуле (19) получим
и'х (X- + 2Л- + 3); 2,v-|-2-|-0 2<Л'+1)
а х- —р 2х —3 х~ ,_j— 2х - 3 —р 2х 3
Пример 3. Дана функция у = f (х) — 1g (.v 1). Найти: а) /' (х);
б) /'(0); в) Г(-3).
Решение. По формуле (18) находим:
(л2+1); . 2х
б) f(O)-of~-lge = O;
в) Г (-3) - р.3^1 • 1gе = - ~ • 0,434 - 0,26.
Пример 4. Дана функция у = 1п(2х — 9). Найти: а) при каких
значениях аргумента х эта функция существует; б) /'(х); в) /'(5).
Решение, а) Функция существует при значениях х, удов-
летворяющих условию 2х— 9^>0. Решаем это неравенство:
2х —9Д>0; х 4,5.
Итак, функция определена в промежутке (4,5; со). По формуле
(19) находим:
__9)' 2 2
б) ух = Г{х) = ^^ = ^у, в) Л(5) = -^-^2.
198
Пример 5. Найти производную функции у = In Ух:1~[- а3.
Решение. 1-й способ. Применяя формулу (19), получаем
(х’+л3)'х
ух =( inV=
J ' ]/х3 + а3 рх3+«3
Зх3
_ 2 р х3 -р Зх3 _ 3 г3
~ /х3 + а3 — 2 /х3 + а3 Ух3 + а3 ~ 2 (х3 + а3) *
2-й способ. Предварительно переписываем эту функцию,
применив правило логарифмирования корня:
у— In Ух3 a3 = In (х3 а3),
а затем находим производную по формуле (19). Получаем
1
2
у'х= у1п(х34-а3)^ = -^ •
(х3 + «’);
х‘ -р аВ * 1
Зх= Зх3
х1 + а* 2 (х3 +. л3) ‘
Как видно из примера, предварительное логарифмирование
значительно упрощает процесс вычисления производной'’.
Пример 6. Найти производную функции/(х) = 1н (sin Зх—cos3x).
Решение. Применяя последовательно формулы (19), (11) и
(12), находим
(sin Зх — соз'Зх)'
/' (х) = Г In (sin Зх — cos Зх)К = ——---5— —
' ' ' i ' ' sin Зх — созЗх
__созЗх(Зх)’— (—sin3x)(3x)' 3 (sin Зх + cos Зх) 3(tg3x-|-l)
sin Зх — cos3x sin Зх — cos3x tg3x—1 *
§ 75. ПРОИЗВОДНАЯ СТЕПЕННО! ФУНКЦИИ ПРИ ЛЮБОМ
ПОКАЗАТЕЛЕ СТЕПЕНИ
В § 69 было установлено, что при п целом и положительное
производная функции у=и", где ц = /(х), находится ио формуле
(tP)'x~ йх.
Покажем, что эта формула справедлива при любом п (дроб-
ном, отрицательном, иррациональном).
Пусть нам дана функция у —и'1, где u = f(x~), имеющая про-
изводную их. Возьмем от обеих частей равенства у = и'1 нату-
ральные логарифмы. Получим
lny = nlnu.
Так как ц = /(х), то очевидно, что у = и11 = [f (х)]п тоже будет
функцией от х. Берем от обеих частей равенства \пу = п]пи
199
производные по формуле (19). Получаем
(Inу)'х== (п In u)i; (In у)'х = п (In и)'х,
пли
Ух и’х
— -П-----.
у и
Решив последнее уравнение относительно у'х, находим
U
Ух = п-у- — .
Подставив в это равенство вместо у его значение (y — url),
получим
U
ух — (и'1)х — П-и ‘ — = пи'1 Ux.
Итак, при любом действительном п получим уже известную
формулу
ух = (ип)'х = пип^и'х, (7)
где
u — f(x).
Замечание. Упражнений на применение этой формулы при
любом действительном п проделано,достаточно. Предлагаемый ниже
пример имеет назначение показать, как можно использовать метод
доказательства, примененный в этом параграфе, при дифферен-
цировании нелогарнфмических функций в случаях, когда непо-
средственное применение соответствующих формул приводит к
громоздким вычислениям.
Пример. Найти производную функции
(2х — а)" \^4х2 — а2
У— (2х + а)'
Решение. Возьмем от обеих частей этого равенства нату-
ральные логарифмы: ,
Прологарифмировав правую часть равенства, получим
1п у — 3 In (2х — й) + у In (4х2 — а2) — 3 In (2х -j- а).
Дифференцируем обе части этого равенства, имея в виду,
что у является натуральным логарифмом функции от х:
(In у\х— |^3 In (2х— a)-|-yln(4x2 — й2)— 3 In (2х-{-о) J ;
У'х о (2х-2);. , 1 (4^-а=)л (2х + а)'х_
у ' 2.V—а 2 4х2—а2 2ха
— ч 2 I J. . 8х _ о. 2 _ 6
— ’ 2х—а*' 2 4,v2 — а2 2х -р а 2х —
, 4х 6 __б (2х + a) -j- 4х— 6 (2г — а)_4(х-рЗи)
Т 4л2 — а2 2х 4- а 4хг — а2 4х2 — а2 ‘
200
Мы нашли
у х 4 (х —1~ 3d)
у 4л3 — а~ ‘
Решим последнее уравнение относительно у’х и заменим у его
выражением из условия
, _4(х + 3о)' ___4 (х + За) . (2.t —a)3/4.t3—а3
Ух 4х3— а3 4.Г3 — а3 ’ (2х-|-а):1
Получим
, _ 4 (х + За) (2х — а)3 К4х3 — а3
~х (2ха)1
§ 76. ДИФФЕРЕНЦИРОВАНИЕ ПОКАЗАТЕЛЬНЫХ ФУНКЦИИ
Дана показательная функция у = ап, где u = f(x). Требуется
найти у'х = (ап)’х.
Прологарифмируем обе части равенства у=ап по основанию е:
In у — Inn", или In у ~и Inn,
у и zz — функции от х, Inn — величина постоянная.
Дифференцируем обе части равенства In у = и Inn, применив
формулы (19) и (5):
Ух <
— = ил1па.
Разрешив это уравнение относительно у\ н заменив у его
значением (z/ = n"), получим у'х = у-их In а=а"и'х Inn. Итак,
(n").v — n"zz'v Inn
(20)
Читается эта формула так: производная показательной функ-
ции при любом (постоянном) основании равна произведению этой
функции на производную показателя степени, умноженному на
натуральный логарифм основания.
В частном случае при и = х формула (20) принимает вид
или
(nv); = ах х'х In п,
(nv)'v = ах In а
(20а)
Если в формуле (20) за основание принять число е, то полу-
чится
(е“)’х — е"йх\пе,
201
пли
(е")'х = е"и'х . (21)
Формулируется это так: производная функции у=еп, где
u = f(x), равна произведению этой функции на производную
показателя степени.
В частном случае при и = х формула (18) примет вид
(е1ух — ехх'х,
пли
(е*ух = ех , (21а)
т. е. производная функция ек равна самой функции.
Пример 1. Построить кривую у = ех и провести к ней каса-
тельную в точке, абсцисса которой равна нулю.
Решение. 1) Строим кривую (рис. 122) по точкам, вычислив
ординаты их с точностью до 0,1 (табл. 12).
Таблица 12
Л' СО —2 —1 0 1 2 3 —•со
у — ех 0 — 1—^0,1 е~‘ 0,4 1 е 2,7 е- «= 7,4 е'Л 20,1 — оо
2) Координаты точки касания уже известны (у—1, когда
л = 0). Находим
угловой коэффициент k касательной в данной
точке. Для этого по формуле (21а) находим
производную данной функции: у'х = (ех)х = ех.
Тогда (см. § 62) получим
k — ех — = 1
при х— 0.
Составляем уравнение касательной по
формуле (9) § 16; получаем у — 1 = 1 (х — 0),
или у — х-|- 1.
Пример 2. Найти производную функции
У = f (*) = ех“ — 4е~х 3.
Решение. По формулам (3), (5) и (21) находим
Ух — (ех? — 4 с—v + ЗД = ех“ (х‘)'х — 4е~х • (— л-Д Д- 0 =
= ех“-2х— 4е~х-(—l) = 2xexS~]- 4е~ж.
Пример 3. Найти наклон кривой у — 2(е2У~е 2) в точке,
абсцисса которой равна: 1) 0; 2) 2; 3) —4.
Р е ш е н и е. Решение этой задачи сводится к нахождению
углового коэффициента касательной в данной точке (см. § 62).
202
Находим производную, последовательно применив формулы (5),
(3) и (21):
Итак, наклон k этой кривой к оси Ох при любом х опреде-
ляется по формуле
X X
k = e‘l — е 9.
1) При х = 0 получаем:
z/ = 2^94-e taj = 2 (1 4-1) = 4;
£ _ ®.
k = f'(O) = e* —е 2 = 1 —1 = 0;
касательная в этой точке (0; 4) параллельна оси Ох.
2) При х = 2 получим
А _ А
ki = f' (2) = е2 * *—е 9=е— е-1^2,3.
3) При х = — 4 находим
^ = с‘2 — 0,1 — 7,4 = — 7,3.
Пример 4. Найти производную функции у — хъе~^х.
Решение. По формулам (4), (21) и (11) находим
или
у' = (х^е-sin3 х)х = 2хе~sin3 х -|- х- (е~sin3 *)' —
= 2хе~ sin!i-': -ф- х2е_ sin2-v (— sin2 х)' =
= 2xe_sin3>; -]-x2e_sin2jc (— 2 sin х cos x) =
= 2xe-sin3 x -ф x2e-sin3 x •. (— s i n 2x),
(x2e_sin3-v)' = .te_sin''-v (2 — x sin 2x).
§ 77. ДИФФЕРЕНЦИРОВАНИЕ ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ
ФУНКЦИИ
1. Производная о б р а т н о й т р и г о н о м е т р н ч е с к о й
функции z/ = arcsin«, где w=/(x).
Напоминание. Равенство z/ = arcsinzz означает, что у есть
наименьший по абсолютной величине угол (| у | sg; -4, синус кото-
203
рого равен и. Так как синус угла может изменяться только от
— 1 до 1, то функция у — arcsin н существует только при таких
значениях аргумента х, при которых удовлетворяются условия
— 1 О<1.
Из равенства у — arcsin н следует:
$ту = и.
Дифференцируем обе части последнего равенства по аргу-
менту х:
(sin у)'х — и'х.
Применив к левой части этого равенства формулу (11), полу-
чим '
cos у • у'х = и'х,
откуда
, и'х
У v----------------------------- ,
J COSJ’
ИЛИ
и'х *
Ух — г . - •
У1 — sin- у
Заменив в этом равенстве sin у его значением и, найдем
или
м'.
Ух — -у==,
J У\-и"-
При и — х получим
х'
(arcsin х)'х — -у=^=
] 1 — х-
или
(arcs in x).v = 1
] 1 - х-
(22а)
Пример 1. При каких значениях аргумента х существует
функция
у = arcsin (2.с— 3)?
* Знак плюс перед корнем берется потому, что УI — sin3 y = cosy > О
при | у | (см. напоминание).
204
Решение. Данная функция существует при значениях аргу-
мента х, удовлетворяющих условиям:
— 1 ;2.t —3 ; 1;
— 1 Д-3-с2л.--с 1 4-3;
- 2 2xsg 4
или
l-gX^g2.
Следовательно, данная функция существует на отрезке [1; 2].
Пример 2. Дана функция г/= / (х) = arcsin Д/^2л:. Найти: 1) /' (х);
2) /'(1); 3) /'(2).
Решение. 1) Применив формулы (22) и (8), находим:
(2х);
№ = -ЛКЧ-.______________________1____.
Г1 - (/2х)3 /1-2х /2х(1-2х)’
3) f (2) = ___L.—— = —— мнимое число, Г (2) не суще-
У 2 -2(1— 2-2) 2)- — 3 J
ствует.
2. Производная обратной тригонометрической
функции у = arccos и, где и — f(x).
Напоминание. Равенство у = arccos и означает, что у есть
угол в промежутке от 0 до и (0 =g у =g it), косинус которого равен и.
Так как косинус угла может изменяться только от —1 до 1,
то функция, у = arccosи существует лишь при таких значениях
аргумента х, при которых удовлетворяются условия
— 1 sg U =g 1.
Из равенства Д/ — arccos и следует
cosy — и.
Дифференцируем обе части последнего равенства по х:
(cos у)'х = и'х.
Применив к левой части этого равенства формулу (12), получим
— sin у- у'х = и'х,
откуда
. _ их
J* sin ’
205
или
и'х *
— cos= 3’
Нам известно, что cos у = и, следовательно,
или
и'.
(arccos и)’х —-------, .
(23)
В частном случае при и — х получим
(arccos х)'х —---, х
У 1 — х
или
1
(arccos х)’х — — тт=
(23 а)
Пример 3. Дана функция у — arccos . Найти у’ж.
Решение. Дифференцирование ведем, пользуясь форму-
лами (23) и (9). Получаем
/х — а\' (х 4- а) (х — а)’х — (х — а) (х 4- а)’х
ti’\л~ -|- а)х (х 4~ а)~
х -У а — х -У а 2 а
(х 4~ «)~ (л- 4- а)" ,(х 4- а)"
х-У а __ а
У ах (х 4- а) У ах ‘
3. Производная обратной тригонометрической
функции у= arctgи, где u — f(x). •
Напоминание. Равенство у — arctg и означает, что у есть
угол в промежутке от —у до тангенс кото-
рого равен н = /(х).
* Перед корнем берется знак плюс потому, что У1—cos"у — sin у с> О
при 0^з'е£л (см. напоминание).
206
Из тригонометрии известно, что тангенс может принимать любые
числовые значения. Вследствие этого функция y = arctgu суще-
ствует при любых значениях аргумента х, удовлетворяющих
условиям
— со<^ц<^оо
пли
— со f (х) со .
Если y = arctg«, то tgz/ = «. Дифференцируем обе части этого
равенства по х:
(tgi/)i = их.
Левая часть данного равенства является тангенсом функции
от х. По формуле (13) получим
Ух . ,
= их или sec- у-ух — их,
откуда следует
«(. и'х
У* sec2 .у l+tg-J'*
Подставив в это равенство вместо tgyero значение (tgz/ = w),
получим
' — и'х
Ух | _|_ ц2 »
или
(arctg«)^ = -j-p? (24)
х' При и = х будем иметь (arctgx)i= 2-, или X2’
(arctgx); = y-p^ (24a)
4. Производная обратной тригонометрической
функции y = arcctg«, где и —/(х).
Напоминание. Равенство y = arcctg« означает, что у есть
угол в промежутке от 0 до (0 <^//<^ ~), котангенс которого
равен и. Из тригонометрии известно, что котангенс может при-
нимать любые числовые значения. Вследствие этого функция
z/ = arcctg и существует при таких значениях аргумента х, при
которых удовлетворяются условия:
— со и со
или
— сю <^ / (х) со.
207
Из равенства r/ = arcctgu следует ctgу = и. Берем от обеих
частей последнего равенства производные, учитывая, что у является
функцией от х. Получаем:
, , ., , У'х
(ctg у}х = их\ ------7-^- — их,
\ ъхцх Л. S1[1- у
или
cosec2 у • у'х = — и'х.
Из этого уравнения находим
и'Х и'х
Vх COSCC2 у 1 +clg2y‘
Так как ctg у = и, то получаем
и'
lJx ~ ~1 + и- ’
пли________________________________________
(arcctg u)i = — .
(25)
При и — х получим (arcctgx)^ =
или
(arcctg х)^ = —
(25а)
Пример 4. Дана функция у = arctg (sin Зх). Найти: 1) /'(х);
2)/'(0).
Решение. 1) Применив формулы (24) и (11), получим
(sin3A)'t cos 3.v (Зл.-)* ЗсозЗх
Vх ‘ i -f- (sin Зд-)2 1 + sin2 Зд 1 ф sin2 Зх ’
3cos3-0 ____ 3cos0 3__q
I (u) i _|_ sin2 3 • 0 1 ф sin2 0 T d‘
Пример 5. Найти производную функции у — arcctg (tg 2х).
Решение. В данном случае zz = tg2x. Последовательно при-
меняя формулы (24), (13), найдем
(tg2x)'
у'х = [arcctg (tg 2х)]1- = — =
(2х); . 2
__ cos2 2.v _____ cos2 2х____ 2 see2 2,t_ Q
• .l+tga-2x ' sec22.v sec82x * .
Этот пример можно решить значительно проще. Из тригоно-
метрии известно, что:
1) tg2x = ctg^y —2х^;
208
2) arcctgjctg — 2x^ = — 2x, '
следовательно, функция у = arcctg (tg 2x) равносильна функции
у = — 2x, откуда y’x = — 2x^ ~ — 2.
§ 78. ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНЫХ ФУНКЦИИ.
ПРОСТЕЙШИЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
1. Функция у называется явной, если известны действия, которые должны
быть произведены над значением аргумента х, чтобы найти соответствующее
значение этой функции, и неявной, если зависимость между функцией/у
и аргументом х дается уравнением, не разрешенным относительно у (см. § 8).
Общее обозначение неявной функции: f (х, у) = 0. Примеры неявных
функций:
А'3 V2
1) + (уравнение эллипса)"
2) у3 — 2рх = 0 (уравнение параболы);
3) ДхSy + С = 0 (общее уравнение прямой).
Дифференцировать неявные функции можно двумя способами.
Первый способ применим тогда, когда уравнение, связывающее х
и у, разрешимо относительно у. Пусть требуется найти производную (у(.)
функции, данной неявно: х84~У8 —— 3 = 0.
Находим у = ± "/3 4х — л3,
откуда
(3 + 4х-х3); _ 2-х *
Ух~ ±2 V 3 4- 4х — л^ ~ ~ У 3 + 4л- — л3
Второй способ. Пусть нам надо найти производную неявной функции:
^4-^. = 1 или 44-4-1=0.
«3 ' о3 а2 1 Ь2
Перепишем для удобства данное уравнение, приведя члены его к общему
знаменателю:
Ь2х~ 4- «3у3 - а3й3 =0.
К левой части этого равенства приложимо правило дифференцирования
суммы, а производная правой части будет равна нулю как производная
постоянной величины:
. й3(х3);4-а3(у3); = о.
Здесь аргументом является X, а на у следует смотреть как на функцию
от х; получаем;
Ь2-2ха2 -2у • у'х = 0;
Ь2х 4- а2уу'х = 0,
откуда находим
—
а2у ‘
2. Простейшие геометрические приложения производной. Уравнение
касательной к кривой У=/(х) в точке М (х0; уп) имеет вид (см. § 61)
У — Уо—Уо(х — х0),
* Знак перед корнем тот же, что у у.
209
где _у,[— частное значение производной при х = ха‘, х и у— текущие
дипаты касательной (рис. 123).
Прямая MN, проходящая через точку касания перпендикулярно
тельной КМ, называется нормалью к кривой в данной точке.
Уравнение нормали напишется в виде
1 .
У-Уа= — -^г(х — Х^,
_>о
так как угловой коэффициент уравнения нормали и но величине, п по
должен быть < '
коор-
каса-
) знаку
быть обратен угловому коэффи-
•циенту уравнения касательной [см.
мулу (15) § 211.
Пример. Составить уравнение
Л’2 у-
тельной к гиперболе = 1 в
фор-
каса-
точке
Решение. Уравнение касательной
к кривой в данной точке имеет вид
У— Уо—У'ч (х — х0),
где у'. — частное значение производной
при х = х0.
Находим производную (у'х) данной функции Ь~х3 — а-у3 = а"Ь3 при любом
допустимом значении аргумента:
v Ь- (х2); - а2 (у3)'х = 0;
2ZAc - 2<уу= 0.
Решив последнее уравнение относительно ух, найдем
а2 у"
При х = х0 и у = у0 получим
Ь~Х„
Подставляем найденное значение углового коэффициента в уравнение
пучка прямых, проходящих через точку (х0, у0), и получаем;
пли
а -ЛО
Мууй — а*у\ = &2xr0 — Мх3,
b°xxa — а‘у% = b3x30 — a-y'i- (а)
Но точка (л'о; у0) лежит на гиперболе и, следовательно, х0 и должны
удовлетворять уравнению гиперболы, т. е.
Ь3х% — а-у^ = a2Z>2.
Заменяем правую часть уравнения (а) ее значением и получаем
— а-уу0 = а-Ь3.
Разделив все члены последнего уравнения на a3bs, получаем уравнение
касательной к гиперболе в простейшем виде:
ХХр yyQ _
а3 bs
где л- иу—текущие координаты точек касательной, а .г0 в — координаты
точки касания.
(б)
210
§ 79. ПРОИЗВОДНЫЕ ВТОРОГО И ВЫСШИХ ПОРЯДКОВ.
МЕХАНИЧЕСКИЙ СМЫСЛ ВТОРОЙ ПРОИЗВОДНОЙ
1. Производная у'х = f'(x) от функции у = f (х) тоже является
функцией от х, следовательно, ее можно дифференцировать, т. е.
найти производную от производной.
Производная от производной называется производной второго
порядка, или просто второй производной, и обозначается симво-
лом у'хх или f” (х). Следовательно, у"хх = {у’х)'х.
Так как вторая производная в свою очередь есть функция
от х, то ее тоже можно дифференцировать. Получается третья
производная: ух'хх — (ухх)'х и т. д.
Пример 1. Дана функция z/ = sinax. Найти третью произ-
водную.
Решение. Первая производная: у'х = a cos ах\
вторая производная: ухх — (a cos ах)' = — a1 sin ах\
третья производная: у'ххх = (— cr sin ах)'х = — ад cos ах.
2. Механический смысл второй производной. Мы знаем (см. § 59,
60), что если в прямолинейном движении пройденный путь s
в зависимости от времени t выражается уравнением
* = Ж
то скорость этого движения в данный момент t определяется как
производная от пути s по времени t, т. е.
« = $/ = /'(0-
Возьмем производную от скорости v — f (/) по времени t, сле-
дуя общему правилу дифференцирования.
1-й шаг. v -ф- Ду — /' (/ -ф- Д/).
Мы нашли выражение скорости движения в момент t -ф- ДЛ
2-й шаг. Ди = (у -ф- До) — o — — f'(t).
Очевидно, 2-й шаг выражает изменение скорости движения за
время от момента t до момента t -ф- Д/.
о-и.шаг, —.
Третий шаг выражает изменение скорости движения за еди-
ницу времени в предположении, что в промежутке (/, /4-Д/)
скорость изменялась равномерно, т. е. среднее ускорение за
промежуток времени от момента t до момента /-ф-ДЛ Обозначив
среднее ускорение через гуср, получим
^ср — &t — д;
. - ,. .. До .. f(t-y М) -f(t)
4-и шаг. lim &уср = lim lim ——1
д/-.о л/-.о м-»о
211
Пределом среднего ускорения (акср) за время от момента / до
момента / —Д/ при Д/ — О, очевидно, является ускорение w
в момент t:
w— lim ti'Cp = lim
Согласно определению производной (см. § 59) утверждаем, что
. • Ду ' / • \»
hm—
следовательно,
w = su — nt).
Это значит, что ускорение прямолинейно движущейся точки
в данный момент t равно второй производной от пути s по вре-
мени t.
Пример 2. Закон прямолинейного движения точки выражается
уравнением s = P*4-^2 (за единицу длины принят метр, за еди-
ницу времени — секунда). Найти:
1) скорость движения точки в момент /;
2) среднее ускорение в промежутке времени (/;
3) среднее ускорение в промежутке времени (2; 3);
4) ускорение в момент t\
5) ускорение в момент t = 3 сек.
Решение. 1) v = St = 3t2-р4t;
2) ц4-Дп = 3(/ + Д/)2 + 4(/ + Д0;
4 Ду = 3 (t 4- Д/)2 4- 4 (/-|- M) — (3/2 + 4t) =
= (6/4-ЗД/4-4) Д/;
__ Ду (6/ -p ЗД J ”p 4) Д/ t Q v 1 Л
= aJ = 6/4~ ЗД/-p 4 .
3) Первый способ. В этом случае: t = 2, Д/ = 3— 2=1.
Среднее ускорение найдем, подставив вместо t и Д/ их значения:
ц,'ср = 6 • 2 -4 3 • 1 4~ 4 = 19 м(сек1.
Второй способ. Подставляя в равенство ц = $) = ЗР24~4/
вместо t последовательно 2 и 3, найдем скорости в эти моменты:
ц = 3-224-4-2 = 20 м(сек\
v1 = 3-324~4-3 = 39 М)Сек.
Зная v и Vi, найдем Ду = У!— v. Тогда среднее ускорение
в промежутке времени (2; 3) найдется как отношение прирагце-
нин Дц и ДР. юср=д^- = —j =19л1/сек2.
4) w — v't — 6t-)-4.
5) Подставив вместо t его значение, получим
ю = 6-34-4 = 22 м[сек\
212
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Как изменяется тангенс угла при изменении угла: 1) от 0 до
2) от у до п; 3) от у до 0; 4). от к до у?
2. Какое геометрическое значение имеет производная данной функции
y=f(x) при данном значении аргумента?
3. Кривая KL (рис. 124) является графиком дифференцируемой функ-
ции у=/(х). Какой знак (плюс или минус) имеет угловой коэффициент
касательной к этой кривой: 1) в точке А; 2) в точке В; 3) в точке С?
4. Кривая АВ (рис. 125) является графиком дифференцируемой функ-
ции y=f(x). Какой знак имеет производная этой функции: 1) в точке
A(.t = .v1); 2) в точке B(.v = .v„)?
5. При каких значениях аргумента функция y = tg.v не имеет произ-
водной?
6. Чему равна производная функции у = sin2 и + cos2 и, где u=f(x),
при любом х?
7. Если у* = О при любом х, то какой функцией является у?
8. Сформулируйте правило дифференцирования частного двух функций.
9. Дана функция у = —' - 0-. При каком значении аргумента эта функ-
ция не имеет производной?
10. При каких значениях аргумента х функция y = -j——не имеет про-
изводной?
11. Указать область существования функции у = 1п (х— 2).
12. Если ll=f(x) и при данном значении аргумента lim — — ц',: то
Дл:_0А.Х
какой величиной является &и, когда A.v—> О?
13. Существует ли функция у = arcsinfv—1): 1) при х— 1,5; 2) при
х = 0,5; 3) при х = —1?
14. Как найти ускорение в данный момент t = t, сек, если закон прямо-
линейного движения выражен уравнением з =/(£)?
15. Чему равен угловой коэффициент касательной к кривой у = sin х
~ 2
в точке, абсцисса которой равна: 1) 0; 2) у; 3) — п?
16. Определить наклон кривой y=cos.v в точке, абсцисса которой равна:
17, Какая линия называется нормалью к кривой в дайной точке?
18. Уравнение касательной к некоторой кривой в данной на ней
э -
точке (3; 4) имеет виду—4 = -,-(.v — 3). Написать уравнение нормали.
О
213
19. Показать, что производная функции, у = х3 непрерывна при любых
значениях аргумента х.
Указан и е. Найти повзводную при любом х и исследовать ее на
непрерывность (см. § 57).
20. Показать, что функция у — \Ах- при х = 0 производной не имеет.
Ответы. 3. 1) Плюс; 2) минус; 3) плюс. 4. 1) Плюс; 2) минус. 5. При х =
= , где /г — любое целое число. 6. 0. 7. у=С, где С — любое дей-
ствительное число. 9. При Л' = 2. 10. При х = >—1 и л'=1. 11. Интер-
вал (2, оо). 12. Бесконечно малой. 13. 1) Существует; 2) существует; 3) не
существует (см. § 77). 15. 1) 1; .2) у; 3)-у ; 18. у — 4 =—(х — 3).
Глава VIII
ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ
СВОЙСТВ ФУНКЦИИ
§ 80. ВВЕДЕНИЕ. СВОЙСТВО НЕПРЕРЫВНОЙ ФУНКЦИИ
В этой главе рассматриваются свойства функций с помощью
первой и второй производных этих функций. Известно (см. § 79),
что первая производная дан-
ной функции у —fix) и ее
вторая производная являются
функциями от х, поэтому все
изложенное ранее об области
существования функции и ее
непрерывности полностью
применимо и к производным
данной функции. В частно-
сти, первая производная
у'х = f'(x) и вторая производ-
ная yxx=f" (х), как и сама дан-
ная функция у — f(x), могут
быть изображены графически.
Возьмем, например, функ-
цию у = ^^—Графи-
ком этой функции является
кривая AF, изображенная на
рис. 126 [график построен по
точкам в промежутке (—1; 6)].
Найдем первую и вторую производные этой функции;
1 2
Ул- = -4-х — х,
У хх — “2 У — 1
214
Графиком первой функции, очевидно, будет парабола, симмет-
ричная относительно прямой, параллельной оси Оу (см. § 38),
а графиком второй — прямая линия (см. рис. 126).
Свойство непрерывной функции. Непрерывная функ-
ция t/ = f(x) может изменять свой знак лишь при переходе аргу-
мента х через такое значение, при котором эта функция обра-
щается в нуль. Это следует понимать в том смысле, что если при
х — а и х=Ь значения непрерывной функции y = f(x) противо-
положны по знаку, например f(a)<^0 и f(&)^>0, то в проме-
жутке (а; Ь) существует по крайней мере
одно такое значение (xi) аргумента х,
при котором эта функция обращается
в нуль: /(Xj) —0.. Справедливость этой
теоремы геометрически можно пояснить _____
так. 0
Если функция t/ = /(x) при х=а
пх=Ь имеет разные знаки, то график /
этой функции имеет точки A [ti; f (а)] '
и В [(&; /(&)], расположенные по разные
стороны от оси Ох. Часть графика не-
прерывной функции y=f(x), соединяющая,
под осью Ох, с точкой В, лежащей над этой
сечь ось в некоторой точке М (рис. 127). Так как ордината лю-
бой точки оси абсцисс равна нулю, то у = /(х1) —0>, т. е. абс-
цисса точки М и будет тем значением х, при котором данная
функция обращается в нуль.
Если в. некотором промежутке непрерывная функция меняет
знак несколько раз, то столько же раз график этой функции
пересекает ось Ох. Так, например, непрерывная функция у’х —
— у х'2—х (см. рис. 126) в промежутке (—1; 6) меняет знак два
раза и график ее пересекает ось Ох тоже два раза в точках
(0; 0) и (4; 0).
'3[Ь;НЬ)/
х,
^A[a;f(aU
Рис. 127
точку А, лежащую
осью, должна пере-
§ 81. ХОД ИЗМЕНЕНИЯ ФУНКЦИИ. ВОЗРАСТАНИЕ
П УБЫВАНИЕ ФУНКЦИИ
Наглядное представление о~ ходе изменения функции y—f(x)
дает график этой функции, т. е. линия, абсциссы точек которой
являются значениями аргумента х, а ординаты — соответствую-
щими значениями этой функции.
Предположим, что нам дан график некоторой функции y=f(x)
(рис. 128). Из чертежа ясно видно, что при возрастании х от
значения, равного а, до значения, равного числу Ь, график функ-
ции поднимается вверх, значения функции возрастают от /(я) до
/'(&); при возрастании х от b до с график функции идет вниз,
215
значения функции убывают от f(b) до /(с). При дальнейшем воз-
растании х от с до е значения функции возрастают в промежутке
(с; d) и убывают в промежутке (d; е).
В промежутках (а; Ь) и (с; d) любому большему значению
аргумента х соответствует и большее значение функции: x.j)>xi
и f(xt)^>fM- в промежутках (&; с) и (d; е), наоборот, боль-
шему значению х соответствует меньшее значение функции: х^>х3,
Функцию, график которой
имеет вид, как на рис. 128, на-
зывают возрастающей в проме-
жутках (a; b), (с; d) и убы-
вающей в промежутках (Ь; с)
и (d; е).
Определение 1. Функция
у — f (х) называется возрастаю-
если в этом промежутке любому
Рис. 128
щей в некотором промежутке',
большему значению аргумента х соответствует и большее значение
функции.
Определение 2. Функция у — f(х) называется убывающей
в некотором промежутке, если в этом промежутке любому боль-
шему значению аргумента х соответствует меньшее значение
функции.
Вопрос о возрастании и убывании функции является основным
вопросом в изучении свойств функции.
Займемся установлением признаков, по которым можно судить
о возрастании или убывании любой функции, заданной анали-
тически (уравнением), не имея ее графика.
§ 82. ПРИЗНАКИ ВОЗРАСТАНИЯ II УБЫВАНИЯ ФУНКЦИИ
Нам известно (см. § 62), что производная функции геометри-
чески выражает угловой коэффициент касательной к графику этой
функции.
Положим, что кривая АС (рис. 129) является графиком функ-
ции y — f(x). Очевидно, что часть АВ этой кривой соответствует
промежутку (а; Ь) возрастания данной функции, а часть ЕС —
промежутку (Ь; с) убывания. Из рисунка видно, что в любой
такой точке (М), где данная функция возрастает, касательная MIC
с положительным направлением оси Ох образует острый угол сц.
Так как тангенс острого угла — число положительное, то угло-
вой коэффициент (ki — tg o-j) касательной МК должен быть числом
положительным, следовательно, должна быть положительна и про-
изводная f(x) при x = xi, т. е. [’ (xj) = tgaj)>0.
Касательная, проведенная к графику той же функции в такой
точке (L), где функция убывает, образует с осью Ох тупой угол а4.
Тангенс тупого угла— число отрицательное. Угловой коэффи-
216
циепт (&2 = tga.>) касательной LF? должен быть отрицательным,
следовательно, должна быть отрицательна и производная f (х)
при х = х3, т. е. /'(xj) = tg а-2 < 0. Эти геометрические соображе-
ния приводят к следующим признакам возрастания и убывания
функции:
1. Если производная функции y = f (х) положительна при зна-
чениях аргумента х, удовлетворяющих условиям а<^х<^Ь, то
в интервале (а-, Ь) эта функция возрастает (см. рис. 128).
2. Если производная функции y — f(x) отрицательна при зна-
чениях аргумента х, удовлетворяющих условиям a<^x<Fb, то
в интервале (а; Ь) данная функция
Примечание. В промежутках
ции в отдельных точках графика
оказаться параллельной оси Ох, и
при соответствующих значениях
аргумента х производная обратится
в нуль (см. пример 4).
Пример 1. Показать, что функ-
2 ,
ция г/ = -; убываете любом про-
межутке, не содержащем нуля.
Решение. Находим произ-
водную данной функции
2
Ух—~
убывает (рис. 130).
возрастания и убывания функ-
функции касательная может
При любом действительном значении аргумента х, отличном
от нуля, производная отрицательна.
При х = 0 функция У = ~ теряет смысл и производной не
имеет. Следовательно, данная функция убывает в промежутках
(—оо; 0) и (0; со) (см. рис. 97).
217
Пример 2. Определить промежутки возрастания и убывания
функции —
Р е ш е н и е. у'х — — 4- х 4-1.
j 1 * * * У
Функция возрастает при тех значениях аргумента, при кото-
рых первая производная положительна. Следовательно, значе-
ния х, при которых функция возрастает, должны удовлетворять
неравенству
-|х+1>0.
Решив это неравенство, получаем
1>-5-х, или х<СЗ.
О
Оказывается, что данная функция возрастает при значениях х,
меньших числа 3 (—оо<^х<^3).
Функция убывает при таких значениях аргумента, при кото-
рых производная отрицательна. Для этих значений аргумента,
очевидно, будет справедливо неравенство
1 1 —уХ-[-1<40. Решив его, получим л\>3-
I Следовательно, функция убывает при изменении
/ Л' от 3 до со (см. рис. 92).
/ Пример 3. Указать промежутки возрастания
. 0 J и убывания функции
1 ,1/=1х‘4-р+з.
/ Решение. у'х = хл-{-х = х(х‘*-[-1).
I Производная представлена в виде произве-
I дения двух сомножителей. Второй сомножитель
положителен при любом значении х, поэтому
Р,1С' 131 знак у'х будет зависеть только от знака первого
сомножителя (х). Производная будет отрица-
тельна, когда л'<^0, и положительна при х^>0. Следовательно,
эта функция убывает в промежутке (—сю; 0) и возрастает в про-
межутке (0; со).
Пример 4. Исследовать на возрастание и убывание функцию
1 3
У —-г х3.
Решение. На рис. 131 дан график этой функции, построен-
ный по точкам. По графику видно, что функция возрастает
в любом промежутке. Найдем производную этой функции:
'/л=/'(х)^^-х2.
21S
Производная больше нуля при любом положительном
и отрицательном значении аргумента х, но при х = 0 она обра-
щается в нуль: /'(0) = 4-• О'3 = 0. График этой функции в точке
(0; 0) имеет касательную, совпадающую с осью Ох.
Пример 5. Исследовать на возрастание и убывание первую
производную функции
II _1_ Щ 1-
У— 12х 2 •
Решение. Имеем у'х = ^х1— х.
Нужно исследовать эту функцию. Производной этой функции
является вторая производная данной (в условии) функции:
Шг = «/.« = у х — 1.
Известно, что функция убывает при тех значениях аргу-
мента х, при которых ее производная отрицательна. Получаем
неравенство
-J>-x — 1<0.
Решив это неравенство, находим х<^2. Это значит, что функ-
ция у'х = ^х‘1— х убывает в промежутке (—оо; 2).
Определим теперь промежуток возрастания. Получим нера-
венство -^-х—1^>0. Решив его, получим х^>2. Функция у'х —
= -i- х3— х возрастает в промежутке (2; оо) (график функции
и ее производной см. на рис. 126).
§ 83. МАКСИМУМ И МИНИМУМ ФУНКЦИИ
Положим, что кривая CD (рис. 132) является графиком функ-
ции г/ = /(х). Из рисунка видно, что при возрастании аргумента
х от с до d график этой функции то поднимается вверх, то опус-
кается вниз. Участки СА и BD графика соответствуют проме-
жуткам возрастания данной функции, а участок АВ—проме-
жутку- ее убывания.
При х = а функция переходит от возрастания к убыванию.
Ордината /(а) точки А больше ординат любых точек графика,
достаточно близких к точке А и находящихся от нее как справа,
так и слева. Такое значение аргумента принято называть точкой
максимума, а, соответствующие значения функции — максимумом
этой функции.
219
Эго следует понимать в том смысле, что /(а) больше любых
значений данной функции при значениях аргумента х, близких
к числу а, т. е.
или короче:
/'(а)>/'(а^/г),
где h — достаточно малое положительное число.
При х — Ь, наоборот, функция от убывания переходит к воз-
растанию. Ордината f(b) точки В меньше ординат всех прочих
точек кривой, достаточно близких к точке В и расположенных
функции при значениях аргумента
лу Ь, т. е.
как слева, так и справа от
точки В. Такое значение ар-
гумента принято называть
точной минимума, а значе-
ние функции при этом зна-
чении аргумента (в данном
случае при х~Ь) — мини-
мумом функции.
Это значит, что f (b) мень-
ше любых значений этой
х, достаточно близких к чис-
где h — любое достаточно малое положительное число.
Определение 1. Функция y=f(x) имеет максимум при
данном значении аргумента х (например, при х = а), если при
любом достаточно малом положительном h выполняется условие
Определение 2. Функция y=f(x) имеет минимум при
данном значении аргумента х (например, при х — Ь), если при
220
любом достаточно малом положительном h выполняется условие
Функция может иметь несколько максимумов и несколько ми-
нимумов. На рис. 133, например, изображена функция, имеющая
максимумы в точках а, с, е и минимумы в точках b и d. При
этом следует отметить, что некоторые максимумы функции могут
оказаться меньше минимумов. Так, на рис. 133 имеем
Термины «максимум» и «минимум» объединяются одним терми-
ном «экстремум». Эти термины латинскими буквами пишутся так:
maximum; minimum; extremum. Слово «extremum» означает «край-
нее» в смысле «крайнее значение».
§ 84. ПРИЗНАКИ СУЩЕСТВОВАНИЯ МАКСИМУМА
И МИНИМУМА ФУНКЦИИ
В . этом и последующих параграфах предполагается (если нет
особой оговорки), что рассматриваемая функция непрерывна,
имеет непрерывную первую производную и непрерывную вторую
производную.
Займемся установлением признаков существования максимума
и минимума функции, удовлетворяющей этим условиям.
1. Необходимый признак. Теорема. Если функция у —
= f(x) имеет экстремум при х — а, то ее производная при этом
значении аргумента равна нулю, т. е. /'(ц) = 0.
Доказательство (способом «от противного»). Если бы при
х — а производная не была равна нулю, то она была бы пли
положительным числом If' (й)Д>0], или отрицательным числом
[/'(а)<^0] и, согласно § 82, при х=а функция у = f (,г) была бы
возрастающей или убывающей, а следовательно, не имела бы ни
максимума, ни минимума.
Геометрически эта теорема представляется очевидной: каса-
тельные, проведенные к графику функции (см. рис. 133) в точках
максимума и минимума, параллельны оси Ох, и согласно геомет-
рическому смыслу производной (см. § 62),
/'(а) = tg 0 = О, f'(c) = O.
Из, этой теоремы следует, что точки максимума и минимума
функции должны быть корнями уравнения
Ш = ' (а)
В числе корней уравнения (а) могут оказаться и такие, при
которых данная функция экстремума не имеет. Так, в точках
х = т и х = п (см. рис. 133) касательная параллельна оси Ох
221
и производная равна нулю [числа тип являются корнями урав-
нения (а)]. Между тем при этих значениях аргумента функция
не имеет ни максимума, ни минимума. Это значит, что равенство
(а), являясь необходимым условием существования экстремума,
не является достаточным, т. е. не всякий корень уравнения
f (х) — 0 является точкой экстремума.
2. Достаточные признаки. Допустим, что производная
функции y = f(x) при х = а— h* положительна [[' (а — Л) Д>0],
а при x = a-j-/z отрицательна [fr (аД- h) О Op При этих условиях
-в интервале (а — 1г, а) функция возрастает и в интервале (a; aA-h)
убывает (см. § 82), а при х = н от возрастания переходит к убы-
ванию, достигнув максимума f(a) (см. § 83). При переходе аргу-
мента через значение х = а производная меняет знак с плюса на
минус, так как
, f(a — /г)>0 и /ДаД-/г)<0.
Нам известно (см. § 80), что непрерывная функция меняет
свой знак лишь при переходе аргумента х через такое значение,
при котором эта функция обращается в нуль. Следовательно,
Ш = о.
Итак, в точке максимума производная обращается в нуль и
меняет знак с плюса на минус.
Допустим далее, что производная этой функции при x — d — h
отрицательна, при x = d-\~h положительна. При этих условиях
в интервале (а — h\ d) функция убывает и в интервале (d; d-|-/i)
возрастает, а при x — d от убывания переходит к возрастанию,
достигнув минимума /(d). При переходе аргумента через значе-
ние x—d производная меняет знак с минуса на плюс, так как
/'(d —/г)<ДО и /'(d Д- h) У> 0. Значит (см. § 80) при x — d произ-
водная обращается в нуль: /'(d) = 0. Следовательно, в точке
минимума производная обращается в нуль и меняет знак с минуса
на плюс. Эти выводы наглядно подтверждает рис. 133, на кото-
ром представлен график функции y = f(x). В точках, располо-
женных левее точки А, касательная образует с осью Ох острый
угол и, следовательно, У (а — /i) = tgaj)>0. В точке А касатель-
ная параллельна оси Ох, следовательно, /'(a) = tgO = O. В точ-
ках, расположенных правее точки А, касательная с осью Ох обра-
зует тупой угол и поэтому fr (а Д- /г) = tg a2 <Д 0.
В точках графика, расположенных левее точки D, касатель-
ная образует с положительным направлением оси Ох тупой угол
и потому f (d — h) = tg a3 ДО. В точке D касательная параллельна
осн Ох, следовательно, /'(d) = tgO = O. В точках, расположен-
ных правее точки D, касательная с осью Ох образует острый
угол и поэтому у (d Д- h) = tg a4 0.
* Под h разумеем любое достаточно малое положительное число. О до-
пустпмых значениях h подробно говорится в § 85.
222
Эти рассуждения приводят к следующим 'до с та то ч н ы м
признакам существования максимума, и минимума
функции у = f (х).
Если производная f (х) функции y = f(x) при некотором зна-
чении аргумента х (например, при х = а) равна нулю и при переходе
аргумента через это значение меняет знак е плюса на минуе, то
при х = а данная функция имеет максимум.
Если производная функции при некотором значении аргумента х
(например, при х = с£) равна нулю и при переходе аргумента
через это значение меняет знак е минуса на плюс, то при x = d
функция имеет минимум.
Если производная, обращаясь в пуль при некотором значении
аргумента, например при х=т, не меняет знака при переходе
аргумента через это значение, оставаясь положительной как при
х=т— h, так и при x=m-\-h, то в этом случае функция, воз-
растая в промежутке (tn\ т — /г), продолжает возрастать и в про-
межутке (/«; т-\-К), а следовательно, при х = т не имеет ни
максимума, ни минимума.
Точно так же функция не имеет ни максимума, ни минимума
и в том случае, когда производная, обращаясь в нуль при неко-
тором значении аргумента, например при х — п, остается отри-
цательной как при х = п — h, так и при x = n~\-h. /
Сделанные выводы кратко представлены в табл. 14.
. Те значения аргумента, при которых производная f' (х) функ-
ции y=f(x) обращается в нуль, называются критическими зна-
чениями аргумента.
Таблица 14
X f (x-h) Г (х) /' U + Л) Заключение /(.V)
а + 0 Максимум. f(a)
d. — 0 + Минимум
т + 0 + Ни максимума, ни минимума
. п 0 — Ни максимума, ни минимума
Из изложенного выше должно быть ясно, что критическими
значениями аргумента х являются все действительные корпи урав-
нения /'(х) = 0.
§ 85. ПРАВИЛО НАХОЖДЕНИЯ МАКСИМУМА И МИНИМУМА
ФУНКЦИИ С ПОМОЩЬЮ ПЕРВОЙ ПРОИЗВОДНОЙ
Пусть нам дана функция
z/ = /(x) = х2 (х—5)3
и требуется исследовать эту функцию на максимум и минимум.
223
Ранее было показано, что функция может иметь экстремум
лишь при таких значениях аргумента, при которых первая про-
изводная обращается в нуль. Отсюда должно быть ясно, что пер-
вым шагом в исследовании функции на максимум и минимум
должно быть нахождение производной данной функции.
По формуле производной произведения двух функций находим
УХ = Г (*) = (X - 5)3 (х‘% + • [(X - 5) ’j;: =
= (х— 5)3 • 2х -ф х- • 3 (х— 5)--(х— 5)л =
— х (х — 5)2 [2 (х — 5) -ф Зх] = х (х — 5)'- (5х — 10).
Итак,
(х) = 5х(х — 2) (х —5)2.
Вторым шагом является нахождение критических значений
аргумента. Для этого достаточно решить уравнение /'(х) = 0.
Получим
5х(х—2) (х — 5)- = 0;
Xi = 0, х.> — 2, х3 — 5.
Мы нашли те значения аргумента, при которых данная функция
может иметь экстремум.
Далее следует определить знаки производной при значениях
аргумента, близких к найденным критическим и расположенных
левее и правее их, т. е. знаки f (х — h) и /Дхф-й), где под х
разумеется критическое значение аргумента, а под h — такое малое
положительное число, при котором интервал (х — /г, x-\-h) не
захватывает соседних критических значений х (справа и слева).
Примечание. Если Xi — наименьший корень уравнения
f'(x) = O, то в интервале (—оо, Xi) производная сохраняет свой
знак без изменения. В этом случае за h можно принять любое
положительное число. Если хк— наибольший корень этого урав-
нения, то за h тоже можно принимать любое положительное
число, так как в интервале (хк, оо) производная знака не меняет.
Эта часть работы явится третьим шагом в процессе исследо-
вания функции на максимум и минимум. Во избежание путаницы
результаты желательно вносить в указанную ниже таблицу, на-
писав под буквой х критические значения аргумента в возраста-
ющем порядке (табл. 15).
Таблица 15
X /' (л-й) /' (л) /' и + Л) Заключение /U)
0 •Ф 0 Максимум 7(0) = 0
2 5 + 0 0 д Минимум Ни максимума, нм минимума /(2) = —108
224
Определим сначала знаки первой производной при значениях
аргумента х<^0, а затем при х^>0. Полагая, например, /г=1,
получим
/'(х —А) = /'(0 —Л) = /'(—D = 5(—1)(—1 — 2)(—1 — 5)* =
= 5(-1)(-3)(+36)>0.
Ставим знак плюс против нуля под /' (х— h). Далее имеем:
Г (x-\-h) = f'(O-\-h) = f'(1) = 5-1 • (1 - 2) • (1 - 5)2<0,
так как число отрицательных множителей нечетное (один).
При переходе" аргумента через значение х = 0 производная
меняет знак с плюса на минус. Следовательно, при х = 0 данная
функция имеет максимум, что и отмечается в таблице в графе
«Заключение», Точно так же ведется исследование дальше. Так,
в точке 2 имеем:
f (х — Л) = f (2 — h) = f (1) -<0 (см. выше);
f (х + /г)==/'(2 + /г) = /'(3) = 5-3(3-2)(3~5)2>О,
'При переходе аргумента через значение х = 2 производная
меняет знак с минуса на плюс. Следовательно, при х= 2 данная
функция имеет минимум. Наконец, в точке х==5
/'(5 —/г) — f (4) = 5 • 4 • (4 — 2) • (4 — 5)2> 0;
/'(5-(-/г) = Г (6) = 5 • 6-(6 — 2) • (6 — 5)2> 0.
При переходе аргумента через значение х = 5 производная
знака не меняет. Это означает, что при х = 5 функция не имеет
ни максимума, ни минимума.
Остается найти максимальное и минимальное значения' функ-
ции. Получаем:
ут^ = №) = (? (9
утш = f (2) = 23 • (2 - 5)’ = - 108.
Признаки существования максимума и минимума функции,
указанные выше, и разбор приведенного примера приводят к сле-
дующему правилу нахождения максимума и минимума функции
с помощью первой производной.
1-й шаг. Найти производную данной функции y — f(x).
2-й шаг. Приравняв производную нулю, найти действитель-
ные корни полученного уравнения f (х) = 0, которые и будут кри-
тическими значениями аргумента.
В случае, когда все корни уравнения f (х) = 0 — числа мнимые,
функция экстремума не имеет.
З-й шаг. Расположить критические значения аргумента в воз-
растающем порядке и определить ' знаки производной при значе-
ниях аргумента, близких к найденным критическим и располо-
женных левее и правее их (см. выше разбор примера). Если при
этом знак производной меняется с плюса на минус, то при дан-
8 П. Е. Агачеа
225
ном значении аргумента функция имеет максимум. Если знак
производной меняется с минуса на плюс, то значение аргумента
является точкой минимума. Если же знак производной не меняется,
то нет ни максимума, ни минимума.
4-й шаг. Вычислить максимальные и минимальные значения
функции, т. е. значения данной функции у = f (х)., соответствую-
щие тем значениям аргумента х, при которых эта функция имеет
максимум или минимум.
Пример 1. Исследовать на максимум и минимум функцию
у = f (х) = у х3 -ф- х2 — Зх.
Решение. 1) Находим производную этой функции:
У' = Г (х) = х2ф-2х —3.
2) Находим критические значения аргумента, приравняв про-
изводную нулю и решив полученное уравнение х!--Г2х— 3 = 0:
*1.2 = — 1 ± 1 + 3; X] = — 3, х.-> = 1.
При определении знака производной работа значительно упро-
щается, если производная разложена на множители. В данном
случае это разложение легко выполняется по правилу разложе-
ния на множители квадратного трехчлена., Получаем
/'(х) = (х-)-3)(х-1).
3) Полагая /г=1, имеем:
Г (_3_ Л)==Г (_4) = (_4 4-3)(—4— 1)>0;
/'(—3+ //)=/'(—2) = (—2 4-3) (—2—1)<0 (табл. 16).
Под h можно разуметь любое, положительное число, при кото-
ром x-f-A меньше следующего критического значения аргумента,
т. е. в данном случае —3 -|- h <ф 1
Г(1 — Л)=г (0)=(04-3) (О — I) <0-
Таблица 16
X f (х — Л) /' (*) Г (ж -ЬЛ) Заключение /W
—3 + 0 — Максимум /(-3) = 9
1 •— 0 + Минимум /0) = -1-з .
В этом случае вместо h можно было взять любое положительное
число, при котором 1——3.
/'(1 (2) = (2 + 3)(2 —1)>0.
226
4) утт = / (- 3) = j (- З)3 + (- З)2 - 3 • (- 3) = 9;
ymin = f (1) = |-13+ 12-3-1 =- 1
Пример 2. Исследовать функцию у — ^-х'*— х—4 на макси-
мум и минимум и построить ее график.
Решение. Из аналитической геометрии известно (см. § 38),
что уравнение вида у = ax’1 Ьх -]- с выражает параболу, симмет-
ричную относительно прямой, параллельной оси Оу.
1) Находим производную: у'х = ['(х) = х—1.
2) Находим критическое значение аргумента:
f'(x)=x—1=0; х=1;
3) /'(1 — Л) = /'(0) = 0—1 <0;
f'(l+/i) = f(2) = 2—1>0 (табл. 17).
4) г/ш1п = /(1) = 1.12-1^4 = -41.
Таблица 17
X /’(-v-Л) г (Л) Г и + Л) Заключение / (х)
1 — 0 + Минимум -4
Следовательно, вершина параболы находится в точке ^1; —4-^J.
Чтобы приближенно (от руки) построить такую параболу,, доста-
точно знать положение ее вершины и точки
пересечения с осями координат. Решив урав- у .
некие t/ = yX2 — х — 4 = 0, получаем: Х\=
=— 2, х3 = 4. Точку пересечения с осью 1 I
Оу находим, решив совместно уравнения: у q /
х = 0, у = -^х2 — х—4=0. Получаем (0; — 4). х
'Построив вершину параболы (1; —4~j /
и точки (—2; 0), (4; 0), проводим через них
плавную кривую, учитывая, что в промежут- 1д4
ке (—оо; 1) данная функция убывает, а ис'
в промежутке (1; оо) возрастает (рис. 134).
Наибольшее и наименьшее значения функции на данном от-
резке. Задачи на наибольшее и наименьшее значения функции.
Наибольшим значением функции на данном отрезке может быть
один из его максимумов или ее значение на одном из концов
8*
227
этого отрезка. Например, наибольшим значением функции y=f(x),
график которой изображен на рис. 133, на отрезке [s, Z] является
ее наибольший максимум: f(e) — eE, а на отрезке [/?, т] — пра-
вый конец этого отрезка: f(m) = mM.
Аналогично, наименьшим значением функции на данном от-
резке является или один из ее минимумов, или ее значение на
конце отрезка. Например, наименьшим значением рассматриваемой
функции на отрезке [s, /] является ее значение на левом конце
отрезка: f(s) — sS, а на отрезке [а, /] —меньший из двух его
минимумов: f(b) = bB.
Отсюда следует, что для нахождения наибольшего и наимень-
шего значений функции y = f(x) на данном отрезке [а, 6] надо
вычислить значения этой функции на концах отрезка (f(a) и f(b))
и найти все ее экстремальные значения в интервале (а, Ь).
Наибольшее из этих чисел будет наибольшим значением функции
на данном отрезке, а наименьшее из тех же чисел — наименьшим
ее значением.
Пример 3. Найти наименьшее и наибольшее значения функции
у = f (х) = х1 (х — 5)3 на отрезке [—1,6].
Решение. Эта функция достигает максимума при х—0:
f(0) = 0 и минимума прих = 2: /(2) = ynii„ =—108 (см. табл. 15).
Находим ее значения на концах данного отрезка: /(—1) = — 216,
/(6) —36. Наименьшим из этих четырех значений функции яв-
ляется число —216, а наибольшим — число 36. Следовательно,
наименьшего и наибольшего значений эта функция достигает на
концах отрезка.
Замечание. Если функция в интервале (а, Ь)' имеет един-
ственный максимум без минимумов, то этот максимум является
ее наибольшим значением на отрезке [а, Ь] (см. рис. 129). Точно
так же, если функция в интервале (а, Ь) имеет только один мини-
мум без максимумов, то этот минимум является наименьшим зна-
чением этой функции на отрезке [а, 6] (см. рис. 134). В таких
случаях для определения наибольшего и наименьшего значений
функции не надо вычислять ее значения на концах отрезка.
С этими случаями мы встретимся ниже при решении задач.
Теория экстремума функции имеет большое практическое при-
менение как в самой математике, так и в технических науках.
До сих пор эта теория прилагалась нами к исследованию данных
функций, на практике же часто случается, что по данным усло-
виям задачи сначала надо составить функцию, а уже затем про-
вести исследование ее на максимум и минимум. Рассмотрим это
на примерах.
Задача 1. Разбить число 14 на два слагаемых так, чтобы
сумма их квадратов была наименьшей.
Решение. Обозначим первое слагаемое через х. Тогда вто-
рое слагаемое выразится в виде разности 14—х. Сумма квадра-
228
тов этих слагаемых будет функцией, подлежащей исследованию.
Обозначив ее через у, получим
т/ = х9 + (14-хЛ
По правилу, приведенному в этом параграфе, найдем:
1-й шаг: y'v = 2x-|-2(14—х)(14— х)'х = 2х-ф- 2 (14—х)(—1) =
— 2х — 28 2х = 4 (х— 7).
2-й шаг. 4(х— 7) = 0; х— 7 = 0; х = 7.
3-й шаг. Определяем знак производной при х<^7, например
при х — 6. Получим:
//1 = 4(6-7)<0.
При х^>7, например при х = 8, получим
//1 = 4(8 — 7)>0.
Итак, при х — 7 производная у'х равна нулю и при переходе
аргумента через это значение (х = 7) меняет знак с минуса на
плюс. Следовательно, при х — 7 данная функция имеет минимум.
Второе слагаемое, очевидно, тоже будет равно 7: 14 — х= 14 —
— 7 = 7.
4-й шаг. Подставив в выражение данной функции вместо х
число 7, находим
Ут1П = 74-Н14-7Г = 98.
Задача 2. Дан треугольник АВС (рис. 135), основание кото-
рого АС = Ь, высота BD = h. Из всех прямоугольников, которые
могут быть вписаны в этот треуголь-
ник так, чтобы две вершины их ле-
жали на основании треугольника,
а две другие —на боковых сторонах,
найти тот, который имеет наиболь-
шую площадь.
Решение. Здесь функция, мак-
симум которой нам надо определить,
не дана. Займемся составлением этой
Рис. 135
функции. Из геометрии известно,
что площадь прямоугольника равна
произведению основания на высоту.
Обозначив высоту вписанного прямоугольника MMiNtN через х
основание—через у (MN — y), получим
S = xy. (а)
Этой формулой площадь прямоугольника выражается как функ-
ция двух переменных: хи у*. Между этими переменными вели-
* Переменная величина z называется функцией двух независимых пере-
менных х и у, если каждой паре допустимых значений этих переменных
соответствует определенное значение z. Тот факт, что z является функцией
от х и у, принято записывать в виде равенства z —f (х, у), или S — q(x,y),
и т. д.
229
чинами х и у существует зависимость: чем больше х, тем меньше
у, и обратно. Эту зависимость можно выразить формулой.
Мы имеем два подобных треугольника: /\MiBN]'y^AABC.
Из геометрии известно, что в подобных треугольниках сходствен-
ные высоты относятся как сходственные стороны. Следовательно,
tv'^Ni________________________BDi
~АС ~ BD ’
Нам известно: MiNi — MN ~у:, АС — Ь\ BD — h', BD! — BD —
— MMt = h — х.
Получаем
у _______________________h — х
~b~~ Л ’
откуда
У=^(Ь — х). (б)
Заменив в формуле (а) у его выражением (б) через х, найдем
S—x-^-(h—х),
или
S=^(hx — х2). (в)
Эта формула выражает площадь прямоугольника как функцию
его высоты х.
Теперь можно приступить к исследованию этой функции на
максимум и минимум. По правилу, изложенному в этом пара-
графе, найдем:
1-й шаг. S'x — ^-(hx — хъ)х — ^{Н — 2х),
или
2-й шаг. —х^ — 0; у — х = 0; x — ^ = 0,5h.
3-й шаг. Определим знак производной при х<^0,5й, напри-
мер при х = 0,4/г. Подставив в (г) вместо х число 0,4й, получим
Х; = ^(0,5й —0,4й)>0.
При х2>О,5/г, например при х— 0,6й,- будем иметь
S* = ^(0,5/i — 0,6й)<0.
Как видим, при переходе аргумента через значение х —0,5/г
производная S’v меняет знак с плюса на минус. Следовательно,
при х — 0,5/г площадь S имеет максимум.
230
4-й шаг. Подставив в формулу (в) вместо х число ,получим
Оказывается, что наибольшую площадь, равную половине пло-
щади данного треугольника, будет иметь такой вписанный пря-
моугольник, высота которого равна половине высоты данного
треугольника.
Указание. Прежде чем приступить к проработке следующего
параграфа, предлагается решить задачи 580—607, к некоторым
из которых даны подробные указания. Рекомендуется добиваться
правильного решения, не пользуясь этими указаниями. Решение
задач 584—587 следует завершать построением графика.
§ 86. ПРАВИЛО НАХОЖДЕНИЯ МАКСИМУМА И МИНИМУМА
ФУНКЦИИ ПРИ ПОМОЩИ ВТОРОЙ ПРОИЗВОДНОЙ
Первая производная функции y = f(x) в свою очередь является
функцией от х (см. § 80). Поэтому она, как и всякая функция,
при возрастании аргумента может возрастать или убывать. Про-
следим ход изменения первой производной функции y — f(x)
вблизи точки максимума.
Мы знаем (см. § 84), что функция имеет максимум при х — а,
если при этом значении аргумента производная равна нулю и
при переходе аргумента х через это значение меняет знак с плюса
на минус, т. е. если
Г(а-й)>0, f'(«) = 0, Г(а + /1)<0.
Отсюда следует
(a-j-A).
Эти неравенства показывают, что в промежутке (а — /г; a~\-h)
большему значению аргумента х соответствует меньшее значение
первой производной f (х). Следовательно (см. § 81), в этом про-
межутке первая производная y'x — f (х) убывает, а потому (см.
§ 82) ее производная, т. е. вторая производная функции y — f(x),
отрицательна:
Г(а + й)<0 и f'(fl)<0.
Проследим теперь ход изменения первой производной вблизи
точки минимума. Нам известно (см. § 84), что функция имеет
минимум при х = с, если при этом значении аргумента производ-
ная обращается в нуль, и при переходе аргумента через это зна-
чение меняет знак с минуса на плюс, т. е. когда
231
Эти условия приводят к неравенствам
из которых видно, что в промежутке (с — h; c-\-h) большему зна-
чению аргумента х соответствует большее значение первой про-
изводной. Это означает (см. § 82), что в данном промежутке
(вблизи точки минимума и в точке минимума) первая производ-
ная возрастает, .а щотому ее производная, т. е. вторая произ-
водная функции y — f(x), положительна:
/" (с zjr й) > 0 и /" (с) > 0.
Эти рассуждения приводят к следующим признакам существо-
вания максимума и минимума функции.
1. Функция y — f{x) при х — а имеет максимум, если при
этом значении аргумента первая производная равна нулю и вто-
рая производная отрицательна'.
f'(a) — O, Г(а)<0.
2. Функция y — f(x) при х = с имеет минимум, если при этом
значении аргумента первая производная равна нулю и вторая про-
изводная положительна:
Г(с) = о, Г(с)>0.
Эти выводы можно пояснить примером. На рис. 126 изобра-
жена функция, имеющая максимум при х — 0 и минимум при
х = 4. По графикам ее процзводнь!х видно, что при'переходе
аргумента через значение х = 0 первая производная убывает,
вторая производная отрицательна, а при переходе через х = 4
первая производная возрастает, вторая производная положи-
тельна: ___
/" (0) = О^<0, f (4) = PPi>0.
На рис. 136 изображен график некоторой функции. Внизу
отмечены знаки первой и второй производной, соответствующие
ходу изменения этой функции в промежутках
(а — h; a-j-h) и (с — h; c~[-h).
Второе правило исследования функции на экстремум.
1-й шаг. Находится первая производная ух —fix') данной
функции.
2-й шаг. Первая производная приравнивается нулю [/'(х) = 0]
и находятся критические значения аргумента, т. е. те его зна-
чения, при которых данная функция может иметь максимум и
минимум.
3-й шаг. Находится вторая производная f" (х) данной функции.
4-й шаг. Во вторую производную последовательно подстав-
ляются критические значения, аргумента, т. е. действительные
корни уравнения /' (х) — 0.
232
Если при данном критическом, значении аргумента, например,
при х = Х[, вторая производная оказывается отрицательной, то
при этом значении аргумента данная функция имеет максимум.
Если при критическом значении аргумента, например, при
x = xit вторая производная имеет знак плюс, то при этом зна-
чении аргумента данная функция имеет минимум.
Рис. 136
Если же при данном критическом значении аргумента, например,
при х — хз, вторая производная обращается в нуль или в беско-
нечность, то вопрос остается нерешенным. В этих случаях иссле-
дование завершается по правилу, изложенному в § 85.
Результаты исследования можно представить в виде таблицы
(табл. 18).
Таблица 18
X /’ (ж) 7" (.V) Заключение / (л)
Xj 0 — Максимум -^max
Хц 0 4- Минимум
0 0 1 Заключения сделать нельзя, необходимо опре-
Л 3 0 со [ делить знаки f (х3 — А) и f (xz + Л)
Следует заметить, что исследование функции на экстремум
по этому правилу в ряде случаев выполняются гораздо проще и
быстрее, чем по первому правилу (см. § 85).
Пример 1. Исследовать на максимум и минимум функцию
f (х) = 2. х1 — х3 — 2х'\
233
Решение. Проведем исследование по второму правилу:
1-й шаг. /'(х) = х3— Зх2— 4х — х(х!— Зх — 4).
2-й шаг. x(xi— Зх — 4) = 0; Xi = 0; х-— Зх — 4 = 0.
Решив последнее уравнение, получим: х2 — —1, х3 = 4. Зано-
сим найденные критические значения аргумента в таблицу, рас-
положив их в возрастающем порядке (табл. 19).
Таблица 19
X /’ (*) /" U) Заключение / (-V)
—1 0 + Минимум то |-^ 1 д 7
0 0 — Максимум
4 0 + Минимум /(4) =—32
При этих значениях аргумента производная /' (х), очевидно,
равна нулю, что и отмечено в соответствующем столбце таблицы.
3-й шаг. f" (х) = (х3 — Зх2 — 4х)Л- = Зх2 — 6х — 4.
4-й ш а г. Определяем знаки второй производной при найден-
ных критических значениях аргумента и делаем заключение о типе
экстремума:
f (—1) = 3.(— I)2 — 6-(—1) — 4 = 3 + 6 — 4>0,
при этом критическом значении аргумента вторая производная
положительна, следовательно, при х = —1 данная функция имеет
минимум;
f” (0) = 3-02 — 6-0 —4<0,
при х = 0 вторая производная отрицательна, следовательно, при
этом значении аргумента функция имеет максимум;
f (4) = 3-4- — 6-4 — 4 = 48 — 24 — 4>0,
следовательно, при х = 4 данная функция имеет минимум.
В заключение находим, если в этом есть надобность, макси-
мальные и минимальные значения данной функции.
Получаем:
i/min = /(-1) = j (-1)4 - (-1)3 - 2 (— 1Г = — 4 ;
//,пах = /(0)=4-04-°3-2-0 = 0; '
ymin = 4 • 44 - 43 - 2 • 42 = -32.
Пример 2. Исследовать на максимум и минимум функцию
234
Решение. 1-й шаг. f’(x) = 2 \х3 — 1) • ух3 = -|-х3 \х3 — 1).
1/1 \ 1 1
2-й шаг. х3 (^х3 — 1) = 0, х3 =0, х3 — 1=0; Xj=0,х23=± 1.
о г 1 -2 / 1 \ 1 -4 11
3-й шаг. /'(х) = у х 3 (х3 — 1)-f-х3 jx3j,
или
4-й шаг. Подставляем во вторую производную (± 1) вместо х.
Получаем
5/(±1)\-1
rw=4-
Следовательно, при х = —1 и при х=1 данная функция
Г 1 I2
имеет минимум: z/min = /(—1) = [(—I)3 — 1] =0, ymin =/(1) = 0.
Подставляем в f" (х) вместо х нуль. Получаем
1
р, 8 5 03 — 1
f (°)=9-------У---=—°°-
. О3
В этом случае, как замечено выше, второе правило остав-
ляет вопрос открытым. Определяем знаки первой производной
при х = 0 — h и при х = 04~й:
/' (0 — й) = у (-/г)-3 [(—й)3 — 1] > 0;
f (04- й) = | h3 (fi3 — <0.
При переходе аргумента через значение х = 0 производная
меняет знак с плюса на минус. Следовательно, в точке х = 0.
функция имеет максимум: г/тах=1.
Задача. Требуется сделать из листового железа цилиндриче-
ский сосуд данной емкости v, закрытый сверху и снизу. Каковы
должны быть его размеры, чтобы затрата материала была наи-
меньшей?
Решение. Очевидно, затрата материала будет тем меньше,
чем меньше поверхность сосуда. Обозначив радиус основания
цилиндрического сосуда через г, высоту — через, й и полную
поверхность — через S, будем иметь
S = 2тсгй 4-2тсг9. (а)
235
Формула (а) выражает функцию S через две переменные вели-
чины: г и h. Между этими переменными величинами существует
зависимость, позволяющая выразить одну из них через другую.
Зависимость эта выражается формулой
v == itr-h, (б)
где v (объем цилиндра) — данная постоянная величина.
Из равенства (б) находим
/г = Д. (в)
ЛГ’
Подставив в формулу (а) вместо Л его выражение через г,
получаем
или
\ Г /
Это равенство выражает S как функцию одной независимой
переменной г.
Исследуем эту функцию на экстремум по второму правилу:
1-й шаг. S', — 2 (~ -I- лг-) — 2 (v г 14- кг)', =
= 2[у. (—1)г“‘2 + 2л4
Итак, .
S’r = 2^r-^.
2-й шаг. 2 ^2л/- — = 2лг — ^=0,
откуда имеем
>-=]/£ (г>
3-й шаг. 54 = [2(21>г-^]' = 2(2л + ^1
или
4-й шаг. Подставляем во вторую производную вместо аргу-
мента г его критическое значение (г). Получаем -
3 Г v
ПРИ Г==У 24’
3 /V
Следовательно, при г — ~\/ функция имеет минимум.
236
Это значит, что при заданной емкости (и) наименьшую полную
поверхность имеет7 такой цилиндрический сосуд, радиус основа-
ния которого определяется по формуле (г).
Высоту этого сосуда найдем, подставив в формулу (в) вместо
г его’ значение. Получаем
Сопоставление равенств (г) и (д) приводит к равенству
h = 2r.
Итак, чтобы при любой заданной емкости v с наименьшей
затратой материала сделать цилиндрический сосуд, закрытый
сверху и снизу, надо высоту его взять равной диаметру осно-
вания.
Пример 3. Исследовать на максимум и минимум функцию
/(x) = sin2x в промежутке (0; 2л).
Решение. 1-й шаг. f' (х) = 2 sin xcosx = sin 2х.
2-й шаг. sin2x —0; 2х = лм; х = |-п, откуда при n = Р, 2‘, 3
получим (табл. 20):
ГС 3
*1 = 2 > = =
3-й шаг. /’(x) = cos2x(2x)x = 2cos2x.
4-й шаг. /* Qj=2cos2-y =?=2cosit==2.(—1)<0;
f (rt) = 2cos2ic = 2-(+l)>0;
/’ itj = 2 cos 2 j л = 2 cos (2л -f- л) = 2 cos л < 0.
Таблица 20
X /' (х) /” <Х| Заключение / U)
ТС 2" 0 — Максимум 1
тс 0 + Минимум 0
3 2 « 0 — Максимум I 1
237
В заключение находим максимальное и минимальное значения
функции. Получим:
= sin2|- = l;
Z/inin == f (тс) =: sin" К = О,
= = sin2| -к —(—1)2= 1.
§ 87. ОСОБЫЙ ТИП ЭКСТРЕМУМА ФУНКЦИИ
При выводе правил нахождения экстремума функции мы предполагали,
что данная функция y=f(x) имеет непрерывную производную f (х), обра-
щающуюся в нуль при определенных значениях аргумента, называемых
критическими. Существуют непрерывные функции, которые имеют экстремум
и при таких значениях аргумента, при которых производная обращается
в бесконечность.
Возьмем, например, функцию у*=-у/гх3, рассмотренную в § 63 (см.
рис. 114). Эта функция непрерывна в любом промежутке. При х = 0 она
не имеет производной: f (0) — оо. По графику видим, что х = 0 является
точкой минимума. В этом легко убедиться и не пользуясь чертежом (см. § 83,
определение 2):
/(0)</(0 + й),
так как
/ (0 + Л) = /(0 + Л)3 = //F > 0.
Возникает вопрос: каковы признаки существования экстремума при
таких значениях аргумента, при которых непрерывная функция у — f (х)
производной не.имеет?
Предположим, что кривая EF (рис. 137) является графиком непрерывной
функции y = f(x). Касательные к этой кривой в точках х = а, х — Ь и х — с
перпендикулярны к оси Ох (см. § 62):
f (а) = lim tg = оо, f (fi) = со и f (с) = со.
а-0 \4 /
При х = а данная функция, очевидно, имеет максимум, прих = с —
минимум, при х — Ь не имеет ни максимума, ни минимума.
238
При значениях х, немного меньших а, функция возрастает, а при значе-
ниях, немного больших а, она убывает и поэтому
/(а-Л)>0,/(в + ЛХО,
где h — малое положительное число.
При значениях аргумента х, немного меньших с, данная функция убывает,
а при значениях, больших с, она возрастает.
Следовательно,
f (с - й) < 0, f (с + й) > 0.
При значениях х, немного больших и меньших й, функция возрастает.
При переходе аргумента через значение х = Ь производная знака не меняет:
/' (й - й) > 0 и f (Ь + й) > 0.
Результаты получаем в виде таблицы (табл. 21).
Таблица 21
X /' (X — Л) Г (х) Г (х + Л) Заключение / (X)
а + со — Максимум
й + со + Ни максимума, ни минимума
с —- со + Минимум Ут^Н')
Итак, при значении аргумента, при котором производная f (х) не
существует (обращается в бесконечность'}, непрерывная функция у—f (х)
имеет экстремум, если при переходе аргумента через это значение произ-
водная меняет знак.
Порядок исследования функции на максимум и минимум с учетом кри-
тических точек, в которых производная обращается в бесконечность, указан
в решении следующего примера.
Пример 1. Исследовать на максимум и минимум функцию
2
Л’=/(х) = (х-5)а(х-1)* 3.
Решение. 1-й шаг. Находим производную данной функции:
2 2--1
y’x=f(*) = (*-I)3 -2 (х -5) + (х— 5)а-~(х - I)3 =
= 2 (х - 5) -У(х - I)2 + 21^=^ =
з j/ х — 1
_ 2 • 3 • (х - 5) у<(х- I)3 • у^х- 1)+ 2 (X - 5)а
3 — 1
= 6(х —5) (х- 1) + 2(х-5)а _ 2 (х - 5) [3 (х - 1) + (х - 5)] =
3 у'х - 1 3 у^хСГТ
_ 2 (х - 5) (4х - 8) _ 8 (х-5) (х — 2)
3 yCv — 1 Зу^х—1
Итак,
/(х)=^Д^2). (а)
3 у х — 1
239
2-й шаг. Приравниваем нулю производную и находим корни получен-
ного уравнения:
8 ~ = 0; 8 (х - 5) (Л- - 2) = 0;
3 у х — 1
х — 2 = 0, xt = 2; х — 5 = 0, х., — 5.
3-й шаг. Ищем те значения аргумента, при которых производная обраща-
ется в бесконечность. Если /'(х)=оо, то величина,
должна быть равна нулю. Получаем
его выражением (а), будем иметь
уравнение
1
Г (а)
ей обратная,
= 0. Заменив
1
Г (А)
Г (А)
1
8(х-5) (х-2)_0
3 у^х — 1
Зг^х~1
-----------=0.
8 (х — 5) (х — 2)
Решаем это уравнение: 3-|/ .v — 1 = 0; j/ х — 1=0; х —1=0; х=1.
Итак, производная данной функции при х — 2 и х = 5 обращается
в нуль, а при х = 1 — в бесконечность. Располагаем эти значения аргумента
в возрастающем порядке (табл. 22) и ведем дальнейшее исследование, как
указано в § 85.
Таблица 22
X /' (х — II) f (X) Г U + A) Заключение / (-< )
1 со + Минимум 0
2 + 0 Максимум 9
.5 0 . + Минимум 0
4-й шаг. Определяем знаки производной при значении аргумента,
немного меньшем каждого критического значения и немного большем этого
критического значения:
/< -»)=/•(») = 8 <°-?>±72) =8-<=^а<»;
Г0 + »)=Г (1+1) = V--
f (2 — h) =f (2 — 2 j =f > 0 (CM- выше);
f (2 + h) =f (3) =8 (3 < o;
f (5 — h) —f (4) < 0 (см. выше);
f (5+h) =/ (6)=8(6~Д£~-^- > о.
3 -у о — 1
* Вместо h можно взять только
ряется неравенство 1 -j- h < 2.
** Следует взять h таким, чтобы
такое число, при котором удовлетво-
удовлетворялось условие 2— Л>1.
240
Теперь можно найти максимальное и минимальное значения функции.
Получим
-Vmin=/(1)
5)3 (1 - 1)' =0;
2
=/(2) = (2 - 5)3 (2 - I)3 = 9 • 1 = 9;
2
Лип =/(5) = (5 - 5)2 (5 - I)3 = 0.
На основании результатов этого исследования
построить график этой функции (рис. 138).
Пример 2. Исследовать на максимум и
минимум функцию у — д/~х.
можно приближенно
Решение. 1-й ш а г. у'х
2-й ш а г.
0.
_1 -з 1
~з/.7
Это уравнение корня не имеет, следо-
вательно, производная нигде в нуль не об-
ращается.
3-й щ а г. Ищем значение аргумента, при котором производная обращается
в бесконечность. Для этого пишем
У
Рис. 139
уравнение вида у,~ — 0. В данном слу-
чае получим/х3 = 0, откуда х = 0.
4-й шаг. /'(0 —/;)=/'(—1) =
= 1 т. = у>0;
3/(0- I)3 3
/(0+4)=П1)-гт=
При переходе аргумента через
значение д==0 производная знака не
меняет, следовательно, при х — 0 данная функция не имеет ни максимума,
ни минимума.
При х = 0 и у = -^/~0 — 0. В точке (0; 0) график этой функции имеет
касательную, совпадающую с осью Оу, так как /'(0)=оо. График этой
функции будет иметь вид, показанный на рис. 139.
§ 88. ВЫПУКЛОСТЬ И ВОГНУТОСТЬ КРИВОЙ
Если две линии y = f(x) и у = <р(х) (рис. 140) в рассматри-
ваемом промежутке (а; Ь) располагаются так, что ордината любой
точки первой из них, например, точки М^[х; f(x)], больше орди-
наты соответствующей точки Л41 [х; ф (х)] второй, то говорят, что
241
в этом промежутке первая кривая y = f(x~) выше второй кривой,
или вторая линия у — ниже первой.
Определение 1. Кривая y = f(x) называется выпуклой
в промежутке (а; Ь), если она лежит ниже касательной, проведен-
ной к этой кривой в любой ее точке М [х; f(x)], абсцисса кото-
рой удовлетворяет условиям а<^х<^Ь (рис. 141).
Определение2. Кривая y — f(x) называется вогнутой в про-
межутке (а; Ь), если она лежит выше касательной, проведенной
к этой кривой в любой ее точке 'М [x; f (х)], абсцисса которой
удовлетворяет условиям а<^х<^Ь (рис. 142).
Займемся установлением признаков, позволяющих судить
о выпуклости или вогнутости кривой в некотором интервале (а; Ь).
Положим, что кривая EF (рис. 143) является графиком функции
y = f(x)*. Возьмем на выпуклой дуге АВ ряд точек Pt, Pt, Р3,
Р1г Рь так, чтобы одна из них (Р4) была наивысшей точкой этой
* Предполагается, что данная функция y—f(x) имеет в любом рассмат-
риваемом промежутке непрерывную первую производную у'х и непрерывную
вторую производную у“х.
242
дуги. Обозначив абсциссы этих точек соответственно через хь х1г
х3, Xi, х3, будем иметь
xi<x2<x3<x4<x8. (а)
Проведем к кривой в этих точках касательные PtTt, Ря1\,...
Эти касательные с положительным направлением оси Ох образуют
di, а3, а4, а3.
углы
Из рисунка видно, что
следовательно,
<Х1>аа>аз>“0,
tg ai>tgaa>tga3>0.
(б)
Угол а3— тупой. Тангенс тупого угла — величина отрицатель-
ная:
0>tga8. (в)
Из неравенств (б) и (в) следует:
tgai>tga2>tga3>0>tgas. (г)
Нам известно (см. § 62), что
tgai = f(^i). tga2 = r(x2), tga3 = /'(x3),
tga4 = 0 = f Сч), tgas = /'(x3).
Поэтому неравенства (г) можно переписать так:
Г(х1)>Г(^)>/,Ы>7'иО>Л(^). (д)
Неравенства (а) и (д) показывают, что в интервале (а; Ь)
большему значению аргумента х соответствует меньшее значение
первой производной f'(x).
Следовательно, в интервале выпуклости (а; Ь) кривой функция
/' (х) убывает (см. § 82), а потому ее производная [/' (х)]^ (см. в § 82
243
признак 2 и рис. 136), т. е. вторая производная функции у = f (х),
отрицательна: /" (х)<^0.
Положим далее, что нам дана функция y = f(x), график кото-
рой в промежутке (а; Ь) вогнут (рис. 144). Возьмем на дуге АВ
точки Plt Р2, Р-А, Pt так, чтобы одна из них (Р2) была наинизшей
точкой этой дуги. Обозначив абсциссы этих точек соответственно
через Xi, Xi, xit х4, будем иметь
, Xl < Х2 < Л'з < Xi.
Проведем к кривой (к графику данной функции) в этих точках
касательные PiT\, Р27’а,... .' Эти касательные с положительным
направлением оси Ох образуют углы
а1( а2 = 0, а3, а4.
Из рисунка видно, что 0<^а3<^а4, вследствие чего получаем
0<tga3<tga4.
Угол а4 — тупой и потому 1
tga4<0.
Из этих неравенств следует:
tg«l<0<tgO3<tga4. (е)
Мы знаем (см. § 62), что
tgai = r(Xi), tga2 = 0 = /'(X2);
tga3 = /'(x3), tga4 = f(x4).
Поэтому неравенства (е) равносильны неравенствам
Г (Xi) <J' (х2) <J' (х3) <J’ (Xi).
244
Следовательно, в интервале вогнутости кривой у = f(x) функ-
ция [' (х) возрастает, а потому ее производная (см. в § 82 приз-
нак 1), т. е. вторая производная данной функции, положительна:
Г(х)>0.
Таким образом, получаем следующие признаки выпуклости
и вогнутости кривой:
1. Кривая у—.[(х) выпукла в интервале (а; Ь), если при всех
значениях аргумента х, заключающихся между а и Ь, вторая
производная f (х) отрицательна.
2. Кривая y = f(x) вогнута в промежутке (а; Ь), если при
всех значениях аргумента х, заключающихся между а и Ь, вторая
производная f" (х) положительна.
Пример 1. Показать, что кривая
у = х2 — 2х — 2^ вогнута в любом
промежутке.
Решение. Найдем вторую про-
изводную функции:
Ух —— щ X 2, ухх — 2~ •
Вторая производная при любом
значении аргумента х положительна:
ухх = L0, следовательно, эта кривая вогнута повсюду (—оо
<^оо). Кривая изображена на рис. 145 (см. решение примера
2, § 85).
Пример 2. Показать, что кривая у =
==-— g-x2—|—х—— l.j выпукла в любом
промежутке.
Решение. Находим вторую произ-
водную функции:
1 1 - 1
Ух = — 4^+1; Ухх = — 4-
Вторая производная отрицательна при любом х:
Ухх = -^<0,
следовательно, эта кривая выпукла повсюду (—оо<^х<^оо)
(рис. 146).
Пример 3. Дана кривая
У = ^-х3 — х2.
Определить: 1) интервал, в котором эта кривая выпукла;
2) интервал, в котором она вогнута.
245
Решение. Находим вторую производную:
у'х^х1 — 2х; ухх = 2х — 2.
Кривая выпукла при таких значениях х, при которых вторая
производная отрицательна. Получаем неравенство
Решив неравенство, находим х<4. Это значит, что кривая
выпукла при значениях х, удовлетворяющих условиям —;оо<^
<л 1-
Нам известно, что кривая вогнута при таких значениях аргу-
мента, при которых вторая производная функции, графиком
Рис. 147
которой она является, положи-
тельна.
Имеем неравенство 2х — 2^>0.
Неравенство удовлетворяется при
значениях х, больших единицы
(х>1). Следовательно, кривая
вогнута в интервале (Г, со).
Из результатов этого иссле-
дования можно усмотреть, что на
кривой у=т!-Л':| — х2 (рис. 147)
имеется точка (1; —1, отделяющая участок выпуклости от
участка вогнутости.
§ 89. ТОЧКА ПЕРЕГИБА
Мы видим (пример 3, рис. 147), что на кривой у = -|-х3— х2
имеется точка А 11; —д), отделяющая дугу, находящуюся на
участке выпуклости, от дуги, находящейся на участке вогнутости.
Такая точка называется точкой перегиба.
Определение. Точка кривой, отделяющая участок выпукло-
сти от участка вогнутости, называется точкой перегиба.
Займемся теперь установлением признака, по которому можно
было бы судить о существовании точки перегиба. Положим, что
кривая, изображенная на рис. 148, является графиком функции
У = /(*)•
Согласно определению, точки В и С, абсциссы которых обо-
значены через b и с, являются точками перегиба. Заметим, что
в этих точках (В и С) кривая пересекает касательную, переходя
с одной ее стороны на другую. Часть АВ этой кривой, распо-
ложенная влево от точки В, вогнута. Известно, что кривая
y = f(x) вогнута при таких значениях х, при которых вторая
246 ,
производная положительна. Значит, прих = й— h, где h — произ-
вольно малое положительное число, будем иметь неравенство
Г(Л-й)>0. (а)
Дуга ВС выпукла. Поэтому (см. § 88) при любом достаточно
малом положительном h будет удовлетворяться неравенство
f'(b + h) <0. (б)
Из (а) и (б) следует, что при переходе х через значение
х = Ь вторая производная меняет знак с плюса на минус. В § 80
было установлено, что непрерывная функция меняет знак при
переходе аргумента через такое значение, при котором эта функ-
ция обращается в нуль. По нашему предположению, f (х) —•
непрерывная функция от х. При переходе х через значение
х — Ь эта функция [/" (х)] меняет знак с плюса на минус. Сле-
довательно, при х = Ь вторая производная обращается в нуль, т. е.
/"W = o.
Аналогичным путем можно доказать, что при х = с вторая
производная обращается в нуль и при переходе аргумента х
через это значение меняет знак с минуса на плюс, т. е.
Г(С)=0,/’(С-/1)<0.и/'(с+/1)>0
при любом достаточно малом положительном h.
Эти рассуждения приводят нас к следующему признаку суще-
ствования точки перегиба: если при некотором значении аргумента
х (например, при х = Ь) вторая производная функции у = [(х)
равна нулю и при переходе аргумента через это значение меняет
знак, то при х — Ь график этой функции имеет точку перегиба.
Из изложенного выше следует правило нахождения точек пере-
гиба кривой.
1-й шаг. Находим вторую производную функции.
2-й шаг. Приравниваем нулю вторую производную и решаем
уравнение f" (х) — Q. Допустим, что в результате решения этого
уравнения получено: хх = а, х^ = Ь, х3 = с.
247
3-й шаг. Определяем знак второй производной при х — а— h
и при х = а-\-1г. Если при переходе аргумента через значение
х = а вторая производная меняет знак, т. е. если /" (а — ft)4>0
и f" (a -j- ft) <4 0 * или f (а — ft) О и f (а -ф- ft) ~^> О, то при х = а
график функции y — f(x) имеет точку перегиба.
Точно так же ведется исследование и дальше (при х — b и
при х — с).
Замечание. По этому правилу могут быть найдены точки
перегиба кривой y — f(x), когда функция /(х) имеет непрерывную
первую производную и непрерывную вторую производную. Суще-
ствуют такие непрерывные функции, графики которых имеют
перегиб при значениях аргумента х,. при которых и первая
и вторая производные обращаются в бесконечность. Ниже в каче-
стве примера такой кривой будет рассмотрен график функции
у = -у/ х — 2 (см. пример 3).
Пример 1. Найти точки перегиба кривой у = х3— 4х.
Решение. 1-й шаг. Находим вторую производную функции
/(х) = х3 —4х;
получаем:
f' (х) = Зх'2 — 4; /" (х) = 6х.
2-й ш а г. 6х = 0; х = 0.
3-й шаг. f (0-ft) = f'(—1) = 6-(—1)<0;
f (0-|-Л) = Л(1) = 6-1 >0. "
При переходе аргумента через значение х = 0 вторая произ-
водная меняет знак, следовательно, при х = 0 существует точка
перегиба. Подставив в данное уравнение вместо х корень урав-
нения fr(x) — O, находим ординату точки перегиба:
1/т.пер = о3 - 4 - 0 = 0.
Итак, кривая у — х3— 4х имеет перегиб в точке (0; 0).
Пример 2. Найти точки перегиба кривой у —
Решение.
1-й шаг.
г/; = /'(х) = 4[(1 + т; = -(Г^р;
о[ X Т „ (1 4-х2)3-1 — х-2(1 +х2)-2х
_ 8 (1 4-х2)(14-х2-4х2)_8(Зх2-1)
(14-х2)4 (1 4-ха)“ •
* Здесь под Л можно разуметь любое число, при котором выполняется
условие а 4~ Л < Ь.,
248
2-й шаг.
8(3x3-l) n. о ’ i n. /З №
(14-х2)1 — °’ Зх 1—0, Xi— 3 ; Х2 — .. .
3-й шаг. Полагая ——ht = —1 и —^-4-й.2==0, имеем:
о О
\ 3
1 \ 3
. Л2 _ 1
= f(0) = 8.2-2_—-<<0.
При переходе х через значение х = — вторая производная
кз
меняет знак, следовательно, при х = — х__ существует точка
перегиба. Абсцисса ее нам уже известна. Найдем ординату:
/ т/з \ '
Этой точкой I — А*-; 31 часть кривой, находящейся на уча-
Г / /зГ
стке вогнутости в промежутке —оо; —Аг* , отделяется от
L \ о i
части, находящейся на участке выпуклости:
/"(Хр— ^ = 7”(0)<;0 (см. выше);
Полученный результат показывает, что при переходе х через
/Т
значение х = -^~ вторая производная меняет знак с минуса на
плюс. Это значит, что точка (Хк; 3 j отделяет часть кривой,
находящейся на участке выпуклости, от части, находящейся на
участке вогнутости (см. рйс. 109). -
Пример 3. Найти точку перегиба кривой у — у^х — 2.
Решение. Эта функция непрерывна при любом х. Находим
первую и вторую производные функции:
1
f (х) = Ух^2 = (х — 2) ’;
f(x) = |(x-2f'5;
Г _ 2 Т _ 4
г w=> - ч Ч=А (-1) (х - 2Гт=- 9-yi=.
249
Ни при каких конечных значениях х вторая производная
в нуль не обращается, но при х— 2 — 0 или при х = 2 она
обращается в бесконечность. При этом для значений х, меньших
2, вторая производная положительна:
/" (2 — й) = /" (1)
2 _ 2
9^(1 -2)*~
а при х^>2 она отрицательна:
Г(24-/1)=Г(3) = -
2
9
2
Это значит, что левее точки х = 2 эта кривая вогнута, правее
(при х^>2)— выпукла. Очевидно, что точка (2; 0) является
точкой перегиба. В этой точке кривая имеет
касательную, перпендикулярную оси Ох:
1
на
/г = /'(2)_ _____
3у (2 - 2)
Примерный график этой функции см.
рис. 149.
§ 90. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
В курсе элементарной математики, а также в гл. II этой
книги вы занимались построением графиков по точкам. Этот
способ построения графиков имеет ряд существенных недостат-
ков, из которых укажем следующие:
1) чтобы получить график, по которому можно судить о ходе
изменения функции в промежутке ее существования, надо вычис-
лить координаты большого числа точек;
2) невозможно точно выявить характерные особенности гра-
фика функции: точки экстремума, точки перегиба и направление
выпуклости в любом малом промежутке.
Изучив ход изменения функции с помощью первой и второй
производных, мы имеем возможность строить графики функций
более совершенным способом и значительно точнее, пользуясь
результатами исследования на максимум и минимум и находя
точки перегиба. В предыдущих параграфах в непосредственной
связи с теорией было построено много графиков. Теперь подве-
дем итоги и укажем план, которого следует придерживаться
при построении графика данной функции y = f(x).
1. Определить промежуток существования функции.
2. По правилу, изложенному в § 85, найти те значения аргу-
мента х, при которых данная функция имеет экстремум, и, вычис-
250
лив соответствующие значения у, построить эти точки и неболь-
шие части графика вблизи этих точек.
3. По правилу, изложенному в § 89, найти координаты точек
перегиба, если они имеются, и построить их.
4. Определить, если это возможно, и построить точки
пересечения графика с осями координат.
5. Если функция существует в любом промежутке (— оо; оо),
найти lim у и lim у.
X —> — СО X—* -|-ОЭ
6. Все отмеченные элементы графика соединить плавной кри-
вой и продолжить ее, учитывая ход изменения у при х->— оо и
при х->-|-оо.
Для большей точности полезно в «сомнительных местах» по-
строить отдельные точки, вычислив их координаты, пользуясь
уравнением кривой.
Пример 1. Построить график функции
у~ 4-х3 — х3—Зх.
J з
Решение. 1) Эта функция существует в любом промежутке.
2) Исследуем ее на максимум и минимум:
1-й шаг. гД = х9 —2х— 3. _____
2-й шаг. х2 — 2х — 3 = 0; x)2= 1 ±1 -ф-3 = 1 ±2;
Xi = — 1, х2 = 3.
3-й шаг. f"(x) = 2x— 2.
4-й ш а г. /" (—1) = 2 • (—1) — 2 <0;
f (3) = 2-3 — 2>0.
Следовательно, при х = — 1 данная функция имеет максимум,
а при х = 3 —минимум (табл. 23):
//тах = |-(-1)3-(-1)3-3.(-1)=1|;
//гп,п = 4-33-32-3-3=-9.
О
Таблица 23
X /'W /" м Заключение f(x)
—1 0 — Максимум . 2 . ^max з
3 0 + Минимум
/ 2 \
Строим точки —1; 1 v и (3; —9) и небольшие части гра-
У о J
фика вблизи этих точек, учитывая, что точка максимума
251
(— 1; 1 — на участке выпуклости, а точка минимума (3; —9) —
на участке вогнутости (рис. 150, а).
3) Находим точку перегиба, решив уравнение f"(x) — O.
Получаем:
2х —2 = 0; х=1, z/T.nep = l • 13-12-3-1 = —
На рисунке эта точка А 1; — 3 v отмечена маленьким кружком.
\ и /
4) Находим точки пересечения графика с осью Ох, решив
совместно уравнения:
х = 0; у — —г1 — х‘2 — рх.
Получаем:
4 х' — х2 — Зх = 0; х (х2 — Зх — 9) = 0;
О _
V, 2 2 ,
43U-l,8;x, = i+r®~4,S
(на рисунке эти точки отмечены крестиками).
5) lim у = lim (4 — 3x4 = lim х3 (4 —
Х—г— СО X -»—СО\ ! X— СО \ ’Э %
вой и продолжаем ее влево от точки
lim-у=( lim х')3- lim (4~V-Д) = (+ °°)3-4== + °°-
Л'- + сс , (л-- + оэ ] XX) а
6) Все отмеченные элементы графика соединяем плавной кри-
3-/45 3
—; 0 I и вправо от
/3 + /45 п\
точки (—; 01, учитывая, что
lim у — — оо, lim у — -/ со (рис. 150,6).
j X -*• — СО Л’-*--^03
252
Пример 2. Построить график функции y = f(x) = -^x(x— 4)3.
Решение. 1) Эта функция существует в любом промежутке
(—с°; +°о)-
2) Исследуем ее на максимум и минимум:
у; = /'(х) = 1[(х-4)3-1+^-3(х-4Л =
=1(х-4)2(х-4 + Зх) = |(л:-4)3(4х-4) = А(х_4)^(х_1);
4 (* — 4)9(х—1) = 0; (х-4)9 = 0; х—1=0;
Xi= 1; х2 = 4;
• Г(х) = 4[(х-4)М + (х-1).2(х-4)] =
= 4(х-4)[х-4 + 2(х-1)] = 4(х-4)(Зх-6) =
= 4(х-4)(х-2);
/"(1) —4(1 — 4)(1 — 2)>0; z/min = 4- 1 (1 — 4)3 = —3;
/" (4) = 1 (4 - 4) (4 - 2)3 = 0.
Вопрос остается нерешенным. Исследуя знак первой произ-
водной, находим/'(4 — /г)2>0 и f h)^>0, т. е. в точке х = 4
нет ни максимума, ни минимума (табл. 24).
Строим точку (1; —3) и небольшую дугу кривой вблизи этой
точки, учитывая, что дуга должна быть вогнута (рис. 151, а).
3) По правилу, изложенному в § 89, находим точки перегиба.
Для этого в первую очередь находим корни второй производной:
/"(х) = 0; 4(х-4)(х — 2) = 0; х2 = 4, х3 = 2;
/" (4 — й) = /"(3) = 4 (3 — 4) (3 — 2) <0;
Г (4 + Л) = /" (5) = А (5 - 4) (5 - 2) > 0.
, 253
Таблица 24
X /' U ) f" U) Заключение /W,
1 0 + Минимум v — — 3 -'ПШ1
4 0 0 Ни максимума, пи ми- нимума, точка перегиба
В точке х = 4 вторая производная равна нулю и меняет свой
знак с /тлюса на минус, значит в этой точке кривая имеет перегиб.
/"(2 —Л) = /"(1) = 4П —4)(1 — 2)>0;
Г (24-Л) = /"(3) = 4(3 —4)(3 —2)<0.
Следовательно, точка с абсциссой, равной 2, есть точка пере-
гиба. Находим ординаты точек перегиба и строим эти точки
(на рисунке они показаны кружками):
^ = /(4) = 1.4-(4-4)а = 0; (4; 0);
й = Н2) = 42-(2-4)3 = -^; (2; —1-1).
4) Находим точки пересечения графика с осью Ох, решив
совместно уравнения:
г/ = 0, г/ = |.г(л-4)3.
Получаем: х = 0, х = 4. Одна из этих точек (4; 0) уже по-
строена на чертеже, а другая является началом координат (0; 0).
5) lim у = ± lim х(х— 4)3 = -i- lim x4fl— 4 =
= 7г( lim х)4• Г lim (1 — 4Т=4 • (— оо)4- 13 = + оо;
lim у — • (4- оо)4 • 1 = -j- оо.
х -> со -У • •
6) Все отмеченные элементы графика соединяем плавной кри-
вой, учитывая, что в промежутке (—оо; 2) кривая вогнута, в про-
межутке (2; 4) выпукла и в промежутке (4; -|-оо) вогнута
(рис. 151, б).
д-2 _ |
Пример 3. Построить график функции у= 8 , ,
А ”Г 1
Решение. 1) Эта функция непрерывна в любом промежутке.
254
. . (Xs + 1) • 2х — (х9 - 1) • lx _ 4х
W— (.r94-l)2 — (x9 + l)9*’
fW=O; cfw=0: 4x=0> x=0:
f и _ 4[(х2+1)9-1-х-2(х9 + П-2х] _
1 (x2 + l)4
_ 4(aj+1)[(a4-1)-Ia--] 4(1 — 3x9).
(x9 + 1Г — (.v9 + l)’ ’
p. 4(l-3.0a)
При x = 0 данная функция имеет минимум. ym-,n = /70) =
Л2 _ 1
= ^-р-Г = —1. Строим точку (0; —1) и небольшую дугу кривой
вблизи этой точки, учитывая знак второй производной (рис. 152).
3) Находим точки перегиба, решив уравнение /" (х) — 0. В дан-
ном случае
4(1-Зх9)_п
(х9+1)3
получаем:
i/1,2 —
- з
(О,-П
Рис. 152
Так как f"(x) в точках х = ±Х^ меняет знак, то данная
Уз
кривая имеет перегиб при х = ±4-д-. На рисунке эти точки
Г/ /Т 1 \ //з 1V
I — —-yl и Ну-;—Ji показаны кружками.
показаны кружками.
4) Находим точки пересечения кривой с осью Ох:
% ~ y = 0; х2—1=0; Xi = 1, х2 =—1.
На рисунке эти точки (—1; 0) и (1; 0) показаны крестиками.
2/. '\
д;-3 I J — _- I
5) lim w= lim Л, ~~ ‘ = lim —7-----------=
' и Г- —4— I / I \
V ь. -+~ v ь. -4- /-/•. 1 1 V —» -Ь- гн _ .9 / 1 I 1 \
1 -~
= lim ---Т= 1-
х -> ± со 1 I
п X3
Прямая линия у—1 является асимптотой данной кривой
(см. § 33).
255
6) Соединяем все отмеченные элементы графика плавной кри-
вой и продолжаем ее в обе стороны (влево и вправо), учитывая,
что при х — ±оэ она неограниченно приближается к прямой
У=1- '
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Какой смысл имеет выражение «функция y—f(x) возрастает в про-
межутке (a; i)»?
2. Как следует понимать выражение «функция y—f(x) убывает в про-
межутке (a; ih?
3. Как изменяется функция y=f(x) в промежутке (а; Ь) (убывает или
возрастает), если при любых значениях аргумента х, заключающихся между
а и Ь, се первая производная поло-
жительна?
4. Как изменяется функция
у=/(х) в промежутке (а; 1>), если
при любых значениях аргумента х,
заключающихся между а и Ь, ее
первая производная отрицательна?
5. Как следует понимать' выра-
жение «при данном значении аргу-
мента функция имеет: 1) максимум;
2) минимум»?
6. Как находятся те значения
аргумента, при которых данная функ-
ция y — f(x) может иметь экстре-
мум?
7. Для того чтобы утверждать,
что при данном значении аргумента
функция y=f(x) имеет экстремум,
достаточно ли знать, что при этом
значении х первая производная этой
функции обращается в нуль?
8. Какое значение аргумента на-
зывается: 1) точкой максимума; 2) точ-
кой минимума?
9. Какие значения аргумента при-
нято называть критическими?
10. Если данная функция имеет
несколько экстремумов (не меньше
ли случиться, что какой-нибудь максимум окажется меньше
непрерывная функция имеет один максимум и один минимум,
трех), может
минимума?
11. Если
может ли минимум оказаться больше максимума? (Если"нс можете ответить
, сразу, постройте график произвольной функции, удовлетворяющей условиям
вопроса.)
12. Сформулируйте правило нахождения максимума и минимума с по-
мощью первой производной.
13. Как изменяется угловой коэффициент касательной (убывает или воз-
растает) к графику функции y=f(x) в точке М (рис. 153, а), если эта точка,
перемещаясь по кривой, последовательно занимает положения Л1(, Л42, М3, Л1,?
14. Как изменится производная функции у— fix] (рис. 153, б), когда
аргумент х, непрерывно возрастая, переходит от значения, равного числу а,
к значению, равному числу Л?
15. Какой знак имеет вторая производная функции у—/(xj (рис. 153, б)
при значениях аргумента, заключающихся между а и й?
256
16. Какой знак имеет вторая производная функции .у =/(л) (см. рис. 153, а)
при х = ОМ!?
17. Если при данном, значении аргумента х первая производная функции
обращается в нуль, то какой знак должна иметь вторая производная, чтобы
при этом значении аргумента данная функция: 1) имела минимум; 2) имела
максимум?
18. Сформулируйте правило нахождения экстремума функции с помощью
второй производной.
19. Как установить существование экстремума в случае, когда при неко-
тором значении аргумента и первая и вторая производные исследуемой функ-
ции обращаются в нуль?
20. При каких значениях аргумента х график функции y=f(x) имеет:
1) участок выпуклости; 2) участок вогнутости?
21. Что называется точкой перегиба?
22. Как располагается дуга графика функции, находящаяся на участке
выпуклости, относительно касательной, проведенной в любой точке этой
дуги?
23. Как располагается часть кривой вблизи точки перегиба относительно
касательной, проведенной в этой точке?
24. Если известно, что функция j'=/(.v) возрастает в промежутке (я, Ь),
можно ли утверждать, что при любых значениях аргумента х, удовлетво-
ряющих условиям acxcb, первая производная этой функции положи-
тельна?
Ответы.
И. Не может. 13. Убывает, переходя при х = 0М'3 через нулевое значение.
14. Возрастает. 15. Плюс (см. § 86). 16. Минус. 17. 1) Плюс, 2) минус.
19. Исследовать с помощью первой производной. 20. При таких значениях ,х,
при которых: 1) /"(х)<0, 2) f (х) > 0. 23. Пересекает касательную.
24. Нельзя: в этом промежутке может быть такое значение х, при котором
Г(х) = 0.
Глава IX
ДИФФЕРЕНЦИАЛ ФУНКЦИИ
§ 91. СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИН
В § 49 мы видели, что отношение двух бесконечно малых
величин может быть величиной: 1) бесконечно малой, имеющей
своим пределом нуль (пример 9); 2) бесконечно большой (пример 10)
и 3) ограниченной, имеющей своим пределом число, отличное от
нуля (пример 8). Уясним смысл каждого пз этих трех случаев.
Пусть нам дано: а —х-, $=х3, у = 2х, 8 = ^х. При х —0 пере-
менные величины а, fl,'(и 8, очевидно, будут бесконечно малыми. Бу-
дем давать аргументу значения х= 0,1; 0,01; 0,001; .... приближаю-
щиеся к пулю. Тогда а, 3, ~( и 3 будут последовательно принимать
значения:
а = х'2 = 0,0Г, 0,0001; 0,000001; ... (а)
р ==хз = 0,001; 0,000001; 0,000000001; ... (б)
7 = 2х = 0,2; 0,02; 0,002; ... (в)
S = ^x = 0,05; 0,005; 0,0005; ... (г)
9 И. Е. Агачев
257
1) Из сопоставления (б) и (а) можно усмотреть, что р стре-
мится к нулю «гораздо быстрее», чем а. При этом — — 0, или
В х3
lim — — lim = lim у—n
Л- —0 “ х-0х" Л-0
В этом случае говорят, что бесконечно малая р более высокого
порядка малости, чем а.
2) Из сопоставления (в) и (а) видно, что бесконечно малая у
стремится к нулю «гораздо медленнее», чем а. При этом — —.оо, или
. т ,. 2х ,. 2
lim lim — = lim —=оо.
Л — 0 а л О Л х О х
В этом случае говорят, что 7 — бесконечно малая величина
низшего порядка малости по сравнению с а.
3) Из сопоставления (в) и (г) видно:
lim 1 = lim =4.
О 1
х -» 0 х -»0 2'^
В этом случае сравниваемые величины называются беско-
нечно малыми одинакового порядка.
Итак, можно сделать следующие определения:
Определение 1. Если а и р — бесконечно малые величины
и lim-|- = 0, то р называется бесконечно малой высшего порядка
малости, чем а..
Определение 2. Если а и бесконечно малые величины
и lim-|- = oo, то р называется бесконечно малой низшего порядка
малости, чем а..
Определение 3. а и р называются бесконечно малыми
одинакового порядка, если предел их отношения равен числу, отлич-
ному от нуля, т. е. если
lim = где а Ф 0.
Определение 4. Бесконечно малые величины а и р назы-
ваются эквивалентными, или равносильными, если предел их отно-
шения равен 1, т. е. если
1 lim —=1.
а
Пример 1. Показать, что при х—>0 величина х1— Зх34~5ха
бесконечно малая высшего порядка малости, чем х.
Решение.
' Пт ~ 3x3 + 5л'~ — Пт х“ ~ Зх + 5) _
х х — 0 х
= lim х (ха — Зх 5) - lim х • lim (х2 — Зх 5) = 0 5 — 0.
Л -. О х ->-0 X -fO
258
Следовательно, xl— Зх3-[-5х2 при х—>0 — бесконечно малая
величина высшего порядка малости, чем х (см. определение 1).
Пример 2. Показать, что при х—> 0 sinx есть бесконечно малая
низшего порядка по сравнению с 1 — cosx.
Решение.
sin v 2 sin "2 cos У t
lim j———= lim -----------;—= lim ctg4y = oo (см. определение 2).
.v — 0 cos x X — 0 2 sin2 — x — 0 2
Пример 3. Показать, что при х —-О бесконечно малая вели-
чина tg3x имеет одинаковый порядок малости с х.
Решение.
lim = ^-f^ lim -—
t q x , q COS
,. 3 sin 3x
= lim
x — 0
sin Зх ,. sin Зх
= lim----------
х — О х
____1
cos 3x
Зх
• lim ——
v _ о COS Зх
= 3 lim —-y—— • 4-= 3 • 1 • 1 =3 (cm. §71).
x - 0 6X 1
Предел отношения tg3x к x при x —О равен числу, отличному
от нуля, следовательно (см. определение 3), tg3x и х — бесконечно
малые одинакового порядка.
Пример 4. Показать, что при х —-О бесконечно малые вели-
чины: 1) tgx, 2) arcsinх и 3) arctgx — эквивалентны х.
Решение.
,. to х .. sin х j. sin х I
lim — — lim------= lim----------
X — 0 X X — 0 COS X x —• О X COS X
= lim —- lim—= 1-1 = 1.
X — О X x 0 cos X
Предел отношения tgx к x равен 1, следовательно (см. опре-
деление 4), при х —0 tgx эквивалентен х.
2) Положим arc sin х = у, тогда х — sin у. При х —О и у—*0.
,. arc sinx ,. у 1 1 1 ,
lim-------= lim =—= lim — =------------:— = -j- = 1.
х-о X у^^ту -y-.osmy ljrn sin у 1
У v-0 У
Следовательно, при х—0 arcsinх эквивалентен х.
3) Положим arctg х = у, тогда x = tgy. При х —0 и у —0.
limarct^=1.y =1.mw =
х-о х y_oxgy о siny
= lim • lim cos y— lim -J— lim cos y = 1=1.
•v_0SIn3’ у —0 V-0 1
У
Итак, arctgx при x —0 эквивалентен x.
9’
259
На основании этих результатов для малых значений х можно
написать приближенные формулы:
sinx^x; tgx^x;
arcsinx^x; arctgx?=«x.
Пример 5. Доказать, что если дуга окружности данного
радиуса /? стремится к нулю, то эта дуга и стягивающая ее
хорда — равносильные бесконечно малые.
Pemeiiu е. Возьмем на окружности радиуса /? точки Л4 и. N
и соединим их с центром (рис. 154). Обозначив радианную меру
угла MON через х, длину дуги MN—через
ч s, получим
®s — Rx.
ч Далее, из прямоугольного треугольника
МОК найдем
МК — ОМ sin — R sin~;
тогда длина хорды MN определится по формуле
п ,г. MN = 2MK = 2Rsiii±
Рис. 154 2
Из равенства s=Rx видно, что при s —0 и х —0. Найдем
предел отношения длины s дуги MN к длине хорды MN при х — 0:
,. s ,. Rx ,. X
111П 1141 ----7= 11111 -----7 =
v о Л1Д1 _ । о ,, . х а п . .v
A U А ' IJ 2/? sm л и 2 sin 2"
1- 1 .. 1 1 1 ,
= 1 пи------; = lim------=------------= -г- = 1.
V fl C) ’ v j 0 • X . X 1
Л u 2 Sin A —> и sin — Sill ___
— — lim -—
X----------------------------x X 0 x
2“ ~2
Следовательно, бесконечно малая дуга окружности эквивалентна
стягивающей, ее хорде (см. определение 4).
П р и м е ч а н и е. В подробных курсах высшей математики
доказывается, что бесконечно малая дуга любой кривой эквива-
лентна стягивающей ее хорде.
§ 92. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
1. Дифференциал функции как главная часть приращения
функции. Пусть нам дана некоторая функция y — f(x). Согласно
определению (см. § 59), производная y'v —f(x) этой функции при
данном значении х есть предел отношения при Дх —0, т. е.
260
Нам известно (см. § 46), что разность между переменной вели-
чиной ^в данном случае такой величиной является и ее пре-
делом— величина бесконечно малая. Имеем
&У
/ Хх
Ух —
или
ДУ
Д.с
где a — бесконечно малая величина при Дх—>0.
Из последнего равенства находим
Ьу=(Ух-\-ь)кх,
или
^У = у'х^х 4- аДх. (а)
Это равенство показывает, что приращение (Ду) функции состав-
ляется из двух слагаемых: у_(Дх и аДх. Первое из этих слагаемых
при любом х, при котором у'х ф 0, — бесконечно малая величина
одинакового порядка с Дх, так как
lim -т—= lim ух = ух
Дх 0 Дх -> 0
(см. § 91, определение 3).
Вторсе слагаемое — бесконечно малая величина высшего по-
рядка малости, чем Дх, потому что
lim lim a = 0
Дл'->0 лх ДХ-.0
(см. § 91, определение 1).
Это означает, что в равенстве (а) при Дх—>0 второе слагаемое
стремится к нулю «гораздо быстрее», чем первое. Поэтому первое
слагаемое принято называть главной частью приращения функции.
Главная часть (у'хЬх) приращения функции у = [(х) иначе на-
зывается дифференциалом этой функции и обозначается символом
dy (читается «дэ игрек»):
dy = y'xkx . (1)
Следовательно, дифференциал функции равен произведению про-
изводной этой функции на приращение Дх аргумента.
Если в формуле dy = y\.-±x принять у = х, получим
dy = dx = x'x- Дх,
или _______
йх = Дх . , (2)
Это равенство показывает, что дифференциал dx аргумента
есть его приращение Ьх.
261
Заменив в формуле (1) Дх равным ему dx, получаем
dy — y'xdx,
или '
dy — f'(x)dx
(3)
Эта формула читается так: дифференциал функции равен про-
изведению производной этой функции на дифференциал аргумента.
Следует знать и помнить, что дифференциал dx аргу-
мента, как и его приращение Дх, не зависит от х.
2. Выражение производной через дифференциал функции и
дифференциал аргумента. Разделив обе части равенства (3) на dx,
получаем
dy уУх
dx dx ’
ИЛИ
(4)
Из формулы (4) видно, что производная (у\.) функции у —
= f (х) есть отношение дифференциала dy этой функции к диф-
ференциалу dx аргумента х. Это отношение читается так: «дэ
игрек по дэ икс».
3. Формулы для нахождения дифференциалов функций. Поль-
зуясь формулой (3) и основными формулами для нахождения
производной, можно легко вывести формулу для нахождения диф-.
ференциала любой функции.
Пусть нам дано
где и = /(х),п = «р (х).
По формулам (3) и (4) (см. § 67) получим
dy = d (uv) — (uv)'xdx — (vu'x uv'x) dx — vu'xdx-|- uv'xdx=
= v (u’xdx) и (v'Adx).
А так как [см. формулу (3)]
u'xdx — du, v'xdx^dv,
то
d (uv) — vdu udv.
(5)
Рассмотрим еще функцию y — -^, где u~f(x) и v = <p(x).
Получим
[ u\ I u V
d — = — I dx
\ V / \ V Jx
vu'x — uv' vu'dx — uv'xdx v (u’xdx) — и (v'xdx)
------;------dx —------------;--------—---------------v---------
v~ v- v
или
vdu — udv
(6)
262
Пример 1. Найти дифференциал'функции у = У1 sin Зх.
Решение. По формуле (3) находим
dy = y'xdx — \y 1 4-sin 3x)vc?x =— - 4 dx =
J J 4 1 ' 2/l + sin3x
cos 3,v • (3x)' 3 cos 3x dx
= —r - dx = —.
2 1 sin 3л- 2 у 1 4 sin 3x
Пример 2. Найти дифференциал функции у — ln(sin£x4-cos At).
Решение. Применяем последовательно формулы (3) и (19)
(см. § 72). Получаем
(sin kx 4 cos kx)'
du — I In (sin kx 4- cos kx)lx dx — ———,--------dx =
J 1 ' 1 " sin kx 4cos kx
(sin kx)' 4 (cos kx)'x cos kx (kx)'x — sin kx • (kx)’
=----------i----i------ dx =-------r----i----:--------dx =
Sin kx 4 cos kx Sin kx 4 COS kx
cos kx k — sin kx k __ k (cos kx — sin kx) 4_
' sin kx 4 COS kx X sin kx 4 COS kx X
' _ sin kx \
dx=k!'~tik^dx.
, , sin kx , , \ tg kx 4 1
COS kx ---г---Pl '
\ cos kx I
k cos kx
Пример 3. Дана функция у = ~ tg’ х -ф- ~ tg3x -ф- tgx. Найти ~.
Решение. На основании формулы (4) получим
% (4 tgs х + у tg3 х + tg = у 5 tgi x <tg x}x +
-ф- -| • 3 tg2 x (tg x).v -ф- sec2 x = tg1 x sec2 x -ф- 2 tg2 x sec2 x -j- sec2 x =
= 5ес2х((§{хф-2 tg2x-ф- l) = sec2x(l -ф- tg2.r)2 =
= sec2 x (sec2 x)2 = sec6 x.
Пример 4. Аргумент x й функция у в зависимости от пара-
метра t выражены формулами: х = Ы— 1, у = (2-\-3t -(-2. Выра-
зить у'х через t.
Решение. По формуле (4) найдем
, _ dy __ d (t3 43/42) _(2/ 4 3) dt_2/4 3
Ux dx d (5/ — 1) 5d/ 5 '
Пример 5. Дана кривая параметрическими уравнениями
(см. § 39):
х==асо53ш, t/ = asin3<p.
Найти угловой коэффициент касательной к этой кривой в
точке, где ср = у.
Решение. Угловой коэффициент касательной к кривой в
данной на ней точке численно равен частному значению произ-
263
годной у'х при значении аргумента, равном абсциссе точки каса-
ния (см. § 62). По формуле (4) найдем производную ух функции у:
dy d(ash\3<f ) а • 3 sin2 <|> (sin <p)^'d<p sin2 <р cos?
dx ' d (a cos3 m) a 3 cos3 tp (cos <f)^ dy cos3 <f (— sin <f)
sin о .
—--------- = —tg'f.
COS tf> 0 1
Теперь можно найти угловой коэффициент касательной в
точке, где = 4. Получим k — у' | п = — tg ~ = —V3.
3 х = 3
§ 93. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА ФУНКЦИИ
Положим, что кривая, изображенная на рис. 155, является
графиком функции y = f(x). Возьмем на этой кривой точку М (х; у)
и опустим из нее перпендикуляр на ось Ох. Получим:
01< = х, КМ=у.
Придав абсциссе х приращение I\P = Дх — dx н восставив к
оси.. Ох перпендикуляр в точке Р, получим .
PM1=_-i/ + Az/ = /(x4-Ax).
Допустим, что касательная МТ к этой кривой в точке 7И (х; у)
образует с положительным направлением оси Ох угол а. Нам
известно (см. § 62), что угловой
коэффициент касательной, про-
веденной к графику функции
y~f(x) в точке М (х; у), равен
производной этой функции при
данном значении х, т. е.
k = iga=yx = f (х).
Проведем прямую MPt па-
раллельно оси Ох. Тогда отре-
зок PiMi будет приращением
(Ьу) ординаты у графика функ-
отрезок PiT — приращением ординаты касатель-
абсцисса х получает приращение Дх.
ции у = f (х), а
ной МТ, когда
Из прямоугольного треугольника MPiT получим
PlT = MPltga.
Это равенство можно переписать в другом виде, приняв во
внимание, что
MPi — КР = dx, tg а = k — /' (х) = у'х.
Получим
Р\Т — y'xdx.
264(
Нам известно (3), что
y’xdx = dy.
Следовательно,
Р\Т = y'xdx-= dy.
Это равенство показывает, что дифференциал функции у = f.(x)
геометрически представляет собой приращение ординаты каса-
тельной к графику этой функции в точке с абсциссой х при пере-
ходе от точки касания в точку с аб-
сциссой х -|- dx.
Из рис. 155 видно, что
пли
Ду — dy Ц- TMt.
Сопоставление этого равенства с
равенством (а) из § 92 приводит к за-
ключению, что
7'Л11=аД.г,
т. е. отрезок TMi изображает ту часть приращения функции,
которая при Дх—>-0 является бесконечно малой высшего порядка
по сравнению с Дх.
В данном случае Ду2> dy, так как
by — dy =-- аДх = TMi Z> 0-
Может оказаться и так, что при данном значении х прира-
щение Ду функции y — f(x) будет меньше дифференциала (dy)
этой функции. Так, например, на рис. 156 получаем
Ьу - dy = P\Mi - РфГ = ТЛГ1 < 0.
§ 94. ДИФФЕРЕНЦИАЛ ВТОРОГО ПОРЯДКА
Дифференциал функции y = f(x) является, как и сама фуик-
, ция, функцией от х. Поэтому можно взять дифференциал диф-
ференциала. Дифференциал дифференциала функции y = f(x) на-
зывается дифференциалом второго порядка и обозначается симво-
лом d2y (читается «дэ два игрек»).
Зададимся целью вывести формулу, выражающую дифферен-
циал второго порядка. Нам известно, что
dy — y'xdx,
где dx является произвольным приращением аргумента и не за-
висит от х. Согласно определению получим
d!y = d (dy) — d (y'xdx).
265
Рассматривая dx как постоянный множитель, не зависящий
от х, ио формуле (3) найдем
d-y — d (у'х) dx = dx] dx — (y'xxdx) dx = y'xxdx dx,
или
d^y’xxdxl (7)
Итак, дифференциал второго порядна равен произведению вто-
рой производной функции y = f(x) на квадрат дифференциала
аргумента.
Разделив обе части равенства (7) на dx1, находим второй сим-
вол для обозначения второй производной:
d'y
dx- ‘dx- ’ dx2 dxx’
или
„ d‘y
Символ читается так: «дэ два игрек по дэ икс квадрат».
Пример 1. Дана функция f (х) — In cos тх. Найти дифферен-
циал второго порядка.
Решение. 1) Находим вторую производную данной функции;
(cos/ил’)'. —sin шх • т
Г (х) —-------—----------- - — т tg тх;
1 ' ' cos тх cos шх
(llix)' III 1111
f" <х) = — т--з-----= — т----з— =------=—.
' ' ' cos- тх cos- тх cos- шх
2) По формуле (7) находим дифференциал второго порядка:
.dV(x)=r(x)^=-^^.
Пример 2. Дана функция z/ = arcsinax. Найти
dy (ал')х а
Решение. 1) — (arcsinax)'t= Г .. = = -т=. - .
’ dx v ,х у 1 _ сРх1 У 1 - а'-л-3
— а'^—-j) (1 — 2 О — лД’Д =— у(1 —а2*8) 2.(—2а-х) -
__ а'!х
~~ /(1 — asxs)3'
§ 95. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛА ФУНКЦИИ
‘ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
1. В § 92 дифференциал функции был определен как главная
часть приращения функции. Докажем, что при Дх->-0 и у' У О
приращение йу функции y — f(x) и ее дифференциал dy — экви-
266
валентные бесконечно малые величины. Нам известно, что
Ду = у‘х^х -j- а-кх;
dy—y'xdx,
где а —бесконечно малая при Дх->0, т. е. lima =0.
Дх —0
Найдем предел отношения Ду к dy при Дх -> 0:
Ху Ух^х + Ух&х “Дх \
1 im —г- = 1 im---гт = 1 im С I
дх-о аУ дх-о Ух^х ^-.оХУх^х ' у.^х/
Получаем
Согласно определению 4 (см. § 91) это значит, что Дуй dy —
эквивалентные бесконечно малые величины. Вследствие этого при
значениях Дх, близких к нулю, можно принять
Ду^г/у = у1Дх. (9)
Вычисление приращения функции по правилу, изложенному
в § 56, обычно приводит к громоздким вычислениям. Формула
(9) при значениях Дх, близких к нулю, дает возможность нахо-
дить приближенное значение приращения (Ду) функции y = f(x)
с незначительным отклонением от его истинного значения, при
этом вычислительная работа значительно упрощается.
Пример 1. Вычислить приращение функции у=2х1 — 3x4-3
при переходе аргумента от значения хх — 1 к значению х2 = 1,001:
1) приближенно; 2) точно; 3) найти разность между его точным
и приближенным значением.
Решение. В данном случае принимаем х=1, Ух = Дх =
= 0,001. По формуле (8) найдем приближенное значение
Ду dy = (2х2 — Зх 4~ 3).'v dx — (4х — 3) dx.
Заменив х и dx их значениями, получим
Ду ^(4-1 -3)-0,001 =0,001. (а)
2) Точное значение приращения функции вычислим по пра-
вилу, изложенному в § 56. Получим
Ду = (У + Ду) - У = 2 (1 + Дх)2 - 3 (1 + Дх) +
4-3-(2- Р-3- 1 4-3) = 2 4-4Дх4-2(Дх)2-3-ЗДх4-3-2 4-
4-3 — 3 = (4 — 34- 2Дх) Дх = (1 4-2• 0,001) • 0,001 = 0,001002. (б)
3) Сравнивая (а) и (б), видим, что точное значение Ду отли-
чается от приближенного значения лишь в шестом десятичном
знаке:
0,001002 - 0,001 = 0,000002.
267
Пример 2. Найти приближенно приращение функции у =
— |/Зх-[-1 при переходе аргумента от значения xj — 5 к значе-
нию х.2 = 5,1.
Решение. Принимаем х = 5, dx = Ax = 0,l:
^у -ф- 1)Л dx — [ (Зх -ф-1)4 [х-dx —
= l(3x+l) 4(3x + l)ldx
4, . -dx.
4 уТ (Зх-f- I) '1
Подставив в полученный результат вместо.х и dx их значе-
ния, находим
Ду 3 - -0,1= 3'°lL • 0,1 = 0,09375 -0,1^ 0,009.
у 4|/(3-5+1)3 4|/(24)3 32
Пример 3. Дана функция у = |3х'-ф- 1. Найти приближенное
значение этой функции при х= 1,02.
Решение. Известно (см. §56), что Д// = /(х—j-Дх) — /(х).
Из этого равенства следует f (х Д- Дх) = f (х) -ф- Ду.
Заменив. Ду его приближенным значением по формуле (9), по-
лучаем
. /(х-фДх)^/(х) + йу . (10)
В данном случае следует принять х=1. Тогда
Дх= 1,02- 1=0,02.
Значение функции при х = 1 определяется просто и точно,
оно равно
/(1) = ]/3. Г2+ 1 =2.
Для приближенного определения значения данной функции
при значении аргумента, равном 1/,02, применима формула (10):
/ (1,02)— /(1 0,02) (1) 4-<iy,
где
dy = (V Зх- + 1 'l (Дх = ?xdx = 'ixdL= =
J 4 1 ' 2/Зх-'+1 /Зх34-1
__ 3 1 • 0,02 _0,06 _„ По
— ---'г —г “о- - U»V«J.
уз.р-pi 2
Следовательно, •
f (1,02) МО) + 0,03 = 2 + 0,03 = 2,03.
В результате вычисления значения этой функции при х— 1,02
приемами элементарной алгебры получается
[ (1,02) = /З • 1,02- +'! = ]/ 4J212 = 2,03007 ...
268
Как мы видим, разность между точным значением (1^4,1212)
данной функции при х= 1,02 и ее приближенным значением, вы-
численным по формуле (10), оказалась числом очень малым:
2,03007... —2,03 = 0,00007...
2. Приближенные формулы. Приближенные формулы получа-
ются в результате применения формулы (10) к отдельным классам
функций.
1) В случае степенной функции у = [(х)=хп, где п — любое
действительное число, находим
/ (х 4- Дх) М (х) 4- df (х) = хп 4- d (хя) = хя 4- пхя-1Дх,
пли
(х4-Дх)я^хя-4/гхя-1Дх.
При х = 1 и Дх = ±р из последней формулы получаем фор-
мулу для определения степеней бинома (1±р):
или
(1 + ?4я^1+^; (П)
(1-р)я^1-цр. (Па)
Формулы (11) и (На) пригодны для приближенного вычисле-
ния (1 ch р)'1 лишь при небольших п и малых, р, в противном
случае может получиться значительное расхождение между точным
и приближенным значениями степеней бинома.
2) Пусть нам дана функция у = [(х)=Ух.
По формуле (10) получим
п ,----- п >— , . п ,— п,— ( — \
у х Дх№ у хуа у х = у х-[-\хп ]х-&х =
, 1 , ,71 — 1
71.-, 1----1 . П/> — 1 — ---
— у х 4* - х п Дх = ух 4~ — х п Дх,
' 1 п г 1 п ’
"ИЛИ
"/-i--Д- ЛГ~ I
У X 4~ Дх «И у х 4- .
лу Хп~
Приняв в последнем равенстве х= 1, Дх = ±р, будем иметь
или ,
. ^ГЕЕр = 1 ±|. (12)
3) Возьмем функцию у = 1пх. Для этой функции формула (10)
примет вид
In (х 4* дх) In х 4~ ,
269
так как dy = -у Дх = . При х—1, Дх — ± р, где р — число
малое по сравнению с единицей, получим
In (1±₽) = 1п 1 + ^р-,
пли
1п(1 ± ₽) = ±₽. (13)
Пример 4. Вычислить приближенно: 1) 1п 1,012; 2) In 0,996.
Решение. По формулам (13) получаем:
1) 1п 1,012 = 1п(1 +0,012)^0,012;
2) In 0,996 — In (1 - 0,004)^ — 0,004.
Пример 5. Вычислить приближенно: 1) 2) д/0,982.
Решение. 1) — 1,02'2. Далее по формуле (11) найдем
(1 + 0,02)-2 = 1 + (— 2) • 0,02 == 1 - 0,04 = 0,96;
2) По формуле (12) получаем +б,982 = +1—0,018= 1 —
_(Ц)18== Ogg?
б
§ 90. ДИФФЕРЕНЦИАЛ ДУГИ
Пусть кривая линия, изображенная на рис. 157, является графиком функ-
ции у=/(х). Возьмем на этой кривой точки А и М Точку А будем счи-
тать неподвижной, а точку М — перемещающейся по кривой. Тогда длина з
дуги AM будет функцией от абсциссы х точки Л1, так как всякому значе-
нию х будет соответствовать одно определенное положение точки Л1 и
вследствие того — определенное значение дли-
ны s дуги AM. Поставим задачей найти про-
изводную н дифференциал этой функции, т. е.
s'x и ds = s'xdx. С этой целью придадим ар-
гументу х приращение Дх = Л11Л?1, восставим
к оси Ох перпендикуляр NtN и проведем па-
раллельно этой оси прямую MN«. Тогда
Л1ЛУ = = Дх, N.N = Ду, = Дз
(приращение дуги з).
Известно, (см. § 59), что производная з'
. Дз
функции з есть предел отношения — при
Дх —0. Преобразуем предварительно, это отношение,
его на длину хорды Л1М Получим
умножив и разделив
Дз _ Дз • MN _ As MN
Дх . \x-MN — MN' Дх ’
При Дх — 0 будем иметь
lim lim lira lim
дх - о Дх дл- - о \MN Дх ] дл- — о MN дх-о Дх
(а)
270
При Дх —О точка W неограниченно приближается к точке М и вслед-
ствие этого Дл —0. В § 91 было указано (примечание в конце), что беско-
нечно малая дуга и стягивающая ее хорда — эквивалентные бесконечно
малые величины. Основываясь на этом, утверждаем, что
1 *
lim -i-
ix-oMN
(б)
Из прямоугольного треугольника по теореме Пифагора найдем
MN = VМ№ + Na№ = V(\х)- (Ьу)3 =
ИЛИ ________
AW=Ax]/ri + ^j3. (в)
Д о
Подставив в равенство (а) вместо lim - и их значения (б) и (в),
д,г->0 MN
найдем
или
Нам известно, что
следовательно, равенство
откуда
,;;,й=''|+И' <г>
. ds
lim — = s = —
a.v —оДх x dx’
(г) равносильно равенству
ds = ]/" 1 + (Уд-)2 dx. (14)
§ 97. КРИВИЗНА КРИВОЙ
Кривая линия будет «искривлена» одинаково во всех своих частях или
будет иметь постоянную «кривизну», если любая ее часть может быть сов-
мещена с другой частью этой кривой. Един-
ственной кривой, удовлетворяющей этому
условию, является окружность.
Возьмем несколько окружностей раз-
ных радиусов, имеющих в некоторой точке
А общую касательную. Из рис. 158 вид-
но, что чем больше радиус окружности,
тем больше ее дуга приближается к пря-
мой АТ (кривизна прямой принимается
равной нулю) и тем меньше ее кривизна.
Поэтому за меру кривизны К окружности
естественно принять величину, обратную
271
радиусу, т. с.
к-л
(15)
Кривизну окружности можно определить и другим способом. Возьмем
на окружности радиуса R какие-нибудь две точки ,М и А' (рис. 159) и соеди-
ним их с центром О. Обозначив длину дуги Л-l.V через з, радианную меру
угла MON — через а, получим s — Ra,
,, s 1 а
откуда /? = - и
Проведем к этой окружности каса-
тельные ЛШ1 и NNt в крайних точках
дуги MML. По теореме об углах с взаим-
но перпендикулярными сторонами,
Z (MMt, AWJ = £NAMt = а.
Следовательно,
1 _ AWJ
R~ s
Сопоставив последнее равенство с
равенством (15), получаем
.. L (Ж ВД)
Л —----------.
т. е. кривизна окружности равна от-
ношению угла между касательными
к длине дуги, заключенной между точ-
ками касания.
Перейдем теперь к установлению
способа измерения кривизны в случае,
когда кривизна кривой является величиной переменной, изменяющейся при
переходе от одной ее точки к другой.
Пусть кривая на рис. 160 является графиком функции у = f (х). Возьмем па
этой кривой точки М и Л' и проведем касательные MMt и AWP При пере-
ходе от точки Л1 до точки Л/ касательная меняет свое направление. Поло-
жим, что касательная в точке А1 образует с положительным направлением
оси Ох угол а; тогда касательная в точке N, близкой к точке А1, образует
с этой осью угол а Да и угол Да явится углом между касательными ЛШх
и AWt, проведенными в крайни^ точках дуги MN, т. с. утлом поворота
первой касательной (AMfJ до второй касательной (AWi). Разделив Да на
длину дуги MN=bs, мы получим среднюю величину угла поворота каса-
тельной, приходящуюся на единицу длины дуги. Полученное частное назы-
вается средней кривизной дуги MN= Дз. Обозначив среднюю кривизну сим-
волом АГср, получим
(а)
Определен и е. Средней кривизной дуги MN = Дх называется отно-
шение угла между касательными, проведенными в крайних точках этой
дуги, к длине этой дуги.
Чем меньше Дх, тем точнее отношение (а) будет характеризовать кри-
визну кривой вблизи точки Л4. Если точка N будет неограниченно прибли-
жаться к точке Л4, то Дз и Да, уменьшаясь, будут приближаться к нулю, а
средняя кривизна (а) будет стремиться к некоторому пределу,, который ц
называется кривизной кривой в данной точке Л-1. Итак,
1НИ _
д4- -+о Аз ’
272
или
[см. (4) § 92].
Определение.' Кривизной кривой у = fix') в данной точке М (х, у)
называется предел, к которому стремится средняя кривизна дуги MN=&s,
когда точка N неограниченно приближается к точке М.
Займемся теперь выводом формулы для нахождения кривизны произ-
вольной кривой y=f(x) в данной на ней точке М (х, у). Нам известно, что
rfs = ]Л1 -I- (y’J! dx.
Остается найти выражение дифференциала (rfa) угла п через производные
функции у =f(x) и дифференциал аргумента. Известно (см. § 62), что
г£а=У'х,
откуда
« = arctgy?;;
Л = (arctg XJ ; lit = npgjt«
,<”=TT<)i4v' (n)
Подставив в равенство (б) вместо с?а и ds их выражения (в) и (14),
получим
- Ухх__________________(iK <
Г=<Ь = ' = Ухх
4 rfs 1/1 4- (К)3 dx
или
=—-х-х - 3.. " (16)
Р + (ОТ
§ 98. РАДИУС КРИВИЗНЫ
Если окружность и дуга AW кривой у — f (х) (рис. 161), направленные
выпуклостью в одну сторону, проходят через некоторую точку А, имеют
общую касательную АТ и кривизна окружности
равна кривизне кривой в точке А, то центр С
окружности называется центром кривизны дан-
ной кривой в точке А, радиус СА этой окружно-
сти — радиусом кривизны кривой в точке А, а
сама окружность — окружностью кривизны.
Кривизна К окружности радиуса А' опреде-
ляется по формуле
откуда
Я = 1
273
По этой же формуле определится и радиус кривизны кривой y = f(x)
в точке А (х, у). Подставив вместо К его выражение (16) через производные,
получим
р-1 1 _Р+(ОТ к Ухх Ухх
Итак, Р + (Л)Т R- у • (17). •?хх
Применив эту формулу к прямой линии y = kx, получим Ji + 0Q2F_(i+fe4 _ « у'„ 0
так как У'х = к’ Ухх = °-
Следовательно, прямую линию можно рассматривать как окружность с
бесконечно большим радиусом.
Заметим, что в зависимости от знака у"хх при данном значении х кри-
\визна и радиус кривизны могут получиться как со знаком «+», так и со знаком
«—». Следует знать и помнить, что кривизна и радиус кривизны — величины
положительные и при вычислении R и Л' по формулам (16) и (17) брать
ухх по абсолютному значению |ухх |.
Пример 1. Дана кривая у = 1пл\ Найти кривизну этой кривой в точке,
абсцисса которой равна: а) 1; б) 5; в) 10.
Решение. 1) Находим первую и вторую производные этой функции;
Отметим, между прочим, что при любом х вторая производная отрица-
тельна: у'хх = —р <0; это указывает (см. § 88), что данная кривая всюду
выпукла.
2) По формуле (16) находим выражение кривизны Д' этой кривой при
любом х. Получим
/ _ Кл-| = |~^1 = Р л-КО+'Г
nW p+gf (ха+1Г’
3) Вычисляем кривизну К при х==1; 5; 10:
* К— i)s — оу ~ 4 1 ’
5/26 5 ,,-лд
(52+1Г 26а
274
ю/Тонгт_ lo/ioi - ю ,ли,-
л (Ю2 + 1)а “ 1012 “ 1013 F
Отсюда видно, что по мере
быстро убывает (рис. 162).
Пример 2. Дана кривая (цеп-
ная линия)
Найти радиус кривизны этой
кривой в точке, абсцисса которой
равна нулю.
возрастания х кривизна кривой у = In.V
Решение. 1) Находим первую и вторую производные этой функции;
При любом х вторая производная положительна: у" >• 0. Это значит,
что кривая всюду вогнута.
2) Подставив в формулу (17) вместо у* и у” их выражения, получаем
формулу, по которой можно вычислить R при любом х:
3
2
2
* Форму этой кривой принимает тяжелая нерастяжимая нить, подвешен-
ная за два конца.
275
3) Теперь можно найти радиус кривизны и точке х = 0; получаем
/ о «V
(рис. 1G3, пунктиром изображена окружность кривизны).
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. При каком условии бесконечно малые величины а п ₽ называются
эквивалентными?
2. При каком условии бесконечно малая величина 0 называется беско-
нечно малой высшего порядка по сравнению с бесконечно малой а?
3. Если а и р — бесконечно малые одинакового порядка, то каким числом
является предел их отношения?
4. Что называется дифференциалом функции у=/(х)?
5. Чему равен: 1) дифференциал аргумента; 2) дифференциал функции?
6. Какими величинами являются приращение ку непрерывной функции
y=f(x) и ее дифференциала dy при Дх — 0?
Ду
7. Какой величиной является разность ~^~УХ 11ри Дх — 0?
8. Какой величиной является разность Ду — dy при Дх —О?
9. При каком условии можно принять Ду а’у ?
10. Что представляет собой геометрически: 1) дифференциал (dy) функ-
ции у=/(х); 2) дифференциал аргумента?
11. Выпукла или вогнута кривая у=/(х) вблизи точки М (х; у), если:
1) Ду> dy, 2) ky<zdy (см. рис. 155 и 156).
,, / • л''2 — fl2V
12. Вычислением найдено arcsin ——И
м (с — любое данное число)?
13. Вычислением найдено d [arctg (In xj] =
2а .. ,
j. Чему будет равна
arcsin
dx
Чему будут
равны:
1) d [arctg (In x) + 117]; 2) d [2 arctg (In x) -f- c]; 3) d arctg (In x) — 15 ?
14. Пусть известно /' (x) — F (x). Чему будут равны: 1) [/(x 4~ <’)] .,
2> [4/<v>+13L? -
276
15. Пусть известно, что dF(x) = flx} dx. Чему будут равны:
1) rf[F(x4-c)]; 2) rf[l/(x)-21]?
16. Написать формулу дифференциала дуги кривой.
17. Что называется кривизной окружности?
18. Если кривизна окружности равна 0,0625, то чему равен се радиус?
19. Как будет изменяться кривизна окружности, если радиус будет
неограниченно возрастать?
20. Чему равна кривизна прямой в любой ее точке?
21. Что называется средней кривизной дуги кривой у=/(х)?
22. Что называется кривизной кривой y=f[x) в данной точке М (х; у)?
23. Чему будет равна кривизна кривой в точке перегиба?
24. Написать формулу радиуса кривизны кривой у~ех.
25. Если dy = 3x3dx, то чему будет равен у>
dx
26. Если dy — —, то чему будет равен у>
27. Если для функций/(х) и F(x) справедливо равенство f (х) = F' (х),
то чем будут отличаться друг от друга эти функции?
Ответы. И. 1) Вогнута; 2) выпукла. 14. 1) F(x); 2)yF(x). 15. l)/(x)dx;
2) ±-f(x)dx. 18. /?=16. 19. Л'—О. 20. /<пр = 0. 23.
з
(1 -L
24. ——. 25. у = х3 + С (следует проверить дифференцированием).
26. _у = 1пх-|-С. 27. Постоянными слагаемыми: /(х) = F(х) + С.
ЧАСТЬ ТРЕТЬЯ
ЭЛЕМЕНТЫ
ИНТЕГРАЛЬНОГО
ИСЧИСЛЕНИЯ
Глава X
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 99. ВВЕДЕНИЕ
Из элементарной математики известно, что всякому прямому
действию соответствует обратное действие. Так, например, воз-
ведению в степень соответствует обратное действие — извлечение
корня, логарифмированию — потенцирование, нахождению триго-
нометрической функции угла — нахождение угла по данному зна-
чению его тригонометрической функции (табл. 25).
Таблица 25
Дано Прямое действие Обратное действие
Основание а и показатель степени п Возведение в сте- пень an — N Извлечение корня a=^N
<г\’Ь Х = -;1Г=~ УС Логарифмирование 1g* = 2 1g а-ф + т *ей--r'gc Потенцирование: 1g х = 2 1g а -ф + 1g Vb — 1g /Г; i i Vb ig* = ig J- ; V c У c
Угол а Нахождение триго- нометрической функции угла tg а. = т Нахождение угла по данному значению его три- гонометрической функции а = arctg т -ф пп
278
В анализе бесконечно малых величин мы также встречаемся
c двумя взаимно обратными действиями. С одним из них, назы-
ваемым дифференцированием и имеющим задачей нахождение
производной или дифференциала данной функции, мы уже зна-
комы. В данной главе изучается действие, обратное дифферен-
цированию, называемое интегрированием. Цель этого действия —
нахождение функции по ее производной, или, что то же, подан-
ному ее дифференциалу.
Следует заметить, что всякое обратное действие усваивается
тем легче, чем лучше усвоено прямое, действие. Поэтому присту-
пать к проработке данной главы следует,, основательно овладев
техникой дифференцирования и зная наизусть формулы диффе-
ренцирования.
§ 100. ИНТЕГРИРОВАНИЕ КАК ДЕЙСТВИЕ,
ОБРАТНОЕ ДИФФЕРЕНЦИРОВАНИЮ.
ПОНЯТИЕ О НЕОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
Дифференцированием, как нам известно, по данной функции
y = F(x) находится ее производная y' = F'(x) или ее дифферен-
циал dg — F'(x)dx = f(x')dx. Так, например, если
Д(х)'=х4,
то
F' (х) = f(x) = 4хя;
dF (х) = f (х) dx = 4x:,dx.
Действие, обратное- дифференцированию, т. е. нахождение
функции F (х) по данной ее производной F' (x)—f (х), или, что
то же, по данному дифференциалу f (х) dx, называется интегри-
рованием. При этом искомая функция F (х) называется первооб-
разной, или интегралом для данной функции.
Определение 1. Функция Т’(х), имеющая данную функцию
f(x) своей производной, или f(x)dx — своим дифференциалом, назы-
вается первообразной функцией для данной функции f(x).
В примере, приведенном выше, для функции
/(х) = 4х3
первообразной функцией, очевидно, является функция
F (х) = х4.
Из дифференциального исчисления известно, что функции,
отличающиеся друг от друга постоянными слагаемыми, имеют
одну и ту же производную и, следовательно, один и тот же
дифференциал. Возьмем, например, функции
F(x) = x4; Fj (х) — х1 11; Г2(х) = х4—119; F3 (х) = х1 ф- С,
где С — любое число.
279
Все эти функции имеют функцию /(х) = 4х3 своей произвол-
ной и f (xj dx — 4хМх— своим дифференциалом. Отсюда следует,
что функции
f(x) = 4xs, (а)
или дифференциалу
/ (х) dx = 4r' dx, ' (б)
соответствует бесчисленное множество первообразных функций
вида
л-Ч-С, (в)
отличающихся друг от друга постоянными слагаемыми.
Двучлен (в) называется неопределенным интегралом от функ-
ции (а) пли от дифференциала (б) и обозначается символом
J 4х:| dx, следовательно, $ 4х3 dx — х1 -|- С.
Точно так же, если /(x) = cosx или f (х) dx = cos х dx,
получим
§ cos xdx — sin x -}- С,
так как л
(sin х—|-C)Lc = cosx
и
d (sin х-}- С) — cos xdx.
Итак, если .известно, что производная некоторой функции F (х)
равняется функции f(x), т. е.
F(x) = /(x),
то
5/(х)^х = Д(х) + С, (г)
где С — произвольная постоянная.
Следовательно, символу \f(x)dx соответствует бесконечное
множество функций (часто говорят «семейство функций»), перво-
образных для данной функции f (х) и отличающихся друг от друга
постоянными слагаемыми. Вследствие многозначности .(неопреде-
ленности) этот символ называется неопределенным интегралом.
С подобными случаями мы встречались и в элементарной мате-
матике. Например, если tg у = х, то z/ = arc tgx-)-wi. Это равенство
утверждает, что существует бесконечное множество углов, тангенсы
которых равны числу х, точно так же как равенство (г) утверж-
дает существование бесконечного множества функций, имеющих
данную функцию /(х) своей производной, пли (что то же)/(х)б/х —
своим дифференциалом.
Определение 2. Совокупность функций F(x)-[-C, перво-
образных для данной функции f (х) или для данного дифференциала
f(x)-dx, называется неопределенным интегралом. Символ § f (х) dx
280
читается так: «неопределенный интеграл эф от икс дэ икс», при
этом f (х) называется подынтегральной функцией, f (х) dx — подын-
тегральным выражением, знак § — знаком интеграла, а х — пере-
менной интегрирования.
В равенстве (г) как левая, так и правая , части называются
неопределенным интегралом, но левая часть ^f(x)dx представляет
собой искомый интеграл, а правая — найденный интеграл, или
совокупность функции, первообразных для данной функции /(х).
Займемся геометрическим истолкованием неопределенного инте-
грала. Из дифференциального исчисления известно, что наклон
k кривой y=f(x) (угловой коэффициент касательной) в точке
с абсциссой х равен производной, т. е.
k = y'x = f' (х).
Пусть теперь нам предлагается обратная задача: зная наклон
k кривой в любой ее точке как функцию абсциссы этой точки,
т. е. зная, что k — f(x), найти уравнение кривой.
Так как k = y'x = ~, то ^ = /(х), dy = f(x)dx, откуда'инте-
грированием найдем
y=\f(x)dx.
Вычислив этот неопределенный интеграл, получим уравнение
r/ = F(x)-[-C, (д)
содержащее произвольную постоянную С. Очевидно, уравнению (д)
на плоскости будет, соответствовать бесконечное множество кри-
вых (семейство кривых), уравнения которых будут отличаться
друг от друга только постоянными слагаемыми.
Пусть нам дано k = у'х — х. Тогда
J^=x, dy — xdx, у = xdx = ~y х2 -|-С.
Следовательно,
. у = ±.е-[-С.
Придавая произвольной С последовательно значения 0, 2,
4, ... —2, —4, ..., получим:
у = ~х\ у=^-х*-\-2\
// = уХ2-С4; г/ = уХ2 —2, ... .
Производные этих функций равны у'х = х, вследствие' чего
промежутки убывания (—оо<х<0) и возрастания (0 <^х<^оо)
28Г
будут одинаковы. Функции имеют минимум при х = 0, наклон
их графиков в точках с одной и той же абсциссой (рис. 164, а)
относительно осп Ох один и тот же, так как
/г — tg а — х! — х,
и при x = xt он будет равен ki = tga — Xi (графики их должны
быть совершенно одинаковы). Построив график одной функции
(например, у = ^-х~ , графики остальных можно получить пере-
мещением его параллельно оси Оу. Очевидно, что неопределенному
интегралу от функции f(x) — x на плоскости соответствует
Рис. 164
семейство одинаковых парабол, симметричных относительно оси Оу
и отличающихся друг от друга лишь смещением вдоль оси Оу.
Как мы знаем, символ ^f{x)dx предлагает найти совокупность
таких функций F{x)--C, производная которых равнялась бы
подынтегральной функции, т. е. [F (х) 4-C]'=j(x). Выясним сущ-
ность этого процесса на примерах.
Пример 1. Найти § 5хМх.
Решение. Предлагается найти такую функцию, производная
которой равна 5х4. Из дифференциального исчисления известно,
что
5х4 — (xs).v,
следовательно, $ 5xldx = Xs -ф- С.
Пример 2. Найти .
r r COS" X
282
Решение. В данном случае ищется функция, производная
которой равна —Из дифференциального исчисления известно,
что
—4—=(tgxK,
COS-' X ° '
следовательно,
Пример 3. Найти ^ехдх.
Решение. Известно, что ех=(ех)’х, откуда \)exdx = ех ф- С.
Из элементарной математики известно, что результат любого
обратного действия проверяется прямым действием. Например,
если 128 = 2, то возвышением числа 2 в седьмую степень
(27= 128) убеждаемся в правильности извлечения корня.
Точно так же прямым действием, действием дифференцирова-
ния, проверяется и результат интегрирования. Если
J f (х) dx — F (х) ф- С,
то
[F(x) + C]; = F(x) = /(x),
или
d [F (х) ф- С] = F’ (х) dx = f (х) dx.
Пример 4. Проверить справедливость равенства
\ x*dx ! д_с
J /2л-3 + 1 3 11
Проверка:
d (1 /2х’+ 1 -ф с) = /2х3+ 1 ф- dx =
1 (2.У4-1); 1 бла xs dx
— — • —л-—' dx --------у—- dx = . .
3 2p2.v‘+l 3 2/2.г’+1 /2х34-1
Получили подынтегральное выражение. Следовательно, инте-
грал найден верно.
§ 101. ОСНОВНЫЕ СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Первое свойство. П роизводная неопределенного интеграла
равна подынтегральной функции, т. е.
[\f(x)dx]’x = f(x).
Это свойство непосредственно вытекает из определения неопре-
деленного интеграла и доказательства не требует. Так, если
283
f(x) = 5xl (см. § 100, пример 1), то
5xMx)x — (лл + С)'х = 5х4,
[$/(x)dx]'.=7(x).
Второе свойство. Дифференциал неопределенного инте-
грала равен подынтегральному выражению, т. е.
d^f(x)dx — f (х) dx.
Это свойство тоже вытекает из определения неопределенного
интеграла (см. § 100). Для пояснения рассмотрим следующий
пример.
Пусть /(x)dx = ^^ (см. § 100, пример 2). Получим
d = d (1g х Д-С) = (tg х Д-С)\dx =—^f—,
J COS- X Volz ' О I /•' cos- x >
ИЛИ
d J f (x) dx — f (x) dx.
Третье свойство. Неопределенный интеграл от диффе-
ренциала функции равен этой функции плюс произвольная по-
стоянная, т. е.
JdF(x) = F(x) + C. <
Например,
d (х4) = § 4хДх — х4 С.
Четвертое свойство. Постоянный множитель подынте-
грального выражения можно вынести за знак интеграла, т. е. если
а — величина постоянная, то
$ af (х) dx — a\f (х) dx,
так как
[a Jj f (х) dx]x — а f (х) dx]x = af (х)
и
[\af (x)dx]^, = a/(x).
Например, § 2 cos xdx = 2 J cos x dx = 2sinx4~ C.
Пятое свойство. Интеграл от алгебраической суммы функ-
ций равен алгебраической сумме интегралов от этих функций, т. е.
51/ W — ? W + F (*)]dx = $ f W dx ~ J ? W dx + $F W dx-
Справедливость этой формулы можно легко обнаружить, сравнив
производные левой и правой частей. По первому свойству неопре-
284
деленного интеграла, имеем
{ $ [/ (х) — ? (х) -ф- F (х)] dx}* = f (х) — v (х) F (х).
Применив к правой части правило дифференцирования алге-
браической суммы функций, получаем
[ / (х) dx — $ ср (х) dx + $ F (х) dx]f (х) dx ] 'х — [ $ ср (х) dx] . -ф-
+ [ $ F (х) dx]= / (х) — ср (х) -ф- F (х).
Следовательно,
$ [/ (х) — Т W + F (х)] dx = J f (х) dx — J ср (х) dx -ф- F (х) dx.
§ 102. ОСНОВНЫЕ ФОРМУЛЫ ИНТЕГРИРОВАНИЯ.
НЕПОСРЕДСТВЕННОЕ ИНТЕГРИРОВАНИЕ
Из определения неопределенного интеграла следует
J F' (х) dx = F (х) С. (а)
Пользуясь этой формулой, можно найти интегралы простейших
функций и составить таблицу основных формул интегрирования.
1. Предположим, F'(x) = хх- Тогда по формуле (а) получим
x'xdx = х -р С,
а так как
Xi- — 1,
ТО
51 dx = х -ф- С,
или
dx ==z х —С. ,
2. Возьмем F'(x) = p——j') .
Подставив в формулу (а) вместо F' (х) его значение, найдем
х'г’ 1
«+1
+ С,
а так как
то
(«+1)х«н-> _ ,
„ I —'л >
vnn
xndx = —г -ф- С.
п + 1 1
Эта формула справедлива при любом постоянном п, не рав-
ном — 1. Для случая л = —1 ниже выводится другая формула.
285
Пусть F' (х) = (In х)'х. Тогда по формуле (а) имеем
§ (In х)'х dx — In х 4- С.
Заменив в этом равенстве (Inх)'х его выражением получаем
1 • dx , i
----= lnx4-
x---1 ’
или
x~ldx = ^=1пх-|-С. (б)
Известно (см. § 74), что областью существования функции
1пх является интервал (0; оо). Поэтому формула (б) приложима
только при х^>0.
Таким же путем можно получить все приводимые ниже основ-
ные формулы интегрирования:
I. ^dx — x-]-C.
IL (ЛЬ=4) + С.
при П ф— 1
Ill. J ^ = 1пх + С* *, х>0.
IV. \e*dx = e*4-C.
V. )“'Л=£+С-
VI. $ sin xdx — — cosx-\-C.
VII. $cosxdx = sinx4~C-
VIII. t -^4-= \ sec2xdx = tgx + C.
J COS’X J 1
IX. t cosec2xdx=—ctgx4~C.
j smJx j
X. jj tg x dx — — In cos x + C.
XI. ^ctgxdx— Insinx4-C-
* Если x<0, to (—x)>0 (см. сноску на стр. 24) и функция In (—х)
существует. Подставив (—х) в формулу 111 вместо х, получаем
С £(—х)_1п(_х)+С1 т_ е_ С = ]11(_Л.) + С (в)
•) - X V X
— формулу, справедливую ири всяком х из интервала (— со; 0).
Формулы 111 и (в) можно объединить в одну формулу
Р /1 у
^ = 1п|х|+С, (Ша)
справедливую в любом интервале, не содержащем нуля.
.286
XII. -r dx = = arc sin x4- C.
/1-х- 1
XIII. 1-^5 = arctg x 4-C.
В справедливости данных формул можно убедиться дифферен-
цированием: производная правой части каждой их них должна
равняться подынтегральной функции левой частгг
Нахождение интегралов, основанное на прямом применении
приведенных формул, называется способом непосредственного ин-
тегрирования. Этот способ охватывает следующие случаи.
I. Данный интеграл находится непосредственно по одной из
формул, приведенных выше (см. далее решение примера 1).
2. Данный интеграл при помощи применения четвертого и
пятого свойств неопределенного интеграла приводится к одному
или к нескольким табличным интегралам, т. е. к интегралам,
которые берутся непосредственно по формулам (см. далее при-
меры 2 и 3).
3. Данный интеграл в результате тождественного преобразо-
вания подынтегральной функции и применения свойств неопре-
деленного интеграла (4-го и 5-го) приводится к одному или не-
скольким табличным интегралам (см. пример 4).
С С dx
Пример 1. Найти интегралы: а) \ dx; б) \ x9dx; в) \ —.
Решение. Из сопоставления этих интегралов с левыми час-
тями формул I, II, III видим:
а) dx = х Д- С', б) x9dx = Д- С = х10 Д- С;
в) ^ — \пх-\-С.
Пример 2. Найти §3xsdx.
Решение. В подынтегральном выражении имеется постоян-
ный множитель 3. Применив последовательно четвертое свойство
неопределенного интеграла и формулу II, находим
\ 3x3dx = 3 \ x3dx = 3-^4-C=3-|x0 + C = lx6 + C.
J 5 + 1 1 о 1 2 1
Пример 3. Найти ^(6х3— Зх2Д-2х— 5) dx.
Решение. В данном случае под знаком интеграла дана 1
алгебраическая сумма функций. По пятому свойству неопреде-
ленных интегралов, имеем
J (6х3 — Зх2 —2х — 5) dx — $ 6х3 dx — J Зх'2 dx Д- J 2х dx — $ 5dx.
Далее последовательно применяем четвертое свойство инте-
гралов и формулы I и II. Получаем
J (6х3 — Зх2 Д- 2х — 5) dx = 6 jj х3 dx — 3 jj х2 dx Д- 2 х dx — 5 J dx =
= 6 • 3^1 - 3 • 4- 2 • - 5x + С = 4 X1—x3+X2 - 5x+C.
287
Примечание. Полученный ответ является результатом че-
тырех интегрирований. Каждое отдельное интегрирование вносит
свою произвольную постоянную С. В таких случаях принято
ставить только одну произвольную постоянную, имея в виду,
что алгебраическая сумма произвольных постоянных есть одна
произвольная постоянная величина.
Проверка:
х4 — х3 ф- х2 — 5х ф- с)к- = -|- • 4х3 — Зх‘* ф- 2х — 5 • 1 =
х = 6х3— Зхаф--2х— 5.
Получилась подынтегральная функция. Следовательно, интег-
рал взят верно.
Пример 4. Найти \ 1 dx.
Решение. В выше приведенных формулах интегралов под-
ходящей формулы не имеется, четвертое и пятое свойства неоп-
ределенного интеграла непосредственно применить невозможно.
- Преобразуем подынтегральное выражение так:
f (2х — I)2 , С 4х2 - 4л- + 1 . С /. . , 1 \ ,
\ д------dx— \---------— dx — \ 4х — 4 ф— dx.
J X J X J \ X /
Затем применим последовательно свойства неопределенных
интегралов (4-е и 5-е) и формулы II, I и III. Получим
С (2л — Ч = 4xdx — { 4dx ф- j — = 4Л x dx — 4 \ dx -ф-
J x j J j x j .) 1
—4-x ф- 1пхф-С = 2х2 — 4x-i-lnx4-C.
Проверка: d (2x~ — 4x -ф- In x -ф- C) = (2x2 — 4x ф- In x ф-
ф- C).v dx — 4x — 4 ф- — ]dx —---- — dx = 2---dx.
Получилось подынтегральное выражение. Следовательно, ин-
теграл найден верно.
Указание. Задачи на интегрирование по формулам I—XI11
расположены в порядке возрастающей трудности. К некоторым
из них даны решения с соответствующими пояснениями. За каж-
дой решенной задачей следует ряд интегралов, вычисляемых теми
же приемами. Ответы и краткие указания к ним даны в конце
книги, однако для более успешного приобретения навыков в вы-
числении интегралов рекомендуется пользоваться ответами и ука-
заниями как можно реже.
Задачи следует решать до полного овладения приемами вы-
числения. Основные формулы интегрирования необходимо знать
наизусть.
288
§ 103. ОПРЕДЕЛЕНИЕ ПРОИЗВОЛЬНОЙ ПОСТОЯННОЙ
ИНТЕГРИРОВАНИЯ
В § 98 было выяснено, что символ
\f(x)dx
означает множество функций
y=F(x)-[-C, (а)
имеющих своей производной подынтегральную функцию /(х) и
отличающихся друг от друга постоянными слагаемыми.
Чтобы из множества первообразных функций (а) выделить
одну определенную функцию, необходимо иметь дополнительное
условие, дающее возможность определить значение произвольной
постоянной С. Рассмотрим несколько примеров.
Пример 1. Найти функцию, производная которой
4х"' — 2.v + 3, (б)
зная, что при х=1 эта функция принимает значение, равное 4.
Решение. Обозначив искомую функцию через у, получим
1/л = 4х3—2х -'-3,
или
^ = 4хз_ 2x4-3.
dx 1
Отсюда
dy == (4х3 — 2х 3) dx,
^dy — 1^ (4х3 — 2х -j- 3) dx,
у-\-С\ = х1 — х- 4- Зх -j- С2,
или
y~xF — х'- 4-Зх —С.
Итак, '
у = х'1 — х2 -{- Зх 4- С. (в)
~ Мы нашли общее выражение функций, имеющих своей про-
изводной данную функцию (б).
Нам предложено найти ту из первообразных функций, кото-
рая при х=1 принимает значение, равное 4. Эти данные (х=1,
у = 4) принято называть начальными значениями аргумента х
"-и функции у, или начальными условиями задачи.
Подста!вив в уравнение (в) вместо х и у их данные значения,
находим:
4 = I4—Г24-3-1 4-С; С=1.
Заменяем в равенстве (в) произвольную постоянную С най-
денным ее значением и получаем искомую функцию
у = х1 — X9 4- Зх 4- I.
10 П. Е. Агачев
289
Пример 2. Написать уравнение кривой, проходящей через
точку (3; 4), зная, что угловой коэффициент касательной к этой
кривой в любой ее точке (.г, у) равен х1— 2х.
Решение. Нам известно (см. § 62), что
В данном случае имеем:
= — 2х; dy = (x?— 2x)dx.
В результате интегрирования получаем:
у = (х9 — 2х) dx\
у=^х? — х<1 + С. (г)
Мы нашли уравнение семейства кривых (см. § 100). Остается
из этого семейства кривых выделить ту, которая проходит через
данную точку (3; 4). Для этого подставляем в уравнение (г)
вместо хну координаты данной точки и находим:
4 =1-3:| —32Д-С; С = 4.
Это значит, что через данную точку проходит та из кривых (г),
для которой С = 4, т. е.
г/х=1%3 —х94-4.
Пример 3. Тело, находившееся в начальный момент, т. е. при
t — Q, в покое, падает при постоянном ускорении g силы тяже-
сти. Найти закон этого движения.
Решение. Нам известно (см. § 79), что
. dv
W=V‘=df
В данном случае w = g и ^(—g; dv = gdt.
Интегрируя, находим
v = \gdt—>gt-\- Ci,
или
v = ^ + Ci. (д)
Так как в начальный момент (при 7 = 0) тело находилось
в покое, то при t — О и и — 0. Подставив эти значения t и v в
равенство (д), находим значение Ct:
0 = £-0 + Сь
откуда
Ci = 0.
290
Следовательно, скорость движения в момент t определяется
по формуле
и = ^4-0; v = gt. (е)
Но (см. § 58) так как
то равенство (е) можно переписать в следующем виде:
rl/ = gt, или ds = gtdt,
at b
откуда, интегрируя, получаем
s = gt dt — -ф- С>.
По условию задачи, при t = 0 и пройденный путь з = 0. Для
определения произвольной постоянной Са получаем уравнение
о = ^+са,
откуда
С2 = 0.
Следовательно, в данном случае пройденный путь s в зави-
симости от времени t выражается формулой
s— 2 •
Пример 4. С земной поверхности вертикально вверх брошено
ядро со скоростью м/сек. Найти скорость движения этого ядра
в момент t.
Решение. Направление по вертикали вверх принимаем за
положительное; тогда ускорение силы тяжести, направленное
вниз, придется взять со знаком минус:
w — ^- —— g, или dv = — gdt.
Интегрируя, получаем
v = $ (— g dt) = — gt + С,
или
v =—gt-\-C. (ж)
В начальный момент (при / = 0) скорость движения была
равна MjceK. Подставив эти значения t и v в равенство (ж),
найдем значение С, соответствующее условиям данной задачи.
Получим:
= — g-0 + C; С— Vo.
10’ 291
Остается в равенстве (ж) заменить произвольную постоянную С
ее найденным значением:
v — (—gt-j-Vo) м)сек.
По этой формуле определяется скорость равнозамедленного
движения под действием силы тяжести. Очевидно, она будет
справедлива в случае любого равнозамедленного движения, т. е
при любом другом ускорении а.
§ 104. ИНТЕГРИРОВАНИЕ СПОСОБОМ ПОДСТАНОВКИ
Нижеприведенные формулы являются обобщением формул,
помещенных в § 102. В них и рассматривается как функция от
х [u = f(x)l, a du — как дифференциал этой функции: du — dfixj —
t= f (х) dx.
Преобразованные основные формулы интегрирования:
I. $ du — и-\-С.
II. ( u'ldu=-^-,+C. III. J--=lnu4-C, »>0.
J n ф 1 1 J и ' ’
при и-p — I
IV. \e" du = e'4-C. V. (a"d« = .- + C.
J 1 j In a 1
VI. ( sin и du — — cos и -p С. VII. $ cos и du — sin и C.
VIII. \ sec2 и du — tg и 4- C.
j COS" и J b 1
IX. -Д'—= cosec2 и du —— ctg и 4-C.
J Sin- U J bl
X. $ tg и du = — In cos u -J- С. XI. ctg и du = In sin и C.
XII. - = arc. sina-t-C. XIII. ( , f = arc tg и -+- C.
Очевидно, что формулы, приведенные в § 102, являются част-
ными случаями этих формул при и = х. Справедливость любой
из них может быть доказана: для этого достаточно показать, что
дифференциал правой части равен дифференциальному выражению,
стоящему под знаком интеграла.
Пусть требуется, например, доказать справедливость формулы
? и’1 du = -1—т-г С, где u=f(x).
Находим дифференциал правой части:
. / n'1+< I /~Л ! иплл I А , Г(н 4 1) ип+1'-1 , П1 ,
d —г-, 4- С = --.-г + С к- dx = v - j-j-----u.v 4- 0 dx —
vA1 J \“+' I L "+1 1 J
= unux dx — u'1 du,
292
так как [см. (3) § 92[
и\ dx = du.
Следовательно, формула II верна.
Ранее мы вычисляли интегралы непосредственно по формулам
1—XIII, (см. § 102). Но этот способ применим лишь к интегри-
рованию простейших функций. В технике интегрирования исклю-
чительно важное значение имеет другой способ, называемый спо-
собом подстановки, или способом замены переменной. Сущность
его заключается в том, что, принимая за и некоторую функцию
от независимой переменной х, мы преобразуем интеграл ^f(x)dx,
который по формулам § 102 не вычисляется, в интеграл \F(u)du,
который уже легко берется по какой-нибудь из формул, приве-
денных в начале этого параграфа. Рассмотрим несколько при-
меров.
Пример 1. Найти (а2 -ф х3) з х dx.
Решение. Среди формул, приведенных в § 102, нет такой,
по которой можно было бы вычислить данный интеграл. Просмат-
ривая формулы I—XIII этого параграфа, мы устанавливаем сход-
ство между данным подынтегральным выражением (а? -ф- х3)3 х dx
и подынтегральным выражением в формуле II, если принять
а1 -ф х3 = и.
Выразится ли при таком значении и множитель xdx через du
независимо от х?
Если a3-J-x3 = u, то 2xdx = du, откуда
xdx — -l^\ (а3-фх3)3 xdx = ( и* ~ =
Г ’1 * 4-м /
= 4- | иЧи=Л--.-----------рС=4и4 ф-С.
J 4+1
Остается в полученный результат вместо и подставить его
выражение через х. Получим
(а3 + х3)3 х dx = | 4- С = 4 рЧя34-х3ф ф- С.
Проверка:
d [| /(а9 + х2)1 + С | = [4 + -4)3 + с] /х =
4 _ 1_
= К ' 4^ х^ 1 ’ (a<L Х^х ^х ~ 2' (d2 4- 4)3 • 2х dx —
।
= (a- -J- х3)3 х dx.
293
Получилось подынтегральное выражение, следовательно, ин-
теграл взят верно.
Пример 2. Найти $ (а3 4" х3)® Зх2 dx.
Решение. Положим а'-\-х3 — и\ тогда
d (а3 4- х:|) — Зх2 dx, или 3x1dx = du.
Вследствие этого данный интеграл преобразуется в другой
интеграл, который берется по формуле II этого параграфа:
(а3 4- х3)0 Зх2 dx — и6 du — у -j- С — *- 4~ С.
Следует приучаться записывать короче, а именно:
(а3 4~ х3)6 Зх2 dx — (а3 4~ х3)® d (а3 4* х3) — (а х - -ф- С.
Пример 3. Найти \
Решение. Числитель (2xdx) подынтегрального выражения
является дифференциалом знаменателя (14-х2). Это наводит на
мысль принять
1 4-х2=«.
Тогда, взяв дифференциалы от обеих частей этого равенства,
получим:
d(l 4-х2) —du, пли 2xdx — dw,
f = f — = lnt/4-C*.
J 1 + Х“ J U 1
Подставив вместо и его выражение через х, найдем:
$^ = 1п(14-х2)4-1нС = 1пС(14-х2).
Решение можно записать короче, а именно:
§ ^Ц^у-,=Лп(14-х2)4-1пС = 1пС(14-х‘-).
Пример 4. Найти Г 4.
J у- (1 + ах‘У
Решение. Этот интеграл может быть переписан в следую-
щем виде:
з
Р 4ах3 dx Р 4ах3 dx Г*/, । л > j
- = I ------5-= 1 (14-ах1) 4.4ax3dx.
/(i + «xv J- Г
J J (1 + ЧХ'1) J
* См. указание к задаче 721.
294
Подынтегральное выражение сходно с подынтегральным вы-
ражением в формуле II. Положим 1 -+-ах'‘ = и. Тогда, продиффе-
ренцировав обё части этого равенства, получаем
4ax3dx = dtr, I (1 -4-ах4)_^-4ax3dx =
J и dn
_з “?+1 Т
и du = ~------|-C=:^- + C = 4yA«+C.
— — 4.1 —
4 - 1 4
Подставив в полученный результат вместо и его выражение
через х, найдем
(• \ах" dx , 4 г-.—;---т ,
\ лт-------: = 4 V 1 + ах14- С.
' /1 + («Х’Р v
______ г 1 Т
Проверка: d(4 ф! -ф- ах4 -ф- С) = [4 (1 -ф- ах4)4 -ф- С] х dx =
= 4 • j • (1 -ф-ах4)4 • (1 ~\~ax'l)xdx =
= (1 -ф- ах4) 4 • 4ах3 dx = -4ах .
Следовательно, интегрирование выполнено верно.
Указание. На вычисление неопределенных интегралов спо-
собом подстановки даны задачи 789—888, причем некоторые из
них снабжены полным решением с подробными пояснениями.
За каждым таким интегралом дан ряд интегралов, которые сле-
дует . вычислить самостоятельно, прибегая к наводящим ука-
заниям только в тех случаях, когда все попытки преобразо-
вать данный интеграл §/(x)dx в один или несколько интегралов
вида ^F(u) du, вычисляемых по формулам I—XIII, окажутся без-
успешными,
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Какое действие называется интегрированием?
2. Какая функция называется первообразной для данной функции /(х)?
3. Чем отличаются друг от друга функции, первообразные для данной
функции /(х)?
4. Если f(x) — F’(x), то как выразится совокупность функций, перво-
образных для функции f(X)?
5. Чему равен J (^Зх3-)-1)^ rfx?
6. Чему равен ) d (cos5x— sin 5х)?
7. Как читается запись ^/(x)rfx?
8. Что называется неопределенным интегралом?
9. Какой геометрический образ соответствует неопределенному интег-
ралу J/(.г) rfx?
295.
10. Каким действием проверяется результат интегрирования?
11. При каком условии справедливо равенство
$ / (х) dx = F (х) + С?
12. Найти f(x), зная, что f(x) dx — (sin 2х — cos 2x) ф- C.
13. Чему равна производная неопределенного интеграла?
14. Чему равен дифференциал неопределенного интеграла?
15. Чему равен неопределенный интеграл от дифференциала функции
F(X)?_
16. Как формулируются четвертое и пятое свойства неопределенных
интегралов?
17. При каком значении п неприменима формула
р ,-я+1
' \ х« dx = -%-г + С?
J « + 1
18. Какую формулу надо применить, чтобы найти
когда п = —1?
19. На сколько интегралов распадается каждый
хп dx в том случае,
из следующих инте-
i pn.I ио,
1) ? -vl ~ + 3а-+-5 dx; 2) ( *'' —</х?
.) х- J х —а
20. Выделить из семейства кривых, соответствующих неопределенному
интегралу \ (2х — 5) dx, кривую, проходящую через точку (—3; 6).
21. Выделить из семейства кривых, угловой коэффициент касательной
к которым в любой точке (х; _у) равен удвоенной абсциссе этой точки, ту
кривую, которая проходит через начало координат.
22. Из функций , первообразных дт.я функции f (х) 'Leos 2х , найти ту,,
которая при х = 0 обращается в нуль.
23. Скорость v материальной точки, движущейся но оси Ох в зависи-
мости от времени t, определяется по формуле v — cos 4Л Найти закон этого
движения, если известно, что в начальный момент эта точка находилась
в начале координат (при ? = 0; х = 0).
24. В каких случаях применяется способ интегрирования подстановкой?
25. Можно ли в подынтегральном выражении вместо dx нависать (х -ф- а),
где а — любое число? Если можно, то почему?
26. Изменится ли величина подынтегрального выражения, если вместо dx
, , 1 . . , о. 1 . , Г г \ ! (ах b 1..
написать: 1) --а (ах); 2) — dlax-^b), 3) — d I—-— ?
Ответы. 19. 1) На четыре; 2) на три. 20. у — х“ — 5х—18. 21. у=-х~.
22. у = sin 2х. 23. sin М. 25. Можно, так как ^dx — x-\-C u ^tZ(x-(-a) =
= х-|-С, где а и С — произвольные постоянные. 26. Во всех трех случаях
величина подынтегрального выражения не изменится.
Глава XI
ОПРЕДЕЛЕННЫЙ интеграл и его приложения
\
§ 105. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ВЫЧИСЛЕНИЕ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Задача 1. Найти приращение функции, первообразной для
функции cos х, когда аргумент х от значения а переходит к зна-
чению р.
296
Решение. Интегрированием находим множество первообраз-
ных функций, отличающихся друг от друга постоянными сла-
гаемыми:
J cos xdx — sin х -j- С.
Очевидно,
sin х -|-Ci,
где Ct — любое данное число, является одной из этих первообраз-
ных функций. Найдем значение этой первообразной функции при
х = ^. Получим
(sin х ф- Ct) | v_r, = sin p(a)
Аналогично, при x = a получим
(sin x 4-Ct) !.<_, = sin a 4-Сь ' (6)
Приращением функции, как известно, называется разность
двух ее значений. Находим эту разность, вычитая (б) из (а);
получаем
sin р 4~ Ст — (sin a 4* Ci) = sin 8 — sina.
Задача 2. Найти приращение функции, первообразной для
функции f(x), при переходе аргумента х от значения а к зна-
чению Ь.
Решение. Положим, что интегрированием найдено
$ f (х) dx = F (х) -PC. 1
Тогда F(x)-|-C1, где Ci — любое данное число, будет одной
из первообразных функций для данной функции f(x). Найдем
ее приращение при переходе аргумента х от значения а к зна-
чению Ь. Получим
[А(х) 4- С1]пр1| Л-_/, — [А (х) 4" Ct]npn х-а ~
— F (6) 4- Ct — F (a) — Ci = А (6) — A (a).
Как видим, в выражении приращения первообразной функ-
ции F(x)4~Ct отсутствует постоянная величина Сь А так как
под Ct разумелось любое данное число, то полученный результат
приводит к следующему заключению: при переходе аргумента х
от значения х — а к значению х — b все функции F(x)-\-C, перво-
образные для данной функции f(x'), имеют одно и то же прира-
щение, равное F (b) — F (а).
Это приращение принято называть определенным интегралом
и обозначать символом
ь
\f(x)dx.
а
Определение. П риращение первообразных функций F (х) 4- С
при переходе аргумента х от значения х — а к значению х = Ь,
297
равное разности F(b) — F (а), называется определенным интегралом
ь
и обозначается символом \f(x)dx, так что если
а
\f(x) dx — F (х) -f- С,
то
ь
\ f(x)dx — F (6) — F (а) *
а
(1)
предполагается при этом, что подынтегральная функция f(x)
непрерывна при всех значениях х, удовлетворяющих условиям
a^xs^b.
ь
Символ ^/(x)dx читается так: «определенный интеграл от а
а
до b эф от икс дэ икс». Число а в этом символе называется
s нижним пределом определенного интеграла, число Ь — его верх-
ним пределом.
Порядок вычисления определенного интеграла принято запи-
сывать так:
b ь
\jf(x)dx = F (х) | — F (b) —F (а)
а а
(1а)
где символ F (х) читается: «.двойная подстановка от а до b
в функцию F(x)», причем под F (х) обычно разумеют ту из перво-
образных функций, у которой С = 0.
Из изложенного видно, что для вычисления определенного
интеграла в первую очередь следует найти неопределенный инте-
грал, пользуясь формулами, приведенными в § 102 и 104, а также
четвертым и пятым свойствами неопределенных интегралов (см.
§ 101), которые применительно к определенным интегралам запи-
шутся так **:
1> ь
\cf(x)dx = c\f(x)dx; (2)
а а
b b ь ъ
$[f(x) — <p(x)4-F(x)]dx = J f(x)dx— 5 <?(x)dx-\-^F(x)dx. (3)
а а а а
9
Пример 1. Вычислить f -Д.
J Ух
4
* Равенство (1) называется формулой Ньютона—Лейбница.
** Пока примем эти формулы без доказательства. Справедливость их
будет доказана в § 109.
298
/L = 2/I
Решение. Находим неопределенный интеграл
. _j_ - i+1 _
*dx = —.------f-C = 2/x-|-C,
J И-v J — — + 1
2 ' 1
а затем по формуле (la) вычисляем определенный интеграл
9
Э = 2/9 — 2/4 = 2-3-2-2 = 2.
4
4
Пример 2. Угловой коэффициент касательной в любой точке
кривой численно равен абсциссе этой точки. Найти приращение
ординаты точки этой кривой при изменении абсциссы от 2 до 3.
Решение. Обозначив абсциссу любой точки кривой через х,
ординату — через у, по условию задачи будем иметь:
k — ~ = x, dy — xdx.
Из этого равенства видно, что ордината у есть первообразная
функция для х, т. е. -
y — ^xdx,
или
у=^-х‘>-\-С (см. рис. 164, б).
Согласно определению найдем, что при изменении абсциссы х
от 2 до 3 ордината у получит приращение, равное
( xrfx = lx2|=|-32—4 -22 = 4 1--2 = 21.
2 2
На рисунке это приращение показано на кривых
I » 1 » I л
’ ^=-2х+4-
Я
т
Пример 3. Вычислить § (3cosx— 3sinx)dx.
О
Решение. По формулам (3) и (2) находим
71 К Л
2 2 2
(2 cos х — 3 sin х) dx' = J 2 cos х dx — § 3 sin x dx —
о о 0
3 —3(—cosx) 3
0 0
= 2 $ cos xdx — 3 J sinxdx = 2 sinx
о 0
sin-| —sino)-j-3(cos| —cos o) = 2(1 — 0)/3(0— 1) = - 1.
299
§ 106. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ КАК ПЛОЩАДЬ
Предположим, что кривая КМ (рис. 165) является графиком
непрерывной функции у —/(х), остающейся положительной при
всех значениях х.
Возьмем на этой кривой точку А с абсциссой OAi—a и точ-
ку В, движущуюся по ней и, следовательно, имеющую перемен-
ную абсциссу ОВ1 — х. Получим фигуру AiABBi, ограниченную
графиком дайной функции y=f(x), осью Ох, ординатой АгА —f (a)
(будем называть ее начальной
ординатой) и переменной ор-
динатой BiB = f(x). Такие
фигуры принято называть
криволинейными трапециями.
Очевидно, что при уменьше-
нии х переменная ордината
BiB будет перемещаться вле-
во и вследствие этого пло-
щадь криволинейной трапе-
ции AtABBt будет умень-
шаться, а при увеличении х
ордината В}В будет переме-
щаться вправо и площадь фигуры AiABBi будет увеличиваться.
Короче, каждому значению х будет соответствовать одно вполне
определенное значение переменной площади AiABBi, следователь-
но, площадь криволинейной трапеции AiABBi является какой-то,
нам еще неизвестной, функцией от х.
Обозначив эту функцию через Р (х) и переменную площадь
криволинейной трапеции^AiABBi— через S, получим
S = P(x).
(а)
Из § 103 известно, как восстанавливать (находить) функцию
по данному выражению ее производной и по одному частному
значению этой функции, соответствующему определенному значе-
нию аргумента. В данном случае такое значение функции (а) нам
известно. При х = а фигура AiABBi обращается в отрезок AiA
и, следовательно, площадь ее обращается в нуль, т. е.
Остается найти
S\x-a~P(a) = 0.
(б)
sx = d/.
dx
Дадим аргументу х приращение BiCi = I±x. Тогда S получит
приращение Д£, равное площади BiBCCt. Через точки В и С
проведем отрезки ВСч и СВ±, параллельные оси Ох. Получим
два прямоугольника с общим основанием BiCi. один BiBC.>Ci
с высотой BiB — [(x), другой В1В>СС1 с высотой CiC — f (х -ф- Дх).
300
Так как площадь криволинейной трапеции B^BCCi является
частью площади прямоугольника BiBiCCs, а площадь прямо-
угольника BiBCiCt — в свою очередь частью площади криволи-
нейной трапеции, то очевидно:
площадь В|В.2СС1^>площади BiBCCt У> площади BtBCaCr,
но площадь QBiBo.CC1 = C1C-B1C1 = f (% + Дх) Дх; :
площадь П BiBCiCt = BiB- BiCi = f(x)‘ Дх;
плошадь ДВ1ВСС1 = Д5;
поэтому предыдущие неравенства можно переписать в следующем
виде:
f (x-f- дх) Д5^>/(х) Дх, (в)
где Дх^>0.
Из алгебры известно, что смысл неравенства не изменится,
если его части разделить на любое положительное число. На
основании этого, разделив части неравенства (в) на Дх, получим
f (х + Дх) Дх AS f (х) Дх
Дх Дх Дх ’
ИЛИ
f(x+Ax)>g>f(x).
Когда Дх будет стремиться к нулю, точка Ct будет стремиться
к совпадению с точкой Bi, а потому ордината С(С будет стре-
миться к совпадению с ординатой BjB, т. е. f (х Дх) ->/ (х).
Так как величина отношения заключается между f(x-\-bx)
и f(x), a limf (x-j- Дх) = / (х), lim f (х) = / (х), то
А.г->0 Д.а—о
Ит =
Д X -* 0 а л
Но мы знаем, что пределом отношения приращения функции
к приращению аргумента, когда приращение аргумента стремится
к нулю, является производная этой функции. Получаем:
S'< = f(x); g = /(x); dS = f(x)dx. .
Интегрируя, находим:.
\dS = \f(x)dx; S-[-Cl = F(x)-^ra..
Это равенство можно переписать в виде S =-F (х) -|- С, — С\, или
еще проще: S = F(x)-)-C, заменив разность двух произвольных
постоянных С-2 и Ci одной произвольной постоянной С. Приняв
во внимание равенство (а), найдем
Р (х) — F (х) С. (г)
Теперь из множества первообразных функций F(x)-\-C надо
выделить ту, которая обращается в нуль при х — а, т. е. найти
301
правая часть равенства
неопределенного интеграла
такое значение С, при котором Р (а) — 0 [условие (б)]. Для этого
в равенстве (г) заменяем х числом а и находим:
Р (а) = F (а)С = Q-, C = — F(a).
Следовательно, при данном а и переменном х, большем а,
площадь криволинейной трапеции определится по формуле
S = Р (х) = F (х) — F (а).
является разностью двух значений
^((xjdx. Мы знаем (см. § 105),
что
F (х) — F (а) = § f (х) dx.
а
Следовательно, площадь криволи-
нейной трапеции AiABBi при данном
а и при любом х)>а найдется по
формуле
х S = \ f (х) dx. (4а)
Рис. 166 а
Чтобы получить формулу для площади AiABBi (рис. 166) при
х=Ь и, следовательно, при вполне определенном положении орди-
наты BBt, достаточно в формуле (4а) заменить х числом Ь. Получим
ь ь
S — I\lf(x)dx, или S = ^ydx
а а
(4)
ь
Следовательно, определенный интеграл [[(x'fdx геометрически
выражает площадь криволинейной трапеции, ограниченной графи-
ком функции y — f(x), осью Ох и прямыми
х~а, х — Ь.
Пример 1. Вычислить площадь фигу-
ры, ограниченной графиком функции у =
= уХ-)-2, осью Ох и прямыми: х=2, х=6.
Решение. В первую очередь строим
фигуру, площадь которой требуется най- pIlc
ти (рис. 167). Площадь S вычисляем по
формуле (4). В данном случае: « = 2, й = 6, у = / (х) — х -ф- 2.
Находим
S = хДх = х 2^ dx = х2 |®-]-2х|® —
= рб2— 22)-ф2(6 — = 8= 16 кв. ед.
302
Фигура AiABBt является прямоугольной трапецией. Вычислим
ее площадь по формуле S — • Параллельные стороны этой
трапеции соответственно равны: с= AtA = f (2) == 4” 2 + 2 = 3;
d — B1B = f(6)=^-6Jr2 = 5. Высота h = A1Bt = OBi — OAt =
= 6-2 = 4.
Подставив найденные значения с, d и h в формулу площади
трапеции, получим
е (3 + 5) -4 ,
S = -- "2 —=16 кв. ед.
Оба способа, как и следовало, ожидать, дали один и тот же
результат.
Пример 2. Вычислить площадь фигуры, ограниченной кривой
у = ^ х"1, осью Ох и прямыми:
х = — 4, х = 6.
Решение. Построим фигуру,
ограниченную данными линиями*
Уравнение у — ~х3 равносильно
уравнению х‘1 = 4у. Параболу, сим-
метричную относительно оси Оу,
строим так, как это делалось в ана-
литической геометрии (рис. 168).
Приемами элементарной геомет-
рии площадь фигуры AiABBt точ-
но вычислить невозможно. Интегрированием она найдется просто
и легко. Получим
f(x)dx = ~x'!dx = --j- х2 dx = 1 у |в , ~
= ’,[+-(-4)^ ='.(216 +64) = 23 ± кв. ед.
Указание. На вычисление площадей даны задачи 959—977.
Задачи 960, 961, 969 снабжены подробными решениями с пояс-
нениями.
§ 107. ВЫЧИСЛЕНИЕ ПУТИ, ПРОПДЕННОГО ТЕЛОМ
Из § 58 мы знаем, что если в прямолинейном движении прой-
денный путь s в зависимости от времени t выражается формулой
s = то скорость этого движения в момент t будет равна
первой производной функции s = f(t) при данном значении t, т. е.
303
В § 79 было установлено, что в неравномерном движении,
определяемом уравнением s = /(Z), ускорение w в момент t равно
значению второй производной от пути s по времени t при данном
значении t, т. е.
В § 101 нами разобрано несколько примеров на выражение
пути через время t по данным выражениям скорости и ускоре-
ния. По ознакомлении с определенным интегралом такие задачи
можно решать значительно проще, не тратя времени и места на
определение произвольной постоянной С по начальным данным.
Рассмотрим примеры, пренебрегая, как и выше, сопротивле-
нием воздуха.
Пример 1. На какую высоту поднимается тело, брошенное
вертикально вверх со скоростью 39,2 м)сек?
План решения:
1) найти момеш времени, когда скорость обратится в нуль,
т. е. когда прекратится движение вверх;
2) найти наибольшую высоту, на которую поднимется тело.
Решение. 1) Здесь движение равнозамедленное. Скорость
такого движения выражается формулой
v = — gtf + vo,
или
V — — gt -1- 39,2, (а)
так как нам дано н0 = 39,2 м)сек.
Приравняв нулю правую часть равенства (а) и решив получен-
ное уравнение, найдем:
— g/4*39,2 = 0; = сек.
2) Равенство (а) можно переписать в виде
g = 39,2-g/.
При определении s пределами интегрирования будут /1 = 0,
6 = 4. Найдем:
ds — (39,2 — gt) dt',
s = (39,2— gZ) d/= 39,2/1‘ — -f/2|* =
0
= 39,2 (4 - 0) - (4- — 0‘2) = 78,4 m.
Пример 2. Реактивный самолет в течение 20 сек увеличил
свою скорость от 240 до 720 км[ч. Считая движение равноуско-
ренным, найти, с каким ускорением летел самолет и какое рас-
стояние пролетел он за это время.
аоч
с.
План решения:
1) найти ускорение;
2) найти расстояние, которое покрыл самолет за 20 сек.
’ • 240.1000 , 200 ,
Решение. 1) = —мсек.—-^ мсек\
' 60-60 ' 3 '
720-1000 /
^ = ЛЮ76(Г=200 м!сек-
Скорость равноускоренного движения в зависимости от уско-
рения w и времени t выражается формулой v = wt и0. В дан-
ном случае 1
/ , , 200\ ,
v = lwt-\- — j м/сек. - (б)
Чтобы найти ускорение w, примем во внимание, что при
/ = 20 сек н = н1 = 200 м/сек. Заменив в уравнении (б) и и t
их значениями и решив полученное уравнение относительно ш,
найдем:
200-200
900 .4 9
200 — w • 20 -ф- - 3- ® = —по— = 6 -у м/сек*.
2) В уравнении (б) v является первой производной от пути
по времени, и, следовательно, оно может быть представлено
в следующем виде:
ds с 2 , , 200
или
, /20 , . 200. ,, 20 . 1Л. ,,
as = l-y t-\- —j at = -3 (t 10) di.
Нам надо вычислить путь самолета за время от момента
/1 = 0 до момента Л = 20 сек. Интегрированием найдем
20 20
С 20,, . 1П. 20 (“ ,, , 1Л. ,, 20 t- [20
s = \ -у (/ -ф-10) dt — у- 1 (/ —j- 10) dt — -у • -ф-
о о
4- . ю/ |*° = у (202 — О2) 4- (20 — 0)
2666,7 ,н ^2,67 км.
§ 108. ЗАМЕНА ПЕРЕМЕННОЙ ПОД ЗНАКОМ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Чтобы по формуле (1) вычислить определенный интеграл
f (х) dx,
а
необходимо в первую очередь найти неопределенный интеграл
\f(x)dx = F\x).-
305
Мы умеем находить неопределенные интегралы: 1) непосред-
ственно по формулам I — XIII, приведенным в § 102, и 2) спо-
собом подстановки (см. § 104). Из предыдущих параграфов этой
главы (и решения приведенных в них задач) известно, как вычис-
лить определенный интеграл в тех случаях, когда неопределен-
ный интеграл берется непосредственно по формулам. В данном
параграфе рассматриваются приемы вычисления определенных
интегралов, когда неопределенный интеграл берется способом
подстановки. Известно (см. § 104), что в этом случае приходится
заменять переменную интегрирования х другой переменной (обо-
значим ее через и), связав ее с переменной х определенным урав-
нением.
Имеют место равенства:
[f (х) dx = jj Ф (u) du,
Ьц.>
/ (х) dx — Ф (u) du *,
a
где th и и-2 должны быть, границами изменения и, соответствую-
щими границам изменения х(а и Ь) (при этом и должна быть
однозначной функцией от х).
Л
6‘ _________
Пример- Вычислить jj 1^1 4-6sinxcosxd%.
а
л -л
Т ________- "б 1
Решение. l)jj рТ-|-6sinxcosxdx = (1 4- 6 sin х)2 cos xdx.
о о
Введем новую переменную и, связав ее с переменной х урав-
нением
1 -6 sin х = и,
откуда
6 cos х с/х = Фи, cosxdx = ^.
Подставив вместо 1 -j- 6 sin х и cosxdx их выражения через и
и du, получим:
7Е
2) J (1 -(-6sinх)2 cosxdx— J u2 • = $ и2 du,
0 И1 ill
1 -1-
где -и2=Ф(и), Ui и и.г — границы изменения и.
* В более полных курса/ анализа справедливость этой формулы дока-
зывается. '
306
При определении е и е рассуждаем так:
а) было принято и = 1 —6 sin х;
б) нижняя граница (ut) изменения и должна соответствовать
нижней границе изменения х (xi = 0), следовательно,
U1 = l + 6sin0=l +6-0=1;
в) верхняя граница (и2) изменения и должна соответствовать
верхней границе изменения х = , откуда
1 +6sin -g- = 4.
3) Теперь подставим вместо е ненайденные их значения, получим
Я Л
"6 б‘ £
1А -|-6sinxcosxdx = ^ (1 + 6sinx)2 cos xdx =
о о
1 , . 4 1 I
с dll 1 f -о , 1 2 3
= \ и2 • -£-==« \и2 du =-=- =
J Ь 6 J 6 з и
III 1 1
§ 109. ПРОСТЕЙШИЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Свойство 1. Перестановка предела интегрирования равно-
сильна изменению знака перед определенным интегралом, т. е.
Ь а
\f (x)dx = — f (х) dx.
a b
Доказательство. Предположим, что
Тогда
$/(x)dx = .F(x) + C.
ь
f(x)dx = F(x)
а
Ъ
= F(b)~F(a);
а
- f(x)dx== — F(x')\b== — [F(a) — F(b)] =
ь
== —F(a)+F(6) = F(&) —F(a).
(а)
(б)
Правые части равенства (а) и (б) равны между собой, следо-
вательно, должны быть равны и левые части, т. е.
$ f (х) dx = — f(x) dx, (5)
а b
что и требовалось доказать.
307
Свойство 2. Промежуток интегрирования (а\ Ь) можно раз-
бить на меньшие промежутки, т. е.
ъ ъ
/ (х) dx — $ f (х) dx $ / (х) dx, (6)
a a bi
где а <4 bi Ь.
Доказательство. Если $ /(х) dx = F (х) Д- С, то
bi ь
\ f^dx^F^-Fta), \f(x)dx = F(b)-F(b1),
a bi
b
\f(x)dx=F(b) — F(a).
a
Отсюда
\f(x)dx+ \f(x)dx=F(bi)-F(a) + F(b)-F(bi)==
a bi
b
= F(b)-F(a)=\f(x)dx.
а к
Итак, доказано, что
b bi ъ
\f{x’)dx = \f{x')dx\-\f{x)dx. __
a a .
В случае, когда график подынтегральной функции y = f(x)
в промежутке (а; Ь) не пересекает оси Ох, справедливость фор-
так как
мулы (6) наглядно подтверждается
рис. 169.
Обозначив площади криво-
линейных трапеций AiA’tBBt,
AiAiA^A-i и AiA'2BBi соответствен-
но через S, Si и St, получим оче-
видное равенство
S = Si St,
или
ь (1, 1>
$ / (х) dx = $ f (х) dx (х) dx,
a a bi
ь
S = \f(x)'dx,
а
Пример. Вычислить
о
Решение. — V х
4
bl
Si = \f(x)dxi,
а
О
— Кх dx.
4
4 1 (?
(х2 dx = — х
•’ о
b
St — У (х) dx.
bi
16
з •
308
Свойство 3. Постоянный множитель можно вынести за
знак определенного интеграла, т. е.
ь ь
^cf (x)dx = c\f(x) dx, (6a)
a a
где c — постоянная величина.
Доказательство. Допустим, что/(х) =77'(х). Тогда будут
справедливы равенства:
ъ ь
\f(x)dx = F(x) + C, ' \f(x)dx=F(x) = F(b) — F(b); Да)
cf (х) = cF' (х). (б)
Из равенства (б) следует: cf (х) = [с/7 (х)]',
ъ ь ь
^cf(x)dx=\[cF(x)]'dx — [cF(x)] = cF(b) —cF(a) = c[F(b) — F(a)J ,
a a a
или (см. (a)]
\cf(x) dx = c \f(x) dx. (66)
’ . a a
Свойство 4. Определенный интеграл от алгебраической сум-
мы функций равен алгебраической сумме определенных интегра-
лов от этих функций, т,- е.
ь ь h
[/ (х) ± ср (х)] dx — У (х) dx ± ср (х) dx.
а а а
Доказательство,-Допустив, чтоf(x)=F’(х) и <р(х) = Ф'(х),
получаем
ь ъ ь -
\[/(x)zb cp(x)]cfx= ^[F'(x)±<5'(-v)]dx= ^/Дх) ± Ф (х)]' dx==
= [F (х) ± Ф (х) ] = Р7 W ± Ф (6)] — [У7 (a) zt Ф (&)]=
= [/7(6)-Г(а)]±[Ф(6)-Ф(а)],
или
b b ь
jj [/ (х) ± ср (х)| dx = f (х) dx zb ср (х) dx.
а а а
Таким же путем можно доказать справедливость этого свой-
ства для любого данного числа слагаемых.
Замечание. На применение 3-го и 4-го свойства уже решено
достаточное число примеров и задач в связи с изучением § 105 —
108. Свойством 2-м воспользуемся в § 111.
309
§ ПО. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ КАК ПРЕДЕЛ СУММЫ
Допустим, что нам дана криволинейная трапеция AiA'tBiB,
сверху ограниченная графиком функции 1/ = /(х), непрерывной
и положительной в промежутке (а; Ь), снизу—осью Ох, слева —
ординатой AiA^^fta) и справа — ординатой BBt—f (6) (рис. 170).
Нам известно [см. (4) § 106], что
ь
£ = пл. /11Л|ДВ = dx. (а)
а
Разобьем отрезок А2В точками Л._>, А:1, Л4, ..., Ап на п час-
тей (я — произвольное число). На рисунке эти части для про-
стоты взяты равными, но могут быть и не равными. Ординатами
А.2А',, Л3Л3, Л4Л[, .... АпА'п криволинейная трапеция AjAjBiB
разобьется на п полосок, ограниченных сверху дугой кривой
y = f(x), снизу — осью Ох.
Через точки А[, А.2, Аз, Л[, ..., А'п проведем отрезки AiA.2,
Л.2Л3 А'л, At, ..., А„В[ параллельно оси Ох. Тогда наша криво-
линейная трапеция разобьется на прямоугольники AjAjA^A-:,
A-tA^A-iА3...АпА'пВ[В и криволинейные треугольники А[А^А^,
А2А3А3, ..., A'nBiB’i (на рисунке заштрихованы). Обозначим
площади прямоугольников соответственно через Si, s.2> s3, ..., sn,
а площади криволинейных треугольников — через О], 32, 83, ... ,8Я.
Сумма площадей всех прямоугольников и криволинейных тре-
угольников, очевидно, будет равна площади фигуры AiA^BiB.
Получим равенство
<s = (si si т sa 'г • • • Ч-Sn) (ч 4~ ^7]-з3-}-... 4-в„). (б)
зю
Примем
OAi=a = xit ОА^ — Хч, ОАл = хл, .... ОАп = хп.
Тогда
AiA'l=f(a) = f(xi), ЛЛ2=Д(х.2),
Л3Л3 = [ (х3), ..., AnAn — f(xn)-
Отрезок А1А-2 является приращением xt. Обозначив его через
Дхь получим AiAi = Ξ аналогично, Л2Лз = Дх.2, /(3X4 = Дх3,
Л4Лз — Дх1, ..., АпВ = ^хп.
Мы знаем, что площадь прямоугольника равна произведению
основания на высоту. Выразив площади st, s2, s3, stl по
этой формуле, получим:
Si — Л]Л( • Л1Л2 = f (xf) Дхь ,
s2 = Л2Л,2 • Л2Лз = j (х.2) Дх2;
8=7(*з)дх3; •••; 8„ = /(х„)Дх„.
Введя найденные выражения площадей прямоугольников в ра-
венство (б), получим
S = Д%1 -ф- f (х-2) Дх.2 -ф- f(x3) Дхз + ... + /(хл)дхя]4-
+ (31 + §2 + ОЗ + ••• +8Д (В)
Ранее уже было сказано, что п — число произвольное. Сла-
гаемых в первых и во вторых скобках равенства (в) может быть
сколько угодно и написать их все нет никакой возможности,
вследствие чего в предшествующих записях мы отмечали лишь незна-
чительную часть их, ставя вместо отсутствующих членов много-
точие будучи уверены, что читатель сумеет написать любое
желаемое число. Уверенность основывается на том, что все сла-
гаемые, заключенные в скобки (например, в первые скобки),
одного вида и отличаются только индексами (указателями) при х
и при Дх.
Для краткой записи суммы однотипных слагаемых вводят
символ 2, называемый «сигма» и заменяющий слово «сумма».
Пользуясь этим символом, суммы, стоящие в скобках в равен-
стве (в), можно записать в таком виде:
/ (х2) Дх( -ф- / (х>) Дх-з -ф~ / (Хз) Дхз -ф- ... -ф-
k = п
+ f (Хп) Ьхп = 2 f (х,г) Дх/г;
Л- — J
k = п
-I- 02 И- °3 4“ • • •
k = 1
k = п.
Символ 2 f(.xk)kxk означает, что надо сложить все слагае-
л = 1
мые данного вида, последовательно придавая индексу k целые
значения, начиная от числа, стоящего под этим символом (в дан-
311
ном случае 1), и кончая числом, стоящим над этим символом
(в данном случае таким числом является п). После введения
вместо сумм, стоящих в скобках, их кратких выражений равен-
ство (в) примет вид
k = П k = п
s= у;/(х,)ДхЛ.+ у ()
1г = 1 к = I
Эта формула, очевидно, будет справедлива при любом п, т. е.
на сколько бы частей ни был
разделен отрезок AtB — b— а.
Из рис. 170 видно, что сумма
У, о/г мала по сравнению с сум-
к = 1
МОЙ f (Х/.) Дх/г *.
Покажем на конкретном приме-
ре, что с увеличением числа делении
п сумма площадей криволинейных
треугольников уменьшается и вслед-
ствие этого площадь ступенчатой
фигуры приближается к площади
криволинейной трапеции.
Возьмем криволинейную траие-
. цию ОА^В'В (рис. 171), ограниченную
графиком функции у = х" -|-4, осью Ох и прямыми х = 0, х=4. Пло-
щадь этой фигуры (ОА[В'В) точно найдется интегрированием. Получим
ь 4 4 4
S = у dx = f-i-.v + dx = -g- x-dx 4-4 dx —
а V U U
1 г’ 14 14 1 2
Впишем в эту криволинейную трапецию ступенчатую фигуру
OA’lA'^A:,A':A',A’A'iB"B, разделив отрезок ОВ = 4 на четыре равные части.
' Получим:
8 '
и
х2 = ОД» = 1, х3 = ОА~ — 2, х4 = ОА4 = 3;
Ад-, = Дх„ = Дх. = Дх4 = 1;
/(л-1) = ОД;=/(0) = 1 -0= + 4 = 4;
f (х2) = Д2Д' =/(1) = 1 . Р + 4 = 4
/(.г3) = ЛЛ = /(2) = т-2“ + 4 = 4
У(х4) = А4А4 =f (3) = 1-3* + 4 = 5 1
О О
* Текст, набранный ниже мелким шрифтом, следует внимательно про-
читать и продумать. Это облегчит понимание и усвоение основного текста,
набранного нормальным шрифтом.
312
с
Обозначив площадь ступенчатой фигуры, составленной из четырех пря-
моугольников, через S4, найдем
+ = У / (xk) Дл-й = / (xj Д.с, 4- / (х„) Дх2 4-/ (.с.) A.v3 +/ (х4) Д.г, =
4=1
= 4.1 + 4-’-. 1+4^ 1+э1- 1^17-J кв. ед.
о £ . о 4 ,
Разность между площадью криволинейной трапеции S и площадью сту-
пенчатой фигуры из четырех полос St окажется равной
S — S4 = 18 — 17 4 = 4 кв. ~ °,92 кв. ед.
Следовательно, на сумму площадей криволинейных треугольников при-
4=4
ходится только 0,92 кв. ед., т. е. У 3* = 0,92 кв. ед.
к — I
Разделим теперь отрезок ОВ на восемь равных частей и впишем в кри-
волинейную трапецию ступенчатую фигуру, состоящую из восьми полосок.
Из рисунка мы видим, что сумма площадей криволинейных треугольников
стала меньше на сумму площадей заштрихованных прямоугольников и, сле-
довательно, площадь ступенчатой фигуры S3 из восьми полосок ближе подо-
шла к S, чем S4.
Беря последовательно п = 16, н = 32, ... мы бы заметили, что
< Ss <+„ < ... < S,
4 = 4 4 = 8 4 = 16
S 84> У 84> У 84>
4=1 4 = 1 4=1
Эти неравенства показывают, что с увеличением числа п сумма пло-
4 = «
щадей криволинейных треугольников 8* уменьшается и вследствие этого
4 = 1
площадь ступенчатой фигуры (.$„) приближается к площади криволинейной
трапеции (S).
Вернемся (см. рис. 170) к формуле
с (г)
4=1 4=1
Эта формула справедлива при любом п, в частности,' оиа
будет справедлива и при п->сю, т. е. когда каждое из прира-
щений Дх* -> 0; при этом S как площадь данной фигуры АГА\В’В
k = n
будет величиной постоянной, ^/(х*)Дх* как площадь ступенча-
4 = 1
той фигуры из п прямоугольных полосок, приближающаяся к S
/г = п
по мере увеличения п, и У) о*, убывающая при увеличении п,
' 4 = 1
будут величинами переменными, имеющими пределы.
313
Следовательно,
~k — п k = п
Sz^ linl У У, ,
п со L/г = 1 > = 1
или (ио теореме о пределе суммы)
<S = lim У /(х*)Дхл+ lim У 8Л. (д)
п -* оз }. _ ] п -»а. ]
Мы уже видели, что с увеличением числа делений сумма пло-
(1{ — п
У <К I убывает. Найдем пре-
* = i /
дел этой суммы, когда п->оо и ДхА->0. Для этого переместим
все заштрихованные криволинейные треугольники на прямоуголь-
ную полоску ВВ'С'С, высотой которой является BBi — f{b), осно-
ОВ — ОА, b — а • „
ванием ВС —----------- = —— = &х. Как видно из рисунка, пло-
щади их занимают только часть площади прямоугольника В^С&ъ
п, следовательно,
k = tl
У площади Q BiBtCjCi,
it = i
или
1< = п
У У B-iB} В,С>, ' (е)
Л = 1
где
В..В, — ВВ, —BBi = BBi — Л1Л' = /(й) — / (а),
В.£ъ = ВС^Ь-^^х-,
и
После замены Д/Л и В.^ их значениями неравенство (е)
принимает вид
(ж)
k = i
В правой части этого неравенства множитель f(b)—/(а) — ве-
ь — а
личина постоянная как длина данного отрезка, множитель ——
при Ti^-oo — величина бесконечно малая. Мы знаем теорему:
произведение постоянной величины на бесконечно малую является
величиной бесконечно малой. Следовательно,
Пт |/(Ь)-/(«)]^-='О.
И—►ГТ.»
314
А так как У при любом п меньше, чем \f(b) — [(a)] -~~
ь=\
[см. неравенство (ж)], то тем более
k = n
lim 2 3л = 0.
Л = 1
k = п
Подставим в равенство (д) вместо lim У, 8* * его значение
k -- 1
k — п k = п k = n'
s— lim У f(xk) Лха4~ lim У = lim У f (xk) Axft -j- О,
«->cofc = l n^'x;, = 1 a-*ooft==1 I
получим
k = n
S=lim (к)
«-’cc*=i
С другой стороны нам известно, что
ь
S = \f(x)dx.
а
(а)
Левые части равенств (к) и (а) равны между собой, следова-
тельно, должны быть равны и правые части, т. е.
b k — n
[f(x)dx= lim y/(xft)Axft. (7a)
a n-co k = !
b — a „
При n->oo и, следовательно, при ----------= Дх/г->0 перемен-
ная х, непрерывно изменяясь, пробегает значения от х = а до
х — Ь. Отмечая под знаком суммы и над ним границы изменения х
(а и 6), формулу (7а) пишут проще, а именно:
(7)
При Дх->0 каждое из слагаемых суммы ^f(x)&x делается
величиной бесконечно, малой и вследствие этого число таких
слагаемых — неограниченно большим. Значит, формула (7) иоказы-
ь
вает, что определенный интеграл f (х) dx является пределом суммы
а
бесконечно большого числа бесконечно малых слагаемых.
k — n
* Сумму У /(.v*)A.v* часто называют интегральной суммой.
А=1
315
Этот вывод сделан нами в предположении, что функция y=f(x)
в промежутке (а; Ь) возрастает. Пользуясь тем же методом, можно
было получить вывод (7) и в том случае, когда функция y=f(x)
убывает в данном промежутке (а; Ь) (рис. 172).
Если указанный вывод справедлив для убывающей функции
так же, как и для возрастающей, он будет справедлив и для
такой функции, которая то убывает, то возрастает. На рис. 173
Рис. 172
Рис. 173
изображен график функции y — f(x), возрастающей в промежутке
(а; Ь) и убывающей в промежутке (Ь; с). Площадь S заштрихо-
ванной фигуры будет равна
ъ с ,
£ = Si-[-S.; = lim У]/(х)Дх-ф ^/(а)Дх =
О с с
= $ f (х) dx -ф- $ / (х) dx — $ / (х) dx.
К определению предела суммы бесконечно большого числа
бесконечно малых слагаемых приводят многие вопросы геометрии,
физики, механики и других наук. Во всех случаях, когда иско-
мая величина может быть представлена в виде суммы однотип-
ных слагаемых /(х)Дх [при условии, что / (х)— непрерывная
функция], нахождение этой величины сводится к вычислению
^f(x)dx как предела суммы таких слагаемых при условии, если
такой предел существует.
§111. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ
Пользуясь вышеуказанным методом, уточним в первую очередь
некоторые вопросы, связанные с вычислением площадей.
Пусть требуется вычислить площадь фигуры, ограниченной
дугой кривой y — f(x), расположенной над осью Ох, прямыми
х = а, х — Ь и осью Ох (рис. 174). В данном случае любой эле-
мент AS — f (х) Дх суммы V]f(x)dx будет величиной положнтель-
316
ной, потому что f(x)^>0 и Дх^>0. Вследствие этого площадь 3,
ь ь
равная \f(x)dx~ lim ^f^dx, выразится числом положительным.
а Лх-*0 а
Если же фигура ограничена дугой кривой у = f (х), располо-
женной под осью Ох, осью Ох и ординатами f(o), f(b) (рис. 175),
то любое слагаемое суммы ^f(x)^x будет величиной отрицатель-
ной, так как f (х)<^0, Дх>0;, поэтому предел суммы
ъ ь
\f(x)dx = lim
а Дх-^О а
будет числом отрицательным.
Указанное обстоятельство необходимо учитывать при вычис-.
лении площадей фигур, особенно в тех случаях, когда кривая
х = [(х) пересекает ось Ох в точке, лежащей
между границами (пределами) интегрирова-
ния. Рассмотрим пример: вычислить площадь
фигуры, ограниченной осью Ох, кривой у — х'
и прямыми х =— 2, х = 2.
По формуле (4) имеем
\хЧх = 1 х41^2 = 1 [24 - (-2)4 = 0.
-2
Полученный ответ ясен из рис. 176. Фи-
гура АВО расположена под осью Ох и площадь
ее выражается отрицательным числом:
о
5 .г' dx = | х4=4 [0 - (-2)4 = —4;
—2
фигура OCD расположена над осью Ох, площадь ее выражается
положительным числом:
х1 dx= х4 = 4.
.) 4 л»
317
2 0 2
Поэтому $ х3 dx, равный сумме интегралов $ х3 dx и ^x3dx
—2 —2 0
(см. свойство 2 определенных интегралов), оказывается равным
нулю. Во избежание подобных ошибок в случаях, когда подынте-
гральная функция y — f(x) в
мает как положительные, так
Рис. 177
пределах интегрирования прини-
и отрицательные значения (рис.
177), следует при вычисле-
нии площадей, разбив про-
межуток интегрирования на
части, сложить абсолютные
значения интегралов:
д_. с d
I S — ^f(x)dx-]~ |Jf(x)dx| +
а с
b
+ 5 f wdx-
d
В примере, приведенном выше, площадь будет равна
О 2
S = | х3 dx 14- х3 dx = 4 -j- 4 — 8 кв. ед.
—2 0
Указание. Предлагается внимательно разобрать решение
задачи 1008 и затем самостоятельно решить задачи 1009—1011.
/
§ 112. ОБЪЕМ ПИРАМИДЫ
Выведем формулу для вычисления объема пирамиды, поль-
зуясь понятием определенного интеграла как предела суммы.
Возьмем пирамиду SABC (рис.
178) с площадью основания Q 1гв.
ед. и с высотой Н ед. Разделим
высоту Н на п частей: Д%1, Дх.2>
Дх3,..., Дх*,..., Дх,г и через точки де-
ления проведем плоскости, парал-
лельные основанию пирамиды. Пи-
рамида рассечется на п частей. На
чертеже изображена ‘одна из таких
частей: AiB^A-diaCi. Обозначим
расстояние от вершины пирамиды
до сечения А2В,С.2 через хк, пло-
щадь этого сечения —через qk. По
теореме о свойствах параллельных
сечений пирамиды найдем:
— О 2
Qk — хк.
*7/г хк
Q—TP’
Рис. 178
318
При достаточно большом п объем (Ди*) части AJiiCiAiBiCt дан-
ной пирамиды SABC можно приближенно принять равным объему
призмы с площадью основания qk и высотой Дх*. Получим
^а = <7а-д^ = ^х|Дх/;;- (а)
тогда объем всей пирамиды (V) найдется приближенно как сумма
слагаемых вида (а). Получим
fc= i
При п->оо и Дх*->0 число слагаемых в этой сумме делается
бесконечно большим и каждое слагаемое бесконечно малым при
непрерывном изменении х от значения, равного нулю, до значе-
ния, равного Н. Следовательно, объем пирамиды является пре-
делом суммы (б), когда п->со, и, значит, Дх*->-0.
По формуле (7) получим
k = n п н п Н
V = Нт у х^Дх*= lim у^х2Дх = £ Q хгйх =
п->п U П A.v-o4jr/ J Н2
k = { О о
н
= = = = (в)
б
При выводе этой формулы была взята треугольная пирамида.
Ход рассуждений во всем остался бы тот же самый, если бы была
взята пирамида с любым, числом боковых
граней. Следовательно, объем любой пира-
миды равен одной трети произведения пло-
щади основания на высоту.
Пример. Дана правильная четырехуголь-
ная пирамида со стороной основания а и
высотой h. Высота пирамиды точками О| и
О> разделена на три равные части и через
точки деления проведены плоские сечения,
параллельные основанию. Вычислить отдель-
но объем каждой из трех частей, на кото-
рые пирамида разбита этими сечениями.
Решение. На рис. 179 изображена
Рис. 179
правильная четырехугольная пирамида
SABCD. Дано: АВ = а, SO = h, SO.3 = O.3O1=O1O = 4 • Требуется
найти Vj, V2, V3. Объем любой из этих трех частей пирамиды опре-
делится как предел суммы слагаемых вида
(г)
где Q — площадь основания пирамиды, Н — ее высота.
319
В данной задаче Q = ai, H = h. Следовательно, каждое, сла-
гаемое (г) будет иметь вид
(I ~ Q 4
,-г Л'-Дх;
Л-
грапицами изменения х (пределами интегрирования) будут:
1) 0 и h при вычислении Уг>
1 9
2) h п v/г при вычислении V2;
3) 4 /г и h при вычислении V3.
О
Получим:
Vj = lini У х-Дх= ( “„x^dx — 4 x’dx =
J Л- h- )
о о о
x-dx =
2
Л-’ з 11 /г №
/ S • о 1 . > I la h
\nh ~~ 2ilr j= ~WKlJ(}iедл
h
V С а~ <? з1Л W/г . .
= \ j?x^dx^^x“I = — куо. ед.
2 , Тй
3
Проверка. По формуле (в) объем данной пирамиды будет
равен
V = ±QH=~a-h.
О о
Сумма объемов ее трех частей должна быть'равна V:
у _1_ у _i_ у — £2! = 27ц~7( — J. d’-h — V
v 2“ v з 8i п 81 1 81 81 з и11 к-
§ 113. ОБЪЕМ ТЕЛА ВРАЩЕНИЯ -
Дана криволинейная трапеция (рис. 180), ограниченная гра-
фиком непрерывной функции у = /(х), осью Ох н прямыми х = а,
х~~Ь. Вращая эту фигуру вокруг оси Ох, получаем тело вра-
щения Л1'ВД’Л[.
320
Зададимся целью вывести формулу для вычисления объема
такого тела. Разделим отрезок AtB точками Д9, А3, At, ..., Ап
на п равных частей и в криволинейную трапецию AtA[B'B впи-
шем ступенчатую фигуру, состоящую из п прямоугольных поло-
сок. Вращаясь вместе с криволинейной трапецией, ступенчатая
фигура образует геометрическое тело, состоящее из п цилиндров.
Введем обозначения:
ОД1==а = Х|, 0Ai = x-2, ОАз~х3, ..., ОАп = хп-, .
AjА%== Axj, А°А3== Ах?, А3А1 = Дхз,...., АПВ = Дхл',
=//j =/(Х|), А-1А^ = у-г = f (х~г),
АзА'з=уз=[(х3).......А„А‘п=уп=[ (хп).
Мы знаем, что' объем цилиндра равен произведению площади
основания на высоту. У наших п цилиндров радиусами основания
будут соответственно yt, у*, у3, ..., у„, а высотами—Дхь Дх2,
Дх3, ... , Дхп. Поэтому объем Vп тела, составленного из п цилинд-
ров, можно будет записать в следующем виде:
> V n = ^yi^Xi -f- "Z/JAXj 4" кУз^Хз 4* • • 4“ кУп^хп —
= к (y'i^Xi 4- у:Дху + у'^Хз 4-. • 4- yh^Xn).
Итак,
k -=п
= У, y№xk. (а)
* = 1
Разность между объемом (V) тела вращения и объемом (Уи)
геометрического тела, состоящего из п цилиндров, очевидно, будет
11 П. Е. Агачео
321
равна сумме объемов колец, образуемых вращением вокруг оси Ох
заштрихованных на чертеже криволинейных треугольников, пло-
щади которых обозначены соответственно через 8Ь 8.2, 83, ..., оп.
В § ПО мы доказали, что при н->со сумма площадей таких
/Л = п \
фигур I У, 8Л делается величиной бесконечно малой. Отсюда
\/г = 1 /
заключаем, что при н->оо бесконечно малой величиной будет
и сумма объемов колец, образуемых вращением заштрихованных
фигур. А это значит, что разность между постоянной величиной V
и переменной величиной Vn при n->i<x> является величиной бес-
конечно малой. Следовательно,
V= lim Vn,
tl —св
или (а)
k = п ь ь
V — lim тс У, у]Дхц = тс lim у у2&х — тс dx.
П-~<л к = ! Дх - 0 ц
Итак,
ь ь
V — Tz^y2 dx, или И = тс $ [/(х)]3 dx
а . а
По этой формуле вычисляется объем тела, образуемого вра-
щением криволинейной трапеции вокруг оси Ох. Для вычисления
объема тела, образуемого вращением кри-
волинейной трапеции вокруг оси Оу, по-
лучается аналогичная формула:
Рис. 181
ъ
V — тс х9' dy.
а
(9)
Пример 1. Вычислить объем тела, об-
разуемого вращением вокруг оси Ох фи-
гуры, ограниченной линиями:
у х -]-4, y — Q,x — 0, х = 6.
Решение. В первую очередь следует построить эту фигуру
(рис. 181) и изобразить на том же чертеже тело вращения.
В данной задаче <7 = 0, Ь—6,у = /(х) = ~х-\-4.
322
По формуле (8) находим
= К[-1- (б3 — °) 4-2 (б2 — °) 4- 16 (б — 0)] = 186- куб. ед.
Результат можно проверить по формуле объема усеченного
конуса:
+ + Н Н
v — 3
Проверку рекомендуется выполнить
самостоятельно.
Пример 2. Вычислить объем тела, об-
разуемого вращением вокруг оси Оу фи-
гуры, ограниченной линиями: х2— if-=d2,
у = — 2а, у = 2а.
Решение. Строим эти линии, при-
няв за а отрезок произвольной длины.
Первая линия является равносторонней Рис. 182
гиперболой, остальные две — прямыми, па-
раллельными оси Ох (рис. 182). В этом случае V вычисляется по
формуле (9). Решив уравнение х2— у1 —а2 относительно х2, по-
лучаем:
х2 = у24- а2;
V — it $ x2dz/ = ~ (у*a3)dy = 2п \ (у2-{-d2)dy=’
—2а —2а 0
= 2it [(2а):| — 0] 4- а2 (2а — 0)| — 2тс а3 4- 2а3 j =-у- па3 куб. ед.
§ 114. РАБОТА, ПРОИЗВОДИМАЯ СИЛОЙ
Положим, что некоторая сила F приводит в движение какое-
то тело по прямой OS, причем направление силы совпадает
с направлением движения. Перемещая тело, эта сила совершает
работу. Из физики известно, что если сила F постоянна по вели-
11
323
чине, то работа, произведенная ею, определяется по.формуле
P^=Fs,
где s — путь, пройденный телом.
Допустим, что F—переменная сила, меняющая свое значение
с изменением пройденного пути s. Тогда, очевидно, эта сила
должна рассматриваться как функция от s, т. е. должно быть
(ь).
Положим далее, что под действием переменной силы тело
было перемещено по оси Os (рис. 183) от точки At (а) до точки
В(Ь). Зададимся целью вычислить работу, произведенную силой
F = f(s) при таком перемещении тела.
О
Рис. 183
4, 61b)
•Д5„
S
Разделим промежуток (а; Ь) точками Ль А<, А3, Ац, ... , Ак, ...
... , Ап на п равных весьма малых участков и обозначим их соот-
ветственно через Даь Дд>, Дз3, ... , Да*, ..., Дз„. Величину силы
f (s) на любом участке приближенно можно будет считать постоян-
ной и равной ее значению в начале участка. Тогда
7(si), /(s-i), 7(s3), .... f{sk), ..., f(sn), ...
будут соответственно приближенными значениями этой силы на
участках Даь Да4, Дхз, ..., Да*, ..., Да„.
Работа, произведенная данной силой на любом уцастке пути
Да*, определится по формуле
Др* = /(а*)Да*,
а вся работа (Р) приближенно будет равна сумме п таких сла-
гаемых. Получится
Р ~ 7 (si) Asi Я- 7 4'4 4~ 7 (5з) Да3 4-... ,
-г7 (s*) As* 4~ • • • 4'7 (s«)
При ?г->оо число слагаемых в последней сумме становится
бесконечно большим и каждое слагаемое — бесконечно малым,
так как при этом &sk -► 0. По формуле (7) получим
Ъ 1 ь
Р= Тип У 7 (s) As = \ 7 (s) ds-
а а
324
Итак, работа (Р) переменной силы f(s) на участке пути от
Si —а до s-2 = b определяется по формуле
ь
P = y(s)ds. (10)
а
Пример 1. Газ заключен в цилиндр с подвижным поршнем.
Вычислить работу, производимую силой давления газа при уве-
личении высоты части цилиндра, заключающей газ, от значения,
равного s1; до значения, равного
s2 (температура газа Т = const).
Решение. Положим, что ра-
диус основания цилиндра (рис. 184)
равен R. Обозначив через s пере-
менную высоту цилиндра (путь,
проходимый поршнем) и через о —
его переменный объем, получим
w = ~P5s. (а)
Рис. 184
Найдем теперь выражение переменной силы, действующей на
поршень через s, т. е. /(s'). Для этого воспользуемся законом
Бойля — Мариотта ' ,
pv = k, ' .
где v — объем газа, р — давление, а А —постоянная величина.
Из последней формулы находим
Это будет величиной давления на одну квадратную единицу
площади поршня. Так как площадь поршня равна ~/?2, то дав-
ление, испытываемое им, найдем, умножив на ^R2. Получи?.!
' V
Подставив в последнее равенство вместо v его выражение (а),
получим
Итак,
Работа Р найдется по формуле
P = $/(s)ds. (10)
а
325
В данном случае границами интегрирования, очевидно, будут
a —Si, b-s-i. Следовательно,
Р — — ds — k ( — = k In s 152 — k (In s.> — In $i) — k In —.
J S J S |S1 ' < St
Si Si
Пример 2. Какая работа произведена при сжатии буферной
пружины железнодорожного вагона на 5 см, если для сжатия
этой пружины на 1 см требуется сила 3000 кГ?
Решение. Мы уже знаем, что работа, производимая пере-
менной силой F — f(s), определяется по формуле
ь
P--y(s)ds.
а
По закону Гука, сжатие винтовой пружины пропорционально
приложенной силе. Если буквой s обозначим сжатие, то получим
F=ks,
где k — коэффициент пропорциональности. В условии задачи дано:
F = 3000 кГ при s=l см = 0,01 м. Подставив эти значения в
уравнение F = ks, найдем:
3000 = ^-0,01; k = -^-.-=300 000 лг/м.
Подставив в равенство F — ks вместо k его значение, полу-
чим выражение переменной силы, соответствующее условию дан-
ной задачи:
F = / (s) = 300 000s кг.
Пределами интегрирования будут: п = 0, 6 = 5 см = 0,05 м.
Теперь по формуле (10) можно найти производимую работу.
Она будет равна
Ь 0,05
Р = (s) ds = j 300 000s ds = 300 000 • у |°’°5 =
a 0
300 000 /IV 300 000 r
= —2~ • Ы =-2Т40(Г = 375 кГм-
§ 115. ДАВЛЕНИЕ ЖИДКОСТИ
Из физики известно, что давление жидкости на горизонталь-
ную пластинку (рис. 185) равно весу столба жидкости, основа-
нием которого является эта пластинка, а высотой — ее расстояние
от свободной поверхности жидкости. Если обозначим через As
326,
площадь пластинки, через h — расстояние ее от свободной поверх-
ности жидкости, а через 7 — вес кубической единицы этой жид-
кости, то давление Др, испытываемое пластинкой, выразится
формулой
Др = рДз./г.
Следовательно, вычисление силы дав-
ления на горизонтальное дно сосуда не
представляет трудностей.
Рассмотрим задачу о вычислении давле-
ния жидкости на вертикальную стенку со-
суда. Допустим, что такая стенка имеет
форму прямоугольника (рис. 186, а). По за-
кону Паскаля, давление жидкости пере-
дается с одинаковой силой во всех направле-
ниях. Разобьем прямоугольник ABCD прямыми, параллельными
свободной поверхности жидкости (CD), на п весьма узких поло-
сок. Пусть KKiMiM будет одной из таких полосок, находящейся
на расстоянии х от поверхности воды. Обозначив через Дх ши-
рину этой полоски, через Дх — площадь, получим
Дх = А В • Дх = b • Дх.
Так как ширина этой полоски весьма мала, то можно считать
давление во всех ее точках одинаковым и приближенно равным
давлению на глубине х. Обозначив давление на эту полоску
через Др, получим
Др 7 • Дх • х = у • 6Дх • х = ^йхДх. (а)
Это и будет давление на одну из п полосок, на которые была
разбита стенка прямоугольной формы.
Давление р на всю стенку ABCD найдется приближенно как
сумма п слагаемых вида (а). При /2—>-00 и Дх->0 каждое сла-
327
гаемое такой суммы сделается величиной бесконечно малой и
число таких слагаемых — бесконечно большим при непрерывном
изменении х от 0 до h. Следцвательно, давление на всю стенку
определится по формуле (7). Получим
h . h ft
р — lim У, -fix&х — $ ^bxdx = ?£> J xdx —
о ,0 0
Задача. Пластинка в виде треугольника, основание которого
Ь — 12 см, высота /i = 5c'.u, погружена вертикально в воду. Найти
давление, испытываемое одной стороной этой пластинки, если
вершина ее лежит на поверхности воды, а основание парал-
лельно ей.
Решение. Представим себе площадь треугольника (рис. 186,6)
состоящей из узких полосок, параллельных поверхности воды.
Пусть КМ будет одной из таких полосок, находящейся от поверх-
ности воды на расстоянии х. Обозначив через Дх ширину поло-
ски и через As ее площадь, получим
As = К М Дх
(вследствие малости Дх полоску принимаем за прямоугольник);
Ир = КМ -Ьх-х
(б)
(см. решение предыдущей задачи).
Из подобия треугольников АВС
и ВКМ имеем пропорцию
КМ _ BE
АС ~ BD'
или
КМ _ х
b — h *
откуда
КМ = £х.
Подставив в равенство (б) вместо КМ найденное его выра-
жение, получаем
Др = ~х‘2Дх. (в)
Давление, испытываемое всей пластинкой, будет равно пре-
делу суммы слагаемых вида (в), когда Дх -> 0, т. е.
л л
p= lim У х‘2Дх = -h x'2dx — -^7—— 100 г.
328
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Дан Зх3 dx. Найти приращение первообразной функции при изме-
нении от значения, равного 1, до значения, равного 3.
ь 1>
2. Дано, что \f(x)dx=p. Чему равны \ cf (х) dx?
а а,.
3. Что называется определенным интегралом?
. , j 3 b
Г /,3 дЛ С Г
4. Найдено \f(x)dx =——«Чем'у равны: 1) dx', 2) j f (x) dx",
J 1 a
a
5
3).j/(x)dx?
L a
5. Чему равен ^/(x)dx?
a b
6. Какой геометрический смысл имеет интеграл 'j / (х) dx?—
а .
7. Сформулируйте свойства определенных интегралов.
ь а
С j3 _ ?
8. Найдено \ f(x)dx =—. Чему равен \f(x)dx?
b а
9. Чему равна сумма f (х) dx -f- J f (x) dx?
, a b
b
(*
10. Найдено \ f(x)dx———• Чему равна разность
a
b a
jj f (x) dx —. \ f (x) dx?
11. Если ^/(x)dr=12, ^/(x)dx = 9, то чему
5 3
12. Если ^/(x)dx=19, ^f(x)dx~6, то чему
*=6
равен
равен
f (x) dx?
5
$/(x) dx?
з
13.
14.
Напишите сумму
Напишите сумму
V x^Axft в развернутом виде.
fe = i
Л—4
V 1 Л
2^ — Дх* в развернутом виде.
15. Сколько слагаемых в сумме f (xb) \хк>
k = 1
4
16. Чему равен lim
2
17. Чему равен Jim^ У 4х3Дх?
329
b b
C a2 — b3 Yi
18. Найдено \f(x)dx~—л-----. Чему равен lim 7 /(л)Дл-?
J ОС Дх->0^
а а
19. Как вычислить площадь фигуры, ограниченной осью Ох и графиком
функции y—f(x) в промежутке (а; Ь), если эта функция в промежутке (а; с)
положительна и в промежутке (с; Ь) отрицательна?
20. Если кривая y-f(x') симметрична относительно оси. Оу и
а а
(х) dx — Q, то чему равен Jj/(x)dx?
0 — а
21. Переменная сила F в зависимости от пути, пройденного телом под
действием этой силы, выражается формулой F=(2s~|-3) кГ. Найти работу,
произведенную этой силой на участке пути от st = 2 м до s2 = 4at.
% „з__м 195
Ответы. 1. 26. 2. ср. 4. 1) — ; 2) „ ; 3) 5. 0. 9. 0.
О О О
10. - . 11.21. 12. 13. 13. л^Д.с1+л?Дх24-... + ^- Дхс. 16.2. 17.15.
d~_№
18. ---. 20. 2Q. 21. 18 к Гм.
3с
Глава XII
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 116. ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Определение 1. Дифференциальным уравнением называется
такое уравнение, которое содержит переменные х, у и производ-
ные или дифференциалы функции у. Так, например, уравнения
а) у' — х-, б) z/"4-4z/ = 0; в) х-\-уу' = Ъ
являются дифференциальными.
Решить или проинтегрировать дифференциальное уравнение
значит найти такую функцию y = f(x), которая удовлетворяет
данному уравнению, т. е., будучи подставлена в это уравнение,
обращает его в тождество. »
С дифференциальными уравнениями мы уже встречались в гл. X
и XI. В § 103 решение каждой задачи приводило к интегрированию
простейшего дифференциального уравнения вида y' = f(x) (см. при-
меры 1—4).
Определение 2. Всякая функция y = f(x), удовлетворяю-
щая данному дифференциальному уравнению, называется решением
этого уравнения. Так например, функции
А) У = 4 х‘ + С и Б) z/ = 3cos2x
будут решениями уравнений (а) и (б). В этом легко'удостовериться
подстановкой этих функций и их производных в соответствующие
уравнения. Получим:
330
а) (у Xs -j- Cj = х или х — х — тождество;
б) (3cos2x)"4“4 (3cos2x) = 0; 3(—4cos2x)-]- 12cos2x = 0
или 0 = 0 — тождество.
Определение 3. Уравнение вида <р(х, у) = 0, определяющее
решение (искомую функцию у) дифференциального уравнения как
неявную функцию у (см. § 78), называется интегралом данного
дифференциального уравнения. Так, например, уравнение
В) х2 + у2 = С или х2-|-у9 — С = 0,
где С — произвольная постоянная, является интегралом уравне-
ния (в): х-\- уу' = 0. Чтобы убедиться в этом, достаточно взять
производные от обеих частей равенств (В). Получим:
(x2+«/2); = C;; 2х4-2уу' = 0 или х-\-уу' = 0. (в)
Функция (А) называется общим решением уравнения (а); любая
функция, получающаяся из этой функции заменой произвольной
постоянной С определенным числом, называется его частным реше-
нием. Так, например, при С = — 4 получается частное решение
у — ^х1 — 4.
Аналогично, х*-\-у*=С называется общим интегралом диф-
ференциального уравнения (в). Придавая С значения 1; 2; 3
и т. д., будем получать частные интегралы'. у
х2-[-у‘а=1; х2Ц-у2 = 2;
х3 + ^ = 3: х2 + у3 = 4
И т. д.
С геометрической точки зрения общий
интеграл (общее решение) выражает семей-
ство кривых, а частный интеграл (частное
решение) — отдельные кривые этого семей-
ства. В данном случае уравнению (В)
соответствует множество окружностей с
центром в начале координат, а частным Рис. 187
интегралам — окружности данных радиу-
сов (рис. 187). Точно так же общему решению (А) диффе-
ренциального уравнения (а) на плоскости соответствует семейство
парабол, а каждому частному решению — одна из парабол этого
семейства (см. рис. 164).
В дифференциальное уравнение могут входить производные
разных порядков, в зависимости от этого различают уравнения
1-го, 2-го и т. д. порядков. Например,
ху'— У = ® — уравнение первого порядка;
у"-[-4у = 0 — уравнение второго порядка;
у'”-\- 5у"4~ бу = 0 — уравнение третьего порядка.
Вообще, порядком дифференциального уравнения называется
наивысший порядок производной, входящей в это уравнение.
331
§ 117. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
Если дифференциальное уравнение первого порядка имеет вид
f (У) У' + W = 0, или /(r/)dz/4-<p(x)dx = 0, (1)
где /(у)— функция от у, <р(х)— функция ог х, то говорят, что
в данном уравнении переменные разделены. Решение такого урав-
нения выполняется непосредственно интегрированием:
(y)dy ^\<?(x)dx = C.
Пример 1. Найти общий интеграл уравнения
у dy — (1 -j- 2х) dx — 0.
Решение.
^ydy—(1 -ф- 2x)dx — C; ---------(х-|-х2) = С,
или .
у^ = 2(ха- + х) + 2С.
Пользуясь произвольностью С, можно 2С обозначить через С
и общий интеграл переписать в следующем виде: у,- = 2(х1-[-х)-\-С.
Если дифференциальное уравнение после приведения его
к общему знаменателю и соединения в один член всех членов, ;
содержащих множителем один и тот же дифференциал, прини-
мает вид
f (х) F (у) dx(у) Ф(х)ду = 0, (2)
то его можно привести к виду (1), разделив все члены на про-
изведение Р(у)Ф(х).
Пример 2. Проинтегрировать уравнение
х2уу' 4- xif — уу’ + х=0.
Решение. Соединяем в один члены, содержащие у':
(х2у — у) у' xif 4- х — 0.
~ Заменяем у' через и приводим уравнение к общему зна-
менателю:
(х2у — у) dy 4- (ху2 4- х) dx == 0.
Разлагаем на множители коэффициенты при дифференциалах:
у(х2— l)dy4-x(y24- l)dx — 0.
Разделив это уравнение почленно на (х2 — 1) (у2 4~ 1), . имеем
V dy । х dx j___,,
З-’2 + I + _v= _ 1 — u-
332
Получилось уравнение вида (1). Интегрируем его:
С у (iy । С х dx п.
J у- + 1 Г J л- - 1 — С ’
11п(//2+1)-|-41п(^-1) = С;
1п(^+1)Ч-1п(х2-1) = 2С.
Пользуясь произвольностью С, заменяем 2С через In С:
In (у* -J- 1) + In (х3 — 1) = In С,
откуда в результате потенцирования получаем
(/+1)(х3-1) = С, или ^ = -^-1.
Пример 3. Найти частное решение дифференциального урав-
нения
(1 — х3) у' ф- ху — ах = О,
удовлетворяющее условию у —2а при х — 0.
Решение.
(1 ~ах = 0;
(1— x”-)dy-}- xiy — a}dx-—0.
Делим члены этого уравнения на произведение (1 — х3) (у — а)-,
dy . xdx _______________________„
у — а 1—х3 ~~L '
Получили уравнение вида (1). Интегрируем это уравнение:
С dy . С х dx ___р' ' . -
J У—а + J 1 — х3 — ’
In (у — а) — 1 In (1 — х1) — In С;
In /~а_— In С; = у^а^СУГ^?.
/1-х3 Rl-.r3 ~ г
Мы нашли общее решение. Определяем значение С, удовлетво-
ряющее начальному условию у = 2а при х = 0:
2а = аС 1^1—О2, откуда С = а.
Следовательно, искомым частным решением будет функция
y — a-j-0,1^1—х2, или у = а(1 -ф1 — х2).
Пример 4. Написать уравнение кривой, проходящей через
точку (д; 0), зная, что угловой коэффициент касательной в любой
ее точке равен — -^2у-.
333
„ IT , Ь-x dy
Решение. Из условия задачи следует у или
Ъ'-х dy . b-x п
u2V ’ dx ' asy
После приведения к общему знаменателю это уравнение при-
нимает вид
а2у dy + b2x dx = 0.
Переменные разделены. Интегрируем:
, d'-ydy \У!х dx = С;
. 1 a2j>2 , £>2х2 __г
2'2 —Ь’
откуда t>V~i~a3y3 = C.
Из этого семейства кривых выделим ту, которая проходит
через данную точку (а; 0): У1 ds а2 • О3 = С, откуда С = а2Ь2.
Следовательно, кривой, удовлетворяющей условиям данной
задачи, является эллипс:
Пример 5. Найти закон движения тела, движущегося со ско-
ростью, пропорциональной пройденному пути, если известно,
что за первые 10 сек тело проходит 100 м, а за 15 сек — 200 м.
Решение. Известно, что у = ^-. В данном случае скорость
пропорциональна пройденному пути. Следовательно, имеем
> = (а)
где k — коэффициент пропорциональности. Разделив переменные,
интегрируем полученное уравнение:
^L = kdt-, \-^-=\kdt; lns = ^4-Ci,
откуда, потенцируя, получаем
s—_£« + <?!, или s = ew,eclt (б)
Так как Ci — произвольная постоянная, то е~1 можно заменить
С (очевидно, С>0). Тогда общее решение (б) дифференциального
уравнения (а) запишется так:
s = Cekt. (в)
Найдем частное решение, удовлетворяющее начальным усло-
виям: s= 100 м при t=\QceK и s = 200 м при £=15 сек. Имеем:
100 = Се,<,А; 200 = Се’8\ (г)
334
Разделив второе уравнение системы (г) на первое, найдем
esft = 2. Извлекая корень пятой степени из обеих частей этого
равенства, получим е* = /2.
_Подставив в одно из уравнений (г) вместо е* его значение
/2, определим С:
100 = С-(efe)’°; 100 = С-(уЛ2)’0; С = 25.
После замены С и ек их найденными значениями уравнение
(в) примет вид _ _
5 = 25(67 = 25(^2/, или 5 = 25/2*.
§ 118. ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПЕРВОГО ПОРЯДКА
Определение. Дифференциальное уравнение первого порядка,
имеющее вид
P(x,y)dx-\-Q(x,y)dy=O, (3)
называется однородным, если Р (х, у) и Q (х, у) являются однород-
ными функциями * переменных х и у одного и того же измерения.
Так, например, уравнение
(х3 + х*у) dx (ху* + у3) dy = O
является однородным, так как в нем Р = х3 х^у и Q = xif~r у'—
однородные функции относительно переменных х и у одного и
того же (третьего) измерения.
Однородное дифференциальное уравнение (3) приводится к виду
уравнения с разделяющимися переменными подстановкой
^ = и, (4)
где и — новая неизвестная функция.
Пример 1. Решить уравнение
у* dx + (х* — xy)dy = 0.
Решение. В данном случае Р~у* и Q = x* 1 2 — ху — однород-
ные функции одного и того же (второго) измерения. Полагаем
~ = и, т. е. у = их, (4)
* Функция двух переменных <р (х, у) называется однородной функцией
k-ro измерения, если при любом t имеет место тождество
<f (tx, ty) — tk® (x, у).
Например:
1) P (x, у) = x3 -|- x2y— однородная функция 3-го измерения, так как
Р (tx, ty) = (tx)3 + (tx)3 ty = t3 (x3 + x3y) = t3-P (x, y);
2) Q (x, y) = x -|- Уху — однородная функция первого измерения, так как
Q (tx, ty) = tx + У tx- ty = t (x + Уху) = t-Q (x, y).
335
откуда dy — udx-\-xdu [см. (5) в § 92].
Подставляем эти выражения у и dy в данное уравнение:
(их)'2 dx (х2 — х их) (udx-\-x du) = 0;
ux-dx-^- х3 (1 — и) du = 0. (а)
Получилось уравнение вида (2). Разделяя переменные, на-
ходим , ,
I С—и) du__q
х ~г и
Интегрируем это уравнение:
4- —\du-C; 1п х -1- in и—и-\-С.
J X 1 J и J 1 1
В результате потенцирования получается общий интеграл
уравнения (а):
Inx-j-lnw — 1пе“ = 1пС; lnux = InCe", их==Сеи. •
Заменив в последнем уравнении функцию и его выражением
(4), находим общий интеграл данного уравнения:
_У „V .
х==Сех, илиу — Сех.
Пример 2, Составить уравнение кривой, проходящей через
точку (1; 1), зная, что угловой коэффициент касательной в любой
ее точке (х, у) равен---
т 1 ' i dy х 4- v
Решение. Из условия следует: у= — —-----------—, или
(х 4- У) dx -ф- х dy — 0.
В этом уравнении Р — х-\-у и Q = x— однородные функции
одного и того же (первого) измерения. Приняв ~ — и, находим:
у = их; dy = и dx -j- х du;
1 (x~^ux)dx-~x(udx-\-xdu) = O,
или
(2u 1) x dx -j- x2 du = 0.
Чтобы разделить переменные, делим члены этого уравнения
на произведения (2^4-1)х2. Получаем
dx , du __________________________„
Т 2« + 1 — У’
Интегрируем это уравнение:
С dx 1 Г du ___
' 34 ) 2«+ 1 —
1пх4-^1п(2«4- 1) = С; 2 lnx-j- in (2и 4~ 1) = 2С;
Inx24* ln(2«4~ 1) = 1пС*; (2и4-1)х2 = С.
Заменив в последнем уравнении функцию и ее выражением
336
(4), находим уравнение семейства кривых, обладающих одним и
тем же свойством [k — il — — •.
\ э -V 1
x‘i = C, или 2ху-}-х1 = С.
Подставив в это уравнение координаты данной точки, получаем
2.Ь1 + 19 = С; С = 3.
Следовательно, уравнение кривой, удовлетворяющей условиям
данной задачи, имеет вид
n I о о 3 — X2
2хух~ = 3, или у—
§ 119. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПЕРВОГО ПОРЯДКА
Определение, Дифференциальное уравнение первого по-
рядка называется линейным, если оно первой степени относи-
тельно неизвестной функции у и ее производной у'. Такое урав-
нение имеет вид , , п
tJ+Pty = Q, (5)
где Р и Q — функции от х или постоянные величины. Такое
уравнение (5) решается подстановкой
y = uv, (5а)
где и и v — неизвестные функции от х, одну из которых можно
выбрать произвольно так, как зто удобно для решения.
Пример 1. Решить уравнение
, । 2 з
у+^у=х-
2
Решение. В этом линейном уравнении Р = ~, Q = x“.
Полагаем y = uv, тогда
,__<7 («о)______L dvv du__ dv , du
dx dx dx 11 dx ' V dx ’
Подставив в данное уравнение вместо у и у их выражения,
получаем .
I dv . du\ , 2 з
\u-j--г V -т- Н-uv — X ,
\ dx 1 dxj 1 х ’
или
!dv , 2 \ . du з , ,
Н— v } и v -т- = хЛ. (а)
\ dx 1 х / . 1 dx ' '
Выше было замечено, что одна из функций (н и о) может
быть выбрана произвольно. Выберем функцию v так, чтобы в
* См. решение примера 2 в § 117.
337
уравнении (а) коэффициент при и обратился в нуль, т. е. чтобы
функция v удовлетворяла уравнению * **
dv . 2
Разделив переменные и
находим
С dv__ 2 С .
J v J х ’
интегрируя полученное уравнение,
In v = 1п In С; v = ^,
Л Л
откуда при С — 1 получаем частное решение:
После замены v его выражением (б) и коэффициента при и
нулем уравнение (а) примет вид
откуда
du = xsdx\ и = g х° + С.
Подставив в равенство y = uv вместо и и v их найденные
выражения, получаем общее решение данного линейного диффе-
ренциального уравнения:
/1 6 | Х,\ 1 1 4 , С
1! = I - ГЬ -I- ( , I . —П.ТТМ 11 = -г Y4 -4-
s \6" 1 x-........... » (
Пример 2. Проинтегрировать уравнение
у' cos х -f- у sin х = 1.
Решение. Разделив все члены данного уравнения
фициент при у', получаем равносильное ему уравнение
У ~гУ^ёх^=-----•
1 Х ° COS X
т, г d (uv) dv . du
Делаем подстановку: y = uv, у = " -
/ dv . du\ , ,
+Uvt&X
1
cosx ’
2 •
на коэф-
вида (5):
получаем
или
{ dv , . \ , du 1 , ,
Н—L- v tgx « + v -=-=------, (в)
\dx 1 ° / 1 dx cosx v '
* Для этого, очевидно, достаточно найти какое-нибудь частное решение
этого уравнения.
** В дальнейшем при нахождении такого частного решения мы совсем
не будем вводить произвольную постоянную С. Будем запись располагать
так:
, , 1 1
In и — 1п-^: V — —2
’ г*5
338
Коэффициент при и приравниваем нулю:
-g.-|-0tgx = O. (г)
В уравнении (г) переменные разделяются: ^- = —tgxdx.
Интегрируем: — tgxdx; In и = In cos х, откуда v —
- COS X.
После замены коэффициента при и и функции и их значениями
уравнение (в) принимает вид
Л , du. 1 , dx
0-wH-cosx-7- =-------, откуда du =——;
1 dx cos x1 J cos- x ’
\ du = ; и =:tgx4-C.
J J COSJ X ’ 1
Подставив в равенство y = uv вместо и и v их найденные
выражения, находим общее решение данного уравнения:
y = (igx-\-C) cosx, или у = sinх-ф-С cosх. (д)
Проверка. Находим производную функции (д):
у' = (sin х -j- С cos х)' = cos х — Csinx.
Подставив в данное уравнение вместо у и у' выражения функции
(д) и ее производной, получаем:
(cos х — С sin х) cos х —(sin х —С cos х) sin х = 1;
cos2 х sin2 х = 1; 1 = 1 — тождество.
§ 120. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА.
УРАВНЕНИЯ ВИДА ;/=/(./)
В дифференциальное уравнение второго порядка могут входить
переменные х, у и производные у', у", причем те или иные из
величин х, у, у' могут и отсутствовать. Простейшее уравнение
второго порядка имеет вид
/ = /(х).
Уравнения этого вида решаются двукратным интегрированием.
Пример 1. Проинтегрировать уравнение у" = cosx.
Решение, у” = (y'Yx=(^] . Полагаем ^ = z, тогда данное
' \ах]х dx
уравнение перепишется в следующем виде:
z.v = cosx, или dz = cosxdx.
Интегрируя это уравнение, находим
^dz = $ cos xdx, или 2 = sinx-(-G.
339
Заменяем в последнем уравнении величину г ее значением:
—= sin х -f- G; dy ^=(sinx-|- C() dx.
Интегрируем второй раз и получаем общее решение данного
уравнения:
^dy — J (sinхCj)dx‘, у=— cosх-ф-CiX-ф-C2.
Как видим, общее решение дифференциального уравнения вто-
рого порядка содержит две .произвольные постоянные *.
Пример 2. Найти частное решение дифференциального урав-
нения у"=х*, удовлетворяющее условиям: 1) у'= 2 — при х=1;
2) у = 12-|- при х = 3.
Решение, у"-— . Положим ^=г. Тогда данное урав-
нение перепишется в следующем виде:
2'х — х1 или dz = xidx.
Интегрируя это уравнение, найдем: dz = xldx\ z = yX!,-|-Ci.
Заменив z его значением, получим
(а)
Определим Сь пользуясь условием у' = 2~ при х— 1:
2‘ = ‘ P + Ci—2.
о о
Подставив в уравнение (а) вместо (ф его значение, будем иметь
t/' = yX3-j-2, или dy = х3 -ф- 2^ dx. .
Проинтегрировав это уравнение, получим
У == J2 ~ф~ “T Ч-
3 1
Для определения С« имеем уравнение 12 — = у2'34-ф-
откуда находим С2 = 0.
Следовательно, частным решением данного уравнения, удов-
летворяющим начальным условиям, будет
z/ = ^x4-j-2x.
* Вообще, общее решение дифференциального уравнения п-го порядка
содержит п произвольных постоянных.
340
Пример 3. Ускорение (w) материальной точки, движущейся
прямолинейно, в зависимости от времени t выражается формулой
w = 2t-[-3. Найти закон этого движения, если у = 0 и s = 0
при t = 0.
Решение. Эта задача сводится к нахождению частного
решения дифференциального уравнения s"t — 2t-]~3 (см. § 79).
о „ dv
Заменив в данном уравнении s его значением получим:
^ = 2^ + 3; dy = (2/4-3)d/;
\dv = \(2t-\-3)dt-, и^^Н-З/^-Сь
Полагая в последнем уравнении п = 0 при / = 0, находим С( = 0.
Следовательно, o = E-]-3f, или ~ — E~j-3f; ds = (E-\-3t)dt.
1 3
Интегрируя еще раз, получим s = g-/3—[— Для определе-
1 3
ния Ci имеем уравнение 0 = д-03-|-2 -О2-}-С®, откуда находим
С2 = 0. Следовательно, в данном случае закон движения выра-
жается уравнением
§ 121. ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Дифференциальное уравнение называется линейным, если оно
первой степени относительно искомой функции у и ее производ-
ных у', у", у'",.... '
Линейное дифференциальное уравнение второго порядка, имею-
щее вид
У’-'гРУ’-\-УУ = в> (6)
где р и q — постоянные величины, называются линейным однород-
ным уравнением второго порядка с постоянными коэффициентами.
Рассмотрим некоторые свойства этих уравнений.
Теорема 1. Если функция у} = [(х) является решением уравне-
ния (6), то функция Сцц, где Ct— произвольная постоянная,
также будет его решением.
Доказательство. Так как, согласно условию, ух— реше-
ние уравнения (6), то (см. § 116)
У’ -\-РУ\-\-ЯУ1 = Ъ- (а)
Подставив в уравнение (6) вместо функции у и её производных
341
соответственно Ciy, (СдуУ)' и (Cir/i)’, получим
С1у{ + pCiy\-\- qCtyi^G, т. е.
(У* + Р1А + Wi) — о
или в силу равенства (а): Ci-О —0; 0 = 0 — тождество.
Следовательно, функция См является решением уравнения (6).
Теорема 2. Если функции у2 и у-2— решения уравнения (6), то
функция y3=yt~\-.yt — также его решение.
Доказательство. Так как у\ и //> — решения уравнения (6),
то
у"1 РУ1+ ЯУ1—о и у* 4“ рУи+яуъ—о* (б)
Подставив в (6) вместо у", у’ и у функцию у3 и ее производ-
ные, будем иметь:
(У1 + Уд" + Р (У1 + Уд'д~.Я (У1 ~г Уд — 0>
или
(У1 + РУ1 + ЯУд + (у* + РУ 2 + ЯУд —
Принимая во внимание равенства (б), получим 0-[-0 = 0 — тож-
дество. Следовательно, функция z/3 = z/j-|-z/.2 — решение уравне-
ния (6).
Пример 1. Проверить, что функции yi — e-^ и z/.2 = e2*-— реше-
ния уравнения
у" ^Чу'-8у = 3. (в)
Подставляя в уравнение (в) последовательно у2 и уч и их
производные, получаем (е"4А)'--[-2(е_4А).'— 8е“4А = 0, или
1 Qeix — 8е 4А — 8е“4* = 0 — тождество;
(ew)" + 2(ea7- 8e2v = 0,
или
4е'А 4еи — 8ё2х — 0 — тождество.
Следовательно, функции у2 — е~и и //.? = е2х — решения уравне-
ния (в).
Определение. Два решения гц и уч дифференциального
уравнения (6) называются линейно независимыми, если одно из
тих не является произведением другого на постоянную величину.
В противном случае решения ух и уч называются линейно зависи-
мыми.
Например, функции е~1х и ё2х являются линейно независимыми
решениями уравнения (в), так как при любом постоянном k
e^lx^ke2x, а функции y1 — e~ix и y.2 = 3e~ix — линейно зависимые
решения этого уравнения, так как уч — kyi ири k — 3.
342 ’
Теорема 3. Если щ и у* — два линейно независимых частных
решения уравнения (6), то функция
у = Схух-\-С^у*, (7)
где Ci и С3 — произвольные постоянные, является его общим реше-
нием.
Доказательство. Так как, по условию, yi и уг— два
частных решения уравнения (6), то, согласно теореме 1, Сур
и С2у2, где Ci и С2— произвольные постоянные, тоже будут его
решениями, а потому (по теореме 2) их сумма [функция (7)] также
будет его решением. Эта функция (7) содержит две произвольных
постоянных (см. § 120) и не может быть преобразована в равно-
сильную ей функцию, содержащую только одну произвольную
постоянную (см. сноску на стр. 340), так как tp и у2— линейно
независимые решения.
Следовательно, эта функция (7) — общее решение уравнения
у''~\-ру'+уу=О- (6)
Так например, общим решением уравнения (в) будет функция
y = Cie-ix + C^x,
где Ct и С2— произвольные постоянные.
Функции yt — C}eix и у2 = С2ем, очевидно, при любых дейст-
' вительных значениях Ci и С2 будут двумя линейно независимыми
частными решениями этого уравнения.
Из этой теоремы следует, что для нахождения общего реше-
ния уравнения вида (6) достаточно найти два линейно независи-
мых частных решения yi и у2. Пример, рассмотренный выше,
наводит на мысль, что такие частные решения можно искать
в виде
= (8)
где k—некоторое число. Тогда
у'= у" = &екх.
Подставив в уравнение (6) вместо у и ее производных их
выражения, получим:
k^ekx-^pkekx-^qekx = Q-,
eft-v(^ + pA + ^) = 0,
или
k^pk-\-q = G, (9)
* Если yL и у3 — линейно зависимые решения уравнения (6), то функ-
цию (7) можно преобразовать в равносильную ей функцию, содержащую
только одну произвольную постоянную:
У — Срц + С2у2 = Сур Са • kyi = (Сх ф- С Ji) yi = Су\.
343
так как екх^0. Корни уравнения (9), очевидно, будут теми
значениями k, при которых функция (8) будет удовлетворять
уравнению (6), т. е. будет его решением. Это уравнение (9) принято
называть характеристическим уравнением по отношению к уравне-
нию (6).
Из алгебры известно, что корни уравнения (9) находятся по
формуле
. (10)
При этом в зависимости от числовых значений р и q возможны
следующие случаи:
1. Корни ki и ki характеристического уравнения (9) — числа
действительные и разные по величине k>).
2. ki и ki — действительные числа, равные между собой (ki = ki).
3. kt и ki — сопряженные комплексные числа.
Рассмотрим эти случаи по порядку.
Первый случай. Если kt и k> — разные по величине действи-
тельные числа, то функции yl=e,''iX и у.> — е1:-х будут частными
линейно независимыми решениями уравнения (6). В этом случае
общее решение будет иметь вид
,/^СцА' Сд?Л (11)
Пример 2. Решить уравнение у" — 4у' Зу — 0.
Решение. Полагая у — екх, получим:
(екху — 4(?А)' + Зе"х = 0; екх (k2 — 4k + 3) = 0,
или
/г2 — 4*4- 3 = 0.
Характеристическое уравнение можно написать сразу, заменив
в данном уравнении у", у' и у величинами k'2, k и 1. Решив это
уравнение, найдем kt = 3, #2=1. Частными решениями будут
функции:
t/i = eJA; у^ = ех.
Следовательно, общее решение имеет вид у — СУ]х-гС-е''.
Пример 3. Решить уравнение у” -j- Зу'— 0.
Решение. Заменив в этом уравнении у" и у' величинами k2
и k, получаем характеристическое уравнение k‘-\-3k — 0. Решив
это уравнение, -находим: &i = 0, =—3, iy1 = e<', у^ — е^.
Следовательно, общим решением является функция
y — C^-yCie^, или у — G C~ie~'ix.
Пример 4. Решить уравнение у" •—ау — 0.
Решение. Решив характеристическое уравнение k‘‘— а — 0
находим; klti — ±V а, yt — e^ax, yi = e~Vax-,
, y — Cie^ax -[- Cg-l a x.
344
Второй случай. Из формулы (10) видно, что характери-
стическое уравнение (9) имеет равные корни = если
—<7=Д). (г)
Непосредственно получаем только одно частное решение
У1=е •
Докажем, что в этом случае вторым частным решением уравне-
ния (6) является функция -
_р х
yt = xyi, т. е. у2 = хе 2 . (д)
Найдем первую и вторую производные этой функции:
/ A' -Р_х
у'3=[хе 2 ) —е 2 ~~^хе 2 ;
(_р __р V __р _р
е 5 )=-ре 5 +4'еС
Подставив выражения функции (д) и ее производных в урав-
нение (6), получаем:
(р р \ / р р \ р
2j+42" -Vе 2
р р р
Л9 -2Х , ~2Х п -2Х /р3 \ п
— ~ хе -\-qxe =0 или —хе (j—<71—0.
Приняв во внимание условие (г), имеем
— хе -0 = 0, или 0 = 0— тождество.
Это значит, что функция (д) —-решение уравнения Д6) в слу-
чае, когда оно имеет равные корни. Эта функция (д)' линейно
независима с функцией уь так как при любом постоян-
ном k.
, Следовательно, при£1=&.2 = у общим решением уравнения
y"-\-P!) 4- W=0 (6)
является функция
у—Ср 2 -j-Cjxe 2 ,
или -
y = (Cl-J[-Cix)e \ . .... (12)
345 :
Пример 5. Решить уравнение у" -ф- 6z/ -ф- 9у = 0.
Решение. Характеристическое уравнение ft2— 6/г9 = 0
имеет равные корни: &1==£.2 = — 2=3- ^астными линейно ^неза-
висимыми решениями этого уравнения являются функции:
z/i = е'м; у2 = хем.
Общее решение имеет вид (12) у = (Ct -ф- С2х) е31'.
Пример 6. Найти частное решение уравнения х"и -ф- 4х/ -ф- 4х = 0,
удовлетворяющее условиям: х—1 и х\ — —1 при t — 0.
Решение. Характеристическое уравнение &24£4 = 0
имеет равные корни: kt=k2 =—— — 2. Функции х1=е-2<
и хг = 1е~2‘ — частные линейно независимые решения данного
уравнения. Общим решением его является функция
х — (С, -ф- C2t) е 21. (е)
Полагая в этом уравнении (согласно начальным условиям) t = 0,
х=1, находим: 1 = (Ci -ф-(X• 0)е-2,0; Ci=l. Далее, продиффе-
ренцировав функцию (е), получим
xt = (C2 — 2Cj — 2Cat)e^‘.
Подставив в это уравнение вместо G его найденное значение
и полагая в нем t — 0, x't — — 1, находим: —1=(С2 —2-1 —
— 2С>-0)е°; Са = 1, следовательно, искомое частное решение
имеет вид
х = (1 -ф/)е'2'.
Третий случай. Уравнение (9) имеет сопряженные комп-
лексные корни тогда, когда ~ — q<^0. Обозначив их кратко
в виде
kt = a-]-bi.-, k2 — a — Ы, (ж)
где а = — у, b=j/~q — частные решения уравнения (6)
можно записать так:
У1^е^ь9х- уг=е(^^х^ (и)
Эти решения можно заменить двумя линейно независимыми
функциями:
У1 = еах cos Ьх-, (л)
t/2 = eaj:sin(>x, (м)
не содержащими мнимых величин.
346
Уравнение (9) будет иметь комплексные корни (ж), если 4
р - — (&1 ki)'= — [(a -j- bi) (а — Ы)] = — Ча-,
q = kiki = (а -|- Ы) (а — bi) = а2 Ц- Ь\
и уравнение (6) имеет вид
у" — Чау' -|- (а2 4“ ^) У — 0- (6a)
Докажем, что функции (л) и (м) являются решениями этого
уравнения.
1) Найдем первую и вторую производные функции (л):
у] = (еах cos bx)x = еах (a cos bx — b sin bx); ,
у’’ = [еах (a cos bx — b sin 6x)]'x = eax [(a2 — 62) cos bx — 4ab sin bx].
Подставив значения ylt у] и y'{ в уравнение (6а), получим:
еах {[(а9 — b*) cos bx — ЧаЬ sin bx] —
— Ча (a cos bx — b sin bx) 4~ (a2 4* 62) cos bx} = 0;
eax (0 • cos bx 4* 0 • sin bx) — 0,
или 0 = 0 — тождество.
Следовательно, функция (л) — решение уравнения (6а) и урав-
нения (6) в случае, когда оно имеет комплексные корни (ж).
2) Аналогично, подставив в уравнение (6а) функцию (м) и ее
производные, получим:
еах {[(п2 — 62) sin bx-\- ЧаЬ cos bx]—
— Ча (a sin bxA-b cos 6x)-J- (a2 -j-62) sin 6х} = 0;
еах (0 • sin bx 4- 0 • cos bx) = 0;
0 = 0 — тождество.
Итак, функции (л) и (м) являются двумя линейно независимыми
частными решениями уравнения (6) в случае, когда уравнение (9)
имеет сопряженные комплексные корни. Поэтому общее решение
его имеет вид
у = Ае?* cos bx 4- Ве'1Х sin bx,
или
y = (A cos 6x4-5 sin 6x) еял;, (13)
где a = — b=~^/~q—А и В— произвольные постоянные.
Пример 7. Найти общее, решение уравнения у" Чу' 5у = 0.
Решение. Находим корни характеристического уравнения
£а-[-2& Ц-5 = 0: ^.2 = —1±]/1^75 = —1±]/4-(—1) =
= —1±2]/—1 = —l±2i. Следовательно, а = —1, 6 = 2.
Подставив эти значения а и 6 в формулу (13), получаем общее
решение:
у = (A cos Чх 4- В sin Чх) ё~х.
* Из алгебры известно (теорема Виета): kl-\-k2 — —р; kL-kn=pq.
347
Пример 8. Решить уравнение s"t -f- 4n-s — 0.
Решение. Характеристическое уравнение k? -|- 4/г2 = 0 имеет
мнимые корни: ki = 2ni, ki = — 2ni. В данном случае а =
= — у = 0, b — j/ q — ~ = V 4ri’ = 2п. Общим решением яв-
ляется функция у — A cos 2nt В sin 2ni.
Задача. Материальная точка массы т притягивается непод-
вижной точкой О с силой, пропорциональной массе т и рас-
стоянию х от точки О; при этом коэффициент пропорциональ-
ности равен «Л Найти закон движения.
Решение. Из механики известно, что если материальная
точка массы т движется прямолинейно под действием силы F, то
F—mx’tt, (н)
где / — время; х"< — ускорение, вызываемое силой F (см. § 79).
Принимая во внимание, что притягивающая сила F пропорцио-
нальна т и \, и учитывая при этом, что эта сила при положи-
тельном х направлена в сторону его убывания, получаем урав-
нение
F =— uFmx.
Заменив в этом, уравнении F его выражением из равенства (н),
получаем дифференциальное уравнение этого движения:
тхн = — uFmx, или х’и -|- Л - 0.
Характеристическое уравнение ^2Ц-ш2 = 0 имеет мнимые корни:
Л1 = и)1, ki — — wL Общим решением является функция
х - A cos ш/ В sin ы1.
Этому уравнению можно придать другой (более простой) вид,
полагая
Л = A? sin a, B = /?cosa,
где 7? и а — произвольные постоянные величины. Получим
х = R (sin wt cos а -ф- cos ut sin a).
В скобках мы имеем развернутое выражение синуса суммы
двух углов <и/ и а. Получается уравнение
x = A?sin (и>/-]-а), (14)
выражающее закон простого гармонического колебательного дви-
жения.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Что называется дифференциальным уравнением?
2. Какая функция называется общим решением дифференциального
уравнения?
3. Что представляет собой общий интеграл дифференциального уравне-
ния с геометрической точки зрения?
348
4. Что представляет геометрически частное решение дифференциального
уравнения?
5. Какой вид имеют дифференциальные уравнения первого порядка:
1) с разделяющимися переменными; 2) однородные; 3) линейные?
6. Какими функциями являются Р и Q в однородном уравнении первого
порядка?
7. Какими величинами являются Р и Q в линейном уравнении первого
порядка?
8. Какой подстановкой решаются дифференциальные уравнения первого
порядка: 1) однородные; 2) линейные?
9. Какой подстановкой решаются линейные однородные уравнения вто-
рого порядка с постоянными коэффициентами?
10. Какой вид имеют общие решения линейных однородных уравнений
второго порядка с постоянными коэффициентами в случае, когда характе-
ристическое уравнение имеет: 1) действительные и разные по величине
корни; 2) действительные и-равные корни; 3) сопряженные комплексные
корни?
Глава XIII
РЯДЫ
§ 122. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ.
ЧИСЛОВЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ
1. Определение. Совокупность чисел at, а-2, a:h ait ..., ап,...,
являющихся частными значениями некоторой функции f(n), когда
аргумент п последовательно принимает значения 1, 2, 3, ..., п, ...,
т. е. «1 — /(1), a2 = f{2), a3 = f(3),, an — f(n),..., называется
числовой последовательностью или просто последовательностью.
Чтобы уяснить себе смысл этого определения, рассмотрим
примеры последовательностей:
В первой из этих последовательностей имеем.'
«г=/(1) = ^ = 1, ^ = /(2) = 24т=4,
^ = /(3) = ^=^, ... , Д„ = /(П) = J_, ... ;
во второй: -
ai = f(l) = 4, a.2 = f(2) = l,
а3 = /(3) = 1, ... , an = f(n) = ^, ... .
Числа t?i, а2, а3, ... , аП, ... называются членами последова-
тельности.
349
Последовательность называется бесконечной, если за каждым
ее членом следует еще один.
Выражение, определяющее п-й член последовательности (при
любом п), называется общим членом последовательности и обо-
значается символом ап.
Можно сказать, что закон образования последовательности
дан *, если дана формула, выражающая ее общий член в зави-
симости от порядкового номера п этого члена. В примерах, рас-
смотренных выше, такими формулами, очевидно, являются:
1) a„=f(n) = 2^; 2) a„ = f(n) = l.
Пример 1. Написать несколько первых членов последователь-
ности по данному общему члену
Решение.
, 1 (2-1 2 2 , . .3_. 3 3
«2 ( О *(2.2— 1)-’ — ‘9’ °3 ' (2 - 3 — 1)2 —25’
Й4 = ( I)4 (2-4 — 1)2 = 49 И Т‘ Д' ,
Получаем:
. _ 2 3 _ 4 5______6_
"9 ’ 25’ — 49’ 8Т’ — ТЗТ’
Пример 2. Написать формулу общего члена последователь-
ности
.11 1 1
*’ 1-2’ 1-2-3’ 12-3-4 ’ 1-2-3-4-5 ’
Решение.
ai = f(l) = |; = «3 = ^; ...;
отсюда видно, что общий член этой последовательности имеет вид
1 1 **
йп= 1.2.3...n = Td •
2. Определение. Выражение вида
Щ -j- а-2 аз -|- ап , (1)
* Закон образования числовой последовательности может быть выражен
и не формулой общего члена. Например, предложение «извлечь корень
квадратный из числа 3 с точностью до 0, 00...01» приводит к следующей
числовой последовательности приближенных значений этого корня (с недо-
статком): 1,7; 1,73; 1,732; 1,7320; 1,73205; ...
** Произведение натуральных чисел от 1 до и-кратко обозначается так:
п\ (читается; «эн факториал»),
350
где а(, й2, ал, ani... являются членами бесконечной последо-
вательности, называется бесконечным числовым рядом или просто
числовым рядом. При этом числа йь сп, аЛ, ... называются чле-
нами ряда. Символ «4-...», поставленный в конце, заменяет
фразу «плюс и так далее до бесконечности».
В качестве примеров можно привести числовые ряды:
1 + '2’+22Н~2з4_24 + ••• + 2^* ‘
1'Ну+4+т+у+ ••• + 4+ ••• >
составленные из членов последовательностей,, рассмотренных
выше.
Из определения и приведенных примеров видно, что числовой
ряд представляет собой сумму бесконечно большого числа сла-
гаемых. Что же понимать под суммой бесконечного множества
чисел и всегда ли такая сумма существует?
Обозначим через Sn сумму п первых слагаемых ряда (1)
Sn = аЛ -j- a<i -ф- йз -ф- ... -ф- ап. (2)
Сумма Sn называется частичной суммой ряда (1). Давая п
последовательно значения 1, 2, 3, ..., будем получать частич-
ные суммы:
Si = fli‘, $2 = й1-j—$з = at -ф- йз -ф- йя;
S4 = Й1 -ф- Й2 “ф'йз -ф- Й4 и т. Д.
Очевидно, с изменением числа слагаемых п изменяется и
сумма Sn. При п->оо могут иметь место, следуюшие три случая:
1) Sn может стремиться к некоторому определенному пре-
делу S, т. е.
lim S„ = S;
2) Sn может неограниченно возрастать, т. е. lim S„ = oo;
n->co
3) Sn хотя и не возрастает неограниченно, но ни к какому
определенному пределу не стремится.
В первом случае ряд (1) называется сходящимся и число S
называется его суммой. В этом случае пишут условное равенство
S = at -ф- а2 -ф- йз -ф- ... -ф- ап -ф- ... (3)
Во втором и третьем случаях ряд (1) называется расхо-
дящимся. Расходящийся ряд, очевидно, суммы не имеет.
3. Если сумма Sn первых п членов числового ряда при п-^-са
стремится к определенному пределу S, т. е. lim S„ = S, то та-
п — со
кой ряд называется сходящимся, а число S — его суммой.
В качестве примера сходящегося ряда можно привести любую
бесконечно убывающую геометрическую прогрессию (см. § 52),
351
так как сумма первых п членов такого ряда при я-*ор имеет
предел, определяемый по формуле
lini
л со 1 Ч
Примерами расходящихся рядов могут служить следующие ряды:
3 + 3-24-3-2а + 3-23+...+3-2"-‘+;
1 — 1 + 1 — 1 + — 1 4-1 — ...
В первом из них сумма S„ первых п членов неограниченно
возрастает при п->оо, во втором, эта сумма равна или 1 (при
п нечетном) или 0 (при п четном), а потому при п->оо она
не стремится ни к какому пределу.
Следует заметить, что вычислить точно сумму S сходящегося
ряда можно лишь в редких случаях; обычно вычисляют ее при-
ближенно, суммируя несколько первых членов и отбрасывая
остальные. Нахождение таких (приближенных) значений суммы
ряда рассматривается в § 131.
§ 123. НЕОБХОДИМЫЙ ПРИЗНАК СХОДИМОСТИ РЯДА
Из предыдущего параграфа мы знаем, что существуют ряды
сходящиеся и расходящиеся, В данном параграфе и в трех после-
дующих параграфах устанарливаются признаки, с помощью кото-
рых можно судить о сходимости или расходимости ряда по его
общему члену ап.
Пусть суммой сходящегося ряда
Hi а> -р а3 -р • • 4~ 4- ап ... Д1)
является число S, т. е.
lini S„ = S. (а)
Л -> СО
Возьмем суммы первых п членов и (и — 1) членов этого ряда
S„ —а\ —f-ct-> —4z3—[— ... an_i-|-ай, (2)
Sn_j = di-L 4“ ••• 4~°ri-i- 4 (2а)
Так как при /г—>-оо и (н — 1) -►оо, то, очевидно (см. § 122),
lim Sn_1 = S. (б)
п-* со
Вычтем из равенства (2) равенство (2а):
ап.
Возьмем от обеих частей этого равенства пределы-при п->оо,
получим
lim (Sn— S„4) = lim а„; lim S„— lim Sn.1= lim On,
• « ^»CO • Я -* CO fl-»CO ' Л-*ОЭ' • П-* CO'
352
или [см. равенства (а) и (б)] S — S— lim ап, откуда следует
/г-* со
lim an = Q.
Zl -♦ ОО
Это значит, что общий член сходящегося ряда (1) стремится,
к нулю, когда п -> сю.
Следовательно, для того чтобы данный ряд сходился, необхо-
димо, чтобы его общий член ап стремился к нулю при п^-со.
Однако это условие не является достаточным, так как ряд может
оказаться расходящимся и тогда, когда общий член его стре-
мится к нулю ири /г->0.
Возьмем,, например, ряд, называемый гармоническим:
1 + 1 + 1 + 1+-- + т+-- W
Этот ряд расходится, несмотря на то что его общий член —
стремится к нулю, когда п неограниченно возрастает. Чтобы убе-
диться в этом, перепишем сумму Sn первых п членов этого ряда,
распределив слагаемые на группы так, чтобы последнее слагае-
мое каждой группы имело своим' знаменателем степень числа 2;
I \ [ 1 I 2т~2 | 2 Г” 2Ш-1 | 3 * *** 2т]
и подобрав п так, чтобы 2т = п.
Сумма (в), очевидно, больше, чем следующая сумма:
так как каждое слагаемое второй суммы равно или меньше соот-
ветствующего слагаемого первой суммы (в), т. е.
или
s«>i+4+(y+-2-+4+•••+4)-
Заметив, что скобки содержат (пг—1) слагаемых, каждое из
Г „
которых равно у, найдем
— 1 +-2 2"(т— 1)—1
12 п. Е. Агачев 353
Заменив в неравенстве '(г) правую часть найденным ее значе-
нием, получим
S„2> 1-j-y/n.
Положим, что т-ь-оо, тогда ^1 Ц-у tnj -> оо и /г = 2т->оо.
Так как Sn больше, чем 1 --j- ут, то, безусловно, S„->oo
при /1->оо. Следовательно, гармонический ряд (4) расходится.
§ 124. ДОСТАТОЧНЫЕ ПРИЗНАКИ СХОДИМОСТИ РЯДОВ
С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
До сих пор сходимость или расходимость того или иного
ряда мы устанавливали, пользуясь выражением суммы первых п
членов ряда. Однако это выражение часто бывает очень сложным
и притом таким, что невозможно определить lim<S„ при п-*оо.
Поэтому возникает потребность установить признаки, по кото-
рым можно бы было судить о сходимости или расходимости ряда,
не пользуясь выражением для S„.
1. Признаки сравнения рядов. Если каждый член
ряда с положительными членами
Щ a.t а3 . + ап ..., , (а)
начиная с некоторого члена, меньше соответствующего члена схо-
дящегося ряда с
bi -j- b-i b3 ... bn ..., (6)
то данный ряд (а) также сходится.
Если же,, наоборот, каждый, член ряда (а), начиная с некото-
рого члена, больше соответствующего члена расходящегося ряда (б),
то данный ряд (а) также расходится.
Примем эти признаки без доказательства.
Пример 1. Исследовать сходимость ряда
2Л* + зТ2’з+ ••• ••• <в)
Решение. Сравнивая этот ряд с рядом
у + + 2» + ‘ ‘ ‘ + 2« “Ь • • • ’ (г)
видим, что каждый член его, начиная со второго, меньше соот-
ветствующего члена ряда (г):
1 1 _ 1 1 _ 1 1 .
2.2а<'22; 3-23<^23’ ’ /1-2" <^2«’
354
но ряд (г) сходится как бесконечно убывающая геометрическая
прогрессия. Следовательно, сходится и ряд (в).
2. Признак Даламбера. Если в ряде с положительными
членами
ai -j- аЛ ... -j- ап Д- an+i
отношение (n-j-l)-eo члена к п-му члену стремится к определен-
ному пределу I при неограниченном возрастании п, т. е.
lim =
ап
то
1) в случае, когда /<Ч, данный ряд сходится;
2) в случае IД-1 — ряд расходится.
(При 1=\ вопрос о сходимости остается нерешенным; в од-
них случаях ряд сходится, в других — расходится.)
Примем этот признак без доказательства.
Пример 3. Исследовать по признаку Даламбера сходимость
ряда
2.4.6
2га
(е)
Решение. Запишем общий член ряда
2га
О-п-- чл •
Подставив в выражение общего члена вместо п число n-f-1,
получаем х
„ __2(га+1)
+1--- зл+1
Находим предел отношения (п-|-1)-го члена к n-му члену при
п —>оо:
ап+1 _2 (га 1) /2га_п -|- 1 .
"оД 3«+* ; 3« Зга ’
Так как / = -д-<^1, то ряд (е) сходится.
Пример 4. Исследовать сходимость ряда
1+ ь2“Ь 1 1 .2.3.4 + ••• + 1.2-3... /г “Ь •" (5)
Решение. Пользуясь условным обозначением 1.2.3; ... п=п\
(см. сноску на стр. 350), данный ряд можно кратко записать так:
Т1+д + д + д+•••+д+
12*
355
Нам известно:
_ 1 _ 1 _ 1
а" zz! 1 -2 -3 -4...ZZ’ а^л ~ 1 -2-3 -4 ... п (п+ 1)’
Далее находим:
- "л+1_Г 1 . 1 1 1
ап ~L1 -2.3.4 ... п (п + 1) • 1 .2-3.4 ... п J ~ zz + 1 ’
Так как I — 0<Д, то данный ряд сходится.
§ 125. ПРИЗНАК СХОДИМОСТИ ЗНАКОЧЕРЕДУЮЩИХСЯ РЯДОВ
Знакочередующимся рядом называется ряд. вида
. Ci—а<1~\~а3 — а^-\- ... 4-(=—1)" •••, (6)
где at, а-2, а3, ... — положительные числа.
Признак Лейбница. Если члены знакочередующегося ряда
убывают по абсолютной величине и, стремятся к нулю при п->оо,
то ряд сходится.
Доказательство. Рассмотрим сначала сумму первых 2//г
членов этого ряда:
— а2 а2 —а3 аг — |— ... < а-2тл а.2гп_з 4~ а2т_] а->т- (а)
Эту сумму можно переписать в следующем виде:
Sim — (<21 — а2) (<23 — й4) • 4" (flim-3 — (Ьт-Ч.) 4" f — О.-1пд- (6)
В этом равенстве все разности в круглых скобках положительны,
так как, согласно условию,
й1 а* > аз 4> ••• 4> atm и lim aim = 0.
Вследствие этого сумма Sim положительна и возрастает с воз-
растанием т. Эту сумму (б) можно еще представить так:
Sim = ai [(Й2 — й3) 4" (а1— ад 4- 4~(a'Zm-S>~ Й-2т-1) 4~ fl-Zzzi|- (в)
Из этого равенства видно, что при любом т сумма остается
меньше первого члена ряда (6), т. е. 5ат<4щ.
Если переменная величина Sim все время возрастает с возра-
станием т, оставаясь при этом меньше данного числа at, то она
имеет предел и этот предел меньше at. Обозначив этот предел
через S, получим
lira S.2,n — S.
т-*оэ ’
356 (
Прибавив к сумме (а) еще один, (2m-1- 1)-й член, будем иметь
SsmM =0] — Оз -f- Оз — Oj-f- • • • -f- 0_>m_i — 02от - j- Oom+1,
пли
*5зт+1 ~~ Sim —|- Ojm+i,
откуда
lim Sim+i= lim S9m+ lim a2m+i.
m -* co m -+ co
но lim Sim = S (по доказанному),
m-* co
lim a2m+i = O (по условию).
m co
Поэтому lim S2m+) = S.
m — co
Следовательно, при любом n, как четном, так и нечетном,
имеем, lim Sn — S, где S — некоторое вполне определенное число.
п -> со
Согласно определению (см. § 122) ряд (6) сходится. Итак, чтобы
знакочередующийся ряд, члены которого убывают по абсолютной
величине, сходился, необходимо и достаточно, чтобы его общий
член ап стремился к нулю, когда п^>-оо.
Пример 1. Исследовать сходимость ряда
J_____L.J_______Li ..
/3 /ё 1 /7 /9 1
Решение.
1 1 1
/2-1 + 1 /2-2+1 /2-3+1
а„ = ——г; lima„=lim -........— 0.
/2л+1 ге-со /2п+1
По признаку Лейбница, данный ряд сходится, так как
1.1.1,.. п
, -r=Z> ~~> • • • и liman = 0.
/3 ^/5 ^/7
§ 126. АБСОЛЮТНО СХОДЯЩИЕСЯ РЯДЫ
Ряд называется знакопеременным., если среди его членов имеются
как положительные, так и отрицательные.
Теорема. Знакопеременный ряд
«1 + аз + аз+ ••• 4~+ + •••
сходится, если сходится ряд
I Ut | -j-1 a21 1 a3 ] + ... | an | -/ ...,
составленный из абсолютных величин его членов.
Примем эту теорему без доказательства.
357
Определение 1. Ряд называется абсолютно сходящимся,
если сходится ряд, составленный из абсолютных величин его членов.
Замечанне. Знакочередующиеся ряды, рассмотренные в пре-
дыдущем параграфе, очевидно, являются частными случаями
знакопеременных рядов.
Пример 1. Знакочередующийся ряд
1 ~2г + зг~4т + 5!~ +(— 1)"-1
является абсолютно сходящимся, так как сходится ряд (5), со-
ставленный из абсолютных величин его членов (см. § 124).
Существуют ряды, которые сходятся и в том случае, когда
ряды, составленные из абсолютных величин их членов, расхо-
дятся.
Пример 2. Знакочередующийся ряд
сходится, так как (см. § 125)
! \ 1 \ 1 \ Г V 1 Л
••• > ЬГП ап= 11П1 —=0,
тогда как ряд (3), составленный из абсолютных величин его чле-
нов, расходится. Такне ряды называются условно сходящимися.
Определение 2. Сходящийся ряд называется условно схо-
дящимся, если ряд, составленный из абсолютных величин его чле-
нов, расходится.
Пример 3. Исследовать сходимость ряда
sin 1 । sin 2 , sin 3 . ' . sin n . . .
-j—+ ...+... (a)
Признаки, изложенные в § 124, в данном случае неприме-
нимы, так как ряд (а) содержит как положительные, так и отри-
цательные члены. Неприменим также и признак Лейбница, потому
что этот ряд не знакочередующийся. Возьмем ряд, составленный
из абсолютных величин его членов:
Так как | sin n|s=g 1 при любом п, то члены этого ряда меньше
соответствующих членов сходящегося ряда:
Следовательно (см. § 124, и. 1), ряд (б) сходится, а потому
ряд (а) сходится абсолютно.
358
§ 127. СТЕПЕННЫЕ РЯДЫ
Выражение вида
Л (*) 4~ А (х) + /з (*) + • • + А» (х) + • •,
где ft (х), ft(x), f»(x), ... являются функциями от х, называется
функциональным рядом. Таким рядом, например, является три-'
тонометрический ряд
sin х ф- у sin 2хф- у sin Зх-ф- ... sin пх-г ...
Среди функциональных рядов в математике и ее приложениях
особо важную роль играет ряд, расположенный ио возрастаю-
щим степеням аргумента х и имеющий, вид
щ (2iX —а.2х! -ф- плх3 -ф- . - • -ф- апхП ~|~ • • • > (7)
где щ, П], а2, а3, ... —постоянные коэффициенты. Такой ряд
называется степенным. Очевидно, при любом данном значении х
этот ряд обращается в числовой. Поэтому вопрос о сходимости
степенного ряда сводится к определению тех значений аргу-
мента х, при которых ряд (7) сходится.
Совокупность тех значений аргумента х, при которых дан-
ный степенной ряд сходится, называется интервалом сходимости.
Интервал сходимости ряда (7) можно, определить, применив при-
знак Даламбера к ряду
| аЛ | -ф-1 atx | 1 а^ | -ф-1 плх31 -ф- ... | апхп | -ф--..., (7а)
составленному из абсолютных величин членов данного ряда:
ряд (7а) сходится и, следовательно, ряд (7) сходится абсолютно
при таких значениях аргумента х, которые удовлетворяют нера-
венству
lim ^<1, (76)
п -> со 11
где ип и «л+1 являются n-м й (п-|-1)-м членами ряда (7а).
Пример 1. Определить интервал сходимости ряда
+ ••• + 4^ + ••• (8)
Решение. Ряд, составленный из абсолютных величин чле-
нов ряда (8), имеет вид:
359
или
Заменив левую часть
иием, получим
и<1
неравенства (76) найденным ее значе-
или — 1<х<1,
следовательно, степенной ряд (8) сходится в интервале (—1; 1)
и притом абсолютно.
Пример 2. Определить интервал сходимости ряда
Решение. В данном случае имеем:
I ХП ;| I ХП I ' I Х" + 1 |
11,1 = |7Г |— 1 -2.3...,г; Un+1= 1 •2-3...н(«+ 1):
1- "п+1 1- [ ! .vn+1 i I хп i
n-co “« -2-3...»(,/ + 1) l-2-3...«J
Предел отношения абсолютных величин (zz—[- 1)-го и п-го
членов ряда (9) при п->оо меньше единицы при любом конеч-
ном х, т. е. при |х|<^со или —оо<^х<^оо. Следовательно,
данный ряд сходится абсолютно при всяком конечном х.
Пример 3. Определить промежуток сходимости ряда
у* уЗ 4*5 v-2/Z 1
T-sr+g!1^-(2Ьйг+-- ' (10)
Решение. Ряд составленных из абсолютных величин членов
ряда (10), имеет вид:
1-yl 1 isi I 1^1 । । ।
1 3! 5! (2н-1)! “Г-
Un~ (2« — 1)! : Ыл+!~(2,г+ 1)1’
(Юа)
,. «л+1 г л-2Л+‘ л-2"-1
lim = lim . —г-г-: ------г-
woo «Л „-.cu L1 2 ^ ... С" — 1)(2/1 + 1) . 1 -2.3... (2п— 1
= lim
Л —* СО
2/г (2п-Ь 1)
0-х2 = 0<1.
При любом конечном х предел отношения (и-|- 1)-го члена
ряда (10а) к его n-му члену меньше единицы. Следовательно,
ряд (10) сходится абсолютно при всяком конечном х.
3G0
§ 128. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ СТЕПЕННЫХ!
РЯДОВ
Производной степенного ряда (7) является тоже степенной
ряд
Ц| 4~ 2арс —Зц3х2 —. —!— папхп 1 ...
В более полных курсах математического анализа доказывается,.
что если степенной ряд сходится в некотором интервале (а; Ь) и
имеет своей суммой функцию f (х), то этот ряд (7) можно почленно
дифференцировать и интегрировать сколько угодно раз, причем
получаемые степенные ряды будут сходиться в том же интервале
(а; Ь), т. е. если
f (к) = а0 4~ atx -j- Ojx2 Озх1 4~... 4~ fln-v”1
то
f (х) — а> 4~ 2ачХ 4- За3х2 . -|- паПхп~1 4~. •; ;
f" (%) = 1.2ач 4- 2 • За3х 4- .. -4“ (w — 1) папхп 2 4“ • • • I
. X X X .V V
J f (х) dx = $ ай dx 4- $ а,х dx-\- $ а%х2 dx 4-... 4~ $ апХп dx 4-...
О 0.0 о о
Поясним смысл изложенного на примере. Возьмем степенной
ряд
1 — х24-х4 — х6 4- Xs — х104-... (а)
При любом х, удовлетворяющем условию |х|<^1, этот ряд
представляет собой геометрическую прогрессию со знаменателем
о — — х2, сходится в интервале (—1; 1) и имеет своей суммой
функцию
/(х) = Гр-?=1-х24-х*-хв + х8-х'в + ...,
отсюда, дифференцируя и интегрируя, получаем:
f (х) = —2х 4- 4х3 — 6xs 4- 8х7 — 10х” — (б)
$ f (х) dx = J (1 — х2 4- х‘х— х6 4- х8 — х’° 4- ...) dx,
о и
пли
f (х) dx = х — у х3 4- j Xs — у X7 4- X9 — пх'1 -р ... /в)
и 4
361
Легко показать, что ряды (б) и (в) сходятся в том же интервале
(—1; 1), в каком сходится и данный ряд (а). Суммой первого из
них служит функция
„ф 1 V _ 2х
второго —
§ f(x)dx= J arctg x|J = arctgx. - (г)
О о
Из равенств (в) и (г) следует
arctgx = x — 1x’4-Axs — yx’ + |xs-^х1’+.„ (11)
Это равенство справедливо при любом х из интервала (—1; 1),
§ 129. РЯД МАКЛОРЕНА
Из предыдущего параграфа нам известно, что если степенной
ряд (7) сходится в некотором интервале (а; Ь) и имеет своей сум-
мой функцию f (х), то при'всех значениях аргумента х, заклю-
чающихся в этом интервале, справедливы равенства:
f (х) — а0 -ф щх -ф а^х1 -ф а3х3 -ф щх1 -ф... -ф- апхп -ф-...; (12)
ф (х) = Цх —j— 2щх —ф Зй3х_ —4й4х3 —ф... —{— папх'1 1 —{—.,.;
ф'(х) = 1 -2а.2 -ф2 • За3х-ф 3 • 4адг-ф.. ,-ф (п — 1) 7ia„x"“2-ф...;
ф" (х) = 1 • 2 За3 -ф 2 • 3 -'4a4x -ф-... ф- (п — 2) (л — 1) папх'1-3 -ф-...;
flv (х) = 1 • 2 3 • 4а4 -ф. -ф (/1 — 3) (/1 — 2) (/г — l)na;ix'1-4 -ф...;
fW (х) = 1.2 • 3-... (л — 3) (п — 2) (/г — 1)7Ш„х'!-'г -ф-... = п,\ап -ф...
Приняв в этих равенствах х = 0, получаем:
f (0) = Йо -ф fli • 0 -ф #2 • О2 -ф_О3 О'1 -ф . . . = <2о>
ф (0) = щ-ф 2щ> • 0-ф За3 • О'-ф... = ад
ф'(0) = 1 2щ-ф 2 3 а3 • 0-ф 3 • 4щ • 0-ф ... —-1 -2а3;
ф" (0) = 1 • 2 • За3-ф 2 • 3 • 4й4 • 0 +.. .= 1 • 2 • Зад
fv(0)= 1-2-3-4а4-ф0-ф0...—1-2-3-4ад
Ф'г) (0) = 1 • 2 • 3 • 4... пап -ф 0 -ф 0... = п\ап.
Из этих равенств находим:
«о = /(0); щ = ф(0); а2 = ^; «3 = ^
362
Подставив в равенство (12) вместо ап, af, аг, аъ... их найденные
значения, получаем равенство, называемое формулой Макларена:
t W=, (0) г+/м х>+ф +Др .<•+
+Дрх>+...+рр^+... ' (13)
Правая часть этой формулы называется рядом Макларена. Эта
формула (13) дает вид тоТо степенного ряда, в который разла-
гается функция y=f(x).
Формула Маклорена встречается во многих разделах высшей
математики, а также во многих технических науках, базирующихся
па математике; с ней приходится иметь дело при различных
практических вычислениях. Эта формула ценна тем, что для раз-
ложения функции y~f(x) в степенной ряд достаточно знать
частные значения этой функции и ее производных при х = 0.
Однако не следует думать, что всякая функция может быть раз-
ложена в ряд Маклорена. Нельзя, например, разложить в этот
ряд функцию f (х) = 1пх, так как при х = 0 эта функция не суще-
ствует и не имеет производных. Может случиться и так, что при
х — 0 функция f (х) существует и имеет производные всех поряд-
ков, но ряд, составленный по формуле Маклорена, расходится и
не имеет своей суммой данную функцию.. Поэтому для установ-
ления того, что степенной ряд, составленный по этой формуле (13),
имеет своей суммой данную функцию, необходимо исследовать
его сходимость.
Из изложенного вытекает следующий порядок разложения
данной функции f (х) в ряд Маклорена:
1) найти производные данной функции;
2) найти частные значения этой функции и ее производных
при х = 0;
3) написать ряд Маклорена для данной функции, подставив
в формулу (13) вместо f(0), /'(0),... /(п) (0),... их значения;
4) определить интервал сходимости полученного, ряда.
Если окажется, что ряд сходится, то сумма его будет пред-
ставлять данную функцию f (х) при всех 'тех значениях аргу-
мента, при которых этот ряд сходится.
§ 130. ПРИМЕРЫ РАЗЛОЖЕНИЯ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ
Пример 1. Разложить в ряд Маклорена функцию /(x) = ev.
Решение.
1) ['(х) = ех, f" (х) = ех, fn(x) — ex, ...
2) f(Q) = en=\, f'(0) = Г (0) = ... = f^(0) = ...=*!.
3) Ряд Маклорена имеет вид:
H0)+^x + ^.v>+^ + ...+^ + ... (|эд
363
Подставив вместо f(0), f (0), /(я) (0), ... их значения, по-
лучаем
' i + t+S+S + -"+^ + --
Из § 127 мы знаем (см. пример 2), что этот ряд сходится при
любом х. Следовательно, по формуле Маклорена имеем
е-1 = 1+х-4-2г + зг + ---+77г + '" (14)
Пример 2. Разложить в ряд Маклорена функцию f(x) = sinx.
Решение.
1) f(x) = cosx; f" (х) =— sinx; f"(x) = — cosx; flv(x) = sinx;
fv(x) = cosx‘, fvl(x) =—sinx; fvli(x) — — cosx; fYU1 (x) — sinx;
fix (x) = cos x и т. д.;
2) f (0) = sin0 = 0; f(0) = cos0=l; (0) = —sin0 = 0;
(0) = — cos 0 — — 1;
/IV(0) = 0; fv(0)=l; P’'(0)=0; /vii(0)=_1.
/VII1(0) = 0; /1Х(0) = 1 й т. д.
3) Подставив найденные частные значения функции и ее про-
изводных в (13а), получдем:
0 + Т х + 4 л'2 + Чг х’ + 7!х" + Il + Б! А'“ +
+ Цг х1 + A's -г -<jj -V<J + • • >
или
а-5 + Й-^+5--(10)
4) В § 127 было доказано, что этот ряд сходится при любом х.
Следовательно, при всяком конечном х справедливо равенство
= + + + (15)
Пример 3. Разложить в степенной ряд функцию f (x) = cosx.
Решение. Разложение этой функции в ряд Маклорена можно
найти таким .же путем, как и разложение функции sinx. Но зна-
чительно проще получить это разложение, воспользовавшись ра-
венством (15). Продифференцировав это равенство почленно, на-
ходим:
/ * Г X’2 I X Х~‘ । Х° । I , \fi—1 Х^ I . 1
(sin х)х |х — -Tjj 5i ~ 7j + Qi — • • • + (—!) ’ (2,г — 1)1 + ’ • J.v =
____ 1 Х“ । х’ Xе | Xs I / , \л-1 Х2п 2
— 2! “Г 41 6! “Г 8] •••.-Г 1 ч '(2п — 2)1 "Т* • • • »
ИЛИ
cosx=l^|1+^-^+... + (-l)-.^l + ... (16)
364
Ряд (10) сходится при любом х Следовательно (см. § 128),
ряд (16) тоже сходится при любом х.
Пример 4. Разложить в степенной ряд Маклорена функцию
/(х) = 1п(14-х).
1 1 1.9
Решение. 1) Пх)^^; /"(х) = - <1^; Г (*)=(Т+^Г:
XIV/ \ 1 - 2-3 fV . , 1 • 2 - 3 - 4
f (х) — (1+-г)3 ’
Г (х) = (-1Г1 • L2(i^^1), • •
2) /(0) = 1п(1 4-0) = 0; /'(0)=т-1--0=1; /"(0)=-—^=-1;
(0) = 1 -2; /IV (0) = — 1 - 2 3; fv (0) = 1 • 2 • 3 • 4; ...,
/<”) (0) = (—I)""1-1-2-3 ... (n—1), ...
3) Подставив эти частные значения данной функции и ее про-
изводных в формулу Маклорена, получаем:
In (1 -|- х) = 0 —у ЛГ —|- ytj- х2 -ф-—2 з х3 4- у. 2.3Т4 х +... +
или
1п(1+л-) = х-| 4-^_^ + ... + (_1Г1.^ + .., (17)
4) В § 127 было доказано, что ряд
.V2 , X3 X* | X5 ,о '
Х ~2 + 3 — 4 + 3 ~' • • • (8>
сходится в интервале (—1; 1). Следовательно, равенство (17)
справедливо только при таких значениях х, которые удовлетво-
ряют условиям —1 <х< 1.
Пример 5. Разложить в степенной ряд Маклорена функцию
j (х) = (1 4- х)т, где т — любое действительное число.
Решение. 1) f’(x) — m (1 4-х)"‘-1; f" (х) = т(т—1) (14-х)т^3;
/"'(х) — т(т'—1) (нг — 2) (1 4~ х)"1-'1, • • •;
(х) = /72 (т— 1)(/72— 2)... [/72— (/2 — 1)[ ( 1 4~ Х)'”-'1, ...
2) Приняв во всех этих равенствах х = 0, находим:
/(0) = (1 4-0)m= 1; /'(0) = т; /"(0) =/тг (m — 1);
f40) = /72 (/72 — 1)(/72 — 2); ...,
(0) =/72 (/72 — l)(ffl — 2)...(/72 — «4- 1), ...
365
3) Подставив найденные частные значения данной функции
и ее производных в формулу Маклорена, получаем
(1+хг=1+/пх+т (,;1~1+т °" т.у ,(з ~2) xj+
I т (т — 1) (>« - 2)... (m - n +J) ,
П „I +••• (18)
4) Можно доказать, что в данном случае ряд Маклорена схо-
дится в интервале (—1; 1); равенство (18) справедливо при
И<1-
При т целом и положительном правая часть формулы (18)
обращается в конечный ряд, состоящий из (т -ф- 1) членов. Полу-
чается равенство, справедливое при любом х. Например, при
т — 4, получим
(1 + х)‘^ 1 + 4х + х- + 4 (<7.0-2) х. +
+ '114~1|>.(2^у-3) ** = Ч-41 + 6х! + 4х> + X1.
§ 131. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ ПРИ ПОМОЩИ РЯДОВ
Пусть, число S является суммой сходящегося ряда
Hi -ф-й2-ф- аз_г • • • Н- ап • • > (1)
т. е.
S = til -ф- й-> -ф- й3 -ф-... -ф- ап -|~... (3)
Тогда сумма Sn первых п членов ряда (1)
S„ = й1 -ф- йг ~ф- а-3 -ф- ап (2)
будет приближенным значением числа S, погрешность которого
Д*5„ будет равна сумме^ отброшенных членов, т. е.
Д5„ = а„+1 -ф- йи+а -ф- а„+з -ф-...
Так как в любом сходящемся ряде, начиная с некоторого
(£-го) члена,
a*>a*+i>a/<+2>... и lima„ —О,
п->оэ
то всегда можно подобрать п так, чтобы абсолютная погрешность
| Д5>„ [ приближенного значения Sn суммы S не превышала на-
перед заданного малого числа. Сравнительно легко найти такое
значение п для знакочередующегося ряда, т. е. когда
<S —Gi— йа-рОз — Щ-{-,..-|-(—1 )"-1 ;
4 Sn = at — Й2йз — й4~|-...-|-(—1)п~1ал;
—— (й«+1 — ~г — ~г • • • )• (а)
366
Абсолютная величина суммы (а), т. е.
I | = | a,I+i — ап+2 4" алгз — ®/iV4 + •••!, (б)
очевидно, является абсолютной погрешностью приближенного зна-
чения Sn суммы S. Равенство (б) можно переписать в следующем
виде:
I ^Sn | = | an+i — [(пл+<г — йл+з) ~г (а>Ш — л„+в)
откуда видно (см. § 125), что
I ASn | пп+1,
т. е. абсолютная погрешность | AS„ | приближенного значения Sn
суммы S меньше абсолютной величины первого отбрасываемого
члена.
Пример 1. Вычислить sin 0,5 с точностью до 0,001.
Решение. Подставив в формулу (15) вместо х его данное
значение (0,5), получаем числовой знакочередующийся ряд
• лк лк 0,5’ . 0,55 0,5’ . . .
sin0,5 = 0,5---^-4-—-------(в)
в котором
А с 0,53 0,5s
а, = 0,5; а,=-----4; а3 = ^-; ...
Нам предложено вычислить sin 0,5 с точностью до 0,001. Во избе-
жание лишних вычислений следует предварительно выяснить,
сколько членов ряда (в) надо сохранить, чтобы абсолютная по-
грешность | | приближенного значения sin 0,5 не превышала
числа 0,001. Выше было установлено, что в случае знакочереду-
ющегося ряда | | 4 fln+i> гДе an+i— первый из отбрасываемых
членов. Попробуем взять /? = 2, тогда
0,5Г| 0,03125 Л г.ллос /л 'пл1
an+i = а3 = упо = 190 = 0,00026 <( 0,001
и
I Д$3|<аз<0,001.
Это значит, что, отбросив все члены ряда, начиная с третьего,
мы можем найти sin 0,5 с требуемой точностью. Получим
sin 0,5 «= 0,5 — ^ = 0,5- 0,021=0,479.
Пример 2. Вычислить cos 15° с точностью до 0,001.
Решение. В данном случае в формуле (16) следует принять
". 15 = 0,2618.
367
Получим числовой знакочередующийся ряд
1К0 пос.о 1 0,2618s , 0.26184
cos 15° — cos 0,2618 1 ------------•••, (г)
в котором
. 0,2618s 0,2618*
а1=1; а.2=-<—; а. — .
Сохранив лишь первые два члена ряда (г), будем иметь воз-
можность вычислить cos 15° с требуемой точностью, так как
| 1 а-s <^yj- <0,001. Получим
' cos 15-^1 — 212^= 1 — 0,034 — 0,966.
Число членов, удерживаемых в формулах (15) и (16), зависит
от требуемой точности и от значения х. Из приведенных приме-
ров видно, что для вычисления синусов и косинусов небольших
углов с точностью до 0,001 достаточно сохранить в этих форму-
лах два первых члена, т. е. принять:
X3 X-
sinx^x — у; cosх1—(19)
Пример 3. Вычислить In 5,12 с точностью до 0,001.
Решение. В книге В. М. Брадиса «Четырехзначные матема-
тические таблицы» имеется таблица, озаглавленная «Натуральные
логарифмы». В ней помещены натуральные логарифмы целых чисел
от 1 до 109.
Пользуясь этой таблицей и формулой (17), можно вычислить
натуральный логарифм всякого числа, которое может быть пред-
ставлено в виде произведения ?V(l-|-a), где N — целое число,
не превышающее 109, |а|<1. В данном случае находим In 5 —
= 1,6094 (по таблице);
In 5,12 = In 5 (1 0,024) = In 5-|-In (1 0,024),
или (см. формулу (17)] .
In 5,12 = 1,6094 + (0,024 - 2^--|-2^ ..
Первое слагаемое дано с точностью до 0,0001. Чтобы иметь
возможность найти In 5,12 с точностью до 0,001, в сумме, заклю-
ченной в скобки, достаточно сохранить первое слагаемое, так как
I Л о I 0,024s лп,
I | <а2<^—<0,001.
Следовательно, In 5,12 «« 1,6094 < (0,024) = 1,633.
Пример 4. Вычислить с точностью до 0,001 основание нату-
ральных логарифмов (число е).
Решение. Приняв в формуле (14) х — 1, получаем числовой
ряд с положительными членами:
1 + 1 + ^+^ + ^ + 5у + 6-1 + .,. + 2|+... (д)
368
Здесь, очевидно, [см. (2а)]. Поэтому по величине
первого отбрасываемого члена нельзя судить о погрешности при-
ближенного значения Sn суммы S [см. (2)]
Покажем, что, сохранив первые семь членов ряда, т. е. приняв
е№1 + 1 дЛ--]-1-4-14-1-4- - (е)
можно вычислить е с точностью до 0,001. В самом деле, обозна-
чив сумму отбрасываемых членов через AS7, получим
А5, _ 71 4- 81- у( -j- IQ14-... _
=1 _i_ _1_ _i_ _J_ 4._____!_____ =
7М 7! 8 Г 7! 8 9 '71 У • 9 10 ’
= 1(14-1 + _L . __J_4_ )
7Г-1 8'8-9 Г 8.9-10 Г
Если в ряде, заключенном в скобки, заменим каждое из чисел-
8, 9, 10, ... числом 7, то знаменатели уменьшатся, а дроби увели-
чатся. Поэтому
Вследствие этого
<Z у (1 + у 4~ уз + yr + • • •)
Преобразуем правую часть этого неравенства, заменив бесконечно
убывающую геометрическую прогрессию ее суммой. Получим
Следовательно, Д5, <40,0003. Это значит, что погрешность, про-
исходящая от замены суммы (д) суммой (е), меньше, чем 0,0003.
Вычислим теперь сумму (е) приближенно, обращая ее слага-
емые в десятичные дроби с точностью до 0,00005:
1 4-1 -1-1 = 2,5000
. 4 = 0.1667
1=4:4^0,0417
v 4=зт;5’=,одаз
1 = 1: 6^0,0014
—/^=2,7.81
369
Абсолютная погрешность, полученная при вычислении при-
ближенного значения суммы S7, ие превысит числа 0,00005-4 =
= 0,0002. Эта погрешность и погрешность Д5, в общей сложно-
сти не превосходят числа 0,0003 4-0,0002 = 0,0005. Следовательно,
с = 2,718 с абсолютной погрешностью, меньшей 0,001.
1
Пример 5. Вычислить dx.
о
Решение. Этот определенный интеграл, можно вычислить
лишь приближенно, предварительно разложив подынтегральную
функцию в степенной ряд. Этот ряд мы получим, разделив обе
части равенства (15) на х:
4
sin х . х2 . Л'4 л'с , '
1 — зГ + бГ ~ 7Г “г • • >
откуда
1 1
С sin х , С !, х2 , х1 х° , \ ,
dx= ^1-з]- + ёТ-7г4-..рх =
-и .0
|о 3! 3 |о^ 5! 5 |о 7! 7 |о ‘ ’
или
1
С sin х , , 1,1 1 ।
3 ~\Tdx~ 1 — зГТз+бРб 71-7-*-'"
о
Этот знакочередующийся ряд сходится очень быстро. Сохра-
нив лишь первые три члена, т. е. приняв
1
С sin х . q , lil
) —^ = ^3=!—зруз 4-5Г5 ,
о
получаем возможность вычислить этот интеграл с точностью до
0,0001, так как (см. решение примера 1)
| Д531 <0,0001.
Следовательно,
I
t 5ВА dx = 1,00000 - 0,05555 4- 0,00166 = 0,9461.
j х 1
о
§ 132. ФОРМУЛЫ ЭЙЛЕРА*
Из алгебры известно, что корень квадратный из минус еди-
ницы обозначается символом i и называется мнимой единицей.
Целые положительные степени мнимой единицы имеют четыре
* Леонард Эйлер (1707—1783) — великий математик, механик, физик
и астровом, член Петербургской Академии наук.
370
периодически повторяющихся значения:
il — i; i1 — (V—I)2 =—1; z:' = i2 i = — 1 • i = — i;
i4 = z9-z2 = (—1)3=1; z4ft+1 = z; zift+3 = —1; /4ft+:i = —
iik=l, где k=\, 2, 3, ....,
Возьмем формулу (14) и заменим в ней действительное число
мнимым числом zx*. Получим
После замены степенных рядов, заключенных в скобки, их сум-
мами [см. формулы (15) и (16)] это равенство принимает вид
eix — cos x-|-z sin x. (20)
Если вместо х возьмем (—х), то получим
' е1 — cos х) i sin (— х),
пли
^'-v = cosx — zsinx. (21)
В результате почленного сложения и вычитания равенств (20)
и (21) будем иметь:
„ й,л’~4й~,л' = 2со8х; е‘х— e~‘x — 2i sinx,
откуда следует .
Посредством формул (20)—(22) устанавливается связь между
тригонометрическими и показательными функциями. Эти формулы
были открыты Эйлером и называются формулами Эйлера.
Формулы Эйлера дают возможность комплексное число г==
= a-[-bi представить в показательной форме, пользуясь его три-
гонометрической, формой
г = г (cos срz' sincp), (23)
где г — модуль комплексного числа, ср — его аргумент,
определяемый из формулы tgcp = y.
По формуле (20)
cos ср —г sin ср = е1<р. (а)
* Законность такой замены доказывается в более полных курсах.
371
Принимая во внимание это равенство, формулу (23) можно пред-
ставить в следующем виде:
z-^re1'. (24)
'Г акая форма (24) записи комплексного числа называется пока-
зательной.
Пример 1. Представить комплексное число z — 3 V 3 -ф- 3z в три-
гонометрической и показательной формах.
Решение. Находим модуль комплексного числа:
’ г = У (3/3)2 + 32 =6.
Так как а^>0 и Ь^>0, то вектор, соответствующий данному
Ь __ 3 ' 71
— — —т-- находим <р — -yr-.
а з/з 6
комплексному числу г, лежит в первой четверти, а потому аргу-
мент О <р <ф у. Из уравнения tg <р —
Следовательно [см. формулу (23)],
6/ । • ТЕ \ ' , _.
(cos g- -j- I Sin -g-1 . (6)
Представим данное комплексное число в показательной форме,
заменив в равенстве (б) выражение, заключенное в скобки, его
значением по формуле (а):
z = 6e6
Пример 2. Представить в тригонометрической и показательной
формах комплексное число z = — 1 — i.
Решение. Находим модуль этого комплексного числа:
г = vVir + (-iy2 = у 2.
Из равенства a -j-- bi = г (cos <р -ф- i sin <р) следует:
а b
COStf ; Sin <Р = - . (в)
Подставив в формулы (в) вместо а, b и г их значения, по-
лучаем:
1 ]/"2 . |/2
C0S'? = -^j = -L2-’ sin<p = -^. •
Такие знаки («—» и «—») имеют косинус и синус в третьей чет? ‘
верти. Поэтому из двух углов = и <р2 = — к, удовлетворяю-
щих уравнению tg ср = 1, следует взять второй, т. е. =
Теперь можно записать данное комплексное число в тригоно-
метрической форме:
z — V 2 ^cos -5- п i ,sin n)
и в показательной форме:
. 5 .
- г—
, 2= I 2с ...
372
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ '
1. Что называется бесконечным рядом? х.
2. Какие ряды называются сходящимися?
3. Что называется суммой сходящегося ряда?
4. Какие ряды называются расходящимися?
5. Имеет ли сумму расходящийся ряд?
6. Может ли’ряд сходиться, если его n-й член не стремится к нулю, когда
п — оо?
7. Можно ли утверждать, что ряд сходится, если его n-й член стремится
к нулю, когда п — оо?
8. Какие признаки сходимости рядов с положительными членами осно-
вываются нй сравнении рядов?
9. В чем состоит признак Даламбера?
10. Какой ряд называется знакочередующимся?
11. Что необходимо и достаточно, чтобы знакочередующийся ряд схо-
дился?
12. Какой ряд называется: 1) абсолютно сходящимся; 2) условно схо-
дящимся?
13. Какой ряд называется геометрической прогрессией?
14. При каких значениях знаменателя q сходится геометрическая про-
грессия?
15. Что называется интервалом сходимости степенного ряда?
16. Какой вид имеет ряд Маклорена?
17. Всякую ли функцию можно разложить в ряд Маклорена?
18. Воспользовавшись формулой 111), вычислить с точностью до 0,001
arctg 0,16.
19. Определить интервал сходимости каждого из следующих степенных
рядов:
у уЗ уЗ уЛ
о 1+т+21 + зт + - + ^г + -:
2)*-у + у-Л+-;
уЗ у5 у7
3^-ЗГ + 5Г-71+-: .
ат 1 А‘Э t х“ I
4) 2! + 4! 61 +•••
Ответы. 18. arctg 0,16 »= 0,159. 19. 1) Сходится в любом интервале; 2) схо-
дится абсолютно в интервале (—1; 1); 3) сходится абсолютно в любом ин-
тервале; 4) сходится абсолютно в любом интервале.
Глава XIV
РЯДЫ ФУРЬЕ
§ 133. ВВЕДЕНИЕ
В последующих параграфах этой главы мы будем иметь дело
с некоторыми интегралами, подобных которым до сих пор не
встречали. В настоящем параграфе займемся изучением приемов
вычисления таких интегралов.
373
1. Преобразование произведения тригонометрических функций
в сумму
Из тригонометрии известно, что
COS a. COS Г = у [cos (а + ₽) + COS (а — Р)[;
sin а sin ₽ = у [cos (а — р) — cos (a -ф- Р)];
sina cos Р = у [sin (а-[~ Р) + sjn (а — р)].
Приняв в этих формулах а = тх, ф = пх, получаем:
cos тх cos пх = у [cos (m у- п) х -ф- cos (m — п) х]; (1)
sin тх sin пх — у [cos (т — п) х — cos (т -J- п) х]; (2)
sin тх cos пх = [sin (m -ф" п) х sin (m — п) х]. (3)
Пример I. Преобразовать в сумму произведение sin5xcos2x.
Решение. По формуле (3) находим
sin 5х cos 2х = у [sin (5 -ф- 2) х—sin (5—2) х] = у (sin 7а; —j— sin Зх).
2. Понятие о четной и нечетной функциях
Определение 1. Функция у = f (х) называется четной, если
она не изменяет своего значения при изменении знака ее аргумента
на обратный, т. е.
/(—х)==Дх). (4)
Определение 2. Функция y = f(x) называется нечетной,
еуш при изменении знака аргумента на обратный меняется на
обратный и знак самой функции, т. е. '
/(—х) = —/(х). (5)
Из тригонометрии известно, что
sin(—х) = — sinx; tg (—х) = —tgx; cos (—x) = cosx;
sec(—x) = secx.
Согласно определениям, cosx и secx-—четные функции, a sinx
и tgx — нечетные функции. Очевидно, это справедливо и для
кратных углов, т. е. для sin их, cosnx и tgnx, где п — любое
целое число. В самом деле, sin/г (—x) = sin(—rtx) = sinnx,
cos п (^- х) = cos (— пх) = cos пх.
Например, функции
1) /(*) = А 2) (х) = лх44-с; 3) ф(х) = —За-
являются четными;
374 -
функции
4) F (х) = Зх, 5) Ф (х) — х3 — 2х : Ф (х) = .
являются нечетными.
Г рафик четной функции симметричен относительно оси Оу,
так как на таком графике любой точке (х; у) будет соответство-
вать точка (—х; у} (см. § 28, 31 н рис. 63 и 69). График не-
четной функции симметричен относительно начала координат:
любой точке (х; у) графика такой функции соответствует точка
(—х; —у\
3. Свойства определенного интеграла от четной и нечетной
функций в случае, когда пределы интегрирования равны по
абсолютной величине, но противоположны по знаку.
а
Рассмотрим интеграл F (х) dx, где а — любое действительное
— а
число, F (х) — функция, непрерывная в интервале (—а; а). Из-'
вестно, что этот интеграл геометрически выражает площадь фи-
гуры, ограниченной графиком функции y—-F(x), осью Ох и
прямыми х = — а и х — а (см. § 106). В случае, когда F(x) —
четная функция, фигура, ограниченная указанными линиями,
симметрична относительно оси Оу и вследствие этого (см. решение
задачи 961 и рис. 208)
S(t, — F (х) dx = 2 jj F (х) dx,
— а О
ИЛИ
J F W dx = 2 § F (х) dx. (6)
— а О
Если F (х) — нечетная функция, то (см. § 111 и рис. 176)
О а
jj F (х) dx = — F (х) dx
— а 0
и поэтому
J F (х) dx* = F (х) dx $ F (х) dx = — $ F (х) dx -[- § F (х) dx,
— <7 —а 0 0 0
ИЛИ
jj F (х) dx — 0. (7)
— Л
4. Вычисление некоторых интегралов, встречающихся в после-
дующих параграфах ' *
л
1) Вычислить интеграл § sinmxdx, где Tn =1, 2, 3,...
• — л
* По формуле (6) § 109.
375
Решение. Нам известно, что sin тх —нечетна я функция. На
основании формулы (7) имеем * .
л
sin тх dx — 0. (8)
— л
л
2) Вычислить интеграл J cosmxdx, где т=\, 2, 3, ...
Р е ш е н и е. Известно, что cos тх— четная функция. По формуле
(6) находим
С 2
\ cos тх dx — — sin тх
J т
G
т. е.
л
cos тх dx 0.
— л
= 0,
о
(9)
3) Вычислить § cos тх cos пх dx, где т и п независимо друг
от друга могут принимать любые целочисленные значения.
Решение. Заменив подынтегральную функцию ей тождест-
венной по формуле (1), получаем
Л .л
cos тх cos пх dx — [cos (т -ф п) х-ф cos (m — п) х] dx =
—л — л
•л л
= у \ cos (m -j-п) х dx-]--} cos (m — n) x dx .
Если n Ф m, to m — n и m-x-n— целые числа, отличные от
нуля. По формуле (9) имеем:
л л
cos (т -ф п) х dx — 0; § cos (т — n'jxdx — O.
— Л -- Л ’ ;
Следовательно, если п Ф т, то
л
§ cos тх cos пх dx — 0. (10а)
— Л
Если п — т (см. указание к задаче 850):
л л л
С о С ч о С 1 4- cos 2тх ,
\ cos тх cos пх dx —2 \ cos,1 тх—2 \ —1—— dx —
— л b — 5
I71 1 • л [л
-ф К-Sin2/7iX —It,
о 1 2//i | о
376
т е.
я ч
cos тх cos пх dx ~ те. (106)
— я
Итак,
* ( 0, если п Ф т,
\ cos тх cos пх dx = { (10)
_п 1 те, если п = т.
4) Вычислить интеграл
- я V
sin mx sin/гх dx.
> —71
Решение. Здесь могут иметь место те же два случая, ко-
торые были рассмотрены в предыдущем примере. Примем сначала
п Ф т. Тогда, заменив подынтегральную функцию ей тождест-
венной (2) й применив к полученным интегралам формулу (9),
найдем
Я .к
sin тх sin пх dx = у [cos (т — п) х — cos (т п)х] dx =
— л — я
Я Я
^2 jcos (т — n)xdx — cos (т-\-п) xdx — ^-0 — 0 =0.
— я — я
Следовательно, если т ф п, то
Я
sin тх sin пх dx = 0. (На)
' — я
При т = п получим
Я 4 я
§ sin тх sin nxdx = § sin2mxdx.
— я — я
Здесь sin2mx— четная функция. Применив формулу (6) и заменив
подынтегральную функцию ей тождественной (см. указание к за-
даче 848), находим
я я я .
sin2 тх dx = 2 ? sin2 mxdx = 2 ( * ~ cos '2тх dx —
— It о о
я я’
С С 1 I я
— \ dx — \ cos 2mxdx = те — sin 2 тх =л.
о J 2.-я [о
Следовательно, если п = т, то
я
sinmxsin nxdx' —те. (116)
— я •
377
Итак,
с ( 0, если т Ф п,
\ sin тх sin пх dx — 1 (11)
дф I тс, если т — п.
ТЕ '
5) Вычислить интеграл J sinmxcos/u'dx.
' —ТЕ
Решение. Разберем сначала случай т Ф п. Заменив подынте-
гральную функцию ей тождественной (3), находим
ТЕ ТС ТС
sin тх cos их dx = у sin(OT4-n)xdA'-|-y sin — n)xdx.
— ТЕ —ТС —ТЕ
К последним двум интегралам применима формула (8), так как
тфп и т — п при т Ф п — числа целые, отличные от нуля.
Получаем
ТЕ ' ТЕ
sin тх cos nxdx • 0 -ру • 0, или sin/zzx cos nxdx = 0.
— ТЕ —ТЕ
При т — п имеем
sin тх cos тх dx ==? у sin 2тх dx = 0.
— It' — ТЕ
так; как sin 2тх — нечетная функция (7). Следовательно, при любых
т и 11 справедливо равенство
ТЕ
sinmxcos/rxdx = 0. (12)
— ТЕ
5. Интегрирование по частям.
Если и и v — функции, от X, то по формуле (5) § 92 диф-
ференцирования произведения двух функций имеем
d (uv) = vdu -ф- udv,
где
du — u'xdx, dv = v'xdx.
Из этой формулы следует
udv = d (uv) — vdu.
Интегрируя обе части этого равенства, получаем
§ udv — \d (uv) — § vdu,
где (см. § 101, свойство 3)
§ d (uv) — uv.
378
Следовательно,
^udv — uv—; J vdu. (13)
Эта формула называется формулой интегрирования по частям.
С ее помощью нахождение интеграла udv сводится к нахождению
другого интеграла J vdu, который может оказаться проще, чем
данный. Для успешного применения этой формулы требуется
подынтегральное выражение представить в виде произведения
двух сомножителей и и dv так, чтобы dv был дифференциалом
известной функции, 'т. е. такой функции, которую можно легко
найти по данному дифференциалу.
Пример 2. Вычислить интеграл х4 In xdx.
Решение. Если подынтегральное выражение представить в
виде произведения х4- In xdx, то окажется, что невозможно найти
« dv
v ~ jj 1 n xdx. Целесообразно принять: u = lnx, dv — xldx. Тогда
, rfx С . 1 ,,
du = —; \ x4ax = -g-xJ;
х ’ j 5
Р . 1 1 1 Р 1 1 rfX "1 'i 1 1 Г
In х • хтх — In х -g-x1— х' •— = ^rx'Inx----x dx,
I __. 5.15 x 5 51 ’
1 !l dv U '-----I '7— I
d v v du J
ИЛИ
\ x4 In x dx — X xs In x — X x!i + C.
J э 25 1
Пример 3. Вычислить интеграл $xsin xdx.
Решение. Этого интеграла нет в таблице, приведенной в
§ 102. Нельзя^ его вычислить и способом подстановки. Применяем
формулу интегрирования по частям (13). В данном случае целе-
сообразно подынтегральное выражение представить в виде про-
изведения x-sinxdx. Примем а = х; dv — sinxdx. Тогда du = dx",
v = sin xdx = — cos x;
xsinxdx = x-Z—cosx'\— /—cosxWx =— xcosx-f-sinx-j-C.
J и dv 11 \ v. / J \ v / du -
Пример 4. Вычислить интеграл \xcos axdx.
Решение. Интеграл вида ^vdu окажется проще данного лишь
в том случае, если принять и — х, dv —cos axdx. Получим:
du = dx-, v = \ cosaxdx = —sinax;
f x cos axdx =x • — sin ax— C — sin axdx — — sin ax 4-
J “ ri» J
4--^-cosax 4- C.
379
Формулу (5) из § 92 можно переписать в следующем виде:
d (uv) — uv'xdx Ч- vu'xdx.
Интегрируя это равенство почленно в пределах от = a до
Xi—b, получаем
b b b b b ь
$ d (uv) ~ $ uv’dx $ vu'dx, или- uv — uv'dx $ vu’dx,
а а а а а а
откуда
' . £ b b
^udv — uv —^vdu. ' (14)
а а а
Мы получили формулу (14) интегрирования по частям для опре-
деленных интегралов.
> л
Пример 5. Вычислить интеграл $xsin3xdx.
и
Решение. Интегрирование ведем по формуле (14). Примем
и = х, dv = sin 3xdx.
Тогда du —dx, v= \ sin 3xdx —— cos Зя;
TC
fxsin3x dx~xl — -yr cos 3x
I о
и dv и \ '—v—'
\ v >
0
— — ~-xcos 3x j*-|- ~ sin 3x — §- h (—1) — 01 +j (0 — 0)
л
У ‘
Пример 6. Вычислить интегралы:
тс тс
1) jj xl cosmxdx; 2) § x'2 sin xdx,
— к . — TC
полагая, что m — целое число. x
Решение. 1) Так как x‘2cosmx—четная функция, то
тс - тс
§ х2 cos тх dx = 2 jj xl cos mx dx.
— л ' о
Этот интеграл можно вычислить, воспользовавшись формулой (14).
В данном случае следует принять:
и — х2, dv = cos mxdx.
Тогда
du = 2xdx, 0= cosmxdx sinmx;
It /
f x2 cos mx dx — 2 I x2 • + sin mx
j и av \ и
—л . . 4
к— 1 — sin тх- 2xdx V
I ------ du /
0 J к /
и '
380
тс
С л < 4тг
или \ х£ со$тхах=—rcosmr,
j Wi
— тс
тс
- 2) J х'2 sin тх dx = 0, так как x'2sinmx— нечетная функция
[см. (7)f.
§ 134. СИНУСОИДАЛЬНАЯ ПЛИ ГАРМОНИЧЕСКАЯ ФУНКЦИЯ.
СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ ФУНКЦИЙ
ОДНОЙ ЧАСТОТЫ И РАЗНЫХ ЧАСТОТ
Во многих вопросах физики и техники приходится встре-
чаться с периодическими функциями времени, т. е. с такими
функциямй, значения которых повторяются через определенные
промежутки времени. Периодическая функция /(/) с периодом Т
характеризуется равенством
/(/-ИГ) = /(/), (15)
где k — любое целое число.
Простейшей из таких функции, часто встречающейся в элек-
тротехнике и радиотехнике, является функция вида
у = f(x) = R sin («>/-]- <pn), (16)
выражающая закон простого гармонического колебательного движе-
ния [см. (14) в § 121]*. На рис. 188 изображены графики трех
таких функций:
1) при /?=1, <о = 2, <р0 = у; 2) при /?=1, <о = 3, <р0 = О;
3) при R = ^-, <о= 1, <ро = О.
* Понятие о таком движении и вывод уравнения (16) см. в книгах:
1) А. Ф. Б е р м а в т, Л. А. Люстерник «Тригонометрия», § 67. 2) «Ма-
тематика для заочных техникумов», часть 1, глава X, § 7.
381
Функции такого вида называются синусоидальными или гармо-
ническими. В формуле (16) постоянная величина R называется
амплитудой колебания, переменная величина ср = о>/-|-ср0 — пере-
менной фазой колебания, а постоянная величина <р0 (значение ?
при / = 0) — начальной фазой. Периодом этой функции (16) явля-
2”
ется величина —} так как
<0
R sin [со р 4- k • ¥0] = sin [((4 -f- ?o) 4" k • 2~] = Rsin (coz' 4- <po) >
t. e. [cm. (15) и (16)]
Эта величина
T = (17)
определяющая промежуток времени, в течение которого совер-
шается одно колебательное движение, называется периодом ко-
лебания.
В тесной связи с периодом Т находится число
» = -(18)
называемое частотой колебания-, оно показывает, сколько колеба-
ний совершает точка в течение единиц времени (секунд).
Правую часть равенства (16) можно преобразовать, пользуясь
формулой для синуса .суммы двух углов:
у=f(t) = R (sin vt cos <po 4- cos sin <p0) = R sin <p0 cos wt 4-
4-/?c°s<f>osinw!f.
Приняв 7?sin tfo = a; 7?cos<po = &> получим
y = f[t) = a cos co/4~ 6 sin co/. (19)
Функцию вида (16) или (19) и ее график называют ^простой гар-
моникой с частотой со.
Легко показать, что сумма функций вида (19) с одной и той
же частотой со является функцией того же вида, т. е. в резуль-
382
тате сложения гармоник с одной и той же частотой получается
гармоника с той же частотой. В самом деле, если
У\ = ai cos mt by sin co/; y-2 — a> cos mt 4- sin «/;
i/3 = a3cosu)/4-&3sin(o^; ..., to ’ .
у—у i ~F Уч 4- У* • • •= (fli Ч~ Ч- • • •)cos 4~
4~ (bi 4~ b<i 4- b3 4" • • •) sin
или , . , . , -
у —a cos со/ 4- о sin со/,
где a=ai4-aa4-a34--”> b — bi 4-Ь.г 4-b3 4~-• •
Если складывать простые гармонические функции:
yi = ai cos со/ 4- bi sin со/; yi = a1cos2wt 4~/>2 sin 2со/; ... (20)
383
2
с частотами ш, 2<о, 3«, и с периодами [см. (17)] Т\ — ~ = Т,
— ~ = Тз — ^ — ^Т, то будут получаться перио-
дические функции с периодом Т, графики которых не имеют того
симметричного вида, какой присущ синусоидам. Так, например,
в результате сложения трех простых гармонических функций:
z/i = sinZ, у-2 — у sin 2/, i/3 = ysin3/
получается периодическая функция
7 //=/(/) = sin / -j- ~ sin 2t -ф- sin 3/
с периодом 2тг (см. табл. 26 и рис. 189), график которой значи-
тельно отличается от синусоиды. Сложение четырех и более гар-
моник с разными частотами и при различных значениях коэффи-
циентов а-2, а-з, .... bi, b-2, Ь-з, ... приводит к еще более слож-
ным периодическим функциям.
Таблица 26
/ 0 ft T - ft T 3ft T к 5ft 4 3ft ~2 7ft ~T . 2ft
3'1 = sill t 0 |/25=0,7 1 0,7 0 -0,7 -1 -0,7 0
= -у sin 2t 0 0,5 0 —0,5 0 0,5 0 -0,5 0
Т = Vi + У 2 0 1.2 1 0,3 0 —0,2 -1 -1.2 0
1 о/ sin 3f 0 ’ /2 ^0,2 V ll 1 1 “1- ° « 0,3 0 —6 1'2- -0,2 9 5 -i” I) -41'2- -0,2 0
v = J’l + y-1 + Va 0 1,4 0,7 0,4 0 -0,4 -0,7 -1.4 0
§ 135. ТРИГОНОМЕТРИЧЕСКИЙ РЯД
В предыдущем параграфе мы видели, что в результате сложе-
ния гармоник разных частот получается сложная периодическая
функция. Естественно, возникает вопрос: нельзя ли произволь-
ную периодическую функцию с периодом Т представить в виде
суммы гармоник с периодами Т, ~Т, ...?
Оказывается, что всякая периодическая функция f(t) с перио-
дом Т — принадлежащая к весьма широкому классу функ-
384
ций* * ***, может быть представлена как сумма постоянной величины
и бесконечного ряда простых гармоник вида (20), т. е.
/ (0 = -j- "Г (ai cos оз/ bi sin art) (а2 cos 2<ot 4- b2 sin 2uf) -f-
4- ... 4~ • + (°Э cos mat bn sin nort)
или кратко,
/(/) = -^--{~ 2^cosn(nlf_b^'1 s*n (21)
n = I
Правая часть равенства (21) называется тригонометрическим
рядом, а числа си, ait ..., bi, bit ... — коэффициентами этого ряда.
Этот ряд принимает более простой вид, если положить о>=1.
Обозначив в этом случае аргумент t через х, получим:
СО
-у-4 V (a„cosnx4-^sinnx); (22)
н= 1
f (х) = -^-4- (алс°8 их 4-sin пх). (23)
п = 1
\
Так как cosnx и sin их (при п=1, 2, 3, ..,) — периодические
функции с периодом 2л, а ~-----величина, сохраняющая свое зна-
чение неизменным при любом х, то правая часть равенства (23)
не изменится от замены х на х4~2л, а потому от этого не должна
меняться и левая часть, т. е. f (х-\-2к) =f (х). Это значит [см. (15)
в § 134], что f (х) должна быть периодической функцией с периодом 2л.
Следовательно, эта функция может быть задана только в про-
межутке длиной 2л. В качестве такого промежутка мы в даль-
нейшем будем брать промежуток (—л; л). Очевидно, в проме-
жутках (±л; сЬЗл), (±Зл; ±5л), (±5л; ±7л), ... значения
функции /(х) будут периодически повторяться.
§ 13(5. КОЭФФИЦИЕНТЫ ФУРЬЕ. РЯД ФУРЬЕ
Чтобы разложить заданную периодическую функцию /(х) с пе-
риодом 2л в тригонометрический ряд, надо найти коэффициенты
.ряда (22) для этой функции. Займемся выводом формул, по кото-
рым они вычисляются.
Равенство (23) предполагает, что в промежутке (—л; л) ряд
(22) сходится и имеет своей суммой данную функцию /(х).
* В следующем параграфе будут изложены условия, которым должны
удовлетворять функции этого класса.
Постоянное слагаемое берется в виде дроби в целях упрощения вы-
числений.
*** Жан Батист Жозеф Фурье (1768—1829)—знаменитый французский
математик.
13 П. Е. Агачев 385
Проинтегрируем * ** обе части этого равенства в пределах от
— -л; до я (предварительно умножив пх на dx):
Я Л Л л
f(x)dx — -^~- dx-\-ai cosxdx-f-&i \ siuxdx-f-
—я —я • —я я —л
ял л
-|- а-2 jj cos 2xdx-ф- b^ jj sin 2xdx -|-... -]-...-j-an jj cos xdx 4-
—я —я —я
л
-J- bn $ sin nx dx-}-...
— Л
Так как [см. (9) § 133]
я л л
Jj cosxdx— cos 2xdx=.. .= J cos nxdx — .. . = 0
—Л — л — я
и [см. (8) § 133]
я я я
jj sinxdx = sin 2x = ...= sin nxdx = .. . = 0,
—n —Л —л
то в правой части этого равенства все члены, кроме первого,
обратятся в нули и мы получим:
Я л л
/(х) dx = ~ dx, или / (х) dx = • 2гс,
—я —л —л
откуда найдем
л
ай — y / (х) dx. (24)
— л
Для определения коэффициентов ап умножим обе части равен-
ства (23) на cosmx**, где т— любое целое число, и проинтегри-
руем в пределах от —гс до гс:
л л ,л
f (х) cos тх dx — cos тх dx-^-at cos х cos тх dx -j-
— л —я —я
л л
4- bi jj sin х cos mxdx-}-..-ф- an ij cos nx cos mx dx-\-
—Я — Л
Л
bn jj sin nx cos mx dx .
—я
* Теорема о сходящемся степенном ряде, набранная в § 128 курси-
вом, приложима и к рядам Фурье.
** В более полных курсах математического анализа доказывается, что
если для некоторой функции /(х) справедливо равенство (23), то будет
справедливо и равенство, полученное от умножения всех членов этого ра-
венства на cos тх или sin тх, где /и — любое действительное число.
386
В правой части этого равенства [см. (9), (12), (10а) в § 133]:
J cos тх dx — Q при любом целом /и;
— тс
тс
sin пх cos тх dx — 0 при любых целых тип;
$ cos пх cos тх dx — 0 при п # т.
Следовательно, в правой части этого равенства сохранится
только один член с коэффициентом ат, и равенство это примет вид
тс тс
J f (х) cos тх dx = ат jj cos тх cos nixdx,
или [см. (106)]
f (х) cos тх dx — am- я,
откуда
тс
. f (х) cos тх dx. (25)
Давая т последовательно значения 1, 2, 3, ..., вычислим коэф-
фициенты at, а-2, ал, ...
Чтобы определить коэффициенты Ьп, умножим обе части ра-
венства (231 na sinmx и проинтегрируем полученное равенство
в пределах от —- до ~. Получим
тс тс тс
f (х) sin тх dx = ~ sinmxdx-^-aj cos х sin/их dx 4-
— ТС — ТС ' — тс
тс тс
-\-bi \ sin xsin mxdx-\-.... • + ап $ cos nxsin/nxdx-j-
— тс — тс
тс
-ф- bn J sin пх sin тх dx-\-...
В правой части этого равенства в силу формул (8), (11), (12)
сохранится только один член с коэффициентом Ьт, и равенство
это примет вид
тс тс
f (х) sinmxdx = bm J sin mx sin mx dx,
или
тс
J f (x) sin mxdx=bm-к,
откуда
TC
= f (x)sinmxdx, где m=l, 2, 3, ... (26)
13*
387
Определение. Числа аа, ат и Ьт, определяемые по форму-
лам (24), (25) и (26), называются коэффициентами Фурье функции
f (х), а тригонометрический ряд (22) с такими коэффициентами —
рядом Фурье функции f{x).
Таким образом, мы установили, что если периодическая функ-
ция / (х) с периодом 2тс может быть разложена в тригонометри-
ческий ряд, то его коэффициенты через данную функцию выра-
жаются по формулам (24), (25), (26) и этот ряд является рядом
Фурье.
Однако существуют периодические функции, ряды Фурье ко-
торых оказываются расходящимися, а также и такие, ряды Фурье
которых сходятся, но не к данной функции. Поэтому' весьма
важно знать те условия, которым должна удовлетворять функ-
ция /(х), чтобы его ряд Фурье сходился и имел своей суммой
эту функцию f (х) во всех точках непрерывности । внутри про-
межутка (—тс; и). Эти условия были установлены французским
математиком Дирихле. - .
Теорема Дирихле. Если данная функция f (х) в промежутке
(—тс; к) непрерывна или имеет конечное число точек разрыва пер-
вого рода (см. сноску на стр. 153 и рис. 107); имеет конечное
число максимумов и минимумов или совсем их не имеет, то\
1) ряд Фурье этой функции сходится и сумма его в каждой
точке непрерывности внутри промежутка (— и) равна значе-
нию самой функции в этой точке;
2) в точках разрыва f(x), лежащих внутри этого промежутка,
сумма ряда равна половине скачка функции *;
3) в концах промежутка (при х — — тс и х = тс) сумма ряда
л /(—тс)+/1тс)
имеет одно и то же значение, равное —-----
Примем эту теорему без доказательства.
Пример. Разложить в ряд Фурье периодическую функцию f(x)
с периодом 2тс, заданную в промежутке (—тс; тс) уравнением
f(x) = Z
Решение. График этой функции изображен на рис. 190
[в промежутке (—тс; тс) сплошной линией, вне этого промежутка —
* Точнее, величине ординаты средней точки скачка функции.
388
пунктиром]. Эта функция удовлетворяет условиям теоремы Ди-
рихле [она непрерывна в промежутке (^-л; л) и имеет в этом
промежутке только один минимум]. Вычисляем для этой функции
коэффициенты Фурье. По формуле (24), учитывая, что х2— чет-
ная функция, находим
ао = -^ f(x) dx—^ x3dx = ^ хМх = -|-гЛ,
— п —к 0 '
по формулам (25) й (26) получаем (см. пример 6 в § 133):
Ьт — — \ х2 sin тхdx = 0;
1 С о , 1 4л
ат — — \ х cos тх dx = — • — cos т~
я j я т-
или ат = cos т~. По этой формуле находим:
4 4 4 „ 4
fli = pCOS-=—-р; = —
4 о 4 4 4
«3 — Va COS Зя--— Ct^ = -т5 : Л;;-77 : ...
о и ’ 4“ ’ 0“7
Заменив в равенстве (23) /(х) и коэффициенты ай, alt blt
bit ... их значениями, получаем
2-^
, 3 4 .4 _ 4 о.4 .
. х2 — --р cos х -]- cos 2х — cos Зх -j- cos 4x —
— p cos 5x-}-...,
или
а я2 ./cosx cos2x , cos3x cos4x . cos5x \ /T.
A~T-4^ + ~P-------------------------t1’
Это равенство справедливо при любом х из промежутка (—л; л).
§ 137. РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ
Если f (х) — четная функция, то произведение f(x)cosmx,
где т— любое целое число, тоже будет четной функцией, а произ-
ведение /(x)sinmx—нечетной функцией [см. формулы (4) и (5)],
так как
f (— х) cos т (— х) — f (х) cos тх\
[ (— х) sin т (— x)= f (х) (— sin тх) = — f (х) sin тх.
В этом случае [когда fix) — четная функция] на основании
формул (6) и (7) из § 133 для коэффициентов Фурье получаем
38D
следующие выражения:
fl0 — ( f (х) dx = -^ • 2 / (x)dx, т. е.
— тс О
f (*) dx; (24 ч)
о
тс
ат — \ f (х) cos тх dx", (25ч)
о
/ (х) sin/nxdx = 0.' (26ч)
Следовательно, четная функция разлагается в ряд Фурье по ко-
синусам:
f (х) = -j1 -J- aj cos х -j- a-2 cos 2x -ф- a3 cos 3x -j-... (23ч)
В качестве примера можно привести четную функцию х2,
рассмотренную в предыдущем параграфе.
Если же f (х) — нечетная функция, то произведение f (х) cos тх
тоже будет нечетной функцией:
[/ (— х) cos т (— х)] = I— f (х)] cos тх — — f (х) cos тх,
а произведение /(—x)sin?nx — четной функцией, так как
f (— х) sin т (— х) = [— / (х)] • (— sin тх) = f (х) sin тх.
Вследствие этого для нечетной функции получим:
йо = -^ /(x)dx = 0; (24н)
— ТС
ТС
ат — -i- f (х) cos тх dx — 0; (25н)
— тс
тс тс
= f (х) shiiiixdx = ^ • 2 f (х) sinmxdx, т. e.
— к -0
тс
bm = \ f (х) sin тх dx', (26н)
о
f (х) = ф sin х -ф- b-i sin 2х -f- sin Зх -I-... (23н)
§ 138. ПРИМЕРЫ НА РАЗЛОЖЕНИЕ ФУНКЦИИ В РЯДЫ ФУРЬЕ
Пример 1. Разложить в ряд Фурье функцию /(х), график
которой изображен па рис. 191.
Решение. В промежутке (—it; it) график функции изобра-
жен сплошной линией, вне этого промежутка — пунктиром; по
390
графику видно, что / (х)— четная непрерывная функция, удовлет-
воряющая условиям Дирихле. Эта функция разлагается в ряд
Фурье по косинусам. Для вычисления коэффициентов а0, аь
а.2, .... достаточно иметь аналитическое выражение функции в про-
межутке (0; -). В этом промежутке она изображается отрезком
прямой линии
£ + т=1>
х it I i
"2
откуда
По формулам (24ч) и (25ч) получаем:
— x cos mx dx =
\ f (х) dx
и
9 С 9
ат = — \ / (х) cos тх dx = --
IT 1 1 v J IT
x cos mx dx.
Пользуясь формулой (14), найдем:
391
или
4Z) ,
am = —^(cosmz—1).
По этой формуле при m = 2k, где k=\, 2, 3, ..., находим
а,п — а-п< : т? (cos — 1)= 0> т- е- «г = «4 = «с =... = °-
При т—1, 3, 5, ... получаем:
4Ь , .. 8Ь
«> = -p7p(cos*--l) = ir-,;
4b . о 86
Из — — (COS Зтс— 1)=зГ^5;
4b , г ., 86
Щ =i (COS 5it—1) = 557^5, ...
Следовательно, для данной функции ряд Фурье имеет вид
г , , 86/cos а । cos Зх . cos5.t , \ /11ч
нх)=^(—+-3»—Ь-б,- , ап
На рис. 192 изображены ^для простоты принято 1,6 «а 1)
первая гармоника z/i = cos.r, третья гармоника у3 — cos Зх
и ломаная линия — график данной функции). На рис. 193 изоб-
ражены кривая, представляющая сумму двух гармоник, и лома-
ная линия. Эти рисунки наглядно показывают, как с увеличе-
нием числа складываемых гармоник кривая, изображающая их
392
сумму, приближается к ломаной линии — графику рассматриваемой
функции.
Пример 2. Разложить в ряд Фурье функцию f(x), график
которой изображен на рис. 194.
Решение. Из рисунка видно, что f(x)— нечетная непре-
рывная функция; она разлагается в ряд Фурье по синусам (23н).
На отрезке [0; -] график этой функции составляется из отрезков
двух прямых:
1) у = х на отрезке ^0; yj;
2) у — — a’-L~ на отрезке .
Следовательно, /(.г) определяется следующим образом:
/(Х) =
X при 0 .
х-|-л при
По формуле (2бн) находим [см. (6) § 109]
Ь,п == \f (х) sin тх dx = ~
и
2 I
/(х) sin inxdx-]- ( f(x) sinmxrfx ,
О
2
пли
393
Последовательно интегрируя по частям, получаем:
(б)
2
ТС
/ л . \ «1 1 I
— I— ) cos -у — sin тх |
2
пли
С, ... , л шт: , 1 • тг. . .
\(—л'4- к) sin mxdx — ^— cos -к- -4 ;>sin^- . (в)
J ' 17 2ш 2 1 ill- 2 4 '
к
Заменив в равенстве (а) определенные интегралы их найденными
выражениями (б) и (в), находим
По этой формуле, давая т последовательно значения 1, 2, 3,
получаем:
. 4 . л 4 . 4 . 2л „
01 = т.,— sin-A- = v«—; т — -а—sin-s- = 0;
1 - • л 2 1 - • л ’ 2-- л 2
I 4 . Зл 4 , п , 4
63 = 3^siiiy = -^; й4 = 0; =
Следовательно,
. , , 4. 4.0,4.- 4 . _ ,
/ (х) — ТЛ, Sin X — л:, Sin Зх н- тл,— sin 5х — — sin IX 4- ...,
' ' 7 1 - • п 3--Л 'П-.л 7 - т: 1 ’
или
г / . 4 /sin х sin 3.v i sin 5.v sin 7x . \ /тттч
/W=vh--------3^- + ^-—(HI)
394
Замечание. Выше мы рассматривали функции, непрерыв-
ные внутри промежутка: (—тс; тс) и имеющие равные значения
на границах этого промежутка: / (—тс) = f (тс) = 0. Согласно тео-
реме Дирихле, ряды Фурье таких функции сходятся и сумма
нх в любой точке этого промежутка равна значению функции f (х)
в этой точке, т. е. равенства (I), (II) и (III) справедливы при
любом х, удовлетворяющем условиям —-</<тс.
В электротехнике и радиотехнике нередко встречаются перио-
дические функции, имеющие разрывы первого рода внутри про-
межутка (—тс; тс) и на границах его. Рассмотрим примеры.
Пример 3. Разложить в ряд Фурье периодическую функцию
[(х) с периодом 2тс, изображенную на рис. 195.
Рис. 195
Решение. В промежутке (—тс; 0) эта функция изображается
отрезком прямой у = —а в промежутке (0; тс) — отрезком пря-
мой у — ~. В точке х = 0 она имеет разрыв и делает скачок,
переходя от значения, равного —, к значению, равному
Из рисунка видно, что. f (х) — нечетная функция; разлагается
она в ряд Фурье по синусам (23н), в промежутке (0; тс) ана-
литически выражается уравнением у — f (х) = . По форму-
ле (26н) получаем
л л п
°C 2 С те 1 1
bm = — \ f (х) sin тх dx — — \ -р sin тхdx — — cos тхI,
л ) ' ' 7 ~ .' 4 2tll |
о и о
или
&«= —2^г (cos ттс—1),
откуда
Ь\ ——уЦ (cos тс — 1) = 1; 6-2 = — (cos 2тс — 1) = 0;
=— уЦ (COS Зтс—!) = --; &4 = 0;
&6 = 0; 1ъ = \-, ...
395
Следовательно, для этой функции ряд Фурье имеет вид
f (х) — sin х у sin Зх 4- -у sin 5.v у sin 7х-\~...
Сумма этого ряда равна —у в интервале (— л; 0) и у в ин-
тервале (0; к). В точке разрыва (x = 0) внутри промежутка (—к; к)
Т Т
и на границах его сумма ряда равна ----------— 0-
На рис. 196 изображены: I) первая гармоника этого разло-
жения у — sin х; II) сумма первой п третьей гармоник; III) сум-
ма первой, третьей и пятой гармоник. Этот рисунок показывает,
как с увеличением числа слагаемых (гармоник) кривая, изобра-
жающая их сумму, подходит к разрывной линии — графику дан-
ной функции.
Пример 4. Разложить в ряд Фурье периодическую функцию,
которая в промежутке (—к; л) задается уравнением у — х.
39G
Решение. f(x) — x (рис. 197) — нечетная функция. Она раз-
лагается в ряд Фурье по синусам. По формуле (26н) находим
°C 9 Г t ] 1 (•
bm = — \ х sin тх dx — -- — — cosтх\ -I— \ cos тх dx =
л j L т I 1 т j
6 о о
2 Г 1 I 1
= —------(tccos/?2~—OcosO)4—ssnimx =
п inv J 1 mr I
‘ - Q
Отсюда следует:
2 ° 2
&i =----p cos к = 2; Ы = — -^-cos2k = — — *
9 9 9 9 9
fe3 = —4-cos37t = -5-; &i = — rrCOs4Tt = — & =_r.
о о 4 4 ’ о ’ '
Следовательно,
। 2 2 2 2
/(х) = у sinx— -у sin 2х -ф- у sin Зх — у sin4x-|-y sinox— ... ,
или
/(х) = 2 ^s in х—у sin 2х-|-у sin Зх — у sin 4x-f~y sin 5х— .
Это равенство справедливо при любом х из интервала (—тс; тс);
f (—4- f (тс)
при х — — г. и х — - сумма этого ряда равна -------- =
Пример 5. Разложить в ряд Фурье периодическую функцию
с периодом 2я, заданную следующим образом:
ч (0 при —тс<7x55 0,
[М — 1
( X при 0-Сх<7~.
Решение. На рис. 198 график этой функции в промежутке
(—тс; тс) изображен сплошной линией, вне этого промежутка —
пунктиром. В ряде Фурье она разлагается по формуле (23).
397
Находим коэффициенты Фурье этой функции:
к 0 тс
T = i § fMdx = ~[^f(x)dx + § f(x)dx] =
— it — к О
+ § xdA: = 2^ [° * +1 X'|o] = T ’
— к О
, О к
ат = ~ [ 0‘cos тх dx -ф- х cos тх dx] =
— it О и dv
1 Г 1 1 1К1
= — — (л sin пк — 0 • sin 0) -I—cos тх ,
7. [«• ' 1 «!' |oj
или
a,„ = ^(cosmrc—1).
Отсюда следует
Oi = (cos 1 • л — 1) = — ; а2 — 2^ (cos 2г. — 1) — 0;
1 9 1
03 = 3^(008 371—1) = — -^; a4 = ^(cos4n — 1) = 0;
т. е.
, 1
Ьт = — - cos тг..
Отсюда следует
. 1 it 1 О 1
01 =---р cos 77=1; bi = —гг cos 2л = — у;
, 1 о 1
М3 --7Г COS 3~ -7Г ’
о О
, 1 3 1 , 1 , 1.1
64 = —^COS4k = —т; 6в = у; Ьй = — -g-; й, = у; ...
-------- b- ь
I 4 Так как С'х — 0, то d'C = 0 dx\ jj 0 • dx = С | —С — С — 0 при любых
а
а и Ь.
398
Подставив найденные значения alt ait bt, Ьг, ...в фор-
мулу (23), получаем
,. , л 2 cos х . 1 • п 2 cos Зх ।
= 4- —-~p--Hsin* —-2 sin2x——Ь
, sin Зх sin 4х 2 cos 5х । sin 5х sin 6х 2 cos 7х ,
' 3 4 + о (Г~ 7= ~Г ’
или ,, , ~ 2 /созх , созЗх । cos5x . cos lx , \ , л [ р ' [ за + 52 4- г + ••) + , /sin х sin 2х , sin Зх sin 4х , sin 5х ‘I Г \ , 1 2 । 3 4 । 5 ’ • J •
Это при равенство справедливо при любом х из интервала (—я х = — л и х = " сумма ряда равна
/(-*)+/(*) _О+2 _Л
2 — 2 —2 '
ЗАДАЧИ И УПРАЖНЕНИЯ
1. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Координаты точки на прямой (к § 1,2)
1. Построить точки: Л (5), В(—3), С (2 yj, —3-^j.
2*. Построить точки, координаты которых удовлетворяют урав-
нениям:
1) 2(х—2) = х-’г Н 2) х3 —4 = 0;
3) х3Ц-x — 6 = 0; 4) х3-|-2х4-5 = 0.
3. Даны точки: А(—10), В(—4), С(—1), 0(2) /< (5), М (8).
Найти величину: 1) АВ; 2) ВД; 3) ОВ; 4) Л4С; 5) В/?; 6) ВС.
4. При условиях предыдущей задачи найти длину отрезков:
1) ДО; 2) ВС; 3) СМ.
5*. Найти координаты точек, симметричных точкам А (-[-3) и
В(—4): 1) относительно начала координат; 2) относительно точки
С(-1).
6. Построить точки: А (У 2), В(—У 3) и С(|/5).
7. Найти координаты точек, симметричных точкам Д(—У7)
п В (У11) относительно начала координат.
8. Показать, что точки В(зУ2) и С(—У2) симметричны
относительно точки М (У 2).
* К упражнениям и задачам, номера которых отмечены звездочкой,
даны подробные указания в разделе „Ответы и указания".
309
Координаты точки на плоскости (к § 3)
9. Построить треугольник по координатам его вершин:
Л (—3; —4), В (1;-3), С (4; —1).
10. Построить четырехугольник по координатам вершин:
А (—6; 0), В (—2; 4), С (4; 0), 0(0; —5).
11. Дана точка А (4; 3). Найти точку, симметричную дан-
ной: 1) относительно оси Ох; 2) относительно оси Оу, 3) относи-
тельно начала координат.
12. Дан отрезок координатами своих концов А (—4; 0), В (0; 5).
Найти концы отрезка, симметричного данному: 1) относительно
оси Ох; 2) относительно оси Оу, 3) относительно начала коор-
динат.
13. Дан треугольник АВС координатами своих вершин А (6; 0),
В (4; 4), С (0; 6). Найти вершины треугольника, симметричного
данному: 1) относительно оси Ох; 2) относительно оси Оу, 3) от-
носительно начала координат.
, 14*. Найти точку, лежащую па биссектрисе координатного
угла, если: 1) абсцисса ее равна 4; 2) ордината ее равна —5.
15*. Дана точка Д(1; 4). Найти точку, симметричную данной
относительно биссектрисы координатного угла.
16*. Дан отрезок АВ координатами своих концов Л (1; 3),
В(3;7). Найти координаты концов отрезка, симметричного дан-
ному относительно биссектрисы координатного угла.
17. Даны точки С(—3; 2) и D (4; —2). Найти проекции на
оси координат: ^направленного отрезка CD; 2) направленного
отрезка DC.
18. Даны точки Д(—4; —2), В(3; 4), С (5; —5). Найти сум-
мы проекций отрезков А В, ВС, С А на осп координат.
Расстояние между двумя точками (к § 4)
19. Найти расстояние между точками:'!) А (1; 4) и В (4; 8);
2)С(--1; 4) и £>(11; 9); 3)Е(3;—2) и £(11; 4).
20. Дано: np.v CD =—3; пр,, CD = 5. Найти длину отрез-
ка CD.
21. Найти периметр треугольника, вершинами которого явля-
ются точки Л(—3; 1), В(1; —2) и С (4; —6).
22*. Показать, что треугольник, вершинами которого являются
точки А (1; 1), В(1; 4) и С (2,5; 2,5), прямоугольный и равно-
бедренный.
23. Показать, что треугольник, вершинами которого являют-
ся точки А (—1; 1), В(1; 3) и С(—КЗ; З-^УЗ), равносторонний.
24. Сторона равностороннего треугольника равна а. Найти
координаты вершин этого треугольника, если одна из них сов-
падает с началом координат и основание лежит на оси Сх.
400
25. Абсциссы концов диагонали квадрата, совпадающей с
биссектрисой координатного угла, равны 2 и 6. Найти коорди-
наты всех вершин этого квадрата.
. 26*. Найти ординату точки, равноудаленной от точек А (1; 3)
и В (4; 6), если абсцисса ее равна —1-3. '
27. Найти абсциссу точки, равноудаленной от двух дан-
ных точек М(—4; 2) и N (2; — 6), если ордината ее равна — 2.
28. На оси Ох найти точку, равноудаленную от двух дан-
ных точек М (—2; 4) и /< (3; —1).
29. На оси Оу найти точку, равноудаленную от точек А (—5; 2)
и В(3; —4). v
30*. На биссектрисе координатного угла найти точку, равно-
удаленную от точек А (4; —6) и В (8; —2).
31. Показать, что точки М (8; 0), К. (0; —6), Р (7; —7) лежат
на окружности, центром которой является точка С (4; —3). Че-
му равен радиус этой окружности?
32*. Даны три точки: А (0; —6), В (7; —7) и С (1;. 1). Найти
координаты точки, равноудаленной от них.
33. Найти центе окружности, проходящей через точки
Л (0; 0), В (4; 2), С (6; 4).
34. Даны вершины треугольника: А (2; 1), В(—3; 2), С(—1; 1).
Найти центр и радиус описанной окружности.
Деление отрезка в данном отношении ( к § 5 )
35. Найти координаты . точки, делящей отрезок, ограничен-
ный точками А(—2; 3) и В(4; 6): 1) в отношении 2:3 (считая
от точки А к точке В);- 2) в отношении 1 :3 (считая от точки В
к точке А); 3) пополам.
36*. Даны координаты вершин треугольника: А (2; 1),
В(—2; 3), С (0; 3). Найти длины медиан этого треугольника.
37. Даны вершины треугольника: А(—5; 4), В (0; 6);
С (2;—4). Найти центр тяжести этого треугольника.
38. Даны две вершины треугольника А (3; 6), В (—6; 9) и
центр тяжести его М (—1; 10). Найти третью вершину.
39*. Точки AI (—3; —3), А (2; 5) и Р (3; 0) — середины сто-
рон треугольника. Найти его вершины.
40. А(—4; 2) к В(0; 6) — вершины параллелограмма; М (2; 4)
— точка пересечения его диагоналей. Найти две другие вершины
параллелограмма. .
41. Точки А(—3; —2), В (0; 3), С (5; —4) — вершины парал-
лелограмма. Найти четвертую вершину, если она лежит против
вершины В.
42. Точки А(—3; —5), В (Г, 3) — концы отрезка АВ. Найти
длину отрезка, соединяющего середину данного отрезка с нача-
лом координат.
401
43. Найти точки, в которых отрезок между точками А (—6; 2)
и В (4; —4) делится на три равные части.
44. Точки А(—2; 0) и В (4; 6) — концы отрезка АВ. Найти
точки С, D и Е, в которых отрезок АВ делится па четыре рав-
ные части.
45*. Найти точку, находящуюся на расстоянии 5 единиц мас-
штаба от осп Ох и от данной точки А (2; 2).
46. Найти точку, находящуюся на расстоянии 5 единиц мас-
штаба от оси Оу и от данной точки Л4(2; 2).
47. Построить точки, абсциссы которых равны —3; —2; —1;
0; 1; 2; 3, а ординаты определяются из уравнений: 1) у=х-2;
2) у = х\
48. Построить точки, координаты которых удовлетворяют
уравнениям:
1) Зх4~2у-12 = 0 и x-y-f-l =0;
2) xi 4- у- = 25 и у — х -j- 1;
3) х2 Уг — 4 и х -j- у — 6 = 0.
Графическое изображение функциональной зависимости (к § 9)
49. Построить графики функций первой степени:
1) у — х\ 2) у —— 2х; 3) г/ = 2х—j-4; 4) у = ~х— 2; 5) у =
= — т?-х + 4; 6) 2x4-3?/—12 = 0; 7) 4х —Зу —9 = 0.
50. Построить графики функций второй степени:
1) у = х- — 4; 2) у = х'--|-4; 3) у = х‘24-х— 2; 4) у =— х2;
5) у = —х24-2x4-3; 6) у = —х24-4х; 7) 2х2 — у — 3 = 0;
8) х2 — Зу — 9 = 0. '
51. Построить графики функций третьей степени: 1) у = х:|;
‘2) у — х3— 4х; 3) у =— х:1-'-2х2; 4) у—х3— х2-|-х4-2.
52. Построить линии, соответствующие уравнениям:
0 У = 2) (х24-4)у = 4х; 3) (1+х2)у = 2х = 0.
53. Построить графики функций:
1) ху = 2; 2).ху =— 4; 3) ху— 2у — 4 = 0; 4) уг = х3.
Уравнение прямой с угловым коэффициентом (к § 11 —13)
54. Построить прямую линию по данному ее уравнению:
1)* у = 2х — 3; 2)* у = —3x4-2; 3) у = -|х; 4) у = — х;
5) у = — х — 2; 6) х = 4; 7) у = —2.
55. Изобразить фигуру, ограниченную прямыми: у = х-}-2;
у = — ~ х-j- 2; х = 4.
402
' 2
56. Изобразить фигуру, ограниченную прямыми: i/ = -^-x-|-2;
У=^х — 2; у = —х—2; у = —х + 2.
57. Изобразить фигуру, ограниченную прямыми:
£/ = -|-х + 6; // = —уХ-|-8; у = 0;у = 4.
58*. Написать уравнение прямой, проходящей через начало
координат, если она с положительным направлением оси Сх
образует угол: 1) 30°; 2) 45°; 3) 60°; 4) 135°; 5) 150°; 6) 0°; 7) 90<
59. Сторона квадрата равна 6 единицам. Точка пересечения
его диагоналей принята за начало координат. Написать уравне-
ния сторон и диагоналей этого квадрата, если стороны его
параллельны осям координат.
60. Написать уравнение прямой, отсекающей на осп Оу
отрезок, равный 4 единицам, и образующей с положительным
направлением оси Ох угол: 1) 0°; 2) 30°; 3) 45°; 4) 120°; 5) 135°.
61. Написать уравнения сторон равностороннего треугольника,
если середина его основания совпадает с началом координат,
а противоположная вершина находится в точке (0; 4).
62. Написать уравнения сторон треугольника, если вершины
его находятся в точках (0; 0), (—4; 0); (0; 5).
63. На прямой у = 2%4-1 найти точки, абсциссы которых
соответственно равны: 1) —3; 2) 0; 3) 4; 4) 7,5.
64*. Найти расстояние от начала координат до той точки
прямой у = — 2х— 2, ордината которой равна -|-4.
65. Найти длину отрезка прямой ?/= Зх —1, ограниченного
точками, абсциссы которых соответственно равны —2 и -|-3.
66. Проходит ли прямая у = 3х — 5 через точки: 1) (1; —2);
2) (3; 4); 3) (-3; 1); 4) (0; -5); 5) (— 1; 3)?
67*. Написать уравнение прямой, проходящей через начало
координат и через точку (5; —2).
68. Написать уравнение прямой, проходящей через начало
координат и через точку (4; 6).
69*. Написать уравнение прямой, проходящей через точку
(3; 5) и наклоненной к оси Ох под углом 45°.
70. Написать уравнение прямой, проходящей через точку
(— 2; 3) п образующей с положительным направлением оси Ох
угол 135°.
71. Написать уравнение прямой, проходящей через точку
(Р 3; 5) и наклоненной к оси Ох под углом 60°.
72. Написать уравнения сторон треугольника, если две из
них проходят через начало координат и образуют с положитель-
ным направлением оси Ох соответственно углы в 30° и 120°,
а третья параллельна осп Ох и отстоит от нее на расстоянии
5 единиц.
403
73. Написать уравнение прямой, проходящей через две дан-
ные точки: (2; 7), (0; 3).
74. Составить уравнение прямой, проходящей через точки
(2; 1), (1; 3).
Уравнение прямой в отрезках (к § 14)
75. Написать уравнение прямой, отсекающей от осей коорди-
нат отрезки -j-2 и 4-5.
76. Диагонали ромба равны 6 и 8 единицам. Написать уравнения
сторон и диагоналей, приняв за оси координат диагонали ромба.
77*. Написать уравнение прямой, отсекающей на оСи Ох
отрезок 4-4 и проходящей через точку (2; —4).
78. Написать уравнение прямой, отсекающей на оси Оу отре-
зок — 6 и проходящей через точку (2; — 3).
79. Написать уравнение прямой, проходящей через точку
(6; —2) и отсекающей на положительных полуосях равные
отрезки.
80. Написать уравнение прямой, проходящей через точку
(6; — 2) и образующей вместе с отрезками, отсекаемыми этой
прямой на положительных полуосях, треугольник, площадь кото-
рого равна 1 кв. ед.
81. Написать уравнения сторон треугольника, две из которых
проходят через точку (5; 4) и параллельны осям координат,
а третья проходит через точку (2; 1) и отсекает от положитель-
ных полуосей отрезки, один из которых в два раза больше
другого.
Общее уравнение прямой (к § 15, 16)
82. Указать особенности в расположении прямых относительно
осей координат: 1) Зх 4_ 4;/= 0; 2) 5х — 7 = 0; 3) Зу^-8 — 0;
4) Зх = 0; 5) 7y = Q.
83. Преобразовать нижеследующие уравнения прямой к виду
уравнения с угловым коэффициентом:
1) Зх — 4//— 8 = 0; 2) 5х—4у = 0;
3) x4-2i/-7 = 0; 4) ^4-|=1.
84. Преобразовать нижеследующие уравнения прямой к виду
уравнения прямой в отрезках:
1) 3x4-4// — 12 = 0; 2) 5х —2г/—10 = 0;
3) 2х4-3//4-9 = 0; 4) 7х — 2//Д-8 = 0; 5) /д=5х —3;
6) у =— 4х'4-2.
85*. Построить прямые: 1) 2x4-3// 4- 6 = 0;
2) 5х4-2у—10 = 0; 3) 2х — у — 6 = 0.
86. Построить треугольник по данным уравнениям его сторон:
1) 2x4-3//—12 = 0; 2).2х — у— 4 = 0; 3) 7х4-2// = 0.
87. Даны прямая у= 4 х — 3 и точки А (6; —2), В (6; 2),
404
С(— 3; —5), £)(9; 3), Е (0; 4), Г(—3; —6). Не пользуясь
чертежом, указать те из них, которые: 1) лежат на данной
прямой; 2) лежат над этой прямой; 3) лежат ниже этой прямой.
88. Найти площадь треугольника, ограниченного осями ко-
ординат и прямой Зх-]-5у—15 = 0.
89. Дана прямая Ах-\-7у—11 = 0. При каком значении
коэффициента А эта прямая пройдет через точку (2; 1)?
90. Дано уравнение одной стороны ромба Зх-ф-бг/Д-15 = 0.
Написать уравнения трех других сторон, принимая за оси коор-
динат диагонали ромба.
91. Дана прямая AxJrBy— 8 = 0. При каких значениях
коэффициентов А и В она пройдет через точки (2; 1), (0; 4)?
92*. Координаты движущейся точки в зависимости от времени t
выражаются уравнениями x = 2t, y=3t-\-2. Написать уравнение
траектории движения этой точки.
93. Координаты движущейся точки в зависимости от времени t
выражены уравнениями x = 3t—1; у — 21 -j- 1. Написать уравне-
ние траектории.
Пучок прямых. Уравнение прямой, проходящей через две
точки. Угол между двумя прямыми. Условия параллельности
и перпендикулярности (к § 17—21)
94. Через точки пересечения прямой Зх-|-2у— 6 = 0 с осями
координат провести прямые, образующие с положительным на-
правлением оси Ох угол 45°.
95. Вычислить острый угол между прямыми:
7 ч
и = 2хД-4 1 п = ттх-4-3 I у—7х—4)
') __Д : 2) " . ; 3)
2)
96. Найти острый угол между прямыми:
1) 2х— 4у — 7 = 0 и Зх-|-2у-1- 7 = 0;
2) 4х— Зу-^б — О н 2х-|- у — 4 = 0;
3) 2х— ЗуД-7 = 0 и 4х— 6z/-j-12 = 0;
4) 2х —ЗуД-9 = 0 и Зх-|-2у — 8 = 0.
з
97*. Даны уравнения сторон треугольника: 1) у =— уХ-[-6;
2) у = 2хД-6; 3) у=х-\- 1. Найти внутренние углы треуголь-
ника.
98. Даны уравнения сторон треугольника:
1) х + у—4 = 0; 2) 4х —уД-4 = 0; 3) 5x-|-2i/+10 = 0.
Найти внутренние углы треугольника.
99*. Написать уравнение прямой, проходящей через точку
(—2; —4) и образующей с положительным направлением оси Ох
угол 60°.
100. Написать уравнения прямых, проходящих через точки
пересечения прямой 7x4- 2у—14 = 0 с осями координат и об-
405
разующпх с положительным направлением осп Ох угол <р =
= arctg(—-J).
101. Написать уравнение прямой, проходящей через точку
(—5; 2) и параллельной данной прямой у = — 2х3.
102. Написать уравнение перпендикуляра, опущенного из точ-
ки (—6; 4) на прямую y=^-x-j-5.
103. Написать уравнение прямой, проходящей через точку
9
(3; 2), зная, что она: 1) перпендикулярна прямой у ——yX-j-2;
2) параллельна прямой у = 2х— 3; 3) параллельна оси Ох\
4) параллельна оси Оу.
104*. Даны две точки: А (5; 2) и В (3; —2). Написать урав-
нение прямой, проходящей через эти точки.
105. Даны вершины треугольника: А (4; 6), В(—4; 0),
С(—1; —4). Написать: 1) уравнения сторон этого треугольника;
2) уравнение медианы стороны АВ.
106. Составить уравнения перпендикуляров, восставленных
к прямой у — Зх— 6 в точках пересечения ее с осями координат.
Пересечение двух прямых (к § 22)
107. Найти координаты точки пересечения прямых:
1) 2х— у — 8 = 0 и 4x-f-3z/4“ 4 = 0;
2) x-|~Z/4~2 = 0 и 2х — Зу—J- 14 = 0;
3) Зх + 2у4-12 = 0 и 6х4-4у—15 = 0.
108. Найти расстояние от начала координат до точки пересе-
чения прямых 2х — у4- 14 = 0 и Зх4~у4_ 16 = 0.
109. Через , точку пересечения прямых 2х — Зу-f-l = 0,
Зх — 2у — 6 = 0 провести прямую, параллельную прямой —
4-4 = 1.
ПО. Через точку пересечения прямых у = 2х—10, 2х-'-Зу—
— 5 = 0 провести прямую, перпендикулярную прямой 5х — 2у 4-
4-10 = 0.
111. Даны уравнения сторон треугольника: х — у = 0, 2х--
4- Зу — 5 = 0, х4~ 2у 4-3 = 0. Найти вершины этого треугольника.
112*. Даны вершины четырехугольника: А (2; 2), В (5; 1),
С (3; 6), D (0; 3). Найти точку пересечения его диагоналей.
113. Даны вершины четырехугольника: /< (—9; 0), L(—3; 6),
М (3; 4), N (6; —3). Найти точку пересечения диагоналей 1(М
п LN и вычислить угол между ними.
114. Даны вершины треугольника: Л (0; 4), В (8; 8), С (4; 0).
Найти внутренние углы треугольника.
115. К прямой у = 2х— 5 восставить перпендикуляр в точке,
.абсцисса которой равна 4.
406
116. Даны вершины треугольника: А(2; 1), В(0; 7), С(—4; —1).
Найти уравнения медиан и точку их пересечения.
117*. Через точку А (6; 6) провести прямые, составляющие
с прямой 5х— 4у— 20 = 0 угол 45°.
118. Через точку (—4; —6) провести прямые, составляющие
с прямой 2х Зу — 9 = 0 угол 45°.
119. Через данную точку (2; 6) провести прямые, образующие
с прямой у = — х — 3 угол ? = arctg у.
2
120. Дана прямая у = -^х-\-4. Найти основание перпендику-
ляра, опущенного на данную прямую из начала координат.
121. Найти длину перпендикуляра, опущенного из точки (8; 4)
на прямую Зх-44у — 10 = 0.
122. Вершиной треугольника служит точка (5; —3), а осно-
ванием— отрезок, соединяющий точки (0; —1), (3; 3). Найти
высоту треугольника и его площадь.
123* . Найти расстояние между параллельными прямыми
Зх -|- 4у — 15 = 0, Зх 4- 4у 4- 5 = 0.
124. Найти расстояние между параллельными прямыми 5x4-
4-12г/—13 = 0, 5x4- 12т/ — 52 = 0.
125. Даны уравнения двух сторон параллелограмма х4~2у4-
4-1—0, 2х -1-у — 3 = 0 и точка пересечения его диагоналей
М (1; 2). Наиисать уравнения двух других сторон. .
Смешанные задачи к гл. III
126. Даны вершины треугольника: Я (8; 12), В(—8; 0),
С (—2; —8). Написать: 1) уравнение биссектрисы угла В;
2) уравнение перпендикуляра, опущенного из вершины В на
противоположную сторону.
127. Даны уравнения сторон треугольника: 5х — Зу—15 = 0;
х-{-5у — 3 = 0, Зх-4 у 4-5 = 0. Написать уравнения всех его
высот.
128. К прямой ^--4^=1 в середине отрезка, заключенного
между осями координат, восставить перпендикуляр.
129. Даны вершины треугольника: Д(—9; 0), В (0; —3),
С (5; 2), Найти координаты точки пересечения перпендикуляров,
восставленных к сторонам в их серединах.
130. Найти координаты вершин треугольника, образованного
прямой у = —2x4-8 и двумя прямыми, проведенными через
начало координат под углом 45° к данной прямой.
131. Даны координаты концов одной диагонали квадрата:
А(—2; 2), С (2; 8). Составить уравнения диагоналей и сторон
квадрата.
132*. Концы большей диагонали ромба находятся на прямой
у — — 2х — 3, причем абсциссы их равны: Xj =— 2, ха = — 6.
407
Составить уравнения сторон ромба, если острый угол его <f =
= 2 arctg
133. Даны уравнения сторон треугольника: 5х— Зу—15 = 0,
л'Д-5у — 3 = 0, Зх-|-у-f- 5 = 0. Написать уравнения прямых,
проходящих через вершины этого треугольника параллельно
противоположным сторонам.
134. Даны уравнения двух сторон параллелограмма х— у—
— 1=0, х—2у = 0 и точка пересечения его диагоналей (3; —1).
Написать уравнения двух других сторон.
135. Вычислить координаты вершин ромба, если известны:
уравнения двух его сторон 2х— 5у—1=0, 2х—5у — 34 = 0 и
уравнение одной диагонали х-\-Зу— 6 = 0.
136. Даны координаты середин сторон треугольника: К (1; 2),
' £(7; 4), Л4(3; —4). Написать уравнения сторон.
137. В параллелограмме ABCD даны: уравнение стороны АВ
Зх-1-4у—12 = 0, уравнение стороны AD 5х—12у — 6 = 0 и
середина стороны ВС точка Л1 (— 2; . Написать уравнения
двух других сторон.
138*. Дана прямая Зх — 4у— 6 = 0 и точка А (2; 3). Найти
точку Ai, симметричную точке А относительно данной прямой.
139*. Луч света, выйдя из точки Л (2; 3), отражается от оси
Ох и попадает в точку В (5; 8). Найти уравнения луча падающего
и отраженного.
140. Луч света, выйдя из точки Л4 (1; 5), отражается от пря-
мой у — х и попадает в точку В (5; 9). Составить уравнения
луча падающего и отраженного.
Геометрические места точек (к.§ 24)
141. Составить уравнение геометрического места точек, равно-
удаленных от точек А (4; 2), В (8; 6).
142. Составить уравнение геометрического места точек, равно-
удаленных от начала координат и точки А (а; 2а).
143. Составить уравнение геометрического места точек, зная,
что расстояния их от точки А (8; 0) в два раза больше их рас-
стояний от точки В (2; 0).
144. Составить уравнение геометрического места точек, равно-
удаленных от точки В (0; 2) и оси Ох, и построить график.
145*. Найти уравнение геометрического места точек, сумма
квадратов расстояний которых от двух данных точек Л (0; 4) и
В (0; —4) — величина постоянная, равная 64.
146. Составить уравнение геометрического места точек, раз-
ность квадратов расстояний которых от начала координат и от
точки В (а; —За) — величина постоянная, равная 4аг.
147. Написать уравнение геометрического места точек, равно-
удаленных от прямой z/ = 2 и точки В (0; 4).
408
148*. Два стержня вращаются вокруг двух неподвижных
точек Л(—а; 0) и В (а; 0), оставаясь все время перпендикуляр-
ными друг другу. Написать уравнение геометрического места
точек пересечения этих стержней.
\
Окружность (к § 25, 26)
149. Составить уравнение окружности, зная, что: а) центр
находится в начале координат и диаметр равен 4; б) центр
находится в точке (0; 3) и диаметр равен 7; в) центр находится
в точке ^2-^-; 0j и диаметр равен 5; г) центр находится в точке
—3-^-; + и диаметр равен 4-^-.
150*. Написать уравнение окружности, имеющей: а) центр
в точке (0; 0) и проходящей через точку (]^2; 1); б) центр
в точке (—1; ,2) и проходящей через точку (3; 5); в) центр
в точке (—5; 12) и проходящей через точку (0; 0); г) центр
в точке (0; —2) и проходящей через точку (—3; 2).
151. Даны координаты концов одного из диаметров окружно-
сти: Л(—3; 1), В (1; —5). Написать уравнение этой окружности.
152. Из данных точек Л(—3; 0), В (5; 0), С (4; 2), 0(2; 7Ц
Е (—4; 6), F (3; —1) и Р(—2; 3) указать те, которые: 1) нахо-
дятся на окружности (xf- l)2-)- (у — 2)2 = 25; 2) лежат вне окруж-
ности; 3) находятся внутри окружности.
153*. Привести к нормальному виду уравнения окружности:
а) .г'3Н- 4х-j- 2//— 4 = 0; б) у1—8х— 4у— 5 = 0; в) 2х3Д-
-р//2-Ц5л; —Зу-'г2 = 0; г) х! + if = 2ах- д) 4ЦД- 4tf — 25 = 0;
е) 2х!-г2у2-7у = 0.
154. Центр окружности находится в точке С (0; 3) и окруж-
ность пересекает прямую 2хЦ-Зу4~6 = 0 в точке, абсцисса кото-
рой равна —3. Написать уравнение этой окружности.
155. Диаметром окружности является отрезок прямой 2х-|-
-1- 5у—10 = 0, заключенный между осями координат. Написать
уравнение окружности.
156. Окружность касается положительных полуосей координат
па расстоянии а единиц от начала координат. Написать уравне-
ние окружности.
157. Составить уравнение окружности, касающейся оси Оу
в начале координат и пересекающей ось Ох в точке (—8; 0).
158. Составить уравнение окружности, касающейся оси Ох
в начале координат и проходящей через точку (0; 6).
159. Составить уравнение окружности, касающейся обеих осей
координат и проходящей через точку М (2; 4).
160. Составить уравнение окружности, касающейся обеих
осей координат и проходящей через точку (—6; —3).
161. Составить уравнение окружности, проходящей через
409
точки А(—1; —3) п В (3; 5), зная, что центр ее находится на
оси Ох.
162. Составить уравнение окружности, проходящей через
точки А (2; 5) и В (3; 2), зная, что центр ее лежит на оси Оу.
163. Составить уравнение окружности, проходящей через три
данные точки: А (9; 3), В(—3; 3), С (11; 1).
Реше н и е. Нормальное уравнение окружности имеет вид
(х-й)2-}-(//-/>)*= А
Так как окружность проходит через точки
координаты этих точек должны удовлетворять
Для определения параметров а, b и г получаем
(9 —й)2 + (3-6)2=г2;
(-3 —а)2 + (3-6)2=г2;
(11 — а)2-|-(1 - Ь)- = А
(1)
А, В и С, то
уравнению (1).
три уравнения:
Правые части уравнений равны, следовательно, должны быть
равны и левые части:
(9 — й)2 + (3 - bf = (— 3 — af + (3 — bf; 1 .
(9 - af -I- (3 = bf = (11 - a2) + (1 - bf. f
Решив полученную систему, найдем: a = 3, b =— 5. Подста-
вив значения а и b в одно из уравнений, определим
/=10.
Следовательно, искомым уравнением будет
(х - З)2 + (у 4- 5)2 = 100
НЛП
х~ -[- I/2 — 6х - р I Оу — 66 = 0.
164. Даны уравнения сторон треугольника: х-\-7у— 56 = 0;
х—Зу—{-14 = 0; 2х— у -[-8 = 0. Написать уравнение окружно-
сти, описанной около этого треугольника.
165. Найти точки, в которых оси координат пересекаются
окружностью: 1) (х -г З)2 if = 25; 2) (х—2)2 (у — 2)2 = 4.
166. Найти точки пересечения окружности л-2 —у2 = 25 с пря-
мой у = х~4 1.
167. Найти точки пересечения окружности х2-}- у2-г 2х— 4у —
— 20 = 0 и прямой х — у — 5 = 0.
168. Найти длину отрезка прямой z/ = x = 4, заключающегося
внутри окружности (х -!- I)2 4~ (У — 2)2 = 25.
169* . Написать уравнение окружности! имеющей центр в точке
(5; 4) и касающейся прямой 5х-[-2у-4 25 = 0.
170. Окружность касается прямой 5х—12у—24 = 0, центр
ее находится в точке (6; 7). Написать уравнение згой окружности.
410
171*. Написать уравнение касательной к окружности х" + if =
= 25 в точке (3; 4).
172. Написать уравнение касательной к окружности x--rif =
= 13 в точке, абсцисса которой равна 2 и ордината положительна.
Эллипс (к § 27 — 29)
173*. Построить все вершины и фокусы эллипса, если даны
его полуоси а и Ь.
174*. Найти координаты вершин и фокусов, а также эксцен-
триситет эллипса:
+ 2)9^+16^=144;
3) х3 + 4у2 = 4; 4) Зх2 + 4у3 — 12 = 0.
175*. Дан эллипс 16лД25z/3 = 400. Построить те точки
этого эллипса, абсциссы которых равны: 0, ±1, Пд 4.
176. Составить уравнение эллипса, зная, что: 1) малая полу-
ось 6=1, полуфокусное расстояние с = 2; 2) большая полуось
4
а= 10, эксцентриситет е = -^; 3) малая полуось 6 = 2, эксцентри-
ситет с=+ 4) полуфокусное расстояние с = 2, эксцентриситет
4
е = .
о
177*. ЭлЛипс проходит'через точку (У"б; Г), большая полу-
ось равна 3. Составить уравнение этого эллипса.
178*. Эллипс проходит через точку (—2]/"з; У 3), полу-
фокусное расстояние его с = 2. Составить уравнение этого эллипса.
179. Составить уравнение эллипса, проходящего через точки:
1) А (Уб; 1) и В(— УЗ; У1); 2) С (2; — У 2) и D(— Уб; 1).
180. Составить уравнение эллипса, зиая, что: 1) он проходит
через точки (—6; 2) и (0; —4); 2) фокусами его являются точки
э
(0; 4) и (0; —4) и эксцентриситет е = + .
181. Найти площадь четырехугольника, вершинами которого
являются фокусы эллипсов:
182. Составить уравнения прямых, проходящих через центр
окружности х--г:/2— 8х— 8у + 28 = 0 и фокусы эллипса 5х‘2+,
~ 9/у’ — 45 = 0, и найти угол между ними.
183*. Доказать, что для любой точки А (хр, гд), лежащей вне
эллипса -~2-1-ys = l, будет справедливо неравенство -А,-+ 1 ,
а для любой точки В (х3; у2), лежащей внутри эллипса, — не-
равенство
411
184. Определить положение точек А (2; 3), В (—3; 2), С (3; —3),
ZK— 2/2; Кб), Е(1; 2), Г(/Г5; 1) относительно эллипса
16^ 12 11
185*. Найти длину отрезка прямой у = -^х, заключающегося
внутри эллипса 164 25у2— 400 = 0.
,186. Найти длину отрезка прямой х— 2y — d, заключающегося
внутри эллипса ха-~}-2у- — 10.
187. Написать уравнение и найти длину диаметра эллипса
34 4-4 у’2— 48 = 0, если известно, что абсцисса одного из концов
его равна 2, ордината отрицательна.
188. Под каким углом видны из центра окружности х~-}-у- —
— 12х— 8t/-[- 43 = 0: 1) большая ось эллипса х24-4^=16;
2) малая ось этого эллипса?
189. В эллипсе х'--г2у-— 8 = 0 через нижний конец малой
осн и через правый фокус проведена хорда. Найти уравнение н
длину этой хорды.
190. Написать уравнения общих хорд кривых х2 Зу- — 16 = 0;
Зх24- у* = 16.
191. Какой геометрический образ соответствует уравнению:
1) ах — Ьу = с; 2) ах2-\-ау--\- bx-^-'by^d — 0 (а> 0);
3) 4-фг/2 = 0; 4) х2+# = — 4;
5)< + i = l; 6) £ + 4 = 1;
7) Ах^Ву- = С, когда Л>0, В>0, С>0;
8) Axi-\-Byi = 0, когда Л)>0, В^>0?
Гипербола (к § 30 — 35)
192. Построить вершины, фокусы и ветви гиперболы (послед-
ние от руки) по данным: 1) полуосям а и й; 2) фокусному рас-
стоянию 2с и мнимой полуоси &; 3) полуфокусному расстоянию с
и действительной полуоси а.
193. Найти вершины, фокусы, эксцентриситет н написать
уравнения асимптот гиперболы:
2)^-у2 = 1; 3) 24-3^=24,
194*. Составить уравнение гиперболы, зная, что: 1) дейст-
вительная ось 2а = 8, а эксцентриситет е = = 2) сумма полуосей
а -j-й = 7, полуфокусное расстояние с = 5; 3) действительная
полуось равна 3 и гипербола проходит через точку (9; —4);
4) гипербола проходит через точки А (4 КЗ; —4) и В (—8; 2Кб).
195. На гиперболе ~ — -у=1 взята точка, абсцисса которой
равна 8 и ордината положительна. Вычислить фокальные
радиусы-векторы этой точки (расстояния от точки до фокусов).
412
196. На гиперболе х2— Зу2=12 дана точка, абсцисса которой
равна 6 и ордината положительна. Написать уравнение окруж-
ности, проходящей через эту точку, зная, что: 1) центр находится
в начале координат; 2) центром является правый фокус гиперболы.
197*. Дана окружность — 2х—15 = 0. Составить
уравнение гиперболы, правый фокус которой находится в точке
пересечения данной окружности с осью Ох, зная, что: 1) эксцен-
триситет гиперболы равен 4; 2) асимптотами гиперболы являются
и
прямые у = ±-^-х. .
198. Дан эллипс 16.С -{- 2t>tf— 400 = 0. Найти уравнение
гиперболы, фокусы которой находятся в вершинах эллипса,
а вершины — в фокусах.
199*. Написать уравнение равносторонней гиперболы, если
она проходит через точку: 1) (КЮ; —Иб'; 2) (]/21; —2]/3).
200. Составить уравнение равносторонней гиперболы, фокусы
которой находятся в фокусах эллипса Зл.---,-7// = 84.
201. Написать уравнение равносторонней гиперболы, отнесен-
ное к асимптотам, если она проходит через точку: 1) (8; 2); 2) (5; 3);
' 3) (—4; -3); 4) (-6; 4).
202. Написать уравнение и найти длину общей хорды кривых
х-— у3 = 3; ху = 2.
203. Найти точки пересечения прямой 2х-ф-у— 18 = 0 с гипер-
болой 2х'2— 5у'2=180.
204. Найти точки, в которых гипербола 9л4—16у3 = 576 пере-
- секается прямыми, проходящими через ее правый фокус парал-
лельно асимптотам.
205. Какие геометрические образы соответствуют уравнениям:
1) bx-\-ay — ab-, 2) 6V— а^у2 = aiba-,
3) = ’ - 4) аД— a’V = ^;
5) rAc3== £>-; 6) x2—y2 = 0;
7) &2х2-)-п2а-2 = 0; 8) —ay = 0;
9) axy=b-, 10) 6'2x'2-L-a2y'2 = —c;
11) (х2-2Г + (У-3)3 = 0?
Парабола (к § 36, 37)
206*. Найти длину хорды параболы у2 = 2рх, проходящей
через ее фокус перпендикулярно к оси Ох.
207. Осью симметрии параболы служит ось Ох, вершина
находится в точке (0; 0). Составить уравнение параболы и пост-
, роить ее (от руки по точкам), если: 1) расстояние от вершины
до фокуса равно 2; 2) парабола проходит через точку (4; 2);
3) парабола проходит через точку (2; —4); 4) парабола прохо-
дит через точку (—2; 4).
208. Парабола симметрична относительно оси Оу, вершина ее
находится в начале координат. Составить уравнение этой пара-
413
болы, если: I) расстояние от вершины до фокуса равно 3;
2) парабола проходит через точку (4; 2); 3) парабола проходит
через точку (—6; 2); 4) парабола проходит через точку (—4;—2);
5) парабола проходит через точку (Кб; —]/з).
209. На параболе у- = 8.с взята точка, находящаяся от фокуса
на расстоянии d = 20. Найти координаты этой точки.
210. На параболе у1 — 4х найти точку, фокальный радиус-
вектор которой равен 3.
211. Найти точки пересечения следующих линий:
1) г/‘2 = 4х и у = х\ 2) у- = — 2х и г/ = Л'ф-4;
3) х--=6у и у = х-\-\2', 4) х2 =— 4у и 2х— у — 5 = 0;
5) № = 4г/ и у'- = 4х-, 6) у' = 2рх и х2 = 2ру.
212. Изобразить фигуру, ограниченную линиями:
1) zf=18.v и 6х-1-у — 6 = 0;
2) № = — 18л/ и Зл'ф-2у —8 = 0;
3) у1 = — 8л' и х- — у.
213. Через фокус параболы у“- = 4х проведена прямая, перпен-
4
дикулярная данной прямой у — ^х-\-4. Найти точку пересечения
этой прямой с директрисой параболы.
214. На рис. 199 представлен эскиз про-
дольного разреза параболического зеркала. По
данным эскиза найти уравнение этого се-
чения.
215*. На параболе у = 4 взяты две точки,
абсциссы которых равны — 1 и 2. Написать
уравнение прямой, проходящей через фокус
параболы перпендикулярно прямой, проходя-
щей через две точки, взятые на параболе.
216. На параболе х = у1 взяты две точки,
абсциссы которых равны 1 и 4, причем орди-
ната первой точки отрицательна, ордината вто-
рой— положительна. Через фокус этой пара-
болы провести прямую, параллельную прямой, проходящей че-
рез две точки, взятые на параболе.
217. Найти длину и уравнение общей хорды параболы у2=\2х
11 эллипса £ 4- ~ = 1.
25 1 16
218. Найти точки пересечения кривых № — У'= 16 н у- = 6д
и изобразить фигуру, ограниченную этими кривыми.
Парабола у = ах2 -ф- Ьх -ф- с (к § 38)
219. Составить уравнение параболы, ось которой параллельна
оси Оу, найти фокус и построить ее, если: 1) вершина находится
в точке (3, 2) и р = 2; 2) вершина находится в точке (—2; 4)
н парабола проходит через точку (2; 6); 3) вершина находится
414
Рис. 2С0
в точке (—6; —4) и параметр равен 1; 4) вершина находится
в точке (—4; 8) и парабола проходит через начало координат.
220. Предполагая, что проволока, соединяющая точки А и В
(рис. 200), приблизительно имеет вид параболы, найти по данным
рисунка уравнение этой параболы.
221*. Камень, брошенный под
острым углом к горизонту, описал
дугу параболы и упал на расстоянии
16.н от начального положения. Наи-
большая высота, достигнутая кам-
нем, 16 м. Составить уравнение траек-
тории камня.
222. Струя воды, выбрасываемая
фонтаном, принимает форму парабо-
лы. Составить уравнение этой пара-
болы, если струя падает обратно в
бассейн на расстоянии 2 м от места '
выхода, достигая высоты 5 м.
223*. Составить уравнение параболы, симметричной относи-
тельно осн Оу, зная, что она отсекает от осн Оу отрезок длиной
Ь единиц, а на оси Ох — хорду, равную 2а единиц.
224. Написать уравнение параболы, ось которой параллельна
оси Оу, а вершина находится в точке (2; 4), зная, что она отсе-
кает на осн Ох хорду, равную 4.
225*. Построить (приближенно от руки) параболу:
1)
3)
1 , , 2 с 1
У=6 Х' + зХ~53’
2) х =
4) x = у;
6) х= —
-5) у= — х — 3;
226. Определить вид кривой по ее параметрическим уравне-
ниям:
1) X = t !• 2) Х = 2<_1 3) % = I
у = t2 — 4 Г у = ’ у = В — 1 J'
227. Какой геометрический образ соответствует
нижеприведенных уравнений:
1) ау2— 4х = 0 при любом действительном а 0;
2) ах2—bif — с при а^>0, Ьф>0, с>0;
3) ах by -ф- с = 0 при любых действительных а,
4) Л-Г-ф Ау2Вх~\-Су A-D = 0 при Лф.>0 и
действительных значениях остальных коэффициентов
5) 5 (у — 3) = (х— 2)ф
6) 4х‘24-fy/3= 16 при Ь<^0;
7) 4у = ах1 -ф- Ьх с;
8) 4х2 -ф- ау2 = 0 при аф>01
9) 9.Н — а2у2 — 0.
У = ?-\
каждому из
b и с;
при любых
415
Смешанное задачи по аналитической геометрии
228. Найти длину общей хорды кривых x‘--j- 2у2 = 24;
(х-2)2-|-у2 = 8.
229. Составить уравнения касательных к окружности (х— 1)‘-|-
(у— 3)2 = 34 в точках пересечения ее с осью Ох.
230. Составить уравнения касательных к окружности х- у2 = 20
в точках пересечения ее с параболой у- = 8х.
231. Уравнения двух сторон треугольника, вписанного в окруж-
ность X2-ф-у" — 4х = 0, суть у=х; у = —~х. Найти уравнение
третьей стороны и длины сторон.
232*. Написать уравнения касательных к окружности x'i-\-y’- =
— 52, проведенных из точки (2; 10).
233*. Дана окружность х-—j—z/-= 4а2. Написать уравнение
геометрического места середин ординат точек этой окружности.
234. Вне эллипса 9л‘2-J-25if = 225 взята точка, абсцисса кото-
рой равна 3, а ордината положительна и в i раза больше
соответствующей ординаты эллипса. Написать уравнения прямых,
проходящих через эту точку и фокусы эллипса.
235. Написать уравнение геометрического места середин орди-
нат точек параболы z/2 = 2px.
236*. Точка М движется по эллипсу 1- Найти
уравнение геометрического места центров тяжести треугольника
Д1Л1Д.2, полагая, что точки Л и Дг являются концами большой
оси этого эллипса.
237. Найти длину и уравнение общей хорды окружности
х2 -И if — 12х -'-11=0 и эллипса Зх2 -ф 4у2 — 48 = 0.
238*. Найти эксцентриситет гиперболы и написать уравнение
ее асимптот, если: 1) мнимая полуось относится к полуфокусному
расстоянию, как 4:5; 2) действительная полуось относится
к мнимой полуоси, как 3:2.
239. Написать уравнения прямых, проходящих через левый
фокус гиперболы 9х2—16z/2—144 параллельно ее асимптотам.
240. Найти длину общей хорды окружностей х2-|-у24-2х—
— 4у—15 = 0, Xе—[—z/2 —4х— 4у— 3 = 0.
241*. Одна из асимптот гиперболы параллельна прямой
Зх — 4z/—{—8 = 0. Расстояние от точки этой прямой, ордината
которой равна 5, до правого фокуса гиперболы равно 1^26.
Составить уравнение гиперболы.
242. Найти угол между касательными, проведенными к окруж-
ности х24-у- — 6х — 2у-j- 5 = 0 в точках, абсцисса которых
равна 4.
243. Написать уравнение окружности, описанной около тре-
угольника, вершинами которого являются точки А (0; 0), В (4; 2),
С(6; 4).
416
X~ v
244. Дана гипербола — -g-= 1. Найти расстояние от точки
Л(1; 7) до ее асимптоты с положительным угловым коэффициен-
том.
245. Прямая 4х-ф- Зу — 20 = 0 перпендикулярна к - одной из
асимптот гиперболы и проходит через ее правый фокус. Составить
уравнение этой гиперболы.
246. Даны кривые х' -)- if — 13, ху = 6. Найти площадь четы-
рехугольника, вершинами которого являются точки пересечения
этих кривых.
247. Вершинами треугольника являются точки пересечения
прямых у=х-\-2, у — — ^-х—1 с гиперболой 4.С— у1 — 16.
Написать уравненйё третьей стороны этого треугольника.
248. Точка М перемещается по гиперболе —р = 1.
Составить уравнение геометрического места центров тяжести треу-
гольника AMAi, где А и Л —вершины гиперболы.
249. Написать уравнение геометрического места точек, орди-
наты которых в два раза больше ординат соответствующих точек
(имеющих ту же абсциссу) данной параболы х‘1 = 4ру.
250. Из фокуса параболы хг = 2ру проводятся лучи, пересе-
кающие эту параболу. Написать уравнение геометрического места
середин отрезков лучей, ограниченных фокусом и параболой.
251. Основанием равнобедренного треугольника, вписанного
в параболу у1 = 4х, является отрезок прямой у — х. Найти вер-
шины этого треугольника.
252* . Канаты, поддерживающие полотно цепного моста, имещт
форму параболы (рис. 201).' По данным рисунка определить
высоту каната над полотном КМ в точках А, В, С и D.
Рис. 201
____г - Л - -2^
’I -------60м——-1
| ’777777777777777777777777777777;
Рис. 202
253. Слабо провисающий провод располагается по параболе.
Зная это, определить величину провеса телеграфного провода
(рис. 202) в точках А и В, 'если стрела провеса ОС — 1 щ,
ED — 3Qm,CA — AB — BD=\Gm.
254. Написать уравнение параболы, ось которой параллельна
оси Ох, зная, что она проходит через точки (0; 0), (2; 3), (4; 4).
14 П. Е, Агачев X 417
255. Найти площадь прямоугольника, вписанного в эллипс
j^4_Tj' = зная> что одна из диагоналей этого прямоугольника
является отрезком прямой х — 2у = 0.
256. Написать уравнение параболы, симметричной относи-
тельно прямой, параллельной оси Оу, зная, что она проходит
через точки: 1) (0; 0), (2; 6) и (1; 4); 2) (1; 1), (2; 3) и (0; 0);
3) (4; 0), (0; 4) и (8; 4).
257. Закон движения точки в зависимости от времени t
определяется уравнениями: x — 3t-—1, y — t--\-2t. Найти траек-
торию движения этой точки в декартовых координатах.
258. Написать в декартовых координатах уравнения следую-
щих кривых:
x = /3 cos ср 1 2 x = 3cos<p 1 х —a = rcoscpl
у— КЗ sin <р /’ 7 у = sin <р J ’ у — b = г sin ср )
2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Примеры на теоремы о пределах (к § 46—52)
259. Urn (х'л — Ех2 Д-6-
260. lim(x— ]/х-|-2).
262*. lim 9 Л ...
а.^32л~+3
264. lim
261*. lim(x3 — 1)(Зл2-[-5).
х-1
4__/,х
263*. lim^^.
1- й + 3
lim -4—.
265.
266*. lim
267. lim ----------А
7\
х2/ '
7
268*. lim
269.
.. 2л-3-2х24-4
lim -----г—!—
1 • 4.v4 — 5л- —|— 6
2Z°' Л 2xi + 2л- + 3 •
Решение. К этому примеру нельзя сразу применить теорему
о пределах, так как при х->-оо ни делимое, ни делитель не имеют
предела (см. § 49, примеры 4—6). Делим делимое и делитель на xi:
lim
Л-» 03
4xi - 5л-- + 6
4л1 — 5л2 + 6 _____ j. х4
2л4 + 2х + 3 ~ 2х4 + 2л- + 3 ;
л4
418
получаем
.. 4х4-5х9 + 6
2 4- — + —
+ л-'1 + х*
При х->оо члены этой дроби — величины конечные и отлич-
ные от нуля. Применяя теорему 3, находим:
4 Л-> _ 5х3 + 6 _ ~х1.Г^с^+л1П^-^_4-0 + 0_9
J^2x‘ + 2x + 3 |шд 2 + ]jm 3 -24-0 + 0-2-
X СО % X —» СО Л
" • "_:^2-4х’- — з + 2х»-8х-
273. lim 274. lim
х_ет 2/г’4-2 л^юлЧ'
„ .. п'— Зя .. 1 4- 2 + 3 +... + п
275. пш ,, , т,. 276*. lim —1———5е—
и^от2я- + 2 я-
Решение. 1\ этому случаю нельзя непосредственно приме-
нить теорему о пределе частного, во-первых, потому, что предел
знаменателя равен нулю, во-вторых, при х = а числитель также
обращается в нуль. Применяем прием, рассмотренный в § 49
(примеры 8—10). Получаем
.. х9 — л9 1. (х — л)(х+л) .. х-С а
lim —=^ — lim 7—1—г- „ \!—г—r; = lim -5-1——i—«.
х^ах а х-оАх — а}(х+ах + а~) Х^ах+ах+а~
При х = а знаменатель дроби, стоящей под знаком предела,
не обращается в нуль, поэтому к разыскиванию предела может
быть применима теорема о пределе дроби. Найдем
. . № — «2 lim (х + о) х-а 1 л ' _ а + а _<2
lim (х2 ах + л2) л2 -j- аа + а2 Зл х -> а
..2 I ? v 278- ii2b4i.<- 280. nm44±-2. л:-* 1 Л Л 282. lim + х-0 х 279*. lim-" \+3. х-З х- — 9 281. lim 3x2 + 5x + b non 1- V a + x — У a x-0 x
Решение. При х = 0 дробь обращается в Непосред-
ственно применить прием, указанный в § 49, невозможно. Преоб-
разуем данную дробь умножением числителя и знаменателя па
14*
419
множитель, сопряженный с числителем, т. .е. на суммууа _|_ х Д- Ya,
в дробь, ей тождественную. Получим
] j m А _ । j m CKa + x — /«) (Y‘ + x + Ya) _
x - о A" x 0 x (I7 a + x + Ya)
—— lllil , - ------,-X - lilll . ,-- f~,
Xu X (]/ a X 4- Ya) .v-»оX (j/g + x 4-P a)
..1 11
= lim _________— = —=----— — —
x^o Ya + x 4- Ya Ya + V a “2 Ya
. ,. Ya + h — Ya — h
284. 11 m -!--r-7-—--.
h о “
285. lim '
.v-.OrgX
Решение. При x = 0 и числитель и знаменатель дроби
обращаются в нули. Преобразуем эту дробь, заменив tgx его
выражением через sinx и cosx:
1- sinx .. sinx sin х cos х—lim ivk y— 1
lim-— = lim-— = lim—:-------------- ишсиьл — i.
.v->0 tgA' A-->OS111A’ л--*0 sin x A'“*°
COS X
286. iim^A. 287*. lim ~-sin x .
л C0S A A->0 Sin X
288. Периодические дроби: a) 0, (315), 6) 2, (36), в) 0,75 (6),
г) 3,3 (54) — обратить в простые дроби.
Символика функциональной зависимости (к § 54)
289. Даны функции f (х) = Зх2 Д- 5х — 6, <р (х) = 2х Д- 1. Найти:
1) Л(х) = /(х) + ?(х); 2)Д2(х)=^;
3) ъ W = / Y) Ef 4) л (х) = 2f (х) - Зх ср (х);
•« f .«=YY,; 6> F‘ w •
290. Дана функция f (х) = 2х2 Д- Зх — 7. Найти частные значе-
ния этой функции: 1) при х = 1; 2) при х — —1; 3) при х = 0;
4) при х=2н; 5) при X — Y3; 6) при х = аД-й.
291. Даны функции: /(х)=х2 —Зх, <р (х) = ха Д- 1. Найти:
1) / (а); 2) <р(6); 3) 4) ? (СД-1); 5) {(а^Ьу, 6) <f(a-by
292. Даны функции: /(х) = х2Д-1, <р(х) = х3. Найти:
1) <р(х-Д/1) —<р(х); 2) lim^(A' + /y~/(^; 3) lim .
h-^О а л-»оэ fix)
420
293. Даны функции: f (х) = sin х-|-cosх, <p(x) = sinx— cosx.
НайтиО
1) /(0); . 2) o = (^; 3)
4)? (I); 5) f(^); 6)?(|к].
Область существования функции (к § 55)
294. Определить область существования функции у = ]Лх—2.
Решение, у будет иметь действительные значения, когда
х — 2 5” 0 или х><-2. Следовательно, эта функция существует
при значениях, х, удовлетворяющих условиям 2^х<^со.
295. Определить область существования функции:
1) у = 2х4~3; 2) у = хя— 2х-|-7; 3) у = sin х; 4) у = х'1—
— 5х3 + бх2 — 7x4-8.
296. Определить область существования функции:
1) у— log3x; 2) у = Кх; 3) у—у^х; 4) y = Y^ — х\
5) y = V^ — 9;. 6) У=^.
297. Определить область существования функции №-\-у*= 16.
Решение. В этом примере зависимость фупкции у от аргу-
мента х дана в неявном виде. Решив это уравнение относительно у,
получаем у = ± 2 ]/Ч — х'2.
Функция существует, когда 4 — x2SsO или | х | -С 2.
Ответ. —2^xsg2.
298. Определить область существования функции:
1) у —4х2; 2) х‘24- if — 16;
,3) х2 —у2 = 4; 4) у2 = — 16х.
Приращение функции (к § 56)
299. Найти формулу приращения функции у = ~, когда аргу-
мент х получает приращение Дх.
Решение. 1-й шаг. Находим наращенное значение функции:
, . 1
у -4- Ду — у—j—-—— .
J 1 J (х + A*)3
2-й шаг. Вычитая из наращенного значения функции ее началь-
1 'ж
ное значение у = —3> находим приращение функции:
д,. = 1________L _ х3 - (х ф- Хху _
и (хф-Дх)3 х’“ х3(хф-Дх)3 ~~
__ х3 — [х3 ф Зх3 Дх ф Зх (Дх)3 ф (Дх)3]_
х3 (х 4- Дх)’
_ — Зх3Дх - Зх (Дх)3 - (Дх)3 [Зх3 ф ЗхДх ф (Дх)3] Дх
-х3 (х Дх)3 — х3 (х 4- Дх)3 .
421
300. Найти приращение функции:
1) у = Л; 2) у=Ух; 3) у = х1 — 3x4-4; 4) у = 1gх.
301*. Найти приращение функции у = 4 — хг, когда: 1) аргу-
мент х переходит от значения, равного 4~2, к значению, рав-
ному 2,1; 2) аргумент х переходит от значения, равного — 2,
к значению — 3; 3) аргумент от значения, равного 0,4, переходит
к значению, равному 0,2.
302. Найти приращение поверхности и объема куба, когда:
1) ребро, равное 6 см, получает приращение 0,1 см; 2) ребро,
равное 10 см, получает прираще-
ние 1 см; 3) ребро, равное 4 см,
получает приращение — 0,2 см.
303. Приращение Ду функции
у,при любом значении аргумента
х определяется по формуле
ху = 1 х 4- ~2~ I Дх.
Построить график этой функ-
ции в промежутке (—5; 5), если
известно, что он проходит через
точку В (0; 2).
Решение. На рис. 203 дан-
ная точка В (0; 2) построена.
Для построения точки с абсцис-
сой, равной 4~ 1, достаточно найти
приращение Ду ординаты, когда абсцисса х переходит от значения,
равного нулю, к значению, равному -[- 1, т. е. в формуле
Ду — (х 4- ^х принять:
x = Xi = 0; Дх = Дл'1=1.
Получим:
Ду = 4—<4 j ДХ1 = (О 4- ~2 j • 1 = у.
^Эта точка отмечена на рисунке буквой С.
Для построения точки с абсциссой, равной 2, следует принять:
(Д^у \
х4~-у1 &х найдем
Л Л I 1\ 1 3
Ьуг— ^4-у) • 1 — у-
На рисунке эта точка (О) построена.
Очевидно, идя таким же путем, можно построить точки,
абсциссы которых равны 3; 4; 5 и т. д. >
422
Для построения точки с абсциссой, равной—1, в формуле
Ly = (x-f- Дх следует принять: х = 0, Дх =—1.
Получим
4<, = (0-ф .(-1) = |
И т. д.
304. Кривая проходит через точку (0; —4). Построить эту
кривую в промежутке (—3; 3), зная, что приращение Ду этой
функции при любом значении аргумента х определяется по фор-
муле
Ду = Дх(2х-ф- Дх).
Понятие о непрерывности функции (к § 57)
305. Показать, что функция у=х1 непрерывна при любых
конечных значениях аргумента.
Решение. 1-й шаг. Находим наращенное значение функции:
у4-Ду=(хД-Дх)*. '
2-й шаг. Определяем приращение функции:
Д# = (хДх)2 — х5 = (2х-|-Дх) Дх.
3-й шаг. Находим lim Ду, когда Дх—«0;
Пт Ду = lim (2х-ф-Дх)-Дх =
Д.у -* 0 A.t 0
lim (2х-ф-Дх)- lim Дх = 2х-0 = 0.
A.V 0 A.V -* 0
Следовательно, при любом конечном значении аргумента х
приращение функции Ду —0, когда Дх —0, что и показывает
непрерывность данной функции при любых конечных значениях
аргумента. Графиком этой функции является парабола с верши-
ной в начале координат и симметричная относительно оси Оу
(см. § 36).
306. Показать, что нижеследующие функции непрерывны в лю-
бом интервале:
1) у — х1 — 2х-|-5; 2) у = ; 3) у = ах, где а~^> 1.
307*. Исследовать на непрерывность функцию: 1) у = sinx;
2) y = cosx.
308. Доказать, что функция у=у х, где п — любое целое
положительное число, непрерывна при всяком Jt, большем нуля.
309. Доказать, что функция у— Д- непрерывна при любых
значениях х, кроме х = 4. Построить график этой функции.
423
310. Определить точки разрыва функции:'
2) У = ^\ 3) У = ^.- .
311. При каких значениях х претерпевает разрыв функция:
1) у = tgx; 2) y = ctgx?
Производная (к § 58—60)
312*. Тогда движется по закону s = t'L-}- 2. Найти среднюю
скорость движения точки за промежуток времени от момента
/ = 4 до момента /1 = 4,2, если за единицу времени принята
секунда, за единицу длины — метр.
- 313. Закон движения дан формулой s = 2/2 -1- 3. Найти сред-
нюю скорость движения за промежуток времени: 1) от момента /
до момента /ф-Д/; 2) от момента / = 3 до момента /1—-5, если
за единицу времени принята секунда, за единицу длины — метр;
3) от момента / = 3 до момента ф = 5, приняв за единицу времени
секунду, за единицу длины — сантиметр.
314. Найти производную функции г/ = х'3—2х-3 при х = 4.
Найти производные функций:
315. у = /гх~ Ь. 316. 2 = г2 — 2х.
317. Дана функция / (х) = х2 —J—4x. Найти: 1) [г (х); 2) /'(0);
3) /'(2); 4) Г (-3); 5) f (а -Ь).
318. Дана функция г/= —. Найти производную этой функ-
ции: 1) при х=1; 2) при х — — 2; 3) при х = 4.
При каком значении аргумента х эта функция не имеет про-
изводной? 1
319. Точка движется по закону 8ф-3/ =/-(единица времени —
секунда, единица длины — метр). Найти закон изменения скорости
этого движения и определить скорость в момент: 1) / = 2 сек;
2) /= 10 се^ \
320. Угол поворота шкива в зависимости от времени / выра-
жается формулой <с = /'2-фЗ/— 5 (единица времени — секунда,
единица угл^ поворота — радиан). Найти угловую скорость в мо-
мент / = 4 сек.
321*. Количество электричества, протекающее через проводник,
начиная, с момента ./ = 0, дается формулой Q = 2/2 ф- 3/ ф-1 (куло-
нов). Найти силу тока: 1) в момент /; 2) в конце 8-й секунды.
Геометрический смысл производной (к § 61—62)
322. На кривой у — х1 взяты точки, абсциссы которых соот-
ветственно равны 2 и 3. Найти угол между секущей, проходящей
через эти точки, и положительным направлением оси Ох.
424
323. Найти угловой коэффициент касательной к кривой у = 2х“
в точке, абсцисса которой равна: 1) 4,-; 2) —2.
324. Найти наклон кривой у =— х*-\-2х в точке,, абсцисса
которой равна: 1) 0; 2) —3; 3) 4.
325. Найти наклон кривой z/ = 4— х1 в точке, абсцисса кото-
рой равна: 1) —3; 2) 0; 3) 3.
326. Написать уравнение касательной к кривой У — ~ в точке,
абсцисса которой равна: 1) —2; 2) 2.
327. На кривой // = х'2— 2х найти точку, в которой касатель-
ная параллельна оси Ох.
Дифференцирование алгебраических функций (к § 64—70)
Найтн производные функций:
328. у=х-\-3.
329. у = 4х — 7.
330. у = х2 — Зх -ф- 6.
331. у = х‘ — 2х64-3х2 — 4.
332. y = xa+l — 4-а.
333. у = у х3 — у х2 4- 5х 4- 2.
335. у
х° — 4х’ 6х2
336.
337.
_ х4 - 2х
2 (« + *)'
Xя - Зх2 + 6х
У =---------'ьГ—
338. у = 2хЛ
339. .y = x ’4-2.v 3 —Зх-:'4^5.
340. » = Д.
J Л'°
341. у= ~ — - 4-2.
J Л- X 1
4 г3 — 3 г 4- 9
342. у=- + л
3 4 6
343. у = 2х'2 — Зх3 4- 5х5 — 7.
_ i _ 1 _ J
344. у —2х ‘2—Зх 3 —4х т.
3 4 9
345. у =--------? + А---------^ + 4-
2х3 Зх4 Зх2
425
346. 2 - л- r- Л"2
347.
348. у = ^х\
349* . y = Vx.
350. У — 2 Vх 3 х — ур.
351* . у — \ах — х3.
352* • у=У ъ-
353. х3 — Зх У з ‘ _Т А~
354* . t/ = (x4+D(2x2 + 3).
355. у = (4х2 + 2) /х.
356. У — (3 /х+1)(2 /хН-1).
357* . у = (ах2 Ьх + с)4.
358. z/ = (x3 + a3)s.
359. у = (ах4-Н)7-
360. у = (4 Кх+ l)s.
/ 3 у
361. у = \ах2 +&/’ .
362. у = у/ (ах3 +
363. у = У4х^З. .
364. 2
У ~ (2л* З)3 * а _ и —Z
365.
\/—s-!—" • )/х- 4- <1-
366. у = ^Уа*-х\
367* *=Ш-
368.
369. а- -4 ь- •
370. /(х)=М-\
371. Г3 — 1
372. »—л,3 + л' + 1 У Л-—Л'+1’
426
373.
J 1-Л-— 1
375*. у = (а24- x-) У a1 — x2.
376. у = x Ух1 + 1 •
377. у = (a x) У a— x.
378*. y = 4x — l)3(x — I)3.
380.
382.
381*.
383. Закон прямолинейного движения точки выражен уравне-
нием s = у jZД — 4 У t -ф- 5 (единица времени — секунда, единица
длины — метр). Найти: а) скорость в момент /; б) скорость в мо-
мент t = 64 сек.
384. Закон движения точки выражен формулой s = 4-^-12/ —
— (единица времени —секунда, единица длины — метр). Опре-
делить момент, когда скорость будет равна: 1) 8 м/сек-, 2) 0.
385. Количество тепла Q, необходимого для нагревания одного
грамма воды от 0° до t°, определяется по формуле
О = 14- 0,00002/3 + 0,0000003/'.
Вычислить теплоемкость воды: 1) для/ = 30°; 2) для/==100°.
386. Тело массой 3 кг движется прямолинейно по закону s =
= /-—42/4“3 (s — в сантиметрах, t — в секундах). Определить
/ г, mvl\ ,
кинетическую энергию = тела через 4 сек от начала
движения.
387. К кривой у = х3 — Зх3 провести касательную в точке,
абсцисса которой равна 3.
. 1
388. На кривой — 4х найти точки, в которых каса-
тельная параллельна оси Ох.
389. Написать уравнения касательных, проведенных к кривой
у — х3 — 4х в точках пересечения ее с осью Ох.
390. Даны кривые у = х\ у = х2— 2x4-4. Написать уравне-
ния касательных, проведенных к этим кривым в точке их пере-
сечения, и найти угол между ними.
427
Дифференцирование тригонометрических функций (к § 71,72)
Найти пределы:
391*. lim^.
Л" —* О л
„„„ sin 2.V
392. 11 tn •------
л' —* О А
ПМП -1- 1 • Sill //Z,V и
393*. lim--------, где т — любое действительное число, отлич-
х — О х
ное от нуля.
. Л"
sin
394. lim ----
л_0 х
2 cos
395. lim--------
а -* О
396. ]im sin (х+а,-sinx
а— О а
397.
.. sin 5х — sin 3.v
Ilin-----------;-------
Л- -»0 А
ОАО* 1- COS (х + с) — COS X
398*. 11П1—51—-------
а-* о .. а
• о Л
sm- -тг _
♦. 2 ЛЛ.Л.,. 1- cosx— cosax
399. lim——. 400\ lim ----------——
Л -> о А х -< О А
401 ]jm sin (-v + Да) — sin <А — Да')
Дх —0 Да‘
402. Дана функция f (х) = sinx-ф- cos х. Найти: 1) /' х; 2) f(0);
3) №; 4)
403. /(х) —1' 2 cos х-j- 1- Найти f' (х); f (0); Г (у)-
404. f (х) = (sinx cos x)2. -Найти /'(x); f (0); /'(-y).
Найти производные функций:
405. z/ = tgx — x.
407. y = sin ax.
409*. y=X-^.
411. z/ = 2siny.
413*. z/ = (tgx—f- 1) cosx.
414. t/ = (ctgx-|- 1) sinx.
415. z/ = sinaxcos bx.
417. t/ = xsin2x'4-cos2x.
.,sin x + cos x ,
419. y = ---1----.
17 Sin X-COS X
421. y — a l^sin 3x.
423. r/ = 2]/tg|.
406. y = a(\— cosx).
408. z/ = cos3x.
4Ю*. ^ctg(4x+n
412. у = 2- cosx2.-
u 2.
416. y — sin 3x cos 4x.
sin ax — cos ax
418"-. z/ = -r—----:---j---.
17 sm ax + cos ax
. sin 2x — cos 2x
420. y = —r-7-i—:-----ГГ-.
17 sin 2x 4- cos 2x
422. y — aVrcos2x.
424. y — sin2x4- cos9x.
428
425*. z/ = cos3x. 426. y=—^-—.
3 • si n- ax 1
427. у={£ ax. ' 428. y = sin2#,.
429. z/ = atg3y. 430. z/ = cos2x3. —
431. г = a sin3 • 432. f (/) = ц0 cos3 / sin Л
433. u = 434. /(x) = — ctg2 4 — tg’#.
cos Лр 1 ' ’ b 2 b 2
435. S= sinia'T^- НЗЙТИ S“; 2> S‘3-
sin (a -j-
436. y= (xtgx)2.
437. y = ytg3x — tg x—}—x ~|-1.
438. y = |tg3# + tg#.
439: z/=-L ctg3 Ax —ctg Ax1.
О
440*. На кривой z/ = cosx найти точки, в которых касательная
параллельна оси Ох.
441. Написать уравнение касательной к кривой z/ = sinx
в точке, абсцисса которой равна к.
442. Найти наклон кривой у= tgx в точке, абсцисса которой
равна # •
443. Найти угол между прямой z/= 2х1 и касательной
к кривой у = sinx в точке, абсцисса которой равна #. '
Решение. Для решения задачи надо знать угловой коэффи-
циент касательной к кривой в данной на ней точке. Он равен
A = tga = z/'v| ,=cosx| n=cos# = #.-
Г=3 3 2
Угол между двумя прямыми, найдем по формуле (13).§ 20.
В данном случае
2 ч 3 3
tg® =------Г = т; <P = arctg7.
1+2-у
444. Под каким углом пересекаются кривые
z; = sinx, y — cosx.
Указание. За угол между двумя кривыми в точке их пере-
сечения принимается угол, образованный касательными, прове-
денными к этим кривым в их общей точке.
429
Решение. 1) Находим общую точку кривых, решив совместно
их уравнения. Имеем: sinх — cosx. Наименьший положительный
корень этого уравнения будет х = ^~.
2) Определяем угловые коэффициенты касательных к данным
кривым в точке х = ^-:
, ., , yi
= l _ ,=cosx = ;
ki = yx\ „=—smx '-.у-.
Н=4 Г =4 2
3) Находим тангенс искомого угла:
tg?
_ /г, — /г2
— 1 +
откуда
? = arctg ]/8 = arctg 2,828 70°32'.
Дифференцирование логарифмических функций (к § 73, 74)
445. f (х) = In х -ф- 1g х -ф- 3. Найти: 1) f (х); 2) /' (1).
446. / (х) = Vx -ф- In х--
V х
Найти производные функций:
447*. y = \vt(ax--\-bx-\-c).
449. r/ = lnx3.
451. у = In (2х — I)4.
453. s = / —|- 2 In cos у.
455.
456. f (?) = In tg4 k<?.
457. /(0 = ln
458. w = ln^r±-tt
u — a'
//=ln[(X2+l)3(X2-l)4].
rr t \2 /
HI — 2 cos yj (1 -ф-
Найти: 1) f (x); 2) /' (4)
448. y = \n(bi— x2).
450. y— In41 x.
452. y = \nV^~\.
454. у = In 1 -ф- sin 4/.
2соз4У].
459.!, = ln/]4|i
460. f (x) = In j/"
1 4- sin X
1 — sin X '
461. ? (x) = In j/i4?co£- -Найти: w>2) (t) ’ 3) (i)'
462. f (x) = In j/Найти: 1) f (x), 2) f (0), 3) f (/a).
430
Дифференцирование показательных функций (к § 76)
463. Дана функция f (х) = ех~[-2х-]-5. Найти: 1) /' (х); 2) /'(0);
3) /'(3); 4) /'Щ.
Решение. По формулам (17оф и (18а) находим: 1) /'(х) =
= ех Д- 2х In 2. Частные значения получим, подставляя в выра-
жение f’ (х) вместо х его данные значения; 2) /' (0) = е° Д-2° • In 2 =
— 1 -j- 1 • In 2 № 1,693 (см. решение примеров в конце § 71);
3) /' (3) = е:| Д- 2:| • In 2 № 20,086Д-8 • 0,693№ 25,25;
4) = + /2 In 2 ^2,629.
464. f(x) = 3x + 4ex + 3. Найти: 1) f' (х); 2) /'(0); 3) f (1).
465*. f(x) = eax. Найти: 1) /' (х); 2) /'(0); 3) /'(—4)-
Найти производные функций:
466. z/ = ew+6. 467. у = аях.
468. у = 7“+й. 469. у = 5^Д-52г —
470. у = ел'3 + 3*+Д 1 471*. у = х2е'2х2.
472. у — ахе2х. 473. f (х)—-lnesin2-t.
474. y__eCOS*X. 475. y = as'n2x.
476. o = esin2z cos 2Л
477. у Z-^ + r
5*"
Решение. Дифференцируем как частное двух функций?
Получаем
(X* + 1) е^х (/x).v - (eVx - 1) X* _
~ . (ХЧО3 “
v 2/х 2/х_ eVx
~ (Х5 + 1)2 “ (Х*+1)3/^’
478. у = 479. у=еХ~е~'Х-.
J 1 + J ех -\-е х
Рх 1 -4- рзх
480*. 4=10-7—;—т. 481. »=1и
J • 1 + ех J елх
482*. у = In (а/?е“). 483. у = ё^т+1.
484. у = ^\еа Д-е а). 485*. г/ = In (ev Д- 1 Д- e2JC).
486. // = 1п(2хф-]/1 Д-4х2).
487. //= In [х (1 Д-х) |/1 — х].
431
488. //=1п3(ах3Ц-6).
Решение. Здесь мы имеем функцию от функции у = и3, где
и = 1п (ах3-}- Ь). Поэтому, дифференцируя по формуле (7) § 69,
находим ' '
у‘х = Зи-их = 3 [In (ах3 -Н &)Г2 • Пп ~г Ж = 9аЛ д”з+Аг> + ~ •
^489. у = In3х. 490*. у — In41'2х^- 1.
491. у — хх.
Решение. В данном случае формула (7а) неприменима, так
как показатель степени — величина переменная; нельзя применить
и формулу (17а), потому что основание — также величина пере-
менная. Для дифференцирования таких функций {у — |/(х)] <р'’Д
применяется следующий прием:
1) логарифмируем данное равенство по натуральному лога-
рифму:
1пг/ = х1пх;
2) берем производные от обеих частей этого равенства:
(1п уУх = (х 1пх),(.
В этом равенстве у — функция от х. Применяя формулы (16),
(4) и (16а), получим:
У'х У'х
— = х(1пх);4-1пх(х)?, у=1-}-1пх;
у»'
3) из уравнения у=1-|-1пх определяем у'х-.
у'х = у (1 -h In х) = х‘(1 + In х).
492. Дана функция f(x) — x'ax. Найти: /' (х); 2) f (е); 3) f (1).
493. При статическом разряде конденсатора закон уменьше-
ния его потенциала v в зависимости от времени выражается
формулой v = voe~at, где и0 — начальный потенциал; а —некото-
рая постоянная, зависящая от характера разряда; t—время,
отсчитываемое от начала разряда. Найти скорость изменения
потенциала проводника в зависимости от времени.
494. Давление атмосферного воздуха на высоте h над уров-
нем моря можно вычислить по формуле P — P^ect, где Д— Дав-
ление на уровне моря; с — величина постоянная. Показать, что
скорость изменения давления в зависимости от высоты прямо
пропорциональна величине этого давления.
432
Дифференцирование обратных
тригонометрических функций (к § 77)
495. Дана функция f (х) — arcsin Зх. Найти: 1) /' (х); 2) f' (0);
3> /(}}•
496. Дана функция f (х) = arctg ах. Найти: 1) /' (х); 2) /ДО);
3>Д-Д-
Найти производные функций:
497. У = arcctg ±. 498. У= arccos (2х — 1).
499. У = ! 1 х\ arccos 1 . \ а) 500. У = arcsin ]/х .
501*. У = . х — а arctg —;—. ь х + а , 2х arctg 1 _ • 502. У = arcctg (х2 — 5).
503. У = 504. У = arccos V 1 — х2 .
505. У = arctg V 1 — х. 506. У = a - arcsinа2
507. » = arcsin - —.
у а- — х-
508. . у = х]Лг2 — х'2-)-a2-arcsin
509. Дана функция /(х) —Найти: 1) /Дх); 2) /ДО);
3> ДД _____
510. Дана функция /(х) = ]/1—х2-arcsinх— х. Найти:
1) /Дх); 2) /ДО); 3) /'(^-).
Дифференцирование неявных функций (к § 78)
Найти производную (у'х) неявных функций:
511*. у*=х\ 512. tf = 2px.
513. x’-ry! = A ' 514. х2Д-у1 — 4х — 9 = 0.
515. (х — а)2ДДу — = 516. у1 — х2— 2ах=0.
517. sin у — 2х = 0.
518. х2Д-у2- 12х8у Д-43 = 0.
519. Написать уравнения касательных и нормалей к пара-
боле у — х?— 4хД-1 в точках, ордината которых равна 6.
520. Написать уравнение касательной и нормали к гиперболе
х2— 2у’ = 8 в точке, -абсцисса которой равна 4, а ордината поло-
жительна.
521. Найти угол между касательными, проведенными к гипер-
v2
боле -д- — Д = 1 в точках, абсцисса которых равна 6.
433
522. Написать уравнение касательной к окружности х2Д-
4~у2 = г! в точке (х0; у0).
523. Найти угол между касательными, проведенными к окруж-
ности х2У1 — 25 в точках (4; 3) и (3; —4).
524. Написать уравнение касательной и нормали к параболе
4 = 4х в точке, ордината которой равна —6.
525. Написать уравнение касательной к эллипсу 1
в точке (х0; z/0).
526. Написать уравнения касательной и нормали к эллипсу
x--[-2yi—6 = 0 в точке, абсцисса которой равна —2 и орди-
ната положительна.
527*. На окружности х2 4" у- = 169 найти точки, касательные
о 5
в которых параллельны прямой у = ^х.
528. Написать уравнения касательных и нормалей к гипер-
боле х1 — у1—12 в точках, ордината которых равна 2.
529. На параболе у2 = 6х найти точку, касательная к кото-
рой была бы перпендикулярна прямой 4x-|-3t/—12 = 0.
530. Написать уравнения касательных к окружности х2 -J- у- —
—4х — бу—12 = 0 в точках, абсцисса которых равна 6.
531. Под каким углом пересекаются кривые х'1— у* — ! и
х1 у2 = 25 (достаточно рассмотреть случай х^>0 и y^>ty?
532. Доказать, что эллипс Зх24у2 = 48 и гипербола Зх2 —
— У2 —3 пересекаются под прямым углом.
Последовательное дифференцирование (к § 79)
Найти производные второго порядка:
533. ахл 4- Ьх1 -4 сх 4- d.. 534. 1/ = Ух\
535. У = С 536. У = а\
537. У— cos£x. 538. У = е1ПХ.
539. 1 — л- 540. У = 1п (ех е~х)
У 1 + Л' ’
541. У = (2ах 4~ by. 542. У = In sin ах.
543. У = 1пУ1+х2. 544. У = sin2x.
545. У = COS2X.
546. Высота s в метрах, достигаемая в t сек телом, брошен-
ным вертикально вверх со скоростью м/сек, определяется фор-
мулой 5 = с„/— 4,9Л При ао=ЮО м/сек найти скорость движе-
ния и ускорение: а) в момент /; б) в конце второй секунды;
в) в конце 10-й секунды.
547. Расстояние (в м), проходимое точкой в i сек, опреде-
ляется формулой з = Найти: а) скорость движения
434
точки в момент t; б) среднее ускорение за промежуток времени
от момента / = 4 сек до момента ZT = 5 сек; в) ускорение в мо-
мент г) ускорение в момент / = 4 сек.
548. Точка движется прямолинейно по закону s — ~(eal — e~at).
Найти скорость и ускорение этого движения в момент t.
549. Тело движется прямолинейно по закону, выраженному
15
уравнением 5 = ^/’—g- /3 -ф- 2f2. Найти: а) ускорение в момент 4
б) момент времени, когда ускорение будет равно нулю; в) момент
времени, когда ускорение будет равно —2 м/сек?.
550. Расстояние (в л«), проходимое точкой в t сек, опреде-
2 Tzt
ляется формулой s^'g-sin^. Найти ускорение: а) в момент t\
б) в конце первой секунды; в) в конце третьей секунды.
551. Точка движется прямолинейно по закону, выраженному
уравнением s= 10 In-g-^ (s — в м, t — ъсек). Найти скорость
и ускорение: а) в момент /; б) в конце первой секунды; в) в конце
16-й секунды.
Смешанные задачи к гл. VII
Найти производные функций:
552. у = (sinx)*.
554. у = ]/4х — 1 — arctg ]/4х — 1.
555. У=1п]/^~-.
557. /(/) = у tg2 /4~ In cos t.
558. s = In (eaJ -ф-1) — 2 arctg e*.
559. у = In у — ^-arctgx.
560. у = arctg 1/c— .
J Г 1 + cos x
553. /y = xt£*.
556. у = |/ 1 4~ cos2 x .
561.
]/х3.+ 1—.e
КТЯИ + х’
562. y = ix:'arctgx —-|x24-yln(x‘!4-1).
563. cp(x) = eftv(sin£x —cos£x).
564. F(x) = — In-^^7- 1 -4~arctg 2% ~ 1 .
' 3 j/ .c'2 - x + 1 1 /3 /3
565. На кривой y = yx3— Зх2— 7x найти точки, в которых
касательная параллельна оси Ох.
566. Найти наклон кривой y = xlnx в точке, абсцисса кото-
рой равна: а) 1; б) е; в) е3.
435
567*. Составить уравнения касательной и нормали к кривой
у*— Xs в точке, ордината которой равна 1 (график этой функции
см. на рис. 242).
568. С крыши дома высотой 20 м брошен вверх металличе-
ский шарик со скоростью 39,2 м}сек. По истечении t сек. шарик
будет находиться от Земли на расстоянии s = (20 —|—39,2/ —
— 4,9/-) м. Определить: а) скорость в момент / = 2 сек; б) мо-
мент начала падения; в) наибольшую высоту, достигнутую шариком.
569. Под каким углом пересекаются равносторонняя гипер-
бола х2— yi = 2di и окружность х2-ф-у-== бас? (Достаточно рас-
смотреть случай, когда хо^>0 и у0^>0, где х0 и у^ — координаты
точки пересечения данных кривых.)
570; Дана гипербола 2х2— 5z/2 = 30. Составить уравнения
касательных к этой гиперболе, параллельных прямой х -ф- у -ф- 4 — 0.
571. К эллипсу х1 2у- — 18 проведена касательная в точке
(4; 1). Показать, что углы, образованные этой касательной с фо-
кальными радиусами данной точки, равны между собой.
Возрастание и убывание функцир (к § 81—82)
- 572*. Показать, что функция у = е* возрастает в любом про-
межутке.
573. Показать, что функция у = — х3 убывает в любом про-
межутке.
574. Исследовать на возрастание и убывание функцию z/—lnx.
575. Показать, что функция у =х3-|-х5 возрастает в лю-
-бом промежутке.
576. Исследовать на .возрастание и убывание первую произ-
водную функций y — e ix.
577. Определить промежутки возрастания и убывания функ-
ций: 1) у=х*; 2) y = xi— 6х —j—4; 3) у=— х2-|-8х-|-5.
578. Указать промежутки возрастания и убывания функций:
i) z/ = x'!Зх-j-4; 2) z/ = lxi + |x34-7.
579. Исследовать на возрастание и убывание первую произ-
водную функций:
1) //=|х‘4-16х-7; 2) у = 1у'-Зхф-4;
3) у — arctg х; 4) y = -^x'd — 2х24*3х— 5.
Максимум и минимум функции (к § 83—85)
Исследовать на максимум и минимум функции:
580*. /(х) = х2 — 6x4-1. - 581. /(х)=х24-4х —3.
582. /(х) = — х24-8x4-2. 583. у = — х2-)- 10x4- 1-
436
Исследовать на максимум и минимум и построить график
функций: -
584*. y = x‘sAr 4х — 12. 585. z/ = x‘a-|-5x — 6.
586. у = уХ2Ч-2.. 587. // = —х2-|-2х —5.
Исследовать на максимум и минимум функции:
588*. f (х) = х‘‘ — Зх2. 589. f (х) = х3 — 12х 15.
5£0. f(x) = — х3. 591. /(х) = (х — а)л-\-а.
592. /(х) — |х3 — Зх2 —5х—1- 593. /(х) =— ~х3 — 4х.
594. f(x) = x(x — 4)3. 595. f(x) = xl — 2х3 — 2х2.
596. Балка (рис. 204) нагружена равномерно распределенной
нагрузкой q кг[см по всей длине I. Изгибающий момент, дейст-
вующий на балку в сечении на расстоянии х от левой опоры А,
выражается формулой М — ^х — ~ х1. Показать, что максималь-
ный изгибающий момент будет посередине балки.
597. При распределении нагрузки балки соответственно за-
кону </ = уХ (рис. 205) изгибающий момент, действующий на
балку в сечении на расстоянии х от левой ее опоры, выра-
жается формулой M = -^hlx — где будет макси-
мальный изгибающий момент у этой балки.
598. Тело движется по закону s= 18/-ф- 9/2 — /3 (единицы —
метр, секунда). Найти момент t, в который скорость будет макси-
мальной.
599. Разделить число 10 на такие две части, чтобы их про-
изведение. было максимальным.
600. Разделить число 12 на две части так, чтобы сумма квад-
ратов их была наименьшей.
601. Разделить число 6 на две части так, чтобы сумма утроен-
ной одной части и куба другой части была наименьшей.
602. Разность двух чисел равна 4. Каковы должны быть эти
числа, .чтобы их произведение было наименьшим?
603. Кусок проволоки длиной 36 см согнуть в виде прямо-
угольника так, чтобы площадь последнего была наибольшей..
437
604. Нужно огородить проволочной сеткой длиной в 100 м
земельный участок прямоугольной формы, прилегающий к стене.
Каковы должны быть длина и ширина участка, чтобы площадь
получилась наибольшей?
605. Из квадратного листа жести, сторона которого равна а,
требуется сделать открытый сверху ящик, возможно большей
емкости, вырезая по углам равные квадраты -и затем загибая
края, чтобы образовать бока ящика. Какова должна быть длина
стороны вырезанных квадратов?
606*. Прочность балки прямоугольного поперечного сечения
пропорциональна произведению ширины балки на квадрат вы-
соты. Определить размеры наиболее прочной балки, которую
можно вырезать из цилиндрического бревна диаметром d.
607. Из круглого бревна, диаметр которого равен d, тре-
буется вырезать балку прямоугольного сечения, чтобы площадь
сечения была наибольшей. Каковы должны быть измерения этого
сечения?
Исследование функции ни максимум и минимум
при помощи второй производной (к § 86)
Исследовать на максимум и минимум функции:
608* . у ——х34х. 609. z/=2x3 —Зх2—12х.
610. /(х) = х3—5х4-j-5х3 + 1.
611*. /(х) = (х—1)2(хЧ-3)2.
612. z/ = (x — 5)Хх-j- 2).
613. f (x) = cos2x, где 0iCx<^2~.
614*. Показать, что из всех равнобедренных треугольников,
вписанных в данный круг, наибольший периметр имеет равно-
сторонний треугольник.
615. Из куска картона 30 X 14 см1 требуется сделать коробку
(без крышки) наибольшей вместимости, вырезая по углам равные
квадраты и загибая выступы для образования боков коробки.
Какова должна быть длина сторон вырезаемых квадратов?
616*. Поверхность открытого сверху резервуара, имеющего
квадратное дно, требуется выложить изнутри свинцом. Каковы
должны быть измерения резервуара, чюбы потребовалось наи-
меньшее количество свинца, если он должен вмещать 32 л воды?
617. В шар диаметром d вписан цилиндр. Каковы должны
быть высота и радиус основания этого цилиндра, чтобы объем
его был наибольший?
618. Гипотенуза прямоугольного треугольника равна с. Каковы
должны быть его катеты, чтобы площадь была наибольшей?
619. Сопротивление трения при движении воды по каналу
будет наименьшим, когда периметр его поперечного сечения будет
иметь наименьшую длину. Если площадь поперечного сечения
438
равна 8 м2 и сечение имеет форму прямоугольника, каковы
должны быть его измерения, чтобы сопротивление трения было
наименьшим?
620*. Кровельщик делает из жести открытый сверху желоб,
имеющий в поперечном сечении форму равнобедренной трапеции.
Основание трапеции и боковая сторона должны быть длиною
2 дм. Чему должно быть равно верхнее основание трапеции,
чтобы площадь поперечного сечения желоба была наибольшей?
621*. Нормандское окно имеет форму прямоугольника, завер-
шенного полукругом. Дан периметр фигуры Р. Каковы должны
быть размеры окна, чтобы оно пропускало наибольшее коли-
чество света?
622. Судно стоит в 9 км от ближайшей точки берега. С него
необходимо послать посыльного в населенный пункт, располо-
женный на берегу в 15 км от упомянутой точки. Зная, что
посыльный проходит пешком 5 км в час и на лодке делает 4 км
в час, определить, в какой точке берега он должен высадиться,
чтобы в кратчайший срок достичь населенного пункта.
Особый тип экстремума функции (к § 87)
Исследовать на максимум и
Z
2
623. f (х) = b -ф- с (х — а)3.
минимум функции:
2
624. f(x) = 3 — 2(х — 4)3.
_2
625. f(x)=x(x— 5)3.
626. f (х) = (х -ф- 1) /(х + 6)3 .
Выпуклость и вогнутость кривой. Точки перегиба.
Построение графиков функций (к § 88—90)
627. Доказать, что парабола у = ах2 -ф- Ьх -ф- с\ 1) выпукла
при а<фО; 2) вогнута при аД>0.
f X X \
628. Доказать, что кривая у = ^\еа Д-е а) вогнута в любом
промежутке.
Исследовать на выпуклость и вогнутость кривые.
629. у = ^х*— 2х2Д-Зх— 3. 630. у = tg х в промежутке
(-2 Д “I-»=*+!•
Найти точки перегиба кривых: v
632. у=^х1— х1. 633. у = sinx,
634. z/ = ctgx. 635. Z/^-ri-з. 636.
1 Л 1 Л
439
Построить-графики функций: ,
637. у = ~х3 — 2х. 638. z/ = — -х3 4-2x4
639. z/ = yx3 — ~х2—Зх. 640. y = -^-xi — 2x‘J.
641. у^^--4)\ 642.
ИЗ. 9=,^.. 644. =
645*. y = cos2x в промежутке (0 sg; х sg; 2я).
646. у=х*(х — 4)4 647*. // = Г(Г—>
Смешанные задачи к гл. VIII
648. Определить промежутки возрастания и убывания функ-
ции у = е~х~. '
Исследовать на максимум и минимум функции:
649. у = х In cos х в интервале ^0; .
650. у = sinx4-cosx в промежутке (0sgxsg2ir).
651*. у = cos х — cos Зх в промежутке (Ч); yj.
Построить графики функций:
652. = + 1 . 653. г/ = 4-(х-2)Ч /
654. =
J 4 1 л'
655*. В эллипс ~ 4- ~ = 1 вписан прямоугольник. Каковы
должны быть его измерения, чтобы площадь была наибольшей?
656*. Через точку (4; 3) провести прямую так, чтобы она
вместе с положительными полуосями образовала треугольник
наименьшей площади.
657*. Известно, что сила освещения, прямо пропорциональна
косинусу угла падения и обратно пропорциональна квадрату рас-
стояния от источника света до освещенной поверхности. Электри-
ческая лампа висит на блоке прямо над центром круглого стола,
радиус которого равен рЛ2 м. На какой высоте надо повесить
дампу, чтобы она максимально освещала книгу, лежащую у края
стола? ' .
658*. Цилиндр вписан в шар. Под каким углом должны пере-
секаться диагонали осевого сечения цилиндра, чтобы полная по-
верхность его была наибольшей?
440
659. Через точку (4; 1) провести прямую так, чтобы сумма
отрезков на положительных полуосях была наименьшей.
648*. Две светящиеся точки А и В находятся одна от другой
на расстоянии 6 м. Какая точка на прямой АВ освещена слабее
всего, если силы света относятся, как 8:1?
661. Образующая конуса имеет длину I. Каковы должны
быть высота и радиус основания конуса, чтобы объем его был
наибольшим?
662. Водоем имеет форму правильной четырехугольной призмы.
Площадь его дна и четырех стенок равна 10 лг. Каковы должны
быть его измерения, чтобы емкость
была наибольшей?
663*. Профиль открытого кана-
ла имеет форму равнобочной трапе-
ции, площадь которой равна 12 лг2,
а угол откоса 60°. Какой глубины
надо сделать этоткаиал, чтобы по-
тери на сопротивление трения были
наименьшими, т. е. чтобы мокрый
периметр был наименьшим?
664*. По одну сторону шоссе
EF = d на расстоянии EA = h
и FB = H расположены пункты
А и В (рис. '206). Эти пункты
надо соединить телеграфным проводом, но не непосредственно,
а так, чтобы из А провод дошел до какого-нибудь пункта М на
шоссе и лишь затем был проведен к В. Где надо взять точку М,
чтобы длина провода оказалась наименьшей?
Сравнение бесконечно малых величин (к § 91)
665. Показать, что при х->0 величина 1 — cos2x есть беско-
нечно малая высшего порядка, чем х.
666. Показать, что при cos 2х и ctg 2х х -> ~ — бесконечно ма-
лые равносильные. ,
667. Показать, что cosx и sin 2х при х->^- бесконечно малые
одинакового порядка малости.
Нахождение дифференциалов функций (к § 92—94)
Найти дифференциалы следующих функций:
668. г/ = 4ах2-|-7&х—12. 669. f (х) = -FL---—
670. 2 = (а2 —у2)\ 671. f(y) = /l у у2.
672. z/ = ln]/l—х2. 673. y = xlnx.
441
674. s = (t’-z2Z)‘-’.
675. y— In (cos ax-j- sin ax).
676. z = -i- tg3ax4- tgax-|- 3.
677. Дана функция 2 = sin2 у. Найти: a) б) в) d*z.
678. Дана функция 2 = ^-tg4x---tg2x—In cosx. Найти:
a) 6) -^4: в) d'Z.
' dx ' dx- '
Найти производные от у по х:
Г^П(\ “И 3
679. х = -—г, у =—.
t — 1 ’ о
680. х =—l^-2cos/, у — 44~2sin/.
681. х= ln(l-|-ег)> У = — arctg г1.
682. Дана окружность своими параметрическими уравнениями:
x = acos<p, y = asin<p. Найти угловой коэффициент касательной
к 5
к этой окружности в точке, где; а) <р = у; б) ? = в) <₽ =
___П
—’ 6’17
Приложение дифференциала к приближенным вычислениям (к § 95)
683. Найти приближенно приращение функции у — Jx2x- -j- 7
при переходе аргумента от значения х = 3 к значению х = 3,1.
684. Найти приближенно приращение функции у — In (х2 1).
при переходе аргумента хот значения х = 3 к значению х = 3,02.
685. Дана функция f (х) = j/3x'- 4. Найти приближенное
значение этой функции прн х = 2,16.
чение этой функции при х = 4,175.
687. Вычислить приближенно: а) 1,013; б) 0,983; в) -р^;
г) 1,012й; д) 0,9983; е) 0,97е.
688. Вычислить приближенно: а) 1,04 3; б) ; в) -рд^-;
г) 1,0064
689. Вычислить приближенно: а) 7/ 1,042; б) ^0,984. в) .
690. Зная, что 1п25 = 3,2189, найти приближенно: а) In25,02;
б) In 24,6.
691*. Зная, что In 50 = 3,9120, найти приближенное значение
функции / (х) = In Iхх-3 —j - 1 при х = 7,02.
692. Найти приближенно: a) In 1,024; б) 1п0,98; в) In 1,148;
г) In 0,976; д) In 0,96. _____ ____________________
693. Найти приближенно: а) In (/'0,997; б) In 1,02е; в) In 7/0,996;
г) 1111/1,04; д) 1п|/1,06.
442
Кривизна кривой. Радиус кривизны (к § 96—98)
694. Найти кривизну параболы у = х1 — 2х в точке, абсцисса
которой равна 1.
695. Найти радиус кривизны кривой у = хл-\-х*— 4 в точке,
абсцисса которой равна 0.
696. Найти радиус кривизны равносторонней гиперболы
ху = 96 в точке, ордината которой равна —24.
697. Найти кривизну кривой у = sinx в точке, абсцисса кото-
рой равна: 1) 2) у.
698. Найти радиус кривизны параболы х^ — Ъру в точке, аб-
сцисса которой равна: 1) х0; 2) 0.
699*. Найти радиус кривизны параболы //3 = 2рх: 1) в точке
; р\; 2) в начале координат.
' “ v2 „2
766*. Найти радиус кривизны гиперболы —^_=\: 1)в лю-
бой точке; 2) в точке (а; 0).
761. Найти радиус кривизны эллипса /Лх3-}-сРу1 — d№\ 1) в лю-
бой его точке; 2) в точке (а\ 0); 3) в точке (0; &).
Смешанные задачи в гл. IX
702. Найти дифференциалы функций: 1) у — Их'2 — а3-|-
a-arcsin 4-; 2) у = In (х-|- l-'x" + <
703. Найти производные от у по
,. 3at 3at2
1) * = T+F: y = VW’ '
2) x=t—у = / +
704. Найти дифференциалы второго порядка: 1) у=In cos ах;
2) f/ = esinnt.
705. Найти приближенно приращение функции f (х) = у
при переходе аргумента от значения х = 3 к значению Xi = 3,2.
706. Найти приближенное значение функции
/(Х)=]^Т+Т ПРИ х =°2-
707. Составить уравнение касательной и нормали к эллипсу
х —4 cos ср, у —2 sin <р при ср = 22.
708. Найти радиус кривизны кривой a‘2y = xt в точке (а; а).
709. Найти кривизну параболы у2 = 8х в точке 3^. '
710. Найти радиус кривизны кривой z/=tgx в точке 1).
443
3. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Непосредственное интегрирование по формулам (к § 100—102)
711. Проверить дифференцированием результат интегриро-
вания:
1) §(2cosx4~ 1) = 2 sin хх —|—С;
2) sin3xdx = -^cos3x-|-C;
3) $(3х2 + 2х+ l)dx = x3-f-x9 + x4-C.
Проверка. 1) (2 sin х-|-* +Qi = 2 cos х-|-1.
Интегрирование выполнено верно;
2) cos Зх -L- С\ . = у (cos Зх)х = у (— sin Зх) • 3 4 sin Зх.
Интегрирование выполнено неверно;
3) (х3 + х9 + х + С)1-= ЗхЧ-2х + 1.
Интегрирование выполнено верно.
Проверить дифференцированием 1 результат интегрирования:
712. 1) x3dx=^x4-|-C; 2) Kxdx = -|]/х3-|-С';
3) 4) j|/ra-=f/xs+c.
713. 1) j (г’-Зх‘Ч-1-1)йх=1х4-х3-1 + ^ + С;
2) ? (2х3 — х- 4- Л — — dx = J-х4 — 4- х3-!— 4 Inх-ф С.
7 J \ x~ x] 2 3 л 1
714. 1) f + ' z
J Л- -I- ar
2) (xJ-fl)sdx = |(x + tz)c + C. .
715. 1) -^^5 — In 1Лх2-L-й2-}- C; 2) ctgxdx = lnsinx-j- C.
Найти интегралы:
716. (jx'dx. 717. 5x'“ dx.
718. J(x9H-3x4-2)dx. 719.. $ (x4 — x3 + x2 -•)- 2x — 3) dx.
720. (2x3 — Зх2 -ф- 2x — 3) dx.
72i*. §-3-. 722.
723. J 724*. *4~2x2 + 3A'+Adx.
725. t Л'5 ~Л'32v + 7 dx. 726*. $x 4dx. .
444.
727*. (4х— Зх 2 4- 2) dx.
728. $ (2х2 — Зх'4- 2 -4 х'1 — х2) dx.
729*
730. U&-^+rx + ^dx-
731. J (x3-|-2x-4 l)x2dx. 732. $ (x2-L3)2dx.
733. 1 C - 3x2 + 2x - 3 , * 734. \ 5 dx. J x3
735. f (^—^dx. J X~ 736*. x^ dx.
737. \ (x1 — x? 4- -V + 2) dx. 738. (x2 — a'1] dx.
739*. \УхЧх. 740. $ (Ух2 — Ух -|-2) dx.
741* e dx ' J Ух' 742-
743. 5 (У\х -4 2) (Ух—3) dx. 744. \ dx . J Ух
745. f xa + Зх — 2 . 1 —4—= dx. J Vх'1 746*. <\.-^+^Ldx. J x 4- a
747. p ’x3-5x + 6 J ,v — 3 ах. x 748. f ~-l ~ a-^dx. J p x — У a
749. C У F — 1 , \ r—r= dx. ' J/x-l 750. [(Уах — VbydX.
751. Доказать справедливость . формул: 1) ax dx =^-|-
Найти интегралы:
752. $(2v + e* — 3) dx. 753*. J(3V)dx.
^54. \aVdx. 755*. \ ~dx. J ex
756. C* pX ( 4s dx. 757*. ynv+l)(ev—l)rfx.
758* . Доказать справедливость формул:
1) sin xdx =— cosx-{-С; 2) Jcosxdx = sinx-|-C;
3) \ ^4- = tgx4-C; COSJ X C i » 4) $ &= — ctg'x + C-
Найти интегралы: 7Я0* _ { (7i me y — h Qin Hy 760 t f a -J-cnsr'l
J \cos2x sinJx 1 J
445
761. с 1 4- cos- х , С 1 — 2 sin2 х , \ —, dx. 762. \ — dx. J COS“ X J Б1П"Х
763. (* sin Зх -4- sin x , . C cos x — cos 3x , , \ r-4 dx. 764. \ —5 dx. j sin 2x A sin 2x
765. Доказать справедливость формул:
1) jj tgxdx — — In cosx 2) ctgxdx — ln sinx-j-C.
Найти интегралы:
766*. Utgx + ctgx-Д-Д dx.
767*. C sin2 x — 2 sin x cos x 4- 3 c J sin x !OSX , — dx.
768. C cos3 x + 2 cos2 x sin x j cos;i X
769. C (sin x +cosx3) J cos^x 770. ^4sec2xdx.
771. j i a cosec2xdx. 772*. $tg'2xdx.
773*. $ ctg- x dx. 774. jj (1 Д-tg x)2 dx.
775. 1 t (1—ctg x)2dx.
776. Доказать справедливость формул:
1) \ = arcs in х Д- С;
«' у 1 — х3
2) гдтп = arctg х + С'
Найти интегралы:
. С /1 — х2 + 1 , ,х С 3 4- х2 ,
777• а) J у i _ Л-з dx’ б) J 1 н- X2 4х-
Определение произвольной постоянной интегрирования
по начальным условиям (к § 103)
778. Найти функцию, производная которой равна 4х — 3,
зная, что при х = 2 эта функция принимает значение, равное 10.
779. Написать уравнение кривой, проходящей через точку
(0; —2), если угловой коэффициент касательной в любой ее точке
(х; у) равен 2х—1.
780. Полагая, что при s = 0 t — 0, найти выражение пути s
в зависимости от времени t, если скорость равна: 1) постоянной
величине г>0; 2) m-^-nt-, 3) 3 — 2t — ЗУ2.
781. Найти расстояние, которое пройдет в t сек тело, брошен-
ное вертикально вниз с начальной скоростью 30 м)сек.
782. Из точки, находящейся на высоте 18 м над уровнем
Земли, брошена вертикально вверх пуля с начальной скоростью
30 м[сек. Пренебрегая сопротивлением воздуха, найти: 1) высоту,
446
на которой будет находиться пуля в момент /; 2) момент, когда
пуля начнет падать вниз; 3) наибольшую высоту, до которой под-
нимется пуля.
783. Найти уравнение кривой, проходящей через точку (4; 4),
• если угловой коэффициент касательной к кривой в точке (х; у)
равен
784. Найти функцию, производная которой равна sin2x-j—
-}-cos2x, зная, что при х=~ эта функция равна
785. Написать уравнение и построить график функции, про-
изводная которой равна —2х-!-2, зная, что при х = 0 эта функ-
ция принимает значение, равное 8.
, 786. Из семейства кривых у=^(3х*— 4x)dx выделить ту,
которая проходит: 1) через начало координат; 2) через точку (1; —2).
787. Скорость v движения материальной точки в момент t
, определяется по формуле v = (3t1 — 4t-'r4) м/сек. Найти закон
движения, если известно, что за время / = 2 сек точка прошла
путь, равный 8 м.
788. Поезд движется со скоростью о = (/3—5/2 —|—50) км/ч
и находится от станции в начальный момент (при 1 — 0) на рас-
стоянии 5 км. Найти уравнение движения относительно станции.
Интегрирование способом подстановки (к § 104)
Найти : интегралы:
789*. V 1 -j- х3 • Зх2 dx. 790. $ (axby-adx.
791. l)3-3dx. 792. $ (x‘4- l)3- 4x3dx.
793. (’ 3,t2 (lx 794. (• 3x3 dx
J a- -|- ,v!' J /a34-x3
795. Г 3x3 dx 796. r 4x3 dx
J (<23 -|- A"1)" ’ J 14-x4‘
797.
798. (ax3 -ф- bx c)3 (2ax -j- b) dx.
799. \(x — 2.C)3(1— 4x)'dx.
800*. (ax3 -j- b)1 x dx. 801*. У x4 4~ 1 x3 dx.
802. L «л. 4/ v J ax' 4- b' 803. V 3x -j- a dx.
804. C dx j x 4- a ‘ 805. C dx • z J (* + <
806. f dx 807*. C x dx
I l/'-v + a J a1 — x3 ’
447
808*. § (ax2 2bx 4- c)4 (ax 4- b) dx.
809. f (Уа+Ух/^. J Vx 810. 0 dx J /a(1+/x)3.
811. 812. C f 2x 1 \ , \ \~—Г— ~гт dx. \x 1 x “H 1 / c / 1 1_ И/х(1+/л) /да- -V~x\ ) dx.
813. C hr1 .v dx ' x 814. In2 (x2 4-а2)
815. С 3a‘ dx 816- C fl — IV —
J yxs + ^ Г(№ J ’-v 818. Доказать справедливость J \ x J X ’4 C a11 формул: 1). \ a" du = ^-4-C;
2) err du— e“-j-С. Вычислить интегралы: 819. §a2Adx. 820*. § e3x2+GA +5 (x -f-1) dx.
Л 821*. $ bax~xdx. 822. $ eax'rb dx.
823. J (e2A — e“2A) dx. 824. $(eM4- ye2xdx.
825. V dix -|- 1 dx. 826. $ (amx — bnx) dx.
827. ak' bkx dx. 828. C ex — e~x , \ r - dx.
829. ? (ev — е~хУ dx. J V ел + e A
830. Проверить справедливость формул:
1) sin udu —— cosu-\-C; 2) jj cos и du — sin и C;
3) = tgu-{~C; 4) ^44— =— ctgu-l-C.
' J cos2 и Ь 1 J Sin" и b
831. Доказать справедливость формул:
1) ^tgada =— ln|cosu|4~C; 2) J ctg и du = In |fsin и | -j- C.
Вычислить интегралы:
832*. $ cos 3xdx. 833. f dx
j cos2 dx ‘
834*. (’ № dx J sin2 x3 ‘ 835. sinaxdx.
836. f dx 837. J sin (4x4- 7) dx.
J sin2 3x '
838. cos (5x— 7) dx. 839. J sin (ax2) x dx.
840. cos (4xJ) x- dx. 841. \ ctg j dx.
448
842. \ [cos у — sin3xj dx.
843. \ sin I 4^-I dt. P
844. COs3^-X
845. $(sinx-|-cosx)2dx. 846. о \ / C / . x xV , к (sinу — cos у 1 dx.
847*. $ (tg ax-}-ctg ax^dx. 848*. sin2 у dx.
849. $sin22xdx. 850. §cos2axdx.
851. jj sin4xcosxeta. 852. i‘ , •> dx \ tg3X j— .
J & COSJ X
853. § sin2 ax cos ax dx. 854*. C cos x 4- sin x j J sin x — cos.v C 1 4- cos c , \ i : j co -j- Sin □ *
855. Jj У 1 -j-sinxcosxdx. 856.
857. ^e’invcosxdx. 858. a} +sin? cos у d'o. f cos x dx
859. \ у/ cos21? sin © d<p; 860.
J sirf1 x
861*. cos3 ? dp. 862. J cos8xdx.
863. $ sin3xdx. 864. §sin”&xdx.
865*. C dx 866*. (• dx
J i 4- 4.e • У У 1 - 9x3 ’
867. f x dx 868*. ex dx
J 1 + x1 ‘
869. (* dx 870*. dx
J 1 4- 25xa ‘ J a- x3 ‘
871. C dx 872*. (* dx
J 25 + x3 ’ J У a2 - X3 ‘
873. {• dx 874. C dx
J У5 - x3 ‘ J 7 4- 4x3 •
875. C dx 876. С -v3 dx
J /3 - 2x3 J У У — b~x1'
877. f 3dx 878. C dx
J У 2 - Зх3 ‘ J a’- 4- (2x 4- ЬУ
879. (* dx 880*. f dx
J У a2 - (x - by ‘ j 2 4- 2x 4- x3 ’
881. (“ dx 882*. f dx
J 13 4-6x + x3‘ J Уз — 2x — x3
883*. f dx 884. J* cos xdx
J хУ1 — 1113 X 1 J a- 4- sin3 x ‘
15 п. E. Агачев 449
885*. ctg:l kxdx.
887. sin9— cos2-?- d'f.
886*. cos'1 xdx.*
888. t -j—^Цг-.
J 1 — COS
Смешанные задачи к гл. X
Найти интегралы:
889. /3 2 i \2x + 1 Зл- - 1 dX. 4x4-8/
890. ' f b\i dx 891. ’ k cos ax — sin ax .
! a J —т. ( dx.
1 \ X~ ] x3 • 3 sin ax -f- cos ax
892. ; v.+c^dx. } sin- ax 893. C Vfl + />tg2x J cos2 2x
894. :(1+in^ dx. ) x 895. cos2^ dx.
896. tg2 ax dx. 897. ) [sin2 2kxdx.
898. i cosdysin dx. 899. Г ctg7-KJ dx. J Kx
C cos3 a t/"x
900. x31/ a4 Д- x4 dx. 901. zr-„ dx.
J V X-
902. \ tg3 (3x2) x dx.
903. Доказать справедливость формул:
1) £ —=^==- = arcsin и Д-С; 2) — arctgи + С.
J у 1 — и- а 1 т
Найти интегралы:
dx
1 — cos х '
ех dx
рДб^72-2'
cos 2tp dy
(sin <f + cos tp)2 '
905.
ex dx
a be“x '
K1 + tg?
COS"’ (p
d'f.
dx
tg x cos2 x ‘
910. Jy4(sin ax -f- cos ax)9 cos 2ax dx.
C cos2x , ( ni'i'T‘xilx
911. \ —j— dx. 912. —
J cos2x J j/x2-|-l
C sin.2x</x
9 ' a2-p &2 sin2 x’
914. $ 62sin2xsin2x,dx.
450
Hl a. \ ,---ГГ-Г.
J a (1 + cos 2x)
916. Найти функцию, производная которой равна — 2"~V’
зная, что при х= 1 эта функция обращается в нуль.
917. Написать уравнение кривой, проходящей через начало
координат, зная, что угловой коэффициент касательной в любой
ее точке (х; у) равен cos 2х.
Найти интегралы:
918' § sin3 <р sin1'? dx>.
920.
921. Vesin ах 4- 1 esin ах cos ах dx.
922. р sin х cos х dx 923. C sin x dx
J )/cos-’ x— sin-’ x j У a cos x + b
924. § sin‘xdx. 925. (tg2x4-tg4x) dx
926*. (“ dx 927. C dx
j sin 2x ’ J, sin3 x cos3 x ‘
928. \ cos4ydx. 929. §sinsaxdt.
930. Найти функцию, производная которой равна зес22хЦ-
-ф- cosec2 2х, зная, что при х = -^- эта функция обращается в нуль.
931. В момент t скорость точки, движущейся по оси Ох, равна
V — у cos ~ (где Т — некоторая постоянная величина). Найти
уравнение движения точки, если известно, что в момент 1 = 0
она находилась в начале координат.
Найти интегралы:
932. . § ctg1 axdx. 933. dx=. J У 1 -x3
934*. У sin22x cos2 2xdx. no_ Г <?ч1п 2jtcos 2x dx УоЭ • 1 —г .
J У 1 + 3esin2-v
936. C dx J 5 4x + 4x3 ‘ S37. ((/+1 x3+[)dX.
938. J V :±>- 939- 5 V !+>
940. f x3 + 4 , \ a 1 dx. 941. [^-^dx.
J x + 1 J x + 1
942. dx
V‘2x-xl
15‘
451
Определенный интеграл (к § 105—108, 111, 113—116)
Вычислить определенные интегралы:
з
943. \&х^х.
.2
Решение. По формуле (1а) находим:
з з
§ Wdx = 6 хЧх = 6 ~ = 2ха£ = 2 • З3 - 2 • 23 = 38.
2 2
944. $ (а3х — xs) dx.
о
Решение.
а а а
( (сгх— x3)dx — a3 xdx— ( x3dx = a1 |а — 4Г =
j J 2 |о 4 |о
о оо-
л
4 а 2" — 3
945. (4^. 946. . 947. 1) ( cosxdx; 2*И —.
4 7 2 -
948. ? Л-. 949. \ sin xdx. 950. \exdx.
3 COS- X J J
It
."2 '9 3
95!. 952. \Vxdx. 953. \¥~xldx.
£ Sin'x О и
4
.к 2
954. (1 -|-*2 + *4) dx. 955. $ (x2 — 2x -|- 3) dx.
и и
ь з '
956. $(x3 — \)dx. 957. J (x3 — 3x2 — x-\- l)dx.
a
/3 — e —
9E8. 1) 2) 3) \
1 1 ~Г Л J Л «V
Гз
3
959. Вычислить площадь, ограниченную прямыми y=2x-\-S,
х=1, х = 3 и осью Ох.
452
960. Вычислить площадь, ограниченную кривой у = х^—:2х-|-3,
прямыми х =—-1, х — 2 и осью Ох.
Решение. Определяем площадь фигуры (на рис. 207 она
заштрихована) интегрированием:
S = § (х1 — 2x-}-3)dx =
-1
2 2 2
= $ х9 dx — 2 $ х dx -|- 3 jj dx =
-[29-(-1Г1 + 3(2 + 1) =
= |(8+l)-(4-l)-|-3-3 = 9/се. ед.
Рис. 207
961. Вычислить площадь, ограниченную кривой у — 9 — х9 и
осью Ох.
Решение. Определив точки пересечения кривой с осью Ох,
находим пределы интегрирования: а — — 3, 6 = 3. Так как фи-
гура симметрична относительно оси Оу
(рис. 208), то площадь ее будет равна удво-
енной площади фигуры ОАВ:
з
з
S = 2 (9 —x3)dx = 2-9 dx — 2 x9cfx =
О 0 0
= 18ХГ — |х3|3 =
|о з |о
' = 18 (3 — 0) — | (З3 - 0) = 36 кв. ед.
962. Вычислить площадь фигуры, ограниченной линиями // =
= — уХ-)-4, х = 0; х=4, // = 0.
Примечание. Решение данной и нижеследующих задач надо
начинать с построения чертежа.
963. Вычислить площадь фигуры, ограниченной кривой у — х2,
осью Ох и прямыми х=1, х = 3.
964. * Вычислить площадь, ограниченную кривой у = 4х— х*
и осью Ох.
965. Вычислить площадь фигуры, ограниченной графиком
функции z/ = sinx и осью Ох от х = 0 до х='.
966. Вычислить площадь фигуры, ограниченной линиями if—
= 4х, х — 4.
967. Вычислить площадь фигуры, ограниченной кривой // =
= 4х9 — х3 и осью Ох.
453
968. Вычислить площадь фигуры, ограниченной линиями ху—4,
у = 0, х — 1,. х — е.
969. Вычислить площадь фигуры, ограниченной линиями у —
= 4 — х2, у = х-ф2.
Решение. Требуется определить площадь фигуры, ограни-
ченной сверху кривой у = 4 — х\ а снизу прямой (рис. 209).
Площадь фигуры, очевидно, равна Sabkl— Sakl- Совместным ре-
шением двух уравнений найдем пределы интегрирования: a — Xi—
-— 2, b = Xi=l. Получим
S — Sahkl — Sakl —
i i
=' \ (4 — x2) dx — \ (x 2) dx =
-2 —2
= 4[l-(-2)]-l[l-(-2)3l-
_l[l-(-2)2]-2[l-(-2)] = 4-3-
— у • 9 — 4 (—3) — 2 •3 = 4,5 кв. ед.
970. Вычислить площадь, ограниченную параболами у2 — 2рх,
х2 = 2ру.
971. Вычислить площадь, ограниченную кривой у — х2 и
прямой y = x-j-2.
972. Вычислить площадь фигуры, ограниченной кривыми
у = х2, у = 8 — х2.
973. Найти площадь фигуры, ограниченной параболой х2—
— 9у = 0 и прямой х — Зу6 = 0.
974. Найти площадь, ограниченную линиями у — х3, у—2х.
975. Вычислить площадь, ограниченную полукубической пара-
болой у2 = х' и прямой у = 2х.
976. Вычислить площадь, ограниченную параболой у2 = 4х и
прямыми у — х, у — 2х.
977. Вычислить площадь фигуры, ограниченной параболой
у — х2 и прямыми у = 4, у— 1.
978. Тело движется прямолинейно со скоростью и = (3/2-|-
-ф- 3/) MfceK. Какой путь пройдет это тело за промежуток времени
gt момента ti = 2 сек до момента Л> = 4 сек?
979. Двигаясь прямолинейно и равноускоренно, тело за 10 сек
увеличило свою скорость с 4 до 12 м)сек. С каким ускорением
двигалось это тело? ' На какое расстояние оно передвинулось за
это время?
980. С аэростата, находящегося от поверхности Земли на
расстоянии 196 м, брошено вертикальнои вниз ядро со ско-
454
ростью 14,7 м/сек. Через сколько секунд это ядро упадет па
Землю?
981. Кусок льда брошен по гладкой ледяной поверхности
со скоростью 12 м/сек. Сколько времени будет двигаться кусок
льда до остановки, если ускорение при этом движении будет
равно — 0,6 м/сек1? Какой путь он за это время пройдет?
982. В момент, когда скорость была равна 43,2 км/ч, поезд
был заторможен и двигался дальше с ускорением, равным
— 0,4 м/сек1. Через сколько времени поезд остановился? Какой
путь он покрыл за время торможения?
983. Автомашина при движении со скоростью 36 км/ч оста-
навливается торможением в течение 2 сек. Какое ускорение со-
общают автомобилю тормоза? Какое расстояние он пробегает до
остановки?
984. Поезд, достигнув скорости 57,6 км/ч, стал двигаться
равнозамедленно с ускорением — 0,4 м/сек1. Через сколько времени
поезд остановился? Какой путь он пройдет до остановки?
Вычислить определенные интегралы:
985. $]/2л'2— 1 xdx.
о
Решение. Этот интеграл вычислим способом подстановки.
Положим 2^ 4-1— и. Тогда 4xdx = du, xdx — ~. Числа 0 и 2
были границами изменения переменной интегрирования х. Если
мы за переменную интегрирования принимаем и, то пределы
интегрирования (гРаниЦы изменения и) будут уже другие. Нижний
предел интегрирования и\ будет соответствовать нижней границе
Изменения х, а верхний — верхней границе изменения х, так
что при u = 2x24- 1
Ul = 2-О24- 1 = 1; ц2 = 2-224- 1=9;
2 //о 9 j а
V 2х24- lxdx=^]fu-~-=-^ u2du—~ • и2 |'^=
В данном случае вычисление можно было вести и иначе:
2 2 !
; V2x!-{-ixdx = | J (2.4 4- 1р 4xdx =
Ь и
2
2 2
(2-i-3 + l)7
_3
2 0
0
(24-j- 1)2 d(2xa+D = |
О
(^+1Ц| =44=44-
455
986. (-7^==-.
J р З - 2л
о
Решение.
3 — 2х = и; — 2dx - dir, dx
du
T’
u1==3—2-0 = 3; u2=3 —2-1=1-,
tg3 Л ,
-b-г- dx
COS- X
990.
992.
993.
3 4
C sin x dx , f о ,
\ —j— . 994. \ cos2 x dx.
J cosJ x 5
•K
995. [Var — x'dx.
о
Решение. Этот интеграл берется легко при помощи триго-
нометрической подстановки: x = «sincp. Тогда dx = acos <р d<p. При
x = 0 имеем 0 = asin<p, <pi = 0. При x = a имеем a = a sin <p,
sin <p= 1, <p.2 = ^-. Новыми пределами интегрирования, следова-
тельно, будут: <pi = 0, <р2 = у.
а ________ <р2
1/Ла'2 — х2 dx = § Vа1 — аг sin3 <р a cos <pd<p =
0 fi
Я . я
"2 _____________ 2"
= $ ]Ла2 (1 — sin2 ср) a cos ср dy — $ a 1 — sin2 ср a cos <р tty =
и 0
Я Я - Л л
7 1 "2 "2
о С « , qf 1 4-cos2<p , а’ С , । а2 С , а"п
= а* \ cos2 ср dtp = а2 \ —Ц,—- dtp — -? \ d<p \ cos 2ср d<p = .
и 0 о о
456
д
d х
з •
(a2 + .v2)f
о
Решение. Этот интеграл берется тоже тригонометрической'
подстановкой, при этом подстановка делается с таким расчетом,
чтобы знаменатель подынтегрального выражения стал рациональ-
ным. Положим х = а tg <р; тогда
. з. _з
dx = ^, (a* + x*)2 = (a* + a3tg2<p)2 =
2
= [а? (1 tg2 tp)]2 = а:| sec3 ®.
При x = 0 имеем O = atg<p, <pi = 0; при x = a находим:
a = atg<?, tg®=l, <p-2=j;
a _
1001.
о
v3
1002. Вычислить площадь эллипса =
Указание. Эллипс симметричен относительно осей коорди-
нат, вследствие чего площадь S эллипса будет равна 4S0AB. Пре-
делами интегрирования при вычисле-
нии заштрихованной площади будут
О и а (рис. 210). Решив уравнение
эллипса относительно у, получим:
У — ^ /а^'х5;
S=4? -Vdl—x2dx=^Ka2—x2dx,
о '>
откуда S = itab,
457
1003. Найти интегрированием площадь-круга: х2-\~у2 = г2.
Найти площадь фигуры, ограниченной кривой у=-г^-
и прямыми х — — а. х —а. а
1004.
осью Ох
1005. Найти площадь фигуры, ограниченной кривой у —
— 4^^?, осью Ох и прямой х = 4.
1006. * Вычислить площадь круга, пользуясь параметрически-
ми уравнениями ограничивающей его окружности x = rcos<p,
у — г sin tp.
1007. Вычислить площадь эллипса, пользуясь его параметри-
ческими уравнениями: x=acos<p, y = bsin<p.
1008. * Вычислить площадь фигуры, ограниченной кривой
y = cosx и осью Ох от х = 0 до х = 2л.
1009. Вычислить площадь фигуры, ограниченной кривой у =
= х2— 4х, осью Ох и прямыми х =— 2, х = 6,
1010. Найти площадь, ограниченную кривой у~х:‘— 4х и
осью Ох.
1011. Найти площадь, ограниченную кривой y = и осью
Ох от х =— 2 до х = 2.
1012. Вычислить объем тела, полученного от вращения эллипса
^4-рГ = 1 вокруг оси Ох.
a- й2
Решение. Из уравнения эллипса находим у2 = -^.(а2— х2).
Крайними, точками эллипса будут х = — а, х — а. По формуле (8)
л,1 получим
' а
в V = л (а2 — х2) dx.
s'" ( \ -а
Вследствие симметричности эллип-
——Г7‘:—i— 3^7—са относительно оси Оу данное тело
Х/""-—"Д-----/------ (эллипсоид вращения) разделится
плоскостью О АВ (рис. 211), проходя-
щей через начало координат перпен-
рис. 211 дикулярно оси Ох, на две равные
части. Поэтому объем его V будет
равен удвоенному объем}' тела, полученного от вращения поло-
вины эллипса, расположенной вправо от оси Оу. Следовательно,
V = п (<г — dx — 2r. (а2 — х2) dx =
— а 0
а
— § (а2 — х2) dx = ~ nab2.
о '
1013. Найти интегрированием объем тела (шара), полученного
от вращения окружности ,х2 -|- у2 — г2 вокруг оси Ох.
458
1014. Найти объем тела (параболоида вращения), полученного
от вращения параболы у^ = 2рх вокруг оси Ох от х = 0 до
х=2р.
1015. Найти объем тела, полученного от вращения вокруг оси
Ох фигуры, ограниченной параболой х1 — 4ау, осью Ох и прямыми
х — — а, х = а.
1016. Найти объем тела, полученного от вращения гиперболы
— ~2 = 1 вокруг оси Ох от х = — а л.0 х = а.
Примечание. Такое тело называется гиперболоидом вра-
щения.
1017. Вычислить объем тела, полученного от вращения во-
круг оси Ох фигуры, ограниченной параболой у = 2х — х1
и осью Ох.
1018. Вычислить объем тела, полученного от вращения вокруг
оси Ох синусоиды у = sinx от х = 0 до х = 2г..
1019. Найти объем тела, полученного от вращения полуку-
бической параболы у* = х* вокруг оси Ох от х = 0 до х — а.
1020. Вычислить объем тела, полученного от вращения вокруг
оси Ох фигуры, ограниченной кубической параболой у — х' — 4х
и осью Ох.
1021 *. Вычислить интегрированием объем конуса, радиус
основания которого равняется R, а высота Н.
1022 *. Вычислить объем тела, полученного от вращения во-
круг оси Ох фигуры, ограниченной параболой t/ = 6 — ха и пря-
мой у = 2..
1023 *. Вывести формулу объема усеченного конуса, радиусы
оснований которого равны R и г, а высота И.
1024. Вычислить работу, которую надо затратить для того,
чтобы выкачать воду, наполняющую ци-
линдрический резервуар, высота которого
И = 5 м, а радиус основания R = 3m.
Решение. Представим себе воду,
наполняющую резервуар, состоящей из
тонких горизонтальных слоев, один из
которых изображен на рис. 212. Величи-
на работы, необходимой для поднятия
этого слоя воды, как известно, будет рав-
на произведению веса воды на высоту
поднятия.
Обозначим через х глубину слоя, че-
рез Дх — его толщину. Тогда объем слоя
будет равен r.R2\x вес воды слоя 1000т: R2 Дх кг (1 м3 весит
1000 кГ), а работа, необходимая для поднятия этой воды на вы-
соту х, равна 1000г/?2Дх-х кГм.
Работа, затрачиваемая на выкачивание всей воды из резер-
вуара, явится пределом суммы таких слагаемых, когда Дх->0
459
и х изменяется от 0 до А/:
к " F
lim V 1000~/?'2 хДх = \ 1000я/?2хг/х = 1000л:/?2 \ х dx =
--I'-' о и
= 1000л/?2 • $ \н = 1000 • 3,14 • З2 353 250 кГм.
2 |о 2
1025. Вычислить работу, которую надо затратить для того,
чтобы выкачать воду из резервуара прямоугольной формы, если
высота его равна 2 м, а основанием служит квадрат со сторо-
ной 4 м.
1026 *. Вычислить работу, которую необходимо затратить,
чтобы выкачать воду, наполняющую котел, имеющий форму полу-
шария, радиус которого равен 0,6 м.
1027 *. Вычислить работу, которую надо затратить, чтобы
выкачать воду из резервуара, имеющего форму конуса, обращен-
ного вершиной вниз, высота которого И м, а радиус основания
равен 7? ль
1028. Найти силу давления, испытываемого плотиной, имею-
щей форму трапеции, основания которой равны 40 и 16 м, а вы-
сота равна 8 м. Верхнее основание плотины лежит на поверх-
ности воды.
Решение. Представим себе площадь данной трапеции
(рис. 213), разбитой на узкие полоски, параллельные ее осно-
ванию. Пусть МК будет
одной из таких полосок,
находящейся на расстоя-
нии х от поверхности
воды. Вследствие малости
ширины Дх эту .полоску
можно принять за прямо-
угольник, а площадь ее
считать приближенно рав-
ной МЛ'Дх. Тогда дав-
1ет приближенно равно
ДР = i - МК • Дх-х.
Принимая во внимание, что вес одного кубического метра
воды равен одной тонне, последнюю формулу применительно
к данному случаю можно переписать в следующем виде (у — 1):
ДР = Л4/<-хДх.
Остается выразить МК в зависимости от данных и глубины х.
Из подобия треугольников АВС и MCF найдем:
ЕМ СЕ . FM _ 8 - х .
АВ CD’ 40 -16 8 '
FM = 3 (8 — х) = 24 — Зх,
МК = 16 + FM — 16 (24 — Зх) — 40 — Зх.
400
Тогда
Др = (40 — Зх)хДх. (а)
Давление, испытываемое всей плотиной, будет пределом суммы
слагаемых вида (а), когда Дх->0 т. е.
8 .8
Р = lim V(40— Зх)хДх=^(40— 3x)xdx =
Дл-0 о о '
8 8
= 40 {xdx — 3 t х2 dx = 40 ’X-18 — х318 = 768.
2 о о
о и
Ответ. Р = 768 т.
1029. Вычислить давление, испытываемое вертикальным прямо-
угольным затвором шлюза, имеющим 10 xi в ширину и 6 м в глу-
бину, если его верхняя грань лежит на поверхности воды.
1030. Вычислить давление на нижнюю половину затвора шлюза
по данным предыдущей задачи.
1031. Вычислить силу давления на одну сторону прямоуголь-
ной пластинки с основанием 8 см и высотой 12 см, погруженной
в воду вертикально так, что верхнее основание находится на
5 см ниже поверхности воды.
1032. Вычислить давление, испытываемое треугольником, вы-
сота которого равна h см, а основание b см, если он погружен
в воду так, что основание его лежит на поверхности воды,
а высота направлена вертикально вниз.
1033. Найти давление, испытываемое плоскостью полукруга,
погруженного в воду вертикально, если его радиус равен 5 см,
а диаметр лежит на свободной поверхности воды.
1034. Вычислить давление ртути, наполняющей стакан, на
боковую поверхность этого стакана, если высота его // = 8 см,
радиус основания R — 3,5 см, удельный вес ртути равен 13,6.
Смешанные задачи к гл. XI
Вычислить определенные интегралы:
1 1035. $/1— xdx. 0 п .4 1037. Jcos2xdx. 0 тс 7 1039. §cos3xdx. о ь 1036. ( + dx. J ах2 + Ьх + с а I Р х dx 1038. 3 у 1 * 0 1 1040. J/1— x*dx.
461
1041. Вычислить площадь фигуры, ограниченной линиями
у- = 8х, х — 2, х — 8.
1042. Вычислить площадь фигуры, ограниченной кривой
у — 2х1 -}- хл и осью Ох.
1043. Вычислить площадь фигуры, ограниченной линиями
ху — ^, у = 0, х = е, х = е\
1044. Вычислить площадь фигуры, ограниченной параболами
у°- = ах, х^ — ау.
1045. Вычислить площадь фигуры, ограниченной кривыми
у = х’ 1, у = — х1 + 9.
1046. Вычислить площадь фигуры, ограниченной линиями
у = хл, у = 4х. •
1047. Вычислить площадь фигуры, ограниченной кривой
у = ~хл и прямой у — х.
1048. Тело движется прямолинейно со скоростью v —
= (2^-ф-3) м'[Сек. За сколько секунд оно пройдет путь 88 м, если
S0 = 0?
1049. В момент, когда скорость была равна 36 км/ч, автомо-
биль затормозил и дальше он двигался с ускорением — 0,5 м!секг.
Определить путь, пройденный автомобилем за промежуток вре-
мени от момента 6 = 2 сек до момента 6 = 6 сек.
1050. Вычислить площадь фигуры, ограниченной линиями
у —sinx, у = 0 в промежутке (0; 2к).
1051. Найти площадь фигуры, ограниченной кривой у —
= 3х-— х3, осью Ох и прямыми х = — 3, х = 3.
1052. Найти объем тела (параболоида вращения), получен-
ного от вращения параболы х- — 2ру вокруг оси Оу от у = 0
до у = 2р.
1053. Найти объем тела, полученного от вращения гиперболы
= 1 вокруг оси Оу от у =— b до у — Ь.
1054. Вычислить объем тела, полученного от вращения вокруг
оси Ох фигуры, ограниченной линиями у — е* -ф-е~х, у = 0-,
х —— а, х = а.
1055. Вычислить объем тела, образованного вращением фигуры,
ограниченной параболами у^ — 2рх и х1 = 2ру, вокруг оси Оу.
1056. Вычислить объем тела, полученного от вращения фигуры,
ограниченной линиями у1 — 4х и у — х, вокруг оси Ох.
1057 *. Вычислить давление, испытываемое полуэллипсом,
погруженным в воду вертикально так, что большая ось его ле-
жит на поверхности воды.
1058. Какую работу надо затратить, чтобы насыпать песок
в виде кучи конической формы, радиус основания которой 1,2 м,
а высота 1 м, если 1 л? песка весит 2000 кг (песок берется
с поверхности Земли).
462
Ь. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Уравнения с разделяющимися переменными (к § 116—117)
Q
1059. Показать, что У = ~ (I) является решением дифферен-
циального уравнения
г/4-хг/' = 0. (II)
Решение. Дифференцируя (I), находим
(HI)
Подставив (I) и (III) во (II), получаем тождество
1060. Показать, что у = С (х -]- 1) — 1 является интегралом
уравнения (х-|- 1) tf=y-\- 1.
1061. Показать, что z/ = sinx—1 -ф-Се~sin* является решением
, , , , sin 2х
дифференциального уравнения у у cos х — —у—.
Проинтегрировать следующие уравнения:
1062*. уdx — xdy = 0. 1063*. if — #ctgx = 0.
1064. x2 dx— y2dy = Q. 1065. x2 dy — y2dx = 0.
1066. (1 Ч-x2) — xy = 0. 1067. +
1068. 6ДД- ачуу’ = 0. 1069. ^ — ^{/ = 0.
1070. + ydy— x dx = °'
1071. (].-\-y)dx — (1—x)dy = 0.
1072*. (x2 - x2y) d/x 4- (y2 + xy2) = 0. 1073*. y’ - 2xy = 0.
1074. x2dyf-(y— a)dx = 0. 1075. if 2y tg 2x = 0.
1076. ex (1 + ey) dx + ey (1 ex) dy = 0.
1077. — e5[nxdx = 0.
1078. Vl—x2dy—VT^y:>dx = Q.
1079. (\-}-x2)dy — (14-y2)dx=,0.
1080. (1 -]- y2) dx —{- x dy = 0.
1081. cosxsinr/dz/ — cos у sin x dx = 0.
1082. ctgydx4-tgxdy = 0.
1083. sec2 у tg x dy -f- sec2 x tg у dx = 0.
463
Найти частные решения или частные
уравнений:
1084. ytf = p,
1085. у’ = у tgx,
1086. b*x— а-уу'~0,
1087. (1 -[-х2)г/' = 2х(£/+3), если
1088. sec2 a tg р 4~ sec2 р tg оф; = 0, если P = j
если
если
если
У = Р
У = 2
</ = 0
У = ~
интегралы следующих
при Л’=у.
при х = 0.
при х = — а.
при х = 0.
при а=£.
1
Задачи на составление дифференциальных уравнений
1089*. Найти уравнение семейства кривых, зная, что угловой
коэффициент касательной во всякой точке любой из кривых этого
семейства равен произведению координат, т. е. ху.
1090. Написать уравнение кривой, проходящей через точку
(0; 0), зная, что угловой коэффициент касательной в любой ее
точке равен у.
1091. Составить уравнение кривой, проходящей через точку
(а; 0), зная, что угловой коэффициент касательной в любой ее
Ь-х
точке равен
1092. Координаты точек некоторой кривой удовлетворяют урав-
нению (2х2—1)гД —4хг/ = 0. Составить уравнение этой кривой,
если известно, что она проходит через точку (1; 2).
1093. Найти уравнение кривой, проходящей через точку (0; —1),
если известно, что угловой коэффициент касательной во всякой
ее точке пропорционален квадрату ординаты этой точки-
1094*. Согласно закону Ньютона скорость охлаждения тела
в воздухе пропорциональна разности между температурой тела Т
и температурой воздуха а. Температура воздуха а = 20°. Известно,
что в течение 20 мин тело охлаждается от 100 до 60° С. Выра-
зить температуру Т охлаждающегося тела в зависимости от вре-
мени i.
1095. Замедляющее действие трения на диск, вращающийся
в жидкости, пропорционально угловой скорости ш. Выразить
угловую скорость ш в зависимости от времени /, если при 1 = 0
угловая скорость была равна ш0.
1096. Давление воздуха Р и высота к точки над урознем моря
связаны уравнением jj) = — kP, где k — постоянная.
Полагая, что Р = Рй при h — О, выразить давление воздуха
в зависимости от высоты h точки над уровнем моря.
1097*. Радий распадается со скоростью, пропорциональной
начальному его количеству. Если половина начального коли-
чества распадается за 1590 лет, то какой процент распадется
за 100 лет?
464
1098*. Некоторое вещество преобразуется в другое со ско-
ростью, пропорциональной количеству непреобразованного веще-
ства. Если количество первого по истечении 1 часа 31,4 г, а по
истечении 3 часов — 9,7 г, то сколько вещества было в начале
процесса?
1099. При определенных условиях размножения бактерий
число их нарастает со скоростью, которая в каждый момент про-
порциональна начальному числу бактерий. Выразить число бак-
терий у в зависимости от времени /, если у = у« при / = 0.
1100*. Тростниковый сахар в присутствии кислот разлагается
на составляющие' вещества. Скорость, с которой идет этот про-
цесс, пропорциональна массе неразложившегося сахара х. Пока-
зать, что x = Ce~kt. Что здесь означает С?
1101. Скорость, с которой вода вытекает из малого отверстия
на дне сосуда, пропорциональна корню квадратному из высоты
воды. Если половина количества воды вытекает из цилиндриче-
ского сосуда за 5 мин, то за какое время вытекает вся вода?
1102*. В резервуаре находится 100 л рассола, содержащего
10 кг растворенной соли. В резервуар со скоростью Зл в 1 мин
вливается вода и одновременно из него со скоростью 2 л в 1 мин
выливается рассол, причем концентрация поддерживается равно-
мерной. Сколько соли будет содержаться в смеси по истече-
нии 1 часа?
Однородные и линейные уравнения первого порядка (к § 118—119)
Проинтегрировать следующие дифференциальные уравнения:
1103. (х 4- у) dx 4- (у — x)dy = 0.
1104. (х— y)dx-[-xdy = 0.
,1105. xy'^dy— (хЛ-\- y")dx = 0.
1106. (x2-J-y2) dx — ‘Ixydy.
1107. (2]/'xy — y^ dx x dy — 0.
1108. y' + ^ = A. 1109. y' —
J 1 X X- J X
1110. tf-\-y=e~x. 1111. i/'-_^T = (x + l)3.
1112. s'sin2 cos/ = sin 2Л
Найти частные решения следующих уравнений:
1113. xy'-j-y^ 3, если у = 0 при х= 1.
1114. — у ctg х = cosec х, если :1 при л X у
1115. , Зу х 4-1 У~х^~1Г’ если У = 1 6 при х= 1.
1116. ху'Ц- у=х-\- 1, если У — 3 при х=2..
465
Дифференциальные уравнения второгс • порядка (к § 120, 121)
1117. У'=1—4х. 1118. z/" = ev.
1И9. |Г-^. 1120. Sit — cos 2t.
1121. х'уу — sin г/ — cos у. 1122. <?£= 12/2-f-6Z-|-2.
1123. z/' —5t/'-j-6z/ = 0. 1124. —2z/ = 0.
1125. у" — ау' — О. 1126. s'tt — s't — 6s = 0.
1127. у" — 2у = 0. 1128. x'tt — 2x't x = 0.
1129. у" — 4z/'4-13z/ = 0. ИЗО. x'yy 4x = 0.
1131. у"+ 10z/'-j-25// = 0 1132. yiz 4yt -\-8y — 0.
пзз. Р;9 - 6Р(;+9Р=0. 1135. 4у"-4у,-]-у = 0. 1134. у"-2у’^у = 0.
Найти частные решения следующих уравнений:
1136. slt = 2, если $ - < 6 и s't = 5 при i= 1.
1137. Р^р = 2 cos 2<р, если р = -i- и p' = 0 при — j .
1138. у"-]-5у'-\-5у = 0, если у = у и у =~-—1 при Л'=0.
1139. 4^" + 9z/ = 0, если у = 1 и у' = — 4 при х = -^-. Z О
1140. у"-2у'-4-2у = 0, если у — 1 и у' —2 при х = 0.
1141. Ускорение движущейся точки в зависимости от пути s
и скорости v выражается формулой w =— 2v— 5s. Найти урав-
нение этого движения, если s = 5 и v — — 5 при / = 0.
5. РЯДЫ
Числовые ряды (к § 122—126)
1142. Написать несколько первых членов последовательности,
n-i\ член которой равен:
2)
1143. Написать несколько первых членов ряда по данному
общему члену:
1) = 2) = 1)п 1' (2/1 — 1)! ;
3) ап== (2я — 1) (2л-f-1) : 4) йп = (~О'11’?-
1144. По данным первым членам ряда написать формулу об-
щего члена ряда:
1)у + у + т+-'-: 2) 1— i + i- ••• •'
466
3) 1 + XL+ :
1 Г J.2T1.2-3 ‘ 1-2-3-4
4) 1—L+-L —4-+•••
’ у 2 1 /3 /4 1
’ Показать, что нижеследующие ряды расходятся:
1“5- | + 1+4 + 1+-+^+ -"
П46. 2 + 4 + 4+.-+”41+-"
1147, ТоТX201'+ 3UT"Ь • • • + 100/1 + 1+•••
С помощью признаков сравнения установить сходимость или
расходимость следующих рядов:
1148.1+4 + ^+--- + ,^+---
Т?з+2^35 + оз+ +пТз«+
1150. + 2733 + -374Т + • • • + n(rt_pi)" + •'’
1151. i + -L+‘ +... * + ...
У 2 . У 3 У п
Исследовать по признаку Даламбера сходимость следующих
рядов:
1152*- 2 + ^ + д + 4+-+(2^1)1+-
1153. 4 + о? + Д+ • • • + 'Тп + ' ‘'
1154*. —21-+ др И" ер + ••• 7^++ •••
1155- 2т + 1г + 1+ •••+++>+ -
Исследовать сходимость следующих рядов:
1156*. 1— -- + +- -J-+ ...+(—l)"-1--Х+...
У2 1 Уз У 4 1 v ’ У п 1
1157. 1-I + 4-4+ -
1158. cosl + c-g+^ + “4-4+...+E7+...
1159. 1-1-+4-±-1-+...+(-!)«.+ +.„
.. z.rt sin а , sin 2а , sin За . sin п а .
П60. _- + _+—+...+ и(2д+-- + ...
467
Степенные ряды (к § 127, 128)
Определить интервал сходимости степенного ряда:
у*~ у-3 .-П
116L х + +I+ ... ч4,+..........................
1162. х + -^=- + -^+...+ ^-4-...
1 /2 1 /3 1 П Vn ' ’
V v*3 v-Zt
,163- 24-J+ff--- + (-1)n-1--w-+-
П64 —-J- x' .-Х! _i_-уП ,_i_ '
1165. x + 2x24-3r‘+...+«хиН-
Разложение функций в степенные ряды (к § 129, 130, 132)
Разложить в степенные ряды функции:
1166. a) f(x)=eax-, б) f(x) — ea-, в) f(x) = e а.
1167*. a) f(x) = sinkx; б) f (х) = coskx.
1168. a) /(x) = sin2x; б) f (x) = cos2х.
1169. а)Кх) = -^-,
1170. a) f(x)==(a-]~x)m-, б) f(x) = (a — x)4;
в) f(x) = (a-bx)G.
1171. Разложить в степенной ряд функцию f(x) = e~x2 и найти
^e^x'dx в виде степенного ряда,
о
1172. Пользуясь формулами Эйлера, вывести формулу
sin3 ср =— sin 3tf> -]- sin ср.
Решение. Известно (см. § 132), что silly —~.е —.
Отсюда
. М‘ — е-<Р‘\3 г3¥1 _ 1 3g-¥i _ e-S9i
S1I13tP = (— й—) = ---------------------ФР-— =
__(g3fi _ t>-3<F‘) _ 3 (е<р/ _ e~<pi)_ 1 es?i_e-s<ei 3 efi _ e~<fl
~ — "4 ‘ 3 Г T 2?
ИЛИ
• з 1 • q I 3 .
Sin3 cp = 4- Sin 3<p 4- Sin Cp.
1173. Пользуясь формулами Эйлера, вывести формулы:
,. « 1 + cos 2и _ . „ 1 — cos 2ш
1) Cos2<p = —Ц)—2) sin2<f—-—2— >
1 3
3) COS3 <p = COS 3 <p -j- COS <p.
468
Приложение рядов к приближенным вычислениям (к § 131)
1174. Вычислить sin 12°, ограничившись двумя первыми чле-
нами ряда (15), и оценить погрешность.
1175. Вычислить cos 6°, ограничившись двумя первыми чле-
нами ряда (16), и оценить погрешность.
1176. Вычислить приближенное значение ]/е, ограничившись
тремя первыми членами ряда (14), и оценить погрешность.
1177. Вычислить Ye с точностью до 0,001.
1178. Вычислить с точностью до 0,0001: 1) 1п 16,32; 2) In 6,79;
3) In 110,7.
Ряды Фурье (к § 133—137)
Вычислить интегралы:
1179. sin 5х cos 3xdx. 1180. ycos (nt -j- n)x cos (m — n)xdx.
1181. ij sin Зх sin xdx. 1182. J xex dx.
1183. ^xsinaxdx. 1184. x sec2 x dx. It 1 12
1185. § x2 cos x dx. К . 1186. $ cos 5xcos xdx. 0 It fe
1187. J xsin xdx. 0 1188. $ x cos Ax dx, 0
где k — любое число.
1189. Разложить
f(х) = | х | с периодом
1190. Разложить в
риодом 2ic, заданную
в ряд Фурье периодическую функцию
2~.
ряд Фурье периодическую функцию с пе-
в промежутке (—я; -) уравнением /(%) =
= — х.
1191. Разложить в ряд Фурье периодическую функцию с пе-
риодом 2s заданную следующим образом:
— х при —-ТС-<Хг^0;
0 при Ос.г
1192. Разложить в ряд Фурье периодическую функцию с пе-
риодом 2~, заданную следующим образом:
Цх) =
0 при —
— у при — у<х<0;
11 Л It
У при 0<^х<^ 2 ;
0 При у
469
ОТВЕТЫ И УКАЗАНИЯ
2. Указание. Решить данные уравнения. 1) А (5); 2) В (2), С (—2);
3) В (—3); D (2); 4) корни мнимые, на оси Ох таких точек ист. 3. 1) АВ = 6;
2) ВА- — 6; 3) DB = —6; 4) = —9; 5) В/<=9; 6) ВС = 3. 4. 1; Д£)= 12;
2) ВС = 3; 3) СМ = 9. 5. 1) AL (—3), Bt (4); А« (—5), В, (2). У к а з а н и е. Две
точки оси Ох будут симметричны относительно третьей, если они находятся
по разные стороны от этой точки, но на равных расстояниях от нее. 6. См.
рис. 214. 7. At ()'7 ), Bt (—I' ll)- 8» MB —— МС. 9. См. рнс. 215. 10. См.
рис. 216. 11. 1) Ai(4; —3); 2) А., (—4; 3); 3) А3 (—4; —3) (рис. 217).
12. 1) Л (—4; 0), В(0; —5); 2) А (4~; 0), В (0; 5); 3) Л (4; 0), В (0; —5).
13. 1) (6; 0), (4; —4), (0; —6); 2) (—6; 0), (—4; 4), (0; 6), 3) (—6; 0), (—4; —4),
(0;—6). 14. 1) А (4; 4), В(—5;—5). Указание. На рис. 218 построена
биссектриса координатного угла хОу. Для любой точки этой биссектрисы ОМ
справедливо равенство х = у. 15. А (4; 1). У к а з а н и е. Точка М лежит на
470
биссектрисе ОМ; ее абсцисса равна 1, поэтому и ордината должна быть
равна 1. Треугольник АА-.М прямоугольный и равнобедренный, катеты его
должны быть равны, т. е. МА = MAt = 3. Отсюда: xAl = 1 + 3 = 4; уА =
= 4—3=1 (рис. 219). Точка А, расположится по отношению к оси Ох
так же, как точка А расположена по отношению к оси Оу, так что абсцисса
точки At будет равна ординате точки А, и наоборот. 16. А (3; 1) и В (7; 3)
(см. указание к задаче 15). 17. 1) прЛС£) = 7; пр;, СО = — 4; 2) прх ~DC = — 7,
пр>,ОС = 4 (см. решение задачи, § 3). 18. 1) 0; 2) 0. 19. 1) АВ = 5;
2) CD = 13; 3) EF=\0 (см. решение примера 2, § 3). 20. 670 = 1^34,-
21. Р = АВ + ВС + АС = 10 + 7 У2 . 22. Указание. Вычислить длины
сторон и воспользоваться теоремой Пифагора. 23. Сравнить длины сторон.
24. Задача имеет четыре решения: 1) (0; 0); (а; 0), %)
(-а; 0), f Кз); 3) (0; 0); (а; 0). ; -у/з)-, 4) (0; 0); (- а; 0),
— |/з). 25. (2; 2), (2; 6), (6; 2), (6; 6). Указание. Сделать
чертеж и воспользоваться указаниями к задачам 14, 15. 26. у = 4. Указа-
ние. Для искомой точки Л1 справедливо равенство АМ = ВМ. Абсцисса
этой точки известна и равна 3. Если обозначим ординату ее через у
(рис. 220), то для определения у получим уравнение
/(3 - 1 )2 + (У - З)3 = у (4-3)* +(6-У)2.
27. .V = —1 (см. указание к задаче 26). 28. (—1; 0). У к а з а н и е. Предва-
рительно следует продумать решение примера 4, § 4. 29. fo; -i-V 30. (1,1).
814,6)
Л ’
"-4 |
Ъ/Ы I
I : !
। । ।
Рис. 221
о .
Рис. 220
Указание. Пусть Л1 (х; у) будет искомая точка. Для определения двух
неизвестных х и у можно составить два уравнения (см. указания к задачам
14 и 26 и рис. 221). 31. Л? = 5. Указание. Если эти точки лежат на
окружности, то СМ = СК = СР. 32. М (4; —3). У к а з а н и е. Пусть М (х; у?)
будет искомая точка. Тогда AM = ВМ = СМ. Для определения х и у получим
два уравнения: AM = ВМ или У(х — О)3 -|- (у -|- 6)3 = J^/x — 7)3 -|- (у 7)3;
ВМ — СМ или /(х-7)3 + (у> + 7)3 = /(х- 1)2 + (у- I)2. 33. М (—3; 11).
31. , Я = 1 /По. 35. !) М (Ь 41); 2) (2±; 5±); 3) (l; 4-1).
36. 1^13, УТО, 1. У казание. Сначала найти координаты середины сторон,
а затем вычислить длины медиан. 37. (—1; 2). 38. (0; 15). Указание.
Воспользоваться формулами (5). 39. А(—4; 2), В (8; 8), С(—2;—8). Указа-
471
и и е. Отрезки будут средними линиями треугольника (рис. 222). Стороны
треугольника параллельны средним линиям, что дает возможность построить
треугольник, вершины которого тре-
буется определить. Для нахождения не-
известных абсцисс хА, хв, хс надо иметь
три уравнения, которые получим, применив
формулы (4а). Так же составляются урав-
нения для определения ординат. Получа-
ются следующие системы уравнений:
40. С (8; 6), D (4; 2). У к аз а ни е. Построить чертеж п воспользоваться
свойством диагоналей параллелограмма. 41. (2; —9) (см. указание к зада-
— / 2 \ / 2 \
че 40). 42. <7 = рЛ2. 43. С (— 2-х-; 0 , D (-х-; —2). У к а з а н и е. Обозначив
\ о / \ о
гч ЛС 1
искомые точки через С и D, получим:
Со 2
0(1; 3), 4.1). 45. (6; 5), (-2; 5).
Указание. Искомая точка должна лежать
на прямой КМ, параллельной оси Ох и от-
стоящей от нее на расстоянии, равном 5.
Следовательно, ордината ее известна. Для оп-
ределения абсциссы следует составить урав-
нение, пользуясь условием .4Л4 = ДАГ = 5
(рис. 223). 46. Задача имеет два решения:
1) (5; 6); 2) (5; —2) (см. указание к преды-
дущей задаче). 47. 1) См. табл. 27; 2) см.
табл. 28. Предлагается данные точки.построить
и обратить внимание на их расположение.
^ = 2.44.С(-
________
--^12,2) [
48. 1) Точка (2; 3); 2) две точки: (3; 4), (—4; —3); 3) такой точки не
существует, так как система уравнений x--j-y2—4, х-^-у — 6 = 0 действи-
472
тельных корней не имеет. 49. Графики функций 1—5 см. на рис. 224,
графики функций 6,7 — на рис. 225. Указание. Предварительно следует
решить уравнения 6 и 7 относительно у. 50. 1) у — х2 — 4 (табл. 29 и
рис. 226); 2) у — х2 + 4 (рис. 227); 3) у — № + х — 2 (рис. 228); 4) у = — х*
(табл. 29 и рис. 229); 5) р = — х2 + %х 3; 6) у = — .с24~4.г (рис. 230);
7) 2х2 - у — 3 = 0; 8) — Зу - 9 = 0 (рис. 231).
Рис. 224 Рис. 225 Рис. 226
473
51. 1) jr = A'3 (рис. 232); 2) y = x3—4x (рис. 233); 3) v = — л-3 -|- 2л-
(табл. 31 и рис. 234); 4) у — л3 — л~ + х + 2. (табл. 32 и рис. 235).
Примечав нс. Кривые на рис. 232—235 называются кубическими
474
4
52. 1) a (табл. 33 и рис. 236); 2) (№ + 4) 4.г (рис. 237).
1 ~г
Указание. Предварительно следует решить уравнение относительно у;
3) см. табл. 34 и рис. 238.
Таблиц а 33
X —4 —3 —2 — 1 0 1 2 3 4 '
У |!^ 2 5 4 5 1 0 1 4 К 2 5 4 17
Таблица 34
X —5 —4 —3 —2 — 1 0 1 2 3 4 . 5
5 8 3 4 —1 4 .3 8 5
У 13 17 5 5 1 0 5 5 17 13
475
53. 1) См. табл. 34 и рис. 239; 2) см. рис. 240; 3) см. решение примера 4,
§ 10, и рис. 242. Примечание. Кривая на рис. 242 называется полу ку-
бической параболой.
Таблица 35
Л' —со . —6 —4 о —1 1 2 1 4. 8 ... —0
У 0 —... 1 3’ 1 2 —1 —2 —4 —8 —16 .* — со
1 0 —... , "1 т _1_ 4 1 "2 1 2 4 8 ... —* СО
У СО 16 8 4 2 1 1 2 1 4 ... — 0
476
54. См. решение примера 1, § 11; 1) Ь = — 3, k = tg а = 2 = у — -у;
3 _3 5
2) 6 = 2, fe = tga = —3 = -2y = -j-; 3) 6 = 0, k = tg a = — (рис. 243);
4) — 7) — см. рис. 244. 55. См. рис. 245. 56. См. рис. 246. 57. См. рис. 247.
у з
58. 1) _у = -^-н- х. У к а з а н и
О
е.
Уравнение прямой, проходящей через начало
тЛз"
координат, имеет вид y—kx, в данном случае A = tg30°=—=• 2) у = х',
О
3*
х\ 6) _у = 0;7)д- = 0. 59. Уравнения
3) у> = /3 х; 4) _у = -лг; 5) у-----
сторон: х = — 3, д- = 3; у = — 3; _у = 3.
Уравнения диагоналей: у = х\ у = — х.
60. 1) \у=4; 2) _у = К^х + 4; 3) у=л' + 4;
О
= /3 х + 4; 2) у = — /3 х + 4; 3) _у = 0
(рис. 248). 62. 1) л = 0; 2) ,у = 0; 3) у =
= |х + 5. 63. (—3; —5); (0; 1); (4; 9); (7,5; 16).
477
64. d — 5. Указание. Абсциссу найдем, решив уравнение 4 = — 2х — 2.
65. d = 5 К10. 66. Проходит через точки (1; —2); (3; 4}; (0; —5); не проходит
2
через точки (—3; 1); (—1; 3) (см. решение примера 2, § 11). 67. у —— — х.
Решение. Уравнение прямой, проходящей через начало координат, имеет
вид _у=/гх. Но так как эта прямая проходит , через точку (5; —2), то коор-
динаты этой точки должны удовлетворять уравнению y = kx, т. е. —2 = 5/г,
2 2 3
откуда к = —у; у ~ — у х. 68. у — у х. 69. у — х 4- 2. Указание. Урав-
нение прямой с угловым коэффициентом имеет вид y = kx-\-b. В данном
случае й = tg 45‘= 1; наше уравнение обращается в уравнение у = х-\-Ь.
Неизвестным остается Ь. Точка (3; 5) . должна лежать на прямой, поэтому
координаты ее должны удовлетворять уравнению прямой, т. е. должно быть
справедливо равенство 5 — 3J- Ь. 70.у = — х 1. 71. у ~ рЛ3-х 4- 2.72. Задача
имеет два решения: 1)у = у’ =— УЗх, у= 5; 2) у— -у-х, У = —Уг3-х,
у = — 5. 73. у = 2х + 3. Указание. Уравнение прямой с угловым коэф-
фициентом имеет вид у = 1гх Ь. В этом уравнении неизвестны параметры к
и Ь. Принимая во внимание, что прямая должна проходить через две данные
точки, для определения неизвестных k и b получим два уравнения: 3 =
= к • 0 Ь и 7 = к • 2 4- b. 74. у = — 2.v 5 (см. указание к предыдущей задаче).
75. Задача имеет два решения: ~ 4~ V" =11 v + Ту = 1> 76. Задача имеет
2, О м 2,
,. X . у , X , у , X у , Л' у ,
два решения: 1) у + у = 1, — у 4~ у = 1, у— у = 1, — ~£ — у = h
_п ч, — 1 ^ — 1—1 Л________L. — ] _Л_____=51—1
л — 0, у — 0, 2) 3 + 4 — 1, 3- 4 — 1, 3 4 — 1, 3 4 — 1.
х = 0, у — 0. 77. — хг = 1- Указание. Задача может быть решена двумя
4 о
XV
способами. 1) Уравнение прямой в отрезках имеет вид —+ у= 1; в данном
случае а = 4. Приняв во внимание, что прямая проходит через точку (2; —4),
для определения Ь получим уравнение у4--у-=1. 2) Принять во внима-
ние, что прямая проходит
2 , —4
4 1 b
через две точки (4; 0), (2; —4), и применить спо-
соб, разобранный при решении задачи 73.
78. у — у = 1. 79. у -j- у = 1. Указание.
а = Ь. 80. ^-4"J=1- Указание. Согласно
~ ab
условию задачи должно быть — 1 (рис. 249).
81. Задача имеет два решения: 1) у4-у = 1,
х =5, у — 4; 2) 4“ 11 х = 5, х = 4. У к а -
у 5
2
з а н и е. Первое решение получим при а = 2Ь,
второе — при b — 2а. 82. 1) Проходит через начало
___. z . . - . оси Оу', 3) параллельна оси Ох; 4) уравнение
оси*7?у; 5) уравнение оси Ох. 83. 1) Решаем уравнение относительно у»:
1) 4,у=3х —8, у = ~х — 2; 2) у = |х;3)у = - 1-х 4-у-, 4)yi=—-|-х4-
4-3. 84. 1) у4-J-1; 2) = 11 3) -2^--''
4 0 4 • £>
координат; 2) параллельна
7 . 3
2 ’ ~ 2
_________ 1- 4) _£_1_2.>= 1
.1 3 ’ ’ 8 л 4
42
478
5) — у = 1; 6) -у- 4- -у = 1. 85. См. § 16 и рис. 250. 86. Указание.
¥
Прямая 7.v-|-2y = 0 проходит через начало координат и для нее а = 0, Ь = 0.
Для построения этой прямой следует данное уравнение преобразовать к виду
y — kx. 87. 1) На данной прямой лежат точки С(—3; —5), D (9; 3); 2) над
прямой расположены точки В (6; 2), Е (0; 4); 3) ниже прямой—точки
Д(6; —2); F(—3; —6). 88. 5 = 7,5 кв. ед. 89. Л = 2. 90. Зх — 5у + 15 = 0;
3,v + 5j>-15 = 0; Зх —5j—15 = 0. 91. Л = 3; В = 2. 92. _у = -|-х + 2.
У к а з а н и е. Текущие координаты (х; у) здесь выражены через переменную
величину t. Такие уравнения называются параметрическими, a t называется
параметром. Из первого уравнения x = clt выражаем t в зависимости от х.
Подставив во второе уравнение вместо t его значение у, получаем: _у =
= уЛ'4-2. 93. 2л: — Зу,-|-5 = 0. 94. у = х + 3; у = х — 2. 95. 1) <р = 71’34';
2) <0 = 71’34'; 3) <р = 0. 96. 1) ? = 82’53'; 2) <? = 63’26'; 3) <р = 0; 4) <р = 90".
Указание. Предварительно решить данные уравнения относительно V.
3
97. Угол (рис. 251) образуется вращением прямой у =-у х^-6 (против
часовой стрелки) до совпадения с прямой у = х + 1, поэтому в формуле (13)
следует принять: k{ = kAC =-у, = kAB = 1. Получим:
_ kAB-kAC _ ’-(-4) _1+4
^21 I ь . ь /3\ 3 »
1 I “ас 1~4
<Pi = 180" — arctg 5 — 180“ — 78°41' — 101’19'. Так же найдем: о« = 60’15',
<р3 = 18’26'. Проверка. 101’19'+ 60"15'+ 18’26'= 180". 98. й; = 180’—
— arctg 4 = 120’58', <f2 = arctg 4 = 23’12', <о3 = arctg 4 = 35"50'. 99. у =
О / 1 о
= х + 2 /3 — 4. Указание. Берем уравнение пучка прямых с центром
в точке (—2; —4). Получаем у 4 = k (х -|- 2). В данном случае fe = tg60° =
= /3, у>4-4 = /3 (,с4-2). 100. 2х + ЗУ- 4 = 0, 2.г + 3v — 21 =0. В дан-
2
ном случае k = tg а =—у. 101. 2х4->4-8 = 0. 102. 4х-|-3.у-|- 12 = 0.
479
103. 1) у=*
Указание.
задачи 83; 2) уравнение прямой, проходящей через точки А и В, имеет вид
у—Уд х — х.
---------=---------. Заменив в данном уравнении хА, уА, хв и ув их
. Уд — J’a а'д — ХА
У—2 х —5 у—2 х—5
значениями, получим: —-------------g , —— > У — 2 = 2х — 10
105. 1) Уравнения сторон: Зх — 4у + 12 = 0; 4х + Зу» + 16 = 0; 2х — у — 2 = 0;
2) уравнение медианы 7х—у» + 3 = 0. 106. х + Зу» + 18 = 0, х-(-Зу»— 2 = 0.
107. ~
109.
х-У-; 2) у = 2х-4; 3) v = 2; 4) х = 3. 104. 2х — у - 8 = 0
Эту задачу можно решить двумя способами: 1) см. решение
1) (2;—4); 2) (—4; 2); 3) прямые параллельны. 108. d = 2 ]/10.
3
'=4
ПО. 4л'+ 10з> —5 = 0.
—1); (19; -11).
У
А(6;6)
О
Рис. 252
Составить урав-
нения диагоналей и решить их совместно.
113. (0; 3); ? = arctg 2 = 63-26’. 114. А =
= С = 1\°Ы', В = 36"52'. 115. х4-2у—10=0.
116. х—у + 3 = 0, х-\-2у— 4 = 0, 7х —у> + 7 = 0,
(— — • I-}. 117.x — 9у + 48 = 0, 9х+у-60 = 0.
\ 3 3/
У казанис. Угловой коэффициент данной пря-
5
мой k — Через точку (6; 6) можно провести
две прямые,
Прямые АВ и АС (рис. 252) принадлежат пуч-
ку у — 6 = k (х — 6). Чтобы написать требуемые
уравнения, достаточно определить их угловые
коэффициенты,
с данной
112.
Указание.
удовлетворяющие условию задачи.
Угол <f, образуется вращением
прямой. Если угловой коэффициент дан-
а угловой коэффициент прямой АВ —
5 ,
4~~fel
1+4 *1
Из последнего уравнения получим fe1 = 4> Уравнение прямой АВ: у — 6 =
= 4 (х — 6) или х — 9у» + 48 = 0. Угол <р2 образуется вращением данной пря-
мой вокруг точки С до совпадения с прямой АС. Поэтому tg ,
где А» — неизвестный угловой коэффициент прямой АС. Подставив извест-
5
5 4
значения tg<j2 = l и k = ~г, получим уравнение 1=----.Решив
уравнение, найдем k, = — 9. Уравнение прямой АС: у — 6 = — 9 (х — 6)
9л' + _у —60 = 0. Примечание. Для решения задач, аналогичных
прямой АВ до совпадения
пой прямой обозначим через k,
через /г1( то получим:
tg45'
1 + ^-А
1 4
иые
это
или
данной, достаточно взять формулу для угла между двумя прямыми с двой-
ным знаком: tg , принимая k за угловой коэффициент данной
прямой, a А, — за угловой коэффициент искомой прямой. В данном частном
случае, при = 45°, зная уравнение прямой АВ, уравнение второй прямой
480
ВС можно было бы написать, пользуясь условием перпендикулярности двух
прямых, так как А = 90°. 118. х — 5у — 26 = 0, 5х-}-у 4- 26 = 0. Указание.
Воспользоваться указанием к предыдущей задаче. 119. 5х-|-у—16 = 0,
х4-5у —32 = 0. Указание. См. примечание к решению задачи 117; при-
2 / 24 36 \ .. ,,
пять' во внимание, что tg с? =. = . 120.-— ; --- | . Указами е. Составить
О \, 1 о 1U у
уравнение перпендикуляра и найти точку пересечения двух прямых. 121. d = 6.
Указание. Составить план решения, как в примере 1, § 23. 122. rf = 5,2;
5 = 13 кв. ед. 123. d — A. Указание (рис. 253). Расстоянием между двумя па-
раллельными прямыми является отрезок общего,перпендикуляра, заключенный
между ними. Пишем уравнение прямой, перпендикулярной данной и проходящей
(для простоты) через "
результате совместного решения
начало коррдинат. В
уравнения перпендикуляра с каждым из уравнений этих прямых найдем
концы искомого отрезка. 124. d — 3. 125. х 2у — 11 = 0, 2х -|-у — 5 = 0.
У к а з а н и е. Составить план решения, как при решении примера 2, § 23.
126. 1) х -|- Чу 8 = 0; 2) х J- 2у -|- 8 = 0. Указание. 1) На основании
теоремы о свойстве биссектрисы внутреннего угла треугольника имеем:
-^- = ^=Х (рис. 254). Так как ВС = 10, АС = 20, то ^- = 1. Коор-
динаты точки (ЛТ) пересечения биссектрисы ВМ со стороной АС найдутся
по формулам деления отрезка в данном отношении. 2) Чтобы написать урав-
нение перпендикуляра из точки В на прямую АС, надо по формуле (11)
найти угловой коэффициент этой прямой и воспользоваться условием пер-
пендикулярности. 127. Зх + 5у -|- 1 = 0, 5л'—у — 5 = 0, х — Зу— 3 = 0.
Указание. Найти вершины треугольника и составить уравнения прямых,
проходящих через вершины перпендикулярно противоположным сторонам.
128. 2х — Зу + 5 = 0. 129. —2 ~ •, 4 yj . 130. Уравнения сторон: у = — 2х-|--
8; у = 3х; у = —у х. Координаты вершины (0; 0);
(см. решение задачи 117). 131. Уравнения диагоналей: Зх— 2у-|-10 = 0;
2х-|-Зу — 15 = 0. Уравнения сторон: х— 5у-)-12 = 0; 5х -|- у Ц- 8 = 0; х —
— 5у + 38 = 0; 5х -f-y — 18 = 0. Указание. Стороны-квадрата проходят
‘через концы данной диагонали и образуют с ней угол 45°. 132. у = уХ-|- 12;
11 I ло 1 1 I С v ? . 3 <р 3
у = уХ-|-42; у=—-2х;у=—^х -j-б. У к а з а н и с. у = arctg у, tg-*-=y.
133. Зх+у—9=0; 5х—Зу+13 = 0; х-|-5у+25=0. 134. х—у—7=0; х—2 у—10=0.
135. (3; 1); (12; —2); lyy; |5 11 (уз» —yd - Указание. Воспользоваться
свойством диагоналей ромба. 136, Зх -f-y — 25 = 0; х — Зу — 15 = 0; у = 2х.
16 П. Е. Агачев
481
Указание. Отрезки ЕК, ЕМ, КМ — средние линии треугольника. Урав-
нения его сторон можно написать, воспользовавшись свойством средней
линии треугольника. 137. 9х -р 12у + 20 = 0, 5х — 12у 36 = 0. Указание.
'Зная точку М на стороне ВС, можно написать уравнение этой стороны.
Определив совместным решением уравнений сторон АВ и ВС координаты
точки В, можно найти 'координаты точки С. Следует сделать чертеж.
/ 122 21\
138. (-щ-; —щ). Указание. Определив основание перпендикуляра,
опущенного из точки А на данную прямую, точку At можно найти по фор-
мулам деления отрезка пополам. 139. 11х-|-Зу — 31=0; Их — Зу — 31=0.
Указание. Пусть AM будет лучом падающим, а ЛЛ1 — лучом отраженным
(рис. 255). Тогда = <р3 = <р3, точка М, удовлетворяющая этому условию,
найдется как точка пересечения прямой, проходящей через данную точку А
и точку симметричную точке В (5; 8) относительно оси Ох. Зная коор-
динаты точки М,
В15;8)
легко составить уравнение
Рис. 255
отраженного луча МВ.
можно воспользоваться указа-
При решении этой задачи
_____, ..._______I к задачам 138 и 139 (рис. 256). 141. Прямая х-|-у — 10 = 0.
Указание. Из геометрии известно, что геометрическим местом точек,
равноудаленных от концов данного отрезка, является перпендикуляр, вос-
ставленный к данному отрезку в его середине. Пользуясь этим свойством
данного геометрического места, можно составить
и его уравнение. Рассмотрим здесь более общий
прием. Пусть /<(х; у) будет произвольная точка
данного геометрического места (рис. 257).
Тогда АК=ВК, пли )Дх — 4)-' (у — 2)-’ =
= |(х — 8)2 -|- (у — 6)2. После преобразований
получим х-|-у—10 = 0. 142. 2х4у— 5а = 0.
143. х2 -j- у2 — 16. Указание. Полагая, что
Л4 (х; у) — произвольная точка геометрического
места, получим AM = 2ВМ. 144. у = 4-х2 + 1 —
парабола (см. решение примера 2, § 25).
145. х2 -}-у2 = 16. Указа н и е. Для любой точки
Л1 (х;у) геометрического места должно быть спра-
ведливо равенство АМ~ -)- ВМ- = 64. 146. Задача
140. х = 5, ^ = 5. 1
пнями, сделанными
имеет два решения:
х — Зу — За = 0; х — Зу — Та = 0. 147. у=-^-х2-|-3—
парабола. Указание. Расстояние любой точки кривой от прямой у = 2
будет, равно | у — 21. 148. х2 + у2 = а-. Указа и и с. На рис. 258 изобра-
482
жено одно из бесчисленного множества возможных положений стержней.
С (х; _у) — точка йх пересечения. Треугольник АВС — прямоугольный.
На основании теоремы о свойстве перпендикуляра, опущенного из вершины
прямоугольного треугольника на гипотенузу, можно написать равенство
CN3 = BN • NA. Выразив отрезки CN, NA и BN через координаты точек
геометрического места 1х; у) и данных точек А и В, после несложных пре-
образований получим уравнение, данное в ответе. 149. а) х3-|-_у3 = 4;
49 / 1 \2. 25
б) х3 + (у- З)3 = или 4х3 + 4^3 - 24_у - 13 = 0; в) х - 2 j + у2 = --
или х3 у3 — 5х = 0; г) ^х 3 -f- (у — I)3 = или 2х3 2_у3 13х —
— 4_у-|-13 = 0. 150. a) x3-|-J’3 = 3. Указание. Уравнение окружности с
центром в начале координат имеет вид х3 + у2 = г'2. Так как окружность '
должна пройти через точку (У2; 1), то должно быть справедливо равенство:
(/2)2+13 = г3; б) (х+1)3 + (у»-2)3 = 25; в) х3 4-/4-10х-24у = 0;
г) х3 + (у + 2)3 = 25 или х3+у»3 + 4у»-21 =0. 151. (х + I)3 + (у> + 2)3 = 13.
152. 1) На окружности лежат точки С, Е и F; 2) вне окружности — точки
В и О; 3) внутри окружности — точки А и Р (см. решение примера 1, § 25).
153. а) (х 2)3 (у I)3 = 9. Ре ш е н и е. Переписываем данное уравнение,
собирая в одну группу члены, содержащие абциссу х, в другую — члены,
содержащие ординату у, перенося свободный член вправо с противополож-
ным знаком: (х3 -|- 4х) (у3 + 2у) = 4. Затем дополняем обе группы до пол-
/ 4 V
ных квадратов суммы (или разности), прибавив к первой группе Ну = 23,
ко второй = I3. Чтобы уравнение осталось равносильным данному, при-
бавим к правой части 23 I3. Получим: (х3 4- 2 • 2х -j- 23) 4- (ys -f- 2 • 1 у -j- Is) —
= 4-|-4 4-1 или (х 4- 2)3 4- (У + I)2 = 9 (см. разбор примеров, § 27);
/ 5 А2 / 3\3 Ч
б) (X - 4)3 4- (,v- 2)2 = 25; в) 1x4-7 + (у-г! = дг. У к аз ан и е. Спа-
\ 4 j \ 4 / о
чала все члены разделить на коэффициент при х3 и у3 (на 2), а затем вос-
пользоваться указаниями, сделанными в § 26 при решении первого примера;
+ =тв-,54- х2 + у3 -
— 6_у— 9 = 0. Указание. Сначала надо найти ординату точки пересече-
--------------- “ ..... ...... - 15б х3 + у>_
25
г) (х - а)2+у3 = <z2; д) л-’ + / =
— 2у = 0.
ния окружности сданной прямой. 155. х3 4т у3— 5х
—2<zx— 2ау-\-а3 = 0. 157. х3 у3 Ц- 8х = 0.
Указание. Окружность касается оси Оу в
начале координат. Но касательная перпенди-
кулярна к радиусу, проведенному в точку ка-
сания, следовательно, центр окружности лежит
на оси Ох и точка (—8; 0) является концом
диаметра. 158. х2-|-_у3—6у=0 (см. указание к
предыдущей задаче). 159. Задача имеет два ре-
шения; .r-J-y3— 20х—20_у-|-100 = 0 и х3 -|-
4-У3— 4х — 4у-[-4 = 0. Указание. Пусть точ-
ка С (а; Ь) (рис. 259) будет центром искомой
окружности. Тогда, по условию задачи, СМ =
= C/V = АС, или а — Ь = г. Точка А (2; 4) лежит
на окружности и, следовательно, координаты ее
должны удовлетворять уравнению окружности.
Подставляя в нормальное уравнение окружности
вместо b и г равное им а, а вместо текущих координат— координаты точки А,
получим уравнение (2 — а)3 (4 — а)3 = а3. Из этого квадратного уравнения
найдем два значения а, соответствующих двум окружностям, удовлетворяю-
щим условиям задачи. 160. Задача имеет два решения: (х + З)3 4- (У + З)3 = 9;
(х 4~ 15)3 + (у + 15)3 = 255 (см. указание к предыдущей задаче)., 161. х3 4*
16* ' 483 '
+yr — Cix — 16 = 0. У казание. Центр окружности должен лежать на оси
Ох; ордината центра должна быть равна 'нулю. Пусть С (х; 0) (рис. 260)
является центром окружности. Тогда АС —ВС, т. 1 е. У(х 4- I)2 + З2 =
= 1^(х — З)352. Решив это уравнение, найдем х = а = 3. 162. х2-\-
+ [у — = ду*. 164. (х — З)2 4“ СУ ~ 4)2 = 25. Указан н е.. По определе-
нии координат вершин треугольника задача решается аналогично предыду-
щей. 165. 1) Пересекает ось Ох в точках (2; 0) и (—8; 0); ось Оу— в точках
(0; 4) и (0; —4); 2) касается оси Ох в точке (2; 0) н оси Оу в точке (0; 2).
Указание. Для определения точки пересечения окружности с осью коор-
динат следует решить совместно уравнение этой окружности с уравнением
оси. 166. (3; 4) и (—4; —3). У к а з а н и е. Решить данные уравнения сов-
местно. 167. Совместное решение уравнений дает мнимые корни. Следова-
тельно, прямая и окружность общих точек не имеют. 168. d = ^2.
169. (х — 5)2 4~ (.У ~ 4)3 = 116. Указание. Координаты центра даны. Чтобы
написать уравнение этой окружности, следует определить радиус г, который
У
6,10 ib)
А, Рг Q
а 1
. b
F, А,(а,0)
Вгю,-Ь)
Рис. 262
В2. Из формулы (46)
будет перпендикуляром, опущенным из цент-
ра на данную прямую. Решив совместно урав-
нения перпендикуляра и данной прямой, най-
дем координаты точки касания, а радиус опре-
делится как расстояние между двумя точками.
170. (х — 6)2 4-(у, — 7)3 = 36. 171. 3x4-4у» —
—25=0. Указание. Подставив координаты
точки А в уравнение окружности, убеждаемся,
х-что она лежит па окружности. Уравнение ка-
; сательной получим, написав уравнение прямой,
проходящей через точку А перпендикулярно
радиусу ОА (рис. 261). 172. 2х 4~ Зу — 13 = 0.
Указание. Пусть данные отрезки а и b
(рис. 262) будут полуосями эллипса. По дан-
ным полуосям строим вершины Л,, Л», В,,
имеем a3 = 62-j-c2. Если Ь и с являются катетами
прямоугольного треугольника, то а будет его гипотенузой. Из вершины В,
как из центра, описываем дугу радиусом, равнцм а. Точки пересечения этой
дуги с осью Ох будут фокусами эллипса, так как B,Fl = ОВ2, 4~ ОЛр и
а2 = Ь2-\-с2. 174. У к аз ан и е. 1) Сравнивая дапное^уравнение с уравнением
(4), видим: а2 = 25, Ь2 = 9, откуда а — 5, 6 = 3, с = ’|/а-— Ь2 = 4; А, (5; 0),
г 4
Л2 (—5; 0), В, (0; 3), В2 (0; —3), F, (4; 0), /•’„ (—4; 0), е = - = 4 = 0,8; 2) раз-
и э __
484
X9 V9
делив все члены уравнения на свободный член, получаем: ~ — 1;
+ (4;0), Л2(—4; 0), (0; 3), В2(0;—3), Ft (/7? 0), Л (- УТ; 0), e =
3) Л2 (2; 0), Л2 (—2; 0), В,(0; 1), В2 (0; — 1), Ft (/3; 0), F2 (- УЗ; 0), е = ;
4) А, (2; 0), Л2 (—2; 0), Bt (0;/3), В, (0; - /3), Ft (1; 0), Fs(-1; 0), е = ~.
175. Указание. Решив данное уравнение относительно^, получим у~
= it 4- ^25 — л'-’. Далее определяем ординаты точек, подлежащих построе-
на Щ г8
нию, и строим эти точки (см. пример 3, §9). 176. 1) у + у = 1; 2) -jpg-+
V3 с 4
== 1. Указание. Из уравнения — = — определяем с, а затем по фор-
оо а о )
,. . . х- , У3 , л У а3 — ь“
муле (4а) находим ft; 3) —+ ^ = I. Приняв во внимание, что е— -----------,
двух уравне-
(— 2 /3 )2
а-
3 ' ’ '
/а3-23 1 х- , У . л-3 , у* , ’
получим уравнение ---------— v- 4) of+tf —*• *77- 7Г~Г~Т='- ^ка-
Д £ Z3 У У о
4 _ ~4
з а н и е. В данном случае а — 3. Точка (+б; 1) лежит на эллипсе. Коорди-
наты этой точки должны удовлетворять уравнению (4). Для определения
. 1 ^._о х3 у .
параметра Ъ получим уравнение —1. 178. ]g । = ^ка*
з а н и е. Чтобы написать уравнение эллипса, надо знать его. параметры а и
Ь. Поэтому дело сводится к составлению и решению системы
ний с неизвестными а и Ь. Эти уравнения получим, принимая во внимание
условия задачи: а2— Ь- = с3 или а2 — Ь~ = 22; + +~ 1 или
(У3 )2 xs V1
+ У = 1. 179. 1) —-|--д- = 1. Указание. Подставив в уравнение (4)
вместо текущих координат координаты
данных, точек, получаем два уравнения
№ у2
с неизвестными а и ft; 2) — 4-2- —1.
8*4
V3 V2 V3 м3
18°. 1) 48+15 = 1; 2) gg + go =1.
181. S = 16 кв. ед. 182. 2х— Зу-^4 = 0,
4
2х — у —4 = 0, tg<p = y (рекоменду-
ется составить план решения). 183, Ука-
зание. Координаты точки С (х0; у»0)г
лежащей на эллипсе (рис. 263), удовлет-
воряют его уравнению, так что
-5 4-+= 1. Абсцисса точки А, лежа-
а1 1 b
щей вне эллипса, равна абсциссе соответствующей точки эллипса х( = х(|,
а ордината ее yt больше ординаты точки С эллипса: yt > у^. Отсюда следует:
^2
Таким же образом можно доказать: 184. На эллипсе лежат
точки А (2; 3), D (—2/2; /б); вне эллипса точки С (3; —3), А (/15;—1);
внутри эллипса точки В (—3; 2), А(1;—2). 185. г/= — ]/34. Указание.
Предварительно найти точки пересечения эллипса
187. Зл'4-2у' — 0, d = 2 /13 (диаметром эллипса
g
проходящая через центр). 188. tg у, = ; .2) lg у
углы между прямыми, проведенными пз центра окружности к концам
шрй осп и к концам малой
„ 1О/з j 10 /3
и прямой. 186. d ’
называется любая
1 v
~ ~2 Указание.
3 •
хорда,
Найти
боль-
8
оси эллипса. 189. х — у» — 2 — 0; d = — У‘2~.
190. у^2, у — — 2, л- = 2, л = — 2, у = х,
у = — х. Указа н и е. Общей хордой двух
кривых будет отрезок, соединяющий точки
пересечения этих кривых. 191. 1) Прямая ли-
ния; 2) окружность; 3) точка (0; 0), так как
это уравнение при вещественных значениях
х и у удовлетворяется лишь тогда, когда
,г —0 и у = 0; 4, мнимая окружность; своим
видом это уравнение похоже на уравнение
окружности с центром в начале координат,
по так как оно на при каких Действительных
значениях х и у не удовлетворяется, то на
плоскости пет точек, ему соответствующих;
5) эллипс; 6) прямая; 7) эллипс; 8) точка (0; 0).
192. Построение вершин AIf А«, Bt, !!.. и
асимптот OL и ясно из рис. 264 без
пояснений. Для построения фокусов
формулой (6а). Из нее следует: с3 = а2 -|- Ь~,
и А» следует воспользоваться
поэтому полуфокуснос расстояние OF, = с должно быть равно гипотенузе
прямоугольного треугольника, катетами которого являются полуоси гипер-
болы, так что- (JF\ = F«O = А1В1. 193. 1J Д1 (4; 0), Д2 (—4; 6), Bi (0; 3),
В2(0; -3), А/5; 0), F, (-5; 0), е = = |, у = +|л-; 2) (2; 0), Л2 (-2; 0),
г- г~ /5 1
/(0;1), Д2(0;-1), Л (У 5; 0), А» (—/5; 0), е = ^-, у=±^-х;
3) At Д+2/3;0), B.s(0', ±2/2), Ab2(± 2/5 ; 0),
194. 1) /=1; 2) задача имеет два решения:/ — 1, —/=1.
7 16 9 1о 9 9 16
У к а з а п и с. Приняв во внимание формулу (6а), для нахождения а и b
получаем два уравнения; 3) — ^2 = 1’’ Тб—195, А —6, г.. —14.
196. л=+/ = 44, (х-4)=+/ = 12. 197. 1) ^-^=1; 2)g-£=L
Указан и е. Для определения параметров а и b надо составить два урав-
нения, пользуясь условиями задачи: одно из этих уравнений получим из
сопоставления данных уравнений асимптот с уравнениями (9), второе — под-
ставив в формулу (6а) вместо с его найденное значение. 198. — j^ = l.
199. 1) л-2— у- — 4. Указание. В уравнение равносторонней гиперболы
(24, 4) входит только один параметр. Для определения этого параметра по-
486
лучим уравнение, приняв во внимание, что гипербола проходит через данную
точку; 2) х2—у2 = 9. 200. х2—у' = 8. Указание. Для равносторонней
гиперболы формула (6а) принимает вид с2 = 2я2. 201. 1) ху=16; 2 х_у=15;
3) ху= 12; 4) ху =—24 (см. решение примера, § 36). 202. у = у х; </ = 2^5.
203. Прямая и гипербола имеют одну общую точку
(10; —2). 204. (8,2; 1,35;; (8,2; —1,35). 205. 1) Прямая
линия: 2) гипербола; 3) эллипс; 4) равносторонняя ги-
пербола; 5) окружность; 6) это уравнение распадается
на два уравнения первой степени: x-f-y = 0, х ~у = 0,
каждому из которых соответствует прямая линия, про-
ходящая через начало координат; следовательно, урав-
нению х3—У=0 соответствует пара прямых; 7) точ-
ка (0; 0); 8) пара прямых Ьх-\-ау = 0; Ьх — ау = 0;
9) равносторонняя гипербола; 10) мнимый эллипс
(ни при каких действительных значениях х и у это
уравнение не удовлетворяется); И) точка (2; 3).
206. 2р. Указа п и е. Чтобы найти длину хорды
AlAIi (рис. 265), надо знать координаты точек М и пе-
ресечения прямой х = ^- с параболой. Решив совмест-
но их уравнения, получим у — ± р, откуда МjМ = 2FM—
— 2р. 2ffl. 1) Задача имеет два решения: у = 8х, если
фокус находится справа от директрисы; У —— 8х, ес
директрисы (см. решение примера 1 в § 37); 2) у2 = х; 3) у = 8х; 4) у =
= — 8х. 208. 1) х-’ = 12_у, х2 = —12у; 2) х3 = 8у; 3) х2 = 18_у; 4) х2 = — 8_у;
5) х2= — 2/зТу 209.(18; 12);(18; —12). 210. (2; /8); (2; —/8). 211. 1) (0; 0),
(4; 4); 2) (-2; 2), (-8; -4); 3) (-6; 6), (12; 24); 4) (2; —1), (—10; —25);
5) (0; 0), (4; 4); 6) (0; 0), (2р; 2/Д. 212. Указан и е. Для более точного по-
строения парабол, кроме обычных точек (0; 0), fy; р\ , fy; —р\ , ip', yj ,
— р; у! следует
принять во внимание точки пересечения линий, образую-
щих фигуру. 213.
, 214. у = 9х. . Данная
парабола проходит через
точку (4; 6). 215. 4хД-4у—1=0. Указание. Данное уравнение может
быть переписано так; х2 = у, откуда 2/>=1. 216. 4х Д- 4у — 1 = 0 (см. ука-
зание к предыдущей задаче). 217. d = 2 у 15, х = -|-. 218. (8; 4 рЛ3),
(8; —4 1/3). При Х =— 2 для у получаются мнимые значения. 219. 1) За-
1 1 „ 3 17
дача имеет два решения: у = уу (х — З)2 Д- 2 или у— — х2—^-хД-у,
если фокус параболы поместить выше директрисы; Ур = 0 Д- у = 2 Д- 1 = 3;
Д(3; 3); _у = —-у\.-2Д-4уХ— у, если фокус ниже директрисы; у, = 0—-^ =
= 2—1 = 1, 27(3; 1). Указание. Значение р находим, подставив в урав-
нение (14) вместо а и 0 их данные значения и заменив текущие коорди-
наты х и у координатами данной точки; 2) задача имеет два решения:
у = 0,5х2 Д-6х Д- 14, если фокус* выше директрисы, F(—6; —3,5); у =
= — ОДУ— 6х — 22, если фокус ниже директрисы, F(—6; —4,5); 4) у —
= — ОДУ — 4х, Г (—4; 7,5). 220. у=Д х2Д-3. 221. у>= 1 9 - х2Д- 16 или
1 J 2(2)
у — — уХ2Д-16. Указание. Дуга параболы, описанная камнем при его
487
движении, может быть изображена, как показано на рис. 266. Осыо сим-
метрии служит ось Оу, вершина се находится в точке (0;.16). Кроме того,
известна точка В (8; 0), через которую проходит парабола. 222. у==
~ о-х° + 5 или -у-=-—5л2 4~ 5 . 223 . Задача имеет два решения'.
. 2 • ( U ,1)
i\ Я
D5- = -^
если принять за вершину точку (0; Ь), и 2) у —
— —-V л'2 —Ь с вершиной в точке (0; —Ь). 224. у =— x24-4x. 225. 1)р = 3,
а =— 2, 0 =— 6, F(—2;—4,5). Легко определяются точки пересечения
параболы с осями координат (см. решение примера 2 в § 38); 2) р=3,
§ 38); 3) р.= -2,
так, как показано
а = 0, ° =— 2, Zr(l,5; —2) (см. решение примера 3 в
а = 8, р = 16, /?(8; 15). Можно преобразовать к виду (14)
в примере 4 в § 38; 4) р = 2, а =—1, 0 = 2, В(0, 2). Данное уравнение
можно привести к виду (15) следующим образом: х = (у2 — 4у -|- 4 — 4);
.г = .1 (у> - 2)2 - 1; 5) р = 2, а = 2, 0 = —4, F (2; -3); 6) р = — 4, а = 2,
0 = 2, /?(0; 2). 226. 1) Парабола у> = дг2 —4; 2) парабола у- = 3.г; 3) пара-
бола у = х2 — 4х 3 (см. § 39). 227. 1) Па-
рабола, симметричная относительно оси О.г;
2) эллипс; 3) прямая линия; 4) окружность;
5) парабола, симметричная относительно пря-
мой, параллельной оси Оу; 6) гипербола; 7) па-
рабола; 8) точка (0; 0); 9) пара прямых:
3.V — ау = 0, Зх 4- ау = 0. 228. d = 4. 229. 5х 4~
4- 3_у 4- 20 = 0; 5х — 3_у — 30 = 0 (см. указание
к задаче 171). 230. х 4- 2у — 10 = 0, х — 2у —•
—10 = 0. 231. Уравнение третьей стороны:
_у = — З.с 4- 8; длины сторон: dl—2 }-/2, гЛ =
=ЦЖ , d 3 =^у^. 232 . 2л- —Зу» 4- 26 =0',
Зх 4-2у> — 26 = 0. Указание. Приняв О Л
за диаметр, построить вспомогательную окруж-
ность (на рис. 268 она показана пунктиром). ’
Z.ANO = lAMO = d как вписанные углы,
опирающиеся на концы диаметра, поэтому
AN и AM будут касательными к данной окружности. Л1 и N яв-
ляются точками пересечения данной окружности с вспомогательной, урав-
нение которой можно написать по данным координатам концов диаметра О А.
В результате совместного решения уравнений двух окружностей найдутся
488
v9
точки касания Л1 (б; 4) и N(—4; 6). 233. 'т-? 4- -{ = 1 эллипс. Указание
4а3
(рис. 269). На окружности возьмем какую-нибудь точку Л), (х; у/) и сере-
дину Л1 (>;; у/,) ординаты этой точки. Кривая L представляет собой геомет-
рическое место точек Л1 (х; По условию задачи, у[ = -у пли у=2у,.
Уравнение кривой L получим, если в уравнении окружности ординату у
заменим ее выражением через у/,: х2 -р (З^)2 — 4л3 или х24у2 = 4а2. В по-
следнем уравнении у/, — текущие ординаты геометрического места точек,
а х — пх абсциссы; следовательно, это уравнение будет служить уравнением
I'3 ! V5
кривой L. После преобразования получим ~= 1. Опуская у его
индекс, уравнение искомого геометрического места можно окончательно
V3
написать в следующем виде: 4—7 + -.? = 1 — эллипс. 234. 4х4-у—16 = 0,
4aJ а~
4х — 7у + 16 = 0. 235. Парабола у2 = рх (см. указание к задаче 233).
236. На рис. 270 изображено одно из положений движущейся точки Л1 <х; у).
Точка /И, (хр, у»,) является точкой пересечения медиан треугольника AsMAt
(центр тяжести). Спрашивается, какую кривую опишет точка Л4,, когда
точка Д4 описывает данный эллипс? По формулам для центра тяжести нахо-
дим (см. решение примера 3, § 5);
-vai + -rn2 + -v.4, х — а-\-а х
Л| ~ 3 ~ “ 3 — "з :
Ли + Ул, + У а , У + 0 + О 'У
Л =--------3=------=——= з-
откуда получаем: х = 3х,( у = Зу/,; х и у — координаты точек данного эллипса
н, следовательно, удовлетворяют его уравнению. Подставив в данное урав-
нение вместо текущих координат х п у их выражения через текущие коор-
(Зх,)3 , (Зу/,)3 , 9х3 , 9у/3 . п
динаты центра тяжести, получим-. '—У- -4- „ = 1 или —— + ~г- = 1- Но-
/г ее о-
следнсс уравнение можно переписать, опустив индексы у х, и у/,. Получим
Оу3 Оу3 5
эллипс: ^-+^-=1 пли Qb2xs+ 9а2у2=а2Ь2.'237. rf=6,x=2. 238.
4 „. J/13 2. ' Ь 4 _
_у = it -j- х; 2) е = ~— ( у = ± — х. Указание. Нам дано: — = , При-
няв b = 4t, c = 5t и выразив а в зависимости от t, пользуясь формулой (6а),
489
найти е и составить уравнения асимптот. 239. 3.v 4~ 4у 15 = 0; Зл — 4у 4-
4-15 = 0. 240. rf = 2/ll. 241. Задача имеет два решения: 1) — ~=1;
2) — — = 1. Указание. Вследствие параллельности асимптоты данной
25 25
3
прямой имеем уравнение асимптот = —х. Отсюда получаем первое урав-
нение ~ = Для определения параметров а и Ь. Данное расстояние /26
от точки прямой до правого фокуса позволяет составить второе уравнение,
а третьим уравнением будет / формула (6а). 242. Уравнения касательных:
4
х 4- 2у — 10 = 0, л--- 2у — 6 = 0. Угол между ними <? = arctg у . 243. х- 4-
4- у“ + 6х — 22у = 0. 244. d = 5. 245. 9л:2 — 16_у2 =144. Указами е. Поль-
зуясь условием перпендикулярности двух прямых, можно написать уравне-
ния асимптот. Данная прямая проходит через правый фокус гиперболы, что
позволяет найти с. 246. Получается прямоугольник, стороны которого равны
2 и 5 /2 > площадь 5=10. Рекомендуется сделать чертеж. 247. 1х — у —
— 18 = 0. 248. Гипербола: §Ь“х- — 9а2уё = а"Ь- (см. указание к задаче 236).
249. л2 = 2ру. 250. х" — р[у — yj — парабола. Указание. Любой луч, вы-
ходящий из фокуса параболы, пересекает се в некоторой точке. Требуется
написать уравнение геометрического места середин отрезков, ограниченных
фокусом и точками параболы. На рис. 271 изображено несколько таких лу-
чей. Возьмем, например, луч Г4Л. Если координаты середины отрезка обо-
х Т +
значим через xt и у„ то, очевидно, л:, =-—, у1 = —-—. Из этих уравне-
ний текущие координаты точек параболы выражены в зависимости от теку-
щих координат искомого геометрического места; получаем: Л' = 2х1, у —
— 2yi — • Подставив в уравнение параболы вместо х и у их выражения
через и получаем: (2x42 = 2^. , xj —р ~j или х2 =
~р(у — • 251. Задача имеет два решения: 1) (0; 0), В (4; 4), С (6 — 2 ^5’,
-24-2/5); 2) (0; 0), В (4; 4), 6/(6 4-2/5; -2-2/5) (рис. 272).
252. Составим уравнение параболы EOJ', приняв за начало координат
точку О. Тогда эта парабола будет симметрична относительно оси Оу, вер-
490
шиной ее будет точка Су (0; 6) и она пройдет через точку 74250; 40). Под-
ставив в уравнение (14) вместо а и р их данные значения, получим у =
= = (л-—0)а-|-6. Для определения 2р будем иметь уравнение 40 = ^- • 2503 +
zp 2р
250а
+ 6, откуда найдем: 2р = -^-г-, Заменив в предыдущем уравнении 2р най-
34
денным значением, получим: .У = + 6, пли = 0,000544л2 + б. Далее
2 CAJ "
задача сводится к определению ординат точек параболы по данным абсцис-
сам. Получим: у, = /1Л, = 0,000544 • 503 + 6 = 1,36 -|- 6 = 7,36 м; уа = ВВ\=2
= 11,44 м‘, у3 = СС\ = 18,24 м\ у, = DD1 = 21>1Q м. 253. Уравнение пара-
18 5
болы EOD". У = ш^х3; м, Вр>' = — м. Указание. В данном
t/CU У У -
случае целесообразно принять за начало координат точку О. 254. х =
= -|-у3--^-у (см. пример 5 в § 38). 255. 5 = 46,08 кв, ед. 256. 1)у =
= -х3+5х;2) y=l.va + y.v; 3) у = 1 х3 - 2х + 4. 257. у=|(х3 +
+ 8х + 7). 258. 1) х3+у3=3; 2) ^+^ = 1; 3) (х - а? + (у - by = г3.
259. —12. 260. 4. 261. 119. Указание. Применить теорему о пределе про-
изведения. 262. ^-.Указанно. В данном случае применима теорема о пре-
деле частного, так как предел знаменателя не равен нулю. 263. 1. 264. 0.
265. 0. 266. 4. Указа и и с. Применяя теорему о пределе суммы, получаем
/ . 5 7 \ 5 7
lim I4-]-----у, = 4 + lim----lim ==4+0— 0 = 4.
X -* СО \ X X / X ->- CO X Л'
267. 4. 268. 1. Указание. Следует предварительно разделить почленно
числитель на знаменатель. 269. 2. 271.-- 272.--. 273. —, У к а з а и ие.
4 2 2
з ... > \ Ч'1 f<
а д_о =—/ —уг. 274, 0. 275. оо. 276.=, Указание. Числитель
"3(24-4)
представляет собой сумму чисел натурального ряда от I до п, определяе-
мую по формуле суммы членов арифметической прогрессии. 278. , 279. —.
Указание. Числитель разложить на множители по формуле х3 + рх +
+ q = (х — xj (х — л-J, где х, и хг—корни квадратного трехчлена х3+
+ рл‘ + <7- 280. — 1. 281. 2. 282. 2а. 284. . 286. 1 (см. решение примера
285). 287. 0. Указа п и е. Разделить почленно числитель на знаменатель и
35 1 S) ”7 39
рассмотреть предел разности. 288. 1) -У—; 2) 2 — ; 3) 4) 3-1—.
ill 1Ц oUv 11v
289. 1) F, (х) = Зх3 + 7х - 5; 2) R (х) = ^+^'~4' 3> Ю = <?'х" +
+ 5х-6)К2ГрТ; 4) F4(x)=7x—12; 5) (х) = j/3**~ 6 ;
6) Fa(x)=g + ^2^ 290. 1} 0) — 2 . I3 + 3 . 1 _ 7 = —2; 2)/(-l) =
= -8; 3) /(0) = —7; 4) /(2a) = 8a3 + 6<7 — 7; 5) / (/3 ) = 3/3 - 1;
491
6) у (д 4-*) = 2 (a + *)я + 3 (л-[ 6) — 7. 291. 1) /(</) = а3-За; 2) <р (&) =
= »4l;3)/W=^;4) т(С + 1)=са+3С343е + 2; 5) f(a-\-b)~
— а2 4 ‘lab 4 b2 — За — ЗЬ; 6) <р (а — Ь) = (а — Ь)3 4 1- 292. 1) ср (.г 4 h) —
— ? (х) = (Зх3 4 ЗЛх 4 Л3) //; 2) 2л-;. 3) 1. 293. 1) /(0) = 1; 2)<р^-) = 1;
з)/^) = /2’; 4> б) •
295. Указание. Любому конечному значению аргумента соответствует
определенное действительное значение функции. Поэтому данные функции
существуют в любом промежутке (—со <’х < со). 296. 1) 0 < х < со. Ука-
зание. Вспомнить свойства логарифмов; 2) 0 л- < 4 е0- Указание.
При х<0 для у получаются мнимые значения; 3) — со < х < со;
4) — со < 4 (л 4); 5) — co<xsg —3 и Зосх<ос; .,6) существует
в любом промежутке, не содержащем начала координат: хуДО-
298. 1) — со<х<оо; 2) —4ccx=cc4, или | х | - 4; 3) — оо-Слоо — 2 и
2 С х < со или | л-|^2; 4) — оо<Л;ссО (при х > 0 у принимает мнимые
значения). 300. 1) Ду =— > %) ~ х + Да' — 3) Ду =
Ду = 1g (х 4 Дх) — lgx = lg(14y). 301. Ь ДУ =
= — 0,41; 2) Ду = — 5; 3) Ду = 0,12. Указание.
Сначала находим приращение функции в общем
виде: у 4 4’ = 4 — (х 4 Дх)3; Ду = 4 — (х 4 Дх)3 —
— (4 — х3) = — 2х Дх — (Дх)3 = — (2х 4 Дх) Дх. Для
определения приращения функции в первом случае
полагаем х — 2, Дх = 0,1; во втором случае х =— 2,
Дх = — 1; в третьем х = 0,4, Дх = — 0,2. 302. 1) Дтг =
= 7,26 см3, Д1/= 10,981 см3; 2) Ди = 126 см2, ДУ =
= 331 см2; 3) Ди= —9,36 сх3, ДУ= —9,128 см3.
Указание. Обозначив ребро куба через х, по-
верхность— через и,, объем — через V, напишем
формулы: и—6х2, 1/ = х3. Дальнейшее решение
аналогично решению задачи 301.304. См. рис. 273. За-
дача решается так же, как предыдущая. 306.3) У к а-
з а н и е. Ду = ах(а^х — 1), lim </* = !. 307. Обе функ-
дл- - о
ции непрерывны в любом промежутке —со<х<со.
(Дл?\ Л
х 4 -g- • sin-g-. При Дх —0
„ / . Дх\ . Дх _ ,
-2 cos I х—2~1 величина ограниченная, sm -%----величина бесконечно малая,
а потому их произведение (§ 47, 2-е свойство) — величина бесконечно малая’.
308. Указана е. Ду = 2-у/~х (1/ 1 — Н . 310. 1) х = 1; 2) х — 2;
3) х = — 2 н х = 2. 311. 1) х = -^- (2/г 4 1)1 2) х = пи, где п — любое целое
число. 312. иС[)=4,1 —Указание. Z = 4 сек. Д£ = 0,2 сек (см. решение
примера 1, § 58). 313. 1) иСр = 2 (2/ 4 д4 2) из формулы, выражающей
среднюю, скорость через t и М при 7 = 3 сек а Д7 = 2 сек, находим: »с„ =
= 2 (2 • 3 4 2) м}сек = 16 м[сек; 3) иср = 16 см/сек. 314. ух — 6. 315. у‘х = k.
316. zx = 2х — 2. 317. /'(х) = 2х 4 4; 2) 4; 3) 8; 4) -2; 5) 2 (а — *) 4 4.
318. Эта функция не имеет производной при х = 0. Разумея под х любое
число, отличное от нуля, по общему правилу дифференцирования найдем:
492
2 1 1
y't—~p. l)yv= — 2; 2) y'x — 4; 3) y'x= — g2. 319. « = 34-2/ (см. ре-
шение примера 3,- § 59). 1) 7 м/сек", 2) 23 м/сек. 320. <л = (2t 3) рад/сек",
<> = (2 • 4 4~ 3) = 11 рад/сек (см. решение задачи 1, § 60). 321. 1) / = (4t 4- 3) Л;
2) / = 35.4. Указание. Сила постоянного тока определяется как отноше-
ние количества электричества, протекающего через поперечное сечение
проводника за некоторый промежуток времени, к величине этого проме-
жутка. В случае переменного тока будем иметь: /ср=^; I=Q't— lim =
= (4/ 4- 3) ампер *. 322. р = arctg 5. У к а з а и и е. При определении tg |3 по фор-
муле (5), § 62, следует принять х = 2, Дх=1. 323. k =у = 4х [см. формулу
(6), § 62]. 1) Л = 2; 2) А = —8. 324. 1) 2; 2) 8; 3) - 6. 325. 1) 6; 2) 0; 3) -6.
4
326. у'х — — 1) х 4-у + 4 = 0; 2) х 4-.У— 4=0. 327. Точка касания (1; —1).
Указание. Абсцисса точки касания определяется из уравнения у'х = 0.
328. у'х = 1. 329. _v’v = 4. 330. у’ = 2х — 3. Указа н и е. Применяются фор-
мулы (1), (2), (3), (5) и /7а) из § 64—67 и 69. 331. = 7х« — 12х5 4- 6х.
332. у?; = (а4-1)л'“ — (а — 3) х"-^1 = (а + Г) х'1 — (а — 3) х'1”1, 333. =
= х3 — .<4~о- 334. y’v = xb~l—хя-1. Указание. Применить формулы (3),
(6) и (7а). 335. у'х = 4х3 — 8х. Указание. Предварительно числитель по-
членно разделить на знаменатель. 336. у'х = Q •
91- _ з
нить формулу (6). 337. ух = —^—. 338. у'х ——
У Казани е. Прпме-
8 ,
— (см. решение при-
149 10 6
мера 1, § 69). 339. <=-±-^4-4. 340. у'=-^ 341.^=-4-
4 3 4'
+ р. 342. у'х =; 4 4- (см. указание к задаче 335). 343. у\—
, 1-1 л ±-t й 6.-1 111 _1
2-3|-х2 -З-fx3 4-5-lx5 =3,г2-4.с3+6х5. 344. -х 2 +
-1 -А / з _1 4 _1 2 -- V- -- --
4-Х 34-х 1345. —ту-X 3+~-х 4—T-V 24-4 =х 3—х 4 4-х 2.
У Z о и / х
346. 4х-2-Зх" 2. 347. (yxyxd^)x=^^. 348. (^)' =
f -^Y 5 1
— \х6 Ух — в.— 349. . Указание. Пример можно решить, как и
два предыдущих, воспользовавшись формулой (7а), но в случае квадратного
корня предпочтительнее писать производную сразу по формуле (8а):
(Кх)х = —Y_. 350. —к-4-т-^=4-Д. 351. — . .1 z Указание.
Т\Г х /х |<х3 Л'3 2]/х 41/*
У ах =Уа Ух. 352.—. У к а з а и и е. (1/"— ) =(Х=) ,353.^-т/х1 —
2 У ах W а/х \уа/х 3
1 7 г2 — 3
_ ——. — - t 354. 4х (Зх4 4- Зх2 4- 1). У к а з а н и е. Применяем фор-
- 5?
* Ампер = 1
кулон
сек. *
493
мулу дифференцирования произведения двух функций: ф(х4 4- 1) (2х* 2 4- 3)]ф =
= (2х* + 3) (л-’ + 1);+(х‘ +1) (2х2+3)* и т. д. 355. 356. •
К х 2 у х
357. 4(2u.v Ц-/?) Z/.v + <):1, Указание. В данном случае у является
степенью функции от х. Полагая ах- -ф- Ьх 4~ с = и, у можно представить
в виде у = и4. Следует применить формулу (7); получаем (и4)^ = 4ы3п^ =
= 4 (ах2 -ф- Ьх -ф- с)3 (ах2 -j- Ьх -ф- с)* и т. д. 358. 15х2 (х3 -|- а3)1 (см. решение
предыдущего примера, и примера 3, § 69). 359. 28<zx3 (ах4 Ц- Ь)в. 360. 8 (4)/"х -ф-
+ и?. 4. ,.Ц = 16(4Ух_+.!/ 361. Qaxi (аХ2 + b) . 362. - 2ах' . У к а-
2Ух Ух ‘ Уах3^Ь
з а н и е. Переписываем данную функцию, заменив радикал дробным показа-
2
телем у = (ах3 -ф- Ь)3 и приняв ах3 -ф- Ь = и, находим производную по фор-
2 —-
муле (7): ух = у (ах3 -ф- Ь) 3(ах3-[-Ь)'х (см. решение примера 4, § 69).
4 v
363. — Указание. Можно взять производную так, как указано
У4х2 + 3
в предыдущем примере, по проще применить формулу (8) (см. решение при-
(4х~ -ф- 3)ж 24 v
мера 6, § 69): ух = — . 364. у'х =--------. Указание. Пред-
2у 4х2 -ф- 3 (2х“ -ф- З)4
варительпо переписать данную функцию в следующем виде: у = 2 (2х2 -ф- 3)~3.
—, ах b (а-— х2)
(а2 д_ 2 2л- = — г . 366.--------г - =
1 ’ У(х2 -ф- а2)3 а 2Уа2—х2
367. а. Применяя формулу (9) § 70 дифференцпро-
365. а • — ~2 j '
__ Ьх
а У а2 — х2
вания частного,
(х -ф- 3)(х -ф- 2)'х — (х -ф- 2) х (х -ф- 3)*
получаем f'(x)^=
(л~ 4~ 3) • 1 -ф- (х -ф- 2) 1
(х -ф- 3)-
, 1 368. — 369. Указа-
(х-ф-З)2 (3x4-1)- а-~(-Ь-
дроби — величина постоянная. Следует взять пропзвод-
(А'4-3)2
Знаменатель
и и е.
ную по формуле (6) § 67. 370. . — И-Ь*2. 371. /'(х) =—Gj_ , u.
л Л (Л "j- 1 }
372 ~ -л~ 1) 373 ____1_________ 374 _______?_______
372- (л-3._л- + 1Г • • ут(Гх-1)* зур (уг+ 1)2 •
о__ х (а2 — Зх2) п ,
375. —Указание. Данная функция является произведением
У а2 — X'1 ______
двух функций: и = (а2 + х2), у = У а2 — х2. Дифференцируя по формуле (4)
§ 67, получаем; [(а‘ + А") У а2 — х2]х = )Лз2—х2 • (а2 -ф- х2)л- + (a2 -j- х2) X
гг______ч, г.__________ (а2 — х2\х г___________
х (У а2 - х2)х — у а2 - X2 -2х + (а2 4- х2) -\ = У а2 - х2 2х —
2 у а2 — х2
__(а2 4- х2) х_(Уа2 — х-’)а 2х — (а2 4- х2) х_(а2—Зх2)х 37(, 2х2 4~ 1
У а2 — х2 , У а2 — х2 У а2—х2 ' Ух2 -ф- 1
377. ° , 378. 3 (5х — 3) (Зх — 1) (х — I)2. У Казани е. Дифференци-
2 У а — х
494
руя как произведение двух функций, получим:
[(Зх-1)3 (х -1)’].; = (х -1)'1 [(Зх - 1)3]; + (Зх -1)3 [(х -1)’]; =
= (x-i)’.2(3x-i)(3x-i); + (3x- 1)3-З(х— 1)3-(х-1); =
= (х - I)3 • 2 (Зх — 1) • 3 + (Зх — I)3 • 3 (X — I)3 и т. д.
379 2<-г+1>
Указание. Дифференцируя как частное двух функций,
получаем:
/ 2х—1 У _ V2х3 + 1 (2х (2х - 1) (/2P~+T)'v
vKirqn/v , (/2^+т)2 “
/2х3 + 1 . 2 - (2х - !) (2-у+^4 2/‘2х3+ 1 — (2х— !)•——-4'V —
2 /2х3 + 1 2 / 2х3 + 1
— 2х3 + 1 2х3 + 1
2(/2х3 + 1)а-(2х-1)2х
(2х3 + 1) J/ 2F+T
380. --------, 381.
(1 4-х3)/1 4-х3
_____2д3х
(а3 + х3) /д1 - х4 ‘
Указан и е.
1/4^4 = 382.
> а“ + /д3 + х3
— 9 Ч
=5/' б) г,=19т
(1-х 4-х2) /1 4-х3 4-х4
383. a) v —
м/сек. 384. 1) £ = 8 сек; 2) t = 24 сек.
385. см = 1,00201, с[00 = 1,013 (см. пример 2 и решение задачи 2, § 60).
386. v = з) = (21 -|- 2) см/сек, Е/г=15-104 эрг. Указание. /« = 3000 г.
387. 9х — у — 27 = 0 (см. решение примера 2, § 62). 388, ^2; —5 уj,
f—2; 5у) (см. указание к задаче 327). 389. 1) у = 8x4-16; 2) у = — 4х;
4 2
3) у = 8х — 16. 3S0. у = 2х; у = 4х — 4, и = arctg у . Предлагается построить
эти параболы. 391. 1. У к а з а и п е'. lim I?— = lim s’n x = lim —!— . ——
x-*0 X .V-.0XCOSX .v — OCOSX x "
392. 2. (Воспользоваться формулой sin 2r =2 sin x cos г.) ЗОЗ.т. У к а з а н и e.
lim — тх = lim s‘n mx (см. решение примера 2 в § 71). 394. 4-.
Л'-‘О X ,v_o тх / г I г г/ / 4
3S5. cos х (см. решение примера 3 а. § 71). 3S6. cosx (следует предвари-
тельно преобразовать разность синусов в произведение). 397. 2. 398. —фпх.
Указание. Преобразовав разность косинусов в произведение, получаем
lim
а-> 0
COS (х 4- “) — COS X
а
П . х 4- а 4- X X + а -— X
— 2 Sin L-yJ— cos —--------
lim -----------=----------------
а —► 0 а
495
/ х\2
1 / Sln 2\ 1
= lim —. 400. 12. У к а зап и е. Преобразовав числитель
\ 2
, cos х — cos 5х , 2 sin Зх sin 2х
в произведение, получаем lim -----------------------— lini ,-----------—
Х-.0 'Л'" х -- о X2
= 2 lim sin lim .401.2cosx. 402.1) f (x) — cosx — sin x; 2)/' (0) = 1;
x -> 0 X x -*• 0 A*
3) /’ w = -1; 4) f (- = 1. 403. 1) f (x) = - ; 2) f (0) = 0,
\ z , V 2 cos x + 1
3) f — 4" Кб • 404. 2 (sin x + cosx) (sin x созх)Л = 2 cos 2x; f (0) = 2;
i\ 3 j 4
/'(41= — 2. 405.
407. y'x = a cos ax.
— cos ax • (ax)'x. 408. — 3 sin 3x. 409.
I(gax\' 1
меняется формула (12) 1-^—j — •
Указание. Применяется формула (13)
у'х — tg2 х. Указа н и е. see2 х — 1 = tg2 х. 406. a sin х.
Указан и с.
Применяется формула (10) (sinax)^ =
a a - V n
я---5sec- ax. Указа н и e. При-
2 cos- ax 2
—J— (ax)' 410. •—Jr cosec2 (4x 4- 1).
cos- ax ' Л 2
"ctg (4x4- !)]'_ 1 (4a'+* 1).c
8 J.v^ ~ 8 ‘ sin2 (4x4-1) ‘
411. cos-^. 412. —xsinx2. 413. cosx —sinx. Указание. Можно диффе-
ренцировать как произведение двух функций: j<( = (tgx-|-l)(cosx)'t-f-
-|-cosx (tg х4~ !)(/> в данном случае дифференцирование значительно упро-
стится, если функцию предварительно переписать так: у =- (tgх + 1) cosx =
= sin х + cos х. 414. cosx—sinx. 415. a cos ax cos bx — b sin ax sin bx. Ука-
зание. Следует дифференцировать как произведение двух функций:
(sin ах cos bx)'x — cos bx (sin ах)'х + sin ах (cos bx)'x. 416. .3 cos Зх cos 4x —
— 4 sin 3x sin 4x. 417. 2x cos 2x — sin 2x. 418. •:—,—— . Решение.
1 -f- sin lax
Дифференцирование ведем по формулам (9), (10) и (11):
(sin ах cosax) • (sin ах — cos ах/*. — (sin ax — cosax) • (sin ax 4~ cos ax)'x
. (sin ax cos ax)2
___(sin ax 4-’cos ax)-(cos ax-a 4- sin ax-a)—(sin ax—cos ax) (cos ax • a — sin ax-a)_
" sin2 ax 4~ 2 sin ax cos ax 4- cos2 ax
a (sin ax 4-cos ax)2 4-a (sin ax — cosax)2 _
1 sin 2ax
a (sin2 ax -|- 2 sin ax cos ax 4- cos2 ax 4- sin2 ax — 2 sin ax cos ax 4- cos5 ax)
1 4- sin 2ax
2a (sin2 ax 4-cos2 ax) 2a
1 4- sin ‘lax . 1 4* sin 2ax ‘
..r. 2 4 3a cos 3x ,,
419. — in . 420. ———r—. 421.-------------. .Указание. Применяются
1 — sin 2x 1-|- sin 4x 2 ]/ sin 3x
иоследователыю формулы (5), (8), (10). 422. — °ДП _ 423.-------=
у cos 2x n <, X / X
r 2 COS-2 I/ tg-2
496
/к?
=-i----—424. у' — 0. Данная функция сохраняет свое значение иеизмсн-
stn X х
ным при любом х. Предлагается проверить ответ дифференцированием
(см. решение примера 3, § 72). 425. —3 sin xcos'-‘x. Указание, (cos3 х)' —
,, 2л cos ах ,, „
— [(cosл')3]v. 426.------—--. У казание. Следует переписать данную
Sill
функцию: —---------= (sina.v)“2, а затем дифференцировать так же. как ука-
J sin- ах •
to4 ах
зано в предыдущем примере. 427. ------1-- (см. решение примера 4, § 72).
cos- ах
3tg2 —
428.---sin — . 429. ----—- = 3 tg2 — sec2 —. 430. —3.v2 sin 2x3. Указа-
№ x <. x ь a a
cos3 —
a
ние. (cos2 A’'')'v = [(cos x3)2]^.. 431. r’v = a sin2 cos . 432. /'(() = vQ cos21 X
X (1 - 4 sin2 (). 433. -—x (1 + tg 2o sin 2o). 434. f (x) = Зам e-
v . cos2tpcos2«> ' 1 ‘ T ' sin3 x
чание. Такой вид принимает производная после тождественного преобра-
зования тригонометрических выражений cos’у — sin1 и sin’у cos3 у .
sin 28 sin 2<х ,г ’ „ ж.
435. а) !—тк . о)--^г-,---• Оказание. При первом дифферсн-
' sin- (а — 3) ’ Sin- (а — 3) Г Г гг <
цировании р принимается за постоянную, а за аргумент, при втором — на-
оборот. 436. 2х tg х (tg х х sec2 х). Указание. [(xtgx)-|'v = (х3 tg2 х)'Л
437. tg2 х sec2 х — sec2x4- 1 = tg1 x. 438. ~ tg1 ~ sec’-sec’-—
| X
— g sed -y .439 . —k t g-ft x coset-fc t —k cosecA x = —k cosc’c/г Л440 {2k я} )
и [(2й + 1) я; —1], где k— любое целое число. У к а з а н и е. Для определе-
ния таких точек получим уравнение у* = 0. Подставив в это уравнение
вместо у'х его выражение, получим — sinx = 0 или sin х = 0. Решив это
уравнение, найдем х=яп, где п — любое целое число. Если n = 2k, то
у = cos 2йл = 1. При п = 2k -j- 1 yi = cos (2й 1) л =—1 (см. график этой
функции на рис. 120). 441. хД-у — я = 0. Указание. Найти ординату
точки касания, угловой коэффициент касательной и написать уравнение
прямой, проходящей через данную точку в данном направлении. 442. k = 4.
445. 1) /4A-) = l + lige = l+Jg_e. 2) /'(l) = l+lge^ 1,434.
Л л л
(\,rx I 1V 9
446. 1) /' (х) = . 2) f (4) = . 447. В данном случае под знаком
2xJ/x
логарифма находится функция от х. Поэтому следует дифференцировать
г. /1с\ ' («х3 + 6х-[-с)х 2ах4~* .,о
по формуле (16): j =----—j--------=— . 448.
ах1 4- Ьх 4* с аха(>х + с
449. = Указание. Сначала следует преобразовать функцию, при-
менив правило логарифмирования степени: у = 3 In х. 450. Указание.
(1п/Г)'х=Ц- lnxV451. у=^Л—\ -452. y^i.453 .s^ = 1 - tg.
2х
497
.r. . cos4x , 2x (7x2 + 1) v n
454. у — у- . 455. у —---[—-. Указание. Предварительно
преобразовать правую часть, -применив правила логарифмирования,
г, , ч 8/г 4 sin t . _ , 4а2х
456. f (<р) = . . 457. /'(/) —------— . 458. у —----------. Указа-
J чт/ sin 2Аи , . » t J xi — ai
т 1—4 cos-
н и с. Чтобы упростить вычисления, следует правую часть предварительно
Л ЛСЛ , 6л"
переписать, применив правило логарифмирования частного. 4а9. _у ——--.
Указан и е. Предварительно преобразовать правую часть, воспользовав-
шись правилами логарифмирования. 460. = 461. 1) </ (х) —
=-2) -1; 3i - 4 /3 • 462- п f /)2) f =0;
з) f (/7) = •461 ЗЛ'1п 3+4rV; f (1)=31113+4<?; f (°)=
= In 3 -j- 4. 465. f (л-) — аеах; f' (0) = a; f = -у . У Казани е. Дан-
ная функция имеет вид у = е", где и = ах; поэтому надо дифференцировать -
по формуле (21): j’’v — е“ их = еах (ах)\. 466. 5е5А'+“. 467. 3<г!л‘1пй.
468. 7ax+b а 1п 7. 469. 5А" 2х 1п 5 -|- 52А • 2 1п 5 4 • 5 х 1п 5 = 111 25 (5А-! • х -|-
। 52л д_ 2 \ 470. (3xs + 3) еА’3 +ЗА+2 = 3 (х2 + 1) eAS+3A+2. 471.2х (2л2 Д- 1) е2х'~..
5Л у
Указан и е. Данная функция является произведением степенной функции
ла показательную. Следует взять производную по формуле (4).
472. ахе2х (2 In а). 473. f (х) = sin 2х. 474. у —— kews кх sin kx. .475. у' =
v't = 2esln2z (cos2 2t — sin 2/). 478. — ~e .
t 4 ' / I - I Ml-
= а
показательную. Следует взять производную
А (2 4- In a). 473. f (x) = sin 2х. 474. у = — kew& кх
In a sin 2,v. 476.
4 1
479. , . 480. •=-/—
получаем у=х—1п(14-еА).
481.
Указание. В результате логарифмирования
3
—. 482. V’ = а. У к а з а н п с. v =
4х .
— In (abcax) = In а Д- In b Д- ax In e — In а Д- In b Д- ax. 483. --I'1' : Х4л
]/4л2 4- 5
484. -i- \,e a — e a / . 485. . Указание, [in (ех Д- Kl 4~ e2A )].v =
2 ' . jz 1 e-x
+ 2 1 1 •; >.':a _ ex (|/ 1 + e2x 4- e-v) ' 4Sfi 2
ex + /1 4- e2x (йа 4-/1 4-e“A )yi +е2Л ’ ' /4л2 + 1 *
487.
2 4- л — 5л2
2л(1 —Х-) •
489.
3 In2 х
X
490.
4 In3 /2х 4- 1
2л- 4- 1
Указание.
(1п4/2л-+ 1)л=41п=/2л-4- 1 (1п /2л- 1)1 = 4 1п3 /2л-4-1[’1п(2л-4-1)]л=
1 (2.v4- l)’v i i
= 4 In3 . 2- • 2х + . 492. /'(л) = 2л 11А— In л; f (е) = 2;
f(l) = 0. 493. Скорость изменения потенциала в зависимости от вре-
мени t выразится формулой v't — — voae~at (см. § 60). 494. P't = Poceci,
а так как P = Poect, то P't = cP. Из этой формулы видно, что скорость P't
изменения давления прямо пропорциональна давлению Р, 495. 1) /' (х) =
498
3)у,Ш=34' ** '> rz+ 2>
1 U j Ч 1 —J— U Л.
“ 498. --—L=. 499. ,_____L^z .
fl“ + х~ vх - х2 у 2ах - х2
500.—\
2 /х V1 - х
/х — а\> (х-\-а) — (х — а)
... 1 got у - \*+~г/ _ (х + а)3
2 ]/гх - х2 ' ’ [х~а\ (х + а)3 + (х —а)3
‘\x-yaj (х + а)3
_______~х 503 504 1
х* — Юл-3+ 26’ • 14-х3- ’ ’ y-j—^ •
505. 1 , . 2 (2 - х) У 1 - х- . а2 506. - а Х = 1/ а — х У а2 — х2 г а + х Лarctg 2.V
507. —------- - -- _. 508. 2 /а3 - х3.509. 1) f (х) = , , 2) f (0) = 2;
(я»--х3)/а2-2х3 1 1 + 4х3 ’
Зг3
54. Л =27-
. 510. 1) f (х) = - р==; 2)./' (0) = 0; 3)/' (^)=-
Указание. Берем производную от обеих частей данного
уравнения, имея в виду, что у является функцией от х: 2yy’v = Зх3, откуда
, Зх3 , р , х ... , 2 — х ... , х — а
V = . 512. У’ = —. 513. v =----. 514. \> =----. 515. у =--------
Хх 2у х у х у ' * у х у—Ь
v -1 а
516. у' =’----. 517. у’ =---. 518. у' ———+ . 519, Уравнения касатель-
Хх у х cosy У+4
иых 6х—у —24 = 0, бх+у = 0. Уравнения нормалей: х + бу — 41=0,
х — бу + 37 = 0. Указание. Чтобы составить эти уравнения, достаточно
в соответствующие формулы § 78 вместо х0 и уп подставить координаты
точек пересечения линий у = 6 и у = х3 —4x4-1. 520. х—у —2 = 0,
12
х +у — 6 = 0. 521. <р = arctg- (угловые коэффициенты касательных легко
можно найти по формуле из § 78). 522. хх0 +уУо = г3. 523. <р = ,
524. х + Зу + 9 = 0; Зх -у - 33 = 0. 525. +-^ = 1. 526. х - у + 3 = 0;
х +у + 1 = 0. Указание. Для составления уравнения касательной можно
воспользоваться ответом предыдущей задачи. 527; (5; —12) и (—5; 12).
Указание. Угловой коэффициент касательной к окружности
х3 -|-у3 = г3 в зависимости от координат х и у точки касания выражается
формулой k = ——(см. ответ задачи 513). Так как касательная должна
быть параллельна данной прямой, то k = или — . Очевидно, коор-
динаты точки касания должны удовлетворять этому уравнению и уравнению
данной окружности. 528. Уравнения касательных: 2х — у — 6 — 0,.2х+у +
+ 6 = 0. Уравнения нормалей: х + 2у — 8 = 0, х — 2у + 8 = 0. 529. [% 4^ .
530. Точки касания (6; 0) и (6; б). Уравнения касательных: 4х — Зу — 24 = 0,
24
4х + Зу — 42 = 0. 531. = arctgу. 532. Кривые пересекаются в точке (2; 3),
угловые коэффициенты касательных к ним в этой точке удовлетворяют
условию перпендикулярности. 533. у" = бах + 2& = 2 (Зах + Ь). Указание.
499
Q
Л =Зах'.+ 7bx + c< +Ьх + сУх- 534- У'^'^'^ух' 535‘
== C'‘ 1 . 536. У'=ал lns a. 537. y" , = — k2coskx. 538. y"— tn2emx.
v/It* • -'XX XX xx
4 4
^^ = 0+^. 54°- Ухх-у^у-
541. y"xx = 48a2 (2ax + b)2.
/>* 1 -- v~
542. y"=~ -A—. 543. y"=, , 544. y" = 2 cos 2л. 545. у" =
xx sinJ ax (1 + x-)J
=—18cos6x. 546. a) v — v0— 9,8/, w =— 9,8 м/сек2; 6) v = 80,4 м/сек;
u) v = 2 м/сек (ускорение — величина постоянная). 547. a) v = (/2 Д- 3/) м/сек;
6) 12 м/сек2; в) w = (2/3) м/сек2; r) 11 м/сек2. 548. v = eal e~at;
— a (eat — e~at). 549. a) w = t2 — 5/ 4- 4; 6) t, ~ 1 сек, Z2 = 4 сек; в) t3 = 2 сек,
ti = 3 сек. 550. a)w =—--sin = м/сек2; б) = м/сек2; в) м/сек2. -
lo Z io lo
10 2
w = (JzpTp i 6)v — — 2 м/сек, w = у м/сек2; в) v =
м/сек2. Указаний. Вычисление производной упро-
10
551. a) v
1 , '1
— —гг м сек, w —
2 ' ’ 40
стится, если предварительно логарифм дроби выразить через логарифм ее
числителя и знаменателя. 552. (sin х)х (In sin х 4-х ctgx) (см. решение за-
лп, , cm tl- х I •п х , tg ,v\ , ]/"4х — 1 , 2
дачи 491). 553. ,vU A —5----Г— . 554. у =---------=-----. 555. у =
\cos-x х J х 2х х е,х-{-1
rin 9 у (pt __ 1 )
556. у' =----, 557. /' (Z) = tg3 1. 558. s'. . 559. у =
4/(14-cos2x)3 1 6^4-1
y2 I ?
- 7-^ • 560‘ У' = V . 561. у = — 562.7 (Л-) - A'2 arc tg x. 563. </(x)=
= 2kekx sin kx. 564. F' (.v) = -Ц-г. 565. (—1; 3 7, {7! —81 4V 566. а) й =
' xJ 4- 1 \ 3/’^ 8 j
= 1; 6) k — 2; в) k = 4. 567. Уравнение касательной Зх — 2y—1=0, урав-
нение нормали 2х 4- Зу — 5 = 0. 568. а) .19,6 м/сек; б) t — 4 сек; в) s=98,4 м.
569. ,£ = arctg 2 )/2 . 570. x-|-y — 3 = 0, х4“У + 3 = 0 (следует построить
гиперболу и касательные). 571. ^ = = arctg3 (рис. 274). 572. У казан ве.
Производная (ех)'х = ех положительна при любом значении аргумента х.
Следовательно, данная функция возрастает в любом промежутке .(—оо <
<х <со) (график этой функции см. рис. 118). 573. Указание. Доста-
точно показать, что производная отрицательна при всяком х. 574. Возрас-
тает в промежутке (0; со). У к а з а н и е. Данная функция при отрицатель-
ном значении аргумента х не имеет смысла. 575. Производная у^ = х“4-1
положительна при любом действительном значении х. 576. Первая произ-
500
водная этой функции возрастает в любом промежутке, так как (у'х) =
= 4e~axz>0 при любом х. 577. 1) Убывает в промежутке (—со; 0), возрас-
тает в промежутке (0; оо); 2) убывает в промежутке (—со; 3), возрастает
в промежутке (3; оо); 3) возрастает в промежутке (—со; 4), убывает в про-
межутке (4; со). 578. 1) Возрастает в любом промежутке (см. указание к
задаче 572), 2) возрастает в промежутке (—1<х<со) и убывает в про-
межутке (—со < х <—1). 579. Производная у’ = х3 16 возрастает в лю-
бом промежутке, так как у"'= Зх2 > 0 при любом х; 2) убывает в проме-
жутке (—оо; 0) и возрастает в промежутке (0; со); 3) возрастает в проме-
жутке (оо; 4) и убывает в промежутке (0, оо); 4) убывает в промежутке
(—со; 0) и возрастает в промежутке (4; оо). 580. х = 3 дает минимум
/(3) = — 8. Указание, f (х) = 2х — 6 = 2 (х — 3). Приравняв пулю про-
изводную и решив полученное уравнение, находим х = 3. f (3 — Л) =
=f (3 -- 1 )•=/ (2) = 2 (2 - 3) < 0; f (3 + Л) =/ (4) = 2 (4 — 3) > 0. 581. При
х = — 2 минимум f (—2) = (—2)2 4 (—2) — 3 — —7. 582. При х = 4 макси-
мум /(4) = 18. 583. При х = 5 максимум /(5) = 26. 584. При х = —2 функ-
ция имеет минимум: ymin =—16. Точки пересечения с осями координат:
(—6; 0), (2; 0), (0; —12). В промежутке (—со; —2) функция убывает, в про-
межутке (—2; со) — возрастает. На основании этого исследования строим
вершину параболы С (—2; —16) и небольшой отрезок кривой вблизи вер-
шины, учитывая, что эта точка является точкой минимума, а также точки
А (—6; 0), В (0; —12), D (2; 0). Затем все элементы соединяем плавной кри-
вой (рис. 275). S85. Предлагается всю работу выполнить самостоятельно.
586. Функция имеет минимум при х = 0, убывает в промежутке (—со; 0)
и возрастает в промежутке (0; оо). Вершиной параболы является точка
С (0; 2), с осыо Ох парабола нс пересекается. Для более точного построе-
ния графика найдем еще две точки, расположенные по разные стороны от
оси симметрии (х = 0) на равных расстояниях: прих = —3 У = 4“ (—3)а -f-
-{-2 = 6-1-, при х —= (рис. 276). 587. Функция имеет максимум
при х=1, возрастает в промежутке (—со; 1), убывает в промежутке (1;со)
(примерный график см. на рис. 277). 588. При х = 0 максимум/(0)=0,
при х — 2 минимум /(2)=—4. Указание. /'(х)=3х(х — 2). Критиче-
ские значения аргумента находим, решив уравнение Зх (х — 2) = 0. Полу-
чаем: X! = 0, х» = 2. f (0 - Л) = f (— 1) = 3 (— 1) (— 1 — 2) > 0; /' (0 + h} =
=/(1) = 3-1 (1— 2)<0; /'(2-ft)=/(l)<0, f (2 + Л) =/' (3) > 0. Ре-
зультаты исследования заносим в таблицу (табл. 36).
501
Таблица 36
X /' (х — 7г) Г (X + Л) Заключение У U)
0 2 + 1 0 0 1 + Максимум Минимум 0 —4
1 Л 1 \ 3
у МИНИМУМ/,-2 16’
2 минимум /(2)= — 8. 596. Произ-
. Без дальнейшего
этом значении аргумента изгибающий момент Л-1
легко это проверить и по знакам производной
,, 7 hl ,, _
При х——^= Л11пах = - - . У к а з а н п е. Про-
уз 9 у 3
при х = В данном случае отрицательный
)п1ах = 45 м1сек. Указан и е.
исследовать па максимум и минимум скорость.
В данной задаче функцией, подлежащей цсследо-
589. При х =— 2 максимум /(—2)=31, при х == 2 минимум /(2) =—1.
590. Ни максимума, ни минимума [при переходе аргумента через критиче-
ское значение х — 0 производная знака пе меняет:/' (0— Zi) = — 3 (0 — h)- < 0
и f (0 h) — — 3 (0 + h)- < 0]. 591. Ни максимума, ни минимума. 592. При
1 ” 28
Л'=1 максимум/(1) = 1 -ту , при Л' = 5 минимум /(5) —----. 593. Ни мак-
симума, ни минимума, так как ни при каком действительном х производная
в нуль не обращается. 594. При х = 1 минимум /(1) =— 27, при х = 4 —
ни минимума, ни максимума. 595. При х = — -у минимум/
при Л‘ = 0. максимум/(0) = 0, при х -
ql ,
водная = ~--------обращается в пуль при х =
исследования ясно, что при
будет иметь максимум. Но
1 I ап
при х < у и х > — . 597.
изводпая обращается, в пуль
корень смысла не имеет. 598. При £ = 3 сек V.
В данном случае надо
599. 5 и 5. У к а з а н и е.
вашпо (см. решение задач 1 и 2, § 85), является произведение двух чисел,
сумма которых равна 10. Обозначив одно из этих чисел через х, получим
у = л'(10 — л'). Дальше исследование ведется по правилу, изложенному в § 85.
600. Каждая часть должна быть равна 6 (см. решение задачи 1, § 85).
601. 1 и 5. 602. 2 и —2. Указание. Составить функцию, подлежащую
исследованию, обозначив одно из двух чисел
через .с. 603. Квадрат со стороной 9 см. У к а-
з а н п е. Если обозначить измерения прямо-
Рис. 279
100-2 х
Рис. 278
угольника через х и у, то площадь его выразится формулой S — ху. Пользуясь
условием задачи, выражаем у» через х: 2х-|- 2у = 36, 'у = 18 — л; Подставив
в выражение площади вместо у его значение, получим в окончательном виде
функцию, подлежащую исследованию: <$ = л-(18 — Л-). 604. Длина должна быть
в два раза больше ширины. Длина ,равна 50 м, ширина — 25 м (рис. 278).
а
605.
Указан и е. Квадрат, ограниченный пунктирными линиями (рис. 279),
502
будет дном ящика, прямоугольники, заштрихованные косыми линиями, — его
боками. Если сторону вырезаемого квадрата обозначить через х, то сторона
основания ящика АВ будет равна а — 2х, а высота х. Тогда интересующая
нас функция (емкость ящика) выразится формулой
У=(а — 2х)3х. 606. Ширина^, высотаy = ^d.
Указание. Если через х обозначить ши-
рину, а через у — высоту балки, то функция,
подлежащая исследованию, выразится формулой
S = kxy2, где k — коэффициент пропорциональ-
ности. Но эта функция — функция от двух пе-
ременных х и у. Пользуясь условием задачи,
выразим у через х: х2у2 = d2 (рис. 280), от-
куда получаем у2 = d2 — х2. После подстановки
вместо у2 его выражения через х функция,
подлежащая исследованию, примет вид S =
= kx(d2—Л'3). 607. Сечение должно быть квадратом
1/2
со стороной, равной —(см. решение предыдущей
задачи п рис. 280).
608. При х — — 2 минимум /(—2) = — 5 — , при х = 2 максимум f (2) =
О
= 5^-. Указание. Ведя исследование по правилу, изложенному в § 86,
находим: 1) у'х = — х2 + 4; 2) xt=— 2, х2 - 2; 3) у’= — 2х, У™„^=_2 =
= — 2 • (— 2) > 0, у’ = (—2) • 2 < 0 (см. решение примера 1, § 86). 609. х = — 1
дает максимум/(—1) = 7; х = 2 дает минимум f (2) = — 20. 610. 1)/'(х) =
= 5л-1 — 20х3 4- 15х3 = 5л- (л3 — 4х + 3); 2) х2 (х3 — 4х + 3) = 0, откуда нахо-
дим xt=0, х3=1, х, = 3; 3) /"(х) = (5х1-20х3 + 15х3); = 10х(2х3 —
— 6х-|-3); 4) (1) = 10 • 1 (2 — 6 + 3) < 0, следовательно, х=1 дает макси-
мум /(1)= 1 -5 + 5+ 1 =2; (3) = 10-3 (2 • З3 — 6-3 + 3)>0, откуда
f (3) = — 26 — минимум; f (0) = 0 — вопрос остается нерешенным. Прибегаем
к первому способу исследования (85):
f(О - Л) =f (-1) = 5 • (- I)3 [(- I)3 - 4 • (- 1) + 3] > 0;
/ 1 \* /1 \ /1 V Г/1 \3 11
/(0 + Л)=/'[0 + ^ =/(!-) =5.у |_у _4.2+з]>0.
Следовательно, при х = 0 пет ни максимума, ни минимума (результаты
исследования следует заносить в таблицу, как указано в § 85). 611. f (— 3)=0 —
минимум,/(— 1) = 16 — максимум,/П) =0—минимум. У к а з а н и е./' (х) =
= 4 [(х + 1) • (х — 1) (х + 3)]'v = 4 (х3 + Зх3 — х — 3)'v. 612. При х = 5 нет пи
максимума, пи минимума, при х = — функция имеет минимум. 613. При
cos 2 • g- =— 1; при х = я — макси-
’t . .
х = — функция имеет минимум: f
3 I о 1
мум; f (я) = cos 2л = 1; при х = =- л — минимум: f + л ) = — 1. Указание.
-> \" j
Приравняв нулю первую производную и решив полученно'е тригонометричес-
кое уравнение — 2 sin 2х = 0, найдем: 2х = лп, х — ^-п. В границах данного
* h следует взять меньше 1, так как при /г = 1 получается:
0 + А1 =0+1=х2.
Л=1
503
промежутка п можно давать значения: 1, 2, 3. Получим х1 — ^, -v2 — п,
3
л'а — 2- «. Дальнейшее исследование надо вести ио второму способу (§ 86).
614. Обозначим через х угол.при основании равнобедренного треугольника
(рис. 281). Тогда угол при вершине будет равен 180° — 2х. По теореме сину-
сов имеем: а —2/? sinx, с — 2R sinx, b — 2R sin (180° — 2x)i= 2R sin 2х.
Периметр .-треугольника выразится формулой: Р = 2R sin х + 2R sin х 4-
2R sin 2х = 2R (2 sin х -ф- sin 2х); Р'х - 2R (2 cos х 2 cos 2х) — 4R (cosх 4-
4~cos2x). Приравняв нулю первую производную, получаем уравнение
cos 2х 4-cos х — 0, или 2 cos cos ^- = 0, откуда находим: cos^=0, x'i=60°;
cos(|=0,x.,=180°. Второй корень (х2= 180°) отбрасываем, как не имеющий смыс-
ла. Итак, х = 60°. Треугольник получается равноугольный, следовательно, рав-
носторонний. Чтобы убедиться, что при х = 60° Р имеет максимум, находим вто-
Рис. 282
рую производную: Р\_х - 4R (— sin х — 2 sin 2х) ~ - — 4R (sin х + 2 sin 2х). При
х — 60° Р" < 0. Следовательно, при этом значении х Р будет иметь макси-
мум. 615. Сторона вырезаемых квадратов должна быть равна 3 см. Указа-
11 и с. Функцией, подлежащей исследованию, является емкость коробки. Опа
выражается формулой У= (30 — 2х) (14 — 2.С)х = 4 (15 — х) (7 — х)х
(рис. 282 и указание к задаче 605). 616. Сторона основания равна 4 дм,
высота — половине стороны основания. Указание. Свинца потребуется
минимум, если подобрать сторону основания х призмы и ее высоту у так,
чтобы при данной емкости 32 л сумма площадей боковых граней и основа-
ния оказалась наименьшей. Функция S, подлежащая исследованию, в зависи-
мости от х и у выразится формулой S = x2-|-4xj> (I). В выражении этой
функции две переменные х и у. Из условия задачи следует, что У — х~у
32
или 32 = х2у, откуда получаемую — (II). Подставив в равенство (I) вместо у
его выражение (11), получаем функцию от одной переменной x:S = x24~
198
(III), которую требуется исследовать на максимум и минимум. Находим
128
производную S'x.=^2x---. Приравняв производную пулю, получим урав-
нение х3 — 64 = 0, которое имеет только один действительный корень: х = 4.
Без дальнейшего исследования видно, что при этом значении аргумента х
функция (III) будет иметь минимум. Легко это установить и по знаку второй
256
производной: S"x = 2 4- —. Очевидно, S’xх > 0 при х — 4. Высоту резер-
вуара найдем, подставив в равенство (11) вместо х его найденное значение.
'0 4
32 ' .
Получим у = да = Оказалось, что высота резервуара должна быть
равна половине основания. 617. Радиус основания г — высота й = ~ а.
г о •>
Указание. Функция, подлежащая исследованию: V=~r'h (на рис. 283
дано осевое сечение цилиндра). Из прямоугольного треугольника АВС можно
выразить, г2 в зависимости от d и й. 618. Треугольник равнобедренный,
каждый из его катетов равен ^2. Указание. Обозначив один из острых
Рис. 284
в зависимости
619. Ширина
углов треугольника через х, выражаем площадь треугольника
от с и х; S = sin 2х, S будет иметь максимум при =
канала, в два раза больше высоты. Ширина 4 м, высота 2 м. 620. Верхнее
основание трапеции 4 дм. Указание. Если обозначить высоту трапеции
через h и верхнее основание через х, то площадь трапеции определится
по формуле: S = . В треугольнике АСЕ катет АЕ = - - (рис.284).
Т 1/^ Iх - 2V / 12 + 4.C-.V2 п '
Тогда й= I/ 2-— I—— 1 — ----------------------. Подставив в выражение пло-
щади вместо й его значение, найдем функцию, подлежащую исследованию:
(х -|- 2) У \2-\-4x — Xs. 621. Радиус полукруга должен быть равен высоте
р
прямоугольника r-=h=~——. Указание. Обозначим диаметр полукруга
через 2г, высоту прямоугольника через '
й (рис. 285). Тогда площадь свето-
вой поверхности окна будет равна
7ГГ3
S — 2rh~y-^-, Для выражения h через
г по условию задачи имеем уравнение
_ , „ . Р — яг — 2г
2г -|-2/г -)-яг = Р, откуда й =------•
Функцией, подлежащей исследованию,
яг2
будет S = Рг-----2" ~ 2г3, где незави-
симой переменной, очевидно, являет-
ся г. 622. В 3 км от населенного пункта.
У к а з а и и е. Допустим, посыльный пристает к берегу в точке Д' (рис. 286),
''отстоящей от населенного пункта на х км. Тогда, время, затраченное им на
весь путь, будет равно где .МД’ — )/9- + (15 — х)3. 623. х = а
505
Н-------—15км—-jr------—
L
М
Рис. 286
дает минимум /(a) = Z>. 624. Нет ни. максимума, ни минимума. 625. При
л'; - 3 максимум /(3) — 3 yZ(3 — 5)2 = 3 у/~4, при х — 5 минимум /(5) = 0.
626. При л-= — 6 максимум /(—6) —О, при х —— 4 минимум/(—4) =
— — 3 у^4. У к аз анис. При х = — 6 эта функция не имеет производной
[/'(—6) = со]. 627. у" = 2а. При а < 0, у" < 0 кривая выпукла, ири а > О,
у" > 0 кривая вогнута (см.§ 88). 628. у^. — ^(еа-[-е а) > 0 при любом х
(график этой функции см. на рис. 163). 629. Выпукла в промежутке (—со; 2),
вогнута в промежутке (2; со). 630. Выпукла в промежутке ~; oj , вог-
нута в промежутке ^0; У Казани е. Вторую производную этой функции
можно представить так: у" = 2 scc2x tg х. Она будет отрицательна при х с 0
(см. рис. 117) и положительна при х > 0. 631. Кривая выпукла в промежутке
(—со; -0), вогнута в промежутке (0; со). 632. 1— 1; —— \ и (1; — — I
(см. решение примера 1, § 89). 633. Точки пересечения этой кривой с осью
Ох (лп; 0), где п — любое целое число (см. рис. 119). 634. Точки пересече-
ния кривой с осью Ох: (м-У j; oj, где /г — любое целое число (см. рис. 122).
v ,, 2 ctg х-
Указание. Приравняв нулю вторую производную, получаем:—, ° =0,
ctg Л- = 0. 635. (-^4) п (’4; т) •636- ~Кг) > (°;°) 11 *т) •
637. Примерный график см. на рис. 287. 638. При х — 0 минимум f (0) = 0,
при Л’= 4 максимум /(4) = 10^-. Точка перегиба 2; — 1 ; Предлагается
О \ о /
построить график, пользуясь указаниями к примеру 1, § 90. 639. Максимум
7 " /1 5 \
/(—1) = 4, минимум/(2) = — 5. Точка перегиба —1 g-1. У кара-
13 '
н и е. Уравнение х~— х — 3 ---0 имеет иррациональные корни; можно
их вычислить приближенно. 640. Примерный график показан па рис. 288.
641. /(—2) = 0 — минимум,/(0) = 16 — максимум,/(2) — 0 — минимум. Для
большей точности чертежа следует взять дополнительно по одной точке вне
/ Уз 1 \
промежутка (— 2; 2). 642. /(0) — 6 —максимум. Точки перегиба: I — 4 ,, I,
506
(1/ 3 1 \ t)
4j-; 4yI . С осью Ох кривая не пересекается, так как О ни при
каких конечных значениях х, lim у = 0. Следовательно, ось Ох служит
асимптотой этой кривой (при-
мерный график на рис. 289).
► 3
643. f (— 1) =— -------мини-
3
мум, / (1) = у — максимум.
Кривая имеет перегиб в
точках f— }^3; —, (0; 0),
(]УЗ; 4 и имеет своей
асимптотой ось Ох (пример-
ный график на рис. 290).
644. Указание. Эта кривая
имеет такую же форму, как
кривая, изображенная на
рис. 152. 645. y'v =—sin2.v.
Критические значения х:хг =
п я 3
= 0, *2 = .у > Хз = ~ 2
х5 = 2я. Находим вторую про-
изводную у" = — 2 cos 2.v и,
подставляя в нее вместо х
найденные критические значения аргумента, последовательно' находим:
f (0) = — 2 cos 0 — — 2 <0, /(0) = 1 — максимум;
f = — 2 cos 2 • = — 2 cos я > 0, /(— 0 — минимум;
f (я) = — 2 cos 2я = — 2 < 0, /(я) = 1 — максимум;
f" я^ = — 2 cos Зя = 2 > 0, f я^ = 0 —- минимум;
f (2я) = — 2 cos 4я = — 2 < 0, /(2я) = I — максимум.
Находим точки перегиба. В этих точках v” = 0 или 2cos2.v = 0. Корнями
. . я 3 о 7 _ „я
этого уравнения будут: ^-я, — я, —я. Ординаты точек: yt = cos- =
/2? 1 „51
= 2’ Уз = соз-^я=у, yt =
2 7 1 И
= cosJ я = 2" • ‘,а основании . этих
данных- строим график (рис. 291).
646. f (г) = 8л'-у-_.Производная об-
3 у .г — 4
ращастся в нуль при Л' = 0 илг = 3,
в бесконечность — при .V = 4. При
х = 0 минимум f (0) = 0, пргцх = 3 мак-
симум f (3) = 9, при л'= 4 минимум
/(4)=0 (см. примерный график на
507
и справа, т. е.
рис. 292). 647. При х=±4 функция не существует и, следовательно, дан-
ная кривая с прямыми х — — 4 и х — 4 (рис. 293, а, б), общих точек не имеет.
Областью существования этой функции являются л промежутки (—со; —4),
(—4; 4) и (4; со). С осью Ох кривая не пересе-
4
кается, так как уравнение = 0 конечных
корней не имеет. При значениях абсциссы х, удовлет-
воряющих условиям (—со < х < — 4) и (4 <х < оо),
ордината у принимает отрицательные значения, так
как л’=16_(-Д--^<°
при любом положительном
промежутках (—оо; —4) и
полагается иод осью Ох.
- когда абсцисса приближается к числу —4 слева
л = — 4 — /z и х — — 4 h при h —- 0. Получим:
4
11 У 16- (44-Л)=<0
h. Следовательно, в
.. (4; со) кривая рас-
Найдем пределы у,
когда
4 4
1) lim у — lim -г---------------——— = litn —г-------——Т--------—
h-*0 Л-0 16 —(—4 —/z)- Л_о 16—16 —8Л —//-
,. 4 — 4 1
= 1,1,1 1—гп----и = Пт о, . ,= — 4 lim , ,ц , .. = — 4 • со — — со.
л —* о— 8/z— h- л—o8/z+/z_ л—оЛ(8 + Л)
4 4 4
2) Нт -Г7------—. , , = lim -гг------,г . ---j-j- = lim =
п-+о 16 —(—4 +Л)- д-о 16— 16-|-8Л — 1г л_0 8Л —/г
4 , '
= 11[|1 -т------гс — Ч-оо, так как h стремится к пулю, оставаясь положитель-
л^оЛ(8 — h)
ным, и 8 — Zz —► 8. Так же можно показать, что у — + со, когда х стремится
к числу 4, возрастая, и у —— со, когда х — 4, убывая. Наносим на чертеж
дуги а, б, в и г, характеризующие полученные результаты. Затем строим
кривую по плану, изложенному в § 90: 1)у* =. — 4 [(16 — х2)-1]^. =
(16-ГТ = <)'
' о Г А- Т 16+Зх2
L(16-x2)2Ja- (16-х2)У-
508
Определяем знак второй производной при х=0. Получаем _y' t=-8 X
16 4-3 -о2 „ п .
v ---!-----^-0. Следовательно, при х=0 данная функция имеет минимум,
4 1 „
-- т6 = 4- • Строим точку
, учитывая направление
Х (16 —О2)2
равный _ymjn
выпуклости. 2) Приравняв нулю вторую производную, получаем уравнение
I6 | зг2
---~ — 0, не имеющее действительных корней. Значит, кривая перегиба
(I6 —
не имеет. 3) Как уже оыло замечено выше, данная кривая с осью Ох общих
4 4
точек нс имеет. 4) lim у = . lim —--------lim ----------———— =0.
- Следовательно, при.х —— со и х—«со кривая неограниченно прибли-
жается к оси Ох (у = 0). 5) Строим график, соединив отмеченные элементы
плавными кривыми, учитывая, что у—* 0, когда х —«-.too (рис. 293).
648. Возрастает в промежутке (—со; 0), убывает в промежутке (0; оо).
649. При х = -^- имеет максимум f ~-----------In 2. 650. Прих = -^- имеет
максимум f , при х = -к — минимум / лj =—V2. 651. При
л / л \ 2 У2 . .
a = -j- максимум yf—1 = —. Указание, f (х) = sin Зх — sin x —
= 2 cos 2x sin x. Уравнение 2 cos 2x sin x = 0 распадается на два уравнения:
cos2x = 0, sinx = 0. Из корней этих уравнений следует отобрать тот, кото-
.. . .с 1 — 2х (3 х )
рыи удовлетворяет условию задачи. 652. ух= , „ . ,-р, , 2 ,т3г .
(х- -f- 1)“ (х -f- 1)
3
При х = —1 максимум /(—1) = —g—,
С осью Ох кривая не пересекается, так
ствнтельных корней не имеет. С осью
(0; 1). Точки перегиба —У 3", j ,
(рис. 294). 653.-При х = 2 максимум /(2) = 4, /'(2) = со. При переходе
при х=1. минимум /(l) = -i-.
_ I |
как уравнение —j - = 0 дей-
Оу кривая пересекается в точке
(О', 1), (КЗ’> 4 ~ УП (Л™ У = 1
\ 4 / ’ х-^-Ьоэ
аргумента через значение х = 2 первая производная меняет знак с плюса
на минус. По обе стороны от точки х = 2 кривая вогнута и пересекается
с осью Ох в точках (—6; 0), (10; 0) (см. рис. 295). 654. Эта функция не
существует при х = 0 (см. решение задачи 647). В промежутке (—оо; 0) она
выпукла, в промежутке (0; со) — вогнута (см. график на рис. 296). 655. Сто-
роны прямоугольника AM = а У2 , ВМ = Ь У2. У к а з а и и е. Предположим,
что одна из вершин прямоугольника находится в точке М (х; у) эллипса
509
(рис. 297). Тогда AM = 2х, ВМ — 2у, площадь прямоугольника S = 2х • 2у.
Точка Л4 находится иа эллипсе, следовательно, координаты ее удовлетворяют
л-2 । У" .. Ь1 , „ b ..г--,--j „ АЪх
уравнению + <- = 1, откуда у- — ~2- (а- — Л'“), у = — У а2 — х“, S = — X
X У аг — х' будет функцией, которую требуется исследовать иа максимум
и минимум. 656. 7r + Ja- = l. Данная точка должна быть серединой отрезка
о b
прямой, заключающегося между осями координат (рис. 298). Указание.
Обозначив отрезки, отсекаемые прямой от осей координат, через а и Ъ для ,
е аЬ
площади треугольника получим выражение 5 = -^- и уравнение прямой
X V
в виде —-|-у = 1. Пользуясь тем, что точка М (4; 3) лежит на прямой,
можно получить уравнение, из которого можно выразить b в
от а
зависимости
657. Лампу
(в полученной функции независимой переменной будет а).
Рис. 299
надо повесить на высоте 1 м. У к аз а ни е. При обозначениях, принятых на
рис. 299, силу освещения у края стола (С) можно выразить формулой
k cos <р , , , , т / ,
у ——> где «— коэффициент пропорциональности, а = у х- _|_ (у 2)'3 =
= VX3 -1-2 , СОЗ <р = -Д- = 1 У .
Функцией, подлежащей исследованию, будет
V = ——. Множитель k при исследовании можно отбросить. 653. Тан-
(|'У + 2)
гене угла ср между диагоналями, обращенного к образующей цилиндра,
должен быть равен 2? = 63“26'. Указание. Обозначив через R, г, h и <р
соответственно радиус шара, радиус основания цилиндра, высоту его и угол
510
между диагоналями (рис. 300), найдем: г = R cos , h = 2R sin —. Полная
поверхность S = 2~rh 4- 2яг3 = 2л . R cos • 27? sin 2л/?3 cos3 = 2л/?3 х
,, /о . to а , , а \ , 1 + cos и\ _ 2 sin <р 4- cos а 4-1
X 12 sin-^-cos-^- + соз-^-1=2л/?И sin to 4---\=2-R-------—=1— —
= л/?3 (2 sin to 4~ cos to 4~ 1 )• Исследуя эту функцию на максимум и минимум,
получим результат, данный в ответе. 659. Уравнение прямой ^-4--< = 1.
Указание. Исследуемая функция у = а 4- —где отрезок на оси Ох
(а) является аргументом. 660. Точка, находящаяся от точки А на расстоя-
нии 4 лг. Указание. Освещенность прямо пропорциональна силе света
Рис. 301
источника и обратно пропорциональна квадрату расстояния. При условиях
данной задачи освещенность точки прямой АВ, находящейся от точки А
8 ,
на расстоянии х м, определяется по формуле Е = ~4
661. й = -^
/з
17=^-л(73Л— й"). 662. Сторона основания х
Указание. Функция, подлежащая исследованию, V
= ——. 663. Высота должна быть, равна 2 /3. У к а з а н и
1
(6 — -V)3 '
Z/б V
—-—. У к аз а ни е. Функция, подлежащая исследованию,
3
/зб , /зб
- -, высота =
.у3 (10 —.у8) _
3
4.V
е. Мокрый
х 4 /3
периметр Р — у 4- 2АС =у 4- 2 • = У 4---—-У Zpnc. 301). Для пыра-
(AB + CD)x
женпя у через х получится уравнение 12=-----, или 12 = уу4-
/Т
4--Ц— х2. 664. Если примем ЕМ = х (см. рис. 206), то MF=d—x и длина
О
I провода определится по формуле I = У'х2 4- Л8 4- /(7Z — .у)3 4“ 77а- Тогда
,, х d — x
I у = -= ---г Приравняв производную пулю, получим
У.у34~Л3 у (d — .с)3 4~/73
V d — х п х d — х
уравнение :----— =0, или =—-----
/л-34-Л3 —лД34-/-/3 /л3 4-й3 /(rf-.v)34-Ha’
т т Л’ d — X „ „
Из чертежа видно — - = cos а, , = соя Я. Следовательно,
Ух2 4- л3 у(rf - х)2 4- н2
cos а = cos 3, а'= р, т. с. точка М должна быть точкой пересечения прямой EF
511
с прямой, соединяющей точку А с точкой Blt симметричной точке В относи-
тельно ЕЕ. 665. lim * 1 ~.cos 2х = 0. 666. lim -°-s 2х =
х ~ 0 X ctg 2х
х~~ 4
668. dy = (fax 4- 7b) dx [применяется формула (3) § 92]. 669. df(x) =
" - • ! 5л‘ 2л' -1рх. 670. dz = z'ydy — ~ 10/(а2 — y-у dy.
xdx
1 SID 2x
667. lini ---= 2.
4 COSX
X~ 2
—j ^,ил — ^а + ь
671. rf/(/) = -?^
a — b
. 672. dy
. 673. dy = (lnx -j- 1) dx.
e(l — tgax)
1 _[_ tg at—dx (CM’ Рсшенис примера 2,
. , an \ = \ d~z.
a sec’ axdx. 677. а г=--=--suu 6—— =
’ x dx 2 ’ dx2
dz < dfz _ ,
Tx = ^*, 6) ^ = 5tg>xsec-.v;
+ (t — l)2. Указан и с. См. решение
О
примера 4, § 92). 680. у'х —— ctg t. 681. у'х = 682. a) k = — ;
б) k =—1; в) k = ]3. 683. Д/«=0,12. 684. Д/ = 0,0Г2. Указание.
Д/«= dy — [In (л'2 l)]xdx. 685. /(2,16) «=2,06 (см. решение примера 3, § 95).
Следует принять х = 2. 686. /(4,175) = (4 4- 0,175) «= 0,8126. 687. а) 1,03;
б) 0,96; в) 0,94; г) 1,024; д) 0,994; е) 0,85. 688. а) 0,88; б) 1,04; в) 0,88; г) 0,988.
689. а) 1,007; б) 0,998; в) 0,99. 690. a) In 25,02 = 3,2197. Указание.
0 07
а) .In 25,02 = 1п (25 4-0,02) = In 25 4--^-; б) In 24,6 = 3,2029. 691.
1,9588. Указание. Вычисляем дифференциал этой функции
х 7
и Дл' = 0,02. Получаем df (х) = 9 , Дх = = • 0,02 = 0,0028, а
Х~ “|- 1 Эм
формуле (10) находим
674. ds = 4 (eil — е~*‘) dt. 675. dy
§ 92). 676. dz = -adx—
J cos1 ax
= cos x; в) d2z = -% cos xdx2. 678, a)
2
в) d2z = 5 tg4 x see2 x dx2. 679. y' = —77
o
при x — 7
затем no
f (7,02) як/ (7) + df (л-) = -% In (72 * + 1) + 0,0028 «= 1,9588.
692. a) 0,024; 6) —0,02; в) 0,148; г) —0,024; д) —0,04. 693. a)—0,001; б) 0,06;
в) —0,001; г) 0,005; д) 0,00325. Указание. Предварительно прологарифмиро-
вать. 694. А' = 2. 695. /? = . 696. R = —-I =^Zp^37 (в этой точке кривая
J I о | о
выпукла). 697. /<= |л Г I • » 698- =
J ' 1(1+ cos- x) 12 | 49
з
(x% д_р42 •
' 11 1 2 ; 2) R —p. У к а з а н и e. Вычисления упростятся, если предва-
/ 2 I „2\ 2
рительно разрешить уравнение параболы относительно/. 699. R =-.
1) R = 2 Y 2р; 2) R z=p. У к а з а и и е. Находим производные у'х и ухх спо-
собом, указанным в § 78: /у’ =р, у' = , /’ =/(/“*)[.=/(—1)/*2/^.=
= _£.Zi = — 700. 1) 7?= (ау-А- Ех2)2 . /? = . у 1С а з а н и е.
у2 у У а Ь1 ’ . а
512
Рассматривая j» как
b- I х\’ й3 V — ху’х
Ухх — у у)х — р
ния гиперболы следует а3у3
производной разность- (а2у2 —
неявную функцию от х (см. § 78), найдем: у’ =
Л3х
Ь*х
а3у ’
&3 У ~ Х ‘ л - ь*х*
= — •------з---= = ------—=---. Из уравпе-
гг у- а2 a-у
_ bax3 = —а-b3. Заменив в выражении-второй
63х3) через (—а2Ь2), получим:
„ _Ь^ — а2Ь2__ Ь'
Ухх а2 а2у3 а‘2у'
1
701. 1)
['+(ЛУГ
702. - 1) dy =
R
= dx; 2) dy = . 703. 1) ^=-Z{2- ; 2) -^ =
x ' ’ J jZx-’ + a3- clx 1 — 2/' ’ dx
= ^+ 1 +2. 704. ly d2y = — a3 sec3 ax dx3; 2) d2y = a3esi,,ax (cos3 ax —
Vr'+x-t
— sin ax) dx2. 705. Д/ «= 0,0562. Указание, x = 3, Ax — 0,2; Д_у «= dy =
= r., , ---------- 70S /(0,2)=^0,8 707. x + 2y>-4|/V= 0;
(л~ + 7)/(.e- -5)(x> + 7)
2x - у - 3 /2 — 0. 708. R = 5g ‘° . 709. К = 0,128. 710. R = -5 5 .
o 4
716. 1 x2 + C. 717. x5 + C. 718. 4 *’ + 4 x2 + 2x + C. 719. ~ _L
О О Zj О О
+ A-3 - 3x + C. 720. 2 _ X» + Xs - ЗЛ' + С. 721. 41n x+C = ln Сх\ где C>0.
P e in с u и e.' Применив четвертое свойство неопределенных интегралов и
формулу (III), § 102, получаем 22 = 4 ~ = 4 In .г 4- С. Здесь С — про-
извольная постоянная, могущая принимать любые числовые значения. Но
In С тоже может принимать любые числовые значения, вследствие чего
в данном случае и в случаях, ему подобных, есть смысл С заменить In С.
Тогда f — = 4 In х 4- С = In лл + In С = 1п Сх'. 722. In Сх». 723. In С j/.v'.
724. ~— а'3 + Зх -|- 5 1п х -|- С. У к а з а п и е. Надо предварительно числитель
подынтегральной функции почленно разделить на ее знаменатель,
а затем интегрировать как алгебраическую сумму дифференциалов:
С х' — 2а-3 -j- Зх -f- 5 С / о п , , 5 \ , _ос 1 [хл х3
~ dx — (л~ — 2х + 3 —J dx. 725. у4~2х4-
4- 7 In х 4- С). Указание. Предварительно вынести за знак интеграла по-
стоянный множитель -j-, а затем взять интеграл так, как указано в преды-
дущем примере. 726. — ^2 _|_ (j у казанце. Применяя формулу (II), § 102,
получим fx“4rfx = —2- - 4- С. 727.---- 4- —- + 2х 4- С. Указание.
J — 4 4- 1 1 х ‘ х 1 1
17 П. Е. Дгачео
513
Основываясь на четвертом и пятом свойствах неопределенных интегралов,
получаем \ (4х~а— Зх~2 2) dx — 4 { х-5 dx — 3 f х~2 dx 4- 2 f dx. Далее
2 3
интегрирование ведется ио формулам (I) и (II), § 102. 728. у .г3 — -^-х2 4~ 2x4-
4-lnx-f-—4-С. 729. —Д + 4з + 2 1пх + С. Указание. Предвари-
х ,у~ X
1 С М 3 , 2\
тсльно следует переписать подынтегральную функцию: \ I—---=
/* / 9 \ Ч 2 Ч 1
= \ 4х-’-Зх-4+ — \dx. 730. - Д+ -й-^+й-1пх + 2х+С. 731. Нгх'Ч-
J \ X / 2Х х u.V’ 2 О
-- xi 4- тгХ34-С. У к а з а н и е. Предварительно следует многочлен,заклю-
2 о
чевный в скобки, почленно умножить на х~, а затем применить пятое свой-
ство. 732. у х5 4~ 2.V1 4- 9х 4- С. Указание. Следует сначала переписать
9
подынтегральную функцию в виде многочлена. 733.-----1- 121пх 4~ 4хС.
734. 1 х2 - Зх 4- 21п х 4- 2 4- С. 735. — — - ЗаЧпх 4- Зах-Д- х2 4- С.
2 х х 2 1
736. — + С. Указание. Применяя формулу (II), § 102, получаем
. 2 3- 1 5 5 3 а
I хУ dx = 4------НС — !хД + С. 737. ~х~4 -4 х1" 4- Д 4- 2х + С
I 2 ' 5 5 3 1 2 '
J 3" +
1 4 г
(см. указание к предыдущему . примеру). 738. — х2 — ах +
4 о
5 _ С — С -3 3 —
739, у y/.v'-’ 4- С. Указание. \ ]/ х3 dx = \ х5 dx. 740. у у^х’ —
—-тх У'х3-Н 2х 4~ С. 741. 2 /х 4- С. Указание, f —f х 2 dx.
'J J I x J
742. 3 Vx2 - 4- /x 4- 2v 4- C. 743. 1 x2 - ~ x/x — 6x 4- C. 744. ~ x X
X Ух 4- 4 Ух 4- С. 745. ~х2У^+~хУ'х—бугх+С. 746. 4~х3 —
( ' 4 ' ' ! о
---х2 4-<*2х 4~ С. Указание. Сначала сократить дробь, стоящую под
। 2 — ___
знаком интеграла. 747. 75-х2 — 2х 4~ С. 748. х Ух 4- У ах 4- С. Указа-
4 о
н и е. Числитель разлагается на множители: (Ух—Уа) (УхУа). 749 *
749. 4- х2 4~ v /х3 4- х 4- С. 750. х2— х Уabx 4- bx 4~ С. Указание.
2 о 4 о
2 Уabx = 2 Уab Ух. 751. 1) d [— 4- (?) = 4- cY dx dx =
г \1п а 1 J \1п а У In а
-t=axdx. Следовательно, формула (V), § 100, верна; 2) =
4- С)'х dx = ех dx, что доказывает справедливость формулы (IV), \§ 102.
2х
752. 4- ех - Зх 4- С.
а-2- 753- т+1^ + с-
У казан и е.
Р е ш е н и е.
В формуле (V), § 102, принимается
3xexdx= ij (3e)xdx. Далее, приме-
514
. (3AX Зхрх
нив формулу (V), § 102, получаем \ Зхех dx=~.—-[~С =—----
J J In Зе 1 In 3 4- In е
а.х£.х ах
= , , , „-+С. 754. +С. 755. ----- , х Л. + С Указ
1 + 1п 3 1 1 -j- 1п а 1 (1па—1)йл 1
(]Х ! Р% лХрХ пХ
- . 756. -j--L——4-С. 757. ---^-^.ех-х^С.
ех \е ] (1 — 1п 4) 4А l-(-lna In а
з а и и е. Предварительно произведение двух функций представить в виде
алгебраической суммы функций. 758. 1) d(—cosx-f-C) = (—cos х -f- С) 'v dx =
=— (—sin X) dx — sin x dx', 2) d (sin x + C) = (sin x 4- C)'x dx = cosx dx\
3) d (tgx+C)=(tgx+C);dx=-i-dx = -J- ; 4) rf(-ctgx+C)=(-ctgx.+
v-C'o X vt'j -x
f 1 X
4- C)’ dx = — --r-з— dx = . 759. a sin x 4- b cos x 4- С. Указание.
•v \—sin xj sm x
(a cos x — b sin x) dx = a cos x dx — b sin x dx = a sin x — b (— cos x) C
[см. формулы (VII) и CVI), § 102]. 760. a tg x 4- b ctg x 4- sin x 4- С. [приме-
няются формулы (VIII) и (IX), § 102]. 761. tgx-f-x-f-C. У к а з а н и e. После
почленного деления числителя па знаменатель под знаком интеграла полу-
чится функция cos*2 д. 4~ 1 • 762. —etgx — 2х 4-С. 763. 2 sin х 4-С. У к а з а-
н и е. Числитель надо преобразовать в произведение и дробь сократить,
предыдущему примеру),
(cosx)' —sinx
------- dx =-------dx=
COS X COS X
3xexdx
+ C?=
ани e.
У к a-
764. —2 cosx 4-С (см. указание к
765, 1) d (— Incos.v-|-C) = (— Incosx + C)'xdx
(sin лг) v coq v
= tgxdx; 2) d (In sin x’’4- C) = (In sin x 4- C)i dx =—:-- dx =—— dx =
x sin x sin x
= ctg xdx. 766. InCxtgx. Решение. \ ftg xetgx 4--д') dx=
С С C dr ' X
= \ tg x dx4~ \ ctg x dx 4- \ = — In cosx In sin x /- In x /- In C =
= In X- = 1 fi Cx tg x. [см. формулы (X) n (XI), § 102, и указание к за-
даче 721]. 767. — cosx — 2 sin х 4- 3 In sin x 4- С. Указан и e. Разделив чис-
литель почленно на знаменатель, под знаком интеграла получим функцию
sin х — 2 cos х 4-3 ctg х. 768. х — 2 In cosx 4-С. 769. tg x — 2 In cos x 4~ C.
v (sin x 4- cosx)2 14-2 sinx cosx __n .. , „
Указание. —i4--------------------=. 1------5-------. 770. 4 tgx-4-C.
COS" x cos2 x .
771. — a ctg x 4- C. 772. tg x — x -]- С. Указан и e. Сначала преобразовать
подынтегральную функцию, воспользовавшись формулой tg3 х = sec3 х — 1.
773. —etgx — х4-С. У к а з а н п е. Преобразовать подынтегральную функ-
цию: ctg2 х = cosec2 х— 1. 774. х — 2 In cosx-|-tgx — хС — tg х—-
— 2 In cosx 4- С. 775. х — 2 In sin х — ctg х — х -]- С — — 2 In sinx — ctg х4~ С.
776. 1) d (arcsin хС) = (arcsin х-[-С)' dx = —- d v = —(1X- ;
V 1 - X3 V 1 - X2
2) d (arctg x + C) = (arctg x 4-C);dx=T-jJ—3dx= (4^. 777. a) x 4-
1 "1* X i —X
1/| _ X- 1 [ 1
4- arcsin x 4- С. У к a 3 a H и e. - r = 14- — 6) x4-2arctgx-4-C.
VT^- x2 T |/1 _ x3'
3 4- л2 2
У к а з а н и e. У 3 = 1 4- —•—5. 778. у = 2x2—3x4-8. 779. _y=x3—x—2.
1 4“ * “T“
780. 1) s = vat', 2) s = 4 + m^ 3) s = ЗГ-H2 - i’. 781. s = 4 4- 30^ .
17*
515
Указание. В этом движении ускорение постоянно и равно g; =
ds
= g; v = gt-^c. При / — О скорость v0 = 30 м/сек, откуда f =-^ = g/4~30.
782. I) s = — -j- 30/ -|- 18; 2) v = — gt + 30. Пуля начинает падать в мо-
. 30 ох Г g /30V , on 30 i id f450 , ,<Л ' '
мент t = — сек', 3) з = —4?- — + 30 •-----1- 18 лг =-----Р 18 л« === 64 м.
g L 2 \g] 1 g J \ g I
783. у — 2 /.v. 784. у = A. (sjn 2x — cos 2x). 785. Парабола у—— .v~ + 2.v-|-8.
786. l)yz = x3— 2x2; 2) y, = x3 — 2x2 - 1.787. s = /3 - 2/2 + 4/. 788. s^/1-
— 4 t3 4- 50/ + 5. 789. 4- /(1 4-х3)3 + С. Указание. /Г4Г? 3.v2 dx —
О o J
_1_
— j (1 + A'3)2 3x2 dx. Приняв 1 4- a3 = и, получаем: 3x2dx = du,
\ (1 4- x3)2 • За2 dx —Д и 2 du. 790. 4- (ax 4- ft)5 4* С. Указание. Приняв
ax 4- ft = и, получаем: adx = du, ((ax-j-ft)1 adx=\u* du.
791. — j/"(3.r 4- I)5 4- С. Указание. 3x 4- 1 : u, 3dx = du.
792. |(X<41)<4-C. 793. In (a3 4-x3) 4-In C = In C (a3 4-a3).
794. 2 /a3 4- x3 4-C. 795. J—. 4- C. 796. In C (14- a1).
797. ~ (1 4- Ka)2 4- С. Указание. Если предположить, что 1 4- /а = и,
то = 798. 1 (ах2 4- Ьх 4- С)\ 4- С. 799. 1 (х - 2л2)1 4- С.
2 у х
800. (ах- -f- ft)5 + С. Указание. В данном случае d (ах~b)— 2ах dx
отличается от множителя х dx постоянным множителем 2а. На основании
четвертою свойства неопределенного интеграла постоянный множитель может
быть введен иод знак интеграла и выведен из-под знака интеграла. Поэтому ин-
тегрирование можно вести так: (ах2 -|- ft)1 х dx — (ах2 4~ ft)1 2ax^dX =
= 4 4- с. 801. -1- v(А1 4- 1 }3 4-С. ' Указание.
Полагая a1 -J- 1 = и, найдем: 4x3dx — du, a3 dx = ,
С г------- С V fl'll 1 0 4 1
\ /а4 4- 1 a3 dx= \ и 2 • -т- =-j- \ и2 du. 802. 5--In (ах3 4- ft) 4- С. Реше-
f x2dx If 3«x2rfx
пне кратко можно записать так: \ —,, , , = тг- \ —., , , =
. J ах3 -j- ft 3 a j ax' 4- b
= Г =^-ln(«A34-Y>)4-C. . 803. /(3л 4- а)3 4- С.
За J ал3 4~ Ь За 4 . 9 ' ‘
804. 1п (л -|- а) + In С = In С (х -р а). Указа н и е. Полагаем х + а = и.
805. - L—j- 4- С. 806. |/'(х4-а/ -f- С. 807. — у In (а2 - х2) 4- In С —
516
= 1n—— Указание. Сделаем подстановку: л2 — х3 = и; тогда
у а- — х~
du .
„ , , , du С хdx С 2 1 С du
— 2х ах = du, х dx =----, \ —=--= \ ------ = — \ —.
2 ’ J а- — л- J и . 2 J и
808. (ах3 4- 2Ьх 4- с)5 + С. Указание. Приняв ах3 4- 2Ьх с = и, полу-
чим: 2 (ах 4- b) dx — du, (ах 4- Ь) dx — , § (ах3-}-2Ьхс)* (ах-[- &) dx =
= \ и' . 809.1 (Уа 4- /4)* 14- С. 810. - 1—г, + С. 811. In (х3 - 1) —
J 2 z (14-ух)'
— 1п(х4-1) + С = 1п^-^-4-1пС = 1пС(х-1). 812. 21п(14./4)4-
4- 2 1п(1—/х) 4- In С = In С (1 — х)2. Указание. (~/ ~(1~-----
1 Д т С dx (• ’ dx
/х(1-/х)/ J Гх(14-/х) . /х(1-/х)
этих интегралов приводится к виду (111), § 104, в результате подстановки
1 /х = и, второй — подстановкой 1 — /х = ъ. 813. — In4 х 4- С- У к а з а-
лпе. Сделать подстановку 1пх=и. 814. -g- In2 (х2 -f- а3) 4* С. Указание.
„ , , 0 । . ,, . , , .. 2х dx xdx du
Приняв In (х2 4~ й") = получаем d In (х1 4~ а3) = ,
6-Ly
815. 2 У (а3 + х3У + С. 816. + С = ДД + С. 817. Д (/24 -
—/2^)**4-С. 819. Ji—4-С. У к аз ан не. Приняв 2х=п, получаем
п., . , da С . С „da If „ , 1 ' ап , „ ,
2dx = du, dx = -=-, \ a--dx = \ a’-- = „- \ andu = •,--------k С 1см. cnop-
2 ’ J J 2 2 J 2 Ina 1 '
мулу (V), § 104].'820. e"-v2+«x+5 -|-C. У казанке. Полагая Зх2 4- 6x 4- 5 = a,
находим: (<oxdx ~ dtt, (x 4- 1) dx = е1Л'2+“v+5 (x-|-1) rfx =
= = e"dLl fCM- ФОРМУЛУ (IV), § 104]. 821. 2^-4-C.
Указание. Сделать подстановку; x2 = и. 822. — ca-v+ft 4~ С. 823. i-(e2x 4~
a ' 2
1 2 ._______ anlx
+ e~3x) 4- C. 824. i (езх 4- I)4 4- C. 825. -±— /(a™ -]- I)2 4- C. 826. Д-
1 1 8 v 1 / 1 9 in a 1 4 1 / 1 m |na
bnx 1 akxbbx r______
----T-b + C- 827- г - ~7г + С. 828. 2 /е-v 4- e~x 4- С. Указание.
И1ПЙ 1 k In ab 1 1
ex 4~ e~x = a, (ex — e~x}dx = da. 829. ~ e3X—2x—-^e~3x-(-C.
832. sin Зх-|-С. Решение. Этот интеграл берется по формуле (VI),
О
3dx = du, dx = ^, ^cos3xrfx =
cos и da = sin a 4- С. Решение можно записать короче:
О
§ 104. Приняв Зх = и, получим:
(* da 1
= \ cos и ъ- = 0
) о о
517
\ cos 3x dx = 5- f cos 3,t 3dx = ~ sin 3x 4- C. 833. — tg ax 4- С. Подстановка
J 3 J 3 1 a b
it du
ax = и [см. формулу (VIIJ), § 104]. 834.
литсль
только
подынтегрального выражения
постоянным множителем 3.
’-ctgx3-|-C. Замечаем, что чис-
отличается от дифференциала дуги (х3)
Приняв х3 = и, получаем: 3xadx = du,
» . du
x-dx =
□
dtt ♦ I z** л—
. = — 5- ctg и 4- С. Следует
sin- и 3 b 1 J
_1 3x°dx 1 £ d (x3)
3 j sin-’x3 3
836. — 1-
0
siirx3
ctg Зх 4- С.
подстановку:
4х + 7 = и.
е. Принять
приучаться записывать решение короче; \ -^„--3 -
= —i-ctgx3-|-C. 835. — —cos их-J-С.
3 a
837. —- cos (4x + 7) -|- С. Указан п e. Сделать
838. — sin (5x — 7) C. 839. — A cos (ax") 4" С. Указан»
ax-= u. 840. — sin (4x3) 4-C. 841. 2 In sin ~ 4~ С [см. формулу (Xl), § 104].
842. 3 sin 5 4-1 cos3x 4- C. 843. - ~ cos f^4-4- C. 844. — tg 4- C =
о о Jz \ 1 I \4 /
= tg 4" C. 845. x — g- cos 2x 4~ С- Указание. Предварительно сле-
дует преобразовать подынтегральную функцию. 846. х 4-cosx 4-С (см. ука-
зание к предыдущему примеру). 847. — (tg ах— ctg ах) 4- С (см. указание
к задачам 772 п 773); j (tg ах 4- ctg ах)" dx =.j (tg2ux 4- 2 1g ax ctg ax 4-
-4- ctg ax) dx = f (sec2dx — 14-2 4- cosec2ax — 1) dx = f —^4-[- f ..
b J J cos ux J sin-ax
848. 2~x—t_sinx-|-C. В формулах интегрирования нет такой, по которой
можно взять этот интеграл непосредственно или подстановкой. Поэтому
. „ X „ 1 — COS X
подынтегральную функцию sinзаменим тождественной ----------- 1|а осно-
вании формулы 1 — cosx = 2 sin- ~silr'^dc — -—J:os ~v dx --
= ~ dx — 1- ? cos х dx. 849. 2- x — t- sin 4x -+- С. Указание. Подынтег-
2 J 2 J 2 о
ральную функцию заменить тождественной, воспользовавшись указанием
к предыдущей задаче. 850. ~ х 4-sin 2ах-|-С. Указание. Сначала
, “ 1 4- cos а
преобразовать подынтегральную функцию по формуле cos- у = —.
851. 1- sin°x -[- С. У к а з а н । е. Приняв sinx = u, получаем: cosx <7х = du,
\ sm'x сс&х dx—\ u^du. 852. tg’x 4- С. 853. 3-sin3ux4-C. 854. In (sinx —
J J 4 3u
— cosx)-|-C. Указание. Приняв sin x — cos x = u, получаем:
, • . , j C (cos x 4-sin x) dx C du 2 ... ._2 .
(cos x -4- sin x) dx ^du, \ -:------- =. \ — . 855 • (1 4“ sin лг) C.
3 1 ' J sm x — cos x Ju 3
518
Указание. Сделать подстановку: 1 sin х =.и. 856. In (ср -J- sin ?) 4* С.
857. е51"* + С. 858. а + С. 859. — f- 4/cos^ + С. 860. \ =
1 Ina 5 ' J sin'x
= \ sin~3xcosx dx = —- —к- С. 861. sin о — sin"? 4~ С- Указание.
,1 2 sm-x 3
Сначала следует преобразовать подынтегральную функцию, заменив cos5?
через 1 — sin5?: cosW? = j cos5? cos ?d? = \ (1 — sin5?) cos <?d<f и т. д.
2 1
862. sinx—g- sin’x g- sin'x 4* С. Указание. cos’'x = cos’x cos x =
= (1 — sin5x)5 cosx. 863. — cosx -]- g- cos5x 4~ C. 864. —1- cos kx -f-
2 1 1
+ cos’ftx — — cos'fex -|- C. 865. arctg (2x) 4~ С. Мы имеем (формула (XIII),
0/2 эй л-
= М nrr>V?=1<arct- (2х) + с- 866- 1-arcsin (Зх) 4-С.
Указание. Этот интеграл приводится к виду С — [см. формулу (XII),
J V1 — 1Г
§ 104] подстановкой Зх = «ч Решение кратко можно записать так:
f dx р dx 1 р d (Зх) 1 . „
I —= - г - --=^- = 5- | —г --- = 5- arcsin (Зх) 4- С.
J У 1 - 9х3 J /1-(Зх)5 3 J •. /1 - (Зх)5 3
1
867. Ff arctg (х5) 4~ С. Указание. Сделать подстановку: х5 — и.
868. arctg е* 4~ С- Указание. Если принять ех = а, то exdx = dtt,
С exdx f du осп 1 . .. . । _ О_Л 1 . х , „
\ ;—сп; = \ -г-;—; . 869. - arctg (ох) 4~ С. 870. — arc tg —PC. Р е ш е и и е.
J 1 4- е J 1 + и* 5 а ь а 1
d v dx
Подынтегральный дифференциал —— похож на =——j [см. формулу (XIII), ।
d" —№ 1 -j- Х“
§ 104], но отличается от него тем, что вместо единицы в знаменателе стоит а-.
Вынеся а5 за скобки, а затем за знак интеграла, приводим интеграл к извест-
ному уже виду:
-j. Принимая = а, полу-
dx
чаем: —=du, dx=adu,
а
adu 1
4- и“ а
du 1 . , _
-j—s- arctg и 4- С =
4- и а °
= — arctg — 4- С. 871. arctg 4* С. 872. arcsin — 4- С. Указание. Дан-
(2d О Э d
0 dx
ныи интеграл отличается от интеграла только тем, что под
квадратным корнем вместо единицы стоит а5. Вынеся а5 за скобки
1
и множитель — за знак интеграла, приводим его к виду форму-
519
лы (XU), § 104:
dx
873. arcsin ^4 4-C. 874.
V5
dx
_ 1_
— T
875.
LZ arctg + С. У к
14 /7
1 -] /”2 . _
— arcsin I/ „ x4~c.
/2 r 3 .
С dx
а з а н и е. \ fZpp =
о_й 1 Ьх'л , „
876. гп- arcsin----С.
ib а
Указание.
x-dx
У
a
x2dx „
—7. После такого преобра-
- /~3
зования следует сделать подстановку: — = ц. 877. р'З arcsin Т,/ ^х-\-С.
878. ~ arctg + С. 879. arcsin С. 880. arctg (х + 1) + С.
Указание. Знаменатель подынтегрального выражения можно переписать
в следующем виде: 2 2х 4- х2 — 1 4- (1 + 2х 4- л2) = 1 + (1 + х)2. После
этого интеграл легко приводится к виду формулы (XIII), § 104.
881. 1 arctg 4. с. 13 + 6х + х2 = 4 + (3 + х)2. 882. arcsin + С.
Указание. Сначала следует преобразовать подкоренное
в знаменателе подынтегральной функции к виду а2 — (Ь±х)2;
3 — 2х — х2 = 3 -j- 1 — 1 ~^2х — л2 — 4 — (х + 1)“. После этого
легко приводится к виду формулы (XII),
Указан и с. Сделать подстановку: In х — и.
2
выражение
получаем
। интеграл
§104. 883. arcsin (In л) + С.
884.
1 sin х
— arctg
а ь
4- С. У к а-
а
заме.
(см.
решение
примера 870).
ctg:!Ax dx =
, 1 . „ ।
А Д - 4 Sin lx -j-
885. —— ctg2£x— -г- In sin kx 4- С.
2k ь k 1
<= ctS с13=^'л' — J ctg (cosec2/ex — 1) dx.
+ sin 4x С. У к а з а и и e. ( cos’.v dx = ( (cos2
==; ~ (1 4- 2 cos 2x + cos2 2x) dx — 1 4~ 2
887. 1- ш — sin 2<p 4- С. У к а з а н и e. sin2 cos2 X- =f (sin X- cos X~') = =
8 T 16 Tl 2 2 \ 2 2 ] \ 2 J
__—. 888. —g- ctg 3s 4~ С. Указание. Предварительно преобра-
зовать подынтегральную функцию, воспользовавшись формулой 1 — cos ах =
= 2sin2y. 889... | In (2л- 4- 1) - ?- In (Зх - 1) - In (4х - 3) 4- 1иС =
Указ
а и п е.
3
8
' 1 4- cos 2л\2
_____:_____ /1 г
886.
2
1 + cos 4х
2
СУ (2x4- I)3
= In . 890.
уЛ(Зх — 1)- у (4х 4" З)5
891. — In (sin ах -|- cos ах) 4~ С.
(ах2-Ьу , п
16Z1X111
892. _J_(l + ctgaxy+C,
520.
1 1 ' 1 X
893. |/ (й + b tg 2х)3 + С. 894. т (1 + In х)’ + С. 895. 2- х + sin £ + С.
о 2 2
896. tg ах — х + С. 897. х — sin 4kx + С. 898. — LCose^ + C.
899. — ctg2 2 V-v — In sin 2 Ух + С (полагаем 2 Ух = и).
900. У (а* -|- -V"1)3 С. 901. sin а Ух — sin’ аУ~х -|- С (полагаем
аУ=У. 902. 1 tg2 (Зх2) + ~ in cos (Зх2) + С. - 904. -ctg^4-C.
905, —L= arctg 1/ — ех
У ab Г а
(принимаем 1 + tg <р = и). 908. in (1 -ф sin 2ср) -J- С. 909. Intgx4-C =
ех о г_____________
+ С. 906. arcsin + С. 907. - /(1 4- tg ср)’ + С
= lnCtgx ^принимаем tgx = u; тогда coFv=^U)‘
910. Д У (1 4- sin 2ах)4 + С. 9П. 2х— tgx + C. 912. ег^х2+1 4- С (полагаем
Ух2 1 = ч). 913, i in (а2 + b2 sin2x) -|- С (полагаем а2 4- b2 sin2 х = и).
а
914. ~ (а2 + Ь2 sin2 х)^ + С. 915. -L tg х 4- С. 916. _у=1пх(2 — х).
917. jy = 2~-sin2x.. 948. — у^ sin3 ср—yj у/ sin11® 4* С- Указание.
С ? С 4 С ?
' Sin3 <0 C0S3W® = J Sin3 ср COS2 ср COS fdtf =: J Sin3 ср ( 1 — Sin2 <p) COS epdep.
919. у tg1 cp 4- C. 920, 5-tg3 cp — tg co -f- ср С. У к а з а и и e. tg1cp = tg2cp • tg2cp =
4 • о
= tg3 cp (sec2 cp - I). 921. ^/(esi"“'v + l)’ + C. 922. - /cTsU + C.
sinxcosx sin 2x nn„ 3 3?------------r-7—, , „
Указан и e. = —...... 923. — =- т/ (a cos x Ц- by -f- C.
У cos2 x — sin2 x 2 у cos 2x ,
924, x — у sin 2x 4- sin 4x 4- C. 925. tg3 x 4- C. 926. I- In tg x 4- C.
Указание. sin 2x = 2 sin xcosx = 2 tgxcos2 x. 927. — 2 ctg 2x4-C.
928. — x4- sin x 4- r- sin 2.v 4- C. 929. —— cos ax 4- cos3 ax —
8 1 2 1 16 1 a 3a
— cos3 ax 4- C. 930. у = i- tg 2x — ~ ctg 2x = i- (tg 2x — ctg 2x).
931. s = sin ^.932. —ctg3 йх 4-ctg «X 4-x 4-C. 933. arcsin x4 4- C-
934. }~ x — Д sin 8x 4- С. Указ а н и c. \ sin2 2x cos2 2xdx — -J- sin2 4x dx.
8 64 „ 4 J
935. 1 /1 4-3esin2v 4- C. 936. --^arctg'^il 4-C. 937. 1 ]n (xa 4-1)-
— 3 In (x 4- 1)4-C —In yv ip ~ • 938. a arcsin —У a2—x2 4~C. У к аз а н не.
Освободившись от иррациональности в числителе подынтегральной функции,
” +Х .7 г = Т a ~+-V ,7 .r= f adX I f XdX
a^xa- J yy^.2 J У^=У2± J У й2-х3'‘
получаем
521
939. arcsin х + У 1 — х2 + С. 940. х -|- 3 arctg х + С. Указами е. Этот инте-
грал можно представить в виде суммы двух
_ е (х2-Н) + з .. с л । з \
“ 3 х2-н d J\1+a'“+V
Указание. Этот интеграл можно представить в
Т л-2 , С х~ >— 1 -f- 1
трех интегралов: \ ах =
= ^х — 1 j dx. 942. arcsin (х — 1) С. У к а з а н и е. Интеграл при-
водится к виду формулы (XII), § 104, в результате следующего преобразо-
вания: f dx = f dx = f dX 945. --^1'' =
J |z2x - x2 J /1 -1 +2л--x2 J /1 - (.v - 1 )2 /x ,|i
С 4 i
интегралов: \ о . ах =
J “г J
у X2 — X 4- 111 1х + 1) + С.
виде алгебраической суммы
С /Л-2 - 1 . 1 \ ,
dx = \ —г 4- —г ах —
/2 2 \ I a
= — -4= — — = 1. 946. lux =ln a. 947. 1) sin x
\/4 1 /
ванне. Следует применить формулу (Illa) (см.
-з *
( — = In I A711 —3 = ln|—3| — ln|— 2|. 948. tgxl 4
x I —2 , I 0
-2 7C
2 = 1; 2) In 1,5. У к a-
o
сноску на стр. 286):
1С
= I. 949, —cosx 12 — I.
Io
950. ez
9 Qfi
I. 951. —ctg A- =l. 952. 18. 953.
& TC 5
954. x + lx2 + 1 x4
4
14 /,1___a< 17
955. у . 956. ° у—— Z> + a. 957. — y. 958.
даче 947); 3) 2. 959. 5=14 /се. ed. (cm.
39 26
-'-962. кв. ед. 963. = кв. ед. (см. решение
0.0
1) А. 2) 1 (см. указание к за-
решение примера 1, § 106).
задачи 940). 964. ~ кв. ед.
О
Указание. Сначала найти пределы интегрирования. 965.5= — cosx =
1 । о
= — (cos л — cos 0) = — (—1:— 1) = 2 кв. ед. 966. 5 = 21 у кв. ед. Указан и е.
Кривая у2 = 4х является параболой, симметричной относительно оси Ох.
Относительно этой осп будет симметрична и фигура, ограниченная данными
Рис. 303
линиями (рис. 302). Следовательно, достаточно вычислить площадь верхней
заштрихованной части фигуры и результат удвоить. Для точек параболы,
лежащих над осью Ох, ордината у положительна, поэтому, решив данное
уравнение относительно у, берем только одно положительное значение его;
_ 1 , 4
у = 2]/х. 967. 5 = 21 = кв. ед. 968. 5 = 4 кв. ед. 970. 5 = =/г кв. ед.
О о
У к а з а н и е. Эта фигура (рис. 303) ограничена сверху кривой у1 2рх или
522
y — Y'lpx, а снизу — параболой
Xs = 2py или у
2р-
Пределы интегриро-
вания найдем совместным решением данных уравнений (см. решение за-
дачи 969). 971. 5 = 4-^- кв. ед. (см. решение задачи 969). 972. 21 4- кв. ед.
2 о
973. 13-^- кв. ед. 974. 16 хе. ед. Указание. Площадь искомой фигуры
(рис. 304, заштрихованная часть) равна удвоенной площади фигуры 0NM.
975. 3— кв. ед. 976. 2кв. ед. Указание. На рис. 305 видно, что
О о
зSqAAi + — SoBBt 9з" кв- е<1-
У к а з а н и е. Эта фигура симметрична относитель-
но оси Оу (рис. 306). 978. з = 74 .и. У к а з а н и е.
Рис. 304 Рис. 305 Рис. 306
4
= 3t2 -|- 2/, s = (З/2 -]- 21) dt (см. решение примера 1, § 107). 979. Уско-
' 2
рение 0,8 щ/егк2, s = 80 м (см. решение примера 2, § 107). 980. t = 5 сек.
(I S '
У казан не. — = §7 + 14,7 = 9,87 14,7. Обозначив момент падения через
Л
7„ получим: з = (9,87 14,7) dt. Момент падения tL определится из уравнения:
й
196 = 4,97; -ф-14,77. 981. 7 = 20 сек, s=120.w. 982. t = 30 сек, s=180 м,
=~^^Г= 12 лг/се/с. 983. Ускорение:—5 м'сек2, s = 10 м. 984. t = 40 сек.,
3500 '
s = 320 .и. 987. 3. Указа н и е. Полагаем х2 4- 4 = и; xdx = , и, = 0э -ф
/5 о _ _|
4-4 = 4, «,=(/5)2 4-4 = 9 , f .3xdx—=3. С и f du. 988. -L In 10.
J J .г -pl 2 J 2
0 4
7t
989. 4. 990. —2 /cosx I 3 = 2-/2. 991. 1 992. 4. 993. —1. 994. "L±2
о 10 4 2 о
(см. указание к задаче 850). 997. . 998. =£-. Указание. Принять
' о Lo
523
х = 3 tg <р. 999.
Уз
За-
Указание. Сделать подстановку х — a sin ср. 1000. л.
Указание. Принять х — 2 sin ср. 1001. па4 (см. решение задачи 995).
1003. №. 1004. кв. ед. 1005. 3 — In (4 + х“) | °=1ц 5- Ю06. №. Указание.
Площадь фигуры, ограниченной кривой у = f(x) и осыо Охотх = ад.ох = Ь,
ь ь
как нам уже известно, определяется по формуле = j f(x)dx— $ ydx.
а а
Рис. 307
х = 0) и <р2 — 0 (при
По этой формуле площадь заштрихованной четвер-
Г
ти круга (рис. 307) будет равна 'j ydxt а площадь
о
г
всего круга S = 4^j^a. Возьмем теперь парамет-
о
X = Г COS » 'I
рические уравнения окружности > (I) и
J’ = г sin J
заменим у и dx их значениями из (1). Получим:
S — 4^* г sin <р (—г sin Так как <?1=-g- (при
?!
л' = г), то но первому свойству определенных интег-
0 2
ралов S ——4г2 J sin2 ydy — 4r2 \ sin2 ydy — 4r2
тс Ь
1 — cos 2y
о
dy и т. д.
2
1007. nab (см. указание к предыдущей задаче). 1008. 4 кв.ед. Кривая у =
:=cosa пересекает ось Ох в точках лу——, л^ = — л. В промежутках
/п Я \ / 3 . Q \ / К 3 \
10; 1~2 л; 2л j функция положительна) в промежутке [у; —
Рис. 308
2
отрицательна (рис. 308). Согласно указаниям в § 111,
2~ ~2К
дем так: S = Si + S2 + =Ц cosAcfx-|- cosatZa*
" г
1
площадь фигуры най-
2it
+ . \ cos xdx = 1 +
з
Г 71
о
+ 1-1 —1-|,+ 1°—(—1)] = 4. 1009. 5 = 32/св.еЛ 1010. 8 = 3кв.ед. 1011. 1п2.
524
1013. V = — куб. ед. (см. решение предыдущей задачи). 1014. И=
= 4л/>’ куб. ед. 1015. 17 = ^- куб. ед. 1016. V— r.ah" куб. ед. Уравнению
— \ соответствует гипербола, у которой мнимой осью является ось
Ох (рис. 309 и решение задачи 1012). 1017. куб. ед. 1018. V—
= кг куб. ед. 1019. v = ^- куб. ед. 1020. = Куб. ед. 1021. V =
= i Указание. Конус образуется вращением прямоугольного
О
треугольника ОАО (рис. 310) вокруг оси Ох. Следовательно, для вывода
формулы объема конуса надо знать только уравнение образующей ОА:
р
y = tga-x= х. 1022. 76,8л куб. ед. У к а з а н и е- Предлагается вычис-
лить объем кольца, полученного от вращения заштрихованной фигуры
(рис. 311) вокруг оси Ох. Объем находится
как разность объемов, полученных от враще-
ния вокруг оси Ох фигуры А..ЛКВВ, и прямо-
угольника AAfBiB. Совместным решением
уравнения найдем пределы интегрирования:
х, ——2 и л'2 = 2. Плоскость, проходящая через начало координат перпен-
дикулярно оси Ох, делит тело вращения на две равные части. 1023. V —
л (А'-' + Дг + г3) Н .,
= —11-------------—. Указание. Для вычисления ооъема усеченного
конуса (рис. 312) надо составить уравнение образующей АВ. Опа проходит
через точки А(0; г) и В (И; и уравнение ее будет иметь вид: у =
525
R — r
уу л I ’ ’ к 1
б
32 000 кГм. Указание.
as • Дх м3 (рис. 313), вес
н
fR — r
\ Ч
Объем слоя воды толщиной Дх будет равен
этого слоя воды 1000 а2Дх кг, работа, (затрачива-
емая на поднятие этого слоя, 1000 а2Дх-х кГм.
Работа, потребная для выкачивания всей воды, бу-
н и 2
дет: lim У 1000а2х = ( 1000a2xdx = \ 16 OOOxrfx.
Дх—о о О О
1026. Вся работа Q— 101,8 кГм. Указание.
Вследствие малости Дх слой АВ можно принять
за цилиндр. При принятых обозначениях (рис. 314)
объем этого слоя определится по формуле
Д1/=л№Дх м3, вес будет равен 1000лг2Дх кг. На
поднятие слоя будет затрачено 1000 л№Дх кГм
работы. Вся работа по выкачиванию воды на-
ходится как предел суммы бесконечно большо-
1025. Вся работа равна
го числа бесконечно малых слагаемых: Q =
Л Я
= lini V 1000г.№хДл—{ 1000 л r2xdx, где 0 и R —
Дх-0 о р
крайние значения глубины х слоев воды. Но при .
изменении глубины слоя х изменяется и г, иначе говоря, г является функцией
от х. Из прямоугольного треугольника AOOt найдем: № — R-—х2. Заменив в
R
подынтегральном выражении г2 его значением, получим ф=1000т:^(А?2—x'2)xdx.
и
250
1027. Q = — л2/?2//2 кГм. Указание. Работа, затрачиваемая на поднятие
о
слоя малой толщины Дх, при обозначениях,
принятых на рис. 315, будет равна 1000 лг2хДх.
слоя
Л,/?!, очевидно, зависит от глубины х. Из подобия треугольников ASO и
г [/______________х R
получим: — =—-pj—> '')• Заменив в подынтегральном выраже-
нии г2 его значением, получим Q — 1000л (И — х)2 xdx. 1029. Р—180т.
о
526
б
1030. Р = 135 т. Указание. В этом Случае Р = \0xdx. 1031. Одна сто-
з
bh2
рола пластинки испытывает давление 1056 г = 1,056 кг. 1032. Р = -у г.
2 250
1033. Давление на одну сторону полукруга равно -g- Д)3 = -у г. 1034. Р =
= ~РН‘--( = 3,14 • 3,5 • 8‘-‘ • 13,6 9565,7 г = 9,57 к Г. Указание. Для жид-
кости, удельный вес которой равен 7, давление, испытываемое цилиндри-
ческим кольцом АВ (см. рис. 212.), приближенно будет равно 2-n.Rx^x~{.
1035. 4. 1036. In aV* + + g . 1037.1. Ю38. 1. 1039. f sin x -
3 <P-j-ab-j-c 2 \
—-1 Sin\lh = 1. 1040. 4. 1041. 5=74-1 кв. ed. 1042.5= 1-1 кв. ед.
3 j |o 3 4 3 3
1043. S = a2 кв. ед. 1044. 5 = у кв. ед. 1045. 5 = 21 -1 кв. ед. 1046. 8 кв. ед.
1047. 2 кв. ед. 1048. 7 = 8 сек. 1049. 32 м. 1050. 5 = 4 кв. ед. 1051. 54 кв. ед.
1052. 4п/Р куб. ед. 1053. -1 -па-b куб. ед. 1
О
19 49
1055. 17 = ~ л/)3 куб. ед. 1056. 17= л,
ваемое одной стороной полуэллипса, равно
2
-у ab2. У к а з а н и е. Площадь полоски АВ
равна АВ Ду (рис. 316), но АВ равняется уд-
военной абсциссе точки В, ордината которой
равна у. Из уравнения эллипса следует х =
1- —-----кУб- ед-
i. ед. 1057. Давление, испыты-
= ~-УЬ‘2 — у2, откуда АВ = ~ УЬ2—у2 .
х У Ь2 —у~ Ду, давление, испытываемое ею,
у УЬ2 — у2 уДу. Одна сторона
ь
С I2 уь2 -y2ydy. 1058. Р =
эллипса испытывает давление, равное Р =
= 240л кГм. У к а з а н и е. Для поднятия слоя песка АВ (рис. 317) нужно
затратить 2000лгал'Д.с кГм работы. Следовательно (см. указание к задаче 1027),
Н 1 3 1
<?=Л 2000-г3.«Лг = 2000л (77 —л)2 лд/л' = 2000л .-Ь|1 (1 _ x f-xdx.
<J и о
10 62.. у = Сх. Указание. Разделив все члены уравнения на ху, получаем:
dx dv n С dx С dy х х
X у J X J у у у
527
откуда следует: у = 2. х или у = Сх. 1063. у = С sin х, У Казани е. Заменив
/б?у'\ f
символу отношением дифференциалов 1зу), привести уравнение к общему
' ’ ‘ 1
знаменателю и все члены разделить на у. 1064. л3—у3 = С. 1065.—— +
2. - с или у -- —А—_ t 1066. In у — -2 In (1 4- л2) = С пли у=С Х1 4-л2.
Л 1 “г” (_•> X £
1067. (x-a)-’4-(y —Z>)2 = C. Ю68. Ь2х2 4- а2у2 = С. 1069. X. — AL = с или
— AL — 1. 1070. У#2 4^у' — Vа2 4- х2 = С (см. решение примера 2, § 117).
1071. (1 4-у) (1 — л-) = С или у = -г-2- - 1. .1072. 1н 4 — = с. У к а-
1 — л у ху
з а н и с. Приводим к общему знаменателю и разлагаем коэффициенты при
дифференциалах на множители: д- (1 — у) dy 4~У2 (1 + х) dx — 0. Делим все
„ » (1— y)dy , (14-xir/x „
члены уравнения на х-у и получаем-. -------2, • + ~—уу-----~ ° илп
dy dy . dx . dx
-----4^?4----------— 0. В результате интегрирования последнего уравнения
У~ у Х“ X
получим:------ — In у----- 4- 1ч х — С или In — — А' А — с. 1073. у — Сех*.
-1 у - J х 1 У ху
Указание. После интегрирования получим: 1пу — х2—С илп 1пу — х2 ==
= In С; In — х2, откуда следует: ~ = ех', y = Cexi. 1074. у — а = Сех
Ci G
или у = Сех а. 1075. y — Ccos2x. 1076. (1 ех) (1 еУ) = С. 1077. у =
= esi” х _|_ с. 1078.
1080, 2 ]Lv— arctgy = C.
1083.
1087.
arcsin у—.arcsin х = С. 1079.
1081. COS X = С cosy.
2
tgxtgy = C. 1084. у' = 2рх. 1085. у — ——-
у = 2х:
arctg у.— arctg х = С.
1082. sin х = С cos у.
1086. 1.
а- и-
1. 1088. Общее решение: р = arctg (С ctg а); частное решс-
’ ние: р = arctg (ctg а) или |3 = ~ — а. 1089. у = Се2. Указан и е. Из условия
1 dy
задачи следует: ^~ =лу. Проинтегрировав это уравнение, получаем: 1пу —
—-1-л~+Сили In у=-2 л~ + 1п С, откуда In у—1нС—L
2 2 ‘ 2
1090. Уравнение семейства кривых: у2 — '.
дящей через данную точку: у2 = 2
~ = С. Уравнение кривой, проходящей через точку (а; 0):
1092. у = 4л’2 — 2 (см. указание к задаче 1089). 1093. у» = — / ? 4- 1 '
н и е. Из условия задачи следует: ух ky2, где /г — коэффициент пропор-
циональности. 1094. 7’ = 80 0,5' 4~ 20. . У к а з а н и е. Искомой функцией
является температура (7’) охлаждающегося тела. Скорость изменения функции
(температуры 7') в зависимости от времени t есть T't = (см. § 60). В дан-
ном случае скорость изменения температуры (функции) пропорциональна
разности между температурой тела 7' и известной постоянной температурой
528
inA.=L. А’
~ С 2 ’ С
у2 — 2рх-\-С. Уравнение кривой, прохо-
2рх. 1091. Уравнение семейства кривых:
--С-ь
Указа-
воздуха а = 20”. Поэтому дифференциальное уравнение напишется в сле-
дующем виде: ^ = fe(T—а), где — коэффициент пропорциональности/
Общий интеграл этого уравнения: In (7"—20) = kt С или (см. решение
примера 5, § 117) Т — 20 = Cekl. Так как Т с течением времени' убывает,
то ^<0, а поэтому k должно быть отрицательным. Дальнейшее решение
аналогично решению примера 5, § 117. 1095. к> = a>ac~kt. У к а з а и и е. Диф-
ференциальное уравнение будет иметь вид = — ka>, где й(й>0) является
коэффициентом пропорциональности. 1096. P = Pae~kl, где k — коэффициент
пропорциональности. 1097. ~ 4°/0. Указан и е. Обозначим через у наличное
количество радия через t лет с момента Л, = 0, когда У=Уа- Тогда, по
условию задачи, получим дифференциальное уравнение = ky, где k — пока
неизвестный коэффициент пропорциональности. Интегрируя это уравнение,
получаем: In = kt -ф- С (I); у =уа при t — 0, откуда следует: lnj’(| = k 0-|- С,
С = \пуа. Уравнение (1) теперь можно написать в.следующем виде: 1n>> =
= kt -|- 1пу/0 или In — = М (II). Решив уравнение (II) относительно у, полу-
Уп 1
чим у =уаеы (III). Hoy —-yjy, при t = 1590. Для определения ек из (III)
получаем уравнение уу0 = у»„с150<)/г, или 0,5 = (е*)1500, откуда следует:
= 1а"-р^0,5. Вследствие этого уравнение (III) представится в виде у =
=у0 (ek)t=y<l 0,5^ (IV). Полагая в формуле (IV) t = 100, найдем наличное
количество радия по истечении 100 лет от начального момента t = 0:
ю _i_
у = у:, ОД"” — у0 Кд/'0,510=_У0 (Q5)159 <=уа (Q5),6^_y0 0,9578 *. Следова-
тельно, по истечении 100 лет наличное количество радия составит 0,9578
части начального количества (_у0); распадается 1—0,9578 = 0,0422 части, т. е.
около 4%. 1098. 56,5 г. Указание. Обозначив наличное количество веще-
ства по истечении t ч от начального момента через jy, а наличное количество
его при ^ = 0 —через _у„, общий интеграл получим такой же, как и в преды-
дущей задаче, т. е. y=Ceki, или у-=у;,ек<, так как при / = 0 yl = j>0. При-
няв во внимание начальные условия, для определения ек и у.-, найдем два
уравнения: 1) 31,4 —у0 • еы', 2) 9,7 = • к-3. Из первого уравнения находим
31 4
. После подстановки значения ek во второе уравнение получаем
Vo v _____
41 дч .41 л-3 - /'.41 43
9.7=j0-jj-, откуда = |/ 56,5 г. 1099. y=yvekt,
где k— коэффициент пропорциональности, а у>0— начальное количество бак-
терий. 1100. Из условия задачи следует: =— kt, откуда x = Ce~kt (V).
При / = 0 получаем: х0 = Се"; х0 = G. Следовательно, в уравнении (V) С
означает начальное количество тростникового сахара (л:0).при t = 0. 1101.
Пусть v — высота жидкости в сосуде в момент t, а уа — в момент t = (1
Тогда объем V7, занимаемый жидкостью в момент t, будет равен ъРУ-у, где
R—внутренний радиус цилиндрического сосуда. Скорость вытекания воды:
dv dу Г, .
= л/?2 . । По условию задачи, эта скорость должна быть пропорцио-
U L ИI I
* Множитель 0,5|в вычисляется при помощи логарифмов.
529
иальна корню квадратному из высоты жидкости в сосуде, т. е. =
= й/у. Проинтегрировав это уравнение, получаем 2пА|2/у — М 4- С (VI).
Но так как .V = y0 при t = 0, то получим уравнение 2тД2 /у0 — k • 0 4- С, от-
куда следует^ С — 2тД- Уу0. Подставив значение С в уравнение (VI), полу-
чим: 2кД2Уу — kt 4- 2пД2 Уу,, или 2-л.Д1 (Уу ~yy<l) = kt (VII). Через 5 сек
от начального момента из сосуда вытекает половина его содержимого, т. е.
у делается равным у Л- Подставив в уравнение (VII) вместо у и t их зна-
] / / 1 _\ 2
чения Г = 5и^=-9-^, получаем: (1/ у 3’0 —/л ) = Л = —
/т /"Т г— \
X I I/ -^-Уо — УУо (VIII). После замены й его значением (VIII) равенство
(VII) принимает вид 2-/<= (Уу — /_у0) = тД2 У о — /Уо) в мо-
мент опорожнения сосуда должно быть
2к/?а(/У-/у\) _ 5(0 -/У)
2 с„ Л| Г
У [ |/j
5/У,
у — 0. Следовательно, t =
5 /У
-/л
5/2
/ J'o
17 м. 1102. 3,9 кг. У к а-
5
cU j.
. по так как рассол выливается из
то скорость уменьшения количества
можно представить и иначе, а именно:
б/.v 2х ,.г. _
уравнение (IX). В нра-
занн е. Количество воды в сосуде ежеминутно увеличивается на 3 л —
— 2 л—1 л, поэтому через t мин в сосуде будет 100 4- t л воды. Обозна--
чим через х.количество соли, оставшееся в сосуде по прошествии t мин
от начального момента (ври t — 0). Скорость изменения х аналитически вы-
разится производной от х по т. е.
еццуда со скоростью 2 л в минуту,
соли (х) в зависим ости от времени t
7777; , - . Получим дифференциальное
1 (JU —f— t
вой части этого равенства знак минус взят потому, что при возрастании t функ-
, dx „
ция х убывает, следовательно, ——величина отрицательная. Проинтегри-
ровав уравнение (IX), найдем: 1п х — — 2 In (100 4- t) 4~ In С, или х =
Q
= (100 4~ ^)2 (X)’ Условию задачи, х=10 кг при i=0. Подставив эти
С
значения х и t в уравнение (X), найдем: — Ю, С = 1С5. После за-
„ /V, 105
мены С его значением уравнение (X) получит вид х
Уравнение (XI) разрешено относительно количества
вию t
(Юо 4- ty (Х1)’
соли. Каждому значе-
будет соответствовать единственное и вполне определенное зна-
105
х. В частности, при t = 60 получим х — go)*:3,9 кг.
In (х2 4~ У) — 2arctg — = С. 1104. Общий интеграл 1п х 4- •— — In С.
X X
Общее решение: _у = х In . 1105. у — хуУ In Сх. 1106. у = л2 4-Се-
чсние
1103.
530
1107. Общий интеграл: In .t + j/" = hi С; общее решение: у = .tin2 1108-
У ал; + (см, решение примера 1 в § 119). 1109. у = хп (ехС). 1110.
у = (х -f- С) е~х. У к а з а и и с: — х=1пе~х. 1111. у — ~ (х -]- 1)4-|-С (x-f-l)2.
1112. s=4 sinZ + —. И13. у = 3^~-^. Ц14. у = sin х — cos х. 1115.
3 sm-1 x
y = x2-~ x-~. 1116. v = l x-|-l + 1117. y = --|x’+y xs +
4-Cpt + C,. 1П8. у — ex С усC1119. у = 4 4-C^ + C,.. 1120. s=
=----~ cos 2t 4- Су + С». H21. x = cosy — siny C,y-|- Cs. 1122. -c = t' 4~
+ G + Cit + C«. 1123. y = Cie'-x~rCy'[X (см. решение примера 2 в § 121).
1124. y=Ciex'-\-C2e~2x. 1125. у = Ci + С2еах (см. решение примера Зв
§ 121). 1126. s = Cle~2t-f-Cse3t. 1127 у= сХ2* + 1128. х = (С1+
C2t) е( (см. решение примера 5 в § 121). 1129. у = A (cos Зх В sin З.г) е2х
(см. решение примера 7 в § 121). 1130. .г = A cos 27 В sin 2i. 1131. у —
= (Cl-\-Cyc) е~'зХ. П32. у = (Л cos2£ + В sin 2>!) <?"='. 1133. /> = (64 + С26)е3».
1134. у = (Д cos Д- х + В sin у .г) ех. 1135. у = (Ct + Сгх)е^ *. 1136. s = t2 +
1 Г 3 3
+ 3^ + 2. Н37.р = —ycos2?. 1138.у=у<?-зх. 1139. y = cos-g .v+sin y.r.
1140. у = ex (cos x -I- sin .v). 1141. Общее решение: s = (Л cos 2t -L В sin 2/) e_/;
частное решение: s = 5e-zcos2i. У к а з а и и e. Обозначив t> и w соответст-
венно через s) и получаем линейное однородное уравнение. 1142.
1) 4, ; 2) 1 |1,... 1143. 1) 1 +лЦ+т4-з+... •
ТГ~зг + б!' ~7Г + ",; 3) ЬЗ +зТ5 +5^7+ 14 + з» “
-1-Ь ...1144. 1) «я==^_2__. 2) «„=(_ 1)^.1. з) = 4) ял =
= (—1)га-1 —L-. 1145. Ряд расходится, так как (см. § 123) 11ш«л =
у П ' п-*со
— lim 2д ~ -?^0. 1146 и 1147. См. указание к предыдущему примеру. 1148.
я-co 2п
Сходится. (Сравнить с геометрической прогрессией, у которой а1 = 1,
= 1149. Сходится. 1150. Сходится. 1151. Ряд расходится (см. ре-
шение примера 3 в § 124). 1152. Ряд расходится, так как lim
п-*оо ап
= lim Г_________2.№)__________.________________l=iim . я+1_ . =
n~OT|_l - 2-3...(2п— 1)>(2«+ 1) * 1 2-3...(2п- 1)] п • 2п • (2я-|-1)
= 0<1 (см. решение примера 4 в § 124). 1153. lim = _L < 1; ряд схо-
п—*со ап 2
дится. 1154. Ряд сходится. 1155. Ряд сходится. 1156. По признаку Лейбница,
знакочередующийся ряд сходится, если «j > д, > ... и lim ап = 0. В данном
п—*00
случае 1 > —1_ >> .2— ... и НтаЛ/=Пт =0. Следовательно, этот
]/"л ]/3 п-со ‘ п-^сп уп
/1 1
ряд сходится. 1157. Ряд расходится, так как Птдл = 11т----= --^:0.
п—.со л-.со 2fl 1 2
531
1158. Сходится абсолютно, так как члены ряда, составленного из абсолют-
ных величин членов данного ряда (см. решение примера 3 в § 126), не
превосходят соответствующих членов сходящегося ряда (5). 1159. Сходится
абсолютно. 1160. Сходится абсолютно. 1161. Сходится в любом интервале
(см. решение примера 2 в § 127). 1162. Сходится в интервале (—1; 1).
1163. Сходится абсолютно в любом интервале (см. решение примеров 1 и 3.
в § 127). 1Ц>4. Сходится в интервале (—2; 2). 1165. Сходится в интервале
Х'2 и3 v3 —
(-1; 1). 1166. a) £^ = 1+tfA. + £A + L^+... + £_!L + ...: б) е« =
£1 О1 /и
-1 + ^ + 1йг+^зг + -+и-йг+-: ‘ а =
х3 х,г
----?—от+ ••• + (—I)'1- -у,—г-4---- Указание. Эти результаты можно
а3 • 3! ап п\ ' 1
получить, подставляя в формулу (14) вместо к последовательно', а) ах', б)
х х , Л3х3 , /У'л5 /ггх7 ,
—! в)------. 1167. a) smjzx = kx----57~T~Ei------щ—Ь-..; б) cosftx —
а ’ ' а 3! 51 71 1 ’
k"x- kex°
= 1----Fjj—h -------g,—[-••• 1168. У к а з а н и e. Можно воспользоваться
91 v2 9'1,1 9s Vе 97ra
формулами (15) и (16). 1168. a) sirr.v = ^-щ- + '7Й------кГ + '”: б>
z! 41 01 Dl
COS3 X = 1--------fjy-
1 9 1
----2 cos — ту
2
1169. a)
, 2
муле (18)
, 1 • 3 - 5-7 8
4- --------v8
4-5
2
\ 2! ~ 41 6!
= 1 - 3.v + 6x2 - Юл-3 + 15x4 -
принять
2-4-6-8
2’x1 2x3x° „ 1 — cos 2x 1
-j- .---gj--... У к а з а и и e. sin- x =-%-= y —
1 cos 2x
cos- x =.-!—2-----.
1-2 2-3 ,
~2 ~2~X +
+... [сходится в интервале (—1; 1)]. У казанне. Вфор-
1 1 1 •> 1 1 - 3 . 1 -3-5 . ,
= =1-2- л- + .771 л--2Т476Л +
Указание. В формуле (18) принять т— — и
in = — 3. 6)
вместо х взять х2. 1170. а) (а -)- х)т = а’п 4- у- ат 1х -|- - am^x'L4-
ш(т-1)(ш-2) щ (ш-1)(ш-2) (ш - 3) 4
1 -2-3 а х 1 .2.3-4 Й Х +
+ _ Указание. /(0)=(а +
4~0)т = ат, f (0) — т (а -[- 0)'“ 1 — шат 1 н т. д. [см: разложение бинома
(1 4-х)яг в ряд Маклорена]; б) (а — х)4 = а4 — 4а3х + a~xs — т В X
l*z 1 • 2. • о
4 • 3 • 2 • 1
X ах3 + ]—j-g—аах^ = а1 — 4а5х+ 6а-х2 — 4ах3 4-х1; в) (а х)6 = ае 4-
4- 6а5х 4- 15а4х3 4- 20а3х3 4- 15а2х4 бах5 ф- х“. 1171. е-*1 = 1 — ^4-
-31 + 41--:У~^Х = Л-ЗМТ + 572!-7£3! + 9^— П74‘ stol2’=
0,20943
= sin 0,2094«= 0,2094 — —g—% 0,2079. Верны все цифры, так как первыР
0 20945
отбрасываемый член as — — < 0,0001 (см. решение примера 2 в § 131).
1175. cos 6° — 0,9945 (верны все цифры). 1176. |/е 1,39; Дз2< 001. Ука-
532
з а н и е. Подставив в формулу (14) вместо х чнсло-л-, получаем: е* = 1 +
О
+ J + 3^21 +3^3!+ ••• 1177- == 1,619. 1178. 1) In 16,32 = 2,7926 (см.
решение примера 3 в § 131); 2) In 6,79 = 1,9154. Указание. in 6,79 =
In (7 — 0,21) = In 7 (1 — 0,03); 3) in 110,7 = 4,7068. Указание. In 110,7 =
= In (109 — 1,7) = In. 109 (1 + 0,0156). 1179. — cos 8x — cos 2x С. У к a-
з а н и e. Воспользоваться формулой (3), приняв n = 3, m=5. 1180. X
(sin 2mx , sin 2nx\ ,,,,,,,, 1 . „ , 1 . . , „ , „
X---------------------+ С. 1181.------г sin 2x + -7Г sin 4x 4- C. 1182. xex —
\ m n j 4 8
—+ C. 1183. — — cos ax + = sin ax + С. 1184. x tg x ф- In cos .v ф- C. 1185.
7 2
(.v2 - 2) sin x + 2x cos x + C. 118S. 1187. л. 1188 . — 1189. |x| =
л 4 / , cos3x , cos 5,v . \ „
—-у-------- I cos.<-j-----1--Это равенство справедливо на всем
отрезке [ — л; л]. У к а з а н и е. f (х)— четная функция, так как/(—х) =
= | — х I = | х | = / (х). 1190. — х = — 2 (sin х —sin 2х ф- sin Зх —
2 о
---i- sin 4х ф- • • ) Равенство справедливо при любом х из интервала (—л);
на границах этого интервала (при х = — л и х = л) сумма ряда равна
л ф ( — л) ... л 2 / cos х cos Зх . cos5x . \ .
---i=0. 1191. /(х) = т--^— — +—js— +...)-(sinx—
---sin 2x + g-sin Зх—~ sin 4x + ...). Это равенство, справедливо при
— л < х < л. 1192./ (х) = sin х + -л- sin Зх -ф- i sin 5х + • • • + 2 sin 2х -|-
о О у 2
i sin 6х j^sinl0x+..-)- Это равенство справедливо в интервалах (—л; ,
ПРИЛОЖЕНИЙ
Латинский алфавит
Аа — a Nn — ЭН
ВЬ — 6c Оо — 0
Се — ЦС РР — ne
Dd — де Qq — ку
Ее — c Rr — эр
Ff — эф Ss — эс
Gg — же rt — тэ
Hh — аш Uu —-у
И — и Vv — ве
Jj — пот Ww — дубль-ве
Kk — ка Xx — икс
LI — эль \ Уу — игрек
Ahn — эм Zz — зет
Греческий алфавит
Аа — альфа
ИЗ — бета
1'7 —гамма
До —дельта
Ее — эпсилон
Z' — дзета
Ит; — эта
еао _ т9та
Ii — йота
К-/. — каппа
АХ — лямбда
Mfr — ми
Nv — ни -
— К СИ
Оо — омикрон
Птс — пп
Pp - ро
Ха — сигма
Тх — тау
1’и- — ипсилон
Ф? — фи
Ух — хи
— пси
— омега
ОГЛАВЛЕНИЕ
Из предисловия к первому изданию . . . /........................ 3
Предисловие ко второму изданию.................................. 4
Введение ....................................................... 5
Часть первая
ОСНОВЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
Глава I. Метод координат....................................... 9
§ 1. Координаты точек на прямой.......................... 9
§ 2. Направленный отрезок. Расстояние между двумя точками
па прямой линии......................................... 10
§ 3. Прямоугольная система координат. Координаты точки
иа плоскости ........................................... 13
§ 4. Расстояние между двумя точками на плоскости...... 15
§ 5. Деление отрезка в данном отношении................. 19
Вопросы для самопроверки ........................ 22
Глава 11. Функциональная зависимость и способы ее выражения
§ 6. Величины переменные и постоянные................... 23
§ 7. Абсолютная величина относительного числа.
Допустимое значение переменной величины................. 24
§ 8. Способы задания функции . ........................ '26
§ 9. Графическое изображение функциональной зависимости,
выраженной аналитически................................. 30
Вопросы для самопроверки ............................... 34
Глава III. Прямая линия........................................ 35
§ 10. Введение ........................................ 35
§ 11. Уравнение прямой с угловым коэффициентом.......... 37
< § 12. Частные случаи уравнения прямой с угловым коэффи-
циентом ............................................... 39
§ 13. Уравнение прямой, параллельной оси Оу ........ 40
§ 14. Уравнение прямой в отрезках....................... 41
§ 15. Общее уравнение прямой ........................... 43
§ 16. Построение прямой по се уравнению, данному в общем
виде.................................................... 45
§ 17. Уравнение прямой, проходящей через данную точку
в данном направлении ................................... 46
535
§ 18. Уравнение пучка прямых с центром в данной точке . . 48
§ 19. Уравнение прямой, проходящей через две данные точки 49
§ 20. Угол , между двумя прямыми ........................ 51
§ 21. Условия параллельности и перпендикулярности двух
прямых............................................ . . 53
§ 22. Пересечение двух прямых............................ 56
§ 23. Составление плана решения задачи .................. 57
Вопро сы для самопроверки............................... 59
Глава IV. Кривые второго порядка................................ 60
§ 24. Геометрическое место точек ........................ 60
§ 25. Окружность п ее уравнение в-нормальном виде .... 63
§ 26. Уравнение окружности как частный вид общего уравне-
ния второй степени с двумя переменными................... 66
§ 27. Эллипс. Вычерчивание эллипса непрерывным движением.
Уравнение эллипса .................................. . 69
§ 28. Исследование формы эллипса по его уравнению .... 71
§ 29. Эксцентриситет эллипса. Связь между эллипсом и окруж-
ностью .................................................. 74
§ 30. Гипербола. Уравнение гиперболы..................... 76
§ 31. Исследование формы гиперболы по ее уравнению ... 79
§ 32. Построение фокусов гиперболы по данным полуосям.
Эксцентриситет гиперболы ........................... . 82
§ 33. Асимптоты гиперболы............................. . 83
§ 34. Равносторонняя гипербола ......................... 86
§ 35. Уравнение равносторонней гиперболы, отнесенной
к асимптотам. • Вычерчивание гиперболы непрерывным
движением ............................................... 88
§ 36. 'Парабола и ее простейшее уравнение......... 90
§ 37. Исследование формы параболы по ее уравнению .... 92
§ 38. Парабола у = ах- Ьх -ф- с.......................... 96
§ 39. Параметрические уравнения кривых................. 101
§ 40. Кривые второго порядка как конические сечения ... 103
Вопросы для самопроверки . . ........................... 105
Часть вторая
ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Глава V. Теория пределов ...................................... 106
§ 41. Абсолютная величина и связанные с~~псй соотношения 106
§ 42. Бесконечно малая величина.....л . х............... 107
§ 43. Бесконечно большая величина ...................... 111
§ 44. Связь между бесконечно малой и бесконечно большой
величинами............................................. 113
§ 45. Ограниченная переменная величина ................. 114
§ 46. Предел переменной величины....................... 115
§ 47. Основные свойства бесконечно малых величин....... 118
536
§ 48. Основные теоремы о пределах................. . . 122
§ 49. Понятие о пределе функции. Некоторые приемы нахож-
дения пределов функций................................. 128
§ 50. Вычисление длины окружности........................ 135
§ 51. Вычисление площади круга.................’....... 138
§ 52. Сумма членов' бесконечно убывающей геометрической
прогрессии ............................................ 139
Вопросы для самопроверки.......................-....... 141
Глава VI. Производная функции 142
§ 53. Введение ........................................ 142
§ 54. Символика функциональной зависимости. Частное значе-
ние функции............................................ 143
§ 55. Область существования функции . . ............... 146
§ 56. Приращение функции............................... 147
§ 57. Непрерывность функции . '........................ 149
§ 58. Скорость движения в данный момент ............... 154
§ 59. Производная функции. Общий метод нахождения про-
изводной .............................................. 159
§ 60. Физический смысл производной'........ .......... 162
§ 61. Касательная и наклон кривой . . . ........... 165
§ 62. Геометрический смысл производной ................ 166
Вопросы для самопроверки .............................. 170
Глава VII. Основные формулы и правила дифференцирования 171
§ 63. Введение. Непрерывность функции, имеющей- произвол- •
ную.................................................... 171
§ 64. Производная постоянной величины.............. 172
§ 65. Производная функции у = х ....................... 173
§ 66. Производная алгебраической суммы функций......... 174
§ 67. .Производная произведения двух функций........... 175
§ 68. Понятие функции от функции. Производная функции от
функции . . . ......................................... 177
§ 69. Производная степенной функции.................... 179
§ 70. Производная частного двух функций............ 182
§ 71. Предел отношения когда х — 0..................... 184
§ 72, -Дифференцирование тригонометрических функций . . . 188
§ 73. Число е. Натуральные логарифмы. Переход от натураль-
ных логарифмов-к десятичным и обратно.................. 193
§ 74. Дифференцирование логарифмических функций ..... 195
§ 75. Производная степенной функции при любом показателе
степени................................................ 199
§ 76. Дифференцирование показательных функций ...... 201
§ 77. Дифференцирование обратных тригонометрических функ-
ций ......................................... ?...... 203
. § 78. Дифференцирование неявных функций. Простейшие гео-
метрические приложения производной...................... 209
537
§ 79. Производные второго и высших порядков. Механический
смысл второй производной . .......................... 211
. Воп росы для самопроверки . . : ................ 213
Глава VIII. Приложение производной к изучению свойств функ-
ций......................................................... 214
§ 80. Введение. Свойство непрерывной функции ......... 214
§ 81. Ход изменения функции. Возрастание и убывание функ-
ции ................................................. 215
§ 82. Признаки возрастания и убывания функции......... 216
§ 83. Максимум и минимум функции..................... 219
§ 84. Признаки существования максимума и минимума функции 221
§ 85. Правило нахождения максимума и минимума функции
с помощью первой производной......................... 223
§ 86. Правило нахождения максимума и минимума функции
при помощи второй производной . . . . .......... 231
§ 87. Особый тип экстремума функции .................. 238
§ 88. Выпуклость и вогнутость кривой.................. 241
§ 89. Точка перегиба................................. 246
§ 90. Построение графиков функций..................... 250
Вопросы для самопроверки ............................. 256
Глава IX. Дифференциал функции . . ....................... ; 257
§ 91. Сравнение бесконечно малых величин.............. 257
§ 92. Дифференциал функции............................ 260
§ 93. Геометрический смысл дифференциала функции .... 264
§ 94. Дифференциал второго порядка ................... 265
§ 95. Приложения дифференциала функции к приближенным
вычислениям ......................................... 266
§ 96. Дифференциал дуги................'.............. 270
§ 97. Кривизна кривой................................ 271
§ 98. Радиус кривизны................................. 273
Вопросы для самопроверки ............................. 276
Частьтретья
ЭЛЕМЕНТЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
Глава X. Неопределенный интеграл............................. 278
§ 99. Введение . ................................. . 278
§ 100. Интегрирование как действие, обратное дифференциро-
ванию. Понятие о неопределенном интеграле ........... 279
§ 101. Основные свойства неопределенного интеграла .... 283
§ 102. Основные формулы интегрирования. Непосредственное -
интегрирование ..................................... 285
§ ЮЗ. Определение произвольной постоянной интегрирования 289
§ 104. Интегрирование способом подстановки........... 292
Вопросы для самопроверки ................./........... 295
538