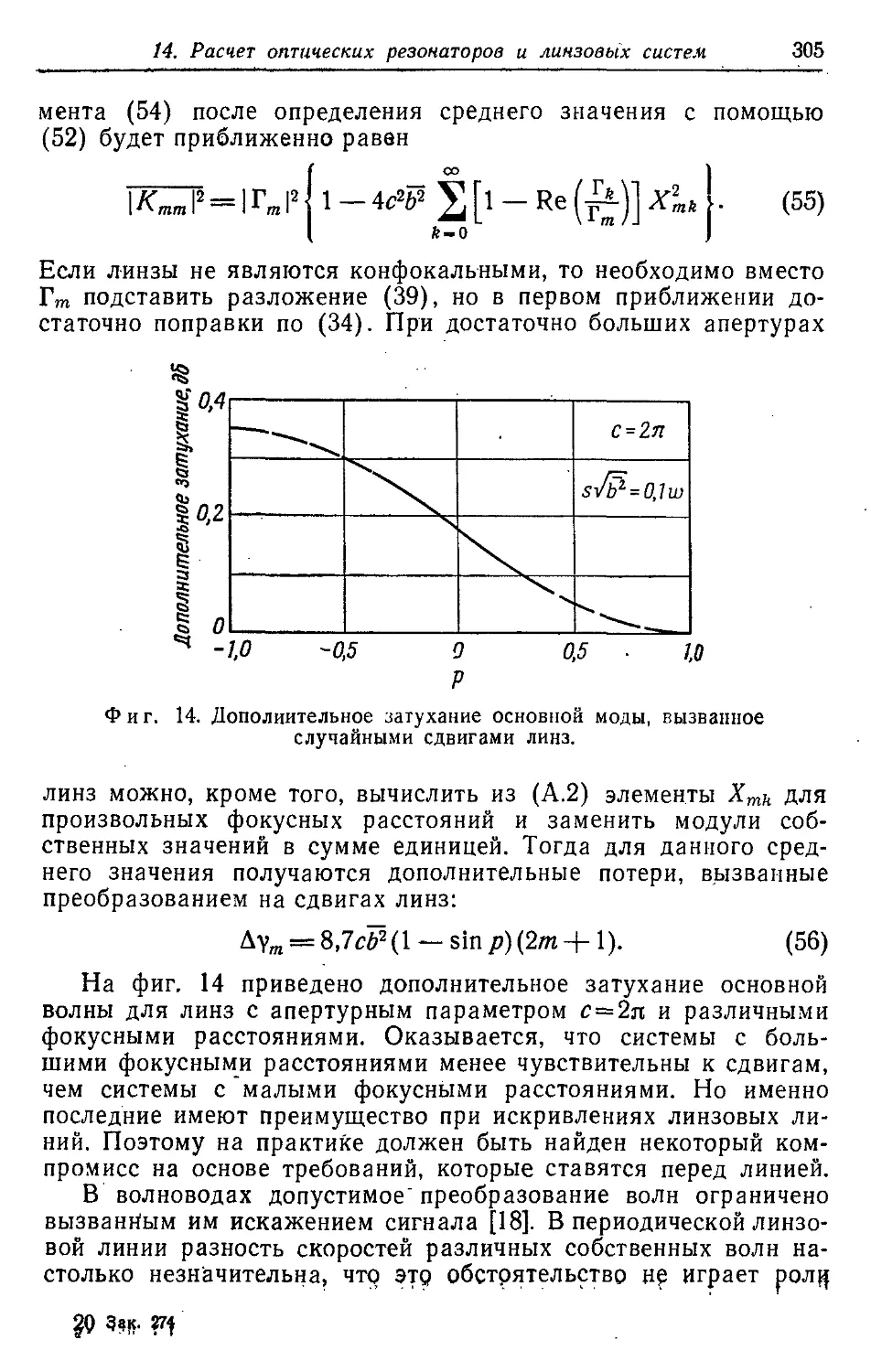
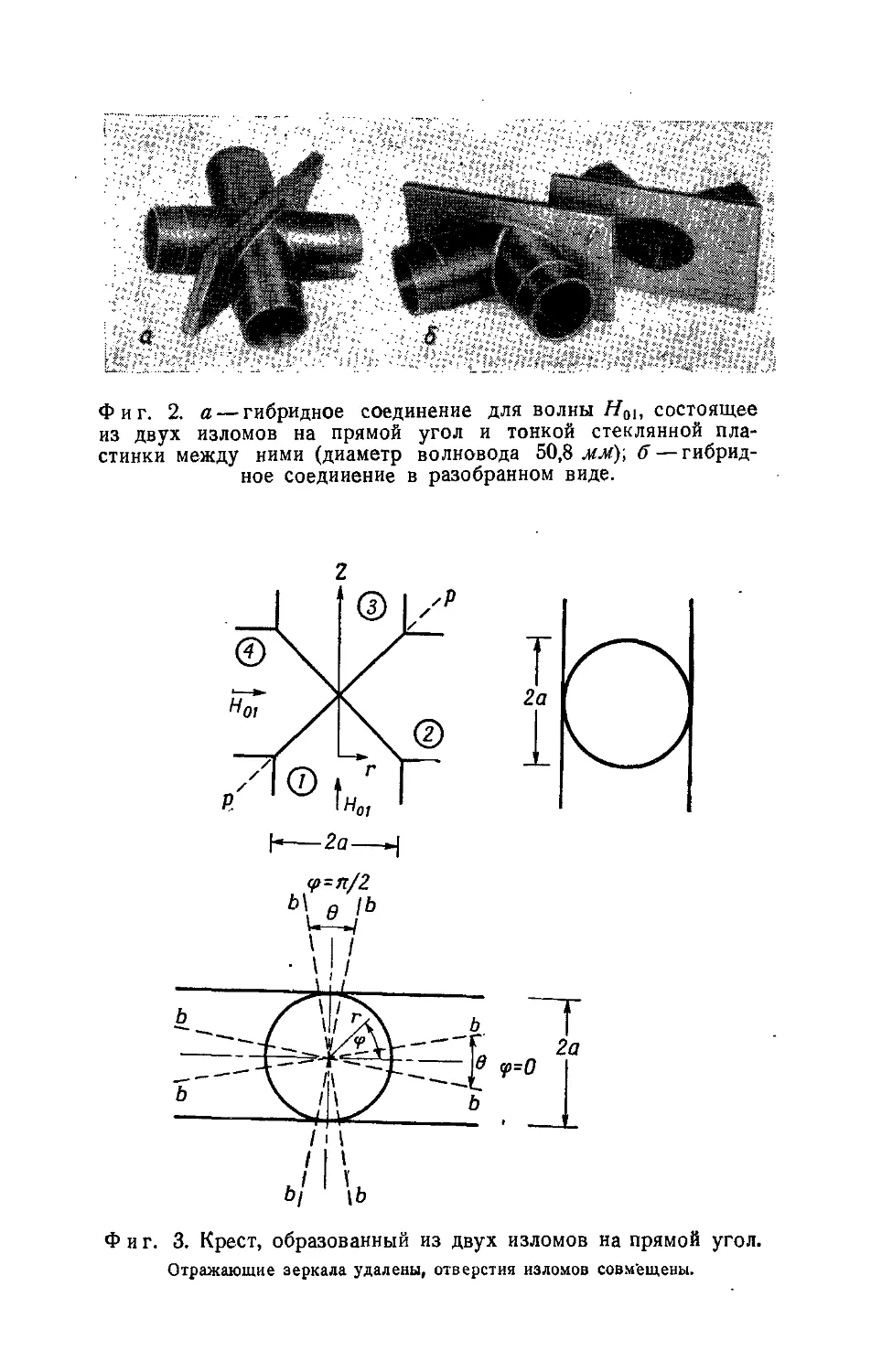
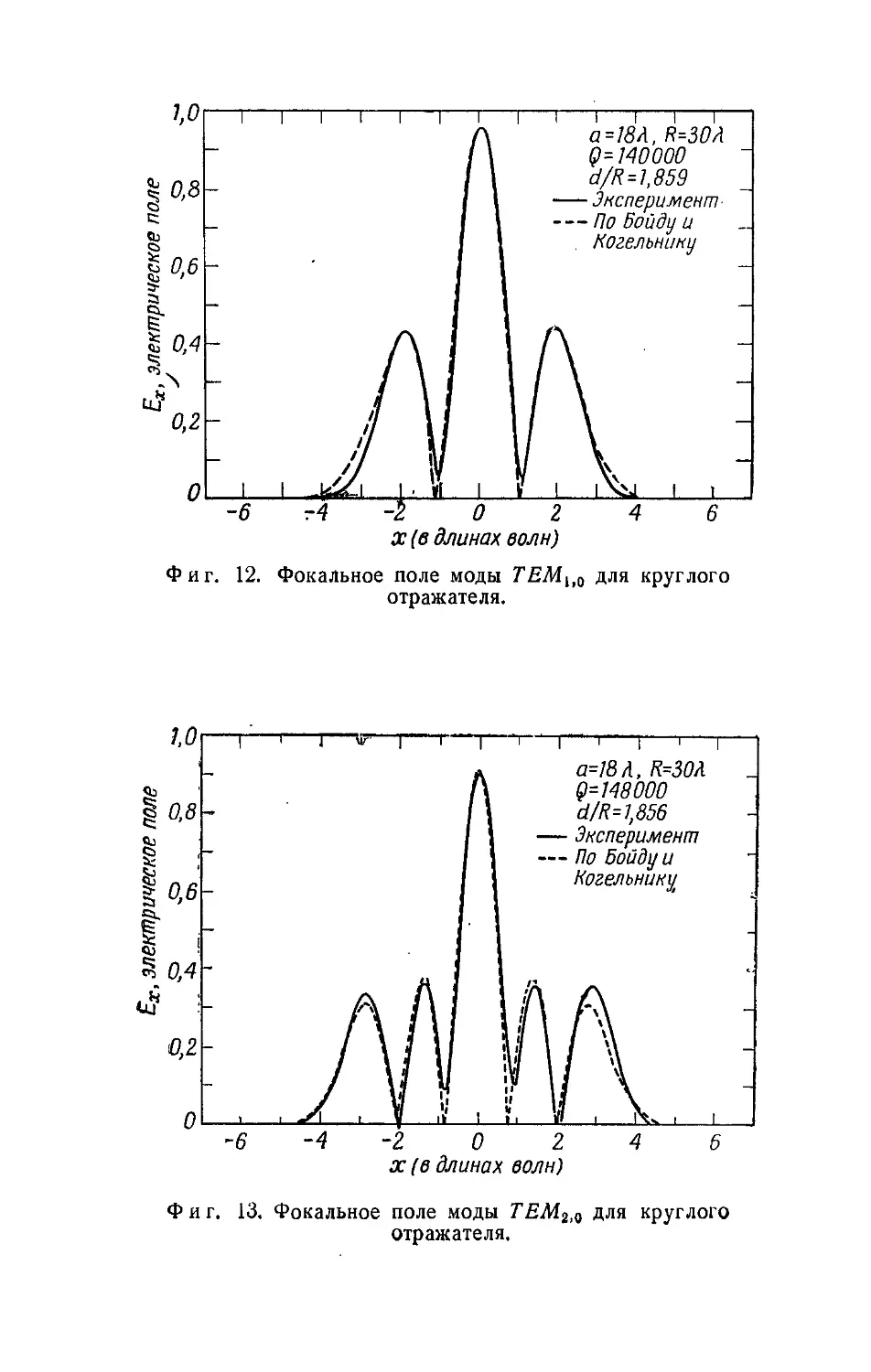
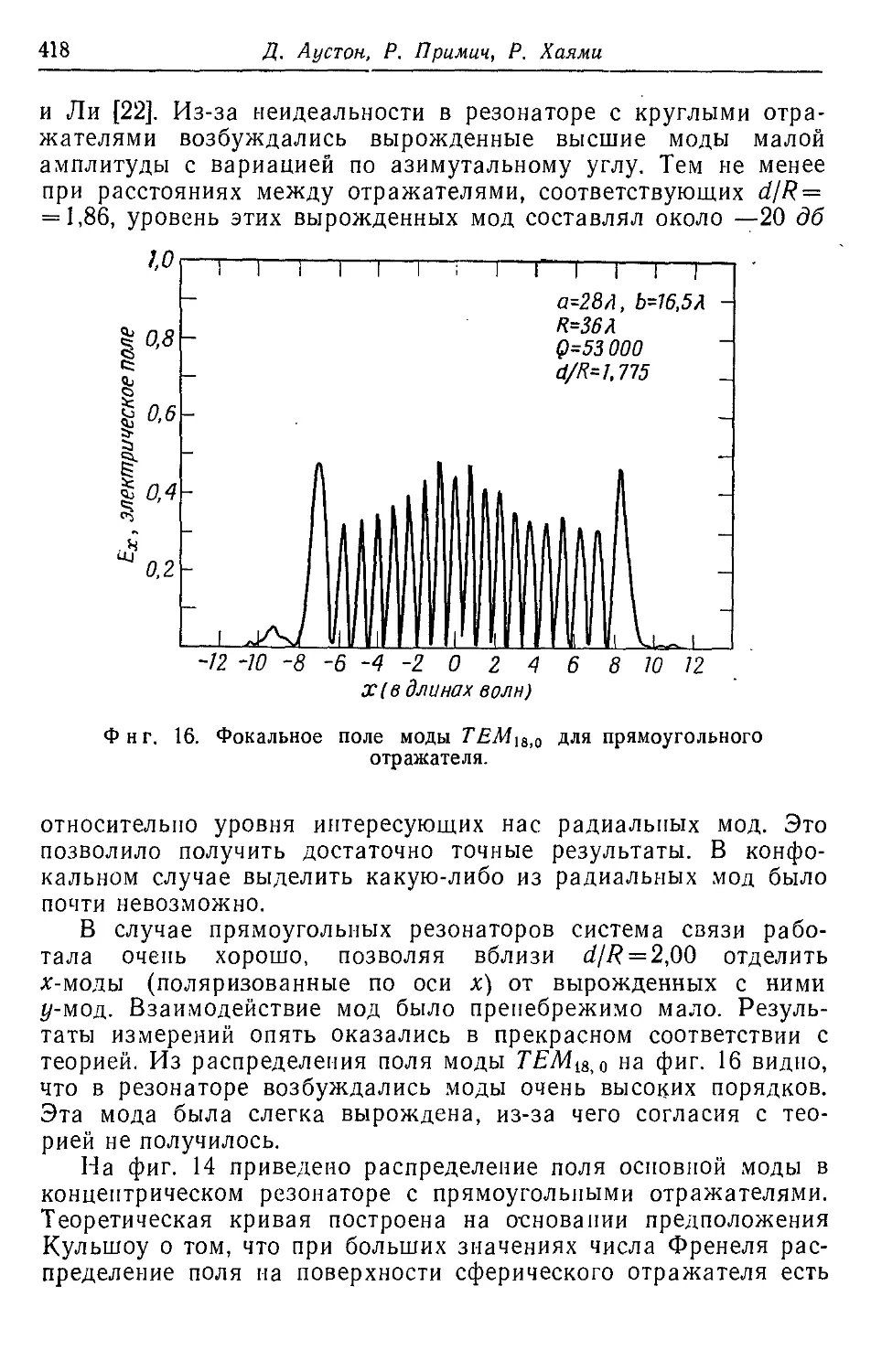
Автор: Кацеленбаум Б.З.
Теги: оптика физика спектроскопия квантовая физика квантовая оптика
Год: 1966
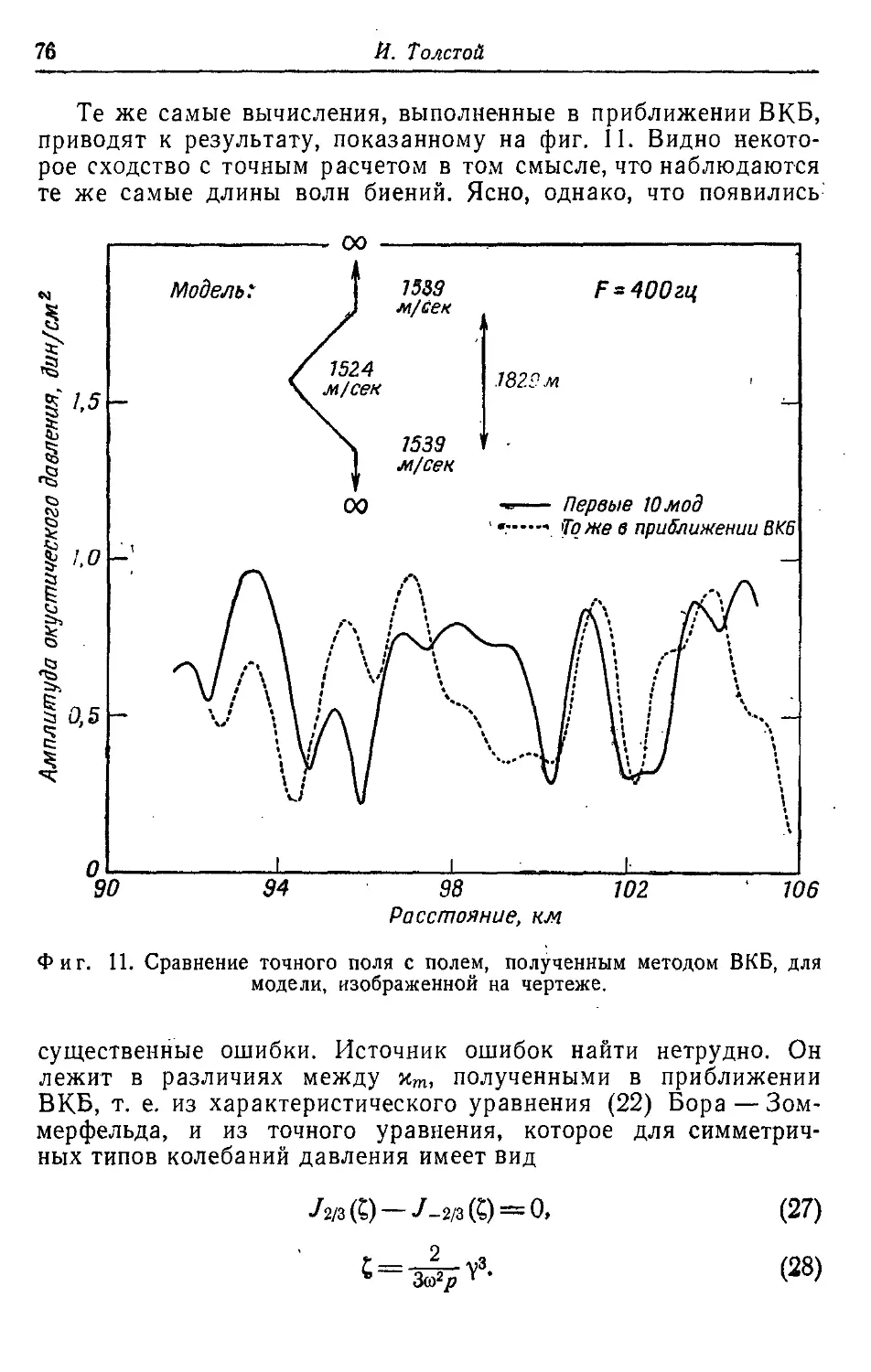
Текст
ВАЗИОПТИКА
Proceedings of the symposium bn
QUASI-OPTICS
New York, N. Y., June 8, 9, 10, 1964
POLYTECHNIC PRESS
OF THE POLYTECHNIC INSTITUTE OF BROOKLYN,
BROOKLYN, N. Y„ 1964
КВАЗИОПТИКА
Избранные доклады
на международном симпозиуме
Перевод с английского и немецкого
Под редакцией
В. 8. КАЦЕНЕЛЕНБАУМА и В. В. ШЕВЧЕНКО
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1966
УДК 535 + 538
Квазиоптика занимает промежуточное положение между
высокочастотной электродинамикой и оптикой. Опа изучает про-
цессы распространения, преломления и отражения очень коротких
волн в ситуациях, где существенную роль играет явление ди-
фракции. Типичным примером такого процесса является распро-
странение волн в линзовой и зеркальной линиях, а также коле-
бания в открытом резонаторе. Эти вопросы приобрели в послед-
нее время важное значение в связи с развитием квантовооптиче-
ских устройств н с освоением миллиметрового и субмиллимет-
рового диапазонов волн.
В основу книги положены наиболее интересные доклады на
международном симпозиуме по квазиоптике, состоявшемся летом
1964 г. в Нью-Йорке. Включено также несколько оригинальных
статей из научных журналов.
Содержание книги освещает следующие разделы: 1)' квази-
оптическая (и вообще асимптотическая) теории дифракции и рас-
пространения волн; 2) теория оптических резонаторов и свето-
водов; 3) теория многоволновых широких волноводов; 4) при-
менение квазиоптических устройств в диагностике плазмы, спек-
троскопии миллиметрового диапазона и субмиллиметровой интер-
ферометрии.
Книга представляет интерес для физиков и инженеров, рабо-
тающих в области СВЧ электроники, квантовой оптики, радио-
спектроскопии и их применений в физике и технике.
Редакция литературы по физике
ПРЕДИСЛОВИЕ
Термин «квазиоптика» появился сравнительно недавно и уже
получил широкое распространение. Квазиоптикой называют
пограничную между физикой и техникой область науки, охва-
тывающую круг вопросов, промежуточных между геометрооп-
тическими и дифракционными. Точнее .говоря, квазиоптика за-
нимается изучением и применениями явлений, в основе которых
лежат геометрооптические процессы распространения, прелом-
ления и отражения очень коротких электромагнитных волн,
однако в ситуациях, в которых волновая природа имеет карди-
нальное значение. Типичным примером таких явлений служит
распространение волн в линзовой или зеркальной линии и ко-
лебания в открытом резонаторе. Например, в открытом резо-
наторе, состоящем из двух расположенных друг против друга
зеркал (плоских или фокусирующих), поле представляет собой
две встречные волны; отражение их от зеркал происходит по
законам геометрической оптики, но расстояние между зерка-
лами столь велико, что при распространении волны от одного
зеркала к другому имеет место значительное дифракционное
возмущение поля. Аналогичная ситуация возникает при анализе
системы, в которой зеркало помещено в изломе широкого
волновода и т. п.
Интерес к квазиоптическим явлениям связан в первую оче-
редь с тем, что открытые резонаторы оказались идеальными
устройствами для квантовых генераторов света (см., напри-«
мер, сборник статей «Лазеры», ИЛ, 1963). Вместе с тем все
большее значение приобретают также и другие типично квазиоп-
тические устройства — открытые линии, геометрооптические эле-
менты в широки^ волноводах и т. д.
В основе настоящей книги лежат доклады, сделанные на
симпозиуме по квазиоптике, который состоялся летом 1964 г.
в Нью-Йорке (США) и собрал весьма квалифицированную и
представительную аудиторию. Доложенные работы относились
в основном к квазиоптическим проблемам в указанном выше
смысле; таких докладов на симпозиуме было большинство.
б
Предисловие
Часть докладов была посвящена общим вопросам асимптоти-
ческой теории дифракции. Наиболее интересные из докладов
этого последнего направления также включены в настоящее
издание, так как на русском языке пока нет последовательного
изложения современного состояния асимптотической теории ди-
фракции. Кроме того, в это издание включено несколько статей
из периодической литературы двух последних лет по вопросам,
непосредственно примыкающим к тематике симпозиума.
Сборник состоит из четырех разделов. В раздел I вошли ра-'
боты по квазиоптической и вообще асимптотической теории ди-
фракции, по распространению и излучению волн. Здесь в первую
очередь следует отметить большой обзор Фельсена (статья 1) по
общим вопросам квазиоптической дифракции. Началом система-
тических исследований в этом направлении принято считать ра-
боты Келлера *) по геометрической теории дифракции. В этой
теории в дополнение к падающему, отраженному и преломлен-
ному лучам постулируется существование различных типов ди-
фрагированных лучей. В данной работе показано, что ряд нестро-
гих результатов геометрической теории дифракции можно полу-
чить при асимптотическом анализе строгого интегрального пред-
ставления поля. Особое внимание при этом уделено анализу поля
в области геометрической границы свет — тень, а также в обла-
стях каустик и фокусов. Эти области не могут быть описаны сред-
ствами лучевой оптики.
Развитию идей Келлера посвящены также работы Льюиса
(статья 3) и Бреммера (статья 4). В первой из них рассматри-
вается нестационарное распространение волн, во второй — рас-
пространение волн в статистически неоднородной среде.
Интересным является сравнение двух возможных представ-
лений поля в граничных задачах: в виде лучей и в виде мод* 2).
Этот вопрос затронут в обзоре Фельсена, и специально ему
посвящена работа Толстого (статья 2). В работах Пальмера
(статья 5), Карпа и Карала (статья 6) рассмотрены вопросы
дифракции волн на дифракционной решетке и ограниченной
структуре, допускающей существование поверхностных волн.
') J. В. Keller в книгах Proc, of the simposium on microwave optics,
McGill University, Montreal, Canada, 1953; Calculus of variations and its
applications, New York, 1958; см. также Journ. Opt. Soo. Am., 52, 116 (1962).
2)' Английский термин «мода» соответствует русскому термину «тип ко-
лебаний», или «тип волны». В случае резонаторов и волноводов он перево-
дится также как «собственное колебание», или «собственная волна.». В по-
следнее время в научно-технической литературе на русском языке все чаще
употребляется сам термин «мода». В переводе в большинстве случаев мы
также используем этот термин.
Предисловие
t
В конце раздела помещена работа Палоча и Олинера (статья 7),
В Которой развита самосогласованная теория излучений Черенко-
О и Смита — Парселла, учитывающая обратное влияние излу-
Шнин па поток зарядов.
В разделе II, посвященном открытым резонаторам и луче-
ВОДпм, следует обратить внимание на работу Дешана и Маста
(статья 8), в которой процесс распространения волнового
Пучка анализируется с помощью диаграммы типа извест-
ной диаграммы Вольперта — Смита для длинных линий, и
работу Когельника (статья 9) по расчету неоднородностей в лу-
ЧСноде. Вопросам математического изучения интегральных урав-
нений теории открытых резонаторов посвящены работы Штрай-
фера и Гамо (статья 10) и Хартли (статья 11). Именно в
Йот раздел включены статьи из периодической литературы.
Это работа Торальдо ди Франчиа (статья 12) по резонаторам
С двугранными зеркалами и две работы Глоге (статьи 13, 14)
ПО расчету оптических резонаторов и. линзовых систем с по-
мощью матриц рассеяния. Этот раздел заканчивается дискус-
сией по резонаторам (статья 15), которая состоялась на сим-
позиуме под председательством проф. Кана. В ней приняли
участие такие известные ученые, как Губо, Морган, Торальдо
Ди Франчиа, Гамо, Карп, Бергштейн, Латуретт.
Раздел III содержит работы Као (статья 16) и )У1аркатили
(статья 17) по элементам в волноводе широкого сечения и Грай-
мемена (статья 18) по расчету желобкового волновода методом
поперечного резонанса.
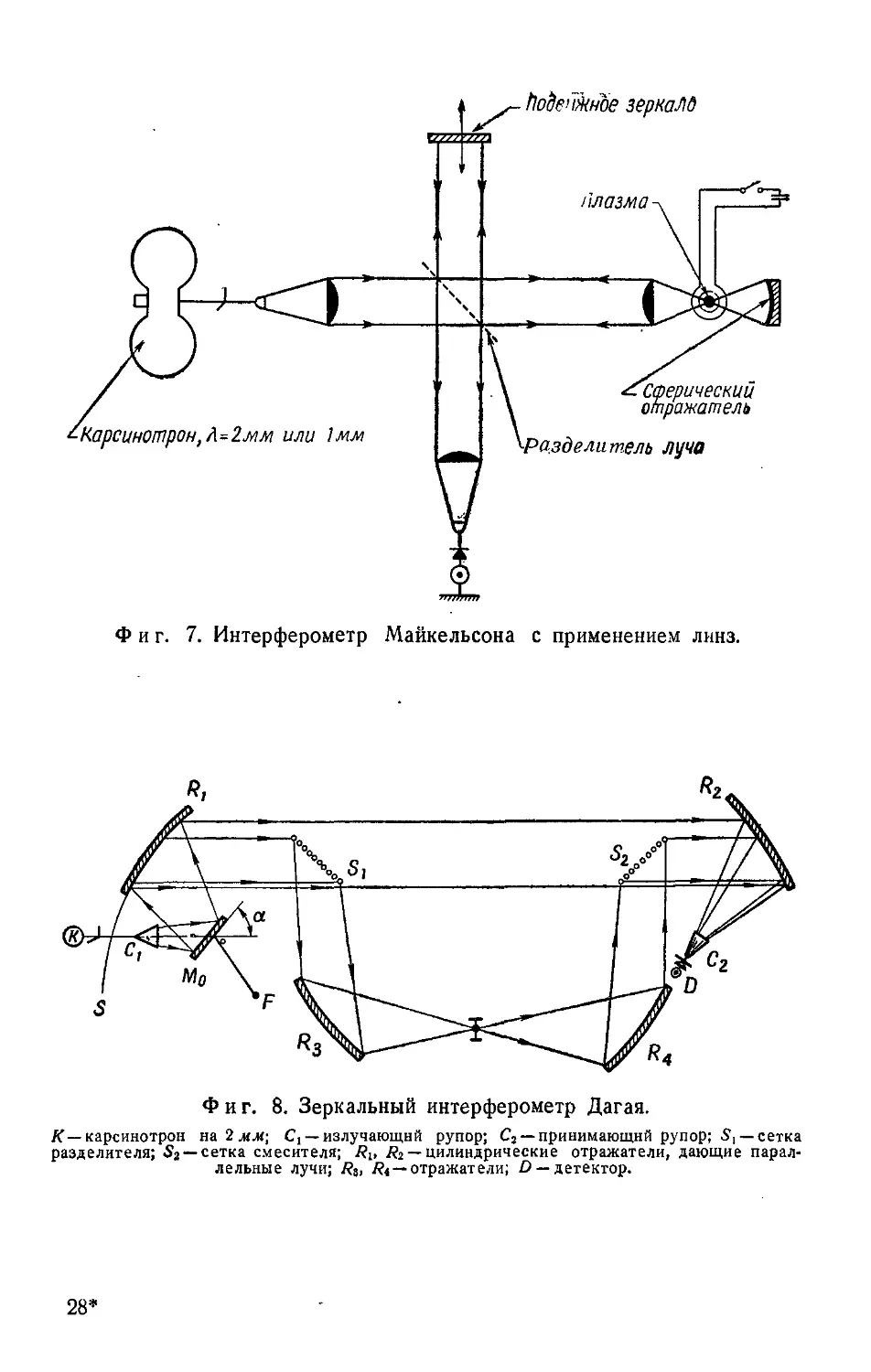
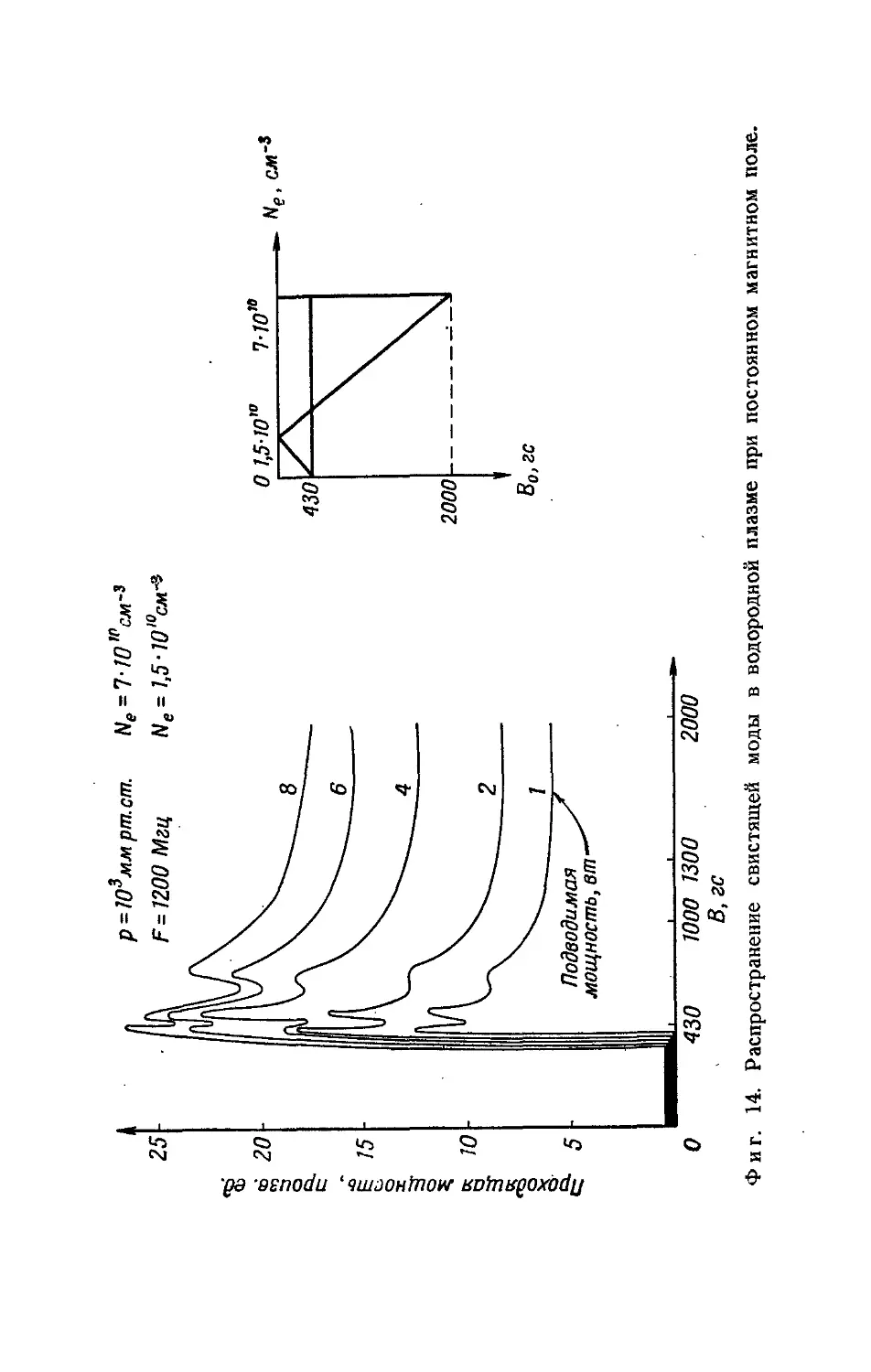
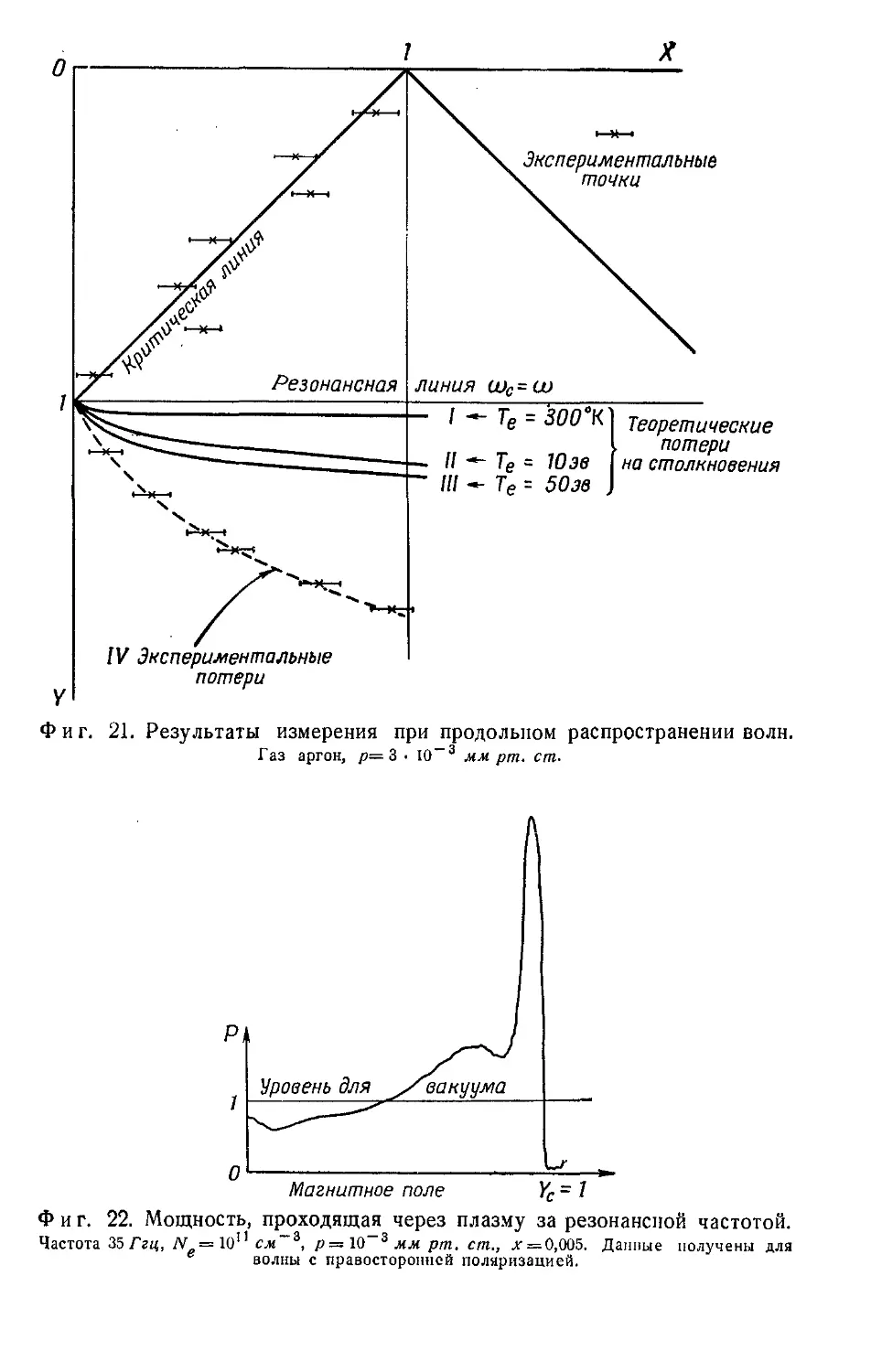
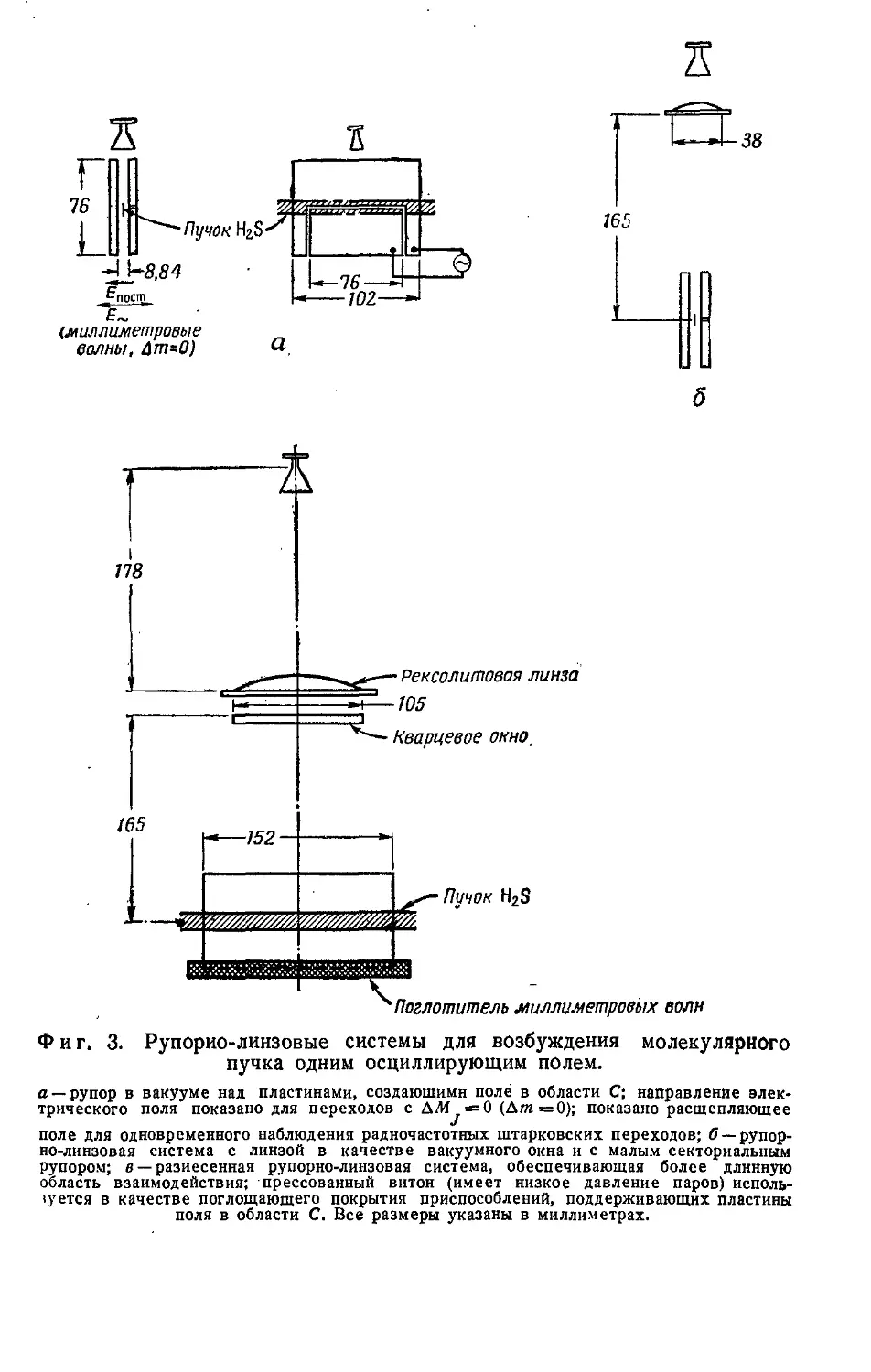
Раздел IV посвящен вопросам применения квазиоптических
устройств в плазменной диагностике (статьи 19, 20), в милли-
метровой спектроскопии (статья 21) и субмиллиметровой интер-
ферометрии (статья 22).
За время, прошедшее с момента проведения симпозиума,
по-видимому, не появилось кардинально новых идей, и подбор
материала в предлагаемом издании, по нашему мнению, позво-
ляет создать правильное представление о современном состоя-
нии вопроса.
При переводе мы не вносили никаких исправлений, кроме,
разумеется, исправления опечаток, и почти не комментировали
текст. Разные авторы по-разному оценивают важность той или
иной проблемы; особенно отчетливо это проявилось в указан-
ной выше интересной дискуссии по резонаторам (статья 15).
Например, известное интегральное уравнение для резонаторов
принадлежит к мало изученному классу; одни авторы считают
необходимым обосновать с математической строгостью суще-
ствование решений этого уравнения, другие, зная, что такое
8
Предисловие
доказательство отсутствует, озабочены разработкой наиболее
эффективного метода его фактического решения. Нам кажется,
что оба направления имеют право на существование.
Вклад советских ученых в квазиоптическую теорию дифрак-
ции является общепризнанным, и это в общем нашло свое
отражение и в статьях этого сборника. Лишь в некоторых слу-
чаях в подстрочных редакционных примечаниях указано на
пропущенные авторами соответствующие советские работы.
Январь 1966 г, Б. 3. Каценеленбаум
В. В. Шевченко
1
ДИФРАКЦИЯ,
РАСПРОСТРАНЕНИЕ
И ИЗЛУЧЕНИЕ ВОЛН
1
КВАЗИОПТИЧЕСКИЕ МЕТОДЫ В ДИФРАКЦИИ
Л. Фельсен*
Квазиоптические методы применяются при изучении явлений распростра-
нения и дифракции волн в случаях, когда длина волны мала по сравнению
с характеристическими размерами рассеивающих или направляющих систем.
При изучении рассеяния в основном используется геометрическая оптика с
учетом дифракционных вкладов, а при анализе явлений распространения в
больших волноводах или каналах более уместны разложения по модам.
Геометрическая теория дифракции Келлера, которая дополнительно к
кидающим, отраженным и преломленным лучам геометрической оптики посту-
лирует существование различных типов дифрагированных лучей, дает после-
довательный подход, объединяющий волновую и лучевую оптики при изуче-
нии рассеяния высокочастотного излучения в однородных и неоднородных
Средах. После краткого обзора теории внимание сосредотачивается на пере-
ходных явлениях в окрестности границ геометрооптической тени, в области
Киустик или фокусов; эти явления нельзя объяснить при простом описании с
помощью оптических лучей. Исследуя асимптотическое поведение точных
интегральных решений типичных дифракционных задач, можно связать по-
явление переходных областей в физическом пространстве с характерными
аналитическими свойствами интегрального представления. Описаны различные
переходные функции и дана их физическая интерпретация. Хотя основное
внимание уделено задачам для изотропных сред, приводятся некоторые ре-
зультаты, относящиеся и к анизотропным средам.
Когда свойства рассеивающего тела изменяются вдоль его поверхности,
метод оптических лучей применим только для медленных изменений. На ряде
примеров показано влияние быстрых изменений свойств поверхности на «ло-
кальный» характер высокочастотной дифракции. Использование метода мод.
(собственных волн) вместо метода оптических лучей ставит интересные во-
просы, особенно при изучении сложных объектов или слоистых сред, где воз-
никают многократные отражения. Даны примеры, в которых дифракционные
эффекты, получающиеся от вытекающих или поверхностных волн при рассмо-
трении с использованием мод, сравниваются с эффектами, получающимися
при геометрическом расчете.
В заключение'-приведен перечень задач, которые, по-видимому, заслужи-
вают дальнейшего рассмотрения.
* L. В. F е 1 s е п, Department of Electrophysics, Polytechnic Institute of
Brooklyn, Long Island Graduate Center, Farmingdale, N. Y.
12
Л. Фельсен
§ 1. ВВЕДЕНИЕ
Дифракционные явления, включающие рассеяние на телах,
размеры которых велики по сравнению с длиной волны падаю-
щего излучения, характеризуются термином «квазиоптика», так
как рассеянное поле можно описать при помощи обычных лу-
чей геометрической оптики с учетом дополнительных дифрак-
ционных вкладов. Локальная природа процессов, в которых
рассеянное поле в данном месте определяется индуцированными
токами в окрестностях особых точек на рассеивающей поверх-
ности, послужила основой систематического изучения высоко-
частотной дифракции. Индуцированные токи в освещенной об-
ласти рассеивающего тела с плавно и медленно меняющейся
кривизной поверхности определяются по существу законами
физической оптики (т. е. равны удвоенной магнитной танген-
циальной компоненте падающего поля, если препятствие имеет
идеальную проводимость); это несправедливо для точек вбли-
зи границ геометрической тени и структурных особенностей
типа края или угла. При расчете излучения в приближении
физической оптики [1] для коротких длин волн (k—»оо, где
k — волновое число в среде) основной вклад в интеграл излу-
чения вносят окрестности стационарных или седловых точек и
упомянутых выше граничных точек. Результирующее асимптоти-
ческое приближение в этом случае дает отраженное поле, амп-
литуду и фазу которого можно рассчитать при помощи геометри-
ческого построения отраженного луча, а также дифракционное
поле, которое проникает в тень, но существует и в освещенной
области. Поскольку особые точки, ответственные за дифрак-
ционное поле, лежат на тех частях поверхности, где приближе-
ние геометрической оптики неудовлетворительно, то эти про-
стые расчеты обычно не дают правильно дифракционной части
поля. Точность можно улучшить путем использования точных
локальных токов в окрестности этих точек [2—4]. Получаю-
щаяся в результате физическая оптика, или метод Кирхгофа,
уже обсуждались в литературе [1—5].
Выводы, которые следуют из предыдущих рассуждений,
были кратко сформулированы Келлером в его геометрической
теории дифракции [6—8]. Эта теория постулирует, что в допол-
нение к падающему, отраженному и преломленному лучам гео-
метрической оптики существует класс дифрагированных лучей,
которые описывают поведение, дифрагированных волн. Эти лучи
возникают тогда, когда падающий луч попадает на край, вер-
шину или угол рассеивающей поверхности или когда он рас-
пространяется по касательной к плавно изогнутой границе. Ди-
фрагированные лучи могут также появиться, если возможно
1. Квазиоптические методы в дифракции
13
полное внутреннее отражение (боковые лучи) или если в не-
которую область пространства проникают только затухающие
ноля (спадающие лучи) (фиг. 1). Эти лучи ведут себя по
особым законам: их амплитуды зависят от падающего
поля и от свойств поверхности в точке, где происходит
Спадающий луч
Лучи,
дифрагированные
от вершины
б) Вершина
Спадающий луч -
Каустика
Боковые
лучи
Многократная
дифракция
е) Сложная структура
г) Поверхность раздела д) Каустика
Фиг. 1. Дифрагированные лучи (по Келлеру).
дифракция (точнее в ее непосредственной окрестности). В этом
методе подчеркнут локальный характер дифракционного про-
цесса, а рассеянное поле в данной точке наблюдения можно
построить, суммируя вклады от всех лучей, проходящих через
эту точку. Поскольку важны только локальные свойства по-
верхностей вблизи точки, в которой происходит дифракция,
амплитуды дифрагированных лучей можно определить из стро-
гого решения соответствующих «эталонных», или «канониче-
ских», задач. Применяемая в этом методе геометрическая теория
дифракции использовалась для построений высокочастотных
полей, возникающих при рассеянии в однородных и неодно-
родных средах [9]. Справедливость результатов проверялась
на ряде специальных задач, для которых получены строгие
решения, а следовательно, и строгие асимптотические прибли-
жения. Достоинство метода состоит в его простоте, а также
в возможности применения к задачам, которые трудно под-
даются строгому решению.
Поскольку геометрическая теория дифракции уже была опи-
сана ранее [6—9], то нет нужды вдаваться в дальнейшие де-
тали. В пределах своей применимости представление в виде
14
Л. Фельсен
оптических лучей (включая геометрооптические и дифракцион-
ные вклады) дает физическую интерпретацию дифракционных
процессов, возникающих на простейших телах или сложных
системах, где может иметь место многократная дифракция.
Вполне возможно, что в некоторых случаях теория в основном
точно предсказывает поведение главных членов при асимптоти-
ческом предельном переходе в строгом решении для поля
(k —»оо), хотя общего доказательства этого еще не существует.
Следовательно, необходимо проверить справедливость теории
на известных результатах, полученных из решений канонических
задач. В «переходных областях», охватывающих границы тени,
каустики или фокусы, теория перестает быть справедливой и
должна быть изменена путем использования подходящего ка-
нонического решения или другими методами [10—13].
Ввиду важности канонических решений, их асимптотической
оценки и последующей интерпретации при помощи лучевой
оптики все эти вопросы здесь детально рассмотрены. Особое
внимание уделено явлениям в переходных областях, которые
не могут быть объяснены при простом описании с помощью
оптических лучей, физическому смыслу характерных ана-
литических особенностей в преобразовании поля, которые по-,
являются в представлении точного решения. В этой связи по-
лезны модовые представления, когда поле записывается в виде
разложения в ряд по собственным функциям, или модам, кото-
рые описывают распространение волн в присутствии заданной
структуры. Вышеупомянутые аналитические особенности заклю-
чены в функции, дающей амплитуды мод, и непосредственно
связаны с характеристиками высокочастотного поля. Следова-
тельно, анализ устанавливает связь между волновой оптикой
и представлением в виде оптических лучей, а также границы при-
менимости последнего, т. е. показывает, где простое описание
с-помощью оптических лучей неприменимо и должно быть мо-
дифицировано [14].
Ниже будет показано, что для асимптотического приближе-
ния требуется фактически только небольшая доля информа-
ции, которая содержится в точном решении. Именно это свой-
ство позволяет просто описать высокочастотное поле. Затем
описание с помощью оптических лучей будет использовано для.
того, чтобы объяснение волновых явлений вести при помощи
геометрических и дифрагированных лучей независимо от того,
получена ли эта форма описания из асимптотического прибли-
жения точного решения или из непосредственного геометрооп-
тического анализа. С другой стороны, использование метода
мод предполагает, что поле представимо в виде суммы или
в виде интеграла в зависимости от того, является ли спектр
1. Квазиоптические методы в дифракции
15
мод дискретным или непрерывным. Мода описывает поведение
волны с заданной периодичностью в сечении, перпендикуляр-
ном оси симметрии, и зависимостью вдоль оси симметрии, опи-
сываемой функцией амплитуд мод. Так как изменение поля ка-
ждой моды в поперечном направлении задано вдоль всей си-
стемы, то концепция мод является существенно нелокальной
и для построения поля с произвольной пространственной зави-
симостью требуется суперпозиция бесконечного числа мод. Гео-
метрическая оптика, наоборот, описывает локальные процессы,
и, следовательно, можно предположить, что модовое и геомет-
рооптическое представления акцентируют наше внимание на
различных аспектах задачи. Поскольку ряд статей, предста-
вленных на этом симпозиуме, связан с. явлениями распростра-
нения волн, которые рассматриваются с геометрооптической,
модовой и комбинированной точек зрения, то одна из целей
настоящей работы состоит в том, чтобы обратить внимание на
преимущества того или иного описания. Как упоминалось выше,
полная суперпозиция мод содержит информацию, которая от-
сутствует в высокочастотном приближении. Ниже будет пока-
зано, что поведение поля вдоль луча локально соответствует
поведению моды (собственной волны), индекс которой зависит
от направления луча (индекс описывает пространственное из-
менение поля волны в поперечном направлении). Хотя пред-
ставление в виде мод не дает преимуществ, когда конфигура-
ция лучей получается простой, оно имеет преимущества в пере-
ходных областях и в тех случаях, когда могут существовать
многократные отражения, так как эти многократные эффекты
часто хорошо объясняются при помощи мод.
Прежде чем продолжить изложение, уместно заметить, что
в ряде работ [15—19] уже даны обзоры по квазиоптическим
методам в дифракции, некоторые из которых [15—17] содержат
обширную библиографию. Поэтому здесь нет необходимости
давать подробный обзор литературы.
§ 2. ПРЕДСТАВЛЕНИЕ В ВИДЕ МОД.
ЛУЧИ И ЯВЛЕНИЯ В ПЕРЕХОДНЫХ ОБЛАСТЯХ
Общие замечания. Выше отмечалось, что высокочастотное
поле в присутствии возмущающих препятствий или протяжен-
ных неоднородностей можно представить в виде лучей, которые
включают дифрагированные лучи в дополнение к обычным па-
дающим, отраженным и преломленным лучам геометрической
оптики. В «переходных областях», которые отделяют области
существования лучей различных типов, описание поля с
помощью лучей непригодно. Невозможность такого описания
16
Л. Фельсен
можно понять из условия, что истинное поле должно быть не*
прерывно во всех точках пространства, в которых нет источни-
ков или резких структурных неоднородностей, тогда как гео-
метрооптическое построение приводит к разрыву поля на гра-
нице, которая отделяет одну область геометрооптических лучей
от другой. Например, освещаемая область предмета, отбрасы-
вающего тень, содержит падающие, отраженные и дифрагиро-
ванные лучи, а в области тени присутствуют только последние.
Так как оба описания справедливы в соответствующих им об-
ластях пространства, переход от области одного вида лучей
к области другого вида должен иметь место в окрестности
границы тени. При k—»оо переходная область сильно сужается
и возникает резкое изменение поля.
Хотя (или, возможно, так как) явления в переходных об-
ластях на высоких частотах имеют место в сравнительно огра-
ниченных областях пространства, они представляют интерес во
многих приложениях. Увеличение напряженности поля в окрест-
ности каустик или фокусов представляет интерес во многих
инженерных задачах и требует для своего расчета использо-
вания методов, выходящих за пределы применимости геомет-
рической оптики. То же самое относится и к расчету поля
вблизи горизонта за препятствием, который является необхо-
димым при исследовании распространения радиоволн над гори-
стой местностью или вдоль земной поверхности. Основная ха-
рактеристика в теории дифракции — полное поперечное сечение
рассеяния — просто связана с амплитудой рассеяния вперед,
для определения которой также необходимо знание полей в пе-
реходной области.
Аналитическое описание поля в переходной области значи-
тельно сложнее, чем в любом другом месте, так как функцио-
нальная зависимость должна описать плавный переход от од-
ного вида поля к другому. В связи с этим используются два
различных асимптотических метода: первый из них сводится по
существу к подходящему видоизменению и последующему ре-
шению дифференциальных уравнений, описывающих лучи, в то
время как второй исходит из разложения решений поля по
модам и исследования аналитических свойств этого разложе-
ния в комплексной плоскости волновых чисел. Методы гранич-
ных слоев и поперечной диффузии служат двумя примерами
применения первого подхода. Асимптотическое выражение для
поля в «граничном слое», т. е. в переходной области, можно
получить после применения «преобразования растяжения»
к дифференциальному уравнению для амплитуд луча, как
это делали Бушель и Келлер [10], а также Заудерер [11].
Этот метод дает обобщение лучевой теории, применимой в
/. Квазиоптические методы в дифракции
17
областях вне граничного слоя, и используется в некоторых
случаях для описания поля в окрестности каустик и границ
тени, возникающих, когда падающая волна дифрагирует, на-
пример на отверстии или препятствии с плавно изогнутой по-
верхностью. В методе поперечной диффузии для выпуклых
тел, развитом независимо в статьях Фока, Малюжинца и
Вайнштейна [12], волновое уравнение для точек наблюде-
ния в переходной области сводится к параболическому урав-
нению, которое затем решается при помощи канонического ин-
теграла, связанного с интегралом, найденным ранее Фоком [20].
Этот метод, детально изложенный Логаном и йи [13], приме-
нялся для изучения полей вблизи границы геометрооптической
тени или вблизи затененной поверхности выпуклого цилиндра.
Поскольку одна из целей настоящей статьи состояла в том,
чтобы определить соотношение между • методом мод и геомет-
рической оптикой, здесь не проводится дальнейшей тщатель-
ной разработки методов граничных слоев и оптических лучей.
Вместо этого мы перейдем ко второму из двух вышеупомянутых
асимптотических методов и попытаемся установить связь ме-
жду аналитическими свойствами разложения по модам и со-
ответствующим поведением реального дифрагированного поля.
Аналитические решения. Из асимптотического анализа неко-
торых задач об излучении, для которых удается построить
точные решения, можно получить многие способы описания
дифракционного поля в переходной области. Многие из этих
задач можно решить методом разделения переменных, при ис-
пользовании которого n-мерное (п = 2, 3) решение представ-
ляется суперпозицией собственных функции (мод), зависящей
от п—1 переменной и модовой функцией Прина, описывающей
зависимость от оставшихся пространственных координат. Для
высокочастотного асимптотического анализа обычно желатель-
но использовать совокупность мод с непрерывным индексом,
так чтобы результирующее представление имело форму инте-
грала по контуру. Если задача двумерная (скажем, отсутствует
зависимость от аксиальных или угловых переменных), то полу-
чается лишь однократный интеграл и решение обычно можно
представить в виде
1= J (1)
с
где £—индекс моды (комплексное волновое число в разло-
жении по плоским волнам), k—волновое число в свободном
пространстве и С — бесконечный путь интегрирования, на-
чинающийся и оканчивающийся в областях комплексной
2 Зак. 274
18
Л. Фелъсен.
плоскости £, обеспечивающих сходимость интеграла. Функции f (С)
и g(£) являются медленно меняющимися функциями k и имеют
известные аналитические свойства как функции £, причем
х, z) зависит также от обеих рассматриваемых ко-
ординат (скажем, х и z). Асимптотическое поведение решения/
при больших k определяется: а) стационарными (седловыми)
точками £s функции g'(C); б) сингулярностями £ функции f(£)
в плоскости Особенно важными являются те значения £s и
для которых величины g(t,s) и gfy действительны; в. этом слу-
чае соответствующие моды в среде без потерь представляют
распространяющиеся волны в отличие от нераспространяю-
щихся (экспоненциально затухающих) волн, которые соответ-
ствуют комплексности величин £(£)• Тот факт, что только от-
дельные точки в интегральном представлении дают вклад
в асимптотическое решение, указывает на локальный харак-
тер высокочастотного дифракционного процесса — свойство, ис-
пользуемое при описании с помощью оптических лучей.
Для проведения асимптотического анализа попытаемся де-
формировать контур С так, чтобы он прошел через одну или
более седловых точек g(Z) и чтобы вдоль получившегося пути
С' выполнялось неравенство
Если бы имелось более одной седловой точки, то было бы не-
обходимо учитывать только те из них, которым соответствуют
наименьшие значения Img,(^s) и которые, следовательно, дают
величины одного порядка. Например, для двух седловых точек
U и £s2, для которых Im g-(£si)<Im g-(£s2), вклад от есть
О (exp [— k Im g О + k Im g(Сл)]}
относительно вклада от Csi и им можно пренебречь при k -> оо.
Очевидно, что основной вклад в решение I получается от тех ча-
стей контура С' (путей «быстрейшего спуска» — SDP), которые
лежат в окрестности седловых точек (фиг. 2), так как подынте-
гральная функция на оставшихся отрезках пути получается от-
носительно экспоненциально малой. Любая сингулярность £ функ-
ции f(Z), которая пересекается при деформации С в С', должна
учитываться, если Im g'(C) =Im g(£s). Таким образом, асимптоти-
ческое приближение для / включает в себя различные типы волн
(т. е. отдельные "Моды), возникающие от соответствующих седло-
вых точек и сингулярностей. Такое выделение мод составляет ме-
ханизм, посредством которого высокочастотные характеристики
выбираются из излищне детального представления в (1).
1. Квазиоптические методы в дифракций
19
Несмотря на то что ниже в основном рассматриваются си-
стемы без потерь, метод мод имеет дополнительное преимуще-
ство, заключающееся в том, что с его помощью можно легко
описать изменения, возникающие при наличии поглощения.
Фиг. 2. Пути интегрирования и особенности в комплексной
плоскости
SDP — путь быстрейшего спуска.
Если £s является седловой точкой первого порядка [т. е.
g'(Ss)=O, g" (£s) =£0, где штрих обозначает d/dQ, а других
седловых точек у g(£) или сингулярностей у f(t) вблизи нет,
то асимптотическое приближение, возникающее от £s, имеет
вид [21]‘)
+0 (1)]. (2а)
где корень выбран так, что фаза третьего сомножителя в пра-
вой части равна фазе элемента пути d£, идущего от точки
Для изолированной седловой точки порядка N(t. е. dng/dZn =
— О, п=\,dN+1g/d^N+i =£ 0) вместо полученного выше
будем иметь асимптотическое выражение вида
/1 .l1/(Ar+1)nw+2>l(g,-a+gzP) (2б)
k(dN+'g/dt,N+1)t N + l >’ W
где углы аир выбраны так, чтобы обеспечить нужную фазу
вдоль отрезков пути, проведенных соответственно к седловой
точке и от нее. Волна типа (2а) характерна для двумерных
задач рассеяния и может описывать падающую, отраженную
и дифрагированную цилиндрические волны, которые легко ин-
терпретировать с помощью оптических лучей. Усиление поля,
') Несмотря на то что рассматривается зависимость только от k, сле-
дует учесть, что g-(g) имеет размерность длины и что за соответствующий
большой параметр можно взять величину kDl где D — некоторая характерная
длина,
2*
20
Л. Фельсен
возникающее из-за различной зависимости от k в формуле (26),
обычно связывают с наличием каустик.
Сингулярность в виде простого полюса С=Ср функции f(£) мо-
жет дать вычет
I lSp ~± [(С - Ср) / elkg ^Usp, (3)
который превышает вклад от седловой точки в формуле (2),
если только Img(£p) не больше Img(£s). Когда Img(£p)=0,
такой полюс поля соответствует обычной плоской волне, тогда
как lmg(£p)>0 соответствует поверхностным волнам или вол-
нам с комплексной постоянной распространения («вытекаю-
щие» волны), которые характеризуют распространение волн
вдоль границ тел, имеющих определенные свойства. Величина
Usp представляет собой функцию единичного скачка, которая
равна единице для тех значений £s, для которых необходимо
пересекать точки £р при деформации С в С', и равна
нулю при всех других значениях £s. Особая точка в виде точки
ветвления первого порядка £=£& функции [или &(£)] дает
вклад, поведение которого часто описывается формулой вида f)
Iк ~ «(Q 7—зтт [14-0 (6’5/2)] Usb, (4)
т. е. он имеет более высокий порядок по k, чем вклад от сед-
ловой точки (2), даже если Im £(£&)== Im g(£s). Здесь Lsb—
параметр длины, который стремится к нулю при £s—
а а(£&) —амплитудный коэффициент. Типичная волна, соответ-
ствующая ветви разреза, описывает дифракционный эффект
в виде «боковой» волны (см. фиг. 1) и является малой по
сравнению с другими вкладами, если только не выполняется
неравенство Im g(£b) <Im g(Zs, P). Величина Usb определяется
подобно Usp, а присутствие этого сомножителя нужно для того,
чтобы подчеркнуть, что волны от полюса и ветви разреза
в асимптотическом представлении решения существуют, вообще
говоря, лишь в ограниченных областях пространства. В связи
с этим следует напомнить, что положение определяется ко-
ординатами источника и точки наблюдения; а это всегда учи-
тывается видом функции g(C).
Если асимптотическое приближение для решения / можно
записать как сумму составных частей (2а), (3) и (4), то ре-
зультирующее поле представимо в виде системы лучей. Такое
описание теряет смысл в переходных областях, где амплитуда
одного из этих просто определенных типов волн стремится
к бесконечности. Это указывает на то, что представление в виде
*) См. работу [14], § 21,
1. Квазиоптические методы в дифракции
21
лучей перестает быть адекватным и что необходимо более
тщательное вычисление исходного интеграла (1). Например,
если ?S->?P, то в формуле (2) f(£s)-*oo и приближение не-
верно. Если предположить, что £s, tp и S (£s> £р) действительны и
что вычет существует только тогда, когда ?s>?p, т0 в переход-
ной области £s~£p должна быть обеспечена зависимость поля
вида k~'li (цилиндрическая волна) в формуле (2а) при -?s<Cp и
вида k° (плоская волна) в формуле (3) при ?s>?p. С другой
стороны, если седловая точка £s стремится к точке ветвления ^ь,
так что в формуле (4) Ls6—>0, то поведение переходной функ-
ции должно обеспечить появление или исчезновение в фор-
муле (4) вклада с зависимостью k~\ для чего требуется изме-
нить в (2а) член но не обязательно изменять главный
член O(kr'h) (поведение в окрестности угла полного внутрен-
него отражения). Приближение (2а), получаемое от седловой
точки, также теряет силу при g"('C.s) —>0, что соответствует слу-
чаю, когда в одновременно находятся две или более седло-
вых точек первого порядка; тогда вместо (2а) должна быть
использована более общая формула (26). Если рассматри-
ваются две седловые точки £si и ?s2 и если g'"(ts)^=O при
£si = £s2 = Cs, так что ?5 является седловой точкой второго по-
рядка, то переходная функция должна описать изменения поля
от до О(й~‘/з) при Типичной является ситуа-
ция, когда g(Csi) и g(^S2) действительны на одной стороне пере-
ходной области и на ее границе (?si и ?s2 действительны) и
комплексны на другой стороне (?si и ?s2 комплексны), при этом
переходная функция должна описывать преобразование двух
интерферирующих распространяющихся полей в экспонен-
циально спадающее поле (такая ситуация наблюдается вблизи
некоторых каустик). Все описанные выше эффекты соответствуют
двум или более типам волн, фазы которых (expfifeg' (?) ]) изме-
няются в области перехода почти одинаково, чем объясняется
их сильное взаимодействие.
Переходные функции для высокочастотного поля, связан-
ные с описанными выше функциональными свойствами подын-
тегрального выражения в формуле (1), можно получить из
сравнения данного интеграла с другим, «эталонным», или «ка-
ноническим», интегралом, который имеет необходимые анали-
тические свойства в простейшей форме [21]. Так, влияние по-
люса первого порядка вблизи седловой точки первого порядка
выражается весьма просто интегралом
-—т- ds, й
s — b
О,
(5а)
22
Л. Фельсен
подынтегральное выражение которого имеет в комплексной
плоскости s седловую точку первого порядка при s = 0 и полюс
первого порядка при s = b. Путь интегрирования взят вдоль
направления быстрейшего спуска (действительная ось), в на-
правлении от точки s = 0. Интеграл Ц можно вычислить точно
через интеграл вероятности: - -
Л = Im6>0, . (56)
где
Q (у) = / е~*2 dx. (5в)
у
Разрывность интеграла Л, когда точка b пересекает действи-
тельную ось, объясняет наличие вклада от вычета, соответ-
ствующего (3), тем самым обеспечивая непрерывность полного
поля. Так как Q (0) = ]/л/2, в то время как
±Q(Tii,VQ)~i7=[l+0(IT.)]. (5г)
то функция /1 ведет себя в соответствии с требованием, которое
было поставлено в предыдущем рассуждении (здесь Q играет
роль большого параметра). Область перехода соответствует
той части области изменения параметра, где неприменимо
асимптотическое приближение (5г), т. е.
b = O(QTi/2), (5д)
а так как величина Q велика, то переход получается резким
и имеет место в очень малой области изменения Ь. Очевидно,
что переходную функцию для полюса более высокого порядка
[в знаменателе подынтегрального выражения в (5а) стоит
(s — b)n при и>1] можно получить путем дифференцирования
/1 по Ь.
Простейшей функцией, которая содержит две различные сед-
ловые точки первого порядка, является полином третьей сте-
пени. Следовательно, удобно использовать интегральное пред-
ставление для функции Эйри:
/2 = +~) ds == 2л Ai (ой2/3) 1/3. (6а)
— СО
Седловые точки расположены при 5=±/)Ло, так что а
является параметром, описывающим расстояние между ними.
1. Квазиоптическим методы в дифракции
23
Если | о | Й2/3 1, то можно использовать асимптотическое
приближение [22]
А1 (т) ~ е-^ [ 1 + О (т-з/2)], | arg т | ;
Z у Л Т <5
Ai(r) ~ Ь-г^3/2 + ie^] [1 + О (т-3'2)],
Z у л т
2л
т
4л
(66)
(6в)
где т“ обозначает |т“| ехр [га arg т]. Итак, интеграл /г содержит
две распространяющиеся волны (вклады от двух различных
седловых точек), когда а — действительная отрицательная ве-
личина (освещенная область), и затухающую волну, когда а —
действительная положительная величина (область тени). Соот-
ветствующая алгебраическая зависимость от Q описывается
функцией [(ай)2/3] 1/4Q-1/3.— Q-1/2, как и должно быть для
вклада от изолированной седловой точки в формуле (2). При-
ближения (66) и (6в) неприменимы в области перехода
jо | й2/3 = О (1), т. е. при
а = О(й"2/3), (6г)
в которой должна быть использована функция Эйри [см. фор-
мулу (6а)]. Как и прежде, соответствующая область о мала,
так как Поскольку Ai(0)=O(l) относительно Q, то сов-
падение двух седловых точек первого порядка повышает по-
рядок амплитудной зависимости с £Г1/2 до Q~V3, что соответ-
ствует седловой точке второго порядка.
Если подынтегральное выражение содержит три седловые
точки, расположенные на одной прямой на равных расстояниях
друг от друга, то простейший канонический интеграл имеет вид
/з= J (/32 а);
n = 0, 1, 2, ..
(7а)
здесь седловые точки расположены при $ = 0 и ± г"|/"а. Инте-
грал выражен через функции параболического цилиндра
а), которые описывают поле в переходной области,
24
Л Фельсен
когда параметр разделения а стремится к нулю. Из приближения
для случая большого аргумента [23] имеем
е~т=/4
D-(n+42) (Т) ~ тП + 1/;
z,-t2/4 Г i
В-(n+'wW— n+i/2 1 + О (
Iargr|<^; (76)
_ г(-1)пК2^ eTi/4 Г. ,
Г(п + '/2) ?/2-« +
5л
— 1 > argr>—
(7в)1)
Видно, что если т движется по прямой, наклоненной под углом
45°, из первого квадранта (argr = n/4) в третий квадрант
(argr = —Зл/4), то характер поля изменяется: от одной рас-
пространяющейся волны переходим к трем [вклады от двух
седловых точек s=±iYа одинаковы и объединены в форму-
ле (7в)]. Различным значениям п можно приписать различные
типы волн. Для п = 0 амплитудная зависимость в /з (при усло-
вии что У 2Й | а | 1) имеет обычный вид Q-1/2• Она изме-
Q-1/4
> характерной для седловой точки
третьего порядка [см. (26) при М=3], при а—>0 [Z)_i/2(0) есть
0(1) относительно Q]. Размер переходной области определяется
в этом случае величиной
a = 0(Q~1/2). (7г)
Мы закончим данное обсуждение исследованием переход-
ных явлений, возникающих в случае, когда точка ветвления
располагается вблизи седловой точки первого порядка. В этом
случае простейший канонический интеграл имеет вид
СО
/4 = (s-ft)“ ds. (8а)
— оо
где a=n/m, n<m; пит обозначают положительные целые
числа, причем Ь представляет собой расстояние от седловой
точки s = 0 до точки ветвления (случай отрицательных а можно
получить дифференцированием по Ь). Заменой переменных и —
= ($ — Ь)а этот интеграл сводится к виду
ОО
z4 = l J ul/ae-Q^la+b^du, (86)
в котором конечные точки пути интегрирования расположены
на бесконечности. Мы рассмотрим только точку ветвления пер-
вого порядка а='/2> т. е. случай, когда интеграл /4 совпадает
Ч При n/4<arg т<5л/4 в {7в) необходимо заменить i на — д
1. Квазиоптические методы в дифракции
25
но форме с /3 в (7а). Следовательно, переходные эффекты, свя-<
ванные с соседством седловых точек и точек ветвления
первого порядка, подобны эффектам, которые возникают от
трех смежных седловых точек первого порядка.
Предыдущие расчеты показывают, как можно проанализи-
ровать переходные явления при помощи выбора соответствую-,
щих канонических интегралов, основные аналитические свой-
ства которых такие же, как и у исследуемого решения с исполь-
зованием мод. Имеется прямой и систематический метод сведе-
ния данного интегрального представления / (1) к соответствую-
щей канонической форме. Детальное изложение метода дано в
работе [21]; этот метод включает в_ себя замену переменной £
на s с помощью равенства g(^)=T(s), где полином t(s) наи-
более просто описывает поведение g(£) вблизи рассматриваемой
седловой точки [например, для седловой точки первого порядка
£(£)—&(£«)—s2, 0<$2<оо]. Несмотря на то что выше обсужда-
лись асимптотические приближения только низшего порядка, мо-
жно также получить и члены высшего порядка при помощи пря-
мого, но большей частью громоздкого расчета.
Примеры. 1. Определения и общие замечания. В качестве
иллюстрации применения изложенных общих принципов мы
рассмотрим ряд типичных дифракционных задач и дадим ха-
рактерные формулы для функций /(£) и g(£). В первом столбце
таблицы показаны 'рассеивающие тела; непрозрачные, отбра-
сывающие тень препятствия с особенностями структуры (клин,
конус), а также плоская слоистая среда с различными диэлек-
трическими свойствами. Соответствующие седловые точки и
сингулярности, которые появляются в асимптотической оценке
интеграла и определяют вторичное поле (т. е. полное поле ми-
нус падающее), указаны соответственно во втором и третьем
столбцах таблицы. Асимптотический расчет часто более удобно
производить с помощью комплексной угловой переменной w,
получающейся из соотношения
£ = Asinw, (9)
которое преобразует действительную ось плоскости £ в «путь
Зоммерфельда» Р, состоящий из следующих трех отрезков
в плоскости w.
Re w = — -у+“0“, “0“ < Im w < оо;
[- | + (1 +/) “0“] < w < [|- (1 + /) “0“];
Re®) —— “0“, —оо < Im w < “0“
Таблица
Аналитические свойства решения в виде собственных функций и соответствующее поведение
квазиоптического поля
Соответствующие седловые точки Соответствующие особенности Типы воли Переходные функции
' . В А 2л-а4' 1. Клин С ft. Oft. в в II II- «с «0 В в © 4i О’ || °з Ч Л Я вех ®$ = Л — |ф — <р'| ®р2 = Я — Ф — ф' = л — 2а -|- Ф + ф7 А: 1г lr 2d В: lz 2d С: 2d АВ-. Ц ВС- it
7 Ц В г'^2^'л-0о 2. Конус ws = 0 На ABw: , = * р = л — 20о + 0 3/ 3(/ 3/ Зг 3(/ АВ: li
Ус У
В полупространстве с е0
Wsr = ЯР. 1 ЯР 1 <
На АВ; wsr =w^
3. Полупространство, за-
полненное диэлектриком,
А < Со
«о
d-----
d
В полупространстве «0
®i = q>- |ф|<у
Изображение
4. а — диэлектрическая'
пластина s( > е0;
б — щель в диэлектрике
«1 < ео
ttl«J Л4
t п
Первоначальный Типичный
путь путь
интегрирования быстрейин
спуска
5. Неоднородный диэлек-
трик
В полупространстве е0:
wsi = sin <рг- |
= sin <₽r |ф) <фи
Wsrr = 31Пфгг J
ip равно углу луча при
Z ">СО
На AB;wST — w^
COS Wp1’ = — (1 4- E)~1/2 At 2,- 2r 1 AB: /3
= 4>e = ± arcsin Bt 2t 2f «</
e = ~<l eo Ct 2„
Поверхностные волны 5d (6d) Действительных
(z) Г Л -1 w„ = -ь га,- p L 2 11 Вытекающие волны ЧЛ==± [₽/ + ZVy] a- Y?>0; 0<P/.<-J w^ = 0, когда Cj < e0 2i, 2r, 6d переходных функций нет; когда wp вбли- зи SDP или ws\ используется Л
^1)=arcsin'/5)<
<pm = arcsin n (г')
At 2i 2r ABt /3
Bt 2i 2r 4d CDt /2
Ct 2i 2„ 4d
Dt 4<z 7d
Bt 4d
Соответствующие
седловые точки
6. Анизотропное полупро-
странство
е — х0х0е0 -|- zozoe, е < О
а—точка наблюдения внутри
is г — * I
_________I в 1 sign q>
V ctg2q> — ctg2<p
ctg2$ = | e |
I Ф | < q> для действи-
тельной
Ha AjA2 или
Ha B2C: gir->oo
Csa = fesinq>a, a = 1, 2,3
. . л
I Фа I < ~2
Ha АВг-. £$2 = ^>s3
Ha AB2.
В В- t,sl ~ ?S2 = Css
о о
V А
б~ точка наблюдения сна-
ружи
Продолжение таблицы
Соотв етству ющие особенности Типы волн Переходные функции
£(? = ± k (<р = q>e) ctg2 фс=|е|(1 + 1е|) Лр 2/ 2Г 4dl 4^2 Л2: 2/ 2Г 4dI Bi- 2Г 4dl 4</2 В2: 2Г 4^ С: 4dl или /3 2 2 ЛГ(ф)_ sin ф = УГ ctg2q>—Ctg2(p (р, ф) — измерен- ное положение изображения (р, ср)—измерен- ное положе- ние источника
to Со iu ю » • • № ND ND nd Л V 3 ^5 «S W ЛВр 12 2 F-.I3
1. Квазиоптические методы в дифракции
29
(символ “0“ обозначает малую положительную величину). Вели-
чины ws, wp и Wb обозначают седловые точки или особенности в
плоскости w, а индексы над wp, Wb или Ср, Сь отмечают порядок
особенности. Области геометрооптических лучей различных
типов обозначены заглавными буквами А, В, ..., а границы
между смежными областями, скажем между А и В, имеют
соответствующие двойные буквы (ЛВ). Различают семь ти-
пов волн: 1 — плоская; 2 — цилиндрическая; 3 — сферическая;
4 — боковая; 5 — поверхностная; 6 — вытекающая; 7 — спа-
дающая.
Индексы I, г, гг и d обозначают падающую, отраженную,
преломленную и дифрагированную волны соответственно. Из
рассмотрения типов волн, помещенных в четвертом столбце
таблицы, видно, что в различных областях геометрооптических
лучей присутствуют вклады от различных волн. (Возбуждение
поля в структурах, помещенных в строке 1, происходит пло-
ской волной, в строке 2 — точечным источником, в строках
3—6 — линейным источником; рассматриваются только скаляр-
ные потенциалы, из которых можно получить сами поля.) По-
явление или исчезновение взятой в отдельности волны, когда
она переходит из одной области в другую, должно описы-
ваться одной из переходных функций Л, /2, 1з [см. выражения
(5) — (7)], которые приведены в последнем столбце таблицы.
Две заглавные буквы обозначают в этом случае, что данная
переходная функция обеспечивает гладкое, хотя и быстрое из-
менение поля при переходе через границу.
В отсутствие потерь (что предполагается для простоты)
волны типов 1—4 представляют незатухающие, распространяю-
щиеся волны [функция действительна], которые отли-
чаются друг от друга различной зависимостью от большого
параметра задачи. Если большим параметром задачи является,
например длина L, то плоские, цилиндрические и сферические
волны имеют соответственно следующие зависимости от L:
O(L°), O(L~'12) и O(L-1), в то время как боковая волна спадает
как O(LA*1‘) или O(L~2) в зависимости от того, возбуждается ли
поле линейным или точечным источником. Боковая волна тес-
но связана с явлением полного внутреннего отражения в зада-
чах для двух сред и фактически возбуждается лучом, падаю-
щим на поверхность раздела из более плотной среды под
углом полного внутреннего отражения (см. фиг. 1). Преломлен-
ные лучи распространяются в очень тонком прилегающем слое,
параллельном поверхности раздела; при преломлении они уно-
сят энергию обратно в более плотную среду, чем объясняется
более быстрое затухание их по сравнению с затуханием обыч-
30
Л. Фельсен
ных геометрооптических полей. Поле боковой волны в тонком
промежуточном слое спадает экспоненциально. Волны типов
5—7 соответствуют полям с комплексной функцией g(£), что
связано с экспоненциальным затуханием. Поверхностные и вы-
текающие волны возникают от вычетов в особых точках типа
полюс, тогда как спадающие волны в общем случае могут
также образовываться от комплексных точек ветвления или
седловых точек. Поскольку рассматриваются комплексные
углы распространения, то границы областей существования по-
верхностных и вытекающих волн определяются не так легко,
как для волн, распространяющихся под действительными
углами. Кроме того, величина рассмотренного малого, экспо-
ненциально затухающего дифрагированного поля должна срав-
ниваться с экспоненциально малой ошибкой, которую делают
(и которой обычно пренебрегают) в асимптотическом прибли-
жении при рассмотрении других, значительно больших соста-
вляющих поля.
Вопрос о том, когда необходимо учитывать экспоненциально
затухающее поле, должен решаться в связи с другими аспек-
тами задачи; при этом ясно, что существенны лишь области
малого затухания. При соответствующих условиях вклад от по-
люса с затуханием, характеризуемым самой низкой степенью
по k [О (ft0) в (3)], можно сравнить с вкладом от седловой точки
[O(ft_,ft) в (2)], если величина g(Zp) имеет малую мнимую часть,
a g(&s) действительна. Это имеет место, например, для точек
в дальней зоне, вблизи диэлектрической пластины (строка
4 таблицы), т. е. в случае, когда величина Img(^p) для поверх-
ностной волны стремится к нулю, делая, таким образом, этот
вклад доминирующим. Аналогичные эффекты могут возникать
в случае щели в диэлектрике (строка 4,6 таблицы), для которого
некоторые из полюсов, соответствующих вытекающим волнам, мо-
гут иметь очень маленькие мнимые части. В этом случае об-
ласть существования волн заключена приблизительно в интер-
вале углов где <л/2 есть действительная часть
координаты полюса в комплексной плоскости w (путь’быстрей-
шего спуска через седловую точку ays=cp пересекает полюс
только при 1ф|>|₽,-|). Спадающее поле (тип 7 по вышеприве-
денной классификации) получается, например, на теневой сто-
роне каустики (строка 5 таблицы), где его вклад может опять-
таки преобладать над вкладами от других составляющих поля
для некоторых областей точек наблюдения.
Теперь мы выпищем строгие интегральные решения для
некоторых конфигураций, указанных в таблице. Они взяты из
литературы, на которую в необходимых местах даны ссылки.
1. Квазиоптические методы в дифракции
31
Если исследование проводится в плоскости w, то интеграл за-
писывается в виде
/= J f (w) elk^w}dw,
р
(10)
где Р — указанный выше путь Зоммерфельда.
2. Клин [24]
[ = е~ /ftPcos (л | ф — ф' |) — е~ cos (ч,+ч,')£7 (л —- <р — <р') —
_ g-iftpcos (2а-ф-ф')/у _ 2а4- ф4-ф') —
g/ftpcos W
sin — (w — л)
cos (w — л) — cos ~ (ф — <р')
, тс . .
sin — (го — л)
ТС / . ТС , I ».
cos “ (w — л) — cos — (ф Ф )
dw. (11)
Здесь (р, ф) — цилиндрические координаты с началом, поме-
щенным на краю клина, a (J(x) = l при х>0 и (7(х)=0 при
х<0. Клин возбуждается плоской волной, падающей под уг-
лом ф', причем на его поверхности поле предполагается рав-
ным нулю. Геометрооптическое поле уже подробно рассматри-
валось, поэтому интеграл в (11) содержит члены, описывающие
только дифракционные и переходные эффекты. Из вида особен-
ностей, указанных в таблице, и из рассуждений, которые при-
ведены в предыдущем параграфе, следует, что переходная
функция есть интеграл Ц, записанный в виде формулы (56),
причем в переходной области АВ
Q = k, b== Vi\g(ws) — g(wp2)]=(]. 4-z)/p cos^±I_
а в переходной области ВС
Q = k, b — (1 4-1) /р cos .
Асимптотическая оценка и последующее представление в виде
лучей следуют непосредственно из формулы (2а).
3. Конус. Точечный источник на оси полубесконечного ко-
нуса возбуждает, как показано в таблице, систему лучей с ко-
нической поверхностью АВ, которая образует границу для от-
раженных лучей. Строгое решение можно преобразовать к виду,
подобному (11), но со значительно большим числом слагаемых,
включенных в функцию f(w) [25]. Известно, что переходные
32
Л. Фельсен
функции вдали от вершины конуса определяются функцией Л
при
Q = £/•', 6 = (1 -|- t) cos '6°~7~'
где г'— расстояние от источника до вершины, 0О— внешний
угол конуса, отсчитываемый от оси, и 0 — угол наблюдения.
Когда конус превращается в плоскую поверхность, т. е. 0о—»
—>л/2, поверхность АВ вырождается в линию вдоль оси сим-
метрии. В этом случае при падении вдоль оси рассеянная на-
зад сферическая волна О (1/Агг) превращается в плоскую волну
O(fer°) при 0о—>л/2. Переходные функции определяются путем
дифференцирования 1\ [26].
4. Полупространство, заполненное диэлектриком. Благодаря
присутствию плоской поверхности раздела двух полубесконеч-
ных диэлектриков вторичное поле можно представить в виде
(10). Если возбуждение производится линейным магнитным то-
ком, а точка наблюдения находится в полупространстве с е = е0
(как показано в таблице), то с точностью до несущественных
постоянных коэффициентов [27, 28] 9 имеем
Г/ , в cos да— Ke — sin2 да
где р и ср — координаты, отсчитываемые относительно зеркаль-
ной точки. Переходная функция при ср>0 есть в этом случае
функция параболического цилиндра /3, приведенная в формуле
(7а), при
п — 0, & = k, a = V — i[g(wj — g(wft)] = (l — i) Vp sinf-^7±c.
Вклад от боковой волны в чистом виде получается вблизи
ср = сре из /3 при
n=l, Q = k, a = V/[g(wJ) — g(wft)]
(см. также |14], стр. 286).
5. Диэлектрическая пластинка или щель в диэлектрике. Вто-
ричное поле от слоя конечной толщины дается выражением
(10) с учетом того, что теперь J(w) имеет следующий вид
[27, 28]!):
-Г/ \ ее cos да cos а — Уе — sin2 да sin а ,, . /---г»—
ГМ =-----------------77===---------, • а — kL у е — sin2®. (13)
ie cos да cos а У е — sin2 да sin а
) См. также [14], § 19, и [21],
1. Квазиоптические методы в дифракции
33
Заметим, что /(w) из (13) переходит в формулу (12), когда
L -> со при 1та = “0“ (внутренние потери). Поскольку приве-
денная функция f(w) является четной функцией а, то точек
ветвления нет. Вместо них есть полюса в нулях знаменателя,
которым соответствуют поверхностные и вытекающие волны.
6. Неоднородный диэлектрик и родственные задачи. Если
неоднородный диэлектрик с ео=8о(г) заполняет полупростран-
ство z>0, то анализ существенно усложняется: собственные
волны в этом случае уже не столь просты, как плоские
волны, характеризующие распространение в однородной среде.
Даже в простейшем случае плоских слоев бо(г)=бо(х) и воз-
буждении линейным электрическим током (последнее означает
отсутствие г-компоненты у электрического поля) решение для
электрического поля Еу имеет вид
оо
Еу — j G (z, z', С) с&, (14)
где G(z, z', 0—одномерная функция Грина, которая удовле-
творяет той части волнового уравнения
[V2 + (г)] Еу = - 6 (х) 6 (г - г'),
которая зависит от z. Конкретное выражение для функции G
можно получить только в особых случаях изменения нормиро-
ванной диэлектрической постоянной e'(z), когда волновое
уравнение приводится к одному из стандартных дифферен-
циальных уравнений.
Когда Бд(г) меняется медленно на расстояниях порядка
длины волны в диэлектрике (более точно, когда \(dn/dz)X
Х(1/^«2)|1> где /г = ]Л-'—показатель преломления), функ-
цию G можно вычислить методом ВКБ и окончательное под-
ынтегральное выражение в этом случае имеет вид подынте-
грального выражения в (10) с функцией gt (ш), равной [29, 30]!)
z>
gi (w) = х sin w ф j ]/zz2(p) — sin’-'wdp. (15a)
г<
Здесь z< и z> обозначают меньшую и большую из координат
ги г’ соответственно.
Функция gi (ш) в формуле (15а) описывает волны от источ-
ника, идущие вверх и вниз (первичное поле). Аналогичное
*) См. также [21].
3 Зак. 274
34
Л. Фельсен
выражение для g2 (w) описывает волны, «преломленные» до того,
как они достигли границы:
Z
g-2(w) = xsin W-+ J У/г2 (р) —sin2wtZp +
z'
+ | ]//г2(Р) — sin2 wdp, n(zw) = sin w. (156)
zw
Для волн, отраженных от границы г = 0; величина zu: в (156)
заменяется нулем. Седловые точки gt находят из условия
dgl/dw = Q, т. е.
г>
л = sinter, [ -у..--. -...., (16)
J У n (Р) — sin2 ws
которое дает уравнение лучей геометрической оптики. Для от-
раженных и преломленных лучей получаются аналогичные со-
отношения. Если ’плотность среды изменяется монотонно от
п2(0) до н2(оо)е=1, то седловая точка ws определяет угол, кото-
рый возникающий луч составляет при z-»oo с положительным
направлением оси г. Следовательно, седловые точки на дей-
ствительной оси плоскости w можно определить непосредствен-
ным исследованием уравнения лучей. Для заданной действи-
тельной величины ws, для которой n2(z') >sin2 wa, уравнение
лучей имеет действительное решение только для тех значе-
ний г, для которых п(г) > sin ws-t значение Zi<z', удовлетво-
ряющее условию n(Z()=sinays, дает граничный уровень, до ко-
торого доходят первичные лучи, распространяющиеся вниз па-
раллельно оси х. После этой «точки поворота» лучи изгибаются
вверх по направлению к г—>оо. Кроме описанных лучей,
имеется непрерывно преломляющийся луч гг, сразу распростра-
няющийся вверх прямой луч г, может существовать также от-
раженный луч г, который имеет излом на границе г=0. Для
того чтобы до этой границы доходили распространяющиеся
лучи, необходимо выполнение условия п2(0)>0. Эти лучи изо-
бражены в таблице. Они описывают геометрооптическое поле.
Если полупространство z<0 занято средой с /г2 — е' < /г2(0),
то может возбуждаться боковая волна d, которая является
прямым аналогом волны, описанной в задаче для изотропного
полупространства (строка 3 в таблице).
Прямой и преломленный лучи в рассматриваемой среде за-
ключены в области полупространства, которая ограничена кау-
стикой CD (таблица). Каустика служит огибающей для семей-
1. Квазиоптические методы в дифракции
35
ства непрерывно преломляющихся лучей и является асимпто-
той при z —»оо для луча, который выходит из источника гори-
зонтально [sin azr^-sin tpm=n(z')]. Для точки наблюдения вблизи
каустики критические углы и w(^r (т. е. углы соответ-
ствующие седловым точкам) двух преломленных лучей стре-
мятся друг к другу, й поле в этом случае описывается переход-
ной функцией /2 [формула (6а)] с параметрами [30] ’)
& = o==||i[i2(w(nr) — g-2«;)]}2/3 (17)
и argo = n; или 0 на освещенной и теневой сторонах каустики
соответственно. При наличии поверхности раздела, показанной
в таблице, появляется ряд характерных областей оптических
лучей. Полностью отраженный луч определяет границу АВ,
причем в любую точку вне области А могут попадать лишь бо-
ковые лучи, которые ведут- себя аналогично лучам в случае
однородного полупространства. Для точек в окрестности АВ
характерна близость к седловой точке и точке ветвления, сле-
довательно, соответствующая переходная функция имеет вид /3
[формула (7а)]. Ни отраженные, ни преломленные лучн не про-
никают .в область Е между каустикой и скользящим лучом
с Z( = 0.
Интересно, что боковые волны играют важную роль в дан-
ной системе лучей. Несмотря на то что их затухание больше,
чем затухание геометрооптических полей [ср. выражения (2)
и (4)], они одни (кроме несущественных экспоненциально за-
тухающих спадающих волн) способны проникать в область
тени D. Поэтому боковые волны представляют основную состав-
ную часть поля в области тени в противоположность случаю
однородного полупространства, где всегда присутствует гео-
метрооптическое поле, а область тени не существует.
Предыдущее рассмотрение справедливо только тогда, когда
вблизи седловых точек справедливо упомянутое выше прибли-
жение ВКБ для функции G(z, z', £) в интеграле (14). Это при-
ближение неприменимо вблизи точки поворота луча, так что
простое уравнение (15) или его аналог для преломленного луча
нельзя использовать для исследования переходных явлений,
связанных со скользящим лучом. Важным примером такого
типа трудности является случай, когда неоднородная среда
ограничена при 2 = 0 идеальным проводником или импедансной
поверхностью. В этой задаче предполагают, что скользящий
луч возбуждает семейство конгруэнтных дифрагированных лу-
чей d, которые, экспоненциально затухая, распространяются
), См. также [21].
3*
36
Л Фельсен
вдоль поверхности и непрерывно переносят энергию в область
тени [9, 13] (фиг. 3). Чтобы описать поле вблизи скользящего
луча, нужно использовать более точные методы, чем приближе-
ние ВКБ. Соответствующее исследование было выполнено
Джонсоном [32] для случая линейно изменяющейся проницае-
мости n2(z) = n^(l +cz), где /г2 и с — положительные по-
стоянные. Функция Грина G(z, z', £) для такой среды выра-
жается через функцию Эйри, строгое интегральное представление
которой было использовано для описания поля в переходной
области вблизи скользящего луча после детального анализа,
потребовавшего асимптотической оценки получившегося двой-
ного интеграла. В окрестности точек касания скользящего
луча с каустикой такой анализ провести не удается, так что
эта область требует дальнейшего исследования. Глубже, в об-
ласти тени £>, поле вдоль дифрагированных лучей можно вы-
числить прямым методом, в котором интеграл (14) вычисляется
с помощью вычетов в комплексных полюсах функции G (это до
некоторой степени аналогично вычислению с помощью вычетов
в задаче о диэлектрическом слое).
Отметим еще раз, что поле в области тени D на фиг. 3 на-
много слабее, чем поле в области»/), показанной в строке 5
таблицы, так как поле на фиг. 3 затухает с расстоянием экспо-
ненциально, т. е. быстрее, чем степенная функция. Далее видно,
что поверхностные дифрагированные лучи имеют значение
(хотя и небольшое) для описания поля вблизи этой поверх-
ности в области тени, тогда как в точках наблюдения, далеких
от границы, но близких к каустике, более важную роль могут
играть спадающие дифрагированные лучи. Хотя описанный ана-
лиз был сделан лишь для частного случая изменения показа-
теля преломления, .можно доказать, что результаты справед-
ливы и для произвольного монотонного изменения п, когда
п(оо) >оо [32]. К тому же преобразование показывает экви-
валентность между прямой границей в неоднородной среде и
кривой границей в однородной среде, что дает возможность
получить результат для перехода через границу тени АС, обра-
зованную выпуклым цилиндрическим рассеивающим телом
(фиг. 4). Эта задача также была успешно решена методом
поперечной диффузии [12, 13] и близкими к нему [11, 33, 34]
методами. Из сравнения задач, показанных на фиг. 3 и 4, видно,
что скользящий луч образует границу тени, каустика отсут-
ствует, а геометрооптическое поле не проникает дальше сколь-
зящего луча.
7. Анизотропный диэлектрик. В анизотропном диэлектрике
характеристики распространения плоской волны зависят от на-
правления, а электромагнитная энергия переносится вдоль
Фиг. 3. Дифрагированные лучи, возбуждаемые
скользящим лучом.
Фиг. 4. Дифракция па гладком выпуклом препятствии.
Фиг. 5. Волповая_пормаль и луч; nk = -/.z0-f~£р0.
38
Л. Фельсен
луча, направление которого в общем отличается от перпендику-
ляра к поверхности равной фазы. Распространение плоской
волны exp(tnk-r) в такой среде удобно рассмотреть с по-
мощью показателя преломления п и диаграммы, описываемой
концом вектора nk (й — волновое число в вакууме). На фиг. 5
изображена типичная диаграмма показателя преломления для
простой анизотропной плазмы, на которой показано, что луч S,
соответствующий волновому вектору к, получается построением
нормали к кривой в рассматриваемой точке; координаты (£, х)
и (р, z) описывают соответственно диаграмму показателя пре-
ломления и направления в пространстве к и S1)-
Поле в дальней зоне, возбуждаемое сосредоточенным источ-
ником в анизотропной среде, ведет себя локально подобно од-
ной или более плоским волнам, каждую из которых можно
охарактеризовать соответствующим лучом [35]. Если среда одно-
родна, то лучи являются прямыми линиями и идут радиально
от источника, который обычно помещают в точке p = z=0. Зна-
ние характеристик луча вблизи заданной точки и использова-
ние закона сохранения энергии для лучевой трубки дают воз-
можность определить последующее распространение луча и из-
менение его интенсивности даже при наличии резких измене-
ний свойств среды (для которых требуется знать законы отра-
жения и преломления луча) или медленно меняющихся неодно-
родностей. Дифракционные эффекты также можно исследовать
при помощи дифрагированных лучей, обобщая соответствую-
щее рассмотрение для изотропной среды [36] (см. также [61]).
Для волновых функций, описывающих лучи в анизотропной
среде, характерно появление «показателя преломления луча»
Л^(0, <р) в функции exp [ikrN], где N = ncosa, а — угол между
нормалью к волне и лучом. Подробное описание некоторых
дифрагированных лучей дано в работах [36, 61].
Отметим, что если среда характеризуется диаграммой пока-
зателя преломления, подобной той, которая изображена на
фиг. 5, то в заданную точку. наблюдения могут попадать не-
сколько лучей.. Например, если точка наблюдения лежит на
оси z, а источник находится в точке z=0, то возможны вклады
от четырех лучей, так как нормали в точках /, 2, 3 и 4 все на-
правлены параллельно оси z. Более того, видно, что только
один распространяющийся луч (от точки 5) достигает точки
наблюдения, лежащей в плоскости z=0, откуда следует огра-
ничение областей существования для некоторых лучей. По мере
того как точка наблюдения движется от положительной полу-
оси- z к положительной полуоси р, точка 1 движется вправо,
*) См. [22], разд. 13 и 18,
1. Квазиоптические методы в дифракции
39
а точка 2 — влево; они встречаются в точке поворота Т. Если
через 0 обозначить угол наблюдения относительно оси z, а че-
рез 01 — угол, характеризующий направление нормали в точ-
ке Т, то областью существования лучей, соответствующих точ-
кам 1 и 2, является внутренность конуса 0<0Ь Угол 0 = 01
определяет границу тени этих лучей. Аналогично точка 4 дви-
жется влево и соответствующий луч существует только тогда,
когда 0<02, где 02—нормаль к асимптоте незамкнутой ветви;
границей тени для этого луча является угол 0 = 02- Только
точка 3 является простой точкой, непрерывно движущейся
в положение 5.
Можно показать, что в разложении полей по собственным
функциям, приводящим к интегралу вида (1), Действительные
седловые точки £s(0), соответствующие углу наблюдения 0,
определяются абсциссами точек на диаграмме волновых нор-
малей, перпендикуляры в которых параллельны направлению
0 [35]. При 0—>01 две седловые точки соединяются и переход-
ная функция выражается через интеграл Эйри (6а). Усиление
соответствующего им поля подобно росту поля, наблюдаемому
вблизи каустики в неоднородном изотропном диэлектрике. Ко-
гда 0 —>02). седловая точка уходит в бесконечность и становится
необходимым специальное исследование. В простом частном
случае линейного магнитного тока, направленного по оси у и
помещенного в бесконечный анизотропный диэлектрик с е=
= xox0eo + z0zog, е<0, единственная не равная нулю компонента
магнитного поля Ну точно выражается в виде [36]
Ну — Но} [^pTV (ф)], /У(ф) = Vcos2ф — |е| sin2ф, (18)
где р — расстояние от источника, ф — угол, отсчитываемый от
оси z, а у — полярная ось в этой двумерной конфигурации.
Можно показать, что диаграмма показателя преломления в этом
случае имеет только две незамкнутые ветви (см. фиг. 5), являю-
щиеся гиперболами, что соответствует одному распространяю-
щемуся лучу. Если М(ф) —>0, то |^| ->оо и поле, которое вблизи
соответствующего угла наблюдения фг описывается функцией
Ханкеля (18), расходится при ф = фг. (Эта расходимость объяс-
няется тем, что дифференциальное уравнение, определяющее
Ну, является гиперболическим, когда диаграмма показателя
преломления имеет указанные незамкнутые ветви.) Если /гр^> 1,
то для функции Ханкеля можно использовать асимптотическую
оценку при условии, что точка наблюдения лежит снаружи от
переходной области N(ф) —>0. Отсюда ясно, что волна распро-
страняется при -IФI < i Ф21 и затухает при | ф [ > | ф21. Следует
40
Л. Фельсен
подчеркнуть, что наличие областей перехода, фокусировки и
тени, имеющих место в бесконечной однородной среде, является
непосредственным следствием анизотропии.
После этого предварительного обсуждения мы можем рас-
смотреть более сложную задачу (см. строку 6 таблицы), когда
упомянутый выше линейный источник помещен в одноосном
анизотропном полупространстве [37]. Можно показать, что
в этом случае лучи отражаются обратно от поверхности раз-
дела и что может иметь место полное внутреннее отражение,
связанное с боковыми волнами 4di и 4d2- Поле внутри анизо-
тропного полупространства состоит из прямых лучей, которые
ограничены клинообразной областью At (раньше оно соответ-
ствовало условию |tg ф| <tg q>2) отраженных лучей, которые ис-
ходят от воображаемого зеркального источника и освещают
области Bi и В2, и боковых лучей, которые являются единствен-
ными лучами, проникающими в область С геометрооптической
тени. Величина g(t,} в выражении (1) для вторичного поля
определяется формулой [37]
g(0 = (z + z')-|A2 + ^+Cr, z, У>0, (19)
г I е I
а /(£) содержит квадратный корень, приведенный в формуле (19),
и величину У k2— £2; это позволяет проверить расположение
седловой точки и сингулярностей, помещенных в таблице. Соот-
ветствующие переходные функции получаются из предыдущего
рассуждения.
Поле в изотропном полупространстве г<0 имеет интересную
особенность, связанную с ранее упомянутым явлением существо-
вания обратных отраженных лучей. В этом случае
g(q==/l-^|2| + -/1 + (19а)
= z < 0, z'>0;
' /(;) =----------1 (196)
+ у *2 +
а условие для седловой точки dgfdt,—Q дает семейство прелом-
ленных лучей, что показано в таблице. Так как вблизи по-
верхности раздела образуются пересечения лучен, то возникает
каустика с фокусом F. Таким образом, плоская поверхность
раздела, ограничивающая однородное анизотропное полупро-
странство, действует подобно оптической линзе [38]. Переходные
функции, определенные из предыдущего рассмотрения, п<5ме-
1. Квазиоптические методы в дифракции
41
щены в последнем столбце. Возле каустики переходные функ-
ции выражаются через функции Эйри по формуле (6а)д в ко-
торой величины Q и а даются формулой (17), где g2(w^f')
и g.,(w^) заменены соответственно на gfat) и g(£s2) или
g(£.,2) и g(Cs3). Величина равна sin фа, где <ра — угол пре-
ломления. Поскольку лучи являются прямыми линиями, эти
углы определяют также направление лучей на бесконечности.
Эти замечания были сделаны для того, чтобы показать, что
функции перехода через каустику определяются одинаково
в однородной и неоднородной средах. Если точка наблюдения
движется по оси г, приближаясь к фокусу, то седловые точки
расположены на одинаковом расстоянии друг от друга (?5з=
= —g.,1, Ss2=0), а переходная функция определяется формулой
(7а), в которой положено
ц = 0, □ = £ и а = /—z[g(C51)—g(0)]
(см. работу [38]). Аналогичные явления имеют место и при
более общих условиях, когда диэлектрическая среда уже не
описывается простым диагональным тензором.
8. Синфазный и противофазный круговые токи. В предыду-
щих примерах явления в области перехода возникали в силу
отличительных особенностей рассеивающих тел, тогда как сам
источник был элементарно простым. Поучительно также рас-
смотреть эффекты, которые возникают из-за особой структуры
источника. Рассмотрим, например, кольцевой ток с равномерно
меняющейся фазой eiai, что изображено на фиг. 6, а [^9]. Если
радиус кольца а велик по сравнению с длиной волны в свобод-
ном пространстве (т. е. ka1), то каждый элемент кольца ds
излучает поле так, как будто он является частью бесконечного
прямого тока, касательного к ds. Ввиду равномерного измене-
ния фазы в зависимости от волнового числа а элемент излу-
чает вдоль лучей, расположенных в угле ф = агс cos (a/k). При
a>k излучение отсутствует и энергия сосредотачивается в не-
посредственной близости от источника. Система лучей, полу-
чаемая путем вращения конуса лучей на фиг. 6, а около оси z,
содержится в области, являющейся внешней по отношению
к гиперболоиду, который образует каустику. Кратчайшее рас-
стояние от каустики до оси z в плоскости кольца равно р=
= а cosip; асимптотой гиперболоида является поверхность двой-
ного конуса р= ctg ф.
Легко видеть, что в каждую точку освещенной области при-
ходят два луча, излучаемые из двух различных точек кольца,
которые сближаются, когда точка наблюдения движется к
42
Л. Фельсен
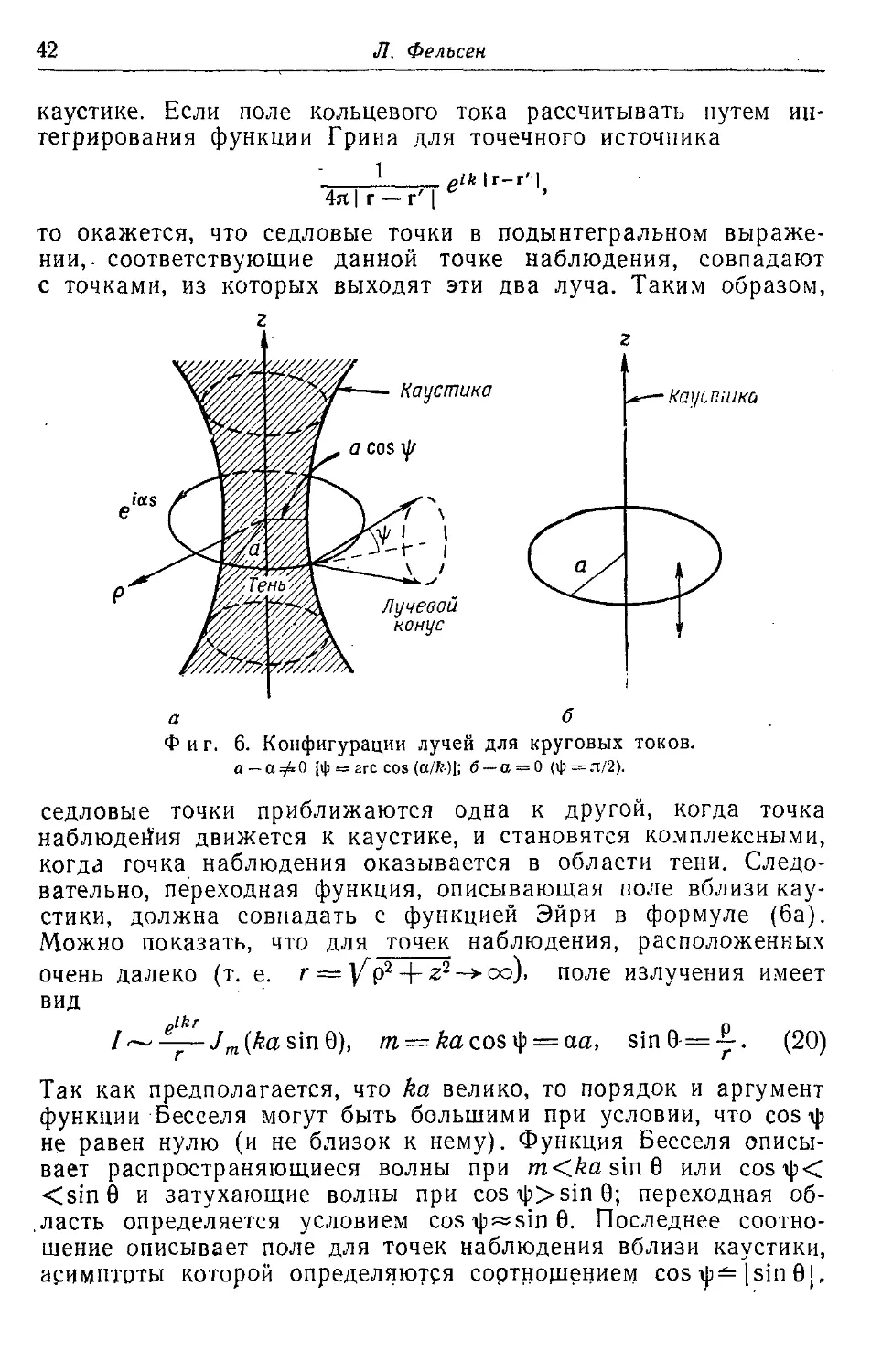
каустике. Если поле кольцевого тока рассчитывать путем ин-
тегрирования функции Грина для точечного источника
то окажется, что седловые точки в подынтегральном выраже-
нии,. соответствующие данной точке наблюдения, совпадают
с точками, из которых выходят эти два луча. Таким образом,
Фиг. 6. Конфигурации лучей для круговых токов.
а — а у. О [ф = arc cos (а/А’)|; б — а =0 (ф — л/2).
седловые точки приближаются одна к другой, когда точка
наблюдения движется к каустике, и становятся комплексными,
когда точка наблюдения оказывается в области тени. Следо-
вательно, переходная функция, описывающая поле вблизи кау-
стики, должна совпадать с функцией Эйри в формуле (6а).
Можно показать, что для точек наблюдения, расположенных
очень далеко (т. е. г = ]/"р2 + г2 сю), поле излучения имеет
вид
plk? - л
Л------ Jm (ka sin 0), т — kacosty — aa, sinO — — . (20)
Так как предполагается, что ka велико, то порядок и аргумент
функции Бесселя могут быть большими при условии, что cos ф
не равен нулю (и не близок к нему). Функция Бесселя описы-
вает распространяющиеся волны при m<ka sin 0 или созф<
<sin0 и затухающие волны при cosip>sin0; переходная об-
ласть определяется условием cosip~sin0. Последнее соотно-
шение описывает поле для точек наблюдения вблизи каустики,
асимптоты которой определяются сортнощением cos ф = | sin 01,
/. Квазиоптические Методы в дифракции ' 43
Замена функции Бесселя ее приближением с помощью функции
Эйри
'm(v)~ m)], | от — v| == О(/п1/3), (20
i ‘ m
подтверждает предполагаемое поведение поля в переходной
области вблизи каустики.
Выражение (20) интересно тем, что оно описывает пове-
дение поля в области перехода также тогда, когда скорость изме-
нения фазы а стремится к нулю. В этом предельном случае луч
из источника на кольце выходит под прямым углом и каустика
вырождается в ось z (фиг. 6,6). Так как в каждую точку полу-
чившейся линейной каустики приходят лучи от всех точек коль-
ца (в противоположность описанному ранее случаю cos
когда в точку наблюдения приходят только два луча), то на
линейной каустике будет очень сильное поле. Это видно и из
формулы (20), откуда для линейной каустики 0 = 0 имеем 1 —
= О[(/га)°] [так как Уо(О) = 1], тогда как на невырожденной по-
верхности каустики в силу (21) I — О[(йа)~1/3]- Линейная кау-
стика интересна также в задачах о дифракции нормально па-
дающей плоской волны на круглом отверстии или диске. В этом
случае ось является каустикой дифрагированных лучей [40].
Целесообразность применения к другим системам. Хотя
в предыдущих примерах мы имели дело с частными и относи-
тельно простыми системами, для которых решение предста-
вимо в виде интеграла, полученные переходные функции можно
применить и в других случаях. Переходные области возникают
в тех частях пространства, где две волны, описываемые, напри-
мер, в виде ехр (г/г^(^1)] и exp [ikg(£2)], имеют почти одинаковые
фазовые зависимости g(£1) «g(g2). Аргументы всех.рассмотрен-
ных выше переходных функций фактически явно зависят от
g(Ci) —g(Ca), т. е. для построения переходной функции доста-
точно знать фазовые характеристики взаимодействующих типов
волн. Итак, если бы различные типы волн и изменения их фаз
были известны в различных областях, заполненных лучами, то
эту информацию можно было бы использовать при весьма общих
условиях для предсказания поведения поля в переходных обла-
стях.
§ 3. ПОВЕРХНОСТИ С ПЕРЕМЕННЫМИ СВОЙСТВАМИ
Методы геометрической оптики, уточненные с помощью гео-
метрической теории дифракции, требуют дальнейшего видо-
изменения, когда рассеивающее тело имеет поверхность с
44
Л. Фельсен
неоднородными свойствами. Хотя высокочастотная дифракция
является существенно локальным процессом и в пределе при
k—»оо определяется свойствами рассеивающего тела только
в точке выхода данного луча, ясно, что величина длины
волны играет роль, когда число k велико, но конечно, а по-
верхность имеет неоднородные свойства. По соображениям,
аналогичным тем, которые применяют для обоснования метода
ВК.Б при изучении распространения волн в средах с перемен-
ными параметрами, можно заключить, что локальный характер
процесса рассеяния нарушается не сильно, если изменения
свойств поверхности незначительны на расстояниях порядка
длины волны. Наличие существенных неоднородностей на дли-
не волны приводит к тому, что представление в виде оптиче-
ских лучей становится неприменимым и возникает необходи-
мость в более детальном исследовании отраженных и ди-
фрагированных полей. Интересно в связи с этим выяснить
более точно границы применимости геометрической оптики и
определить поправки, которые необходимо ввести в случае, ко-
гда геометрическая оптика неприменима. В этом направлении
предстоит провести большую работу. Ниже обсуждаются не-
которые задачи из описанного круга вопросов. Как и в преды-
дущем рассмотрении, наиболее перспективны два способа ис-
следования: первый есть приближенное изучение весьма об-
щего класса задач, а второй — отыскание точных решений и
асимптотических представлений полей в частных случаях.
Одной из простейших структур, которая допускает отно-
сительно простой и точный анализ, является клин, поверхност-
ный импеданс которого Zs (или адмиттанс) изменяется линейно
в зависимости от расстояния от края [41]. Если на этот клин
падает плоская волна, то можно предположить, что в высоко-
частотном приближении рассеянное поле будет содержать отра-
женные и дифрагированные лучи, причем последние будут пред-
ставлять единственный механизм попадания энергии в область
геометрооптической тени. Дифрагированное поле получается
в виде цилиндрической волны ~ (йр^'^ехр (i/гр), которая ка-
жется исходящей от края (т. е. обычный краевой дифракцион-
ный луч), умноженной на амплитудную функцию («коэффи-
циент дифракции») f(c; <р, q/), где с — коэффициент пропорцио-
нальности в выражении для линейного импеданса Zs = ckp, а q;
и <р' — углы наблюдения и падения соответственно. Так
как на краю р = 0 импеданс Zs = 0, то в силу локального харак-
тера дифракции амплитуда дифрагированной волны будет та-
кой же, как и от клина с нулевым импедансом. Изучение вида
функции f показывает, что сформулированное утверждение
верно, когда 1, причем в этом частном случае Zs растет мед-
I. Квазиоптические методы в дифракции.
45
ленно с ростом р. При с^>1 коэффициент дифракции такой же,
как у клина с бесконечным импедансом. В последнем случае,
когда импеданс растет быстро, значение Zs на самом краю не
играет роли, однако некоторая часть импедансной поверхности
в окрестности края оказывается все же существенной. Точное
поведение функции f при изменении коэффициента с от малых
величин до больших описывается специальной функцией
[41]. Для других законов изменения импеданса следует
ожидать другие функциональные зависимости. Данное рассмо-
трение показывает, что необходимы новые канонические реше-
ния задач по рассеянию на телах с переменными свойствами
поверхности для понимания подобных дифракционных процес-
сов. Найдено, что аналогичные рассуждения применимы и к от-
раженному полю, которое в случае медленного изменения
свойств поверхности можно построить методом геометрической
оптики, используя то, что амплитуда отраженного луча опреде-
ляется локальным значением поверхностного импеданса в точке
отражения. В связи с этим интересно отметить, что поведение
переходной функции на границе тени по существу не зависит
от импеданса поверхности (здесь основную роль играет эффект
перекрытия препятствием части лучей), тогда как в окрестности
границы, которую образует отраженная волна, ноле зависит
от материала клина. Следовательно, при наличии сильных из-
менений свойств поверхности могут понадобиться другие пере-
ходные функции. Сравнение вкладов отраженных и дифрагиро-
ванных лучей необходимо проводить очень тщательно, так как
эффекты высщих порядков, отсутствующие для структур с по-
стоянным импедансом, могут иметь важное значение при рас-
чете отраженных полей.
В предыдущем примере мы имели дело с некоторыми явле-
ниями, возникающими при монотонном изменении импеданса.
Картина поля совершенно меняется, когда импеданс периоди-
чен. Были исследованы две эталонные структуры, на поверх-
ности которых импеданс Zs меняется синусоидально: плоская
поверхность [42] и цилиндр [43, 44]. Теперь нужно обобщить
понятие геометрооптического поля, чтобы включить в рассмо-
трение не только зеркально отраженные лучи, но и дифраги-
рованные скользящие лучи. Когда пространственный период L
функции, описывающей импеданс, велик, существует очень
много дифрагированных лучей, причем направления возникших
дифрагированных лучей первого порядка отличаются незначи-
тельно от направления зеркального отражения. Если амплитуда
изменений импеданса мала, то нужно рассматривать дифра-
гированные лучи только первого порядка; тогда в точку наблю-
дения Р, лежащую над поверхностью, приходят три луча, один
46
Л. ФельСёН
из которых кажется выходящим из точки зеркального отраже-
ния А, а два других — из точек Bt и В2, расположенных по
разные стороны от точки А (фиг. 7). Эти три точки совпадают,
когда импеданс не меняется, а расстояние между ними харак-
женный луч и дифрагиро-
ванные лучи первого по-
рядка для периодической
поверхности.
теризует изменение импеданса вбли-
зи А. Все это наводит на мысль о том,
что дифрагированные лучи как бы
зондируют окрестность точки зер-
кального отражения, что имеет место
даже в том случае, когда импеданс-
ная функция не периодична, так как
в окрестности любой отдельной точки
пространственная периодичность не
сказывается.
Эти рассуждения можно использо-
вать, чтобы установить критерий при-
менимости геометрической оптики
[45]: считают, что геометрическая оп-
тика применима, если три указанных
выше луча можно объединить в один
зеркально отраженный луч, коэф-
фициент отражения которого зави-
сит только от свойств поверхности
в точке отражения. Для точек, находящихся на плавно изог-
нутой выпуклой цилиндрической поверхности с конечным зна-
чением поверхностного импеданса Zs, получены следующие
оценки:
| X (dZs!dx) |
1, когда
X
—, когда
s
X
—, когда
(22)
где X — длина волны, х — координата на поверхности, s—рас-
стояние от точки отражения А на поверхности до точки наблю-
дения и а— радиус кривизны в точке А. Из этих условий, полу-
ченных для периодического поверхностного импеданса, но при-
менимых и для некоторых непериодических неоднородностей,
можно оценить влияние кривизны поверхности и изменения им-
педанса на геометрооптическое поле.
Интересно указать на другую интерпретацию выбора рас-
стояния Ло между точками В4 и В2 на фиг. 7. Максимальную
величину s = So, удовлетворяющую второму из неравенств (22),
можно также записать как 5о~4лАо/Х, что совпадает по виду
1. Квазиоптические методы в дифракции
47
с формулой для величины зоны Френеля, соответствующей
апертуре диаметром Ео. Это можно использовать для доказа-
тельства того, что геометрическая оптика применима в преде-
лах зоны Френеля, т. е. при таких расстояниях на поверхности,
на которых свойства поверхности изменяются незначительно.
В предыдущих расчетах неоднородности на поверхности
учитывались при помощи поверхностного импеданса, завися-
щего от свойств материала, но не зависящего от геометрических
свойств самой поверхности. Другой важный класс задач связан
с рассеивающими телами, которые имеют неоднородную струк-
туру поверхности [46, 47]1). Если эти возмущения малы, то
можно определить приближенный поверхностный импеданс (он
может быть анизотропным), к которому затем можно приме-
нить предыдущие рассуждения. Интересно, что оценка границ
применимости геометрической оптики, из которой получаются
условия (22), содержит зависимость от периода неоднород-
ности L, совпадающей с зависимостью, найденной для среды со
случайно изменяющимися свойствами, где она определяет об-
ласть неоднородности [49]. С последними работами по распро-
странению волн в среде со случайными неоднородностями
можно ознакомиться в статье [50].
§ 4. ДАЛЬНЕЙШЕЕ СРАВНЕНИЕ ОПИСАНИЙ
С ПОМОЩЬЮ МОД И ЛУЧЕЙ.
РЕЗОНАНСЫ
Рассуждение, проведенное в § 2, послужило иллюстрацией
того, как можно определить основные особенности геометрооп-
тических и дифракционных полей из модового представления
типичных решений. Как указывалось выше, вклады в асимпто-
тическое поле получаются не от всех мод поля, а только от
тех, у которых волновое число находится в окрестностях сед-
ловых точек или сингулярностей. Следовательно, решение с по-
мощью мод содержит больше информации, чем это требуется
для представления поля в виде лучей. Для исследования
свойств поля при описании его с помощью оптических лучей
можно использовать другие, более прямые методы. Однако
такое упрощение невозможно при изучении явлений в областях
перехода, описание которых содержится лишь в точном реше-
нии в виде разложения по модам. Несмотря на то что решение
с помощью мод ограничивается конечным классом разрешимых
задач, оно имеет то важное преимущество, что объединяет все
Детальное изложение теории многократного рассеяния дано в рабо-
48
Л. Фельсен
асимптотические свойства решения и дает ценный инструмент
для проверки применимости более широко используемых при-
ближенных теорий, таких, как геометрическая теория ди-
фракции.
Кроме анализа явлений в переходной области, решение
в виде разложения по модам часто бывает полезно в случае,
когда в рассеянное поле входят многократно отраженные и
дифрагированные лучи. В то время как при лучевом подходе
надо проследить путь каждого луча между последователь-
ными точками, в которых происходит отражение или дифрак-
ция, представление по модам дает сразу результирующее
поле. Полный эффект от бесконечного числа вкладов при много-
кратном отражении лучей обычно можно записать в замкну-
той форме, которая содержит «резонансный знаменатель»,—
свойство, естественное в представлении ио модам. Комплекс-
ные резонансы играют важную роль в представлении решения
с помощью мод,- причем появление их не так просто объяснить,
поскольку они не получаются при лучевом подходе. Они воз-
никают, например, в открытых областях, в которых каждое от-
ражение или дифракция связаны с некоторым излучением.
Подчеркнем, однако, что после того, как попята важность ком-
плексных резонансов, действительный резонансный знаменатель
в представлении решения в виде оптических лучей дает ключ
к решению вопроса о существовании и размещении комплекс-
ных корней. Таким образом, геометрическая оптика может
быть использована для решения задач, которые не поддаются
прямому анализу с помощью мод. Не следует пренебрегать
этим обратным методом нахождения комплексных резонансов.
Известная задача о точечном источнике, помещенном внутри
идеально проводящей цилиндрической трубы с произвольным
поперечным сечением, служит наглядной иллюстрацией преи-
мущества модового метода над методом построения оптических
лучей. Очевидно, что геометрооптическое поле представляет
очень сложное распределение лучей, отраженных много раз от
границ (или преломленных, когда среда внутри трубы неодно-
родна). Если размеры поперечного сечения не очень велики по
сравнению с длиной волны, то сложный результат суммирова-
ния вкладов от всех лучей на некотором расстоянии вдоль
волновода значительно удобнее представить с помощью не-
скольких ортогональных мод, которые распространяются вдоль
оси волновода х. Этот пример напоминает еще об одном часто
используемом свойстве метода, а именно о возможности иссле-
дования решения методами теории функций. Поэтому было бы
весьма удобно записать формальное решение для волноводной
задачи при помощи интегрального разложения по продольному
I. Квазиоптические методы в дифракции'
49
волновому числу [например, с помощью преобразования Фурье,
как в формуле (14), если задача является двумерной и свой-
ства среды, заполняющей слой, зависят от z], а потом дефор-
мацией контура и нахождением вычетов построить ряд, показы-
вающий зависимость мод от поперечных координат. Первое пред-
ставление по существу включает волны, распространяющиеся пер-
пендикулярно оси х, а результирующая амплитудная функция мод
[G(z, z', £) в формуле (14)] содержит тогда явно «резонансный
знаменатель», описывающий многократное отражение. С дру-
гой стороны, из представления по ортогональным модам реше-
ние получается в виде ряда
£ф;(2)ФХг')±^1 (23)
I
где Ф;(г)—собственная функция, описывающая поведение
поля в поперечном сечении, а &— соответствующее собствен-
ное продольное волновое число. Для трубы небольшого попе-
речного сечения существенны только несколько первых чисел £4,
так что ряд (23) быстро сходится. Разлагая резонансный зна-
менатель в G(z, z'; £) в степенной ряд, получают ряд интегра-
лов, асимптотические вклады которых являются вкладами от
распространяющегося геометрооптического луча, подвергше-
гося многократному отражению или преломлению. Нетрудно
сопоставить сложную форму полученного соотношения и про-
стую и удобную формулу (23). Полученное разложение по
ортогональпЫхМ модам [51, 52] ) уже нашло важное применение
в теории электрических волноводов, при изучении распростране-
ния радиоволн низкой частоты между“землей и ионосферой,
в акустике при изучении подводного распространения волн
в океане и во многих других случаях. Так как статья Тол-
стого* 2), также представленная на этом симпозиуме, специально
посвящена сравнению методов ортогональных мод и лучей
при подводном распространении звука, то мы заканчиваем об-
суждение этого вопроса.
Интересно сравнить описания с помощью оптических лучей
и мод в случае, когда возникают комплексные резонансы. Как
указывалось ранее, эти явления связаны с излучением, так что
в этом случае отражение будет неполным. Пластина, возбу-
ждаемая линейным магнитным током (см. строку 4 таблицы),
служит наиболее простым примером. Решение с помощью мод
для этой задачи получается в виде соотношений (10) и (13);
если ei<e0 (щель в диэлектрике), то резонансный знаменатель
*) См. также обзор [14], гл. 5, и работу [27], гл. 6.
2) См. настоящий сборник, стр. 63. — Прим. ред.
4 Зак. 274
50
Л Фельсен
J\w) в формуле (13) допускает только счетное множество ну-
лей wp в комплексной плоскости, которым соответствуют вы-
текающие волны, представленные в таблице. Вклад любой
Затухание по
Фиг. 8. Поведение вытекающей и боковой волн (е( < е0).
Сплошная линия—поверхность постоянной амплитуды; пунктирная — поверхность по-
стоянной фазы.
вытекающей волны [т. е. любого полюса, соответствующего нулю
/(&>)] представляется в виде формулы
' (24)
описывающей неоднородную плоскую волну, фазовые фронты
которой распространяются в направлении <pp = Reayp, а ам-
плитуда в плоскости постоянной фазы затухает экспоненциаль-
но вдоль перпендикулярного ему направления фа = (Re wp)+л/2
(фиг. 8, а). Так как путь быстрейшего спуска пересекает полюс
только тогда, когда угол наблюдения фа удовлетворяет условию
Ф^фа>фР (см. фиг. в таблице), то величина /р отлична от
нуля только тогда, когда ф>ф«, а экспонента в (24)
уменьшается в зависимости от р для всех точек наблюдения,
находящихся в области возбуждения вытекающей волны (фо
обозначает угол наблюдения, для которого путь быстрейшего
спуска пересекает полюс). Из фиг. 8, а видно, что поле выте-
кающей волны возрастает экспоненциально с увеличением z при
фиксированном х. Таким образом, волна этого типа, когда она
рассматривается в отсутствие возбуждения, расходится на бес-
конечности. Поэтому вытекающие волны не являются собствен-
ными решениями уравнений для поля без источников [53]; они
возникают только в специальном представлении поля, исполь-
зующем метод быстрейшего спуска.
Асимптотическое решение для поля в полупространстве
z>0 определяется вкладами от седловой точки ws = cp (отра-
женное поле) и от всех полюсов wp, которые пересекаются
1. Квазиоптические методы в дифракции
51
контуром при его деформации (дифрагированное поле). Как
уже указывалось, последние вклады затухают экспоненциально
и обычно пренебрежимо малы по сравнению с вкладами от
седловой точки; поэтому в таблице они не показаны. Волна,
соответствующая седловой точке, отражается по законам гео-
метрической оптики и имеет коэффициент отражения /(<р) [см.
выражение (2а)]. Он содержит в сложной форме вклады от
геометрооптических лучей, которые выходят из источника, па-
дают на поверхность раздела и, преломляясь, попадают внутрь
диэлектрической щели. Отразившись однократно или много-
Источник
Фиг. 9. Построение отражен-
ного поля с помощью лучей
. (Е; < е0).
и в виде оптических
кратно от границ, они попадают в
область z>0. Отсюда видно, что ко-
эффициенты отражения для мод
/(ф) зависят только от угла зеркаль-
ного отражения <р, тогда как пре-
ломленные и многократно отражен-
ные лучи достигают точки наблюде-
ния в целом спектре углов д/, ср",. . .
(фиг. 9). Спектр углов близок
к <р, когда точка наблюдения нахо-
дится далеко от поверхности раз-
дела, что обеспечивает эквивалент-
ность представлений поля по модам
чей (с очевидным. предпочтением первого). Однако при дру-
гом положении точки наблюдения может возникнуть противоре-
чие. Эта задача в -настоящее время исследуется. Сильный ма-
ксимум 7(<р) при некотором угле <pt обычно указывает на при-
сутствие комплексного полюса wp функции f(w) с КеаУр^фь
|1таур|<С1. Изучение комплексных модовых резонансов может
поэтому обеспечить непосредственную информацию о направ-
ленности поля излучения [53].
Упомянутое выше описание с помощью оптических лучей
есть результат освобождения от знаменателя в формуле (13)
при помощи разложения функции J(а?) в степенной ряд
СО
Нти)=
m=0
Асимптотическое значение каждого члена дает один из много-
кратно отраженных лучей фиг. 9. Поскольку знаменатель в вы-
ражении (13) теперь отсутствует, то отсутствуют и полюса, со-
ответствующие вытекающим волнам, а особенностями fm(w)
являются точки ветвления, как в выражении (12). Поэтому
дифракционное поле, получаемое при пересечении точек ветвле-
ния для достаточно больших значений угла наблюдения <р,
имеет форму боковых волн, главная из которых (см. фиг. 8)
52
Л. Фельсен
имеет те же самые характеристики, как и для бесконечно ши-
рокой щели. Вклады высшего порядка обусловлены конечной
шириной щели и могут быть объяснены взаимодействием быстро
затухающего поля боковой волны при z<0 (см. фиг. 1) с гра-
ницей при z==—L. Как видно из формулы (4), поле боковой
волны распространяется в области z>0 в направлении <рс и за-
тухает как степенная функция вдоль поверхности равной фазы.
Описание с помощью оптических лучей приводит поэтому
к предположению, что дифракционное поле для широкой щели
имеет вид боковой волны, которая является такой же, как
если бы щель была бесконечно широкой (строка 3 в таблице).
С другой стороны, из описания с помощью мод следует, что
дифракционное поле представляется в виде вытекающих волн,
которые для больших L соответствуют полюсам wp, сосредото-
ченным вокруг точки ау = фс, с очень малой величиной Im wp
(т. е. фа~фр~фс на фиг. 8). Можно показать [54], что набор
экспоненциально затухающих вытекающих волн может дать
в итоге одну волну, имеющую затухание в виде такой же сте-
пенной функции, как и у боковой волны. Тем самым показы-
вается эквивалентность обоих описаний. Очевидно, что представ-
ление дифракционного поля в виде оптических лучей имеет
более быструю сходимость и поэтому более удобно, когда щель
широкая. Однако для не слишком широкой щели, когда нельзя
пренебречь взаимодействием боковых волн со второй грани-
цей, описание с помощью мод может оказаться предпочтитель-
нее, так как в этом случае из бесконечного числа вытекаю-
щих волн только несколько волн являются слабо затухаю-
щими. Этот пример служит иллюстрацией использования мето-
дов мод, лучей и смешанного метода, причем выбор зависит
от параметров рассматриваемой области.
§ 5 НАПРАВЛЕНИЯ ДАЛЬНЕЙШЕГО ИССЛЕДОВАНИЯ
В предыдущем обсуждении была сделана попытка дать об-
зор основных свойств высокочастотной теории дифракции и
установить границы применимости анализа при помощи оп-
тических лучей и мод (волновой оптики). Цель нижеследую-
щих замечаний состоит в том, чтобы выделить направле-
ния, которые заслуживают дальнейшего исследования. Некото-
рые из сделанных здесь замечаний подобны тем, которые
имеются в других обзорах [15—19]; они включены сюда для
полноты.
Канонические задачи. Так как высокочастотная дифракция
является существенно локальным процессом, то соответствую-
1 Квазиоптические методы в дифракции
53
щую информацию, касающуюся начальных амплитуд вдоль от-
раженных, преломленных и дифрагированных лучей, можно
получить из решения упрощенных «канонических» задач, кото-
рые содержат в себе различные важные локальные особенности
в простейшей форме. Эти задачи должны решаться по возмож-
ности точно; тогда последующее асимптотическое приближе-
ние будет базироваться на точном результате. Для максималь-
ного использования канонических решений в рамках квазиоп-
тической теории дифракции асимптотическое решение должно
быть преобразовано к виду, в котором выделен в первую оче-
редь лучевой характер распространения и дифракции волн. Это
даст подтверждение тем общим методам, которые основы-
ваюкя на постулатах геометрической теории дифракции. Кано-
нические решения являются ценным материалом при изучении
явлений, которые недостаточно точно описываются методами
лучевой оптики, и служат для исследования явлений, которые
не поддаются описанию с помощью лучей.
1. Простейшие рассеивающие тела. Чтобы проанализировать
поведение поля вблизи сложных структур при падении на них
высокочастотного излучения, необходимо знать поле рассеяния
от простых составных частей структуры (т. е. от края, угла, из-
гиба и г. д.). До настоящего времени еще не решены удовле-
творительно задачи о дифракции на диэлектрическом клине и
конусе, а также задача о дифракции на идеально проводящем
конусе с некруговым поперечным сечением, в которую как част-
ный случай входит задача о дифракции на тонком плоском
секторе (коэффициенты дифракции от края или вершины можно
получить при решении этих задач). Несмотря на то что задача
о рассеянии волн, наклонно падающих на идеально проводящий
конус, уже решена и найден соответствующий коэффициент ди-
фракции от вершины, остается исследовать еще асимптотиче-
ское решение в области геометрической тени и вблизи границы
сложной тени.
Задачи рассеяния на длинных, тонких, сигарообразных те-
лах или на почти плоских, «блинообразных» структурах также
заслуживают дальнейшего изучения, так как такие тела содер-
жат участки поверхности, имеющие как большую, так и малую
кривизну *).
Прозрачные тела (например, диэлектрические сферы и ци-
линдры или сферические и цилиндрические оболочки) представ-
ляют собой интересный объект изучения в связи с возникнове-
нием на них сложного геометрооптического поля [56]. Не менее
интересны дифракционные эффекты на изогнутых поверхностях
!) Последние результаты в этой области изложены в работе [551.
5.4
Л. Фельсен
(например, скользящие, поверхностные и боковые волны). Тре-
буется дальнейшее изучение связи между оптическими лучами
и модами для таких структур. Скользящие лучи в геометриче-
ской теории дифракции и вытекающие волны в описании с по-
мощью мод имеют похожие характеристики. Однако скользя-
щие лучи соответствуют собственным волнам, тогда как выте-
кающие волны являются «несобственными». Диэлектрические
тела могут приводить к образованию разнообразных каустик и
фокусов.
2. Неоднородная среда. Когда рассеивающее тело поме-
щается в неоднородную среду, локальные коэффициенты отра-
жения, преломления и дифракции должны измениться. И хотя
для решения этой задачи пригодны методы модифицированной
геометрической теории дифракции [9], законность применения ее
постулатов и в этом случае должна быть проверена сравне-
нием с точными решениями. Такая проверка была сделана для
бесконечного плоского рассеивающего тела, помещенного
в плоско слоистую среду, а также для цилиндрического п сфе-
рического рассеивающих тел, помещенных в радиально слои-
стые среды. Однако во всех этих случаях показатель прелом-
ления считался постоянным на поверхности тела. В связи с этим
желательно рассмотреть ряд таких задач на рассеяние для тел,
на поверхности которых направление и величина градиента по-
казателя преломления в какой-то степени произвольны..
Задачи такого типа возникают при рассмотрении поля в сре-
де, относительная проницаемость которой изменяется' по закону
е'= 1 — (a/kz)2, где а — половина нечетного целого числа, аг —
прямолинейная координата. Если поле в среде возбуждается ли-
нейным электрическим ток'ом, направленным параллельно оси х,
то строгое решение можно получить для случаев, когда в среду
помещены круглый или эллиптический цилиндр (ось которого
параллельна координатной оси х) или наклонная плоскость [57].
Можно ожидать, что асимптотические решения, полученные для
таких частных случаев, дадут строгие результаты более об-
щего характера, чем асимптотические решения, полученные для
.других моделей.
Такая среда интересна также тем, что. и в отсутствие рас-
сеивающего тела лучи образуют каустику. При внесении в среду
рассеивающего тела возникает явление переходной области,
вызванное одновременным присутствием границы тени (вдоль
луча, касательного к поверхности тела) и каустики. Эти явле-
ния еще не изучены, особенно в зоне, где касательный луч и
каустика совпадают. Дифракционные и переходные явления,
вызванные разрывностью функции е' или одной из ее производ-
ных (см. строку 5 в таблице), также могут быть исследованы
1. Квазиоптические методы в дифракции
55
на модели среды с приведенным выше изменением е', обратно
пропорциональным квадрату координаты, которая служит удоб-
ным эталоном для области с монотонно меняющимся показа-
телем преломления. В настоящее время эти вопросы находятся
в стадии изучения.
Следует отметить, что выполненные нами расчеты в основ-
ном были проделаны для случаев, когда при г—>оо проницае-
мость неограниченно увеличивается [31, 32], в то время как про-
ницаемость, обратно пропорциональная квадрату z, а равно и
с другими зависимостями, поддающимися анализу, стремится
при г-*оо к конечной величине. Это различие несущественно
при геометрооптическом подходе, когда рассматривается ло-
кальная дифракция при каком-либо конечном значении z (на-
пример, на плоской границе раздела z=Z\, как показано на
фиг. 3); при модовом описании эти .случаи принципиально отли-
чаются. Это связано с тем, что спектр собственных волн, рас-
пространяющихся перпендикулярно оси z, является дискретным
для случая е(оо)=оо, но имеет непрерывную часть, если вели-
чина е(оо) конечна. (Если проницаемость изменяется обратно
пропорционально квадрату г, то весь спектр непрерывен.) По-
скольку дифрагированные лучи (лучи d на фиг. 3) связаны
с полюсами в модовом представлении, то эти полюсы соответ-
ствуют собственным волнам, когда спектр дискретный, и несоб-
ственным, когда он непрерывный.
Возникает вопрос, каждый ли из этих полюсов описывает
поле дифрагированного луча. По-видимому, это так, поскольку
поля собственных и несобственных дифрагированных волн в об-
ласти тени ведут себя аналогично: они затухают в направле-
нии, параллельном границе, и растут в перпендикулярном к ней
направлении (ср. со случаем, изображенным на фиг. 6, а). То
обстоятельство, что поле собственной моды в конце концов за-
тухает, в то время как поле несобственной моды растет при
удалении от поверхности, сказывается мало из-за ограничен-
ности области существования дифрагированных волн.
3. Анизотропная среда. Если среда, окружающая источник
или рассеивающее тело, анизотропна, то возникает целый класс
новых задач. Особый интерес в настоящее время представляют
гиротропные диэлектрики, которые в некотором приближении
можно использовать как модель плазмы, находящуюся в по-
стоянном магнитном поле. Для. источников, находящихся в не-
ограниченных областях, в квазиоптическом приближении полу-
чены канонические решения, так что соответствующие ампли-
туды лучей известны [35, 58, 59]; проанализированы также неко-
торые явления отражения, преломления и дифракции [36—38,
60, 61]. Однако в этом направлении предстоит еще многое
56
Л. Фельсен
сделать: необходимо провести более общее исследование и вы-
разить результаты в виде, допускающем геометрооптическую ин-
терпретацию. Полученные таким образом решения можно бу-
дет использовать для проверки геометрической теории дифрак-
ции (в анизотропных средах), многие детали которой еще
необходимо доработать. Не исследован также ряд новых явле-
ний в переходных областях.
Некоторые электромагнитные явления в гиротропных ди-
электриках подобны явлениям, имеющим место при распростра-
нении акустических волн в упругих средах1). Например, связь
мод на поверхности раздела, которая приводит к тому, что
падающий луч может создавать два или более лучей, отражаю-
щихся под разными углами; или боковые волны, которые могут
распространяться по обе стороны от границы раздела воз-
дух—диэлектрик. Следует заметить, что, несмотря на такие
аналогии, встречается множество явлений, которые требуют
специального исследования.
4. Рассеивающие тела с переменными свойствами поверх-
ности. Как было отмечено в § 3, поведение поля вблизи направ-
ляющих и рассеивающих структур, имеющих переменные
свойства поверхности, требует дальнейшего изучения. К сожа-
лению, для структур такого типа трудно получить точное ана-
литическое решение. Исключением является специальный слу-
чай изменения импеданса как функции метрических коэффи-
циентов в естественной системе координат, соответствующей
форме рассеивающего тела.
Прямые; асимптотические методы. 1. Теория граничного слоя.
Метод граничных слоев дает многообещающие возможности
расширения рамок применимости таких асимптотических мето-
дов, как геометрическая теория дифракции для переходных об-
ластей вблизи каустик, фокусов, границ тени и структурных осо-
бенностей. Можно надеяться, что применение этого метода к бо-
лее сложным задачам рассеяния даст новые результаты.
2. Геометрическая теория дифракции для анизотропных ди-
электриков. Для ряда задач, в которых рассматривалась анизо-
тропная среда с осью симметрии, результаты опубликованы
[61], однако остаются неразработанными детали теории для об-
щего случая анизотропии.
Сравнение модового и лучевого представлений. Как уже
отмечалось, хотя геометрооптическое и модовое рассмотрения
иногда и эквивалентны, однако чаще всего они дополняют друг
') См. [14], § 24.
1. Квазиоптические методы в дифракции
57
друга. Этот факт заслуживает особого внимания, так как не-
редко комбинация двух методов дает мощный аппарат для 'ре-
шения некоторых типов задач, и в особенности задач, связан-
ных с многократным отражением или дифракцией.
Из сказанного в § 2 ясно, что существует прямая связь ме-
жду квазиоптическими типами волн и аналитическими свой-
ствами решения в модовом представлении (седловые точки,
полюсы и точки ветвления). При наличии многократных отра-
жений анализ в модовой области (т. е. в области соответствую-
щим образом преобразованного реального поля) может при-
вести к выделению комплексных особенностей, влияние которых
в физическом пространстве учитывается затем в асимптотиче-
ском решении.
Применение этой методики будет особенно полезно к зада-
чам геометрической оптики, когда комплексные особенности
ярко выражены. Например, в задаче о щели в диэлектрике,
схематически изображенной в строке 4 'таблицы, диаграмма
излучения может иметь сильный максимум, направление кото-
рого нетрудно предсказать, зная координаты полюса, соответ-
ствующего вытекающей волне, который расположен вблизи
действительной оси [53]. Из отдельных же вкладов в диаграмму
излучения отраженного и преломленного лучей эту информа-
цию получить не так просто. Остается применить аналогичные
методы для систематического описания рассеяния телами или
апертурами конечных размеров, для которых многократную ди-
фракцию в реальном пространстве можно интерпретировать как
итерационный процесс в преобразованном пространстве, приводя-
щий к комплексному резонансу. С другой стороны, для сложных
задач, анализ которых с помощью мод неудобен, но которые ре-
шаются геометрооптическими методами, информацию о комп-
лексных резонансах можно получить с помощью резонансного
знаменателя, возникающего в результате суммирования много-
кратных отражений.
Уже указывалось на преимущества представления поля
в виде «нормальных мод» в волновых каналах и волноводах не
очень больших поперечных размеров. Комбинация геометрооп-
тического и модового представлений оказывается плодотворной
в применении к многомодовым волноводам, особенно при иссле-
довании нарушений структурной непрерывности, резких изме-
нений направления, открытых резонаторов и в других случаях,
когда имеет место связь между собственными волнами (мо-
дами). Геометрическую оптику можно использовать для при-
ближенного построения поля в плоскости разрыва; в свою оче-
редь это поле можно использовать при точном расчете ампли-
туд прошедших и отраженных волн.
58
Л. Фельсен
Такая методика составляет основу многих работ, представ-
ленных на данном симпозиуме1). Первое строгое исследование
с одновременным использованием геометрооптического и модо-
вого представлений, было проведено Вайнштейном [63], который
показал, что поле, излученное из конца полубесконечного пло-
ско-параллельного многомодового волновода, можно найти при
рассмотрении дифракции на концах двух полуплоскостей, обра-
зующих волновод. Совместное применение модового и геометро-
оптического подходов использовалось в недавно опубликованной
работе [64] при анализе рассеяния на диэлектрическом теле.
Численные методы, С ростом использования быстродей-
ствующих вычислительных машин все чаще отдается предпочте-
ние численным методам решения задач перед аналитическими
методами. Численные результаты имеют неоспоримое преиму-
щество, если необходимо детальное изучение какого-либо част-
ного вопроса, например рассеяния на теле заданной формы или
распространения волн в некоторых неоднородных средах.
Однако в исследованиях общего характера возможности чис-
ленных методов не используются полностью, если не выяснен
физический смысл результата или не сделано сравнение с при-
ближенным аналитическим решением, позволяющее определить
границы применимости результата.
Квазиоптические методы основываются на предположении,
что kD~>оо, где D — некоторая характеристическая длина дан-
ной структуры. Полученные в таком предположении формулы
обычно с достаточной точностью применимы и для не слишком
больших значений kD. Поскольку аналитическую оценку ошибки
(а не только ее порядок) получить трудно, то для реше-
ния вопросов, связанных с определением области, в которой
справедлива данная формула, могут служить численные ме-
тоды, позволяющие перекрывать область критического значе-
ния параметра. Численная информация необходима также для
.изучения поведения поля в переходных областях и особенно по-
.лезна, когда переходные функции являются характерными для
целого класса явлений. Хорошо поддаются, изучению с по-
мощью численных методов, например, задачи, связанные с рас-
пространением в плоской слоистой среде. В этом случае можно
исследовать влияние пространственного изменения величины
показателя преломления в виде быстрого монотонного изме-
нения, отдельного острого максимума или близко расположен-
) Этот метод эффективен также при расчете полей, излученных боль-
шими апертурами или большими рефлекторами. В этих приложениях он сво-
дится к приближениям классической физической оптики [62],
1. Квазиоптические методы в дифракции 59
ных максимумов (близко расположейные волновые каналы).
Эти результаты можно сравнить с вычислениями, основанными
на асимптотическом приближении.
Еще один класс задач, удобных для применения численных
методов, связан с дифракцией на составных объектах, центры
рассеяния которых расположены не слишком далеко друг от
друга.
Экспериментальные методы. Использование эксперименталь-
ных методов подобно использованию упомянутых выше числен-
ных методов. И в этом случае основная цель состоит в том,
чтобы получить результаты, необходимые для специальных при-
ложений, установить пределы применимости приближенных вы-
ражений или охватить такие области значений параметров, для
которых нет адекватной теории. Численный и эксперименталь-
ный подходы могут дополнять друг друга в тех случаях, когда
один из них предпочтительнее. Например, на практике трудно
создать плоскую слоистую среду, в то время как численный
расчет выполнить можно. С. другой стороны, если имеется экс-
периментальное оборудование, то почти любое рассеивающее
тело можно смоделировать и провести соответствующие изме-
рения.
§ 6. ЗАКЛЮЧЕНИЕ
Многие явления распространения и дифракции высокоча-
стотных полей хорошо описываются на базе лучевого представ-
ления, основные положения которого можно получить из гео-
метрической теории дифракции и из асимптотических решений
соответствующих канонических задач.
Для задач, связанных с дифракцией, полезными также ока-
зались модовые представления. Сделана попытка установить
связь между некоторыми аналитическими свойствами решения
в модово.м представлении и поведением высокочастотного поля.
Поскольку применения геометрической теории дифракции до-
статочно полно обсуждались в ранее опубликованных рабо-
тах, то в данной статье основное внимание было уделено явле-
ниям в переходных областях и явлению модового резонанса,
которые невозможно изучить при геометрооптическом подходе.
После обсуждения ряда типичных задач перечислены некото-
рые нерешенные проблемы и те, которые заслуживают дальней-
шего изучения.
ЛИТЕРАТУРА
1. Siegel К. М., Appl Sei. Res., В7, 293 (1958).
Far Field Scattering from Bodies of Revolution.
2. Braunbek W„ Z. J. Phys., 127, 381 (1950).
Neue Ndherungsmethode fur die Beugung am Ebenen Schirm.
60
Л. Фельсен
3. Фок В. A., Journ. of Phys. (СССР), 10, 130 (1946).
The Field of a Plane Wave Near the Surface of a Conducting Body.
4. Levine H., Wu T. T., Report. 71, Appl. Math, and Statistics Lab., Stan-
ford University, December 1957.
Diffraction by an Aperture at High Frequencies.
5. К e 11 e г J. B., Lewis R. M., S e c k 1 e r B. D., Report EM-96, Inst, of
Math. Sciences, New York University, August 1956.
Diffraction by an Aperture, II.
6. Keller J. В., в книге Calculus of Variations and its Applications, New
York, 1958. '
A Geometrical Theory of Diffraction.
7. К e 11 e r J. B., IRE Trans., AP-4, 312 (1956).
Diffraction by a Convex Cylinder.
8. К eller J. B., Journ. Opt. Soc. Am., 52, 116 (1962).
Geometrical Theory of Diffraction.
9. Sec kier B. D., Keller J. B-, Journ. Acoust. Soc. Am., 31, 192 (1959).
Geometrical Theory of Diffraction in Inhomogeneous Media.
10. Buch al R. N., Keller J. B„ Report EM-131, Inst, of Math. Sciences,
New York University, April 1959.
Boundary Layer Problems in Diffraction Theory.
11. Z a u d e r e r E., Journ. Math, and Meeh., 13, 187 (1964).
Wave Propagation around a Convex Cylinder.
12. Фок В. А., Вайнштейн Л. А., в книге Electromagnetic Theory and
Antennas, New York, 1963, p. 11.
On the Transverse Diffusion of Short Waves Diffracted by a Convex Cy-
linder.
13. Logan N. A., Y e e K. S., в книге Electromagnetic Waves, Madison, 1962.
A Mathematical Model for Diffraction by Convex Surfaces.
14. Бреховских Л. M., Волны в слоистых средах, изд-во АН СССР,
1957.
15. Миллер М, А., Таланов В. И., Report on Soviet contributions to
diffraction theory, presented at URSI General Assembly, London, 1960.
16. Felsen L. B., Siegel К- M., Journ. Res. (NBS), 64D, Nov. — Dec. issue
(1960). (Обзор за период 1957—1959 rr.)
Diffraction and Scattering.
17. Felsen L. B., Weston V. H., Radio Science (NBS), 68D, 440 (1964).
(Обзор за период 1960—1962 rr.)
Diffraction and Scattering.
18. F e 1 s e n L. B., Alta Frequenza, 31, 266 (1962).
High-Frequency Diffraction.
19. К e 11 e r J В., в книге Electromagnetic Theory and Antennas, New York,
1963, p. 3.
A Survey of Short Wavelength Diffraction Theory.
20. Фок В. А, ЖЭТФ, 19, 916 (1949).
Поле вертикального и горизонтального диполей, расположенных над зем-
ной поверхностью.
21. Felsen L. В., Marcuvitz N., Report R-776-59, Microwave Res., Inst.,
Polytechnic Inst, of Brooklyn, October 1959.
Modal Analysis and Synthesis of Electromagnetic Fields,
22. Budden K. G., Radio Waves in the Ionosphere, London, 1961.
23. Magnus W., Oberhettinger F., Functions of Mathematical Physics,
New York, 1954, p. 92.
24. Sommerfeld A., Optik, Wiesbaden, 1950. (Имеется перевод: A. 3 ом-
мер ф e л ь д, Оптика, ИЛ, 1953.)
25. F е 1 s е n L. В., IRE Trans., АР-7, 168 (1959).
Radiation fiom Ring Sources in the Presence of a Semi-Infinite Cone.
1. Квазиоптические методы в дифракции
61
26. Fel s е п L. В., Journ. Appl. Phys., 26, 138 (1955).
Back-Scattering from Wide-Angle and Narrow-Angle Cones.
27. Wait J. R., Electromagnetic Waves in Stratified Media, New York, 1962,
Ch. 2.
28. Reports P1BMR1-841-60 and 1057-62.
29. Sec kier B. D., Keller J. B., Journ. Acoust. Soc. Am., 31, 206 (1959).
Asymptotic Theory of Diffraction in Inhomogeneous Media.
30. Report PIBMR1-1225-64.
31. F r i e d 1 a n d e r F. G., Sound Pulses, London, 1958, p. 174. (Имеется
перевод: Ф. Фри длеиде р, Звуковые импульсы, ИЛ, 1962.)
32. J о n е s D. S., Phil. Trans. Roy. Soc.. London, Ser. A, 255, 341 (1963).
High-Frequency Refraction and Diffraction in General Media,
33. Wait J. R„ Con da A. M„ Journ. Res. (NBS), 63D, 181 (1959).
Diffraction of Electromagnetic Waves by Smooth Obstacles for Grazing
Angles.
34. Rub in о w S. 1., Keller J. B., Report EM-162, Inst, of Math. Sciences,
New York University, December 1960.
The Shift of the Shadow Boundary and the Scattering Cross Section of
an Opaque Object.
35. Arbel E., Fel sen L. В., в книге Electromagndtic Theory and Antennas,
New York, 1963, p. 391.
Theory of Radiation from Sources in Anisotropic Media. Part I — General
Sources in Stratified Media; Part II — Point Sources in Infinite Homoge-
neous Medium.
36. Felsen L. B., Proc. ГЕЕ (London), 111, 445 (1964).
Propagation and Diffraction in Uniaxially Anisotropic Regions. Part I —
Theory; Part II — Applications.
37. Felsen L. B., IEEE Trans., AP-11, 469 (1963).
Radiation from a Uniaxially Anisotropic Plasma Half Space.
38. Felsen L. B., IEEE Trans., AP-12, 624 (1964).
Focusing by an Anisotropic Plasma Interface.
39. Levey L„ in Report R-452, 23-63, Microwave Research Institute, Poly-
technic Institute of Brooklyn. (Отчет за период октябрь 1962 г. — март
1963 г.)
40. К е 11 е г J. В„ Journ. Appl. Phys., 28, 429 (1957).
Diffraction by an Aperture.
41. F e 1 s e n L. B., Appl. Sci. Res., B9, 170 (1961).
High-Frequency Diffraction by a Wedge with a Linearly Varying Surface
Impedance.
42. H e s s e 1 A., Doctoral Dissertation, Polytechnic Inst, of Brooklyn. 1960.
43 Clem mow P. C., Weston V. H., Proc. Roy. Soc. (London), A264, 246
(196!).
Diffraction of a Plane Wave by an Almost Circular Cylinder.
44. M а г c i n k о w s k i C. J., Felsen L. B., Journ. Res. (NBS), 66D, 699
(1962).
On the Geometrical Optics of Curved Surfaces with Periodic Impedance
Properties.
45. M a r c i n k о w s k i C. J., Felsen L. B., Journ. Res. (NBS), 66D, 707
(1962).
On the Limitation of Geometrical Optics Solutions for Curved Surfaces
with Variable Impedance Properties.
46. ФайнбергЕ. Л., Изв. АН СССР, сер. 'физич., 8, 107 (1944).
47. Seni or T. B. A„ Appl. Sci. Res., B8, 437 (1960).
Impedance Boundary Conditions for Statistically Rough Surfaces.
48. T w e r s k у V., Journ. Res. (NBS), 64D (1960).
On Multiple Scattering of Waves.
62
Л. Фельсен
49. Чернов Л. А., Распространение волн в среде со случайными неоднород-
ностями, Изд-во АН СССР, 1958.
50. Hoffman W. С., Radio Science (NBS), 68D, 455 (1964).
Electromagnetic Wave Propagation in a Random Medium.
51. Bud den K. G., The Wave-Guide Mode Theory of Wave Propagation,
г Englewood, 1961.
52. В r e m m e r H., Terrestrial Radio Waves, New York, 1949.
53. Tamir T., Oliner A. A., Proc. IEE (London), 110, 310 (1963).
Guided Complex Waves. Part 1 —Fields at an Interface; Part 2 — Relation
to Radiation Patterns.
54. Tamir T., Felsen L. B., IEEE Trans., AP-13, No. 3, 410 (1965).
On Lateral Waves in Slab Configurations and their Relation to other
Wave Types.
55. G о о d г i c h R. F., Karzarinoff N. D., Weston V. H., в книге
Electromagnetic Theory and Antennas, New York, 1963.
Scalar Diffraction by a Thin Oblate Spheroid.
56. Ko dis R. D., в книге Electromagnetic Theory and Antennas, New York,
1963.
The Radar Cross Section of a Conducting Cylinder with a Dielectric Sleeve
at the Optical Limit.
57. Felsen L. B., Report R-765-59, Microwave Research Institute, Polytechnic
Institute of Brooklyn, July 1959.
Diffraction by Objects in a Certain Variable Plasma Medium.
58. К о g e 1 n i k H., M о t z H., в книге Electromagnetic Theory and Antennas,
New York, 1963, p. 477.
Electromagnetic Radiation from Sources Embedded in an Infinite Anisotro-
pic Medium, and the Significance of the Poynting Vector.
59. M i 11 r a R., Deschamps G. А., в книге Electromagnetic Theory and
Antennas, New York, 1963, p. 459.
Field Solution for a Dipole in an Anisotropic Medium.
60. Seshadri S. R„ Report 366, Cruft Lab. Harvard Univ., May 1962.
Excitation of Surface Waves on a Perfectly Conducting Screen Covered
with Anisotropic Plasma.
Report 402, Cruft Lab., Harvard University, February 1963.
Scattering of Unidirectional Surface Waves.
61. Rulf B., Felsen L. B., Proc. Symposium on Quasi-Optics, New York,
1964.
Diffraction by Objects in Anisotropic Media.
62. Silvers. Journ. Opt. Soc. Am., 52, 131 (1962).
Microwave Aperture Antennas and Diffraction Theory.
63. В а й н ш т e й н Л. A , Изв. АН СССР, Сер. физич., 12, 166 (1948).
К теории дифракции на двух параллельных полуплоскостях.
64 Kouyoumjian R. G., Peters L., Thomas D. T., IEEE Trans.,
AP-11, 690 (1962).
A Modified Geometrical Optics Method for Scattering from Dielectric Bo-
dies.
2
СРАВНЕНИЕ ДВУХ ТЕОРЕТИЧЕСКИХ ТРАКТОВОК
РАСПРОСТРАНЕНИЯ АКУСТИЧЕСКИХ ВОЛН
В ОКЕАНЕ-ТЕОРИИ НОРМАЛЬНЫХ ТИПОВ
КОЛЕБАНИЙ И ЛУЧЕВОЙ ОПТИКИ
И. Толстой*
Если отношение длины волны к некоторому линейному размеру среды или
тела невелико, а их характеристические параметры изменяются сравнительно
медленно, то обе точки зрения в теории распространения волн — модовая и
лучевая — могут быть справедливы и полезны. Это область квазиоптики, в
которой число типов колебаний (мод) может быть достаточно большим и вы-
полнены критерии справедливости лучевого приближения и приближения
ВКБ. Подводная акустика дает много примеров поведения волн в таких
случаях. Сравнение численных результатов и формул для этих двух прибли-
жений— лучевого и ВКБ — имеет методологическое значение. Физическое
соотношение между типами колебаний и лучами наглядно продемонстриро-
вано на модели А Вуда. В области подводной акустики выявляется также
важная роль неизвестных неоднородностей среды Действительно, в конечном
счете именно эти неоднородности определяют относительную практическую
полезность различных теоретических подходов.
§ 1. ВВЕДЕНИЕ
Типы колебаний (моды) и лучи являются двумя централь-
ными понятиями, господствующими в теории распространения
волн. Первое из них в наиболее общем смысле соответствует
точному решению волнового уравнения, хотя в частных слу-
чаях оно также может быть приближенным (например, когда
используется метод ВКБ). Наоборот, лучевой подход обычно
является приближенным (за исключением специального случая
однородной среды, где, конечно, он является точным).
На практике возникает известная трудность определе-
ния точности и применимости лучевого и модового методов
в конкретных условиях. Причина заключается в том, что
если не прибегать к численным расчетам, то трудно оценить
ошибки, которые вносятся при использовании лучевого и ВКБ
* I. 1 о 1 s I о у, Hudson Laboratories, Columbia University, Dobbs Ferry.
N. Y.
64
И, Толстой
приближений. Особенно это касается подводной акустики, где
часто работают в таких частотных диапазонах, в которых при-
годны и лучевой и модовый методы.
Рассмотрение связи между модовым и лучевым представле-
ниями дает много интересного и полезного. Эти два представле-
ния являются дополнительными подобно волновой и классиче-
ской механике. Каждое из них может быть использовано для
того, чтобы разъяснить и углубить второе — соотношение, кото-
рое имело место между классической и квантовой физикой
в начальный период существования атомной теории. Модифи-
цированная лучевая теория Келлера [1] ‘) представляет собой
хороший пример совместного использования обоих представ-
лений.
§ 2. ОПРЕДЕЛЕНИЯ
Теорию нормальных типов колебаний можно представить
себе в традиционном духе теоретической механики как обобще-
ние метода нормальных координат в неограниченной среде. Эта
концепция (ей оказывал предпочтение Релей [3]) была широко
использована в теории поля [4] и распространена на любые
механические и смешанные поля излучения [5]. В ней рассма-
триваются все возможные частоты колебаний и соответствую-
щие конфигурации поля или типы колебаний среды, а также
определяется степень возбуждения каждого типа колебаний.
Тогда сумма этих возбуждений дает результирующее возмуще-
ние, вызываемое источником:
(1)
где Ф,„ есть вещественное решение уравнения
(Т2 + ^)Ф = 0, (2)
т. е. той части волнового уравнения, которая зависит от коор-
динат; <о—угловая частота, с—локальное значение скорости
волн (например, звуковых), k — волновое число. Решение пред-
ставляет собой стоячие волны, удовлетворяющие граничным
условиям (собственные функции). Величины qm — функции вре-
мени, определенные возбуждающими силами, или нормальные
координаты. Во многих случаях функция (1) представляется
двойной или многократной суммой по нескольким индексам
(комнатная акустика), иногда — суммой интегралов и ряда
(волноводы) или многократным интегралом. Действительно,
*) См. также [2].
2. Распространение акустических волн в океане
65
суммирование по дискретному индексу m возникает всякий раз,
когда энергия данного типа колебаний Фт заключена внутри
ограниченной области. Говорят, что в этом случае соответствую-
щий спектр дискретный. Конечно, все встречающиеся в природе
системы обладают дискретным спектром. Рассматриваем ли мы
кристалл, атмосферу, океан или Землю как целое — все эти
системы ограничены. Но размеры си-
стемы могут быть настолько велики
по сравнению с длиной волны, что для
упрощения спектр можно считать не-
прерывным и перейти в формуле (1)
к интегралу.
Заметим, что все стандартные фор-
мы решения независимо от того, имеют
ли они форму интегралов или разло-
жений в ряд по собственным функ-
циям, эквивалентны решению типа (1)
(или его интегральной форме).
Естественные среды обычно неод- г
нородны. В первом приближении они
часто просто слоистые, т. е. описы-
ваются функциями одной координаты z (например, сама Зем-
ля, океаны и атмосфера). Здесь важно различать вертикаль-
ную компоненту у волнового вектора k и горизонтальную ком-
поненту х (фиг. 1). В соответствии с законом Снеллиуса х есть
константа и
Л2 _ у2 z2.
(3)
Особенно удобную аппроксимацию для слоистой среды дает
метод ВКБ. Он приводит к хорошо известным соотношениям
если
_v-l/2 m
m m \cossm/
z
S = j у dz 4- s0,
«0
(4)
(5)
(6)
Это условие хорошо выполняется для медленно меняющихся
сред и высоких частот, но не имеет места вблизи точек пово-
рота у = 0, где е—>оо. Подстановка (4) в (1) дает решение ВКБ
для источника.
Лучевая теория совершенно отлична по характеру от теории
нормальных типов колебаний, хотя в некоторых отношениях
5 Зак. 2Z4
66
И. Толстой
весьма похожа на метод ВКБ. На практике она состоит из
двух приближений. Первое приближение — решение в виде сво-
бодной волны для слабых градиентов и достаточно высоких
Фиг. 2.
частот. В случае слоистой среды, как легко показать,—это бе-
гущий волновой фронт (4), т. е.
Ф — Ае1<‘3+кх\ (jrj
опять при условии (6). Типы колебаний ВКБ суть стоячие вол-
ны, полученные суперпозицией плоских бегущих волн в луче-
вом приближении; таким образом, в данном случае оба под-
хода тождественны (А = у~1/2В . Во втором же приближении,
т. е. при вычислении поля данного источника, результаты луче-
вой теории отличаются от любого приближения теории нор-
мальных типов колебаний. По существу из лучевой теории сле-
дует, что энергия распространяется вдоль лучей (направляю-
щие косинусы х/й, y/k) или лучевых трубок. Предполагается,
что поток энергии сохраняется вдоль лучевой трубки. Так,
в акустике (фиг. 2) при постоянной плотности имеем
<8>-
Это соотношение теряет смысл на каустиках, где
doi/doo—»0. В лучевом представлении мы по существу рассма-
триваем локализованный пучок энергии, движущийся вдоль лу-
чей, перпендикулярных волновым фронтам s+xx=const. С точ-
ки зрения теории нормальных колебаний среда представляет
собой суперпозицию гармонических осцилляторов — ситуация,
которая, пожалуй, имеет более наглядный характер для огра-
ниченных систем. Этот подход идентичен методу нормальных
координат в теоретической механике и теории поля. Лучи и
типы колебаний так же дополняют друг друга, как классиче-
ская и волновая механики.
2. Распространение акустических волн в океане
67
§ 3. ПРИМЕРЫ ДВОЙСТВЕННОСТИ ЛУЧ-ТИП КОЛЕБАНИЙ
Подводная акустика дает много примеров взаимосвязи и
взаимовлияния понятий «тип колебаний» и «луч». Мы ограни-
чимся здесь двумя примерами, причем оба относятся к волно-
водным эффектам. Большую часть вопросов, связанных с рас-
пространением звука в океане, можно рассмотреть по существу
тем же способом. Спектр в данном случае дискретный, и для
гармонического источника поле акустического давления будет
иметь следующую форму [6, 7]:
s 2PnPmCosr ДхгаЛ1/2г~1/2С08(®<4-ф), (9)
\ m пфт т )
где
= —(10)
есть разность между .соседними корнями некоторого характе-
ристического уравнения, а Рт, Рп — функции г, учитывающие
тот факт, что источник и приемник находятся на некоторой
глубине. Акустическое давление представляет собой колеблю-
щуюся функцию г, возникающую в результате суперпозиции
приблизительно периодических составляющих с длинами волн
Amn = v~Г, (П)
которые представляют собой длины волн биений колебаний
различных типов.
Многие свойства этого представления, и в частности его
связь с лучевым представлением, хорошо поясняются на при-
мере однородного волновода с идеально отражающими стен-
ками. Такой волновод будет нашим первым примером, проил-
люстрированным очень хорошими экспериментальными данны-
ми А. Вуда [8], которые получены на макете, но тем не менее мо-
гут быть применены и к распространению волн в мелководье.
Рассмотрим слой однородной жидкости с поверхностями
нулевого давления при г=0 и z=h. Зависимость давления от
глубины приемника для каждого типа колебаний описывается
формулой
Pra«=Arasinyraz, (12)
а характеристическое уравнение имеет вид
ymh = tnn, (13)
где (см. фиг. 1)
Ym = XmCtg9m. (14)
5*
68
И. Толстой
Предположим, что возбуждаются только два типа колебаний
т=1, 2 (низкочастотный источник). Тогда амплитуда давления
меняется с расстоянием согласно соотношению
р = Г~'/2(Р? + Pl + 2ЛР2 cos г Дх12)1/2. (15)
На любой глубине г, такой, что Pi и Р2 имеют один и тот же
порядок, амплитуда давления поля как функция расстояния
имеет форму (фиг. 3), из которой хорошо видно наличие опре-
деленной длины волны биений Л12.
С лучевой точки зрения, которая в этом случае (однородная
жидкость) является точной, поле в идеальном волноводе такого
типа можно представлять как результат бесконечного множества
отражений. Такое множество дает для каждой частоты один или
несколько лепестков или предпочтительных углов излучения: они.
являются разрешенными углами передачи в теории типов ко-
лебаний [уравнения (13) и (14)].
Указанное соответствие между двумя представлениями
можно развить следующим образом. Учитывая (12) и (13), мы
видим, что произведение PiP2 меняет знак на оси волновода.
Следовательно, амплитуда давления р(г) в уравнении (15) для
z>h/2 по существу та же самая, как и для z<h/2, но сдвинута
по горизонтали на Л12/2. Это схематически показано на фиг. 4:
максимумы давления р вдоль уровня, расположенного между
осью и верхней поверхностью волновода, имеют место при тех
значениях г, для которых вблизи дна р принимает минималь-
ное значение. Таким образом, зона максимальной освещенности
(заштрихована на фиг. 4) покрывает область синусоидальной
формы, похожую на размытый луч, бегающий вверх и вниз
между ограничивающими поверхностями. Покажем, что это
действительно есть первое приближение к реальной картине лу-
чей при низких частотах и малом числе типов колебаний.
Для этого размытого луча можно определить средний угол
падения 0' (фиг. 4), такой, что
<16)
или
2h tgd'=^~
& Дх,2
и
Л (xj — х2) tg 0'= л. (17)
Рассмотрим теперь характеристическое уравнение (13) и урав-
нение (14). Допустим, что m достаточно велико, так что Дт=1
соответствует малым приращениям 0 и х, ,
А*га+1, ctg А0ш+1. m cosec2 0m == л. (18)
р
Фиг. 3. Биения колебаний двух типов (давление как функция
расстояния в волноводе).
Фиг. 4. Интерференционная структура в верхней половине волно-
вода сдвинута на Л.ц/2 относительно интерференционной структуры
в иижией половине.
В результате получаются полосы максимальной освещенности (заштрихованная
область), имеющие синусоидальную форму. Они напоминают размытый дуч, бегающий
вверх и вниз между границами волновода.
70
И. Толстой
Рассматривая фиг. 1, видим, что изменение 0 при фиксирован-
ной частоте а означает изменение х:
40=~tg0; (19)
подставляя это выражение в (18), получаем
0 == Л, (20)
т. е. соотношение (17) при m=l и 0 = 0'. Это соотношение по-
лучено для т» 1; - интересно, однако, что оно близко к дей-
ствительности и для типов колебаний низких порядков1).
Хорошей иллюстрацией этих рассуждений служит серия опы-
тов А. Вуда, проведенная им на модели. Он использовал слой
воды толщиной несколько сантиметров с дном различного ха-
рактера и частоту порядка 0,5 Мгц. Сканирующий механизм
давал ему возможность построить двумерную (г, г) картину
путем фотографирования с экрана осциллографа.
При использовании поглощающего резинового дна высшие
типы колебаний затухают очень быстро, в результате чего
появляется простая двумодовая интерференционная структура,
показанная на фиг. 5. Это именно тот тип структуры, который
мы только что рассматривали: ясно виден широкий размытый
луч, полученный при интерференции только двух типов колеба-
ний. Когда же Вуд использовал дно в виде стеклянной пла-
стинки и более толстый слой воды, эффективное число типов
колебаний возросло приблизительно до 20. Картина интерфе-
ренции, наблюдавшаяся в этом случае, показана на фиг. 6:
лучи видны теперь очень четко. То, что они появляются боль-
шей частью под одним углом, объясняется, несомненно, селек-
тивным действием упругой пластинки. Относительно высокая
четкость лучей обусловлена большим числом типов колебаний
(т»1).
В качестве второго примера мы рассмотрим типичный про-
филь с (г), минимальное значение с которого расположено на
некоторой глубине (фиг. 7). Чтобы упростить задачу и исклю-
чить все отражения от дна, мы предположим, что слой воды
лежит на бесконечной «жидкой» подложке, скорость распро-
странения звука в которой равна скорости распространения
звука в воде вблизи дна2). Два граничных луча, исходящих
. *) Подобные рассуждения были использованы Вестоном в его муаровых
аналогиях [9].
. 2) В действительности в донных подложках скорость звука является
функцией с(г), которая быстро нарастает с глубиной. К тому же подложки
сильно поглощают звук. Таким образом, лучи, претерпевшие более одного-
двух донных отражений или преломлений, большей частью значительно мень-
ше основного луча звука. Итак, наща модель вполне приемлема.
Фиг. 5. Эксперимент А. Вуда [8] на модели, иллюстрирующей эффект,
изображенный на фиг. 4.
Доминируют два типа колебаний; Л =1,9 см, f = 563 к г и.
Фиг. 6. В этом случае эффективная глубина модели была больше, а по-
глощение высших типов колебаний — меньше. Лучи видны намного лучше,
чем на фиг. 5, так как присутствовали многие высшие типы колебаний.
Фиг. 7. Модель, иллюстрирую пая некоторы? особенности распространения
звука на дальние расстояния в глубоком океане.
п
/7. Толстой
от источника, соответствуют первоначальному конусу полного
отражения, т. е. донному скользящему лучу. Однако если ис-
точник находится очень близко к поверхности, то достаточно
рассмотреть один из них вместе с лучом, выходящим из источ-
ника горизонтально (фиг. 7). Прямые лучи, проходящие слева
от этих двух лучей, достигают дна и проникают в него без от-
ражения. С точки зрения теории типов колебаний это есть та
область, в которой непрерывный спектр вносит значительный
вклад в звуковое поле. Справа (в основном для больших рас-
стояний) только циклические лучи, т. е. полностью отражен-
ные лучи, вносят вклад в общее поле: преобладают типы коле-
баний дискретного спектра. Мы ограничимся здесь только этим
полем (легко показать, что возникающие ошибки пренебрежи-
мо малы).
Хорошо видны две особенности хода лучей, изображенных
на фиг. 7:
1) существование зон, которые совершенно не облучаются
(зоны тени)',
2) заметная фокусировка энергии в довольно равномерно рас-
положенных точках (зоны сходимости).
При вычислении амплитуд звукового поля хорошо видна
разница между двумя решениями: приближенным лучевым и
точным модовым. Так, немодифицированный лучевой подход
дает кривые р(г), изображенные на фиг.’ 8: уровень звука
в тени равен нулю, причем измеримые амплитуды поля резко
ограничены зонами сходимости; имеются также каустики, на ко-
торых решение расходится. Модовое решение дает расчетные
кривые, показанные на фиг. 9: пики интенсивности весьма остры
в зонах сходимости, каустикам соответствуют едва заметные
колебания на их склонах, а уровни в тени малы, но изме-
римы ').
С другой стороны, оба метода дают похожие результаты
при описании геометрии поля, например при определении рас-
стояния между зонами сходимости. Если мы обозначим это рас-
стояние через D (фиг. 7), то ясно, что в лучевом приближении
гт
£> = 2jtg9<fe. (21)
о
С модовой точки зрения величина D есть длина волны биений.
Итак, если условия справедливости приближения ВКБ удовле-
творяются (за исключением точек поворота), то характеристи-
Метод, использованный для вычисления этого поля, описан в работе [7],
Фиг. 8. Звуковое поле как функция расстояния.
Расчет произведен обычным методом лучевой оптики для модели фиг. 7.
Амплитуда акустического давления, дин/смг
Фиг. 9; Результат точного расчета звуковых полей методом теории типов
колебаний для модели фиг. 7.
Амплитуда давления для непрерывного источника мощностью 1 вт и с частотой 30 гц как
функция расстояния; с (б)= 1524 м/сек, с 1г0| = 1487,4 м/сек, с (z,) = 1539,2 м/сек, zQ = 1281 Л,
74
И. Толстой
ческое уравнение для типов колебаний есть известное уравнение
Бора — Зоммерфёльда
s = {т — у) л, (22)
где s определяется уравнением (5). Предполагая, что т до-
статочно велико, так что бт = 1 соответствует малым прираще-
ниям х и 0, мы имеем приближенно
гТ
6s 6х ds , \ д г , /п„,
6т ~ 6т ди ди J У dz ~ - (23)
о
(24)
и, следовательно,
гг
АИ_1,Л1 = 2 j tgQdz — D. (25)
о
Этот результат еще раз демонстрирует дуализм луч — тип ко-
лебаний в случае слоистой среды.
§ 4. ТЕОРЕТИЧЕСКАЯ И ЭКСПЕРИМЕНТАЛЬНАЯ ТОЧНОСТЬ
Полезно отметить, что метод ВКБ дает в пределе более вы-
сокую точность, чем точность, которую может обеспечить не-
модифицированная лучевая оптика. Правда, типы колебаний
ВКБ суть просто стоячие волны, полученные из противопо-
ложно распространяющихся волновых цугов в приближении
лучевой оптики; с этой точки зрения оба метода неразличимы
и вносят одинаковые ошибки. Однако при вычислении ампли-
туды поля, создаваемого источником, согласно модовой. тео-
рии в приближении ВКБ следует просто подставить эти моды
в точную формулу, т. е. в уравнение (1); таким образом, от-
сутствуют какие-либо дополнительные источники ошибок. В то
же время в лучевом методе делаются дополнительные допуще-
ния при использовании амплитудной формулы (8). Таким обра-
зом, ясно, что в задачах с заданным источником обычное при-
ближение лучевой оптики в общем случае несколько менее
точно, чем решение ВКБ. Сказанное иллюстрируется, в част-
ности, тем, что последнее решение хорошо ведет себя вблизи
каустики {10], тогда как лучевой метод дает в этих точках
расходящееся решение.
Фиг. 10. Точное звуковое поле для модели, изображенной на чертеже.
Мощность источника 1 вт.
На фиг. 10 изображено точное поле в симметричном канале
типа, показанного на фигуре, скорость звука в котором описы-
вается соотношением
7 =
с со
(26)
На фиг. 10 иллюстрируется тот .интересный факт, что для опи-
сания средних свойств акустического поля достаточно ограни-
читься в этом случае низшими типами колебаний; тогда бы-
стрые осцилляции поля, соответствующие интерференции ме-
жду низшими и высшими типами колебаний '), исчезают.
-. ) Заметим, что наименьшую длину волны биений Лот
по крайним значениям х:
можно оценить
х0
<»
Со ’
2л
и Лот
. V__________V
CpCl
Лс
с7
76
И. Толстой
Те же самые вычисления, выполненные в приближении ВКБ,
приводят к результату, показанному на фиг. 11. Видно некото-
рое сходство с точным расчетом в том смысле, что наблюдаются
те же самые длины волн биений. Ясно, однако, что появились
Фиг. 11. Сравнение точного поля с полем, полученным методом ВКБ, для
модели, изображенной на чертеже.
существенные ошибки. Источник ошибок найти нетрудно. Он
лежит в различиях между хт, полученными в приближении
ВКБ, т. е. из характеристического уравнения (22) Бора — Зом-
мерфельда, и из точного уравнения, которое для симметрич-
ных типов колебаний давления имеет вид
J2/3 (?) — J-2/Z (?) — О,
(27)
(28)
?
—s— №.
Y
2. Распространение акустических волн в океане
77
В этом случае уравнение (22) записывается как
s — 2Z={m— у)л; т=1, 3, 5........... (29)
В таблице точные корпи уравнения (27) сравниваются с кор-
нями уравнения (29).
m Xm. м 1
для уравнения (27) для уравнения (29)
1 1,64867 1,64862
9 1,64388 1,64387
19 1,640197 1,640194
Необходимо показать, к каким ошибкам в Дх0- для низшего
типа колебаний или для комбинаций из низших и высших ти-
пов приводят расхождения, представленные в таблице. Так,
чтобы относительная фаза г&хц в уравнении (9) была значи-
тельной, необходимо выполнение соотношения
гб(Аи/;)~гбхгу< 10-1.
Используя наибольшую ошцбку в таблице (т=1), получаем
г < 2 • 103 м. (30)
Итак, уже после нескольких первых километров относительные
фазовые соотношения между низшими типами колебаний, вы-
численные по методу ВКБ, становятся весьма сомнительными.
Конечно, это особенно неблагоприятный случай, так как мы
взяли самые низшие типы колебаний. Но даже если мы возь-
мем только высшие типы колебаний, то при обычных условиях
в океане невозможно расширить этот предел более чем на один
порядок величины. Таким образом, метод ВКБ, как и обычные
методы лучевой оптики, не дает возможности найти детальное
распределение амплитуд акустического поля в глубине океана
на расстояниях, больших приблизительно 20 км.
Весьма интересно, что неопределенность наших знаний о за-
коне изменения с(г) в океане вместе с флуктуациями среды [11]
являются источниками ошибок, которые сравнимы с рассмот-
ренными выше ошибками, вносимыми лучевым приближением
или приближением ВКБ.
78
И. Толстой
Рассмотрим гармоническую волну, которая выходит из- ис-
точника, находящегося на оси звукового канала, и вновь пере-
секает ось после касания поверхности воды (фиг. 12). Пусть Дс
есть разность скоростей звука на оси канала (с0) и на его по-
верхности (С|). Если в определении Ci допущена ошибка и соот-
ветствующая неопределенность в Дс равна 6Дс, то фаза луча,
Параметры приблизительно те же, что и для фиг. 9.
рассчитанная согласно принятой модели, будет содержать
ошибку. Простой лучевой расчет показывает, что ожидаемая
ошибка в фазе равна
(31)
где f есть частота в герцах. Типичными для океана являются
Дс~30 м!сек, 6Дс~0,3 м!сек, т. е.
• 10-2/ рад.
Таким образом, для частот порядка 50 гц или более все сведе-
ния о фазах оказываются ложными после первого же полупе-
риода, т. е. на расстоянии порядка 20 км.
Из сказанного следует, что естественные причины и экспери-
ментальные ошибки ограничивают использование точных реше-
ний приблизительно в той же самой степени, в какой ошибки
при расчете ограничивают использование ВКБ или обычных лу-
чевых методов. Действие естественных причин мешает провести
любое детальное и чисто детерминистское сравнение между тео-
рией и экспериментом на расстояниях, превышающих несколько
километров. Чтобы избавиться от непредсказуемой части в из-
меренных данных, следует использовать статистическую обра-
ботку, перекрестную корреляцию, усреднение и т. д. Этот про-
2. Распространение акустических волн в океане 79
цесс нужно произвести также и над вычисляемыми полями, что
позволит расширить диапазон использования лучевого метода и
метода ВКБ. Можно ожидать, что в этих направлениях будут
проведены успешные исследования. Тогда модифицированные и
улучшенные методы ВКБ, а также более сложные и общие ме-
тоды лучевой оптики (например, метод Келлера [1]) следует зна-
чительно более широко использовать в подводной акустике.
ЛИТЕРАТУРА
1. Keller J. В., Proc. Symposium on Microwave Optics, McGill University,
Montreal, Canada, 1953.
2. Seckier B. D., Keller J. B., Journ. Acoust. Soc. Am., 31, 192 (1959).
3. Rayleigh, The Theory of Sound, New York, 1930. (Имеется перевод:
Релей, Теория звука, М., 1955.)
4. Heitler W„ The Quantum Theory of Radiation, Oxford, 1954. (Имеется
перевод более раннего издания: В. Г а й т л е р, Квантовая теория излу-
чения, М. — Л., 1940.)
5. Biot М. A., Tolstoy I., Journ. Acoust. Soc. Am., 29, 381 (1957).
6. Tolstoy 1., Journ. Acoust. Soc. Am., 30, 348 (1958).
7. Tolstoy 1., M a у J., Journ. Acoust. Soc. Am., 32, 655 (1960).
8. W о о d А. В., в книге Underwater Acoustics, ed. V. M. Albers, New York,
1963, p. 159.
9. Weston D. E., Journ. Acoust. Soc. Am., 32, 647 (1960).
10. Skudzyk E. J., в книге Underwater Acoustics, ed. V. M., Albers, New
York, 1963, p. 199.
11. Б p e x о в с к и x Л. M., Волны в слоистых средах, М., 1957.
3
ФОРМАЛЬНАЯ ТЕОРИЯ БЕГУЩЕЙ ВОЛНЫ
Р. Льюис*
Метод бегущей волны, которая является обобщением геометрической
оптики, позволяет получить приближенные решения краевых задач для вол-
нового уравнения и других линейных гиперболических уравнений. Эта теория
включает как особый случай асимптотическую (высокочастотную) теорию
приведенного волнового уравнения и родственных ему уравнений. Она позво-
ляет проанализировать не только гармонические во времени поля, но и вол-
ны, модулированные по амплитуде, распространение скачков и других сингу-
лярностей, а также поведение произвольных волн в окрестности волнового
фронта. Кроме того, она позволяет рассмотреть отражение от движущихся
поверхностей и излучение движущихся источников.
§ 1. ВВЕДЕНИЕ
Современные теории, обобщающие геометрическую оптику,
такие, как «геометрическая теория дифракции» [7, II] Келлера,
обычно основаны на асимптотических методах решениях крае-
вых задач для приведенного волнового уравнения
[?2 + ^(Х)]-ц(Х) = 0 (1.1)
и родственных ему уравнений. В уравнении (1.1) &о = соо/со,
п(Х) =со/с(Х), с(Х)—скорость распространения волн и с0 —-
некоторая постоянная. Это уравнение описывает распростране-
ние гармонических во времени полей с частотой соо- Подставляя
в уравнение (1.1) асимптотический ряд
СО
2 [(^о)^^ЗД(Х)]гт(^), k0^, (1.2)
zra=0
получаем дифференциальные уравнения для ф(Х) и функций
zm(X). Эти уравнения можно решить с помощью «лучей», кото-
* R. М. Lewis, New York University, Division of Electromagnetic Re-
search, Courant Institute of Mathematical Sciences, New York, N. X.
3. Формальная теория бегущей волны
81
рые представляют собой некоторые пространственные кривые.
Для получения асимптотических решений краевых задач для
уравнения (1.1) часто можно использовать комбинацию разло-
жений вида (1.2). Главный член этого разложения совпадает
с геометрооптическим полем.
Метод бегущей волны позволяет решать краевые задачи для
волнового уравнения
*)=° П-3)
и других гиперболических уравнений. Подставляя в уравнение
(1.3) ряд вида
u(t, Х) = 2 ет[<р(Л X)]zlm'’(t, X), (1.4)
получаем дифференциальные уравнения для функций <р(/, X) и
z<m)(/, X). Эти уравнения можно решить с помощью «бихарак-
теристик», являющихся некоторыми пространственно-временны-
ми кривыми. В выражении (1.4) е0(т) —произвольная функция,
однако функции ет(т) (т = 1, 2, ...) должны удовлетворять ус-
ловиям <(т) = ет_1(т).
Интерпретация разложения по бегущим волнам (1.4) зави-
сит от выбора «формы волны» е0(т). Если
<?0(т) = е~г'°°т и ср (Л X) = t — ф (X),
с0
то (1.4) сводится к (1.2), причем
u(t, X) = v(X)e-l<n,>t.
Таким образом, в этом случае метод бегущей волны сво-
дится к асимптотической теории уравнения (1.1). Если, однако,
мы положим
^0(т) = а(т)е-г®»т,
где too—большой параметр, то получим асимптотическую тео-
рию высокочастотных волн, модулированных по амплитуде.
Если е0(т) —скачок или даже обобщенная функция, то функ-
ции ет(т) будут сглаживаться с повышением номера m и раз-
ложение (1.4) можно использовать для того, чтобы свести
задачи с сингулярными исходными данными к задачам с глад-
кими данными. В этом случае метод бегущей волны стано-
вится теорией «распространения» сингулярностей. Если е0(т)—
любая функция, обращающаяся в нуль при т<0, и последова-
тельные интегралы ет(т) также обращаются в нуль при т<0,
то можно показать, что разложение (1.4) сходится в достаточно
82
Р. Льюис
малой окрестности точки <р = 0. В этом случае разложение (1.4)
правильно описывает поведение решений уравнения (1.3) в ма-
лой области непосредственно за распространяющимся волновым
фронтом.
Для всех этих интерпретаций можно изучить отражение и
преломление бегущих волн на границах и поверхностях раз-
дела сред. При фиксированных границах вычисления анало-
гичны тем, которые проводятся при асимптотическом решении
краевых задач для приведенного волнового уравнения. При
движущихся границах появляются новые интересные особенно-
сти. Довольно просто показать, что и стационарный и движу-
щийся точечные источники вызывают бегущие волны; следова-
тельно, теория бегущей волны идеальна для изучения распро-
странения, отражения и преломления волн, вызываемых такими
источнцками.
Уже давно известны некоторые частные случаи выражения
(1.4). «Плоские волны»
г,
« — е0 /---—
L Со J
и «сферические волны»
1 Г/ г ч
и — — eQ \t + —
г °L CoJ
являются точными решениями уравнения (1.3) (при постоянной
величине с) для произвольной функции е0(т). (Здесь I — по-
стоянный единичный вектор, г=\Х— Хо|.) Эти функции являют-
ся «бегущими волнами первого порядка», т. е. функции zm тож-
дественно равны нулю при т>1. Для плоской волны г0^1, в то
время как для сферической волны г0=1/г. Бегущие волны бо-
лее высокого порядка можно получить, например, посредством
дифференцирования приведенных выше выражений. Однако
бегущие волны конечного порядка имеют ограниченную приме-
нимость при решении краевых задач для уравнения (1.3), по-
этому мы будем иметь дело в основном с распространяющимися
волнами бесконечного порядка, т. е. с решениями уравнения
(1.3) в виде (1.4).
Метод бегущей волны применительно к асимптотической тео-
рии приведенного волнового уравнения был детально развит
главным образом Келлером и его сотрудниками в Нью-Йорк-
ском университете [1, 3, 6—8, И]. Другие приложения теории
бегущих волн были изучены Людвигом [12, 13], Фридлендером
[5], а также Бабичем и Алексеевым [2]. Некоторые результаты
важных работ Людвига и Фридлендера суммированы в § 3.
[\а^ указал Курант [4], работа Лакса [9] об асимптотическом р§-
3. Формальная теория бегущей волны
83
шении начальных задач с осциллирующими начальными данны-
ми является частным случаем теории бегущей волны.
Хотя решения в виде бегущих волн получены для широкого
класса линейных гиперболических уравнений и систем уравнений
и эти решения дают важный теоретический инструмент для изу-
чения соответствующих уравнений в частных производных, в
этой статье основное внимание уделено практическим приложе-
ниям. Мы попытаемся показать, что метод бегущей волны спо-
собен дать полезные приближенные решения разнообразных
задач, которые с трудом решаются другими методами (если
вообще решаются). Мы ограничимся рассмотрением волнового
уравнения, поскольку сущность и применения метода хорошо
иллюстрируются задачами для этого уравнения.
В § 2 мы дадим основы теории разложения по бегущим вол-
нам, а в § 3 применим ее к важному частному случаю «бегу-
щих волн, не зависящих от времени». В § 2 и 3 мало оригиналь-
ного, за исключением рассмотрения в конце § 3 волн, модулиро-
ванных по амплитуде. Однако материал, изложенный в этих
параграфах, служит введением в теорию. Рассматривая про-
стейший случай (т. е. волновое уравнение), мы пытались сде-
лать теорию насколько возможно легко понимаемой. Излучения
движущихся источников (§ 4) и отражения от движущихся по-
верхностей (§ 5) приводят к бегущим волнам, которые не яв-
ляются «не зависящими от времени». Исследование этих явле-
ний является, насколько нам известно, оригинальным.
Настоящая работа была названа «формальной теорией бегу-
щей волны» именно потому, что эта теория является в значи-
тельной степени формальной. Выкладки производятся по обыч-
ным правилам без рассмотрения вопросов сходимости и без
определения -произвольной функции е0(т). Как отмечено выше,
результирующее формальное разложение им'еет полезные при-
менения для различных функций е0(т). Заманчиво предполо-
жить, что это разложение полезно для класса функций е0, более
широкого, чем тот, который мы рассмотрим. Рассмотренные
нами задачи, конечно, не исчерпывают применимости метода.
§ 2. РАЗЛОЖЕНИЕ ПО БЕГУЩИМ ВОЛНАМ
Мы ищем решения однородного волнового уравнения
Lu ~ Uxvxv с2 (jq utt = 0 (2-1)
вида
u(t, X)~u(t, %i, х2> *з) — S em [ф(/, X)\zSm)(t, X), (2.2)
m =>0
6*
84
Р. Льюис
где е0(т)— произвольная функция и
-^-ет(т) = ет_1(т); /п=1, 2, .... (2.3)
Как обычно предполагается, что по повторяющимся индексам
производится суммирование от 1 до 3. Векторы обозначаются
прописными буквами. Верхний символ (т) является просто ин-
дексом. В некоторых случаях ряд (2.2) будет сходящимся или
даже конечным. В других случаях он может представлять со-
бой асимптотическое разложение; как мы увиди.м ниже, возмож-
ны и другие интерпретации. Подставим (2.2) в (2.1) и исполь-
зуем выражение (2.3) для производных ет. Ниже мы прирав-
ниваем нулю коэффициент при каждой функции ет(<р). Если
предположить, что z<0)=#0, то приходим к характеристическому
уравнению
с2 Ф?= 0 (2-4)
для фазовой функции <р и к последовательности уравнений пе-
реноса
2 [фл гл”> — ^Ф/г/"г>]4-г(Я1)£ф4-0; m = 0, 1,2.....(2.5)
для амплитудной функции z<m>. В уравнениях (2.5) предпола-
гается, что г<-1)=0.
Удобно ввести функции a>(t, X) и kv(t, X), определенные вы-
ражениями
о = — фр ^ = фЛ^; v=l, 2, 3. (2.6)
Тогда характеристическое уравнение (2.4) принимает вид
a2 = c2kvkv или
d) = h(X, K) = h(x1, х2, х3, kx, k2, k3\,
h — ±c(X)k, k = Vk^kv. (2.7)
Дифференциальное уравнение в частных производных первого
порядка (2.7) можно решить «методом характеристик»1)- Та-
ким образом мы получаем систему обыкновенных дифферен-
циальных уравнений
'-1- “=°- «=1.2.3, (2.8)
которые являются «характеристическими уравнениями» диффе-
ренциального уравнения в частных производных (2.7). Посколь-
ку уравнение (2.7) эквивалентно (2.4), которое само является
См. [4], гл. 2.
3. Формальная теория бегущей волны
85
«характеристическим уравнением» для (2.1), то уравнения (2.8)
называют бихарактеристическими. Из первого уравнения (2.8)
видим, что независимую переменную в этих уравнениях можно
отождествить с t. Тогда если ввести функции
= = v=l, 2, 3, (2.9)
то можно записать (2.8) в эквивалентной форме
-dF = Sv = v=l, 2, 3; -^ = 0. (2.10)
Последнее уравнение в (2.10) является следствием остальных
шести уравнений. Каждое решение уравнений (2.8) или (2.10)
определяет кривую [/, Х(/)] в (/, X)-пространстве, называемую
бихарактеристикой. Вдоль этой кривой
== Ф, + Ф^ ® (c2kvkv — со2) = 0, (2.11)
т. е. фазовая функция ф(/, X) постоянна на бихарактеристиках.
Следовательно, бихарактеристики лежат на поверхностях уров-
ня <р(/, X). Эти поверхности уровня называются характеристи-
ческими гиперповерхностями уравнения (2.1).
Решения бихарактеристических уравнений определяют также
некоторые кривые X = X(t) в Х-пространстве, которые мы будем
называть лучами. Лучи являются просто проекциями бихарак-
теристик на Х-пространство. Если через s обозначить длину дуги
вдоль лучей, то
ds \2_ dxv dxv
~dt) ~~dT~dT
(2-12)
gvgv = C2.
Систему шести уравнений первого порядка (2.11) можно заме-
нить системой трех уравнений второго порядка. Используя «как
независимую переменную и вводя показатель преломления
(здесь Со—некоторая постоянная), легко получаем систему
= v=l. 2, 3. (2.14)
Это известные дифференциальные уравнения для лучей геомет-
рической оптики [11].
Бихарактеристические уравнения и уравнение (2.11) являют-
ся инструментом для решения начальной задачи для характери-
стического уравнения (2.4) относительно ф(/, X).
86
Р. Льюис
Пусть S=(oi, 02, 03), и пусть параметрические уравнения
/ = /°(S), xv = xO(S); v = l, 2, 3, (2.15)
описывают гиперповерхность Г в пространстве — времени, на
которой <р имеет заданные значения
ф[/»(2), х»(2)] = ф0(2). (2.16)
Требуется найти решение уравнений (2.4) и (2.16). Диффе-
ренцируя (2.16) по oj, получаем
dX°v dt° Эф°
kv-^- — о /=1,2,3. (2.17)
v OCfj OQj j J ' *
Эти уравнения вместе с (2.7) составляют четыре аглебраических
уравнения для определения со = со0 (2) и £v = £®(2); v=l, 2, 3,
в каждой точке 2 исходной гиперповерхности (2.15). Далее, ве-
личины /°(2), х®(2), о)°(2) и £0(2) представляют исходные
данные для решения бихарактеристических уравнений (2.10),
причем, как видно из (2.11), на каждой определенной таким
образом бихарактеристике ф = ф°(2). Соответственно значениям
(2.7) это дает два решения начальной задачи для ф. Если, на-
пример, исходное множество является плоскостью /=0, то мож-
но отождествить crv и xv; в этом случае уравнения (2.17) и (2.7)
приводят к ________
£0v(^) = ^-,cd0(X)=±C(X)-/' (2.18)
* t/л.^ у .
Таким образом, мы видим, что функцию ф(/, X), входящую в
разложение (2.2), можно определить, если задано ее значение
на некоторой гиперповерхности Г. Аналогично можно опреде-
лить функции z<m) (/, X), если известны их значения на гиперпо-
верхности Г. Чтобы убедиться в этом, запишем сначала урав-
нения переноса (2.5) в виде
4m) + 2^)^v + '^2(m)z-T = —£2(т-1); т — о, 1,2.........(2.19)
Здесь мы использовали (2.6) и (2.9). Поскольку
d __ д , dxv д _____ д . д
dt dt' dt dxv dt 'ov QXyi '
то для каждого m (2.19) является обычным дифференциальным
уравнением для z<m> вдоль бихарактеристики
£ф')г<'я> = — m = 0, 1, 2..... (2.20)
Функция г(°) = г удовлетворяет однородному уравнению
т + («£*)г = г<+^ + (ж£'1>)г = 0- (2.21;
3. Формальная теория бегущей волны
87
Если функция z определена путем решения уравнения (2.21), то
функции z(‘), £(* 2>, ... могут быть определены последовательно
путем решения уравнения (2.20).
Решение уравнения (2.21) приведено в приложении. Чтобы
описать это решение, необходимо сначала ввести несколько
важных определений. Пусть С — любая характеристическая ги-
перповерхность, заданная выражением
Ф(Л А’) = ф1; (2.22)
она содержит двухпараметрическое семейство бихарактеристик.
Соответствующее двухпараметрическое семейство лучей (полу-
ченных проектированием этих бихарактеристик на Х-простран-
ство) назовем семейством лучей, связанных с С. Каждому фик-
сированному значению Л соответствует поверхность
ф(Л, Х) = Ф1 (2.23)
в Х-пространстве, которую мы назовем волновым фронтом; когда
/1 изменяется, соответствующее однопараметрическое семейство
поверхностей образует семейство волновых фронтов, связанных
с С. Теперь выберем фиксированную точку (/i, Л\) на гиперпо-
верхности С. Эта точка лежит на некоторой бихарактеристике
поверхности С, а точка Х{ лежит на соответствующем луче, а
также на волновом фронте (2.23). Из выражений (2.9) и (2.10)
видно, что этот луч параллелен вектору G=(glt g2, gs), а следо-
вательно, и вектору К=(йь k2, #з)=^ф(^1, ^i), который ортого-
нален к волновому фронту (2.23). Отсюда ясно, что семейства
лучей и волновых фронтов, связанных с любой характеристиче-
ской поверхностью С, всюду ортогональны, т. е. лучи являются
ортогональными траекториями волновых фронтов1).
Чтобы описать решения уравнения (2.21) вдоль некоторой
бихарактеристики В, заданной выражением [/, Х(0], предполо-
жим, что С есть характеристическая гиперповерхность, на кото-
рой . лежит В. Образуем из семейства лучей, связанных с С,
бесконечно малую трубку лучей, содержащую проекцию R биха-
рактеристики В. Пусть da(t)—площадь поперечного сечения
такой трубки в точке X(t) на R2). Тогда решение (2.21) есть
<2-24>
Этот результат выведен в приложении. В нем с(/) обознача-
ет функцию с[Х(01, а г(0 —функцию z[t, Х(01- Формула (2.24)
’) Такое семейство лучей часто называют нормальной конгруэнтностью
лучей.
2) Тогда da(t)—площадь части волнового фронта, связарогр с С, кото-
рая вырезается трубкощ
88
Р. Льюис
дает значение z в любой точке t на бихарактеристике, если из-
вестно его значение в некоторой точке Очевидно, что выра-
жение da(t0) lda(t) является пределом отношений площадей, ко-
гда трубка лучей стягивается к лучу R. Его можно также интер-
претировать как якобиан преобразования вдоль лучей от вол-
нового фронта ф(/0, А’)=ф1 к волновому фронту ф(/, Х)=фЬ
Поскольку (2.24) есть решение обыкновенного однородного
дифференциального уравнения (2.21), то решение соответствую-
щего неоднородного уравнения (2.20) можно получить из (2.24)
методом «вариации параметров». В результате получаем
-i "*=ri >• 2......<2-25)
Л»
Из соотношений (2.12) видно, что решение можно также запи-
сать, используя в качестве параметра длину дуги $:
ж_о. 1.2....... (2.26)
So
Здесь zm(s) обозначает-функцию z<m>{/(s), X[f(s)]}, c(s) —функ-
цию c{X[/(s)]} и т. д.
Волновое уравнение (2.1) описывает распространение возму-
щения в среде, характеризуемой функцией с(Х). Говорят, что
среда является однородной, если величина с постоянна. В этом
случае из (2.10) видно, что бихарактеристики и лучи — прямые
линии. Кроме того,
da (Sp) _ (Pi 4~$о) (Р2 4~5о) /9 971
da(s) (pi 4- s) (p2 +s) ’ k '
где pi и p2 — главные радиусы кривизны волнового фронта (свя-
занного семейства волновых фронтов) в точке s = 0 на луче R').
Таким образом, (2.26) принимает вид
/ ч _ (Ш) /_ ч Г (Р1 + ^о) (Рг + ^о)11/2 _
z (s)-z (ЗД[ (pi + s)(p2 + s) J
_ [ Г (.Р2±-^11/2 Lz<*-» (s') ds'-, m = 0,1,2,.... (2.28)
2<B J L (Pi + S) (p2 + S) J V / ’ V /
So
') Вывод выражения (2.27) и обсуждение главных радиусов, каустик
ц т. д. проводятся в [1Ц; см. также [7, 8).
3. Формальная теория бегущей волны
89
Из (2.26) видно, что функции z<m>(s) бесконечны в точках, где
da(s) равняется нулю, а из (2.28) ясно, что для однородной
среды это происходит тогда, когда s = —pi или s = —рг. В этих
точках лучи проходят через фокус или каустическую поверхность
соответствующего семейства лучей. Таким образом, ряд (2.2)
не может представлять решение и на каустике, и в окрестности
таких точек метод бегущей волны нужно модифицировать1).
В последующих параграфах теория будет применена к реше-
нию краевых задач для уравнения (2.1). Как мы увидим, реше-
ние принимает вид одной или более бегущих волн (2.2), и исход-
ные данные задачи дают значения каждой волны на некоторой
гиперповерхности Г. Полученные выше результаты дают воз-
можность определить бегущую волну вдоль бихарактеристик,
исходящих из Г, поскольку наше решение начальной задачи для
характеристического уравнения определяет сначала бихаракте-
ристики, а потом значения функции <р (которая постоянна на
них), а (2.25) или (2.26) дают значения функции z<m) вдоль би-
характеристики. Таким образом, функции <р и z<m> определяются
их значениями на Г, которые известны.
Чтобы понять возможные интерпретации формального разло-
жения (2.2), удобно получить уравнение для остаточного члена
ряда /(”>, когда ряд (2.2) ограничивается п членами. Таким об-
разом, полагаем
«<">(/, Х)= 3 еш[ф(/, X)]z<m>(/, X), (2.29)
О
где функции ет(т) удовлетворяют равенству (2.3). Далее, если
<р удовлетворяет (2.4), a z<m>— (2.5), то легко показать, что
£«<") = еп [ф (Л X)] Lz(n} [t, X). (2.30)
Теперь положим
u(t, X) = u^(t, X) + r<ni(t, X). (2.31)
Тогда если а —решение однородного уравнения (2.1), то
LrW = -enLz<n\ (2.32)
Здесь уместно сделать небольшое замечание относительно
некоторых приложений метода бегущей волны. Если функ-
ция е0(т) такова, что ее последовательные интегралы ет(т)
становятся малыми при больших т, то из (2.32) видим, что
г(п) — решение волнового уравнения с источником, причем член,
соответствующий источнику, сколь угодно мал, если «достаточно
*) См, работы [6, 12].
90
Р. Льюис
велико. Опираясь на этот факт, иногда можно показать,
что остаточный член И”) сам мал и что, следовательно, —
хорошее приближение для и.
§ 3. БЕГУЩИЕ ВОЛНЫ, НЕ ЗАВИСЯЩИЕ ОТ ВРЕМЕНИ
Рассмотрим важный частный случай разложения по бегу-
щим волнам, который был детально изучен в связи с асимпто-
тической теорией приведенного волнового уравнения [11].
Бегущую волну (2.2) будем называть не зависящей от вре-
мени, если функции z<m)(/, X) не зависят от t, т. е.
z^(t, X) = (-c0)mzm(X), (3.1)
а <р(/, X) имеет только тривиальную зависимость от времени
вида
<Р(Л X)-t — -(3.2).
1-0
Множители, содержащие постоянную с0, введены в (3.1) и (3.2)
для удобства. Тогда из (2.4) и (2.6) следует, что ф(Х) является
решением уравнения эйконала
(?Ф)2 = «2РО; = (3-3)
и (о =—1. Кроме того, из (3.2), (2.11) и (2.12) имеем
S
Ф(5) = Ш) + J n(s')ds'. (3.4)
Sq
Характеристические гиперповерхности ф(/, X) =<pi можно тогда
представить в виде
= (3.5)
С0
Из (3.5) непосредственно видно, что все характеристические
гиперповерхности (соответствующие всем возможным значениям
постоянной ф1) параллельны. Отсюда следует, что каждая ха-
рактеристическая гиперповерхность имеет одно и то же связан-
ное с ней семейство лучей и одно и то же связанное с ней се-
мейство волновых фронтов.
Уравнение (2.26) дает формулу для величины zm вдоль луча
zm^> — da(s)J
1 [Г£^1^211/2 ’ Az (S')^S'; m = Q, 1,2,...; (3.6)
2 J L n (s) da (s) J n (s') m ’
*0
3. Формальная теория бегущей волны
91
здесь Дг = zx х^. Для однородной среды величины с и п,
постоянны и (2.27) дает
~ г \Г (Р1 + $о) (Рг + so) ~|1/2
— (P1 + s)(P2 + 5) J
_ 1 Г Г (Р. + И (Р2 +ZL11/2 дг (s') ds'-, m = Q, 1,2______ (3.7)
2n J L (Pl +s) (p2 + s) J m v ’ v
Jo
Функции em(r), входящие в выражение для не зависящей от
времени бегущей волны, подчиняются, конечно, условию (2.3),
однако в остальном произвольны. Рассмотрим теперь не зави-
сящую от времени бегущую волну, соответствующую следую-
щему выбору ет(т):
ет (т) = (— г©0)_'и (3.8)
В этом случае из соотношений (2.2), (3.1) и (3.2) имеем
«(/, Х) = е-;“»^(Х), (3.9)
где
00
®(X) = e<Mffl У (ik0Ymzm(X)-, (ЗЛО)
ЛИ и О
от>“0
Кроме того, из (3.9) и (2.1) следует, что v(X) есть решение
приведенного волнового уравнения
. + (3.11)
Выражение (3.10), рассматриваемое как асимптотическое
разложение при ko~+<x>, является отправным пунктом асимпто-
тической теории приведенного волнового уравнения, которая
детально рассмотрена в работе [11]. Уравнения лучей (2.14),
формула (3.4) для «фазовой функции» ф(Х), а также формулы
(3.6) и (3.7) для «амплитудных функций» zm образуют основу
этой теории. Поскольку ни одно из этих выражений не зависит
от конкретного выбора функции ет(т) в виде (3.8), то резуль-
таты, полученные при изучении приведенного волнового уравне-
ния, можно применить и к задачам, содержащим произвольные,
не зависящие от времени бегущие волны1). В частности, могут
быть использованы многочисленные специальные формулы, ко-
торые были получены (для частных случаев) путем оценки
сложного интегрального члена в (3.7) (см. [8]).
Это было показано Фридлендером [5], который довольно детально
изучал не зависящие от времени бегущие волны.
92
Р. Льюис
В качестве примера рассмотрим задачу об отражении пло-
ской волны ’)
= = vI{X) = eik'>x', (3.12)
от поверхности* 2) S, находящейся в однородной среде (с — с0,
п=Г). Полное поле на этой поверхности («74~«) или (^74-^)
удовлетворяет граничному условию
(а7 + и) = 0, (х»74-т) = 0 на S. (3.13)
Отраженное поле v является решением приведенного волнового
уравнения
Дг> + ^ = 0, (3.14)
а также удовлетворяет условию излучения Зоммерфельда на
бесконечности и условию
v = — Vj — — eik°x' на S. (3.15)
Асимптотическое разложение (3.10) для v определяется сле-
дующим образом. Подставляя (3.10) в (3.15), убеждаемся, что
Ф(А')е^лс1 на S (3.16)
и
z0(X) = —1, zm(X)zzO; т = \, 2, на S. (3.17)
Из (3.16) легко находим3), что отраженные лучи вместе с па-
дающими лучами (которые параллельны оси Xi) удовлетворяют
«закону отражения», а если отраженные лучи найдены, то функ-
ции ф и zm определяются из (3.4), (3.7), (3.16) и (3.17).
На практике вычисление функций zm при т>0 обычно весь-
ма затруднено. Однако эти функции найдены для многочис-
ленных частных случаев [8]. Рассмотрим, например, параболи-
ческий цилиндр S с фокусным расстоянием р (фиг. 1). Уравне-
ние поверхности S в полярных координатах имеет вид
= <80 = ^. (3.18)
Плоская волна (3.12) падает снаружи вдоль оси параболиче-
ского цилиндра; благодаря фокусирующему свойству параболы
отраженные лучи являются радиальными линиями, которые про-
*) Индекс / означает «падающее» поле.
2) Чтобы избежать осложнений, связанных с дифракцией, необходимо
предположить, что поверхность S гладкая и так уходит на бесконечность, что
ни один падающий луч не является тангенциальным к ней (см. [И]).
3) См. [11] или [8],
3. Формальная теория бегущей волны
93
ходят через фокус (т. е. через линию Xi = p, *2 = 0), если их
продолжить назад. Следовательно, отраженные волновые фрон-
ты являются круговыми цилиндрами (r=const), т. е. отражен-
ная волна является цилиндрической волной. Функции ф и zm
Фиг. 1. Отражение плоской волны от параболического цилиндра
с фокусным расстоянием р.
вычислены в работах [8, И]1)- Они выражаются формулами
ф = г — р, (3.19)
= (3.20)
Здесь
/>»(©) = a)mp'^+i-m (sec |)27+1, (3.21)
а постоянные ajm даются рекуррентными формулами
= — />1. m>l; (3.22)
aOm = —m>l, a00 = —1. (3.23)
Подставляя эти результаты в (3.10), для асимптотического
разложения отраженной волны получаем
a7m(pr-‘sec2-J)У+Л; (3.24)
т=0 /«0
’) Результаты, приводимые здесь, могут быть получены из соответствую-
щих формул в работах [8, 11] подстановкой у—х2, z=xg, х=р — xlt k=k0 и
и=е~ lkopv.
94
Р. Льюис
Этот результат был проверен в [8] посредством асимптотического
разложения точного решения задачи, которое в этом случае
можно получить методом разделения переменных в параболиче-
ских координатах.
Задача об отражении гармонической во времени плоской
волны (3.12) была сформулирована выше как краевая задача
для приведенного волнового уравнения. Бесконечные гармони-
ческие во времени волны вида (3.12) не существуют в природе,
и решение рассмотренной выше задачи об отражении можно фи-
зически интерпретировать как установившееся1) состояние для
отраженного поля, когда падающая волна представляется по-
лубесконечной последовательностью волн и является гармони-
ческой, за исключением окрестности ее «фронта».
Задачу об отражении плоской волны
(3-25)
при произвольной форме волны е(т) можно сформулировать
как гранично-начальную задачу для волнового уравнения
Lu — uXvX -д utt = 0. (3.26)
со
Прежде всего заметим, что волна (3.25) является решением на-
чальной задачи для уравнения (3.26) с начальными условиями
«(0, *) = е(-^-), й/(0, Х) = е'(-^-). (3.27)
Если полное поле обращается в нуль на поверхности S, то
волна (3.25) будет решением гранично-начальной задачи (3.26),
(3.27) и
«(/, А") = 0 на S. (3.28)
Чтобы обеспечить совместность условий (3.27) и (3.28), пред-
положим, что S лежит в полупространстве Xi>0 [это условие
удовлетворяется в частном случае параболического цилиндра
(3.18)] и что
е(т) = 0 при т<:0. (3.29)
Сначала мы решим гранично-начальную задачу (3.26) —
(3.28) методом бегущей волны, а затем обсудим интерпретацию
полученного таким образом формального разложения при раз-
личном выборе функции е. Положим, что
и = U/ —(— Ид» (3.30)
‘J См. работу [10],
3. Формальная теория бегущей волны
05
где Uj задается выражением (3.25), а отраженную волну пред-
ставим не зависящей от времени бегущей волной
СО
= 2 em[t—^-](-СоГгт(Л). (3.31)
т=0
Заметим, что волна (3.25) тоже является не зависящей от вре-
мени бегущей волной первого порядка1). Подставляя (3.25) и
(3.31) в (3.28), заключаем, что выражения (3.16) и (3.17) ос-
таются в силе и что е0—е. Как и прежде, функции ф и zm можно
определить из (3.4), (3.16), (3.7) и (3.17). Заметим, однако, что
из уравнения (2.3) последовательные функции еь е2, ... опре-
деляются через е0=е только с точностью до произвольной адди-
тивной постоянной; например,
X
^1(т)= J e(s)rfs + ci- (3.32)
о
Для определения этих постоянных заметим, что (3.25) удовлет-
воряет начальным условиям (3.27) и, следовательно, uR и
duRfdt должны обращаться в нуль при /=0. Однако поверхность
S лежит в полупространстве Xi>0, поэтому тождество (3.16)
означает, что ф^О на S. Поскольку функция ф возрастает
вдоль отраженных лучей, то она всюду неотрицательна. Далее,
тождество (3.29) означает, что 6i(t)=Ci при т40; следова-
тельно,
L Со J
И
обращаются в нуль при t = 0 тогда и только тогда, когда С! = 0.
Так как функция Zi, вообще говоря, не равна тождественно
нулю, то Ci=0 и
т
("О — J £ (s) ds. (3.33)
о
Аналогично находим
Т X m
J ет-1(т)с/тх= J e(s)ds; /п=1, 2, .... (3.34)
о о
9 То есть для нее 1, a при zn> 1,
96
Р. Льюис
Таким образом, отраженная волна uR полностью определена.
В частном случае параболического цилиндра (3.18) функции ф
и zm даются выражениями (3.19) —(3.23) и
00 т -и
«Я = 2 р ~ -4^] (— -у)”1 S (РГ~1 Sec2 ’ • <3-35)
/««О
Для таких задач, как задача о параболическом цилиндре, не
существует каустик в области определения решения и бегущая
отраженная волна может быть построена во всей области. (Для
параболического цилиндра область определения лежит вне ци-
линдра, в то время как единственная каустика находится в фо-
кусе внутри цилиндра.) Для задач с каустиками в области
определения наше построение дает решение вдоль всех отра-
женных лучей вплоть до первой каустической точки, но не
за ней.
Построив решение краевой задачи (3.26) — (3.28) в виде бе-
гущих волн, рассмотрим смысл полученного формального раз-
ложения. Заметим сначала, что uR является решением гранич-
но-начальной задачи
LuR = Q, ur(Q, X) = ^ur(0, Х) = 0,
если положить
4" = i М' - (- w- (3-37)
т-0
ТО
Л / \ (3.38)
4л)(0. X) = 4«W(0, Х)=0, = на S.
Эти уравнения вытекают из (2.30) и нашего построения uR.
Следовательно, функция
r^(t, X) = tiR — u.W
является решением гранично-начальной задачи
Lr™ = -en\t-(- с0У \zn (X),
L Co J
ГИ)(О, X) = -^.r^(0, X)=0, r^>(0, Х)эО на S.
(3.39)
(3.40)
3. Формальная теория бегущей волны 97
Заметим также, что функции ф(Х) и zm(X) действительны и
не зависят от выбора е(т). Кроме того, нетрудно показать, что
эти функции (которые были построены вплоть до первой кау-
стики на каждом отраженном луче) являются сколь угодно
гладкими при условии, что S — достаточно гладкая поверх-
ность1).
Решение нашей задачи в виде бегущей волны интересно по
крайней мере в трех случаях (в дополнение к асимптотическому
решению приведенного волнового уравнения, рассмотренному
прежде).
1) Предположим, что начальные данные являются сингуляр-
ными, т. е. функция е(т) является разрывной или даже обобщен-
ной функцией2). При достаточно большом п последовательные
интегралы еп(т) являются обычными функциями, сколь угодно
гладкими, если п достаточно велико. Тогда из (3.40) следует,
что остаточный член Нп>, являясь решением задачи с гладкими
начальными данными и гладкой функцией источника, есть тоже
гладкая функция. Поскольку г<п> — гладкая функция, то дол-
жно иметь те же сингулярности, что и и. Таким образом, тео-
рия бегущей волны дает описание «распространения» сингуляр-
ностей начальных данных на решение. На такое приложение
бегущих волн указал Людвиг [12], который изучал сингулярные
решения гиперболических уравнений с гораздо более общей
точки зрения, чем в настоящей работе.
2) Фридлендер [5] показал, что при произвольных функциях
е(т) разложение бегущей волны (3.31) сходится в достаточно
малой окрестности характеристической гиперповерхности
/=ф(Х)/со, а Людвиг [12] доказал подобное утверждение в более
общей постановке. Их результаты имеют следующую физиче-
скую интерпретацию. Отраженная волна приходит в данную
точку X в момент времени /=ф(Х)/со- В течение небольшого
времени, начиная с этого момента, ряд (3.31) сходится и, следо-
вательно, является хорошим приближением к действитель-
ному решению при достаточно большом п.
3) Пусть
е (т) = е~ 1<ЛаХа (/); a(x)sO при т<0. (3-41)
Тогда функция
') Термин гладкий в применении к функции означает, что функция обла-
дает соответствующим числом производных, а в применении к поверхности —
что функция, представляющая поверхность, является гладкой.
4) «Обобщенные функции», или «идеальные функции», такие, как S-функ-
ция Дирака, рассматриваются в книге [4], гл, 6.
7 Зак. 274
98
Р. Льюис
представляет собой модулированную по амплитуде плоскую вол-
ну с частотой йо- Мы покажем, что если функция а(т) является
действительной и гладкой, то наше разложение по бегущим
волнам (3.31) является асимптотическим разложением при
йо-► оо решения гранично-начальной задачи (3.26) — (3.28).Ти*
пичная кривая
у — а (т) cos йот = Re е (т)
приведена на фиг. 2.
Из (3.34) и (3.41) видно, что
т
еп+А^= f e-l<i>>sgn(s)cls; gn (s) = —)Я a (s); n = 0, 1, 2......
о
(3.42)
Если Л==0, 1, 2, .... n—1, to k-я производная g„(s) выра-
жается формулой
fe л у
( 5)(-1)у-(т=^лГ«(й-л(4 (3.43)
7-0 -
а если k = n, n+1, n + 2, ..., то формулой
n n J
g™ W = 2 (kj) (-I/.(T^g7~ aS*-» (s). (3.44)
7-o
Здесь aV} (s) обозначает j-ю производную a(s). Так как a(s)
и все её производные обращаются в нуль при $ = 0, то
g(/)(T) = 0; А = 0, 1, 2, .... (3.45)
Кроме того, из формулы (3.43) следует, что
g(*)(T) = 0; А=0, 1, 2.......л—1, (3.46)
3. Формальная теория бегущей волны
99
в то время как (3.44) означает, что
А = л> л + !> « + 2. .... (3.47)
Теперь для любого неотрицательного целого числа р инте-
грируем (3.42) по частям р-\-п раз. С учетом известной фор{
мулы
г р+п-1
J «($) V ($) ds = У} (—1/ ф(й) Io 4-
О k-0
+ (—1)Р4Л J и!~р-пЧр+п} ds (3.48)
О
из соотношений (3.44) — (3.46) получаем
р+Л-1 .
k-п и/
г
I* о""
+ ds- <3'49>
J z<oo)'
Следовательно,
е-
(- ^0)т
\m — 1 J
x .
У /и — l + а|Л(т> , n /_lx I
y“o\ z”-1 / \®o+Jf
p — Q, 1, 2, ...; m=l, 2................
(3.50)
Выражение (3.50) дает асимптотическое разложение при <оо—>со
для гт(т). Если в этом выражении положить р = п — т и. под-
ставим его в (3.37), то найдем
И(«) = е-1<^+ tk^ да | Zq (X) а [/ — -^2-] +
n-l V-1
V-1 7-0
]+0«) -’(3.51)
здесь А) = ®о/со- Если мы сможем показать, что
г(«=иЛ —и^ = О(©о-я),
(3.52)
7*
100
Р. Льюис
то формула (3.51) даст нам асимптотическое разложение ыд
при <й0-*оо. Строгое доказательство равенства (3.52) можно
получить следующим образом: выражения (3.40) и (3.50) озна-
чают, что
LrW = g(t, X); г(я> (О, X)^±r^(Q, Х)=0;
(и.Ои)
г(л) (0, Х)~0 на S,
где
]g(t, X)\ = a-"b(t, X), (3.54)
a b(t, X)—функция, ограниченная при Остаток rW
можно оценить из (3.53) и (3.54) посредством энергетических
неравенств (см. [4]):
||rW||,< «-"&(/), . (3.55)
где функция b(t) ограничена, когда «о-*оо; l|«llt — «энергети-
ческая норма»:
II «11? = J + utu^dX. (3.56)
Оценивая подобным образом производные остатка Нп) и при-
меняя лемму Соболева [4], можно получить оценку (3.52) с по-
мощью обычной нормы. Мы не пытались, однако, получить эту
оценку и довольствуемся результатом в виде (3.55).
В начале настоящего параграфа мы обсуждали асимптоти-
ческое разложение (3.10) решения краевой задачи для приве-
денного волнового уравнения. Интересно отметить, что общего
доказательства асимптотической природы этого разложения
(такого, как доказательство, которое мы наметим для гранич-
но-начальной задачи) еще не дано. Также невозможно аппрок-
симировать асимптотическое разложение функции установив-
шегося состояния с помощью результата (3.55), поскольку наша
оценка не является равномерной по t.
Заметим, что если положить а(т)^1 при т^То>О, то падаю-
щая плоская волна
является полубесконечной последовательностью волн, гармони-
ческой всюду, за исключением окрестности ее «фронта» Xi. = cot.
В этом случае я<й(т)=0 при т>то и /== 1, 2, .... При
3. Формальная теория бегущей волны
101
выражение (3.51) принимает вид
U.W = e-w+iw да 2 (ikQyvzv (X) + 0 (V)- (3-57)
Интересно сравнить этот результат с рядом (3.10).
§ 4. ИЗЛУЧЕНИЕ ДВИЖУЩИХСЯ ИСТОЧНИКОВ
Начальная задача для неоднородного волнового уравнения
Lu = uXvXv~c^uit=-g(t, X), «(0, X) = ut(0, X)=zp, (4.1)
при постоянной величине с имеет хорошо известное решение [4]
= I X')dX'-, р = \Х-Х'\. (4.2)
P<ct
Точечный источник, движущийся по траектории X=Y(t) и излу-
чающий сигнал e(t), можно описать функцией источника
g(t, X) — e(f)6[X — Y(t)]. (4.3)
Здесь 6[Х] — трехмерная 6-функция Дирака. Подставляя (4.3)
в (4.2), находим, что e(t)=O при /<0, поэтому можно опустить
ограничение области условием р^Сс/. Итак,
пимж-’ф-т)]"'; (44)
Р = |^-Х'\.
Каждая точка X', для которой .
= е-), (4.5)
дает вклад в интеграл (4.4).
Чтобы упростить вычисление интеграла, введем единичный
вектор Л =(04, аг, ссз) и двухпараметрическое семейство лучей
Л' = Г(т)4-гД, xv = t/v(T)4-rav; 0<г, (4.6)
исходящих из точки У(т) во всех направлениях. Эти равенства
совместно с
/ = (4.7)
определяют двухпараметрическое семейство бихарактеристик,
которое порождает характеристический гиперконус с вершиной
102 Р. Льюис
в точке [т, У(т)]. Каждая бихарактеристика, проходящая через
точку (/, X), исходит из точки X'=Y(r), где
с с с с
и, следовательно, дает решение уравнения (4.5). Обратно, для
каждого решения уравнения (4.5) можно положить
т = /-|, г = р = \Х-У(х)\, А = ^^,
и тогда соотношения (4.6) и (4.7) удовлетворяются. Таким об-
разом, существует взаимно однозначное соответствие между
бихарактеристиками, проходящими через точку (/, X), и реше-
ниями уравнения (4.5).
В окрестности каждого решения X' уравнения (4.5) мы вве-
дем преобразование Z=Z(X'), определяемое формулами
Z = р = \Х — Х'\.
Тогда если якобиан
/ = (4’8)
d(*i,x2, х3)
не равен нулю в окрестности каждого решения, то это преобра-
зование имеет единственное обращение в окрестности Z = 0 и
интеграл (4.4) принимает вид
“ЗтН'-т)' <4-9)
Здесь р и j вычислены при Z = 0, а суммирование производится
по решениям уравнения (4.5), т. е. по бихарактеристикам, про-
ходящим через точку (t, X). При Z=0 величина X' удовлетво-
ряет (4.5) и
р = г. (4.Ю)
Чтобы вычислить j, заметим, что
P2=.2«-xv)2;
следовательно,
рД-=<-*,. (4.11)
3. Формальная теория'-бегущей волны
ЮЗ
Тогда поскольку
то
гч = Хч~У. -7)’
(4-12)
При Z — 0
P = r> t — ^ = v, ,x'k^yk(x), x'k — xk — —rak,
и
Теперь якобиан вычисляется просто:
г» = ^(т)ау = У(т)А.
где
(4.13)
(4-14)
(4.15)
Заметим, что v есть составляющая скорости источника в на-
правлении луча (4.6) в «момент излучения» т.
Подставим теперь (4.10) и (4.14) в (4.9). Будем считать, что
решение u(t, X) является суммой членов, причем каждый член
соответствует бихарактеристике, проходящей через точку (I, X).
Тогда член, связанный с любой данной бихарактеристикой, ра-
вен
« = е[ф]г, (4.16)
где ср и г выражаются вдоль бихарактеристик (4.6) и (4.7) фор-
мулами
Ф=т=/— у, (4.17)
г = ~; z (т, av) = 1 . (4.18)
4=ФА|
Нетрудно показать, что и является бегущей волной первого по-
рядка, т. е. и имеет вид (2.2), причем ?т=0 для т>1. Из фор-
мулы (4.17) видно, что функция ф постоянна на каждой биха-
рактеристике (и на всем характеристическом гиперконусе); ниже
прямым вычислением мы убедимся, что ф удовлетворяет харак-
теристическому уравнению (2,4). Семейство лучей, связанных
с характеристической гиперповерхностью ф=т = const, имеет фо-
кус (т. е. точечную каустику) при Х = Y(т). Для такого семейства
104
Р. Льюис
лучей в выражении (2.28) нужно положить pi=p2 = 0, если s
отсчитывается от фокуса. Тогда для /и = 0 имеем
z(s) = z(s0)-^. (4.19)
При $ = 0 функция г бесконечна, однако предел величины sz(s)
при $—»0 конечен. Таким образом, если в (4.19) положить s0—>0
и отождествить s с г, то равенство (4.19) дает
г — —; z = limrz(r). (4.20)
г г->0
Для волны (4.16) функция z дается формулой (4.18).
Рассмотренная задача в известном смысле тривиальна, так
как точное решение уже задано формулой (4.2). Однако наше
представление решения в виде бегущей волны показывает, что
с помощью теории бегущей волны можно рассмотреть два типа
нетривиальных задач.
Первый тип — это краевая задача, в которой к гранично-на-
чальной задаче (4.1) добавлено однородное граничное условие
на некоторой поверхности S. В этом случае необходимо только
добавить к (4.16) «отраженную бегущую волну», которая опре-
деляется аналогично тому, как это делалось при рассмотрении
задач отражения в § 3 (или в § 5, если S движется).
Второй тип — это начальная задача (4.1), в которой с не
является постоянной, a g по-прежнему выражается формулой
(4.3). В этом случае разумно предположить что, как и прежде,
бихарактеристики исходят из каждой точки [т, У(т)], а /функ-
ция q> имеет на них постоянное значение т. Для неоднородной
среды функция z должна быть получена из выражения (2.26),
которое при т = 0 принимает вид
2(5) = г(5о)[т^Т^Г^]1/2- (4-21)
Точка Х=У(т) снова является фокусом соответствующего се-
мейства лучей (которые теперь, вообще говоря, изогнуты), и
если s отсчитывается от фокуса, то функция z снова бесконеч-
на при z=0. Однако
da (s0) ~ si dQ, s0->0, (4.22)
где dQ— элемент телесного угла с вершиной в фокусе. Если
подставить (4.22) в (4.21) и положить $о->О, то получим
<4-23>
где
z = lira soz (s0). (4.24)
“►О
3. Формальная теория бегущей волны.
105
Выражение (4.23) определяет значение г вдоль каждой бихарак-
теристики, за исключением коэффициента z, являющегося
функцией т и единичного вектора А. Вектор А определяет на-
чальное направление соответствующего луча.
Теперь предположим, что функция z выражается формулой
(4.18), где скорость v определяется по формуле (4.15), а вели-
чина с заменена на с[У(т)]. Тогда функции z и q> полностью
определены. Полагая е0=е, мы завершаем построение главного
члена (т = 0) решения нашей задачи в виде бегущей вол-
ны (2.2).
Описанный метод решения очень похож на метод, развитый
Келлером в связи с асимптотической теорией приведенного вол-
нового уравнения [11]. Основная черта этого метода состоит в
нахождении некоторых неопределенных величин’) в разложении
по бегущим волнам (в приведенном выше примере — функция?)
путем сравнения с решением канонической задачи, которая мо-
жет быть решена точно и которая имеет те же локальные черты,
что и данная задача. В нашем примере канонической задачей
является задача с постоянной величиной с. Не было дано ника-
кого общего доказательства справедливости метода, однако он
успешно применялся в многочисленных частных случаях. Метод,
который мы изложили, нельзя непосредственно обобщить так,
чтобы он давал следующие члены в разложении, но для этих
целей предложены «методы пограничного слоя» [1, 3], которые
применимы к рассмотренной здесь задаче. Во многих прило-
жениях достаточно найти главный член разложения.
Можно получить некоторые интересные свойства- нашего ре-
шения (4.16), вычисляя производные т и г по t и xv. Диффе-
ренцируя неявную функцию (4.6) и учитывая (4.7) и выраже-
ние avav=l, получаем
% =^y.+ \av+ %(%),. ==° (4-25)
и
0 = i/vT/ + r(av + r(av)/, 1=д + с?-Др аДаД = 0. (4.26)
Далее, из (4.26) и (4.15) имеем
0 = ^vavT/ + r/ = v// + c(l—тД (4.27)
и, следовательно,
С4-28)
*) В работе Келлера неопределенные величины часто называются «ди-
фракционными коэффициентами» (см. [7, 11]).
106
Р. Льюис
Аналогично из (4.25)
“j = Wx, + ГХ) = (^ ~ с) (4.29)
и поэтому
а< / v\-1 / v\-1
t:Xj = — (1 — -j . rXj = av(l—. (4.30)
Можно проверить, что <р = т удовлетворяет характеристиче-
скому уравнению (2.4) [это является непосредственным след-
ствием (4.28) и (4.30)] при
В фиксированной точке X мы определим принимаемую ча-
стоту v, которая пропорциональна <р<, т. е.
v = v0<p/t (4.32)
где vo зависит от выбора формы волны е(т) ’)• В движущейся
точке X=X(t) принимаемая частота определяется формулой
v = vo4<Pl/- + (4-33)
Из (4.17), (4.28) и (4.30) получаем
Xt Ч1 “7/ L1-“"*r]Vo==T=^rvO’ <4-34>
где
dxi
— (4.35)
Заметим, , что w является составляющей «скорости приемника»
dX/dt в направлении источника, в то время как v есть состав-
ляющая скорости источника У в направлении приемника. Мно-
житель (1 + щ/с)/(1—v/c) в (4.34)—хорошо известный множи-
тель Допплера, вызванный одновременным движением источ-
ника и приемника.
Как уже отмечалось выше, каждая точка Х=У(т) является
фокусом семейства лучей, связанных с характеристической ги-
перповерхностью (т. е. гиперконусом) <р(/, X) =т, причем каж-
дое такое семейство не имеет никакой другой каустики, посколь-
ку лучи имеют вид просто радиальных линий, исходящих из фо-
*) Так, например, если е(т)=# 1апХ, io и = е x^z(t, X) и у =
~ т. е. vfl = wp.
3. Формальная теория бегущей воЛны
107
куса. Однако в случае |У|>с однопараметрическое семейство
характеристических гиперконусов имеет огибающую. Чтобы убе-
диться в этом, запишем семейство гиперповерхностей в виде
[X — У (т)]2 = с2 (/— т)2.
(4.36)
Это выражение получено посредством исключения г и А из (4.6)
и (4.7). Дифференцирование по т дает
[Х-У(т)].У(т)=:С2(/-т).
(4-37)
На пересечении двух гиперповерхностей (4.36) и (4.37)
Д.У(т) = с.
(4.38)
Таким образом, две гиперповерхности пересекаются вдоль одно-
параметрического семейства бихарактеристик (4.6) и (4.7), для
которого вектор А удовлетворяет уравнению (4.38). Когда т ме-
няется, эти бихарактеристики порождают огибающую, которая
описывается формулами (4.6), (4.7) и (4.38).
Из (4.15) и (4.38) мы видим, что на огибающей
V = с,
(4.39)
поэтому из (4.16) и (4.18) следует, что функция и является син-
гулярной. Если | Y | > с, то более чем одна из бихарактеристик,
исходящих из точек нахождения источника [т, У (т)], может прой-
ти через заданную точку (Л X). Действительно, чтобы найти все
Фиг. 3. Бихарактеристики, выходящие из источников в двух
пространственно-временных точках [ть Y (тг)] и [т2, Y (т2)];
а — | Y (т) | < с; б — | Y (т) | > с.
В случае 6 через данную пространственно-временную точку Р может прохо-
дить более чем одна бихарактеристика (на рисунке показаны две бихаркте-
ристнкн). В случае а характеристические гиперконусы не пересекаются н
через точку Р может проходить самое большее одна бихарактеристика.
бихарактеристики, достигающие точки (i, X), нужно лишь по-
строить обратный характеристический гиперконус из этой точки
и найти его пересечения с линией источника [т, У(т)]. Если д
108
Р. Льюис
бихарактеристик проходит через точку (t, X), то решение и в
этой точке является суммой q членов вида (4.16). Если ни одна
бихарактеристика не проходит через точку (/, X), то эта точка
находится вне «области влияния» источника и функция и в ней
равняется нулю.
Если I Ё|<с, то (4.38) никогда не удовлетворяется и семей-
ство характеристических гиперконусов не имеет огибающей.
В этом случае линия источника может пересекать обратный ха-
рактеристический конус самое большее один раз и лишь одна
бихарактеристика проходит через каждую точку (t, X).
Конечно, все результаты настоящего параграфа применимы
и к частному случаю неподвижного точечного источника
£(Л X) = e{t)b[X-Y\, (4.40)
где У — постоянный вектор. Случаи |У.|<с и |У|>С схематиче-
ски изображены на фиг. 3.
§ 5. ОТРАЖЕНИЕ ОТ ДВИЖУЩЕЙСЯ ПОВЕРХНОСТИ
В задачах об отражении бегущей волны от движущейся по-
верхности мы предположим, что падающая волна возбуждает
отраженную, и потребуем, чтобы сумма этих волн удовлетво-
ряла заданному краевому условию на отражающей поверхности
S. Если через <р* и <рг обозначить фазовые функции падающей
и отраженной волн, то граничное условие означает, что
<рг(/, А')^=ф/(/, X) на S. (5.1)
Чтобы найти <рг, нужно решить начальную задачу для характе-
ристического уравнения с начальными данными (5.1).
Если подставить (5.1) в (2.17), то это уравнение примет вид
дх° т dt° ___ d<fl [f° (2), Х(2)] _ ( dx°v г dt°
v дО] W да/ ~ ddj v doj daj ’
(5-2)
или
>)v-0
(^_^)_L_(^_(0')__ = 0; /=1,2,3. (5.3)
Здесь klv = d<f>l/dxv, a a1 — — dql/dt. Предположим, что S можно
представить в виде xv = x^(op о2, т), t = x. Тогда (5.3) можно
записать следующим образом:
дх°
«-*Э-^=0; у = 1.2; -(»'-»')=о. (5.4)
3. Формальная теория бегущей волны
109
Пусть Af=(ni, «2, п3) —мгновенная единичная нормаль к по-
верхности S в направлении, показанном на фиг. 4. Определим
нормальную (со знаком) скорость о0 поверхности как
= = (5.5)
и дт дт v 4 '
Тогда (5.4) означает, что
Кт-К1 = ^ (5.6)
и
..Г I ___ ([/-Г rsl\ _
to — to = (л — Л ) • -fo- =
= Mr.-^- = W. (5.7)
ОХ ' 7
Здесь X — скаляр, который нужно оп-
ределить.
Из (5.6) видно, что векторы Кт, К1
и N лежат в одной и той же «плоско-
сти падения». Кроме того, равенства
(2.9) и (2.10) означают, что падающие
и отраженные лучи имеют направле-
Фиг. 4. Плоскость падения
для случая отражения от
движущейся поверхности S.
N— мгновенный единичный век-
тор нормали в точке Р; 0* и
0Г —углы падения и отражения;
векторы G1 и Gr имеют направле-
ния соответственно падающего н
отраженного лучей. Фигура изо-
бражает плоское сечение Х-про-
страиства, а не сечение простран-
ства-времени.
ния
(5-8)
Здесь лучам была приписана ориентация, соответствующая уве-
личению значений параметра t\ они показаны на фиг. 4.
Непосредственно из (5.6) следует, что КгХЛ^ = КгХМ; следо-
вательно, из (5.8) имеем
&rGrXN = v>lGlXN. (5.9)
Из (5.6) и (5.7) видно, что
т°Кг N — т°К1 N = &r -&1,
поэтому из (5.8) следует, что
v°(prGr • N — т)°а‘О1 • N = с2 (сог — о?). (5.10)
Поскольку | Gr | = | G11 = с, то (5.9) означает, что
tor sin 0r = to‘sin 0г, (5-11)
а (5.10) означает, что
юг (с — и0 cos 0r)== to'(t?+ t°cos 0г). (5.12)
110
Р. Льюис
Здесь 0’ и 0Г— углы падения и отражения, показанные на фиг. 4.
Наконец, (5.11) и (5.12) дают
sin О'’ sin ..ox
1 — (у о/с) cos 1 + (у o/c) cos 0z
Выражение (5.13) определяет 0Г неявно через 0’ и v0/c. Те-
перь мы определим 0Г, <вг и Gr= (c2/ar)Kr явно. Для этого удоб-
но положить x=cos0r и t/ = cos0!. Возводя обе части равенства
(5.13) в квадрат, освобождая от знаменателя и группируя
члены, получаем квадратное уравнение
ах2 -J- 2(3х + у = 0, (5.14)
где
V = -4+2(i) + (i),!,].
Непосредственно решить уравнение (5.14), конечно, можно, но
сложно, поэтому мы поступим иначе. Заметим, что одно решение
(5.13) дается формулой
0r=n— 0г, cos0r = — cos 0г, sin 0r = sin 0Z.
Это решение соответствует просто падающей волне, т. е.
<рг^<р’. Аналогично.одно решение (5.14) есть х =—у. Чтобы
найти второе решение, х—z, можно положить
ах2 4- 2рх + у = а (х 4- у) (х — z) = ах2 4- ах (у — z) — ayz. (5.16)
Из этого уравнения непосредственно видно, что у = — ayz,
поэтому
v_ —у _ у [1 ч-(Ур/с)2] н-2 (Ур/с) 1 ~
ay — [1 4-(Уо/С)2] + 2 (Уо/с) У • { 1 ’
Отсюда следует, что
rns 0r — cos9' + fl • а = 2 (г?о/с)
1 a cos 0г 14- (Уо/с)2
(5.18)
Эту формулу можно назвать законом отражения для движу-
щихся тел. Она переходит в обычный «закон отражения» при
-5»о = 0.
Из (5.17) получаем
i До. г _ [1 — (уо/с)2] [1 4- (t'o/c) У] .
с л 1 4-(Ур/с)2 4-2 (vjc)y •
(5.19)
S. Формальная теория бегущей волны
Ш
далее (5.11), (5.13) и (5.19) дают
ог _ sin 9Z _ 1 + (у0/с) у _ 1 4- (у0/с)2 4- 2 (Уо/с) у __
®г sin 9r 1 — (Уо/с) х 1 — (Уо/с)2 5
_ 1 + 2 (ур/с) cos 9* 4- (уц/с)2
1 — (vo/c)2
(5.20)
Из (5.7) и (5.20)
X = -L (о/ — о/) == (®L — 1 \
у° v ' У° \ <0z )
Следовательно, (5.6) дает
С 1 — (Vo/C)
=K‘+^x^^N-
2®г (y0/c) + cos9' /п
с 1-(Уо/с)2 ’
Соотношения (5.18), (5.20) и (5.22) дают искомые формулы для
0Г, аг и & = (с2/<))г)Кг. В каждой точке отражения
[т, №(ap о2, т)] = [т, х», 4 х°]
(5.18), (5.20) и (5.22) дают значения
(ог = (ог(а1( о2, т), kTv = krv(av о2, т) и grv = ^v(av <у2, т).
Эти значения используются для того, чтобы определить отра-
женный луч X — X(t', Ор о2, т)> Для которого X (т; оь о2, т) =
= №(Op о2, т). Тогда, согласно (2.Г1), функция <рг постоянна
вдоль соответствующей бихарактеристики; следовательно, из
(5.1) имеем
<рг [/, X (/; Ор о2, т)] = <рг [т, X (т; Ор о2, т)] =
= <р'’[т, Х°(ор о2, т)] == <pz [т, A"0(ap о2, т)]. (5.23)
В качестве иллюстрации теории отражения движущимися
поверхностями рассмотрим задачу об отражении плоской бегу-
щей волны в однородной среде, наклонно падающей на движу-
щуюся плоскую границу S. Граница остается нормальной к оси
%1 и пересекает ее в точке Xi=f(O, как показано на фиг. 5.
Пусть c=const, и пусть на S имеет место граничное условие
и—0.
Падающую волну возьмем в виде
ul(t, X) = e[(pz(/, X)l, <pz = /-X—ct = — cos-0z H-x2sin0z—ct
(5.24
Здесь Х*=(хь Xz), 0’— постоянный угол падения и е(<р)—про-
извольная функция. Легко видеть, что <р’ удовлетворяет харак-
112
Р. Льюис
теристическому уравнению (2.4), а «{ есть бегущая волна (пер-
вого порядка); в действительности «’ есть точное решение вол-
нового уравнения.
Фиг. 5. Отражение плоской бегущей волны от плоской
поверхности S, движущейся параллельно самой себе.
I н 7?—единичные векторы в направлении падающего и отраженного лучей.
Чтобы удовлетворить граничному условию, положим
и = и1 + иг. Отраженная бегущая волна равна
u'(t, Х)=2^^(Л X); e'm — em_v (5.25)
m=0
Введем граничные параметры ти а, с помощью которых поверх-
ность S выразится формулами
х1=/(т), х2 = о, t = x. (5.26)
Тогда граничное условие примет вид
е[фг(т, f, ff)]+ 2 ет [<рг(т, f, <j)]z(m)(T, f, о) = 0. (5.27)
m-0
Из этого уравнения заключаем, что •
<рг(т, f, о) = (р'(т, f, о) = — f (т) cos 0Z + о sin 0Z — ex, (5.28)
eQ — e, (5.29)
и
z<°> (T, f, о) = — 1; (т, f, о) = 0; «1=1,2.....(5.30)
Из (5.18) находим угол отражения 0Г = 0г(т):
cos0Г= ic°s9f+a-, а = -Л-, ~Ь = ^, Ь = Ш. (5.31)
l-]-acos0z 1 -j- (b)2 dx с '
Отраженные бихарактеристики являются, конечно, прямыми ли-
ниями, исходящими из 5. С помощью параметра s (s обозначает
3. Формальная теория бегущей волны 113
длину дуги вдоль соответствующего луча) бихарактеристики вы-
ражаются формулами
Xi = Xi (s; т, а) = f (т) -|- s cos 0r (т), (5.32)
х2 — х2 ($; т> а) = ° ~Ь $ sin 0Г (т), (5.33)
/ = / (s; т, o) = T-|-<?_1s, (5.34)
причем на каждой бихарактеристике <рг имеет постоянное зна-
чение, даваемое формулой (5.28).
Функцию г<°> можно получить из (2.28). В связи с тем что
задача не зависит от третьей пространственной переменной Хз,
один радиус кривизны является бесконечным, и из- (2.28) полу-
чаем
Г А 11/2 Г с-1-’/2
2(0)(s)==z(0)(0)[_^_] + . (5.35)
Здесь мы использовали (5.30), чтобы получить г<°>(0)=—1.
Для нахождения р заметим, что, как следует из (5.28), если
фо—какая-либо постоянная, то «отраженная характеристиче-
ская поверхность» фг(/, Х)=ф0 пересекает S по кривой
— f (т) cos 0Z -|- о sin 0z — ex = ф0;
следовательно,
а = о (т) = . (5.з6)
v sin6z v '
Из этого выражения и из (5.13) получаем
А м — c+f COS 6г _ С—/COS О' , е
( ' sin 9^ sine'- ( '
Бихарактеристики, исходящие из кривой сг=сг(т), лежат на дан-
ной характеристической поверхности, и соответствующее семей-
ство лучей дается формулами ')
хг — f + s cos 0Г, х2 = о (т) -1- s sin 0Г,
или
* = [/. + (5.38)
Здесь 7?=(cos0r, sin 0r)—единичный вектор в направлении от-
раженного луча. Так как, по определению, р — радиус кривизны
волнового фронта при s = 0, то каустика, или огибающая этих
лучей получается, когда s = —р(т), т. е. уравнение каустики
есть
Х = Х(т) = (Ь а) — р/?. (5.39)
’) Это семейство лучей является однопараметрическим семейством, так
как задача не зависит от третьей пространственной переменной х3.
8 Зак. 274
114
Р. Льюис
Значение р может быть получено из условия, что тангенциаль-
ный к каустике вектор Х(т) параллелен направлению луча
R>= (cos 0r, sin 0r), т. e. перпендикулярен вектору U= (—sin 0r,
cos 0r). Тогда условие X • U=0 дает
f sin 0r — о cos 0r + p0r == 0,
или с учетом (5.37)
__ c cos 0r — f_c(b — cos 0r)
P 0rsin0r cos 0r
Далее, из (5T31) имеем
• 2?(l-d2)
(1+*2)2 ’
(cos 0ГУ = a sin‘ 9‘ = 2'b(1 ~ sin2 Ql
k ' (1 4- a cos 0')2 (1 — 2i cos 0г 4-ft2)2
и
b _ cos 0Г = £ _ (1+fo cos 0' + 2fr = (6 +cos 0') (»2-l)
14-24 cos 0'4-ft2 1-|-26со8 0г4-£2
(5.40)
(5.41)
(5.42)
(5.43)
. (5.44)
Наконец, (5.41), (5.43) и (5.44) дают
о = р (т) = — с $ +cos + 2*cos 9<) _
1 7 26 sin2 0'
— _ (I + с cos Ql) [1 + (f/c)2 + 2 (f/c) cos 0г] _ .
2 (f/c) sin2 0' ’
Заметим, что величина р была вычислена при использовании
семейства лучей, связанного с единственной характеристической
поверхностью фг(/, Х)=фо.
Теперь мы можем выразить главный член отраженной бегу-
щей волны параметрически через параметры т, а и s. Из (5.25),
(5.28), (5.29) и (5.35) имеем
UT (t, Xj, Х2) — ~е[—f СО cos 0Z4“OSin 0' — ст] р 4- +•••;
(5.46)
здесь р(т) выражается формулой (5.45), 0г(т)—формулой
(5.31) и (xi, Х2, 0 — параметрически формулами (5.32) — (5.34).
Из (5.32) — (5.34) можно вычислить якобиан
. d (xt, х2, i)
' д (з, а, т)
3. Формальная теория бегущей волны
115
(5-47)
(5.48)
Результат получается следующий
J = cos 0Г с-1 [/ -j- s (cos 0r)'],
что при s = 0 с учетом (5.44) дает
1 + 2b cos 0Z -I- b‘
Из этого выражения видно, что в окрестности поверхности 5
/=#0, и (5.32) — (5.34) можно разрешить относительно т, о и s
как функции t, Xi, х2 при условии, что
b 4= ± 1, т. е. f = v0 4= ± с, (5.49)
и
b Ф — cos0£, т. е, | = -и0=£= — ccos0£. (5.50)
Эти условия имеют интересную интерпретацию. Если и0=±с,
то граница S движется со скоростью распространения с; если
же и0=—с cos 0’, то падающие бихарактеристики в простран-
стве— времени тангенциальны к границе, т. е. падающий сигнал
никогда не достигает удаляющейся границы. Последнее утверж-
дение справедливо также, если и0<—ccos0*. Поэтому на f(t)
мы налагаем условие
— с cos 0Z </(/)< с. (5.51)
Это условие, в частности, означает, что граница является вре-
менноподобной [4].
Рассмотрим теперь частный случай равномерного перемеще-
ния границы: f(/)=u0^ где и0 — постоянная. Тогда угол 0г по-
стоянен и дается формулой (5.31). Из (5.28), (5.32), (5.34) и
(5.13) имеем
Г • al Г / с -4- Va COS 0‘ XI • л/Г I /VnCOS0r — с XI
mr = sin 0‘ а — т | ~ °-------- = sin 0 а 4- т I —---------- =
L V sin 0Z I] L \ sin 0r /]
= S'in fy- [цот cos 0r -j- о sin 0r — ctl ==
sin 0r 1 u 1 J
= Iх!cos 0r + *2sin 0r - = Sr • * - <4 (5.52)
Olli V _| oill V
a из (5.45) видим, что p=oo. Следовательно, (5.46) принимает
вид
ur (t, X) = - е [-^-(Я • X - с/)]. (5.53)
Выражение (5.53) есть точное решение волнового уравнения;
легко проверить, что граничное условие и{ + иг — 0 выполнено.
Из (5.13) получаем
sin 0f с v0 cos Ql (C. -
sin0r c — v0 cos 0r ' ' '
8*
116
Р. Льюис
следовательно, при нормальном падении 0г = О, 0Г = О и (5.53)
дает
«г (Л Х) = — е (X! - с/)]. (5.55)
ПРИЛОЖЕНИЕ. РЕШЕНИЕ УРАВНЕНИЯ ПЕРЕНОСА
Для решения уравнения переноса (2.21) определим вектор
F с компонентами
f Л = г = 1,2,3. (П. 1)
/г <о с2 ’ v '
Поскольку ©л-г = — ф^ = — (k^
V(0==-^; (П.2)
так как К2 = № — аР/с2, то
Kt • к=4 (п=4 (-Я=с~2^- (п- з)
Следовательно,
= Д w + Д»,] = I [ф„А - 7- Ф„] = I Со- (П. 4)
Подставляя (П.4) в (2.21), получаем
тН+^г+4г777=0- <п-5)
Пусть (t0, Хо) —любая пространственно-временная точка, и
пусть фо = ф(^о, Хо). Тогда характеристическая гиперповерхность
ф(/, Х)=фо проходит через данную точку. Поскольку характери-
стическая гиперповерхность нигде не параллельна оси t, то
ф(/, Х)=фо можно представить в виде /=т(Х), отсюда
ф[т(Х), Х] = Фо. (П. 6)
Дифференцирование (П. 6) дает
(₽<\+(₽хгв-®\+^=0;
следовательно,
s=4-1‘- м
Теперь положим
2(X)^z[r(X), X], М*) = Ыт(*), X], (П.8)
^ = (/b к /з)
3. Формальная теория бегущей волны
117
и заметим, что zr =zx, -L-Zx. — f.z,4-ги. Следовательно, так
xi I xl I I I I
как ^ = £2/<о2= 1/с2, то
р. •гЖг = ^[^ + гХ/] = А-г< + ^г- (п- 9)
Кроме того,
(м(ь=|ш=|(|)=о;
поэтому
(П-10)
Если подставить (П. 8) — (П. 10) в (П. 5), то получим
V.(z2F) = 2z[A Vz + |zV-F]=0. (П.11)
Таким образом мы свели левую часть уравнения переноса к
дивергенции.
Заметим, что z(X) и fi(X)—просто значения z(t, X) и
f(t, X) на характеристической гиперповерхности t=r(X), прохо-
дящей через точку (/0, Хо). Пусть
(t, X) —любая другая точка на
этой бихарактеристике. Проекция
бихарактеристики есть луч, ко-
торый проходит через точки Хо
и X. Это иллюстрируется на
фиг. 61). Поверхности ф(/0, X) =
= ф0 И ф(/, Х)=фо являются вол-
новыми фронтами, связанными с
характеристической гиперповерх-
ностью t=T(X). Согласно (2.10),
лучи всюду параллельны векто-
ру G, а следовательно, и векто-
ру F. Образуем бесконечно ма-
лую трубку этих лучей (два из
которых показаны на фигуре
Фиг. 6. Бесконечно малая трубка
лучей, которые проходят через
точки Ха и X.
Трубка образована лучами, ортогональ-
ными к 'волновым фронтам ф Цо, X) — ф0
и ф Ц, X) = ф0. Трубка находится в Х-про-
странстве, а фигура представляет ее про-
дольное сечение.
пунктирными линиями) и приме-
ним теорему Гаусса к части этой трубки, отсекаемой двумя
волновыми фронтами. Поскольку вектор F всюду параллелен
>) В данном случае наглядное геометрическое представление затруднено
четырехмерным характером (t, ^-пространства. Поэтому полезно представить
себе трехмерный случай двух пространственных переменных. В этом слу-
чае гиперповерхность является поверхностью, волновой фронт — кривой,
а трубка — полосой и- фиг, 6 правильно представляет двумерное Х-про-
странство.
.18
Р. Льюис
этим лучам и |^|= \1с(Х), то (П. 11) дает
z* (X) da (X) - z* (Хо) da (Хо) ==
= j $z2F-Nda = j J J V- (z2F)dX = 0. (П. 12)
Здесь da(X) —площадь поперечного сечения трубки в точке X.
Пусть X — X(t) —уравнение луча на фигуре, тогда X(t0)=X0.
Положим также, что z(t)=z[t, Х(/)]. Тогда z(t0) =z[t0, X0] = z(X0)
и аналогично z(t) =z(X). Положим наконец, чтоda(t) = da[X(t)]
и c(t) = c[X(t)]. Тогда формула (П. 12) принимает вид
г(')=гМтеттЖ- <п-13)
ЛИТЕРАТУРА
1. Avila G. S. S., Keller J. В., Comm. Pure Appl. Math., 16, 363 (1963).
The High-Frequency Asymptotic Field of a Point Source in an Inhomoge-
neous Medium. .
2. Бабич В. M„ Алексеев А. С., Изв. АН СССР, сер. геофиз, 9 (1958).
Лучевой метод вычисления интенсивностей волнового фронта.
3. Buchal R. N, Keller J. В, Comm. Pure Appl. Math., 13, 85 (1960).
Boundary Layer Problems in Diffraction Theory.
4. С о u r a n t R., Hilbert I)., Metoden der matematische Physik, Berlin,
1931. (Имеется перевод: P. Курант, Д. Гильберт, Методы матема-
тической физики, ч. II, М. — Л, 1951.)
5. F г i е d 1 а п d е г F. G., Sound Pulses, London, 1958. (Имеется перевод:
Ф. Фридлендер, Звуковые импульсы, ИЛ, 1962)
6 К а у I., Keller J. В., Journ. Appl. Phys., 25, 876 (1954).
Asymptotic Evaluation of the Field at a Caustic.
7. Keller J. B., Proc. Simposium on Microwave Optics, McGill University,
Montreal, Canada, 1953.
The Geometrical Theory of Diffraction.
См. также Journ. Opt. Soc. Amer., 52, 116 (1962).
8. Keller J. B., Lewis R. M, Seckier B. D., Comm. Pure Appl. Math.,
9, 207 (1956).
Asymptotic Solution of Some Diffraction Problems.
9. Lax P. D, Duke Math. Journ., 24, 627 (1957).
Asymptotic Solutions of Oscillatory Initial Value Problems.
10 LewisR. M, Journ Math. Meeh , 7, 593 (1958).
Asymptotic Expansion of Steady-State Solutions of Symmetric Hyperbolic
Linear Differential Equations.
11. Lewis R. M, Keller J. B., NYU Research Report, E. M.-194, 1964.
Asymptotic Methods for Partial Differential Equations: The Reduced Wave
Equation and Maxwell’s Equations.
12. Ludwig D, Comm. Pure Appl. Math., 13, 473 (1960).
Exact and Asymptotic Solutions of the Cauchy Problem.
13. L u d w i g D„ NYU Research Report, A. E. C„ N. Y. 0.-9351.
The Singularities of the Riemann Function. - '
4
ПОЛУГЕОМЕТРИЧЕСКОЕ ПРИБЛИЖЕНИЕ
К ЯВЛЕНИЮ РАССЕЯНИЯ
X. Бреммер*
Основные эффекты, возникающие при распространении волн в слабо не-
однородной среде со случайными нерегулярностями, можно описать через
искажения волнового фронта, а также флуктуации амплитуды и фазы. Эти
эффекты можно получить, применяя борновское приближение в строгой тео-
рии дифракции к случаю малых углов Полученные выражения для флук-
туаций амплитуды позволяют рассмотреть вопрос о том, составляют ли по-
следовательные рассеяния марковский процесс,
§ 1. ВВЕДЕНИЕ
Рассеивающее влияние локальных нерегулярностей на рас-
пространение волны в слабо неоднородной среде можно иссле-
довать, сочетая оптическое рассмотрение со статистикой. Ис-
пользование статистического подхода (изложенного в общем
виде в работе [5]) необходимо в обычных приложениях, если
локальные неоднородности полагаются случайными. В первом
приближении влияние неоднородностей можно выразить через
малые изменения амплитуды и фазы проходящей волны или
через искажения волнового фронта последней. Другая возмож-
ная интерпретация этого явления подчеркивает рассеивающие
эффекты, вызываемые такой средой. Первое (главным образом
геометрооптическое) описание непосредственно зависит от авто-
корреляционной функции пространственного распределения от-
клонений показателя преломления бп. Второе же описание не-
посредственно связано с функцией изменения дифференциального
поперечного сечения а, которая дает распределение рассеянной
энергии по различным направлениям. Эти основные функции
связаны соотношением Винера — Хинчина.
Для обоих упомянутых выше описаний результаты первого
порядка можно получить из борновского приближения. Это при-
ближение не учитывает величин более выского порядка малости,
♦ Н В rem me г, Philips Research Laboratories, N. V. Philips GIpnilam
penfabrihen, Eindhoven, Netherlands
120
X. Бреммер
чем бп, что эквивалентно пренебрежению эффектами, связанны-
ми с многократным рассеянием. Для неоднородной среды гео-
метрооптическое описание особенно удобно при не слишком
глубоком проникновении внутрь среды. Эффекты отклонения
геометрооптических траекторий от прямой доминируют в этом
случае над дифракционными эффектами. Область, в которой
рассеяние вполне изучено (см., например, [7]), можно назвать
зоной Френеля. Действительно, свойства этой области подобны
свойствам соответствующей области для оптического изображе-
ния, где распределение волновой функции в области Френеля
лишь слегка отличается от распределения в начальной плоско-
сти, в которой оно определяется, например, данным объектом.
С другой стороны, описание явлений с точки зрения теории
рассеяния соответствует более глубокому проникновению внутрь
неоднородной среды. Дифракционные эффекты, связанные с
общей функцией распределения би, становятся здесь более су-
щественными, чем эффекты, связанные с отклонениями геомет-
рооптических траекторий, которые в этом случае очень сложны.
Мы можем использовать для этой области термин «зона
Фраунгофера», так как ее свойства можно уподобить свойствам
области того же названия в теории оптических изображений,
расположенной на большом расстоянии от выше упомянутой
начальной плоскости; в обоих случаях дифракционные эффекты
преобладают. В существующей теории рассеяния действие ко-
герентно рассеивающего элемента («шарика») изучается в пред-
положении о прямолинейном распространении волн от источ-
ника до рассеивающего элемента и от последнего до точки
наблюдения. Эффекты, связанные с кривизной траекторий, ис-
следованы в работе [6]. Изложенная в ней теория позволяет
рассматривать среды, содержащие большие неоднородности.
В настоящей статье исследуется слабо неоднородная рассеи-
вающая среда, к которой применимо борцовское приближение.
Кроме того, предполагается, что изменения показателя прелом-
ления на расстояниях порядка длины волны малы. Последнее
эквивалентно тому, что среда рассеивает в основном вперед.
Свойства среды в данной задаче представлены так, чтобы
четко показать переход от зоны Френеля к зоне Фраунгофера.
Вначале рассматривается среда с фиксированным распределе-
нием отклонения бп, после чего делается переход к случайной
среде. Для последней результаты даны частично с помощью
автокорреляционных функций, частично с помощью функций
рассеяния.
Среда, подобная рассматриваемой в этой статье, исследова-
лась Фаннином [4] для весьма частного вида автокорреляцион-
ной функции. Один из наиболее интересных результатов Фан-
4. Полугеометрическое приближение к явлению рассеяния
121
нина, а именно простое соотношение между флуктуациями фазы
в зонах Френеля и Фраунгофера, выводится в настоящей работе
для произвольной случайной среды, рассеивающей главным
образом вперед.
§ 2. БОРНОВСКОЕ ПРИБЛИЖЕНИЕ ДЛЯ СЛУЧАЯ ПЛОСКОЙ ВОЛНЫ,
ПАДАЮЩЕЙ НА СЛАБО НЕОДНОРОДНУЮ СРЕДУ
Допустим, что слабо неоднородная среда занимает полупро-
странство г>0 и имеет следующее распределение коэффициента
преломления:
п(х, у, z) = 1 + бга (х, у, z)._
Распространение монохроматической волны с волновым числом
в вакууме kQ описывается (в пренебрежении величинами поряд-
ка бп2) скалярным волновым уравнением .
V2u-|-^« = — 2£2бга(х, у, z)u.
Пусть плоская волна (с временным множителем
е-ги() распространяется в положительном направлении оси z
и входит в исследуемую среду при z=0. В борцовском прибли-
жении общая волновая функция при z>0 записывается следую-
щим образом:
62 ik.(z+QP\
Rn г С С .„ Р Я >
и (Р) = el ozp -ь J J j dxq Ъп (Q) Qp , (1)
г?>0
где QP есть расстояние от точки наблюдения Р до точки интег-
рирования Q, расположенной в элементарном объеме dxq =
= dxqdyqdzq.
Проведем ось z через точку наблюдения Р(0, 0, d) и огра-
ничим неоднородную среду слоем 0<z<d; среда вне z — d бу-
дет давать лишь малый эффект обратного рассеяния. Рассеян-
ная компонента поля запишется в виде
k2n ? [z+VjP-uP + (d-zi)l
[dz^dxdybntx, у.
Это выражение можно преобразовать следующим образом. Вве-
дем полярные координаты с помощью соотношения х + 1у = Хе‘Ч
и заменим отклонение бп(х, у, г) его разложением в ряд Мак-
лорена в символической форме
д в , ( О д \
6п (х, у, г) ~ е* да нг/ дЬ Ъп (a, b,z)~e' '°s Ф да т s ° Ф дЬ' бга {а, Ь, г)
при а — Ь = 0.
122
X. Бреммер
Производя интегрирование по <р, получаем
, d со_______________________________________
ирас (Р) — k2eik°z j J dz j rfXX/o у X
I о о
J*orv+(d-z)=
X ;> =гбга(а, b, z)
y\2 + (d —г)2 v ’
Интеграл по А хорошо известен из представления функции
поля точечного источника егкг]г с помощью мод в цилиндриче-
ских координатах при условии, что (—дуда2—(92/(962)V2 есть рас-
стояние по радиусу (число k расположено в первом квадранте
комплексной плоскости). Формальное применение здесь инте-
грала к символическому квадратному корню можно обосновать
с помощью замены отклонения би (a, b, z) его двойным интегра-
лом Фурье по а и Ь. Производя таким образом интегрирование
по X, получаем формулу
^рас (^)
d
— ikQ J" dzeik<iZ
. о
6n (a,b,z)
d-b-0
(2)
Здесь на отклонение 8п(а, Ь, с) действует оператор, яв-
ляющийся функцией двумерного поперечного оператора Лап-
ласа дУда2 + дУдЬ2 для распределения показателя преломления
в плоскости, перпендикулярной оси z, т. е. направлению распро-
странения волны. В частном случае синусоидального распреде-
ления
бга(х, у, z) = ф(з) cos cos^^p-^
поперечный оператор Лапласа
д2 д1 8т£_
дх* ду2 ~ /2
приводит к следующей величине для параметра, входящего
в формулу (2):
1 Р2 —
a0^x2 + M- z i2 •
Следовательно, величина, стоящая слева, имеет, вообще говоря,
порядок (А//)2, где / — характерная длина, на которой существен-
но меняется переменная часть показателя преломления. В даль-
нейшем мы будем предполагать этот параметр малым, т. е. огра-
4. Полугеометрическое приближение к явлению рассеяния
123
ничимся рассмотрением структур, показатель преломления кото-
рых плавно меняется на расстояниях порядка длины волны.
Известно, что данное ограничение означает преобладание эф-
фекта рассеяния вперед. Это позволяет заменить квадратный
корень в формуле (2) единицей в знаменателе и двумя первыми
членами его биномиального разложения в показателе экспоненты.
Таким образом, вместо формулы (2) получаем
Ирас(^) = ^гМ
d d-z / d2 д2 \ |
J dze 2k° {даг db2) bn(a,b,z) . (3)
° Jfl = (>=0
Полное поле можно представить в виде
е1^ + ирас (Р) = eik°d (1 + 6Д) е16ф, (4)
где М — относительное изменение амплитуды, а 6Ф — фазовая
поправка из-за неоднородности среды. Обе эти величины имеют
порядок отклонения показателя преломления бп. Поскольку бор-
цовское приближение ограничивается учетом величин первого
порядка по би, то, используя его, следует пренебрегать членами
второго порядка, такими, как 6Д6Ф и 6Ф2. Поэтому уравнение
(4) можно переписать в виде
_|_ Ирас (р) = (1 4- /бФ),
откуда
6Д + i 6Ф = е~ (Р).
Соотношение (3) можно теперь записать в виде
6Д —/ 6Ф — i^q
J dze 2*« z 'dx2 + dyl ' bn (x, y, z)
о
x-y=0
Символический оператор можно исключить с помощью дву-
мерного интеграла Фурье для функции бп(х, у, г) по х и у.
Дальнейшее преобразование производится с помощью полных
интегралов Френеля при интегрировании по пространственным
гармоникам, связанным с интегралом Фурье. Окончательное вы-
ражение
Л2 г dz Гс
дд + /бФ=^у^_ jjdxdybn(x, у, z)e2(d} (6)
О —оо
представляет борцовское приближение для плоской волны, про-
шедшей через слабо неоднородный слой 0<z<d, в котором Ьп
меняется мало в пределах длины волны.
Возникает вопрос, можно ли пренебречь рассеянием назад,
имеющим место в среде вне плоскости z=d. Его вклад дается
124
X. Бреммер
выражением, подобным (2), а именно
Иобр. рас (^) ^0
ik^z-d) Уц. 1 (&L +Ji)
OO Q ' dfl2 db2'
f dze1^-------r ] b> 2)
а у 1+pV6e»'l"d51/
r . K0
Используя метод и приближения, аналогичные предыдущим, по-
лучаем относительную величину амплитуды поля, рассеянного
назад:
i (z—d) / d2 d2 \
2ik0Z 4- I 4- - д.,- )
' 2ft. \d<* db>)
иобр. рас (P)
wpac (T5)
d
d i (d—z) / й!
\ да1 + db2 J <_ , , .
on («, b, Z)
a=b^0
(7)
2ft0
0
Заметим, что наряду с плавно меняющейся величиной бп под-
ынтегральные функции в (7) содержат осциллирующие множи-
тели. Осцилляции множителя в числителе происходят значитель-
но быстрее, чем в знаменателе; следовательно, числитель будет
много меньше знаменателя. Учитывая малые изменения бп на
длине волны в направлении z, находим, что отношение (7) имеет
порядок величины (&о*О-1. Это означает, что при d^>% рассея-
нием назад можно пренебречь,
§ 3. ПЕРЕХОД ОТ ЗОНЫ ФРЕНЕЛЯ К ЗОНЕ ФРАУНГОФЕРА,
ПЕРЕХОДНЫЙ ПАРАМЕТР
Выражения (5) и (6) дают искажения плоской волны, про-
шедшей расстояние d в слабо неоднородной среде. Действи-
тельная и мнимая части этих выражений представляют собой
изменения относительной амплитуды и фазы соответственно. Эти
выражения дополняют друг друга, поскольку первое более удоб-
но при малых значениях d, а второе — при больших.
Рассмотрим сначала выражение (5). Экспоненциальный мно-
житель в этом выражении допускает разложение в элементар-
ный экспоненциальный ряд, два первых члена которого дают
следующие приближения, справедливые для малых расстояний:
d
6Ф ±= k0 J dzbn (0, 0, z), (8а)
о
d
6Д = -1 (d - z) {бп (х, у, Z)} _о. (86)
л *
4. Полугеометрическое приближение к явлению рассеяния
125
Таким образом, фазовая поправка 6Ф задается изменением
длины оптического пути вдоль траектории ОР, ведущей к точке
наблюдения вдоль линии (z=0) невозмущенного прямолиней-
ного распространения вперед. Второе выражение для изменения
амплитуды бД указывает на наличие небольшого линзового эф-
фекта, который вызван неоднородностью среды и не зависит от
волнового числа и частоты. Действительно, величина 6Д оказы-
вается положительной в том случае, ко-
гда действие поперечного оператора Лап-
ласа д21дх2 + д21ду2 вдоль всего невозму-
щенного пути ОР сводится к умножению
на отрицательный коэффициент. Это оз-
начает, что среднее значение бп внутри
небольшой окрестности рассматриваемой
точки больше значения бп в самой точ-
ке. В результате в окрестности такой
точки имеет место некоторое фокусирую-
щее действие, а следовательно, и воз-
растание амплитуды волны, проходящей
через эту область (бД>0). Области же
с положительным . поперечным операто-
ром Лапласа д21дх2 + д21ду2 вызывают
некоторую дефокусировку, а значит, для
них бД<0.
Следующие члены полного разложе-
ния экспоненты в (5) определяют поправ-
ки к простому геометрооптическому пред-
ставлению. Выражения (8) можно также
получить, применив к (1) метод перева-
ла. Для точечного источника этот метод
чей.
описан в работе [2].
Получим теперь другое выражение для бД, отличное от пред-
ставления (6). Кроме коэффициента ik0, экспонента в формуле
(6) содержит разность путей QP—Q'P прямого невозмущен-
ного луча ОР и луча O'QP (фиг. 1), который приходит в точку
наблюдения после рассеяния на элементе объема, расположен-
ном в точке Q(x, у, г). Действительно,
QP-Q'P~
X2 + у2
2(d —г)
при условии, что угол QPQ' не слишком велик. Таким образом,
формула (6) представляет суммирование по всем дифракцион-
ным эффектам, связанным с различными элементами объема.
Такая дифракция характерна для распространения на большие'
расстояния.
126
X. Бреммер
В соответствии с принятой в оптике терминологией область
на близких расстояниях мы назовем областью геометрической
оптики или зоной Френеля. Ее лучше всего описывать выраже-
нием (5). Дальнюю область, которую лучше описывать выра-
жением (6), мы назовем зоной Фраунгофера.
Покажем, что переход из одной области в другую зависит
от численного значения некоторого безразмерного параметра q,
который мы введем ниже. Трехмерное распределение бп пред-
ставим в виде
б/1(л, у, z) = v(y, у), (9)
где с помощью масштабной длины I введены новые безразмер-
ные пространственные переменные
« X у
5 = -. n-f.
ъ z >
выражение (5) преобразуется к виду
1“ 1 12. 1 Л ( д2 \ 52 \
п, С) , (Ю)
° h-n-o
где, кроме того, введен безразмерный параметр q
_____ 2nd ______dA_
q ~ kal2 ~ I2 '
(П)
В случае справедливости наших допущений, которые можно
объединить соотношением X<gmin(d, /), оказывается, что бор-
новское приближение зависит от параметра q и от отноше-
ния d/l. Однако в практически интересных случаях по-
этому при d/l оо и можно считать, что борновское приближе-
ние зависит только от параметра q.
Введение безразмерных переменных в выражении (6) при-
водит его к виду
Ь / * Й? а а I ъ Л1
6Л + /6Ф==-^ J —J J Т), £)е о . (12)
0 1 — ? -со
Зону Френеля, характеризуемую малыми значениями па-
раметра q, удобно исследовать с помощью выражения (10) или
с помощью степенного ряда по а, полученного разложением экс-
4. Полугеометрическое приближение к явлению рассеяния
127
поненты. Для действительной и мнимой частей получаем сле-
дующие ряды:
/ п \2т + 1 ,
со г \т (_Д_ | f dll
m=0 (О
Щ + 03а)
со k—ynf_9_ym dll
m=0 О
<13б)
С другой стороны, зона Фраунгофера соответствует боль-
шим значениям q, и ее лучше описывать выражением (12) или
подходящим разложением этого выражения.
Геометрическую интерпретацию «переходного параметра» q
можно получить из представления о «шарике», вводимом в тео-
риях рассеяния для случайных сред. Такой шарик образует ко-
герентно рассеивающую область с линейными размерами по-
рядка характеристической длины. Эту длину можно отожде-
ствить с масштабной длиной I, которую мы ввели выше. Вспом-
ним, что лежащее в основе наших расчетов допущение о том,
Что %//<§; 1 (связанное с Преимущественным рассеиванием впе-
ред), ограничивает угловое отклонение при рассеянии величи-
нами порядка X//. Поэтому луч, входящий в неоднородную
среду и имеющий бесконечно малое поперечное сечение, после
прохождения расстояния d в этой среде будет иметь поперечное
сечение с линейным размером порядка d/Jl. Следовательно, ли-
нейный размер поперечного сечения луча в среднем оказывается
сравнимым с размером I шарика после прохождения лучом
пути d, определяемого из соотношения d^l^l, т. е. d=/2/£ Те
же рассуждения применимы ко второму шарику и т. д. Таким
образом, величина q~d7.ll2 представляет собой среднее число
шариков после прохождения расстояния d. Такое рассмотрение
обсуждается в работе [7].
§ 4. БОРНОВСКОЕ ПРИБЛИЖЕНИЕ
ДЛЯ СЛАБО НЕОДНОРОДНОЙ СРЕДЫ
СО СЛУЧАЙНЫМИ ПАРАМЕТРАМИ
Для такой среды распределение величины отклонения пока-
зателя преломления точно не известно, а известны лишь' его
статистические характеристики, например- пространственная
128
X. Бреммер
автокорреляционная функция. Эта функция описывает отклоне-
ния в двух различных точках Pi и Р2. Предполагая отклонение
однородным и изотропным (как это часто делается при рассмо-
трении распространения волн в тропосфере), можно предста-
вить эту функцию в следующем нормализованном виде:
(би (Р.) (Р2)) „ / Р,Р2 \
Эта функция зависит только от расстояния Р±Р^. Используя
безразмерные переменные £, ц и £, получаем
№ П1> £l)v(U П2> ?2)) =
= С [/& - |2)2 + (ш - п2)2 + & - с2)2 ]. (14)
Рассмотрим пространственную корреляцию (включая дис-
персии, полученные для бесконечно малого расстояния PiP2) из-
менений амплитуды и фазы, вызванных неоднородностью среды.
В силу (10) изменения бЛ и 6Ф в точке наблюдения можно
одновременно представить следующим образом (х, у, d — де-
картовы координаты точки наблюдения):
бФ(х, у, d) J [0J cos ' d '
x№+^)}v(x+e’
Исследуем корреляцию между величинами в точках Pi (0,0,d)
и Р2(а, b, d+c), где с — расстояние между этими точками в
продольном направлении (т. е. в направлении распространения
волны); (а2+б2)'/2 = /(а2 + р2)есть расстояние в поперечном
направлении, совпадающем с фронтом невозмущенпой волны,
перпендикулярным оси z. С помощью (14) находим соответ-
ствующие средние величины:
(d+0/Z
J ',cos[ta-1 rf + c/U|'2^ dT]'2 / J Л
xcW
Очевидно, что оператор d2/d£2+d2/di')2 можно заменить на
d2/da2 + d2/dp2; тогда мы можем положить | = ц = 0. Кроме того,
4. Полугеометрическое приближение к явлению рассеяния 129
можно заменить д2 * * * * * * 9/д1'2 + д2/дт]'2 на д2/да2 + д2/д$2 и затем поло-
жить £' = т)'=0. Дальнейшее упрощение с помощью формул
sin a sin В ) 1 . 1 . ,
cosa cosfJ [= 2COS(a-0)+ 2CoS(a + 0)
приводит к окончательным выражениям
(6Л(Р1)6Д(Р2))1 $2(би2) f
(дФ(Р1)бФ(Р2)) J 2 J J а!°Х
V cos < — —___ь I — |- V Т
А L I 4л \ d. rf + с Д ба2 ' др2 Л +
т Н5Г (2 - 71-7Т7) (•»- + »} ]С i/»1+ ₽+«'-№]
Положим далее d^>l и возьмем предел подынтегральной
функции при dll —» оо. Этого нельзя сделать для пределов ин-
тегрирования, так как возникнет расходимость двойного интег-
рала. Далее в двойном интеграле по сделаем подстановку
№ = £' — изменим порядок интегрирования и возьмем предел
при djl —> оо. Принимая во внимание, что C(s) —четная функ-
ция, получаем
(дД(Р1)бД(Р2))|
(6Ф(А)6Ф(Р2)> |
kfyd (fin2) f q ( d2 d2 \ 1
2 P + cos j 2л W + dF/ |
X 2 J rflFC(/a2 + p2+ W2) + j- J tfU7C(/a2 + p2+ W2) (15)
при условии, что интегралы
ОО 00
^dWC(W) и ^dWWC(W)
о о
сходятся.
Таким образом, оказывается, что корреляция в продольном
направлении (а = Ь — 0) зависит в основном от величины
(16)
2 j dWC(W)+± j dWC(W).
О C/Z
В поперечном же направлении (с = 0) аналогичная зависимость
дается формулами
0Д (Pi) 6Д (Р2)) 1 _ г ( q j д2
(6Ф(Р1)6Ф(Р2)) J —+ cos\2n (da2 + жШ*
00
х J rflFC(Va2 + p2+ IF2). (17)
о
9 Зак. 274
130
X. Бреммер
Дисперсии (6А2) и (6Ф2) определяются как частный случай
при а = Ь = 0.
§ 5. СВОЙСТВА СТАТИСТИЧЕСКИ СЛАБО НЕОДНОРОДНОЙ СРЕДЫ
Прежде всего из выражения (16) мы заключаем, что для
такой среды существует значительная корреляция волновой
функции в продольном направлении. Действительно, в рассмат-
риваемом приближении автокорреляционная функция для этого
направления отличается от нуля даже в случае бесконечного
расстояния с.
Ниже мы будем рассматривать корреляцию только в попе-
речных направлениях. Аргумент автокорреляционной функции
в соответствующей этому случаю формуле (17) имеет величину
по меньшей мере порядка единицы, если относительное рас-
стояние (a2 + p2)'/s превосходит единицу. С другой стороны, кор-
реляция постепенно исчезает на расстояниях, превышающих
масштаб когерентности /, т. е. для значений безразмерной вели-
чины s в C(s), больших единицы. Следовательно, заметная кор-
реляция в поперечных направлениях ограничивается относи-
тельными расстояниями (<х2 + р2)1/2 порядка единицы, что соот-
ветствует расстояниям порядка масштаба турбулентности I. Эти
доводы применимы как к фазовой, так и к амплитудной кор-
реляции. Фазовая корреляция рассматривалась подробно в
статье [8] вплоть до расстояний порядка масштаба турбулент-
ности. Очевидно, оба вида корреляции постепенно уменьшаются
при переходе от поперечного направления к продольному.
Общее выражение (17) включает два интересных частных
случая: q = 0 и q = oo. Первый случай описывается приближен-
ным выражением
(М (₽,) м (/>,», i+х
х / dWC (/а2 + Р2 + VT) (18)
о
для амплитудной корреляции и точным выражением
(6Ф(А) 6Ф (А)\=о = 262Zrf(6«2) J rfrc(/a2 + 02+U72) (19)
о
для фазовой корреляции. Оба эти выражения можно было бы
получить и из более простых приближений (8а) и (86), выве-
денных для начальной области зоны Френеля в случае регуляр-
ной неоднородной среды. Оказывается, что в этой области дис-
4. Полугеометрическое приближение к явлению рассеяния 131
Персия отклонений амплитуды растет пропорционально кубу
расстояния.
Соотношения для другого предельного случая (q -> оо, зона
Фраунгофера) можно получить заменой автокорреляционной
функции С(]/"а2-|-р24- W2) в (17) ее представлением как функ-
ции от (а2+р2)1/г, согласно тождеству Ханкеля. Действие опера-
тора д2/да?+д2/д$2 можно раскрыть с помощью тождества
а+w)
Используя далее в формуле (17) соотношение, известное из
теории функций Бесселя1), окончательно получаем следующее
выражение:
<дД(Л)6Л(Р2)) ) Г г° / г ч
оо оо
q: - J dW J dssC (/s2 + IF2)sin{-£- (a2 + P2 + $2)} X
oo
xUys/^ + P2) • (20)
\ 4 /
Отсюда следует интересное соотношение
I (Р1)6Л I = k2ld{bn2} f dWC (/a2 + p2+U72),
W,W2))U 0 x 7
(21)
согласно которому статистические свойства амплитудного и фа-
зового отклонений становятся одинаковыми в конце зоны
Фраунгофера. Кроме того, выражение (21) составляет поло-
вину соответствующей величины (19) для фазовых отклонений
в начальной области зоны Френеля.
Применительно к дисперсии (она получается при <х=р = О)
полученные результаты можно суммировать следующим обра-
зом. Переход из зоны Френеля в зону Фраунгофера связан с по-
степенным ростом дисперсии амплитудных отклонений. В на-
чале этот рост пропорционален d3, а предельное значение равно
оо
$ld{bn} J dWC(W). (22)
о
С другой стороны, дисперсия отклонений фазы уменьшается
от значения, вдвое большего (22) в начале зоны Френеля, до
’) См. [91, формула (1) иа стр. 395,
а*
132
X. Бреммер
предельного значения, равного (22) в конце зоны Фраунгофера.
Согласно (20), рост дисперсии амплитудных отклонений (6Д2)
оказывается совершенно симметричным уменьшению дисперсии
фазовых отклонений (6Ф2). Это обстоятельство иллюстрируется
фиг. 2, где для нормировки (бД2) и (6Ф2) как функций q они
Фиг. 2. Дисперсии флуктуаций амплитуды и фазы как функции
переходного параметра q.
разделены на (6Ф2) при <7 = 0. Ветви, изображающие (бД2) и
<6Ф2), стремятся при q—* оо к одному и тому же пределу х/2-
При фиксированных значениях (а2 + р2)'^ такое симметричное
поведение имеет место и для автокорреляционных функций от-
клонений бД и 6Ф. Последнее утверждение следует, например,
из суммы двух членов выражения (20)
<6Д (Р,) бД (Р2)) + (6Ф (Л) 6Ф (Р2)) =
=2 Z&rf (бп2) J dVTC (/а2 + р2 + W2).
о
Эти свойства рассматривались Фанииным [4] для частного
случая гауссовской автокорреляционной функции C(s)=e~s2 для
поля, возбуждаемого точечным источником (а не для плоской
волны, как в нашем случае). Оказалось, что упомянутые общие
свойства не зависят от конкретного вида автокорреляционной
функции C(s), однако он определяет структуру зависимости
(бД2) и (6Ф2) от параметра q. Для малых q эту зависимость
можно получить из (17) путем разложения в степенной ряд,
4. Полугеометрическое приближение к явлению рассеяния
133
а для больших q — из (20) соответствующим разложением по
обратным степеням q [ср. формулы (32) и (34), приведенные
ниже].
Мы видим, что такие свойства характерны для статистически
неоднородной среды и не имеют места для регулярной неодно-
родной среды, рассмотренной в § 3.
§ 6. СВЯЗЬ ПРЕДЕЛЬНЫХ СООТНОШЕНИЙ
В ЗОНАХ ФРЕНЕЛЯ И ФРАУНГОФЕРА
СО СРЕДНЕЙ ДЛИНОЙ СВОБОДНОГО ПРОБЕГА
ПРИ РАССЕЯНИИ
Из замечаний, относящихся к уравнению (22), ясно, что
ОО
(«П-о = ^»=2^»=2^ \dWC(W). (23)
о
Этот параметр определяет в общем поведение функций корре-
ляции типа тех, которые входят в уравнения (15) и (20), хотя,
разумеется, конечный вид зависит и от базовой функции C(s).
Важность соотношения (23) подтверждается также тем, что
оно связано с основным параметром теории рассеяния для сла-
бо неоднородной среды, а именно с «длиной свободного пробега
при рассеянии».
Теория рассеяния обычно излагается с помощью дифферен-
циального поперечного сечения (функция рассеяния) о(В), оп-
ределяемого следующим образом. Величина o(fi)dldQ представ-
ляет часть энергии, которая при прохождении волной бесконеч-
но малого расстояния dl вдоль прямого невозмущенного пути
рассеивается внутрь бесконечно малого конуса с телесным уг-
лом сШ, центральная ось которого составляет угол 0 с траек-
торией луча. В соответствии с этим определением расстояние
=----—-------- (24)
2тс J а (0) sin 0 d0
о
представляет «длину свободного пробега при рассеянии», по-
скольку при прохождении этого расстояния вся энергия волны
будет полностью рассеяна.
В теории тропосферного рассеяния волн СВЧ используется
известная формула Винера — Хинчина, связывающая о(0) с
функцией автокорреляции C(s). Эта формула получается из
предельного значения в зоне Фраунгофера в борновском при-
ближении. При этом исходят из представления о среде как о
134
X. Бреммер
когерентно рассеивающих шариках, находящихся на больших,
но конечных расстояниях от источника (передающая антенна)
и от точки наблюдения (приемная антенна). В общем случае,
который включает и анизотропное рассеяние, соответствующее
уравнение имеет вид
Интегрирование производится по всему пространству (на прак-
тике же только по объему одного шарика), координаты кото-
рого являются компонентами вектора х; векторы ипад, ирас яв-
ляются единичными векторами в направлениях падающего и
рассеянного излучений соответственно.
Аргумент функции С показывает, что она может зависеть
как от длины, так и от направления вектора х- соединяющего
две точки наблюдения, в которых сравниваются флуктуации по-
казателя преломления. В случае изотропной турбулентности С
зависит только от длины вектора х- Учитывая в этом случае,
что 9 есть угол между ипад и ирас, выражение для о (В) можно
свести к одномерному интегралу
k-l2 {fin2') f? ( 0 1
о (6) —------д- | dssC (s) sin (2£0/ sin 4 s). (25)
16л sin у oJ '
Изменяя порядок интегрирования в двойном интеграле в (24),
получаем
J_ = k° 1 J dsC (s) sin2 (kols).
о
Этот интеграл можно преобразовать к следующему выраже-
нию:
| J dsC (s) -1 J dsC (s) е2^.
О —оо
Вклад второго члена стремится к нулю при kol—> оо, согласно
теореме Арсела — Лебега. Поэтому вторым членом можно пре-
небречь при больших kol, т. е. при (что предполагалось
в начале работы). Итак, окончательно
4
do=----------. (26)
^{fin^l [ dsC(s)
L 0.
4. Полугеометрическое приближение к явлению рассеяния 135
Таким образом, используя понятие длины свободного пробега,
соотношения (23) можно преобразовать к виду
<6Ф2\=О = 2 0Ф2\=те = 2 (6Л2\_ = %. (27)
Существование такой простой связи между дисперсией фа-
зовых флуктуаций и длиной свободного пробега рассеяния
было установлено Бугноло [3] для предельного значения в зоне
Френеля и для частных видов автокорреляционной функции C(s).
. § 7. СВЯЗЬ БОРНОВСКОГО ПРИБЛИЖЕНИЯ
ДЛЯ СТАТИСТИЧЕСКИ НЕОДНОРОДНОЙ СРЕДЫ
С МОМЕНТАМИ РАССЕЯНИЯ
Согласно формуле (17), все свойства борновского прибли-
жения для слабо неоднородной среды со случайными параметр
рами зависят от интеграла
J rfVTC(/a2 + p2+^), (28)
о
который можно связать со средними, зависящими от угла рас-
сеяния 0. Соответствующие соотношения (они выводятся ниже)
связаны с параметром перехода q.
Так как для случая изотропной однородной турбулентности
функция C(s) является четной, то выражение (25) эквивалентно
выражению
о (0) = ——---3- dssC(s)e 2 .
32л sin у .со
Соответствующее обратное преобразование Фурье имеет вид
C(s)~-----,8f 2\.. f d80<j(2 arc sin (29)
v 7 k2l(t>n2}s J \ 2; v >
Изменим порядок интегрирования в двойном интеграле, ко-
торый получается, если в (28) подставить последнее выраже-
ние при s=(a2 + ₽2+r2),/J. В результате интегрирования
по W, введения новой переменной ф согласно соотношению
136
X. Бреммер
£= (а2 + fl2)1/2 sh ф и использования известного представления для
Но ’ (® V4- р2) получаем
[ dW С (]/а2 4~ Р2 ~+- U72)= [ dO 80(2 arc sin-|)х
J k-J {bn ) J \
0 ° ' ' -co
xH^(V0= ,2J* 2<- f de 0 X
X o (2 arc sin -j-j J0(kQie |Лх2 4- p2).
Действие оператора 4- d2/dp2 сводится к умножению
подынтегрального выражения на — koi 0 , поэтому действие
произвольной функции от этого оператора дает
<Х> 00
J' рееЦ-й/^х
О 0 ' ' о
X о (2 arc sin Jo(^o/0'|/ra24- Р2)- (30)
Ввиду того что рассеяния вперед по-прежнему считается
преобладающим, углы рассеяния 0 можно считать малым. Это
позволяет заменить аргумент функции о на 0.
С учетом (30) соотношение (17) дает
(6Л(Л)М(Р2)) ) г°°, < /„ 2 2 2П
(6Ф (Л) 6Ф (Р2)> J ~ 8л£/ / rf9 00 (0 5 1 + C0S ( 2^ 0) Iх
x;s(V9/a“44). (31)
При малых углах рассеяния выражение для среднего зна-
чения любой функции от 0 по всем направлениям рассеяния
с учетом распределения вероятности запишется в виде
Л со
2л J ДО sin 0a (0) i|> (0) J Д0 0a (0) ф (0)
W0)> = _±_----------------
2л J1 ДО sin 0a (0) J1 ДО sin 0a (0)
о о
Согласно (24) эту формулу можно привести к виду
(ф(0))==2лйГо J 0о(0)ф(0).
О
4. Полу геометрическое приближение к явлению рассеяния
137
Таким образом, оказывается, что (31) эквивалентно выражению
(6Л (/-*!) 6Л 1 d / ( 1 _ I q ,2/2ft2\ \ , (t, /а-./"о '| п21\
<6Ф(Л)6Ф(Р2)) 1 “ 4 м + C°S k°l ° ) > J°
Результирующие разложения для дисперсий, получаемые
при а = р = О и при использовании выражения (11) для пере-
ходного параметра q, имеют вид
Такие разложения особенно полезны для зоны Френеля. Чле-
ны этого разложения уменьшаются как среднее (94п). Если ряд
быстро сходится, как, например, для ярко выраженного рассеи-
вания вперед, то зона Френеля распространяется на большие
расстояния. Соответствующее разложение для зоны Фраунго-
фера будет получено в следующем параграфе.
§ 8. СВЯЗЬ БОРНОВСКОГО ПРИБЛИЖЕНИЯ
ДЛЯ СТАТИСТИЧЕСКИ НЕОДНОРОДНОЙ СРЕДЫ
С МОМЕНТАМИ АВТОКОРРЕЛЯЦИОННОЙ ФУНКЦИИ
Мы ограничимся рассмотрением дисперсий, считая а = р = 0.
Второй член в правой части выражения (20) после элементар-
ных преобразований принимает вид
оо оо
- ] dW j ds sC (/s2+ U72) sin s2) =
о 0
OO 0
-%- f rfooC(o) f -y=ss- - sin (-Д s2k
<7 J v ’ J /a2 — s2 \ 2? J
о о r
Разложение синусоидальной функции приводит к интегралу
Эйлера первого рода. Учитывая (26), разложения для диспер-
сий можно записать следующим образом: 33 * *
(33)
Мы получили удобное выражение для зоны Фраунгофера
(область больших ц). Его коэффициенты зависят от моментов
138
X. Бреммер
автокорреляционной функции C(s), а не от моментов функции
рассеяния, как это было в предыдущем параграфе. Однако
коэффициенты можно выразить через функцию рассеяния о (9),
если для C(s) использовать формулу (29), заменив в ней аргу-
мент 2 arc sin(0/2) на 9 (угол рассеяния считается малым). Из-
меняя порядок интегрирования и учитывая, что C(s)—четная
функция, получаем
j dsC (s) s4'" =
о
CO оо
----f rf9 0ff(9) f dssim~xeik^s
u ' —oo — co
Интеграл no s равен
2лг6(4'п-1)(Ао/0) = 2л/-^-^ ,
(M)
так что двойной интеграл сводится к следующим производным
высшего порядка от о(0) в точке 0 = 0:
— 2зп
d4"1"1
dO4”2-1
W)4m
{0а (0)} е=0
— (4W " о(4т-2)/0\
(M4m ’
Для дисперсий (33) опять-таки с учетом (26) и (11) полу-
чаем следующие окончательные выражения:
(6Ф2) J 4»
1 Т 4Яз/Ц, £
Г gOm-2) (0)
3), (4Aod)2m
(34)
Итак, дисперсии в зоне Фраунгофера очень просто связаны
с поперечным сечением рассеяния. Это и понятно, так как вы-
вод последнего выражения связан с приближением фраунгофе-
ровского типа.
§ 9. ДАЛЬНЕЙШЕЕ ОБСУЖДЕНИЕ МЕХАНИЗМА РАССЕЯНИЯ
Рассеяние становится заметным только после того, как вол-
на, вошедшая в неоднородную среду, пройдет в ней достаточ-
ное расстояние. С самого начала для отклонения амплитуды
можно применить формулу (19). Вычисление дисперсии
4. Полугеометрическое приближение к явлению рассеяния
139
(а = р = О) приводит в этом случае к следующему выражению,
в котором, согласно (26), введена длина свободного пробега:
о
Численный коэффициент этого уравнения зависит от функции
C(s), но эта зависимость не очень критична. Например, для мо-
дели Фаннина C(s)=e~s2 получаем
(6 А2} ~ 8 У л . (35)
Эта формула дает удовлетворительное приближение для
зоны Френеля, которая характеризуется, неравенством q<l или
d</2/X. Следовательно, максимально возможное значение для
(бЛ2> в этой области будет порядка
В случае распространения радиоволн в турбулентной тропо-
сфере или ионосфере эти величины таковы, что рассеяние в
зоне Френеля незначительно. Рассеяние становится заметным
только в зоне Фраунгофера, в которой, согласно (27), (М2)
порядка d/d0. Таким образом, рассеяние становится существен-
ным только тогда, когда волна проходит расстояние порядка^-
Это становится понятным, если интерпретировать d0 как длину
свободного пробега. С физической точки зрения главной при-
чиной, вызывающей рассеяние, является дифракция, а не гео-
метрооптические явления, которые доминируют в области Фре-
неля.
Рассмотрим теперь другой случай, когда рассеяние стано-
вится заметным уже в зоне Френеля. Такое предположение рав-
носильно тому, что (бп2)(//Х)3>1. В случае турбулентной тропо-
сферы и ионосферы этот, случай реализуется для оптических
длин волн. Приближение (35) можно применить теперь для
определения критического расстояния dvp, на котором рассея-
ние становится значительным. Очевидно, что это расстояние бу-
дет иметь порядок величины
I
«бп2))1/3 ’
которая больше, чем I для слабо неоднородной среды. Таким
образом, рассеяние начинается на расстоянии d1<p, которое имеет
140
X. Времмер
величину порядка d0 при <6/г2> (Z/X)3 < 1 и порядка //(6/г2),/з при
(бп2)(//Х3)>1. Оба случая можно описать одним неравенством
dKp~max{d0, (36)
где порядок величины do определяется из соотношения (26) и
равен Х2//(бп2).
Итак, для всех условий мы можем определить расстояние,
на котором рассеяние становится заметным. Это расстояние мо-
жет соответствовать как зоне Френеля, так и зоне Фраунгофера.
Исследуем далее возможность многократного рассеяния. Для
этого введем специальную единицу энергии проходящей волны,
равную среднему количеству энергии, которое рассеивается на
длине порядка dltp. Таким образом, среднее расстояние между
точками двух последовательных рассеяний оказывается порядка
г/Кр, причем эти рассеяния независимы одно от другого при ус-
ловии, что величины 8п для этих точек не коррелированы. Неза-
висимость в данном случае понимается в том смысле, что угол
последующего рассеяния не связан с углом предыдущего. Итак,
мы приходим к условию dKp>l, при котором последовательные
рассеяния оказываются в среднем независимыми друг от друга.
Поэтому последовательные рассеяния можно рассматривать как
марковский процесс. Такое рассмотрение справедливо, если вы-
полняется неравенство
( , I к ,
max 1 do, ---гп ) > I-
I и <дп2)1/3 J
С учетом вышеприведенного выражения для порядка величины
получаем условие
f л2 IV,
max (------, -----пг ) > 1,
1 /2 <<л2> (6п2>1/3 J
которое обычно выполняется.
Представляет интерес попытка подтвердить это условие мар-
ковского характера процесса многократного рассеяния, либо
сравнивая точные значения вкладов в поле, связанных с после-
довательными рассеяниями [1], либо непосредственно применяя
строгие вероятностные методы.
§ 10. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ.
СВЯЗЬ С ТЕОРИЕЙ ОПТИЧЕСКОГО ИЗОБРАЖЕНИЯ
С помощью борновского приближения, рассмотренного для
слабо неоднородной среды с малым изменением показателя
преломления на расстояниях порядка длины волны, можно чет-
ко проследить переход из зоны Френеля в зону Фраунгофера
4. Полугеометрическое приближение к явлению рассеяния
141
по мере того, как расстояние, пройденное волной, увеличивается.
Одним из наиболее интересных результатов для такой среды
является одинаковая предельная зависимость дисперсий фазы
и амплитуды (относительно амплитуды падающей волны) на
больших расстояниях. Дисперсия фазы на близких расстояниях
в 2 раза больше дисперсии фазы на больших расстояниях. Дис-
персия амплитуды на близких расстояниях пропорциональна
кубу расстояния.
Теорию, развитую здесь, можно рассматривать как обобще-
ние теории оптического изображения, которая исходит из рас-
пределения волновой функции в некоторой начальной плоскости
(например, плоскости двумерного объекта или плоскости его
параксиального изображения). Последнюю ситуацию можно
формально рассмотреть, введя отклонения эффективного пока-
зателя преломления, которые ограничены непосредственной
окрестностью начальной плоскости, от его значения в свобод-
ном пространстве. Таким образом, оказывается возможным по-
лучить общепринятую дифракционную теорию оптических изо-
бражений в качестве частного случая вышеизложенной теории,
предполагая, что показатель преломления бп(х, у, z) содержит
дельта-функцию 6(г) и ее производную 6'(г) (г=0 есть на-
чальная плоскость, перпендикулярная оптической оси рассма-
триваемой системы).
В этом случае падающая плоская волна соответствует пло-
ской волне, которая освещает начальную плоскость. Прямые
вычисления приводят к выражению
6Д-Н'6Ф = 4- e2k' ду" Ы{х, у)=
Го
00
= I J’ ^«(1. П)^(х‘5)г+М\ (37)
U[ о j j
— оо
в которо.м величина /o+W(x, у) представляет Собой коэффи-
циент прохождения, на который необходимо умножить падаю-
щую волну, идущую слева (г<0), чтобы получить волновую
функцию по другую сторону этой плоскости (г=4-0). Эти вы-
ражения дают отклонения фазы и амплитуды, наблюдаемые в
точке (х, у, d), по отношению к амплитуде и фазе плоской
волны tQeihaZ, которая была бы в плоскости изображения г>0,
если бы первоначальная волна изменялась не статистически, а
лишь соответственно средней прозрачности to объекта в плос-
кости г=0. Соотношения (37) соответствуют формулам (5) и
(6) для рассмотренной нами слабо неоднородной среды, если
6/ — малая величина.
142
X. Бреммер
Статистически неоднородной среде, рассматриваемой в этой
статье, соответствует прозрачность t(x, р)=/о + 6/(*, у), вклад
которой 6/(х, у) можно определить ^ишь статистическими ме-
тодами. Кроме того, все приближения, которыми мы пользова-
лись, требуют, чтобы в плоскости ху величина б/(х, у) изме-
нялась незначительно на расстояниях порядка длины волны.
Таким образом, можно вывести свойства, аналогичные тем, кото-
рые мы получили в этой статье для корреляций и дисперсий не-
больших изменений амплитуды, и фазы, вызванного неоднород-
ной структурой объекта, расположенного в начальной плоско-
сти. Этот объект может слегка поглощать и изменять фазу про-
ходящей волны, что эквивалентно комплексной функции t(x, у).
С другой стороны, частные случаи чистого поглощения или
полной прозрачности (изменяется только фаза) соответствуют
действительной или мнимой функции t(x, у) соответственно. На-
помним, что в большинстве случаев отклонения амплитуды
уменьшаются пропорционально d-2, а фазовые флуктуации —
пропорционально d“‘ в зоне Фраунгофера, где d -»оо (при ис-
пользовании линз эта область передвигается на более короткие
расстояния).
ЛИТЕРАТУРА
1. В rem mer Н., National Bureau of Standards Circular, 527 (1954), p. 145.
On a Phase-Contrast Theory of Electron-Optical Image Formation.
2. В rem mer H., в книге Handbuch der Physik, Bd. 16, Berlin, 1958, S. 423.
Propagation of Electromagnetic Waves.
3. В u g n о 1 о H., Journ. Geoph. Res^, 65, 879 (1960).
Multiple Scattering into the Ionosphere.
4. F a n n i n В. M., Line-of-sight wave propagation in randomly inhomoge-
neous medium, Dissertation, Univ, of Texas, Austin, Texas, June 1956.
5. Keller J. B., Journ. Am. Math. Soc., 11, 227 (1962).
Wave Propagation in Random Media.
6. Keller J. B., Levy B. R., New York Univ. Courant Inst. Math. Science,
Res, Rept. EM-182, 1963.
Scattering of Short Waves.
7. Muchmore R. B„ Wheel on A. D„ Proc. IRE, 43, 1437 (1955).
Line-of-Sight Propagation Phenomena; 1. Ray Treatment.
8. Robieux J., Ann. Radio Electr., 15, 331 (1960).
Lois generales de la liaison entre radiateurs d’ondes, application aux ondes
de surface et a la propagation, III: Proprietes des liaisons par diffraction
et diffusion.
'9. Watson G. N., A Treatise on the Theory of Bessel Functions, Cambridge,
England, 1944. (Имеется перевод: Г. И. Ватсон, Теория бесселевых
функций, ИЛ, 1949.)
10. Wheel о п A. D., Muchmore R. В., Proc. IRE, 43, 1450 (1955).
Line-of-Sight Propagation Phenomena; 2. Scattered Components,
5
ДИФРАКЦИОННЫЕ АНОМАЛИИ В РЕШЕТКАХ
НА МИЛЛИМЕТРОВЫХ ВОЛНАХ
К. Пальмер*
Полвека назад Вуд обнаружил аномальное поведение дифракционных
решеток; с тех пор по этому вопросу был опубликован ряд статей, как теоре-
тических, так и экспериментальных Теоретические работы лишь частично
объяснили это явление. Экспериментальные работы были выполнены в основ-
ном на дифракционных решетках в оптическом и ближнем инфракрасном
диапазонах. Недавно Хессель и Олинер сделали многообещающую попытку
теоретического рассмотрения этой проблемы с точки зрения распространения
поверхностной волны в открытых гофрированных волноводах. Этот метод
позволяет анализировать случай очень глубоких канавок в решетке. Автор
исследовал проблему экспериментально, используя миллиметровый спектро-
метр на длине волны 4 мм. Прецизионные решетки размером 100X150 см
наносились на воск и частично или полностью покрывались проводящей кра-
ской. Приводятся предварительные результаты проведенных экспериментов.
Например, решетка с 30-градусным пилообразным профилем, у которой только
освещенные грани являются проводящими, проявляет резко выраженные ано-
мальные свойства. Даже полностью диэлектрическая решетка проявляет ано-
малии.
§ 1. ВВЕДЕНИЕ
Аномальное поведение спектра, полученного на оптической
дифракционной решетке, впервые наблюдал Вуд в 1902 г. [1].
Он обнаружил, что у одной из исследуемых отражательных ре-
шеток обычные гладкие спектры пересекались яркими или тем-
ными линиями. Кроме того, длины волн, на которых появлялись
эти полосы, смещались по мере того, как изменялся угол паде-
ния волн на решетку. Вуд также заметил, что полосы появ-
ляются только в той компоненте падающего света, электриче-
ский вектор которой поляризован перпендикулярно направле-
нию канавок (5-компонента). Для параллельной поляризации
* С. Н. Palmer, Jr., Department of Electrical Engineering, Th? John®
Hopkins University, Baltimore, Maryland
144 .
К. Пальмер
(P-компонента) каких-либо аномальных свойств не наблюда-
лось.
В 1907 г. Релей [2] выдвинул теорию, которая объяснила не-
которые особенности аномалий, наблюдавшихся Вудом. Он рас-
смотрел полностью отражающую периодическую структуру бес-
конечной протяженности, описываемую рядами Фурье. Суммар-
ное поле (т. е. поле падающей волны плюс дифрагированные
спектры) должно было удовлетворять одному из двух гранич-
ных условий. Условие равенства нулю этого поля на поверхно-
сти решетки соответствовало электрическому полю, параллель-
ному штрихам, т. е. P-компоненте. Условие равенства нулю
производной поля по нормали на поверхности решетки соответ-
ствовало 5-компоненте.
Релей получил, что решетки должны давать необычно яркие
линии при таких длинах волн X, для которых в каком-либо дру-
гом порядке N происходит дифракция под углами ±90°. Таким
образом, аномалии должны иметь место при длинах волн,
удовлетворяющих соотношению /VX = d(sin i± 1), где d— пе-
риод решетки, I — угол падения, W — «порядок Релея» и X —
длина волны Релея. Далее Релей установил, что эти яркие
линии должны иметь место в спектрах всех порядков и
что они будут иметь место для 5-поляризации, как и наблю-
дал Вуд.
Теория Релея правильно предсказала длины волн аномалий,
но не объяснила природу темных линий. Дальнейшие наблюде-
ния Вуда [3], Ингерсола [4], Стронга [5], а также более точные
теории Фано [6] и Артмана [7] подтвердили заключение Вуда,
что аномалии появляются лишь для 5-поляризации. Аномалии
для P-компоненты, описанные автором [8] в 1952 г., по-види-
мому, возникают, когда глубина канавки сравнима или больше
длины волны. В такой периодической структуре могут существо-
вать как ТЕ-, так и ТТИ-поверхностные волны, соответствующие
Р- и 5-поляризации. Мелкие канавки, рассматриваемые Релеем,
не поддерживают ТЕ-волны, поэтому он заключил совершенно
правильно, что для мелких поверхностных решеток Р-аномалии
не должны иметь места.
На фиг. 1 изображен яркий случай Р- и 5-аномалий, полу-
ченных на грубой (d= 10,55 мк) решетке с глубокими канав-
ками, нанесенными на серебро. Видно, что Р- и 5-аномалии
различаются между собой.
На фиг. 2 приведена микрофотометрическая запись Р- и
5-спектров при угле падения 25°. Индексы I, II, III на шкале
длин волн указывают порядок спектров. Точки на кривых отме-
чают длины волн, рассчитанные по Релею. В некоторых слу-
чаях порядки Релея указаны вместе с наблюдаемыми поряд-
5 Дифракционные аномалии в решетках
145
ками спектров, обозначенными индексами I, II, III. Следует от-
метить крайне высокие порядки Релея вплоть до 42-го.
Аномальные свойства решеток зависят от угла падения и
отношения длины волны к периоду решетки; это видно из фор-
мулы Релея (которая относится как к Р-, так и к 5-аномалиям).
Фиг. 1. Аномальное поведение грубой оптической решетки
(d = 10,55 мк) при нескольких углах падения, указанных справа
для каждой тройки спектров.
Верхний спектр в каждой тройке — ртутный спектр сравнения; средний —
спектр белого света в P-компоненте, нижний —то же в S-компоненте. Линия
слева отмечает нулевой порядок; спектр слева —первый порядок; спектр
справа —второй и частично третий порядки
Помимо очевидной зависимости от поляризации, аномальное по-
ведение определяется также профилем канавки и условиями на
поверхности. Если поверхность решетки покрыта слоем диэлек-
трика толщиной не более, чем приблизительно 2Х, то аномалии
видоизменяются. Если толщина диэлектрика составляет много
длин волн, то аномалии смещаются в соответствии с формулой
10 Зак. 274
146
К. Пальмер
NX = d(sin i±[i), где р— показатель преломления диэлектрика.
Свойства решетки с диэлектрическим покрытием можно объяс-
нить непосредственно из рассмотрения того, как покрытие
влияет на распространение поверхностной волны.
Фиг. 2. Микрофотометрическая запись Р- и S-спектров фиг. 1 при угле
падения 25°.
Точками отмечены длины волн, рассчитанные по Релею. Некоторые порядки Редея указаны
вместе с наблюдаемым порядком спектра.
За последние десять лет Липпман и Опенгейм [9], Миллер
[10] и в особенности Тверский [II]1) выполнили теоретические
работы по исследованию аномалий. Совсем недавно Хессель и
Олинер [12] предприняли многообещающую попытку решения
проблемы. Дальнейшая экспериментальная работа с оптически-
ми решетками была выполнена Стюартом и Галловеем [13], а
также автором [14].
Для проведения количественных исследований этой трудной
проблемы был сконструирован спектрометр, работающий на
миллиметровых волнах. Хотя прибор не обладал еще достаточ-
ной точностью, однако удалось получить некоторые новые дан-
) В работе [11] дана весьма полная библиография, включающая и статьи
Тверского,
5. Дифракционные аномалии в решетках
147
ные, что почти невозможно было сделать на оптических решет-
ках. В настоящей статье описана методика измерений и неко-
торые результаты.
§ 2. ОПИСАНИЕ УСТАНОВКИ
Спектрометр. На фиг. 3 схематически изображен спектро-
метр. Источником служит модулированный меандром 4,2-мил-
лиметровый отражательный клистрон с обычными СВЧ элемен-
тами для контроля мощности и частоты, а также для пере-
стройки. Выходная мощность попеременно подается через одну
из двух сменных антенн в виде открытого конца волновода для
освещения с Р- или S-поляризацией параболического зеркала
со смещенной осью. Ширина коллимированного пучка 1 м, вы-
сота 0,5 м. Решетки устанавливаются на вращающемся столе
примерно на расстоянии 3,5 м от зеркала. Дифрагированный
пучок фокусируется полистироловой линзой Френеля диаметром
45 см. Своей искривленной поверхностью линза обращена к ре-
шетке, поэтому луч, отраженный от линзы назад к решетке, бу-
дет расходящимся, а не параллельным и, следовательно, будет
давать минимальные интерференционные помехи при измере-
ниях. Кроме того, такая ориентация линзы дает меньшие кому
и астигматизм. Сферическая аберрация может быть исправлена
выбором ориентации. Для экономии дорогостоящего материала
линза была сделана ступенчатой, однако число ступеней было
ограничено двумя, чтобы сделать минимальными интерферен-
ционные эффекты на каждой ступени.
Излучение, сфокусированное линзой, принимается согласо-
ванным рупором, апертура которого перекрывает диск Эйри
фраунгоферовой дифракционной картины линзы. Кристалличе-
ский детектор вмонтирован в короткую волноводную секцию,
присоединенную к рупору (детектор, показанный на фигуре,
представляет собой камеру Голея; впоследствии он был заме-
нен рупором и кристаллом). Приемный рупор, разумеется, не-
обходимо ориентировать в соответствии с принимаемой поляри-
зацией. Обе поляризации хорошо разделяются; когда рупор
установлен под прямым углом к правильному положению, не
наблюдается заметного сигнала даже при максимальной падаю-
щей мощности.
На фиг. 4 показан вид сбоку телескопической системы и
стола с решеткой. Ось установки определяется центральным
опорным столбиком; опорное колесо используется для того, что-
бы обеспечить компенсирующий момент, уменьшающий давле-
ние на центральные подшипники. Так как пол неровный, то ис-
пользуется пружинная подвеска колеса. Точность измерения
10*
Фиг. 3. Схема спектрометра миллиметровых волн.
Фиг. 4. Вид сбоку на телескопическую систему и стол
с решеткой.
5. Дифракционные аномалии в решетках
149
углов падения и дифракции 0,1°, что составляет примерно */5 уг-
лового разрешения телескопической системы.
Сигнал с выхода кристаллического детектора поступает на
узкополосный усилитель с большим коэффициентом усиления,
который перестраивается синхронно с частотой модуляции кли-
строна. Выходной сигнал усилителя регистрируется либо
встроенным в установку ламповым вольтметром, либо само-
писцем.
Решетки. Прецизионные решетки произвольного профиля с
размерами вплоть до 50X100 см наносятся на специальную
основу из воска (точка плавления около 65°С). Этот воск пред-
ставляет собой смесь парафина с высокой точкой плавления,
микрокристаллического парафина и туффина. Он прозрачен для
миллиметровых волн и имеет удовлетворительные механические
свойства. Смесь плавят, а затем или отливают в виде толстой
пластины, или наносят на неметаллическую подложку.
Заготовка решетки помещается на специальную делительную
машину с ручным управлением, изображенную на фиг. 5. Алю-
миниевый резец необходимого профиля устанавливается на ка-
ретке, скользящей по прецизионным продольным и поперечным
направляющим. Заготовка решетки перемещается с помощью
прецизионного направляющего винта, который задает шаг ре-
шётки с точностью, большей чем 0,001 дюйма (0,025 мм), или
примерно 1/160 длины волны. Точность профиля решетки, по-
видимому, околи 1/30 длины волны.
Угол падения, град
Фиг. 6. Коэффициент отражения нулевого порядка в Р- и S-компонентах
для решетки с 30°-ным пилообразным профилем, d = 12,7 мм, % = 4,2 мм.
Угол падения, град
Фиг. 7. Дифракционные спектры нескольких порядков в обеих поляриза-
циях для решетки с 30°-ным пилообразным профилем и d — 19,0 мм.
В данном случае только более широкая сторона каждой канавки была окрашена серебряной
проводящей краской.
5. Дифракционные аномалии в решетках
151
Изготовленную решетку можно покрыть полосками из алю-
миниевой фольги, которые прикрепляются к стенкам канавок
тонким слоем парафина с очень низкой точкой плавления
(28°С); кроме того, ее можно покрыть серебряной проводящей
краской или краской, имеющей сопротивление. Главную труд-
ность при изготовлении решеток представля-ет незначительное
искривление подложки, которое может вызвать отклонение от
заданной поверхности до */2 длины волны на ширине 1 м.
§ 3. РЕЗУЛЬТАТЫ
На фиг. 6 приведены типичные результаты измерений, полу-
ченные для спектра нулевого порядка от решетки с 30-градус-
ным пилообразным профилем при шаге 12,7 мм, т. е. с отно-
шением шага к длине волны 3,02. При монохроматическом излу-
чении спектр нулевого порядка так же легко исследовать, как
и любой другой. Следует отметить, что вблизи угла падения
—42° 5-компонента резко уменьшается примерно на 13 дб по
мощности. Положение аномалии хорошо совпадает с порядком
Релея +1. Интенсивность P-компоненты изменяется более плав-
но. Поведение описанной решетки очень похоже па поведение
оптических решеток.
Было высказано предположение, что аномалии можно устра-
нить, если посеребрить только освещенную сторону каждого
выступа решетки — операция, трудновыполнимая в оптике, но
легкодоступная в диапазоне миллиметровых волн. Результаты
измерений с такой решеткой представлены на фиг. 7. Эта была
решетка с 30°-ным пилообразным профилем, более грубая, чем
предыдущая; шаг канавки равен 19,0 мм (d/X=4,53). Порядок
спектра и поляризация указаны для каждой кривой; при соот-
ветствующих углах указаны порядки Релея. На фиг. 8 произве-
дено сравнение решетки с частично посеребренными канавками
(пунктирные кривые) и полностью посеребренной решетки
(сплошные линии) в спектрах двух порядках. Аномалии ярко
выражены в обоих случаях, но сильно различаются. Эти кри-
вые включают четыре различных порядка Релея.
Так как аномальные свойства очень тесно связаны с харак-
тером распространения поверхностной волны и так как чисто
диэлектрические структуры могут поддерживать поверхностные
волны, то, по всей вероятности, диэлектрическая решетка так-
же может вызывать аномалии. На фиг. 9 приведены резуль-
таты, полученные для описанной выше решетки, когда с нее
было снято все металлическое покрытие. На кривых ясно видны
аномалии для 5-поляризации (спектры отражения). Результаты
серии измерений, проведеншдх с Р-цодяризацией, цоказаны на
Фиг. 8. Сравнение мощностей дифрагированных полей в S-комноненте
для решеток с частично и полностью посеребренными канавками (профили
решеток как для фиг. 7).
-40 -50 -г 60
Угол падения, град
Фиг. 9. Аномалии в S-поляризации для диэлектрической решетки (профиль,
решетки как для фиг. 7}.
5. Дифракционные аномалий в решетках
153
фиг. 10. Здесь также наблюдается аномальное поведение при
углах, даваемых формулой Релея.
Из оптики хорошо известно, что проводимость поверхности
решетки оказывает значительное влияние на аномалии: поведе-
ние чисто диэлектрической решетки и поведение полностью по-
серебренной решетки резко различны. Средняя кривая была по-
лучена при покрытии чистого диэлектрика смесью парафина с
Фиг. 10. Аномалии в Р-поляризации для чисто диэлектрической
решетки.
низкой точкой плавления и угольного порошка. Это покрытие
имеет высокое сопротивление—порядка 105 ом!квадрат. На
фиг. 11 сравниваются данные измерений S-компоненты в нуле-
вом порядке для трех случаев: для чистого диэлектрика, поверх-
ности с большим сопротивлением и серебряной проводящей по-
верхности. Кривые для диэлектрической поверхности и поверх-
ности с большим сопротивлением очень схожи, но не совпадают.
Недавно для решетки с низким сопротивлением были получены
результаты, менее различающиеся с данными для решетки с ме-
таллическим покрытием (не'показаны на рисунке). Кривая рас-
полагается между кривыми для решеток с высоким сопротив-
лением и высокой проводимостью поверхности. Поведение спек-
тров других порядков для решетки с большим сопротивлением
имеет довольно резкие аномалии в —1-м, —2-м и -3-м поряд-
ках для обеих поляризаций. Уже неоднократно наблюдалось, что
154
К. Пальмер
в некоторых порядках имеется увеличение интенсивности на
длине волны аномалии, соответствующей яркой линии, в то
время как в других порядках наблюдается четко выраженный
Фиг.' 11. Сравнение нулевого порядка S-ко.мпонеиты для решеток
с серебряной проводящей поверхностью, угольным покрытием с боль-
шим сопротивлением и без покрытия.
спад. Создается впечатление, что энергия, обычно принадлежа-
щая к одному порядку, переходит из него в другой порядок при
интерференционном эффекте, в котором участвуют вытекающие
поверхностные волны.
Несколько лет назад на грубой оптической решетке автор
пытался определить, сколько канавок должно быть освещено,
чтобы появились аномалии. Было найдено, что приблизительно
50 штрихов достаточно, однако минимальное число штрихов
определить не удалось. На фиг. 12 приведены недавно полу-
ченные экспериментальные данные для S-компоненты; на ре-
шетке были посеребрены 24, 12 и 6 линий. Видно, что при
—51,3° аномалия (порядок Релея +1) имеет место даже на
Фиг. 12. Результаты измерений в S-поляризации для решетки
с 24, 12, 6 посеребренными канавками и решетки без серебрения.
Кривая для диэлектрической решетки дана в увеличенном виде, чтобы пока-
зать характер аномалии; мощность, конечно, много меньше, чем в случае ре-
шетки с проводящими канавками.
Фиг. 13 Аномалии в Р-поляризации при различном числе
посеребренных канавок.
Кривая для диэлектрической решетки также даиа в увеличенном виде, чтобы
показать характер аномалии.
156
К- Пальмер
решетке с шестью посеребренными линиями. Кроме того, можно
видеть, что, когда серебро снимается полностью и остается
только диэлектрик, аномалия сохраняется (хотя и другого вида).
Следует заметить, что отражение от чисто диэлектрической ре-
шетки много меньше, чем от проводящей решетки, поэтому кри-
вая дана в увеличенном масштабе, чтобы показать характер
аномалии. Фиг. 13 иллюстрирует результаты для Р-компо-
ненты. Чтобы убедиться, что шести посеребренных линий дей-
ствительно достаточно, была изготовлена и исследована новая
узкая решетка с шестью линиями, покрытыми алюминиевой
фольгой. Поведение решетки оказалось таким же, как и поведе-
ние полной решетки с шестью посеребренными канавками.
Можно заметить, что вторичные максимумы ведут себя несколь-
ко неожиданно, однако для объяснения этого требуется даль-
нейшее изучение.
§ 4. ЗАКЛЮЧЕНИЕ
Предварительные измерения на описанном приборе пока-
зали, что его можно использовать для проверки новых теорети-
ческих исследований и для детального количественного изуче-
ния различных аспектов проблемы аномалий решеток. Вместе
с тем необходимо дальнейшее усовершенствование эксперимен-
тальной техники, особенно метода определения относительного
распределения падающей мощности по спектральным порядкам.
ЛИТЕРАТУРА
1. Wood R. W,. Proc. Phys. Soc. (London), 18, 396 (1902); Phil. Mag.
(September 1902).
2. Rayleigh, Proc. Roy. Soc. (London), A79, 399 (1907); Phil. Mag., 14,
60 (1907).
3. Wood R. W.. Phil. Mag., 23, 310 (1912); Phys. Rev., 48, 928 (1935).
4. Ingersoll L. R., Phis. Rev., 17, 493 (1921).
5. Strong J., Phys. Rev., 46, 326 (1934); 48, 480 (1935); 49, 291 (1936).
6. Fa no U„ Phys. Rev., 50, 573 (1936); 51, 288 (1937); Ann. d. Phys., (5)32,
393 (1938).
7. Artmann K., Zs. Phys., 119, 529 (1942).
8. P a 1 m e г С. H., Journ. Opt. Soc. Am., 42, 269 (1952).
9. L i p p m a n n B. A., Oppenheim A., Technical Research Group Report,
Contract No. OSR-TR-54-25 (June 30 1954).
Toward a Theory of Wood’s Anomalies.
10. M i 11 a r R. F., Can Journ. Phys., 39, 81, 104 (1961).
11. Twer sky V., Journ. Res. Natl. Bur. Standards, 64D, 715 (1960).
12. Hess el A., О liner A. A., Symposium on Electromagnetic Theory and
Antennas, Copenhagen, June 1962.
13. Stewart J. E., Gallaway W. S., Appl. Optics, 1, 421 (1962).
14. Palmer С. H., Journ. Opt. Soc Am., 46, 50 (1956); 53, 1005 (1963);
A Symposium on Electromagnetic Warfare, Paper 13, The Johns Hopkins
University, Baltimore, Maryland, November 1963.
6
ФЕНОМЕНОЛОГИЧЕСКАЯ ТЕОРИЯ СИСТЕМ
СО МНОГИМИ ПОВЕРХНОСТНЫМИ ВОЛНАМИ
С. Карп *, Ф. Карал *
Дано феноменологическое описание системы со многими поверхностными
волнами. При этом вводится обобщенное импедансное граничное условие.
Качественные особенности электромагнитного поля остаются такими же, как
и в случае обычного импедансного граничного условия, которое используется
для описания направляющей системы с одной поверхностной волной. Новое
граничное условие допускает распространение большего количества волн. Ойо
вводится для облегчения аналитического исследования ряда интересных задач.
§ 1. ВВЕДЕНИЕ
1. Описание нового граничного условия. Одна из целей на-
стоящей статьи состоит в том, чтобы дать обобщенное гранич-
ное условие, которое можно было бы использовать в граничных
задачах (включая исследование сложных структур), и описать
способ их применения. Вводимые здесь граничные условия со-
держат ряд параметров Zm, которые в целом позволяют по-но-
вому описать систему, ограниченную некоторой поверхностью.
Их более точное определение дается ниже. Если и есть функ-
ция, удовлетворяющая, например, волновому уравнению, то гра-
ничные условия записываются в виде
N
П(1 + хЬ'^)м(х,у) = 0'при у = 0’
где предполагается, что поверхность у = 0 ограничивает иссле-
дуемую систему. Если система имеет несколько сторон- (напри-
* S. N. К а г р, F. G. К а г g 1, Jr., Qpurant Institute of Mathematical Scien-
ces, New York University, New York, N. r.
158
С. Карп, Ф. Карал
мер, заключена в области у<0, x=±L), то такие граничные ус-
ловия записываются для каждой стороны, а д/ду заменяется
производной по нормали. Если же система кусочно неоднород-
на (например, состоит из двух однородных частей), то для
различных частей (например, по оси х) нужно применять раз-
личные граничные условия. Это выражается в том, что для
другой части {Хщ} заменяется другим рядом чисел, скажем {цп}.
Случай N=l хорошо изучен; выбирая соответствующим обра-
зом Ал, можно описать тонкий диэлектрический слой [1], гофри-
рованную поверхность [2], неидеально проводящую поверх-
ность [3] и поглотитель [4, 5]. При описании векторного поля
во всех этих случаях имеет место-более сложный оператор, осо-
бенно для поверхности с анизотропной проводимостью [4, 6].
Случай N = 2 детально описан в работах [7, 8], где рассматрива-
лось поле на поверхности диэлектрика. Случай поверхностных
волн рассматривался также в работе [9].
2. Применение метода к ограниченным структурам. Вторая
цель статьи состоит в том, чтобы показать, как можно исследо-
вать ограниченные структуры при использовании одного или бо-
лее описанных граничных условий, после того как решены соот-
ветствующие предварительные задачи. Основная идея метода
подробно излагается ниже на примере диэлектрического слоя
толщиной t, нанесенного на торец металлической пластинки ши-
риной 2L. Диэлектрик занимает область —L<x<L, 0>y>—t.
Металлическая пластинка занимает область —оо<у<—t,
|х|< L. Если мы зафиксируем какой-нибудь угол, а положение
другого устремим к +оо или —оо вдоль оси х, то в пределе по-
лучим геометрическую поверхность в виде бесконечного клина.
Мы покажем, как использовать решения, получаемые при спе-
циальном возбуждении бесконечного клина, чтобы, составляя
их линейную комбинацию, получить приближенное решение пер-
воначальной задачи о пластине конечной толщины. Коэффи-
циенты, входящие в эту линейную комбинацию, можно получить
из решения небольшого числа алгебраических уравнений. Тре-
бование нетривиальное™ решения при отсутствии внешнего воз-
буждения можно использовать для нахождения резонансных
частот, в общем случае комплексных.
3. Определение оператора и задача обратного рассеяния. Как
видно из сказанного выше, анализ зависит от решения задач
с полубесконечпыми границами (в нашем примере от геометри-
ческих параметров клина). Результат для клина можно полу-
чить экспериментально, но нам нужно вычислить его теорети,-
6. Теория систем со многими поверхностными волнами
159
чески. Еще более простой геометрией обладает слой на метал-
ле, простирающийся от — оо до +оо. (Конечно, на практике
«слой» может представлять собой искусственный диэлектрик,
решетку и т. д.) Для нас важно определить операторное гра-
ничное условие. Если свойства слоя (в нашем примере — ди-
электрического слоя на металле, —оо<х< + оо, —/<у<0) из-
вестны, то можно определить коэффициент отражения теорети-
чески (как функцию угла падения). В противном случае его
можно определить экспериментально. Затем определяем пара-
метры {Хт} из условия, что коэффициент как функция угла от-
ражения соответствует функции, определенной с помощью опе-
раторного граничного условия. Нетрудно решить эту задачу и
при экспериментальном определении коэффициента отражения.
Когда подходящий оператор, учитывающий существование по-
верхностных волн, определен, его можно- использовать для ре-
шения задачи о клине, а затем и для случая ограниченного с
двух сторон тела.
План статьи следующий. В соответствии со сказанным во
введении последовательно (но в обратном порядке) обсуждают-
ся вопросы, поставленные в п. 1—3. А именно в § 2 опреде-
ляются импедансы и граничные условия и обсуждается особый
случай обратного отражения. В § 3, п. 1, рассматривается по-
лубесконечная задача. В § 3, п. 2, обсуждается решение задач
для двусторонне ограниченных систем.
§ 2. ОПРЕДЕЛЕНИЕ ИМПЕДАНСОВ Хт
И ОБРАТНАЯ ЗАДАЧА ОТРАЖЕНИЯ
Предположим, что импеданс неограниченной системы можно
описать с помощью простого коэффициента отражения. Кроме
того, предположим, что полная эффективная диэлектрическая
проницаемость среды за поверхностью раздела, учитывающая
распределенную диэлектрическую проницаемость слоя, а так-
же наличие проводника (при этом образуется «искусственный»
диэлектрик), является такой, что падающая волна отражается
от этой поверхности, как от идеального металла, но с измене-
нием фазы; при этом абсолютная величина коэффициента отра-
жения равна единице. (Противоположный случай, когда эффек-
тивная диэлектрическая постоянная за поверхностью раздела
такая же, как и у обычного диэлектрика, был разобран Кейпом
и Карпом [7] и далее в диссертации Кейна [8]. Этот пример взят
для получения соответствия с некоторыми математическими
выражениями.) Коэффициент отражения для действительных
160
С. Карп, Ф. Карал
углов падения, полученный из эксперимента или аналитически,
аппроксимируем выражением
N
ik cos 0
-------------------------
\
выбирая подходящим образо.м Кт. Параметры Ат выбираются
действительными или комплексными (попарно комплексно-
сопряженными), чтобы обеспечить |Д|=1, как требуется в рас-
сматриваемом примере. Степень приближения для Кт зависит
от количества сомножителей, т. е. они не постоянны и зависят
от N. Таким образом, мы запишем = А,^1. Действительные
параметры Кт соответствуют поверхностным волнам, если имеет-
ся источник, который их возбуждает.
Теперь допустим, что мы имеем дополнительную информа-
цию из аналитического решения задачи для системы с беско-
нечной поверхностью раздела или из эксперимента, т. е. знаем
некоторые параметры Кт. Тогда сомножитель, следующий после
некоторого N-ro члена, можно заменить соответствующим со-
множителем, который включает известную величину Кт. Полу-
ченная таким способом последовательность будет сходиться
к истинному значению R в расширяющейся области комплекс-
ного параметра 0. При этом те корни, которые известны с са-
мого начала, будут оставаться постоянными по величине. Вели-
чины же остальных корней К^т при фиксированном т будут
изменяться вместе с N, Они сходятся к точным значениям К^-
Предельное значение для R будет иметь вид
ika cos 0
Л оо
ik0 cos 0
Л оо
cos 0.
ika cos 0 \
Л оо I
Л'т /
1 \
Для приближенного представления, которое содержит N со-
множителей, по-видимому, нельзя пользоваться точными значе-
ниями Кт (т. е. Кт), поскольку при этом возникают фазовые
ошибки из-за экспоненциально сходящихся сомножителей в бес-
конечном произведении. Наличие такой фазовой ошибки требует
выбора поверхности отсчета, на которой должны быть заданы
граничные условия, чтобы скорректировать эту ошибку, при-
6. Теория систем со многими поверхностными волнами
161
чем поверхность отсчета будет изменяться с изменением чис-
ла N. Конечно, можно было бы использовать точные значения
корней (щ ДА), ио тогда экспоненциально сходящийся со-
множитель должен быть приближенно представлен в виде про-
изведения, т. е.
(л । iAo2cOS0\Ar
exp(z£0Scos 0) — 11 -)-—j ,
как это часто делают в теории фильтров. Это приводит к. появ-
лению дополнительного многократного полюса или нуля, кроме
того полюса, который сильно удален от той области значений
cos 0, для которой справедливо приближение N-ro порядка.
Обратный процесс отражения (заслуживающий детального
изучения) оказывается тесно связанным с вопросом реализации
цепей и с теорией предсказания Винера. Однако мы не можем
пока установить однозначное соответствие, чтобы использовать
теорию Винера в нашем случае.
После того, как подходящее число N и соответствующий
ряд выделены, мы можем построить эквивалентное гранич-
ное условие:
ОО
П(1 + ^_ \ 0.
\ А.та ду)
1
Теперь мы можем решить задачу о точечном источнике над бес-
конечной структурой и сравнить полученное решение с экспе-
риментом или с точным решением, если оно имеется. Результат
сравнения будет, по-видимому, удовлетворительным, и в даль-
нейшем нам не нужно будет каждый раз выверять оператор.
Чтобы было понятно, как эТо делается, заметим, что для ре-
шения при наличии источника полное поле зависит от вида ана-
литической функции коэффициента отражения. Например, в
двумерной задаче для диэлектрического слоя толщиной /, нане-
сенного на идеальный проводник, при падении Т£-волны имеем
, . . sin/p
cos tp + ip0—-f-
______________и .
, , sinZp ’
cos tp — lp0-
Где po=^ocos0, p'1 = k'1 — ko-j-po, a kQ и & —постоянные рас-
пространения соответственно во внешней и внутренней средах.
И Зак. 274
162
С. Карп, Ф. Карал
Таким образом, если вместо косинусов и синусов взять пер-
вые N сомножителей их разложений, в виде бесконечных про-
изведений, то получим
ПЛГ — ipatnN ’
где
'II
о
I 1 \2
(”+2) »
П»=п[1,
1
(у2+д§К
т2л2
pt
здесь yi = ki — k20.
Следовательно, в представлении (2Л1+1)-го порядка знаме-
натель является полиномом, и его корнями будут Для
достаточно больших N приближение будет хорошим в расши-
ряющейся области значений р0, при этом корни Х(иЛГ+1) изме-
няются с номером N так, что достигается хорошее приближение.
Если остановиться на некотором фиксированном значении N, то
получим корни, соответствующие одной или нескольким поверх-
ностным волнам. Если необходимо, эти корни (например, корни,
соответствующие вытекающим волнам) можно заменить их дей-
ствительными значениями (если они известны), оставляя прочие
сомножители без изменения. При изменении N такой процесс
можно повторить. Итак, если Xi известно, то для каждого N
можно определить № для т<.п, а затем заменить Х^’ на ХН
так, чтобы получить последовательность корней ?Л°°); X?*,
Xf°>, Х^; Х(Л Х^, Х<3>; ХП Ч, и т. д.
В рассматриваемом примере /?(ОО) и R(N} известны; мы знаем
также, что RIN> -> Таким образом, с ростом N Х^-> Х^,
так что ’изложенный метод будет вполне удовлетворительным,
хотя, возможно, и не наилучшим. Подобные расчеты желательно
проделать и для коэффициента отражения, полученного из экс-
перимента, но тогда и проверку подходящего представления
необходимо провести экспериментально.
Определив числа Хт, необходимые для дальнейшего, очень
легко рассчитать поле источника, т. е. функцию Грина. Авторы
уже пользовались этим удобным методом в работе [11], однако
результаты можно получить и методом преобразования Фурье.
Методы изображения дают решение задачи о пластинке конеч-
ных размеров в волноводе. Следует подчеркнуть, что этот пред-
варительный анализ может быть полезен в случаях, когда
структура слоистой среды является сложной или неизвестной.
6. Теория систем со многими поверхностными волнами
163
Тогда аналитическое решение можно приближенно получить при
помощи описанного выше обратного метода. Применение ре-
зультирующего оператора позволяет определить функцию Гри-
на даже тогда, когда измерены только коэффициент отражения
и, быть может, характеристики вытекающих и поверхностных
волн.
§ 3. ПРИМЕНЕНИЯ ТЕОРИИ
1. Полубесконечная задача. Главное применение оператор-
ного граничного условия заключено не в предварительных
вычислениях, проделанных выше. Основная цель данной ра-
боты состоит в учете -влияния концов и неоднородностей. На-
пример, задачи, в которых рассматривается полубесконечная ди-
электрическая пластина, вообще не поддаются решению дру-
гими методами. Использование изложенного здесь метода
для бесконечной диэлектрической пластины бессмысленно,
поскольку более строгие решения могут быть получены одина-
ково легко.
В задачах с кусочно-однородными системами для каждого
участка границы мы используем свойственный ей оператор. Для
одноволнового случая метод хорошо известен (см., например,
работы [11—19]). Использование оператора с двумя членами,
как предложено в [7], проиллюстрировано в работах [8, 9]. Дока-
зательство единственности задачи о диэлектрической поверхно-
сти раздела опубликовано Кейном [10]. Решение для бесконеч-
ной пластины получено Карпом и Каралом [11] в случае дей-
ствительных X для W=l, 2, 3. Решение для прямоугольного
клина найдено Каралом и Карпом и будет опубликовано в се-
рии «Электромагнитные волны» Нью-Йоркского университета,
а также и в других изданиях. Интересно, что анализ многовол-
новой системы ненамного труднее, чем одноволновой. Существо-
вание решений установлено его построением. Единственность
доказана в диссертации Моргана для плоского /V-волнового слу-
чая (см. также работу [21] о задаче для прямоугольного клина
в случае одной волны). Результаты этих работ показывают, что
краевые задачи с описанными выше граничными условиями по-
ставлены корректно, несмотря на наличие производных высо-
кого порядка, входящих в граничное условие.
2. Конечная задача и метод взаимодействия. В действитель-
ности все реальные системы конечны. Поэтому наибольший ин-
терес представляет применение изложенного метода к системам,
ограниченным с двух сторон. Случай одноволновой системы
был рассмотрен Карпом и Каралом (работа не опубликована)
11*
164
С. Карп, Ф. Карал
методом самосогласованного взаимодействия. В этом методе
предполагается, что внешнее падающее поле возбуждает на ка-
ждом угле поверхностную волну, причем так же, как и на бес-
конечном клине с тем же углом. Однако коэффициент возбу-
ждения неизвестен. Кроме того, имеется радиальное поле, но
это поле быстро спадает вдоль импедансной поверхности. Пред-
полагается, что, кроме внешней падающей волны, поле на ка-
ждом углу возбуждается еще поверхностной волной, приходя-
щей от другого угла, причем амплитуда этой поверхностной
волны для данного момента времени неизвестна. Следователь-
но, полное поле в силу влияния каждого угла приближенно яв-
ляется линейной комбинацией поля, возбуждаемого внешней
падающей волной, и поля, возбуждаемого приходящей поверх-
ностной волной неизвестной амплитуды. Отраженная поверх-
ностная волна может быть определена из решения задачи для
бесконечного клина — через амплитуду неизвестной падающей
поверхностной волны. Она складывается с поверхностной вол-
ной, возбуждаемой внешним падающим полем, и результирую-
щая амплитуда должна быть амплитудой поверхностной волны,
идущей к другому углу. При таком рассмотрении задача сво-
дится к решению двух алгебраических уравнений с двумя неиз-
вестными. Полное поле определяется суммой вкладов от углов,
возбуждаемых падающей и поверхностной волнами. Похожий
самосогласованный метод уже использовался Карпом в рабо-
тах [22, 23], а также был описан в работах [24—27]. Этот метод
особенно подходит к нашему случаю (импедансные граничные
условия), так как именно в этом случае стремление к нулю
функции, описывающей поле, вдоль поверхности раздела сводит
к минимуму другие взаимодействия между краями, кроме вза-
имодействия через поверхностные волны. Задача о слое с ко-
нечным импедансом в неограниченном проводнике решена не-
зависимо этим же методом Кейном для случая одной волны [28].
Описанный выше пример ограничивается случаем одной вол-
ны. Читатель может легко проверить, что он применим также и
в случае W волн с учетом того, что каждый угол может излу-
чать и в свою очередь возбуждаться несколькими поверхностны-
ми волнами, неизвестные амплитуды которых определяются, как
указывалось выше, из требования согласованности. Главными
составными частями в таком расчете являются задачи рассея-
ния от углов поля падающей волны и любых распространяю-
щихся над данной структурой поверхностных волн. Следует под-
черкнуть, что этот метод расчета можно применить и в отсут-
ствие падающего поля, так как видно, что коэффициенты
возбуждения волн, записанные в виде отношений, определяют
6. Теория систем со многими поверхностными волнами 165
возможные комплексные резонансные частоты системы, когда
их знаменатели стремятся к нулю. Метод может оказаться так-
же полезным при анализе работы лазера.
ЛИТЕРАТУРА
1. Barlow Н. М„ Cullen A. L., Proc. IEE, Pt. Ill, 100, 329 (1953).
Surface Waves.
2. Barlow H. M., Karbowiak A. E., Proc. IEE, Pt. Ill, 101, 182 (1954).
An Experimental Investigation of the Properties of Corrugated Cylindrical
Surface Waveguides.
3. G r ii n b e r g G. A., Phys. Rev., 63, 185 (1943).
Suggestions for a Theory of Coastal Refraction.
4. Karal F. C., Karp S. N., Comm. Pure Appl. Math., 11, 495 (1958).
Diffraction of a Skew Plane Electromagnetic Wave by an Absorbing Right
Angled Wedge.
5. К a r p S. N., Karal F. C., IRE Trans. (Toronto Symposium on Electro-
magnetic Theory), AP-7, S91 (1959).
A New Method for the Determination of Far Fields with Application to the
Problem of Radiation of a Line Source at the Tio of an Absorbing Wedge.
6. C h u T. S., К a r p S. N„ Quart. Appl. Math., 21, 257 (1964).
The Field of a Dipole Above an Infinite Corrugated Plane.
7. К a n e J., К a r p S. N„ Journ. Res. Nat. Bur. Stds., 68D (Radio Science),
303 (1964).
A Simplified Theory of Diffraction at an Interface Separating Two Dielec-
trics.
8. Kane J., Karp S. N., Res. Rep. EM-154, New York University, Inst.
Math. Sci., Div. Electromagnetic Res., 1960.
Radio Propagation।Past a Pair of Dielectric Interfaces.
9. J о n e s W. R., Hughes Res. Rep. FL62-1, Hughes Aircraft Co., Culver
City, Calif., 1962.
An Approximate Approach to the Problems Involving Surface Waves.
10. Kane J., Proc. Am. Math. Soc., 12, 967 (1961).
A Uniqueness Theorem for the Reduced Wave Equation.
11. Karal F. C., Karp S. N., Res. Rep. EM-198, New York University,
Inst. /Math. Sci., Div. Electromagnetic Res.
Phenomenological Theory of Multi-Mode Surface Wave Excitation, Propaga-
tion and Diffraction; I. Plane Structures.
12. Senior T. B. A., Comm. Pure Appl. Math., 12, 337 (1959);
Diffraction by an Imperfectly Conducting Wedge.
13. C h u T. S., К о u у о u m j i a n R. G., Karal F. C., Karp S. N., IRE
Trans., AP-10, 679 (1962).
The Diffraction of Surface Waves by a Terminated Structure in the Form
of a Right-Angle Bend.
14. К a r a 1 F. С., К a r p S. N„ Quart. Appl. Math., 20, 97 (1962).
Diffraction of Plane Wave by a Right Angled Wedge which Sustains Sur-
face Waves on One Face.
15. К a r a 1 .F. C., Karp S. N., C h u T. S., К о u у о u m j i a n R. G., Comm.
Pure Appl. Math., 14, 35 (1961).
Scattering of a Surface Wave by a Discontinuity in the Surface Reactance
on a Right Angled Wedge.
16. Karp S. N., Res. Rep. EM-129, New York University, Inst. Math. Sci.,
Div. Electromagnetic Res., 1959.
Two Dimensional Green’s Function for a Right Angled Wedge Under an
Impedance Boundary Condition.
166 С. Карп. Ф. Карал
17. Karp S. N., Kara! F. С., Comm. Pure Appl. Math., 12, 435 (1959).
. Vertex Excited Surface Waves on Both Faces of a Right Angled- Wedge.
18. Karp S. N., Karal F. C., Quart. Appl. Math. 18, 235 (1960).
Vertex Excited Surface Waves on One Face of a Right Angled Wedge.
19. Williams W. E., Quart. Journ. Meeh. Appl. Math., 13, 278 (1960).
Propagation of Electromagnetic Surface Waves along Wedge Surfaces.
20. Малюжинец Г. Д., ДАН, 121, 436 (1958).
Возбуждение, отражение и излучение поверхностных воли на клине с за-
данными импедайсами граней.
21. Morgan R. С., Karp S. N„ Comm. Pure Appl. Math., 16, 45 (1963).
Uniqueness Theorem for a Surface Wave Problem in Electromagnetic Dif-
fraction Theory. См. также Res. Rep. EM-178, New York University, Inst.
Math. Sei., Div. Electromagnetic Res.
22. Karp S. N„ Phys. Rev. (Bull. Amer. Phys. Soc. Meeting), 86, 586 (1952).
Diffraction by Finite and Infinite Gratings.
23. К a r p S. N, The McGill Symposium on Microwave Optics, Pt. II, Pub-
lished AFCRC, Bedford, Mass., April 1959.
Diffraction by Combinations of Obstacles.
24. Karp S. N., Res. Rep. EM-85, New York University, Inst. Math. Sci., Div.
Electromagnetic Res., 1955.
Diffraction by an Infinite Grating of Cylinders.
25. Karp S. N„ Rad low J., Res. Rep EM-90, New York University, Inst.
Math. Sci., Div. Electromagnetic Res., 1956.
On Resonance in Infinite Gratings of Cylinders.
См. также IRE Trans., AP-4, 654 (1956).
26. Karp S. N., Russek A., Res. Rep. EM-75. New York Univ., 1955.
Diffraction by a Wide Slit.
См. также Journ.. Appl. Phys., 27, 886 (1956)
27. К e 11 e r J. В., К a r p S. N„ Optica Acta, 8, № 1, 61 (1961).
Multiple Diffraction by an Aperture in a Hard Screen.
28. Kane J., в книге Proc. Symp. on Electromagnetic Theory and Antennas
(Copenhagen, June 1962). ed. E. C. Jordan, New York, 1963, Pt. 2, p. 891.
A Surface Wave Antenna as a Boundary Value Problem.
7
САМОСОГЛАСОВАННАЯ ТЕОРИЯ ИЗЛУЧЕНИЙ
ЧЕРЕНКОВА И СМИТА—ПАРСЕЛЛА
И. Палоч *, А. Олинер **
В предшествующих работах по эффекту Черенкова предполагалось, что
источник возбуждения (движущийся электрон или модулированный пучок
электронов) задан и не подвергается воздействию со стороны излучения
В данной работе предлагается новый метод анализа излучений Черенкова и
Смита — Парселла, вызванных модулированным электронным пучком; послед-
ний рассматривается как самосогласованный, т. е. учитывается эффект обрат-
ного воздействия на пучок со стороны излучения При таком подходе пучок
и замедляющая структура (диэлектрическая среда или периодическая решет-
ка) рассматриваются при получении решения как единое целое, т. е требо-
вание самосогласоваиности выполняется автоматически. Таким образом, в ре-
шении учитывается воздействие на пучок волн пространственного заряда.
Получены строгие решения в двух случаях: а) для излучения Черенкова,
которое возникает при прохождении плоского электронного пучка конечной
толщины, модулированного малым сигналом, между двумя полубесконечными
диэлектрическими областями, и б) для излучения Смита — Парселла, которое
возникает при прохождении такого же пучка между двумя плоскопараллель-
ными ленточными дифракционными решетками. Применительно к последнему
случаю необходимо было сперва рассчитать эквивалентную схему для волны,
падающей иа такую решетку, с учетом многомодовости. Численные данные
для различных случаев были получены с помощью простого, но достаточно
точного метода возмущений
Метод собственных значений позволяет обнаружить новые эффекты в из-
лучениях Черенкова и Смита — Парселла. Показано, что для обоих указан-
ных случаев волновые числа комплексны и что спектр излучений состоит из
бесконечного ряда быстрых и медленных волн. Даже в идеальном моно-
эиергетическом случае излучение не сосредоточено в определенном направле-
нии. Разброс по углу составляет обычно менее 1°, однако ни эксперимента-
торы, ни теоретики не обнаружили пока тонкой структуры излучения. Иссле-
довались различные свойства быстрых и медленных волн; показано, что
амплитуды медленных волн растут вдоль оси пучка. Среди прочих результа-
тов следует отметить существование оптимальной толщины пучка
* 1. Р а 1 б с z, IBM Thomas J. Watson Research Center, Yorktown Heights,
N. Y.
** A. Oliner, Department of Electrophysics, Polytechnic Institute of
Brooklyn, Brooklyn, N. Y.
168
И. Палоч, А. Олинер
§ 1. ВВЕДЕНИЕ
Исторический обзор: теория заданного источника. Объясне-
ние эффекта Черепкова было дано Франком и Таммом [1] в
1937 г. Анализируя поле, созданное движущимся в диэлектри-
ческой среде электроном, они нашли, что излучение возможно,
а '''//////Л АЛ/W
77/////Л
г ~ ~
Фиг. 1. Различные конфигурации, соответствующие излучениям
Черенкова и Смита—Парселла.
если заданная постоянная скорость частицы превышает фазовую
скорость волн в среде. Излучение представляет большой инте-
рес и с теоретической и с практической точек зрения. По этому
вопросу существует многочисленная литература [2—4].
Эффект Черенкова можно использовать для генерации мил-
лиметровых волн. При этом по практическим соображениям
наиболее удобной является такая конструкция, при которой пу-
чок движется не внутри диэлектрика, а в непосредственной бли-
зости от его поверхности (фиг. 1,а) или вдоль щели, образован-
ной в диэлектрике. Первые расчеты для таких конструкций были
проделаны Гинзбургом [5]; позднее они были развиты Гинзбур-
гом и Франком [6], Линхартом [7], Торальдо ди Франчиа [8],
Фельсеном и Хесселем [9] и другими. Каждая из этих работ вне-
сла свой вклад в понимание физических или математических
характеристик излучения Черенкова.
Известно, что частотный спектр излучения отдельной частицы
(возбуждение типа б-фупкции) является непрерывным; при этом
можно вычислить все представляющие интерес величины. Не-
обходимо отметить, что в вышеупомянутых работах по исследо-
ванию эффекта Черепкова предполагалось, что источник возбу-
ждения задан и не подвергается изменению при появлении из-
лучения. Поэтому волновые числа, полученные в этом прибли-
жении, были действительными.
7. Теория излучений Черенкова и Смита — Парселла 169
В 1953 г. Смитом и Парселлом [10] был описан новый тип
излучения, который родствен излучению Черенкова. Они пред-
сказали теоретически и затем наблюдали экспериментально из-
лучение, вызванное электроном, движущимся вблизи идеально
проводящей периодической структуры (фиг. 1,6). При объясне-
нии природы этого явления представляется удобным рассмот-
реть электрон и его изображение, которые образуют диполь.
Изображение имеет горизонтальную и вертикальную компонен-
ты скорости. В соответствии с этим в плоскости, перпендикуляр-
ной оси пучка, мы будем видеть осциллирующий диполь, со-
здающий излучение. Так как последний движется относительно
наблюдателя, то будет наблюдаться также эффект Допплера.
Этот тип излучения можно использовать для генерации волн
от миллиметрового до оптического диапазонов включительно.
В связи с этим следует отметить работу Солсбери [11], который
запатентовал генератор высокочастотного излучения, возникаю-
щего при прохождении электронного пучка через стоячую волну,
образованную решеткой и отражателем. Бредшоу [12] предло-
жил конструкцию СВЧ умножителя миллиметровых волн, в ко-
тором используется излучатель Смита — Парселла, состоящий
из ряда полусфер, вмонтированных в плоскость. Ишигуро и
Тако [13] провели эксперименты в инфракрасном диапазоне, они
исследовали эффективность различных решеток и указали на
связь между излучениями Черенкова и Смита — Парселла. Ин-
тересно отметить, что Торальдо ди Франчиа [8] обнаружил эту
связь независимо от них и пользовался представлением о волно-
вом пакете, которое значительно облегчает понимание эффекта
и дает возможность вычислить полную энергию излучения. По
словам Фельсена и Хесселя [9], метод Торальдо ди Франчиа
представляет изящную технику теории одномерных цепей, по-
зволяющую’получать численные данные.
Из этого краткого обзора ясно, что метод анализа, предпо-
лагающий заданным источник возбуждения, позволяет получить
много сведений о характере излучения Смита — Парселла, од-
нако до сих пор оно изучено гораздо меньше, чем эффект Че-
ренкова.
Выше мы говорили, что излучение возбуждается отдельным
электроном, движущимся по прямой с заданной скоростью. Прак-
тически в генераторе Миллиметровых волн возбуждение осуще-
ствляется модулированным пучком электронов. Это обстоятель-
ство было учтено Деносом [14], который проанализировал излу-
чение Черенкова, возбуждаемое сконцентрированным электрон-
ным пучком, проходящим вблизи полубесконечной диэлектриче-
ской пластины (фиг. 1,в). Он предполагал, что пучок движется
подобно твердому телу, т. е. плотность заряда в системе коорди-
170
И. Палоч, А. Олцнер
нат, связанной с движущимся электроном, принимается по-
стоянной.
Самосогласованное решение. Во всех исследованиях, на ко-
торые мы ссылались выше, излучение вычислялось в предполо-
жении заданного источника возбуждения, тем самым не учиты-
валось обратное воздействие на движущуюся частицу или пучок
со стороны излучения. Многие авторы отмечали тот факт, что
обратная реакция должна иметь место и что, используя метод
заданного источника, можно рассчитать в первом приближе-
нии поправку на эту реакцию. Однако это не было сделано, воз-
можно, потому, что обычно эту поправку считают пренебрежимо
малой. Это пренебрежение справедливо лишь для пучков и за-
рядов, движущихся с релятивистскими скоростями, но в том
случае, когда эти скорости имеют порядок 1/10 скорости света
(этот диапазон скоростей, как указал Коульман1), является
наиболее интересным для ферромагнитных сред), вышеупомя-
нутой поправкой пренебрегать не следует.
Самосогласованное решение, автоматически учитывающее
влияние излучения на пучок, важно не только с точки зрения
того, что оно позволяет осуществить уточнение численных расче-
тов при различных условиях. С его помощью удалось обнару-
жить целый ряд новых эффектов, которые не были обнаружены
с помощью методов анализа, предполагающих неизменным ис-
точник возбуждения.
Одним из выводов самосогласованной теории явилось то, что
в излучении принимают участие быстрые и медленные волны
пространственного заряда и что эти волны по природе своей
являются вытекающими. Быстрые волны затухают вдоль оси
пучка, а медленные, наоборот, растут. Более детально свойства
этих волн будут обсуждены ниже. Далее, существует бесконеч-
ное число этих вытекающих/волн пространственного заряда, но
отличие по углу между ними обычно мало (меньше 1°). Хотя
даже в моноэнергетическом случае излучение не сосредоточено
строго в одном направлении, это свойство весьма трудно обна-
ружить экспериментально. Какая из вытекающих волн простран-
ственного заряда будет давать наибольший вклад в излучение,
зависит от параметров пучка и замедляющей структуры. Для
различных параметров будут преобладать различные волны;
ниже это иллюстрируется численно. Теория указывает на суще-
ствование оптимальной скорости и оптимального диаметра пуч-
*) Р. О. С о 1 е m а п, частное сообщение, 1953,
7 Теория излучений Черенкова и Смита — Парселла 171
ка, а также дает прямой метод расчета этих важнейших пара-
метров излучений Черенкова и Смита — Парселла.
Некоторые авторы указывают, что излучение Черенкова, про-
цессы в лампе бегущей волны (ЛБВ) [7, 15] и волны простран-
ственного заряда типа Хана — Рамо [16] тесно связаны. Однако
существующие между ними различия затрудняют использование
теории ЛБВ для получения аналитических результатов в случае
излучения Черепкова.
Мурье установил необходимость комплексных собственных
волновых чисел в полном решении и исследовал случай первой
моды для бесконечно тонкого пучка. Дарней и Гроу [15] учли
толщину пучка, но получить выражения для собственных волно-
вых чисел им не удалось. Поэтому аналогия с ЛБВ имеет огра-
ниченное применение; предлагаемый вместо этого подход, осно-
ванный на теории антенн вытекающих волн, является более
удачным.
Целесообразно указать основные различия между излуче-
нием Черенкова и излучением в ЛБВ, которые станут более по-
нятными после изложения сущности самосогласованной теории:
1) В отличие от ЛБВ для получения излучения Черенкова
выполнение условия синхронизма необязательно; требуется лишь,
чтобы скорость пучка превышала некоторую критическую ве-
личину.
2) В отличие от ЛБВ в излучении участвуют как быстрые,
так и медленные волны пространственного заряда. (Свойства
этих волн изложены ниже более подробно.)
3) В ЛБВ взаимодействие волн пространственного заряда
и пучка осуществляется с дискретными модами медленной вол-
ны; в противоположность этому в случае излучения Черен-
кова взаимодействие осуществляется с волнами непрерывного
спектра. Можно ожидать поэтому, что выходная мощность ЛБВ
больше, чем мощность излучения Черенкова, и мы покажем это
численным расчетом. С другой стороны, излучению Черенкова
присуща большая широкополосность, что можно использовать
в усилительных и антенных устройствах.
§ 2. САМОСОГЛАСОВАННАЯ ТЕОРИЯ ИЗЛУЧЕНИЙ
ЧЕРЕНКОВА И СМИТА-ПАРСЕЛЛА
Введение. Здесь мы изложим новый метод анализа излуче-
ний Черенкова и Смита — Парселла, в котором при расчете по-
лей, создаваемых токами, учитываются и токи, наводимые по-
лями. При этом предполагается, что пучок и структура, с кото-
рой он взаимодействует (периодическая решетка или диэлектри-
ческая среда), рассматриваются в решении как единое целое,
172
И. Палоч, А. Олинер
т. е. требование самосогласованное™ выполняется автоматиче-
ски. Как было отмечено выше, аналогия между рассматривае-
мым классом проблем и антеннами вытекающих волн позволяет
создать методику расчета собственных значений с учетом реаль-
ных условий.
'-Электронный
пучок
а
Фиг. 2. а — плоский луч в свободном пространстве; поле вне
луча спадает в поперечном направлении экспоненциально, как
в волноводе с докритическими размерами; б — волны, возни-
кающие благодаря наличию диэлектрического материала.
Рассмотрим два случая: а) излучение Черенкова, обуслов-
ленное плоским электронным пучком конечной толщины, про-
модулированным малы.м сигналом и проходящим между двумя
полубесконечными диэлектрическими полупространствами, и
б) излучение Смита — Парселла, обусловленное таким же пуч-
ком, проходящим между двумя плоскопараллельными ленточ-
ными дифракционными решетками.
Природу волн в рассматриваемых явлениях можно понять
из фиг. 2. Каждый электрон в пучке (фиг. 2, а) движется пря-
молинейно слева направо вдоль сильного внешнего постоянного
магнитного поля. На фиг. 2, б показан пучок, помещенный меж-
ду двумя диэлектрическими полупространствами, которые воз-
мущают поле пучка. Из фиг. 2, а видно, что поле волны про-
странственного заряда модулированного пучка спадает экспо-
ненциально в поперечном направлении от границы пучок — сво-
бодное пространство. Если же теперь поместить пучок в диэлек-
трическое пространство с высокой диэлектрической постоянной
(фиг. 2,6), то возмущение и сопутствующее ему излучение пре-
вратят волны пространственного заряда, занимающие ограни-
ченную область, в вытекающие волны. В математической интер-
претации это означает, что в первом случае волновые числа
действительны, а во втором (т. е. когда происходит излучение
Черенкова) комплексны.
В случае излучения Смита — Парселла природа волн анало-
гична (фиг. 3). Действительно, легко видеть (фиг. 3,а), что
7. Теория излучений Черенкова и Смита — Парселла 173
амплитуда волн пространственного заряда имеет экспоненциаль-
ный спад от границ пучка, когда последний проходит между
двумя плоскопараллельными проводящими пластинами. Если
теперь в пластинах прорезать щели с некоторым периодом, то
возникнут пространственные гармоники и при определенном
периоде появится несколько пространственных гармоник, рас-
пространяющихся в поперечном направлении. Из-за возмущения
а 5
Фиг. 3. а — луч, проходящий между двумя идеально прово-
дящими плоскопараллельными пластинами; б — при наличии
периодического возмущения некоторые из пространственных
гармоник могут распространяться в поперечном направлении.
волны пространственного заряда превращаются в вытекающие
волны пространственного заряда, другими словами, их волно-
вые числа становятся комплексными, тогда как в случае, изо-
браженном на фиг. 3, а они были действительными.
Таким образом, излучение Черенкова, излучение Смита —
Парселла и процессы в антеннах вытекающих волн подобны
друг другу. Выход энергии излучения в двух последних случаях
происходит через щели, прорезанные в волноводе (фиг. 3,6);
в случае же эффекта Черенкова это осуществляется благодаря
присутствию диэлектрика.
Вышеизложенная точка зрения не только дает новое каче-
ственное понимание этих явлений, но и метод, с помощью ко-
торого можно найти комплексные волновые числа в условиях
многомодовости.
Математическая трактовка. Изложим в общих чертах мате-
матический аппарат, с подробностями которого можно ознако-
миться в работах [17, 18]. Используя выражения, строгие в слу-
чае малых амплитуд, мы выведем точные соотношения, учи-
тывающие влияние возмущения и позволяющие сравнительно
просто получить необходимые численные данные.
Вначале мы исследуем волны пространственного заряда, воз-
буждаемые плоским электронным пучком конечной толщины,
проходящим между двумя плоскопараллельными пластинами
(фиг. 3,а). Если последние отодвинуть в бесконечность, то пу-
чок окажется в свободном пространстве (фиг. 2, а). В дальней-
ших расчетах учитывается тот факт, что некомплексные соб-
ственные значения, полученные для случаев, изображенных на
174
И. Палач, А. Олинер
фиг. 2, а и 3, а, тесно связаны с комплексными собственными
значениями, характеризующими излучения Черенкова и Сми-
та— Парселла; следовательно, последнее можно вычислить ме-
тодом теории возмущений.
Свойства волн пространственного заряда хорошо известны;
первыми их исследовали Хан [19] и Рамо [20]. Бранч и Миран
[21] исследовали свойства этих волн для различных конфигу-
раций. Маркувиц [22] предложил очень удобную для данного
случая схему, в которой электронный пучок рассматривается
как матричный элемент изотропного диагонального многопо-
люсника. Для наших расчетов можно успешно применить также
метод поперечного резонанса, должным образом обобщенный
на релятивистский случай (т. е. когда средняя скорость пучка
vQ сравнима со скоростью света с в свободном пространстве}.
Для электронного пучка, движущегося между двумя плоско-
параллельными пластинами, необходимо решить следующие
нормализованные уравнения:
x;tg(Bx;)=A'cthnn (1)
Л'2 = ^2-1, (2)
< = (1 - (3)
Здесь хь и —jh суть поперечные волновые числа в пучке и в сво-
бодном пространстве соответственно, a kz — продольное волно-
вое число. Штрихи над соответствующими буквами означают,
что искомые волновые числа безразмерны, т. е. разделены на
k—волновое число в свободном пространстве.
Нормализованные параметры определяются следующим об-
разом:
A — ak, (4)
В = bk, (5)
(В \2 е IZ I / \2~13/2
М =---------lol , (6)
k / znoeo v^k \ с ) I
= (7)
где а — расстояние между пучком и пластиной, 2Ь — толщина
пучка, р₽ —волновое число распространения плазмы электрон-
ного пучка, обобщающее обычное волновое число на реляти-
вистский случай.
Легко показать, что эта система уравнений имеет бесконеч-
ное число действительных решений для чисел kz, лежащих
между D — С1/2 и D, а также между D и D Д- С1/2. Во всех
интересующих нас случаях постоянная С мала по сравнению
7. Теория излучений Черенкова и Смита — Парселла 175
с D, поэтому корни системы очень близки друг к другу. Данную
систему уравнений можно использовать и в случае излучения
Черенкова (фиг. 2,6), для чего необходимо заменить правую
часть уравнения (1) выражением
zdh cth {Ah ) +J{ed — kz )
Л / / /2Д/2 . t •
tdh +/ (ed — kz ) cth(JA)
Здесь e<i — относительная диэлектрическая проницаемость среды.
На фиг. 4 представлена половина структуры Черенкова и схема,
а
Zb, ХЬ za>xa %d>xd
Фиг. 4. а — плоский луч, про-
ходящий между двумя полу-
бесконечными диэлектрически-
ми областями (показана поло-
вина структуры); б — эквива-
лентная схема для половины
структуры.
Фиг. 5. Эквивалентная схема
решетки (для половины струк-
туры).
эквивалентная только что рассмотренным уравнениям. Воз-
можны два основных случая:
1) Волновое число k'z действительно, причем > ed~>
Имеет место качественно такой же случай, как и для пучка, на-
ходящегося в свободном пространстве, т. е. излучение отсутствует.
2) Все собственные значения комплексны и e</>Re(&').
В этом случае происходит излучение Черенкова.
Переход между этими случаями соответствует критическому
значению диэлектрической проницаемости
= (8)
при этом излучение направлено почти параллельно пучку. Урав-
нение (8) является условием наличия излучения Черенкова под
скользящим углом к оси пучка. Если имеется решение для пуч-
ка, движущегося в свободном пространстве, то вышеприведен-
ную систему уравнений, описывающую излучение Черенкова,
176
И. Палоч, А. Олинер
можно решить методом линейных возмущений. С подробностями
такого расчета можно ознакомиться в работе [17].
Заметим, что анализ излучения Черенкова осуществляется
в три этапа: I) составление и решение уравнений для пучка,
движущегося в свободном пространстве; 2) составление уравне-
ний для излучения Черенкова, являющихся строгими для сиг-
нала малой амплитуды; 3) решение этих уравнений простым, ио
весьма точным методом линейных возмущений. Аналогично
можно произвести и анализ излучения Смита — Парселла, но
расчеты усложняются из-за того, что периодическая структура
(фиг. 3, б) порождает пространственные гармоники высших
порядков. Анализу излучения Смита — Парселла должно пред-
шествовать тщательное изучение свойств используемой перио-
дической структуры.
Ввиду того что анализ идеально проводящей многомодовой
плоской решетки в свободном пространстве, используемой здесь
(фиг. 3,6), весьма громоздок, мы дадим лишь его схему. В ка-
честве источника излучения Смита — Парселла (при исследо-
вании решетки в свободном пространстве) рассматривается
£-мода, падающая поперек плоскости решетки. После выбора
подходящего представления по модам составляется интеграль-
ное уравнение для искомого поля в районе щели. Параметры
эквивалентной статической схемы вычисляются путем ортого-
нализации ядра интегрального уравнения и последующего при-
менения аппарата рядов Фурье. Выражения для импедансных
параметров получаются в явной форме как функции коэффи-
циентов Фурье при условии, что размер щели много меньше
периода дифракционной решетки р.
На фиг. 5 изображена эквивалентная схема половины струк-
туры для случая, когда учитываются две поперечные моды: ос-
новная (т = 0) и первая (т=1). Номер гармоники определяется
из соотношения
где р— период решетки. Элементы эквивалентной схемы для
половины структуры равны
Уто’ = -i- /сое0/? In cosec ~ ,
у = ae.op = 2jo_
15 7 2л 2a2 ’
1
a =-----------,
лд
Sin
2p
p^-co^.
(9)
(10)
(И)
(12)
7. Теория излучений Черенкова и Смита — Парселла
177
Можно показать, что если геометрия решетки выбрана пра-
вильно, то для вычисления поля в дальней зоне достаточно рас-
смотреть лишь две моды. Мы будем анализировать излучение
Смита — Парселла при этих условиях.
б
I
I_______________________________________________________________________________________________________________________________________
в
*b,Yb
Xa>Ya
Т'
Ф н г. 6. а — плоский пучок проходит между двумя пластинами
(показана половина структуры); б и в — эквивалентные схемы
для половины структуры.
На фиг. 6, а показана половина структуры, для которой про-
водится анализ. Расстояние между пучком и поверхностью ре-
шетки и полуширина пучка обозначены соответственно а и Ь;
пучок движется вертикально. В нижней части фиг. 6 представ-
лены две эквивалентные схемы структуры Смита — Парселла,
на одной из которых проводимость YT представлена более де-
тально. Из схемы видно, что полная проводимость Уг является
12 Зак. ??4
178
И. Палач, 4. Олинер
функцией параметров решетки и полных проводимостей пере-
дающих линий для первой гармоники (m = I). Следует напом-
нить, что для этой моды
(13)
так как разность между D и k'z незначительна по сравнению
с Х/р; с другой стороны, для обычных значений параметров
Ср2/Х2<С1. С учетом этого в случае первой моды (т=1) можно
заменить две последовательные передающие линии одной. Пара-
метры этой линии равны
(И)
<1 = 1
Уравнение поперечного резонанса имеет вид
XP + 2pA'Qr = 0,
где величины Р, Q, R, S и Т даются формулами
Р — h' — -л'ь tg(Zta') cth (Ah'),
Q — h' cth (Ah') — x' th (Z?x'),
R = x;, cosec2 -g,
(15)
(16)
(17)
Уравнение поперечного резонанса (16) вместе с уравнениями
(2) и (3) определяют собственные значения, причем в случае
излучения они комплексны. Как уже было отмечено выше, для
получения простых по форме, но точных аналитических выра-
жений собственных функций следует использовать метод линей-
ных возмущений.
§ 3. РЕЗУЛЬТАТЫ
Свойство волн. Мы уже говорили, что возмущение, вызывае-
мое присутствием диэлектрической области или решетки, и со-
путствующее ему излучение превращают полностью связанные
с электронным потоком волны пространственного заряда с дей-
ствительными собственными значениями в вытекающие волны
7. Теория излучений Черенкова и Смита — Парселла 179
пространственного заряда, у которых собственные значения ком-
плексны.
Свойства этих вытекающих волн можно пояснить с помощью
фиг. 7, которая относится к излучению Черенкова. В левой ча-
сти фигуры показаны быстрые вытекающие волны простран-
ственного заряда (быстрые по сравнению со скоростью немоду-
лированного пучка). Излучение Черенкова схематически пред-
ставлено лучами, густота которых является мерой плотности
мощности излучения. Как показано на фигуре, амплитуда волн
пространственного заряда экспоненциально спадает вдоль оси z,
т. е. количество излучения на единицу длины уменьшается с
увеличением z. Это уменьшение показано уменьшением густоты
лучей вдоль оси z.
Вдоль вертикальной линии z=z' в направлении от плоско-
сти возбуждения амплитуда экспоненциально нарастает, причем
имеется максимум при z' tg0 (0 — угол между лучом и положи-
тельным направлением оси z). По другую сторону максимума
амплитуда быстро спадает. Видно, что поле сосредоточено глав-
ным образом в области, имеющей форму клина, при этом из-за
поперечного экспоненциального роста оно представляет’ собой
неспектральное решение.
В правой части фиг. 7 представлены в графической форме
свойства медленных волн. Все вышесказанное относительно
свойств быстрых волн (за исключением двух последних заме-
чаний) справедливо и для медленных волн, если поменять ме-
стами слова «уменьшение» и «увеличение». Более детально
свойства этих волн рассмотрены в работе [17].
На фиг. 8 показаны основные свойства вытекающих волн
пространственного заряда в излучении Смита — Парселла. Изо-
бражен случай, когда параметры решетки и.длина волны тако-
вы, что в расчетах надо учитывать две поперечные моды. Вид-
но, что при этих условиях возбуждаются обратные волны. Ха-
рактер изменения амплитуды волн пространственного заряда
в продольном направлении такой же, как и для излучения Че-
ренкова. Поведение поля в поперечном направлении для излу-
чения Смита — Парселла прямо противоположно, так как оно
связано с обратными волнами. Другими словами, в поперечном
направлении быстрые (медленные) волны в излучении Смита —
Парселла ведут себя так же, как медленные (быстрые) волны
в излучении Черенкова. В обоих излучениях амплитуда бы-
строй волны определяется глубиной модуляции электронного
пучка, а медленная волна является нарастающей и обладает
обычным свойством «отрицательной» энергии, связанной с та-
кими медленными волнами пространственного заряда.
12*
Диэлектрик
Диэлектрик
Фиг. 7. Природа волн в излучении Черенкова
Линии поля н амплитуда для быстрой (а) и медленной (б) волн.
Фиг. 8. Природа обратных волн в излучении Смита — Парселла.
Линии поля и амплитуда для быстрой (а) и медленной (б) волн.
Амплитуда
5
7. Теория излучений Черенкова и Смита — Парселла 181
Результаты численных расчетов. Как уже отмечалось,
все численные расчеты проводились методом 'возмущений. Ре-
зультаты этих расчетов представлены в графической форме.
Следует отметить, что для проверки методом итераций были
найдены и точные решения, причем было получено хорошее со-
ответствие. Как мы увидим ниже, излучения Черенкова и Сми-
та— Парселла ведут себя одинаково, хотя количественно имеют-
ся некоторые различия.
Фиг. 9. Нормализованная постоянная затухания (мера излучае-
мой мощности) в случае излучения Черенкова для первой
и второй воли как функция толщины пучка.
На фиг. 9, относящейся к излучению Черенкова, представ-
лена зависимость нормализованной постоянной затухания от
толщины пучка для первой и второй быстрых волн. Аналогичная
зависимость для соответствующих медленных волн мало отли-
чается от представленной на фиг. 9. На этой фигуре представ-
лен случай, когда толщина пучка имеет оптимальное значение,
при котором мощность первой волны максимальна. Если тол-
щину луча увеличивать, то весьма быстро возрастает мощность
второй и высших волн. Так, при Ь/Х>0,25 вклад второй быстрой
волны в излучение уже больше, чем вклад первой. На фиг. 10
изображена аналогичная зависимость для излучения Смита —
Парселла, причем для сравнения здесь же пунктиром нанесены
кривые фиг. 9 для излучения Черенкова. Видно, что кривые
подобны по форме и даже численные различия для выбранных
значений параметров не велики.
На фиг. 11 представлена излучаемая мощность (нормализо-
ванная постоянная затухания) для первой быстрой волны в
функции относительной диэлектрической проницаемости е<г-
Фиг. 10. Постоянная затухания для случая излучения Смита —
Парселла как функция толщины пучка (сплошные линии).
Для сравнения пунктирными линиями нанесена аналогичная зависимость (фиг. 9)
для излучения Черенкова.
Фиг. 11. Постоянная затухания первой быстрой волны как
функция диэлектрической проницаемости.
Фиг. 12. Постоянная затухания в случае излучения Черенкова
как функция плотности тока для первой и второй быстрых
волн.
Фиг. 13. Постоянная затухания как функция плотности тока
для случая излучения Смита—Перселла.
Для сравнения пунктирными линиями показана аналогичная зависимость для
излучения Черенкова.
184
И. Палоч, А. Олинер
Начало кривой на оси абсцисс соответствует точке ed = k'*\
она имеет в этой точке вертикальную касательную. Кривая так-
же имеет оптимальное значение проницаемости е<г, причем опти-
мумы для других волн находятся вблизи от оптимума для пер-
вой быстрой волны (на фигуре это не показано). Кривая
Фиг. 14. Направление излучения Черенкова для различ-
ных вытекающих волн пространственного заряда как
функция плотности тока.
на фиг. 11 относится к случаю излучения Черенкова. Струк-
тура Смита — Парселла, которую мы уже подробно обсуждали
(фиг. 3), не содержит диэлектрика.
На фиг. 12 вдоль оси ординат отложена величина, являю-
щаяся мерой энергии излучения Черенкова, а вдоль оси абс-
цисс— плотность тока. В этих осях построены графики для двух
первых быстрых волн. Как и следовало ожидать, излучаемая мощ-
ность растет с ростом плотности тока в пучке. На фиг. 13 пред-
ставлена та же зависимость, но в случае излучения Смита —
Парселла, причем здесь же приведены для сравнения и преды-
дущие данные; аналогия очевидна.
На фиг. 14 представлена зависимость угла излучения от
плотности тока для эффекта Черенкова. При практически осу-
ществимых плотностях тока углы излучения для первых бы-
строй и медленной волн отличаются незначительно (см. шка-
лу 0). Из-за этого до сих пор не удалось обнаружить экспе-
риментально тонкой структуры излучения. Теория заданного
источника вообще не содержит данных об угловом расхождении
ролн,
7. Теория излучений Черенкова и Смита — Парселла 185
Фиг. 15 подобна фиг. 14, но относится к излучению Смита —
Парселла. Для рассматриваемых значений параметров угол,
Фиг. 15. Направление излучения Смита—Парселла для
различных волн как функция плотности тока.
измеренный от положительного направления продольной оси,
больше л/2 в соответствии с тем, что это излучение связано с
обратной волной.
ЛИТЕРАТУРА
1. Франк И. М„ Тамм И. Е„ ДАН СССР, 14, № 3, 109 (1937).
2. J el ley J. V., Cerenkov Radiation and its Aplications, New York, 1958.
3. Болотовский Б. M„ Усп. физич. наук, 62, 372 (1957).
Теория эффекта Вавилова — Черенкова.
4. Lashinsky Н., в книге Advances in Electronics and Electron Physics,
cd. L. Marton, New York, 1961.
Cerenkov Radiation at Microwave Frequencies.
5. Г и н з б у р г В. Л., ДАН СССР, 56, № 3, 253 (1947).
Использование эффекта Черенкова для генерации радиоволн.
6. Гинзбург В. Л., Франк И. М., ДАН СССР, 56, № 7, 699 (1947).
Излучение электрона или атома, движущихся вдоль оси канала в плот-
ной среде.
7. Linhart J. G„ Journ. Appl. Phys., 26, 527 (1955).
Cerenkov Radiation of Electrons Moving Parallel to a Dielectric Bondary.
8. Toraldo di Fran ci a G., Nuovo Cimento, Ser. X, 16, 61 (1960). On
the Theory of Some Cerenkovian Effects.
9. F e 1 s e n L. B., Hessel A., Nuovo Cimento, Ser. X, 19, 1065 (1961).
A Network Approach to the Analysis of Cerenkov Radiation Problems.
186
И. Палач, А. Олинер
10. Smith S. J., Purcell Е. М., Phys. Rev., 92, No. 4, 1069 (1953).
Visible Light from Localized Surface Charges Moving Across a Grating.
11. Salisbury W. W., U. S. Patent 2634 372, Patent granted April 7, 1953.
Super High Frequency Electromagnetic Wave Generators.
12. В r a d s h a w J. A., Proc. Symposium on Millimeter Waves, New York,
1960, p. 22Й.
A Millimeter Wave Multiplier Using the Purcell Radiator.
13. I s h i g u г о К., T а к о T., Optica Acta, 8, No. 1, 25 (1961).
An Estimation of Smith-Purcell Effect as a Light Source in the Infra-Red-
Region.
14. Danos M., Journ. Appl. Phys., 26, No. 1, 2 (1953).
Cerenkov Radiation from Extended Electron Beams.
15. Durney С. H., Grow R. W., Technical Report ONR-2, University of
Utah (May 1, 1961).
Cerenkov Microwave Radiation to an Infinite Dielectric Medium.
16. M о u r i e r G., L’Onde Electrique, 38, No. 371, 132 (1958).
L’Effect Cerenkov et la Gendration d’Ondes Hertzienes.
17. P a 1 6 c z L, О 1 i n e r A. A., Proc. IEEE, 53, No. 1, 24 (1965).
Leaky Space Charge Waves I: Cerenkov Radiation.
18. P a 1 6 c z I., О 1 i n e r A. A., Proc. IEEE, в печати.
Leaky Space Charge Waves 11: Smith-Purcell Radiation.
19. H ah n W. C„ Gen. Elec. Rev., 42, 258 (1939).
Small-Signal Theory of Velocity Modulated Electron Beams.
20. R a m о S., Proc. IRE, 27, 757 (1939).
The Electron Wave Theory of Velocity Modulated Tubes.
21. Branch G. M„ Mihran T. G„ IRE Trans., ED-2, No. 2, 3 (1955).
Plasma Frequency Reduction Factors in Electron Beams.
22. Marcuvitz N., Proc. Symposium on Electronic Waveguides, New York,
1958, p. 63.
General Electronic Waveguides.
23. В r i 11 о u i n L., P a г о d i M., Propagation des ondes dans les milieux
periodiques, Paris, 1956. (Имеется перевод: Л. Бриллюэн, М. П а р о-
. ди, Распространение волн в периодических структурах, ИЛ, 1959.)
II
РЕЗОНАТОРЫ
И ЛУЧЕВОДЫ
8
ПРЕОБРАЗОВАНИЕ ПУЧКА ПРИ РАСПРОСТРАНЕНИИ
В СИСТЕМЕ КВАДРАТИЧНЫХ ЛИНЗ
, Ж. Дешан*, П. Маст*
Введены графические методы описания преобразования пучка при его
прохождении через оптическую систему. Рассматриваемые здесь пучки опре-
деляются синфазным распределением поля по гауссову закону в некотором
поперечном сечении (плоскости сравнения). Однако могут быть включены
в рассмотрение также моды высших порядков [3—5], которые определяются
функциями Эрмита — Гаусса, и «пучковые моды», исследованные Губо [1, 2].
Введен комплексный варианс, который одновременно определяет эффективное
поперечное сечение пучка и кривизну его фазового фронта. При распростра-
нении пучка в свободном пространстве и при его прохождении сквозь линзу
комплексный варианс преобразуется простым способом. Это преобразование
можно сравнить с преобразованием импеданса в реактивной многозвенной
цепи.
Описанные графические построения позволяют проследить за изменением
сечения пучка и кривизны фазового фронта в оптической системе. Они соот-
ветствуют некоторым формулам, уже полученным Губо [2], но приводят так-
же к пониманию процессов в неконфокальных резонаторах и лучевых волно-
водах с неэквидистантными линзами. Для иллюстрации дано несколько при-
меров, “В том числе расчет узконаправленной антенны. Приведено графиче-
ское построение для многопробеговых резонаторов, причем резонансные
условия в этом случае можно сравнить с резонансными условиями для мод
высших порядков.
§ 1. ОПРЕДЕЛЕНИЕ ПУЧКА
В ряде статей [1—5] подробно рассмотрены поля между дву-
мя отражателями резонатора или внутри эквивалентной перио-
дически повторяющейся структуры. Эти поля анализировались
в понятиях мод (типов волн), общим свойством которых являет-
ся то, что они состоят из совокупности плоских волн, угловой
спектр которых занимает малый конус около общего направле-
ния распространения. Для каждой моды некоторая характери-
стическая функция описывает распределение амплитуды поля в
* G. A. Deschamps, Р. Е- Mast, Antenna Laboratory, University of
Illinois, Urbana, 111.
190
Ж- Дешан, П. Маст
каждом поперечном сечении. Масштаб этого амплитудного рас-
пределения и кривизна фазового фронта меняются с расстоя-
нием (в направлении распространения), причем закон измене-
ния не зависит от номера моды. Моду, имеющую эти свойства,
мы назовем пучком. Это понятие объединяет не только поля,
которые Губо назвал пучковыми модами, но также и поля, свя-
занные с итерационными структурами различной геометрии.
Цель настоящей статьи состоит в том, чтобы перевести
некоторые известные свойства этих мод в простые геометриче-
ские построения, которые внесут ясность в соотношения между
различными расчетными параметрами и могут быть использо-
ваны в приложениях. Отправной точкой является описание пуч-
ка системы посредством его фазовых поверхностей и амплитуд-
ных распределений поля. Преобразование пучка при прохождении
его через оптическую систему нетрудно найти путем согласо-
вания амплитуды и фазы на каждой поверхности. Таким об-
разом, могут быть получены формулы, данные Губо [2]. По-
строение позволяет проследить ход луча через сложную систему.
В резонаторе становится важным параметром абсолютная фаза
поля. Характер ее зависимости от z определяется порядком
моды. Построение укажет форму этой зависимости и приведет
к простому виду резонансных условий.
. § 2. ОПИСАНИЕ ГАУССОВА ПУЧКА
Чтобы упростить рассмотрение, мы начнем с двумерной за-
дачи. когда поле в поперечном сечении является функцией един-
ственной переменной х. Результаты легко обобщаются на дву-
мерные поперечные сечения, по крайней мере для наиболее ча-
сто встречающихся случаев.
Если поле f0(x)=f(x, 0) известно в поперечном сечении z=0,
то поле fz(x)=f(x, z) может быть определено в любом попереч-
ном сечении. Преобразование от f0 к fz получается проще всего,
если представить эти два поля через угловые спектры плоских
волн:
(1)
= Рг^е-^dl. (2)
При переходе от (1) к (2) каждая плоская волна в спектре
просто сдвигается по фазе на величину гУ №— £2. Для спек-
тра, который сконцентрирован вблизи £=0, мы можем аппрок-
симировать /~ I2 выражением k — g2/2fe и, следовательно,
= г/:т2- 13)
8. П реобразование пучка в системе квадратичных линз 191
Соответствующее соотношение между f0 и fz представляет собой
свертку
/г(х) = е-^гф_Гг(л)*/0(х). (4)
Здесь
p-in/4
m = —-------е~1 (й/2г>xI
~iz /И
есть фурье-преобразование функции
ei
Следует отметить, что q>_,z есть гауссова функция с комплек-
сным вариансом —i(z/k) '). Вспоминая, что свертка двух гаус-
совых функций дает другую гауссову функцию, мы видим, что,
если поле /о при z=0 является гауссовой функцией, то оно будет
также гауссовой функцией во всех других поперечных сечениях.
Эти гауссовы распределения имеют комплексные вариансы, и
их можно интерпретировать как амплитудные распределения по
гауссову закону в сочетании с кривизной фазового фронта. Здесь
целесообразно ввести нормированный варианс, умножив ва-
рианс на k, и определить функцию <рд
Фд(х) = (^л)“1/2^-™, ' (5)
для которой
Фд'*Фв = Фд+В" (6)
В теории вероятностей это означает, что сумма независимых
случайных величин с нормальным законом распределения также
подчиняется нормальному закону, и дисперсия ее равна сумме
дисперсий слагаемых.
Применяя (6) к соотношению (4) и учитывая, что/о=фдо (х)„
получаем
= (7)
где
V = A0 — iz. (8)
’) В теории вероятностей этот параметр нормального (гауссова) распре-
деления называется дисперсией (variance). Мы используем термин «варианс»,
во-первых, из-за того, что «дисперсия» в оптике означает совсем другое по-
нятие, а во-вторых, желая подчеркнуть, что речь здесь идет не о случайных
величинах и что аналогия с теорией вероятностей чисто формальная. Ва-
рианс— комплексный параметр, характеризующий площадь и кривизну фазо-
вого фронта пучка. — Прим, ред.
192
Ж. Дешан, П. Маст
Варианс (нормированный) при z-О может быть записан в виде
Л0=£аб; он имеет размерность длины. При z¥=0, согласно фор-
муле (7), варианс становится равным V и
1 х3
= у (9)
Коэффициент 1/V можно разложить на действительную и мни-
мую части:
7 = 4 + 4- <10>
Величина fz, равная ехр {—(6/2) (х2Д4)], представляет собой
функцию Гаусса со среднеквадратичной величиной а, такой,
что A = ka2. Длина а с точностью до коэффициента ]/~2 равна
величине пятна, введенной Бойдом и Гордоном [4]. Длина А
представляет собой эффективную площадь пучка па2, умножен-
ную на k/n, и будет для краткости называться шириной пучка.
Фаза fz содержится в множителе ехр (—ikx2/2R), который
пропорционален <p_1R, где R есть радиус кривизны фазового
фронта в точке z. Этот радиус считается положительным для
расходящегося пучка и отрицательным для сходящегося.
Чтобы получить А и R из Ао и z, удобно ввести фазу вариан-
са V — угол и, определив его следующим образом:
z = ?lotg«. (И)
Это новая переменная, которая может заменять z и использо-
ваться при описании изменения фазы на оси. Рассмотрим
фиг. 1,а. Если нанести на чертеж точку с координатами х =
= А0~ка2й, z = 0, то угол и будет равен /ФМ. Точка Ф будет
играть важную роль в геометрических построениях, которые
следуют ниже. Формула (8) принимает вид
= До(1 ~jtg«) = Л sec (12)
действительная часть величины 1/V равна
1 COS^ ll t zi
Д’ —
следовательно, размер пятна составляет
а (г) = <г0 sec и. (14)
Кривая а (г), которая показывает, как расширяется пучок,
является гиперболой (фиг. 1,а).
Радиус кривизны получается из формул (8), (10) и (11):
R — . (15)
Sin и COS Ur ' '
8. Преобразование пучка в системе квадратичных линз 193
Центр кривизны С на фиг. 1,6 получен путем графического по-
строения. Он находится па пересечении осн z с перпендикуля-
ром к МФ, проведенным через точку Ф. В то же время ширина
Фиг. 1. Построение радиуса пучка и фазового центра,
а —радиус пучка; б —фазовый фронт пучка.
пучка А—ka2 получается при пересечении МФ с прямой, парал-
лельной оси х и проведенной через точку М. При изменении z
точка Р описывает параболу.
Предположим, что в точке z=0 поле имеет комплексный
варианс Vo, т. е.
f — (р == ______5____^-(»/2)U2/Ko)
'О (|х е
13 Зак. 274
194
Ж- Дешан., П. Маст
тогда в точке z поле будет иметь комплексный варианс
V(z) = V0 — iz. (16)
Эта простая формула учитывает как изменение поперечного
сечения пучка, так и изменение кривизны фазового фронта в
зависимости от z.
Теперь рассмотрим коэффициент в формуле (9), который
определяет, в частности, изменение фазы на оси z. Используя
(8) и (11), этот коэффициент можно переписать в виде
—L_e','*z=--^X^V'coswe-!'(*z-,''2) = ^=L=r- (17)
/ЛУ /Мо F /Mcos« ’
откуда ясно, что фаза в точке z есть kz—(u/2). Она отличается
от набега фазы при распространении в свободном пространстве
на половину угла и.
§ 3. ГАУССОВЫ ПУЧКИ ВЫСШЕГО ПОРЯДКА
Применение описанных выше построений не ограничивается
простейшим случаем, рассмотренным в § 2.
Для одномерной апертуры гауссовы пучки высших поряд-
ков могут быть описаны с помощью функций Эрмита — Гаусса
. <Рдл (•«) = //„ (x-jZ-j) фд (•*)• (18)
Свертка [см. (4)] двух таких функций также является функцией
Эрмита — Гаусса; но в то время, как фЛо(*) преобразуется с
точностью до коэффициента в
ФЛп(х)ф_//?(х)е-г<*г-и/2), (19)
функция Флл(х) преобразуется в
фля(х)ф_;я(х) е~1 _ (20)
Мы можем снова рассмотреть комплексное число V, такое,
что
1=4+4' <2»
и хотя его интерпретация как «варианса» ) является спорной,
оно будет меняться при изменении z так же, как и в случае
простого гауссова пучка. Фаза на оси получает, однако, поправ-
ку (« + ‘/2)«, зависящую от порядка п пучка.
!) То есть «дисперсии» — по формальной аналогии с теорией вероятно-
стей. — Прим. ред. .
8. Преобразование пучка в системе квадратичных линз
195
Мы можем рассматривать пучки с двумерным поперечным
сечением, когда поле при z=0 определяется формулой
fo(x, у) = фЛя(х)<рЛт(у) (22)
(см. формулу (20) в работе Бойда и Гордона [4]). Поправка,
вносимая в набег фазы на оптической оси, равна теперь сумме
поправок для каждого сомножителя: (п + т+1)и. Для пучко-
вых мод, рассмотренных Губо [1, 2], изменения ширины пучка
и кривизны фазового фронта подчиняются тем же законам, од-
нако фазовая поправка становится равной (2n + v+l)«, где п и
v — индексы волн в цилиндрических координатах.
Общий метод описания свойства полей, распространяющих-
ся почти в одном направлении, найден Пирсом [6]. Нетрудно видеть,
что его формулы (16) и (17) согласуются с нашими формула-
ми (14) и (15), которые лежат в основе построений преобразо-
вания пучка. Более того, фаза на оси, которая получается инте-
грированием его формулы (12), как и в нашем случае, равна
kz—(п+т+\)и.
Все предыдущие рассуждения основывались на параксиаль-
ной аппроксимации. Поля, близкие к этой оси, были описаны с
точностью до второго порядка малости. Это ограничение может
быть в какой-то степени снято, если рассматривать моды сфе-
роидальных полых резонаторов, как было предложено Цимме-
рером [9]. С точностью до второго порядка малости эти послед-
ние совпадают вблизи оси с модами, описанными выше. Точ-
ка Ф и ее зеркальное изображение относительно оси z являются
фокусами семейства эллипсов и гипербол. Гипербола на фиг. 1, а
принадлежит к этому семейству. Центр кривизны эллипса, про-
веденного через точку М, находится в точке С, показанной на
фиг. 1,6. Благодаря этим свойствам точку Ф можно назвать бо-
ковым фокусом пучка.
§ 4. ПРЕОБРАЗОВАНИЕ ПУЧКА ОПТИЧЕСКОЙ СИСТЕМОЙ
Рассмотрим пучок, падающий на линзу L. Пучок опреде-
ляется своей центральной точкой / и минимальным размером
пятна а0, или, что то же самое, своим боковым фокусом Ф.
Задача состоит в том, чтобы описать пучок, прошедший через
линзу. Рассмотрим фиг. 2, а. Центр кривизны С пучка, падаю-
щего в точку О, получается пересечением оси Oz с перпендику-
ляром к ОФ, проведенным через точку Ф. Центр кривизны С'
пучка справа от линзы должен быть оптическим изображением
центра кривизны С в линзе.
Чтобы дополнить определение преломленного пучка, мы
можем согласовать амплитуды поля по обе стороны линзы, счи-
13*
196
Ж. Дешан. П. Маст
тая последнюю тонкой и идеально прозрачной. Поскольку фор-
ма амплитудного распределения является характеристикой мо-
ды, то достаточно приравнять размер пятна а или ширину пучка
а
Фиг. 2. Преобразование пучка при прохождении через линзу,
а —тонкая линза; б —сферическая поверхность раздела.
A = ka1 по обе стороны линзы. Это приводит к построению, пока-
занному на фиг. 2, а: ширина пучка равна расстоянию ОА от О,
причем точка А определяется пересечением прямой СФ с пло-
скостью линзы. Проводя перпендикуляр из точки О на линию
С'А, получаем боковой фокус Ф' преломленного пучка. Зная
Ф', сразу находим центральную точку I' и размер пучка. Это
построение эквивалентно формулам Губо [2].
Очевидно, что подобное построение применимо и к сфериче-
скому зеркалу. В случае толстой линзы приходится определять
преобразование пучка при прохождении через каждую из двух
поверхностей линзы. Так как волновое число k различается на
8. Преобразование пучка в системе квадратичных линз
197
обеих сторонах поверхности преломления, согласование разме-
ров пучка требует, чтобы k^a2 и k2a2 находились в отношении
k2lki, которое представляет собой отношение показателя пре-
ломления второй среды к показателю преломления первой.
Итак, после того как точка А построена способом, указанным
выше, положение точки А' определяется из соотношения ОА' =
= (kzlkfiOA.
Таким образом, можно проследить за преобразованием пуч-
ка в любой сложной оптической системе, например в лучевом
волноводе с линзами, расположенными на неодинаковом рас-
стоянии. Сравнение размера пучка на каждой поверхности си-
стемы с размером этой поверхности будет показывать величину
дифракционных потерь при каждом переходе. Для гауссовой
моды нулевого порядка с круговой симметрией нетрудно найти
[1] величину потока энергии, протекающей внутри круга опреде-
ленного радиуса, в q раз превышающего размер пятна; в пер-
вом приближении можно предположить, что энергия, которая
не попадает в пределы апертуры линзы, теряется.
Преобразование пучка в линзе можно описать и другим спо-
собом— с йомощью комплексного варианса пучка V. Пусть У —
комплексный варианс падающего пучка, а V' — варианс прошед-
шего пучка, причем оба определены на линзе. В соответствии с
формулой (10) имеем
1 _ J__, г
V ~~ А "г R '
1 i . i
V' ~ А' R' '
Согласование амплитуд требует, чтобы А = А', а «преобразова-
ние сходимости» пучка приводит к соотношению
~Rr~~R~J' (23)
где f — фокусное расстояние, которое считается положительным
для собирающей линзы. Мы можем объединить эти два условия
и описать преобразования пучка линзой соотношением
§ 5. АНАЛОГИЯ МЕЖДУ ЭЛЕКТРИЧЕСКОЙ ЦЕПЬЮ
И ЛУЧЕВЫМ ВОЛНОВОДОМ
Преобразование пучка в оптической системе полностью опи-
сывается изменением комплексного варианса V(z) как функ-
ции 2,
198
Ж- Дешан, П. Маст
Два важных результата, выраженных формулами (16) и
(24), состоят в следующем:
а) преобразование V на длине Zi в свободном пространстве
V (z + Zi) = V (г) — Zzp,
б) преобразование V с тонкой линзой с фокусным расстоя-
нием fi ,
J_ = ±+_L
V V if.
Эти две формулы напоминают преобразование импеданса
в многозвенной электрической цепи, состоящей из последова-
Фиг. 3. Преобразование пучка при прохождении
через систему линз.
а — линзы и пучок; б — эквивалентная электрическая цепь.
тельно включенных реактивных сопротивлений — iz^ и шунти-
рующих реактивных проводимостей if,.
На фиг. 3 мы изобразили преобразование пучка системой
линз и соответствующую электрическую модель. Преобразова-
ние V-* V' можно описать цепной дробью:
V = — /г3 Ч------------——j-----------.
-]----------—.—-------
— г>2 Ч--------;----
8. Преобразование пучка в системе квадратичных линз 199
Эта электрическая модель позволяет рассматривать соответ-
ствующие преобразования на диаграмме Вольперта — Смита.
На фиг. 4, где V соответствует импедансу, размер пятна постоя-
нен, когда V находится на окружности активной проводимости,
R>0
Расходящийся
пучок
Фиг. 4. Комплексный варианс пучков, представленный на диаграмме
Вольперта — Смита.
а радиус кривизны R постоянен на окружностях реактивных
проводимостей. Действительно, ширина пучка А соответствует
обратной величине активной проводимости, а радиус кривизны
R—обратной величине реактивной проводимости. Точки на
окружности соответствуют предельному случаю геометрической
200
Ж- Дешан, П. Маст
оптики, когда частота, а следовательно, и ширина пучка беско-
нечны. Тогда V сводится к —iR. Так как ширина пучка всегда
положительна, то физическим пучкам соответствуют только точ-
ки внутри круга.
Общее преобразование, которое может быть реализовано си-
стемой линз, соответствует преобразованию импеданса, произ-
водимому обратимым четырехполюсником без потерь. Такая
цепь определена, когда известен ее входной импеданс для трех
различных реактивных нагрузок или для двух различных не-
реактивных нагрузок, расположенных на выходе. В переводе на
язык оптики это означает, что действие системы на любой пучок
будет известно, если известно преобразование двух пучков с
конечным сечением или трех пучков с бесконечным сечением.
Смысл последней части этого утверждения заключается в том,
что геометрические свойства системы полностью определяют ее
воздействие на конечные пучки.
В результате этого отпадает необходимость следить за пре-
образованием пучка шаг за шагом в каждом элементе системы,
как это делалось выше. Однако такая процедура необходима,
если нужно определить потери из-за конечных размеров линз
и убедиться, что квадратичная аппроксимация остается справед-
ливой при каждом шаге преобразования.
Четырехполюсники без потерь можно классифицировать
по типу неевклидова вращения, которое соответствует им на
диаграмме Вольперта — Смита [10, 11]. Это вращение может
быть эллиптическим (имеющим действительную инвариантную
точку внутри круга), гиперболическим (имеющим две инвари-
антные точки на круге) или параболическим (имеющим един-
ственную инвариантную точку на круге). Эти типы обозначают-
ся для краткости символами (£), (Я) и (Р). Та же самая
классификация применима и к оптическим системам, причем
каждому типу систем соответствуют определенные характери-
стические свойства. Например, для эллиптической системы су-
ществует пучок с конечным поперечным сечением, который при
прохождении через нее не изменяется. Другими словами, па-
дающий пучок в начале системы и пучок, выходящий из нее,
являются частью единого пучка, который существовал бы, если
бы система была удалена. Для гиперболической системы подоб-
ных пучков не существует.
В случае периодических структур необходимо рассматривать
преобразование от некоторой входной плоскости к выходной
плоскости, расположенной на расстоянии одного периода. Это
преобразование также можно классифицировать в соответствии с
типом вращения. Тип (£) соответствует стабильным конфигура-
циям, которые были определены Фоксом и Ли [3]. В этом случае
8. Преобразование пучка в системе квадратичных линз
201
существует пучок с характеристическим комплексным вариапсом
1/0 на входной плоскости, имеющий тот же самый варианс на
выходной плоскости. Следовательно, этот пучок повторяется
периодически. Если начать с пучка, имеющего произвольный
Фиг. 5. Преобразование комплексного варианса стабильной периодической
системой.
варианс V, отличный от Vo, то его последовательные преобразо-
вания Vi, V2, Vn, будут лежать на регулярной много-
угольной линии, вписанной в круг с центром Уо- (Все эти утвер-
ждения следует понимать в смысле неевклидовой геометрии.)
Ширина пучка будет колебаться между двумя границами Лмип
и Дмакс, как показано на фиг. 5. Если угол вращения вокруг Ёо
выражается рациональной дробью, умноженной на 2л, то мно-
гоугольная линия замкнется и пучок станет периодическим с
периодом, кратным периоду структуры.
Структуры типа (Н) и (Р) нестабильны. Они не допускают
повторяющегося пучка конечного поперечного сечения, и если
начать с произвольного варианса V, то ширина пучка при по-
следовательных преобразованиях будет увеличиваться до беско-
нечности.
202
Ж. Дешан, П. Маст
§ 6. РЕЗОНАТОРЫ
В резонаторе, образованном двумя сферическими зеркалами,
за преобразованием пучка, колеблющегося между зеркалами,
можно проследить тем же самым способом, что и на фиг. 4.
Резонансное условие будет включать, однако, абсолютную фазу
волны, а не только форму фазового фронта.
Чтобы существовал пучок, который преобразуется в себя
при каждом отражении, фазовый фронт на каждом зеркале
Фиг. 6. 'Стабильное и нестабильное расположение зеркал.
а — стабильное; б — нестабильное.
должен совпадать с поверхностью зеркала и, следовательно,
фазовый центр должен быть центром зеркала. Это значит, что
боковой фокус Ф, как показано на фиг. 6, а, должен нахо-
диться одновременно на окружностях П и Гг с диаметрами
SjCj и S2C2 соответственно. Для любого сферического зеркала
окружность диаметром SC будем называть окружностью, при-
соединенной к этому зеркалу. Условие существования пучка,
соответствующего паре сферических зеркал, состоит в том, что
их присоединенные окружности пересекаются. Можно показать,
что это условие тождественно условию стабильности, получен-
ному Фоксом и Ли. На фиг. 6,6 приведен пример нестабильной
конфигурации.
Фазовое условие состоит в том, что фазовый сдвиг па одном
пробеге от Si и S2 кратен л. Используя формулу (20), получаем
kSxS2 — [гг Д- и = qn
для одномерного гауссова пучка порядка п их
kSlS2 — (n-\-m-\- V)u = qn,
для двумерного гауссова пучка порядка (т, п); число q целое.
Угол и есть полный угол SiOS2, под которым видна длина про-
8. Преобразование Пучка в системе квадратичных линз 203
бега из точки Ф. Он равен половине угла между присоединен-
ными окружностями в точке их пересечения.
При конфокальном расположении зеркал, показанном на
фиг. 7, две присоединенные окружности Г\ и Г2 совпадают и точ-
ка Ф может быть выбрана где угодно на общей окружности Г.
Фиг. 7. Конфокальный резонатор,
а— симметричный пучок; б — асимметричный пучок.
Все соответствующие пучки удовлетворяют резонансному усло-
вию, если ему удовлетворяет хоть один из пучков, т. е. если
kSiSz имеет вид qn для мод четных порядков и (q + 4z)n для
мод нечетных порядков. Симметричный пучок соответствует
наименьшему размеру пятна на зеркалах и, следовательно, ми-
нимальному затуханию для зеркал данных размеров.
•
. § 7. МНОГОПРОБЕГОВЫЕ РЕЗОНАТОРЫ
Если конфокальный резонатор рассматривается с точки зре-
ния геометрической оптики, то изображение в первом зеркале
любой точки на оси имеет во втором зеркале изображение, ко-
торое совпадает с первоначальной точкой. Если 1\ обозначает
преобразование, которое переводит точку на оси в ее изображе-
ние в зеркале i, то
Т2Т\ = \,
где 1 —тождественное преобразование.
Это наводит на мысль отыскать такие расположения зеркал,
при которых (Г27'1)2=1 или в более общем виде (Т2Т1)п=\.
В последнем случае резонаторы могут быть названы п-пробего-
выми резонаторами [7]. Резонансы, соответствующие этим уело-
204
Ж. Дешан, П. Маст
виям, наблюдались и использовались Жерардо и Вердейе-
ном [8].
Некоторые из построений, использованных выше, приводят
к решению этой задачи. На оси z преобразование
Т-М^М',
связывающее точку’ и ее изображение в сферическом зеркале,
представляет собой инверсию по отношению к присоединенной
окружности Г. Из фиг. 8 в соответствии с хорошо известной
Фиг. 8. Построение изображения М' точки М в сферическом
зеркале.
формулой мы имеем FM • FM' — f2. Рассмотрим любую точку Ф
на Г и окружность Й с диаметром Ф/, перпендикулярным оси z.
Проекция оси Oz через точку Ф на окружность Й преобразует
точки S, С, М, М! в s, с, т, т'. Линия cs есть диаметр окруж-
ности Й, а точка т' может быть получена из т путем зеркаль-
ного отражения относительно cs. Таким образом, преобразова-
ние Т на оси переходит в более простое преобразование.
t :т—>т'
на окружности Й.
Если мы возьмем теперь два зеркала с общей осью, а. в ка-
честве Ф точку пересечения присоединенных окружностей Г1
и Г2, то сможем заменить 7\ и Т2 на их отображения Ц и /2, дей-
ствующие на окружности Й. Произведение есть просто вра-
щение окружности Й на угол 2и. Условие
(^1Г = 1
сводится к тому, что угол и должен быть равен числу л, умно-
женному на рациональную дробь. На фиг. 9 и 10 приводится
несколько иллюстраций.
Фиг. 9. Двухпробеговый резонатор. Эквивалентные
конфигурации.
Фиг. 10. Трехпробеговый резонатор.
206
Ж. Дешан, П. Маст
Двухпробеговый резонатор можно рассчитать, задавшись
окружностью Q с диаметром Ф/. Построив любые два диаметра
SiG и s2c2, пересекающиеся под прямым углом, и спроектиро-
вав точку Ф на перпендикуляр к Ф/, получим точки Si, Cb S2, С2,
которые полностью определяют положение и кривизну двух зер-
кал. С теми же самыми двумя диаметрами можно получить
четыре эквивалентные конфигурации путем переставления букв
S и С. Заметим, что соответствующие углы и различны. На
фиг. 10 изображен трехпробеговый резонатор, полученный та-
ким же образом.
§ 8. ЛУЧЕВОДНАЯ АНТЕННА
Метод построения антенны, излучающей энергию из луче-
вого волновода Губо [1] в свободное пространство, показан на
фиг. 11. Мода, имеющая наименьшие дифракционные потери в
лучевом волноводе, линейно поляризована и имеет гауссово рас-
пределение амплитуды в радиальном направлении.
Гауссово распределение обеспечивает идеальное облучение
антенны с малыми боковыми лепестками, так как теоретически
оно дает диаграмму направленности без боковых лепестков,
если освещается бесконечная поверхность. Параметры лучевого
волновода обычно выбираются так, чтобы получить наивысшую
возможную концентрацию энергии на фазовом преобразователе
и таким образом свести к минимуму дифракционные потери.
Вогнутая рассеивающая линза используется для рассеяния кон-
центрированной энергии лучевого волновода, причем гауссово
распределение по амплитуде сохраняется. Собирающая излу-
чающая линза дает фазовую коррекцию, необходимую для того,
чтобы получить однородную фазу на всей выходной плоскости.
Фиг. 12 иллюстрирует построение, позволяющее определить
требуемые рассеивающую и излучающую линзы. Рассмотрим
сначала случай, когда рассеивающая линза расположена в экви-
фазной плоскости лучевого волновода. Размер пятна as на рас-
сеивающей линзе, расстояние D до излучающей линзы и раз-
мер пятна на излучающей линзе считаются известными. Точки
Ф,- и Ф6 определяются из выражений
Фс = ka?r,
ф. = ^>
а окружности Qr и Qs вычерчиваются с диаметрами £>ФГ и ОФ3
соответственно. Пересечение окружностей Qr и Qs дает возмож-
ный боковой фокус Ф для пучка между рассеивающей и излу-
Фиг. 12. Преобразование пучка в лучеводной антенне,
208
Ж. Дешан, П. Маст
чающей линзами. Проекция Фг через точку Ф на ось z опреде-
ляет точку Сг, которая является фазовым центром пучка на вы-
ходе рассеивающей линзы. Зная фазовые центры Сг и С„ мож-
но определить требуемые рассеивающую и излучающую линзы.
В случае если рассеивающая линза располагается не в эквифаз-
ной плоскости лучевого волновода, требуемая рассеивающая
линза есть комбинация двух линз. Одна из них является вы-
пуклой линзой, которая необходима для получения эквифазной
поверхности из волны лучевого волновода, а другая — вогнутой
линзой, такой же, как и рассмотренная выше.
§ 9. ЗАКЛЮЧЕНИЕ
Здесь были рассмотрены два графических построения, по-
зволяющих проследить за преобразованием гауссова пучка в
оптической системе, образованной коаксиальными линзами или
сферическими зеркалами. Эти построения применимы и к пуч-
кам высших порядков, но в этом случае фаза поля на оси за-
висит от порядка пучков. В одном из построений используется
боковой фокус пучка — точка, расположенная в плоскости ми-
нимального поперечного сечения на расстоянии от оси, пропор-
циональном эффективному сечению пучка в этой точке. Другое
построение основывается на описании поперечного сечения пуч-
ка (радиус пятна или ширина пучка и радиус кривизны фазо-
вого фронта) одним комплексным числом V, которое называется
вариансом. Варианс меняется простым способом при изменении
расстояния вдоль оси пучка и при пересечении линзы (или отра-
жении от сферического зеркала). Формулы указывают на ана-
логию с преобразованием импеданса в электрической цепи. Это
приводит к построениям в комплексной V-плоскости или на диа-
грамме Вольперта — Смита, которые можно использовать, на-
пример, для нахождения некоторых свойств итерационных си-
стем, периодических или резонансных.
При таком подходе становится более ясным соотношение ме-
жду геометрической оптикой и оптикой волновых пучков. Пере-
ход от первой ко второй можно рассматривать как процесс
аналитического продолжения. Преобразование объект —♦ изобра-
жение для точек на оси системы есть проективное преобразова-
ние, выраженное билинейной функцией z'=f(iv). Та же самая
билинейная функция iV'=f(iv) связывает комплексные вариан-
сы. На диаграмме Вольперта — Смита или проективной диа-
грамме [11] точки на окружности соответствуют точкам на оси
оптической системы, а точки внутри круга представляют пучки
С конечными эффективными сечениями. Преобразование пучка
8. Преобразование пучка в системе квадратичных линз
209
оптической системой представляется некоторым неевклидовым
вращением всех точек диаграммы.
Если сделать угол вращения рациональной дробью полного
угла 2л, то решается проблема многопробеговых резонаторов.
Таким образом, построения, описанные в § 7, связаны с преды-
дущими.
Эти построения используются для расчета антенны, позво-
ляющей сконцентрировать излучение лучевого волновода или
лазера.
ЛИТЕРАТУРА
1. Goubau G., Schwering F., Trans. IRE, АР-9, 248 (1961). (Имеется
перевод: 1. Губо, Ф. Ш в е р и н г, Зарубежная радиоэлектроника, № 11,
1961, стр. 3.)
2. Goubau G., Electromagnetic Theory and Antennas, Pt. 2, New York,
1963, p. 907.
3. Fox A. G., Li T., Bell Syst. Tcchn. Journ., 40, 453 (1961). (Имеется
перевод в сб. «Лазеры», ИЛ, 1963, стр. 325.)
4. В о у cl G. D., Gordon J. Р., Bell Syst. Tcchn. Journ., 40, 489 (1961).
(Имеется перевод в сб. «Лазеры», ИЛ, 1963, стр. 363.)
5. Boyd G. D„ Kogelnik IL, Bell Syst. Tcchn. Journ., 41, 1347 (1962).
6. P i e r c e J. R., Proc. Nat. Acad. Sci., 47, 1808 (1961).
7. Г о r a 1 d о d i F г a n c i a G., Proc. Symposium on Optical .Masers, Vol. 13,
New York, 1963, p. 157.
8. Gerardo J. B., Ver deyen J. T„ Proc. IEEE, 52, No. 6, 690 (1964).
9. 7 im mer er R. W„ Trans. IEEE, MTT-11, 371 (1963).
10. Deschamps G. A., Proc. Symposium on Modern Network Synthesis,
New York, 1952, p. 277.
Geometric Viewpoints in the Representation of Waveguides and Waveguide
Junctions.
IL Deschamps G. A., Federal Telecommunication Laboratories (1953).
A Hyperbolic Protractor.
14 Зак. 274
9
КОЭФФИЦИЕНТЫ связи
И КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ ВОЛН
В ОПТИЧЕСКИХ СИСТЕМАХ
X. Когелышк, *
Собственные колебания и волны оптических систем, таких, как резона-
торы лазеров, интерферометры со сферическими зеркалами или оптические
линии передачи, описываются функциями Эрмита — Гаусса или Лагерра —
Гаусса. Если волну, выходящую из такой системы, скажем из лазера, подать
в другую систему, например в оптическую линию передачи, то возбуждается
набор собственных волн этой последней системы. Связь с различными волна-
ми зависит от параметров системы, параметров падающей волны и от степени
оптической юстировки. Вычисляются коэффициенты связи и коэффициенты
преобразования, которые описывают переход мощности в различные волны.
§ 1. ВВЕДЕНИЕ
В данной статье рассматриваются резонаторы со сфериче-
скими зеркалами и оптические линии передачи типа системы
эквидистантных линз. Резонатор со сферическими зеркалами
широко используется в лазерах, а системы эквидистантных линз
используются для передачи когерентных световых пучков на
дальние расстояния. С хорошим приближением можно считать,
что собственные волны таких оптических систем являются вол-
нами ТЕМ.
В прямоугольных координатах поперечное (координаты х, у)
распределение поля волны ТЕМтп можно приближенно запи-
сать [1, 3, 4] следующим образом:
ТЕМтп = ^т(х)^„(у), (1а)
где
Фт (х) = w2mml) (оГ ^2) еХР { —(16)
* Н. о g е 1 n i k, Bell Telephone Laboratories, Inc., Murray Hill, N. J.
9. Коэффициенты связи и коэффициенты преобразования волн 211
Здесь нормировка произведена таким образом, что переноси-
мая волной мощность равна единице, т. е.
+ СО
/ (1в)
— 00
где Ф*П(Х) — комплексно сопряженная функция, Нт(х)—поли-
номы Эрмита, т и п — индексы поперечных волн и & = 2лД—
волновое число.
В цилиндрических координатах (г, ф) распределение поля
волны TEMpi можло приближенно записать [2, 4] в виде
ТЕМр1 = —4= 1/ р- Г /2?Lp /2 х
р w К1 4- 6ог г л (/ р)! \ w I \ w! I
Xexp{-4-y-4JU C°SM, (2)
zx к I w2 J 2R f I sin /<p ) v '
где нормировка проведена также на единичную мощность. Здесь
р й / — индексы волн, Лр(г2)— обобщенные полиномы Лагер-
ра, а до/ —символ Кронекера (6=1 для 1=0, 6 = 0 для 1^=0).
Заметим, что как в прямоугольных, так и в цилиндрических ко-
ординатах распределение поля основной волны (0, 0) является
гауссовым. «Ширина» этой гауссовой кривой определяется па-
раметром w, который называется радиусом пучка или размером
пятна. Этот параметр, а также параметр Е зависят [1, 2, 4] от
устройства и размеров интересующей нас оптической системы;
они изменяются [1, 2, 5] по мере распространения пучка вдоль
оптической оси г. Параметр Е описывает изменение фазы поля
в некотором поперечном сечении пучка. Точнее говоря, Е есть
радиус кривизны фазового фронта (поверхности постоянной
фазы).
Приведенные выше выражения (1) и (2) дают хорошее при-
ближение, если апертуры используемых зеркал или линз до-
статочно велики и только малая часть направляемой световой
мощности теряется на излучение. Для заданных апертур при-
ближение ухудшается с увеличением индексов волн.
Теперь предположим, что волна одной системы переходит во
вторую систему. В качестве примера рассмотрим пучок, кото-
рый выходит из резонатора лазера и поступает в оптическую
линию передачи (фиг. 1). Так как параметры волн обеих си-
стем в общем случае не согласованы, то одномодовый пучок из
лазера будет связан с несколькими модами линии передачи, т. е.
будет происходить преобразование волн. Чтобы устранить пре-
образование волн, можно поставить на пути пучка соответ-
ствующие оптические элементы [6], которые согласуют волны
14*
Фиг. I. Световой пучок, выходящий из резонатора лазера, подается
в оптическую линию передачи.
ТЕМ тп
ТЕМтп
TEMfi
Оптическая
система
Фиг. 2. Световой пучок из резонатора подается в другой резонатор,
проходя при этом через оптические элементы согласования.
Z
TEMpi
Фиг. 3. Параметры волн пучка: R и R — радиусы кривизны фазовых фрон-
тов на плоскости отсчета; w и w—соответствующие радиусы пучков;
wa и wa — радиусы пучков в шейке пучка, где фазовые фронты плоские.
9. Коэффициенты связи и коэффициенты преобразования волн 213
обеих систем (фиг. 2). На фиг. 2 вместо линии передачи изобра-
жен резонатор, который можно использовать в качестве резо-
натора перестраиваемой интерферометрической системы Фа-
бри — Перо для анализа спектра излучения лазера [7]. Если вол-
ны систем согласованы не полностью, то опять-таки будет про-
исходить преобразование волн.
В данной статье исследуются связь и преобразование волн.
Как показано на фиг. 2, величины, относящиеся к входящему
световому пучку, помечаются черточкой. Мы определим и вычис-
лим коэффициенты, которые характеризуют связь и преобразо-
вание волн.
§ 2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ СВЯЗИ
Предположим, что волна ТЕМ— единичной мощности па-
дает слева. Пусть параметры падающего пучка в некоторой под-
ходящим образом выбранной плоскости отсчета будут w и Ё,
как показано на фиг. 3. Параметры собственных волн системы,
расположенной справа, на этой плоскости отсчета равны соот-
ветственно w и R. Параметры R и 11 считаются положительными,
если наблюдатель слева видит вогнутый фазовый фронт (для
волн, распространяющихся вправо). Падающая волна ТЕМ—
единичной мощности будет возбуждать в системе набор волн
ТЕМтп с полями С—тлфтф„. Комплексные амплитуды С—тп
называются коэффициентами связи. Мощность возбужденной
волны ТЕМтп равна С—тп • С— тп при характеристическом
импедансе, равном единице.
Коэффициенты связи находим из условия равенства функ-
ций распределения полей в плоскости отсчета:
Фт (*) • = 2 2 С- т$т (х) • (у). (3)
т п
Используя ортогональность функций (1), получаем интеграль-
ные выражения для коэффициентов связи.
Подобным же образом вычисляются коэффициенты связи в
случае цилиндрических координат.
§ 3. коэффициенты связи
В СЛУЧАЕ ПРЯМОУГОЛЬНЫХ КООРДИНАТ
Принимая во внимание ортогональность собственных функ-
ций (1) в уравнении (3), можно записать коэффициенты связи
следующим образом:
Стптп ^тт пп’
214
X. Когельник
где
j ^ (*)€(*)•
(46)
Такая же формула имеет место для с-я. Подставляя собствен-
ные функции (16) в эту формулу для коэффициентов связи, по-
лучаем
2
с~ = (----=--------
тт \nww2m+m-т\т\
X j dxHm (Х Нт (х V ₽) еХР (— ^2)- (4в)
где введены обозначения:
1 , 1
Я
W2 W2
_1\
Я/
(4г)
2
а = -=г-
w2
Р 2
(4д)
W2
(4е)
Из формулы (4в) видно, что между четными и нечетными
типами волн нет связи (взаимодействия). Действительно, если
один из номеров волны четный, а другой нечетный, т. е. если
m+tn нечетно, то подынтегральная функция является нечетной
функцией х и
с==0. (5)
тт ' '
Производя интегрирование в (4в), нужно различать два слу-
чая: 1) т и т четные (связь между четными волнами) и 2) т
и т нечетные (связь между нечетными волнами).
Рассмотрим сначала связь и преобразование четных волн;
положим
m = 2v; /га = 2ц. (6а)
Результат интегрирования в формуле (4в) можно представить
в виде конечного гипергеометрического ряда [8]
- = /_ ±^+V 1/_2 (2H + W (4-«)у(4-Р)ц х
тт \ 2/ У wwq 2v!
гГ ,1 q(q —« —Р)1 юхх
Xf[-V, -н; -v-m-2 - (g_a)(g_P)J- (66)
9. Коэффициенты связи и коэффициенты преобразования волн 215
где гипергеометрический ряд определяется следующим об-
разом:
F(a, b; с, .... (6в)
Формула (66) описывает связь и преобразование волн с любым
четным номером. С помощью этой формулы выпишем некоторые
коэффициенты-для волн низших порядков:
Соо = 1/-1-. (7 а)
г wwq
(7б>
<7в>
С22 ~ 7^ (С00 + СО2С2о)’ (^Г)
п /~ 3 ^02
<^ = У 7^’ ™
= (7е)
С00
(7ж)
Эти коэффициенты являются комплексными числами. Связь
между двумя основными (нулевыми) волнами описывается ко-
эффициентом с00. Ниже мы рассмотрим этот коэффициент более
подробно. Остальные коэффициенты для простоты выражены
через Соо- При полном согласовании Соо = С22=1, а остальные ко-
эффициенты в формулах (7) равны нулю.
При вычислении коэффициентов связи между нечетными вол-
нами положим
771 = 2v 4-1 И 777 = 2 Ц -|- 1.
(8)
Как и в предыдущем случае, интеграл в формуле (4в) можно
представить с помощью гипергеометрического ряда [8]
- = I— rf+V ( 2 У/2 (2у + 2|1+1)! _
mm 2/ \wwqj (V_2|_jx)! V"(2v-4-1)! (2^4- 1)!
<Щ)>- -И; 1, (9)
216
X. Когельник
где гипергеометрический ряд F определяется формулой (6в).
Выпишем некоторые коэффициенты для волн низших порядков:
C11 ~ coo> (10a)
C13 “ C00C02’ (Ю6)
C31 ~ C00C20’ (Юв)
C33 C00 (C00 "b 3co2C2o)’ (Юг)
П/"ЗУ 2 C!5 У 2 C00C02’ (Юд)
,/з/Г , с51 У 2 C00^20‘ (Юе)
Как видно из формул, эти коэффициенты также довольно
просто выражаются через сОо, С20 и с02. При полном согласовании
коэффициенты си и с33 равны единице. При неполном согласо-
вании । too i < 1 и, следовательно, | сн | = | с$01 < | с001. Мы ви-
дим, что основная волна менее чувствительна к рассогласова-
нию, чем волна высшего порядка.
§ 4. КОЭФФИЦИЕНТЫ СВЯЗИ
В СЛУЧАЕ ЦИЛИНДРИЧЕСКИХ КООРДИНАТ
Собственные функции в выражении (2) также ортогональны.
Воспользовавшись этой ортогональностью, вычислим коэффи-
циенты связи. Из ортогональности функций sin /ф и cos/ф сле-
дует
= ° ПРИ 1 + (И а)
Между волнами с различными индексами по углу нет связи;
чтобы упростить обозначение, мы можем определить
CFiPi=cpP,i ПРИ l=l- (11б>
Используя соотношения ортогональности [2] для собственных
функций (2), получаем коэффициенты связи
е_ =fJ_V+I]/__________
РР: 1 \wtul У (I р) 1 (Z р)!
j dr2r2lL-p (ar2) Llp (pr2) e ' qr\ (12)
Q
9. Коэффициенты связи и коэффициенты преобразования волн 217
где параметры а, |3 и q даются формулами (4г) — (4е). Интеграл
вычисляется так же, как и в предыдущем параграфе [8], а ре-
зультат можно представить в виде гипергеометрического ряда
с- ;-(_2 Г г-_ + - -p-fy
РР' \wwq / V (^ + P)' (/ + /’)!/’!/’! V q' ' q'
xf[-p.-p-.-p-p-i. ,*2;^)]. оз»
где F дается формулой (6в).
Используя коэффициент сОо из предыдущего параграфа, вы-
пишем некоторые коэффициенты для волн низшего порядка, по-
лучаемые из формулы (13):
соо, о = соо! (14а)
Уо, i = 4(Z+,)- О46)
со1,о==соо(1 -|гсоэ)’ (14в)
-лу). (14г)
%.,-4l,t'>/3^R|-j4,)'’- (14а)
= (14=)
=11, ! = cw.i (=«. А|<! ,+ соог+2))- (14ж)
Из формулы (146) следует, что для заданного рассогласова-
ния связь между волнами более высокого порядка по углу
уменьшается в значительно большей степени, чем связь между
основными волнами. При полном согласовании коэффициенты
Соо, о=Соо, г=сц, (=1, а остальные коэффициенты в формулах (14)
равны нулю.
§ 5. связь ОСНОВНЫХ волн
Определим теперь ту часть мощности, которая переходит из
падающей волны ТЕМОо в основную (0, 0) волну системы, рас-
положенной справа. Так как и в прямоугольных, и в цилиндри-
ческих координатах основные волны одни и те же, мы можем
использовать или коэффициент Соо, или Соо, о- Коэффициенты свя-
зи для комплексных амплитуд равны соответственно Соо^оо или
Соо, о- Следовательно, доля мощности х, переходящая из одной
волны в другую, определяется следующим образом:
х (с0!/00)2 Cqo, осоо, о* (15а)
218
X. Когельник
Учитывая (7а), получаем
Л " •
I wwq |2
Подставим сюда q из (4г):
(156)
(16)
4
Таким образом, связь по мощности выражается через парамет-
ры падающего пучка (w, R) и параметры системы, расположен-
ной справа (да, У?,). Мы можем переписать это выражение
______4_____
' W , W \2 w2
—И— + р —“
L® W I W2
(17а)
и понимать под w/w меру рассогласования радиусов пучков, а
под
(176)
меру рассогласования радиусов кривизны обоих фазовых фрон-
тов. Множитель о определяется соотношением
яу2
о=:Лт₽- (17в)
Мы называем а «параметром системы», так как он описывает
чувствительность различных резонаторов и линий передачи к
рассогласованию фазовых фронтов. Для конфокальной системы
этот параметр равен единице. Для симметричных неконфокаль-
ных резонаторов [1] с расстоянием между зеркалами d и радиу-
сом кривизны зеркал R параметр а запишется следующим об-
разом:
"-(2-J-I) (18)
На фиг. 4 приводится график параметра системы, рассчитан-
ного по формуле (18). Из графика видно, что системы, в кото-
рых расстояние между зеркалами (или линзами) много меньше
конфокального расстояния, сравнительно мало чувствительны к
рассогласованию фазовых фронтов.
На фиг. 5 изображена зависимость х от (w/w)2, данная фор-
мулой (17а) для различных значений ±р. Из этих кривых при
заданных параметрах пучков может быть найдена часть мощ-
ности, переходящая из одной основной волны в другую. Возь-
мем, к примеру, случай почти конфокальной системы (о^1) и
предположим, что рассогласование кривизны фазовых фронтов
d/R
Фиг. 4. Параметр системы о.
фиг. 5- Коэффициент связи ОСНОВНЫХ волн,
220
X. Когелышк
составляет 20% (R=\,2R)). Из формулы (176) следует, что
р = 0,2. Для разницы в радиусах пучков приблизительно 35%
(w = l,35ay) из кривой находим, что около 90% мощности пере-
ходит из падающей волны в основную волну системы.
Из графиков на фиг. 5 видно, что для данного рассогласо-
вания фазовых фронтов (р¥=0) величина и максимальна при
значениях w/w, несколько меньших единицы. Следовательно,
если нельзя полностью согласовать фазовые фронты, то для
получения лучшего согласования надо сделать радиус падаю-
щего пучка меньше, чем радиус основной волны системы.
Строго конфокальная система является вырожденным слу-
чаем, который заслуживает специального рассмотрения. Пока
апертуры системы достаточно велики, всегда существует набор
волн, у которых радиусы пучка на зеркалах могут быть любой
величины. Эти волны были названы конфокальными волнами
с продольной асимметрией [4]. В этом случае радиусы пучков
автоматически согласованы, поскольку всегда имеется одна
волна, радиус пучка которой равен радиусу падающего пучка.
Для полной связи этих воли необходимо еще согласование фа-
зовых фронтов.
Если собственная волна системы имеет плоский фронт, сов-
падающий с плоскостью отсчета, т. е. Д = оо, то формула (176)
упрощается:
(19)
Иногда вместо параметров w, w, R и R на плоскости отсчета
удобно использовать расстояния z и z от этой плоскости до
наиболее узких мест (шеек) пучка [5] и радиусы пучка wQ и wa
в этих местах. Связь между этими параметрами иллюстрирует
фиг. 3. Старые параметры можно выразить через новые [5]:
(20а)
(206)
такие же формулы справедливы для w и R (в соответствии с
нашим выбором знака параметр R отрицателен, как показано
на фиг. 3). Согласно (4г), величина q может быть выражена че-
рез эти новые параметры:
__ 1 । 1
Q —^.Xz ? . Xz ’
(21)
9. Коэффициенты связи и коэффициенты преобразования волн 221
а коэффициент связи по мощности для основных волн запи-
шется следующим образом:
_________4________
+ММ2 <?+
. Wq / \ЛШ0Ш0/
(22)
где z + z— расстояние между шейками пучков этих двух волн.
Здесь коэффициент и выражен через параметры обеих волновых
систем, которые не зависят от выбора плоскости отсчета.
§ 6. КОЭФФИЦИЕНТЫ связи по мощности
В предыдущем параграфе мы описали связь между двумя
основными волнами с помощью коэффициента х. Для воли выс-
ших порядков переход мощности из одной волны в другую
описывается модулями коэффициентов, приведенных в форму-
лах (6), (7), (9), (10), (12) и (14). Доля мощности, переходя-
щая из волны ТЕМ— в волну ТЕМтп, равна | с-т |2 • |с-л |2,
а д<?ля мощности, переходящая из волны TEM-t в волну
TEMpi— |c-pZ|2. Эти коэффициенты связи могут быть выраже-
ны через х.
Для прямоугольных координат после некоторых алгебраиче-
ских преобразований получаем:
1 С00 |2 = V (23а)
|С02 I2 = 1 С20 I2 = J /х (1 — И). (236)
1 СО4|2 - к4о12 = 4 /%(1-X)2, (23в)
сОт I2 = 1 сто I2 = /х (1 - х)т/2-. 2т(-у!) (23г)
k22|2 = j/x(l — Зх)2 (23д)
кп |2 = хЧ (24а)
ki312 = кз112 = 4 у-3 2 (1 — (246)
kul2 = k51 I2=-¥-x8-(1 -X)2, (24в)
k3312 = 4 х3/‘к — 5х)2. (24г)
222
X. Когелышк
В цилиндрических координатах
koo, о12 = х> (25а)
koo, i l2 = *z+1. (256)
kol.o I2 = х (1 — и)> (25в)
koi, г|2 = (/4~1)х/+1 (1 -х), (25г)
I сОр, 112 = |^, г I2 = xz+1(1 - х)', (25д)
I cu, 112 = х/+] [(/ + 2) х - (Z + 1 )]2. (25е)
Записанные выше формулы для передачи мощности между
волнами удивительно просты. В соответствии с формулой (22)
коэффициент х может быть выражен через параметры пучка,
которые не зависят от выбора исходной плоскости. Следователь-
но, коэффициенты связи для волн высшего порядка не зависят
от выбора плоскости отсчета.
Из приведенных формул следует, что коэффициенты связи
между волнами различного порядка могут принимать макси-
мальные значения. Мы имеем:
। ,2 1 1
ког 1макс Туу ПРИ z-y’
. ,2 6 1
l'’«U‘=WT "Р"
= 4 "Р" х = 7 " т- л-
Максимальный переход мощности из прямоугольной волны
ТЕМо2 в основную волну ТЕМа0 имеет место при х = 7г
(Jс0212 koo12)макс = Ч&, т. е. максимальная величина переходящей
мощности составляет 12,5%. Максимальный коэффициент пере-
дачи мощности из круглой волны ТЕМ10 в основную волну
TEMqo составляет 25%.
§ 7. ОТРАЖЕНИЕ ОТ НЕСОГЛАСОВАННОГО РЕЗОНАТОРА
СО СФЕРИЧЕСКИМИ ЗЕРКАЛАМИ
В качестве другого примера использования коэффициентов
связи рассмотрим случай падения несогласованной волны
ТЕМ— на резонатор со сферическими зеркалами. Допустим,
что мы хотим определить, какая часть этой волны отражается
от резонатора в виде волны ТЕМ— (с теми же индексами!).
Для простоты будем предполагать, что резонатор состоит из
двух одинаковых зеркал, которые имеют коэффициент отраже-
ния по амплитуде г (комплексный), коэффициент передачи t
и радиус кривизны /%• Расстояние между зеркалами равно ci.
9. Коэффициенты связи и коэффициенты преобразования волн 223
Собственными колебаниями ' резонатора являются волны
ТЕМтп с радиусом пучка [1]
(26)
на зеркалах. Волны ТЕМтп отражаются от резонатора по тому
же закону, что и плоская волна от плоскопараллельного резо-
натора (интерферометр Фабри — Перо). Если собственная вол-
на резонатора ТЕМтп падает на резонатор, то она отражается
с коэффициентом отражения по амплитуде гтп
где 0mn — фазовый сдвиг волны ТЕМтп при прохождении от
одного зеркала к другому. Он определяется формулой [1—4]
Qm„ = kd — (т ф- п +1) ггД-7775лт • (28)
тп ' ' 1 ’ cos [1—(d//?0)] v ’
В общем случае фазовый сдвиг неодинаков для волн с разными
индексами. Следовательно, коэффициенты гтп также неодина-
ковы.
Падающая волна ТЕМ— обычно не является собственной
волной резонатора. Она связана с целым набором собственных
волн резонатора
т, п
(предполагается, что падает волна единичной мощности). Каж-
дая из собственных волн резонатора отражается с коэффициен-
том отражения по амплитуде гтп. После отражения мы имеем,
следовательно, ряд волн, бегущих налево с амплитудами
ОО
Ус- с- г ф* (х) ф’ (и)
тт пп тп* т V / тп\У /
mt п
в исходной плоскости. Мы должны взять комплексно сопряжен-
ные собственные функции, гак как волны, бегущие влево, опи-
сываются множителем exp (jkz), в то время как волнам, бегу-
щим вправо, соответствует ехр (—jkz). Этот набор отраженных
собственных воли резонатора переходит в набор волн первона-
чальной волновой системы. При этом могут возбудиться волны
и других порядков. Комплексные амплитуды отраженных волн
ТЕМ- Рав"Ь1
ОО
г^-п= 2 4птс-ппг (29)
т, «—О
2-4
Л. Цогелъник
§ 8. КОЭФФИЦИЕНТЫ СВЯЗИ ДЛЯ СИСТЕМ
СО СМЕЩЕНИЕМ И ИЗЛОМОМ
Связь между падающими волнами и волнами данной опти-
ческой системы изменяется, если ось падающего пучка смещена
или расположена под углом по отношению к оси рассматривае-
мой системы. Для простоты мы будем здесь обсуждать только
связь между основными волнами.
Во-первых, предположим, что ось падающего светового пуч-
ка смещена на относительно оси системы. Собственные функ-
ции системы определяются из выражений (1). Из-за сдвига оси
распределение поля основной волны пучка, падающего слева,
определяется теперь следующим образом:
Фо(*) = (]/||У/2ехр1- -(-^Т^)2 - jk {х^ ) (30)
\* л w / ( w2 2R )
для собственных функций, не зависящих от у. Используя (46),
находим коэффициенты связи между основными волнами
Г dx exp I — (L x°~
J \ ( w2
Вычисляя интеграл, находим
д.Д.2 /И^'Д^2 х21й
w2 [ 2R 2/?])/’
(31)
cvq — с00 exp
-ур / 1 jk \! j jk \
q \ w2 ' 2R / \ w2 R /
(32)
где Coo и q имеют тот же смысл, что и в предыдущих парагра-
фах. Эта формула позволяет рассчитать часть мощности х , пе-
реходящую из одной основной волны в другую. Для малых сме-
щений х0 после несложных преобразований получаем
хх — | сХа |2 • I с0012 = х —- Ф ( —р -Х-Д ф -f —'j 1,
“ 1 1 001 2 Д 4/?2П
(33а)
где х дается выражением (15). Как и следовало ожидать, связь
между основными волнами уменьшается при наличии смещения
хй. Выражение (33а) может быть записано следующим образом
через параметры wo и w0 [см. (20)]:
1 2
(336)
Рассмотрим теперь случай, когда ось падающего пучка на-
клонена по отношению к оси системы, и выберем плоскость от-
счета в том месте, где эти две оси пересекаются. Для наклонной
9. Коэффициенты связи и коэффициенты преобразования волн 225
оси пучка x = gz, а угол излома В предполагается малым. С уче-
том излома собственная функция падающей волны в точке х
запишется в виде
Фо(*) = (1Z- -i-V’ exp [ — — jk~ — jk^x 1. (34)
\ г л w / ( w2 2Z? J
Как и раньше, воспользуемся для расчета коэффициента
связи формулой (46). Получаем
+ оо
f dxe-^^M. (35)
\ 31WW I J
' —оо
После вычисления интеграла имеем
с^соое-^. (36)
Отсюда окончательно определяем часть мощности, переходящую
из одной волны в другую:
^ = 1^12-коо|2 = и-4^2(^2 + да2)- <37)
где предполагается, что угол наклона В достаточно мал, чтобы
можно было пренебречь членами второго порядка малости в
разложении экспоненты. Уравнение (37) описывает уменьшение
связи, вызванное изломом оси падающего пучка.
ЛИТЕРАТУРА
1. Boyd G. D., Gordon J. Р., Bell Syst Techn. Journ., 40, 489 (1961).
(Имеется перевод в сб. «Лазеры», ИЛ, 1963. стр. 363.)
Confocal Multimode Resonator for Millimeter through Optical Wavelength
Masers.
2. Goubau G., Schwering F., Trans. IRE, AP-9, 248 (1961). (Имеется
перевод: Г. Губо, Ф. Шверин г, Зарубежная радиоэлектроника, № 11,
1961, стр. 3.)
On the Guided Propagation of Electromagnetic Wave Beams.
3. Pierce J. R., Proc. Nat. Acad. Sci., 47, Г808 (1961).
Modes in Sequences of Lenses.
4. Boyd G. D., Kogelnik H., Bell Syst. Techn. Journ., 41, 1347 (1962).
Generalized Confocal Resonator Theory.
5. Y a r i v A., G о r d о n J. P., Proc. IEEE, 51, 4 (1963).
The Leser
6. Kogelnik H., Bell Syst. Techn. Journ., 43, 334 (1964).
Matching of Optical Modes.
7. Fork R. L., Herriott D. R„ Kogelnik H., Appl. Optics, 3 (1964).
A Scanning Spherical Mirror Interferometer for Spectral Analysis of Laser
Radiation.
8. Erdelyi A., Magnus W., Oberhettinger F., Tricomi F. <3.,
Tables of Integral Transforms, Vol. I, Bateman Manuscript Project, New
York, 1954.
15 Зак, 274
10
ПРИМЕНЕНИЕ РАЗЛОЖЕНИЯ ШМИДТА
К АНАЛИЗУ КОЛЕБАНИЙ
В ОПТИЧЕСКОМ РЕЗОНАТОРЕ
В. Штрайфер *, X. Гамо*
С помощью интегрального уравнения, получаемого из принципа Гюйген-
са в параболическом приближении, рассматриваются оптические резонаторы
с неодинаковыми сферическими зеркалами. К ядру интегрального уравнения,
не являющемуся эрмитовым, применяется теорема разложения Шмидта, и
интегральное уравнение сводится к матричному уравнению. Последнее ре-
шается аналитически методами теории возмущений. Решение дает структуры
мод, включая фазу и условие резонанса.
§ 1. ВВЕДЕНИЕ
Эта статья посвящена аналитическому методу определения
мод оптического мазера путем решения однородного интеграль-
ного уравнения Фредгольма. Ядро интегрального уравнения яв-
ляется, вообще говоря, комплексным и симметричным, но не
эрмитовым. Поэтому интегральное уравнение резонатора не при-
надлежит к хорошо изученному классу интегральных уравнений
с эрмитовыми ядрами. Однако существует математическая тео-
рия, первоначально сформулированная Шмидтом [1] (см. также
[2—4]), позволяющая решать интегральные уравнения с пеэрми-
товыми ядрами. Наиболее хорошо известный результат теории
Шмидта обычно называют теоремой разложения Шмидта.
Применяя эту теорию, мы можем разложить ядро интеграль-
ного уравнения резонатора по так называемым функциям
Шмидта. Это делается для того, чтобы свести интегральное
уравнение к матричному уравнению. Некоторые исследователи,
а именно Губо и Шверинг [5, 6], Шахтер и Бергштейн [7], исполь-
зовали в подобных задачах другие функции для разложения.
Однако мы попытаемся показать, что теория Шмидта и его
разложение обладают многими преимуществами.
* W. S t г е i f ег, Н. Gamo, Department of Electrical Engineering, Uni-
versity of Rochester, Rochester, N. Y.
10. Анализ колебаний в оптическом резонаторе
227
В § 2 выводится интегральное уравнение резонатора с двумя
разными сферическими зеркалами, а в следующем параграфе
к нему применяется теория Шмидта. В § 4 методами теории
возмущений аналитически определяются структуры мод и усло-
вия резонанса, а затем в § 5 рассматриваются некоторые чис-
ленные примеры.
§ 2. ПОСТАНОВКА ЗАДАЧИ
В этом параграфе мы выведем интегральное уравнение, ко-
торое описывает моды в резонаторе. Резонатор образован двумя
неодинаковыми прямоугольными зеркалами А и В различной
Фиг. 1. Геометрия резонатора.
сферической кривизны с общей линией центров, параллельными
краями и параллельными касательными плоскостями (фиг. 1).
Поскольку зеркала неодинаковы, мы должны определить моду
как структуру поля, которая преобразуется в себя после того,
как волна проходит через резонатор и возвращается обратно.
Ядро интегрального уравнения, описывающего весь процесс,
должно быть симметричным, поскольку два ядра для прохода
волны туда и обратно в силу теоремы взаимности (см., напри-
мер, [8]) получаются друг из друга путем транспонирования.
15*
228
В. Штрайфер, X. Гамо
Сформулируем это, используя формулу Кирхгофа — Френеля,
чтобы описать каждое прохождение, как это делали Фокс и
Ли [9]. Тангенциальная составляющая электромагнитного поля
^i(xA, у а) на зеркале А порождает на В поле
+₽л +аА
^2(xs, Ув)= / J Ка{ха, уа, хв, yB)&i(xA, yA)dxAdyA, (la)
~ал
где
^(Хл, уА; хв, ув) =
ike~ikd f Г (х —ха)г (у —у \2 "|
], (16)
а волна, пришедшая обратно, описывается формулой
&з(Хд. УА)= / / Ка(ха, уА; хв, Ув)&2(хв, yB)dxBdyB. (1в)
~ав
Волнистая черта обозначает перестановку. В (16) мы использо-
вали параболическое приближение, пренебрегая в показателе
экспоненты членами порядка
^(т)2 и м(т)4- <1г)
Здесь k — волновое число, а другие величины являются разме-
рами, указанными на фиг. 1. Чтобы получить симметричное ядро
для полного прохождения туда и обратно, нам нужно было бы
скомбинировать ядра и КА. Прежде чем пытаться их комби-
нировать, заметим, что для сферического зеркала радиусом b в
параболическом приближении отклонение разделяется по коор-
динатам:
®(х. </) = -^- + -fp (2)
Таким образом, мы можем рассматривать только одномерные
эквиваленты уравнений (1а) и (1в):
+“л
£2(хд) = х'/2 J LA(xA. x^E^x^dx^ (За)
10. Анализ колебаний в оптическом резонаторе
229
где
X — ie~lkd,
LA (хА, хв) = (ехр | [иАх2А + авх2в - 2хАхв]} (36)
и
+“в
£зС*-д) = Х^ J LA(xA> хв)ei(xb)^xb- (Зв)
-“в
Здесь мы использовали параметры иА и ив, которые являются
мерой отклонения от конфокальной геометрии:
«л.в = 1-т4- (4)
° А, В
Функции, описывающие изменение поля моды в зависимости
от координаты х, одновременно удовлетворяют условию
Е3(хл) = оЕ1(хл)
и уравнениям (За) и (Зв), т. е. являются собственными функ-
циями £(Ха) комбинированного уравнения
+“л
(О = X J LAB (хл, Х’А} Е (хд) dxA (5 а)
-“л
с симметричным комплексным, но не эрмитовым ядром:
• +“в
LAB (хд, хд) = J LA (хл, хд) LA (хА, хв^ dxB. (56)
~ав
Соответствующие собственные значения о определяют резо-
нансные частоты и потери мод. Ньюмен и Морган [10] показали,
что у этого уравнения имеется по крайней мере одно решение.
§ 3. ТЕОРИЯ ШМИДТА И МАТРИЧНАЯ ФОРМУЛИРОВКА
Интеграл (56) обычно не выражается через элементарные
функции, поэтому мы начнем с разложения ядра ЬА. Исполь-
зуемые функции разложения находятся из теории Шмидта, ко-
торая фактически применима к более общим ядрам, чем непре-
рывные ядра, определенные в конечных областях, которые воз-
никают в задачах о резонаторах.
230
В. Штрайфер, X. Гамо
Шмидт определяет два положительных полуопределенных
эрмитовых ядра
Л (•*'£’ Хд)— J ^А(хА, хв')^ха—
-“л
— ехр
и
£п = (хА,
_±„ /.,2 Sin[(^/rf)(4- *Д)]
2d 11В {ХВ ХВ) J л(4-хв)
(6а)
+“в
Хл) = J ^Л+(ХЛ’ Xb)LA(Xa> Хв)^ХВ~
~ав
= ехр
«л (*л~*л)
П(ХА — Ха)
(66)
Их собственные функции {<рл} и {фл}, являющиеся решениями
уравнений
+ав
IN4(хв)= J ^i(xb’ хв)^п(хв)^хв (7а)
~ав
и
+аА
|H„|4(^)= J Ln(XA> XA^n(XA)dXA’ (7б)
-“л
образуют полные ортонормированные системы, т. е.
+ав
(Фл> Фт)В= J Ф*Я(Хв)фтЫ^В = 6лт.
(Фл. Фт)л= J Ф’я (Хл) Фте (Хл) dXA = Ъпт.
-“л
Собственные функции имеют одинаковые собственные значе-
ния и связаны между собой первоначальным ядром:
+“л
НлФ„(хв)= J La(xa, xB)^n(xA)dxA (8а)
-“л
10. Анализ колебаний в оптическом резонаторе
231
+ав
(ХА> Хв)(Рп(.Хв)^ХВ‘ (86)
~ав
Крестик обозначает эрмитово сопряжение. Для рассматривае-
мых здесь прямоугольных зеркал собственные функции можно
выразить через угловые функции вытянутого сфероида [11—13]:
£ / X \21 — / х \
Фп (-*в) = е‘пп,4ав12 exp icSOn \с, ) (9а)
и
фп (хл) == е~1пп^а-'^ ехр
(96)
Мы использовали черту сверху для того, чтобы обозначить нор-
мированную функцию Son (с, х/а), которая удовлетворяет усло-
вию
+i
J Son(c, t)SOm(c, t)dt = bnm. (10)
В формулах (9а) и (96) для краткости использованы обозна-
чения: и ,а, [ d \ а, = = (На) ав \ °а) ав <х„ / d \ <х_ ь = и В=1 В (116) А \ В / А
и ka С = (Ив)
Последияя величина приблизительно равна геометрическому
среднему зон Френеля, наблюдаемых на каждом зеркале из
центра другого, умноженному на 2л. Интересно заметить, что
в пределах наших параболических приближений (1г) и (2) си-
стема {фп), определенная на зеркале В, не зависит от кривизны
зеркала А, т. е. от иА, и аналогично система {фп}, определенная
на А, не зависит от ив.
При малых с функции SOn аппроксимируются полиномами
Лежандра
Мс- (12а)
232
В. Штрайфер, X. Гамо
Это приближение тесно связано с функциями Фурье, использо-
ванными Шахтером и Бергштейном [7]; действительно, при ма-
лых с первые два члена в (12а) воспроизводят их результат.
Фиг. 2. Зависимость (с) от п (по Слепяну [14]).
При больших с SOn аппроксимируется функциями Гаусса — Эр-
мита или Вебера:
(126)
Эти функции использовал Шверинг [6].
При тех мультипликативных постоянных, которые выбраны
для <рп и в (9а) и (96), собственные значения ц в (8а) яв-
ляются действительными и положительными. Флеммер [12] при-
водит значения ц при а Слепян [16] показал, что при боль-
ших с и фиксированном значении п невырожденные (см. [13])
определяются формулой
1 2 4л1/28',с"+1/2е-2с Г1 бп2 — 2п-|-3 . _2J ,
------[1-------32Г^+°(С )? <13а)
При больших п, и с Слепян получил
lim ji2 — [1 -|-0яО]~1,
С->оо
(136)
где D — фиксированное число:
г»___ (лп/2) — с
In (2с1/2) '
(13в)
10. Анализ колебаний в оптическом резонаторе
233
Зависимость jin от п при трех значениях с показана на
фиг. 2. Видно, что вблизи 2с/л величина jin быстро уменьшается
от 1 до 0 при увеличении п. Этот факт является особенно важ-
ным при оценке усеченного разложения ядра, рассмотренного
ниже. В данной статье мы будем предполагать, что распреде-
ление jin имеет простой вид:
(14)
Теперь вернемся к разложению ядра по функциям Шмидта:
LA (хл> хв) = 2 Нлфл (хв) ф*л (хл). (15а)
Когда ядро квадратично интегрируемо (какими являются встре-
чающиеся на практике ядра), равенство в (15а) понимается
в среднеквадратичном смысле. Однако если ряды сходятся рав-
номерно относительно любой из двух переменных, то они схо-
дятся равномерно относительно обеих переменных. Теперь вы-
разим интеграл (56) через функции Шмидта:
LAB(*л- хл) = ₽ (х'д)(Фр. Ф’л)л (ф’л. Фт)в Мт(*л)> С56)
где
+ав
(фл. Фт)в= J ФЯ(*в)Фт(*вМ*В (16а)
~ав
и
+“л
ф*ДЛ(хл)=1Х(хл) J фжмч-
р р -ад
(166)
Если переписать (156) в виде
£ЛВ(Хл> S Фт(лл) ^трфр(хл)> (^)
/п, р
то будет определена бесконечная матрица L:
Ь=='КрФ(г. (18)
Здесь — диагональная матрица с элементами
Нят = Мпт
(19а)
234
В. Штрайфер, X. Гамо
и симметричные матрицы Т и Ф имеют элементы
^=(Ъ€)Л- (,196)
фпт-^„>К)в- (19в)
Матрицы Т и Ф являются унитарными, поскольку каждая
представляет изоморфное преобразование в гильбертовом про-
странстве. Хорошо известно, что такие унитарные преобразова-
ния соответствуют передаче без потерь, поэтому информация о
потерях содержится в матрице ц; ее элементы дают потери в
конфокальном резонаторе с одинаковым значением с [формула
(Ив)].
Разложим теперь поле Е(хА) моды в ряд по функциям
Шмидта {фр}:
£(хл) = 2Г,Ш (20)
р
Если Е— непрерывная функция, то, согласно теореме разло-
жения Шмидта, ряд (20) сходится абсолютно и равномерно.
Если на ряд (20) подействовать ядром LAB в виде (17), то
интегральное уравнение (5а) превращается в бесконечную си-
стему линейных алгебраических уравнений. Эта система уравне-
ний имеет нетривиальные решения при таких значениях or, ко-
торые удовлетворяют характеристическому уравнению
detfxL —о!] = 0. (21)
Для каждого собственного значения or, скажем огп, существует
по крайней мере одно собственное распределение поля Еп(хд).
Таким образом, мы имеем матрицу Т с элементами Трп, кото-
рая удовлетворяет уравнению
XLT = Tor. (22)
Следовательно, элементы n-го столбца матрицы Т являются
коэффициентами разложения для n-й мода.
§ 4. НАХОЖДЕНИЕ МОД
Теперь наша задача состоит в том, чтобы вычислить Т и
Ф, а потом определить Тип. Ограничимся рассмотрением прак-
тически важного случая с^>1. Тогда при /<^1 можно написать
асимптотическую формулу
= 2.я(д|),в (28)
10. Анализ Колебаний в оптическом резонаторе
235
где Нп — полином Эрмита, а нормировка выбрана так, что
f SOn(c, t)SOm(c, = J
+оо
Ошибка, обусловленная расширением пределов интегрирования,
незначительна, если величина ег^1 Hn(w)Hm(w) пренебрежимо
мала при w>c'/a. Слепян показал, что формула (23) является
хорошим приближением только при и n<Sc. Однако при-
сутствие матрицы ц, элементы которой равны нулю при
п>2с/л, препятствует тому, чтобы ошибка стала большой при
увеличении п. Таким образом, элементы матриц У иФ прибли-
зительно равны
.1(п + т)л/4
~i е~(w)(w)
где
Jnm== ДЛЯ с, = И ®пт ДЛЯ
В случае почти конфокальных зеркал и поэтому полез-
но разложить ехр (—ilw2) в ряд. Ряд интегралов, получающий-
ся после перемены порядка суммирования и интегрирования:
4-оо 4-оо
J e-^PHn(w)Hm(W)dW,
р—0 — оо
сходится при |В|<1. Эти интегралы можно оценить, используя
ортогональность полиномов Эрмита и рекуррентные формулы
для них. Значения первых четырех коэффициентов разложения
4-со
»=0
приведены в таблице. Заметим, что матрица Зпт является сим-
метричной и все члены, для которых п+т— число нечетное,
равны нулю. Поскольку, согласно (14), ц— конечная единичная
матрица, матрица L легко вычисляется (см. приложение). Ко-
гда -> 0, остаются только диагональные члены
L°nm==ein*bnm (25)
236
В. Штрайфер, X. Гамо
Значения Avnm
х. m п п-2 П — 4 л-6
0 1 0 0 0
1 |(2п+1) 1 2 0 0
2 |(2n2 4-2n + l) 4(2«-п 2_ 8 0
3 Д(4пз + 6п2 + 8п + 3) 4(«2-«+d к 4(2«-3) 1
сильно вырожденной матрицы L, Но вырождение снимается во
многих встречающихся на практике случаях, когда выполняется
условие
(26)
т. е. £в—£a = OU2). Используем для вычисления Тио методы
теории возмущений. В случае bB>d>bA, когда конфигурация
резонатора дает большие потери («неустойчивость») [14, 15], не-
равенство (26) не выполняется.
Применяя теорию возмущений (см. приложение) для соб-
ственного значения оп интегрального уравнения резонатора при
л<2с/л, получаем
х-1ол = ^ 2 о<лЧ (27а)
а—О
где
0(0) = 1,
00)== —/1(2л + 1)(|д--Нв),
= - 7 (2л2 + 2л - 1) (^ + %) —| (2л2 4- 2п +1) |А1В,
= i 1 (2п + 1) { 4 (2л2 + 2п + 3) + £3,) +
+1 (2«2+2л - 9) (ь -нв) + 2д~} • (276)
До третьего порядка модуль ап равен единице. Когда ап ком-
бинируется с подобным членом для вариации по у (скажем, ато)
10. Анализ колебаний в оптическом резонаторе
23?
двумерной моды, резонансная частота определяется из уравне-
ния
апот — е~2я1я, (28а)
где q — целое число, знак которого выбирается так, чтобы в по-
лости существовало положительное число стоячих волн. Запи-
шем фазу On в виде пл+л/2—kd—уп, тогда условие резонанса
примет вид
Ы = Л7 + (1+/п + л)^ —(286)
где величина у„ (или ут) должна быть вычислена из уравнения
(276). Сравнивая (286) с условием Бойда и Когельника [15]
kd = nq + (1 4- т + п) | у — arc sin [(aAus)1/2] |,
видим, что наше решение зависит от дополнительного парамет-
ра — отношения размеров зеркал. Если эти отношения аА/ав и
₽а/₽в (для вариации по у) равны единице (зеркала одинакового
размера, но не обязательно с одинаковыми радиусами кривиз-
ны), то ^=и=\ — d/b и формулы совпадают. Здесь уместно на-
помнить, что
&в £л ~11 в u-a — O (и2)>
т. е. разница в кривизне зеркал мала.
В настоящее время проводятся расчеты для того, чтобы про-
верить, насколько согласуются при больших значениях £в— |д
и 1а представленное выше приближение матрицы g и более точ-
ные значения, полученные Слепяном [16].
Структура моды с учетом лишь возмущений первого порядка
описывается тремя членами разложения по полиномам Эр-
мита:
(хА) =
=e-^-iKA) (да)+Нп+2 (w) _ п (п _ п Нп_2 (w)] _
— t [4Нп+2№) +«(« — 1)//л-2(®)]}> (29а)
где
(296)
5в Г 5Л
и
да = с112 ——. (29в)
ал
Здесь использован результат, полученный в приложении (П.8)
238
В. Штрайфер, X. Гамо
§ 5. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
В этом параграфе мы рассмотрим некоторые численные ре-
зультаты, полученные на основании выражения (29а), при вы-
воде которого учитывались лишь возмущения первого порядка.
На фиг. 3 приведена нормированная величина |En|2 для пер-
вых четырех мод, причем ее максимальные значения приняты
за единицу. По горизонтальной оси отложена величина
w=c'l*xla. Отметим, что если на зеркале А существует поле,
соответствующее £=+0,4, то на зеркале В имеется поле, соот-
ветствующее £ =—0,4, причем в последнем случае w = c'/2xB/aB;
справедливо и обратное утверждение. Для основной моды
(п = 0) сравним размеры пятен [расстояние Xs., для которого
i-EoCv8) i2= i-Eo(O) |2*е~2], вычисленные по нашей формуле и фор-
муле Бойда и Котельника. В конфокальном случае bA=bB = d и
результаты, конечно, совпадают. В случае bA=f=bB4=d анализ
Бойда и Котельника не содержит размеров зеркала, но в первом
порядке размер пятна не зависит от отношения ад/ав, которое
обозначает масштаб по горизонтали. Что касается зависимости
от радиусов кривизны зеркала, то результаты тоже совпадают.
Размер пятна для мод более высокого порядка определить не
так просто. Отметим, однако, что увеличение параметра, содер-
жащего радиусы кривизны и размеры зеркал, сказывается во
всех случаях одинаковым образом.
Вопрос о фазе Еп тоже является интересным, поскольку в
предыдущих работах о сферических зеркалах [11, 15] предпола-
галось, что зеркала являются поверхностями постоянной фазы.
Аналитическое рассмотрение фазы в выражении (29а) для £=0
(одинаковые зеркала) показывает, что в первом порядке это
предположение справедливо. Это видно на фиг. 4, где для
£А = 0,1 и £=±0,4 показан фазовый сдвиг относительно кон-
фокальных мод £д = £=0. Эти кривые требуют пристального рас-
смотрения. Во-первых, фазовый сдвиг в начале координат
(центр зеркала) не равен нулю и различен для различных зна-
чений £ и различных мод; фаза, приведенная для нечетных мод,
является предельной. Фазовый сдвиг в центре зеркала опреде-
ляет возмущение резонансной частоты для каждой моды по
сравнению с конфокальным случаем. Во-вторых, существуют
определенные точки, в которых пересекаются кривые для трех
различных значений £; можно показать аналитически, что фаза
в этих точках (в первом порядке) не зависит от £ (но зависит от
£а) и что ненормированные величины, содержащиеся в выраже-
нии (29а), в точках пересечения также равны. В-третьих, фазо-
вые кривые для п = 2, п = 3 имеют разрывы в определенных точ-
ках. Эти точки соответствуют значениям, в которых конфокальная
Фиг. 3. Нормированная интенсивность мод.
t> и г. 4. Фазовые сдвиги мод относительно мод конфокального резонатора.
10. Анализ колебаний в оптическом резонаторе
241
мода меняет знак; на фиг. 4, в и г фазовый сдвиг конфокаль-
ной моды вычтен. Большие фазовые сдвиги не означают, что
нельзя пользоваться формулой Кирхгофа — Френеля, поскольку
вблизи этих точек поле очень мало (ср. фиг. 3,в и г). Нако-
нец, сравним кривые для £=±0,4. Заданные значения £л и £
определяют £в; при £л = 0,1 и'£=+0,4 £в = 0,2333. Поэтому не-
удивительно, что кривая £=—0,4, относящаяся к зеркалу В, по-
казывает более сильный фазовый сдвиг, чем для зеркала А.
Если £=—0,4 и £л = 0,1, то £в=0,0428 и фазовый сдвиг на зер-
кале В (теперь £=+0,4) изменяется менее быстро.
§ 6. ЗАКЛЮЧЕНИЕ
В заключение укажем на некоторые преимущества исполь-
зования теории Шмидта при решении задач для резонатора.
Наиболее важное из них связано с теоремой приближения Шмид-
та, которая утверждает, что если множество цп упорядочено,
т. е.
то лучшее в среднеквадратичном смысле Af-членное конечное
приближение для ядра дается первыми N членами разложения
Шмидта, иначе говоря, величина
/ j La(xa,xb) — ^fntx^gnixA) dxAdxB
минимальна тогда и только тогда, когда
TV—1 N-1
S fn (хв) gn (хл) = S Н„Ф„ (хв) Ф*„ (Хл).
Теорема приближения особенно важна ввиду того, что мы почти
всегда имеем дело с конечными рядами.
Другое преимущество теории Шмидта связано с типом мат-
риц, которые возникают в разложении ядра. В противополож-
ность матрицам, используемым в других работах, в данном слу-
чае имеется четкое различие между матрицами ц, несущими
информацию о потерях, и унитарными матрицами У и Ф. Та-
ким образом, в случае когда потери отсутствуют, ц является
единичной матрицей и матрица ядра L унитарная.
Применимость рассматриваемого метода была бы сильно
ограничена, если бы нахождение функций Шмидта становилось
затруднительным в более сложных случаях, например когда,
в формулу Кирхгофа — Френеля включаются члены более
16 Зак. 274
242
В. Штрайфер, X. Гамо
высокого порядка. Однако ядра Шмидта и Лц суть положи*
тельно полуопределенные и эрмитовы, поэтому для нахождения
функций Шмидта можно использовать известные приближенные
методы.
Заметим также, что для любой пары прямоугольных зеркал
в пределах области Френеля и в параболическом приближении
функции Шмидта можно выразить через функции вытянутого
сфероида независимо от характера отклонения w(x, у) —даже
в том случае, когда оно не разделяется:
w (х, у)Ф и (х) 4- -п (у).
Эти и другие результаты будут рассмотрены в статье авторов,
которая в настоящее время готовится к печати.
В случае резонаторов с круглыми зеркалами функции Шмид-
та можно выразить через «гиперсфероидальные» функции, кото-
рые были независимо исследованы Слепяном и Хэртли1).
ПРИЛОЖЕНИЕ
ВЫЧИСЛЕНИЕ Т И <т МЕТОДАМИ ТЕОРИИ ВОЗМУЩЕНИИ
Как говорилось выше, результаты, представленные выраже-
нием (24) и таблицей, определяют Y иФ. Умножая их на и
[формула (14)] и замечая, что |в —|а = О(|2), имеем при
л<2с/л
L=2L<s), (П. 1)
L®=einslbnm,
Lnm = йгля{ - / | (2л + 1) (|л 4- |в) }
-Ub|(2«2 + 2«-1)-
— (5л-Нв)|(2л2 + 2л-Н) для п, п,
1<2)=ймя] /П9^
L>nm — е ,1/о Г 1 1 л (II. 2)
[л(л-1)]1/2[1(|л~|в) + /|л|в] для п, п -2/
\п(п— 1)]1/2[4(Ь — Вл) + ^дЬ] для П, — 2, п,
Ц3> = ?ля-^ (2л +1) [(|3 + II) 4 (2«2 + 2л + 3) +
+ Ub (Ь + Ь) (2«2 + 2л - 9)],
*) См. статью 11 в настоящем сборнике. — Прим. ред.
10. Анализ колебаний в оптическом резонаторе
243
где кубические члены сохранены только на главной диа-
гонали.
Теперь запишем Т и диагональную матрицу а как сумму
убывающих матриц, каждая из которых содержит высшие
степени Вл и
Т=2Т(Ч (П. За)
v—Q
Х-’а = 2 (П. 36)
V-0
где
Т(0) = I, (П. 4а)
o(0) = L(0). (П.46)
Подставляя эти выражения в (22),
xLT = Ta, (22)
и приравнивая члены одинакового порядка, находим
L(0) = o(0), (П.ба)
L(1) + L(0)T(1) = T(1)or<0) + ог(1), (П. 56)
L(2) + L(1>T(1) + L(0)T(2) T(2)a(0) + T(l)a(l) + a(2)t (П 5в)
L(3) -|- l(2)T(1) + l(1)T(2) L(0)T<3) =
= T(3)ff(0) + T(2)a(l) + T(l)a<2) + a(3). (n 5r)
Используя далее (П. 5a), из (П. 56) получаем
ff(1) = L(,); , (П.6)
продолжая процесс, находим
Т^)л±2[Ц1Цл±2-ЬЙ] = Ц2,)„±2, (П.7а)
✓т(З) _। (3) I । (2) *р(1) । I (2) Т'(1) /гл
Опп — -f- Л-21Л-2, /I -Г~ L/J, Л4-2* л4-2, л* (11. / О)
Из этих результатов получаем выражения (276) для <з и
у(>) [n(n — 1)]/г Г» — 1
yf1) + ___yU),
т. е.
__ тЧ1)*
* л-2, л — 1л, л—2»
что дает нам в первом порядке матрицу Т.
244
В. Штрайфер, X. Гамо
ЛИТЕРАТУРА
1. Schmidt Е., Math. Ann., 13, 433 (1907).
2. Yoshida К., Lectures on Differential and Integral Equations, New York,
1960, p. 127.
3. S m i t h i e s F., Integral Equations, London, 1958, p. 142.
4. Gamo H., в книге Progress in Optics, vol. 3, Amsterdam, 1964, p. 253.
5. Goubau G., S ch w ering F., Trans. IRE, AP-9, 248 (1961). (Имеется
перевод: Г. Губо, Ф. Шверииг, Зарубежная радиоэлектроника, № 11,
1961, стр. 3.)
6. S с h w е г i n g F., Arch. Electr. Ubertrag., 15, 555 (1961).
7. Schachter H., Bergstein L., в Proc. Symposium on Optical Masers,
New York, 1963, p. 173.
8. Rubinowicz A., Acta Phys. Polonica, 20, 725 (1961).
9. Fox A. G., Li T., Beil Syst. Techn. Journ., 40, 453 (1961).
10. Newman D. J., Morgan S. P., Bell Syst. Techn. Journ., 40, 113
(1964). (Имеется перевод: в сб. «Лазеры», ИЛ, 1963, стр. 325.)
11. Boyd G. D., Gordon J. Р., Bell Syst. Techn. Journ., 40, 489 (1961).
(Имеется перевод в сб. «Лазеры», ИЛ, 1963, стр. 363.)
12. F1 a m m е г С., Spheroidal Wave Functions, Stanford, 1957.
13. Si epi an D., Pollack H. O., Bell Syst. Techn. Journ., 40, 43 (1961).
14. Fox A. G„ Li T„ Proc. IEEE, 51, 80 (1963).
15. Boyd G. D., Kogelnik H„ Bell Syst. Techn. Journ., 41, 1347 (1962).
16. S 1 e p i a n D„ готозится к печати.
Some Asymptotic Expansions for Prolate Spheroidal Functions.
и
ГИПЕРСФЕРОИДАЛЬНЫЕ ФУНКЦИИ
И ОПТИЧЕСКИЕ РЕЗОНАТОРЫ
С КРУГЛЫМИ ЗЕРКАЛАМИ
Дж. Хэртли*
Моды в оптических резонаторах с круглыми конфокальными сферически-
ми зеркалами могут быть описаны однородным интегральным уравнением
Фредгольма, полученным из дифракционной формулы Френеля — Кирхгофа.
Случай системы с круглыми апертурами тоже приводит к такому же уравне-
нию Фредгольма. Решениями этих интегральных уравнений являются гипер-
сфероидальиые функции, взаимно обратные при конечном преобразовании
Хаикеля. Для этих функций методом коммутирующих операторов получено
дифференциальное уравнение и показано, что при малых значениях числа
Френеля функции можно разложить по круговым полиномам Цернике. При
больших значениях числа Френеля получается асимптотическое разложение
по полиномам Лагерра, которое в пределе соответствует бесконечной апер-
туре или решениям с неограниченными пучковыми модами.
§ 1. ВВЕДЕНИЕ
Моды в оптических резонаторах с круглыми конфокаль-
ными сферическими зеркалами могут быть описаны однородным
интегральным уравнением Фредгольма, выведенным из ди-
фракционной формулы Френеля — Кирхгофа [1]. Анализ процес-
са направленного распространения в системе с круглыми апер-
турами тоже приводит к такому же уравнению Фредгольма [2].
Решениями этого интегрального уравнения являются так назы-
ваемые гиперсфероидальные функции Snm, которые, кроме того,
взаимно обратны при конечном преобразовании Ханкеля. Для
этих функций получено дифференциальное уравнение и изучены
его решения.
* J. Heurtley, Department of Electrical Engineering, University of
Rochester, Rochester, N, Y,
246
Дж. Хэртли
§ 2. ГИПЕРСФЕРОИДАЛЬНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
Фокс и Ли [1] показали, что в случае резонатора, состоящего
из двух одинаковых круглых конфокальных сферических зеркал
радиусом а, отстоящих друг от друга на расстояние d и имею-
щих общую линию центров, моды являются решениями однород-
ного уравнения Фредгольма
а
&пт (4 ’ Г1) = У пт 4 / &пт (4 ’ Гз) Jn (4 Г2 ^2- (О
О
П₽ИЧеМ
Здесь п — порядок изменения поля по углу, т — целое положи-
тельное число и Jn — функция Бесселя.
Удобно нормировать уравнение (1) и записать его в виде
1
пт (^» y)J„(cxt/)(xi/)1/24Zi/, (2)
0
где величина c = ka?ld связана с числом Френеля. Решения это-
го интегрального уравнения ортогональны на интервале [0, 1] и
были изучены Слепяном’) и автором независимо друг от друга.
Метод решения состоит в определении самосопряженного
дифференциального оператора, который коммутирует с симмет-
ричным интегральным оператором на замкнутом интервале [0, 1].
Тогда решения результирующего однородного дифференциально-
го уравнения, удовлетворяющие соответствующим граничным
условиям, будут решениями интегрального уравнения.
Поскольку мы ограничиваемся конечными полями структур,
гиперсфероидальные функции должны быть конечными в замк-
нутом интервале [0, 1]. Далее, поле на одном зеркале будет из-
лучаться и непрерывным образом освещать всю поверхность,
на которой лежит следующее зеркало, воспроизводя на зеркале
свое распределение с точностью до положительной постоянной.
Поэтому функция распределения поля по радиусу — гипер-
сфероидальная функция — и ее производная должны быть не-
прерывны в замкнутом интервале [0, 1]. Мы не требуем, чтобы
функция или ее производная принимали заданное значение в
какой-либо точке внутри или на краю зеркала. Этим условиям
могут удовлетворять решения дифференциального уравнения
второго порядка.
Образуя коммутатор между общим самосопряженным диф-
ференциальным оператором второго порядка и симметричным
*) Слепян [10] рассматривает функции х*^8лт(с, х) как обобщенные
функции вытянутого сфероида.
11. Гиперсфероидальные функции и оптические резонаторы
247
интегральным оператором, интегрируя по частям и используя
свойства функции Бесселя, находим, что коммутирующий диф-
ференциальный оператор имеет вид
(3)
где Гпт — произвольная постоянная.
Изменяя зависимую переменную, можно получить из выра-
жения (3) дифференциальное уравнение для гиперсфероидаль-
ных функций:
(1 — X2) Km (с, X) 4- — Зх) &'пт (с, X) 4-
4- (глт - 4 - с*х* - J) (с, х) = 0. (4)
Требования коммутации и непрерывности приводят к гра-
ничному условию
Кт(.С, Х)-~О(1) При Х->0.
Анализ уравнения (4) показывает, что оно имеет устранимые
особенности в точках 0 и ±1 и неустранимые особенности на
бесконечности. Классификация уравнения согласно порядку его
особенностей (по методу Муна и Спенсера [3]) дает
[2 2 2:4] гиперсфероидальное уравнение
[0 2 2:4] сфероидальное уравнение
[1 1 1:2] уравнение Ламе,
где первые три целых числа указывают порядок особенностей
в конечной части плоскости, а последнее — порядок полюса на
бесконечности.
Таким образом, мы видим, что гиперсфероидальное диффе-
ренциальное уравнение для радиального распределения поля по-
добно сфероидальному уравнению, но сложнее последнего, имея
еще одну особенность в конечной части плоскости.
Следует подчеркнуть, что число Френеля с является важным
параметром гиперсфероидальных функций; оно примерно равно
числу зон Френеля, которые видны на одном зеркале из центра
другого, умноженному на 2л. Теперь рассмотрим гиперсферои-
дальное уравнение в интервалах больших и малых значений с.
§ 3. МАЛЫЕ ЗНАЧЕНИЯ с
Рассматривая малые значения с, находим, что гиперсферои-
дальное уравнение вырождается при с=0 в уравнение кру-
говых полиномов Цернике
(1 - Л2) Rnm (X) 4- (у - Зх) /?"' (х) + [т (т 4- 2) - -g-] Rnm (х) = 0,
/п>«, т — п четно, (б)
248
Дж. Хэртли
которое выводится в дифракционной теории аберраций [4, 5].
Эти полиномы, образующие полную ортогональную систему на
интервале [0, 1], непрерывны и имеют непрерывные первые про-
изводные в замкнутом интервале [0, 1]. При х—>0 они имеют
порядок 0(1). Таким образом можно получить решение гипер-
сфероидального уравнения в виде разложения в ряд по поли-
номам Цернике
4-со
&пт (С, X) = 2 An2’r т (С) ^2r (х). (6)
г-0
Подставляя ряд (6) в гиперсфероидальное дифференциальное
уравнение и используя дифференциальное уравнение Цернике
(5) и рекуррентные соотношения, мы получаем разностное,
уравнение второго порядка для коэффициентов разложения
— — Г 2г(2г + 2п) ] т ,
4 L (2г + п -1) (2> + n) J Л2г"2
[Q
Гдт (с) — т — (2Г Н~ п) (2г 4- п 4- 2) 4-
I С2 (2г я) (2г -|- д ~Н 2) -|- Пг ~| .п, т , V_
2- (2г 4-я) (2г4-я4-2) ,]Л2г
_£ Г (2г + 2)(2г4-2я4-2) 1 т , , _ п
4 [(2г4-я4-2) (2г4-я4-3) J Л2г+2(<?) —О. (7)
Сохраняя только сходящееся решение разностного уравнения,
получаем разложение собственного значения Гпт(с) по степе-
ням с, которое обеспечивает сходимость разложения Цернике
при х=1 (см. приложение Д). Тогда коэффициенты разложения
вычисляются как степенные ряды по с. Для моды наинизшего
порядка имеем
$оо(с> х) = ^°{$(х)-[4 + Й$(*) +
+ [^]$(x)4W)}- (8)
Очевидно, что ряд быстро сходится при с<1. Последнее усло-
вие эквивалентно следующему утверждению: относительные
размеры резонатора таковы, что дифракционная структура на
одном зеркале, обусловленная структурой на другом, может
быть вычислена с помощью дифракционного интеграла Фраун-
гофера. Это приводит к тому же однородному уравнению Фред-
гольма для структур мод, и приближения, приводящие к этой
постановке, таковы, что мы не можем различить конфокальные
и плоские зеркала. Поэтому в области малых значений о, т
И. Гиперсфероидальные функции и оптические резонаторы
249
и п для плоских зеркал пригодно разложение Цернике. Разло-
жение Цернике при с=п/4 и т=п = 0 согласуется с результа-
тами, опубликованными Бергштейном и Шахтером [6].
§ 4. БОЛЬШИЕ ЗНАЧЕНИЯ С
Случай больших с очень интересен, поскольку он „соответ-
ствует размерам резонатора, которые обычно употребляются в
газовых лазерах. Форма асимптотического решения определяет-
ся решением уравнения (1) для бесконечных апертур [2, 7]
/г г2
rne~^Lnp(^-), (9)
где Lp— присоединенный полином Лагерра, а р— целое число.
Анализ гиперсфероидального уравнения показывает, что оно до-
пускает решение такого типа в предельном случае бесконеч-
ного с и x<d 1, т. е. вблизи центра зеркала. Поэтому рассмотрим
следующее разложение в ряд по присоединенным полиномам
Лагерра:
СХ2 00
(Ю)
S-P
для решения уравнения (4) в случае больших, но конечных с.
Чтобы определить, какой из присоединенных полиномов Ла-
герра пропорционален гиперсфероидальным функциям в пре-
дельном случае бесконечного с, мы сравним асимптотическое
решение с решением в случае с=0. Напомним, что коммутирую-
щий дифференциальный оператор является непрерывной функ-
цией параметра с, и, следовательно, число нулей гиперсферои-
дальной функции не будет зависеть от с [8]. При с = 0 решениями
будут полиномы Цернике Rm(x), которые имеют (m + n)/2 ну-
лей в интервале [О, 1]. Асимптотическое решение
сх2
&пт(с, X) ~ Хпе 2 ЛрСсХ2) (11)
с->со
при фиксированных пир имеет п+р нулей в области изменения
переменной сх2. Поэтому мы должны брать
т — п ,Лп.
Р = (12)
Подставляя ряд (10) в гиперсфероидальное дифференциальное
уравнение и используя дифференциальное уравнение для при-
соединенных полиномов Лагерра и рекуррентные соотношения,
250
Дж. Хартли
получаем другое разностное уравнение второго порядка для
коэффициентов разложения
— f [(^ — 4~ 2s) (tn — п 4- 2s — 2)] Bs’-i (с) 4~
4~ — 2с(пгЧг 1) — 4cs 4~2s(s -\-ш ф-1)4-
+ (m + n+2)(m-n)+ д m (f) _
-I[(/ra_n4-2s + 2)(/n —n4-2s4-4)]B?+2(c) = 0. (13)
Способом, аналогичным тому, который был использован в слу-
чае малых с, можно получить асимптотическое разложение для
собственного значения и потом вычислить коэффициенты раз-
ложения решения в ряд (см. приложение Б). Асимптотическое
решение с точностью до О (1/с2) таково:
$пт(с> х)~хпе 2 $Lnm_n (сх2)—
4“ з^-[И4-п)И4-« — 2)Lnm-n ?(сх2) —
- (от - n 4- 2) (fft - n + 4) , 2 (ex2)] + О (c~2)l. (14)
§ 5. ЗАКЛЮЧЕНИЕ
Мы получили взаимно обратные функции, являющиеся ре-
шениями конечного преобразования Ханкеля, которое описы-
вает моды в конфокальных резонаторах с круглыми зеркалами.
Эти функции могут оказаться полезными в некоторых приложе-
ниях. Например, они могут играть роль, аналогичную той, кото-
рую играют угловые функции в вытянутых сферических коорди-
натах для квадратных апертур при изучении мод в резонаторах
с неконфокальными круглыми зеркалами1)- Ими можно поль-
зоваться также как функциями разложения в дифракционной
теории аберраций подобно полиномам Цернике. Эти и другие
результаты рассмотрены в статье [9].
ПРИЛОЖЕНИЕ А
В данном приложении кратко излагается способ вычисления
коэффициентов разложения в виде рядов (6). При этом мы в
основном повторяем работу Флэммера [8].
') См. статью Штрайфера и Гамо в настоящем сборнике (стр. 226).—
Прим. ред.
11. Гиперсфероидальные функции и оптические резонаторы
251
Анализ отношения двух последовательных членов в разност-
ном уравнении (7) показывает, что
с2
16г2
или
16г2
—при г->оо.
сг
2г(2г + 2тг) A"; m (с)
Мы хотим получить для Snm сходящееся разложение, поэтому
выберем первую возможность и таким образом получим значе- -
ния Гит (с), которые гарантируют сходимость при целых г.
Следуя Флэммеру, удобно определить величины
с2
N& =----------------------------------.
4 (2г + я) (2г + п + 1) 4;_т2(с)
рП, m _ ________(2г)г(2г + 2»)г
Р2г — 16 (2r+ п — 1) (2г —|-п)2 (2г —|-п —|-1) ’
vn, m__A I 79r I (Or I и I 9\ I !?_ -|- П) (2r -|~п ~Н 2) ~|- П2
Y2r — 4 + (2Г +«)(27-4-71-1-2)4- 2 (2г-|_п) (2г4-га4-2)
Тогда разностное уравнение (7) можно записать так:
ой, m
N^ m =------------—-------------,
zr v t^\ m лтп> m
Гпт (c) — Y2r N2r+2
или
Nn- m = г (с) — v"' m
•'v2r+2 пт Iе/ *2r
(15)
(16)
Р2;т
N^m ’
Теперь пусть в (15) 2r->- (2r+2); разложим это выражение в
бесконечную, сходящуюся цепную дробь, а выражение (16) в
конечную цепную дробь. После вычитания получаем следующее
уравнение для Гпт(с):
ой, m
Г (с) = у"; m 4-----------------------------------—
/г/n \ ' '2г т /гл «Л» m Rnt m
1 nm (c> ~ У2г-2 ~ P2r-2
rnm(0-Yo’m
on, m
__________Р2ГЧ 2________
Г„т (C) - tfr+m2 - M______________ ,17)
r„mG)-v2";+m4-••• (
252
Дж. Хартли
При малых значениях параметра с удобно разложить Г„т(с) в
степенной ряд
СО
(18)
й-0
Далее, видно, что 2г будет при некотором г принимать значение
2г = пг—п. (19)
Поэтому, подставляя (18) и (19) в (17) и приравнивая коэффи-
циенты при одинаковых степенях с, мы получаем следующие
значения для коэффициентов разложения собственного значе-
ния:
пп> ио т = т (т 4- 2) 4- —, (20a)
а2"’ т _ 1 т(т + 2) + п2 . , ~ 2 т (tn + 2) ’
а4"’ т = 1 Г (w —n)2(m + n)2 _ (m — n-|-2)2(m + n-|-2)2 ] . „ 4-16 L(« —l)m3(m-|-l) (m-|-l) (m-|-2)2 (m-j-3) J’
а"- иб m 1 Г — (m — n)2 (m n)2 n2 . 8 • 16 L (tn — l)2 (tn)5 (tn 4-1) (tn 4- 2) । (m —n4-2)2(m4-n4-2)2n2 1 ,„п , 1 m (m-|-1) (m 4-2)5 (m 4-3) (m 4" 4) J ’ 'zul'
а"» m 1 (m — n)2 (m 4~n)2 f 4n4 4-16-16 L (m — 1)и5(я + 1) [ (tn—2)2m2(m-|-2)2 _a„, m , РяЛ-2 | _ (m-n + 2)2(m + n + 2)2 4 a”’ m J (m_|_i)(m_|_2)5(m + 3) X X + 2)^ + 4) ~a4> m ’ (2°Д) ( Tu \tn -f- Z) Oq J
где последний член полностью не раскрыт. Первые члены
a"’ m, а£> т и а"’ т нужно положить равными тождественно ну-
лю для случая /п = п=0, поскольку процесс деления, путем кото-
рого они были получены, незаконен в данном случае.
Теперь сосредоточим внимание на коэффициентах разложе-
ния. Так как
К.т (С, Х) -> (х),
с->0
то главный член в разложении Цернике (6) равен
(21)
11. Гиперсфероидальные функции и оптические резонаторы
253
Поэтому структура разностного уравнения показывает, что мы
можем получить следующее разложение в степенной ряд:
дп, m °°
nm-n±2r\''> VI опт 21 ,П!Л
' Лп> т (с} =24^'21С • <22)
Эти разложения получены путем использования разложения для
собственной функции и последовательного вычисления из (22)
Ля, яг лп, т лп, т лп, т
2 4 т — п т —п + 2
лп, т * лп, т * ’ * лп, т 9 ап, т > • • •»
^0 л2 лт-п
где как результат (21) мы ожидаем, что каждое и'З разложе-
ний от Л2М0 до Xm_nMm-n-2 будет содержать обратную степень
с2, тогда как разложения от Лт_п+2/Лт-п и дальше будут иметь
вид (22). Эти степенные ряды или их инверсии можно затем
перемножить, чтобы получить разложение (22).
ПРИЛОЖЕНИЕ Б
В данном приложении кратко излагается метод определения
разложения (10).
Подставляя х"е_"!/20(сх2) в гиперсфероидальное уравнение
и полагая с->сои г2<1, находим
0 (сх2) — Lp (сх2),
(23)
а собственное значение в этом случае принимает вид
Г„т(с)~2с(2р+-п+-1).
Однако поскольку
то
Гят(с)~2с(/п + 1).
Таким образом, в пределе при с->оо собственное значение ока-
зывается вырожденным, так как не зависит от п.
Анализ разностного уравнения для коэффициентов разло-
жения показывает, что и собственное число, и коэффициенты
можно разложить следующим образом:
ОО
r„m(c) = 2c(/n+l)+S^"Z. (24)
i =0
Drt, т /_ч 00
<25)
"0 (c) k-r
254
Дж. Хэртли
Подставляя эти соотношения в разностное уравнение (13) и при-
равнивая коэффициенты при степенях с, мы получаем следую-
щие соотношения:
bnQm = — |[И — /г)(т + /г + 2) + 2/г + |], (26а)
b"m = 158 [(т ~ я — 2) (т — /г) (т 4- /г — 2) (т + /г) —
— (m — п + 2) (m — п -|- 4) (т п + 2) (т -|- п + 4)], (266)
bT = [(т — п)(т — п — 2)k +
+ (m + «4-2)(m-Ь/г4-4)е«'”р> 1, (26в)
e2,"i = — ^2<т~ п + 2)(т — п + 4), (27а)
е«^1 = -^-(/п4-/г)(т + /г —2), (276)
(28а)
6™==|(т + 3)6™ (286)
ЛИТЕРАТУРА
1. Fox A. G„ Li Т., Bell Syst. Techn. Journ., 40, 453 (1961).
2. G о u b a u G., S c h w e r i n g F., Trans. IRE, AP9, 248 (1961).
3. Moon P., Spencer D., Field Theory Handbook, Berlin, 1961, p. 144.
4. Nijboer B„ The Diffraction Theory of Aberrations, Thesis, Groningen,
1942.
5. Born M., Wolf E., Principles of Optics, London, 1959, p. 764.
6. Bergstein L., S c h a c h t e r H., Journ. Opt. Soc. Amer., 54, 887 (1964).
Resonant Modes of Optic Interferometer Cavities.
7. Boyd G„ Kogelnik H„ Bell Syst. Techn. Journ., 41, 1347 (1962).
8. Fla miner C., Spheroidal Wave Functions, Stanford, 1957.
9. H e u r 11 e у J., Paper presented at Meeting of Opt. Soc. Am., New York,
N. Y„ Oct. 7—9, 1964.
Optical Resonators with Circular Mirrors.
10. S 1 e p i a n D., готовится к печати.
Prolate Spheroidal Wave Functions, Fourier Analysis and Uncertainty —
IV: Extensions to Many Dimensions; Generalized Prolate Spheroidal Func-
tions.
12
РЕЗОНАТОРЫ С ДВУГРАННЫМИ ОТРАЖАТЕЛЯМИ
Г. Торальдо ди Франчиа*
G. Toraldo di Francia, Appl. Optics, 4, 1267 (1965)
Теоретически исследуется резонатор открытого типа для СВЧ диапазона
или для лазера с двугранными отражателями. Если угол между гранями от-
ражателя очень мал (порядка 10*3 рад в случае СВЧ резонаторов или 10~3—
10~6 рад в случае оптических резонаторов), то такой резонатор в некоторых
отношениях сходен с конфокальным резонатором.
§ 1. ВВЕДЕНИЕ
Резонаторы открытого типа широко используются в послед-
нее время в лазерной технике [1] и для точных измерений на СВЧ
[2, 3]. Предпочтение отдается интерферометру Фабри — Перо с
плоскими отражателями, а также конфокальным или неконфо-
кальным резонаторам со сферическими отражателями. Иногда
используются резонаторы других конфигураций, например обыч-
ный интерферометр Фабри — Перо с прямоугольными призмами
в качестве отражателей [4, 5] или с призмами в виде трехгран-
ного угла куба [6].
Резонатор с двугранными отражателями, у которых угол
между гранями очень мал (фиг. 1, at), имеет ряд положительных
черт, общих с конфокальным резонатором.
Применяя принцип Гюйгенса для этого резонатора и исполь-
зуя обычные аппроксимации [7], легко показать, что интеграль-
ное уравнение для его поля распадается на два независимых
интегральных уравнения, для каждой из «боковых коорди-
нат». Следовательно, собственные типы колебаний резонатора
образуются из двумерных колебаний в резонаторе с бесконеч-
ными двугранными отражателями и из собственных колеба-
ний в интерферометре Фабри — Перо с отражателями в виде
*G. Toraldo di Francia, Institute of Physics of the University of
Florence, Italy.
256
Г. Торальдо ди Франчиа
бесконечных полос. Более удобным является расположение от-
ражателей, изображенное на фиг. 1,6, при котором отражатели
развернуты на прямой угол. В этом случае каждый собственный
тип колебаний образуется двумя собственными типами коле-
бания двугранных бесконечных отражателей.
Фиг. 1. Резонатор с двугранными отражателями,
а —грани параллельные; б —грани скрещиваются.
Ниже показывается, что такой резонатор характеризуется
очень малыми дифракционными потерями и сравнительно мало
чувствителен к перекосам отражателей. Поэтому он может со-
перничать с конфокальным резонатором. Что касается простоты
конструкции, то в оптическом диапазоне двугранные отража-
тели, может быть, менее удобны, чем сферические отражатели,
а в диапазоне СВЧ они, несомненно, более удобны.
В противоположность сферическому отражателю, который
характеризуется линейной величиной — радиусом кривизны, дву-
гранный отражатель характеризуется углом между его гранями.
Именно поэтому условия геометрической стабильности [8] суще-
ственно различны в обоих случаях. Любой резонатор с двугран-
ными отражателями стабилен при условии, что ширина грани
достаточно велика.
§ 2. РЕЗОНАТОРЫ РОМБОВИДНОГО СЕЧЕНИЯ
Поперечное сечение исследуемой системы представлено на
фиг. 2. Каждая пара отражателей АВ, ВС и DE, EF составлена
под малым углом (обычно а=10-3—10~6 рад у резонаторов для
лазеров и а=10~3 рад у СВЧ резонаторов). Обозначив через d
12. Резонаторы, с двугранными отражателями х 257
расстояние между вершинами В и Е, положим d-q^fe, где Та-
ллина волны в свободном пространстве и q0 — большое положи-
тельное число не обязательно целое. Обычно <7о=Ю5—107 у резо-
наторов для лазеров и q0—102 у СВЧ резонаторов.
На некоторое время забудем, что отражатели ограничены,
и рассмотрим резонатор в виде полного ромба GBHE. На левой
половине резонатора введём цилиндрическую систему коорди-
нат г, z, ф с осью, проходящей через G. Подобным же образом
Фиг. 2. Резонатор ромбовидного сечения.
правой половине введём симметричную цилиндрическую си-
стему координат с осью г, проходящей через Н. В обеих частях
решение волнового уравнения для электрического поля дается
выражением
£=A(^r)Xs(vq>). ’ (О
где k = 2n/k.
Граничное условие на пластинах дает
v = -^>
а
(2)
где q — целое положительное число. Нас интересует случай, ког-
да q^qo при q<qo. В этом случае поле в центральной области
резонатора принимает вид стоячей волны между двумя критиче-
скими сечениями в волноводе из двух пластин. И электрический,
и .магнитный векторы практически параллельны пластинам.
Порядок величины у оказывается очень большим, примерно
108—1013 у резонаторов для лазеров и 105 у СВЧ резонаторов.
В интересующей нас области, а именно в центре резонатора, ве-
личина kr также велика. Очевидно, что fer«fed/a=n?o/a~v. Сле-
довательно, мы можем заменить функцию Бесселя в формуле
17 Зак. 274
258
Г. Торальдо ди Франчиа
(1) .ее асимптотическим выражением для больших значений по-
рядка и аргумента. Оно имеет вид [9]
exp [v (th д — д)]
У2лу th д
при kr < v; th а = 1 — I — 1 ;
Jv(kr) =
sin (л/3) Г (1/3)
Зя (£г/6)1/3
sin (2л/3) Г (2/3) ,, ч ,
—:—'-!—— у) при йг^у;
Зя (/гг/6)'
2 \1/2 Г я) ,
—т-т- cos v(tg b — b) — -т- при яг>у;
jiv tg я / Lv& ' 4 J r
(3)
Теперь поля двух половинок резонатора должны быть сшиты в
средней плоскости BE. В общем случае это очень трудная за-
дача. Но мы можем воспользоваться тем фактом, что угол а
очень мал, и пренебречь кривизной поверхностей вблизи центра
резонатора. В этом приближении, о законности которого речь
будет идти в следующем параграфе, средняя плоскость пред-
ставляется в виде г=сЦгх. Для сшивания поля с обеих сторон
плоскости потребуем только, чтобы эта плоскость совпадала
либо с узлом, либо с пучностью поля. Из третьего выражения
в формулах (3) получим
y(tg£ — b) — = = 1]'/2. (4)
Это соотношение сразу же дает нам частоты колебания резо-
натора.
В дальнейшем мы будем пользоваться приближенными вы-
ражениями (3). Если потребуется большая точность, то можно
учесть большее число членов асимптотических выражений (3).
§ 3. РЕЗОНАТОР С ДВУГРАННЫМИ ОТРАЖАТЕЛЯМИ
Рассмотрим две плоскости A'D' и C'F' (фиг. 2), в которых
расстояние между отражателями равно q • Х/2. Легко видеть, что
эти плоскости проходят вдоль критических сечений для рассма-
триваемых типов колебаний. Обозначим через х0 расстояние от
критического сечения до средней плоскости. Тогда имеем
= (5)
Плоскости в критических сечениях представляют собой гра-
ницы между тремя областями (3), поскольку радиальные коор-
динаты этих плоскостей r0= (dja) —х0 точно соответствуют ра-
12. Резонаторы, с двугранными отражателями
259
венству kr0—v. Целесообразно отсчитывать боковые координаты
от критических сечений, положив
х=г0— г. (6)
Теперь видно, что во внутренней области резонатора |х|<Сго.
Пренебрегая величиной х/г0 по сравнению с единицей и проводя
несложные вычисления, легко показать, что (3) может быть пе-
реписано так:
А (£г) =
ехр —з- W J
— ----------—- при х > 0;
2я (дх/аА.)1'4
а ОЛЕ / «\1/3 , ОЛ ( а \2/3 х л
0,305 —1,20^—j у при х«0;
Г 8л I а | х |3 V/2 я I
cos ---------Г
I 3 \ ал3 I 4 J _ п
-----------—----'-ур.------ при X < 0.
я (q | х|/аА)1/4
(7)
Воспользовавшись этой аппроксимацией и подставив (2) в (4),
получим условие резонанса в виде
1 = — И — - Г3ct <2w + Ч ~12/31
9 (. 1 2 L 4q J J ’ ' '
Как и следовало предполагать, резонансная длина волны даже
для аксиального типа колебаний (/п=0) немного меньше 2d/q.
Никакого вырождения, кроме случайного, нет. Частотное разде-
ление поперечных мод может быть ненамного меньшим, чем
частотное разделение аксиальных мод.
Подставив (8) в (5), получим
= (9)
Расстояние х0 между первыми несколькими боковыми мо-
дами (/п<10) будет малой величиной порядка 10~2—IO-3 d у
резонаторов для лазеров и 10-1 d у СВЧ резонаторов. Первое
же выражение в (7) говорит нам, что поле вне области, огра-
ниченной критическими сечениями, спадает экспоненциально.
Величина x — w, при которой экспонента уменьшается вдвое, мо-
жет быть выбрана как показатель скорости спадания интенсив-
ности поля. Для него имеем z
о»)
Таким образом,, в типичном случае пу=102Л или 103Х у резона-
торов для лазеров и w равно нескольким А, у СВЧ резонато-
ров. Спад поля настолько быстрый, что уже не очень важно,
17*
260
Г. Торальдо ди Франчиа
смыкаются пластины резонатора (фиг. 2) или нет. Следователь-
но, мы можем считать, что выражение (7) с хорошим приближе-
нием описывает виды колебаний резонатора открытого типа с
. ,.ЛЛ. 2
-1.6 -1.2 -0.8 -0,4 0 0,4 0,8 1,2 1,6
-1,6 -1.2 -0,8 -0,4 0 0.4 0,8 1.2 1.6
Боковая координата в единицах 1,12(q/U)’^ Л
Фиг. 3. Распределения поля для первых трех типов колеба-
ния (m=0, 1, 2) и для 11-го типа колебаний (т ~ 10) в резо-
наторе с двугранными отражателями.
двугранными отражателями. Если только ширина граней отра-
жателей у такого резонатора будет немного больше х0, его ди-
фракционные потери будут очень малы.
На фиг. 3 показано распределение интенсивности поля вдоль
одного из отражателей при /п=0, 1, 2, 10. Диаграммы вычис-
лены по формуле (7). Конечно, две области сшивания трех ана-
литических выражений требуют некоторых предположений и,
12. Резонаторы с двугранными отражателями 261
следовательно, допускают некоторый произвол. Тем не менее
диаграммы, по-видимому, достаточно точны, особенно для /п = 0.
Теперь мы можем рассмотреть вопрос о законности предпо-
ложения, сделанного в предыдущем параграфе, о том, что кри-
визной поверхностей узлов или пучностей можно пренебречь.
Максимальная выпуклость (отклонение от плоскости) такой по-
верхности в центре резонатора дается выражением d2/8r—ad/8.
Чтобы наше предположение было справедливым, эта. величина
должна быть намного меньше расстояния между узлом и пуч-
ностью поля. Предположим, что последнее — порядка х0 [см. (9)]
при /п=0. Таким образом, мы получаем условие
Это условие будет почти всегда выполнено, если а<10~3 у резо-
натора для лазера и а<10-’уСВЧ резонатора. Во всяком слу-
чае этим соотношением устанавливается граница применимости
данной приближенной теории. Но можно думать, что теория бу-
дет качественно верна даже в том случае, если условие (II) не
будет выполнено строго.
Наконец, будет полезно обсудить вопросы стабильности с
точки зрения геометрической оптики. Легко показать, что при
a<a/d, где 2а — общая ширина каждого двугранного отража-
теля, любой луч, идущий параллельно оси на расстоянии, мень-
шем ad от нее, возвращается на прежний путь после четырех
последовательных отражений. Следовательно, он стабилен вну-
три резонатора, -Возможность нестабильности следует из того,
что при =a>4a/d луч, выходящий .из любой точки первого отра-
жателя и отраженный от второго отражателя, не попадает
снова на первый отражатель.
Так как практически всегда а>х0, то условия геометрической
стабильности будут автоматически выполняться, если выпол-
няется (11).
§ 4. АСИММЕТРИЧНЫЕ РЕЗОНАТОРЫ
На практике очень трудно обеспечить условия абсолютной
симметрии в резонаторе. Наиболее вероятная погрешность свя-
зана с тем, что углы а' и, а" в точках G и Н резонатора в виде
ромба (фиг. 2) могут быть не совсем одинаковыми. В этом слу-
чае мы все же можем пользоваться решением (1) для обеих ча-
стей резонатора с одинаковой величиной q, но с разными вели-
чинами v:
V'=V-- ’"=?• <12’
262
Г. Торальдо ди Франчиа
Средняя плоскость резонатора уже не будет плоскостью симме-
трии, и ей не будет соответствовать узел или пучность. Все, что
мы можем потребовать, — это то, чтобы на средней плоскости
Боновая координата в единицах 1,1Z (q/a)’/s Л
Фиг. 4. Типичное распределение поля в асимметричном
резонаторе.
оба решения были равны и средняя плоскость отстояла на оди-
наковом расстоянии от узлов или пучностей.
Условие резонанса (4) перепишется так:
(tg b' — Ь') — пг’ у + -J. + е,
v"(tgy'-y') = /n"-J + ^-e, (13)
, ,, Г/ kd \2 .-11/2 г/ kd \2 11/2
где т' и т” — произвольные, но близкие по величине числа, а
е — произвольно. Положив т'+т"—2т и сложив первые два
уравнения (13), получаем
v' (tg b' - b') + v" (tg У' - b") = (2m +1) . (14)
Подставляя выражения (12) для v', v" и произведя ту же ап-
проксимацию, что и раньше, получаем прежнее условие резо-
нанса (8), если а определяется выражением
<’5)
Величины %о и w с обеих сторон различные и получаются из
(5) и (10) простой заменой а на а' или а".
Можно заключить, что на юстировке резонатора с двугран-
ными отражателями не очень сильно сказываются малые пово-
роты отражателей вокруг их вершин, При этом диаграмма поля
12. Резонаторы с двугранными отражателями
263
просто смещается в сторону от оси, так что максимум оказы-
вается наибольшим с той стороны, где меньше угол а. На фиг. 4
приведен пример для случая а'7а'=17/9.
Более серьезные потери могут быть вызваны (кад и для
плоских зеркал) недостаточной параллельностью ребер отража-
телей; чтобы устранить эти потери, нужно расположить их реб-
ра под прямым углом друг к другу. В таком случае каждая из
двух плоскостей симметрии резонатора представляет - собой
практически резонатор с двугранным отражателем, с одной
стороны, и плоским отражателем — с другой. Такой резонатор
имеет свойства, подобные полуконфокальному резонатору. Для
него не требуется очень точной юстировки. Можно предполо-
жить, что его диаграмма поля будет описываться произведе-
нием выражений (7) для координаты х на аналогичные выра-
жения для координаты у.
§ 5. ЗАКЛЮЧЕНИЕ
Резонаторы Фабри — Перо, образованные двугранными от-
ражателями, можно использовать вместо более распространен-
ных резонаторов со сферическими отражателями. Резонаторы с
двугранными отражателями характеризуются очень малыми
дифракционными потерями и не боятся небольших перекосов
отражателей. Они не обнаруживают вырождения, кроме слу-
чайного, и могут быть всегда сделаны стабильными в смысле
геометрической оптики при условии, что ширина боковой грани
отражателя достаточно велика.
Что касается возможных применений, то резонатор с дву-
гранными отражателями, вероятно, больше подходит для ра-
боты на СВЧ, чем в оптическом диапазоне.
ЛИТЕРАТУРА
1. Townes С. Н„ Quantum Electronics and Coherent Light; Enrico Fermi
International School of Physics, New York, 1964, p. 53.
2. Culshaw W., Trans. IRE, MTT-8, 182 (1960); MTT-9, 135 (1961). (Имеет-
ся перевод в сб. «Лазеры», ИЛ, 1963.)
3. Zim merer R. W., Rev. Sci. Instr., 33, 858 (1962); Trans. IRE, MTT-ll,
371 (1963).
4. Peck E. R., Journ. Opt. Soc. Am., 52, 253 (1962).
5. Bergstein L„ Kahn W., Shulman C., Proc. IRE, 50, 1833 (1962).
6. Rabinowitz P., Jacobs S. F., Chultz T., Gould G., Journ. Opt.
Soc. Am., 52, 452 (1962).
7. Fox A. G., Li T., Bell Syst. Tehn. Journ., 40, 453 (1961). (Имеется пере-
вод в сб. «Лазеры», ИЛ, 1963.)
8. Boyd G. D., Kogelnik Н., Bell Syst. Tehn. Journ., 41, 1347 (1962).
9. Morse P. M.,. Feshbach H., Methods of Theoretical Physics, New York,
1953, p. 631. (Имеется перевод: Ф. M. Морс, Г. Ф е ш б а х, Методы тео-
ретической физики, т. 1, ИЛ, 1958.),
13
РАСЧЕТ РЕЗОНАТОРОВ ФАБРИ-ПЕРО
ДЛЯ ЛАЗЕРОВ С ПОМОЩЬЮ МАТРИЦ
РАССЕЯНИЯ
Д. Г логе*
D. Gloge, Arch. Elektr. Ubertrag., 18, 197 (1964)
Резонаторы Фабри —Перо применяются для построения лазеров. Их ха-
рактеристики позволяют также определять свойства периодических линзовых
линий передачи света. В статье развит метод возмущений, учитывающий сис-
тематические ошибки зеркал или линз. Для демонстрации эффективности этого
метода он применен к комбинации произвольно искривленных зеркал, кото-
рые рассматриваются как результат возмущения зеркал конфокального резо-
натора, свойства которого известны. Таким способом с высокой точностью
вычисляются дифракционные потерн произвольных резонаторов; при этом
точность тем лучше, чем выше дифракционные потери. Метод возмущений
обобщен на усложненные системы с линзами, имеющими различные апертуры
и находящимися на различных расстояниях друг от друга. Дан способ пре-
образования для линз с достаточно большими апертурами.
§ 1. ВВЕДЕНИЕ
С открытием лазеров особое значение приобрела новая груп-
па электромагнитных резонаторов. Эти системы, известные из
оптики под названием интерферометров Фабри — Перо, состоят
из двух находящихся друг перед другом зеркал. Остальная часть
объема, резонатора открыта. Колебания могут распространяться
лишь вдоль оси резонатора (фиг. 1); поперечные колебания,
распространяющиеся под углом к этой оси, быстро покидают ре-
зонатор. Фокс и Ли [1, 2] показали, что продольные колебания
нужно считать основным типом в системе собственных колеба-
ний резонатора, а поперечные колебания — типами высших по-
рядков в этой системе.
Если пространство между зеркалами заполнить усиливающим
материалом, то получится лазерная система. Резонатор должен
возбуждаться на основном типе колебаний по возможности без
* D. Gloge, Institut ftir Hochstfrequenztechnik der Technischen Hoch-
schule, Braunschweig.
13. Расчет резонаторов Фабри — Перо для лазеров
265
потерь (используются зеркала с отражающим слоем без по-
терь), в то время как поперечные колебания не должны само-
нозбуждаться. Поверхности зеркал должны быть поэтому до-
статочно малыми, чтобы все поперечные колебания быстро
исчезали, но, с другой стороны, достаточно большими, чтобы
потери основной моды из-за дифракции на краях зеркал были
малы.
Фиг. 1. Устройство резонатора Фабрн — Перо с зеркалами
в виде симметричных полос.
Нерегулярности поверхностей зеркал и ошибки их юстиров-
ки приводят к изменению полей мод и, вообще говоря, увеличи-
вают потери. Ниже исследованы способы расчета таких возму-
щений; эти способы приводят к простому приближенному мето-
ду определения дифракционных потерь, который дает резуль-
таты, хорошо сходящиеся в области значительных дифракцион-
ных потерь, неизбежных в лазерах.
§ 2. МАТРИЦА РАССЕЯНИЯ
Для расчета распределения поля в резонаторе одно зеркало
(например, правое на фиг. 1) рассматривается как поверхность
лучей Гюйгенса, возникающих из волны с амплитудой ЧТ(Х, У);
вклады этих лучей суммируются на левом зеркале. Такой под-
ход является достаточно точным, когда размеры резонатора зна-
чительно больше длины волны. Тогда свойства резонатора пол-
ностью описываются поперечным линейно поляризованным
электромагнитным полем с амплитудой ^(Х, Y) [11, 12, 15].
Кроме того, интегрирование можно проводить раздельно по X
И по У. Поскольку оба суммирования осуществляются одним и
266
Д. Глогё
тем же способом, общность не нарушится, если рассматривать
систему цилиндрических зеркальных полос, бесконечных в на-
правлении У, что и будет сделано ниже. Для слабо искривлен-
ных зеркал такое интегрирование дает [1, 6, 16]
= / ¥(Х)/^e-^dX. (1)
-S
Здесь k — постоянная распространения в пустоте, остальные
величины показаны на фиг. 1. Целесообразно ввести безразмер-
ные величины
А” [ ___ X' _ k г, /0.
х — ~—; х ' — — c^-rS2. (2)
s s а ' '
Тогда уравнение (1) принимает вид
Ф'(*') = J ф(х)]/-^e-^dx. (3)
-1
Для р достаточно разложения по координатам до второго по-
рядка
, а2 Г г It d \ х2 /, d \ х'2 1 ...
--------j- \хх — 1--Hr— 1------ -75- • (4)
r d L \ r / 2 \ r') 2 J v ’
Если оба зеркала имеют одинаковую кривизну, то из-за сим-
метрии в установившемся состоянии должно быть ф'=ф. При
этом предполагается, что в резонаторе нет никаких потерь, или
же что между зеркалами имеется усиливающий материал, ко-
торый непосредственно поддерживает стационарное состояние.
Пусть потери при отражении от зеркал отсутствуют (их можно
легко учесть позже); тогда остаются лишь потери на излучение
в открытое пространство. Последние мы в дальнейшем будем
называть дифракционными потерями, так как их величины
определяются дифракцией электромагнитных волн на краях
зеркал.
Предположим ради простоты, что никакого усиливающего
материала внутри резонатора нет; тогда амплитуда ф при каж-
дом пробеге туда-обратно будет несколько уменьшаться, что
должно быть учтено в множителе распространения Г. Из (3)
получается следующее уравнение Фредгольма [17]:
1
Гф(х')= J ф(х)Л-(х, x'}dx (5)
-I
с симметричным ядром ___
№ = х) = ]/(6)
13. Расчет резонаторов Фабри — Перо для лазеров
267
Это интегральное уравнение имеет полную систему собственных
функций фт, ортонормированных в области интегрирования 1)
Каждой собственной функции отвечает собственное значение Гт.
В области интегрирования ядро можно разложить в билиней-
ную форму
К (х, х') = 5 ГАфй (х) (х'). (8)
й—О
Нерегулярности зеркала, например деформация поверхности
или ошибки юстировки, входят в ядро через показатель экспо-
ненты р. Когда отклонения малы по сравнению с длиной волны
и медленно меняются на поверхности зеркал, ошибка правого
зеркала а(х) не зависит от ошибки левого зеркала р(х').
Собственные функции возмущенной системы зеркал будут
отличаться от фт, в частности они будут различны на обоих
зеркалах. Однако их можно разложить по фт:
ОО
«т (х) = S Umityl (*)> (9 а)
м
оо
^m(<)== S ^тгФг(х')- (96)
г-о
Возмущенные собственные функции должны быть также орто-
нормированными. Поэтому Umi и Vmi суть элементы ортонорми-
рованных матриц2), имеющих то свойство, что их обратная мат-
рица равна транспонированной
и~х = ит. ’ (10)
Если обозначить собственное значение возмущенного интег-
рального уравнения через Гт, то для возмущенного резонатора
имеем
ОО оо 1
Г(т> 2 УтгФг (*') = I Ф» (*К(х, •*') eicdx. (11)
z-о г-о -г
В дальнейшем будет видна целесообразность выделения пос-
тоянного множителя гс/2 из величин ошибок. Величины аир
П См., впрочем, ниже стр. 283. — Прим. ред.
2) В последующем изложении элементы матриц обозначены теми же
прописными буквами, что и матрицы, отличаясь от них только индексами.
268 Д. Глоге
являются теперь действительными при деформациях , поверхно-
сти, влияющих лишь на фазу поля, но становятся комплексными
при деформациях, вносящих потери. Если умножить обе части
(11) на фп(х') и проинтегрировать, по х', учитывая при этом
разложение (8) и ортогональность фп, то получим
оо оо 1 I
тп — SS ЦЛ J Фге/са/2Фл dx J фАе/сР/2Ф„ dx. (12)
Z-0 А-0 -1 -1
Обоим интегралам в этом уравнении можно поставить в со-
ответствие две матричные функции еА и ев, аргументы А и В
которых являются матрицами с коэффициентами
1
А™ = 4 J Фта(-*)Ч’Я^ ОЗа)
-1
1
втп~-^ J фтр(х)фп</х. (136)
-1
Экспоненциальная функция матрицы определяется, как извест-
но, своим представлением в виде ряда. Справедливость (13а)
и (136) можно легко показать, если разложить экспоненты в
интегралах уравнения (12) в ряды и приравнять их члены чле-
нам матричного ряда. Уравнение (12) можно записать теперь
в виде
или после умножения на У-1 справа
Г(1)= UeAVeBV'\ (14а)
Здесь Г(1) и Г — диагональные матрицы определенных выше
собственных значений Гт и Гт.
Уравнение (14а) означает следующее: оператор U превра-
щает собственные функции um(x) возмущенной системы в соб-
ственные функции невозмущенной системы, еА описывает их
рассеяние на правом зеркале, Г — передачу к левому зеркалу,
ев — рассеяние на нем и У-1 превращает результат в собствен-
ные функции Vm(x') этого зеркала. Для обратного прохождения
к правому зеркалу получается аналогичное матричное урав-
нение
Г(2,= УевГеАи~\
(146)
13. Расчет резонаторов Фабри — Перо для лазеров
269
Здесь Г<2>— диагональная матрица постоянных распространения
для обратного пробега. Перемножая (14а) и (146), окончатель-
но получаем
Q = Г(,)Г(2) = UeAT'e2BTeALJ~l. (15)
Это однородная система линейных уравнений относительно ко-
эффициентов разложения Umn. Матрица G является диагональ-
ной матрицей собственных значений Gm. Их в принципе можно
найти из характеристического уравнения системы; подставляя
полученные коэффициенты Umn в (9), можно найти также соб-
ственные функции цт(х). Ниже мы найдем приближенное ре-
шение для малых значений а и р. В этом случае величины
Итп| и |Bmn| будут все время значительно меньше единицы,
поэтому еА и ев можно разложить в ряд. Разлагая матрицу
Н = еАГе2ВГеА
по степеням Атп и Втп и предполагая, что возмущения на
обоих зеркалах имеют один и тот же порядок величины, по-
лучаем
/у — Г2 4-/7(1) 4-/У(2) 4- ....
Матрица собственных значений G, разложенная по порядкам И,
имеет вид
Gm==r2m+^m+ 5} + .... (16)
п^т 1т
Если подставить вместо Н<У> и //<2> выражения из разложе-
ний, то после ряда преобразований получаем
От — Гт
1+2(Лтт 4- втт) 4~ 2 (Лтт Втт)24-
со
оо
+ У' (Л-+5-)2 + S' (л- - в^2
n=fctn п^т
(17)
Это приближение учитывает лишь члены до второго порядка,
однако оказывается, что уже в этом случае получаются вполне
удовлетворительные результаты.
§ 3. РАСЧЕТ ДИФРАКЦИОННЫХ ПОТЕРЬ
При условии, что оба зеркала имеют равные радиусы кри-
визны, справедливо интегральное уравнение (3), из которого
можно определить собственные значения и собственные функции
270
Д. Глоге
невозмущенного резонатора. Правда, это уравнение не может
быть точно решено в общем виде. Наиболее полные из су-
ществующих результатов были получены итерационным путем
[4, 2], применимым к общему случаю, но весьма трудоемким.
Для частных случаев [3, 5, 11, 13] существуют приближенные
решения. Лишь для конфокальных резонаторов, когда радиусы
кривизны зеркал равны расстоянию между ними, получается
интегральное уравнение, решения которого известны [6, 7]. В этом
случае в разложении (4) пропадают некоторые члены и из (6)
получается ядро
К(х, = e-ikdeicxx'. (18)
Интегральное уравнение (5) с этим ядром имеет собственные
значения
= ~.2imRm(c, 1) (19)
и собственные функции
фт(х) = 5я(с, х), (20)
где Rm(cr х) и Sm(c, х)—присоединенные волновые функции
первого рода нулевого порядка в вытянутых сфероидальных ко-
ординатах, называемые кратко сфероидальными функциями. Эти
функции подробно исследованы в литературе и для них имеется
богатый табличный материал [8, 9]. В дальнейшем будет ис-
пользоваться нормировка
1
J S2m(c, x)dx — \, (21)
как это и требовалось для решений фт.
Результаты для неконфокальных резонаторов можно полу-
чить, рассматривая их отклонение от конфокальной формы как
возмущение этой известной системы. Тогда ошибки обоих зер-
кал как раз и даются в виде добавочного квадратичного чле-
на в (4)
а(х) = -(1-4)^. (22)
Р(х') = -(1-4) х'\
Если ввести для краткости
а = 1~4. ^=1~4 (23)
13. Расчет резонаторов Фабри — Перо для лазеров
271
И
1
Qm«= J Sm(c, x)x2S„(c, x)dx, (24)
-1
то из (13a) и (136) получаем
2~ iC&Qmn> ^mn= icbQmn- (25)
Функции Sm при четном m четны, а при нечетном m не-
четны. Поэтому исчезают все Qmn с нечетной суммой индексов
пг+п, т. е. не возникает никакой связи между четными и нечет-
ными функциями. Этого следовало ожидать, так как возмущаю-
щая функция Сама четна. Следовательно, можно рассматривать
раздельно систему четных и нечетных функций; одна из них бу-
дет давать четные, а другая — нечетные собственные функции
возмущенной системы. В дальнейшем будет рассматриваться
только система четных функций, содержащая особенно важную
основную функцию. В расчете это обстоятельство скажется в
том, что встречающиеся индексы будут пробегать лишь четные
значения.
Для вычисления интеграла (24) воспользуемся разложением
сфероидальных функций Sm по полиномам Лежандра Р&, быстро
сходящимся при с<10,
Sm (с, х) = У dk (с) Ри (х), ш, k четные. (26)
к-О
Коэффициенты d™ (с) достаточно хорошо протабулированы во
многих источниках, но при использовании другой нормировки
для функций [8, 9]. Учитывая свойства полиномов Лежандра
[14], интеграл (24) можно представить в виде суммы
. 1 / 2k 2 ,m । 2k -|- 4 ,m \ x,
mn — 4^4-6 \2A-I-1 * 2^4-5 Uk + 2} x
A=0
. z / 2^-4-2 in । 26-4-4 in \ i /n_.
x dk 2k + 5 2) ’ m и четные. (27)
Этот ряд настолько быстро сходится, что при с< 10 нужно учи-
тывать лишь несколько членов. Оказывается, что коэффициенты
Qmn вещественны, поэтому матрицы А и В чисто мнимые. В чле-
ны разложения (17) входят, кроме этого, лишь отношения раз-
личных собственных значений. В силу (19) эти отношения для
четных индексов вещественны, и поэтому в разложении (17)
диненные члены являются чисто мнимыми, а . квадратичные
272
Д. Глоге
вещественными. Если выделить модули и аргументы комплекс-
ных чисел, то получается
От«Г2т(1-Д)</ф, (28а)
ОО оо
nds т nds т
(286)
и
Ф = 2с - Qmn, тип четные. (28в)
На фиг. 2 каждому резонатору Фабри — Перо поставлена
в соответствие точка плоскости (а, Ь). В частности,, точка
Фиг. 2. Линии равных потерь основного колебания в резона-
торах Фабри — Перо.
Сплошные линии —приближенный метод матриц рассеяния; пунктир —метод
итераций Фокса и Ли. (Для потерь в 5% кривые совпадают в пределах гра
фической точности.)
а=Ь = 0 соответствует конфокальному резонатору, точка а—Ь =
= 1 — плоскому, а точка а=Ь =—1 —концентрическому резона-
тору. , На прямой а = Ь лежат все симметричные резонаторы.
Резонаторы на прямой а=— Ъ выделяются как резонаторы с
13. Расчет резонаторов Фабри — Перо для лазеров 273
особой асимметрией. Кривые равных потерь, получающиеся из
(286) при A=const, являются на этой плоскости эллипсами с
главными осями, лежащими на диагоналях а = Ь и а = —Ь.
Собственные значения и коэффициенты связи конфокального
резонатора при с = л
п 0 2 4
cQon 0,5194 0,6158 0,1154
Гл 0,9909 —0,4930 0,0327
В качестве примера была рассчитана’реальная система с па-
раметром с = л. Собственные значения конфокального резона-
тора Гп и коэффициенты QOn приведены в таблице; при этом
А = 0,1415 ( -j2 -j- 1.2549 (g ~ j2 для с —л.
Для различных значений потерь |1 —Go\ основного колеба-
ния были найдены эллипсы (фиг. 2) и проведено сравнение со
значениями, полученными Фоксом и Ли [2]. Кривые потерь всех
симметричных резонаторов (фиг. 3) и резонаторов с особой
асимметрией (фиг. 4) получаются в этом приближении парабо-
лами. Оказалось, что особенно хорошее приближение к значе-
ниям, вычисленным Фоксом и Ли, имеет место на диагоналях.
На них равен нулю член четвертого порядка, не учтенный в (28),
(W)’
На фиг. 5 приводится и сравнивается с результатами Фокса
и Ли дополнительный фазовый угол множителя распростране-
ния основного колебания; установлено полное совпадение.
Вообще говоря, апертуры обоих зеркал различны. Пусть
в дальнейшем правое зеркало на фиг. 1 имеет ширину 2s, а ле-
вое— 2s'. Целесообразно ввести новые величины
х = т, х' = —, c = -jSS. (29)
Ядро конфокальной системы (18) сохраняется с точностью до
постоянного множителя. Это значит, что решениями являются
те же собственные функции S(c, х). В этом проявляется выро-
ждение конфокальной системы, на что уже указывалось в других
18 Зги- 274
Фиг. 3. Дифракционные потери основного колебания
в симметричных резонаторах Фабри — Перо.
Сплошные линии —приближенный метод матриц рассеяния; пунктир —
метод итераций Фокса и Ли.
Фиг. 4. Дифракционные потери основного колебания
в асимметричных резонаторах Фабри—Перо.
Сплошные линии--приближенный метод матриц рассеяния; пунктир —
доетод итераций Фокса и Ли.
13. Расчет резонаторов Фабри — Перо для лазеров
работах [6, 10]1)- Собственные значения для прямого и обрат-
ного прохождения отличаются при этом множителем s/s'; вме-
сто (19) имеем __
= 1), (30а)
y^2imRm(c, 1). (306)
Видно, что для пробега в обе стороны множитель распро-
странения тоже сохраняется
Г2т =ГтГт.
Новые характеристики возмущения вновь получаются из разло-
жения (4) с учетом (29)
' “Н1—»=(>-(31>
Различие множителей распространения Гт и Гт пропадает
уже при образовании матрицы полного обращения Н (собствен-
Ф и г. 5. Дополнительный набег фазы Ф основного колебания
симметричных (а = Ь) и асимметричных (а = — Ь) резонаторов
Фабри — Перо.
Результаты Фокса и Ли совпадают с этими данными.
ные значения входят в, нее лишь в виде произведения ГтГп);
поэтому выражение для дифракционных потерь различных
*) Обычно под вырождением понимается совпадение нескольких собствен-
ных значений. — Прим, ред, »
18*
276
Д. Глоге
по размерам зеркал произвольной кривизны легко получается
из (15) или из приближения (28), если вместо а и b подставить
в него выражения (31).
Таким образом, любой резонатор с различными апертурами
зеркал можно свести к соответствующему резонатору с одина-
ковыми апертурами; эта эквивалентность будет весьма точной,
так как при этом переходе не используются никакие предполо-
жения, кроме разложения р. Поэтому свойства любого резона-
тора с зеркалами различных размеров можно определить на
плоскости (а, Ь), применяя определения (31).
§ 4. ОБОБЩЕННЫЕ РЕЗОНАТОРЫ
И ПЕРИОДИЧЕСКИЕ ЛИНИИ
Бойд и Котельник [10] показали, что для каждого резона-
тора Фабри — Перо существует эквивалентная последователь-
ность линз. Соответственно матрицы рассеяния можно приме-
нять и к линзам. На фиг. 6 приведены два резонатора, связан-
ные линзой. Параметры этих резонаторов суть
k k
S1SO> С%~~сЦ S2S0- (22)
Все размеры показаны на фиг. 6. Для невозмущенной системы
справа собственными функциями являются (ср л), а сле-
ва (с2, л). В плоскости линзы, обозначенной пунктиром, эти
полные системы можно перевести одну в другую
*)= S 4 (зз)
Коэффициенты
I
см= J (34)
принадлежат ортонормированной матрице С, для которой так-
же справедливо С'1 = СГ.
Если имеют место возмущения и А& на зеркалах, а так-
же ВЮ и В<2> соответственно на левой и правой сторонах линзы,
то для одного прохождения справа налево получаем
tf=ZW(,W(2W(2). (35)
Для сложной системы необходимо было бы записать друг за
другом много таких-операторов.»
13. Расчет резонаторов Фабри — Перо для лазеров 277
На практике важно, что каждую идеальную линзу с беско-
нечной апертурой (практически достаточно апертуры, несколько
большей, чем размеры соседних элементов) можно выбросить,
Фиг. 6. Резонатор Фабри — Перо с линзой в резонирующем
пространстве.
а —система с линзой, имеющей апертуру 2$0 и фокусное расстояние Го/2;
б—эквивалентный резонатор для случая, когда апертура линзы в системе а
очень велика»
5
если при этом правильно изменить параметры соседних элемен-
тов. Это нетрудно показать с помощью принципа Гюйгенса, од-
нако здесь это доказательство опущено. Результаты можно объ-
яснить частично с помощью геометрической оптики.
Порядок преобразований объясним с помощью фиг. 6. Когда
находящаяся там линза имеет большую апертуру, то ее можно
убрать, сохранив апертуры соседних элементов, но изменив рас-
стояние на
D = dx + d2 —
и взяв радиусы, равными
1 1 | О ^2
— rt "Г z Dr0 ’
1 . _ 1 , о rf.
Т?2 Г*2 Dr о
(36)
(37)
(38)
И этот принцип можно обобщить на последовательность
линз. Это дает простую возможность сводить к известным
278
Д. Глоге
простым резонаторам резонаторы, в которых поперечные коле-
бания подавляются диафрагмой в резонирующем пространстве.
В качестве примера на фиг. 7 показан конфокальный резонатор
Фиг. 7. Преобразование резонатора с диафрагмой в резони-
рующем пространстве.
а — исходная система; б и в —эквивалентные системы.
с диафрагмой в плоскости симметрии, в которой ищется ампли-
тудное распределение. Заменяя линзы и зеркала, резонатор а
можно перевести в резонатор б; резонатор в получается, если
учесть соотношения (36) — (38). Следовательно, в плоскости диа-
фрагмы системы а имеет место то же распределение, что и на
конфокальных зеркалах системы в; это сфероидальная функция
с параметром c = ks2ld.
Особого внимания заслуживает случай r0=dl = d2, для кото-
рого такое преобразование невозможно. Физически этот случай
соответствует концентрическому резонатору с бесконечной
апертурой зеркал и линзой или диафрагмой посредине (фиг. 7, а).
Так как собственные функции такого резонатора имеют по-
средине особеннЬсть, там не может эффективно работать ни-
какой элемент. Потери системы описываются лишь свойствами
концентрических зеркал, поэтому преобразование таких зеркал
невозможно.
13. Расчет резонаторов Фабри — Перо для лазеров
279
§ 5. ЗАКЛЮЧЕНИЕ
Ошибки на зеркалах резонатора Фабри — Перо можно опи-
сать матрицами рассеяния, имеющими вид экспоненциальных
функций от некоторой матрицы. Из-за таких ошибок изменяются
собственные колебания и потери резонаторов; изменения мож-
но представить в виде функции ошибок. Это показано на при-
мере конфокального резонатора, причем его известные соб-
ственные значения и собственные функции использовались для
расчета другой зеркальной системы. Этот метод работает тем
лучше, чем выше сами потери. Его можно распространить на
еще более общий вид резонаторов, которые содержат дополни-
тельные линзы и диафрагмы различных апертур.
ЛИТЕРАТУРА
1. Fox A. G., Li Т., Bell Syst. Techn. Journ., 40, 453 (1961). (Имеется пере-
вод в сб. «Лазеры», ИЛ, 1963, стр. 325.)
Resonant Modes in a Maser Interferometer.
2. Fox A. G., Li T., Proc. IEEE, 51, 80 (1963).
Modes in a Maser Interferometer with Curved and Tilted Mirrors.
3. В arone S. R., Journ. Appl. Phys., 34, 831 (1963).
Resonances of the Fabry Perot Laser.
4. H a r d e r C., Studienarbeit am Institut fur Hochstfrequenztechnik der
Technischen Hochschule, Braunschweig, 1963.
Berechnung der Beugungsverluste eines nichtkonfokalen optischen Resona-
tors.
5. Culshaw W„ Trans. IRE, MTT-10, 331 (1962).
Further Considerations on Fabry Perot Type Resonators.
6. Boyd G. D„ Gordon J. P., Bell Syst. Techn. Journ., 40, 488 (1961).
(Имеется перевод в сб. «Лазеры», ИЛ, 1963, стр. 363.)
Confocal Multimode Resonator for Millimeter through Optical Wavelengths
7. Slepian D., Pollak H. O., Bell. Syst. Techn. Journ., 40, 43 (1961).
Prolate Spheroidal Wave Functions; Fourier Analysis and Uncertainty — I.
8. F 1 a m m e r C., Spheroidal Wave Functions, Stanford, 1957.
9. Stratton J. A., et al., Spheroidal Wave Functions, New York, 1957.
10. Boyd G. D., Kogelnik H. W., Bell Syst. Techn. Journ., 41, 1347
(1962).
Generalized Confocal Resonator Theory.
11. Goubau G„ Schwering F„ Trans. IRE, AP-9, 248 (1961).
On the Guided Propagation of Electromagnetic Wave Reams.
12. S c h w e r i n g F., Arch, elektr. Ubertrag., 15, 555 (1961).
Reiterative Wave Beams of Rectangular Symmetry.
13. T a n g C. L„ Appl. Opt., 1, 768 (1962).
On the Diffraction Losses in Laser Interferometers.
14. E r d ё 1 у i A. et al., Higher Transcendental Functions, New York, 1953,
Vol. 2, p. 179.
15. Pierce J. R„ Proc. Nat. Acad. Sci., 47, 1808 (1961).
Modes in Sequences of Lenses.
16. Born M., Wolf E., Principles of Optics, New York, 1959, p. 374.
17. Morse P. M., Feshbach H., Methods of Theoretical Physics, vol. I,
New York, 1953, p. 949. (Имеется перевод: Ф. M. Морс, Г, Ф е Щ б а X,
Методы теоретической физики, т. 1, ИЛ, 1958.)
14
ОБЩИЙ МЕТОД РАСЧЕТА ОПТИЧЕСКИХ РЕЗОНАТОРОВ
И ПЕРИОДИЧЕСКИХ ЛИНЗОВЫХ СИСТЕМ
Д. Глоге *
D.Gloge, Arch. Elektr. Obertrag., 19, 13 (1965)
Оптические системы, в которых распространяется когерентный свет в виде
собственных волн, целесообразно описывать с помощью коэффициентов связи
и коэффициентов распространения этих волн. Это дает наглядный метод
расчета лазерных резонаторов и периодических линзовых систем с произ-
вольными фокусными расстояниями и размерами апертур. Таким способом
можно учесть как систематические деформации, так и случайные ошибки.
В работе исследованы искривления линзовой линии, случайные поперечные
сдвиги отдельных линз, перекос в зеркальном резонаторе и влияние неодно-
родного усиливающего материала между зеркалами.
§ 1. ВВЕДЕНИЕ
Простой оптический резонатор представляет собой два
искривленных, хорошо отражающих зеркала (фиг. 1), между
которыми может распространяться система собственных ко-
лебаний [1]. Полное математическое описание этих собствен-
ных колебаний удалось пока найти лишь для случая, когда
система зеркал является конфокальной, т. е. когда она состоит
из одинаковых вогнутых зеркал с общим фокусом [2]. Во всех
других случаях даже доказательство существования собствен-
ного значения сопряжено со значительными математическими
трудностями [3]. Поскольку такие системы являются важным
средством для получения и передачи когерентного света, Фокс
и Ли [4] с помощью трудоемкого численного метода нашли пер-
вые собственные функции и их собственные значения для про-
извольных зеркальных резонаторов.
Как эти исследования, так и эксперименты с газовыми ла-
зерами [5] показывают, что в большинстве систем из вогнутых
зеркал энергия первой моды концентрируется в луче, имеющем
♦ D. Gloge, Institut fur Hochstfrequenztechnik d?r Technischcn Hoch-
SChule, Braunschweig.
14. Расчет оптических резонаторов и линзовых систем
281
несколько миллиметров в поперечном сечении и направленном
вдоль оптической оси. Если апертура зеркала значительно боль-
ше этого поперечного сечения, то дифракционные явления на
краю зеркала почти не влияют на форму собственного колеба-
ния; пренебрегая этим искажением, можно довольно просто
Фиг. 1. Общий вид резонатора с зеркалами в виде
цилиндрических полос.
вычислить распределение энергии [6]. Однако это пренебреже-
ние становится недопустимым в тех случаях, когда зеркала
либо плоские, либо столь сильно искривлены, что их центры
кривизны совпадают. Кроме того, недостатком Ьтого метода яв-
ляется то, что он не дает затухания собственной волньц обу-
словленного потерями на краю зеркал. А это необходимо знать,
если требуется подавить определенные типы колебаний в резо-
наторе.
Резонатор с вогнутыми зеркалами эквивалентен периодиче-
ской линии с собирающими линзами [7]. Если линзы имеют то
же фокусное расстояние, что и зеркало, то на каждой линзе
имеет место такая же фокусировка, что и на зеркале, однако
собственные волны распространяются теперь лишь в одном на-
правлении. Такая линзовая линия пригодна для связи на коге-
рентном свете с малыми потерями. Для определения размеров
линии необходимо знать распределение поля и потери собствен-
ных волн для линз с- различными фокусными расстояниями и
различными размерами апертур.
Этот вопрос исследовался в предыдущей работе автора [8]
с помощью метода возмущений, который для малых апертур
приводит к вполне удовлетворительным результатам. В настоя-
щей работе эти результаты обобщены настолько, что с их по-
мощью можно, находить распределение поля и коэффициент
передачи собственных волн с любой точностью, причем и в том
случае, если система регулярно или случайно деформирована.
282
Д. Глоге
Особый интерес представляет случай больших апертур, для
которого получаются простые выражения для затухания невоз-
мущенных собственных волн и дополнительных потерь на воз-
мущение.
§ 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ
Если размеры зеркала достаточно велики по сравнению с
длиной волны, то для расчета зеркального резонатора (фиг. 1)
достаточно предположить, что поле на правом зеркале является
поперечнььм линейно поляризованным электромагнитным полем
с амплитудой ф(х, у). Тогда амплитуда у') на левом
зеркале вычисляется согласно принципу Гюйгенса интегрирова-
нием по поверхности правого зеркала. При этом можно либо
интегрировать раздельно по х и у, либо с самого начала рас-
сматривать двумерную модель, бесконечную в направлении у.
Такая модель содержит все наиболее существенные черты ре-
ального резонатора, а распределение поля в ней является лишь
функцией х.
Ограничимся пока резонаторами с одинаковыми зеркалами;
из соображений симметрии распределения полей на них должны
совпадать. Это приводит к интегральному уравнению [8]
1
Ф(аг') = Х J ф(х)ЛГ(х, x')dx, (1)
-1
где х — нормированная по ширине s поперечная координата,
% —комплексный множитель распространения, учитывающий
затухание и фазовый сдвиг волны при пробеге от зеркала
к зеркалу. Так как в этой модели зеркало не вносит потерь
(потери при отражении можно потом легко учесть), то % опи-
сывает исключительно потери на излучение в открытое про-
странство. В дальнейшем будем называть их дифракционными
потерями, поскольку их величина определяется дифракцией
электромагнитных волн на краях зеркала. Ядро интегрального
уравнения имеет вид __
К(х, = (2)
где £=2лД—постоянная распространения в свободном про-
странстве, р — расстояние между точками на противоположных
зеркалах, а
As2
/ с = — (3)
есть параметр резонатора, учитывающий его размеры. Этот па-
раметр представляет собой число Френеля, умноженное на 2л;
в дальнейшем мы будем называть его апертурным параметром.
14. Расчет оптических резонаторов и линзовых систем 283
Ядро /С(х, х')' является комплексным симметричным ядром.
Об интегральных уравнениях с таким ядром известно лишь то,
что они имеют хотя ‘бы одно собственное значение [3]. Однако
ниже будет показано, что по крайней мере для физически инте-
ресных случаев это уравнение всегда имеет полную систему соб-
ственных функций, ортогональных, хотя и не в эрмитовом
смысле.
Для этого прежде всего рассмотрим в качестве системы
сравнения конфокальный резонатор, для которого ядро имеет
вид [8]
Кконф (X, х') = e-ikdeicxx\ (4)
Интегральное уравнение (1) с этим ядром имеет собственные
значения
= 1) (5)
и собственные функции
фт(х) = 5т(с, х). (6)
Обычно под собственным значением интегрального уравнения
понимают величину \/Gm. Ниже будет встречаться лишь зна-
чение Gm, на которое мы ради простоты перенесем название
«собственное значение». Логарифм Gm является постоянной рас-
пространения, описывающей затухание и фазовый сдвиг волны
при пробеге от зеркала к зеркалу. Выражения (5) и (6) пол-
ностью описывают типы собственных колебаний конфокального
резонатора. Функции Rm(c, х) и Sm(c, х) вещественны. Это так
называемые присоединенные волновые функции первого рода
нулевого порядка в вытянутых сфероидальных координатах, или
просто сфероидальные функции [9, 10]. Функцию So можно ап-
проксимировать для с>2л функцией е~схгР (фиг. 2). Ампли-
туда основной моды на зеркалах в этом случае очень быстро
спадает вне некоторого пятна, радиус которого можно опреде-
лить как расстояние, на котором функция Гаусса уменьшается
в е раз. Из условия сх2 = 2 можно определить полуширину пятна
‘па = Уdk/л. К этому случаю больших апертур мы еще вер-
немся в § 4.
Сфероидальные функции составляют полную ортогональную
систему. Ниже в отличие от работ [9, 10] они будут нормиро-
ваны следующим образом:
„ „ , (0 при т ¥= п,
SmSn dx = i>mn — ( ,
(1 при т — п.
284
Д. Глоге
Если оба зеркала имеют одинаковые отклонения от конфокаль-
ной формы, то распределения полей на обоих зеркалах вслед-
ствие симметрии остаются одинаковыми. Предположим сначала,
что возмущенная таким образом конфокальная система всегда
Фиг. 2. Амплитудное распределение основной моды
в конфокальном резонаторе для различных с = s2k!d.
Вне зеркала функции обозначены пунктиром.
имеет собственные функции и что последние можно разложить
по сфероидальным функциям
ОО
«т(х)=2 ЦпЛ(х).
1-0
(8)
Если в дальнейшем будет показано, что этот ряд сходится,
то предыдущее предположение можно считать физически оправ-
данным. С тем же условием предполагается существование ди-
скретных собственных значений 0^ возмущенной системы. То-
гда из уравнения (1) следует1)
1
0{т11т (/) = J ит (х) F (х) /Сконф (х, х') F (х') dx. (9)
-1
Функции F(x) и F(x') описывают отклонение от конфокальной
системы.
Относительно системы сфероидальных функций уравнение (9)
можно записать в матричной форме [8]
0MU= UF(X)0F(X). (10)
*) Ядро уравнения (1) обозначено ₽ . уравнении (9) через
Г(х)Киовф(«, x')F(x'l. —Прим, ped.
14. Расчет оптических резонаторов и линзовых систем
285
Здесь G^> и G — диагональные матрицы собственных значений
От и Gm; 17—матрица коэффициентов разложения Umi; X —
матрица с элементами
1
Хтп= J Sm (х) xSn (х) dx, (11)
-1
a F(X) — функция матрицы, определяемая рядом Тейлора функ-
ций F(x).
Умножая правую часть уравнения (10) на I7-1, получаем
Qm = UF(X)GF(X)U~\ (12)
Согласно (12), необходимо преобразовать к главным осям ма-
трицу F(X)GF(X), которая является комплексной симметрич-
ной матрицей бесконечного ранга. В принципе это лишь другое
представление возмущенного ядра; поэтому относительно его
собственных значений делать какие-либо высказывания можно
не с большим основанием, чем о собственных значениях инте-
грального уравнения. Однако в практических случаях ранг ма-
трицы можно, по-видимому, ограничить, так как, начиная с не-
которого порядкового номера, собственные волны полностью
исчезают за один пробег; следовательно, исчезают и соответ-;
ствующие собственные значения. Поведение величины Gm для.
конфокальной системы подтверждает справедливость этого
предположения. Как будет, показано ниже, чтобы иметь воз-
можность ограничить матрицу F(X)GF(X), достаточно равно-
мерной сходимости функции F(X). Но комплексная симметрич-
ная матрица ранга п ортогонально подобна некоторой (обобщен-
ной) диагональной матрице [11], т. е. матрица U существует и
в общем случае является комплексной и ортогональной; ее об-
ратная матрица равна транспонированной
CTl = Ur. (13)
Отсюда с учетом (7) следует, что
1
J umundx = 6mn. (14)
-1
Вообще говоря, функции и комплексны, поэтому есть разница
между общей ортогональностью по (14) и эрмитовой ортого-
нальностью, которая получилась бы, если бы под интегралом
(14) одна из функций и была заменена на комплексно сопря-
женную. Согласно условию (7), функции Sm ортогональны как
в эрмитовом, так и в обычном смысле, так как они вещественны.
286
Д. Глоге
Однако ортогональности (14) достаточно, чтобы использовать
функции и в качестве базисной системы некоторой матричной
записи, как это имеет место в случае сфероидальных функций.
Это обстоятельство еще будет использовано.
Матрицу F(X) GF(X) можно интерпретировать следующим
образом. На правом зеркале сфероидальные функции рассеи-
ваются согласно матрице F(X), а затем переносятся с помощью
матрицы собственных значений G на левое зеркало, где снова
подвергаются рассеянию согласно матрице F(X). Собственные
волны, которые при этом переходят сами в себя, можно найти
с помощью трансформации к главным осям.
Резонаторы с различными зеркалами, характеризуемые раз-
ными отклонениями F(x) и F'(x) от конфокальной системы,
имеют различные распределения поля на обоих зеркалах. Тогда
матрица перехода имеет вид F(X) GF'(X). Однако этой матрицы
недостаточно, чтобы вычислить собственные функции возмущен-
ной системы, поскольку в исходное положение система возвра-
щается лишь после полного пробега туда-обратно. Трансфор-
мация к главным осям матрицы полного пробега дает собствен-
ные значения
r = GrF(zV)OF'2(X)(?F(X)^-1. (15)
Это равенство справедливо и тогда, когда зеркала имеют раз-
личную ширину [8], но тогда в (5) и (6) следует подставить
C^JSS', (16)
где 2s — ширина правого зеркала, a 2s' — ширина левого зер-
кала. С точки зрения дифракционных потерь каждый резонатор
полностью определяется апертурным параметром (16) и функ-
циями F(x) и F'(x), которые описывают отклонение этого резо-
натора от конфокального.
Зеркала или линзы являются взаимными элементами; их ма-
трицы рассеяния должны быть симметричны. Матрица F(X)
удовлетворяет этому условию, так как матрица X, согласно ее
определению (11), симметрична. Если собственные волны мож-
но описать системой функций, ортогональных в эрмитовом смыс-
ле, то матрица рассеяния не вносящих потерь рассеивающих
элементов унитарна [12]. Матрица F(X) будет унитарной тогда,
когда зеркала или линзы отличаются от конфокальной системы
только формой поверхности, и при этом неравномерные погло-
щения и отражения не учитываются. Симметричную матрицу
можно представить с помощью матричной функции eiA [11], где
А — вещественная симметричная матрица. Как будет показано
ниже, такое представление.является целесообразным.
14. Расчет оптических резонаторов и линзовых систем 287
Так как матрица (15) ограничена, то элементы матрицы
F(X) должны исчезать для больших разностей индексов: воз-
мущение не должно связывать собственные волны, порядковые
номера которых слишком сильно отличаются друг от друга. Ма-
трица X удовлетворяет этому условию (см. приложение А), а
матричная функция F(X) удовлетворяет ему, если степенной ряд
для F(x) сходится. В принципе достаточно потребовать, чтобы
функция F (х) была аналитической в области интегрирования.
В практических случаях достаточно самое большее несколько
членов разложения F(x), и при этом существенны лишь не-
сколько коэффициентов матрицы вне главной диагонали. Таким
образом можно оценить, сколько собственных волн следует учи-
тывать при заданной точности.
Если ранг матрицы (15) установлен таким способом, то для
вычисления собственных значений Гт часто целесообразно идти
следующим путем. Поскольку матрица X вещественна, симмет-
рична и после принятых нами предположений ограничена, то она
должна быть ортогонально подобна некоторой диагональной ма-
трице, Обозначим эту матрицу через Z. Матрицу F(X) можно
преобразовать к тем же главным осям, получив при этом диа-
гональную матрицу F(Z), коэффициенты которой F(Zm) не за-
висят от с. Тем же способом следует преобразовать матрицы G,
превратив их в комплексную симметричную матрицу W. Тогда
равенство (15) примет вид
r = VT(Z) WF^WF (Z)V~X. (17)
Собственные функции системы можно получить из комплексной
ортогональной матрицы V. Описанный способ позволяет точно
вычислить собственные значения Гт, не требуя при этом разло-
жения функции F(x) по степеням х. Правда, когда необходимо
учитывать очень большое число собственных волн и, следова-
тельно, ранг матричного уравнения становится большим, то
удобнее не только F(X), но и Г разлагать по степеням X. Этот
путь будет описан в следующем параграфе. Точный метод
уравнения (17) затем будет использован для проверки прибли-
женных результатов.
§ 3. ЛИНЕЙНЫЕ ОШИБКИ ПОВЕРХНОСТИ
Важнейшими отклонениями от конфокальной системы яв-
ляются деформации поверхности зеркал или линз, не вносящие
локальных потерь. При этом матрица рассеяния является уни-
тарной. Простым выражением e~ieX можно описать три важней-
ших возмущения резонаторов и линзовых линий. На фиг. 3, а
показан конфокальный резонатор, зеркала которого повернуты
288
Д. Глоге
так, что их центры кривизны находятся на расстояниях bs' и b's
от оптической оси. Такие искажения имеют место в интерфе-
рометре вследствие ошибок юстировки и в дальнейшем будут
называться перекосом. Если углы перекоса равны по величине и
направлению, то такой интерферометр соответствует линзовой
Фиг. 3. Линейные ошибки поверхности.
а —интерферометр, полученный перекосом конфокальных зеркальных полос,
б —искривленная по дуге окружности линзовая линия.
линии с постоянным искривлением оси. Этот случай представлен
на фиг. 3,6. Третий случай относится к случайным сдвигам от-
дельных линз линии и будет рассмотрен в § 5.
При наличии перекоса выражение для расстояния между
точками на противоположных зеркалах можно получить из
фиг. 3, а:
— ~~(хх'— bx — b'x'). (18)
Выражение хх' принадлежит ядру конфокальной системы, а
остальные слагаемые дают функции возмущения
F (x) — e~icbx, F' (x') = e~lcbx' (19)
При этом матрица (15), разложенная по степеням X до первого
порядка, принимает вид
e.icbXQe-2icb’XGe-Mx — 1с(ЬХ(Р + 2b'QXQ + bCPX). (20)
14. Расчет оптических резонаторов и линзовых систем 289
Отсюда с учетом уравнения (Б.6) получаются в первом прибли-
жении коэффициенты матрицы собственных векторов
2GmGn
G2m-G*J
Xтп
для т =# п,
(21)
для т = п.
В члене первого порядка разложения (20), кроме X, стоят
лишь диагональные матрицы. Сама матрица X не имеет элемен-
тов на главной диагонали, следовательно, их не имеет также и
член первого порядка. Но, согласно (Б.6), эти элементы как раз
образуют член первого порядка матрицы собственных значений.
Поскольку последний равен нулю, в матрице собственных значе-
ний не содержится линейных: членов относительно b и Ь'. Возму-
щение имеет более высокий порядок. С учетом (Б.7) получаем
разложение собственного значения
Г — G2
* /п — Um
°0 /^2 1^2
1 _ 2С2 (&2 + Ь>г) -
Gm-Gk
СО
— №bb'.
Gnfik
G\-G\
X2mk (22)
Матрица X является нечетной, поэтому элементы Xmh отлич-
ны от нуля лишь тогда, когда разность между т и k является
нечетным числом.
Аргументы Gm таковы, что первая сумма в (22) действитель-
на, а вторая мнима. Выражение для Гт не содержит мнимой
части, если учитывать только члены до второго порядка.
Значение мнимой части становится ясным, если рассмотреть
предельный случай больших, апертур. Для собственного значе-
ния невозмущенной системы имеет место соотношение
lim |Gm| = 1.
С->оо
(23)
Однако из-за аргумента Gm знаменатель в сумме (22) не исче-
зает, а принимает значение 2. С другой стороны, числитель пер-
вой суммы при предельном переходе с->оо становится нулем.
Величины b и Ь' являются безразмерными переменными, от-
несенными к ширине зеркала s и принимающими значение 1,
когда центр кривизны одного зеркала находится на краю вто-
рого. Если при постоянном отношении d/k величина s, а вместе
с ней и /с стремятся к бесконечности^ то конечному углу пе-
рекоса отвечает конечная величина У с Ь. В случае больших
19 Зак. 274
290
Д. Глоге
апертур для tfcX справедливо выражение (А.2). Как уже упо-
миналось, первая сумма исчезает из-за Om-^Gln остается вы-
ражение
lim -Дг = 1 — 2icbb'. (24)
С->оо Gm
Этот результат можно, интерпретировать с помощью выраже-
ния (18), если последнее немного преобразовать: -
+ (25)
В таком виде р представляет собой расстояние между точками
некоторой конфокальной системы без перекоса, оптическая ось
которой определяется точками х = Ь' и х'=Ь, т. е. просто цен-
трами кривизны зеркал (фиг. 3, а). Расстояние между зерка-
лами должно быть увеличено по сравнению с исходной системой
на величину ebb'. Такой резонатор будет работать, если на соб-
ственные колебания не будут оказывать влияния края зеркал.
Мнимая часть уравнения (24) или (22) представляет собой до-
полнительный фазовый сдвиг, обусловленный изменением рас-
стояния между зеркалами.
Проводя несколько точнее предельный переход при с->оо,
можно учесть также и первую сумму в (22). Поскольку раз-
ность т — k в (22) является нечетным числом и поэтому в зна-
менатели всех членов суммы входят разности, а в числители —
суммы квадратов собственных значений, то для отдельных чле-
нов можно приближенно написать
С учетом X, согласно (А.2), это приводит к приближению
с->оо
rm ~Q\e-Ucbb’ /1G>2-/)[(«+1)In
c->oo I L I I
+ и|"1^=7|]}- <27>
Можно показать, что влияние углов перекоса на обеих сто-
ронах аддитивно и не зависит от Направления поворотов. Прав-
да, это справедливо лишь для конфокальной системы. На фиг. 4
представлены три первых собственных значения конфокальной
системы, возмущенной перекосом, в зависимости от относитель-
ной величины поворота. Апертурный параметр выбран равным
с = л; число Френеля соответственно равно 0,5. Это значение
Фиг. 4. Потери первых трех собственных колебаний резо-
натора из конфокальных зеркальных полос, обусловленные
перекосом.
Фиг. 5. Затухание основной моды искривленной по дуге
окружности линзовой линии с различными апертурными пара-
метрами (двумерная модель).
19*
292
Д. Глоге
примерно отвечает резонаторам газового лазера: потери основ-
ной моды еще достаточно малы для самовозбуждения, в то вре-
мя как следующие собственные волны подавляются, так как за
один пробег они теряют более 20% своей амплитуды. Видно, что
хотя перекос увеличивает потери всех волн, он все же сильнее
влияет на высшие собственные волны, чем на основную моду.
Для линзовой линии целесообразно выбирать апертурный
параметр больше л, чтобы иметь возможность управлять лу-
чом. Уже при с=2л ошибка, которую мы делаем, используя для
определения Го выражение (27) вместо (22), лежит в пределах
точности вычислений. Поэтому можно относительно просто вы-
числить потери искривленной по дуге окружности линзовой ли-
нии. При этом вместо собственного значения лучше использо-
вать величину затухания волны на одну итерацию в децибелах,
получающуюся из собственного значения
Ym= lOlgirj,
= — 20 lg| Om|.
Приближение (27) имеет для этих величин простой вид
Ym —^2[(2m+l)gm —(rn+l)gm+i—(29)
C->co
На фиг. 5 приведены коэффициенты затухания основной моды
различных искривленных конфокальных линзовых линий.
Для с>2л затухание собственного колебания первого поряд-
ка более чем в 10 раз превышает затухание основной волны [2].
Поэтому можно положить
Yo ~g\
при с&2=1.
t?->co
Отсюда видно, что для перекоса
основная волна затухает так, как мода с порядковым номером 1
в невозмущенной системе. Интерферометру с таким углом пере-
коса соответствует искривленная по дуге окружности линия с
радиусом искривления ___
^?искр = ~%bs~d }/Г'2х- (30)
Например, при расстоянии между линзами Юли длине вол-
ны 0,63 мк (длина волны лазера на смеси Не—Ne) радиус ис-
кривления получается порядка 50 км. Провести линзовую линию
14. Расчет оптических резонаторов и линзовых систем
293
так прямолинейно кажется едва возможным. Поэтому на прак-
тике апертуры линз нужно делать настолько большими, чтобы
высшие типы колебаний не имели заметных затуханий. Это при-
водит к апертурному параметру с = 30ч-40. Для основной вол-
ны, не слишком эксцентрично падающей на линзу, такая си-
стема имеет практически неограниченные раскрывы, и прохо-
ждение таких волн можно рассчитать на основании геометриче-
ской оптики [12, 13].
§ 4. КВАДРАТИЧНЫЕ ОШИБКИ ПОВЕРХНОСТИ
Сводя ядро интегрального уравнения, получающееся из вы-
ражения (2), к конфокальному ядру и двум функциям ошибок [8]
F (х) — 1сах2/2 и F'(x') = e-lca'x'2/2, (31)
идеальный зеркальный резонатор с произвольно искривленными
зеркалами можно преобразовать к конфокальной системе. Здесь
а и а' описыйают свойства зеркал и в обозначениях фиг. 1
имеют значения
Это выражение можно получить, ограничившись квадратичными
членами в разложении по х расстояния между точками на про-
тивоположных зеркалах. Для краткости целесообразно ввести
следующие два параметра:
Матрицы рассеяния из функций ошибок (31) имеют сильно
выделяющиеся диагональные элементы, которые с учетом (15)
дают первое приближение для собственных значений
Q^ = Qme-lc^m,
(34)
где
оо
Дт= 3 x2mk (35)
ft-о
есть диагональные элементы матрицы X2. Остальные элементы
матрицы X2 объединяются в новую матрицу Q с коэффициен-
тами
ОО
Qmn — 3 XmkXiiv т^=П. (36)
ft=0
294
Д. Глоге
Окончательно с учетом (Б.7) имеем
k т
Gtf+GP
k т
Q^-G^
(37)
По причинам, которые будут объяснены ниже, кубический и выс-
шие члены в q представляют лишь незначительный интерес. Ес-
ли пренебречь элементами матрицы Q3, то добавочный член
третьего порядка в р примет вид
СО
QL(Ara-A,). (38)
k
Так же как и матрица X3, матрица Q является четной, по-
этому индексы т и k в (37) отличаются всегда на четное число,
и все отношения GwJGk с учетом фазы Qm вещественны и отри-
цательны.
Поэтому (37) и (38) можно записать в виде
г —
* т — v т
2 2 ’
— Cq
fi&rn
1 - с^р2 2' In | | - icp -
k ф m
co
S' <&.. cth (1 In | | _ icp _
/
00
— Qmk(bm-bk)
k^s m
(39)
Коэффициенты разложения матрицы собственных векторов
U получаются путем, аналогичным описанному в § 3
Umn = - icpQmn th (4 In | | - icp -
— icqQmn cth (4ln I I — icP 7 j ПРИ (40)
Этот результат лучше всего продемонстрировать на плоско-
сти (а, а') (фиг. 6), где каждому резонатору ставится в соот-
ветствие одна точка. На прямой а = а' лежат все симметрич-
ные системы. Точка а = а' = О обозначает конфокальный, точка
Фиг. 6. Линии равных потерь основной моды для резонаторов
с зеркалами в виде цилиндрических полос.
Фиг. 7. Дифракционные потери первых трех типов колебаний
в симметричном резонаторе с зеркалами в виде полос.
296
Д. Глоге
а = а'=\ — плоский, а точка а = а' — — 1 — концентрический резо-
натор, зеркала которого являются частями одной сферы. Пере-
ход от переменных а, а' к переменным р, q представляет собой
поворот осей на 45° в плоскости (а, а').
Выражение (39) для малых апертур принимает в этой пло-
скости простое выражение. Для
ср С
In | О0/О2 I
Д2 — До
(41)
в аргументах гиперболических функций в (39) преобладает дей-
ствительная часть, а членом третьего порядка можно прене-
бречь. Это справедливо для всех т, если справедливо для т = 0.
Выражение в квадратных скобках уравнения (39) становится
тогда действительным; считая его постоянным, получаем кри-
вые равных потерь в плоскости (а, а'). Получаются эллипсы с
главными осями р и q [8].
Точный расчет по (39) дает линии равных потерь, которые
для с=л приведены на фиг. 6. Для ср<1,5 их действительно
с хорошим приближением можно представить эллипсами [см.
(41)]. Чем больше с, тем сильнее сжимаются эти кривые по оси
q. Поэтому резонаторы, соответствующие точкам, которые ле-
жат во втором и четвертом квадрантах, имеют очень большие
потери на основной моде. Согласно (39), эти потери возрастают
тем сильнее, чем больше апертура зеркала. Естественно, что
на практике такое поведение является нежелательным, а по-
этому такие резонаторы (в частности, «асимметричные» в осо-
бом смысле) представляют незначительный интерес. По этой
причине в (39) можно ограничиться малыми значениями q,
стремясь в то же время к хорошему приближению для р.
Дальнейшее разложение собственного значения для оценки
ошибки наталкивается на значительные трудности. Поэтому точ-
ность данного приближения проверялась путем точного вычис-
ления с помощью (17) собственного значения Го для некоторых
предельных форм резонаторов. Для этого были выбраны точки
а=1, а'=1; а = 0,5, а'= —0,5 и а=1, а'=0, которые на фиг. 6
отмечены кружками. Во всех трех случаях точный результат
совпал с приближенным.
На фиг. 7 приведены первые три собственных значения сим*
метричных резонаторов для того же значения с = л. Результаты
фиг. 6 и 7 совпадают с результатами Фокса и Ли [4], которые
'численно определили потери первых двух собственных волн при
значении апертурного параметра с=л.
Из фиг. 2 видно, что в конфокальном резонаторе края зер-
кал практически не сильно влияют на амплитуду основной мо*
14. Расчет оптических резонаторов и линзовых систем
297
ды, если зеркало вдвое шире пятна; под радиусом пятна подра-
зумевается расстояние, на котором кривая гауссова распреде-
ления спадает в е раз.
Например, в лазерном резонаторе длиной 1 м при длине вол-
ны 0,63 мк этот радиус равен ш = 0,45 мм. Практически исполь-
зуют зеркала с гораздо большими апертурами, а если нужно
приблизиться к случаю с=л, чтобы подавить высшие типы ко-
лебаний, то резонирующее пространство ограничивают допол-
нительной диафрагмой. Передающая линзовая линия с расстоя-
нием между линзами 100 м при той же длине волны будет иметь
радиус пятна 4,5 мм. В действительности же, чтобы вести луч,
нужны линзы с диаметром несколько сантиметров [12, 13]. Та-
ким образом, случай больших апертурных параметров имеет
важное практическое значение.
Бойд и Когельник [6] показали, что при больших аперту-
рах зеркал амплитуда основной моды в неконфокальном резо-
наторе удовлетворяет гауссовому распределению, а высшие мо-
ды получаются умножением на полиномы Эрмита. Правда,
эффективный радиус пятна различен’ для разных резонаторов.
Учитывая введенные в (32) параметры формы, для правого и
левого зеркал получаем соответственно
VdK/л , ,.п.
" 7771 ( ’
Это приближение не дает дифракционных потерь; поэтому
соответствующие собственные значения равны по модулю еди-
нице. Для фазы справедливо выражение
—g-2ikdgl (2m + D arccos Vaa' (43)
C~>CO
Если а и а' имеют разные знаки, то из (42) величина w полу-
чается комплексной, функция arccos У аа' становится мнимой
и поэтому собственные значения быстро убывают; собственные
волны такого интерферометра имеют большие потери. То же са-
мое получается при применении разложения (39) во втором и
четвертом квадрантах плоскости (а, а'). Такие же свойства по-
являются при аа'>\. На границе этих областей высоких потерь
(фиг. 8), описываемых уравнениями аа' = 0 и аа'=\, производ-
ная функции (43) разрывна; поэтому следует ожидать, что на
этой границе при больших‘с разложение (39) не сходится.
Чтобы в дальнейшем избежать критических точек, будем рас-
сматривать лишь область, где p>q. Это первый и третий ква-
дранты цлрс^ости (а, а'). Цодставдяд (33) в (43), разлагая
298
Д. Глоге
корень в аргументе арккосинуса при q<p и оставляя члены до
третьего порядка, получаем
Р — (2m+ 1) (Л/2-р) Г|
?->СО L
— Z(2m+l)(| р3
(44)
Это разложение умышленно доведено до той же степени, что и
(39). Ниже будет показано, что оба эти приближения совпа-
Ф и г. 8. Области малого затухания и линии равной фазы раз-
личных резонаторов с зеркалами в виде цилиндрических полос.
Для этого подставим в (39) вместо гиперболических функ-
ций первые члены их разложений в ряд Тейлора. Условие p>q
обеспечивает ограниченность гиперболического котангенса при
любом с. Коэффициенты cQmk и сДт получаются путем возве-
дения в квадрат матрицы У с X (см. соотношение А.2). Пред-
С->СО
положим, что
„ „ In I Gm/Gk I
Это не является большим ограничением; например, при с=2л
для основного колебания это значит, что р>4 • 10-5. Для боль-
ших с граница лежит еще ниже,
14. Расчет оптических резонаторов и линзовых систем
299
При этом предположении
= G2me-1 <2m+1)' { 1 - (р* -^) р-и + 1^. + 2.)-1 п | | +
+ M^znln|^_|]_|i(2/n+1)^+j/(2/7z+1)±.|. (45)
Если подставить вместо модулей всех собственных значений их
величины (единицу), то выражения (44) и (45) совпадут. Но
(45) дополнительно дает еще и приближение для потерь. Здесь
целесообразно вновь использовать величину затухания в де-
цибелах, согласно определениям (28):
Ут = gm — 4- О’2 + $ — -у) К"* +1) ("* + 2) (gm — gm+2) +
+ /?z(m—l)(gm —gm_2)]. (46)
Это равенство справедливо для области 01,5 и р<0,7.
Для остальной части фиг. 9 приведены величины затухания ос-
новной моды, полученные из выражения (39), а для плоской си-
стемы— соответственно из (17), и совпадают с результатами
Фокса и Ли [4] (с теми значениями, которые там имеются).
Кривые равных потерь на плоскости (а, а') получаются из
(46), если положить
, । а2 а2 .
Р24--Ц----V = const.
г ' р2 3
Результаты приведены на фиг. 10. Это кривые четвертой сте-
пени с особенностью в точке а = а'=0. Эллипсы, показанные па
фиг. 6, с ростом с становятся все более «перетянутыми»; это
значит, что потери в направлении q растут все быстрее. Резо-
наторы, лишь немного отличающиеся от конфокального, будут
обладать высокими потерями, если это отклонение лежит в кри-
тическом направлении. Чем больше апертура зеркала, тем мень-.
шего отклонения достаточно, чтобы имело место большое отли-
чие от конфокальной системы. Это отличие относится не только
к затуханию основной моды, но и ко всем другим свойствам ин-
терферометров, соответствующих второму и четвертому квадран-
там, как, например, затухание высших собственных волн.
При экспериментах с газовыми лазерами наблюдалось, что
конфокальный резонатор очень критичен к таким отклонениям.
Из-за ничтожной разницы в фокусных расстояниях зеркал или
вследствие локальных нерегулярностей их поверхностей резона-
тор очень легко переходит в нежелательную область; редко по-
лучаются чистые собственные колебания низших порядков, что,
несомненно, должно происходить в системах из первого и треть-
его квадрантов.
Затухание на итерацию, 38
Фиг. 9. Затухание основной моды линзовой
линии с различными фокусными расстояниями и
апертурами.
Фиг. 10. Линии равных потерь основной моды
для больших апертур.
14. Расчет оптических резонаторов и линзовых систем
801
§ 5. СОСТАВНЫЕ И СЛУЧАЙНЫЕ ОШИБКИ
Исследуем сначала влияние перекоса на резонаторы, не яв-
ляющиеся конфокальными, а имеющие произвольно искривлен-
ные зеркала. Результат позволяет одновременно получить по-
тери в искривленной по дуге окружности неконфокальной лин-
зовой линии.
Если выбрать в качестве системы сравнения конфокальный
резонатор, то фаза функций ошибок будет содержать члены, ли-
нейные и квадратичные относительно х. Эти функции можно
разложить и получить собственные значения методом теории
возмущений. Этот метод применим, но приводит к не очень на-
глядным результатам.
В принципе любой интерферометр может служить системой
сравнения. Следовательно, потери за счет перекоса можно рас-
считывать так же, как и в конфокальном резонаторе, подстав-
ляя при этом вместо используемых там собственных значений и
собственных функций соответствующие собственные значения и
собственные функции новой системы сравнения. В дальнейшем
будут рассматриваться лишь те системы, для которых справед-
ливы полученные в § 4 приближения, а именно резонаторы в
первом и третьем квадрантах плоскости (а, а'), для которых
имеет место неравенство аа'<\. Тогда из разложенных по р и q
собственных функций (40) можно получить новую матрицу X.
Подставляя ее вместе с разложенными по р и q собствен-
ными значениями в (22), получим собственные значения си-
стемы, возмущенной перекосом. Обозначим их через Г^.
Первый член разложения по р и q сохранится, если в (22) оста-
вить неисправленной матрицу X, и лишь подставить 0$ из
(34) вместо входящих в слагаемые собственных значений Gm.
Тогда (22) дает
Г(тК) = Гт[1-2с2^ + И
кфт т *
—8c2bb' 0(Py_ Q(Py > (47)
k^m m k J
где Гт есть m-e собственное значение системы сравнения без
перекоса. Собственные значения О(т отличаются от собствен-
ных значений конфокального резонатора Gm лишь фазой, но не
модулем. Учитывая, что (т—k)—нечетное число (иначе Xmk — 0),
302
Д. Глогё
можно выделить в G(m модуль и фазу и записать
р(^)___р
1 т — 1 т
СО
l-2c2(62+H |-
кфт
г-»-т^2
— icp(Am — Д*)1 — №bb' У —r- -,-Q- -j-----——
J k^m ch In кЛ — icp (Am
(48)
В случае больших апертур это приближение можно упростить
дальше, разложив гиперболические функции по их аргументам
и вычислив X и Л при с —> оо из (А2). После некоторых преоб-
разований с использованием определений (28) получаем
= Ут - 7 К* + И2 (1 + Р) + (Ь - ЬУ (1 - />)] X
X |АР (Sm — gm+l) — -^-(gm— gm-1)] • (49)
Фиг. 11 дает потери основной волны симметричного резо-
натора при с = 2л для различных типов перекоса. Сильно ис-
Фиг. 11. Дополнительное затухание основной моды в искри-
вленной по дуге окружности линзовой линии с радиусом кри-
визны d У nd/2h.
зеркалах критичны перекосы в одну сторону. Это можно объяс-
нить качественно следующим образом. На фиг. 12 представлен
интерферометр, зеркала которого перекошены в одну сторону.
Если собственные колебания такой системы не возмущаются
14. Расчет оптических резонаторов и линзовых систем 303
краями зеркал, то они концентрируются вокруг оси, проходящей
через центры кривизны обоих зеркал. Это было уже доказано
на конфокальной системе. На фиг. 12 показаны центры кривизны
зеркал, искривленных в различной степени. Оказывается, что
Фиг. 12. К объяснению чувствительности различных резонаторов
к углам перекоса.
при слабо искривленных зеркалах собственные колебания силь-
нее сдвинуты относительно центров зеркал, чем при сильно ис-
кривленных. Соответственно на них сильнее влияют края, что
вызывает большие дифракционные потери. При перекосах в
противоположные стороны имеют место обратные соотношения.
Оба вида перекосов появляются при юстировке резонаторов с
одинаковой вероятностью. Следовательно, наименее чувствитель-
ной к ошибкам юстировки является конфокальная система.
Резонатор с зеркалами, перекошенными в одну сторону,
имеет те же свойства, что и искривленная по дуге окружности
линзовая линия, состоящая из линз с соответствующими фо-
кусными расстояниями. Из фиг. 11 видно, что наиболее жела-
тельны короткие фокусные расстояния. Отсюда следует, что
для линзовой линии оптимальной будет концентрическая си-
стема или по крайней мере система, близкая к концентриче-
ской, но гарантирующая в соответствии с (42) ограниченное
пятно собственной волны. Правда, ниже будет показано, что
другие точки зрения противоречат этому требованию.
При изготовлении и установлении линзовой линии отдель-
ные линзы будут несколько смещены относительно друг друга.
Поворот линз относительно оси луча не приводит в первом при-
ближении к возмущениям, но при смещении линз луч не будет
следовать этим смещениям и дифракционные потери на краях
увеличатся. Предположим, что взаимные смещения соседних
линз принимают случайные величины и направления, но для
среднего значения имеет место соотношение
’=Дт„т2*"=°- (50)
304
Д. Глоге
Мерой возмущения является средний квадрат всех отдельных
смещений
N
г2=пт4 5Х (5i)
«-0
Это равнозначно
N
lim 4- S(^ - ^+1)2. (52)
N -> co 2V •ЛТ!
я-0
так как слагаемые bnbn+i выпадают, если сдвиги от линзы
к линзе некоррелированы. На фиг. 13 показаны две линзы, сдви-
нутые относительно друг друга. Такое устройство соответствует
резонатору, зеркала которого перекошены в противоположных
направлениях на одинаковую величину. Матрица передачи от
линзы к линзе имеет вид
#(") = e~ic *«+i) хГе~1с х. (53)
Разложение (53) по смещению Ьт — bn+i дает для диагональ-
ных элементов
ОО
К$т — Гт — с2(b„- bn+l)2 s (Гт-ГА)X2mk. (54)
k = 0
Это приближение учитывает лишь потери на преобразование
в другие типы колебаний, но не учитывает обратного преобра-
зования.
Фиг. 13. К вычислению затухания, вызванного смещением
линз.
В результате перемещений, случайных по величине и направ-
лению, матрица передачи меняется от линзы к линзе. Можно
высказать лишь некоторые соображения относительно интенсив-
ности каждой собственной волны и квадратов модулей элемен-
тов матрицы передачи [17]. Квадрат модуля диагонального эле-
14. Расчет оптических резонаторов и линзовых систем
305
мента (54) после определения среднего значения с помощью
(52) будет приближенно равен
СО
1 - [1 - Re (^)] X2mk
s-о m
(55)
Если линзы не являются конфокальными, то необходимо вместо
Гт подставить разложение (39), но в первом приближении до-
статочно поправки по (34). При достаточно больших апертурах
Фиг. 14. Дополнительное затухание основной моды, вызванное
случайными сдвигами линз.
линз можно, кроме того, вычислить из (А.2) элементы Xmk для
произвольных фокусных расстояний и заменить модули соб-
ственных значений в сумме единицей. Тогда для данного сред-
него значения получаются дополнительные потери, вызванные
преобразованием на сдвигах линз:
Аут==8,7с#2(1 — sin р) (2/п +1). (56)
На фиг. 14 приведено дополнительное затухание основной
волны для линз с апертурным параметром с = 2л и различными
фокусными расстояниями. Оказывается, что системы с боль-
шими фокусными расстояниями менее чувствительны к сдвигам,
чем системы с малыми фокусными расстояниями. Но именно
последние имеют преимущество при искривлениях линзовых ли-
ний. Поэтому на практике должен быть найден некоторый ком-
промисс на основе требований, которые ставятся перед линией.
В волноводах допустимое" преобразование волн ограничено
вызванным им искажением сигнала [18]. В периодической линзо-
вой линии разность скоростей различных собственных волн на-
столько незначительна, что это обстоятельство НО играет рол$
Ft
306
Д. Глоге
Даже в очень длинных передающих линиях. Поэтому преобра-
зование волн является здесь нежелательным лишь в связи с
увеличением затухания, которое возникает при появлении выс-
ших собственных волн. Это увеличение совпадает с вычислен-
ным по формуле (56) лишь тогда, когда затухание всех высших
волн настолько больше затухания основной волны, что обрат-
ным преобразованием можно пренебречь. Это справедливо, ко-
гда
Юо12 — IG. |2> <&.
что при с=2л делает допустимым средний сдвиг sV Ь2 <0,14®.
Фактически же линзовые линии нужно делать с большими
апертурами, чем при с = 2л. Тогда собственные колебания низ-
ших порядковых номеров различаются очень слабо и обратное
преобразование должно учитываться.
Для очень больших апертур нецелесообразно производить
разложение по собственным волнам невозмущенной системы.
Дело в том, что сначала амплитудное распределение не изме-
няется от линзы к линзе, а лишь сдвигается относительно оси
на основании призменного действия сдвинутой линзы. Это дей-
ствие можно понять с помощью законов геометрической оптики.
В прямой передающей линии с одинаковыми несдвинутыми
линзами ход луча описывается разностным уравнением
хп+х — 2рхл + л„_1 = 0, (57)
где хп — расстояние от луча до центра n-й линзы. Для прос-
тоты рассмотрим двумерную задачу. Ход луча в третьем изме-
рении описывается таким же независимым уравнением.
Если линзы сдвинуты на величину Ьп относительно оси си-
стемы, то (57) превращается в неоднородное разностное урав-
нение [12, 13]
xn+i — 2px„ + x„_i = 2(l — р)Ьп. (58)
Это уравнение в принципе решается так же, как и соответ-
ствующее дифференциальное уравнение. Если правильно вы-
брать начальные условия, то получим
п
*«=]/j-zrj Е 2bk sin (n — k) <р. (59)
k-o
Здесь для краткости временно положено
р = cos ф. (60)
Среднее значение сдвига равно нулю по предположению; от-
сюда с учетом (59) следует, что среднее значение отклонений
14. Расчет оптических резонаторов и линзовых систем
307
луча также равно нулю. Но для среднего квадрата отклонений
получается
л п
= Т ^46ft6zsin(« — £)<psin— (61)
k-0 1-0
Это среднее значение все еще зависит от номера линзы, отсчи-
танного от начала линии, так как усреднение нужно проводить
Фиг. 15. Среднее отклонение луча (после прохождения через
200 линз) по отношению к среднему смещению линз в линии.
не по всем линзам линии, а по всем п-м линзам ансамбля. Так
как сдвиги от линзы к линзе некоррелированы, то в (61) все
слагаемые с &=#/ равны нулю. Остается
п
2sin2
ьо
Эту сумму можно записать в свернутом виде [15]
Р = р Г2й + 1 _ . (62)
”1 + ^1 sin <р J ' '
Корень этого выражения дает среднеквадратичное отклоне-
ние, которое для линзовых систем с различными фокусными
расстояниями приведено на фиг. 15. Луч все больше удаляется
от оси системы и тем быстрее, чем короче фокусное расстояние.
В соответствии с результатом предыдущего параграфа здесь
можно установить, что системы с большими фокусными расстоя-
ниями нечувствительны к сдвигам. Сдвиги очень больших линз
вызывают сначала весьма малые потери, но после определен-
ного числа линз луч может так далеко уйти, что он достигнет
края линзы и там пропадет. При меньших апертурах луч дол-
гое время центрируется, но обусловливает при этом постоянно
высокие потери.
20*
308
Д. Глоге
§ 6. НЕОДНОРОДНОЕ УСИЛЕНИЕ В РЕЗОНАТОРЕ
Предыдущие три параграфа были посвящены исключительно
различного рода поверхностным нерегулярностям. Такие нере-
гулярности имеют очень важное значение в резонансной оптике.
Если в оптических элементах вносятся потери, то они очень
мало или даже совсем не изменяются на апертуре и поэтому не
вызывают связи между' модами.
Фиг. 16. Эскиз резонансной системы с неоднородным усилением
(газовый лазер).
Напротив, усиливающий множитель в большинстве случаев
нельзя считать постоянным по поперечному сечению. Напри-
мер, в лазерах на смеси Не—Ne усиливающий газ находится в
стеклянной трубке между зеркалами, которая должна быть по
возможности тонкой, чтобы энергия возбужденных электронов
достигала достаточно большого значения [16]. Практически для
возбуждения основной моды выбирают поперечное сечение
трубки немногим более 4а>, т. е. порядка удвоенного диаметра
пятна. Для лазера длиной 1 м, работающего на длине волны
0,63 мк, 2w — 0,9 мм. Светящаяся часть трубки по ширине ока-
зывается менее 2 мм. Это сечение одновременно ограничивает
резонансный объем и обеспечивает подавление высших типов
колебаний. Если трубка подходит вплотную к зеркалам, то эф-
фективный диаметр зеркала разумно взять равным диаметру
трубки (фиг. 16). Коэффициент усиления приблизительно про-
порционален плотности возбужденных электронов. Распределе-
ние этих электронов определяется диффузией через стенки
трубки [16], поэтому постоянную распространения электромаг-
нитных волн можно представить в виде
k = k' -j- ik" (х), (63)
где k' — постоянная распространения в свободном пространстве,
a k” — коэффициент усиления, для которого приближенно спра-
ведливо соотношение
Г = ^'(1-х2).
(64)
14. Расчет оптических резонаторов и линзовых систем Э09
Здесь ko — усиление на оптической оси. Ядро интегрального
уравнения (1) теперь принимает вид [19]
Х(х,х') = У^-е ₽ . (65)
С учетом (63) и (64) интеграл в этом выражении для конфо-
кального резонатора равен
k"d
— i J k dp = — ik'd 4- k'^d 4- icxx'-y- (x2 4- xx' 4- x'2)- (66)
₽
Выражение k'd дает среднюю фазу, a k" — среднее усиление при
пробеге волны от зеркала к зеркалу. Третье слагаемое образует
ядро конфокальной системы, а остаток — функцию возмущения
р xtj _ e-(*od/3) G2+"'+*2). (67)
В этой функции х и х' не разделяются. Возмущение является
связанным между зеркалами. Каждому зеркалу нельзя поста-
вить в соответствие собственную матрицу рассеяния.
Однако пока усиление не превышает 1%, что соответствует
лучу с длиной волны 0,63 мк, функцию (67) можно разложить
по аргументу и получить для матрицы перехода выражение
я ’d
к == e°dG + (ХЮ + ХОХ -Н О АГ2) 4- .... (68)
Разложение матрицы собственных векторов имеет вид
Uma =
V Gm 4~ Qfe у V ппи т п
3 q Q mk^ kn при т п,
ЬО т п
1 при т = п.
(69)
Для модуля собственного значения получаем
|Г^ = Л"|С^2(1-|^Дт).
(70)
На фиг. 17 приведено усиление за пробег 1—|Гт| в зависимо-
сти от kQd для первых трех типов колебаний. Как видно, не-
однородное усиление оказывает благоприятное влияние на по-
давление высших типов колебаний. Чем выше среднее усиление
kod, тем сильнее различаются усиления отдельных типов
310
Д. Глоге
колебаний. Максимум усиления на оптической оси благоприятст-
вует прежде всего основному типу колебаний. Правда, это нельзя
практически доказать при малых усилениях (порядка 10—12%
Фиг. 17. Усиление первых трех собственных волн конфокального
резонатора при неоднородном усилении.
на 1 ж), какие дает гелий-неоновый лазер (Х = 0,63 мк). Иная
ситуация имеет место при очень большом усилении многих га-
зовых лазеров с инфракрасным излучением.
§ 7. Заключение
Расчет дифракции на краях и вызванных ею потерь в опти-
ческих резонаторах связан в общем случае с очень большими
математическими трудностями. В данной работе эти трудности
удалось обойти, для чего все исследуемые системы приводились
к конфокальной, для которой имеется полное описание. Благо-
даря этому оказалось возможным решить относительно просто
многие задачи теории оптических резонаторов. Важнейшим сред-
ством при этом оказывается матрица рассеяния, с помощью ко-
14. Расчет оптических резонаторов и линзовых систем
311
торой можно быстро и наглядно представить совокупность соб-
ственных колебаний системы.
Исследования ограничивались двумерной моделью. Поскольку
в декартовых координатах для трехмерной модели можно раз-
дельно вычислять распределение на зеркалах в обоих коорди-
натных направлениях, то для этого достаточно двумерного пред-
ставления. Собственные значения общей системы получаются
как произведение собственных значений обеих двумерных си-
стем.
При круглых апертурах целесообразно проводить расчеты в
цилиндрических координатах, на которые в принципе можно
перенести приведенный здесь метод, если в этих координатах
есть система сравнения, свойства которой известны. До сих пор
известно лишь одно приближение для собственных функций при
больших апертурах, а именно гауссова функция, умноженная на
полиномы Лагерра [20]. Собственных значений пока получено
очень мало, причем в основном численным путем [1].
Однако основные результаты этой работы справедливы так-
же для систем с радиальной симметрией. Хотя конфокальная
система как резонатор является неустойчивой, в конфокальной
линзовой линии никаких трудностей не встречается; наоборот,
эта система представляет собой хороший компромисс, когда не-
обходимо преодолеть трудности, связанные с изгибами и слу-
чайными сдвигами.
ПРИЛОЖЕНИЕ А. МАТРИЦА Х(с)
В случае малого апертурного параметра с функции Sm мож-
но заменить полиномами Лежандра [9]. С помощью рекуррент-
ной-формулы для этих полиномов из (11) имеем
Jim Xm> m+i = hm ATra+1, m = y=^==, (A. 1)
m — 0, 1.....
В случае большого апертурного параметра с функции Sm имеют
вид функций Гаусса, умноженных на m-й полином Эрмита. На
основании справедливой при этом рекуррентной формулы из
(11) имеем
lim /с Xmi m+i = lim /с Xm+li m = 1/, (A.2)
m — 0, 1, ....
Выражение (A. 1) действительно для уm > С, а (Д.^) — дл$
Ут < р.
312
Д. Глоге
В обоих предельных случаях исчезают те элементы матри-
цы X, для которых пД=т±\. Если с'принимает бесконечное зна-
чение, то в точности это не выполняется, но и тогда коэффи-
циенты матрицы быстро убывают при удалении от главной диа-
гонали.
ПРИЛОЖЕНИЕ Б. ТЕОРИЯ ВОЗМУЩЕНИЙ
ДЛЯ РЕШЕНИЯ ЗАДАЧИ О СОБСТВЕННЫХ ЗНАЧЕНИЯХ
Пусть требуется найти собственное значение
Г = ики-1 (Б.1)
комплексной симметричной матрицы К, имеющей разложение
К=О + 1К("е-/<(2}е2 — /ЯГ(3)е3 ± ... . (Б.2)
Разложим Г и U по тому же параметру
U = £7(0> + ZtZ(1)e — £7(V — ZtZ(3)e3 ± ... , (Б.З)
Г = Г(0) + /Г(,)е - Г(2)е2 — /Г(3)е3± ... (Б.4)
и приравняем коэффициенты в (Б.1). Отсюда получаются мат-
рицы разложения для собственных значений. Правда, матрица
собственных векторов будет полностью определена лишь тогда,
когда будет учтена их ортогональность
UTU = E. (13)
Приравнивание коэффициентов в этом равенстве дает диаго-
нальные элементы матрицы собственных векторов.
Для нулевого порядка получаем
р(О)^у(О) . £/(°) Т£/(°) £
а отсюда можно видеть, что
г(°)__Q //(°> _______Д
L т —'~>т> и пп— Отп-
(Б.5)
Члены первого порядка дают
r(1) + GtZ(1) = 47(1>G + ^1),
откуда
Umr 4- £/(1) = О,
р(1)____zz(U //П) ___________
l'mn
Gm — Gn
: о
*
при
при m = ri.
(Б.6)
14. Расчет оптических резонаторов и линзовых систем
313
Наконец, можно учесть еще второй порядок
Г(2) Г(1)^у(!) _|_ Ot/2) = ^(1)^(1) Д'Ф
Это дает
V' , „(2)
2j ат — ck ~т-^тт'
k^m
1
Gm Gn
Gm-Gk
/г(1) /z(i)
mm‘x тп
[_fey=m
при т$п,
,,т _ 1 у' кг
Gm Gn
(Б.7)
Л
ЛИТЕРАТУРА
1. Fox A. G., Li Т., Bell Syst. Techn. Journ., 40, 453 (1961). (Имеется
перевод в сб. «Лазеры», ИЛ, 1963, стр. 325.)
Resonant Modes in a Maser Interferometer.
2. Boyd G. D., Gordon J. P., Bell Syst. Techn. Journ., 40, 488 (1961).
(Имеется перевод в сб. «Лазеры», ИЛ, 1963, стр. 363.)
Confocal Multimode Resonator for Millimeter through Optical Wavelength
Masers.
3. Newman D. J., Mo r g a n S. P., Bell Syst. Techn. Journ., 43, 113 (1964).
Existence of Eigenvalues of a Class of Integral Equations Arising in Laser
Theory.
4. Fox A. G., Li T„ Proc. IEEE, 51, 88 (1963).
Modes in a Maser Interferometer with Curved and Tilted Mirrors.
5. Gloge D., Frequenz, 16, 196 (1962).
Gesichtspunkte zum Bau von He-Ne-Lasern ftir die Nachrichtentechnik.
6. Boyd G. D., Kogelnik H. W., Bell Syst. Techn. Journ., 41, 1347
(1962).
Generalized Confocal Resonator Theory.
7. Goubau G., S ch w ering F., Trans. IRE, AP-9, 248 (1961).
On the Guided Propagation of Electromagnetic Wave Beams.
8. Gloge D., Arch, elektr. Ubertrag., 18, 197 (1964). (Статья 13 настоящего
сборника.)
Berechnung von Fabry-Pdrot-Laser-Resonatoren mit Streumatrizen.
9. F1 a m m e r C., Spheroidal wave functions, Standford, 1957, p. 49.
10. S t r a 11 о n J. A. et al., Spheroidal wave functions, New York, 1957.
11. Ф. P. Гантмахер, Теория матриц, M., 1953.
12. Montgomery С. G, et al., Principles of Microwave Circuits, New York,
1953, p. 149,
314
Д. Глоге
13. G е 11 е г m а n n W. D., Diplomarbeit am Institut fiir Hochstfrequenz-
technik der Technischen Hochschule, Braunschweig, 1964
Strahlfiihrung in periodischen Linsensystemen.
14. Marcuse D., Bell Syst. Techn. Journ., 43, 741 (1964).
Propagation of Light Rays through a Lens—Waveguide with Curved Axis.
15. Град штейн И. С., Рыжик И. М., Таблицы интегралов, сумм, рядов
и произведений, М., 1963.
16. Gordon Е. I., White A. D., Appl. Phys. Lett. 3, 199 (1963).
Similarity Laws for the Effects of Pressure and Discharge Diameter on
Gain of He-Ne-Lasers.
17. M i 11 e r S. E , Bell Syst. Techn. Journ., 42, 2741 (1963).
The Nature of and System Interferences of Delay Distorion due to Mode
Conversion in Multimode Transmission Systems.
18. Unger H G., Arch, elektr. Ubertrag., 15, 393 (1961).
Regellose Stdrungen in Wellenleitern.
19. G1 oge D., Arch elektr. Ubertrag., 18, 451 (1964).
Biindelung koharenter Lichtstrahlen durch ein ortsabhangiges Dielektrikum.
20. E a g 1 e s f i e 1 d C. G., Proc. IEE, 111, 610 (1964).
Mode-Conversion Loss in a Sequential Confocal lens System,
15
КВАЗИОПТИЧЕСКИЕ РЕЗОНАТОРЫ*
Проф. Кан **
Предметом настоящей дискуссии являются квазиоптические
резонаторы, т. е. открытые структуры, размеры которых велики
по сравнению с длиной волны, способные поддерживать одно-
временно много типов колебаний. Работы участников дискуссии
относятся к модовой и лучевой оптике, интегральным уравне-
ниям и вариационным методам. Разумеется, влияние резона-
торов на электромагнитное взаимодействие с помещенными в
них активными веществами будет широко обсуждаться в на-
стоящей дискуссии, поскольку названная тема в значительной
степени охватывает вопросы, связанные с лазерами.
Д-р Губо сделает замечания вводного характера. Затем я
сделаю ряд замечаний относительно оптической теории резона-
торов. Профессора Гамо, Торальдо ди Франчиа и Бергштейн
обсудят различные аспекты дифракционной теории резонаторов.
Наконец, Латурет расскажет о некоторых теоретических иссле-
дованиях, проведенных вариационным методом, и о некоторых
экспериментальных результатах.
Д-р Губо***
Историческая справка. Плоскопараллельный резонатор был
впервые исследован в диапазоне СВЧ в 1954 г. Шайбом, Кин-
гом и Тацугути в Висконсинском университете. Сферический от-
ражательный резонатор имеет своим прообразом пучковый вол-
новод, в котором распределение поля в поперечном сечении пучка
периодически восстанавливается через определенные интервалы.
* Отчет о дискуссии по резонаторам под председательством проф. Ка-
на на симпозиуме по квазиоптике.
**W. К. К a h n, Polytechnic Institute of Brooklyn.
*** G. J. E. G о u b a u, U. S. Army Electronics Labs., Fort Monmouth, N. J.
316
Дискуссия
В линзовой линии (фиг. 1) повторение происходит за счет
восстановления распределения фазы' в поперечном сечении по-
средством фазокорректоров, имеющих форму линз.
Если пучок распространяется между двумя плоскими реф-
лекторами 7?! и R2, помещенными в средних плоскостях двух
последовательных линз, то получается резонатор, который имеет,
конечно, ту же самую систему мод, что и линзовая линия. Пло-
ский отражатель с половиной линзы эквивалентен сферическому
рефлектору, имеющему такое же фокусное расстояние, как и
Фиг. 1.
у полной линзы. Такие резонаторы были впервые использованы
в субмиллиметровом диапазоне волн для определения дифрак-
ционных потерь пучкового волновода.
Различие между плоскопараллельным и сферическим резона-
торами.-Системы мод в плоскопараллельном и сферическом ре-
зонаторах совершенно различны. Моды, существующие между
плоскими пластинами, существенно зависят от размеров пла-
стин, тогда как моды сферического резонатора слабо зависят от
диаметра рефлекторов (если только он достаточно велик) и, по
существу, определяются лишь кривизной рефлекторов.
Имеет также место различие резонансных свойств. Если оба
резонатора возбуждаются посредством отверстий связи в цен-
тре рефлекторов, то плоскопараллельный резонатор (согласно
Шайбу и др.) имеет сильно асимметричную резонансную кри-
вую, в то время как резонансная кривая резонаторов со сфе-
рическими отражателями вполне симметрична при перепаде ам-
плитуд во много децибелл. Частотная зависимость резонаторов
вблизи резонанса для различных видов возбуждений теорети-
чески еще не исследована.
Проф. Торальдо ди Франчиа *
Может ли асимметрия быть вызвана недостаточной парал-
лельностью пластин?
* С. ToraldodiFrancia, University of Florence, Italy. ‘
15. Квазиоптические резонаторы
817
Д-р Губо
Не думаю» так как было произведено множество измерений
в различное время и с различными зеркалами. Все кривые
имели одни и те же виды асимметрии.
В этой связи я указывал, что резонансы имеют место и в
гипотетическом случае рефлекторов бесконечной протяженности.
Поле, создаваемое дипольным источником, можно представить
распространяющимися или затухающими в радиальном направ-
лении цилиндрическими волнами. Резонанс происходит при пре-
образовании затухающей нераспространяющейся волны в рас-
пространяющуюся. Если зеркала не имеют потерь, то резонанс-
ный пик имеет логарифмическую особенность.
Проф. Кан
Д-р Губо только что указал на тесную связь, существующую
между типами колебаний внутри оптического резонатора и вол-
нами в аналогичной линии передачи. Одним из простых спосо-
бов описания электромагнитных процессов, происходящих в этих
двух структурах, является рассмотрение параксиальных лу-
чей. Эти лучи либо сосредоточены внутри структуры, либо не-
ограниченно расходятся из нее. Критерий, позволяющий разли-
чить эти состояния, был развит Пирсом и использован недавно
Бойдом и Котельником для разделения конфигураций поля оп-
тических резонаторов, образованных двумя зеркалами различ-
ной кривизны, на конфигурации, связанные с большими и с ма-
лыми потерями. Так как такое разделение весьма важно для
эксперимента, то я приведу далее более удобную и общую фор-
мулировку критерия Пирса.
Большинство прежних результатов по оптическим резона-
торам получено без учета свойств заполняющей среды, иными
словами, среда предполагается однородной и изотропной. В ла-
зерных приложениях среда является, по-видимому, неоднород-
ной и, кроме того, рассеивающей.
Лучевое рассмотрение приводит к очень интересным и важ-
ным выводам. Если мы занумеруем ряд плоскостей, перпенди-
кулярных к оси оптической системы ..., N—1, N, AZ+1, ..., то
на каждой из этих плоскостей луч характеризуется двумя пара-
метрами — расстоянием от оси а и наклоном луча Ь. Эти два
параметра можно объединить в матрицу-столбец. Для указан-
ных последовательных плоскостей эти столбцы связаны матри-
цей преобразования, присущей данной оптической системе.
318
Дискуссия
На фиг. 2 показаны плоскости с номерами N и М+1, отстоя-
щие на расстояние I. Ясно, что
(aN+i\ /1‘ .
\bN+J~ко ш
Для поперечных плоскостей, разделенных только простой лин-
зой (нулевой толщины), матрица преобразования есть
где величина с (обратная фокусному расстоянию) считается
положительной для собирающих линз.
Наиболее простой тип резонатора показан в верхней части
фиг. 3. Под ним изображена аналогичная (эквивалентная) ре-
зонатору оптическая линия передачи. Матрица преобразова-
ния Т единичной ячейки передающей линии является произведе-
нием матриц преобразования ее составляющих.
/ 1 0\/1 2l\ 1 0\
Т= =
с 1Д0 1 /к— с 1/
/ cos 0 Z sin 0\
к—Y sin 0 cos 0/ ’
(За)
(36)
где
COS0 = 1— 21с и Z = = у tg-|-.
У k z
Можно показать, что критерий Пирса для матрицы преобра-
зования единичной ячейки имеет вид
-1 <|Sp Т < 1,
*
(4)
15. Квазиоптические резонаторы
319
В частности, для простого случая, представленного фиг. 3
и уравнениями (3), получается хорошо известный результат
(в наших обозначениях)
0</с<1.
Соотношения (1) — (36) являются основой для формальной ана-
логии с четырехполюсниками, на что указали также Дешан и
Маст ').
Единичная
ячейка
Фиг. 3. Простой резонатор и эквивалентная ему оптическая
линия.
1с = 1/Фокусное расстояние зеркала = 1/Фокусное расстояние линзы.
Как я уже указывал в своем вступлении, необходимо учесть,
что среда внутри резонатора является неоднородной. С оптиче-
ской точки зрения существуют два простых случая: среда яв-
ляется либо фокусирующей, либо рассеивающей. Пусть z— ко-
ордината вдоль оси резонатора, а у — координата в попереч-
ном направлении. Этим случаям соответствует следующее изме-
нение показателя преломления вблизи оси резонатора:
«(^Ла + лУ2. (5)
причем для фокусирующей среды т|<0, а для рассеивающей
среды т|>0. Дифференциальное уравнение для лучей в такой
среде записывается в параксиальном случае в виде
d?y _ 2г)
' По
) См. статью 8 настоящего сборника. — Прим. ред.
320
Дискуссия
Таким образом формула, эквивалентная (1), легко записывает-
ся в тригонометрических функциях для любой длины 2=2/.
Умножая слева и справа на матрицу (2) для учета наличия
зеркал, можно получить матрицу преобразования для резона-
тора (или единичной ячейки).
Рассеивающая
среда
Фокусирующая
*'' среда /
Однородная
среда
Фиг. 4. Общее рассмотрение резонатора, заполненного
неоднородной средой.
Абсцисса пропорциональна расстоянию между зеркалами резонатора. Величины
по осям отложены в произвольных единицах.
Главная особенность результатов, которые следуют из при-
менения критерия (4), становится понятной из фиг. 4. Для резо-
наторов, заполненных рассеивающей средой, единственными
конфигурациями с низкими потерями являются системы с ма-
лым расстоянием между зеркалами. С другой стороны, для ре-
зонаторов, заполненных фокусирующей средой, конфигурации
с низкими потерями существуют периодически и при бесконечно
больших расстояниях между зеркалами; между ними располо-
жены конфигурации с большими потерями.
В переходной области лазерная среда является также рас-
сеивающей. Когда рассеивающийся характер сочетается с не-
однородностью рассматриваемого типа, можно ожидать возник-
новение больших динамических изменений добротности оптиче-
ских резонаторов.
Проф. Гамо *
Я хочу обсудить два вопроса Теории оптических резонато-
ров: линейную теорию резонаторов, основанную на функцио-
♦ Н, G a m о, University of Rochester,
15. Квазиоптические резонаторы
321
нальном анализе, и нелинейное взаимодействие оптических ла-
зерных мод.
Линейная теория резонаторов, основанная на линейном функ-
циональном анализе. Линейная теория резонаторов развита уже
настолько, что объясняет многочисленные экспериментальные
результаты. Например, теория сферических резонаторов, разви-
тая Бойдом и Кагельником, довольно хорошо согласуется с экс-
периментами, как отмечали Аустон и др. ‘).
Остается, однако, несколько серьезных вопросов в линейной
теории резонаторов. Назову для примера три из них. Во-пер-
вых, развитие наиболее удобной техники приближений (напри-
мер, метод возмущений и вариационный метод), базирующейся
на полученных результатах и позволяющей удобным образом
применять этот аппарат к расчету практически важных случаев.
Надеюсь, что доклады, представленные нашей группой от Ро-
честерского университета, смогут указать здесь некоторые буду-
щие направления. Во-вторых, определение границ применимости
приближений существующей теории, таких, как скалярная вол-
на, формула Кирхгофа — Френеля, параболическое приближе-
ние, функции Гаусса — Эрмита и т. д. Вторая проблема яв-
ляется, по существу, общей для дифракционной теории в оптике.
В-третьих, линейная теория резонаторов, основанная на линей*
ном функциональном анализе «анормальных преобразований»
в'пространстве обобщенных функций. Такой анализ позволяет
глубоко исследовать природу резонаторных мод.
Остальная часть этой короткой дискуссии по линейным ре-
зонаторам имеет отношение к последнему вопросу. Допустим,
что однородное интегральное уравнение Фредгбльма для резо-
наторных мод имеет вид
»
of(s)= f K(s, t)f(t) dt, (6)
a
где ядро K(s, t) удовлетворяет следующим условиям: оно не-
прерывно, квадратично интегрируемо, определено внутри огра-
ниченной области и комплексно симметрично. Последнее свой-
ство отличает линейную теорию резонаторов от многих других
подобных задач математической физики. Вследствие симметрии
оптической передачи от зеркала А к зеркалу В и обратно,
к А, функция передачи, т. е. ядро интегрального уравнения сим-
метрично, но, вообще говоря, комплексно. Выбирая надлежа-
щим образом разложение собственного колебания по полной
) См. статью 19 настоящего сборника, — Прим, ред,
21 Зак. 274
322
Дискуссия
ортогональной системе функций, можно привести интегральное
уравнение резонатора к матричной форме
Кх — ох, . (7)
где матрица К симметрична,
КТ = К, (8)
а х есть вектор, компонентами которого являются коэффи-
циенты разложения резонаторной моды.
Согласно матричной теории оптической передачи, основан-
ной па теории Шмидта для линейных интегральных уравнений
(1), симметричную матрицу оптической передачи можно пред-
ставить в факторизованном виде
K=UMJT, (9)
где U — унитарная матрица, а Л — диагональная матрица с не-
отрицательными элементами. Для резонатора без потерь диаго-
нальная матрица становится тождественной матрицей. Так как
произведение унитарных матриц является также унитарной мат-
рицей, то матрица передачи К для резонатора без потерь также
является унитарной. Матрицы K^KKj и Кц — КАК являются
положительно-полуопределенными и эрмитовыми. Диагональные
элементы А являются квадратными корнями из неотрицатель-
ных собственных значений Ki и Кп, которые одинаковы.
Из уравнения (9) следует, что К есть в общем случае анор-
мальная матрица. Нормальная матрица А удовлетворяет ра-
венству АА+=А+А и всегда может быть диагонализирована
унитарным преобразованием U к форме A = J7AJ7+. Как было
упомянуто выше, ядро для резонатора без потерь описывается
унитарной матрицей, которую всегда можно диагонализировать
унитарной матрицей. Таким образом, ядро для резонатора
без потерь всегда нормальное. Необходимым и достаточным усло-
вием того, чтобы ядро для резонатора с потерями К было нор-
мальным, является равенство U—U*. Ядро для резонатора с
потерями К является нормальным в том и только в том случае,
когда К можно разложить на множители ортогональной матри-
цей, для которой UUT=UTU—1. Следовательно, ядро К обычно
является анормальным. Для конфокального сферического резо-
натора в обычном приближении ядро, как легко видеть, нор-
мально. Для пеконфокальной геометрии оно уже ненормально.
Следовательно, линейная теория резонатора связана, вообще
говоря, с математическими проблемами, касающимися анор-
мальных ядер и их диагонализации.
Отметив свойства симметрии ядра, можно легко показать,
что собственные векторы ц(') и и<2\ соответствующие модам с
15. Квазиоптические резонаторы
323
различными невырожденными собственными значениями, удов-
летворяют следующему соотношению ортогональности:
2^ = 0. (10)
I
Можно также показать, что собственные значения комплексно*
симметричных ядер являются стационарными значениями отно-
(И)
i
Условие (10) и квадратичная форма в (11) отличаются от
тех, которые используются для эрмитовых симметричных ядер
в гильбертовом пространстве [2]. Это показывает, что линейная
теория резонатора обычно связана с (анормальными) линейны-
ми преобразованиями в более общем пространстве, чем про-
странство Гильберта, т. е. в комплексном пространстве Банаха.
Согласно Риссу и Секефальви-Надь [3], общая спектральная
теория анормальных линейных преобразований все еще сравни-
тельно плохо развита по сравнению с интенсивно изучаемой
теорией нормальных преобразований. К счастью, ядро нашего
резонатора непрерывное, ограниченное и квадратично интегри-
руемое в ограниченной области, принадлежит к хорошо изучен-
ному классу абсолютно непрерывных ядер [3—5]. Собственные
значения абсолютно непрерывного ядра не могут иметь точку
сгущения в ограниченной части комплексной области и обра-
зуют либо ограниченную последовательность, либо неограничен-
ную последовательность, стремящуюся по модулю к нулю.
В случае вырожденных собственных значений число вырож-
дений ограничено. Совершенно непрерывное ядро можно с про-
извольной погрешностью по норме аппроксимировать ядрами
конечного ранга. Наилучшее приближение ядрами конечного
ранга дают первые N членов шмидтовского разложения ядра, на-
чиная с члена, имеющего самое большое собственное значе-
ние, |. Ошибка приближения дается выражением
b Ъ оо
/ t)\*dsdt = JI l^l2’ (12)
a a 1—N+1
где
АГ
H(s, t) = K(s, f) — 2 (s) vt (/)>
i-I
a m,(s) и Vi(t}—функции шмидтовского разложения [4]. Более
того, ядро для резонатора можно привести к комплексно
21*
324
Дискуссия
симметричной матрице в конечномерной области посредством
процесса разложения Шмидта [3, 4].
Существований собственных функций, представляющих моды
резонатора [6], можно доказать методом' такого разложения.
Итак, математические основы линейной теории резонатора
должны рассматриваться как вполне установившиеся. Основной
проблемой в линейной теории резонатора должно стать разви-
тие методов удобного и обоснованного приближения, базирую-
щегося на упомянутом выше линейном функциональном ана-
лизе. Таким образом, я думаю, что в оптике линейного резона-
тора все еще остаются серьезные математические проблемы.
Нелинейное взаимодействие мод оптического мазера. Да-
вайте обсудим другую сторону вопроса о модах резонатора,
а именно, нелинейное взаимодействие мод. Когда нелинейность
материала мазера из-за насыщения становится существенной,
как бывает в практически применяемых мазерах, наблюдаются
интересные явления, такие, как сильная связь между модами,
конкуренция мод, комбинационные тона, затягивание фаз раз-
личных мод и т. д. [7].
Нелинейная теория мазеров была развита Лэмбом [8] до
такой степени, что она объяснила и предсказала многие резуль-
таты экспериментов. Остается однако очень много важных фи-
зических, математических и экспериментальных задач, касаю-
щихся нелинейных свойств мазера.
Рассмотрим коротко типичный пример нелинейного взаимо-
действия мод. Предположим, что три соседние продольные
моды возбуждаются на частотах Vi, V2, v3 в газовом мазере не-
прерывного действия с бегущей волной. Если длина резонатора
постепенно изменяется так, что эти три моды размещаются
симметрично вокруг центра линии Допплера с широким пиком,
и разность частот биений v2—Vi и v3—v2 является малой вели-
чиной порядка 1 кгц, то происходит скачкообразное изменение
частоты. После этого скачка колебания этих трех мод происхо-
дят с согласованными фазами. Согласно теории Лэмба, колеба-
ния на частоте Vi возмущаются сигналами с «внешней» комби-
национной частотой v = 2v2 — v3, генерируемым поляризацией
третьего порядка в нелинейной активной среде.
Интересно отметить, что такие согласованные по фазе коле-
бания не были известны в оптике до развития техники оптиче-
ских мазеров, и фазовые соотношения между этими модами
нельзя проанализировать обычными спектроскопическими при-
борами, например, интерферометрами и решетчатыми или приз-
матическими спектрометрами.' Если разрешающая сила этих
приборов была бы достаточна, то можно было бы наблюдать
15. Квазиоптические резонаторы
325
только три спектральные линии: vi, v2, v3. Чтобы определить фа-
зовые соотношения между этими модами, необходимо разрабо-
тать новые типы интерферометров, измеряющих коэффициен-
ты корреляции высших порядков между амплитудами колеба-
ний [9].
Вариационный принцип в линейной теории резонатора. Ка-
саясь вариационного принципа применительно к анормальным
ядрам для резонатора, мы должны отдавать себе отчет в серьез-
ных ограничениях этого принципа — еще не изучены условия,
при которых функции сравнения в вариационном принципе обес-
печат приближение к истинному решению [10]. Численные ре-
зультаты, полученные Таном [11] и Бароном [12], и основанные
на вариационном принципе, совпали особенно хорошо в случае
малого числа Френеля с замечательными расчетами Фокса и
Ли [2] для резонатора с плоскими зеркалами. Функциями срав-
нения были собственные функции закрытого металлического
резонатора, которые можно рассматривать как собственные
функции симметричного нормального ядра.
В случае резонатора с числом Френеля порядка единицы соб-
ственные значения симметричного нормального ядра, представ-
ляющего конфокальный сферический резонатор, сильно отли-
чаются друг от друга. Разница между сферическим и плоскозер-
кальным резонаторами в случае очень малых чисел Френеля не
является столь очевидной, как в случае больших чисел Френеля.
Собственные функции конфокального резонатора были бы хоро-
шим приближением для собственных функций плоскозеркаль-
ного резонатора с малым числом Френеля.
Следовательно, комплексно сопряженное ядро К для резо-
натора с плоскими зеркалами и малым числом Френеля можно
представить через симметричное нормальное ядро L для кон-
фокального сферического резонатора
K—L-\-H, (13)
где ядро Н=К—L удовлетворяет условию
ь ь v,
||Я|| = J J |f7(s, fytdsdt < е.
а а
(14)
Так как К и L — ограниченные операторы, то оператор Н
также ограничен. Таким образом, к вышеупомянутой задаче
можно применить общую теорию возмущений для ограничен-
ного возмущения, считая Н возмущением.
Общая теория возмущения была вначале разработана для
эрмитовых операторов и затем обобщена Секефальви-Надь [14]
326
Дискуссия
и Като [15] для более общих операторов. Как было упомянуто
выше, собственные значения ядра L невырождепы и расстоя-
ние изоляции, обозначенное через d, определяется минимальным
расстоянием собственного значения Хо от остального спектра.
Тогда, согласно теории возмущения, ряд возмущений для
собственных значений и собственных функций безусловно схо-
дится, если величина возмущения ||Я|| меньше половины рас-
стояния изоляции собственного значения Хо ядра L.
Как нетрудно видеть, собственные значения, полученные в
первом порядке вариационным методом при использовании соб-
ственной функции ядра L, по существу, совпадают с первым
членом в вышеупомянутом ряду возмущений. Следовательно,
если удовлетворено вышеупомянутое условие, то функция срав-
нения в вариационном методе дает приближение к истинному
значению. Я надеюсь обсудить эту проблему более подробно
и с использованием числовых примеров.
Ввиду полного согласования теории Бойда — Когельника с
экспериментом, а также с нашими расчетами, в которых ис-
пользовался метод возмущения, следует продолжить исследо-
вания вариационного метода и метода возмущения для реше-
ния других задач.
Д-р Морган* *
Интегральные уравнения квазиоптических резонаторов —
комментарии к выступлению проф. Гамо. В дополнение к вы-
ступлению проф. Гамо я хотел бы сказать о современном со-
стоянии теории интегральных уравнений квазиоптических резо-
наторов и, в частности, обсудить применение процесса Шмидта
для нахождения собственных значений и собственных функций.
Хотя отчасти верно, что, как говорит проф. Гамо, «ядро резо-
наторного уравнения можно привести к комплексно симметрич-
ной матрице в конечномерном пространстве при помощи метода
разложения Шмидта», внимательное рассмотрение показывает,
что ситуация несколько сложнее, чем может показаться.
Рассмотрим уравнение
Kf = of, (15)
где К — интегральный оператор, соответствующий ядру K\s, t).
В методе Шмидта ) К разлагается на оператор в виде ко-
нечного ряда плюс оператор с малой нормой:
K—L-^-H, (16)
* S. Р. .Morgan, Bell Telephone Laboratories, Murray Hill, N. J.
’) Cm. [4], стр. 41.
15. Квазиоптические резонаторы
327
где
L(s, 0 = 2 ап ($) bn (t)
Л-1
И
||Я|| = |/ j\H(s, t)\2dsdt\112 <г.
(17)
(18)
Величина е несущественна для анализа, хотя в конце концов она
будет принята малой.
Оператор, обратный Н — о/, обозначим через
(Я-о/Г^-^/Н-Го). (19)
Рассматриваемый как функция о резольвентный оператор Го
нигде (кроме, быть может, значения о = 0) не имеет других осо-
бенностей, кроме полюсов, и его полюсы расположены в ограни-
ченной области о-плоскости. Вне окружности, заключающей эти
полюсы, и в частности для всех резольвента дается
рядом Неймана
(20)
п-1
где Нп есть п-й итерированный оператор от Н.
Уравнение (15) можно записать как
(21)
и преобразовать, согласно (19), к виду
(L-+-raL)f = of. , (22)
Если L(s, t) дается формулой (17), то
L (s, t) + Г0А (s, t) = S ап (s, о) Ьп (/), (23)
Л-1
где
an(s, о) = ая ($) + !>„($). (24)
Из формулы (20) видно, что
lim an(s, o) = an(s). (25)
0->0О
Решение (22) должно иметь вид
f = 2 о), (26)
ГЛ-1
328
Дискуссия
где fm — неопределенные коэффициенты. Так как функции an(s)
можно считать линейно независимыми, то подстановка (23)
и (26) в (22) приводит к системе линейных уравнений
S dnm(a)fm — afn, Д=1, 2........N, (27)
т=1
где .
dnm(o) — [ bn(t)am(t, d)dt, n=l, 2,'..., N; m=l, 2,..N.
(28)
Как известно, ненулевое решение (27) существует,
если
A(a) = det[^(a)-6nma] = 0. (29)
Величины о, для которых функция Д(а) равна нулю, являются
(если они существуют) собственными значениями первоначаль-
ного интегрального уравнения (15). Но (и это очень важно)
уравнение (29) не эквивалентно задаче о собственных значениях
для обыкновенной матрицы порядка N. Разница в том, что все
элементы в Д (о) являются функциями о, а не только диаго-
нальные элементы. Функция Д(а) в общем случае даже не мно-
гочлен от о. Так как корни Д(а) точно соответствуют собствен-
ным значениям оператора К, то число корней должно быть не-
зависимым от выбора N.
Можно, конечно, рассмотреть постоянную матрицу D=(dnm),
где
dnm = lim dnm (о) = f bn (/) am (t) di, (30)
0->oo. *
n = \, 2, .... N-, яг = 1, 2, ..., N.
Матрица D имеет не более N собственных значений, которые
являются корнями уравнения
— 6„mo]=0, (31)
в котором левая часть — многочлен от о.
Если Oj есть собственное значение D и если разность
dnm(csi) —dnm мала для всех п и пг, то можно предположить,
что Д(о) имеет корень около oj. В некоторых случаях суще-
ствование такого корня можно доказать, используя теорему
Руше и неравенства для детерминантов, но доказательство
обычно нетривиально. Трудность заключается в том, что начав
с данного ядра K(s, t), нельзя независимо устанавливать и
порядок N для вырожденного ядра L и малость остатка Н.
15. Квазиоптические резонаторы
329
Для интегральных уравнений квазиоптических резонаторов
трудность возрастает с ростом числа Френеля. Насколько мне
известно, современное состояние теории следующее. Ньюмен и
Морган [6] использовали специальное доказательство того, что
ядро К(s, t) = exp ik (s — t)2, соответствующее плоскопараллель-
ным лентам, имеет по меньшей мере два ненулевых собствен-
ных значения. Согласно теореме Фредгольма [18], каждое непре-
рывное ядро с ненулевым следом имеет по меньшей мере одно
Ненулевое собственное значение. На применимость этой теоремы
в данном случае указал Кохран [19]. Пока не доказано, что
любое ядро для резонатора, кроме как для конфокального, т. е.
ядра exp(2ikst), имеет более чем два ненулевых собственных
значения, хотя естественно предположить, что все ядра, кото-
рые возникают в теории резонаторов, имеют бесконечно много
собственных значений.
Известный метод приближенного решения линейных интег-
ральных уравнений заключается в разложении.ядра и неизвест-
ной функции в ряд по полной системе базисных функций, что
приводит к преобразованию интегрального уравнения в беско-
нечную систему линейных алгебраических уравнений. Затем
бесконечная система сводится к ограниченной усеченной системе,
и численными методами находится решение для собственных
значений и собственных векторов усеченной матрицы. Здесь
появляется возможность выбора оптимальных базисных функ-
ций. Например, как указал проф. Гамо, лучшее среднее ква-
дратичное приближение к произвольному ядру J?2 при помощи
ядра фиксированного конечного ранга получается при использо-
вании функций разложения Шмидта (сингулярных функций)
[22] ядра, т. е. собственных функций эрмитовых ядер КЮ и
К+К. Можно надеяться получить хорошее приближение для не-
скольких первых собственных значений и собственных функций,
если усеченный ряд для ядра является в некотором смысле до-
статочно хорошим приближением к точному ядру. Однако на
практике бывает нелегко найти такую оценку ошибки, вызван-
ной усечением, которая была бы строгой и в то же время эф-
фективно применимой. В этом случае вычислитель вынужден
делать проверки, проводя, например, несколько просчетов и вы-
ясняя, насколько результаты чувствительны к тому, где произ-
ведено усечение уравнений.
Самый существенный недостаток этого метода применительно
к квазиоптическим резонаторам заключается в том, что он прак-
тически ограничен теми случаями, в которых число Френеля и.но-
мер моды малы, в то время как наибольший интерес представ-
ляет резонатор, в котором число Френеля, а возможно й номер
моды, велики. Я не знаю каких-либо обоснованных расчетов^
330
Дискуссия
сделанных этим методом, которые содержали бы что-нибудь но-
вое по сравнению с первоначальными расчетами Фокса и Ли
[2] с помощью метода итераций.
Что . касается вариационных методов для квазиоптических
резонаторов, то недостатки последних для приближенного на-
хождения собственных значений комплексно симметричных ядер
хорошо известны [10, 20, 21]. Основная трудность заключается
в том, что для комплексно симметричных ядер нет ничего по-
добного методу Релея — Ритца, который для действительного
симметричного или комплексного эрмитового ядра позволяет по-
степенно улучшать приближенные собственные значения. Кро-
ме того, в случае комплексного ядра нельзя сказать, которое
из двух вариационных приближений к собственным значениям
лучше. Если проф. Гамо в состоянии доказать, что при опреде-
ленных условиях какой-либо вариационный метод дает наилуч-
шее приближение к точным собственным значениям (или соб-
ственным функциям), которое может быть получено с помощью
данного ряда функций сравнения, то это будет, насколько мне
известно, первая теорема этого типа для комплексно симметрич-
ных ядер.
Проф. Гамо
Выступление д-ра Моргана по поводу метода разложения
Шмидта для меня особенно интересно, так как разъясняет важ-
ный момент, который, по-видимому, обсужден недостаточно по-
дробно в книгах по интегральным уравнениям. Конечно, приве-
денная матрица dnm(o) конечной размерности должна быть
функцией неизвестного собственного значения о. Если расстоя-
ние между собственным значением ц для L(s, t) и неизвестным
собственным значением а мало, то мы можем с некоторым при-
ближением заменить dnm(a) на <Лпт(ц). Я думаю, что процесс
разложения может оказаться полезным при выводе и оценке
приближенных методов для оптических резонаторов.
Для резонаторов, у которых число Френеля велико, мы
пытаемся выполнить некоторые надежные расчеты при помощи
метода разложения Шмидта. Замечу, что наибольший практи-
ческий интерес представляют резонаторы, в которых существует
только одна мода. После открытия нескольких типов высоко-
добротных переходов резонаторы со сравнительно малым чис-
лом Френеля стали практически возможными и могут быть
полезны с точки зрения получения одномодового режима; точ-
ные расчеты и эксперименты с резонаторами, имеющими малое
число Френеля, будут тоже важны.
15. Квазиоптические резонаторы
331
Проф. Торальдо да Франчаа
Я собираюсь сделать необычную для ученого вещь. Я буду
говорить не о своей работе, а о работе другого ученого. Более
того, я собираюсь признать, что его работа гораздо значитель-
нее моей. Я хотел бы говорить о последних работах советских
ученых в области теории резонаторов, а именно об исследова-
ниях Вайнштейна [22], который развил очень изящный и мощ-
ный метод решения задачи о резонаторе с плоскими зеркалами.
Идея метода очень проста и, кажется, приходила на ум мно-'
гим, но только Вайнштейн смог развить ее количественно, так
как он разработал необходимую для этого теорию излучения с
открытого конца волновода.
Пусть мы имеем плоский волновод. Волна изнутри волно-
вода идет к открытому концу, причем часть энергии излучается,
а часть отражается внутрь волновода или в виде той же моды,
что и падающая, или в виде другой моды. Вайнштейн решил эту
сложную задачу дифракции методом Винера — Хопфа, который
слишком сложен, чтобы его здесь обсуждать. Он вычислил ко-
эффициент отражения для различных типов волн, возбу-
жденных падающей волной. В частности, если мы имеем
моду, частота которой лишь немного выше критической, так
что она еще может распространяться в волноводе, то коэффи-
циент отражения этой моды велик и приближается к еди-
нице.
Теперь предположим, что плоский волновод открыт не только
с одного конца, но также и с другого. Тогда получаем резона-
тор с плоскими зеркалами. Мы видим, что исследуемая мода
в точности совпадает с модой такого резонатора. Вблизи своей
критической частоты волна в волноводе состоит из двух волн,
распространяющихся в двух направлениях, почти перпендику-
лярных пластинам. Именно это и происходит в резонаторе. Если
мы умеем вычислить коэффициент отражения от открытых кон-
цов, то мы можем найти и резонансную частоту.
Мы можем определить резонансную частоту, добротность
(т. е. потери), сдвиг фаз и т. д. Замечательно то, что Вайн-
штейн решил задачу для любых значений параметров и реше-
ние, как оказывается, выражается через некоторые сложные
функции, которые в принципе можно найти. При высоких зна-
чениях Q все упрощается. Мы можем найти асимптотическое
представление решения, которое очень удобно и дает выраже-
ние для интересующих нас параметров в очень простой форме.
С помощью этой теории можно получить замкнутую аналитиче-.
скую форму для параметров, вместо того чтобы численно ре-
шать интегральные уравнения на вычислительной машине.
332
Дискуссия
Совпадают ли результаты, полученные Вайнштейном, с выво-
дами теории, развитой, например, Фоксом и Ли? Что касает-
ся Q и смещения фаз, то результаты согласуются очень хорошо,
я бы сказал, необыкновенно хорошо. Некоторая разница наблю-
дается в распределении амплитуд на зеркалах. В распределении
амплитуд, рассчитанном Фоксом и Ли, есть небольшая волни-
стость. Эта волнистость отсутствует в приближенной теории
Вайнштейна, так как она не учитывает отражение высших мх>д.
Он мог бы в принципе учесть это отражение, но для расчетов Q
они не представляют интереса, и нужны только для вычисления
точного распределения энергии мод.
Нет необходимости подчеркивать, что такой метод очень
ценен, потому что позволяет найти нужные параметры для лю-
бого числа мод, а не только для одной или двух.
Д-р Губо
Рассчитал ли Вайнштейн форму резонансной кривой? Экс-
перименты Шайба, Кинга и Тацугути с возбуждением диполь-
ным источником показали, что резонансная кривая очень асим-
метрична по сравнению с контрольным резонатором.
Проф. Торальдо ди Франчиа
Насколько мне известно, Вайнштейн рассчитал самую низ-
шую из мод, но нет и намека на то, что упоминаемая кривая
должна быть асимметричной.
Проф. Карп *
Проф. Торальдо ди Франчиа говорил о некоторых работах
Вайнштейна, в которых было показано, как рассчитать резо-
нансные свойства открытого резонатора, образованного парой
параллельных пластин. На мой вопрос, как далеко зашел Вайн-
штейн в решений этой задачи, Торальдо ответил, что Вайнштейн
рассмотрел тадже случай с параллельными круглыми дисками,
а возможно, и с прямоугольными пластинами.
Отмечу, что диапазон применения таких методов гораздо
шире, чем скалярные задачи, упомянутые выше. Необходимую
* S. Karp, Courant Institute of Mathematical Sciences, New York Uni-
versity.
15. Квазиоптические резонаторы
333
информацию можно получить из решения соответствующей диф-
ракционной задачи. Эту задачу решают для действительного
волнового числа k и заданного возбуждения, а затем для комп-
лексного числа k, так что решение для данного падающего поля
исчезает. Задача сводится к нахождению комплексных волно-
вых чисел, для которых существует решение однородной задачи,
т. е. задачи без возбуждения. Анализ можно сильно упростить
для широкого круга задач, для которых он сводится к решению
алгебраических уравнений, что приводит в случае низких по-
терь к решению трансцендентного уравнения .методом возму-
щения.
Предположим, что исследуемую систему можно разделить
на конечное число М подсистем и что ответная реакция каждой
подсистемы на возбуждение произвольным падающим полем
при отсутствии других систем найдена- экспериментально или
аналитически. По существу, нужно знать реакции только на
ограниченный набор различных полей. Реакция каждой си-
стемы, рассчитанная вблизи любой другой системы, должна
представлять собой линейную комбинацию некоторых базисных
функций. Эта другая система возбуждается, таким образом, ли-
нейной комбинацией базисных функций. Ее реакция в свою оче-
редь должна быть линейной комбинацией реакций на эти базис-
ные функции. Эти реакции, просуммированные по всем систе-
мам, должны затем привести в соседстве с каждой системой
к другой комбинации базисных функций.
Базисные функции включают функции, представляющие ре-
акции каждой отдельной системы на внешнее падающее поле.
Математическая запись этих соображений приводит к алгебраи-
ческим уравнения.м для коэффициентов базисных функций. Со-
ответствующий детерминант включает реакцию изолированных
подсистем и зависит от волнового числа k. Он является анали-
тической функцией волнового числа, и однозначность решения
не позволяет ему обратиться в нуль для Im &>0 [здесь прини-
мается зависимость от времени в виде ехр (—twZ)]. Однако его
корни в нижней полуплоскости дают нужные комплексные ре-
зонансные частоты. Если индивидуальные реакции известны
экспериментально только для действительного k, то можно при-
менить аналитическое продолжение. В интересующем нас случае
низких потерь оно упрощается, так как мнимая часть k должна
быть малой. Поэтому достаточно использовать несколько пер-
вых членов ряда Тейлора. Разлагая, например, детерминант
F(k), получаем
F (fe) = F (а + /т) = F (а) + ixF' (а) - F" (а) ...,
334
Дискуссия
где т — мнимая часть k, которая считается малой. Затем нахо-
дим от и im. Исследование упрощается тем, что корни о=от
должны быть близки к резонансным значениям для закрытого
объема, а возможно, и к действительным корням псевдорезо-
нанса для дифракционной задачи об открытом объеме.
Чтобы проиллюстрировать характер разложения и выбор ба-
зисных функций, заметим, что для двух тел конечных размеров
поле, возбуждаемое каждым телом, действует на другое тело
как конечная сумма мультиполей при условии, что расстояние
между телами достаточно велико по сравнению с их размерами
и с длиной волны. Если отношение размера тела к длине волны
невелико, то на второе тело падает поле, состоящее из плоской
волны и из ее производных (по углу падения), т. е. членов
типа
eikx — ехр (х cos р _|_ у Sin р) |
ikyeikx = ехр Ik (х cos р -|-у sin р) |р=0.
Аналогично, сравнительно длинную секцию волновода можно
рассматривать как два противоположно ориентированных полу-
бесконечных волновода. На каждый конец падают по одной или
более распространяющихся волн, приходящих с другого конца,
а также волны, идущие по внешней стороне волновода. Если
возможны поверхностные волны, они тоже действуют как воз-
буждение и при этом преобладают. Следует также отметить,
что реакция каждой подсистемы на волне одного типа при паде-
нии волны другого типа удовлетворяет условию взаимности, что
приводит к некоторым упрощениям.
Следует отметить, что частичные реакции часто можно вы-
числить приближенно, пользуясь грубыми, но простыми и хо-
рошо испытанными методами, например методом Кирхгофа —
Релея. Это делает излишним дальнейшее разложение на более
простые подсистемы.
Проф. Бергштейн *
Практически все исследования оптических резонаторов, ко-
торые мы имеем в литературе, основаны на интегральных урав-
нениях для мод резонатора, получающихся из скалярной
формулировки математически не последовательной теории Кирх-
гофа (или, что то же самое, из скалярной формулировки прин-
ципа Гюйгенса). Чтобы решить это уравнение для мод резона-
* L, Bergstein, Polytechnic Institute of Brooklyn,
15. Квазиоптические резонаторы
335
торов, его упрощают, используя параболическое приближение
для расстояния между двумя точками на поверхности двух тор-
цовых отражателей резонатора.
Верно, что почти во всех исследованных до сих пор практи-
ческих случаях результаты, вычисленные с помощью этого при-
ближенного интегрального уравнения, находятся в полном
соответствии с экспериментальными данными. Есть, однако,
случаи, где необходим другой подход или где параболическое
приближение может привести к неверным результатам.
Например, очевидно, что принцип Гюйгенса можно эффек-
тивно применить только к резонаторам, наполненным изотроп-
ной и однородной средой. Для резонаторов, заполненных анизо-
тропной средой, принцип Гюйгенса неприменим; для резонато-
*ров, заполненных неоднородной средой, нужны дальнейшие
приближения, чтобы вывести интегральное уравнение для мод
резонаторов. Кроме того сомнительно, можно ли использовать
параболическое приближение для резонаторов с торцовыми
рефлекторами, размеры которых не малы по сравнению с рас-
стоянием между ними.
Можно вывести более общее интегральное уравнение, если
вместо метода Кирхгофа использовать более строгий метод, ос-
нованный на дифракционных формулах Релея. Решение можно
получить с помощью разложения электромагнитного поля внутри
полости резонатора на составляющие волны, характерные для
заполняющей среды и геометрии резонатора. Однако в литера-
туре нет ни одного общего вывода интегрального уравнения,
основанного на формулировке Релея.
Используя самосогласованную формулировку Релея и разла-
гая поле внутри резонатора в угловой спектр плоских или ци-
линдрических волн, получаем интегральное уравнение для мод
оптических резонаторов с плоскопараллельными торцовыми от-
ражателями и однородной (и линейной) средой. Интегральное
уравнение можно решить относительно распределения поля или
относительно углового спектра плоских волн. Для резонаторов,
заполненных изотропной средой, мы решили интегральное урав-
нение относительно спектра (квазичисленным методом), не на-
кладывая каких-либо ограничений на относительные размеры
зеркал и расстояние между ними. Мы сравнили полученные ре-
зультаты с предсказанными по интегральному уравнению в при-
ближении Гюйгенса (т. е. интегральным уравнением с парабо-
лическим приближением). Мы получили превосходное соответ-
ствие между решениями этих двух интегральных уравнений для
резонаторов, линейные размеры зеркал которых меньше их
взаимного удаления или равны ему. Однако даже для резонато-
ров с линейными размерами зеркал, значительно превосходящими
336
Дискуссия
расстояние между ними, получено хорошее совпадение ме-
жду результатами, предсказанными обоими интегральными
уравнениями. До тех пор пока линейные размеры рефлектора'
больше, скажем, расстояния в 10Х, распределение поля резона-
торных типов зависит в основном от числа Френеля и только
в малой степени от отношения линейных размеров зеркал к рас-
стоянию между ними. Дифракционные потери и резонансные
частоты также мало зависят от отношения размеров зеркал к
удалению. Например, для чисел Френеля, меньших 100, дифрак-
ционные потери увеличиваются менее чем на 20% при измене-
нии отношения размеров рефлектора к удалению от 0 до 10
(при фиксированном числе Френеля).
Были исследованы также плоскопараллельные резонаторы
(из бесконечных лент и круглых торцовых зеркал), погружен-
ные в линейную неоднородную среду с диэлектрической прони-
цаемостью, изменяющейся как квадрат расстояния. В этом слу-
чае получено, что вырождение моды, предсказанное приближен-
ным интегральным уравнением, не имеет места для решения
более точного интегрального уравнения.
Сравнение более общего характера решений приближенного
интегрального уравнения, выведенного из принципа Гюйгенса,
и более точного интегрального уравнения, основанного на фор-
мулировке Релея, представляло бы значительный интерес.
Л ату ре т *
Я кратко опишу работу по теории резонаторов, проделанную
моими коллегами. Работа основана на вариационных расчетах
потерь мод и резонансных частот плоскопараллельного ленточ-
ного резонатора. Интегральное уравнение, описывающее эту за-
дачу, представляется как условие стационарности и, применяет-
ся вариационный метод Релея — Ритца. Этот способ имеет, од-
нако, недостаток, заключающийся в том, что ядро интегрального
уравнения, хотя и симметрично, но не эрмитово, и поэтому нель-
зя предсказать, насколько хороши будут результаты для соб-
ственных значений. Барон использовал условие стационарности
и применил разложение, асимптотически справедливое для
больших чисел Френеля, и таким образом сконструировал мо-
дель открытого резонатора, который можно описать через соот-
ветствующие величины для закрытого резонатора с импеданс-
ными стенками. Ему удалось точно решить дифференциальное
уравнение, описывающее эту модель.
* J. Т. La Tourrette, TRG, Melville, N. Y.
15. Квазиоптические резонаторы
337
Несколько слов об экспериментальных работах, проделан-
ных нашей группой. Недавно мы исследовали резонаторы с
очень малым числом Френеля. Если стоит задача максимизи-
ровать выходную мощность лазера в одномодовом режиме (т. е.
при наличии в резонаторе колебания низшего порядка — един-
ственной частоты и единственного пространственного распреде-
ления), то можно показать, что выходная мощность резонатора
зависит от избирательности.
Насколько можно поднять усиление среды лазера выше по-
рога возникновения колебания в одномодовом режиме? Усиле-
ние лазера будет в этом случае в большей степени ограничено
порогом возникновения следующей моды, чем средой лазера.
Можно показать, что дискриминация мод, т. е. величина, на ко-
торую усиление лазера может превысить порог для моды низ-
шего порядка, растет при уменьшении числа Френеля.
Мы экспериментировали с резонаторами, для которых числа
Френеля порядка 0,1 и меньше. Был испытан гелий-неоновый
лазер на 3,39 мк с рефлектором на одном конце лазера, огра-
ниченным площадью в один квадратный миллиметр, и с рас-
стоянием между зеркалами 60 см. В подтверждение этой ра-
боты Барон и Ньюстейн [23] рассмотрели задачу о резонаторах
с малыми числами Френеля. Ядро интегрального уравнения
для круглого рефлектора есть функция Бесселя. При помощи
полиномиального разложения, которое пригодно для малых чи-
сел Френеля, можно точно решить эту задачу. Получен есте-
ственный результат, что коэффициент потерь для моды низ-
шего порядка изменяется как квадрат числа Френеля, а для
последующей моды высшего порядка он изменяется как четвер-
тая степень числа Френеля. Эти результаты скоро будут опуб-
ликованы.
ЛИТЕРАТУРА
1. Gamo Н., в книге Progress in Optics, ed. E. Wolf, vol. 3, 1964, § 5.
2. Fox A. G., Li T„ Bell Syst. Techn. Journ., 40, p. 453 (1961).
3. R i e s z F., Sz. Nagy В. V., Lemons d’Analyse Fonctionelle, Budapest,
1952. (Имеется перевод: Ф. Рисе,- Б. Секефальви-Надь, Лекции
по функциональному анализу, М., 1954.)
4. Smithies F„ Integral Equations, London, 1958.
5. Yoshida K., Lectures on Differential and Integral Equations, New York,
1960.
6. Newman D. J., Morgan S. P., Bell Syst. Techn. Journ., 43, 113 (1964).
7. Bennett W. R., Jr., Appl. Optics, 1, Suppl., p. 24 (1962).
8. Lamb W. E„ Jr., Phys. Rev., 134A, 1429 (1964).
9. G a m о H., Journ. Opt. Soc. Am., 54, 571 (1964).
10. Morgan S. P., IEEE Trans., MTT-11, 191 (1963); MTT-12, 254 (1964).
11. Tang C. L„ Appl. Optics, 1, 768 (1962).
12. BaroneS. R., Journ. Appl. Phys., 34, 831 (1963),
22 Зак. 274
338
Дискуссия
13. Kato Т., Progress Theory. Phys., 4, 514 (1949).
14. Sz. Nagy В. V., Acta Sci. Math. Szeyed, 14, 125 (1951).
15. Kato T., Journ. Math. Soc. Japan, 4, 323 (1952).
16. Cop son E. T., Theory of Functions of a Complex Variable, London, 1935,
p. 119.
17. Канторович Л. В., Крылов В. И., Приближенные методы высшего
анализа, М. — Л., 1962.
18. Fredholm I., Acta Math., 27, 365 (1903).
19. С о с h г a n J. A., Bell System Techn. Journ., в печати.
The Existence of Eigenvalues for the Integral Equations of Laser Theory.
20. F о x A. G., Li T., Morgan S. P., Appl. Optics, 2, 544 (1963).
21. Kaplan S., Morgan S. P., IEEE Trans., MTT-12, 254 (1964).
22. В а й н ш т e й н Л. А., ЖЭТФ, 44, № 3, 1050 (1963).
Открытые резонаторы для квантовых генераторов света.
23. BaroneS. R., N е w s t е i n M. C., Applied Optics, в печати,
Research on Properties of Laser Devices,
Ill
КВАЗИОПТИЧЕСКИЕ
ВОЛНОВОДНЫЕ
ЭЛЕМЕНТЫ
22’
16
ТЕОРИЯ И КОНСТРУИРОВАНИЕ
КВАЗИОПТИЧЕСКИХ ВОЛНОВОДНЫХ ЭЛЕМЕНТОВ
К. Као*
Изложена квазиоптическая теория, развитая для анализа волноводных
элементов большого сечения. Теория основывается на представлении поля в
волноводе в виде суммы плоских волн, и раздельно рассматривает возбу-
ждение волновода каждой волной через некоторую апертуру или на неодно-
родности. Для подтверждения справедливости теории приводятся эксперимен-
тальные данные.
Обсуждаются теоретические и практические вопросы измерений, основан-
ных иа резонансных методах. Эти методы дают возможность эксперимен-
тально определить свойства волн в волноводных элементах широкого се-
чения.
Рассматриваются общие вопросы, касающиеся работы таких волновод-
ных систем.
§ 1. ВВЕДЕНИЕ
В дециметровом и сантиметровом диапазонах одноволновые
волноводные устройства обладают превосходными свойствами.
В большинстве случаев у них достаточно низкие потери и впол-
не приемлемые размеры. Кроме того, одноволновый волновод
имеет то преимущество, что все моды высшего порядка являют-*
ся быстро спадающими и с ними не связан поток энергии. Этот
реактивный эффект может быть соответствующим образом уч-*
тен или использован в зависимости от обстоятельств.
В диапазоне же миллиметровых и субмиллиметровых волн
одноволновые волноводные устройства имеют ряд существен-
ных недостатков. Во-первых, потери резко возрастают, так что
на длине волны 4 мм потери в волноводах часто доходят до
5 дб]м. Во-вторых, размеры этих устройств настолько малы, что
почти невозможно выдержать требуемые относительные до-
пуски.
* К. С. Као, Standard Telecommunication Laboratories Ltd., Harlow,
Essex, England,
342
К. Као
Поэтому для работы в миллиметровом и субмиллиметровом
диапазоне были предложены «многоволновые волноводные» эле-
менты. «Многоволновым волноводом» мы называем здесь вол-
новод, работающий на основном типе волны, размеры которого,
однако, таковы, что в нем может распространяться большое
число высших типов волн в случае их возбуждения. В таких
устройствах можно ожидать значительного уменьшения потерь,
а также некоторого улучшения допустимой ширины полосы. При
выборе подходящей конструкции допуски на размеры могут
быть менее жесткими.
Элементы, которые будут рассматриваться ниже, предназна-
чены для металлических волноводов прямоугольного сечения,
в которых электромагнитное поле распространяется в основном
в виде волны Hi0. Основой всех устройств является 3-децибель-
ный направленный ответвитель, изображенный на фиг. 1. Из
него могут быть получены следующие волноводные элементы: ат-
тенюатор, фазовращатель, индикатор стоячей волны, волномер
и т. д. Такая система была предложена в работе [I], и было
16. Квазиоптические волноводные элементы
343
опубликовано несколько сообщений [2—4], в которых описыва-
лись способы практического выполнения этой системы.
В данной работе рассматриваются методы расчета парамет-
ров волноводных элементов, теоретические и практические во-
просы методики измерений и основные проблемы, касающиеся
работы многоволновой системы.
Обозначения
0 — угол падения фронтов плоских волн, отсчитываемый
от оси волновода;
— Др-компонента n-го типа волны;
W — результирующая амплитуда фп;
—дипольный момент;
hn — волновое число для n-го типа волны, равное
У № + у2 = ПЛ]с1',
d — ширина волновода вдоль оси х;
Хо — длина волны в свободном пространстве;
(0)—фазовый множитель e~je.
В основе теории лежит новый квазиоптический метод'). Сущ-
ность его заключается в том, что поле в волноводе представ-
ляется в виде двух пересекающихся плоских волновых фронтов
(плоских волн), и рассматривается раздельно возбуждение каж-
дой волной через некоторую апертуру или на неоднородности.
Результирующее поле описывается распределением по типам
волн. Для измерений в многоволиовой волноводной системе осо-
бенно удобны методы, в которых используется явление резо-
нанса на паразитной волне, когда определенная волна высшего
порядка оказывается «запертой» в системе. Такой метод ис-
пользовался раньше, правда, довольно ограниченно, при иссле-
дованиях многоволнового волноводного конусного перехода
[5—8}. В настоящей работе анализируются две схемы, и на ос-
нове каждой из них дается примерный способ практического из-
мерения.
§ 2. КВАЗИОПТИЧЕСКАЯ ТЕОРИЯ
Как хорошо известно, электромагнитное поле волн типа Нп0,
распространяющихся в прямоугольном волноводе, может быть
представлено в виде двух бегущих плоских волн, распростра-
няющихся под углами ±0 с осью волновода. В плоскости апер-
туры или в месте неоднородности облучение, обусловленное
электромагнитным полем собственной волны, можно рассматри-
вать как облучение, обусловленное двумя плоскими волнами,
*) См. примечание к стр. 361. — Прим, ред.
344
К. Као
взятыми по отдельности. Предполагается, что путь распростра-
нения фронтов плоских волн в этой области определяется зако-
нами геометрической оптики. Результирующее поле получается
из решения задачи возбуждения волновода при заданном рас-
пределении поля в апертуре.
Свойства основного элемента — 3-децибельного ответвите-
ля — можно понять, рассматривая прямоугольный уголок, изо-
браженный на фиг. 2, так как из двух таких уголков образуется
крестообразный узел ответвителя. Задача об уголке формули-
руется следующим образом. Фронты плоских волн 1 и 2 под-
ходят к месту соединения волноводов (фиг. 3). По законам
геометрической оптики волновые фронты 1 и 2' после отраже-
ния от наклонного зеркала могут быть разложены на 4 состав-
ляющие, отмеченные цифрами 1', 2', 2" и 1" (фиг. 4). Первые
три составляющие освещают апертуру волновода 2, создавая
прямую бегущую волну. Последняя, освещает волновод 1 так,
что образуется обратная волна. Результирующее поле вычис-
ляется следующим образом. Распределение на апертуре пред-
ставляется в виде решетки линейных диполей с определенными
фазовыми и амплитудными соотношениями. Затем решается за-
дача возбуждения волновода единичным линейным диполем.
Результирующее действие всей решетки диполей дает возбуж-
дение, вызванное заданным облучением.
Решение для возбуждения волновода линейным электриче-
ским диполем, расположенным в точке г=0 и х=хх, приводится
в приложении 1. Запишем Ду-компоненту для волны Нп0 в виде
(Еу)п = ^n=j(—1)" sin A«X1 sin hn ~
где К — величина дипольного момента, являющаяся функ-
цией хг, K(xi) соответствует определенному освещению апер-
туры. Результирующая амплитуда возбужденной волны п-го
порядка есть суперпозиция всех таких компонент. Она полу-
чается интегрированием по апертуре
a d
Чп = j
о о
Для случая многоволнового волновода, т. е. когда угол па-
дения 0 плоской волны мал и sin 0«s0, апертурное распределе-
ние можно вывести из геометрической оптики. Полученные
результаты дают возможность описать действие уголка. Для
удобства интерпретации действие уголка характеризуется сле-
дующими параметрами:
dxx = /' sin hn (fi — d)^ /C(xi) sin hnxx dxx.
Фиг. 3. Фронты плоских волн, падающих
на соединение.
Фиг. 4. Волновые фронты после отражения.
346
К. Као
а) прямым преобразованием волн, т. е. мощностью, пере-
шедшей в каждую прямую бегущую волну высшего порядка;
б) обратным преобразованием волн, т. е. мощностью, пере-
шедшей в каждую обратную бегущую волну высшего порядка;
в) потерями на преобразование, т. е. потерями основной
волны, вызванными переходом мощности во все волны высшего
порядка;
г) частотной характеристикой;
д) обратным преобразованием, т. е. свойством уголка, по
отношению к падающей волне высшего порядка.
В работе [9] показано следующее:
1. На уголке возбуждаются все распространяющиеся моды
высшего порядка Нп0. В волнах высшего порядка мощность
распределяется таким образом, что относительная мощность
каждой волны увеличивается с возрастанием порядка волны.
3-сантиметровый диапазон Размер 12А
Теория Эксперимент Теория Эксперимент
Прямые рас- пространяю- щиеся вол- ны Семейство Нп0 до п = 5. Амплитуда увеличивается с увеличе- нием п Волны с п = 2, 3, 4 обнаружи- ваются четко; волна с п = 5 присутствует Семейство Нпо до и== 11. Амплитуда увеличивается с увеличе- нием п Волны с п = 3, 4, 5, 6, 7, 8, 9 обнаружи- ваются четко; волны с п = 2, 10 присутст- вуют; волны с п = 11 нет
Обратные распростра- няющиеся волны Семейство Нпо до п = 5* Амплитуда волн с п = 3 и 4 порядка 60—100% от амплитуды прямых волн Семейство Нпо до п = 11 * Амплитуды, по-видимому, имеют тот же порядок, что прямые волны
Потери на преобразо- вание, дб 0,4 0,5 0,04 0—0,3
* Теория дает, что в обоих случаях амплитуда увеличивается с увеличением л. Волны
с четными номерами —прямые. Амплитуда волн с нечетными номерами того же порядка,
что н амплитуды прямых волн.
16. Квазиоптические волноводные элементы 347
В идеальном волноводе максимальной мощностью обладает
волна порядка гамакс, где гаМакс равно 2Я/Л0 или самому близкому
целому числу, меньшему 2d/io- В реальном волноводе из-за влия-
ния омических потерь максимальная мощность заключена в
волне, порядок которой несколько меньше пмаКс>
2. Амплитуды прямой и обратной распространяющихся волн
высшего порядка имеют одинаковый порядок величины.
3. При постоянной частоте потери па преобразование умень-
шаются по мере того, как размеры волновода увеличиваются.
4. Частотную зависимость можно записать в виде функции
угла падения 0. Для волновода с очень большим количеством
волн ширина полосы может быть большой.
5. Эффект обратного преобразования также можно харак-
теризовать изменением угла падения 0.
Свойства З-децибелыюго ответвителя можно определить на
основе характеристики прямоугольного уголка в Я-плоскости.
Тем самым мы найдем свойства всех устройств, получаемых из
3-децибельного ответвителя.
В таблице представлены некоторые экспериментальные дан-
ные, иллюстрирующие согласие между результатами измерения
и теорией.
§ 3. ИЗМЕРЕНИЯ
Оценка характеристик многоволновых устройств может быть
проведена различными специальными методами, сложность ко-
торых зависит от объема необходимых данных. Требуются дан-
ные двоякого рода:
а) поведение волны Яю, т. е. отражение и потери при про-
хождении волны Яю;
б) поведение волн Яп0, т. е. мощность отдельных паразит-
ных волн и общая мощность паразитных волн, распространяю-
щихся как в прямом, так и в обратном направлении (прямое
направление — направление потока мощности волны Я10).
Если измерительное устройство не вызывает заметного пере-
распределения энергии волн, при измерении коэффициента стоя-
чей волны и затухания волны Яю может быть использован обыч-
ный одноволновый метод. Но в измеренное затухание вероятно
будут все же входить и потери на преобразование. Истинная ве-
личина омических потерь может быть получена только путем
измерения всей мощности, содержащейся в паразитных волнах.
Существует ряд методов измерения мощности паразитных
волн, но они требуют больших затрат времени и довольно тру-
доемки, и, хотя теоретически можно получить полную информа-
цию о типдх волн, практически, если число воли больше пяти,
трудно добиться успеха, используя любой из этих методов.
348
К. Као
Основная трудность определения типов волн состоит в том,
что каждая волн-а является членом гармонического ряда Фурье
и поэтому характеризуется амплитудным и фазовым коэффи-
циентами. Таким образом, число требуемых уравнений равно
удвоенному числу волн. Каким бы методом мы ни пользова-
лись, если число волн равно п, то для получения полной инфор-
мации требуется найти (2п)2 коэффициентов.
По-видимому, наиболее перспективной для анализа свойств
волноводных элементов является методика измерения, основан-
ная на явлении резонанса паразитной волны. Она представляет
большие возможности для анализа распределения мод. Это
обусловлено тем фактом, что при резонансе задача может быть
сведена к задаче двух волн.
Разработанный нами метод дает возможность:
а) показать наличие паразитных волн в схеме известной кон-
фигурации и определить наиболее опасный эффект, который
при этом может иметь место, т. е. эффект резонанса паразит-
ной волны;
б) определить действительное число присутствующих волн;
в) определить мощность волны определенного вида;
г) определить отношение прямой и обратной компонент па-
разитной волны.
Таким образом, с помощью этого метода можно быстро
произвести оценочный анализ свойств устройства, а в случае
необходимости получить также все сведения о типах волн.
Теоретически преобразование волн на-^неоднородности в мно-
говолновой волноводной системе описывается 4Д^-полюсником
без потерь, который характеризуется унитарной матрицей рас-
сеяния порядка 2N, где N — число распространяющихся собст-
венных волн. В системе с малым преобразованием волн, где
мощность всех паразитных волн очень мала, можно заставить
одну из паразитных волн резонировать в соответствующем кон-
туре и тогда по величине она будет преобладать над всеми дру-
гими паразитными волнами. При таких условиях схема может
быть описана с помощью четырехполюсника, который характе-
ризуется матрицей рассеяния 4-го порядка.
Следуя общепринятым обозначениям, неоднородность можно
представить так, как показано на фиг. 5. Здесь а и b — «падаю-
щее» и «отраженное» напряжения соответственно, нормализо-
ванные таким образом, что средняя падающая мощность была
равна Угаа*. Они связаны соотношением
b = Sa,
где S — матрица рассеяния соединения.
16. Квазиоптические волноводные элементы
349
При условии резонанса, как показано выше, матрица рас-
сеяния приводится с понижением порядка к следующей:
•$11 •$12 •$13 •$14
•$12 •$22 •$23 •$24
•$13 •$23 •$33 •$34 индексы относятся к линиям.
_ *$14 •$24 •$34 •$44 _
Линия 1 представляет собой входную линию искомой волны,
линия 2 — выходную линию искомой волны, линия 3 — линию
прямой бегущей паразитной волны и линия 4 — линию обрат-
ной бегущей паразитной волны.
Если с помощью согласующих устройств настроить систему
так, чтобы линия 1 была согласована при условии согласования
линий 2, 3 и 4, то матрица рассеяния запишется следующим об-
разом:
- 0 1 *$12 1 [((S13|2-|S24I2) + 1 -$131 |«$141
1 *$121 +(1ЗД-1-$2з12)],/! | -$231 1 -$24 1
[(|512|2 -[•$34 |2) +
1 «$131 I *$23 1 +(1*$14 12-|523 |2)]’/2 1-$34|
' [(IS12I2- 1534П +
_|5ц1 1 *$241 l*$34 1 + (l‘$13|2+l‘$24l2)],/,_
350
К. Као
При исследовании неоднородности резонансным методом воз-
можны два варианта схемы (фиг. 6 и 7). Плечи 3 и 2 четырех-
полюсника замкнуты накооотко.
Оба варианта анализируются в приложении 3 для случая,
когда обратная связь пренебрежимо мала, т. е. когда матрица
4-го порядка сводится к матрице 3-го порядка (см. приложе-
ние 2). Устанавливаются соотношения между измеряемыми ве-
личинами, такими, как коэффициенты передачи и отражения и
коэффициенты связи волн; пользуясь этими соотношениями,
можно выразить коэффициент связи через измеряемые вели-
чины. Отсюда вытекают различные методы измерения. В прило-
жениях 4 и 5 рассматривается метод измерения для каждой из
двух возможных конфигураций схемы.
Если обратной связью нельзя пренебречь, то задача сильно
усложняется математически. Тем не менее влияние обратной
связи можно оценить путем анализа матрицы (1) на основе
конкретных физических соображений.
Матрица (1) описывает случай, когда линия 1 предполагает-
ся согласованной. Коэффициенты отражения в плечах выра-
жаются через коэффициенты связи. Можно доказать, что коэф-
фициенты отражения имеют тот же порядок, что и коэффи-
16. Квазиоптические волноводные элементы
351
циенты связи. К этому можно прийти, рассуждая следующим
образом.
В пределе, т. е. когда обратная связь незначительна, связь
линий 1 и 2 равна связи линий 3 и 4, а связь линий 1 и 3 равна
связи линий 2 и 4. Тогда вполне естественно ожидать, что при
малой обратной связи коэффициент связи Si2 мало отличается
от S34, a S13 мало отличается от S24- Следовательно, отражение
мало. Прэтому при резонансных измерениях должны получаться
дополнительные резонансы с низким Q, когда длины линий 2,
3 или 4 составляют целое число полуволн.
В условиях опыта, когда добиваются согласования на входе
при закороченной линии 4 и при согласованных на концах ли-
ниях 2 и 3, из-за изменения длины линии 4, очевидно, будет ме-
няться фаза волны, переходящей в линию 1 и, следовательно,
согласование на входе будет нарушено. Изменение длины ли-
нии 4 приводит к периодическому изменению согласования.
Эффективное преобразование волн, измеренное в резонанс-
ной схеме, зависит от фазового соотношения между прямой и
обратной преобразованными паразитными волнами. Это соотно-
шение зависит от длины линий 3 и 4.
Следовательно, наблюдаемое преобразование волн периоди-
чески изменяется от максимальной величины, когда фазы скла-
дываются до минимальной, когда фазы вычитаются. Этот эф-
фект наиболее резко выражен, если два коэффициента связи
равны по величине. Различные эффекты, описанные выше, мож-
но наблюдать экспериментально, получая, таким образом, дан-
ные о коэффициенте обратной связи,
§ 4. ПРАКТИЧЕСКИЕ ВОПРОСЫ
Для многоволновых систем большое значение имеют чис-
тота возбуждения и стабильность типов волн. Волна Дю обычно
возбуждается одноволновым волноводом через прямолинейные
или криволинейные конусные секции. Можно сконструировать
настолько плавные конусные секции, что волна Яю будет воз-
буждаться с очень высокой степенью чистоты. На практике лег-
ко получить чистоту ~0,1%. Возбужденная таким способом
волна Яю устойчива в идеальном волноводе. В реальном волно-
воде устанавливается некоторая квазисобственная волна [12].
Но на любой неоднородности или переходе может происходить
преобразование волн и обратное преобразование, что приводит
к нарушению устойчивости волн.
Система устройств, сконструированных на основе многовол-
нового 3-децибельного ответвителя, имеет только один тип не-
однородности — в форме прямоугольного уголка в Я-плоскости.
352
К. Као
Легко видеть, что в предельном случае, когда длина волны на-
много меньше размеров волновода, на уголке не происходит
заметного преобразования волн. Следовательно, естественно
предположить, что эта форма неоднородности вызывает мини-
мальное преобразование волн. Тем не менее система не сво-
бодна от паразитных волн как из-за нечистого возбуждения
волны, так и из-за преобразования волн на неоднородностях;
но паразитные волны, вероятно, малы.
Присутствие паразитных волн в системе требует определен-
ных мер предосторожности при работе с многоволновой систе-
мой. 1) Необходимо, чтобы, паразитные типы не имели резонан-
сов с высоким Q. Паразитные волны не будут резонировать в
системе, если в схему включить фильтры этих волн или сделать
так, чтобы паразитные волны не оказались «запертыми». Для
этого в схему включается 3-децибельный ответвитель по край-
ней мере с двумя плечами, оканчивающимися согласованными
нагрузками для всех типов волн. 2) В схеме не должно быть
никакой неоднородности, кроме уголка, закороченная цепь ко-
торого перпендикулярна к оси волновода; в схему должны быть
включены согласованные нагрузки для всех типов волн.
Для улучшения рабочих характеристик многоволновых эле-
ментов необходимо сводить к минимуму преобразование волн.
В данном случае это достигается коррекцией уголка по харак-
теристикам преобразования. Используются диэлектрические
вставки длиной в 1/2Х, которые позволяют производить компен-
сацию волн в полосе частот с ограниченной шириной [13]. При
другом способе с помощью диэлектрической вставки с потерями
можно обеспечить различное поглощение волн и тем самым
также уменьшить преобразование волн.
§ 5. ЗАКЛЮЧЕНИЕ
Квазиоптические многоволновые волноводные элементы мо-
гут работать в миллиметровом и субмиллиметровом диапазо-
нах. Характеристики, полученные для таких устройств, вполне
обнадеживающие. Можно думать, что преимущества подобных
элементов — низкие потери, широкая полоса, простота конструк-
ции— окажутся более существенными, чем их недостатки, а
именно неполная чистота и неполная устойчивость волны на
выходе.
Представленный здесь квазиоптический метод дает возмож-
ность анализировать работу устройств при условии, что волно-
вод достаточно многоволновый. Он углубляет понимание работы
многоволновой системы и подсказывает возможные способы
улучшения ее характеристик.
16. Квазиоптические волноводные элементы 353
Трудности определения характеристик собственных волн в
значительной мере устраняются благодаря резонансному ме-
тоду. Как показано, этот метод универсален. С его помощью
можно легко обнаруживать присутствие паразитных волн, что
очень важно с точки зрения быстрой проверки элементов. Ме-
тод позволяет также получить полную информацию о распреде-
лении энергии по типам волн.
ПРИЛОЖЕНИЕ 1. ВОЗБУЖДЕНИЕ ВОЛНОВОДА
ЛИНЕЙНЫМ ЭЛЕКТРИЧЕСКИМ ДИПОЛЕМ,
РАСПОЛОЖЕННЫМ ВДОЛЬ ОСИ у
Волновод состоит из двух бесконечных параллельных идеаль-
но проводящих пластин в Н-плоскости, расположенных прих = 0
и x*=d. Линейный электрический диполь помещается параллель-
но оси у на расстоянии от одной пластины.
Из уравнений Максвелла для данной системы получаем сле-
дующее уравнение:
дЕ 2Е д2Е
-d^ + ^- + k2Ey=^Jk4z^(x-x^
Это уравнение может быть решено методом преобразований.
Вводя преобразование
Е = j* Eye-^dz,
о
мы получаем для области 0^x<Xi
Е ~ axe)hx -[-bxe~lh’c,
Н = jhaxejhx — jhbxe~lhx,
где
Д2 = Л2 —у2;
для области Xi
Е = a2elhx -|- b2e~ihx,
Н = jha2elhx — jhb2e~ihx.
Запишем граничные условия в виде
£(0)^£(</) = 0,
£(xI-F-0) = £(xl —0),
Н (хх + 0) - //(%! - 0)=jK.
23 Зак. 274
354
К. Као
Подставляя граничные условия и решая уравнения относитель-
но Я1, Ь}., а2 и Ь2, получаем
А — * 51пЛл» cihd
°2~~ 2h s\nhd е ’
_ К sinhXl fkd
“2 ~ 2Л sin hd е
, ___ К sin Л (d— X])
1 2Л sin hd
___ К sin Л (d — xi)
2h sin hd
Для любой из двух областей может быть получено обратное
преобразование. Для области имеем
о . К sin hxi . , ,
E = j-i,—sin h (x — d).
J h sin hd v ’
Возьмем обратное преобразование
/со
о 1 Г • К sin hx, . , ,, ,
= г j — . J-sin(x — d\e~^zdy.
у 2nj j J h sin Ad v ’ 1
-Zoo
Следовательно,
T = (Eu)„ =J(— 1)" sin hnXi • sin h„ (x — d) e~v"z,
где hn = nn/d.
ПРИЛОЖЕНИЕ 2.
ПОНИЖЕНИЕ ПОРЯДКА МАТРИЦЫ РАССЕЯНИЯ 4-ГО ПОРЯДКА,
КОГДА ОБРАТНАЯ СВЯЗЬ ПРЕНЕБРЕЖИМО МАЛА
Легко показать, что если вход 1 согласован и <Si4=S23=0,
то матрица (1) сводится к матрице
- о |Sl2|(e12) |S13|(e13) о
|512|(012) 0 0 |513|(624)
|513|(013) 0 0 1^1(034)
. О |S13|(024) 1^1(034) 0 .
где (0)—фазовый множитель е~^в. Если 012 = 034=0, а 013=л/2,
то 024 равно л + 2012—013=л/2 и матрица может быть представ-
лена в виде
‘О р jq 0 “
Р 0 0 jq
jq 0 0 р '
_0 JQ Р 0 _
16. Квазиоптические волноводные элементы
355
где Siz = p и Si3~q. Это — матрица для- направленного ответ-
вителя.
В измерительной схеме линия 4 обычно закорочена. Если
линия 4 закорочена на расстоянии Z.4 от плоскости отсчета и не
имеет потерь, то единичное напряжение на входе линии 1 бу-
дет возбуждать в линии 2 напряжение р, а в линии 3 напряже-
ние jq. При единичном напряжении на входе линии 2 в линии 4
установится напряжение jq. Это напряжение будет иметь сдвиг
фазы 29, где 9 = p4L4 и возбуждать напряжение g2(n + 29) в ли-
нии 2, в виде отраженной волны, и напряжение pq(a/2 + 2Q)
в линии 3, равное коэффициенту связи между линиями 2 и 3.
Аналогично единичное напряжение на входе линии 3 будет вы-
зывать отражение р2(29) и pq(n/2 + 2Q) из-за связи.
Следовательно, эквивалентная матрица рассеяния 3-го по-
рядка запишется в следующем виде:
'О р(0) <?(я/2) -
р(0) q2 (л 4-29) р<7(л/2 4~29)
-<?(я/2) ^(л/24-29) р2^29) _
При смещении плоскости отсчета в линиях 2 и 3, так что
912=9 и 01з=л — 9, матрица принимает вид
’ 0 р(-9)
р(—9) ?2
q(— 0) pq
-qt-ЪУ
pq
p2
ПРИЛОЖЕНИЕ 3. РЕШЕНИЕ МАТРИЧНЫХ УРАВНЕНИЙ
Запишем матричное уравнение
фиг. 6, в виде
для схемы, изображенной на
О
р(-0)
-<7(-9)
^2
- ^3 ,
р(_в) _9(_0)-|г ] -
q2 pq b2c~2',,f-2
pq p2 J L й3е~2^Лз-
где Y2 = 04“/₽2 — постоянная распространения в линии 2.
Следовательно, у2 = /Р2> и Тз = аз4~/Рз—постоянная распро-
странения линии 3. Раскроем матричное уравнение:
bi — р (— 9) Ь2е~}’2^ — q(— 0) Ь3е~2УзС-3,
Ь2 = р(— 9) 4~ q2b2e~ ]'2^L14- pqb^e-2^,
Ьъ — — q(— 9) 4- pqb2e~2^iLi 4- p2bie~'2'i'iL\
23*
356
К. Као
Для Ь\, Ь2 и &з получаем
Jt,2g-/2^2 ^-2v3Zs — jj-/2paZ2e-2YaZ!
-------------р-----------(— й)>
б!=И1^1(_0),
t3==d^^(_e).
(2)
D
где
Запишем
фиг. 7,
£) == 1 — 2у8д8 — J^2^2t
матричное уравнение для схемы, изображенной на
'bl '
- h -
О
р(-0)
L —?(—0)
Р(-е) (-в)]
я2
РЯ
РЯ
Р2
1
О
- 63е“2’1’‘Л’.
Пусть
^“2у8£а --г 2<Хз£з£—27$3Л3 —
Решение дает
_ (Х-р^ае-ЖР-*
Ь1~ Х-р^ае-М^ ( 29)’
, __ 1 — ae~^’Li .
62— 1_/,2^-/23,Zs7’( 6)>
&3= 1
(3)
(4)
\-p^ae-^q^ 6)’
ПРИЛОЖЕНИЕ 4. МЕТОД ИЗМЕРЕНИЯ НА ОСНОВЕ
АНАЛИЗА ОТРАЖЕННОЙ МОЩНОСТИ
Схема изображена на фиг. 6. Этот метод основан на изме-
рении входного коэффициента отражения. Подставим р2=1 —
— q2, а = е20^ и пренебрежем фазовым множителем (20). Тогда
из уравнения (2) в приложении 3 получаем
bl = l-ae~ + q2 (ae' ^L> - e~ >2^) ’
Пусть bi исследуется в зависимости от ^2L2, при наличии резо-
нанса в линии 3. Таким образом, мы определяем огибающую-
кривую для амплитуды bi при изменении $2L2-
16. Квазиоптические волноводные элементы
357
Подставляем ехр (—/'2p3L3)=l и берем квадрат модуля:
\h 12 — 2а?2 (1 — д — g2) cos 2р2£2 + (! — д ~ ?2)2 + g2g4
*011 — — 2?Ч1—« + «g2)cos2p2£24-(l—a4-ag2)24-?4 *
Представляют интерес два положения огибающей кривой
cos ₽2£2 = 1
при &i=0, и
cos 2р2£2 = — 1,
при |&i|2 равном минимуму величины 6>д2, где 1 —б = а, в слу-
чае докритической связи и максимуму величины 6<д2 в случае
закритической связи.
Рассмотрим bi при cos2p2L2 =—1 для 8>q2, как уже было
сказано. При этом pi.|2 минимально. Подставляя это условие
в выражение (1), получаем
А - — (1 — Д).Ч-У2 (!+«)
01 — (l-a) + g2(14-a) ’
откуда следует, что если д2=(1—а)/(1+а), то &i=0. Это со-
ответствует случаю критической связи.
Для нахождения двух неизвестных а и q необходимы два
уравнения. Чтобы получить эти уравнения, нужно выбрать зна-
чения для Pz^-2 и p3L3, которые можно определить. В экспери-
менте легче фиксировать какое-то постоянное p2L2 и изменять
величину р3£3. В нашем случае p2L2 выбрано так, что =
= — 1. Величина при этих условиях получается в виде
(1 +<72)йг-'2^-(1 -q1)
1=(-l+g2)^-W1+(l + ?2) '
Произведем замену (1—<у2)/(1 ~\-q)-=x и возьмем квадрат мо-
дуля-:
., .2 a2-j-x2 — lax cos 2Рз^з
‘ 1' 1 а2х2 — 2ах cos 2₽3Л3 ‘
Если выбираются такие значения р3£3, что е~}^— 1, то
|А I2 __ (« — -О2
I *мии (1 — ах)2 ' ' '
Если же р313 = ф, где <р мало (cos ср = 1 —1/2 <р2), то
Уравнения (5) и (6) можно решить и получить следующее при-
ближенное уравнение:
(1 — 1^1.|мив),
4 "»
358
К. Као
где ф1Д определяется из соотношения |6il2 = -g-(l 1 Ьх |мин) при
Ф = Ф,/2. По измеренным значениям |&1|мин и ф,д можно рассчи-
тать коэффициент связи q.
Различные типы волн распознаются по положению недостаю-
щих резонансов и расстоянию между соседними резонансами.
Именно такой метод используется при исследованиях волновод-
ных переходов в работах [5—8], где можно найти описание
методики эксперимента.
ПРИЛОЖЕНИЕ 5. МЕТОД ИЗМЕРЕНИЯ НА ОСНОВЕ
АНАЛИЗА ПРОШЕДШЕЙ И ОТРАЖЕННОЙ МОЩНОСТЕЙ
Схема изображена на фиг. 7. При резонансе паразитной
волны выполняется условие ехр (—/2p2L3) = l. Из уравнений (3)
и (4) приложения 3 имеем
(7)
= <8)
Следовательно,
l»il _ (1 — д2)/д ,ПЧ
|*2| (1-а)/л •
Исключая из (7) и (8) величину а, получаем
Р3 (х — 1) — р (х — 1) + р*у — у = 0,
где
х = |М и у = 1Ь21-
Отсюда
Подставляя в (9), получим
_ х(1— х) _ х
— Х-ур-
Таким образом, если измерены |&i| и |&2|, можно опреде-
лить коэффициент связи и коэффициент затухания определен-
ной паразитной волны:
1*11
/7 ---——-----
1-1*2||512Г
где
Q, =
16. Квазиоптические волноводные элементы
359
Существуют разные способы практической реализации схемы
и выполнения измерений величин 1^1 и |&2|. Можно использо-
вать вариант блок-схемы, представленный на фиг. 8. Метод не
сложен и может дать достаточно точные результаты.
Кмосту
Фиг. 8.
Методика измерений. Эксперимент может быть выполнен на
любой интересующей нас частоте. Согласованный детектор кон-
тролирует прошедшую мощность, т. е. \Ь2\. При изменении
длины раздвижного сочленения получаются резонансные кривые
величины j b21. Регулировкой длины раздвижного сочленения до-
биваются минимума величины |&2|. На мосте измеряется раз-
ность значений проходящей мощности в этом случае и в отсут-
ствие резонанса и регистрируется изменение отраженной мощ-
ности— по величине КСВ, которая в сущности равна |&±|. После
этого остается лишь определить тип волны. Это можно сделать
путем регистрации последовательных резонансов. Так как Q ре-
зонатора очень медленно меняется при изменении его длины
(особенно если длина резонатора намного больше длины волны;
а требуемое изменение длины резонатора составляет несколько
длин волн), резонансы будут одинаковыми по величине. Они
будут отличаться от резонансов других паразитных волн, кото-
рые будут иметь свои характерные амплитуды.
Кроме того, можно уточнить тип волны, определяя расстоя-
ние между резонансами, которое должно быть равно l/akg для
данного типа волны. Если нельзя использовать раздвижное со-
членение, измерения могут быть выполнены путем изменения
частоты. В этом случае нужно быть уверенным, что длина ко-
нуса мала по сравнению с длиной резонатора. Если коэффи-
циент связи с высшей волной больше 0,1, достаточно измерять
360
К Као
только прошедшую и отраженную мощности при резонансе. При
точности измерений ~1% данным методом можно измерить
коэффициент преобразования и потерь волны высшего порядка
с точностью до 5%. Если коэффициент связи меньше 0,1, то, что-
бы получить тот же порядок точности, необходимо измерять
также прошедшую и отраженную мощности на уровне 0,5 резо-
нансной кривой.
ЛИТЕРАТУРА
1. Lewin L., Proc. Symposium on Millimeter Waves, New York, I960, p. 469.
A Note on Quasi-Optical Methods at Millimeter Wavelengths.
2. T a u b J. J. et al., Proc. Symposium on Millimeter and Submillimeter Wa-
ves, IEEE Trans., MTT-11, No. 5, 338 (1963).
Submillimeter Components Having Oversize Quasi-Optical Waveguide.
3. Garnham R. H., Symposium on Millimeter and Submillimeter Waves,
Qrlando, Florida (January 7—10, 1963).
Optical and Quasi-Optical Transmission Techniques and Component Systems
for Millimeter Wavelengths.
4. Wort D. J. H., Journ. Sci. Instr., 39, 317 (1962).
Directional Coupler in Oversize Waveguide.
б. К 1 i n ger Y., Proc. IEE, Suppl., 106, 89 (1959).
The Measurement of Spurious Modes in Overmoded Waveguides.
6. Ваганов P. Б., Радиотехника и электроника, 5, № 5, 31 (1960).
Экспериментальный анализ электромагнитио'го поля в волноводных пере-
ходах, содержащих критические сечения.
7. King А. Р., Marc at i И Е. A., Bell Syst. Techn. Journ., 35 (1956).
Transmissions Loss Due to Resonance of Loosely Coupled Modes in a
Multimode System.
8. В u 11 e r w о r t h J. S. et al., Proc. IEE, 110, 848 (1963).
Overmoded Rectangular Waveguide for High Power Transmission.
9. Ka о К. C., Proc. IEE, Hl, 624 (1964).
An Approximate Solution of the Я-plane Right-Angled Corner in Rectangu-
lar Waveguide Operating in Яю Mode.
10. Un ge r H. G., Bell Syst. Techn. Journ., p. 899 (July 1958).
Circular Waveguide Taper of Improved Design,
11. Tang С. С. H., IRE Trans, on Microwave Theory and Techniques, p. 422
(September 1961).
Optimization of Waveguide Taper Capable of Multimode Propagation.
12. К a r b о w i a k A. E„ Proc. IEE, 102, Pt. B, No. 5 (1955).
Theory of Imperfect Waveguides — The Effect of Wall Impedance.
13. L e w i n L., E a g 1 e s f i e 1 d С. C., British Patent No. 905 774.
14. Kao К. C., British Patent Case No. 15072/63,
17
ИЗЛОМ ВОЛНОВОДА С ПЛОСКИМ ЗЕРКАЛОМ
ДЛЯ СИММЕТРИЧНОЙ ЭЛЕКТРИЧЕСКОЙ волны
Е. Маркатили *
В цилиндрическом миоговолиовом волноводе можно изменять направле-
ние распространения волны HOi на перпендикулярное, так чтобы омические
потери и потери на преобразование в паразитные волны при этом были
незначительными, если использовать для этого волноводный уголок, т. е.
излом волновода с плоским зеркалом. Такое устройство весьма эффективно,
поскольку в 'первом приближении оио ведет себя как идеальное зеркало.
Электродинамический расчет излома с зеркалом представляет собой сложную
задачу, так как его поверхность не выражается в аналитической форме. Эти
трудности можно преодолеть, если свести трехмерную граничную задачу к
двум двумерным задачам. Двумерную задачу удобно решать одновременно
как волноводную и антенную, особенно, если отношение Х/а — длины волны
в свободном пространстве к радиусу волновода — мало
Потери волны Н<» равны 201g [1—0,279(Z/a)’2 ] дб, а уровень волны Hot
составляет 201g 0,51 (Х/а)’/адб. Эти формулы подтверждаются эксперименталь-
но для значений Х/а до 0,5.
Соединив два уголка и выбрав соответствующую форму отражающих
поверхностей, можно не только повернуть ось выходного волновода относи-
тельно оси входного на любой заданный угол, но и уменьшить преобразова-
ние волны Яо1 в волну Но2 в широкой полосе частот').
§ 1. ВВЕДЕНИЕ
Для преодоления сосредоточенных изгибов многоволнового
цилиндрического волновода с волной HOi можно использовать
уголки — изломы на прямой угол с плоским зеркалом [1]
(фиг. 1). Такие простые и компактные устройства могут быть
интересны не столько как элементы волноводных линий, сколько
* М а г с a t i 1 i Е A. J., Crawford Hill Laboratory, Bell Telephone Labora-
tories, Inc., Holmdel, N J.
) Задача о зеркале в изломе волновода на любой угол была ранее ины-
ми методами полнее решена в работах Б. Кацеиелеибаума, Б. Кострова и
Е. Нефедова, Р. Ваганова, И, Котика и А. Сивова; см. литературу в обзоре
3 Усп. физич. наук, 83, 81 (1964). — Прим. ред.
362
Е. Маркатили
как элементы многоволновых трактов и устройств типа гибрид-
ных мостов [2] (фиг. 2), фильтров для разделения частотных
каналов [2]., чрезвычайно широкополосных направленных ответ-
вителей и т. д.
Опыт показывает, что излом на прямой угол в волноводе
диаметром 50,8 мм на частоте 55 Ггц вносит потери порядка
0,25 дб [2]. Это значит, что отражающее плоское зеркало уголка
Фиг. 1. а — излом на прямой угол для волны /701 (диаметр волновода
50,8 мм); б — излом для волны (в разобранном виде).
действует практически как идеальное. Мощность потерь сле-
дует почти полностью отнести к возникающим на уголке пара-
зитным волнам, идущим в прямом направлении. Из этих волн
представляют интерес только волны типа Н02, Hos и т. д., так
как все остальные могут быть значительно ослаблены с по-
мощью спирального волновода. Поэтому в данной работе мы
вычисляем преобразование Н01 в Н02, Hos и т. д„ хотя матема-
тический аппарат можно легко обобщить на волны других ти-
пов и изломы с иной геометрией.
§ 2. ПОСТАНОВКА И РЕШЕНИЕ ЗАДАЧИ
Рассмотрим два уголка, соединенные в волноводный крест
(фиг. 2 и 3). Общее плоское зеркало удалено.
Пусть в этом четырехполюснике слева и снизу (плечи 4 и 1)
подходят две синфазные волны с равными амплитудами. Из
соображений симметрии очевидно, что электрическое поле, тан-
генциальное к плоскости р, будет равно нулю. Следовательно,
эту плоскость можно заменить металлической плоскостью, не
изменяя конфигурации поля. Но тогда вместо креста у нас ока-
жется два независимых друг от друга уголка. Это значит, что
Фиг. 2. а — гибридное соединение для волны Hoi, состоящее
из двух изломов на прямой угол и тонкой стеклянной пла-
стинки между ними (диаметр волновода 50,8 мм); б — гибрид-
ное соединение в разобранном виде.
Фиг. 3. Крест, образованный из двух изломов на прямой угол.
Отражающие зеркала удалены, отверстия изломов совмещены.
364
Е. Маркатили
граничная задача о дифракции на уголке может быть решена,
если мы решим граничную задачу о дифракции на кресте. Снова
рассмотрим крест, на этот раз не разделяя его на части. Так
как диаметр волновода велик по сравнению с длиной волны, то
большая часть энергии, идущей в плече /, пройдет в плечо 3,
а большая часть энергии, идущей в плече 4 — в плечо 2. Этот
факт и соображения симметрии говорят нам о том, что боль-
шая часть мощности симметричной электрической волны из пле-
ча 1 пройдет в плечо 3 и очень немного — в плечо 4. Следова-
тельно, коэффициенты рассеяния для симметричных электриче-
ских волн в противоположных плечах креста совпадают с коэф-
фициентами рассеяния между теми же волнами в уголке.
Пусть теперь симметричные электрические волны падают
только со стороны плеча 1 волноводного креста. Определим ко-
эффициент связи этих волн с волнами того же типа в плече 3.
Граничную задачу решить чрезвычайно трудно из-за того,
что металлические поверхности не выражаются в аналитической
форме. Мы будем искать приближенное решение, путем сведения
трехмерной задачи к двум двумерным.
Если смотреть со стороны плеча 1 (нижняя часть фиг. 3), то
нетрудно заметить, что поле возбуждающей симметричной элек-
трической волны и металлические стенки симметричны относи-
тельно плоскостей ф=0 и ф = л/2. Поэтому электрическое поле
в каждой точке этих плоскостей должно быть перпендикулярно
плоскостям. Введем четыре фиктивные металлические плоско-
сти Ь. Если углы 9 между ними исчезающе малы, то плоскости
не внесут в поле никакого возмущения.
Проанализируем поле внутри каждого клина с углом 9.
Сначала рассмотрим клин, содержащий плоскость ф = 0. Элек-
трическое поле перпендикулярно обеим металлическим плоско-
стям и не зависит от 9, до тех пор пока 0—*0. Поэтому оно сов-
падает с полем в любой радиальной плоскости некоторой
простой волноводной структуры. Последняя состоит из двух ци-
линдрических волноводов с общей осью, разделенных проме-
жутком, ширина которого равна диаметру волноводов; слева
падает волна Но1.
Пользуясь тем же приемом, можно найти эквивалентную
более простую структуру для анализа поля в клине, содержа-
щем плоскость ф=л/2 (см. фиг. 3). Оказывается, что такой
структурой является просто регулярный цилиндрический вол-
новод диаметра 2а, который не содержит никаких неоднородно-
стей.
Пусть нам известно решение уравнений Максвелла для двух
простых цилиндрических структур: волновода со щелью и волно-
вода без щели. В таком случае мы знаем только поля Ео и Еп/2
17. Излом волновода с плоским зеркалом
365
на плоскостях <р = 0 и <р=л/2 креста, показанного на фиг. 3. Но
поле Е в области, общей для обоих плеч креста, должно изме*
няться непрерывно. Следовательно, поле при любом угле близ*
ко к
Е = Ео cos2 <р + Ея/2 sin2 ф = (Ео + Ея/2) + (Ео — Еяц) cos 2ф.
Игнорируя член с азимутальной зависимостью по ф, которым
определяется связь волны Н01 с несимметричными волнами, ис*
ключенными нами из рассмотрения, и пренебрегая обратным
рассеянием, которое, как известно, в многоволновых структу-
рах мало [5], мы формально записываем электрические поля Ei
и Es в плечах 1 и 3 волноводного креста и поле Е в области ме-
жду плечами в виде
(v! £-) (1)
со
+ H (2)
О
со
где kn = k — (ynlka)2, k = 2л/Х, X — длина волны в свободном
пространстве, vn — n-й корень бесселевой функции первого по-
рядка и Sn — коэффициент связи волны Н01 в плече 1 с волной
Ноп в плече 3.
Сшивая поле Et с полем Е при z=0 и Е3 с Е при z=2a и
пользуясь ортогональностью функции Бесселя, мы получаем сле-
дующие уравнения:
СО
Л (vi = J А (у) л (yr) dy (4)
О
И [со
о _ 1 ^nJо СУд) ___ 0_______________ [
^“2^) * -1-
о
оо ___ а
j А (у) e~l2a (r j j, (Yr) jn p L) r dr
PPPW
о
366
Ё. МаркаТили
Функция Л (у), полученная преобразованием Ханкеля [6] из
выражения (4), имеет вид
A (Y) = -rJU- 'о W -A (М (6)
\ Vj )
Подставляя это значение в (5) и производя интегрирование по г
[7], мы получим коэффициент рассеяния
о со 9 — iZatVk2—у2-1 M 1
„ _а f V п' , . -2 ПРИ Я = 1>
Io "Р”
(7)
Основной вклад в величину этого интеграла вносят области у,
близкие к vi/a и чп1а- Следовательно, если выполняется условие
то квадратный корень в (7) можно заменить первыми двумя
членами разложения в ряд по степеням у2. Мы отбрасываем все
члены, содержащие Х/а в степени большей 3/2. При этом интегри-
рование дает
S1 = l—0,019v2[|)3/2= 1 —0,279 (9)
S„=(-l)W19V1v„(|)3/2. (10)
Таблица
Дифракция волны Hoi на уголке
(сравнение теории и эксперимента)
К мм а. мм Теория Эксперимент Эксперимен- татор
S,, Вб S„ дб S„ дб S2, W
5,4 25,4 0,25 26,2 0,22±0,05 0,25 ±0,05 22 27 Кинг Бисби Баррус Маркузе
5,4 11,1 0,76 0,75 ±0,05 Кинг
31,9 63,5 0,93 14,8 0,9±0,5 13,7 ±1 У ортерс
В таблице эти теоретические результаты сравниваются с резуль-
татами, полученными экспериментально различными исследова-
17. Излом, волновода с плоским зеркалом
367
телями. Налицо очень хорошее согласие теории с эксперимен-
том для величин (vnX/2na)2 до 0,315 или, что то же самое, для
величин \/а до 0,5.
§ 3. УМЕНЬШЕНИЕ ВОЗБУЖДЕНИЯ ВОЛНЫ Ню В УГОЛКЕ
Фиг. 4. Излом иа прямой угол
с коаксиальными винтами для
устранения преобразования в сим-
метричную электрическую волну
высшего порядка.
Экспериментально было найдено, что при помощи двух коак-
сиальных винтов, закрепленных в отражающей поверхности
уголка (фиг. 4), можно устранить на одной частоте преобразо-
вание Hoi в Но2- В общем слу-
чае одного винта недостаточно.
Идеализируем задачу, считая S2
коэффициентом преобразования
в волну Ног, который обуслов-
лен исключительно уголком с
плоским зеркалом, a St — коэф-
фициентом преобразования, об-
условленным только винтом. Ни-
какого преобразования в Нщ нет,
если S2 + S2 —0. Но чтобы это
равенство было выполнено, диа-
метр винта следует подбирать
очень точно. ’ В противном слу-
чае при идентичных амплитудах
| S21 и | S21 коэффициенты S2 и
S2 окажутся не в противофазе, и
наоборот — при правильных фа-
зовых соотношениях не будет вы-
полняться равенство амплитуд. Если же имеются два коаксиаль-
ных винта с коэффициентами преобразования S2 и S2, то число
комбинаций S2 и S2, при которых удовлетворяется равенство
S2-I-S24-S2 =0, бесконечно.
§ 4. РАСШИРЕНИЕ ПОЛОСЫ ЧАСТОТ,
В КОТОРОЙ ПРЕОБРАЗОВАНИЕ /701 В Я02 МАЛО
Один уголок дает нам возможность изменить направление
оси волновода на 90°, а два уголка, связанных вращающимися
сочленениями (фиг. 5), допускают поворот выходного волновода
относительно входного на любой угол. Кроме того, как сейчас
мы качественно покажем, можно подобрать расстояние L ме-
жду уголками таким образом, чтобы преобразование волны Н01
в волну Н02 было мало в широкой полосе частот.
368
Е. Маркатили
Рассмотрим два идентичных уголка. Преобразование волны
Hot в волну Ног, на каждом из них мы сведем к нулю на длине
волны используя описанный выше метод коаксиальных
Фиг. 5. Два уголка с тремя вращающимися сочленениями.
винтов. Зависимость уровня волн Н02, возникающих на обоих
уголках, одинакова; она показана качественно пунктирной ли-
нией на фиг. 6. Выберем теперь расстояние L между двумя
___________Отдельный излом с подстроечными винтами
; I2 _______Два излома, расположенных на расстоянии,
21 равном половине длины волны оиении
, между волнами H0J и Нв2
Фиг. 6. Зависимость мощности 13212 от длины волны.
уголками (фиг. 5) равным половине длины волны биений ме-
жду Hot и Ног при Х=Ло. Если неравенство (8) удовлетворяется, то
, (4ла)2 •
17. Излом волновода с плоским зеркалом
369
При таком выборе расстояния L обе волны Н02, возникшие на
уголках из волны Н01, на длине волны Х = Х0 компенсируют друг
друга. Сплошная линия на фиг. 6 дает представление о суммар-
ной зависимости уровня волны Н02 на выходе двойного уголка
от длины волны.
§ 5. ЗАКЛЮЧЕНИЕ
Волноводный уголок в многоволновых цилиндрических вол-
новодах вносит малые потери в волну Н01, а преобразование
Hot в Н02 может быть сделано малым в широком диапазоне
частот.
Найден сравнительно простой метод расчета потерь на пре-
образование. Этот метод может быть легко обобщен как на из-
ломы прямоугольных волноводов с увеличенным поперечным се-
чением, так и на изломы двух многоволновых волноводов.
ЛИТЕРАТУРА
1. Miller S. Е., Bell Syst. Techn. Journ., 33, 1209 (1954). (Имеется перевод
в сб «Волноводные линии передачи с малыми потерями», 1960, стр. 13.))
Waveguide as a Communication Medium.
2. М а г с a t i 1 i Е. A. J., Bisbee D. L., Bell Syst. Tech. Journ., 40, 197
(1961).
Band-Splitting Filter.
3. M a r c a t i 1 i E. A. J., Ring D. H., IRE Trans., MTT-10, 251 (1962).
Broadband Directional Couplers.
4. Morgan S. P., Young J. A., Bell Syst. Techn. Journ., 35, 1347 (1956).
(Имеется перевод в сб. «Волноводные линии передачи с малыми поте-
рями», ИЛ, 1960, стр, 404.)
Helix Waveguide.
5. Morgan S. P., Journ. Appl. Phys., 21, 329 (1950). (Имеется перевод в сб.
«Волноводные линии передачи с малыми потерями», ИЛ, 1960, стр. 228.)
Mode Conversion Losses in Transmission of Circular Electric Waves Through
Slightly Noncylindrical Guides.
6. Magnus W., Oberhettinger F., Formulas and Theorems for the
Functions of Mathematical Physics, New York, 1954, p. 136.
7. J a m k e E., E m d e F., Funktionentabeln, Leipzig, 1933. (Имеется перевод:
E. Янке, Ф. Э м д e, Таблицы функций с формулами и кривыми, изд. 2-е,
М. — Л., 1949.)
24 Зак. 274
18
ЖЕЛОБКОВЫЙ ВОЛНОВОД
Д. Граймсмен *
В линии из параллельных пластин с продольными прямоугольными же-
лобами могут распространяться слабозатухающие Я-волны, которые характе-
ризуются сравнительно малыми продольными токами в стенках. Для волн
сантиметрового и миллиметрового диапазонов сравнительно мелкий желоб мо-
жет вызвать значительное спадение полей в поперечном от желоба направле-
нии. Следовательно, такая структура может быть использована на практике
для создания линий с малыми потерями. Правильность приближенного ана-
лиза поперечного резонанса подтверждается результатами измерений длины
волны в экспериментальном волноводе. Описан преобразователь волн прямо-
угольного волновода в волну желобкового волновода.
§ 1. ВВЕДЕНИЕ
Желобковый волновод представляет собой разновидность
плоскопараллельного волновода большого сечения; как видно
на фиг, 1, на обеих его пластинах имеются продольные желоба.
Одна из низших волн ТЕ, распространяющихся в такой струк-
туре, резко спадает в поперечном направлении в обе стороны
от желоба и может быть эффективно передана при конечной
ширине пластин волновода. При соответствующей конструкции
продольные токи можно сделать достаточно малыми и получить
плоскопараллельный волновод с очень малыми потерями. Же-
лобковый волновод может быть использован при конструирова-
нии таких квазиоптических элементов, как изгибы и направлен-
ные ответвители. Для желобкового волновода из-за быстрого
спадания поля в боковом направлении можно не учитывать ди-
фракционные эффекты, тогда как для круглого и прямоуголь-
ного волноводов широкого сечения эти эффекты должны быть
учтены на поворотах волновода. Для волны низшего порядка,
* J. W. Е. G г i е m s m а п n, Department of Electrophysics, Polytechnic
Jpstitpte of Brooklyn, Long Island Graduate Center, Farmingdale, N. Y,
18. Желобковый волновод
371
рассматриваемой в данной статье, волновод не является широ-
ким в направлении, перпендикулярном плоскостям; благодаря
этому можно сконструировать некоторые стандартные волно-
водные устройства типа ответвителей и изгибов1). На практике
такой волновод мог бы быть выполнен в виде закрытой волно-
водной металлической трубы с тонким слоем поглощающего ма-
териала на узких стенках для поглощения излучения, возникаю-
щего на неоднородностях. Для возбуждения желобкового волно-
вода можно использовать специальный конусный переход от
прямоугольного волновода.
Идею желобковой формы волновода впервые мне сообщил
Цунео Накахара летом 1962 г.; в то время он работал в Брук-
линском политехническом институте, приехав из Японии для об-
мена научным опытом. С тех пор он продолжал исследование
этого волновода и применил его в форме асимметричного вол-
новода вытекающих волн для передачи сигналов на экспрессной
линии Токио — Осака2). Описываемый в настоящей статье вол-
новод Отличается от волновода Накахары меньшей глубиной
желоба. Такой волновод может быть использован в качестве
линии передачи с малыми потерями. Цель данной статьи — по-
казать, в какой степени в таком волноводе могут быть достиг-
нуты свойства идеальной волны плоскопараллельного волновода
с низкими потерями. Так же как Накахара, мы используем при
анализе метод поперечного резонанса. Наши результаты под-
тверждаются экспериментально. Этот анализ следует отличать
от анализа Тишера [3, 4], который предлагает метод конформ-
ных преобразований, подобный методу, ранее известному Мейн-
ке [5]3).
§ 2. АНАЛИЗ ПОЛЕЙ
На фиг. 1 показаны все необходимые размеры для волновода
и компоненты для волн типа ТЕ, а также приведена эквивалент-
ная схема для анализа поперечного резонанса. Выделены три
области: область желоба А и две боковые области В с быстрым
спаданием поля, отделенные от А плоскостями, содержащими
края желоба. Поскольку сечение симметрично отнрсительно оси
х, достаточно рассмотреть только одну половину волновода.
В дальнейшем для удобства анализа предполагаем, что ширина
боковых пластин бесконечно велика. Так как волновод имеет
однородное диэлектрическое заполнение, полная система
) Эти утверждения основаны на данных анализа элементов //-волново-
да — передающей линии (см. [1]);, по типам воли похожей на линию, опи-
сываемую в настоящей статье. Модовое описание дается в работе [2],
2) Т. Nakahara, частное сообщение,
3) См. также ссылку [8] в работе [5].
24*
372
Д. Граймсмен
собственных волн состоит из типов ТЕ и ТМ. При конечной ши-
рине желобкового волновода следует учитывать также волну
ТЕМ. В случае идеального возбуждения желобковой волны ТЕ
волна ТЕМ не возбуждается, и во всяком случае ее можно легко
—*-оо
~ Н2 куВ
о-...о .
Фиг. 1. Схема конструкции и детали анализа.
контролировать с помощью поперечной металлической или по-
глощающей пластины, расположенной в центре. Такая перего-
родка не оказывает влияния на интересующую нас волну ти-
па ТЕ.
Строго говоря, чтобы удовлетворить граничным условиям на
краях прямоугольного желоба для любого типа колебаний, тре-
буется бесконечный набор волн, являющихся нечетными гармо-
никами по b в области А, и точно так же по Ь' в области В. Для
анализа же преобладающих волн ТЕ и ТМ методом поперечного
резонанса удобнее рассмотреть соответствующую эквивалентную
схему для неоднородности. Эквивалентная неоднородности про-
водимость должна быть подключена на зажимах между отрез-
ками эквивалентных двухпроводных линий, изображенных на
фиг. I. Из опыта известно, что для мелкого желоба влияние
краев желоба мало по сравнению с тем влиянием, которое ока-
зывает различие в характеристических импедансов двух частей
сечения волновода. Поэтому в первом приближении эквивалент-
ная схема выглядит так, как показано на фиг. 1. Необходимо
иметь в виду, что этот упрощенный анализ справедлив для ча-
стот, на которых все возбуждаемые высшие гармоники по b яв-
ляются сильно закритичными.
!S. Желобковый волновдб
873
Уравнения для полей основной ТЕ волны в области желоба
могут быть записаны следующим образом:
— х) sin kYAye~lk^z, (la)
eya = eoa cos (y x) cos kYAy e~ik*z, (16)
HxA = — (^) em cos (y x) cos kYAy e~ik*z, (1b)
Hya = (w) E°a s!n (7 *) s!n кУлУ e~lk*z, (lr)
hza=J—~Jya—E0A^[-b xj cos kYAye , (1д)
где n/b, kYA и kz— волновые числа по осям х, у и г. Мы пред-
полагаем, что в направлении распространения z линия беско-
нечна; со— угловая частота и р, — магнитная проницаемость
среды.
Уравнения для полей основной волны ТЕ справа в области
быстрого спада поля таковы:
Ехв = Еов sin (-J х) е~\к™ I и'е-}кЛ (2а)
EYB —-Еов(-^~\cos x\e~^kYB^y'e~jk^z, (26)
Нхв = - Ш (ТТЛ) Е™ cos (у х) е"1к ™ । v'e-^z, (2в)
Нг, = Ш В«‘ см НЧ <' *ril (2Г)
V1'si"<2д)
ши II \и !
где п/b', kYB и kz — волновые числа по осям х, у и г. Для удоб-
ства по оси у выбрана переменная у' = у—а/2. Так как интере-
сующие нас решения должны быть затухающими, то
^YB = J I ^YB I •
Распределение поля основной волны ТЕ, приближенно вы-
раженное приведенными выше уравнениями, представлено на
фиг. 2. Как нетрудно видеть, мгновенные магнитные силовые
линии (пунктирные линии) лежат на изогнутых поверхностях.
Соотношения (2в), (2г) и (2д) показывают, что эти поверхности
имеют постоянную кривизну, определяемую только отношением
374
Д. Граймсмен
Hyb к Нхв, которое не зависит от у'. Уравнения (1в), (1г)
и (1д) дают кривизну, зависящую от у, а при у=0 получается
плоская магнитная силовая линия. Действительное поле, по-ви-
димому, будет мало отличаться от поля, изображенного на
Продольное сечение
Пунктиром показаны линии магнитного поля
Фиг. 2. Картина линий поля желобковой волны TExi.
фиг. 2, поскольку кривизна линий Н изменяется плавно при пе-
реходе из области желоба в боковые области, а не устанавли-
вается сразу постоянной. Некоторое различие может быть вы-
звано наличием полей волн высших типов на краях желоба.
Из-за разной зависимости по х в уравнениях (1) и (2) нель-
зя непосредственно сшивать поля на границе областей А и В.
На поверхностях раздела сшиваются «напряжения», т. е.
<ЕХА\.^Ь = (Ехв\_ь^ (3)
у-ар у1—О
и плотность бокового ятока“, или
ZA)x-bp ~ № ZB^x-W (4)
у—ар у'-О
18. Желобковый волновод
375
Из уравнений (1а), (2а) и (3) для постоянной величины Еов
получаем
b k,, .а
E0B = vEQAsin^-, (5)
а из уравнений (1д), (2д) и (4)
Р ____ |аув| (л#)2-(-Ауд ,, kYAa
°В~ kYA °Л 2
(6)
Уравнения- (5) и (6) должны удовлетворяться одновременно.
Поделив (5) на (6), мы получим условие поперечного резонан-
са, из которого можно получить конкретные значения волновых
чисел.
Итак, определим значения волновых чисел. В области А
уравнение волновых чисел записывается следующим образом:
(у)2 + ^д+^ = ^ (7)
а в области В
(^-\kyB\2A-k^k\ (8)
где 6 = 2лД — волновое число волны ТЕМ в диэлектрике, запол-
няющем волновод, а X — длина волны ТЕМ в этой среде. Вычи-
тая (8) из (7), получим
(1) — |£ув12 = £кр, (9)
где /?I!p=2n/7.Kp — критическое волновое число, которое полу-
чается из (7) или (8), если положить kz = Q, а А1ф— длина волны
ТЕМ при критической частоте. Как указывалось выше, условие
поперечного резонанса получается при делении (5) на (6).
С учетом равенств (7) —(9) это условие может быть записано
в следующем виде:
кУА tg kYA "2 = I ^yb I ~ • (Ю)
Полагая, что
= (11)
q = \kyB\%, (12)
уравнения (9) и (10) можно записать следующим образом:
^+’!==[(H~(f)W- <13>
е^р=(-т)ч- (И)
376
Д. Граймсмен
Очевидно, что одновременно уравнения (13) и (14) удовлетво-
ряются при значениях куд и kyB, не зависящих от частоты. Сле-
довательно, распределение поля в поперечном сечении, соответ-
ствующее приближенным решениям для открытого волновода,
не будет зависеть от частоты, так же как для закрытых волно-
водов с однородным диэлектрическим заполнением. В конструк-
ции с мелким желобом величина Ь' близка к b и, как видно из
уравнений (13) и (14), значения р и q малы. Тогда из уравне-
ний (7) и (8) получим, что
Чр«26~26'. ' (15)
Это означает, что в конструкции с мелким желобом критическая
длина волны желобковой моды приблизительно равна критиче-
ской длине волны идеальной слабо затухающей моды ТЕ в пло-
скопараллельной линии приблизительно с таким же расстоянием
между пластинами. В действительности более детальный анализ
показал бы, что
2Ь' А.кр 2Ь.
Заметим, что в соответствии с конструкцией линии есть
не что иное, как коэффициент затухания поля в боковых обла-
стях.
§ 3. РАСЧЕТНЫЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ
ХАРАКТЕРИСТИКИ ЛИНИИ
Ниже приведены волноводные характеристики, рассчитанные
для желобкового волновода с расстоянием между боковыми
пластинами 6 = 7,110 мм и коэффициентом затухания в боковом
направлении, приблизительно равным 8 d6jcM:
а Ъ bf, мм Хкр "2ЙА* ’ град
3,0 6,85 1,0205 48,4
1,0 6,60 1,0189 30,7
0,6 6,32 1,0174 21,2
Для получения затухания 8 дб!см в случае широкого желоба
необходимо, чтобы глубина желоба в каждой пластине состав-
ляла 0,127 мм. Следовательно, необходимы жесткие допуски на
внутренние размеры плоскостей в желобковой линии. Последний
столбец таблицы иллюстрирует величину изменения поля в об-
18. Желобковый волновод
377
ласти желоба в поперечном направлении параллельно плоско-
стям. Для случая а/6 = 3,0 после интегрирования вектора Пойн-
тинга по поперечному сечению с учетом указанных выше соот-
ношений получаем, что 77% мощности передается в области
желоба и 23%—в боковых областях. Другим интересным ре-
зультатом для вышеуказанного случая (а/6 = 3,0) является тот
факт, что 98,4% передаваемой мощности определяется произве-
дением Е?-Нх. Все указанные характеристики желобкового
волновода близки к характеристикам плоскопараллельной ли-
нии, обладающей малыми потерями.
Для случая а/6 = 3,0 получено хорошее экспериментальное
подтверждение приближенной теории. Эксперимент производился
на перестраиваемом резонаторе реактивного типа с парамет-
рами 6 = 7,11 мм, 6' = 6,85 й шириной боковой плоскости, прибли-
зительно равной 12,7 см. Резонатор возбуждался через емко-
стную диафрагму в торцевой стенке, а положение другой торце-
вой стенки можно было изменять в направлении оси z. При
перемещении этой регулируемой стенки между последовательны-
ми резонансами измерялась длина волны волйовода на данной ча-
стоте. Несмотря на то, что возбуждающая резонатор диафрагма
вносила дополнительные потери, добротность Q была достаточ-
но высокой, чтобы провести с необходимой точностью измерения
длины волны волновода.
В таблице дана зависимость трех значений длины волны
волновода от частоты. Во втором и третьем столбцах таблицы
измеренные значения длин волн желобкового волновода сравни-
ваются с теми значениями, которые рассчитаны по приближен-
ной теории. Видно, что теория хорошо подтверждается экспе-
риментом. В последнем столбце приведены расчетные значе-
ния длины волны плоскопараллельного волновода, имеющего
Расчетные и экспериментальные длины волн волновода
/. Ггц мм
Эксперименталь- ная Расчетная Расчетная плоско- параллельной линии
27,62 17,279 17,272 17,907
28,82 15,636 15,621 16,104
30,02 14,279 14,275 14,707
31,96 12,705 12,700 12,979
33,90 11,400 11,430 12,421
35,86 10,393 10,439 10,617
38,00 - 9,586 9,576 9,703
378
Д. Граймсмен
расстояние между пластинами 6'=6,85 мм. В этом случае раз-
ница значений длин волн волновода третьего и четвертого столб-
цов, хотя и небольшая, но заметна на каждой частоте.
§ 4. РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ ЗАТУХАНИЯ
Вышеприведенный анализ поля желобкового волновода по-
казывает, что продольные токи, пропорциональные величине HY,
малы на металлических плоскостях. Строго говоря, желобковую
линию нельзя считать линией с малыми потерями, даже теорети-
чески нельзя показать, что затухание бесконечно уменьшается
с ростом частоты. Но в случае линии с мелким желобом, кото-
рый рассматривается в данной статье и который интересен для
практики, кривая затухания имеет минимум на очень высо-
кой частоте, так что в рабочей полосе частот желобковый вол-
новод имеет характеристику затухания, близкую к характерис-
тике плоскопараллельного волновода, обладающего малыми по-
терями.
В любом регулярном волноводе, заполненном однородным
диэлектриком, затухание волны типа ТЕ, обусловленное конеч-
ной проводимостью металлических стенок, может быть записано
в форме [6]
где Rs— действительная часть импеданса металла, t] — волновое
сопротивление диэлектрика, заполняющего волновод, d — харак-
терный поперечный размер волновода, А и В — постоянные, ко-
торые зависят от выбора d, но не зависят от частоты.
Для волновода с малыми потерями постоянная А рав.на
нулю. Одной из задач этой статьи является исследование фор-
мулы затухания для волновода с мелким желобом с целью по-
казать путем сравнения постоянных А и В волноводов двух
типов, что затухание волны желобкового волновода прибли-
жается к затуханию волны плоскопараллельного волновода.
§ 5. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ
По плоскопараллельному волноводу можно передать мощ-
ность, большую чем по прямоугольному, благодаря тому, что
в первом случае больше площадь поперечного сечения волно-
вода. Мы не пытаемся дать точные величины, которые получи-
лись бы при учете закруглений на краях желоба, поскольку
18. Желобковый волновод
379
соответствующие данные можно получить только эксперимен-
тально, а эксперименты еще не проводились. В данной части
статьи находится лишь соотношение между мощностью и no-
постоянной Еоа, используемой в уравнениях (1) и (2), и, кроме
того, соотношение между мощностью, переносимой желобковой
частью волновода, и мощностью, проходящей между боковыми
плоскостями. Также указано различие между относительной
мощностью, рассчитанной для главной пары компонент ЕуНх и
для пары ЕХН?, связанной с продольными токами.
Ниже приводится распределение мощностей:
в области желоба
в боковых областях
где _________
t] — волновое сопротивление диэлектрика, заполняющего волно-
вод. Полная мощность равна сумме этих мощностей.
В случае очень мелких канавок (а=21,336; 6 = 7,11;
Ьс = 6,85 мм) распределение мощности таково:
область желоба
РАЕу = 0,7611 Рт, РАЕх = 0,0063 рт-,
боковые области
РВЕу = 0,2236 Рт, РВЕх = 0,0090 Рт,
полная мощность в области желоба, равна 0,7674 полная
мощность в боковых областях равна 0,2326 Рт, где Рт — пол-
ная мощность, передаваемая по линии. Заметим, что в этом слу-
чае значительная величина мощности переносится боковыми
областями, а величина мощности, определяемая произведением
ЕхНу, мала. Это еще раз показывает степень приближения
волны желобкового волновода к волне плоскопараллельного
волновода.
380
Д. Граймсмен
Формула для полной мощности может быть более удобно
записана в следующем виде:
§ 6. ЗАТУХАНИЕ
Затухание волновода, заполненного воздухом,
где Rs — поверхностный импеданс внутренних металлических
стенок волновода; t] — волновое сопротивление диэлектрической
среды (воздуха) в волноводе в предположении, что эта среда
обладает малыми потерями.
Величины А и В выражаются следующим образом:
В этих выражениях пренебрегается потерями на краях желоба,
так как для мелкого желоба они малы.
Соотношение (21) дает общий вид затухания волн типа ТЕ
регулярного волновода, заполненного диэлектриком. Для волны
с малыми потерями в бесконечно широкой плоскопараллельной
линии величина Л = 0, а В=2 [это видно из соотношений (22) и
(23), где величина b — расстояние между пластинами]. Для ли-
нии с мелким желобом при а/Ь — 3,0, Ь'/6 = 27/28 соотношения
(22) и (23) дают
А =0,0454 и В=2,871.
На фиг. 3 нанесены расчетные графики затухания желобкового
волновода, стандартного прямоугольного (7,11 мм X 3,55 мм)
18. Желобковый волновод
381
и плоскопараллельного (7,11 мм) волноводов. Все эти волно-
воды изготовлены из меди и имеют одну и ту же критическую
Фиг. 3. Сравнение кривых зависимости затухания от частоты.
частоты волны ТЕ^о прямоугольного и плоскопараллельного вол-
новодов. Из фигуры нетрудно видеть сходство в поведении кри-
вых затухания желобкового и плоскопараллельного волноводов.
Точные размеры желобкового волновода для той же самой кри-
тической частоты следующие:
6 = 7,054 мм\ 6'= 6,995 я#; .« = 21,762 мм,
382
Д. Граймсмен
Его кривая затухания имеет минимум на частоте, которая
зависит от отношения В/A. Выше этой частоты затухание желоб-
кового волновода растет в противоположность затуханию пло-
скопараллельной линии, которое бесконечно уменьшается при
увеличении частоты. Для волновода с мелким желобом мини-
мум затухания соответствует частоте, которая в 13,9 раза боль-
ше критической частоты. Эта частота оказывается далеко от
рабочего диапазона волновода.
§ 7. ВОЛНЫ ВЫСШЕГО ПОРЯДКА
Приближенный метод поперечного резонанса применим толь-
ко в ограниченном частотном диапазоне для первых распростра-
няющихся волн ТЕ и ТМ и для ограниченного числа волн ТЕ
и ТМ. следующих порядков. На высоких частотах можно счи-
тать, что на краях желоба имеет место постоянная связь двух
или более распространяющихся волн. Здесь эти волны опреде-
лены в том смысле, что неоднородность вызывает в поперечном
направлении только изменение характеристического импеданса.
Из-за связи на краю желоба поперечное распределение поля
для различных типов становится функцией частоты, поэтому
необходимо дальнейшее выяснение вопроса.
На фиг. 4 представлено распределение поля для волн низ-
ших порядков. Это распределение поля получено с помощью
метода поперечного резонанса, в котором учитывается только
изменение характеристического импеданса. При вычислении пре-
небрегается дополнительной энергией поля, запасенной на раз-
рыве, и связью между волнами, которые могут распространяться
одновременно. При таких упрощениях общие соотношения для
определения постоянных распространения волн типа TMN<M и
TEn.m принимают вид
, ( Ь' \
Р^Р=[—)Я-
Индекс N означает число полуволн между плоскостями в х на-
правлении; индекс М на единицу больше, чем целая часть 2р!п.
В этом методе все моды ТЕ и ТМ одного и того же индекса
имеют одну и ту же критическую частоту.
§ 8. ВОЗБУДИТЕЛЬ ВОЛНЫ
На фиг. 5 изображен эскиз предлагаемого преобразователя
волны прямоугольного волновода в волну желобкового волно-
вода. В нижней части фигуры показан вид сбоку. Заметим, что
i
—— Линии электрического поля
—— Линии магнитного поля
х-0 Ex=Hv*Q
i TMlt
у-0 £у=Нк<=0:
Фиг. 4. Распределение поля в поперечном сечении для различных
типов волн.
384
Д. Граймсмен
преобразование осуществляется в два этапа. Сначала осущест-
вляется переход прямоугольного волновода в специальный же-
лобковый волновод, у которого размер Ь' меньше, чем оконча-
тельный размер Ь' и меньше критического размера для вол-
ны ТЕ01 плоскопараллельной линии для наиболее высокой ра-
бочей частоты. Во второй части преобразователя размер Ь'
Фиг. 5. Преобразователь волны прямоугольного волновода в волну
желобкового волновода.
увеличивается до нужной величины желобковой линии переда-
чи. В результате испытания полного преобразователя радиа-
ционные потери оказались малыми. Величина потерь вставки
была порядка 0,1 дб.
ЛИТЕРАТУРА
1. Griemsmann J., Politechnic Institute of Brooklin Report No.
P1B-MRI-1166-63 (Signal Corps Contract DA-36-039-50-85321).
Final Repoit on Design of Millimeter Waveguide Components (1 June
1960 — 31 January 1963).
2. Birenbaum L., Griemsmann J., в книге Proc. Symposium on Milli-
meter Waves (MRI Symp. Series, Vol. IX), New York, 1960.
A Low-Loss Я-guide for Millimeter Wavelengths.
3. Ti scher F. J., Proc. IRE, 51, 1050 (1963).
Conformal Mapping in Waveguide Considerations.
4. Ti scher F. J., Wescon Conv. Record, Paper 4, 5, August 1963.
The Groove Guide, a Low-Loss Waveguide for Millimeter Uses.
5. Meinke H. H., Lange К. P., Ruger J. F., Proc. IEEE, Nov. 1963,
p. 1463.
ТЕ- and TM-Waves in Waveguides of very General Cross-Section.
6. G an net D. K., Szekelyz, Proc. IRE, 48, 1161 (1960).
A Simple General Equation for Attenuation.
IV
ПРИМЕНЕНИЕ
КВАЗИОПТИЧЕСКИХ
УСТРОЙСТВ
19
ОБ ИСПОЛЬЗОВАНИИ РЕЗОНАТОРОВ ФАБРИ-ПЕРО
ДЛЯ СВЧ ДИАГНОСТИКИ ПЛАЗМЫ
Д. Аустон*, Р. Примич*, Р. Хаями*
В статье приведены результаты теоретических и экспериментальных ис-
следований, касающихся изучения структуры поля внутри резонаторов Фаб-
ри— Перо и его взаимодействия с плазмой с целью СВЧ диагностики
плазмы.
Эксперименты проводились, используя резонатор со сферическими отра-
жателями иа частоте около 70 Ггц. Рассмотрена зависимость различных
характеристик резонатора таких, как добротность, распределение поля в
фокальной плоскости для различных мод и дифракционные потери, от рас-
стояния между отражателями и их формы. Расстояние между отражателями
изменялось от конфокального до концентрического для случаев сплошных
круглых, перфорированных круглых и сплошных прямоугольных отражателей.
Найдено, что оптимальное с точки зрения диагностики плазмы расстояние не-
много меньше концентрического; при этом добротность максимальна. Размер
пятна для основного типа колебания немного больше длины волны, а ди-
фракционные потери сравнимы с потерями конфокального резонатора. При
приближении к концентрическому расстоянию добротность быстро растет, ди-
фракционные потери быстро убывают, но в то же время появляются боковые
лепестки в распределении поля основной моды в фокальной плоскости. Более
подробно были рассмотрены моды высших порядков для сплошных круглых
отражателей и был замечен так называемый «воловий глаз», или коль-
цо Френеля. Были выполнены измерения на резонаторах с прямоуголь-
ными отражателями и получены данные для некоторых мод высших по-
рядков.
При теоретическом исследовании другими авторами было найдено, что
скалярная теория дифракции дает удовлетворительные результаты при -усло-
вии, что расстояние не слишком близко к концентрическому. В данной статье
основное внимание уделено случаю концентрического расстояния. Была раз-
вита приближенная скалярная теория дифракции, которая подтверждает ос-
новные экспериментальные результаты, а именно малый размер пятна и суще-
ствование боковых лепестков для распределения поля в фокальной плоскости.
Обсуждается также приближенный математический анализ, который показы-
вает, что моды высших порядков можно использовать для зондирования из-
менений плазмы в фокальной плоскости.
* D. Н. A u s t о п, R. I. Р г i m i с h, R. A. H a у a m i, G. M. Defence
Research Laboratories, General Motors Corp., Santa Barbara, Calif.
25*
388
Д. Аустон, Р. Примич, Р. Хаями
§ 1. ВВЕДЕНИЕ
В настоящее время существует большая потребность в таких
методах СВЧ диагностики плазмы, которые обладали бы одно-
временно высокой пространственной разрешающей способностью
(доли сантиметра) и хорошей чувствительностью, т. е. по-
зволяли бы измерять малые электронные плотности порядка
107—108 см~3. С помощью сфокусированных СВЧ пучков можно
измерять электронные плотности до 1010 см~3 с пространствен-
ным разрешением около 1 см [1].
При внесении в такой пучок концентрического резонатора
Фабри — Перо фокусировка пучков сохраняется, а чувствитель-
ность измерения электронной плотности возрастает из-за эф-
фекта резонанса по крайней мере на два порядка [1, 2]. Это уве-
личение чувствительности было оценено в предыдущей статье
авторов [2]. Там же было получено экспериментальное подтвер-
ждение увеличения чувствительности и изучено влияние фоку-
сировки пучка. В то время существовали значительные трудно-
сти в измерении поля в фокальной плоскости. Из-за сильного
искажения поля размер фокального пятна удалось оценить лишь
с точностью порядка 50%.
Кроме чувствительности важной характеристикой резонато-
ров Фабри — Перо, предназначенных для диагностики плазмы,
является распределение поля различных мод вблизи фокальной
плоскости. Изучение этих распределений поля и, в меньшей сте-
пени, взаимодействия полей с плазмой и составляет основное
содержание данной работы.
Начнем с обсуждения распределений поля в резонаторах
Фабри — Перо. Будут рассмотрены распределения поля, наибо-
лее желательные как при обычных применениях резонаторов,
так и при использовании резонаторов для диагностики плазмы.
Затем мы дадим подробный обзор тех работ, которые могут
быть полезны для интерпретации взаимодействия поля в резо-
наторе Фабри — Перо с плазмой. Детальное исследование взаи-
модействия полей с плазмой будет проведено в другой статье.
Здесь мы ограничимся выяснением общего характера взаимодей-
ствия, поскольку знать его необходимо для правильного кон-
струирования измерительных резонаторов. Мы рассмотрим резо-
наторы, состоящие из сферических отражателей с круглыми и
прямоугольными апертурами, считая, что расстояние между от-
ражателями может изменяться от конфокального до концентри-
ческого.
Экспериментальная часть работы включала измерения доб-
ротности и распределения электрического поля основной моды,
а также нескольких высших мод в зависимости от формы апер-
19. Резонаторы Фабри — Перо в диагностике плазмы 389
туры отражателей и расстояния между ними. Все отражатели
были сферические. Мы опишем также новый метод измерения
распределения поля в фокальной плоскости, который позволяет
получить высокую точность измерения распределения поля, при-
чем искажения поля в процессе измерений можно сделать пре-
небрежимо малыми и контролируемыми.
При измерениях была обнаружена интересная особенность,
свойственная отражателям любой из рассмотренных форм. Ко-
гда расстояние между отражателями изменялось от концентри-
ческого до конфокального, оптимальные условия для диагности-
ки плазмы всегда соответствовали расстоянию, несколько мень-
шему концентрического. В этом случае при работе на основной
моде добротность максимальна, полные потери близки к поте-
рям в конфокальном резонаторе, а размер фокального пятна
слегка превышает длину волны. В концентрическом резонаторе
размер фокального пятна еще меньше (порядка длины волны),
однако из-за дифракционных потерь заметно снижается доб-
ротность. Следовательно, концентрический резонатор для диаг-
ностики плазмы не подходит и расстояние между отражателями
должно быть несколько меньше концентрического.
Было детально измерено распределение поля в фокальной
плоскости резонатора со сплошными круглыми отражателями.
Распределение имело известную форму «воловьего глаза», или
колец Френеля1). Исследованы распределения поля для трех
первых мод при различных расстояниях между отражателями,
исключая близкие к концентрическому. Экспериментальные дан-
ные находятся в хорошем согласии с результатами расчета, ос-
нованного на скалярной теории дифракции.
В случае перфорированных отражателей характеристики ос-
новной моды (добротность, распределение поля, полные потери
в функции расстояния между отражателями) мало отличались
от случая сплошных отражателей. Однако в поведении высших
мод были отмечены интересные различия. Так, в случае перфо-
рированных отражателей в фокальной плоскости обнаружена
четко выраженная азимутальная асимметрия распределения поля
первой высшей моды. Причина этого явления неясна, но, по-ви-
димому, его можно объяснить возбуждением азимутальных мод
из-за асимметрии отверстий в отражателе относительно оси.
Было найдено, что поля в резонаторах со сплошными прямо-
угольными отражателями соответствуют рассчитанным методом
разделения переменных в прямоугольной системе координат.
В одном измерении поле в фокальной плоскости можно сделать
сосредоточенным внутри узкой полосы, т. е. хорошо сфокусиро-
). См. книгу [3], стр. 330, фиг. 7.60.
390
Д. Ay стон, Р. Примич, Р. Хаями
ванным, а в другом измерении можно получить ряд пиков при-
близительно одинаковой интенсивности. Число пиков зависит от
номера моды. Эти пики в принципе можно использовать для
зондирования плазмы на малых участках, расположенных поч-
ти равномерно с интервалом порядка одной длины волны. Ниже
приведены результаты, полученные для трех первых мод. И в
этом случае было получено хорошее совпадение с выводами
скалярной теории дифракции.
Статья заканчивается обсуждением многомодовых резонато-
ров, закрытых по крайней мере в одном измерении. В ряде слу-
чаев такие резонаторы имеют преимущества перед открытыми
резонаторами. В случае осесимметричной плазмы (ось симме-
трии плазмы совпадает с осью резонатора) предполагается, что
взаимодействие полей с плазмой, включая и перекрестную связь
мод, можно описать с помощью модовых решений для незапол-
ненного резонатора. Резонаторы такого типа могут успешно
применяться для диагностики плазмы в том случае, если удаст-
ся интерпретировать взаимодействие поля с плазмой, когда она
не локализована вдоль оси резонатора.
§ 2. ОСОБЫЕ ТРЕБОВАНИЯ К ДИАГНОСТИКЕ ПЛАЗМЫ
В аэродинамике гиперзвукового полета подробно изучается
участок свободного полета по баллистической кривой [4]. Не-
давнее теоретическое [5] и экспериментальное [6] доказательство
двойного масштабного копирования (особенно применительно к
ионизации) в ближней спутной струе за гиперзвуковым снаря-
дом, создание предпосылок для осуществления точных измере-
ний излучения и ионизации [7] поля гиперзвукового потока, а
также серьезное внимание, которое сейчас уделяется защите от
межконтинентальных баллистических ракет — все это выдви-
нуло баллистический участок.траектории на первый план в изу-
чении физики вхождения баллистических ракет в плотные слои
атмосферы.
В связи с этим возникла особая задача — измерение степени
и пространственного распределения ионизации в спутной струе
(электронной плотности и частоты столкновений) в области
за снарядом малых размеров, движущимся со скоростями до
7200 м!сек. Для осесимметричных тел при малых углах атаки
спутные струи сильно асимметричны и обладают большими гра-
диентами ионизации как в радиальном, так и в осевом направ-
лениях. Измерение этих градиентов является важной частью
упомянутой задачи и требует пространственного разрешения по-
рядка 6 мм и менее.
«4
/9.' Резонаторы Фабри — Перо в диагностике пЛазмы 391
Для тупых тел, движущихся со скоростями 6000—7200 м]сек
в воздухе на представляющих практический интерес высотах,
электронные плотности лежат в пределах 1010—1014 см~3. Такие
плотности можно легко измерить на частотах 35—70 Ггц с по-
мощью сфокусированных зондов [1]. Например для зонда, рабо-
тающего на частотах около 70 Ггц [1] в плоскости, перпендику-
лярной траектории полета, располагается ряд сфокусированных
пучков. Каждый пучок сфокусирован так, что размер пятна со-
ставляет около 6 мм при фокусном расстоянии около 2,5 см.
Осевые градиенты на участке длиной 6 мм определяются непо-
средственно по изменению показаний одного зонда во время
прохождения мимо него ионизованной области. Радиальные гра-
диенты (на участке длиной 6 мм) определяются с помощью на-
бора пучков подобно тому, как это делается в оптике;
С другой стороны, для тонких тел при тех же условиях ди-
апазон электронных плотностей лежит в пределах 108—10н см~3.
Такие плотности измерить сфокусированными зондами обычно
не удается. Чувствительность можно увеличить, если пользо-
ваться низкими частотами, когда при той же плотности взаи-
модействие между электромагнитной волной и плазмой стано-
вится сильнее. Однако при уменьшении частоты уменьшается и
разрешающая способность, вследствие чего получить разреше-
ние радиальных градиентов ионизации не удается. Проблема
решается с помощью сфокусированного резонатора Фабри —
Перо, предложенного в работе [1] и рассмотренного в работах
[1, 2]. В этом резонаторе свойства сфокусированного зонда соче-
таются с высокой чувствительностью.
Дополнительным требованием к любому методу СВЧ диагно-
стики, применимому к свободно летящим объектам, является
требование невозмущения поля струи. В частности, было уста-
новлено, что влияние отражений от фронта ударной волны, об-
разованной снарядом вне участка, прилежащего к траектории,
может быть достаточно сильным, чтобы изменить ионизацию
в спутной струе. Этот эффект достаточно- мал при размещении
зондов вдали от траектории. Мы увидим далее, что резонатор
Фабри — Перо может удовлетворять этим требованиям.
В заключение следует подчеркнуть, что, кроме достаточной
пространственной разрешающей способности и чувствительно-
сти, метод должен обеспечивать возможность измерения ра-
диальных градиентов. Этого можно достигнуть, применяя ряд
резонаторов, работающих на основной моде и соответствующим
образом смещенных по радиусу, подобно решетке зондов со
сфокусированными пучками [1].
Такая система из-за ее громоздкости и неэкономичности в
дальнейшем рассматриваться не будет. Однако имеется по
392 Д. Аустон, Р. Примич, Р. Хаями
меньшей мере два других способа применения резонаторов Фаб-
ри — Перо, каждый из которых позволяет определять радиальные
градиенты ионизации плазмы. В одном способе за счет выбора
подходящей конфигурации зеркал создается плоская решетка
пучков, соответствующая суперпозиции различных поперечных
мод. Тогда для определения градиентов можно использовать
совместное рассмотрение взаимодействия с плазмой каждой из
мод. В другом способе резонатор диафрагмируется в поперечной
плоскости, в результате чего с плазмой взаимодействуют лишь
радиальные моды с сильной концентрацией поля вблизи оси
плазмы. Радиальные градиенты определяются так же, как и в
предыдущем случае, но сделать это проще из-за присущей та-
кому резонатору симметрии.
Резюмируя, можно сказать, что многомодовые резонаторы
Фабри — Перо в принципе удовлетворяют всем сформулирован-
ным выше требованиям. Хотя мы рассмотрели весьма специфи-
ческую задачу, тем не менее результат анализа можно, очевид-
но, применить и к любым другим задачам диагностики осесим-
метричной плазмы с радиальными градиентами.
§ 3. РАСПРЕДЕЛЕНИЯ ПОЛЕЙ В РЕЗОНАТОРЕ
Несмотря на широкое и разнообразное применение резонато-
ров Фабри — Перо, в литературе рассматривались в основном
не заполненные веществом резонаторы. Такие резонаторы яв-
ляются первым приближением в задачах по диагностике плазмы.
Поэтому результаты, полученные для «пустых» резонаторов, мо-
гут быть полезны и для резонаторов с плазмой. Ниже будет дан
исторический обзор и проведено подробное обсуждение работ,
относящихся к «пустым» резонаторам.
Несмотря на широкое и разнообразное применение резонато-
ров Фабри — Перо1), они почти не применялись для диагно-
стики плазмы. В своем первоначальном виде [8] резонатор Фаб-
ри— Перо состоял из двух разнесенных, плоскопараллельных
пластин, обладающих очень высокой отражающей способностью.
Чрезвычайно высокая частотная избирательность этого устрой-
ства позволила применить его для изучения тонкой структуры
спектральных линий и измерения длины волны. По мере расши-
рения спектральных исследований они стали включать изучение
спектра ионизированного газа, что можно считать одной из
форм диагностики плазмы.
В СВЧ технику настраиваемые резонаторы Фабри — Перо
были введены Кульшоу, который в работах [8—12] рассмотрел
1) См. книгу [3], стр. 328.
19. Резонаторы Фабри — Перо в диагностике плазмы
393
их применение для измерения параметров диэлектриков, в спек-
троскопии, а также в качестве фильтров и волномеров. Позд-
нее он исследовал такие резонаторы, как резонансные элементы
квантовых генераторов диапазона миллиметровых и субмилли-
метровых волн [13]. Им были изучены и нашедшие затем приме-
нение в лазерах резонаторы со сферическими отражателями.
При анализе Кульшоу пользовался аналогией с линией передачи,
считая, что на вход плоской системы поступает однородная пло-
ская волна. Позднее было показано [14], что такой подход спра-
ведлив для концентрических резонаторов при отсутствии ди-
фракционных потерь. Используя подобный подход, Примич и
Хаями [2] показали, что резонатор Фабри — Перо позволяет
с чрезвычайно высокой чувствительностью измерять плотность
электронов и нейтрального газа.
Рэвид [50] предложил использовать плоскопараллельный
СВЧ резонатор Фабри — Перо для определения пространствен-
ных вариаций изменений электронной плотности плазмы в тру-
бах с ударной волной. Однако возможности и эффективность
этого метода изучены пока недостаточно.
Использовать плоские резонаторы Фабри — Перо в качестве
резонансных элементов лазеров предложили независимо друг
от друга Шавлов и Таунс [15], Прохоров [16] и Дик [17], а впер-
вые успешно применили Мейман [18] и Коллинз и др. [19].
Резонатор со сферическими отражателями первоначально
был использован в качестве интерферометра (Коннес [20]).
Позднее такой резонатор был применен в лазере и исследован
для этой цели Фоксом и Ли [22, 25], Бойдом и Гордоном [23],
Бойдом и Котельником [24], Яривом и Гордоном [26], Суху [27],
Кульшоу [14], Тангом [28], Хардингом и Ли [31], Ли [32] и Вайн-
штейном [53, 54].
Эшби и Джефкотт [51] использовали плоский резонатор Фа-
бри — Перо, имеющий сильную связь с лазером, для измерения
электронной плотности. Жерардо и Вердьен [52] заменили в ре-
зонаторе плоское зеркало сферическим, значительно повысив
благодаря этому чувствительность. Однако в обоих случаях ин-
терпретация экспериментальных данных была сильно упрощен-
ной, а абсолютная чувствительность недостаточной для решения
рассматриваемой здесь задачи.
Параллельно развивались исследования пучковых СВЧ вол-
новодов. Благодаря аналогии между линзовой системой и систе-
мой конфокальных параболических отражателей многие резуль-
таты, полученные для линзовых волноводов, оказались полез-
ными и для резонаторов Фабри — Перо. Резонансы в системе из
параллельных пластин были обнаружены еще в 1955 г. Шайбе
[33]. Позднее, после появления теоретических работ Губо и
394 Д. Ay стон, Р. Примич, Р. Хаями
Шверинга [34], а также Фокса и Ли [22] Шайбе возобновил 'экс-
перименты на этот раз с конфокальными параболическими отра-
жателями. Как в случае плоских круглых отражателей, так и в
случае конфокальных параболических отражателей имело место
превосходное совпадение измеренных и расчетных дифракцион-
ных потерь. Измерения проводились также Кристианом и Губо
[35, 36], а также Бейером и Шайбе [37]. Последние авторы дали
расчет дифракционных потерь для высших пучковых мод [38].
Маркуз [39] успешно применил сферический резонатор в не-
сколько иной области СВЧ техники, а именно для квантового
генератора миллиметрового диапазона волн. Циммерер и др. [40]
использовали плоский и сферический’ резонаторы для газовых
спектрометров и рефрактометров. Кроме того, Циммерер [41]
провел измерения полей,и потерь в сферическом СВЧ резона-
торе. Наконец, Циммерером [42] и Олтманом [43] были описаны
волномеры диапазона миллиметровых волн, использующие сфе-
рические резонаторы Фабри — Перо.
Перейдем теперь к более подробному обсуждению работ, от-
носящихся к рассматриваемой здесь задаче. Фокс и Ли [22] с
помощью электронной вычислительной машины рассчитали соб-
ственные функции и собственные значения ряда мод для
следующих случаев: а) прямоугольные плоские отражатели;
б) круглые плоские отражатели и в) конфокальные параболи-
ческие отражатели. На основании принципа Гюйгенса для ска-
лярного поля им удалось получить интегральное уравнение, свя-
зывающее поле на одном отражателе с полем на другом отра-
жателе. В обычном приближении дальней зоны (т. е. считая,
что размеры отражателя велики по сравнению с длиной волны,
но малы по сравнению с расстоянием между точкой наблюде-
ния и источником) [44] уравнение было упрощено и для всех
трех случаев решено численно методом итераций. Были найдены
зависимости дифракционных потерь от числа Френеля, что при-
дало результатам большую общность. Собственные функции
были найдены лишь для некоторых значений числа Френеля и
поэтому могут быть использованы в более ограниченном числе
случаёв. Число Френеля определяется соотношением
где а — радиус или полуширина отражателя, d — расстояние
между отражателями, % — длина волны.
Бойд и Гордон [23] исследовали конфокальный параболиче-
ский резонатор с прямоугольными апертурами. Они получили
интегральное уравнение, подобное уравнению Фокса и Ли [22],
и сумели записать его решение в замкнутой форме. Решение
/5. Резонаторы Фабри — Перо в диагностике плазмы 395
выражается через присоединенные сферические волновые функ-
ции, а собственные значения могут быть получены непосред-
ственным расчетом. Собственные функции также могут быть
непосредственно рассчитаны, однако было показано, что их
можно аппроксимировать функцией Гаусса, умноженной на по-
лином Эрмита. Аппроксимация хороша для точек на оси и ухуд-
шается по мере удаления от оси. Интересным свойством распре-
деления поля является то, что оно подобно на всех плоскостях
равной фазы. Использовав далее простую подстановку, Бойд и
Гордон предположили, что распределение поля и дифракцион-
ные потери для некоторой области неконфокальных расстояний
между отражателями можно найти из рассмотрения конфокаль-
ного резонатора. Расстояния, при которых это справедливо, за-
ключены между конфокальным и концентрическим, исключая
последнее.
Циммерер [41] высказал интересную точку зрения, позволяю-
щую объяснить, почему Бойд и Гордон смогли получить для от-
крытого резонатора замкнутое решение в виде полной системы
ортогональных мод. Он показал, как конфокальный параболиче-
ский резонатор может быть образован из системы конфокаль-
ных сплющенных сфероидальных поверхностей. Если размеры
резонатора велики по сравнению с длиной волны, то собствен-
ные функции будут заметно отличаться от нуля только вблизи
оси. Если на соответствующих конфокальных поверхностях пер-
пендикулярно оси поместить отражатели конечных размеров,
то между ними будет заключена большая часть поля резона-
тора. Если учесть к тому же, что присоединенные сферические
волновые функции образуют полную систему и ортогональны
как на бесконечном, так и на конечном интервалах, и так как
открытый конфокальный резонатор можно получить из закры-
того резонатора, то становится очевидным, что в обоих случаях
замкнутое решение можно записать через эти функции. Разу-
меется, с тем отличием, что для конечных отражателей из-за
дифракционных потерь собственные значения открытого резона-
тора суть комплексные величины, тогда как в закрытой системе
они действительны.
Бойд и Когельник [24] распространили теорию Бойда и Гор-
дона [23] на отражатели с неравными размерами апертур и
радиусами кривизны. Если расстояние между отражателями
больше одного радиуса и меньше другого, то имеют место об-
ласти высоких и низких потерь. Практически это означает, что
хотя идеально конфокальная система с идентичными зеркалами
и обладает наименьшими среди всех систем дифракционными
потерями, однако уже малое различие в радиусах кривизны
зеркал вызывает резкое увеличение потерь. Этот эффект в кон-
396
Д. Ay стон, Р. Примич, Р. Хаями
фокальном резонаторе можно устранить, увеличив или умень-
шив расстояние между отражателями. В лазерной технике
имеется тенденция к уменьшению расстояния между отражате-
лями, что вызывает увеличение числа мод. Из дальнейшего бу-
дет ясно, что для диагностики плазмы предпочтительнее увели-
чивать расстояние. Следует отметить, что область высоких по-
терь, вызванная неоднородностью радиусов кривизны отража-
телей, была обнаружена экспериментально Циммерером [41] до
появления соответствующей теории.
В своей второй статье Фокс и Ли [25] исследовали числен-
ными методами отражатели различной кривизны при различных
расстояниях между зеркалами. Они ввели двумерную диаграмму,
показывающую области больших и малых потерь в зависимости
от расстояния между отражателями и их кривизны. Потери, рас-
считанные для области малых потерь, хорошо согласуются с
результатами Бойда и Гордона [23]. Однако на некотором уча-
стке области больших потерь последние оставались постоянными
при возрастании числа Френеля.
Вайнштейн исследовал резонаторы Фабри — Перо как с пло-
скими [54], так и со сферическими [55] отражателями конечных
размеров. В случае плоских зеркал он установил близкую ана-
логию между излучением из такого резонатора и из открытого
конца волновода. Это позволило использовать для резонатора
с бесконечными плоскими отражателями существующее строгое
решение задачи об излучении из полубесконечного волновода.
Предполагалось, что в резонаторе можно возбудить некоторую
моду. Преобразование этой моды в другие при отражениях
вблизи краев пластин не учитывалось. Несмотря на это огра-
ничение, собственные значения и собственные функции на по-
верхности отражателей оказались в очень хорошем согласии
с результатами Фокса и Ли [22]. Подобным образом анализиро-
вались и круглые плоские зеркала, для которых были сделаны
дополнительные упрощения. Отражение моды от краев пластин
резонатора определялось на модели волновода, образованного
двумя дисками, между которыми распространяется волна с ци-
линдрическим фронтом. Собственные значения и собственные
функции на отражателях также оказались в хорошем согласии
с полученными Фоксом и Ли [22].
Для случая сферических зеркал с прямоугольной и круглой
апертурой Вайнштейн получил дифференциальное уравнение и
записал его приближенное решение черёз сферические волновые
функции при любых расстояниях между отражателями, исклю-
чая концентрическое. Сначала были найдены собственные функ-
ции в предположении отсутствия дифракционных потерь. Затем
были вычислены собственные значения с учетом дифракционных
19. Резонаторы Фабри — Перо в диагностике плазмы
397
потерь. Последняя поправка представляется несколько произ-
вольной, так как она получена на основании предыдущего опы-
та решения задач теории дифракции. В конфокальном случае соб-
ственные функции переходили в полученные Бойдом и Гордоном
[23]. Вайнштейн в отличие от интуитивных представлений Бойда
и Гордона [23], а также Бойда и Котельника [24], по-видимому,
впервые получил аналитическое решение для неконфокальной
геометрии.
Суху [27] также рассматривал зависимость дифракционных
потерь от расстояния между сферическими зеркалами. Для од-
ного частного значения отношения N к djR. (R— радиус кри-
визны зеркала) он провел и численный расчет. Взятое отноше-
ние слишком мало для наших целей. Однако результаты расчета
показывают, что вблизи концентрического расстояния имеет ме-
сто быстрый переход от области с большими потерями к обла-
сти с малыми потерями.
Кульшоу [14] применил вариационный метод для решения
интегрального уравнения резонатора Фабри — Перо. Он рассчи-
тал собственные функции и собственные значения сферического
конфокального резонатора и собственные значения плоского ре-
зонатора. Результаты хорошо согласуются с результатами Бойда
и Гордона [23] и Фокса и Ли [22] соответственно. Танг [28] также
использовал вариационный метод для расчета дифракционных
потерь. Однако, как указал Кульшоу, им была допущена ошиб-
ка в одной из формул. Морган [29, 30] показал, что класс инте-
гральных уравнений с комплексным симметричным ядром, встре-
чающихся в задачах о резонаторах Фабри — Перо, не обладает
хорошо известными свойствами интегральных уравнений с эрми-
товыми ядрами. В частности, к ним не применим обычный прин-
цип экстремума, с помощью которого в случае эрмитовых ядер
можно оценить собственные значения методом Релея — Ритца.
Морган считает, что расчет дифракционных потерь вариацион-
ным методом приводит к результатам, корректность которых
вызывает сомнение.
Ярив и Гордон [26] сделали полезное обобщение свойств ре-
зонаторов Фабри — Перо, применяемых в лазерной технике.
В частности, ими приведена полученная Бойдом и Гордоном [23]
формула для вычисления дифракционных потерь сферического
резонатора при различных расстояниях между отражателями.
Губо и Шверинг [34] исследовали лучевой волновод. Задача
эта по существу та же, что и решенная Бойдом и Гордоном [23].
Результаты Губо и Шверинга были использованы Бейером и
Шайбе [37] для расчета дифракционных потерь высших мод.
Как и следовало ожидать, все результаты совпали с получен-
ными Бойдом и Гордоном, а также Фоксом и Ли.
398 Д. А у ст он, Р. Примич, Р. Хаями
Многие из упомянутых авторов обсуждали вопрос о вырож-
дении колебаний в различных типах резонаторов Фабри — Перо.
Так, имеется почти полное вырождение в сферическом конфо-
кальном резонаторе, в котором половина поперечных мод резо-
нирует на одинаковой частоте. Это вырождение снимается при
увеличении расстояния между зеркалами в сторону концентри-
ческого. Однако при этом появляется возможность вырождения
между некоторыми поперечными и продольными модами. Если
при конфокальном расстоянии между отражателями некоторая
(-я поперечная мода вырождена с /-Й продольной модой, то при
неконфокальном расстоянии указанная i-я мода может оказать-
ся вырожденной с продольной модой индекса /±1. Однако,
строго говоря, вырождение всегда снимается из-за различия ди-
фракционных потерь у мод.
Это обстоятельство играет важную роль в лазерах. Там
моды с большими дифракционными потерями вообще не воз-
никают, если условия таковы, что коэффициент усиления этих
мод на длине резонатора меньше единицы. Применительно же
к диагностике плазмы такое снятие вырождения проявляется
лишь в перераспределении энергии между модами в соответ-
ствии с их дифракционными потерями. Критерий порога гене-
рации моды в этом случае отсутствует. Это означает, что распре-
деление поля, условия резонанса и дифракционные потери для
всех мод в сферическом резонаторе с пластинами круглой
или прямоугольной формы можно легко рассчитать по суще-
ствующим формулам. Расстояние между пластинами может изме-
няться от несколько меньшего, чем конфокальное, до концентри-
ческого, исключая последнее. (Разумеется, эти величины всегда
можно найти численными методами.) В соответствии с теорией
размеры зеркала должны быть велики по сравнению с длиной
волны и малы по сравнению с расстоянием между зеркала-
ми. Другими словами, число Френеля должно быть достаточно
малым.
Так как в рассматриваемой нами задаче первостепенное зна-
чение имеет хорошая фокусировка поля, а в случае концентриче-
ского резонатора, когда можно ожидать наилучшей фокусиров-
ки, теория Бойда — Гордона перестает быть справедливой, то
необходима дальнейшая разработка теории концентрического
резонатора.
Хотя Кульшоу [14] и Вайнштейн [54] показали, что поля на
отражателях плоского резонатора можно строго преобразовать
в поля на отражателях концентрического резонатора и что ди-
фракционные потери в обоих случаях одинаковы, тем не менее
поле в фокальной плоскости концентрического резонатора
найдено не было. Норсовер [45] исследовал сферический кон-
19. Резонаторы Фабри — Перо в диагностике плазмы
399
центрический резонатор с круглыми апертурами. Используя
скалярный принцип Гюйгенса и приближение параболического
уравнения, он получил для очень больших апертур решение в
замкнутом виде. Дифракционные потери при этом не учитыва-
лись, однако найденные таким образом собственные функции,
по-видимому, весьма точно описывают поле, так как напряжен-
ность поля быстро спадает при удалении от оси. Чрезвычайно
интересны распределения полей различных осесимметричных
мод в фокальной плоскости, где, очевидно, имеют место боковые
лепестки. В частности, основная мода имеет более узкий, чем в
конфокальном случае, центральный лепесток. Однако с обеих
сторон от него имеются боковые лепестки. Их можно было ожи-
дать, исходя из теории антенн, поскольку любое, исключая га-
уссово, синфазное распределение на одном из сферических
зеркал дает в дальней зоне распределение поля, имеющее в
фокальной плоскости боковые лепестки. Если предположить,
что зеркала являются параболическими и учесть, что фазы на
отражателях не постоянны, то распределение поля в дальней
зоне будет отличаться от идеального. Фазовое распределение
играет особенно большую роль в создании нулей в картине поля.
Боковые лепестки, несмотря на их низкий уровень, уносят за-
метную энергию. Это приводит к увеличению дифракционных
потерь по сравнению со случаем распределения Гаусса, имею-
щего тот же размер фокального пятна. Следующим этапом ис-
следования концентрического резонатора является нахождение
дифракционных потерь и учет малых отклонений расстояния ме-
жду отражателями от концентрического.
В литературе имеются факты, подтверждающие такое пред-
положение. Например, Кульшоу [14] показал, что поле в плоском
резонаторе можно строго преобразовать в поле концентриче-
ского резонатора. Этот результат также можно было предвидеть,
исходя из теории антенн и свойств фокусирующих апертур. Ли
[32] предложил использовать диафрагму в фокальной плоскости
концентрического резонатора для селекции мод. Его идея осно-
вана на расширении эффективного радиуса поля с увеличением
номера моды.
Численным методом было показано, что дифракционные по*
тери двух первых мод испытывают колебания по мере увеличе-
нйя апертуры диафрагмы в фокальной плоскости, что, очевидно,
связано с перекрыванием апертурой боковых лепестков. Фокс и
Ли [25] произвели специальный расчет распределения поля в фо-
кальной плоскости концентрического резонатора. Было обнару-
жено присутствие первого нуля и бокового лепестка !). Наконец,
') См. [25], фиг, 15,
400
Л. Аустон, Р. Примич, Р. Хаями
в той же работе [25] были рассчитаны большие, но конечные
дифракционные потери в резонаторах с плоскими зеркалами
прямоугольной и круглой формы. Эти результаты непосредствен-
но применимы к случаю концентрических резонаторов.
Основные сформулированные выше теоретические положения
были подтверждены экспериментально. Так, Шайбе [33] измерил
дифракционные потери основной моды в плоском и конфокаль-
ном параболическом резонаторах. Результаты находятся в хо-
рошем согласии с теорией Бойда и Гордона [23], а также Губой
Шверинга [34]. Аналогичные измерения и с тем же результатом
были проведены Кристианом и Губо [35, 36], Бейером и Шайбе
[37]. В частности, Кристиан и Губо [36] показали, что теория со-
гласуется с экспериментом вплоть до весьма больших значений
числа Френеля. Эти авторы получили также распределение поля
основной моды в лучевом волноводе. Циммерер [41] предпринял
попытку измерить распределение поля основной моды в фокаль-
ном резонаторе. Однако он обнаружил флуктуации распределе-
ния поля, не следующие из теории. Получить какое-либо
подтверждение существования в конфокальном резонаторе с
круглыми зеркалами мод типа «воловий глаз» Циммереру не
удалось. Примич и Хаями [2] провели аналогичные измерения в
сферическом резонаторе и снова безуспешно. Это вынудило их
сделать вывод, что измеряющий объект слишком сильно возму-
щает резонатор.
Когельник и Ригод [46] наблюдали присутствие нескольких
поперечных мод в лазерах с прямоугольными конфокальными
зеркалами, работающих в непрерывном режиме. Поскольку в
этом случае модовые распределения разделяются в прямоуголь-
ных координатах, то, наклоняя зеркала, им удавалось устранить
паразитные моды. При этом наблюдались распределения поля,
которые хорошо описываются полиномами Эрмита.
Насколько нам известно, моды типа «воловий глаз» в резо-
наторах с круглыми зеркалами так и не были обнаружены. В ла-
зерах это, по-видимому, объясняется наклоном круглых зеркал,
мешающих возникновению чистых мод. В СВЧ резонаторах при-
чина, по всей вероятности, в отсутствии удовлетворительных ме-
тодов измерения поля.
Некоторые доказательства существования таких мод уда-
лось получить Олтману [43]. Он определял, при каких смеще-
ниях от оси напряженность поля спадала до нуля. Найденные
смещения хорошо соответствовали рассчитанным по теории
Бойда и Гордона [23]. Резонансные частоты мод достаточно хо-
рошо определяются по измерениям с СВЧ резонаторами и из
наблюдения частот биений лазеров, работающих в непрерыв-
ном режиме.
19. Резонаторы Фабри — Перо в диагностике плазмы
401
§ 4. ВЗАИМОДЕЙСТВИЕ ПОЛЯ С ПЛАЗМОЙ
Хотя в диагностике плазмы с помощью резонаторов Фабри —
Перо основное значение имеет распределение поля различных
мод, тем не менее нельзя не учитывать и взаимодействия этих
полей с плазмой. Без ясного понимания этого взаимодействия
и при отсутствии методов его измерения и интерпретации де-
тальное изучение полей в пустом резонаторе было бы практи-
чески бесполезным. Поэтому ниже проведено предварительное
обсуждение взаимодействия поля с плазмой. Детальное рассмот-
рение этого вопроса будет дано в других статьях.
В нашем случае плазму можно рассматривать как диэлек-
трик с соответствующим комплексным показателем преломле-
ния. Плазма предполагается имеющей низкую !) плотность, хотя
во многих случаях понятие низкая плотность нуждается в более
точном определении, так как зависит от степени принятого мате-
матического приближения.
При рассмотрении проблемы взаимодействия можно исполь-
зовать по меньшей мере два подхода. Первый — это метод
матриц рассеяния, когда моды рассматриваются как волны, ко-
торые, рассеиваясь, распространяются через плазму. Этот под-
ход, очевидно, аналогичен методу, применяемому в теории ли-
ний передачи. Он позволяет рассчитать увеличение чувствитель-
ности за счет резонаторов Фабри — Перо [2]. Второй подход к
явлениям в резонаторе заключается в применении квантовоме-
ханического метода возмущений.
Метод матриц рассеяния или линий передачи применим
при очень низких электронных плотностях плазмы. По мере рос-
та плотности плазмы точность этого метода нарушается по двум
причинам. В реальном резонаторе поля мод можно представить
в виде суперпозиции неоднородных квазиплоских волн. Если
плотность плазмы очень мала, то прохождение этих волн через
плоский плазменный слой приблизительно эквивалентно прохо-
ждению через такой слой однородной плоской волны, поскольку
явлениями дифракции и многократных отражений можно прене-
бречь. С ростом плотности плазмы приближение однородной
плоской волны начинает давать серьезные ошибки. Вначале ос-
новную роль в этом играет рефракция, а при достижении кри-
тической плотности плазмы важным фактором становятся мно-
гократные отражения. Описание взаимодействия волны с плаз-
мой становится настолько сложным, что теряет практический
смысл. Однако поскольку рефракция начинает играть роль при
') В оригинале использован термин underdence, буквальный перевод ко-
торого «поДплотная». — Прим, ред,
20 Зак. 274
402
Д. А у стон, Р. Примич, Р. Хаями
значительно более низких плотностях плазмы, чем многократ-
ные отражения, то имеет смысл рассмотреть лишь ту область,
где погрешности определяются рефракцией. Высокая чувстви-
тельность резонатора связана с многократным (несколько сот
раз) прохождением волны через плазму. Поэтому в резонаторе
рефракция начинает играть существенную роль при значитель-
но более низких плотностях плазмы, чем в обычных сфоку-
сированных индикаторах. Таким образом, ограничения на об-
ласть применимости такого рассмотрения могут быть весьма
жесткими.
Область применимости метода можно в принципе расширить,
если включить в рассмотрение истинные распределения полей
мод в резонаторе с плазмой и рассматривать последний как
совокупность неоднородных линий передачи. Так, конфокальный
резонатор можно анализировать на модели гиперболических
линий. Это было бы справедливо для всех мод и позволило бы,
кроме того, учесть их взаимодействие. Тем самым можно было
бы учесть рефракцию, так как именно она и вызывает взаимо-
действие. В сущности расширение области применимости ме-
тода требует решать дифракционную задачу при заданной моде
на входе, параметрах плазмы и граничных условиях, опреде-
ляемых резонатором. Практических результатов можно ожидать,
по-видимому, лишь после введения ряда упрощающих предпо-
ложений. Тем не менее этот метод стоит развивать, так как с
его помощью можно получить информацию о плазме достаточно
высокой плотности.
Вторым способом интерпретации результатов является метод
возмущений. Этот метод с успехом применяется для анализа
малых возмущений в закрытых резонаторах, поэтому естествен-
но попытаться обобщить его и на открытые резонаторы.
Рассмотрим эту возможность. Следуя стандартной формули-
ровке метода возмущений, данной Морсом и Фешбахом [47], бу-
дем искать решение возмущенного скалярного волнового урав-
нения *)
?2ф + ^2 —Ш(г)]ф —0
при заданных условиях на границах резонатора. Здесь
Ш(г) ~ ЛЦг)
й2 ~ Мф'
Скалярное приближение применимо, разумеется, лишь в случаях, когда
градиенты плотности плазмы н локальных полей малы по сравнению с длиной
волны. Если градиенты велики, то нужно пользоваться векторной формули-
ровкой; см., например, Ван Владел [55].
19. Резонаторы Фабри — Перо в диагностике плазмы 403
(в пренебрежении частотой столкновений); М(г)—простран-
ственное распределение электронной плотности; Мкр— критиче-
ская электронная плотность.
Задача сводится затем к интегральному уравнению, содер-
жащему функцию Грина резонатора
Ф(г) = — 1 J О (г | г0) U (г0) Ф (г0) dx0.
Для решения этого уравнения нужно знать функцию Грина
G(r/r0), являющуюся решением дифференциального уравнения
FO + W = 6(r-r0).
Для закрытых резонаторов функция Грина выражается через
невозмущенные (т. е. при % = 0) волновые функции (или моды)
с помощью соотношения Гильберта — Шмидта
Морс и Фешбах, используя метод итераций, показали, что
при подстановке этой формулы в интегральное уравнение по-
лучается следующее приближенное соотношение для нахожде-
ния возмущенных собственных значений (или собственных ча-
стот) :
k .—kt
рфп л Р
где
Первый член в правой части есть невозмущенное волновое
число. Второй член соответствует формуле Слэтера для поправ-
ки первого порядка [48]. Третий член учитывает изменение
структуры поля (в первом порядке) из-за возбуждения других
мод. Можно получить поправки и более высокого порядка. В об-
щем случае для любого хорошо ведущего себя возмущения (/(г)
можно найти решение с любой степенью точности.
Однако в случае открытых резонаторов возникают серьез-
ные математические трудности. Для применения соотношений
Гильберта — Шмидта необходимо, чтобы невозмущенные волно-
вые функции образовывали полную ортогональную систему. К со-
жалению, это не имеет места для открытых резонаторов. Тем
не менее полезно рассмотреть возможность использования не-
полной системы. Бойд и Гордон [23] показали, что моды с ма-
лыми дифракционными потерями с хорошей точностью взаимно
26*
404
Д. Ay стон, Р. Примич, Р. Хаями
ортогональны во всем объеме резонатора; это, конечно, неверно
для мод с большими потерями. Поэтому, если возмущения вы-
зывают связь лишь между «высокодобротными» модами, то мо-
жно ожидать, что проведенный выше анализ даст вполне хоро-
шие результаты.
Однако это накладывает серьезные ограничения на допу-
стимую геометрию возмущений. Пусть имеется, например, кон-
фокальный резонатор, работающий на основной моде. Введем
в такой резонатор возмущение в виде сплющенного сфероида из
плазмы малой плотности. Если сфероид расположен вдоль син-
фазных линий поля и его размеры велики по сравнению с раз-
мером фокального пятна, то связь с высшими поперечными
модами будет мала. Для получения довольно точных результа-
тов будет достаточно учесть лишь связь с продольными модами.
Если, однако, в тот же резонатор поместить цилиндрическую не-
однородность так, чтобы ее ось находилась в поперечной пло-
скости, а диаметр был сравним с размером фокального пятна,
то связь волн будет очень сильной, особенно между вырож-
денными модами. Чрезвычайно сильная связь таких мод на-
блюдалась экспериментально в резонаторах Фабри — Перо диа-
пазона частот 50—52 Ггц. Эти явления сейчас внимательно изу-
чаются; результаты будут опубликованы позже [49].
Возможное решение этой задачи состоит в разбиении функ-
ции Грина открытого резонатора на две части: сумму дискрет-
ных мод, имеющих малые потери, и интеграл по непрерывному
спектру мод, учитывающий потери на излучение из-за рассеяния
энергии на возмущающем объекте. Это разбиение аналогично
выделению «связанных» и «свободных» состояний в квантовой
механике.
Более удобным решением проблемы было бы упрощение ана-
лиза путем изменения геометрии резонатора. Очевидно, что пол-
ностью закрытый резонатор использовать для диагностики плаз-
мы нельзя. Наоборот, весьма перспективен для этой цели резо-
натор, закрытый по одному измерению и открытый по двум
другим. Таким резонатором является, например, круглая секция
удлиненного сфероида, получающаяся путем удаления двух
«шапок» от каждого конца. Это позволяет осуществить ввод и
вывод исследуемого плазменного столба. В большом сфероиде
с такими срезами структура полей резонирующих мод будет
приблизительно такой же, как и в закрытом сфероиде, т. е. бу-
дет описываться присоединенными сферическими волновыми
функциями [47]. Моды в поперечном сечении, описываемые про-
изведением радиальной присоединенной волновой функции на
синусоиду, будут иметь, грубо говоря, то же значение Q и с хо-
рошей точностью могут использоваться для построения полной
19. Резонаторы Фабри — Перо в диагностике плазмы
405
системы. Кроме того, в цилиндрической плазме (такой тип
плазмы встречается наиболее часто) моды связаны главным об-
разом по радиальной компоненте, поэтому расчет связи можно
произвести методом возмущений. Такой тип резонатора весьма
удобен при работе в многомодовом режиме и позволяет получить
информацию о радиальных распределениях в цилиндрических
столбах плазмы. Сейчас проводится более детальное исследова-
ние этого вопроса, результаты которого будут опубликованы.
До сих пор пространственное распределение изучаемой плаз-
мы мы предполагали известным. В действительности это не так.
Одно из наиболее интересных и полезных применений резона-
тора Фабри — Перо как раз и заключается в извлечении из
экспериментальных данных информации о пространственном
распределении плазмы1). Этого можно достигнуть, измеряя
сдвиги резонансных частот основной и высших мод. Неизве-
стное распределение плазмы можно представить в довольно об-
щем виде как линейную комбинацию известных радиальных
функций
Функции fi(r) могут быть, например, семейством распределений
Гаусса с различной дисперсией. Тогда, используя приближение
первого порядка теории возмущений (дающее хорошую точность
лишь при очень низкой плотности плазмы, т. е. при
WKp<0,001), можно получить систему линейных алгебраиче-
ских уравнений с неизвестными коэффициентами сг
J = |<Мг)Шг)Л,
O]=iw,i.
где
Ьц= / I Фу (г) |2 ft (г) dr,
а (Дсо/со)у—-наблюдаемый нормированный сдвиг частоты/-й моды.
Таким образом, при подходящем выборе функций А (г) и
знании невозмущенных волновых функций фу (г) можно в прин-
ципе определить приближенное пространственное распределение
*)) На принципиальную возможность использования различных мод в ре-
зонаторе для зондирования пространственных распределений ионизации впер-
вые указал одному из авторов Н. Кролль (Калифорнийский университет)
в июне 1962 г.
406
Д. А у стон, Р. Примич, Р. Хаями
плотности изучаемой плазмы. При более строгом анализе сле-
дует принять во внимание связь мод. Интуитивно принцип ис-
пользования резонатора Фабри — Перо для зондирования рас-
пределения плазмы можно понять, если вспомнить, что распре-
деления полей высших мод резонатора имеют ряд пиков и
нулей. Поэтому высшие моды могут рассматриваться как инстру-
мент для определения параметров плазмы в ряде выделенных
точек. Разрешающая способность метода, естественно, ограни-
чена расстояниями порядка длины волны. Экспериментальные
результаты, полученные таким методом, показывают, что он мо-
жет быть весьма полезным.
§ 5. ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ
Экспериментальная программа предусматривала измерение
распределений поля и добротности резонаторов Фабри — Перо
миллиметрового диапазона волн. Изучалось три различных типа
резонаторов на частоте 70 Ггц. Как видно из фиг. 1, резонаторы
отличались главным образом способом возбуждения. В каждом
резонаторе использовалась система с зеркальным отражением,
состоящая из сферического и плоского отражателей; поэтому
требовалось по одному отражателю каждого типа.
Фиг. 1. Конструкции миллиметровых резонаторов Фабри — Перо.
Первая из изучавшихся систем состояла из перфорирован-
ного сферического отражателя. Возбуждение осуществлялось
системой из рупора и линзы. Такой способ возбуждения должен
был обеспечить возбуждение только продольных мод. Это ДО’
19. Резонаторы Фабри — Перо в диагностике плазмы
407
стиралось путем согласования поля на входе (после линзы) с
полем основной моды на поверхности отражателя. Было уста-
новлено, что для оптимального возбуждения поля, имеющего в
зависимости от расстояния между зеркалами тот или иной эф-
фективный размер пятна на отражателе, можно использовать
возбуждающие рупоры с различными апертурами. Перфорация
на отражателе состояла из квадратной сетки отверстий разме-
ром 0,4 X, отстоявших друг от друга на 0,7%.
Во второй системе имелось лишь одно отверстие связи диа-
метром 0,25%, расположенное в центре отражателя. Это было
сделано для преобразования энергии в предсказанные Фоксом
и Ли [22] высшие радиальные моды (типа «воловий глаз»), а
также в основные продольные моды.
Третья система предназначалась для изучения высших мод,
предсказанных Бойдом и Гордоном [23]. Поля этих мод в по-
перечной плоскости резонатора разделяются в прямоугольной
системе координат. Для устранения вырождения применялся от-
ражатель прямоугольной формы, а система возбуждения была
рассчитана на преобразование энергии только в те высшие мо-
ды, которые имеют вариации вдоль большего из размеров пря-
моугольной поверхности отражателя. Это достигалось использо-
ванием ряда отверстий, расположенных вдоль меньшей оси отра-
жателя. Резонатор возбуждался системой, состоявшей из рупора
с раскрывом 20° в плоскости Н и линзы, как показано на фиг. 2.
Линза обеспечивала такое преобразование фазы и амплитуды
входного поля, чтобы при расстоянии между плоским и сфери-
ческим отражателями, немного меньшем радиуса кривизны сфе-
рического отражателя (т. е. вблизи так называемой концентри-
ческой геометрии), в резонаторе возбуждалась основная 1/-мода
(ось у направлена вдоль большой оси отражателя). Отверстия
имели диаметр 0,2% и располагались на расстоянии 0,6% друг
от друга. Во всех трех случаях отражатели изготавливались из
полированного алюминия при допусках на точности изготовле-
ния ±0,0127 мм (±0,003%).
Как видно из фиг. 3, плоский и сферический отражатели
монтировались на прецизионной станине токарного станка. Схе-
ма установки, включая вспомогательные устройства, приведена
на фиг. 4. Сферический отражатель был неподвижен, а плоский
отражатель мог свободно перемещаться во всех трех измере-
ниях. Для измерения распределения поля в плоском отражателе
было сделано отверстие, через которое из резонатора отбира-
лась малая часть энергии. Было установлено, что при достаточ-
но малом диаметре отверстия (менее 0,1 %) искажение поля в
резонаторе весьма мало и не вызывает заметных изменений до-
бротности резонатора и его резонансной частотьг,
Фиг. 2. Прямоугольный отражатель.
Фиг. 3. Экспериментальная установка.
19. Резонаторы Фабри — Перо в диагностике плазмы
409
Система перемещения зеркала тщательно юстировалась; по-
этому при перемещении плоского зеркала в поперечной плоско-
сти изменения резонансной частоты изучавшихся мод не наблю-
далось. Максимальное отклонение резонансной частоты состав-
ляло менее 20% от полуширины резонансной кривой (т. е. око-
ло ±100 кгц на 70 Ггц при Q= 140 000). Это соответствует точ-
ности юстировки порядка 2,5- 10-4 мм.
Для еще большего уменьшения влияния малых сдвигов ре-
зонансной частоты использовалось линейное качание частоты.
Это позволило усреднить принимаемую энергию по полосе ча-
стот усилителя промежуточной частоты (10 Мгц). Малая связь
с резонатором компенсировалась большим коэффициентом уси-
ления усилителя промежуточной частоты (90 дб). Для по-
лучения линейной характеристики использовался балансный
смеситель с двумя хорошо согласованными кристаллами. Харак-
теристика смесителя была линейной с точностью ±4% и про-
верялась путем сравнения с калиброванным аттенюатором.
Распределение напряженности электрического поля в фо-
кальной плоскости (т. е. на поверхности плоского отражателя)
записывалось непосредственно Х-У-самописцем. Для этого
плоский отражатель перемещался в сечении, перпендикулярном
оси резонатора. Для обеспечения пренебрежимо малых искаже-
ний поля резонанс в системе контролировался по отраженной
волне.
Добротность измерялась путем наблюдения частотной харак-
теристики резонатора на осциллографе. Частотная калибровка
производилась ЧМ-методом, примененным ранее Циммерером [1].
Модулированный сигнал известной частоты (около 1 Мгц) по-
давался на отражатель клистрона и вызывал генерацию боко-
вых частот. Резонатор работал как спектр-анализатор, давая
непосредственную калибровку частоты по расстоянию на экране
осциллографа между боковыми полосами. Величина Q находи-
лась путем измерения ширины резонансной кривой на уровне
3 дб. Точность такой методики составляла около ±3%.
Результаты измерения Q для трех изучавшихся систем при-
ведены на фиг. 5—7 для ряда расстояний между отражателями
при конфокальной и концентрической геометрии резонатора.
Для сравнения там же приведены результаты расчета Q по
полуэмпирической формуле Бойда и Гордона [23], учитывающей
дифракционные потери и коэффициент связи через отверстия
в отражателе и предполагающей линейную зависимость Q от d
Q =______—______.
aD + 2a* + ас
Фиг. 4. Схема экспериментальной установки.
Фиг. 5. Добротность перфорированного круглого отражателя.
Фиг. 7. Добротность прямоугольного отражателя.
412
Д. Ay стон, Р. Примич, Р. Хаями
Здесь
, 2л
aR = омические потери =
= 0,0009 для А1 на частоте 70 Ггц\
ас = коэффициент связи =
0,0020 для системы 1,
= 0,0009 для системы 2,
. 0,0007 для системы 3;
aD — дифракционные потери =
= 10,9ехр(—4,947V), или
л,=лг»[^-1Г •
^2
No = -эд- = число Френеля для конфокального случая =
9,3 в системе 1,
= 9,3 в системе 2,
. 12,8 в системе 3;
2а = размер отражателя (ширина или диаметр);
d .
-g- = расстояние между плоским и сферическим отража-
телями;
/?= радиус кривизны сферического отражателя.
Во всех трех случаях добротность Q линейно возрастала
с увеличением расстояния между отражателями вплоть до зна-
чений d, близких к концентрическому. При концентрической
геометрии резко возрастали дифракционные потери, вызывая
быстрое уменьшение Q. Этот быстрый спад следовало ожидать,
учитывая большие значения числа Френеля изучавшихся резо-
наторов. Максимальное значение Q имело место в области
1,90<d/R< 1,95. Имелся ряд значительных отклонений Q от
плавной зависимости Q — Q(d/R). Эти отклонения нельзя объ-
яснить несовершенством метода измерения. Наиболее вероятной
причиной этих отклонений является случайное вырождение ме-
жду основной модой и какой-либо из низкодобротных высших
мод. В ряде случаев это явление действительно наблюдалось на
осциллографе.
Для измерения эффективного размера пятна поля основной
моды в фокальной плоскости каждой из трех систем применял-
ся описанный ранее метод измерения распределения электриче-
ского поля. Результаты приведены на фиг. 8—10. Там же для
d/R
Фиг. 8. Размер пятна в фокальной плоскости для перфориро-
ванного отражателя.
Фиг. 9. Размер пятна в фокальной плоскости для круглого
отражателя.
Размер пятна (в длинах лам)
Фиг. Ю. Размер пятиа в фокальной плоскости
для прямоугольного отражателя.
Фиг. 11. Фокальное поле моды ТЕМм для круглого
отражателя.
19. Резонаторы Фабри — Перо в диагностике плазмы
415
сравнения приведены теоретические результаты Ярива и Гор-
дона [26]. За исключением концентрической геометрии d/R = 2,
когда теория перестает работать, предсказывая нулевые раз-
меры фокального пятна, совпадение эксперимента и теории
очень хорошее. Как и при измерениях Q ряд точек кривых вы-
падает из-за вырождения мод. Имеется интересное различие ре-
зультатов для сплошного и перфорированного круглых отража-
телей. В последнем случае отличие результатов измерения от
теоретических было значительно большим из-за того, что подав-
ление высших мод было таково, что их амплитуды составляли
около 0,1 амплитуды основной моды. Эта аномалия объясняет-
ся, по-видимому, тем, что перфорация действовала как решет-
ка. Этот эффект, вероятно, можно устранить, если уменьшить
расстояние между отверстиями.
На фиг. 11 —16 приведен ряд примеров распределений поля
в резонаторах с круглыми и прямоугольными отражателями.
Измерялось электрическое поле лишь для мод одной из двух
ортогональных поляризаций. Проверка показала, что уровень
мод второй поляризации был на 15 дб ниже, а распределение
их полей было близко к распределению полей основных про-
дольных мод. Однако для мод высших порядков уровень кросс-
поляризованных мод был значительно выше, хотя распределе-
ния полей по-прежнему оставались одинаковыми. Сейчас прово-
дится более детальное исследование этого вопроса.
Результаты измерений сравнивались с теоретическими ре-
зультатами Бойда и Гордона [23], Губо и Шверинга [34] и Бойда
и Котельника [24]. Поле моды TEMpiq в фокальной плоскости
резонатора с круглыми отражателями можно записать на осно-
вании скалярной теории дифракции Следующим образом:
Е(г, ®) //2rV ,z/2r2\ -г2/™?
--«--- — I Lp I-o' I с ' »
Е0 \ ws / \™SJ
где ws — эффективный радиус фокального пятна основного мода
и Lp — присоединенный полином Лагерра. Поле моды TEMmnq
в фокальной плоскости резонатора с прямоугольными отража-
телями имеет вид
Е (•* У) и (У~2х\ „ (У^уУ^-^+у2)/^
Ео ~Пт\ ws I П\ ws Г
где Нт, Нп — полиномы Эрмита.
Все три распределения (фиг. 11—13) для круглых отражате-
лей имеют очень слабую зависимость от угла ср. Распределения
на фиг. 12 и 13 в пределах ошибок эксперимента действительно
соответствуют модам типа «воловий глаз», предсказанным Фоксом
, электрическое поле Ех, электрическое поле
Фиг. 12. Фокальное поле моды TEMll0 для круглого
отражателя.
1,0
0,8
0,6
0,4
0,2.
О
-6-4-2 О 2 4 6
х (в длинах волн)
Фиг. 13. Фокальное поле моды ГЕЛГ2,0 для круглого
отражателя.
х (в длинах волн)
Фиг. 14. Фокальное поле моды ТЕМал для прямоугольного
отражателя.
Фиг. 15. Фокальное поле моды ТEM2lD для прямоугольного
отражателя.
27 Зак. 274
418
Д. Ay стон, Р. Примич, Р. Хаями
и Ли [22]. Из-за неидеальности в резонаторе с круглыми отра-
жателями возбуждались вырожденные высшие моды малой
амплитуды с вариацией по азимутальному углу. Тем не менее
при расстояниях между отражателями, соответствующих d[R =
= 1,86, уровень этих вырожденных мод составлял около —20 дб
Фнг. 16. Фокальное поле моды ТЕМ\йл для прямоугольного
отражателя.
относительно уровня интересующих нас радиальных мод. Это
позволило получить достаточно точные результаты. В конфо-
кальном случае выделить какую-либо из радиальных мод было
почти невозможно.
В случае прямоугольных резонаторов система связи рабо-
тала очень хорошо, позволяя вблизи d/R = 2,00 отделить
х-моды (поляризованные по оси х) от вырожденных с ними
1/-мод. Взаимодействие мод было пренебрежимо мало. Резуль-
таты измерений опять оказались в прекрасном соответствии с
теорией. Из распределения поля моды ТЕМ1&< 0 на фиг. 16 видно,
что в резонаторе возбуждались моды очень высоких порядков.
Эта мода была слегка вырождена, из-за чего согласия с тео-
рией не получилось.
На фиг. 14 приведено распределение поля основной моды в
концентрическом резонаторе с прямоугольными отражателями.
Теоретическая кривая построена на основании предположения
Кульшоу о том, что при больших значениях числа Френеля рас-
пределение поля иа поверхности сферического отражателя есть
19. Резонаторы Фабри — Перо в диагностике плазмы
419
полупериод косинуса. Согласие теории с экспериментом, в ча-
стности в уровнях боковых лепестков, очень хорошее. Для
области больших потерь d/R>2 из-за низких значений Q,
а, следовательно, и амплитуд мод диаграммы поля получить не
удалось.
Фиг. 17. Поперечное распределение поля вблизи осн резонатора
Фабри — Перо 6-сантиметрового диапазона.
Резонансная частота 5015 ЛГгц; изменение z при качании частоты ±Л/4; сферы 9,0;
диаметр сферы 0,94 см; расстояние между отражателями 20Л.
Кроме описанных экспериментов, была проведена еще одна
серия измерений [49] с использованием иного метода зондирова-
ния поля. В резонатор, работающий на частотах порядка 5 Ггц,
с помощью тонкой нейлоновой нити вводилась малая диэлек-
трическая сфера и фиксировалось изменение резонансной часто-
ты и добротности Q. По изменению резонансной частоты в за-
висимости от положения сферы можно оценить поле в резо-
наторе. Так, используя приближение первого порядка (для за-
крытого резонатора), имеем
f |х|Мт,
©0 J 1
по сфере
— сфере (ЛЛЯ МаЛЫХ СФеР)‘
Предварительные результаты этих измерений обнадеживаю-
щие. На фиг. 17 и 18 приведены примеры полученных таким
образом распределений поля основной моды в поперечном сече-
нии и картины стоячей волны в продольном направлении. Фор-
ма и эффективный размер пятна поля основной моды хорошо
согласуются с ожидавшимися результатами. Однако очень
27*
420
Д. Аустон, Р. Примич, Р. Хаями
большое отличие величины Q указывает на то, что большая
часть энергии переходит в низкодобротные моды и (или) рас-
сеивается из резонатора наружу. Лишь 20% наблюдавшегося
отклонения Q можно отнести за счет поглощения в сфере. Таким
1 1 1 J 1 1
1,5 I 0,5 0
Смещение вдоль оси резонатора г/Ла
^1000
п)
:е
ч 800
3
Е
§ 600
о
§ 400
<о
200
О
Фиг. 18. Продольное распределение поля в резонаторе Фабри —
Перо 6-сантиметрового диапазона.
Резонансная частота 5015 Мгц; диаметр сферы 0,95 см; e,f сферы 9,0; расстояние
между отражателями 20А,.
образом интерпретация результатов несколько сомнительна.
Сейчас проводится работа по улучшению этого метода, о чем
будет сообщено в следующей статье [49].
§ 6. ЗАКЛЮЧЕНИЕ
Можно сделать заключение, что миллиметровые резонаторы
Фабри — Перо могут быть весьма полезными для диагностики
плазмы. Особенно ценны их высокая чувствительность и потен-
циальная способность к измерению пространственного распре-
деления поля в многомодовом режиме.
Полученные экспериментальные результаты показывают, что
существующая теория неконфокальных резонаторов справедлива
при больших значениях числа Френеля и больших расстояниях
между отражателями (за исключением концентрического). Стро-
гое решение задачи о возмущениях, вносимых в резонатор Фаб-
ри — Перо плазмой, все еще отсутствует. Однако можно пред-
19. Резонаторы Фабри — Перо в диагностике плазмы 421
положить, что при определенной конфигураций плазмы, имею-
щей очень низкую плотность, применимы первое приближение
теории возмущений или метод матрицы рассеяния (см. § 4).
При более плотной плазме с большими пространственными
градиентами необходимо учитывать ряд дополнительных эффек-
тов, например, связь мод и рассеяние энергии наружу из резо- -
натора. Задача значительно упрощается при использовании ре-
зонаторов, закрытых в одном измерении. Этот случай сейчас
детально изучается и результаты будут опубликованы позднее.
Анализ концентрического резонатора будет опубликован Нор-
совером. Экспериментальные работы ведутся сейчас в направ-
лении изучения возмущения резонатора диэлектрическими объ-
ектами, а также проверки применимости различных подходов
теории возмущений.
ЛИТЕРАТУРА
1. Prim i ch R. I., Hay ami R. A., Millimeter and Submillimeter Conf.,
Orlando, Fla., January 8—10, 1963.
Millimeter Wavelength Focused Probes and Focused, Resonant Probes for
Use in Studying Ionized Wakes behind Hypersonic Velocity Projectiles.
2. Primich R. I., Hay ami R. A., IEEE Trans. MTT-12, 33 (1964).
The Application of the Focused Fabry — Perot Resonator to Plasma Diagno-
sties
3. Born M., W о 1 f E., Principles of Optics, New York, 1959.
4. High Speed Aerodynamics and Jet Propulsion, Vol. VIII, Princeton, 1961.
5. Hall J. G., Eschenroeder A. Q., Marrone P. V., Journ. Aero. Sci.,
29, 1039 (1962).
Blunt — Nose Inviscid Airflows with Coupled Nonequilibrium Processes.
6. E s c h e n г о e d e r A. Q., Chen T., H a у a m i R. A., Thermochemical Si-
militude in Hypersonic Flows (готовится к изданию).
7. Hansen C. F., Primich R. 1., Steinberg M., Maiden C. J.,
AIAA Meeting, Los Angeles, Calif., June 17—20, 1963, Preprint No. 63—204.
Measurement and Analysis of Optical and Microwave Observables in Flow
about Hypersonic Models.
8. Culshaw W„ IRE Trans., MTT-7, 221 (1959).
9. C u 1 sh a w W„ IRE Trans., MTT-8, 182 (1960).
High Resolution Millimeter Wave Fabry — Perot Interferometer.
10. Cui shaw W., Anderson M. V., Proc. Conf. Microwave Measurements
Techniques, IEE, London, September 1961,
Measurements of Dielectric Constants and Losses with a Millimeter Wave
Fabry — Perot Interferometer.
11. Cui shaw W., Advances in Electronics and Electron Phys., 15, 197 (1961).
Millimeter Wave Techniques.
12. Culshaw W„ Proc. IEE, 109, Pt. B, Suppl. No. 23, 820 (1961).
Measurement of Permittivity and Dielectric Loss with a Millimeter Wave
Fabry — Perot Interferometer.
13. Culshaw W„ IRE Trans., MTT-9, 135 (1961).
Resonators for Millimeter and Submillimeter Wavelengths.
14. Culshaw W„ IRE Trans., MTT-10, 331 (1962).
Further Considerations on Fabry — Perot Resonators.
15. Schawlow A. L., Townes С. H., Phys. Rev., 112, 1940 (1958).
Infrared and Optical Masers.
422
Д. Ay стон, Р. Примич, Р. Хаями
16. Прохоров А. М., ЖЭТФ, 34, 1658 (1958).
17. Dicke R. Н., U. S. Patent 2 851 652, September 9, 1958.
18. Maiman Т. Н., Nature, 187, 493 (I960).
Stimulated Optical Radiation in Ruby.
19. С о 1 1 i n s R. J., Nelson D. F., S c h a w'l о w A. L., Bond W., G a r-
rett C G. B, Kaiser W., Phys. Rev. Lett., 5, 303 (1960).
Coherence, Narrowing, Directionality and Relaxation Oscillations in the
Light Emission from Ruby.
20. С о n n e s P., Revue d’Optique, 35, 37 (1956).
Increase of the Product of Luminosity and Resolving Power of Interfero-
meters by Using a Path Difference Independent of the Angle of Inci-
dence.
21. С о n n e s P., Journ. Phys. Rad., 19, 261 (1958).
The Spherical Fabry — Perot Etalon.
22. Fox A. G., Li T., Bell Syst. Techn. Journ., 40, 453 (1961). (Имеется
перевод в сб. «Лазеры», ИЛ, 1963.)
Resonant Modes in a Maser Interferometer.
23. В о у d G. D., Gordon J. P., Bell Syst. Techn. Journ. Vol., 40, p. 489
(1961). (Имеется перевод в сб. «Лазеры», ИЛ, 1963.)
Confocal Multimode Resonator for Millimeter through Optical Masers.
24. Boyd G. D., Kogelnik H., Bell Syst. Tech. Journ., 41, 1347 (1962).
Generalized Confocal Resonator Theory.
25. Fox A. G„ Li T„ Proc. IEEE, 51, 80 (1963).
Modes in a-Maser Interferometer with Curved and Tilted Mirrors.
26. Yariv A., Gordon J. P„ Proc. IEEE, 51, 3 (1963).
The I я ser
27. Soohoo R. F„ Proc IEEE, 51, 70 (1963).
Nonconfocal Multimode Resonators for Masers.
28. Tang C. L., Appl. Optics, 1, 768 (1962).
On Diffraction Losses in Laser Interferometers.
29. Morgan S. P„ IEEE Trans., MTT-11, 191 (1963).
On the Integral Equations of Laser Theory.
30. К a p 1 a n S„ IEEE Trans., MTT-12, 254 (1964).
The Use of the Rayleigh— Ritz in Nonselfadjoint Problems.
31. H a r d i n g G. O., L i T„ Journ. Appl. Phys., 35, 475 (1964).
Effect of Mode Degeneracy on Output of Gaseous Optical Masers.
32. Li T., Bell Syst. Techn. Journ., 42, 2609 (1963).
Mode Selection in an Aperture — Limited Concentric Maser Interfero-
meter.
33. Scheib e E. H„ Proc. IRE, 49, 1079 (1961).
Measurements on Resonators Formed from Circular Plane and Confocal
Paraboloidal Mirrors.
34. Goubau G., Schwerin g F., IRE Trans. AP-9, 248 (1961). (Имеется
перевод в сб. «Зарубежная радиоэлектроника», № 11, 1961.)
On the Guided Propagation of Electromagnetic Wave Beams.
35. C h r i s t i a n J., Goubau G., IRE Trans. AP-9, 256 (1961). (Имеется
перевод в сб. «Зарубежная радиоэлектроника», № 11, 1961.)
Experimental Studies on a Beam Waveguide for Millimeter Waves.
36. C h r i s t i a n J., Goubau G., Proc. IRE, 49, 1679 (1961).
Some Measurements on an Iris Beam Waveguide.
37. В e у e r J., S h e i b e E., IEEE Trans. MTT-11, 18 (1963).
Loss Measurements of the Beam Waveguide.
38. В e у e r J„ S h e i b e E„ IRE Trans., AP-10, 349 (1962).
Higher Modes in Guided Electromagnetic Wave Beams.
39. M a r c u s e D„ IRE Trans., 1-11, 187 (1962).
HCN Molecular Beam — Type Maser.
19. Резонаторы Фабри — Перо в диагностике плазмы 423
40. Z i m m е г е г R. W., Anderson М. V., S t г i n е G. L., Beers Y., IEEE
Trans., МТТ-12, 142 (1963).
Millimeter Wavelength Resonant Structures.
41. Zimmer er R. W., IEEE Trans., MTT-12, 371 (1963).
Spherical Mirror Fabry — Perot Resonators.
42. Z i m m e r e r R. W , Rev. Sci. Instr., 33, 858 (1962).
New Wavemeter for Millimeter Wavelengths.
43. Oilman G., IRE WESCON Convention Record, 1963.
A 2MM (Non)-Confocal Resonator for Use as a Wavemeter or Filter Ele-
ment.
44. S i 1 v e r S., Microwave Antenna Theory and Design, New York, 1949,
p. 167.
45. N о r t h о v e r F. H. N., в печати.
Fabry — Perot Interferometer as the Center of a Focused Microwave Sy-
stem.
46. Kogelnik H., Rigod W. W., Proc. IRE, 50, 220 (1962).
Visual Display of Isolated Optical-Resonator Modes.
47. Morse P. M., Feshbach H„ Methods of Theoretical Physics, Pt. II,
New York, 1953, Ch. 9. (Имеется перевод: Ф. M. Морс, Г. Ф еш б а х,
Методы теоретической физики, ИЛ, 1960, т. II, гл. 9.).
48. Maier L, С.. Slater J. С., Journ. Appl. Phys., 23, 68 (1952).
Field Strength Measurements in Resonant Cavities.
49. F a u 1 k n e r .1. R., Hay ami R. A„ Au st on D. H., в печати.
Experimental Studies of a C-band Fabry — Perot Resonator for Use in
Plasma Diagnostics.
50. R a v i d E., Phys. Fluids, 5, 1026 (1963).
Determination of Longitudinal Shock Wave Profiles in a Microwave Fab-
ry — Perot Interferometer.
51. Ashby D. E. T. F., Jephcott D. F., Appl. Phys. Lett., 3, 13 (1963).
Measurement of Plasma Density Using a Gas Laser as an Infrared Inter-
ferometer.
52, Gerardo J. B., Ver deyen J. T., Proc. IEEE, 52, 690 (1963).
The Laser Interferometer: Application to Plasma Diagnostics.
53. В а й и ш т e й и Л. А., ЖЭТФ, 44, 1050 (1963).
Открытые резонаторы для квантовых генераторов света.
54. Вайнштейн Л. А., ЖЭТФ, 45, 684 (1963).
Открытые резонаторы со сферическими зеркалами.
55. V а п В lade 1 J., Electromagnetic Fields, New York, 1964, Ch. 10,
p. 330.
20
ПРИМЕНЕНИЕ ТЕХНИКИ СВЧ
ДЛЯ ИССЛЕДОВАНИЯ ВЗАИМОДЕЙСТВИЯ ВОЛН
С ПЛАЗМОЙ-ДИАГНОСТИКА ПЛАЗМЫ
Т. Консоли*, Д. Лепешинский*, Ф. Парлянж*, М. Кадар*
В данной статье обсуждаются вопросы применения техники СВЧ для
диагностики плазмы. В § 2 дается обзор некоторых основных положений тео-
рии распространения электромагнитных волн в ионизированной среде. Теоре-
тические положения развиваются затем для случаев поперечного и продоль-
ного (по отношению к направлению магнитного поля) распространения волн
в горячей и холодной плазме. В §; 3 изложены экспериментальные методы
СВЧ, развитые в плазменной лаборатории Института прикладной физики в
Сакле для случаев поперечного и продольного распространения волн и осо-
бенно для правостороннего вращения плоскости поляризации. Этимя мето-
дами рассматривается направленное и свободное распространение волн; при
этом используется оптическая техника: металлические и диэлектрические лин-
зы и антенны, сетчатые разделители луча, волноводы больших сечений и т. д.
В § 3 дается также обзор экспериментальных результатов, полученных:
а) при исследовании областей распростраиеиия воли; б) при изучении эффек-
тов, связанных с распространением волн с круговой поляризацией при право-
стороннем вращении плоскости поляризации; в) при применениях «свистящей
моды» для нагревания и ускорения плазмы.
§ 1. ВВЕДЕНИЕ
Исследование взаимодействия между волнами СВЧ и плаз-
менными образованиями с целью применения для диагностики
плазмы представляет особый интерес. В данной статье мы изло-
жим общие черты взаимодействия волн СВЧ с плазмой и рас-
скажем о некоторых технических устройствах, которые были
сконструированы нами для изучения распространения волн в
плазме и которые подчас тесно связаны с оптикой. Настоящие
исследования открывают новые пути в диагностике плазмы, в
методах разогрева плазмы и ускорения ее электромагнитными
полями и приводят к первоначально непредвиденным возмож-
ностям.
* Т. Consol i, D. Lepechinsky, F. Parlang e, M. Cadart, Co-
missariat a L’Energie Atomique, Centre D’Etudes Nucleates de Saclay,
Seine-et-Oise, France.
20. Исследование взаимодействия волн с плазмой
425
Прежде всего определим слово «волны СВЧ». Мы будем по-
нимать под этим; такие электромагнитные волны, длина волны
которых достаточно мала, чтобы они могли распространяться
в волноводах или чтобы были применимы упомянутые выше оп-
тические методы исследования. Изучение распространения волн
в плазме мы'будем проводить в предположении, что эффектив-
ная длина волны меньше, чем поперечный размер плазменного
образования (эффективная длина волны определяется как от-
ношение длины волны в вакууме к показателю преломления
среды). При этих условиях можно пренебречь влиянием границы
и с хорошей точностью применять формулы, справедливые для
распространения волн в неограниченной среде. Плазма, рас-
сматриваемая в § 2 работы, предполагается «холодной» и до-
статочно однородной, чтобы можно было без всяких ограниче-
ний применять формулы Апльтона — Хартри. Далее мы рас-
смотрим распространение волн в полностью ионизированной
«горячей» среде, помещенной в магнитное поле, вызывающее по-
явление дрейфовой скорости. В этом случае потребуется уже
рассмотреть дисперсионное уравнение.
В § 2 мы дадим также обзор основных теоретических соот-
ношений, описывающих распространение волн в холодной и го-
рячей плазме. Эти формулы составляют основу для понимания
экспериментальных результатов, представленных ниже. В § 3
мы опишем СВЧ устройства, которые были сконструированы
нами для экспериментальных исследований. Там же предста-
влены типичные результаты и их анализ.
§ 2. КРАТКИЙ ОБЗОР ТЕОРЕТИЧЕСКИХ РЕЗУЛЬТАТОВ
Рассмотрим СВЧ луч, пронизывающий плазму, которая по-
мещена в постоянное магнитное поле, направленное перпенди-
кулярно или параллельно лучу.
Хорошо известно, что первый случай можно подразделить
на два частных случая. Когда электрическое поле волны парал-
лельно направлению внешнего постоянного магнитного поля
(К±В0, Е||В0), критическая электронная плотность определяет-
ся такой же формулой, как и при отсутствии магнитного поля,
т. е. Лге=пгво®2/^2. Если исследуемая волна имеет Х = 0,6 мм
(эта волна представляет собой нижнюю границу, получаемую
от некоторых ламп карсинотронного типа), то электронная
плотность равна 3*1015 сдг3. Она определена путем интерферо-
метрических измерений (т. е. методом сравнения волн, движу-
щихся в свободном пространстве и в плазме).
При более высокой электронной плотности необходимо при-
менять более короткие волны, а именно волны светового диапа-
426 Т. Консоли, Д. Лепешинский, Ф. Парлянж, М. Кадар
зона от источников типа рубинового или газового лазера. Тре-
буемая длина волны как функция электронной плотности, встре-
чающейся в различной плазме, показана на фиг. 1.
В случае, когда оба вектора Е и К перпендикулярны на-
правлению магнитного поля (поперечное распространение) ме-
тод сравнения может оказаться неприменимым. В этом случае
показатель преломления определяется с помощью дифферен-
циального метода, который требует измерения сдвига фаз меж-
ду обыкновенным и необыкновенным лучами после их прохожде-
ния через плазму (см., фиг. 2) [1]. Это дает возможность опре-
делить профиль электронной плотности плазменного столба, если
известны две величины [2],
i
<Р = 7 J <l—nr)dz,
О
~ юг
= а
О L
2ра2р
az,
где Ne — электронная плотность, пг — действительная часть по-
казателя преломления, I — длина плазменного столба.
До сих пор экспериментаторы, работающие с лабораторной
плазмой, редко использовали распространение волн параллель-
но магнитному полю, которое в этом случае либо не учитыва-
лось, либо рассматривалось как возмущающий фактор. Однако
представляется интересным использовать присутствие магнит-
ного поля, с тем, чтобы продвинуть границу измеряемой элек-
тронной плотности с помощью волны данной частоты далеко за
граничную частоту, соответствующую поперечному распростра-
нению. Это оказывается возможным благодаря использованию
волны с правосторонней круговой поляризацией — так называе-
мой «свистящей моды»:
«с >
где Ир, ®с, и представляют собой соответственно круговую
плазменную частоту, циклотронную частоту электронов и ча-
стоту зондирующей волны.
В случае продольного распространения дисперсионное соот-
ношение, взятое с учетом анизотропии и температуры, можно
записать следующим образом [1]:
df<>_dfo 1 ,.2
^v° dv V°
dv0 dvz,
ю2
, = 1 -Л ~ I I -------------
О 1 Ю2 J J I
vz 0
, 1 1 l2kT\'h
fo = ^7^ — е ' • ®о== ------
у л Vq \ m /
ю т юс — Kvz
ft&H л
Ne, слг3
Фиг. 1. Критическая электронная плотность как функция длины зонди-
рующей волны.
Z—линейный пинч-эффект и импульсный разряд Пеннинга; //—0-пинч и дуговой раз-
ряд при атмосферном давлении с ионизацией / в диапазоне 1% < 1 < 100%; /// — быстрая
ударная волна при давлениях, больших атмосферного; /И — металлы и внутренние
области звезд.
Фиг. 2. Дифференциальный интерферометр с поперечным распростра-
. нением волн.
ОЛ — обыкновенный луч; НЛ — необыкновенный луч; ГС — гибридйое соединение; Д- де-
тектор; СН — согласованная нагрузка; Хь Х3, Х3—детектируемые сигналы.
428 Т. КонСйЛи, Д. Лепешинский, Ф. Парлянж, М. Кадар
Для максвелловской функции распределения это соотношение
имеет вид
1 1
Vo
2 cd
®р Г е ° dvz
щ2 J <о ± Cl)c — kvz — jvz
— ОО
где Т — электронная температура, k — постоянная Больцмана и
пг — масса электрона.
Рассматривая действительные части, можно получить обла-
сти распространения волн. В приближении первого порядка
имеем
. (l-f-Г—JT) —(1 ± Г)
V2 —
{\±Y)^-X~-VA
(величина А в знаменателе описывает анизотропию).
Силин и Рухадзе [4] получили следующее выражение для по-
казателя преломления с учетом магнитного поля и электронной
температуры, но без учета столкновений:
1 = (0 + Ф)ei ± — l)2 + 4g2<p],
где
— 1 х __ XY , 2kT Л (1-f-ЗУ2)
E1 ~ 1 1— У2’ 1 — У2 ’ r — ^mc2 (1—У2)2 '
Достоинство этой формулы состоит в том, что она учитывает
влияние температуры. Нетрудно видеть, что показатель прелом-
ления практически не зависит от температуры. Исключением яв-
ляется область циклотронного резонанса, где влияние электрон-
ной температуры велико.
Когда температурный эффект и анизотропия пренебрежимо
малы, обычное дисперсионное соотношение Апльтоиа — Хартри
получается из обоих выражений. Формула Апльтона — Хартри
для чисто продольного распространения волн с учетом столкно-
вений записывается следующим образом:
со2
«2 __ j______2____
\±Y—jZ'
7 v Ne\ еВ
Z = — , со* =-----, © = —
<о со Р те0 с т
где Ne — электронная плотность, v — частота столкновений.
Действительную часть показателя преломления можно пред-
ставить некоторой поверхностью, проекция которой на пло-
скость (где электронная плотность Ne отложена по оси ординат,
а магнитное поле В — по оси абсцисс) показана на фиг. 3 и 4,
20. Исследование взаимодействия волн с плавмой
429
Диаграмма на фиг. 3 подобна той, которая имеется в работе
Клеммова, Миллали и Аллиса [5], но здесь, вдоль осей х и у от-
ложены соответственно величины Ne и В, чтобы для данной зон-
дирующей частоты диаграмма сразу давала области распро-
странения волн как функции физических параметров {Ne и В).
В этих областях в холодной плазме могут распространяться
волны с правосторонней и левосторонней поляризациями. Когда
присутствуют обе поляризации одновременно, можно наблю-
дать эффект Фарадея.
Фиг. 4 представляет ту же диаграмму для горячей плазмы.
На ней представлены области, где можно наблюдать черенков-
ский эффект и направленное распространение. Направление по-
тока энергии совпадает с групповой скоростью, если среда не
имеет потерь. Но в анизотропной среде, как известно, направле-
ние движения энергии vg отличается от направления волнового
вектора К [6]. Угол а между К и vg дается выражением
1 (da>/dQ)K 1 ди 1 д
tg “ IКI (да/д | К I )0 — п дв ~ 2пг д& '•
где 0 есть угол между направлением вектора К и направлением
постоянного магнитного поля.
Для свистящей моды при 1 угол между направлением
луча и направлением магнитного поля меньше, чем 19°28'. Энер-
гия же волны распространяется вдоль силовых линий магнит-
ного поля, так что можно сказать, что свистящая мода распро-
страняется направленно вдоль этих линий.
Нам удалось проверить эти явления, хорошо известные из
ионосферных исследований, на наших экспериментальных уста-
новках. Указанный эффект направленного распространения не
следует путать с тем, который может наблюдаться, когда усло-
вия существования свистящей моды не удовлетворяются, т. е.
при <ос<®. Последний имеет место при радиальном изменении
плотности плазмы (т. е. в неоднородной плазме), например, в
полом разряде.
Для корректного наблюдения свистящей моды должны удов-
летворяться три основных условия:
1) векторы К и В, т. е. направления распространения волны
и магнитного поля должны быть параллельны;
2) переход поля от источника в плазму должен быть хорошо
согласован;
3) должно быть обеспечено плавное согласование между по-
казателем преломления в вакууме, равном единице, и показа-
телем преломления плазмы для свистящей моды, который мно-
го больше единицы.
Фиг. 3. Области продольного распространения волн в холодной
плазме.
7, 11 — распространение волн с правосторонней и левосторонней поляризациями:
наблюдается эффект Фарадея. 777, IV — распространение волн с левосторонней
н правосторонней поляризациями соответственно; И —распространения нет. Длина
волны зондирующего излучения 8,6 мм.
Ne
В
Фиг. 4. Эффекты, наблюдаемые в горячей плазме. Термические
эффекты, эффект Черенкова, направленное распространение и
ускорение даны для случая распространения волн с правосторонней
поляризацией.
20. Исследование взаимодействия волн с плазмой
431
В § 3 будет показано, как эти условия могут быть удовлет-
ворены на практике.
В заключение рассмотрим случай, когда в плазме присут-
ствует электрическое поле, параллельное В. Это поле изменяет
условия распространения волн. Бриффорд [7] показал, что дис-
персионное соотношение для этого случая имеет вид
О
+ а v~
(О2 - с2К2 — ®2-^z f ----------------------= со2 G (со, KY
У л 4 о ± а>с — Kvz — jv р v0V л mv
где
J-а
О (со, К) — ~ J
—а
со ± — jv — Kvz
„ +а v„
__ 2jv f Уге u dvz ।
Vq J co ± coc — Kvz — jv
+^z j (ю;Юс^)3
-а
Разложение этого выражения с точностью до двух членов,
справедливое для области далекой от циклотронного резо-
нанса, имеет вид
со г
со2 = с2К2 + со2 —-----г- 1 4- —
1 Р (о ± — jv L 2 (со ± — jv)2
Kvz J [2 (w ± ас) — jv] w 4- ] I
w ( 2 (w ± wc — jv)2 ... J J ‘
Таким образом, оказывается, что волны, условия распростра-
нения которых изменяются, имеют фазовую скорость, близкую
к дрейфовой скорости. Экспериментально хорошо подтвержда-
ется, что фазовая скорость распространения приближается г
дрейфовой, возникающей благодаря наличию электрического
поля или из-за собственного ускорения плазмы.
Переход энергии от волны к электронам и от электронов к
ионам через столкновения или пространственный заряд может
быть полным. Если СВЧ мощность достаточна, поперечный по-
ток энергии стремится увеличиться до релятивистских величин
при условии, что переход энергии будет поддерживаться. Дрей-
фовая скорость является фактором, способствующим этому пе-
реходу. Действительно, электроны под влиянием градиента СВЧ
поля (вызываемого затуханием волны в плазме и постоянным
432
Т. Консоли, Д. Лепешинский, Ф. Парлянж, М. Кадар
магнитным полем) стремятся ускориться в направлении умень*
шения поля. Таким образом, резонанс возникает при
/ vz\ ( у2| V/!
и — =а>с,
где т0 — масса покоя. Если бы а>' уменьшалась с увеличением г
и условие (0/=®с сохранялось вдоль всего интервала г, то энер-
гия перешла бы от волны к электронам и ионам (через про-
странственный заряд) и волна полностью бы затухла.
Рассмотрим внимательнее причину перехода энергии от вол-
ны к электронам. Когда частота столкновений мала по сравне-
нию с частотой электромагнитного поля, безразлично, как изу-
чать поведение плазмы в самосогласованном электромагнитном
поле — с помощью уравнения Власова или в приближении сво-
бодных зарядов.
Изучение поведения электронов и ионов в самосогласован-
ном электромагнитном поле (включая электрическое поле про-
странственного заряда и уменьшающееся магнитное поле) вбли-
зи резонанса показывает, что электроны и плазма в целом мо-
гут ускоряться и приобретать аксиальную скорость vz, которая
может быть порядка фазовой скорости волны. В этой модели
частицы плазмы оказываются обладающими тензорной массой—
релятивистской массой электронов в поперечной плоскости и
массой ионов в продольной плоскости.
Если предположить, что постоянное магнитное поле неодно-
родно и уменьшается с увеличением z и что в некоторой точке z
оно имеет значение В, которое соответствует резонансу между
циклотронной частотой и частотой электромагнитного поля, то
путем точного решения уравнения движения можно показать,
что плазма ускоряется [8].
§ 3. ЭКСПЕРИМЕНТАЛЬНАЯ ТЕХНИКА И РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
1. Нестандартная интерферометрия. Обычный интерферо-
метр, элементы которого включают волновод стандартных раз-
меров (фиг. 5), не может быть использован при длине волны
2; 1 или 0,6 мм из-за слишком больших потерь в волноводе.
Приходится прибегать либо к волноводам большого сечения
с потерями, меньшими на порядок (использовать волноводы
для волны 8 мм), либо использовать смешанную конструкцию,
состоящую из волноводов и открытых линий, причем последние
следует использовать на наиболее длинных участках системы.
Мы применили оба эти способа. Использование волноводов
Выход отраженного
Передаваемый сигнал
Фиг. 5. Обычный рупорный интерферометр на волноводах.
Фиг. в. Интерферометр Мах-Цендера с применением линз.
28 Зак. 274
434
Т. Консоли, Д. Лепешинский, Ф. Парлянж, М. Кадар
большого сечения имеет то преимущество, что для них не тре-
буется жесткая юстировка, которая необходима в открытых
квазиоптических устройствах. Тем не менее эта техника еще
не применялась из-за задержки в разработке переходов от вол-
новодов с Л=8 мм к волноводам с Х=1 и 0,6 мм.
В методе, использующем распространение в свободном про-
странстве, можно выбрать один из следующих вариантов:
а) интерферометрические измерения с использованием линз
(диэлектрических или металлических) (на интерферометрах
Мах-Цендера или Майкельсона);
б) интерферометрические измерения с использованием фоку-
сирующих зеркал (на интерферометре Дагая).
Первый вариант схематически представлен на фиг. 6 и 7.
Линзы и фазовые корректоры основного плеча сделаны из фто-
ропласта. Линзы имеют параболический профиль и фокусное
расстояние 14 см, так как требуется получить параллельный
луч от передающего рупора, смонтированного прямо на выходе
карсинотрона. Фиг. 8 показывает систему, использующую зерка-
ла. Эта система описана в статье [9].
Типичные результаты. Интерферометрические исследования
с помощью поперечного распространения волн были проведены
для измерения электронной плотности импульсного разряда Пен-
цинга с горячими катодами. На фиг. 9 показаны теоретическое
изменение плотности как функции импульсного тока (а), тео-
ретическая интерферограмма с колебаниями, соответствующими
ионизационному и послетлеющему периодам (б), и действитель-
ная интерферограмма, полученная путем суперпозиции 50 иден-
тичных импульсов тока (в). Следует отметить, что область, со-
ответствующая плоской части кривой плотности, воспроизводит-
ся плохо.
Интерферометрические измерения при продольном распро-
странении волн. При зондировании плазмы параллельно маг-
нитному полю оказывается возможным изучить свойства плаз-
мы, связанные с распространением волн с правосторонней и ле-
восторонней круговыми поляризациями, с линейной поляриза-
цией и особенно с распространением свистящей моды. Основ-
ным условием для этого является обеспечение строгой парал-
лельности волнового вектора К и магнитного поля В. Этого
можно достигнуть следующими тремя способами:
а) В случае импульсной плазмы, помещенной в постоянное
магнитное поле В, можно применить металлические линзы с от-
верстиями, параллельными вектору В, помещенные внутрь плаз-
менного столба. Эти линзы не только обеспечат параллельность
векторов К и В, но и создадут достаточно резкую продоль-
ную границу для плазмы. При этом линзы должны облучаться
йодепМиое зеркало
Фиг. 7. Интерферометр Майкельсона с применением линз.
Фиг. 8. Зеркальный интерферометр Дагая.
К— карсинотрон на2.«Л; С! —излучающий рупор; Сг — принимающий рупор; $,— сетка
разделителя; Sj —сетка смесителя; Rlt У?2 — цилиндрические отражатели, дающие парал-
лельные лучи; Rt, Rt~отражатели; D — детектор.
28*
436 Т. Консоли, Д. Лепешинский, Ф. Парлянж, М. Кадар
высокочастотным источником, через герметическое стеклянное
окошко.
б) Когда плазма и магнитное поле импульсные (0-пинч), ме-
таллические линзы нельзя помещать в плазму из-за возмущаю-
щего эффекта, возникающего в переменном магнитном, поле и
приводящего к искажению импульсного поля на поверхности
Фиг. 9. Показания СВЧ интерферометра для случая нестационарной
плазмы импульсного разряда Пеннинга с горячим катодом.
д — изменение плотности при действии импульса постоянного тока; б — детектированный
сигнал (теоретическая кривая для полной длины пробега через плазму D=4Z); в—де-
тектированный сигнал (экспериментальное наложение 50 импульсов тока).
линз. В этом случае линзы можно расположить с внешней сто-
роны стеклянных окошек, которые ограничивают плазму. Когда
это возможно, лучше использовать рупоры, помещенные в плаз-
му и закрытые в раскрыве фторопластовой пластинкой, которая
предотвращает затекание плазмы, находящейся под давлением.
Однако этот последний способ нельзя использовать, если в вол-
новоде, соединяющем генератор с рупором, может возникнуть
локальная резонансная (ис=и) ионизация.
в) Когда такая ионизация имеет место, связь высокочастот-
ного поля с плазмой можно обеспечить с помощью третьего
способа, в котором используются диэлектрические антенны,
Фиг. 10. Кварцевая антенна и ее конструкция.
'"зо"' 2,0 ' io b ‘idr' го' ^о‘
Фиг. 11. Диаграмма направленности кварцевой антенны.
438
Т. Консоли, Д. Лепешинский, Ф. Парлянж, М. Кадар
укрепленные на выходе волновода. Чтобы обеспечить хорошую
направленность, мы использовали кварцевую антенну со, спе-
циально рассчитанным профилем (фиг. 10).
2. Диаграмма излучения кварцевой антенны. Результаты
сравнения. Кривая фиг. 11 представляет собой диаграмму излу-
чения кварцевой антенны, смонтированной на выходе 8-милли-
/ — продольная интерферометрия, Л=:5л<.и; 2 — продольная интерферометрия,
Х = 8.илг: «3 —продольное прохождение. Газ аргон, р = 8 • 10~2 мм рт. ст.,
/с = 32Ггц</.
метрового волновода. Видно, что направленность такой антен-
ны лучше, чем у обычного рупора. Мы использовали эту систему
для измерения электронной плотности импульсного разряда и
сравнили соответствующие интерферограммы с полученными
обычным рупорным интерферометром.
На фиг. 12 представлены интерферограммы, полученные при
продольном распространении волн с помощью рупора и диэлек-
трической антенны. Следует отметить сходство результатов по-
лученных для разных импульсов разряда, за исключением вре-
мени жизни плазмы. Вследствие рекомбинации на поверхности
20. Исследование взаимодействия волн с плазмой
439
антенны плазма охладилась и время ее жизни (5 мсек) сокра-
тилось на 250 мксек.
3. Продольное распространение волн. Свистящая мода. Из
диаграммы фазовых скоростей КМА (Клеммова — Миллали —
Аллиса) [6] следует, что в плотной плазме (алр‘^>т) при условии
о)с>ю может распространяться волна с правосторонней круго-
вой поляризацией. Эффективная Длина волны в плазме равна
5 __ Хр
лэфф п >
где Хо — длина волны в свободном пространстве, п — действи-
тельная часть показателя преломления холодной плазмы (v = 0),
которая может достигать довольно большой величины
л X \% /х\'/2
п~ V 1— У1) ’
здесь y=Y—1 отклонение от циклотронного резонанса.
Проверка в статическом режиме. Экспериментальная уста-
новка; прохождение волны. В установке, показанной па фиг. 13,
плазма образуется при разряде рефлексного типа. Распределе-
ние электронной плотности, измеренное зондом Ленгмюра, дано
на фиг. 13, а. Антеннами в этом случае были электрические ди-
поли, помещенные в плазменный столб в зону, где магнитное
поле однородно. В эксперименте была использована большая
длина волны (Х = 25 см). Эта волна в случае отсутствия магнит-
ного поля соответствует критической электронной плотности
jVe = 2- 1010 см~3. Волна отражается плазмой при (ос<ю, при
этом уровень проходящего сигнала равен нулю. Прохождение
волн обнаруживается сразу же после достижения резонансной
частоты (юс^ю), причем уровень сигнала выше, чем при про-
хождении в волноводе, вследствие эффекта направленности сви-
стящей моды (фиг. 14).
Проверка в динамическом режиме. В описанном выше экс-
перименте была использована большая длина волны, поэтому
оставался неясным вопрос о законности применения в этом слу-
чае уравнений, справедливых для волн, распространяющихся в
неограниченной среде.
Для измерения электронной плотности в 0-пинче с помощью
свистящей моды мы использовали установку, показанную
на фиг. 15. Металлические линзы располагались вне разряд-
ной трубки; плазма образовывалась с помощью разряда ба-
тареи конденсаторов через катушку с несколькими витками;
торцы трубки представляли собой стеклянные окошки. В мо-
мент максимума тока катушка закорачивалась, чтобы увеличить
Фиг. 13. Распространение свистящей моды.
а —схема опыта; б —распределение магнитного поля по оси; в —эксперимен-
тальная СВЧ установка.
А, А' — аноды; М — катушки, создающие постоянное магнитное поле; К, К' — ка-
тоды; СН—согласованная нагрузка; НО — направленный ответвитель; Ф —фер-
ритовый вентиль; ЯЛ —клистрон; Д — детектор; ППК — переход от прямоуголь-
ного к круглому волноводу; П— поляризатор; ВО —вакуумное окно; Р — круг-
лый рупор.
Фиг. 14. Распространение свистящей моды в водородной
плазме при постоянном магнитном поле.
Источник волн
Фиг. 15. Установка для получения 0-пинч-эффекта.
Интерферометры с поперечным и продольным (свистящая мода) распростра-
нением.
Фиг. 16. Области плоскости (Ne, В), обследованные во время
сжатия (0-пинч).
Фиг. 17. Интерферометрия О-пинч-эффекта. Распростра-
нение в продольном направлении.
а — интерферограмма свистящей моды (X = 8,6 мм); б—интерферо-
грамма для случая распространения в поперечном направлении
(К = 2,2 мм); в — изменение полного магнитного поля; газ Н2,
= 0,1 мм рт. ст.
Фиг. 18. Экспериментальная установка для изучения
эффекта направленного распространения.
ИРи ЯР2 — излучающие рупоры; ПРи ПР2, ПРа — принимающие
рупоры; 0О, 01( 02 — углы между векторами К и Во; Ah Д2 —аноды;
Л’п Яг —горячие катоды; Р —35 Ггц.
Диаграммы направленности: 6(К,Во)=0°10'>,90*
Типичный результат: газ Н2, р=2,4-103ям рт.ст.г 1^=10
Фиг. 19. Диаграммы направленности для эффекта направленного
распространения.
20. Исследование взаимодействия волн с плазмой
445
продолжительность магнитного сжатия. Волна была линейно
поляризована и имела Z=8,6 мм.
Поперек трубки располагался интерферометр оптического ти-
па, работающий на длине волны 2,2 мм. Это дало возможность
сравнить измерения при поперечном и продольном распростра-
нении волн. Фазы сжатия и расширения плазмы представлены
на фиг. 16, а типичные результаты измерений даны на фиг. 17.
Легко видеть, что в продольном направлении волна 8,6 мм в
свистящем режиме распространяется лучше, чем волна 2,2 мм
в поперечном направлении. Искажение колебания при продоль-
ном распространении должно быть приписано большей неодно-
родности разряда в этом направлении [10].
4. Эффект направленности свистящей моды. В случае рас-
пространения волны с правосторонней круговой поляризацией
направленность волн в плазме изучалась на установке, пока-
занной на фиг. 18. Для измерения падающей прошедшей и отра-
женной мощности использовалось несколько приемных рупоров,
которые устанавливались под углами 0, 10, 90 и 180° к направ-
лению прямого прохождения волны. Плазма находилась в маг-
нитном поле, интенсивность которого можно было произвольно
изменять. Полученные диаграммы направленности показаны на
фиг. 19. Можно отметить два эффекта направленности: один ни-
же резонанса ((ос<и) из-за радиальной неоднородности плаз-
мы, второй, значительно более резко выраженный и не дающий
излучения в поперечном направлении, появляется сразу после
достижения циклотронного резонанса.
5. Исследование распространения волны с правосторонней
круговой поляризацией вблизи критической и резонансной ли-
ний. Аномальное затухание. На фиг. 20 представлена установка
для волны 8,6 мм с круговой поляризацией, которая позволяет
исследовать выбранные области диаграммы фазовых скоростей
для постоянных Ne или В. На ней было подтверждено наличие
критической линии У=1 — X в аргоне при давлении 3- 10-3 мм
рт. ст. Однако измерение затухания волны вблизи циклотрон-
ного резонанса дало величину, которую нельзя объяснить как
результат потерь на столкновения. На фиг. 21 показаны теоре-
тические кривые, вычисленные с учетом столкновений электро-
нов с нейтральными атомами при значениях температуры 300° К,
10 эв и 50 эв. Здесь же приведены экспериментальные резуль-
таты. Несоответствие между теорией и экспериментом нельзя
объяснить экспериментальными ошибками. Наблюдаемое зату-
хание имеет другую природу. Возможно, что этот результат
446 Т. Консоли, Д. Лепешинский, Ф. Парлянж, М. Кадар
Г. ёамёры
Ф и г. 20. СВЧ устройство для измерений при прохождении
волн через плазму. Интерферометр с волной, поляризованной
по кругу (Л = 8 мм).
связан с термическим эффектом или с дрейфом всей среды как
целого, если не с обоими эффектами вместе.
На фиг. 22 дается типичный результат измерения прохожде-
ния волны через плазму. Увеличение проходящей мощности за
резонансной частотой (со>сос) связано не со свистящей модой,
а с радиальным изменением концентрации плазмы.
ПРИЛОЖЕНИЕ 1. УСКОРЕНИЕ ПЛАЗМЫ ПОД ДЕЙСТВИЕМ
НЕОДНОРОДНОГО ПОСТОЯННОГО МАГНИТНОГО поля
И ВОЛН С ПРАВОСТОРОННЕЙ КРУГОВОЙ ПОЛЯРИЗАЦИЕЙ
Механизм такого ускорения подробно описан в недавно опу-
бликованной статье [8]. В высокочастотном поле правосторонне
поляризованной волны при достаточном затухании в ионизиро-
ванной среде возникают градиенты поля. Мы также предполо-
жили, что и магнитное поле уменьшается с расстоянием. Можно
показать, что в этом случае электронная и ионная компоненты,
связанные через пространственный заряд, ускоряются в направ-
лении уменьшения полей. Параллельная дрейфовая скорость
электронов и ионов мала по сравнению с поперечной скоростью.
Она имеет порядок величины I07—108 см/сек, т. е. порядок фазо-
вой скорости правосторонпе поляризованной волны в резонанс-
ной зоне. Это совпадение фазовой скорости и параллельной
Фиг. 21. Результаты измерения при продольном распространении волн.
Газ аргон, р= 3 • I0”3 мм рт. ст.
Фиг. 22. Мощность, проходящая через плазму зарезонансной частотой.
Частота 35 Ггц, N =10!1 с.и~3, р=10 3 мм рт. ст., л = 0,005. Данные получены для
е волны с правосторонней поляризацией.
Фиг. 23. Ускоритель плазмы на бегущей волне.
а — профиль статического магнитного поля; б —положение волновода; а —профиль амплитуды
СВЧ поля; г —сечение плазменного луча; б —волновод в вакуумной камере; е —вид луча
плазмы.
20. Исследование взаимодействия воЛн t плазмой
449
дрейфовой' скорости благоприятствует взаимодействию волны
с электронами и расширяет зону, в которой энергия передается
частицами во всей области, где это свойство удовлетворяется.
Экспериментальные измерения действительно показали су-
ществование ускорения. Оказалось возможным построить ца
этом принципе (и мы это сделали) ускоритель или плазмен-
ный инжектор. На фиг. 23 представлены схема ускорителя бе-
гущей волны, экспериментальная установка и производимый
ею луч.
ПРИЛОЖЕНИЕ 2. НАГРЕВАНИЕ ПЛОТНОЙ ПЛАЗМЫ
ВЫСОКОЧАСТОТНЫМ ПОЛЕМ В СВИСТЯЩЕЙ МОДЕ
Как было показано ранее, свистящая мода может распро-
страняться в плотной плазме и затухает в зоне резонанса. Это
дает возможность разогревать плотную плазму, если использо-
вать профиль поля типа того, который изображен па фиг. 24 и 25.
Вид.поля в'.
- идеальный
реальный
Фиг. 24. К нагреванию плазмы с помощью свистящей моды.
I. а>с < со, распространения нет (отражение); //. > со, область распро-
странения с малым поглощением; III. = область с сильным поглоще-
нием, или электронный циклотронный резонанс.
Высокочастотная установка для такого разогрева представлена
на фиг. 26.
Волны распространяются в области coc>w и затухают при
когда параллельный дрейф усиливает поглощение. При-
менение к электронам принципа «магнитного берега», предло-
женного Стиксом для ионов, можно использовать в этом случае
без ограничений на плотность ионизированной среды и массу
частиц. Это возможно благодаря хорошему согласованию полей
в вакууме и плазме с помощью рупора или диэлектрической
кварцевой или нитридбариевой антенны с высокой диэлектри-
ческой проницаемостью. Эксперимент, в котором были исполь-
зованы кварцевые окна, показал, что такое нагревание доста-
точно эффективно.
29 Зак. 274
Фиг. 25. Экспериментальное устройство для нагревания плазмы
волной с правосторонней поляризацией (10-сантиметровый диапазон).
Цепь СВЧ
Фиг. 26. Высокочастотная секция экспериментального устройства,
показанного на фиг. 25.
20. Исследование взаимодействия волн с плазмой
451
НРЙЛОЖЕНИЕ 3. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ДИЭЛЕКТРИЧЕСКОЙ АНТЕННЫ
Такую антенну следует изготавливать из материала с хоро-
шими вакуумными свойствами, небольшую по величине, но даю-
щую достаточно высокую направленность. Использованная в
опытах диэлектрическая антенна была сделана из кварцевого
стержня, представлявшего собой диэлектрический волновод. Она
возбуждалась открытым концом обычного металлического вол-
новода. Мощность, распространяющаяся в диэлектрике, мала
по сравнению с мощностью, распространяющейся вблизи ди-
электрика, тем не менее последняя эффективно направляется
диэлектриком. Цилиндрический излучатель можно рассматри-
вать как совокупность однородных излучающих дисков с диа-
метром, равным диаметру излучателя, и. с малой толщиной. Об-
ратную волну, отраженную от конца днтенны, можно значи-
тельно уменьшить, если сделать стержень слегка коническим,
так чтобы на его конце фазовая скорость волны в таком диэлек-
трическом волноводе была близка к фазовой скорости волны
в свободном пространстве [12]. Для того чтобы направленность
антенны была наилучшей, необходимо ее диаметр на выходе
возбуждающего устройства сделать таким, чтобы отношение
длины волны в диэлектрическом волноводе такого диаметра к
длине волны в воздухе-было равно примерно 0,9 (Xg/X~0,9).
Мальбах предложил следующие формулы для вычисления
наибольшего и наименьшего диаметров диэлектрической ан-
тенны
. _ Л , __ Л
макс“ [л(е —1)],/2 ’ мии ~ [2,5л (е—1)]1/2 ’
где X — длина волны в воздухе, а 8 — диэлектрическая прони-
цаемость антенны. Что касается длины антенны, то величина в
5Z, согласно Буи и Мальбаху, вполне удовлетворяет как требо-
ванию направленности, так и согласованию с-волноводом. Так,
например, для Z = 8,6 мм и 8 = 3,8 (кварц) фмакс=2,9 мм, с?мип=
= 1,85 мм\ длина антенны 5Х = 43 мм. Конец антенны, вставляю-
щийся в возбуждающий волновод, заостряется, чтобы поле втя-
гивалось в диэлектрик постепенно. Параметры антенны были
следующие: ширина диаграммы направленности на уровне 3 дб
равна 22°, 10 дб — 38°, подавление боковых лепестков не хуже
13 раз, КСВ< 1,15 на частоте 35 Ггц.
Заключение. По уровню боковых лепестков и ширине
диаграммы направленности описанная выше антенна далека от
оптимальной. Тем не менее она оказалась годной для наших
экспериментов.
29*
452
Г. Консоли, Д. Лепешинский, Ф. Парлянж, М. Кадар
ЛИТЕРАТУРА
1. Motley R. W., Heald М. A., Proc. Symposium on Millimeter Waves,
New York, 1960.
Use of Multiple Polarization for Electron Density Propofile Measurements
in High-Temperature Plasma.
2. Con soli T., CEA Report, No. 1703, Centre d’Etudes Nucleaires de Saclay,
France, 1960.
Mesure de la densite electronique des millieux ionises par des methodes
hyperfrequences.
3. Briffod G., Internal Report No. PA.IGn/RT. 110, Centre d’Etudes Nuc-
leaires de Saclay, France, 1960.
Diffusion dans les milieux faiblement ionises — Etudes des instabilites.
4. С и л и и В. П., Р у х а д з е А. А., Электромагнитные свойства плазмы,
М, 1961.
5. AU is W. Р., TID 7582 (1959).
6. S t i х Т. Н., The Theory of Plasma Waves, New York, 1962. (Имеется'
перевод: T. Стикс, Теория плазменных волн, М., 1965.)
7. В г 1 f f о d G., Gregoire M., Internal Report No. PA IGn/RT. 292,
Centre d’Etudes Nucleaires de Saclay, France, 1964; см. также International
Symposium on Diffusion across a Magnetic Field, Munich, Germany, July,
1964.
Origines et effets des instabilites microscopiques dans les decharges reflex.
8. Bar det R., Con soli T., Geller R., Parlange F., Weill M.,
Comptes rendus de I’Academie des Sciences (France), 258, No. 18, 4454
(1964).
Accelerateurs a plasma a ondes progressives — Etude theorique.
9. Dagai M., Proc. 5th International Conference on Ionization Phenomena
in Gases (Miinich, 1961), Amsterdam, 1962, p. 417.
Techniques et Equipements de mesure de densite de plasma de 1’ordre de
IO’4 e/cm3.
10. С о n s о 1 i T., D u p a s L., I c h t c h e п k о G., Phys. Lett., 1, No. 7 p. 267
(1962).
Transparence d’un plasma dense aux ondes a polarisation circulaire.
11. Consoli T., Clement M., Dupas L., Leroy J., Weill M., Comptes
rendus de la 6-me Conference Internationale sur les Phenomenes d’lonisa-
tion dans les Gaz, Paris, 1963, vol. Ill, p. 75.
Etude du mecanisme physique de transfert de I’energie d’une onde electro-
magnetique a polarisation circulaire droite a un millieu ionise.
12. Bouix M., Ann. des Telecomm. (France), 7 (1952).
21
КВАЗИОПТИЧЕСКИЕ МЕТОДЫ
В МИЛЛИМЕТРОВОЙ СПЕКТРОСКОПИЙ
Р. Штраух*, Р. Капп.*, М. Лихтенштейн*, Дж. Галлагер*
В области миллиметровых и субмиллиметровых волн имеется много воз-
можностей для спектроскопических исследований газов и твердых тел. В этой
области широко используются квазиоптические методы, поскольку длина вол-
ны мала, а для получения заметного поглощения или излучения необходимо
присутствие достаточного числа частиц. Ниже описываются методы, которые
в настоящее время используются в миллиметровой спектроскопии.
В качестве миллиметрового спектрометра в нашей лаборатории исполь-
зовались интерферометры Фабри — Перо, Штарка и Зеемана. Описываются
поляризационные опыты для определения знака g-фактора молекул, обла-
дающих поглощением в диапазоне 1—2 мм. Фильтрация гармоник для опре-
деления частот перехода может быть осуществлена с помощью сеточных
интерферометров.
Обсуждается использование интерферометров и рупорно-линзовых систем
в электрорезонансном миллиметровом спектрометре и в приборе с поглоще-
нием молекулярного пучка. Описываются также исследования на миллимет-
ровых мазерах. Обсуждается спектроскопия свободных радикалов на милли-
метровых волнах, которую можно производить в стеклянных камерах, облу-
чаемых рупорами с линзами.
Квазиоптические методы могут быть использованы также при исследова-
нии резонансных явлений в твердом теле на миллиметровых волнах. Обсу-
ждается возможность приложения квазиоптических методов к исследованиям
многоквантовых систем и другим проблемам квантовой электроники в области
субмиллиметровых и миллиметровых волн.
До недавнего времени работы по миллиметровой спектроско-
пии проводились в основном в волноводных поглощающих каме»
рах. Обычно эти камеры представляют собой газонаполненные
секции волновода широкого сечения с окнами из слюды. Они
с успехом используются при изучении прямого поглощения мо-
лекул с достаточно большими дипольными моментами. За по-
следние годы значительно возрос интерес к таким спектроско-
* R. G. S t г а и с h, R. Е. Cupp, М. Lichtenstein, J. J, Gallag-
her, The Martin Company, Orlando, Florida.
30 Зак. 274
454 Р. Штраух, Р. Капп, М. Лихтенштейн, Дж. Галлагер
пическим исследованиям, которые не могут быть выполнены
обычными волноводными методами. Из-за малости рабочей дли-
ны волны становится необходимым применять квазиоптические
устройства. Ниже сделана попытка рассмотреть некоторые ква-
зиоптические методы исследования взаимодействия электромаг-
нитного излучения с молекулярными системами. Главная за-
дача практически всех обсуждаемых методов — создать для
молекулярной системы наиболее выгодные условия для взаимо-
действия с излучением. Мы кратко обсудим следующие вопросы:
1) миллиметровая электрорезонансная спектроскопия; 2) газо-
вая спектроскопия в интерферометрах; 3) зеемановские измере-
ния с помощью излучения, поляризованного по кругу; 4) милли-
метровые газовые мазеры; 5) многоквантовые устройства;
6) спектроскопия свободных радикалов; 7) использование ква-
зиоптических методов в исследованиях твердого тела; 8) некото-
рые другие приложения квазиоптики в спектроскопии.
§ 1. ЭЛЕКТРОРЕЗОНАНСНАЯ СПЕКТРОСКОПИЯ
НА МИЛЛИМЕТРОВЫХ ВОЛНАХ
Долгое время спектроскопия на молекулярных пучках про-
изводилась только на радиочастотах и в нижней части СВЧ
диапазона. До сих пор методы пучковой спектроскопии не ис-
пользовались в миллиметровом диапазоне из-за трудности полу-
чения достаточно стабильной мощности в миллиметровом диа-
пазоне и из-за сложности систем, обеспечивающих излучение
пучков. Использование же этих методов в миллиметровом диа-
пазоне может дать некоторые преимущества.
Во-первых, было предложено использовать миллиметровый
электрорезонансный спектрометр в качестве стандарта частоты
[1, 2] и была показана возможность практического осуществле-
ния такого прибора [3]. Как будет показано ниже, успех такого
прибора сильно зависит от применения квазиоптических мето-
дов. Во-вторых, эта техника позволяет создать чрезвычайно
чувствительный спектрометр с высоким разрешением, пригодный
для исследования сверхтонкой ядерной структуры и внутриядер-
ных взаимодействий. В миллиметровом диапазоне можно изу-
чать сверхтонкую структуру отдельных вращательных перехо-
дов (что не всегда возможно в более длинноволновой области),
а также независимо определять электрические дипольные мо-
менты и вращательные константы. С помощью квазиоптических
методов можно создать спектрометр с высокой разрешающей
способностью.
Прежде чем описывать проведенные нами эксперименты в
миллиметровом диапазоне, мы опишем в общих чертах метод
21. Квазиоптические методы в спектроскопии
455
электрического резонанса в том виде, в каком мы его исполь-
зовали. Этот метод более подробно описан в литературе по мо-
лекулярным пучкам [1, 2, 4, 5]. На фиг. 1 изображена схема
электрорезонансного молекулярного спектрометра. Молекулы
Фиг. 1. Схема электрорезонансного спектрометра на молекулярном пучке.
3 —источник молекулярного пучка; г —щель коллиматора; А и В — области неоднородных
электрических полей; С —область однородного электрического поля, содержащая также
осциллирующее электрическое поле; D — ионизатор с электронной бомбардировкой; Ж — масс-
спектрометр; ЗУ —электронный умножитель. Пунктирная линия —траектория молекулы,
которая проходит через прибор в своем первоначальном состоянии. Штрихпунктирная кри-
вая-траектория молекулы, которая претерпевает переход в области С.
испускаются источником S через щель. Пучок ограничивается до-
полнительными щелями коллиматора. Траектория молекулы за-
висит от ее электрического дипольного момента и формируется
при прохождении молекулы через неоднородные электрические
поля; отклонение молекулы в этих полях зависит от ее дипольного
момента. Эти неоднородные электрические поля сосредоточены
в областях А и В, в которых молекулы отклоняются в направ-
лении, перпендикулярном плоскости пучка.
В области С имеется осциллирующее электромагнитное по-
ле, которое может вызывать переходы молекулы из одного со-
стояния в другое. В нашем приборе неоднородные поля подо-
браны так, что если молекула, вылетевшая из источника, не
совершает в области С переход в другое состояние, то она,
двигаясь по траектории, попадает в ионизатор с электронной
бомбардировкой и далее движется с ускорением через масс-
спектрометр к электронному умножителю-детектору. Если же ос-
циллирующее поле в области С имеет такое значение (или близ-
ко к нему), что происходит молекулярный вращательный пере-
ход из первоначального состояния молекулы, то в этом случае
молекула, перейдя в другое состояние, будет испытывать иное
отклонение в области В и таким образом не попадет в умножи-
тель. Однородное электрическое поле в области С поддерживает
частицу в определенном квантовом состоянии на протяжении
всего пути прохождения через прибор при отсутствии индуци-
30*
456
Р. Штраух, Р. Капп, Л4. Лихтенштейн, Дж. Галлагер
рованного перехода, а также обеспечивает штарковское рас-
щепление, по которому можно определить электрический ди-
польный момент.
Фиг. 2. Миллиметровый электрорезонансиый спектрометр
на молекулярном пучке.
На фиг. 2 изображен спектрометр на молекулярном пучке,
который использовался в опытах, описанных ниже. Источник
находится на переднем плане справа. Магнит масс-спектромет-
ра виден за системой. Миллиметровая аппаратура, не показан-
ная на фотографии, монтируется наверху центральной части
большой камеры. Во всех наших опытах миллиметровый сигнал
поступал с гармонического клистронного генератора, который
был синхронизован по фазе стабильным низкочастотным гене-
ратором. В этих экспериментах можно использовать фазовую
модуляцию в цепи умножителя, модуляцию путем прерывания
21. Квазиоптические методы в спектроскопии
457
молекулярного пучка или, как в наших экспериментах, штар-
ковскую модуляцию поля в области С. Сигнал пучка, продетек-
тированный электронным умножителем, поступает затем в уси-
литель, синхронизируемый сигналом модулятора, а выходной
сигнал выдается на самописец.
Использованию электрорезонансного спектрометра в каче-
стве стандарта частоты или спектрометра с высоким разреше-
нием препятствовали два фактора, а именно, чистота спектра
источника сигнала и трудность ввода сигнала в молекулярный
пучок; последний фактор интересует пас здесь больше всего. Же-
лательно, чтобы молекулярный пучок синфазно взаимодейство-
вал с однородным полем вдоль большей части своего пути че-
рез область С. Получение на миллиметровых волнах однород-
ного поля большой протяженности представляет собой трудную
задачу. Оптимальная ширина линии зависит, кроме прочих фак-
торов, от времени, которое молекула проводит в поле излучения,
и от допплер-эффекта. Ширина линии (равная разности ча-
стот dv между точками кривой интенсивности па уровне 0,5) не
может быть уже, чем естественная ширина, определяемая соот-
ношением неопределенности dvT^{, где Т — промежуток вре-
мени, в течение которого молекула подвергается действию ос-
циллирующего поля, вызывающего переход.
Первый электрорезонансный эксперимент в миллиметровом
диапазоне [6] производился па Li6F19 в области 90 Ггц\ для вво-
да миллиметрового сигнала использовался 20-децибельный ру-
пор, расположенный примерно на 5 см выше молекулярного
пучка. Рупор был ориентирован так, чтобы электрическое поле
волны было направлено параллельно штарковскому полю. При
такой ориентации имеют место переходы, для которых ДЛ4/=0.
В предположении, что ширина линии определяется в основном
соотношением неопределенности и допплеровским уширением
из-за углового разброса излучения рупора, было получено, что
ширина линии составляет приблизительно 200 кгц. При уровне
мощности приблизительно 1 мквт -имело место насыщение уши-
рения линии. Конфигурация рупора была такая же, как на
фиг. 3, где также изображено поле в щели с, которое вызывает
радиочастотные переходы между штарковскими компонентами.
В недавно проведенных экспериментах мы применили метод
электрического резонанса к вращательным переходам в несим-
метричной молекуле H2S на частотах 168,7 и 216 Ггц. В этих
экспериментах сразу же обнаружилась необходимость в более
совершенных облучающих устройствах. В первых экспериментах
использовался рупор внутри вакуумной системы, который был
ориентирован только для переходов с ДЛ4/=0. На фиг. 3, а
показано положение рупора. Ширина линии в этом устройстве
165
Фиг. 3. Рупорио-линзовые системы для возбуждения молекулярного
пучка одним осциллирующим полем.
I =
5
а —рупор в вакууме над пластинами, создающими поле в области С; направление элек-
трического поля показано для переходов с Д2И «О (Дот=0); показано расщепляющее
поле для одновременного наблюдения радиочастотных штарковских переходов; б — рупор-
но-линзовая система с линзой в качестве вакуумного окна и с малым секториальным
рупором; в — разнесенная рупорно-линзовая система, обеспечивающая более длинную
область взаимодействия; прессованный витон (имеет низкое давление паров) исполь-
зуется в качестве поглощающего покрытия приспособлений, поддерживающих пластины
поля в области С. Все размеры указаны в миллиметрах.
21. Квазиоптические методы в спектроскопии
459
была значительно шире (приблизительно 100 кгц) и слабее, чем
в последующих экспериментах с рупорно-линзовым возбужде-
нием.
В рупорно-линзовом устройстве, изображенном на фиг. 3, б,
в котором линза использовалась в качестве вакуумного окна,
при вращении рупора можно было наблюдать переходы с ДЛ4/=
= 0 и ДЛ4,Г=±1. На фиг. 4, а и б приведены графики перехода
с ДЛ4/=0 на частоте 168,7 Ггц. В обоих случаях использовалась
штарковская модуляция. Видна только одна штарковская ком-
понента Мг=±1, ДМ/=0, так как переход с Д7 = 0, ДЛ4/=0,
Mj=0 имеет очень малый коэффициент интенсивности. На
фиг. 4, а показан график перехода при штарковской модуляции
поля в области С меандром 0—500 в. При отсутствии поля на-
чинает проявляться ядерная сверхтонкая структура, состоящая
из шести компонент. Однако в присутствии штарковского поля
сверхтонкое расщепление уменьшается; теоретическая ширина
линии для длины пути 3,8 см равна 14 кгц. При этом интенсив-
ность излучения на протяжении пути 3,8 см изменяется. На
фиг. 4, б показаны две штарковские компоненты при модуляции
поля в области С меандром 800—1000 в. На фигуре видно, что
линия сужается. Исчезновение сверхтонкой структуры и суже-
ние линии, вероятно, являются результатом изменения кванто-
вомеханического состояния от 1IFMf для нулевого поля к
JIMjMj для сильного поля. При нулевом поле компоненты
сверхтонкой структуры должны проявляться в соответствии с
правилом отбора ДР = 0, ±1. В случае сильного поля осуще-
ствляются правила отбора AMj=0, ±1, ДЛ1/ = 0. Исходя из
факта сужения линий, можно предположить, что отдельные пе-
реходы сверхтонкой структуры происходят приблизительно на
одинаковой частоте и что постоянные сверхтонкой структуры
приблизительно равны для двух вращательных уровней пере-
хода.
В дополнение к уширению, обязанному излучающему устрой-
ству, происходит уширение из-за неоднородности налагаемого
штарковского поля и из-за нечистоты спектрального состава из-
лучения источника. Уширение, вызванное последним обстоятель-
ством, уменьшалось при использовании мазера на аммиаке в
качестве опорного генератора, от которого источник сигнала
был синхронизован по фазе. Это в свою очередь приводит к
дальнейшему сужению ширины линии при наложении штарков-
ского поля и к дополнительному разрешению сверхтонкой струк-
туры в нулевом поле.
Чтобы гарантировать оптимальную ширину линии или раз-
решение, необходимы определенные меры предосторожности
при облучении молекулярного пучка. В частности, это касается
168 762 7 34КЗЦ 16В 762 804Х2Ц
168 762 769КЗЦ
5008
168 762 993к2ц
Фиг. 4. Электрические резонансные вращательные переходы в сероводороде.
а —переходи H2S32 на частоте 168,7 Ггц-, j% = (т =±1) <--> Jx ~ l_j (т = ±1); возбуждение рупорно-линзовое; миллиметровая мощность —
семнадцатая гармоника клистрона с фазовой синхронизацией гармоникой кварцевого генератора; модуляция поля в области С осуществлялась
меандром 0 — 500 в; средний масштаб развертки по частоте 16,7 кги,1деление\ б— переход такой же, как на фиг. 4, а, ко модуляция поля произ-
водилась меандром 800—1000 в; средний масштаб развертки по частоте 19,32 кгц/деление.
21. Квазиоптические методы в спектроскопии
461
уровня СВЧ мощности в области пучка. На фиг. 5 приводятся
результаты эксперимента по определению мощности, которую
достаточно ввести в пучок. Обе кривые сняты почти при одина-
ковых условиях, но при разной СВЧ мощности. Ширина линии
и форма линии на фиг. 5 слева имеют такой вид из-за большой
мощности миллиметровых волн и из-за отражений от пластин и
держателей в области С. При уменьшении мощности (график
справа) и при использовании поглощающего материала влияние
эффектов насыщения и отражения на ширину линии уменьша-
лось.
На фиг. 3, в показана последняя рупорно-линзовая конструк-
ция, которую мы использовали в своих опытах. Она обеспечи-
вает наиболее длинный путь, на котором молекула взаимодей-
ствует с СВЧ сигналом и, таким образом, сужает линию при-
близительно до 7 кгц при сильных штарковских полях, а при
нулевом поле еще больше повышает разрешение сверхтонкой
структуры. На фиг. 6 изображена используемая рупорно-линзо-
вая система. Эти эксперименты выявили несколько особенно-
стей взаимодействия пучка с электромагнитным полем и, в част-
ности, влияние длины пути на ширину линии. Однако для увели-
чения длины пути, на котором происходит взаимодействие, в
обычной схеме возбуждения Раби необходимо увеличить протя-
женность поля в области С, что в свою очередь накладывает
жесткие требования на однородность электрического поля вдоль
всей области С. Чтобы ослабить требования на однородность
протяженного поля в области С, Рамзей [7] предложил метод
разнесенных осциллирующих полей, которые сосредоточены в
двух малых областях, расположенных в начале и в конце обла-
сти, где должен происходить переход. В этом случае неоднород-
ности установившегося электрического поля вызывают значи-
тельно меньшее уширение резонансной линии, чем в случае, ко-
гда осциллирующее поле существует во всей области. В методе
Рамзея не только уменьшается уширение линии из-за неодно-
родности электрического поля, но и форма линии отличается
от фор'мы, полученной в обычной схеме Раби.
На фиг. 7 изображена форма линии, полученная со схемой
Рамзея; сверху дана типичная схема низкочастотной резонанс-
ной установки. Полуширина центрального пика равна dv =
= 0,64а/А, в то время как для обычного метода возбуждения
Раби одинарным полем она равна l,07a/L. Здесь а — наиболее
вероятная скорость молекул, т. е. a = y2kT/m, L — расстояние
между осциллирующими полями в схеме Рамзея или длина об-
ласти перехода в методе Раби.
Фиг. 5. Переход в H2S32 на частоте 168,7 Ггц. Jx = 1] (т = ±1) J. =
= l_i (т = ±1).
Левая кривая снята полностью при тех же условиях, что и правая, ио при большей мощ-
ности миллиметровых волн и при вдвое меньшем коэффициенте усиления. Возбуждение
рупорно-линзовое; мощность миллиметровых волн —третья гармоника клистрона с фазовой
синхронизацией гармоникой кварцевого генератора; модуляция поля в области С произво-
дилась меандром 800—1000 в.
Фиг. 6. Квазиоптические устройства, используемые в спектроскопических
исследованиях.
В центре слева —рупоры, используемые для возбуждения схем фиг. 3. В центре —линзы,
используемые для возбуждения электрического резонанса в протяженном поле. В центре
вверху—две рупорно-линзовые системы, используемые в методе Рамзея. Справа—ромб
Френеля, используемый в исследованиях зеемановского эффекта при круговой поляризации.
Вверху —пластина с вакуумными окнами для ввода сигнала в пучок. Слева —зонная френе>
левская линза»
21. Квазиоптические методы в спектроскопии
463
В спектрометре на молекулярном пучке, изображенном на
фиг. 2, длина поля в области С увеличена до 40,65 см, так что
если применяется возбуждение одним полем по всей длине
Фиг. 7. Линия, полученная на устройстве по схеме Рамзея.
Вверху —схема устройства для возбуждения разнесенного поля.
системы, то результирующая теоретическая полуширина линии
сероводорода будет приблизительно 900 гц при условии, что
сверхтонкая структура не скрывает это сужение. Два рупора с
линзами, изображенные на фиг. 6, использовались в схеме Рам-
зея с разнесенными полями, причем расстояние между полями
равнялось 30,5 см, так что при оптимальных условиях полуши-
рина составляла бы приблизительно 670 гц. Как видно из фиг. 6,
обе рупорно-линзовые системы возбуждались стандартным вол-
новодом прямоугольного сечения типа RG-138/U. Сигнал с гене-
ратора гармоник разветвляется посредством четырехполюсного
ответвителя, в одно плечо которого включен фазовращатель для
получения надлежащего фазового соотношения между разне-
464
Р. Штраух, Р. Капп, Л1. Лихтенштейн, Дж. Галлагер
сенными полями. Для сравнения с волноводными устройствами
на стандартных волноводах типа RG-138/U были сконструи-
рованы квазиоптические делитель луча и фазовращатель [8] на
волноводе широкого сечения.
Возбуждение одним полем вдоль всей области С можно, оче-
видно, осуществить, применяя одну из антенных схем: парабо-
лическую антенну, большой секториальный рупор, линейные ре-
шетки [9] и решетки Парселла [9]. Метод разнесенных полей
даст, по-видимому, неплохие результаты, если вместо двух ру-
порно-линзовых систем будут использованы два интерферомет-
ра. Из проведенных нами экспериментов следует, что наиболь-
шее возможное разрешение в миллиметровом спектрометре
будет достигнуто тогда, когда для электрорезонансного спектро-
метра будет создана наиболее подходящая излучающая система.
§ 2. СПЕКТРОСКОПИЯ ГАЗОВ С ПОМОЩЬЮ ИНТЕРФЕРОМЕТРОВ
Интерферометр Фабри — Перо представляет наибольший ин-
терес как резонатор оптического диапазона. Однако еще до при-
менения его в оптическом диапазоне Кульшоу [10] использовал
его в качестве резонатора на миллиметровых волнах, а совсем
недавно эта работа была продолжена Циммерером и др. [11].
Поскольку вопрос о резонаторах подробно рассмотрен в других
статьях настоящего сборника, то здесь нам хотелось бы кратко
обсудить некоторые спектроскопические наблюдения, которые
мы провели, и обсудить дальнейшие возможности применения
интерферометров для спектроскопии газов. В миллиметровом
диапазоне уровни мощности обычно малы, так что наблюдение
слабых линий поглощения часто оказывается невозможным. Во
многих случаях, особенно в случае слегка асимметричных моле-
кул, таких, как вода или сероводород, наблюдение этих линий
необходимо, чтобы получить достаточное количество данных для
определения вращательных постоянных. С помощью интерферо-
метра можно обнаружить очень слабые линии поглощения, так
как при многократном пробеге сигнала через газ в высокодо-
бротном резонаторе обеспечивается длинный путь, на котором
происходит поглощение, и, кроме того, поле в интерферометре
имеет большую величину по сравнению с полем в волноводе.
Можно показать, что эквивалентная длина пути поглощения в
свободном пространстве имеет величину порядка QX/2n. Отсюда
получаем, что для Х = 2 мм и резонатора Q = 40 000 эквивалент-
ная длина пути равна приблизительно 13 м, в то время как дли-
на наших обычных миллиметровых спектрометров примерно
30 см. Отношение электрического поля внутри резонатора к по-
21. Квазиоптические методы в спектроскопии
465
лю в подводящей линии передачи, как показал Циммерер [11],
приблизительно равно
IQtAA'1'
где Ql — нагруженная добротность, Аг и Ао — эффективные пло-
щади поверхности резонатора и поперечного сечения линии пе-
редачи на входе соответственно, am — целое положительное
число, которое в данном случае принимается за единицу. Таким
образом в интерферометре, который имеет Ql = 40 000, диаметр
пластин 3,8 см и записывается стандартным волноводом типа
RCi-138/U, внутреннее электрическое поле приблизительно в
9 раз больше, чем поле в волноводе. При таких полях возмож-
ны эффекты насыщения в газе, и действительно были получены
довольно интересные результаты.
Для получения высокой чувствительности величина Q дол-
жна быть большой; однако она не может быть слишком боль-
шой, чтобы при визуальных наблюдениях ширина резонансной
кривой была достаточна для получения всей линии и любой
сверхтонкой структуры, если последняя имеет место. При спек-
троскопических исследованиях величина Q не должна быть на-
столько большой, что резонансная кривая становится много уже,
чем ширина линии. Для работы в электрорезонансном спектро-
метре большая добротность резонатора не требуется, так как в
этом случае интерферометр служит только для ограничения из-
лучения в определенной области, через которую проходит мо-
лекулярный пучок, а также для установления определенного
распределения поля, с которым молекулы должны взаимодей-
ствовать.
Наконец, следует рассмотреть использование интерферомет-
ра с применением модуляции для получения более высокой чув-
ствительности, чем при визуальном наблюдении. Если исполь-
зуется модуляция источника и сигнал регистрируется с помощью
синхронизованного усилителя и самописца, то из-за высокой до-
бротности резонатора происходят большие отклонения на само-
писце, когда сигнал проходит через резонанс. Для высокочув-
ствительной спектроскопии гораздо лучше подходят зееманов-
ская и штарковская модуляции; эти методы в настоящее время
и используются. Ниже описываются некоторые интерферометры,
которые или находятся в рабочем состоянии, или уже сконструи-
рованы и проходят предварительные испытания.
Миллиметровая спектроскопия с полуконфокальным интер-
ферометром для визуального наблюдения была описана ранее
[12]. Интерферометр, который использовался в этих эксперимен-
тах, показан на фиг. 8. Зеркала смонтированы на каретке
466
Р. Штраух, Р. Капп, М. Лихтенштейн, Дж. Галлагер
небольшого токарного станка, так что вогнутое зеркало можно
перемещать в вакууме через уплотнение (заглушку) Вильсона.
Полуконфокальный интерферометр имеет то преимущество
перед плоскопараллельным, что юстировка его менее критична.
Число Френеля a2jbK было выбрано равным примерно единице
Фиг. 8. Полуконфокальный интерферометр, применяемый
в спектрометрах с прямым поглощением.
для 168,7 Ггц. Добротность этого резонатора первоначально рав-
нялась 88 000, но когда для получения большей связи отверстия
были увеличены, она уменьшилась примерно до 50 000.
Оказалось, что прибор является очень чувствительным спек-
трометром, и он был использован при наблюдении линий H2S
для различных изотопов и различных интенсивностей перехо-
да. Спектрометр проверялся в частотном диапазоне от 155 до
220 Ггц, причем резонансная характеристика резонатора не пре-
терпевала в этом диапазоне никаких резких изменений. Изме-
ренная добротность менялась от 56 000 на 167,9 Ггц до 38 000
на 215,5 Ггц, что не мешает использованию прибора в качестве
спектрометра.
Легко были получены интенсивные линии H2S32, соответ-
ствующие переходам l-i~*- h и20-*22 на 168,7 и 216,7 Ггц соот-
ветственно. На фиг. 9, а линия 168,7 Ггц показана в центре ха-
рактеристики интерферометра. Линия 216,7 Ггц была даже
более интенсивной (см. фиг. 4 в статье [12]) и, по-видимому, по-
глощала всю мощность, проходящую через газ. Переход l_i->li
Фиг. 9. Осциллограммы вращательных переходов
сероводорода в полуконфокальном интерферометре.
а —линия поглощения H2S82 на частоте 168,7 Jx = I— 1 -> J =
б — тот же вращательный переход в n2S84.
468 Р. Штраух, Р. Капп, М. Лихтенштейн, Дж. Галлагер
в H2S34, который происходит из 167910 Мгц, показан на фиг. 9, б.
Эта линия значительно слабее, чем линия на фиг. 9, а, так как
концентрация изотопа S34 равна 4,2%, в то время как для S32
она равна 95,1%. Были получены линии H2S33 на 168 319 и
215 502 Мгц (см. фиг. 6 в статье [12]). Изотоп S33 имеет есте-
ственную концентрацию 0,74%; помимо уменьшения интенсив-
ности линий H2S33 из-за малой концентрации изотопов серы, изо-
топ ее S33 имеет ядерный квадруполь, который при взаимодей-
ствии с градиентом молекулярного электрического поля расщеп-
ляет каждую вращательную линию дальше в сверхтонкий муль-
типлет: шесть компонент в случае линии 168 Ггц и восемь ком-
понент в случае линии 215 Ггц. Линии H2S33 являются самыми
слабыми линиями, которые еще наблюдаются визуально в мил-
лиметровом диапазоне.
Эти эксперименты продемонстрировали высокую чувстви-
тельность интерферометрического спектрометра при визуальном
наблюдении. Однако возникает ряд других вопросов, которые
представляют интерес для спектроскописта. Так, он заинтересо-
ван, например, в возможности использования систем модуля-
ции, которые обеспечивают повышенную чувствительность спек-
трометра; возникает также вопрос, какой резонатор наиболее
пригоден для получения высокого разрешения в спектрометре
на молекулярном пучке. Могут возникнуть и другие вопросы,
касающиеся влияния резонатора на ширину линии и влияния
насыщения на наблюдение. Мы начали исследование этих эф-
фектов; проведены некоторые предварительные наблюдения.
Была сконструирована небольшая спектрометрическая ка-
мера, которая позволила вести наблюдения и на молекулярном
пучке, и на стационарном газе при фиксированном давлении
внутри спектрометра (фиг. 10). Газ втекает внутрь камеры че-
рез множество отверстий в верхнем зеркале. В верхней камере
имеется азотная ловушка; в нее можно поместить также откло-
няющее устройство для пучкового мазера. На фигуре видна ка-
мера для наблюдений, в которой линзы используются в качестве
вакуумных окон. Использовались прямолинейные рупорно-лин-
зовые системы для передачи волн СВЧ через газ и плоскопарал-
лельный интерферометр, вмонтированный между линзами. В ин-
терферометре применялись кварцевые пластины с фотогравиров.
кой на алюминиевых поверхностях. На фигуре видны три
подстроечных плунжера, которые расположены около линзы и
служат для юстировки одного плоского зеркала по отношению
к другому. Плоскопараллельный интерферометр имел малое Q,
вероятно, что-то около 12 000 для тех зеркал, которые исполь-
зовались в опытах. Однако потери при прохождении волн СВЧ
были весьма малы, меньше 10 дб на частоте 168,7 Ггц.
Фиг. 10. Небольшая спектроскопическая камера
на молекулярном пучке.
Фиг. 11. Полуконфокальный интерферометр с зеемановской
модуляцией.
470
Р. Штраух, Р. Капп, М. Лихтенштейн, Дж. Галлагер
Пара штарковских пластин устанавливалась перпендикуляр-
но зеркалам интерферометра, так что на молекулы в интерфе-
рометре можно было наложить горизонтальное электрическое
поле. Молекулярный пучок проходил через прибор в вертикаль-
ном направлении и подвергался действию штарковского поля;
в дальнейшем это устройство позволяло наблюдать переходы
как с ДЛ1 = 0, так и с ДЛ4=±1. Если штарковское напряжение
приложено к пластинам интерферометра, то можно наблюдать
только переходы с ДЛ1=±1.
Спектрометр, изображенный на фиг. 10, использовался для
исследований как молекулярных пучков, так и газов в замкну-
тых объёмах. Исследовалось поглощение молекулярного пучка
в системе со штарковской модуляцией при давлении внутри ка-
меры порядка 10~6 мм рт. ст. Наблюдения линии поглощения
H2S32 на частоте 168,7 Ггц выявили сильное насыщение линии
при сравнительно низких значениях входной мощности. Обычно
в интерферометр поступает мощность меньше 1 мет. При ви-
зуальном наблюдении мощность должна быть уменьшена до та-
кого уровня, чтобы отношение сигнал/шум стало близко к. еди-
нице, когда насыщение линии уже не происходит. Следователь-
но, для уровней поля внутри интерферометра, при которых на-
сыщение не имеет места, потери сигнала при прохождении че-
рез интерферометр, по-видимому, достаточно велики, чтобы от-
ношение сигнал/шум на детекторе было мало. Для резонаторов
с более высоким Q, чем в данном эксперименте, этот эффект
был бы выражен более резко.
Что касается эффектов насыщения, то необходимо быть
очень осторожным при определении местонахождения линии мо-
лекулярного поглощения на резонансной характеристике интер-
ферометра. Оказывается, что при уровне мощности, достаточ-
но высоком, чтобы имело место насыщение, линия в центре ха-
рактеристики интерферометра значительно слабее линии на
ее краю. Линии на краях резко искажаются. Это надо иметь
в виду при измерениях формы линии с помощью интерферо-
метров.
Помимо тех преимуществ, которые дает интерферометр, изо-
браженный на фиг. 10, часто бывает полезно использовать зее-
мановскую или штарковскую модуляцию молекулярной, систе-
мы. Первый метод представляет большую ценность для иссле-
дования парамагнитных молекул NO, NO2 или О2. На фиг. 11
изображен полуконфокальный интерферометр, который запиты-
вается одним волноводом. Радиус кривизны вогнутого зеркала
равен 25,4 см, диаметр обоих зеркал 7,12 см. Модуляция осу-
ществляется с помощью катушки, намотанной на стеклянную
трубку. Вогнутое зеркало направляется через вакуумное уплот-
21. Квазиоптические методы в спектроскопии
471
нение Вильсона. На спектрометре сейчас проводятся предвари-
тельные опыты с линиями О2 на 3 мм, но он может с успехом
использоваться для спектроскопии и субмиллиметровых линий
кислорода. Чувствительность этого прибора по сравнению с волно-
водным зеемановским спектрометром должна бцть значительно
выше.
Для исследовательских целей интерферометрический спек-
трометр желательно сделать перестраиваемым в возможно бо-
лее широкой полосе частот, чтобы можно было использовать мо-
дуляционный метод, обеспечивающий высокую чувствитель-
ность, и чтобы была предусмотрена возможность одновременной
перестройки интерферометра и источника сигналов в широкой
полосе.
Интерферометр Фабри — Перо с плоскими зеркалами отве-
чает этим требованиям при условии, что перестройку одного зер-
кала относительно другого можно производить в широкой по-
лосе частот, не нарушая юстировку интерферометра. Штарков-
ское напряжение можно подать на зеркала интерферометра,
хотя при этом возможности наблюдения ограничиваются пере-
ходами с ДЛ1=±1, а при изменении расстояния между пласти-
нами изменяется штарковский эффект. Ни один из этих эффек-
тов не представляет серьезного ущерба для исследовательских
целей. Источник сигнала можно синхронизовать с интерферо-
метром, и при перестройке последнего источник настраивается
на соответствующую частоту [13]. Веллинг и Андресен проде-
монстрировали этот метод синхронизации в широкой полосе пе-
• рестройки миллиметрового клистрона.
На фиг. 12 изображен плоскопараллельный резонатор, кото-
рый предназначен для исследовательских целей и проходит в
настоящее время предварительные испытания. Прибор состоит
из двух строго концентрических диэлектрических цилиндров,
причем во внутреннем цилиндре расположено подвижное зер-
кало. Другое зеркало (в дальнем конце интерферометра) укреп-
ляется на внешнем цилиндре центрирующими винтами. Внутрен-
ний цилиндр подстраивается с помощью винта, который можно
вывести через вакуумное уплотнение, если цилиндр помещается
в вакуумную камеру. С помощью этого винта одно из зеркал
перестраивается относительно другого, укрепленного на внеш-
нем цилиндре. Если допуски на цилиндры выдержаны достаточ-
но точно, то первоначальная юстировка допускает перестройку
резонатора в довольно больших пределах. Зеркала представ-
ляют собой фотовытравленные поверхности с кварцевыми под-
ложками; на фотографии видно отделенное от камеры зеркало,
которое крепится на внешнем цилиндре. Другое зеркало не уста-
новлено на свое место.
472 Р. Штраух, Р. Капп, М. Лихтенштейн, Дж. ГаЛЛаеер
До сих пор мы обсуждали только некоторые предваритель-
ные результаты исследований по резонаторам для миллиметро-
вой спектроскопии. Для получения положительных результатов
Фиг. 12. Плоскопараллельный интерферометр со штарковской модуляцией
в этой области должна быть проделана большая работа. Осо-
бенно тщательно должно быть исследовано взаимодействие мо-
лекулярных систем с резонатором. В связи с этим интересны но-
вые данные о распределении поля в резонаторе, о числе типов
волн, возбуждаемых в резонаторе, и количестве молекул, вза-
имодействующих с полем в различных частях резонатора. Было
обнаружено, что как в плоскопараллельном интерферометре (см.
фиг. 10), так и в полуконфокальном мазерном интерферометре
(см. фиг. 16) может наблюдаться необычная форма линий. На
фиг. 13 представлена фотография линии H2S32 на 168,7 Ггц, из-
меренной более тщательно, чём на фиг. 9. Заметно небольшое
расщепление линии на два максимума, причина этого расщепле-
ния пока не выяснена.
Это могло произойти по следующим причинам: из-за пере-
возбуждения системы молекул, поглощения в различных частях
интерферометра или некоторого влияния поля модуляции. Пред-
положение о том, что это происходит из-за насыщения усили-
21. Квазиоптические методы в спектроскопии
473
теля, маловероятно, так как применялись различные усилители,
а эффект расщепления появлялся при достаточно малых детек-
тируемых сигналах. Измерение частоты показало, что один пик
соответствует центральной частоте для того случая, когда систе-
ма облучается слабым сигналом и насыщение не имеет места.
Фиг. 13. Осциллограмма перехода H2S32 на частоте 168,7 Ггц в плоско-
параллельном интерферометре.
Виден эффект расщепления линии.
Для практического использования интерферометров в спектро-
скопии требуется дальнейшее исследование этих и подобных им
эффектов взаимодействия молекул с полем излучения.
§ 3. ЭФФЕКТ ЗЕЕМАНА ПРИ ИЗЛУЧЕНИИ,
ПОЛЯРИЗОВАННОМ ПО КРУГУ
Зеемановский эффект для молекулы, находящейся в основ-
ном состоянии *2, дает возможность определить вращательный
магнитный момент молекулы. Обычно эти магнитные моменты
малы, порядка долей ядерного магнетона. Если магнитное поле
достаточно сильно, а источник имеет высокую стабильность, то
получающееся разрешение спектра позволяет определить вели-
чину вращательного магнитного момента для каждого состоя-
ния, из которого происходит вращательный переход. Недавно
это было выполнено [14], причем использовались магнитные по-
ля порядка 14 кгс и синхронизованные по фазе миллиметровые
источники. Камера поглощения представляла собой малень-
кую стеклянную камеру примерно 15,25 см длиной и 3,68 см в
31 Зак. 274
474
Р. Штраух, Р. Капп, М. Лихтенштейн, Дж. Галлагер
диаметре. Она помещалась между полюсами магнита длиной
30,5 см, а для пропускания сигнала через газ использовались
рупорно-линзовые системы. При вращении рупоров можно было
наблюдать переходы с ДЛ4 = 0 и ДЛ4 = ±1 в зависимости от того,
было ли миллиметровое излучение поляризовано параллельно
или перпендикулярно приложенному магнитному полю.
Из этих наблюдений нельзя определить знак магнитного мо-
мента (или ^/-фактор спектроскопического расщепления). Для
его определения нужно, используя излучение с круговой поля-
ризацией, возбудить переходы без ДЛ4 =— 1, но с ДЛ1= + 1, или
наоборот. Если магнитное поле параллельно направлению рас-
пространения волны с круговой поляризацией, то возбуждается
лишь одна из зеемановских о-компонент и в ней заключена вся
интенсивность нерасщепленной линии. Переход с ДЛ1 = +1 воз-
буждается в случае, когда электрический вектор вращается по
часовой стрелке, если смотреть в направлении магнитного поля,
а переход с ДЛ1 = — 1 возбуждается, если вращение происходит
против часовой стрелки.
Для данных СВЧ экспериментов излучение с круговой поля-
ризацией удобно получать с помощью ромба Френеля [15, 16].
В этом приборе вследствие изменения фазы при полном вну-
треннем отражении линейно поляризованное излучение преобра-
зуется в излучение, поляризованное по кругу. В таком ромбе
полное внутреннее отражение происходит па двух границах ди-
электрик— воздух. Используется рексолит с диэлектрической
проницаемостью 2,55. Обе поверхности срезаны под углом 58°39'
для получения правильного фазового сдвига между компонен-
той, перпендикулярной к плоскости падения, и компонентой, па-
раллельной плоскости падения. После того как электрический
вектор поляризуется под углом 45° к плоскости падения, волна
входит с одного конца параллелепипеда, претерпевает два пол-
ных внутренних отражения и выходит с другого конца поляри-
зованной по кругу. На лицевой входной стороне ромба сделан
желоб для согласования импедансов на границе диэлектрик —
воздух. Детектор регистрирует одну из компонент, а после по-
ворота на 90° — другую.
На фиг. 14 представлена экспериментальная аппаратура,
предназначенная для измерений с волной, поляризованной по
кругу. Для наблюдения линии H2S на 168,7 Ггц использовался
клистрон на 55 Ггц с умножителем частоты. Система из четырех
катушек создает магнитное поле 1000 гс в направлении излу-
чения. Это поле вызывает смещение линии примерно на 0,4 Мгц,
что вполне достаточно для наблюдения. На фотографии виден
ромб перед отверстием катушки; в катушках можно также за-
метить стеклянную камеру с газом.
21. Квазиоптические методы в спектроскопии
475
Полученные с помощью такой системы результаты для серо-
водорода показывают, что при правостороннем вращении поля-
ризации (ДЛ4= + 1) линия поглощения смещается в сторону бо-
лее высоких частот. Поворот электрического вектора или ромба
Фиг. 14. Аппаратура для зеемановских измерений при круговой
поляризации.
на 90° дает излучение с левосторонней поляризацией (ДЛ1 =— 1),
если смотреть со стороны источника; при этом смещение линии
поглощения происходит в сторону более низких частот. Для се-
роводорода это соответствует положительной величине фактора
gj. В этом эксперименте можно определить не только величину
магнитных моментов молекул, но и знаки этих моментов. Не-
большая стеклянная камера использовалась для исследования
поглощения на частотах вплоть до 368 Ггц, а ромб пригоден,
по-видимому, во всем субмиллиметровом и миллиметровом диа-
пазоне.
31*
476
Р. Штраух, Р. Капп, М. Лихтенштейн, Дж. Галлагер
§ 4. МАЗЕРНЫЕ УСТРОЙСТВА В МИЛЛИМЕТРОВОМ ДИАПАЗОНЕ
В диапазоне более длинных волн мазеры можно построить
на нескольких веществах [17], в миллиметровом же диапазоне —
только на линейной молекуле HCN [18]. Существует несколько
видов молекул, на которых можно построить газовые мазеры,
но большинство из них требует сильных отклоняющих полей
для разделения состояний. Молекула цианистого водорода не
требует больших отклоняющих полей. Для выбора системы,
обеспечивающей пучок достаточной интенсивности, было опробо-
вано большое количество источников и отклоняющих устройств.
С точки зрения спектроскопии предпочтительнее использовать
малые пучки (порядка тех, которые применяются в сантимет-
ровом диапазоне), так чтобы мазер с учетом усиления мож-
но было использовать в качестве спектрометра с высоким раз-
решением. Как показали Таддеус и др., на более низких часто-
тах с помощью этих методов можно получить довольно пол-
ную информацию о сверхтонкой структуре асимметричных мо-
лекул.
Мы исследовали возможность создания тазовых миллиметро-
вых мазеров, не прибегая к использованию нескольких молеку-
лярных пучков. Однако для этого необходимо иметь соответ-
ствующий резонатор и использовать интерферометр, как это сде-
лано у Маркузе [18]. Мы пытались получить генерацию на
частоте 618 Ггц в дейтерированном аммиаке ND3, используя
плоскопараллельный интерферометр [19]. Не зная природы ре-
зонатора, здесь, по-видимому, нельзя добиться успеха. Ис-
пользуя вторую гармонику имеющегося у нас карсинотрона на
300 Ггц, мы сможем, наверное, исследовать резонатор на час-
тоте 618 Ггц.
Одновременно мы исследовали возможность создания мазе-
ра на более низких, более доступных частотах миллиметрового
диапазона. Мы сконструировали резонатор с Q — 40 000 для ра-
боты с линией сероводорода 168,7 Ггц. Интерферометр был по-
луконфокальпый с четырехполюсным волноводным облучателем.
Радиус кривизны вогнутого зеркала равен 20,3 см, диаметр
обоих зеркал — 3,8 см. Прибор изображен на фиг. 16. Слева
видны два волноводных облучателя, связанных с неподвижным
плоским зеркалом; вогнутое зеркало (с правой стороны) укреп-
лено на штативе, который перемещается по трем линейным на-
правляющим с помощью стержня, проходящего через вакуум-
ное уплотнение. Первоначально в экспериментах с этим резона-
тором использовалась аксиальная квадрупольная фокусировка.
До сих пор не было получено сколько-нибудь заметного усиле-
ния. Это может быть вызвано несколькими причинами, а имен-
21. Квазиоптические методы в спектроскопии
477
но недостаточной интенсивностью пучка, низкой добротностью
и плохой конфигурацией поля в области пучка.
Из опытов, проведенных с аммиачным мазером на частоте
23 870 Мгц, следует, что можно добиться того, чтобы непригод-
ные области интерферометра пересекали малые пучки. В ам-
миачном мазере использовался интерферометр, сконструирован-
ный Шеппардом для другой цели. Этот резонатор, изобра-
женный на фиг. 15, помещался вместо объемного резонатора
аммиачного мазера, который имел порог генерации приблизитель-
но при 12 кв на стержнях откло-
няющего устройства; доброт-
ность резонатора была менее
10 000, в то время как доброт-
ность интерферометра равнялась
приблизительно 30 000. Интер-
ферометрический мазер не гене-
рировал, но усиливал.
Фиг. 15. Полуконфокальный ин-
терферометр, используемый в ам-
миачном мазере (частота порядка
30 000 Мгц).
Фиг. 16. Полуконфокальный
интерферометр для исследова-
ния миллиметрового мазера.
Усиление имело место при напряжении на стержнях откло-
няющего устройства приблизительно 30 кв, причем только для
некоторых частных типов колебаний, полученных с интерферо-
метром. Измерение распределения поля интерферометра пока-
зало, что усиление имеет место на тех типах колебаний, кото-
рые, вероятно, связаны с основным колебанием TEM00q, и что те
типы, для которых усиление не имеет места, по-видимому, при-
надлежат к классу TEMWq. Таким образом, очень важно точно
знать типы колебаний генерации мазера и положение пучка в
интерферометре. Ясно, что в противном случае для опытов на
миллиметровом мазере потребуются большие пучки, порядка тех,-
которые использовал Маркузе. Было рассмотрено применение
478 Р. Штраух, Р. Капп, М. Лихтенштейн, Дж. Галлагер
отклоняющих устройств поперечного ступенчатого типа [20]’)
и кольцевых отклоняющих устройств [21, 22] для создания
больших пучков при использовании интерферометра.
§ 5. МНОГОКВАНТОВЫЕ УСТРОЙСТВА
Доказано, что при взаимодействии квантовомеханической
системы с полем излучения, могут иметь место миогоквантовые
процессы, которые могут приводить к нелинейным эффектам,
Фиг. 17. Интерферометр для исследования многоквантовых устройств.
например, генерации гармоник. Эти эффекты довольно полно
освещены в литературе-[23, 24]; мы хотим только рассказать о
системе, которая сейчас изготовляется и в которой будет осуще-
ствлен многоквантовый переход в миллиметровой области. Уже
описано несколько экспериментальных исследований в миллиме-
тровом диапазоне; в большинстве их использовался HCN и не-
резонансный метод [23]. В опытах нашей лаборатории исполь-
зовался переход симметричной молекулы фтористого метила
J=I ->2, К=1 и резонансная субгармоника миллиметрового пе-
рехода. Вращательный переход фтористого метила происходит
на частоте 102 140,86 Мгц; этот переход накачивался на частоте
х *) См, также работу [19]. '
21. Квазиоптические методы в спектроскопии 479
в три раза меньшей с помощью 20-киловаттного магнетрона.
Использованный в этом опыте резонатор показан на фиг. 17.
Он конструировался по типу резонатора Стрейна и Коульмана
[25]. Сигнал частоты 34 Ггц вводится в резонатор при помощи
четвертьволнового трансформатора, который облучается рупор-
но-линзовой системой; этот трансформатор описан Стрейном и
Коульмапом. Полуконфокальный резонатор поддерживает ко-
лебания на частотах 34 и 102 Ггц, причем сигнал с частотой
102 Ггц выводится с помощью стандартного волновода RG-138/U.
Связь с колебаниями интерферометра можно -осуществить так-
же с помощью некоторых других схем; однако основная труд-
ность связана с тем, что резонатор должен работать одновре-
менно на двух частотах. Интерферометр, показанный на фиг. 17,
отвечает этому требованию, холя на частоте 102 Ггц и в мень-
шей степени.
Молекула фтористого метила имеет дипольный момент
1,79 дебая, т. е. много меньший, чем у HCN. Однако с этой мо-
лекулой проще иметь дело, чем с HCN; она имеет переход на
утроенной частоте имеющегося в наличии магнетрона. В рассма-
триваемых приборах можно использовать переходы намного
менее токсичных цианистого метила и изоцианистого метила,
так как эти молекулы имеют дипольные моменты, большие, чем
у HCN.
§ 6. СПЕКТРОСКОПИЯ СВОБОДНЫХ РАДИКАЛОВ
При использовании волноводов или других металлических
конструкций сокращается время жизни нестабильных молекул и
свободных радикалов. Этот факт, а также трудность производ-
ства свободных радикалов ограничивали исследования в этой
области. Возможность использования стеклянных камеф ДЛЯ
спектроскопии свободных радикалов была показана в более ран-
них исследованиях [26, 27], а совсем недавно эти камеры были
использованы для исследования радикалов CS и SO [28, 29].
Рупорно-линзовые системы вместе с большими стеклянными
камерами могут с успехом применяться в миллиметровом диа-
пазоне [27, 28]. На фиг. 18 показана камера, которая использо-
валась в нашей лаборатории для исследования линий СМ. Йтобы
избежать отравления цианистыми соединениями, которые ис-
пользуются в опыте, камеру помещают в вытяжной колпак. Дли*
на камеры примерно 1 м. Камера имеет зеемановскую катуШку
Для модуляции свободных радикалов. Свободные радикалы соз-
даются высокочастотным разрядом в боковом плече, соединен-
ном с камерой, и они быстро прокачиваются через стеклянную
камеру. Гальванопластические рупоры и рексолитовые линзы
480
Р. Штраух, Р. Капп, М. Лихтенштейн, Дж. Галлагер
служат для пропускания сигнала через стеклянную камеру, со-
держащую протекающий газ. В качестве окоп этой камеры ис-
пользуются стеклянные пластины, но могут быть использованы
Фиг. 18. Камера для спектроскопии свободных радикалов.
также фторопластовые и рексолитовые окна. На длинах волн
порядка 2 мм потери в этих камерах составляют 3—5 дб.
§ 7. СПЕКТРОСКОПИЯ ТВЕРДЫХ ТЕЛ
Квазиоптические методы широко используются в спектро-
скопии твердых тел в миллиметровом диапазоне. Исследуется
возможность использования интерферометра в качестве резона-
тора для исследования циклотронного резонанса. Для проводи-
мых до сих пор экспериментов вполне подходил настроенный
объемный резонатор. Однако по мере продвижения в область
более высоких частот становится все труднее конструировать
подходящие резонаторы. В опытах с твердым телом необходимо
также подавать оптический сигнал для получения дырок или
электронов, над которыми проводятся наблюдения. Интерферо-
метр представляет собой удобную резонансную конструкцию
для более высоких частот; поскольку он является открытой
структурой, то к нему легко подвести оптический сигнал.
На фиг. 19 изображен интерферометр, который используется
в экспериментах по циклотронному резонансу в миллиметровом
21. Квазиоптические методы в спектроскопии
481
диапазоне. Интерферометр небольшой, примерно 1,9 см в диа-
метре, так что его можно поместить в гелиевый дюар. Сигнал
подается в резонатор с помощью стандартного волновода RG-
98/U. Нижнее вогнутое зеркало (радиус кривизны 3,8 см) мо-
жет подстраиваться с помощью двух настроечных стержней, на
которых крепится зеркало. На частоте 70 Ггц дифракционные
Фиг. 19. Малый интерферометр для исследования циклотронного
резонанса.
потери из-за малых размеров зеркал вызывают уменьшение Q,
но с ростом частоты эти потери уменьшаются. Изменяя отвер-
стие связи в плоском зеркале, можно использовать интерферо-
метр на любой частоте миллиметрового диапазона.
§ 8. НЕКОТОРЫЕ ДРУГИЕ ПРИЛОЖЕНИЯ КВАЗИОПТИКИ
в спектроскопии
В спектроскопии на миллиметровых волнах можно использо-
вать и другие методы, основанные на принципах квазиоптики.
К сожалению, спектроскописты не использовали до сих пор эти
методы, хотя с помощью их можно, по-видимому, исследовать
весьма широкий круг явлений, а также повысить чувствитель-
ность. Эти методы еще предстоит изучить, мы упомянем лишь
некоторые из них.
Обычно спектроскопист контролирует гармонику, на кото-
рой имеет место изучаемая линия, используя две различные ча-
стоты, которые перемножаются, поскольку в его распоряжении
были только высокочастотные фильтры. Эти фильтры представ-
ляют собой сужающиеся волноводы, отсекающие частоты ниже
некоторой фиксированной частоты. Волновод должен иметь весьма
Малые размеры, чтобы не пропускать низкие частоты, потери kq-
482
Р. Штраух, Р. Капп, М. Лихтенштейн, Дж. Галлагер
торых в волноводе должны быть очень большими. Интерферо-
метр можно использовать в качестве полосового фильтра: гар-
монику, на которой происходит переход, можно определить по
расстоянию между параллельными зеркалами. В этом случае
можно использовать фильтры на волноводах широкого сечения.
В случае электрорезонапсного спектрометра квазиоптические
методы необходимо исследовать дальше, чем это сделано в на-
стоящей работе. Возможность получения многоквантовых пере-
ходов в приборах на молекулярных пучках миллиметрового диа-
пазона можно положить в основу создания интересной разно-
видности спектрометра, в котором не требуются ни умножители,
ни детекторы излучения. Квазиоптические методы можно ис-
пользовать при облучении пучка субгармоникой перехода
молекулы в миллиметровом диапазоне.
В миллиметровом диапазоне для спектроскопических иссле-
дований не применялись импульсные методы, хотя в области
более низких частот эти методы очень эффективно использовали
Дикк, Аллей и другие. Интерферометрические резонаторы дол-
жны способствовать применению этих методов.
Идея использования интерферометра в исследованиях сво-
бодных радикалов была высказана авторам Сестри. Однако
присутствие в интерферометре стеклянной камеры приводило
к уничтожению резонанса. В открытых резонаторах нестабиль-
ные молекулы проходят через резонатор, имея относительно
малый контакт с зеркалами резонатора.
Использование квазиоптических методов в исследованиях
твердого тела обещает быть полезным. Кажется вполне осуще-
ствимым использование биконического резонатора для получе-
ния интенсивных полей в акустических исследованиях. Исследо-
вание свободных радикалов, вымороженных в матрицу на зер-
кале интерферометра, должно способствовать продвижению этих
методов в миллиметровый диапазон.
ЛИТЕРАТУРА
1. Н u g h е s V. W., Rev. Sci. Instr., 30, 689 (1959).
2. Zorn J. C., Chamberlain Q. E., Hughes V. W., Quantum Electro-
nics, ed С. H. Townes, New York, 1960, p. 156.
3. Gallagher J. J., Strauch R. G., Cupp R. E., Quaterly Progress
Reports, Contract DA-36-039-SC-90753.
4. Ramsey N. F., Molecular Beams, London, 1956.
5. Kusch P., Hughes V. W., в книге Handbuch der Physik, Bd. 37/1, Ber-
lin, 1959.
Atomic and Molecular Beam Spectroscopy.
6. Wharton L.. Klemperer W., Gold L. P., Strauch R. G., Gal-
lagher J. J„ Derr V. E., Journ. Chem. Phys., 38, 1203 (1963).
21. Квазиоптические методы в спектроскопии 483
7. Ramsey N. F., Phys. Rev., 78, 695 (1950).
8. Taub J. J., Hindin H. J., Hinckelmann O. F., Wright M. L.,
IEEE Trans. MTT-11, No. 5, 338 (1963).
9. Honey R. C., Proc. Symposium on Millimeter Waves, New York, 1959,
p. 563.
10. C u 1 s h a w W., IRE Trans., MTT-7, 221 (1959).
11. Zimm er er R. W., Anderson M. V., S trine G. L., Beers Y.,
IEEE Trans., MTT-11, 142 (1963).
12. Lichtenstein M., Gallagher J. J., Cupp R. E., Rev. Sci. Instr.,
34, 843 (1963).
13. Welling H., Andersen H. G., Paper 4.6, The Millimeter and Submil-
limeter Conference, Orlando, Florida, January, 7—10, 1963.
14. C u p p R. E„ S t r a u c h R. G., G a 11 a g h e r J. J., в печати.
15. Born M., Wolf E., Principles of Optics, London, 1959, p. 46.
16. В u i z e r t IL, Warren F. G. R., Technical Report ASD-TDR-63-55,
RCA — Victor Co., Research Laboratories, Montreal, Canada (January
1963).
17. Thad deus P., Krisher L. C., Loubser J. H. N., Journ. Chem.
Phys., 40, 257 (1964).
18. Marcuse D„ Journ. Appl. Phys., 32, 743 (1961).
19. Derr V. E., Gallagher J. J., Lichtenstein M., Proc. 15th Annual
Symposium on Frequency Control, U. S. Army Signal Research and Deve-
lopment Laboratory, Fort Monomouth, N. J. (1961).
20. Peter M., S t r a n d b e r g M. W. P., Tech. Rept. 336, Res. Lab. of Electro-
nics, M. I. T. (August 26, 1957).
21. Becker G., Zs. angew. Phys., 15, 281 (1963).
22. Басов H. Г., Зуев У. 3., Приб. и техн, экспер., № 1, 120 (1961).
23. Pantell R. Н„ Smith R. G., IEEE Trans., MTT-11, No. 5, 317 (1963).
24. Andersen H. G., Paper 6.5, The Millimeter and Submillimeter Confe-
rence, Orlando, Florida, January 7—10, 1963.
25. Strain R., Coleman P., IRE Trans., MTT-10, No. 6 (1962).
26. D о u s m a n i s G. C., Sanders T. M., Townes С. H., Phys. Rev., 100,
1735 (1955).
27. G a 11 a g h e r J. J., Derr V. E., Bull. Am. Phys. Soc., 3, No. 4, 263
(1958).
28. К e w 1 e у R., S a s t г у К. V. L., W i n n e w i s s e r M., Gordy W.,
Journ. Chem. Phys., 39, 2856 (1963).
29. Powell F. X., Li de D. R., Jr., Bull. Am. Phys. Soc., Ser. 11, 9, No. 3,
255 (1964).
22
ИНТЕРФЕРОМЕТРИЧЕСКАЯ СЕЛЕКЦИЯ
ДЛИНЫ ВОЛНЫ В СУБМИЛЛИМЕТРОВОЙ
РАДИОМЕТРИИ
Р. Вильямс *, У. Чанг *
В своей более ранней статье авторы теоретически рассмотрели некоторые
аспекты радиометрии в области субмиллиметровых волн и, в частности, воз-
можность использования интерферометрической модуляции в субмиллиметро-
вой радиометрии с минимальной различимой температурой до ГК. На этом
принципе впоследствии был сконструирован и испытан радиометрический
приемник. Прибор был построен так, что может работать как в периодиче-
ском, так и в апериодическом режиме. В первом случае график спектраль-
ной плотности излучения получается прямо с прибора; во втором случае при-
бор выдает только интерферометрические данные (т. е. «интерферограмму»),
которые должны быть обработаны на вычислительной машине для определе-
ния функции спектральной плотности. В данной статье описываются кон-
струкция, принцип действия и экспериментальные характеристики этого при-
бора (т. е. минимальная различимая температура, ширина полосы и т. д.).
Приводятся спектральные характеристики и чувствительность для различных
приемников излучения (элемент Голея, угольный болометр, германиевый бо-
лометр и термопара), а также обсуждается способ улучшения формы спек-
тральных характеристик. Сообщается об использовании этого прибора в соче-
тании с целостатом для измерения атмосферного и солнечного излучения в
области субмиллиметровых волн,
$ 1. ВВЕДЕНИЕ
В области субмиллиметровых волн, которая простирается от
50 мк до 1 мм, имеется ряд проблем, возникающих из-за неко-
торых особенностей этой области спектра и из-за отсутствия
приборов высокой точности, которыми располагают эксперимен-
таторы, работающие в других участках спектра. Для этого диа-
пазона характерны низкая энергия квантов, сильное атмосфер-
ное поглощение и низкий коэффициент излучения черного тела
по сравнению с полным излучением черного тела. Последнее об-
стоятельство хорошо иллюстрируется тем, что на всех длинах
* R. A. Williams, W. S. Chang, Antenna Laboratory, Department of
Electrical Engineering, The Ohio State University, Columbus, Ohio.
22. Интерферометрическая селекция длины волны
485
волн больших 100 мк излучение солнца на шесть порядков
меньше (10~б), чем полное солнечное излучение. Если учесть
еще то, что здесь нет приемников с высокой избирательностью и
чувствительностью1), таких, как супергетеродин на более длин-
ных волнах или же квантовых приемников для более коротких'
длин волн, то станет очевидным, что задача обнаружения ма-
лого количества энергии в субмиллиметровой области в присут-
ствии интенсивного излучения более коротких длин волн являет-
ся чрезвычайно сложной.
В данной статье обсуждаются практические стороны исполь-
зования детектора теплового излучения в сочетании с интерфе-
рометрическим модулятором Майкельсона для создания радио-
метрического приемника субмиллиметровых волн от 50 до
1000 мк. В статье [1] было показано, что подобный приемник с
3-метровым собирающим зеркалом будет иметь геометрически
ограниченную ширину луча 0,06° и даст возможность обнару-
живать изменение температуры в пределах от 0,23 до 23° К (в
зависимости от используемого детектора) у источника, который
перекрывает угол больший, чем ширина луча приемника, и
имеет эквивалентную температуру черного тела 300° К.
§ 2. ТЕОРИЯ ИНТЕРФЕРОМЕТРИЧЕСКОГО МОДУЛЯТОРА
Принцип действия интерферометра Майкельсона, вероятно,
знаком большинству инженеров и ученых. Используемый в суб-
миллиметровой области делитель луча (частично посеребренное
зеркало в оптическом варианте) представляет собой сетку из
тонкого провода, вделанную в металлическую рамку (фиг. 1).
В нашем приборе были использованы различные сетки с числом
линий на 1 см приблизительно от 30 до 200.
Апериодический режим. Если менять скачком излучение на
входе и регистрировать величину сигнала на выходе детектора,
то по мере того, как подвижное зеркало смещается от «зеркаль-
ного положения» (при котором расстояния от делителя до ка-
ждого из зеркал одинаковы), получаем кривую, называемую «ин-
терферограммой». Ее абсцисса есть разность длины путей у,
равная двойному смещению подвижного зеркала, а ордината
VD(Y) — величина выходного напряжения квадратичного детек-
тора излучения.
На фиг. 2 приведены интерферограммы для различных типов
входного излучения. Эти интерферограммы представляют собой
’)' Низкая избирательность и чувствительность приемников субмиллимет-
рового диапазона объясняется отсутствием мощных источников когерентного
излучения и устройств усиления, фильтрации и преобразования, работающих
в этом диапазоне.
486
Р. Вильямс, У. Чанг
не что иное, как фурье-преобразования по косинусам для спек-
тральных плотностей входных излучений, несколько видоизме-
ненные спектральными характеристиками проволочного дели-
теля луча и приемника излучения. Если бы мы могли выполнить
Пружины
Детектор
Кулачок и
толкатель
Проволочный
делитель луча
Фотоэлектрический
прерыватель и лампа
облучателя
Передающее устройство
с переменной
скоростью р
(под станиной) х” >
Точка опоры
Плоское зеркало
Апертура
на входе
Фиг. 1. Общий вид интерферометрического приемника.
Параболическое
зеркало
Неподвижное
зеркало
Подвижное
зеркало
обратное фурье-преобразование интерферограммы, то получили
бы искомую функцию спектральной плотности
ОО
^(v)= / yD(T)Cos2nvY(Zy, (1)
— ОО
где v — волновое число излучения в см~\ а у — смещение в см.
Как видно из формулы (1), для этого нужно иметь интерферо-
грамму в интервале от у =—оо до у = 0 или от у = 0 до у= + оо.
Практически это невозможно, но мы можем рассмотреть интер-
ферограммы в интервале от у = 0 до у=уМакс, предполагая, что
VD(y) = 0 при |у|>умакс- Ее фурье-преобразование представляет
измеряемую на практике функцию спектральной плотности
''макс ’’’макс
£(V)— | Пд (Yj cos 2nvy rfy — 2 j VD (v) cos 2nvy dy. (2)
— v 0
’макс
22. Интерферометрическая селекция длины волны
487
Однако так как Vdm содержит некоторую постоянную состав-
ляющую, это уравнение справедливо только при тех v, для кото-
рых в аргументе косинуса стоит целое число л радиан в интер-
вале у = 0 И У = Умакс, т. е. при V = Vn = rt/2yMaKC- Величины f(vn)
Фиг. 2. Интерферограммы монохроматического сигнала (а),
сигнала с постоянной спектральной плотностью ((7) и произ-
вольного сигнала (в).
представляют собой коэффициенты ряда Фурье функции ]Zd(y) в
интервале —уМакс ЬуМакс, которая продолжена как периоди-
ческая функция. Коэффициент f(vn) имеет размерность мощ-
ности (ватт) и соответствует области волновых чисел от v„ до
Vn+i шириной '/гУмакс см~х. Величина E(vn) связана с Ем через
характеристическую функцию прибора ^?(v-vn)
E\vn)= j £(v)^(v - dv, (3)
488
Р. Вильямс, У. Чанг
где
n _ sin {2лумакс (V — Уя)} (Л \
(v-vn) 2лумакс (v — vn) ' '
Функция /?(v-v„) изображена на фиг. 3. По радиотехнической
терминологии функция /?(V-vn) соответствует частотной харак-
теристике перестраиваемого усилителя, где vn — центральная
частота, на которую настроен усилитель.
Следует сделать два замечания относительно характеристи-
ческой функции фиг. 3: во-первых, ширина полосы зависит от
максимальной разности хода Ду=1/уМакс; во-вторых, форма ха-
рактеристической кривой оставляет желать лучшего, так как
она имеет покатый главный максимум и большие боковые ле-
пестки. Можно улучшить форму характеристической функции
прибора, если использовать наложение нескольких функций ти-
па sin х/х, как показано на фиг. 4, где x = 2nyMaKc(v— vn). Для
случая трех налагаемых функций вместо соотношения (2) полу-
чаем
/
^макс
£(vn) = 2 f ^(у)Гсо8/гл-Д—|-cos (П-Н)«7— +
' nr J L гмакс гмакс
О
-ф-cos (п — 1)л —— 1 dx. (5)
гмакс J
Чтобы (Av)' = Av, мы должны положить Тмакс = 2умакс. Можно
пойти дальше, комбинируя пять, семь, девять и т. д. функций
вида sin х/х. В таблице представлено в процентах отношение
площади боковых лепестков к площади главного максимума при
наложении k функций вида sin х/х.
k (число функций sin х/х) 1 3 5 7 9 11 13
боковые лепестки главный максимум. ’ 15,18 4,70 2,69 1,87 1,43 1,16 0,97
На практике умакс должно быть достаточно большим, чтобы
Av было меньше, чем ширина самой узкой измеряемой линии,
которая ожидается в спектральной области, а & = 3; 5 или 7 дает
удовлетворительную форму характеристической функции в боль-
шинстве случаев. Измеряемая спектральная плотность полу-
чается при обработке интерферограммы с помощью простой
цифровой вычислительной программы.
22. Интерферометрическая селекция длины волны
489
Периодический режим. В апериодическом режиме мы скач-
ком изменяли входное излучение и очень медленно меняли раз-
ность хода. При этом на выходе детектора получали интерферо-
грамму, которую мы обрабатывали, чтобы получить измеряе-
мую спектральную плотность. Пусть теперь входное излучение
Фиг. 4. Улучшенная характеристическая функция прибора.
не меняется, а вместо этого периодически изменяется разность
хода, как показано на фиг. 5. Тогда напряжение на выходе де-
тектора будет периодической во времени функцией, один период
которой будет не что иное, как рассмотренная выше интерферо-
грамма. На выходе приемника будут присутствовать гармоники
fn = n)T, где Т — период колебательного движения зеркала. Та-
ким образом, если Т=1 сек, то будут присутствовать только
частоты f=l, 2, 3, ..., 12, 13, 14 ... гц. Если провести фурье-
анализ выходного сигнала, то получим, что на частоте fn ампли-
32 Зак. 274
490
Р. Вильямс, У, Чанг
туда пропорциональна £(vn), измеряемой спектральной плот-
ности уп, связанной с fn соотношением
V tп п
" v Умакс 'Умакс?' ’ ' '
где v — скорость изменения длины пути, равная dyfdt па линей-
ной части хода. Теперь можно было бы получить приближен-
ную спектральную плотность без дополнительных вычислений,
Фиг. 5. Изменение во времени разности хода y при периодическом режиме
работы.
измерив лишь величины fn и считая другие факторы постоян-
ными. Однако из-за ряда технических трудностей, таких, как
изменение чувствительности приемника с изменением звуковой
частоты, трудности перестройки по частоте при постоянстве
коэффициента усиления и т. д., все измерения удобнее выпол-
нить на одной звуковой частоте fn и перестраивать уп во всей
изучаемой спектральной области v, варьируя соотношение ме-
жду vn и fn путем изменения умакс- Хотя Ду=1/уМакс, относитель-
ная ширина (Av)/vn = 7'/nT«2/n остается приблизительно по-
стоянной в перестраиваемой области (7'/т~2).
Строго говоря, необходимо, чтобы в конце каждого переме-
щения зеркала изменение направления происходило практиче-
ски мгновенно. Однако так как механически это сделать невоз-
можно, то лучше всего устранить нежелательные эффекты,
возникающие в моменты поворота, путем отключения выхода де-
тектора излучения в эти промежутки времени с помощью огра-
ничительных переключателей, встроенных в механизм управле*
ния зеркалом. Так как выходной сигнал прибора интегрируется
по нескольким периодам, то это отклонение вызовет лишь не-
большое уменьшение выходного сигнала и соответственно умень-<
шение отношения сигнала/шум. При апериодическом режиме
22. Интерферометрическая селекция длины волны.
491
можно улучшить характеристическую функцию прибора, комби-
нируя fn, fn+l, fn-i и Т. Д.
С практической точки зрения селекцию интересующей нас
звуковой частоты (или частот) можно выполнить с помощью
узкополосного звукового усилителя или коррелятора, исполь-
зующего опорный сигнал, генерируемый механизмом перемеще-
ния зеркала. Однако если выделяется не одна звуковая частота,
то следует позаботиться р том, чтобы не появились относитель-
ные фазовые сдвиги между различными интересующими нас
частотами. По этой причине, если требуется улучшить характе-
ристическую функцию, то лучше использовать коррелятор, а не
узкополосный усилитель.
§ 3. ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
На фиг. 6—9 показан общий вид радиометрического прием-
ника, собранного для испытаний в периодическом режиме
(фиг. 6) и в апериодическом режиме (фиг. 9). На фиг. 10 при-
ведена блок-схема прибора для каждого режима работы.
Испытания были проведены как в периодическом, так и в
апериодическом режимах, причем испытания в апериодическом
режиме были более успешными, несмотря на задержку во вре-
мени при обработке интерферограммы на цифровой вычисли-
тельной машине. Данные, полученные в апериодическом режи-
ме, приведены на фиг. 11. Сплошная линия представляет резуль-
таты измерений при использовании сетки с 200 линиями на 1 см,
источника в виде черного тела при 230° С и внешнего фильтра
из черного полиэтилена толщиной порядка 0,137 см в допол-
нение к фильтрам из кристаллического кварца и черного поли-
этилена (толщиной 0,01 см) в детекторе. Пунктирной линией
представлены результаты опыта при тех же условиях, только в
качестве делителя луча использовалась сетка с 80 линиями на
1 см. В обоих случаях сетка была ориентирована таким образом,
что провода составляли 45° с горизонталью. Видно, что функ-
ция спектральной плотности излучения имеет всплеск вблизи
90 мк для сетки с 200 линиями на 1 см, а для сетки с 80 ли-
ниями на 1 см вблизи 240 мк. При использованном здесь разре-
шении (Av= 1,284 см~}) пики и провалы функции спектральной
плотности хорошо соответствуют атмосферным окнам и полосам
поглощения, которые были определены другими исследованиями
[2, З]1). Низкая интенсивность излучения на длинах волн мень-
ше 80 мк вызвана сильной фильтрацией ближнего инфракрас-
) R. F. R о w n t г е е, М. Е. Vance, Е. Е. Bell и др., частное сооб-
щение.
32*
Фиг. 6. Интерферометрический приемник, собранный для работы
в апериодическом режиме.
Кулачковый механизм, расположенный на переднем плане, приводится в действие
с помощью передающего устройства с переменной скоростью (размещено под столом);
в свою очередь он линейно перемещает кулачковый толкатель (полное смещение 7,6 см).
Этот толкатель содержит генератор опорного сигнала и фотографическую пленку, пере-
мещающуюся между фотоэлементом и облучающей лампой. Подвижное зеркало приво-
дится в движение посредством пропорционального рычага, причем пропорция регули-
руется путем движения точки опоры плеча.
Фиг. 7. Точка опоры пропорционального рычага.
Точка опоры может перемещаться в пределах нескольких сантиметров. Видны индика-
тор, который регистрирует положение подвижного зеркала, и мотор с устройством авто-
матического сканирования (для работы в периодическом режиме), которое плавно пере-
страивает прибор в исследуемой области волновых чисел, смещая точку опоры.
2.-Интерферометрическая селекция длины волны
493
Фиг. 8. Оптическая часть интерферометрического приемника.
На переднем плане слева расположено подвижное зеркало, справа — непо-
движное зеркало, в центре —делитель луча. На заднем плане слева располо-
жено черное тело для калибровки, справа — детектор излучения (элемент
Голе я).
кого излучения (кристаллическим кварцем и черным полиэти-
леном, использованным в этих опытах). Совершенно очевидно,
что если изготовленная электролитическим способом сетка
ориентирована под углом 45°, то ее эффективность как делителя
луча резко возрастает в том случае, когда длина волны прибли-
зительно в два раза меньше, чем расстояние между проволоч-
ками в проекции под 45°. Результаты опыта, проведенного с
сеткой, имеющей 30 линий на 1 см, также хорошо соответствуют
имеющимся данным для поглощения паров воды [3], хотя
эффективность этого делителя луча была несколько ниже на
длинах волн короче 500 мк.
Более ранние попытки проведения измерений подобного типа
с элементом Голея в качестве индикатора не увенчались успе-
хом из-за того, что элемент Голея вносит спектры звукового ка-
нала и имеет более высокий уровень шума.
494
Р. Вильямс, Р. Чанг
Фиг. 9. Интерферометрический приемник, собранный
для работы в апериодическом режиме.
Кулачок и кулачковый толкатель заменены устройством перемещения с малой
скоростью. Виден генератор опорного сигнала, который используется при ра-
боте в периодическом режиме.
Опыты, проведенные в периодическом режиме, выявили сле-
дующие трудности: 1) большая инерционность детектора излу-
чения вызывает задержку в канале сигнала, которая затруд-
няет синхронизацию выходного сигнала детектора с опорным
сигналом; 2) необходимость устранения каких-либо механиче-
ских люфтов в моменты поворота и 3) трудность получения в
периодическом режиме высокой разрешающей способности.
Первую трудность, по-видимому, можно разрешить, если в
опорном канале использовать линию задержки. Вторая трудность
устраняется при тщательном выполнении механических деталей.
Мы также проделали несколько измерений, используя узкий
акустический фильтр вместо корреляционного детектора, что-
бы выделить нужную частотную компоненту детектора. Из-за
низкой разрешающей способности получилось хорошее совпа-
дение результатов этого опыта и опыта в апериодическом ре-
жиме.
Из данных опытов в апериодическом режиме было устано-
влено, что, используя сетки с 200 линиями на 1 см и подбирая
Умане соответственно полосе пропускания 1,284 елг1 при сред-
ней длине волны 90 мк, с помощью этого прибора можно об-
наружить изменение температуры значительно меньшее, чем
3°К У источника с 300° К и диаметром входной апертуры 1,6 см.
Эта точность находится в пределах, предсказанных в статье [1].
| Самописец~\
Детектор
излучения
УсилительИКоррелятор \
Детектор
излучения
Н Синхронный
детектор
Вход —
излучения_
—I
Неподвижное
зеркало
♦
t
Опорный
сигнал
Подвижное
зеркало
Делитель луча
Механизм управ
ления зеркалом _ _
Вращающийся
прерыватель
излучения
Вход —
излучения.
I Неподвижное
зеркало
Делитель луча
Подвижное зеркало
К закорачивающим
контактам
_L механизм
управления
I зеркалом
7смалои скоростью)
Опорный сигнал
а
5
Фиг. 10. Блок-схемы системы, работающей в периодическом (д) и апериодическом {б)
режимах.
В периодическом режиме работы выход умножителя закорачивается в моменты поворота. В усилителе приме-
няется умножитель на эффекте Холла; ои запускается двумя транзисторными усилителями мощности. Если исполь-
зуется германиевый болометр, то элемент Голея и его предварительный усилитель заменяются болометром и его
транзисторным предварительным усилителем.
Спектральная плотность (в относительных единицах)
6,00
5,00
4,00
3,00
2,00
1,00
О
0,20
-1,00
Характеристическая
функция
/\
— £и=1,284см~'
Длина волны, мк,и волновое число, слг'
Фиг. 11. Спектральная плотность, полученная в апериодическом режиме при использовании сетки с 200 ли-
ниями на 1 см (сплошная линия) н 80 линиями на 1 см (пунктирная линия).
Обе сетки были ориентированы под углом 45°; Умакс = 7800 мк\ использовался болометр с фильтром нз черного полиэтилена; темпера-
тура источника 230° С.
22. Интерферометрическая селекция длины волны
497
§ 4. ИЗМЕРЕНИЯ СОЛНЕЧНОГО ИЗЛУЧЕНИЯ
В начале 1964 г. была предпринята попытка определить,
можно ли наблюдать какое-либо солнечное излучение в диапа-
зоне 50—500 мк в месте расположения города Колумбуса
(шт. Огайо). Для слежения за солнцем и для направления из-
лучения в прибор был использован небольшой целостат. Все
опыты проводились в апериодическом режиме. Хотя некоторые
опыты были проделаны в холодную сухую погоду, когда содер-
жание паров воды было весьма низким, никаких различий в
результатах, полученных при слежении за солнцем и при напра-
влении вертикально вверх, не было замечено. Только вблизи
длины волны 90 мк была обнаружена едва различимая величи-
на солнечного излучения, проникающего сквозь атмосферу до
такой малой высоты (около 250 м над уровнем моря).
Попытки измерить солнечное излучение выявили трудности
фильтрации исследуемого излучения на фоне видимого и ближ-
него инфракрасного излучения. При апериодическом режиме все
входящее излучение модулируется с помощью обтюратора. Хотя
некоторая часть видимого и ближнего инфракрасного излучения
рассеивается проволочным делителем луча, большая часть его
все же попадает на приемник и дает вклад в выходной сигнал.
Так как излучение этих более коротких длин волн значительно
интенсивнее, чем излучение субмиллиметровых волн, то на
фоне флуктуаций уровня сильного сигнала будут совершенно
незаметны изменения выходного сигнала детектора, вызванные
интерференционным эффектом на субмиллиметровых волнах.
Следовательно, необходимо использовать какой-то способ филь-
трации излучения. Однако любой фильтр, помещенный на входе
прибора перед обтюратором, будет разогреваться и добавлять
к измеряемой величине свой собственный спектр излучения.
Тонкий фильтр, помещенный после прерывателя, будет, конечно,
попеременно разогреваться и охлаждаться, по обычно это про-
исходит с запаздыванием во времени и в общем случае вносит
искажения в любые измерения. С другой стороны, толстый
фильтр, помещенный после прерывателя, даже если температура
его остается постоянной и он отфильтровывает большую часть
нежелательного излучения, будет сильно отфильтровывать и ин-
тересующее нас полезное излучение, часто до такой степени, что
шумы детектора становятся настоящей проблемой. В этом смыс-
ле периодический режим имеет некоторые преимущества, так
как сетка рассеивает большую часть ближайшего инфракрас-
ного и видимого излучений; поэтому лишь излучение субмилли-
метровых волн будет сильно модулировано и, следовательно,
только оно даст вклад в выходной сигнал детектора. Однако
498
Р. Вильямс, У. Чанг
обычно перед детектором все же ставят какой-либо фильтр, что-
бы излучение на более коротких длинах волн, рассеянное дели-
телем луча, не попадало в детектор и не увеличивало уровень
шума.
§ 5. ЗАКЛЮЧЕНИЕ
С учетом проведенных опытов мы считаем, что если есть
время и возможность использовать цифровую вычислительную
машину, то лучше использовать апериодический режим, так как
он дает более точные конечные результаты и лучшее разреше-
ние. Возможны, однако, два случая, когда следует отдать пред-
почтение периодическому .режиму, а именно при измерениях на
одной определенной длине волны за короткий промежуток вре-
мени и в присутствии ближнего инфракрасного излучения вы-
сокой интенсивности. Измерения солнечного излучения по-
падают во вторую категорию. Для радиометра, установленного
на спутнике, предпочтительнее использовать апериодический ре-
жим, если, кроме измерений солнечного излучения, должны
производиться и некоторые другие измерения. В этом случае'
можно было бы построить простой и легкий прибор, потребляю-
щий малую электрическую мощность.
Согласно полученным нами результатам, в данной спектраль-
ной области имеется очень сильное атмосферное поглощение.
Мы намерены продолжить эти исследования и провести в лабо-
раторных условиях измерения прохождения сигнала па сравни-
тельно большие расстояния методом многократного пробега,
моделируя различные атмосферные условия в больших камерах.
Мы намерены также провести ряд радиометрических измерений
в условиях малой влажности на большой высоте. Следует под-
черкнуть, что данный прибор, работая в апериодическом режиме,
дает возможность определить спектральный состав для любого
излучающего устройства, которое может быть промодулировано
импульсами с частотой повторения несколько герц (устройство
типа субмиллиметрового газового лазера).
Л ИТЁРАТУРА
1. Williams R. A, Chang W. S. С., IEEE Trans., МТТ-11, 513 (1963),
2. Oetj en R. A. et al., Journ. Opt. Soc. Am., 42, 559 (1952).
3. Yosbinage H. et al., Journ. Opt. Soc. Am., 48, 315 (1958).
4. Gebbie H. A., 5th Annual Conference of ICO, Stockholm, Sweden, 1959.
5. Strong J., Vanassee G. A., Journ. Opt. Soc. Am., 49, 844 (1959).
6. F e 11 g e 11 P., Journ. Phys, et Rad., 19, 237 (1958),
7, Genzel L., Journ. Mol, Spectr., 4, 241 (1960).
СОДЕРЖАН ИЕ
Предисловие ................................................... 5
I. ДИФРАКЦИЯ, РАСПРОСТРАНЕНИЕ И ИЗЛУЧЕНИЕ ВОЛН
1. Л. Фельсен. Квазиоптические методы в дифракции (Перевод
В. В. Семенова).................................................11
§ 1. Введение ...............................................12
§ 2. Представление в виде мод. Лучи и явления в переходных об-
ластях ......................................................15
§ 3. Поверхности с переменными свойствами...............43
§ 4. Дальнейшее сравнение описаний с помощью мод и лучей. Ре-
зонансы .....................................................47
§ 5. Направления дальнейшего исследования....................52
§ 6. Заключение ................................59
Литература ...................................................59
2. И. Толстой. Сравнение двух теоретических трактовок распростра-
нения акустических волн в океане — теории нормальных типов коле-
баний и лучевой оптики (Перевод Р. Б. Ваганова).................63
§ 1. Введение .................................................63
§ 2. Определения ..............................................64
§ 3. Примеры двойственности луч — тип колебаний...............67
§ 4. Теоретическая и экспериментальная точность .............. 74
Литература ....................................................79
3. Р. Льюис. Формальная теория бегущей волны (Перевод О. Е. Шу-
шпанова) ..................................................80
§ 1. Введение .....................'.........................80
§ 2. Разложение по бегущим волнам............................83
§ 3. Бегущие волны, не зависящие от времени..................90
§ 4. Излучение движущихся источников.........................101
§ 5. Отражение от движущейся поверхности.....................108
Приложение. Решение уравнения переноса.......................116
Литература ..................................................118
4. X. Бреммер. Полугеометрическое приближение к явлению рассея-
ния (Перевод В. А. Ирикова).......................................119
§ 1. Введение ..............................................119
§ 2. Борцовское приближение для случая плоской волны, падаю-
щей на слабо неоднородную среду........................... . 121
500
Содержание
§ 3. Переход от зоны Френеля к зоне Фраунгофера. Переходный
параметр .....................................................124
§ 4. Борновское приближение для слабо неоднородной среды со
случайными параметрами........................................127
§ 5. Свойства статистически слабо неоднородной среды .... 130
§ 6. Связь предельных соотношений в зонах Френеля и Фраунго-
фера со средней длиной свободного пробега при рассеянии . 133
§ 7. Связь борновского приближения для статистически неодно-
родной среды с моментами рассеяния............................135
§ 8. Связь борновского приближения для статистически неодно-
родной среды с моментами автокорреляционной функции . . 137
§ 9. Дальнейшее обсуждение механизма рассеяния..............138
§ 10. Заключительные замечания. Связь с теорией оптического изо-
бражения ................................................. ... 140
Литература ..................................................142
5. К. Пальмер. Дифракционные аномалии в решетках на миллиметро-
вых волнах (Перевод Л. Н. Вершининой)............................143
§ 1. Введение ...............................................143
§ 2. Описание установки......................................147
§ 3. Результаты..............................................151
§ 4. Заключение .............................................156
Литература ..................................................155
6. С. Карп, Ф. Карал. Феноменологическая теория систем со многими
поверхностными волнами (Перевод В. В. Семенова)..................157
§ 1. Введение ............................................. 157
§ 2. Определение импедансов >.т и обратная задача отражения 159
§ 3. Применения теории......................................163
Литература ..............................................'. . 165
7. И. Палоч, А. Олинер. Самосогласованная теория излучений Че-
ренкова и Смита—Парселла (Перевод Е. Н. Коршуновой)...............167
§ 1. Введение ...............................................168
§ 2. Самосогласованная теория излучения Черенкова и Смита—
Парселла ....................................................171
§ 3. Результаты............................................. 178
Литература ...................................................185
II. РЕЗОНАТОРЫ И ЛУЧЕВОДЫ
8. Ж. Д е ш а и, П. Маст. Преобразование пучка при распространении
в системе квадратичных линз (Перевод Р. Б. Ваганова) ... . . . 189
§ 1. Определение пучка.................•....................189
§ 2. Описание гауссова пучка................................190
§ 3. Гауссовы пучки высшего порядка.........................194
§ 4. Преобразование пучка оптической системой...............195
§ 5. Аналогия между электрической цепью и лучевым волноводом 197
§ 6. Резонаторы .......................................... 202
§'7. Мяогопробеговые-резонаторы.............................203
Содержание 501
§ 8. Лучеводная антенна.....................................206
§ 9. Заключение ...................................... • • 208
Литература .................................................209
9. X. Котельник. Коэффициенты связи и коэффициенты преобразо-
вания воли в оптических системах (Перевод Л. Н. Вершининой) 210
§ 1. Введение ................•....'........................210
§ 2. Определение коэффициентов связи........................213
§ 3. Коэффициенты связи в случае прямоугольных координат . . 213
§ 4. Коэффициенты связи в случае цилиндрических координат . . 216
§ 5. Связь основных волн....................................217
§ 6. Коэффициенты связи по мощности........................ 221
§ 7. Отражение от несогласованного резонатора со сферическими
зеркалами ................................................. 222
§ 8. Коэффициенты связи для систем со смещением и изломом . . 224
Литература ................................................ 225
10. В. Ш т р а й ф е р, X. Г а м о. Применение разложения Шмидта к ана-
лизу колебаний в оптическом резонаторе (Перевод О. Е. Шушпанова) 226
§ 1. Введение .......................................... 226
§ 2. Постановка задачи .................................... 227
§ 3. Теория Шмидта и матричная формулировка.................229
§ 4. Нахождение мод.........................................234
§ 5. Численные результаты...................................238
§ 6. Заключение.............................................241
Приложение. Вычисление Тио методами теории возмущений . . 243
Литература ............................................... 244
11. Дж. Хэртли. Гиперсфероидальные функции и оптические резонато-
ры с круглыми зеркалами (Перевод О. Е. Шушпанова) . • . . . . 245
§ 1. Введение ............................................ 245
§ 2. Гиперсфероидальное дифференциальное уравнение .... 246
§ 3. Малые значения с.......................................247
§ 4. Большие значения с ....................................249
§ 5. Заключение.............................................250
Приложение А................................................250
Приложение Б................................................253
Литература .................................................254
12. Г. Торальдо ди Франчиа. Резонаторы с двугранными отража-
телями (Перевод И. П. Башкатова).................................255
§ 1. Введение ..............................................255
§ 2. Резонаторы ромбовидного сечения........................256
§ 3. Резонатор с двугранными отражателями...................258
§ 4. . Ари^мстричпые резонаторы ............................261
§ 5. Заключение ............................................263
Литература -.................................. 263
502
Содержание
13. Д. Г л о г е. Расчет резонатором Фабри—Перо для лазеров с помощью
матриц рассеяния (Перевод Н. Н. Войтовича) . ..................... 264
§ 1. Введение ...............................................264
§ 2. Матрица рассеяния ......................................265
§ 3. Расчет дифракционных потерь.............................269
§ 4. Обобщенные резонаторы и периодические линии...........276
§ 5. Заключение..............................................279
Литература ..................................................279
14. Д. Глоте. Общий метод расчета оптических резонаторов и периоди-
ческих линзовых систем (Перевод Н. Н. Войтовича)......................280
§ 1. Введение ..............................................280
§ 2. Математическое описание................................282
§ 3. Линейные ошибки поверхности............................287
§ 4. Квадратичные ошибки поверхности........................293
§ 5. Составные и случайные ошибки...........................301
§ 6. Неоднородное усиление в резонаторе.....................308
§ 7. Заключение ............................................310
Приложение А. Матрица Х(с).............................. ... 311
Приложение Б. Теория возмущений для решения задачи о соб-
ственных значениях......................................312
Литература .................................................313
15. Квазиоптические резонаторы (Перевод А. Н. Сивова)..............315
Литература .................................................. 337
III. КВАЗИОПТИЧЕСКИЕ ВОЛНОВОДНЫЕ ЭЛЕМЕНТЫ
16. К. Као. Теория и конструирование квазиоптических волноводных
элементов (Перевод Л. Н. Вершининой).............................341
§ 1. Введение ..............................................341
§ 2. Квазиоптическая теория.................................343
§ 3. Измерения..............................................347
§ 4. Практические вопросы...................................351
§ 5. Заключение ............................................352
Приложение 1. Возбуждение волновода линейным электрическим
диполем, расположенным вдоль оси у ...............353
Приложение 2. Понижение порядка матрицы рассеяния 4-го поряд- -
ка, когда обратная связь пренебрежимо мала.............3.54
Приложение 3. Решение матричных уравнений...................355
Приложение 4. Метод измерения на основе анализа отраженной
мощности ...............................................356
Приложение 5. Метод измерения на основе анализа прошедшей
и отраженной мощностей............................358
Литература .............................................. 366.
17. Е. М а р к а т и л и. Излом волновода с плоским зеркалом для снимет- ’
ричной электрической волны (Перевод Р. Б. Ваганова) ...... 361
§ 1. Введение ............................................. 361
§ 2. Постановка и решение задачи.............................362
§ 3. Уменьшение возбуждения волны Яоа в уголке...............36*
Содержание 503
§ 4. Расширение полосы частот, в которой преобразование Я01 в
Ног мало.....................................................367
§ 5. Заключение .............................................369
Литература ...................................................369
18. Д. Граймсмен. Желобковый волновод (Перевод Е. Н. Коршуно-
вой) ....................................................... 370
§ 1. Введение ............................................. 370
§ 2. Анализ полей...........................................371
§ 3. Расчетные и экспериментальные характеристики линий . . . 37.6
§ 4. Расчетные характеристики затухания.....................378
§ $• Распределение мощности ................................378
§ 6. Затухание ............................................ 380
§ 7. Волны высшего порядка..................................382
§ 8. Возбудитель волны........................•.............382
Литература .................................................384
VI. ПРИМЕНЕНИЕ КВАЗИОПТИЧЕСКИХ УСТРОЙСТВ
19. Д. А у стон, Р. Примич, Р. Хаями. Об использовании резонато-
ров Фабри—Перо для СВЧ диагностики плазмы (Перевод В. В. Ме-
риакри) .................................................. ..... 387
§ 1. Введение .............................................388
§ 2. Особые требования к диагностике плазмы................390
§ 3. Распределения полей в резонаторе......................392
§ 4. Взаимодействие поля с плазмой.........................401
§ 5. Экспериментальные исследования........................406
§ 6. Заключение ...........................................420
Литература ................................................421
20. Т. Консоли, Д. Лепешинский, Ф. П а р л я н ж, М. Кадар.
Применение техники СВЧ для исследования взаимодействия волн с
плазмой—диагностика плазмы (Перевод В. А. Ирикова)............424
§ 1. Введение ..............................................424
§ 2. Краткий обзор теоретических результатов .............. 425
§ 3. Экспериментальная техника и результаты измерений .... 432
Приложение 1. Ускорение плазмы под действием неоднородного
постоянного магнитного поля и волн с правосторонней круго-
вой поляризацией .......................................... 446
Приложение 2. Нагревание плотной плазмы высокочастотным по-
лем в свистящей моде....................................449
Приложение 3. Технические характеристики диэлектрической ан-
тенны ..................................................451
Литература .................................................452
Квазиоптические методы в миллиметровой спектроскопии (Перевод
Л. Н. Вершининой) ..............................................453
§ 1. Электрорезонансная спектроскопия на миллиметровых волнах 454
§ 2. Спектроскопия газов с помощью интерферометров...........464
504
Содержание
§ 3. Эффект Зеемана при излучении, поляризованном по кругу . . 473
§ 4. Мазерные устройства в миллиметровом диапазоне..........476
§ 5. Многоквантовые устройства............................ 478
§ 6. Спектроскопия свободных радикалов.......................479
§ 7. Спектроскопия твердых тел..............................480
§ 8. Некоторые другие приложения квазиоптикн в спектроскопии . 481
Литература ................................................ 482
22. Р. Вильямс, У. Чанг. Интерферометрическая селекция длины вол-
ны в субмиллиметровой радиометрии (Перевод Л. Н. Вершининой) 484
§ 1. Введение ..............................................484
§ 2. Теория интерферометрического модулятора................485
§ 3. Экспериментальные результаты...........................491
§ 4. Измерения солнечного излучения ........................497
§ 5. Заключение ............................................498
Литература ................................................. 498
КВАЗИОПТИКА
Редакторы В. Рабин и Е. Куранский Художественный редактор И. Некунвй
Технический редактор Ю. Энке
Сдано в производство 13/VII 1966 г. Подписано к печати 1/XII 1966 г. Бумага бОхЭО1/^
15,75 бум. л. 31,50 печ. л. Уч.-ивд. л. 28^64. Изд. № 2/3552. Цена 2 р. 26 к. Зак. № 274.
Темплан изд-ва «Мир» 1966 г., Хе 58
ИЗДАТЕЛЬСТВО «1МИР» Москва, 1-й Рижский пер., 2.
Ленинградская типография № 2 имени Евгении Соколовой Главполиграфпрома
Комитета по печати при Совете Министров СССР. Измайловский проспект, 29.