Автор: Галин Л.А.
Теги: механика деформируемых тел упругость деформация физика механика теория упругости
Год: 1980
Текст
Л.А.ГАЛ ИН
КОНТАКТНЫЕ ЗАДАЧИ
ТЕОРИИ УПРУГОСТИ
И ВЯЗКОУПРУГОСТИ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
22.25
Г 15
УДК 539.3
ГАЛИН JI. А. Контактные задачи теории упругости и вяз·
коупругости.— М.: Наука, Главпая редакция физико-математиче¬
ской литературы, 1980.— 304 с.
Книга посвящена плоским и пространственным контактным за¬
дачам теории упругости и вязкоупругости.
Кроме контактных задач, которые в настоящее время принято
называть классическими, решаемых методами теории функций
комплексной переменной и теории потенциала, рассматривается
важный случай качения вязкоупругого цилиндра по вязкоупругой
полуплоскости в наиболее общем случае, когда площадка контак¬
та имеет участки с трением и сцеплением. Даются решения кон¬
тактных задач при наличии износа, приводящиеся к однородным
уравнениям Фредгольма, а также решения контактных задач для
шероховатых тел, приводящиеся к нелинейным интегральным урав¬
нениям типа Гаммерштейна. Большинство результатов получено в
конечном виде.
Книга рассчитана на специалистов в теории упругости, инже¬
неров, аспирантов и студентов втузов.
(g) Издательство «Наука»,
20305—084 ,κο on i7rwunnnn Главная редакция
■ loo-oU. l/UoU4UUUU физико-математическои
053 (02)-80 литературы, 1980
ОГЛАВЛЕНИЕ
Предисловие 5
Глава I. Плоские контактные задачи теории упругости 7
§ 1. Основные соотношения плоской задачи теории уп¬
ругости 7
§ 2. Напряжения и перемещения для упругой полу¬
плоскости 15
§ 3. Граничные условия в плоских контактных задачах 24
§ 4. Решение задачи Римана — Гильберта для полу¬
плоскости 28
§ 5. Давление штампа при отсутствии сил трения . 38
§ 6. Давление штампа при отсутствии сил трения (про¬
должение) 48
§ 7. Задачи при наличии сил трения 55
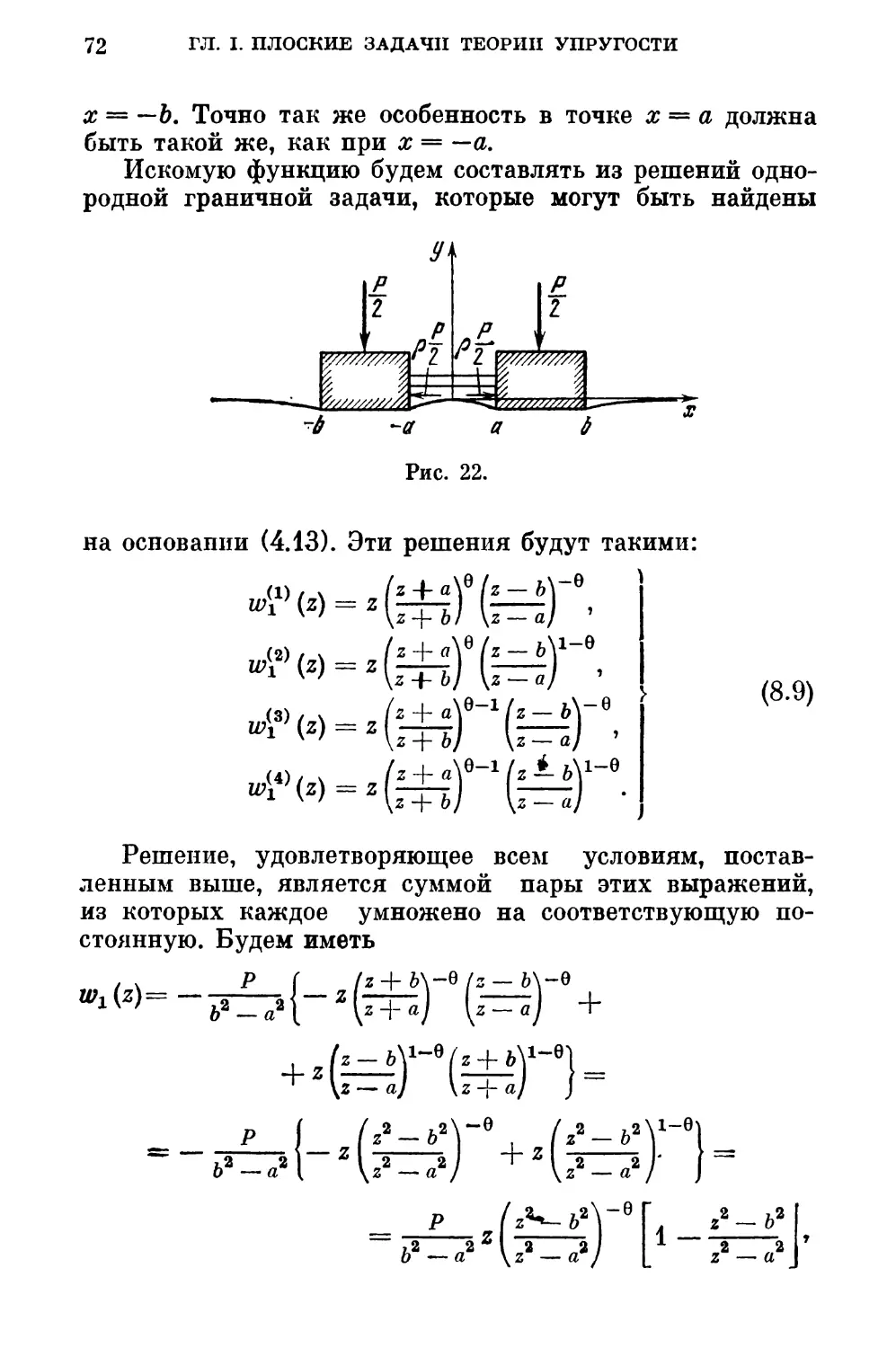
§ 8. Задачи при наличии сил трения (продолжение) 67
§ 9. Давление движущегося штампа 75
§ 10. Задачи для анизотропного тела 78
§ И. Задачи для анизотропного тела (продолжение) . 92
§ 12. Вдавливание штампа при наличии трения и сцеп¬
ления ЮЗ
§ 13. Задача о контакте двух упругих тел . . . . 119
§ 14. Приближенный учет пластических деформаций,
возникающих под штампом 124
Глава II. Пространственные контактные задачи теории уп¬
ругости 127
§ 1. Напряжения и перемещения для упругого полу¬
пространства 127
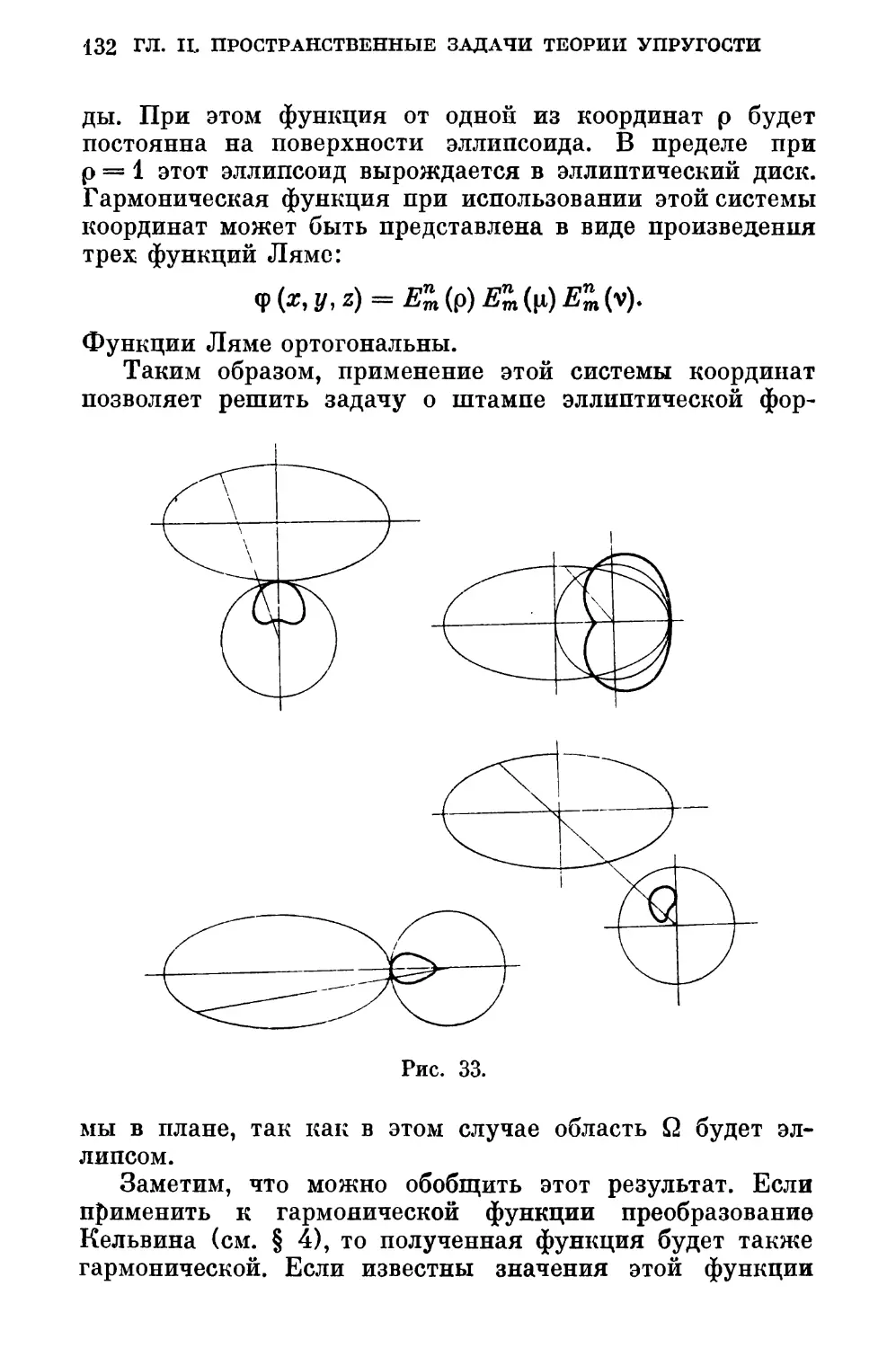
§ 2. Решения уравнений Лапласа в некоторых криво¬
линейных координатах 131
§ 3. Задачи для штампов круговой формы в плане. Об¬
щий случай 13
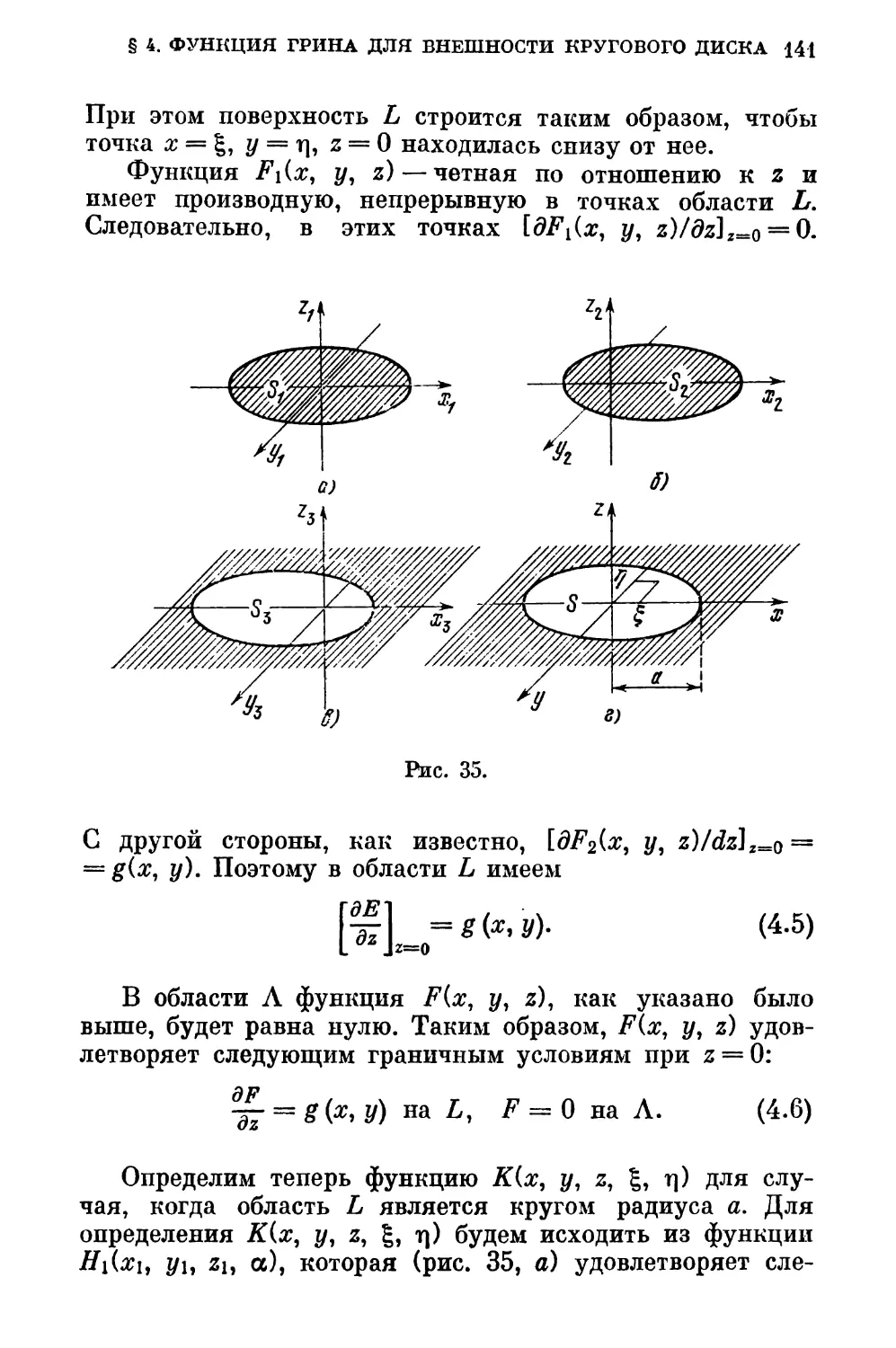
§ 4. Функция Грина для внешности кругового диска 138
§ 5. Осесимметричная задача без сил трения . . . 144
§ 6. Задача для штампа круговой формы в плане. Вли¬
яние нагрузки, действующей вне штампа . . . 158
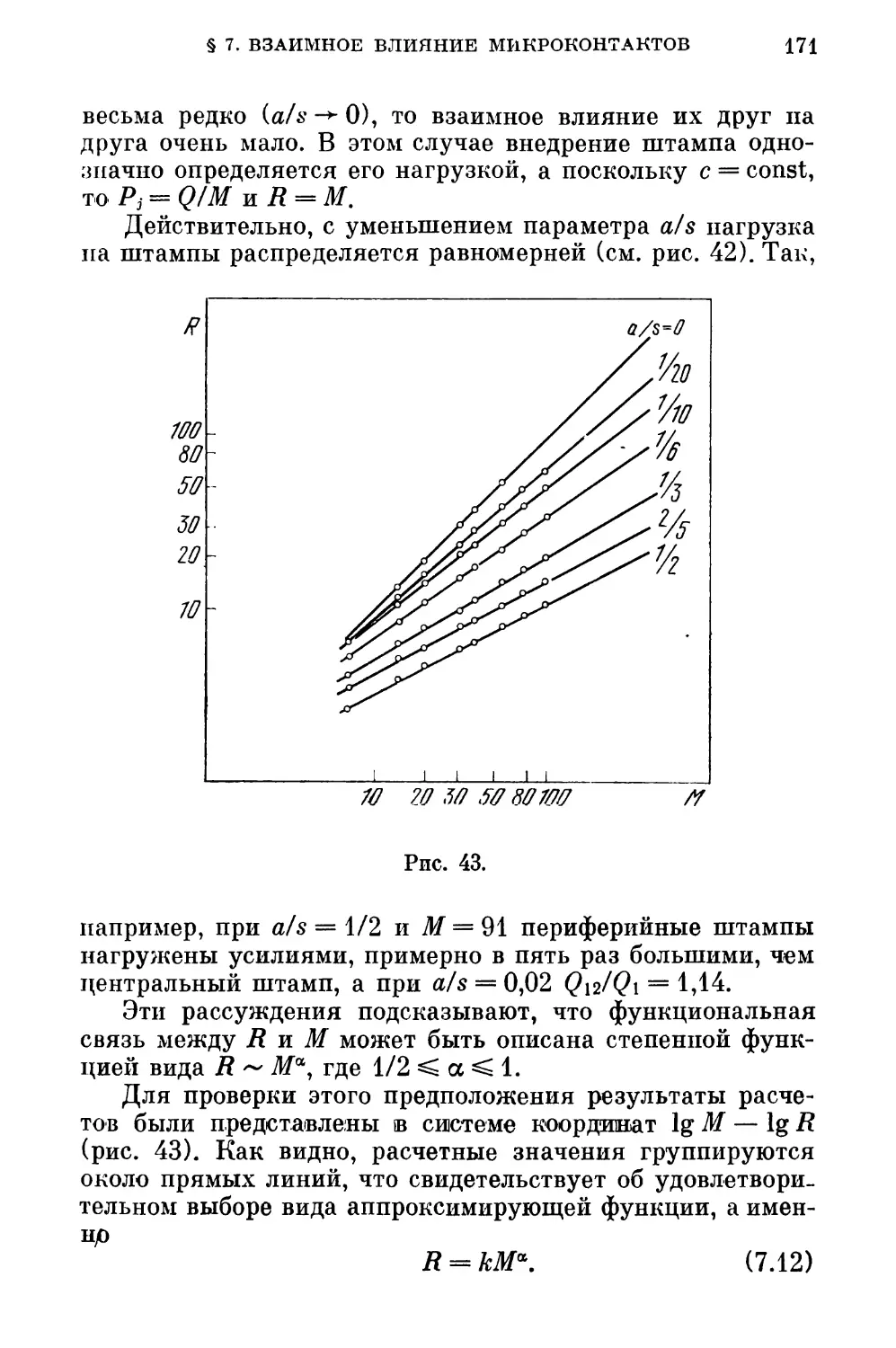
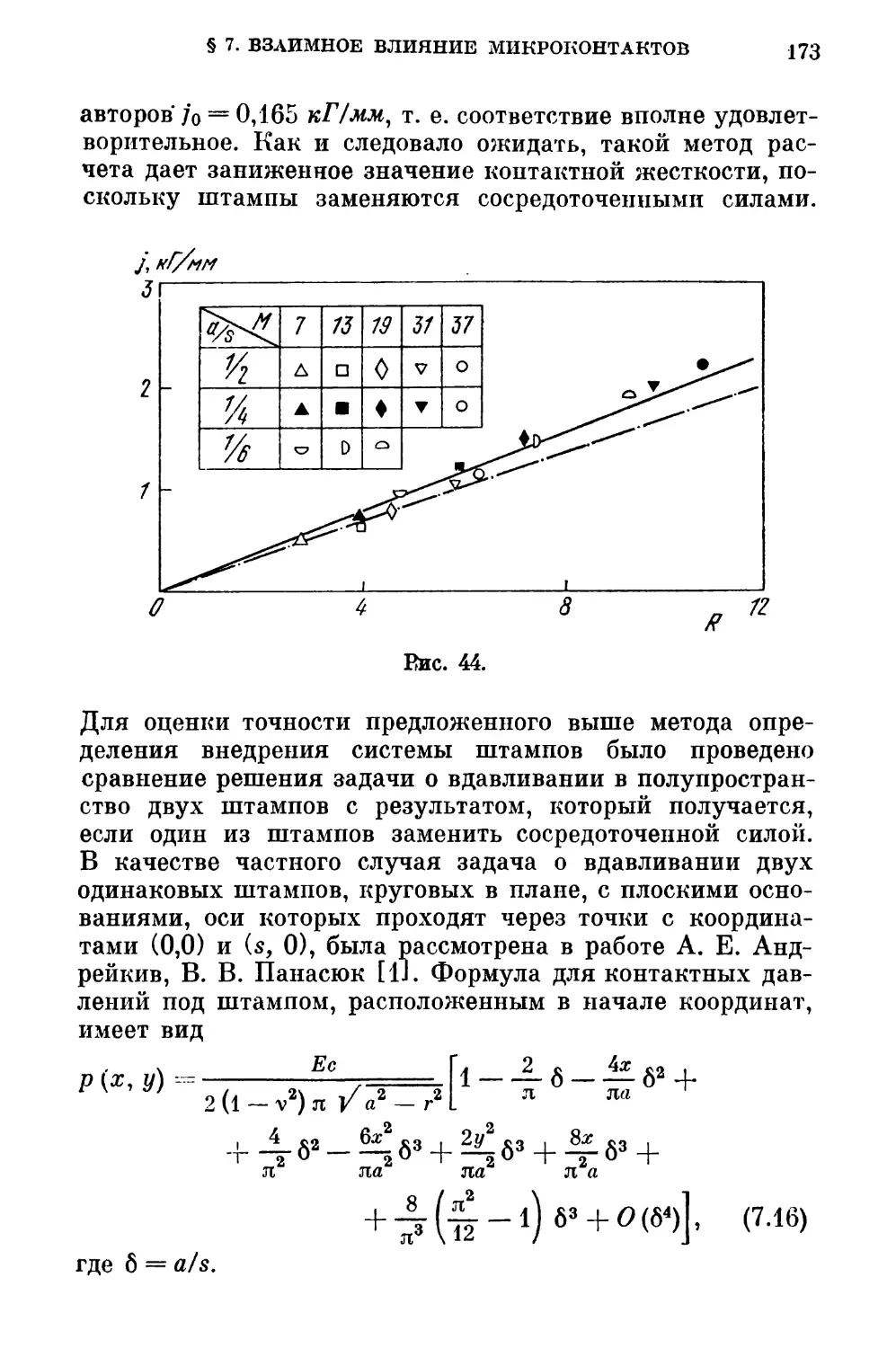
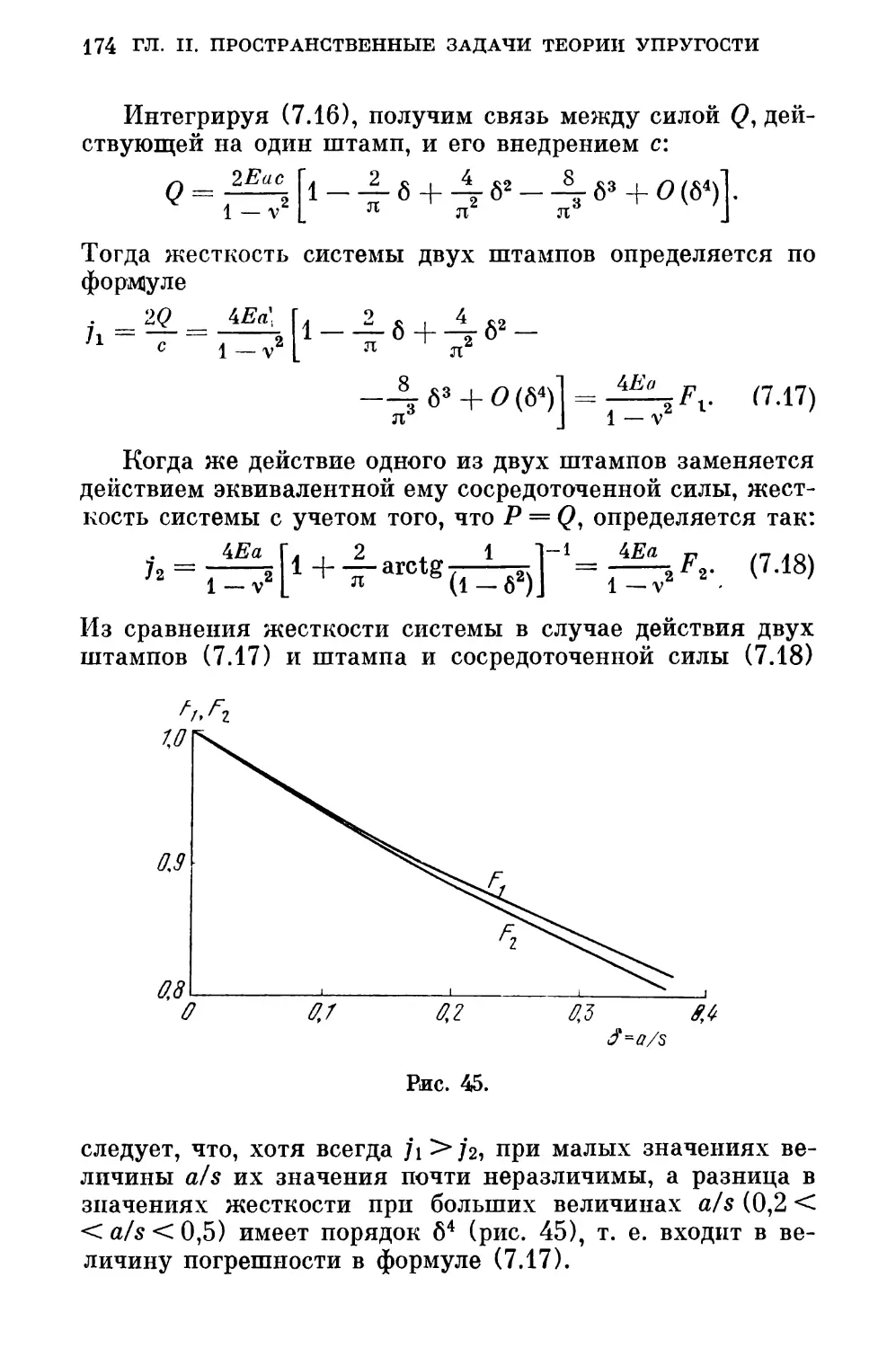
§ 7. Взаимное влияние микроконтактов при расчете
жесткости стыка шероховатых тел 165
§ 8. Осесимметричные контактные задачи с силами тре¬
ния 178
ОГЛАВЛЕНИЕ
§ 9. Давление штампа эллиптической формы в плане
на упругое полупространство ,
§ 10. Штамп эллиптической формы в плане под дейст¬
вием силы и моментов
§11. Оценка перемещений для штампа произвольной
формы в плане
§ 12. Давление штампа с плоским основанием клипооб¬
разной формы в плане
§ 13. Давление узкой балки на упругое полупространство
§ 14. Пространственная задача о контакте двух упругих
тел
§ 15. Давление твердого тела па пластинку .
Глава III. Контактные задачи для вязкоупругих и упругих
тел с учетом шероховатости и износа их поверхности
§ 1. Деформация ортотропного вязкоупругого тела в ус¬
ловиях плоской задачи
§ 2. Задача о давлении штампа, жестко связанного с
изотропной вязкоупругой полуплоскостью
§ 3. Контактная задача качения вязкоупругого цилинд¬
ра по основанию из того же материала
§ 4. Предельный случай качения цилиндра по вязкоуп¬
ругому основанию
§ 5. Одномерные контактные задачи теории упругости
при наличии износа
§ 6. Плоская контактная задача теории упругости прп
наличии износа
§ 7. Осесимметричная контактная задача теории упру¬
гости при наличии износа
§ 8. Плоские контактные задачи для шероховатых упру¬
гих тел
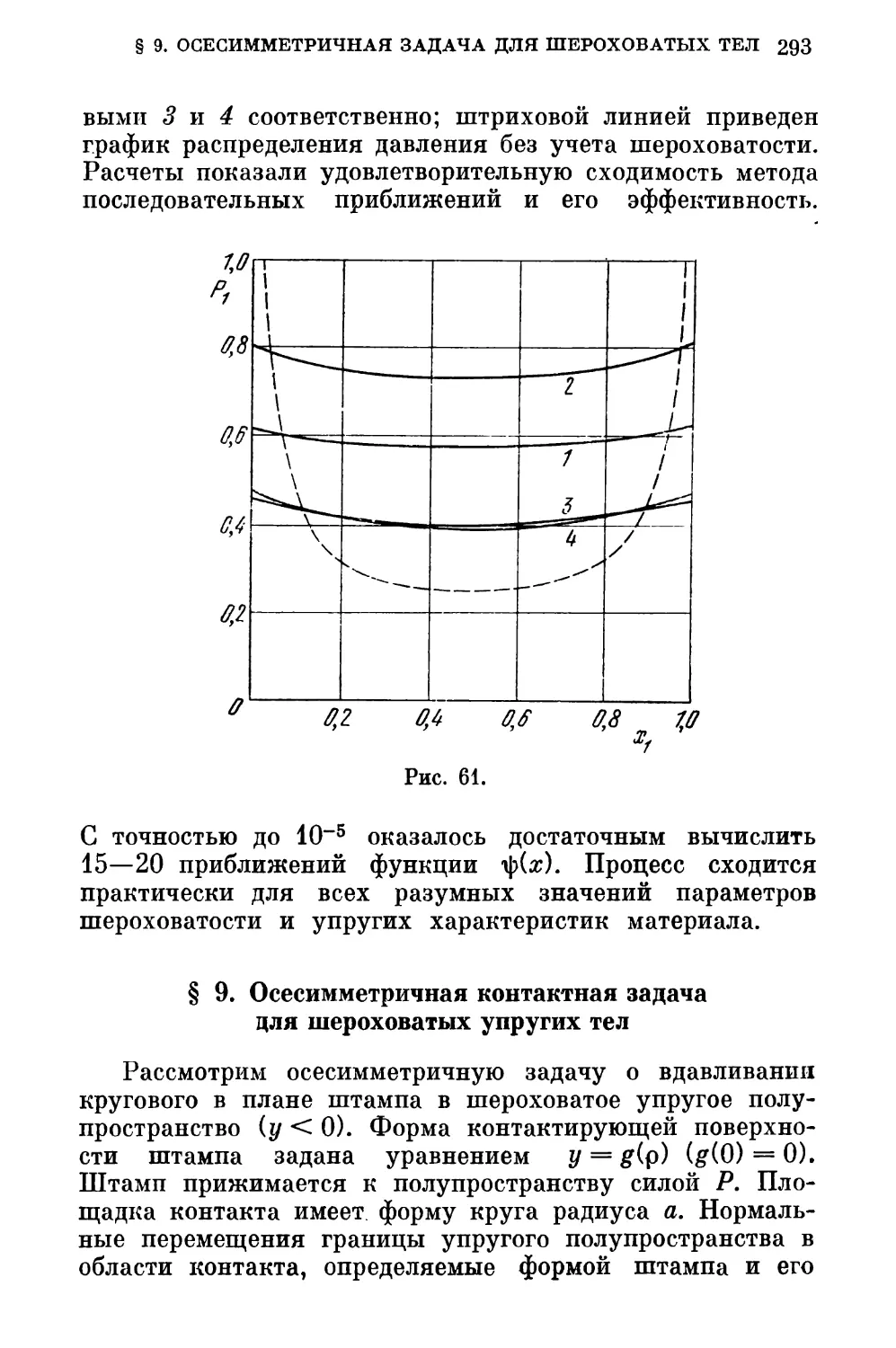
§ 9. Осесимметричная контактная задача для шерохова¬
тых упругих тел
Литература
Именной указатель
184
189
199
204
211
229
231
241
242
247
252
264
273
277
279
286
293
297
303
ПРЕДИСЛОВИЕ
Книга автора «Контактные задачи теории упругости»,
изданная в 1953 году, была посвящена плоским и прост¬
ранственным контактным задачам теории упругости, т. е.
задачам о касании упругих тел. Главное внимание в этой
книге было уделено задачам о давлении штампа (т. е.
твердого тела) на упругое тело. В первой главе, посвящен¬
ной плоским задачам, и во второй главе, в которой изло¬
жены пространственные задачи, показано, каким образом
полученные результаты могут быть распространены на
случай касания двух упругих тел.
В настоящее время возникло много новых видов кон¬
тактных задач. Это, во-первых, контактные задачи для
вязкоупругих тел, в том числе и такие, когда происходит
перекатывание вязкоупругого цилиндра по вязкоупругой
полуплоскости и площадка контакта делится на участки с
трением и сцеплением. Эта задача позволяет получить
важные результаты, относящиеся к определению сопро¬
тивления перекатыванию.
В контактных задачах, которые рассматривались ра¬
нее, предполагалось, что упругие тела ограничены абсо¬
лютно гладкими поверхностями. В действительности эти
поверхности являются шероховатыми, что очень сущест¬
венно для определения контактной жесткости. Решение
этой сложной нелинейной задачи было выполнено И. Г. Го¬
рячевой и составляет содержание § 8 третьей главы.
В книге содержатся работы Л. А. Галина, одна из ко¬
торых была выполнена вместе с Η. М. Бородачевым (§ 13
второй главы), и И. Г. Горячевой (§ 7 второй главы и
§ 2, § 3, § 4, § 7, § 8 и § 9 третьей главы). Работы дру¬
гих авторов затронуты лишь в той мере, в какой они
примыкают к содержащимся в книге исследованиям.
В книге «Контактные задачи теории упругости» содер¬
жался обзор работ, относящихся к этому разделу механи¬
6
ПРЕДИСЛОВИЕ
ки. Несмотря на свою краткость, в нем довольно полно
были изложены результаты, доведенные до 1953 года.
В настоящей книге помещение такого обзора нецелесооб¬
разно, поскольку обширный литературный обзор имеется
в опубликованной в 1976 году издательством «Наука»
коллективной монографии «Развитие теории контактных
задач в СССР».
Автор приносит благодарность Е. И. Галиной за уча¬
стие в работе над книгой.
ГЛАВА I
ПЛОСКИЕ КОНТАКТНЫЕ ЗАДАЧИ
ТЕОРИИ УПРУГОСТИ
§ 1. Основные соотношения плоской задачи
теории упругости
Напряженное состояние в упругом теле в случае плос¬
кой задачи (рис. 1) определяется тремя компонентами
напряжения: σχ, ау и τ^. Они удовлетворяют условиям
равновесия
Деформация упругого тела может быть выражена че¬
рез относительные удлинения гх и гу по направлению
Рис. 1.
осей х и у и через относительный сдвиг при этом ве¬
личины εχ, гу п чху определяются через и, т. е. перемеще¬
ния точки упругого тела по направлению оси х, и через
8
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
(1.3)
Компоненты деформации связаны с компонентами на¬
пряжения соотношениями
(1.4)
Здесь Θ = гх + гу — относительное объемное расширение,
а λ и μ — так называемые коэффициенты Ляме.
На основании этих уравнений компоненты деформации
могут быть выражены через компоненты напряжения:
(1.5)
Модуль упругости Е и коэффициент Пуассона ν опре¬
деляются через коэффициенты λ и μ по формулам
(l.fi)
(1.7)
ν, т. е. перемещения по направлению оси у:
(1.2)
Так как три компонента деформации гх, гу и *(ху выра¬
жены через два компонента перемещения гг и у, то между
ними должно существовать некоторое соотношение. Оно
носит название условия совместности и имеет следующий
вид:
Коэффициенты Ляме выражаются через Е и ν следу¬
ющим образом:
§ 1. ОСНОВНЫЕ СООТНОШЕНИЯ ПЛОСКОЙ ЗАДАЧИ 9
Если в условие совместности (1.3) подставить выраже¬
ние (1.5), то будет получено
(1.8)
Условия равновесия (1.1) будут удовлетворены, ког¬
да ах, оу и Хху выражаются через функцию напряжений
Ф(х, у) следующим образом:
Если подставить (1.9) в условие (1.8), то окажется, что
функция напряжений должна удовлетворять бигармони-
ческому уравнению
(1.10)
При решении плоских контактных задач мы будем
пользоваться методами теории функций комплексной пе¬
ременной.
Приведем краткий вывод основных соотношений плос¬
кой задачи теории упругости. Подробное изложение этих
вопросов можно найти в книге Н. И. Мусхелишвили [1].
Если подставить в соотношения (1.4) εχ, гу и γ^, вы¬
раженные через и и ν согласно (1.2), и воспользоваться
представлениями а*, ау и хху через функцию напряжений
(1.9), то в результате получим
(1.11)
ди
dv
Из первых двух уравнений можно определить и
Введя обозначение
(1.12)
(1.9)
10
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
получим
Так как Ф(я, у) удовлетворяет бигармоническому урав¬
нению, то Р(я, у), очевидно, будет функцией гармониче¬
ской. Если обозначить функцию, сопряженную с ней, че¬
рез Qix, г/), то найдем
Здесь f(z) зависит от комплексной переменной z = x + iy.
Найдем теперь необходимые в дальнейшем выражения
для перемещений. Для этой цели введем еще две гармо¬
нические функции ряд. При этом
В таком случае
Условия Коши — Римана дают соотношения
из которых, воспользовавшись (1.15), будем иметь
На основании (1.16) выражения (1.13) могут быть за¬
писаны следующим образом:
(1.17)
(1.16)
(1.15)
(1.14)
§ 1. ОСНОВНЫЕ СООТНОШЕНИЯ ПЛОСКОЙ ЗАДАЧИ
И
После интегрирования получим
Если подставить эти выражения в третье уравнение
исходной системы (1.11), то найдем следующее соотноше¬
ние между функциями f\ и /2:
Так как каждое из слагаемых может быть равно толь¬
ко некоторой постоянной, то функции f\(y) и /г(#) будут
такими:
Очевидно, они соответствуют смещению недеформирован-
ного тела.
Образуем теперь функцию Ф — рх — qy.
Если воспользоваться соотношениями (1.12) и (1.14),
то путем непосредственного вычисления можно убедиться
в том, что эта функция будет гармонической, т. е.
Если обозначить через χ(ζ) функцию комплексной пе¬
ременной, вещественной частью которой является (Ф —
— px — qy), то, принимая во внимание (1.14), получим
или, иначе,
(1.19)
Пользуясь (1.19), составим следующую комбинацию про¬
изводных от Ф:
(1.20)
При этом введем следующее обозначение:
На основании (1.20) может быть найдено выражение
для комплексной комбинации перемещений упругого тела.
12
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Рис. la.
Если пренебречь функциями f\(y) и /2W, дающими толь¬
ко жесткое смещение, то на основании (1.18), принимая
также во внимание (1.14), получим
2 μ(« + iv) = κφ(ζ) — ζφ'(ζ) — ψ(ζ). (1.21)
Коэффициент κ выражается через коэффициенты Ляме
λ и μ или через коэффициент Пуассона V, причем это вы-
ражение будет различным в
случае плоской деформации и
в случае плоского напряженно¬
го состояния.
При рассмотрении плоских
контактных задач теории упру¬
гости в большинстве случаев
приходится иметь дело с плоской
деформацией. При этом выра¬
жение для κ будет следующим:
(1.22)
В случае плоского напряженного состояния (когда
происходит деформация тонкой пластинки в ее плоскости)
будем иметь такое выражение:
(1.23)
Приведем численные значения κ и κ*. Если коэффи¬
циент Пуассона ν = 0,3, то κ = 1,80, а κ* = 2,08.
Выразим через функции <ρ(ζ) и ψ(ζ) компоненты на¬
пряжения σ*, ϋυ, Тху, а также некоторые комплексные ком¬
бинации от этих величин.
Рассмотрим дугу АВ, расположенную в области, заня¬
той упругим телом (рис. 1а).
Обозначим через L длину дуги, которую будем отсчи¬
тывать в положительном направлении от А к В.
Будем считать положительным направление нормали
вправо по отношению к наблюдателю, движущемуся по
дуге от А к В. Компоненты усилия, действующего на выб¬
ранный элемент дуги АВ со стороны внешней нормали,
обозначим через Xnds, Ynds. При этом компоненты усилия
направлены по осям хну. Имеет место следующее соот¬
ветствие между употребляемыми нами обозначениями для
§ 1. ОСНОВНЫЕ СООТНОШЕНИЯ ПЛОСКОЙ ЗАДАЧИ
13
(1.24)
напряжении σ*, оу и тху и компонентами напряжения в
тех обозначениях, которые приняты, например, в книге
И. И. Мусхелишвили [1] и более удобны для данного
случая:
Οχ === Хх, Оу = Yyi Т ху Ху·
Компоненты напряжения Хп и Yn могут быть выраже¬
ны следующим образом:
V д2Ф , V д2Ф , ч
п = 1>7cos (га’х) ~ эщ,cos (”’г/)’
v д2Ф , . д2Ф , .
Уп = в? 008 (”’ ~~ ~дхТу C0S <"· ^
Эти соотношения могут быть записаны так:
γ — JL (дф\ ν —
71 ds \ ду /’ 11 ds\d«r /’
или, если образовать комплексную комбинацию этих ве¬
личин, будем иметь на основании (1.20)
= — id [φ(ζ) + ζφ'(ζ) + ψ(ζ)]· (1.25)
Выберем теперь дугу АВ таким образом, чтобы эле¬
мент ds был параллелен оси Оу. Тогда
σ* + ixxy = Хх + iXv = φ' (ζ) + φ' (ζ) — ζ φ" (ζ) — ψ' (ζ).
(1.26)
Если выбрать элемент ds так, чтобы он был располо¬
жен параллельно оси Ох, то будем иметь
Оу i'txy = Yу iXy = (ζ) +
+ φ'(ζ) + ζφ" (ζ) + ψ'(ζ). (1.27)
Если ввести обозначения
Φ(ζ) = ф'Ы, Ψ(ζ) = ψ'(ζ),
то формулы (1.26) и (1.27) могут быть записаны так:
Οχ + Пху = Φ (ζ) + φ (ζ) — Ζφ' (ζ) — Ψ (ζ), (1.28)
<Уу ~ ΐτχν = Φ (ζ) + Φ (ζ) + ζΦ' (i) + ψ (ζ). (1.29)
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Если (1.28) и (1.29) сложить, то будет получена фор¬
мула для суммы нормальных напряжений а* + ау. Если из
(1.29) вычесть (1.28) и в результате, полученном после
вычитания, поменять + ь на — £, то найдем формулу для
комбинации напряжений ау — <зх + 2ixxy. Таким образом,
получаются следующие выражения:
— 2 [Φ(ζ) + Ф (ζ)], (1.30)
оυ + 2irxy = 2 [ζΦ' (ζ) + ψ(ζ)]. (1.31)
Комбинации величин σ* + <5У и <sy — σχ + 2ixxy очень
удобны для исследования напряженного состояния упру¬
гого тела. Сумма нормальных напряжений ох + оу являет¬
ся инвариантной величиной и характеризует объемное
сжатие в точке упругого тела. Модуль су — а* + 2ixxy равен
удвоенному максимальному тангенциальному напряже¬
нию. В самом деле,
— I ву σχ “Ь 2ixхУ | = — ]/~(оу σ*)2 4- 4τ%у =
= |/ (^^)г+т^ = ттах.
Так как сумма и разность главных напряжений вы¬
ражаются формулами
σι + σ2 = ^х ~1“ Gy, σλ сг2 ~ 2ттах,
то
^ _°х + °У , ах + °У
<*1 2 ^тах» ^2 — 2 ^тах*
Использовав выражения для указанных комбинаций
напряжений через функции φ(ζ) и ψ(ζ) [(1.30) и (1.31)],
получим формулы для максимального тангенциального
напряжения ттах и главных напряжений σι и 02:
τη^ = \ζΦ'(ζ) + Ψ(ζ)\, (1-32)
σχ = [Ф (ζ) + Ф (i)] + I iφ (ζ) + ψ (ζ) |, (1.33)
σ2 = [Φ (ζ) + Φ (i)] - I 'ζΦ (ζ) + Ψ (ζ) |. (1.34)
Эти формулы позволяют определить величины, пред¬
ставляющие наибольший интерес при исследовании на¬
пряженного состояния упругого тела.
§ 2. НАПРЯЖЕНИЯ И ПЕРЕМЕЩЕНИЯ ДЛЯ ПОЛУПЛОСКОСТИ 15
§ 2. Напряжения и перемещения
для упругой полуплоскости
Величина площадки контакта в большинстве случаев
невелика по сравнению с величиной радиусов кривизны
соприкасающихся тел. Поэтому при рассмотрении плос¬
ких контактных задач предполагается, что упругое тело,
в которое вдавливается штамп, является полупространст¬
вом. В том случае, когда рассматривается плоская задача,
считают, что упругое тело занимает полуплоскость. По¬
добное предположение, само собой разумеется, несколько
искажает картину напряженного состояния, однако это
искажение будет иметь заметную величину только доста¬
точно далеко от площадки контакта. Итак, мы будем пред¬
полагать, что упругое тело, в котором возникают контакт¬
ные напряжения, занимает полуплоскость.
В главе I этой книги излагается решение ряда плоских
контактных задач. Некоторые результаты даются здесь
впервые, другие излагались ранее, в частности, в книге
Н. И. Мусхелишвили [1].
Однако здесь применяется несколько отличный метод
решения указанных задач. В книге Н. И. Мусхелишвили
решение приводится к непосредственному определению
функций Φ(ζ) и Ψ(ζ) (см. § 1). В данной работе вводятся
в рассмотрение функции W\(z) и Шг(г), являющиеся ин¬
тегралами типа Коши, у которых плотности равны соот¬
ветственно нормальному давлению и тангенциальной на¬
грузке, действующим на поверхности. Через эти функции
W\(z) и ιυ2(ζ) весьма просто определяются Φ(ζ) и Ψ(ζ),
на основании которых находится напряженное состояние
в упругой полуплоскости.
Введение здесь функций W\(z) и 1^2(2) представляет
известные преимущества, так как контактные задачи для
анизотропного тела, для случая движущегося штампа,
а также более сложные задачи (с участками различных
типов на площадке контакта) приводятся к граничным
задачам смешанного типа для отыскания этих функций.
Итак, будем определять напряжения и перемещения
в упругой полуплоскости, на границе которой приложено
нормальное давление и распределены тангенциальные на¬
пряжения.
16 гл. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Используем формулу (1.15), которая дает выражение
для комплексной комбинации нормального напряжения
Gy π тангенциального напряжения хху\ при этом обозначим
φ'(ζ) = Φ(ζ) и ψ'(ζ) = Ψ(ζ).
Тогда будем иметь
— ίτχυ = Φ (ζ) + Φ (ζ) + ζΦ' (ζ) + Ψ{ζ).
Будем рассматривать эту комплексную комбинацию
напряжений для полуплоскости, т. е. для полубесконечной
области, полагая при этом, что компоненты напряжения
на бесконечности стремятся к нулю. Это обусловливает
следующее поведение на бесконечности (т. е. при больших
значениях Ы) функций Φ(ζ), Ф'Ы и Ψ(ζ):
ф(!)=т + °(т)· ЧЧ‘>=^ + о(4-),
«>'<*> =-£ + о(Х).
Если теперь перейти к точке, расположенной на гра¬
нице нижней полуплоскости, занятой упругим телом, то,
так как при у = О имеет место ζ = ζ, получим
(σ„ - iXxy)v=о = [Ф(*} + Φ (ζ) + ζ Φ' (ζ) + Ψ(ζ)1ν=ο· (2-1)
Взяв сопряженное значение, найдем
(О у + iXxy)^ = [Ф(*) + φ (ζ) + ζΦ' (ζ) + ψ (Z)]y=0. (2.2)
Умножим теперь каждое из этих выражений на
t и проинтегрируем по t от — <» до + °°. Известно,
что если g(z) — функция, регулярная в нижней полу¬
плоскости и ведущая себя на бесконечности так, как
функции Φ(ζ) и Ψ(ζ), то на основании известных свойств
интегралов Коши имеем
2Й1 Jril*=-g(z), = 0.
§ 2. НАПРЯЖЕНИЯ II ПЕРЕМЕЩЕНИЯ ДЛЯ ПОЛУПЛОСКОСТИ 17
Следовательно, получим
+ оо
— оо
+°°
_L_ J К + «V Wf _ = - [ф (2) + ζΦ' (2) + ψ(Ζ)],
—оо
Отсюда найдем следующие выражения:
— (X)
Φ (ζ) + ζΦ'(ζ) + Ψ (ζ) = - ± j к +;**>W* , (2.4)
— оо
Обратимся теперь к формуле (1.21) для комплексной
комбинации перемещений:
2 μ(ι* + ίι;) = κφ(ζ) — ζφ'(ζ) — ψ(ζ).
Перемещения на границе нижней полуплоскости, т. е.
при у = О (на том основании, что при этом ζ = ζ), будут
2μ (u + if)j,=o = [κφ (z) — ζφ' (ζ) — ψ (z)]y=0. (2.5)
Продифференцировав (2.5) по х, получим
0 (да ди\
2^[д7 + 1 w)y=0 =
= {κφ' (ζ) — [q7(z) + ζφ" (ζ) + ψ' (ζ)]}„=0,
или, вводя обозначения φ'(ζ) = ФЫ, ψ'(ζ) — Ψ(ζ),
(£+* £Lo=κ [φ {z)]y=° ~ ^+
+ ζΦ7!^ + T(ij]y=0. (2.6)
Исходя из выражений (2.3) и (2.4), найдем правую
часть в (2.6). При этом воспользуемся формулой, даю¬
щей предельное значение интеграла типа Коши при
стремлении к точке, расположенной на действительной
2 Л. А. Галин
18
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
оси, являющейся границей нижней полуплоскости. Если
f(t) — некоторая функция, то
[+°о “I +<*=
2л? J- 7^1 = - -γΐ <*>+т J <2·7)
— oo J 2=x—io —oo
Интеграл в правой части этого выражения понимается
в смысле главного значения. Обозначение у = О, кото¬
рым мы также пользуемся, в данном случае эквивалент¬
но обозначению ζ — х — Ю, так как мы приходим к точ¬
ке, расположенной на действительной оси, приближаясь
к ней снизу.
На основании (2.3) и (2.7) получим
- 1 Λτ _ ,·τ ^ -J-Т (аУ ~ iT*»)»=»dt
[Φ(ζ)]„=0 — 2 ( ϊ/ ιτχν)ν=ο 2πι J г — я
— ОО
(2.8)
Точно так же, пользуясь (2.4) и (2.7), найдем
[Ф (ζ) + ζΦ' (ζ) + Ψ (ζ)]^^ =
-j-ΟΟ
1 . , V If (σ.«l\y)M=0dt
-—\συ~Τ пху)у=о 2πΐ J J _ д.
— σο
Поэтому сопряженное значение будет следующим:
[Φ^ + ΖΦ^+ΨΙ^Ο^
-foo
__ 1 / · \ I ]_ Г (°У ίτχν)ν=0^* /9 Q\
2 у ху)у=о "Ь 2дг J ί — х ' v*-*’-)
— оо
Подставим теперь (2.8) и (2.9) в (2.6) и разложим
интегралы, входящие сюда, на отдельные слагаемые.
В результате получим
2» [(£)_+ 4 Ш - ^ -
-foo -foo
κ + 1 С , \ dt , κ + 1 Г , ч dt /п , Α4
~ ~Έΰ~ J Ю*=--о + it J ^2Л0^
§ 2. НАПРЯЖЕНИЯ II ПЕРЕМЕЩЕНИЯ ДЛЯ ПОЛУПЛОСКОСТИ 19
Отделяя в этом выражении действительную и
мнимую части, найдем производные от перемещений
по х:
0 [ ди\ κ — 1 , ν . κ -j- 1 Г / \ dt
2,48*/ip=о — ^-(σί')ί/=ο + “ST J (τ«)!/=0 7ΤΓ^’
— оо
-j-oo
с\ (θν\ κ — 1 t 4 κ 1 Г , ч cfa
2-иЫУ=о - 2“ (τ**)ν=» + ~ΈΓ J (σ*)*=ο *=■£·
(2.11)
Умножив каждое из этих выражений на 2π/(κ+1),
получим
-foo
4μπ / ди\ _κ —1/^\ if/ \ ^
κ+Τ \0жД.=о — *(+1 Я ( v'v=° 1 .) VT*»b=
— oo
+ oo
4μπ /diA f / \ dt κ — 1 , 4
ίΓΓιϋο- J Κ)ν=0 7ΖΓ;--5ΓΜπ(τ^)ι/=0*
Введя обозначение (κ — 1)/(κ + 1) = β, найдем окон¬
чательно
dt
IT+lOv-e- J (Gy)v=0T^.-Pn(xxy)u^0·
(2.12)
Интегралы здесь берутся в пределах от — °° до + оо.
(Заметим, что во всех случаях интегралы понимаются в
смысле главных значений.) Однако, если давления и
тангепциальные усилия распределены на некоторых ко¬
нечных участках границы полуплоскости, как это имеет
место в контактных задачах, то указанные выше интег¬
ралы будут браться в конечных пределах. В таком слу¬
чае, когда нагрузка распределена на участке а<х<Ь,
2*
20
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
будем иметь
ΖΤΊ [dijy=о = (σ^=° + J (т^»)у=»Г=^’
а
κ+l (te)y=0 = I^v=0 t~ ~ ^τ^ν=0'
(2.13)
где
κ = 3 — 4ν, β =
1 — 2ν
2 — 2ν*
После интегрирования этих выражений по х получим
формулы, дающие перемещения:
-^г~. и -f- const =
κ +1 1
х Ъ
= βπ j* (Оу)у=о Ах + J (τ*Β)»=ο In 11 — * | df,
4μπ
κ + 1
ο χ
= j (°у)у=0 In 11 — x I dt — βπ J (txy)y=o
dx.
(2.14)
Эти формулы для перемещений границы полуплоскости
даны Н. И. Мусхелишвили [2L
Если воспользоваться более употребительными по¬
стоянными — модулем упругости Е и коэффициентом
Пуассона ν, то выражения (2.12) могут быть переписа¬
ны так:
ιΕ (ди\ _ 1 — 2ν ( \ , Г / \ dt
_ v*) \Щу^~ π Ισ»)»=» ·+■ J ντ*!/)ί/=0 t _ *.
πΕ
2 (l — ν2)
nE I Ου
2 (l — v2) Wy=0
4-00
(2.15)
Г \ dt 1 — 2ν , v
J (<Μν-ο ^ _ д. 2 — 2v Я 'τ^)ί/·=ο·
§ 2. НАПРЯЖЕНИЯ И ПЕРЕМЕЩЕНИЯ ДЛЯ ПОЛУПЛОСКОСТИ 21
Точно так же выражения (2.14) будут
пЕ
■ и 4- const =
2 (1 - v2)
х Ъ
= п j (ay)v=o dx + J (*ху)у=о In 11 — х I dt,
пЕ
2 (l-v2)
ъ
v -f const =
— «ί ^у^у=0 И x\dt 2 2v π J
do:.
(2.16)
Иногда мы будем пользоваться следующими обозна¬
чениями для напряжений, действующих на границе:
(^г/)*/=о = Р {χ)ι (^ху)у=о = ^ (#)·
Введем в нижней полуплоскости две функции комп¬
лексной переменной, являющиеся интегралами типа Ко¬
ши, плотности которых равны соответственно величинам
нормального давления и тангенциальных усилий, дейст¬
вующих на границе полуплоскости:
+ оо \
Ч (*) = Щ — щ = j (σ„)„=0 j^-z,
и?.
— oo
+ 00
U)t
(z) — u2 iu2 — J (τxy)y=o t z·
(2.17)
Если найти предельные значения этих интегралов,
приближая ζ снизу к точке, расположенной на дейст¬
вительной оси, то получим выражения
wi (z) \z-*x — [^l —
+ oo
= 1 (Gy)y=o JZL'x ni(ay)y=о»
^2 (^) \z-*x — [^2 ^2^1J=0 —
-j-oo
~ j* (Xxy)v=о ~ZL~x κϊ{τχν)ν=ο·
(2.18)
22
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Теперь можно выразить нормальное давление и тан¬
генциальные усилия, действующие на границе полупло¬
скости:
(Оу)у=о = {Vl)v=0 = Im К (*)Ь=*.
(τ*,)*=0 = i (v'i)y=0 = — т Im (W2 (2))г=х·
(2.19)
На основании (2.18) действительные части функций
u>i(z) и u?2(z) на оси х таковы:
+ о°
(Ul)y=0 = J (ay)y=0 t _ хч
+оо
{и2)у=о = J (хху)у=0
Отсюда, пользуясь (2.17), можно дать выражения
для производных по х от перемещений и и г; на грани¬
це полуплоскости:
пЕ (ди\ ( . 1 — 2v
“ г2+ViL·*
2v
2(1 - ν2) V
пЕ fdv\ ( 1 —
W=f) “ Г1 “
' у=0
TvV*
У=0
(2.20)
если же принять сокращенное обозначение
κ — 1 1 — 2ν
β
κ Η- 1
2ν’
то получим
ηΕ
2 (1 - ν2) \д*)у=0
— (w2 + Pyl)y=0»
пЕ
2 (1 - v2) \дх1у=,
(лг) ~~ Рг;2)у=0
(2.21)
Установим теперь некоторые свойства введенных
функций W[(z) и Мнимые части этих функций при
у = 0, будучи умножены на π, дают величины давлений
(оу)у=о и распределенных тангенциальных усилий
(тХу)у=о, действующих на поверхности. Эти величины мо¬
гут в некоторых точках обращаться в бесконечность.
§ 2. НАПРЯЖЕНИЯ II ПЕРЕМЕЩЕНИЯ ДЛЯ ПОЛУПЛОСКОСТИ 23
Установим характер особенностей, которыми могут об¬
ладать функции w\(z) и w2(z).
Если к границе полуплоскости приложена сосредото¬
ченная сила, то это можно представить как передачу
давления посредством предельно узкого штампа. В та¬
ком случае функции W\{z) и будут обладать по¬
люсами первого порядка.
Когда же давление передается посредством штампа
конечпой ширины, возникновение под штампом (в том
числе и у его краев) сосредоточенных сил, очевидно,
невозможно. Отсюда следует, что мнимые части w\(z)
и Wiiz) могут иметь на действительной оси интегрируе¬
мые особенности. А это будет выполнено, когда будет
иметь место следующее свойство функций W\(z) и w2(z),
являющихся интегралами типа Коши: они могут иметь
особенности вида ζ~θ, где 0 < θ < 1.
Если нормальное давлепие и тангенциальные усилия
распределены на некотором конечном отрезке оси х, то
выражепия для w\(z) и будут такими:
dx
о Z~~,
о о
и\ (2) = j* (Gy)y=0 х _ z, (2) = J (tjcy)^
а а
Из этого следует, что при ζ -> °°
Ц7г(2)-* j, W2(Z)^Q,
причем
ъ ь
Р — J (σν)ν=о Q — \ (1:ху)у=о άχ·
а а
Таким образом, Р иQ — силы, приложенные к
штампу, которые действуют параллельно осям х и у.
Таким же будет поведение па бесконечности w\{z) и
когда нормальные давления и тангенциальные
усилия распределены на конечной совокупности отрез¬
ков ограниченной длины.
В контактных задачах, рассматриваемых в этой кни¬
ге, wiiz) и W2(z) всегда будут обладать указанными
свойствами.
24
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Выразим теперь функции <р'Ы и ψ'(ζ), на основа¬
нии которых могут быть определены напряжения, воз¬
никающие в упругом теле, через функции w\(z) и w2(z).
Воспользуемся для этого соотношениями (2.3) и (2.4),
откуда получим после некоторых преобразований
-foo -foo
φ/ № = - ш $ (σ^=<> Γ~~ζ + т ί irh'
— оо —оо
-foo -foo
ψ' = ~Έ S *— + z 2Hi ί (ау)у=ь -
(t-z)
~ ZL· ί (x*v)v=o7fZ
—oo
-foo
(t - *)\
Пользуясь (2.17), принимая также во внимание, что
-foo -foo
J (Gy)y-= 0 ^ _ ν2 == W1 (z)’ J (Xxy)y=0 /t_"T2 =
(г-ζγ ^ ' J '
— ^ —oo
найдем окончательно
4>' (2) = (ζ) + 2Hi ^ (z) - έ <*>·
(2.22)
После определения φ'(ζ) и ψ'(ζ) по формулам (1.30)
и (1.31) могут быть найдены напряжения, возникающие
в упругом теле.
§ 3. Граничные условия
в плоских контактных задачах
В контактных задачах, которые служат предметом
рассмотрения в этой книге, мы будем иметь дело с та¬
кими случаями, когда внешние усилия, создающие на¬
пряженное состояние, прилагаются на различных участ¬
ках поверхности различными способами. Можно, одна¬
ко, установить несколько достаточных общих типов гра¬
ничных условий, к различным комбинациям которых
приводится большинство контактных задач. Внешние
§ 3. ГРАНИЧНЫЕ УСЛОВИЯ В ПЛОСКИХ ЗАДАЧАХ
25
силы, действующие на упругое тело, могут прилагаться
или непосредственно к поверхности (например, гидро¬
статическое давление), или посредством другого твердо¬
го или упругого тела. В этом параграфе мы рассмотрим
случай, когда тела, посредством которых передаются
усилия, действующие на данное упругое тело, будут
твердыми.
Если силы, действующие на упругое тело, приложе¬
ны к нему непосредственно, на его поверхности будут
заданы значения нормального и тангенциального напря¬
жений σν и τδν. Если усилия передаются посредством
твердого тела, то упругое тело или может быть жестко
сцеплено с перемещающимся твердым телом, или же
может скользить по его поверхности. В случае жест¬
кого сцепления на поверхности будут заданы значения
перемещений в направлении осей координат и и υ*
В случае скольжения упругого тела по поверхности
твердого на границе этого упругого тела будет задана
величина перемещения νν, нормального к поверхности,
и соотношение между нормальным и тангенциальным
напряжениями, указывающее на наличие трения, под¬
чиняющегося закону Кулона: τδν + ρσν = 0. Знак при ко¬
эффициенте трения р обусловлен направлением переме¬
щения точки на поверхности упругого тела относитель¬
но твердого тела. При отсутствии сил трения между эти¬
ми телами р = 0 и граничное условие будет иметь вид
Tsv = 0.
Итак, основные типы граничных условий в контакт¬
ных задачах теории упругости будут следующими:
I тип. На участке поверхности упругого тела заданы
внешние усилия (в частности, равные нулю, когда этот
участок свободен от внешних сил):
σν = /ι00, τsv = f2(s)·
II тип. Участок поверхности упругого тела жестко
связан с перемещающимся твердым телом. В этом слу¬
чае известны перемещения по осям координат:
u = gi(s), v = g2(s).
III тип. На участке поверхности упругого тела, где
в него вдавливается твердое тело, имеют место силы
сухого трения:
vv = h (s), tsv + ρσν = 0.
26
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
IV тип. На участке поверхности упругого тела, где
имеет место давление твердого тела, силы трения от¬
сутствуют (р = 0):
В двух последних случаях vv — перемещение по на¬
правлению, нормальному к поверхности. Последний тин
граничных условий является частным случаем предыду¬
щего, однако, в силу особой простоты, должен быть рас¬
смотрен отдельно. Во всех перечисленных типах гранич¬
ных условий /1(5), /2(5), g\is)y £2(5), his) — заданные
функции точки контура.
Приведенные здесь типы граничных условий даны
для случая, когда упругое тело занимает область, огра¬
ниченную произвольным контуром. Так как в этой кни¬
ге предметом рассмотрения являются контактные зада¬
чи для упругого тела, занимающего полуплоскость, при¬
ведем типы граничных условий для этого случая:
I тип: о у = f1 (х), ххУ = /2 (х);
Если вдоль отрезка оси х задана величина переме¬
щения и или перемещения ν, то на основании этого мо¬
гут быть определены и величины их производных по х.
В таком случае основные типы граничных условий мо¬
гут быть записаны в таких формах:
vv — h(s), tsv = 0.
II тип: и = gx (х), v = g2 (х)\
III тип: v = h (я), ххУ + ρσ*, = 0;
IV тип: v — h(x), хху = 0.
(3.1)
I тип: о у = /х (х), ххУ = /2 (ж); ’
III тип: -zz = h' {х), ххУ + роу = 0;
(3.2)
На отдельных участках границы полуплоскости мо¬
гут быть заданы условия каждого из этих трех типов.
Иногда эти условия на разных участках принадлежат
§ 3. ГРАНИЧНЫЕ УСЛОВИЯ В ПЛОСКИХ ЗАДАЧАХ
27
только двум типам. Это обстоятельство, как мы увидпм
дальше, значительно упрощает задачу.
В контактных задачах о давлении штампа без сил
трения будем иметь граничные условия первого типа
(там, где поверхность свободна от усилий) и четвертого
типа (там, где упругое тело соприкасается со штампом).
Если в местах контакта имеют место силы трения, то
будут наблюдаться условия первого и третьего типов.
Если штампы жестко связаны с упругим телом, гранич¬
ные условия будут первого и второго типов. Наконец,
если штамп соприкасается с упругим телом таким обра¬
зом, что площадка контакта делится на участки с тре¬
нием и участки со сцеплением, граничные условия будут
принадлежать первому, второму и третьему типам.
Итак, граничные условия в контактных задачах тео¬
рии упругости таковы, что на ее границе даются или
напряжения ау и тяу, или линейная комбинация напря¬
жений гху + ρσν = 0, или перемещения и и ι;, а следова¬
тельно, их производные ди/дх и dv/dx.
Как было показано в предыдущем параграфе, каж¬
дая из этих величин может быть представлена как ли¬
нейная комбинация действительных и мнимых частей
функций W\(z) =Щ — iV[ И W2(z) =и2 — iv2.
Таким образом, принимая во внимание (2.19) и
(2.21), основные типы граничных условий могут быть
записаны следующим образом:
I тип:
= π/ι (х),
1>2 -^/2 (*^)t
II тип:
»1 ~ f>V2 = g2 (*);
III тип:
IV тип:
(3.3)
28
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
В этих формулах β, как и раньше, выражается через
коэффициент Пуассона ν:
Итак, в наиболее общем случае решение основных
контактных задач для полуплоскости приводит к оты¬
сканию двух аналитических функций на основании та¬
ких граничных условий: на различных участках оси х
известны значения двух различных линейных комбина¬
ций действительных и мнимых частей функций W\iz) ш
w2(z). Напомним выражения для функций w\(z) и w2(z):
В ряде случаев вопрос может быть приведен к оты¬
сканию одной аналитической функции на основании
граничного условия смешанного типа. Эта задача носит
название задачи Римана — Гильберта.
§ 4. Решение задачи Римана — Гильберта
для полуплоскости
Для решения ряда контактных задач нам потребу¬
ется решение задачи Римана — Гильберта. Как извест¬
но, она заключается в следующем: необходимо найти
функцию wiz) = u— ίν, которая на контуре области
должна удовлетворять условию
a(s)u + b(s)v = f{s).
В нашем случае область является полуплоскостью,
поэтому условия будут заданы на оси х и, следователь¬
но, могут быть записаны в такой форме:
Будем рассматривать нижнюю полуплоскость и по¬
этому будем полагать w(z)=u — iv. В условии (4.1) а(х)
и Ь(х) — функции точки контура, причем для наших
задач — функции кусочно-непрерывные. Будем пола¬
гать, что а(х) и Ых) одновременно не обращаются в
нуль.
а{х)и + b(x)v = fix).
(4.1)
§ 4. ЗАДАЧА РИМАНА — ГИЛЬБЕРТА ДЛЯ ПОЛУПЛОСКОСТИ 29
Что касается w(z)y то эта функция на основании
особенностей контактных задач, как это показано в § 2,
должна удовлетворять следующим условиям:
а) Она регулярна в области, исключая границу; на
границе в точках разрыва а{х) и Ь(х) она может иметь
особенности вида ζ~θ, где IθI <1.
Могут быть также задачи, в которых ιυ(ζ) должна
быть ограничена в точках разрыва а(х) и Ъ(х). Заметим,
что это налагает некоторые дополнительные условия на
fix) — правую часть граничного условия задачи Рима¬
на — Гильберта (4.1).
б) На бесконечности функция w{z) ведет себя как
cz~l.
Подробное исследование задачи Римана — Гильберта
дано в книге Н. И. Мусхелишвили [5]. Здесь мы не бу¬
дем касаться решения этой задачи в наиболее общей
постановке.
При указанных выше условиях выражение для
функций w(z) будет пеединственным. Как мы увидим
в дальнейшем, в него будет входить несколько произ¬
вольных постоянных.
Будем представлять w(z) в таком виде:
w(z) = Wi(z) + w0(z), (4.2)
причем w0(z) = ио — iv0 является решением однородной
задачи, когда отыскивается функция, удовлетворяющая
граничному условию
а(х)щ + b(x)v о = 0. (4.3)
Найдем функцию wq(z). Введем в рассмотрение вы¬
ражение
ω (х) = arclg (4.4)
При этом мы будем брать значение arctg, меньшее по
абсолютной величине чем π/2, т. е. находящееся в пер¬
вой и четвертой четвертях.
Если а(х) и Ых) разрывны, то ω(χ) может быть так¬
же разрывна, причем точки ее разрыва будут совпадать
с соответствующими точками для а(х) и Ь(х).
Аналитическая фупкция, регулярная в нижней полу¬
плоскости, действительная часть которой на оси х рав¬
30 ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
на со(.г), выражается так:
Ω (2) = Ω, — iQt = - -L j ω (х)(4.5)
— oo
Следовало бы, вообще говоря, написать
+ оо
Ω = ~к ί ω τ=Γζ +ic■
— oo
Однако из условия, налагаемого на w(z), а значит, и на
Wq(z) и W\(z) и состоящего в том, что эти функции стре¬
мятся к нулю при стремлении ζ к бесконечности, выте¬
кает, что постоянная с должна быть принята равной
нулю.
Формулу (4.5) нетрудно доказать на основании
свойств интегралов типа Коши. В самом деле, рассмот¬
рим функцию Ω(ζ):
-j-oo
ОЮ-В,-®,-—i j »(*)^.
— оо
Предельное значение интеграла типа Коши при подходе
к точке z = x снизу будет
Ω (2) го ~ Ωι (#) ^£^2 {ρέ) ==·
-foo
= j ω(ί)^ + ω(χ), (4.6)
— oo
или, иначе,
Re [Ω (я)]?—x—го = φ (*^)·
Таким образом, действительная часть Ω(ζ) на оси х
равна плотности интеграла типа Коши, распределенной
на этой оси, что и доказывает высказанное выше ут¬
верждение. Заметим, что в правой части выражения (4.6)
интеграл понимается в смысле главного значения. В ре¬
зультате получим
Ω W = а. — №... = - Λ J [«„ §£>] (4.7)
§ 4. ЗАДАЧА РИМАНА — ГИЛЬБЕРТА ДЛЯ ПОЛУПЛОСКОСТИ 31
На оси х при подходе к точке ζ = х снизу будем
иметь
Ωχ (х) — ?Ώ2 (х) = arctg-^y^ — /Ω2 (ж). (4.8)
а \х)
Если для arctg, как уже указывалось, брать значе¬
ние, меньшее по абсолютной величине чем π/2, то бу¬
дут иметь место следующие соотношения:
Гб (гг) I а (х)
cosarctg !-Ы = -
"(*)| Уа2(х)+Ь2(х)
sin arctg I 1 — l>-^ -
.p(*)l
la (*)J у „
V a2 (x) + b2 (x)
(4.9)
(при другом значении arctg, находящемся во второй или
в третьей четверти, в правых частях этих равенств нуж¬
но брать знаки минус). Следовательно, условием одно¬
родной задачи Римана — Гильберта будет
а (х) и0 + Ь (х) νΌ =
= Уа2{х) + ЬЦх)\ ria(x) ' -и0+ / ;&(χ)_=ι;0] =
|_ У а (х) + Ъ2(х) 1 а (х) + b (х) J
= 1 Га2 (ж) + Ь2 (х) [cos arctg ^ и0 + sin arctg Щ v0j = 0.
Принимая во внимание (4.8), придадим этому усло¬
вию такой вид:
я (х) и0 + Ь (х) v0 =
= У а2 (х) + b2 (х) [cos Ωχ (х) и0 + sin Ωχ (х) f0] =
= У а2 (х) + Ь2 (х) Re[etQl(iC) (м0 — iv0)] =
= /а2 (х) + Ь2 (х) Re \еш*х)и;0 {х - *0)] = 0. (4.10)
Так как а(х) и Ь(х) одновременно не обращаются в
нуль и поэтому j /а2 (х) + Ь2 (х) Ф 0, то на основании
(4.10) будем иметь
Re [eiQ*x)w0 (х - Ю)] - 0. (4.11)
Умножая это выражение на βχρΩ2(ζ) и принимая во
32
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
внимание (4.7), получим
Re (Ио _ ^о)] = Re (Uq _ ^о)] =
= Re jexp Г- ±- J (arctg £Ц) ^-1 w, (ζ) 1 = 0.
* L _οο J ) z=x—io
(4.12)
Это условие будет выполнено, если выражение, от
которого берется действительная часть в уравнении
(4.12), будет равно некоторой функции, принимающей
на действительной оси мнимые значения. Поскольку
u?q(z) должна быть регулярна в нижней полуплоско¬
сти, то в качестве такой функции может быть взята ра¬
циональная функция с действительными коэффициента¬
ми и притом такая, чтобы ее полюсы находились на
действительной оси. Итак, условие (4.12) будет удовлет¬
ворено, если
ехр [_ 4- J (агс1^Щ) г^-г] ю« <z) =* Ш (4ЛЗ>
При этом рациональная функция, находящаяся в
правой части, должна быть такой:
Р (ζ) _ Р (ζ)
ew Π(ζ-β»)'
(4.14)
Здесь βη — действительные коэффициенты, а полином
Ρ(ζ) принимает действительные значения на оси х. На
основании этого будем иметь следующее выражение для
wq(z):
Так как согласно первому из исходных условий, на¬
лагаемых на wo(z), она может иметь полюсы только в
точках разрыва коэффициентов а(х) и Ь(х) [и, следова¬
тельно, в точках разрыва arctg (b(x)/a(x))], то отсюда
следует, что значения βη должны совпадать с коорди-
§ 4. ЗАДАЧА РИМАНА — ГИЛЬБЕРТА ДЛЯ ПОЛУПЛОСКОСТИ 33
патами этих точек разрыва. Однако количество значе¬
ний β„, т. е. количество корней полинома, находящегося
в зпаменателе, может быть и меньше общего числа то¬
чек разрыва.
Таким образом, решение однородной задачи Рима-
на — Гильберта оказывается ;неедивственньш, так как
в выражение для полинома Ρ(ζ) может входить несколь¬
ко произвольных постоянных. Количество этих постоян¬
ных можно уменьшить, если предписать искомой функ¬
ции определенный вид особенностей в точках разрыва
коэффициентов а(х) и Ь(х), а также определенное по¬
ведение на бесконечности. В нашем случае условия, на¬
лагаемые на эту функцию, содержат, во-первых, требо¬
вание, касающееся характера особенности в точке раз¬
рыва коэффициентов а(х) и Мя), а во-вторых, требова¬
ние, заключающееся в том, чтобы она вела себя на
бесконечности как cz~l.
Таким образом, учет этих требований при построе¬
нии функции wo(z) позволяет сократить количество про¬
извольных постоянных, входящих в ее выражение. За¬
метим, что в случае, когда а(х) и Ь(х) имеют разрывы
в двух точках (это соответствует контактной задаче о
давлении одного штампа), удовлетворение указанным
требованиям вполне определяет искомую функцию.
В частном случае, когда рациональная функция,
входящая в выражение (4.15), равна постоянной, будем
иметь
w0 (z) = ic exp ^ J arctgj (4.i6)
Найдем теперь решение неоднородной задачи Рима-
на — Гильберта, т. е. дадим выражение для функции
Wi(z) = щ — ivi, удовлетворяющей на действительной оси
граничному условию
а(х)щ + b(x)v ί = fix). (4.17)
Будем при этом исходить из найденного выше ре¬
шения однородной задачи. Функция Wo(z) = щ —■ iv0 при
ζ = х — Ю, т. е. при подходе к оси х снизу, удовлетво¬
ряет граничному условию
а(х)щ + b{x)v о==0.
Л. А. Галин
34
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
При этом действительная и мнимая части этой функции
будут иметь следующие значения:
Ъ(х)
V а\х) + ъг(х)
IVо(х — iO) |,
vn =
а (х)
V а\х) + Ь2(х)
| w0 (х — Ю)|.
(4.18)
Это следует непосредственно из выражения (4.12), если
в нем отделить действительную и мнимую части, для
чего в интеграле типа Коши необходимо перейти к пре¬
дельному значению, устремляя ζ к точке х. При этом
должно быть принято во внимание, что значение
arctg(6(^)/a(^)), на основании которого определяется ар¬
гумент и>оЫ, мы берем по абсолютной величине мень¬
шим чем π/2.
Определим теперь действительную часть от
iwi(z)/w$(z) при z = x — Ю. Будем иметь
Re
1^1
wo
= Re
i (иг - iPj)
Re
1 (и0 + ^0)(“ι -
ul + vt
ll + vl
I wo I*
(4.19)
Подставляя значения Щ и г:о из (4.18), получим
iw-
Re
ul + ί,·2
о
а (х)
_ / а2 (х) + Ъ2(х)
и1 +
ъ (х)
I а2 (х) + Ь2(х)
\w0{x—г0)|·
Из условия (4.17) следует, что это выражение может
быть представлено так:
Re
('ш1 (х — ί'0)
«’о (X — «0)
/ (ж)
у а (х)
Ь2(х)
I ш0 (ж — Г
(4.20)
Функция, действительная часть которой на оси х
равна правой части (4.20), выражается на основании
§ 4. ЗАДАЧА РИМАНА — ГИЛЬБЕРТА ДЛЯ ПОЛУПЛОСКОСТИ 35
(4.5) следующим образом:
+ оо
*■<*>--И
/(*)
у а2 (*) + Ь2(х)
| w0 {х — iO) |
dx
(4.21)
Если будет иметь место равенство
iw. (ζ)
то оно повлечет за собой и равенство действительных
частей этих функций на оси х и, таким образом, будет
удовлетворено выражение (4.20). Итак, имеем
iw1 (ζ) 1 +f° Г f(x) 1 1 dx
' (*) + F (*) I
_! l_i
•0 (x — Ю) I ] a? -
Отсюда определяется функция W\(z), которая явля¬
ется решением неоднородной задачи Римана — Гильбер¬
та:
+ оо
/ (я) 1 dx
•«И I
L — оо
(4.22)
Так как в это выражение входит и?оЫ, которая оп¬
ределяется неединственным образом, то, следовательно,
w\(z) будет также неедипственной. Можно было бы
представить функцию, решающую неоднородную задачу
Римана — Гильберта, также в других формах, однако
для наших целей приведенное здесь выражение является
наиболее удобным.
В частном случае, если в качестве решения однород¬
ной задачи взять формулу (4.16), будем иметь
+ оо
<2) = - * еХР [ί ί arCtS (Ш) ^]
f+oo
— oo
X
X exp
f (*)
(*) + b2 (x)
X
X
[+oo
-i J arctg
— oo
b (t) dt
a (t) t — ;
dx
(4.23)
36
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Общее решение задачи Римана — Гильберта может
быть, согласно (4.2), представлено в виде суммы двух
слагаемых:
w (ζ) = Wl (ζ) + w*0 (ζ) == wQ (z) x
X
π \ V a2 (x) + Ьг (,) ί0) I * - *] + ^ (Z)’ (4,24)
где wq{z) и w*0 (z) — решения однородной задачи (не обя¬
зательно одинаковые), которые определяются на осно¬
вании (4.15).
Здесь мы пользуемся несколько иной формой ре¬
шения задачи Римана — Гильберта для полуплоскости,
чем это приведено в книге Н. И. Мусхелишвили [5]. По¬
кажем, что эти выражения тождественны.
В книге Н. И. Мусхелишвили [1] дано решение этой
задачи для верхней полуплоскости, причем отыскивается
функция ФЫ = и + iv, удовлетворяющая условию
а(х)и — b(x)v = с(х). (4.25)
Обозначим решение однородной задачи
Χ(ζ) = и0 + iv о,
причем
а{х)и0 — b{x)v о = 0. (4.26)
Решепие неоднородной задачи выражается следую¬
щим образом:
ф « - Ψ i (!)- (4'27>
— ОО
Здесь X+(t) — значение X(t) при подходе к оси х свер¬
ху. [В наших обозначениях X+(t) = X{t + z*0)J Второе
слагаемое является решением однородной задачи.
Выражение, находящееся в знаменателе под знаком
интеграла, может быть представлено так (будем для
краткости опускать аргументы):
(а + ib)(uQ + ivQ) = (auo — bv0) + i{bu0 + αν0).
§ 4. ЗАДАЧА РИМАНА — ГИЛЬБЕРТА ДЛЯ ПОЛУПЛОСКОСТИ 37
Но на осповании (4.26)
аио — bv о = О,
и поэтому
(а + ib)(u0 + ivo) = i(buo +αν 0). (4.28)
Если Χ(ζ) строить таким же образом, как была по¬
строена u?o(z), т. е. ее аргумент определять так же, как
и аргумент wq(z), то мнимая и действительная части бу¬
дут определяться следующим образом:
М0 = \Х+\, У0 = \Х+\.
Уа* + Ъг V7~Tbz
В таком случае (4.28) будет
ί (К + «>.) = I (i7==| IX* I + р4=, Iх+1) =
\Кя2 + 6г V а + b /
= «1/о« + Ь*|Х+|.
Следовательно,
(а + ib) (и0 + iv0) = i а? -4- Ъг \ Х+1.
На основании этого (4.27) принимает такую форму:
®<г> = Ψ ] т+штгъ-ё-'+сХ (2> =
— с»
= XJz) Г _ с (t) dt_ сХ ^ =
— ОО
= - ^ Г с^\ + cX(z). (4.29)
π J к» (<) + * (<) x I
—00
Это выражение эквивалентно ранее полученной фор¬
муле (4.24). Различие между ними состоит в том, что
(4.29) определяет функцию в верхней полуплоскости.
Кроме того, в данном случае у граничного условия (4.25)
приняты другие знаки коэффициентов при действитель¬
ной и мнимой частях, чем те, которые принимались на¬
ми ранее.
38
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Выражение (4.29) представляет некоторые удобства
для вычисления, так как в нем плотность в интеграле
типа Коши является вещественной функцией.
Аналогично можно показать (Н. И. Мусхелишвили
[l])t что решение однородной задачи эквивалентно при¬
меняемой нами функции w<y(z).
§ 5. Давление штампа при отсутствии сил трения
Если между штампом и упругим телом, занимающим
полуплоскость, отсутствуют силы трения, то граничные
условия на площадке контакта, согласно изложенному в
§ 3, принадлежат четвертому типу. В этом случае вслед¬
ствие отсутствия сил трения между штампом и упругим
телом тангенциальные уси¬
лия на границе упругой
полуплоскости равны ну¬
лю. Кроме того, при этом
известна величина переме¬
щения v. Будем полагать*
что поверхность упругого
тела вне штампа свобод¬
на от усилий. Гранич¬
ные условия на свобод¬
ной поверхности принад¬
лежат первому типу. Если предположить, что на поверх¬
ности упругого тела впе штампа усилия отсутствуют,
то будут равны нулю ау и %ху. Таким образом, %ху равно
нулю на всей границе упругой полуплоскости. Это об¬
стоятельство, как мы увидим из дальнейшего, значи¬
тельно упрощает решение задачи. Итак, на основании
(3.1) на границе упругой полуплоскости имеем условия
(рис. 2):
на участках СА и ВС (на свободной поверхности)
а у = 0, %ху =0; (5 1)
на участке АВ (под штампом)
v = f (х) -\- с, хху = 0.
При этом fix) — функция, соответствующая поверх¬
ности, ограничивающей основание штампа.
Вис. 2.
§ 5. ДАВЛЕНИЕ ШТАМПА ПРИ ОТСУТСТВИИ СИЛ ТРЕНИЯ 39
Здесь мы полагаем, что штамп, производящий дав¬
ление, перемещается параллельно оси у, не поворачи¬
ваясь при этом, и, таким образом, величина перемеще¬
ния границы упругой полуплоскости определяется функ¬
цией fix), к которой прибавлена некоторая постоянная.
р
'г
\
Pi
(
p3
ί © ;
У////'/”',
у//////''/·
С
Aj В7 /42 ^2
Рис. 3.
На штамп действует сила Р, которая является равно¬
действующей давления, имеющего место на площадке
контакта. Величина силы Р может быть любой, однако
точка ее приложения будет в этом случае вполне опре¬
деленной.
В случае давления на упругую полуплоскость не¬
скольких штампов (например трех, как это показано на
рис. 3) будем иметь следующие граничные условия:
на совокупности участков L, состоящей из участков
СА\, В1А2, В2Аз и ВЪС (на свободной поверхности),
ау = 0, тху = 0; (5.2)
па совокупности участков Li, состоящей из участков
АхВи А2В2, А$ВЪ (под штампами),
v = fn ix) + const, τxy = 0. (5.2')
Здесь fnix) — функции, представляющие уравнения по¬
верхностей, которые ограничивают основание каждого из
штампов. Так, на участке Α\Βχ (под первым штампом)
будем иметь v = f\ix) + const; на участке А2В2 v =
= f2ix) + const; на участке А$ВЪ v = %ix) + const.
Здесь, так же как и в предыдущем случае, мы по¬
лагаем, что каждый из штампов перемещается парал¬
лельно оси у, но не поворачивается в процессе деформа¬
ции. На каждый из штампов действует сила, величина
40
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Рис. 4.
которой может быть произвольной, по точка приложения
является вполне определенной.
Задача может быть поставлена иначе: можно пред¬
полагать, что штампы жестко связаны друг с другом.
В таком случае каждая из сил, действующих на отдель¬
ный штамп, и точки их приложения определяются из
решения задачи; величина же равнодействующей всех
сил может быть произ¬
вольной.
Хотя, как мы увидим
из дальнейшего, оба ука¬
занных случая приводят
к одной и той же смешан¬
ной задаче для отыскания
функции комплексной пе¬
ременной, т. е. к задаче
Римана — Гильберта (см. § 4), однако вследствие неедин¬
ственности ее решения произвольные постоянные можао
подобрать так, что будет получено решение или для пер¬
вого, или для второго случая.
В задачах, которые были рассмотрены выше, пред¬
полагалось, что на один штамп или на несколько штам¬
пов действуют силы, приложенные во вполне определен¬
ных точках. В том случае, когда сила приложена в про¬
извольной точке или же действует некоторая система
сил, которая приводится к силе и моменту, будет проис¬
ходить не только перемещение штампа по направлению,
параллельному оси у, но одновременно с этим и его
поворот (рис. 4).
Приведем граничные условия, которые в этом случае
будут иметь место, применительно к случаю одного
штампа:
на участках С А и ВС (на свободной поверхности)
Ух у — 0»
на участке АВ (под штампом)
ν = f (х) + ах + с, хху
= 0.
(5.3)
Кроме того, имеют место дополнительные условия,
определяющие величины действующих на штамп силы
и момента:
§ 5. ДАВЛЕНИЕ ШТАМПА ПРИ ОТСУТСТВИИ СИЛ ТРЕНИЯ 41
b
b
р = j р(х) dx = — j (σ„)ν=0 dx,
a a
a
a
(5.4)
b b
a
a
Эти условия позволяют определить неизвестную ве¬
личину а — наклон штампа или, что то же самое ввиду
малости а, угол поворота штампа. В следующем парагра¬
фе будет рассмотрена одна задача такого типа.
До сих пор мы считали, что размеры площадки кон¬
такта являются заданными. В этом случае, если на
штамп действует ироиз-
чено гладкой поверхностью
(рис. 5). Первоначально штамп касается упругой полу¬
плоскости в точке. Затем, по мере возрастания силы,
размеры площадки контакта увеличиваются, однако до
тех пор, пока края площадки контакта не дойдут до то¬
чек А и В, давление будет, очевидно, оставаться огра¬
ниченным всюду, в том числе и в точках А\ и В\. Усло¬
вие ограниченности позволяет однозначно определить
давление, действующее на штамп, и, таким образом, най¬
ти вполне определенную силу, которая будет иметь ме¬
сто при заданных размерах площадки контакта.
Для решения контактных задач были введены две
аналдаические функции:
вольная сила, у его углов
возникают, вообще говоря,
бесконечно большие на¬
пряжения. Однако могут
быть задачи несколько
иного типа. Рассмотрим
давление на упругую по¬
луплоскость штампа, ос¬
нование которого ограни-
't
7
Рис. 5.
-foo
—оо
(5.5)
-foo
—оо
42
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
причем для отыскания этих функций в § 3 указаны гра¬
ничные условия, пригодные для различных случаев.
На основании (3.1) и (3.3) можно прийти к выводу,
что выражениям (5.1) соответствуют следующие условия
для определения функций W\iz) и w2iz) (см. рис. 4):
на С А и ВС
на АВ
пЕ
2 (ΐ — ν2)
νλ = 0, ν2 = 0;
f{x), v2 = 0.
(5.6)
Здесь β следующим образом выражается через коэффи¬
циент Пуассона ν:
Р =
1 — 2ν
2 — 2ν*
Аналогичные условия могут быть получены при оты¬
скании функций W\iz) и w2iz) в контактных задачах,
граничные условия которых даны выражениями (5.2) и
(5.3).
Обратимся к условиям (5.6) для определения функ¬
ций W\iz) и w2iz), При этом v2 — мнимая часть функции
w2iz) — равна нулю на всей оси х. Так как эта функция
регулярна в нижней полуплоскости и ведет себя на бес*
конечности как cz~l, то из указанного выше условия сле¬
дует, что она должна быть равна нулю всюду в полу¬
плоскости. Итак, w2iz) = 0.
В таком случае условие (5.6) будет таким:
на СА и ВС
0;
на АВ
ил =
пЕ
2 ('1 — ν2)
Г (*)·
(5.7)
Таким образом, для определения W\iz) получаем
частный и притом наиболее простой случай задачи Ри¬
мана— Гильберта с разрывными коэффициентами. Плос¬
кие контактные задачи теории упругости при отсутствии
сил трения исследовались многими авторами. Изложение
§ 5. ДАВЛЕНИЕ ШТАМПА ПРИ ОТСУТСТВИИ СИЛ ТРЕНИЯ 43
большинства результатов, относящихся к этому вопросу,
можно найти в монографии Н. И. Мусхелишвили [5] и
в третьем издании его книги [1]. Поэтому в этом пара¬
графе мы только кратко изложим некоторые результаты,
которые относятся к данному классу задач.
am*t a(x)-ff а(хН
b(x)=0 6(х)=1 Ь(х)=0
сГ(х)=0 А FW=£^ifte) в FW=(} $
Функция W\iz) удовлетворяет граничному условию
на оси х (рис. 6):
а{х)щ + b{x)v\ = Fix)\
при этом на участках С А и ВС имеем aix) = 1, Ых)=0,
а на участке АВ aix) = 0, Ых) = 1. Правая часть в этом
условии — функция Fix) —- определена таким образом:
F(x) = 0 на С А и ВС,
Функция W\iz), для определения которой даны гра¬
ничные условия (5.7), может быть найдена при помощи
выражений, приведенных в § 4. В данном случае функ¬
ции aix) и Ых) обладают двумя точками разрыва при
х = а и при х = Ь.
На основании (4.22) и (5.7) W\iz) выражается так:
а
Рдс. 6.
ИЧ (2) = Wо (ζ)
г 6
1 Г *Е к
L π j 2 (1 — ν2)
dx
. (5.8)
X — Ζ
Здесь принято во внимание, что Fix) — правая часть в
граничном условии задачи Римана — Гильберта — от-
44
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
лпчпа от нуля только па участке АВ, где она равна
πΕ (l-v2)-1/^).
При этом w0(z) — решение однородной задачи Гиль¬
берта — дается формулой (4.15):
Wo (*) = exp h f ω (x) др^· (5.9)
L — oo J n
В этом выражении
I π/2 на СА,
О на АВ,
π/2 на ВС.
Полином Ρ(ζ) имеет действительные коэффициенты,
а βη может принимать значения координат точек раз¬
рыва коэффициентов а(х) и Ь(х), т. е. а и Ъ.
Выполняя вычисления, находим следующее выраже¬
ние для Wq(z):
,ч Г π . 1 , Ь — zl iP(z)
w0(ζ) = exp г - T In — jn{zl’K) =
П
- i \/b~z iP (z) - _ l/b ~2 p {z) 10Ί
~г V a - г Π (ζ - Pn) ~ V в-гП(^-Рп)· ( }
n n
Для того чтобы искомая функция W\(z) обладала не¬
обходимым поведением на бесконечности и имела допу¬
стимые особенности, -следует положить
Р<*) = -1, П(*-Рп) = г-Ь.
п
В таком случае будем иметь
w0 (ζ) = 1 (5.11)
0W y{a-z){b-z) '
Подставляя (5.11) в (5.8) и принимая во внимание,
что У а? (х) + 62 (х) = 1, получим
(z) =
ь
= , Е 2ч 1 —Jjr (х) К(а-х)(х- Ь) (5.12)
2(l — v)Y(a — z)(b — z)J М '*-2 ' >
§ 5. ДАВЛЕНИЕ ШТАМПА ПРИ ОТСУТСТВИИ СИЛ ТРЕНИЯ 45
Общее решение, как было показано в § 4, слагается
из полученного выражения и решения однородной за¬
дачи. На основании этого окончательно получим
Для определения давления, действующего па штамп,
согласно (2.17), устремляем в этом выражении ζ к х и
отделяем мнимую часть:
Постоянная с определяется из условия, что давление,
действующее на штамп, равно заданной величине. Сле¬
довательно,
Итак, W\{z) выражается формулой (5.13). Как было
ранее установлено, w2(z) = 0. Согласно (2.22) могут быть
определены функции φ'(ζ) и ψ'(ζ), на основании кото¬
рых можно найти напряжения, возникающие в упругом
теле:
Формулы (1.30) и (1.31) позволят определить ком¬
поненты напряжения σΧι оу и гху, а максимальные, тан-
Wi (ζ) =
ь
Е
1
j Г (z)Y(a-x)(x-b)-^-z +
2(1 -νηγ(α-ζ)(ΰ-ζ)
а
а
р(*) = — Юу=о =
Ъ
а
а
Ь
(5.15)
а
46
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
гепциальпые п главные нормальные напряжения могут
быть найдены на основании (1.32), (1.33) и (1.34).
Если на основании полученных выражений для W[(z)
и w2(z) определить <р'Ы и ψ'(ζ), а затем найти <ρ(ζ) и
if (г), то окажется, что эти последние функции будут об¬
ладать на бесконечности логарифмическими особенно¬
стями. Однако перемещения и и ν определяются соглас¬
но формуле (1.21) через φ(ζ) и ψ(ζ) и поэтому также
Рис. 7.
будут иметь логарифмические особенности на бесконеч¬
ности. Следовательно, в задаче о давлении штампа на
полуплоскость перемещения па бесконечности обраща¬
ются в бесконечность. Поведение перемещения в данном
случае будет таким же, как и при действии сосредото¬
ченной силы на границу полуплоскости. Это будет иметь
место также и в других контактных задачах, аналогич¬
ных той, которая рассмотрена в этом параграфе., Нужно
сказать, что плоская задача теории упругости является
некоторой идеализацией, так как в действительности
давление оказывает тело конечных размеров. На осно¬
вании ее решения могут быть определены напряжения,
однако определение перемещений в этом случае невоз¬
можно.
Приведем выражения для давления, возникающего
под штампом, при некоторых формах поверхности, ог¬
раничивающей его основание. При этом Р — сила, дейст¬
вующая на штамп.,
1. Штамп с плоским прямолинейным основанием.
Ширина 2а (рис. 7, а и б). Давление иа площадке кон¬
§ 5. ДАВЛЕНИЕ ШТАМПА ПРИ ОТСУТСТВИИ СИЛ ТРЕНИЯ 47
такта равно
Р
р(х) =
пУ а2-х
2. Штамп с наклонным прямолинейным основанием.
Ширина 2а, наклон а; давление равно
Р Еах
р(х) =
л У а2 — х2 2 (ί — ν2) У а2 — х2'
Эта формула будет иметь смысл тогда, когда всюду
на площадке контакта давление будет положительным.
Рис. 8.
3. Давление кругового цилиндра (рис. 8, а и б). Если
радиус цилиндра велик по сравнению с размерами пло¬
щадки контакта, то уравнение поверхности, ограничива¬
ющей основание штампа, будет приближенно выражать¬
ся формулой
/(*)=24
а давление, возникающее под штампом:
, ч Е (а2 — 2х2) , Р
р (х) = _ -{ ^ ■
4(l-v2UK«2-*2 ηγα2-χ2
На рис. 8, б показано распределение давлений под
штампом при том значении силы, действующей на
штамп, когда оно остается ограниченным.
48
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
4. Штамп с закругленными краями (рис. 9, а и б).
Будем рассматривать цилиндр, контуром которого явля-
Рис. 9.
ется парабола четвертой степени. Давление, действую¬
щее под штампом:
/>(*) = - ^4 [(«2 + 2х2)
ока
§ 6. Давление штампа при отсутствии сил трения
(продолжение)
Рассмотрим задачу о давлении штампа с плоским ос¬
нованием, на который действует сила, приложенная к
середине штампа, и момент
или, что то же самое, слу¬
чай, когда точка приложения
силы является произвольной
(рис. 10, а и б).
Будем полагать, что тре¬
ние между штампом и упру¬
гой полуплоскостью отсутст¬
вует. В случае возникнове¬
ния отрицательного давления
штамп должен отрываться
от упругой полуплоскости.
Одна из границ площадки
контакта в этом случае из¬
вестна; другая граница под¬
лежит определению из усло¬
вия ограниченности давления
δ)
Рис. 10.
§ 6. ДАВЛЕНИЕ ШТАМПА ПРИ ОТСУТСТВИИ СИЛ ТРЕНИЯ /кг)
л этой точке. Аналогичная задача была рассмотрена
Я. Б. Львиным [1]. Мы приведем здесь решение кон¬
тактной задачи, при отрыве от основания, в качестве
примера приложения метода, который изложен в преды¬
дущих параграфах. Результаты этого исследования мо¬
гут быть применены при установлении условий устой¬
чивости фундамента, имеющего плоское основание.
Если считать основание, на котором покоится фун¬
дамент, абсолютно жестким, то при различных значе¬
ниях момепта возможны два случая:
М <Ра — фундамент неподвижен,
М = Ра — фундамент опрокидывается.
В действительности, так как основание является уп¬
ругим телом, при каждом значении момента М, не пре¬
вышающем Ра, фундамент будет иметь определенное
положение.
При некотором значении момента М произойдет от¬
рыв фундамента от основания. Очевидно, это следует
считать началом опасного состояния фундамента.
Определим положение фундамента под действием си¬
лы и момента. Введем функцию w\(z), которая в данном
случае будет
п
wx (ζ) = щ — ii\ = j {ov)y=0 (6.1)
—a
причем на основании (2.19) имеем
(°у)у=о = ^ (Im Щ (z))y=o· (6.2)
Уравнение основания штампа следует принять в виде
fix) = — ах + с. (6.3)
Здесь а — угол поворота штампа. Из (6.3) следует
/'(*) =-а. (6.4)
На основании (5.7), используя (6.4), получим следующее
граничное условие для определения функции ινχ(ζ):
= О, — оо <я< —а,
ы1 = т———«г ос, — а<ж<а, I (6.5)
2 (1 — ν )
= 0, а <х< + оо.
4 л. А. Галин
50
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
На бесконечности функция w{(z) должна вести себя
следующим образом:
к (я))^оо -У — |, Р = - { j (ау)у=0 dxJ. (6.6)
Момент сил, действующих на штамп, относительно
точки с координатой а равен
+а
М = Ра + j (ву)у=0 (а — t) dt. (6.7)
—а
Применяя формулу (5.13), нетрудно найти решение
граничной задачи (6.5). Будем иметь
Н+ (М>
Для определения постоянной с рассмотрим поведение
полученной функции на бесконечности- При ζ -> <»
, ν пЕа Г1 fz —а а
<г) = - ЛТ—7)[Угт^~1.
+
Y(z — a) (z + а)
[пЕа , 1 2
Отсюда, принимая во внимаиие (6.6), получаем сле¬
дующее соотношение:
пЕ а
2 (1 - V2)
щм посто
с = — Р —
а 4- с = — Р, (6.9)
из которого находим постоянную
тсЕа
2(1-/)“·
Таким образом, функция W\(z) будет
+{-ρ-πτ^)ή^· (610)
Определим теперь значение угла поворота а и зна¬
чение действующего на фундамент момента, при кото¬
§ 6. ДАВЛЕНИЕ ШТАМПА ПРИ ОТСУТСТВИИ СИЛ ТРЕНИЯ
51
ром происходит отрыв от основания, причем будем по¬
лагать, что отрыв происходит в точке х = — а.
В этой точке давление в момент отрыва должно быть
ограниченным. Но давление является плотностью в ин¬
теграле типа Коши (6.1), а из свойств этих интегралов
следует, что при ζ = — α функция W\(z) должна быть
ограниченной.
Подставляя в выражение для функции w{(z) (6.10)
значение z = — a и выделяя коэффициент при (z — a)~ч%
который должен быть равен нулю в том случае, если
функция W\(z) будет в этой точке ограниченной, нахо¬
дим следующее соотношение между силой Р и углом
поворота а:
пЕа ( ъ„\У± х I η пЕаа \, 0 ч_!4 ^
-2ТГГ7)(-2,>) +(-р-2-(Г37|)(-2“> =0'
откуда следует, что
- ,πΕα 2\ 2 а = -Р- -*Еа\; (6.11)
2 (1 - ν2) 2 (1 - ν2) V '
и что Р получает выражение
р = ~Еаа* (6.12)
2(l — v ) V '
Таким образом, угол поворота в момент отрыва фун¬
дамента от основания будет
« = 2(‘„д«>'’· (в·13)
Функция W\(z) при отрыве от основания в точке
ζ = а примет следующее выражение:
2 Р
(6.14)
Давление, возникающее под фупдаментом, будет
[Wi (z)],=0c
Ργα-χ_ ^_ ^615)
а Ψ а х -ш г * о ' '
Р (*) = — {Оу)у=о = - j Im [li’x (z)],=0c =
+ * Y a2 — хг
52
ГЛ. I ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
На осповании (6.15) может быть определен момент,
под действием которого произошел поворот фундамента:
-j-o.
М = Ра + ( у)у—ъ (а — х) dx,
пли, подставляя сюда выражение для давления (6Л5),
будем иметь
- ■ ■ ' 2
М = Ра + - f Г- \^а-тг =
Ч |«Г “ + * у а
2
X
(а — х) dx. (6.16)
Для вычисления этого интеграла вводим безразмер¬
ную величину % = х/а. Тогда получаем
М =
= JpL^l Г \±-лГlnl_ 1 -JL·
I 1 я ЗД « ^ 1 + 6 ay 1_]
= J VT4Fd|j = P|·. (6.17)
Итак, отрыв фундамента от основания произойдет,
если момент, действующий на фундамент, достигнет ве¬
личины, большей Ра/2, и, следовательно, сила будет при¬
ложена в точке, находя¬
щейся от середины фун¬
дамента на расстоянии,
большем а/2 (рис. 11).
Если М<Ра/2, то сопри¬
косновение между фунда¬
ментом и упругим основа¬
нием будет происходить
на всем участке — а < х <
< а.
Определим теперь угол поворота фундамента и дав¬
ление, возникающее под ним в случае, когда М>Ра/2.
В этом случае следует определить положение одной из
границ площадки контакта. Будем полагать, что точка
имеет координату х = —Ь (см. рис. 10). В таком случае
§ 6. ДАВЛЕНИЕ ШТАМПА ПРИ ОТСУТСТВИИ СИЛ ТРЕНИЯ
53
для функции w\iz) будем иметь
(г> “ - лγΝ*!=τ - *)+с <6-18)
Условия, которые послужат для определения а и Ъ
при заданной силе Р, таковы:
1) w\(z) при z-+ оо должна стремиться к — P/z\
2) W\{z) должна быть ограничена в точке ζ = Ь;
3) дана величина момента, действующего на фунда¬
мент.
Первое из этих условий приводит к соотношению,
которое получается аналогично (6.9):
πΕα а — Ъ , п
iTTv)— + ' = ~ρ·
откуда находим постоянную
'~-ρ-ΤίΓ=7Γ· <6М>
и, следовательно, выражение для w\(z) будет таким:
j_ р пЕа (а — Ъ)^ 1
\ 4 (l — v2) )V(z — a) (z — b).
Использовав второе из условий — ограниченность в
точке ζ = &, получим по аналогии с (6.11)
+ <6-20)
ИЛИ
Р = пЕ*{п ~6). (6.21)
4 (1 - ν2) 4 '
Принимая во внимание это соотношение, найдем дав¬
ление
Р («) = — 4~ [И>1 (z)L=* =
-,-Ebs(vl=i+v,<°·22>
54
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
или, после преобразований,
р (х) = ·
- Е
hV—·
г а — х
/ 24 \ п · (6.23)
2 (1 — ν2) r а —х 4 '
Но согласно (6.21) коэффициент в этой формуле равен
Еа
2 Р
2 (1 — ν2)
(а — Ь) π *
Тогда выражение для дав¬
ления будет
/\ 2^ х — Ъ
Р (я) п (а — ΐή у а — х·
(6.24)
Найдем теперь величину
момента, под действием ко¬
торого происходит поворот
штампа:
1 Р
М=-Ра
X
π а — Ъ
а
(6.25)
a -j- Ь
= —Р
На основании (6.25) положение границы участка
определится следующим образом:
, 2 М
Ь = -р а.
(6.26)
Подставляя (6.26) в (6.24), находим окончательное
выражение для давления
р(х) =
»(-f)
Г 2 М
1/ X — -р- + а
(6.27)
Для определения угла поворота штампа воспользу¬
емся выражением (6.21), подставляя в которое (6.26),
§ 7. ЗАДАЧИ ПРИ НАЛИЧИИ СИЛ ТРЕНИЯ
55
найдем
При стремлении М к Ра величина угла поворота стре¬
мится к бесконечности, т. е. фундамент опрокидывается.
Итак, формула (6.22) для давления, возникающего
под фундаментом, справедлива тогда, когда момент, дей¬
ствующий на фундамент, находится в следующих пре¬
делах:
Ц- СМС Ра.
На рис. 12 даны графики, показывающие распределе¬
ние давлений, возникающих под фундаментом при раз¬
личных соотношениях между моментом М и величи¬
ной Ра.
§ 7. Задачи при наличии сил трения
Будем решать задачу о напряженном состоянии,
возникающем в упругом теле при вдавливании в него
одного или нескольких штампов, причем между штам¬
пами и упругим телом имеют место силы трения. При
этом мы будем полагать, что штампы находятся в со¬
стоянии предельного равно¬
весия, когда каждый из них
подвержен действию силы,
равной произведению коэф¬
фициента трепия на вели¬
чину силы, прижимающей
штамп (рис. 13). Дальше бу¬
дет показано, что если штам¬
пы перемещаются по поверх¬
ности упругого тела, причем
скорость этого перемещения
невелика по сравнению со скоростью звука в упругой
среде, то при решении этой задачи можно пренебречь
динамическими явлениями и рассматривать ее так же,
как и задачу этого параграфа.
Результаты, содержащиеся в этом параграфе, были
кратко изложены в статье автора [1]. Граничные условия
Рр
Р
ζ
/ - у ■■
&
Ряс. 13.
56
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
при этом будут следующими (рассмотрим вначале слу¬
чай одного штампа): на свободной поверхности отсутст¬
вует внешняя нагрузка, поэтому при у = О
Gy = 0, τχΰ = 0. (7.1)
Под штампом имеет место линейное соотношение
между нормальным давлением и тангенциальной нагруз¬
кой. Кроме того, дана величина перемещения ν. Следо¬
вательно, при у = 0
гху + ptfy = 0, ν = fix) + const. (7.2)
Здесь р — коэффициент трения между штампом и
упругим телом, fix) — уравнение контура штампа. Таким
образом, граничные условия принадлежат, согласно на¬
шей терминологии, к первому и третьему типам.
Для нескольких штампов будем иметь такие гранич¬
ные условия:
па участках свободной поверхности iy = 0)
Оу — 0, хху = 0; (7.3)
на участках, где штампы соприкасаются с упругим
телом,
Хху +ρΛσν = 0, v = fkix) + const. (7.4)
Здесь Дix)— уравнение контура штампа на к-м участке,
pft — коэффициент трения на к-м участке. Коэффициент
трения рА может быть различным на различных участках.
Например, если один штамп перемещается по поверхности
упругого тела в положительном, а другой в отрицатель¬
ном направлении, то коэффициенты трения будут иметь
одинаковую абсолютную величину, но противоположные
знаки.
В § 2 было показано, каким образом перемещение
выражается через компоненты напряжения, действую¬
щего на поверхности, су и гху.
На основании (2.16) имеем следующее выражение
для перемещения ν при у = 0:
ъ
2 (l?-~7) V + C°nSt = I (σν^=° ln It ~ ХI dx ~~
' а
х
-|Ξ^"ί(-τ*Λ=βΛ. (7.5)
а
§ 7. ЗАДАЧИ ПРИ НАЛИЧИИ СИЛ ТРЕНИЯ
57
Производная от перемещения дается выражением
(2.15):
2(ι - ν2) )у=0 = J ^σ^=0Τ^Τχ ~ 2^Γ2ν П ху)у=ош (7·6)
Так как компоненты напряжения оу и τотсутствуют
на участках свободной поверхности, то в выражении
(7.6) интегрирование производится или в интервале от
а до b для одного штампа, или на некоторой совокуп¬
ности участков для нескольких штампов.
На основании соотношения (7.4) выражение (7.6)
будет таким:
ziE j ди \ Г / \ dt .1 — 2v . ч
2 (l — ν2) \ дх )у=о J №у)у=0 t — х 2 ~ 2v^^h (cfy)y==0'
(7.7)
Это последнее выражение написано применительно к
случаю нескольких штампов.
Для одного штампа будем иметь выражение
2("J ν*)(ΐ)ϊ=0 = ί Т=~х + ibdbπΡ(σν)ί/=ο* (7·8)
Рассмотрим вначале этот случай. Введем функцию
ь
wi (z) — ui ~ J (ау)у = о х _ ζ (7-9)
а
Правая часть (7.8) может быть выражена через дей¬
ствительную и мнимую части функции (7.9) при у = 0:
лЕ ί ди \ ί 1 — 2ν /гη i ач
ίΰ37)Μ»=Γ“1 + ρ~’1’1' <7-10)
Принимая во внимание условие (7.2), получим
= Ъ + (7.11)
На участках свободной поверхности (оу)у=о = 0, поэтому
мнимая часть введенной функции w\iz) при у = 0 будет
равна нулю. Таким образом, имеем граничные условия:
58
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
па участках вне штампа {у — 0)
V\ = 0, —оо < X < а, Ъ<Х< оо; (7.12)
на участке, где штамп соприкасается с упругим те¬
лом (у = 0),
и1 + Р Г {Х)' а<х<Ь■ (7Л2'>
Для нескольких штампов, исходя из (7.3) и (7.4), по¬
лучим условия:
на участках свободной поверхности (у = 0)
VI = 0;
на участках, где штампы соприкасаются с упругим
телом,
“‘+^>=лгЬ>';и· (7'13>
Здесь fk (я) — уравнение поверхности, ограничивающей
штамп на &-м участке, pft — коэффициент трения на к-м
участке (как было указано выше, знак коэффициента
трения определяется направлением перемещения штампа).
В § 2 было показано, что функция w\(z) должна
удовлетворять следующим требованиям:
а) она может иметь особенности на действительной оси
вида ζ_α, где 0<а<1; что является следствием того,
что под штампами не могут иметь места сосредоточен¬
ные силы;
б) на бесконечности w\(z) должна вести себя как Ρζ~ι,
где Р — сила, прижимающая штамп к упругому телу,
или сумма сил, действующих на несколько штампов.
Нужно принять во внимание также следующее об¬
стоятельство: при дифференцировании fk(x) на каждом
из участков akbk утрачена постоянная; постоянные вой¬
дут в выражение функции, определяемой на основании
условий (7.13), и должны быть найдены на основании
дополнительных данных.
Таким образом, задача о вдавливании штампов в
упругое тело приводится к частному случаю граничной
задачи смешанного типа по отысканию функции комп¬
лексной переменной (задачи Римана — Гильберта), ко¬
торая была рассмотрена в § 4.
§ 7. ЗАДАЧИ ПРИ НАЛИЧИИ СИЛ ТРЕНИЯ
59
Необходимо отыскать функцию, которая на оси х
удовлетворяет условию а(х)и + b(x)v = fix). При этом
для а(х) и Ых) будем иметь
а(х) — 0, Ь(х) = 1, — оо <£<а, Ь <Z x<Z оо;
Найдем вначале решение задачи о вдавливании одно¬
го штампа в упругое тело при наличии сил трения. Здесь
па штамп действует сила Р, причем будем полагать, что
штамп не может поворачиваться и сила рР, сдвигающая
его, не создает момента.
Для определения этой функции воспользуемся форму¬
лами (4.15), (4.22) и (4.29), данными в § 4. Решения
однородной задачи в данном случае имеют следующий
вид:
Здесь P(z)— некоторый полином (который, в частности,
может быть принят равным (z — a)(z — b), когда будет
получено простейшее решение).
Пользуясь этим выражением и беря различные поли¬
номы РЫ, получим решения однородной задачи, которые
могут быть использованы для нашей цели:
при этом I θ I <1 и, таким образом, удовлетворяется одно
из требований, налагаемых на функцию W\(z), которая
может иметь только интегрируемые особенности.
На основании полученных функций, применяя форму¬
лы (4.22) и (4.24), найдем следующие выражения для
а(х) = 1, Ь{х) = р^—aCxCb.
wi (z) = ехР
(z— a) (z — b)'
(7.14>
iP (ζ)
(7.15)
6\θ 1
a I ζ — b
(ζ — α)Θ(Ι — б)1'0
1
Здесь
60
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
функции w\(z):
w{х) (г) = Ь ==х
X.-И)/,+,·(£! )■
X
<7-16>
И’18) (2) f Е Т-—=Т х
(brir’i/'w^r1^· <7·ΐ7>
а
Е
ъ
г5 i=S f -0 r (Х) rfe-i · (7·18)
— α)θ(ζ — Ь) ® J (х — a) Q (Ь — х)θ 1 (аг — ζ)
Очевидно, эти решения не являются вполне общими,
так как дают вполне определенное, а не произвольное
значение для силы, прижимающей штамп к упругому
телу. Для того чтобы решение было общим, к нему нуж¬
но прибавить функцию, удовлетворяющую однородным
граничным условиям. В таком случае получим
wx (ζ) =
Е
X
ь
ΐ^θ ί Г И , \-θ /и_
(ζ — α)θ (ζ — b)1 (x — a) θ (b — x)® 1 (x — z)
+ W7 ГГ- (7·19)
(z —a)e(z —6)ΧΓΘ
§ 7. ЗАДАЧИ ПРИ НАЛИЧИИ СИЛ ТРЕНИЯ
61
На основании (7.19) давление может быть определено
согласно формуле
р(х) = — Im [ιυλ (z)]2=x_i0.
Если трение между штампом и упругим телом от-
1 1 2v 1
сутствует, то р = 0 и поэтому Θ = — arctg __ ^ .
Подставляя в (7.19) значения р и 9=у, получим вы¬
ражение для w\{z), эквивалентное (5.14), которое было
Таблица I. Значения Θ
<
II
о
to
ν=0,30
Ρ
θ
1 θ
Ρ
θ
i-e
0
од
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
0,500
0,489
0,482
0,469
0,457
0,447
0,438
0,428
0,416
0,406
0,397
0,000
0,011
0,018
0,031
0,043
0,053
0,062
0,072
0,084
0,094
0,103
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
ι,ο
0,500
0,492
0,479
0,473
0,464
0,455
0,447
0,437
0,429
0,420
0,411
0,000
0,008
0,021
0,027
0,036
0,045
0,053
0,063
0,071
0,080
0,089
получено ранее для случая отсутствия силы трения.
Значения Θ при различных значениях коэффициента
трения р и для значений коэффициента Пуассона ν =
= 0,25 и ν = 0,30 приводятся в табл. I.
Функции w(iUz) и ιυψ(ζ) будут давать решения, ог¬
раниченные в одной из крайних точек площадки контак¬
та, причем для первой из этих функций это будет в
точке х = а, а для второй — в точке х = &.
Так, например, ιοψ (ζ) позволяет найти решение зада¬
чи, приведенной на рис. 14. Здесь штамп является глад¬
ким в окрестности точки b и негладким вблизи точки а.
Поэтому в точке а решение будет неограниченным, так
как dv/dx при подходе к точке х — а слева будет равно
бесконечности. Неограниченность этой величины влечет
за собой неограниченность самой функции ινψ {ζ)
62
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
В точке же х = Ъ поверхность штампа гладка, и это
приводит к тому, что H>i2)(z) в этой точке ограничена.
Функция (7.19) позволяет найти решение контактной
задачи для штампа, у которого бесконечно большие дав¬
ления могут возникать на
обоих краях площадки кон¬
такта (рис. 15).
Рассмотрим теперь давле¬
ние штампа, который гладок
в окрестности обеих крайних
точек (рис. 16). В этом слу¬
чае w\{z) должна быть огра¬
ниченной при х = а и х = Ъ.
Вследствие этого ди/дх в
этих точках будет ограни¬
ченным, а также будет ограниченным (и притом, как
мы увидим далее, равным нулю) давление, возникающее
в этих точках.
Будем исходить из функции
(ζ) Е
ιυψ
(ζ):
2 (1 - ν2) У ί - р2
X
2ν
■ 2ν
X
—‘)“|/'(Ι)(|5ΙΓι#ι· σ-т
Ζ —
В точке х = Ъ эта функция ограничена. Предельное
значение интеграла при подходе к этой точке будет иметь
особенность вида (ζ — 6)_θ, однако множитель при интег¬
рале содержит (ζ — 6)θ.
Исследуем теперь поведение этого выражения в точке
х = а. Найдем предельное значение интеграла при под¬
ходе к этой точке:
J / <5) - - »< [/ <*> (йГХ. +
о о
+ jV (I) Д = jV (I) (b-lf -1 (l-afdt (7.20)
§ 7. ЗАДАЧИ ПРИ НАЛИЧИИ СИЛ ТРЕНИЯ
63
Для ограниченности Η>ιυ(ζ) необходимо, чтобы эта
величина была равна нулю, так как только в этом слу¬
чае, будучи умноженной на {ζ — 6)θ(ζ — α)_θ, она может
дать величину, равную нулю, т. е. ограниченную.
Рис. 15. Рис. 16.
Итак, условие ограниченности решения контактной
задачи на обоих краях площадки касания тел заключа¬
ется в том, чтобы имело место равенство
ъ
j1 Г (I) (b-lf-1 (ξ - α)-0<Ζξ = 0. (7.21)
а
При выполнении этого условия функция W\{z), реша¬
ющая задачу, может быть представлена в форме
wx (ζ) = Е . X
2<.-v·)/
х(йП''®(НГ‘^· <7'22)
а
Нетрудно убедиться, что она удовлетворяет необхо¬
димым условиям на бесконечности, так как интеграл
типа Коши, входящий в это выражение, при ζ ->■ оо ведет
себя как ζ~\ а множитель при нем стремится к единице.
Итак, если штамп вдавливается в упругое тело при
наличии сил трения, то величина площадки контакта не
может быть произвольной.
Если дано положение одной из крайних точек, на¬
пример х = а, то для определения другой точки х = Ь
64
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
следует решить уравнение
ь
J г (I) (Ъ - |)θ_1 (| - a)-*dl = 0. (7.23)
а
Покажем, что решение этого уравнения может быть
во многих случаях получено достаточно просто. Рассмот¬
рим в качество примера контактную задачу о давлении
кругового цилиндра при на-
При этом мы помещаем начало координат в одной из
крайних точек площадки контакта; здесь с — координата
середины штампа, a R — радиус окружности. Длину пло¬
щадки контакта обозначим через I.
В таком случае для определения I получаем следую¬
щее уравнение:
ι ι
j Г (I) (I )е-1гЧ = -JT j (5 - с) гв (I - = 0.
Введем безразмерную переменную ξι = \/1. Тогда по¬
лучим
личии сил трения (рис. 17).
Принимая обычное прибли¬
жение, т. е. заменяя окруж¬
ность параболой, уравнение
поверхности, ограничиваю¬
щей штамп, запишем следу¬
ющим образом:
Ряс. 17.
«
о
(7-24)
1
j (igj - ο) Гв|Г®<* - =
*0
= I j (|x - -f) 179 (1 - ξι)β_1<ϋι = 0,
§ 7. ЗАДАЧИ ПРИ НАЛИЧИИ СИЛ ТРЕНИЯ
65
или отсюда
1
ί!
I'
Ιί~θ (1 - hf-'dh —Γ.ίΐΓθ (1 - Ιι)0-1^! = о. (7.25)
о
Воспользуемся следующим представлением для ин¬
теграла
,7.26,
о
Применяя эту формулу к (7.25), найдем
Г (2 — Θ) Г (Θ) с Г (1 — Θ) Г (Θ) . 0
Г (2) I Г(1)
после чего, принимая во внимание, что Г(1) = 1, Г(2) =
= 1, получим
с _ Г (2 — Θ) Г (Θ) Г (1). Г (2 — Θ)
I Г(2)Г (1 - θ) Γ(θ) Г (1 - Θ)*
Так как имеет место соотношение
Γ(2-Θ) = (1-Θ)Γ(1-Θ),
то окончательно найдем
-j- = 1 — Θ. (7.27)
Вследствие того, что согласно (7.15)
Θ = arctg —^—трг,
π р (2 — 2ν)
получим искомое соотношение (см. рис. 17)
4- = 1 Х~ arctg
1 — 2v
I π 6 ρ (2 — 2ν) ’
Это соотношение полностью определяет положение
площадки контакта. Изменяя величину Ζ, получим раз¬
личные значения для силы Р, действующей на штамп.
При этом можно заметить следующее: если между штам¬
пом и упругим телом силы трения отсутствуют и, следо¬
вательно, коэффициент трения р = 0, то отношение с к
I равно 1/2. Таким образом, в этом случае ось симмет¬
рии штампа делит пополам площадку контакта. Если
5 Л. А. Галин
66
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
коэффициент трения между штампом и упругим телом
будет увеличиваться, то с стремится к нулю и, следова¬
тельно, площадка контакта перемещается таким образом,
что в пределе она будет располагаться на одной половине
контура симметричного штампа.
Подобное определение положения площадки контакта
можно достаточно легко произвести и для других случаев.
В частности, если уравнение кривой, ограничивающей
штамп, является некоторым полиномом, то определение
положения крайних точек площадки контакта, т. е. ре¬
шение уравнения (7.23), приводит к нахождению корня
алгебраического уравнения, степень которого на единицу
ниже степени полинома.
Функция w\(z), формулы для нахождения которой
приведены в этом параграфе, позволяет определить дав¬
ление, возникающее под штампом. В большинстве слу¬
чаев именно это представляет наибольший интерес.
Если необходимо определить напряжение в упругом теле,
то следует найти также функцию w2(z). Она определяется
согласно выражению
При этом интегрирование должно производиться по L,
т. е. по совокупности участков границы, где штампы
соприкасаются с упругим телом.
Здесь (гху)у=о — тангенциальная нагрузка, которая
определяется после нахождения давления, что можно
сделать после того, как будет найдена функция w\(z).
Если известны W\(z) и ιυ2(ζ), то определение компонентов
напряжения и максимальных нормальных и тангенциаль¬
ных напряжений может быть произведено по формулам
Можно отметить, что наличие сил трения для глад¬
кого штампа, например такого, как круговой цилиндр,
вызывает перемещение по направлению к поверхности
тела точки, где тангенциальное напряжение достигает
максимального значения. Это перемещение может оказать
влияние на прочность поверхностей контактирующих тел.
Указанное обстоятельство может быть проиллюстрирова¬
но фотографиями, полученными методом оптической
аналогии (рис. 18 и 19), которые взяты из книги М. М. Са-
L
(2.21), (2.22), (1.30) —(1.34).
§ 8. ЗАДАЧИ ПРИ НАЛИЧИИ СИЛ ТРЕНИЯ
67
верина [1], где показаны изоклины, т. е. линии равных
главных касательных напряжений в случае наличия и в
случае отсутствия сил трения. Эти результаты получены
для случая, когда оба контактирующих тела имеют
равные упругие постоянные. Однако общий характер
ш
т
Щ}\
1
|Ц, vflW'
Рис. 18. Рис. 19.
зависимости будет таким же и в случае, когда штамп
будет твердым.
На рис. 18 силы трения отсутствуют. На рис. 19 тан¬
генциальная нагрузка составляет 0,2 от нормальной, что
соответствует коэффициенту трения р = 0,2. При этом
точка, находящаяся в центре семейства изоклин, где
будет иметь ме^то максимальное тангенциальное напря¬
жение, переместилась по направлению к поверхности
тела.
§ 8. Задачи при наличии сил трения (продолжение)
Рассмотрим более подробно задачу о вдавливании в
упругое тело штампа с плоским основанием. Вначале
будет рассмотрен случай одного штампа, затем случай
двух штампов.
Пусть штамп прижимается к упругому телу силой Р.
В направлении оси х дей¬
ствует сила рР, которая сдви¬
гает штамп так, что он сколь¬
зит по поверхности упруго¬
го тела (рис. 20). При этом рР
предполагается, что штамп '
находится в состоянии пре¬
дельного равновесия или же Рис. 20.
5*
- 6
68
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
что скорость этого скольжения весьма невелика, так что
динамическим характером задачи можно пренебречь.
Будем полагать, что штамп перемещается так, что не
может поворачиваться под действии приложенных сил.
Так как уравнение контура штампа /(#)= с, то /'(#)=
= 0 и условия для определения функции W\{z) = щ — ivi
запишутся следующим образом [см. (7.12)]:
Таким образом, w\(z) определяется из решения одно¬
родной задачи и поэтому может быть построена из
функций
Разница между этими выражениями и выражениями
(7.15) обусловлена тем, что в данном случае взято про¬
тивоположное направление силы трения. Пусть
Подберем постоянные А и В таким образом, чтобы
при ζ
(Выше было указано, что таким должно быть поведение
функции w\{z) на бесконечности. При этом Р — сила,
действующая на штамп.) Для этой цели следует принять
v± = 0, — оо<С#<я,
Vi = 0, Ь<х<. оо,
(8.2)
р
Z
В таком случае
§ 8. ЗАДАЧИ ПРИ НАЛИЧИИ СИЛ ТРЕНИЯ
69
эго может быть преобразовано к виду
^(ζ) = — г·—— tl=>)e\Lz±- i] />(ΐ^)θ —
1X7 b — a\z — a) \_z — b J \z— a] z —<
_ p 1 1 1 1
, .Vi , ( .О-Уг . 7Ν/^-θ
(ζ — a) (ζ — b) (ζ — a) {ζ — Ъ)
iH -θ
(НН) · (*·3)
V(z — ο) (ζ — b)
Здесь
θ = — arctg -Ir—^rv
π & ρ (1 — 2v)
При отсутствии сил трения р = 0, поэтому Θ = 1/2. Из
(8.3) следует, что w\(z) в этом случае определяется вы¬
ражением
/ ч р
Щ (2) = - \ ί -7V
у (ζ — fl) (ζ — г.)
На поверхности упругого тела давление будет
Р (*) = — -J- Im [ϊ^! (z)]z=x_i0 = 1 р
π V(rt — Λ) (& — *)'
Таким образом, получена формула, приведенная ранее
в § о.
Следовательно, для w\(z) получено выражение, кото¬
рое только множителем отличается от той же функции
для случая отсутствия сил трения. Такая структура фор¬
мулы позволяет легко исследовать влияние трения.
Определим давление, действующее на границу упру¬
гого тела при наличии сил трения. Будем исходить из
выражения
р (х) = — Im [и?! (Z)h=*_i0.
В интервале а< х<Ъ будем иметь
70
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
отсюда
Р (я) = — Im wi (z) \z=x = ~ p^^
X
X
~Ϋ(x — a) (b — x)
(Ιξ-;)*"· (8·5>
Расположим начало координат в середине штампа,
причем · введем новые обозначения. Будем обозначать а
Таблица II. Значения коэффициентов λ и λ0
-1,00
-0,95
-0,90
-0,80
-0,60
-0,40
-0,20
0,00
1,019
0,730
0,530
0,398
0,347
0,327
0,318
оо
1,498
0,988
0,649
0,437
0,357
0,315
0,290
0,20
0,40
0,60
0,80
0,90
0,95
1,00
0,327
0,347
0,398
0,530
0,730
1,019
оо
0,282
0,283
0,302
0,360
0,449
0,578
вместо Ъ и —а вместо а. В таком случае получим
р{х) = -Р^ 1 fz+a\K-* =
^ W тг .4 /.__*) \а — х)
1
У(х + а) (а — х)
, sin πθ
= -Р-
а-\- х\
а — х)
(8.6)
Введем
найдем
π Уа2-
безразмерные координаты ξ = α;/α; тогда
ρ (I) =
sin πθ Ρ
π
/i-i:
1 (1 + 1)
Ά-θ
(8.7)
при этом —1 < ξ < +1.
Значения давления ρ(ξ) в различных точках под
штампом могут быть определены с помощью табл. И,
при составлении которой коэффициент Пуассона принят
равным ν = 0,3, а коэффициент трения р = 0,5. Давление,
которое будет иметь место в случае отсутствия сил
трения, обозначим ^ο(ξ). Формулы для ^(ξ) и ρ0(ξ)
§ 8. ЗАДАЧИ ПРИ НАЛИЧИИ СИЛ ТРЕНИЯ
71
представим следующим образом:
р «) = -£-λ, Po«)=4v
Значения коэффициентов λ и λ0 приведены в табл. II.
На основании полученных результатов построен гра¬
фик (рис. 21).
Рассмотрим теперь один случай контактной задачи
для двух плоских штампов, когда между штампами и
упругим телом возникают си¬
лы трения. В качестве при¬
мера рассмотрим задачу о
вдавливании двух штампов,
когда штампы при возраста¬
нии силы Р могут скользить
по упругому телу.
Пусть в упругое тело
вдавливаются два плоских
штампа, жестко связанных
друг с другом и находящих¬
ся на одной высоте (рис. 22).
Сила Р направлена по оси
симметрии штампов. При
вдавливании такого твердого
тела в упругое тело поверх¬
ность этого упругого тела перемещается относительно
него и скользит по нему. Будем полагать, что на площад¬
ке контакта не будут возникать участки со сцеплением.
Граничные условия для определения функции W\(z)
будут следующими [см. (7.13)1:
Ъ,
ν1 = О,
I 1 — 2v А
г1 + Р 9 — 2vVl ~
νι = О,
1 — 2ν
Mi-P2=2^ = 0’
= О,
— оо <
— Ъ<Сх<С — а,
— а < х<С а,
a <ix
Ъ<х<оо.
(8.8)
При этом w\(z) ->■ P/z, когда ζ ->■ оо. В точках х = а,
х = —а, х = Ь, х = —Ъ функция может иметь особенности
вида (ζ — с)а, где 0 < а < 1. В силу симметрии особен¬
ность в точке х — Ъ должна быть такой же, как в точке
72
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
х = —Ь. Точно так же особенность в точке х = а должна
быть такой же, как при х = —а.
Искомую функцию будем составлять из решений одно¬
родной граничной задачи, которые могут быть найдены
ψ/ш/щ
Ύ//////Δ/Λ
п
£
г
.ρ
щшщ
м
а
Рис. 22.
на основапии (4.13). Эти решения будут такими:
-рм-Ы’Ыг·
\1—Θ
(8.9)
Решение, удовлетворяющее всем условиям, постав¬
ленным выше, является суммой пары этих выражений,
из которых каждое умножено на соответствующую по¬
стоянную. Будем иметь
->«~?ЬИЗГ(£Г+
ч^язя-
р I , (z*-b
~ Ь*-а*\ ZU-«V +ZW-a·
= -£-ζ(£ζιΐ’Γίΐ
W-α*)
§ 8. ЗАДАЧИ ПРИ НАЛИЧИИ СИЛ ТРЕНИЯ
73
что может быть преобразовано следующим образом:
/ч Р (z2 — b2\~6
г2 λ2
л ζ — Ь
1 2 2
ζ — а
\Z
U2 —a2/ U2 —&*/ 22 — a2
— Pz
(z2 - b2) V* (z2 - b2f~1/2 (z2 - a2)1/2 (z* - a2) % “0‘ (8Л0)
Таким образом, окончательно для W[(z) получим сле¬
дующее выражение:
Pz fz2-b2\'A-e
V(z2-a*)(z2·
ί\ **ζ (z2—b2\Vz-n to *i\
^ (дГ?) · («-И)
При отсутствии сил трения р = 0 и Θ = 1/г? и мы по¬
лучаем
Pz
wx (ζ) =
V(z2-a2) (ζ2 — b2)
Аналогичное выражение приведено в работе А. И. Бе-
гиашвили [1].
Определим давление, действующее на упругое тело.
Воспользуемся фор»1улой
Р (*) = — Im [Щ (z)lz=*+io·
Для нахождения давления определим значение
W[{z) при ζ = х + Ш в интервале а< х < Ь:
(z)];=x+i0 = - ρη=======τχ
Отсюда давление
Р (*) — ~ 4- lIm W1 («)]*-*+« =
π
sin πθ Ρχ I b2 — х2\Уи —θ
Я j/(**_a2)(62
(b2-x2\Vz
-x2)[x2-a2j
(8.12)
74
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Рассмотрим следующий пример; допустим, что а =
= В/8, Ъ = 55/8 (В — общая длина участка, где штамп
соприкасается с упругим телом), коэффициент трения
р = 0,5, коэффициент Пуассона ν = 0,3. Введем безразмер¬
ные координаты % = х/В; в таком случае будем иметь
р{1)
4 sin πθ Ρ
π
* J/U2-1)(25-|2)U:
~ξ2|1/2-θ
Значения давления р(\) в различных точках под
штампами определяются с помощью табл. III. Для срав-
Таблица III. Значе¬
ния коэффициентов λ и λ0
нения приводятся также дан¬
ные в случае, когда трение
отсутствует. Давление /?(ξ)
выражается следующим об¬
1
1
λο
λ
1,0
-1
оо
оо
1,1
—1,1
0,6276
1,0800
1,2
—1,2
0,4888
0,7608
1,4
—1,4
0,3872
0,5412
1,8
—1,8
0,3272
0,4048
2,2
—2,2
0,3196
0,3640
2,6
-2,6
0,3208
0,3524
3,0
-3,0
0,3360
0,3364
3,4
-3,4
0,3640
0,3432
3,8
-3,8
0,4060
0,3588
4,2
-4,6
0,6672
0,4872
4,6
-4,6
0,6672
0,4872
4,8
-4,8
0,9296
0,6132
4,9
-4,9
1,3036
0,7800
5,0
-5,0
оо
оо
разом: ρ{ζ) = λ-β\ давление />ο(ξ), которое будет иметь
ι р
место в случае отсутствия сил трения, р0 = Λο ~β-
Значения коэффициентов λ и λο приведены в табл. III.
По данным табл. III построен график (рис. 23). Из
результатов, полученных для плоских штампов, можно,
очевидно, сделать вывод, что влияние сил трения сказы¬
вается особенно сильно у краев штампов. При этом зона,
где напряжения становятся выше некоторой предельной
величины, увеличивается у одного края штампа и умень¬
шается у другого.
§ 9. ДАВЛЕНИЕ ДВИЖУЩЕГОСЯ ШТАМПА
75
§ 9. Давление движущегося штампа
Пусть скорости движения одного или нескольких
штампов W. Уравнения Ляме для неподвижной системы
координат, связанной с телом, имеют вид
дГ
, д\
^ ^ ду[ μΔϊ7 ^ д? ~
Здесь λ и μ — постоянные Ляме, Θ = ^ + J—-, δ — масса
в единице объема. Эти уравнения будут удовлетворены,
если
и = —
λ -j- [I д Θ
,2ft*
λ + 2μ 9 θ ,
V = —■—- +
'μ βχ\
μ dXjdy^
d20* δ_ Λ)*
μ at
2
2 »
причем
ί1_μ —
дх\ ду\
λ + 2μ dt2
Введем подвижную систему координат, связанную со
штампом:
X = XI- wt, у = г/1.
Тогда функция напряжений θ(χ, у) в новой системе коор¬
динат будет удовлетворять уравнению
1 — 4- — \ (ί — — Л- — '
с\ )дх% + ду*\ [[ с\ )дх2 + ду2 _
=О. (9.1)
При этом
и = т
д2в
дхду ’
52θ . Θ2Θ
ν = η&+·&'
д% , , д3в
2 l·»—5.
дя ду ду
аУ — f
d*Q d^Q
дх2ду ^ dyz’
= I
(TQ
дх3
_^θ
дхду
2’
76
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
где
λ “f Μ· λ "f 2μ
m —, η ——!— -,
μ ’ μ c|’
β = -(λ+2μ)-λ4. ά = λ,
/ — (3λ -j- 4μ} — (λ + 2μ) ——, g — λ -)- 2μ,
W
72
2
„2
Ζ = λ -f- 2μ — μ —г-» h ~ — λ,
С\ и с2 — скорости распространения волн расширения и
волн искажения. Мы будем рассматривать случай, когда
w<c\ и w<C2. Уравнение (9.1) будет удовлетворено,
если
θ(*, у) = Ке[Ф(ζι) + ψ(ζ2)].
Здесь
ζ\ = х + iK\y, z2 = x + iK2y,
*■= V’‘-f· *·=ιΛ
(9.2)
Обозначим
Φ'(*,)-φ(2,), Ψ"(ζ2) = ψ(ζ2).
Тогда будем иметь
а у = ΐ [G<p' (ζχ) — G<p' (zj + Щ' (ζ2) — Я ψ' (ζ2) ],
χχυ = Μ<(' (ζχ) + Μφ' fo) + Νψ (ζ2) + Mjj' (ζ2),
ν = 2Re [C<p (Zi) + (z2)b
где
G^fKr -gKl Η = fK2 — gK\, M = l- hK\,
N — I — hK\, С = n-K\, D = n - /<:!·
Составим две линейные комбинации из оу и τ«, так, чтобы
в одной было исключено φ'(ζι), а в другой ·ψ'(ζ2), и умно-
dt dt ηη
жим их соответственно на г и 1огда, принимая
2 — ν Ζ — С
§ У. ДАВЛЕНИЕ ДВИЖУЩЕГОСЯ ШТАМПА
77
/ ΛΓι
во внимание, что Ζ\ = ζ2 = ζ = х при у = 0, что (ζι)“^
Zj->oo ι
,,, Ν2
φ (ζ2)->—-, и пользуясь известными свойствами инте-
22-»оо 2 2
гралов Коши, в результате интегрирования от — <» до
+ оо будем иметь
т'(г\- -1 Т (Να« ~ iHx*v)u=o dt
ф " — 2п (GN — МН) J zi — t d ’
— ОО
\ - 1 т (Μσ»~ί6τ*ν)ν=ο at
Ψ ^ ~ 2л (GN — МН) J 2 — t
— ОО
В случае скольжения серии штампов будем иметь гранич¬
ные условия (7.3), (7.4). Принимая во внимание условие
(τα!/)1/=ο = ρ(σν)!/=ο, преобразуем выражения для φ'(ζι) и
фЧ^г) и проинтегрируем их соответственно по ζ\ и ζ2.
Тогда, используя (9.2), получим для ν следующее выра¬
жение:
+оо
pVy=o = j (<*y)v=o lg IX — 11 dt + qh J (Oy)y=0dt + const.
L x
(9.3)
Здесь
- я[fhK1K2 + ghK\K\ + If-gl (K\ + KtK2 + *|)]
P (I- nh)(KX + Kt)
- «pJ»/ + fK^ - ng (Kf + KtKt + JT|) + gK\K\\
9k +
Λ» ^
Вводя функцию W (z) = J (ay)y==0 —- = U + iV, полу-
L
чим для ее определения условия, вполне аналогичные
(7.12), (7.120:
V = 0 на участках Ьк-гак, 1
U + qhV = — pf'h (х) на участках ahbh. )
78
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
§ 10. Задачи для анизотропного тела
В предыдущих параграфах рассмотрен ряд контактных
задач для изотропного тела, причем область, занятая уп¬
ругим телом, представляла полуплоскость. В этом и сле¬
дующих параграфах приводится решение основных кон¬
тактных задач для анизотропной полуплоскости. Эти
задачи, так же как и аналогичные задачи для изотроп¬
ной полуплоскости, приводятся к отысканию одной из
двух аналитических функций на основании граничных
условий смешанного типа.
Рассмотрим вдавливание штампа в анизотропное упру¬
гое тело, ограниченное полуплоскостью. Будем полагать,
что упругое тело обладает при этом анизотропией общего
вида. Рассмотрим задачу, когда между штампом и анизо¬
тропным телом имеют место силы трения. Напряженное
состояние при отсутствии сил трения будет получено как
частный случай для коэффициента трения, равного нулю.
Закон Гука устанавливает в упругом теле связь между
компонентами деформации ε*, гу и уху и компонентами
напряжения σ*, су и хху. Мы рассматриваем здесь плоскую
задачу и поэтому ограничиваемся величинами, связанны¬
ми с координатами х и у.
У анизотропного тела каждый из компонентов дефор¬
мации представляет собой линейную комбинацию компо¬
нентов напряжения. Подобные соотношения имеют место
в случае изотропного тела. Однако при этом в формулы,
выражающие закон Гука, входят две постоянные — мо¬
дуль упругости и коэффициент Пуассона. Для анизотроп¬
ного тела этих постоянных больше. Анизотропными тела¬
ми являются, например, кристаллы, дерево, грунты, гор¬
ные породы и т. д.
Контактные задачи для анизотропной полуплоскости
представляют интерес, например, при определении давле¬
ний, возникающих под фундаментами, под основаниями
гидротехнических сооружений, так как грунты часто об¬
ладают заметной анизотропией. Как будет видно из даль¬
нейшего, определение давлений в этом случае не сложнее,
чем в случае изотропного тела. Необходимо только знать
коэффициенты, характеризующие упругую анизотропию.
Заметим также, что, сравнивая результаты предыдущего
параграфа с результатами этого, можно сделать заключе-
§ 10. ЗАДАЧИ ДЛЯ АНИЗОТРОПНОГО ТЕЛА
79
пие, что упругое тело, по которому с постоянной ско¬
ростью движется нагрузка, приобретает как бы некото¬
рую упругую анизотропию.
Закон Гука для анизотропного тела имеет следующую
форму:
гх — = βΐΐσΛ: + βΐ2σΣ/ + Pie***,
Еу ~ Ту ~ Ρΐ2σΛ: + $22°У + P26T^2/’
xy = — βιβσχ ”Ь Ргв^г/ “Ь ββ6τΛ'ΐ/·
(10.1)
В частном случае, когда тело является изотропным,
коэффициенты, входящие в эти выражения, будут такими:
ft _ λ + μ —λ V ο η
μη μ (3λ + 2μ) Ε’ Ρΐ2 ~ 2μ (3λ + 2μ)~“ΈΓ’ Ρΐ6-υ>
β λ ~{~ μ ι ^ π β t ι + ν
μ22 μ (3λ + 2μ) Ε ’ Рг6 ~ U’ Ρ66 "2μ — ~ЁГи
Здесь λ и μ — постоянные Ляме, Ε — модуль упругости,
ν — коэффициент Пуассона.
Эти значения коэффициентов имеют место для случая
плоского напряженного состояния. Для плоской деформа¬
ции εζ = 0 и первые три уравнения, связывающие компо¬
ненты деформации и компоненты напряжения, таковы:
1 ν ν
εχ ~β~ σχ ~е °у Ж
1 ν ν
£у — -γ Оу Е ох 2Г °Ζ1
1 V V
εζ — 0 -γ Οζ -β- Οχ Ύ О у.
Из последнего уравнения σζ определяется в зависимо¬
сти от σχ и оу:
Οζ = ν(σ* + Оу).
Подставляя это выражение в первые два уравнения, нахо¬
дим соотношения
1 — ν2 ν + ν2
80
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Поэтому для плоской деформации коэффициенты, вхо¬
дящие в уравнение (10.1), будут
о _ 1 —ν ν + Λ> Q η
Ри — —β » Pl2 β » Pie —
α 1 v л л о 1 + ν
Ρ22 — β j Ρ26 — Рбв — β ·
(10.2)
Для так называемого ортотропного тела, которое явля¬
ется одним из видов анизотропного, βιβ = 0 и ^26 = 0.
Компоненты деформации гх, гу и уху определяются на
основании соотношений (1.2) через переменные и и ν:
ди
дх ’
dv 1 fди . ди\
~ Ту' ^ху ~ ~\Тх ~Т~~дх)'
Кроме того, компоненты напряжения должны удовлетво¬
рять условиям равновесия (1.1):
дх ~ ду v’ дх ^ ду
Таким образом, две последние группы условий анало¬
гичны тем, с которыми мы имеем дело в случае изотроп¬
ного тела. Это естественно, так как связь между компо¬
нентами деформации устанавливается на основании
геометрических соотношений, а уравнения равновесия яв¬
ляются следствием условий статики. Всем этим условиям
удовлетворяет функция напряжений φ (см. работы
С. Г. Лехницкого [1, 2]), через которую напряжения оп¬
ределяются следующим образом:
0 ^д\ Лр =_ Λρ.
* дуг' U дх%' хУ дхду
Эта функция должна удовлетворять уравнению
<10·3)
Из уравнения (10.3) следует, что φ, а также напряже¬
ния и компоненты деформации можно выразить в зави¬
симости от двух функций комплексных величин:
Zi=x + \)Liy, Ζ2 = #+μ2ίΛ (10.4)
§ iO. ЗАДАЧИ ДЛЯ АНИЗОТРОПНОГО ТЕЛА
81
Здесь μι, а также величины, им сопряженные, μι и
μ2 — корни уравнения
βιιS4 - 2β1653 + (2β12 + βδб)52 - 2fc6s + β22 = о. (10.5)
Обозначаем эти корни так:
*ι = μι, s2 = μι, *3 = μ2, 54 = μ2. (10.6)
Выражения для компонентов напряжений σ*, оу и гху
и перемещений и и ν имеют следующую форму:
σ, = μΐΦ'ι К) + μ?Φί (50 + μ*Φ' (ζ2) + μ\Φ' (*0,
О у = Φ! (ζχ) -j- Φ (zt) + Φ2 (ζ2) -J- Φ2 (2-2)1
τхУ = — [μιΦι (ζχ) + μιΦ (ζι) + μ2Φϊ (2з) + Ц2Ф2 (ζ)] >
u = (ζχ) + ΡιΦι (ζ0 + Ρ2Φ2 (ζ2) + РгФ (ζ2),
ν = ?1Φ1 (ζι) + 9ιΦι («0 + ?2φ2 (ζ2) + ?гФ (*г)·
(10.7)
При этом
Pi = βιιμί + βΐ2 — βίβ^Ι ’
Ρ2 = βΐΐμΐ + β 12 βΐ6μ2.
Ρΐί^ϊ + Ρ22 - β20μχ
?1 =
μχ
βΐ2^2 + β22 ~ β26^2
(10.8)
Комплексные числа, которые входят в выражения для
Ζ[ и ζ2, являются корнями уравнения четвертой степени.
В том случае, когда тело будет ортотропным и, следо¬
вательно, β 16 = ββ6 = 0, это уравнение станет биквад¬
ратным.
Будем здесь рассматривать случай упругого тела с
произвольной анизотропией. При этом μ! и μ2 будут про¬
извольными комплексными числами.
Дадим решение задачи о вдавливании одного или нес¬
кольких штампов в анизотропное упругое тело. На к-й
штамп действует сила Рк (рис. 24). Мы рассмотрим слу¬
чай, когда между телами имеют место силы трения, под-
6 Л. А. Галин
82
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
чиняющиеся закону Кулона. Отсутствие сил трения по¬
лучится как частный случай этой задачи при коэффици¬
енте трения р = 0.
Граничные условия для первого и третьего типов (см.
§ 3) в данном случае при у = 0 будут такими:
Будем полагать также, что коэффициент трения р оди¬
наков на всех участках, где штампы соприкасаются с уп¬
ругим телом. Обозначим совокупность площадок контакта
через L. Найдем выражения для производных от переме¬
ны. dv
щении на границе полуплоскости и в зависимо¬
сти от внешней нагрузки. В результате будут получены
равенства
оу — 0, τхУ = 0 на участках bk-idk;
v = f(x), Хху = ρσυ па участках ahbk.
} (Ю.9)
Рис. 24.
оо
ХУ)У=01
+ А4 § (Ъху)у=0 ^ΖΓΧ + π54 (τ^
хУ)У=Οι
—оо
§10. ЗАДАЧИ ДЛЯ АНИЗОТРОПНОГО ТЕЛА
83
аналогичные тем, которые были ранее найдены для слу¬
чая изотропного тела [см. (2.15)].
Определим первое из этих выражений, необходимое
для решения поставленной здесь контактной задачи.
Применим метод, которым мы пользовались в преды¬
дущем разделе этого параграфа, для случая движущейся
нагрузки. Так же, как и там, воспользуемся свойствами
интегралов Коши, обобщенными на комплексные числа
вида ζ\ = х + \лу:
— ОО —оо
Воспользуемся (10.7) и составим выражения для ком¬
бинации μισν + хху и μ2σ!/ + тху. Получим
И1°у + Хху = (μι — μι) Φί (ζι) + (μι — μ2) Φ2 (ζ2) +
+ (μι — μ2)Φ2(ζ2)’
μ2σ!/ + τχυ =(μ2 — μι)Φι (ζι) + (μ2 — μι) Φι (%) 4-
-Ь (μ2 — μ2) (^*2 (ζ2)-
Используя приведенные выше свойства интегралов Коши,
будем иметь
+ оо
φ1 (ζι) = — Ιπί 7μΓ~μ ) ί (μ2σί/ +τ*ί/)ί/=0ζ-=ΓΓ>
— ΟΟ
+ οο
’2 ^ = 2πί (μχ - μ2) j + Xxv)u=ο
/.. .. 4 \ (iLllO'w Т^7/)ц=0 ζ ~·
(10.10)
Найдем теперь выражение для производной перемеще¬
ния ν по координате х. На основании одного из соотноше¬
ний (10.7) получим
= чМ (Ζ1) + ?ΐΦί (*ΐ) + д2φ2 (z2) + Ы,
или, иначе,
= 2Re [?1Φί (z,) + q,Φ; (z.2)] . (10.11)
6*
84
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Выражения для функций Oi(zj) и Φ2(ζ2) (10.10) за¬
пишем таким образом:
Φι (*> = - ί^μ; Έύ ί (σ^=» “
— οο
-foo
ί L Γ (τ «%
>*ι — 2πί J χν/ν—ο ζ _
— οο
<*<’.>=■ jq^ai ί K),..J^ +
—οο
-(-ΟΟ
+ ?Ρϊζ ^ ^ ^х^у=0
(10.12)
ε-V
Подставляя (10.12) в (10.11), получим выражение для
dv/dx:
8» о Rr ( 1 Т (д ч К дг ν
j — μ2 2πΐ J ( y^~aZ, — z1 μχ —μ2
" —ΟΟ
V, 1 V /- 4 « , «Λ !?/„> <*ζ ,
ΧΰΙ J + J ^=οξΤΓΓ2 +
— ΟΟ —οο
+ μΡ^Η; ί <*»Ь-.Д}· (la,3>
— ΟΟ '
Используя предельные свойства интегралов типа Ко¬
ши, найдем значение dv/dx при у = 0:
§ 10. ЗАДАЧИ ДЛЯ АНИЗОТРОПНОГО ТЕЛА
85
+ [ά J ξ~1ο — ΊΓ (°ri/)i/=oJ +
+ μι_!μ2 2Ηϊ ί (τ*^"=0 ·ζ=~χ ~~ Τ (Χχν)«=0
L. — οο
После преобразований получаем
L — oo
/ϊΛ-ϊΛ (9*~ЯЛ 1 ΐ(τ ) άζ
['μ-μΤ ){σ^ Ux-^J 11 J '*«·*-· С —
— OO
^Г^)(Т^=о]·
Λ
Это выражение может быть записано и так:
* —оо
+ R· V.)»-. -Im (ϊ^) 4 _((*->».. х
xf-.
Введем обозначения:
(10.14)
Определим действительные и мнимые части комплек¬
сных величин, находящихся в правых частях (10.14). При
86
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
этом используем выражения (10.8) для q\ и q2. Будем
иметь
Ял — У* 1 Г Ρΐ2μι + 022 — 026^1
Pl2^2 022 026^2
~ΐν=^;[βΐ2(μι_μ2) +
+ р22^г ]= βΐ2 ~р22 ά
На основании этого
Re (ЧЛ !*Л = β - !W._1_ _]_ =4-У
\Н-^) Н12 2 [w, μχμ2)
Im ( ?1 ~ ?2 \ ί — =Χτ-
\μ1-μ2;Ι 21 νμιμ2 μΛ
(10.15)
Другое выражение может быть преобразовано так:
Vl2-^i
μ
1 2
1
Отсюда находим
^2 (Pla^l + Р-22 ~ Pae^l) μΐ(Ρΐ2^+Ρ22-Ρ26·α2)
μι μ2
—Ргг -?гт—■ + β2« (μ2 μι)
μ, μ,
1^2
--Р22(]^+^)+Р2в·
Rc/^2-g2^l\ Р22/ 1 , 1 , 1 j
R I ^-ι», )~ 2 U ' μ7 μ J Ргв’
Im
1*1 -1*2
Р22/ 1 1,1 _L
' 2i [ 1*1 μχ + ^ f*2
(10.16)
На основании (10.15) и (10.16) получаем выражения
для коэффициентов Л3, Ζ?3, А4 и В4:
§ 10. ЗАДАЧИ ДЛЯ АНИЗОТРОПНОГО ТЕЛА
87
A (Л L +J L\
3 2i \ μ, μ, + μβ ~ I*
“ί Μί f*2 μ2
D ^22 ί 1 I 1 J 1 I ^
3~ o~ I 77 l· ■= r~ |- 7.
1 μι μ2 **2
A = _!W_i ί_\
2i ^,μ, μ,μ, )’ ,
β26>
в* =
ηΑ+άϊ+ν
12*
(10.17)
Таким образом, выражение для dv/dx может быть за¬
писано в такой форме:
+ оо
(-£i=o= Аэ ^ ί{<Jy)v=o &+Бз (<Jy)y=°+
— 00
+00
+ А,-i- J (хху)у=0^-+В,(ххУ)и=ο· (10.18)
— СХ»
Перейдем теперь к решению нашей контактной зада¬
чи. Рассмотрим случай, когда между штампом и анизот¬
ропным упругим телом возникают силы трения, подчиня¬
ющиеся закону Кулона. Отсутствие сил трения получим
как частный случай этой более общей задачи, полагая
коэффициент трения р = 0.
На основании (10.9) на поверхности тела будем иметь
такое соотношение между компонентами напряжения
Су и хху:
(гху)и=о — Р №у)у=о·
Тогда условие (10.18) приобретет следующую форму:
( £),=„= + рАл) -±- j (оу)и=0 Д +
— оо
+ (вз + р54)
Принимая во внимание граничное условие (10.9), учи¬
тывая при этом, что компоненты напряжения ау и гху дей¬
ствуют на совокупности участков L, получаем условие в
88
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
таком виде:
Η" (Β3 Η” Ρ^) (σί/)ί/=ο· (10.19)
Введем функцию w\iz):
Wi (z) = ul— ivx = I (ay)u==0-2L·. (10.20)
L
При этом на действительной оси будем иметь
L
Теперь на основании (10.9) может быть составлено
условие для определения функции w\(z); при г/= 0
Здесь L означает совокупность участков, где штампы со¬
прикасаются с упругим телом. Функция fix), равная пере¬
мещению поверхности упругого тела под штампом, оп¬
ределяется таким образом, что на &-м участке она равна
Условие (10.22) совершенно эквивалентно условию
(7.13), полученному для изотропного упругого тела, зани¬
мающего полуплоскость, когда между штампом и упругим
телом действуют силы трения.
В случае отсутствия сил трения (при р = 0) условие
(10.22) будет таким:
Если 5з=5^0, условие (10.23) при отсутствии сил тре¬
ния будет такого же типа, как и при наличии сил треиия.
Рассмотрим случай одного штампа, когда компоненты
напряжения отличны от нуля на одном участке, где
/' (я) — (Л3 + рЛ4) — uL -f (53 -f pi?4) —
ь\ = 0
vx на L,
вне L.
(10.22)
fk(x).
f (x) = Аз^ и1 + 53 “ на L,
ь\ = 0 вне L.
(10.23)
§ 10. ЗАДАЧИ ДЛЯ АНИЗОТРОПНОГО ТЕЛА
89
— 1<х<1. Тогда можно построить решение по аналогии
с (7.19). При наличии сил трения функция W\(z), удовлет¬
воряющая условию (10.22), будет такой:
Коэффициенты 4з, #з, Ва определяются на основа¬
нии (10.17).
Таким образом, все сказанное о решении смешанной
задачи с силами трения целиком применимо и к этой за¬
даче об анизотропном упругом теле.
В частном случае, когда анизотропное тело является
ортотропным, а оси упругой анизотропии параллельны
осям координат, коэффициенты βΐ6 = = 0. При этом
уравнение (10.3) будет биквадратным. Кроме того, его
корни — числа μι и μ2 — оказываются чисто мнимыми.
Пусть μι = ivi, μ2 — iv2, где vi и v2 действительны.
Определим значения коэффициентов Л3, А^ В3, ВА.
Воспользовавшись (10.17), получим
1
X
вз + РВЛ* <2 + г)е (z - *)1_θ
При этом давление
Здесь коэффициент Θ равен
(10.25)
90
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Тогда условие (10.22) преобразуется к виду
v± = 0
вне L.
Условие (10.23) при отсутствии сил трения приобретает
следующую форму:
Контактная задача для ортотропного тела при отсутст¬
вии сил трения была исследована Г. Н. Савиным [1].
Как видно из (10.27), она вполне аналогична задаче о
давлении штампа без сил трения на изотропную полу¬
плоскость.
Получим из общих уравнений (10.26) ранее выведен¬
ное граничное условие для определения функции W\{z)
в случае изотропного тела. При этом для плоской дефор¬
мации коэффициенты βπ, βΐ2, βΐ6, β;22» β26, βθ6, как было по¬
казано выше, выражаются так:
ft _ 1 —γ3 ft _ V + Vs а п )
Ριι — > Ρΐ2 — β ι Pie — u>
« 2 , ^ (10.28)
a 1 — v a _ n « _ * +v
P22 β » P26 Рбб β *
На основании (10.28) уравнение (10.3) для определе¬
ния μι, μ2, μι, μ2 становится биквадратным, а его корпи:
s\ = μι = iv 1 = i, 52 = μ2 = iv2 = i, S3 = μι = — ivi = — i, s4 =
=μ2 = — iv2 = i, vi = 1, V2 = 1. Отсюда
u± на Z/,
вне L.
(10.27)
1 — v — 2v2
E
(1 + ν) (1 — 2v)
§ 10. ЗАДАЧИ ДЛЯ АНИЗОТРОПНОГО ТЕЛА
91
Следовательно, (10.26) приобретет следующий вид:
Это условие совпадает с ранее выведенным для изо¬
тропного тела условием (7.13).
Приведем в качестве примера решение задачи о давле¬
нии штампа с плоским основанием на упругое анизотроп¬
ное тело, занимающее полуплоскость, в случае, когда на
площадке контакта действует сила трения.
Функция W\(z), удовлетворяющая (10.22), будет иметь
по аналогии с (8.3) следующий вид:
Итак, результаты этого параграфа позволяют сделать
заключение о том, что контактная задача для анизотроп¬
ной полуплоскости при наличии сил трения решается
точно так же, как и аналогичная задача для изотропной
полуплоскости.
Сравнивая результаты этого параграфа с результатами
предыдущего, где исследовалось вдавливание движущего-
(1 + v) (1 2v) j
ul + P V1 Ha L'l
vx = 0
вне L,
или, иначе,
на L, ]
(10.29)
νλ = 0
вне L.
При этом
а =
(10.30)
Давление, действующее под штампом:
р(х) = — ps»lfg-==,1
π V(x + l){x — l) 14-е
(10.31)
92
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
ся с постоянной скоростью штампа в упругое тело, можно
установить аналогию между рассмотренными задачами.
И в том и в другом случае функция напряжений удов¬
летворяла дифференциальным уравнениям четвертого по¬
рядка одного и того же вида [ср. уравнения (9.1) и (10.3)].
Этим обусловлено сходство решений обеих задач.
§ 11. Задачи для анизотропного тела (продолжение)
Рассмотрим теперь контактную задачу для анизо¬
тропной полуплоскости, когда штампы жестко связаны с
упругим телом. Согласно нашей терминологии (см. § 3),
в этом случае имеют место граничные условия первого
и второго типов (следовательно, на одной части поверхно¬
сти заданы напряжения, а на другой — перемещения).
Аналогичная задача для изотропной полуплоскости была
решена В. М. Абрамовым [1] и Н. И. Мусхелишвили [1,2].
Так как в нашей задаче на площадке контакта даны
перемещения и и ι; и, следовательно, их производные по
х, необходимо иметь выражения для этих фупкций, опре¬
деленные на основании нагрузки, действующей на грани¬
це полуплоскости. Функция {dv/dx)y=o была определена
в предыдущем параграфе [см. (10.18)]. Дадим аналогич¬
ное выражение для (ди/дх)у== о.
Согласно (10.7) перемещение и будет
и = ριΦ^Ζι) + ριΦ^Ζ!) + ρ2Φ2(ζ2) + ρ2Φζ(ζ2) =
Воспользуемся формулами (10.12), дающими Φι(ζι) и
Φ2(ζ2) на основании напряжений, действующих по по¬
верхности. Подставим их в (11.1) и устремим ζ\ и ζ2 к
точке, расположенной на действительной оси. В резуль¬
тате получим [по аналогии с тем, как это было сделано
для (dv/dx) у=01
= RetpiCPi(zi) + ρ2Φ2(ζ2)]. (11.1)
4-00
§11. ЗАДАЧИ ДЛЯ АНИЗОТРОПНОГО ТЕЛА
93
L ~ ^(σ,,)ί,=ο]+
+ μ1-μ2|"ώ ί (τ*Λ=0ζΤ7ϊ — \(χχυ)ν=0
L —oo
Отсюда находим
P^i - PiH
μ, - μ.
(τ ) ^ .
\lxy)y=0 ζ_ χ
U-;J (τ*^=ο];
иначе это может быть записано следующим образом:
!/ \ +°°
+ Re(^)K),=t_Im(^)x
х I· I ζ4ϊ + Re (5^) (τ»Α-ο1· (11.2)
— oo /
Введем обозначения:
1 V ^-μ* / \ μχ-μ2 Г
А2 = -lmi-1—- М, Вг = RefPl~P2).
2 \μ! — μ3/’ 2 \μ1-μ8/
Преобразуем эти формулы, используя при этом выра¬
жения (10.8) для р\ и p,2i
(11.3)
р. - р.
Η,Τ+τΚβι^+^-^μχ)-
ί1! - I1* 1*1 ~ ^2
— (βιιμΙ + βχ2 — βιβμζ)] = βη (μι + μί) — βιβ·
94
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Отсюда находим
Л = ^) = -^(μι + μ2_μ1_μ2),
Вг — Re = -j1 (μι + μ2 + μι + μ2) — βιβ·
Другое выражение будет
Ρχμ2 - Ρ2μχ _
μ>-μ2
ζγϊγ [(βιιμ* + βι*~ βι«μι)μ*—(Ριιμ*+Ρι*~βΐ6μ2)μι]=
= Plll·1!^ βΐ2*
^1-^2
Из этого получаем
= — Im (Pl^ _ μ^1) - - ^ (μχμ2 - μχμ2),
Βΐ = ΚΘ (Ρΐμ^ - μ^) = ΊΓ ^ιμ2 + ^г) — Ρ12'
Итак, коэффициенты (11.3) могут быть представлены
гак:
β
Αι = —-^(μιμ2 — μιμ2)>
β
Βι = -γ (μιμ2 + μιμ2) — β^
β
А = — -^-(μι + μ2 — μι — μ2).
β
(11.4)
Β2 γ (μχ + μ2 + μι + μ2) — βι«·
На основании (11.4) выражение (11.2) для производ¬
ной перемещения и по х будет
+ оо
(й)у=о = Al ^ J (σ^=° ΐ~=Τχ + В1 (°у)у=о +
— ОО
+ оо
Н“ Л2 7^ J (Гху)у=0 ζ~~ϊ ·®2 (1'ху)у=0' (11-5)
§ it. ЗАДАЧИ ДЛЯ АНИЗОТРОПНОГО ТЕЛА
95
Итак, из (10.18) и (11.5) находим производные по х
от перемещений границы упругой полуплоскости и и ν:
+ оо
(11.6)
Я [di}y=о ~ ^ J (σ^=0
— со
+ оо
“Ь ^2 J ('txy)v=0 ζ — х π^2 (T5Ci/)y=0i
— оо
+ оо
π (S)„=o = Лз ί (σ^=° + πβδ (0Г^=° +
— οο
+ οο
+ ^4 J (^3CZ/)l/=0 ζ Λ· + Я^4 (Тл:у)у=0·
Значения коэффициентов Ль 5Ь Л2, 52, Л3, 53, А4
и В4 таковы:
β
Λ = —-^(μιμ2 — μιμ2)ι
β
Βι = -γ (μιμ2 + μιμ2) — βχ2>
β _
A = — -jy- (μι + μ2 — μι — μ2),
β
^2 = -τ·(μχ + μ2 + μι + μ2) — βι«>
А~ =
022
f-
^13
2i
Ui
μχ
СО
II
—
%l
(£+
Л4 —
—
Is!
( 1
V^2 '
#4 =
—
¥(
^ 1
μ^2ι ’
12*
(11.7)
Формулы (11.6) являются обобщением формул (2.15),
выведенных для изотропного упругого тела.
96
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Введем две функции [см. (2.17)]:
—оо
(11.8)
—оо
Предельные значения этих функций при подходе к
точке, расположенной на границе полуплоскости, таковы:
[и?! (z)L=*-io = их — ivx =
Пусть в анизотропную полуплоскость вдавливается
несколько штампов, жестко с ней связанных. На /-й
штамп действуют сила Р,·, направленная параллельно оси
г/, и сила Th направленная параллельно оси х; число
штампов будем полагать равным п.
В нашей задаче имеют место следующие граничные
условия при у = 0:
Участки, где а,<х< образуют совокупность L. Умно¬
жим первое из условий (11.6) на АГ, а второе на N и сло-
—оо
(11.9)
(z)L=*_i0 = Щ — iv2 =
j* (^'Jcy)l/=0 ζ χ Я ΐ {Ъху)у=о·
— оо
Кроме того,
§11. ЗАДАЧИ ДЛЯ АНИЗОТРОПНОГО ТЕЛА
97
жим. Будем иметь
■(*£+*£L-
= (АгМ + A3N) J (ау)у=-_й + (пВ^'1 + πΒ3Ν) (ау)у==0+
L
+ {АгМ + AtN) J(хху)у=о + (пВ2М + nBtN) {гху)у^0.
L
(11.11)
Подберем постоянные М и N таким образом, чтобы
АгМ + A3N пВгМ + πΒ3Ν {
АгМ + ΑχΝ = пВ2М + nB^N = Τ'
Прп этом может быть принято Μ — 1. Для определе¬
ния N будем иметь условие
Аг + Α3Ν Βχ + BSN
At +AtN ~ Bt +BaN’
которое приводится к следующему квадратному урав¬
нению:
и3Я4 - A4B3)N2 + (А3В2 - В3А2 + AlBi- AABy)N +
+ (А1В2-А2В1) = 0. (11.12)
Решая это уравнение, получаем два значения N я N
(в случае, если N комплексно):
Ν, N = 2 (А β 1_ А β \ 1— (^з^2 — BjA2 -J- A1Bi г- AtBt) ±
V 3 4 4 3/
[(^3^2 ^3^2 ~Ь ^4-®l)2
- 4 (А3Ва - ΒζΑα) (АгВъ -А^)]172}. (11.13)
Если принять первое из значений, равное Ν, то будем
иметь
Аг + Α3Ν = К, А2+ Α,Ν = KS, 1
Вг + Β3Ν = <?, В2 + B,N = QS. j (ИЛ4)
7
Л. А. Галшн
98
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Отсюда получим
π (ё + Ν £)у==0 ^71 Ьи (») + Nf't} (*)] =
= К (оу + Sxxy)y=0 + Qπ [σ» + $хху]у=ο· (11-15)
L
Обозначим
w
з (ζ) = J (Oy + Sxxy)y=ο = и?! (ζ) + £и>2 (ζ). (11.10)
L
На основании свойств интегралов типа Коши имеем
IP, (я + *0) = J (σ^ + Sxxy)y=0 + ni (ay + Stx„)y=s0,
L
w3 (x — ί0) = J (σ„ + Sxxy)y=0 ^-x — ni (aу + Sxxy)y=0.
Здесь w${x + Ю) и w3(x — iO) — значения функции w3(z)
при подходе к точке z = х, расположенной на действи¬
тельной оси, соответственно сверху или снизу. В таком
случае
w (х + Ю) + w (х — iO)
w (х + Ю) — w (х — Ю)
— j" (^г/ + 8тху)у=о ζ ,
— ni (Gy + SxxlJ)y,.=ο·
(11.17)
Если взять другое значение Ν, сопряженное с первым,
то тогда вместо К7 S, Q будем иметь соответственно
К, S, Q. В таком случае
П\ flj (х) + Nfu (*)] =
= К j* (συ + Sxxy)y=0 ξ~^ + Qn (σ& + 8τχν)μ=ο· (11-18)
§11. ЗАДАЧИ ДЛЯ АНИЗОТРОПНОГО ТЕЛА
99
Введя функцию w4{z), получим
(z) = J К + $Хху)и=ο ζΤΤ~ζ = Щ (ζ) + Sw2 (ζ). (11.19)
L
Следовательно,
(х + ίΌ) + u>4 (х — iO) f* _ άζ
— J (&У Stxy)y=ο ζ .
w
2 j \~y ι - *χυ/υ=υζ_
L
..„ + ,0, -“.<«-,0) = л|(а> + ^А_0,
(11.20)
Таким образом, правая часть в выражении (11.15),
равная известной функции, может быть выражена на ос¬
новании (11.16) через предельные значения функции
w^iz) при подходе сверху или снизу к точке, расположен¬
ной на действительной оси:
I [и>3 (х + г0) + w3(x — Ю)] + i | [w3 (х+Ю)— w3(x— i0)] =
= -j [K + iQ] w3 (x + iO) + j [K — iQ] w3 (x — iO) =
= n[fii(x) + Nf'2j(x)}.
Точно так же, используя (11.18), найдем аналогичное
условие, которое послужит для определения функции
w4(z):
~2 [К iQ] (х ~l· iO) + “2 [К — iQ] Wi (х — Ю) =
= п [f[j (χ) + Nftf (ж)].
Каждое из этих условий будет иметь место на участ¬
ках, принадлежащих совокупности L.
На остальных участках действительной оси
Wz(x + Ю) — w3(x — Ю) = 0,
w4(x + Ю) — w4{x — Ю) = 0,
так как здесь W\{x + Ю) — wx(x — Ю) = 0 и w2(x + i0) —
— w2(x — i0) =0.
Итак, окончательно получаем следующие условия для
определения wz(z) и w4(z):
7*
100
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[К + iQ] ы>з (я + *0) + [К — iQ] w3 (х — ί0) =
= 2π [fy (χ) + Nf'i} (χ)] α} < χ <bh 1 < /<и,
[К + г@] ^4 (* + ί0) + [Κ — *#1 wt (χ — *0) =
= 2η [/ij (χ) + Nf'2j (ж)],
(a: + г0) — w^{x— Ю) = 0, fcj_i <Cx<C.dj,
wA (x + Ю) — w4(x — Ю) = 0.
Таким образом, при определении w$(z) и w^(z) мы
приходим к частному случаю задачи Гильберта или зада¬
чи о линейном сопряжении граничных условий (по тер¬
минологии Н. И. Мусхелишвили).
В § 4 были рассмотрены случаи, когда на границе
одной области (нижней полуплоскости) заданы гранич¬
ные условия смешанного типа. В данном случае на ли¬
нии, отделяющей две области (верхнюю и нижнюю полу¬
плоскости), дано условие, в которое входят граничные
значения функций в первой и второй областях.
Мы занимались подробно задачей, когда N и N — со¬
пряженные комплексные числа, так как в случае анизо¬
тропного тела, близкого по своим свойствам к изотроп¬
ному, уравнение (11.12) будет иметь комплексные корни.
Если определены функции w^(z) и ιυ^(ζ), то W\{z) п
w2(z) находятся следующим образом:
Щ (*) = J^~s 1вщ, (Ζ) - Swt (ζ)],1
(2) = =4— [— 1»ζ (Ζ) + (*)!·
Ο ο
(11.22)
Итак, определение функций w^iz) и w^iz) свелось к
решению задачи Гильберта, точно так же, как и для
аналогичной контактной задачи в случае изотропного
тела (Н. И. Мусхелишвили [1]).
Приведем в качестве примера решение задачи о дав¬
лении одного штампа с плоским основанием на анизотроп¬
ную полуплоскость. Пусть его ширина равна 21, причем
начало координат расположено в середине штампа. На
штамп, жестко связанный с упругой анизотропной полу¬
плоскостью, действуют нормальная сила Р и тангенци¬
альная Т.
§11. ЗАДАЧИ ДЛЯ АНИЗОТРОПНОГО ТЕЛА
101
Условия (11.21) в этом случае приобретают следую¬
щий вид:
ю3 (х + i0) + Кк w3(x—i0) = 0, — I < х < + Z,
(х + Щ + .5 ~ l% (х — Ю) = 0,
ιν3 (х + Ю) — w3 (х — 10) = 0, χ<Ζ — I, х>1,
(х + Ю) — (χ — ίΟ) = 0.
(11.23)
Применяя метод, изложенный в указанной выше кни¬
ге Н. И. Мусхелишвили, найдем следующие выражения
для wz(z) и и;4Ы:
u;3 (г) = C3(z- l)~y* (ζ + i)V3_1, Τα = jk1η (~
и’* (ζ) = C4 (ζ - Ι)-'* (ζ + 1?*+1, γ4 = ± 1η |±|).
(11.24)
Постоянные С3 и С4 могут быть установлены на осно¬
вании поведения w3(z) и м>4Ы на бесконечности. Соглас¬
но определению будем иметь
[w3 (2)]г_оо = ί f {Оу + SxXy)y=о =
L-I ζ —*оо
= [- ί (Оу)у,о « - 5 ( (τ^.0 (ίζ j i- = (/> + ST) -1.
Точно так же получим
[И>4 (Z)b^co = (Р + ST) 4".
С другой стороны, из (11.24) следует
[^3 (Z)]z-»oo = С3 -J—, [и?£ (z)]2-*oo = С4
Сопоставляя эти выражения, находим
С3=(Р + 5Г), С4=(Р + т
102
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
На основании этого получаем окончательно
w3 (2) = (Р + ST) (2 - 0“ТЗ (2 + 1)Уз~\
Wt (2) = (Р + ST) (2 - l)~y* (2 + Z)V4_1.
(11.25)
Подставляя (11.25) в (11.22), находим W\(z) и w,2(z),
на основании которых могут быть определены напряже¬
ния, возникающие на площадке контакта, а также в лю¬
бой точке упругого тела:
wt (2) = =4— [5 (Р + ST) (2 - I)-*з (Z + if 3-1 _
о — о
- 5 (Р + ST) (2 -1(2 + г)’*-1],
Ц>2 (2) = =4— [(Р + ST)(z- 1)~Ъ (2 + if*~l +
— *3
Напряжения, возникающие на площадке контакта:
Итак, выражения для функций w\{z) и ιν<ι(ζ), а также
для напряжений, возникающих на площадке контакта,
получаются весьма простыми. Необходимо только для
определения коэффициентов произвести ряд алгебраиче¬
ских операций. Из уравнения (10.5) определяются корни
μι и μ2. Формулы (11.7) позволяют найти коэффициенты
А ι, В\, А2, #2, As, В3, А4 и В4. На основании этих коэф¬
фициентов, пользуясь (11.3), находим Λί и IV, а из соот¬
ношений (11.14) определяем К, Q и S.
+ (P + ST) (z-l)-^(z + If*-1].
(11.26)
Здесь
(Ру)у=0 = — Im [wt (2)];=x_i0,
(Уху)у— 0 = [U72 (z)]z=x—iо·
§ 12. ЗАДАЧИ ПРИ НАЛИЧИИ ТРЕНИЯ И СЦЕПЛЕНИЯ ЮЗ
§ 12. Вдавливание штампа при наличии трения
и сцепления
В предыдущих параграфах этой главы были рассмот¬
рены контактные задачи теории упругости, причем между
упругим телом и штампом действовали силы трения, под¬
чиняющиеся закону Кулона. Так будет обстоять дело в
том случае, когда штамп
скользит по поверхности уп¬
ругих тел. Однако в ряде
случаев картина сложнее.
В частности, когда происхо¬
дит вдавливание штампа в
упругое тело (будем здесь,
как и в предыдущих пара¬
графах, полагать, что упру- Рис. 25-
гое тело занимает полупло¬
скость), иа площадке контакта будут участки и со сце¬
плением.
Будем рассматривать процесс вдавливания штампа в
упругое тело, считая, что площадка контакта разбивается
на три участка, на одном из которых имеет место сцепле¬
ние, а на других — трение.
Если штамп прижимается к упругой полуплоскости
силой Р (одновременно на него может действовать на¬
правленная по оси х сила Г, не превышающая некоторого
предельного значения и не вызывающая поворота штам¬
па), то на участках проскальзывания АВ и CD (рис. 25)
имеем
tix) — ppix) = 0 на АВ,
t{x) + ppix) = 0 на CD.
Здесь tix) и pix) — тангенциальные и нормальные напря¬
жения на поверхности. Разные знаки перед рpix) указы¬
вают, что проскальзывание на АВ и CD происходит в
противоположных направлениях.
На участке сцепления ВС значения тангенциальных
напряжений на поверхности контакта недостаточны для
того, чтобы вызвать проскальзывание, т. е.
I Цх)
I pW
<р. (12.1)
Нормальное давление под штампом должно быть всю¬
ду положительным, следовательно, pix) > 0 на участках
104
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
АВ, ВС и CD. Отсюда вытекает
р(х) ^0 на
(12.2)
На свободной поверхности (участки и DE) будем
иметь
р(х) = 0, t(x) = 0.
Перемещения под штампом
v(x) = с2 на Л2?, CD, иЫ = ci на ВС.
Таким образом, граничные условия будут следующими:
t (х) = 0, р (х) = 0 на ЕА (— оо <£<—/),
t (х) — рр (#) = 0, г; (я) = с2 на ЛВ (— I < я < — а),
гг (я) = cls г; (я) = с2 на ВС (— а < х < + а),
ί (a:) + РР (я) = 0, у(а;) = с2 на CZ) (+а<я<-М),
г(я) = 0, p(x) = 0 DE (+/<£< + оо). )
При этом на участке ВС должно иметь место еще усло¬
вие (12.1), а на участках АВ, ВС и CD — условие (12.2).
В случае неплоского штампа одно из условий на уча¬
стке AD будет иметь вид и(х) —fix) + Сг.
Воспользуемся выражениями для ^ н при г/ = 0,
которые были установлены в § 2 [см. (2.15)]:
(12.3)
оо
(12.4)
Введем две функции [см. (2.17)]:
+J
(*) = j Ρ (ζ) = «1 + ^1» (12.5)
-I
+ι
wt (Ζ) = j* t (ζ) ^ = u2 + ii;,. (12.6)
-I
§ 12. ЗАДАЧИ ПРИ НАЛИЧИИ ТРЕНИЯ II СЦЕПЛЕНИЯ Ю5
Эти функции, очевидно, аналогичны ранее введенным
функциям (2.17), отличаясь от них только знаком. Здесь,
в отличие от того, как это делалось в предыдущих пара¬
графах, мы будем полагать, что упругое тело занимает
верхнюю полуплоскость. Поэтому в выражениях для
u?i(z) и u>2(z) перед мнимыми частями берутся знаки плюс.
При у = 0 будем иметь [ср. с (2.19) и (2.20)]
ди (х)
л ±7 v ' л дх
ρ(χ) = — 4rvi’ *{χ) = —^Γυ 2>
ди (х) 0
-ST=Ul + Vv2.
(12.7)
Функции u)\{z) и w2(z) должны удовлетворять усло¬
виям:
Р_
Ζ
w2(z)-> при ζ —*■ оо. (12.8)
Кроме того, функции w\(z) и ιυ2{ζ) должны быть та¬
ковы, чтобы их особенности в точках действительной оси
были вида
(ζ-β)-θ (0 < θ < 1). (12.9)
На основании (12.7) граничные условия (12.3) при¬
мут вид:
на ЕА (— оо < χ < — I)
ь\ = Im wl — 0, v2 = Im ιυ2 = 0;
на АВ (— 1<Сх<С — а)
V2 — Р^1 = Im (^2 — P^l) — 0»
ui + P^2 = Im + β^) = 0;
на ВС (— а<х< + а)
«г — β^ι = Im (iwi — β^ι) = 0, I (12.10)
u\ + β^ ~ {iw\ + β^) — 0;
на CD (+a<x< + 0
v2 + pi^ = Im (w2 + pu^) = 0,
Ui -f βι>2 = Im (iwt + βΜ>2) = 0;
на DE (+ I <C x < + oo)
vL = Imiu1 = 0, i>2 = Im w2 = 0.
106
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
При этом на участке ВС должно иметь место условие
\ν2/ν\\ < р, а на участках А В, ВС и CD — условие ν\ Ф 0.
Рассмотрим первое условие (12.10) на участке ЕЛ.
Так как граничные значения функций W\ и т2 действи¬
тельны, то и их частное будет также действительным.
Поэтому получим Im (w2/w\) = 0.
На участке АВ имеем Im (w2 — pw\) = 0, откуда
Im $w2 = Im βρί^. Второе из условий примет вид Im[(i +
+ βρ)α?ι] = 0. Разделив второе из условий на этом участ¬
ке на полученное, находим
Im£L+£i=Im(T
(ί + βρ)α>1 \l
β
+ βρ ' + βρ Wj
= 0. (12.11)
Аналогичное преобразование можно провести и для
других участков. Обозначим для краткости
s(z) =
w^z)
w1 (ζ) *
Для функции s(z) будем иметь:
на ЕА (— оо < х < — I)
Im s(z) = 0;
на АВ (— I < х < — а)
(12.12)
Im
(т
+ Г
β
+ βρ 1 i + βρ
на ВС (— а<#< + я)
Im (Щ^т) -
на CD (4- + /)
<*)) = 0;
Im
Ml
+ г
β
βρ
' (ζ)) = 0;
на DE (+/<£<+=·с)
Im s (z) = 0.
(12.13)
Пусть функция s(z) отображает некоторую область S
на полуплоскость. Тогда для каждой линии, являющейся
§ 12. ЗАДАЧИ ПРИ НАЛИЧИИ ТРЕНИЯ И СЦЕПЛЕНИЯ Ю7
частью контура области S, будем иметь условие вида
im (ШШ)=°· <12-,4>
Это значит, что каждая из таких линий посредством
дробно-линейного преобразования переходит в действи¬
тельную ось, т. е. прямую. Следовательно, эти линии бу¬
дут дугами окружностей. В самом деле, подставляя в
приведенное выше условие комплексное число, соответ¬
ствующее точке, расположенной на контуре области £,
мы находим некоторое комп¬
лексное число, которое соот- -а +а +1 ®
ветствует точке, находящей- ^ ^ ^
ся на контуре области, полу- q
ченной после преобразова- ~
пня. Однако у этого комп¬
лексного числа мнимая часть
равна нулю, следовательно,
оно будет действительным.
Поэтому участок контура об¬
ласти, полученной после пре¬
образования, будет отрезком
действительной оси. Таким
образом, область S, части гра¬
ницы которой после дробно¬
линейных преобразований Рис. 26.
переходят в отрезки прямых,
ограничена дугами окружностей. Эта область, очевидно,
аналогична годографу скоростей в задачах теории филь¬
трации.
Условиям на ЕА и DE соответствует прямая GH
(рис. 26), условиям на АВ и CD — прямые KL и MN,
а условию на ВС — окружность F. Покажем теперь, что
если за S принять область, заштрихованную на рис. 26,
т° будут удовлетворены условия (12.3), а также допол¬
нительные условия (12.1) и (12.2). Таким образом, мы
удовлетворим всем условиям и тем самым найдем полное
решение поставленной задачи.
Установим соответствие между областью S и верхней
полуплоскостью.
Точка Еи соответствующая Е, находится на прямой
GH. Так как lw2(z)/w\(z)]z^OQ = TIP, то, принимая во
108
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
внимание (12.8), найдем, что координата точки Е\
Отсюда, между прочим, следует, что сдвигающая сила
Т по абсолютной величине не может быть больше чем рР,
так как в противном случае точка Е\ уходит за пределы
области S. При |Я>рР штамп, очевидно, будет сдви¬
гаться и мы получим задачу с другими условиями.
Точка А\ совпадает с точкой пересечения прямых KL
и GH. Так как w\(z) и ιν2(ζ) согласно (12.5) и (12.6) яв¬
ляются интегралами типа Коши, плотности которых на
участке АВ пропорциональны вследствие условия t(x) —
— р/Кя) = 0, то, рассматривая эти функции в окрестности
точки А, можно показать, что они будут иметь особенно¬
сти одного и того же порядка, т. е. соответственно вида
Αχ(ζ — α)~θ и Α2(ζ — α)~θ. Следовательно, функция s(z),
равная отношению w2(z) к w\(z), будет ограниченной в
точке А, и поэтому А\ находится не в бесконечности, а в
точке, показанной на рис. 26. Рассуждая подобным же
образом, найдем положение точки D\.
Таким образом, мы установили полное соответствие
между областью S и верхней полуплоскостью (соответ¬
ствие между точками Е\, А\, D\ и точками Е, А и D).
Неизвестное положение точек В и С при этом опреде¬
ляется.
Рассмотрим теперь дугу, соединяющую точки В\ и С\.
На участке ВС имеем условие, которому удовлетворяет
Ег=*( оо) = Х.
(12.15)
откуда
Допустим, что в точках х = и и х = ν
На основании (12.16) имеем
i + β$ (и) i -f (ν)
§ 12. ЗАДАЧИ ПРИ НАЛИЧИИ ТРЕНИЯ II СЦЕПЛЕНИЯ Ю9
В силу однозначности дробно-линейной функции это
приводит к условию
s(u) = s(v). (12.18)
Итак, если выражение (12.16) меняется на участке не¬
монотонно, что влечет за собой условие (12.17), то это
приводит к условию (12.18). Однако условие (12.18) яв¬
ляется признаком того, что при перемещении по контуру
области S от В\ к С\ мы пройдем часть дуги круга дваж¬
ды. В этом случае на дуге, соединяющей точки В\ и Сι,
будет точка возврата и, следовательно, область будет об¬
ладать некоторым разрезом. С другой стороны, монотон¬
ность изменения выражения. (12.16) влечет за собой от¬
сутствие точек возврата на дуге В\С\.
Положим теперь, что отношение t{x)/p(x) меняется
монотонно па участке ВС. Тогда в силу граничных усло¬
вий (12.3)
+ Р>Я7)>-Р или Ш1<р (12-19)
и, следовательно, условие (12.1) будет выполнено.
Согласпо (12.12) имеем
j + Р.9 (Z) _ + Р^2
— β + is (ζ) “ — βι^ + iu>2'
Принимая во внимание, что на участке ВС
Im(— βι^ι + iw2) = 0, Imdwi + $w2) = О,
пайдем
i + (z) Ro {ш1 + β^2) vt + β“2 ,,2 20.
— β + ^ (ζ) Re (— βΐί^ + iw2) ν2 — βι^’
Но из (12.10) следует, что u2 — = 0 и ΐίι + βΐ’2 = 0
па участке ВС. Поэтому и\ — — βι>2 и и2 = βι>ι. Следова¬
тельно,
Г1 + β“·2 _ ν, + β\ _ _^1_ _ Р (х)
Подставляя это условие в (12.20), получим на участ¬
ке ВС
110
ГЛ. Т. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Монотонность t(x)/p(x) влечет за собой монотонность
pix)/tix) и, следовательно, выражения (12.16), а это
последнее свойство приводит к тому, что точки В\ и С{
должны соединяться дугой без точек возврата. Должна
быть принята именно дуга, показанная иа рис. 26, а не
другая, дополняющая эту последнюю по окружности.
Только в этом случае в результате уменьшения р до нуля
область S, непрерывно изменяясь, превращается в линию
и функция s(z) будет равна нулю почти всюду (см. ни¬
же). В результате этого в пределе будет получено извест¬
ное решение для вдавливания штампа с плоским основа¬
нием без сил трения. Итак, вид дуги, ограничивающей
область S на участке В\С\, влечет за собой выполнение
условия (12.1).
Воспользуемся одним из условий (12.12), общим для
участков АВ, ВС и CD:
u\ + $V2 = Imiiwi + $ιυ2) = 0. (12.22)
Но согласно (12.13) имеем w2(z) = s{z)w\(z)\ поэтому из
(12.22) получим
Im [{i + βδ (х) шх)] = 0 на AD\ \
Imw^ 0 на ЕА и DE. J I - '
Таким образом, для определения w\(z) получаем част¬
ный случай задачи Римана — Гильберта. Функция W\(z)
может быть определена на основании результатов, изло¬
женных в § 4. Выражение для w\(z) в случае, когда бу¬
дут удовлетворены условия (12.8) и (12.9), имеет вид
ί 1 ί\ Г * + β*(ζ) 1 άζ \ P(z)
wi (z) — exp j 2n J^q_j + p-(D ]ξ_ζ| {z_l)(z + i) ■
(12.24)
Если функция s(z) будет известна, то входящий в это
выражение полипом Piz) может быть определен таким
образом, чтобы были удовлетворены условия (12.8)
и (12.9).
Функция w\(z), удовлетворяющая этим условиям, мо¬
жет быть построена также для случая, когда на поверх¬
ности упругого тела приложены сосредоточенные нор¬
§ 12. ЗАДАЧИ ПРИ НАЛИЧИИ ТРЕНИЯ* И СЦЕПЛЕНИЯ Щ
мальные и тангенциальные силы, связанные некоторым
соотношением. Будем иметь также
u>2(z) = s(z) χ
+г
- ST ί ^ ϊ^-J <r=^fVr>- <12·25>
Χ - I
' —I
Нормальное давление и тангенциальные усилия опре¬
деляются формулами
p(x)=-L [lmw1{z)]:^i0, t(x) = ± llmw2(z)]z=x+i0.
(12.26)
Покажем, что если удовлетворено условие (12.23), то
тем самым удовлетворяются условия (12.10). Рассмотрим,
например, участок ВС. Если имеет место 1тШ +
+ β$(ζ)]w\(z)} = 0, το на основании (12.12) выражение
iw\(z) + ^1^2(2) на этом участке действительной оси дей¬
ствительно.
Но из определения функции s(z) следует, что на уча¬
стке ВС должно выполняться условие (12.13):
im (LhtM)=,m f =0.
\ (2) — β/ \ lw2 (2) ^ β^!^ J
Таким образом, на ВС
iwi (ζ) + βκ?2(ζ)
iw2 “ Ρ^ΐί2)
имеет действительное значение. Выше было показано,
что в этом выражении действительным будет числитель.
Раз это так, то действительным будет также знамена¬
тель. Поэтому имеем на ВС
\m[iw2iz) — βι^ι (ζ)] =0. (12.27)
Следовательно, удовлетворены оба условия (12.10) на
ВС. Рассуждая подобным же образом, можно показать,
что эти условия будут выполнены на всех участках дей¬
ствительной оси.
Покажем теперь, что при выборе области 5, который
был сделан выше, давление р(х) на участке AD нигде ие
112
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
будет обращаться в нуль, т. е. будет выполнепо усло-
BPie (12.2).
Необходимо рассмотреть два случая: во-первых, когда
w\{z) = Q в какой-нибудь точке отрезка AD и, следова¬
тельно, р(х) = + Ю)] = 0; во-вторых, когда w\{z)
на участке AD нулю не равно, обращается в нуль лишь
р(х) = Iml.M?iCr + Ю)]. Первый случай будет, если \ w\iz) I =
= 0; второй, когда arg iv\\x + Ю) = кп, где к — целое число.
Заметим прежде всего, что величина έ + β$(ζ) будет
комплексным числом; так как β — действительная кон¬
станта, то (см. рис. 26)
Из рис. 26 видно, что величина έ+β$(ζ) меняется на
участке AD непрерывно, не обращаясь нигде в нуль.
Покажем теперь, что невозможен первый случай
Ιμ?ι(ζ)| =0. Из (12.24) следует, что для этого необходимо,
чтобы на участке AD интеграл
был в некоторой точке неограниченным. Так как плот¬
ность этого интеграла типа Коши повсюду ограничена, то
интеграл будет принимать бесконечно большие значения
только в тех точках, где lg {[ ί + $s (ζ)]/[ — ί
будет иметь разрывы. Однако, согласно установленному
выше, ί + β$(ζ) (а следовательно, и сопряженная величи¬
на), изменяясь непрерывно, нигде не обращается в нуль.
Поэтому
будет непрерывным и интеграл (12.28) повсюду ограни¬
чен. Из (12.24) следует, что в таком случае w\(z) нигде
не будет обращаться в нуль и поэтому на AD не может
иметь места \ιν\(ζ) \ =0.
arg (P — Q) = arg [s (z) — y]|
= “*14-1* +
|-p- [I + β« (*)]} = arg [i + βί (z)].
(12.28)
1 glli + β* (ζ)]/ [_ί + βί(ζ)]}
§ 12. ЗАДАЧИ ПРИ НАЛИЧИИ ТРЕНИЯ II СЦЕПЛЕНИЯ ЦЗ
Перейдем к рассмотрению второго случая. Из рис. 26
видно, что на AD
-γ — arctg -j^- < arg (P — (?) =
= arg [i + β« (z)] <~~ + arctg
Так как постоянные β и ρ конечны н положительны,
то arctgd/βρ) < л/2 и поэтому на AD
О < argti + β$(ζ)] < π. (12.29)
Допустим, на этом участке Ιπιμ?ι(ζ)=0. Это будет
иметь место, если argw\(z) = кп, где к— целое число.
Но из условия:
Im[(i + βδ(ζ))ιι;ι(ζ)] =0 на AD
следует, что
argU + β$(ζ)] + arg W[(z) = k\n, argU + β$(ζ)] = к2л,
где k\ и k2 — целые числа. Однако из (12.29) следует, что
это не будет иметь места; таким образом, мы доказали,
что ImwiGs) ^0 на AD.
Итак, мы построили функции w\(z) и которые
удовлетворяют всем условиям (12.10) и, следовательно,
также условиям (12.3). При этом качественный анализ
решения оказалось возможным произвести, не зная точно
выражения для s(z). Перейдем теперь к определению
этой функции.
Для построения s(z) необходимо найти функцию, ото¬
бражающую четырехугольник S, ограниченный дугами
окружностей на полуплоскость. Покажем, что углы при
вершинах этого четырехугольника будут равны между
собой.
Из рис. 26 имеем а = ^-В\А\Е\ — х/2 л — ^-B\Q\E\.
С другой стороны, А\В\Р + ι/2 п + 7г BiQE\ = л.
Отсюда
a^AlBlP=l/2n-1/2BlQEl.
Таким образом, доказывается, что все углы четырех¬
угольника S равны между собой. Как известно, нахожде¬
ние функции, отображающей такую область на полуплос¬
кость, приводится к отысканию интегралов дифференци-
8 Л. А. Галин
114
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
ального уравнения класса Фукса (В. В. Голубев til)
„ , /l — α/π , 1 — α/π , 1 — α/π^ λ, ,
S +\~ζ h z-l + 2-α Is +
(1 — α/π) (1 —2α/π) (ζ - λ) g = Q (12.30)
ζ (ζ — 1) (ζ — α)
Трудности этой задачи заключаются в определении
параметров а и λ. Только при р = 0 и, следовательно,
а = Ч2 π мы получим частный случай дифференциального
уравнения Ляме, причем задача становится элементарной.
Однако этот случай не представляет интереса для иссле¬
дования контактных задач, так как при р = 0 единственно
возможным решением будет решение о давлении штампа
с плоским основанием, когда силы трения отсутствуют
на всей площадке контакта. При этом область S выродит¬
ся в линию.
Мы применим здесь приближенное конформное ото¬
бражение области S, причем на основании некоторых
оценок можно показать, что точность получается вполне
удовлетворительной.
Проведем через точки А\, В\ и через точки Dь С\
окружности, ортогональные к окружности F и прямой
A\D\ (рис. 27). Дугами этих окружностей А\В\ и D\C\,
дугой В\С\ и прямой A\D\ ограничена область Si, геомет¬
рически весьма близкая к S при всех значениях р и β,
с которыми приходится иметь дело в реальных условиях.
(В этом легко убедиться из рис. 27, где область Si по¬
строена для случая р = 0,6 и β = 0,286, т. е. коэффици¬
ента Пуассона ν = 0,3.)
Найдем функцию, отображающую область Si на по¬
луплоскость. При этом точкам А ι, Е\ и D\ мы будем при¬
водить в соответствие точки Л, Е и D действительной
оси. Рассмотрим вначале случай, когда сдвигающая сила
Т отсутствует и, следовательно, Z?i = 0.
Путем элементарных, но довольно длинных вычисле¬
ний устанавливается, что координаты точек К и L равны
соответственно +i и —L
Если посредством дробно-линейного преобразования
перевести точку К в бесконечность, Е в +i и L в О, то
область Si перейдет в четырехугольник, ограниченный
двумя концентрическими окружностями и двумя радиуса¬
ми. Этот последний отображается на прямоугольник, ко-
§ 12. ЗАДАЧИ ПРИ НАЛИЧИИ ТРЕНИЯ И СЦЕПЛЕНИЯ Ц5
Рис. 27.
(12.31)
(12.32)
8*
торый в свою очередь отображается на верхнюю полу¬
плоскость.
Здесь F(z\, к) — эллиптический интеграл первого рода:
Таким образом, имеем ряд зависимостей
116
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
На основании соотношений (12.31) получим выраже¬
ние для s\(z), причем, полагая s(z)~si(z), будем иметь
(12.33)
ξ = exp {- -L lg xF (JL ή - lg κ}. (12.34)
Обратная функция имеет вид
2 (s) » Iksn [lg £±i + ± π] + i lg κ}. (12.35)
Область S\ после ряда преобразований переходит в
прямоугольник со сторонами 4 arctg р и lgx. На основа¬
нии этого определяется модуль к. Он находится таким
образом, чтобы имело место равенство
К _ 2 arctg р
К' lgx
(12.36)
По известным формулам для тета-функции (Г. Н. Ват¬
сон и Е. Т. Уиттекер [1]) имеем
к' = к^[т)'
Ъ\ (0. Я) (2 qlfi + 2 q1* + + ... )*
к =
θ|(0,q) (l + 2? + 2q* + 2q9 + ... )2
На основании этого получим
Ί ^2 (0, q) ( Jllgxl /1 O Q7\
к = , где σ = βχρι f—\. (12.3/)
<>5(0,g) L arctg pj v '
Эллиптический интеграл (12.32) переводит прямоуголь¬
ник в верхнюю полуплоскость, причем положение точек
Ci и Ог, соответствующих точкам С\ и D\ области Si,
будет Ci — 1, Dx = 1/А*. Последнее пз преобразований со¬
стоит в умножении на постоянную к, поэтому
^ =-Г· <12·38)
Таким образом, определено искомое отношение длины
площадки сцепления ко всей линии контакта.
§ 12. ЗАДАЧИ ПРИ НАЛИЧИИ ТРЕНИЯ И СЦЕПЛЕНИЯ Ц7
Приведем значения отношения а/l при коэффициенте
Пуассона ν = 0,3 и различных значениях коэффициента
трения р:
Р
afl
Р
all
0
од
0,2
0,3
0,4
0,5
0
0,0369
0,366
0,695
0,868
0,942
0,6
0,7
0,8
0,9
1,0
0,974
0,989
0,993
0,996
0,997
На рис. 28 эта зависимость изображена графически.
Постараемся получить представление о точности при¬
мененного конформного отображения. Функция s\(z)
отображает область S на область £2, представляющую по¬
луплоскость, из которого вырезаны две, вообще говоря,
весьма неглубокие лунки. В частности, при р = 0,6, ν = 0,3
и I= 1,000 концы этих лу¬
нок будут соответственно
в точках х = —1,000, х =
= — 0,974 и х = 1,000, х =
= 0,974. Максимальная
глубина этих лунок равна
0,0010.
Если обозначить функ¬
цию, отображающую об¬
ласть 1S2 на полуплоскость,
через $2(2), то
s(z) = s\[s2(z)].
Для таких областей,
весьма близких к полупло¬
скости, функция мо¬
жет быть определена с до¬
статочной степенью точности. Метод построения функции,
отображающей на полуплоскость область, близкую к по¬
луплоскости, можно найти, например, в книге М. А. Лав¬
рентьева [1].
Вычисления, на деталях которых мы не будем здесь
останавливаться, позволяют уточнить значение а/1, опре¬
деленное для данного случая, и найти его с точностью до
Рис. 28.
118
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
третьего знака. Это значение будет 0,973. Таким образом,
приближенное конформное отображение дает, очевидно,
вполне достаточную точность.
Рассмотрим теперь два предельных случая, когда р = 0
и когда коэффициент Пуассона ν = 0,5 и, следовательно,
β = 0. Как видно из рис. 26, в этих случаях область S
превращается в линию. Пользуясь внутренней теоремой
площадей (см., например, И. И. Привалов [1]), легко
показать, что при этом s'(z) = 0.
В самом деле, площадь области S пропорциональна
интегралу от U'(z)l2, причем областью интегрирования
является полуплоскость. Если этот интеграл равен нулю,
то в силу положительности подынтегрального выражения
это будет иметь место только тогда, когда s'(z) равно ну¬
лю почти всюду. Кроме того, s(z) = с также почти всюду,
причем эта постоянная должна быть принята равной нулю.
Но если это так, то w2(z) = W[(z)s(z) будет равна нулю
почти всюду. Следовательно, в обоих этих случаях тан¬
генциальные усилия на поверхности будут отсутствовать
почти везде.
Остановимся в заключение на случае, когда сдвигаю¬
щая сила Τ Ф 0. При этом в соответствие точке TIP плос¬
кости s приводится бесконечно удаленная точка Е плос¬
кости ζ; соответствие других точек остается прежним.
Определим функцию s*(z) в этом случае. Функция s(z)
переводит точку Е\ = Т/Р на контуре области S в точку
z* = z(T/P) на действительной оси. [Приближенное вы¬
ражение для функции 2(5), обратной 5(2), дано формулой
(12.35).] Дробно-линейная функция, отображающая полу¬
плоскость саму на себя, переводит Е\ в бесконечно уда¬
ленную точку. Поэтому окончательное выражение для
s*(z) будет таким:
**(*) = *[тй£]· (12·39)
Результаты, содержащиеся в этом параграфе, позволя¬
ют сделать следующие выводы (см. рис. 28). Если коэф¬
фициент трения между штампом и упругой полуплоско¬
стью невелик, меньше чем 0,1, то размеры участка, где
имеет место сцепление, незначительны и поэтому для
определения давления следует пользоваться формулой,
полученной в предположении отсутствия сил трения. Ес¬
§ 13. ЗАДАЧА О КОНТАКТЕ ДВУХ УПРУГИХ ТЕЛ
119
ли же трение значительно, а коэффициент трения больше
чем 0,5, сцепление будет иметь место почти на всей пло¬
щадке контакта и для нахождения давления целесооб¬
разно воспользоваться предположением о жестком сцеп¬
лении между штампом и упругим телом.
В работе В. И. Моссаковского и В. В. Петрова [1]
приведены результаты ряда экспериментов, где исследу¬
ется изменение фактической площади контакта в зависи¬
мости от прикладываемой нагрузки и получена некоторая
кривая. Она качественно совпадает с результатами, уста¬
новленными в этом параграфе при решении задачи о вда¬
вливании штампа с плоским основанием, контактная пло¬
щадка которого разбита на центральную зону сцепления
и две зоны проскальзывания.
§ 13. Задача о контакте двух упругих тел
В предыдущих параграфах при рассмотрении контакт¬
ных задач предполагалось, что одно из тел, находящихся
в соприкосновении, является абсолютно твердым. Приме¬
няя установившуюся терминологию, мы называли это
тело штампом.
Однако подобное предположение не является слишком
ограничительным. Мы покажем здесь, что в ряде случаев,
когда соприкасаются два упругих тела, для решения за¬
дачи необходимо определять
аналитические функции на У
основании смешанных уело- к
вий таких же типов, с каки- %
ми мы имели дело ранее. \
Мы будем полагать, что
радиусы кривизны обоих тел
велики по сравнению с раз¬
мерами площадки контакта
и поэтому каждое из этих
тел будем заменять полупло- Рис. 29.
скостью (рис. 29).
Установим соотношение между перемещениями, кото¬
рое должно иметь место на площадке контакта. Пусть
Уравнения поверхностей, ограничивающих первое и вто¬
рое тела, до деформации таковы:
yi = fi(x), Уг = —/г(я)· (13.1)
120
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Начало координат поместим в точке первоначального
касания тел. Под действием сил первое тело получит пе¬
ремещение δι, а второе тело — перемещение б2. Кроме
того, точка А, расположенная на поверхности первого те¬
ла, и вступающая с ней в контакт точка J5, которая на¬
ходится на поверхности второго тела, в результате проис¬
шедшей упругой деформации получат соответственно пе¬
ремещения vi и ν2 в направлении оси г/.
Так как координаты точек А и В после вступления
их в контакт становятся одинаковыми, то это позволяет
найти следующее условие, связывающее перемещения
обоих тел:
fi(x) + νι—δ[ = — f2(x) — ν2 + δ2,
или отсюда получаем при у = 0 (мы полагаем, что гра¬
ничные условия могут быть снесены на ось х)
νχ + ν2 = δ{ + δ2-fi(x) - /2(х). (13.2)
В дальнейшем придется иметь дело с производными
от перемещений v\ и ν2 по координате х. Из (13.2) на¬
ходим
(аГ+ а7)у=о = -Μ*)-/ι(ζ)· (13.3)
Нормальное давление, действующее на первое тело
вдоль площадки контакта, совпадает с нормальным дав¬
лением, которое действует на второе тело. Точно так же
равны по абсолютной величине и тангенциальные усилия.
Таким образом, dv\/dx и dv2/dx могут быть выражены
по формулам (2.15) на основании одних и тех же нор¬
мальных давлений и тангенциальных усилий. Имеем сле¬
дующие выражения:
пЕ1 (dvx) К I 1 ~ 2ν1 π fт )
2(1 _ν») VUo ~ j ( ϊ,!/=0 ζ - * + 2 - 2ν, π (τ*^=ο.
яЕ0 (dv,} άζ 1-2v2 ( ^
2(1 +ν?) Wi/=o_ j {°у)у~0 2 - 2ν2 π
§ 13. ЗАДАЧА О КОНТАКТЕ ДВУХ УПРУГИХ ТЕЛ
121
Отсюда находим
(13.4)
(ϊλ _2(‘-».')L·' _s_,
\ дх Jy--=Q - лЕ J Ισβ)ν— ζ _ х +
а
, (t + v1)(l-2v1)
τ /? vlwy=o>
1
tei -2(‘-»«)L·'
\dxjy=0- лЕ
a
(1 + v2)(1-2v2)
Vl^;i/=0·
Знак минус перед (тху)у=о во втором из выражений (13.4)
обусловлен обратным направлением тангенциального на¬
пряжения.
Подставляя (13.4) в условие для перемещений (13.3),
будем иметь
(дЛ + дЛ)
\ дх ' дх )у=о
2 (1 — vf) 2(1-у22)
JVi/Wo^
а
(1 + Vl)(l - 2va) (1 + ν2)(1 - 2ν2)
βι Ег
(T3Ci/)i/=0 —
= —/l (*)—/*(*)»
пли, после преобразований,
Ь V + \)(1~2νι) „ (1 + ν2) (1 - 2у2)
[σ,Λ„_„
2
2(1~νΐ) , 2(1~V2)
Η ^
х
Et
X π (тжу)*/= о —
1
[2(1 —vf) 2(1 —v^) I
L πΕ1 ЛЕ2 J
X
122
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Если ввести обозначения
2(l-v*) 2(1 -v|)
1 “ πΕ1 “Τ' πΕ2 '
(l + v1)(l-2v1) (1 + v2)(1-2v2)
2(l-v*) l2(1-v|)
Ea
то окончательно найдем
ь
a
(13.7)
Итак, получено условие, совершенно аналогичное од¬
ному из выражений (2.15). Введем, так же как это дела¬
лось ранее, функции w\(z) и w^<z)\
Эти функции определены в нижней полуплоскости.
Таким образом, задача о контакте двух тел, из которых
одно заменяется верхней, а другое нижней полуплоско¬
стью, приводится к отысканию функций только в нижней
полуплоскости.
Приведем граничные условия для нескольких контакт¬
ных задач.
1. Случай, когда на площадке контакта отсутствуют
силы трения. Так как в этом случае тангенциальные уси¬
лия отсутствуют, W2(z) = 0. В результате получаем гра¬
ничные условия [см. формулы (3.3) в § 3J. Вне площадки
контакта
ь
а
b
(13.8)
а
VI = 0;
(13.9)
§ 13. ЗАДАЧА О КОНТАКТЕ ДВУХ УПРУГИХ ТЕЛ
123
на площадке контакта
ui = — -χ /ί И·
2. Случай, когда на площадке контакта имеют место
силы трения.
Пусть коэффициент трения равен р. В таком случае
на основании (3.3) вне площадки контакта
V\ = О, v2 = 0,
на площадке контакта
иг — mv.2 = — 4-[f'l (χ) + /г (ζ)], ν2 — pvt = 0.
Условие V2 — = 0 позволяет свести задачу также
к определению одной функции w\(z). Принимая во вни¬
мание это соотношение, получим:
вне площадки контакта
иг = 0;
на площадке контакта
иг — тро1 = — -J- [fi (х) + /г (ж)].
(13.10)
Таким образом, граничные условия (13.8) для опреде¬
ления функций w\(z) в случае контакта двух упругих тел
при отсутствии сил трения имеют точно такую же форму,
как и условия (5.7), полученные для решения этой зада¬
чи, когда исследовалось давление жесткого штампа. Точ¬
но так же условия (13.10) при наличии сил трения ана¬
логичны выражениям (7.12), которые были получены в
§ 7 для такого же случая.
Итак, решения задач, о которых идет речь в этом
параграфе, имеют точно такую же форму, как и решения
задач, рассмотренных ранее, отличаясь от них только не¬
которыми построениями.
В случае, когда между двумя упругими телами на
площадке контакта имеет место жесткое сцепление, также
могут быть получены граничные условия для определения
двух функций w\{z) и w2(z), аналогичные тем, которые
имеют место при наличии жесткого штампа.
124
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Заметим, что задачи о контакте двух упругих тел
становятся особенно простыми, когда упругие постоянные
обоих тел одинаковы. Тогда в выражении (13.5) исчезает
член, содержащий тангенциальную нагрузку. Поэтому на
основании заданной формы штампа может быть сразу
определено нормальное давление.
§ 14. Приближенный учет пластических деформаций,
возникающих под штампом
Будем рассматривать воздействие штампа, имеющего
плоское основание, на упругую полуплоскость. При этом
под штампом будет возникать давление, которое опреде¬
ляется по формуле
р(х)= Z—-. (14.1)
π у с? — я2
Таким образом, в точках, где х = + а и я = — а, т. е. у
углов штампа, давление равно бесконечности. Однако в
действительности в окрестности точек А и В возникают
области пластических деформаций, в результате чего дав¬
ление становится конечным.
Попытаемся приближенно исследовать вопрос об из¬
менении давления, возникающего под штампом, а также
вопрос о виде пластических областей. Будем полагать, что
после перехода материала в пластическое состояние для
него будут справедливы уравнения идеальной пластично¬
сти, т. е. величина максимального тангенциального на¬
пряжения будет равна константе пластичности к. Итак,
положим, что при той нагрузке, которая приложена к
штампу, в окрестности его углов возникают небольшие
области пластических деформаций (области предельного
равновесия).
Сделаем также допущение, что одной частью контура
пластической области будет граница упругой полуплоско¬
сти, свободная от усилий. Другая часть контура пласти¬
ческой области будет находиться под штампом, который
согласно условию обладает плоским основанием.
В таком случае, значение давления /?, при котором
область, указанная на рис. 30, будет находиться в состоя¬
нии предельного равновесия (см., например, В. В. Соко¬
§ 14. ПРИБЛИЖЕННЫЙ УЧЕТ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ 125
ловский [1]), будет равно
к(п + 2), (14.2)
где к — константа пластичности.
На рис. 31 показана пунктиром предполагаемая форма
пластической области, где АВ — площадка контакта.
Сделаем достаточно естественное предположене о том,
что давление справа от точки С (границы пластической
Ряс. 30.
области) будет меньше, чем максимальное давление, рав¬
ное к(п + 2), при котором будет иметь место состояние
предельного равновесия. Такое же соотношение будет
иметь место также слева от точки D. Само собой разу¬
меется, что это предположение нуждается в строгом до¬
казательстве. При удалении от пластических областей
давление, очевидно, будет приближаться к тому, которое
дается формулой (14.1). Действительная кривая будет
проходить примерно так, как показано пунктиром на
рис. 31.
Указанные выше соображения позволяют приближен¬
но оценить изменение давления на площадке контакта,
а также размеры пластических областей.
Решение песколько более простой задачи об опреде¬
лении формы пластических областей в случае, когда па
границе полуплоскости действует заданное нормальное
давление, может быть получено посредством применения
метода аналогии для решения упруго-пластической зада¬
чи. В этом случае областями пластических деформаций
126
ГЛ. I. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
будут те зоны, где упругая пластинка, находящаяся под
воздействием моментов, приложенных на контуре, сопри¬
касается с твердыми телами, поверхности которых соот¬
ветствуют функциям напряжений в пластической области.
Подробное обоснование метода аналогии содержится в
статье автора [3J.
На рис. 32 изображено устройство, посредством кото¬
рого может быть произведено это моделирование. Тело К
соответствует функции напряжений в пластической обла¬
сти. Оно состоит из двух параболических цилиндров С\,
одного параболического цилиндра С2, обладающего боль¬
шой кривизной, и двух тел F\ и F2, уравнения которых
в цилиндрических координатах (начала координат распо¬
лагаются в точках А и В) будут z = kr2Q. Упругая плас¬
тинка, жестко защемленная вдоль отрезков СА и BD,
касается на отрезке АВ тела К, причем на нее на этом
отрезке действует заданная моментом нагрузка. Величина
момента, приложенного в данной точке, пропорциональна
нормальному давлению, которое действует в этой точке
границы полуплоскости. Под действием моментов упругая
пластинка изгибается и прижимается к телу К. При этом
зонам пластических деформаций будут соответствовать
области, ограниченные штриховой линией, в окрестно¬
стях точек А и В.
Заметим, что предлагаемый метод моделирования при¬
меним в том случае, когда пластические области не силь¬
но развиты и функции напряжений для них будут имен¬
но такими, которые соответствуют телу К.
ГЛАВА II
ПРОСТРАНСТВЕННЫЕ КОНТАКТНЫЕ ЗАДАЧИ
ТЕОРИИ УПРУГОСТИ
§ 1. Напряжения и перемещения
для упругого полупространства
Мы будем рассматривать задачу о давлении штампа
на упругое тело, занимающее полупространство, в слу¬
чае, когда между упругим телом и штампом не возника¬
ют силы трения. Предположим, что на границу полупро¬
странства при ζ = 0 действует заданная нагрузка р{х, у).
Для нахождения напряженного состояния и перемеще¬
ний в теле удобно воспользоваться, как это было сделано
А. И. Лурье [1], функциями, введенными для решения
трехмерной задачи П. Ф. Папковичем [1] и НейберомШ.
При этом перемещения и, ν и w выражаются через гар¬
монические функции Фо, Фь Ф2 и Ф3:
и _ фх — — — (ф0 + χφχ -]- уф2 -f- ζΦ3),
ν = ^2 “ 4 1_J ν) Ту (Φ° + χΦι + У®* + *фзЬ
W = φ3 - 4 (1 — ν) Τζ (φ0 + жф1 + УФ* + 2фз)·
(1.1)
Здесь ν — коэффициент Пуассона.
На границе упругого полупространства равны нулю
компоненты напряжения
— О, х1У — 0 при 2 = 0. (1.2)
ьхх
Выражая эти величины через перемещения и, у, w,
найдем соотношения между введенными функциями:
4. 2(1~v> L_ A ί г ίίί + ^ 4- ^ = О
дх ' 1 — 2v dz 1 — 2v dx \ dz ^ dz dz j ’
128 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
£Ф3
ду
+
2 (1 — у) дФ2 1 д
1 — 2v dz 1—2ν ду
I дФ. дФ9 <?ФП\
1*ТГ+!'15- + -Зг) = 0·
Таким образом, между граничными значениями (при
; = 0) функций Ф0, Φι, Ф2 и Ф3 существуют соотношения
дФг
dz
1 — 2v ^ф2
2 (1 — ν) дх ’ dz
2 (1 — ν) ду щ
д%
dz
i_2v I дф3 ^ф3\
2 (1 - ν) \ дх ^ У ду У
Однако, если две гармонические функции, исчезаю¬
щие на бесконечности и удовлетворяющие некоторым ус¬
ловиям, касающимся их регулярности, совпадают на гра¬
нице области, то они равны между собой всюду в обла¬
сти. На основании этого получаем
дФ1
dz
д%
dz
дфл
1 - 2v дф3
2 (1 — V) дх'
1 — 2v д®3
2 (1 - ν) ду'
<-2v I », £«,\
) \ дх ш ' У ду ' dz )
(1.3)
dz 2 (1 — ν)
Если ввести новую гармоническую функцию
Φι '■=
4ν
Фз»
8 (1 - ν)
то Фо, Φι и Ф2 выражаются следующим образом:
(1.4)
§ 1. НАПРЯЖЕНИЯ II ПЕРЕМЕЩЕНИЯ
129
Подставляя (1.5) в (1.1), получим перемещения
u = (l-2v)j^4z-z^:\
2
ОО
С дф* д(р ί
ζ
dW%
w = 2(1 — ν)φ! —
Компоненты напряжения таковы:
7' д\, , й2<р.
1 + ν
1 + V« -9«3<P1
Е х — 2 dz
Е
Лч
dydz'
l±-v = 2v 5 + (1 - 2v) J d, -1 i£‘,
1 + v _ ^2φχ
E Xzx~ z dzdx'
1 +
Ρ τχν = (1 - 2v) J <fa _ z _*J,
1 + ν* 5Φι θ2Φι
E ~ dz z dz* ‘
(1.6)
(1.7)
Будем теперь полагать, что нормальное давление
р(х, у) распределено на некоторой области Ω, располо¬
женной на границе полупространства. Таким образом,
имеем
σΗ"
р (х, у) внутри Ω,
О вне Ω.
(1.8)
Из соотношений (1.7) следует, что величина компо¬
нента напряжения ог при ζ = 0 и, следовательно, величи¬
на давления — р(х, у) выражаются через производную от
9 л. А. Галин
130 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
введенной выше гармонической функции
<σ.)·—= 2й(5-‘),-.· -25'’<*'»> = (srL.· <19>
где 0 = 27IW·
Итак, на основании (1.8) получаем для определения
функции φι(χ, г/, ζ) следующий случай задачи Неймана:
~^р(х,у) внутри Ω,) (110)
0 вне Ω. ■
ί-1) =
\ д* /ζ-*+о
Из теории потенциала известно, что такая функция
может быть представлена в виде потенциала простого
слоя:
JaJ V <* - 6) + fo - ч) + =
Принимая во внимание последнее из уравнений (1.6),
устанавливающее связь между м; и φι, получим выраже¬
ние для перемещения w, имеющего место на границе
полупространства (ζ = 0):
Из (1.12) следует, что если известно перемещение штам¬
па в области Ω (и при этом отсутствует тангенциальная
нагрузка, т. е. силы трения), то известна гармоническая
функция φι(χ, у, ζ) на одной стороне этой области, а в
силу четности потенциала простого слоя также и на
другой.
Таким образом, для определения гармонической функ¬
ции cpiU, г/, ζ) мы получаем частный случай задачи Ди¬
рихле, когда значения функции, исчезающей на беско¬
нечности, заданы па двух сторонах плоской области, рас¬
положенной в плоскости ζ = 0.
Если определена функция <pi(;r, у, ζ), соотношения
(1.6) и (1.7) позволяют определить перемещения и
компоненты напряжения в любой точке полупростран¬
ства.
§ 2. РЕШЕНИЯ УРАВНЕНИЙ ЛАПЛАСА
131
В дальнейшем часто будет вводиться в рассмотрение
гармоническая функция φ, причем
φ = — 2(1 — ν)φι. (1.13)
Значение этой функции при 2 = 0 согласно (1.6) совпада¬
ет с величиной перемещения поверхности w(x, у, 0).
§ 2. Решения уравнений Лапласа
в некоторых криволинейных координатах
В предыдущем параграфе установлено, что задача о
давлении штампа па упругое полупространство в случае,
когда на площадке контакта не возникает сил трения,
может быть приведена к частному случаю задачи Дирих¬
ле. При этом значения некоторой гармонической функ¬
ции заданы на двух сторонах плоской области, располо¬
женной в плоскости ζ. Естественно попытаться устано¬
вить, в каких случаях эта задача допускает эффектив¬
ное решение.
Такое решение оказывается возможным получить в
следующем случае: необходимо ввести систему криволи¬
нейных координат так, чтобы двухсторонняя поверх¬
ность Ω, о которой говорилось выше, была одной из ко¬
ординатных поверхностей. Необходимо также, чтобы
решение уравнения Лапласа при переходе к этой системе
координат «расщеплялось», т. е. гармоническую функцию
можно было бы представить в виде произведения трех
функций от каждой из координат. Кроме того, нужно,
чтобы полученные системы функций были ортогональ¬
ными. Этим условиям удовлетворяют следующие системы
координат:
1. Эллиптические координаты. Вводятся координаты
ν, μ и р, связь которых с прямоугольными дается сле¬
дующими соотношениями:
гх2 = а2 ρ2μ2ν2, |
(1 — ε2) г2у2 = а2 (р2 — ε2) (μ2 — ε2) (ε2 — ν2), 1 (2.1)
(1 - ε2) ζ2 = α2 (ρ2 - 1) (1 - μ2) (1 - ν2); J
при этом 1^ρ<οο, ε^μ^Ι, Ο^ν^ε.
Координатными поверхностями будут в этом случае
эллипсоиды, однополостные и двуполостные гиперболои-
9*
132 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
ды. При этом функция от одной из координат р будет
постоянна на поверхности эллипсоида. В пределе при
р = 1 этот эллипсоид вырождается в эллиптический диск.
Гармоническая функция при использовании этой системы
координат может быть представлена в виде произведения
трех функций Ляме:
φ (х, у, z) = Em (р) EZ. (μ) Ε„ (ν).
Функции Ляме ортогональны.
Таким образом, применение этой системы координат
позволяет решить задачу о штампе эллиптической фор¬
мы в плане, так как в этом случае область Ω будет эл¬
липсом.
Заметим, что можно обобщить этот результат. Если
применить к гармонической функции преобразование
Кельвина (см. § 4), то полученная функция будет также
гармонической. Если известны значения этой функции
§ 2. РЕШЕНИЯ УРАВНЕНИЙ ЛАПЛАСА
133
на двух сторонах плоской эллиптической области Ω, рас¬
положенной в плоскости 2 = 0, то в том случае, когда
центр преобразования находится также в плоскости
2 = 0, будут известны значения этой функции на двух
сторонах плоской области Ωι, являющейся инверсией эл¬
липса. Таким образом, задача Дирихле может быть ре¬
шена для плоской области Ωι, когда ее контур получает¬
ся посредством инверсии эллипса. На рис. 33 приведены
различные формы этих областей (кривые даны жирными
линиями). Такие формы в плане могут иметь штампы,
причем решение будет выражаться в конечном виде через
функции Ляме.
Уравнение кривой, полученной при инверсии эллипса
в параметрической форме, таково:
д-... ^ R(P + l)
У(Р + if + (? ± ZbV^a2 — 62|aj2'
R \q±YbVΛ* - δ2!2) ί2'2*
У = — ■ ■ — а
λί(р + If + (g ± jj У- 62ξ2)2
Здесь р и q — координаты центра эллипса относительно
центра инверсии, а и Ъ — полуоси эллипса.
2. Сфероидальные координаты. Эти координаты г, η
и φ являются частным случаем эллиптических координат.
Координатными поверхностями будут эллипсоиды вра¬
щения, однополостные и двуполостные гиперболоиды вра¬
щения. При этом эллипсоид вращения вырождается в
круговой диск. Связь между прямоугольными коорддна-
тами и сфероидальными такова:
х = j/r2 + a2 sin η cos φ,
у = Υг* + λ2 sin η sin<p, ζ — r cos η.
Эта координатпая система может быть применена в
том случае, когда штамп будет иметь круговую форму
в плане.
Заметим, что в этом случае, как это показано в § 3
и следующих, более удобное решение ряда задач может
быть получено без привлечения специальных функций.
(2.3)
134 гл. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
3. Сферические координаты. Связь между прямо¬
угольными и сферическими координатами такова:
# = rcos0, y = r sin Θ cos θ, z = r sin Θ sin θ. (2.4)
Эта система координат, хотя и не обладает всеми ука¬
занными выше свойствами, также оказывается удобной
при решении задачи о клинообразном штампе (см. § 12).
Заметим, что в работе Η. Н. Лебедева [1] введена ко¬
ординатная система, в которой одно из семейств коорди¬
натных поверхностей является семейством торов оваль¬
ного сечения. При этом торы в предельном случае вы¬
рождаются в плоское кольцо. Эта система координат
могла бы быть применена к решению задачи о давлении
штампа кольцеобразной формы в плане. Однако связан¬
ные с ней специальные функции не табулированы, что
затрудняет их применение.
§ 3. Задачи для штампов круговой формы в плане.
Общий случай
В настоящем параграфе дается решение задачи о дав¬
лении на упругое полупространство штампа круговой
формы в плане с произвольно изогнутым основанием. Как
будет показано в дальнейшем, эта задача на основании
некоторых результатов теории потенциала, полученных
достаточно давно, может быть решена в конечном виде.
Следует заметить, что такая весьма общая постановка
представляет, может быть, меньший интерес, чем реше¬
ние, и притом достаточно эффективное, ряда более част¬
ных задач. Однако решение в общей постановке позволит,
в частности, найти в дальнейшем некоторые важные
оценки (§ 11).
Будем полагать, что на абсолютно твердое тело (кото¬
рое в дальнейшем называется штампом), находящееся па
упругом полупространстве, действуют силы, вследствие
чего в упругом теле возникает напряженное состояние.
Одной из целей исследования является установление рас¬
пределения давлений на площадке контакта, а также на¬
хождение зависимости между силой, действующей на
штамп, и величиной его перемещения. Параграфы, отно¬
сящиеся к штампам круговой формы в плане, воспроиз¬
водят статьи автора [2, 3].
§ 3. ЗАДАЧИ ДЛЯ ШТАМПОВ КРУГОВОЙ ФОРМЫ В ПЛАНЕ 135
Граничные условия в контактной задаче для упругого
полупространства iz ^ 0) при отсутствии сил трения име¬
ют следующий вид:
на площадке контакта L при ζ = 0
w = f(x,V) + c, τχζ — 0, τυζ — 0;
на свободной поверхности, вне L при ζ—0
σζ = 0, τχζ = 0, хУ2 = 0.
Здесь w — перемещение точек упругого полупространства
в направлении оси ζ, с — перемещение штампа, σ2, τΛΖ,
Tyz — компоненты напряжения.
Уравнение поверхности штампа:
z — fix, у):
Функция <р(я, у, ζ) может быть, согласно (1.11), пред¬
ставлена в виде потенциала простого слоя:
φ(^,Ζ) = ί^Γίρ(ξ,η) *** (3.2)
nh |/(^_ξ)2+(2/_η)2 + 22
Здесь pix, у) — давление, действующее на поверхности
упругого тела.
Таким образом, определение φ(#, у, ζ) в случае отсут¬
ствия сил трения сводится к следующему случаю задачи
Дирихле: необходимо найти гармоническую функцию,
исчезающую на бесконечности и непрерывную всюду,
кроме кругового диска. На верхней и на нижней сторо¬
нах диска она принимает равные по величине заданные
значения.
Рассмотрим случай, когда в упругое полупространство
вдавливается штамп круговой формы в плане (круг ра¬
диуса а, который мы будем обозначать через S). Его ос¬
нование является поверхностью, представляющей функ¬
цию двух координат (рис. 34). Пусть уравнение этой по¬
верхности ζ = fix, у).
Для определения гармонической функции, равной
fix, у) на верхней и на нижней сторонах диска и исче¬
зающей на бесконечности, воспользуемся выражением,
данным Гобсоном [2] (см. также книгу Гейне [1]).
Если ввести сфероидальные координаты г*, η*, φ*,
которые связаны с прямоугольными следующими соотно-
136 гл. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
шениями:
х = У г*2 a2 sin η* cos φ*,
у = У г*2 -f a2 sin η* sin φ*, ζ = r* cos η*
(3.3)
(причем 0 < г* < оо, 0 < η* < π/2, 0 < φ* < 2π), то будем
иметь
2π π/2 *
С С / * 2α sin η,
φ(Γ*,η*,φ*)= /(ηι,φι)-^ ; X
J J яг cos η
о о
( a cos η! cos η* a cos ть cos η*) * *
X |l Η arctg j d\\idy t. (3.4)
Здесь r — расстояние между точками с координатами со¬
ответственно г*, η*, φ* и г* = 0, ηχ, ψχ.
Если перейти теперь к прямоугольным координатам,
приняв при этом во внимание, что элемент площади в
2 i
{P
1
УШФ/Ά
L a J
Рис. 34.
сфероидальных и прямоугольных координатах соответ¬
ственно будет
dS = a2 sin r\*cos ηί^ηι^φι, dS = d\ di),
то получим
φ (χ, У, ζ) = J J / (ξ, η) j”^ -f arctg M j j dl ώη.
(3.5)
§ 3. ЗАДАЧИ ДЛЯ ШТАМПОВ КРУГОВОЙ ФОРМЫ В ПЛАНЕ 137
Здесь
П/Г ζ Ϋ2 У~а2 — ξ2 — η2
г х2 -f- у2 -f- ζ2 — а2 + R
г = V (х — ξ)2 + (у — η)2 + ζ2,
Л = 7/ (а2 — х2 — у2 — ζ2)2 -f 4 α2ζ2.
Ha основании (3.5) по формулам (1.7) могут быть
определены напряжения в упругом теле. Что касается
давления, действующего на площадке контакта, то для
него согласно (1.10) будем иметь
p(i’rt=2-<dbK*L' <з-б>
Воспользуемся выражением (3.4) для определения си¬
лы, действующей на штамп, которая имеет такое значе¬
ние, что поверхность упругого тела под штампом будет
определяться уравнением ζ = /(х, у). Из (3.2) следует,
что при s = (х2 + у2 + ζ2)Ίι -*· о© будем иметь
[<р(я, У, z)]SH.oo= (З·7)
Здесь Р — сила, действующая на штамп:
Р= f |ρ(ξ,η)^<Ζη. (3.8)
s
С другой стороны, из (3.4) следует, что
2π п'2 *
[φ(Γ*, η*, <р*)]г*-*оо=^
о о
Кроме того, при г* -*■ оо будет иметь место z!cos η* s.
Отсюда при s
2 π π/2
φ (ж. У, ζ) = 4- ί \ f (η*, φ*) sin η^η^φΓ· (3.9)
ο ο
Если теперь сравнить (3.7) и (3.9) и перейти от сфе¬
роидальных координат к полярным на диске S, восполь¬
зовавшись для этого соотношениями (3.3), то получим
выражение для силы, действующей на штамп.
ГГ,/* * \ ^ sm η * *
/UUi<Pi)-2 T2dlfUd(Pi
) J n cos η*6·
138 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Результат может быть сформулирован следующим об¬
разом: на штамп круговой формы в плане (радиуса а),
основание которого ограничено поверхностью z = f(x, у),
находящийся на упругом полупространстве, действует
сила Р. Для того чтобы соприкосновение происходило по
всей площадке контакта, нужно, чтобы
2Л а
Р = Е f f / (Ρι, θ) —4= dPldB. (3.10)
π (l — ν ) J J V«*-p!
Следует заметить, что здесь перемещение штампа в
направлении оси ζ входит в качестве постоянного слагае¬
мого в функцию fix, у).
Рассмотрим случай, когда /(ρ, Θ) = с. При этом штамп
с плоским основанием вдавливается на глубину, равную с,
и, следовательно,
Р = .—2 с I -7=r=i ^ с· <ЗЛ1>
1 - V J У а2 - р2 1 - V
Это совпадает с результатами Буссинеска [1].
§ 4. Функция Грина для внешности кругового диска
В следующем параграфе будет рассмотрена осесим¬
метричная контактная задача при дополнительном требо¬
вании относительно давления под штампом, которое
должно быть ограничено на контуре площадки касания.
Решение можно было бы получить, исходя из общей фор¬
мулы (3.5). Однако удобнее определение функции φ(χ,
г/, ζ) свести к задаче Неймана. При этом для построения
решения будет необходима функция Грина, которая об¬
ращается в нуль на внешности кругового диска и ведет
себя как 1/г в окрестности точки, расположенной на ди¬
ске. Так как эта функция представляет значительный
интерес, в частности, для задачи о крыле круговой фор¬
мы в плане, дадим элементарный способ ее определения.
Установим некоторые свойства введенной функции Грина.
Пусть построена К{х, г/, ζ, ξ, η) — гармоническая
функция переменных х, у и ζ, удовлетворяющая следую¬
щим условиям:
§ 4. ФУНКЦИЯ ГРИНА ДЛЯ ВНЕШНОСТИ КРУГОВОГО ДИСКА 139
1. В области Λ функция К(х, у, ζ, ξ, η) = 0, причем
Λ — полубесконечная область в плоскости ζ = 0, внешняя
к некоторой области L, также находящейся в плоскости
2=0.
2. Функция К(х, у, ζ, ξ, η) ведет себя как
1 1
r Y(x — I)2 + (У - η)2 + Ζ2
в окрестности точки (# = ξ, г/ = rj, 2 = 0), находящейся
в области L.
3. Функция К(х, г/, 2, ξ, η) непрерывна во всем про¬
странстве.
4. Функция дК(х, г/, 2, ξ, η)/$2 непрерывна в точках
области L.
Функцию К(х, у, 2, η) можно представить в виде
К (х, у, 2, I, η) =
= J J?(S, η, I', η') -r . +
V ν (*-!') +(»-η')+**
+ —r - 1 —■· (4-1)
— i)2 + (у — η)2 τ г2
При этом плотность простого слоя #(ξ, η, ξ', η') под¬
бирается так, чтобы выполнялось условие 1. Это всегда
можно сделать, если известно решение задачи Дирихле
для пространства, внешнего по отношению к области А.
В самом деле, если
К(х, у, ζ, I, η) =
= К* (х, у, ζ, I, η) + 1 ,
У (χ — 1) (у — η) 4-ζ
то для того, чтобы на Λ (на двух сторонах этой плоской
области, расположенной в плоскости 2 = 0) имело место
равенство
К(х, у, 0, η) = 0,
необходимо, чтобы также на двух сторонах области А,
следовательно, при 2 = 0, выполнялось условие
К* (х, У, ζ, I, η) = - 1 ■
у (х — |)2 + (у — η)2
140 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Если известно решение задачи Дирихле для простран¬
ства, внешнего по отношению к области Л, то может
быть определена функция K*ix, у, ζ, ξ, η). После того
как отыскана эта функция, находится ее производная по
zy т. е. по нормали к области Л при ζ — 0. Это позволит
определить плотность qi\, η, η') в потенциале просто¬
го слоя и получить представление
Таким образом, находится выражение (4.1).
Из (4.1) следует, что Kix, у, ζ, ξ, η) — четная функ¬
ция ζ. Следовательно, в точках, где ζ = 0 и где К(х, у, ζ,
ξ, η) и dKix, у, ζ, ξ, y\)/dz непрерывны, т. е. согласно ус¬
ловиям 3 и 4, в области L будет иметь место dKix, у, ζ,
ξ, η)/5ζ = 0. Это будет соблюдаться везде, кроме точки
# = У = Ц, 2 = 0, в которой dKix, у, л, ξ, η)/5ζ = «>.
Образуем теперь функцию
Очевидно, F(x, у, ζ) будет гармонической функцией пере¬
менных х, у и ζ. Так как подынтегральное выражение в
этой формуле согласно условию 1 равно нулю в точках
области Л, то и Fix, у, ζ) в этих точках равна нулю. Она
может быть представлена в виде суммы
К*(х, у, ζ, ξ, η) =
F (*, У, z) = J J g (ξ, η) К (;г, у, ζ, ξ, η) dr). (4.2)
L
Fix, y, z)=F\ix, y, z)+F2ix, y, z), (4.3)
причем
L
x . η.ξ',η')
Ϋ (Χ-1'Ϋ+(У -·η')*+ ζ2
X
A
(4.4)
X dl·, dt],
(*» У· z) —
Я*<Ы>
/(* -1)2 + (г/ - η)3 + г2
L
§ 4. ФУНКЦИЯ ГРИНА ДЛЯ ВНЕШНОСТИ КРУГОВОГО ДИСКА 141
При этом поверхность L строится таким образом, чтобы
точка # = ξ, £/ = η, 2 = 0 находилась снизу от нее.
Функция F\(x, у, ζ) — четная по отношению к ζ и
имеет производную, непрерывную в точках области L.
Следовательно, в этих точках [сМ^я, у, z)/dz]z=0 = 0.
С другой стороны, как известно, [дР2(х, у, z)/dz]z=0 =
= g(x, у). Поэтому в области L имеем
В области Λ функция F(x, г/, ζ), как указано было
выше, будет равна нулю. Таким образом, Fix, у, ζ) удов¬
летворяет следующим граничным условиям при ζ = 0:
Определим теперь функцию К(х, у, ζ, ξ, η) для слу¬
чая, когда область L является кругом радиуса а. Для
определения К(х, у, ζ, g, η) будем исходить из функции
Их(хи У и zu ос), которая (рис. 35, а) удовлетворяет сле¬
Рис. 35.
(4.5)
-57 = ё(х, У) на L, F = 0 на Λ. (4.6)
142 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
дующим условиям при ζι = 0:
Hi (*ι> Уи α) = 1 на St,
β
{χχ, уг, ζχ, а) = 0 вне Sx,
где Sί —* круг радиуса а.
Если ввести «сфероидальные координаты г*, η*, φ* по
формулам (3.3), полагая при этом а = а, то можно пока¬
зать, что
Здесь Qo(ir*/a) —- функция Лежакдра второго рода нуле¬
вого порядка.
Как известно, Qo{ir*/a) = arcctg (г*/а). Выражая r*/a
через #i, yi и ζι, будем иметь
Если теперь введем новые переменные х2 = χι + β, у2 = ί/ь
Ζ2 = Ζι, то получим функцию
равную единице на некотором круге S2, центр которого не
совпадает с началом координат (рис. 35, б).
Применим к #2(#2, У2, ζ2, а) преобразование инверсии
относительно начала координат. Преобразование инвер¬
сии, или преобразование Кельвина, как известно, заклю¬
чается в следующем. Если Ф(я, г/, ζ) является гармони¬
ческой функцией, то также гармонической функцией
будет
Здесь у Ф(я, г/, ζ) вместо х, у, ζ берутся новые значения
н, {х1У у 1( zlt а) = 1 — arctg Θ,
Я2(ж2, г/2, Z2, а) = //ι(^2 — β, г/2, гг, а),
Ф* (х, у, ζ) =
1
ф(.
Ж
ί/
)
§ 4. ФУНКЦИЯ ГРИНА ДЛЯ ВНЕШНОСТИ КРУГОВОГО ДИСКА 143
аргументов, равные соответственно
X у
2 , 2 ι 2’
* + У +ζ
2 ι 2 ι 2’ 2 ι 2ι 2*
х ~\~ у Л~ζ χ у ζ
Полученная функция в нашем случае будет равна
{*1 + У\ + ZD' на внешности круга S3 и плоскости
ζ = 0. Если вычесть ее из (х\ + у\ + z\) 2, го полу¬
ченное выражение будет равно нулю на внешности кру¬
га S3 и будет вести себя как (х% + у\ + zl) 2 в на¬
чале координат (рис. 35, в). В результате этих преобра¬
зований найдем
#, (я3, ζ/з, z3, а)
X
X
1 -я,
, а
Для того чтобы получить функцию, равную нулю на
внешности круга Sz в плоскости ζ = 0, центр которого
совпадает с началом координат, введем переменные
β
Х4 = Ха
а — β"
Ζλ ΖО.
В таком случае будем иметь
1
НЛхи Уп z4> °0
X 1-я,
х
. (*4-^)2+^+24
(*4
h )*+»!+*;
1.
(*4-&ΐΓ+»ί + *5 J
(4.8)
Введем систему координат х, у, ζ, повернутую отно¬
сительно £4, г/4, "4 на некоторый угол (рис. 35, г) вокруг
оси Ζ4. Имеем следующие соотношения:
I2 + η2 = i?, х2 + у* = х\ + yl,
(х - |)2 + (у - η)2 = (*4 - 8 + У*·
144 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Кроме того, если обозначить радиус круга S через а, то
Jll
а--Ц 1 а*-If
Если подставить (4.7) в (4.8) и заменить в П\(х\, у\,
ζι, а) величины х\, у\ и ζχ на новые переменные, приняв
во внимание также (4.9) и (4.10), то в результате будет
получена гармоническая функция К(х, у, ζ, |, η), удов¬
летворяющая поставленным условиям:
К (х, у, ζ, I, η) =
(«ί»
π г ° у 2 аг
где
г = /(a: — i)2 + (у — η)2 + z2, R =
= /(α2 - χ2 — у2 — ζ2)2 + 4α2ζ2 .
Эта функция была определена Η. Е. Кочиным [1] на
основании результатов А. Зоммерфельда [1]. Метод
А. Зоммерфельда, использующий потенциал в римаповом
пространстве, весьма сложен.
§ 5. Осесимметричная задача без сил трения
В этом параграфе дается решение контактных задач
теории упругости, когда в упругое полупространство
ζ ^ 0 вдавливается штамп, ограниченный поверхностью
вращения. При этом предполагается, что между штампом
и упругим телом сил трения нет. На штамп действует
сила Р, направленная по оси симметрии. Будем полагать,
что поверхность, ограничивающая штамп, обладает про¬
изводными в точках, расположенных на краях площадки
контакта. При этом давление, возникающее под штам¬
пом, будет ограниченным на окружности, являющейся
контуром этой площадки (рис. 36).
Если штамп имеет такую форму, что при увеличении
силы Р выше некоторой величины в соприкосновение не
входят новые участки поверхности, то размеры площад¬
§ 3. ОСЕСИММЕТРИЧНАЯ ЗАДАЧА БЕЗ СИЛ ТРЕНИЯ
145
ки контакта будут заданными (рис. 37). В этом случае
поверхность, ограничивающая штамп, будет обладать
ребром на краях площадки контакта. Давление в этих
точках будет, вообще говоря, неограниченным. Решение
этой задачи также дается в настоящем параграфе.
Ζ,
Р
V/
I
.
L— х
Рис. 37.
Граничные условия для определения напряженного
состояния будут:
на площадке контакта — круге S радиуса а
при ζ = О
w = Ap)+c? τζθ = 0, τ2Ρ = 0;
на свободной поверхности вне S при ζ — 0
σ2 = 0, τ2θ = 0,
= 0.
(5.1)
)
Здесь р = |/я2 + у2. Уравнение поверхности, ограничи¬
вающей штамп, ζ = /(ρ), причем /(0) = 0. Плоскость ζ = 0
совпадает с поверхностью недеформированного полупро-
Ю Л. А. Галин
146 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
страпства. Поэтому с — величина перемещения штампа,
σζ, τζθ, τζρ — компоненты напряжений в цилиндрических
координатах. При этом аг ограничено на контуре круга S.
Перемещение в направлении оси ζ обозначено иВ пря¬
моугольных координатах эти условия будут:
на круге S при ζ = О
w = / (Р) + с, τχζ 0, xyz = 0;
вне круга S при ζ — 0
σζ = 0» = тУ2 = 0.
(5.2)
Компонент напряжения σζ ограничен на контуре кру¬
га S.
Согласно изложенному в § 1 условия для определения
ф(я, г/, ζ) [при этом φ(#, г/, 0) = w(x, г/, 0)] таковы:
при ζ = 0
ер =- / (х, г/) -f с на 5, = 0 вне 5. (5.3)
Здесь /(#, г/) является функцией радиуса р = у х2 + г/2.
Так как функция φ(#, г/, ζ) удовлетворяет уравнению
Лапласа (д2/дх2 +д2/ду2 +d2/dz2)ф = 0, то, использовав
первое из условий (5.3), получим равенство, которое бу¬
дет иметь место на круге S:
j? - - (S+0) = - (έ+$) <'{χ·у) ~ -А1 <*■
(5-4)
Здесь и в дальнейшем Δ обозначает двумерный оператор
Лапласа. Введем функцию
ψ {х, у, ζ) = (5.5)
Согласно (1.6) и (1.10) нормальное давление на по¬
верхности следующим образом выражается через функ¬
цию ψ(#, г/, ζ):
р (х, у) = - (аг)г=0 = 2(''f =
Е ψ (а;, г/, ζ). (5.6)
2 (l — ν2)
§ 5. ОСЕСИММЕТРИЧНАЯ ЗАДАЧА БЕЗ СИЛ ТРЕНИЯ
147
Обозначим
s = Y х% + у2 + za. (5.7)
На основании (3.2) устанавливается поведение ψ(χ, у, ζ)
на бесконечности:
[ψ (я, У, 2)U~ = J
д_
dz
S
__ 1 — ν2 р Z 1 — у2 ρ ζ /гг 04
TlE ^ (** + у* + ^3/2 пЕ Г 8Г
Здесь Р — сила, действующая на штамп,— определяется
на основании (3.8).
Для определения г|э(;г, г/, ζ) имеем следующие условия
при ζ = 0:
ψ = 0 вне 5, ^ = — Δ/(χ, у) на S. (5.9)
Таким образом, мы получили условия вида (4.6) и со¬
гласно установленным свойствам функции К(х, у, ζ, ξ, η)
на основании (4.11) будем иметь
ψ (я, г/, z) = — ^ j*] Δ/ (I, η) Κ (х, у, ζ, ξ, η) d% d\\ =
s
= ~4ίίΔ,(ξ’η) x
S
—arctg|^fl2~ξ2^^г_~**~У*.—dgdt). (5.10)
яг [ У 2 а г )
X
Рассмотрим поведение ψ(^, г/, ζ) на бесконечности.
Нетрудно показать, что при s -> оо п? следовательно, при
Г “> 5
2 arctg^«*-£*-чУα2_-^2-/-ζ2 + Τ?
ЛГ аг
-У*‘- е-ч’?·
10*
148 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
так как
У а2 — х2 — уг — г2 + R > У 2 az Уs2 — а2 ^ ί
V2ar (s2 — а2) Ϋ2, as s* ‘
На основании этого
lim ψ (ж, у, z) = / =
S->0O \v / S->oo
= - {4 JJ д/M f /*2 -12 - η2« <*η} (5·ΐΐ)
Сравнивая (5.8) и (5.11), находим выражение для си¬
лы, действующей на штамп:
р = ί fΔ/ (ξ’η) /β2 _ ξ2 ~η2 dn* (5,12)
s
или, припимая во внимание зависимость /(ξ, η) только
от радиуса, получим
а
Р = ^ j Δ/ (Pl) Pl >V-p? dp,, (5.13)
О
Согласно (5.6) имеем следующее выражение для нор¬
мального давления на поверхности:
Р (х, у) = — 2^Е_ v2) 41 [ Δ/ (S. η) Я (*. у. О, ξ, η) df\.
S
(5.14)
Величина pix, i/) будет ограничена всюду на круге 5,
так как К(х, ι/, ζ, ξ, η) имеет особенность того же поряд¬
ка, что и 1/г. Поэтому интеграл в выражении (5.14) бу¬
дет иметь всюду конечное значение (при условии, что
Δ/(ξ, η) является ограниченной величиной).
Таким образом, выполнено требование ограниченности
давления под штампом, которое содержится в услови¬
ях (5.2).
Подставляя в (5.14) из (4.11) значение Жх, у, ζ, ξ, η)
при ζ = 0 и замечая, что при этом
г = У (χ — ξ)2 4- {у — η)2, R — а2 —х2 —у2,
§ 5. ОСЕСИММЕТРИЧНАЯ ЗАДАЧА БЕЗ СИЛ ТРЕНИЯ
149
получим
К (х, у, О, I, η) =
X
. Υ α2 — I2 — η2 j/ а2 —X2 — у2 ..
X arctg ¥- Τ' ГГ ■ · (5-15)
Введем полярные координаты
# = pcos0, у = psinO, ξ = pi cos θι, η = ρι8ΐηθι. (5.16)
Принимая во внимание, что fix, у) — функция только
радиуса р, получим из (5.14), используя также (5.15),
р*(р) = ~Е
4π (1 —- ν2)
X
а 2Я
X J | А/*(рх) К (р cos 0, р sin 0, рх cos 0Х, рА sin 0Х) рх d0x dp1?
о о
или, окончательно,
а
Р* (Р) = ~ 4π(ΐ- ν21 ί (Pl) H (P’ Pl) Φΐ’
где
H
2Л
(plp‘)=L-7?r
2px
X
У^р2 — 2ρρχ cos θχ + p2
— ρ2 V a2 — p?
X arctg— a dQv
a > ρ — 2ρρχ cos θχ + p®
(5.17)
При этом
Можно показать, что при том убывании ψ(χ, у, ζ)
с приближением к бесконечности, которое имеет место в
данном случае, функция
150 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
будет также гармонической. Отсюда находим величину
перемещения поверхности упругого полупространства:
о
φ (х, у, 0) = J ψ (х, у, z) dz =
— оо
О
= — Δ/(ξ,rj) j* K(x,y,z,l,4])-dzdldr\. (5.18)
S —оо
Подставляя вместо К(х, у, ζ, ξ, η) выражение (4.14),
установим, что ядро интеграла является функцией сле¬
дующих величин:
о
j K(x,y,z,l,4)dz =
— оо
= G* (У(х — 1)г + (у — η)2, у 'х2 + у2, ΥΨΤη5)·
Если ввести теперь полярные координаты по форму¬
лам (5.16), то в нашем случае, когда /(ξ, η) является
функцией только рь будем иметь
<p(x,y,z) = -1 Δ/(ξ, η) X
s
X G* (τ/(χ — I)2 + (у — η)2, У χ2 + у2, -/Iй + η2) άξάη =
ci i
" ~4ί(ί А/<й) x
0 vo
X G* {Уpf — 2pxp cos (θχ — Θ) + p2, pi, p) dQt | dpv '
(5.19)
Если заменить Θ через θ* = θ + α и θι через θι =
= θι + α и взять пределы интегрирования а < θ ι < 2π +
+ а, что, очевидно, возможно, то, так как dQ = d0*, dQι =
= ί, θ — θχ = θ* — θι, значение интеграла (5.19) не бу¬
дет зависеть от а. Таким образом, φ(χ, г/, ζ), определенная
по (5.19), не зависит от угла Θ.
Согласно условию (5.4) имеем Δφ = Δ/*(ρ), поэтому
Ф = /(р) + причем Δφ* = 0.
§ 5. ОСЕСИММЕТРИЧНАЯ ЗАДАЧА БЕЗ СИЛ ТРЕНИЯ 151
Но так как φ* на основании доказанного выше может
зависеть только от радиуса и, кроме того, ограничена, то
она будет постоянной величиной. Поэтому
w(x, у, 0)=φ(.ζ, у, 0)=/*(р) + с.
Так как согласно определению /*(0) = 0, то с будет
величиной перемещения точки упругого полупростран¬
ства в начале коордипат или, что то же, перемещения
штампа, на который действует сила такой величины, что
радиус площадки контакта будет равен а.
Таким образом, функция φ(.ζ, у, 0) = w(x, у, 0), опре¬
деленная на основании ψ(^, у, ζ), на круге S будет дей¬
ствительно совпадать с уравнением поверхности штам¬
па /(р).
Определим величину перемещения. Так как переме¬
щение жесткого штампа повсюду одинаково, то найдем
его в начале координат:
W (0,0,0) - φ (0,0,0) =
(° 1
j *(0,0,ζ,ξ,η)ώ d£dn =
— оо )
- - JJ Δ/ (ξ, η) G** а, η) dg dt). (5.20)
s
Здесь
о
η) = j ΛΓ(0,0,ζ,ξ,η)ίζ.
— OO
Если теперь ввести согласно (5.16) полярные коорди¬
наты, то выражение (5.20) будет иметь следующий вид:
с = w (0, 0, 0) = — ~ JJ Δ/ (ξ, η) G** (I, η) d\ йц =
S
2 тс a η
= ~ ίη J J Af (Pi) G = ~ J ^ (pl> d(>1·
0 0 0
(5.21)
152 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Это имеет место, так как выше было показано, что
£**(ξ, η) зависит только от Ρι = ι^ξ2 + η2. Определим
функцию £**(ξ, η). Принимая в (4.11) х = 0, г/ = 0, по¬
лучим
Я (0, о, ;-Ц-— X
π V I ч- η + г'
χ , rrt[- А* - ξ2 - г,2 УУ - *2 Ч- /(а2 - **) + 4аУ =
Y2»V I2 Ч- η® Ч- г2
2 ·»/ а2 — ξ2 — η2
arctg s ‘
nVl* + r? + z2 Y? + r? + z
Отсюда
6*·(ξ,η)= j -у--2·- - arctgdz;
+4 +z У! Ч-1+!
введя же ξ2 + Ή2 = Ρι и принимая во внимание чет¬
ность подынтегрального выражения относительно ζ, бу¬
дем иметь
2 С 1 Υя2 — Р?
G (Pl) = А -4== arctg —=L dz, (5.22)
ϊ νρϊ + ζ2 Υρ! + ζ2
или, иначе,
2 CV α* — Pi — Pi
£(Pi) = 2 2J у - --■ 2arctg dz. (5.23)
π V a — p2 " У p2 — z у p2 + z
Имеем разложение, которое справедливо при τ2 < + °°:
J& у
3 ’
τ ν 22W ( τ2 V
aretgt = _Si^^_j
или
j. v 22ft 2 (k — i)\2 ( τ2 \k /к n/\
τ arctg τ = Σ ■ (5.24)
§ 5. ОСЕСИММЕТРИЧНАЯ ЗАДАЧА БЕЗ СИЛ ТРЕНИЯ
153
Если
ϊ/V-p» ea-Pi
1+τ2 α2+22'
Следовательно, подынтегральное выражение (5.23)
будет таким:
^а*-Рх 1rptr^al-Pi ^ 22ft~a (& — !)! (дД — P?)ft
/pITI2 VpT+7a ~ <*-*>■ («2+*2)*·
Отсюда получим
(2fc-D! ( Pl) j(a2 + 2T“
_ у Σ2*"1 (fc —1)1а / , _ 24ft_ % f dz -
2d я (2*-1)1 ^ Ρ^ J^ + z2)*’ ' '
А=1 о
Имеем следующее выражение:
оо
Г dz я (2Ас 2)1 1 /с ос\
J (a2 + **)* “ г*-» (А - 1)!а a**"1- К }
Подставляя (5.26) в (5.25), найдем
Полученный ряд легко суммируется. Окончательно най¬
дем
G (Pl) = Arth [/1 - (£)*]· (5.27)
Подставляя (5.27) в (5.21), будем иметь
а
. (О, 0,0) = - JΔ/ (Pl) Pl Arth [V 1 - (£)*] d9l.
о
(5.28)
С = W I
154 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Итак, получено следующее решение поставленной за¬
дачи.
Штамп, являющийся телом вращения, уравнение по¬
верхности которого ζ=/(ρ), причем /(0) = 0, прижимает¬
ся к упругому полупространству силой Ρ, действующей
по оси вращения таким образом, что радиус площадки
контакта будет равен а. Силы трения между штампом и
упругим телом отсутствуют. Давление под штампом всю¬
ду ограничено. В таком случае сила, прижимающая
штамп, равна
а
р = (Τ^ί Δ/ (pl) Ρι ^ ^ (5·29>
0
Перемещение штампа будет
с = - J Δ/ (Pl) Pl Arth [ ~\f 1 - (5)2] dPl. (5.30)
О
Давление под штампом равно
а
Р(Р) = — 4π v2) j д/ (Pi)H (P. Pi) dPi> (5·31)
0
где H(p, pi) дается выражением (5.17).
В работах А. И. Лурье [1], И. Я. Штаермана [1] рас¬
смотрен осесимметричный штамп в виде параболоида с
уравнением ζ = Α р\ С помощью примененного здесь ме¬
тода может быть установлено в конечном виде соотно¬
шение между силой и перемещением. Пусть
f(p) = ApK (5.32)
В таком случае
4/<р) “ ($+i &) ><р)=^ν_!· (533)
Вводя новую переменную р = a sin τ, получим следую¬
щее выражепие для силы, действующей на штамп:
а
Р = f Δ/ (Pl) Ρι У а2 - P!dPl =
1 — V о
§ 5. ОСЕСИММЕТРИЧНАЯ ЗАДАЧА БЕЗ СИЛ ТРЕНИЯ 155
π/2
1 — ν2'
= у2——з Ααλ+1λ2 j (sin^~1 τ — sir^+1 τ) dx =
ό
2^ ^ „λ + 1^ 2 ί ολ — 2 Γ (λ/2) Q
“ΐ_ν2Αα AL Γ (λ) Ζ Γ (λ + 2) J*
,λ Γ2 (λ/2)
После некоторых преобразований находим оконча¬
тельно
d Ε ^/τλ+12λ~1 ^ ^ /5 34\
ι 2 λ+l г (λ) ·
Принимая во внимание (5.28) и (5.33), получим выра¬
жение для перемещения в следующей форме:
а
с = —|δ/(ρι) рх Arth У 1-(γ)
Φι =
π/2
= — Αλ2(ΐ" J sin*" 1 τ Arth (cos τ) cos τ dx,
но
Arth (cos τ) = — In tg -г-.
В таком случае, интегрируя по частям, находим
π/2
с = Αλ2αλ j In tg -у sin*·-1 τ cos τ dx =
=-л*«Ч 2*-*r4tf·
Окончательно получим
= - Ααλ2λ_2λ У^2)·. (5.35)
На основании (5.34) и (5.35) можно установить зави¬
симость между Рже:
2 λ—1 12 1
λ+ι
156 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Иначе эта зависимость может быть записана следую¬
щим образом:
ι λ+1
Р =
Е
При этом
λ-1
2 ΛΊΓ 1
κ(λ) = 2ϊ^ΤΪΓϊ(λ)Γ
Приведем значения κ(λ) для нескольких значений λ:
λ
1
2
3
4
κ
0,636
0,942
1,127
1,253
На рис. 38 представлена за¬
висимость κ(λ) от λ.
В случае, рассмотренном
Герцем [1], когда штамп пред¬
ставляет параболоид второй степени, будем иметь
/(ρ) = Ар2, Δ/(ρ) = 44.
Тогда
р = ~ГЕ?л fa ■= - зТгЬ) ^
О
а
С = — 4Л J Arth [ 1 — j Φι = ~ 2α2-4’
а
Ρ {х, У) - - J 2(Γ^~ν5)4Α έ ίί ■Κ (χ’ ·ν’°’1 η) dl
§ 5. ОСЕСИММЕТРИЧНАЯ ЗАДАЧА БЕЗ СИЛ ТРЕНИЯ 157
Подставляя в последнее выражение значение внутрен¬
него интеграла (его можно найти в статье Η. Е. Кочина
[1]), получим
о (х υ\ _ ~ Е^А JL -tin2 — χ2 — υ2 — ~~ 4ЕА г/а2 — о2
Р{ " У У ~n(i-vYa Р*
Эти выражения совпадают с результатами, полученными
Герцем.
В заключение рассмотрим случай, когда в упругое по¬
лупространство вдавливается штамп, форма которого при¬
ведена на рис. 37. В этом случае радиус площадки кон¬
такта будет заданной величиной и давление на ее краях
будет, вообще говоря, неограниченным. Рассмотрим задачу,
когда задано перемещение штампа. В этом случае гармони¬
ческая функция φ*(χ, у, ζ) должна удовлетворять следую¬
щим граничным условиям при ζ = 0:
φ* = / (р) -j- с* на 5, =0 вне 5, (5.37)
где с* — заданная величина, S — круг радиуса а.
Будем искать φ*(χ, ι/, ζ) в виде суммы
φ* (х, у, ζ) = <р* (я, у, ζ) + ср* (х, г/, ζ),
причем Ф* (я, г/,2), определенная по формуле (5.18),
как это следует из (5.28), удовлетворяет условиям при
2 = 0:
фГ = /(р)+£ на S, ~ =0 вне S. (5.38)
Здесь
а
dpv (5.39)
С = jA/(p1)p1Arth[yF 1-(^)2
о I
Функция Ф2 должна удовлетворять условиям при 2 = 0:
2 Ф
φ* = С* — С на S, = 0 вне S. (5.40)
В таком случае φ* = ф* + Ц>*удовлетворяет (5.37).
158 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
На основании (4.7) функция φ2{x,y,z) выражается
следующим образом:
<р* = (С* — С) arctg Θ,
Θ = 1Ajp2 + 22 — «а +
Итак,
ф* (х, у, z) = — ^ J j* Δ/ (ξ, η) j J К (x, г/, ζ, ξ, η) όζ| <ίη +
+ (С* — C) — arcctg θ,
θ = ^]/'x2-j-y2-^-z2—α2+|/(χ2+ι/2+ζ2—α2)2+4α2ζ2 j.
(5.41)
Определим давление на поверхности, принимая во вни¬
мание, что
1 ■
прлучим
р*(р) = -м^)х
X ί Δ/ (р.) И (,), (,,) ф, + (С* - О , ,4 , . (5.42|
I ) “/ 11 ψ> ^1/ “^1 ~Г W ■
Ιο У
2 2
а — р
Здесь tf(p, pi) определяется согласно (5.17), причем С
имеет значение (5.39).
§ 6. Задача для штампа круговой формы в плане.
Влияние нагрузки, действующей вне штампа
Рассмотрим случай, когда на поверхности упругого
полупространства в области Σ, лежащей вне круга S ра¬
диуса а, приложено нормальное давление, равное q(x, у).
§ G. ВЛИЯНИЕ НАГРУЗКИ, ДЕЙСТВУЮЩЕЙ ВНЕ ШТАМПА 159
В таком случае для определения гармонической функ¬
ции будем иметь следующие условия при ζ = 0:
Ф = f(x, У) на S, ^ = ^-jf^q(x,y) на Σ. (6.1)
Функция φ может быть представлена в виде суммы
двух слагаемых φ = φι + ф2, причем для φι имеем гранич¬
ные условия при ζ = 0:
дц>л
Φι = f(x, У) на S, = 0 на Σ. (6.2)
Функция φι, удовлетворяющая (6.2), определяется сог¬
ласно (3.5) и (3.6). Для определения ψ2 имеем граничные
условия при ζ = 0:
φ2 = 0 на S, ^ = 2(l~v )q{x, у) на Σ. (6.3)
Таким образом, получаем условия, аналогичные (4.6).
Для нахождения ф2 необходимо построить функцию Гри¬
на К\{х, у, ζ, ξ, η), равную нулю на диске S и ведущую
себя как 1 /г в окрестности точки с координатами # = ξ,
у = η, ζ = 0 на плоскости Σ, внешней по отношению к
диску S.
Искомая функция должна удовлетворять следующим
условиям:
KL (х, у, ζ, ξ, η) = 0 на S,
§-ζΚι(χ, ί/,ζ,ξ,η) = 0 на Σ,
кроме точки А с координатами х = ξ, у = η, ζ = 0, в ок¬
рестности которой
(я,у,г,£,г])->оо.
Будем исходить из найденной выше (4.11) функции
К{х, у, ζ, ξ, η), причем применим к этой функции преобра¬
зование инверсии. Пусть круг S имеет радиус 1/а. Функ¬
ция К(х, у, ζ, ξ, η) удовлетворяет следующим условиям:
gj К (х, У, ζ, 1, η) = 0 на 5,1
(0.0)
к (х, у, ζ, ι, η) = 0 на Σ,
кроме точки А с координатами # = ξ, г/ = η, ζ = 0.
(6.4)
160 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
= Н7 arctg —" :γί · (6-с)
Функция К(х, у1 ζ, ξ, η) имеет следующее выражение:
К (х, у, ζ, I, η) =
Κτ-ΐ2-η2/Λ-*2-?2-*2 + *
п (i
V21-
Здесь
г = /(а: — I)2 + (г/ — η)2 + ζ2,
Применяя к этой функции преобразования инверсии,
получим выражение
(Х> У* ΖΊ Л) = г п 2 2 ^
j/V + ^+s2
χκ( х у z 5 -Л—\
^ I 2 I 2 I 2’ 2 I 2 I 2’ 2 I 2 ■ 2 ’ уЧ . 2’ f2 ι 2 Г
^ ж* + / + ζ'5 + у-5 + ζ'5 ξ^+η δ +η /
При этом /£* (χ, у, ζ, ξ, η)— гармоническая функция пе¬
ременных χ, у и ζ.
Введем обозначения:
5 = yf X* + у2 + ζ2, σ = /ξ2 + η2.
Выражение R после замены переменных будет иметь
следующий вид:
я* = 2 / 2 ,1 2 , 24 / (х2 + У2 + ζ2 — а2)2 — 4α2ζ2.
л \д; -j- у -j- 2 )
Точно так же радикал
У“5 — χ2 — ί/2 — ζ2 + Д
после замены переменных становится таким:
— У s2 — а2 + у (?= α2)2 + 4α2ζ2.
§ 6. ВЛИЯНИЕ НАГРУЗКИ, ДЕЙСТВУЮЩЕЙ ВНЕ ШТАМПА 161
Выражение
\-12- η2
при этом превратится в
±.yV-a2.
Наконец, выражение 1 /г после замены переменных бу¬
дет таким (обозначим его через 1/г*):
1 1
г*
2 2
SO
/(*σ2 - Is2)2 + (ус2 - η*2)2 + (ζσ2)2
Окончательно получим
* 1/2 1
Κι (х, у, ζ, ξ, η) - 7^7* Χ
77 Vo* - α2 |Λ2 - a2 + /(s2 _ ay + 4αΓ^
. aa $
X arctg
20 . V |Λ*-«* + /(.*-.*)*+4A*
Jf7r · (6'7)
Для того чтобы получить функцию К\(х, I/, 2, ξ, η),
которая ведет себя как 1/г в окрестности точки # = ξ,
ϊ/ = η, 2 = 0, необходимо Κι (х, у, 2, ξ,η) разделить на σ.
На основании этого окончательно найдем следующее
выражение:
к, (х, I/, 2, ξ, η) =
где
7? = у' (а2 — х2 — у2 — z2 )2 + 4α2ζ2,
г = >/(х — |)2 + (у —η)2 + ζ2.
11 Л. А. Галин
102 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Найдем теперь производную функции К{(х, у, ζ, ξ, η)
по переменной ζ. Будем иметь
£Кг (*,*,*,ξ,η)
j_h±
dz [ π г
X
X arctg
T7 i2 + η2 - а2 |/ X2 + у2 + г2 - Я2 + Д
= Ίγ I—%aretg ^4 +
1 + Л
X
X
[ г +
L ,2 ι7 *2+у2
*2 + / + z2 - а2 + R
ζ2 — а2 + И
Tarct2 А +
71 ^ 1
1 + А*
X
X
ζ 1 z(a2 + x2 + y2 + z2+ R)
Г3 Г я (х2 -I- У2 + г2 _ а2 + К)
(6.9)
При этом введены обозначения:
г = у (х—1)2 + (у — η)2 + ζ2,
R = у [а2 — х% — у2 — z2) -f 4α2ζ2,
А
V12
+ η2 - д2, у х2 + у2 -|- Σ2 _ а2 + д
У2 аг
(6.10)
Определим теперь предельное значение выражения
(6.9) на круге х2 + у2 <а2 при ζ 0.
Выполняя переход к пределу, находим
lim j·^ А\(х, г/, ζ, ξ, η)|
= lim|·
dz
λ 1 arctg 17 ξ2 + η2 ~ q2 *1+ y2 + z2~ « + R
π г у 2 ar
— lim f ^ arctg A
π :-o I '·
ν Г * , 1 г(а2 + *г+у2 + г2
X[ r3+ ' л(*« + / + **_в;
1 +
2 , 2 ι 2 ι 2
+ Д
+ R
§ 6. ВЛИЯНИЕ НАГРУЗКИ, ДЕЙСТВУЮЩЕЙ ВНЕ ШТАМПА 163
2 1 /ξ2 + η2 — а8
2 2 У ^
г а — х
У 2 а
/|2 + т)2-«2
π (Ж - i)2 + (у — η)ν а2 — *2 —Уг '
(6.11)
На рис. 39 геометрически интерпретированы отдельные
величины, входящие в эту формулу.
Выражение (6.11) может быть представлено следую¬
щим образом:
1 AD
π (Лд)« не¬
определим давление, воз¬
никающее под штампом в ре¬
зультате действия нормаль¬
ного давления, равного
—q(x, у) на поверхности уп¬
ругого полупространства вне
штампа.
На основании (6.3) функция <рг(#, у, ζ) будет
φ2(χ, у, 2) = Jg(|, η) Кг(х, у, 2, ξ, η)ώ|(ίη. (6.12)
Давление выражается через <рг:
Р (*, у) = — (<Ь)г=0 = +
—-—
2 (l - ν2) \ <?ζ У2=0
Отсюда
P(^,!/) = +^(f j?(S, η)[^ΛΓι(«, !/, ζ, ξ, η) dg <1т|. (6.13)
Таким образом, на основании (6.13) и (6.11) получим
следующее решение поставленной задачи.
Если на поверхности упругого полупространства вне
штампа приложено давление q(x, у), то под штампом воз-
11*
164 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
никает дополнительное давление
,./ξ2 + η2-«2
Уа2-х2-у2
d%dr\. (6.14)
Здесь Σ — внешность круга S в плоскости ζ = 0. В слу¬
чае, когда на штамп с плоским основанием действуют си¬
ла Ρ, направленная по оси
женная в точке А с координатами х = I, у = 0 (рис. 40)
давление будет
Это выражение получено для случая, когда штамп пе¬
ремещается так, что его основание остается параллельным
плоскости ζ = 0. Если фиксировать положение силы Ρ,
то результат будет несколько иным.
На рис. 41 приведены графики, изображающие вели¬
чину дополнительных давлений, возникающих под штам¬
пом радиуса а=1 в случае, когда в точке А с коорди-
р(^,0)
Вис. 40.
Вис. 41.
Р (я. у) = —
+ пг [(« - I)2 + у2] /
/га-а2
§ 7. ВЗАИМНОЕ ВЛИЯНИЕ МИКРОКОНТАКТОВ
165
натами у = О, χ = Ζ = 1,5 приложена сосредоточенная си¬
ла. При этом р(О, у) означает давление, которое имеет
место вдоль диаметра, где х = 0, а р(х, 0) — давление
вдоль диаметра, совпадающего с осью х.
Дополнительное давление может быть выражено сле¬
дующим образом:
р(х,у) = -^к(х,у), к (х, У) = - -τ/L· а22 , ,·
п l\* — l)+y\Va—x—y
(6.16)
Приведем значения к(х, у) в разных точках под штам¬
пом:
(z=0, у)
к(х, у)
(я, У=0)
к(х, у)
-1,0
ОО
—1,0
оо
—0,8
0,646
—0,8
0,354
-0,6
0,536
—0,6
0,318
-0,4
0,508
-0,4
0,339
-0,2
0,500
-0,2
0,396
-0,0
0,498
0,0
0,498
0,2
0,500
0,2
0,676
0,4
0,508
0,4
1,011
0,6
0,536
0,6
1,729
0,8
0,646
0,8
3,810
1,0
оо
1,0
оо
§ 7. Взаимное влияние микроконтактов
при расчете жесткости стыка шероховатых тел
При расчете сближения и фактических площадей ка¬
сания шероховатых тел чаще всего заранее задаются фор¬
мой индивидуальной неровности и законом их распреде¬
ления по высоте. Далее, предполагая определенный харак¬
тер деформирования (упругий, пластический), авторы счи¬
тают, что каждая неровность деформируется независимо
от всех остальных. При таком подходе к проблеме (см.
В. А. Журавлев [1], И. В. Крагельский [1], Н. Б. Дёмкин
[1], J. A. Greenwood [1], F. F. Т. Ling [1]) плотность пя¬
тен касания и их число не влияют на жесткость стыка и
166 гл. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
закономерности формирования фактических площадей ка¬
сания.
Между тем известен ряд работ, из которых следует,
что с повышением плотности контакта меняется несущая
способность индивидуального пятна контакта (см. Т. Н. С.
Childs [1], S. D. Probert, А. Н. Uppal [1], Г. М. Бартенев,
В. В. Лаврентьев [1]). Это обстоятельство исследователи
связывают с эффектом взаимного влияния микроконтак¬
тов друг на друга (R. Т. Hunt, Т. В. P. Williamsonll]).
Здесь предлагается новый подход к решению контакт¬
ных задач для шероховатых тел, который состоит в тюм,
что рассматривается поведение под нагрузкой всей сово¬
купности контактов.
Рассматривается задача о давлении штампа на упру¬
гое полупространство в случае, когда между ними отсут¬
ствуют силы трения. Предполагается, что вдавливается
штамп круговой формы в плане с плоским основанием,
поэтому размеры площадки контакта заранее определены.
На штамп действует .сила Ρ, вне его ,на расстоянии I от
центра площадки контакта (I > а, где а — радиус основа¬
ния штампа) действует сосредоточенная сила Q. Тогда
граничные условия для упругого полупространства (ζ ^ 0)
имеют вид:
на площадке контакта х2 + у2 ^ а2 при ζ = 0
ιν = с, ххг = 0, х уг = 0;
на свободной поверхности х2 + г/а> а2 (ζ = 0)
αζ = — Q8(x— ξ, у — η), τχζ = 0, xyz = 0
(I2 + η2 = г2).
Здесь w — перемещение точек ушругого полупространства
в направлении оси ζ, с — перемещение штампа, σζ, τ*ζ, xyz —
компоненты напряжения.
Задача решается методом, изложенным в § 6, и сво¬
дится к определению гармонической функции ф(;г, г/, ζ),
удовлетворяющей следующим условиям на границе (ζ=0):
φ = с при х2 + у2 ^ а2,
ду /dz = 2(1 — v2) Q8(x — l·, у — η)/£ . (7.1)
при х2 + у2 > а2.
§ 7. ВЗАИМНОЕ ВЛИЯНИЕ МИКРОКОНТАКТОВ
107
На основании найденного выражения для функции φ
(§6) могут быть определены перемещения и напряжения
в упругом; теле.
Для давления, действующего на площадке контакта
штампа с упругим полупространством, будем иметь (х2 +
+ у2 ^ а2)
/ ч Е (дЧ>\ Ес
Р У) ~ 2(1 - ν2) («* )г=0 (! _ ν)« πв» '
?/ξ2 + η2-«2
(7.2)
Первое слагаемое в этом выражении представляет собой
давление, возникающее под круглым штампом с плоским
основанием, когда он вдавлен в упругое полупространство
на глубину с. Второе слагаемое есть дополнительное дав¬
ление, возникающее вследствие действия вне штампа на
расстоянии I от него соцредоточенной силы Q. Принимая
во внимание уравнение равновесия штампа
Р = ί ί P(x>y)dx dy%
можно найти связь внедрения с штампа с приложенной к
нему нагрузкой Р:
р=2аЕс _2£_arctg «
i — v2 « *
Пусть теперь в окрестности штампа круговой формы
в плане с плоским основанием, вдавливаемого в упругое
полупространство, действует М сосредоточенных сил Qh
расположенных на окружности радиуса I (Z > а) от его
центра.
Тогда граничные условия для определения гармони¬
ческой функции ф(х, ι/, ζ) будут иметь вид
ф = с, х2 + у2 < a2, j
ду/dz = 2 (1 — v2) Qfi {χ — gm, у — r\m)/E, (7.3)
m = 1, 2, ..., Μ, χ2 + i/2 > a2. J
Рассуждая так же, как и в предыдущем параграфе, полу¬
чим следующее выражение для гармонической функции
168 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
<р(я, у, ζ), удовлетворяющей всем граничным услови¬
ям (7.3) (Θ определено формулой (5.41)):
4(1 -ν2)<?<
<p(a;,j/,z) = c-arctg0 ^ х
м
VI ι + αθ| /7/ч
X 2t \ — arctg - , (7.4)
j \ ' /
771— 1
где rm =у(X — |т)2 + (!/ — η™)2 + Ζ2, |т, η™— координаты
точек приложения сосредоточенных сил.
Учитывая (7.4), для давления, действующего под
штампом, получим следующее выражение в полярных
координатах (г, φ):
/ % Ес
Р (Г’ = 24 ~
π (1 — ν2) у а — г
м
а
π2 /а2 - г2 (Г cos ? “ * C0S 0m)2 + ί»- sin Φ - * sin ‘
(7.5)
Определим, как и в предыдущем параграфе, связь
между внедрением штампа с и действующей на него нор¬
мальной силой Р:
P(l — ν2) , MQt(l-va) _ β /7β4
C— 2α^ πα£ ]/1ПТ^‘
Следовательно, внедрение штампа не зависит от взаимно¬
го расположения сосредоточенных сил на окружности,
а определяется лишь их расстоянием от штампа I и сум¬
марной интенсивностью MQt.
Изложенные выше результаты были использованы для
расчета внедрения системы штампов в упругое полупро¬
странство. Разберем случай М цилиндрических штампов,
каждый радиуса а, заделанных в жесткую плиту так, что
их оси проходят через узлы гексагональной решетки с
межузловым расстоянием s, а основания лежат в одной
плоскости (рис. 42).
Совокупность штампов, оси которых расположены на
одинаковом расстоянии от оси некоторого фиксированного
штампа, будем называть слоем штампов. Номер слоя мо¬
дели определяется относительно ее центрального штампа.
§ 7. ВЗАИМНОЕ ВЛИЯНИЕ МИКРОКОНТАКТОВ
169
Под действием нормальной силы Q, приложенной к
этой системе, все штампы внедряются на одинаковую глу¬
бину с. По причине осевой симметрии всей системы штам¬
пы, расположенные в /-м слое модели, будут нагружены
равными усилиями Qj.
Выделим в /-м слое модели любой штамп, а действие
всех остальных штампов модели на полупространство
9]/0,
'5
Система штамло#
о о о о о о
о о о о о о о
оооооооо
О О О СИ>Ч) о о о
oooioood^ooo
О О О ό О 2-2-^-— Λ*
о о о'о о οψ О О О J
О О о V Q JCГ ООО
оооооооо
о о о о о о о
о о о о о о
LLU
τα/s =0,5
ша/s =$02
0 12 3
Вис. 42.
заменим действием сосредоточенных сил. Тогда внедре¬
ние выделенного штампа согласно (7.6) определится со¬
отношением
Здесь / — порядковый номер слоя модели (/ = 1, 2, ... к),
i — порядковый номер слоя штампов относительно штампа,
расположенного в /-м слое (i=l, 2, ..., &Д, Мц — число
170 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
штампов, одновременно находящихся в i-м и /-м слоях,
U — радиус i-то слоя штампов.
Из таких соотношений, составленных для каждого слоя
модели, образуют систему линейных уравнений относи¬
тельно неизвестных (λ,. Дополняя ее условием равновесия
системы
где Mj — число штампов в у-м слое модели, можно устано¬
вить связь между действующей нагрузкой Q и внедрением
системы штампов.
Введем новую переменную
С учетом (7.9) соотношения (7.7) и (7.8) примут вид
С использованием системы определяющих уравнений в
виде (7.10) и (7.11) на ЭЦВМ «Минск-22М» был проведен
расчет моделей с числом слоев от 2 (7 штампов) до 12
(91 штамп) при различной плотности размещения штам¬
пов, определяемой параметром а/s.
Для того чтобы описать закономерности внедрения та¬
кой систе1мы штампов, надо изучить связь характеристики
R с параметрами модели: плотностью размещения штам¬
пов на плоскости и числом этих штампов.
Здесь целесообразно провести следующий анализ. Если
разместить штампы предельно плотно (a/s = 1/2), то всю
систему их можно отождествить с одним штампом, имею¬
щим радус RMj при этом, очевидно, RM ~ М1/2. Посколь¬
ку жесткость уединенного штампа пропорциональна его
радиусу, то жесткость такой системы должна быть про¬
порциональна Ми2. Напротив, если штампы расположить
к
Q = Σ QjMj,
(7.8)
(7.9)
Q = joRC
(7.11)
Здесь обозначено: jo = 2αΕ/(ί — ν2) — жесткость уединен-
k
ного цилиндрического штампа; li = rriiS, R — ^jMjqj.
j=i
§ 7. ВЗАИМНОЕ ВЛИЯНИЕ МИКРОКОНТАКТОВ
171
весьма редко (α/s-^O), то взаимное влияние их друг на
друга очень мало. В этом случае внедрение штампа одно¬
значно определяется его нагрузкой, а поскольку с = const,
то Pj — Q/Μ и R = М.
Действительно, с уменьшением параметра a/s нагрузка
на штампы распределяется равномерней (см. рис. 42). Так,
Рис. 43.
например, при a/s — 1/2 и М = 91 периферийные штампы
нагружены усилиями, примерно в пять раз большими, чем
центральный штамп, а при a/s = 0,02 Q^/Qx = 1,14.
Эти рассуждения подсказывают, что функциональная
связь между R и М может быть описана степенной функ¬
цией вида R ~ Ма, где 1/2 < а < 1.
Для проверки этого предположения результаты расче¬
тов были представлены в системе координат lg М — lg R
(рис. 43). Как видно, расчетные значения группируются
около прямых линий, что свидетельствует об удовлетвори¬
тельном выборе вида аппроксимирующей функции, а имен-
нр
R = кМа. (7.12)
172 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Связь показателя а с параметром a/s может быть вы¬
ражена соотношением
(т-тГ + ^-^^т· (7ЛЗ)
В отношении коэффициента к было установлено, что
при a/s = 0 и a/s = 1/2 он равен 1, при промежуточных
значениях a/s он больше 1 и принимает максимальное зна¬
чение 1,35 при a/s ^ 1/8. Таким образом, связь между
нагрузкой и внедрением описанной выше модели, учиты¬
вающей взаимное влияние контактов друг на друга, может
быть выражена в виде
Q = kj0Mac. (7.14)
Если же пренебрегать эффектом взаимного влияния,
то расчет внедрения следовало бы вести по формуле
<?« = ]0Мс. (7.15)
Сравнивая эти выражения, легко убедиться в том, что
неучет взаимного влияния штампов приводит к завышен¬
ным значениям жесткости контакта, причем это различие
становится тем ощутимей, чем больше число штампов.
Для того чтобы оценить погрешность, вносимую в рас¬
чет предположением, что действие соседних штампов мож¬
но заменить действием сосредоточенных сил, и оценить
тем самым пригодность метода для расчета сближений
шероховатых тел, нами были обсчитаны результаты экспе¬
риментов К. Kendall, D. Tabor [ll. На плоской поверхно¬
сти мягкой резины были установлены в узлах гексагональ¬
ной решетки стальные цилиндрики одинакового радиуса.
Поверх цилиндров располагалась плоская плита и вся си¬
стема нагружалась нормальной нагрузкой Q. Меняя число
цилиндров и шаг между ними, авторы определяли соответ¬
ствующие значения контактной жесткости системы. На
рис. 44 эти данные нанесены в системе координат j — R (j =
= “)· Характеристика жесткости рассчитывалась по
изложенному выше способу. Экспериментальные точки
наилучшим образом группируются около прямой с угло¬
вым коэффициентом /о = 0,19 κΓ/мм, а по данным тех же
§ 7. ВЗАИМНОЕ ВЛИЯНИЕ МИКРОКОНТАКТОВ
173
авторов /о = ОД65 кГ/мм, т. е. соответствие вполне удовлет¬
ворительное. Как и следовало ожидать, такой метод рас¬
чета дает заниженное значение контактной жесткости, по¬
скольку штампы заменяются сосредоточенными силами.
/ иГ/мм
О 4 8 12
Вис. 44.
Для оценки точности предложенного выше метода опре¬
деления внедрения системы штампов было проведено
сравнение решения задачи о вдавливании в полупростран¬
ство двух штампов с результатом, который получается,
если один из штампов заменить сосредоточенной силой.
В качестве частного случая задача о вдавливании двух
одинаковых штампов, круговых в плане, с плоскими осно¬
ваниями, оси которых проходят через точки с координа¬
тами (0,0) и (s9 0), была рассмотрена в работе А. Е. Анд-
рейкив, В. В. Панасюк [1J. Формула для контактных дав¬
лений под штампом, расположенным в начале координат,
имеет вид
Ес
174 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Интегрируя (7.16), получим связь между силой (^дей¬
ствующей на один штамп, и его внедрением с:
Тогда жесткость системы двух штампов определяется по
формуле
Когда же действие одного из двух штампов заменяется
действием эквивалентной ему сосредоточенной силы, жест¬
кость системы с учетом того, что Р = Q, определяется так:
Из сравнения жесткости системы в случае действия двух
штампов (7.17) и штампа и сосредоточенной силы (7.18)
следует, что, хотя всегда /ι > /2, при малых значениях ве¬
личины a/s их значения почти неразличимы, а разница в
значениях жесткости при больших величинах a/s (0,2 <
< a/s < 0,5) имеет порядок δ4 (рис. 45), т. е. входит в ве¬
личину погрешности в формуле (7.17).
2Еас Г _2_δ + А δ2 — 4г δ3 + 0(δ4)1.
ι — ν L π Л Я J
J'=a/s
Вис. 45.
§ 7. ВЗАИМНОЕ ВЛИЯНИЕ МИКРОКОНТАКТОВ
175
Поскольку замена каждого штампа сосредоточенной си¬
лой сопряжена с внесением определенной погрешности, то,
очевидно, при увеличении числа штампов в системе рас¬
хождение в значениях жесткостей двух сравниваемых
систем должно возрастать. С другой стороны, увеличение
числа штампов при сохранении неизменной плотности их
размещения неизбежно приводит к увеличению размеров
всей системы, в частности площади, па которой размеща¬
ются штампы, а, следовательно, у каждого фиксированного
штампа увеличивается число более далеких «соседей»,
влияние которых на штамп с тем большим основанием
можно отождествить с влиянием сосредоточенных сил,
чем дальше они расположены от него.
Приведенные результаты свидетельствуют о том, что
учет взаимного влияния микроконтактов при расчете жест¬
кости стыков шероховатых тел может существенно уточ¬
нить известные методы расчета, расчеты по предложенно¬
му методу дают значение жесткости стыка, заниженное
на 7 -т-10% по сравнению с наблюдаемым в опытах.
До сих пор мы рассматривали контуры, ограниченные
окружностью. Однако известно, что при контакте шерохо¬
ватых тел форма контурной площадки коптакта часто бы¬
вает близкой к эллиптической (Н. Б. Дёмкин [1]). Для оп¬
ределения степени влияния этого фактора на связь между
внедрением и нагрузкой были выполнены расчеты для мо¬
делей А, А1 и А2 (см. табл. IV), отличающихся степенью
вытянутости контуров, характеризуемой эксцентриситетом
е. В моделях А1 и А2 штампы расположены симметрично
относительно большой и малой осей эллипса, поэтому в
расчетах принималось заранее, что симметрично располо¬
женные штампы нагружены одинаковыми усилиями. Ре¬
зультаты этих расчетов приведены на рис. 46, где 1 — тео¬
ретическая зависимость для модели А, 2 — для штампов,
расположенных в одну линию, 3 — для модели А1, 4 —
для модели А2.
Как и в случае кругового контура, зависимость внед¬
рения от нагрузки носит линейный, характер. С увеличе¬
нием вытянутасти контура жесткость системы возраста¬
ет, ΙΗΟ отличия ее от значения жесткости для кругового
контура весьма незначительны. Так, например, отношение
жесткости модели А2 к жесткости А составляет 1,08. Та¬
кой же результат соотношения жесткостей приведен в
176 гл. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
§11 для штампов с эллиптическими в плаие основаниями.
Там же высказывалась мысль о том, что штампы с плоски¬
ми основаниями, одинаковые по площади, но имеющие
форму, далекую от круговой, при одинаковых нагрузках
внедряются приблизительно на одинаковую глубину. Как
Таблица IV. Характеристики контурных площадок контакта
Условное
обозначе¬
ние моде¬
ли
Число
штампов
модели М
Диаметр
штампа
2а, мм
a/s
Форма контура и
его характеристика
Суммар¬
ная пло¬
щадь
штампов,
мм2
А
55
3
1/8
Окружность
в=0
ak=43,26 мм
388,7
А1
55
3
1/8
Эллипс
е=0,8660
ak=60 мм
388,7
А2
.
55
3
1/8
Эллипс
*=0,9428
ak = 72 мм
388,7
D
55
3
1/8
Равносторонний
треугольник
длина стороны
е—108 мм
388,7
Примечание. afe — большая полуось эллипса, е —
триситет.
- эксцен-
показали расчеты, этот тезис может быть принят и в слу¬
чае системы штампов и сформулирован следующим обра¬
зом: модели, различающиеся лишь формой контура, харак¬
теризуются примерно одинаковой жесткостью. Это иллюст¬
рируется данными, в частности экспериментальными, по¬
лученными на модели D, контур которой очерчен пра¬
вильным треугольником.
Предельная вытянутость контура получается в слу¬
чае расположения штампов вдоль прямой линии. При
этом следует ожидать максимальной жесткости системы.
Этот случай был рассчитан и соответствующая зависи¬
§ 7. ВЗАИМНОЕ ВЛИЯНИЕ МИКРОКОНТАКТОВ
177
мость внедрения от нагрузки приведена на рис. 46. По¬
скольку круговая форма контура является наиболее ком¬
пактной и поэтому характеризуется минимальной жестко¬
стью, то в секторе, ограниченном прямыми 1 и 2, будут
располагаться зависимости внедрения от нагрузки для лю¬
бых размещений 55 штампов диаметром 2а = 3 мм, распо¬
ложенных с шагом a/s = 1/8.
1
а — модель А /
о - модель А/ 1 /
0 — модель А 2 /
ν - модель U /
0
νΟ
0 ΎΛ
1
/ 0
/
/ ^rSv
f
о 200 Ш 600
с,мкм
Рис. 46.
Однако, имея в виду реально наблюдаемые формы
контурных площадок при контакте шероховатых тел
(Н. Б. Дёмкин [1]), случай, описываемый линией 2, сле¬
дует отнести к маловероятным и считать жесткость не за¬
висящей от формы контура.
‘2 д. А. Галин
178 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
§ 8. Осесимметричные контактные задачи
с силами трения
В этом параграфе дается решение контактных задач
теории упругости, когда в упругое полупространство вдав¬
ливается штамп, ограниченный поверхностью вращения,
причем между штампом и упругим телом имеют место си¬
лы трения. Рассматриваемый вопрос представляет интерес
для некоторых задач машн-
строения, например, для оп¬
ределения давления, возни¬
кающего между пятой и под¬
пятником. До сих пор вели¬
чина сил трения в этих слу¬
чаях определялась лишь при¬
ближенными методами.
На штамп, находящийся
па упругом полупространстве,
действует сила Р, направлен¬
ная по оси вращения. Кроме
того, он поворачивается во¬
круг этой оси моментом М.
Угловая скорость вращения
равна ω. Между штампом и
упругим полупространством
имеют место силы трения,
направление которых проти¬
воположно направлению вра¬
щения, т. е. является перпен¬
дикулярным к радиусу пло¬
щадки контакта, имеющеи в плане форму круга (рис. 47).
Так как сила трения равна произведению нормального
давления на коэффициент трения, то на площадке контак¬
та имеет место граничное условие τΖθ = μσζ. Скорость дви¬
жения различных точек штампа, различная в зависимости
от угловой скорости и расстояния до оси вращения, будет
νθ = ωρ.
Так как коэффициент трения между твердыми телами
зависит, вообще говоря, от скорости вращения, то будем
полагать
Рис. 47.
(8.1)
§ 8. ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ С СИЛАМИ ТРЕНИЯ 179
Для определения напряженного состояния имеем сле¬
дующие граничные условия на площадке контакта при
на круге S радиуса а
и* = / (ρ) + с, τζ0 = F (ρω)σζ, трг = 0;
вне круга S на свободной поверхности
οζ = 0, τ2θ = 0, τΡ2 - 0.
Здесь мы пользуемся выражениями для перемещений (а
также для компонентов напряжения) в полярных коорди¬
натах. При этом иг соответствует употребляемому в пре¬
дыдущих параграфах w.
Напряжение σζ ограничено на контуре круга S. Напи¬
шем уравнение Ляме в цилиндрических координатах ρ, ζ и
Θ (см. А. Ляв [1], Е. Reisstier [1]):
где объемное расширение δ следующим образом выражает¬
ся на основании перемещений и9, uz и ив:
1 д (Рцр)
Р д9
Величины ωρ, ωθ и ωζ таковы:
\ ди ди.
180 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Компоненты напряжения в цилиндрических координа¬
тах будут
\
Тп
λδ + 2μ^,
др
ди
σζ — λδ + 2μ-^,
Л диЙ
σ0 = λδ + 2μ -τβ,
(\ дит диЙ\
J¥ + ir)=
_ ( 1 ди0 . д /“ΘΥ\
τΡβ -μ(— ~ш + р^1т//*
(8.4)
В случае осесимметричной задачи компоненты напря¬
жения и деформации не зависят от угла Θ. Если принять
это во внимание и подставить в уравнения (8.3) и (8.4)
значения б, ωρ, ω* и ωβ, то получим следующие выраже¬
ния для уравнения Ляме:
а ι д ί1 δ(ρ“ρ) ι диА ι а д \ди?- -^1-0 '
(λ + 2μ)^-[-^ ^_+'дГ] + Н- dz[dz <?e]~U’
д (дие\ ι 9 [ ι ^(Ρ“θ)1_η
н- V аг у + μ Lt ’
(λ -t-
ад -k [у
д (Р“р)
с?р
+
ди2
dz
]-
1 8 Г дип диЛ
-^ίκ-ρ^]=0·
(8.5)
Для компонентов напряжений найдем следующие вы¬
ражения:
[4 д (ои А ди "I ди
Т-^Т + ^ + ^-ёГ’
ди2
дР.
Р“р
rpz — μ [ dz
Г 1 ^ (ргО ди "Ι ди
σθ = λ[-±
др
д (ри
Р дР
,)+^1
^ dz J’
τΡθ = μρ
τ:θ = μ
Α.(11)
\ Ρ /"
<4
dz
(8.6)
Можно убедиться, что в первое и третье из уравнений
Ляме входят только и2 и ир, а во второе — только uQ. Точ¬
но так же компоненты напряжения σρ, ае, σζ и τρζ зависят
от ир и uZj а τρθ и τζθ — от ие.
§ 8. ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ С СИЛАМИ ТРЕНИЯ
181
Таким образом, в осесимметричном случае в упругом
теле существуют две независимые системы деформаций
и напряжений.
Мы получим первую из них, если положим uQ = 0. При
этом щ Ф 0 и иг Ф 0. В этом случае компоненты напряже¬
ния τΡθ ит2θ будут равны нулю, а σζ,<τρ, Οθ и τρζ отличны
от нуля.
Вторая система будет получена, если щ = 0, иг = 0,
ивФ 0. При этом компоненты напряжения Οθ, σρ, σζ и τρζ
будут равны нулю, а тр0 и τζθ отличны от нуля.
Напряженное состояние в нашей задаче, когда в уп¬
ругое полупространство вдавливается штамп в виде тела
вращения (причем имеют место силы трения, обусловлен¬
ные вращением штампа вокруг своей оси), может быть
разбито на два независимых напряженных состояния.
Для определения первого из них имеем следующие
граничные условия на площадке контакта при ζ = 0:
на круге S
«* = /(р) + с, Tpz — 0, t2*e = 0;
п (l/· ί )
вне круга S
a*z = 0, τρ*ζ = 0, = 0.
Для определения второго напряженного состояния
пмеем условия при ζ = 0:
на круге S
иГ = 0, тр*; = 0, т*е* = F (ρω) σ!*;
0 (o.o)
вне круга S
♦ р. % И1
о2 = 0, тР2 = 0, tzq = 0.
Сумма этих двух напряженных состояний (т. е. на-
пряжения σζ = σ*+ σ**, τΡζ = Трг+ Тр*и т. д.) будет удов-
летворять исходным граничным условиям (8.2) и, таким
образом, даст решение поставленной задачи. [Для опреде¬
ления напряженного состояния, удовлетворяющего усло¬
виям (8.8), нужно положить ир = 0, и2 = 0, иеФ0. При
этом будет получено иг = 0 и σζ = 0 как на круге, так и
вне круга SJ
182 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Итак, согласно, (8.8) для определения компонента на¬
пряжения τζθ при ζ = 0, которая в данном случае пред-
41
ставляет интерес, нужно определить οζ , удовлетворяю¬
щую условиям (8.7), эквивалентным условиям (5.1), и
умножить на фунцию Τ^ρω).
Очевидно, τ2θ = τzq, так же как и oz = σ2. Поэтому
момент, необходимый для поворота штампа, равен
а а
М = j ρχ2πρχ (τΡιθ)ζ=0^Ρι = j 2πρ?/Τ(ρ1ω) ρ* (ρχ) dpr
(8.9)
Таким образом, здесь решена следующая задача.
Штамп, представляющий собой тело вращения, урав¬
нение поверхности которого z = f(р), причем /(0) = 0, при¬
жимается к упругому полупространству силой Р, дейст¬
вующей по оси вращения таким образом, что радиус пло¬
щадки контакта равен а. Между штампом и упругим по¬
лупространством имеют место силы трения, причем коэф¬
фициент трения равен ί4ω, р). Штамп также поворачи¬
вается вокруг оси симметрии моментом М.
В таком случае сила Р определяется согласно (5.29),
перемещение с в направлении оси ζ — согласно (5.30),
нормальное давление под штампом /?*(р) — на основании
(5.31) и (5.17). Момент, поворачивающий штамп, будет
М
a f а
= YliS?) j F(ωρ)pa ί Δ/(pl)Η(ρ’ pi)dpl
О ^0
dp,
(8.10)
где Ж ρ, pi) определяется из (5.17).
Определим величину момента, необходимого для по¬
ворота штампа при различных его формах. Будет пола¬
гать, что коэффициент трения μ — постоянная величина.
i.Штамп с плоским основанием. Площадка контакта —
круг радиуса а. Распределение давления под штампом
Р*(Р) = А а'·
2ла У а2— р3
(8.11)
§ 8. ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ С СИЛАМИ ТРЕНИЯ 183
Здесь Р — сила, действующая на штамп. Представляя это
выражение в (8.9), находим
2. Равномерное распределение давления под штампом.
Рассмотрим случай, когда штамп имеет такую форму, что
на площадке контакта, радиус которой равен а, возникает
равномерно распределенное давление. Если сила, дейст¬
вующая на штамп, равна Р, то /?*(р) =Р/па2.
В таком случае на основании (8.9) момент равен
3. Штамп в виде параболоида второй степени. Пусть
на штамп действует сила Р такая, что площадка контакта
имеет радиус а. Он следующим образом зависит от вели¬
чины силы:
Здесь Е и ν — упругие постоянные, R — радиус кривиз¬
ны параболы, вращением которой получен параболоид, на
ее оси симметрии или, что то же, радиус сферы, которая
приближенно заменяется параболоидом.
Распределение давления под штампом дано в виде
Воспользовавшись (8.9), получим следующее выраже¬
ние для момента:
(8.12)
п
а
Μ = 2πμ ( р* (рх) ρϊ% = —2 (* μ/’α. (8.13)
JC CL °
J πα fJ
о 0
a
0
1
0
184 гл. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Таким образом, величина момента, необходимого для
поворота штампа при наличии сил трения, в значитель¬
ной степени зависит от его формы.
§ 9. Давление штампа эллиптической формы
в плане на упругое полупространство
Как было указано в § 1 данной главы, задача о дав¬
лении штампа эллиптической формы в плане на упругое
полупространство сводится к задаче Дирихле для внеш¬
ности эллиптического диска. Она может быть решена
посредством разложения в ряд по функциям Ляме. Одна¬
ко при выполнении этого разложения возникает ряд
трудностей, поэтому целесообразно установить некоторое
общее свойство получаемых решений.
Пусть в упругое полупространство ζ < 0 вдавливается
штамп, представляющий в плане эллипс, полуоси которо¬
го равны а и Ъ. При этом силы трения между штампом
и полупространством отсутствуют и поверхность полу¬
пространства вне штампа свободна от усилий. Если
уравнение поверхности, ограничивающей основание штам¬
па, является некоторым полиномом Рп(#, у) степени тг, то
давление, действующее под штампом, может быть пред¬
ставлено в виде
р (X, у) = (l - ^ - £)" * Pl (*, У), (9.1)
где Р*п {х, у) — полином, степень которого также равна /г.
Большинство контактных задач, рассмотренных выше,
представляет частные случаи этой задачи.
Приведенное здесь решение (9.1) позволяет, в част¬
ности, все задачи указанного вида привести к решению
системы линейных уравнений. Так как форма решения
заранее известна, то для определения конечного числа
содержащихся в нем неизвестных коэффициентов может
быть получена система линейных уравнений.
Для доказательства (9.1) введем эллипсоидальные ко¬
ординаты, которые связаны с прямоугольными следующи¬
ми соотношениями:
§ 9. ДАВЛЕНИЕ ШТАМПА ЭЛЛИПТИЧЕСКОЙ ФОРМЫ В ПЛАНЕ 185
е2х2 = α2ρ2μ2ν2, Ϊ
(1 - е2) е2у2 = а2 (р2 — е2) (μ2 — е2) (е2 - ν2), (9.2)
(1 — е2) ζ2 = а2 (р2 — 1) (1 — μ2) (1 — v2). J
При этом, если 1 ^ ρ ^ оо, β ^ μ ^ 1, 0<v^e, эллип¬
соид, соответствующий ρ = 1, вырождается в эллиптиче-
ский диск, полуоси которого равны а и b = aj^l — е2.
Известно, что задача, поставленная здесь, приводится
к следующему случаю задачи Дирихле: необходимо найти
гармоническую функцию во внешности эллиптического
диска, которая принимает значения, равные Рп(я, У) на
верхней и нижней сторонах этого диска, а на бесконеч¬
ности обращается в нуль. Заметим, что искомая функция
будет четной относительно ζ. Давление, возникающее под
штампом, пропорционально плотности простого слоя, по¬
тенциалом которого является эта гармоническая функция.
Известно, что произведение трех функций Ляме:
А? (*, У, ζ) = Е™ (ρ) El (μ) ЕТг (ν), (9.3)
которое мы в дальнейшем будем называть тройным про¬
изведением Ляме, является гармонической функцией.
Функции Ляме удовлетворяют уравнению Ляме при опре¬
деленном значении некоторого параметра, входящего в это
уравнение, при котором произведение этих функций в
прямоугольных координатах будет полиномом от х, у, ζ.
(см. Г. Н. Ватсон, Е. Т. Уиттекер [1]).
Построим в пространстве xyz гармоническую функцию
W\(x, у, ζ), четную относительно ζ, которая при 2 = 0
совпадает со значением полинома Рп(х, у).
Будем искать W\(x, у, ζ) в следующей форме:
Wiix, у, z) = Рп(х, y) + z*P'2)U\ y) + z*P™(x, у) + ...
Применяя к W\(x, у) оператор Лапласа, получим
+ i-2Pi2)(x,y)\+[AP%)(x,y) + 3-iPU)(x,y)]z*+... (9.4)
Здесь
а д2 , д2
186 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Пользуясь выражением (9.4), находим рекуррентные
формулы для jP(2ft)(x, у), на основании которых получаем
т
Wx (х, у, ζ) = 2 (— 1)кщ &»Рп (х, у) z*k. (9.5)
к=о
Здесь т равно целой части величины п/2, где п — наи¬
высшая степень переменной х или переменной у, а Δ(Λ) —
полигармонический оператор степени к.
Итак, W\{x, ι/, ζ) является гармоническим полиномом.
Его степень относительно ζ будет 2т п. Поэтому он
имеет степень, равную тг, так как наивысший показатель
степени у одной из переменных будет равен п.
Построим эллипсоид, поверхность которого соответст¬
вует некоторому значению ρ = κ. Гармоническая функция
W\(x, у, ζ), которая на куске плоскости ζ = 0, находящем¬
ся внутри эллипсоида, равна Рп(#, у), определяется на
основании (9.5).
Докажем, что функция W\{x, у, ζ) может быть пред¬
ставлена в виде суммы конечного числа тройных произве¬
дений Ляме.
Известно (Г. Н. Ватсон и Ε. Т. Уиттекер [11), что су¬
ществует (д+1)2 линейно независимых гармонических
полиномов, степени которых равны или меньше п. С дру¬
гой стороны, известно (там же, стр. 422), что существует
также (д+1)2 линейно независимых тройных произведе¬
ний Ляме. Эти условия являются достаточными для того,
чтобы каждый гармонический полином, степень которого
равна /г, мог быть представлен в виде линейной комбина¬
ции тройных произведений Ляме со степенями, равными
или меньшими д.
Нетрудно показать, что эти условия являются также
и необходимыми. Если перенумеровать линейно независи¬
мые гармонические полиномы, обозначив их через Р\(х,
г/, ζ), Р2(х, У, z), P3U, У, ζ), ..., и перенумеровать также
тройные произведения Ляме, введя для них обозначения
Aiix, у, ζ), А2(х, у, z), A3U? у, ζ), ..., то на основании
указанного выше можно написать систему r=(n+1)2
линейных уравнений
ВпР{ + В$Р2 + ... + BjrPr = Aj(x, у, ζ)
(/ = 0, 1, ..., г). (9.6)
§ 9. ДАВЛЕНИЕ ШТАМПА ЭЛЛИПТИЧЕСКОЙ ФОРМЫ В ПЛАНЕ 187
Для того чтобы каждое тройное произведение Ляме
можно было представить в виде линейной комбинации
гармонических полиномов, принадлежащих указанной вы¬
ше совокупности, и для того чтобы можно было обратить
это преобразование, нужно, чтобы определитель ||| Bjk || |
был отличен от нуля. Но определитель системы линейных
уравнений будет равен нулю тогда и только тогда, когда
его строки или колонны линейно зависимы. Линейная
зависимость строк невозможна, так как она приведет к
линейной зависимости правых частей — тройных произве¬
дений Ляме, которые все линейно независимы. Линейная
зависимость колонн также невозможна, так как, умножая
строки на соответствующим образом подобранные числа и
складывая их, можно при наличии подобной линейной за¬
висимости получить определитель с двумя равными стро¬
ками и таким образом прийти к линейной зависимости
правых частей, что невозможно.
Итак, определитель ||| Bjk\\\^0, и поэтому каждый гар¬
монический полином на основании (9.6) может быть пред¬
ставлен в виде линейной комбинации тройных произведе¬
ний Ляме. Отсюда следует также, что любой гармоничес¬
кий полином степени п является линейной комбинацией
тройных произведений Ляме, степени которых равны п
или ниже п. На основании этого имеем
w, (х, у, ζ) = Σ *Σ AklE{ (р) Е{ (μ) Elk (ν). (9.7)
h=0 1=1
Найдем гармоническую функцию W2(x, у, ζ) во внеш¬
ности эллипсоида р = κ, которая на его поверхности сов¬
падает с W\{x, г/, ζ). Для ее построения используем функ¬
ции Ляме второго рода, которые определяются формулой
(Г. Н. Ватсон и Ε. Т. Уиттекер [11)
и
Fn (р) = (2п + 1) Я™ (р) J (9.8)
Переменная и находится из следующего соотношения
(там же, стр 409):
£>И = р + |-(Л2 + я2 + с2).
188 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
При этом инварианты g2 и gz эллиптической функции
Вейерштрасса определяются из тождества
4 μ2 + ρ) (δ2 + р) (С2 + р) = 4гР (и) + gjp («) - *,·
Здесь i, δ и С - полуоси эллипсоида.
Гармоническая функция у, ζ), совпадающая на
поверхности эллипсоида ρ = κ со значением W\(x, у, ζ),
имеет следующее выражение:
Отсюда плотность слоя, распределенного на поверх¬
ности эллипсоида:
Если в выражении (9.9) устремить κ к 1, мы получим
в пределе гармоническую функцию, которая на эллипти¬
ческом диске с полуосями а и b будет равна Рп(х, У).
Устремляя κ к 1 в выражении (9.10) и умножая полу¬
ченную плотность на 2, мы найдем плотность простого
слоя, распределенного на эллиптическом диске, такую,
что потепциал этого простого слоя будет принимать на
нем значение, равное Рп(х, У). В результате получим
п 2fe+l
^4(Ρ)^(μ)4(ν). (9.9)
W,, (x, у, ζ) = 2 2 Ам
k=0 1=1
x [£ к (p) - & (p>L Ei (μ) Ei (ν)· (9-10)
n 2ft+l
причем имеем следующее .(выражение:
id о\ 1 / .2 ,Λ-Vz
§ 10. ШТАМП ПОД ДЕЙСТВИЕМ СИЛЫ И МОМЕНТОВ
189
Кроме того, нетрудно убедиться, что другой множи¬
тель, содержащийся в (9.11), будет равен некоторому по¬
линому на эллиптическом диске, так как на поверхности
эллипсоида тройное произведение Ляме Elk(i) Elh(\k) 2?/t(v)
будет полиномом. При этом двойная сумма будет полино¬
мом степени п, так как под знаком суммы содержатся
функции Ляме, порядок которых не выше п.
Вследствие того, что давление, возникающее под штам¬
пом, пропорционально определенной выше плотности
простого слоя, окончательно получим следующий резуль¬
тат:
р{х,у) = (l — Х-г — У*Р*п(х,у)· (9.12)
§ 10. Штамп эллиптической формы
в плане под действием силы и моментов
В этом параграфе исследуются штампы эллиптической
формы в плане, причем их основания ограничены поверх¬
ностями, уравнения которых представляют собой произ¬
вольные функции двух переменных: даются выражения
для перемещений и поворотов штампа на основании силы
и моментов, действующих на штамп. Таким образом, ес¬
ли известна система сил, кото¬
рая действует на штамп, то его
положение после вдавливания
в упругое полупространство
вполне определяется. При этом
предполагается, что эти силы
должны быть таковы, чтобы со¬
прикосновение между штампом
и упругим телом происходило
по всей площадке контакта.
Пусть на штамп эллиптиче¬
ской формы в плане действуют
сила Р и моменты Мх и Му от¬
носительно осей х и у (рис. 48). Область в форме эллипса
будем обозначать буквой Э. Для определения напряжен¬
ного состояния, возникающего в теле, необходимо, как
это показано в § 1, определить гармоническую функцию
ф(#, У, ζ), которая должна быть равна fix, у) на верхней
PIbgc. 48.
190 гл. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
и па нижней частях разреза в пространстве в виде эллип¬
тического диска. При этом f(x, у) — перемещения точек
поверхности упругого полупространства под штампом.
Условия для определения ср(я, г/, ζ) можно представить
в виде
Ф = f(x, У) на Э, ^ = 0 вне 3; (10.1)
при этом для s оо
φ(χ,ι/,ζ)->0 (s = >/£2 + i/2 + z2).
Давление под штампом определяется формулой
р <*, „) = - <σ,)_ = (g) ^, (10.2)
где Е — модуль Юнга, σ — коэффициент Пуассона (бук¬
вой ν обозначена дальше эллиптическая координата). По¬
этому <р(ж, у, ζ) может быть также представлена в виде
φ (х, у, z) = i-~ JJ ρ (ξ, η)
dl·,
У (* — If + (y — η)2 + z:
, (10.3)
Определим силу и моменты относительно осей х и у,
действующие на штамп. Имеем
р= P(l,4)<%dr\,
"а
МУ =■ Я Р (6. Ί) Idldr], Мх=^р (I, η) η dl·, dr\.
(10.4)
Найдем значение <р(я, г/, ζ) при стремлении s -*■ оо.
Имеем соотношение
φ (х, у, z)y_»oo =
1
-Цг^- f f Ρ <δ. Ή) “7=—Γ-5 2—2
э ν (*-ξ)*+(0-η)'+*2.Ι(
^||ρ<?,η)ίξίη = 1^->/>· <10·5>
πΕ
Для определения моментов Μχ и Μν воспользуемся
выражением
§ 10. ШТАМП ПОД ДЕЙСТВИЕМ СИЛЫ И МОМЕНТОВ 191
££ = — 1 ~ °2 Г Г р (I. η) <Щ, dr\
дх дх ЛЁ JJ Г- _t.a ,
1 — д2 JJ р (ξ, η) (* — ξ) <*η
π* J0J [(^-i)2 + (y-n)2 + 22]3/2
1—σ* iff Ip(E,T))dS<hi
*E IJ J 3/2
I» [(* —i) 4-(v —η) +* 1
• X
Я
P (ξ, η) d|dr|
9 [(χ-Ι)2 + (^-η)2 + ζ2]
21 2
/,
(10.6)
Устремим теперь в функции ду/дх величину s к °°,
причем будем оставаться в плоскости
х = 0 (рис. 49). На основании (10.4)
имеем
(S), — > ί Я Р «. ч) i <*6 -п -
- * J J Р (ξ, η) dl Λι| = -
9 I
(10.7)
Если теперь мы будем устремлять рИс. 49.
я к 0, т. е. будем находить значение
ду/дх на плоскости £ = 0, то из выражения (10.7) получим
Применяя аналогичные рассуждения, найдем выраже¬
ние для ду/ду в плоскости г/ = 0:
(10.9)
/£φ\ _ 1 - ог J_
\ду )s~>oo,y=Q лЕ х53
Представим теперь φ(#, у, ζ) в виде ряда, расположен¬
ного по функциям Ляме. Введем эллипсоидальные коорди¬
наты р, ν, μ, которые связаны с прямоугольными коорди-
192 гл. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
натами соотношениями (9.2):
(10.10)
е2х2 = α2ρ2μ2ν2,
(1 — е2) е2у2 = а2 (р2 —- е2) (μ2 — е2) (е2 — ν2),
(1 — е2) ζ2 = а2 (р2 — 1) (1 — μ2) (1 — ν2).
Пределы изменения переменных μ, ν и р таковы:
е < μ < 1, 0 < ν < β, 1 < р <
Полуоси эллиптического диска, в который вырождается
эллипсоид, будут а и Ъ = а)/1 — е2. Пусть
сю 2П+1
φ (*, у, ζ) = φ* (ν, μ, р) = 2 2 АптЕ% (ν) Д™ (μ) F% (р).
rj=o т=о
(10.11)
Функции Ляме второго рода F™ (р) определяются со¬
отношениями
^(ρ) = ^(ρ)ΨΓ(ρ),
где
(10.12)
Это выражение эквивалентно представлению (9.8) для
функций Ляме второго рода, которым мы пользовались в
предыдущем параграфе. Поэтому разложение по функци¬
ям Ляме можно представить в виде
φ (х, у, ζ) = φ* (ν, μ, р) =
оо 2П + 1
= Σ Σ Апт [£п (V) (μ) ЕТг (р)] Ψη (р). (10.13)
п—о т=о
Тройное произведение Ляме Ε™ (ν) Ε™ (μ) Еп (р) в
прямоугольных координатах будет некоторым полиномом
от переменных х, у и ζ. Порядок функции Ляме равен
сумме степеней при переменных х, у и ζ у главного члена
в этом полиноме. Полиномы, которые соответствуют про-
§ 10. ШТАМП ПОД ДЕЙСТВИЕМ СИЛЫ И МОМЕНТОВ
493
изведениям Ляме, могут иметь одну из следующих форм:
θ(ζ2, y\z>).
х ху
j 1 у yz xyz
ζ ζχ
Здесь θ(^, у2, ζ2) — полином от переменных x2,y2,z2, т. е.
полином, четный относительно х, у, ζ. Если полином
9U2, у2, ζ2) умножить на одну из величин, находящихся
в первой, второй, третьей или четвертой колонне, то полу¬
чаются произведения Ляме, соответствующие функциям
Ляме первого, второго, третьего или четвертого рода. Су¬
ществуют 2гс + 1 функций Ляме порядка η, причем при
четном п они будут состоять из функций первого и треть¬
его рода, а при нечетном п — из функций второго и чет¬
вертого рода.
В разложении функции φ(#, у, ζ) выделим три первых
члена; заметим, что в силу четности функции φ(#, у, ζ)
относительно переменной 2 произведения Ляме, нечетные
относительно 2, например, состоящие из 2?χ3)(μ), (ν),
Е[3) (ρ), Ψχ3) (р) и т. д., будут отсутствовать. Имеем
φ (*, у, ζ) =
= φ* (μ, ν, ρ) = А0 [Е0 (ν) Е0 (μ) Е0 (ρ)] Ψ0 (р) +
+ Аг [Ε[ι) (ν) Μυ(μ) Ε[ι) (ρ)] Ψ?» (р) +
+ А2 [M2)(v) Е[2) (μ) М2)(Р)] Ψί (Р) +
ОО 2П+1
+ Σ Σ Апт [еТ} (V) £(nm) (μ) £nm> (ρ)] Ψη (ρ). (10.14)
η=2 τη=1
Найдем асимптотические значения функций Ψ0 (ρ), Ψ^ρ),
Ψι (ρ) при ρо©. При этом воспользуемся (10.12) и
примем во внимание, что
я0(р) = 1, Я(11}(Р) = Р, 42)(р) = /^72. (10.15^
Тогда получим
[Ψο (р)1р->°° —
13 л. А. Галин
J ,,, dpW2 2> 1 = £. (10.16)
% У (р2- l)(p2-e2) Jp-,οο Р
194 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Г Ψι1)(ρ)]ρ-»οο = [ψΐ2) (р)]р-»оо =
-)(>■-.,1--^' (10·,7)
Заметим также, что
(ν) (μ) Е[1} (ρ) = х, Εψ (ν) Εψ (μ) Εψ (ρ) = у.
(10.18)
Кроме того, при ρ -*■ «> будет р s. Таким образом, огра¬
ничиваясь тремя первыми членами разложения (10.14),
имеем
Ф (я, У у ζ) = φ* (μ, ν, ρ) =
= Λτ + γΑι^+±Α^+ ... (10.19)
Нетрудно показать, что предельные значения последу¬
ющих членов будут содержать в знаменателях s в более
высоких степенях.
Выше в (10.5) было определено значение φ(χ, у, ζ)
при s °°. С другой стороны, на основании (10.19) нахо¬
дим
[φ (х, у, ζ)]^» = А0 -р (10.20)
Сравнивая (10.5) и (10.20), определяем
Р = -^А0. (10.21)
1 — σ
На основании ортогональности функций Ляме коэффи-
ент Aq определяется следующим образом:
4, = £ J J / (ν, μ) 1Е0 (V) Е0 (μ) Е0 (1) Ψ0 (1) dF =
э
= <10'22)
э
где
/* - J J I [Е0 (ν) Е0 (μ) Е0 (1) Ψ0 (I)]2 dF = [ψβ (l)]2 J j ί dF,
э Э
§ 10. ШТАМП ПОД ДЕЙСТВИЕМ СИЛЫ И МОМЕНТОВ
195
1 =
/(ΐ-μ2)(ΐ-ν2)
Если перейти к прямоугольным координатам, пользу¬
ясь (10.10), то для Р будет получено выражение
Е \
Р = 2 (1 - σ2) Ψ0 (1) Х
χτίί /(*.») (1-^-fa) А dxdy’ (10.23)
оо
Ψ0(1)= f r dp = W~,A
* A>2-0(p2-*2) V2 '
Здесь ^О/гл;, e) — полный эллиптический интеграл перво¬
го рода. В чаютном случае, когда е = 0 и, следовательно,
штамп будет обладать круговой формой в плане, получим
ψ.(ΐ) = J
Ϊ р/р!-1 2*
После введения полярных координат г cos θ = х,
г sin Θ = у формула (10.23) примет вид
2Л а
J?
π (1 — о*)
о о
Это выражение совпадает с формулой (3.10), получен¬
ной другим путем в § 3.
Найдем теперь на основании (10.19) выражение для
ду/дх при х = 0 и s Имеем
2 л а
<10'24>
3£
ь
'4° ,“ 3 А‘ ( ,■ т
-т^*? +<10-25>
Сравнивая (10.6) и (10.25), находим
(9Л\ ί-о2 ,f 1 1 л 1
1 у s3 3 153
13*
196 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Отсюда
П/Г пЕ 1 л
Му о
,_σ.3··>· <10'26>
Но коэффициент А\ определяется следующим образом:
Л = 7- / / / (ν, μ) ΙΕψ (ν) (μ) Ε[ι) (1) ψ?> (1) dF,
Э
J = j j г [Мг) (ν) МХ) (μ) (1) ΨΐΧ) (l)]2 dF,
Э
1
z =
/(ΐ-μ2)(ΐ-ν2)·
(10.27)
Если перейти от эллипсоидальных координат к прямо¬
угольным, то получим следующее выражение для мо¬
мента:
му= , Ε·-- χ
2 (l — σ2) b
1 ί ί χΐ (χ ’ V ^
X
4f>(i)
2 2
л
α2 Ъ2
dxdy\ (10.28)
при этом
ψ(χ1)(ΐ)= f
Ϊ pV(p2-l)(p:
2 ,2)
= ,т[^(тя-е)-£(тл'е)]· <10·29>
Здесь ίτ(1/2π, е) и £'(1/2я,е)— полные эллиптические ин¬
тегралы первого и второго рода.
Пользуясь аналогичными рассуждениями, можно на
основании (10.9) и (10.19) определить выражение для
Мх. В результате получим
Мх = Е X
2(1 — σ2) Ъ
X
Ψ2(1)(ΐ-«2)
2 2
1
о - о
-Ч
dxdy; (10.30)
§ 10. ШТАМП ПОД ДЕЙСТВИЕМ СИЛЫ И МОМЕНТОВ
197
при этом
Ψ
i2)(l) = j
с?р
1 <p’-«W-iMp*-«!)
Здесь П (V2^, — e2, e) и F (1/2π, e)—полные эллиптические
интегралы третьего и первого рода.
На основании (10.23), (10.28) и (10.30), полагая в них
fix, у) = ах + β*/ + δ, можно получить выражения для сил
и моментов, найденные А. И. Лурье [3] для частного слу¬
чая штампа с плоским основанием.
Рассмотрим теперь случай, когда даны Р, Мх и Му.
Примем уравнение поверхности упругого полупространст¬
ва под штампом в виде
fix, у) = foix, у) + ах + $у + δ. (10.31)
Здесь δ — перемещение штампа по оси ζ, а а и β — нак¬
лоны штампа относительно осей хну.
Применяя выражение (10.28), найдем на основании
(10.31)
М»~2 (! - Д С) {ijХ/(Х’ »)[*-? ~ 'У\А “*“« +
ixd*\
При этом интегралы, у которых подынтегральная величи¬
на содержит в качестве множителей величины β*/ и δ, бу¬
дут равны нулю. Полученное выражение позволит опре¬
делить угол поворота штампа а на основании момента
Му. Аналогичные выражения для Р и Мх можно найти по
формулам (10.23) и (10.30). Они позволят определить ве¬
личины β и δ на основании Мх и Р.
Итак, результат этого параграфа можно сформулиро¬
вать следующим образом: пусть на штамп эллиптической
формы в плане, основание которого ограничено поверх¬
ностью z — foix, у), действуют сила Р, направленная по
оси ζ, и моменты Мх и Му. В таком случае δ — перемеще¬
198 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
ние штампа в направлении оси ζ, а также а — его пово¬
рот относительно оси у и β — его поворот относительно
оси х определяются по следующим формулам:
-И )
dxdy I,
(10.32)
dx dyj,
(10.33)
dxdy{. (10.34)
-H
-H
Здесь введены следующие обозначения:
■Ά
dxdy,
A =
E
2 (l - σ2) ь¥? (1) ’
-И
dxdy,
В =
E
2 (l — σ2) b (l — e2) ψ<*) (1) ’
-Я
dxdy,
E
2 (l — σ2) 6Ψ (1) '
(10.35)
При этом Ψ0(1), Ψι^ίΐ) и ψ[2) (1) определяются на осно¬
вании (10.23), (10.29) и (10.30).
В настоящем параграфе изложено подробное содержа¬
ние статьи автора [6]. В работе В. И. Моссаковского [1]
предложен другой метод определения сил и момен¬
тов, действующих на штамп эллиптической формы
§11. ОЦЕНКА ПЕРЕМЕЩЕНИЙ
199
в плане. Этот метод позволяет определить указанные ве¬
личины также для штампа произвольной формы в плане.
Однако для этой цели необходимо знать решение задачи
о вдавливании штампа с плоским основанием, форма ко¬
торого в плане произвольна. Так как подобная общая
задача не имеет эффективного решения, то оказывается
возможным определить силы и моменты только для штам¬
па эллиптической формы в плане, т. е. получить формулы
(10.23), (10.28) и (10.30), что и сделано в упомянутой
статье. Тем не менее обобщение, полученное В. И. Мос-
саковским, представляет несомненный интерес.
Большое количество исследований контактных задач
для штампов эллиптической и, в частности, круговой фор¬
мы в плане было выполнено В. И. Довноровичем [1]. При
этом были использованы несколько модифицированные
методы, изложенные в двух предыдущих параграфах.
§ 11. Оценка перемещений
для штампа произвольной формы в плане
Результаты, полученные в предыдущем параграфе,
позволяют найти оценки для перемещения штампа с плос¬
ким основанием, на который действует заданная сила.
Будем рассматривать штамп произвольной формы в пла¬
не, причем будем полагать,
что он перемещается так, что
его основание остается пер¬
пендикулярным к оси ζ
(рис. 50). Найдем двусторон¬
нюю оценку для силы, прило¬
женной к штампу, который
под ее действием перемеща¬
ется на заданную величину.
Согласно условию, указан¬
ному в § 1, гармоническая
функция <φ(χ, у, ζ), которая
совпадает с величиной перемещения поверхности упругого
полупространства, в этом случае на обеих сторонах разреза
в виде области L в пространстве будет равна постоянной
величине δ. При этом ΰ — перемещение штампа. На беско¬
нечности φ(#, у, ζ) обращается в нуль. Гармоническая
Рис. 50.
200 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
функция φ(.ζ, у, ζ) будет обладать максимумом на поверх¬
ности, ограничивающей область. В данном случае этим
максимумом будет ее значение на ограничивающей по¬
верхности, т. е. величина δ. Таким образом, всюду вне
области L будет иметь место <р(х, у, ζ) < δ.
Опишем вокруг области L в плоскости ху некоторый
эллипс. В таком случае область «9, представляющая эл¬
липс, разобьется на две подобласти L и М так, что
Ь + М = Э.
На основании указанного выше
φ(χ, ι/, 0) = δ на L, <pU, у, 0) = g(x, у) ^ δ на М. (11.1)
Определим теперь силу, действующую на штамп, вос¬
пользовавшись формулой (10.23). На основании (11.1)
найдем неравенство
Вычисляя значение последнего интеграла, найдем
окончательно
Найдем для силы Р оценку снизу. Предварительно вве¬
дем одну электростатическую аналогию. Пусть на плос¬
кой проводящей пластинке, имеющей такую же форму L,
как и основание штампа, распределены электрические
заряды, плотность которых qlx, у). В таком случае элект¬
ростатический потенциал будет
Р
< 2 (ί — σ2) 6Ψ0 (1)
iff 9(1, η) dl *ι
§ ii. ОЦЕНКА ПЕРЕМЕЩЕНИЙ
201
Общее количество электричества на пластинке будет
<? = f Ji(S,4)dS*|. (И.5)
Здесь ко — диэлектрическая постоянная, ε — диэлектриче¬
ский коэффициент среды.
Будем рассматривать пластинку, от которой удалены
на бесконечно далекое расстояние поверхности, обладаю¬
щие зарядом противоположного знака. В таком случае
потенциал на пластинке постоянен:
[ψΟτ, у, z)]L = ·ψο.
Таким образом, для определения q(x, у) имеем уравнение
Ψο = ГТГ f f * &'****' = const. (11.6)
V(x-l)2 + (v-tf + S
Емкость пластинки С, точнее конденсатора, образован¬
ного пластинкой и бесконечно удаленной поверхностью,
будет в наших условиях следующей:
С = |, (11.7)
Сравнивая эти выражения с выражениями, получен¬
ными для контактной задачи, нетрудно заметить, что
(11.6) аналогично (10.3), а (11.5) аналогично первому из
выражений (10.4). Емкость С представляет собой анало¬
гию с коэффициентом λ, связывающим величину силы,
действующей на штамп с плоским основанием, с величи¬
ной перемещения этого штампа δ, т. е.
Ρ = λδ. (11.8)
В дальнейшем при нахождении оценки для силы, дей¬
ствующей на штамп, мы будем пользоваться понятием
емкости.
Для установления нижней оценки воспользуемся неко¬
торыми результатами Полиа и Сегё Ш. Они заключаются
в следующем: пусть даны тело S, тело вращения S\ и
линия Z, которая является осью тела S\. Пусть плоскость,
перпендикулярная к линии Z, пересекает оба тела S и S\,
причем площади плоских фигур, полученных при пересе¬
чении, одинаковы. Пересечение плоскости с телом S\ дает,
202 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
очевидно, круговой диск. Построение тела S\ на основа¬
нии S называется симметризацией относительно линии.
Далее, пусть поверхность тела S и поверхность, уда¬
ленная на бесконечность, образуют конденсатор. В таком
случае доказывается, что С\ — емкость поверхности сим-
метризованного тела S\ — будет меньше С — емкости по¬
верхности тела S. Это неравенство будет справедливо и в
предельном случае, когда тело S превратится в плоскую
пластинку L. В таком случае симметризованное тело Si
превратится в круговой диск, равновеликий с L по пло¬
щади.
Таким образом, будет справедливо неравенство
Здесь CL — емкость пластинки L, а Со — емкость круговой
пластинки, равновеликой с ней по площади.
На основании этого применительно к контактным за¬
дачам получаем следующий результат: штамп с плоским
основанием произвольной формы в плане при заданной
силе будет обладать меньшим перемещением, чем штамп
с основанием в виде круга равной площади. Пусть пло¬
щадь области L будет А. Сила Р<>, действующая на круго¬
вой штамп с площадью А при перемещении б, согласно
(10.24) будет равна
На основании (11.10) и (11.9) получаем неравенство
Результаты этого раздела можно сформулировать сле¬
дующим образом: если штамп с плоским основанием L
и с площадью А перемещается на величину б, то для ве¬
личины силы Р, действующей на штамп, получаем сле¬
дующие неравенства:
(11.9)
(11.10)
(11.11)
Здесь Е — модуль упругости, σ — коэффициент Пуассона,
а — большая полуось, е — эксцентриситет эллипса, опи-
§ ii. ОЦЕНКА ПЕРЕМЕЩЕНИЙ
203
санпого вокруг L, и Ρ(42π, е) — полный эллиптический
интеграл первого рода.
Приведем оценки для силы Р, действующей на плос¬
кий штамп, имеющий заданное перемещение б в случае,
когда этот штамп имеет квадратную форму в плане.
Пусть сторона квадрата равна 2h, площадь штампа
А — Ah2. Вокруг квадрата опишем окружность, т. е. эл¬
липс, эксцентриситет которого е = 0. Радиус этой окруж¬
ности равен У 2ft. Он может быть в данном случае принят
равным большой полуоси эллипса. Поэтому а = j/2ft.
Полный эллиптический интеграл /''О/гЯ, е) при е = 0
равен
Подставляя эти значения в формулу (11.12), получаем
δЕ о ι [ΰ? ^ п ^ № nyih
1_σ2- V " ^ΐ-σ2 π/2 ’
На основании этого находим следующую оценку:
J^j/f </><-^4/S, (11ЛЗ)
или, после вычислений,
2,26 2,82 J^L-,/ι. (Ц.14)
1 — σ2 1 — σ '
Среднее значение будет
2,54 -^-5 А.
1 — σ
Неравенства (11.14) позволяют сделать заключение,
что отклонение силы Р от этого среднего значения не бу¬
дет превышать 10%. В некоторых случаях подобная точ¬
ность является достаточной. Однако, как будет показа¬
но в дальнейшем, есть основание предполагать, что ниж¬
няя оценка является более точной и поэтому в данном
случае сила Р будет близка к значению, равному
2,26h.
1—0
204 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Предположение, что из всех пластинок данной площа¬
ди круговая пластинка будет обладать наименьшей ем¬
костью, было высказано Дж. В. Стреттом (лорд Рэлей)
[1]. При этом, сравнивая емкости эллиптических пласти¬
нок равной площади, но с различными эксцентриситета¬
ми, он пришел к выводу, что изменение эксцентриситета
незначительно влияет на емкость.
Приведем некоторые из этих результатов примени¬
тельно к нашему случаю контактной задачи. Пусть
к = бо/бэ, где бэ — перемещение штампа с эллиптическим
основанием, а бо — перемещение штампа с круговым ос¬
нованием. Основание обладает одинаковой площадью,
и на каждый штамп действуют одинаковые силы. В этом
случае для к можно привести (следуя Рэлею) числовые
значения, соответствующие эксцентриситету е с полуося¬
ми а и Ь:
е
Ь/а
к
0,00000
0,34204
0,50000
0,64279
0,76604
0,86603
0,93969
0,98481
1,00000
1,00000
0,93969
0,86603
0,76604
0,64279
0,50000
0,34202
0,17365
0,00000
1,0000
1,0002
1,0013
1,0044
1,0122
1,0301
1,0724
1,1954
Эти данные позволяют, по-видимому, сделать вывод,
что довольно значительное изменение формы штампа
в плане, при котором его площадь остается неизменной,
весьма слабо влияет на величину перемещения штампа.
Поэтому в неравенствах (11.12) сила Р\ для штампов,
даже довольно далеких от круговой формы в плане, бу¬
дет, вероятно, весьма близка к нижнему пределу.
§ 12. Давление штампа
с плоским основанием клинообразной формы в плане
Рассмотрим задачу о давлении на упругое полупрост¬
ранство ζ < 0 штампа, который в плане имеет форму бес¬
конечного клина и обладает плоским основанием (рис. 51).
§ 12. ШТАМП КЛИНООБРАЗНОЙ ФОРМЫ В ПЛАНЕ
205
Угол между прямыми, ограничивающими бесконечный
клин, равен 2а. Предполагается, что между штампом
и основанием силы трения отсутствуют. Штамп переме¬
щается на некоторую величину, оставаясь параллельным
плоскости ху.
В этом параграфе мы дадим решение одной задачи
о давлении штампа с плос¬
ким основанием клинообраз¬
ной формы в плане. В § 1
было показано, что это реше¬
ние задачи приводит к отыс¬
канию гармонической функ¬
ции cpU, г/, ζ), совпадающей
при z = 0 с величиной пере¬
мещения поверхности упру¬
гого полупространства, так
что cpU, г/, 0) = w(x, у, 0), и
удовлетворяющей следующим
на L
граничным условиям:
вне L
ф = с,
dy/dz = 0.
(12.1)
Здесь L — часть плоскости ζ = 0, находящаяся внутри
клина, с — величина перемещения штампа.
Давление, возникающее под штампом, определяется
следующим образом:
р (х, у) = —(<т2)2=о = [згЦ; (12.2)
Е — модуль упругости, ν — коэффициент Пуассона.
Из (12.1) следует, что φ(χ, у, ζ) может быть представ¬
лена в виде потенциала простого слоя, распределенного
на плоском клине L. Ее определение можно привести
к следующему случаю задачи Дирихле: найти гармони¬
ческую функцию, непрерывную во всем пространстве,
кроме разреза L, имеющего форму плоского клина; на
верхней и нижней сторонах разреза она должна прини¬
мать значения, равные постоянной величине. На беско¬
нечности должны обращаться в нуль первые производ¬
206 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
ные от функции ср (что соответствует обращению в нуль
напряжений).
Введем сферические координаты г, Θ и # по фор¬
мулам
z = rsia0sia#, у = г sin Θ cos Ф, x = r cosO. (12.3)
Тогда уравнение Лапласа будет иметь следующий вид:
^1 + 2й+ ' !(si„e®+ ->«^ = 0. (12.4)
г дг г2 sjn dQ J r2 sin2 0 Qftb
Найдем некоторое решение, полагая, что <р(я, г/, ζ)
не зависит от радиуса так же, как и ее граничные зна¬
чения на плоском клине L. Тогда φ(#, г/, ζ) будет сфери¬
ческой гармонической функцией нулевой степени. Если
положить
φ{χ, г/, ζ)=Φ(θ, θ), (12.5)
то функция Φ(Θ, θ) будет удовлетворять уравнению
sme^0(sineg?)+^ = O. (12.6)
Если ввести новые переменные
ξ = tg -|· cos ή, (12.7)
то, как известно (см. Ε. W. Hobson [ID, функция
Φ*(ξ, η) = Φ(Θ, О) (12.8)
будет удовлетворять уравнению
д2Ф* , д2Ф*
df дц
= 0. (12.9)
При преобразовании переменных (12.7) сфера пере-
ходит во всю плоскость комплексной переменной
S = E + ^ = tg-|ei#,
причем следу от пересечения плоского клина L со сфе¬
рой соответствует прямоугольный разрез, идущий от точ-
ки i = — tg-p η = 0 до точки ξ = + tg γ, η = 0.
§ 12. ШТАМП КЛИНООБРАЗНОЙ ФОРМЫ В ПЛАНЕ
207
Согласно (12.1), (12.5) и (12.8) Φ*(ξ, η) принимает
значение, равное с на верхнем и нижнем краях этого
разреза. Кроме того, мы будем считать, что функция
Φ*(ξ, η) обладает на бесконечности логарифмической
особенностью; тогда производные от <р(я, г/, ζ) будут на
бесконечности исчезать, что соответствует исходному тре¬
бованию [функция Φ*(ξ, η) не может быть регулярной
всюду, так как в этом случае она была бы равна посто¬
янной] .
Нетрудно показать (см. Н. И. Мусхелишвили [1]), что
Ф*(|, T])=Rei^) + c, (12.10)
где
U;(Q = Klg^ + |/>-tg2|),
или, выражая через Θ и
Φ (Θ, Ъ) = Re [к lg {tj je^ + Ytg21 е2й> - tg2 f-)] + с.
(12.11)
Выразим эту функцию в прямоугольных координатах.
На основании (12.3) установим следующие соотношения
между функциями сферических координат, входящих
в (12.11), и координатами х, у, ζ:
COS θ = , tg -f = λ/j
-,2 ι _2 b 2 f 1
— COS Θ
V^a + 02 + *2’ 2 1 + cos Θ
Отсюда следует
Θ = л[Vэ? + У2 + *2 — *
2 V /я2 + у2 + Ζ2 + *
Кроме того,
cos 0 = _ , sin θ =
У у2 -j- г2 + ζ2
На основании этого
=cosO + i sin ϋ=
2 ι 2’
У У + ζ
208 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Подставляя эти выражения в (12.11), получим
Это выражение может оказаться удобным для нахож¬
дения напряжений, возникающих внутри упругого тела.
Однако для определения давления, имеющего место на
поверхности упругого тела, целесообразно воспользовать¬
ся исходной формулой (12.11) в сферических коорди¬
натах.
Обратимся к формуле (12.11) для того, чтобы устано¬
вить смысл полученного решения. Нетрудно заметить,
что функция Φ(θ, θ) имеет логарифмическую особенность
вдоль радиуса, которому соответствует значение Θ = π,
или, иначе, приведенная выше функция Ф(я, г/, ζ) будет
иметь подобную особенность при ζ = 0, т. е. на поверх¬
ности упругого полупространства вдоль отрезка действи¬
тельной оси от х = 0 до —
Логарифмическая особенность функции напряжений
вдоль некоторой линии на поверхности упругого тела со¬
ответствует давлению, приложенному вдоль этой линии.
При этом давление будет меняться по закону С/r, где
г — расстояние от точки, где оно определяется, до вер¬
шины клина. Это обстоятельство следует из того, что
производная от гармонической функции нулевой степени,
т. е. не зависящей от радиуса г, будет вести себя как
1/г. В выражении же для давления, как было указано
выше, входит производная от функции напряжений
φ по ζ.
Таким образом, полученное решение соответствует
давлению клинообразного штампа при наличии некоторой
нагрузки, действующей на поверхности упругого полу¬
пространства.
Будем определять это давление. Имеем
Λ, Е /д<р\
§ 12. ШТАМП КЛИНООБРАЗНОЙ ФОРМЫ В ПЛАНЕ
209
На половине разреза, где Ό1 = 0, между точками ξ = 0,
η = 0 и ξ = t:* η = 0 будем иметь
дФ (θ,θ)] Г0Ф (Θ, 0)1
ζ 1=0 L д* Ъ=о1.^>=о*
dz
На основании (12.3)
\**] = Г ! 1 = _1-.
[ dz Jd==0 у г sin 0 cos О ]fl.=0 г sin Θ
С другой стороны,
рф (0,0)1 = рФ* (I, η)1 Γ£η]
dti Jd=0 [ dv\ ]л=0[^^=0
Из (12.7) следует, что
p»],.0-[,gl-cosdL=‘8^
поэтому
ГдФ (0, ϋ)
Г<?Ф(0, Щ _ рФ* (£, η)1 Γ^η] г
[ dz }z=0 L ^ h=oMi>=oL
djy
dz
θ'—о
аф* (ξ, η)
5η
Но если Φ*(ξ, η) = Re Η>(ζ) + с, то
дф* (ξ, η) т г /е.ч
J£iJi=-Imu/ (ζ).
Из (12.10) получим
u/(o = |/ng(s + / s»-tg»|) =
К
ν
r'b t„2 α
ζ — tg τ
(12.14)
(12.15)
Под штампом —α/2<θ<α/2. Следовательно, при
η = 0 и ξ <С tg будем иметь
я
9 θ'
■tg-τ
14
Л. А. Галии
210 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Из (12.13) следует, что при |<tg γ
= — Im ц>' (О = , К
На основании (12.12), (12.13) и (12.16) получим
(12.10)
2 Θ
2 -*а2
или, после некоторых преобразований,
В 1
р (г, Θ) = К
2 (ί — ν2) 1 / о а * Θ
?-(l+cos Θ) у tg -т — tg -2
. (12.17)
Здесь Θ отсчитывается от биссектрисы угла при верши¬
не клина. В выраже¬
ние для величины
давления входит мно¬
житель К; он может
быть определен, если
известно суммарное
Рдс. 52.
давление, действующее на какой-нибудь ограниченный
сектор.
На рис. 52 и 53 показаны распределения давлений
под штампами в виде бесконечного клина с углами при
вершине π/2 и π/4; на них нанесены кривые, вдоль ко¬
торых давление остается постоянным.
§13. ДАВЛЕНИЕ УЗКОЙ БАЛКИ НА ПОЛУПРОСТРАНСТВО 211
Нетрудно также заметить, что при стремлении угла а
к нулю распределение давлений вдоль прямой, перпенди¬
кулярной к биссектрисе, стремится к тому, которое по¬
лучается на основании решения плоской задачи (см.
гл. I, § 5). Если ввести переменную s = tg0 [причем
вдоль указанной прямой, находящейся на расстоянии Я
от вершины угла, будем иметь —a<s<a (a = tga)], то
из (12.16) получим при а-^0
р* (s) = К —г Е -4=гг, (12.18)
w 2(1 _v2)ff/a2_s2· V '
Итак, полученное простое решение соответствует слу¬
чаю, когда на прямой, являющейся продолжением сред¬
ней линии клина, действует некоторая пригрузка.
Можно, однако, указать примеры, когда будет иметь
место решение подобного типа, т. е. такое, при котором
функция напряжений не зависит от радиуса и поверх¬
ность упругого тела свободна от усилий.
Логарифмическая особенность функции напряжений
является следствием того, что давление, действующее на
сектор ограниченных размеров, выделенный из площади
контакта, конечно, а полное давление, которое оказывает
клинообразный штамп на упругое полупространство, бес¬
конечно велико. Если рассмотреть задачу, когда в сопри¬
косновении с упругим телом находится клинообразный
штамп, повернутый относительно средней линии на не¬
который угол так, что на одной половине площадки кон¬
такта действует положительное, а на другой отрицатель¬
ное давление, и общее давление равно нулю, то указан¬
ное обстоятельство не будет иметь места.
В этом случае может быть построена гармоническая
функция, не зависящая от радиуса, которая будет всюду
регулярна и которая позволит решить эту контактную
задачу.
§ 13. Давление узкой балки
на упругое полупространство
В технической теории изгиба балок на упругом осно¬
вании часто принимается предположение, что между пе¬
ремещением балки, т. е. осадкой упругого основания,
н средним давлением, приходящимся на единицу длины
14*
212 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
балки, существует прямая пропорциональность (гипотеза
Циммермана — Винклера).
В некоторых случаях это предположение является не¬
достаточно удовлетворительным. Поэтому был выполнен
ряд работ, о которых упоминалось во введении, в кото¬
рых упругое основание рассматривается как полупрост¬
ранство и решается приближенно полученная контактная
jpi:
ж
-t
Рис. 54.
задача. Однако это приводит к значительно более слож¬
ным выкладкам, и поэтому представляется целесообраз¬
ным установить пределы применимости указанного выше
предположения.
В настоящем параграфе устанавливаются случаи, ког¬
да это предположение будет близко к действительности,
а также определяется величина коэффициента постели,
который до сих пор определялся лишь экспериментально.
Будем рассматривать задачу о вдавливании в упругое
полупространство абсолютно жесткой балки конечной
длины. Основание контура поперечного сечения балки
представляет собой отрезок прямой. Если балка является
упругой и изгибается под действием приложеннной на¬
грузки и реактивных сил, то вывод о пропорционально¬
сти между осадкой и давлением, который устанавлива¬
ется в дальнейшем, будет справедливым также и в этом
случае.
В самом деле, безразлично, имеет ли балка заданную
форму, или приобрела ее под действием приложенных сил.
Предполагается, что балка (рис. 54) в плане является
достаточно узким прямоугольником, длину которого обо¬
значим через 2а, ширину — через 26. Считаем, что рас¬
пределение давления в поперечном направлении будет
§ 13. ДАВЛЕНИЕ УЗКОЙ БАЛКИ НА ПОЛУПРОСТРАНСТВО 213
таким же, какое получается на основании решения соот¬
ветствующей плоской задачи. Следовательно (см. гл. I,
§ 5), давление на прямой х = ξ
Ρ*&ν) = ··-·/Ρ® 2.
ft У δ — у
Функция p(l·) — величина давления на единицу дли¬
ны балки — подлежит определению. Она находится та¬
ким образом, чтобы перемещение упругого полупростран¬
ства на оси х было равно заданной функции w(x), кото¬
рая определяется на основании контура сечения балки
в направлении оси х. Принятая предпосылка аналогична
предположению, на котором построена теория узкого
крыла конечного размаха.
Перемещение поверхности упругого полупространства
равно значению на плоскости ζ = 0 гармонической функ¬
ции φ(χ, г/, ζ), определенной при ζ < 0. Для ее нахожде¬
ния имеем условия:
1) перемещение вдоль отрезка оси х, равного длине
балки, является заданным:
φ(#, 0, 0) = w(x)
при
z = 0, у = 0, — а<х< + а;
2) распределение давления под балкой определяется
через функцию /?(|):
дер = 2 (ί — у2) р (I)
dz пЕ у 62 _ у2
при
ζ = 0, # = ξ, — δ < у < + 6;
3) давление на свободной поверхности отсутствует:
д(р (— оосус— б, —ОО <х<—а,
~~ при ζ = 0 и при j . л ^ ^ .
dz I +б<г/<+оо, +а<х<+оо;
4) поведение функции на бесконечности:
Ф (x,y,z)-+ r Р ■■■■:■:= при Ζ = ]/ X2 + у2 +Ζ2 ОО.
У X -\- у +2
Здесь Е — модуль упругости, ν — коэффициент Пуассона.
В таком случае [см. (1.12)] для перемещения вдоль оси х
214 ГЛ. II, ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
имеем
w(х) = Lz*! Г +f ■■ ■ .ρ(ξ) dydi.
Произведя интегрирование по у, получаем для опреде¬
ления функции р(х) интегральное уравнение
+а
w (х) = j ρ (ξ) Hi (х — ξ) dt, (13.1)
—а
где через Нь(х— ξ) обозначено ядро этого интегрально¬
го уравнения,
=iW3[rhi*(rrO· <«·2>
причем К f—
( ίδ
скии интеграл первого рода от модуля ух __ |
Рассмотрим новое ядро
Нь{х-1) = Нь(Х~1\ (13.3)
Л6
где λδ определено следующим образом:
+ а Л
λδ β Цл2 Г Г .* — *. (13.4)
пЕ L l-β / («а - у) (sa + л!
Покажем теперь, что
1) ядро #бЫ монотонно убывает при s>0 и монотон¬
но возрастает при s < 0, причем s = х — ξ;
2) при 6-^0 Ihix — ξ) = 0, если х — ξ Ф 0,
Нб(х — ξ) σο, если х — ξ = 0;
эллиптиче-
§ 13. ДАВЛЕНИЕ УЗКОЙ БАЛКИ НА ПОЛУПРОСТРАНСТВО 215
3) интеграл
-fa
j H6(s)ds = 1.
Очевидно, что при s > О
-f δ
^ тт ι п\ ^ ^ ν Г —s ^ о
так как выражение, находящееся под знаком интеграла,
будет в этом случае всегда отрицательным. Следователь¬
но, Ht(s) монотонно убывает при возрастании s, если
5 > 0. Так как функция H6(s) является четной, то она
монотонно возрастает при возрастании s, если s < 0.
Таким образом, первое положение доказано.
Найдем теперь предельное значение λδ при б 0.
Исходя из выражения (13.4), будем иметь
Легко убедиться, что
lg^n + lg (1 + /2)> arsh ^ =
= lgfe + 1//(ίδ)2 + 1]>1δίδ + 1δ2·
Следовательно,
4U-v*)f(· *1 , a Γι drj_
** 6 i gVr^?+
+ lg (l + /2) j ;/==,] > λ«·
216 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Из этих неравенств получим, что при δ -*■ О
^ = 2jW^‘e(-s)· <13·β>
Установим теперь предельное значение Нь (s) при s Ф 0.
Пользуясь (13.2), имеем
2 (1 — ν2) π 1
Л? 2~М'
lim Hi (s) = lim[2(l-~v2) 1 К (-)
6^o β-,ο l η*Ε s W J
Отсюда следует, что
ι. tj i \ н6 (у) 11 1
limtf6(s)- λβ -=|,| 2ΐ8(β/β)·
Если 5 = 0, т. е. х = ξ, то #бЫ -*■ 00 при s О и δ -*■ О,
так как δ и s стремятся к нулю независимо друг от дру¬
га. Таким образом, доказано второе положение.
Третье положение непосредственно следует из опреде¬
ления ядра:
и , t4 И*6(х-Ъ)
Н 6 (х — ι )= J ,
Аб
где
+а
λδ = | Нь (s) ds.
Таким образом,
(13.5)
§ 13. ДАВЛЕНИЕ УЗКОЙ БАЛКИ НА ПОЛУПРОСТРАНСТВО 217
Вследствие этого
-fa
j* He (s) ds = 1.
—a
Но если выполнены условия 1, 2 и 3, то —
представляет собой ядро сингулярного интеграла и эти
условия являются необходимыми и достаточными (см.,
например, Д. К. Фадеев [1]) для того, чтобы существо¬
вало асимптотическое представление функции р(х):
-fa
lim f р (ξ) Я б (x-l)dl = p (χ). (13.7)
6-»0 —а
Таким образом, выражение (13.1) при стремлении δ
к нулю вырождается в сингулярный интеграл.
Из (13.1) и (13.3) имеем
~fa ~fa
j р (ξ) #6 (χ — I) dl·, = λδ j P (I) Hb {x—Q d|= w (x), (13.8)
—a —a
и, следовательно, согласно (13.7)
I
lim τ- w(x) = p{x),
δ->0 δ
или, подставляя вместо λβ выражение (13.6), получим
lim пЕ g 1 / -/T, w (χ) — ρ (,χ). (13.9)
6_0 2 (1 - ν2) lg (β/δ) w ^ν ' ν 7
Таким образом, имеет место предельная пропорцио¬
нальность. Предельное равенство (13.7) будет иметь ме¬
сто при достаточно широких предположениях о поведе¬
нии функции р(х). Однако в действительности ширина
балки δ является величиной конечной.
Постараемся найти некоторые соотношения, которые
позволят установить, насколько быстро может меняться
давление, возникающее под балкой, чтобы предельная
пропорциональность имела место.
Исследуем более подробно сингулярный интеграл
(13.7). Выведем равенство (13.7) для нашего случая и
установим на основании этого условие, необходимое для
асимптотического представления функции посредством
такого интеграла.
218 гл. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Разобьем в интеграле (13.7) промежуток изменения
переменной следующим образом:
χ-ζδ х+£б
j р®Нф-$Ъ+ j p(l) H6(x-t)dt +
-а х-ζδ
-f а
+ j p(l)H6(x-t)<%.
я-ί-ζβ
Определим величину ζβ так, чтобы при δ -*■ 0 имело
место
χ—ζδ а
j р(|)Яб(.т-|)^+ j p(l)H6(x-l)dl
— ΪΤ5 — ►<>. <«·«»
*-ζβ
Это равносильно тому, что при δ О
χ—ζδ -fa
f ρ(ξ)Η*6*(χ-ΙΜΙ + j Ρ(1)Η*6*(x~i)di
— ад — -0’ ί13·11)
j ρ (I) Η*6* (х — ξ) d%
χ-Ιδ
где
+б
НТ(х-\) = Г ■ .·ιί=_?(?_ .
(δ2 — у2) [(ж — ξ)2 + у%\
Заменим числитель выражения (13.11) величиной,
принимающей заведомо большие значения. Рассмотрим
неравенство
+б +б
j’ dy ^ 1 Г dy __ π
^У{.ьг-у*)[(х-1?+у*\ ι*-δΓ
Вследствие монотонного возрастания Нь(х — ξ) макси¬
мум этого выражения при данных значениях ξ будет до¬
стигнут при ξ = х — ξ6, а также в силу четности при
§ 13. ДАВЛЕНИЕ УЗКОЙ БАЛКИ НА ПОЛУПРОСТРАНСТВО 219
ξ = X + ξβ. Поэтому
(— ad<x — ζδ, X + ζδ <ξ<+α).
Если обозначить максимальное значение р(х) при
— а< х< + а через ро (функция р(х) предполагается ог¬
раниченной и положительной), то будем иметь
χ—1δ -fo
j p{t)Hl*(x-l)dZ+ j р(|)ЯГ(*-|)й|<
-α зс+ζδ
<ρ°ξ(2α-2ζ6)<ρ0
Определим величину, заведомо меньшую чем знаме¬
натель. Вследствие того, что каждый из множителей ρ(ξ)
и Не (χ — ξ), из которых составлено подынтегральное
выражение, всегда положителен, будем иметь
Λ+ζυ £δ
j Р (I) Нь (x — l)dl=p (х0) j ЯГ (s) ds
x~t6 —ζδ.
{Χ — ζδ < Χ0 < X + ζδ)·
Аналогично тому, как в (13.5) была произведена оцен¬
ка λ», имеем для интеграла правой части:
+εδ
j* Hi* (s) ds > j^2jt lg ^ -f- 2π lg 4].
-ίδ
Следовательно,
χ+U
j р(1)НГ(х-|)dg =
*-Εδ
+£δ
= Ρ (*ο) J (S) ds > ρ (χ0) ^2η lg J + 2π lg 4| >
ζδ
>ρ(*„)2π lgi6.
220 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Подставим величину, большую числителя и меньшую
знаменателя, в дробь (13.11); предельное равенство будет
иметь место во всяком случае тогда, когда выполняется
pji2 а ра
9 Ί >-/04 = “7—\"г ί /У ,Я\ == 0· (13.12)
6-»0 (хо)1* (Ы6) Р (*0) 1ё (Сб/δ) V '
Покажем, что равенство (13.12) будет справедливо,
если ζ6 определяется следующим образом:
Ь-ТОЭТ,· <<3'13>
Подставляя это выражение в (13.12), будем иметь
Р0а Р0 lg lg (д/δ) _
ρ (*„) ζβ ig (Se/6)— ρ (χ0) tte (β/δ)— ^ ig lg («/δ)] —
_ -Ρρ /( lg (а/δ) _ lg lg lg (a/6))
P(*o)/llglg(a/6) lg lg (a/б) J'
Ho x/\g x -*■ oo при x -*■ oo, следовательно, при δ О будем
иметь
lg (а/δ) ^ ^ lg lg lg (а/б) q
lg lg (а/δ) ’ lg lg (a/6)
Поэтому
iP^CL Λ
?(^WW6)J
- limi If _ IglglgWSAl = 0
6-»o I P (*„)/ \lg lg («/δ) lglg(a/6) I) ’
так как po/p(xo) — конечная величина. Таким образом,
доказаны (13.12) и, следовательно, исходные предельные
равенства (13.10) и (13.11).
Однако, если имеет место (13.10), то это обусловит
выполнение условия (13.7); будем иметь при 6-^0
+α *+£δ
j P it) Нь (X - 0 dg - .f ρ (t) Нь (X -1) dt -
-α χ-ζβ
“Ь ζό "f·^
ρ (χ0) j Ял (s) ds p (x0) j H6 (s)ds-*p{x0). (13.14)
§13. ДАВЛЕНИЕ УЗКОЙ БАЛКИ НА ПОЛУПРОСТРАНСТВО 221
При этом χ — < хо < # + ζβ. Для возможности пред¬
ставления функции р(х) посредством сингулярного ин¬
теграла нужно, чтобы lim х0 — х, а для этого необходимо,
Если а будет бесконечно большим, а δ — конечным,
то это не будет иметь места. Таким образом, эти рассуж¬
дения, в которых на рост функции р{х) не налагается
никаких требований (предполагается только, что функ¬
ция р{х) конечна и ограничена), будут справедливы для
балки конечной длины.
Для приближенного представления функции посредст¬
вом сингулярного интеграла нужно, чтобы величина
ζδ = α/lglg (α/δ) была достаточно малой или чтобы функ¬
ции р{х) не менялись на этом участке значительно. За¬
метим, что оценка для ζδ является довольно грубой.
Таким образом, при уменьшении ширины балки по
сравнению с длиной (увеличении α/δ) отношение давле¬
ния на единицу длины балки к осадке стремится к вели¬
чине, постоянной по ее длине. Следовательно, гипотеза
о пропорциональности между давлением и осадкой спра¬
ведлива для достаточно узкой балки.
Эта предельная пропорциональность будет иметь ме¬
сто везде, кроме, может быть, углов балки, где в неко¬
торых случаях давление может достигать бесконечно
большой величины.
Для коэффициента постели на основании (13.9) полу¬
чено следующее предельное значение:
Коэффициент постели будет близок к этому предель¬
ному значению во всяком случае тогда, когда на участке
длиной lg lgfl(a/6) осаДка не меняется значительно. Все
это будет иметь место, следовательно, для балки конеч¬
ной длины.
Как указывалось выше, полученные выводы справед¬
ливы как для абсолютно жесткой балки, так и для упру¬
гой балки, так как безразлично, имеет ли балка ранее
6-*0
чтобы
222 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
заданную форму, или приобрела ее под действием прило¬
женных сил.
Эти результаты в дальнейшем были уточнены в рабо¬
те Л. А. Галина и Η. М. Бородачева [1], а также в рабо¬
тах Η. М. Бородачева [1, 2]. Приведем результаты, содер¬
жащиеся в одной из этих работ.
1. Рассмотрим штамп, имеющий в плане форму узкого
прямоугольника длиной 2а и шириной 26, причем ε =
= δ/α< 1. Пусть этот штамп вдавливается под действием
вертикальной силы Р в упругое изотропное полупрост¬
ранство х ^ 0. Сила Р проходит через центр тяжести
штампа и направлепа вдоль оси ζ.
Применяя к уравнениям равновесия Ляме в прямо¬
угольных координатах xyz двумерное интегральное пре¬
образование Фурье, находим
W (х, у, 0) = — х
оо оо
X j* j (α* + Ρ*ΓκσΓ (α, β, 0) e~iiax+(iy)dad$. (13.10)
—οο —οο
Здесь Ε, ν — соответственно модуль Юнга и коэффициент
Пуассона материала упругого полупространства, w — про-
**
екция вектора перемещения на ось ζ, σζ — двумерная
трансформанта Фурье нормального напряжения σζ. Фор¬
мула (13.16) справедлива при условии, что касательные
напряжения на границе полупространства (при ζ = 0) от¬
сутствуют. Эта формула устанавливает связь вертикаль¬
ных перемещений границы полупространства с нормаль¬
ными напряжениями на границе:
р{х,у) = — oz{x,y, 0). (13.17)
Вернемся к задаче о штампе. Положим, что трение
между штампом и полупространством не возникает, а на¬
грузка на полупространство вне штампа отсутствует. Для
упрощения задачи примем также, что основание штампа
плоское.
Пусть р(х) — давление на единицу длины штампа.
Тогда
Pl*'*)**—ΤΨ=Ί (Μ<α> \у\<8)· (13.18)
я у δ — у
§13. ДАВЛЕНИЕ УЗКОЙ БАЛКИ НА ПОЛУПРОСТРАНСТВО 223
Найдем двумерную трансформанту Фурье функции
р(х, г/). Имеем
оо оо
ρ** (α, β) = 2^ j* J ρ (χ, у) ег(ах+м dx dy.
—oo —oo
Подставляя сюда выражение для pix, у) из (13.18) и
выполняя интегрирование, находим
Р** (α, β) = (^) " Jo (δβ) Ρ* (а), (13.19)
где Jn(x) — бесселева функция первого рода, р*(а) — од¬
номерная трансформанта Фурье функции р(х). Используя
(13.16), (13.17), (13.19), имеем
ν, “
w Iх) = Чпг (т) j р* ^ А ^ е~ШХ<1а’
А (а) = J (а2 + β2) /0(δβ)ίΖβ, w (χ) == w (χ, 0, 0).
Известно (см. И. С. Градштейн, И. М. Рыжик [1]),
что Λ (α) =/ο(1/2δ|αΙ)Α'ο(1/2δΙαΙ), где /о(#), К0(х) — моди¬
фицированные функции Бесселя соответственно первого
и второго рода.
В рассматриваемом случае w(x) и р{х) — четные функ¬
ции. Поэтому получаем
пЕ
X
1/ 00
(Ί·) jр* ^1 ° (τδα) κ° (τδα) cos χα da"
(13.20)
2. Учитывая, что
w(x) = с при Ы < а, /?(#)=() при \х\ >а
224
ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
и используя соотношения (13.20), приходим к парным
интегральным уравнениям
оо
j F(£)/0(i-8£)tf0(i-ei)cosiid| = fc, 0<*<1,
о
оо
j F (ξ) cos t\ dt = 0, 1 < t с oo;
ό
(13.21)
f(?) = p*(i).
e = -j-. i = 7- t = aa. (13.22)
Здесь с — величина, на которую штамп вдавливается в уп¬
ругое полупространство под действием силы Р.
Решение уравнений (13.21) ищем в виде
оо
F © = ъ 2 (- ι)”Λη/2η (ξ). (13.23)
п=0
Известно (см. И. С. Градштейн, И. М. Рыжик [1]),
что [Тп(х) — полиномы Чебышева первого рода]
оо
J Лп (i) COS tt dt = (—1)'
и T2n(t) /1, 0<ί<1,
ΐΛ-ί2 1°» 1 <ί<οο.
(13.24)
Подставляя (13.23) во второе уравнение (13.21) и учи¬
тывая (13.24), убеждаемая, что второе уравнение (13.21)
удовлетворяется. Подставляя затем (13.23) в первое урав-
пение (13.21), получаем
§ 13. ДАВЛЕНИЕ УЗКОЙ БАЛКИ НА ПОЛУПРОСТРАНСТВО 225
Далее имеем
cos tg = J0 (g) + 2 Σ (- l)m Тш (ί) J2m (ξ), 0 < t < 1.
m=l
(13.26)
Подставляя (13.26) в (13.25), приходим к соотношению
2 ^2пС0п “Ь 2 2 ^2П 2 (— 1) CmnTzmty) =1,
w=o η—0 m=l
О < ί < 1. (13.27)
Здесь
оо
Cmn = (- 1)” j /2т (I) Λη (ξ) /о (у εξ) Я0 (у ε|) dg,
О
m, η = 0,1, 2, ... (13.28)
Необходимо и правую часть в (13.27) разложить по
полиномам Чебышева. Имеем
i — b0T0(t)-{- 2
771=1
Ь0 — 1, Ьцп — 0, ш — 1,2,..., Т0 (ί) — 1.
(13.29)
Сравнивая в (13.27) и (13.29) коэффициенты разложе¬
ния, получаем (бпт — символ Кронекера)
О0
2 СтпА2п — 8moi т = Oy 1, 2, ... (13.30)
71=0
Система (13.30) является бесконечной системой ли¬
лейных уравнений для коэффициентов разложения А2п-
В общем случае решение системы (13.30) можно выпол¬
нить лишь приближенно, обрывая ее на m = n = N и вы¬
числяя из полученной конечной системы первые N +1
коэффициентов А2п>
3. Теперь можно получить формулу для р(х). На ос¬
новании (13.20), (13.22) и (13.23) имеем
1/ оо 00
Р (л) = (-f-) 2 ν 2 !)П j ^ ® cos (^) dg.
П=0 о
15 Л. А. Галин
226 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Учитывая (13.22) и (13.24), окончательно получаем
«та (*-?)’ ‘ 2*л.(т)
X
,1 при |χ|<;α,
X n L (13·31)
'О при |ζ|>·α.
Сила, действующая на штамп:
а б
Р = j dx j р(х, у) dy.
—а —б
Подставляя сюда выражение для pix, у) из (13.18),
учитывая (13.31) и выполняя интегрирование, находим
(l— v2)P 2 /лоооч
С ~У Ёа ’ γ = ^ζ· (13,32)
По формуле (13.32) можно определить глубину вдав¬
ливания штампа. На основании (13.31) и (13.32) имеем
ί’Μ = έ(1-?Γ,ί2τ!Γ»(τ)· и<«· (13.33)
\ а / п=о О
Таким образом, величина с и функция pix) определя¬
ются формулами (13.32), (13.33). В эти формулы входят
коэффициенты А2п (/г = 0, 1, ...), которые можно найти
из системы уравнений (13.30).
Система (13.30) может быть представлена и в таком
виде:
оо
А2т = $то i^mn δ?ηη) А^п·
η=ο
Эту систему можно решить и методом итераций, по¬
лагая
1} = бто - 2 (стп - ьтп) 4гп>, (13.34)
п=О
где А^т — г~е приближение. Некоторая модификация
формулы (13.34), которая имеет определенные преиму-
§ 13. ДАВЛЕНИЕ УЗКОЙ БАЛКИ НА ПОЛУПРОСТРАНСТВО 227
щества, дается соотношением
л(г+1) L
л2ТП —
п
тт
J77l0
Σ (ί - бт„) ст„4гД
п=о J
4. Формулу (13.28) для коэффициентов Стп приведем
к виду, более удобному при выполнении вычислений. Из¬
вестно (см. Г. Бейтмен, А. Эрдейи [1]), что
л
/„ (z) = -i- J cos (ηθ — z sin θ) d0,
о
π/2
Λη (ζ) /η (ζ) = -|- J Jm+n (2ζ cos θ) cos [(ffi — re) θ] d0,
О
Re (т + η) > — 1.
(13.35)
Первую из формул (13.35) после некоторых преобра¬
зований можно записать так:
π/2
J2n (ζ) = .“ J cos 2и0 cos (z sin Θ) d0. (13.36)
0
Учитывая (13.35) и (13.36), находим
π/2
Js.mil) J*n(i)=4 cos [2 (/n— re)<p]d<px
Jl t/
0
π/2
X j cos [2 (m + η) Θ] cos [2ξ cos φ sin Θ] dQ.
о
Подставляя это выражение в (13.28) и выполняя ин¬
тегрирование по ξ, окончательно получаем [К (к) — пол¬
ный эллиптический интеграл первого рода]
π/2
Стп = \(— 1)” (* cos [2 (т — η) φ] d<p:
π J
о
π/2
xfC0s [2 (^ +") Θ] к Г
J g (φ. Θ; 8) Lg (φ, Θ; e)J
0
15*
>x
228 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
g (φ, θ; ε) = (4 cos2 φ sin2 θ + ε2)^ , m, η = 0,1, 2, ...
(13.37)
Коэффициенты Стп теперь можно вычислить с помо¬
щью ЭВМ, заменяя интегралы, входящие в (13.37), по
одной из квадратурных формул.
Бесконечную систему уравнений (13.30) приближен¬
но заменяем конечной системой из 11 уравнений с 11 не¬
известными. Эта конечная система решалась несколько
раз применительно к разным значениям параметра ε. Ре¬
зультаты вычислений приведены в табл. V. Зная коэффи¬
циенты А2п, нетрудно найти величины с и р(х).
Таблица V. Значения коэффициентов Л2п
А
ε
2 п
0,02
0,05
0,10
0,15
0,20
А0
Α,.10
А4102
Αβ·102
а8-юз
Α1ο·108
Α12·1ΰ3
Aj.4-104
Аи-10*
Α1β·104
α20·ιο*
0,13279
—0,68209
-1,3115
-0,43721
-0,86645
-8,1259
1,0691
2,7912
2,5506
2,5964
1,6284
0,16117
-0,73630
0,083613
-0,45794
-4,2548
0,97589
0,33955
1,0673
4,3947
2,3446
1,0846
0,19403
-0,72402
-0,84254
-0,0035444
1,4015
1,1747
0,65397
2,5336
0,41799
—0,34982
-0,30902
0,21982
-0,70868
-0,50500
0,18313
1,8660
0,91164
0,24670
-0,18771
—0,61749
—0,36215
—0,11260
0,24252
—0,68526
-0,20875
0,28892
1,7295
0,49437
-0,0085908
-0,82858
-0,39833
-0,11618
—0,027086
Ниже приведены значения коэффициента γ [формула
(13.23)] для некоторых ε:
ε
0,02
0,05
0,10
0,15
0,20
У
1,5260
1,2573
1,0444
0,92184
0,83555
При вычислении функции р(х) по формуле (13.33) ис¬
пользовались таблицы полиномов Чебышева. В табл. VI
приведены значения величины aP~lpix) для некоторых ε
и х/а.
§ 14. ЗАДАЧА О КОНТАКТЕ ДВУХ УПРУГИХ ТЕЛ 229
Таблица VI. Значения величины аР~гр(х)
χία
ε
0,02
0,05
0,10
0,15
0,20
0,00
0,481
0,496
0,474
0,475
0,474
0,10
0,471
0,497
0,474
0,475
0,474
0,20
0,450
0,497
0,473
0,475
0,474
0,30
0,440
0,493
0,474
0,475
0,476
0,40
0,474
0,481
0,476
0,475
0,471
0,50
0,483
0,473
0,478
0,475
' 0,470
0,60
0,502
0,439
0,478
0,474
0,468
0,70
0,490
0,431
0,481
0,473
0,464
0,80
0,479
0,456
0,485
0,470
0,457
0,85
0,497
0,481
0,484
0,466
0,456
0,90
0,553
0,522
0,488
0,477
0,475
0,95
0,632
0,588
0,524
0,539
0,562
0,975
0,712
0,703
0,650
0,697
0,747
0,99
0,874
0,986
0,963
1,061
1,152
§ 14. Пространственная задача
о контакте двух упругих тел
До сих пор мы рассматривали контактные задачи,
предполагая, что тело, производящее давление, является
абсолютно твердым. В этом параграфе мы покажем, что
в случае, когда оба контактирующих тела упруги, вопрос
приводится к решению смешан¬
ной задачи теории потенциала
такого же типа, как и в рас¬
смотренном ранее случае.
Будем полагать, что радиу¬
сы кривизны обоих тел, входя¬
щих в соприкосповение, велики
по сравнению с размерами пло¬
щадки контакта. Поэтому заме¬
ним каждое из этих тел упру¬
гим полупространством.
Пусть Ει и vi — упругие по- Рис> 55>
стояпные тела / (рис. 55)
или, что тоже самое, верхнего полупространства; Е2 и
v2 — упругие постоянные тела II — нижнего полупрост¬
ранства. Поместим начало координат в точке первона¬
чального касания двух тел. Уравнения поверхностей,
230 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
ограничивающих каждое из тел, будут
Zi = fi(x, у), Z2 = у). (14.1)
В результате воздействия силы на каждое из соприка¬
сающихся тел они сблизились на величину, равную δ.
Рассмотрим две точки А\ и А2, которые будут совме¬
щены после происшедшей упругой деформации. Обозна¬
чим через w\ упругое перемещение точки А\, расположен¬
ной па теле /, а через zx ее координату, определяемую
согласно (14.1). Для точки А2 на теле II соответственно
будем иметь упругое перемещение w2 и координату на
поверхности z2.
Расстояние между двумя точками Αχ и А2 после про¬
исшедшей упругой деформации равно сближению упругих
тел (см. по этому вопросу аналогичные рассуждения в
§ 13 гл. I).
Таким образом, имеем
Ui — w{) — (z2 — w,2) = δ,
или, принимая во внимание (14.1), получим
lf\(x, у) — W{] — [/2U, у) — w2] = δ.
Окончательно это может быть записано в такой форме:
i»2 — Wi = δ — f{(x, y)—f2{x, у). (14.2)
Но нормальное давление, приложенное к первому те¬
лу на площадке контакта, равно нормальному давлению,
приложенному на этой площадке ко второму телу.
Если обозначить через Ω площадку контакта, то вели¬
чины перемещений w\ и w2 согласно (1.12) будут
1,2 '-.η) dl dx\
1 ~νχ ГГ dL·
π£ι JoV(*-£!
ξ)2 + (у - η)2
1 - ν2 ГГ p(l,r\)dldx\
π£2 JQJ /(* - ξ)2 + (у - η)2'
(14.3)
Подставляя эти выражения в (14.2), найдем инте¬
гральное уравнение для определения />(ξ, η):
6 — fi (х, У) — и (х, у) =
ч
1 — ν* 1 — v\
пЕj
ГГ ρ (ξ. η) dl лц (14 4)
У(х— ξ)2 + (у — η)2
§ 15. ДАВЛЕНИЕ ТВЕРДОГО ТЕЛА НА ПЛАСТИНКУ
231
Это уравнение совершенно аналогично уравнению
(1.12), на основании которого решались все контактные
задачи о давлении жесткого штампа.
Таким образом, зная решения этих задач, можно лег¬
ко найти решения более общих задач о контакте двух
упругих тел, если площадка контакта Ω будет такой же.
§ 15. Давление твердого тела на пластинку
Zi
Р
*
1
В предыдущих параграфах этой главы мы полагали,
что упругое тело, па которое производит давление штамп,
является достаточно протяженным и поэтому может быть
заменено полупространством. В этом параграфе будет рас¬
смотрен другой крайний случай, когда упругое тело пред¬
ставляет собой тонкую пластинку.
Следует заметить, что сосредоточенная сила обычно
прилагается к пластинке через посредство некоторого уп¬
ругого или твердого тела. Таким образом, подобная задача
является в большинстве слу¬
чаев контактной задачей тео¬
рии упругости. При этом под¬
лежат определению размеры
площадки контакта и распре¬
деление по ней давлений.
Здесь дается решение одной
задачи такого типа.
Пусть на круговую пла¬
стинку радиуса а, заделан¬
ную по контуру, давит твер¬
дое тело, причем начальное соприкосновение будет иметь
место в центре пластинки (рис. 56). В уравнении для по¬
верхности, ограничивающей твердое тело, сохраним толь¬
ко главные члены, подобно тому, как это делается в теории
Герца. Таким образом, уравнение этой поверхности будет
z = Ах2 + By2.
На тело действует сила Р, направленная по оси сим¬
метрии. Примем следующие предположения:
1) толщина пластинки мала по сравнению с размера¬
ми площадки контакта;
2) размеры площадки контакта малы по сравнению с
радиусом пластинки;
h
Рис. 56.
232 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
3) размеры площадки контакта малы по сравнению
с величинами радиусов кривизны тела.
Будем определять форму площадки контакта. На дос¬
таточном удалении от площадки контакта прогиб пла¬
стинки определяется выражением (см. J. Н. Michell [1])
Здесь h —■ толщина пластинки, Е —■ модуль упругости ма¬
териала пластинки, ν — коэффициент Пуассона. Это вы¬
ражение будет иметь место при достаточно больших г,
так как действие твердого тела в таком случае можно
рассматривать как действие сосредоточенной силы. Вне
площадки контакта функция w2 будет удовлетворять би-
гармоническому уравнению
так как пластинка свободна от давления.
На площадке контакта пластинка будет прилегать к
твердому телу, поэтому уравнение для ее прогибов опре¬
деляется следующим образом:
При этом δ — перемещение твердого тела. Функция
будет также бигармонической:
На контуре площадки контакта L, который подлежит
определению, должны выполняться условия:
1) Wl = ш2;
(15.1)
ААи>2 = 0,
(15.2)
W{ = б — Ах2 — By2.
(15.3)
ΔΑινι = 0
(15.4)
(15.5)
Эти равенства являются следствием непрерывности
прогибов пластинки, наклона касательной к пластинке и
величины изгибающих моментов. Условия 3 необходимы
§15. ДАВЛЕНИЕ ТВЕРДОГО ТЕЛА НА ПЛАСТИНКУ
233
для того, чтобы были выполнены условия 1 и 2. Однако
в результате удовлетворения условий 3 функции w\ ш
определяются с некоторой степенью произвола, именно с
точностью до некоторого слагаемого, которое является ли¬
нейной функцией от х и у. В данном случае вследствие
симметрии задачи эта линейная функция равна нулю.
Итак, на контуре L, ограничивающем площадку кон¬
такта, должны выполняться условия
d2wx 02м>2 d*wx 02м>2 diw1
дх2 ~ ~ ~дуГ’ дх ду ~~ дх ду
(15.6)
Образуем функцию
w$ = wl — w2. (15.7)
Далее ее определения и нахождения контура L имеем
условия
d2w dZw^ d2w„
^ = Vе0’ ^ = 0HaL· (15·8)
Очевидно, можно продолжить аналитически функции
(15.1) и (15.3) на всю плоскость. Следовательно, на осно¬
вании (15.1) и (15.3) будем иметь при г->- <»:
”> = -ттг214>-тш(аг-г2) + 8-А*-вУ* =
~ — ~ — ^) +
+ (i^v - ^ + («Ιλγ - ») »г· (15.9)
Построим теперь функцию
= а* “δ· (15.10)
Для определения этой функции и контура L будем
иметь условия
d2w. d2w
4 П
234
ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
при г-*
оо
lg ί + (ϊέν - ■4*2 + (шаг - ВУ- (15Л1>
Автором рассмотрен один случай плоской упруго-пла¬
стической задачи [4], причем для нахождения некоторой
функции <рз и для одновременного определения контура L
имели место условия
На бесконечности функция фз удовлетворяла услови¬
ям, аналогичным (15.11).
Следует заметить, что существует аналогия между
давлением твердого тела на пластинку и упруго-пластиче¬
ской задачей для плоской деформации. Это обстоятельство
может быть использовано для моделирования упруго-пла¬
стических задач (см. работу автора [8J).
Применим метод, посредством которого были решены
упруго-пластические задачи для нахождения решения в
нашем случае. Если представить в следующем виде:
w4 = Re [ζφ*(ζ) +x*(z)J,
(15.12)
то будем иметь
(15.13)
Здесь
Ф*Ы = <р*'Ы, ψ*ω = χ*" ы. (15.15)
Установим, к каким выражениям на бесконечности
стремятся (15.13) и (15.14). На основании (15.11) получим
следующие выражения:
§15. ДАВЛЕНИЕ ТВЕРДОГО ТЕЛА НА ПЛАСТИНКУ
235
Точно так же
d2w д2 w d2w р
—Г 2 - 2i *—я-4 = - 2А + 2В - 1^ме ■ (15·17)
дх2 ду2 дх дУ 4π^
На контуре L вследствие (15.8)
d2w, d2wt d2w. d2wd
4
НО, ^ ‘-2W = 0. (15.18)
дх2 ду2 ’ дх2 ду2 дхдУ
Отобразим область, внешнюю по отношению к L, на
внешность единичного круга γ(|ζ| >1) так, чтобы беско¬
нечно удаленная точка одной области переходила в бес¬
конечно удаленную точку другой. Контур единичного
круга будем обозначать буквой γ. Тогда отображающая
функция ω(ξ) может быть представлена в следующем
виде:
ζ = ω(ξ) = οξ + £(ξ). (15.19)
Здесь g(£) — некоторая функция, регулярная вне γ, при¬
чем можно положить g(oo) = 0. Если обозначить
Φ(ξ) = Φ*[ω(ξ)], Ψ(ξ) = Ψ*[ω(ξ)], (15.20)
то из (15.13) и (15.14) получим
JT + -JT = 4Re ф (£). (15-21)
дх ду
d2w д2iv ^2и> Г 7Т (7\ — 1
17 ~ 1? ~ 21Ш, = 2 [5f,ф' <0 + Ψ ю]· <‘5-22)
Точкам иа контуре L будут соответствовать точки на
контуре γ. Поэтому вследствие (15.18) и на основании
(15.21) и (15.22) будем иметь на γ
4ReO(C) = 0, (15.23)
2[^!φ,(ζ)+ψ(ζ)]=0· (15·24)
При ξ оо на основании (15.16) и (15.19) имеем
Ϊ? + 17 = 2Л*(- тг л - ψ В - 4 + lg а - 1;g 121) =
236 ГЛ. И. ПРОСТРАНСТВЕННЫЕ ЗАДАЛИ ТЕОРИИ УПРУГОСТИ
Точно так же при ξ °° из (15.17) получим
д\
дх* ду2 аъ*ду
= -2А + 2В-^егЩ (Q^argy. (15.26)
Из (15.25) и (15.26) имеем условия для определения
функций Φ(ξ), Ψ(ξ) и ω(ξ):
[О на γ,
4Re Φ (ζ) = { ρ ί 4πΛΓ . 4πΝ D
\ш I—τΑ~—Β-
— j + lga — lgc — lg I ζ I) для ζ-*οο; (15.27)
[Цф,«>+'!’<э]-
О на γ,
>
4 πΝ
I — 2A + 2B - т^гт е*1 ДЛЯ ζ-^οο. (15.28)
На основании условия (15.27) определяется Φ(ξ). Эта
функция может быть представлена следующим образом:
ФК) = -^Ы + Н1)·
Здесь М£) — функция, регулярная вне единичного круга.
Из (15.27) следует, что действительная часть Φ(ζ)
равна нулю на контуре единичного круга и ограничена
повсюду, в том числе и на бесконечности. На основании
этого Λ(ξ) =0. Таким образом,
Φ®--β1^· (,5-29>
Так как Μζ)=0, то действительная часть Φ(ζ) на
р
бесконечности равна ζ|· Поэтому на основании
(15.27) будем иметь
4лЛг л 4ηΝ -η 1,ι , л
б-А -B — - + lga — lgc = 0.
§ 15. ДАВЛЕНИЕ ТВЕРДОГО ТЕЛА НА ПЛАСТИНКУ
237
Отсюда определяется величина с:
(4πΝ л 4ηΝ п 1 1 /л г Плч
~р~ А -р— В — |. (15.30)
Подставляя (15.29) в одно из условий (15.28), получим
при ζ оо;
= -2А + 2Я-^Га1\ (15.31)
Но согласно (15.19) в этом случае
ω(ξ) = οξ, о'(£) = с. (15.32)
На основании (15.31) при ζ оо
2 [- f &т + ψ«)] = - 2Л + 2fi -
Так как
!=*-*«» (e^argo,
ГО при ζ оо
Ψ(ζ) = -4+Α (15.33)
Из (15.28) следует, что для определения Ψ(ζ), регу¬
лярной вне единичного круга и равной А — В на беско¬
нечности, необходимо воспользоваться условием
ιψ <01. = Ует ·!-§!]»· (1М4)
Функция ω(ζ) может быть представлена в виде (15.19),
причем
оо
8(ζ)=Σα*7ϊ· <15·35)
71=1 *
Преобразуем выражение (15.34) следующим образом:
[ώ(ζ)]ν = [^ω'(ζ)ζψ(ζ)]ν.
Здесь правая часть представляет собой функцию, регу¬
лярную вне единичного круга, кроме бесконечно удален-
238 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
ной точки, где она имеет полюс первого порядка, так как
на основании (15.32) и (15.33) при ξ
^ ω' (ζ) ζψ (ζ) = 8ψ οζ (Β - Α) = 8πΛ4|~-^ €ζ. (15.36)
Функция ω(ζ) имеет следующую форму:
οο
ω (ζ) = °ζ + 2
П=1 Ь
причем вследствие симметрии контура L относительно
оси х коэффициенты ап действительны. Следовательно,
в силу того, что на контуре единичного круга ξ = 1/ζ,
оо
[ω(ξ)]ν = с4- + 2 αη^η·
п—1
Итак, имеем
[сτ + Σ α«εη] = [^г <*' β>]τ· (15·37>
В левой части под знаком суммы нужно взять толь-·
ко один член αιζ. В самом деле, применим к обеим ча¬
стям равенства (15.37), умноженным на ζ“ίη, формулу
Коши:
j [с -L + 2 „„£»] £«=Л1“ <■>' ω ετ <о] «·
у L n=i J ь у *
Выражение ω'(ζ)ζΨ(ζ) согласно (15.36) представляет
собой функцию, регулярную вне единичного круга, кроме
бесконечно удаленной точки, где она имеет полюс перво¬
го порядка. Поэтому интеграл в левой части будет равен
нулю при всех m > 1. Если взять величину вычета рас¬
сматриваемой функции в бесконечно удаленной точке, то
из (15.36) придем к выводу, что в правой части коэффи¬
циенты должны быть следующими:
8ηΝ·(Β — А) η t ^
ах — р ? (in — 0 (^ 1)·
Бесконечная последовательность рассмотренных инте¬
гралов вполне определяет функцию, находящуюся под
*15. ДАВЛЕНИЕ ТВЕРДОГО ТЕЛА НА ПЛАСТИНКУ
239
знаком интеграла в левой части равенства. Поэтому кон¬
турные значения выражений в правой и левой частях
(15.37) будут действительно совпадать. Таким образом,
имеем
у , 8ηΝ(Β-Α) 1 />|с ооч
ω(ζ) = ΰζΗ ^ ’-с-ζ·. (15.38)
Эта функция отображает внешность эллипса на внеш¬
ность круга. Таким образом, граница площадки контакта
будет эллипсом. Подставляя в (15.38) выражение (15.30),
получим
m /«. . bnN (В - А) 1 \ Г 4лЫ . 4πN D 1
ω(ζ)= (ζΗ j, --ξ-]αβχρ|- — Л-—5- у
(15.39)
На основании (15.37) полуори этого эллипса (рис. 57)
будут
ехр [_ _ Ц
п = « (l - ЫЯ % - А>) ехр [- ™ У + g> - ±].
(15.40)
Величина Ρα2/16πΝ, т. е. величина прогиба в центре
пластинки радиуса а, должна быть мала по сравнению
с а, или, иначе, безразмерная величина
-Р а- < 1
16πΝ А‘
При выполнении этого условия будут справедливы
обычные уравнения теории пластинок, которые исполь¬
зованы в этой работе.
Интересно отметить, что площадка контакта в рас¬
смотренной задаче будет эллиптической, так же как и в
задаче о давлении тела в форме эллипсоида на упругое
полупространство.
Что касается давлений, действующих на площадке
контакта, то в данном случае они будут приложены по
контуру, так как па площадке контакта
ΔΔωι = 0 и р(х, у) = 0.
240 ГЛ. II. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
В том, что это обстоятельство имеет место, можно убе¬
диться из рассмотрения более простой задачи, когда
жесткий круговой (почти параболический) цилиндр да¬
вит на балку, находящуюся на двух опорах, причем
таким образом, что площадка контакта расположена
симметрично относительно
середины балки. Нетрудно
увидеть, что цилиндр будет
контактировать с балкой на
среднем участке тогда, ког¬
да на краях площадки кон¬
такта приложены силы, рав¬
ные опорным реакциям (из¬
гибающий момент на участке
контакта будет в этом слу¬
чае постоянен, и этот участок
будет отрезком параболы).
Для более точного уста¬
новления распределения дав¬
лений аппроксимация, при¬
нятая для уравнения поверхности, ограничивающей тело,
является, очевидно, недостаточной.
ГЛАВА III
КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ ВЯЗКОУПРУГИХ
И УПРУГИХ ТЕЛ С УЧЕТОМ ШЕРОХОВАТОСТИ
И ИЗНОСА ИХ ПОВЕРХНОСТИ
В этой главе даны решения ряда новых контактных за¬
дач для упругого и вязкоупругого тела. В частности, ис¬
следовано качение вязкоупругого тела по границе вязко-
упругой полуплоскости. При этом определяются размеры
участков с трением и сцеплением. Это позволяет решить
задачу о качении в наиболее общем виде. При определе¬
нии коэффициента трения качения удается учесть эф¬
фекты трения скольжения, а также влияние последей¬
ствия.
Другая категория новых контактных задач — это за¬
дачи при наличии износа. При контактировании упругие
тела обычно перемещаются одно относительно другого.
Это обстоятельство обусловливает износ упругих тел, ко¬
торый приводит к существенному перераспределению
давления.
До недавнего времени предполагалось, что упругие
тела, которые контактируют между собой, являются иде¬
ально гладкими. На самом деле тела обладают шерохова¬
тостью, которая обусловлена их механической обработкой.
Таким образом, на поверхности упругого тела имеется
некоторый слой, который деформируется нелинейно, и за¬
дача приводится к решению некоторых нелинейных ин¬
тегральных уравнений. Результаты, которые содержатся
в этом разделе, очень важны для изучения контактной
жесткости.
Данная глава составлена по работам Л. А. Галина
[1, 2], Л. А. Галина, И. Г. Горячевой [1] и И. Г. Горяче¬
вой [1—4].
16 Л. А. Галин
242 ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
§ 1. Деформация ортотропного вязкоупругого тела
в условиях плоской задачи
В настоящем параграфе рассматривается деформация
стеклопластиков в условиях плоской задачи. Мы будем
полагать, что стеклопластик является ортотропным те¬
лом как в отношении упругих, так и в отношении вязко-
упругих свойств. При этом устанавливается, что для ряда
плоских задач определение изменения во времени дефор¬
мации сводится к вычислению однократных квадратур по
определенным контурам. Для относительно небольших
времен действия нагрузки эта задача может быть све¬
дена к ряду рекуррентных алгебраических операций.
Соотношения между деформациями и напряжениями
в ортотропном вязкоупругом теле будут следующими:
ех = вц(Ух -j-
t t
+ j Kn (t — τ) σχάτ + α12συ + j Κ12 (t — τ) συάτ,
0 ο
Sjj = Cli2&x Η”
t t
J Кΐ2 — τ) -f- α22Gy -f- j K22 (t — τ)
Уху — a33^xy “l·" J ^33 it Ό 'bxyd'X*
(1.1)
Будем, кроме того, полагать, что это соотношение спра¬
ведливо как для сжатия, так и для растяжения.
Экспериментальные исследования позволяют сделать
заключение о том, что для некоторого, относительно не¬
большого интервала времени ядра в выражении (1.1) мо¬
гут быть достаточно удовлетворительно аппроксимирова¬
ны посредством степенных функций. При этом показате¬
ли степени относительно близки друг к другу (их значе¬
ния в большинстве случаев находятся в интервале 0,74—
0,78). В последующем изложении они будут полагаться
равными. Поэтому в соотношениях (1.1) примем
(1.2)
§ 1. ДЕФОРМАЦИЯ ОРТОТРОПНОГО ВЯЗКОУПРУГОГО ТЕЛА 243
В этих уравнениях коэффициенты, характеризующие
вязкоупругие свойства, обладают симметрией относитель¬
но диагонали. Это обстоятельство, во всяком случае, будет
иметь место тогда, когда стеклоткань, на основании кото¬
рой изготовлен стеклопластик, обладает переплетением
типа «рогожки», причем уток и основа одинаковы.
В случае вязкоупругого материала, обладающего толь¬
ко сдвиговой ползучестью,
*11 = *12 = *22 — 0, *33 Ф 0.
Как показывают эксперименты, таким свойством облада¬
ют во многих случаях стеклопластики. В дальнейшем
более подробно будет исследован именно этот случай.
Заметим, что при определении напряжений не возник¬
нет дополнительных трудностей в том случае, если в
качестве ядра будет использовано выражение
(1.3)
Если ввести в рассмотрение операционные преобразо¬
вания напряжений и деформаций: о*, ау, , ε*, εν, γ*ν, то
на основании (1.1) и (1.2) будем иметь
&х — С1цОх + а12ву,
Еу = CL12GX 4" <Ζ22σ?/ ϊ
Уху = Я33 %ху.
(1.4)
При этом
«11 = «11 + *цГ (а) р-а, а*2 = а12 + *12Г (а) р~а,
«22 ~ «22 *22^ (®0 Р а» «33 = «33 *33^ (®0 Р~а·
(1.5)
Соотношения (1.4) эквивалентны соотношениям зако¬
на Гука для ортотропного тела. Таким образом, для ре¬
шения плоской задачи о деформации вязкоупругого тела
необходимо решать задачу о деформации ортотропного
упругого тела. Однако отыскание компонентов деформа¬
ции и напряжения, т. е. нахождение оригиналов по изоб¬
ражениям, часто связано со значительными трудностями.
Это обусловлено тем обстоятельством, что для вычисле¬
ния интегралов необходимо знать все особенности подын-
16*
244 гл. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
тегральной функции на плоскости комплексного перемен¬
ного р.
Ниже будет указан класс задач, для которых
определение искомых величин является относительно
простым. В этом случае оказывается возможным устано¬
вить все точки разветвления функции в интеграле Ри¬
мана — Меллина и, таким образом, вычислить его зна¬
чение. Заметим, что для изотропного вязкоупругого тела
этот переход несложен (см. Ю. Н. Работнов [1]).
В некоторых случаях оказывается возможным искать
подлежащие определению величины в форме рядов, одна¬
ко это не всегда оказывается возможным. Кроме того,
указанный метод часто недостаточно эффективен.
Исследуем случаи, когда выражения для компонентов
напряжений могут быть даны в виде однократных квад¬
ратур.
Рассмотрим в качестве примера деформацию пластин¬
ки из стеклопластика под действием приложенной к гра¬
нице силы, которая равна нулю при t < 0 и равна Р при
t > 0. Вводим полярные координаты г и Θ.
Изображения напряжений, возникающих в полуплос¬
кости, определяются по формулам, приведенным в моно¬
графиях С. Г. Лехницкого [1, 2]:
~ Р , . ч -ι г~ *“ cos Θ
°г — — (Wi + и2) \ ^11^22 rL
σθ = 0,
где
L(Q) =
= αζ2sin4 θ + (2а?а + ^зз) sin2 Θ cos2 θ + «η cos4 θ, (1.7)
а щ и U2 — корни уравнения
Я22И4 — (2а*2 + азз) и2 + «и = 0. (1.8)
В случае, когда имеет место только сдвиговая ползу¬
честь,
* * *
(2ц = <2П, (2i2 — ^12, 0,22 = а22»
(1.6)
азз — азз “Ь (®) Ρ α·
(1.9)
§ 1. ДЕФОРМАЦИЯ ОРТОТРОПНОГО ВЯЗКОУПРУГОГО ТЕЛА 245
В таком случае (1.6) может быть преобразовано сле¬
дующим образом:
о г = — У αηα22 q (ρ) — , (1.10)
π V 11 22 ч \Г9 Γ ρ ^ G ^ ρ (X* V >
где
F = cole (Й22 sin* θ + (2αΐ2 + α33^δίη2 θ cos2 θ +
+ «11 COS4 θ),
G (θ) = &Γ (α) sin2 θ co^G.
Кроме того,
я(р) =
= Ul + щ = c{V(A + Bp-) + V(A + Bp-«r- 1 +
+ V(A + Bp-*) -V(A + Bp-»)· -1},
A = (2 an + a33)/2 / αηα22,
В = кГ (α)/2 Vαηα22, С = (αη/α23) У*.
(1.11)
Единственной точкой разветвления выражения qip)
будет р = 0, так как при вещественном р > 0 величина
(А + Вр~а)2 — 1 будет положительной; это является след¬
ствием того обстоятельства, что в данном случае для ор¬
тотропного тела А > 1, корни щ и и2 вещественны.
Для установления изменения с течением времени ра¬
диального напряжения по сравнению с мгновенно уста¬
навливающимся значением о°г рассмотрим величину
σ,_σί = _!-ν^-4 ^
** \F (Θ) + G (Θ) р~“ ΜΘ) J
где (1.12)
д0 = с\У А + + Ул-VA*- lj.
При этом
v+ioo
σ'“σ?=ϊά j γ{ον-ο4)άρ.
246 ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
В данном случае, в силу указанных выше особенно¬
стей подынтегральной функции, контур интегрирования
может быть продеформмрован; интегрирование должно
производиться ПО пути ОТ — оо до 0 при р = ξ — Ю и от
О до оо при ρ = ξ + Ю с обходом начала координат (здесь
ρ = ξ + έη). Если положить р = ре1*, то будем иметь окон¬
чательно
Нетрудно найти мнимую часть выражения, находяще¬
гося под знаком интеграла.
В предыдущем рассмотрении было использовано ядро
вида (1.2). Если воспользоваться ядром (1.3), пригодным
для описания процессов, длительность которых как угод¬
но велика, и рассматривать также случаи, когда имеет
место только сдвиговая ползучесть, то одно из выражений
(1.9) приобретет вид
Таким образом, в формуле (1.10) р~а должно быть за¬
менено на (р + а)~а. Вычисление контурного интеграла
в этом случае также не встречает затруднений. Однако
характер полученного решения (стремление к асимптоти¬
ческому значению при £-*■ оо) будет особенно очевидным,
если воспользоваться следующим, легко доказываемым
соотношением:
чае, когда имеет место ядро (1.3).
Выражения в виде однократной квадратуры могут
быть получены также в следующих случаях: растяжение
пластинки с эллиптическим отверстием, действие штампа,
жестко связанного с пластинкой из стеклопластика, и
деформация полосы из стеклопластика, Во всех этих слу¬
чаях оказывается возможным определить точки развет¬
СГГ — Jj“V^ll#22^
(1.13)
<4 = *33 + *Γ(α )(ρ + θ)"α. (1.14)
а(г1} (0 — Or = e at (аг (t) — а?) +
t
+ α$β-<*(σΓ(1)-σϊ)άΙ. (1.15)
Здесь o^(t)—значение радиального напряжения в слу-
§ 2. ШТАМП, ЖЕСТКО СВЯЗАННЫЙ С ПОЛУПЛОСКОСТЬЮ 247
вления подынтегрального выражения в интеграле Рима¬
на — Меллина и получить формулы, аналогичные (1.13).
Заметим, что задача становится значительно более про¬
стой для относительно малых времен (причем эта малость
зависит от характеристик вязкоупругости). Используя не¬
которые соотношения, относящиеся к преобразованию
Лапласа, можно показать, что при этом достаточно огра¬
ничиться нахождением асимптотического значения ориги¬
нала при больших значениях р\ иными словами, необхо¬
димо знать разложение в окрестности бесконечно удален¬
ной точки, что в большинстве случаев не представляет
труда.
Соотношения между компонентами деформации и на¬
пряжения в изотропном вязкоупругом теле примем, как и в
предыдущем параграфе этой главы, в следующей форме
(случай плоского напряженного состояния):
§ 2. Задача о давлении штампа,
жестко связанного с изотропной
вязкоупругой полуплоскостью
о
(0 = i σν (0 + -g· J K1 (* - *) °y (τ) άτ — ^-σ* (t)
0
t
Уху (t) = Xxy (t) + цр J К (t — τ) xxy (τ) dx
Уху (t) — E XXy
0
(^(0 = πΓϊ«ι(ί) + ϊψ-ν^,(ί)).
(2.1)
248 ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
Рассмотрим задачу о давлении жесткого штампа с
прямолинейным плоским основанием на изотропную вяз¬
коупругую полуплоскость. Пусть штамп жестко связан
с полуплоскостью. На штамп действуют внешние силы,
имеющие равнодействующую, направленную по оси у так,
что X = О, Y = — Pq, где Ро — заданная положительная
постоянная. Будем полагать, что поверхность вязкоупру¬
гого тела вне штампа свободна от усилий.
Воспользуемся решением этой задачи для упругой
полуплоскости, которое приводится в монографии
Н. И. Мусхелишвили [1], причем в случае изотропного
вязкоупругого тела, обладающего объемной ползучестью,
выражения для изображений давления Р(р, х) и каса¬
тельного напряжения Т(р,х) будут следующими:
Р (p. X) = cos in *
nV 1г — хг Vх Ср) L 2π I χ
τ (ρ, Χ) = ■ l+ш sin fcM In *±f
π/Ζ2_^2 yx(p) l 2π l-x
(2.2)
При этом изображение κ (κ— постоянная, введенная
Мусхелишвили) будет таким:
, ч 3 — ν* (р) * , ч 1 +к2 (р)/р 0.
к(р) i —J— ν* (р) ’ V ~ V 1 + К1 (р)/р’ (2^
Введем обозначение
1 , 1 + х
а = — 1п т——.
2п I — х
Тогда выражение для давления в С2.2) можно преобразо¬
вать к следующему виду:
Р (р, х) = /; [κ (р)-й «* + κ (р)4 -<° +
2л у I — я2
+ χ(ρΓ^-ία + κ(ρ)^+ία]· (2.4)
Таким образом, задача сводится к нахождению на¬
чальной функции для изображения [κ(ρ)]τ, где γ — пока¬
затель степени при κ(ρ) в выражении (2.4).
На основе результатов экспериментальных исследова¬
ний для многих материалов ядра ползучести могут быть
§ 2. ШТАМП, ЖЕСТКО СВЯЗАННЫЙ С ПОЛУПЛОСКОСТЬЮ 249
достаточно удовлетворительно аппроксимированы посред¬
ством экспопенциальной функции. Поэтому в соотноше¬
ниях (2.1) примем
Оригинал для [р/(р— а)]т представляется в виде вы¬
рожденного гипергеометрического ряда
сходящегося для любого t. Это позволяет найти оригинал
для [κ(/?)]τ = Кар + b)/(cp + d)]\ Он будет следующим:
Таким образом, давление Pit, х), которое возникает
под штампом, действующим на вязкоупругую полупло¬
скость, выражается в виде (суммы четырех рядов, сходя¬
щихся при любом t. Воспользовавшись соотношениями
для гамма-функций, окончательно получим
Ki(t-%) = /cie-p(<-T) (ί = 1,2).
Воспользовавшись (2.3), найдем
Σ(Υ + Λ-1) ... У _.ktk
к\ α kV
- e~bt/a 2 i-^-)”+1 ft (Λ - 1) ... (ft - η +1) f~n\
71=1 J
a — Vi + ία + & .
r. 1/ _L '
Г (-Ы + ia + fc) ^
T(-tt+ia) X
(b/a — d/o)k ^
TTa *
250 ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
(2.5)
Это решение может быть исследовано для различных
времен действия нагрузки, а также в различных местах
под штампом. Вблизи углов штампа — I и + Z, так же как
и в случае упругой задачи, напряжения бесконечное чис¬
ло раз меняют знак, однако величина этих участков весь¬
ма мала.
Если нагружение происходит мгновенно, т. е. в
(2.5), то найденный результат совпадает с решением, ко¬
торое получено для упругой полуплоскости Н. И. Мусхе¬
лишвили [1] и В. А. Абрамовым [1].
Для больших времен имеем следующее асимптотиче¬
ское выражение:
Это выражение для давления можно представить как
сумму трех гипергеометрических функций
Для давления под серединой штампа (х = 0) имеем
§ 2. ШТАМП, ЖЕСТКО СВЯЗАННЫЙ С ПОЛУПЛОСКОСТЬЮ 251
При мгновенном нагружении давление в середине
штампа определяется формулой
При длительном нагружении давление монотонно из¬
меняется и стремится к некоторому пределу
Воспользовавшись значениями для некоторых гипер-
геометрических функций, это выражение для давления
можно преобразовать к более простому виду
Отношение bid выражается следующим образом через
постоянные материалы:
ь 3(β + Μ-ν(β + *2) 3-νη ί β + *2\
d β + *ι + ν(β + ^) 1 + νη [Ά β + fcj*
Формула для давления при t -*· оо (2.8) имеет такой же
вид, как для давления в начальный момент времени (2.7),
но с измененным значением κ; этого и следовало ожидать.
Из сопоставления выражений (2,7) и (2.8) следует, что
давление под серединой штампа будет возрастать с уве¬
личением времени при η<1 и η>2ν“ι— 1 и убывать
при 1 < η < 2ν-1 — 1. (Коэффициент Пуассона для реаль¬
ных материалов изменяется в пределах 0<ν<1/2.)
(2.7)
(2.8)
252 ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
§ 3. Контактная задача качения вязкоупругого цилиндра
по основанию из того же материала
При качении реальных тел возникает сила сопротивле¬
ния перекатыванию. Одной из главных причин возникно¬
вения этой силы является относительное скольжение со¬
прикасающихся поверхностей вследствие их деформации
(см. Рейнольдс [1] и А. В. Орлов, С. В. Пинегии [Ш.
Другая не менее важная причина — это несовершенная
упругость реальных материалов. Вследствие наличия по¬
следействия имеет место несимметричное распределение
давления цилиндра на основание на площадке контакта и
возникает момент трения качения.
В данном параграфе рассматривается одновременное
действие указанных выше причин, влияющих на сопро¬
тивление качению, и решается задача о качении вязко-
упругого цилиндра по вязкоупругому основанию при
наличии на площадке контакта участков со сцеплением
и проскальзыванием соприкасающихся поверхностей.
Соотношения между компонентами деформации и на¬
пряжения в изотропном вязкоупругом теле примем в сле¬
дующем виде:
+ α if = 4·(σ*° + β“βτ) “ ΊΓ (‘V+P-dfJ’
V + = ^(<V + P“df) — Ίτ(σ*’ + P"ef)»
γ*ν + « ^ - 2-ΤΓ^ (τ* ν + β %-’)·
Здесь а и β — параметры, характеризующие вязкие свой¬
ства среды (α> β).
Пусть вязкоупругий цилиндр движется по вязкоупру¬
гому основанию со скоростью w, которая много меньше
скорости звука в вязкоупругом теле, что позволяет пре¬
небречь инерционными членами в уравнениях равновесия.
Считая, что радиус кривизны цилиндра R велик по срав¬
нению с размерами площадки контакта, заменим цилиндр
верхней полуплоскостью. Будем рассматривать задачу о
контакте двух полуплоскостей, причем площадка контакта
перемещается по ним со скоростью w.
Введем подвижную систему координат х = х° — wt,
У = У°-
§ 3. КАЧЕНИЕ ВЯЗКОУПРУГОГО ЦИЛИНДРА ПО ОСНОВАНИЮ 253
При равномерном движении цилипдра двия^ение среды
можно считать установившимся по отношению к системе
координат, движущейся поступательно вместе с центром
цилиндра. Тогда смещения и напряжения не будут зави¬
сеть явно от времени и будут функциями только коорди¬
нат. Обозначим
. дВгз дггз * , ч
гч + αΊΓ = ευ -aw-^r = εϋ (*»»)»
до..
+ $ —
^ V dt
ди
дх
до..
= Oi
u~awte = u* (*· у)»
dv . . .
V — WDj-x — V* (X, I/).
(3.1)
♦ ♦ ♦ 4!
Для введенных таким образом величин εχ, еу, ухуу ох,
σ*, т*у будут выполняться уравнения, эквивалентные
уравнениям равновесия, совместности деформаций и за¬
кону Гука для изотропного упругого тела.
Будем считать, что вся площадка контакта состоит из
двух участков: на одном из них, (— а, с), имеет место
скольжение соприкасающихся поверхностей, на другом,
(с, Ь),— сцепление. Вследствие малости деформаций гра¬
ничные условия на поверхности будем относить к неде-
формированному состоянию среды (у = 0). Между нор¬
мальными перемещениями на площадке контакта имеет
место такое соотношение (см. гл. I):
(S+SL—''<*>· <3·2»
Здесь Vi и V2 — нормальные перемещения цилиндра и
полуплоскости соответственно, а fix) — уравнение контура
цилиндра до деформации. Вследствие малости деформа¬
ций примем fix) = x?/2R.
Кроме того, на участке проскальзывания (—а, с) име¬
ет место линейное соотношение между нормальным дав¬
лением оу и тангенциальными усилиями тху, действующи¬
ми в нижней полуплоскости:
Ххсу 4” ‘рОу= 0,
где р — коэффициент трения скольжения.
254 гл. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
На участке сцепления (с, Ь) равны скорости горизон¬
тальных перемещений точек цилиндра w — gxR + du\/dt
(ω — угловая скорость вращения цилиндра) и точек полу¬
плоскости du<i!dt. В системе координат, связанной с ци¬
линдром, условие равенства скоростей запишется следую¬
щим образом:
На движущийся цилиндр действуют нормальное давле¬
ние Р, уравновешивающее вес единицы длины цилиндра,
и вращающий момент М. Поверхность вязкоупругого
тела вне площадки контакта свободна от усилий.
Введем в нижней полуплоскости две функции комп¬
лексной переменной W\(z) и w2(z), являющиеся интегра¬
лами типа Коши, плотности которых равны соответствен¬
но величинам нормального давления и тангенциальных
усилий, действующих на границе полуплоскости:
Здесь учтено, что напряжения на границе площадки кон¬
такта в точках —а и Ъ должны быть равны нулю вслед¬
ствие гладкости контура катка.
(dut/dx)y== о, {dut_/dx)lJ=0, {ди\/дх)у=0, (ди*/дх)у^0
через действительные и мнимые части функций w\(z) и
со/? — IV
ь
—а
Ъ
—а
—а
причем на бесконечности
ь ь
Выразив изображения давления (сг^)г/=0^ тангенци¬
альных усилий (v*y)y=oj производных от перемещений
§ 3. КАЧЕНИЕ ВЯЗКОУПРУГОГО ЦИЛИНДРА ПО ОСНОВАНИЮ 255
ιν2(ζ) (см. гл. I) и подставив их в граничные условия, не¬
сколько видоизмененные с учетом (3.1), получим заддчу
сопряжения для отыскания двух аналитических в нижней
полуплоскости функций Wi(z) и w2(z):
VL = О, V2 == 0, — оо<х<—- а, 6<х< + оо,
иг = — (х — aw)/KR, V2 = —- pF1? — а < х < с,
U1 = — (х — a w)/KR, U2 = 6/К, с <х <Ь
(Я = 4(1- ν2)/π£).
(3.3)
Здесь £ — модуль Юнга, ν — коэффициент Пуассона ма¬
териалов цилиндра и основания.
Функции, решающие задачу линейного сопряжения с
перечисленными условиями (3-3), имеют вид
wi 00 =
у (ζ + а) (2 — ft) _о
°1 tfi-iVi,
У (2 + α) (ζ — 6)
— х dx
— Λ (V -—--^-1 . С1,..^,,-=и2-1Уг.
πΚ J Я — СЯ — У(2_С)(2_6) 2 2
(3.4)
Здесь C\ и C2 — некоторые постоянные, с которыми вхо¬
дят решения однородной задачи сопряжения. Из условий
на бесконечности сразу следует, что С\=Р. Найденные
функции на действительной оси обладают интегрируемыми
особенностями, но это обстоятельство не повлечет за собой
нерегулярности компонентов напряжений.
Изображения напряжений на площадке контакта вы¬
ражаются через мнимые части функций W\(z) и w2(z) по
формулам
°у)у=о — п (^ib=o> (T*y)?/=o — ~ (^2)2/—о*
256 гл. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
Отделяя в (3.4) мнимые части при ζ = χ — Ю, получим
при — а< х < Ъ\
У (а + х) (ь — х)
y^V(a + t){b-t)JL
+
(3.5)
V(« + х) [ъ — х)
па участке проскальзывания — а<х< с
(V2)y=0= - ptFO^o; (3.6)
па участке сцепления с < х<Ъ
if!!', «)!„.. V'Bi i4
—a
ь η
δ Γ ί Γb — t dt
л К J V t — с t — x I
C J
l/(x — c) (b — x)
Вычислив интеграл
ь
С t — aw η ; .ч/т г: dt
J -ШГ* (* + №-*) — =
— a
(a b)2 (x — aw) (b — о — 2x)
8 KR
2 KR
x — aw
KR
(b-x)
b — x
V>
(3.7*
(— oo CxC — a, k<x< + oo),
0 (—a<.x<.b)
для функции (Fi)v=0 (3.5) при —a<x<b, получим сле¬
дующее выражение:
(V ,),=<> =
1
~\/(а + х) (Ь — х)
(а + Ъ) . (х — аw) (Ь — а — 2х)
8KR
■ +
2KR
+ р
— 71 (°у)у=о* (3-8)
§ 3. КАЧЕНИЕ ВЯЗКОУПРУГОГО ЦИЛИНДРА ПО ОСНОВАНИЮ 257
Введем обозначение
F(x) =
(а + Ь)л
(х — aw) (Ь — а — 2х)
8 KR 1 2 KR
и вычислим значения интегралов
+ р
(3.9)
с
j l^i(i)lv=o/7Ξ7 г=Ь = Йя(& “ с - 2* +2aw) +
(ж) I с ж ι ι ^ ^ ■ \
7ΊΓ7|α—| (-00 <*<-«, с<х<+ оо),
О (—а<а;<с); (3.10)
ίνϋ? *
С ί — Ж
— π [ ^ —
V> Ί
b — χ I /2
с — χ j
(
— π
(с<£ < b).
оо<х<с, Ь<х<+оо),
Тогда на участке сцепления
(Vt)y=0 = - р(Fj),^,, + (b-c- 2х + 2aw) +
i| l/izL
κ\ν b —;
+
У (χ — c) (b — x)
= π (τ*Λ=0· (3-11)
Зная выражения для изображений напряжений (3.8)
и (3.11), воспользуемся (3.1) и найдем истинные напря¬
жения в любой точке на площадке контакта при
— а< х< Ь:
K)y=o = -„-jLexp(^)X
X f I (t-am) (b-a-2t) J 6XP( gg) ** .
JoL 8kr + 2KR + F\ у-+-)Ть~)' ( ’
на участке проскальзывания — a< x< с
(τχυ)ν=ο = P (ау)у=οϊ
17 л. а. Галин
258 ГЛ. III. ЙЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
на участке сцепления с< х<Ь
(*ху)у=о = — Р (ff!/)y=o — exp (pj x
X
С
X
Ildb (b-c~2t + 2aw) + £}Vj=1texv[-fr)dt-
n$w Vlt_e) (b_i)
(3.13)
V (i — c) (6 — i)
В эти выражения входят четыре неизвестные посто-
яннные — a, &, с, Сч. Их можно определить, удовлетворяя
граничным условиям для истинных напряжений и пере¬
мещений в вязкоупругом теле.
Определяя диг/дх = и1Х и dvjdx = v2X из уравнений
-Θφ + Αν'.χ = ±(ν'.χγ (j = 1 2),
дх 1 aw г awv 1 v ’ n
будем иметь
(νιχ + V2x)y=0 ~
X
=- -Lехр Ш 5 (”'ιχ+ехр (- i)dt=
—oo
= - ά exP fe) ίя βχΡ (- i) ώί· (314>
— oo
Деформации на бесконечном удалении от площадки
контакта исчезают, поэтому должно выполняться следую¬
щее условие:
+ оо
j (tfj)v.-=o ехр (— 5^) dt = 0. (3.15)
— ОО
Из (3.14) с учетом (3.2) и (3.15) для точки х = Ъ полу¬
чим уравнение
+ оо
- ^ ехр (- ±) = j (ί/^ο ехр (- dt. (3.16)
§ 3. КАЧЕНИЕ ВЯЗКОУПРУГОГО ЦИЛИНДРА ПО ОСНОВАНИЮ 259
Отделив в функции W\{z) (3.4) в интервале (Ь, + °°)
действительную часть и воспользовавшись (3.7), (3.9),
найдем вид функции (U\)y=о при Ь<х<+ оо:
{тт v F (х) x — aw
Wi)y=o ~ у{х + ауС-—) ' KR ·
После проведения всех необходимых вычислений и
преобразований уравнение (3.16) примет вид
η (<* + fr)2
8 KR
где К0(х) и К\{х) — цилиндрические функции мнимого
аргумента·
Второе уравнение для определения границ площадки
контакта (точек — а и Ъ) получим из условия равенства
нулю нормального давления в точке Ь:
ь
j взср (— -р^) Аг = о.
Подставляя сюда значение функции (Fi)y==o (3.8) и
произведя интегрирование, получим уравнение, в которое
входят бесселевы функции от мнимого аргумента 1о(х)
и /\(х):
Гр («+ &)21 j l·а + ь\ .
Г ШГ] \2fto ) +
+ (т —+ »*)®'·(Ϊγ) = ο· (3.W)
Обозначим: I = а + Ъ — длина площадки контакта,
d = (Ь — а)/2 — координата середины площадки контакта.
Из (3.17) и (3.18) получим уравнение для определения
длины площадки контакта I: 1
[р - «и] ['· ШЩ+к° Ш7· Ш]+
+ ИР - a) it Λ (2i)= 0., (3.19)
Координата середины площадки d определяется сле-
17*
260 ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
дующим образом:
Л = [Р-ш]¥*.ШМ 2=)' (3-20)
Найдем значения постоянных с и С2. Из условия ра¬
венства скоростей на участке сцепления получим урав¬
нение
J (U2)y=0 exp (- dx = ϊψ exp (- A), (3.21)
ь
которое выводится аналогично (3.16). Из (3.4) и (310)
определим вид функции Ш2)у=о при b < х < + <»:
(U2)yc=o —
Wr (b-c~2x + 2aw) + У V ΊΓ=Τ> +1 +
pF (x) C2
У (χ-\- a) (χ — b) Y (χ — с) (χ — b)
Из уравнения (3.16) следует, что
+ *>
dx
j F(z)exp(--i)
Υ (χ + α) (χ — Ь)
= 0.
Поэтому после вычисления интеграла в левой части
(3.21) получим уравнение
[/-. Р(Ь — с) (6+с—2aw) , б (b — с)] v lb — c\
Г2 4KR 1 2K J · 0 \ 2ш1Г)
<3·22>
Наконец, требование равенства нулю тангенциальных
усилий на границе площадки контакта, в точке х = Ь|,
приводит к условию |
ь
| [^2(*)](/=оехр(-^;)Лг = 0.
§ 3. КАЧЕНИЕ ВЯЗКОУПРУГОГО ЦИЛИНДРА ПО ОСНОВАНИЮ 261
Подставив сюда выражения для (Уг)у=о (3.6), (3.11)
и произведя необходимые вычисления, получим уравнение
г р (Ь — с) (Ь + с — 2aw) . Ь(Ь — с)1 ^ /V— с\
_ ~TKR h 2К J +
, f p (b — с) (b + с — law + 2$w) δ (b — с)] T (b — c\ A
+ [ ш\
(3.23)
Обозначим длину участка сцепления m = b — с. Тогда
с учетом введенных ранее обозначений Ь + с = 2d + l — ш-
Из (3.22) и (3.23) получим уравнение для определения
длины участка сцепления ш:
α {[ά (2Й+г - - 2α» + 2И - δ] Λ (jjk) К. (i) +
+ [jL{U + l-m)- δ] /. (£) К, (£)} = 0. (3.24)
Постоянная Сч определяется следующим образом:
С2 = ^ (2d + I — тп — 2а w) — δ — (2d + I — m —
- 2α» + 2М - в] 7, (jjfc)//. (i)). (3.25)
Таким образом, определены все неизвестные постоян¬
ные задачи.
Из решения уравнения (3.19) можно найти длину пло¬
щадки контакта I. В большинстве случаев это уравнение
решается численно (см., например, Хантер Ш). В работе
было проведено решение уравнения (3.19) для значений
параметров а и β порядка от 10“1 до 106 сек; для скорости
ψ брались значения 10, 100, 1000 см/сек- Во всех этих
Случаях длина площадки контакта была близка к величи¬
не }^8KRP$/а, которая равна длине площадки контакта
при качении цилиндра по упругому материалу ,с модулем
упругости Н = аЕ/$. Модуль Н есть мгновенный модуль
упругости для рассматриваемого материала. Зная длину
площадки контакта, можно определить координату сере¬
дины площадки d по формуле (3.20). Очевидно, что d> 0,
т. е. площадка смещена в направлении движения цилинд¬
262 ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
ра. Из решения уравнения (3.24) находится длина участ¬
ка сцепления т и по формуле (3.25)—постоянная С2.
Если а = β, то эти уравнения дают решение задачи о
качении упругого цилиндра по основанию из того же ма¬
териала (с модулем упругости Е).
Воспользуемся соотношением
ЫхЖМ + 1{(х)К0(х) =
Тогда из (3.19) и (3.20) следует, что длина площадки
контакта 1 = У8KRP и она располагается симметрично
относительно центра цилиндра (d = 0). Из уравнения
(3.24) получаем, что в случае существования участка со
сцеплением (тФ 0) участок с проскальзыванием имеет
длину Z —га = 2б/?/р. Подставив найденные значения
неизвестных постоянных в (3.12) и (3.13), получим выра¬
жения для давления и тангенциальных усилий на пло¬
щадке контакта упругого цилиндра с упругим основанием:
/ \ У а2 —а:2 , _
\^у)у=о — яКЕ ’ d<C.x<Z.CL\
(Хху)у=0 —
а2 — х2, —а<Сх<.с,
nKR
с<Сх < а
Са = /2КНР, с = - /2KRP + 26Я/р).
Определим силу сопротивления движению цилиндра.
Суммарное касательное напряжение на площадке контак¬
та Q вычисляется следующим образом:
ъ ъ ъ
Q = j (τ*„)*-οdx = j (τ*!/)ί/=ο dx= j ^ (Vi)v=odx, (3.26)
так как в силу непрерывности напряжений на границе
площадки контакта
§ 3. КАЧЕНИЕ ВЯЗКОУПРУГОГО ЦИЛИНДРА ПО ОСНОВАНИЮ 263
Последний интеграл в (3.26) легко вычисляется. С уче¬
том (3.25) и введенных ранее обозначений для Q получим
выражение
Q = -рР + — 2к ^ + I — т— %aw +
+2ы-б]^Ш1г‘Ш· (3'27)
На ось цилиндра действует сила сопротивления движе¬
нию цилиндра (?*, равная по величине силе Q и противо¬
положно направленная.
Кроме того, при качении цилиндра по вязкоупругому
оонованшо вертикальная составляющая реакции вязко-
упругой среды не проходит через центр тяжести цилинд¬
ра. Поэтому движению цилиндра еще будет препятство¬
вать пара с моментом
ь ь
мх = J X (0„)у=о dx= j* X (Fx)y=o ώχ — PwP. (3.28)
—a —a
Здесь принято во внимание, что
ъ
—а
в силу непрерывности напряжений на границе площадки
контакта. Подставив в (3.28) значение (κι)ν=0 (3.8), полу¬
чим следующее выражение для момента М{\
мх = p(d— βΐί>) + (aw — d).
Момент Μi вместе с моментом силы Q (3.27) относи¬
тельно центра цилиндра М2 = QR создают момент трения
качения М* = М\ + М2. Для того чтобы имело место рав¬
номерное движение цилиндра, приложенный к нему мо¬
мент М должен быть равен по абсолютной величине
моменту трения качения М*. Величина момента трения
качения М = М\ + рRP соответствует состоянию, пред¬
шествующему буксованию. Характеристикой трения ка¬
чения является также коэффициент трения качения
f = M/P.
264 ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
§ 4. Предельный случай качения цилиндра
по вязкоупругому основанию
В данном параграфе рассматривается задача о каче¬
нии вязкоупругого цилиндра по вязкоупругому основа¬
нию, когда на всей площадке контакта имеет место сколь¬
жение соприкасающихся поверхностей. Этот предельный
случай качения соответствует состоянию, которое пред¬
шествует буксованию.
Будем считать, что материалы цилиндра и основания
являются изотропными и линейно вязкоупругими, соот¬
ношения между компонентами деформации и напряже¬
ния имеют вид
дгхо \ [ д(УхЛ vil г» *V\
ε*° + α ~W = Ei + β~5Π’
ι I Λ d(J,A Л д(Ух°\
εν° + α ж = (σ^° + β ~дГ/ ~ (σχ0 + β ~дг)'
. дУх°и° __ 2I1 + νί) ( ιβ0,
Ух°у° + α dt — -щ -f β j (ι — 1, 2).
Здесь а и β — параметры, характеризующие вязкие свой¬
ства среды (α>β), νί, Е\ и v2, Е2— упругие постоянные
материалов цилиндра и основания соответственно.
Инерционные члены в уравнениях движения не учи-*
тываются, поэтому полученное решение будет справед¬
ливо для скоростей w, малых по сравнению со скоростью
распространения звука в вязкоупругой среде. Считая, что
радиус кривизны цилиндра R велик по сравнению с
размерами площадки контакта, заменим цилиндр верхней
полуплоскостью. Будем рассматривать задачу о контакте
двух полуплоскостей, причем площадка контакта пере¬
мещается по ним со скоростью w = const.
При равномерном движении цилиндра движение
среды можно считать установившимся по отношению к
системе координат (χ, ι/), движущейся поступательно
вместе с центром цилиндра х = х° — wt, у = у°. Тогда
деформации, перемещения и напряжения не будут зави¬
сеть явно от времени и будут функциями только коорди¬
нат (χ, у). Введем обозначения:
дг13 dGij * , Ч
ε« + а ~dt = εν ~ = у)·
§ 4. ПРЕДЕЛЬНЫЙ СЛУЧАЙ КАЧЕНИЯ ЦИЛИНДРА
265
и —а и>д-х = и*{х,у), v — awTx = v*(x,y).
^ ^ ^ •ic •Jt ^
Для величии гх, уху, σχ, σν, тху выполняются уравне¬
ния, эквивалентные уравнениям равновесия, совместности
деформаций и закону Гука для изотропного упругого тела.
Вследствие малости деформаций граничные условия
на поверхности будем относить к недеформированному
состоянию среды (у = 0). Будем считать, что на всей
площадке контакта (—а, Ъ) выполняется соотношение
где р — коэффициент трения скольжения. Знак р выби¬
рается в зависимости от направления проскальзывания,
которое в свою очередь зависит от относительной твер¬
дости контактирующих материалов (Рейнольдс [1]).
Кроме того, нормальные перемещения цилиндра νχ и
полуплоскости ν2 на площадке контакта связаны следую¬
щим соотношением (см. гл. I):
где fix) — уравнение контура цилиндра до деформации.
Вследствие малости деформаций примем fix) = x2/2R.
На движущийся цилиндр действуют нормальное дав¬
ление Р, уравновешивающее вес единицы длины ци¬
линдра, и вращающий момент М. Поверхность вязкоуп¬
ругого тела вне площадки контакта свободна от усилий.
Введем в нижней полуплоскости две функции комп¬
лексной переменной W\(z) и ιυ2(ζ), являющиеся интегра¬
лами типа Коши:
Тху “Ь рОу 0,
(4.1)
(4.2)
66 гл. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
Если ζ °°, то
где
о о
Р — J (°у)г/-=о @ — J (Tjcy)i/—о
—α —α
(Здесь учтено, что напряжения на границе площадки
контакта, т. е. в точках —а и 6, должны быть равны
нулю вследствие гладкости контура катка.)
Из граничных условий (4.1) и (4.2) получим соотно¬
шения для величин со звездочками, которые должны
выполняться на границе полуплоскости (г/ = 0):
σ* = 0, τ*,/ 0, — оо < х < —я, Ь < х < -}- оо,
д 1'л dll -γ fVii) £ £
SF +-3Ϊ = - -7Г^· ^ + = -α<*<δ.
Левые части этих соотношений могут быть выражены че¬
рез действительные и мнимые части функций W\{z) и
w2(z) (см. гл. I), в результате чего получим задачу сопря¬
жения для отыскания двух аналитических в нижней
полуплоскости функций W\(z) и w2(z):
Fi = 0, T^2 = 0, — оо<х<— а, Ь<х<+ оо,
Ux — mV2 = — Fjj-fpF^O, —а<х<ь.
Здесь введены обозначения:
2 (ί — ν2) ι 2 (1 — ν2)
~ π£3 ’ (4.3)
т 1 [О+^Н1-^!) ^1+ν2)(1-2ν2)'
л К L £·χ £'
2
Соотношение V2 + — 0 при —а < х < Ъ позволяет
свести задачу к определению одной функции w{(z), для
которой будем иметь такие условия на границе:
Fi = 0, —оо < χ < —а, b <х <+оо,
(4.4)
t/i+mpFi=0, —а<х<Ь.
§ 4. ПРЕДЕЛЬНЫЙ СЛУЧАЙ КАЧЕНИЯ ЦИЛИНДРА
267
Функция, решающая задачу линейного сопряжения с ус¬
ловиями (4.4), имеет вид
и>1 (Z) = U1-iV1 = г—гр T7-Z —
(г + а) /2 (2 — Ь) Δ ~θ
1 χ
ЯК]/ 1 + т2рг (z + α)θ+ ^ (z — b) ^ -θ
х1Цг?(‘ + «>в+к<(,-,»и^<^· <4·5>
— О
где θ=— arctgmp, а С\ — некоторая постоянная, с ко¬
торой входит решение однородной задачи сопряжения.
Из условия на бесконечности следует, что С\=Р. Функ¬
ция W\(z) на действительной оси обладает интегрируемы¬
ми особенностями (ΙΘΙ<1/2). Но, как будет показано,
это обстоятельство не повлечет за собой нерегулярности
компонентов напряжений.
Для определения величины (сг^^о устремляем в вы-
ражении (4.5) ζ к х и отделяем мнимую часть:
(аг/)г/=о — (ν^=ο —
I ( Р sin π (Υι — θ) (χ — aw) cos π (]/2 -θ)
π |(α + ζ) ^+θ (6 — χ)^~θ KRV1 + m2p2
sin π (У2 — θ)
πΚ|/ 1 + m2p2 (a + χ) ^ +θ (b — χ) ^ “θ
ь
x j L=p {a + ί) ^ (6 - t)1/2 -θ ^L
—a
Вычислив интеграл
b
J L^(a + <)^+f>(b_i)^-9_i£_ =
—о
= -ft-(a + &)2я(х + θ· -§■ — θ) —
(—a <x<b).
268 ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
=^ϊ2(α + δ)β(-§- + θ, -1-е) + (* ·
«(*+·) чшП
π cosec:
(χ<-α, x>b),
X Г VI
π cosec π + θ| 1 — cos π + θ j j j
(—aCx<.b)
и воспользовавшись следующими соотношениями
(Г. Ватсон, Э. Уиттекер [1]):
Г(*)Г(у) Г(1+х) = хГ(х),
’Г(ж + у)* Г(х)Г(1—χ) = π cosec (πχ),
будем иметь '
(a!)j,=0 = —гг JT— Г РЯД +
π£Я К1 + тУ (я + ж) (6 — ж) θ [
+4-(« “ί- (т”^- (*2— ®)——аи^ ^(Ί"
+ (х — aw)(b— ж)|. (4.7)
Из решения дифференциального уравнения
ау-$и>^ = о*и (у = 0)
получим значение давления в любой точке на площадке
контакта:
gX/fiw ? Г
( y)v-0 a,,,n fCf> л/1 _l m2n2 J I
. . PKR +
$umKR V 1 + m2p2 ia L
+4-«.+6>·(4-+θ)(1-θ)-
— (ί — aw) (a + &) (4" + θ) +
+ (!-««,) (i, -<)] ,'*11 (4.8)
(α + t) (6 — <)
§ 4. ПРЕДЕЛЬНЫЙ СЛУЧАЙ КАЧЕНИЯ ЦИЛИНДРА
269
Значение тангенциального напряжения τху на границе
полуплоскости определяется из граничного условия (4.1):
Тху= р(Ту
В выражения для напряжений входят неизвестные
пока границы площадки контакта — точки —а и Ъ. Пер¬
вое уравнение для определения постоянных а и Ъ можно
найти, удовлетворяя условию непрерывности напряже¬
ний на границе площадки контакта — в точке Ъ. Тогда
получим
Πτ<<· + »>,ίτ + β)(4-β)-
—а
— (i — aw) (α + b) [γ + θ) +
+ {t- aw) (b-t) + PKR1 f—W.dt.—_ = 0.
J(a + i)K2+e(6-0/2-e
Воспользовавшись интегральными представлениями для
вырожденных гипергеометрических функций Φ(αι, ci, χ)
(Г. Ватсон, Э. Уиттекер [1]), преобразуем это уравнение
к виду
[РИ _ | (а + „).(! + θ)(± _ θ)]φ(ΐ + θ, 1;*- + -») +
+[(«+ч (4+β) - <«+«»- р»)] ip? (у+β) (4 -θ) χ
:Φ(τ + β'3^)"0· <4·9>
χ<
Второе уравнение получим, удовлетворяя соотноше¬
нию между нормальными перемещениями (4.2). Определяя
ди2 ,
— = vlx и — = v2x из уравнений
дигх ,1 ' 1 / ' \* /. а с\\
"д— 4“— (Ujx) (i — 1, 2)
дх 1 aw 1 aw 4 % v '
и учитывая, что при значении х — +°°, соответствующем
моменту времени £ = —«>, деформации цилиндра и
270 ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
основания отсутствуют, будем иметь
X
+00
= ^е*/а№ j К (Ui)j/=o e~tlawdt.
X
Из граничного условия (4.2) для точки х = Ъ получим
уравнение
+ оо
j {Ux)v-be-*/*"dt = —Щe-v™. (4.10)
b
Отделив в функции w\(z) (4.5) в интервале (b, +оо) дей¬
ствительную часть и воспользовавшись значением инте¬
грала (4.6) найдем вид функции (f/i)y=o при b < х < +
=~ ^(а+ь)’х
X
(τ + θ)(τ-θ) + ρ-Α<*-»“’)<“ + ί'»(τ + 9) +
+ — α»)(δ — ι)] — — «»)■ (4.11)
Подставляя (4.11) в (4.10) и пользуясь интегральными
представлениями вырожденной гипергеометрической функ¬
ции Ψ(αι, Сь х) (Г. Ватсон,Э.Уиттекер tlJ), преобразуем
уравнение (4-10) к виду
[^Λ-τ(β + 6)1(τ + θ)(τ--θ)]ψ(-|- + θ.ΐ;^)-
-[(α + 6)(γ + θ)~α ^Γ"(τ + θ)Χ
χψ(4 + θ,3;^) = 0. (4.12)
Обозначим: l = a + b — длина площадки контакта, d =
= (Ь — α)/2 — координата середины площадки контакта.
Из (4.9) и (4.12) можно получить уравнение для опреде-
§ 4. ПРЕДЕЛЬНЫЙ СЛУЧАЙ КАЧЕНИЯ ЦИЛИНДРА
271
ления длины площадки контакта I:
[™ - т (т +е) (т -θ)] [ψ (т + 9·3; =)х
χφ(τ+ θ·1'έ)+§(τ-θ)'1'(4- + β·1'ά)χ
хф(-| + 9·3; £)] + 4-(l - f)■Ρ(1 + θ)(4- - θ)χ
χψ(τ+θ·3^)*(τ+θ·3;έ)-°· <4·,3>
Смещение площадки контакта d определяется по
формуле
d = - IQ +
[**Л - γ г2 (4- + θ) [γ - θ)1 α*Ψ (γ + θ, 1;
+ ίΐ /~з~ π "· (4·14>
ί2(Τ + θ)ψ(Τ + θ, 3;-]
Таким образом, соотношения (4.13) и (4.14) пол¬
ностью определяют положение площадки контакта.
Так как второе (слагаемое в (4.13) отрицательно (α>β,
IθI < 1/2), то первое должно быть положительным, поэто¬
му длина площадки контакта I всегда меньше величины
У 2PKR/(l4 — Θ2).
Если в (4.8), (4.13) и (4.14) положить т = 0, а следо¬
вательно, и 0 = 0, то получим решение задачи о качении
вязкоупругого цилиндра по основанию из того же мате¬
риала. При этом длина площадки контакта будет опреде¬
ляться из уравнения
[ί-кд - 4] [/. (л.) к, (JL) + Λ (jjL) к. У;)] +
+ »> «>-«)■у'. (4-15)
в которое входят модифицированные функции Бесселя
/0Ы, К0(х), К\(х). Для координаты середины пло¬
щадки контакта получим юле дующее выражение:
d=[pkr- 4] f *·Ш1 к‘Ш- <41б>
272 ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
Соотношения (4.15) и (4.16) будут справедливы и для
задачи о качении цилиндра по вязкоупругому основа¬
нию, когда силы трения отсутствуют (р = 0), что совпада¬
ет с результатом Хантера Ш.
Наконец, полагая в (4.8), (4.13) и (4.14) а = β, получим
решение задачи о качении упругого цилиндра по упруго¬
му основанию, причем модули упругости материалов ци¬
линдра и основания будут равны длительным модулям
упругости рассматриваемых вязкоупругих материалов.
Давление па площадке контакта будет определяться но
формуле
(оу)у.^ о = 1 ■■■ {а + t)% -θ (Ъ - t)1/2 +θ.
nKR У 1 + т ρ
Площадка контакта в этом случае смещена на величину
d = — Ю, а ее длина 1 = У2PKR/( ι4 — Θ2).
Определим момент трения качения при движении вяз¬
коупругого цилиндра по вязкоупругому основанию. В этом
случае вертикальная составляющая реакции вязкоупругой
среды не проходит через центр тяжести цилиндра. Поэто¬
му качению цилиндра будет препятствовать пара с мо¬
ментом
ъ ь
Мх = j* х ((Jy)y=o dx — J x dx fiwP, (4.17)
—a —a
так как
Ιχ9ίάχ=-ρ
—α
в силу непрерывности напряжений на площадке контакта.
Подставив в (4.17) значение (σ^)ν=ο (4.7), получим сле¬
дующее выражение для момента:
+ P(d-fiu> — ei). (4.18)
Момент Μ ι вместе с моментом силы сопротивления Q =
= — ρР относительно центра цилиндра М2 = QR создают
момент трения качения Μ* = Мι + М2.
§ 5. ОДНОМЕРНЫЕ ЗАДАЧИ ПРИ НАЛИЧИИ ИЗНОСА
273
Заметим, что полученные выражения для давления на
площадке контакта (4.8), для определения положения пло¬
щадки контакта и ее длины (4.13) и (4.14), для момента
(4.18) будут справедливы и для задачи о качении жест¬
кого цилиндра по вязкоупругой полуплоскости (с парамет¬
рами вязкости а и β) при замене в них величин
Θ = “ arctg τηρ на Θ* = arctg р * ~ тп и К [см. (4.3)]
I 2v 2 (l ν2)
— на /τι* = 2~2ν> ~ ' · Такой вывод можно
сделать на основании того, что при решении задачи о ка¬
чении жесткого цилиндра для определения аналитической
в нижней полуплоскости функции W\{z) имеем аналогич¬
ные рассмотренным выше условия на границе, в которых
вместо постоянных тп ж К фигурируют тп* и К*.
§ 5. Одномерные контактные задачи
теории упругости при наличии износа
В данном параграфе рассматриваются задачи, когда
первоначально изогнутая балка контактирует с полупло¬
скостью.
Одно из исходных предположений в рассматриваемых
задачах состоит в том, что расстояние между некоторыми
\ш0(Х)
а)
Ряс. 58.
направляющими, в которых скользит контактирующее те¬
ло, и границей полуплоскости остается неизменным. Речь
идет о контактировании изогнутой балки с полуплоскостью
при предположении, что происходит износ этой полу¬
плоскости.
Будем полагать, что первоначальная форма достаточно
тснкой балки определяется начальным прогибом Wq(x)
(рис. 58, а)· После деформации в результате контактиро¬
вания с жесткой полуплоскостью ее форма будет такой,
18 д. А. Галин
274 гл. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
как на рис. 58, б. Считаем, что в данном случае балка
симметрична и контактирует с упругой полуплоскостью
на участке — а< х< а.
Будем в дальнейшем полагать, что износ носит абра¬
зивный характер. В этом случае количество удаленного
материала при износе можно считать пропорциональным
работе сил трения. Результаты экспериментальных иссле¬
дований, касающихся абразивного износа, содержатся в
работах М. М. Хрущова, М. А. Бабичева [1] и В. Хирста
[1]. В случае, когда при износе происходит приработка
поверхностей, в особенности когда материалы контакти¬
рующих тел одинаковы, износ может носить нелинейный
характер.
При сделанных предположениях скорость изменения
прогиба δ будет
δ = Κ*ντ = Λα, к = μνΚ*. (5.1)
Здесь ν — осредненный модуль скорости перемещения
балки (в направлении, перпендикулярном к плоскости чер¬
тежа), тангенциальное усилие τ = μσ, μ —коэффици¬
ент трения, К* — коэффициент пропорциональности меж¬
ду работой сил трения и количеством удаленного мате¬
риала.
Выше было указано, что при исследовании делается
предположение о равенстве нулю давлений на краях пло¬
щадки контакта. Это будет иметь место, например, в слу¬
чае, когда коэффициент пропорциональности между ско¬
ростью износа и интенсивностью работы сил трения не
всегда постоянный, а при достаточно малых значениях
давления равен нулю, причем достаточно, чтобы это имело
место только для начальной стадии процесса. Ряд экспе¬
риментальных данных подтверждает сделанное предпо¬
ложение.
В результате износа может несколько измениться по¬
ложение крайних точек площадки контакта. Однако в свя¬
зи с тем, что величина износа мала по сравнению с разме¬
рами площадки контакта, этим обстоятельством можно
пренебречь. В результате прогиб балки в момент времени
t будет
t
w (я, t) = w0 (χ) — к j ρ (χ, τ) άτ. (5.2)
ο
§ 5. ОДНОМЕРНЫЕ ЗАДАЧИ ПРД НАЛИЧИИ ИЗНОСА
275
Давление р(х, t) связано с прогибом следующим соот¬
ношением:
ρ(χ, t) = EI^iW(х, t).
dx
На основании этого получим из (5.2)
t
d4 С
w (x, t) = w0 (x) — IcEI —ι \ w (χ, τ) dr. (5.3)
dx J
о
Будем искать частное решение этого уравнения в сле¬
дующей форме:
шр (х, t) = (ж). (5.4)
Подставляя (5.4) в (5.3), найдем
(в-р* - 1) и>э (*) = kEI -J (в-Р‘ -1) ·
Это равенство будет иметь место в случае, когда w$(x)
удовлетворяет уравнению
ά*υ>£(χ*) ( π\4 р л
Общее решение этого уравнения:
ιν$ (χ*) = λχ sin vx* + λ2 cos ν.ζ* + λ3 sh νζ* + λ4 ch va?*,
(5.6)
ν = ΛΥ JLjl
У Elk а
Elk а ‘ *
Можно указать в явном виде собственные значения и
собственные функции для уравнения (5.5). При этом дол¬
жны быть использованы краевые условия для функции
Шр(я*) в точках я* = —π, χ* = +π. Эти условия сле¬
дующие:
Щ (я*) = (®*) — О
при χ* = ± π (подпертые концы),
Щ (х*) = Щ ix*) = о
при #* = ± π (заделанные концы).
18*
(5.7)
276 гл. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
Используя условия (5.7) применительно к функции
(5.6), получим четыре однородных уравнения:
Σ Uki (ν) = О (I = 1, 2, 3, 4).
k=l
Это приводит к следующему условию:
|α« (ν) | = 0.
В результате получим трансцендентное уравнение для
определения собственного значения νη. Каждому собствен¬
ному значению νη соответствует фундаментальная функ¬
ция φη. Эти функции могут быть нормированы, причем,
как известно, они образуют полную систему ортогональ¬
ных функций.
На основании второго равенства (5.6) получим выра¬
жение для §п:
о & Elk 4
Ρ η — Ζ η’
η
Заданная функция wo(x), которая представляет собой
значение wit, х) при t = 0, может быть разложена в ряд
по указанным выше ортогональным функциям φη:
оо
w0 (х*) = 2 Κηψη(χ*)·
71=1
В таком случае решение задачи получаем в следую¬
щем виде:
w(3?,t)= 2 ^ехР ί—~τ~ν«ί'ΐ (5·8)
tS \ П /
Исследование трансцендентных уравнений, на основа¬
нии которых определяются собственные значения vn, по¬
зволяет сделать заключение, что эти значения образуют
возрастающую последовательность. Поэтому, если пред¬
ставляет интерес асимптотика при больших значениях
времени, то достаточно ограничиться только одним или
несколькими членами ряда (5.8).
Таким образом, получено точное решение поставленной
задачи. Ниже будет рассмотрена значительно более слож¬
ная двумерная задача, для которой также можно найти
точное решение, причем она приводит к нахождению соб¬
§ 6. ПЛОСКАЯ ЗАДАЧА ПРИ НАЛИЧИИ ИЗНОСА
277
ственных значений и собственных функций, но уже для
некоторых интегральных уравнений.
Заметим, что рассмотренная задача близка к задаче
о колебаниях прямолинейного стержня постоянного сече¬
ния. Однако подобный метод может быть применен и для
решения более сложной задачи об износе стержня в виде
кривого бруса, форма которого близка к части кругового
кольца, контактирующего с жестким круговым цилиндром.
§ 6. Плоская контактная задача теории упругости
при наличии износа
Найдем теперь решения некоторых двумерных кон¬
тактных задач при наличии износа. Будем рассматривать
давление штампа на границу упругого слоя. Штамп совер¬
шает перемещения относительно этого слоя. Движение
происходит в направлении,
перпендикулярном плоскости
чертежа (рис. 59). Как и в
случаях, рассмотренных в § 5,
штамп перемещается в неко¬
торых направляющих так, что
расстояние между этими на¬
правляющими и границей уп¬
ругого слоя остается неиз¬
менным. В этом случае при
наличии износа давление, действующее на границу слоя,
будет уменьшаться. Полагаем, что силы трения между
штампом и слоем (в направлении оси х) отсутствуют.
При этом исследуются контактные задачи при следую¬
щих условиях:
1°. Слой покоится на жестком основании, причем силы
трения в направлении оси х между ними отсутствуют.
2°. Слой жестко связан с жестким основанием.
3°. Модуль упругости материала, из которого состоит
слой, представляет собой функцию координаты у (не рав¬
ную нулю, когда у = 0). Нижняя граница слоя может по¬
коиться на основании без сил трения или быть с ним
жестко связана.
Во всех указанных задачах перемещение поверхно¬
сти и давление, возникающее под штампом, связаны
9‘
V,
\
/~\ ^
-/Г*-*
Я
V7/77777V>
У7'/^7777'^7777777777т.
Рис. 59.
278 ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ. ИЗНОС
следующим интегральным соотношением:
а
ϊφ) = ] КIX — i I p{Q dl·,. (6.1)
-а
Заметим, что ядро в данном соотношении симметрично.
Последнее обусловлено тем, что перемещение границы в
результате действия силы представляет собой функцию
расстояния между координатой приложенной силы и ко¬
ординатой точки, где имеет место перемещение. Простей¬
шее соотношение подобного рода известно для полуплос¬
кости:
а
ю = A J In | χ — ξ I ρ (ξ) dl·.
—a
Следует отметить, что все ядра К\х — ξ| в (6.1) будут
иметь также логарифмическую особенность (но не более
высокого порядка). Отсюда следует, что ядра такого вида
будут интегрируемыми вместе с квадратом, что сущест¬
венно для их дальнейшего исследования. Таким образом,
имеем ядра Кг | χ — ξ |, | χ — ξ |, Κζ | χ — ξ |, | χ — ξ |
(последние два ядра относятся к третьей задаче, где мо¬
гут иметь место два различных условия на нижней гра¬
нице упругого слоя).
Нужно сказать, что задача, в которой упругий слой
покоится без сил трения на полуплоскости, не вполне кор¬
ректна, так как при этом может иметь место отставание
слоя от основания. Однако она будет корректной при опре¬
деленных условиях для весомого слоя, когда подобного
отставания не будет. При этом для построения интеграль¬
ного соотношения нужно воспользоваться несколько иной
функцией Грина.
Будем полагать, что имеет место абразивный износ,
и, следовательно, используя соотношение (5.1), получим
следующее уравнение:
t
w (х, t) = w0(x) — k f ρ (χ, τ) dx. (6·2)
ο
Здесь функция w®(x) описывает поверхность штампа в
начальный момент времени и является заданной.
§ 7. ОСЕСИММЕТРИЧНАЯ ЗАДАЧА ПРИ НАЛИЧИИ ИЗНОСА 279
Из (6.1) и (6.2) следует уравнение для определения
давления:
а
j Κ\χ — ξ|ρ(ξ, ί)άξ =
—а
a t
= j K\x-l\p(t, 0)dt-k$p(x,x)dx.
—a 0
Представляя частное решение рп(х, t) в виде
Рп (х, t) = exp γ- ^ рп {х),
получим, что функция рп(х) удовлетворяет однородному
уравнению Фредгольма
а
j' ^|*-ξΙρ(|)«-λ/»(*) = 0, (6.3)
—а
все λη положительные вследствие вещественности и поло-
жительности ядра К\х — \\.
Вследствие симметрии ядра собственные функции рп(х)
этого уравнения ортогональны. Разлагая функцию для дав¬
ления р(х, 0) в начальный момент времени по ортогональ¬
ной системе собственных функций интегрального уравне¬
ния (6-3), получим выражение для коэффициентов Ап:
оо
ρ (х, 0) = 2 ΑηΡη {χ)·
71=1
Давление в произвольный момент времени имеет вид
оо
р (х, <) = 2 АпРп ехр (~ Т
71=1 ' П '
§ 7. Осесимметричная контактная задача
теории упругости при наличии износа
На штамп, уравнение торцевой поверхности которого
я = /(р), находящийся на упругом полупространстве, дей¬
ствуют сила Р, направленная по оси вращения, и момент
Л/, поворачивающий его вокруг этой оси, которые будут
280 гл. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
меняться с течением времени (рис. 60). Постоянная угло¬
вая скорость вращения равна ω. При этом площадка кон¬
такта имеет в плане форму круга радиуса а ^ Ь, где Ь —
радиус цилиндрической поверхности штампа. При враще¬
нии штампа на площадке контакта возникают силы тре¬
ния τζθ, направление которых сов¬
падает с направлением вращения,
т. е. они перпендикулярны к ра¬
диусу площадки контакта, причем
Τζθ == \iOzt
где σζ — нормальное давление на
площадке контакта, а μ — коэф¬
фициент трения между контакти¬
рующими телами. Надо иметь в
виду, что в рассматриваемой зада¬
че величины напряжений σζ, σρ, σβ,
Ίρζ» Τζθ» Τρθ и перемещении Wp,
uQ — функции времени t.
Для определения напряжен¬
ного состояния имеем следую¬
щие граничные условия на пло¬
щадке контакта при ζ = 0 в на¬
чальный момент времени (S —
круг радиуса а, условие вне
круга S ставится на свободной поверхности):
»* = /(Ρ). τ2θ = μσζ, τΡ2 = 0 на S, J
σ2 = 0, τ2θ = 0, τΡ2 = 0 вне S. J
Перемещение основания и>(р, t) в направлении оси 2
в любой момент времени представляет собой разность на¬
чального перемещения ι#ο(ρ) = /(р) и перемещения осно¬
вания, обусловленного износом, поэтому напряженное сос¬
тояние упругого полупространства в произвольный мо¬
мент времени определяется следующими граничными
условиями:
uz — W (ρ, ί), τ2θ = μσ2, тР2 = 0 на S, )
σζ = 0, τζθ = 0, τΡζ = 0 вне S. J
Для решения задачи воспользуемся уравнениями Ляме,
записанными с учетом осевой симметрии задачи в цилин¬
§ 7. ОСЕСИММЕТРИЧНАЯ ЗАДАЧА ПРИ НАЛИЧИИ ИЗНОСА 281
дрических координатах:
м , о , д ί 1 3(Р“р) , , д <41 л ^
(λ, + 2μ) I — ^ μ J +μ^[ΐ7--^] = 0.
(7.3)
В § 8 главы 2 было показано, что в осесиммет¬
ричном случае в упругом теле существуют две неза¬
висимые системы деформаций и напряжений. Первая
из них получается, если положить ив = О, щ Ф 0, иг Ф 0.
При этом компоненты напряжения τρθ и τζβ равны нулю,
а остальные отличны от нуля. Вторая система может быть
получена, если положить щ = иг = 0, uQ Ф 0. Тогда компо¬
ненты напряжения σβ = σρ = τρζ = σζ = 0, а τρβ Φ 0, χζθΦ0.
Напряженное состояние в рассматриваемой задаче о
вдавливании в упругое полупространство штампа круговой
формы в плане, вращающегося вокруг своей оси, может
быть разбито на два независимых напряженных состоя¬
ния. Для определения первого из них имеем следующие
граничные условия на площадке контакта при ζ = 0:
u* = w (р, t), τ*β = 0, τ*ζ = 0 на S, |
♦ л ί л ^ Λ О I
аг = 0, τ2θ = 0, τΡζ = 0 вне S. J
Второе напряженное состояние определяется из таких
условий на границе ζ = 0:
**/%** * ** . л
uz =0, τζθ = μσζ, τΡζ = 0 на £, I
** Λ ** Λ ** Λ ο I (^*^)
οζ = 0, τζθ = 0, τΡζ = 0 вне S. J
Сумма этих двух напряженных состояний (т. е. напря-
9|С Э|С 3|( j|( ф ф
жения сг2 = σζ + σζ , xzQ = rzQ -f τ2θ и т. д.) будет удов¬
летворять граничным условиям (6.2), т. е. будет решением
поставленной задачи.
Как видно из (7.4), величины orz, xzQ и т. д. определя¬
ются из решения задачи о вдавливании в упругое полу¬
пространство штампа, представляющего собой тело враще¬
п . 2,л 1 Γ-Lд(ри*) -U - JLI
(λ + Ζμ) dz + dz J P dp
я 1дил\
282
ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ. ИЗНОС
ния, когда между контактирующими телами отсутствуют
силы трения. Перемещения uz при ζ = 0 в этой задаче
связаны с. нормальными напряжениями oz (ζ = 0) соот¬
ношением, которое в полярных координатах в случае осе¬
вой симметрии задачи имеет вид (см. гл. II)
а 2Я
*/ 1 — v2 f f a2(r,t)rdrdq>
Uz (Р, t) = - -ш- (7.6)
0 0 ' г + Ρ — 2rp «*■«« m
cos φ
Из решения задачи, удовлетворяющей граничным ус¬
ловиям (7.5), следует, что и**= 0 и σζ = 0 как на
круге, так и вне круга S. Тангенциальное напряжение
τΖθ при ζ = 0 можно определить, зная решение гранич¬
ной задачи (7.4) для нормального напряжения я?, дей¬
ствующего на площадке контакта. Очевидно, что τ2θ ~
= τ2θ, °* = °г = — Р (Рт t) и ut = uz = w ф, t). Таким
образом, перемещения мДр, £), имеющие место на площад¬
ке контакта, связаны с нормальным давлением р(р, ί),
действующим на границе упругого полупространства, сле¬
дующим соотношением, справедливым для любого мо¬
мента времени:
а 2П
ИМ>=^Я . (7.7,
оо Уг +p-2rpc°s(p
Тангенциальные напряжения на границе упругого
полупространства определяются следующим образом:
τζθ(ρ, t) = — μρ(ρ, ί). (7.8)
Здесь надо иметь в виду, что радиус площадки контакта
в процессе износа меняется. Но так как величина износа
мала по сравнению с размерами площадки контакта, то
этим обстоятельством можно пренебречь·
Запишем уравнение (7.7) в безразмерных коордипатах
1 271
0 0 ^'ι + ΡΪ —21-jPjCOsq) ι
Pi = Р/α, >ι = r/a, (plt t) — w (pxa, t)/a,
Pi (Pn t) = p (рха, ί).
§ 7. ОСЕСИММЕТРИЧНАЯ ЗАДАЧА ПРИ НАЛИЧИИ ИЗНОСА 283
Определим теперь перемещение w(р, t) границы упру¬
гого полупространства, которое в процессе износа будет
меняться. При абразивном износе количество удаленного
при износе материала можно считать пропорциональным
работе сил трения (М. М. Хрущов, М. А. Бабичев [1] и
В. Хирст [1]). В этом случае, с учетом формулы (7.8),
модуль скорости изменения перемещений точек границы
полуплоскости будет определяться следующим образом:
|5ш(р, t)/dt\ =ΛωρΙτζθΙ = &ωρμρ(ρ, ί), (7.10)
где к — коэффициент пропорциональности между работой
сил трения и количеством удаленного материала. Тогда
для перемещений точек площадки контакта получим
(в безразмерных переменных)
1
«>1 (Pi> t) = woi (Pl) — ^'ωρ1μ j (plt τ)άτ,
о
^01 (Pl) = w (Ρια> 0)/α.
Если положить коэффициент пропорциональности к и
коэффициент трения μ постоянными, то перемещения в
центре площадки контакта, обусловленные износом, будут
равны нулю, что должно привести к росту напряжений
в этой точке. Этот процесс в свою очередь приведет к не¬
обратимым пластическим деформациям в центре площадки
контакта. Таким образом, хотя необратимые формоизме¬
нения будут иметь место на всей площадке контакта, из¬
лагаемое ниже решение задачи теории упругости будет
справедливо во всей зоне контакта, за исключением малой
области вблизи центра площадки контакта.
Введем в рассмотрение функцию g(pi, £), которая свя¬
зана с давлением pi(pi, t) следующим образом:
pi(pb t) = q(pi, i)/pi· (7.12)
Из (7.9) и (7.11) тогда следует уравнение для опреде¬
ления функции g(pi, t) в любой момент времени
1 ая
1 —у2 Г Г Я (rv t) d^dff
ЛЕ ο ο ^rl + P\ — гг^совф ^
^“’οιίΡι) — Λωμ (7.1Я)
(7.11)
284
ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ. ИЗНОС
Здесь u>oi(pi)— уравнение торцевой поверхности штампа
в безразмерных координатах. Этому начальному переме¬
щению соответствует начальное распределение давления
/>i(pb 0) = #(рь 0)/pi, которое определяется из решения
граничной задачи (6.1) и связано с перемещением M>oi(pi)
соотношением
1 2Л
„.2
и>.
(Рх) = f f ?(гг °) drid4> (7 14)
оо ^ ι "t" Pi 2'"jP1 cos φ
Будем искать частные решения уравнения (7.13) в виде
? (Pi> t) = (pi) е-β».
Тогда для определения величин ^β(ρι) с учетом (7.14) по¬
лучим однородное уравнение Фредгольма с симметричным
ядром:
1
ΪΡ (Ρι) - Ρ ί Н (Γι> Pi) (ri) dri = °.
2Л
Я(г1)Р1) = ^-Г
Α:ωμπ^ J _)_ p2 _ 2^ cos φ
(7.15)
Ядро Н(г\, ρι) можно записать с помощью полного эл¬
липтического интеграла первого рода следующим образом:
гг/„ . ч 4(l-v2) ν(2-/№λ
Н <г1’ Р" - ku>\inE (^ + Р*) U + Pi /
Уравнение (7.15) позволяет определить собственные
значения βη, которые все будут вещественны вследствие
симметрии и вещественности ядра. Покажем также, что
все собственные значения βη положительны. Для этого
необходимо и достаточно доказать, что ядро Жп, pi) по¬
ложительно, т. е.
ι 1
j (?) = Я я (ru Pl) q (гг) q (Pl) dr,d9l > 0
о о
для любой непрерывной функции q(r\), не равной тождест¬
венно нулю в интервале (0, 1). Функционал J(q) можно
§ 7. ОСЕСИММЕТРИЧНАЯ ЗАДАЧА ПРИ НАЛИЧИИ ИЗНОСА 285
представить в виде [с использованием структуры формул
(7.14) и (7.12)]
1
= άμ ί л to»» °) wn (Pi) PidPi·
0
Таким образом, функционал J(q) с точностью до положи¬
тельного множителя предствляет собой суммарную работу,
производимую произвольными силами давления jMpi, 0) =
= ff(pi)/pi на соответствующих перемещениях точек пло¬
щадки контакта в начальный момент времени, которая
для отличных от нуля давлений всегда неотрицательна.
Собственные функции интегрального уравнения (7.15)
будут ортогональными вследствие симметрии ядра. На¬
чальное давление ρι(ρι, 0) представлено формулой
(см. гл. И)
1
Pi (Ри 0) = — j Δ w01 (rx) L (r lf px) drlt
- (ri, Pi) = j
)o
2Л
2ri
1 X
π V+ ΡΪ — 2r1p1 cos φ
Vi — r\Vi — pj
X arctg οφ,
V r? + p?— гг^созф
Δ
[ ri dri ^ dr\
(7.16)
Разложив функцию g(pi, 0) = ρiι(pi, 0), где величи¬
на ρ ι (ρ ι, 0) определена формулой (7.16), в ряд по полной
ортонормированной системе собственных функций ?η(ρι)
интегрального уравнения (7.15), найдем коэффициен¬
ты Ап·.
оо
ff (Ри 0) = 2 АпЯп (pi)·
286 гл. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
Тогда давление в последующие моменты будет вычи¬
сляться по формуле
Видно, что выражение для давления в осесимметрич¬
ной контактной задаче при наличии износа представимо
в таком же виде, как и в двумерной контактной задаче о
дЕижении штампа по границе упругого слоя (см. § 6 этой
главы).
Контактные задачи теории упругости для шероховатых
тел в линейной постановке рассматривались в работах
И. Я. Штаермана [1], Г. Я. Попова, В. В. Савчука [1],
Б. П. Митрофанова [1]. И. Я. Штаерманом [1] впервые
было получено уравнение плоской контактной задачи для
упругого шероховатого тела па основании предположе¬
ния о пропорциональности дополнительных локальных
перемещений за счет смятия неровностей в зоне контакта
нормальному давлению. Однако, как показывают резуль¬
таты ряда экспериментальных исследований (Н. Б. Дем-
кин [1] и М. Н. Добычин, В. С. Комбалов, И. В. Крагель-
ский [1]), сближение контактирующих шероховатых тел
за счет деформации микровыступов пропорциональпо дав¬
лению в степени α (α ^ 1). В такой постановке некото¬
рые плоские контактные задачи были рассмотрены в ра¬
ботах А. С. Рабиновича [1, 2] и С. М. Мхитаряна,
JI. А. Шекяна [1]. Приближенное решение осесимметрич¬
ной задачи приведено в работе А. С. Рабиновича [3].
Рассмотрим плоскую контактную задачу для упругой
шероховатой полосы Ы < °°, 0 <г/<А. В верхнюю гра¬
ницу полосы силой Р вдавливается жесткий штамп, форма
поверхности которого задана уравнением у = g(x) (g(0) =
= 0). Вне участка контакта (—а, а) верхняя граница
полосы не нагружена. Исследуются параллельно два
случая закрепления полосы:
1) Полоса лежит на жестком основании без сил тре¬
ния; в этом случае граничные условия имеют вид (б —
оо
т- 2 AnQn (Pi) е ^л <
71=1
§ 8. Плоские контактные задачи
для шероховатых упругих тел
§ 8. ПЛОСКИЕ ЗАДАЧИ ДЛЯ ШЕРОХОВАТЫХ УПРУГИХ ТЕЛ 287
осадка штампа)
гхУ (х, 0) = 0, 1;(я,0) = 0, \х\ < оо, |
Txy(x,h) = 0, oy{x,h) = 0, а < \х\ < ооД (8.1)
(з, й) = 0, ι>(£,Λ) = g(s) + δ, |χ| < a. J
2) Полоса жестко закреплена по основанию; тогда в
(8.1) изменяются условия на линии раздела у == 0, кото¬
рые примут вид
и{х, 0) = 0, ν(χ, 0) = 0.
Будем считать, что нормальные перемещения грани¬
цы упругой полосы v(x, h) складываются из перемещений
V\ за счет деформации микровыступов, которые определя¬
ются следующим образом:
vx=Alp(x)]*, (8.2)
Здесь р(х) — функция распределения контактных давле¬
ний, А — коэффициент, характеризующий деформацион¬
ные свойства шероховатого слоя, а — показатель, который
находится из кривой опорной поверхности (ос ^ 1). Кроме
того, имеют место упругие перемещения полосы v2, ко¬
торые на основании граничных условий определяются
следующим образом (см. монографию «Развитие теории
контактных задач в СССР» [1]):
Ι’> = ίίΪΓ1>Ι*(Ι-^)ί’5№)· (8.3)
—а
Функция kit) имеет вид
оо
к (t) = j* cos ut du. (8.4)
a
Конкретный вид функции Liu) зависит от граничных ус¬
ловий.
Для случая 1
^“>=ИТГИ· (8-5)
Для случая 2
т 2xsh2w — 4м о / /о о\
ьУи) — ~—г , ;—κ = 3 — 4ν. (8.6)
2κ ch 2u + 4 и + 1 + κ '
288 ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
Запишем условие контакта штампа с полосой и усло¬
вие равновесия в безразмерных координатах. Для этого
введем обозначения:
__х + а _6 « __2а
1 _ 2а ’ η — 2а' Л ’
е. Μ - έ «1“ <21· - ‘И· = s Иг2]"”·
Ρι(*ι)
2 (l — ν*)
пЕ
Тогда получим
ί — у18
(8.7)
j.
j к [λ (ί — χχ)] pt (ί) dt + At [рг fo)]» = gl (жх) -f η, (8.8)
О
1
ρι = j Pl (xi) dxv (8-9)
0
Таким образом, решение поставленной задачи сводит¬
ся к решению нелинейного интегрального уравнения (8.8)
при условии (8.9), в результате чего определяются давле¬
ние под штампом и осадка штампа.
Уравнение (7.8) является уравнением типа Гаммер-
штейна. Приведем его к канонической форме. Для этого
введем новую функцию
ψ(;τι) = Αχ[ρι(χι)]α — g\(x\) — η. (8.10)
Тогда
ι
ATVa J к [λ (t - ^)][ψ (t) + gl (t) + η]dt +
+ Ψ (*i) = 0,
1
P, = Λ~1/α J [ψ fo) + gl (Xi) + η11/α dx1.
(8.11)
Для решения уравнения типа Гаммерштейна (8.11)
можно применить метод последовательных приближений.
Например, положить ψο(#ι) Ξ0 и последовательно
I
ψ»+ι (*ι) = - АТ1>Л j к [λ (t - xj] [ψη (t) + gl (ί) + W4t.
о
§ 8. ПЛОСКИЕ ЗАДАЧИ ДЛЯ ШЕРОХОВАТЫХ УПРУГИХ ТЕЛ 289
Докажем выполнимость достаточных условий сходи¬
мости этого метода для уравнения (8.11), исходя из
условий:
1) Ядро kit) интегрального уравнения (8.11), прини¬
мая во внимание (8.4) — (8.6), можно представить в виде
kit) = -ln\t\+Fit), O^lilCoo,
где Fit) — непрерывная функция. Очевидно, что ядро kit)
принадлежит классу L2.
2) Функция / (£, и) = АТ1/а [и + gx (ί) + η]ι/α равно¬
мерно удовлетворяет условию Липшица вида
I fit, щ) — fit, и2)\ <cit)\u,i — и2\ (8.12)
в интервале изменения функции ^ = ψ(.τι). Действитель¬
но, так как нормальное давление p\ix\) неотрицательно,
то из (8.10) и свойств ядра в уравнении (8.11) следует
—g\ix\) — η < и < 0.
Производная df (t, и)/ди = а~МГ1/а[гг + gx (t) -f- ηρ/α-ι
в интервале изменения аргумента и ограничена значением
α-^Γ1/α lg! (t) + η]ΐ/«-ι (0 < α < 1).
Поэтому выполняется условие Липшица (8.12), в котором
ί(ί) = ^Λ'1/“[^(ί)+η]1/“-1·
3) Функция / {t, 0) = Αΐ1Ι(Χ> [£х (ί) η]1/α, очевидно,
принадлежит классу L2.
При выполнении условий 1—3 метод последовательных
приближений сходится (Ф. Дж. Трикоми [1]), если толь¬
ко параметры задачи удовлетворяют неравенству
α ~2Αΐ2ΐα | [#! (χ) + η]2/α-2 j J £2 ^ ^ dx < 1. (8.13)
При выполнении условия (8.13) последовательность
функций (ψη(#ι)} имеет предел, который и будет единст¬
венным решением уравнения (8.11).
Докажем, что это решение единственно. Допустим про¬
тивное, т. е. что существует два решения уравнения (8.11),
ψι(χι) и ψ^(^ι). Тогда должно существовать нетривиальное
19 Л. А. Галин
290 ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ. ИЗ*ЮС
решение уравнения
1
Ψ fo) + ЛГ1/а J к [λ (t - хх)] φ [ί, Ψ (ί)] dt = 0
ο
(Ψ (X,) = Ь (*,) - ψ2 (xj, φ [ί, Ψ (ί)1 = > (8·14)
= [ψ2 (ί) + Ψ (ί) + g, (ί) + η]1/** -
-[yAV + gAV + nV'*)·
Умножим уравнение (8.14) на функцию φ[χι, Ψ(#ι)1
и проинтегрируем на отрезке (0, 1). Получим
ι 1
А~1/а j* j* & [χ ^ __ Χι)] ф ψ ф ψ dt dxA=
о о
1
= — j Ψ (Xj) φ [χΧ) Ψ (Xj)] dxx. (8.1δ)
О
Функция φ[χι, Ψ(*ι)] положительна при Ψ(#ι)>0 и
отрицательна при Ψ(χ\) < 0. Следовательно,
ι
j‘ Ψ (χ,) φ [χΧ) Ψ (χ,)] dxx > 0, Ψ (χχ) ^ 0.
0
Ядро k[X(t — χ)] неотрицательно, т. е. для любой не¬
прерывной функции ω(,ζ), не равной тождественно пулю
на интервале (0, 1), имеет место неравенство
ι 1
/ (со) = j J к [ λ (t — x)\ω (ί) ω (χ) dt dx ^ 0.
о о
Действительно, функционал Лео) можно представить
в виде
/ (со) = ^ ω (я) | ( к [λ (t — χ)] ω (t) dt 1 dx.
о lo j
Выражение в фигурных скобках представляет собой,
как следует из (8.3), с точностью до постоянного положи¬
тельного множителя перемещение, которое будет иметь
граница полосы на площадке контакта при действии
распределенной нагрузки соЫ. Таким образом, функцио¬
нал /(ω) с точностью до положительного множителя пред-
g 8. Плоские задачи для шероховатых упругих тел 291
ставляет собой суммарную работу, производимую произ¬
вольными силами давления ω(χ) на соответствующих пе¬
ремещениях точек площадки контакта, которая всегда
неотрицательна. В силу неотрицательности ядра левая
часть соотношения (8.15) неотрицательна. Таким образом,
соотношение (8.15) справедливо тогда и только тогда,
когда Ψ(χ\) s 0.
Зпая решение уравнения (8.11) как предел последо¬
вательности функций ψη(#), по формуле (8.10) можно
найти давление в безразмерных координатах. Осадка
штампа η находится из условия (8.9).
Отметим, что давление не может обращаться в беско¬
нечность на концах площадки контакта. Действительно,
предполагая, что давление имеет интегрируемую степен¬
ную особенность вида (0<θ< 1) в точке х\ = 0,
и учитывая, что ядро интегрального уравнения (8.8) име¬
ет особенность вида ln#i, получим, что левая часть в (8.8)
имеет особенность порядка яГав? в правой же части осо¬
бенностей нет, что и доказывает высказанное выше ут¬
верждение.
В случае контактирования гладкого штампа с шерохо¬
ватым упругим слоем для определения неизвестных гра¬
ниц площадки контакта (—а, а) существует дополнитель¬
ное условие р(—а) = р(а) = 0, выражающее собой не¬
прерывность функции для давления на границе упру¬
гого слоя.
Изложенным методом можно решать разные плоские
контактные задачи для шероховатого слоя, определяя при
этом характер распределения давления на границе шеро¬
ховатого слоя в зависимости от толщины слоя, парамет¬
ров шероховатости, упругих характеристик слоя и т. д.
Рассмотрим в качестве примера контактную задачу
о вдавливании без трения жесткого штампа с плоским
основанием g(x) = 0 в толстый шероховатый слой. Для
определения давления в этом случае имеем интегральное
уравнение (8.8) и условие (8.9), в котором £ι(£ι)=0,
а ядро представимо в виде
k(t) = —In I ί I + ао,
где ао = —0,352 для первой граничной задачи и ао =
= —0,527 для второй граничной задачи. Такое асимпто¬
тическое представление ядра (8.4) справедливо для до¬
19*
292
ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, ийнос
статочно толстых полос, когда λ2 = [2a/ti\2 = о(1) (см.
монографию «Развитие теории контактных задач в
СССР» Ш).
При этих условиях, решая уравнение (8.8) методом
последовательных приближений, получим для давления
на площадке контакта выражение
Ρι (^ι) — ^Γ1/α [ψ (^χ) + η]1/α»
где ψ(#ι) — предел последовательности функций {ψη(#ι)},
причем
1
ψη+1 (^ι) = Αχ1,α j [In 11 — χγ I + c0] [ψη (ί) + i\V->adt,
0
c0 = In (2 alh) — a0.
Этот предел существует, если выполняется условие
(8.13), которое в данном случае принимает вид
(с2 _ ЗСо + 3 5) < L
На основании результатов экспериментальных иссле¬
дований (Н. Б. Демкин [1] и И. В. Крагельский, М. Н. До-
бычин, В. С. Комбалов [1]) для численных расчетов
были взяты следующие значения безразмерных парамет¬
ров: а = 0,4, А ι = 1, Со = —3. Графики распределения
давления в случае действия на штамп безразмерных на¬
грузок = 0,6 · 10~2, Р[2)= 0,75 · 10~2 представлены
на рис. 61 кривыми 1 и 2 соответственно. Значения Р\
связаны с истинными значениями нагрузок последней
формулой в (8.7). Углубления, соответствующие нагруз¬
кам Р^ и Ρι2) , равны η(1) = 0,15, η(2) = 0,17, где η =
= 6/(2а). Как видно из графика, при действии большей
нагрузки давление возрастает, особенно на концах пло¬
щадки контакта. При действии одинаковых нагрузок, рав¬
ных 0,41 · 10-2, как показали расчеты, углубление штам¬
па и давление под ним меняются в зависимости от чисто¬
ты обработки поверхности, которая характеризуется без¬
размерными параметрами а и А\. При а = 0,4 и А\ =0,75
штамп углубится на величину η = 0,1, а при а = 0,4 и
^ι = 0,35 (более чистая обработка) штамп углубится на
меньшую величину, η = 0,06. Графики распределения
давления в этих двух случаях показаны на рис. 61 кри¬
§ 9. ОСЕСИММЕТРИЧНАЯ ЗАДАЧА ДЛЯ ШЕРОХОВАТЫХ ТЕЛ 293
выми 3 и 4 соответственно; штриховой линией приведен
график распределения давления без учета шероховатости.
Расчеты показали удовлетворительную сходимость метода
последовательных приближений и его эффективность.
0,4
02
т
1
1
1
■J
I
I
I
L
/
/
1
\
\
\
—
1
з
/
/
—
\
\
/
/
0,2 Оуи 0,0 0,8 т 7,0
Рис. 61.
С точностью до 10“5 оказалось достаточным вычислить
15—20 приближений функции г|>(я). Процесс сходится
практически для всех разумных значений параметров
шероховатости и упругих характеристик материала.
§ 9. Осесимметричная контактная задача
для шероховатых упругих тел
Рассмотрим осесимметричную задачу о вдавливании
кругового в плане штампа в шероховатое упругое полу¬
пространство (у < 0). Форма контактирующей поверхно¬
сти штампа задана уравнением у = g(p) (g(0) = 0).
Штамп прижимается к полупространству силой Р. Пло¬
щадка контакта имеет форму круга радиуса а. Нормаль¬
ные перемещения границы упругого полупространства в
области контакта, определяемые формой штампа и его
294
ГЛ. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
осадкой δ, складываются из упругих перемещений точек
границы полупространства v2j которые на основании гра¬
ничных условий определяются так (см. монографию
«Развитие теории контактных задач в СССР» [11):
а 2Я
v = 1 — У2 Г Г Р (r) rdrdy
ЛЕ о о /г2 + р2-2гр cos φ
(p(r)— функция распределения контактных давлений),
и перемещений v\ за счет деформации микровыступов,
которые определяются формулой (8.2).
Запишем условие контакта штампа с границей полу¬
пространства и условие равновесия в безразмерных ко¬
ординатах в канонической форме. Для этого введем обо¬
значения:
Г1 = Т» Мгх) = Цлг-Р(г1а)> Si{ri) = g^p,
п-1 А -Л
η а ’ Αί — а
πΕ
*1 =
пЕа
р,
(9.1)
Ψ (Pi) = A [Pi (р,)]“ - g! (рг) — η.
Тогда получим
1
АТ1/а j к (rlt Ρχ) гх [ψ (гх) + {гг)+ η]ΐ/« drx +
О
+ ψ (Pl) = О,
dy #
^ (ги Ра) j _j_ р2 — 2ггрг cos φ’
ι
Pi = 2л j р1 (гх) rtdrv
Уравнение типа Гаммерштейна [первое уравнение в
(9.1)], как и в § 8, будем решать методом последователь¬
ных приближений. Очевидно, что ядро Мгь pi) интеграль¬
ного уравнения (9.1) принадлежит классу L2. Можно про¬
верить также, что функция
/(г, и) = ЛГ1/аг [u + gt (г) + η] 1/« и < 0У
§ 9. ОСЕСИММЕТРИЧНАЯ ЗАДАЧА ДЛЯ ШЕРОХОВАТЫХ ТЕЛ 295
равномерно удовлетворяет условию Липшица
I/(г, Ui) — /(г, M2)|<c(r)K — Ц2|,
с (г) = аАГ1/(*г [gx (г) + η]1/α_1
и что функция / (г, 0) = Αχ1/αΓ [gx (г) + η]1/® принадле-
жит классу L/2· Поэтому при выполнении неравенства
ι 1
а-МГ2/“ j ] ρ2 [£х (р) + η12/“-2 к2 (г, р) dr dp < 1
0 ί)
последовательность функций {ψ„(ρι)ί сходится почти всю¬
ду к решению уравнения (9.1) (Ф. Дж. Трикоми [1]).
Доказательство единственности решения уравнения (9.1)
0,5
Pi
О,k
о,ъ
о,г
0,7
О 0,2 О, Ь 0,5 О,δ 1,0
Вис. 62.
проводится аналогично тому, как это было проделано
в § 8.
Рассмотрим в качестве примера численное решение
задачи о вдавливании кругового цилиндрического штампа
с плоским основанием g(р) = 0 в шероховатое упругое
полупространство. Были взяты следующие численные
296 гл. III. ВЯЗКОУПРУГОСТЬ. ШЕРОХОВАТОСТЬ, износ
значения безразмерных параметров: а = 0,4, А\ = 0,9,
η = 0,1. С точностью решения до 10"5 оказалось доста¬
точным вычислить 12 приближений функции ψ(#). Полу¬
ченный график функции ρι(π), представляющей собой
безразмерное давление, приведен на рис. 62. Штриховой
линией дан график распределения давления под штам¬
пом, когда не учитывается шероховатость основания.
В обоих случаях на штамп действует нагрузка
Р = 0,8625 · 10“2.
ЛИТЕРАТУРА
К главе I
Абрамов В. М. [1] Проблема контакта упругой полуплоскости с
абсолютно жестким фундаментом при учете сил трения.—
Докл. АН СССР, 1937, т. 17, № 4.
Бегиашвили А. И. [1] Решение задачи давления системы жестких
профилей на прямолинейную границу упругой полуплоско¬
сти.— Докл. АН СССР, 1940, т. 27, № 9, с. 914—916.
Бицадзе А. В. [1] О местных деформациях при сжатии упругих
тел.— Сообщ. АН Груз. ССР, 1942, т. 3, № 5.
Ватсон Г. Я., Уиттекер Е. Т. [1] Курс современного анализа. Ч. 2.—
М.: Физматгиз, 1963.
Галии Л. А. [1] Смешанные задачи теории упругости с силами
трения для полуплоскости.— Докл. АН СССР, 1943, т. 39, № 3,
с. 88-93.
[2] Вдавливание штампа при наличии трения и сцепления.— ПММ,
1945, т. IX, вып. 5, стр. 413—424.
[3] Аналогия для плоской упруго-пластической задачи.— ПММ,
1948, т. XII, вып. 6.
[4] Контактные задачи теории упругости.— М.: Гостехиздат, 1953.
[5] Развитие теории контактных задач в СССР. / Под ред. JI. А. Га¬
лина.— М.: Наука, 1976.
Глаголев Н. И. [1] Определение напряжений при давлении систе¬
мы жестких профилей.— ПММ, 1943, т. VII, вып. 5, с. 383—388.
Голубев В. В. [1] Лекции по аналитической теории дифференциаль¬
ных уравнений.— М.: Гостехиздат, 1941.
Карцивадзе И. Η. [1] Основные задачи теории упругости для уп¬
ругого круга.—Труды Тбилисского матем. ин-та, 1943, т. XII,
с. 95-104.
Лаврентьев М. А. [1] Конформные отображения с приложениями
к некоторым вопросам механики,—М.: Гостехиздат, 1946, с. ИЗ.
Лехницкий С. Г. [1] Плоская статическая задача теории упруго¬
сти анизотропного тела.— ПММ, 1937, т. I, вып. 1.
[2] Анизотропные пластинки.— 2-е изд.— М.: Гостехиздат, 1957.
Львин Я. Б. [1] Устойчивость жестких стен и колонн на упругом
и упруго-пластическом основании.— Инж. сборник, 1950, т. 7.
Михлин С. Г. [1] Задача о соприкасании двух упругих полупло¬
скостей—ПММ, 1945, т. IX, вып. 2.
Моссаковский В. И., Петров В. В. [1] О влиянии трения на мик¬
роскольжение.—Докл. АН СССР, 1976, т. 231, № 3, с. 603—606.
Мусхелишвили Я. И. [1] Некоторые основные задачи математиче¬
ской теории упругости.— М.: Наука, 1966.
298
ЛИТЕРАТУРА
[2] Решение основной смешанной задачи теории упругости
для полуплоскости.— Докл. АН СССР, 1935, т. VIII, № 2,
с. 51—54.
[3] Основные граничные задачи для полуплоскости — Сообщ.
АН Груз. ССР, 1941, т. 2, № 10.
[4] К задаче равновесия жесткого штампа иа границе упругой
полуплоскости при наличии трения. Сообщ. АН Груз. ССР, 1942,
т. 3, № 5, с. 413—418.
Ш Сингулярные интегральные уравнения.— М.: Физматгиз, 1962.
родецкий М. 3. [1] Об одной контактной задаче.— Докл.
АН СССР, 1943, т. XII, № 6.
Привалов И. И. [1] Введение в теорию функций комплексного пе¬
ременного.— М.: Физматгиз, 1960.
Савин Г. Η. [1] Тиск абсолютно твердого штампа на пружне ани-
зотропне середовище.— Доповиди АН УССР, виддил тех. наук,
1939, № 6, с. 27—34.
[2] Давление жесткого ленточного фундамента на упругое анизо¬
тропное основание.—Вестник инж. и техн., 1940, № 5.
[3] О дополнительном давлении, передающемся по подошве абсо¬
лютно жесткого штампа на упругое анизотропное основание,
вызванном близлежащей нагрузкой.— Докл. АН УССР, 1940,
№ 7.
[4] Давление системы абсолютно жестких штампов на упругую
анизотропную полуплоскость.—Сообщ. АН Груз. ССР, 1940,
т. 1, № 10.
[5] О некоторых контактных задачах теории упругости.—Труды
Тбилисского матем. ин-та, 1946, т. XIV.
[6] Смешанная задача для анизотропной полуплоскости — Науч.
зап. Львовского гос. ун-та им. Франко, 1940, т. 5, вып. 2.
Саверин Μ. М. [1] Контактная прочность материала в условиях
одновременного действия нормальной и касательной нагруз¬
ки.— М.: Машгиз, 1946.
Соколовский В. В. [11 Теория пластичности.—М.: Высшая школа,
1969.
Фалъкович С. В. [1] О давлении жесткого штампа н-а упругую по¬
луплоскость при наличии участков сцепления и скольжения.—
ПММ, 1945, т. IX, вып. 5, с. 425—432.
Флорин В. А. [1] Расчеты оснований гидротехнических сооруже¬
ний.—М.: Стройиздат, 1948.
Чаплыгин С. А. [1] Давление жесткого штампа на упругое осно¬
вание. Собрание сочинений, т. III, М.— JL: Гостехиздат, 1950,
с. 317-323.
Шерман Д. И. [1] Плоская задача теории упругости со смешанны¬
ми предельными условиями.—Труды сейсмологического пп-та
АН СССР, 1938, № 88.
[2] Смешанная задача теории потенциала и теории упругости для
плоскости с конечпым числом прямолинейных разрезов.— Докл.
АН СССР, 1940, т. 27, № 4.
[3] Смешанная задача статической теории упругости для плоских
многосвязных областей.—Докл. АН СССР, 1940, т. 28, № 1,
с. 29-32.м
[4] Об одной смешанной задаче теории упругости.— ПММ, 1943.
т. VII, с. 413-420.
ЛИТЕРАТУРА
299
Штаерман И. Я. [1] Местные деформации при сжатии упругих
круговых цилиндров, радиусы которых почти равны.— Докл.
АН СССР, 1940, т. 29, № 3, с. 182—184.
[2] Контактная задача теории упругости.— М.: Гостехиздат, 1949.
Fromm Н. [1] Berechnung des Schlupfes beim Rollen deformierbaren
Scheiben.— ZAMM, 1927, т. 7, вып. 1.
К главе II
Андрейкив А. Е., Панасюк В. В. [1] Давление системы круговых
штампов на упругое полупространство.— Докл. УССР.Сер. А,
1971, вып. 6, с. 534:—536.
Бартенев Г. М., Лаврентьев В. В. [1] Трение и износ полимеров —
М.: Химия, 1972, с. 240.
Бейтмен Г., Эрдейи А. [1] Высшие трансцендентные функции.
Т. 2.— М.: Наука, 1966.
Бородачев Η. М. [1] Вдавливание штампа с основанием в виде уз¬
кого прямоугольника в упругое полупространство.— Изв. АН
СССР, МТТ, 1970, № 4.
[2] Контактная задача для штампа с прямоугольным основанием.—
ПММ, 1976, т. 40, вып. 3.
Бородачев Н. М., Галин Л. А. [1] Контактная задача для штампа
с основанием в виде узкого прямоугольника.— ПММ, 1974, т. 38t
вып. 1.
Ватсон Г. Н., Уиттекер Е. Т. [1] Курс современного анализа. Ч. II.—
М.: Физматгиз, 1963.
Галин Л. А. [1] О гипотезе Винклера — Циммермана для балок.—
ПММ, 1943, т. VII, вып. 4.
[2] Пространственные контактные задачи теории упругости для
штампа круговой формы в плане.— ПММ, 1946, т. X, вып. 4.
[3] Контактная задача теории упругости с осевой симметрией.-—
Докл. АН СССР, 1946, т. 53, № 9.
[4] Плоская упруго-пластическая задача: Пластические области у
круговых отверстий в пластинках и балках.— ПММ, 1946, т. X,
вып. 3.
[5] О давлении штампа эллиптической формы в плане на упругое
полупространство — ПММ, 1947, т. XI, вып. 2.
[6] Оценка перемещений в пространственных контактных задачах
теории упругости— ПММ, 1948, т. XII, вып. 3.
[7] О давлении твердого тела на пластинку —ПММ, 1948, т. XII,
вып. 3.
[8] Аналогия для плоской упруго-пластической задачи.— ПММ,
1949, т. I, вып. 6.
Градштейн И. С., Рыжик И. М. [1] Таблицы интегралов, сумм, ря¬
дов и произведений.—М.: Наука, 1971.
Д'емкин Н. Б. [1] Контактирование шероховатых поверхностей.—
М.: Наука, 1970, с. 227.
Довнорович В. И. [1] Пространственные контактные задачи теории
упругости.— Изд-во Белорусского университета им. В. И. Ле¬
нина, Минск, 1959.
Журавлев В. А. [1] К вопросу о теоретическом обосновании закона
Амонтона — Кулона для трения несмазанных поверхностей.—
ЖТФ, 1940, т. 10, вып. 17.
300
ЛИТЕРАТУРА
Кочин //. Ε. [1] Влияние шага решетки на ее гидродинамические
характеристики.— ПММ, 1941, т. V, вып. 2.
Крагельский И. В. [1] Влияние различных параметров на величину
коэффициента трения несмазанных поверхностей.— ЖТФ, 1943,
т. 13, вып. 3.
Лурье А. И. [1] Некоторые контактные задачи теории упругости.—
ПММ, 1941, т. V, вып. 3.
[2] Исследование случая несимметричного давления жесткого
плоского штампа эллиптического сечения на упругом полупро¬
странстве.— Докл. АН СССР, 1939, т. 23, № 8.
ГЗ] Теория упругости.— М.: Наука, 1970.
Ляв А. [1] Математическая теория упругости.— М.— JL: ОНТИ,
1935, с. 300.
Моссаковский В. И. [1] К вопросу об оценке перемещений в про¬
странственных контактных задачах.— ПММ, 1951, т. XV, вып. 5.
Мусхелишвили Н. И. [1] Некоторые основные задачи математиче¬
ской теории упругости.— М.: Наука, 1966.
Папкович П. Φ. [1] Теория упругости.—М.: Гостехиздат, 1939.
Стретт Дж. В. (лорд Рэлей) [1] Теория звука.— М.: Гостехжздат,
ч. II, 1955.
Таблицы полиномов Чебышева Sn(x) и Сп(х).— М.: ВЦ АН СССР,
1963
Фадеев Д. К. [1] Полное решение одного класса неопределенных
уравнений третьей степени с отрицательным дискриминан¬
том.— Труды II математического съезда.— Л. — М.: Изд-во
АН СССР, 1936.
Штаерман И. Я. [1] Контактная задача теории упругости.— М.— Л.:
ОНТИ, 1949.
Boussinesque J. [1] Applications des potentiels a l’e ude de l’equilib-
re at d. mouvement des solides elastiques, 1885.
Childs Т. H. С. [1] The presistence of asperities in indentation expe¬
riments.— Wear, 1973, v. 25, pp. 3—16.
Greenwood /. A., Williamson L В. P. [1] Contact of Nominally Flat
Surfaces.— Proc. Roy. Soc., 1966, Ser. A., v. 295, p. 300.
Heine E. [1] Handbuch der Kugelfunctionen. Bd. II, 1881.
Hertz H. [1] Gesammelte werke. Bd. I, 1895, pp. 179—195.
Hobson Ε. M. [1] Sustems of spherical harmonics.— Proc. London
math. Soc., 1891, v. 22, p. 431—449.
[2] On Greens function for a circular disk, with applications of
electrostatic problems.— Cambridge Philosophical Trans, 1900,
v. 18.
Hunt R. Т., Williamson Т. В. P. [1] The real aren of contact between
plastically loaded surfaces.— Mecanique Mater, Electr. L’USURE,
1972, № 1, pp. 22-25.
Kendall КTabor D. [1] An ultrasonic study of the area of contact
between stationary and sleding surfaces.— Proc. Roy. Soc., 1971,
A 323, pp. 321—340.
Lebedev N. [1] The functions associated with a ring of oval cross-
section.— Technical Physics, 1938, № 1, pp. 3—24.
Ling F. F. T. [1] An asperity distributions of metallic surfaces.—
J. Appl. Phys., 1958, v. 29, p. 1168.
Love A. Ε. H. [1] Boussinesq’s problem for a rigid cone.— The
Quarterly Journal of Mathematics, Oxford series 10, 1939, № 39.
ЛИТЕРАТУРА
301
Michell J. Я. [11 The flexure of a circular plate.— Proc. London
Math. Soc., 1902, v. 34, pp. 223-238.
Mindlin R. D. [1] Complianse of elastic bodies in contact.— Journal
of applied Mechanics, 1949, v. 16, № 3.
Neuber H. [11 Ein neuer Ansatz zur Losung raumlicher Probleme der
Elastizitatstheorie.— ZAMM, 1934, Bd. 14, № 4, pp. 203—306.
Polya G., Szego G. [1] Unequalities for a capacity of condenser.—
American Journal of Mathematics, 1945, v. 17, № 1.
Probert S. D., Uppal A. H. [1] Deformation of single and multiple
asperities on metal surfaces.— Wear, 1972, v. 20, pp. 381—400.
Reissner E. [1] Freie und erzwungene Torsionsschwingungen des
elastischen Halbraumes.— Ingenieur-Archiv, 1937, ν. VIII, № 4,
pp. 229—245.
Sneddon /. N. [1] Boussinesg’s problem for a flatened cylinder.— Pro¬
ceedings* of the Cambridge philosophical Society, 1946, v. 42,
p. 1.
[2] Boussinesq’s problem for a rigid cone.—Proceedings of the
Cambridge philosophical Society, 1948, v. 44, p. 4.
Sommerfeld A. [11 Uber verzweigte Potentiale im Raum.— Proc. Lon¬
don math. Soc., 1897, Bd. 28, pp. 395—429.
К главе III
Абрамов В. М. [1] Проблема контакта упругой полуплоскости с
абсолютно жестким фундаментом при учете сил трения.—
Докл. АН СССР, 1937, т. 17, № 4.
Хрущов М. М., Бабичев М. А. [1] Исследование изнашивания ме¬
таллов— М.: Изд-во АН СССР, 1960.
Брызгалин Г. И. [1] К расчету на ползучесть пластинок из стек¬
лопластиков.— ПМТФ, 1963, № 4.
[2] К описанию анизотропной ползучести стеклопластиков.—
ПМТФ, 1963, № 6.
Ватсон ГУиттекер Э. [1] Курс современного анализа.— М.: Физ-
м;атгиз, т. 1, 1961; т. 2, 1962.
Галин Л. А. [1] Деформация ортотропного упруговязкого тела
в условиях плоской задачи.— Докл. АН СССР, 1967, т. 177,
№ 4.
[2] Контактные задачи теории упругости при наличии износа.—
ПММ, 1976, т. 40, вып. 6.
Галин Л. А., Горячева И. Г. [1] Осесимметричная контактная за¬
дача теории упругости при наличии износа.— ПММ, 1977, т. 41,
вып. 5.
Горячева И. Г. [1] Об одной контактной задаче для вязкоупругой
полуплоскости.— ПММ, 1970, т. 34, вып. 4.
[2] Контактная задача качения вязкоупругого цилиндра по осно¬
ванию из того же материала.— ПММ, 1973, т. 37, вып. 5.
[3] Об одном предельном случае качения цилиндра по вязкоупру¬
гому основанию.— Сб. № 1 научных работ аспирантов отд.
механики. Изд-во МГУ, 1973.
[4] Плоские и осесимметричные контактные задачи для шерохова¬
тых упругих тел.— ПММ, 1979, т. 43, вып. 1.
Дёмкин Я. Б. [1] Контактирование шероховатых поверхностей.—
М.: Наука, 1970.
302
ЛИТЕРАТУРА
Крагельский И. В., Добычин М. Н., КомбаловВ.С. [1] Основы рас¬
четов на трение и изпос.—М.: Машиностроение, 1977.
Лехницкий С. Г. [1] Анизотропные пластинки.— М.: Гостехиздат,
1947.
[2] Теория упругостас анизотропного тела.— М.: Наука, 1977.
Мелентьев П. В. [1] Механические испытания полимерных мате¬
риалов.— Пластические массы, 1961, № 12.
Митрофанов Б. П. [1] Плоская контактная задача для упругого
тела с учетом влияния поверхностного слоя — Изв. Томск,
политехи, ин-та, 1970, т. 157.
Мусхелишвили Н. И. [1] Некоторые основные задачи математиче¬
ской теории упругости.— Изд. 5-е.— М.: Наука, 1966.
Мхитарян С. М., Шекян Л. А. [1] Плоская контактная задача для
двух шероховатых упругих тел, изготовленных из степенно
упрочняющихся материалов.—Изв. АН Арм. ССР, Механика,
1977, т. 30, № 3.
Орлов А. В., Пинегип С. В. [11 Сопротивление движению при не¬
которых видах свободного качения.— Изв. АН СССР. Сер. мех.
и маш., 1961, № 3.
Попов Г. Я., Савчук В. В. [11 Контактная задача теории упругости
при наличии круговой области контакта с учетом поверхност¬
ной структуры контактирующих тел.— Изв. АН СССР, МТТ,
1971, № 3.
Рабинович А. С. [1] Плоская контактная задача для шероховатых
упругих тел.— Изв. АН СССР, МТТ, 1974, № 3.
[2] Плоская контактная задача о давлении штампа с прямолиней¬
ным основанием на шероховатую упругую полуплоскость.—
Изв. АН Арм. ССР, Механика, 1974, т. 27, № 4.
[3] Осесимметричная контактная задача для шероховатых упругих
тел.- Изв. АН СССР, МТТ, 1975, № 4.
Работное Ю. Η. [1] Равновесие упругой среды с последействием.—
ПММ, 1948, т. 12, № 1.
Развитие теории контактных задач в СССР [1].— М.: Наука, 1976.
Reinolds О. [11 On rolling friction.— Phil. Trans. Roy. Soc. London,
1876, v. 166.
Трикоми Ф. Дон:. [1] Интегральные уравнения.— М.: ИЛ, 1960.
Хантер [1] Контактная задача качения жесткого цилиндра по вяз¬
ко-упругому полупространству.— Прикл. 1^ехан., Тр. Америк,
об-ва инж.-механ. Сер. Е, 1961, т. 28, № 4.
Хирст В. [1] Износ хрупких материалов.— В сб.: Контактное взаи¬
модействие твердых тел и расчет сил трения и износа—. М.:
Наука, 1971.
Штаерман И. Я. [11 Контактная задача теории упругости.— М.—
Л.: Гостехиздат, 1949.
ИМЕННОЙ УКАЗАТЕЛЬ
Абрамов В. М. 92, 250, 301
Андрейкпв А. Е. 173, 299
Бабичев М. А. 274, 283, 301
Бартенев Г. М. 166, 299
Бегиашвили А. И. 73, 297
Бицадзе А. В. 293
Бородачев Η. М. 5, 222, 299
Брызгалин Г. И. 301
Буссинеск Ж. (Boussinesgue J.)
138, 300
Ватсон Г. Н. (Watson G. N.) 116,
185—187, 268—270, 297, 299
Вплиамсон Т. (Williamson Т. Б. Р.)
166,300
Галин Л. А. 5, 55, 126, 222, 234,
241, 297, 299, 301
Гейне (Heine Е.) 135, 300
Герц Г. (Hertz Н.) 156, 300
Глаголев Н. И. 297
Гобсон (Hobson Е. W.) 135, 206, 300
Голубев В. В. 297
Горячева 5, 241, 301
Градштейн И. С. 223, 224, 299
Гринвуд (Greenwood J. А.) 166, 300
Дёмкин Н. Б. 165, 175, 177, 286,
292, 299, 301
Добычин М. Н. 286, 292, 302
Довнорович В. И. 199, 299
Журавлев В, А. 165, 299
Заоммерфельд A. (Sommerfeld А.)
144, 301
Карцнвадзе И. Н. 297
Кендал К. (Kendall К.) 172, 300
Комбалов В. С. 286, 292, 302
Кочип Η. Е. 144, 157, 300
Крагельский И. В. 165, 286, 292,
300, 302
Лаврентьев М. А. 117, 166, 297,
299
Лебедев Н. П. 134, 300
Лехннцкий С. Г. 80, 244, 297, 302
Линг (Ling F. F. Т.) 165, 300
Лурье А. И. 127, 154, 197, 300
Львин Я. Б. 49, 297
Ляв A. (Love А. Е. Н.) 179, 300
Мелентьев П. В. 302
Миндлин P. (Mindlin К. D.) 301
Митрофанов Б. И. 286, 302
Михлин С. Г. 297
Мичелл Дж. (Michell J. Н.) 232,
301
Моссаковский В. И. 119, 198, 297,
300
Мусхелишвили Н. И. 9, 13, 15, 20,
29, 36, 38, 92, 100, 101, 134, 207,
248, 250, 297, 300, 302
Мхитарян С. М. 286, 302
Народецкий М. 3. 298
Нейбер Г. (Neuber Н.) 127, 301
Орлов А. В. 263, 302
Панасюк В. В. 173, 299
Папкович П. Ф. 127, 300
Петров В. В. 119, 198, 297
Пинегин С. В. 263, 302
Полна (Polya G.) 201, 301
Попов Г. Я. 286, 302
Привалов И. И. 118, 298
Рабинович А. С. 286, 302
Работнов Ю. Н. 244, 302
Рейсснер Э. (Reissner Е.) 179
Рыжик И. М. 223, 224, 299
Саверин М. М. 66, 67, 298
Савин Г. Н. 90, 298
Савчук В. В. 286, 302
Сегё (Szego G.) 201, 301
Снеддон (Sneddon I. N.) 301
Соколовский В. В. 298
Стретт Дж. В. (лорд Рэлей) 204,
300
Табор Д. (Tabor D.) 172, 300
Трикоми Ф. Дж. (Tricomi F. G.)
289, 295, 302
Уиттекер Е. (Witteker Е.) 116, 185 —
187, 268—270, 297, 299
Фадеев Д. К. 217, 300
Фалькович С. В. 298
Флорин В. А. 298
Хант P. (Hunt К. Т.) 166, 300
Хантер (Hunter) 261, 272
Хирст В. 273, 274
Хрущов М. М. 274, 283, 301
Чайлдс Т. (Childs Т. Н. С.) 166, 300
Чаплыгин С. А. 298
Шекян Л. А. 286, 302
Шерман Д. И. 298
Штаерман И. Я. 154, 286, 299, 302
Эрдейи А. 227, 299
Лев Александрович Галин
КОНТАКТНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
И ВЯЗКОУПРУГОСТИ
М., 1980 г., 304 стр. с илл.
Редактор А. А. Наседкин
Техн. редактор Н. В. Вершинина
Корректоры Л. Н. Боровина, В. П. Сорокина
ИБ М 11305
Сдано в набор 03.10.79. Подписано к печати 12.06.80.
Т-08173. Бумага 84x108*/з2, тип. №2. Обыкновенная гар¬
нитура. Высокая печать. Условн. печ. л. 15,96. Уч.-
изд. л. 16,49. Тираж 3500 экз. Заказ № 700. Цена
книги 2 р. 70 к.
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
4-я типография издательства «Наука»
630077, Новосибирск, 77, Станиславского, 25