Текст
КИЕВ
§
ИНТЕГРИРОВАННАЯ СИСТЕМА АНАЛИЗА КОНСТРУКЦИЙ
>
CD
Перельмутер SCAD OFFICE
ООО SCAD Soft
А.В.Перельмутер
SCAD OFFICE. РАСЧЕТ МАЧТ НА ОТТЯЖКАХ
Киев — 2004
УДК 658.512:681.3
Рекомендовано к печати кафедрой строительной механики и кафедрой
конструкций из металла, дерева и пластмасс Киевского национального
университета строительства и архитекту ры
Перельмутер А.В.
SCAD Office. Расчет мачт на оттяжках. К.: Издание ООО SCAD Soft, 2004.—
46 с.
Изложены основные теоретические положения и практические рекомендации по
выполнению расчета мачт на оттяжках в среде SCAD Office. Описаны приемы
линеаризации задачи и совместного использования результатов линейного и нелинейного
моделирования. Изложение проиллюстрировано детально разобранными примерами.
Предназначено для пользователей системы SCAD Office, может быть использовано
при изложении курсов «Строительная механика» и «Стальные конструкции» для
студентов строительных специальностей.
© Перельмутер А.В., 2004
3
Оглавление
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ.............................................6
1. Вантовые элементы...........................................6
2. Задание параметров преднапряжения.........................10
3. Варианты нагружения........................................И
4. Линеаризация модели.......................................12
5. Альтернативный способ линеаризации задачи.................13
ПРИЕМЫ РАБОТЫ С ПРОГРАММОЙ. ПРИМЕРЫ.............................15
6. Предварительные замечания.................................15
7. Описание вантовых элементов...............................17
8. Определение ветровой uai рузки............................19
9. Решение нелинейной задачи.................................22
10. Создание линеаризованных моделей..........................26
11. Динамический расчет.......................................27
12. Проверка устойчивости.....................................30
13. Объединение результатов расчета по разным моделям.........31
14. Использование упрошенной расчетной схемы ствола...........37
15. Использование секущего модуля.............................38
Заключительные замечания......................................47
Литература....................................................47
4
Часть 1
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
Мачта на оттяжках является достаточно специфическим объектом расчета,
который характеризуется следующими особенностями (см. [1], [3], [5], [7], [8]):
• нелинейной работой вантовых элементов (оттяжек);
• необходимостью задания усилий предварительного напряжения;
• необходимостью учета «эффекта силы направленной в полюс» для
передаче усилий от оттяжки на ствол;
• критичностью проверок устойчивости равновесия ствола.
Со мание адекватной расчетной модели такого объекта имеет ряд
особенностей и их описанию посвящена настоящая работа. Изложение
иллюстрируется примером расчета, к которому следует относиться именно как к
примеру, а ие как к рекомендации по проектированию.
1. Вантовые элементы
Простейшая модель вантового элемента имеет вид стержня, способного
воспринять растяжение и выключающегося из работы при появлении сжатия
(рис. 1). Этот стержень может быть установлен с зазором в односторонней
связи или же иметь преднапряжение Но > 0, что может быть интерпретировано и
как наличие отрицательного зазора, то есть До < 0.
Рис I. Односторонне работающий стержень
Два варианта диаграммы работы такого элемента в виде зависимости
продольной силы Н от увеличения расстояния между концевыми точками Л
представлены на рис. 2, где случаю по рис. 2, а) соответствует вариант с
предварительным напряжением, а случаю по рис. 2, Ь) — вариант системы с
зазором
Тангенс угла наклона диаграммы равен величине EA/L (ЕА— жесткость
стержня на растяжение, L — длина стержня).
Такая упрощенная модель вантового элемента на самом деле представляет
собой упругую одностороннюю связь и не учитывает эффект распрямления
провисшей оттяжки при смещении ствола мачты, что допустимо лишь в случае
6
невысоких мач| с сильно пагянузыми и, следовательно, мало провисающими
о пялками.
Более адекватный по постановке задачи вариант расчетной модели
ваиювою cicMenia ио I ибкая нить с малой стрелкой провисания. В исходном
состоянии, характеризуемом температурой То и натяжением Но, нить нагружена
некоюрон поперечной нагрузкой qo(x), а при удлинении хорды на величину Л,
нмепснии поперечной нагрузки до величины q(x) и температуры до значения Т
княжение с1анов!пся равным //.
Уравнение, связывающее эти величины, для пологих нитей имеет вид
(H-H0)L D Do
-----Fo(/ -T0)L---уЧ----- ,
2Н2 2Н%
(1)
ЕА
ле
D = / e2(x)dr, Do = f C02(x)dx, (2)
о о
£Л-г) - поперечная сила, возникающая в шарнирно опертой балке пролета L от
действия нагру зки q(x), направленной поперек хорды вантового элемента;
£?о(т) — го же, но от нагру зки qo(x)\
а - коэффициент температурного расширения;
Е - модуль упру гости материала нити;
А - площадь поперечного сечения нити.
1.СЛИ ввести безразмерный параметр К, характеризующий влияние
поперечной нагрузки на нп!ь
2L(EA)2
и безразмерные переменные
7
b=A/L, 50 = Д<А, Г=Н/(Е4), (4)
где обозначено
д,=^_а(Т_вд^Д. (5)
то у равнение (1) приобретает форму
6 = '-4-^0- (6)
Г
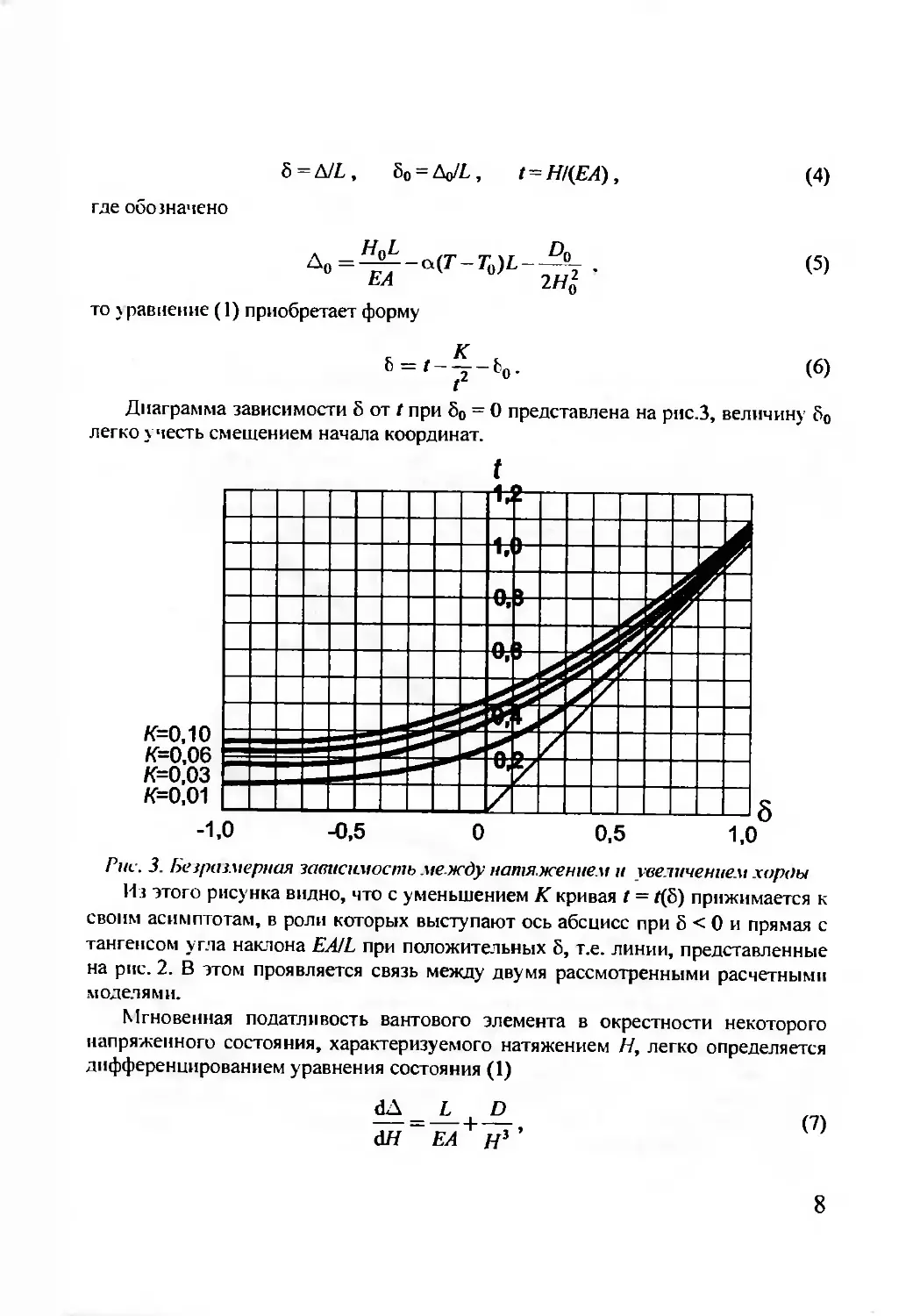
Диаграмма зависимости 5 от t при 60 = О представлена на рис.З, величину б0
легко учесть смещением начала координат.
Рис. 3. Безразмерная зависимость между натяжение м и увеличением хорды
Из этого рисунка видно, что с уменьшением К кривая t — Г(б) прижимается к
своим асимптотам, в роли которых выступают ось абсцисс при 5 < 0 и прямая с
тангенсом утла наклона EA/L при положительных 5, т.е. линии, представленные
на рис. 2. В этом проявляется связь между двумя рассмотренными расчетными
моделями.
Мгновенная податливость вантового элемента в окрестности некоторого
напряженного состояния, характеризуемого натяжением Н, легко определяется
дифференцированием уравнения состояния (1)
— = — + (7)
dH ЕА Н3
8
и, с.'1е'1ок:ие.'1ыю, матрица .мгновенной жесткости такого элемента имеет ипл
К(/7) = 1 1 L D L D ЕЛ Н3 ЕА Н3 1 1 L D L D ЕА И3 ЕА И3 (8)
В опяжечпо.м у тле (рис. 4,</) совместно работают несколько ттяжек и
диаграмма зависимости «сила-смещение» имеет более сложный характер. Если
оттяжки сильно преднаиряжены, то первоначальная жесткость узла,
определяемая тангенсом угла наклона р, с ростом силы R падает, поскольку
постепенно ослабевает одна из оттяжек (рис. 4,6). Если же оттяжки установлены
с малым преднапряжеиием, то угол р увеличивается при увеличении силы R
поскольку .хотя бы одна из обвисших оттяжек распрямляется.
Рис. 4. Работа оття.ясечного ума
Таким образом, видно, что наличие вантовых элементов в расчетной схеме
мачты делает задачу расчета нелинейной. Надо сказать, что ванты не являются
единственным источником порождения геометрической нелинейности, второй
источник нелинейности связан с тем обстоятельством, что имеется сильно
сжатый ствол мачты. Учет влияния продольных сил на изгибающие моменты в
сжатых злементах системы (явление продольного изгиба) приводит к
необходимости проведения расчетов по деформированной схеме, т.е. вновь-таки
к решению нелинейной задачи.
9
2. Задание параметров преднапряжения
При расчете вантовых систем важно правильно задать отсчетное состояние,
которое характеризуется начальными значениями поперечных нагрузок на
вантовых элементах <?0 (как правило, это перпендикулярная к хорде вантового
элемента составляющая нагрузки от собственного веса ванты) и значениями
натяжений Но > 0.
Основная сложность состоит в том, что все значения Но должны
соответствовать равновесному состоянию системы, в котором предварительные
напряжения создают некоторую картину внутренних сил, соответствующую
начальной внешней нагрузке qn (в частном случае нулевой внешней нагрузке).
Обычно существует множество возможных равновесных состояний системы,
каждое из которых отвечает своему распределению усилий предварительного
напряжения в вантах HOi (i = 1,...л»), где т - количество вант в системе. В связи
с этим при проектировании вантовых конструкций перед инженером стоит
задача выбора рационального начального напряженного состояния из множества
допустимых, основываясь на некоторых критериях оптимальности и
конструктивных ограничениях. Сами эти критерии и ограничения могут
варьироваться в зависимости от конкретной проектной задачи.
При проектировании мачтовых
конструкций обычно требуют, чтобы ствол
мачты находился в безизгибном состоянии и
озтяжечные узлы имели достаточную
жесткость. При этом необходимо помнить,
что, задав избыточную величину
преднапряжения, мы передаем на ствол
дополнительные усилия сжатия, что может
привести к преждевременной потере
устойчивости.
Задание преднапряжений, соответствую-
щих состоянию равновесия, не представляет
труда в конструкциях мачт с симметрично
расположенными оттяжками, когда в каждом
ярусе эти значения необходимо попросту
сделать одинаковыми. Однако, в более
Рис. 5. Неравновесное
преднапряжение
сложных ситуациях здесь необходимо
выполнить некоторые предварительные
расчеты.
Для облегчения этих расчетов при работе с вантовыми элементами в системе
SCAD предусмотрена следующая операция — ванты удаляются и усилия
преднапряжения прикладываются к оставшейся части конструкции (для мачты
— к стволу). Если усилия преднапряжения окажутся неуравновешенными, то
система будет сильно деформирована (ствол изогнется). Просматривая значения
10
перемещений можно увидеть к чему приводит нарушение условии
еамоу равновешентюсти нредпапряжений, в частности в какой мере пару шаются
грсбовапия о безнзгнбном состоянии ствола мачты (рис. 5).
Может оказаться, что после удаления вант система окажется изменяемой,
чк> характерно для мачт с шарнирным опиранием ствола на фундамент. Чтобы
у тип от пой неприятности необходимо в опорном шарнире или же в каким-либо
трутом месте .поставить упругую связь с малой жесткостью, которая с одной
стороны сделала бы систему неизменяемой, а с другой (в силу малости своей
жесткости) практически не повлияла бы на работу системы.
3. Варианты нагружения
Поскольку в нелинейной системе не действует принцип суперпозиции, то
нсобхотимо выбирать самостоятельно все необходимые случаи комбинаций
тейству тощих назру зок:
• собственный вес;
• ветровая нагрузка по опасным направлениям;
• । ололедное затру жение с ветром по опасным направлениям;
• температурные воздействия.
Для мачт с тремя и четырьмя оттяжками в плайе рекомендуется рассмотреть
характерные направления действия ветровой натрузки, показанные на рис. 6.
Следует сказать несколько слов о варианте для расчета мачт с тремя
от тяжками в плане. Он часто оказывается расчетным по устойчивости поскольку
оттяжка 2 оказывается провисшей и практически не работает, а оттяжка 1 не
воспринимает нагрузку в направлении, ортогональном ее плоскости
Для всякой нелинейной задачи, в том числе и для расчета мачты, полезно
промоделировать цикл «нагрузка - разгрузка». Сопоставление окончательного
результата (после разгрузки) с исходным состоянием дает прекрасную оценку
точноегн выполненного расчета.
И
Кроме того, можно потребовать, чтобы расчет выполнялся не до расчетного
значения нагрузок, а, например, до их полуторного значения. Если такой расчет
будет доведен до конца (не будет обнаружена вырожденность задачи), то это
значит, что фактически выполнено требование об обеспечении коэффициента
запаса устойчивости А/=1,5 (п.16.13 СНиП 11-23-85* требует, чтобы kv >1,3), хотя
его точное значение останется неизвестным.
4. Линеаризация модели
Кроме выполнения статических расчетов требуется и проведение расчетов
на свободные колебания, поскольку в противном случае невозможно определить
пульсационную составляющую ветровой нагрузки, выполнить расчет на
сейсмические воздействия и т.д.
Вместе с тем, спектральный анализ системы (определение частот и форм ее
свободных колебаний) имеет смысл только в линейной постановке. В
нелинейных же задачах можно говорить о разложении движения системы по
формам свободных колебаний в окрестности изучаемого равновесного
положения при линеаризации поведения системы в этой окрестности.
Определение напряженно-деформированного состояния (НДС) системы при
статическом ее нагружении должно выполняться с учетом отмеченных выше
геометрически нелинейных эффектов. При динамическом же анализе, зная НДС
конструкции от действующих статических нагрузок, необходимо построить
динамическую модель так называемой линеаризованной системы.
Под этим термином понимается конструкция, работающая в геометрически
линейной постановке, но учитывающая достигнутый уровень усилий в вантах в
состоянии, предшествующем линеаризации, а также достигнутый уровень
усилий сжатия в соответствующих сжатых элементах расчетной схемы.
Обычно под линеаризованной системой понимается исходная система, в
которой все составляющие ее элементы рассматриваются в линейной
постановке, но с касательными (мгновенными) матрицами жесткости.
Построение такой системы можно выполнить путем замены вантовых
элементов стержнями, жесткость которых вычисляется по формуле
— + z±
ЕА LH3
которая легко получается из (8) и учитывает тот факт, что вантовый элемент
может быть нагружен в двух плоскостях.
Для линеаризованной системы можно выполнить расчет на устойчивость.
Коэффициент запаса устойчивости, вообще говоря, будет отличаться от того,
который можно получить увеличивая интенсивность нагрузки на нелинейную
систему, поскольку в линеаризованной системе «заморожены» жесткости
вантовых элементов. Но расчет линеаризованной системы может дать форму
12
потери устойчивости, что окажется важным при выборе способа усиления
недостаточно устойчивой мачты.
5. Альтернативный способ линеаризации задачи
Ранее под линеаризованной системой понималась исходная система, в
которой все вантовые элементы рассматриваются в линейной постановке с
касательными (мгновенными) матрицами жесткости.
Рис. 7. Линеаризация по методу секущих
Можно использовать другой способ линеаризации, когда используются
секущие модули (рис. 7.а). В этом случае по результатам нелинейного расчета
определяются перемещения оттяжечных узлов z, и те силы R,, которые вызвали
эти смещения (последние в системе SCAD могут быть определены в режиме
«Нагрузка от фрагмента схемы»). Тогда величины Ct = Rt I будут равны
жесткостям эквивалентных пружин, которые могут быть установлены взамен
оттяжек в линеаризованной системе (рис. 7.6).
13
Чтобы иметь возможность получить суммарный результат расчета на
статические и динамические нагружения использоваться режим «Вариации
моделей» системы SCAD. Но для этого в нелинейной и в линейной задаче
необходимо иметь полный комплект одинаково пронумерованных элементов,
только некоторые из них (отмеченные пунктиром на рис. 8) выключаются из
работы, для чего ей присваивается нулевая жесткость.
Каждый из представленных способов линеаризации имеет свои достоинства
и недостатки. В частности, метод касательных жесткостей легче поддается
автоматизации1, а метод секущих жесткостей в большей мере соответствует
традиции выполнения расчетов вручную [5,7, 8].
1 Режим автоматического построения линеаризованной схемы программно реализован не
во всех версиях системы SCAD, он имеется в версиях 7.33 и более старших. В связи с
этим при дальнейшем изложении мы продемонстрируем ручной способ линеаризации.
14
Часть 2
ПРИЕМЫ РАБОТЫ С ПРОГРАММОЙ. ПРИМЕРЫ
6. Предварительные замечания
При расчете мачт в системе SCAD Office в основном используются обычные
приемы работы с программным комплексом [6]. Определенные особенности
имеются в методах задания исходных данных об оттяжках, а также в создании и
использовании линеаризованной модели конструкции. Далее эти особенности
описываются совместно с рассмотрением характерных примеров,
заимствованных из практики реального проектирования. Что касается обычных
проблем построения расчетной схемы и задания исходных данных, то
предполагается, что читатель владеет необходимыми навыками работы в среде
SCAD Office и соответствующие вопросы подробно здесь не разбираются.
В качестве примера рассматривается
мачта высотой 105,75 м с двумя ярусами
оттяжек. Ствол мачты — сквозная
трехгранная решетчатая конструкция с
поясами и распорками трубчатого сечения
и крестовыми раскосами из круглой стали.
Ствол набирается из секций длиной 6,75 м
(рис. 9), для поясов используется труба
0159x10 для распорок — 057x6, диаметр
раскосов 28 мм.
Ствол опирается на фундамент
шарнирно. Оттяжки из стального каната
диаметром 27 мм расположены полярно
симметрично и крепятся к стволу на
отметках 45,0 и 92,25 м, а к анкерным
фундаментам — на расстоянии 30,0 и 61,5
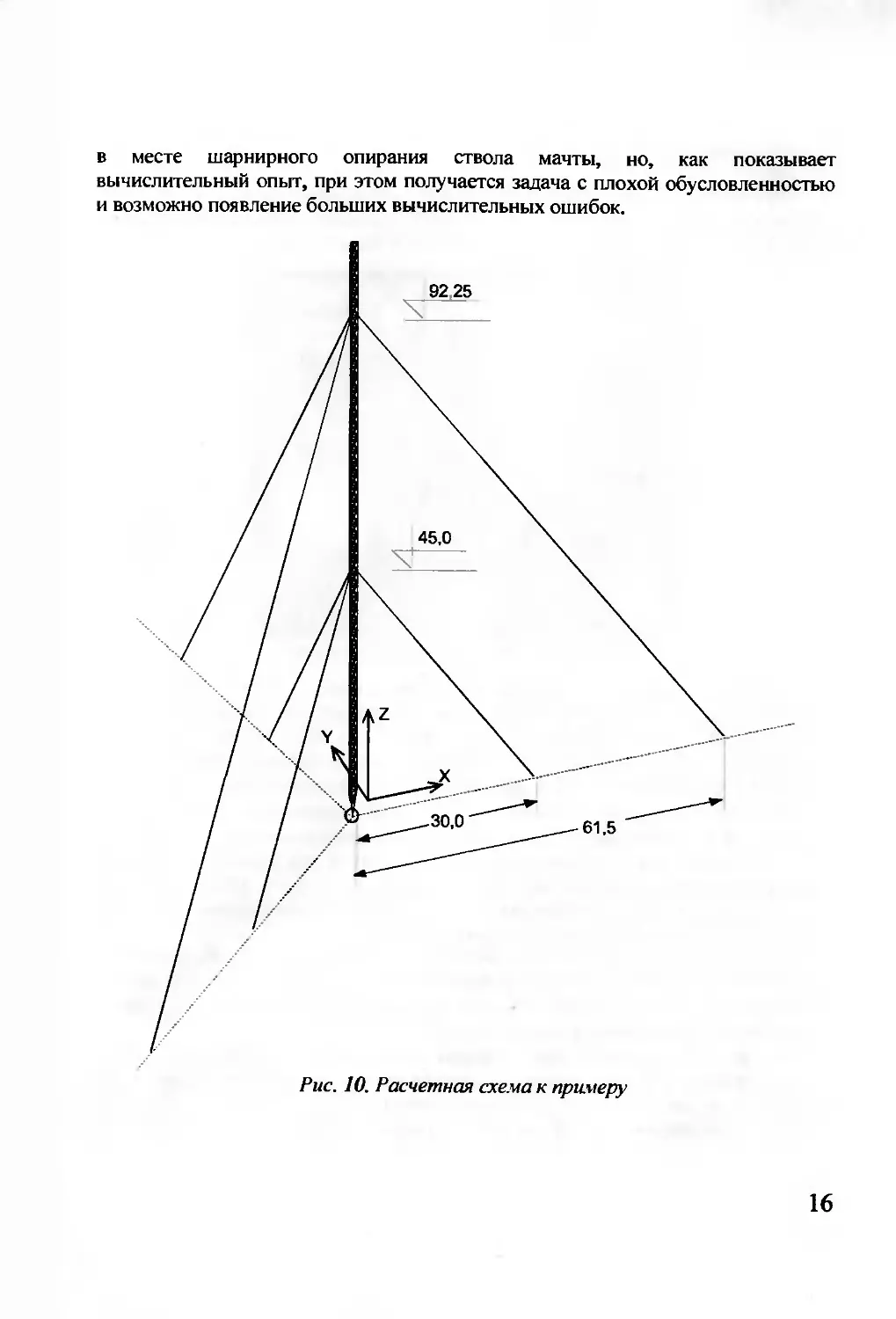
м от оси ствола. Расчетная схема показана
на рис. 10.
Как было указано в конце параграфа 2,
необходимо обеспечить возможность
решения вспомогательной задачи об
уравновешивании заданных усилий
преднапряжения.
Для этого в расчетную схему на вершине мачты введены упругие связи
очень малой жесткости (0,001 тс/м), препятствующие горизонтальным
смещениям. Можно было бы ввести упругие связи поворота с малой жесткостью
15
в месте шарнирного опирания ствола мачты, но, как показывает
вычислительный опыт, при этом получается задача с плохой обусловленностью
и возможно появление больших вычислительных ошибок.
16
7. Описание вантовых элементов
Н' I
-=sJ Данные об оттяжках задаются в окне «Характеристики вант» (рис. 11),
доступ к которому открывает кнопка «Задание данных для вантового элемента»
в разделе «Узлы и элементы» инструментальной панели комплекса.
Рис. 11. Окно «Характеристики вант»
Следует помнить, что модуль упругости канатов, который необходимо
задавать по СНиП П-23-81*, в версиях SCAD, предшествовавших 7.31-R4, не
присутствует в списке материалов и его задают вручную. Необходимо также
обязательно задать объемный вес, поскольку предполагается, что в момент
создания преднапряжения на оттяжку действует ее собственный вес.
Основные проблемы возникают с заданием преднапряжения. Так, например,
в мачте, показанной на рис. 12 первоначальное преднапряжение было задано так,
что не выполнялись условия равновесия. При этом под влиянием разности
неуравновешенных усилий в узлах ствол отклоняется на 3,1 м. После уточнения
значений парметров преднапряжения в соответствии с равновесным состоянием
оказалось, что ствол отклоняется только на 0,041 м.
Если пользователь не уверен в точности задания и хотел бы себя проверить,
то он может выполнить нелинейный расчет мачты на очень малую нагрузку (см.
в следующем разделе). Тогда результатом такого расчета окажется состояние
мачты под воздействием преднапряжения.
Для рассматриваемого нами примера проблема уравновешивания усилий
преднапряжения решается просто в силу симметрии конструкции, однако здесь
возникает другая задача уже не только расчетного характера — оптимизация
значений преднапряжения. При ее решении можно, например, исходить из того,
17
что все оттяжки получают одинаковые относительные стрелки прогиба, которые
определяются по формуле
VL = yAsmaL/(8Ho),
где L — длина оттяжки; у —объемный вес оттяжки; А — площадь ее
поперечного сечения; a — угол наклона оттяжки к вертикали; Но — усилие
преднапряжения.
Рис. 12. Отклонение ствола мачты при неравновесных параметрах
преднапряжения
В рассматриваемом примере мы приняли значение fiJL = 0,05. Вычисления
представлены в табл. 1.
______________ Таблица 1
Ярус оттяжек L, м sina у-А, кг/м Но, кг
Расчет Принято
1 110,44 0,556863 4,5 690,3 700
2 49,97 0,45027 4,5 252,6 250
18
8. Определение ветровой нагрузки
Мачта набирается из сквозных трехгранных секций с расстоянием в осях
между поясами 1350 мм (рис. 9). Для определения аэродинамических коэффици-
ентов используется схема 17 из приложения 4 к СНиП 2.01.07-85*, в
соответствии с которой аэродинамический коэффициент, отнесенный к площади
контура наветренной грани для треугольной сквозной призмы, равен
С, = 0,9(1 +11)0..
Аэродинамические коэффициенты Cxi отдельных элементов конструкции
принимаем равными 1,2 как при числе Г йнольдса не превышающем 1,5x10s.
Тогда для плоской грани
Сх = 1,2х(2х 168x6759 + 3x57x1182 + 6х28х2620)/(1518х6750)
= 1,2x0,283 = 0,34,
где значение 0,283 является коэффициентом сквозности <р. Этому коэффициенту
соответствует значение т] = 0,65 и, следовательно,
О = 0,9х(1 + 0,65)х0,34 = 0,112.
Для мачты, располагающейся в Ш-ем ветровом районе (w0 — 38 кгс/м2) на
местности типа В, в соответствии с п.6.7 СНиП 2.01.07-85* имеем расчетные
нагрузки, подсчет которых приведен в табл. 2.
Таблица 2
Высота (м) Коэффи- циент к Расчетная нагрузка на 1 метр высоты: 1,4x38x0,112x1,68x1,0х к= 10,01 х к (кгс/м) Приведенная к одному поясу
5 0,50 5,0 1,67
10 0,65 6,5 2,17
20 0,85 8,5 2,83
30 0,97 9,7 3,23
40 1,10 11,0 3,67
50 1,20 12,0 4,00
60 1,30 13,0 4,33
70 1,37 13,7 4,57
80 1,45 14,5 4,83
90 1,52 15,2 5,07
100 1,60 16,0 5,33
В этой таблице подсчитаны и нагрузки, приведенные к одному поясу ствола
мачты, поскольку именно в такой форме их удобно задавать в системе SCAD.
Для оттяжек в расчете обычно принимается равномерно распределенная по
хорде нагрузка, соответствующая высоте 2/3 от отметки лацменного узла [5, 8],
т. е на высотах 60 и 30 метров. Сама погонная нагрузка на оттяжку, казалось бы,
может быть подсчитана в соответствии с рекомендациями схемы 18 приложения
4 к СНиП 2.01.07-85*, однако она соответствовала бы только случаю действия
ветра в плоскости провисания оттяжки (нагрузка qz на левой оттяжке по рисунку
19
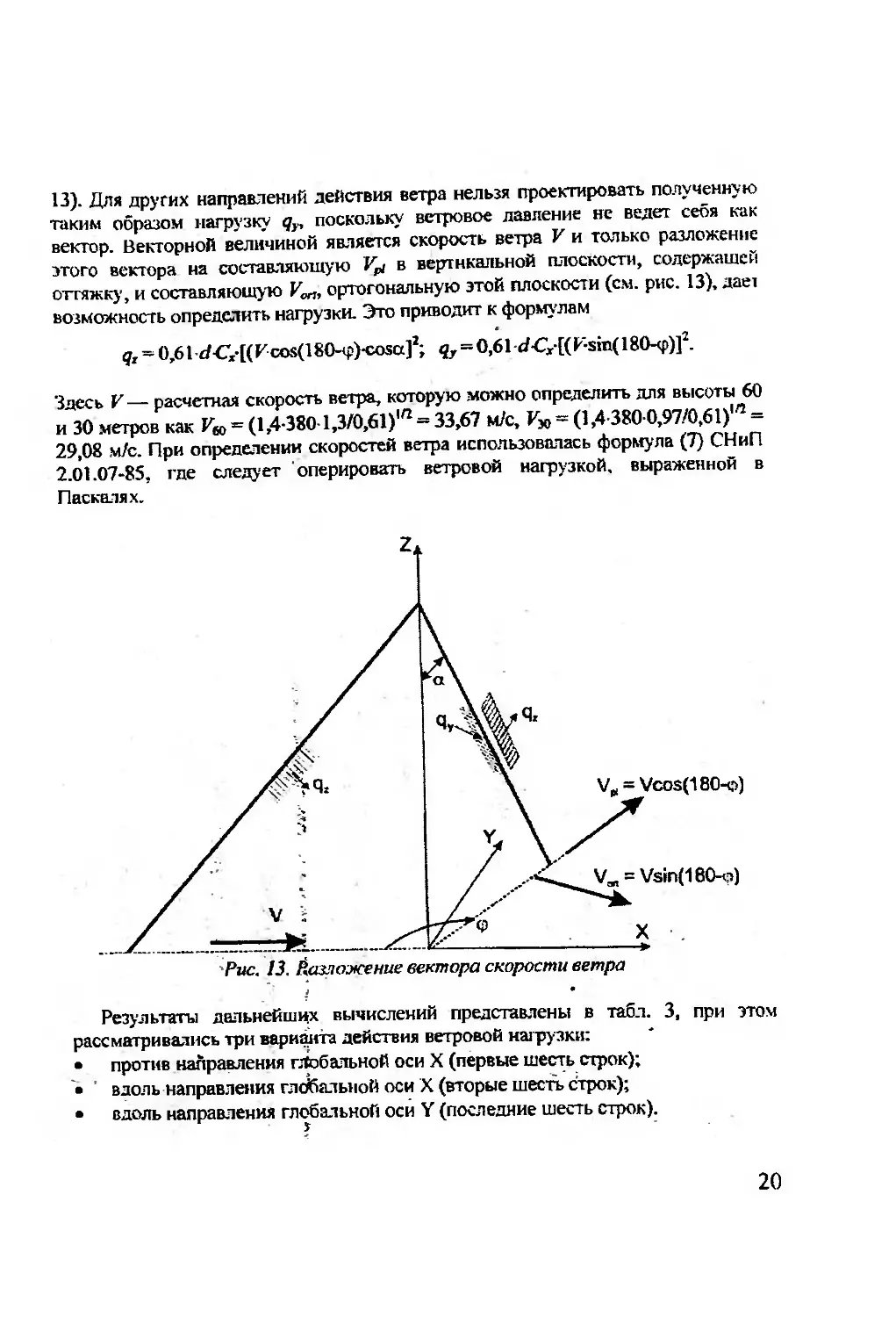
13). Для других направлений действия ветра нельзя проектировать полученную
таким образом нагрузку qr, поскольку ветровое давление не ведет себя как
вектор. Векторной величиной является скорость ветра V и только разложение
этого вектора на составляющую Vpi в вертикальной плоскости, содержащей
оттяжку, и составляющую V^, ортогональную этой плоскости (см. рис. 13), дает
возможность определить нагрузки. Это приводит к формулам
q, ~ 0,61d<;-[(rcos(180-(₽)-cosa]2; qr = 0,61 </-Сх[(K-sin(180-<p)]2.
Здесь V— расчетная скорость ветра, которую можно определить для высоты 60
и 30 метров как У№ = (1,4-380 1,3/0,61)'п = 33,67 м/с, F» = (1,4-380-0,97/0,61),я =
29,08 м/с. При определении скоростей ветра использовалась формула (7) СНиП
2.01.07-85, где следует оперировать ветровой нагрузкой, выраженной в
Паскалях.
Результаты дальнейших вычислений представлены в табл. 3, при этом
рассматривались три варианта действия ветровой нагрузки:
• против направления глобальной оси X (первые шесть строк);
• вдоль направления глобальной оси X (вторые шесть строк);
• вдоль направления глобальной оси Y (последние шесть строк).
20
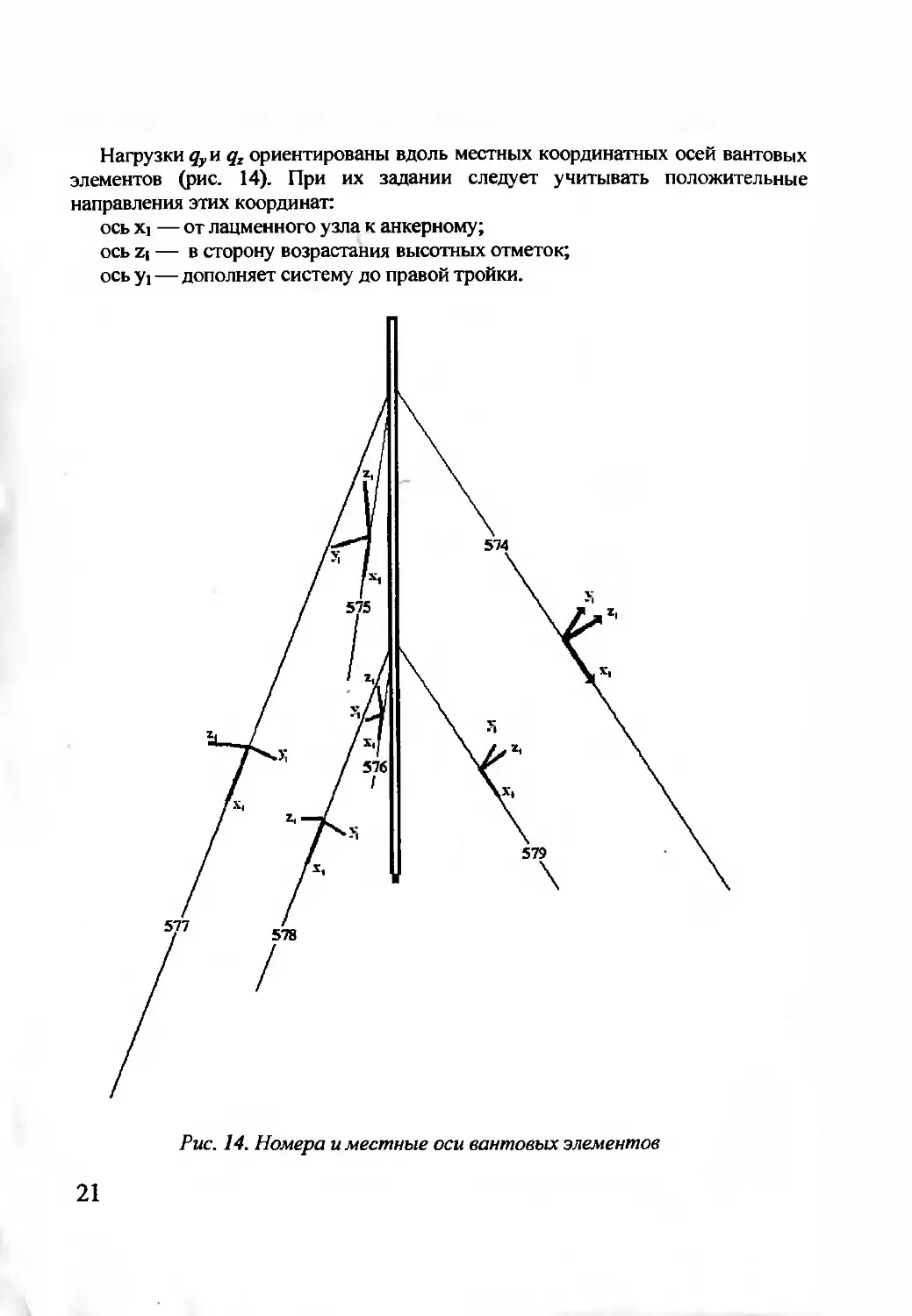
Нагрузки qyH qz ориентированы вдоль местных координатных осей вантовых
элементов (рис. 14). При их задании следует учитывать положительные
направления этих координат:
ось X] — от лацменного узла к анкерному;
ось Z| — в сторону возрастания высотных отметок;
ось yi — дополняет систему до правой тройки.
Рис. 14. Номера и местные оси вантовых элементов
21
Таблица 3
Номер V, м/с Ф, град Vpi, м/с Уш* м/с q„ кгс/м кгс/м
574 33,67 0 -33.670 0.000 + 1.400 0,000
575 33,67 120 16,836 29,159 - 0,350 - 1,722
577 33,67 240 16,836 -29,159 - 0,350 +1,722
579 29,08 0 -29,080 0,002 +1,045 0,000
576 29,08 120 14,541 25,184 - 0,261 -1,284
578 29,08 240 14,541 -25,184 -0,261 + 1,284
574 33,67 180 33,670 0,000 - 1,400 0,000
575 33,67 60 -16,834 29,160 + 0,350 + 1,722
577 33,67 300 -16,834 -29,160 + 0,350 - 1,722
579 29,08 1801 29,080 0,000 - 1,045 0,000
576 29,08 60 -14,539 25,185 + 0,261 + 1,284
578 29,08 300 -14,539 -25,185 + 0,261 -1,284
574 33,67 90 0,001 33,670 0,000 - 2,296
575 33,67 150 29,159 16,835 - 0,350 + 0,574
577 33,67 270 0,001 -33,670 + 0,350 - 0,574
579 29,08 90 0,001 29,080 0,000 - 1,712
576 29,08 150 25,184 14,540 - 0,261 + 0,428
578 29,08 270 0,001 -29,080 + 0,261 -0,428
Эти данные учтены при формировании знаков нагрузок qy и q2, показанных в
последних двух столбцах табл. 3.
9. Решение нелинейной задачи
В соответствии с общими правилами [6] для решения нелинейной задачи
следует задать данные, представляемые в диалоговом окне «Управление
шаговым процессом» (рис. 15), которое открывается из раздела «Специальные
исходные данные» дерева проекта.
Нелинейное загружение 1 представлено здесь как совокупность двух
воздействий: линейного загружения 1 («Собственный вес»2) и линейного
загружения 2 («Ветер на оттяжку» действующий вдоль оси X в направлении
уменьшения координат). Нелинейное загружение 2 представлено совокупностью
линейного загружения 1 и линейного загружения 3 («Ветер против оттяжки»,
действующий вдоль оси X в направлении возрастания координат). Нелинейное
загружение 3 представлено совокупностью линейного загружения 1 и линейного
загружения 4 («Ветер поперек оттяжки», действующий вдоль оси У в
направлении возрастания координат). Наконец, нелинейное нагружение 4
2 Необходимо заметить, что при создании загружения “Собственный вес» следует
исключить вантовые элементы, поскольку для них нагрузка от собственного веса
учитывается автоматически при определении состояния преднапряжения.
22
представлено только линейным нагружением 1 и выполняется с коэффициентом
нагружения
загружений
значения.
0,01 в один шаг для проверки заданного преднапряжения. Для
1—3 величина шага роста нагрузки выбрана как 0,1 от общего
Рис. 15. Диалоговое окно «Управление шаговым процессом»
В системе SCAD можно, вообще говоря, использовать три метода решения
нелинейной задачи:
• простой шаговый - на каждом шаге решается линеаризованная задача, в
которой жесткость вантового элемента определяется при значении
натяжения, полученного на предыдущем шаге;
• шаговый с итерационным уточнением — здесь учитывается, что результат
решения на каждом шаге может быть неточным и выполняется его
итерационное уточнение, но жесткости все равно принимаются по
предыдущему шагу;
• шагово-итерационный - отличается от предыдущего тем, что жесткости
вантовых элементов пересчитываются на каждой итерации.
В рассматриваемом примере мы остановились на выборе шагово-
итерационный метода с десятью шагами роста нагрузки и не более чем с
десятью итерационными уточнениями, что оказалось вполне достаточным. Об
этом свидетельствует протокол решения задачи, из которого видно, что для
достижения заданной точности не понадобилось более семи итерационных
уточнений. Но следует помнить, что общих рекомендаций по выбору метода не
существует и в сложных случаях не стоит ограничиваться только одним
методом. Для этого можно повторить задание нелинейного загружения под
другим номером и заказать в нем решение другим способом.
23
Расчет дал следующие значение перемещений узла 130, расположенного на
вершине мачты:
Номер загружен ия 11еремещения, мм
X Y Z
1 -944 -7
2 1582 1
3 -221 1285 -12
Из этой таблицы видно, что в загружениях 2 и 3 перемещение вершины
мачты превышают допускаемую п.16.8 СНиП П-23-81* предельное значение
/7/100 (и это без учета пульсационной составляющей ветрового нагружения).
Необходимо увеличить жесткость мачты, что можно сделать повысив
преднапряжение.
Новые значения преднапряжения увеличены в полтора раза и взяты равными
0,375 Т для нижнего яруса оттяжек и 1,05 Т — для верхнего. Исходные данные
этой задачи содержатся в файле E1-MNL.SPR, который представлен на дискете.
На рис. 16 по результатам нового расчета показаны деформированные схемы
при трех основных загружениях, численные значения перемещений узлов ствола
представлены в табл. 4, значения усилий в вантах — в табл. 5. Другие
результаты можно получить самостоятельно, решив задачу E1-MNL.SPR как
нелинейную.
Рис.16. Перемещения в загружениях 1-3 задачи E1-MNL.SPR
24
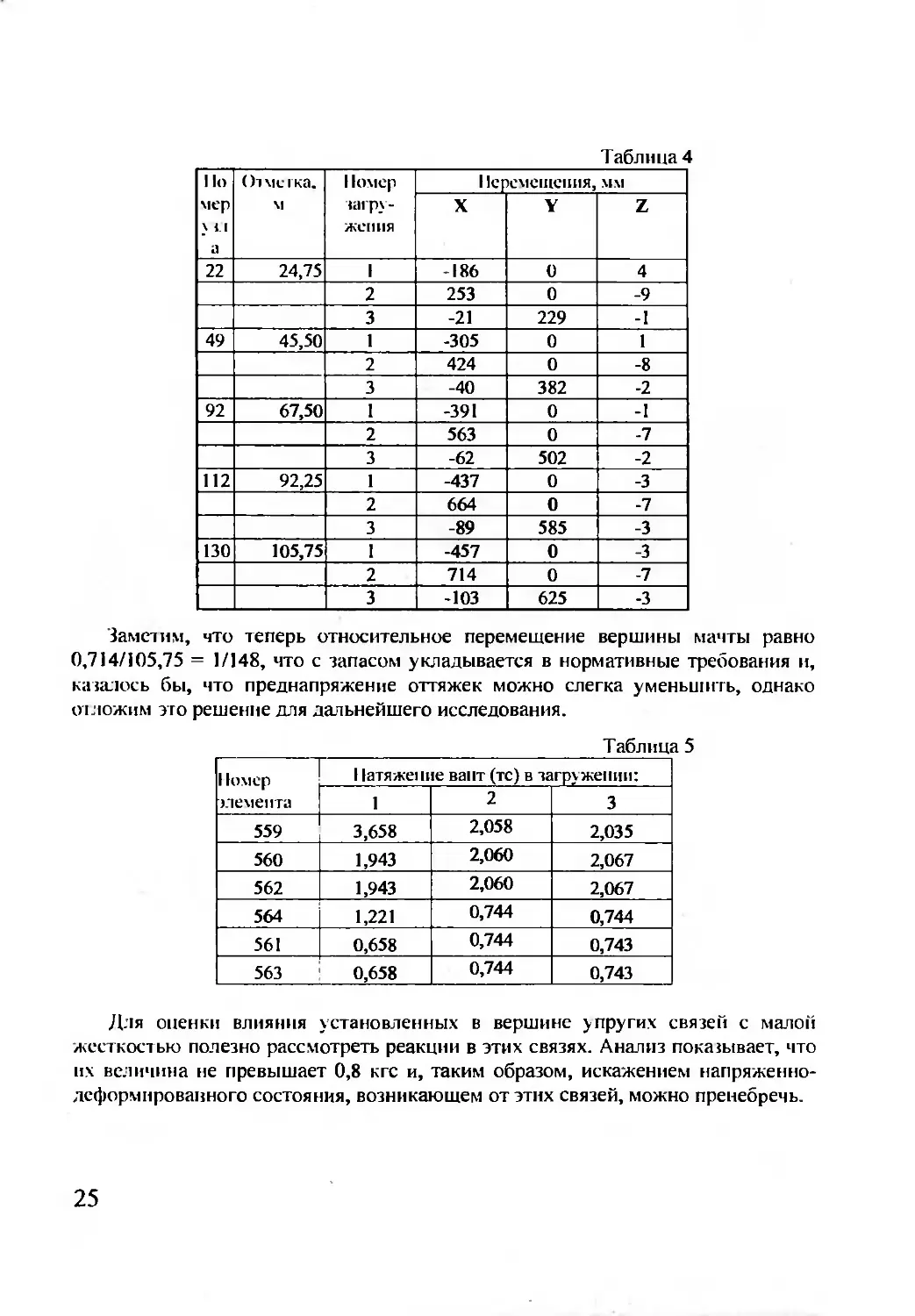
Таблица 4
По мер \ 4.1 а От мс-гка. м 11омер загру- жспия 11еремс1цепия, мм
X Y Z
22 24,75 1 -186 0 4
2 253 0 -9
3 -21 229 -1
49 45,50 1 -305 0 1
2 424 0 -8
3 -40 382 -2
92 67,50 1 -391 0 -1
2 563 0 -7
3 -62 502 -2
112 92,25 1 -437 0 -3
2 664 0 -7
3 -89 585 -3
130 105,75 1 -457 0 -3
2 714 0 -7
3 -103 625 -3
Заметим, что теперь относительное перемещение вершины мачты равно
0,714/105,75 = 1/148, что с тапасом укладывается в нормативные требования и,
казалось бы, что преднапряжение оттяжек можно слегка уменьшить, однако
отложим это решение для дальнейшего исследования.
Таблица 5
11омср элемента 11атяжеиие вант (тс) в загружеиии:
1 2 3
559 3,658 2,058 2,035
560 1,943 2,060 2,067
562 1,943 2,060 2,067
564 1,221 0,744 0,744
561 0,658 0,744 0,743
563 0,658 0,744 0,743
Для оценки влияния установленных в вершине упругих связей с малой
жесткостью полезно рассмотреть реакции в этих связях. Анализ показывает, что
их величина не превышает 0,8 кгс и, таким образом, искажением напряженно-
деформированного состояния, возникающем от этих связей, можно пренебречь.
25
10. Создание линеаризованных моделей
В линеаризованной задаче оттяжка моделируется стержнем с приведенной
жесткостью на растяжение-сжатие, которая вычисляется по формуле (9).
Поскольку в ней фигурируют значения натяжений вантовых элементов,
различные для разных загружений, то будем создавать три линеаризованные
расчетные модели, соответствующие интересующим нас загружениям I - 3.
Подсчет эквивалентной жесткости представлен в табл. 6.
При вычислениях учитывалось первоначальное значение ЕА = 9156,11т и
длины оттяжек по хорде 110,44м (верхний ярус) и 53,57м (нижний ярус), кроме
того, в составе местной нагрузки qz учтена составляющая от собственного веса.
У казанные в табл. 6 значения DJL и DJL увеличены в 10000 раз.
Величины интегралов (2) в случае нагрузок, равномерно распределенных по
хорде вантового элемента, подсчитываются по простой формуле
7 <-3 2 3
Dy = f =%-; dz = f a2«dx=(io)
*J 1Z Iz
о 0
Полезно заметить, что для линеаризации модели совсем не требуется
удалять оттяжку и заменять ее стержнем — просто после задания вантовым
элементам жесткости ЕА следует выполнить линейный расчет, во время
которого вантовый элемент ведет себя как стержень. Само по себе задание
упомянутой жесткости реализуется заданием новой площади поперечного
сечения, которая представлена в последнем столбце табл. 6. Ввести новые
значения удобно с помощью изменения жесткости в маркере «Информация об
элементе», если воспользоваться режимом «Численно-аналитическое описание»
(рис. 17).
26
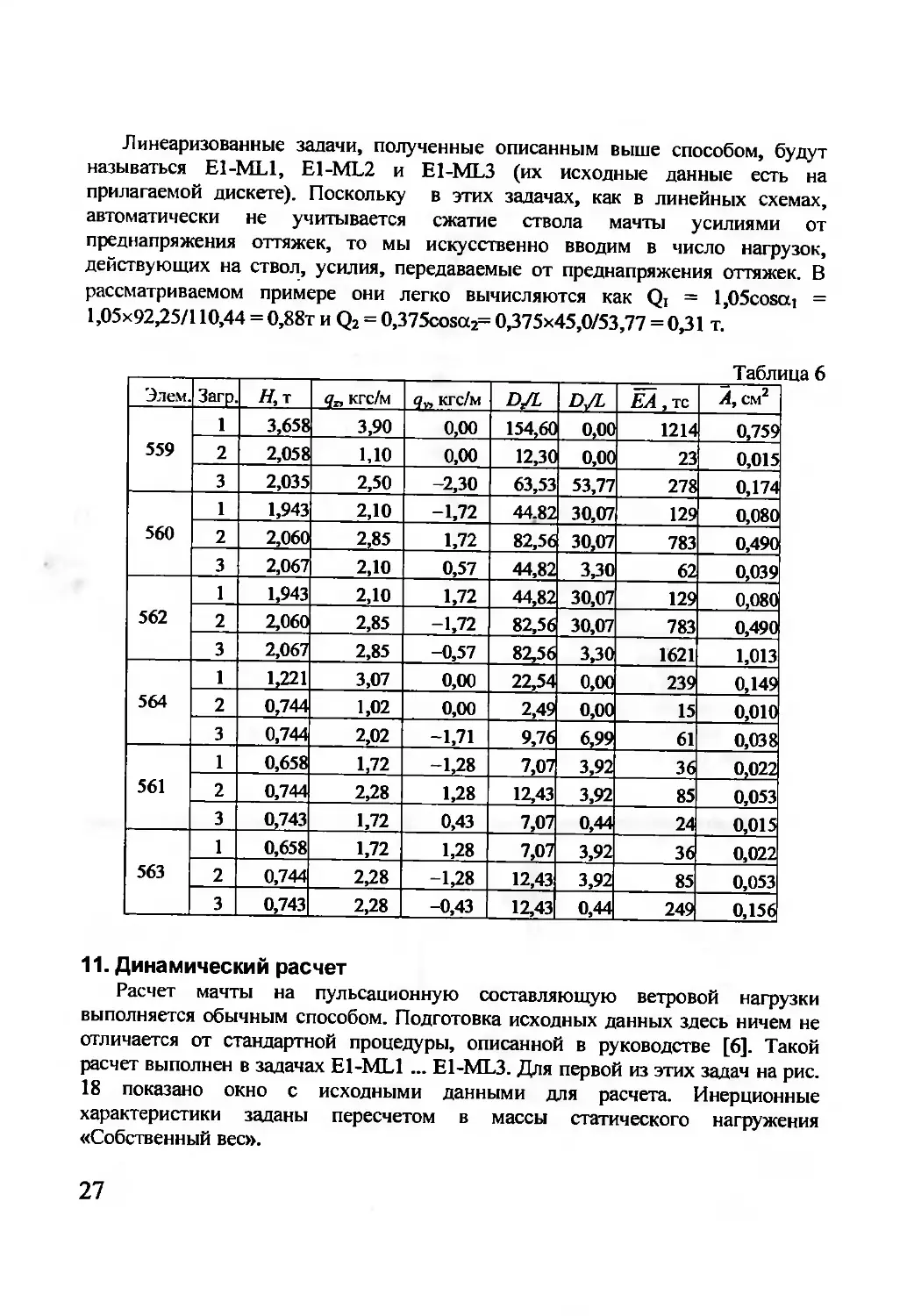
Линеаризованные задачи, полученные описанным выше способом, будут
называться E1-ML1, E1-ML2 и E1-ML3 (их исходные данные есть на
прилагаемой дискете). Поскольку в этих задачах, как в линейных схемах,
автоматически не учитывается сжатие ствола мачты усилиями от
преднапряжения оттяжек, то мы искусственно вводим в число нагрузок,
действующих на ствол, усилия, передаваемые от преднапряжения оттяжек. В
рассматриваемом примере они легко вычисляются как Q, = l,05coscti =
1,05x92,25/110,44 = 0,88т и Q2 = 0,375cosa2= 0,375x45,0/53,77 = 0,31 т.
_____________________________________________ Таблица 6
Элем. Загр. Я,т q„ кгс/м <j„ кгс/м D/L D/L ЕА, тс А, см2
559 1 3,658 3,90 0,00 154,60 0,00 1214 0,759
2 2,058 1,10 0,00 12,30 0,00 23 0,015
3 2,035 2,50 -2,30 63,53 53,77 278 0,174
560 1 1,943 2,10 -1,72 44.82 30,07 129 0,080
2 2,060 2,85 1,72 82,56 30,07 783 0,490
3 2,067 2,10 0,57 44,82 3,30 62 0,039
562 1 1,943 2,10 1,72 44,82 30,07 129 0,080
2 2,060 2,85 -1,72 82,56 30,07 783 0,490
3 2,067 2,85 -0,57 82,56 3,30 1621 1,013
564 1 1,221 3,07 0,00 22,54 0,00 239 0,149
2 0,744 1,02 0,00 2,49 0,00 15 0,010
3 0,744 2,02 -1,71 9,76 6,99 61 0,038
561 1 0,658 1,72 -1,28 7,07 3,92 36 0,022
2 0,744 2,28 1,28 12,43 3,92 85 0,053
3 0,743 1,72 0,43 7,07 0,44 24 0,015
563 1 0,658 1,72 1,28 7,07 3,92 36 0,022
2 0,744 2,28 -1,28 12,43 3,92 85 0,053
3 0,743 2,28 -0,43 12,43 0,44 249 0,156
11. Динамический расчет
Расчет мачты на пульсационную составляющую ветровой нагрузки
выполняется обычным способом. Подготовка исходных данных здесь ничем не
отличается от стандартной процедуры, описанной в руководстве [6]. Такой
расчет выполнен в задачах E1-ML1 ... E1-ML3. Для первой из этих задач на рис.
18 показано окно с исходными данными для расчета. Инерционные
характеристики заданы пересчетом в массы статического нагружения
«Собственный вес».
27
При задании числа учитываемых форм собственных колебаний принималось
во внимание, что в соответствии с п.6.8 СНиП 2.01.07-85* учитываются только
те формы собственных колебаний, для которых частоты не превышают
предельное значение fi, которое для Ш-го ветрового района равно 3,8 Гц.
Поэтому для поиска частот и форм собственных колебаний можно использовать
метод Ланцоша, позволяющий провести анализ в заданном частотном диапазоне
и указать границы этого диапазона от 0,0 до 3,8 Гц (рис. 17).
Рис. 18. Данные для расчета на ветровые пульсации в задаче МЫ
Полезно проанализировать вклад каждой из учтенных форм собственных
колебаний, для чего рассмотреть сведения о работе внешних сил,
представленные в протоколе решения задачи. Для задачи E1-ML1 они имеют
вид:
4-1 1.53894е-29
4 - 2 1.50856е-31
4 - 3 3.21026е-06
4-4 3.096е-32
4 - 5 0.00121241
4 - 6 1.00455е-29
4 - 7 0.00121707
Очевидно, что наибольший вклад вносят пятая и седьмая формы, которая, как
нетрудно убедиться, ориентирована вдоль линии действия статического ветра.
Для задачи E1-ML2 картина будет другой:
4 -1 2.72144е-29
4 - 2 1.16594е-05
4 - 3 1.53303е-33
4-4 0.0012766
4 - 5 3.21961е-33
28
4 - 6 1.27974е-31
4 - 7 0.00145539
Здесь основную роль играют четвертая и седьмая формы, и, наконец, в задаче
E1-ML3 мы имеем:
4 -1 4.13865е-05
4 - 2 1.59666е-06
4 - 3 1.03308е-06
4-4 0.000314639
4 - 5 0.00026864
4 - 6 7.54696е-07
4 - 7 0.00143568
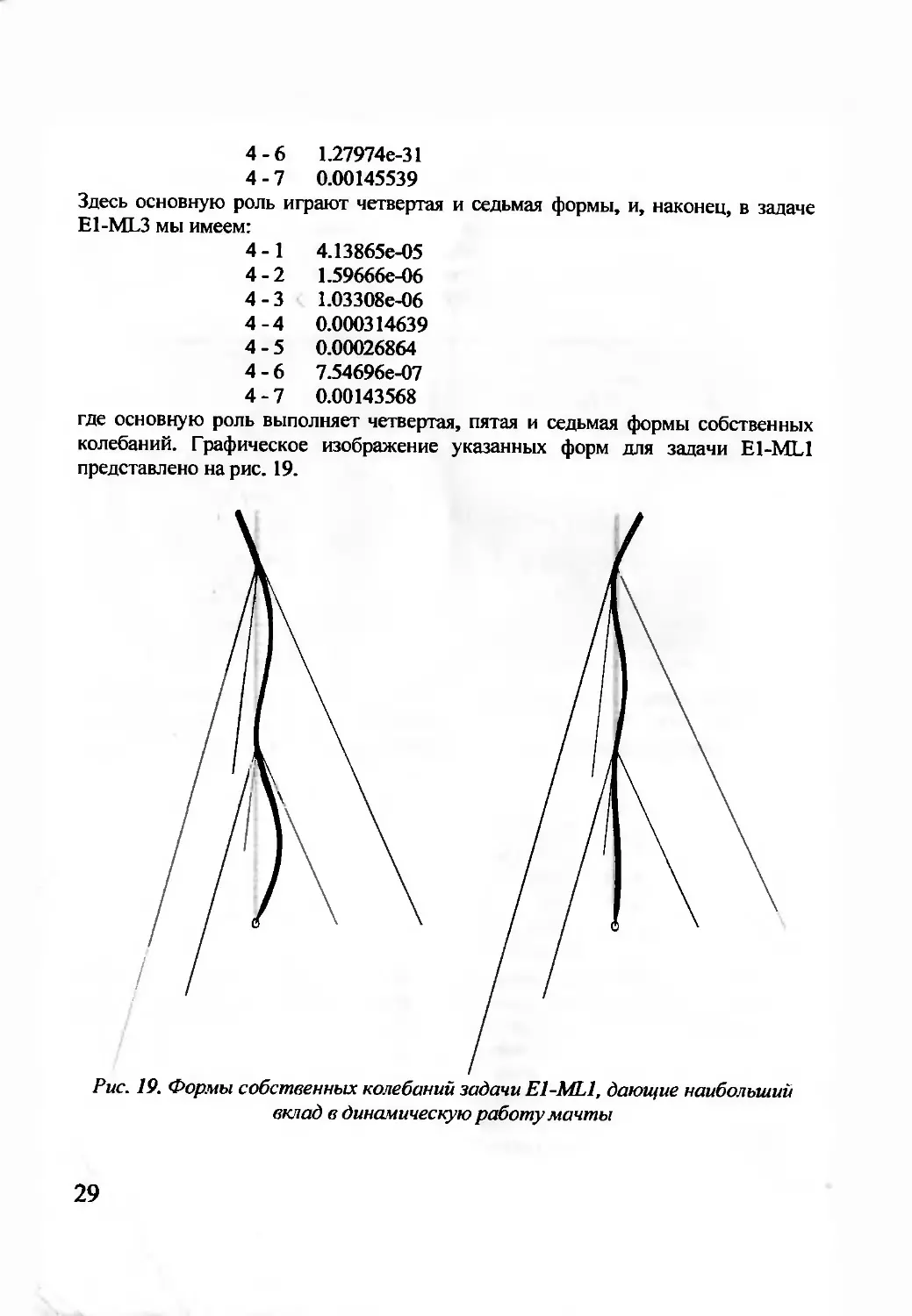
где основную роль выполняет четвертая, пятая и седьмая формы собственных
колебаний. Графическое изображение указанных форм для задачи E1-ML1
представлено на рис. 19.
Рис. 19. Формы собственных колебаний задачи E1-ML1, дающие наибольший
вклад в динамическую работу мачты
29
12. Проверка устойчивости
В соответствии с указаниями п.16.13 СНиП П-23-81* мачты с оттяжками
должны быть рассчитаны на устойчивость в целом при нагрузках:
• от монтажного натяжения оттяжек при отсутствии ветра;
• ветровой — в направлении на одну из оттяжек;
• гололедной — при отсутствии ветра;
• гололедной и ветровой — в направлении на одну из оттяжек.
При этом коэффициент запаса устойчивости не должен быть меньшим 1,3-
Сжатие ствола создавалось путем приложения узловых нагрузок (см.
рис. 19), которые возникают от действия вертикальных компонент натяжения
оттяжек. Эти компоненты найдены с использованием функции «Нагрузки от
фрагмента схемы» (рис. 20). Значения этих нагрузок показаны в табл. 7.
Рис.20. Окно «Нагрузки от фрагмента схемы»
Таблица 7
Номер узла Нагрузки Fz. тс
Загр. 1 Загр. 2 Загр. 3
49 0,701 0,116 0,393
50 0,283 0,431 0,217
51 0,283 0,431 0,582
112 2,363 0,214 1,249
113 0,819 1,778 0,550
114 0,819 1,778 2,149
Для проверки устойчивости создана специальная комбинация загружений
«Собственный вес» + «Сжатие ствола». Поиск коэффициента запаса
30
устойчивости осуществлялся в диапазоне от 0 до 10 и это значит, что если
фактическое значение коэф ицнента запаса превышает 10, то его величина не
будет вычисляться (рис. 21)
Расчеты показали, что коэффициенты запаса устойчивости для схем E1-ML1
— E1-ML3 равны соответственно 4,604; 5,253 и > 10,0. В связи с этим можно
было бы вернуться к назначению преднапряжеиий в оттяжках и несколько их
снизить, однако мы не будем заниматься этой проблемой.
Рис. 21. Окно /(Проверка общей устойчивости системы»
13. Объединение результатов расчета по разным моделям
Для объединения результатов расчета, выполненных с использованием
различных расчетных моделей? используется режим SCAD- «Вариация
моделей». Соответствующая задача E1-VMM создается с использованием ранее
решенных задач E1-ML1, E1-ML2 , E1-ML3 и E1-MNL (рис. 22).
Рис. 22. Формирование пакета моделей
31
Все загружения, для которых имеются результаты расчета, объединяются в
общий список и каждому из них присваивается определенный вид (см. табл. 8).
При подготовке данных для вычисления расчетных сочетаний усилий,
решается вопрос о составлении групп взаимоисключения загружений, которые в
рассматриваемом случае представлены следующим образом:
группа 1 —дает возможность лишь однократного учесть собственный вес;
группа 2 —дает возможность учесть только одно направление ветра.
Кроме того, присвоением нулевых значений всем расчетным коэффициентам
из рассмотрения исключены вспомогательные загружения 3 — «[E1-ML1]
Сжатие ствола», 7 — «[E1-ML2] Сжатие ствола» и 11 — «[E1-ML3] Сжатие
ствола». Нулевые значения расчетных коэффициентов автоматически
присваиваются загружениям 4, 8 и 12 поскольку в линейных расчетных моделях
загружение статической ветровой нагрузкой уже учтено в результатах расчета на
ветровые пульсации.
Таблица 8
Номер загру- же- ния [Задача] Имя загружения Вид загружения
1 [E1-ML1] Собственный вес Постоянное
2 [E1-ML1] Ветер на оттяжку Статическое ветровое
3 [E1-ML1] Сжатие ствола Постоянное
4 [E1-ML1] Пульсации ветра на оттяжку Кратковр. длит, мала
5 [E1-ML2] Собственный вес Постоянное
6 [E1-ML2] Ветер против оттяжки Временное
7 [E1-ML2] Сжатие ствола Постоянное
8 [E1-ML2] Пульсации ветра против оттяжки Кратковр. длит, мала
9 [E1-ML1] Собственный вес Постоянное
10 [E1-ML1] Ветер поперек оттяжки Статическое ветровое
11 [E1-ML1] Сжатие ствола Постоянное
12 [E1-ML1] Пульсации ветра поперек оттяжки Кратковр. длит, мала
13 [E1-MNL] Собственный вес Постоянное
14 [E1-MNL] Ветер на оттяжку Временное
15 [E1-MNL] Ветер против оттяжки Временное
16 [E1-MNL] Ветер поперек оттяжки Временное
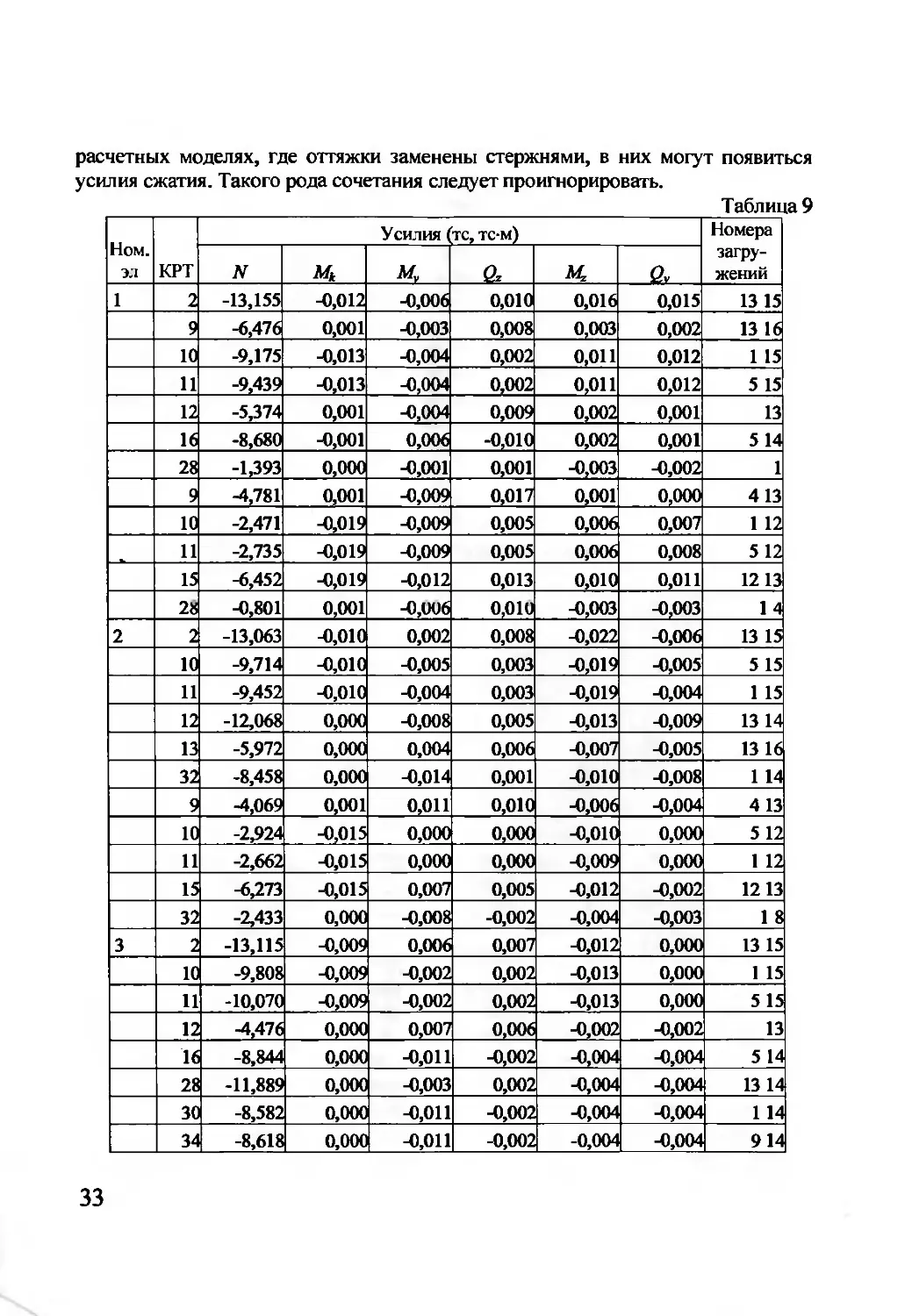
Для нескольких первых элементов расчетной схемы результаты вычисления
расчетных сочетаний усилий приведены в табл. 9. Из таблицы видно каким
образом отбирались загружения-претенденты в состав РСУ: всюду присутствует
пара «собственный вес + ветер», но для разных элементов и различных
критериев (см. столбец КРТ) второе составляющее пары принимается то из
линейного динамического расчета, то из нелинейного расчета.
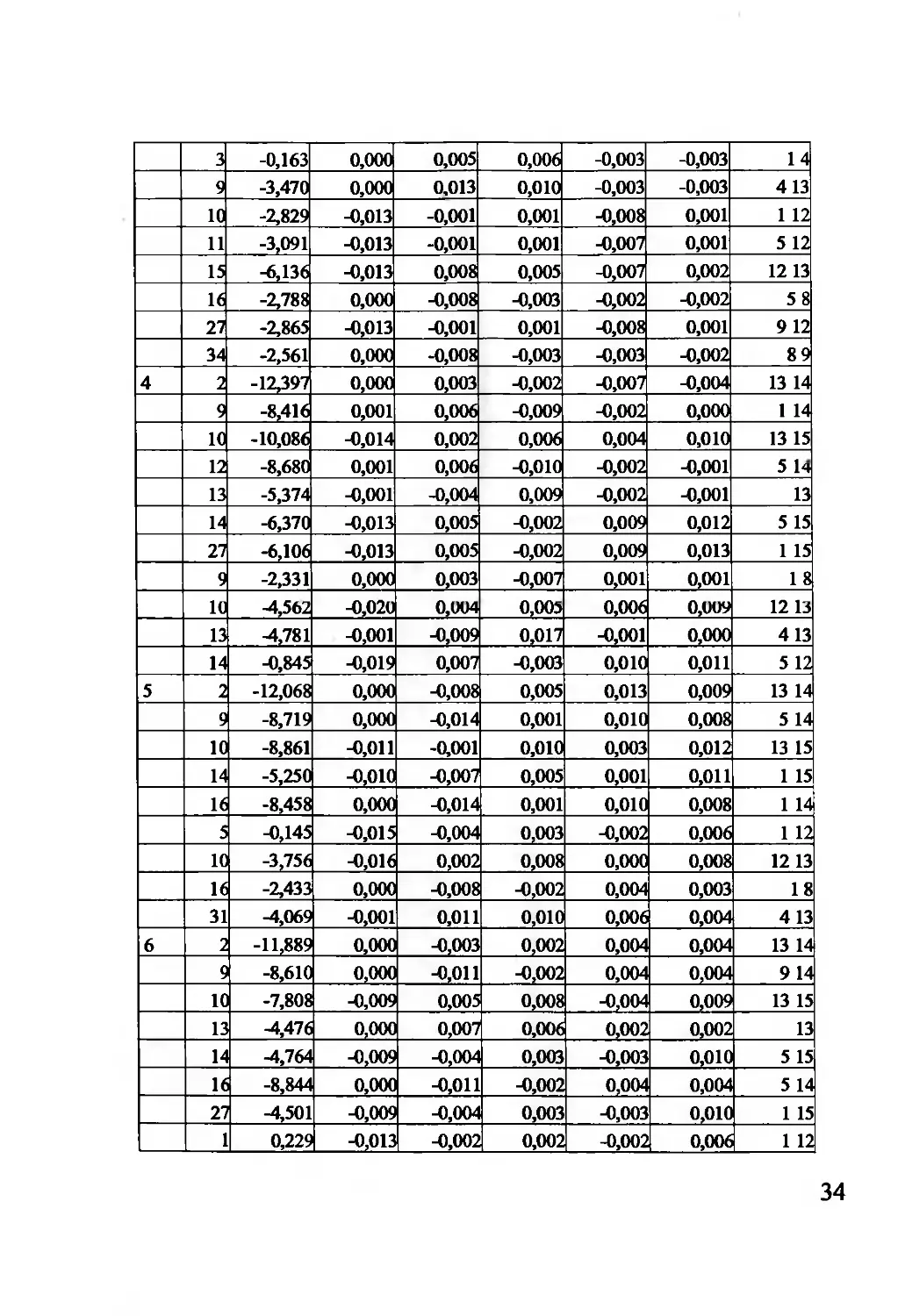
В табл. 10 аналогичные данные приведены для оттяжек. Здесь, однако,
следует проявить определенную осторожность, поскольку в линеаризованных
32
расчетных моделях, где оттяжки заменены стержнями, в них могут появиться
усилия сжатия. Такого рода сочетания следует проигнорировать.
___________________________________________________________Таблица 9
Ном. ЭЛ КРТ Усилия (тс, тс-м) Номера загру- жений
N Mv & И Q,
1 2 -13,155 -0,012 -0,006 0,010 0,016 0,015 13 15
9 -6,476 0,001 -0,003 0,008 0,003 0,002 13 16
10 -9,175 -0,013 -0,004 0,002 0,011 0,012 1 15
11 -9,439 -0,013 -0,004 0,002 0,011 0,012 5 15
12 -5,374 0,001 -0,004 0,009 0,002 0,001 13
16 -8,680 -0,001 0,006 -0,010 0,002 0,001 5 14
28 -1,393 0,000 -0,001 0,001 -0,003 -0,002 1
9 -4,781 0,001 -0,009 0,017 0,001 0,000 413
10 -2,471 -0,019 -0,009 0,005 0,006 0,007 1 12
11 -2,735 -0,019 -0,009 0,005 0,006 0,008 5 12
15 -6,452 -0,019 -0,012 0,013 0,010 0,011 12 13
28 -0,801 0,001 -0,006 0,010 -0,003 -0,003 1 4
2 2 -13,063 -0,010 0,002 0,008 -0,022 -0,006 13 15
10 -9,714 -0,010 -0,005 0,003 -0,019 -0,005 5 15
11 -9,452 -0,010 -0,004 0,003 -0,019 -0,004 1 15
12 -12,068 0,000 -0,008 0,005 -0,013 -0,009 13 14
13 -5,972 0,000 0,004 0,006 -0,007 -0,005 13 16
32 -8,458 0,000 -0,014 0,001 -0,010 -0,008 1 14
9 -4,069 0,001 0,011 0,010 -0,006 -0,004 4 13
10 -2,924 -0,015 0,000 0,000 -0,010 0,000 5 12
11 -2,662 -0,015 0,000 0,000 -0,009 0,000 1 12
15 -6,273 -0,015 0,007 0,005 -0,012 -0,002 12 13
32 -2,433 0,000 -0,008 -0,002 -0,004 -0,003 1 8
3 2 -13,115 -0,009 0,006 0,007 -0,012 0,000 13 15
10 -9,808 -0,009 -0,002 0,002 -0,013 0,000 1 15
11 -10,070 -0,009 -0,002 0,002 -0,013 0,000 5 15
12 -4,476 0,000 0,007 0,006 -0,002 -0,002 13
16 -8,844 0,000 -0,011 -0,002 -0,004 -0,004 5 14
28 -11,889 0,000 -0,003 0,002 -0,004 -0,004 13 14
30 -8,582 0,000 -0,011 -0,002 -0,004 -0,004 1 14
34 -8,618 0,000 -0,011 -0,002 -0,004 -0,004 914
33
3 -0,163 0,000 0,005 0,006 -0,003 -0,003 14
9 -3,470 0,000 0,013 0,010 -0,003 -0,003 413
10 -2,829 -0,013 -0,001 0,001 -0,008 0,001 1 12
11 -3,091 -0,013 -0,001 0,001 -0,007 0,001 5 12
15 -6,136 -0,013 0,008 0,005 -0,007 0,002 12 13
16 -2,788 0,000 -0,008 -0,003 -0,002 -0,002 58
27 -2,865 -0,013 -0,001 0,001 -0,008 0,001 9 12
34 -2,561 0,000 -0,008 -0,003 -0,003 -0,002 89
4 2 -12,397 0,000 0,003 -0,002 -0,007 -0,004 13 14
9 -8,416 0,001 0,006 -0,009 -0,002 0,000 1 14
10 -10,086 -0,014 0,002 0,006 0,004 0,010 13 15
12 -8,680 0,001 0,006 -0,010 -0,002 -0,001 5 14
13 -5,374 -0,001 -0,004 0,009 -0,002 -0,001 13
14 -6,370 -0,013 0,005 -0,002 0,009 0,012 5 15
27 -6,106 -0,013 0,005 -0,002 0,009 0,013 1 15
9 -2,331 0,000 0,003 -0,007 0,001 0,001 18
10 -4,562 -0,020 0,004 0,005 0,006 0,009 12 13
13 4781 -0,001 -0,009 0,017 -0,001 0,000 413
14 -0,845 -0,019 0,007 -0,003 0,010 0,011 5 12
5 2 -12,068 0,000 -0,008 0,005 0,013 0,009 13 14
9 -8,719 0,000 -0,014 0,001 0,010 0,008 5 14
10 -8,861 -0,011 -0,001 0,010 0,003 0,012 13 15
14 -5,250 -0,010 -0,007 0,005 0,001 0,011 1 15
16 -8,458 0,000 -0,014 0,001 0,010 0,008 1 14
5 -0,145 -0,015 -0,004 0,003 -0,002 0,006 1 12
10 -3,756 -0,016 0,002 0,008 0,000 0,008 12 13
16 -2,433 0,000 -0,008 -0,002 0,004 0,003 18
31 -4,069 -0,001 0,011 0,010 0,006 0,004 413
6 2 -11,889 0,000 -0,003 0,002 0,004 0,004 13 14
9 -8,610 0,000 -0,011 -0,002 0,004 0,004 9 14
10 -7,808 -0,009 0,005 0,008 -0,004 0,009 13 15
13 -4,476 0,000 0,007 0,006 0,002 0,002 13
14 -4,764 -0,009 -0,004 0,003 -0,003 0,010 5 15
16 -8,844 0,000 -0,011 -0,002 0,004 0,004 5 14
27 -4,501 -0,009 -0,004 0,003 -0,003 0,010 1 15
0,229 -0,013 -0,002 0,002 -0,002 0,006 1 12
34
10 -3,078 -0,014 0,007 0,006 -0,002 0,006 12 13
13 -3,470 0,000 0,013 0,010 0,003 0,003 413
14 -0,033 -0,013 -0,002 0,002 -0,002 0,006 5 12
34 -2,553 0,000 -0,008 -0,003 0,003 0,002 89
Таблица 10
Номер элемента КРТ Н, тс Загру- жения
559 1 4,286 13 15
2 -1,460 1
1 7,287 413
560 1 3,121 13 14
2 -1,461 1
1 5,242 8 13
562 1 3,559 13 15
2 -1,461 1
1 5,361 12 13
564 1 1,289 13 15
2 -1,604 9
13 -1,578 1
1 3,601 413
2 -3,222 89
561 1 0,860 13 14
2 -1,599 9
13 -1,573 1
1 2,148 8 13
2 -2,970 912
563 1 1,031 13 15
2 -1,602 9
13 -1,573 1
1 2,422 12 13
После выбора расчетных сочетаний можно войти в постпроцессор
«Проверка сечений из металлопроката» и, действуя в нем обычным способом
проверить, например пояса мачты, для чего создать соответствующую группу
конструктивных элементов (рис. 23).
35
Рис. 23. Создание группы элементов «Пояса»
Выполненная проверка показывает, что предварительно заданные сечения
имеют большой запас прочности и устойчивости. Если воспользоваться
режимом «Подбор сечений», то окажется, что можно значительно уменьшить
сечения поясов (рис. 24), однако из конструктивных соображений вряд ли стоит
принимать предлагаемое сечение трубы 095x4 мм, а лучше взять трубу 0159x5
мм, использование которой позволяет лучше решить конструкцию узловых
соединений.
Результаты подбора сечений
П
Имя трупы [ Исходное сечв!ме | Результат подбора |
Группа унификации Трубы стальные бесшовные Трубы стальные бесшовные 303.3
пояса горячедеформированные, ГОСТ 8732-78 горячедеформированные, ГОСТ 8732-78
159x10 95x4
С Прииекоь подобрамяе сечения (потребуется пересчет)
С Прк»«»*пъ подобраьмяе сечения (без пересчета]
Продолжить без применения
Отчет | |£215ы«д"| Справка |
Рис. 24. Результаты подбора сечений
36
14. Использование упрощенной расчетной схемы ствола
Для получения более обозримых результатов расчета сквозной ствол мачты
может быть представлен приведенным стержнем, жесткость которого
определяется в программе «Конструктор сечений» [9], имеющейся в составе
системы SCAD Office (рис. 25). Чтобы иметь возможность сопоставить
результаты расчета использовано сечение поясов 0159x10 мм, с которыми
выполнен предыдущий расчет, а также введены узлы на границах секций.
Рис. 25. Определение жесткости ствола в «Конструкторе сечений»
аНЕц-тасчЕТ
Эксцентричность крепления оттяжек в новой расчетной схеме учитывается
введением соответствующих консольных элементов, соединяющих оттяжечный
узел ствола с концами оттяжек. Сама расчетная схема помещена в одной задаче
рядом со старой, что позволяет легко сопоставлять результаты расчета (рис. 26).
37
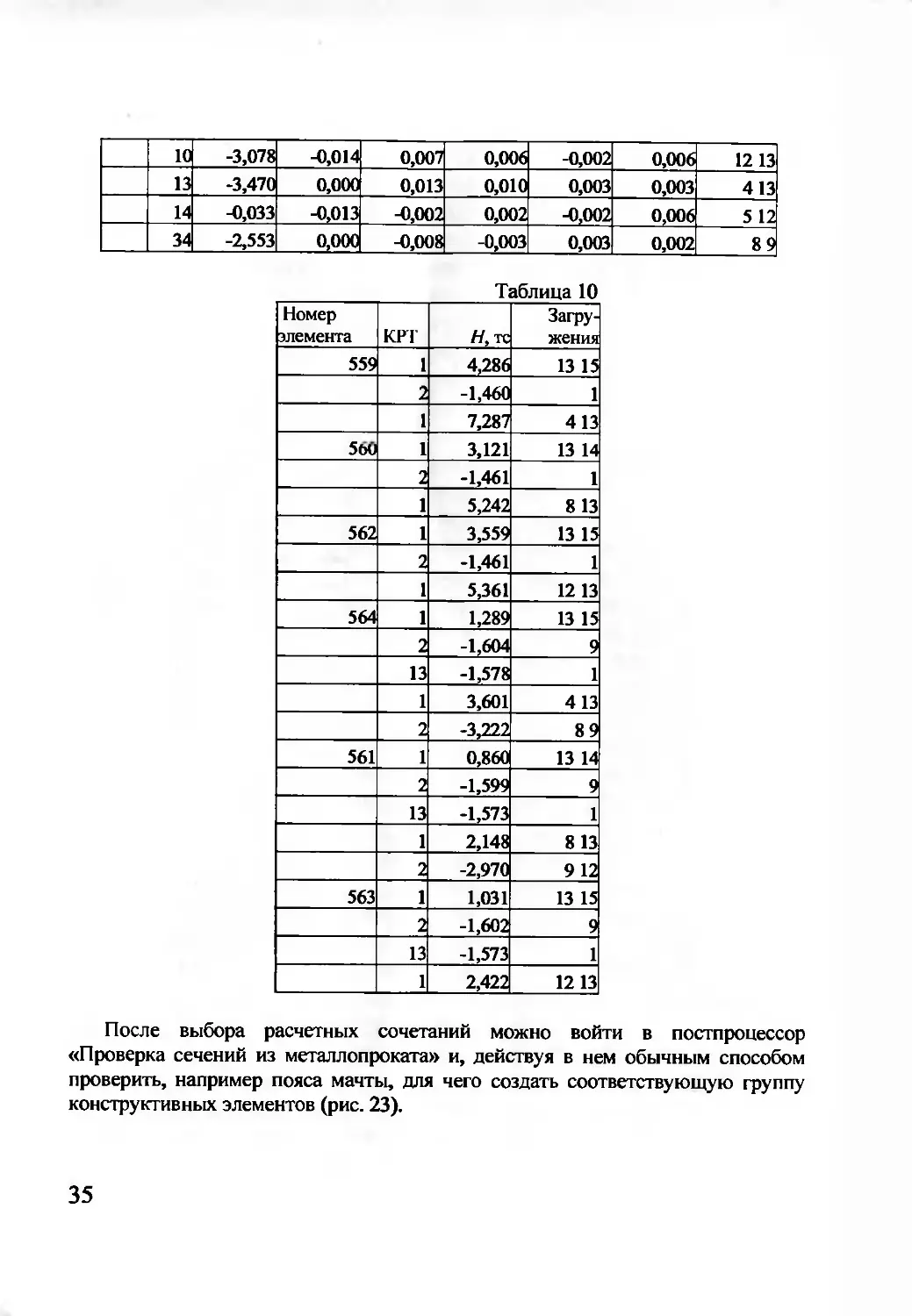
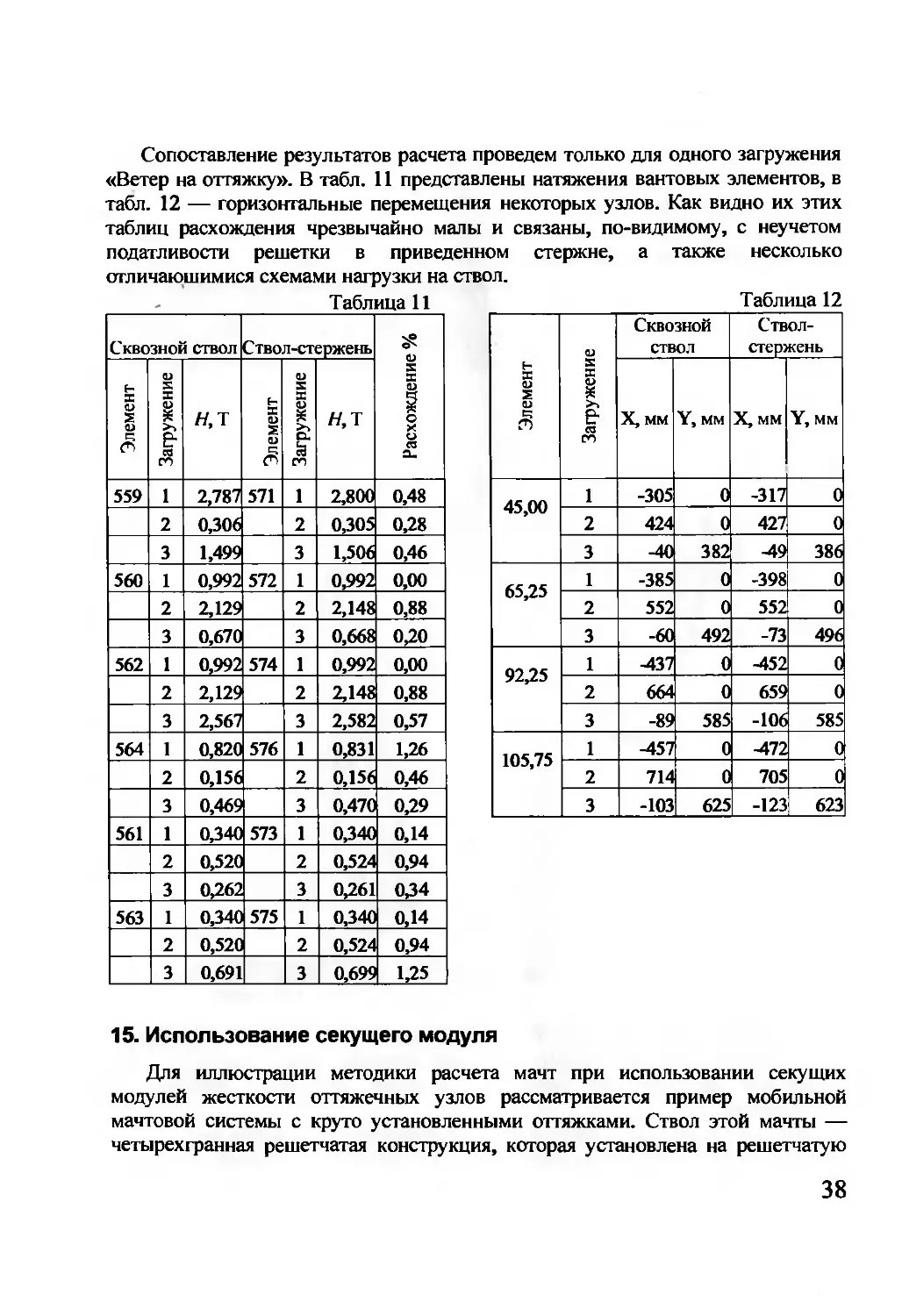
Сопоставление результатов расчета проведем только для одного загружения
«Ветер на оттяжку». В табл. 11 представлены натяжения вантовых элементов, в
табл. 12 — горизонтальные перемещения некоторых узлов. Как видно их этих
таблиц расхождения чрезвычайно малы и связаны, по-видимому, с неучетом
податливости решетки в приведенном стержне, а также несколько
отличающимися схемами нагрузки на ствол.
.________________Таблица 11 ________________________Таблица 12
Сквозной ствол Ствол-стержень Расхождение %
Элемент Загружение Я,Т Элемент Загружение Я,Т
559 1 2,787 571 1 2,800 0,48
2 0,306 2 0,305 0,28
3 1,499 3 1,506 0,46
560 1 0,992 572 1 0,992 0,00
2 2,129 2 2,148 0,88
3 0,670 3 0,668 0,20
562 1 0,992 574 1 0,992 0,00
2 2,129 2 2,148 0,88
3 2,567 3 2,582 0,57
564 1 0,820 576 1 0,831 1,26
2 0,156 2 0,156 0,46
3 0,469 3 0,470 0,29
561 1 0,340 573 1 0,340 0,14
2 0,520 2 0,524 0,94
3 0,262 3 0,261 034
563 1 0,340 575 1 0,340 0,14
2 0,520 2 0,524 0,94
3 0,691 3 0,699 1,25
Элемент Загружение Сквозной ствол Ствол- стержень
X, мм Y, мм X, мм Y, мм
45,00 1 -305 0 -317 0
2 424 0 427 0
3 -40 382 -49 386
65,25 1 -385 0 -398 0
2 552 0 552 0
3 -60 492 -73 496
92,25 1 -437 0 -452 0
2 664 0 659 0
3 -89 585 -106 585
105,75 1 -457 0 -472 0
2 714 0 705 0
3 -103 625 -123 623
15. Использование секущего модуля
Для иллюстрации методики расчета мачт при использовании секущих
модулей жесткости оттяжечных узлов рассматривается пример мобильной
мачтовой системы с круто установленными оттяжками. Ствол этой мачты —
четырехгранная решетчатая конструкция, которая установлена на решетчатую
38
металлическую пирамидальную подставку (рис. 27). Между собой ствол и
подставка соединены шарнирно и для того, чтобы обеспечить возможность
решения вспомогательной задачи об уравновешивании заданных усилий
преднапряжения в месте этого шарнирного сопряжения, в расчетную схему
введены упругие связи поворота с малой жесткостью 1,0 кН-м/рад.
Рис. 27. Секция ствола и
конструкция подставки
Рис. 28. Схема к примеру
В расчетной схеме (рис. 28) ствол моделируется одним стержнем с
приведенными характеристиками жесткости, которые определены с помощью
программы «Конструктор сечений» (влияние стержней решетки не
учитывается).
Нелинейная задача представлена двумя загружениями: ветер по оси X, т.е. в
плоскости оттяжек и ветер по диагонали между плоскостями оттяжек. На рис. 29
39
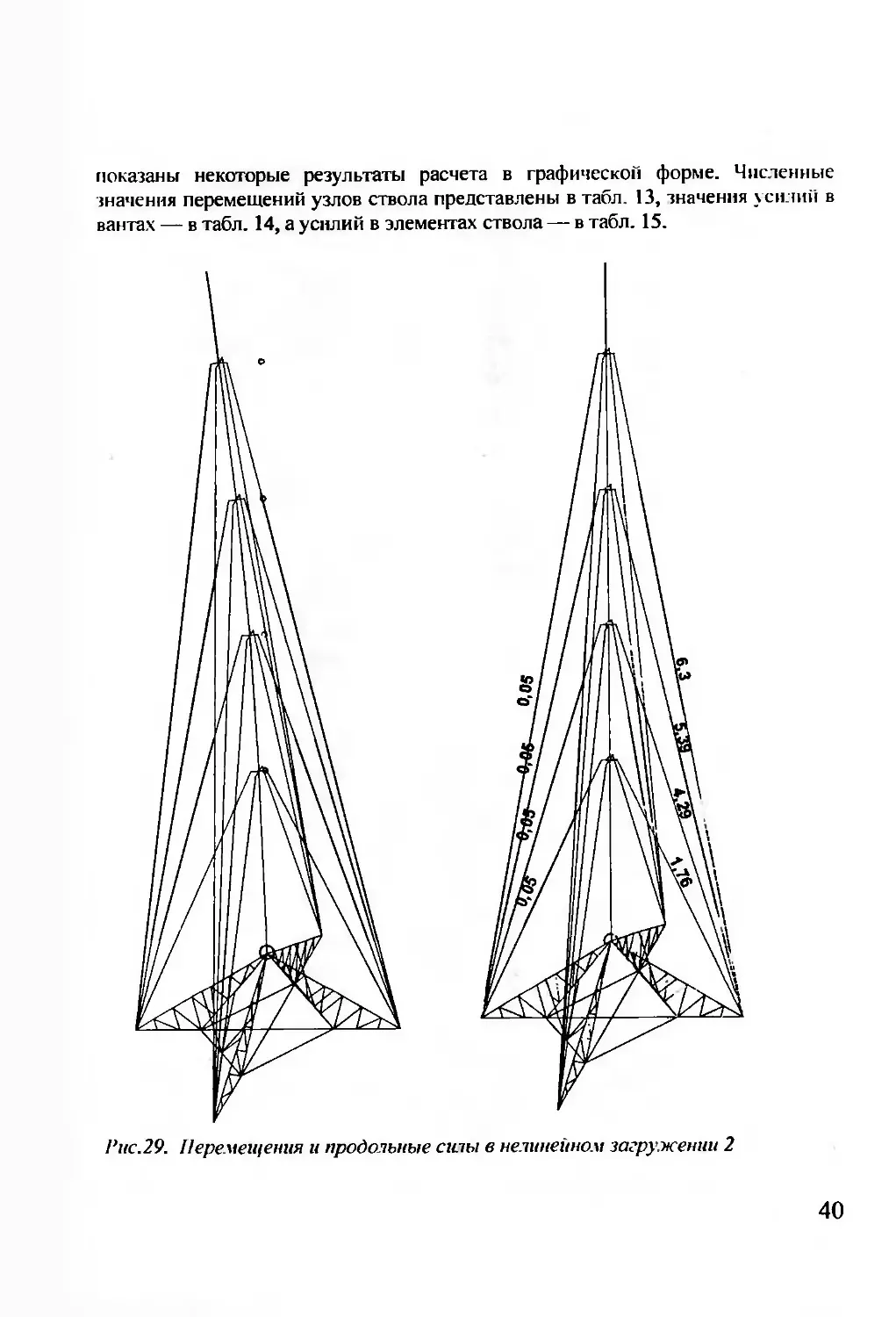
показаны некоторые результаты расчета в графической форме. Численные
значения перемещений узлов ствола представлены в табл. 13, значения усилий в
вантах — в табл. 14, а усилий в элементах ствола — в табл. 15.
I’uc.29. Перемещения и продольные силы в нелинейном загружении 2
40
Таблица 13
Помер узла Перемещения, мм
Загруженне 1 Загруженне 2
X Y X Y
2 (oim. +17 м) -108,1 -0,9 -124,6 -124,6
3 (oim. +26 м) -220,6 -1,3 -238,7 -238,7
4 (oim. +35 м) -394,4 -1,5 -399,9 -399,9
5 (о гм. +44 м) -624,1 -1,8 -602,3 -602,3
6 (oim. +50 м) -792,4 -1,9 -748,0 -748,0
11омер злеменза Усилия, тс
Нелинейное загруженне 1 Нелинейное загруженне 2
153 0,074 0,032
154 0,074 4,786
155 0,017 0,032
156 6,269 4,786
157 0,020 0,030
158 5,357 4,214
159 0,063 0,030
160 0,063 4,214
161 0,055 0,029
.162 0,056 3,588
163 0,022 0,029
164 4,260 3,588
165 0,023 0,026
166 1,716 1,539
167 0,043 0,026
168 0,043 1,539
Таблица 14
Необходимо отметить, что прогиб вершины мачты в загружении 2 составил
0,792 м, что составляет примерно 1/63 ее высоты. Это превышает предельное
значение 1/100, установленное п.16.8 СНиП П-23-81*, однако может быть
лонушено, если в техническом задании установлен отличный от СНиП П-23-81*
41
предел допустимого отклонения. В дальнейшем будем исходить ш пою
предположения.
В линеаризованной задаче оттяжечный узел моделируется линейной
пружиной, жесткость которой равна передаваемой на оттяжки реакцией ствола,
деленной на соответствующее перемещение указанного узла. Как узловые
перемещения, так и реакции меняются от загружения к загружению поэтому и
жесткости пружин будут разными в различных загружениях. Значение реакции
можно получить, воспользовавшись режимом «Нагрузки от фрагмента схемы».
Для рассматриваемого примера они представлены в табл. 16, а жесткости
и GyW), вычисленные с их помощью и с помощью перемещений по табл. 2,
показаны в табл. 17.
Таблица 15
Эл-т Сечен. Загруж N,r М„ тс-м 2z,T М„ те м
1 1 1 -17,505 -0,018 0,002 -0,696 0,072
2 -27,435 0,832 0,229 -0,832 0,229
2 1 -17,505 -0,017 0,002 -1,116 0,395
2 -27,435 1,178 0,502 -1,178 0,502
3 1 -17,505 -0,015 0,002 -3,708 0,797
2 -27,435 3,360 0,841 -3,360 0,841
2 1 1 -15,858 -0,015 0,001 -4,472 0,060
2 -24,610 4,043 0,166 4043 0,166
2 1 -15,858 -0,012 0,001 -4,765 0,401
2 -24,610 4,202 0,455 -4,202 0,455
3 1 -15,858 -0,009 0,001 -6,636 0,761
2 -24,610 5,703 0,762 -5,703 0,762
3 1 1 -11,667 -0,009 0,001 -8,657 -0,533
2 -17,713 7,399 -0,369 -7,399 -0,369
2 1 -11,667 -0,006 0,001 -6,264 -0,155
2 -17,713 5,233 -0,047 -5,233 -0,047
3 1 -11,667 -0,004 0,001 -5,606 0,238
2 -17,713 4,542 0,287 -4,542 0,287
4 1 1 -6,315 -0,003 0,001 -8,201 -1,040
2 -9,458 6,576 -0,777 -6,576 -0,777
2 1 -6,315 -0,002 0,001 -3,775 -0,632
2 -9,458 2,966 -0,432 -2,966 -0,432
3 1 -6,315 0,000 0,001 -1,224 -0,207
2 -9,458 0,936 -0,075 -0,936 -0,075
169 1 1 0,000 0,000 0,000 -4,292 -1,098
2 0,000 3,269 -0,854 -3,269 -0,854
42
)л-г - ICH. Загруж N, т М„ тс м 6z, T Л/2, тем 6г, т
2 1 0,000 0,000 0,000 -2,066 -0,880
2 0,000 1,553 -0,672 -1,553 -0,672
3 1 0,000 0,000 0,000 -0,332 -0,662
2 0,000 0,249 -0,488 -0,249 -0,488
170 1 1 0,000 0,000 0.000 -0.332 -0,295
2 0,000 0,249 -0,228 -0,249 -0,228
2 1 0,000 0,000 0,000 -0,138 -0,221
2 0,000 0,101 -0,166 -0,101 -0,166
3 1 0,000 0,000 0,000 0,000 -0,148
2 0,000 0,000 -0,104 0,000 -0,104
Таблица 16
11омер узла 1 laipy iKii, передаваемые oi стола, т
Загружение 1 Загружение 2
Ех_, ^.1
2 0,736 0,000 0,675 0,675
3 1,294 0,000 1,131 1,131
4 1,278 0,000 1,064 1,064
5 0,891 0,001 0,779 0,779
Таблица 17
Номер узла Жесткости эквивалентных пружин, т/м
Загружение 1 Загружение 2
Gz.! Gy.i G,2
2 6,751 0,593 5,419 5,419
3 5,787 0,488 4,689 4,689
4 3,203 0,391 2,635 2,635
5 1,416 0,342 1,282 1,282
Таким образом мы приходим к необходимости рассмотрения трех моделей:
нелинейная модель мачты с оттяжками и двумя упругими связями по
направлениям X и Y в оттяжечных узлах, которые обладают практически
нулевыми жесткостями G, = Gy = 1 кН/м (задача E2-MNL);
линеаризованная модель с отключенными (но сохранившими свою
ну мерацию) оттяжками, у которой упругие связи имеют жесткость Gxj и Gyi
(задача E2-ML1);
43
• линеаризованная модель с отключенными (но сохранившими свою
нумерацию) оттяжками, у которой упругие связи имеют жесткость GX2 и Gy2
(задача E2-ML2).
Соответствующие расчетные схемы представлены на рис. 30, где
неактивные элементы и их номера показаны бледным цветом.
Необходимо отметить, что в задачах E2-ML1 и E2-ML2 дезактивация
вантовых элементов реализуется с помощью процедуры удаления элементов, но
при этом не следует включать процедуру «Упаковка данных», которая
уничтожит и номера удаленных элементов.
Расчет мачты на пульсационную составляющую ветровой нагрузки
выполняется таким же способом, как и в предыдущем примере.
Задача E2-MNL
Задачи E2-MLl(Gxj и Gyi); E2-ML2 (Gx,j и Gyi)
Рис. 30. Расчетные схемы задач E2-MNL, E2-ML1 и E2-ML2
44
Aiiivnn решения нелинейной задачи показал, что проверку устойчивое™
ic.ieeooopajMo выполнить только при действии ветра по диагонали между
нтяжками (задача E2-ML2), где сжатие ствола является наибольшим (рис. 31).
( жаше ствола создавалось путем приложения узловых нагрузок (см. рис.
И). Koipue реализуют соответствующую эпюру продольных сил. При проверке
>б|ией устойчивости системы определялись как коэффициент запаса
.сюйчивости, так и форма потери устойчивости (рис. 32).
Пре (напряжение
Ветер но.iiiaioiia.ni
Рис 31 Эпюры см iLMimupix ст в стволе и эквивалентное загружение
Расчет показал, что коэффициент запаса устойчивости равен 0,49 и это
потребует переработки проекта. Для оценки направления такой переработки
полезно рассмотреть форму потери устойчивости (рис. 32). После увеличения
сечений пирамидальной подставки был получен коэффициент запаса
устойчивости 1,195, что также недостаточно. В связи со сказанным детальный
разбор рассматриваемого варианта проекта не представляется необходимым,
поскольку требуется внесение кардинальных изменений в конструктивное
решение.
Рис. 32. Форма потери устойчивости
После усиления опорной пирамиды (жесткость ее элементов увеличена
переходом к трубчатым элементам большего диаметра) новый расчет показал,
46
ио котффициент запаса устойчивости системы стал равным 1,195, что также
недостаточно.
Детальный разбор рассматриваемого варианта проекта и внесение
затызсйших изменений в конструктивное решение не является предметом
рассмо! рения настоящей работы и оставляется на откуп читателю.
Заключительные замечания
В приложении к настоящей брошюре имеется дискета с условиями
раесмо!репных выше примеров. Мы рекомендуем читателю решить эти задачи и
в качестве упражнения модифицировать рассматриваемые проекты с тем, чтобы
в первом примере уменьшить, по возможности, расход стали, а во втором —
добиться надежности рассматриваемой схемы. Естественно, что и первая и
вторая задача не имеют единственного решения и читатель может проявить свою
изобретательность в произвольном направлении, включая и полную замену
копстрх ктивного решения.
Литература
I Башмаков 10.11., Лурье Л X., Нерельмутер А.В., Перепои А.А. Проектування та монтаж
вцепких опор. — К.: Б) .’пве.тызик, 1968.
2. Медведева Н.М., Мнкигарснко М./\., 11ерсльмутер А.В. Система программ для расчсза
мачз па оттяжках//Исследование систем автоматизированного проектирования
сзальиых конструкций. I руды ЦНИИПСК им. Мельникова.— М.: 1983. — С. 67 71.
3 Ilepe.iiiMxiep А.В. Основы расчета вантово-стержневых систем. — М.: Стройизлат,
1969.
4. Нерельмутер А.В., Слпвкер В.II. Расчетные модели сооружений и возможность их
анализа / Изд. 2-е, переработанное и дополненное.— Киев: Изл-во «Стать», 2002.
5. Савицкий I .А. Основы расчета радиомачт.— М.: Связьиздат, 1953.
6. SCAD Office. Вычислительный комплекс SCAD / В.С. Карпиловский, Э.З.Крнксу нов,
А.А.Маляренко, A.B.11ерельмутер, М.А. 1[ерельмутер. — М.: Изд-во АСВ, 2004.
7Соколов A.I. Металлические конструкции антенных устройств.— М.: Стройизлат,
1973
8. Справочник проектировщика. Металлические конструкции (в 3 томах). Том 3. .— М.:
Нздазе зьство АСВ, 1999.
9 Формирование сечений и расчет их геометрических характеристик / В.С. Карин
ловекий, СЗ.Крнксунов А.В.Перельмутер, М.А. Перезьмутер — К.: ВПП «Компас»,
2000.— 80 с.— (Structure CAD: Пшсгрированная система анализа конструкций)
47