ЭЛЕМЕНТАРНАЯ
ГЕОМЕТРІЯ
для среднихъ ткыіъ аидуіШ.
Съ приложеніемъ большого количества упражненій
и статьи: главнѣйшіе методы рѣшенія геометриче-
скихъ задачъ на построеніе.
сое? «Ліи
А. К м <• е .іев -ъ.
Ціьна I р. 25 и.
8. 8. ДУИН08А
ПОАТ. АПуАІОЮ
ЛОДЛЮІІХ ІМІМІЪ иышаѵ
МО СНВ А.
ТппоЛнт. .іошхсжііЪ, Зішхсисхіб и К*. Чясгио ирули, X. X 103.
1892.
ЭЛЕМЕНТАРНАЯ
ГЕОМЕТРІЯ
ДЛЯ СРЕДНИХЪ УЧЕБНЫХЪ ЗАВЕДЕНІЙ.
Съ приложеніемъ большого количества упражненій
и статьи: главнѣйшіе методы рѣшенія геометриче-
скихъ задачъ на построеніе.
СОСТАВИЛЪ
А. Киселевъ.
Ц-Ьна і р. 25 к.
ИЗДАНІЕ КНИЖНАГО МАГАЗИНА
В. В. ДУМНОВА
ххол-х» -хчірхгою
„НАСЛІЪДНИКН БРАТЬЕВЪ САЛАЕВЫХЪ."
МОСКВА.
Типо-Лит. Дашкевичъ, Знаменскій и К°, Чистые пруды, д. й 199.
1892.
ПРЕДИСЛОВІЕ.
Главнѣйшія особенности предлагаемаго руководства гео-
метріи состоятъ въ слѣдующемъ:
1. Въ большинствѣ нашихъ учебниковъ геометріи понятіе
о длинѣ окружности и вообще кривой линіи принимается
за элементарное, не требующее никакихъ оговорокъ и разъ-
ясненій, и выводъ, что длина окружности есть предѣлъ пе-
риметровъ правильныхъ вписанныхъ и описанныхъ много-
угольниковъ основывается на скрытомъ допущеніи или на
не строго доказываемой теоремѣ, что объемлющая линія длин-
нѣе объемлемой. Въ предлагаемомъ руководствѣ, въ согласіи
«о многими авторитетами учебно-математической литературы,
проведено иное воззрѣніе, которымъ признается, что понятіе
о длинѣ элементарно только въ примѣненіи къ прямой:, но
когда рѣчь идетъ о сравненіи конечной кривой съ прямо-
линейнымъ отрѣзкомъ, тогда (вслѣдствіе несовмѣстимости
элементовъ кривой съ элементами прямой) понятіе о длинѣ ста-
новится сложнымъ и требуетъ опредѣленія.*) Сообразно этому
взгляду мы не доказываемъ, а принимаемъ за опредѣленіе,
что длиною конечной кривой называется предѣлъ периметра
вписанной ломаной линіи, когда стороны ея стремятся къ
нулю. Конечно, въ среднихъ классахъ учебныхъ заведеній было
бы затруднительно вполнѣ обосновать это опредѣленіе, т. е. до-
казать, что такой предѣлъ существуетъ и что онъ не за-
виситъ отъ закона вписыванія ломаной линіи; но въ педа-
гогическомъ отношеніи, какъ намъ кажется, нѣкоторѣіе
пробѣлы въ доказательствѣ (не скрываемые, впрочемъ, отъ
учащихся) не имѣютъ такого вреднаго значенія, какъ не-
опредѣленность, неясность и сбивчивость въ понятіяхъ, а
тѣмъ болѣе въ основныхъ. При повтореніи геометріи .въ
старшемъ классѣ (особенно въ реальныхъ училищахъ, гдѣ
*) Отсылаемъ интересующихся этимъ вопросомъ къ статьѣ ДГ. По-ѣру-
женко „О длинѣ** помѣщенной въ „Вѣстникѣ оп. физики и Элем. математики.
\1891 г.,	122 и 123).
— VI —
равны ихъ приближенныя значенія, вычисленныя съ про-
извольною, но одинаковою точностью. Принявъ это предло-
женіе за опредѣленіе равенства, мы не Нуждаемся болѣе въ
косвенномъ и тяжеломъ доказательствѣ отъ противнаго; его
всегда можно замѣнить прямымъ доказательствомъ, и болѣе
простымъ, и болѣе яснымъ.
5. Нѣкоторыя статьи изложены въ прилагаемомъ руко-
водствѣ, какъ кажется, проще, чѣмъ въ распространенныхъ
нашихъ учебникахъ. Таковы, напр., статьи: о параллельныхъ
прямыхъ, объ относительномъ проложеніи окружностей, о
пропорціанальныхъ линіяхъ, о правильныхъ многоугольни-
кахъ, о нахожденіи объема всякаго параллелопипеда, о по-
добіи многогранниковъ и нѣкоторыя другія. Сравнительная
простота достигается нѣкоторымъ измѣненіемъ въ распредѣ-
леніи матеріала, а иногда упрощеніемъ пріемовъ доказа-
тельства.
Кромѣ указанныхъ главнѣйшихъ особенностей читатель
встрѣтитъ въ этой книгѣ и нѣкоторыя другія. Отступая
мѣстами отъ обычнаго пріема изложенія, мы стремились
или упростить доказательства, или сократить количество
запоминаемаго матеріала, или облегчить усвоеніе предмета
во всей его цѣлости. Изложеніе нѣкоторыхъ теоремъ существенно
измѣнено (напр., теорема Птоломея); теоремы, близкія другъ
къ другу по ихъ логической связи или по общности дока-
зательства, соединены въ одну группу. Нѣкоторыя обыкно-
венно помѣщаемыя въ руководствахъ теоремы отнесены нами
къ упражненіямъ, или выпущены совсѣмъ, какъ не имѣ-
ющія примѣненія въ логической цѣпи другихъ теоремъ и не
представляющія самостоятельнаго интереса (напр., обратная
теорема о вертикальныхъ углахъ, или случай равенства пря-
моугольныхъ треугольниковъ по катету и противолежащему
острому углу). Съ цѣлью облегчить учащимся усвоеніе распре-
дѣленія матеріала мы сочли полезнымъ вездѣ, гдѣ возможно,
давать той или другой группѣ теоремъ соотвѣтствующій
заголовокъ, указывающій на характеръ теоремъ этой группы.
Замѣтимъ еще, что относительно обратныхъ теоремъ,
слѣдуя нѣкоторымъ Французскимъ учебникамъ, мы стремились
провести идею— что «если въ теоремѣ или рядѣ теоремъ
— VII —
разсмотрѣны всевозможные случаи, которые могутъ предста-
виться относительно величины или расположенія нѣкоторыхъ,
частей Фигуры, причемъ оказалось, что въ различныхъ слу-
чаяхъ получаются различные выводы относительно величины?
или расположенія другихъ частей Фигуры, то можемъ утвер-
ждать & ргіогі, что обратныя предложенія вѣрны». Освоив-
шись съ этимъ логическимъ принципомъ, учащіеся во мно
гихъ случаяхъ могутъ сами составлять и доказывать обрат-
ныя предложенія безъ помощи учителя и учебника.
Книга снабжена значительнымъ количествомъ упражне-
ній, состоящихъ частію изъ нѣкоторыхъ не вошедшихъ въ
текстъ, но представляющихъ интересъ теоремъ, а главнымъ
образомъ изъ задачъ на построеніе и вычисленіе. Въ концѣ,
планиметріи мы помѣстили*) нѣкоторыя задачи на вычисленіе
изъ « Сборника геометрическихъ задачъ для повторительнаго,
курса планиметріи» г. М. Понруженко (Воронежъ, 1891 г.).
Эти задачи обладаютъ прежде всего тѣмъ достоинствомъ, что онѣ-
содержатъ много чисто геометрическаго матеріалу, а не пред-
ставляютъ еобоютолько ариѳметическихъ или алгебраическихъ
упражненій съгеометрическпми данными. Въ концѣ курса, въ
видѣ дополненія, мы сочли не лишнимъ приложить небольшую-
статью о методахъ рѣшенія геометрическихъ задачъ на построе-
ніе съ примѣрами задачъ, рѣшаемыхъ этими методами. Суще-
ствующіе у насъ сборники подобнаго рода, устрашая уча-
щихся своимъ объемомъ, употребляются ими лишь въ рѣд-
кихъ случаяхъ. Мы изложили въ самомъ сжатомъ видѣ
только главнѣйшіе методы и помѣстили наиболѣе типичныя
задачи.
Слѣдуя учебнымъ планамъ гимназій и реальныхъ учи-
лищъ, мы помѣщаемъ основныя задачи на построеніе и вы-
численіе въ самомъ текстѣ книги непосрественно послѣ
тѣхъ теоремъ, на которыхъ основано ихъ рѣшеніе. Въ со-
кращенномъ видѣ мы указываемъ также сущность прило-
женія алгебры къ геометріи и построеніе простѣйшихъ ал-
гебраическихъ Формулъ.
Считаемъ не лишнимъ сдѣлать слѣдующее замѣчаніе. Съ
*) съ согласія составителя.
— VIII —
точки зрѣнія строгой теоріи къ задачамъ па построеніе возмож-
но приступать только тогда, когда-ученики усвоили основныя
предложенія объ окружности. Но съ педагогической точки
зрѣнія ото едва ли было бы удобно: отодвинуть практиче-
скія упражненія такъ далеко отъ начала курса значило бы
сдѣлать начало геометріи, и безъ того трудное для начина-
ющихъ, еще болѣе сухимъ и тяжелымъ. Мы поступились
строгостью въ пользу практическаго интереса и помѣстили
основныя задачи на построеніе тотчасъ послѣ разсмотрѣнія
свойствъ треугольниковъ.
Книга напечатана двумя шрифтами: въ обыкновенномъ
изложено все то, что должно быть пройдено въ среднихъ
классахъ, въ мелкомъ — то, что желательно дополнить при
повтореніи геометріи въ старшемъ классѣ. Не желая рас-
ширять объема учебника, мы не помѣстили въ немъ ничего
такого, что не входило бы въ программы или гимназій, или
реальныхъ училищъ.
При составленіи этого руководства мы пользовались, какъ
пособіемъ, кромѣ извѣстныхъ оригинальныхъ и переводныхъ
учебниковъ па русскомъ языкѣ., еще слѣдующими сочиненіями
ВоисЪё еі СотЬегошяе — Ёіётепіз ёе §ёотёігіс (дпаігіёте
её., 1888);
Тѣхъ же авторовъ—Тгаііё ёе ^ёотёігіе (сіпдніёте её.)-,
Ѵасдцапі—Сонгз ёе ^ёотёігіе (ёепхіёте её.);
Воигуеі — Сонгз ёе §ёотёігіе (8іхіёпіе её.);
Ваег—ЁіётеГііз ёе ^ёотёігіе ріапе (1887);
ТотЬеск — ТгаПё ёе ^ёошёігіе (13-е её., 1890);
Сошрадпоп — Ёіётепіз ёе ёёотёігіе (зесопёе её.);
Ноиеі — Еззаі сгійцие знг Іез ргіпсірез (опёатепіапх ёе
^ёотёігіе ёіётепіаіге;
Н. Всііоиеп — ёпііаіі ппё МеЙюёе ёез ріапітеігізсііеп ІІп-
іеггісМз (1890);
ВаияепЬегдег (ОНо)— ёіеЕІетепіаг^еотеігіе ёез Рнпсіез, ёег
(Іегаёеп ппё ёег ЁЬепе (1887);
и нѣкоторыми другими.
Харьковъ, 8 марта 1892 г.
А. Киселевъ.
ВВЕДЕНІЕ.
Математическія предложенія.
Во всякой математической наукѣ могутъ встрѣтиться
слѣдующія предложенія:
Опредѣленія. Такъ называютъ предложенія, въ которыхъ
разъясняется, какой смыслъ придаютъ тому или другому наз-
ванію. Паприм., въ ариѳметикѣ мы встрѣчаемъ опредѣленія
наименьшаго кратнаго, общаго наибольшаго дѣлителя и т. и.
АКСІОМЫ. Такъ называютъ истины, которыя, вслѣдствіе
своей очевидности, принимаются безъ доказательства. Таковы,
напр., предложенія:
Если двѣ величины равны порознь одной и той же третьей
величинѣ, то онѣ равны и между собою.
Если къ равнымъ величинамъ придадимъ поровну, или
отъ равныхъ величинъ отнимемъ поровну, то равенство не
нарушится.
Если къ неравнымъ величинамъ придадимъ поровну, или
отъ неравныхъ величинъ отнимемъ поровну, то смыслъ нера-
венства не измѣнится, т.-е. большая величина останется большей.
Теоремы. Такъ называются предложенія, которыхъ истин-
ность обнаруживается только послѣ нѣкотораго разсужденія
(доказательства). Примѣромъ можетъ служить ариѳметическая
истина: „если сумма цыфръ дѣлится на 9, то число дѣ-
лится на 9“.
Слѣдствія. Такъ наз. предложенія, которыя составляютъ
непосредственный выводъ изъ аксіомы или теоремы. Напр.,
изъ теоремы: „въ геометрической пропорціи произведеніе край-
А. П. КИСЕЛЕВЪ.	1
2 —•
нихъ членовъ равно произведенію среднихъ" выводится слѣд-
ствіе: „крайній членъ равенъ произведенію среднихъ, дѣлен-
ному на другой крайній".
ж. Составъ теоремы. Во всякой теоремѣ можно разли-
чить двѣ части: условіе и заключеніе. Условіе выражаетъ то,
что предполагается даннымъ; заключеніе содержитъ въ себѣ
то, что требуется доказать. Напр., въ теоремѣ: „если сумма
цыфръ дѣлится на 9, то число дѣлится на 9", условіемъ
служитъ первая часть теоремы: „если сумма цыфръ дѣлится
на 9", а заключеніемъ — вторая часть: „то число дѣлится на
9;“ другими словами, намъ дано, что сумма цыфръ дѣлится
па 9, а требуется доказать, что въ такомъ случаѣ и число
дѣлится на 9.
Условіе и заключеніе теоремы могутъ иногда состоять
изъ нѣсколькихъ отдѣльныхъ условій и заключеній; папр., въ
теоремѣ: „если число дѣлится на 2 и на <?, то оно раздѣ-
лится на 6“, условіе состоитъ изъ двухъ частей: если число
дѣлится на 2 и если число дѣлится на 3.
Полезно замѣтить, что всякую теорему можно подробно
выразить такъ, что ея условіе будетъ начинаться словомъ
„если“, а заключеніе—словомъ „тои.
3.	Обратная теорема. Теоремою, обратною данной теоремѣ,
наз. такая, въ которой условіемъ поставлено заключеніе пли
часть заключенія данной теоремы, а заключеніемъ — условіе
или часть условія данной теоремы. Напр., слѣдующія двѣ
теоремы будутъ обратны другъ другу:
Если сумма цыфръ дѣлится ‘	“
на 9,
то число дѣлится на 9.
Если одну изъ этихъ теоремъ назовемъ прямою, то дру-
гую слѣдуетъ назвать обратною.
Въ этомъ примѣрѣ обѣ теоремы: и прямая, и обратная,
оказываются вѣрными. Но не должно думать, что такъ бы-
ваетъ всегда. Напр.. теорема: „если каждое слагаемое дѣлится
на одно и то же число, то п сумма раздѣлится на то же
число" — вѣрна, но невѣрно обратное предложеніе: „если
сумма дѣлится на какое-нибудь число, то и каждое слагаемое
раздѣлится на него".
Если число дѣлится иа 9.
то сумма цыфръ дѣлится
на 9.
— 3 —
4.	Противоположная1 теорема. Теоремою, противоположной
данной теоремѣ, наз. такая, которой условіе и заключеніе
представляютъ отрицаніе условія и заключенія данной теоремы.
Напр., теоремѣ: „если сумма цыфръ дѣлится на 9, то число
дѣлится на 9“ сооотвѣтствуетъ такая противоположная: „если
сумма цыфръ не дѣлится на 9, то число не дѣлится на 9".
И здѣсь должно замѣтить, что вѣрность прямой теоремы
еще не служитъ доказательствомъ вѣрности противоположной:
напр., противоположное предложеніе: „если каждое слагаемое
не дѣлится на одно п то же число, то и сумма не раздѣ-
лится па это число"—не вѣрно, тогда какъ прямое предло-
женіе вѣрно.
5.	Зависимость между теоремами: прямой, обратной и проти-
воположной. Для лучшаго уясненія этой зависимости выразимъ теоремы
сокращенно такъ:
1°. Прямая: если есть Л, то есть и В.
2°. Обратная: если есть Л, то есть п А.
3°. Противоположная прямой: если нѣтъ А, то нѣтъ и В.
4°. Противоположная обратной: если нѣтъ Б, то нѣтъ и А.
Разсматривая эти предложенія, легко замѣтимъ, что первое изъ нихъ
находится въ такомъ же отношеніи къ четвертому, какъ второе къ
третьему, а именно: предложенія первое и четвертое обратимы одно въ
другое, равно какъ второе и третье. Дѣйствительно, изъ предложенія:
„если есть А, то есть и В“ непосредственно слѣдуетъ: „если нѣтъ В,
то пѣтъ и А-7 (такъ какъ, еслп бы А было, то, согласно первому пред-
ложенію, было бы и В)' обратно, изъ предложенія: „если пѣтъ В, то
нѣтъ и А“ выводимъ: „если есть Л, то есть и В (такъ какъ, если бы
Б пс было, то ве было бы и ЛЬ Совершенно такъ же убѣдимся, что
изъ второго предложенія слѣдуетъ третье, и наоборотъ.
Вслѣдствіе этого, для того, чтобы имѣть увѣренность въ справед-
ливости всѣхъ четырехъ теоремъ, пѣтъ надобности доказывать каждую
изъ нихъ отдѣльно, а достаточно ограничиться доказательствомъ только
двухъ: прямой и обратной, пли прямой и противоположной.
Прямая линія, плоскость. Понятіе о геометріи.
О. Геометрическія фигуры. Часть пространства, занимае-
мая какимъ-нибудь предметомъ, называется іео.ѵетрическимъ
тѣломъ, пли просто тѣломъ.
1*
— 4 —
То, чѣмъ ограничено тѣло отъ остального пространства,
называется поверхностью.
Граница, отдѣляющая одну часть поверхности отъ другой,
называется линіей.
Граница, отдѣляющая одну часть линіи отъ другой, на-
зывается точкой.
Тѣло, поверхность, линія и точка не существуютъ въ
природѣ раздѣльно. Однако, при помощи отвлеченія, мы мо-
жемъ разсматривать геометрическое тѣло независимо отъ ма-
теріальнаго предмета, поверхность—независимо отъ тѣла, ли-
нію—независимо отъ поверхности и точку—независимо отъ
линіи.
Совокупность какихъ бы то ни было точекъ, линій, по-
верхностей или тѣлъ, расположенныхъ извѣстнымъ образомъ
въ пространствѣ, называется вообще фиіурой.
Я. Геометрія. Наука, разсматривающая свойства фигуръ,
паз. геометріей, что въ переводѣ съ греческаго языка озна-
чаетъ землемѣріе. Такое названіе этой наукѣ дапо было по-
тому, что въ древнее время главною цѣлью геометріи было
измѣреніе разстояній па земной поверхности.
8. Въ самомъ началѣ геометріи должно быть указано
слѣдующее общее свойство фигуръ:
Аксіома пространства. Всякую фигуру можно перенести
изъ одного мѣста пространства въ какое угодно другое, не
нарушая ни величины составляющихъ фгауру частей, ни
ихъ взаимнаго расположенія.
». Прямая ЛИНІЯ. Всякій знаетъ, что такое прямая ли-
нія, или просто прямая, представленіе о которой намъ даетъ
туго натянутая нить. Понятіе о прямой элементарно, т.-е.
оно не можетъ быть опредѣлено посредствомъ другихъ болѣе
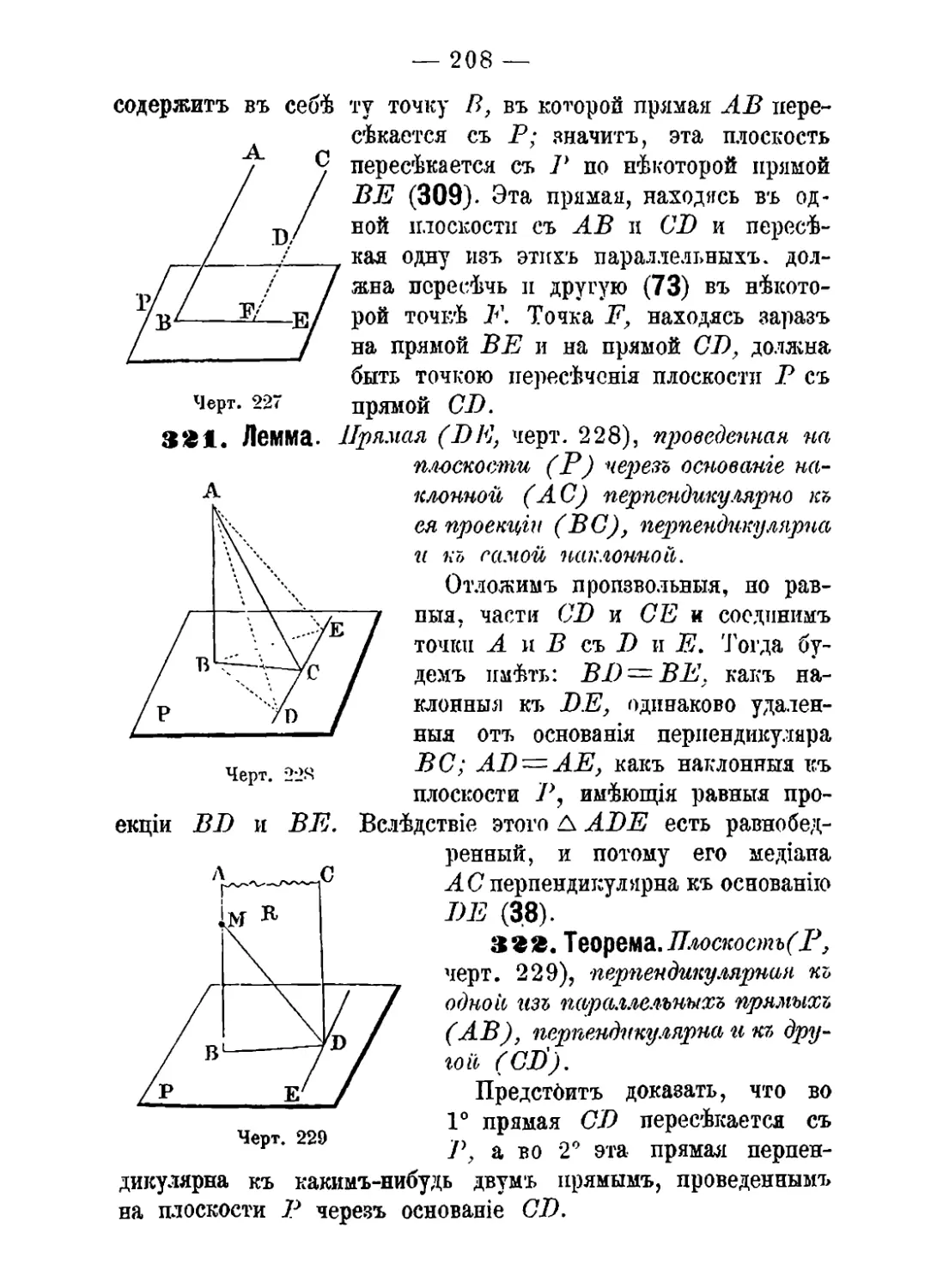
простыхъ понятій.
Прямая линія обладаетъ слѣдующими основными свой-
ствами:
АКСІОМЫ прямой. 1’. Черезъ всякія двѣ точки простран-
ства можно провести прямую и притомъ гполько одну.
2е. Прямую можно продолжать безъ конца въ обѣ сто-
роны отъ каждой ея точки.
3°. Если двѣ прямыя имѣютъ только одну общую
точку, то оиѣ пересѣкаются, гп.-е. каждая изъ нихъ рас-т
полагается по обѣ стороны другой.
Изъ первой аксіомы непосредственно слѣдуетъ:
Двѣ прямыя, будучи наложены одна на другую такъ, что
двѣ точки одной прямой совпадаютъ съ двумя точками дру-
гой прямой, сливаются и во всѣхъ остальныхъ точкахъ
(потому что въ противномъ случаѣ черезъ двѣ точки можно
было бы провести двѣ различныя прямыя, что противорѣчитъ
аксіомѣ первой).
По той же причинѣ двѣ прямыя могутъ пересѣчься только
въ одной точкѣ.
На чертежѣ прямую изображаютъ въ видѣ тонкой черты,
проведенной отъ руки пли помощью линейки черезъ какія-
нибудь двѣ точки прямой.
ІО. Прямая конечная и безконечная. Если прямую пред-
ставляютъ продолженною въ обѣ стороны безконечно, то ее
называютъ безконечною или неопредѣленною прямой. Такую
прямую обозначаютъ обыкновенно двумя буквами, поставлен-
ными у двухъ какихъ-нибудь ея точекъ. Такъ, говорятъ:
япрямая ЛВ пли ВАи (черт. 1).
А-----------------В с |---------------1 В
Черт. 1	Чсрт. 2
Часть прямой, ограниченная съ обѣихъ сторонъ, наз.
конечною прямой, или отрѣзкомъ прямой; такая прямая обо-
значается двумя буквами, поставленными у концовъ ея (от-
рѣзокъ СВ, черт. 2). Отрѣзокъ прямой, соединяющій двѣ
точки, наз. разстояніемъ между пими.
Иногда разсматриваютъ прямую, ограниченную только съ
одной стороны, ианр. въ точкѣ А (черт. 3). О такой пря-
мой говорятъ, что опа исходитъ изъ точки А.
АI..............................
Черт. 3
— 6
II. Равенство конечныхъ прямыхъ. Два отрѣзка прямой
считаются равными, если они при наложеніи совмѣщаются.
А I-------------1В СI--------------1 О
м	X	р
-------1-------------1-------------1------
Черт. 4
Положимъ, напр., что мы накладываемъ отрѣзокъ АВ на
СВ (черт. 4) такъ, чтобы точка А упала въ С и чтобы
прямая АВ пошла по СВ; если при этомъ концы В и В
совпадутъ, то АВ-^=СВ; въ противномъ случаѣ отрѣзки счи-
таются пе равными, причемъ меньшимъ будетъ тотъ, кото-
рый составитъ только часть другого.
Чтобы па какой-нибудь прямой отложпть отрѣзокъ, рав-
ный данному отрѣзку, употребляютъ циркуль—приборъ, извѣст-
ный учащимся изъ опыта.
I». Сумма конечныхъ прямыхъ. Суммою нѣсколькихъ
данныхъ отрѣзковъ прямой наз. такой новый отрѣзокъ пря-
мой, который составленъ изъ частей, соотвѣтственно равныхъ
даннымъ отрѣзкамъ. Положимъ, напр., требуется найти сумму
двухъ отрѣзковъ АВ и СВ (черт. 4). Для этого па какой-
нибудь неопредѣленной прямой беремъ произвольную точку
М и откладываемъ отъ нея часть АШ, равную АВ, затѣмъ
отъ точки въ томъ же направленіи откладываемъ часть
^Р, равную СВ. Отрѣзокъ А1Р будетъ сумма данныхъ от-
рѣзковъ АВ и СВ. Подобнымъ образомъ можно получить
сумму трехъ и болѣе отрѣзковъ.
Изъ понятія о суммѣ выводятся понятія о разности, про-
изведеніи и частномъ отрѣзковъ. Такъ, разность отрѣзковъ
А В и СВ есть третій отрѣзокъ, котораго сумма съ СВ
образуетъ АВ; произведеніе отрѣзка АВ на отвлеченное число
3 есть сумма трехъ отрѣзковъ, изъ которыхъ каждый равенъ
АВ; и т. п.
13. Плоскость. Такъ наз. поверхность, обладающая тѣмъ
свойствомъ, что прямая, проходящая черезъ какія-нибудь двѣ
точки этой поверхности, лежитъ въ ней всѣми остальными
7
своими точками. Положимъ, напр., мы желаемъ убѣдиться,
будетъ ли плоскостью поверхность стола. Для этого беремъ
хорошо вывѣренную линейку и прикладываемъ ее въ различ-
ныхъ направленіяхъ къ поверхности стола такъ, чтобы ка-
кія-нибудь двѣ точки липейки лежали па этой поверхности.
Если при этомъ окажется, что, въ какомъ бы направленіи
лы линейку ни приложили, всѣ остальныя точки ея будутъ
лежать на поверхности стола, то эта поверхность есть плос-
кость.
Укажемъ еще слѣдующее свойство плоскости, которое мы
примемъ здѣсь безъ доказательства*):
Всякую частъ плоскости можно наложитъ всѣми ея
точками на другое мѣсто этой илгі другой плоскости, при-
чемъ накладываемую частъ можно предварительно перевер-
нутъ другою стороною.
14. Раздѣленіе геометріи. Геометрія раздѣляется па двѣ
части: геометрія па плоскости пли плангіметрія, и геометрія
въ пространствѣ пли стереометрія. Первая разсматриваетъ
свойства такихъ фигуръ, которыя всѣ размѣщены въ одной
плоскости; вторая—свойства такихъ фигуръ, которыя не "по-
мѣщаются въ одной плоскости.
*) Доказательство излагается вт, началѣ курса стереометріи.
ПЛАНИМЕТРІЯ.
КНИГА I.
ПРЯМАЯ ЛИНІЯ
ГЛАВА I.
Углы.
Предварительныя понятія.
15. Опредѣленія. Когда двѣ прямыя (ОА и ОВ, черт. 5)
исходятъ изъ одной точки, то онѣ образуютъ то, что наз.
угломъ.- Прямыя, образующія, уголъ, паз. сторонами, а точки,
изъ которой онѣ исходятъ, —вер-
д ...''	шиною угла. Стороны должно пред-
ай . В ставлять себѣ продолженными отъ
/ ...	вершины неопредѣленно.
/	Е	У голъ обыкновенно обозначается
’.. в	тремя буквами, изъ которыхъ срсд-
0 "	няя ставится у вершины, а край-
Черт- 5	пія у какихъ-нибудь точекъ сто-
ронъ; паир., говорятъ: „уголъ А ОВ или уголъ В О А
(черт. 5)“. По можно обозначать уголъ и одною буквою, по-
ставленною у вершпны, если при этой вершинѣ нѣтъ дру-
гихъ угловъ. Мы иногда будемъ обозначать уголъ цыфрою,
поставленною внутри угла, около вершины.
Если изъ вершины угла (черт. 5) проведемъ внутри его
какія-нибудя прямыя 01), ОЕ,..., то образовавшіеся при этомъ
углы АО1). 1)ОЕ, ЕОВ... разсматриваются, какъ части
угла АОВ.
Слово „уголъ® па письмѣ замѣняется иногда знакомъ
1в. Равенство угловъ. Два угла считаются равными или
неравными, смотря по тому, совмѣщаются ли они при нало-
9
женіи или нѣтъ. Положимъ, напр., что мы накладываемъ
уголъ АОВ на уголъ АХОХВХ (черт. 6) такъ, чтобы вер-
шина О упала въ прямая ОВ пошла по ОХВХ и чтобы
углы покрыли другъ друга. Если при этомъ сторона О А со-
Черт. 6
вмѣстится съ ОХАХ, то углы равны; если же О А пойдетъ
внутри угла АХОВАІ или внѣ его, то углы не равны, при-
чемъ тотъ изъ нихъ будетъ меньше, который составитъ часть
другого угла.
13* Сумма угловъ. Суммою двухъ угловъ АОВ и Ах ОХВХ
(черт. 7) наз. такой уголъ МНф, который составленъ изъ
Черт. 7
частей, соотвѣтственно равныхъ угламъ АОВ и АХОХВХ.
Подобнымъ образомъ можетъ быть со-
ставлена сумма трехъ и болѣе угловъ.
Изъ понятія о суммѣ угловъ вы-
водятся понятія объ ихъ равности,
произведеніи и частномъ. Замѣтимъ,
ч’го прямая, дѣлящая уголъ пополамъ,
наз. биссектриссою угла (черт. 8).
Черт. 8
10 —
Свойства прямого угла.
18. Опредѣленія. Два угла (ЛОВ и ВОС, черт. 9)
наз. смежными, если одна сторона у нихъ общая, а двѣ
другія стороны составляютъ продолженіе одна другой. Когда
Л--------о]-------_с
Черт. 9
Черт. 10
два смежные угла равны (черт. 10), то общая ихъ сторона
ОВ наз. перпендикуляромъ къ прямой АС, на которой ле-
жатъ другія стороны; если же смежные углы неравны (черт.
9), то ОВ наз. наклонною къ АС. Въ томъ и другомъ слу-
чаѣ точка О наз. основаніемъ (перпендикуляра или наклонной)
Каждый ггзъ равныхъ смежныхъ угловъ наз. прямымъ.
Говорятъ: „возставитъ къ прямой перпендикуляръ“, если
этотъ перпендикуляръ приходится проводить черезъ точку,
взятую на прямой, и .,опустипгь па прямую перпендикуляръ“,
если онъ проводится черезъ точку, взятую внѣ прямой. Го-
ворятъ: „перпендикуляръ къ срединѣ прямой", разумѣя подъ
этимъ перпендикуляръ къ конечной прямой, проведенный че-
резъ ея средину.
Что смежные углы могутъ быть равны, видно изъ слѣ-
дующей теоремы.
1®. Теорема. Взъ всякой точки прямой можно, но ту
гі другую сторону отъ этой прямой, возставитъ къ ней
перпендикуляръ и притомъ только одинъ.
Пусть дана какая-нибудь прямая АВ (черт. 11) и на ней
произвольная точка О. Требуется доказать: во 1) что изъ
этой точки можно, по каждую сторону отъ прямой АВ, напр.
по верхнюю, возставить къ АВ перпендикуляръ, и во 2), что
этотъ перпендикуляръ можетъ быть только одинъ.
— 11
Для доказательства проведемъ
изъ точки О прямую ОС, почти
сливающуюся съ О А, и затѣмъ
станемъ ее вращать вокругъ точки
О въ направленіи, указанномъ на
чертежѣ стрѣлкою, приближая ОС
все болѣе и болѣе къ ОВ. Тогда
Д СОА будетъ непрерывно увс-	Черт. п
личиваться, а /_ СОВ непре-
рывно уменьшаться, причемъ послѣдній уголъ можетъ быть
сдѣланъ такъ малъ, какъ угодно. Изъ этого слѣдуетъ, что
при вращеніи прямая ОС можетъ занять такое положеніе ОВ,
при которомъ углы АОВ и ВОВ окажутся равными; тогда
ОВ и будетъ перпендикуляромъ къ АВ. Такъ какъ при вся-
комъ иномъ положеніи вращающейся прямой ОС равенство
между смежными углами нарушается, то другого перпенди-
куляра къ АВ изъ точки О возставить нельзя, по крайней
мѣрѣ по ту же сторону отъ АВ, по какой лежитъ перпен-
дикуляръ ОВ.
80, Теорема. Всѣ прямые углы равны между собою.
Пусть смежные углы при вершинахъ О и О, (черт. 12)
будутъ прямые, т.-е. /_АОВ — /_ВОС и /„АХОХВХ —
/ Вх 01 Сх. Требуется доказать, что прямые углы первой пары
равны прямымъ угламъ второй пары.
В	я
Черт. 12
о,
С,
Наложимъ фигуру АОВС на фигуру АІОІВІС1 такъ,
чтобы точка О упала въ О , прямая АС пошла по АХСХ,
и чтобы прямая ОВ упала по ту же сторону отъ АХСХ, по
которой расположена ОХВХ. Тогда ОВ совпадетъ съ ОХВХІ
12 —
потому что въ противномъ случаѣ изъ одной точки 0^ пря-
мой А} можно было бы возставить къ ней, по одну и ту
же сторону, два перпендикуляра, что, по доказанному выше,
невозможно. Если же прямыя ОВ и О1В1 совпадутъ, то это
значитъ, что /_ АОВ = АгОхВг и / СОВ = /. СгОгВ^
что и требовалось доказать.
Зі. Опредѣленія. Изъ доказанной теоремы слѣдуетъ, что
прямой уголъ представляетъ собою постоянную величину (ее
обыкновенно обозначаютъ знакомъ сі, т.-е. начальною буквою
франц. слова йтоіі, прямой}. Вслѣд-
ствіе этого другіе углы сравниваютъ
по величинѣ съ прямымъ угломъ.
Черт. 18
Всякій уголъ АОС (черт. 13),
мепыпій прямого угла АОВ, наз. ост-
рымъ, а всякій уголъ АОВ, большій
прямого, наз. тупымъ.
33. Черченіе прямого угла. Пря-
мой уголъ легко начертить помощью прибора, называемаго
наугольникомъ, у котораго одинъ изъ трехъ угловъ дѣлается
прямымъ. Чтобы начертить прямой уголъ при точкѣ С пря-
мой АВ (черт. 14), при-
ставляютъ къ этой прямой
линейку, а къ линейкѣ на-
угольникъ, какъ указано на
чертежѣ, и двигаютъ на-
угольникъ вдоль линейки до
тѣхъ норъ, пока вершила
прямого угла не совпадетъ
съ точкой С. Остается за-
Че т 14	тѣмъ провести по сторонѣ
прямого угла прямую СВ.
аз. Доказательство наложеніемъ. Пріемъ доказательства,
которымъ мы пользовались въ § 20, весьма часто употре-
бляется въ геометріи для обнаруженія равенства или нера-
венства фигуръ. Онъ извѣстенъ подъ именемъ доказательства
наложеніемъ. Замѣтимъ, что наложеніе одной плоской фигуры
на другую всегда можно выполнить въ такой послѣдовательности:
— 13 —
1°. Мы можемъ любую точку одной фигуры совмѣстить
съ любою точкою другой фигуры; напр. (черт. 12) Іючку
О съ ОР
2°, По совмѣщеніи двухъ точекъ мы можемъ, вращая на-
кладываемую фигуру вокругъ совпавшей точки, совмѣстить
въ обѣихъ фигурахъ любыя двѣ прямыя, исходящія изъ сов-
павшихъ точекъ; напр. (черт. 12) прямую ОС съ ОАА-
3°. По совмѣщеніи двухъ точекъ и двухъ прямыхъ мы
можемъ, вращая накладываемую фигуру вокругъ совпавшей
прямой, какъ около оси, расположить эту фигуру или по ту,
или по другую сторону отъ совпавшей прямой. Напр. (черт.
12) по совмѣщеніи точекъ О и О; и прямыхъ ОС и ОХСІУ
мы можемъ расположить фигуру АОВ О или такъ, что пря-
мая ОВ пойдетъ къ верху отъ 0{Сѵ или же къ ниву отъ
нея (въ послѣднемъ случаѣ будетъ такъ называемое прило-
женіе фигуры).
Послѣ этого нашъ произволъ заканчивается; совпадутъ ли
другія части фигуръ, зависитъ отъ свойствъ самихъ фигуръ.
Свойства смежныхъ и вертикальныхъ угловъ.
Теорема. Сумма двухъ смежныхъ угловъ равна двумъ
прямымъ.
Даны два смежныхъ угла: АОВ и ВОС; требуется до-
казать, что АОВ-\-ВОС~2сІ.
Возставивъ изъ точки О къ пря-
мой АС перпендикуляръ 01), мы	В в
разобьемъ уголъ АОВ па двѣ части:	/
АОТ) и ВОВ, такъ что можно па-	і /
писать:	| /
АОВ = АОВ + ЯОВ	Л/
А.
Приложимъ къ обѣимъ частямъ
Этого равенства по углу В О С; тогда Че₽т* 5
получимъ:
АОВ-\-ВОС=АОВ + ВОВ + ВОС
14 —
Но сумма БОВ + 2?ОС составляетъ прямой уголъ БОС;
слѣдовательно:
АОВ+ВОС— АОБ+БОС=а+а=М
Ж5. Слѣдствія. 1°. Сумма угловъ: АОВ, ВОС, СОБ,
БОЕ (черт. 16), расположенныхъ вокругъ общей вершины О
по одну сторону прямой ЛЕ, равна 2сІ,
Черт. 16
Черт. 17
потому что эта сумма составляетъ сумму двухъ смежныхъ
у г ловъ, напр. такихъ: А О С + С ОЕ.
2°. Сумма угловъ: АОВ, ВОС, СОБ, БОЕ, ЕОА
(черт. 17), расположенныхъ вокругъ общей вершггны О по
обѣ стороны какой-нибудь прямой БМ, равны Ы,
потому что эта сумма равна (МОВ-\-ВОС-\-СОБ)-\-
+ (БОЕ+ЕОА + АОМ) = (1& + Ы = ±&.
90. Обратная теорема. Если сумма двухъ угловъ, имѣ-
ющихъ общую сторону и не покрывающихъ другъ друга, рав-
на двумъ прямымъ, то такіе углы смежные, т.-е. двѣ дру-
гія стороны ггхъ составляютъ продолженіе одна другой.
Пусть даны два угла: АОВ и ВОС, имѣющіе общую
сторону ОВ и не покрывающіе другъ «друга; пусть, кромѣ
того, сумма ихъ равна 2й; требуется доказать, что ОС есть
продолженіе АО.
в	Для доказательства допустимъ
\	временно, что продолженіе сто-
ропы АО пойдетъ по нѣкоторому
_________________\^0______________—с направленію ОБ, не сливающе-
А________________....-0 муся съ ОС. Посмотримъ, къ
Челт 18
1 ’	чему приведетъ насъ это допуще-
— 15 —
ніе. Такъ какъ углы АОВ и ВОІ) смежные, то по дока-
занному выше (24):
АОВ+ВОВ~ 2сІ
Въ то же время, согласно условію нашей теоремы, мы
имѣемъ:
АОВ-\-ВОС=2сІ
Правыя части этихъ двухъ равенствъ равны, слѣд. равны
и лѣвыя:
АОВ+ВОВ=АОВ+ВОС
Отнявъ отъ равныхъ суммъ по одному и тому же углу
АОВ, мы должны получить равные остатки:
ВОВ=ВОС.
Это равенство невозможно, такъ какъ изъ чертежа не-
посредственно видно, что /_ВОВ больше /_ВОС.
Если въ результатѣ разсужденія мы получаемъ невозмож-
ный (нелѣпый) выводъ, то это можетъ произойти отъ двухъ
причинъ: или мы невѣрно разсуждали, или же мы основыва-
лись на невозможномъ допущеніи. Разсужденіе наше было
правильно; значитъ, причина нелѣпаго вывода заключается въ
невозможности допущенія, будто продолженіе АО не сливается
съ ОС. Если же это предположеніе невозможно, то остается
только одно: продолженіе АО есть ОС (слѣд., нашъ чер-
тежъ сдѣланъ неправильно); что и требовалось доказать.
Слѣдствіе. .Вели гізъ одной точки О прямой АВ
возставимъ къ ней, по каждую ея сторону, перпендикуляры
ОС и ОВ, то эти перпендикуляры
образуютъ одну прямую СВ, по-	(
тому что сумма угловъ СОВ и
ВОВ равна 2 с?.
Опредѣленіе. Неопредѣлен- л о в
пая прямая СВ (черт. 19), кото-
рой части ОС и ОВ служатъ пер-
пендикулярами къ прямой АВ, наз.
линіей, перпендикулярной къ АВ.	„ ' л
Черт. 19
ксли СВ перпендикулярна къ
— 16 —
АВ, то и АВ перпендикулярна къ СВ, потому что части
ОА и ОВ служатъ также перпендикулярами къ СВ. Поэтому
прямыя АВ и СВ наз. взаимно-перпендикулярными.
Что двѣ прямыя АВ и СВ взаимно перпендикулярны,
выражаютъ письменно такъ: АВ I СВ.
Доказательство отъ противнаго. Способъ доказатель-
ства, которымъ мы пользовались въ § 26, наз. доказатель-
ствомъ отъ противнаго, или приведеніемъ къ нелѣпости (ге-
(Іисііо ад аЬзигбит). Первое названіе этотъ способъ получилъ
потому, что въ началѣ разсужденія дѣлается предположеніе.
противное (противоположное) тому, что требуется доказать.
Приведеніемъ къ нелѣпости опъ наз. вслѣдствіе того, что.
разсуждая на основаніи сдѣланнаго предположенія, мы при-
ходимъ къ нелѣпому выводу (къ абсурду). Полученіе такого
вывода заставляетъ пасъ отвергнуть сдѣланное въ началѣ до-
пущеніе и принять то, которое требовалось доказать.
30.	Опредѣленіе. Два угла наз. вертикальными, если
стороны одного составляютъ продолженіе сторонъ другого.
Такъ, при пересѣченіи двухъ прямыхъ АВ и СВ (черт.
20) образуются двѣ пары вертикальныхъ угловъ: АОВ и
СОВ, АОС и ВОВ.
31.	Теорема. Вертикальные углы равны.
Пусть даны два вертикальныхъ угла: АОВ и СОВ, т.-е.
ОВ есть продолженіе О А, а ОС продолженіе ОВ. Требуется
доказать, что А ОВ = СОВ.
По свойству смежныхъ угловъ можемъ
В написать:
\	/	А0В-\-В0В = (1сІ
\ /	ООБ+ В0С=Ы
°д	Значитъ: А ОВ-}-ВОВ— ВОВ4- ВОС.
/ \	Отнявъ отъ обѣихъ частей этого равеп-
/ \ ства по углу ВОВ, получимъ:
с/ \в	АОО=ВОС
черТ. 20	Подобнымъ же образомъ докажемъ, что
и А0С= ВОВ.
— 17 —
39. Теорема. Изъ всякой точки внѣ прямой можно
опуститъ на эту прямую перпендикуляръ и притомъ только
одинъ.
Пусть дана какая-нибудь прямая АВ и внѣ ея произволь-
ная точка М; требуется доказать, что во 1) изъ этой точки
можно опустить на прямую АВ перпендикуляръ, и во 2) что
этотъ перпендикуляръ можетъ быть только одинъ.
Перегнемъ чертежъ по прямой
АВ такъ, чтобы верхняя его часть
упала на нижнюю. Тогда точка М
займетъ нѣкоторое положеніе И.
Отмѣтивъ это положеніе, приведемъ
чертежъ въ прежній видъ и затѣмъ
соединимъ точки М и И прямою.
Теперь докажемъ, что прямая МИ
перпендикулярна къ АВ, а всякая
иная прямая, исходящая изъ Л/,
А
в
Черт. 21
напр. МВ, не перпендикулярна къ АВ. Для этого перегнемъ
чертежъ вторично. Тогда точка М снова совмѣстится съ И,
а точки С и В останутся на свопхъ мѣстахъ; слѣд., пря-
мая МС совпадетъ съ СИ, а МВ съ ВИ. Изъ этого слѣ-
дуетъ, что /_МСВ —ВСИ п /_МВС=/_СВИ. Но
углы МСВ и ВСИ смежные и, какъ теперь видимъ, равные;
слѣд., каждый изъ нихъ есть прямой, а потому МИ | АВ.
Такъ какъ линія МВИ не прямая (между точками М и И
не можетъ быть двухъ различныхъ прямыхъ), то сумма двухъ
равныхъ угловъ МВС и СВИ не равна '2(1; поэтому уголъ
МВС не есть прямой, и, значитъ, МВ не перпендикулярна
къ АВ. Такимъ образомъ, другого перпендикуляра изъ точки
М на прямую АВ опустить нельзя.
Замѣчаніе. Чтобы опустить перпендикуляръ на прямую
изъ данной точки, можно пользоваться линейкой и науголь-
никомъ (см. черт .14).
Упражненія. Доказать, что:
1-	Бпссектриссы двухъ вертикальныхъ угловъ составляютъ продол-
женіе одна другой.
2.	Бпссектриссы двухъ смежныхъ угловъ перпендикулярны.
А- П. КИСЕЛЕВЪ.	2
18 —
3.	Если при точкѣ О прямой ЛВ (черт. 20) построимъ, по разныя
стороны отъ ЛВ, равные углы ЛОЛ и ВОС, то стороны ихъ ОВ и ОС
(вставляютъ одну прямую.
4.	Если изъ точки О (черт. 20) проведемъ прямыя ОЛ, ОВ, ОВ, ОС
такъ, что / ЛОС—/ ВОВ и А Л0В=А СОВ, то ОВ есть продолженіе
ОЛ и ОВ продолженіе ОС. 
ГЛАВА II.
Треугольники и многоугольники.
Понятіе о многоугольникѣ и треугольникѣ.
33.	Ломаная ЛИНІЯ. Линія наз. ломаною, когда она со-
стоитъ нзъ отрѣзковъ прямой, не расположенныхъ на одной
прямой (черт. 22 или 23). Эти отрѣзки наз. сторонами ло-
маной. а вершины угловъ, образуемыхъ сосѣдними отрѣзка-
ми, — вершинами ея. Ломаная линія обозначается рядомъ
буквъ, поставленныхъ у ея вершинъ и концовъ.
Черт. 22	Черт. 23
Ломаная АВСВЕ наз. выпуклою, если она вся располо-
жена по одну сторону отъ каждаго составляющаго ее отрѣз-
ка, продолженнаго неопредѣленно.
Выпуклая ломаная не можетъ пересѣчься съ прямою
линіей болѣе, чѣмъ въ двухъ точкахъ. Дѣйствительно, если
бы ломаная пересѣкалась съ какою-нибудь прямою въ трехъ
точкахъ А, В и С (черт. 23), то она была бы расположена
по разныя стороны того отрѣзка, который проходитъ черезъ
среднюю точку В; значитъ, такую ломаную нельзя было бы
назвать выпуклою.
Когда концы ломаной сходятся въ одну точку, то она
наз. замкнутой.
19
Сумма всѣхъ сторонъ ломаной наз. ея периметромъ или
длиной.
34.	Многоугольникъ. Часть плоскости, ограниченная
замкнутою ломаной линіей, наз. многоугольникомъ (черт. 24).
Стороны этой ломаной наз. сторонами многоугольника, углы,
составленные каждыми двумя сосѣдними сторонами,—углами
многоугольника, а ихъ вершины—вершинами его.
Черт. 24
Многоугольникъ наз. выпукломъ, если онъ ограниченъ
выпуклою ломаною линіей. Таковъ, напр., многоуг. АВСБЕ
(черт. 24); но нельзя назвать выпуклымъ мпогоуг.
(тотъ же черт.).
Всякая прямая АВ, которая соединяетъ вершины двухъ
угловъ многоугольника, не прилежащихъ къ одной сторонѣ,
наз. діагональю.
Сумма сторонъ многоугольника наз. периметромъ его.
Два многоугольника, какъ и вообще двѣ какія-нибудь гео-
метрическія фигуры, считаются равными, если они при на-
ложеніи совмѣщаются.
Наименьшее число сторонъ въ многоугольникѣ гири. По
Числу сторонъ многоугольникъ наз. треугольникомъ, четыре-
угольникомъ, пятиугольникомъ и т. д.
35.	Раздѣленіе треугольниковъ. Треугольники раздѣ-
ляются или по сторонамъ, или по угламъ. Относительно сто-
ронъ они бываютъ: разносторонніе (черт. 25), когда всѣ
стороны различной длины, равнобедренные (черт. 26), когда
Двѣ стороны одинаковы, и равносторонніе (черт. 27), когда
ьсѣ стороны равны.
2*
— 20 —
Относительно угловъ треугольники бываютъ: бстроуголь~
ные (черт. 25), когда всѣ углы острые, прямоугольные (черт,
28), когда въ числѣ угловъ есть прямой, и тупоугольный
(черт. 29), когда въ числѣ угловъ есть тупой. Въ прямоу-
гольномъ треугольникѣ стороны, образующія прямой уголъ,
назыв. катетами, а сторона, лежащая противъ прямого-
угла,—гипотенузой.
КАІЕТЬ
Черт. 28
Черт. 29
зв. Главнѣйшія линіи въ треугольникѣ. Одну изъ сторонъ
треугольника обыкновенно называютъ основаніемъ, вершину
противолежащаго угла—вершиною тр.-ка, а перпендикуляръ,
опущенный изъ вершины па основаніе или на его продолже-
ніе,— высотою его. Такъ если въ тр.-кѣ АВС (черт. 30
или 31) за основаніе взята сторона АС, то В будетъ вер-
шина, ВВ высота тр.-ка.
Въ равнобедренномъ тр.-кѣ основаніемъ называютъ обык-
новенно сторону, не принадлежащую къ равнымъ.
Прямая ВЕ (черт. 30 пли 31), соединяющая вершину
какого-нибудь угла тр.-ка съ срединою противоположной сто-
21 —
роны, наз. медіаною (средней линіей). Прямая ВЕ (черт. 30),
дѣлящая какой-нибудь уголъ тр.-ка пополамъ, наз. биссект-
риссою.
На письмѣ слово „ треугольникъ “ замѣняется иногда зна-
комъ д.
Свойства равнобедреннаго треугольника.
33. Теорема. Въ равнобедренномъ треугольникѣ бгіссек-
гприсса угла пргь вергиинѣ служитъ одновременно медіаной,
высотой- и перпендикуляромъ къ средингь основанія.
Пусть тр.-къ АВС равнобед-
ренный и прямая ВВ дѣлитъ по-
поламъ уголъ В при вершинѣ.его.
Требуется доказать, что ВВ есть
также и медіана, и высота, и пер-
пендикуляръ къ срединѣ основанія.
Вообразимъ, что Д АВВ повер-
нутъ вокругъ стороны ВВ такъ,
чтобы онъ упалъ на Д ВВ С. Тогда,
вслѣдствіе равенства угловъ 1 и
2, сторона АВ упадетъ на ВС,
а вслѣдствіе равенства этихъ сторонъ точка А совпадетъ
съ С. • Поэтому ВА совмѣстится съ ВС и уголъ 4 съ уг-
ломъ 3; значитъ, ВА — ВО и ДЗ = /_4. Изъ того, что
ВА = ВС, слѣдуетъ, что ВВ есть медіана; изъ того, что уг-
лы 3 и 4 равны, выходитъ, что эти углы прямые, и ВВ
— 22 —
есть высота тр.-ка АВС; наконецъ, изъ того и другого вмѣстѣ
выводимъ, что ВВ есть перпендикуляръ къ срединѣ основанія.
38. Слѣдствіе. 1°. Такимъ образомъ мы видимъ, что въ
равнобедрепяомъ тр.-кѣ АВС (черт. 32) одна и та же пря-
мая ВВ обладаетъ 4-мя свойствами: опа есть биссектрисса
угла при вершинѣ, медіана, проведенная къ основанію, вы-
сота, опущенная на основаніе, и, наконецъ, перпендикуляръ
къ срединѣ основанія. Такъ какъ каждое изъ этихъ 4-хъ
свойствъ вполнѣ опредѣляетъ положеніе прямой ВВ, то су-
ществованіе одного изъ нихъ влечетъ за собой всѣ осталь-
ныя. Напр.:
высота, опущенная на основаніе равнобедреннаго треу-
гольника, служитъ одновременно бгіссектр косою угла при вер-
гиггнѣ, медіаною, проведенною къ основанію, и перпендику-
ляромъ къ срединѣ основанія.
Дѣйствительно, во 1, эта высота должна служить биссек-
триссою угла при вершинѣ, потому что въ противномъ слу-
чаѣ, проведя такую биссектриссу, мы имѣли бы двѣ высоты
на одну и ту же сторону тр.-ка, что невозможно. Во 2, эта
высота, будучи биссектриссою, должна быть, по доказанному,
и медіаной, и перпендикуляромъ къ срединѣ основанія.
30. Слѣдствіе 2°. Изъ того, что тр.-ки АВВ и ВВС
(черт. 32) совмѣщаются всѣми своими частями, слѣдуетъ,
что /_А — /__С, т.-е.
въ равнобедренномъ треугольникѣ углы при основаніи
равны.
Признака равенства треугольниковъ.
40.	Предварительныя понятія. Такъ какъ равными тре-
угольниками наз. такіе, которые при наложеніи совмѣщаются,
то въ такихъ тр.-кахъ равны всѣ соотвѣтствующіе элементы
ихъ, т.-е. сторопы, углы, высоты, медіаны и биссектрпссы.
Однако, для того, чтобы утверждать равенство двухъ тре-
угольниковъ, не необходимо знать равенство всѣхъ элементовъ
ихъ; достаточно убѣдиться въ равенствѣ только нѣкоторыхъ
изъ нихъ. Слѣдующія теоремы излагаютъ три главнѣйшіе
признака равенства тр.^ковъ.
— 23 —
41.	Теоремы. Два треугольника равны, если:
1°, двѣ стороны и уголъ, заключенный между ними, од-
ного треугольнггка соогпвгьтсгпвенно равны двумъ сторонамъ,
и углу, заключенному между ними, другого треугольника;
или 2°, два угла и прщгежащая къ нимъ сторона одного
треугольника соотвгьтственно равны двумъ угламъ и глриле-
жащей къ нимъ сторонѣ другого треугольника;
иди 3 °, три стороны одного треугольника соотвѣтственно
равны гпремъ сторонамъ другого треугольника.
1°. Пусть АВС и АІВІС1 будутъ два тр.-ка, у которыхъ:
А = АІ, АС=А1С1 и АВ=А,ВГ
Требуется доказать, что эти тр.-ники равны.
Черт. зз
Наложимъ Л АВС на Л А1ВІСІ такъ, чтобы точка А
совпала съ А1 и сторона АС пошла по АД^. Тогда, вслѣд-
ствіе равенства этихъ сторонъ, точка С совмѣстится съ С,;
вслѣдствіе равенства угловъ А и А} сторона АВ пойдетъ по
а вслѣдствіе равенства этихъ сторонъ точка В упадетъ
въ В{; поэтому сторона СВ совмѣстится съ С\В{ (между
двумя точками можно провести только одну прямую) п треу-
гольники совпадутъ: значитъ, они равны.
2°. Пусть АВС и Л151С'1 будутъ два тр.-ка, у которыхъ:
СВ—С.ВХІ О=С1гіВ=В1.
Требуется доказать, что эги тр.-ники равны (черт. 34).
Наложимъ Д АВС на Л А1В1СІ такъ, чтобы точка С
совпала съ С1 и сторона СВ пошла по С1ВІ; тогда, вслѣд-
— 24 —
ствіе равенства этихъ сторонъ, точка В упадетъ въ Вх. а
вслѣдствіе равенства угловъ В и Си Сі сторона ВА
пойдетъ по В1АІ и сторона СА по С^А^. Такъ какъ двѣ
прямыя могутъ пересѣчься только въ одной точкѣ, то вер-
шина А должна совпасть съ А{. Такимъ образомъ, тр.-ники
совмѣстятся; значитъ, опи равны.
3°. Пусть АВС и АІВІСІ будутъ два тр.-ка, у которыхъ:
АВ = АІВ1, ВС=ВІС1 и СА=СХАГ
Требуется доказать, что эти тр.-ники равны (черт. 35).
Доказывать этотъ признакъ равенства наложеніемъ, какъ
мы это дѣлали для первыхъ двухъ признаковъ, было бы не-
удобно, такъ какъ, не зная ничего о величинѣ угловъ, мы
не можемъ утверждать, что при совпаденіи двухъ равныхъ
сторонъ совпадутъ и остальныя. Употребимъ иной пріемъ до-
казательства.
— 25 —
Приложимъ Л АВС къ Д АІВІО1 такъ, чтобы у нихъ
«лились равныя стороны АС и А^. Тогда А АВС займетъ
доложеніе А1С1В11. Соединивъ прямою точки 7^ и Вп,мы
получимъ два равнобедренные тр.-ка АІВ1ВІ1 и ВІС1ВІІ
съ общимъ основаніемъ В1В1І. Докажемъ, что въ каждомъ
изъ нихъ прямая АЛС} служитъ биссектриссою угловъ при
вершинѣ. Для этого допустимъ временно, что биссектрисса
угла В1А1ВІІ будетъ не А1С1, а какая-нибудь иная прямая
^7), и биссектриссой угла ВіС\Вп будетъ не С1АІ, а ка-
кая-нибудь иная прямая С1В. Такъ какъ въ равнобедренномъ
тр.-кѣ биссектрисса угла при вершинѣ служитъ въ то же
время и медіаною, и высотою (37), то прямыя А1В и СХВ,
во 1-хъ, должны пройти черезъ одну и ту же точку прямой
В^В^ именно черезъ средину ея, во 2-хъ, онѣ должны со-
ставить одну прямую (26). Но черезъ двѣ точки Ах и С}
можно провести только одну прямую; значитъ, биссектриссы
АгВ и С^В должны слиться съ прямой А1С1. Изъ этого
слѣдуетъ, что /_1 = ДЗи/_2 = Д4. Но въ такомъ слу-
чаѣ данные тр.-ки должны быть равны, такъ какъ два угла
и прилежащая къ нимъ сторона одного равны соотвѣтственно
двумъ угламъ и прилежащей къ нимъ сторонѣ другого.
Замѣчаніе. Въ равныхъ тр.-кахъ противъ равныхъ сто-
ронъ лежатъ равные углы и противъ равныхъ угловъ лежатъ
равныя стороны.
Соотношеніе между углами и сторонами треугольника.
48. Теорема. Если какуго-нибудь сторону треугольника
продолжимъ аъ одномъ направленіи, то образовавгаійся при
этомъ внѣшній уголъ больше каждаго внутренняго угла, не
смежнаго съ нимъ.
Напр., продолжимъ въ тр.-кѣ АВС (черт. 36) сторону АС
за точку С и докажемъ, что внѣшній уголъ ВСВ больше каж-
даго изъ внутреннихъ угловъ А и В, не смежныхъ съ внѣш-
нимъ. Черезъ средину Е стороны ВС проведемъ медіану АЕ и
продолжимъ ее на длину ЕЕ, равную АЕ. Соединимъ Е съ
Тр.-ки АВЕ и ЕЕС равны, такъ какъ при точкѣ Е
— 26 —
они имѣютъ по равному углу, заключенному между двумя соот-
вѣтственно равными сторонами. Изъ равенства ихъ заключаемъ,
что углы В и ЕСЕ, лежащіе противъ равныхъ сторонъ АЕ
и ЕЕ, равны; по уголъ ЕСЕ, составляя часть внѣшняго угла
уголъ В меньше ВСВ.
Продолживъ сторону В С
за точку С, мы получимъ внѣш-
ній уголъ АСІІ, равный углу
ВСѢ (какъ вертикальный съ
нимъ). Ясли изъ вершины В
проведемъ къ сторонѣ АО ме-
діану и продолжимъ ее на та-
кую же длину за сторону АС,
то совсршенпо такъ же дока-
жемъ, что уголъ А меньше АСН,
т.-е. меньше ВСВ.
ВСВ, меньше его; слѣд., и
43.	Слѣдствіе. Если въ треугольникѣ одинъ уголъ при-
мой, гіли тупой, то два другіе угла острые.
Дѣйствительно, допустимъ, что какой-пибудь уголъ С
тр.-ка АВС (черт. 36) будетъ прямой или тупой; тогда
смежный съ нимъ внѣшній уголъ долженъ быть прямой или
острый; вслѣдствіе этого углы А и В, которые, по доказан-
ному, меньше внѣшняго угла, должны быть оба острые.
44.	Теоремы Во всякомъ треугольникѣ: Е, протгівъ рав-
ныхъ сторонъ лежатъ равные углы; 3°, протгівъ бдльгией
стороны лежитъ большій уголъ.
1°. Если двѣ стороны треугольника равны, то онъ равно-
бедренный; тогда углы, лежащіе противъ этихъ сторонъ,
должны быть равпы, какъ углы при основаніи равнобедреннаго
треугольника (39).
2°. Пусть ъъ^АВС (черт. 37) сторона АВ больше ВС;
требуется доказать, что ДО больше/„Л.
Отложимъ на ВА часть ВВ, равную ВС, и соединимъ
В съ О. Тогда получимъ равнобедренный Д ВВ С, у котораго
углы при основаніи равны, т.-е. / ВВС— /_ВСВ. Но уголъ
ВВС, какъ внѣшній по отношенію къ А АВС, больше угла А;
слѣд., и уг. ВСВ больше А, а потому и подавно, уг. ВСА
больше угла А; что и требовалось доказать.
— 27 —
в
Черт. 37
45.	Слѣдствіе. Въ равностороннемъ треугольникѣ вегъ
углы равны; въ разностороннемъ треугольникѣ нгьтъ равныхъ
угловъ.
4в. Обратныя теоремы. Во всякомъ
треугольникѣ: 7°, противъ равныхъ уг-
ловъ лежатъ равныя стороны;
противъ ббльгиаго угла лежитъ боль-
шая сторона.
1°. Пусть углы А и С равны
(черт. -37); требуется доказать, что
АВ—ВО.—Предположимъ противное,
т.-с. что АВ не равно ВС. Тогда
могутъ представиться два случая: или АВ>ВС, ми АВ <
ВС. Въ первомъ случаѣ, по доказанному въ теоремѣ прямой,
уг. С долженъ быть больше угла А, что противорѣчитъ усло-
вію; значитъ, этотъ случай надо исключггть. Во второмъ слу-
чаѣ, когда АВ < ВС, уг. С. долженъ быть меньше угла А,
что также противорѣчитъ условію; значитъ, и этотъ случай
надо ггсклгочггть. Остается одинъ возможный случай, что
АВ — ВС.
2°. Пусть въ томъ же тр—кѣ уг. С больше угла А;
требуется доказать, что АВ > ВС.— Предположимъ противное,
т.-е. что АВ не больгие ВС. Тогда могутъ представиться два
случая: или АВ = ВС, или АВ<ВС. Въ первомъ случаѣ,
согласно прямой теоремѣ, углы А и С были бы равны, во
второмъ случаѣ уг. А былъ бы больше С; и то, и другое
противорѣчитъ условію; значитъ, оба эти случая исключаются.
Остается одинъ возможный случай, что АВ>ВС.
49.	Слѣдствія. 1°. Равноугольный треугольникъ есть-
равносторонній:
2°. Въ треугольникѣ сторона, лежагцая противъ тупого'
ггли прямого угла, больгие другихъ сторонъ (43).
4$. Замѣчаніе объ обратныхъ теоремахъ. Если въ те-
оремѣ или рядѣ теоремъ мы разсмотрѣли всевозможные слу-
чаи, которые могутъ представиться относительно величины или
расположенія нѣкоторыхъ частей фигуры, причемъ оказалось,
Что въ различныхъ случаяхъ получаются различные выводы
28 —
относительно величины или расположенія другихъ частей фи-
гуры, то можемъ утверждать заранѣе (й ргіогі). что обрат-
ныя предложенія вѣрны.
Приведемъ этому примѣръ. Относительно величины двухъ
сторонъ треугольника, напр. АВ и ВС, могутъ представиться
только слѣдующіе три различные случая:
АВ = В0, АВ>ВС, АВ<ВС.
Въ теоремахъ § 44-го мы разсмотрѣли всѣ эти случаи,
причемъ оказалось, что въ каждомъ изъ нихъ получаются
различные выводы относительно величины противолежащихъ
угловъ А и С, а именно:
А=С, А<С, А> С.
И мы видѣли (46), что обратныя предложенія оказались
вѣрными, въ чемъ легко было убѣдиться доказательствомъ отъ
противнаго.
Впослѣдствіи намъ неоднократно придется убѣждаться въ
вѣрности этого замѣчанія.
Сравнительная длина объемлющихъ и объемлемыхъ
ломаныхъ линій.
49.	Теорема. Въ треугольникѣ одна сторона меньше
суммы двухъ другихъ сторонъ.
Пусть въДЛ7?(7 сторона АС будетъ наибольшая. Дока-
жемъ, что даже эта наибольшая сторона меньше суммы другихъ
I) сторонъ, т.-е. меньше	—
Продолживъ АВ, отложимъ ВВ = ВС
и проведемъ ВС. Такъ какъ {\ВВС
равнобедренный, то / В — / В СВ; по-
этому уголъ В меньше угла ВСА, и,
слѣд.. въАВС сторона АС меньше
АВ (46), т.-е. А0САВА-ВВ. За-
Черт. 38 мѣнивъ ВВ на ВС, получимъ
АССАБ + ВС.
— 29 —
50.	Слѣдствіе. Отнявъ отъ обѣихъ частей выведеннаго
неравенства по АВ или по ВС, найдемъ:
АС—АВ<ВС и АС—ВС<АВ.
Читая эти неравенства справа налѣво, можемъ ихъ вы-
разить такъ:
въ треугольникѣ одна сторона больше разности двухъ
другихъ сторонъ.
51.	Теорема. Отрѣзокъ прямой короче всякой ломаной,
проведенной между его конг^ами.
Пусть АЕ будетъ прямая, а АВСВЕ какая-нибудь лома-
ная, проведенная между копцами прямой. Требуется доказать,
что А Е короче АВ + В С -р ОВ + ВЕ.
Соединивъ А съ С и В,
находимъ, согласно предыдущей	^х*^**^*^
теоремѣ:	^****Л°
АЕ<АВ + ВЕ; АВ< АС~г	\
+ СЛ; АС<АВ + ВС. А	Е
Черт. 39
Сложимъ почленно эти не-
равенства и затѣмъ отнимемъ отъ обѣихъ частей по АВ и
АС; тогда получимъ:
АЕ <АВ + ВС+СВ + ВЕ.
5®.	Теорема. Выпуклая ломаная короче всякой объемлю-
щей ломаной.
Еслп изъ двухъ ломаныхъ линій, проведенныхъ между
Двумя точками А и В (черт. 40) и расположенныхъ по одну
сторону отъ прямой АВ, одна вся заключена внутри много-
угольника, образованнаго другою ломаной съ прямой АВ, то
внѣшняя изъ нихъ наз. объемлющей, а внутренняя — объем-
лемой.
Пусть АВСВ будетъ выпуклая ломаная, а АЕЕСВ ка-
кая-нибудь объемлющая ломаная. Требуется доказать, что АВСВ
короче АЕЕСВ.—Продолживъ стороны АВ ъ ВС, какъ ука-
^но на чертежѣ, найдемъ (49 и 51):
— 30
АВ + ВІКАЕА-ЕН
ВС+ СК< ВНА-НЕА- вс 4- ск
СВ < ОКА~ кв.
Черт. 40
Сложивъ эти неравенства, сок-
ратимъ результатъ на вспомога-
тельные отрѣзки ВН п СК и за-
тѣмъ замѣнимъ ЕН + НЕ черезъ
ЕЕ и СК + КВ черезъ СВ;
тогда получимъ:
АВ+ВС-Ѵ СВ<АЕА~ЕЕ+
А-ЕСА- СВ; что и тр. док.
53. Слѣдствіе. Периметръ выпуклаго многоугольника
меньше периметра, всякаго другого многоугольника, внутри
котораго заключенъ первый.
Пусть АВСВ будетъ выпуклый многоугольникъ, а РЕКРфВ
какой-нибудь многоугольникъ, внутри котораго заключенъ пер-
вый. Требуется доказать, что
АВА-ВС А- СВ 4- ВА < ВМ+ МКА- ЯРА-Р$А~ ЦК
Продолживъ въ обоихъ направ-
леніяхъ какую-нибудь сторону АВ
выпуклаго многоугольника, будемъ
имѣть:
АВ А-ВО А- СВ<АТА- тм+
+ МК+ КР 4~ РЦ + <№+ 8В;
АТА- АВА- В8< 8В-А ВТ.
Сложивъ эти неравенства, сок-
ратимъ результатъ на АТ и В8; затѣмъ замѣнимъ ВТА~ ТМ
черезъ ВМ и В8~]г(Ц8 черезъ В(р тог^а получимъ:
АВ + вс+ СВ -ь ВА < ВМА- НЕ
'-Р^А-^в.
— 31 —
Треугольники съ двумя соотвѣтственно равными сторонами.
54. Теоремы. Если двѣ стороны одного треугольника
соотвѣтственно равны двумъ сторонамъ другого треуголь-
ника, то
1°, противъ большаго изъ угловъ, заключенныхъ между
нггми, лежигпъ большая сторона;
2°, обратно: противъ большей изъ остальныхъ сторонъ
лежитъ большій уголъ.
1°. Пусть АВС и А1В1СІ будутъ два треугольника, у
которыхъ:
АС—А1С1, АВ = АХВХ и А>А^
Требуется доказать, что ВОВ^.—Наложимъ Д А^В^
на А АВС такъ, чтобы сторона А1С1 совпала съ АС. Такъ
какъ Аг< А, то сторона АгВА пойдетъ внутри угла А; пусть
А АІВ1СІ займетъ положеніе АСВгі (вершина Вхі можетъ
упасть или впѣ А АВС, или внутри его, или же на сто-
ронѣ ВС; доказательство можетъ быть примѣнено ко всѣмъ
этимъ случаямъ). Проведемъ биссектриссу АВ угла ВАВІ}
и соединимъ В съ Ви; тогда получимъ два тр —ка АВВ и
которые равны, потому что у нихъ АВ общая сто-
рона, АВ = АВп по условію и / ВАВ = / ВАВи по дѣ-
ленію. Изъ равенства тр.—ковъ слѣдуетъ: ВВ — ВВ^. Те-
перь изъ Д ВСВ1Х выводимъ: ВпС<.ВХГВ-[-ВС (49). или
(замѣнивъ В^В на ВВ):
— 32 —
ВиС<ВВ + ВС, т.-е. В^СВС.
2°. Пусть въ тѣхъ же треугольникахъ будетъ дано усло^
віемъ:
АВ = А1В1 АС=АХС, кВОВ^.
Требуется доказать, что А > Аг.—Предположимъ противное,
т.-е. что А не больше тогда могутъ представиться два слу-
чая: или А — Аа, или Л<ЛК Въ первомъ случаѣ тр. — ки
были бы равны и, слѣд., сторона ВС равнялась бы ВХСХ,
что мротиворѣчитъ условію; во второмъ случаѣ сторона ВС
была бы меньше ВХСХ, что также противорѣчитъ условію.
Значитъ, оба эти случая исключаются; остается одинъ воз-
можный случай, что А> Ах.
ГЛАВА III.
Перпендикуляры и наклонныя.
55. Теоремы. Когда изъ одной точки проведены къ одной
прямой перпендикуляръ и нѣсколько наклонныхъ, то:
1°, перпендикуляръ короче всякой наклонной;
2°, если двѣ наклонныя одинаково удалены отъ основанія
перпендикуляра, то онѣ равны;
3°, если двѣ наклонныя неодинаково удалены отъ осно-
ванія перпендикуляра, то та изъ нихъ больше, которая
дальше отстоитъ отъ перпендикуляра.
1°. Пусть изъ точки А къ
прямой МУ проведены перпен-
дикуляръ АВ и какая-нибудь
наклонная АС. Требуется до-
казать, что АВ < АС. — Въ
А АВС уголъ В прямой, а
противъ прямого угла должна
лежать большая сторона (47,2°);
слѣд., АОАВ.
А
Черт. 43
— 33 —
2°. Пусть АС и ЛР будутъ двѣ такія наклонныя къ пря-
мой А[ВТ, которыхъ основанія С и 2) одинаково удалены отъ
основанія перпендикуляра, т.-е. ОВ = ВІ); требуется дока-
зать. что АС=АВ.—Въ тр—кахъ АВС и АВВ есть об-
щая сторона АВ и сверхъ того ВС=ВВ (по условію) и
/_АВО — ^АВС (какъ углы прямые); значитъ, эти тр—ки
равны и потому АС— АТ).
3°. Пусть АС и АЕ будутъ двѣ такія наклонныя къ пря-
мой 21 Вт, которыхъ основанія неодинаково удалены отъ осно-
ванія перпендикуляра; напр., пусть ВЕ>ВС; требуется до-
казать, что АЕ > А О.—Отложимъ ВВ = ВС и проведемъ АВ.
По доказанному выше АВ = АС. Сравнимъ АЕ съ АВ.
Уголъ АВЕ есть внѣшній по отношенію къ Л АВВ и по-
тому опъ больше прямого угла АВВ; слѣд., /_АВЕ тупой;
въ А АОЕ противъ тупого угла должна лежать большая
сторона (4-7,2°); значитъ, АЕ>АВ и, слѣд., АЕ>АС.
5в. Обратныя предложенія. Въ доказанныхъ теоремахъ
разсмотрѣны всевозможные случаи относительно разстояній
наклонныхъ отъ основанія перпендикуляра; при этомъ полу-
чились различные выводы относительно длины наклонныхъ;
вслѣдствіе этого обратныя предложенія должны быть вѣрны
(48). а именно:
1°. Кратчайшее разстояніе точки отъ прямой есть
перпендикуляръ;
2°. Если двѣ наклонныя равны, то онѣ одинаково уда-
лены отъ основанія перпендикуляра;
3°. Если двѣ наклонныя не равны, то большая изъ нихъ
дальше отстоитъ отъ основанія перпендикуляра.
Предоставляемъ учащимся самимъ доказать эти предложе-
нія (отъ противнаго).
Замѣчаніе. Когда говорятъ: „разстояніе точки отъ пря-
мой то разумѣютъ „кратчайшее“ разстояніе, т.-е. перпен-
дикуляръ, опущенный изъ этой точки на прямую.
П. КИСЕЛЕВЪ.
3
— 34 —
Равенство прямоугольныхъ треугольниковъ.
53. Такъ какъ въ прямоугольныхъ тр—кахъ углы, со-
держащіеся между катетами, всегда равны, какъ прямые, то:
Прямоугольные треугольники равны, если:
1°, катеты одного треугольника, соогпвѣгпсгпоенно равны-
кагпетамъ другого;
или 2°, категпъ и прилежащій къ нему острый уголъ-
одного треугольника равны оотвѣгпственно катету гг при-
лежащему къ нему острому углу другого гпреугольнгіка.
Эти два признака не требуютъ особаго доказательства,
такъ какъ они представляютъ лишь частные случаи общихъ,
признаковъ (4-1,1° и 2°). Укажемъ еще два признака, относя-
щіеся только до прямоугольныхъ треугольниковъ.
58. Теоремы. Прямоугольные треугольники равны, если:
1°, гиггогпеиуза и острый уголъ одного треугольника со-
отвѣтственно равны гипотенузѣ и острому углу другого;
или 2°, гипогпенуза и кагпетъ одного треугольника со-
Огнвгьтсгнвенно равны гипотенузѣ и катету другого.
1°. Пусть АВО іг
лв	/1В' Ц будутъ два пря-
/	/	моугольные тр—ка, у
/	/ которыхъ: АВ — А^В^
/	/	и А = Аг; требуется до-
/	/	казать, что эти тр—-ки
/	/	равны. — Налояыімъ А
дХ----------Іс д/--------------Іс АВС на А1В1О1 такъ,
„	*	1 чтобы у нихъ совмѣсти-
лись равныя гипотенузы.
Тогда, по равенству угловъ А и Аг, катетъ уі(7 пойдетъ по Аг С{.
При этомъ катетъ ВО не можетъ не совмѣститься съ ВІС1І
потому что въ противномъ случаѣ изъ точки Вх можно было
бы на прямую А1СІ опустить два перпендикуляра, что не-
возможно.
2°. Пусть въ тѣхъ же тр—кахъ будетъ дано: АВ=АІВІ
и ВС~В1С1; требуется доказать, что тр—ки равны.—На-
— 35 —
долгимъ Л АВС па Л АІВІС1 такъ, чтобы у нихъ совмѣ-
стились равные катеты ВС и ВІСІ. Тогда, по равенству
прямыхъ угловъ, СА пойдетъ по С1А1. При этомъ гипоте-
нузы не могутъ не совмѣститься, потому что двѣ равныя на-
клонныя должны быть одинаково удалены отъ основанія пер-
пендикуляра В1С1.
ГЛАВА IV.
Свойства перпендикуляра къ срединѣ прямой и
биссектрисой угла.
50.	Теоремы. 1°. Если точка одинаково удалена отъ
концовъ прямой, то она лежитъ на перпендикулярѣ къ сре-
динѣ этой прямой.
2°. Обратно: если точка лежитъ на перпендикулярѣ къ
срединѣ прямой, то она одинаково удалена отъ концовъ
этой прямой.
1°. Пусть точка М одинаково удалена отъ концовъ пря-
мой АВ, т.-е. МА = МВ; требуется доказать, что М лежитъ
на перпендикулярѣ къ срединѣ пря-
мой АВ.—Проведемъ биссектрпссу	|м
МО угла АМВ. Такъ какъ тр.-къ	А
АМВ равнобедренный, то эта бис-	/ '\
сектрисса служитъ въ немъ и пер-
пендикуляромъ къ срединѣ основанія
(37); значитъ, точка М лежитъ па дН--------—-------в
перпендикулярѣ къ срединѣ прямой
АВ.
2°. Пусть ОМ (черт. 45) будетъ	Черт* 4о
перпендикуляръ къ срединѣ отрѣзка АВ и М какая-нибудь
точка на немъ; требуется доказать, что эта точка одинаково
удалена отъ Л и В, т.-е. что МА = МВ.—Прямыя МА п
МВ суть наклонныя къ АВ, одинаково удаленныя отъ осно-
ванія перпендикуляра МО; а такія наклонныя равны; слѣд.,
МА — МВ.
з*
— 36 —
во. Слѣдствіе. Изъ двухъ доказанныхъ теоремъ, прямой
и обратной, можно вывести слѣдствіе, что противоположныя
теоремы также вѣрны (4), т.-е., что
если точка не одинаково удалена отъ концовъ прямой,
то она не лежитъ на перпендикулярѣ къ срединѣ этой прямой;
если точка не лежитъ на перпендикулярѣ къ срединѣ
прямой, то она не одинаково удалена отъ концовъ этой прямой.
Предлагаемъ учащимся самимъ доказать эти противопо-
ложныя предложенія разсужденіемъ отъ противнаго.
ві. Теоремы. 1°. Если точка одинаково удалена отъ
сторонъ угла, то она лежитъ на его биссектриссѣ.
2°. Обратно: если точка лежитъ на биссектриссѣ угла,
то она одинаково удалена отъ его сторонъ.
1°. Пусть точка М одинаково удалена отъ сторонъ угла
АБС, т.-е. перпендикуляры МЕ и МЕ, опущенные изъ этой
точки на стороны угла, равны; требуется доказать, что точка
М лежитъ на биссектриссѣ угла
Л	АВС.— Соединимъ ІІГ съ В,
/	Р Прямоугольные тр.-ки МВЕ и
МВЕ равны, такъ какъ у нихъ
/	общая гипотенуза, и катеты МЕ,
/МЕ равны по условію. Изъ
:Е	равенства тр.-ковъ слѣдуетъ,
----------------с что /_МВК= ^МВР, т.-с.
ч	4б	прямая МВ есть биссектрисса
угла АВС.
2°.	Пусть	ВВ	(черт.	46) есть биссектрисса угла АВС,
и М какая-нибудь	точка	на	пей; требуется доказать, что
перпендикуляры МЕ, МЕ, опущенные изъ этой точки на
стороны угла, равны.—Прямоугольные тр.-ки МВЕ и МВЕ
равны, такъ какъ у нихъ общая гипотенуза, и углы МВЕ,
МВЕ равны по условію. Изъ равенства тр.-ковъ слѣдуетъ,
что МЕ=МЕ.
в®. Слѣдствіе. Изъ двухъ доказанныхъ теоремъ, прямой
и обратной, можно вывести слѣдствіе, что противоположныя
теоремы также вѣрны, т.-е. что
если точка не одинаково удалена отъ сторонъ угла, то
она не лежитъ на его биссектриссѣ;
— 37 —
если точка не лежитъ на биссектриссѣ угла, то она не
одинаково удалена отъ сторонъ его.
03. Геометрическое мѣсто. Геометрическимъ мѣстомъ
точекъ, обладающихъ нѣкоторымъ свойствомъ, наз. такая ли-
нія, или совокупность линій, или поверхность, которая содер-
житъ въ себѣ всѣ точкп, обладающія этимъ свойствомъ, и не
содержитъ ни одной точкп, не обладающей имъ.
Изъ теоремъ предыдущихъ параграфовъ слѣдуетъ:
Геометрическое мѣсто точекъ, одинаково удаленныхъ
отъ двухъ данныхъ точекъ, есть перпендикуляръ къ срединѣ
прямой, соединяющей эти точки.
Геометрическое мѣсто точекъ, одинаково удаленныхъ
отъ сторонъ угла, есть биссектрисса этого ума.
ГЛАВА V.
Основныя задачи на построеніе.
04. Теоремы, доказанныя нами въ предыдущихъ главахъТ
позволяютъ рѣшать нѣкоторыя задачи на построеніе. Замѣ-
тимъ, что въ элементарной геометріи разсматриваются только
такія построенія, которыя могутъ быть выполнены помощью
линейки и циркуля (употребленіе наугольника и нѣкоторыхъ
другихъ приборовъ хотя и допускается ради сокращенія вре-
мени, но не составляетъ необходимости). Посредствомъ ли-
нейки проводятся прямыя линіи, посредствомъ циркуля чер-
тится окружность. Свойства этой линіи мы разсмотримъ
впослѣдствіи, теперь же ограничимся только общимъ понятіемъ
объ ней.
Если дадимъ циркулю произвольное	\ с
раствореніе и, поставивъ его ножку съ / \
остріемъ въ какую-ппбудь точку О, ста- /	\ /	\
немъ вращать циркуль вокругъ этой точки, АГ 0 I
т9 Другая его ножка, снабженная каран- у	!
дашемъ или перомъ, опишетъ непрерыв-
иуіб линію, которой всѣ точкп одина-
Черт. 47
— 38 —
ково удалены отъ точки О. Эта линія наз. окружностью,
а точка О — центромъ ея. Прямыя О А, ОВ, ОС, соеди-
няющія центръ съ какими-нибудь точками окружности, наз.
радіусами. Всѣ радіусы одной окружности равны между со-
бою. Часть окружности, напр. АВ (черт. 47), наз. дугою.
05. Укажемъ теперь рѣшеніе основныхъ задачъ на по-
строеніе.
Задача 1. Построить треугольгшкъ по даннымъ его сто-
ронамъ а, Ь и с.
На неопредѣленной прямой
АШ откладываемъ часть СВ,
равную одной пзъ данныхъ сто-
ронъ, напр. а. Изъ точекъ С
и В, какъ центровъ, описыва-
емъ двѣ небольшія дуги, одну
.С/а\В................к радіусомъ, равнымъ Ъ, другую
радіусомъ, равнымъ с. Точку
А, въ которой эти дуги пере-
Черт. 48
сѣкаются. соединяемъ съ В и С. Треугольникъ АВС будетъ
искомый.
Замѣтимъ, что не всякіе тргг отрѣзка прямой могутъ
служить сторонами треугольника; для этого необходимо,
чтобы ни одинъ изъ нихъ не былъ больше суммы двухъ ос-
тальныхъ (49).
Задача 2. На данной прямой МП при данной на ней
точкѣ О построитъ уголъ, равный данному углу АВС.
Черт. 49
Изъ вершины В, какъ центра, описываемъ произвольнымъ
радіусомъ между сторонами даннаго угла дугу ЕЕ; затѣмъ,
— 39 —
не измѣняя растворенія циркуля, переносимъ его остріе въ
точку О и описываемъ дугу Р(^. Далѣе, изъ точки Р, какъ
центра, описываемъ дугу аЪ радіусомъ, равнымъ вспомога-
тельной прямой Л'ІЛ Наконецъ, черезъ точки О и Р (пере-
сѣченіе двухъ дугъ) проводимъ прямую. Уголъ ВОР равенъ
углу АБС, потому что тр.-ки РОР и ЕБЕ, имѣя соотвѣт-
ственно равныя стороны, равны.
Задача 3. Раздѣлитъ данный уголъ АБС пополамъ.
Изъ вершины В, какъ центра,
произвольнымъ радіусомъ опишемъ
между сторонами угла дугу БЕ. За-
тѣмъ изъ точекъ Б и Е, какъ цент-
ровъ, описываемъ однимъ гі тѣмъ
же раствореніемъ циркуля небольшія
.дуги, которыя пересѣклись бы въ
какой-пибудь точкѣ Е. Прямая БЕ
Черт. 50
будетъ биссекгриссою угла АБС. Для доказательства соеди-
нимъ точку Е съ Б и Е; тогда получимъ два тр.-ка БЕЕ
и ББЕ, которые равны, такъ какъ у нихъ БЕ общая сто-
рона, ВБ —БЕ и БЕ~ЕЕ по построенію. Изъ равенства
тр.-ковъ слѣдуетъ: /^АБЕ=/_ СВЕ.
Задача 4-. Изъ данной точки С прямой АВ возставитъ
къ ней перпендикуляръ.
Отложимъ на АВ по обѣ
•стороны отъ данной точки С
равные отрѣзки (произвольной	/ \
.длины) СБ и СЕ. Изъ точекъ
Е и Б однимъ и тѣмъ же рас-
твореніемъ циркуля (большимъ	С Е
СБ) опишемъ двѣ небольшія а----------1------6--------1—В
.дуги, которыя пересѣклись бы	Черт 51
въ, нѣкоторой точкѣ Е. Прямая
СЕ будетъ искомымъ перпендикуляромъ. Дѣйствительно, какъ
видно изъ построенія, точка Е одинаково удалена отъ Б
и Е; слѣд., опа должна лежать на перпендикулярѣ къ сре-
динѣ отрѣзка БЕ (59); но средина этого отрѣзка есть С;
значитъ, ЕС | БЕ.
— 40 —
Задача 5. Изъ данной точки А опуститъ перпендику-
ляръ на данную прямую ВС.
Изъ точки А, какъ центра, произвольнымъ раствореніемъ
циркуля опишемъ такую дугу, которая пересѣклась бы съ ВС
въ какихъ-нибудь двухъ точкахъ В и Е. Затѣмъ изъ этихъ
точекъ произвольнымъ, но однимъ и тѣмъ же раствореніемъ
А	циркуля проводимъ двѣ не-
о	большія дуги, которыя пере-
сѣклись бы между собою въ
нѣкоторой точкѣ В. Прямая
АВ будетъ искомымъ перпеп-
С дикуляромъ. Дѣйствительно,
какъ видно изъ построенія,
каждая изъ точекъ А и В оди-
наково удалена отъ В и Е; а.
такія точки лежатъ на пер-
нендикулярѣ къ срединѣ от-
рт‘	рѣзка ВЕ (59).
Задача 6. Провести перпендикуляръ къ срединѣ данной,
конечной прямой АВ.
Изъ точекъ А и В произвольнымъ, по одинаковымъ, рас-
твореніемъ циркуля описываемъ двѣ дуги, которыя пересѣк-
лись бы между собою въ нѣкоторыхъ
точкахъ С и I). Прямая СВ будетъ иско-
мымъ перпендикуляромъ. Дѣйствительно,
какъ видно изъ построенія, каждая изъ
точекъ С и В одинаково удалена отъ
А и В; слѣд., эти точки должны ле-
жать на перпендикулярѣ къ срединѣ от-
рѣзка АВ (59).
Задача 7. Раздѣлить пополамъ
данную конечную прямую АВ (черт. 53).
Рѣшается такъ же, какъ предыдущая задача.
вв. При помощи этихъ основныхъ задачъ можно рѣшать
задачи болѣе сложныя. Для примѣра рѣшимъ слѣдующую
задачу:
Задача. Построитъ треугольникъ, зная его основаніе
Черт. 53
— 41 —
уголъ а, прилежащій къ основанію, и сумму 8 двухъ боко-
выхъ сторонъ.
Чтобы составить планъ рѣшенія, предположимъ, что задача
рѣшена, т.-е. найденъ такой тр.-викъ АВС (черт. 54), у
котораго основаніе АС=^Ь, уголъ А = а и АВ-\- ВС~з
(гдѣ Ъ, а и а суть данныя величины, не помѣщенныя у насъ
на чертежѣ). Разсмотримъ теперь полученный чертежъ. Сто-
рону АС, равную Ъ, и уголъ А, равный а, мы построитъ
умѣемъ. Значитъ, остается найти на сторонѣ угла А такую
точку В, чтобы сумма АВ-\~ВС равнялась 5.
Продолживъ АВ, отложимъ АВ, равную 8. Теперь, оче-
видно, вопросъ приводится къ тому, чтобы на прямой АВ отыс-
кать тйкую точку В, которая была бы одинаково удалена отъ С и В.
Такая точка, какъ мы знаемъ (59), должна лежать на пер-
пендикулярѣ къ срединѣ отрѣзка СВ. Этотъ перпендику-
ляръ мы построить умѣемъ. Точка В найдется въ пересѣче-
ніи перпендикуляра съ АВ.
Итакъ, вотъ рѣшеніе за-
дачи: строимъ уголъ А, рав-
ный данному углу а; на
сторонахъ его откладываемъ
АС=Ь и АВ = 8. Черезъ
средину разстоянія ВС про-
водимъ перпендикуляръ ВЕ;
пересѣченіе его съ АВ, т.-е.
точку В, соединяемъ съ С.
Тр.-ппкъ АЬС будетъ иско-
мый, такъ какъ онъ удовле-
творяетъ всѣмъ требованіямъ
и АВ-\- ВС=8, потому чтс
Разсматривая построеніе,
задачи: у него АС=Ь, /_А~а
> вв=вс.
мы замѣчаемъ, что задача воз-
можна но при всякихъ данныхъ. Дѣйствительно, если сумма.
5 задана слишкомъ малою относительно Ь, то перпендикуляръ
ЕВ можетъ и не пересѣчь отрѣзка АВ (пересѣчетъ его про-
долженіе за точку Л); въ этомъ случаѣ задача будетъ невоз-
можна. И независимо отъ построенія можно видѣть, что за-
дача невозможна, если 8<Ь, потому что не можетъ быть
— 42 —
такого треугольника, у котораго сумма двухъ сторонъ была бы
равна или меньше третьей стороны.
Въ томъ случаѣ, когда задача возможна, она имѣетъ
только одно рѣшеніе, т.-е. существуетъ только одинъ тр.-никъ,
удовлетворяющій требованіямъ задачи, такъ какъ пересѣченіе
перпендикуляра ВЕ съ прямой АВ можетъ быть только въ
одной точкѣ.
03. Замѣчаніе. Изъ приведеннаго примѣра видно, что
рѣшеніе сложной задачи на построеніе состоитъ изъ слѣдую-
щихъ четырехъ частей:
1°. Предположивъ, что задача рѣшена, дѣлаютъ отъ руки
приблизительный чертежъ искомой фигуры и затѣмъ, внима-
тельно разсматривая начерченную фигуру, стремятся найти
такія зависимости между данными задачи и искомыми, кото-
рыя позволили бы свести задачу на другія, извѣстныя ранѣе.
Эта самая важная часть рѣшенія задачи (имѣющая цѣлью со-
ставить планъ рѣшенія) носитъ названіе анализа.
2°. Когда такимъ образомъ планъ рѣшенія найденъ, вы-
полняютъ сообразно ему построеніе.
3°. Для провѣрки правильности плана доказываютъ за-
тѣмъ, на основаніи извѣстныхъ теоремъ, что полученная фи-
гура удовлетворяетъ всѣмъ требованіямъ задачи. Эта часть
рѣшенія называется синтезомъ.
4°. Затѣмъ задаются вопросомъ, при всякихъ ли данныхъ
задача возможна и допускаетъ ли она одпо рѣшеніе, или нѣ-
сколько. Эта часть рѣшенія наз. изслѣдованіемъ задачи.
Когда задача весьма проста и не можетъ быть сомнѣнія
относительно ея возможности, то обыкновенно анализъ и из-
слѣдованіе опускаютъ, а указываютъ прямо построеніе и при-
водятъ доказательство. Такъ мы дѣлали, излагая рѣшеніе
первыхъ 7-ми задачъ этой главы; такъ же будемъ дѣлать и
впослѣдствіи, когда намъ придется излагать рѣшеніе неслож-
ныхъ задачъ.
— 43 —
УПРАЖНЕНІЯ.
Домазать теоремы:
5.	Въ равнобедренномъ треугольникѣ двѣ медіаны равны, двѣ бпс-
сектриссы равны, двѣ высоты равны.
6.	Если изъ средины каждой изъ равныхъ сторонъ равпоб. тр -ка
возставимъ перпендикуляры до пересѣченія съ другою изъ равныхъ сто-
ронъ, то эти перпендикуляры равны.
7.	Перпендикуляры, возстановленные къ двумъ сторонамъ угла па
равныхъ разстояніяхъ отъ вершины, пересѣкаются па биссектрпссѣ.
8	Прямая, перпендикулярная къ биссектрпссѣ угла, отсѣкаетъ отъ
его сторонъ равные отрѣзки.
9.	Медіана тр.-ка меньше его периметра, но больше полуперпметра.
10.	Медіана тр.-ка меньше полусуммы сторонъ, между которыми она
заключается. Указаніе: продолжить медіану на разстояніе, равное ей, по-
лученную точку соединить съ однимъ концомъ стороны, къ которой про-
ведена медіана, л разсмотрѣть образовавшуюся фигуру)
11.	Сумма разстояній какой-нибудь точки, взятой внутри тр.-ка, отъ
трехъ его вершинъ меньше периметра, во больше полуперпметра.
12.	Доказать прямо, что всякая точка, не лежащая па перпендику-
лярѣ къ срединѣ отрѣзка прямой, неодинаково удалена отъ концовъ этого
отрѣзка.
13.	Доказать прямо, что всякая точка, не лежащая на биссектрпссѣ
угла, неодинаково отстоитъ отъ сторонъ его.
Задачи на построеніе:
14.	Построить сумму двухъ, трехъ и болѣе данныхъ угловъ.
15.	Построить разность двухъ угловъ.
16.	По данной суммѣ и разпостп двухъ угловъ найти эти углы.
17.	Раздѣлить уголъ на 4, 8, 16 равныхъ частей.
18.	Черезъ вершину даннаго угла провести внѣ его такую прямую,
которая со сторонами угла образовала бы равные углы.
19.	Построить Д: а) по двумъ сторонамъ и углу между ппмп; Ъ) по
сторонѣ и двумъ прилежащимъ угламъ; с) по двумъ сторонамъ и углу,
лежащему противъ большей изъ нихъ.
20.	Построить разнобедренпъЛ Д: а) по основанію и боковой сторонѣ;
Ь) по основанію и прилежащему углу; с) по боковой сторонѣ и углу при
вершинѣ; 4) по боковой сторонѣ и углу при основаніи.
— 44 —
2і)	Построить прямоуіѳ.іъный Д: а) по двумъ катетамъ; Ъ) по катету
и гипотенузѣ; с) по катету и прилежащему острому углу.
22)	Построить раѳнобедренн й Д: а) по высотѣ п боковой сторонѣ;
Ъ) по высотѣ и углу ирлі вершинѣ; с) по основанію и перпендикуляру,
опущенному изъ конца основанія на боковую сторону.
23	Построить прямоугольный Л по гипотенузѣ и острому углу.
24?	Черезъ точку, данную внутри или внѣ угла, провести такую пря-
мую, которая отсѣкала бы отъ сторонъ угла равныя части.
25.	По данной суммѣ п разности двухъ прямыхъ найти эти прямыя.
26.	Раздѣлить данную конечную прямую на 4, 8, 16 равныхъ частей.
27.	На данной прямой пайтп точку, одинаково удаленную отъ двухъ-
данныхъ точекъ (внѣ прямой).
28.	Найти точку, равноотстоящую отъ трехъ вершилъ Д.
29.	На прямой, пересѣкающей стороны угла, пайтп точку, одинаково
удаленную отъ сторонъ этого угла.
30.	Найти точку, одинаково удаленную отъ трехъ сторонъ Д.
31.	На данной прямой АВ найти такую точку С. чтобы прямыя С’ДГ
н СіѴ, проведенныя изъ С къ даннымъ точкамъ ІИ и IV, расположеннымъ
но одну сторону отъ АВУ составлялп съ прямыми СА и СВ равные углы.
32.	Построить прямоугольный Д по катету п суммѣ гипотенузы съ
другимъ катетомъ.
33,	Построить А по основанію, углу, прилежащему къ основанію, и
разности двухъ другихъ сторонъ (разсмотрѣть два случая: 1) когда данъ
м.нъшій изъ двухъ угловъ, прилежащихъ къ основанію, 2) когда данъ
бдлѵшій изъ нихъ).
34.	Построить прямоугольный А по катету и разпости двухъ дру-
гихъ сторонъ.
35.	То же—по гипотенузѣ и суммѣ катетовъ.
36.	То же-по гипотенузѣ и разности катетовъ.
ГЛАВА VI.
Параллельныя прямыя.
Основныя теоремы.
08. Опредѣленіе. Двѣ прямыя наз. параллельными, если,
находясь въ одной плоскости, онѣ но пересѣкаются, сколько
бы ихъ пи продолжали.
Возможность существованія такихъ прямыхъ доказывается
слѣдующей теоремой.
— 45 —
69.	Теорема, Черезъ всякую точку внѣ прямой можно
провести параллельную этой прямой.
Пусть АВ прямая и С какая-нибудь точка внѣ ея; тре-
буется доказать, что черезъ С можно провести прямую, па-
раллельную АВ.—Опустимъ на АВ изъ точки С перпенди-
куляръ СВ и затѣмъ проведемъ СЕ_І_ СВ, что всегда воз-
можно сдѣлать (19). Прямая СВ будетъ параллельна АВ.
Для доказательства допустимъ
противное, т.-е. что СЛ’пере- %	к
сѣкается съ АВ въ нѣкоторой	"х
точкѣ М Тогда изъ точки
АІ къ прямой СВ мы имѣли д----------ІР----------
бы два перпендикуляра АІВ
и МС, что невозможно; зна-	Черт‘ 55
читъ, СЕ не можетъ пересѣчься съ АВ, т.-е. СЕ парал-
лельна АВ.
90.	Слѣдствіе. Два перпендикуляра (СЕ и ВВ, черт. 55)
къ одной прямой (СВ) параллельны.
91.	Замѣчаніе. Что прямая АВ параллельна прямой СВ,
выражаютъ на письмѣ такъ: АВ\\СВ.
93. Аксіома параллельныхъ линій. Черезъ одну и туже
точку нельзя провести двухъ-различныхъ прямыхъ, парал-
лельныхъ одной и той же прямой.
Такъ, если черевъ точку С
проведена прямая СВ, параллель- с ....................15
ная АВ, то всякая другая пря-	...Е
мая СЕ, проведенная черезъ точ-
ку С, пересѣчется при продолже- А.	В
ніи съ АВ.
Всѣ попытки доказать эту пе	Черт’ 56
вполнѣ очевидную истину остались безуспѣшными; поэтому
ее принимаютъ безъ доказательства, какъ допущеніе (розіиіаіиш).
93. Слѣдствія. 1°. Если прямая (СЕ, черт. 56) пе-
ресѣкается съ одной изъ параллельныхъ (СВ), то она пе-
ресѣкается и съ другой (АВ),
потому что въ противномъ случаѣ черезъ одну и ту же
точку С проходили бы двѣ прямыя, параллельныя АВ, что
невозможно.
— 46 —
В-------------------------
С-------------------------
Черт. 57
2°. Если двѣ прямыя (А и В, черт. 57) параллельны
третьей прямой (С), то онѣ параллельны между собою.
Дѣйствительно, если пред-
А положимъ, что А и В пере-
> М	сѣкаются въ нѣкоторой точкѣ
АЕ, то тогда черезъ эту точку
проходили бы двѣ прямыя,
параллельныя О, что невоз-
можно.
34.	Теорема. Если прямая перпендикулярна къ одной
изъ параллельныхъ прямыхъ, то она перпендикулярна къ
другой параллельной.
Пусть АВЦ СВ и ЕЕ | АВ; требуется доказать, что
ЕЕ | СВ.—Перпендикуляръ ЕЕ, пересѣкаясь съ АВ, непре-
мѣнно пересѣчетъ и ОВ (73,1°). Пусть точка пересѣченія бу-
детъ ЕЕ. Предположимъ теперь,
|Е	что СВ не перпендикулярна къ
I	ЕЯ. Тогда какая-нибудь другая
А________ЕІ_________в прямая, напр. ЕЕ ЕЕ, будетъ пер-
пендикулярна къ ЕЕЕ и, слѣд.,
черезъ одну и ту же точку ЕЕ
будутъ проходить двѣ прямыя, па-
раллельныя АВ: одна СВ, по усло-
вію, а другая ЯК по доказанному
выше (70); такъ какъ это невоз-
можно, то нельзя допустить, чтобы СВ была не перпенди-
кулярна съ ЕЕЕ.
35.	Опредѣленія. Когда какія-либо двѣ прямыя АВ и
СВ (черт. 59) пересѣчены третьей прямой АІЯ, то образовав-
шіеся приэтомъ углы получаютъ попарно слѣдующія названія:
соотвѣтственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;
внутренніе накрестъ лежащіе углы: 3 и 5, 4 и 6;
внѣшніе накрестъ лежащіе углы: 1 и 7, 2 и 8;
внутренніе односторонніе углы: 3 и 6, 4 и 5;
внѣшніе односторонніе углы: 1 и 8, 2 и 7.
36.	Теоремы. Если двѣ параллельныя прямыя пересѣ-
чены третьей прямой, то:
Черт. Г 8
— 47 —
1° внутренніе накрестъ лежащіе углы равны;
2° внѣшніе накрестъ лежащіе углы равны;
3° соотвѣтственные углы равны;
4° сумма внутреннихъ одно-
стороннихъ угловъ равна 2сІ;
5° сумма внѣшнихъ односто-
роннихъ угловъ равна 2(1.
Пусть прямыяЛІ? и С7) (черт. 60)
параллельны и пересѣчены третьею
прямою ЛГУ; требуется доказать,
что:
г = И АЗ = А 5
2° /_2 =/.8 И /.1=/.7	Черт. бэ
3° А2 = А 6,	=	/.3 = ^7, Д4 = Д8
4° А3 + Дб = 2с/ и /.4 + А5 = 2с?
5° /1 2-НгІ 7 = 2с? и /.14-^8 = 26?.
Г Изъ средины Е отрѣз-
ка прямой заключеннаго
между параллельными прямыми,
опустимъ па СВ перпендику-
ляръ ЕК и продолжимъ его до
пересѣченія съ АВ въ точкѣ Е,
Такъ какъ перпендикуляръ къ
одной изъ параллельныхъ есть
также перпендикуляръ и къ дру-
гой параллельной, то образо-
вавшіеся при этомъ треугольни-
ки (покрытыя на чертежѣ штри-
хами) будутъ оба прямоугольные
имѣютъ по равной гипотенузѣ и
при точкѣ Е. Изъ равенства тр.-
репніе накрестъ лежащіе углы
впутр. пакр. лежащіе углы 3 и 5
2 А къ равнымъ угламъ 4 и 6.
. Они равны, потому чта
по равному острому углу
—ковъ слѣдуетъ, что внут-
4 и 6 равны. Два другіе-
равны, какъ дополненія да
— 48 —
2°. Внѣшніе накрестъ лежащіе углы равны соотвѣтственно
внутреннимъ накр. лежащимъ угламъ, какъ углы вертикаль-
ные; такъ, уг. 2=^уг. 4 и уг. 8 = уг. 6; но, по доказан-
ному, уг. 4 = уг. 6; слѣд., уг. 2=уг. 8.
3°. Соотвѣтственные углы 2 и 6 равны, потому что
уг. 2=уг. 4, а уг. 4 = уг. 6. Такъ же убѣдимся въ ра-
венствѣ другихъ соотвѣтственныхъ угловъ.
4°. Сумма впут. одностороннихъ угловъ 3 п 6 равна 2б?
потому, что сумма смежныхъ угловъ 3 и 4 равна 2й, а уг. 4
можетъ быть замѣненъ равнымъ ему угломъ 6. Такъ же убѣ-
димся, что сумма угловъ 4 и 5 равна 2сІ.
5°. Сумма внѣшнихъ одностороннихъ угловъ равна 2^
потому, что эти углы равны соотвѣтственно внутреннимъ
одностороннимъ угламъ, какъ углы вертикальные.
3 3. Обратныя теоремы. Если при пересѣченіи двухъ
прямыхъ какою-нибудь гпретъею прямою:
1° внутренніе накрестъ лежащіе углы равны;
или 2° внѣганіе накрестъ лежащіе углы равны;
или 3° соотвѣтственные углы равны;
или 4° сумма внутреннихъ одностороннихъ угловъравна2сІ;
или 5° сумма внгъшнгіхъ одностороннихъ равна 2сІ,
то такія прямыя параллельны.
Всѣ эти предложенія легко доказываются отъ противнаго.
1°. Пусть внутр. накр. лежа-
щіе углы 1 и 2 равны; требуется
доказать, что АВ\\СВ.— Пред-
положимъ, что линіей, параллель-
ной СВ и проходящей черезъ точ-
ку будетъ не АВ, а какая-ни
будь иная прямая 1І8. Тогда,
вслѣдствіе параллельности этихъ
линій, мы получимъ, по доказан-
ному равенство: уг. 3 = уг. 2; но
по условію уг. 1=уг. 2; слѣд.,
уг. 3=уг. 1, что невозможно.
Подобное же разсужденіе примѣняется во всѣхъ осталь-
ныхъ случаяхъ.
— 49 —
38. Слѣдствіе. Если сумма внутреннихъ одностороннихъ
угловъ не равна 2(1, то прямыя при достаточномъ продолженіи
пересѣкаются, такъ какъ, если бы прямыя не пересѣкались,
то онѣ были бы параллельны, и тогда сумма внутреннихъ
одностороннихъ угловъ равнялась бы 2сІ.
Это предложеніе было допущено греческимъ геометромъ
Эвклидомъ (жившимъ въ III вѣкѣ до Р. Хр.) безъ доказатель-
ства, какъ аксіома параллельныхъ линій. Въ настоящее время
предпочитаютъ принимать за такую аксіому болѣе простую
истину, изложенную выше въ § 72.
39. Полезно замѣтить еще слѣдующіе два "признана не-
параллельности прямыхъ.
1*. Перпендикуляръ (АВ, черт. 62) и наклонная (СВ)
къ одной и той-же прямой (ЕЕ) при продолжены пере-
сѣкаются,
потому что сумма внутреннихъ одностороннихъ угловъ
1 и 2 не равна 2сІ.
Черт. 62	Черт. 63
2°. Двѣ прямыя (АВ и СВ, черт. 63), перпендикуляр-
ныя къ двумъ пересѣкающимся прямымъ (ЕЕ и ЕС), при
продолженіи пересѣкаются.
Дѣйствительно, если предположимъ, что АВЦ СВ, то пря-
мая ЕВ, будучи перпендикулярна къ одной изъ параллельныхъ
(къ СВ), была бы перпендикулярна и къ другой параллельной
(къ АВ), и тогда изъ одной точкп Е къ прямой АВ были бы
проведены два перпендикуляра: ЕВ и ЕВ, что невозможно.
80.	Задача. Черезъ данную точку М провести прямую,
параллельную данной прямой АВ (черт. 64).
Наиболѣе простое рѣшеніе этой задачи состоитъ въ слѣ-
дующемъ: изъ точки М, какъ центра, описываемъ произволь-
А. п. Киселевъ.	4
— 50 -
Р\
нымъ радіусомъ дугу СВ и изъ точки С тѣмъ же радіусомъ
дугу ЗЖ. Затѣмъ, давъ циркулю раствореніе, равное раз-
стоянію отъ Е до М, описываемъ изъ точки С небольшую
дугу, которая пересѣклась бы
съ СВ въ нѣкоторой точкѣ Е.
Прямая МЕ будетъ параллель-
на АВ.— Для доказательства
проведемъ МС; образовавшіеся
при этомъ углы 1 и 2 равны
по построенію (65, зад. 2); а
если внутренніе накрестъ ле-
параллельны.
Параллельныя прямыя весьма удобно проводятся также
помощью наугольника и линейки. Приставивъ наугольникъ
Черт. 64
жащіе углы равны, то линіи
одною стороною прямого угла
къ данной прямой АВ, при-
кладываютъ къ другой его сто-
ронѣ линейку; затѣмъ, придер-
живая линейку въ этомъ по-
ложеніи, двигаютъ наугольникъ
вдоль пея до тѣхъ поръ, пока
сторона его, совпадавшая съ
АВ, не будетъ проходить че-
резъ точкѵ АІ: послѣ чего про-
Черт. 65	*	' *
г	водятъ вдоль этой стороны пря-
мую. Эта прямая будетъ параллельна АВ, такъ какъ обѣ
прямыя перпендикулярны къ краевой линіи линейки.
Углы съ соотвѣтственно параллельными пли перпендику-
лярными сторонами.
81.	Теорема. Если стороны одного угла соотвѣтственно
параллельны сторонамъ другого угла, то такіе углы гіли
равны, или- въ суммѣ составляютъ два прямыхъ.
Разсмотримъ особо три случая (черт. 66).
1°. Пусть стороны угла 1 соотвѣтственно параллельны сторо-
намъ угла 2 и, сверхъ того, имѣютъ одинаковое направленіе отъ
— 51 —
вершины (на чертежѣ направленія указаны стрѣлками). —
Продолживъ одну изъ сторонъ угла 2 до пересѣченія съ не-
параллельной ей стороной угла
1. мы получимъ уголъ 3, рав-
ный и углу 1, и углу 2 (какъ
соотвѣтственные при параллель-
ныхъ); слѣд. / 1 = / 2.
2°. Пусть стороны угла 1 соот-
вѣтственно параллельны сторонамъ
угла 4, но имѣютъ противополож-
ное направленіе отъ вершины. — Продолживъ обѣ стороны угла
4, мы получимъ уг. 2, который равенъ углу 1 (по доказан-
ному выше) и углу 4 (какъ вертикальные); слѣд. =
3°. Пусть, наконецъ, стороны угла 1 соотвѣтственно парал-
лельны сторонамъ угла о, причемъ двѣ изъ этихъ сторонъ
имѣютъ одинаковое направленіе, а двѣ другія противоположное.
Продолживъ одну сторону угла 5, мы получимъ уг. 2, кото-
рый равенъ, по доказанному, углу 1; но	— 2сІ
(по свойству смежныхъ угловъ); слѣд. и 5 +/_ 1 = 2<7.
Такимъ образомъ углы съ параллельными сторонами ока-
зываются равными, когда ихъ стороны имѣютъ или одинако-
вое. или противоположное направленіе; если же это условіе
не выполнено, то углы составляютъ въ суммѣ 2а.
8®. Теорема. Если стороны одного угла соотвѣтственно
перпендикулярны къ сторонамъ
другого угла, то такіе углы илгі
равны, или въ суммѣ состав-
ляютъ два прямыхъ.
Пусть уголъ АВС, обозна-
ченный цыфрою 1, есть одинъ
изъ данныхъ угловъ. Проведемъ
изъ его вершины двѣ вспомо-
гательныя прямыя: ВВ | ВС
и I ^А • Образованный ими
уголъ 2 равенъ углу 1 по слѣ-
дующей причинѣ: углы ВВС
и ЕВА равны, такъ какъ оба
Черт. 67
4*
— 52 —
ино прямые; отнявъ отъ каждаго изъ нихъ по одному и
тому же углу ЕВС, получимъ:/_ 2 = /_ 1 • Теперь вообра-
зимъ, что при какой-нибудь точкѣ Н намъ данъ уголъ 3,
пли уголъ 4, у котораго стороны соотвѣтственно перпендику-
лярны къ сторонамъ угла 1. Тогда стороны этого угла будутъ
параллельны сторонамъ угла 2 (потому что два перпендику-
ляра къ одной прямой параллельны); слѣд., уголъ при точкѣ
№ или равенъ углу 2, или составляетъ съ нимъ въ суммѣ
2(1. Замѣнивъ уг. 2 равнымъ ему угломъ 1, получимъ то,
что требовалось доказать.
Сумма угловъ треугольника п многоугольника,
83.	Теорема. Сумма угловъ пгреуіолъника равна двумъ
прямымъ.
Пусть АВС какой-нибудь треугольникъ; требуется дока-
зать, что сумма угловъ А, В и С равна 2(1.
Продолживъ сторону АС п проведя
найдемъ: І_А — / ЕОВ
(какъ углы соотвѣтственные при па-
раллельныхъ), /_В = /_ВСЕ (какъ
углы накрестъ лежащіе при парал-
лельныхъ); слѣд.:
^А+^В + ^С=^ЕС^ +
в
Че₽т- б8<	+ /1 ВСЕ +	С— 2&.
84.	Слѣдствія. 1°. Внѣшній уголъ треугольника равенъ
суммѣ двухъ внутреннихъ угловъ, не смежныхъ съ нимъ
(такъ, / ВСВ — С А-р ЛВ).
2°. Если два угла одного треугольника соотвѣтственно
равны двумъ угламъ другого, то и третьи углы равны.
3°. Сумма двухъ острыхъ угловъ прямоугольнаго тре-
угольника равна одному прямому углу.
4°. Въ равнобедренномъ прямоугольномъ тр-кѣ каждый
острый уголъ равенъ \/2 4.
5°. Въ равностороннемъ тр.-кѣ каждый уголъ равенъ 2/ас?.
— 53 —
85.	Теорема. Сумма угловъ выпуклаго многоугольника
равна двумъ прямымъ, повтореннымъ столько разъ, сколько
въ многоугольникѣ сторонъ безъ двухъ.
Взявъ произвольную точку О
внутри многоугольника, соеди-
нимъ ее со всѣми вершинами. ..	/_____ѵ........
Тогда многоугольникъ разобьст- \	/\	/ х.
ся на столысо тр.-ковъ, сколь ко	\/	\ /	\
въ немъ сторонъ. Сумма угловъ V............ о /
каждаго тр.-ка равна 2с/; слѣд..	\ /	\	/
сумма угловъ всѣхъ тр.-ковъ .................... \/
равна 2с/п, если гг означаетъ
число сторонъ многоугольника.
Эта величина, очевидно, пре-
Черт. 69.
вышаетъ сумму угловъ много-
угольника на сумму угловъ, расположенныхъ вокругъ точки О;
но послѣдняя сумма равна 4с/; слѣд., сумма угловъ много-
угольника равна
2с/и— 4с/ = 2с/ (п—2).
86.	Слѣдствіе. Лри данномъ числгъ сторонъ сумма угловъ
выпуклаго многоугольника есть велггчина постоянная. Такъ,
во всякомъ выпукломъ четыреугольникѣ сумма угловъ равна
4с/, въ пятиугольникѣ она равна 6 с/ и т. п.
83, Теорема. Если каждую сторону выпуклаго много-
угольника продолжимъ въ одномъ наггравленіи, то сумма об-
разовавшихся при этомъ внѣшнихъ угловъ равна четыремъ
прямымъ.
Каждый изъ такихъ внѣшнихъ угловъ (черт. 69) составляетъ
дополненіе до 2с/ къ смежному съ нимъ внутреннему углу много-
угольника; слѣд., если тсъ суммѣ внутреннихъ угловъ прило-
жимъ сумму внѣшнихъ угловъ, то получимъ 2с/>? (гдѣ п число
сторонъ); но точно также если къ суммѣ внутреннихъ угловъ
приложимъ сумму угловъ при точкѣ О, то получимъ тоже
2с/п; значитъ, сумма внѣшнихъ угловъ равна суммѣ угловъ
при точкѣ О, т.-е. равна 4с/.
— 54 —
ГЛАВА VII.
Параллелограммы и трапеціи.
Главнѣйшія свойства параллелограммовъ.
88. Опредѣленія. Четыреугольникъ, у котораго противо-
положныя стороны параллельны, наз. параллелограммомъ.
Параллелограммъ, у котораго одинъ изъ угловъ прямой,
наз. прямоуюлъникомъ.
Параллелограммъ.
Прямоугольникъ.
Квадратъ.	Трапеція.
Черт. 70
а
Параллелограммъ, у котораго двѣ сосѣднія стороны равны,
наз. ромбомъ.
Параллелограммъ, у котораго двѣ сосѣднія стороны равны
п одинъ изъ угловъ прямой, наз. квадратомъ.
Четыреугольникъ, у котораго двѣ противоположныя сто-
роны параллельны, наз. трапеціей. Параллельныя стороны ея
наз. основаніями.
Возможность существованія перечисленныхъ фигуръ не
требуетъ доказательства.
89. Теорема. Во всякомъ параллелограммѣ:
1°, противоположные, углы равны;
2°, сумма угловъ, прилеоісащихъ къ одной сторонѣ, равна
двумъ прямымъ.
55 —
ПустьЛ5(77)(черт.71) есть параллелограммъ, т.-е. АВ П СВ
п ВС\\АВ; требуется доказать, что:
1°, ЛЛ = ^С и /_В = ^В;
2°, /~А~г /_В = 2сІ, ^В-{- /_С=2(1 и т. д.
1°. Углы А и С равны, потому что в	с
стороны этихъ угловъ соотвѣтственно г	7
параллельны и имѣютъ противополож- /	/
ное направленіе отъ вершины (81).	/	/
То же самое можно сказать объ у г-	//
лахъ В п В.
2°. Каждая изъ суммъ: А-\-В,	черт. ті
В~~ С, СА-В и В-\-А равна 2(1, по-
тому что это суммы угловъ внутреннихъ одпостороннпхъ при
параллельныхъ прямыхъ.
ЭО. Слѣдствіе. Вели въ параллелограммѣ одинъ изъ
угловъ прямой, то и остальные углы прямые. — Въ прямо-
угольникѣ всѣ углы прямые.
Э1. Теорема. Во всякомъ параллелограммѣ противо-
положныя стороны равны.
Пусть АВОВ есть параллелограммъ, т.-е. АВ\\СВ и
ВС\\АВ; требуется доказать, что АВ—СВ и ВС=АВ.
Проведя діагональ ВВ, по-
лучимъ два тр.-ка АВВ и в ____________________________С
ВОВ, которые равпы, потому	/1^7	/
что у нихъ: ВВ общая сто-	/
рона, /11 — д_4 и /1 2 = /_ 3	/ мСГ/
(какъ внутренніе накрестъ ле- д/---------------^1)
жащіе при параллельныхъ пря-	Че т 72
мыхъ). Изъ равенства тр.-ковъ
слѣдуетъ: АВ=СВ и АВ = ВС (ъъ равныхъ тр.-кахъ про-
тивъ равныхъ угловъ лежатъ равныя стороны).
ЭЗ. Слѣдствія. Г. Еслгі въ параллелограммѣ двѣ сосѣд-
нія стороны равны, то всѣ стороны равны.—Въ ромбѣ и
квадратѣ всѣ стороны равны.
— 56 —
2° Параллельныя прямыя (АВ и СВ, черт. 73) вездѣ
одинаково удалены одна отъ другой.
Дѣйствительно, если изъ ка-
р _______________К р кихъ-нпбудь двухъ точекъ М и
Т	Т .№ прямой СВ опустимъ па АВ
перпендикуляры МР и то
эти перпендикуляры параллельны
А——--------------—В	(70) п потому фигура А1П(^Р па-
Чсрт. 73	раллелограммъ; отсюда слѣдуетъ,
что МР = ИС.
ѲЗ. Теорема. Во всякомъ параллелограммѣ діагонали
дѣлятся пополамъ.
Пусть АВСВ есть параллелограммъ, а АС и ВВ его
діагонали; требуется доказать, что В0~0В и АО=ОС.
Тр.-ки АОВ и ВОС равпы,
Черт 74
Теорема. Во
равны.
Черт. 75
потому чго у лихъ: ВС=АВ (какъ
противоположныя стороны парал-
лелограмма), / 1 - /_2 и /. 3 =
/ 4 (какъ внутренніе накрестъ
лежащіе углы при параллельныхъ
прямыхъ). Изъ равенства тр.-ковъ
слѣдуетъ: ОВ= ОВ и ОС = ОА.
всякомъ прямоугольникѣ діагонали
Пусть АВСВ есть прямоуголь-
никъ, а АС и ВВ его діагонали;
требуется доказать, что АС—ВВ.
Прямоугольные треугольники А СВ
и А.ВВ равны, потому что у нихъ:
АВ общій катетъ и АВ = СВ (какъ
противоположныя стороиы параллело-
грамма). Изъ равенства тр.-ковъ слѣдуетъ: АС—ВВ.
Теорема. Во всякомъ ромбѣ діагонали перпендику-
лярны гі дѣлятъ углы ромба пополамъ.
Пусть АВСВ есть ромбъ, а АС и ВВ его діагонали:
требуется доказать, что АС | ВВ и что каждый изъ угловъ
ромба дѣлится діагональю пополамъ.
— 57
Черт. 76
Черт. 77
Тр.-ки АВО и ВОС равны, потому что у нихъ: ВО
общая сторона, АВ — ВС (такъ какъ у ромба всѣ стороны
равны) и АО — ОС (такъ какъ діагонали
всякаго параллелограмма дѣлятся попо-
ламъ). Изъ равенства тр.-ковъ слѣдуетъ:
/ 1 = /_ 2, т.-е. ВВ_\_АС, и3 —Д 4.
Эв. Замѣчаніе. Такъ какъ квадратъ
есть параллелограммъ, прямоугольникъ и
ромбъ, то онъ соединяетъ въ себѣ всѣ
свойства этихъ фигуръ.
93. Теорема. Если у четыреугольника: 1°, противо-
положныя стороны равны, или 2°, двѣ противоположныя
стороны равны и параллельны, то такой четыреугольникъ
есть параллелограммъ.
1°. Пусть АВСВ есть четыреуголь-
никъ, у котораго:
ЛВ=СВ и ВС=АВ.
Требуется доказать, что АВСВ есть
параллелограммъ, т.-е. АВ || СВ и
ВС |) АВ. — Проведя діагональ ВВ,
получимъ два тр.-ка, которые равны,
такъ у нихъ: ВВ общая сторона, АВ—СВ и ВС=АВ
(по условію). Изъ равенства ихъ слѣдуетъ: / 1 —/_ 4 и
/ 2 — / 3 (въ равныхъ тр.-кахъ противъ равныхъ сторонъ
лежатъ равные углы), вслѣдствіе этого АВ Ц СВ и ВСЦ АВ
(если внутр. накрестъ лежащіе углы равны, то прямыя па-
раллельны).
2°. Пусть въ томъ же четыреугольникѣ дано условіемъ:
ВС—АВ и ВС || АВ. Требуется доказать, что АВСВ есть
параллелограммъ, т.-е. что АВ\\СВ.—Треугольники АВВ
и ВСВ равны, потому что у нихъ: ВВ общая сторона.
ВС—АВ (по условію) и Д2 = /^3 (какъ внутренніе на-
крестъ лежащіе углы при параллельныхъ ВС и АВ и сѣ-
кущей ВВ). Изъ равенства тр.-ковъ слѣдуетъ: /_1 = /_4;
поэтому АВ |) СВ.
— 58
пряА
сторону отъ нея, есть
О
В
Черт. 78
98.	Слѣдствіе. Геометрическое мѣсто точекъ, одина-
ково удаленныхъ отъ данной прямой и находящихся по одну
ая, параллельная данной.
Дѣйствительно, пусть ЛГи Лг
будутъ какія-нибудь двѣ точки,
находящіяся по одну сторону
отъ прямой АВ и удаленныя
отъ нея на одно и то же раз-
стояніе т, т.-е. перпендикуляры
МР и опущенные изъ
этихъ точекъ на АВ, равны т.
Проведемъ черезъ ЛЛ и 2Ѵ прямую СВ. Такъ какъ ЛІР — Х(Э
и сверхъ того МР[\В(^, то фигура АШ(^Р есть параллело
граммъ; слѣд., СВ || АВ. Такимъ образомъ, всѣ точки,
удаленныя отъ АВ на разстояніе т и расположенныя по
верхнюю сторону отъ нея, лежатъ па прямой СВ, параллель-
ной АВ. Обратно: всякая точка В, взятая па этой прямой,
отстоитъ отъ АВ на столько аіе, какъ и точки М и №,
т.-е. на данное разстояніе т (92, 2°).
99.	Предлагаемъ самимъ учащимся доказать слѣдующія
обратныя теоремы:
1°. Всякій четыреугольникъ, у котораго противополож-
ные углы равны, есть параллелограммъ.
2°. Всякій чегпыреугольникъ, у котораго діагонали дѣ-
лятся пополамъ, есть параллелограммъ.
3°. Всякій параллелограммъ, у котораго діагоналгі- равны,
есть гірямоугольникъ.
4°. Всякій параллелограммъ, гу котораго діагонали ггер-
пендикулярны, есть ромбъ.
Нѣкоторыя теоремы, основанныя на свойствахъ паралле-
лограмма,
1ОО.	Теорема. Если на одной сторонѣ угла отложимъ
равныя части гг черезъ точки дгьленія проведемъ параллель-
ныя прямыя до пересѣченія съ другой стороной угла, то и
на этой сторонгъ отложатся равныя части.
— 59 —
Пусть АВС какой-нибудь уголъ и на его сторонѣ ВС
отложены равныя части: ВВ = ВЕ=ЕЕ.... Проведемъ че-
резъ точки В, Е, Е... параллельныя прямыя ВА[, ЕЕ, ЕР...
до пересѣченія съ АВ; требуется доказать, что
ВАЕ=МЕ=ЕР=...
Проведя ВК і | АІЕ, по-
лучимъ Д ВКЕ, равный
Л ВМВ, потому что у
нихъ: ВВ = ВЕ (по усло-
вію), / В = / КВЕ (какъ
соотвѣтственные углы при-
параллельныхъ ВА1 и ВК
и сѣкущей В С) и / ВВМ
— ДВЕК (какъ соотвѣт-
Черт. 79
ственные углы при па-
раллельныхъ ВМ и ЕЕ и сѣкущей ВС). Изъ равенства
тр.-ковъ выводимъ: ВК=ВМ; но ВК~МЕ (какъ противо-
положныя стороны параллелограмма ВНАЕК); потому МЕ=
= ВМ. Подобнымъ же образомъ докажемъ, что ЕР = ВМ~
~ МЕ и т. д.
1О1, Задача. Данную прямую раздѣлитъ на т рав-
ныхъ частей.
Эта задача рѣшается на основаніи предыдущей теоремы.
Пусть ВР (черт. 79) будетъ данная прямая, которую
требуется раздѣлить, положимъ, на 3 равныя части. Изъ конца
ея В проводимъ прямую ВС, образующую съ ВР произволь-
ный уголъ; откладываемъ на ВС отъ точки В три произ-
вольной длины, но равные между собою, отрѣзка: ВВ, ВЕ
и ЕЕ; точку Е соединяемъ съ Р; наконецъ, изъ Е и В
проводимъ прямыя ЕЕ, ВА[, параллельныя ЕР. Тогда пря-
мая ВР, по доказанному, раздѣлится въ точкахъ М и У на
три равныя части.
102. Теорема. Прямая, соединяющая средины двухъ
сторонъ треугольника, параллельна третьей его сторонѣ и
равна ея половишь.
— 60
Пусть В есть средина стороны АВ и Е—средина сто-
роны ВС тр.-ка АВС; докажемъ сначала, что ВЕ || АС.
Для доказательства проведемъ че-
резъ В прямую, параллельную АС;
пусть это будетъ ВЕ}. Такъ какъ
на сторонѣ ВА угла В отложены
равныя части ВВ = ВА, и изъ то-
чекъ дѣленія къ другой сторонѣ угла
проведены параллельныя прямыя ВЕ}
и АС, то (100) па сторонѣ ВС
должны отложиться равныя части;
В
Черт. 80
значитъ: ВЕ^ — Е^С, т.-е. точка есть средина ВС. Но,
по условію, средина ВС есть точка Е; слѣд. Ег должна сов-
мѣститься съ Е, и параллельная прямая ВЕг должна слиться
съ ВЕ. Остается теперь доказать, что ВЕ^'/^АС. Для
этого изъ Е проведемъ	тогда фигура ЕВА Е бу-
детъ параллелограммъ и, слѣд., ВЕ=АЕ. Такъ какъ па сто-
ронѣ СВ угла С отложены равныя части СЕ = ЕВ и изъ
точекъ дѣленія проведены къ другой сторонѣ параллельныя
прямыя ЕЕ и ВА, то СЕ=ЕА; слѣд. ВЕ^А/^АС.
ІОЗ. Теорема, прямая, соединяющая средины непарал-
лельныхъ сторонъ трапеціи, параллельна основаніямъ тра-
ихъ.
Пусть Е есть средина сторо-
ны АВ и Е—средина стороны
СВ трапеціи АВСВ; требуется
доказать, что ВС (и слѣд.
ЕЕ\\ АВ) и кромѣ того, что
ЕЕ^/ъ (АВ-\-ВС).
1°. Проведемъ черезъ Е пря-
мую, параллельную ВС; пусть
пеціи и равна полусуммѣ
Черт. 81
это будетъ ЕЕ*. Тогда, обращая вниманіе я&^АВС, за-
мѣчаемъ. что діагональ АС должна раздѣлиться въ точкѣ
Сг1 пополамъ (] 00), а обращая вниманіе на &АСВ, нахо-
димъ, что сторона СВ должна раздѣлиться въ точкѣ Е1 по-
поламъ. Но средина СВ есть Е; значитъ. Е1 совмѣщается съ
Е, и параллельная прямая ЕЕг сливается съ ЕЕ.
— 61
2°. Изъ Л АВС, а затѣмъ изъ Л АСВ находимъ:
ЕС — 7» ВС и (гЕ— 73 АВ; слѣд.:
ЕЕ^ЕС+СЛ^1/* ВС-\~Х/^ АВ—1^ (ВС+АВ).
Замѣчаніе. Прямая, соединяющая средины непараллель-
ныхъ сторонъ трапеціи, наз. среднею линіей,.
У II Р А Ж II Е II I Я.
Доказать теоремы:
37.	Соединивъ послѣдовательно средины сторонъ какого-нибудь че-
тыреугольника, получимъ параллелограммъ.
38.	Въ прямоугольномъ А медіана, преведенпая кь гипотенузѣ,
равна ея половинѣ. (Указаніе: слѣдуетъ продолжить медіану па равное
разстояніе).
39.	Обратно: если медіана равна половинѣ стороны, къ которой она
проведена, то тр.-никъ прямоугольный.
40.	Въ прямоугольномъ А медіана и высота, проведенныя къ гипо-
тенузѣ, образуютъ уголъ, равный разности острыхъ угловъ Д.
41.	Если въ прямоугольномъ А одинъ острый уголъ равенъ ’73с?, то
противолежащій ему катетъ составляетъ половину гипотенузы.
42.	Обратно: если катетъ вдвое меньше гипотенузы, то противоле-
жащій ему острый уголъ равенъ
43.	Всякая прямая, проведенная внутри параллелограмма черезъ
точку пересѣченія діагоналей (черезъ центръ параллелограмма), дѣлится
въ эртй точкѣ пополамъ
44.	Всякая прямая, проведенная внутри трапеціи между ея основа-
ніями, дѣлится среднею линіей пополамъ.
45.	Выпуклый многоугольникъ не можетъ имѣть болѣе трехъ острыхъ
угловъ.
46.	Черезъ вершины угловъ А проведены прямыя, параллельныя
противоположнымъ сторонамъ. Образованный ими А въ 4 раза болѣе
даннаго; каждая сторона его въ 2 раза болѣе соотвѣтствующей стороны
Даннаго Д.
47.	Въ равнобедренномъ А сумма разстояній каждой точки основа-
нія отъ боковыхъ сторонъ есть величина постоянная, а именно опа рав-
на высотѣ, опущенной на боковую сторону.
48.	Какъ измѣнится эта теорема, если взять точку на продолженіи
основанія?
— 62 —
49.	Данъ квадратъ АВСВ. На сторонахъ его отложены равныя части:
ААі, ВВѴ ССі и ВВѴ Точкп Лъ Б(, Сг и В{ соединены послѣдова-
тельно прямыми. Доказать, что Л^С^ есть квадратъ.
Найти геометрическія мѣста:
50.	Срединъ всѣхъ прямыхъ, проведенныхъ изъ данной точки къ
различнымъ точкамъ данной прямой.
51.	Точекъ, равноотстоящихъ отъ двухъ параллельныхъ прямыхъ.
52.	Вершпнъ тр.-ковъ, имѣющихъ общее основаніе и равныя высоты.
Задачи на построеніе:
53.	Даны два угла Д, построить третій.
54.	Данъ острый уголъ прямоугольнаго Д; постропть другой острый
уголъ.
55.	Провести прямую, параллельную данной прямой и находящуюся
отъ нея на данномъ разстояніи.
56.	Раздѣлить пополамъ уголъ, вершина котораго не помѣщается на
чертежѣ.
57.	Черезъ данную точку провести прямую подъ даннымъ угломъ къ
данной прямой.
58.	Черезъ данную точку провести прямую такъ, чтобы отрѣзокъ
ея, заключенный между двумя данными параллельными прямыми, равнялся
данной длинѣ.
59.	Между сторонами даннаго остраго угла помѣстить прямую дан-
ной длины такъ, чтобы опа была перпендикулярна къ одной сторонѣ
угла.
60.	Между сторояамп даннаго угла помѣстить прямую данной длппы
такъ, чтобы она отсѣкала отъ сторонъ угла равныя части.
61.	Построить прямоугольный А по даннымъ острому углу и противо-
лежащему катету.
62.	Построить А по двумъ угламъ и сторонѣ, лежащей противъ од-
ного изъ нихъ.
63.	Построитъ равнобедренный А по углу при вершинѣ и основанію.
64.	То же-по углу прп основаніи и высотѣ, опущенной на боковую
сторону.
65.	То же—по боковой сторонѣ и высотѣ, опущенной па нее.
66.	Построить равносторонній А по его высотѣ.
67.	Раздѣлить прямой уголъ на 3 равныя части (пли постропть усолъ,
равный Чз^)-
68.	Построитъ А по основанію, высотѣ и боковой сторонѣ.
69.	То же—по основанію, высотѣ и углу при основаніи.
70.	То .же—по углу и двумъ высотамъ, опущеннымъ на стороны этого
угла.
— 63 —
71.	То же—по сторонѣ, суммѣ двухъ другихъ сторонъ и высотѣ,
опущенной на одну п этихъ сторонъ.
72.	То же—но двумъ угламъ и периметру.
73.	То же—по высотѣ, периметру и углу при основанія.
74.	Провести въ Д прямую, параллельную основанію, танъ, чтобы
она была равна суммѣ отрѣзковъ боковыхъ сторонъ, считая отъ основанія.
75.	Провести в'Ь Д прямую, параллельную основанію, такъ, чтобы
верхній отрѣзокъ одной боковой стороны равнялся нижнему отрѣзку
другой боковой стороны
76.	Построить многоугольникъ, равный данному {указаніе', діагоналями
не разбиваютъ мп.-никъ на тр -ки).
77.	Построить четыреугольникъ по тремъ его угламъ и двумъ сторо-
намъ, образующнмл> четвертый уголъ {указаніе: падо пайтп 4-й угодъ)
78.	То же—по тремъ сторонамъ и двумъ діагоналямъ.
79.	Построить параллелограммъ по двумъ неравнымъ сторонамъ и од-
ной діагонали.
80.	То же—по сторонѣ п двумъ діагоналямъ.
81.	То же—По дйумъ діагоналямъ и углу между ними,
82.	То же—по основанію, высотѣ и діагонали.
83.	Построить прямоугольникъ по діагоналямъ и углу между ними.
84.	Построить ромбъ по сторонѣ и діагонали.
85.	То же—по двумъ діагоналямъ.
86.	То же—по высотѣ п діагонали.
87.	То же—по углу и діагонали, проходящей черезъ этотъ уголъ.
88.	То же—по діагонали и противолежащему углу.
89.	То же-по суммѣ діагоналей и углу, образованному діагональю
со стороною.
90-	Построить квадратъ по данной діагонали.
91.	Построить трапецію по основанію, прилежащему къ нему углу и
двумъ непараллельнымъ сторонамъ (могутъ быть два рѣшенія, одно м ни
одного).
92.	То же-по разности основаній, двумъ боковымъ сторонамъ и
одной діагонали.
92*. То жс-»-по четыремъ сторонамъ.
93.	То же—по основанію, высотѣ п двумъ діагоналямъ.
94.	То же—по двумъ основаніямъ и двумъ діагоналямъ.
95.	Построить квадратъ по суммѣ стороны съ діагональю.
96.	То же—по разности діагонали и стороны.
97.	Построитъ параллелограммъ по двумъ діагоналямъ и высотѣ.
98.	То же—по сторонѣ, суммѣ діагоналей и углу между ними.
99	Построить Л по двумъ сторонамъ и медіанѣ, проведенной къ
третьей сторонѣ.
100	То же—по основанію, высотѣ п медіанѣ, проведенной къ боко-
вой сторонѣ.
— 64 —
КНИГА II.
ОКРУЖНОСТЬ.
ГЛАВА I.
Форма и положеніе окружности.
104.	Опредѣленія. Окружностью называется замкнутая
плоская линія, всѣ точки которой одинаково удалены отъ
одной и той же точки О, называемой центромъ. Прямыя О А,
ОВ,ОС,..., соединяющія центръ
съ точками окружности, называют-
/	Иж\	ѵі радіусами. Неопредѣленная пря-
/	Цг \	мая А1Е, проходящая черезъ ка-
ре--------------------А Я кія-шібудь двѣ точки окружности,
\	называется сѣкущею, а часть ея
\		Е1-\	заключенная	между этими
точками, наз. хордою. Всякая хор-
'	да АВ, проходящая	черезъ центръ,
Черт 8°	наз.	діаметромъ.	Какая-нибудь
часть	окружности,	напр. ЕтЕ,
наз. дугою. О хордѣ ЕЕ, соединяющей концы дуги, гово-
рятъ, что она стягиваетъ, дугу. Дуга обозначается иногда зна-
комъ ч->; напр., пишутъ такъ: ^ЕтЕ.
Часть плоскости, ограниченная окружностью, паз. кругомъ.
Часіь круга, напр. СОВ, ограниченная дугою и двумя ра-
діусами, проведенными къ концамъ дуги, паз. секторомъ;
часть круга, напр. ЕтЕ, ограниченная дугою и стягивающею
се хордою, наз. сегментомъ.
105.	Слѣдствія: 1°, всѣ радіусы одной окружности
равны;
2°, діаметръ равенъ двумъ радіусамъ;
3°, точка, лежащая внутри круга, ближе къ центру,
а точка внѣ круга дальше отъ центра, чѣмъ точки окруж-
ности.
— 65 —
ІОв. Теорема. Прямая и окружность не могутъ имѣть
О
М
Л
Черт. 83
болѣе двухъ общихъ точекъ.
Для доказательства предпо-
ложимъ, что прямая ЛЛѴимѣетъ
съ окружностью, которой центръ
находится въ точкѣ О, три оо-
щія точки: Л.,7? и С. Тогда
прямыя О А, ОВ, ОС должны
быть равны между собою, какъ
радіусы, вслѣдствіе чего тр.-ки
ОАВ и ОАО будутъ равнобедренные и, слѣдов,, /_! = /_ 2
и /_1 = Х_3; откуда: Д2 — /_3; но это невозможно, такъ
какъ /_2, будучи внѣшнимъ по отношенію къ тр-пику ОВС,
больше внутренняго пе смежнаго съ нимъ угла 3 (42).
1О1. Слѣдствіе. Никакая частъ окружности не мо-
жетъ совмѣститься съ прямой, потому что въ противномъ
случаѣ окружность съ прямою имѣла бы болѣе двухъ общихъ
точекъ.
108. Опредѣленіе. Линія, которой никакая часть не
можетъ совмѣститься съ прямой, наз. кривою.
Изъ предыдущаго параграфа слѣдуетъ, что окружность
есть кргівая линія.
109. Теорема. Черезъ три точки, не лежащія на
одной 'прямой, можно провести окружность и притомъ
только одну.
Если возможно провести окружность черезъ три точки
-А. П. КИСЕЛЕВЪ.	5
— 66 —
А,В и С, не лежащія на одной прямой, то должна суще-
ствовать такая точка, которая одинаково удалена отъ А,Ві& С,
Чтобы найти ее, разсуждаемъ такъ: геометрическое мѣсто
точекъ, одинаково удаленныхъ отъ А и В, есть прямая ЛЛѴ,
перпендикулярная къ срединѣ отрѣзка АВ (63); геометриче-
ское мѣсто точекъ, одинаково удаленныхъ отъ В и С, есть
прямая Р(^ перпендикулярная къ срединѣ отрѣзка ВО.
Прямыя ЛТѴ' и Р(^. будучи перпендикулярны къ пересѣкаю-
щимся прямымъ АВ и ВС, должны пересѣчься (79,2°) въ
нѣкоторой точкѣ О. Эта точка, находясь на обоихъ геомет-
рическихъ мѣстахъ, одинаково удалена отъ А,В и С; по-
этому окружность, описанная изъ точки О, какъ центра,
радіусомъ ОА, пройдетъ черезъ эти точки. Итакъ, черезъ
три точки, не лежащія на одной прямой, можно провести
окружность.
Такъ какъ точка, одинаково удаленная отъ А,В и С,
должна непремѣнно находиться въ пересѣченіи прямыхъ
М1Т и Р(^, а двѣ прямыя могутъ пересѣчься только въ
одной точкѣ, то искомая окружность имѣетъ только одинъ
центръ О; такъ какъ, сверхъ того, длина ея радіуса можетъ
быть только одна, равная разстоянію точки О отъ А, или
отъ В, или отъ С, то искомая окружность есть един-
ственная.
440. Слѣдствіе. Точка О (черт. 84), находясь на оди-
наковомъ разстояніи отъ А и С, должна лежать на перпен-
дикулярѣ В8 къ срединѣ хорды АО (59). Такимъ образомъ:
Три перпендикуляра къ срединамъ сторонъ треугольника
(АВС, черт. 84) пересѣкаются въ одной точкѣ.
414. Задача. Найти центръ, данной окружности.
Взявъ на данной окружности какія-нибудь три точки
А,В и С (черт. 84), проводятъ черезъ нихъ двѣ хорды,
наир. АВ и ВС, и изъ срединъ этихъ хордъ возстановляютъ,
перпендикуляры МИ и Р(^. Искомый центръ, будучи оди-
наково удаленъ отъ А,В и С, долженъ лежать и па МИ,,
и на Р(^; слѣд., онъ будетъ въ пересѣченіи этихъ перпен-
дикуляровъ.
— 67 —
ГЛАВА И.
Равенство и неравенство дугъ.
Черт. 85

ца. Теорема. Два круга одинаковаго радіуса равны.
Пусть О и 01 будутъ центры двухъ круговъ, которыхъ
радіусы равны. Наложимъ кругъ
О на кругъ 01 такъ, '^обы
ихъ центры совпали. Тогда обѣ
окружности совмѣстятся, такъ
какъ въ противномъ случаѣ ихъ
точки неодинаково отстояли бы
отъ центра и, слѣд., радіусы
были бы неравны.
113.	Слѣдствіе. Вращая одинъ изъ совпавшихъ круговъ
вокругъ общаго центра, мы не нарушимъ совмѣщенія. Изъ
этого слѣдуетъ, что части- одной окружности или равныхъ
окружностей совмѣстимы.
ІІ4.	Опредѣленія. Двѣ дуги одного радіуса считаются
равными, если онѣ при наложеніи совмѣщаются. Положимъ,
напр., что мы накладываемъ дугу АВ
па дугу СВ такъ, чтобы точка А упала
въ точку С и дуга АВ пошла по
дугѣ СВ (что возможно, какъ мы ви-
дѣли въ предыдущемъ слѣдствіи); если
при этомъ копцы В и В совпадутъ,
то'—1 АВ='—' СВ; въ противномъ слу-
чаѣ дуги неравны, причемъ та будетъ
меньше, которая составитъ только
частъ другой.
Суммою нѣсколькихъ данныхъ дугъ
одинаковаго радіуса наз. такая дуга
того же радіуса, которая составлена
ственпо равныхъ даннымъ дугамъ. Такъ, если отъ произволь-
ной точки М (черт. 86) окружности отложимъ часть ЛПѴ,
равную АВ, и затѣмъ отъ точки въ томъ же направле-
Черт. 86
частей, соотвѣт-
ИЗЪ
— 68 —
ніи часть КР, равную СВ, то дуга МР будетъ сумма
дугъ АВ и СВ. Подобно этому можно составить сумму
трехъ и болѣе дугъ.
Изъ понятія о суммѣ дугъ одного и того же радіуса вы-
водятся понятія объ ихъ разности, произведеніи и частномъ
въ томъ же смыслѣ, какъ и для отрѣзковъ прямыхъ.
ІІ5.	Теорема. Всякій діаметръ дѣлитъ окружность и
кругъ пополамъ.
Вообразимъ, что кругъ перегнутъ по
какому-нибудь діаметру АВ такъ, чтобы
часть АтВ упала на часть АпВ. Тогда
всѣ точки дуги т совмѣстятся съ точ-
ками дуги п, потому что въ противномъ
случаѣ точки одной дуги лежали бы ближе
къ центру, чѣмъ точки другой дуги, что
невозможно.
Такимъ образомъ, всякій діаметръ раздѣляетъ окружность
на двѣ полуокружности и кругъ на два полукруга.
ІІв. Замѣчаніе. Всякая хорда ОВ (черт. 87), не про-
ходящая черезъ центръ, стягиваетъ двѣ неравныя дуги: одну,
большую полуокружности, другую—меньшую ея. Когда гово-
рятъ: „дуга, стягиваемая хордой“, то обыкновенно разумѣютъ
дугу, мепыпую полуокружности.
ІІ’З. Теоремы. 1°. Діаметръ,, перпендикулярный къ
хордѣ, дѣлитъ эту хорду и обѣ стяггіваемыя ею дуги по-
поламъ.
2°. Дуги, заключенныя между параллельными хордами,
равны.
1°. Пусть діаметръ АВ перпендику-
ляренъ къ хордѣ СВ] требуется дока-
зать, что

СК= КВ и — СВ=^ВВ, — СА =
=^ВА.
в
Черт 88
Перегнемъ чертежъ по діаметру АВ
такъ, чтобы его лѣвая часть упала на
правую. Тогда полуокружность А.ЕСВ
— 69 —
совмѣстится СЪ полуокружностью АЕВВ, а перпендикуляръ
КС пойдетъ по КВ. Изъ этого слѣдуетъ, что точка С со-
впадетъ съ В’, поэтому:
КС— КВ; ^ВС=^ВВ] ^АС—^АВ.
2°. Пусть (черт. 88) хорды ЕР и СВ параллельны;
требуется доказать, что СЕ—^ВЕ.—Проведя діаметръ
АВ, перпендикулярный къ хордамъ (74), перегнемъ чертежъ
по этому діаметру. Тогда одна полуокружность совпадетъ съ
другою, перпендикуляръ КС пойдетъ до КВ, а перпенди-
куляръ ВЕ по ВЕ. Изъ этого слѣдуетъ, что точка С со-
вмѣстится съ В, а точка Е съ Е] значитъ, СЕ—^ ВЕ.
118. Задача. Раздѣлить данную дугу (СВ, черт. 88)
пополамъ.
Проведя хорду СВ, опускаемъ на нее перпендикуляръ
изъ центра и продолжаемъ его до пересѣченія съ дугою.
По доказанному въ предыдущей теоремѣ дуга СВ раздѣлится
этимъ перпендикуляромъ пополамъ.
ГЛАВА III.
Зависимость между дугами, хордами и разстояніемъ хордъ
отъ центра..
119. Теоремы. Въ одномъ кругѣ или въ равныхъ кругахъ:
1°, еелгі дуги равны, то стягивающія гіхъ хорды равны
и одинаково удалены отъ центра]
2°, если дуги не равны ад при-
томъ меньше полуокружности, -то	о
бдльгиая изъ нгіхъ стягивается боль- /я \	\
шею хордою, и эта большая хорда	\ И/
ближе къ центру.	‘ к....	...
1°. Пусть дуга АВ равна дугѣ СВ]
требуется доказать, что хорды АВ и
СВ равны, а также равны перпенди-
куляры ОЕ и ОЕ, опущенные изъ
— 70
центра на хорды. — Повернемъ секторъ ОАВ вокругъ цент-
ра О въ направленіи, указанномъ стрѣлкою, на столько,
чтобы радіусъ ОВ совпалъ съ ОС. Тогда дуга ВА пойдетъ
по дугѣ СВ, и вслѣдствіе ихъ равенства эти дуги совмѣ-
стятся. Значитъ, хорда АВ совмѣстится съ хордою СВ (между
двумя точками можно провести только одну прямую) и пер-
пендикуляръ ОЕ совпадетъ съ ОЕ (изъ одной точки можно
опустить на прямую только^ одинъ перпендикуляръ); т.-е.
АВ=СВ и ОЕ=ОЕ.
2°. Пусть дуга АВ (черт. 89) меньше дуги СМ, и при-
томъ обѣ дуги меньше полуокружности; требуется доказать,
что хорда АВ меньше хорды СМ, а перпендикуляръ ОЕ
больше перпендикуляра ОВ.—Отложимъ на дугѣ СМ часть
СВ, равную АВ, и проведемъ вспомогательную хорду СВ,
которая, по доказанному, равна хордѣ АВ. У тр.-ковъ СОМ
и СОВ двѣ стороны одного равны двумъ сторонамъ другого
(какъ радіусы), а углы, заключенные между этими сторонами,
не равны; въ этомъ случаѣ, какъ мы знаемъ (54). противъ
большаго изъ угловъ, т.-е. СОМ, должна лежать большая
сторона; значитъ, СМ>СВ, и потому СМ>АВ.
Для доказательства того, что ОЕ~> ОВ, примемъ во вни-
маніе, что, по доказанному въ 1-ой часги этой теоремы,
0Е~0Е; слѣд., намъ достаточно сравнить ОЕ съ ОВ.
Въ прямоугольномъ тр.-кѣ ОКВ гипотенуза ОК больше ка-
тета ОВ', но ОЕ> ОК-, значитъ, и подавно, ОЕ> ОВ и
потому ОЕ^ОВ.
Теорема, доказанная нами для одного круга, остается
вѣрною и для равныхъ круговъ, потому что такіе круги ни-
чѣмъ другъ отъ друга не отличаются, кромѣ своего поло-
женія.
Обратныя предложенія. Такъ какъ въ предыдущемъ
параграфѣ разсмотрѣны всевозможные случаи относительно ве-
личины двухъ дугъ одного радіуса, причемъ получились раз-
личные выводы относительно величины хордъ и разстоянія
ихъ отъ центра, то обратныя предложенія должны бытъ
вѣрны (48), а именно:
Въ одномъ кругѣ ѵлн въ равныхъ кругахъ:
— 71 —
1°, равныя хорды стягиваютъ равныя дуги и одинаково
удалены отъ центра',
2°, хорды, одинаково удаленныя отъ центра, равны и
стягиваютъ равныя дуги',
3°, изъ двухъ неравныхъ хордъ большая стягиваетъ боль-
шую дугу и ближе къ центру,
4°, изъ двухъ хордъ, неодинаково удаленныхъ отъ центра,
та, которая ближе къ центру, болгье и стягиваетъ боль-
шую дугу.
Эти предложенія легко доказываются отъ противнаго.
Напр., для доказательства перваго изъ нихъ разсуждаемъ
такъ: если бы данныя хорды стягивали неравныя дуги, то,
-согласно прямой теоремѣ, онѣ были бы неравны, что про-
тиворѣчитъ условію; значитъ, равныя хорды должны стяги-
вать равныя дуги; а если дуги равны, то, согласно прямой тео-
ремѣ, стягивающія ихъ хорды одинаково удалены отъ центра.
Теорема. Діаметръ есть нагібольгиая гізъ хордъ.
Если соединимъ съ центромъ концы какой-нибудь хорды,
не проходящей черезъ центръ, то получимъ тр.-къ, въ ко-
торомъ одна сторона есть эта хорда, а двѣ другія—радіусы.
Но въ тр.-кѣ одна сторона мепѣе суммы двухъ другихъ сто-
ронъ; слѣдовъ взятая нами хорда менѣе двухъ радіусовъ;
тогда какъ всякій діаметръ равенъ двумъ радіусамъ. Значитъ,
діаметръ больше всякой хорды, не проходящей черезъ центръ.
ГЛАВА IV.
Свойства касательной.
Опредѣленіе. Прямая ЛІУ, имѣющая съ окруж-
ностью только одну общую точку	А
А, наз. касательною къ окруж- м
ности.	/	\
Возможность существованія ка- /	.	\
сательной, и при томъ во всякой 1	]
точкѣ окружности, доказывается \	/
слѣдующей теоремой.
Черт. 90
12
1ЖЗ. Теорема. Если прямая перпендикулярна къ радіусу'
въ концѣ его, лежащемъ на. окружности, то она есть ка-
сательная .
М
Пусть О есть центръ круга»
и О А какой-нибудь радіусъ. Че-
резъ конецъ его А проведемъ
МЕ I О А; требуется доказатьг
что прямая МЕ есть касательная,
т.-е. что эта прямая "имѣетъ съ.
окружностью только одну общую*
точку А. — Допустимъ противное: пусть МЕ имѣетъ съ ок-
ружностью еще другую общую точку, напр. В. Тогда прямая
ОВ была бы радіусомъ и, слѣд., равнялась бы ОА; но этого-
быть не можетъ, такъ какъ, если О А есть перпендикуляръ,
то ОВ должна быть наклонная къ МЕ, а наклонная больше
перпендикуляра.
04. Обратная теорема. Если прямая касательпа къ-
окружности, то радіусъ, проведенный въ точку касанія, пер-
пендикуляренъ къ ней.
Пусть МЕ (черт. 91) есть касательная къ окружности,
А точка касанія и 0 центръ окружности; требуется дока-
зать, что ОА | МЕ.— Допустимъ противное, т.-е. предполо-
жимъ, что перпендикуляромъ, опущеннымъ изъ 0 на МЕ,
будетъ не ОА, а какая-нибудь другая прямая, напр. ОВ.
Возьмемъ ВС=ВА и проведемъ ОС. Тогда О А и ОС бу-
дутъ наклонныя, одинаково удаленныя отъ перпендикуляра.
ОВ, и слѣд. 0С= О А. Изъ этого слѣдуетъ, что окруж-
ность, при пашемъ предположеніи, будетъ имѣть съ прямою
2И2Ѵ двѣ общія точки: А и С, т.-е. МЕ будетъ не каса-
тельная, а сѣкущая,
что противорѣчивъ условію.
125. Теорема. Касательная, па-
раллельная хордѣ, дѣлитъ въ точкѣ
касанія дугу, стягиваемую хордой, по-
поламъ .
Пусть прямая АВ касается окруж-
ности въ точкѣ М и параллельна хордѣ
СВ; требуется доказать, что СМ—
= — МВ.
— 73 —
Проведя черезъ точку касанія діаметръ МЕ, будемъ
имѣть: ЕМ I АВ (124) и слѣд. ЕМ \_^СВ (74); поэтому
СМ=МВ (117).
1%6. Задача. Черезъ данную точку провести касатель-
ную къ данной окружности.
Проведеніе касательной черезъ точку, данную на окруж-
ности, выполняется на основаніи теоремы § 123: проводятъ
черевъ эту точку радіусъ и черезъ конецъ его перпендику-
лярную прямую. Разсмотримъ тотъ случай, когда точка дана.
внѣ окружности.
Пусть требуется провести къ
окружности О касьіельпую черезъ
точку А. Для этого изъ точки А,
какъ центра, описываемъ дугу ра-
діусомъ А О, а изъ точки О,
какъ центра, пересѣкаемъ эту дугу
въ точкахъ В и С раствореніемъ
циркуля, равнымъ діаметру дан-
наго круга. Проведя затѣмъ хорды
ОВ и ОС, соединимъ точку А
съ точками В и Е, въ которыхъ
эти хорды пересѣкаются съ дан-
ною окружностью. Прямыя АВ
и АЕ будутъ касательными къ
Черт. 93
окружности О. Дѣйствительно, изъ построенія видно, что
тр.-ки АОВ и АОС равнобедренные (АО — АВ = АС) съ
основаніями ОВ и ОС, равными діаметру круга О. Такъ
какъ ОВ и ОЕ суть радіусы, то В есть средина ОВ и Е
средина ОС\ значитъ, АВ и АЕ суть медіаны, проведенныя
къ основаніямъ равнобедренныхъ тр.-ковъ, и потому пер-
пендикулярны къ этимъ основаніямъ (37). Если же прямыя
ВА и ЕА перпендикулярны къ радіусамъ ОВ и ОЕ, то
онѣ касательныя (123).
Другой способъ проведенія касательной будетъ указанъ
ниже (158).
183. Слѣдствіе. Двѣ касательныя, проведенныя изъ од-
ной точки къ окружности, равны.
— 74 —
Такъ, АВ~АЕ (черт. 93), потому что прямоугольные
тр.-ки АОИ и АОЕ, имѣющіе общую гипотенузу АО и рав-
ные катеты ОЕ и ОЕ (какъ радіусы), равны.
ІЙ8. Задача. Провести касательную къ данной окруж-
ности О параллельно данной прямой АВ,
Опускаемъ па АВ изъ центра
Е к	О перпендикуляръ 00 и черезъ точ-
( \	ку В, въ которой этотъ перпепди-
--------\ \ \ куляръ пересѣкается съ окружностью,
/-------ЧР \с	проводимъ ЕЕ || АВ. Искомая каса-
/ о\ тельная будетъ ЕЕ. Дѣйствительно,
у	А \	такъ какъ ОС_\_АВ и ЕЕ || АВ,
./ \ \ то ЕЕ | 01); а прямая, перпенди-
Г кулярная къ радіусу въ концѣ его,
Черт. 94	лежащемъ на окружности, есть ка-
сательная.
199. Задача. Еъ двумъ окружностямъ О и 01 про-
вести общую касательную.
1°. Предположимъ, что за-
дача рѣшена. Пусть АВ бу-
с/Ч^7*'*,*****-*^В дегъ °бщая касательная, А и
В точки касанія. Очевидно, что
О^.-Л..-I...) если мы найдемъ одну изъ этихъ
..._точекъ> напр. А, то затѣмъ
-------------В, легко найдемъ и другую. Про-
ведемъ радіусы О А и 0}В. Эти
Чсрс. 95	радіусы, будучи перпендикуляр-
ны къ общей касательной, па-
раллельны между собою; поэтому если изъ Ог проведемъ
0Т С И ВА, то тр.-къ 000І будетъ прямоугольный при вер-
шинѣ С; вслѣдствіе этого, если опишемъ изъ 0, какъ центра,
радіусомъ 00 окружность, то она будетъ касаться прямой
01С въ точкѣ С. Радіусъ этой вспомогательной окружности
извѣстенъ: онъ равенъ О А—0А=0А—0{В, т.-е. онъ равенъ
разности радіусовъ данныхъ окружностей. Такимъ образомъ
построеніе можно выполнить такъ: изъ 0 описываемъ окруж-
ность радіусомъ, равнымъ разности данныхъ радіусовъ; изъ Ог
— 75 —
проводимъ къ этой окружности касательную О1 С (способомъ,
указаннымъ въ предыдущей задачѣ); черезъ точку касанія (7
проводимъ радіусъ 00 и его продолжаемъ до встрѣчи съ
данною окружностью въ точкѣ А. Наконецъ, изъ А прово-
димъ АВ параллельно СО{.
Совершенно такимъ же способомъ мы можемъ построить
другую общую касательную А1ВІ. Прямыя АВ и А^В^
наз. внѣшними общими касательными. Можно еще провести
двѣ внутреннія касательныя слѣдующимъ образомъ.
2°. Предположимъ, что
задача рѣшена. Пусть АВ	\
будетъ искомая касатель-	"*’Х.
ная. Проведемъ радіусы /
О А и ОгВ въ точки ка- /	.
санія А и В. Эти радіу- і I 0/	\ іХИ "'-О )
сы, будучи оба перпенди- у
кулярпы къ общей каса- \ \
тельной, параллельны меж- \ ХА, /
ду собою. Поэтому если
изъ О1 проведемъ 0^11
|| ВА и продолжимъ О А	Черт- 96
до точки С, то ОС будетъ перпендикуляръ къ 01 С; вслѣд-
ствіе этого окружность, описанная радіусомъ ОС изъ точки
О, какъ центра, будетъ касаться прямой ОгС въ точкѣ С.
Радіусъ этой вспомогательной окружности извѣстенъ: онъ ра-
венъ О А -\-АС= 0А-\- ОгВ, т.-е. онъ равенъ суммѣ радіу-
совъ данныхъ окружностей. Такимъ образомъ, построеніе мо-
жетъ быть выполнено такъ: изъ О, какъ центра, описываемъ
окружность радіусомъ, равнымъ суммѣ данныхъ радіусовъ;
изъ 01 проводимъ къ этой окружности касательную О^С;
точку касанія С соединяемъ съ О; наконецъ, черезъ точку
А, въ которой ОС пересѣкается съ данною окружностью,
проводимъ АВ |) СОг.
Подобнымъ же способомъ можемъ построить другую вну-
треннюю касательную А1В1.
130.	Общее опредѣленіе касательной. Пусть къ окружности о
проведены черезъ точку А касательная АТ н какая-нибудь сѣкущая АМ.
— 76
Станемъ вращать эту сѣкущую вокругъ тонки А такъ, чтобы другая
точка пересѣченія В все ближе и ближе придвигалась къ Л. Тогда пер-
пендикуляръ ОВ, опущснпыймзъцент-
т Ра яа сѣкущую, будетъ все болѣе и
—-—___	болѣе приближаться къ радіусу ОА,
/ //\\\ А и уголъ А ОВ можетъ сдѣлаться мень-
ше всякаго малаго угла. Уголъ 21 АТ,
' образованный сѣкущею и касатель-
ною, равенъ углу АОВ (вслѣдствіе
М перпендикулярности ихъ сторонъ);
поэтому при неограниченномъ при-
ближеніи точки В къ А уголъ 21 А Т
также можетъ быть сдѣлапъ какъ-
угодно малъ. Это выражаютъ иными
словами такъ: касательная есть предѣльное положеніе, къ которому стре-
мится сѣкущая, проведенная черезъ точку касанія, когда вторая точка пере-
сѣченія неограниченно приближается къ точкѣ касанія.
Это свойство принимаютъ за опредѣленіе касательной, когда рѣчь
идетъ о какой угодно кривой.
Такъ, касательною къ кривой ЛВ
~ въ точкѣ ЛГ паз. предѣльное поло-
, жсніе 2І'Р, къ которому стремится
— Ы сѣкущая ЛГЛ7, когда точка лере-
сѣченія Р неограниченно приб.іи-
жается къ ЛГ.
Замѣтимъ, что опредѣляемая
1 такимъ образомъ касательная мо~
*6	жетъ имѣть съ кривою болѣе од-
ной общей точки (какъ это видно на черт. 98).
131. Выпуклая кривая. Кривая, или часть кривой, наз. выпуклою,
если она расположена по одну сторону отъ каждой своей касательной.
Выпуклая кривая обладаетъ тѣмъ же свойствомъ, какъ и выпуклая ло-
маная: она не можетъ пересѣчься съ прямою болѣе, чѣмъ въ двухъ точкахъ..
Окружность есть выпуклая кривая.
ГЛАВА V.
Относительное положеніе окружностей.
133. Опредѣленія. Если двѣ окружности имѣютъ только
одну общую точку, то говорятъ, что онѣ касаются; если же-
двѣ окружности имѣютъ двѣ общія точки, то говорятъ, что
онѣ пересѣкаются.
— 77
Трехъ общихъ точекъ двѣ не сливающіяся окружности
имѣть не могутъ, потому что въ противномъ случаѣ черезъ
три точки можно было бы провести двѣ различныя окруж-
ности, что невозможно (109).
133» Теорема. Если двѣ окружности имѣютъ общую
точку по одну сторону отъ линіи ихъ центровъ, то онѣ
имѣютъ общую точку и по другую сторону отъ линіи
центровъ, т.-е. такія окружности пересѣкаются.
Пусть окружности О и О1 имѣютъ общую точку А, ле-
жащую внѣ линіи центровъ ООІ; требуется доказать, что
эти окружности имѣютъ еще общую точку по другую сторо-
ну отъ прямой ОО1.
Опустимъ изъ А на пря-
мую ОО1 перпендикуляръ АЕ
и продолжимъ его па разстоя-
ніе ВАЛ, равное АВ. Докажемъ
теперь, что точка А1 принад-
лежитъ обѣимъ окружностямъ.
Изъ построенія видно, что точ-
ки О и О1 лежатъ на перпен-
Черт. 99
дикулярѣ къ срединѣ отрѣзка АА^. Изъ этого слѣдуетъ, что
точка О одинаково удалена отъ А и А^ (59, 2°); то же можно
сказать и о точкѣ значитъ, обѣ окружности, при продол-
женіи ихъ, пройдутъ черезъ А{. Такимъ образомъ, окруж-
ности будутъ имѣть двѣ обіція точки: А (по условію) и Ау
(по доказанному); слѣд., онѣ пересѣкаются.
134. Слѣдствіе. Общая хорда (АА1? черт. 9 9) двухъ
пересѣкающихся окружностей перпендикулярна къ линіи
центровъ гі дѣлится ею пополамъ.
135. Теоремы. 1°. Если двѣ окружности имѣютъ об-
щую точку на линіи центровъ или на ея продолженіи, то
онѣ касаются.
2°. Обратно: еелгі двѣ окружности касаются, то общая
гіхъ точка лежитъ на линіи центровъ или на ея продол-
женіи .
1°. Пусть общая точка А двухъ окружностей лежитъ на
линіи центровъ ОО1 (черт. 100) или на продолженіи ея
— 78 —
(черт. 101). Требуется доказать, что такія окружности ка-
саются, т.-е. что онѣ не имѣютъ никакой другой общей точ-
ки.— Окружности не могутъ имѣть другой общей точки внѣ
Черт. 101
линіи центровъ, потому что въ противномъ случаѣ опѣ имѣли
бы еще третью общую точку по другую сторону линіи цент-
ровъ (133) и, слѣд., должны были бы слиться (109). Опѣ
не могутъ имѣть другой общей точки и на линіи центровъ,
такъ какъ на этой прямой, очевидно, пѣтъ другой точки,
которая отъ обоихъ центровъ была бы удалена на столько же,
какъ и точка А. Слѣд., окружности имѣютъ только одну
общую точку, т.-е. онѣ касаются.
2°. Пусть двѣ окружности О и О1 (черт. 100 или 101)
касаются, т.-е. опѣ имѣютъ только одну общую точку А;
требуется доказать, что эта точка лежитъ на линіи центровъ
или на ея продолженіи. — Точка А не можетъ лежать внѣ
линіи центровъ, потому что въ противномъ случаѣ окруж-
ности пересѣклись бы (133).
136. Слѣдствіе. Двѣ касательныя окружности имѣютъ
общую касательную въ точкѣ касанія, потому что прямая
1ДУ (черт. 100 или 101), перпендикулярная къ О А, пер-
пендикулярна также и къ (ДА.
139. Признаки различныхъ случаевъ относительнаго по-
ложенія окружностей. Пусть имѣемъ двѣ окружности, кото-
рыхъ центры суть О и О15 радіусы И и и разстояніе
между центрами (I. Эти окружности могутъ находиться въ
слѣдующихъ 5-ти относительныхъ положеніяхъ:
— 79 —
1°. Окружности лежатъ одна внѣ другой, не касаясь;
въ этомъ случаѣ, очевидно, ^>2? + ^.
2°. Окружности гсмѣютъ внѣшнее касаніе; тогда & =
= .ВтЯр такъ какъ точка касанія лежитъ на линіи цент-
ровъ ООХ.
3°. Окружности пересѣкаются; тогда	и
й>_В—_й1? потому что въ тр.-кѣ 04-О-і сторона ООІ
меньше суммы, но больше разности двухъ другихъ сторонъ.
4°. Окружностгь имѣютъ внутреннее касаніе; въ этомъ,
случаѣ I — II — потому что точка касанія лежитъ па
продолженіи линіи 00^.
5°. Одна окружность лежитъ внутри другой; тогда,
очевидно,	(въ частномъ случаѣ с? можетъ рав-
няться нулю, т.-е. окружности могутъ имѣть общій центръ;
такія окружности наз. конгъетрическими').
138.	Обратныя предложенія. Такъ какъ различные слу-
чаи расположенія двухъ окружностей сопровождаются различ-
ными соотношеніями между разстояніемъ центровъ и величи-
ною радіусовъ, то обратныя предложенія должны быть вѣрны
(48), а именно:
— 80 —
1°. Если СІ> .8 + Д, то окружности расположены
одна внѣ другой, не касаясь.
2°. Если СЬ-Е^Е^, то окружности касаются извнѣ.
3°. Если ^<Е-\~ЕХ и &> Е — Еі, то окружности
пересѣкаются.
4°. Если сі—Е— Еі, то окружности касалотся из-
онутри.
5°. Если 6<Е— Ех, то одна окружность лежитъ
внутри другой, не касаясь.
Эти предложенія легко доказываются отъ противнаго.
Напр., для доказательства перваго предложенія разсуждаемъ
такъ: предположимъ противное, т.-е. что окружности не
расположены одна внѣ другой. Тогда могутъ представиться
4 случая относительно ихъ расположенія. Какой бы изъ
этихъ случаевъ мы ни взяли, нп въ одномъ изъ нихъ не бу-
детъ такой зависимости между разстояніемъ центровъ и ве-
личиною радіусовъ, какая намъ дана условіемъ (<Е> Е-\- Ег);
значитъ, всѣ эти случаи исключаются. Остается одинъ воз-
можный, именно тотъ, который требовалось доказать.
Такимъ образомъ, перечисленные признаки различныхъ
случаевъ относительнаго положенія двухъ окружностей не
только необходимы, но и достаточны.
УПРАЖНЕНІЯ.
Найти геометрическія мѣста:
101.	—точекъ, из'ь которыхъ касательныя, проведенныя къ данной
окружности, равны данной длинѣ.
102.	— точекъ, изъ которыхъ данпая окружность видна кодъ дан-
нымъ угломъ (т.-е. двѣ касательныя, проведенныя изъ каждой точки къ
окружности, составляютъ между собою данный уголъ).
103.	— центровъ окружностей, описанныхъ даннымъ радіусомъ и ка-
сающихся данной прямой.
104.	—центровъ окружностей, касающихся данной окружности въ
данной точкѣ.
105.	— центровъ окружностей, описанныхъ даннымъ радіусовъ и ка-
сающихся данной окружности (два случая: касаніе внѣшнее и касаніе
внутреннее).
— 81
106.	Прямая данной длины движется параллельно самой себѣ такъ,
чю одинъ ея конецъ скользить по окружности. Найти геом. мѣсто, опи-
сываемое другимъ концомъ.
107.	Прямая данной длины движется такъ, чго концы ед скользятъ
по сторонамъ прямого угла. Найти геом. мѣсто, описываемое срединою
эгоіі прямой.
Доказать теоремы:
108.	Если черезъ центръ окружности и данную точку внѣ ея про-
ведемъ сѣкущую, то часть ея, заключенная между данною точкою и
ближайшею точкою пересѣченія, есть кратчайшее, а часть, заключенная
между дайною точкою и другою точкою пересѣченія, есть наибольшее
разстояніе точки отъ окружности.
109.	Кратчайшее разстояніе между двумя окружностями, лежащими
одна внѣ другой, есть отрѣзокъ линіи центровъ, заключенный между
окружностями.
ПО. Изъ всѣхъ хордъ, проведенныхъ въ окружности черезъ одпу
точку, наименьшая есть та, которая перпендикулярна къ радіусу, про-
ходящему черезъ эту точку.
111.	Если черезъ точку пересѣченія двухъ окружностей будемъ про-
водить сѣкущія, ие продолжая ихъ за окружности, то наибольшая изъ
нихъ будетъ та, которая параллельна линіи центровъ.
112.	Если къ двумъ окружностями, касающимся извнѣ, провести три
общія касательныя, то внутренняя изъ никъ дѣлитч, двѣ другія въ точ-
кахъ, одинаково удаленныхъ отъ точекъ касанія.
113.	Всѣ хорды данной длины, проведенныя въ данной окружности,
касаются нѣкоторой другой окружности.
114.	Если черезъ одну изъ точекъ пересѣченія двухъ окружностей
проведемъ діаметры въ каждой окружности, то прямая, соединяющая
концы ихъ, пройдетъ черезъ другую точку пересѣченія.
Задачи на построеніе:
115.	Раздѣлить дугу на 4, 8, 16... равныхъ частей.
116.	По суммѣ и разности дугъ найти эти дуги.
117.	Изъ данной точки, какъ центра, описать такую окружность,
которая раздѣлила бы данную окружность пополамъ.
118.	На дайной прямой найти точку, наименѣе удаленную отъ дан-
ной окружности.
119.	Въ кругѣ дана хорда. Провести другую хорду, которая дѣли-
лась бы первою пополамъ и составляла съ нею данный уголъ.
120.	Черезъ данную въ кругѣ точку провести хорду, которая дѣли-
лась бы этою точкою пополамъ.
121.	Изъ точки, данпой на сторонѣ угла, описать окружность, кото-
рая отъ другой стороны угла отсѣкала бы хорду данной длины.
А. и. КИСЕЛЕВЪ.	6
— 82 —
122.	Даннымъ радіусомъ описать окружноеіь, которой центръ де-
жадъ бы на сторонѣ даннаго угла и которая отъ другой стороны его
отсѣкала бы хорду данной длины.
123.	Даннымъ радіусомъ описать окружность, которая касалась бы
данной прямой въ данной точкѣ.
124.	Описать окружность, касательную къ сторонамъ даннаго угла,
причемъ одной изъ нихъ въ данпой точкѣ.
125.	Описать окружность, касающуюся трехъ сторонъ тр.-пика.
126.	Между двумя параллельными прямыми дана точка; провести окруж-
ность, проходящую черезъ эту точку и касающуюся данныхъ прямыхъ.
127.	Провести къ данной окружности касательную подъ даннымъ
угломъ къ данной прямой.
128.	Изъ точки, дапной внѣ окружности, провести къ пей сѣкущую
такъ, чтобы внутренняя ея часть равнялась данной длинѣ (изслѣдовать
задачу).
129.	Даннымъ радіусомъ описать окружность, проходящую черезъ
данную точку и касательную къ данной прямой.
130.	На данной прямой найти такую точку, чтобы касательныя, про-
веденныя изъ нея къ данной окружности, были дапной длины.
131.	Построить Д, зная одинъ уголъ и двѣ высоты, изъ которыхъ
одна проведена изъ вершины .даннаго угла.
132.	Ц,аны двѣ окружности; провести къ нимъ сѣкущую такъ, чтобы
внутреннія части ея равнялись давнымъ прямымъ.
133.	Даны двѣ точки; провести прямую такъ, чтобы перпендикуляры,
опущенные на нее изъ этихъ точекъ, имѣли данныя длины.
134.	Описать окружность, ксторая проходила бы через’ь данную
точку и касалась бы данной окружности въ дапной точкѣ.
135.	Описать окружность, которая касалась бы двухъ данныхъ па-
раллельныхъ прямыхъ и къ кругу, находящемуся между ними.
136.	Даннымъ радіусомъ описать окружность, которая касалась бы
даннаго круга и проходила черезъ данную точку.
137.	Даннымъ радіусомъ описать окружность, которая касалась бы
данпой прямой и даннаго круга.
138.	Даппымъ радіусомъ описать окружность, которая отъ сторонъ
дапнаго угла отсѣкала бы хорды данной длины.
139.	Описать окружность, касающуюся даннаго круга въ данной
точкѣ и данной прямой (2 рѣшенія).
140.	Описать окружность, касающуюся данпой прямой въ данной
точкѣ и даннаго круга (2 рѣшенія).
141.	Описать окружность, касающуюся двухъ данныхъ круговъ, при-
чемъ одного изъ ппхъ въ данной точкѣ (разсмотрѣть три случая: 1, ис-
комый кругъ лежитъ внѣ данныхъ; 2, одинъ изъ данныхъ круговъ ле-
житъ внѣ искомаго, другой внутри», 3, оба данные круга лежатъ внутри
искомаго).
— 83 —
142.	Одпсать окружность, касающуюся трехъ равныхъ круговъ извнѣ
зіли извнутрп.
143.	Въ данный секторъ вписать окружность, касающуюся къ радіу-
самъ и дугѣ сектора.
144.	Вписать въ данный кругъ три равные круга, которые каса-
лись бы попарно между собою и даннаго круга.
145.	Черезъ точку внутри круга провести хорду такъ, чтобы разность
ея отрѣзковъ равнялась данной длинѣ.
146.	Черезъ точку пересѣченія двухъ окружностей провести сѣку-
щую такъ, чтобы часть ея, заключенная внутри окружностей, равнялась
данной длинѣ.
147.	Изъ точки, данной внѣ окружоостп. провести сѣкущую такъ,
чтобы внѣшняя ея часть равнялась внутренней.
ГЛАВА VI.
Измѣреніе величинъ.
130. Общая мѣра. Общею мѣрою двухъ конечныхъ
прямыхъ называется такой отрѣзокъ прямой, который въ
каждой изъ нихъ содержится цѣ- м
лое число разъ. Такъ, если от-	д|----1;------{--1-----|В
рѣзокъ АМ содержится въ АВ
и СВ цѣлое число разъ (напр.,	с'----]---1---|р
5 разъ въ АВ и 3 раза въ СБ),	т 103
то АМ есть общая мѣра АВ и СІ>.	ері *
Подобно этому можетъ быть общая мѣра двухъ дугъ оди-
наковаго радіуса, двухъ угловъ и вообще двухъ значеній
одной и той же величины.
140. Нахожденіе наибольшей общей мѣры. Чтобы най-
ти -наибольшую общую мѣру двухъ конечныхъ прямыхъ, упот-
ребляютъ способъ иослѣбовательна'іо	а
дѣленія, подобный тому, какимъ въ
ариѳметикѣ находятъ общаго наи- 1	1	:	•
большаго дѣлителя двухъ цѣлыхъ . ... Ч
чиселъ. Этотъ способъ основывается . ’і
на слѣдующихъ двухъ предложеніяхъ:	ЧеРт- Ю4
1°. Бела большая прямая А содержитъ меньшую прямую
В цѣлое число ралъ, то В есть наиболыѣая общая мѣра АиВ.
6*
84
Это предложеніе не требуетъ доказательства по своей
очевидности (черт. 104).
2°. Если большая прямая А содержитъ меньшую пря-
мую В нѣкоторое число разъ съ остаткомъ В, то наиб.
общая мѣра- А и В есть и наиб. общая мѣра В и В.
л	Пусть, папр., А содержитъ
..........	В три раза съ остаткомъ В,;
I ""	]-----{----тогда можно положить, что
В	А =В-гВ+В + В
Изъ этого равенства мы' мо-
Черт. 105	жемъ вывести два заключенія:
1°, всякая прямая, содержащаяся цѣлое число разъ въ А и
В, содержится также цѣлое число разъ и въ В; 2", обратно:
всякая прямая, содержащаяся цѣлое число разъ въ В и В>,
содержится также цѣлое число разъ и въ А; значитъ, у
двухъ паръ прямыхъ:
А и В В и II
однѣ п тѣ же общія мѣры; поэтому у лихъ должна быть
одна и та же наиб. общая мѣра.
Пусть теперь требуется найти наиб. общую мѣру пря-
мыхъ АВ и ОВ. Для этого на большей прямой отклады-
к ваемъ меньшую столько разъ,
д|_______]________।_______।__сколько можно. Если 67)уло-
жится въ АВ безъ остатка,
। . Еі	то искомая мѣра, согласно-
I 1	предложенію Г, и есть ОВ;
Черт. 106	если же этого не произойдетъ,
то, согласно предложенію 2°, вопросъ приведется къ нахож-
денію наиб. общей мѣры двухъ меньшихъ прямыхъ, именно
СІ) и остатка ЕВ. Чтобы найти ее, поступаемъ по предыду-
щему: откладываемъ ЕВ на ОВ столько разъ, сколько можно.
Если ЕВ уложится въ СВ безъ остатка, то искомая мѣра п
будетъ ЕВ; если же этого не произойдетъ, то вопросъ при-
ведется къ нахожденію наиб. общей мѣры двухъ меньшихъ
прямыхъ, именно ЕВ и новаго остатка ЁВ. Если, продолжая
— 85 —
этотъ пріемъ далѣе, мы дойдемъ до того, что какой-нибудь
остатокъ уложится въ предшествующемъ остаткѣ цѣлое число
разъ, то этотъ остатокъ и будетъ искомая мѣра.
Чтобы удобнѣе вычислить, сколько разъ найденная общая
мѣра содержится въ данныхъ прямыхъ, выписываемъ рядъ
равенствъ, получаемыхъ послѣ каждаго отложенія. Положимъ,
напр., что
АВ^ЪСВ + ЕВ
СВ = 2ЕВ+ГВ
ЕВ~±Е1)
Переходя въ этихъ равенствахъ отъ нижняго къ верхнему,
«послѣдовательно находимъ:
ЕВ~4ЕІ)\ С1) = 2 (ІЕВ) -Ь ЕВ^=ЪЕВ\
АВ = 3 (<)ЕВ) -\-4:ЕВ = 311'79.
Подобно этому можно находить наиб. общую мѣру двухъ
дугъ одинаковаго радіуса, двухъ угловъ и т. и.
Замѣтимъ, что, найдя наибольшую общую мѣру, мы мо-
жемъ затѣмъ получить сколько угодно другихъ меньшихъ
мѣръ; стоитъ только брать V , ’/3, */ и т. д. наибольшей
мѣры.
141. Соизмѣримыя и несоизмѣримыя величины. Можетъ
случиться, что при нахожденіи общей мѣры мы никогда не
дойдемъ до того, чтобы не получилось никакого остатка;
тогда данныя прямыя пе будутъ имѣть общей мѣры.
Два значенія одной величины наз. соизмѣримыми, если
они имѣютъ общую мѣру, и несоизмѣримыми, когда такой
мѣры не существуетъ.
Ыа практикѣ пѣтъ возможности убѣдиться въ существо-
ваніи несоизмѣримыхъ прямыхъ, потому что, продолжая по-
слѣдовательное наложеніе, мы всегда дойдемъ до столь малаго
остатка, который въ предшествующемъ остаткѣ, повиди-
мому, укладывается цѣлое число разъ. Быть можетъ, при
этомъ и долженъ былъ бы получиться нѣкоторый остатокъ,
но по причинѣ неточности инструментовъ мы не въ состоя-
— 86 —
что АВ несоизмѣрима съ АС.
В
Черт. 107
ніи его замѣтить. Однако можно доказать, что несоизмѣри-
мыя прямыя существуютъ. Приведемъ наиболѣе простой при-
мѣръ такихъ прямыхъ.
14$. Теорема. Если у равнобедреннаго треугольника
каждый уголъ при основаніи равенъ 'ІА, то боковая сто-
рона его несоггзмгг>рима съ основаніемъ.
Пусть АВС будетъ равнобедренный тр.-къ, у котораго
каждый изъ угловъ А. и С равенъ І/А1; требуется доказать,
Для доказательства ста-
немъ находить наиб. об-
щую мѣру между АС и
АВ. Прежде всего опре-
дѣлимъ, которая изъ этихъ,
прямыхъ больше. Для это-
го достаточно сравнить уг-
лы, противъ которыхъ ле-
жатъ эти стороны. Такъ какъ, по условію, А— С—^/^й, то
В = 2(1 —	— */р:1 — 6/8й; слѣд.. В > С; поэтому^О АВ.
Теперь найдемъ, сколько разъ въ АС можетъ уложиться АВ.
Такъ какъ АС<АВ-\-ВС и АВ—ВС, то АС<2АВ;
значитъ. АВ въ АС можетъ уложиться только одинъ разъ
съ нѣкоторымъ остаткомъ.
Итакъ, если гу равнобедреннаго гпрегуголъника каждый
уголъ, при основаніи равенг, гпо боковая его сторона
содержится въ основаніи одинъ разъ съ нѣкоторымъ остат-
комъ.
Замѣтивъ это, приступимъ теперь къ послѣдовательному
наложенію. Отложимъ на АС часть А]), равную АВ: тогда
подучимъ остатокъ ВС, который надо накладывать на АВ,
или, что все равно, па ВС. Чтобы узнать, сколько разъ
ВС уложится въ ВС, соединимъ В съ В и разсмотримъ,
какой будетъ А ВВС. Для этого найдемъ его углы. Такъ,
какъ А АВВ равнобедренный, то его углы АВВ и АВВ
равны; слѣд.. каждый изъ нихъ равенъ у., (2<7 —Л9~У2
(2й — %) = у„й. Но уголъ АВС, какъ мы выше нашли,
равенъ 73^; слѣд.. /_ ВВС— У-/? — Такимъ об-
— 87
разомъ, у тр.-ка ВВС есть два равныхъ угла при ВС;
слѣд., онъ равнобедренный, при чемъ каждый уголъ при его
основаніи ВС равенъ 2/5^. Вслѣдствіе этого, по доказанному
выше, боковая сторона его ВС уложится въ основаніи ВС
одинъ разъ съ нѣкоторымъ остаткомъ. Пусть этотъ остатокъ
будетъ ВВ. Соединивъ Е съ В, мы снова получимъ равно-
бедренный тр.-къ ВВЕ, у котораго каждый уголъ при осно-
ваніи ВВ равенъ Къ этому тр.-ку можно примѣнить
тѣ же разсужденія^ значитъ, его бокъ ЕВ содержится въ
основаніи ВВ (или, все равно, въ ВС) одинъ разъ съ нѣко-
торымъ остаткомъ. Продолжая эти разсужденія далѣе, мы
постоянно будемъ приходить къ равпоб. тр.-ку, у котораго
углы при основаніи равны -/АІ, и. слѣд.. постоянно будемъ
получатъ остатки. Изъ этого слѣдуетъ, что А.В несоизмѣ-
рима съ АС.
Подобно этому можно доказать, что Оіаюна.іъ квадрата
несоизмѣрима съ его стороною.
143. Понятіе объ измѣреніи. Чтобы составить себѣ ясное
представленіе о данной длинѣ, ее измѣряютъ при помощи
другой, извѣстной намъ, длины, напр., посредствомъ метра.
Эта извѣстная длина, съ которой сравниваютъ другія длины,
наз. единицей длины. При измѣреніи могутъ представиться
два различныхъ случая: пли измѣряемая длина соизмѣрима
съ единицей, или несоизмѣрима съ ней.
1°. Измѣритъ длину, соизмѣримую съ единицей, зна-
читъ узнать, сколько ралъ въ ней, содержится единггца или
доля единицы.
Пусть, напр.. надо измѣрить какую-нибудь длину А при
помощи единицы В, соизмѣримой съ А.
Тогда находятъ ихъ общую мѣру и уз-	А.......
наютъ, сколько разъ она содержится ।	।	। ;'Ч
въ В и А. Если общей мѣрой ока- ~
жется сама единица В, то результатъ Р.. (
измѣренія выразится цѣгымъ числомъ: ।	1 5 I
такъ, когда В содержится въ А три Чррт
раза, то говорятъ, что длина А равна
3 ед. Если же общей мѣрой будетъ доля В, то результатъ
— 88 —
измѣренія выразится дробнымъ числомъ; такъ, если общая мѣра
есть 74 доля В и она содержится въ А девять разъ (какъ изобра-
жено на черт. 108), то говорятъ, что длина А равна !'Д единицы.
Число, получившееся послѣ измѣренія, наз. часто мѣрою
того значенія величины, которое измѣрялось. Числа цѣлыя и
дробныя наз. соизмѣримыми числами.
2°. Когда данная длина А. несоизмѣрима съ единицей В,
тогда измѣреніе выполняется косвенно: вмѣсто длины А. из-
мѣряютъ двѣ другія длины, соизмѣримыя съ единицей, изъ
которыхъ одна меньше, а другая больше А, и которыя раз-
нятся отъ А. такъ мало, какъ угодно. Чтобы найти такія
соизмѣримыя длины, поступаютъ такъ: положимъ, что мы
желаемъ найти соизмѣримыя длины, которыя отличались бы
отъ А. меньше, чѣмъ на */10 единицы. Тогда дѣлимъ единицу
В на 10 равныхъ частей (черт. 109) и одну такую долю
укладываемъ въ длинѣ А столько разъ, сколько можно. Пусть
она уложится 13 разъ съ нѣкоторымъ остаткомъ, меньшимъ
Черт. 109
У10І?. Тогда мы будемъ имѣть длину Ат, соизмѣримую съ
единицей и меньшую, чѣмъ А. Отложивъ г/пВ еще одинъ
разъ, получимъ другую длину А.,, тоже соизмѣримую съ еди-
ницей, но большую, чѣмъ А}, и которая разнится отъ А
менѣе, чѣмъ на д/10 единицы. Длины Аг и 4 выражаются
числами 1:’/10 и г710. Эти числа разсматриваются, какъ при-
ближенныя мѣры длины А, первое съ недостаткомъ, вто-
рое съ избыткомъ; причемъ, такъ какъ длина А разнится
отъ Аг и Ал менѣе, чѣмъ на '/1й единицы, то каждое изъ
этихъ чиселъ выражаетъ длину А съ точностью до ’/10.
Вообще, чтобы найти приближенныя мѣры длины А съ
точностью до х/п единицы, дѣлятъ единицу В на п равныхъ
частей и узнаютъ, сколько разъ \:п доля содержится въ А;
— «9
если она содержится болѣе т разъ, то менѣе т 1 разъ,
то числа яу7?, и »' -г і/7г будутъ приближенныя мѣры А съ
точностью до уп, первое съ недостаткомъ, второе съ из-
быткомъ.
Предположимъ теперь, что число п рапныхъ частей, па которыя мы
дѣлимъ единицу В, неограниченно увеличивается (напр., п = 10,100,1000
и т. д.1; тогда разность между длиною Л и каждою изъ соизмѣримыхъ
длинъ и Л2 будетъ все болѣе и болѣе уменьшаться и можетъ сдѣ-
латься такъ малой, какъ угодно. Это выражаютъ такъ: при неоъраітчен-
номъ возрастаніи числа равнымъ частей, на которыя мы дѣлимъ единицу В,
соизмѣримыя длины и Ла стремятся къ общему предѣлу, который есть не-
соизмѣримая длина А. Числа, выражающія длины А{ и Л2, также при
этомъ стремятся къ нѣкоторому общему предѣлу, называемому несоизмѣ-
римымъ числомъ. Это число принимаютъ за точную мѣру несоизмѣримой
длины А.
Сказанное объ измѣреніи длины прямой вполнѣ примѣ-
нимо къ измѣренію всякой величины, напр., дуги, угла и пр.
144. Отношеніе. Отношеніемъ двухъ значеній А и В
одной и той же величины наз. число, гізмѣряющее А, когда
В принято за единицу.
Такъ, если говорятъ, что отношеніе прямой А къ другой
прямой В ость 23/і? то это значитъ, что А. равна 2:’Д В,
т.-е. А. содержитъ въ себѣ 2 раза В, причемъ получается
остатокъ, равный 3/{ В.
Когда А соизмѣримо съ В, отношеніе А къ В можно
выразить точно, цѣлымъ пли дробнымъ числомъ; въ против-
номъ случаѣ его выражаютъ приближенно съ желаемою точ-
ностью. Такъ, если хотятъ найти отношеніе А къ В съ точ-
ностью до УІ0, то дѣлятъ В на 10 равныхъ частей и узна-
ютъ наибольшее содержаніе 1/10 В въ А; если это будетъ,
положимъ, число 27, то 4”/10 или ІЯ/10 будутъ приближенныя
значенія отношенія А къ В, съ точностью до У10, первое
съ недостаткомъ, второе съ избыткомъ.
Когда А несоизмѣримо съ В, отношеніе между ними на-
зываютъ несоизмѣримымъ.
Два несоизмѣримыя отношенія считаются равными, если
равны ихъ приближенныя значенія, вычисленныя съ произ-
вольною, но одинаковою точностью.
— 90 —
145. Свойства отношеній. Если Л и В измѣрены прц
помощи одной и той же единицы С, то отношеніе А къ В
можно выразить частнымъ отъ дѣленія числа, измѣряющаго А,
па число, измѣряющее В (это частное, какъ извѣстно изъ
ариѳметики, наз. кратнымъ или геометрическимъ отношеніемъ
двухъ чиселъ). Напр., положимъ, что А — ^/^С и В=-^ІгС.
Приведя эти дроби къ общему знаменателю, получимъ:
Л — 2!-С В = уС
6	о
Отсюда видпо, что % доля С содержится 10 разъ въ В и
21 разъ въ А; значитъ, */10 доля В содержится въ А ровно
21 разъ, т.-е. отношеніе А къ В есть число -'/10. Но это
число получится, когда 21/е раздѣлимъ на 10Д; значитъ:
отношеніе А къ В — 11 • 19 — 2- ♦ А — А
л 6 • 6	2	3	10*
Вообще, если измѣривъ А и В при помощи одной и той же-
единицы С, мы получимъ для А число т, а для В число-
то
отношеніе Л къ ^ — 1^. О.
Вслѣдствіе этого отношеніе А къ В принято обозначать
помощью тѣхъ же знаковъ, какіе употребляются для обозна-
ченія отношенія чиселъ, а именно такъ:
А : В или
Когда члены отношенія выражены числами, то къ нему
могутъ быть отнесены всѣ свойства числовыхъ отношеній.
Напр., если имѣемъ два равныя отношенія (т.-е. пропорцію),
то произвденіе крайнихъ равно произведенію среднихъ,
и т. п.
*) Въ алгебрѣ доказывается, чго это вѣрно и тогда, когда числа
т и п несоизмѣримыя. См. напр. ^Элементарная алгебра**, сост. А. Ки-
селевъ, 2-ое изданіе, стр. 161.
— 91
Г.ІАВА ѴІГ.
Измѣреніе угловъ помощью дугъ.
14в. Опредѣленія. Уголъ АОВ,
радіусами, паз. иенгпрагънымъ угломъ:
уголъ ОБЕ, образованный двумя хор-
дами, исходящими изъ одной точки ок-
ружности, наз. вписаннымъ» угломъ.
О центральномъ углѣ и дугѣ, зак-
люченной между его сторонами, гово-
рятъ, что они соотвѣтствуютъ другъ
другу; о вписанномъ углѣ говорятъ,
что онъ отдается на дугу-, заключен-
ную между его сторонами.
141. Теоремы. Въ одномъ пругѣ
гахъ:
образованный двумя?
1°, если 'центральные углы рахты, то и соотвѣтствую-
ги,ія имъ дуги равны;
2°, еслгі гі/внтралъиые углы не равны, то большему изъ
нихъ соогпвгглпствуетъ бдлыиая дуга-.
Пусть АОВ и СОВ будутъ два цент-
ральные угла, равные пли неравные. По-
вернемъ секторъ АОВ вокругъ центра въ	/ дЕ
направленіи, указанномъ стрѣлкою, на
столько, чтобы радіусъ О А совмѣстился А ’о^'-..........у
съ ОС. Тогда, если центральные углы \	/
равны, то радіусъ ОВ совпадетъ съ ОВ
и дуга АВ съ дугою СВ; значитъ, эти „
дуги будутъ равны; если же центральные
гулы не равны, то радіусъ ОВ пойдетъ не по ОВ, а по ка-
кому-нибудь иному направленію, напр. по ОЕ или по ОЕ;
въ томъ и другомъ случаѣ большему углу, очевидно, будетъ
соотвѣтствовать большая дуга.
Теорема, доказанная нами для одного круга, остается вѣр-
ною для равныхъ круговъ, потому что такіе круги ничѣмъ,
другъ отъ друга не отличаются, кромѣ своего положенія.
92 —
148.	Обратныя предложенія. Такъ какъ различные слу-
чаи относительно величины двухъ центральныхъ угловъ со-
провождаются различными выводами относительно величины
соотвѣтствующихъ дугъ, то обратныя предложенія должны
быть вѣрны (48), а именно:
Бъ одномъ кругѣ илгь въ равныхъ кругахъ:
1°, если дуги равны, то гь соотвѣтствующіе имъ и,ент-
ралъгѵые углы равны;
2°, еслгі дуги гіе равны, то ббльиіей гізъ нихъ соонклът-
ствуегѣъ больгиій гыттралъгіый уголъ.
Доказательство отъ противнаго предоставляемъ самимъ
учащимся.
149.	Теорема. Бъ одномъ кругѣ или въ равныхъ кру-
гахъ ценгпралъные углы относятся, какъ соотвѣтствующія
гімъ дуги.
Пусть АОБ и СОБ будутъ два центральные угла; тре-
буется доказать, что
/. АОБ : А СОБ=^АБ : ^СБ.
ные углы па равныя части
равные центральные углы).
1°. Допустимъ сначала, что'
дуги АВ и СБ соизмѣримы, т.-е.
имѣютъ общую мѣру. Полояіимъ,
что эта общая мѣра содержится
т разъ въ дугѣ АВ и г: разъ
въ СБ'. тогда
АВ'.^СО^т.'.гі [I].
Соединивъ точки дѣленія дугъ съ
центромъ, мы раздѣлимъ централь-
(равяымъ дугамъ соотвѣтствуютъ
Такъ какъ этихъ частей будетъ т
въ углѣ АОВ и п въ углѣ СОБ, то
/_АОБ'./_, СОБ=т-.н	12].
Сравнивая пропорціи [Г] и [2], замѣчаемъ, что вторыя отноше-
нія у нихъ равны; слѣд., равны и первыя отношенія, т.-е.
^АОБ: Д СОБ=^ АВ'. — СБ.
— 93
2°. Предположимъ теперь, что дуги АВ и СВ несоиз-
мѣримы. Тогда и соотвѣтствующіе имъ центральные углы бу-
дутъ также несоизмѣримы. Дѣйствительно, если бы углы имѣли
какую-нибудь общую мѣру, напр. уголъ ЕОР, то п дуги
имѣли бы общую мѣру, именно дугу ЕР, что противорѣчитъ.
условію. Чтобы доказать равенство двухъ несоизмѣримыхъ
отношеній, достаточно доказать равенство ихъ приближенныхъ,
значеній, вычисленныхъ съ произвольною, но одинаковою,
точностью (144). Найдемъ приближенное значеніе отношенія
дугъ АВ и СО съ точностью до 1/п, Для этого раздѣлимъ
СВ на н равныхъ частей и одну часть отложимъ на АВ
столько разъ, екольно можно. Пусть */,> доля СВ содержится
въ АВ болѣе т разъ, но менѣе ш+1 разъ; тогда
Лрибл. ОТПОІ1І.	(съ нсд.).
С.Т) п
Соединивъ точки дѣленія дугъ съ центромъ, мы раздѣлимъ
уголъ СОВ па м такихъ равныхъ частей, какихъ въ углѣ
АОВ содержится болѣе ш. но мепѣе ш-’гі; слѣд.:
ирибл. отнош.	(съ нсд.).
Сравнивая приближенныя отношенія угловъ и дугъ, видимъ,
что они равны при всякомъ //; а въ этомъ и состоитъ ра-
венство несоизмѣримыхъ отношеній.
150.	Опредѣленіе. Двѣ зависящія другъ отъ друга ве-
личины наз. пропорціаналънымн, если зависимость между
ними состоитъ въ слѣдующемъ: 1°, каждому значенію одной
величины соотвѣтствуетъ только одно значеніе другой вели-
чины; 2°, отношеніе двухъ какихъ бы то ни было значеній
одной величины равно отношенію соотвѣтствующихъ значеній
Другой величины.
Изъ предыдущихъ теоремъ слѣдуетъ, что центральный
уіо.г,, пропорціоналеш, соотвѣтствующей ему дугѣ.
151.	Измѣреніе угловъ. Измѣреніе угловт> сводится на
измѣреніе соотвѣтствующихъ ихъ дугъ слѣдующимъ обра-
зомъ.
За единицу угловъ берутъ угодъ, составляющій У90 часть
прямого угла; эту единицу называютъ угловымъ градусомъ.
94 —
За единицу дугъ одинаковаго радіуса берутъ такую дугу
того же радіуса, которая соотвѣтствуетъ центральному углу,
равному угловому градусу. Такая дуга наз. дуговымъ граду-
сомъ. Такъ какъ прямому центральному углу соотвѣтствуетъ
У4 окружности, то угловому градусу соотвѣтствуетъ У90 чет-
верти окружности; значитъ, дуговой градусъ есть Узв0 цѣлой
окружности.
Пусть требуется измѣрить уголъ АОВ, т.-е. найти от-
ношеніе этого угла къ угловому градусу А'ШР. Для этого
Черг. 113
опишемъ изъ вершинъ угловъ дуги СО и ЕЕ произвольнымъ,
но одинаковымъ радіусомъ. Тогда (149) будемъ имѣть:
^АОВ:/_ МЕР =	'-'ЕЕ.
Лѣвое отношеніе этой пропорціи есть число, измѣряющее
уголъ АОВ въ угловыхъ градусахъ (144); правое отношеніе
есть число, измѣряющее дугу 01) въ дуговыхъ градусахъ,
Слѣд., эту пропорцію можно высказать такъ:
Число, измѣряюгцее уголъ въ угловыхъ градусахъ, равно
числу, измѣряющему соотвѣтствующую дугу съ дуговыхъ
градусахъ.
Для краткости эту фразу выражаю іъ обыкновенно
такъ:
Уголъ измѣряется соо-твгглисггшующелг ему дугой.
Подраздѣленіе градусовъ. Градусы угла и дуги
подраздѣляются па 60 равныхъ частей, называемыхъ мггну-
гпамгг (угловыми или дуговыми); минуту подраздѣляютъ па 60
равныхъ частей, называемыхъ секундами (угловыми или ду-
говыми).
— 95 —
Изъ сказаннаго выше слѣдуетъ, что въ углѣ содержится
•столько угловыхъ градусовъ, минутъ и секундъ, сколько въ
соотвѣтствующей ему дугѣ заключается дуговыхъ градусовъ,
минутъ и секундъ. Если, напр., въ дугѣ СВ (черт. 113)
содержится 40 град. 25 мин, п 13.5 секунды (дуговыхъ),
то п въ углѣ АОВ заключается 40 град. 25 мин. 13.5 сек.
•(угловыхъ); это выражаютъ сокращенно такъ:
/_ ЛО# —40°25'13,5"
обозначая значками (°), (') и (") соотвѣтственно градусы,
минуты и секунды.
153.	Такъ какъ прямой уголъ содержитъ 90°, то:
1°, сумма угловъ тр.-ка равна 180°;
2°, сумма острыхъ угловъ прямоугольнаго тр.-ка равна 90°;
3й, каждый уголъ равносторонняго тр.-ка равенъ 60*’;
4°, сумма угловъ выпуклаго многоугольника, имѣющаго
п сторонъ, равна 180°(// — 2); и т. и.
154.	Транспортиръ. Такъ наз. приборъ, употребляемый
для измѣренія угловъ. Онъ представляетъ собою полукругъ,
котораго дуга раздѣлена на 180 градусовъ. Чтобы измѣрить
уголъ АОВ, накладываютъ
на него приборъ такъ, чтобы
центръ полукруга совпадалъ
съ вершимою угла, а радіусъ
ОМ. совпадалъ со стороною
О А. Число градусовъ, содер-
жащееся въ дугѣ РЛ7. по-
кажетъ величину угла АОВ.
При помощи транспортира
можно также чертить уголъ, содержащій данное „число градусовъ.
Конечно, на такомъ приборѣ пѣтъ возможности отсчиты-
вать не только секунды, но и минуты; построеніе и измѣре-
ніе можно выполнять только приближенно.
155.	Теорема. Вписанный  уіолъ измѣряется половиною
душ, на которую онъ опирается.
Эту теорему надо понимать такъ: вписанный уголъ со-
держитъ въ себѣ столько угловыхъ градусовъ, минутъ и се-
96 —
Черт. 115
кундъ, сколько въ половинѣ дуги, на которую онъ смиряется,,
заключается дуговыхъ градусовъ, минутъ и секундъ
При доказательствѣ теоремы разсмотримъ особо три случая:
1°, центръ О (черт. По) лежитъ на сторонѣ вписан-
наго угла АВС. — Проведя радіусъ АО,
мы получимъ А АВО, въ которомъ ОА =
= ОВ (какъ радіусы) и, слѣд., /_АВО~
ВАО. По отношенію къ этому тр.-ку
уголъ А ОС есть внѣшній: поэтому онъ
равенъ суммѣ угловъ АВО и ВАО, или
равенъ двойному углу АВО\ значить,
уг. АВО равенъ половинѣ центральнаго
угла А ОС. Но послѣдній измѣряется ду-
гою АС (151); слѣд., вписанный уголъ
АВО измѣряется половиною дуги АС.
2”, центръ О лежитъ между сторонами вписаннаго
угла АВВ (черт. 115).
Проведя діаметръ В С, мы раздѣлимъ уголъ АВВ на два
угла, изъ которыхъ, но доказанному въ первомъ случаѣ,
одинъ измѣряется половиною дуги АС, а другой—половиною
дуги СВ\ слѣд., уголъ АВО измѣряется (АС-\- СВ),
ч\-с. % АВ.
3°, центръ О лежитъ внѣ вписаннаго угла ВВЕ
(черт. 115).
Проведя діаметръ ВС, мы будемъ имѣть:
/_ ВВЕ= Д СВЕ —/1 СВВ.
Но углы СВЕ и СВО измѣряются, по
доказанному, половинами дугъ СЕ и СВ',
слѣд., уг. ВВЕ измѣряется ’/2 (СЕ —
СВ), т.-е. половиною дуги ВЕ.
150. Слѣдствіе 1°. Вписанные углы,
опирающіеся на одну и ту же дугу, равны
(черт. 116), потому что каждый изъ нихъ
измѣряется половиною одной и той же
дуги. Если величину одного ивъ такихъ
угловъ обозначимъ а, то можно сказать, что сегментъ АтВ
вмѣщаетъ въ себѣ уголъ, равный а.
т
Черт.
116
— 97
В
Черт. 117
ИСКОМЫЙ,
примѣнить
159. Слѣдствіе 2°. Вписанный у іолъ, опирающійся на
діаметръ, есть прямой (черт. 117), потому что каждый такой
уголъ измѣряется половиною полуокруж-
ности и, слѣд., содержитъ 90°.
158. Задача. Построить прямо-
угольный треугольникъ по гипотенузѣ
АВ и катету АС (черт. 117).
На основаніи слѣдствія 2° эта задача
рѣшается такъ: на гипотенузѣ АВ, какъ
на діаметрѣ, описываемъ полуокружность
и изъ копца А проводимъ хорду АС,
равную данпому катету. Тр.-къ АСВ будетъ
Это построеніе можно, между
томъ случаѣ, когда изъ данной
точки А требуется провести ка-
сательную къ данной окружности
О (см. § 126). Соединивъ А съ О,
строятъ укізанпымъ способомъ на
прямой АО, какъ на гипотенузѣ,
прямоугольный тр.-къ Л ВО, у ко-
тораго катетъ ОВ есть радіусъ
данной окружности. Другой ка-
тетъ АВ будетъ касательной, по-
тому что онъ перпендикуляренъ
къ радіусу ОВ въ концѣ его, лежащемъ на окружности.
159. Задача. Изъ копца А данной прямой АВ, не про-
должая ея, возставить къ ней перпендикуляръ (черт. 119).
Вз івъ внѣ прямой произвольную
точку О, опишемъ изъ пея радіусомъ
О А окружность; черезъ точку С, въ
которой эга окружность пересѣкается съ
прямой АВ, проведемъ діаметръ СВ и
конецъ его В соединимъ съ А. Прямая
АВ будетъ искомый перпендикуляръ,
потому что уголъ А прямой, такъ какъ онъ вписанный и
опирается на діаметръ.
1<М». Теорема. Уголъ, вершина котораго лежитъ внутри
А. П. КИСЕЛЕВЪ.	7
прочимъ,
в.
Черт. 118
въ
в
Черт. 119
— 98 —
круга, измѣряется полусуммою дуга, изъ которыхъ одна заклю-
чена между его сторонами, а другая меледу продолженіями
сторонъ.
Пусть вершина угла АВС лежитъ
— внутри круга. Продолживъ его стороны
Д° пересѣченія съ окружностью въ точ-
/ /	\ кахъ В и Е, докажемъ, что этотъ уголъ
[	। измѣряется половиною суммы д^гъ АС и
\ I ВЕ. — Проведя хорду АВ, мы получимъ
\	\ / Л АВВ, относительно котораго уголъ
АВС есть внѣшній; слѣд.:
черт. 120	/1 АВО~/_. А-\~ Л В.
Но углы А и В, какъ вписанные, измѣряются половинами
дугъ- ВЕ и АС; поэтому уголъ АВС измѣряется полусум-
мою этихъ дугъ.
161. Теорема. Уголъ, вершина котора >о лежитъ внѣ
круга, измѣряется полуразпостыо оугъ, заключенныхъ между
ею сторонами.
Пустъ вершина угла АВС лежитъ внѣ
в	круга. Требуется доказать, что этотъ
Л	уголъ измѣряется половиною разности дугъ
АС и ЕВ.—Проведя хорду АВ, мы по-
/ [ / . \\ лучимъ А АВВ, отяосителі но котораго
/ / /	\\ уголъ АВС есть внѣшній; слѣд.:
у'	\	/_В = {_АВС-/_А.
\І/	г
X	/ Но углы АВС и А, какъ вписанные,
измѣряются половинами дугъ АС и ЕВ;
поэтому уголъ В измѣряется полураз-
Черт. 121 ностыо этихъ дугъ.
Слѣдствіе. Геометрическое мѣсто точекъ, изъ
которыхъ данный отрѣзокъ прямой виденъ подъ даннымъ
угломъ а и которыя расположены по одну сторону отъ
этого отрѣзка, есть дуга сегмента, вмѣщающаго грюлъ а.
Пусть М будетъ одна г въ точекъ, изъ которыхъ дапный
отрѣзокъ АВ виденъ подъ угломъ а, т.-е. допустимъ, что'прямыя
— 99 —
АГА и МВ образуютъ уголъ а. Проведемъ черезъ точки А,
АІ и. В окружность. Тогда часть этой
АтВ, будетъ искомымъ геометриче-
скимъ мѣстомъ. Дѣйствительно, изъ
каждой точки этой дуги прямая АВ
видна подъ угломъ а, потому что всѣ
вписанные углы, опирающіеся на АВ,
равны углу АМВ, который есть а.
Обратно: всякая точка, напр. изъ
которой прямая АВ видна подъ угломъ
а, и которая расположена по ту же
сторону отъ АВ, какъ и точка АІ,
должна находиться на дугѣ сегмента
АтВ, потому что въ противномъ слу-
чаѣ у голъ ААВ не измѣрялся бы поло-
окружности, именно
Черт. 122
виною дуги АпВ (160 и 161) и слѣд., не былъ бы равенъ а.
По другую сторону отъ АВ существуютъ также точки,
изъ которыхъ эта прямая видна подъ угломъ а; онѣ распо-
ложены па дугѣ сегмента АРВ, равнаго сегменту АтВ, но
расположеннаго по противоположную сторону отъ АВ.
163. Теорема. Уголъ, составленный касательною и хор-
дой, измѣряется половиною дуги, заключенной внутргі его.
Пусть уголъ АОВ составленъ ка-
сательною А О и хордою СВ; требуется
доказать, что этотъ уголъ измѣряется
половиною дуги СтВ.—Проведя діа-
метръ СЕ, будемъ имѣть:
/_ А СВ = А СЕ - /_ В СЕ.
Уголъ АСЕ, какъ прямой (124), из-
мѣряется половиною полуокружности
СтЕ; уголъ ВСЕ, какъ вписанный,
Е
Черт. 123
измѣряется половиною
В
дуги ВЕ; слѣд., уголъ АСВ измѣряется полуравностью дугъ
СтЕ и БЕ, т.-е. половиною ;уги ВС.
Подобнымъ образомъ можно доказать, что уголъ ВСВ,
также составленный касательною и хордой, измѣряется поло-
виною дуги СпВ; разница въ доказательствѣ будетъ только
— 100 —
та, что этотъ уголъ надо разсматривать не какъ разность, а
какъ сумму прямого угла ВСЕ и остраго ЕОВ.
164. Теорема. Уголъ, составленный двумя касатель-
ными, измѣряется полуразно сгпъю дугъ, заключенныхъ между
точками касанія.
в	Пусть уголъ АВС составленъ двумя
касательными; требуется доказать, что
одъ измѣряется половиною разности
ДУГЪ и ВнЕ (7) и Е суть точки
У	касанія).—Проведя хордуВЁ, мы по-
/1	)\ лучимъ Л ВВЕ, относительно кото-
\	/ с раго уголъ СЕВ есть внѣшній; слѣд.:
^В = ^СЕВ — ^ВВЕ.
Чорі. 124 Но углы сер) и ВВЕ, какъ состав-
ленные касательною и хордою, измѣряются соотвѣтственно
половинами дугъ ЕтВ и ВпЕ\ поэтому уголъ В измѣряется
полуразностью этихъ дугъ.
165. Задача. На данной прямой АВ построитъ сег-
ментъ, вмѣщагощій данный уголъ а (черт. 125).
С
Черт. 125
Предположимъ, что задача рѣшена;
пусть сегментъ АСВ будетъ такой, кото-
рый вмѣщаетъ въ себѣ уголъ а. Центръ
О этого сегмента долженъ лежать на пер-
пендикулярѣ ВО, возстановленномъ изъ
средины прямой АВ. Съ другой стороны
онъ долженъ лежать и на перпендикуля-
рѣ АО, возстановленномъ къ касательной
АЕ изъ точки касанія А. Поэтому поло-
женіе центра опредѣлится, если мы съумѣ-
емъ построить касательную АЕ. Уголъ
ВАЕ, составленный касательною и хор-
дою, измѣряется половиною дуги АтВ\ вписанный уголъ АСВ'
также измѣряется половиною этой дуги; значитъ, / ВАЕ=
=^/_АСВ. Но послѣдній уголъ, по условію, долженъ рав-
няться а; слѣд., и /^ВАЕ—а, а потому положеніе каса-
тельной АЕ опредѣлено. Отсюда выводимъ слѣдующее по-
— 101 —
строеніе: при концѣ прямой АВ строимъ уголъ ВАЕ, рав-
ный углу а; къ срединѣ прямой ЛВ возстановляемъ пер-
пендикуляръ ВО и изъ точки А перпендикуляръ къ АЕ.
Пересѣченіе этихъ двухъ перпендикуляровъ принимаемъ за
центръ и радіусомъ О А описываемъ окружность. Сегментъ
АОВ будетъ искомый, потому что всякій вписанный въ немъ
уголъ равенъ углу ВАЕ, т.-е. углу а.
ГЛАВА VIII.
Вписанные и описанные многоугольники.
166. Опредѣленіе. Если вершины какого-нибудь много-
угольника АВСВЕ лежатъ на окружности, то говорятъ, что
зтотъ мн.-къ вписанъ въ окружность,
или что окружность описана около	—Л
него.	-Чч I
Если стороны какого-нибудь мпо-	у!	сГм
тоуголі.ника М1РР0 касаются окруж-	I /	\ |
пости, то говорятъ, что этотъ мн.-къ Д/	\ А
/ ѴА-	тп/І
описанъ около окружности, или что /	РУ
•окружность вписана, въ него.	/	|
161. Теоремы. 1°. Около вся- м „	'	®
г	Черт. 126
каю треугольника можно описать
окружность и притомъ только одну.
2°. Во всякій треугольникъ можно вписать окружность
и притомъ только одну.
Пусть АВС будетъ какой ни будь тр.-къ; требуется до-
казать: 1°, что около него можно описать окружность и
притомъ только одну и 2°, что въ него можно вписать окруж-
ность и притомъ только одну.
1°. Вершины А, В п С суть три точки, пс лежащія
на одпой прямой; а черезъ такія точки, какъ мы видѣли
(109), всегда можно провести окружность п притомъ только
Одну.
2°. Если возможна такая окружность, которая касалась
•бы всѣхъ сторонъ тр.-ка АВС, то ея центръ долженъ быть
— 102 —
В
Черт. 127
точкой, одинаково удаленной отъ этихъ сторонъ. Докажемъ,
что такая точка существуетъ. Геометрическое мѣсто точекъ,
равноотстоящихъ отъ сторонъ АВ и АС,
есть биссектрисса АМ угла А (63); гео-
метрическое мѣсто точекъ, равноотстоя-
щихъ отъ сторонъ ВА и ВС, есть бис-
сектрисса В№ угла В. Эти двѣ биссек-
трисой, находясь внутри замкнутаго про-
странства (треугольника), должны пере-
сѣчься внутри ого, въ нѣкоторой точкѣ
: О. Эта точка и будетъ равноудатенной
отъ сторонъ тр.-ка, такъ какъ она заразъ,
находится на обоихъ геометриі. мѣстахъ.
Итакъ, чтобы вписать кругъ въ тр.-къ, дѣлимъ какіе-нибудь,
два угла его, напр. А и В, пополамъ и точку пересѣченія
биссектриссъ беремъ за центръ. Радіусомъ будетъ служить одинъ
.изъ перпендикуляровъ ОР, 0<Э, ОВ, опущенныхъ изъ.
центра на стороны тр.-ка. Окружность каснется сторонъ въ.
точкахъ Р, <д, В, такъ какъ стороны въ этихъ точкахъ пер-
пендикулярны къ радіусамъ (123).
ности не можетъ быть, такъ какъ
Черт. 128
Другой вписанной окруж-
двѣ биссектриссы могутъ
пересѣчься только въ од-
ной точкѣ, а изъ одной
точки на прямую можно^
опустить только одинъ пер-
пендикуляръ.
І68. Слѣдствіе. Точ-
ка О, находясь на одина-
ковомъ разстояніи отъ сто-
ропъ^Си ВС(черт. 127),
должна лежать на биссек-
триссѣ угла С (61); слѣд.:
биссектриссы трехъ
уг ювъ треугольника схо-
дятся въ одной точкѣ.
169. Внѣвписанные-
НРУ ГИ. Такъ называются круги (черт. 128), которые касаются одной сто-
— 103 —
роны тр.-ка и продолженій двухъ другихъ сторонъ (они лежатъ внѣ тр.-ка,
вслѣдствіе чего и получили названіе внѣвписанныхъ). Такихъ круговъ для
всякаго треугольника можеть быть три. Чтобы построить ихъ, проводятъ
бпссектриссы внѣшнихъ угловъ тр.-ка ЛВС и точки ихъ пересѣченій бе-
рутъ за центры. Такъ, цеатромъ окружности, вписанной въ уголъ А, 6у-
детъ точка О, т.-е. пересѣченіе биссектрпссъ ВО и СО внѣшнихъ угловъ,
де смежныхъ съ А; радіусомъ этой окружности будетъ перпендикуляръ
ОдІ, опущенный изъ О па как)Ю-ллбо сторону треугольника.
1?О. Теоремы. 1°. Во всякомъ вписанномъ четыре-
угольникѣ сумма противоположныхъ уіловъ равна двумъ
прямымъ.
2°. Обратно: около четыреугольника можно описать ок-
ружность. если въ немъ сумма противоположныхъ угловъ
равна двумъ прямымъ.
1°. Пусть АВСВ будетъ вписанный	в
четыреугольникъ; требуется доказать, что
1_В-\-/_В~Ъд, и / Л + /	\ \
Углы В и В, какъ вписанные, измѣря-	\)
ются: первый — половиною дуги АВС, \\.
второй — половиною дуги АВС\ слѣд.,
сумма В + В измѣряется полусуммою дугъ Чс^ 129
АВС и АВС, т.-е половиною окруж- с₽т’
ностп; значитъ, ВД-В — 'ІсІ. Подобно этомѵ убѣдимся, что
А-ѴС=Ы.
2". Пусть АВСВ (черт. 129) будетъ такой четыреуголь-
никъ, у котораго В-\- В~2сІ. Требуется доказать, что около
такого четыреугольника можно описать окружность.—Черезъ
какія-нибудь три его вершины, папр. А, В и С, проведемъ
окружность (что всегда можно сдѣлать). Тогда четвертая
вершина В непремѣнно окажется на этой окружности, по-
тому что въ противномъ случаѣ уголъ В лежалъ бы своею
вершиною пли внутри круга, или внѣ его, и тогда этотъ
уголъ не измѣрялся бы половиною дуги АВС (160 и 161);
поэтому сумма В-}-В не измѣрялась бы полусуммою дугъ
АВС и АВС, т.-е. сумма В В не равнялась бы 2й. что
лротиворѣчитъ условію.
— 104 —
131. Слѣдствія. 1°. Изъ всѣхъ параллелограммовъ мож-
но описать окружность только около прямоугольника.
2°. Около трапеціи можно описать окружность толы.о
тогда, когда она равнобочная,
133. Теоремы. 1°. Во всякомъ описанномъ четыре-
угольникѣ суммы противоположныхъ сторонъ равны.
2°. Обратно: въ четы} еуго.іьпккъ можно вписать окружность, если «ь
немъ равны, суммы противоположныхъ сторонъ.
1°. Пусть АВСВ будетъ описан-
ный четыреугольникъ, т.-е. стороны
его касаются окружности; требуется
= доказать, что АВСВ ~ ВС-\- АВ.
р Обозначимъ точки касанія черезъ М,
И, Р и Такъ какъ двѣ касатель-
ныя, проведенныя изъ одной точки къ
окружности, равны (127), то АМ=А@,
Черт. 130 ВИ~ВИ, СЯ=СР и вр = вд.
Слѣд.
АМ-I- мв + СР + РВ = А 4- $В -ь ВИ+ ХС
т.-е. АВ+СВ — АВ + ВО.
2°. Пусть АВС?) будетъ такой четыреугольникъ (черт 131), у котораго:
Требуется доказать, что въ него можно вписать окружность. — Проведемъ
ІЕ( пыхъ изъ О на стороны угловъ В и С, то
окружность каснется сторопт>^.^9.БО, и СВ.
Докажемъ, что она каснется и четвертой
стороны АВ. Для этого предположимъ, что касательная, проведенная къ
нашей окружности изъ точки А, будетъ не АВ, а какая-пибудь ипая
прямая, напр. АВ, Тогда получится описанный четыреугольникъ АВСЕ,
въ которомъ, по доказанному выше, будемъ имѣть:
ВС + АЕ= АВ + СЕ
— 105 —
Но по условію:
ВС + АРг=ЛВ + СР
Вычтя почленно первое равенство изъ второго, найдемъ:
ЛР — АЕ = СР — СЕ=РЕ
-т.-е. разность двухъ сторонъ ДЛРЕ равна третьей сторонѣ РЕ, что
невозможно (50); значитъ, нельзя допустить, чтобы касательною къ на-
шей окружности была прямая АЕ, лежащая ближе къ центру О, чѣмъ ЛР.
Такъ же можно доказать, что касательною не можетъ быть никакая пря-
мая ЛЕѴ лежащая дальше отъ центра, чѣмъ ЛР; значитъ, ЛР должна
касаться окружности, т.-ѳ. въ четыреугольникъ АВСР можно вписать
окружность.
133. Слѣдствіе. Изъ всѣхъ гшраллелоіраммовъ окружность можно
вписать только въ ромбъ и квадратъ.
ГЛАВА IX.
Четыре замѣчательныя точки въ треугольникѣ.
І34. Мы видѣли, что во всякомъ треугольникѣ:
іо, перпендикуляры къ срединамъ сторонъ сходятся въ одной точкѣ,
которая есть центръ описаннаго круга (110);
2°, бпссектрпссы угловъ сходятся въ одной точкѣ, которая есть
центръ вписаннаго круга (168).
Слѣдующія двѣ теоремы указываютъ еще двѣ замѣчательныя точки
треугольника: 3°, пересѣченіе высотъ и 4°, пересѣченіе медіанъ.
11«і. Теорема. Три высоты треугольника пересѣкаются въ одной точкѣ.
Черезъ каждую вершину тр.-ка ЛВС (черт. 132) проведемъ прямую,
параллельную противоположной сторонѣ его. Тогда получимъ вспомога-
тельный Д АІВ1С1, къ сторонамъ ко-
тораго высоты даннаго тр.-ка пер-
пендикулярны. Такъ какъ С1Б =
— АС = БЛг (какъ противоположныя
стороны параллелограмма), то точка
В есть средина стороны По-
добно этому убѣдимся, что С есть
средина и А — средина Б^.
Такимъ образомъ, высоты ЛР, ВЕ
и СЕ служатъ перпендикулярами къ
срединамъ сторонъ тр.-ка уЦБ,^; а
такіе перпендикуляры, какъ извѣстно,
пересѣкаются въ одной точкѣ.
Замѣчаніе. Точка, въ которой пересѣкаются высоты треугольника,
наз. ортоцентромъ.
— 106 —
13в. Теорема. Тримедіапы треуіолъникапересѣкаются въ одпойточкѣ;
эта точка отсѣкаетъ отъ каждой медіаны третью частъ, считая отъ соот-
вѣтствующей стороны.
Возьмемъ въ тр.-кѣ АВС какія-нибудь двѣ медіаны, нппр. АЕкВВ,
пересѣкающіяся въ точкѣ О, и докакемъ,.
что
ОВ - ^ВВ и ОЕ - і/3АЕ.
Для этого, раздѣливъ О А и ОВ пополамъ^
въ точкахъ Г и О, проведемъ ЕС я ВЕ.
Такъ какъ прямая ЕС соединяетъ средины
двухъ сторонъ тр.-ка А ВО, то (102) ЕС || А В
и ЕС^'/^АВ. Прямая .О.Е также соеди-
няетъ средины двухъ сторонъ тр.-ка АВС;
поэтому: ІЛЕЦЛ.В п ВЕ:=А/<,АВ. Отсюда
выводимъ, чтоЛ^ЦТ^б? и ВЁ=ЕС. Срав-
нивая теперь тр.-ки ОВЕ и ОЕО, замѣ-
чаемъ, что у нихъ ВЕ — ЕС и углы, прилежащіе къ этимъ сторонамъ,
равны (какъ углы накрестъ лежащіе при параллельныхъ прямыхъ), слѣд.,.
эти тр.-ки равны. Изъ равенства ихъ выводимъ: ОВ — ОС — ВС и ОЕ —
= ОЕ—АЕ; поэтому ОВ — ^ВВ и ОЕ= Ч3АЕ.
Такъ какъ это доказательство можетъ быть повторено о любой парѣ
медіанъ, то заключаемъ, что всѣ медіаны треугольника сходятся вь одной
точкѣ, которая отъ каждой изъ нихъ отсѣкаетъ третью часть, считая
отъ соотвѣтствующей стороны.
Замѣчаніе, Изъ физики извѣстно, чго пересѣченіе медіанъ тр.-ка
есть его центръ тяжести.
УПРАЖНЕНІЯ.
Доказать теоремы:
148.	Если двѣ окружности касаются, то всякая сѣкущая, проведен-
ная черезъ точку касанія, отсѣкаетъ отъ окружностей двѣ противо-
лежащія дуги одинаковаго числа градусовъ.
149.	Еслп черезъ точку касанія двухъ окружностей проведемъ двѣ
сѣкущія п концы ихъ соединимъ хордами, то эти хорды параллельны.
150.	Если черезъ точку касанія двухъ окружностей проведемъ какую-
либо сѣкущую, то касательныя, проведенныя въ копцахъ этой сѣкущей,
параллельны.
151.	Если основанія высотъ тр.-ка соединимъ прямыми, то получимъ
новый тр -къ, для котораго высоты перваго тр.-ка служатъ бнссект-
риссамп.
152.	Если около тр.-ка опишемъ окружностыі нзъпропзвольпойточки
ея опустимъ перпендикуляры на стороны тр.-ка, то ихъ основапія лежатъ
на ОДНОЙ прямой (прямая Симпсона').
— 107 —
Задачи на построеніе.
153.	Па данной неопредѣленной прямой найти точку, изъ которой-
другая данная конечная прямая была бы видна подъ даннымъ угломъ.
154.	Построимъ Л по основанію, углу при вершинѣ и высотѣ.
155.	Къ дугѣ даннаго сектора провести касательную, чтобы часть ея,,
заключенная между продолженными радіусами (ограничивающими секторъ),
равнялась данной длинѣ (свести эту задачу па предыдущую).
156.	Построить Л по основанію, углу при вершинъ и медіанѣ, про-
веденной къ основанію.
157.	Даны ио величинѣ и положенію двѣ. конечныя прямыя а и Ъ.
Найтп такую точку, изъ которой прямая а была бы видна подъ даннымъ,
угломъ а, а прямая Ъ подъ даннымъ угломъ /3.
158.	Въ тр -кѣ найти точку, изъ которой его стороны были бы видны,
подъ равными углами {указаній: обратить вниманіе на то, что каждый изъ.
этихъ угловъ долженъ равняться 4/3й).
159.	Построить Л по углу при вершинѣ, высотѣ и медіанѣ, прове-
денной къ основанію {указаніе:продолживъ медіану па равное разстояніе
и соединивъ полученную точку съ концами основанія, разсмотрѣть обра-
зовавшійся параллелограммъ).
160.	Построить Д, въ которомъ даны: основаніе, прилежащій къ нему
уголъ и уголъ, составленный медіаною, проведенною изъ вершины даннаго
угла, со стороною, къ которой эта медіана проведена.
161.	Построить параллелограммъ по двумъ его діагоналямъ и одному
углу.
162.	Построить А по основанію, углу при вершинѣ и суммѣ или раз-
ности двухъ другихъ сторонъ.
163.	Построить четыреугольникъ по двумъ діагоналямъ, двумъ сосѣд-
нимъ сторонамъ и углу, образованному остальными двумя сторонами.
164.	Даны три точки А, Б и С. Провести черезъ Л такую прямую,,
чтобы разстояніе между перпендикулярами, опущенными на эту ирянукь
изъ точекъ В и С, равнялось данной длинѣ.
165.	Въ данный кругъ вписать А, У котораго два угла даны.
166.	Около даннаго круга описать А, У котораго два угла даны.
167.	Построить А по радіусу оппсапнаго круга, углу при вершинѣ
и высотѣ.
168.	Вписать въ данный кругъ А, У котораго изрѣстны: сумма двухъ,
сторонъ и уголъ, противолежащій одной изъ этихъ сторонъ.
169.	Вписать въ данный кругъ четыреугольникъ, котораго сторона и
Два угла, пе прилежащіе къ этой сторонѣ, даны.
170.	Въ даппый ромбъ вписать кругъ.
171.	Въ равносторонній Д вписать три круга, попарно касающія
Другъ друга и изъ которыхъ каждый касается двухъ сторонъ тр.-ка.
172.	Построить четыреугольникъ, который можно было бы вписать,
въ окружность, по тремъ его сторонамъ и одной діагонали
— 108 —
173.	Построить ромбъ по даннымъ: сторонѣ и радіусу вписаннаго
круга.
174.	Около даннаго круга описать равнобедренный прямоугольный/\.
175.	Построить рав нобсдренный Л по основанію и радіусу вписан-
наго круга.
176.	Построить Л по основанію и двумъ медіанамъ, исходящимъ изъ
концовъ основанія.
177.	То же — по тремъ медіанамъ.
178.	Дана окружность и на ней три точки А, В и С. Вписать въ эту
окружность такой Д, чтобы его бпссектриссы, при продолженіи, встрѣ-
чали окружность въ точкахъ А, В и С.
179.	Та же задача, съ замѣною бпссектрпссъ тр.-ка его высотами.
180.	Дана окружность и па пей три точки И, X п Р, въ которыхъ
пересѣкаются съ окружностью <при продолженіи) высота, биссектрисса
и медіана, исходящія изъ одной вершины вписаннаго тр.-ка. Построить
этотъ Д.
181.	На окружности даны двѣ точки А и 7?. Изъ этихъ точекъ про-
вести двѣ параллельныя хорды, которыхъ сумма дана.
Задачи на вычисленіе.
182.	Вычислить вписанный уголъ, опирающійся па дугу, равную Ѵіг
части овружпостп.
183.	Кругъ раздѣленъ на два сегмента хордою, дѣлящею окружность
па части въ отношеніи 5: 7. Вычислить углы, которые вмѣщаются этими
сегментами.
184.	Двѣ хорды пересѣкаются подъ угломъ въ 36е 15' 32". Вычислить
въ градусахъ, минутахъ и секундахъ двѣ дуги, заключенныя между сто-
ронами этого угла и ихъ продолженіями, если одна изъ этихъ дугъ отно-
сится къ другой, какъ 3 : 2.
185.	Уголъ, составленный двумя касательными, проведенными изъ
одной точки къ окружности, равенъ 25° 15'. Вычислить дуги, заключен-
ныя между точками касанія.
186.	Вычислить уголъ, составленный касательною и хордою, если
хорда дѣлитъ окружность па двѣ части, относящіяся какъ 3:7.
187.	Двѣ окружности одинаковаго радіуса пересѣкаются подъ угломъ
въ 2/а<7; опредѣлить въ градусахъ меньшую изъ дугъ, заключающихся
между точками пересѣченія.
Примѣчаніе. Угломъ двухъ пересѣкающихся дугъ наз. уголъ, состав-
ленный двумя касательными, проведенными къ этимъ дугамъ изъ точки
пересѣченія.
188.	Изъ одного конца діаметра проведена касательная, а изъ другого
сѣкущая, которая съ касательною составляетъ уголъ въ 20° 30'. Какъ
велика меньшая изъ дугъ, заключенныхъ между касательною и сѣкущею.
— 109 —
КНИГА III.
ПОДОБНЫЯ ФИГУРЫ.
ГЛАВА I.
Подобіе треугольниковъ и многоугольниковъ.
13Э. Опредѣленія. Два многоугольника съ одинаковымъ
числомъ сторонъ называются подобными, если углы одного
равны соотвѣтственно угламъ другого и сходственныя стороны
ихъ пропорціональны.
Сходственными называются тѣ стороны, которыя приле-
жатъ къ равнымъ угламъ. Выраженіе: „сходственныя стороны
пропорціапальньГ означаетъ, что отношеніе какихъ-нибудь двухъ
сходственныхъ сторонъ равно отношенію всякихъ другихъ сход-
ственныхъ сторонъ.
Такимъ образомъ, мно-
гоугольники Л В СВЕ и
2?! Вг Ех считаются
подобными, если они удо-
влетворяютъ слѣдующимъ
условіямъ:
Г’, А=АѴ В=ВХ,
0=0,, В~В^ Е=Е.
Б
АВ _ ВС   СВ_  	__ ЕА_
Щ В{ ВРі С\р ВІЕ1 ЁХА,
Этимъ условіямъ удовлетворяютъ, напр.. всякіе два квад-
рата или всякіе два равносторонніе треугольника.
Замѣтимъ, что могутъ быть два многоугольника, у кото-
рыхъ углы соотвѣтственно равны, но стороны не пропорціа-
йальны, и наоборотъ; напр., у квадрата и прямоугольника
Углы соотвѣтственно равны, а стороны не пропорціональны;
У квадрата и ромба, наоборотъ, стороны пропорціональны, а
Углы не равны. Въ этомъ отношеніи треугольники рѣзко вы-
— 110 —
.дѣлаются изъ многоугольниковъ: у нихъ, какъ увидимъ ниже,
равенство угловъ влечетъ за собою пропорціональность сто-
ронъ и обратно.
Изъ опредѣленія подобія слѣдуетъ, что если изъ двухъ
равныхъ многоугольниковъ одинъ подобенъ третьему, то и дру-
гой подобенъ ему.
138.	Лемма.*) Прямая, проведенная внутри треуголь-
ника параллельно какой-нибудь его сторонѣ, отсѣкаегпъ отъ
него другой гпреуголъиикъ, подобный первому.
Пусть въ тр.-кѣ АВС проведена прямая ВЕ\\АС; тре-
буется доказать, что А ВВЕ подобенъ А АВС.— Углы этихъ
тр.-ковъ соотвѣтственно равны между собою (В общій уголъ,
В = А и Е=С, какъ углы соотвѣтственные при параллель-
ныхъ прямыхъ). Остается доказать,
что сходственныя стороны пропорціо-
нальны. Разсмотримъ отдѣльно два
случая.
1°, стороны АВ и ВВ имѣюгпъ
общую мѣру. Раздѣлимъ АВ на части,
равныя этой общей мѣрѣ. Тогда ВВ
раздѣлится на цгьлое число такихъ
частей. Пусть этихъ частей содер-
жится гп въ ВВ и п въ АВ. Про-
ведемъ изъ точекъ дѣленія рядъ пря-
мыхъ, параллельныхъ АС, и другой рядъ прямыхъ, парал-
лельныхъ ВС. Тогда ВЕ и ВС раздѣлятся на равныя частя
(100), которыхъ будетъ гп въ ВЕ и п въ ВС, Точно также
ВЕ раздѣлится на гп равныхъ частей, а АС на п равныхъ
частей, причемъ части ВЕ равны частямъ АС (какъ противо-
положныя стороны параллелограммовъ). Теперь очевидно, что
БВ___гп	ВЕ___пі	ВЕ____т
ВА	п’’	НС	п '>	АС'	п
~ х	ВВ НЕ ВЕ
ВА~ ВС~ АС
Такимъ образомъ у тр.-ковъ ВВЕ и АВС углы соотвѣтственно
*) Леммою паз. вспомогательная теорема, излагаемая то ько для того, чтобьі
'при ея помощи доказать послѣдующія теоремы.
с
Черт. 135
Черт, 136
—111 —
равны и сходственныя стороны пропорціональны; значитъ, оии
подобны.
2°, стороны АВ и ВВ не гімѣготъ общей мѣры. Най-
демъ приближенное значеніе каждаго
изъ отношеній:
1)В ВЕ І)Е
АВ’ ВС И АС
съ произвольною точностью до ДД. Для
этого раздѣлимъ АВ на п равныхъ
частей и черезъ точки дѣленія про-
ведемъ рядъ прямыхъ, параллельныхъ
АС, и другой рядъ прямыхъ, парал-
лельныхъ В С. Тогда каждая изъ сто-
ронъ ВС и АС раздѣлится также на п .равныхъ частей (100).
Предположимъ теперь, что Т/п доля АВ содержится въ ВВ
болѣе т разъ, но менѣе ш4"1 разъ; тогда, какъ видно изъ
чертежа, доля ВС содержится въ ВЕ также болѣе т, но
менѣе гп-\- 1 разъ, и г/п доля АС содержится въ ВЕ болѣе т,
но менѣе т-Ь1 разъ. Слѣд.:
„ ВВ т.	, ВЕ т.	ВЕ т
прибл. отн. — , прнбл. отн. 2^=^, прпбл. отн. ХС~1І
Такимъ образомъ, приближенныя отношенія, вычисленныя съ
произвольною, но одинаковою точностью, равны другъ другу;
а въ этомъ п состоитъ равенство несоизмѣримыхъ отношеній.
13©. Теорема. Два треугольника подобны, если:
1°, два угла одного соотвѣтственно равны двумъ угламъ
другого;
или 2°, двѣ стороны одного пропорціональны двумъ сто-
ронамъ другого, и углы, лежащіе между этими сторонами,
равны;
или 3°, три стороны одного пропорціаналъны тремъ сто-
ронамъ другого.
1°. Пусть АВС и А1В1С} будутъ два тр.-ка, у которыхъ:
А = А1І В = ВІ и, слѣд.; (7= Ц (черт. 137).
Требуется доказать, что такіе тр.-ки подобны. — Отложимъ
на АВ часть ВВ, равную А^, и проведемъ ВЕ || АС.
— 112 —
Тогда получимъ вспомогательный тр.-къ ВВЕ, который
Черт. 137
согласно предыдущей
леммѣ,подобенъ тр.-ку
АВС. Съ другой сто-
роны Л ВВЕ = А
Аг С1, потому что
у нихъ: ВВ—АхВг
(по построенію), В =
— Ву (по условію) и
В — Ах (потому что
В = А и А — Аг).
Но если изъ двухъ равныхъ тр.-ковъ одинъ подобенъ третьему,
то и другой ему подобенъ; слѣд., А подобенъ В.АВС.
2°. Пусть въ тр.-кахъ АВСр А1ВІ 01 дано (черт. 138):
7?-р	— в2_
В Вг К а1В1~В1С1
и
тр.-ки подобны. — Отложимъ
снова часть ВВ, равную А1 В}, и
проведемъВЕ || АС.Тогда полу-
чимъ вспомогательный &.ВВЕ,
подобный Л АВС. Докажемъ,
что онъ равенъ А А1 Вг С1. Изъ
подобія тр.-ковъ ВВЕ и АВС
слѣдуетъ (черт. 138):
ВВ — ВЕ ВЕ
Сравнивая этотъ рядъ равныхъ
отношеній съ даннымъ рядомъ (1), замѣчаемъ, что первыя от-
ношенія обоихъ рядовъ одинаковы (ВВ~- А^В} но построе-
нію); слѣдовательно, остальныя отношенія этихъ рядовъ также
равны, т.-е.
вс вс	п 7?/І
0ТКУда В1С, = -ВЛ
Теперь видимъ, что тр.-ки ВВЕ и А1В1С\ имѣютъ но рав-
ному углу (В = В1), заключепному между равными сторо-
нами; значитъ, эти тр.-ки равны. Но А ВВЕ подобенъ
и ЛА^ВІСІ подобенъ А АВС.
— 113 —
3°, Пусть въ тр.-кахъ АВС и А1В1С1 (черт. 139) дано:
АВ _ ВС _ АС	т
АХВХ~~ ВХСХ ~АХСХ	Ш
Требуется доказать, что такіе тр.-ки подобны. — Сдѣлавъ по-
строеніе такое же,
какъ и прежде, дока-	В
жемъ, что Л ВВЕ—	/\
— /\А1ВІСГ Изъ	/ \	в
подобія тр.-ковъБВЕ	/	\
и АВС слѣдуетъ:	/ \
ля__зс_лс |9-і	/	\	/	\
вв~вв-^вв аА-------------------------\с АХ---------1ц
Сравнивая этотъ рядъ	Черт 139
съ даннымъ рядомъ
[1], замѣчаемъ, что первыя отношенія у нихъ равны; слѣд.,
и остальныя отношенія равны, т.-е.
откуда: В.С^ВЕ
«Ор 1 ПАѢ	*	11
А С	(У	а _____ -у-ч 777
и — откуда: А1С^ = ])Е
•Теперь видимъ, что тр.-ки ВВЕ и АІВ1С1 имѣютъ по три
соотвѣтственно равныя стороны; значитъ, они равны. Но одинъ
изъ нихъ, именно ВВЕ, подобенъ &АВС; слѣд., и другой,
т.-е. А1В1С1 подобенъ ЛВС,
180. Замѣчаніе. Полезно обратить вниманіе на то, что
пріемъ доказательства, употребленный нами въ трехъ случа-
яхъ предыдущей теоремы, одинъ и тотъ же; а именно: от-
ложивъ на сторонѣ большаго треугольника часть, равную
сходственной сторонѣ меньшаго, и проведя прямую, парал-
лельную другой сторонѣ, мы образуемъ вспомогательный тр.-къ.
подобный большему данному. Послѣ этого, беря во вниманіе
условія разсматриваемаго случая и свойства подобныхъ тр.-ковъ,
мы доказываемъ равенство вспомогательнаго тр.-ка меньшему
данному и, наконецъ, заключаемъ о подобіи данныхъ тр.-ковъ.
181. Слѣдствіе. Въ подобныхъ треугольникахъ сход-
ственныя стороны пропорггганальны сходственнымъ высо-
А. П. КИСЕЛЕВЪ.
8
— 114 —
тамъ, т.-е. тѣмъ,
стороны.
Черт. 140
которыя опущены на сходственныя
Дѣйствительно, если
тр.-ки АВС н
подобны, то прямоугольные
тр.-ки АВВ и
также подобны (А— Ах и
В — Вх); поэтому
ВП___АВ _ ВС______АС
ВХВХ — АХВ\ ~~ ВХСХ~ АХСХ
Подобно этому можно доказать, что въ подобныхъ тр.-кахъ
сходственныя стороны пропорціанальны сходственнымъ ме-
діанамъ, сходственнымъ биссекпгриссамъ, радіусамъ круговъ
вписанныхъ и радіусамъ круговъ описанныхъ,.
<88. Теорема. Если стороны одного треугольника со-
отвѣтственно параллельны или перпендикулярны сторонамъ
другого треугбльнгіка, то такіе треугольники подобны.
Такъ какъ на чертежѣ затруднительно изобразить всевоз-
можные случаи расположенія указанныхъ въ теоремѣ треуголь-
никовъ, то мы будемъ вести разсужденіе независимо отъ
чертежа.
Пусть стороны угловъ А,В и С одного треугольника со-
отвѣтственно параллельны или перпендикулярны сторонамъ
угловъ А{, В1, Сх другого треугольника. Тогда углы А и
Л1 или равны другъ другу, или составляютъ въ суммѣ два
прямыхъ (81 и 82); то же самое можно сказать объ углахъ
В и В,, С и Сѵ Чтобы доказать подобіе данныхъ тр.-ковъ,
достаточно убѣдиться, что какіе-нибудь два угла одного изъ.
нрхъ равны соотвѣтственно двумъ угламъ другого. Предполо-
жимъ, что этого нѣтъ. Тогда могутъ представиться два
случая:
1°, У гпреугольнгіковъ нѣтъ вовсе попарно равныхъ, угловъ.
Тогда:
А~\~ А ^2(1; В -\-В<1=2(1; С~}~С1~2сІ
и, слѣд., сумма угловъ обоихъ треугольниковъ равна
Такъ какъ это невозможно, то этотъ случай исключается.
— 115 —
2°, У треугольниковъ только одна пара равныхъ угловъ;
напр., пусть А = Аа. Тогда
В + В=М; С+С^Ы
и, слѣд., сумма угловъ обоихъ тр.-ковъ больше <к?. Такъ
какъ это невозможно, то и этотъ случай исключается.
Остается одно возможное допущеніе, что тр.-ки имѣютъ
двѣ пары равныхъ угловъ; но тогда они подобны.
183. Теорема. Прямоугольные треугольники подобны,
еслгь гипотенуза и катетъ одного ггропорціанальны гипоте-
нузѣ и катету другого.
Пусть АВС и Л1В1О1 два тр.-ка (черт. 141), у которыхъ
углы В и Ві прямые и
А1І   АС	г 11
Требуется доказать, что такіе тр.-ки подобны.—Для доказа-
тельства употребимъ тотъ же пріемъ, которымъ мы пользо-
вались выше (180). Отложимъ ВБ — АуВ' и проведемъ
Черт. 141
ВЕ\\АС. Тогда получимъ вспомогательный А ВВЕ, подоб-
ный &АВС (178). Докажемъ, что онъ равенъ ЛА^В/^.
Изъ подобія тр.-ковъ АВС и БВЕ слѣдуетъ:
ѴЕ
[2]
Сравнивая эту пропорцію съ данной [1], находимъ, что пер-
выя отношенія ихъ одинаковы; слѣд., равны и вторыя отно-
шенія, т.-е.
°™Уда: і'Е=А6'і
Теперь видимъ, что тр.-ки ВВЕ и А1В1С1 имѣютъ по рав-
ной гипотенузѣ и равному катету; слѣд., они равны; а такъ.
—116 —
какъ одинъ изъ нихъ подобенъ &АВС. то и другой ему
подобенъ.
1 84. Задача. На данной сторонѣ построитъ трсуіолъ-
нггкъ, подобный данному треугольнику.
При концахъ данной стороны строимъ углы, соотвѣтственно
равные угламъ даннаго тр.-ка и одинаково съ ними располо-
женные. Полученный тр.-къ будетъ подобенъ даппому (179,1”).
185. Теорема. Два многоугольника подобны, если они
состоятъ изъ одинаковаго числа подобныя?, гг одинаково рас-
положенныхъ треугольниковъ.
Пусть мн.-ки АВСВЕ и АІВ1С1ВІЕІ составлены изъ
одинаковаго числа попарно
5	подобныхъ тр.-ковъ: А А/
/	С, подобенъ А 21^, Л И по-
/ /	\о	добенъ и т. д.; пусть
в\м/ X /х7	КР°М'Ь того эти тр.-ки оди-
\ /	/	’\м/ ц1 наково расположены; тре-
Р / Ѵ/р / буется доказать, что такіе
А	Е А, * Е, многоугольники подобны,
Черт. 142	т.-е. что У нихъ: Г, равны
попарно углы и 2е, сход-
ственныя стороны пропорціанальпы (177).
1°. Равенство угловъ мн.-ковъ слѣдуетъ изъ равенства
угловъ тр.-ковъ; такъ, В = В^ и Е=ЕХ, какъ равные углы
подобныхъ тр.-ковъ (М и М±, Р и Рг), А — А^ С=С},
В = І)І, какъ суммы угловъ, соотвѣтственно равныхъ другъ
другу.
2°. Изъ подобія тр.-ковъ слѣдуетъ:
Изъ подобія ІИ и ЛІ,	Изъ подобія Р и Р,
_ ВС _ СЛ1 _ СП _ 112) _ ЕВ __ А^
АХВ1~~ВХСІ'— СХАХ ~~ СХВХ ~ ЛіРі ~ Ех — АХЕ\
Изъ подобія Аг и А7!
Возьмемъ изъ этого ряда равныхъ отношеній только тѣ,
въ которыя входятъ стороны данныхъ многоугольниковъ: тогда
получимъ:
АВ _ ВС __ СВ _______ ВЪ _ трр
Ах ВХ ~ Вх С\ — Сх Т)х — Вх'Ъх ~ Ех А і
— 117 —
Такимъ образомъ, данные многоугольники, имѣя соотвѣтственно
равные углы и пропорціанальпыя стороны, подобны.
І8<і. Обратная теорема. Подобные мноюуюлъники можно
разложитъ на одинаковое кисло подобныхъ и одинаково рас-
положенныхъ треугольниковъ.
Пусть мн.-ки АВСВЕ и А^В^С^В^ подобны. Ихъ
можно разложить па одинаковое число подобныхъ тр.-ковъ
различными способами.
Возьмемъ внутри мн.
АВСВЕ произвольную
точку О и соединимъ
ее со всѣми вершинами.
Тогда мн. АВСВЕ ра-
зобьется на столько тре-
угольниковъ. сколько въ
ремъ сторонъ. Возьмемъ
Укажемъ самый общій способъ,—
одинъ изъ нихъ, напр.	Черг> 143
АОЕ, и на сходствен-
ной сторонѣ АІЕІ другого многоугольника построимъ Л Ах О1Е11
подобный А АОЕ. Вершину его О1 соединимъ съ прочими
вершинами мн. А1В1С1В1Е1. Тогда и этотъ мног.-къ ра-
зобьется на то же число тр.-ковъ. Докажемъ, что тр.-ки пер-
ваго многоугольника соотвѣтственно подобны тр.-камъ второго
многоугольника. Л АОЕ подобенъ ѢА1О1ЕІ по построенію.
Чтобы доказать подобіе сосѣднихъ тр.-ковъ АВО и АІВІО1,
примемъ во вниманіе, что изъ подобія мн.-ковъ, между про-
чимъ слѣдуетъ:
<__ / Ллі _____ Л Л	г 11
А—4 “	01
а изъ подобія тр.-ковъ АОЕ и А1ОІЕІ выводимъ:
/_ОАЕ=АОІАІЕ1 и =	И
Изъ равенствъ [1] и [2] слѣдуетъ:
ЛВАО = /_В1АІО1 п |т;'-=Д
Теперь видимъ, что тр.-ки АВО и А1ВІО1 имѣютъ по рав-
— 118 —
ному углу, заключенному между пронорціанальнымн сторонами:
значитъ, они подобны.
Совершенно такъ же докажемъ подобіе слѣдующихъ тре-
угольниковъ ВСО и ВХСХО^ затѣмъ СОБ и С1О]Л1 и т. д.
18 3. Сходственныя точки и линіи. Если на плоскостяхъ подоб-
ныхъ многоугольниковъ возьмемъ такія точки О и Ох (черт. 148), что
тр.-ки ОЛВ и ОіА'Ві, полученные отъ соединенія этихъ точекъ съ кон-
цами какихъ-нибудь двухъ сходственныхъ сторонъ, подобны, то такія
точки наз. сходственными. Изъ предыдущей теоремы слѣдуетъ, что если
точки О и О1 сходственныя, то воь треугольники, получаемые соедине-
ніемъ этихъ точекъ съ концами какихъ угодно сходственныхъ сторонъ,
•будутъ соотвѣтственно подобны.
Сходственныя точки могутъ быть взяты и па сторонахъ многоуголъ^
никовъ, и въ ихъ сходственныхъ вершинахъ, и даже внѣ многоуголь-
никовъ.
Если точки О и Р и Р, (черт. 144) попарно сходственныя, то
прямыя ОР п ОѴРХ наз. сходственными линіями. Эти линіи обладаютъ
•слѣдующимъ свойствомъ.
188.	Теорема. Сходст-
венныя линіи двухъ подобныхъ
многоугольниковъ пропориганаль-
ны ихъ сходственнымъ сторонамъ.
Соединимъ сходственныя
точки съ концами двухъкакпхъ-
нибудь сходств. сторонъ, напр.
ЛВ и Изъ подобія тре-
угольниковъ АОВ и Л1б>1В1
слѣдуетъ:
ОЛ____АВ	ГII
а изъ подобія тр.-ковъ РАВ и РХАХВХ выводимъ:
/РЛВ-/ДАЛ и	[2]
Изъ сравненія равенствъ [1] и [2] находимъ-.
Черт. 144
/ОАВ=/О1ЛіВл и
/_ ОЛР=>^ О1ЛХР1 ц
ОЛ _ РА
ОХЛХ ~ РіЛІ
Теперь видимъ, что тр.-ки ОАР и ОХЛ1РІ имѣютъ по равному углу,
заключепному между иропорціаяальпыми сторонами; слѣд.. они поюбны
я потому
ОР ___ ОА __ ЛВ
ОѴРХ~ О1А1~ А^Ві
— 119 —
189.	Теорема. Периметры подобныхъ многоугольниковъ
огпносягпся, какъ сходственныя стороны.
Пусть мн.-ки АВСВЕ и АІВІС1ВІЕ1 (черт. 143) по-,
добны: тогда, по опредѣленію:
АВ __ ВС __ СЛ _ ЛЕ _ ЕА
А1В1 ~~ В/’і ~ (\П1 л^і Е^
Изъ алгебры извѣстно, что если имѣемъ рядъ равныхъ отно-
шеній, то сумма предыдущихъ относится къ суммѣ послѣдую-
щихъ, какъ какой-нибудь изъ предыдущихъ къ своему послѣ-
дующему: поэтому:
АВ 4- ВС 4- СЛ -^ЛЕА- ЕА _ АВ _ ВС
а1в1 4- А А +'^7?! 4- А А + АА ~ А А ~ А А...
Примѣръ. Если сторона одного многоугольника болѣе
сходственной стороны другого многоугольника, подобнаго ему,
въ 2 раза, 3 раза, 4 раза и т. д., то и периметръ перваго
многоугольника болѣе периметра второго въ 2 раза, 3 раза,
4 раза и т. д.
190.	Задача. На данной сторонѣ АІЕ1, (черт. 142)
построить многоугольникъ, ггодобный данному многоугольнику
АВСВЕ.
Разбивъ данный многоугольникъ на тр.-ки (М, Е, Р),
•строятъ на данной сторонѣ Л1^І тр.-къ Р]} подобный тр.-ку
Р, затѣмъ на сторонѣ АуВ} тр.-къ , подобный тр.-ку
Е, и т. д. Полученный такимъ образомъ мног.-къ
•будетъ подобенъ данному (185).
ГЛАВА II.
Нѣкоторыя теоремы о пропорціональныхъ линіяхъ.
191.	Теорема. Деѣ прямыя, пересѣкаемыя рядомъ па-
раллельныхъ прямыхъ, разсѣкаются имгг на гіроггорціаналь-
ныя части.
Пусть АВ и Л1 Ву (черт. 145) будутъ двѣ какія-нибудь прямыя,
разсѣкаемыя рядомъ параллельныхъ прямыхъ СО,, ВВ^ ЕЕІ,
— 120 —
ЕВг и т. д.; требуется доказать, что отношеніе двухъ какихъ-
нибудь отрѣзковъ прямой АВ равно отношенію соотвѣтствую-
щихъ отрѣзковъ прямой А1ВІ. Докажемъ, напр., что:
01) _
і Проведя СМ и параллельно
/	будемъ имѣть: С^В—СМ
/	и Е.Е^ЕХ (91). Тр.-ки СВМ
/	/ / И ВВХ подобны, потому что углы
/ I	одного равны соотвѣтственно уг-
А /	/	/ /	ламъ другого (вслѣдствіе парал-
л (у Ц/ К/ Е/ ц лельности линій). Изъ ихъ подо-
'/ 7	77	* бія слѣдуетъ:
СВ СМ	СВ с.ві
Черт. 145	ЕЕ = Е2^ откуда: ЁЁ=1&
Подобнымъ образомъ легко доказать пропорціанальность вся-
кихъ другихъ соотвѣтствующихъ отрѣзковъ.
192.	Теорема. Стороны угла, пересѣкаемыя рядомъ
параллельныхъ прямыхъ, разсѣкаются ими на пропори/іаналь-
ныя части.
Пусть стороны угла АВС пересѣкаются рядомъ парал-
лельныхъ прямыхъ ВВу, ЕЕ{, ЕІ<\ и т. д.; требуется до-
казать, что отношеніе двухъ какихъ-нибудь отрѣзковъ стороны
ВС равно отношенію соотвѣтствующихъ отрѣзковъ стороны
ВА. Докажемъ, напр., что:
вр_ ВВі
ВЕ~ ВІЕ1
А^о^^ВМ || ВА., будемъ имѣть:
В^Е^ — ВМ. Изъ подобія тр.-ковъ
ВВВг и ВЕМ находимъ:
ВВ ВВ. л ВВ ВВ.
ВЕ ~~ ВМ ’ отКУДа: ВЕ ~В^
Подобнымъ образомъ легко дока-
зать пропорціанальность всякихъ дру-
Нерт. 146	гихъ соотвѣтствующихъ отрѣзковъ.
193. Обратная теорема. Если на сторонахъ угла отло-
— 121 —
оюимъ отъ вершины нропорціанальныя части, то прямыя,
Соединяющія соотвѣтственные концы ихъ, параллельны.
Пусть на сторонахъ угла АВС (черт. 146) отложены отъ
вершины части ВВ, ВЕ, ВВг и В1Е1, удовлетворяющія
пропорціи:
ВВ\ВЕ = ВВХ гВ^
Требуется доказать, что прямыя ВВг и ЕЕу параллель-
ны.—Предположимъ, что прямая, параллельная ВВѴ и про-
ходящая черезъ точку Е, будетъ не ЕЕ±, а какая-нибудь
иная, напр. ЕЕи. Тогда, согласно прямой теоремѣ, будемъ
имѣть:
вв вв,	. вв вв,
-ВЁ=В-Е~и и по УСЛОВ1Ю: 7^ = 7^
Откуда: ВіЕп—В1Е1, что невозможно.
194. Теорема. Прямыя (ОА, ОВ, ОС.... черт. 147),
•исходящія изъ одной точки (О),
и пересѣкаемыя рядомъ парал-
лельныхъ прямыхъ (АВ,А1 Вг....),
разсѣкаются ими на пропорці-
анальныя части и сами дѣлятъ
'зти параллельныя на пропорці-
анальныя части.
1°. Примѣняя теорему § 192
сначала къ углу АОВ, затѣмъ
къ углу ВОС и т. д., получимъ:
О
Черт. 147
для угла АОВ	для угла СОВ
ОА, __ ОВі _ ОС, _
А.А ~ В.В ~~ С.С ~~ В,В~~"-
1_________I
для углаВОС
2°. Изъ подобія тр.-ковъ
и В1ОС1, выводимъ:
АОВ и А1ОВ1, затѣмъ ВОС
Откуда:
АВ _ ВО ВО _ ВС
~ В,0 И ВгО В,С,
АВ __ ВС
А,В, ~~В,С,
— 122 —
Подобнымъ же образомъ доказывается пропорція ВС .3^0.=
—СВ.С.В^
195. Задача. -Раздѣлитъ конечную прямую ЛВ на ча-
сти пропорціаналъно конечнымъ прямымъ т:п:р.
т	Проведя неопредѣленную
1 п [ * 1	прямую А С подъ произвольнымъ
]___р___)	угломъ къ АВ, отложимъ на
Е ________ ней части, равныя т, п и р.
/------у-------Точку Р, составляющую конецъ
ч	- Р' соединяемъ съ В и черезъ
г	; і точки отложенія проводимъ пря-
/ мыя, параллельныя ВВ. Тогда
АВ раздѣлится въ точкахъ В
с и Е на части, пропорціаналь-
ЧеРт- 148	ныя т:п:р (192).
Если т, п ир означаютъ какія-нибудь числа, напр. 2,5.3,
то построеніе выполняется такъ же, съ тою разницей, что
па АС откладываются части, равныя 2, 5 и 3 произволь-
нымъ единицамъ длины.
19В. Задача. Еъ тремъ конечнымъ прямымъ а, Ъ и с
найлпи четвертую пропорціаналъную,
а	т.-е. найти такую прямую
1	1	я, которая удовлетворяла бы
1--------1	пропорціи а : Ь=с : х.—На сто-
\~й-----------1 ронахъ произвольнаго угла АВ С
•.....   ;р______-,е Л откладываемъ части: ВВ = а,
У'" -	ВЕ—Ъ, ВЕ=с. Соединивъ
і затѣмъ В и Е, проводимъ
с ”ЕС [; ВЕ. Отрѣзокъ ЕС будетъ
’і	искомый (192).
Задача. На неопре-
С,’і	С	дѣленной прямой МН найти
Черт. 149	точки, которыхъ	разстоянія
отъ двухъ данныхъ точекъ	А	и В этой прямой	относились
бы, какъ т : п.—Черезъ А и В проводимъ двѣ произвольныя
параллельныя прямыя и на нихъ откладываемъ: АС — т,
ВВ~п и ВЕ=п. Проведя затѣмъ СВ и СЕ, получимъ
— 123 —
двѣ искомыя точки: Е и С. Дѣйствительно, изъ подобія тре-
угольниковъ АСЕи ЕВЕ,
а затѣмъ изъ подобія
тр.-ковъ АС& и ВВС	/\ о
находимъ:	у
ЕА :ЕВ=АС:ВЕ~ А/ \ В/	м
= т : п	М ® ЁѴу О
СА.СІВ=ЛС'-.ВІ)=	р
т •	Черт. 150
Замѣчаніе. Болѣе двухъ точекъ, удовлетворяющихъ тре-
бованію задачи, не можетъ быть, потому что при измѣненіи
положенія точки Е между А и В отношеніе ЕА: ЕВ измѣ-
няется; то же самое можно сказать объ отношеніи 6гЛ: СВ.
Когда т = п, существуетъ только одна точка (лежащая
на брединѣ между А и В), которая удовлетворяетъ требо-
ванію задачи.,
198. Теорема. Биссектрисса внутренняго или внѣшняго
угла треугольника пересѣкаетъ противоположную сторону
или ея продолженіе въ такой точкѣ, которой разстоянія
огпъ концовъ эгпой стороны пропоргуганальны двумъ другимъ
сторонамъ треугольника.
Пусть ВВ есть биссектрисса внутренняго, а ВВу—бис-
сектрисса внѣшняго угла тр.-ка АВС. Требуется доказать, что
Черезъ вершину С проведемъ ЕЕХ II АВ до пересѣченія
— 124 —
съ обѣими биссектриссами. Тр.-ки АВВ и ВЕС подобны?
(углы при В равны, какъ вертикальные, уг. 1 =уг. 5, какъ,
углы накрестъ лежащіе при параллельныхъ); точно также по-
добны тр.-ки АВВг и СЕ1ВІ. Изъ подобія ихъ находимъ:
ра__ав	т	дл 
РС~~ ЕС	Ш	І\С~СЁ\
12]
Чтобы перейти отъ этихъ пропорцій къ тѣмъ, которыя тре-
буется доказать, достаточно убѣдиться, что ЕС = ВО и:
СЕ^-ВС. И дѣйствительно, такъ какъ уг. 2 —уг. 1 (по
условію) и уг. 5 = уг. 1 (какъ накр. леж.), то уг. 2=уг. 5,
и потому [\ЕВО равнобедренный, т.-е. ЕС—ВС; съ дру-
гой стороны уг. 3—уг. 4 (по условію) и уг. 6=уг. 4 (какъ
накр. леж.); значитъ, уг. 3~уг. 6, и потому А ВОЕ} рав-
нобедренный, т.-е. СЕа = ВС. Замѣнивъ теперь въ пропор-
ціяхъ [1] и [2] отрѣзки ЕС и ОЕХ на ВС, получимъ тѣ.
пропорціи, которыя требовалось доказать.
Численный примѣръ. Пусть ЛВ=10, ВО =7 ъАС=В.
Тогда биссектриссы ВВ и ВВу опредѣлятъ точки В и В1У
которыхъ разстоянія отъ А и С можно найти изъ про-
порцій:
откуда:
т.-е.
значитъ:
ра_іо рха _ іо
РС~ 7 и	7
РА+РС_^УІ Р^А—РуС _3
РА “16 и ДА’” “16
6 _ 17	6 _ 3
ВЛ~10 И РѴА —10
РА=^=3°7 и ЦА = $=20
199. Обратная теорема. Если прямая, исходящая изъ
вергиины треугольника, пересѣкаетъ противоположную сто-
рону гіли ея продолженіе въ такой точкѣ, которой разсто-
янія до концовъ этой стороны пропорціональны двумъ дру-
гимъ сторонамъ, то она есть биссектрисса внутренняго гіли-
внѣшняго угла треугольника.
Пусть В и Ву (черт. 151) будутъ двѣ точки, удовлетво-
ряющія пропорціямъ:
^4 —-в?	т	Р1А — ВА	г9-|
РС~ ВС	Ш	Р^С-ВС
— 125 —
Требуется доказать, что прямыя ВВ И' ВВХ дѣлятъ пополамъ:
первая внутренній, а вторая внѣшній уголъ тр.-ка АВС.—
Проведя снова прямую ЕЕГ\\АВ, найдемъ изъ подобія тре-
угольниковъ :
гп, ВХА_ВА	г.п
ВС~ВС
Сравнивая пропорціи [3] съ [1] и [4] съ [2], находимъ:
ЕС= ВС и СЕг = ВС
Поэтому въ тр.-кѣ ВЕС равны углы 2 и 5, а въ тре-
угольникѣ ВЕХС равны углы 3 и 6: но уг. 5—уг. 1 (какъ
пакр. леж.) и уг. 6 = уг. 4 (по той же причинѣ); слѣд.
уг. 2=уг. I и уг. 3=уг. 4, т.-е. ВВ и ВВѴ суть бис-
сектриссы.
Теорема. Геометрическое мѣсто точекъ, которыхъ разсто-
янія отъ двухъ данныхъ точекъ А и В находятся въ постоянномъ отно-
шеніи т:п, есть окружность, когда т не равно п.
Еслп т не равно п, то на неопредѣленной прямой, проходящей че-
резъ А и В, можно найти двѣ точкп, принадлежащія искомому геометр.
мѣсту (197). Пустъ это будутъ точкп С и С], т.-е.
СА : СВ = т: п и (\А : С\В = т : п
Предположимъ теперь, что существуетъ еще какая-нибудь точка М,
удовлетворяющая пропорцію
МА : МВ = т : П
Проведя МС и 2ИС\, мы должны заключить (199), что первая изъ
этихъ прямыхъ есть бпссектрисса углаЛЛ/Д а вторая—бпссектрисса угла
ВМХ; вслѣдствіе этого уголъ СМС), составленный изъ двухъ половинъ
смежныхъ угловъ, долженъ быть прямой, а потому вершина его Млежптъ,
на окружности, описанной на СС1. какъ на діаметрѣ. Такимъ образомъ
— 126 —
мы доказали, что всякая точка ЛГ, принадлежащая искомому геометр. мѣ-
сту, лежитъ на окружности СС^ Теперь докажемъ обратное предложеніе,
т.-е , что всякая точка этой окружности принадлежитъ геометр. мѣсту.
Пусть М есть произвольная точка этой окружности. Требуется до-
казать, что МА : МВ—пі: п. Проведя черезъ В прямую ВЕ || АМ, будемъ
имѣть слѣдующія пропорціи:
МА : ВВ — СіА : СгВ = т : п	[11
МА :ВЕ—СА: СВ = т : п	[2]
Откуда	ВВ — ВЕ
т.-е. точка В есть средина прямой ВЕ. Такъ какъ уголъ СМСХ вписан-
ный и опирается на діаметръ, то онъ прямой; поэтому Л ВМЕ прямо-
угольный. Вслѣдствіе этого, если средину В гипотенузы ВЕ примемъ за
центръ и опишемъ окружность, то она пройдетъ черезъ М; значитъ,
ВВ—МВ. Подставивъ теперь въ пропорцію [1] намѣсто ВВ равную ей
прямую МВ, будемъ имѣть
МА : МВ = т : п
ГЛАВА III.
Числовыя зависимости между элементами треугольника и
нѣкоторыхъ другихъ Фигуръ.
®О1. Теорема. Перпендикуляръ, опущенный изъ вершины
прямого угла на гипотенузу-, есть средняя пропори,іанальная
между гипотенузой гс прилежащимъ отрѣзкомъ.
Пусть АП есть перпендикуляръ, опущенный изъ вертилы
прямого угла А на гипотенузу ВС. Требуется доказать слѣ-
дующія три пропорціи:
ВВ — АР'
Тв~ вс'1
9о вс
2 • АВ
С
В
Черт. 153
ихъ сторонъ (82). Возьмемъ
АВ . чо ВС_АС
ВВ> ^-АС~~ВС
Первую пропорцію мы до-
кажемъ изъ подобія тр.-ковъ
АВВ и АВС, у которыхъ АВ
общая сторона. Эти тр.-ки по-
добны, потому что острые углы,
обозначенные на чертежѣ однѣ-
ми и тѣми же цыфрами, равны
вслѣдствіе перпендикулярности
въ А АВВ тѣ стороны ВВ и
- 127 —
АВ, которыя составляютъ первое отношеніе доказываемой
пропорціи; сходственными сторонами (177) въ Д АВС бу-
дутъ АВ и ВС; поэтому
ВВ: АБ = АБ :БО
Вторую пропорцію докажемъ изъ подобія тр.-ковъ АВС
и АВВ, у которыхъ АВ общая сторона. Эти тр.-ки подоб-
ны, потому что они прямоугольные и острый уголъ В у нихъ
общій. Въ А АВС возьмемъ тѣ стороны ВС и АВ, кото-
рыя составляютъ первое отношеніе доказываемой пропорціи;
сходственными сторонами въ Д АВБ будутъ АВ и ВБ:
поэтому
ВС:АВ = АВ:ВВ
Третью пропорцію докажемъ изъ подобія тр.-ковъ АВС
и АБС, у которыхъ АС общая сторона. Эти тр.-ки подобны,
потому что они оба прямоугольные и имѣютъ общій острый
уголъ О. Въ Д АВС возьмемъ стороны ВС и АС; сход-
ственными сторонами въ Д АВС будутъ АС и ВС; по-
этому
ВС: АС=АС:БС
909. Слѣдствіе. Пусть А есть произвольная точка окруж-
ности,, описанной на діаметрѣ ВС. Соединивъ копцы діа-
метра съ этою точкою, мы получимъ
прямоугольный тр.-къ АВС, у кото-
раго гипотенуза ВС есть діаметръ, а
катеты суть хорды. Примѣняя дока-
занную выше теорему къ этому тре-
угольнику, приходимъ къ слѣдующему
заключенію:
А
Черт. 154
ІІерпендикуляруъ, опущенный изъ какой либо точки окруж-
ности на діаметръ, есть средняя пропорціаналъная между'
отрѣзками діаметра, а хорда есть средняя пропори,іаналъ-
ная между діаметромъ и прилежащимъ отрѣзкомъ ею.
903. Задача. Построить среднюю пропорціанальную
между двумя конечными прямыми а и Ъ.
— 128 —
Предыдущее слѣдствіе позволяетъ рѣшить эту задачу двоя-
кимъ путемъ.
1°. На произвольной прямой откладываемъ части ВВ = а
и ВС~Ъ (черт. 154); па ВС, какъ па діаметрѣ, описы-
ваемъ полуокружность; изъ В возстановляемъ до пересѣченія
съ окружностью перпендикуляръ ВА. Этотъ перпендикуляръ
и будетъ искомою среднею пропорціональною между ВВ и ВС.
2°. На произвольной прямой откладываемъ части (черт.
154) ВВ = а и ВС~Ъ. На большей изъ этихъ частей опи-
сываемъ полуокружность. Проведя перпендикуляръ ВА, соеди-
няемъ А съ В. Хорда АВ будетъ среднею пропопорціональ-
ною между ВС и ВВ.
204. Теорема. Если стороны прямоугольнаго треуголь-
ника измѣрены одною единицею, то квадратъ числа, выра-
жающаго гипотенузу, равенъ суммѣ квадратовъ чиселъ, вы-
ражающихъ катеты.
а	Пусть АВС есть пря-
Xх \	моугольный треуголъ-
\	никъ и АВ перпепди-
с //	\ь куляръ. опущенный на
//	\ гипотенузу изъ верши-
//\ .... Я..	\ пы прямого угла. Тогда,
Р..................1.---....по доказанному выше.
а I5	можемъ написать:
Черт. 155
ВС: АВ = АВ:ВВ и ВС: АС=АС: ВС
Когда стороны даннаго треугольника и отрѣзки гипотенузы
выражены числами, то мы можемъ примѣнить къ этимъ про-
порціямъ свойства числовыхъ пропорцій; тогда:
АВ- = ВС.ВВ и АС* = ВС.ВС
Сложивъ эти два равенства, получимъ:
АВ2 + АСІ = ВС(ВВ + ВС) = ВС.ВС=ВС2
Эту теорему обыкновенно выражаютъ сокращенно, хотя и
неправильно, такъ:
- 129 —
Квадратъ гипотенузы равенъ суммѣ квадратовъ ка-
тетовъ,
«Ой. Численныя примѣненія. Пусть а, Ъ, с, 1і, Ъ' и с
(черт. 155) будутъ числа, выражающія въ одной единицѣ
стороны, высоту и отрѣзки гипотенузы прямоугольнаго тр.-ка
АВС. На основаніи доказанныхъ выше теоремъ, мы можемъ
вывести слѣдующія 5 уравненій, связывающія эти 6 чиселъ:
с2 = ас; Ь2 = аЬ'; Ъ2 = Ь'с; Ь'-\-с=а; Ь2-\-с2 = а2
Изъ этихъ уравненій только первыя четыре самостоятель-
ны, а послѣднее составляетъ слѣдствіе двухъ первыхъ; вслѣд-
ствіе этого уравненія позволяютъ по даннымъ двумъ изъ шести
чиселъ находить остальныя четыре.
Для примѣра положимъ, что намъ даны отрѣзки гипо-
тенузы: Ь' = о метровъ и с=7 метр.; тогда
а = Ь' + с= 12; с = і'ас' = )/12.7 =]/84 = 9,165...
Ъ = угі' = уА~2Тб = у/(М = 7,74:4...
й = ]/1/с' = у5. 7=|/35 = 5,916...
«06. Слѣдствіе. Квадраты катетовъ относятся между
собою, какъ отрѣзки гипотенузы. Дѣйствительно, изъ урав-
неній предыдущаго параграфа находимъ:
с2: Ь2 = а-с: аЬ1 = с': Ъ'
«09. Замѣчаніе. Въ послѣдующихъ теоремахъ мы бу-
демъ сокращенно говорить: „квадратъ стороны“ вмѣсто: квад-
ратъ числа, выражающаго сторону, или: „произведеніе пря-
мыхъ “ вмѣсто: произведеніе чиселъ, выражающихъ прямыя.
При этомъ будемъ подразумѣвать, что прямыя измѣрены одною
и тою же единицею.
«08. Теорема. Въ треугольникѣ квадратъ стороны,
лежащей противъ остраго угла, равенъ суммѣ квадратовъ
двухъ другихъ сторонъ безъ удвоеннаго произведенія одной изъ
Л. и. КИСЕЛЕВЪ.	Я
— 130 —
этихъ сторонъ на отрѣзокъ ея отъ вершины остраго угла
до высоты.
Черт. 156	Черт. 157
Пусть ВС будетъ сторона тр.-ка АВС (черт. 156 или
157), лежащая противъ остраго угла А, и ВВ высота, опу-
щенная на какую либо изъ остальныхъ сторонъ, напр. па АС.
Требуется доказать, что
ВС2 = АВ2-\-АС2 — 2АС.АВ
Изъ прямоугольныхъ тр.-ковъ ВВС и АВВ выводимъ:
ВС2 = ВВ2~\-ВС2 [1] ВВ2 = АВ2 — АВ2 [2]
Съ другой стороны: ВС=АС — АВ (черт. 156) или
ВС=АВ — АС (черт. 157). Въ обоихъ случаяхъ для ВС2
получимъ одно и то же выраженіе:
ВС2—(АС—АВ)2 = АС2 — 2 АС. АВ-г АВ2}
ВС2 = (АВ — АС)2 = АВ2 — 2АВ.АС-( АС2]
Подставивъ въ равенство [1] на мѣсто ВВ2 и ВС2 ихъ
выраженія изъ равенствъ [2] и [3], получимъ:
ВС2 = АВ2 — АВ2-\-АС2 — 2 АС. АВ + АВ2
Это равенство, послѣ сокращенія членовъ —АВ2 и -}-АВ2,
и есть то самое, которое требовалось доказать.
Замѣчаніе. Доказанная теорема остается вѣрною и тогда,
когда уголъ С прямой; тогда отрѣзокъ СВ обратится въ 0,
т.-с. АС сдѣлается равною АВ, и мы будемъ имѣть:
В С2 А Вг -|- А С2 — 2АС2 — АВ2 — А С2
что согласуется съ теоремою о квадратѣ гипотенузы (204).
Теорема. Въ треугольникѣ квадратъ стороны, лс-
— 131 —
жащей противъ тупого угла, равенъ суммѣ квадратовъ двухъ
другихъ сторонъ, сложенной, съ удвоеннымъ произведеніемъ
одной изъ этихъ сторонъ на отрѣзокъ ея продолженія отъ
вершины тупого угла до высоты.
Пусть АВ будетъ сторона тр.-ка АВС (черт. 158), лежа-
щая противъ тупого угла С, и ВВ—высота, опущенная на
какую либо изъ остальныхъ сторонъ; требуется доказать, что
АВ2 — АС2-\-ВС2А2 АС. СВ
Ивъ прямоугольныхъ тр.-ковъ в
АВВ и СВ О имѣемъ:	к.
АВ2~ВВ2-ѴАВ2
вв2—вс2--св2
Но АВ2 — (АСА- СВ)2 =
= АС2А~2АС. СВ А СВ2
[1]
[2]
[3]
Черт. 158
Замѣнивъ въ равенствѣ [I] ВВ2 в АВ2 ихъ выраженіями
изъ равенствъ [2] и [3] найдемъ:
АВ2 — ВС2 — СВ2 + А С2 + 2 А С. СВ + СВ2
что. послѣ сокращенія, даетъ доказываемое равенство.
МО. Слѣдствіе. Изъ трехъ послѣднихъ теоремъ выво-
димъ, что квадратъ стороны треугольника равенъ, меньше или
больше суммы квадратовъ другихъ сторонъ, смотря по тому,
будетъ ли противулежащій уголъ прямой, острый или тупой.
Отсюда слѣдуетъ обратное предложеніе:
Уголъ треугольника окажется прямымъ, острымъ или
тупымъ, смотря по гному, будетъ ли квадра/тъ противолежа-
щей стороны равенъ, менъгае или больше суммы квадратовъ
другихъ сторонъ.
Примѣры. 1°. Стороны тр.-ка АВС (черт. 159) суть: а = 5,
с=3. Такъ какъ 52 = 42+ 32, то уголъ А прямой.
2°. а = 8, 6 = 7, с = 4. Такъ какъ 82< 72 + 42, то уголъ
А острый.
3°. а = 8, 6 = 5, с = 4. Такъ какъ 82 > 52-{-42, то уголъ
А тупой.
9*
— 132 —
В
211. Вычисленіе высотъ треугольника по его сторонамъ
Обозначимъ высоту, опущенную на
4 сторону а тр.-ка АВС, черезъ Ка
/ \ Чтобы вычислить ее. предварительно
/	\ изъ уравненія:
/	\	Ъ2 ~ а2 И- с2 — 2 ас
/........ Ь \ находимъ отрѣзокъ основанія с':
....А с
а В	/___+ с2 — Ъъ
Черт. 159
Послѣ чего изъ Д АВВ опредѣляемъ высоту какъ катетъ:
*.=Ѵ>Ч"Ѣ?І3’)7 •’
Такимъ же путемъ можно опредѣлить высоты Л* и кс,
опущенныя па стороны Ъ и с.
312» Теорема. Сумма квадратовъ діагоналей параллело-
грамма равна суммѣ квадратовъ его сторонъ.
Изъ вершинъ В п С паралле-
лограмма АВСВ опустимъ па осно-
ваніе АВ перпендикуляры ВЕ и СЕ.
Тогда изъ тр.-ковъ АВВ и АСВ
находимъ:
ВВ^АВЦ-АВ'—ЪАВ.АЕ
Черт, 160
А С'2 =.-.АВ*+ СВ^АВ.ВЕ
Прямоугольные тр.-ки АВЕ и ВСЕ равны, такъ какъ
они имѣютъ по равной гипотенузѣ и равному острому углу;
поэтому АЕ=ВЕ. Замѣтивъ это, сложимъ два выведенныя
выше равенства; тогда подчеркнутые члены сократятся, и мы
получимъ:
ВВ2+А Сг=АВ'+АВ2+АВ2+ СВ2=АВ2+АВ2+В С>+СВ2
213. Вычисленіе медіанъ треугольника по его сторонамъ.
Пусть даны стороны тр.-ка АВС (черт. 160) и требуется вы-
числить его медіану ВН. Для этого продолжимъ ее на раз-
*; Ниже, въ § 278, будетъ дана болѣе простая формула для высоты.
— 133-
стояніе НВ=ВН и точку I) соединимъ съ А и (7. Тогда
получимъ параллелограммъ АВСВ (99,2). Примѣняя къ нему
предыдущую теорему, найдемъ:
ВВ2=2 А ВЧ-2 В Сг—А С2
слѣд. ВН=±ВВ=У<ІАВІ+ЪВ&—А<?
914. Вычисленіе діагоналей вписаннаго четыреугольника.
Обозначимъ стороны вписаннаго четыреугольника АВСВ че-
резъ а, Ь, с, <і и его діагонали
черезъ х и у. Проведемъ АК I
ВС и СВ ! Л О. Такъ какъ сумма
противоположныхъ угловъ впиган.
четыреугольника равна 2(1, то если
уголъ В острый, уголъ В долженъ
быть тупымъ; поэтому изъ тр.-ковъ
А.ВС и АВС можемъ написать (208,
209):
х2=а2+Ъ2—2Ъ.ВК	[1]
х2=с2+сі2-\-2ВВВ	[2]
Прямоугольные тр.-ки АВК и СВВ подобны, такъ какъ
они содержатъ по равному острому углу (углы В и СВЬ
равны, потому что каждый изъ лихъ служитъ дополненіемъ
до 2с/ къ углу АВС). Изъ подобія ихъ выводимъ:
ВК: а~ВВ: с
откуда В1І. с~ВВ. а	[3]
Такимъ образомъ мы получили три уравненія съ тремя
неизвѣстными х, ВК и ВВ. Чтобы исключить ВК и ВВ,
уравняемъ въ первыхъ двухъ равенствахъ послѣдніе члены,
для чего умножимъ равенство [1] на Ы, а равенство [2] на
аЬ. Сложивъ затѣмъ результаты и принявъ во вниманіе ра-
венство [3], найдемъ:
(аЬ^с4)х2==агссІ-\-ЪісЛ']-с2аЪА-
—ас^аЛ-^-Ьс^ЬсІіЪс-^гаВ)
=(ас+&с/)(ас/+&с)
Откуда
— 134 —
Замѣтимъ, что въ числителѣ подкоренной величины пер-
вый множитель есть сумма произведеній противоположныхъ
сторонъ, а второй — сумма произведеній сторонъ, сходящихся
въ копцахъ опредѣляемой діагонали, знаменатель же пред-
ставляетъ сумму произведеній сторонъ, сходящихся въ кон-
цахъ другой діагонали; послѣ этого мы можемъ, но аналогіи,
написать слѣдующую формулу для діагонали у:
у— !(
у	ай -|- Ъс
Ж15. Слѣдствіе 1°. Произведеніе діагоналей вписаннаго
четыреугольника равно суммѣ произведеній противополож-
ныхъ сторонъ.
Дѣйствительно, перемноживъ формулы, выведенныя для
х и для т/, получимъ:
ху—\}( ас-\~ЬдІ)г=ас-^-Ъ(1
Это предложеніе извѣстно подъ именемъ теоремы Птоломея.
21в. Слѣдствіе 2°. Отношеніе діагоналей вписаннаго
четыреугольника равно отногиенію суммы произведеній сто-
ронъ, сходящихся въ конггахъ первой діагонали, къ суммѣ
произведеній сторонъ, сходягцихся въ концахъ второй діаго-
нали.
Дѣйствительно, раздѣливъ тѣ же два равенства, найдемъ:
я__ І(ав-\-Ь р_а<1~\-Ъс *)
у у (аЬ+с<1р аЬ+С(1
Эти два слѣдствія удобны для запоминанія; изъ нихъ мож-
но, обратно, вывести формулы для х и для у (перемножені-
емъ или дѣленіемъ равенствъ, опредѣляющихъ ху и р.
217. Заіача. По двумъ сторонамъ а и Ъ треугольника АВС ирадіусу
В описаннаго круга вычислить третью сторону х треугольника.
Проведя діаметръ СИ и хорды ЛТ) и В7), получимъ вписанный
четыреугольникъ АСВЯ, въ которомъ ВС=2В, А Т)~У - ЛС'2=
*) Изложенный способъ вычисленія діагоналей виисанного четыреугольника
сообщенъ намъ г. Поѣруженко (инспекторомъ Неплгосвскато Оренбургскаго
ворпуса).
— 135 —
С
Л
Черт. 162
4Л2~~/^(изъ прямоугольнаго тр.-ка Л СВ) и ВВ^У ~ВС2 — ВС2~
-=г]/4№— «2 (изъ прям. тр.-ка ВСВ).
Примѣняя къ атому четыреугольнику теорему Птоломея, будемъ имѣть:
2Вх~аУШ^^ьУ^й^а2
откуда легко найдемъ .т.
Задача будетъ имѣть другое рѣшеніе, если
предположимъ, что стороны а и Ъ лежатъ по
одну сторону отъ центра. Примѣняя къ этому
случаю теорему Птоломея, мы получимъ слѣдую-
щее уравненіе:
2]Іх=аУТІІ^Ъ2-Ь У
®18. Теорема. Если черезъ одну и
ту же точку внутри круга проведены нѣсколько хордъ, то
произведеніе двухъ отрѣзковъ каждой хорды есть
постоянная.
Пусть черезъ точку АІ проведены
двѣ хорды АВ и СІ)'^ требуется дока- лС
•зать, что	/ і~\
АЯЕМВ=ВМ.МС	I ! /\
Проведемъ вспомогательныя хорды АС
и ВВ} тогда получимъ два тр.-ка А МС дК
и ВАГВ, которые подобны, потому что
углы А. и С одного изъ нихъ равны
соотвѣтственно угламъ В и В другого Че т
(какъ углы вписанные, опирающіеся на
одну и ту же дугу). Изъ подобія ихъ выводимъ:
АМ:МВ=СМ:МВ
Откуда: АЪ'І.МВ=СМ.МВ
2 ІЯ. Теорема. Если черезъ одну и ту же точку внѣ
круга проведены нѣсколько сѣкугцйхъ и касательная, то:
1°, проггзведеніе каждой сѣкущей на ея внѣшнюю часть
есть величина постоянная;
2°, этапастоянная величина равна квадрату касательной.
величина.
163
— 136 —
Черт. 164
Пусть черезъ точку М проведены двѣ сѣкущія М4 кг
МВ и касательная МС; требуется доказать, что
МА. МА1 =МВ. МВ, =МС2
1° Проведемъ вспомогательныя хор-
ды АВ, и ВА,; тогда получимъ тр -ки>.
МАВ, и АГА,В, которые подобны,
потому что у нихъ уголъ М общій, а-.,
углы А и В равны, какъ вписанные,
опирающіеся на одну дугу. Изъ подо-
бія ихъ слѣдуетъ:
Откуда: МА.МА=МВ.МВ,
2°. Проведемъ вспомогательныя хор-
ды В,С и ВС; тогда получимъ два.
тр.-ка МВС и МВ,С, которые подобны, потому что у нихъ
уголъ М общій, и углы МСВ} и СВМ равны, такъ какъ
каждый изъ пихъ измѣряется половинкою дуги В,С, (155*
163). Возьмемъ въ Д МВС стороны МВ и МС; сходствен-
ными сторонами въ А МВ, С будутъ МС и МВ,; поэтому:
МВ;МС=МС;МВ,
Откуда: МВ.МВ ,~МС2
Значитъ: МА.МА,=МВ.МВ,=МС2.
Теорема. Произведеніе двухъ сторонъ треугольника равно:
1°, произведенію діаметра описаннаго кру- -
га на высоту, проведенную къ третьей сторонѣ;
2Э, квадрату биссекпгриссы угла, заключен-
наго между этими сторонами, сложенному съ
произведеніемъ отрѣзковъ третьей стороны.
1° Обозначимъ стороны тр.-ка ЛВС. че-
резъ а, Ъ и с, высоту, опущенную на сторону
а, черезъ 7*а, а радіусъ описаннаго круга че
резъ Л. Проведемъ діаметръ ЛВ и соединимъ
Р съ В. Тр. ки АВВ и ЛЕСподобны, потому
что углы В и Е прямые и Р=:С, какъ углы-
вписапные, опирающіеся на одну и ту ткс-
с-.Ъ,а —2В:Ь
Ъсг^2ВЛа.
Черт. 165
дугу. Изъ подобія выводимъ:
Откуда:
СИ
— 137 —
2° Обозначимъ биссѳктриссу угла Л черезъ «(черт. 166). Продолжимъ
ее до пересѣченія съ описанною окружностью въ точкѣ і>’(эта точка лежитъ
въ срединѣ дуги ВС, такъ какъ углы ВАЕ и ЕАС, по условію, равны).
Тр.-ки АВЕ и АВС подобны, потому что углы при точкѣ А равны по
условію, п С—Е, какъ углы вписанные, опирающіеся на одну дугу. Изъ
подобія ихъ слѣдуетъ:
с:а=Л1?:Ь; откуда Ьс=ѵ. АЕ
или Ьс=2л(»+ВЕ')—ѵ.2+а..ВЕ
Но *.ВЕ=ВП.ВС (218)
Поэтому Ъс^с^+ВВ.ВС [2]
Вычисленіе радіуса описаннаго
круга и биссектриссъ угловъ. Изъ равенст-
ва [1] предыдущаго параграфа находимъ:
II---
2/>.
Если вставимъ па мѣсто Ііа выраженіе, найденное для высоты рань-
ше (211), то получимъ формулу, опредѣляющую В въ зависимости отъ
а, Ь п с.
Изъ равенства [2] того же параграфа выводимъ:
^=Ъс~ ВВ.ВС
Отрѣзки ВВ и ВС можно найти изъ пропорціи ВВ-ВС—е-.Ь (198);
откуда*
ВВ+ВС_Ъ+<: ВВ+ВС—Ъ+с
ВВ ~ с ’ л ВС — ъ
Замѣтивъ, что ВВ+ВС=а, получимъ:
ас	_ аЪ
ВІ)~Ъ+с	Т)С~ЬѴс
С1*». «»=6г-(Д^2=(^-)2[ (6+с)2-а’]=(^^[(Ь+е+<г)(і>+с-о)]
Это выраженіе можно упростить, если обозначимъ периметръ тр.-ка,.
т. е. а+й+е, черезъ 2р; тогда Ъ+с—а=2.р—2а=2Ср—а) и
2	,_______
ГЛАВА IV.
Понятіе о приложеніи алгебры къ геометріи.
222. Задача. Данную конечную прямую раздѣлитъ въ
среднемъ и крайнемъ отношеніи.
Эту задачу надо понимать такъ: раздѣлить данную пря-
— 138 —
мую на такія двѣ части, чтобы большая изъ нихъ была сред-
нею пропорціанальною между всею линіей и меньшею ея
частью.
Задача, очевидно, будетъ рѣшена, если мы найдемъ одну
изъ двухъ частей^ на которыя требуется раздѣіить данную
прямую. Будемъ находить большую часть, т.-е. ту, которая
должна быть среднею пропорціональною между всей линіей
и меньшею ея частью. Предположимъ сначала, что рѣчь идетъ
не о построеніи этой части, а только объ ея вычисленіи. Тог •
да задача рѣшается аліебрагічески такъ: если длину данной
прямой обозначимъ а, а большей ея части .г, то длина дру-
гой части выразится а—х, и согласно требованію задачи мы
будемъ имѣть пропорцію:
а: х—х — х
откуда:	х? = а(а — х)
пли	х2 4- ах — а2 = 0.
Рѣшивъ это квадратное уравненіе, находимъ:
Отбросивъ второе рѣшеніе, какъ отрицательное*), возь-
мемъ только первое, положительное, рѣшеніе, которое удоб-
нѣе представить такъ:
Чтобы убѣдиться, годится ли это рѣшеніе для предложен-
ной задачи, необходимо показать, что величина хі меньше а.
Въ этомъ легко убѣдиться, преобразуя радикалъ такъ:
/1 а\2 ।	2	/ а* і 4а2 ІЬа2 « /7
ѴІ2-) +« = ѵт+ т=Ѵт=2І/5
Такъ какъ \/б< 3, то '^д/5 и потому разность
| меньше разности —а—т. е. меньше а. Та-
*) Не трудно было бы показать, что отрицательное рѣшеніе, буяучи взято
со знакомъ -р, дпетъ отвѣтъ ня измѣненную задачу: данную прямую а продол-
жить на столько («а ж), чтобы продолженіе было средней пропорціональной
между а и а 4- х.
— 139 —
кимъ образомъ, мы прежде всего видимъ, что задача всегда
возможна и имѣетъ только одно рѣшеніе. Если бы ламъ те-
перь удалось построить такую прямую, которой длина вы-
ражается формулой [1]. то, нанеся эту длину на данную
прямую, мы раздѣлили бы ее въ среднемъ и крайнемъ отно-
шеніи. Итакъ, вопросъ сводится къ построенію формулы. [1].
Разсматривая отдѣльно выраженіе	мы замѣ-
чаемъ, что оно представляетъ собою длину гипотепузы такого
прямоугольнаго тр.-ка, у котораго одипъ катетъ равенъ а,
а другой °/2. Построивъ такой тр.-къ, мы найдемъ прямую,
выражаемую формулой \/(уУ+л2' Чтобы получить затѣмъ
длину достаточно изъ гипотенузы построеннаго треуголь-
ника вычесть 72.
Такимъ образомъ, построеніе можно выполнить такъ:
Дѣлимъ данную прямую АВ пополамъ	,
въ точкѣ С. Ивъ копца В возстаповля-	1
емъ перпендикуляръ ВВ и откладываемъ
на немъ ВБ^=ВС. Соединивъ А съ В,	у
получимъ прям. тр.-къ АВБ, у котораго '	в
катетъ АВ~а, а другой катетъ ВБ—*}*. 'ІОРТ- 167
Слѣд., его гипотенуза АВ равна \/- Чтобы вычесть
изъ гипотепузы длину а/і, опишемъ изъ Л, какъ центра, ду-
гу радіусомъ ВВ~а/^. Тогда отрѣзокъ АЕ будетъ равенъ
\Ду)2~гг/2 — у т-"е- будетъ равенъ .г,. Отложивъ АЕ па
АВ (отъ Л до Сг), получимъ точку <7, въ которой АВ раз-
дѣлится въ среднемъ и крайнемъ отношеніи.
«гз. Алгебраическій способъ рѣшенія геометр. задачъ.
Мы рѣшили предложенную задачу путемъ приложенія алгебры
къ геометріи. Этотъ весьма плодотворный пріемт, состоитъ
въ слѣдующемъ: сперва опредѣляютъ, какую линію должно
отыскать, чтобы можно было рѣшить задачу. Затѣмъ, обоз-
начивъ данныя линіи буквами а, Ъ, с...., а искомую буквою
составляютъ изъ условій задачи и извѣстныхъ теоремъ
уравненіе, связывающее искомую линію съ данными: получен-
— 140 —
ное уравненіе рѣшаютъ по правиламъ алгебры. Найденную
формулу изслѣдуютъ, т. е. опредѣляютъ, при всякихъ ли
заданіяхъ эта формула даетъ возможныя рѣшенія, или только
при нѣкоторыхъ, и получается ли одно рѣшеніе или нѣсколь-
ко. Затѣмъ строятъ формулу, т. е. находятъ построеніемъ
такую линію, которой численная величина выражается этой
формулой.
Такимъ образомъ, алгебраическій пріемъ рѣшенія геомет-
рическихъ задачъ состоитъ изъ слѣдующихъ 4-хъ частей: 1°,
составленіе уравненія, 2°, рѣшеніе его, 3°, изслѣдованіе по-
лученной формулы и 4°, построеніе ея.
Иногда задача приводится къ отысканію нѣсколькихъ ли-
ній. Тогда, обозначивъ ихъ буквами х, у, г,..., стремятся
составить столько уравненій, сколько неизвѣстныхъ.
Построеніе простѣйшихъ формулъ. Укажемъ про-
стѣйшія формулы, которыя можно построить посредствомъ
циркуля и линейки; при этомъ будемъ предполагать, что бук-
вы а, 6, с.... означаютъ данныя прямыя, а х искомую. Не,
останавливаясь па такихъ формулахъ:
х — а 4- Ь -|- с, х = а — Ь, х=2а, За,....
построеніе которыхъ весьма просто, перейдемъ къ слѣдующимъ:
_ т	а а	2
1.	Формулы: х=-,-^.... х=2-а.... строятся посред-
ствомъ дѣленія прямой а на равныя части (65,7, 101) и за-
тѣмъ, если нужно, повтореніемъ одной части слагаемымъ
2, 3.... раза.
2.	Формула х = ^- представляетъ собою четвертую про-
порціаналъную къ прямымъ с, а и Ъ, Дѣйствительно, изъ
этого равенства выводимъ:
сх—аЬ] откуда с : а = Ь : х.
Слѣд., х найдется способомъ, указаннымъ выше (196) для
построенія 4-ой пропорціапальной.
3.	Формула х = ^ выражаетъ четвертую пропорціональ-
ную къ прямымъ Ъ, а и а, или, какъ говорятъ, третью про-
— 141 —
порціаналъную къ прямымъ Ь и а. Дѣйствительно, изъ дан-
наго равенства выводимъ:
Ъх = а2; откуда Ъ : а = а : х.
Слѣд., х найдется тѣмъ же способомъ, какимъ отыски-
•вается 4-я пропорціанальная (прямую а придется откладывать
два раза).
4.	Формула х = \/аЬ выражаетъ среднюю пропорціональ-
ную между а и Дѣйствительно, изъ нея выводимъ:
х2= аЬ; откуда а : х = х: Ъ.
Слѣд., х найдется способомъ, указаннымъ раньше для
построенія средней пропорціональной (203).
5.	Формула х = у/а? -|- Ь2 выражаетъ гипотенузу прямо-
угольнаго тр.-ка, у котораго катеты суть а и 6.
6.	Формула х — ^(Р—у представляетъ катетъ прямоуг.
тр.-ка, у котораго гипотенуза есть а, а другой катетъ Ь.
Построеніе всего удобнѣе выполнить такъ какъ указано въ § 158.
Указанныя формулы можно считать основными. При по-
мощи ихъ строятся болѣе сложныя формулы. Напр.:
7.	х = ~^~. Разобьемъ дробь на множителей такъ:
аЪ с <і 	аЪ і П1	і „
•ж = — . у • - и положимъ, что — =к. Тогда к найдемъ, какъ
4-ю пропорціапальпую къ е, а и Ь. Найдя А;, будемъ имѣть:
,х=у.^. Положимъ, что	Тогда I найдемъ, какъ 4-ю
пропорціанальную къ линіямъ /*, к и с. Найдя /, будемъ имѣть
:х=^‘. слѣд., х есть 4-я пропорціанальная къ г;, I и
Подобнымъ образомъ строятся также и формулы вида:
’т. е. такія формулы, въ которыхъ числитель и знаменатель
представляютъ произведеніе линейныхъ множителей (т.-е. буквъ,
означающихъ линіи), причемъ числитель содержитъ этихъ мно-
жителей на одинъ больше, чѣмъ знаменатель.
8.	х=а\^~- Подведя а подъ знакъ радикала, получимъ:
— 142 —
Отсюда видимъ, что х есть средняя пропорціанальная меж-
ду прямыми а и 2/3а.
9.	—0*4-сі*. Положимъ, что а2-]-Ъ' — /г2. Тогда
к найдется, какъ гипотенуза прямоуг. тр.-ка, у котораго ка-
теты суть а и Ь. Построивъ к, положимъ, что к2—с*=1*.
Тогда / найдется, какъ катетъ такого прям. тр.-ка, у кото-
раго гипотенуза есть /г, а другой катетъ с. Построивъ I. бу-
демъ имѣть:	Слѣд., х есть гипотенуза тр.-ка,
у котораго катеты суть I и сі.
10.	х=\!аі'—Ь*. Положимъ, что
<73	а! а? а а
а — ігу, т.-е. « = -п=-г-. т .-г
ьл ъ ъ ъ
Отсюда видно, что у найдется посредствомъ троекратнаго
построенія 4-ой пропорціапальной. Построивъ у, будемъ имѣть:
х — \/Ь лу — Ь '= У \/Ъ\у — Ь) = V Ь\/Ь(у — Ь)
Выраженіе \/Ь(у — Ь) представляетъ линію, которая есть
средняя пропорціапальная меледу Ь и у — Ь. Пусть эта линія
будетъ к. Тогда х — \[Ък\ значитъ, х найдется, какъ средняя
пропорціапальная между Ь и к.
Ограничимся этимп примѣрами. Замѣтимъ, что подробное
разсмотрѣніе способовъ построенія алгебраическихъ формулъ
приводитъ къ слѣдующему важному выводу:
помощью циркуля и линейки возможно строить только
такія алгебраическія выраженія, которыя или вовсе не со-
держатъ радикаловъ, или же содержатъ радикалы съ пока-
зателемъ 2, 4, 8...., т. е. съ показателемъ, равнымъ сте-
пени 2-хъ.
УПРАЖНЕНІЯ.
Доказать теоремы:
189.	Прямая, проведенная черезъ средины основаній трапеціи, про-
ходитъ черезъ точку пересѣченія непараллельныхъ сторонъ п черезъ
точку пересѣченія діагоналей.
190.	Если два круга касаются извнѣ, то часть внѣшней общей каса-
тельной, ограниченная точками касанія, есть средняя пропорціанальная
между діаметрами круговъ.
— 143 —
191.	Сумма квадратовъ сторонъ треугольника равна утроенной суммѣ
квадратовъ разстояній точки пересѣченія медіанъ отъ вершинъ треуголь-
ника (§ 212).
192.	Если въ прямоугольный тр.-къ АВС вписать квадратъ ВЕЕС
такъ, чтобы сторона ВЕ совпадала съ гипотенузой ВС, то эта сторона,
есть средняя проііорціапальпая между отрѣзками гипотенузы ВВ и ЕС.
193.	Если двѣ конечныя прямыя АВ и СВ пересѣкаются (хотя бы и
при продолженіи) въ точкѣ Е такъ, что
ЕА . ЕВ~ ЕС. ЕВ
то точки А, В, С и В лежатъ па одной окружности (эта теорема обратна,
изложеннымъ въ 218 и 219).
194.	Дана окружность О п двѣ точки А и В внѣ ея. Черезъ эти точки
проведены нѣсколько окружностей, пересѣкающихъ окружность О, или
касающихся ея. Доказать, что всѣ хорды, соединяющія точки пересѣче-
нія каждой изъ этихъ окружностей съ окружностью О, а также и общія
касательныя, сходятся (при продолженіи) въ одной точкѣ, лежащей на
продолженіи прямой АВ.
195.	Основываясь на этомъ, вывести способъ построенія такой ок-
ружности, которая проходитъ черезъ 2 данныя точки А и В и касается
данной окружности О.
196.	Даны два какіе-нибудь круга па плоскости. Если два радіуса
этихъ круговъ движутся, оставаясь постоянно параллельными, то пря-
мая, проходящая черезъ концы ихъ, пересѣкаетъ линію центровъ всегда
в.ъ одной точкѣ (эта точка наз. г^мпромъ подобія двухъ круговъ).
197.	Медіана тр.-ка дѣлитъ пополамъ всѣ прямыя, проведенныя
внутри тр.-ка параллельно той сторонѣ, относительно которой взята
медіана.
198.	Дапы три прямыя, исходящія изъ одной точки. Если по одной
изъ нихъ движется какая-нибудь точка, то разстоянія ея отъ двухъ дру-
гих'ь прямыхъ сохраняютъ всегда одно и то же отношеніе.
199.	Если двѣ окружности концентрическія, то сумма квадратовъ
разстояній всякой точки одной изъ ппхъ отъ концовъ какого угодно діа-
метра другой есть величина постоянная (§ 212).
200.	Если изъ трехъ вершинъ тр.-ка и изъ точки пересѣченія его
медіанъ опустимъ перпендикуляры па какую-нибудь внѣшнюю прямую,
то послѣдній изъ 4-хъ перпендикуляровъ равенъ третьей части суммы
первыхъ трехъ.
201.	Если соединимъ прямыми основанія трехъ высотъ какого-нибудь
тр.-ка, то образовавшіеся при этомъ 3 тр -ка у вершинъ даннаго подобны
ему. Вывести отсюда, что для чр.-ка, имѣющаго сторонами прямыя, со-
единяющія основанія высотъ даннаго тр.-ка, эти высоты служатъ бпе-
Еектрпссами.
202.	Діаметръ АВ данпой окружности продолженъ за точку В, Черезъ
какую-нибудь точку этого продолженія проведена неопредѣленная прямая
— 144 —
СОДЛВ. Если произвольную точку М этого перпендикуляра соединимъ
съ А, то (обозначивъ черезъ Аі вторую точку пересѣченія съ окруж-
ностью этой прямой) произведеніе АМ,ААі есть величина постоянная.
Найти геометрическія мѣста:
203.	— срединъ всѣхъ хордъ, проходящихъ черезъ данную точку ок-
ружности.
204.	— точекъ, дѣлящихъ въ одномъ и томъ же отношенія т: п всѣ
хорды, проходящія черезт, данную точку окружности.
205.	— точекъ, которыхъ разстоянія отъ сторонъ даннаго угла имѣ-
ютъ одно и то же отношеніе т: п.
206.	— точекъ, для которыхъ сумма квадратовъ разстояній отъ двухъ
данныхъ точекъ есть величина постоянная (§ 212).
207.	— точекъ, для которыхъ разность квадратовъ разстояній отъ
двухъ данныхъ точекъ есть величина постоянная.
208.	— точекъ, изъ которыхъ касательныя, проведенныя къ двумъ
даннымъ окружностямъ, раины (это геометр. мѣсто есть прямая, перпен-
дикулярная къ линіи центровъ; опа наз. радикальною осью двухъ
круговъ).
209.	— точекъ, дѣлящихъ въ данномъ отношеніи т: п всѣ прямыя,
соединяющія точки окружности съ данною точкою О (лежащую внѣ или
внутри окружности).
210.	Даны двѣ извнѣ касающіяся окружности. Черезъ точку касанія
А. проводятъ въ окружностяхъ двѣ перпендикулярныя хорды АВ и АС.
Концы ихъ В и С соединяютъ прямой. Найти геометр. мѣсто точекъ;
дѣлящихъ ВС въ данномъ отношенія т : п.
211.	Данный уголъ вращается вокругъ своей вершины. Иа сторонахъ
его, отъ вершины, откладываютъ перемѣнныя длины, но которыхъ отно-
шеніе постоянно. Если конецъ одной стороны описываетъ даппую по по-
ложенію прямую, какую линію опишетъ другой конецъ?
Задачи на постооеніе:
212.	Черезъ точку, данную внутри или внѣ угла, провести прямую
такъ, чтобы части ея, заключенныя между этой точкой и сторонами угла,
имѣли данное отношеніе »< : п.
213.	Найти въ треугольникѣ такую точку, чтобы перпендикуляры,
опущенныя изъ нея на стороны, находились въ данномъ отношеніи
пг:п:р(см упражненіе 205).
214.	Построить тр.-къ но углу, одной изъ сторонъ, прилежащихъ къ
нему и отношенію этой стороны къ третьей сторонѣ (сколько рѣ-
шеній?).
215.	То же—по углу при вершинѣ, основанію и отношенію его къ
одной изъ боковыхъ сторонъ.
216.	То же—по высотѣ, углу при вершинѣ и. отношенію отрѣзковъ
основанія.
— 145 —
217.	То же—по углу при вершинѣ, основанію и данной на основаніи
точкѣ, черезъ которую проходитъ биссектрисса угла при вершпнѣ.
218.	То же—по двумъ угламъ и суммѣ или разности основанія съ
высотою.
219.	Построить равнобедренный тр.-къ но углу при верщпнѣ и сум-
мѣ основанія съ высотою.
220.	Вписать въ данный кругъ тр.-къ, у котораго даны: основаніе и
отношеніе двухъ другихъ сторонъ.
221.	Вписать въ дапиый кругъ тр.-къ, у котораго даны: основаніе
и медіана относительно одной пзъ неизвѣстныхъ сторонъ (см. упраж-
неніе 203).
222.	Вписать квадратъ въ данный сегментъ такъ, чтобы одна его сто-
рона лежала на хордѣ, а вершины противолежащихъ угловъ на дугѣ.
223.	Вписать квадратъ въ данный тр.-къ такъ, чтобы одна сторона
его лежала на основаніи тр.-ка, а вершины противолежащихъ угловъ на
боковыхъ сторонахъ тр.-ка.
224.	Въ данный треугольникъ вписать прямоугольникъ (см. ирсд. за-
дачу), у котораго стороны относились бы, какъ тѣ: п.
225.	Около даннаго квадрата описать тр.-къ, подобный данному.
226	Дана окружность и па пей двѣ точки А и В. Найти на этой
окружности третью точку С, чгобн разстоянія ея отъ А и В находились
въ данномъ отношеніи.
227.	На дапной прямой пайтп точку, которая одинаково была бы уда-
лена отъ другой дапной прямоп и данной точки.
228.	Построить тр -къ по двумъ сторонамъ и бнссектрнссѣ угла между
ними (см. черт. 151. Сначала находимъ прямую ВЕ изъ пропорціи ЛВ :ЕС
(т.-с. ВС) = ВВ: ВЕ: затѣмъ строимъ ВСЕ;...).
229.	Построить прямую х, которая относилась бы къ даппой прямой
т, какъ «2:А'2 (а и Ъ данныя прямыя).
230.	Пайтп внѣ даннаго круга такую точку, чтобы касательная, про-
веденная изъ нея к-ь этой окружпости, была вдвое менѣе сѣкущей, про-
веденной изъ этой же точки черезъ центръ (приложеніемъ алг. къ геом).
231.	Черезъ данную внѣ окружности точку провести такую сѣкущую,
которая раздѣлилась бы этою окружностью въ даппомъ отношеніи (прил.
.алг. къ геом.).
232. Построить тр.-къ ио тремъ его высотамъ Ль Ла и 7і8. (Предва-
рительно изъ подобія прямоуг. тр. ковъ надо доказать, что высоты об-
ратно пропорѵ/іапалъны соотвѣтствующимъ сторонамъ. Если стороны, на
которыя опушены высоты А2 и Л3) обозначимъ соотвѣтственно черезъ
*і, т2 и <е3, то
а'і: «з = 712^'1
а'2 •' Л’з = Л3 : 7і2 «= 1 :
Лх
7>Л
откуда
я*і :	: я’з — «э :	:	’
А. И. КИСЕЛЕВЪ.
10
— 146 —
Выраженіе есть четвертая пропорціанальная къ Л3, й2 и Ях. Пост-
"з
роивъ ее, мы будемъ имѣть три прямыя: Л9. и ~2, которымъ искомыя сто--
лз
ропы ироіюрціанальны; значитъ, тр.-къ,. имѣющій эти прямыя сторонами,
будетъ подобенъ искомому, и потому вопросъ сведется къ построенію та-
кого тр.-ка, который, будучи подобенъ данпому, имѣлъ бы даппую вы-
соту. Задача будетъ невозможна, если по тремъ прямымъ: Л-2 и
нельзя построить треугольникъ (49).
Задачи на вычисленіе:
233.	По данпому основанію а и высотѣ Л остроугольнаго тр.-ка вы-
числить сторону х квадрата, вписаннаго въ этотъ тр.-къ такъ,, чтобы
одна сторона квадрата лежала на основаніи тр.-ка, а двѣ вершили квад-
рата па боковыхъ сторонахъ тр.-ка.
234.	Стороны гр.-ка суть !О ф., 12 ф. п 17 ф<. Вычислить отрѣзки
стороны, равной 17 ф , на которые опа дѣлится биссектриссою противо-
лежащаго угла.
235.	Перпендикуляръ, опущенный изъ вершины прямого угла на ги-
потенузу, дѣлитъ се па два отрѣзка т и п. Вычислять катеты.
236.	Вычислить высоту тр.-ка, опущенную па сторону, равную 20.
если двѣ другія стороны суть 12 и 15.
237.	Вычислить медіаны тр.-ка, котораго стороны суть а = 5, Ъ — 7
и с = 9
238.	Въ тр-кѣ АВС стороны суть:	= 7, ВС — 15 и АС— 10.
Опредѣлить, какого вида уголъ Л, и вычислять высоту, опущенную изъ
вершины К
239.	Изъ точки внѣ круга проведены касательная а и сѣкущая. Вы-
числить длину сѣкущей, зная, что отношеніе внѣшней ея части къ внут-
ренней равно т: п.
240.	Къ двумъ кругамъ, которыхъ радіусы суть В и г, а разстояніе
между центрами Л, проведена общая касательная. Опредѣлить вычисле-
ніемъ положеніе точки пересѣченія этой касательной съ линіей центровъ
во 1, когда эта точка лежитъ но одну сторону отъ центровъ, во 2, когда,
опа расположена между ними.
ГЛАВА IV.
Правильные многоугольники.
Опредѣленія. Ломаная линія наз. правильной, если
она удовлетворяетъ слѣдующимъ тремъ условіямъ: 1°, отрѣзки
— 147 —
прямыхъ, составляющіе ее, равны, 2°, углы составленные каж-
дыми двумя сосѣдними отрѣзками, равны, и 3°, изъ каждыхъ
трехъ послѣдовательныхъ отрѣзковъ первый и третій распо-
ложены по одну сторону отъ второго.
Черт. 168
Таковы, напр., линіи АВСВЕ и Е&ІТКЕ; но ломаную
ЛІЕРфВ нельзя назвать правильною, потому что она не
удовлетворяетъ третьему условію.
Правильная ломаная можетъ быть выпуклой (33), какъ
напр,, линія АВСВЕ.
Многоугольникъ наз. правильнымъ, если онъ ограниченъ
замкнутою правильною ломаною линіей. Таковы, напр.,
квадратъ, равносторонній треугольникъ и другіе.
Черт. 169
Черт. 170
Многоугольникъ, изображенный на чертежѣ 169. есть вы-
пуклый правильный пятиугольникъ; мн.-къ чертежа 170 так-
же правильный пятиугольникъ, но по выпуклый (звѣздчатый}.
Мы будемъ разсматривать только выпуклые прав. мп.-ки.
Слѣдующая теорема показываетъ, что выпуклые пра-
вильные многоугольники возможны съ произвольнымъ числомъ
сторонъ (большимъ двухъ).
10е
— 148 —
22в. Теорема. Если окружность раздѣлена на произ-
вольное число равныхъ частей (ббльшее двухъ), то
1°, соединивъ хордами каждыя двѣ сосѣднія точки дѣле-
нія, получимъ правильный вписанный многоугольникъ;
2°, проведя черезъ всѣ точки дѣленія касательныя до
взаимнаго пересѣченія, получггмъ правильный описанный мно-
гоугольникъ.
Пусть окружность раздѣлена на нѣсколько равныхъ ча-
стей въ точкахъ АВС... и черезъ эти точки проведены
хорды АВ, ВС... и касательныя МЕГ, ЪТР......... Тогда:
10. Мпог.-къ АВСВЕЕ бу-
детъ правильный, потому что всѣ
его сторопы равны (какъ хорды,
стягивающія равныя дуги) и всѣ
его углы равны (какъ вписан-
ные, опирающіеся на равпыя ду-
ги).
2°. Чтобы доказать правиль-
ность описаннаго многоугольника
М№Р(^)В8, разсмотримъ тр.-ки
АМВ, ВЕТС и т. д. У нихъ
основанія АВ, ВС ит.д. рав-
ны; углы, прилежащіе къ осно-
ваніямъ, также равны, потому что каждый изъ нихъ имѣетъ
одинаковую мѣру (уголъ, составленный касательною и хордой,
измѣряется половиною дуги, заключенной внутри его). Зна-
читъ, всѣ эти тр.-ки равнобедренные и равны между собою;
а потому д'ЕЕГ—НР—... и М=ЪГ=... т. е. мн.-къ МЕРфВЗ
есть правильный.
Замѣчаніе. Если возьмемъ средины дугъ АВ, ВС,
СВ,... (черт. 171), то получимъ точки, которыя дѣлятъ окруж-
ность на столько же равныхъ частей, на сколько она раздѣ-
лена въ точкахъ А, В, С.... Поэтому, если черезъ эти сре-
дины проведемъ касательныя до взаимнаго пересѣченія, то
получимъ также правильный описанный многоугольникъ;’ сто-
роны этого многоугольника будутъ параллельны сторонамъ
вписаннаго мн.-ка АВСВЕЕ.
м В и
в Е Ч
Черт. 171
— 149 —
998. Теорема. Если многоугольникъ правильный, то
1°, около него можно описать окружность;
2°, въ него можно вписать окружность.
1°. Проведемъ окружность черезъ
какія-пибудь три сосѣднія вершины
А, В и С (черт. 172) правильнаго
мн.-ка АВСВЕ и докажемъ, что оиа
пройдетъ черезъ четвертую вершину
В. Опустимъ изъ центра О перпен-
дикуляръ ОК на хорду ВС и соеди-
нимъ О съ А и В. Повернемъ четыре-
угольникъ АВКО вокругъ стороны
ОК такъ, чтобы онъ упалъ на че-
тыреуг.-къ ОВСК. Тогда КВ пой-
детъ по КС (вслѣдствіе равенства прямыхъ угловъ при точкѣ
К), точка В упадетъ въ С (такъ какъ хорда ВС дѣлится
въ точкѣ К пополамъ), сторона ВА пойдетъ по СВ (вслѣд-
ствіе равенства угловъ В и С) и, наконецъ, точка А упа-
детъ въ В (вслѣдствіе равенства сторонъ ВА и СВ). Изъ
этого слѣдуетъ, что ОА= ОВ, т.-е. точки А и В одина-
ково удалены отъ центра; поэтому вершина В должна лежать
па окружности, проходящей черезъ А, В и С Точно такъ же
докажемъ, что эта окружность, проходя черезъ три точки,
В, С и В, пройдетъ черезъ слѣдующую вершину Е и т. д.
2°. Изъ доказаннаго слѣдуетъ, что стороны правильнаго
мн.-ка всегда можно разсматривать, какъ равныя хорды одной
окружности; но такія хорды одинаково удалены отъ центра;
значитъ, всѣ перпендикуляры ОМ, ОЕ..., опущенные изъ О
па стороны многоугольника, раввы между собою, и потому
окружность, описанная радіусомъ ОМ изъ центра О, будетъ
вписанной въ мн.-къ АВСВЕ.
990. Слѣдствіе. Изъ предыдущаго видно, что окруж-
ности описанная около правильнаго мп.-ка и вписанная въ
него имѣютъ одинъ и тотъ же центръ. Этотъ общій центръ,
будучи одинаково удаленъ отъ всѣхъ вершинъ мн.-ка, дол-
женъ лежать па перпендикулярѣ, возстановленномъ изъ сре-
дины любой стороны, а будучи одинаково удаленъ отъ сторонъ
— 150 —
каждаго угла, онъ долженъ находиться на его биссектрпссѣ.
Поэтому, чтобы найти центръ описаннаго или вписаннаго
круга, достаточно опредѣлить точку пересЬченія двухъ перпен-
дикуляровъ къ срединамъ сторонъ, или двухъ бпссектриссъ
угловъ, или перпендикуляра съ биссекриссой.
930. Опредѣленія. Общій центръ окружности, описан-
ной около правильнаго мн.-ка или вписанной въ него, наз.
центромъ этого мп.-ка, радіусъ описанной окружности наз.
радіусомъ мн.-ка, а радіусъ вписанной окружности — апоѳе-
мою его.
Уголъ, составленный двумя радіусами, проведенными къ
концамъ какой-нибудь стороны правильнаго мп.-ка, паз. гъент-
ральнымъ угломъ. Такихъ угловъ въ ми.-кѣ столько, сколько
сторонъ; всѣ они равны, какъ измѣряющіеся равными дугами.
Такъ какъ сумма всѣхъ центральныхъ угловъ равна 4г/
или 360°, то каждый изъ пихъ равенъ 4б//п или 360,)/п. если
п означаетъ число сторонъ ми,- ка.
331. Теорема. Правильные одноименные многоугольники
подобны, и стороны ихъ относягпся, какъ радіусы или
аповемы.
Іерт. 173
1°. Чтобы доказать подобіе правильныхъ одноименныхъ
мн.-ковъ АВСВЕР и А1 Вг С\ Е1 Рі, достаточно обнару-
жить, что у нихъ углы равны и стороны пролорціанальпы.
И дѣйствительно, углы равны, такъ какъ каждый изъ нихъ
содержитъ одно и тоже число градусовъ, а именно —
(85), если п означаетъ число сторонъ каждаго мн.-ка; сто-
роны же, очевидно, пропорціанальны.
— 151 —
2”. Пусть О и Ол будутъ центры данныхъ мн.-ковъ,
ОА и ихъ радіусы, ОМ и О^МХ—апоѳемы. Тр.-ки
ОАВ и ОХАІВІ подобны, такъ какъ углы одного соотвѣт-
ственно равны угламъ другого. Изъ подобія ихъ слѣдуетъ:
— 0А — 0 ѵ
~ о1л1 “ ог мА
(181).
939. Слѣдствіе. Периметры правильныхъ многоугольни-
ковъ относятся, какъ радіусы или апооемы (189).
933. Задача. Вписать въ данный кругъ, квадратъ и
опредѣлить ею сторону въ зависимости отъ радіуса,
1°. Предположимъ, что АВ есть
сторона квадрата, вписаннаго въ дан-	В
ный кругъ О. Тогда дуга АВ долаша //І\\
равняться 2/4 окружности, и уголъ АОВ	(/	\\
долженъ быть прямой. Поэтому, для	____!<)_
построенія вписаннаго квадрата, доста-	у\	/>
точно провести два перпендикулярныхъ Ѵ\ / >'
діаметра АС и ВВ и копцы ихъ
соединить хордами. Четыреугольнкъ	174
АВСВ будетъ правильнымъ, потому
что дуги АВ, ВС, СВ и ВА равны, какъ соотвѣтствующія
равнымъ центральнымъ угламъ.
2°. Изъ прямоугольнаго тр.-ка АОВ находимъ:
АВ2 = АО2-±ВО2, т.-е. АВ2 = 2АО2
откуда	АВ — АО у 2
Условимся всегда обозначать черезъ ап численную вели-
чину стороны прав. вписан. мн.-ка, имѣющаго н сторонъ, а
черезъ В радіусъ круга; тогда выведенное равенство изобра-
зится такъ:
= В /2
931. Задача. Вписать въ данный кругъ правильный
‘^шестиугольникъ и опредѣлить его сторону въ зависимости
^тъ радіуса.
— 152 —
Предположимъ, что АВ есть сторона правч вписап. шести-
угольника. Тогда дуга АВ должна быть Ус часть окружности,
и, слѣд., уголъ АОВ долженъ содержать
60°. Такъ какъ тр.-къ АОВ равнобед-
ренный (АО-~ОВ), то углы А и В
равны и каждый изъ нихъ содержитъ по
(180°—60°). т.-е. по 60°. Такимъ,
образомъ, тр.-къ АОВ оказывается равно-
угольнымъ и, слѣд.. равностороннимъ, т.-е.
АВ — АО—ОВ. Итакъ, сторона прав.
впис. гиестиугольника равна радіусу, что,,
по принятому нами обозначенію, можно выразить такъ:
лс — В
Отсюда возникаетъ весьма простой способъ построеніи прав.
впис. шестиугольника (или дѣленія окружности на 6 равныхъ,
частей): давъ циркулю раствореніе, равное радіусу, отклады-
ваютъ этимъ раствореніемъ по окружности, одна за другою,
равныя дуги и точки дѣленія соединяютъ хордами.
%3а. Задача. Вписать въ данный кругъ правильный тре-
угольникъ и опредѣлить его сторону въ зависимости отъ
радіуса.
1°. Чтобы, раздѣлить окружность на 3-
равныя части, дѣлятъ ее сначала на 8
равныхъ частей (какъ указано въ преды-
/ /  \	\ ДУЩей задачѣ) и затѣмъ соединяютъ по
। /	\	части въ одну.
\/	’	\/	2°. Для опредѣленія стороны АВ про-
і ~~/С ведемъ діаметръ ВВ и хорду АВ. Тр.-къ
АВВ прямоугольный при вершинѣ А;
Черт. 176	поэтомуАВ=\]ВВ2— АВ2.Но ВВ=2В
и АВ — В (потому что дуга АВ есть.
7в часть окружности и, слѣд., хорда ^41) есть сторона прав..
впис. шестиугольника); значитъ:
а3 = ^(2 Д)2 — В2 = і/3 В2 = В
ЖЗв. Задача. Вписать въ данный круіъ правильный де-
— 153 —
сятиуголъникъ и опредѣлитъ его сторону въ завгісимосгни отъ
радіуса.
Предварительно докажемъ одно важное свойство прав.
десятиугольника. Пусть хорда АВ (черт. 177) будетъ сторона
такого многоугольника. Тогда уголъ АОВ равенъ 36°, а каж-
дый изъ угловъ А и В содержитъ по і/і (180° — 36°), т.-е..
по 72°. Раздѣлимъ уголъ А пополамъ прямою АО. Каждый:
изъ угловъ, образовавшихся при точкѣ А, будетъ равенъ 36°;
слѣд., Л АСО, имѣя два равные
угла, будетъ равнобедренный, т.-с.
АС= СО. А АВС также равно-
бедренный, потому что В=72° и
(7—180° —72°—36°=72(,;слѣд.,
АВ = АС— СО. По свойству бис-
сектриссы угла тр.-ка (198) можемъ
паписать:
АО: АВ — ОС: СВ [1]
Замѣнивъ АО и АВ равными
получимъ:
ОВ: ОС=ОС
т.-е. радіусъ ОВ раздѣленъ въ точ
немъ отношеніи (222), причемъ ОС есть его большая часть.
Но ОС равна сторонѣ прав. впис. десятиугольника; значитъ:
сторона правильнаго вписаннаго десягпиуголъника равна
большей части радіуса, раздѣленнаго въ среднемъ и- крайнемъ
отношеніи.
Теперь задача рѣшается легко!
1 °. Дѣлятъ радіусъ круга въ среднемъ и крайнемъ отно-
шеніи (222); затѣмъ, давъ циркулю раствореніе, равное боль-
шей части радіуса, откладываютъ имъ по окружности дуги,
одна за другою, и точки дѣленія соединяютъ хордами (этО'
построеніе указано на черт. 177; хорды ВЕ и ВЕ суть двѣ.
смежныя стороны прав. 10-угольника).
2°. Пропорцію [2] можно переписать такъ:
“ аіо ’
откуда	4-7Ц0 — ІВ — о
Черт. 177
имъ прямыми ОВ и ОС,
: СВ	[2]
ѣ О въ среднемъ и край-
— 154 —
Рѣшивъ это квадратное уравненіе, найдемъ:
«39. Замѣчанія. 1". Формулы, выведенныя нами въ пре-
дыдущихъ задачахъ для ае>. и а10, позволяютъ вы-
числитъ радіусъ описаннаго круга, по данной сторонѣ прав.
многоугольника. Такъ, изъ выраженія, опредѣляющаго «1(Р
находимъ:
р___ 2«ю	-ст10 (V 5+1) — 1	/ / е і і \
В~	------2 Мѵ5 4-1)
2°. Чтобы вписать въ данный кругъ прав. пятиугольникъ,
дѣлятъ окружность на 10 равныхъ частей (какъ указано выше)
и точки дѣленія соединяютъ чередъ одну хордами.
338.	Задача. Вписать въ данный кругъ ггравильиыа
п ят н адцатиугольни к ъ.
Чтобы найти 71» окружности, достаточно изъ 7С ея части
вычесть 710. Это видно изъ слѣд ющаго тождества:
і _ _і__ 5__ _з _ 2___1
6 іо—зо 30“ 30—15
Поэтому, если дуга АВ есть
в.-----7« окружности, а дуга ЛС есть
7ю часть ея, то дуга СВ будетъ
\	7і .ч окружности, а хорда СВ —
У/ \	сторона прав. вппс. 15-угольника.
\	\	/ Вычисленіе стороны СВ можно выпол-
\	)	/ пить, примѣняя теорему Птоломея (215)
\Ѵ у / к'ь четыреугольнику АСѢВ, въ которомъ
А С = «ю, СВ = «1Г). А О — 2Л, А В — ай —
Черт. 178	= В,СВ = \'4№- а2’іо, ВВ=а3 (такъ какъ
дуга равна 1/а окружности).
Теорема Птоломея даетъ:
АВ . СВ = АО . СВ + АС. ВВ
т.-е.	П 1 42?2 — а^10=^К . «15 + «іоа-
Подставивъ на мѣсто а10 и «3 ихъ выраженія, получимъ послѣ упро-
щеній:
а,5 = А И 4- 21/5 - 1 3" (у 5 - 1 ^)]
— 155 —
в ЗЭ. Задача. Но данному радіусу круга и сторонѣ
правильнаго вписаннаго многоугольника вычислить сторону
нравилгмаго одноименнаго описаннаго многоугольника.
Пусть АВСВ... будетъ прав.
впис. мн.-къ, а 7ИЛГР... одно-
именный прав. описанный. Такъ какъ
стороны правильныхъ одноименныхъ
мн.-ковъ относятся, какъ ихъ ра-
діусы или апоѳсмы (231), то:
МИ'. АВ—ОВ: ОВ
Черт. 179
Откуда:
°*--4Б — ()в •лв
ОЕ ѴО&—ВЯ*
Обозначивъ АВ и ОВ соотвѣтственно черезъ Ьп,
аѣ и В и замѣтивъ, что ВЕ=г/2АВ, будемъ имѣть:
Примѣръ. Вычислимъ сторону прав. описаннаго 10-уголь-
ника:
Ь — ^21®-— о#./— 22? / О'о —і)3 __
=2ДѴ/?^=Д2/!-?!н^[)^
ѴЮ + 2Ѵ5	V (5 +/5) (5 — Ѵ'5)	V Ю
240. Замѣчаніе. Формула, опредѣляющая Ьп, позволяетъ
вычислить а„ по даннымъ Ьл и В. Для эгого стоитъ только
рѣшить уравненіе, принимая ап за неизвѣстное:
Ѵ(Л’-6, Л1 = «Д-В’+У)
241. Задача. Удвоить число сторонъ правильнаго впи-
саннаго многоугольника.
Въ этомъ сокращенномъ выраженіи разумѣются собственно
— 156 —
двѣ задачи: 1°, по данному правильному впие. мп.-ку по-
строить другой мн.-къ, вписанный въ ту же окружность и
имѣющій вдвое болѣе сторонъ; 2°. вычислитъ сторону этого
мн.-ка по данной сторонѣ перваго мн.-ка и данному радіусу
круга.
1°. Пусть АВ есть сторона прав.
впис. мп.-ка, имѣющаго и сторонъ,
и О центръ круга. Проведемъ
00 і АВ и соединимъ А съ С.
Дуга АВ дѣлится въ точкѣ С по-
поламъ; слѣд., хорда АС будетъ сто-
рона прав. впис. мн.-ка, имѣющаго
2и сторонъ.
2°. Изъ тр.-ка АС О нахо-
димъ (208):
АС*=ОА2+ОС2~ 2ОС . ОВ
т.-е. а\п=Е2-\-В2-2В. ОВ = 2ВІ-2В. ОВ
Изъ прямоугольнаго тр.-ка А ВО опредѣлимъ катетъ ОВ:
ОІ) — )/ ОАг	—	= у/ № -
Такова формула удвоенія числа сторонъ прав. впис. много-
угольника
Примѣръ. Вычислить сторону прав. впис. 12-угольника:
ам=фв?—
2І?г^/? = ^/2ЛГ-7г\/3 = Л^2-?3
На сколько равныхъ частей можно дѣлить окруж-
ность помощью циркуля И линейки. Примѣняя указанные въ
предыдущихъ задачахъ способы, мы можемъ помощью циркуля
— 157 —
и липейки дѣлить окружность па такое число равныхъ частей,
которое заключается въ слѣдующихъ рядахъ:
3,	3.2,	3.2.2....	вообще	3.2*
4,	4.2,	4.2,2....	вообще	2я
5,	5.2,	5.2.2....	вообще	5.2я
15,	15.2,	15.2,2,...	вообще	3.5.2*
Германскій математикъ Гауссъ (умершій въ 1855 г.) до-
казалъ, что посредствомъ циркуля и липейки можно дѣлить
окружность на такое число равныхъ частей, которое, будучи
простымъ, выражается формулою 2* + 1. Напр., окружность
можно раздѣлить на 17 равныхъ частей, такъ какъ 17 есіь
число простое вида 2*-г 1 (17 = 2І-|-1). Доказательство
Гаусса выходитъ изъ предѣловъ элементарной математики.
На всякое иное число равныхъ частей окружность можетъ
быть раздѣлена только приближенно.
943.	Построеніе правильнаго многоугольника по данной
сторонѣ. Для различныхъ правильныхъ мн.-ковъ существуютъ
различные способы. Но можно указать слѣдующій общій спо-
собъ. Чертятъ окружность произвольнаго радіуса и вписыва-
отъ въ пее прав. мп.-къ съ такимъ числомъ сторонъ, кото-
рое должно быть у искомаго мн.-ка; затѣмъ на данной сто-
ронѣ строятъ мп.-къ, подобный вписанному (190).
УПРАЖНЕНІЯ.
241.	Составить формулу для стороны правильнаго вписаннаго 24-
угольника.
242.	Составить формулы для сторонъ правильныхъ вписанныхъ 8-
угольника и 16-угольплка.
243.	Исходя изъ формулы удвоспія. опредѣлить сторону прав. впис.
5-угольника.
244.	Составить формулы для сторонъ правильныхъ оппсапныхъ тре-
угольника и шестиугольника.
245.	Доказать, что если въ прав. о-угольппкѣ проведемъ всѣ діаго-
нали, то онѣ своими пересѣченіями образуютъ внутренній нрав. 5-уголь-
нпкъ.
— 158 —
246.	Пусть АВ, ВС и СВ будутъ три послѣдовательныя стороны пра-
вильнаго мн. ка, имѣющаго центръ въ О. Если продолжимъ стороны АВ
и СВ до взаимнаго пересѣченія въ точкѣ Л’, то четыреугольникъ ОАВС
можетъ быть вписанъ вт. окружность.
247.	Доказать, что: 1°, всякій вписанный равпостороппій многоуголь-
никъ есть правильный; 2°, равноугольный вписанный мн - къ есть пра-
вильный, когда число сторонъ его нечетное; 3°, всякій оппсапный равно-
угольный мн.-къ есть правильный; 4°, описанный равносторонній мн.-къ
есть правильный, когда число сторонъ его нечетное.
248.	Доказать, что двѣ діагонали правильнаго 5-угольника, по исхо-
дящія изъ одной вершины, пересЕкаются въ среднемъ и крайнемъ от-
ношеніи.
249.	На данной сторонѣ постропть прав. 8-уго.іьникъ.
250.	На дайной сторонѣ построить прав. 10-угольникъ.
251.	Срѣзать отъ даннаго квадрата углы такъ, чтобы образовался
правильный 8-угольникъ
252.	Въ данный квадратъ вписать равносторонній тр -къ, помѣщая
одну изъ его вершинъ или въ вершинѣ квадрата, пли съ срединѣ какой
либо стороны.
253.	Вписать въ разносторонній тр.-къ другой равносторонній тре-
угольникъ, котораго стороны были бы перпендикулярны къ сторонамъ
даннаго.
254.	Построить углы: въ 18, въ 30, въ 7', въ 72 градуса.
КНИГА IV.
ОПРЕДѢЛЕНІЕ ДЛИНЫ ОКРУЖНОСТИ И ІЯ ЧАСТИ.
ГЛАВА I.
Основныя свойства предѣловъ.
Величины постоянныя и перемѣнныя. Рѣшая какой
либо вопросъ, въ который входятъ нѣсколько величинъ, мы
иногда предполагаемъ, что нѣкоторыя изъ этихъ величинъ
сохраняютъ одно и то же значеніе, тогда какъ другія спо-
собны принимать безчисленное множество различныхъ значеній.
Первыя величины наз. постоянными, вторыя — перемѣнными.
Такъ, разсматривая зависимость между длиною хорды и ея
разстояніемъ отъ центра, мы считаемъ радіусъ круга величи-
— 159 —
ною постоянною, а длину хорды и ея разстояніе отъ центра—•
величинами перемѣнными.
245. Величины, стремящія я къ нулю. Если перемѣнная
величина, измѣняясь, дѣлается меньше какого угодно малаго
даннаго значенія и при дальнѣйшемъ измѣненіи постоянно
остается меньше этого значенія, то говорятъ, что эта пере-
мѣнная величина стремится къ нулю.
Напр., если изъ одной точки окружности проведемъ ка-
сательную и сѣкущую (см. черт 97) и затѣмъ станемъ вра-
щать сѣкущую вокругъ точки касанія такъ, чтобы вторая точка,
пересѣченія все ближе и ближе придвигалась къ точкѣ каса-
нія, то при этомъ уголъ, составленный касательною и сѣку-
щею, будетъ стремиться къ пулю, потому что онъ можетъ сдѣ-
латься меньше какого угодно малаго угла, напр. меньше угла,
въ Г, и, при дальнѣйшемъ сближеніи точекъ пересѣченія,
будетъ постоянно оставаться меньше этого угла. Точно также
центральный уголъ правильнаго многоугольника стремится къ О,
если число сторонъ этого мн.-ка неограниченно возрастаетъ.
246. Величины, стремящіяся къ предѣлу. Иногда слу-
чается, что перемѣнная величина, измѣняясь, стремится къ
нѣкоторому предѣлу.
Предѣломъ перемѣнной величины наз. такая постоянная
величина, къ которой перемѣнная приближается все ближе и
ближе такъ, что разность между ними стремится къ нулю.
Приведемъ два примѣра перемѣнныхъ величинъ, стремя-
щихся къ предѣламъ.
А
А,
Черт. 181
Для перваго примѣра разсмотримъ процессъ измѣренія
какой-нибудь длины А, несоизмѣримой съ единицею В. Чтобы
измѣритъ такую длину (143,2°), мы дѣлимъ В на п равныхъ
частей и одну изъ нихъ откладываемъ на А столько разъ,
— 160 —
сколько можно. Тогда мы получаемъ соизмѣримую длину Ах,
которая меньше А; если же отложимъ 1Д долю В еще одинъ
разъ, то получимъ другую соизмѣримую длину Л2, которая
больше Л; при этомъ каждая изъ разностей А— Аг иА3-—А
меньше 1Д доли В. Предположимъ теперь, что число п рав-
ныхъ частей, па которое мы дѣлимъ В, увеличивается не-
ограниченно. Тогда длины Ах и Л2 становятся перемѣнными:
каждая изъ нихъ стремится къ предѣлу А, такъ какъ раз-
ности между этою постоянною величиною и перемѣнными А{
и А3 стремятся къ О, т.-е. дѣлаются й остаются меньше
какой угодно малой данной длины.
Изъ этого примѣра мы видимъ, что перемѣнная, прибли-
жаясь къ своему предѣлу, можетъ быть или больше его, пли
меньше; такъ, длина постоянно остается меньшею, чѣмъ
А, а длина А3. наоборотъ, всегда больше А.
Для второго примѣра возьмемъ величину угла правильнаго
многоугольника, имѣющаго п сторонъ. Эта величина равна
2(7 (п-2)__^	4(7
п	и
Предположимъ, что число сторонъ многоугольника неогра-
ниченно увеличивается; тогда, какъ видно изъ написанной фор-
мулы, величина угла мн.-ка будетъ все болѣе и болѣе при-
ближаться къ 2(7, такъ что разность между ними, равная
4(7 ѵ
дѣлается и остается меньше какого угодно малаго угла.
Поэтому можно сказать, что уголъ прав. мп.-ка, при неогра-
ниченномъ увеличеніи числа его сторонъ, имѣетъ предѣлъ 2(7.
Величины, увеличивающійся безпредѣльно. Если
перемѣнная величина, измѣняясь, дѣлается и остается больше
какого угодно большого даннаго значенія, то говорятъ, что
она увеличивается безпредѣльно (или неограниченно).
Напр.^ сумма угловъ выпуклаго многоугольника, равная
2(7 (н—2), при неограниченномъ возрастаніи числа сторонъ,
увеличивается безпредѣльно *).
*) Величины, увеличивающіяся безпредѣльно, принято въ математикѣ на-
зывать безконечно большими, а величины, стремящіяся къ пулю, — безконечно
малыми. Въ этой книгѣ мы не будемъ однако употреблять этихъ терминовъ для
избѣжанія нѣкоторой неясности представленія въ умѣ учащагося.
—161 —
948. Теорема. Если двѣ перемѣнныя величины, стре-
мящіяся къ предѣламъ, при всѣхъ своихъ измѣненіяхъ оста-
ются рвными между собою, то равны и ихъ предѣлы.
Пусть а и Ъ будутъ двѣ перемѣнныя величины, а А и В
ихъ предѣлы, и положимъ, что при всѣхъ послѣдовательныхъ
измѣненіяхъ перемѣнныя а и Ъ всегда равны между собою:
требуется доказать, что въ такомъ случаѣ А = В.—Предпо-
ложимъ противное. Пусть, напр., А>В. Тогда разность
А — В должна равняться какой-пибудь постоянной величинѣ,
не равной нулю. Обозначимъ эту разность черезъ А. Чтобы
опровергнуть наше предположеніе, положимъ, что
а = Л + и Ъ — В-\~у
гдѣ х и у, означая разности между перемѣнными и ихъ пре-
дѣлами, суть величины, стремящіяся къ О. Такъ какъ, по
условію, а = 1), то значитъ:
А + х = В у
откуда:	А — В — у — х
т.-е.	д~у — х
Но это равенство невозможно, такъ какъ разность между ве-
личинами у и х, изъ которыхъ каждая стремится къ О,
не можетъ равняться постоянной величинѣ д. Невозмож-
ность равенства доказываетъ невозможность допущенія, что
А>В. Такъ же докажемъ, что А не можетъ быть меньше В.
Слѣд., А=В.
949. Теорема. Если двѣ перемѣнныя величины, стре-
мящіяся къ предѣламъ, при всѣхъ своихъ измѣненіяхъ сохра-
няюютъ одно и то же отношеніе, то въ томъ же отноше-
ніи находятся и ихъ предѣлы.
Пусть а и Ъ будутъ двѣ перемѣнныя величины, а А и В
ихъ предѣлы, и положимъ, что при всѣхъ измѣненіяхъ вели-
чины а и Ь постоянно удовлетворяютъ пропорціи:
а : Ъ = т : п
А. а. КИСЕЛЕВЪ.
11
— 162 —
гдѣ т и п какія-нибудь данныя числа. Требуется доказать,
чго въ такомъ случаѣ и
А : В — т : п
Положимъ снова, что а = А~І-х іл. Ъ = В-\-у, гдѣ х и у,
означая разности между перемѣнными и ихъ предѣлами,
должны быть величинами, стремящимися къ нулю. Подставивъ
въ данную пропорцію на мѣсто а и Ь суммы Я + а? и В-\~У,
получимъ:
А + х : В + у — т : п
Откуда:	Ап -|- пх — Вт + ту
Такъ какъ величина х стремится къ нулю, то и произведе-
ніе пх сгремится къ нулю;*) поэтому сумма Ап-\-пх представ-
ляетъ собою перемѣнную величину, которой предѣлъ есть по-
стоянная величина Ап. Подобно этому сумма Вт^-ту есть
перемѣнная величина, имѣющая предѣлъ Вт. Но если равны
перемѣнныя, то должны быть равны и ихъ предѣлы; значитъ:
Ап = Вт
Откуда:	А : В = т : п
Э5О. Основное начало способа предѣловъ. Двѣ преды-
дущія теоремы составляютъ частные случаи слѣдующаго важ-
наго предложенія:
Если какое либо равенство, содержащее перемѣнныя ве-
личины, остается вѣрнымъ при всѣхъ измѣненіяхъ перемѣн-
ныхъ, то оно останется вѣрнымъ и тогда, когда на мѣсто
перемѣнныхъ подставимъ ихъ предѣлы.
Это предюженіе служитъ основаніемъ такъ называемому
способу предѣловъ, которымъ иногда пользуются для дока-
зательства нѣкоторыхъ геометрическихъ истинъ.
Способъ Предѣловъ. Онъ состоитъ въ слѣдующемъ.
Положимъ, что мы желаемъ найти зависимость между нѣко-
торыми постоянными величинами Л и В, и допустимъ, что
*) Мы принимаемъ безъ доказательства, что если въ произведеніи одинъ
сомнож-ітель постоянный, а другой стремится къ О, то и произведеніе стре-
мится къ О.
— 163 —
эту зависимость трудно (или даже невозможно) найти непо-
средственно. Тогда задаемся вопросомъ: нельзя ли величины
Л и В разсматривать, какъ предѣлы нѣкоторыхъ перемѣн-
ныхъ величинъ а и Ъ, и если можно, то какова зависимость
между а и Ь. Положимъ, оказалось, что эта зависимость вы-
ражается равенствомъ:
а = 37/
которое остается вѣрнымъ при всѣхъ измѣненіяхъ а и Ь; въ
такомъ случаѣ можемъ принять, что это равенство остается
вѣрнымъ и тогда, когда на мѣсто а и Ь подставимъ ихъ пре-
дѣлы, т.-е. чго и
А^ЗВ*
Такимъ образомъ, зависимость между Л и В мы найдемъ
косвеннымъ путемъ, отыскавъ предварительно зависимость
между перемѣнными.
ГЛАВА II.
Вычисленіе длины окружности.
«.»«. Предварительное разъясненіе. Конечную прямую
можно сравнивать съ другою конечною прямою, принятою за
единицу, вслѣдствіе того, что прямыя линіи при наложеніи
совмѣщаются. Дѣйствительно, только но этой причинѣ мы
можемъ совершенно точно установить, какія прямыя считать
равными и неравными, что такое сумма прямыхъ, какая пря-
мая болѣе другой въ 2, 3. 4.... раза, и т. п. Точно также
дуги окружностей одинаковаго радіуса можно сравнивать между
собою вслѣдствіе того, что такія дуги прп наложеніи совмѣ-
щаются. Но извѣстно, что никакая часть окружности или
какой бы то ни было другой кривой не можетъ совмѣститься
съ прямой (107); поэтому нельзя установить путемъ наложе-
нія, какой криволинейный отрѣзокъ должно считать равнымъ
данному прямолинейному отрѣзку, а слѣд. и то, какой кри-
11й
— 164 —
волинейный отрѣзокъ больше даннаго прямолинейнаго въ 2,
3, 4.... раза. Такимъ образомъ является необходимость опре-
дѣлитъ, что мы разумѣемъ подъ длиною кривойлиніи, когда
сравниваемъ ее съ прямолинейнымъ отрѣзкомъ. Слѣдующее
опредѣленіе приводитъ понятіе о длинѣ кривойкъ элементар-
ному понятію о длинѣ прямой.
«33. Опредѣленіе длины кривой. Пусть мы имѣемъ ка-
кую-нибудь конечную кривую АВ. Впишемъ въ пее произ-

IС/С
пь
р?
іЛ
Черт. 182
вольную ломаную АСВВ, которой концы совпадаютъ съ кон-
цами кривой. Найдемъ периметръ этой ломаной, т.-е. сумму
всѣхъ ея сторонъ; пусть это будетъ прямая І\. Впишемъ
теперь другую ломаную, напр. АЕЕ&В, у которой стороны
были бы меньше, чѣмъ у первой ломаной, и слѣд. число сто-
ронъ больше; найдемъ ея периметръ; пусть это будетъ пря-
мая Р2. Впишемъ далѣе третью ломаную, напр. АНКМЕВ,
у которой стороны были бы еще меньше, а число сторонъ
еще больше, и найдемъ ея периметръ; пусть это будетъ Р3.
Вообразимъ теперь, что мы продолжаемъ вписывать въ дан-
ную кривую все новыя и новыя ломаныя линіи, у которыхъ
стороны неограниченно уменьшаются, и каждый разъ нахо-
димъ ихъ периметры. Тогда получимъ безконечный рядъ пе-
риметровъ (Р1У Р ,	Доказано (265), что этотъ рядъ
стремится къ нѣкоторому предѣлу (напр. къ длинѣ Ь), вполнѣ
опредѣленному для данной кривой. Этотъ-то предѣлъ и при-
нимаютъ за длину кривой АВ.
-165-
Такимъ образомъ, длиною конечной кривой называется пре-
дѣлъ, къ которому стремится периметръ вписанной лома-
ной линіи, когда стороны ея неограниченно уменьшаются.
Слѣдствіе 1. Отрѣзокъ прямой короче всякой кри-
вой, проведенной между его концами.
Что отрѣзокъ прямой короче всякой ломаной, проведен-
ной между его концами, было доказано ранѣе (51). Теперь мо-
жемъ доказать ту же истину въ примѣненіи къ кривой. Пусть
АВ будетъ отрѣзокъ прямой, а АСВ какая-нибудь кривая,
проведенная между концами А и В.
Впишемъ въ кривую произвольную
ломаную, напр. АСВ, и затѣмъ во-
образимъ, что число сторонъ этой
ломаной неограниченно удваивается,
т.-е. что вмѣсто ломаной АСВ, со-
стоящей изъ двухъ сторонъ, берется
вписанная ломаная АВСЕВ, состоящая изъ 4-хъ сторонъ.
Черт. 183
затѣмъ вмѣсто этой берется вписанная ломаная, состоящая
изъ 8-ми сторонъ, и т.-д. безъ конца. Отъ этого периметръ
ломаной будетъ все увеличиваться (папр., АВ-^-ВС^СЕ-^ЕВ
болѣе ЛС-гСД потому что АВ ВО АС и СЕ-\-
-і-ЕВ'>СВ); значитъ, предѣлъ, къ которому опъ стре-
мится. будетъ больше ломаной АСВ, а потому, и по-
давно, больше прямой АВ. Но предѣлъ периметра вписанной
ломаной есть то, что наз. длиною кривой; слѣд. длина кри-
вой АСВ больше прямой АВ.
»55. Слѣдствіе 2. Выпуклая
гой линіи, объемлющей ее.
Для ломаныхъ линій это пред-
ложеніе было доказано ранѣе (52).
Убѣдимся теперь, что во 1° вы-
пуклая ломаная короче объемлю-
щей' кривой, и во 2° выпук-
лая кривая короче всякой объем-
лющей (кривой или ломаной).
1°. Пусть АОВ есть выпуклая
линія короче всякой дру-
ломаная, а АтпВЕрцВ какая нибудь объемлющая линія (кри-
—166 —
вая или составленная изъ частей кривыхъ и прямолинейныхъ).
Возьмемъ на ней какія-нибудь точкиЛІ и Л’ и проведемъ хорды
АМ, МВ, ЕЕ и ЯВ. Тогда получимъ ломаную АМВЕЯВ,
которая по отношенію къ ломаной АСВ будетъ объемлющая;
слѣд. (52):
АМ + МВ -гВЕ4- ЕЯ+ ЯВ >ЛО-'г СВ
Такъ какъ дуга АтМ больше хорды АМ, дуга МпВ больше
хорды МВ и т. д., то длина линіи АттВЕрцВ больше пе-
риметра ломаной АМВЕЯВ; слѣд.. она л подавно больше
ломаной АСВ.
2°. Пусть АСВ есть выпуклая крп-
— В —---------ч вая, ѣАВВ какая-нибудь объемлю-
	у щая линія (кривая или ломаная).
[	Л**-I Выберемъ на объемлющей линія та-
\ //	А/	кія двѣ точки Е н Е, чтобы пря-
.....-.........мая ЕЕ не пересѣкалась съ крп-
Черт 185.......вою АСВ. Всѣ ломаныя линіи, впи-
санныя въ эту кривую, будутъ тогда
меньше объемлющей линіи АЕЕВ (по доказанному въ первой
части этого предложенія); вслѣдствіе этого предѣлъ перимет-
ровъ вписанныхъ ломаныхъ, т.-е. длина кривой АСВ, не
можетт, быть больше линіи АЕЕВ; но эта линія короче кри-
вой АВВ; значитъ, длина кривой АСВ меньше длины кри-
вой АВВ.
		Длина окружности. Согласно
данному выше опредѣленію, м длину
н/___________Ѵ\ окружности принимагогпъ предѣлъ, къ
и	\\	которому стремится периметръ вті-
Ы	М	саннаго многоугольника, когда стороны
Л.	У]	сю неограниченно уменьшаготсн, и,
У/ слѣд., число сторонъ неограниченно уве-
ли чивается.
«59. Сравненіе длины окружности
Черт 186 съ периметрами вписанныхъ и опи-
санныхъ многоугольниковъ. Пусть въ данную окружность впи-
санъ какой-нибудь многоугольникъ АВСВ и описанъ какой-
— 167 —
Черт. 187
іта; значитъ,, окруж-
нибудь многоугольникъ МЫРі^В. Такъ какъ дуга АВ боль-
ше хорды АВ, дуга ВС больше хор-
ды ВС и т. д., то окружность
больше периметра всякаго вписаннаго
многоугольника. Съ другой стороны,
такъ какъ дуга аЪ меньше аМ-\-МЬ,
дуга Ъс меньше	и т. д., то
окружность меньше периметра всякаго
.описаннаго многоугольнггка.
Напр., окружность больше периметра
правильнаго вписаннаго шестиугольника
и меньше периметра описаннаго квад
постъ больше 6-ти радіусовъ и меньше 8-ми радіусовъ (такъ
какъ сторона прав. впис. шестиугольника равна радіусу, а
•сторона описаннаго квадрата — діаметру).
Для болѣе точнаго вычисленія длины окружности въ зави-
симости отъ радіуса докажемъ слѣдующую теорему.
Теорема. Окружноспѵи относятся, кань радіусы
гіли діаметры.
Пусть В и 7?] будутъ радіусы двухъ окружностей, а С
и С, ихъ длины; требуется доказать, что
27^:2^
Впишемъ въ данныя окружности какіе-ппбудь правильные
одноименные многоугольники (напр., шестиугольники) и затѣмъ
вообразимъ, что число ихъ сторонъ неограниченно удваивается
(т.-е. вмѣсто шестиугольниковъ берутся 12-угольники, за-
тѣмъ 24-угольники и т. д. безъ конца). Обозначимъ перемѣн-
ные периметры этихъ многоугольниковъ черезъ р и р}. Тогда
будемъ имѣть пропорцію (232):
р : рг — В: Вг
Но если перемѣнныя величины сохраняютъ одно и то же от-
ношеніе, то и предѣлы ихъ находятся въ томъ же отношеніи
(249): предѣлы же периметровъ р и рх будутъ длины окруж-
ностей С и С\; значитъ:
С: С = В: Вх
— 168 —
Умноживъ оба члена второго отношенія на 2, получимъ:
О:(\= 27?: 2В1
959. Слѣдствія. 1°. Переставивъ въ послѣдней пропор-
ціи средніе члены, будемъ пмѣть:
0:27?=^: 27?,
т.-е. отношеніе окружности къ своему діаметру есть числа
постоянное для всѣхъ окружностей.
Это число обозначаютъ греческою буквою я.
2°. Зная радіусъ и число к, мы можемъ вычислить длину
окружности изъ равенства:
С: 27?=^; откуда С=2^1І
т.-е. длина окружности равна произведенію ея радіуса на
удвоенное отношеніе окружности къ діаметру.
990. Понятіе 0 вычисленіи г., Доказано, что отношеніе
окружности къ діаметру есть число несоизмѣримое *) и потому
не можетъ быть выражено точно пп цѣлымъ, ни дробнымъ
числомъ. Но можно найти приближенное значеніе ~ съ ка-
кою угодно точностью. Укажемъ одинъ изъ способовъ этого
вычисленія.
Если радіусъ примемъ за единицу длины, то длина окруж-
ности выразится числомъ 2 и. Поэтому можно сказать, что ъ
есть длина полуокружности единичнаго радіуса. Чтобы вы-
числить полуокружность съ нѣкоторымъ приближеніемъ, на-
ходятъ полупериметры правильныхъ вписанныхъ мн.-ковъ, ко-
торые получаются черезъ удвоеніе какого-нибудь одного изъ
нихъ, напр. шестдугольника. Для этого предварительно на-
ходятъ длины сторонъ этихъ мн.-ковъ, а затѣмъ полупери-
метры. Обозначая, но принятому, черезъ ап сторону прав.
впис. мн.-ка, имѣющаго п сторонъ, будемъ имѣть:
«с —
*) и даже, болѣе того, число трансцендентное, т.-е. такое, которое не можетъ
служить корнемъ никакого алгебраическаю уравненія. См. брошюру А. ЛГар-
коѳа: „Доказательство трансцендентности чиселъ е л 77.“, С.-Петербургъ, 1883 г,
— 169 —
Примѣняя теперь формулу удвоенія (241). т.-е. а22)1 =
= 21?2—21? </I?2 — находимъ:
V 4__________
«212= 2 — 2 у/1 — 1=2 —/3 = 0,26795...
Послѣ этого, пользуясь тою же формулою, послѣдова-
тельно вычисляемъ:
«224 = 2 — 2 ^/1 — а2іѣ= 2 — 2^/1 — и т. д.
Положимъ, что мы прекратили удвоеніе на 96-угольникѣ.
Чтобы получить его полупериметръ, надо сторону умножить
на 48. Сдѣлавъ всѣ упрощенія и вычисленія, найдемъ (обоз-
начая периметръ буквою _/? съ соотвѣтствующимъ знакомъ):
„ = 48^2 —^2+ ^2+^2 +1/3 = 3,1410319...
Если полупериметръ 9 6-угольника примемъ за длину
полуокружности, то, конечно, сдѣлаемъ нѣкоторую погрѣш-
ность. Чтобы судить о величинѣ ея, вычислимъ еще полу-
периметръ правильнаго описаннаго 96-угольника. Для этого
воспользуемся формулою, дающей выраженіе для стороны опи-
саннаго мн.-ка по сторонѣ вписаннаго (239):
гдѣ означаетъ периметръ описаннаго 96-угольника. Под-
ставивъ на мѣсто 7А« и Л9С найденныя прежде числа и сдѣ-
лавъ вычисленія, найдемъ:
-ІР96 = 3,1427146...
Полуокружность болѣе полупериметра вписаннаго, но меньше
полупериметра описаннаго 96-угольника (257); поэтому она
отличается отъ каждаго изъ этихъ полупериметровъ меньше,
чѣмъ они разнятся между собою. Сравнивая два числа, пай-
— 170 —
денныя для '/.2р*6 и	замѣчаемъ, что у нихъ одина-
ковы цѣлыя, десятыя п сотыя доли; слѣд.. разность между
полу периметрами меньше */1п. Поэтому если положимъ, что
~ =3,14, то сдѣлаемъ ошибку, меньшую 0,01.
Если подобнымъ образомъ продолжимъ вычисленіе до по-
лученія полупериметра мн.-ка о 6144 сторонахъ, то получимъ
число, точное до одной милліонной:
к = 3,141 592
Полезно также запомнить нѣсколько цыфръ числа
^0,318 309 886...
часто встрѣчающагося при вычисленіяхъ.
«ві. Архимедово и Меціево отношенія, Архимедъ, зна-
менитый Сиракузскій геометръ, жившій въ III вѣкѣ до Р. Хр.,
нашелъ для и весьма простое число "/?, т.-е. Зг/7. Это чисто
нѣсколько болѣе г. и разнится отъ него менѣе, чѣмъ на 2
тысячныхъ.
Адріанъ Мецій, голландскій геометръ XVI столѣтія, далъ
для отношенія окружности къ діаметру число заи/ш, точное
до одной милліонной*): его легко запомнить по слѣдующему
правилу: написавъ по 2 раза первыя три нечетныя цыфры
113 | 355
слѣдуетъ послѣднія три взять числителемъ, а первыя знаме-
нателемъ.
Ученые позднѣйшаго времени, пользуясь упрощенными спо-
собами (которые указываются высшей математикой), вычислили т.
съ точностью, далеко превосходящею всякія практическія требо-
ванія (такъ, ІПенксъ нашелъ 530 десятичныхъ знаковъ числа к**).’)
Длина дуги въ п0. Такъ какъ длина всей окруж-
*)	Какъ разъясняетъ г. Энештремъ (Стокгольмъ) въ № 94 „Вѣстника
опытной физикп и элементарной математика", число это было найдено отцемъ
Адріана Мсція, математикомъ Андріаномъ Антонисомъ.
*•	) Для запоминанія довольно длиннаго ряда цифръ, выражающихъ число
1:, можво пользоваться слѣдующимъ французскимъ двустишіемъ:
$не у'аіте а /аііе аррі епйге
Гп потЬге гііііе аих Ъоттез1
Если выписать въ рядъ числа буквъ, заключающихся въ каждомъ словѣ
этой Фразы, то иолучимъ д.ія 7: число 3,141о9?б53б, вѣрное до одной половины
десяти билліонной.
— 171 —
ности есть 2~7Л то длина дуги въ 1° будетъ = слѣд.,
длина <$ дуги, содержащей и0, выравитси такъ:
-Цуі
Тйо
Если дуга выражена въ минутахъ (?/) или секундахъ (п"),
то длина ея опредѣлится формулами:
~Ііп' , _______ —Яп"
Т80.6О	“ 180.60 60
963.	Задача. Вычислитъ съ точностью до 1 миллиметра
радіусъ, такой окружности, которой дуга, содержащая
85*21'42", равна 0,452 метра.
Обративъ 85’21'42" въ секунды, получимъ число 307302".
Изъ уравненія:
дг о —	.307302
180.60^60
Р _ 0.452.180.60.60 _ Л о Л о
' - -п, 307302 — 0,303 (метра)
находимъ:
964.	при доказательствѣ нижеслѣдующей теоремы мы будемъ осно-
вываться па слѣдующихъ почти очевидныхъ истинахъ:
1°. Если перемѣнная величина, измѣняясь, все увеличивается, но при этомъ
остается менігие нѣкоторой постоянной величины, то она имѣетъ предѣлъ.
2°. Если перемѣнная величина, измѣняясь, все уменьшается, но при этомъ
остается больше нѣкоторой постоянной величины, то она имѣетъ предѣлъ.
3°. Если разность двухъ перемѣнныхъ величинъ стремится къ О, гі одна
изъ этихъ величинъ имѣетъ предѣлъ, то другая имѣетъ тотъ же предѣлъ.
96 Теорема. Нереметръ ломаной линіи, вписанной въ данную конеч-
ную кривую, стремится кх предѣлу и притомъ единственному, когда стороны
ломаной стремятся къ О.*)
Еслп данная кривая ис выпукла, мы можемъ разбить ее па части,
изъ которыхъ каждая выпукла. Поэтому теорему достаточно доказать
только для выпуклой кривой.
Пусть ЛБСБ (черт. 188) есть ка-
кая-нибудь ломаная, вписанная въ ко-	ѣ.
печную выпуклую кривую АБ. Ирове-
демъ черезъ всѣ ея вершины касатель-	хЧх.
ныя до взаимнаго пересѣченія. Тогда \//к
получимъ описанную ломанную АКЪМБ. у/ ѵ
Условимся называть такую описанную А-	1
линію соотвѣтственную для вписанной	Черт. 188
ломаной АБСБ.
*) Излагаемое доказательство взято (съ нѣкоторыми измѣненіями) изъ книги;
„Еіётепія -<1с ^отёЬгіе, раг Ііоисііё'еі СотЬегоиззе", диаігіёте ёйібіоп, 1888.
— 172 —
Доказательство наше будетъ состоять изъ трехъ частей.
1°. Пусть р означаетъ периметръ какой угодно вписанной, а Р периметръ
соотвѣтственной описанной линіи. Докажемъ, что разность Р—р стремится
къ О, когда стороны вписанной линіи стремятся къ О. Для этого предва-
рительно найдемъ предѣлъ отношенія Р:р. Изъ вершинъ описанной ло-
маной опустимъ перпендикуляры на стороны вписанной (черт. 188).
Тогда:
р=ак + КВ + ВР + РС + см + ю
р = Ак + кВ + РІ + ІС 4- Ст 4- тО
Изъ алгебры извѣстно *), что величина дроби
АК + КР + ВЪ+РС +СМ+ Ш) _Р
Ак 4- к'В 4- РІ 4- ІС 4- Ст 4- тІ) ~ р
заключается между меньшею п большею изъ дробей:
АК КВ ВР	Мр	г
Ак’ кВ ’ ВІ ”* тѴ	1 -
Найдемъ предѣлъ, къ которому стремятся эти дроби. Когда стороны впи-
санной ломаной стремятся къ О, стороны соотвѣтственной описанной линіи
также, очевидно, стремятся къ О; поэтому каждая изъ дробей ряда [2] пред-
ставляется въ предѣлѣ подъ видомъ %. Чтобы раскрыть истинный смыслъ
этой неопредѣленности, возьмемъ отдѣльно (черт.
1890 какой-нибудь изъ прямоугольныхъ тр.-ковъ
чертежа 188-го, наир., Л АКк. Продолживъ сто-
рону Ак, отложимъ па пей какую-нибудь по-
стоянную длину А8 и построимъ Л АВ8, подоб-
ный А АКк. Тогда:
АК-.Ак = АВ.А8
Когда стороны вписанной ломаной стремятся къ О, уголъ А, составлен-
ный касательною и хордою, стремится къ О (130, 245); слѣд., гипоте-
нуза АВ приближается какъ угодно близко къ равенству съ катетомъ
А8, и потому отношеніе АВ: А8, а слѣд. и отношеніе АК: Ак, стре-
мится къ 1. Такъ какъ это разсужденіе можно примѣнить ко всякому
треугольнику чертежа 188-го, то, значитъ, каждая дробь изъ ряда [21
имѣетъ предѣломъ 1; слѣд., и дробь [Г| имѣетъ тотъ же предѣлъ.
Доказавъ это, возьмемъ разность Р—р н представимъ ее такъ:
В
Черт. 189
Отношеніе ^]р стремится къ 1; слѣд., разность — 1 стремится къ О.
Влѣдствіе этого и произведеніе — въ которомъ множимое вели-
чина конечная (такъ какъ периметръ р не можетъ сдѣлаться больше
•) См., иаир., „Элементарная алгебра, сост. А. Киселевъ-', второе изданіе,
стр. 231.
— 173 —
периметра любой описанной линіи), также стремится къ О; значитъ,
<1’0 же самое можно сказать о разности Р —р.
2°. Докажемъ теперь, что периметръ вписанной ломаной стремится
къ предѣлу при слѣдующемъ частномъ законѣ вписыванія. Концы данной
кривой соединимъ хордою. Изъ средины этой хорды возставимъ перпен-
дикуляръ до пересѣченія съ кривою. Соединивъ точку пересѣченія съ
концами хорды, получимъ первую ломаную о двухъ сторонахъ. Изъ сре-
динъ ея сторонъ возставимъ перпендикуляры до пересѣченія съ кривою.
Соединивъ точки пересѣченія съ сосѣдними вершинами первой ломаной,
получимъ вторую ломаную съ 4-мя сторонами. Возставивъ изъ срединъ
сторонъ этой ломаной перпендикуляры до пересѣченія съ кривою и со-
единивъ полученныя точки съ сосѣдними вершинами второй ломаной,
образуемъ третью ломаную съ 8-ю сторонами. Вообразимъ, что по этому
закону мы строимъ неограниченный рядъ вписанныхъ ломаныхъ. Тогда
периметръ этихъ линій будетъ все увеличиваться, оставаясь однако
меньше периметра любой описанной линіи; вслѣдствіе этого онъ стре-
мится къ нѣкоторому предѣлу. Обозначимъ этотъ предѣлъ черезъ Р.
Тотъ же предѣлъ имѣетъ и периметръ соотвѣтственной описанной
ломаной, такъ какъ, по доказанному, разность между этими периметра-
ми стремится къ О.
3°. Докажемъ, наконецъ, что къ тому же предѣлу Ь стремится пе-
риметръ вписанной ломаной, которой стороны уменьшаются по какому
у > одно закопу.
Пусть рі есть перемѣнный периметръ такой вписанной линіи, которой
стороны стремятся къ О по произвольному закону, а р периметръ впи-
санной линіи, образуемой по указанному выше частному закону; поло-
жимъ еще, что Рі и Р будутъ периметры соотвѣтственныхъ описан-
ныхъ, линій. По доказанному въ части 1° этого изложенія разности:
и Р-р
стремятся къ О. Поэтому и сумма ихъ должна стремиться къ О. Но эту
сумму можно представить такъ:
(Рі—р) + (Р—.р^
Такъ какъ Рх>>р и Р>Рі (53), то обѣ разности, стоящія внутри ско-
бокъ, положительны. Но сумма положительныхъ слагаемыхъ будетъ стре-
миться къ О только тогда, когда каждое слагаемое стремится въ О; слѣд.,
разности Р) — р и Р—Р\ стремятся къ О. Отсюда слѣдуетъ, что
пред. Рі=пред.р п пред. Р = пред.рг
Но	пред. р~пред. Р—Ь
Слѣд.	пред. рг =. пред. Рг — пред.р — пред. Р — Ъ
т.-е. этотъ предѣлъ существуетъ п есть единственный для данной ко-
нечной кривой.
— 174 —
У Л Р А Ж 11 Е Н I Я.
255.	Доказать, что въ двухъ кругахъ отношеніе центральныхъ угловъ,
соотвѣтствующихъ дугамъ, имѣющимъ одинаковую длину, равно обрат-
ному отношенію радіусовъ.
256.	Какъ велика будетъ ошибка, если вмѣсто полуокружности возь-
мемъ сумму стороны правильнаго вписаннаго треугольника и стороны
вписаннаго квадрата?
257.	На окружности взята точка А и черезъ нее проведены: діаметръ
АВ, сторона правильною вписаннаго 6- угольника А С и касательная ЛТК.
Изъ центра О опущенъ па АС перпендикуляръ и продолженъ до пере-
сѣченія съ касательнаго въ точкѣ В. Отъ этой точки отложена по ка-
сательной (черезъ точку А) прямая ВЕ, равная 3 радіусамъ. Точка Е
соединена съ концомъ діаметра В. Опредѣлить, какт» велика погрѣшность,
если прямую ВЕ возьмемъ за длину полуокружности *).
258.	На діаметрѣ данной полуокружности построены двѣ равныя по-
луокружности и въ пространство, заключенное между тремя полуокруж-
ностями, вписанъ кругъ. Доказать, что діаметръ этого круга относится
къ діаметру равныхъ полуокружностей, какъ 2:3.
259.	Вычислить въ градусахъ, минутахъ и секундахъ дугу, равную
радіусу.
260.	Вычислить длину одного градуса земного экватора, принимая
радіусъ земли въ 859 геогр. миль.
КНИГА V.
09
ИЗМѢРЕНІЕ ПЛОЩАДЕЙ.
ГЛАВА I.
Площади многоугольниковъ.
Опредѣленія. Площадью наз. величина части пло-
скости, ограниченной со всѣхъ сторонъ линіями.
*) Доказано, что посредствомъ циркуля и линейки нѣтъ возможности по-
строить такую конечную прямую, которая въ точности равнялась бы длинѣ
окружности (задача о спрямленіи окружности). Однако есть нѣсколько спо-
собовъ для приближеннаго спрямленія. Въ задачахъ 256 и 257 указаны два.
изъ этихъ способовъ. Послѣдній изъ нихъ, принадлежащій польскому іезуиту
Ііоханскому (1683), замѣчателенъ тѣмъ, что можетъ быть выполненъ однимъ
раствореніемъ циркуля.
— 175 —
Напр., еслп прямо-
Черт. 191
квадрата, у котораго
Равныя фигуры, т.-е. такія, которыя совмѣщаются при
наложеніи, имѣютъ и равныя площади. Но и у неравныхъ
фигуръ площади могутъ быть равны,
угольникъ АВСВ раздѣлимъ пополамъ
діагональю АС и перенесемъ тр.-къ
АВС въ положеніе ВСЕ, то получимъ
параллелограммъ АСЕВ, котораго пло-
щадь, очевидно, равна площади прямо-
угольника.
Двѣ фигуры, имѣющія равныя пло-
щади, наз. равновеликгіми.
гв?. Единица площади. За еди-
ницу площадей берутъ площадь такого
сторона равна линейной единицѣ. Такъ, употребительны квадр.
футъ, квадр. метръ и т. п.
Измѣреніе площади только въ рѣдкихъ случаяхъ можетъ
быть выполнено непосредственнымъ наложеніемъ квадратной
единицы. Большею частію площади приходится измѣрять кос-
венно, посредствомъ измѣренія нѣкоторыхъ линій фигуры.
Основаніе И высота. Условимся одну изъ сторонъ
треугольника или параллелограмма называть основаніемъ этихъ
фигуръ, а перпендикуляръ, опущенный на эту сторону изъ
вершины тр -ка пли изъ какой-нибудь точки противоположной
стороны параллелограмма будемъ называть высотою.
Вь прямоугольникѣ за высоту можно взять сторону, пер-
пендикулярную къ той, которая принята за основаніе.
Въ трапеціи основаніями называютъ обѣ параллельныя
стороны, а высотою общій перпендикуляръ между ними.
Основаніе и высота прямоугольника наз. его измѣре-
ніями.
2Ф9. Лемма 1°. Площади двухъ прямоугольниковъ, имѣю-
щихъ равныя основанія, относятся, какъ ихъ высоты.
Пусть АС и АХСГ (черт. 192) будутъ два прямоуголь-
ника, у которыхъ основанія АВ и ААВу равны; требуется
Доказать, что площади такихъ прямоугольниковъ относятся,
какъ высоты АВ и А1ВІ.
При доказательствѣ разсмотримъ особо два случая.
— 176 —
1°. Высоты соизмѣримы. Найдя общую мѣру высотъ,
А. В. С. В. на п такихъ же
отложимъ ее на каждой изъ
нихъ столько разъ, сколько
можно. Пусть общая мѣра со-
держится т разъ въ АВ и п
разъ въ АуВу. Проведемъ че-
резъ точки дѣленія прямыя, па-
раллельныя основаніямъ. Тогда
площадь АВСВ раздѣлится на
т равныхъ частей, а площ.
частей. Поэтому
Слѣд.:
площ. АВСВ  т	АВ  т
площ,. АуВуСуВу	п	И АуВу	п
плоіц. АВСВ _____ АВ
площ. АуВу СуВу АуВу
2°. Высоты несоизмѣримы. Раздѣлимъ АуВу на п рав-
ныхъ частей и одну часть отложимъ на АВ столько разъ,
сколько можно. Пусть она содержится въ АВ болѣе т, но
менѣе яі+1 разъ. Черезъ точки дѣленія проведемъ прямыя,
параллельныя основаніямъ. Тогда площадь Ау ВуСуВу раздѣ-
лится на п такихъ равныхъ частей, какихъ въ площ. АВСВ
содержится болѣе т, но менѣе т +1 разъ. Поэтому:
площ. АВСВ	т I 1 \
прибл. ОТН.----——— 3=:— (до—)
площ. АуВуСуВу	п \ п/
, АВ т /	1 \
и прибл. отн. —- (до -
АуВу	п \ п/
Такимъ образомъ, приближенныя отношенія, вычисленныя
съ произвольною, но одинаковою, точностью, оказываются
равными; а въ этомъ и состоитъ равенство несоизмѣримыхъ
отношеній (144).
930. Слѣдствіе. Площади двухъ прямоугольниковъ, имѣю-
щихъ равныя высоты, относятся, какъ ихъ основанія, по-
тому что въ прямоугольникахъ основанія могутъ быть при-
няты за высоты, а высоты за основанія.
Лемма 2°. Площади двухъ прямоугольниковъ от-
носятся, какъ произведенія основаній на высоты.
— 177 —
Пусть Р и будутъ два прямоугольника, Ь и — ихъ
основанія, Ь и — высоты; требуется доказать, что
Р'.І^ЪкЛ^
Черт. 193.
Возьмемъ вспомогательный прямоугольникъ Д у котораго ос-
нованіе равно Ъ,
будемъ имѣть:
а высота Л1. Тогда, по предыдущей леммѣ,
Р __ Ъ_ Р _ь_
'/г — X 11
равенства, получимъ (по сокращеніи на Р):
р__ъь
а
Теорема. Число, выражающее площадь прямо-
угольника въ квадратныхъ единицахъ, равно произведенію чи-
селъ, выражагоги/ихъ основаніе и высоту его въ соотвѣт-
ствуюгцихъ линейныхъ единицахъ.
Это сокращенно выражаютъ такъ: площадь прямоуголь-
ника равна произведенію основанія на высоту.
Доказываемую теорему можно разсматривать, какъ слѣдствіе
предыдущей леммы. Дѣйствительно, если Ресть данный прямо-
угольникъ, а квадратная единица,
то, называя основаніе и высоту
ваго Ь и к, а основаніе и высоту
рого с, будемъ имѣть:
р
<2 се
что можетъ быть написано такъ:
р__
Это равенство и есть то, которое требовалось доказать, такъ какъ
А. П. КИСЕЛЕВЪ.	12
Перемноживъ эти
пер-
вто-
1ь
Черт. 194
— 178 —
отношеніе есть число, выражающее площадь прямоугольника
въ квадратныхъ единицахъ, а отношенія -- и -у суть числа,
выражающія его основаніе и высоту въ соотвѣтствующихъ ли-
нейныхъ единицахъ.
Полагая и с= 1, получимъ:
Р~Ъ1і
гдѣ Р, Ь и 1і суть числа, выражающія площадь. основаніе и
высоту прямоугольника въ соотвѣтствующихъ единицахъ.
303. Слѣдствіе, Площадь квадрата равна квадрату его
стороны.
304. Въ послѣдующихъ теоремахъ мы будемъ сокращенно
говорить: „площадь равна произведенію такихъ-то линій“, раз-
умѣя подъ этимъ, что число, выражающее площадь въ квадр.
единицахъ, равно произведенію чиселъ, выражающихъ такія-то
линіи въ соотвѣтствующихъ линейныхъ единицахъ.
305. Теорема. Площадь параллелограмма (АВСВ,
черт. 195) равна произведенію основанія на высоту.
На основаніи АВ построимъ пря-
Е----—-	моугольникъ АЕЕВ, у котораго вы-
сота такая же, какъ и у параллело-
грамма. Докажемъ, что АВСВ ра-
вновеликъ АЕЕВ. Параллелограммъ
АВСВ получится, если изъ четыре-
угольника АЕСВ отдѣлимъ тр.-къ
АЕВ; прямоугольникъ АЕЕВ по-
лучится, если изъ того же четыре-
угольника АЕОВ отдѣлимъ тр.-къ ВЕС. Отдѣляемые тр.-ка
равны, потому что они прямоугольные и АЕ = ВЕ, АВ = СВ
Черт. 196
изведенія основанія
(какъ противоположныя стороны паралле-
лограммовъ). Изъ этого слѣдуетъ, что
АВСВ равновеликъ АЕЕВ. Но площадь
АЕЕВ равна Ыі; слѣд., и площадь АВСВ
равна Ыі.
3 06. Теорема. Площадь треугольника
(АВС, черт. 196) равна половинѣ про-
ка высоту.
— 179 —
Проведемъ ВЕЦАС и АЕ\\ВС. Тогда получимъ паралле-
лограмъ АЕВС, котораго площадь, по доказанному, равна
произведенію Ьк. По площадь АВС составляетъ половину
площади АЕВС; слѣд.
площ. АВ С ~ Ыі
ЯВЗЯ. Слѣдствія. 1°. Треугольники съ равными основа-
ніями и равными высотами равновелики.
Если, напр., вершину В тр.-ка	в
АВС будемъ перемѣщать по пря- /Х/ѴИхУ
мой, параллельной основанію АС, \ /СЛ/к /
а основаніе оставимъ то же са- \ ///х\\ /
мое, то площадь тр.-ка не из-	хА/
мѣнится.	V
2°. Площадь прямоугольнаго	ЧеРт- 197
треуголънгѵка равна половишь произведенія его катетовъ,
потому что одинъ катетъ можно взять за основаніе, а другой
за высоту.
3°. Площади треугольниковъ относятся, какъ произведе-
нія основаній на высоты.
Ж38. Теорема. Площадь 8 треугольника въ зависимости
отъ его сторонъ а, Ъ и с выражается формулой:
8=\]р(р — а\р-Ъ\р—с)
гдѣ р есть гголупергіметръ треугольника, гп.-е.
р =у(а + &+с)
Пусть высота тр.-ка АВС, опущен-
ная па сторону а, есть Ъа, Тогда:
Чтобы найти высоту //о, возьмемъ
уравненіе (208):
/? = а2 Ч- с2 ~ 2«с	" а И
ѵ	ѵ	,	Черт.1й8
я опредѣлимъ изъ него отрѣзокъ с:
,__а2 + с2—
С — ~ 2а ‘
12*
— 180 —
Тецерь изъ треугольника АВВ находимъ:
Преобразуемъ подкоренную величину такъ:
(2ас)2-(а2+с2-&2)2=(2«с+а2+с2-&2)(2ас--а2-г+&2)
=[(а2+с2+^ае)— &2][&2— (а2~і~с2- 2ас)]
=І(а+С)’-6>г--(«-<0Ч
=(а+г4-&)(а-}-с— &)(&+»— с)(6—а-рс)
Если положимъ, что а-\-Ъ-\-с=^2р> то
а+с— Ъ=[а-\-Ъ-\-с}—2Ъ—2р—2Ь—2(р~~Ъ')
Подобно этому:	Ъ-\-а~-с=2(р~с)
Ь-\-с— а~2(і)—а)
Теперь подкоренная величина представится такъ:
16р(р-а)(р--Ь)(р-~ с)
Слѣд.	Л.=|\/?(?—«)(2>—>)(Р—е)
и 8= і А.— \]р(р—а)(р—Ъ}(р—с)
Частный случай. Площадь равносторонняго треугольника
со стороною сѵ выразится формулой:
®=	=Ѵ-2 в(і“)М
939. Задача. Наѵлпи площадь треугольника АВС по двумъ сто-
рннамъ АВ и АС и углу А между ними.
Геометрически эта задача рѣшается только для нѣкоторыхъ частныхъ
значеній углаЛ.. Положимъ, напр., что Л—18®.
Тогда можно найти Ь въ зависимости отъ сто-
роны АВ такимъ образомъ. Продолживъ ВВ
на разстояніе РБ —БР, соединимъ Е съ А.
Тогда въ равнобедренномъ тр.-кѣ АВЕ уголъ
ВАЕ будетъ равенъ 36®. Изъ этого заключаемъ,
что ВЕ, т.-е. двойная высота, есть сторона
правильнаго 10-угольнпна, вписаннаго въ кругъ
котораго радіусъ есть АВ. Поэтому ЕЕ най-
дется по формулѣ, опредѣляющей сторону
прав. впнсан. 10-уголь нива (236). Опредѣливъ
высоту, найдемъ затѣмъ площадь тр.-ка 1К>
формулѣ 8—~Ыі.
— 181 —
290. Теорема. Площадь трапеціи равна произведенію
полусуммы основаній на высоту.
Проведя въ трапеціи АВСВ
діагональ АС, мы можемъ раз-
сматривать ея площадь, какъ
сумму площадей двухъ тр.-ковъ
АСВ и АВС. Поэтому
площ. АВСВ = АВ.Іі-у
+ '• ВС.к = -’ (АО-\-ВО)к
281.	Слѣдствіе. Проведя въ трапеціи среднюю линію
АНЯ, будемъ имѣть (103):
ЛІЛТ= * (ЛР+ВО)
Поэтому:	площ. АВСВ = МВГ. 1і
т.-с. площадь трапеціи равна произведенію средней линіи
на высоту.
282.	Теорема. Площадь описаннаго многоугольника равна
произведенію периметра на половину апооему.
Соединивъ центръ О со всѣми вер-
шинами описаннаго многоугольника, мы
раздѣлимъ его па треугольники, въ ко-
торыхъ за основанія можно брать сто-
роны многоугольника, а за высоту —
радіусъ круга. Обозначивъ этотъ ра-
діусъ черезъ В, будемъ имѣть:
площ. АВО^АВ.^В}
илощ. АОЕ=АЕ. 2 В и т. д.
Слѣд. ,иощ. АВСѴЕ=(АВ + ВС+СВ+ВЕ+ЕВ).12 в.
283.	Слѣдствіе. Площадь правильнаго многоугольника
равна произведенію периметра на половину апоѳемы, потому
что всякій прав. многоугольникъ можно разсматривать, какъ
списанный около круга, у котораго радіусъ есть апоѳема.
— 182 —
Задача. Превратить многоугольникъ АВСВЕ* въ
равновеликій треуголъникъ.
Черезъ вершину В проведенъ
2.	ВЕЦАС до пересѣченія съ лро-
долженіемъ ЕА. Точку Е соеди-
ЪішШШ \нимъ съ С. Тр.-ки СВ А и СГА
\ \А равновелики, такъ какъ у нихъ
\ /ѵ общее основаніе АС, а вершины
В и Е лежатъ на прямой, парал-
А	лельпой основанію (277). Если отъ
Черт. 202	даннаго многоугольника отдѣлимъ
тр.-къ СВА и вмѣсто него приложимъ тр.-къ СЕА, то ве-
личина Площади не измѣнится; слѣд., данный пятиугольникъ
равновеликъ четыреугольнику ЕСВЕ. Такимъ же пріемомъ
можно превратить этотъ четыреугольникъ въ равновеликій тре-
угольникъ (напр. ЕС6г).
885. Задача. Превратить многоугольникъ въ равнове-
ликій квадратъ.
Сначала превращаютъ многоугольникъ въ равновеликій
треугольникъ, а затѣмъ этотъ треугольникъ въ квадратъ.
Пусть основаніе и высота треугольника будутъ Ь и 1ъ, а сто-
рона искомаго квадрата х, Тогда площадь перваго равна
1/фй, а второго я2; слѣд.
Ыі = ж2; откуда * Ъ : х = х :1і
т.-е. х есть средняя пропорціанальная между * І/ІЪ и 1і. Такимъ
образомъ, сторону квадрата можно построить способомъ, ука-
заннымъ раньше (203) для нахожденія средней пропорціа-
нальной.
Замѣтимъ, что предварительное превращеніе даннаго мно-
гоугольника въ треугольникъ не всегда необходимо. Напр.,
если рѣчь идетъ о превращеніи въ квадратъ данной трапеціи,
то достаточно найти среднюю пропорціанальную между высо-
тою трапеціи и ея среднею линіею и на полученной прямой
построить квадратъ.
— 183 —
Г ЛАВА II.
Теорема Пиѳагора и основанныя на ней задачи.
286. Теорема. Сумма квадратовъ, построенныхъ на
катетахъ прямоугольнаго треугольника, равновелика квад-
рату, построенному на гипотенузѣ.
Это предложеніе, извѣстное подъ названіемъ теоремы Пи-
ѳагора (греческаго философа, жившаго въ VI вѣкѣ до Р. Хр.),
имѣетъ многочисленныя доказательства. Приведемъ простѣйшія
изъ нихъ.
Первое доказательство. Пусть АВС будетъ прямоуголь-
ный треугольникъ, а ВВЕА, АЕ(хС и ВС КН квадраты,
построенные на его катетахъ и гипотенузѣ; требуется дока-
зать, что сумма двухъ первыхъ квадратовъ равновелика треть-
ему квадрату.—Проведемъ ААІ ВС. Тогда квадратъ ВСКН
раздѣлится на два прямоуголь-
ника. Докажемъ, что прям.
ВЪМН равновеликъ квадрату
ВВЕА, а прямоуг. ВСКЗІ
равновеликъ квадрату АЕСгС.
Проведемъ вспомогательныя пря-
мыя ВС п АП. Тр.-къ ВСВ,
имѣющій основаніе ВВ, общее
съ квадратомъ ВВЕА, и вы-
соту СЁ, равную высотѣ А В
этого квадрата, равновеликъ по-
ловинѣ его. Тр.-къ АВП, имѣю-
щій основаніе ВП, общее съ
прямоугольникомъ ВЕМН, и
высоту АВ, равную высотѣ
ВЪ этого прямоугольника, равновеликъ половинѣ его. Срав-
нивая эти два треугольника между собою, находимъ, что у
нихъ ВВ = ВА и ВС~ ВН (какъ стороны квадрата); сверхъ
того /_ВВС— /_АВН, такъ какъ каждый изъ этихъ угловъ
состоитъ изъ общей части АВС и прямого угла. Значитъ,
тр.-ки ВВС и АВН равны. Отсюда слѣдуетъ, что прямо-
угольникъ ВІАПІ равновеликъ квадрату ВВЕА.
в
Черт. 204
— 184 —
Соединивъ (т съ В и А съ К, мы совершенно такъ же
докажемъ, что прямоугольникъ ЪСКМ равновеликъ квадрату
ЛЕСС. Отсюда слѣдуетъ, что ВС КП равновеликъ суммѣ
ВВЕА и АЕСС.
Второе доказательство. Пусть а, Ь и с будутъ числа,
выражающія гипотенузу и катеты прямоугольнаго треугольника
въ одной и той же линейной единицѣ. Тогда, какъ мы ви-
дѣли раньше (204):
а2 — 62 -Ь с1
Но а2, 7/ и с2 суть числа, измѣряющія плоіцади квадратовъ,
которыхъ стороны суть а, 1> и с: слѣд.. написанное равен-
ство выражаетъ, что квадратъ, построенный на гипотенузѣ,
равновеликъ суммѣ квадратовъ, построенныхъ на катетахъ.
$8 Я. Задачи. Построитъ квадратъ, равновеликій:
7°, суммѣ, 2°. разности двухъ данныхъ квадратовъ.
1°. Строимъ прямоугольный треугольникъ, у котораго ка-
тетами были бы стороны данныхъ квадратовъ. Квадратъ, по-
строенный на гипотенузѣ этого треугольника, будетъ равно-
великъ суммѣ данныхъ квадратовъ.
2°. Строимъ прямоуг. треугольникъ, у котораго гипоте-
нузой была бы сторона большаго изъ данныхъ квадратовъ, а
катетомъ сторона меньшаго квадрата. Квадратъ, построенный
на другомъ катетѣ этого треугольника, будетъ равновеликъ
в
В
Черт. 205
разности данныхъ квадратовъ.
$88. Задача. Построитъ квадратъ, котораіо площадь
относилась бы къ площади даннаіо квадрата, какъ т: -«•.
На неопредѣленной прямой отклады-
ваемъ АВ^=т и ВС—п. и на АС,
какъ на діаметрѣ, описываемъ полуокруж-
ность. Изъ точки В возстановляемъ пер-
пендикуляръ ВВ до пересѣченія съ ок-
С ружностью. Соединивъ В съ Л и С, по-
лучимъ прямоугольный тр.-къ, у кото-
раго (206):
АВ2: ВС2 = АВ : ВС= т : п
А
Отложимъ теперь на одномъ изъ катетовъ этого треуголъ-
— 185 —
ника, напр. на ВС, отрѣзокъ ВЕ, равный сторонѣ даннаго
квадрата, и проведемъ КР|| СА. Прямая ВЕ будетъ стороною
искомаго квадрата потому что
ВЕ: ВЕ = АВ:ВС
и слѣд. ВЕ2: ВЕ2 = АВ2: ВС2 ~т : п
ГЛАВА III.
Отношеніе площадей подобныхъ фигуръ.
980. Теорема. Площадгі двухъ треугольниковъ, содержа-
щихъ по равному углу, относягпся, какъ гіроизведенгя сто-
ронъ, заключаюгцгіхъ эти углы.
В
Черт. 206
Пусть АВС и АуВ^С^ будутъ два тр.-ка, у которыхъ
А = АГ Проведя высоты ВВ и В^ВѴ будемъ имѣть:
іілощ. АВС_ _ ас. вп_ _ ас ВІ)
іілоіц. А'ад —	— ДС'і' А А
Тр.-ки АВВ и АХВХВГ -подобны (А=Аг и В = В^); по-
этому отношеніе ВВ: В^В^ равно отношенію АВ: АхВу; за-
мѣнивъ первое вторымъ, получимъ:
НЛОЩ. АВС _ АС АВ __ АС. АВ
Ійоіц.	~ ЛіСі • АіВі ~ АуС\. А^
990. Замѣчаніе. Предлагаемъ самимъ учащимся дока-
зать, что если у двухъ треугольниковъ АВС и АІВ1СІІ
(черт. 206) углы А и Ах составляютъ въ суммѣ 2Л, то
площади такихъ тр.-ковъ также относятся, какъ произведенія
сторонъ, заключающихъ углы А и А±.
— 186 —
991. Площади подобныхъ треугольниковъ или много-
угольниковъ относятся, какъ квадраты сходственныхъ сто-
ронъ.
1°. Пусть АВС и АІВ1С1 (черт. 206) будутъ два по-
добные треугольника, у которыхъ А = А19 В = Вг и
Примѣняя къ нимъ предыдущую теорему, получимъ:
площ. АВС ___ АВ. АС _	АВ	АС	г. ।
площ. А1Іі1С1	АіВі. АіС} ~	А^ * А&
Но изъ подобія треугольниковъ слѣдуетъ:
АВ	_ АС _ ВС	г ,
А1В1~ А1С1~~‘В^^	ЬЧ
Поэтому въ равенствѣ [1] мы можемъ каждое изъ отношеній
и-^7 замѣнить любымъ отношеніемъ ряда [2]. Слѣд.:
ПЛОШ,. АВС ___/АВ у___/ А С у___/ ВС у
площ. АуВ^г ~ \А[вр — и'ібѴ \В/Ѵ
_ ЛВ2 _ АС2 _ ВС2
АГВ^ ~~ АіС^ — В1 СУ
2°. Пусть АВСВЕ и А^В^С^В^Е^ будутъ два подобные
многоугольника. Ихъ можно, какъ мы видѣли (186), разло-
жить на одинаковое число подобныхъ и одинаково располо-
С
Черт. 207
женныхъ тр.-ковъ. Пусть эти тр.-ки будутъ: АВО и Ах Вх
АОЕ и А^^ и т. д. Согласно доказанному въ первой части
этой теоремы, мы будемъ имѣть:
площ. АОВ __/ АВ у. илощ. ВОС ____/ ВС у
площ. ЛіОТВі—ІЛіВУ ’ илощ, В^С]"-(в^У И Т* Д*
— 187 —
Но изъ подобія многоугольниковъ слѣдуетъ:
— \В^) ~ \СгРг)---------
Значитъ- ИЛ0Щл Л0^ _____ илощ. ВОС____ площ. СОР ___
площ.	площ. В1О1С1 площ. С^Р^ ’ ‘
/ч	пл- л0-в + пл. -ВОС+пл. СОР+.. _____ АВ*
ѵткуда. пь а1о\в1 4- ІІЛ. Б/О/^+ пл.’ С&Р' +.. ~А1В1*
292.	Слѣдствіе. Площади правильныхъ одноименныхъ
многоугольниковъ относятся, какъ квадраты сторонъ, или
квадраты радіусовъ, или квадраты апоѳемъ (231).
293.	Задача. Раздѣлить данный треугольникъ на )П
равновеликихъ частей прямыми, параллельными одной его
сторонѣ.
Пусть, напр.,
равновеликія части прямыми,
параллельными основанію АС.
Предположимъ, что задача рѣ-
шена, и искомыя прямыя бу-
дутъ ВЕ и ЕС. Очевидно, что
если мы найдемъ отрѣзки ВЕ
и ВС, то затѣмъ опредѣлятся
и прямыя ВЕ и ЕС. Тр.-ки
ВВЕ, ВЕС и ВАС подобны;
поэтому:
площ. ВВЕ ___ВЕ*
площ. ВАС ВС* И
требуется раздѣлить тр -къ АВС на 3
площ. ВЕС  ВС*
площ. ВАС ВС*
Но изъ требованій задачи видно, что:
площ. ВРЕ_____________ 1	площ. ВЕСг _ 2
площ. ВАС'	3	И	площ. ВАС	3
Р	ѵ,	.	ВЕ2 — 1	,	Я(?з_ 2
Слѣд..	^с.2	3	и	ВСІ—3
Откуда:	ВЕ= \^ВС2 = ^ВС.ВС
и ва—\!^вс'‘=^^вс.в(;
Изъ этихъ формулъ видимъ, что ВЕ есть средняя пропор-
ціанальная между ВС а ГІ3ВС, а ВС есть средняя пропор-
ціанальная между ВС и ^ВС (224,4). Поэтому построеніе
— 188 —
можно выполнить такъ: раздѣлимъ ВС на три равныя части
въ точкахъ а и Ь; опишемъ на ВС полуокружность- изъ а
и Ъ возставимъ къ ВС перпендикуляры аН и ЪК. Хорды
ВН и ВВ будутъ искомыми средними пропорціанальными:
первая между всѣмъ діаметромъ ВС и ого третьею частью
Ва, вторая между ВС и ВЬ, т.-е. между ВС и ^ВС (202).
Остается отложить эти хорды на ВС отъ точки В; тогда
получимъ точки Е и С.
Подобнымъ образомъ можно раздѣлить тр.-къ на какое
угодно иное число равновеликихъ частей.
ГЛАВА IV.
Площадь круга и его частей.
294.	Лемма 1. При неограниченномъ удвоеніи числа
сторонъ правильнаго многоугольника, вписанная въ окруж-
ность, разность между радіусомъ и апоѳемою этого много-
угольника стремится къ
Черт. 209
нулю.
Пусть АВСВ будетъ какой-нибудь
правильный впис. многоугольникъ.
О А радіусъ и ОЕ апоѳема. Изъ
тр.-ка ОАЕ находимъ (50):
ОА—ОЕ<АЕ
или	О А — ОЕ < АВ
т.-е. разность между радіусомъ и
апоѳемою меньше половины стороны
правильнаго многоугольника. Но при
неограниченномъ удвоеніи числа сто-
ронъ прав. впис. многоугольника каждая сторона его, оче-
видно, стремится къ нулю; поэтому разность между радіусомъ
и апоѳемою, и подавно, стремится къ нулю.
295.	Лемма 2. Площадь круга есть общій предѣлъ пло-
щадей правильныхъ вписанныхъ и описанныхъ многоугольни-
ковъ при неограниченномъ удвоеніи числи ихъ сторонъ.
— 189 —
Впишемъ въ данный кругъ и опишемъ около него по ка-
кому-нибудь правильному одноименному многоугольнику (папр.,
шестиугольнику).
Пусть К, <2 и 1 будутъ соотвѣт-
ственно площади круга, описаннаго и
вписаннаго многоугольниковъ. Изъ чер-
тежа мы непосредственно видимъ, что
ЦЖ и К>д
Когда станемъ удваивать число сто-
ронъ обоихъ многоугольниковъ, пло-
щади ихъ д сдѣлаются величинами
перемѣнными (причемъ очевидно, что будетъ уменьшаться,
а д увеличиваться). Мы должны доказать, что постоянная
величина К будетъ при этомъ служить общимъ предѣломъ
для и д; другими словами, мы должны доказать, что каж-
дая изъ разностей:
(} — К и К—д
стремится къ нулю. Для этого возьмемъ третью, вспомогатель-
ную, разность
—Я
которая, очевидно, больше каждой изъ двухъ первыхъ разно-
стей, и докажемъ, что даже и эта, бблыпая, разность стре-
мится къ нулю. Обозначивъ апоѳемы описаннаго и вписаннаго
многоугольниковъ черезъ И и а, будемъ имѣть (292):
<?_ да
Составимъ изъ этой пропорціи производную (разность чле-
новъ перваго отношенія относится такъ къ предыдущему
члену этого отношенія, какъ....):
—ч___да—а2
Откуда:	( $ — #) .й2 = ф (К2 — а2)
или	(() — д) Н2= ()(7г + а) (Д — а)
Такъ какъ при неограниченномъ удвоеніи числа сторонъ
— 190 —
многоугольниковъ разность 2? — ^. по доказанному въ преды-
дущей леммѣ, стремится къ нулю, а сомножители $ и ІІ-\-а
не увеличиваются безпредѣльно, то правая часть послѣдняго
равенства (а слѣд. и лѣвая часть) стремится къ нулю. Но про-
изведеніе (()— ^) Д можетъ стремиться къ нулю только тогда,
когда сомножитель — д стремится къ нулю (такъ какъ другой
сомножитель 1$ есть число постоянное). Если же разность
— д стремится къ нулю, то, и подавно, то же самое можно
сказать о меньшихъ разностяхъ — К и К—д. Изъ этого
слѣдуетъ, что
/Г=пред. $ = пред. д.
29в. Теорема. Ллогцадъ круга- равна произведенію длины
окружности на половину радіуса.
Пусть Д К и С означаютъ радіусъ, площадь и длину
данной окружности, а и Р—площадь и периметръ какого-
нибудь правильнаго описаннаго многоугольника. Тогда можемъ
написать (283):
[і]
Вообразимъ теперь, что число сторонъ описаннаго многоугольни-
ка неограниченно удваивается. Тогда величины и Р сдѣ-
лаются перемѣнными, стремящимися къ предѣламъ: первая къ
площади круга К, вторая—къ длинѣ окружности С. Такъ
какъ равенство [1] остается вѣрнымъ при всѣхъ измѣненіяхъ
и Р, то оно должно остаться вѣрнымъ и тогда, когда вмѣсто
перемѣнныхъ подставимъ ихъ предѣлы (251) значитъ:
к=с.\п
Подставивъ на мѣсто С выраженіе (262,2°), по-
лучимъ:
т.-е. площадь круга равна прогізведеніго квадрата радіуса
на отногиеніе окружности къ діаметру.
Слѣдствіе. Площади круговъ относятся, какъ квадраты
радіусовъ, илгі діаметровъ.
— 191 —
Дѣйствительно, если К и 7^ будутъ площади двухъ кру-
говъ. а Л и 7?, ихъ радіусы, то
К=ъВ2 и К.—т.В^
Откуда •	~
ѵікуда.	— -я12 — ^2 — 4дг2 — (2^)2
999. Задача 1°. Вычислить площадь круга, окружность ко-
тораго равна 2 метрамъ.
Для этого предварительно найдемъ радіусъ В изъ урав-
вненія:
2 г. В — 2 : откуда В =
Затѣмъ опредѣляемъ площадь круга:
В^т.В2^^.^)2 —	0.3183 квадр. метра.
Задача 2°. Построгать квадратъ, равновеликій данному кругу.
Эта задача, извѣстная подъ названіемъ квадратуры круга, не можетъ
быть точно рѣшена при помощи циркуля и линейки. Дѣйствительно, если
обозначимъ черезъ ,т сторону искомаго квадрата, а черезъ 1? радіусъ
круга, то получимъ уравненіе:
.г2 — ті?2; откуда: тЛ : .т ~ х: И.
т.-е. х есть средняя пропорціанальная между полуокружностью и радіу-
сомъ. Но доказано, что помощью циркуля и линейки нельзя построить
прямую, которая въ точности равнялась бы длинѣ полуокружности (см.
выноску къ задачѣ № 257); слѣд., нельзя въ точности рѣшить задачу о
превращеніи круга въ квадратъ. Приближенное же рѣшеніе можно вы-
полнить, еслп предварительно найти приближенную длину полуокружности
и затѣмъ построить среднюю пропорціональную между этою длиною и
радіусомъ.
998. Теорема. Площадь сектора равна произведенію
его дуггі на половину радіуса.
Пусть дуга АВ сектора АОВ содер-	з
житъ п°. Очевидно, что площадь сектора,
котораго дуга содержитъ 1°, равна /	\
т:К2	|	\
360	I 0	/
Слѣд., площадь сектора котораго дуга \	/
содержитъ п°, равна
е тЛ&ь гЛ Н
*	’36(Г	180 ‘ 2	Чс₽т- 211
— 192 —
Н° выражаетъ длину дуги АВ. Обозначивъ ее черезъ 8,
получимъ:
О---------------------------С
999. Задача. Вычислить площадь сегмента, зная радіусъ круга
и число градусовъ, заключающееся въ дугѣ сегмента.
3	Чтобы получить площадь сегмента А8В,
достаточно изъ площади сектора АОВ вы-
честь площадь тр.-ка АОВ. Проведя АС і ОВ,
/ д\	\ будемъ имѣть:
\ ѵ  •'•-•'р	1
I 0	I площадь сектора — ^В&
\.	/ площадь тр.-ка = | ОВ. АС = ~ Я. АС
Черт 21 •> Слѣд. площ. сегмента = Я (я — АС).
Такимъ образомъ вопросъ прзводится къ вычисленію высоты АС.
Геометрически ее можно найти только въ нѣкоторыхъ частныхъ слу-
чаяхъ слѣдующимъ способомъ.
Продолживъ АС до пересѣченія съ окружностью въ точкѣ В, мы
увидимъ, что АС = СВ и АВ= ВВ; значитъ, АС есть половина хор-
ды, стягивающей дугу, вдвое большую дуги сегмента. Отсюда заключаемъ,
что если хорда, стягивающая двойную дугу, будетъ сторона такого пра-
вильнаго вписаннаго многоугольника, для котораго мы знаемъ формулу
его стороны, то высота АС опредѣлится геометрически. Напр., пусть
дуга сегмента содержитъ 60°. Тогда АО есть сторона правильнаго впи-
саннаго треугольника; значитъ, АС —1/2ВѴ'3. Дуга ЛВ въ этомъ случаѣ
равна ’/о окружности, т.-с. Ч&В; поэтому:
площ. сегмента — | В	~ ~ Я2(2г. — 313)
ЗОО.	Теорема. Сумма площадей подобныхъ многоуголь-
никовъ (илгь круговъ), построенныхъ на катетахъ прямо-
угольнаго треугольника, равна площади подобнаго многоуголь-
ника (или круга), построеннаго на гипотенузѣ, еслгь катеты
и гипотенуза служатъ сходственными сторонами этихъ
многоугольниковъ (или діаметрами круговъ).
Пусть (), II п 8 будутъ площади подобныхъ фигуръ (иля
— 193 —
круговъ), построенныхъ на катетахъ и гипотенузѣ прямо-
угольнаго тр.-ка ЛВС. Тогда (292,296. слѣдствіе).
_ лв*	и _ вс*
д'“Т(3	5 — 'ас*
Сложивъ эти равенства, найдемъ:
<2 + в _ ав* + вс*
8 ~ ~ АС*
Но АВ2-у-ВС2=А С2(2МУ, поэтому:
Ц + В~ 8
301.	Слѣдствіе. Іье.пі на сторонахъ прямоугольною треугольника
АБС (черт. 214) построимъ полукруггі, расположенные въ одну сторону,
то сумма образовавшихся при этомъ фигурѣ АМВР и В№СЦ равна
плогиади треугольника.
Дѣйствительно.сумма полукруговъ, постро-
енныхъ на катетахъ, равновелика полукругу,
построенному на гипотенузѣ; если же отъ
обѣихъ частей этого равенства отнимемъ
сумму сегментовъ ЛРВ п ВЦС, то по-
лучимъ:
АМВР 4- ВПС^ — АВС
Фигуры АМВР и извѣстны въ гео-
метріи подъ названіемъ І^іппокрагповыхъ луночекъ.
Когда треугольникъ равнобедренный, то обѣ луночки одинаковы и
каждая изъ нихъ равновелика половинѣ треугольника.
ГЛАВА V.
Соотношеніе между сторонами треугольника и радіусами
вписаннаго и описаннаго круговъ.
303.	Для радіуса В описаннаго около треугольника круга мы вывели
(221) слѣдующее выраженіе;
Исключимъ изъ этой формулы высоту Ло- для этого умножимъ числителя
А. П. КИСЕЛЕВЪ.
13
— 194 —
и знаменателя дроби на а; тогда, замѣнивъ произведеніе Лва удвоенною
площадью треугольника, (которую обозначимъ 8), получимъ:
аЬс 	аЪг
48	I	Гр"—
В
Черт. 215
= ’/а	+ Ъ -I" с).
Чтобы найти радіусъ г внутренняго вписан-
наго круга (черт. 215) примемъ во вниманіе, что
прямыя О А, ОВ и ОС раздѣляютъ данный тр.-къ
на три другіе тр.-ка, у которыхъ основаніями
служатъ стороны даннаго тр.-ка, а высотою
радіусъ т. Поэтому:
<5 — - аг + * Ьг + * сг — г. (« + Ь + с) = гр
Отсюда г = ? =.
р V р
Радіусъ рв внѣвппсанпаго
Черт. 216
_ 8
К—р-Ъ
круга, (черт. 216) касающагося стороны
«, можно опредѣлить изъ равенства:
ил. АВС=ил. ЛСО +
4- ил. АВО — пл. ВОС
О 1 ,	,	1	1
т.-с. 8 ~~1)ба ч- — сра — 2 арв
Откуда:
— ___2<? — *8 — 5
?в Ь + с — а 2{р — а) р^а
Подобно этому найдемъ:
Между четырьмя радіусами-, г, р0, и ос существуютъ нѣкоторыя
зависимости. Укажемъ простѣйшую изъ нпхъ:
1	1	1 „ Зр	— а — 6 —	с _ Зр —2р _ р_
Ра	РЬ	Рс ~	#	~	8	8
ІІО ; = -л-; СЛѢД.
Г й
Рб
— 195 —
УПРАЖНЕНІЯ.
Доказать теоремы:
261.	Въ параллелограммѣ разстоянія какой-нибудь точки діагонали
отъ двухъ прилежащихч, сторонъ обратно пропорціапальпы этимъ сто-
ронамъ.
262.	Площадь трапеціи равна половинѣ произведенія одной изъ не-
параллельныхъ сторонъ на перпендикуляръ, опущенный изъ средины дра-
гой непараллельной стороны на первую.
263.	Два четыреугольника равновелики, если у нихъ равны порознь
діагонали и уголъ между ними.
264.	Если площади двухъ треугольниковъ, прилежащихъ къ основа-
ніямъ трапеціи и образуемыхъ отъ пересѣченія ея діагоналей, равны со-
отвѣтственно р* и «у2, то площадь всей трапеціи равна (р 4- <у)2.
265.	Площадь правильнаго вписаннаго шестиугольника равна 3/4 пло-
щади правильнаго описаннаго шестиугольника.
266.	Въ четыреугольникѣ АВСВ черезъ средину діагонали ВВ про-
ведена прямая, параллельная другой діагонали АС-, эта прямая пересѣ-
каетъ сторону АВ въ точкѣ Е. Доказать, что прямая СЕ дѣлитъ четы-
реугольникъ пополамъ.
267.	Еслп медіаны треугольника взять за стороны другого треуголь-
ника, то площадь послѣдняго равна а/4 площади перваго.
268.	Въ кругѣ съ центромъ О проведена хорда АВ. На радіусѣ ОА,
какъ на діаметрѣ, описана окружность. Доказать, что плоіцадн двухъ
сегментовъ, отсѣкаемыхъ хордою АВ отъ обоихъ круговъ, относятся,
какъ 4:1.
Задачи на вычисленіе.
269.	Вычислить площадь прямоугольной трапеціи, у которой одинъ
изъ угловъ равенъ 60°, зная или оба основанія, или одно основаніе и
высоту, или одно основаніе и боковую сторону, наклонную къ осно-
ванію.
270.	Вычислить площадь равносторонняго треугольника, зная его
высоту к.
271.	Даны основанія трапеціи В и Ь и ея высота Я. Вычислить вы-
соту треугольника, образованнаго продолженіемъ непараллельныхъ сто-
ронъ трапеціи до взаимнаго пересѣченія.
272.	Составить формулу для площади правильнаго вписаннаго
12-угольника въ зависимости отъ радіуса круга.
273.	Въ треугольникъ вписанъ другой треугольникъ, котораго вер-
шины дѣлятъ пополамъ стороны перваго треугольника; въ другой тре-
угольникъ вписанъ подобнымъ жо образомъ третій тр.-къ; въ третій —
13*
— 196 —
четвертый; и т. д. безъ конца. Найти предѣлъ суммы площадей этихъ,
треугольниковъ.
274.	Въ данпомъ треугольникѣ извѣстны стороны а, Ъ и г. Изъ сре-
динъ этихъ сторонъ возстановлены перпендикуляры х, у и г до взаим-
наго пересѣченія въ центрѣ описаннаго круга. Найти въ зависимости
отъ а, /> и с величины х, у, г и радіусъ 7? описаннаго круга (указаніе:
пользуясь теоремою Птоломея (.215), можно вывести уравненія: Ь? + су —
— аЛ, сх \~аг^ЪЛ, ау 4- Ьх~сЛ и ах + Ъу + сз — 26’, гдѣ Я есть пло-
щадь треугольника).
Задачи на построеніе.
275.	Раздѣлить треугольникъ прямыми, проходящими черезъ его вер-
шину, на три части, которыхъ площади относились бы, какъ т-.п-.р.
276.	Раздѣлить пополамъ тр.-къ прямою, проходящею черезъ данную
точку его стороны.
277.	Найти внутри тр.-ка такую точку, чтобы прямыя, соединяющія
ее съ вершинами тр.-ка, дѣлили его иа три равновеликія части.
278.	— то же — на три части въ отношеніи 2 ; 3 :4 (или вообще
т : П : р).
279.	Раздѣлить параллелограммъ па три равновеликія части прямыми,
исходящими изъ вершины его.
280.	Раздѣлить параллелограммъ на двѣ части въ отношеніи т: п
прямою, проходящею черезъ данную точку.
281.	Раздѣлить параллелограммъ на 3 равновеликія части прямыми,
параллельными діагонали.
282.	Раздѣлить площадь тр.-ка въ среднемъ и крайнемъ отношеніи
прямою, параллельною основанію.
283.	Раздѣлить тр.-къ на три равновеликія части прямыми, перпен-
дикулярными къ основанію.
284.	Раздѣлить кругъ на 2, па 3,... равновеликія части концентриче-
скими окружностями.
285.	Раздѣлить пополамъ трапецію прямою, нараллельною основані-
ямъ (указаніе: продолживъ непараллельныя стороны до взаимнаго пере-
сѣченія, взять за неизвѣстную величину разстояніе конца искомой линіи
до вершины тр.-ка; составить пропорціи, исходя изъ площадей подобныхъ
тр.-ковъ....)
286.	Данный прямоугольникъ превратить въ другой равновеликій пря-
моугольникъ съ даннымъ основаніемъ.
287.	Построить квадратъ, равновеликій 3/3 даннаго квадрата.
288.	Превратить квадратъ въ равновеликій прямоугольникъ, у кото-
раго сумма <? пли разность Л двухъ смежныхъ сторонъ дана.
289.	Построить кругъ, равновеликій кольцу, заключенному между
двумя данными концентрпчеекпмп окружностями.
290.	Построить тр.-къ, подобный одному и равновеликій другому изъ
двухъ данныхъ тр.-ковъ.
— 197 —
291.	Данный тр.-къ превратить въ равновеликій равносторонній (по-
средствомъ приложенія алгебры къ геом.).
292.	Въ данный кругъ вписать прямоугольникъ съ дапною площадью
пг2 (посредствомъ приложенія алгебры къ геом.).
293.	Въ данный тр.-къ вписать прямоугольникъ съ данною площадью
«г2 (прллож. алг. къ геом.).
Числовыя задачи на разные отдѣлы планиметріи*).
294.	Катеты нрямоуг. тр.-ка суть 3 ф- и 4 ф. Найти площадь круга,
котораго окружность проходитъ черезъ средину меньшаго катета и ка-
сается гипотенузы въ ея срединѣ.
295.	'Гонка касанія окружности, вписанной въ прямоугольный тр.-къ,
дѣлитъ гипотспузу на отрѣзки а и Ъ. Найти млоігадь тр.-ка.
296.	Катеты прям. тр.-ка суть Ь и с фут. Найти биссектриссу пря-
мого угла.
297.	Радіусы двухъ концентрическихъ окружностей суть 15 д. и 8 д.
На продолженномъ діаметрѣ взята точка па разстояніи 17 д. отъ общаго
центра и изъ пея проведены касательныя къ этимъ окружностямъ. Найти
разстояніе точекъ» касанія (указаніе: примѣнить теорему Птоломея).
298.	Часть площади круга, заключенная между стороною вписаннаго
квадрата и параллельною ей стороною правильнаго впис. 6-угольника,
равна 1/12 (тг + 3^3 — 6). Найти сторону квадрата, равновеликаго дан-
ному кругу.
299.	Въ ромбъ, который раздѣляется діагональю па два равносторон-
ніе тр -ка, вписанъ кругъ. Найти сторону ромба въ зависимости отъ ра-
діуса этого круга.
300.	Въ тр.-кѣ, котораго стороны суть 4 ф., 5 ф. и 6 ф., проведены
биссектрпссы мепыпаго угла п смежнаго съ нимъ внѣшняго угла. Найти
отрѣзокъ противолежащей стороны, заключенный между этимп бпссект-
рпссамп.
301	Въ равностороннемъ тр.-кѣ со сторопою а вписанъ кругъ, а
изъ вершины тр.-ка радіусомъ, равнымъ половинѣ его сторопы, описала
другая окружность. Найти площадь, общую обоимъ кругамъ.
302	Въ треугольникѣ двѣ стороны суть а п Ъ. Найти третью сто-
рону и площадь, если уголъ между сторонами а и Ь равенъ: 45°; 60°; 150°;
120»; 75о; 1350.
303.	Длины двухъ параллельныхъ хордъ круга суть 30 д. и 16 д., а
разстояніе между ними 7 д. Найти площадь круга.
304.	Черезъ точку, удаленную отъ центра круга на длину ^діаметра,
проведена такая сѣкущая, которая дѣлится окружностью пополамъ.
Найти длпну сѣкущей, если радіусъ круга равенъ ^/6.
*) Взяты изъ „Сборника геометрическихъ задачъ для повторительнаго
курса планиметріи", составилъ М. Попруженко, Воронежъ, 1889 года.
— 198 —
305.	Въ кругѣ радіуса 11 проведена хорда, стягивающая дугу въ 10817.
Найти ея длиниу.
306.	Па діаметрѣ полукруга радіуса В построенъ равносторонній
тр.-къ. Найти площадь той его части, которая лежитъ впѣ круга.
307.	Найти радіусъ окружности, касательной къ сторонамъ а и Ъ
треугольника, и центръ которой лежитъ на третьей его сторонѣ с.
308.	Къ двумъ извнѣ касающимся въ точкѣ Д окружностямъ, радіусы
которыхъ суть 3 д. и 1 д., проведена внѣшняя касательная ВС. Найти
площадь фигуры ЛВС, ограниченной двумя дугами и касательной.
309.	Полуокружность радіуса 11 раздѣлена па три равныя части и
точки дѣленія соединены съ концомъ діаметра. Найти площадь, ограни-
ченную двумя хордами и заключенною между ними дугою.
310.	Стороны тр.-ка АВС продолжены въ одномъ направленіи до то-
чекъ В1 и Си такъ что АА^-ЗАВ, ВВ^ЗВС и СС^ЗСА. Найти
отношеніе площадей тр.-ковъ АВС и Л^Сі.
311.	Изъ вершины тр.-ка проведена къ его основанію прямая, дѣля-
щая основаніе на два отрѣзка т и п. Найти длину этой прямой, если
стороны тр.-ка, прилежащія къ отрѣзкамъ т и ѣ> суть а и Ь.
312.	Кругъ радіуса В, обложенъ тремя равными кругами, касающи-
мися даннаго и взаимно. Найти радіусъ одного изъ этихъ круговъ.
313.	Опредѣлить высоту башни, если извѣстно, что нужно отойти на
а футовъ отъ ея основанія, чтобы башпя была видна подъ угломъ въ 30°.
314.	По даннымъ хордамъ а и Ъ, стягивающимъ двѣ дуги въ кругѣ
единичнаго радіуса, найти хорду, стягиваюпі,ую разность этихъ дугъ
(указаніе: примѣнить теорему Птоломея).
315.	Прямая, параллельная основаніямъ трапеціи, раздѣляетъ ее на
двѣ части въ отношеніи 7:2 (считая оть большаго основанія). Найти,
длину этой прямой, если основанія трапеціи суть 5 ф. и 3 ф.
316.	Изъ точки, дѣлящей основаніе тр.-ка въ отношеніи т : п, про-
ведены прямыя, параллельныя двумъ другимъ сторонамъ. Найти отноше-
ніе площади каждой изъ частей, на которыя раздѣлится тр.-къ, къ пло-
щади всего тр.-ка.
317.	Изъ нѣкоторой точки внутри тр.-ка па стороны его а, Ь и с опу-
щены перпендикуляры рх, р.> и рл. Найти отношеніе площади тр.-ка, ко-
торый образуется отъ соединенія основаній этихъ перпендикуляровъ, къ
площади даннаго тр.-ка. (Указаніе: см. § 290).
318.	Вычислить діагонали трапеціи по четыремъ ея сторонамъ а, Ь,
с и Л. (Указаніе: надо примѣнить къ діагопалп теорему о квадратѣ сто-
роны тр.-ка).
319.	Найти площадь трапеціи по четыремъ ея сторонамъ а, 6, с и Л.
320.	Па противоположныхъ сторонахъ квадрата построены внутри,
его два равносторонніе тр.-ка. Пересѣченіе сторонъ этихъ тр.-ковъ
опредѣляетъ нѣкоторый четыреугольникъ. Найти его видъ, стороны, углы,
л площадь, если сторона квадрата равна а.
— 199 —
321.	Проведена окружность, касающаяся одной стороны прямого угла
и пересѣкающая другую сторону въ точкахъ, отстоящихъ отъ вершины
угла на 6 д. и 24 д. Вычислить радіусъ этой окружности и разстояніе
точки касанія отъ вершины угла.
322.	Вычислить площадь тр.-ка по двумъ сторонамъ а л Ь и медіанѣ
х относительно третьей стороны.
323.	На общей хордѣ АВ построены (ко одну сторону отъ АВ) два
сегмента, изъ которыхъ одинъ вмѣщаетъ уголъ 135°, а другой 120°. Найти
площадь луночки, заключенной между дугами сегментовъ.
324.	Па радіусахъ квадранта (четверть круга) внутри его построены
два полукруга. Найти площадь той части квадранта, которая лежитъ внѣ
полукруговъ, еслп радіусъ квадранта есть В.
325.	Въ прямоугольномъ тр.-кѣ АВС опущенъ перпендикуляръ А})
на гипотенузу ВС. Зная радіусы г, и г8 окружностей, вписанныхъ въ
тр.-ки АВВ и АС/), найти радіусъ г окружности, вписанной въ тре-
угольникъ АВС.
326.	На окружности радіуса В отложены отъ точки А (по обѣ ея
стороны) двѣ дуги; АС=::30° и ЛВ —60<>. Найти площадь тр.-ка АВС.
СТЕРЕОМЕТРІЯ.
КНИГА I.
ПРЯМЫЯ иділоскости.
ГЛАВА I.
Опредѣленіе положенія плоскости.
303.	Опредѣленіе. Плоскостью наз. поверхность, обла-
дающая тѣмъ свойствомъ, что прямая, проходящая черезъ
какія-нибудь двѣ точки этой поверхности, лежитъ въ ней
всѣми остальными своими точками. Возможность существо-
ванія такой поверхности принимается за аксіому.
304.	Изъ понятія о плоскости и прямой линіи слѣдуетъ:
1°. Плоскость есть поверхность пеогранпчениая.
2°. Прямая, имѣющая съ плоскостью только одну общую
точку, пересѣкаетъ плоскость, т.-е. изъ пространства, лежа-
щаго по одну сторону отъ плоскости, переходитъ въ про-
странство. лежащее по другую ся сторону.
— 200 —
3°. Черезъ всякую прямую можно провести плоскость.
305.	Плоскость изображается на
чертежѣ въ видѣ нѣкоторой ея части,
обыкновенно въ формѣ параллелограмма
или прямоугольника. Обозначается пло-
скость большею частію одною или дву-
Черт. 217
Черт. 218
мя буквами; такъ, говорятъ: плоскость
Р, плоскость МУ.
ЗОв. Аксіома. Ріели вращать ка-
кую-нибудь плоскость (М, черт. 218)
вокругъ прямой (АВ), лежащей въ ней,
•то она можетъ пройти черезъ любую
точку (С) пространства.
303. Теорема. Черезъ три точки
(А, В и С, черт. 219). не лежагція
на одной прямой, можно Провести
плоскость и притомъ только одну.
1°. Черезъ какія-пибудь двѣ ивъ
трехъ данныхъ точекъ, напр. черезъ А
и В, проведемъ прямую и черезъ нее
произвольную плоскость. Станемъ вращать эту плоскость во-
кругъ прямой АВ до тѣхъ поръ,
пока она не пройдетъ черезъ
точку С (306). Тогда будемъ
имѣть плоскость, которая про-
ходитъ черезъ три данныя точки.
2°. Вообразимъ, что черезъ
тѣ же три точки А, В и О
можно провести двѣ плоскости.
Обозначимъ одну черезъ Р, а
другую черезъ РА. Докажемъ, что эти двѣ плоскости слива-
ются въ одну.—Предварительно замѣтимъ, что прямыя АВ,
ВС и АС, проходящія черезъ каждую пару данныхъ точекъ,
принадлежатъ обѣимъ плоскостямъ, такъ какъ эти прямыя
имѣютъ по двѣ общихъ точки и съ плоскостью Р, и съ пло-
скостью Рх. Возьмемъ теперь на плоскости Р произвольную
тючку М и проведемъ черезъ нее на этой плоскости какую-
— 201 —
нибудь прямую МВ. Эта прямая, находясь въ одной плоско-
сти Р съ прямыми АВ, ВС и АС, должна пересѣчься по
крайпей мѣрѣ съ двумя изъ нихъ, папр. съ АВ и АС, въ
нѣкоторыхъ точкахъ Е и Е. Такъ какъ прямыя АВ и АС
принадлежатъ другой плоскости то и точки ихъ Е и Е
также принадлежатъ этой плоскости. Вслѣдствіе этого пря
мая МВ, проходящая черезъ Е и Е, лежитъ вся въ пло-
скости Рг (по опредѣленію плоскости), а потому и ея точка
М лежитъ въ этой плоскости. Такимъ образомъ, всякая точка
М плоскости Р принадлежитъ л плоскости 7\; значитъ, эти
плоскости сливаются.
308.	Слѣдствія. 1°. Черезъ прямую и -точку внѣ ея
можно провести плоскость и притомъ только одну, потому что
точка внѣ прямой вмѣстѣ съ какими-нибудь двумя точками
прямой составляютъ три точки, черезъ которыя, по доказан-
ному, можно провести плоскость и притомъ одну.
2°. Черезъ двѣ пересѣкающіяся прямыя можно провести
плоскость и притомъ только одну, потому что, взявъ точку
пересѣченія и еще по одной точкѣ на каждой прямой, мы
будемъ имѣть три точки, черезъ которыя и т. д.
3°. Черезъ двѣ параллельныя прямыя можно провести
плоскость и притомъ -только одну, потому что параллельныя
прямыя, по опредѣленію, лежатъ въ одной плоскости; эта
плоскость единственная, такъ какъ черезъ одну изъ парал-
лельныхъ и какую-нибудь точку другой можно провести не
болѣе одной плоскости.
4°. Всякую часть плоскости можно наложить всѣми
ея точками на другое мѣсто этой или другой плоскости,
причемъ накладываемую часть можно предварительно пере-
вернуть другою стороною, потому что всегда возможно на-
ложить одну плоскость на другую такъ, чтобы у нихъ со-
впали какія-нибудь три точки, не лежащія на одной прямой,
а тогда совпадутъ и остальныя точки.
309.	Теорема. Если двѣ не сливающіяся плоскости
имѣютъ общую точку, то онѣ имѣютъ и общую прямую,
проходящую черезъ эту точку.
— 202 —
Пусть плоскость Р
Черт. 220
другой стороны, эта
общихъ точки В и Р.
имѣетъ точку А, общую съ другою
плоскостью (ие указанною на чер-
тежѣ). Проведемъ па плоскости
черезъ точку А какія-нибудь двѣ
прямыя СВ1 и ВОр, изъ нихъ каж-
дая подраздѣлится плоскостью Р на
двѣ части, расположенныя по раз-
ныя стороны отъ этой плоскости.
Возьмемъ на частяхъ АВ и АВ^
какія-нибудь точки В и В1 и про-
ведемъ прямую ВВ1. Эта прямая
пересѣчется съ плоскостью Р въ
нѣкоторой точкѣ Е. Такъ какъ, съ
зямая имѣетъ съ плоскостью двѣ
то она принадлежитъ ей вся. По-
этому точка Е прямой ВВ1 также принадлежитъ плоскости (}.
Итакъ, плоскости Р и $ имѣютъ двѣ общія точки А и Е;
значитъ, онѣ имѣютъ и общую прямую АЕ, проходящую че-
резъ эти точки.
310.	Слѣдствіе. Пересѣченіе двухъ плоскостей есть
прямая линія.
Дѣйствительно, чтобы плоскости пересѣкались, необходимо,
чтобы онѣ нмѣли общую точку; но въ такомъ случаѣ онѣ
будутъ имѣть и общую прямую. Какой-нибудь еще общей
точки, сверхъ точекъ этой прямой, плоскости имѣть пе мо-
гутъ, такъ какъ въ противномъ случаѣ онѣ должны были бы
слиться въ одну (308,1°).
— 203 —
ГЛАВА II.
Перпендикуляръ и наклонныя.
311.	Опредѣленіе. Прямая наз. перпендикулярною къ
плоскости, если ояа пересѣкается съ этою плоскостью и при
этомъ образуетъ прямые углы со всѣми прямыми, проведен-
ными на плоскости черезъ точку пересѣченія. Въ этомъ слу-
чаѣ говорятъ также, что плоскость перпендикулярна къ
прямой.
Прямая, пересѣкающаяся съ плоскостью, но не перпен-
дикулярная къ ней, наз. наклонною. Точка пересѣченія пря-
мой съ плоскостью наз. основаніемъ (перпендикуляра или на-
клонной) .
Возможность существованія взаимно перпендикулярныхъ
прямой и плоскости обнаружится изъ нижеслѣдующихъ те-
оремъ.
313. Теорема. Прямая, перпендикулярная къ двумъ
прямымъ, проведеннымъ на плоскости черезъ ея основаніе,
перпендикулярна къ самой плоскости.
Пусть прямая АВ перпендикулярна къ прямымъ ВО и
ВВ, проведеннымъ на плоскости
Р черезъ основаніе В. Чтобы до-	до-
казать перпендикулярность прямой	/
АВ къ плоскости Р, достаточно	/ \ \
показать, что АВ перпендикуляра / Г \\	7
па ко всякой третьей прямой ВЕ, /	/ \ \с/
проведенной па той же плоскости	/ Р	Г/>'''/7
черезъ точку В. — Продолживъ /
АВ, отложимъ произвольныя, НО	/ •
равныя, длины ВАХ и ВА и про-	\ /
ведемъ на плоскости прямую ВО,
которая пересѣкала бы прямыя
ВС, ВЕ и ВВ въ какихъ-ни-	е₽т’
будь точкахъ С, Е и В. Соединимъ эти точки съ А и А1
и убѣдимся, что тр.-ки АВЕ и АХВЕ равны. Для этого
— 204 —
сначала беремъ тр.-ки АБС и АХВС; они равны, потому
что у нихъ ВС общая сторона, АС~АІС, какъ наклонныя
къ ААГ, одинаково удаленныя отъ основанія перпендикуляра
ВС; по той же причинѣ АВ=АІВ. Изъ равенства этихъ
тр.-ковъ слѣдуетъ, что / АСВ — / Аг СВ. Послѣ этого пе-
рейдемъ къ тр.-камъ АСВ и ЛгСЕ; опіі равны, потому что
у нихъ ЕС общая сторона, АС = Аг С и/_ АСВ = /_ АХСВ;
изъ равенства этихъ тр.-ковъ выводимъ, что АЕ=-АГЕ.
Теперь оказывается, что тр.-ки АВЕ и А^ВЕ имѣютъ со-
отвѣтственно равныя стороны и потому равны; значитъ,
^АВЕ^/^ВЕ, т.-е. АВ±ВЕ.
313. Теорема. Черезъ всякую точку, взятую на пря-
мой или внѣ ея. можно провести къ этой прямой перпен-
дикулярную плоскость и притомъ только о^ну.
1°. Пусть С будетъ точка, взятая на прямой АВ. Про-
ведемъ черезъ эту прямую какія-нибудь
А	двѣ плоскости Р и () и на нихъ возь-
мемъ прямыя СВ и СЕ, перпепдику-
5 ______ парныя къ АВ. Черезъ эти двѣ пере-
/	/ сѣкающіяся прямыя проведемъ пло-
скость В. Это и будетъ плоскость,
перпендикулярная къ АВ въ точкѣ С,
потому что двѣ ея прямыя СВ и СЕ
перпендикулярны къ АС. Такая пло-
скость можетъ быть только одна. Дѣй-
ствительно, всякая плоскость, перпен-
дикулярная къ АВ въ точкѣ С, дол-
Черт. 222
жна пересѣчься съ плоскостями В и по прямымъ, пер-
пендикулярнымъ къ АС и проходящимъ черезъ точку С; та-
кими прямыми будутъ только СВ и СЕ; а черезъ СВ и СЕ
можетъ приходить только одна плоскость.
2°. Пусть В будетъ точка, взятая внѣ прямой АВ
(черт. 222). Проведемъ черезъ В и АВ плоскость Р и черезъ
АВ еще какую-нибудь плоскость (р. па первой опустимъ на
АВ изъ точки В перпендикуляръ ВС, а па второй возста-
вимъ къ АВ изъ точки С перпендикуляръ СЕ. Плоскость В,
проходящая черезъ ВС и СЕ, будетъ перпендикулярна къ
— 205 —
АВ (312). Другой перпендикулярной плоскости черевъ точку
I) провести нельзя. Дѣйствительно, всякая плоскость, пер-
пендикулярная къ АВ и проходящая черезъ В, пересѣчется
съ плоскостью Р пп прямой, перпендикулярной къ АВ п
проходящей черезъ В, т.-е. по ВС; тогда съ плоскостью ф
опа можетъ пересѣчься только по прямой СЕ; а черезъ ВС
и СЕ можетъ проходить только одна плоскость.
314. Слѣдствіе. Всѣ перпендикуляры, которые можно
провести въ пространствѣ къ одной прямой черезъ одну ея
точку, лежапп, въ одной плоскости, перпендикулярной къ
этой прямой.
Проведемъ черезъ прямую АВ
сколько угодно плоскостей Р, О1, В,8..
и на каждой изъ нихъ черезъ точку
В проведемъ по прямой, перпенди-
кулярной къ АВ. Пусть это будутъ
ВС, ВВ, ВЕ... Черезъ двѣ изъ
нихъ, напр. черезъ ВС и ВВ, во-
образимъ плоскость АІ. Эта плоскость
перпендикулярна къ АВ (312). Что-
бы доказать, что она содержитъ въ
себѣ всѣ прочія изъ проведенныхъ
линій, вообразимъ, что какая-нибудь изъ нихъ, напр., линія
ВЕ, не лежитъ въ плоскости М; тогда па плоскости В
можно провести къ АВ черезъ точку В два перпендику-
ляра: одинъ ВЕ, а другой пересѣченіе плоскостей В и М;
такъ какъ это невозможно, то прямая ВЕ и всякая дру-
гая, перпендикулярная къ АВ въ точкѣ В, должна лежать
на плоскости М.
зі5. Теорема. .Изъ всякой
точки (О, черт. 224) плоскости
(М) можно возставить къ этой
плоскости перпендикуляръ и при-
томъ только одинъ.
Возьмемъ какую-нибудь пря-
мую АВ и черезъ произвольную
ея точку В проведемъ къ ней
Черт. 224
— 206 —
перпендикулярную плоскость В. Совмѣстимъ эту плоскость
съ плоскостью М такъ, чтобы точка В совпала съ О. Тогда
прямая ВА, занявъ нѣкоторое положеніе ОК, будетъ пер-
пендикулярна къ М въ точкѣ О. Чтобы доказать теперь, что
эготъ перпендикуляръ единственный, предположимъ, что пря-
мая О1( будетъ другимъ перпендикуляромъ къ М. Проведемъ
черезъ ОК и ОКХ плоскость и возьмемъ ея пересѣченіе ОЬ
съ плоскостью 717. Тогда углы КОІ> и КХОВ должны быть
оба прямые; но это невозможно, такъ какъ одинъ изъ нихъ
составляетъ часть другого; значитъ, другого перпендикуляра
къ 7И въ точкѣ О возставить нельзя.
31в. Когда изъ одной точки А (черт. 225) проведены
къ плоскости перпендикуляръ АВ и наклонная А.С, усло-
вимся разстояніе ВС ихъ основаніями называть про-
екціей наклонной на плоскость Р.
313. Теоремы. Если ивъ одной точки (А, черт. 225)
проведены къ плоскости перпендикуляръ (АВ) и наклонныя
(АС, АВ, АЕ..), .то:
1°, перпендикуляръ короче всякой наклонной;
2°, двѣ наклонныя, имѣющія равныя проекціи, равны;
3°, изъ двухъ наклонныхъ та больше, которой проекція
больгие.
Вращая прямоугольные тр.-ки АВС
и АВВ вокругъ катета АВ, мы мо-
жемъ совмѣстить ихъ плоскости съ
плоскостью тр.-ка АВЕ. Тогда всѣ
наклонныя будутъ лежать въ одной
плоскости съ перпендикуляромъ, и всѣ
проекціи расположатся на одной пря-
мой. Такимъ образомъ, доказываемая
теорема приводится къ аналогичной
теоремѣ планиметріи (55).
319. Обратныя теоремы. 1°. Крат-
чайшее разстояніе точки отъ плоскости есть перпен-
дикуляръ;
2°. Равныя наклонныя гімѣюгпъ равныя проекціи;
— 207 —
3°. Изъ двухъ проекцій та больше, которая соотвѣт-
ствуетъ большей наклонной.
Доказательство (отъ противнаго) предоставляемъ самимъ
учащимся.
ГЛАВА Ш.
Параллельныя прямыя и плоскости.
Параллельныя прямыя.
Черт. 226
319. Двѣ прямыя могутъ быть расположены въ про-
странствѣ такъ, что черезъ нихъ нельзя провести плоскости.
Возьмемъ, напр., двѣ такія прямыя
АВ и ВЕ, изъ которыхъ одна пе-
ресѣкаетъ плоскость Р, а другая
лежитъ въ ней, но не проходитъ
черезъ точку пересѣченія С. Черезъ
такія двѣ прямыя нельзя провести
плоскости, потому что въ против-
номъ случаѣ черезъ прямую ВЕ и
точку С проходили бы двѣ различныя плоскости: одна Р,
пересѣкающая прямую АВ, и другая, содержащая ее; а это
невозможно (308,1°).
Двѣ прямыя, не лежащія въ одной плоскости, конечно,
не пересѣкаются, сколько бы ихъ не продолжали; однако ихъ
не называютъ параллельными, оставляя это названіе только
для такихъ прямыхъ, которыя, находясь въ одной плоскости,
не пересѣкаются, сколько бы ихъ не продолжали.
Въ планиметріи мы видѣли (69 и 72), что черезъ всякую
точку плоскости можно провести прямую, и притомъ только
одну, параллельную данной прямой. То же самое можно ска-
зать о всякой -точкѣ пространства, потому что черезъ точку
и данную прямую можно провести плоскость и только одну.
330. Теорема. Плоскость (Р, черт. 227), пересѣкаю-
щая одну изъ параллельныхъ прямыхъ (АВ), пересѣкаетъ
и другую ( СВ).
Проведемъ черезъ АВ и СВ плоскость. Эта плоскость
— 208 —
содержитъ въ себѣ ту точку В, въ которой прямая ЛВ пере-
сѣкается съ Р; значитъ, эта плоскость
пересѣкается съ Г по нѣкоторой прямой
ВЕ (309). Эта прямая, находясь въ од-
ной плоскости съ АВ и СР и пересѣ-
кая одну изъ этикъ параллельныхъ, дол-
жна пересѣчь и другую (73) въ нѣкото-
рой точкѣ Е. Точка Е, находясь заразъ
на прямой ВЕ и на прямой СВ, должна
быть точкою пересѣченія плоскости Р съ
Черт. 22“ прЯМОЙ СР.
ЗЙІ. Лемма. Прямая (РЕ, черт. 228), проведенная на
плоскости (Р) черезъ основаніе на-
клонной (АС) перпендикулярно къ
ея проекціи (ВС), перпендикулярна
и къ самой наклонной.
Отложимъ произвольныя, но рав-
ныя, части СР и СЕ и соединимъ
точки А и В съ В и Е. Тогда бу-
демъ имѣть: ВР = ВЕ, какъ на-
клонныя къ РЕ, одинаково удален-
ныя отъ основанія перпендикуляра
ВС; АВ — АЕ, какъ наклонныя къ
плоскости Р7 имѣющія равныя про-
екціи ВВ и ВЕ. Вслѣдствіе этого А АРЕ есть равнобед-
ренный, и потому его медіана
ЛСперпендикулярна къ основанію
ВЕ (38).
з®®. Теорема. Плоскость(Р,
черт. 229), перпендикулярная къ
одной изъ параллельныхъ прямыхъ
(АВ), перпендикулярна и къ дру-
гой ( сВ).
Предстоитъ доказать, что во
1° прямая СР пересѣкается съ
Р, а во 2° эта прямая перпен-
дикулярна къ какимъ-нибудь двумъ прямымъ, проведеннымъ
на плоскости Р черезъ основаніе СВ.
— 209 —
1°. Плоскость Г должна пересѣчь СВ, потому что опа,
по условію, пересѣкаетъ прямую АВ, параллельную СВ.
2°. Проведемъ черевъ АВ и СВ плоскость В и возьмемъ
ея пересѣченіе ВВ съ плоскостью Р. Такъ какъ, по усло-
вію, АВ перпендикулярна къ Р, то АВ | ВВ; поэтому и
СВ I ВВ (74). Проведемъ на плоскости Р прямую ВЕ,
перпендикулярную къ ВВ, и возьмемъ какую-нибудь наклон-
ную МВ, для которой проекціей служитъ ВВ. Прямая ЕВ,
будучи перпендикулярна къ проекціи ВВ, должна быть пер-
пендикулярна и къ наклонной МВ (321) и, слѣд., перпенди-
кулярна къ плоскости В (312), значитъ, и къ прямой СВ.
Такимъ образомъ, прямая СВ оказывается перпендикулярною
къ двумъ прямымъ плоскости Р, именно къ ВВ и ВЕ;
слѣд., она перпендикулярна къ этой плоскости.
з»з. Обратная теорема. Два пер?
иендикуляра (АВ и СВ, черт. 230)
і;<> одноіь плоскости (Р) параллельны.
Предположимъ, что линіей, параллель-
ной АВ и проходящей черезъ точку В,
будетъ не СВ, а какая-нибудь иная пря-
мая СГВ. Тогда, согласно прямой теоре-
мѣ, С^В будетъ перпендикуляромъ къ Р,
что невозможно, такъ какъ перпендику-
ляромъ къ Р, по условію, служитъ СВ.
Черт. 220
394. Слѣдствіе. Изъ всякой точки (А,
плоскости (Р) можно опуститъ
на эту плоскость перпендикуляръ
и притомъ только одинъ.	А
Дѣйствительно, всегда возможно
изъ какой-нибудь точки В плоскости
Р возставить къ ней перпендику- /
ляръ ВС (315) и затѣмъ черезъ А / і
провести АВ І] СВ. Прямая АВ	/г I
будетъ перпендикуляромъ къ Р (322).	------
черт. 230) внп.
В
Другого перпендикуляра изъ точки А	Черт. 231
опустить нельзя, потому что перпендикуляръ къ Р дол-
А. П. КИСЕЛЕВЪ.
14
— 210 —
женъ быть параллеленъ ВС (323), а черезъ А можно про-
вести только одну прямую, параллельную ВС.
335. Теорема. Двѣ прямыя (А и В, черт. 231), па-
раллельныя третьей прямой (С), параллельны между собою.
Проведемъ плоскость Р, перпендикулярную къ С. Тогда
А и В будутъ перпендикулярами къ этой плоскости (322).
и, слѣд., ЛII В (323).
ІІрямыя, параллельныя плоскости.
ЗЗв. Опредѣленіе. Прямая и плоскость паз. параллельны-
ми, если онѣ не пересѣкаются, сколько бы ихъ пе продолжали.
Слѣдующія двѣ теоремы выражаютъ признаки параллель-
ности прямой съ плоскостью.
333. Теорема 1. Прямая
і	(АВ, черт. 232), и плоскость
д;________(1>), перпендикулярныя къ од-
|	ной и той же прямой (АС).
|	\	параллельны.
|г--------------з.--- Предположимъ, что АВ пе-
р/іС..............  \м/	ресѣкается съ Р въ точкѣ Аі;
/ •:__________________/ тогда, соединивъ М съ С, мы
і	будемъ имѣть два перпендпку-
Че т 9>й	ляра МС и МА на прямую
АС изъ одной точки М, что
невозможно; значитъ, АВ не пересѣкается съ Р, т.-е. АВ
параллельна Р.
Теорема 2. Прямая (АВ. черт. 233), параллельная ка-
кой-нибудь прямой (СВ), проведенной на плоскости (V),
параллельна самой плоскости.
Черт. 233
АВ не пересѣкается съ
Проведемъ черезъ АВ и СВ
плоскость В. Такъ какъ прямая АВ
па всемъ протяженіи лежитъ па пло-
скости В, то ома могла бы пере-
сѣчься съ плоскостью Р не иначе,
какъ пересѣкаясь съ прямой СВ,
что невозможно по условію. Значитъ,
Р, т.-е. АВ карательна Р.
— 211 —
398. Теорема. Если плоскость (В,, черт. 233) прохо-
-дитъ черезъ прямую (АВ), параллельную другой плоскости
(Р), и пересѣкаетъ эту плоскость, то линія пересѣченія
(СВ) параллельна первой прямой (АВ).
Дѣйствительно, во 1°, СВ лежитъ въ одной плоскости съ
АВ; во 2°, СВ не можетъ пересѣчься съ АВ, потому что
въ противномъ случаѣ АВ пересѣкалась бы съ Р, что не-
возможно.
Слѣдствіе. Прямая (АВ, черт. 234), параллельная двумъ
пересп>каюги,имся плоскостямъ (Р и ()), параллельна линіи
ихъ пересѣченія.
Вообразимъ плоскость черезъ АВ и ка-
кую-нибудь точку М прямой СВ. Эта пло-
скость должна пересѣчься съ Р и () по
прямымъ, параллельнымъ АВ, и проходя-
щимъ черезъ М. Но черезъ М можно про-
вести только одну прямую, параллельную ЛВ;
значитъ, два пересѣченія воображаемой пло-
скости съ плоскостями Р и () должны слить-
ся въ одну прямую, которая не можетъ че т 234
быть иною, какъ ОВ; слѣд., СВ||ЛВ.	р*
399. Теорема. Всѣ точки, прямой (АВ, черт. 235),
параллельной плоскости (Р), одинаково удалены отъ этой
плоскости.
Изъ двухъ какихъ-нибудь точекъ
М и Вт прямой АВ опустимъ на Р
перпендикуляры М С и РВ. Такъ
какъ эти перпендикуляры параллель-
ны (323), то черезъ нихъ можно
провести плоскость. Эта плоскость
пересѣчется съ Р по прямой СВ,
параллельной АВ (328); поэтому
фигура МРВС будетъ параллело-
граммъ и, слѣд., МС—РВ.
Черт. 235
14*
— 212 —
Параллельныя плоскости.
330. Опредѣленіе. Двѣ плоскости наз. параллельными,
если опѣ не пересѣкаются, сколько бы
ихъ не продолжали.
Слѣдующія двѣ теоремы выражаютъ
признаки параллельности двухъ пло-
скостей.
331. Теорема 1. Двѣ плоскости
(Р и (), черт. 236), перпендикулярныя
къ одной и той же прямой (АВ), па-
раллельны.
Если бы плоскости Р и () пересѣка-
лись, то черезъ всякую точку ихъ пере-
сѣченія проходили бы двѣ плоскости Р
и (), перпендикулярныя къ прямой АВ,
что невозможно.
А
Г' 7
в
Черт. 236
Теорема 2. Двѣ плоскости (Р и Ц, черт. 237), парал-^
лельны, если двѣ пересѣкающіяся пря-
мыя одной изъ нихъ (АВ и АС) соот-
вѣтственно параллельны двумъ пере-
сѣкающимся прямымъ друіой (А1 Вг
и АД\).
Изъ точки А опустимъ на плоскость
() перпендикуляръ ААп и проведемъ
прямыя АпВ{1 и	Ц!. соотвѣт -
ственно параллельныя прямымъ А1В1
и А1 Сх; тогда эти прямыя будутъ так-
же параллельны п линіямъ АВ и АС
(325). Такъ какъ ААІЛ I А„В„ и
и АВ || АаВп. то АА,< I АВ; по той же причинѣ АА^ , АС.
Слѣд., прямая ААп перпендикулярна къ плоскости Р (312).
Такимъ образомъ, плоскости Р и перпендикулярны къ
прямой ААп и потому параллельны.
Черт. 237
— 213 —
339. Теорема. Если дай, параллельныя плоскости (Р
и (), черт. 238) пересѣкаются третьею
плоскостью (В,), то линіи пересѣченія
(АВ и СВ) параллельны.
Дѣйствительно, прямыя АВ и СВ,
находясь вт» одной плоскости В, не мо-
гутъ пересѣчься, такъ какъ въ про-
тивномъ случаѣ псресѣкались-бы пло-
скости Р и (^, что противорѣчитъ ус-
ловію.
333. Теорема. Прямая или пло-
скость, пересѣкающая одну изъ па-
раллельныхъ плоскостей, пересѣкаетъ
1°. Пусть прямая АВ пересѣкаетъ
въ точкѣ В плоскость Р, параллель-
ную (). Опустимъ изъ В м § пер-
пендикуляръ ВС и черезъ АВ и ВС
проведемъ плоскость. Эта плоскость,
содержа въ себѣ точкп В и С, пере-
сѣкается съ Р и <2 по нѣкоторымъ
прямымъ ВЕ и ЕН, которыя парал-
лельны (332). Прямая АВ лежитъ въ
одной плоскости съ ВЕ и ЕН и пере-
Черт. 238
и другую.
сѣкаетъ одну изъ этихъ параллельныхъ; Че т 2зд
слѣд., какъ мы знаемъ изъ планимет-	р *
ріи (73,1°), она пересѣчетъ и другую; значитъ, пересѣчетъ и
плоскость
2°. Пусть какая-нибудь плоскость пересѣкаетъ плоскость
Р (черт. 239), параллельную (). Тогда на ней можно взять
прямую АВ, которая тоже пересѣкаетъ плоскость Р: по до-
казанному, эта прямая пересѣчетъ и плоскость ф; значитъ,
съ этою плоскостью пересѣчется и та плоскость, въ которой
взята АВ.
334. Теорема. Прямая (АВ, черт. 240), перпендику-
лярная къ одной изъ параллельныхъ плоскостей (къ Р),
перпендикулярна и къ другой (къ
Прямая АВ, пересѣкая одну изъ параллельныхъ плоско-
— 214 —
стей, пересѣчетъ и другую въ нѣкоторой точкѣ Вх. Про-
ведемъ черезъ АВ какія-нибудь двѣ
плоскости, которыя пересѣкутся съ Р
I	и по параллельнымъ прямымъ: одна
/	| с 7 по ВС и ВАС1, другая по ВВ и
у	Согласно условію, прямая АВ
/__перпендикулярна къ ВС и ВВ; слѣд.,
она также перпендикулярна къ Вх Сх
,—|------------] и ВХВ1У а потому перпендикулярна и
<у	—С' / къ плоскости &
/. /	335. Слѣдствіе. Черезъ всякую
Черт 240 точку (В, черт. 240) пространства
можно провести плоскость (Р), параллельную данной пло-
скости (0), и притомъ только одну.
Предоставляемъ учащимся самимъ доказать это слѣдствіе г
на основаніи теоремъ §§ 331 и 334.
ЗЗв. Теорема. Отрѣзки параллельныхъ прямыхъ (АВ
и СВ, черт. 241), заключенные между параллельными пло-
скостями (Р и 0), равны.
Черезъ параллельныя прямыя АВ и
СВ проведемъ плоскость; она пересѣ-
четъ () и ? по параллельнымъ пря-
мымъ ВВ и АС; слѣд., фигура.
АВВС будетъ параллелограммъ и по-
тому СВ.
33 9. Слѣдствіе. Параллельныя пло-
скости вездѣ одинаково удалены одна
отъ другой, потому что. когда парал-
Черт. 241 лельныя прямыя АВ и СВ (черт. 241)
перпендикулярны къ Р, онѣ будутъ также перпендикулярны
къ (I и въ то же время равны.
338. Теорема. Два угла (ВАС и В'А^С^ черт. 242)
съ соотвѣтственно параллельными и одинаково направлен-
ными сторонами равны и лежатъ въ параллельныхъ плоско-
стяхъ (Р и 0).
Что плоскости Р и О параллельны, было доказано выше
(331,2°); остается доказать, что углы А и Ах равны.—
— 215 —
Черт. 242
Отложимъ АВ — А1В1^ АС=АІС\ и проведемъ ААг, ВВ1
СС1} ВС и ВхСг. Такъ какъ отрѣзки
АВ и Ау Ву равны и параллельны, то
фигура АВВхАг есть параллелограммъ
(97,2°); поэтому отрѣзки АА{ и ВВ1
равны и параллельны. По той же при-
чинѣ равны и параллельны отрѣзки ААг
и СО^ слѣд., ВВ^=С(\ и ВВ^\\
СС1. Поэтому ВС—В^^ Ц и ЛАВС—
= Ё^ВІСІ (по тремъ сторонамъ);
значитъ, /_А=~-/)А1.
ГЛАВА IV.
Двугранные углы.
339. Опредѣленія. Двѣ плоскости Р и <), исходящія изъ
одной прямой АВ, образуютъ деу-
іранный уголъ.
Прямая АВ наз. ребромъ, а
плоскости Р и () — сторонами или
гранями двуграннаго угла. Такой
уголъ обозначается обыкновенно
двумя буквами, поставленными у
его ребра (двугр. уголъ АВ).
Но если при одномъ ребрѣ ле-
жатъ нѣсколько двугр. угловъ, то
каждый изъ нихъ обозначаютъ
4-мя буквами, изъ которыхъ двѣ среднія стоятъ при ребрѣ,
а двѣ крайнія у граней (напр.. двугр. уголъ 80В<)).
Если изъ произвольной точки В ребра АВ (черт. 244)
проведемъ на каждой грани по перпендикуляру къ ребру,
то образованный ими уголъ (УВЕ наз. линейнымъ угломъ
двуграннаго. Величина линейнаго угла не зависитъ отъ поло-
женія точки В на ребрѣ. Такъ, линейные углы СВЕ и (\В1Е1
— 216 —
равны, потому что ихъ стороны соотвѣтственно параллельны и
одинаково направлены.
Черт. 244
ныхъ угловъ въ
метріи. Подобно
Не трудно видѣть, что плоскость линей-
наго угла перпендикулярна къ ребру (312).
340. Равенство двугранныхъ угловъ.
Два двугранные угла считаются равными,
если они при вложеніи совмѣщаются; въ
противномъ случаѣ тотъ изъ угловъ считается
меньшимъ, который, будучи вложенъ въ дру-
гой такъ, чтобы у нихъ совпали ребра, со-
ставитъ часть этого другого угла.
Такъ какъ двугранный уголъ есть ве-
личина, то можно разсматривать сумму,
разность, произведеніе и частное двугран-
томъ же смыслѣ, какъ и для угловъ плани-
этимъ угламъ двугранные углы могутъ быть
смежные, прямые, вертикальные...
341. Теоремы. 1°. Равнымъ двуграннымъ угламъ соот-
вѣтствуютъ равггые линейные углы.
2°. Большему двугранному углу соотвѣтствуетъ большій
линейный уголъ.
Черт. 245
Пусть РАВ$ и	будутъ двугранные углы съ
линейными углами СВВ и С^В^В^. Вложимъ уголъ А^ВХ
.въ уголъ АВ такъ, чтобы у нихъ совпали: во 1, точки В
я В1, во 2, ребра А1В1 и АВ, и въ 3, грани Р± и Р.
— 217 —
При этомъ также совпадутъ и плоскости линейныхъ угловъ,
такъ какъ онѣ перпендикулярны къ одной прямой въ одной
точкѣ. Положимъ, теперь, что наши двугранные углы равны:
тогда грань совпадетъ съ и. слѣд., уголъ С1В1ВІ
совмѣстится съ угломъ СВВ, т.-е. эти линейные углы ока-
жутся равными. Если же двугранные углы неравны, напр.
уголъ АХВХ меньше угла АВ, то грань <^х пойдетъ внутри
угла АВ, напр., займетъ положеніе @п. Тогда линейный
уголъ С1В1В1 займетъ положеніе СІХВВ и. слѣд., будетъ
меньше линейнаго угла СВВ.
349. Обратныя теоремы. 1°. Равнымъ линейнымъ угламъ
соо)нв)мпстоуютъ равные двугранные углы.
2°. Болглаемоу линейному углу соотвѣгпствуетъ бблъгигй
двугранной н уголъ.
Эти теоремы легко доказываются отъ противнаго (48).
343. Замѣчаніе. Наложеніе, или, лучше сказать, вло-
женіе одной фигуры въ другую, часто употребляемое въ сте-
реометріи, всегда можетъ быть выполняемо въ такой послѣ-
довательности: во 1°, совмѣщаемъ какія-нибудь двѣ точки фи-
гуръ; во 2°, какія-нибудь двѣ прямыя, исходящія изъ совпав-
шихъ точекъ и въ 3°, какія-нибудь двѣ плоскости, исходящія
изъ совпавшихъ прямыхъ. Совмѣстятся ли при этомъ другіе
элементы фигуръ, зависитъ отъ свойствъ ихъ.
344. Слѣдствія. Г’. Прямо му двугранному углу соот-
вѣтствуетъ прямой линейный уголъ и обратно.
Пусть уголъ РАВ(^ будетъ прямой.
Это значитъ, что онъ равенъ смежно-
му углу (^АВРг. Но въ такомъ слу- /С\
чаѣ линейные углы СВЕ и СВЕХ	|в
также равны; а такъ какъ они смеж- /	...у 7
ные, то каждый изъ нихъ долженъ	/р
быть прямой. Обратно, если равны /___________д/________
смежные линейные углы СВЕ и СВЕХ,
то равны и смежные двугр. углы, т.-е. Черг* 246
каждый изъ нихъ долженъ быть прямой.
2°. Прямые двугранные углы равны, потому что у нихъ
равны линейные углы. По той же причинѣ:
— 218 —
3". Вертикальные двугранные углы равны.
4°. Двугранные углы съ соотвѣтственно параллельными
и одинаково направленными гранями равны.
34&, Теорема. Двугранные углы относятся, какъ гіхъ
линейные углы.
При доказательствѣ разсмотримъ особо два случая:
Поэтому:
/ СВВ__ін
2^вД)\—п 11
1° Линейные уллы ОВВ
и СІВІВ1 соизмѣримы. Пусть
ихъ общая мѣра содержится
въ первомъ углѣ т разъ, а
во второмъ и разъ. Прове-
демъ черезъ ребра и прямыя,
дѣлящія линейные углы па рав-
ныя части, рядъ плоскостей;
тогда мы раздѣлимъ уголъ АВ
на т. ‘ а уголъ А1ВІ на п
частей, которыя всѣ равны
между собою (вслѣдствіе ра-
венства линейныхъ угловъ).
дв. дг. АВ_т
дв. уг. АіВі п
Откуда:
дв. уг. АВ_/_СВР
дв. уг. АІВ1 А^В^
2° Линейные углы несоизмѣримы. Раздѣлимъ уголъ С^ВДс^
на н равныхъ частей. Пусть х/а этого угла содержится въ
углѣ СВВ болѣе т, но менѣе разъ. Тогда приближен-
ное отношеніе угловъ СВВ и С^ВД)^ съ точностью до
;/Л, будетъ равно и/„. Проведя плоскости такъ же, какъ и
въ первомъ случаѣ, найдемъ, что приближенное отношеніе
двугранныхъ угловъ АВ и АХВ1У съ точностью до ул, также
равно ’Л/Я. Такимъ образомъ, мриближеяныя отношенія оказы-
ваются равными при всякомъ м; а въ этомъ и состоитъ
равенство несоизмѣримыхъ отношеній.
34в, Слѣдствіе. Если за единицу двугранныхъ угловъ
взять такой уголъ, который соотвѣтствуетъ единицѣ линейныхъ
— 219 —
угловъ, то можно сказать, что двугранный уголъ измѣряется
ею линейнымъ угломъ.
Перпендикулярныя плоскости.
34 9. Опредѣленіе. Двѣ плоскости наз. взаимно перпен-
дикулярными, если пересѣкаясь, онѣ образуютъ прямые дву-
гранные углы.
348. Теорема. Плоскость (Р, чер. 2489, проходящая
черезъ перпендикуляръ (АВ) къ другой плоскосгпи (пер-
пендикулярна къ ней.
Черт. 243.
Проведемъ на плоскости () пря-
мую ВС, перпендикулярную къ ВЕ.
Тогда уг. АВС будетъ линейнымъ
двугр. угла РВЕ(). Такъ какъ
АВ, по условію, перпендикулярна
къ (), то АВ1 ВС; значитъ, уг.
АВС прямой, а потому и двугр.
уголъ прямой, т. е. пл. Р пер-
пендикулярна къ ф.
349.	Обратная теорема. Перпендикуляръ (АВ, чер. 249).
имѣющій общую точку (А) съ одною изъ двухъ взаимно пер-
пендикулярныхъ плоскостей (Р и ()), лежитъ весь въ этой
плоскости.
Предположимъ, что АВ не ле-
житъ въ плоскости Р (какъ изоб-
ражено у насъ на чертежѣ). Про-
ведемъ на пл. Р изъ точки А пря-
мую АС, перпендикулярную къ ВЕ,
и на пл. () изъ точки С прямую
СЕ, перпендикулярную къ ВЕ.
Тогда уголъ АСЕ, какъ линейный
уголъ прямого двугр. угла, будетъ	ч 249
прямой. Поэтому линія АС, обра-
зуя прямые углы съ СВ и СЕ, будетъ перпендикуляромъ къ.
— 220 —
ил. (). Но изъ точки А нельзя опустить на плоскость О
двухъ различныхъ перпендикуляровъ;
значитъ. АВ сливается съ АС.
350.	Теорема. Пересѣченіе (АВ,
черт. 251) двухъ плоскостей (Р и ()),
перпендикулярныхъ, къ третьей плос-
кости (В), есть перпендикуляръ къ
этой плоскости.
Черезъ какую-нибудь точку А ли-
ніи пересѣченія вообразимъ перпенди-
куляръ къ пл. В. Этотъ перпендику-
ляръ долженъ лежать и въ пл. О (349),
и въ пл. В; значитъ, опъсольется съ ЛВ.
Черт. 251
Уголъ двухъ непересѣкающихся пряныхъ.
351.------------Опредѣленіе. Угломъ двухъ непересѣкающихся пря-
мыхъ АВ и СВ, которыхъ
дано положеніе и направле-
у н*е> наз. уголъ МОП. кото-
----------------х'	4 рыйполучится,ес.г/< изъ про-
С—	о-извольной точки простран-
ства О проведемъ прямыя
ОМ и ОП, соотвѣтственно
Черт. 252
параллельныя прямымъ АВ и СВ и одинаково съ ними
направленныя.
Величина угла МОП не зависитъ отъ положенія точки
О. Въ самомъ дѣлѣ, если построимъ указаннымъ путемъ
уголъ Мі 01П1 при какой-нибудь другой точкѣ . то М0П=
~М101Пі, такъ какъ эти углы имѣютъ соотвѣтственно па-
раллельныя и одинаково направленныя стороны.
__221
Уголъ прямой СЪ ПЛОСКОСТЬЮ.
353.	Опредѣленіе. Когда прямая АВ наклонна къ плос-
кости Р, то уголъ ея съ этою плос-
костью называютъ уголъ АВС, со-
ставленный наклонною АВ съ ея
проекціей ВС.
Этотъ уголъ есть шишенъшііъ
изъ всѣхъ угловъ, которые наклон-
ная образуетъ съ прямыми, прове-
денными на плоскости Р черезъ осно-
ваніе наклонной. Докажемъ, напр.,
что /_АВ Сменьше /_АВБ. Для этого
отложимъ ВБ—ВС и соединимъ!) съ Л, У тр.-ковъ АВС
и АВБ двѣ стороны одного равны соотвѣтственно двумъ сто-
ронамъ другого, но третьи стороны не равны, а именно АБ
>АС (наклонная больше перпендикуляра). Вслѣдствіе этого
/_АВБ больше А^АВС (54).
ГЛАВА V.
Многогранные углы.
353.	Опредѣленія. Возьмемъ нѣсколько угловъ (черт.
254): А8В, В8С, С8Б,..., которые расположены въ одной
плоскости вокругъ общей вершины 8. Повернемъ уголъ А8В
— 222 —
вокругъ общей стороны 8В такъ, чтобы плоскость АВВ соста-
вила нѣкоторый двугранный уголъ съ пл. ВВС. Затѣмъ, не
измѣняя получившагося двуграннаго угла, повернемъ его во-
кругъ прямой ВС такъ, чтобы пл. ВВС составила нѣкото-
рый двугр. уголъ съ пл. СВВ. Продолжаемъ такое послѣ-
довательное вращеніе вокругъ каждой общей стороны. Если
при этомъ послѣдняя сторона ВЕ совмѣстится съ первою сто-
роною ВЛ, то образуется фигура (черт. 255), называемая
многограннымъ угломъ. Углы АВВ, ВВС... наз. плоскимгг
углами или гранями, стороны ихъ ВА, ВВ... наз. ребрами,
а общая вершина 8—веришного многограннаго угла. Каждому
ребру соотвѣтствуетъ двугр. уголъ; поэтому въ многогранномъ
углѣ столько двугранныхъ угловъ и столько плоскихъ, сколько
въ немъ всѣхъ реберъ. Наименьшее число граней въ многогр.
углѣ три; такой уголъ наз. гпреграннымъ. Могутъ быть углы
четырегранные, пятигранные и т. д.
Многогранный уголъ (черт. 255) обозначается или одною
буквою 8, поставленною у вершины, или же рядомъ буквъ
ВАВСВЕ^ изъ которыхъ первая обозначаетъ вершину, а про-
чія— ребра по порядку ихъ расположенія.
Многогранный уголъ наз. выпуклымъ, если онъ весь располо-
женъ по одну сторону отъ каждой своей грани. Таковъ уголъ,
изображенный на черт. 255. Наобо-
8	ротъ, уголъ на черт. 256 нельзя наз-
вать выпуклымъ, такъ какъ онъ рас-
/ | \\	положенъ по обѣ стороны отъ грани
/ \ *е\	АВВ, пли грани ВВС. Если всѣ
/ /.--Г Ѵ\\ грани многогр. угла пересѣчь пло-
|	скостью, то въ сѣченіи образуется
д/ /	\ многоугольникъ (аЪсйе, черт. 255 и
в / в 256). Въ выпукломъ углѣ этотъ мно-
с ' гоугольникъ тоже выпуклый.
Черт. 256	Мы будемъ разсматривать только
выпуклые многогранные углы.
354.	Теорема. Въ /прегранномъ углгъ каждый плоскій
уголъ менъгие суммы двухъ другихъ плоскихъ угловъ.
Пусть въ углѣ 8АВС наггбо.гъигій изъ плоскихъ угловъ
— 223 —
Черт. 257
будетъ А8С. Докажемъ, что даже этотъ наибольшій уголъ
меньше суммы двухъ остальныхъ. Отложимъ
на углѣ А8С часть А8В, равную А8В.
Проведемъ въ плоскости угла А8С какую
нибудь прямую АС, пересѣкающую 8В въ
точкѣ В. Отложимъ 8В=ВВ. Соединивъ В
съ А и С, получимъ Л АСВ, въ которомъ:
АВ4-ВС<АВ~\-ВС
Тр.-ки А8І) и А8В равны, такъ какъ
они содержатъ по равному углу, заключен-
ному между равными сторонами; слѣд. АВ —
— АВ. Поэтому въ выведенномъ неравенствѣ можно отбро-
сить равныя части АВ и АВ, послѣ чего получимъ:
ВС<ВС
Теперь замѣчаемъ, что у тр.-ковъ 8СВ и 8СВ двѣ стороны
одного равны двумъ сторонамъ другого, а третьи стороны
неравны; въ такомъ случаѣ противъ бблыпей изъ этихъ сто-
ронъ лежитъ большій уголъ; значитъ:
уголъ С8В < угла С8В
Приложивъ къ лѣвой части этого неравенства уголъ А8В,
а къ правой равный ему уголъ А8В, получимъ неравенство,
которое требовалось доказать:
уг. ЛЯС<уг. Л&#-|-уг. 08В.
355.	Теорема. Въ выпукломъ много-
иранномъ углѣ сумма плоскихъ угловъ
меньше 4А.
Пересѣчемъ грани выпуклаго угла
8АВСВЕ какою-нибудь плоскостью;
отъ этого въ сѣченіи получимъ выпук-
лый «-угольникъ АВСВЕ. Примѣняя
теорему предыдущаго параграфа къ каж-
дому изъ трегранныхъ угловъ, образовав-
шихся при точкахъ А, В, С, В и
Е. находимъ:
АВС<АВ8+8ВС; ВСВ < ВС8+ 8СВ:............

Черт, 258
__ 224 _
Сложимъ почленно всѣ эти неравенства. Тогда вг» лѣвой части
получимъ сумму всѣхъ угловъ многоугольника АВСІ)Е, ко-
торая равна 2йп — 4й (85), а въ правой — сумму угловъ
тр.-ковъ А8В, В8С...., кромѣ тѣхъ угловъ, которые лежатъ
при вершинѣ 8. Обозначая сумму этихъ послѣднихъ угловъ
буквою х, мы получимъ послѣ сложенія:
2<іп — 4(1- < 2сіи — х
Откуда:
х < Асі
Равенство трегранныхъ угловъ.
350. Дополнительный уголъ. Изъ вершины 6' треграннаго угла
5АВС возставимъ къ грани АЗВ перпендикуляръ ЗСІУ направляя его въ
ту сторону отъ этой грани, въ которой
расположено противоположное ребро
8С. Подобно этому проведемъ пернен-
Ц дикуллръ 6'Лі къ грани В8С н 8ВІУ къ
грани АЗС. Трегранный уголъ, у ко-
тораго ребрами служатъ прямыя 6’ЛР
8Вг и .9(71, наз. дополнительнымъ для
угла 6' АВС.
Замѣтимъ, что если для угла 8АВС
дополнительнымъ служитъ уг. ЗА^Ср
то и наоборотъ: для уг. 8АІВ1 Сг допол-
Черт, 259
нительнымъ угломъ будетъ 8АВС, Дѣйствительно, плоскость ЗАХВЪ про-
ходя черезъ перпендикуляры къ плоскостямъ В8С и А8С, перпендику-
лярна къ нимъ обѣимъ, а слѣд. п къ линіи ихъ пересѣченія 8С\ значитъ,
прямая 8С есть перпендикуляръ къ грани ЗА^ и, кромѣ того, она рас-
положена по ту же сторону отъ этой грани, но которую лежитъ проти-
воположное ребро 8СѴ Подобно эгому убѣдимся, что прямыя ЗВ и 8А
соотвѣтственно перпендикулярны къ гранямъ ЗА^ п ЯВ^ и располо-
жены по ту сторону отъ нихъ, по которую лежатъ ребра 8ВХ и «9Ар
Значитъ, углы 8АВС и <9ЛІВІ(7Х взаимно дополнительны.
359. Лемма I. Если два трегранные угла взаимно дополнитель-
ны, то плоскіе умы одного служатъ дополненіемъ до къ противополож-
нымъ двуграннымъ умамъ другого.
Каждый плоскій уголъ одного изъ взаимно дополнительныхъ трегран-
ныхъ угловъ образованъ двумя перпендикулирнми, возстановленными къ
— 225 —
гранямъ противоположнаго двуграннаго угла другого треграннаго, изъ
одной точкп его ребра Замѣтивъ это и принявъ во вниманіе направле-
ніе перпендикуляровъ, возьмемъ какой-нибудь дву.
грапный уголъ АВ и изъ произвольной точки В его
ребра возставимъ перпендикуляры: ВЕ къ грани
А.В и ВЕ къ грани АС и затѣмъ черезъ ВЕ и ВЕ
вообразимъ плоскость, которая должна быть пер-
пендикулярна къ ребру АВ (348,350). Пусть пере-
сѣченія этой плоскости съ гранями угла АВ будутъ
прямыя ВС п ВВ. Тогда уголъ СВІ) долженъ быть
линейнымъ угломъ двуграннаго АВ. Такъ какъ сто-
роны угла ЕВЕ соотвѣтственно перпендикулярны
къ сторонамъ угла СВТ), и эти углы не равны, то
сумма ихъ равна 2*7 (82); что и требуется до-
казать.
'Е
Черт. 260
358. Лемма 2. Равнымъ трсіраннымъ угламъ соотвѣтствуютъ
равные дополнительные углы и обратно.
Равные трегранные углы при вложеніи совмѣщаются; поэтому совмѣ-
щаются и тѣ перпендикуляры, которые образуютъ ребра дополнитель-
ныхъ угловъ; значитъ, дополнительные углы также совмѣщаются.
Обратно: еслп совмѣщаются дополнительные углы, то совмѣщаются
и данные углы.
359.	Теоремы. Трегранные уілы равны, если они имѣютъ:
1*>, по равному двугранному углу, заключенному между двумя соот-
вѣтственно равными и одинаково расположенными плоскими утами;
пли 2°, по равному плоскому углу, .заключенному между двумя соот-
вѣтственно ргавными и одинаково расположенными двугранными углами;
или 3°, по три соотвѣтственно равныхъ и одинаково расположен-
ныхъ плоскихъ узла;
Черт. 261
или 4°, по три соотвѣтственно равныхъ и одинаково расположен-
ныхъ двугранныхъ угла.
А. Я. КИСЕЛЕВЪ.
15
— 226 —
1®. Пусть 5 и два треугольные угла (черт. вбі), укоторыхъ: /^А8В—
=/А5і-Ві>/ ЛВС — / «Двугр, уг. А8~ двугр. уѵ. Вложимъ
уголъ Я] въ уголъ 8 такъ, чтобы у нихъ совпали: точка съ 8, прямая
съ 8А и плоскость АІ8ІВІ съА8В. Тогда ребро 8}ВІ пойдетъ по 8В(по
равенству угловъ и А8В), плоскость А^С^ пойдетъ по А8С (по
равенству двугранныхъ угловъ), и ребро по 8С (по равенству уг-
ловъ А^С'і п А8С). Такимъ образомъ, трегранные углы совмѣстятся
во всѣхъ своихъ частяхъ, т.-е. они будутъ равны.
2°. Второй признакъ доказывается вложеніемъ подобно первому.
3®. Пусть 8 и (.черт. 262) будутъ два трегранные угла, у кото-
рыхъ плоскіе углы одного равны соотвѣтственно плоскимъ угламъ дру-
гого, и кромѣ того, равные углы одинаково расположены.
Черт. 262
Отложимъ на всѣхъ ребрахъ произвольные, по равные, отрѣзки:
8А — 8В = 8С=8А1=.... и построимъ тр.-ки АВС и АІВ1СІ. Изъ ра-
венства тр.-ковъ АВ8 и	находимъ: АВ — АІВІ. Подобно этому
изъ равенства другихъ боковыхъ тр.-ковъ выводимъ: АС—А^і н
Слѣд., Л АВС~ Л АіВіСі. Опустимъ на плоскости этихъ тр.-ковъ пер-
пендикуляры 80 п 8х0ѵ Такъ какъ наклонныя 8 А, 8В и 8С равны, то
должны быть равны ихъ проекціи ОА, ОВ и ОС; значитъ, точка О есть
центръ круга, описаннаго около тр.-ка АВС. Точно также точка Оі есть
центръ круга, описаннаго около тр-ка А^С^ У равныхъ тр.-ковъ ра-
діусы описанныхъ круговъ равны; значитъ, 08 = 0^. Поэтому Д8В0~
— Д 8\В1О1 (по гипотенузѣ и катету), и, слѣд., 08— О^. Вложимъ те-
перь фигуру ВхА^ВіСі въ фигуру 8АВС такъ, чтобы равные тр.-ки АІВІС1
и АВС совмѣстились; тогда совмѣстятся описанныя окружности, н, слѣд.,
ихъ центры Оі н 0; вслѣдствіе этого перпендикуляръ пойдетъ по
08, и точка упадетъ въ 8. Такимъ образомъ трегранные углы совмѣ-
стятся всѣми своими частями, т.-е. они будутъ равны.
4°. Четвертый признакъ легко доказывается при помощи дополни-
тельныхъ угловъ. Если у двухъ трегранныхъ угловъ соотвѣтственно равны
и одинаково расположены двугранные углы, то у нхъ дополнительныхъ
угловъ будутъ соотвѣтственно равны и одинаково расположены плоскіе
— 227 —
углы (357); слѣд., дополнительные углы равны; а если равны дополяп-
гельные. то равны и данные углы (358).
360.	Симметричные многогранные углы. Какъ извѣстно, верти-
кальные углы равны, если рѣчь идетъ объ углахъ, образованныхъ пря-
мыми или плоскостями.
Посмотримъ, примѣнима ли эта истина къ
угламъ многограннымъ.
Продолжимъ всѣ ребра угла 8АВСЕЕ за
вершину; тогда образуемъ другой многогран-
ный уголъ	который можно на-
звать вертикальнымъ по отношенію къ перво-
му углу. Не трудно видѣть, что у обоихъ уг-
ловъ равны соотвѣтственно и плоскіе углы,
и двугранные; по тѣ п другіе расположены
въ обратномъ порядкѣ. Дѣйствительно, если
мы вообразимъ наблюдателя, который смот-
ритъ извнѣ многограннаго угла па его вер-
шину, то ребра 8А, 8'В, 8С. 8Е, 8Е будутъ
казаться ему расположенными противъ дви-
женія часовой стрѣлки, тогда какъ, смотря
на уголъ ЗАрВхСіЕхЕі, онъ увидитъ ребра
ЗВ^.. расположенными по движенію ча-
совой стрѣлки.
Черт. 263
Многогранные углы съ соотвѣтственно равными плоскими и двугран-
ными углами, но расположенными въ обратномъ порядкѣ, вообще не
могутъ совмѣститься при влоасеніи; значитъ, они не равны. Такіе углы
называются симметричными.
КНИГА II.
МНОГОГРАННИКИ.
ГЛАВА I.
Свойства параллелопипеда и пирамиды.
361.	Многогранникъ. Многогранникомъ наз. тѣло, огра-
ниченное со всѣхъ сторонъ плоскостями. Многоугольники, об-
разованные пересѣченіемъ этихъ плоскостей, наз. гранями,
ихъ стороны—ребрами, а вершины—вершинами многогран-
15*
— 228 —
ными сторонами, а
Чтобы показать
ника. Прямыя, соединяющія двѣ какія-нибудь вершины, не-
прилежащія къ одной грани, наз. діагоналями.
Мй будемъ разсматривать только выпуклые многогранники,
т. е. такіе, которые расположены по одну сторону отъ каж-
дой своей грани.
Наименьшее число граней въ многогранникѣ четыре: та-
кой многогранникъ получается отъ пересѣченія треграннаго-
угла какою-нибудь плоскостью.
Призма. Призмою наз. многогранникъ, у котораго-
двѣ грани—равные многоугольники съ отвѣтственно параллель-
всѣ остальныя грани — параллелограммы,
возможность существованія такого много-
гранника, возьмемъ какой-нибудь мно-
гоугольникъ АВСВЕ и черезъ его-
вершины проведемъ рядъ параллель-
ныхъ прямыхъ, не лежащихъ въ его-
плоскости. Взявъ затѣмъ на одной изъ.
этихъ прямыхъ произвольную точку
проведемъ черезъ нее плоскость, парал-
лельную плоскости ЛВСВЕ\ черезъ
каждыя двѣ послѣдовательныя парал-
лельныя прямыя также проведемъ,
плоскости. Пересѣченіе всѣхъ этихъ,
плоскостей опредѣлитъ многогранникъ
АВСВЕА1 Вх Сх ВХЕ}, удовлетворя-
ющій опредѣленію призмы. Дѣйствительно, параллельныя плос-
кости АВ СВЕ и Ах Вг Ц В1 Еа пересѣкаются боковыми плос-
костями по параллельнымъ прямымъ (332); поэтому фигуры
АА^Е^Е, ЕЕ1В1В и т. д. параллелограммы. Съ другой
стороны у многоугольниковъ АВСВЕ и А1В1С1В1ЕІ равны
соотвѣтственно стороны (какъ противоположныя стороны па-
раллелограммовъ) и углы (какъ углы съ параллельными и
одинаково направленными сторонами); слѣд., эти многоуголь-
ники равны.
Параллельные многоугольники АВСВЕ и А1В1 С1В1Е1
наз. основаніями призмы; перпендикуляръ опущенный
изъ какой-нибудь точки одного основанія на другое, паз.
,Е
Черт. 261
— 999 —
-высотою призмы. Параллелограммы наз. боковыми гранями
призмы, а ихъ стороны, соединяющія соотвѣтственныя вер-
шины основаній—боковыми ребрами. У призмы всѣ боковыя
ребра равны, какъ отрѣзки параллельныхъ прямыхъ, заклю-
ченные между параллельными плоскостями.
Призма наз. прямою или наклонною, смотря потому, бу-
дутъ ли ея боковыя ребра перпендикулярны или наклонны
къ основаніямъ. У прямой призмы боковыя грани суть пря-
моугольники. За высоту такой призмы можно принять боковое
ребро.
Прямая призма паз. правильною, если
ея основанія правильные многоугольники.
У такой призмы всѣ боковыя грани суть
равные прямоугольники (черт. 265).
Призмы бываютъ: треугольныя, четы-
реугольныя и т. д., смотря по тому, ле-
житъ ли въ основаніи треугольникъ, че-
тыреугольникъ и т. д.
:зоз. Параллелопипедъ. Такъ назы-
ваютъ призму, у которой основаніями слу-
жатъ параллелограммы (черт. 266).	Черт' 2бэ
Параллелопипеды могутъ быть прямые и наклонные. Пря-
мой параллелопипедъ паз. прямоугольнымъ, если его основа-
нія прямоугольники (черт. 267).
Черт. 266	Черт. 267
Изъ этихъ опредѣленій слѣдуетъ:
1°, у параллелопипеда всѣ шесть граней параллелограммы.
— 230 —
2°, у прямого параллелопипеда четыре боковыя грани пря-
моугольники.
3°, у прямоугольнаго параллелопипеда всѣ грани прямо-
угольники.
Три ребра прямоугольнаго параллелопипеда, сходящіяся
въ одной вершинѣ, наз. его измѣреніями’, одно изъ нихъ можно-
разсматривать, какъ длину, другое, какъ ширину, а третье,
какъ высоту. Прямоугольный параллелопипедъ, имѣющій рав-
ныя измѣренія, наз. кубомъ. У куба всѣ грани — квадраты.
364. Пирамида. Это есть многогранникъ, у котораго-
одна грань, называемая основаніемъ, есть какой-нибудь много-
угольникъ, а всѣ остальныя грани, называемыя боковыми,-—
треугольники, имѣющіе общую вершину.
Чтобы получить пирамиду, достаточно какой-нибудь мно-
гогранный уголъ $ (черт. 268) пересѣчь произвольною плос-
костью АВСБ.
Общая вершина $ боковыхъ треугольниковъ наз. верши-
ною пирамиды, а перпендикуляръ 80, опущенный изъ вер-
шины на основаніе,—высотою ея.
Обыкновенно, обозначая пирамиду буквами, пишутъ сна-
чала ту, которая поставлена у вершины; напр.: 8АВСІУ
(черт. 268).
Пирамиды бываютъ: треугольные, четыреугольные и т. д.,
смотря по тому, лежитъ ли въ основаніи треугольникъ, че-
тыреугольникъ и т. д. Треугольная пирамида (черт. 269)
- 231 —
грани правиль-
тр.-ки.
наз. иначе тетраэдромъ} у такой пирамиды всѣ четыре гра-
ни треугольники.
Пирамида наз. правильною (черт. 270), если ея основа-
ніе есть правильный многоугольникъ, и высота проходитъ че-
резъ центръ этого многоугольника. Въ правильной пирамидѣ
всѣ боковыя ребра равны между собою (какъ наклонныя съ
равными проекціями). Поэтому всѣ боковыя
ной пирамиды суть равные равнобедренные
ХЛГ (черт. 270) какого либо одного изъ
этихъ тр.-ковъ наз. апоѳемою. Всѣ апо-
ѳемы въ одной пирамидѣ равны.
365. Усѣченная пирамида. Отрѣ-
зокъ пирамиды, заключенный между
основаніемъ АВСВВ и сѣкущею плос-
костью А.В.О^Е^ параллельною
основанію, наз. усѣченною пирамидою.
Параллельные многоугольники наз. ос-
нованіями, а разстояніе между ними
00,—высотою. Усѣченная пирамида
наз. правильною, если она составляетъ
отрѣзокъ правильной пирамиды.
Высота
Равенство призмъ и пирамидъ.
366. Теорема. Двѣ призмы или двѣ пирамиды равны, если основа-
ніе и боковая гранъ одной и основаніе и боковая гранъ другой соотвѣт-
ственно равны, одинаково наклонены и одинаково расположены.
Черт. 272	Черт. 273
Пусть в'ь двухъ призмахъ соотвѣтственно равны и одинаково распо-
— 232 —
ложепы основанія и боковыя грани Л]) и >417>|, и сверхъ того равны
двугранные углы АВ и ЛрЬ’,. Вложимъ одну призму въ другую такъ,
чтобы у пикъ совпали равныя основанія. Тогда, по равенству двугр. уг-
ловъ, грань ЛгІ>і пойдетъ по ЛВ, и такъ какъ эти грани равны и оди-
наково расположены, то опѣ совпадутъ; по тогда совпадутъ и верхнія
основанія (какъ параллельныя и равныя нижнимъ основаніямъ), т.-е.
призмы совмѣстятся.
То же доказательство примѣняется и къ пирамидамъ (черт. 273).
Свойства граней и діагоналей параллелопипеда.
Въ параллелопипедѣ противоположныя
звз. Теорема.
Чѳрт. 271
звз. Теорема. Въ
каются въ одной точкѣ
ірани равны и параллельны.
Такъ, грани ВВ^(\С и АА{В^)
параллельны, потому что двѣ пересѣ-
кающіяся прямыя ВВ^ и Ві С1 одной
грани параллельны двумъ пересѣка-
ющимся прямымъ ААг и АгВ{ другой
(331/2°); эти грани и равны, такъ
какъ Ві ---А1В1, ВІВ=АІ А (какъ
противоположныя стороны паралле-
лограммовъ) и / ВВХ С= / АА1В1
(338).
параллелопипедѣ діагонали пересѣ-
и дѣлятся въ ней пополамъ.
ются пополамъ.
Это доказательство
Возьмемъ въ параллелопипедѣ АС\
какія-нибудь двѣ діагопами, напр.
АСг и ВВХ, и проведемъ прямыя
в. АВГ и ВСѴ Такъ какъ ребра АВ
и Д С\ соотвѣтственно равны и па-
раллельны ребру ВС, то они равны
и параллельны между собою; вслѣд-
ствіе этого фигура АВСГВ{ есть
параллелограммъ (97,2°), въ которомъ
АС} и ВВ}—діагонали; а въ па-
раллелограммѣ діагонали пересѣка-
можно повторить о каждыхъ двухъ,
— 233 —
Черт. 276
діагоналяхъ; поэтому діагональ АС\ пересѣкается съ ВВ1
пополамъ, діагональ ВВХ пересѣкается съ Аг С пополамъ;
такимъ образомъ, всѣ четыре діогонали пересѣкаются попо-
ламъ, и слѣд. въ одной точкѣ.
369. Теорема. Во прямоугольномъ параллелопипедѣ квао-
рагнъ діагонали равенъ суммѣ квадратовъ трехъ его измѣреній.
Пусть АСГ есть діагональ прямоуголь-
наго параллелопипеда. Проведя АС, по-
лучимъ два тр.-ка: АС\С и АСВ. Оба
они прямоугольные: первый потому, что
параллелопипедъ прямой, и, слѣд., ребро
ССѴ перпендикулярно къ основанію; вто-
рой потому, что параллелопипедъ прямо-
угольный, значитъ, въ основаніи его ле-
житъ прямоугольникъ. Изъ этихъ тр.-ковъ
находимъ:
АС2=АС2-'ГСС2 и АС2=АВ2-\-ВС\
Слѣд. А С\2 = А В2 +ВС2 + СС\2 = А В2 + А В2 + А А12.
3 90. Слѣдствіе. Въ прямоугольномъ параллелопипедѣ
осѣ діагонали равны.
Свойства параллельныхъ сѣченій въ пирамидѣ.
3 31. Теоремы. Вслгг пирамида (черт. 277) пересѣчена
плоскостью, параллельною основанію, то:
1°, боковыя ребра и высота дѣлят-
ся этою плоскостью на частгі пропор-
ціанальныя;
2°, въ сѣченіи получается многоуголь-
никъ (аЪссІе), подобный основанію;
3°, площади сѣченія и основанія от-
носятся, какъ квадраты ихъ разстояній
отъ вершины.
1°. Прямыя аЬ и АВ можно разсмат-
ривать, какъ пересѣченія двухъ параллель-
ныхъ плоскостей (основанія и сѣкущей)
третьею плоскостью А8В; поэтому аЬ (| АВ
ъ
Черт. 277
— 234 —
(332). По той же причинѣ Ъс И ВС,сс1 || СВ., и ат || АМ^ вслѣд-
ствіе этого (192).
8а___8Ъ__8с___	__8т
а А ЬВ сС " тМ
2°. Изъ подобія тр.-ковъ АВВ и аВЪ, затѣмъ ВВС и ЪВс
и т. д., выводимъ:
АВ В8 В8 ВС	АВ ВС
аЬ ~ Ъ8 ’ Ь8 ~ 'Ъс ’ 0ТКуДа: пъ ~ Ьс
ВС С8 С8 СП	ВС СБ
Ъс~~ сЗ'^ с8~ сЛ' 0ТЕуда: Ьс—'с(1
Такъ же докажемъ пропорціональность остальныхъ сто-
ронъ мн.-ковъ АВСВЕ и иЪс&е. Такъ какъ, сверхъ тогог
у этихъ мн.-ковъ равны соотвѣтственно углы (какъ образо-
ванные параллельными и одинаково направленными сторонами),
то они подобны.
3°. Площади подобныхъ многоугольниковъ относятся, какѣ,
квадраты сходственныхъ сторонъ; поэтому:
площ. АВСБЕ АВ2 /АВ\2
площ. аЪсде	аЬ2	\аЪ /
АВ___ А8_ М8
° аЬ ~ а8~— т8
о	площ. АВСБЕ ,М8\2	М82
Значитъ: ----------;—= —5) =. -
площ. аЪсае X т8'	т82
303. Слѣдствіе. У правильной усѣченной пирамиды
верхнее основаніе есть правильный многоугольникъ, а боко-
выя грани суть равныя и равнобочныя трапеціи (см. черт.
271).
Высота какой-нибудь изъ этихъ трапецій наз. апооемоа
прав. усѣч. пирамиды.
3 03. Теорема. Если двѣ пирамиды съ равными высо-
тами разсѣчены на одинаковомъ разстояніи отъ вершины
плоскостями, параллельными основаніямъ, то площади сѣ-
ченій пропорціональны площадямъ основаній.
Пусть В и ВА будутъ площади основаній двухъ пира-
— 235 —
мидъл II высота каждой изъ нихъ, Ъ и площади сѣченій
плоскостями, параллельными основаніямъ и удаленными отъ.
Черт. 278
вершинъ на одно и то же разстояніе к, Согласно предыду-
щей теоремѣ мы будемъ имѣть:
ь _ л.2 Ьі________ля
М и б/'—я
ъ ъ.
Откуда:
334. Слѣдствіе. Если В = В^ то и 5 = ^, т. е. если
у двухъ пирамидъ съ равными высотами основанія равнове-
лики, то равновелики и сѣченія, равноотстоящія отъ вер-
шины.
ГЛАВА II.
Боковая поверхность призмы и пирамиды.
33&. Теорема. Боковая поверхность призмы равна про-
изведенію периметра перпендикулярнаго сѣченія на боковое
ребро.
Перпендикулярнымъ сѣченіемъ (черт. 279) наз. много-
угольникъ аЬсЛ, получаемый отъ пересѣченія призмы плоскостью,,
перпендикулярною къ боковымъ ребрамъ. Стороны этого много-
угольника перпендикулярны къ ребрамъ.
— 236 —
В
Черт. 279
Боковая поверхность призмы есть сумма площадей па-
раллелограммовъ; въ каждомъ изъ ппхъ
за основаніе можно взять боковое реб-
ро, а за высоту сторону перпендику-
лярнаго сѣченія. Поэтому:
Бок. нов. = АА{ .	. Ьс -г
+ ССІ . ссі 4" 1)1) { • (Іа—(аЬ 4" Ьс 4" ссі4*
сіа). АА1
31в. Слѣдствіе. Боковая поверх-
ность прямой призмы равна произве-
денію периметра основанія на высоту.
потому что въ такой призмѣ за пер-
пендикулярное сѣченіе можно взять само основаніе, а боко-
вое ребро ея равно высотѣ.
331. Теорема. Боковая поверхность правильной пира-
произведенію периметра основанія на половину
миды равна
апоѳемы.
$
Пусть 8АВ 07)18 есть прав. пирамида
и 837 ея апоѳема. Боковая поверхность
этой пирамиды есть сумма площадей рав-
ныхъ равнобедренныхъ тр.-ковъ. Площадь
одного изъ пихъ, папр. А8В. равна АВ.
1/І8АГ. Если всѣхъ тр.-ковъ п. то боковая
поверхность выразится (АВ. п). 1/.2 831.
гдѣ АВ.п есть периметръ основанія,, а
О 8М апоѳема.
318. Теорема. Боковая поверхность
правильной усѣченной пирамиды равна
произведенію полусуммы периметровъ обо-
аповему.
Черт. 280
ихъ основаніи на
Эта поверхность есть сумма площадей равныхъ трапецій.
Площадь одной изъ нихъ, напр. АаЪВ (черт. 280) равна
л/2 (Л2?4~ аЬ). Мт (280). Если число всѣхъ трапецій есть п> то
АВ + «Ь	__ЛВ.іі аІ>.п тГ
оок. иов. — —-—. Мт. п---------- —о - -. 31 т
— 237 —
гдѣ АВ.п и аЬ.п суть периметры нижняго и верхняго осно-
ваній.
Задачи.
327.	Высота прямой призмы, которой основаніе есть правильный
треугольникъ, равна 12 метрамъ, а сторона основанія 3 метр. Вычислить
полную поверхность призмы.
328.	Полная поверхность прямоугольнаго параллелопипеда равна 1714
кв. футовъ, а неравныя [стороны основанія равны 25 и 14. Вычислпть-
боковую поверхность и боковое ребро.
329.	Въ прямоугольномъ параллелопипедѣ съ квадратнымъ основаніемъ
и высотою к проведена сѣкущая плоскость черезъ два противополож-
ныя боковыя ребра. Вычислить полную поверхность параллелопипеда,
зная, ч*го площадь сѣченія равна А.
330.	Правильная шестиугольная пирамида имѣетъ сторону основанія
а и высоту к. Вычислить боковое ребро, аиоѳему, боковую поверхность
и полную поверхность.
331.	Вычислить полную поверхность и высоту треугольной пирамиды,
у которой каждое ребро равно а.
332.	Правильная шестиугольная пирамида, у которой высота 25 саптим.,
а сторона основанія 5 сант., разсѣчепа плоскостью, параллельною осно-
ванію. Вычислить разстояніе этой плоскости отъ вершины пирамиды,
зная, чіо площадь сѣченія — 10)/3 квадр. сант.
333.	Высота усѣченной пирамиды съ квадратнымъ основаніемъ равна
к. сторона нижняго основанія а, а верхняго Ъ. Найти полную поверх-
ность усѣч. пирамиды.
334 Высота усѣченной пирамиды равна 6, а площади основаній 18
и 8. Пирамида разсѣчена плоскостью, параллельною основаніямъ, и дѣ-
лящею высоту пополамъ. Вычисли?ь площадь сѣченія
ГЛАВА III.
Объемъ призмы и пирамиды.
3 5». Объемъ. Объемомъ геометрическаго тѣла наз. ве-
личина той части пространства, которую занимаетъ это тѣло.
Равныя тѣла, т. е. совмѣщающіяся при вложеніи, имѣютъ и
равные объемы. Но и неравныя .тѣла могутъ имѣть одинаковые
объемы. Если, напр., мы разрѣжемъ діагональною плоскостью
параллелопипедъ (черт. 281) на части Р и <2 и затѣмъ часть-
— 238 —
Р приложимъ къ такъ, чтобы она заняла положеніе то
Черт. 282
получимъ другой параллелопипедъ, не
равный первому, но имѣющій съ нимъ
| одинаковый объемъ.
І Два тѣла, у которыхъ объемы оди-
; наковы, наз. равновеликими.
380. Единица объема. За еди-
..'/ ницу объема берутъ объемъ такого ку-
ба, у котораго измѣреніе равно линей-
ной единицѣ. Такъ, употребительны:
куб. аршинъ, куб. метръ и т. п. Замѣ-
тимъ что куб. метръ наз. иначе стеръ, а куб. дециметръ—литръ.
Объемъ прямоугольнаго параллелопипеда.
381. Лемма 1. Объемы прямоугольныхъ параллелопипедовъ,
имѣющихъ равныя основанія, относятся, какъ ихъ высоты.
Если прямоуг. параллелопипеды имѣютъ равныя основа-
нія, то ихъ можно вложить одинъ въ другой. Пусть АСг и
ЛР (черт. 282) будутъ такіе два параллелопипеда. Разсмот-
римъ два случая.
1°. Высоты ВР и ВР соизмѣримы. Пусть общая мѣра-
высотъ содержится т разъ въ ВР и п разъ
въ ВР. Проведемъ черезъ точки дѣленія
рядъ плоскостей, параллельныхъ основанію.
О- Тогда пар.-дъ А О раздѣлится на т, а пар.-дъ
АР на п равныхъ частей; такимъ образомъ
р мы получимъ:
ВЕ___ѵі Объемъ АС____т
ВЯ	п И Объема. АР	п
р ѵ	,	Объемъ АС____ВЕ
ѴЛВД..	Объемъ АР~ВХ
2°. Высоты ВР и ВРнесоизмѣримы.
О Раздѣлимъ ВР на п равныхъ частей и одну
Черт. 282 часть отложимъ на ВРстолько разъ, сколь-
ко можно. Пусть доля ВР содержится
въ ВР болѣе т разъ, но менѣе нг+1 разъ. Тогда, проведя
— 239 —
по прежнему рядъ плоскостей, параллельныхъ основанію, мы
раздѣлимъ пар.-дъ ЛР на п такихъ равпыхъ частей, какихъ
въ пар.-дѣ А& содержится болѣе ?п, но менѣе Слѣд.:
. ВГ т , об. А(х т
г	ЛЛ' п 1	об. ЛР п
Такимъ образомъ, приближенныя отношенія, вычисленныя
съ произвольною, но одинаковою точностью, равны; а въ этомъ
и состоитъ равенство несоизмѣримыхъ отношеній.
38®. Лемма 2. Объемы прямоугольныхъ параллелопипедовъ,
имѣющихъ равныя высоты, относятся, какъ площади ихъ
основаній.
Пусть Р и Р] два прямоугольные параллелопипеда. Обо-
значимъ неравныя стороны основанія одного изъ нихъ черезъ
а и 6, а другого черезъ и 6,, Возьмемъ вспомогательный
прямоугольный пар.-дъ О, у котораго высота такая же какъ
у данныхъ тѣлъ, а основаніемъ служитъ прямоугольникъ со
сторонами а и . У иар.-довъ Р и 0 переднія грани (по-
крытыя на чертежѣ горизонтальными штрихами) равны. Если
примемъ эти грани за основанія, то высоты будутъ Ь и
и слѣд. (381):
Объемъ Р Ъ	|--. і
Объемъ ф Ь.	I- -*
У пар.-довъ 0 и Рн боковыя грани (покрытыя на чер-
тежѣ вертикальными штрихами) равны. Если примемъ эти гра-
ни за основанія, то высоты будутъ а и аі, и слѣд.:
Объемъ 0___а
Объемъ Р, аг
И
— 240
Перемноживъ равенства [1[ и [2], найдемъ:
Объемъ Р _ аЬ
Объемъ Ру ахЪу
Такъ какъ аЬ выражаетъ площадь основанія пар.-да Р,
а аД — площадь основанія пар.-да Рп то лемма доказана.
383.	Теорема. Объемъ прямоугольнаго параллелопипеда
равенъ прогізведенію площади основанія на высоту.
Черт. 284
Пусть Р есть прямоугольный параллелопипедъ, а Р,—
какая нибудь кубическая единица. Обозначимъ площадь осно-
ванія и высоту перваго черезъ В и 7/, а втораго черезъ
и Возьмемъ вспомогательный прямоуголъный пар.-дъ
у котораго площадь основанія 7^, а высота Н. Сравнивая.
Р съ 0. а затѣмъ О съ Рп находимъ (382 и 381):
06. Р__В об. Ц _Н
06. <?“'«, и иб р—~Лу
Перемноживъ эти равенства, получимъ:
Об^ р __в_ л_
Об. Р ~Ву Лу
Отношенія, входящія въ это равенство, суть числа, вы-
ражающія объемъ, площадь основанія и высоту даннаго па-
раллелопипеда въ соотвѣтствующихъ кубическихъ, квадрат-
ныхъ и линейныхъ единицахъ; поэтому послѣднее равенство
можно высказать такъ:
Число, выражающее объемъ прямоугольнаго параллелопи-
педа, равно прогізведенію чиселъ, выражающихъ площадь ос-
нованія и высоту въ соотвѣтствующихъ едигпщахъ.
— 2-11 —
Это выражаютъ сокращенно такъ: объемъ прямоугольнаго
параллелопипеда равенъ произведенію п гощади основанія
на высоту, т. с.	у-р#
гдѣ подъ К, В и Н разумѣются числа, выражающія въ соот-
вѣтствующихъ единицахъ объемъ, площадь основанія и вы-
соту прямоугольнаго параллелопипеда.
Обозначая буквами а, Ъ и с три измѣренія прям. пар.-да
(выраженныя въ числахъ), можемъ написать:
I— аЬс
потому что площадь основанія выражается произведеніемъ двухъ
изъ этихъ измѣреній, а высота равна третьему измѣренію.
384.	Слѣдствія. Iй. Объемъ куба равенъ третьей сте-
пени ею ребра.
2°. Отношеніе двухъ куб. единицъ равно третьей сте-
пени отношенія соотвнтіспівуіоіи/ихъ линейныхъ едингщъ; такъ,
отношеніе куб. метра къ куб. дециметру равно ІО3, т. е. 1000.
Объемъ всякаго параллелопипеда.
385.	Лемма. Наклонная призма равновелика такой пря-
мой призмгь, у которой основаніе равно перпендикулярному
сѣченію наклонной призмы, а высота—ея боковому ребру.
Черезъ какую пибудь точку а одного изъ боковыхъ ре-
беръ наклонной призмы АХБ проведемъ перпендикулярное сѣ-
ченіе аЬсйе. Затѣмъ, продолживъ всѣ боко-
выя грани внизъ, отложимъ аа1—АА1 и че-
резъ точку а^ проведемъ перпендикулярное
сѣченіе а^ср^е,. Такъ какъ плоскости
двухъ сѣченій параллельны, то части боко-
выхъ реберъ, заключенныя между ними, рав-
ны, т. е. 7Д—(х\—сІс11~сеі=ша1=АА1 (336)
Вслѣдствіе этого многогранникъ а,сІ есть
прямая призма, у которой основаніемъ слу-
житъ перпендикулярное сѣченіе, а высота
(пли, что все равно, бокбвое ребро) равно
боковому ребру наклонной призмы. Дока-
жемъ, что наклонная призма равновелика
Ъ, с.
Черт. 285
16
А. П. КИСЕЛЕВЪ.
— 242 —
этой прямой. Для этого предварительно убѣдимся, что много-
гранники аВ и агД равны. Основанія ихъ Ме и а&с^е^
равны, какъ основанія призмы съ другой стороны, изъ
равенства А^А-а^ь слѣдуетъ: АгА—Ага^=аха—Ага, т. е.
аА=агАг\ подобно этому: ЪВ=Вф1, сС=схС^ и т. д. Во-
образимъ теперь, что многогранникъ аВ вложенъ въ а^В^ такъ,
чтобы основанія ихъ совпали; тогда боковыя ребра, будучи
перпендикулярны къ основаніямъ и соотвѣтственно равны, так-
же совпадутъ; поэтому многогранникъ аВ совмѣстится съ
ахВх, значитъ, эти тѣла равны. Теперь замѣтимъ, что если отъ
цѣлаго многогранника ахВ отнимемъ часть аР, то получимъ
прямую призму; а если отъ того же многогранника отнимемъ
часть а2Рі, то получимъ наклонную призму. Изъ этого слѣ-
дуетъ, что эти двѣ призмы равновелики.
386.	Теорема. Объемъ параллелопипеда равенъ произ-
веденію плогцади основанія на высоту.
Сначала мы докажемъ эту теорему для параллелопипеда
прямого, а потомъ и наклоннаго.
1°. Пусть А Сх будетъ прямой пар.-дъ,
т.-е. такой, у котораго основаніе АВСВ
есть параллелограммъ, а всѣ боковыя
С, грани — прямоугольники. Возьмемъ въ
немъ за основаніе грань ААгВгВ;
тогда параллелопипедъ будетъ наклон-
ный, Согласно леммѣ предыдущаго §.
этотъ пар.-дъ равновеликъ такому пря-
мому, у котораго основаніе есть пер-
пендикулярное сѣченіе МНР$, а вы-
Чсрт. 286 сота ВС. Четыреугольникъ РШРО
есть прямоугольникъ, потому что его
углы служатъ линейными углами прямыхъ двугранныхъ уг-
ловъ; поэтому прямой пар.-дъ, имѣющій это основаніе, дол-
женъ быть прямоугольнымъ, и, слѣд., его объемъ равенъ
произведенію площади основанія МХР(^ на высоту ВС. Но
площадь АГКРф равна ЛУ.З/(); значитъ:
Объемъ АС. = ЛУ. МО . ВС
— 243 —
Произведеніе МО. ВС выражаетъ площадь параллело-
грамма АВСВ; поэтому:
Объемъ АС\ =(нлощ. АВСВ) . МЫ
2°. Пусть АСу будетъ
пар.-дъ наклонный. Онъ равно-
великъ такому прямому, у ко-
тораго основаніе есть перпен-
дикулярное сѣченіе МЫР(^, а
высота ВС. Но, по доказан-
ному, объемъ прямого парал-
лелопипеда равенъ произведе-
нію площади основанія на вы-
соту; значитъ:
Объемъ АС\ — (плош,. МЫР@) . ВС
Если ВВ есть высота сѣчеиія МЫРО, то площадь МЫР0~
= Мф. ВВ; поэтому:
Объемъ АС1 = МО . ВВ. ВС
Произведеніе ВС. МО выражаетъ площадь параллелограмма
АВСВ; слѣд.
Объемъ АС} =(елоіц. АВСВ) . ВВ
т.-е. объемъ всякаго параллелопипеда равенъ произведенію
площади основанія на высоту.
381. Слѣдствіе. Если V, В и И суть числа, выра-
жающія въ соотвѣтствующихъ единицахъ объемъ, площадь
основанія и высоту какого пи на есть параллелопипеда, то
можемъ писать:
ѵ= вн
Объемъ призмы.
388. Теорема. Объемъ призмы равенъ произведенію пло-
щади основанія на высоту.
16*
— 244 —
Сначала докажемъ эту теорему для треугольной призмы,
а потомъ для многоугольной.
Черт. 288
1°. Проведемъ черезъ ребро АА1 тре-
угольной призмы ЛС, плоскость, параллель-
пую грапи ВВг С\ О, а черезъ ребро СС1
плоскость, параллельную грани АА1ВІВ;
затѣмъ продолжимъ плоскости обоихъ осно-
ваній призмы до пересѣченія съ ранѣе про-
веденными плоскостями. Тогда мы получимъ
параллелопипедъ ВВ}. который діагональ-
ною плоскостью АА{С\С дѣлится на двѣ
треугольныя призмы (изъ нихъ одна есть
данная). Докажемъ, что эти призмы равно-
велики. Для этого проведемъ перпендику-
лярное сѣченіе іМ. Въ сѣченіи получится
параллелограммъ, который діагональю ис дѣлится на два рав-
ные тр,-ка. Данная призма равновелика такой прямой, у ко-
торой основаніе есть А аЬс, а высота — ребро ААХ (385).
Другая треугольная призма равновелика такой прямой, у ко-
торой основаніе есть а высота — ребро ААѴ Но двѣ
прямыя призмы сь равными основаніями и равными высотами
равны (потому что при вложеніи онѣ совмѣщаются): значитъ,
призмы АВСА^В^Сі и АВОА^В^С^
Ел___ равновелики. Изъ этого слѣдуетъ, что
 \ объемъ данной призмы составляетъ по-
ловинУ объема параллелопипеда ВВ^,
I	/ поэтому, обозначая высоту черезъ
/ / 7	/ получимъ (386):
/ :Е I /]) / Об. тр. ирігзмы — 1 (площ. А ВСВ)Н
А^А-—-ГѢ	площ_ (7/)) /-/ — (илощ. АВС}Н
в	2°. Проведемъ черезъ ребро ААг
Черт. 289 данной многоугольной призмы (черт .289)
и черезъ всѣ остальныя боковыя ребра, кромѣ двухъ ближайшихъ,
плоскости АА/\С и ААХВХВ. Тогда данная призма разсѣ-
— 245 —
чстся па пѣскоіько треугольныхъ призмъ. Сумма объемовъ
.этихъ призмъ составляетъ искомый объемъ. Если обозначимъ
площади изъ основаній черезъ Ьг Ь.}, а общую высоту
черезъ Н, то получимъ:
Объемъ МП. прпзмы _1! -\-1)ЛІТ—	Ч"&2
= (іиощ. АВСВЕ)Н
38В. Слѣдствіе. Если V. В и /Л будутъ числа, выра-
жающія въ соотвѣтственныхъ единицахъ объемъ, площадь
•основанія и высоту призмы, то, по доказанному, можемъ
писать:

Объемъ пп р а м и ды.
300. Лемма, Треугольныя пирамиды съ равновеликими
основаніями и равными высотами равновелики.
Ь,
с	’
Черт. 290
Раздѣлимъ высоту каждой изъ данныхъ пирамидъ па про-
извольное число п равныхъ частей и черезъ точки дѣленія
проведемъ рядъ плоскостей, параллельныхъ основанію-(па чер-
тежѣ высота, а слѣд. и. боковыя ребра, раздѣлены на 4 рав-
ныя части). Такъ какъ, по условію, основанія АВС и А1ВІС1
— 246 —
равновелики, то тр.-ки, получившіеся въ сѣченіяхъ одной пи-
рамиды, соотвѣтственно равновелики тр.-камъ, получившимся
въ сѣченіи другой пирамиды (374). Построимъ теперь въ
каждой пирамидѣ рядъ внутреннихъ призмъ такихъ, чтобы
верхними основаніями у нихъ были треугольники сѣченій, бо-
ковыя ребра были параллельны ребру 8А въ одной пирамидѣ
и ребру 8}Аг въ другой, а высота каждой призмы равня-
лась бы 1/п высоты пирамиды. Такихъ призмъ въ каждой пи-
рамидѣ будетъ т?—1. Объемы призмъ пирамиды $ обозначимъ
по порядку, начиная отъ вершины, черезъ рѵ рг. р3,.
а объемы призмъ пирамиды также по порядку отъ вер-
шины, черезъ др д3.......дп. 1
Тогда:
Рі=^ Р^Ч*' Р^'ы..........Ря-і=^-і
потому что у каждой пары соотвѣтственныхъ призмъ основа-
нія равновелики и высоты равны. Поэтому:
а+а+аН---------Нр.- і=й+а+аН--------Ь «.-і
Предположимъ теперь, что п, т.-е. число равныхъ частей,,
на которыя мы дѣлимъ высоту пирамидъ, неограниченно воз-
разстаетъ. Тогда обѣ части послѣдняго равенства сдѣлаются
величинами перемѣнными. Докажемъ, что каждая изъ нихъ
стремится въ предѣлѣ къ объему той пирамиды, въ которую
призмы вписаны. Это достаточно доказать для какой-нибудь
одной пирамиды, папр. дяя $. Для этого построимъ въ ней
рядъ призмъ, выходящихъ частью изъ пирамиды, такихъ, чтобы
нижними основаніями ихъ служили треугольники сѣченій (и
основаніе пирамиды), высоты были бы равны, по прежнему,.
1 /?? высоты пирамиды, а боковыя ребра параллельны тому же-
ребру 8А, Такихъ призмъ будетъ п. Обозначимъ ихъ объ-
емы, начиная отъ вершины пирамиды, по порядку, черезъ.
Р^’ Рз.....Р'п--і’ Рп' ТРУДПО видѣть, что
„	Л'=Л’ Р*'-Ѵі' Рз=Р*‘ ’ * •Р'п-і-Рп-і
Поэтому:
(А'+А '+а Н-----Н?! +А') —
(а+а+аН---------І-А-1)=А'
— 247 —
Если объемъ пирамиды обозначимъ черезъ V, то очевидно,
что:
Рі'+Л'+йН-------Н\'> ѵ> Р!+д+- --І-р,-!
Откуда:	V— (д+дЧ------|-р._1)<р;'
При неограниченномъ увеличеніи числа п объемъ призмы рп
стремится къ нулю (потому что высота ея стремится къ нулю, а
основаніе не измѣняется); слѣд. разность Г—(Рі_г?.>+-
и подавно стремится къ нулю; а это, по опредѣленію предѣла,
означаетъ, что
К=пред.	-----|-Д-і)
Подобно этому можно доказать, что Г’15 т.-с. объемъ пира^
миды 8^ есть предѣлъ перемѣнной суммы
Но если двѣ перемѣнныя величины, имѣющія предѣлы,
всегда остаются равными, то равны и ихъ предѣлы (248);
поэтому:
г=г,
что и требовалось доказать.
391. Теорема. Объемъ пирамиды равенъ произведенію
площади основанія на третъ высоты.
Черт. 291
Сначала докажемъ эту теорему для пирамиды треугольной^
а затѣмъ многоугольной.
— 248 —
1°. На основаніи треугольной пирамиды 8.АВС постро-
имъ такую призму АВС1)8Е. у которой высота равна вы-
сотѣ пирамиды, а одно боковое ребро совпадаетъ съ ребромъ
8В. Теперь докажемъ, что объемъ пирамиды составляетъ
третью часть объема этой призмы. Отдѣлимъ отъ призмы
данную пирамиду. Тогда останется четыреугольная пирамида
8АВЕС, (которая для ясности изображена отдѣльно). Про-
ведемъ въ пей сѣкущую плоскость черезъ вершину 8 и діа-
гональ основанія ВС. Получившіяся отъ этого двѣ треуголь-
ныя пирамиды имѣютъ общую вершину 8 и равныя основа-
нія ВЕС и ВАС, лежащія въ одной плоскости: значитъ,
согласно доказанной выше леммѣ, пирамиды 8ВЕС и 8ВАС
равновелики. Сравнимъ одну изъ нихъ, наир. 8ВЕС, съ дан-
ной пирамидой. За основаніе пирамиды 8ВЕС можно взять
А 8ВЕ: тогда вершина ея будетъ въ точкѣ С, и высота
равна высотѣ данной пирамиды. Такъ какъ Л 8ВЕ = ЛАВС,
то, согласно той же леммѣ, пирамиды С8ВЕ и 8АВС рав-
новелики. Такимъ образомъ, сумма объемовъ трехъ пирамидъ,
равновеликихъ данной, составляетъ объемъ призмы: слѣд.
Об. 8АВС~ -о об. 81)ЕАВС~ (імоіц. АВС}
гдѣ // означаетъ высоту пирамиды.
2°. Черезъ какую-нибудь вершину
Е основанія многоугольной пирамиды
8АВСВЕ проведемъ діагонали ЕВ и
ЕС. Затѣмъ черезъ ребро 8Е и каж-
дую изъ этихъ діагоналей проведемъ
сѣкущія плоскости. Тогда многоуголь-
ная пирамида разобьется на нѣсколько
треугольныхъ, имѣющихъ высоту, об-
щую съ данной пирамидой. Обозначивъ
площади основаній треугольныхъ пира-
мидъ черевъ	и высоту черезъ
//, будемъ имѣіь:
Объмп. 8АГ,С!)Е= 1 6, Н 4-1 Ъі И -|- ’ 6 , Н
=	Ч-Г,) " = АВСВЕ)
8
Чер г. 292
— 249 —
393. Слѣдствіе. Если V, В и Н означаютъ числа,
выражающія въ соотвѣтственныхъ единицахъ объемъ, площадь
основанія и высоту какой угодно пирамиды, то
Г=-| БІГ-
Объемъ усѣченной пирамиды и усѣченной призмы.
393. Теорема. Объемъ усѣченной пирамиды равенъ сум-
мѣ объемовъ трехъ пирамидъ, имѣющихъ высоту одинаковую
съ высотою усѣченной пирамиды, а основаніями: одна—
нижнее основаніе усѣченной пирамиды, другая—верхнее ос-
нованіе этой пирамиды, а третья—среднее про пори,іоналъ-
ное между ними.
Сначала докажемъ эту теорему для треугольной пирамиды,
а потомъ многоугольной.
Г’. Пусть АВСВЕЕ есть усѣ-
ченная треугольная пирамида. От-
дѣлимъ отъ пея сѣкущею плос-
костью АЕС треугольную пира-
миду ЕАВС. Эта пирамида, имѣя
основаніе АВ С п вершину въ Е,
удовлетворяетъ требованію теоремы.
Оставшаяся часть есть четыре-
угольная пирамида ЕАВЕС. Про-
ведя въ ней сѣкущую плоскость
черезъ точки Е, В и С, мы раз-
дѣлимъ ее па двѣ треугольныя
пирамиды. Изъ нихъ одна имѣетъ
основаніемъ А ВЕЕ, т. е. верх-
нее основаніе усѣченной пирамиды, а вершину въ точкѣ С;
слѣд., эта пирамида удовлетворяетъ требованію теоремы. Ос-
тается разсмотрѣть третью пирамиду ЕАВС. Превратимъ ее
въ другую равновеликую пирамиду слѣдующимъ образомъ.
Проведемъ прямую ЕК\\ВА и точку К примемъ за вершину
повой пирамиды, которой основаніемъ оставимъ тотъ же тре-
угольникъ АВС. Пирамиды ЕАВС и КАВС равновелики,
потому что у нихъ общее основаніе АВС и высоты равны
— 250 —
(такъ какъ вершины лежатъ на прямой ЕК, параллельной
плоскости основанія). Примемъ за вершину новой пирамиды
точку 2), а за основаніе Л АСК. Тогда высота ея будетъ
равна высотѣ усѣченной пирамиды. Остается доказать, что
основаніе АСК есть средняя пропорціанальная величина между
АВС и ВЕЕ, т. е. что
площ. АВС___площ. АСК^
илощГЛОТ? площ. ВЕЕ
У тр.-ковъ АВС и АСК за основанія можно взять сто-
роны АВ и АК\ тогда вершина у нихъ будетъ общая О, и,
слѣд., высоты будутъ одинаковы; поэтому:
площ. АВС__АВ___АВ	г-,-»
площТЛ СК — АК~^ ВЕ	*-1 •>
(вмѣсто АК можно взять равный отрѣзокъ ВЕ).
Треугольники АСК и ВЕЕ имѣютъ по равному углу при
вершинахъ А и В\ поэтому (289):
площ. АСК АС. АК_____АС
площ. ВЕЕ ВЕ.ВЕ ВЕ
(отрѣзки АК и ВЕ, какъ равные, сокращаются).
[2]
Изъ подобія тр.-ковъ АВС и ВЕЕ слѣдуетъ, что пра-
выя части равенствъ [1] и [2] равны; слѣд., равны и ихъ
лѣвыя части, т. е.
площ. авс___________________щющ^ястг
"площ. АСК площ. ЛЕЕ
2*. Возьмемъ те-
перь многоуголь-
ную усѣченную пи-
рамиду А(1, сос-
тавляющую часть
полной пирамиды
8АВСВЕ. Прев-
ратимъ мн. - къ
АВСѴЕ въ рав-
новеликій тр.-къ
Р$В и, принявъ
этотъ тр.-къ за
основаніе, построимъ вспомогательную пирамиду МР(^В съ
такой же высотою, какъ у пирамиды 8. Пересѣчемъ пира-
миду Л/- плоскостью рцг, параллельною основанію, на такомъ
— 251 —
разстояніи отъ вершины, на какомъ въ пирамидѣ 8 прове-
дена плоскость адссіе. Въ сѣченіи получится Л рдг, равно-
великій мп.-ку аЬсде (374). Пирамиды 8АВСВЕ и МРфВ>
равновелики, такъ какъ у нихъ равновелики основанія и вы-
соты равны; по той же причинѣ пирамиды 8аЪсИе и Мрдг
тоже равновелики; отсюда слѣдуетъ, что усѣч. многоугольная
пирамида Асі равновелика усѣч. треугольной пирамидѣ Рг,
такъ какъ у этихъ двухъ усѣченныхъ пирамидъ основанія, и
нижнее, и верхнее, соотвѣтственно равновелики, а высоты
равны, то теорема, доказанная для усѣченной треугольной
пирамиды, остается примѣнимой и кь многоугольной.
ЗОД. Слѣдствіе. Пусть V, В, Ъ и ІІ будутъ числа,
выражающія въ соотвѣтствующихъ единицахъ объемъ, пло-
щадь нижняго основанія, площадь верхняго основанія и вы-
соту усѣченной пирамиды; тогда
V—	ВЪ= ^Н(в + Г>+^ВЬ)
гдѣ \/ВЕ> есть величина, средняя пропорціональная между Ви Ь.
395. Теорема. Объемъ треугольной призмы, усѣченной
непараллельно основанію, равенъ суммѣ объемовъ трехъ пи-
рамидъ, имѣющихъ общее основаніе съ усѣченной призмой, а
вершины въ трехъ вершинахъ непараллельнаго сѣченія.
Пусть АЕ есть усѣченная тре-
угольная призма. Проведя сѣкущую
плоскость черезъ точки Е, А и С,
мы отдѣлимъ одну изъ трехъ пира-
мидъ, указанныхъ въ теоремѣ, имен-
но пирамиду ЕАВС, имѣющую об-
щее основаніе А ВС съ усѣченной
призмой и вершину въ точкѣ Е.
Проведемъ еще сѣкущую плоскость
черезъ точки Е, В и О; тогда по-
лучимъ двѣ другія пирамиды: ЕВАС
и ЕВЕС. Теорема будетъ доказана,
если мы обнаружимъ, что эти пира-
миды равновелики такимъ, у кото-
рыхъ основаніемъ служитъ А АВС, а вершины лежатъ:
— 252 —
одной въ V. другой въ К Дѣйствительно: пирамиды ЕЕ АС
и ВАВС равновелики, потому что за основаніе ихъ можно
взять общій тр.-къ І)АС, и тогда вершины Е п В будутъ
лежать на прямой ВЕ, параллельной плоскости основаній:
пирамиды ЕВЕС и ЕАВС равновелики, потому что за ос-
нованія ихъ можно принять равновеликіе тр.-ки: для первой
])ЕС, для второй АЕС', и тогда ихъ вершины Е и В бу-
дутъ лежать на прямой ВЕ. параллельной плоскости основаній.
390. Слѣдствіе. Пусть V, В,1Ч. 7/,, Л3 будутъ числа,
выражающія въ соотвѣтствующихъ единицахъ объемъ, пло-
щадь основанія и высоты, опущенные па основаніе изъ трехъ
вершинъ непараллельнаго сѣченія; тогда
Ѵ= 'ВЪ. +1 ВЛ.-І- ^В1і.--= В
о 1 о - О 4	О
Когда призма прямая, высоты //„ и Л3 равны боко-
вымъ ребрамъ ея.
ГЛАВА ІА’.
Подобіе многогранниковъ.
393. Опредѣленіе. Два многогранника наз подобными, если они
имѣютъ соотвѣтственно равные многогранные углы и соотвѣтственно по-
добныя грани. Соотвѣтственные элементы подобныхъ многогранниковъ
наз. сходственными.
Изъ этого опредѣленія слѣдуетъ, что въ подобныхъ мноюгран-
нккахъ:
1°. Двугранные уілы соотвѣтственно равны и одинаково расположе-
ны, потому что многогранные углы равны.
2°. Сходственныя ребра пропориіана.ѣны, потому что въ кажіыхъ
двухъ подобныхъ граняхъ отношеніе сходственныхъ реберъ одно п то же,
и въ каждомъ многогранникѣ сосѣднія грани имѣютъ по общему ребру.
Возможность существованія подобныхъ многогранниковъ доказы-
вается слѣдующей теоремой:
399. Теорема. Если въ пирамидѣ (черт. 296) проведемъ сѣкутую
— 253 —
плоскость (АД\СД)Д\)параллельно основанію, то отсѣчемъ отъ нея другую
пирамиду(ХАіВіСіѴіЕ^ подобную данной.
Такъ какъ АДЗ^ || АВ, ВѴС, || ВС и т. д. (332),
-го боковыя грани двухъ пирамидъ подобны; ос-
нованія ихъ также подобны (371). Остается до-
казать равенство многогранныхъ угловъ. Уголъ
5’ у обѣихъ пирамидъ общій; трегранные углы
иь Вь Ср... равны соотвѣтственно угламъ А,
В, С’,.. , потому что у каждой пары этихъ угловъ
плоскіе углы соотвѣтственно равны и одинаково
расположены (359;8°).
Теорема. Двѣ призмы, или двѣ пира-
миды, подобны, если основаніе и боковая грань
ооной и основаніе и боковая грань другой соот-
Черт. 296
вѣтственно подобны, одинаково наклонены и ода-
наново расположены.
1°. Пусть у двухъ призмъ будутъ соотвѣтственно подобны и одина-
ково расположены основа-
нія АВСІ)Е, аЬсде и грани
аа^Ъ и кромѣ того
равны двугранные углы АВ
и аЬ. Для доказательства
подобія этихъ призмъ, раз-
суждаемъ въ такой послѣ-
довательности. Трегранные
углы В и Ъ равны, потому
чго опп имѣютъ по равному
двугранному углу (АВ и аЪ),
заключенному между двумя
соотвѣтственно равными и
одинаково расположенными
плоскими углами (АВС—аЬс
и ЛВВг= «ЬЪД, отсюда слѣдуетъ, что равны плоскіе углы ВДЗС и ЬДс,
а также и двугранные ВС и Ьс. Если же у двухъ параллелограммовъ
ВВ{С\С и Ы>р\с имѣется по одному равному углу, то и остальные углы
ихъ соотвѣтственно равны: такъ какъ, сверхъ того,
1/0 АВ ,
— (изъ подобія основаній)
и — (изъ подобія бок. граней),
ВС ВВі
Т0	Ъс ~~ Ыч
Значитъ, грани ВВ^С и ЬЬ^с нодобны. Переходя теперь къ трегран-
нымъ угламъ С и <*, совершенно также убѣдимся, что они равны и что
— 254 —
8
грани СС^Рр и сс^Л подобны. Такимъ образомъ, мы переберемъ всѣ
трегранные углы при основаніи и всѣ боковыя грани. Верхнія основанія
и	подобны, потому что они равны нижнимъ основа-
ніямъ; трегранные углы при верхнихъ основаніяхъ соотвѣтственно равны,
потому что у нихъ равны и одинаково расположены плоскіе углы. Зна-
читъ, разсматриваемыя призмы подобны.
2®. Пусть теперь мы имѣемъ двѣ пирамиды, у которыхъ соотвѣт-
ственно подобны п оди-
наково расположены ос-
нованія АВСВЕ, абеде и
боковыя грани 8АВ, заЬ
и кромѣ, того равны дву-
гранные углы АВ и аб.
Совершенно такъ, какъ
это было сдѣлано для
призмъ, мы докажемъ,
что всѣ трегранные углы,
прилежащіе къ основа-
ніямъ, соотвѣтственно
равны, и что всѣ боко-
выя грани соотвѣтствен-
но подобны. Тогда мно-
потому что, имѣя всѣ
плоскіе и двугранные углы соотвѣтственно равные п одинаково распо-
ложенные, они при вложеніи одного въ другой совмѣщаются.
400. Теорема. Подобные мноипратаіки мнутъ быть разложены
на одинаковое число соотвѣтственно подобныхъ и одинаково расположен-
ныхъ пирамидъ.
Черт. 298
гогранные углы 5 и з также будутъ равны,
Черт. 299
Указанное въ теоремѣ разложеніе можетъ быть выполнено различ-
ными способами. Мы поступимъ такъ.
— 255 —
Возьмемъ въ одномъ изъ данныхъ подобныхъ многогранниковъ вер-
шину А какого-нибудь многограннаго угла. Возьмемъ далѣе всѣ тѣ грани
многогранника, которыя не прилежатъ къ углу А. Въ нашемъ много-
гранникѣ такихъ граней четыре: ЕВКЪ, ВСНК, СВСгІІ и Е&НКВ.
Каждую изъ этихъ граней примемъ за основаніе такой пирамиды, кото-
рой вершина лежала бы въ А. Тогда многогранникъ разбивается на
пирамиды, сходящіяся вершинами въ точку А. Въ другомъ многогран-
никѣ возьмемъ сходственную вершину и тѣмъ же путемъ разложимъ
ого на одинаковое число пирамидъ. Докажемъ, что эти пирамиды соот-
вѣтственно подобны. И дѣйствительно, какую бы пару соотвѣтствен-
ныхъ пирамидъ мы пс взяли, легко найдемъ, что основаніе и грань
одной ппрамиды и оспованіе и грань другой пирамиды соотвѣтственно
подобны, одинаково наклонены и одинаково расположены. Напр., у пира-
мидъ ЛЛ.КХ7С, А1В1Е1І.'ГК1 основанія ВЕІ.К, ВХЕ ^Кі подобны, какъ
сходственныя грани подобныхъ многогранниковъ, грани АВЕ, А1В1Е1
подобны, потому что подобные многоугольники АВСВЕ, А1В1СІВ1Е1 раз-
биваются на соотвѣтственно подобные тр.-ки; двугранные углы ВЕ, ВХЕХ
равны, какъ сходственные углы подобныхъ многогранниковъ. Изъ этого
слѣдуетъ, что взятыя нами пирамиды подобны. То же самое можно ска-
зать о другихъ пирамидахъ.
401» Теорема. Поверхности подобныхъ многранниковъ относятся
какъ квадраты сходственныхъ реберъ.
Пусть Ръ Р2, РЭ,....РЛ будутъ площадп отдѣльныхъ граней одного изъ
подобныхъ многогранниковъ, а рир2, Ри-'--Рп площади сходственныхъ гра-
ней другого; положимъ еще, что X и I будутъ длины двухъ какихъ- ппбудь
сходственныхъ реберъ. Тогда, вслѣдствіе подобія сходственныхъ граней
и проиорціанальности всѣхъ сходственныхъ реберъ, будемъ имѣть (291):
Л __ І?_.
/і’“ & ’ Ръ~ Р~’ р3 “	рп ~ 1?
А_+Р_2+?Н-_ +Лѵ Ь2
• • • +Рп	1*
Откуда:
409» Теорема. Объемы
подобныхъ многогранниковъ от-
носятся, какъ кубы сходствен-
ныхъ реберъ.
1®. Сначала докажемъ тео-
рему для подобныхъ пирамидъ.
Пусть пирамиды 8АВСВЕ и
подобны. Вло-
жимъ вторую пирамиду въ пер-
вую такъ, чтобы у нихъ сов-
пали равные многогранные уг-
лы 8 и Тогда основаніе
А^СіВіЕ^ ,займетъ нѣкото-
рое положеніе аЪсйе^ причемъ стороны аЪ, Ьс,.... будутъ соотвѣтственно
параллельны сторонамъ АВ, ВС..... (вслѣдствіе равенства плоскихъ угловл»
трегранныхъ Л и В и и т д.): вслѣдствіе этого плоскость аЬссІе
будетъ параллельна АВС ПК (331,2°). Пусть 80 и 8о будутъ высоты двухъ
пирамидъ. Тогда:
Об. 8АВСПК— (площ. АВСРК). \38О
Об. 8аЪс(Іе — (площ. аЪсЛе) . ]/8Л'о
Об. 8АВСРЕ_ площ. АВСРЁ 80
Об. 8аѢс<іе площ аЬсгіе ' 8о
Но	(371.3»)
площ. а,Ьс(іе, 8оі
уг	об. 8АВСІЖ 80*	8А*
Поэтому:	——...................................... (371,1'0
об. 8аМе 8 о* 8а*
20. Теперь докажемъ теорему для двухъ какихъ угодно подобныхъ
многогранниковъ, объемы которыхъ назовемъ V и г. Разобьемъ пхъ на
подобныя пирамиды (400). Пусть V), И2,	11 ’ѵ г2> будутъ
объемы сходственныхъ пирамидъ, а В и I длины какихъ-нибудь сходствен-
ныхъ реберъ. Тогда, согласно доказанному, будемъ имѣть:
21- Л --Р. '	»
ѵ, ~ I* ’ г2'~ ?з".......\	- I*
Г1+Га4-...УП _
1-1-І-М-	?3
г _
ѵ I*
Откуда:
т.-е.
ГЛАВА V.
Симметричныя фигуры
403» Опредѣленія. Различаютъ ѵри рода симметріи: относительна
точки, относительно прямой и относительно плоскости.
«____X*
А
О
Черт. 301
Черт. 303
У
Черт. 302
Двѣ точки А и А-і (черт. 301) паз. симметричными относительно точ-
— 257 —
ки О (центра симметріи), если прямая ААХ проходитъ черезъ точку О
п дѣлится ею пополамъ. Двѣ точки А и Ах (черт. 302 и 303) наз. сим.
метричными относительно прямой ху (оси симметріи) или относительно
плоскости Р {плоскости симметріи}, если прямая ААг перпендикулярна
къ ху пли къ плоскости Р и дѣлится ими пополамъ.
Двѣ фигуры наз. симметричными относительно центра (черт. 301),
оси (черт. 305), или плоскости (черт. 306), если каждой точкѣ одной фи-
гуры соотвѣтствуетъ симметричная точка другой. Симметричныя точки
двухъ такихъ фигуръ паз. сходственными.
404. Замѣтимъ прежде всего, что двн, фигуры, симметричныя от-
носитс.іъно оси. равны. Въ этомъ убѣдимся, если повернемъ одну изъ фи-
Черг. 304
гуръ (черг. 305) вокругъ
оси на 180'1. Тогда каждая
точка А одной фигуры сов-
ладаетъ съ сходственной
точкой Л другой фигуры,
и, слѣд., обѣ фигуры совмѣ-
стятся.
4-05. Теорема. Фигу-
ры, симметричныя съ одной
и гной же фигурой отиоеи-
те.ияіо риз.ыічиыхъгіентровъ.
равны.
Пусть фигуры 1’1 и -Т7’!!
Черг. 30?
симметричны съ одной фигурой 1<' относительно центровъ О и (черт. 307).
А. П. КИСЕЛЕВЪ.
17
— 258 —
Возьмемъ въ фигурѣ Е произвольную точку А и въ фигурахъ Е{ и Ри точка
Аі и Лп, симметричныя съ А; затѣмъ проведемъ прямыя О(\ и ААі-
Такъ какъ АО~АХ О и	то Л^ц || ООХ и Л^ц^аоОі. Такимъ об-
разомъ, всѣ соотвѣтственныя точки фигуръ Ех и Рп (паир., Ах и Аи, Ех и
Би, Сі п Сп и т. д.) лежатъ на разстояніяхъ, параллельныхъ прямой <%\ и
равныхъ 200Р Поэтому если перемѣстимъ фигуру Ех такъ, чтобы каж-
дая ея точка описала прямую, параллельную ООХ и равную удвоенной
этой линіи, то обѣ фигуры совмѣстятся; значитъ, онѣ равны.
406. Теорема. Если фигуры. Г и Е (черт. 308) симметричны
относитесь но плоскости»
Р, то ихъ можно помѣ-
стить такъ, что онѣ бу-
дутъ симметричны от-
носительно любой точки
О, взятой на плоскости
Р; и обратно; если фи-
1 уры Е и Рц симметрич-
ны относительно точки
О, то ихъ можно помѣ-
стить такъ, что онѣ бу-
дутъ симметричны от-
носительно любой плос-
кости Р, проходящей че-
резъ точку О.
Если фигуры Е и
симметричны относительно плоскости Р, то прямая ААХ, соединяющая
какія-нибудь двѣ сходственныя точки, перпендикулярна къ плоскости Р'
и дѣлится ею пополамъ; значитъ: Аа-=Лха. Ели фигуры Г и Рп симмет-
ричны относительно точки О, то прямая АА1Ь соединяющая двѣ сход-
ственныя точки, проходитъ черезъ О и дѣлится этою точкою пополамъ;
значитъ: АО=АиО. Замѣтивъ это, соединимъ Ах съ Ли и проведемъ ОЛС
перпендикулярно къ Р. Такъ какъ АО=АиО и Аа=А}а, то ./ЦЛцПаО;
слѣд. ^АцАіА— /_ОаА=д. Такъ какъ ОЛГЦ. Ри ААХ I Р, то ОМ|і АА^
изъ этого слѣдуетъ, что, во 1°, ОМ пересѣкается съ ЛіЛц въ нѣкото-
рой точкѣ Ъ, во 2», /_А^хЪО—/_АххАхА~д,, въ 3°, А1Ъ=Аіф (такъ какъ
ЛІІ0=0Л). Если мы теперь повернемъ фигуры и вокругъ оси ОМ
на 180°, то точки Аг и Лп, а слѣд. и всѣ другія сходственныя точки, по-
мѣняются мѣстами; значитъ, фигура Е{ можетъ быть сдѣлана симметрич-
ною съ Е относительно точки О, а фигура Рп можетъ быть сдѣлана сим-
метричною съ Г относительно плоскости Р; что и требовалось доказать.
409. Слѣдствіе. 1°. Фигуры, симметричныя съ одной и той же
фигурой относительно различныхъ плоскостей, равны между собою, пото-
му что эти фигуры всегда можно сдѣлать симметричными съ одной и
той же фигурой относительно двухъ центровъ, а такія фигуры равны (405)^
— 259 —
21*. Если будемъ обращать вниманіе только па форму фигуры, а не на ея
положеніе въ пространствѣ, то можемъ сказать, что данная фигура Еимѣ-
етъ только единственную симметричную съ него фигуру (относительно
точки, пли относительно плоскости, все равно), такъ какъ всѣ фигуры,
симметричныя съ Е, равны между собою. Вслѣдствіе этого, при изслѣ-
дованіи свойствъ симметричныхъ фигуръ, зависящихъ только отъ ихъ
формы, мы можемъ по произволу разсматривать эги фигуры или какъ
симметричныя относительно центра, пли какъ симметричныя относитель-
но плоскости.
409. Теоремы, выражающія свойства симметричныхъ фигуръ.
1». Фиіура, симметричная съ плоской фпиурой, сетъ также плоская
фиіура, равная первой.
Это свойство сдѣлается очевиднымъ, если возьмемъ за плоскость сим-
метріи плоскость данной фигуры; тогда симметричная фигура сливается
съ данной.
Въ частности, фигура, симметричная съ отрѣзкомъ
прямой, есіь равный отрѣзокъ прямой; фигура, симмет-
ричная съ угломъ, есть равный уголъ; фигура, симмет-
ричная съ плоскимъ многоугольникомъ, есть равный
плоскій многоугольникъ; фигура, симметричная съ кру-
гомъ, есть равный кругъ; и т. п.
2®. Фигура, симметрична я съ двуграннымъ угломъ
(РАВф, черт. 309), есть равный двугранный уголъ.
Это свойство сдѣлается очевиднымъ, если за плос-
кость симметріи возьмемъ биссектриссную плоскость И.
Тогда фигура, симметричная съ гранью Р, будетъ другая
грань и наоборотъ; слЬд. фигура, симметричная съ
угломъ РАВ& будетъ уголъ фАВР.
3°. Фигура, симметргічная съ многограннымъ угломъ, (ЯАВСВЕ черт,
310), есть мноюгранныгг уголъ, у котораго двугранные и плоскіе углы со-
отвѣтственно равны двуграннымъ гі плоскимъ уг-
ламъ перваго многограннаго угла, но расположены
въ обратномъ порядкѣ.
Это свойство сдѣлается очевиднымъ, если
возьмемъ за центръ симметріи вершину 8. Тогда
получимъ два симметричные угла ВАВСЛЕ и
ЗА^С^Е^ у которыхъ двугранные и плоскіе
углы соотвѣтственно равны, но расположены въ
обратномъ порядкѣ (360).
Слѣдствіе. Симметричные многогранные уг-
лы вообще не равны, такъ какъ, вслѣдствіе об-
ратнаго расположенія равныхъ двугранныхъ уг-
ловъ, они не могутъ совмѣститься. По той же
причинѣ симметричные многогранники вообиіе не
равны.
9
Черт. 309
В е С
Черт. 310
— 260 —
4’. Два си.уі.иет/пічиые мноіоіриннѵка равновелики.
Докажемъ сначала эту теорему для
симметричныхъ пирамидъ 8АВСВ іг
Л'рІВСІ), которыя мы размѣстимъ такъ,
чтобы плоскостью симметріи служило
осповапіе АВСВ. Такч» какъ точки Я и
Л*! симагетричпы относительно плоскости
основанія, то высоты 6’0 и $ХО равны;
вслѣдствіе этого пирамиды, имѣя общее
основаніе и равныя высоты, равнове-
лики. Два какіе угодно симметричные
многогранника всегда могутъ быть раз-
ложены па одинаковое число симметрич-
ныхъ пирамидъ; поэтому теорема візрпа
и для многогранниковъ произвольной
формы.
Г л А В А И.
Понятіе о правильныхъ многогранникахъ.
409.	Опредѣленіе. Многогранникъ наз. правильнымъ.
если всѣ его грани суть равные правильные многоугольники
и всѣ многогранные углы равны. Изъ этого опредѣленія слѣ-
дуетъ. что въ правильныхъ многогранникахъ равны всѣ плос-
кіе углы, всѣ двугранные углы и всѣ ребра.
410.	Чтобы опредѣлить, какіе правильные многоуголь-
ника могутъ служить гранями правильныхъ многогранни-
ковъ, примемъ во вниманіе, что во всякомъ многогранномъ
углѣ сумма плоскихъ угловъ меньше 4с/ (355). Каждый уголъ
правильнаго треугольника равенъ Повторяя -Дс/ слага-
емымъ 3 раза, 4 раза и 5 разъ, мы получаемъ суммы, мень-
шія 4с/; а повторяя 2Дс/ слагаемымъ большее число разъ,
мы получаемъ въ суммѣ 4с/ или болѣе. Поэтому изъ плоскихъ
угловъ, равныхъ угламъ правильнаго тр.-ка, можно образо-
вать многогранные углы только трехъ видовъ: треграапые.
четырегранные и пятигранные. Уголъ квадрата равенъ с/, а
уголъ правильнаго пятиугольника равенъ с/:.с/і повторяя эти
углы слагаемымъ не болѣе 3-хъ разъ, получаемъ, суммы.
— 261 —
меньшія ±сІ. Поэтому изъ плоскихъ угловъ, равпыхъ угламъ
квадрата пли правильнаго пятиугольника, можно образовать
только трегранные углы. Уголъ правильнаго шестиугольника
равенъ поэтому изъ такихъ угловъ нельзя образовать
даже треграннаго угла. Ивъ угловъ правильныхъ многоуголь-
никовъ, имѣющихъ болѣе 6-ти сторонъ, и подавно нельзя
образовать никакого многограннаго угла.
Черг. 312	Черт. 813	Черт. 314
Черт 315.
Черт 316.
-<11. Изъ сказаннаго слѣдуетъ, что правильныхъ много-
гранниковъ не можетъ быть болѣе слѣдующихъ пяти:
1°. Правильный четырегранникъ (или тетраэдръ), кото-
раго поверхность составлена изъ 4-хъ правильныхъ треуголь-
никовъ (черт. 312).
2°. Правильный восьмшраннггкъ (или октаэдръ), котораго
поверхность составлена изъ 8-ми правильныхъ тр.-ковъ (черт.
313).
3°. Правильный двадцатигранникъ (пли икосаэдръ), об-
разованный 20-ю правильными тр.-ками (черт. 315).
4°. Правильный шестигранникъ (или эксаэдръ), образован-
ный 4-мя квадратами (черт. 314). Онъ наз. иначе кубомъ.
5°. Правильный двѣнадцатигранникъ (или додекаэдръ), об-
разованный 12-ю правильными пятиугольниками (черт. 316).
— 262 —
ЗАДАЧИ.
335.	Вычислить поверхность и объемъ прямой призмы, у которой осно-
ваніе правильный тр.-къ,'вписанный въ кругъ радіуса7=2 метрамъ, а высота
равна сторонѣ правильнаго 6-угольника, описаннаго около того же круга.
336.	Опредѣлить поверхность и объемъ правильной 8-уголыюй призмы,
у которой высота 7е=6 арш., а сторона основанія а—8 вершк.
337.	Опредѣлить боковую поверхность и объемъ прав. шестиугольной пи-
рамиды, у которой высота равна 1 метру, а апоѳема составляетъ съ высо-
тою уголъ въ 30°.
338.	Вычислить объемъ тре^г. пирамиды, у которой каждое боковое реб-
ро равно I, а стороны основанія суть «, Ъ и с.
339.	Данъ трегранный уголъ 8АВС, у котораго всѣ три плоскіе угла
прямые. На его ребрахъ отложены длины: 8А=а, 8В—Ь и 8С=с. Черезъ
точки А, В и С проведена плоскость. Опредѣлить объемъ пирамиды 8АВС.
340.	Высота пирамиды равна Л, а основаніе—правильный шестиуголь-
никъ со стороною а. На какомъ разстояніи х отъ вершины пирамиды слѣду-
етъ провести плоскость, параллельную основанію, чтобы объемъ образовав-
шейся усѣченной пирамиды равнялся V.
341.	Опредѣлить объемъ правильнаго тетраэдра съ ребромъ а.
342.	Опредѣлить объемъ прав. октаэдра съ ребромъ а.
343,	Усѣченная пирамида, которой объемъ Ѵ=1465 куб. сантим., имѣ-
етъ основаніями правильные шестиугольники со сторонами: а=23 и 6=17
сант. Вычислить высоту этой пирамиды.
344.	Объемъ V усѣченной пирамиды равенъ 10,5 куб. метра, высота
7і=]/3 метр. и сторона а правильнаго шестиугольника, служащаго нижнимъ
основаніемъ, равна 2 метр. Вычислить сторону прав. шестиугольника, слу-
жащаго верхнимъ основаніемъ.
345.	Вычислить объемъ треугольной усѣченной призмы, у которой сто-
роны основанія суть: а=7,5, 6=7 и с=6,5, а ребра, перпендикулярныя къ
основанію, суть: 7с=2, 7=3 и ш=4.
346.	На какомъ разстояніи отъ вершины 8 пирамиды 8АВС надо про-'
вести плоскость, параллельную основанію, чтобы отношеніе объемовъ частей,
на которыя разсѣкается этою плоскостью пирамида, равнялось т.
347.	Вычислить объемъ усѣченнаго параллелопипеда, у котораго основа-
ніе есть В, а 7іі, 11 СУТЬ длины перпендикуляровъ, опущенныхъ изъ вер-
шинъ верхняго основанія па плоскость нижняго основанія.
348.	Пирамида съ высотою 7і раздѣлена плоскостями, параллельными ос-
нованію, на три части въ отношеніи т:п:р. Опредѣлить разстояніе этихъ
плоскостей до вершины пирамиды.
349.	Сумма объемовъ двухъ подобныхъ многогранниковъ равна V, а от-
ношеніе сходственныхъ реберъ равно т:п, Опредѣлить объемы ихъ.
350.	Раздѣлить объемъ усѣченной пирамиды плоскостью, параллельною
основаніямъ В и Ь, на двѣ части въ отношеніи т:п.
— 263 —
КНИГА III.
КРУГЛЫЯ ТѢЛА.
ГЛАВА I.
Цилиндръ и конусъ.
Поверхность вращенія. Такъ наз. поверхность, ко-
торая получается отъ вращенія какой-нибудь неизмѣннющейся
линіи ЛАГ, называемой образующею.
вокругъ неподвижной прямой АВ, на-
зываемой осью; при этомъ предпола-
гается, что образующая іОГ, при-
своенъ вращеніи, неизмѣнно связана
съ осью АВ.
Возьмемъ на образующей какую-ни-
будь точку Р п опустимъ изъ нея на
ось перпендикуляръ РО. Очевидно,
что при вращеніи не измѣняются ни
в
Черт. 317
длина этого перпендикуляра, ни вели-
чина угла АОР, пи положеніе точки
О. Поэтому каждая точка образующей описываетъ окружность,
которой плоскость перпендикулярна къ оси и центръ лежитъ
на пересѣченіи этой плоскости съ осью. Отсюда слѣдуетъ.
что плоскость, перпендикулярная къ оси.
пересѣкаясь съ поверхностью вращенія,
даетъ въ сѣченіи окружность.
Всякая сѣкущая плоскость, проходя-
щая черезъ ось, наз. меридіональною
плоскостью, а пересѣченіе ея съ поверх-
ностью вращенія—меридіаномъ. Всѣ ме-
ридіаны равпы между собою, потому что
при вращеніи каждый изъ нихъ прохо-
дитъ черезъ то положеніе, въ которомъ
ранѣе былъ всякій другой меридіанъ.
XI з. Цилиндрическая поверхность.
Такъ наз. поверхность, производимая дви-
м
в
Черт. 318
— 264 —
С
жопіемъ прямой АВ (черт. 318), перемѣщающейся въ про-
странствѣ параллельною данпому направленію и пересѣкающей
при этомъ данную линію Прямая АВ наз. образую-
щею, а линія МК направляющею,
4І4. Цилиндръ. Тѣло, ограниченное
цилиндрическою поверхностью и двумя па-
раллельными плоскостями, наз. цилиндром7>
(черт. 319). Часть цилиндрической поверх-
ности, заключенная между плоскостями,,
наз боковою поверхностью цилиндра, а.
части плоскостей, отсѣкаемыя этою по-
верхностью,—основаніями цилиндра. Раз-
стояніе между основаніями есть высота
Черт 319 цилиндра. Цилиндръ наз. прямымъ или
наклоннымъ, смотря по тому, перпендикулярны или наклонны
къ основаніямъ его образующія.
Прямой цилиндръ (черт. 320) наз. круго-
вымъ, если его основанія круги. Такой ци-
А лпндръ можно разсматривать, какъ тѣло, про-
исходящее отъ вращенія прямоугольника ОААТ Оі
вокругъ стороны ОО1? какъ оси: при этомъ
В сторона АА{ описываетъ боковую поверхность,
а стороны О А и ОІАІ—круги основаній.
Всякая прямая ВС, параллельная О А, оппсьт-
А ваетъ также кругъ, перпендикулярный къ оси.
Отсюда слѣдуетъ, что сѣченіе прямого круго-
Черт. 320 вого цилиндра плоскостью, параллельною ос-
нованіямъ, есть кругъ. Въ элементарной геометріи разсмат-
ривается только прямой круговой цилиндръ; для краткости
его называютъ просто цилиндромъ.
Иногда приходится разсматривать такія прямыя призмы,
которыхъ основанія суть многоугольники, вписанные въ осно-
ванія цилиндра, пли описанные около нихъ; такія призмы
наз. описанными въ цилиндрѣ, или описанными около него.
445. Коническая поверхность. Такъ наз. поверхность, про-
изводимая движеніемъ прямой АВ (черт. 321), перемѣщающейся
въ пространствѣ такъ, что опа при этомъ постоянно проходить
— 265 —
черезъ неподвижную точку 8
МУ. Прямая ЛВ наз. обра-
зующею, линія МХ—направ-
.іяющею, а точка $ вершиною
конической поверхности.
416. Конусъ. Тѣло, огра-
ниченное коническою поверх-
ностью и плоскостью, пересѣ-
кающею всѣ образующія по одну
сторону отъ верпіипы, наз. ко-
иусомъ (черт. 332). Часть кони-
ческой поверхности, ограничен-
ная этою плоскостью, наз. бо-
и пересѣкаетъ данную линію-
в
новою поверхностью, а часть	черТ. 321
плоскости, отсѣкаемая боковою поверхностью,—основаніемъ ко-
нуса. Перпендикуляръ, опущенный изъ
вершины па основаніе, есть высота конуса.
Конусъ наз. прямымъ круговымъ, если
его основаніе есть кругъ, а высота про-
ходитъ черезъ центръ основанія (черт.
323). Такой конусъ можно разсматри-
вать, какъ тѣло, происходящее отъ вра-
щенія прямоугольнаго тр.-ка 80А во-
кругъ катета 80, какъ оси. При этомъ
гипотенуза 8А производитъ боковую по-
верхность, а катетъ О А—основаніе ко-
пуса. Всякая прямая ВОХ, параллельная
8
Черт. 322
АО, описываетъ-
при вращеніи кругъ, перпендикулярный къ оси.
Отсюда слѣдуетъ, что сѣченіе прямого кру-
гового конуса плоскостью, параллельною осно-
ванію, есть кругъ. Въ элементарной геомет-
ріи разсматривается только прямой круговой
конусъ, который для краткости паз. просто
конусомъ.
Иногда приходится разсматривать такія пи-
рамиды, которыхъ основанія суть многоуголь-
ники, вписанные въ основаніе конуса, иля оіш-
8
Черт .323
— 266 —
нные около него, а вершина совпадаетъ съ вершиною конуса.
Такія пирамиды наз. вписанными въ конусъ, или описан-
ными около него.
413. Усѣченный конусъ. Усѣченнымъ конусомъ (черт.
Черт. 321
324) наз. часть полнаго конуса, заклю-
ченная между основаніемъ и сѣкущею
плоскостью, параллельною основанію'. Па-
раллельные круги, ограничивающіе усѣ-
ченный конусъ, наз. основаніями его.
Усѣченный конусъ можно разсматривать,
пакъ тѣло, происходящее отъ вращенія
А лрямоугольной трапеціи ОАА} вокругъ
стороны О Оі, перпендикулярной къ ос-
нованіямъ трапеціи.
Поверхность цилиндра и конуса.
418. Замѣчаніе. Боковыя поверхности цилиндра и ко-
нуса принадлежатъ къ поверхностямъ кривымъ, т. е. такимъ,
которыхъ никакая часть не можетъ совмѣститься съ плос-
костью. Поэтому мы должны опредѣлить, что разумѣютъ подъ
величиною боковой поверхности цилиндра или конуса, когда
сравниваютъ эти поверхности съ плоскою квадратною единицею.
419. Опредѣленія. Боковою поверхностью цилиндра (при
измѣреніи ея квадратною единицею) наз. предѣлъ, къ кото-
рому стремится боковая поверхность правильной вписанной
призмы, при неограниченномъ удвоеніи чгісла ея боковыхъ
граней.
Боковою поверхностью конуса (при измѣреніи ея квад-
ратною единицею) наз. предѣлъ, къ которому стремится
боковая поверхность правильной впгьсанной пирамиды при
неограниченномъ удвоеніи числа ея боковыхъ граней.
490. Теорема. Боковая поверхность цилиндра равна
произведенію окружности основанія на высоту.
Впишемъ въ цилиндръ какую-нибудь правильную призму и
— 267 —
обозначимъ черезъ 8, р и Н числа, выражающія въ соот-
вѣтствующихъ единицахъ боковую поверх-
ность, периметръ основанія и высоту этой
призмы. Тогда будемъ имѣть (376):
з -=рН
Предположимъ теперь, что число боко-
выхъ граней вписанной призмы неограни-
ченно удваивается; тогда величины 8 и рІІ
«дѣлаются перемѣнными, но равенство между
ними не нарушится. Поэтому (250) равен-
ство останется вѣрнымъ и тогда, когда
вмѣсто перемѣнныхъ подставимъ ихъ предѣлы. Предѣлъ р
есть длина окружности основанія (256), а предѣлъ 8 есть
то, что наз. боковою поверхностью цилиндра. Значитъ, обо-
значивъ первую черезъ С, а вторую черезъ $, получимъ:
8= СВ
49І. Слѣдствія. 1°. Если В означаетъ радіусъ основа-
нія цилиндра, то С=2ъВ\ поэтому боковая поверхность
цилиндра выразится:
2°. Чтобы получить полную поверхность цилиндра, доста-
точно къ боковой поверхности приложить сумму площадей
двухъ основаній; поэтому, обозначая пол-	$
ную поверхность черезъ ]\ будемъ имѣть:	Д
Т=	пВ* + пВ~ = 2 тсіг(7?+//)	/Ж
499. Теорема. Боковая поверхность	/// і ѴД
конуса равна произведенію окружности	/-7 і \\\
основанія на половину образующей. Ду./...:........
Впишемъ въ конусъ какую-нибудь пра- I : \
вильную пирамиду и обозначимъ черезъ I
х, р и I числа, выражающія въ соотвѣт-	в—“—С
ствующихъ единицахъ боковую поверх- Черт. 326.
ность, периметръ основанія и апоѳему этой пирамиды. Тогда
будемъ имѣть (377):
5 = ^-рі
— 268 —
Предположимъ теперь, что число боковыхъ граней впи-
санной пирамиды неограниченно удваивается; тогда величины
ч и рі сдѣлаются перемѣнными, по равенство между яимп
пе нарушится. Поэтому оно останется вѣрнымъ и тогда, когда
вмѣсто перемѣнныхъ подставимъ ихъ предѣлы. Предѣлъ р
есть длина окружности основанія, предѣлъ / есть образую-
щая конуса, а предѣлъ « есть то, что наз. боковою поверх-
ностью конуса. Значитъ, обозначая этп величины соотвѣт-
ственно черезъ С, I, и $. получимъ:
5=1 СЛ
423. Слѣдствіе. 1°. Такъ какъ С= 2-7?, то боковая по-
верхность конуса выразится:
8— * • 2т.НЬ=т.Шу
2°. Полную поверхность копуса получимъ, если къ боко-
вой поверхности приложимъ площадь основанія; поэтому:
Т— кВЬ -I- т: 7?’ = тМ {II Ч- Г)
424. Теорема. Кокован поверхность усѣченнаю конуса
равна произведенію полусуммы окружностей основаній на
образующую.
Впишемъ въ усѣченный конусъ какую-
О,...	пибудь правильную усѣченную пирамиду
\ и обозначимъ черезъ $, р, 1\ и I числа,
/ -І . X \ выражающія боковую поверхность, пери-
у. метРъ нижняго, периметръ верхняго ос-
нованій и апоѳему этой пирамиды. Тогда'
будемъ имѣть (378):
Изъ этого равенства, разсуждая подобно
предыдущему, выводимъ:
О*
Чеот. 327
5=.‘(СЧ-С1) I
гдѣ 5 есть боковая поверхность усѣченнаго конуса. С и Сг
длины окружностей основаній, а I образующая.
— 269 —
445. Слѣдствія. 1°- Если й и Д будутъ радіусы ок-
ружностей нижняго и верхняго основаній, то боковая поверх-
ность усѣченнаго конуса выразится:
5= | (2т. К + 2т.Л,) Ъ=т. (I? +	Ь
2°. Проведемъ въ трапеціи ОО1А1А (черт. 327). отъ
вращенія которой получается усѣченный конусъ, среднюю
линію ВС (103). Тогда получимъ:
лс’=1(ол+о1л])=|(л+А)
Откуда:	В +	= 2 В С
Слѣд.:	8 = 2 кВ С. В
т.-е. боковая поверхность усѣченнаго конуса- равна произ-
веденію окружности средняго сѣченія на образующую.
3°. Полная поверхность 7'усѣченнаго конуса выразится такъ:
т=г, (& н- В; -і- ВВ 4- В, В)
4*46. Замѣчаніе. Въ предыдущихъ теоремахъ боковыя
поверхности цилиндра и конуса разсматривались, какъ пре-
дѣлы боковыхъ поверхностей правильныхъ вписанныхъ призмъ
или пирамидъ. Если бы, подобно тому, какъ мы это дѣлали
при доказательствѣ этихъ теоремъ, мы стали находить пре-
дѣлы описанныхъ призмъ или пирамидъ, то нашли бы, что
эти предѣлы тѣ же самые, какъ и для вписанныхъ призмъ
пли пирамидъ. Вслѣдствіе этого боковыя поверхности цилиндра
и конуса можно разсматривать, какъ общій предѣлъ боковыхъ
поверхностей правильныхъ призмъ или пирамидъ, какъ впи-
санныхъ, такъ и описанныхъ.
Черт. 328
4® 9. Развертка цилиндра и конуса. Впишемъ въ цилиндръ (черт. 328)
— 270 —
какую-нибудь правильную призму и затѣмъ вообразимъ, что боковая
ея поверхность разрѣзана, вдоль какого-нибхдь бокового ребра. Очевидно,
что враіцая ся грани вокругъ реберъ, мы можемъ развернутъ эту поверх-
ность въ одну плоскость, безъ разрыва и безъ складокъ. Тогда получится
то, что паз. разверткою боковой поверхности прав. призмы. Она предста-
вляетъ собою прямоугольникъ КЪМН, составленный изъ столькихъ рав-
ныхъ прямоугольниковъ, сколько въ призмѣ боковыхъ граней. Основаніе
его равно периметру основанія призмы, а высота 7ЙѴ есть высота
призмы.
Вообразимъ теперь, что число боковыхъ граней вписанной призмы не-
ограниченно удваивается; тогда ея развертка будетъ все удлиняться, приб-
лижаясь къ 'предѣльному прямоугольнику КР<№\ у котораго основаніе
равно длинѣ окружности основанія цилиндра, а высота есть высота ци-
линдра. Этотъ прямоугольникъ наз.	боковой поверхности ци-
линдра.
Подобно этому вообразимъ, что въ конусъ вписана правильная пира-
мида (черт. 329). Мы можемъ разрѣзать ея боковую поверхность по ка-
кому-нибудь ребру п затѣмъ, повертывая грани вокругъ реберъ, получить
ея развертку въ видѣ многоугольнаго сектора 8КЪ, составленнаго изъ
Черт. 329
столькихъ равныхъ равнобедр. тр.-ковъ, сколько въ пирамидѣ боковыхъ
граней. Прямыя 8К, 8а, 8Ь... равны боковому ребру пирамиды (или об-
разующей конуса), а длина ломаной КаЪ...Ь равна периметру основанія
пирамиды. При неограниченномъ удвоеніи числа боковыхъ граней вписан.
пирамиды развертка ея увеличивается, приближаясь къ предѣльному сек-
тору 8КМ, у котораго дуга ЛГМ равна окружности основанія, а радіусъ
8К—-образующей конуса. Этотъ секторъ наз. разверткою боковой поверх-
ности конуса.
Подобно этому можно получить развертку боковой поверхности усѣчен.
конуса (черт. 329) въ видѣ части кругового кольца КМЯР.
— 271 —
Объемъ цилиндра п конуса.
4® 8. Лемма 1. Объемъ цилиндра есть общій предѣлъ
объемовъ правильныхъ вписанныхъ и описанныхъ призмъ прѣ
неограниченномъ удвоеніи числа ихъ боковыхъ граней.
Впишемъ въ цилиндръ и опишемъ около него по какой-
нибудь правил. одноименной призмѣ. Обозначимъ объемъ,
площадь основанія и высоту соотвѣтственно: для цилиндра—
V, В, И, для вписанной призмы—Т^, 7?,, Н и для опи-
санной призмы— К2, В*, Н. Тогда будемъ имѣть (388):
Ѵ2 = В9/І \=В,Н
Откуда:	Гй—	= (В9—Вг) Н
При неограниченномъ удвоеніи числа боковыхъ граней
призмъ, разность В2—Вх стремится къ нулю (295), а множи-
тель 77 есть число постоянное: поэтому правая часть послѣд-
няго равенства, а слѣд. и его лѣвая часть стремится къ нулю.
Объемъ цилиндра, очевидно, больше объема вписанной призмы,
но меньше объема описанной: поэтому каждая изъ разностей
V—Ѵ\ и V*-—К меньше разности —У; но послѣдняя, по
доказанному, стремится къ нулю; слѣд., и первыя стремятся
къ нулю; а это, по опредѣленію предѣла, означаетъ, что
Ѵ'-= пред. = пред. Ѵг
4®9. .Лемма 2. Объемъ конуса есть обгціѣ предѣлъ
объемовъ ггравильныхъ вписанныхъ и описанныхъ пирамидъ
при неогрангьченномъ удвоеніи числа ихъ боковыхъ граней.
Впишемъ въ конусъ и опишемъ около него по какой-нибудь
прав. одноименной пирамидѣ. Употребляя тѣ же обозначенія,
какъ и въ предыдущемъ параграфѣ, будемъ имѣть (391):
Откуда:	Уг——В,)
Изъ этого равенства видно, что разность Ѵг— Ѵ\ стре-
мится къ нулю, когда число боковыхъ граней вписанной и
— 272 —
описанной пирамиды неограниченно удваивается; а такъ какъ
каждая изъ разностей: І7^— V и К—меньше Г2—Т7, то
эти разности и подавно стремятся къ нулю; а это значитъ, что
V— пред. Ѵр=иред.
430.	Теоремы. 1°. Объемъ цилиндра равенъ произве-
денію площади основанія на высоту.
2°. Объемъ конуса равенъ произведенію площади основа-
нія на третъ высоты.
Впишемъ въ цилиндръ прав. призму, а въ конусъ прав.
пирамиду; тогда, употребляя прежнія обозначенія, будемъ имѣть:
для призмы...... Ѵ1 = ВІП
для пирамиды....Ур= 2?1 ТУ
Эти равенства остаются вѣрными, сколько бы мы не удва-
ивали числа боковыхъ граней призмы и пирамиды; поэтому
онп останутся вѣрными и тогда, когда на мѣсто перемѣнныхъ
подставимъ ихъ предѣлы (250); слѣд.:
для цилиндра....Ѵ~ВІІ
для конуса......Ѵ= ; ВН
431.	Слѣдствіе. Если радіусъ основанія цилиндра или
конуса обозначимъ черезъ В, то В = -В/і; поэтому:
Общи.	об. коп. Ѵ=~
433.	Теорема. Объемъ усѣченнаго конуса равенъ суммѣ
объемовъ трехъ конусовъ, имгмощихъ одинаковую высоту съ
усѣченнымъ конусомъ, а основаніями: одинъ — тгжнее основа-
ніе этого конуса, другой—верхнее, третій—среднее про-
пориіаналъное между ними.
Подобно предыдущему можно доказать, что объемъ усѣ-
ченнаго конуса есть общій предѣлъ объемовъ прав. вписан-
ныхъ и описанныхъ усѣченныхъ пирамидъ. Но объемъ V1
прав. вписанной усѣченной пирамиды, которой высота есть 77,
а площади основаній Вк и выражается равенствомъ (393):
Г1=ІЯ(Д + б,+ѵ/ДІ1)
— 273 —
іВъ предѣлѣ, при неограниченной ь удвоеніи числа боковыхъ
(граней вписанной пиррамиды, эго равенство дастъ:
Ѵ-~Н(В+Ь + /ВЪ)
гдѣ V есть объемъ, В и Ь площади основаній и Н высота
усѣченнаго конуса.
433. Слѣдствіе. Если В и г будутъ радіусы нижняго
к верхняго основаній усѣченнаго конуса, то В = т:В2. Ь = ^г ц
)/ВЪ—у^В2?2 = т>В>", поэтому:
Об. А С. КОИ. Ѵ = -“7; ІЕ(В2 “Г Г2 “Ь В?)
Подобные цилиндры и конусы.
434.	Опредѣленіе. Два цилиндра пли конуса наз. подобными, если
они произошли отъ вращенія подобныхъ прямоугольниковъ или треугольни-
ковъ вокругъ сходственныхъ сторонъ. Обозначимъ черезъ 7і и 7^ высоты
Черт. 330	Черт. З^1
двухъ подобныхъ цилиндровъ пли конусовъ, черезъ г и ихъ радіусы и че-
резъ I и Іі образующія: тогда, согласно опредѣленію, будемъ имѣть:
43®. Теорема. Боковыя и полныя поверхности подобныхъ цилинд-
ровъ или конусовъ относятся, какъ квадраты радіусовъ или высотъ, а объ-
емы—какъ кубы радіусовъ или высотъ.
Обозначимъ черезъ 5, У п V соотвѣтственно боковую поверхность,
полную поверхность и объемъ одного цилиндра или конуса, а черезъ 8и 1\
•п Ѵ1 тѣ ;ке величины для другого цилиндра или конуса, подобнаго первому.
Тогда будемъ имѣть:
а. и. киселекъ.	18
— 274 —
Для цилиндровъ:
,-9__2тсг/>__г7і _г к_____г2____№
51~2іГг1ЛІ ггк~гг 7і1~г^—кіі
Т _ 2кг(г-|-Л) _г д г-і-Д_?-2__ДЗ
7\ 2кг1(г14-7?І) гх гг	к^
Ѵ_ _ т:г2Л _у . к _г‘і_ _7і»
Ѵ7!-ТО^!- ’ Л1“г7»“"Л7
Для конусовъ:
А’___ 7ІГІ__Г . I _»-2_7<2
^“^71“ Д * Гі~г]2— /72
Т тѵг(г 4-7)  г . г—(-7  /г2
7і То'і^у^рі)-і\ гг	7і^
V уІлТіг^і & к г3 _ 7г3
Уі	ГГ2 гі3 М
ГЛАВА И.
Шаръ.
Сѣченіе шара плоскостью.
436. Опредѣленіе. Тѣло, происходящее отъ вращенія*
полукруга вокругъ діаметра, ограничивающаго его, наз. .ша-
ромъ, а поверхность, образуемая при этомъ полуокружностью,
наз. шаровою пли сферическою поверхностью. Эта поверх-
ность представляетъ собою геометрическое мѣсто точекъ, оди-
наково удаленныхъ отъ неподвижной точки, называемой цент-
ромъ шара.
Прямая, соединяющая центръ съ какою-нибудь точкою
поверхности, наз. радіусомъ, а прямая, соединяющая двѣ
точки поверхности и проходящая черезъ центръ, наз. діамет-
ромъ шара. Всѣ радіусы одного шара равны между собою,
а діаметръ равенъ двумъ радіусамъ.
Два шара одинаковаго радіуса равны, потому что при;
вложеніи они совмѣщаются.
— 275 —
433. Теорема. Сѣченіе шара плосноетъю есть кругъ.
1°. Предположимъ сначала, что сѣкущая плоскость АВ
проходитъ черезъ центръ О шара: тогда
всѣ точки линіи пересѣченія, принадлежа
шаровой поверхности, одинаково удалены
отъ точки О, лежащей въ сѣкущей пло-
скости; слѣд., сѣчепіе есть кругъ.
2°. Положимъ теперь, что сѣкущая
плоскость СВ не проходитъ черезъ центръ.
Опустимъ па нее изъ центра перпендикуляръ ОК и возьмемъ
на линіи пересѣченія какую-нибудь точяу М. Соединивъ ее
съ О и К, получимъ прямоугольный тр.-къ МОК, пзъ ко-
тораго находимъ:
МК=>]ОМГ— ОІС	[1]
Черт. 332
Такъ какъ длины ОМ и ОК не измѣняются при измѣненіи
положенія точки М на линіи пересѣченія, то разстояніе МК
есть величина постоянная: значитъ, линія пересѣченія есть
окружность.
438.	Слѣдствіе. Пусть В, г и еі означаютъ: радіусъ
шара, радіусъ круга сѣченія и разстояніе сѣкущей плоскости
отъ центра: тогда равенство [1] приметъ видъ:
/	— сІ2
Изъ этой формулы выводимъ:
Г’. Наибольшее сѣчепіе получается при И = т.-е, когда
сѣкущая плоскость проходитъ черезъ центръ шара, Въ этомъ
случаѣ г=В.
Сѣчепіе шара плоскостью, проходящею черезъ центръ,
наз. большимъ кругомъ.
2°. Сѣченія, равноотстоящія отъ центра шара, равны.
3°. Изъ двухъ сѣченій, неодинаково удаленныхъ отъ
центра шара, то больше, которое ближе къ центру.
18*
— 276 —
Свойства большихъ круговъ.
439.	Теорема. Большой кругъ дѣлитъ гиаръ и его по-
верхность попо. іамъ.
Вообразимъ, что мы разрѣзали шаръ по
какому-нибудь большому кругу и, перевер-
нувъ верхнюю часть шара, вложили ее въ
нижнюю такъ, чтобы у нихъ совпали круг-
лыя основанія# Тогда всѣ точки одной части
>. шаровой поверхности совмѣстятся съ точ-
' ками другой части, потому что тѣ и другія
одинаково удалены отъ общаго центра. Изъ
этого слѣдуетъ, чго большой кругъ дѣ-
Черт. ззз литъ шаръ и его поверхность пополамъ.
440.	Теорема. Черезъ двѣ точки иьаровой поверхности
можно провести окружность большого круга и притомъ
только одну, если эгпи точки не лежатъ на концахъ одного
діаметра.
Пусть на шаровой поверхности, имѣющей центръ О, взяты
какія-нибудь двѣ точки А и В. Черезъ три точки А, О и.
В всегда можно провести плоскость и притомъ только одну,
если эти точки не лежатъ па одной прямой (т.-е. на діа-
метрѣ). Эта плоскость, проходя черезъ центръ О, дастъ въ
пересѣченіи съ шаровою поверхностью, окружность большого
круга.
441.	Теорема. Окружности двухъ большихъ круговъ пе-
ресѣкаются пополамъ.
Дѣйствительно, плоскости двухъ
большихъ круговъ АВ и СБ прохо-
дятъ черезъ центръ О; значитъ, онѣ
пересѣкаются по прямой КГБ, прохо-
дящей черезъ центръ, т.-е. по общему
ихъ діаметру; а діаметръ дѣлитъ ок-
ружность пополамъ.
44®. Теорема. Кратчайшее раз-
стояніе на шаровой поверхности ме-
жду двумя ея точками есть дуга большого круга, прове-
денная между ними.
Пусть гп есть дуга большого круга,
проведенная на шаровой поверхности
между двумя ея точками А и В, а к
какая-нибудь кривая, проведенная па
шаровой поверхности между тѣми же
точками. Докажемъ, что а длиныие гп.
Возьмемъ па кривой з произвольную
точку В и соединимъ ее съ А и В
дугами большого круга. Проведя ра-
діусы ОА, ОВ, ОВ, примемъ ихъ за
Черт. 335
ребра треграннаго угла. Въ этомъ углѣ, какъ во всякомъ
трегранномъ (354), сумма плоскихъ угловъ АОВ и ВОВ
больше третьяго плоскаго угла АОВ. Но эти углы измѣря-
ются дугами АВ, ВВ и АВ, проведенными изъ вершины
угловъ однимъ и тѣмъ же радіусомъ; слѣд.. сумма дугъ АВ
и ВВ больше дуги АВ. Возьмемъ теперь на кривой а про-
межуточныя точки Е и В и проведемъ дуги большого круга
черезъ каждыя двѣ сосѣднія точки: А, Е, В, В и В.
Такъ же, какъ и прежде, убѣдимся, что АЕ + ЕВ > А О п
ВВ+ЕВ>1)В; значитъ, сумма АЕ-^ЕВД- ВВ-\- ВВ
больше АВ-'ГВВ, а потому и подавно больше дуги гп. Во-
образимъ теперь, что число промежуточныхъ точекъ, взятыхъ
на кривой з, неограниченно увеличивается, и между каждыми
двумя сосѣдними точками постоянно проводятся дуги большихъ
круговъ; тогда линія, составленная изъ этихъ дугъ, все уве-
личивается и постоянно остается больше дуги гп; значитъ,
и предѣлъ, *) къ которому опа стремится, долженъ быть боль-
ше т; а этотъ предѣлъ принимается за длину дуги а.
*) Мы принимаемъ здѣсь безъ доказательства, что предѣлъ кривой АЕ.ІУ&В,
составленной изъ дуіъ большихъ круговъ, существуетъ и что онъ не зависитъ
отъ закона, по которому увеличивается число точекъ па кривой
— 278 —
есть касательная.
Плоскость, касательная къ шару.
<143. Опредѣленіе. Плоскость, имѣющая съ шаровою по-
верхностью только одну общую точку, наз. касательною пло-
скостью.
Возможность существованія такой плоскости доказывается
слѣдующей теоремой.
Теорема. Плоскость (Р черт. 336). перпендикулярная къ
ѵадіусу (ОА) въ концѣ его, лежащемъ на поверхности тара,
Возьмемъ на плоскости Р произ-
вольную точку В и соединимъ ее съ
центромъ О. Такъ какъ ОВ наклон-
ная, а ОА перпендикуляръ къ Р, то
ОВ>ОА. Поэтому точка В не мо-
жетъ лежать на шаровой поверхности;
слѣд., у плоскости Р есть только одна
общая точка А съ шаровою поверх-
ностью: значитъ, эта плоскость каса-
тельная .
444.	Обратная теорема. Касатель-
ная плоскость <Р, черт. 336) перпендикулярна къ радіусу
(ОА), проведенному въ точку касанія.
Такъ какъ, по опредѣленію, точка А есть единственная,
общая у плоскости съ шаровою поверхностью, то всякая дру-
гая точка плоскости лежитъ внѣ шаровой поверхности и,
слѣд., дальше отстоитъ отъ центра, чѣмъ А: такимъ обра-
зомъ, прямая О А есть кратчайшее разстояніе точкп О отъ
плоскости Р. т.-с. О А есть перпендикуляръ къ Р.
)т. 336
Поверхность шара и его частей.
445.	Опредѣленія. Часть шаровой поверхности, .заклю-
ченная между двумя параллельными сѣкущими плоскостями ААУ
— 279 —
и ВВ}, наз. шаровымъ поясомъ или зоною. Окружности
сѣченій ААГ и ВВ^ паз. основаніями,
а разстояніе КЬ между параллельными
плоскостями — высотою пояса.
Часть шаровой поверхности, отсѣкаемая
какою-нибудь плоскостью АА}, наз. сег-
ментною поверхностью; окружность АА^
есть основаніе, а отрѣзокъ 70/ радіуса,
перпендикулярнаго къ плоскости сѣченія,
есть высота сегментной поверхности.
Сегментную поверхность можно разсматривать, какъ частный
случай пояса, а именно: если одна изъ параллельныхъ пло-
скостей сдѣлается касательною къ шару, тогда поясъ обращается
въ сегментную поверхность.
Шаровой поясъ и сегментную поверхность можно разсмат-
ривать, какъ поверхности вращенія: въ то время, какъ по-
луокрожпость МАВЕ, вращаясь вокругъ діаметра 3/2/, опи-
сываетъ шаровую поверхность, часть ея АВ опишетъ поясъ,
.а часть МА—сегментную поверхность.
446.	Лемма. Боковая поверхность каждаго изъ трехъ
тѣлъ: конуса, усѣченнаго конуса и цилиндра равна произ-
веденію высоты тѣла на длину окружности, у которой ра-
діусъ есть перпендикуляръ, возстановленный изъ средины об-
разующей до пересѣченія съ осью.
1°. Пусть конусъ образуется вращеніемъ тр.-ка АВС
вокругъ катета АС. Если В есть средина
-образующей АВ, то (422):
Боков. іюв. конуса = 2~ВС.АВ [1]
Проведя ВЕ АВ, получимъ два по-
добныхъ тр.-ка АВС и АВЕ (они прямо-
угольные и имѣютъ‘общій )голъ Л): изъ
ихъ подобія выводимъ:
ВС:ЕВ = АС:АВ;
откуда:	ВС. АВ — ЕВ . А С
Теперь равенство [1] можно написать
такъ:
Боков. нов. конуса = 2~ЕВ . А С. Что
А
Е'
Черт. 338
и треб. доказ.
— 280 —
2°. Пусть усѣченный конусъ производится вращеніемъ тра-
пеціи АВСВ вокругъ стороны АВ. Про-
х н	ведя среднюю линію ЕЕ, будемъ имѣть
\	(425, 2Л):
______\	Боков. ков. >с. конуса = 2^ЕЕ. ВС [2]
7\	Приведемъ	ЕС _}_ВС н	ВП\\АВ;	тогда
п /,	\р получимъ два подобныхъ тр.-ка ЕЕС и
& и ' ВСИ (стороны одного перпендикулярны
I	къ сторонамъ	другого);	изъ	ихъ	подобія
Черт. 339	ВЫВОДИМЪ:
ЕЕЕВП^ЕС-.ВС
Откуда:	ЕЕ.ВС= ВІ1.ЕС ~ АВ.ЕС
Теперь равенство [2] можно написать такъ:
Бок. пов. ус. кон.= ЕС .АВ. Что и треб. доказ.
3°. Теорема остается вѣрной и въ примѣненіи къ цилиндру
•такъ какъ окружность, о которой говорится въ теоремѣ, равна
окружности основанія цилиндра.
449. Опредѣленіе. За величину поверхности, образуемой
вращеніемъ какой-нибудь части ВЕ полуок 
ружности АСЕ вокругъ діаметра АЕ, прини-
маютъ предѣлъ, кь которому стремится по-
верхность, образуемая вращеніемъ вокругъ того
же діаметра правильной вписанной ломаной
линіи ВСВЕ, когда число ея сторонъ неогра-
ниченно удваивается.
Это опредѣленіе распространяется и на ша-
Черт. 340 ровую поверхность; въ этомъ случаѣ правильная
ломаная линія вписывается въ полукружность.
448.	Теорема. Поверхность шаровою пояса (и сег-
ментная поверхность) равна произведенію окружности боль-
шого круга на высоту.
Пусть въ дугу АЕ, производящую поверхность пояса,
Ьписана правильная ломаная линія А СВЕЕ съ произвольнымъ-
числомъ сторонъ.
— 281 —
Поверхность, образуемая вращеніемъ этой ломаной, со-
стоитъ изъ частей, образуемыхъ сторонами
АС, СВ, ВЕ.... Этя отдѣльныя поверхно-
сти представляютъ собою боковыя поверхности
или копуса (отъ вращенія АС), пли усѣ-
ченнаго конуса (отъ вращенія СВ. ЕЕ...).
или цилиндра (отъ вращенія ВЕ, если
ВЕ\\АВ). Поэтому мы можемъ примѣнить
къ нимъ лемму предыдущаго §. При эгомъ
замѣтимъ, что перпендикуляры, возстанов-
ленные изъ срединъ образующихъ до пере-
сѣченія съ осью, равны апоѳемѣ правильной
вписанной ломаной. Обозначивъ ее черезъ а
ііонерхи. А С~ 2~а . Ас
Черт. 341
получимъ:
повсрхп. СВ = 2т.а . ССІ
повсрхп, ВЕ~2тш . сіе
Сложивъ эти равенства почленно, пайдемъ:
повсрхн. АСВЕГ~2т,а. А{‘
При неограниченномъ удвоеніи числа сторонъ вписанной ло-
маной апоѳема а стремится къ предѣлу, равному радіусу піара-
В, а прямая АС остается безъ измѣненія; слѣд.:
преі. новерхи. АСВЕЕ^=2ъ11. А/
Но предалъ поверхности АСВЕЕ есть то, что принимаютъ
за величину поверхности шарового пояса (пли сегментной
поверхности), а прямая Л/' есть высота пояса: поэтому:
повсрхп. пояса — 2т^Ті,Н
Замѣчаніе. Доказательство нисколько не измѣнится, если
предположимъ, что ломаная линія вписана не въ дугу АЕ,
образующую частный случай пояса (сегментную поверхность),
а въ какую угодно дугу. напр. въ СЕ.
449.	Теорема. ^Іовсрхносгпъ мара равна -произведенію
окружности большою круга на діаметръ.
Или: поверхность шара })авна учетверенной, площади
большого круга.
— 282 —
Поверхность шара, производимую вращеніемъ полуокруж-
ности АВВ (черт. 341), можно разсматривать, какъ сумму
поверхностей, образуемыхъ вращеніемъ дугъ АВ и ВВ.
Поэтому, согласно предыдущей теоремѣ, можемъ писать:
пои. іпдра — 2т.В. ЛИ	2т: ВлІВ = ЪъВ (ЛИ 4"НВ) =
>кВЛВ~ АкВ2
450.	Слѣдствіе. Поверхности шаровъ относятся, какъ
квадраты радіусовъ или діаметровъ, потому что. обозначая
черезъ 11 и Вх радіусы, а черезъ В и X поверхности двухъ
шаровъ, будемъ имѣть:
X: X = Аг.В2: 4^Д2= Д : Д2 = (2 Д2: (2 Д)2
451.	Замѣчаніе. Если бы, вмѣсто того, чтобы въ дугу
^^(черт. 341) вписывать правильную ломаную линію, мы опи-
сали около пея правильную ломаную, то совершенно такъ же
доказали бы, что предѣлъ поверхности, образуемой этой лома-
ной, равенъ ЧъВІІ. Такимъ образомъ, поверхность шарового
пояса (сегментной поверхности и цѣлаго шара) можно разсмат-
ривать, какъ общій, предѣлъ поверхностей, образуемыхъ враще-
ніемъ правильныхъ ломаныхъ линій, какъ внисапиныхъ, такъ
и описанныхъ.
Объемъ шара н его частей.
45®. Опредѣленія. Тѣло, получаемое отъ вращенія круго-
вого сектора СОВ вокругъ діаметра ЛВ, не пересѣкающаго его
в
Черт. 343
поверхности, наз. шаровымъ секторомъ;
это тѣло ограничено боковыми поверх-
ностями двухъ конусовъ и поверхностью
шарового пояса; послѣдняя поверхность
\ наз. основаніемъ шарового сектора. Въ
' частномъ случаѣ одинъ изъ радіусовъ
: кругового сектора можетъ совпадать съ
осью вращенія; напр.. секторъ ЛОС,
вращаясь вокругъ ЛО, производитъ ша-
ровой секторъ ОСЛС\, ограниченный
боковою поверхностью конуса и сег-
ментною поверхностью.
Часть шара, заключенная между параллельными плоскос-
тями Е7І! и ВВ}, наз. шаровымъ слоемъ. Круги параллель-
нихъ сѣченій суть основанія слоя, а разстояніе е/ между
ними—его высота.
Часть шара ВВ\В, отсѣкаемая какою-нибудь плоскостью
ВЕг, наз. шаровымъ сегментомъ. Кругъ сѣченія есть основаніе
сегмента, а отрѣзокъ В/ радіуса, перпендикулярнаго къ ос-
нованію, остъ высота сегмента. Шаровой сегментъ представ-
ляетъ частный случай шарового слоя, а именно: если одна
изъ параллельныхъ плоскостей сдѣлается касательною къ шару,
то слой обратится въ шаровой сегментъ.
Шаровой слой и сегментъ можно разсматривать, какъ
тѣла вращенія: когда полукругъ АВВ (черт. 343) произво-
дитъ своимъ вращеніемъ шаръ, часть его Ее/В производитъ
с юй. а часть /ЕВ—шаровой сегментъ.
453. Лемма. Если тр.-къ АВС вращается вокругъ оси
ху, которая лежитъ въ плоскости тр.-ка, проходитъ чрезъ
его вершину А, но не пересѣкаетъ его гговерх- х
иости, гно объемъ тѣла, получаемаго при этомъ
вращеніи, равенъ произведеніи) поверхност/и,
образуемой противоположною стороною ВС,
на одну третг, высотгя 1і, опущенной эту Л
сторону.
При доказательствѣ разсмотримъ три случая
1°. Осъ совпадаетъ сгпороною АВ. Въ этомъ
случаѣ искомый объемъ равенъ суммѣ объемовъ
двухъ конусовъ, получаемыхъ вращеніемъ прямо-
угольныхъ тр.-ковъ ВО!) н ВС А. Первый объемъ равенъ
’/а ъСВг.ВВ, а второй—^т.СВ',ВА; поэтому:	,г
Об. АВС— Лт.СЩІ)В+І>А)= ' -ВС.ВС.ВА
Произведеніе ВС.ВА равно ВС.Іі, такъ какъ
каждое изъ этихъ произведеній выражаетъ двой-
ную площадь тр.-ка АВС; поэтому:
об. авс= ±т.і)с.ваі’
Но произведеніе кВС.ВС равно боковой по-
верхности конуса ВВС; значить
Об. ЛВС=(ио». ВС).'Л>
У
Черт. 345
— 284 --
2°. Осъ не совпадаетъ съ АВ и не параллельна ВС.
ѵ	Въ этомъ случаѣ искомый объемъ равенъ
разности объемовъ, производимыхъ вращеніемъ
' В	тр.-ковъ АМС и АМВ. По доказанному въ
/\	первомъ случаѣ объемъ АМС~ уз4(пов. МС).
/ \ а объемъ АМВ — 1 ДА (нов. АГВ)‘, слѣд.:
/	Об. Л7?С=у Л (пов. МС—
—нов. МВ) — 1 к (нов. ВС)
3°. Осъ параллельна сторонѣ ВС. (черт. 347).
У	Тогда искомый объемъ рйвенъ объему ВЕВ С безъ
Черт. 346	объема АЕВ и безъ объема АСВ-, первый изъ
нихъ равенъ тсТЭС2. ЕВ, второй—^/^ЕВ^.ЕА и третій—
х/^ВСг.АВ. Принявъ теперь во вниманіе, что ЕВ = ВС.
Черт. 347
получимъ:
Объемъ АВС=г.В(У(ЕІ)~ * ЯЛ)=|ЛР)
— т.ВСЧЕВ— ‘ ЕП) = т.І)Сг‘. ~ЕБ
Произведеніе Ч-ВС.ЕВ выражаетъ боковую
поверхность цилиндра, производимую стороною
ВО; поэтому:
Об. АВС—(пт. ВСУ^ЕС—^оо- ВО}.\іі
454. Теорема. Объемъ шарового сектора
равенъ произведенію поверхности его основанія на третъ,
радіуса.
Пусть шаровой секторъ производится вращеніемъ вокругъ
діаметра ЕЕ (черт. 348) сектора АОВ. Поведемъ разсуж-
деніе въ слѣдующей послѣдовательности.
1°. Впишемъ въ дугу АВ правильную ломаную линію
АВСВ съ произвольнымъ числомъ сторонъ и затѣмъ опи-
шемъ около нея соотвѣтствующую ломаную А^В^В^ Мно-
гоугольные секторы ОАВСВ и ОА^С^ произведутъ при
вращеніи нѣкоторыя тѣла, объемы которыхъ обозначимъ: пер-
ваго черезъ Ѵ\, а второго черезъ и2. Объемъ уг есть
сумма объемовъ, получаемыхъ вращеніемъ тр.-ковъ ОАВ,
ОВС, ОВВ вокругъ оси ЕЕ\ объемъ Г2 есть сумма объе-
 - 285 —
мовъ. получаемыхъ вращеніемъ вокругъ той же оси тр.-ковъ
ОА^В^ ОВіС^. ОС^В^ Примѣнимъ къ
этимъ объемамъ лемму предыдущаго §, при-
чемъ замѣтимъ, что высоты первыхъ тр.-ковъ
равны апоѳемѣ а вписанной ломаной, а
высоты вторыхъ тр.-ковъ равны радіусу В
.шара. Согласно этой леммѣ будемъ имѣть:
Т/’1=(пов. АВ) ^-"І-пов.(7^С)-^-[-(иов. СВ)
=0юв. авсв) "
у1=(ков.лІд)д-|-(по1.. дед-з+О'ов-СД) з У -

Черт. 348.
2°. Вообразимъ теперь, что число сторонъ обѣихъ лома-
маныхъ линій неограниченно удваивается Тогда поверхности
АВСВ и	будутъ стремиться къ общему предѣлу,
именно къ поверхности шарового пояса АВ. а апоѳема а
будетъ имѣть предѣломъ радіусъ 7?; слѣд.:
пред,	^—(поп.АВ)^
3“. Теперь докажемъ, что общій предѣлъ объемовъ и
V* есть объемъ V шарового сектора ОАВ.— Очевидно, что
Ѵ> и	значитъ, каждая изъ разностей V—Ѵі и
Г*— V меньше разности У,— Такъ какъ, по доказанному,
объемы К, и стремятся къ общему предѣлу, то разность
Г2— стремится къ нулю; слѣд., разности V — и Г4— Г<
и подавно стремятся къ нулю; а это значитъ, что Ѵ=пред.
Ѵ\~пре<), Г2 .Но было доказано, что пред. уі=(пов. АВ)~;
значитъ:
Г—-(ков. А В)Л
Замѣчаніе. Теорема и ея доказательство не зависятъ оть
того, будетъ ли одинъ ивъ радіусовъ кругового ерктора сов-
ладать съ осью вращенія, или пѣтъ.
— 286 —
455, Теорема. Объемъ шара равняется произведенію его
поверхности на третъ радіуса.

Т)
Черт. 349
Разбивъ полукругъ АВСВ, произво-
дящій шаръ, на какіе-нибудь секторы А ОВ,
ВОС, СОВ, мы замѣтимъ, что объемъ
шара можно разсматривать, какъ сумму
объемовъ этихъ секторовъ. Такъ какъ,
согласно предыдущей теоремѣ:
Объемъ ЛОЛ = (пов. АВ) 1/3 В
Объемъ ВОС= (пов. ВС) В
Объемъ СОВ~(\шѵ. СВ) В
то объемъ шара = (пов. АВ-}- пов. 7?С*-!-пов. СВ) ^В —
= (нов. АВСВ) В
456. Слѣдствіе. Обозначимъ высоту шарового пояса пли сег-
мента черезъ II, а радіусъ шара черезъ В\ тогда поверхность
пояса или сегмента выразится, какъ мы видили (448) формулой
ЪъВН, а поверхность шара (449) формулой 4ітІ?,2: поэтому:
Об. шар. сектора = с2пВН. }І2В = іІ3г.ВЧІ
Об. шара “ 4т7Л	В — Э/Зт: Ръ
Отсюда видно, что объемы шаровъ относятся, какъ кубы
радіусовъ или діаметровъ.
459. Теорема. Объемъ шаровою сегмента равенъ объему гѵгшімдра,
у котораго радіусъ основанія есть высота сегмента, а высота равна ра-
діусу гиара. уменъгаенному на трепа» высоты сегмента,
т. с. ’ V—-гсЯ2(Ы-і,3Я)
гдѣ Я есть высота сегмента, а Я радіі съ піара.
Объемъ сегмента АВВ, найдется, если изъ
объема шарового сектора ОВАВ, вычтемъ объ-
емъ конуса Орвѵ Первый изъ нихъ равенъ
й/з^дая, а второй V{т.СВ^.СО. Такъ какъ ІЯ'
есть средняя иропорціапалыіая между АС и СО
то СВі= 1І(2В~П)- поэтому СВі.СО.—Н(2іі—
Я)(Я—Я)~2Я4Я ЯЯ2-27?Я-2+ЯЗ=2Я2Я-
ЗЯЯ2ФЯЗ; слѣд.:
1	о
Об. АВВ,—об. ОЛЛ^-об. ОВВ1—--ІИІІ-
^г.сві. со^г.в^н—т.вніАт.іші-^ и*=
э	а о	о
г.Яі(Я-^Я)
— 287 —
Теорема. Объемъ шарового слоя равенъ объему шара, имѣю-
щаго діаметромъ высоту слоя, сложенному съ полусуммою объемовъ двухъ
цилиндровъ, у г;оторыхъ высота равна высотѣ слоя, а основанія: у одного
нижнее, у другое, верхнее основаніе слоя.
т. с.	Г—’
гдѣ Н есть высота слоя, а гх л г2 радіусы основаніи слоя.
Предварительно найдемъ объемъ, получае-
мый вращеніемъ вокругъ діаметра ЛЕ круго-
вого сегмента ВС (покрытаго на чертежѣ штри-
хами). Этотъ объемъ есть разность между объе-
момъ шарового сектора ОВС и объемомъ тѣла,
получаемаго вращеніемъ тр.-ка ОВС. Первый
равенъ 2/3ітІ?2Я, а второй будетъ
(нов. ВС) }-0Е—(:2г.0Е.Н)\ ОЕ—ІТ.ОГЛ.П
о	•>	•>
Слѣд., объемъ отъ вращенія сегмента выразит-	Чэрт. 351
ея такъ:
Щ 1С-0Еі)=Іт.Л.СЛ2—=-1[\вС*=±гЛІС*. Я
о	3	3 4о
Чтобы получить объемъ слоя, достаточно къ найденному объему приложить-
объемъ усѣченнаго конуса ВВ^С; поэтому объемъ слоя будетъ:
^~ВС*	С7<2 ^В&-\- Са. ВЪ)	- 7/(Я С2-|-2 С«2-|-2 ВѴ>- 4-2 Са. ВЪ)
Проведя ВВ ‘ Са, будемъ имѣть:
ВСі=ВВ^\-СП^=ІГі-\-{С.а—ВЪА—П*+ Са*-\-В& 'ІСа.ВЪ
Подставивъ это выраженіе въ предыдущую формулу, найдемъ:
об. с.іоя=іт:Я(/Г2-!-3 С«24-зт?62)=:^ЯЗ-]-1^С«24-Віз Н
или, обозначая Са черезъ т15 а ВЪ черезъ г2:
об. СЛ0Я=^7ѵВ3-)-^г.(.-12-Н 2“)77
Положивъ въ этой формулѣ т2~0, получимъ новое выраженіе для объема ша-
рового сегмента:
об. согм.^-У/з-і-^ттг^Я
6	‘2
— 288 --
ЗАДАЧИ.
353.	Объемъ цилиндра, у котораго высота вдвое болѣе діаметра, равенъ
1 куб. метру. Вычислить его высоту.
354.	Діаметръ основанія цилиндра =16 сапт., а полная поверхность его
содержитъ 1546 квадр сант; вычислить высоту этого цилиндра.
355.	Найти вѣсъ желѣзной цилиндрической трубки, которой внутренній
діаметръ =17 сант., внѣшній діаметръ =18 сапт., а длина 74 сапт.; удѣль-
ный вѣсъ желѣза 7,7.
356.	Въ сосудъ, имѣющій форму конуса, обращеннаго вершиною внизъ,
вливаютъ 345 граммовъ ртути. Зная, что уголъ при вершинѣ конуса равенъ
600, а уд. вѣсъ ртути 13.596, вычислить высоту, до которой налита въ сосу-
дѣ ртуть.
357.	Вычислить боковую поверхность и объемъ усѣченнаго конуса, у ко-
тораго радіусы основаніи суть 27 и 18 сапт., а образующая 21 сапт.
358.	На какомъ разстояніи отъ центра піара, котораго радіусъ равенъ
2,425 метра, слѣдуетъ провести сѣкущую плоскость, чтобы отношеніе по-
верхности меньшаго сегмента къ боковой поверхности конуса, имѣющаго
общее съ сегментомъ основаніе, а вершину въ центрѣ шара, равнялось 1:4.
359.	Найти объемъ тѣла, происходящаго отъ вращенія прав. 6-уго.тьии-
ка со стороною а вокругъ одной изъ своихъ сторонъ.
360.	Вычислить радіусъ шара, описаннаго около куба, котораго ребро
равно 1 метру.
361.	Желѣзный пустой шарь, котораго внѣшній радіусъ =0,154 метра,
плаваетъ въ водѣ, погружаясь вь нее па половину. Вычислить толщину это-
го шара, зная, что уд. вѣсь желѣза равенъ 7,7.
362.	Вычислить объемъ тѣла, пропехо (яіцаі о отъ вращенія прав. тре-
угольника со стороною а вокругъ оси, проходящей черезъ -его вершину и
параллельной противоположной сторонѣ.
363.	Данъ равносторонній А ЛВС со стороною с: па ВС строятъ
квадратъ ВОВЕ, располагая его въ противоположную сторону отъ треу-
гольника. Вычислить объемъ тѣла, происходящаго отъ вращенія 5-у голышка
АВЕВС вокругъ стороны АВ.
364.	Данъ квадратъ АВСВ со стороною а. Черезъ вершину Л проводятъ
прямую АВ, перпендикулярную къ діагонали ЛС, и вращаютъ квадратъ во-
кругъ АВ. Вычислить поверхность, образуемую периметромъ квадрата, н
объемъ, образуемый площадью квадрата.
365.	Данъ прав. 6-угольппкъ АВСВЕЕ со стороною а. Черезъ вершину
Л проводятъ прямую АВ, перпендикулярную къ радіусу ОЛ, и вращаютъ
6-уголышкъ вокругъ АВ. Вычислить поверхность, образуемую периметромъ»
и объемъ, образуемый площадью нрав. 6-у голышка.
366.	Въ шарѣ, котораго радіусъ равенъ 2, просверлено цилиндрическое
отверстіе вдоль его діаметра. Вычислить объемъ оставшейся часі и, если ра-
діусъ пилипдр. отверстія равенъ 1.
— 289 —
ПРИЛОЖЕНІЕ
Главнѣйшіе методы рѣшенія геометрическихъ задачъ на
построеніе.
1. Методъ геометрическихъ мѣстъ, извѣстный еще ео временъ Пла-
тона (IV вѣка до Р. Хр.), состоитъ въ слѣдующемъ. Положимъ, что рѣшеніе
предложенной задачи сводится къ нахожденію нѣкоторой точки, которая
должна удовлетворять извѣстнымъ условіямъ. Отбросимъ изъ этихъ условій
какое-нибудь одно; тогда задача сдѣлается неопредѣленною, т. с. ей могутъ
удовлетворять безчисленное множество точекъ. Эти точки составятъ нѣко-
торое геометрическое мѣсто. Построимъ его, сели это окажется возможнымъ.
Затѣмъ примемъ во вниманіе отбровіепное нами условіе и откинемъ какое-
нибудь другое; тогда задача будетъ снова удовлетворяться безсчисленпымъ
множествомъ точекъ, которыя составятъ новое геометрическое мѣсто. По-
строимъ его, если это возможно. Искомая точка, удовлетворяя всѣмъ
условіямъ, должна лежать на обоихъ геометрическихъ мѣстахъ, т. е. она
должна находиться въ ихъ пересѣченіи. Задача окажется возможной или не-
возможной, смотря по тому, пересѣкаются пли пѣть найденныя геометр. мѣ-
ста; и задача будетъ имѣть столько рѣшеній, сколько окажется точекъ пе-
ресѣченія.
Приведемъ на этотъ методъ одинъ примѣръ, который вмѣстѣ съ тѣмъ
покажетъ намъ, какъ иногда приходится вводить въ чертежъ вспомогатель-
ныя линіи съ цѣлью принять во вниманіе всѣ данныя условія задачи.
Задача. Построитъ треугольникъ по основанію а, углу пргі вершинѣ
А и суммѣ 8 боковыхъ сторонъ.
Пусть АВС будетъ искомый Д. Чтобы
принять во вниманіе данную сумму боко-
выхъ сторонъ, продолжили. ВА и отло-
жимъ ВМ~х. Проведя МС, получимъ вспо-
могательный тр.-къ ВМС. Если мы по-
строимъ этотъ тр.-къ, то затѣмъ легко
построить и тр.-къ АВС. Построеніе тр.-
ка ВМС сводится къ нахожденію точки
М. Замѣтивъ, что тр.-къ АМС равнобед-
ренный (АМ==АС~) и слѣд.,
/.Л), мы видимъ, что точка
ЗГдолжпа удовлетворять двумъ условіямъ:
I) она удалена отъ В на разстояніе в, во
2) изъ нея данная конечная прямая ВС
Черт. 352
19
видна подъ угломъ, равнымъ уа А. Отбросивъ второе условіе, мы получимъ
А. П. КИСЕЛЕВЪ.
— 290 —
безсчисленноо множество точекъ ЛГ, лежащихъ на окружности, описанной
изъ В радіусомъ, равнымъ <-?. Отбросивъ первое условіе, мы получимъ также
бсзсчислсппос множество точекъ М, лежащихъ на дугѣ сегмента, построен-
наго на ВС и вмѣщающаго уголъ, равный І/ІЛ. Такимъ образомъ нахожде-
ніе точки М сводится къ построенію двухъ геометрическихъ мѣстъ, изъ
которыхъ каждое мы построить умѣемъ. Задача окажется невозможною,
если эти геометрическія мѣста не будутъ имѣть общихъ точекъ; задача
будетъ имѣть одно или два рѣшенія, смотря по тому, касаются ля, или же
пересѣкаются эти мѣста (на пашемъ чертежѣ дуга сегмента пересѣкается
съ окружностью; вслѣдствіе этого получаются два тр.-ка АВС. и АіВС, удо-
влетворяющіе условіямъ задачи).
Иногда задача сводится не къ опредѣленію точки, а къ нахожденію
прямой, удовлетворяющей нѣсколькимъ условіямъ Если отбросимъ одно
изъ нихъ, то получимъ безчисленное множество прямыхъ; при этомъ мо-
жетъ случиться, что эти прямыя опредѣляютъ нѣкоторую линію (напр.,
всѣ будутъ касательными къ нѣкоторой окружности). Отбросивъ другое
условіе и принявъ во вниманіе то, которое было откинуто ранѣе, мы по-
лучимъ снова безчисленное множество прямыхъ, которыя, быть можетъ,
опредѣлятъ нѣкоторую другую линію. Построивъ, если возможно, эти двѣ
линіи, мы затѣмъ легко найдемъ и искомую прямую. Пусть, напр., намъ
предложена задача: провести сѣкущую къ двумъ даннымъ окружностямъ
О и Ог такъ, чтобы части сѣкущей, заключенныя внутри окру-
жностей, равнялись соотвѣтственно даннымъ длинамъ а и а4. Если
возьмемъ только одно условіе, напр., чтобы часть сѣкущей, лежащая вну-
три круга О, равнялась а, то получимъ безчисленное множество сѣкущихъ,
которыя всѣ должны быть одинаково удалены отъ центра этого круга
(такъ какъ равныя хорды одинаково удалены отъ центра). Поэтому, если
въ кругѣ О гдѣ-нибудь построимъ хорду, равную а, и затѣмъ радіусомъ,
равнымъ разстоянію этой хорды отъ центра, опишемъ окружность, кон-
центрическую съ О, то всѣ сѣкущія, о которыхъ идетъ рѣчь, должны ка-
саться этой вспомогательной окружности. Подобнымъ образомъ, принявъ
во вниманіе только второе условіе, мы увидимъ, что искомая сѣкущая дол-
жна касаться второй вспомогательной окружности, концентрической съ Оѵ
Значитъ, вопросъ приводится къ построенію общей касательной къ двумъ
окружностямъ.
Кромѣ тѣхъ геометрическихъ мѣстъ, которыя указаны въ текстѣ этой
книги (§§ 63, 98, 162, 200), полезно замѣтить еще слѣдующія (доказатель-
ство предоставляемъ самимъ учащимся):
1®. Геометрическое мѣсто точекъ, дѣлящихъ въ данномъ отношеніи
отрѣзки параллельныхъ прямыхъ, заключенные между сторонами даннаго
угла, есть прямая, проходящая черезъ вершину угла и какую нибудь одну
изъ этихъ точекъ.
2®. Геометрическое мѣсто точекъ, которыхъ разстоянія отъ сторонъ
даннаго угла находятся въ данномъ отношеніи, состоитъ изъ двухъ пря-
— 291 —
мыхъ, проходящихъ черезъ вершину угла, и изъ которыхъ одна лежитъ
внутри угла, а другая внѣ его.
3°. Геометрическое мѣсто точекъ, дѣлящихъ въ данномъ отношеніи всѣ
равныя хорды данной окружности, есть окружность, концентрическая съ
данною.
4°. Геометрическое мѣсто точекъ, изъ которыхъ касательныя, прове-
денныя къ данной окружности, имѣютъ данную длину, есть окружность,
концентрическая съ данною.
50. Геометрическое мѣсто точекъ, квадраты разстояній которыхъ отъ
двухъ данныхъ точекъ А и В имѣютъ постоянную сумму, есть окруж-
ность, которой центръ лежитъ въ срединѣ прямой АВ (доказательство осно-
вывается на теоремѣ § 212).
6«. Геометрическое мѣсто точекъ, квадраты разстояній которыхъ отъ
двухъ данныхъ точекъ А и В имѣютъ постоянную разность, есть прямая,
перпендикулярная къ прямой АВ.
70. Геометрическое мѣсто точекъ, сумма разстояній которыхъ отъ сто-
ронъ даннаго угла постоянна, есть лежащій внутри угла отрѣзокъ прямой,
отсѣкающей отъ угла равнобедренный тр.-къ. Продолженія этого отрѣзка (въ
обѣ стороны) представляютъ геомеср. мѣсто точекъ, разность разстояній
которыхъ отъ сторонъ угла постоянна.
8°. Геометрическое мѣсто точекъ, дѣлящихъ въ данномъ отношеніи хор-
ды, проведенныя изъ одной точки А данной окружности, есть окружность,
пастельная къ данной въ точкѣ А.
Послѣднее геометрическое мѣсто составляетъ частный случай слѣдую-
щею болѣе обищю:
Черт. 353
9<». Если изъ данной точки О (черт 353) къ различнымъ точкамъ А,
Аи Лп... какой-нибудь фигуры В1 проведемъ прямыя ОА, ОА1г ОАи.... и
на каждой изъ нихъ отложимъ части Оа, Оа1г Оа11г,.. такія, что
Оа: ОЛ—Оаг: ОА^Оац: ОАп=......
19*
— 292 —
то геометрическое мѣсто точекъ а, есть фигура /, подобная фигурѣ
Е и одинаково съ ней расположенная относительно точки О.
Такимъ образомъ, если фигура Р есть прямая, то и { есть прямая
(параллельная^); если есть многоугольникъ, то и/'есть многоугольникъ,
подобный 1Г и одинаково съ нимъ расположенный; если Е есть окружность
то и /‘ есть окружность.
Когда пропорціональныя части Оа, Оа^, Оагі... откладываются на про-
долженіяхъ линій ОА, ОА^.. (за точку (9), то получается тоже подобная
фигура, по расположенная обратно относительно точки О.
Замѣтимъ, что точка О въ этихъ случаяхъ наз. центромъ подобія фи-
гуръ Р и Д точки А и а, Аг и аг и т. д ііаз. сходственными точками, а
прямыя Оа, ОА1...—лучами подобія.
Методъ подобія. Онъ состоитъ въ томъ, что, пользуясь нѣкото-
рыми данными задачи, строятъ сначала фигуру, подобную искомой, а за-
тѣмъ переходятъ къ послѣдней. Этотъ методъ особенно удобенъ тогда,
когда только одна данная величина есть длина, а всѣ прочія суть или уг-
лы, или отношенія линій; таковы, напр., задачи:
Построитъ треугольникъ по данному углу, сторонѣ гі отношенію
овухь другихъ сторонъ, или по двумъ угламъ гь длинѣ нѣкоторой прямой
(высотѣ, медіанѣ, биссектриссѣ п т. д.);
Построитъ квадратъ по данной суммѣ или разности между діаго-
налью и стороною-, и т. п.
Въ этихъ задачахъ положеніе искомой фигуры остается произволь-
нымъ; по во многихъ вопросахъ требуется построить фигуру, которой по-
ложеніе относительно данныхъ точекъ или линій вполнѣ опредѣлено. При
этомъ можетъ случиться, что, отрѣшившись отъ какого-нибудь одного изъ
условій положенія и оставивъ всѣ остальныя, мы получимъ безчисленппое
множество фигуръ, подобныхъ искомой Въ такомъ случаѣ метолъ подобія
можетъ быть употребленъ съ пользою. Приведемъ примѣръ.
Черт. 354
Задача. Въ данный уголъ АВС вписать окружность, которая про-
ходила бы черезъ данную точку М Ччерт. 354).
— 293 —
Отбросимъ на время требованіе, чтобы окружность проходила черезъ
точку М. Тогда вопросу будетъ удовлетворять безчисленное множество ок-
ружностей, которыхъ центры лежатъна биссектриссѣ ВВ. Построимъ одну изъ
такихъ окружностей, напр. ту, которой центръ есть о. Возьмемъ па ней точ-
ку т, сходственную точкѣ 71/, т. с. лежащую па лміѣ подобія ЗІВ, и про-
ведемъ радіусъ то. Если теперь построимъ МО |] то, то точка О бул&гь
центромъ искомаго круга. Дѣйствительно, проведя къ сторонѣ АВ перпен-
дикуляры ОК и оп, мы получимъ подобные тр -ки МВО и тВо, КВ О и
пВо, изъ которыхъ будемъ имѣть:
МО:то=ВО :Во
КО:по=ВО:Во
Откуда МО:то=КО:по
Но то=по; слѣд. и МО—КО, т.-е. окружность, описанная изъ центра О
радіусомъ ОМ, будетъ касаться стороны ЛВ; а такъ какъ ся центръ ле-
житъ на биссектриссѣ угла, то опа каснется и стороны ВС.
Если за сходственную точку возмемъ другую точку тх пересѣченія луча
ВМ съ окружностью о, то найдемъ драгой центръ искомаго круга.
Слѣд,, задача допускаетъ два рѣшенія.
3. Методъ параллельнаго перенесенія. Весьма часто бываетъ полезно
перемѣстить нѣкоторыя части данной или искомой фигуры въ другое по-
ложеніе, при которомъ легче обраружпть зависимость между данными эле-
ментами и искомыми. Существуютъ различные пріемы такого перемѣщенія.
Разсмотримъ сначала параллельное перенесеніе.
Задача. Построитъ четыреугольникъ АВСВ, зная всѣ его стороны и
прямую ЕЕ, соединяющую средины ігротмвоггомжнъехъ сторонъ АВ и СВ.
Чтобы сблизить между собою данныя
линіи, перенесемъ параллельно самимъ
себѣ стороны ЛВ п ВС въ положенія
ЕВХ и ЕСХ. Тогда прямая ВВХ будетъ
равна и параллельна АЕ, а прямая ССХ
равна и параллельна ЕВ; по такъ какъ
АЕ=ЕВ, то ВВ^СС\ л В1\ || ССХ.
Вслѣдствіе этого тр.-ки ВВі?' и СС\Е
будутъ равны (такъ какъ у нихъ:
ВВ^СС, ВЕХ—СЕ и ^_ВХВЕ~
ЕССХУ, значитъ, аВхЕ1)=/_ СЕСХ,
и потому линія ВХЕСХ должна быть
прямая, т.-е. фигура ЕВХЕСХ окажется треугольникомъ. Въ этомъ тр.-кѣ
извѣстны двѣ стороны (ЕВХ=АВ н 7'?С,=ВС) и медіана ЕЕ, проведенная
къ третьей ^сторонѣ. Но этимъ даннымъ легко построить тр.-къ (если про-
должимъ медіану ЕЕ за точку Е на длину, равную ей, и полученную точку
соединимъ съ Вх и С], то получимъ параллелограммъ, у котораго извѣстны
стороны и одна діагональ).
— 294 —
Найдя (7і, строимъ затѣмъ тр.-ки В^ВВ м С\СЕ, а затѣмъ и
весь четыреугольникъ АВСВ.
Замѣтимъ, что иногда бываетъ полезно перенести параллельно данному
направленію цѣлую фигуру, напр.: окружность. Въ атомъ случаѣ всѣ точки
перемѣщаемой фигуры описываютъ параллельныя и равныя прямыя (см.,
напр., задачу 383).
•Я. Методъ вращенія вокругъ точки. д.ш уясненія этого особеннаго
вида перенесенія приведемъ слѣдующій примѣръ:
Задача. Даны по положенію точка С ѵ двѣ неопредѣленныя прямыя
а и Ъ. Построитъ треугольникъ АВС, котораго одна вершина была бы въ
С, а двѣ другія лежали бы на прямыхъ а и Ъ, и который кромѣ тою былъ бы
подобенъ данному треугольнику (не помѣщенному на чертежѣ).
Пусть задача рѣшена. Замѣтивъ, что углы искомаго тр.-ка даны, обоз-
Черт. 356
ряющихъ пропорціи:
начпмъ одинъ изъ нихъ, который нахо-
дится при точкѣ (7, черезъ со. Повер-
немъ всю фигуру вокругъ точки С въ
направленіи, указанномъ стрѣлкою, на
уголъ ю п найдемъ положеніе, которое
займетъ послѣ вращенія прямая а. Для
этого достаточно опустить на а пер-
пендику.іяръ СВ, затѣмъ повернуть
его на у голъ со въ положеніи СВ1 и
провести черезъ В{ прямую а1г перпсп-
дикулярн\ю къ С7>і Прямая «і и бу-
детъ то положеніе, которое займетъ
послѣ вращенія прямая а. Такъ какъ
при вращеніи всѣ части фигуры по-
вертываются на одинъ и тотъ жоуголъ,
то СЛ, послѣ вращенія, пойдетъ по СВ; вслѣдствіе этого точка А упадетъ
въ въ точку пересѣченія СВ съ а(. Такъ какъ отношеніе СЯ къ СВ,
пли все равно, отношеніе Сл^ къ СВ, дано (пусть это будетъ т : п), то теперь
вопросъ сведенъ къ тому, чтобы черезъ точку Спровести таку ю прямую САЪ
которая пересѣкалась бы съ прямыми Ь и «і въ точкахъ В и Л1, удовлетво-
СА[: СВ=.»г : н
Чтобы провести такую прямую, достаточно раздѣлить СВг па части въ
отношеніи т : п и черезъ точку дѣленіи провести прлмхіо параллельную аь*
пересѣченіе этой прямой съ Ь опредѣлитъ точку В.
3. Методъ вращенія вокругъ прямой (или методъ симметрія). Иногда
пріемъ построенія легко обнаруживается, если перегнемъ часть чертежа во-
кругъ нѣкоторой прямой такъ, чтобы эта часть заняла симметричное поло-
женіе по другую сторону отъ этой прямой. Приведемъ примѣръ.
— 295 —
Задача. На неопредѣленной прямой АВ найлпи такую точку х, чтобы
сумма ея разстояній отъ данныхъ
точекъ ІИ и И была наименьшая.
Если, перегнувъ чертежъ вокругъ
т17?, приведемъ точк^ 3/ въ симмет-
ричное относительно АВ положеніе
Л/,, то разстоянія точки М отъ какой
угодно точки прямой АВ сдѣлается
равнымъ разстоянію точки 2І1І отъ
той же точки прямой АВ. Поэтому
суммы Мх+хИ, Мхі+х^.... равны
соотвѣтственно суммамъ іИ^+л:^
З^аі+а;^7....; по изъ послѣднихъ суммъ
наименьшая будетъ та, при которой
линія МххИокажется прямою. Отсюда становится яснымъ пріемъ построенія.
То же самое построеніе рѣшаетъ и другую задачу: на прямойАВ найти
такую точку х, чтобы прямыя хМ и хИ, проведенныя отъ нея къ дан-
нымъ точкамъ М и В, составляли съ АВ равные углы.
О. Методъ обратности. Иногда бываетъ полезно, такъ сказать, пе-
ревернуть задачу, т.-е. данныя условія задачи взять за искомыя и на-
оборотъ. Примѣромъ служитъ слѣдующая задача.
Задача. Въ данный треугольникъ АВС вписать другой треугольникъ,
у котораго стороны были бы параллельны сторонамъ другого даннаго тре-
угольника ЛШР.
Перевернемъ вопросъ: опишемъ около тр.-ка ЛГУР другой тр.-къ А^В^,
у котораго стороны были бы параллельны сторонамъ тр-.ка АВС (что,
конечно, легко выполнить). Тогда мы получимъ фигуру, подобную искомой;
раздѣливъ затѣмъ какую-нибудь сторону тр.-ка АВС на двѣ части, про-
порціаиадьныя отрѣзкамъ сходственной стороны т.-ка АіВгСъ мы получимъ
одну изъ вершинъ искомаго тр.-ка.
Примѣры задачъ, рѣшаемыхъ этими методами.
іо. Методъ геометрическихъ мѣстъ.
367.	Построить четыреугольникъ АВСВ, около котораго можно было
бы описать окружность, зная его стороны АВ и ВС, діагональ АС н уголъ
между діагоналями.
368.	Построить треугольникъ по основанію, углу при вершинѣ и суммѣ
или разности квадратовъ двухъ другихъ сторонъ (напр., основаніе Ъ, уголъ
при вершинѣ А, и сумма квадратовъ боковыхъ сторонъ А:2).
369.	Около равносторонняго треугольника описать квадратъ такъ,
чтобы обѣ фигуры имѣли общую вершину.
— 296 —
370.	Найти точку, изъ которой три отрѣзка данной прямой: ЛВ, ВС
и СВ были бы видны подъ равными углами.
371.	Внутри тр.-ка найти такую точку, которой разстоянія до сторонъ
тр.-ка относились бы между собою, какъ 6:3:2.
372.	Найти точку изъ которой три данные круга были бы видны подъ
равными углами {указаніе: надо сначала найти гсометр. мѣсто точекъ, изъ
которыхъ два данные круга видны подъ равными углами).
373.	Дана окружность и какія-нибудь двѣ прямыя. Найти па окруж-
ности такую точку, чтобы сумма ся разстояній отъ этихъ прямыхъ была
наименьшая.
374.	Превратить данный тр.-къ въ равновеликій другой тр.-къ съ дан-
нымъ основаніемъ и съ даннымъ угломъ при вершинѣ.
375.	Въ данной окружности провести двѣ хорды данной длины такъ,
чтобы онѣ пересѣкались подъ даннымъ у г.юмъ и одна изъ нихъ проходила
черезъ лдниую точку.
2®. Методъ подобія.
376.	Построить тр.-къ по углу при вершинѣ, высотѣ и отношенію от-
рѣзковъ, на которыя основаніе дѣлится высотою.
377.	Вписать квадратъ въ данный тр.-къ, въ данный секторъ, въ дан-
ный сегментъ.
378.	Черезъ данную точку провести прямую такимъ образомъ, чтобы
три данныя прямыя, исходящія изъ одной точки, отсѣкали отъ искомой
прямой отрѣзки, находящіеся въ даномъ отношеніи.
379.	Черезъ данную точку А окружности провести хорду АВ, которая
пересѣкалась бы съ данною хордою ВС въ такой точкѣ Е, чтобы прямыя
ВЕ п ВС находились въ данномъ отношеніи.
380.	Провести внутри тр.-ка прямую, параллельную основанію, такъ,
чтобы эта прямая была средней пропорціональной между отрѣзками одной
боковой стороны.
381.	Построить равнобедренный тр.-къ, зная его боковую сторону и
сумму высоты съ основаніемъ.
382 Па данной прямой найти такую точку, чтобы ся разстоянія отъ
данной точки и другой данной прямой находились въ данномъ отношеніи.
3». 'Методъ параллельна! о перенесенія.
383.	Между двумя данными окружностями, провести прямую данной
длины а параллельно данной прямой МЕ.
(Указаніе: Надо одинъ кругъ приблизить къ другому, перенеся его па-
раллельно прямой МЕ на разстояніе а).
384.	Въ кругѣ даны двѣ хорды АВ и СВ. Пайтп на окружности та-
кую точку х, чтобы прямый хА и хВ отсѣкали отъ хорды СВ отрѣзокъ,
равный данной длинѣ (мет. парал. пересѣченія и геом. мѣстъ).
— 297 —
385.	Въ данномъ тр.-кѣ ЛБС найти такія точки: х на сторонѣ АВ и
у на сторонѣ ВС, чтобы прямая ху была данной длины ц кромѣ того от-
ношеніе Ах: Су было бы данное (парал. перенесеніе и методъ подобія).
386.	Постропть трапецію по одному ея углу, двумъ діагоналямъ и
средней линіи.
387.	Построить четыреугольникъ по тремл, сторонамъ «, ь и с и двумъ
угламъ а и и, прилежащимъ къ неизвѣстной сторонѣ.
388.	Къ двумъ даннымъ кругамъ провести общую сѣкущую, парал-
лельную данной прямой такъ, чтобы сумма или разность хордъ, опредѣля-
емыхъ точками перенесенія, была равна данной длинѣ.
389.	Съ корабля видны два маяка, положеніе которыхъ на картѣ из-
вѣстно, подъ даннымъ угломъ. Когда корабль прошелъ извѣстную длину
въ данномъ направленіи, тѣ же самые маяки видны подъ другимъ даннымъ
угломъ. Опредѣлить на картѣ мѣсто корабля (геом. мѣсто и параллельное
перенесеніе).
40. Методъ вращенія вокругъ точки.
390.	Построить тр.къ, подобный данному тр.-ку, такъ, чтобы одна
его вершина лежала въ данной точкѣ А, а двѣ другія вершины находились
бы на данныхъ окружностяхъ О и Ог (одна на О, другая на С^).
391.	Данъ кругъ и внѣ его двѣ» точки А и В; провести къ кругу ка-
сательную такъ, чтобы разстоянія точки А до этой касательной и до пер-
пендикуляра, опущеннаго изъ В на касательную, были въ данномъ отношеніи.
(Указаніе: надо повернуть вокругъ точки А на 90» прямоугольный т.-къ,
у которого гипотенуза есть АВ, а одинъ катетъ—разстояніе точки А до
перпендикуляра, опущеннаго на касательную изъ точки В. Эту же задачу
можно рѣшить при помощи одновременнаго пользованія методомъ подобія
и методомъ геометр мѣстъ).
392.	Построить тр.-къ, котораго стороны были бы проиорціаиальны
числамъ 3, 4 и 5, и котораго вершины лежали бы па трехъ данныхъ па-
раллельныхъ прямыхъ.
5°. Методъ вращенія вокругъ прямой.
393.	Построить по четыремъ сторонамъ четыреугольникъ АВСВ, зная,
что его діагональ АС дѣлитъ уголъ А пополамъ.
394.	Конечная прямая АВ пересѣчена въ точкѣ С прямой М№, найти
на такую точку, изъ которой отрѣзки АС и СВ видны йогъ равными
углами (эту задачу можно также рѣшить методомъ геометр. мѣстъ).
395.	Построить квадратъ, двѣ противоположныя вершины котораго
находились бы па двухъ данныхъ окружностяхъ, а двѣ другія на данной
прямой, расположенной между окружностями.
396.	На прямоугольномъ билліардѣ дано положеніе двухъ шаровъ А и
В. Въ какомъ направленіи надо толкнуть шаръ А, чтобы онъ, отразившись
послѣдовательно отъ всѣхъ четырехъ бортовъ, ударилъ затѣмъ шаръ В.
— 298 —
397.	Данъ уголъ к внутри его точка. Построить тр.-къ наименьшаго
периметра такой, чтобы одна его вершина лежала въ данной точкѣ, а двѣ
другія па сторонахъ угла.
398.	Рѣшить методомъ симметріи задачу, которая выше была рѣшена
методомъ подобія: въ данный уголъ вписать окружность, которая прохо-
дила бы черезъ точку, данную внутри угла.
6°. Методъ обратноети.
399.	Въ даннный секторъ вписать тр.-къ, равный данному тр.-ку.
400.	Построить тр.-къ, равный данному тр.-ку, такъ, чтобы его вер-
шины лежали на трехъ данныхъ прямыхъ, исходящихъ изъ одной точки.
401.	Построить тр.-къ, подобный данному тр.-ку, такъ, чтобы его
вершимы лежали на трехъ данныхъ концетричсскнхъ окружностяхъ.
102.	Въ данный тр.-къ вписать тр.-къ, подобный фугому данному тр.-ку,
такъ, чтобы одна изъ его вершинъ лежала въ точкѣ, данной на основаніи.
.... ----------------------------
ОГЛАВЛЕНІЕ.
Цыфры означаютъ нумера страницъ.
Предисловіе,
Введеніе. Матемаптическія предложенія, 1—Прямая линія, плоскость.
Понятіе о геометріи, 3.
П .1А II П М Е Т РI Я.
КНИГА I. ПРЯМАЯ ЛИНІЯ.
Глава I. Углы. Предварительныя понятія, 8—Свойства прямого >гла.
10. Свойства смежныхъ и вертикальныхъ чгловъ, 13.
Глава II. Треугольники и многоугольники. Понятіе о многоугольникѣ
и треугольникѣ, 18—Свойства равнобедреннаго треугольника, 21,—Приз-
наки равенсіва треугольниковъ, 22.—Соотношеніе между углами и сторо-
нами треугольника, 25.—Сравнительная длина объемлющихъ п обгоняемыхъ
ломаныхъ линій, 28.— Треугольники съ двумя соотвѣтственно равными
сторонами, 31.
Глава III. Перпендикуляры и наклонныя, 32. -- Равенство прямо-
у гольныхъ треугольниковъ,—34.
Глава IV. Свойства перпендикуляра къ срединѣ прямой и биссект-
рисой угла, 35.
Глава V. Основныя задачи на построеніе, 37.
Упражненіи, 43.
Глава VI. Параллельныя прямыя. Основныя теоремы, 44.—Углы съ
соотвѣтственно параллельными или перпендикулярными сторонами, 50.—
Сумма угловъ треугольника и многоугольника, 52.
Глава VII. Параллелограммы и трапеціи. Главнѣйшія свойства па-
раллелограммовъ, 54—Нѣкоторыя теоремы, оспованныя на свойствахъ
параллелограмма, 58.
Упражненія, 61.
— II —
КНИГА II. ОКРУЖНОСТЬ.
Глава I. Форма и положеніе окружности. 64.
Глава И. Равенство и неравенство дугъ, 67.
Глава III. Зависимость между дугами, хордами и разстояніемъ
хордъ отъ центра, 69.
Глава IV. Свойства касательной, 71.—Основныя задачи па проведеніе
касательной, 73.
Глава V. Относительное положеніе окружностей, 76.
Упрам ненія, 80.
Глава Ѵ1. Измѣреніе велечинъ, 83.
Глава VII. Измѣреніе угловъ помощью дугъ, 91.
Глава VIII. Описанные и описанные многоугольники, 101.
Глава IX. Четыре замѣчательныя точки въ треугольникѣ, 105.
Упражненія, 106.
КНИГА III. ПОДОБНЫЯ ФИГУРЫ.
Глава I. Подобіе треугольниковъ и многоугольниковъ, 109.
Глава II. Нѣкоторыя теоремы о пропорціанальныхъ линіяхъ, 119.
Глава III. Числовыя зависимости между элементами треугольника и
нѣкоторыхъ другихъ фигуръ, 126.
Глава IV. Понятіе о приложеніи алгебры къ геометріи, 137.
Упражненія, 142.
Глава V. Правильные многоугольники, 146.
Упражненія, 157.
КНИГА IV. ОПРЕДѢЛЕНІЕ ДЛИНЫ ОКРУЖНОСТИ И ЕЯ ЧАСТЕЙ.
Глава I. Основныя свойства предѣловъ, 158.
Глава 11. Вычисленіе длины окружности, 163.
Упражненія, 174.
— 111 —
КНИГА V. ИЗМѢРЕНІЕ ПЛОЩАДЕЙ.
Глава I. Площади многоугольниковъ. 174.
Глава II. Теорема Пиѳагора и основанныя на ней задачи, 183.
Г лава III. Отношеніе площадей подобныхъ фигуръ, 185.
Глава IV. Площадь круга и его частей, 188.
Глава V. Соотношеніе между сторонами треугольника и радіусами
вписаннаго и описаннаго круговъ, 193.
Ун])ажиеиі,і, 195.
Числовыя задачи на разные отдѣлы планиметріи, 197.
СТЕРЕОМЕТРІЯ.
КНИГА I. ПРЯМЫЯ И ПЛОСКОСТИ.
Глава I. Опредѣленіе положенія плоскости, 199.
Глава II. Перпендикуляръ и наклонныя, 203.
Глава III. Параллельныя прямыя и плоскости. Параллельныя пря-
мыя, 207.—Прямыя, ларл.і іе.іып.ія п іоско"іп, 210. — Параллельныя плос-
кости, 212.
Глава IV. Двугранные углы, 215. — Псрлсіідику.іяркыя плоскости,
219.—Уголъ двххь иеперссѣкаюіцпхся прямыхъ, 220,—Уголъ прямой съ
и кд костью, 221.
Глава V. Многогранные углы, 221—і'двспство гр<ч раипыхъ угловъ, 224.
КНИГА II. МНОГОГРАННИКИ.
Глава I. Свойства параллелопипеда и пирамиды. Опредѣленія, 227.—
Равенство иризмь и пирамидъ, 231—Свошгва граней и діагоналей па-
ра ллолоиппеда,—232. Свойства параллельныхъ сѣченій въ пирамидѣ, 233.
Глава II. Боковая поверхность призмы и параллелопипеда, 235.
Задачи,—237.
Глава III. Объемъ призмы и параллелопинеда. Опредѣленія, 238—
Объемъ лрямсуго іі.наго параллелопипеда, 238. — Объемъ призмы, 243.—
Объемъ пирамиды, 245.—Объемъ усѣченной пирамиды и призмы, 249.
Глава IV. Подобіе многогранниковъ, 252.
Глава V. Симметричные многогранники, 256.
Глава VI. Понятіе о правильныхъ многогранникахъ, 260.—Задачи,262.
— IV -
КНИГА III. КРУГЛЫЯ ГБЛА.
Глава I. Цилиндръ и конусъ Опредѣленія, 263—Поверхность ци-
линдра и конуса, 266.-Обьсмл. цилиндра и конуса, 271.—Подобіе ци-
линдровъ и конусовъ, 273.
Глава II. Шаръ. Сѣченіе шара плоскостью, 274—Свойства большихъ
круговъ, 276.—Плоскость,касательная къ шару, 278.—Поверхность шара
и его частей, 278. Объемъ шара и ого частей, 282.
Задачи, 268.
Приложеніе: Главнѣйшіе методы ріилепія геометрическихъ задачи на-
нестроеніе, 289.
ЗАМѢЧЕННЫЯ 01ІЕЧАТКИ.
Стр. 8. строка6 снизу, напечатано: какія-ппбудя; слѣдуетъ: какія-нибудь.
Стр. 15, строка 3, напечатано: Л0В-\-В0В+2(1'. слѣдуетъ: А0В+
вов—2 а.
Стр. 52, строка 1, напечатано: ино прямые: слѣдуетъ: они прямые.
Стр. 57, строка 14 снизу, иапеч.: такъ у нихъ; слѣдуетъ: такъ какъ
у пнхь.
Стр. 126, напечатано: Теорема. П.ерпендикуляръ, опущенный изъ вер-
шины прямою угла на гипотенузу, есть средняя пропорціональная между
гипотенузой и прилежащимъ отрѣзкомъ.
Слѣдуетъ: Теорема. Перпендикуляръ, опушенный узъ вершины прямою-
угла на гипотенузу, есть среди)ія пропорціональная между отрѣзками
гипотенузы, а каждый катетъ есть средняя пропорціональная между
гипотенузой и прилежащимъ отрѣзкомъ.
Стр. 131,строка 6 снизу, напечатано: а~Ъ е—3; слѣдуетъ: а~-5, Ь=А, е—Ъ.
Стр. 146, напечатано: глава IV; слѣдуетъ: глава V.
Стр. 150, строка 5, напечатано: съ биссскрнсой: слѣдусіъ: съ бис-
сектриссой.
Стр. 155, строка 9 снизу,- напечатано: В. 2; слѣдуетъ: 2 К.