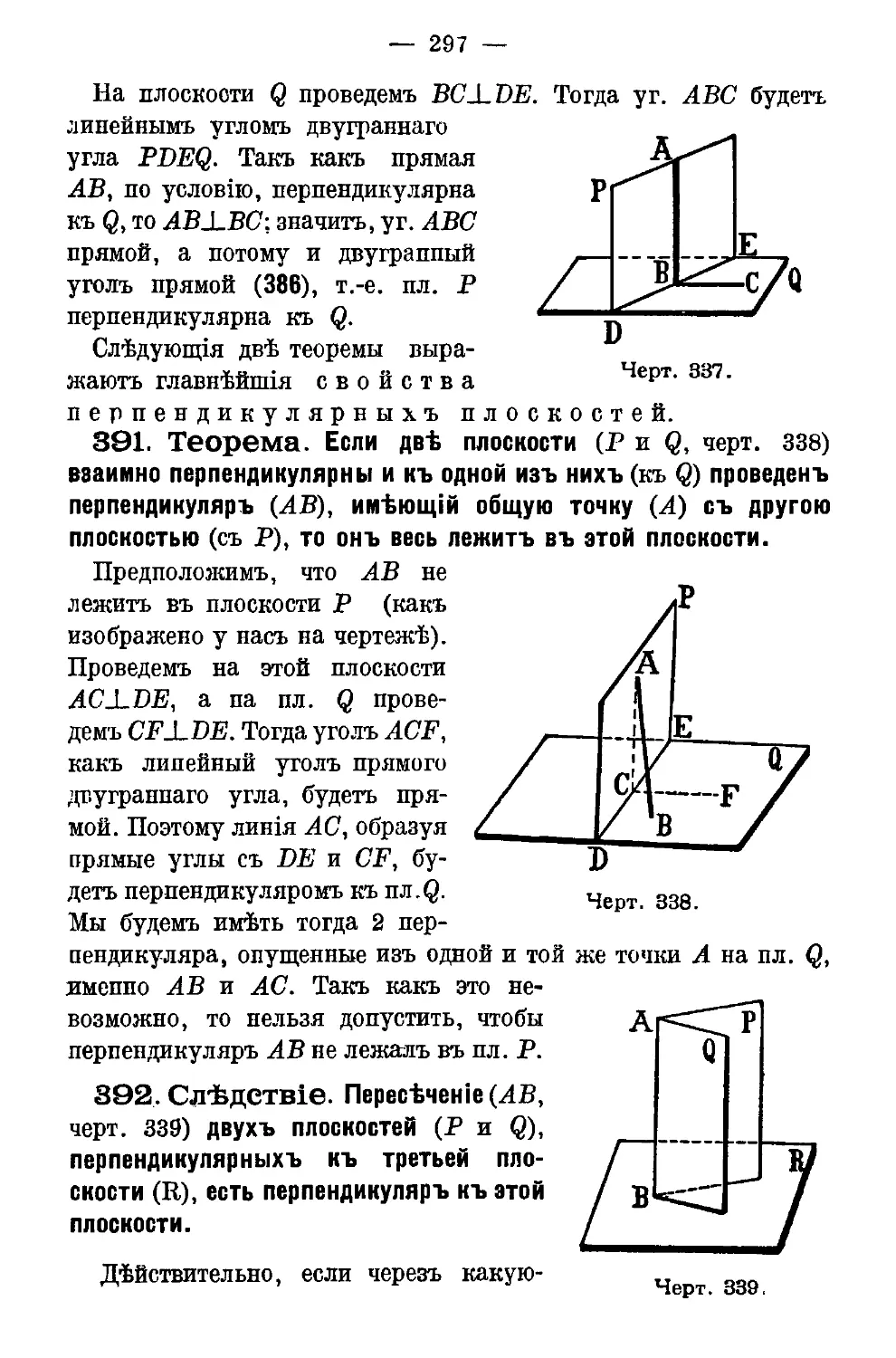
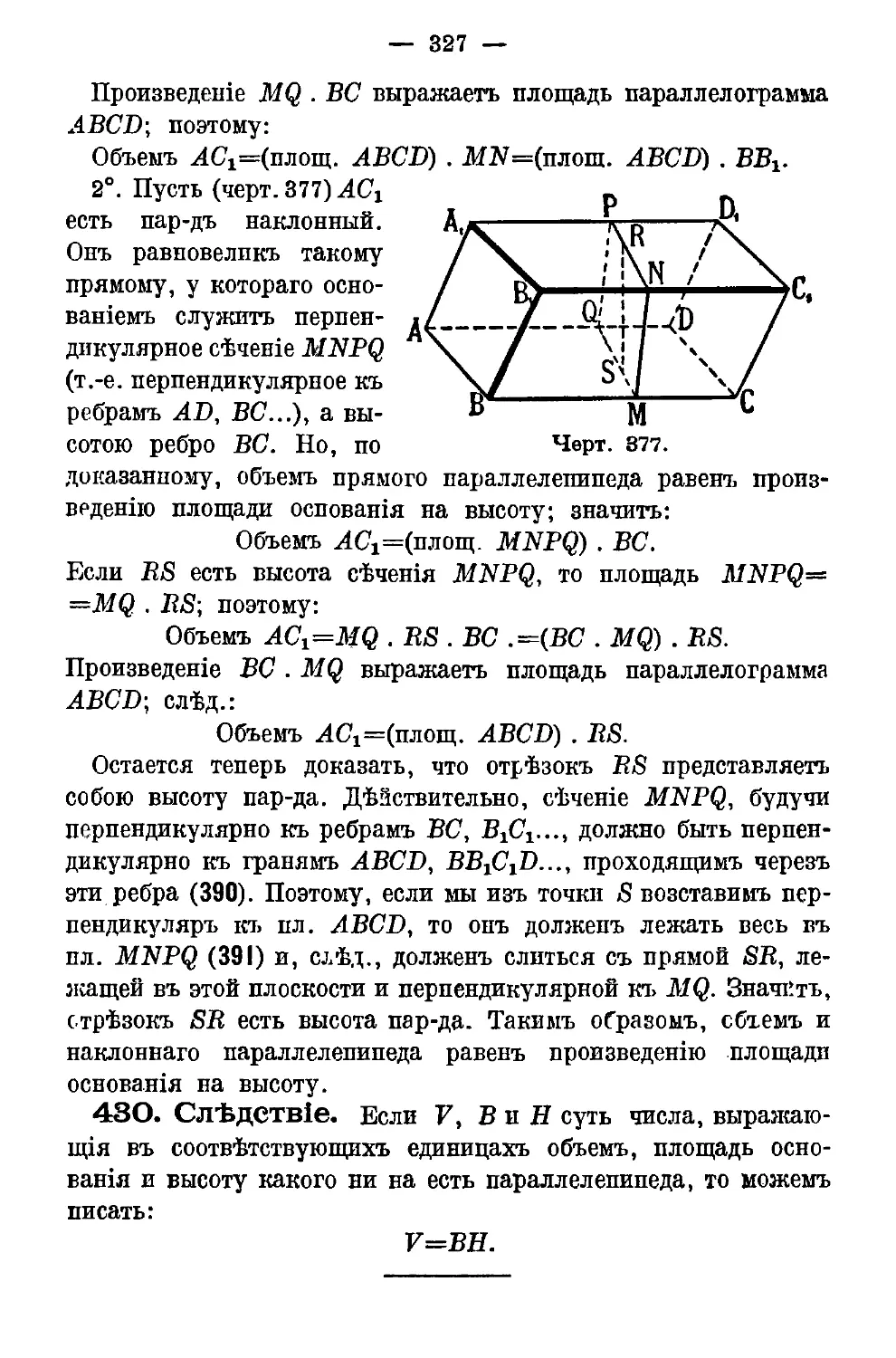
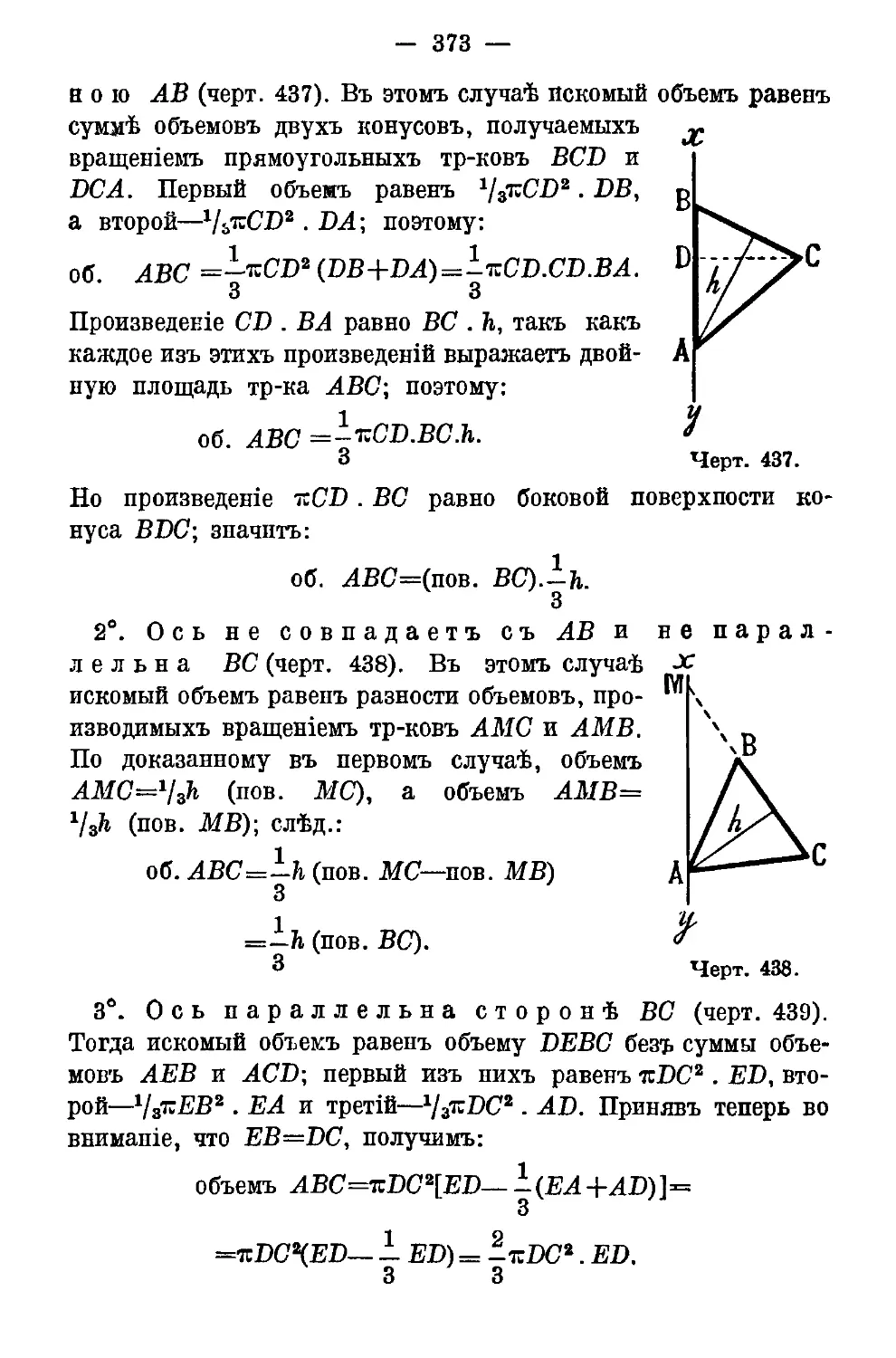
Текст
А. Киселевъ.
ЭЛЕМЕНТАРНАЯ
ГЕОМЕТРІЯ
ДЛЯ СРЕДНИХЪ УЧЕБНЫХЪ ЗАВЕДЕНІЙ.
Съ приложеніемъ большою количества упражненій и статьи: Главнѣйшіе методы рѣшенія геометрическихъ задачъ на построеніе.
Изданіе двадцать третье.
Допущена Уч. Ком. М. Н. Пр. въ качествѣ руководства для среднихъ учебныхъ заведеній, мужскихъ и женскихъ („Журн. М. Н. П.“ 1913. апрѣль), рекомендована Учеби. Ком. при Св. Синодѣ для употребленія въ духовныхъ семинаріяхъ въ качествѣ учебнаго пособія („Церк. Вѣд.“, 1893, № 32); ОДОбрена Деп. Торг. и Мануф. для коммерческихъ училищъ въ качествѣ пособія (извѣщеніе отъ 30 мая 1898 г., № 14128). Рекомендована, какъ РУКОВОДСТВО для кадетскихъ корпусовъ.
Изданіе Т-ва
ПОДЪ ФИРМОЙ „В. В. Думновъ—насл. Бр. Силаевымъ'!
с
МОСКВА.
Типографія П. П. Рябушинскаго, Страстной бульваръ, собственный домъ.
19 14.
Изъ предисловія къ первому изданію.
(1892 г.).
Главнѣйшія особенности предлагаемаго руководства геометріи состоятъ въ слѣдующемъ.
1. Въ большинствѣ нашихъ учебниковъ геометріи понятіе о длинѣ окружности и вообще о кривой линіи принимается за элементарное, не требующее никакихъ оговорокъ и разъясненій, и выводъ, что длина окружности есть предѣлъ периметровъ правильныхъ вписанныхъ и описанныхъ многоугольниковъ, основывается на скрытомъ допущеніи или на не строго доказываемой теоремѣ, что объемлющая линія длиннѣе объемлемой. Въ предлагаемомъ руководствѣ, въ согласіи со многими авторитетами учебно-математической литературы, проведено иное воззрѣніе, которымъ признается, что понятіе о длинѣ элементарно только въ примѣненіи къ прямой; но когда рѣчь идетъ о сравненіи конечной кривой съ прямолинейнымъ отрѣзкомъ, тогда (вслѣдствіе несовмѣстимости элементовъ кривой съ элементами прямой) понятіе о длинѣ становится сложнымъ и требуетъ опредѣленія *). Сообразно этому взгляду мы не доказываемъ, а принимаемъ за опредѣленіе, что длиною конечной кривой называется предѣлъ периметра вписанной ломаной линіи, когда стороны ея стремятся къ нулю. Конечно, въ среднихъ классахъ учебныхъ заведеній было бы затруднительно вполнѣ обосновать это опредѣленіе, т.-е. доказать, что такой предѣлъ существуетъ и что онъ не зависитъ отъ закона вписыванія ломаной линіи; но въ педагогическомъ отношеніи, какъ намъ кажется, нѣкоторые пробѣлы въ доказательствѣ не скрываемые, впрочемъ, отъ учащихся) не имѣютъ такого вреднаго значенія, какъ неопредѣленность, неясность и сбивчивость въ понятіяхъ, а тѣмъ болѣе въ основныхъ. При повтореніи геометріи въ старшемъ классѣ (особенно въ реальныхъ училищахъ, гдѣ въ седьмомъ классѣ пола
*) Отсылаемъ интересующихся втимъ вопросомъ къ статьѣ М. Попру жѳн ко «О длинѣ», помѣщенной въ «Вѣстникѣ опытной физики и элементарной математикѣ» (1801 г. ММ 122 и 123).
— IV —
гается обстоятельно пройти статью о предѣлахъ) ученики не затруднятся усвоить и необходимое обоснованіе указаннаго опредѣленія (оно помѣщено нами въ мелкомъ шрифтѣ).
Замѣтимъ еще по тому же вопросу о длинѣ, что, придерживаясь «Началъ Эвклида» и лучшихъ современныхъ иностранныхъ учебниковъ, мы не приписываемъ прямой линіи, какъ аксіому, свойства быть короче всякой другой линіи, проведенной между концами прямой, а доказываемъ эту истину въ тѣхъ мѣстахъ курса, гдѣ въ этомъ является надобность и возможность, сначала въ примѣненіи къ ломаной, а потомъ и къ кривой. И дѣйствительно, разъ мы стали на ту точку зрѣнія, что длина кривой есть понятіе сложное, разрѣшающееся только при посредствѣ другого сложнаго понятія— о предѣлѣ, становится совершенно невозможнымъ принимать за очевидную истину такое предложеніе, однимъ изъ терминовъ котораго служитъ это вдвойнѣ сложное понятіе. Съ другой стороны, и нѣтъ логической необходимости въ предварительномъ признаніи принципа Архимеда, такъ какъ онъ вполнѣ строго доказывается на ряду съ другими теоремами.
2. Въ согласіи съ изложеннымъ взглядомъ на длину кривой линіи, мы полагаемъ также, что кривыя поверхности, вслѣдствіе несовмѣстимости пхъ элементовъ съ элементами плоскости, не могутъ быть непосредственно сравниваемы съ плоскими поверхностями; поэтому мы не доказываемъ, что поверхность круглаго тѣла есть предѣлъ нѣкоторой плоской поверхности, а принимаемъ это предложеніе за опредѣленіе.
Замѣтимъ, что аналогичный вопросъ по отношенію къ площадямъ криволинейныхъ фигуръ или по отношенію къ объемамъ, ограниченнымъ кривыми поверхностями, разрѣшается совсѣмъ иначе. Въ самомъ дѣлѣ, мы совершенно ясно представляемъ себѣ, что площадь круга больше площади вписаннаго многоугольника, какъ цѣлое больше своей части, и меньше площади описаннаго многоугольника, какъ часть меньше цѣлаго; и далѣе, что при неограниченномъ удвоеніи числа сторонъ вписаннаго и описаннаго многоугольниковъ разность между ихъ площадями стремится къ нулю; поэтому предложеніе: «площадь круга есть общій предѣлъ площадей правильныхъ вписанныхъ и оппсанныхъ многоугольниковъ» должно быть разсматриваемо не какъ опредѣленіе, а какъ теорема, подлежащая доказательству. То же самое можно сказать объ объемѣ цилиндра, конуса и шара.
— V —
3. Какъ извѣстно, въ алгебрѣ существуютъ статьи, которыя не могутъ быть строго обоснованы въ элементарномъ курсѣ, но безъ которыхъ этотъ курсъ не обходится (напр., дѣйствія надъ несоизмѣримыми числами). Въ элементарной геометріи къ такого рода статьямъ относится способъ предѣловъ. Дня строгаго доказательства этого способа потребовалось бы ввести въ курсъ геометріи теорію предѣловъ почти въ такомъ размѣрѣ, въ какомъ эта статья проходится въ седьмомъ классѣ реальныхъ училищъ. Чтобы научно обосновать, напримѣръ, нахожденіе предѣла формулы объема усѣченной пирамиды [\/=1/зН(В+Ь+]/ВЬ)], слѣдовало бы предварительно установить теоремы о предѣлѣ суммы, произведенія и корня, а для этого, въ свою очередь, пришлось бы ввести нѣкоторыя теоремы о безконечномалыхъ величинахъ. Само собою разумѣется, что въ такомъ видѣ статья о предѣлахъ не можетъ быть пройдена въ среднихъ классахъ нашихъ учебныхъ заведеній. Съ другой стороны, обойтись совсѣмъ безъ способа предѣловъ въ элементарной геометріи невозможно. По необходимости здѣсь приходится поступиться строгостью изложенія въ пользу его краткости и доступности. Поэтому мы сочли за лучшее, доказавъ двѣ извѣстныя теоремы о предѣлахъ, указать затѣмъ безъ доказательства основной принципъ способа предѣловъ, состоящій въ томъ, что равенство, вѣрное при всевозможныхъ значеніяхъ перемѣнныхъ, остается вѣрнымъ и тогда, когда вмѣсто перемѣнныхъ подставимъ ихъ предѣлы.
4. Въ большинствѣ русскихъ оригинальныхъ учебниковъ геометріи теоремы о равенствѣ несоизмѣримыхъ отношеній доказываются отъ противнаго. Мы предпочли другой путь. Прежде чѣмь доказывать равенство, необходимо точно установить, что разумѣется подъ этимъ терминомъ. Если же поставимъ вопросъ, что такое равенство несоизмѣримыхъ отношеній, то наиболѣе простой отвѣтъ на него будетъ слѣдующій: несоизмѣримыя отношенія считаются равными, если равны ихъ приближенныя значенія, вычисленныя съ произвольною, но одинаковою точностью. Принявъ это предложеніе за опредѣленіе равенства, мы не нуждаемся болѣе въ косвенномъ и тяжеломъ доказательствѣ отъ противнаго; его всегда можно замѣнить прямымъ доказательствомъ, и болѣе простымъ, и болѣе яснымъ.
5. Нѣкоторыя статьи изложены въ предлагаемомъ руководствѣ, какъ кажется, проще, чѣмъ въ распространенныхъ нашихъ учебникахъ. Таковы, напр., статьи: о параллельныхъ прямыхъ, объ отно
- VI —
сительномъ положеніи окружностей, о пропорціональныхъ линіяхъ, о правильныхъ многоугольникахъ, о нахожденіи объема всякаго параллелепипеда, о подобіи многоугольниковъ и нѣкоторыя другія. Сравнительная простота достигается нѣкоторымъ измѣненіемъ въ распредѣленіи матеріала, а иногда упрощеніемъ пріемовъ доказательства. Книга снабжена значительнымъ количествомъ упражненій, состоящихъ частію изъ нѣкоторыхъ, не вошедшихъ въ текстъ, но представляющихъ интересъ теоремъ, а главнымъ образомъ изъ задачъ на построеніе и вычисленіе. Въ концѣ планиметріи мы помѣстили *) нѣкоторыя задачи на вычисленіе изъ «Сборника геометрическихъ задачъ для повторительнаго курса планиметріи» г. М. Попруженко. Эти задачи обладаютъ прежде всего тѣмъ достоинствомъ, что онѣ содержать много чисто геометрическаго матеріала, а не представляютъ собою только ариометическихъ или алгебраическихъ упражненій съ геометрическими данными. Въ концѣ курса, въ видѣ дополненія, мы сочли не лишнимъ приложить небольшую статью о методахъ рѣшенія геометрическихъзадачъ на построеніе съ примѣрами задачъ, рѣшаемыхъ этими методами. Существующіе у нась сборники подобнаго рода, устрашая учащихся своимъ объемомъ, употребляются ими лишь въ рѣдкихъ случаяхъ. Мы изложили въ самомъ сжатомъ видѣ только главнѣйшіе методы и помѣстили наиболѣе типичныя задачи.
Слѣдуя учебнымъ планамъ гимназій и реальныхъ училищъ, мы помѣщаемъ основныя задачи на построеніе и вычисленіе въ самомъ текстѣ книги непосредственно послѣ тѣхъ теоремъ, на которыхъ основано ихъ рѣшеніе. Въ сокращенномъ видѣ мы указываемъ также сущность приложенія алгебры къ геометріи и построеніе простѣйшихъ алгебраическихъ формулъ.
Считаемъ не лишнимъ сдѣлать слѣдующее замѣчаніе. Съ точки зрѣнія строгой теоріи къ задачамъ на построеніе возможно приступить только тогда, когда ученики усвоили основныя предложенія объ окружности. Но съ педагогической точки зрѣнія это едва ли было бы удобно: отодвинуть практическія упражненія такъ далеко отъ начала курса значило бы сдѣлать начало геометріи, и безъ того трудное для начинающихъ, еще болѣе сухимъ и тяжелымъ. Мы поступились
*) Съ согласія составителя.
— ѴП —
строгостью въ пользу практическаго интереса и помѣстили основныя задачи на построеніе тотчасъ послѣ разсмотрѣнія свойствъ треугольниковъ.
Книга напечатана двумя шрифтами: въ обыкновенномъ изложено все то, что должно быть пройдено въ среднихъ классахъ, въ мелкомъ—то, что желательно дополнить при повтореніи геометріи въ старшемъ классѣ.
Предисловіе къ 21-му изданію.
(1912 г.).
21-е изданіе «Элементарной геометріи» значительно переработано сравнительно съ изданіями предыдущими.
Главнѣйшія измѣненія слѣдующія (перечисляемъ ихъ въ порядкѣ слѣдованія параграфовъ).
1°. Въ началѣ главы «Параллельныя прямыя», раньше опредѣленія такихъ прямыхъ, поставлена вспомогательная лемма (§ 73) о взаимной связи извѣстныхъ 5-и соотношеній между углами, образующимися при пересѣченіи двухъ прямыхъ третьею. Предварительное установленіе этой связи, не представляя собой большой трудности для учащагося, значительно облегчаетъ усвоеніе дальнѣйшей теоріи параллельныхъ прямыхъ. Изложеніе самой этой теоріи тоже отличается теперь отъ прежняго. Такъ, ранѣе опредѣленія параллелизма мы показываемъ (§ 74) возможность существованія такихъ прямыхъ, которыя не пересѣкаются, сколько бы мы ихъ ни продолжали; затѣмъ мы сначала указываемъ признаки параллельности прямыхъ (§ 76), а уже потомъ излагаемъ, въ видѣ обратной теоремы (§ 81), свойства параллельныхъ прямыхъ, а не наоборотъ, какъ это дѣлалось въ предыдущихъ изданіяхъ. Иначе, чѣмъ прежде (болѣе общимъ способомъ) доказывается теорема (§ 77), что «черезъ всякую точку, лежащую внѣ прямой, молено провести параллельную этой прямой»; излагаемый теперь пріемъ доказательства даетъ больше возможности выяснить (§ 78) логическую потребность въ извѣстномъ постулатѣ параллельныхъ прямыхъ (§ 79). Признаки непараллельности прямыхъ (§ 83) изложены теперь нѣсколько подробнѣе, чѣмъ прежде.
— VIII —
Въ концѣ главы о параллельныхъ прямыхъ мы помѣстили теперь (мелкимъ шрифтомъ) добавленіе, могущее, какъ намъ кажется, заинтересовать многихъ любознательныхъ учениковъ: «О постулатѣ параллельныхъ линій»; въ этомъ добавленіи мы даемъ понятіе о важной роли этого постулата, а также и о «не-Эвклидовыхъ» геометріяхъ.
2°. Въ главѣ «Параллелограммы и трапеціи» мы теперь излагаемъ и тѣ теоремы, доказательство которыхъ въ предыдущихъ изданіяхъ предоставлялось самимъ учащимся; таковы, напр., обратныя теоремы: «всякій четыреугольникъ, котораго діагонали дѣлятся пополамъ, есть параллелограммъ» (§ 101), «всякій параллелограммъ, у котораго діагонали равны, есть прямоугольникъ» (§ 105), и т. п.
3°. Въ главѣ «Свойства касательной» болѣе подробно и систематично, чѣмъ прежде, разсматривается относительное положеніе прямой и окружности (§ 135), вслѣдствіе чего дальнѣйшее изложеніе свойствъ касательной упрощается. Въ той же главѣ теперь мы подробно излагаемъ (§ 142) доказательство (которое прежде предоставлялось самимъ ученикамъ) правильности рѣшенія задачи о проведеніи касательныхъ, общихъ двумъ даннымъ окружностямъ.
4°. Въ главѣ «Измѣреніе величинъ» нѣсколько упрощено (§ 156) доказательство теоремы о несоизмѣримости основанія и боковой стороны равнобедреннаго треугольника, у котораго уголъ при основаніи равенъ а также добавлена (мелкимъ шрифтомъ, § 157) классическая теорема о несоизмѣримости діагонали квадрата съ его стороной.
5°. Въ книгѣ III подобіе треугольниковъ отдѣлено отъ подобія многоугольниковъ болѣе, чѣмъ это дѣлалось прежде, причемъ, ранѣе опредѣленій подобія тѣхъ и другихъ, предварительно устанавливается (въ леммахъ §§ 196 и 205), возможность существованія тѣхъ фигуръ, о которыхъ будетъ затѣмъ говориться въ опредѣленіяхъ.
6°. Существенному измѣненію подверглось доказательство теоремы Птолемея. Въ прежнихъ изданіяхъ эта теорема (§ 215 прежнихъ изданій) излагалась мелкимъ шрифтомъ, какъ слѣдствіе изъ формулъ, найденныхъ раньше, путемъ довольно сложныхъ вычисленій, для діагоналей вписаннаго четыреугольника; теперь мы даемъ классическое доказательство (§ 242) этой весьма важной теоремы и излагаемъ ее обыкновеннымъ шрифтомъ. Вычисленіе же діагоналей вписаннаго четыреугольника (оставляя его въ мелкомъ шрифтѣ) мы основы
— IX —
ваемъ на теоремѣ Птолемея и на другой, добавленной теперь (§ 244), объ отношеніи діагоналей такого четыреугольника.
Нѣкоторымъ измѣненіямъ (и дополненіямъ) подверглись также теоремы о пропорціональныхъ линіяхъ въ кругѣ (§§ 246, 247, 248, 249).
7°. Нѣсколько измѣнено изложеніе опредѣленія длины окружности и ея частей (§ 286) и упрощено доказательство теоремы (§ 288), что «длина дуги больше стягивающей ее хорды, но меньше всякой ломаной линіи, описанной около этой дуги и имѣющей съ нею одни и тѣ же концы».
8°. Существенно передѣлано теперь изложеніе теоремы: «площадь прямоугольника равна произведенію его основанія на высоту» (§ 305). Въ предыдущихъ изданіяхъ доказательство этой теоремы основывалось на двухъ предварительныхъ леммахъ объ отношеніи площадей прямоугольниковъ, причемъ приходилось перемножать между собою двѣ пропорціи, сокращая послѣдующій членъ одной пропорціи съ предыдущимъ членомъ другой, т.-е. приходилось скрытымъ образомъ предполагать, что площади, представляющія собою эти члены, уже выражены числами. Теперь мы даемъ прямое, болѣе строгое и вмѣстѣ съ тѣмъ болѣе ясное, доказательство этой теоремы и только, какъ слѣдствіе изъ ноя, выводимъ (§ 306) заключеніе объ отношеніи площадей двухъ прямоугольниковъ.
9°. Въ началѣ главы «Площади многоугольниковъ» мы помѣстили замѣчаніе (мелкимъ шрифтомъ, § 301), указывающее на важный вопросъ, возникающій относительно основныхъ допущеній о площадяхъ, а также дали наглядное понятіе о томъ (§ 303), что слѣдуетъ разумѣть подъ числомъ, измѣряющимъ каку ю-н и б у д ь данную площадь въ квадратныхъ единицахъ.
10°. Въ нѣкоторыхъ случаяхъ, не ограничиваясь обычнымъ доказательствомъ равновеликости фигуръ, мы дали дополнительное замѣчаніе о возможности разложенія этихъ фигуръ на соотвѣтственно конгруептныя части (въ § 309—о превращеніи параллелограммовъ, въ § 312—о превращеніи треугольника въ прямоугольникъ и въ § 315—о превращеніи трапеціи въ прямоугольникъ).
11°. Для большей наглядности мы привели третье доказательство теоремы Пиоагора (§ 321), показывающее, какъ разложить сумму квадратовъ, построенныхъ на катетахъ, на такія части, изъ которыхъ, перемѣщеніемъ ихъ, можно образовать квадратъ, построенный на гипотенузѣ.
— X —
12°. Въ стереометріи, въ главѣ «Перпендикуляръ и наклонныя», ради большей систематичности, мы помѣстили теперь и ту теорему (изъ точки, взятой внѣ плоскости, можно опустить на эту плоскость перпендикуляръ), которая въ предыдущихъ изданіяхъ отрывалась отъ родственной ей теоремы (изъ точки, взятой на плоскости, можно возставить къ этой плоскости перпендикуляръ), и доказывалась позже, въ концѣ главы о параллельныхъ прямыхъ.
13°. Извѣстное предложеніе о трехъ перпендикулярахъ, которое прежде излагалось нами, какъ лемма (§ 321 прежнихъ изданій), теперь поставлено въ видѣ самостоятельной теоремы въ концѣ главы о перпендикулярѣ и наклонныхъ (§ 359).
14°. Изложеніе главы «Объемъ призмы и пирамиды» измѣнено теперь въ соотвѣтствіи съ измѣненіемъ главы о площадяхъ; такъ, объемъ прямоугольнаго параллелепипеда находится непосредственно, а не на основаніи двухъ леммъ объ отношеніи объемовъ, какъ это дѣлалось прежде.
Мы перечислили только главнѣйшія измѣненія, сдѣланныя въ 21-мъ изданіи. Есть много другихъ болѣе мелкихъ отличій, введенныхъ главнымъ образомъ съ цѣлью достигнуть большей ясности изложенія или большей точности въ формулировкѣ опредѣленій и теоремъ.
Кромѣ того, частью съ цѣлью выполнить всѣ требованія офиціальныхъ программъ, а главнымъ образомъ съ цѣлью удовлетворить любознательность учениковъ, мы ввели и нѣкоторые новые параграфы и даже цѣлыя главы; напр., о симметріи фигуръ (§§ 33, 102,109, 264), о постулатѣ параллельныхъ линій (§§ 91—95), о признакахъ, необходимыхъ и достаточныхъ (§ 187), о фигурахъ, подобно расположенныхъ (гомотетія §§ 211—218), объ однородности уравненій, получаемыхъ при рѣшеніи геометрическихъ задачъ (§ 342), о построеніи корней квадратнаго уравненія (§ 343), опредѣленіе проэкціи прямой на плоскость (§ 394) и нѣкоторые другіе.
Предисловіе къ 22-му изданію.
Приступая къ 22-му изданію, мы тщательно просмотрѣли изложеніе предыдущаго изданія съ цѣлью устранить всѣ замѣченныя опечатки, а также и неточности, неясности или шероховатости слога. При этомъ, для большей полноты или для достиженія большей ясности и большей строгости изложенія, пришлось сдѣлать нѣкоторыя небольшія измѣненія и добавленія (послѣднія, главнымъ образомъ, въ мелкомъ шрифтѣ). Укажемъ главнѣйшія изъ нихъ.
Къ § 35 сдѣлана выноска, въ которой разъясняется, что конгруенція на плоскости различается двухъ родовъ: прямая и не-прямая.
Въ § 130 добавлены 2 слѣдствія, представляющія собою предложенія, обратныя теоремѣ 1° этого параграфа. Въ нихъ встрѣчается надобность при доказательствѣ теоремы 2° (обратной) § 138, введенной для обоснованія содержащагося въ § 258 построенія правильнаго списаннаго многоугольника, стороны котораго параллельны сторонамъ правильнаго вписаннаго многоугольника.
Въ выноскѣ къ § 224 указано иное отложеніе прямыхъ а, в и с къ которымъ отыскивается 4-ая пропорціональная.
Равнымъ образомъ, въ выноскѣ къ § 255, 3° указывается другой способъ построенія 3-й пропорціональной.
Въ концѣ того же § 255 добавлена выноска, въ которой говорится о невозможности рѣшенія помощью циркуля и линейки задачи объ удвоеніи куба.
Въ § 301 добавлены два замѣчанія (2° и 3°), въ которыхъ разъясняется, что равновеликость фигуръ можетъ быть двоякаго рода: равновеликость «по разложенію» и равновеликость «по дополненію».
Къ § 433 добавлена выноска о томъ, что равновеликость двухъ пирамидъ, имѣющихъ равновеликія основанія и равныя высоты, не можетъ быть сведена ни на равновеликость «по разложенію», ни на равновеликость «по дополненію».
Изложеніе §§ 299 и 300 («Основныя допущенія о площадяхъ») теперь нѣсколько болѣе систематизировано; то же самое сдѣлано и относительно изложенія соотвѣтствующихъ §§ 422 и 423 объ объемахъ.
Измѣнено изложеніе конца § 429 съ цѣлью подробнѣе, чѣмъ было прежде, выяснить, что отрѣзокъ К8 представляетъ собою высоту параллелепипеда.
Весьма многіе чертежи для 22-го изданія передѣланы вновь съ цѣлью ихъ улучшенія.
— XII —
23-е изданіе существенно не отличается отъ изданія 22-го; лишь въ немногихъ мѣстахъ нѣсколько улучшено изложеніе (напр.. о перпендикулярѣ и наклонныхъ, §§ 59,х, 59,2 и 60), или сдѣланы небольшія добавленія (напр., § 160,2 „О пропорціи11).
ВВЕДЕНІЕ
Математическія предложенія.
1. Во всякой математической наукѣ могутъ встрѣтиться слѣдующія предложенія:
Опредѣленія. Такъ называютъ предложенія, въ которыхъ разъясняется, какой смыслъ придаютъ тому или другому выраженію или названію. Наприм., въ ариѳметикѣ мы встрѣчаемъ опредѣленія наименьшаго кратнаго, общаго наибольшаго дѣлителя и т. п.
Аксіомы. Такъ называютъ истины, которыя, вслѣдствіе своей очевидности, принимаются безъ доказательства. Таковы, напр., предложенія:
Если двѣ величины равны порознь одной и той же третьей величинѣ, то онѣ равны и между собою.
Если къ равнымъ величинамъ придадимъ поровну, или отъ равныхъ величинъ отнимемъ поровну, то равенство не нарушится.
Если къ неравнымъ величинамъ придадимъ поровну, или отъ неравныхъ величинъ отнимемъ поровну, то смыслъ неравенства не измѣнится, т.-е. бдлыпая величина останется большей.
Теоремы. Такъ называются предложенія, которыхъ истинность обнаруживается только послѣ нѣкотораго разсужденія (доказательства). Примѣромъ можетъ служить ариѳметическая истина: «если сумма цыфръ дѣлится на 9, то число дѣлится на 9».
Слѣдствія. Такъ называются предложенія, которыя составляютъ непосредственный выводъ изъ аксіомы или теоремы. Напр., изъ теоремы: «въ пропорціи произведеніе крайнихъ членовъ равно произведенію среднихъ», выводится слѣдствіе: «крайній членъ пропорціи равенъ произведенію среднихъ членовъ, дѣленному на другой крайній».
А. Киселевъ. Геометрія. 1
— 2 —
2. Составъ теоремы. Во всякой теоремѣ можно различить двѣ части: условіе и заключеніе. Условіе выражаетъ то, что предполагается даннымъ; заключеніе — то, что требуется доказать. Напр., въ теоремѣ: «если сумма цыфръ дѣлится на 9, то число дѣлится на 9», условіемъ служитъ первая часть теоремы: «если сумма цыфръ дѣлится на 9», а заключеніемъ — вторая часть: «то число дѣлится на 9»; другими словами, намъ дано, что сумма цыфръ нѣкотораго числа дѣлится на 9, а требуется доказать, что въ въ такомъ случаѣ и само число дѣлится на 9.
Условіе и заключеніе теоремы могутъ иногда состоять изъ нѣсколькихъ отдѣльныхъ условій и заключеній; напр., въ теоремѣ: «если число дѣлится на 2 и на 3,то оно раздѣлится на 6», условіе состоитъ изъ двухъ частей: если число дѣлится на 2 и если число дѣлится на 3.
Полезно замѣтить, что всякую теорему можно подробно выразить словами такъ, что ея условіе будетъ начинаться словомъ «е с л и», а заключеніе — словомъ «т о».
3. Обратная теорема. Теоремою, обратною данной теоремѣ, паз. такая, въ которой условіемъ поставлено заключеніе или часть заключенія данной теоремы, а заключеніемъ— условіе или часть условія данной теоремы. Напр., слѣдующія двѣ теоремы обратны другъ-другу:
Если сумма цыфръ дѣлится Если число дѣлится на 9,
на 9, т о число дѣлится на 9. то сумма цыфръ дѣлится на 9.
Если одну изъ этихъ теоремъ назовемъ прямою, то другую слѣдуетъ назвать обратною.
Въ этомъ примѣрѣ обѣ теоремы, и прямая и обратная, оказываются вѣрными. Но такъ бываетъ не всегда. Напр., теорема: «если каждое слагаемое дѣлится на одно и то же число, то и сумма раздѣлится на то же число» — вѣрпа, но невѣрно обратное предложеніе: «если сумма дѣлится на какое-нибудь число, то каждое слагаемое раздѣлится на него».
4. Противоположная теорема. Теоремою, противоположною данной теоремѣ, наз. такая, которой условіе и заключеніе представляютъ отрицаніе условія и заключенія
— 3 —
данной теоремы. Напр., теоремѣ: «если сумма цыфръ дѣлится на 9, то число дѣлится на 9» соотвѣтствуетъ такая противоположная: «если сумма цыфръ НС дѣлится на 9, то число НС дѣлится на 9».
И здѣсь должно замѣтить, что вѣрность прямой теоремы еще не служитъ признакомъ вѣрности противоположной; напр., противоположное предложеніе: «если каждое слагаемое н е дѣлится на одно и то же число, то и сумма н е раздѣлится на это число»,— не вѣрно, тогда какъ прямое предложеніе вѣрно.
5. Зависимость между теоремами: прямой, обратной И ПРОТИВОПОЛОЖНОЙ. Для лучшаго уясненія этой зависимости выразимъ теоремы сокращенно такъ:
1°. Прямая теорема: если есть А, то есть и В.
2°. Обратная теорема: если ость В, то есть и А.
3°. Противоположная прямой: если нѣтъ А, то нѣтъ и В.
4°. Противоположная обратной: если нѣтъ В, то нѣтъ и А.
Легко обнаружить, что предложенія первое и четвертое обратимы одно въ другое, равно какъ второе и третье. Дѣйствительно, изъ предложенія: «если есть А, то есть и В», непосредственно слѣдуетъ: «если нѣтъ В, то нѣтъ и А» (такъ какъ если бы А было, то, согласно первому предложенію, было бы и В); обратно, изъ предложенія: «если нѣтъ В, то нѣтъ и А», выводимъ: «если есть А, то есть и В» (такъ какъ если бы В не было, то не было бы и А). Совершенно такъ же убѣдимся, что изъ второго предложенія слѣдуетъ третье, и наоборотъ.
Поэтому, чтобы быть увѣреннымъ въ вѣрности всѣхъ четырехъ теоремъ, нѣтъ надобности доказывать каждую изъ нихъ отдѣльно, а достаточно ограничиться доказательствомъ только двухъ: прямой и обратной или прямой и противоположной.
Прямая линія, плоскость. Понятіе о геометріи.
в. Геометрическія фигуры. Всякая ограниченная часть пространства называется геометрическимъ тѣ-л о м ъ.
Геометрическое тѣло можно подраздѣлять на части; каждая часть геометрическаго тѣла есть также геометрическое тѣло.
Граница геометрическаго тѣла, т.-е. то, чѣмъ оно отдѣляется отъ остального пространства, наз. поверхностью.
1*
— 4 —
Поверхность можно подраздѣлять на части; всякая часть поверхности есть также поверхность.
Граница поверхности называется линіей.
Линію можно также подраздѣлять на части; каждая часть линіи есть также линія.
Граница линіи называется точкой.
Геометрическое тѣло, поверхность, линія и точка не существуетъ раздѣльно. Однако при помощи отвлеченія, мы можемъ разсматривать поверхность независимо отъ геометрическаго тѣла, линію — независимо отъ поверхности и точку —независимо отъ линіи. При этомъ поверхность мы должны представлять себѣ не имѣющею толщины, линію — не имѣющею ни толщины, ни ширины, и точку — не имѣющею ни длины, ни ширины, ни толщины.
Всякая линія содержитъ въ себѣ безчисленное множество точекъ. Принято говорить, что эти точки лежатъ на линіи, или что эта линія проходитъ черезъ эти точки. Ихъ можно разсматривать, какъ послѣдовательныя положенія одной и той же точки, движущейся вдоль этой линіи. Поэтому можно сказать,что линія есть слѣдъ движенія точки. Если, папр., мы острее карандаша двигаемъ по бумагѣ, то слѣдъ этого движенія на бумагѣ есть приблизительно линія; приблизительно потому, что острее карандаша не представляетъ собою геометрической точки, вслѣдствіе чего проведенная на бумагѣ линія имѣетъ нѣкоторую ширину (и даже толщину). Чѣмъ острѣе очиненъ карандашъ, тѣмъ болѣе острее его приближается къ геометрической точкѣ и тѣмъ болѣе линія, проведенная этимъ карандашомъ, приближается къ геометрической линіи.
Подобно этому поверхность можно разсматривать, какъ слѣдъ движенія линіи, двигающейся въ пространствѣ нѣкоторымъ образомъ.
Совокупность какихъ бы то ни было точекъ, линій, поверхностей или тѣлъ, расположенныхъ извѣстнымъ образомъ въ пространствѣ, называется вообще геометрической фигурой.
7. Геометрія. Наука, разсматривающая свойства геометрическихъ фигуръ, наз. геометріей, что въ переводѣ съ
— 5 —
греческаго языка означаетъ землемѣріе. Такое названіе этой наукѣ дано было потому, что въ древнее время главною цѣлью геометріи было измѣреніе разстояній и площадей на земной поверхности.
8. Въ самомъ началѣ геометріи должно быть указано слѣдующее общее свойство фигуръ:
Аксіома пространства. Всякую геометрическую фигуру можно перенести изъ одного мѣста пространства въ другое, не нарушая ни величины составляющихъ фигуру частей, ни ихъ взаимнаго расположенія.
9. Прямая линія. Всякій знаетъ, что такое прямая л и н і я, пли просто прямая, представленіе о которой намъ даетъ туго натянутая нить. Понятіе о прямой элементарно, т.-е. оно не можетъ быть опредѣлено посредствомъ другихъ болѣе простыхъ понятій.
На чертежѣ прямую изображаютъ въ видѣ тонкой черты, проведенной отъ руки или помощью чертежной линейки.
Прямая линія обладаетъ слѣдующими очевидными свойствами:
Аксіомы прямой. 1°. Черезъ всякія двѣ точки пространства можно провести прямую и притомъ только одну.
2°. Прямую можно продолжать безъ конца въ обѣ стороны отъ каждой ея точки.
Изъ первой аксіомы слѣдуетъ:
Если двѣ прямыя наложены одна на другую такъ, что какія-нибудь двѣ точки одной прямой совпадаютъ съ двумя точками другой прямой, то эти прямыя сливаются и во всѣхъ остальныхъ точкахъ (потому что въ противномъ случаѣ черезъ двѣ точки можно было бы провести двѣ различныя прямыя, что противорѣчитъ аксіомѣ первой).
По той же причинѣ двѣ прямыя могутъ пересѣчься только въ одной точкѣ.
ІО.Прямая конечная и безконечная. Если прямую представляютъ продолженною въ обѣ стороны безконечно, то ее называютъ безконечною или неограниченною прямой. Конечно, такую прямую изобразить на чертежѣ не
— 6 —
возможно. Изображаютъ только какую-нибудь часть ея и мысленно воображаютъ, что эта часть продолжена въ обѣ стороны безконечно. Прямую обозначаютъ обыкновенно двумя буквами, поставленными у двухъ какихъ-либо ея точекъ. Такъ говорятъ «прямая АВ или ВА» (черт. 1).
А -------------- В С I--------' О
Черт. 1. Черт. 2.
Часть прямой, ограниченная съ обѣихъ сторонъ, наз. отрѣзкомъ прямой или конечною прямой; такая прямая обозначается двумя буквами, поставленными у концовъ ея (отрѣзокъ СВ, черт. 2). Отрѣзокъ прямой, соединяющій двѣ точки, наз. иногда разстояніемъ между ними.
Иногда разсматриваютъ прямую, ограниченную только съ одной стороны, напр., въ точкѣ А (черт. 3). О такой прямой
А -----------------------------
Черт. 3.
говорятъ, что она исходитъ изъ точки А; ее называютъ полупрямою (или л у ч е м ъ).
11. Равенство и неравенство конечныхъ прямыхъ. Два отрѣзка прямой считаются равными, если они могутъ быть наложены другъ на друга такъ, что совмѣщаются. Положимъ, напр., что мы накладываемъ отрѣзокъ АВ на отрѣзокъ СВ (черт. 4) такъ, чтобы точка А упала на С и чтобы прямая АВ пошла по СП; если при этомъ концы В и В совпадутъ, то отрѣзки АВ и СВ считаются равными; въ противномъ случаѣ отрѣзки будутъ неравны, при чемъ меньшимъ считается тотъ, который составляетъ часть другого.
Чтобы на какой-нибудь прямой отложить отрѣзокъ, равный данному отрѣзку, употребляютъ ц и р к у л ь—приборъ, извѣстный учащимся изъ опыта.
12. Сумма конечныхъ прямыхъ. Суммою нѣсколькихъ данныхъ отрѣзковъ прямой наз. такой новый отрѣзокъ прямой, который составленъ изъ частей, соотвѣтственно равныхъ даннымъ отрѣзкамъ. Положимъ, напр., требуется найти сумму трехъ отрѣзковъ: АВ, СВ и ЕР (черт. 4). Для
— 7 —
этого на какой-нибудь прямой беремъ произвольную точку М и откладываемъ отъ нея часть ІИ#, равную АВ\ затѣмъ
А ------------- В С і----------1 В Е1------Г
М Ы Р С
- — । .....। .........। <----
Черт. 4.
отъ точки Е въ томъ же направленіи откладываемъ часть ЕР, равную СВ, и часть Р(^, равную ЕР. Отрѣзокъ будетъ сумма данныхъ отрѣзковъ АВ, СВ и ЕР, которые по отношенію къ этой суммѣ называются слагаемыми. Подобнымъ образомъ можно получить сумму какого угодно числа отрѣзковъ.
Сумма отрѣзковъ прямой обладаетъ свойствами всякой суммы; такъ, она не зависитъ отъ порядка слагаемыхъ (перемѣстительное свойство) и не измѣняется, если нѣкоторыя слагаемыя будутъ замѣнены ихъ суммою (сочетательное свойство). Напр., легко убѣдиться (черт. 4), что
ав+св+ер=св+ер+ав=ер+ав+св=... и АВ+СВ+ЕР=АВ+(СВ+ЕР).
Изъ понятія о суммѣ выводятся понятія о разности, произведеніи и частномъ отрѣзковъ. Такъ, разность отрѣзковъ АВ и СВ (если АВ^>СВ) есть такой третій отрѣзокъ, котораго сумма съ СВ образуетъ АВ-, произведеніе отрѣзка АВ на число 3 есть сумма трехъ отрѣзковъ, изъ которыхъ каждый равенъ АВ, частное отъ дѣленія отрѣзка АВ на число 3 есть третья часть АВ и т. п.
Мы принимаемъ за очевидную истину, что каждый отрѣзокъ прямой можетъ быть подраздѣленъ (хотя бы только мысленно) на 2, на 3, на 4 и т. д. равныя части.
13. Плоскость. Плоскостью наз. поверхность, обладающая тѣмъ свойствомъ, что прямая, проходящая черезъ любыя двѣ точки этой поверхности, лежитъ на ней всѣми остальными своими точками. Положимъ, напр., мы желаемъ убѣдиться, будетъ ли плоскостью поверхность стола. Для этого беремъ хорошо вывѣренную линейку и прикладываемъ ее краемъ въ различныхъ направленіяхъ къ поверхности стола такъ, чтобы какія-нибудь
— 8 —
двѣ точки линейки лежали на этой поверхности. Если при этомъ окажется, что, въ какомъ бы направленіи мы линейку ни приложили, всѣ остальныя точки ея будутъ лежать на поверхности стола, то эта поверхность есть плоскость.
Существованіе плоскости въ пространствѣ принимается за аксіому.
Укажемъ слѣдующее свойство плоскости, которое мы примемъ здѣсь безъ доказательства:
Всякую часть плоскости можно наложить всѣми ея точками на другое мѣсто этой или другой плоскости, при чемъ накладываемую часть можно предварительно перевернуть другою стороною.
14. Раздѣленіе геометріи. Геометрія раздѣляется на двѣ части: планиметрія и стереометрія. Первая разсматриваетъ свойства такихъ фигуръ, которыхъ всѣ части помѣщаются на одной плоскости; вторая—свойства такихъ фигуръ, которыхъ не всѣ части помѣщаются на одной плоскости.
ПЛАНИМЕТРІЯ,
КНИГА I.
ПРЯМАЯ ЛИНІЯ.
ГЛАВА I.
У г д ы.
Предварительныя понятія.
15. Опредѣленія. Фигура, образованная двумя полупрямыми (ОА п ОВ, черт. б), исходящими изъ одной точки, вмѣстѣ съ частью плоскости, ограниченной ими, наз. угломъ. Полупрямыя, образу- ,
ющія уголъ, наз. сторонами, А /*
а точка, изъ которой онѣ исхо- / , Б
дятъ,—в ершиною угла. Сто- /
роны должно представлять себѣ /
продолженными отъ вершины без- / конечно. X''
Уголъ обыкновенно обозначает- 0^---------------в
ся тремя буквами, изъ которыхъ Черт. 5.
средняя ставится у вершины, а крайнія у какихъ-нибудь точекъ сторонъ; напр., говорятъ: «уголъ АОВ или уголъ БОА» (черт. б). Н) можно обозначать уголъ и одною буквою, поставленною у вершины, если при этой вершинѣ нѣтъ другихъ угловъ. Мы иногда будемъ обозначать уголъ цыфрою, поставленною внутри угла, около вершины.
Слово «уголъ» на письмѣ замѣняется часто знакомъ
Если изъ вершины угла (черт. б) проведемъ внутри его (т.-е. въ той частп плоскости, которая принадлежитъ углу) какія-нибудь прямыя ОБ, ОЕ..., то образовавшіеся при этомъ углы АОБ, БОЕ, ЕОВ... разсматриваются, какъ части угла АОВ.
10 —
16. Равенство и неравенство угловъ. Два угла считаются равными, если при наложеніи они могутъ совмѣститься. Положимъ, напр., что мы накладываемъ уголъ АОВ на уголъ АіОіВі (черт. 6) такъ, чтобы вершина О упала въ Оь сторона ОВ пошла по 0^ и чтобы углы покрыли другъ друга.
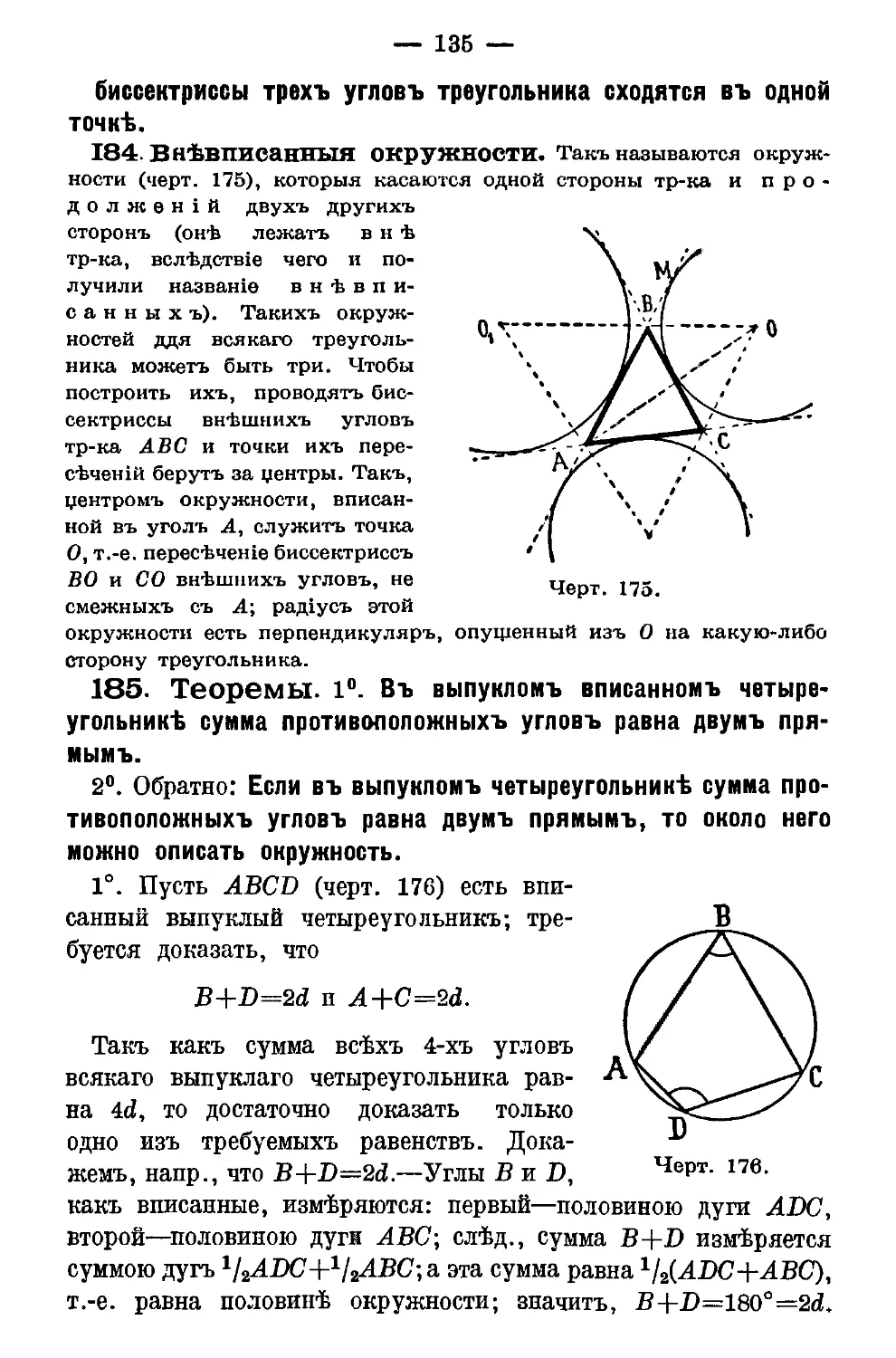
Если при этомъ сторона О А совмѣстится съ ОгАг, то углы равны; если же О А пойдетъ внутри угла А^Вх, или внѣ его, то углы не равны, при чемъ тотъ изъ нихъ будетъ меньше, который составитъ часть другого угла.
17. Сумма угловъ. Суммою данныхъ угловъ наз. уголъ, составленный изъ частей, соотвѣтственно равныхъ даннымъ угламъ. Такъ, чтобы получить сумму угловъ АОВ и А^Ві (черт. 7), строятъ уголъ ІМ^Р, равный одному изъ данныхъ угловъ, напр., АОВ, и къ нему пристраиваютъ уголъ Р^, равный другому данному углу ЛіОіВі, такъ, чтобы у обоихъ угловъ оказалась общая вершина и общая сторона и чтобы углы были расположены по разныя стороны отъ общей стороны №. Полученный такимъ образомъ уголъ МЫО есть сумма угловъ АОВ и А^іВ^ Подобнымъ образомъ можетъ быть составлена сумма трехъ и болѣе угловъ.
Черт. 7.
Сумма угловъ, какъ и сумма отрѣзковъ прямой (12), обла
— 11
При нахожденіи суммы угловъ могутъ особенные случаи, которые полезно раз-
что послѣ сложенія нѣсколькихъ угловъ,
даетъ свойствами перемѣстительнымъ и сочетательнымъ.
Изъ понятія о суммѣ угловъ выводятся понятія объ ихъ разности, произведеніи и частномъ.
Мы принимаемъ за очевидную истину, что каждый уголъ можетъ быть раздѣленъ (хотя бы только мысленно) на 2, на 3, на 4 и т. д. р а в н ы я части.
Замѣтимъ, что полупрямая дѣлящая уголъ пополамъ (черт. 8),
наз. биссектриссою этого угла (или равнодѣлящею) *).
18. Замѣчаніе 1-е. представиться нѣкоторые смотрѣть особо.
1°. Можетъ случиться,
напр., трехъ: АОВ, ВОС и СОВ (черт. 9), сторона ОВ угла СОВ составитъ продолженіе стороны ОА угла АОВ. Мы получимъ тогда фигуру, образованную двумя полупрямыми (ОА и ОВ), исходящими изъ одной О точки (О) и составляющими продолженіе одна другой. Такую фи-
гуру (вмѣстѣ съ частью плоскости, расположенную по одну сторону прямой АВ) принято тоже называть угломъ (развернутымъ, или выпрямленнымъ).
2°. Можетъ случиться, что послѣ сложенія нѣсколькихъ угловъ, напр., пяти угловъ: АОВ, ВОС, СОВ, ВОЕ и ЕОА (черт. 10), сторона ОА угла ЕОА совмѣстится со стороной ОА угла АОВ.
Фигура, образованная такими совпавшими полупрямыми (вмѣстѣ со всею плоскостью, расположенною кругомъ общей вершины О) также называется угломъ (полнымъ).
') Въ нѣкоторыхъ руководствахъ линія эта наз. также биссекторомъ.
12 —
3°. Наконецъ, можетъ случиться, что, строя сумму угловъ, мы не только заполнимъ всю плоскость кругомъ ихъ общей вершины, но даже будемъ вынуждены налагать углы одинъ на другой, покрывая плоскость вокругъ общей вершины во второй разъ, въ третій разъ и т. д.
Въ этомъ случаѣ понятіе о суммѣ угловъ должно быть расширено на основаніи слѣдующихъ опредѣленій:
1°. Двѣ суммы угловъ: «і+«2 + аз + -” + ап и Ьі+Ь2+Ьз + "- + ЬОТ счи-таются равными, если, строя ихъ указаннымъ путемъ, начиная отъ одной и той же полупрямой О А въ одномъ направленіи вокругъ общей вершины О, мы для каждой суммы, во-первыхъ, обойдемъ по плоскости все пространство вокругъ точки О одинаковое число разъ и, во-вторыхъ, послѣдняя сторона угла ап совпадетъ съ послѣднею стороною угла Ът.
2°. Если же эти условія не выполнены, суммы считаются неравными, при чемъ та будетъ меньше, къ которой надо приложить еще нѣкоторый уголъ или нѣсколько угловъ, чтобы получить вторую сумму.
19. Замѣчаніе 2-е. Когда двѣ полупрямыя исходятъ изъ одной точки, то, строго говоря, онѣ образуютъ не одинъ уголъ, а два угла. Возьмемъ, напр., черт. 5-й и вообразимъ, что полупрямая ОА вращается вокругъ О до совпаденія съ полупрямой ОВ. Это вращеніе можетъ быть двоякое: или О А вращается по направленію движенія часовой стрѣлки, или же, наоборотъ, противъ движенія часовой стрѣлки. Если обратимъ вниманіе на часть плоскости, которую ОА проходитъ до совпаденія съ ОВ при первомъ вращеніи, то будемъ имѣть одинъ уголъ, образованный полупрямыми О А и ОВ и содержащій эту часть плоскости; если же обратимъ вниманіе на часть плоскости, проходимую О А до совпаденія съ ОВ при другомъ вращеніи, то получимъ другой уголъ, образованный тѣми же сторонами О А и ОВ, но содержащій эту другую часть плоскости. Эти два угла равны другъ ДРУгу лишь въ томъ случаѣ, когда полупрямыя О А и ОВ составляютъ одну прямую, т.-е. когда оба угла развернутые; въ остальныхъ случаяхъ углы эти не равны, но всегда въ суммѣ составляютъ полный уголъ. Обыкновенно, говоря объ углѣ АОВ, разумѣютъ только тотъ изъ двухъ угловъ, образованныхъ полупрямыми ОА и ОВ, который меньше развернутаго угла.
Свойство прямого угла.
20. Опредѣленія. Два угла (АОВ и ВОС, черт. И и черт. 12) наз. смежными, если одна сторона у нихъ общая, а двѣ другія стороны составляютъ продолженіе одна другой.
Изъ этого опредѣленія видно, что если возьмемъ произвольный уголъ (напр., АОВ, черт. 11) и продолжимъ одну его сто-
— 13 —
рону (напр., АО) за вершину, то получимъ другой уголъ (ВОС), смежный со взятымъ угломъ.
Черт. 12.
Общая сторона (ОВ) двухъ смежныхъ угловъ наз. наклонною къ прямой (АС), на которой лежатъ другія стороны, въ томъ случаѣ, когда смежные углы пе равны (черт. 11).
Общая сторона (ОВ) двухъ смежныхъ угловъ наз. перпендикуляромъ къ прямой, на которой лежатъ другія стороны, въ томъ случаѣ, когда смежные углы равны (черт. 12).
Въ первомъ случаѣ общая вершина (О) наз. основаніемъ наклонной, во второмъ случаѣ — основаніемъ перпендикуляра.
Говорятъ «возставить къ прямой перпендикуляръ», если этотъ перпендикуляръ приходится проводить черезъ точку, взятую на прямой, и «опустить па прямую перпендикуляръ», если онъ проводится черезъ точку, взятую внѣ прямой.
Каждый изъ равныхъ смежныхъ угловъ наз. прямымъ (черт. 12).
Что смежные углы могутъ быть равны, видно изъ слѣдующей теоремы.
21. Теорема. Изъ всякой точки прямой можно, по ту и другую сторону отъ этой прямой, возставить къ ней перпендикуляръ и притомъ только одинъ.
Пусть дана какая-нибудь прямая АВ (черт. 13) и на ней произвольная точка О. Требуется доказать, что: во 1) изъ этой точки можно, по каждую сторону отъ прямой АВ, возставить къ АВ
— 14 —
перпендикуляръ, и во 2) этотъ перпендикуляръ можетъ быть только одинъ (по каждую сторону отъ прямой).
1°. Проведемъ изъ точки О какую-нибудь полупрямую ОС. Тогда образуются 2 смежныхъ угла: АОС и СОВ. Если случится, что углы эти равны другъ-другу, то тогда ихъ общая сторона ОС будетъ перпендикуляромъ къ АВ-, если же углы АОС и СОВ окажутся неравными, то одинъ изъ нихъ долженъ быть меньше другого. Пусть АОС меньше СОВ. Тогда отъ большаго угла СОВ мы можемъ отдѣлить часть С'ОВ, равную р г углу АОС-, послѣ чего отъ
угла СОВ останется нѣко-! торый уголъ СОС'. Вообра-
і । зимъ, что этотъ уголъ раз-
дѣленъ пополамъ; пусть * ''' биссектрисса будетъ нѣкото-
А-------------------------В рая полупрямая ОЛ. Эта полу-
прямая и будетъ перпенди-Черт’ 13, куляромъ къ АВ, такъ какъ
смежные углы АОВ и БОВ, состоящіе изъ соотвѣтственно равныхъ частей (АОС=С'ОВ и СОБ=БОС), равны между собою.
2°. Всякая другая полупрямая ОБ', исходящая изъ Точки О и расположенная по ту же сторону отъ АВ, по которой лежитъ ОБ, не можетъ образовать съ АВ равныхъ смежныхъ угловъ, такъ какъ АОБ'^>АОБ, а Б'ОВ<^БОВ и, слѣд., углы АОБ’ и Б'ОВ не могутъ быть равны. Такимъ образомъ, нельзя возставить другого перпендикуляра къ АВ изъ точки О по ту сторону отъ АВ, по какой лежитъ перпендикуляръ ОБ.
Точно такъ же убѣдимся, что по другую сторону отъ АВ можно возставить изъ точки О перпендикуляръ къ АВ и притомъ только одинъ.
22. Теорема. Всѣ прямые углы равны между собою.
Пусть смежные углы при вершинахъ О и О' (черт. 14) прямые, т.-е. ^ЛАОВ=/_ВОС и Требуется
доказать, что прямые углы первой пары равны прямымъ угламъ второй пары.
— 15 —
Наложимъ фигуру АОВС на фигуру А^В^ такъ, чтобы точка О упала на Оь полупрямая ОС пошла по 0^! и чтобы полупрямая ОВ упала по ту же сторону отъ А^, по которой расположена 0^. Тогда полупрямыя ОА и ОіАх совмѣстятся,
С А
Черт. 14.
такъ какъ онѣ составляютъ продолженіе совпавшихъ полупрямыхъ ОС и ОхСі, полупрямая ОВ совпадетъ съ ОіВх, потому что въ противномъ случаѣ изъ одной точки Ог прямой А1С1 можно было бы возставить къ ней, по одну и ту же сторону, два перпендикуляра, что, по доказанному, невозможно. Если же полупрямыя ОВ и ОхВі совпадутъ, то это значитъ, что ^АОВ= =,І/А1О1В1 и 2/^ОВ=С1(71В1, что и требовалось доказать.
Замѣчаніе. Изъ доказанной теоремы слѣдуетъ, что прямой уголъ представляетъ собою постоянную величину (ее обыкновенно обозначаютъ знакомъ й, т.-е. начальною буквою французскаго слова бгоіі, прямой). Вслѣдствіе этого обыкновенно углы сравниваютъ по величинѣ съ прямымъ угломъ. Если уголъ меньше прямого (какъ уголъ АОС, черт. 15), то его называютъ острымъ, если же уголъ боль- р С
ше прямого (какъ уголъ АОВ, черт. \ /
15), то его называютъ тупымъ. \ /
23. Доказательство надо- \ / женіемъ. Пріемъ, которымъ мы \ /
доказывали предыдущую теорему, 0^"" А
наз. доказательствомъ посредствомъ наложенія. Чѳрт‘ 16,
Мы принимаемъ за очевидное, что
наложеніе одной пло-
— 16 —
ской фигуры на другую всегда можно выполнять въ такой послѣдовательности :
1°. Мы можемъ любую точку одной фигуры совмѣстить съ любою точкою другой фигуры; напр. (черт. 14), точку О съ Ог.
2°. По совмѣщеніи двухъ точекъ мы можемъ, вращая накладываемую фигуру вокругъ совпавшей точки, совмѣстить въ обѣихъ фигурахъ любыя двѣ полупрямыя, исходящія изъ совпавшихъ точекъ, напр. (черт. 14), ОС съ ОХСХ; тогда, конечно, совмѣстятся и продолженія этихъ полупрямыхъ, ОА съ ОХЛХ, т.-е. совмѣстятся прямыя АС и проходящія черезъ точки О и Ох.
3°. По совмѣщеніи двухъ точекъ и двухъ прямыхъ мы можемъ, вращая накладываемую фигуру вокругъ совпавшей прямой, какъ около оси, расположить эту фигуру или по ту, или по другую сторону отъ совпавшей прямой. Напр. (черт. 14), по совмѣщеніи точекъ О и Ох и прямыхъ АС и ЛХСХ, мы можемъ расположить фигуру АОВС или такъ, что полупрямая ОВ пойдетъ кверху отъ ОХС'Х, или же такъ, что она пойдетъ книзу отъ нея (въ послѣднемъ случаѣ будетъ такъ называемое п р и-л о ж е н і е фигуры).
Послѣ этого нашъ произволъ заканчивается; совпадутъ ли другія части фигуръ,—зависитъ отъ свойствъ самихъ фигуръ.
24. Черченіе прямого угла. Прямой уголъ легко на
чертить помощью прибора, называемаго наугольникомъ,
у котораго одинъ изъ трехъ угловъ дѣлается прямымъ. Чтобы начертить прямой уголъ при точкъ С прямой АВ (черт. 16),
можно поступить такъ: приставимъ къ этой прямой линейку,
а къ линейкѣ наугольникъ, какъ указано на чертежѣ, и будемъ двигать наугольникъ вдоль линейки до тѣхъ поръ, пока вершина прямого угла не совпадетъ съ точкой С. Остается затѣмъ провести по сторонѣ прямого угла прямую СВ.
— 17 —
Свойства смежныхъ и вертикальныхъ угловъ.
25. Теорема. Сумма двухъ смежныхъ угловъ равна двумъ прямымъ.
Даны два смежныхъ угла: АОВ и ВОС (черт. 17); требуется
доказать, что АОВ+ВОС=сІ+сІ—2^
Возставивъ изъ точки О къ прямой АС перпендикуляръ ОВ, мы разобьемъ уголъ АОВ на два угла АОВ и ВОВ.
Отнявъ отъ угла АОВ уголъ ВОВ, мы получимъ прямой уголъ АОВ-, прибавивъ къ углу ВОС тотъ же уголъ Черт. 17.
ВОВ, мы получимъ тоже прямой уголъ, именно ВОС. Но если
мы одно слагаемое уменьшимъ, а другое увеличимъ па одну и ту же величину, то сумма не измѣнится; значитъ, сумма АОВА-ВОС должна быть такая же, какъ и сумма АОВ+ВОС. Но эта сумма равна т.-е. 2й; значитъ, и АОВ-{-ВОС—2й.
26. Слѣдствія. 1°. Суммаугловъ (АОВ, ВОС, СОВ, ВОЕ, черт. 18), расположенныхъ вокругъ общей вершины (О) по одну сторону прямой
(АЕ), равна 2<1, потому что эту сумму можно разсматривать (согласно сочетательному свойству), какъ сумму двухъ смежныхъ угловъ, напр., угловъ АОВ и ВОЕ, или угловъ АОС и СОЕ, и т. п.
2 А. Киселевъ. Геометрія.
— 18 —
2°. Сумма угловъ (АОВ, ВОС, СОВ, ВОЕ, ЕОА, черт. 19), расположенныхъ вокругъ общей вершины (О) по обѣ стороны отъ какой-нибудь прямой (ВМ), равна 4й, потому что, сложивъ углы ВОС, СОВ и ВОМ, расположенные по одну сторону отъ прямой МВ, мы получимъ въ суммѣ 2й, и сложивъ углы МО А, АОЕ и ЕОВ, расположенные по другую сторону отъ МВ, мы въ суммѣ еще получимъ 2й; значитъ, сумма всѣхъ этихъ угловъ равна 2й4~2й, т.-е. 4й.
27. Обратная теорема. Если сумма двухъ угловъ, имѣющихъ общую вершину и общую сторону и не покрывающихъ другъ друга, равна двумъ прямымъ, то такіе углы—смежные, т.-е. двѣ другія стороны ихъ составляютъ продолженіе одна другой.
Пусть даны (черт. 20) два угла: АОВ и ВОС, имѣющіе общую вершину О и общую сторону ОВ и не покрывающіе другъ друга; пусть, кромѣ того, извѣстно, что сумма ихъ равна 2й; требуется доказать, что при этихъ условіяхъ ОС есть продолженіе АО.
Допустимъ противное (про-тивоположное) тому, что тре-буется доказать, а именно до-О ..._____Р пустимъ, что ОС не есть про-
А---------_ _ _ _ С
долженіе АО. Посмотримъ, къ
Черт. 20. чему приведетъ насъ это пред-
положеніе. Такъ какъ всякая прямая можетъ быть продолжена въ обѣ стороны, то и прямая АО можетъ быть продолжена за точку О. Пусть это продолженіе будетъ нѣкоторая полупрямая ОВ, которая, согласно нашему допущенію, не сливается съ ОС. Тогда углы АОВ и ВОВ будутъ смежные и потому, по доказанному прежде (25):
А0В-\-В0В=2в.
Съ другой стороны, согласно условію нашей теоремы:
А0В+В0С=2<1.
— 19 —
Правыя части этихъ двухъ равенствъ равны, слѣд., равны и лѣвыя (двѣ величины, равныя порознь одной и той же третьей величинѣ, равны между собою):
АОВ+ВОВ=АОВ+ВОС.
Отнявъ отъ равныхъ суммъ по одному и тому же углу АОВ, мы должны получить равные остатки:
ВОВ=ВОС.
Но это равенство невозможно, такъ какъ уголъ ВОС составляетъ часть угла ВОВ, а часть не можетъ равняться цѣлому.
Если въ результатѣ разсужденія мы получаемъ невозможный (нелѣпый) выводъ, то это можетъ произойти или отъ того, что мы невѣрно разсуждали, или отъ того, что наше разсужденіе было основано на невозможномъ допущеніи. Разсужденіе наше было правильно; значитъ, причина нелѣпаго вывода заключается въ невозможности допущенія, что ОС не есть продолженіе АО. Но если это предположеніе невозможно, то остается только одно: ОС есть продолженіе АО *); что и требовалось доказать.
Слѣдствіе. Если изъ како й-н ибудь точкиО прямой АВ (черт. 21) возставимъ къ ней, по
каждую ея сторону, перпендикуляры ОС и 0.0, то эти перпендикуляры образуютъ одну прямую СВ, потому что сумма угловъ СОВ и ВОВ равна 2й. А
28. Опредѣленіе. Прямая СВ (черт. 21), которой части ОС и ОВ служатъ перпендикулярами къ другой прямой АВ, наз. прямой, перпендикулярной къ АВ.
Черт. 21.
Если прямая СВ перпендикулярна къ прямой АВ, то и обратно: АВ перпендикулярна къ СВ, потому что части О А
) Слѣд., нашъ чертежъ сдѣланъ неправильно.
2*
— 20 —
и ОВ служатъ также перпендикулярами къ СВ. Поэтому прямыя АВ и СВ наз. взаимно перпендикулярными.
Что двѣ прямыя АВ и СВ взаимно перпендикулярны, выражаютъ письменно такъ: АВ±СВ.
29. Доказательство отъ противнаго. Способъ, которымъ мы доказали обратную теорему о смежныхъ углахъ (27), наз. доказательствомъ отъ противнаго, или приведеніемъ къ нелѣпости (гейисНо асі аЪзигйшп). Первое названіе этотъ способъ получилъ потому, что въ началѣ разсужденія дѣлается предположеніе, противное (противоположное) тому, что требуется доказать. Приведеніемъ къ нелѣпости онъ наз. вслѣдствіе того, что, разсуждая на основаніи сдѣланнаго предположенія, мы приходимъ къ нелѣпому выводу (къ абсурду). Полученіе такого вывода заставляетъ насъ отвергнуть сдѣланное въ началѣ допущеніе и принять то, которое требовалось доказать.
80. Опредѣленіе. Два угла наз. вертикальными, если стороны одного составляютъ продолженія сторонъ другого.
Такъ, при пересѣченіи двухъ прямыхъ АВ и СВ (черт. 22) образуются двѣ пары вертикальныхъ угловъ: АОВ и СОВ, АОС и ВОВ.
31. Теорема. Два вертикальныхъ угла равны.
Пусть даны (черт. 22) два вертикальныхъ угла: АОВ и СОВ\ другими словами, пусть дано, что ОВ есть А. /В продолженіе О А и ОС есть продолженіе ОВ.
\ / Требуется доказать, что АОВ=СОВ.
\ / Уголъ АОВ, сложенный съ угломъ ВОВ, составляетъ 2й (по свойству смежныхъ уг-Оу ловъ); уголъ СОВ, сложенный съ тѣмъ же
/\ угломъ ВОВ, составляетъ также 2й (по тому же / \ свойству). Значитъ, каждый изъ угловъ АОВ / \ и СОВ равенъ одной и той же разности 2Л—ВОВ-,
! \ поэтому углы эти равны.
1 В Подобнымъ же образомъ докажемъ, что и
Черт. 22. АОС=ВОВ.
32.Теорема. Изъ всякой точки, взятой внѣ прямой, можно опустить на эту прямую перпендикуляръ и притомъ только одинъ.
— 21 —
Пусть дана какая-нибудь прямая АВ (черт. 23) и внѣ ея точка М\ требуется доказать, что во 1) изъ этой точки можно опустить на прямую АВ перпендикуляръ и во 2) что этотъ перпендикуляръ можетъ быть і М
только одинъ.
1) Перегнемъ чертикъ по прямой АВ такимъ образомъ, чтобы верхняя его часть (со- д С \ р
держащая точку М) упала на нижшою часть *). Тогда точка
М займетъ нѣкоторое положеніе IV. Отмѣтивъ это положеніе, приведемъ чертежъ въ преж-ній видъ и затѣмъ черезъ точки 1
проведемъ прямую. До- Черт' 23,
кажемъ, что эта прямая перпендикулярна къ АВ. Для этого перегнемъ чертежъ вторично по прямой АВ. Тогда точка М снова совмѣстится съ IV, а точка С, въ которой пересѣкаются прямыя М^ и АВ, останется на мѣстѣ; слѣд., полупрямая СМ пойдетъ по полупрямой СН1?, уголъ МСВ, совмѣстится съ угломъ ВС1Ѵ, а уголъ МСА совмѣстится съ угломъ ЛСІѴ; значитъ, смежные углы МСВ и ВС^ равны, а также равны и смежные углы МСА и ЛСІѴ. Такъ какъ каждый изъ равныхъ смежныхъ угловъ наз. прямымъ, то всѣ 4 угла, образовавшіеся при точкѣ С, будутъ прямые; значитъ, М1Ѵ_ЬАВ.
2) Докажемъ теперь, что другого перпендикуляра черезъ точку М къ прямой АВ провести нельзя. Предположимъ противное, т.-е. что черезъ М къ АВ можно провести, кромѣ М1Ѵ, еще какой-нибудь другой перпендикуляръ, напр., МВ (черт. 24).
*) Выражаясь болѣе точно, вообразимъ, что верхняя часть плоскости чертежа, вращаясь вокругъ прямой АВ, пришла въ совмѣщеніе съ нижней частью этой плоскости.
— 22 —
Чтобы опровергнуть это допущеніе, перегнемъ чертежъ снова
по прямой АВ. Тогда точка М по прежнему совмѣстится съ
Черт. 24.
а точки В и С останутся на своихъ мѣстахъ; слѣд., уголъ МВВ займетъ положеніе ВВ1У. Разогнувъ чертежъ, расмотримъ линію МО.ІѴ. Такъ какъ, по предположенію, МВ X АВ, то уголъ МВВ долженъ быть прямымъ, а потому и равный ему уголъ ВВ^ также долженъ быть прямымъ. Но тогда мы будемъ имѣть два угла, МВВ и ВВ1У, которые, имѣя общую вершину и общую сторону, составляютъ въ суммѣ 2й; слѣд., по доказанному раньше
(27), двѣ ихъ стороны ВМ и ВН должны составлять продолже-
ніе одна другой, и, значитъ, линія МВ^ должна окапаться прямою. Но тогда черезъ точки М и будутъ проходить 2 раз
личныя прямыя линіи: одна МП, которую мы раньше провели, и другая МВ1Ѵ, которую мы получили теперь. Такъ какъ это невозможно (9), то нельзя допустить, чтобы черезъ точку М къ прямой АВ можно было провести еще какой-нибудь ппой перпендикуляръ, кромѣ М1Ѵ.
Замѣчаніе. Чтобы опустить перпендикуляръ на прямую изъ данной точки, можно пользоваться линейкой и наугольникомъ (см. черт. 16).
33. Симметричныя ТОЧКИ. Если точки М и X (черт. 24) расположены по разныя стороны отъ прямой АВ, на одномъ къ ней перпендикулярѣ и на одинаковомъ разстояніи отъ основанія этого перпендикуляра, то такія двѣ точки принято называть симметричными относительно оси АВ. Здѣсь слово «ось» примѣнено потому, что если мы часть плоскости, расположенную по одну сторону отъ прямой АВ, станемъ вращать вокругъ этой прямой, какъ вокругъ оси, до совмѣщенія ея съ частью плоскости, расположенною по другую сторону отъ АВ, то симметричныя точки М и X совмѣстятся.
— 23 —
Упражненія. Доказать, что:
1. Биссектриссы двухъ смежныхъ угловъ взаимно перпендикулярны.
2. Биссектриссы двухъ вертикальныхъ угловъ составляютъ продолженіе одна другой.
3. Если при точкѣ О прямой АВ (черт. 22) построимъ по разныя стороны отъ АВ равные углы АОВ и ВОС, то стороны ихъ ОВ и ОС составляютъ одну прямую (теорема, обратная теоремѣ § 31-го).
4. Если изъ точки О (черт. 22) проведемъ полупрямыя О А, ОВ, ОВ, ОС такъ, что ^АОС—^ВОВ и ^АОВ — ^СОВ, то ОВ есть продолженіе ОА и ОВ продолженіе ОС.
— 24 —
ГЛАВА II.
Треугольники и многоугольники.
Понятіе о многоугольникѣ и треугольникѣ.
34. Ломаная линія. Линія наз. ломаною, когда она состоитъ изъ отрѣзковъ прямой, не расположенныхъ на одной прямой (черт. 25 или 26). Эти отрѣзки наз. сторонами ломаной, а вершины угловъ, образуемыхъ сосѣдними отрѣзками,—в ершинами ея. Ломаная линія обозначается рядомъ буквъ, поставленныхъ у ея вершинъ и концовъ; напр., говорятъ: ломаная АВСВЕ (черт. 25 и 26).
Черт. 26.
Ломаную линію мы будемъ называть выпуклою, если она вся расположена по одну сторону отъ каждаго составляющаго ее отрѣзка, продолженнаго неопредѣленно въ обѣ стороны. Такова, напр., линія, изображенная на черт. 25-мъ, тогда какъ ломаная чертежа 26-го не будетъ выпуклой.
Когда концы ломаной сходятся въ одну точку, то она наз. замкнутой.
35. Многоугольникъ. Фигура, образованная замкнутою ломаной линіей (вмѣстѣ съ частью плоскости, ограниченною этою ломаною), наз. многоугольникомъ (черт. 27). Стороны этой ломаной наз. сторонами многоугольника, углы, составленные каждыми двумя сосѣдними сторонами,— углами многоугольника, а ихъ вершины—в ершинами
— 25 —
его. Сама ломаная линія, ограничивающая многоугольникъ, наз. контуромъ его.
Многоугольникъ наз. выпуклымъ, если онъ ограниченъ выпуклою ломаной линіей; таковъ, напр., многоуг. АВСВЕ, изображенный на черт. 27 (многоуг. МЕРфВ.8 нельзя назвать выпуклымъ).
Всякая прямая (какъ АВ, ВЕ, МВ...), которая соединяетъ вершины двухъ угловъ многоугольника, не прилежащихъ къ одной сторонѣ, наз. діагональю многоугольника.
Сумма всѣхъ сторонъ многоугольника наз. периметромъ его.
Два многоугольника, какъ вообще двѣ какія-нибудь геометрическія фигуры, считаются равными, если они при наложеніи могутъ быть совмѣщены *).
Наименьшее число сторонъ въ многоугольникѣ—три. По числу сторонъ многоугольникъ наз. треугольникомъ, четыреугольникомъ, пятиугольникомъ и т. п.
•) Фигуры, могущія совмѣститься при наложеніи, наз. к о н г р у-ентными, а самое совмѣщеніе —к онгруѳнціей. Различаютъ конгруенцію прямую и непрямую. Прямою кон-груенція наз. тогда, когда совмѣщеніе можетъ быть выполнено посредствомъ передвиженія одной изъ конгруентныхъ фигуръ по плоскости, въ которой фигуры лежатъ; если же для совмѣщенія фигуръ такого передвиженія недостаточно, но надо еще перевернуть одну изъ фигуръ другою стороною, то конгруенція наз. непрямою. Напр., тр-ки, изображенные на черт. 37-мъ, прямо конгруентны, а тр-ки АВС и 41В11С1 черт. 39-го непрямо конгруентны.
— 26 —
Для краткости слова: «многоугольникъ», «треугольникъ», «четыреугольникъ» и т. п. мы часто будемъ писать такъ: мн-къ, тр-къ, четыре-къ и т. п. Слово «треугольникъ» на письмѣ иногда замѣняется также знакомъ Д.
36. Раздѣленіе треугольниковъ. Треугольники раздѣляются или по сравнительной длинѣ ихъ сторонъ, или по характеру ихъ угловъ. Относительно длины сторонъ они бываютъ: разносторонніе (черт. 28), когда всѣ стороны различной длины, равнобедренные (черт. 29), когда двѣ стороны одинаковы, и равносторонніе (черт. 30), когда всѣ стороны равны.
Относительно характера угловъ треугольники бываютъ: остроугольные (черт. 28). когда всѣ углы острые,
Черт. 28. Черт. 29. Черт. 30.
прямоугольные (черт. 31), когда въ числѣ угловъ есть прямой, и тупоугольные (черт. 32), когда въ числѣ угловъ есть тупой *).
Въ прямоугольномъ треугольникѣ стороны, образующія пря-
Черт. 31. Черт. 32.
мой уголъ, наз. катетами, а сторона, лежащая противъ прямого угла,—гипотенузой.
•) Возможность существованія всѣхъ этихъ видовъ треугольника легко показать теперь же, за исключеніемъ треугольника равносторонняго, существованіе котораго можно обнаружить только впослѣдствіи.
— 27 —
37. Главнѣйшія линіи въ треугольникѣ. Одну изъ сторонъ треугольника обыкновенно называютъ основаніемъ, вершину противоположнаго угла — вершиною тр-ка, а перпендикуляръ, опущенный изъ вершины на основаніе или на его продолженіе, — высотою его. Такъ, если въ тр-кѣ АВС (черт. 33 или 34) за основаніе взята сторона АС, то В будетъ вершина, ВВ—высота тр-ка.
Въ равнобедренномъ тр-кѣ основаніемъ называютъ обыкновенно ту сторону, которая не принадлежитъ къ равнымъ; тогда вершина равнобедреннаго тр-ка будетъ вершина того угла его, который образованъ равными сторонами.
Конечная прямая ВЕ (черт. 33 и 34), соединяющая вершину какого-нибудь угла тр-ка съ серединою противоположной стороны, наз. среднею линіей или медіаною. Конечная прямая ВЕ (черт. 33 и 34), дѣлящая какой-нибудь уголъ тр-ка пополамъ, наз. равно дѣлящею угла тр-ка или его биссектриссою (биссектрисса вообще не совпа-
Черт. 33. Черт. 34.
даетъ ни съ медіаною, ни съ высотою). Во всякомъ тр-кѣ есть три медіаны, три биссектриссы и три высоты (опущенныя на каждую изъ трехъ сторонъ).
Свойства равнобедреннаго треугольника.
38. Теорема. Въ равнобедренномъ треугольникѣ биссектрисса угла при вершинѣ служитъ одновременно и медіаной, и высотой.
Пусть тр-къ АВС (черт. 35) равнобедренный и прямая ВВ дѣлитъ пополамъ уголъ В при вершинѣ его. Требуется доказать, что эта биссектрисса ВВ есть также и медіана, и высота. Вообра-
— 28 —
зимъ, что Д.АВБ повернутъ вокругъ стороны ВБ, какъ около оси, такъ, чтобы опъ упалъ на ДВБС. Тогда, вслѣдствіе равенства угловъ 1 и 2, сторона АВ упадетъ на ВС, а вслѣдствіе равенства этихъ сторонъ точка А совпадетъ съ С. Поэтому БА совмѣстится съ БС и уголъ 4 съ угломъ 3; значитъ, БА=БС и Изъ того, что
БА=БС, слѣдуетъ, что ВБ есть медіана; изъ того, что углы 3 и 4 равны, выходитъ, что эти углы прямые, и слѣд., ВБ есть высота тр-ка АВС.
39. Слѣдствіе 1-е. Такъ какъ, С то доказанному, биссектрисса ВБ представляетъ собою и медіану, и высоту, то
Черт. 35. можно сказать, что она есть также и перпендикуляръ къ основанію АС, возстановленный изъ его середины Б.
Такимъ образомъ, въ равнобедренномъ тр-кѣ АБС (черт. 35) одна и та же прямая ВБ служитъ одновременно: 1) биссектрис-сою угла при вершинѣ, 2) медіаною, проведенною къ основанію, 3) высотою, опущенною на основаніе, и, наконецъ, 4) перпендикуляромъ къ основанію, возстановленнымъ изъ его середины. Такъ какъ каждое изъ этихъ 4-хъ свойствъ вполнѣ опредѣляетъ положеніе прямой ВБ, то существованіе одного изъ нихъ влечетъ за собой всѣ остальныя. Напр., высота равнобедрен
наго треугольника, служитъодновременно биссектриссою, медіаною и перпендикуляромъ къ основанію въ его серединѣ. Дѣйствительно, во-1-хъ, эта высота должна служить биссектриссою, потому что въ противномъ случаѣ, проведя такую бис-сектриссу, мы имѣли бы двѣ различныя высоты на одну и ту жу сторону тр-ка, что невозможно. Во-2-хъ, эта высота, будучи биссектриссою, должна быть, по доказанному, медіаной и, слѣд., перпендикуляромъ къ основанію въ его серединѣ.
40. Слѣдствіе 2-е. Изъ того, что тр-ки АВБ и ВБС (черт. 35) совмѣщаются всѣми своими частями, слѣдуетъ, что т-“е-
въ равнобедренномъ треугольникѣ углы при основаніи равны.
— 29 —
41. Понятіе Объ ОСИ симметріи. Мы видѣли, что равнобедренный ДАВС (черт. 36) дѣлится биссектриссою ВО на такіе 2 тр-ка (лѣвый и правый), которые вращеніемъ вокругъ биссектриссы, какъ около оси, могутъ быть совмѣщены другъ съ другомъ. Изъ этого можно заключить, что какую бы точку на лѣвой половинѣ равнобедреннаго тр-ка мы ни взяли, всегда можно на правой его половинѣ найти другую точку, симметричную первой относительно оси ВО (33).
Возьмемъ, напр., па сторонѣ АВ какую-нибудь точку М. Опустимъ изъ нея на ВО перпендикуляръ МК и продолжимъ его до пересѣченія со стороною ВС. р
Мы получимъ тогда на этой сторонѣ а
точку М', симметричную точкѣ М отно- /\
сительно оси ВО. Дѣйствительно, если, / \
вращая ДАВО вокругъ ВО, мы его совмѣ- .. / і/\ іИ стимъ съ ДВСО, то при этомъ КМ пойдетъ К1А.---<>"*
по КМ' (по равенству прямыхъ угловъ), / \
а сторона ВА упадетъ на сторону ВС (по / \
равенству угловъ при точкѣ В)\ значитъ, / \
точка М, которая лежитъ и на КМ, и на ВА, /___________\ р
упадетъ въ точку М', которая лежитъ и ** ) **
на КМ', и на ВС. Отсюда видно, что Черт 36
КМ= КМ'. Такимъ образомъ, точки М и М' лежатъ по разныя стороны отъ биссектриссы ВО, на одномъ къ ней перпендикулярѣ и на равныхъ разстояніяхъ отъ основанія этого перпендикуляра; значитъ, эти точки симметричны относительно оси В.
Если въ какой-нибудь геометрической фигурѣ существуетъ прямая, которая раздѣляетъ эту фигуру на такія 2 части, что любой точкѣ на одной части соотвѣтствуетъ на другой точка, симметричная относительно этой прямой, то такая прямая наз. осью симметріи этой фигуры.
Въ равнобедренномъ треугольникѣ бисѳк-трисса угла при вершинѣ есть его ось симметріи.
Въ геометріи мы будемъ иногда встрѣчаться съ фигурами, имѣющими одну или нѣсколько осей симметріи.
Симметрія относительно оси наз. часто «осевая симметрія» (въ отличіе отъ «центральной» симметріи, о которой говорится ниже, въ § 102).
Признаки равенства треугольниковъ.
42. Предварительныя понятія. Такъ какъ равными треугольниками наз. такіе, которые при наложеніи могутъ быть совмѣщены, то въ такихъ тр-кахъ равны всѣ соотвѣтствующіе элементы ихъ, т.-е. стороны, углы, высоты, медіаны и биссектриссы.
— 30 —
Однако для того, чтобы утверждать равенство двухъ треугольниковъ, не необходимо знать равенство всѣхъ элементовъ ихъ; достаточно убѣдиться въ равенствѣ только нѣкоторыхъ изъ нихъ. Слѣдующія теоремы излагаютъ три главнѣйшіе признака равенства тр-ковъ.
43.Теоремы. Два треугольника равны:
1°, если двѣ стороны и уголъ, заключенный между ними, одного треугольника соотвѣтственно равны двумъ сторонамъ и углу, заключенному между ними, другого треугольника;
или 2°, если два угла и прилежащая къ нимъ сторона одного треугольника соотвѣтственно равны двумъ угламъ и прилежащей къ нимъ сторонѣ другого треугольника;
или 3°, если три стороны одного треугольника соотвѣтственно равны тремъ сторонамъ другого треугольника.
1°. Пусть АВС и ЯіВіСі два тр-ка (черт. 37), у которыхъ: А=Аі, АС=А1С1, АВ^=А1В1.
Требуется доказать, что эти тр-ки равны.
Черт. 37.
Наложимъ ДЯВС на ^АуВ^і такъ, чтобы точка А совпала съ Аі и сторона АС пошла по АХСГ *). Тогда вслѣдствіе равенства этихъ сторонъ, точка С совмѣстится съ С^, вслѣдствіе равенства угловъ А и Ах сторона АВ пойдетъ по а вслѣдствіе равенства этихъ сторонъ точка В упадетъ въ В^, поэтому сторона СВ совмѣстится съ СіВі (между двумя точками можно провести только одну прямую), и треугольники совпадутъ; значитъ, они равны.
*) Для выполненія указанныхъ въ этомъ параграфѣ наложеній иногда приходится треугольникъ АВС перевернуть другою стороною.
— 31 —
2°. Пусть АВС и ЛХВХСХ (черт. 38) два тр-ка, у которыхъ: СВ^іВі, С=СУ и В=ВХ.
Требуется доказать, что эти тр-ки равны.
Наложимъ ДАВС на ДЛХВХСХ такъ, чтобы точка С совпала съ Сі, и сторона СВ пошла по СХВХ. Тогда, вслѣдствіе равенства этихъ сторонъ, точка В упадетъ въ Вх, а вслѣдствіе ра-
Черт. 38.
венства угловъ В и Вх, С и Сх сторона ВА пойдетъ по ВХЛХ, и сторона СА по СХЛХ. Такъ какъ двѣ прямыя могутъ пересѣчься только въ одной точкѣ, то вершина А должна совпасть съ Их. Такимъ образомъ, тр-ки совмѣстятся; значитъ, они равны.
3°. Пусть АВС и ЛХВХСХ (черт. 39) два тр-ка, у которыхъ: ЛВ=ЛХВХ, ВС=В1С1 и СА=С1А1.
Требуется доказать, что эти тр-ки равны.
Доказывать этотъ признакъ равенства наложеніемъ, какъ мы это дѣлали для первыхъ двухъ признаковъ, было бы неудобно, такъ какъ, не зная ничего о величинѣ угловъ, мы не можемъ утверждать, что при совпаденіи двухъ равныхъ
— 32 —
сторонъ совпадутъ и остальныя стороны. Вмѣсто наложенія примѣнимъ здѣсь приложеніе.
Приложимъ /\АВС къ /\А1В1С1 такъ, чтобы у нихъ совмѣстились равныя стороны АС и А^. Тогда ДАВС займетъ положеніе А^Вц. Соединивъ прямою точки Вх и Ви, мы получимъ два равнобедренные тр-ка А^Вц и В^Вц съ общимъ основаніемъ ВХВП. Но въ равнобедренномъ треугольникѣ углы при основаніи равны (40); слѣд., ^/1=^/2 и а потому
/А-^В-^х— /А^ВГ^Г=/В. Новъ такомъ случаѣ данные тр-ки должны быть равны, такъ какъ двѣ стороны и уголъ, заключенный между ними, одного тр-ка равны соотвѣтственно двумъ сторонамъ и углу, заключенному между ними, другого треугольника.
Можетъ случиться, что прямая ВХВХ1 не пересѣчется съ Лх С1, а пойдетъ внѣ треугольниковъ (если сумма угловъ С и Си больше 2і), или сольется съ линіей Вх Сх Ви (если С + Сх = 26). Доказательство остается то же самое, съ тою только разницей, что углы Вг и Вп будутъ равны другъ другу, не какъ суммы равныхъ угловъ, а какъ ихъ разности, (черт. 40), или какъ углы при основаніи равнобедреннаго тр-ка (черт. 41).
Черт. 41.
Замѣчаніе. Въ равныхъ тр-кахъ противъ равныхъ сторонъ лежатъ равные углы и противъ равныхъ угловъ лежатъ равныя стороны.
Соотношенія между углами и сторонами треугольника.
44. Опредѣленіе. Уголъ, смежный съ какимъ-нибудь угломъ треугольника (или многоугольника), наз. внѣшнимъ угломъ этого треугольника (или многоугольника).
— 33 —
При каждомъ углѣ тр-ка (и мн-ка) можно построить по 2 р а в-
н ы х ъ смежныхъ угла. Напр., продолживъ стороны угла А (черт. 42) тр-ка АВС за вершину, мы получимъ два внѣшнихъ угла ВАВ и САЕ, которые равны между собою, какъ углы кальные.
верти-
Въ отличіе отъ нихъ углы самого (или мн-ка) наз. тренними.
45. Теорема,
больше каждаго внутренняго угла, не
внѣш- ® ~ тр-ка вну-
Въ треугольникѣ
Черт. 42.
всякій внѣшній уголъ смежнаго съ нимъ.
Е
Напр., докажемъ, что внѣшній уголъ ВСВ тр-ка АВС (черт. 43) больше каждаго изъ внутреннихъ угловъ А и В, не смежныхъ съ этимъ внѣшнимъ. Для этого черезъ средину Е стороны ВС проведемъ медіану АЕ и продолжимъ ее на длину ЕЕ, равную АЕ. Соединимъ Е съ С. Тр-ники АВЕ и ЕЕС (покрытые штрихами) равны, такъ какъ при точкѣ Е они имѣютъ по равному углу, заключенному между двумя соотвѣтственно равными сторонами. Изъ равенства ихъ заключаемъ, что углы В и ЕСЕ, лежащіе противъ равныхъ сторонъ АЕ и ЕЕ, равны; но уголъ ЕСЕ, составляя часть внѣшняго угла ВСВ, меньше его; слѣд., и уголъ В меньше ВСВ.
Продолживъ сторону ВС за точку С, мы получимъ внѣшній уголъ АСН, равный углу ВСВ. Если изъ вершины В проведемъ къ сторонѣ АС медіану и продолжимъ ее на такую же длину за сторону АС, то совершенно такъ же докажемъ, что уголъ А меньше АСН, т.-е. меньше ВСВ.
Черт. 43.
А. Киселевъ. Геометрія.
3
— 34 —
46. Слѣдствіе. Если въ треугольникѣ одинъ уголъ прямой или тупой, то два другіе угла острые.
Дѣйствительно, допустимъ, что какой-нибудь уголъ С тр-ка АВС (черт. 44) будетъ прямой или тупой; тогда смежный съ нимъ внѣшній уголъ ВСВ долженъ быть прямой или острый; вслѣдствіе этого углы А и В, которые, по доказанному, меньше внѣшняго угла, должны быть оба острые.
47. Теоремы. Во всякомъ треугольникѣ: 1°, противъ равныхъ сторонъ лежатъ равные углы; 2°, противъ ббльшей стороны лежитъ ббльшій уголъ.
1°. Если двѣ стороны треугольника равны, то онъ равнобедренный; тогда углы, лежащіе противъ этихъ сторонъ, должны быть равны, какъ углы при основаніи равнобедреннаго тре-
2°. Пусть въ ДАВС (черт. 45) сторона АВ больше ВС-, требуется доказать, что больше
Отложимъ на ббльшей сторонѣ ВА отъ вершины В часть ВБ, равную меньшей сторонѣ ВС, и соединимъ В съ С. Тогда получимъ равнобедренный /\ВВС, у котораго углы при основаніи равны, т.-е. 2/ВВС= ~ /ВСВ. Но уголъ ВВС, какъ внѣш
ній по отношенію къ ДЛВС, больше угла А-, слѣдовательно, и уголъ ВСВ больше А, а потому и подавно уголъ ВС А больше угла Л; что и требовалось доказать.
угольника (40).
Черт. 45.
— 35 —
48. Слѣдствія. 1°. Въ равностороннемъ треугольникѣ всѣ углы равны;
2°, въ разностороннемъ треугольникѣ нѣтъ равныхъ угловъ.
49. Обратныя теоремы. Во всякомъ треугольникѣ 1°, противъ равныхъ угловъ лежатъ ц
равныя стороны; 2°, противъ ббль- А
шаго угла лежитъ большая сторона. / \
1°. Пусть въ ДАВС углы А и С / \
равны (черт. 46); требуется дока- / \
зать, что АВ=ВС.— Предполо- / \
жимъ противное, т.-е., что стороны у \
АВ и ВС не равны. Тогда одна изъ А С
этихъ сторонъ должна быть боль- Черт. 46.
ше другой, и, слѣд., согласно
прямой теоремѣ, одинъ изъ угловъ А и С долженъ быть больше другого. Но это противорѣчитъ условію, что А=С; значитъ, нельзя допустить, что стороны АВ и ВС не равны; остается принять, что АВ=ВС.
2°. Пусть въ тр-кѣ АВС (черт. 47) уголъ С больше угла А; требуется доказать, что АВ^>ВС.—Предположимъ противное, т.-е. что АВ не больше ВС. Тогда могутъ представиться два случая: или АВ=ВС, или АВ<^ВС. Въ первомъ случаѣ, согласно прямой теоремѣ, уголъ С былъ бы равенъ углу А, во второмъ случаѣ уголъ С былъ бы меньше А; и то, и другое противорѣчитъ условію; значитъ, оба эти случая исключаются. ®
Остается одинъ возможный случай, /\
что АВ>ВС. / \
50. Слѣдствія. 1°. Равноуголъ- / \
ный треугольникъ есть и равносто- / \
ронній. / \
2°. Въ треугольникѣ сторона, ле- / \
жащая противъ тупого или прямого А ~ 1С
угла, больше другихъ сторонъ (46). Черт 47.
51. Замѣчаніе объ обратныхъ теоремахъ. Относительно равенства или неравенства двухъ сторонъ тре-8*
— 36 —
угольника, напр., сторонъ АВ и ВС, могутъ представиться только слѣдующіе три возможные случая:
АВ=ВС, АВ>ВС, АВ<ВС.
Каждый изъ этихъ случаевъ исключаетъ собою всѣ остальные; такъ, если имѣетъ мѣсто 1-й случай, что АВ=ВС, то одновременно съ нимъ не могутъ существовать ни 2-й случай, ни 3-й. Въ теоремѣ § 47 мы разсмотрѣли всѣ эти случаи; оказалось, что въ каждомъ изъ нихъ получаются такіе выводы относительно равенства или неравенства противолежащихъ угловъ С и А (именно: С=А, С^>А, С<^Л), изъ которыхъ каждый исключаетъ собою всѣ остальныя. И мы видѣли (49), что обратныя предложенія оказались вѣрными, въ чемъ было легко убѣдиться доказательствомъ отъ противнаго.
Вообще, если въ теоремѣ, или въ рядѣ теоремъ, мы разсмотрѣли всевозможные взаимно исключающіе случаи, которые могутъ представиться относительно величины или расположенія нѣкоторыхъ частей фигуры, при чемъ оказалось, что въ этихъ случаяхъ получаются различные взаимно исключающіе выводы относительно величины или расположенія нѣкоторыхъ другихъ частей фигуры, то мы можемъ заранѣе (а ргіогі)утверждать,что обратныя предложенія вѣрны.
Впослѣдствіи мы неоднократно будемъ встрѣчаться съ этимъ закономъ обратимости.
Сравнительная длина объемлющихъ и объемлемыхъ ломаныхъ линій.
52. Теорема. Въ треугольникѣ каждая сторона меньше суммы двухъ другихъ сторонъ.
Данъ тр-къ АВС (черт. 48); требуется доказать, что любая сторона его, напр., сторона АС, меньше суммы двухъ другихъ сторонъ.
— 37 —
В
Черт. 48.
Если сторона АС равна или меньше какой-нибудь изъ двухъ другихъ сторонъ, то тогда, очевидно, АС<С.АВ+ВС. Значитъ, намъ надо разсмотрѣть только тотъ случай, когда АС есть наибольшая изъ трехъ сторонъ.
Продолживъ сторону АВ, отложимъ ВБ—ВС и проведемъ БС. Такъ какъ Л ВБС равнобедренный, А то ^/Б=^/БСВ-, поэтому уголъ Б меньше угла БСА, и слѣд., въ
ДЛВС сторона АС меньше АБ (49), т.-е. АС<АВ+ВБ. Замѣнивъ ВБ на ВС, получимъ:
АС<АВ+ВС.
Слѣдствіе. Если АС есть наибольшая изъ сторонъ, то мы можемъ отъ обѣихъ частей выведеннаго неравенства отнять по АВ или по ВС-, тогда получимъ:
АС—АВ<ВС и АС—ВС<АВ.
Читая эти неравенства справа налѣво, видимъ, что каждая изъ сторонъ ВС и АВ больше разности двухъ другихъ сторонъ; такъ какъ это же можно, очевидно, сказать и о третьей, наибольшей сторонѣ АС, то заключаемъ:
въ треугольникѣ каждая сторона больше разности двухъ другихъ сторонъ.
53. Теорема. Отрѣзокъ прямой, соединяющій двѣ какія-нибудь точки, короче всякой ломаной, проведенной между этими точками.
Пусть (черт. 49) АЕ есть отрѣзокъ прямой, соединяющій точки А и Е, а АВСБЕ какая-нибудь ломаная, проведенная между тѣми же точками. Требуется доказать, что АЕ короче суммы АВ+ВС+СБ+БЕ.
Соединивъ А съ С и Б, находимъ, согласно предыдущей теоремѣ:
аб<ас+сб-, АС<АВ+ВС.
— 38 —
Сложимъ почленно эти неравенства и затѣмъ отъ обѣихъ частей полученнаго неравенства отнимемъ по АБ и АС; тогда получимъ:
АЕ<АВ+ВС+СБ+БЕ.
54. Опредѣленіе. Если между двумя точками А и Б (черт. 50) по одну сторону отъ прямой АБ проведены такія двѣ ломаныя линіи, что одна изъ нихъ — АВСБ — вся заключена внутри фигуры, образованной другою линіей — АЕЕСБ — съ отрѣзкомъ прямой АБ, то первая ломаная наз. о б ъ е м л е-м о й, а вторая объемлющей.
55. Теорема. Выпуклая ломаная короче всякой другой ломаной, объемлющей ее.
Пусть (черт. 50) АВСБ есть вы-„ п у к л а я (34) ломаная, а АЕГСБ
/ ''У "і какая-нибудь другая ломаная (вы-
/ \ пуклая или невыпуклая — все
// \\ равно), объемлющая первую; тре-
-----------------------буется доказать, что:
А У АВ+ВС+СБ<АЕ+ЕЕ+
ЧерТ. 50. +ЕС + Ш).
Продолживъ стороны выпуклой линіи, какъ указано на чертежѣ, можемъ написать слѣдующія неравенства (53):
АВ+ВН<АЕ+ЕН ВС+СК<ВН+НЕ+ЕС+СК СБ<СК+КБ.
Сложимъ почленно всѣ эти неравенства и затѣмъ отъ обѣихъ частей полученнаго неравенства отнимемъ вспомогательные отрѣзки ВН и СК; далѣе замѣнимъ сумму ЕН+НГ черезъ ЕЕ и сумму СК+КБ черезъ ОБ; тогда получимъ то неравенство, которое требовалось доказать.
56. Теорема Если выпуклый многоугольникъ заключенъ весь внутри какого-нибудь другого многоугольника, то периметръ перваго меньше периметра второго.
— 39 —
Пусть АБСБ (черт. 51) есть выпуклый многоуголь
никъ, а БМР'Р(^В какой-нибудь (выпуклый или невыпуклый), внутри котораго заключенъ первый. Требуется доказать, что АВ + ВС + СБ + БА меньше ЬМ+1!№+№+Р(Э+дВ+ВЬ.
Продолживъ въ обоихъ направленіяхъ одну какую-нибудь сторону АБ выпуклаго мн-ка, примѣнимъ къ ломанымъ линіямъ АВСБ и АТМХРдВЗБ, проведеннымъ между точками А и Б, теорему предыдущаго параграфа:
другой многоугольникъ
Черт. 51.
АВ + ВС + СБ< АТ + ТМ + МіѴ + №+Р(2+дВ+ІІі8+8Б.
Съ другой стороны, такъ какъ отрѣзокъ 8Т короче ломаной 8БТ, то можемъ написать:
А Т+АБ+Б8<ТЬ+Ь8.
Сложимъ почленно эти два неравенства и отнимемъ отъ обѣихъ частей вспомогательные отрѣзки АТ и Б8; затѣмъ замѣнимъ сумму ТЪ-РТМ черезъ БЫ и сумму В8+В.8 черезъ ЪВ,\ тогда получимъ то, что требовалось доказать.
57. Замѣчаніе. Двѣ предъидущія теоремы перестаютъ быть вѣрными, если объемле-мая ломаная или объемлемый многоугольникъ не выпуклые. Такъ, на черт. 52-мъ объ-емлемая ломаная, проведенная между точками А и В, можетъ оказаться длиннѣе объемлющей, проведенной между тѣми же точками.
Черт. 52.
— 40 —
Треугольники съ двумя соотвѣтственно равными сторонами.
58. Теоремы. 1°. Если двѣ стороны одного треугольника соотвѣтственно равны двумъ сторонамъ другого треугольника, а углы, заключенные между этими сторонами, не равны, то противъ ббльшаго изъ этихъ угловъ лежитъ ббльшая сторона.
2°. (Обратная). Если двѣ стороны одного треугольника соотвѣтственно равны двумъ сторонамъ другого треугольника, а третьи стороны не равны, то противъ большей изъ этихъ сторонъ лежитъ ббльшій уголъ.
1°. Пусть въ тр-кахъ АВС и А^Сі (черт. 53) дано:
АС=А1С1, АВ^А^; но А^Аі.
Требуется доказать, что если то и ВС^>В1С1, а если
Л<С4Ь т0 и ВС<ВСХ.— Предположимъ, что Л^>ЛХ. Нало-
черт. бз.
жимъ Д АіВіСі на Д АВС такъ, чтобы сторона А^ совпала съ АС. Такъ какъ, согласно предположенію, А^>Аг, то сторона АіВі пойдетъ внутри угла А, и А А^Сі займетъ нѣкоторое положеніе АВиС (при чемъ вершина Вхх можетъ лежать или внѣ А АВС, какъ изображено на нашемъ чертежѣ*), или внутри его, или же на сторонѣ ВС; доказательство остается одно и то же во всѣхъ этихъ случаяхъ). Проведемъ биссектриссу угла ВАВи до пересѣченія со стороною ВС въ точкѣ Л и эту точку соединимъ прямою съ Вхх; тогда получимъ два тр-ка АВБ и
*) На чертежѣ вмѣсто буквы В„ ошибочно поставлена буква Ь.
— 41 —
ВАВ1Ъ которые равны, потому что у нихъ: АВ общая сторона, АВ=АВи по условію и^ВЛВ=^РЛВи, такъ какъ прямая АВ дѣлитъ пополамъ уголъ ВАВи. Изъ равенства тр-ковъ слѣдуетъ: ВВ=ВВи. Теперь изъ Д ВСВи выводимъ: ВцВ+ВСУВцС (52), или (замѣнивъ ВиВ на ВВ):
ВВ+ВСУВ^С, т.-е. ВСУВ^.
Если допустимъ, что А<^Аг, то такъ же докажемъ, что тогда ВС<В1С'1.
2°. Пусть въ тѣхъ же треугольникахъ дано:
АВ=А1В1, АС=А1С1, но ВС^В^.
Требуется доказать, что если ВСУВ^, то и 20>Лх, если же ВС<ВіСх, то и А<Аі-— Предположимъ, что ВСУВ^Сі, докажемъ, что аУаг. Допустимъ противное, что А не больше Аг\ тогда могутъ представиться два случая: или А=А1г или А^А^ Въ первомъ случаѣ тр-ки были бы равны и, слѣд., сторона ВС равнялась бы В^, что противорѣчитъ условію; во второмъ случаѣ сторона ВС, согласно теоремѣ 1°, была бы меньше В^, что также противорѣчитъ условію. Значитъ, оба эти случая исключаются; остается одинъ возможный случай, что аУАг.
Если допустимъ, что ВС<ВхСх, то такъ же докажемъ, что тогда и А<^Аг.
ГЛАВА III.
Перпендикуляры и наклонныя.
59 ,1. Теорема. Перпендикуляръ, опущенный изъ точки напрямую, короче всякой наклонной, проведенной изъ той же точки на эту прямую.
Пусть АВ (черт. 64) есть перпендикуляръ, опущенный изъ точки А на прямую М1Ѵ, и АС какая-нибудь наклонная, проведенная изъ той же точки А къ прямой М1Я. Требуется доказать, что АВ < АС.— Въ А АВС уголъ В прямой, а противъ прямого угла лежитъ бблыпая сторона (50 ,2°); слѣд., АСУАВ.
— 42 —
Замѣчаніе. Когда говорятъ: «разстояніе точки отъ прямой», то разумѣютъ разстояніе, измѣряемое по перпендикуляру, опущенному изъ этой точки на прямую.
59, 2. Теорема. Если изъ одной и той же точки, взятой внѣ прямой, проведены къ этой прямой перпендикуляръ и какія-нибудь наклонныя, то:
1°, если основанія двухъ наклонныхъ одинаково удалены отъ основанія перпендикуляра, то такія наклонныя равны;
2°, если основанія двухъ наклонныхъ не одинаково удалены отъ основанія перпендикуляра, то та изъ наклонныхъ больше, которой основаніе дальше отстоитъ отъ основанія перпендикуляра.
1°. Пусть АС и ЛР (черт. 54) будутъ двѣ такія наклонныя, прямой МЕ, которыхъ основанія С и Р одинаково удалены отъ основанія перпендикуляра АВ, т.-е. СВ = ВР; требуется доказать, что ЛС=ЛР.ДВъ тр-кахъ АВС и АВВ есть общая сторона АВ и сверхъ того ВС=ВВ (по условію) и / АВС — / АВВ (какъ углы прямые); значитъ, эти тр-ки равны, и потому АС=АВ.
2°. Пусть АС и АЕ (черт. 54) будутъ двѣ такія наклонныя, проведенныя изъ точки А къ прямой 2Ю7, которыхъ основанія неодинаково удалены отъ основанія перпендикуляра АВ- напр., пусть ВЕ^>ВС-, требуется доказать, что АЕ^>АС.—Отложимъ ВВ=ВС и проведемъ АВ. По доказанному выше, АВ=АС. Сравнимъ АЕ съ АВ. Уголъ АВЕ есть внѣшній по отношенію А АВВ и потому онъ больше прямого угла ЛВР; слѣд., ХЛРВ тупой; но въ А противъ тупого угла должна лежать бблыпая сторона (50, 2°); значитъ, АЕ>АВ и, слѣд., АЕ^>АС.
60. Обратныя предложенія. Въ предыдущей теоремѣ разсмотрѣны всевозможные взаимно исключающіе случаи относительно равенства или неравенства разстояній основаній наклонныхъ отъ основанія перпендикуляра; при этомъ получились взаимно исключающіе выводы относительно равенства или
проведенныя изъ точки л къ
А
Черт. 54.
— 43 —
неравенства наклонныхъ; вслѣдствіе этого обратныя предложенія должны быть вѣрны (51), а именно:
Если изъ одной и той же точки, взятой внѣ прямой (черт. 54), проведены къ этой прямой перпендикуляръ и какія-нибудь наклонныя, то:
1°, если двѣ наклонныя равны, то ихъ основанія одинаково удалены отъ основанія перпендикуляра;
2°, если двѣ наклонныя не равны, то основаніе ббльшей изъ нихъ дальше отстоитъ отъ основанія перпендикуляра.
Предоставляемъ учащимся самимъ доказать эти предложенія (способомъ отъ противнаго).
Равенство прямоугольныхъ треугольниковъ.
61. Такъ какъ въ прямоугольныхъ тр-кахъ углы, содержащіеся между катетами, всегда равны, какъ прямые, то:
Прямоугольные треугольники равны:
1°, если катеты одного треугольника соотвѣтственно равны
катетамъ другого;
или 2°, если катетъ и прилежащій къ нему острый уголъ одного треугольника равны соотвѣтственно катету и прилежа
щему къ нему острому углу другого треугольника.
Эти два признака не требуютъ особаго доказательства, такъ
какъ они представляютъ лишь частные случаи общихъ признаковъ (43, 1° и 2°). Докажемъ еще два слѣдующіе признака, относящіеся только къ прямоугольнымъ треугольникамъ.
62. Теоремы. Прямоугольные треугольники равны:
1°, если гипотенуза и
острый уголъ одного треугольника соотвѣтственно равны гипотенузѣ и острому углу другого;
или 2°, если гипотенуза и катетъ одного треугольника соотвѣтственно равны гипотенузѣ и катету другого.
1°. Пусть АВС и АіВіСі (черт. 55) два прямоугольные тр-ка, у которыхъ: АВ=А1В1 и А=Аг-, требуется доказать, что эти
— 44 —
тр-ки равны.— Наложимъ Л АВС на Л А^Сх такъ, чтобы у нихъ совмѣстились равныя гипотенузы. Тогда по равенству угловъ А и Аг катетъ АС пойдетъ по А^. При этомъ точка С должна совмѣститься съ точкой Сь потому что если предположимъ, что она упадетъ въ точку С2 или точку С3, то тогда катетъ ВС занялъ бы положеніе ВхС2 или В^з, что невозможно, такъ какъ изъ одной точки Вх нельзя на прямую АгСі отпустить два перпендикуляра (В/?! и ВіС2, или В^ и В^з).
Тогда, по равенству прямыхъ угловъ,
2°. Пусть (черт. 56) въ прямоуг. тр-кахъ дано: АВ = А1В1 и ВС=В1С1; требуется доказать, что тр-ки равны. — Наложимъ Л АВС на Д А^іСг такъ, чтобы у нихъ совмѣстились равные катеты ВС и В^. СА пойдетъ по С^А^.
При этомъ гипотенуза АВ не можетъ не совмѣститься съ гипо
тенузой ЛіВі, потому что если бы она заняла положеніе А2ВГ
или Л3Ві, то тогда мы имѣли бы двѣ равныя наклонныя (Л^
и А2В1, или АіВі и АзВі), которыя не одинаково удалены отъ основанія перпендикуляра, что невозможно (59, 2).
ГЛАВА IV.
Свойство перпендикуляра, проведеннаго къ прямой черезъ ея середину, и свойство биссентриссы угла.
63. Теоремы. 1°. Если какая-нибудь точка одинаково удалена отъ концовъ отрѣзка прямой, то она лежитъ на перпендикулярѣ къ этому отрѣзку, проходящемъ черезъ его середину.
2°. Обратно: если какая-нибудь точка лежитъ на перпендикулярѣ къ отрѣзку прямой, проходящемъ черезъ его середину, то она одинаково удалена отъ концовъ этого отрѣзка.
— 46 —
1°. Пусть точка М (черт. 67) одинаково удалена отъ концовъ отрѣзка прямой АВ, т.-е. пусть МА-МВ-, требуется доказать, что точка М лежитъ на перпендикулярѣ, проведенномъ къ
прямой АВ черезъ ея середину. — Проведемъ биссектриссу МО угла АМВ. Такъ какъ тр-къ АМВ равнобедренный, то эта
биссектрисса служитъ въ ней высотою и медіаною (38); значитъ, точка М летятъ на перпендикулярѣ къ прямой АВ, дѣлящемъ ее пополамъ.
2°. Пусть ОМ (черт. 57) есть перпендикуляръ, проведенный къ отрѣзку АВ черезъ его середину, и М какая-нибудь точка па немъ; требуется
доказать, что эта точка одинаково Черт. 57.
удалена отъ концовъ АВ, т.-е. что МА=МВ. — Прямыя МА и МВ суть наклонныя къ АВ, одинаково удаленныя отъ основанія перпендикуляра МО\ а такія наклонныя равны; слѣд., МА=МВ.
64. Слѣдствіе. Изъ двухъ доказанныхъ теоремъ, прямой и обратной, молено вывести слѣдствіе, что теоремы, противоположныя имъ, также вѣрны (4), т.-е. что (черт. 58):
если какая-нибудь точка (М) н е одинаково удалена отъ концовъ отрѣзка прямой (ЛВ), то она н е лежитъ на церпендикулярѣ (СВ) къ этому отрѣзку, проведенномъ черезъ его середину (О);
если какая-нибудь точка н е лежитъ на перпендикулярѣ къ отрѣзку прямой, проведенномъ черезъ его середину, то она не одинаково удалена отъ концовъ этого отрѣзка.
Предлагаемъ учащимся самимъ доказать эти противоположныя предложенія (разсужденіемъ отъ противнаго).
— 46 —
65. Теоремы. 1°. Если какая-нибудь точка одинаково удалена отъ сторонъ угла, то она лежитъ на его биссектриссѣ.
2°. Обратно: если какая-нибудь точка лежитъ на биссектриссѣ
угла, то она одинаково удалена отъ его сторонъ.
1°. Пусть точка М (черт. 59) одинаково удалена отъ сторонъ угла АВС, т.-е. пусть перпендикуляры МЕ и МЕ, опущенные изъ этой точки на стороны угла, равны; требуется доказать, что
точка М лежитъ на биссектриссѣ угла АВС. — Проведемъ прямую черезъ В и М. Прямоугольные треугольники МВЕ и МВЕ равны, такъ какъ у нихъ общая гипотенуза и катеты МЕ, МЕ равны по условію. Изъ равенства тр-ковъ слѣдуетъ, что
^/МВЕ=^МВЕ, т.-е. прямая МВ есть биссектрисса угла АВС. 2°. Пусть ВВ (черт. 59) есть биссектрисса угла АВС, и М
какая-нибудь точка на ней; требуется доказать, что перпендикуляры МЕ и МЕ, опущенные изъ этой точки па стороны
угла, равны.— Прямоугольные тр-ки МВЕ и МВЕ равны, такъ какъ у нихъ общая гипотенуза, и углы МВЕ, МВЕ равны по условію. Изъ равенства тр-ковъ слѣдуетъ, что МЕ=МЕ *).
66. Слѣдствіе. Изъ двухъ доказанныхъ теоремъ, прямой и обратной, можно вывести слѣдствіе, что теоремы, п р о-
Черт. 60.
тявоположныя имъ также вѣрны, т.-е., что (черт. 60):
если какая-нибудь точка (М) н е одинаково удалена отъ сторонъ угла (АВС), то она н е лежитъ на его биссектриссѣ (ВВ);
если какая-нибудь точ
*) Предлагаемъ самимъ учащимся разсмотрѣть свойства точекъ, одинаково удаленныхъ отъ продолженій сторонъ угла (за вершину).
— 47 —
ка не лежитъ на биссектриссѣ угла, то она н е одинаково удалена отъ сторонъ его.
67. Геометрическое мѣсто. Геометрическимъ мѣстомъ точекъ, обладающихъ нѣкоторымъ свойствомъ, наз, такая линія, или поверхность, или совокупность линій и поверхностей (вообще такая фигура), которая содержитъ въ себѣ всѣ точки, обладающія этимъ свойствомъ, и не содержитъ ни одной точки, не обладающей имъ.
Изъ теоремъ предыдущихъ параграфовъ слѣдуетъ:
Геометрическое мѣсто точекъ, одинаково удаленныхъ отъ двухъ данныхъ точекъ, есть перпендикуляръ, проведенный къ отрѣзку прямой, соединяющему эти точки, чрезъ его середину.
Геометрическое мѣсто точекъ, одинаково удаленныхъ отъ сторонъ угла, есть биссектрисса этого угла *).
ГЛАВА V.
Основныя задачи на построеніе.
Черт. 61.
68. Понятіе объ окружности. Теоремы, доказанныя нами въ предыдущихъ главахъ, позволяютъ рѣшать нѣкоторыя задачи на построеніе. Замѣтимъ, что въ элементарной геометріи разсматриваются только такія построенія, которыя могутъ быть выполнены помощью линейки и циркуля (употребленіе наугольника и нѣкоторыхъ другихъ приборовъ хотя и допускается но не Посред-прямыя чертится
ради сокращенія времени, составляетъ необходимости), ствомъ линейки проводятся линіи, посредствомъ циркуля
окружность. Свойства этой линіи мы разсмотримъ впослѣдствіи, теперь же ограничимся только краткимъ понятіемъ о ней.
*) Предлагаемъ самимъ учащимся убѣдиться, что геометрическое мѣсто точекъ, равноотстоящихъ отъ двухъ пересѣкающихся прямыхъ, состоитъ изъ двухъ прямыхъ, дѣлящихъ пополамъ углы, образованные пересѣкающимися прямыми.
— 48 —
Если дадимъ циркулю произвольное раствореніе и, поставивъ его ножку съ остреемъ въ какую-нибудь точку О (черт. 61), станемъ вращать циркуль вокругъ этой точки, то другая его ножка, снабженная карандашомъ или перомъ, опишетъ непрерывную линію, которой всѣ точки одинаково удалены отъ точки О. Эта линія наз. окружностью, а точка О — центромъ ея. Прямыя ОА, ОВ,ОС..., соединяющія центръ съ какими-нибудь точками окружности, наз. радіусами. Всѣ радіусы одной окружности равны между собою. Часть окружности, напр., АВ (черт. 61), наз. дугою.
69. Основныя задачи на построеніе. Укажемъ рѣшеніе слѣдующихъ задачъ на построеніе.
Задача 1. Построить треугольникъ по даннымъ его сторонамъ а, Ъ и с (черт. 62).
На какой-нибудь прямой МУ откладываемъ часть СВ, рав-
Черт. 62.
ную одной изъ данныхъ сторонъ, напр. а. Изъ точекъ С и В, какъ центровъ, описы-
ваемъ двѣ небольшія дуги, одну радіусомъ, равнымъ Ъ, дру-
гую радіусомъ, равнымъ с. Точку А, въ которой эти дуги пересѣкаются, соединяемъ съ В и С. Треугольникъ АВС будетъ искомый.
Замѣчаніе. Невсякіе три отрѣзка прямой могутъ служить сторонами треугольника; для этого необходимо, чтобы большій изъ нихъ былъ меньше суммы двухъ остальныхъ (52).
Задача 2. На даннойпрямой при данной
— 49 —
на ней точкѣ О построить уголъ, равный данному углу АВС (черт. 63).
Изъ вершины В, какъ центра, описываемъ произвольнымъ радіусомъ между сторонами даннаго угла дугу ЕР-, затѣмъ, не измѣняя растворенія циркуля, переносимъ его острее въ точку О и описываемъ дугу Р(^. Далѣе, изъ точки Р, какъ центра, описываемъ дугу аЪ радіусомъ, равнымъ разстоянію между точками Е и Р. Наконецъ черезъ точки О и В (пересѣченіе двухъ дугъ) проводимъ прямую. Уголъ ВОР равенъ углу АВС, потому что тр-ки ВОР и РВЕ, имѣющіе соотвѣтственно равныя стороны, равны.
Задача 3. Раздѣлить данный уголъ АВС п о-пополамъ (черт. 64).
Изъ вершины В, какъ центра, произвольнымъ радіусомъ опишемъ между сторонами угла дугу ВЕ. Затѣмъ, взявъ произвольное раствореніе циркуля, большее однако половины разстоянія между точками Е и В (см. замѣчаніе къ за
дачѣ 1-й), описываемъ этимъ раствореніемъ изъ точекъ В и Е небольшія дуги, которыя пересѣкались бы въ какой-нибудь точкѣ Р. Проведя прямую ВР, мы получимъ биссектриссу угла АВС.—Для доказательства соединимъ прямыми точку Р съ В и Е; тогда получимъ два тр-ка ВЕРи ВВР, которые равны, такъ какъ у нихъ ВР общая сторона, ВВ=ВЕ и ВР=ЕР по построенію. Изъ равенства тр-ковъ слѣдуетъ: ^АВР=А^СВР.
Л. Киселевъ. Геометрія. 4
— 50 —
Задача 4. и з ъ возставить къ л я р ъ (черт. 65).
данной точки С прямой АВ этой прямой перпендику-
Отложимъ на АВ по обѣ
Черт. 65.
стороны отъ данной точки С равные отрѣзки (произвольной длины) СБ и СЕ. Изъ точекъ Е и Б однимъ и тѣмъ же раствореніемъ циркуля (большимъ однако СБ) опишемъ двѣ небольшія дуги, которыя пересѣкались бы въ нѣкоторой точкѣ Е. Прямая, проведенная че
резъ точки С и Е, будетъ искомымъ перпендикуляромъ.—Дѣйствительно, какъ видно изъ построенія, точка Е одинаково
удалена отъ Б и Е; слѣд., она должна лежать на перпендикулярѣ, проведенномъ къ отрѣзку БЕ черезъ его середину (63); но середина этого отрѣзка есть С, а черезъ С и Е можно провести
только одну прямую; значитъ, БСЛ.БЕ.
Задача 5.Изъ данной точкиЯопустить перпендикуляръ па данную прямую ВС (черт. 66).
Изъ точки А, какъ центра, произвольнымъ раствореніемъ циркуля (большимъ однако разстоянія отъ Л до ВС) опишемъ такую дугу, которая пересѣкалась бы съ ВС въ какихъ-нибудь двухъ точкахъ Б и Е. Затѣмъ изъ этихъ точекъ произвольнымъ, но однимъ
и тѣмъ же, раствореніемъ циркуля (большимъ однако 1/2 БЕ) проводимъ двѣ небольшія дуги, которыя пересѣкались бы между собою въ С нѣкоторой точкѣ Е. Прямая АЕ будетъ искомымъ перпендикуляромъ .—Дѣйствительно, какъ видно изъ построенія, каждая изъ точекъ А и Е одинаково удалена отъ Б и Е\ а такія точки лежатъ на перпендикулярѣ,
проведенномъ къ отрѣзку БЕ черезъ его середину (63).
— 61 -
Задача 6. Провести перпендикуляръ къ данной конечной прямой (АВ) черезъ ея середину (черт. 67).
Изъ точекъ А и В произвольнымъ, но одинаковымъ, раство-
реніемъ циркуля (большимъ х/2 АВ) описываемъ двѣ дуга, которыя пересѣкались бы между собою въ нѣкоторыхъ точкахъ Си Б. Прямая СІ)будетъ искомымъ перпендикуляромъ. — Дѣйствительно, какъ видно изъ построенія, каждая изъ точекъ С и Б одинаково удалена отъ А и В; слѣд., эти точки должны лежать на перепендикулярѣ, проведенномъ къ отрѣзу АВ черезъ
Черт. 67.
его середину (63).
Задача 7.Раздѣлить пополамъ данную конечную прямую АВ (черт. 67).
Рѣшается такъ же, какъ предыдущая задача.
70. Примѣръ болѣе сложной задачи. При помощи этихъ основныхъ задачъ можно рѣшать задачи болѣе сложныя. Для примѣра рѣшимъ слѣдующую задачу.
Задача. Построить треугольникъ, зная его основаніе Ь, уголъ а, прилежащій къ основанію, и сумму я двухъ боковыхъ сторонъ (черт. 68).
Чтобы составить планъ рѣшенія, предположимъ, что задача рѣшена, т.-е. найденъ такой тр-никъ АВС, у котораго основаніе АС=Ь, уголъ А=а и АВ+ВС=8. Разсмотримъ теперь полученный чертежъ. Сторону АС, равную Ь, и уголъ А, равный а, мы построить умѣемъ. Значитъ, остается найти на сторонѣ АБ угла А такую точку В, чтобы сумма ЛВ+ВС равнялась з. Продолживъ АВ, отложимъ отрѣзокъ АБ, равный «. Теперь вопросъ приводится къ тому, чтобы на прямой АБ отыскать такую точку В, которая была бы одинаково удалена отъ С и В. Такая точка, какъ мы знаемъ (63), должна лежать на перпендикулярѣ, проведенномъ къ отрѣзку прямой СБ черезъ его середину.
4
— 62 —
Этотъ перпендикуляръ мы построить умѣемъ. Точка В най-
дется въ пересѣченіи перпендикуляра съ АВ.
Итакъ, вотъ рѣшеніе задачи: строимъ (черт. 68) уголъ А, равный данному углу а; на сторонахъ его откладываемъ АС=Ь и АВ=з. Черезъ середину отрѣзка прямой ВС проводимъ перпендикуляръ ВЕ\ пересѣченіе его съ АВ, т.-е. точку В, соединимъ съ С. Тр-нпкъ АВС
будетъ искомый, такъ какъ онъ удовлетворяетъ всѣмъ требованіямъ задачи: у него АС=Ъ, Х.А—а и АВ-{-ВС=8, (потому что ВВ=ВС).
Разсматривая построеніе, мы замѣчаемъ, что задача возможна не при всякихъ данныхъ. Дѣйствительно, если сумма в задана слишкомъ малою сравнительно съ Ъ, то перпендикуляръ ЕВ можетъ и не пересѣчь отрѣзка АВ (или пересѣчетъ его продолженіе за точку А или за точку В)-, въ этомъ случаѣ задача окажется невозможной. И независимо отъ построенія можно видѣть, что задача невозможна, если з<^Ь, или 8—Ъ, потому что не можетъ быть такого треугольника, у котораго сумма двухъ сторонъ была бы меньше или равна третьей сторонѣ.
Въ томъ случаѣ, когда задача возможна, она имѣетъ только одно рѣшеніе, т.-е. существуетъ только одинъ тр-никъ, удовлетворяющій требованіямъ задачи, такъ какъ пересѣченіе перпендикуляра ВЕ съ прямой АВ можетъ быть только въ одной точкѣ.
71. Замѣчаніе. Изъ приведеннаго примѣра видно, что рѣшеніе сложной задачи на построеніе состоитъ изъ слѣдующихъ четырехъ частей:
1°. Предположивъ, что задача рѣшена, дѣлаютъ отъ руки приблизительный чертежъ искомой фигуры и затѣмъ, внимательно разсматривая начерченную фигуру, стремятся найти такія зависимости между данными задачи и искомыми, кото
— 53 —
рыя позволили бы свести задачу на другія, Извѣстныя ранѣе. Эта самая важная часть рѣшенія задачи, имѣющая цѣлью составить планъ рѣшенія, носитъ названіе анализа.
2°. Когда такимъ образомъ планъ рѣшенія найденъ, выполняютъ сообразно ему построеніе.
3°. Для провѣрки правильности плана доказываютъ затѣмъ, на основаніи извѣстныхъ теоремъ, что полученная фигура удовлетворяетъ всѣмъ требованіямъ задачи. Эта часть рѣшенія называется синтезомъ.
4°. Затѣмъ задаются вопросомъ, при всякихъ ли данныхъ задача возможна, допускаетъ ли она одно рѣшеніе, или нѣсколько, и нѣтъ ли въ задачѣ какихъ-либо особенныхъ случаевъ, когда построеніе упрощается, или, наоборотъ, усложняется. Эта часть рѣшенія наз. изслѣдованіемъ задачи.
Когда задача весьма проста и не можетъ быть сомнѣнія относительно ея возможности, то обыкновенно анализъ и изслѣдованіе опускаютъ, а указываютъ прямо построеніе и приводятъ доказательство. Такъ мы дѣлали, излагая рѣшеніе первыхъ 7-ми задачъ этой главы; такъ же будемъ дѣлать и впослѣдствіи, когда намъ придется излагать рѣшеніе несложныхъ задачъ.
УПРАЖНЕНІЯ.
Доказать теоремы.
5. Въ равнобедренномъ треугольникѣ двѣ медіаны равны, двѣ биссектриссы равны, двѣ высоты равны.
6. Если изъ середины каждой изъ равныхъ сторонъ равнобедреннаго тр-ка возставимъ перпендикуляры до пересѣченія съ другою изъ равныхъ сторонъ, то эти перпендикуляры равны.
7. Перпендикуляры, возставленные къ двумъ сторонамъ угла на равныхъ разстояніяхъ отъ вершины, пересѣкаются на биссектриссѣ.
8. Прямая, перпендикулярная къ биссектриссѣ угла, отсѣкаетъ отъ его сторонъ равные отрѣзки.
9. Медіана тр-ка меньше его полуперимѳтра.
10. Медіана тр-ка меньше полусуммы сторонъ, между которыми она заключается. Указаніе: продолжить медіану на разстояніе, равное ей, полученную точку соединить съ однимъ концомъ стороны, къ которой проведена медіана, и разсмотрѣть образовавшуюся фигуру.
10. а. Сумма медіанъ тр-ка меньше периметра, но больше полупериметра.
11. Сумма разстояній какой-нибудь точки, взятой внутри тр-ка, отъ трехъ его вершинъ меньше периметра, но больше полупериметра.
— Б4 —
11,о. Сумма діагоналей четыреугольника меньше его периметра, но больше полуперимѳтра.
12. Доказать прямо, что всякая точка, не лежащая на перпендикулярѣ, проведенномъ къ отрѣзку прямой черезъ его середину, не одинаково удалена отъ концовъ этого отрѣзка.
18. Доказать прямо, что всякая точка, не лежащая на биссектриссѣ угла, не одинаково отстоитъ отъ сторонъ его.
18,а. Если на сторонахъ угла А отложимъ равныя длины АВ и АВХ, затѣмъ равныя длины АС и АСГ, то прямыя ВС, и ВгС пересѣкаются на биссектриссѣ угла А.
Задачи на построеніе.
14. Построить сумму двухъ, трехъ и болѣе данныхъ угловъ.
15. Построить разность двухъ угловъ.
16. По данной суммѣ и разности двухъ угловъ найти эти углы.
17. Раздѣлить уголъ на 4, 8, 16 равныхъ частей.
18. Черезъ вершину даннаго угла провести внѣ его такую прямую, которая со сторонами угла образовала бы равные углы.
19. Построить А', а) по двумъ сторонамъ и углу между ними; Ь) по сторонѣ и двумъ прилежащимъ угламъ; с) по двумъ сторонамъ и углу, лежащему противъ ббльшѳй изъ нихъ; б) по двумъ сторонамъ и углу, лежащему противъ меньшей изъ нихъ (въ этомъ случаѣ получаются два рѣшенія или ни одного).
20. Построить равнобедренный Д: а) по основанію и боковой сторонѣ; Ь) по основанію и прилежащему углу; с) по боковой сторонѣ и углу при вершинѣ; б) по боковой сторонѣ и углу при основаніи.
21. Построить прямоугольный Д: а) по двумъ катетамъ; Ь) по катету и гипотенузѣ; с) по катету и прилежащему острому углу.
22. Построить равнобедренный Д: а) по высотѣ и боковой сторонѣ, Ь) по высотѣ и углу при вершинѣ; с) по основанію и перпендикуляру, опущенному изъ конца основанія на боковую сторону.
23. Построить прямоугольный Д по гипотенузѣ и острому углу.
24. Черезъ точку, данную внутри или внѣ угла, провести такую прямую, которая отсѣкала бы отъ сторонъ угла равныя части.
25. По данной суммѣ и разности двухъ прямыхъ найти эти прямыя.
26. Раздѣлить данную конечную прямую на 4, 8, 16 равныхъ частей.
27. На данной прямой найти точку, одинаково удаленную отъ двухъ данныхъ точекъ (внѣ прямой).
28. Найти точку равноотстоящую отъ трехъ вершинъ А.
29. На прямой, пересѣкающей стороны угла, найти точку, одинаково удаленную отъ сторонъ этого угла.
30. Найти точку, одинаково удаленную отъ трехъ сторонъ А.
31. На безконечной прямой АВ найти такую точку С, чтобы полупрямыя СМ и СИ, проведенныя изъ С черезъ данныя точки М и М,.
— 65 —
расположенныя по одну сторону отъ АВ, составляли съ полупрямыми СА и СВ равные углы.
82. Построить прямоугольный Л по катету и суммѣ гипотенузы съ другимъ катетомъ.
83. Построить Л по основанію, углу, прилежащему къ основанію, и разности двухъ другихъ сторонъ (разсмотрѣть два случая: 1) когда данъ меньшій изъ двухъ угловъ, прилежащихъ къ основанію, 2) когда данъ б 6 л ь ш і й изъ нихъ).
34. Построить прямоугольный Л по катету и разности двухъ другихъ сторонъ.
ГЛАВА VI.
Параллельныя прямыя
Основныя теоремы.
72. Опредѣленіе. Когда какія-нибудь двѣ прямыя АВ и
СБ (черт. 69) пересѣчены третьей прямой М1У, то образова-
вшіеся при этомъ углы получаютъ попарно слѣдующія названія:
соотвѣтственные углы:
1 и 5, 4 и 8, 2 и 6, 3 и 7;
внутренніе накрестъ лежащіе углы: 3 и 5, 4 и 6;
внѣшніе накрестъ лежа-
щіе углы: 1 и 7, 2 и 8;
внутренніе односто-
ронніе углы: 3 И 6, 4 и 5;
внѣшніе односторон-
ніе углы: 1 и 8, 2 и 7.
Черт. 69.
73. Лемма. *) Если между углами, образовавшимися при
пересѣченіи двухъ прямыхъ третьею (черт. 69), существуетъ какое-нибудь одно изъ слѣдующихъ 5-и соотношеній:
1°, соотвѣтственные углы равны,
2°, внутренніе накрестъ лежащіе углы равны,
3°, внѣшніе накрестъ лежащіе углы равны,
4°, сумма внутреннихъ одностороннихъ угловъ равна 2<1.
5°, сумма внѣшнихъ одностороннихъ угловъ равна 2й, то существуютъ и всѣ остальныя изъ этихъ соотношеній.
Сначала докажемъ, что первое изъ указанныхъ соотно
шеній влечетъ за собою, какъ слѣдствіе, всѣ остальныя; послѣ
*) Леммою наз. вспомогательная теорема, излагаемая только для того, чтобы при ея помощи доказать послѣдующія теоремы.
— 56 —
этого докажемъ, что, обратно, каждое изъ этихъ остальныхъ соотношеній (т.-е. 2-е, 3-е, 4-е и Б-е) влечетъ за собою первое; отсюда мы заключимъ, что каждое изъ указанныхъ соотношеній влечетъ за собою всѣ остальныя.
1) Пусть дано, что соотвѣтственные углы 2 и 6 равны между собою (черт. 70); требуется доказать, что въ такомъ случаѣ будутъ имѣть мѣсто и всѣ остальныя указанныя соотношенія.
Прежде всего покажемъ, что И равенство одной пары соотвѣт-
С/ ственныхъ угловъ, напр. угловъ
Д ...— ----В 2 и 6, влечетъ за собою равен-
/ ство и всѣхъ остальныхъ паръ
/ соотвѣтственныхъ угловъ. Дѣй-
5/ь\__________п ствительно, 224 = 22 8, такъ
я/7 у какъ первый изъ этихъ угловъ
' равенъ углу 2, а второй—углу 6,
м какъ вертикальный; 22 1 = 22 6,
Черт. /0. такъ какъ эти уГЛЫ составляютъ
дополненія до къ равнымъ угламъ 2 и 6; по той же причинѣ 22 3 = 22 7.
Обращая теперь вниманіе на внутренніе накрестъ лежащіе углы, находимъ: X 4 = /_ 2, какъ углы вертикальные; 222=226 по заданію; слѣд., ^/4=226.
Если же ^/4 = / 6, то равны и внутренніе накрестъ лежащіе углы 3 и 5, какъ дополненія до 2й къ равнымъ угламъ 4 и 6.
Обращая вниманіе на внѣшніе накрестъ лежащіе утлы, нахо-димъ:228=226, какъ углы вертикальные; 216=222 по заданію; слѣд. 228=222.
Если же 222 =228, то равны и другіе внѣшніе односторонніе углы 1 и 7, какъ дополненія до 2й къ равнымъ угламъ 2 и 8.
Обращая вниманіе на внутренніе односторонніе углы, находимъ: ^/3-Н/2=2й, такъ какъ эти углы смежные. Замѣнивъ въ этой суммѣ уголъ 2 равнымъ ему угломъ 6, получимъ: 2^3+^6=2й. Точно такъ же: 224+^1=2(2, 2І1=22б; слѣд., ^4+^5=2(2.
Обращая, наконецъ, вниманіе на внѣшніе односторонніе углы, совершенно такъ же, какъ это было сдѣлано для внутрен-
— 57 —
нихъ одностороннихъ угловъ, докажемъ, что 2І7+2І2—2о! и ^8+^1=2й.
2) Докажемъ теперь, что каждое изъ соотношеній: 2-е, 3-е, 4-е и 5-е влечетъ за собою соотношеніе 1-е.
Пусть, напр., дано (черт. 70), что ^2+^І7=2й; требуется доказать, что соотвѣтственные углы 2 и 6 равны. Дѣйствительно, 2І7+2І6=2й, такъ какъ углы эти смежные; но ^2+^7=2й по заданію; слѣд., 2І7+^6=2І2+^7. Отнявъ отъ этихъ равныхъ суммъ по одному и тому же углу 7, получимъ 2І6=2І2.
Подобно этому докажемъ, что и любое иное изъ соотношеній: 2-е, 3-е, 4-е и 5-е влечетъ за собою соотношеніе 1-е.
3) Теперь заключаемъ, что каждое изъ 5-ти указанныхъ соотношеній влечетъ за собою всѣ остальныя, такъ какъ каждое влечетъ 1-е, а это влечетъ всѣ остальныя.
74. Теорема. Два перпендикуляра къ одной и той же прямой не могутъ пересѣчься, сколько бы мы ихъ ни продолжали.
Пусть къ одной и той же прямой АВ (черт. 71) проведены два перпендикуляра СВ и ЕР-, требуется доказать, что эти перпендикуляры не пересѣкаются, сколько бы мы ихъ ни продолжали.
Предположимъ противное, т.-е что прямыя СІ) и ЕР, будучи продолжены достаточно далеко, пересѣкаются въ нѣкоторой точкѣ М (или ЛГ). Тогда изъ этой точки на прямую АВ были бы опущены 2 различные перпендикуляра. Такъ какъ это невозможно (32), то нельзя допустить, чтобы перпендикуляры СВ и ЕР гдѣ-нибудь пересѣкались.
ѵм’
Черт. 71.
75. Опредѣленіе. Двѣ прямыя наз. параллельными, если, находясь въ одной плоскости, онѣ не пересѣкаются, сколько бы
ихъ ни продолжали.
— 68 —
Возможность существованія паралелльныхъ прямыхъ обнаруживается предыдущей теоремой, которую теперь можно высказать такъ:
два перпендикуляра къ одной и той же прямой параллельны.
Параллельность прямыхъ обозначается письменно знакомъ II , поставленнымъ между обозначеніемъ прямыхъ; такъ, если прямыя СБ и ЕЕ параллельны, то пишутъ: СБ || ЕЕ.
Предыдущая теорема, показывая возможность существованія параллельныхъ прямыхъ, выражаетъ одинъ изъ признаковъ параллельности (перпендикулярность къ одной и той же прямой). Слѣдующая теорема выражаетъ еще другіе признаки параллельности.
76. Теорема. Если при пересѣченіи двухъ прямыхъ какою-нибудь третьей прямой окажется, что:
1°, соотвѣтственные углы равны;
или 2°, внутренніе накрестъ лежащіе углы равны, или 3°, внѣшніе накрестъ лежащіе углы равны, или 4°, сумма внутреннихъ одностороннихъ угловъ равна 2гі, или 5°, сумма внѣшнихъ одностороннихъ угловъ равна 2й, то первыя двѣ прямыя параллельны.
Мы видѣли (73,) что если существуетъ какое-нибудь одно изъ 5-ти соотношеній, перечисленныхъ въ теоремѣ, то существуютъ и всѣ остальныя. Поэтому намъ достаточно обнаружить, что прямыя АВ и СБ (черт. 72) параллельны при существованіи какого-нибудь одного изъ этихъ соотношеній. Пусть, напр., дано, что соотвѣтственные углы 2 и 6 равны; требуется доказать, что въ такомъ случаѣ АВ || СБ.—Предположимъ противное, т.-е. что прямыя АВ и СБ не параллельны; тогда эти прямыя пересѣкутся въ какой-ни-_В_. будь точкѣ Р, ле-
''-,р кащей направо отъ _ МЕІ, или въ какой-Б____________нибудь точкѣ Р', ле-
жащей налѣво отъ МЕ. Если пересѣче-
черт. 72. ніе будетъ въ Р, то
образуется тр-къ, въ которомъ ^/2 будетъ внѣшнимъ, а 2^6 внутреннимъ, не смежнымъ съ внѣшнимъ угломъ 2, и, значитъ,
— 59 —
тогда ^2 долженъ быть больше 2І6 (45), что противорѣчитъ заданію; значитъ, пересѣчься въ какой-нибудь точкѣ Р, лежащей направо отъ ЛГ2Ѵ, прямыя АВ и СВ не могутъ. Если предположимъ, что пересѣченіе будетъ въ точкѣ Р', то тогда образуется тр-къ, у котораго /І4, равный ^2, будетъ внутреннимъ, а внѣшнимъ, не смежнымъ съ внутреннимъ 2І4; тогда долженъ быть больше А^А и, слѣд., больше ^2, что противорѣчитъ заданію. Значитъ, прямыя АВ и СВ не могутъ пересѣчься и въ точкѣ, лежащей налѣво отъ МЕ-, слѣд., эти прямыя нигдѣ не пересѣкаются, т.-е. онѣ параллельны.
77. Теорема. Черезъ всякую точку, лежащую внѣ прямой, можно провести параллельную этой прямой.
Черт. 73.
Дана прямая АВ (черт. 73) и какая-нибудь точка С, лежащая внѣ этой прямой; требуется доказать, что черезъ точку С можно провести прямую, параллельную АВ.—Черезъ какую-нибудь точку В прямой АВ и черезъ точку С проведемъ прямую СВ. Эта прямая образуетъ съ АВ нѣкоторый уголъ а. Построимъ при точкѣ С уголъ Ь, равный углу а, располо- А живъ его такъ, чтобы онъ оказался соотвѣтственнымъ углу а. Тогда прямая СЕ будетъ параллельна
АВ, такъ какъ соотвѣтственные углы а и Ъ равны (76).
78. Замѣчаніе. Такъ какъ точку В на прямой АВ (черт. 73) мы можемъ брать произвольно, то построеній, подобныхъ указанному, можетъ быть . , ,
выполнено сколько угодно. При Е’
этомъ возникаетъ вопросъ, бу- <7^
детъ ли при разныхъ построе- ' /\
ніяхъ всегда получаться одна и / \
та же прямая СЕ, параллельная / у
АВ, или могутъ получаться и д /ѵ \ А ц другія прямыя, параллельныя /В В’\ АВ? ' '
Черт. 74.
— 60 —
Если, напр., вмѣсто точки Б мы возьмемъ точку Б' (черт. 74) и сдѣлаемъ для сѣкущей СБ' такое же построеніе, какое раньше было сдѣлано для сѣкущей СБ (т.-е. построимъ ^.Ъ’—АІа'), то получится ли при этомъ та же прямая СЕ или окажется нѣкоторая новая прямая СЕ'? Вопросъ этотъ другими словами можетъ быть высказанъ такъ: черезъ точку С, взятую внѣ прямой АВ, можно ли провести только одну прямую, параллельную АВ, или нѣсколько? Отвѣтомъ на этотъ вопросъ служитъ слѣдующая аксіома параллельныхъ линій.
79. Аксіома параллельныхъ линій. Черезъ одну и ту же точку нельзя провести двухъ различныхъ прямыхъ, параллельныхъ одной и той же прямой.
Такъ, если (черт. 74) СЕ || АВ, то всякая другая прямая СЕ', проведенная черезъ точку С, не можетъ быть параллельной АВ, т.-е. она при продолженіи пересѣчется съ АВ.
Доказательство этой не вполнѣ очевидной истины оказывается невозможнымъ; ее принимаютъ безъ доказательства, какъ необходимое допущеніе или требованіе (постулатъ — розіиіаіипі).
80. Слѣдствія. 1°. Если прямая (СЕ', черт. 74) пересѣкается съ одной изъ параллельныхъ (СЕ), то она пересѣкается и съ другой (АВ),
потому что въ противномъ случаѣ черезъ одну и ту же точку С проходили бы двѣ различныя прямыя, параллельныя АВ, что невозможно.
2°. Если каждая изъ двухъ прямыхъ А и В (черт. 75) параллельна одной и той же третьей прямой (С), то онѣ параллельны между собою.
Дѣйствительно, если предположимъ, что пря->м мыя А и В пересѣкаются въ нѣкоторой точкѣ М, то тогда черезъ эту точку проходили бы двѣ различныя прямыя, параллельныя С, что невозможно.
А------------------
В-----------------
С-----------------
Черт. 75.
— 61 —
8. Теорема, (обратная теоремѣ § 76). Если двѣ параллельныя прямыя (АВ и СВ, черт. 76) пересѣчены третьей прямой (ЛШ), то:
1°, соотвѣтственные углы равны;
2°, внутренніе накрестъ лежащіе углы равны;
3°, внѣшніе накрестъ лежащіе углы равны;
4°, сумма внутреннихъ одностороннихъ угловъ равна
5°, сумма внѣшнихъ одностороннихъ угловъ равна
Достаточно доказать, что параллельность прямыхъ АВ и СВ влечетъ за собою какое-нибудь одно изъ 5-ти указанныхъ
соотношеній, потому что, какъ мы видѣли (73), если существуетъ одно изъ нихъ, то должны существовать и всѣ остальныя.
Докажемъ, напр., что если АВ II СВ, то соотвѣтственные углы а и Ь равны.
Предположимъ противное, т.-е. что эти углы не равны (напр., пусть с^>Ъ). Построивъ ^/_МЕВ1=Х))-‘ мы получимъ тогда прямую А&, не сливающуюся съ АВ, и, слѣд., будемъ
имѣть 2 различныя прямыя, проходящія черезъ точку Е и параллельныя одной и той же прямой СВ (именно: АВ II СВ согласно условію теоремы и А& II СВ вслѣдствіе равенства соотвѣтственныхъ угловъ МЕВг и Ь). Такъ какъ это противорѣчитъ аксіомѣ параллельныхъ линій, то наше предположеніе, что углы а и Ъ не равны, должно быть отброшено; остается принять, что а=Ъ.
82. Слѣдствіе. Перпендикуляръ къ одной изъ двухъ параллельныхъ прямыхъ есть также перпендикуляръ и къ другой.
Дѣйствительно если АВ || СВ (черт. 77) и МЕЛ.АВ, то, во 1, МЕ, пересѣкаясь съ АВ, пересѣкается и съ СВ въ нѣкоторой
— 62 —
точкѣ Е (80,1°); во 2, соотвѣтственные углы а и Ъ равны. Но уголъ
М
Черт. 77.
а прямой; значитъ и уголъ Ъ прямой, т.-е. МЕЛ.СБ.
83. Признаки непараллельности прямыхъ. Изъ двухъ теоремъ: прямой, выражающей признаки параллельности (76), и ей обратной (81), можно вывести заключеніе, что противополс-жныя теоремы также вѣрны, т.-е. что
если при пересѣченіи двухъ пря
мыхъ третьею окажется, что: 1°, соотвѣтственные углы н е равны, или 2°, внутренніе накрестъ лежащіе углы н е
равны, и т. д., то прямыя не параллельны;
если двѣ прямыя не параллельны, то при пересѣченіи ихъ третьею прямой: 1°, соотвѣтственные углы не равны, 2°, внутренніе накрестъ лежащіе углы не равны, и т.д.
Изъ этихъ признаковъ непараллельности (легко доказываемыхъ способомъ отъ противнаго) полезно обратить особое вниманіе на слѣдующій:
если сумма внутреннихъ одностороннихъ угловъ (а и Ь, черт. 78) не равна 2Л, то прямыя (АВ и СИ) при дозтаточномъ продолженіи пересѣкаются, такъ какъ если бы эти прямыя не
Черт. 78.
пересѣкались, то онѣ были бы параллельны, и тогда сумма внутреннихъ одностороннихъ угловъ равнялась бы 2й (81), что противорѣчитъ условію.
Это предложеніе (дополненное утвержденіемъ, что прямыя пересѣкутся по ту
сторону отъ сѣкущей линіи, по которой сумма внутреннихъ одностороннихъ угловъ меньше 2й) было принято знаменитымъ греческимъ геометромъ Эвклидомъ (жившимъ въ III вѣкѣ до Р. X.) въ его «Началахъ» геометріи безъ доказательства, какъ аксіома параллельныхъ линій, и потому оно
— 63 —
извѣстно подъ именемъ постулата Эвклида. Въ настоящее время предпочитаютъ принимать за такую аксіому болѣе простую истину, а именно ту, которую мы изложили раньше (79).
Укажемъ еще 2 слѣдующіе признака непараллельности, которые понадобятся намъ впослѣдствіи:
1°. Перпендикуляръ (АВ, черт. 79) и наклонная (СВ) къ одной и той же прямой (ЕР) пересѣкаются,
потому что сумма внутреннихъ одностороннихъ угловъ 1 и 2 не равны 2й.
Черт. 79.
2°. Двѣ прямыя (АВ и СВ, черт. 80), перпендикулярныя къ двумъ пересѣкающимся прямымъ (РЕ и РС), пересѣкаются.
Дѣйствительно, если предположимъ противное, т.-е. что АВ II СБ, то прямая РБ, будучи перпендикулярна къ одной изъ параллельныхъ (къ СБ), была бы перпендикулярна и къ другой параллельной (къ АВ), и тогда изъ одной точки Р къ прямой АВ были бы проведены два перпендикуляра: РВ и РБ, что невозможно.
84. Задача. Черезъ данную точку М провести прямую, параллельную данной прямой АВ (черт. 81).
Наиболѣе простое рѣшеніе этой задачи состоитъ въ слѣдующемъ: изъ точки М, какъ центра, описываемъ произвольнымъ радіусомъ дугу СБ и изъ точки С тѣмъ же радіусомъ дугу МЕ.
— 64 —
М
Черт. 81.
Затѣмъ, давъ циркулю раствореніе, равное разстоянію отъ Е до М, описываемъ изъ точки С небольшую дугу, которая пересѣкалась бы съ СВ въ нѣкоторой точкѣ Е. Прямая МЕ будетъ параллельна АВ.—Для доказательства тельную вавіпіеся равны по
а если внутренніе накрестъ лежащіе углы равны, то линіи параллельны.
Параллельныя прямыя весьма удобно проводятся также помощью наугольника и линейки. Приставивъ наугольникъ
проведемъ вспомога-прямую МС\ образо-при этомъ углы 1 и 2 построенію (69, зад. 2);
А
Черт. 82.
одною стороною (напр., гипотенузой) къ данной прямой АВ, прикладываемъ къ другой его сторонѣ (напр., къ длинному катету) линейку; затѣмъ, придерживая рукой линейку въ этомъ положеніи, двигаютъ наугольникъ вдоль нея до тѣхъ поръ, пока сторона его, совпадавшая съ АВ, не пройдетъ черезъ точку М\ послѣ чего проводятъ вдоль этой стороны прямую. Эта прямая будетъ параллельна АВ, такъ какъ соотвѣтственные углы 1 и 2 равны.
Углы съ соотвѣтственно параллельными или перпендикулярными сторонами.
85. Теорема. Если стороны одного угла соотвѣтственно параллельны сторонамъ другого угла, то такіе углы или равны, или въ суммѣ составляютъ два прямыхъ.
— 65 —
Черт. 83.
Разсмотримъ особо слѣдующіе три случая (черт. 83);
1°. Пусть стороны угла 1 соотвѣтственно параллельны сторонамъ угла 2 и, сверхъ того, имѣютъ одинаковое направленіе отъ вершины (на чертежѣ направленія указаны стрѣлками.)—Продолживъ одну изъ сторонъ угла 2 до пересѣченія съ непараллельной ей стороной угла 1, мы получимъ уголъ 3, равный и углу 1, и углу 2 (какъ соотвѣтственные при параллельныхъ), слѣд., ^1=^2.
2°. Пусть стороны угла 1 соотвѣтственно параллельны сторонамъ угла 4, но имѣютъ противопо
ложное направленіе отъ вершины.—Продолживъ обѣ стороны угла 4, мы получимъ уг. 2, который равенъ углу 1 (по доказанному выше) и углу 4 (какъ вертикальные); слѣд., ^4=<(/1-
3°. Пусть, наконецъ, стороны угла 1 соотвѣтственно параллельны сторонамъ угла 5 или угла 6, при чемъ двѣ изъ этихъ сторонъ имѣютъ одинаковое направленіе, а двѣ другія противоположное. Продолживъ одну сторону угла 5 или угла 6, мы получимъ уг. 2, который равенъ, по доказанному, углу 1; но /І5 (или 2^6) +^.2=2й (по свойству смежныхъ угловъ); слѣд., п 2І5 (пли 2І6)+^1=2й.
Такимъ образомъ, углы съ параллельными сторонами оказываются равными, когда ихъ стороны имѣютъ или одинаковое, или противоположное направленіе отъ вершины; если же это условіе не выполнено, то углы составляютъ въ суммѣ 2Л.
86. Теорема. Если стороны одного угла соотвѣтственно перпендикулярны къ сторонамъ другого угла, то такіе углы или равны, или въ суммѣ составляютъ два прямыхъ.
А. Квселсп. Геометрія. 5
Черт 84.
— 66 —
Пусть уголъ АБС, обозначенный цыфрою 1 (черт. 84), есть одинъ изъ данныхъ угловъ. Проведемъ изъ его вершины двѣ вспомогательныя прямыя: ВБЛ-ВС и ВЕ-ЬВА. Образованный пми уголъ 2 равенъ углу 1 по слѣдующей причинѣ: углы ВВС и ЕВА равны, такъ какъ оба они прямые; отнявъ отъ каждаго изъ нпхъ по одному и тому же углу ЕВС, получимъ: ^2=^11.
Теперь вообразимъ, что намъ данъ гдѣ-нибудь такой уголъ 3 (пли уг. 4, пли уг. 5, или уг. 6), у котораго стороны соотвѣтственно перпендикулярны къ сторонамъ угла 1. Тогда стороны этого угла будутъ параллельны сторонамъ угла 2 (потому что два перпендикуляра къ одной прямой параллельны); слѣд., новый уголъ пли равенъ углу 2, или составляетъ съ нимъ въ суммѣ 2й. Замѣнивъ уголъ 2 равнымъ ему угломъ 1, получимъ то, что требовалось доказать.
87. Замѣчаніе. Если намъ заранѣе извѣстно, что два угла съ соотвѣтственно параллельными или перпендикулярными сторонами оба острые, пли оба тупые, то можемъ утверждать, что такіе углы равны, такъ какъ два острыхъ или два тупыхъ угла не могутъ въ суммѣ составить 2й.
Сумма угловъ треугольника и многоугольника.
В
88. Теорема. Сумма угловъ всякаго треугольника равна двумъ прямымъ.
Пусть АВС (черт. 85) какой-нибудь треугольникъ; требуется доказать, что сумма угловъ А, В и С равна 2й.
Продолживъ сторону АС и проведя СЕ II АВ, найдемъ: Х.А=Х.ЕСВ (какъ углы соотвѣтственные при параллельныхъ), /1 В = Х.ВСЕ (какъ углы накрестъ лежащіе при параллельныхъ); слѣд.:
Черт. 85. ^.А
^ЕСВ+^ВСЕ+^.С=2<і (26).
67
Слѣдствія. 1°. Внѣшній уголъ треугольника равенъ суммѣ двухъ внутреннихъ угловъ, пе смежныхъ съ нимъ (такъ, ^ІВ(77)=2ІЛ+^В).
2°. Если два угла одного треугольника соотвѣтственно равны двумъ угламъ другого, то и третьи углы равны.
3°. Сумма двухъ острыхъ угловъ прямоугольнаго треугольника равна одному прямому углу.
4°. Въ равнобедренномъ прямоугольномъ тр-кѣ каждый острый уголъ равенъ
5°. Въ равностороннемъ тр-кѣ каждый уголъ равенъ 2/3 <2.
89. Теорема. Сумма угловъ всякаго выпуклаго многоугольника равна двумъ прямымъ, повтореннымъ столько разъ, сколько въ многоугольникѣ сторонъ безъ двухъ.
Взявъ внутри многоугольника (черт. 86) произвольную точку О, соединимъ ее со всѣми вершинами. Тогда выпуклый Х\ч ।
многоугольникъ разобьется на / I столько тр-ковъ, сколько въ Л---------------/
немъ сторонъ. Сумма угловъ \ \ /
каждаго тр-ка равна 2^; слѣд., \ \ /
сумма угловъ всѣхъ тр-ковъ \У У равна 2йп, если п означаетъ Черг. 86.
число сторонъ многоугольника.
Эта величина, очевидно, превышаетъ сумму угловъ многоугольника на сумму всѣхъ тѣхъ угловъ, которые расположены вокругъ точки О; по эта сумма равна 4й (26, 2°); слѣд., сумма угловъ многоугольника равна 2йп—4сІ=2й (п—2).
Слѣдствіе. При данномъ числѣ сторонъ сумма угловъ выпуклаго многоугольника есть величина постоянная. Такъ, сумма угловъ во всякомъ выпукломъ четыреугольникѣ равна 2й(4—2)=4й; въ пятпугольнпкѣ=2<3(5—2)=6й; въ шестиуголь-нпкѣ=2й(6—2)=8й; и т. Д.
90. Теорема. Если изъ вершины каждаго угла выпуклаго многоугольника проведемъ продолженіе одной изъ сторонъ этого угла, то сумма образовавшихся при этомъ внѣшнихъ угловъ
5*
— 68 —
равна четыремъ прямымъ (независимо отъ числа сторонъ много* угольника).
Черт. 87.
Каждый изъ такихъ внѣшнихъ угловъ (черт. 87) составляетъ дополненіе до 2й къ смежному съ нимъ внутреннему углу многоугольника; слѣд., если къ суммѣ всѣхъ внутреннихъ угловъ приложимъ сумму всѣхъ внѣшнихъ угловъ, то получимъ 2сІп (гдѣ п число сторонъ); но сумма внутреннихъ
угловъ, какъ мы видѣли,
равна 2йп—4й; слѣд., сумма внѣшнихъ угловъ равна:
2йп—(2 йп—4й) =2 д,п—2д,п+4й =4й.
Слѣдствіе. Въ выпукломъ многоугольникѣ не можетъ быть болѣе 3-хъ внутреннихъ острыхъ угловъ. Дѣйствительно, если бы существовало 4 (или болѣе) внутреннихъ острыхъ угла, то тогда бы было 4 (или болѣе) тупыхъ внѣшнихъ угла, и потому сумма всѣхъ внѣшнихъ угловъ мн-ка была бы болѣе 4й, что невозможно.
О постулатѣ параллельныхъ линій.
91. Легко показать, что такъ называемый 5-й постулатъ Эвклида (указанный въ § 83 этой книги) и постулатъ, принятый нами (§ 79) въ основаніе теоріи параллельныхъ линій (введенный впервые англійскимъ математикомъ Джономъ Плейферомъ въ 1795 г.) обратимы одинъ въ другой, т.-е. изъ постулата Плейфера можно вывести, какъ логическое слѣдствіе, постулатъ Эвклида (что и сдѣлано въ этой книгѣ, § 83) и, обратно, изъ этого постулата можно логически получить постулатъ Плейфера. Послѣднее можно выполнить, напр., такъ:
Пусть черезъ точку Е (черт. 88), взятую внѣ прямой СО, проведены какія-нибудь 2 прямыя АВ и АіВі; докажемъ, исходя изъ постулата Эвклида, что эти прямыя не могутъ быть обѣ параллельны одной и той же прямой СО.
— 69 —
Для этого проведемъ черезъ Е какую-нибудь сѣкущую прямую МН-,
обозначимъ внутренніе односторонніе углы, образуемые этсго сѣкущею съ пря‘мыми СО и АВ, буквами
а и Ъ. Тогда одно изъ двухъ: или сумма а-ЬЬ не равна 2<і, или она равна 2й. Въ первомъ случаѣ согласно постулату Эвклида, прямая АВ должна пересѣчься съ СО и, слѣд., она не можетъ быть параллельной СО\ во второмъ случаѣ сумма а-\-В1Е^ окажется не равной 2<і (такъ какъ уголъ ВХЕК не равенъ углу ВЕ№)’, значитъ, тогда, согласно тому же постулату, прямая -А}#, должна пересѣчься съ СО и, слѣд., эта прямая
Черт. 88.
не можетъ быть параллельной СО. Такимъ образомъ, одна
изъ прямыхъ АВ и А1В1 непремѣнно окажется непараллельной прямой СО-, слѣд., черезъ одну точку нельзя провести двухъ различныхъ прямыхъ, параллельныхъ одной и той же прямой.
62. Существуетъ очень много и другихъ предложеній, также логически обратимыхъ съ постулатомъ Эвклида (и, слѣд., ему логически равноси л ь н ы х ъ). Укажемъ, напр., слѣдующія предложенія, которыя нѣкоторыми извѣстными геометрами ставились въ основаніе
теоріи параллельныхъ линій:
Существуетъ по крайней мѣрѣ одинъ треугольникъ, у котораго сумма угловъ равна 2И (французскій математикъ Л е ж а н д р ъ, въ началѣ XIX столѣтія).
Существуетъ выпуклый четыреугольникъ (прямоугольникъ), у котораго всѣ четыре угла прямые (французскій математикъ Клодъ К л ѳ р о, ХѴІП столѣтіе).
Существуетъ треугольникъ, подобный, но не равный, другому треугольнику (итальянекій математикъ С а к к е р и, начало ХѴІП столѣтія).
Черезъ всякую точку, взятую внутри угла, меньшаго 2Л, можно провести прямую, пересѣкающую обѣ стороны этого угла (нѣмецкій математикъ Лоренцъ, конецъ ХѴІП стол.); и другія.
Такъ какъ постулатъ Эвклида и всѣ другіе, равносильные ему, не обладаютъ качествомъ очевидности, то весьма многіе математики, начиная съ древнихъ временъ и до конца первой четверти XIX столѣтія, дѣлали неоднократныя попытки доказать постулатъ Эвклида (или какой-нибудь другой, ему равносильный), т.-е. вывести его, какъ логическое слѣдствіе, изъ другихъ аксіомъ геометріи. Всѣ эти
попытки оказались однако неудачными: въ каждомъ изъ такихъ «дока
— 70 —
зательствъ», послѣ подробнаго разбора его, можно было всегда найти какую-нибудь логическую ошибку.
93. Постоянныя неудачи въ поискахъ доказательствъ Эвклидова постулата привели нѣкоторыхъ математиковъ къ мысли, что этотъ постулатъ (или ему равносильный) и не можетъ быть выведенъ изъ другихъ аксіомъ геометріи, а представляетъ собою независимое отъ нихъ самостоятельное допущеніе о свойствахъ пространства. Впервые эту мысль обстоятельно развилъ русскій математикъ, профессоръ Казанскаго университета, Н. И. Лобачевскій (1793—1856). Въ своемъ сочиненіи «Новыя начала геометріи», появившемся въ 1836—1838 годахъ, онъ обнародовалъ особую геометрію (названную потомъ геометріей Лобачевскаго), въ основаніе которой положены тѣ же геометрическія аксіомы, на которыхъ основана геометрія Эвклида, за исключеніемъ только его постулата параллельныхъ линій, вмѣсто котораго Лобачевскій взялъ слѣдующее допущеніе: ч е р е з ъ т о ч к у, л о ж а щ у ю внѣ п р я м о й, м о ж и о п р о-ножество параллельныхъ этой прямой; именно, онъ допустилъ, что если АВ (черт. 89) есть прямая и С какая-нибудь точка внѣ ея, то при этой точкѣ существуетъ нѣкоторый уголъ БЕС, обладающій тѣмъ свойствомъ, что всякая прямая, проведенная черезъ С внутри этого угла (напр., прямая СЕ), а также
и обѣ стороны его не пересѣкаются съ АВ, сколько бы ихъ ни продолжали, тогда какъ всякая прямая, проведенная черезъ С внѣ этого угла, пересѣкается съ АВ. Понятно, что такое допущеніе отрицаетъ постулатъ Эвклида, такъ какъ при существованіи этого угла нельзя утверждать, что всякія 2 прямыя пересѣкаются, коль скоро онѣ съ сѣкущей образуютъ внутренніе односторонніе углы, которыхъ сумма не равна двумъ прямымъ угламъ. Несмотря однако на это отрицаніе, геометрія Лобачевскаго представляетъ собою такую же стройную систему геометрическихъ теоремъ, какъ и геометрія Эвклида (хотя, конечно, теоремы геометріи Лобачевскаго существенно отличаются отъ теоремъ геометріи Эвклида); въ ней, какъ и въ геометріи Эвклида, не встрѣчается никакихъ логическихъ противорѣчій ни теоремъ съ аксіомами, положенными въ основаніе этой геометріи, ни однѣхъ теоремъ съ другими теоремами. Между тѣмъ, если бы постулатъ Эвклида могъ быть доказанъ, т.-е. если бы онъ представлялъ собою нѣкоторое, хотя бы и очень отдаленное, логическое слѣдствіе изъ другихъ геометрическихъ аксіомъ, то тогда отрицаніе этого постулата, положенное въ основу геометріи вмѣстѣ оъ п р и н я-
вести оезчисленное м
А-----------------------В
Черт. 89.
— 71 —
т і е м ъ всѣхъ другихъ аксіомъ, непремѣнно привело бы къ логически противорѣчивымъ слѣдствіямъ. Отсутствіе такихъ противорѣчій въ геометріи Лобачевскаго служитъ указаніемъ на независимость 5-го постулата Эвклида отъ прочихъ геометрическихъ аксіомъ и, слѣд., на невозможность доказать его *).
94. Почти одновременно съ Лобачевскимъ, независимо отъ него, Венгерскій математикъ Іоаннъ Вольэ (1802—1860) также построилъ новую геометрію, исходя изъ того же допущенія, какъ и Лобачевскій, что черезъ точку, взятую внѣ прямой, можно провести безчисленное множество параллельныхъ этой прямой.
Позже ихъ нѣмецкій математикъ Риманъ (1826—1866) показалъ возможность построенія еще особой, также лишенной противорѣчій, геометріи (названной потомъ геометріей Римана), въ которой вмѣсто постулата Эвклида принимается допущеніе, что черезъ точку, взятую внѣ прямой, нельзя провести ни одной параллельной этой прямой (другими словами, всѣ прямыя плоскости пересѣкаются).
Всѣ тѣ геометріи (какъ Лобачевскаго и Римана), въ которыхъ въ основаніе положено какое-нибудь допущеніе о параллельныхъ линіяхъ, не согласное съ постулатомъ Эвклида, носятъ общее названіе не-Эвклидовыхъ геометрій.
95. Приведемъ нѣкоторыя теоремы геометріи Лобачевскаго, рѣзкоразличающіяся отъ соотвѣтствующихъ теоремъ геометріи Эвклида:
Два перпендикуляра къ одной и той же прямой, по мѣрѣ удаленія отъ этой прямой, расходятся неограниченно.
Сумма угловъ треугольника меньше 2й (въ геометріи Римана она больше 2гі), при чемъ эта сумма не есть величина постоянная для разныхъ треугольниковъ.
Чѣмъ больше площадь треугольника, тѣмъ больше сумма его угловъ разнится отъ 2й.
*) Замѣтимъ, однако, что одно только отсутствіе противорѣчій въ геометріи Лобачевскаго еще не служитъ доказательствомъ независимости Эвклидова постулата отъ другихъ аксіомъ геометріи; вѣдь всегда можно возразить, что это отсутствіе противорѣчій есть только случайное явленіе, происходящее, быть можетъ, отъ того, что въ геометріи Лобачевскаго не сдѣлано еще достаточнаго количества выводовъ, что со временемъ, быть можетъ, и удастся кому-нибудь получить такой логическій выводъ въ этой геометріи, который окажется въ противорѣчіи съ какимъ-нибудь другимъ выводомъ той же геометріи. Подробная теорія этого вопроса (см. Энциклопедія элем. математики Вебера и Вѳльштейна, т. II, кп. 1, стр. 74 и др.) устанавливаетъ: 1) что если бы въ геометріи Лобачевскаго или въ какой-нибудь другой не-Эвклидовой геометріи оказалось противорѣчіе, то и въ Эвклидовой геометріи было бы соотвѣтствующее
— 72 —
Если въ выпукломъ четыреугольникѣ 3 угла прямые, то 4-й уголъ острый (значитъ, въ этой геометріи прямоугольники невозможны).
Если углы одного тр-ка соотвѣтственно равны угламъ другого тр-ка, то такіе тр-ки равны (слѣд., въ геометріи Лобачевскаго не существуетъ подобія).
Геометрическое мѣсто точекъ плоскости, равностоящихъ отъ какой-нибудь прямой этой плоскости, есть нѣкоторая кривая линія.
ГЛАВА VII.
Параллелограммы и трапеціи.
I. Главнѣйшія свойства параллелограммовъ.
ѲѲ. Опредѣленіе. Четыреугольникъ, у котораго противоположныя стороны попарно параллельны, наз. параллелограммомъ.
Такой четыреугольникъ (АВСВ, черт. 90) получится, напр., если какія-нибудь двѣ параллельныя прямыя КВ и ММ пересѣчь двумя другими параллельными прямыми В8 и Рф.
Для краткости слово «параллелограммъ» мы часто будемъ писать такъ: пар-мъ.
97. Теорема. Во всякомъ параллелограммѣ:
1°, противоположные углы равны;
2°, сумма угловъ, прилежащихъ къ одной сторонѣ, равна двумъ прямымъ.
Пусть АВСБ (черт. 91) есть параллелограммъ, т.-е. АВ II СВ и ВС II АВ\ требуется доказать, что
1°, /_А=/_С и Л.В=Л.В-.
2°, /^4+/СВ=2гі, /^В+/^С=2й и т. д.
противорѣчіе; но 2) въ Эвклидовой геометріи противорѣчій быть не можетъ. Отсюда, конечно, необходимо слѣдуетъ, что постулатъ Эвклида не представляетъ собою слѣдствія другихъ аксіомъ и потому онъ недоказуемъ.
— 73 —
1°. Углы А п С равны, потому что стороны этихъ угловъ соотвѣтственно параллельны и имѣютъ противоположное направленіе отъ вершины (85). То же — самое можно сказать объ углахъ І ]
В и Р. / /
2°. Каждая изъ суммъ: А+В, / /
В+С, С+Р и Б+А равна 2Л, по- д I ч)
ТОМУ ЧТО ЭТО СУММЫ внутреннихъ Черт. 91.
одностороннихъ угловъ при параллельныхъ прямыхъ.
98. Теорема. Во всякомъ параллелограммѣ противоположныя стороны равны.
Пусть фигура АВСБ (черт. 92) есть параллелограммъ, т.-е. АВ II СБ и ВС II АБ-, требуется доказать, что АВ—СБ и ВС=АБ.
Проведя діагональ БР, получимъ два тр-нпка АВБ ""
и ВСБ, которые равны, по- /
тому что у нихъ: БР общая / сторона, /^1=^4 и д / ^4)
/ІЗ (какъ внутренніе накрестъ лежащіе при парал- Черт. 92.
лельныхъ прямыхъ). Изъ равенства тр-ковъ слѣдуетъ: АВ=СБ и АБ—ВС (въ равныхъ тр-кахъ противъ равныхъ угловъ лежатъ равныя стороны).
Замѣчаніе. Теорему эту можно выразить еще и такъ: отрѣзки параллельныхъ, заключенные между параллельными, равны.
99. Обратныя теоремы. Если въ выпукломъ *) четыреугольникѣ:
•) Четыреугольникъ, какъ и всякій многоугольникъ (35), наз. выпуклымъ, если онъ ограниченъ такою ломаною линіей,
Черт. 96.
которая вся расположена по одну сторону отъ каждаго изъ 4-хъ составляющихъ ее отрѣзковъ. Четыреугольники могутъ быть и не-пыпуклыѳ, какъ, напр., тѣ, которые изображены на черт. 96-мъ.
— 74 —
1°, противоположныя стороны попарно равны, или 2°, двѣ противоположныя стороны равны и параллельны, то такой четыреугольникъ есть параллелограммъ.
1°. Пусть фигура АВСВ (черт.93)
Л г- -с есть выпуклый четыреугольникъ, / у котораго:
/ А/ АВ=СВ и ВС=АВ.
д / и, Требуется доказать, что эта
фигура—параллелограммъ, т.-е.
черт. 93. АВ у св и ѢС || АІ) _проведя діа-
гональ ВВ, получимъ два тр-ка, которые равны, такъ какъ у нихъ: ВВ общая сторона, АВ=СВ и ВС=АВ (по условію). Изъ равенства ихъ слѣдуетъ: ^1=^І4 и 2І2=/І3 (въ равныхъ тр-кахъ противъ равныхъ сторонъ лежатъ равные углы); вслѣдствіе этого АВ II СВ и ВС II АВ (если внутренніе накрестъ лежащіе углы равны, то прямыя параллельны).
2°. Пусть въ четыреугольникѣ (АВСВ, черт. 94) дано усло-р _ віемъ: ВС—АВ и ВС II АВ.
Требуется доказать, что
/ х. / АВСВ есть параллелограммъ,
/ х. / т.-е. что АВ || СВ.—Тре-
X Лм/ угольники АВВ и ВСВ рав-
У ны, потому что у нихъ: ВВ
Черт. 94. общая сторона, ВС=АВ
(по условію) и 2І2=2ІЗ (какъ внутренніе накрестъ лежащіе углы при параллельныхъ ВС и АВ и сѣкущей ВВ). Изъ равенства тр-ковъ слѣдуетъ: ^11=2І4; поэтому АВ II СВ.
Черт. 95.
100. Теорема. Во всякомъ параллелограммѣ діагонали дѣлятся пополамъ.
Пусть АВСВ (черт. 95) есть параллелограммъ, а АС и ВВ его діагонали; требуется доказать, что ВО=ОВ и АО=ОС.
Тр-ки ВОС и АОВ (покрытые на чертежѣ штрихами) равны, потому что у нихъ: ВС—АВ (какъ противоположныя стороны параллелограмма), /^1=/^2 и Х.з=2^4 (какъ внутренніе на
75 —
крестъ лежащіе углы при параллельныхъ прямыхъ). Изъ равенства тр-ковъ слѣдуетъ: ОС=ОА и ОВ=ОВ.
1О1. Обратная теорема. Всякій четыреугольникъ, діагонали котораго дѣлятся пополамъ, есть параллелограммъ.
Пусть фигура АВСБ (черт. 95) есть четыреугольникъ, у котораго: АО—ОС и ВО=ОВ-, требуется доказать, что эта фигура—параллелограммъ.
А АОВ—^ВОС, такъ какъ этп тр-ки имѣютъ по равному углу (при вершинѣ О), заключенному между соотвѣтственно равными сторонами. Изъ ихъ равенства слѣдуетъ: Л.1—Л.2 и 2^.3 =2^.4 (въ равныхъ тр-кахъ противъ равныхъ сторонъ лежатъ равные углы); но если внутренніе накрестъ лежащіе углы равны, то прямыя параллельны (76); поэтому АВ II ВС. Такъ какъ изъ равенства тѣхъ же тр-ковъ слѣдуетъ еще, что АВ=ВС, то фигура АВСВ есть параллелограммъ (99, 2°).
102. Центръ симметріи. Полезно замѣтить еціе слѣдующее свойство параллелограмма: ес и черезъ точку пересѣченія діагоналей парал-
лолограмма (черезъ точку О, черт. 97) проведемъ какую-нибудь прямую (Л2Ѵ), то эта прямая пересчетъ контуръ параллелограмма въ двухъ точкахъ (Р и ($, симметричныхъ относительно точки пересѣченія діагоналей, т.-е. въ 2-хъ такихъ точкахъ, которыя, во 1, лежатъ по разныя стороны отъ точки О и, во 2, на равныхъ разстояніяхъ отъ этой точки. Дѣйствительно, тр-ки ОАР и ОСф равны, такъ какъ у нихъ: АО —ОС (по свойству діагоналей параллелограмма), углы при общей вершинѣ О равны (какъ вертикальные) и
(какъ углы внутренніе накрестъ лежащіе при параллельныхъ). Изъ равенства этихъ тр-ковъ слѣдуетъ: ОР = Оф.
Черт. 97.
Если въ какой-нибудь фигурѣ существуетъ точка, обладающая указаннымъ свойствомъ, то такая точка наз. центромъ симметріи этой фигуры; значитъ, въ паралеллограммѣ пересѣченіе его діагоналей есть центръ симметріи.
Симметрія относительно центра наз. центральной симметріей.
— 76 —
Черт. 98.
2. Особыя формы параллелограммовъ: прямоугольникъ, ромбъ и квадратъ.
103. Опредѣленіе. Параллелограммъ, у котораго всѣ углы прямые, паз. прямоугольникомъ.
Такой параллелограммъ можно, напр., получить, если па сторонахъ прямого угла А (черт. 98) отъ его вершины отложимъ произвольной длины отрѣзки АВ п АС и черезъ точки В и С проведемъ прямыя ВВ и СЕ, параллельныя сторонамъ прямого угла. Прямая ВВ, пересѣкаясь въ точкѣ В съ прямой АВ, должна пересѣчься и съ прямой СЕ, параллельной АВ (80, 1°) въ пѣкоторой точкѣ Е. Мы получимъ такпмъ образомъ параллелограммъ АВЕС, у котораго одинъ уголъ, именно А, есть прямой по построенію; но
въ такомъ случаѣ, по свойству угловъ параллелограмма (97), и всѣ остальные углы его должны быть прямые, такъ какъ уголъ при вершинѣ Е равенъ А, а углы при В и С дополняютъ А до 2(1.
104. Теорема. Во всякомъ прямоугольникѣ діагонали равны.
Пусть фигура АВС О (черт. 99) есть прямоугольникъ; требуется доказать, что ЛС=ВВ.
Прямоугольные тр-ки ЛСВ и АВВ равны, потому что у нпхъ: ЛВ общій катетъ и АВ=СВ (какъ противоположныя стороны паралле
лограмма). Изъ равенства тр-ковъ слѣдуетъ: АС=ВВ.
105. Обратная теорема. Всякій параллелограммъ, у котораго діагонали равны, есть прямоугольникъ.
Пусть фпгура АВСВ (черт. 99) есть параллелограммъ, у котораго АС=ВВ-, требуется доказать, что эта фигура—прямоугольникъ.—Тр-ки АВВ и АСВ равны, такъ какъ у нихъ АВ общая сторона, АС=ВВ (по условію) и АВ=СВ (по свой
Черт. 99.
11
ству противоположныхъ сторонъ параллелограмма). Изъ ихъ равенства слѣдуетъ: /_ВАВ=/_АВС. Но сумма этпхъ 2-хъ угловъ равна (по свойству угловъ параллелограмма); слѣд., каждый изъ нихъ есть гі. Но тогда и углы В и С должны быть прямые, и потому фигура АВСВ есть прямоугольникъ.
1ОѲ. Опредѣленіе. Параллелограммъ, у котораго всѣ
стороны равны, наз. ромбомъ.
Такой пар-мъ можно получить, если па сторонахъ произ-
вольнаго угла А (черт. 100) отъ его вершины отложимъ равные
отрѣзки АВ и АС и черезъ точки В п С проведемъ прямыя ВВ и СЕ, параллельныя сторонамъ угла А. Эти прямыя должны пересѣчься между собою (80,1°) въ нѣкоторой точкѣ Е. Мы получимъ такимъ образомъ пар—мъ, у котораго двѣ
смежныя стороны АВ и АС
равны по построенію. Но тогда, по свойству сторонъ пар—ма (98), у него всѣ 4 стороны окажутся равными, такъ какъ ВЕ=АС п СЕ=АВ.
107 Теорема. Во всякомъ ромбѣ діагонали взаимно перпендикулярны.
Пусть АВСВ (черт. 101) есть ромбъ, а АС к ВВ его діаго-
нали; требуется доказать, что АСЛ-ВВ.
Тр-ки АВЭ и ВОС равны, потому что у нихъ: ВО общая сто-
рона, АЕ=ВС (такъ какъ у ромба всѣ стороны равны) и АО=ОС (такъ какъ діагонали всякаго параллелограмма дѣлятся пополамъ). Изъ равенства тр-ковъ слѣдуетъ:
/^1=2^2, т.-е. ВВЛ.АС.
Черт. 101.
Замѣчаніе. Изъ равенства тѣхъ же тр-ковъ слѣдуетъ, что /^,3=^4, т.-е. что уголъ В дѣлится діагональю пополамъ. Изъ равенства тр-ковъ ВОС и СОВ (которое доказы -вается такъ же, какъ и равенство тр-ковъ АВО и ВОС) слѣ
— 78 —
дуетъ, что уголъ С дѣлится діагональю пополамъ; и т. д. Значитъ, діагонали ромба дѣлятъ его углы пополамъ.
108. Обратная теорема. Всякій параллелограммъ, у котораго діагонали взаимно перпендикулярны, есть ромбъ.
Пусть фигура АВСВ (черт. 101) есть параллелограммъ, у котораго діагонали АС и ВВ перпендикулярны; требуется доказать, что эта фигура есть ромбъ, т.-е. что АВ=ВС=СВ—ВА. Тр-ки АОВ и ВОС прямоугольные (по условію); у нихъ катетъ ОВ общій и катеты АО и ОС равны (такъ какъ діагонали всякаго параллелограмма дѣлятся пополамъ). Значитъ, эти тр-ки равны, и потому равны ихъ гипотенузы АВ и ВС. Но АВ=СВ и ВС=АВ (по свойству противоположныхъ сторонъ пар-ма); слѣд., АВ—ВС=СВ=ВА, т.-е. фигура АВСВ есть ромбъ.
109. ОСИ симметріи ромба. Полезно замѣтить еще слѣдующее свойство: каждая діагональ ромба есть его ось симметріи.
Такъ, діагональ ВО (черт. 102) есть ось симметріи ромба АВС О, потому что, вращая Л АВО вокругъ ВО, мы можемъ совмѣстить его съ А ВСО-, вслѣдствіе этого любой точкѣ М, взятой на одной половинѣ контура ромба, соотвѣтствуетъ точка К на другой половинѣ контура, симметричная относительно діагонали ВО (33). То же самое можно сказать о діагонали АС.
\ / НО. Опредѣленіе. Параллело-
\ / граммъ, у котораго всѣ стороны равны
р и всѣ углы прямые, наз. к в а д р а -
Черт. 102. томъ.
Такой пар-мъ можно получить, если при построеніи прямоугольника (103) мы возьмемъ отрѣзки АВ и АС равными, или если при построеніи ромба (106) возьмемъ уголъ А прямой.
Такъ какъ квадратъ есть параллелограммъ, прямоугольникъ и ромбъ, то онъ соединяетъ въ себѣ всѣ свойства этихъ фигуръ; напр., относительно діагоналей квадрата можно сказать, что онѣ: 1) дѣлятся пополамъ, 2) равны между собою, 3) взаимно перпендикулярны и 4) дѣлятъ углы квадрата пополамъ.
— 79 —
3. Нѣкоторыя теоремы, основанныя на свойствахъ параллелограмма.
111. Теорема. Параллельныя прямыя (АВ и СВ, черт. 103) вездѣ одинаково удалены одна отъ другой; другими словами: всѣ точки одной параллельной одинаковы удалены отъ другой параллельной.
Дѣйствительно, если изъ какихъ-нибудь двухъ точекъ М и №
прямой СВ опустимъ на АВ перпендикуляры МР и
то эти перпендикуляры параллельны (74), и потому фигура М^Р параллелограммъ; отсюда слѣдуетъ (98), что МР— =^^,т.-е. точкиМиЯ одинаково удалены отъ прямой АВ.
Черт. юз.
112. Теорема. Геометрическое мѣсто точекъ, удаленныхъ отъ данной прямой на одно и то же разстояніе и находящихся по одну сторону отъ нея, есть прямая, параллельная данной.
Пусть М и М (черт. 104) будутъ какія-нибудь двѣ точки, находящіяся по одну сторону отъ прямой АВ н удаленныя отъ нея на одно и то же разстояніе т\ тогда перпендикуляры МР и опущенные изъ этихъ точекъ на АВ, равны т. Проведемъ черезъ М и прямую СВ. Такъ какъ МР=Н(^ и сверхъ того МР II (74), то фпгура М^Р есть параллелограмъ (99, 2°); слѣд., СВ II АВ. Мы видимъ такимъ образомъ, что всякія 2 точки (какъ Мп №), которыя удалены отъ прямой АВ
на разстояніе т и расположены по одну сторону отъ этой прямой, лежатъ на прямой, параллельной АВ и удаленной отъ АВ на разстояніе т. Такъ какъ такая прямая можетъ быть только одна (по одну сторону отъ АВ), именно СВ, то мы должны заключить, что всѣ точки, удаленныя отъ АВ на одно и то же разстояніе т и расположенныя по одну сторону отъ нея, лежатъ на прямой СВ, параллельной АВ. Обратно, всякая
К ы
Черт. 104.
в
— 80 —
точка В, взятая на этой прямой, отстоитъ отъ АВ па столько же, какъ и точки М и Е, т.-е. па данное разстояніе т (III).
113. Теорема. Если на одной сторонѣ угла отложимъ какіе-нибудь равные между собою отрѣзки и черезъ ихъ концы проведемъ параллельныя прямыя до пересѣченія съ другой стороной угла, то и на этой сторонѣ отложатся равные между собою отрѣзки.
Пусть АВС (черт. 105) какой-нибудь уголъ и на его сторонѣ ВС отложены равные отрѣзки ВВ=ВЕ=ЕЕ... Проведемъ черезъ точки В, Е, Е... параллельныя прямыя ВМ, ЕЕ, ЕР... до пересѣченія съ АВ; требуется доказать, что
ВМ=МЕ=ЕР...
Возьмемъ какіе-нибудь два изъ этнхъ отрѣзковъ, напр., МЕ и ЕР, и докажемъ, что они равны.
Черт. 105.
Для этого проведемъ А прямыя ВК и ЕЬ, параллельныя АВ. Полученные при этомь тр-ки ВКЕ п ЕЬЕ рав-вны, такъ какъ у нихъ: ВЕ=ЕЕ (по условію), АІКВЕ = АЬЕЕ и А_КЕВ = АЬГЕ (какъ углы соотвѣтственные
при параллельныхъ прямыхъ). Изъ равенства этихъ тр-ковь слѣдуетъ: ВК=ЕЬ. Но ВК==МЕ и ЕЬ=ЕР (какъ противоположныя стороны параллелограммовъ); значитъ, МЕ=ЕР.
Черт. 100.
Такъ же докажемъ равенство и другихъ отрѣзковъ стороны АВ (для отрѣзка ВМ мы должны взять тр-къ ВМВ).
Замѣчаніе. Теорема не требуетъ, чтобы равные отрѣзки откладывались на
— 81 —
4В
Б
Г'-С
Черт. 107.
Докажемъ сначала, что
сторонѣ угла непремѣнно отъ его вершины; они могутъ быть отложены отъ произвольной точки стороны и даже могутъ раздѣляться какими-нибудь промежутками (черт. 106).
114. Задача. Данный отрѣзокъ прямой раздѣлить на пь равныхъ частей.
Эта задача рѣшается на основаніи предыдущей теоремы.
Пусть АВ (черт. 107) дан-ный отрѣзокъ прямой, кото- АН:-------V--------ц-
рый требуется раздѣлить, положимъ, на 3 равныя части. Изъ конца его А проводимъ прямую АС, образующую съ АВ произвольный уголъ; откладываемъ на АС отъ точки А три произвольной длины, но равные между собою, от
рѣзка: АВ, ВЕ и ЕЕ: точку Е соединяемъ съ В; наконецъ, изъ Е и В проводимъ прямыя ЕЕ и ВМ, параллельныя ЕВ. Тогда отрѣзокъ АВ, по доказанному, раздѣлится въ точкахъ М и Л7 на три равныя части.
115. Теорема. Прямая, соединяющая середины двухъ сторонъ треугольника, параллельна третьей его сторонѣ и равна ея половинѣ.
Пусть ВЕ (черт. 108) есть прямая, соединяющая середины двухъ сторонъ треугольника АВС. ВЕ II АС. Предположимъ противное, т.-е. что прямая ВЕ не параллельна АС. Проведемъ черезъ точку В прямую, параллельную АС (77). Эта прямая, при нашемъ предположеніи, не можетъ быть ВЕ-, пусть это будетъ нѣкоторая прямая ВЕ^ Такъ какъ на сторонѣ ВА угла В отложены равные отрѣзки ВВ и ВА, и изъ ихъ концовъ проведены къ другой сторонѣ угла В параллельныя прямыя ВЕг
и АС, то на сторонѣ ВС должны получиться равные отрѣзки (113); значитъ, ВЕ^ЕгС, и потому точка Ех должна быть серединой
А. Киселевъ. Геометрія 6
— 82
стороны ВС. Мы приходимъ, такимъ образомъ, къ нелѣпому заключенію, что сторона ВС имѣетъ 2 середины: точку Е по условію и точку Еі согласно нашему выводу. Нелѣпость этого заключенія заставляетъ насъ отбросить сдѣланное допущеніе, что ВЕ не параллельна АС-, значитъ, ЛЕЦЛС. Остается теперь доказать, что ВЕ=г/2АС. Для этого изъ Е проведемъ ЕЕ II ВА-, тогда фигура ЕВАЕ будетъ параллелограммъ и, слѣд., ВЕ=АЕ. Такъ какъ на сторонѣ СВ угла С отложены равные отрѣзки (СЕ=ЕВ) и изъ точекъ, разграничивающихъ эти отрѣзки, проведены къ другой сторонѣ параллельныя прямыя ЕЕ н ВА, то СЕ=ЕА- слѣд., ВЕ=г/2АС.
4. Опредѣленіе и свойство трапеціи.
116. Опредѣленіе, котораго какія-нибудь двѣ лелыіы, наз. трапеціей.
Выпуклый четыреугольникъ, у противоположныя сторопы парал-
Такой четыреугольникъ Вл""— іС можно получить, если между
/ \ двумя параллельными пря-
/ \ мыми ВС и АВ (черт. 109)
/ \ проведемъ двѣ какія-нибудь
А* 1,11 Б сѣкущія прямыя АВ и СВ.
Черт. 109. Параллельныя стороны тра-
пеціи наз. ея основаніями, непараллельныя—б о к а м и.
117. Теорема. Прямая, соединяющая середины боковъ трапеціи, параллельна основаніямъ трапеціи и равна полусуммѣ ихъ.
Пусть прямая ЕЕ (черт. 110) соединяетъ середины боковыхъ сторонъ трапеціи АВСВ-, требуется доказать, что ЕЕ || АВ (и, слѣд.,ЕГ || ВС)
и, кромѣ того, что ЕЕ=1/2 (АВ+ВС).—Черезъ точки В и Е проведемъ прямую до пересѣченія съ продолженіемъ стороны АВ
— 83 —
въ нѣкоторой точкѣ О. Тогда получимъ два тр-ка ВСР пБРО, которые равны, такъ какъ у нихъ: СР=РБ (по условію), Х.ВРС=Х.БРС (какъ углы вертикальные) и ^.ВСР=^.РБСг (какъ углы внутренніе накрестъ лежащіе при параллельныхъ прямыхъ). Изъ равенства тр-ковъ слѣдуетъ: ВР=РС и ВС=БС. Теперь видимъ, что въ &АВО прямая ЕР соединяетъ середины двухъ сторонъ; значитъ (115), ЕР II АВ и ЕР—1/2(АБ+ВО)\ другимп словами, ЕР II АБ и ЕР=Ч2 (АБ+ВС).
Замѣчаніе. Прямая, соединяющая середины боковъ трапеціи, наз. ея среднею линіей.
УПРАЖНЕНІЯ.
Доказать теоремы.
37. Соединивъ послѣдовательно середины сторонъ какого-нибудь четыреугольника, получимъ параллелограммъ.
38. Въ прямоугольномъ Л медіана, проведенная къ гипотенузѣ, равна ея половинѣ. (Указаніе: слѣдуетъ продолжить медіану па равное разстояніе).
39. Обратно: если медіана равна половинѣ стороны, къ которой она проведена, то тр-никъ прямоугольный.
40. Въ прямоугольномъ Д медіана и высота, проведенныя къ гипотенузѣ, образуютъ уголъ, равный разности острыхъ угловъ Д.
41. Если въ прямоугольномъ Д одинъ острый уголъ равенъ 1/3 Л, то противолежащій сму катетъ составляетъ половину гипотенузы.
42. Обратно: если катетъ вдвое меньше гипотенузы, то противолежащій ему острый уголъ равенъ ’/3й.
44. Всякая прямая, проведенная внутри трапеціи между ея основаніями, дѣлится среднею линіей пополамъ •).
46. Черезъ вершины угловъ Д проведены прямыя, параллельныя противоположнымъ сторонамъ. Образованный ими Д въ 4 раза болѣэ даннаго; каждая сторона его въ 2 раза болѣе соотвѣтствующей стороны даннаго Д.
*) Упражненія подъ №№ 43 и 45 выпущены, такъ какъ содержаніе перваго изъ нихъ изложено теперь въ § 102, а второго—въ слѣдствіи къ § 90.
6'
— 84 —
47. Въ равнобедренномъ Д сумма разстояній каждой точки основанія отъ боковыхъ сторонъ есть величина постоянная, а именно она равна высотѣ, опущенной на боковую сторону.
48. Какъ измѣнится эта теорема, если взять точку на продолженіи основанія?
48,а. Въ равностороннемъ А сумма разстояній всякой точки, взятой внутри этого Д, до сторонъ его ость величина постоянная, равная высотѣ Д.
49. Данъ квадратъ АВСВ. На сторонахъ его отложены равныя части: ААи ВВг, ССг и ВВѴ Точки Ви СІУ Вг соединены послѣдовательно прямыми. Доказать, что Л1В1С1Д1 есть квадратъ.
49,а. Если середины сторонъ какого угодно четыреугольника взять за вершины новаго четыреугольника, то (упр. 37) послѣдній есть параллелограммъ. Опредѣлить, при какихъ условіяхъ этотъ пар-мъ будетъ: 1) прямоугольникомъ, 2) ромбомъ, 3) квадратомъ (рѣшается на основаніи § 115).
Найти геометрическія мѣста:
50. —серединъ всѣхъ прямыхъ, проведенныхъ изъ данной точки къ различнымъ точкамъ данной прямой.
51. —точекъ, равноотстоящихъ отъ двухъ параллельныхъ прямыхъ.
52. —вершинъ тр-ковъ, имѣющихъ общее основаніе и равныя высоты.
Задачи на построеніе.
53. Даны два угла Д; построить третій.
54. Данъ острый уголъ прямоугольнаго Д; построить другой острый уголъ.
55. Провести прямую, параллельную данной прямой и находя щуюся отъ нея на данномъ разстояніи.
56. Раздѣлить пополамъ уголъ, вершина котораго не помѣщается на чертежѣ.
57. Черезъ данную точку провести прямую подъ даннымъ угломъ къ данной прямой.
58. Черезъ данную точку провести прямую такъ, чтобы отрѣзокъ ея, заключенный между двумя данными параллельными прямыми, равнялся данной длинѣ.
59. Между сторонами даннаго остраго угла помѣстить прямую данной длины такъ, чтобы она была перпендикулярна къ одной сторонѣ угла.
60. Между сторонами даннаго угла помѣстить прямую данной длины такъ, чтобы она отсѣкала отъ сторонъ угла равныя части.
61. Построить прямоугольный А по даннымъ острому углу и противолежащему катету.
62. Построить А по двумъ угламъ и сторонѣ, лежащей противъ одного изъ нихъ.
— 85 —
63. Построить равнобедренный Л по углу при вершинѣ и основанію.
64. То же—по углу при основаніи и высотѣ, опущенной на боковую сторону.
65. То же—по боковой сторонѣ и высотѣ, опущенной на нее.
66. Построить равносторонній Л по его высотѣ.
67. Раздѣлить прямой уголъ на 3 равныя части (другими словами построить уголъ, равный
68. Построить Л по основанію, высотѣ и боковой сторонѣ.
69. То же—по основанію, высотѣ и углу при основаніи.
70. То же—по углу и двумъ высотамъ, опущеннымъ на стороны ото го угла.
71. То же—по сторонѣ, суммѣ двухъ другихъ сторонъ и высотѣ, опущенной на одну изъ этихъ сторонъ.
72. То же—по двумъ угламъ и периметру.
73. То же—по высотѣ, периметру и углу при основаніи.
74. Провести въ А прямую, параллельную основанію, такъ, чтобы она была равна суммѣ отрѣзковъ боковыхъ сторонъ, считая отъ основанія.
75. Провести въ А прямую, параллельную основанію, такъ, чтобы верхній отрѣзокъ одной боковой стороны равнялся нижнему отрѣзку другой боковой стороны.
76. Построить многоугольникъ, равный данному (указаніе: діагоналями разбиваютъ данный мн-къ на тр-ки).
77. Построить четыреугольникъ по тремъ его угламъ и двумъ сторонамъ, образующимъ четвертый уголъ (указа-н і е: надо найти 4-й уголъ).
78. То же—по тремъ сторонамъ и двумъ діагоналямъ.
79. Построить параллелограммъ по двумъ неравнымъ сторонамъ и одной діагонали.
80. То же—по сторонѣ и двумъ діагоналямъ.
81. То же—по двумъ діагоналямъ и углу между ними.
82. То же—по основанію, высотѣ и діагонали.
83. Построить прямоугольникъ по діагонали и углу между діагоналями.
84. Построить ромбъ по сторонѣ и діагонали.
85. То же-—по двумъ діагоналямъ.
86. То же—по высотѣ и діагонали.
87. То же—по углу и діагонали, проходящей черезъ этотъ уголъ.
88. То же—по діагонали и противолежащему углу.
89. То же—по суммѣ діагоналей и углу, образованному діагональю со стороною.
90. Построить квадратъ по данной діагонали.
91. Построить трапецію по основанію, прилежащему къ нему углу и двумъ непараллельнымъ сторонамъ (могутъ быть два рѣшенія, одно и ни одного).
— 86 —
92. То же—по разности основаній, двумъ боковымъ сторонамъ и одной діагонали.
92,а. То же—по четыремъ сторонамъ (всегда ли задача возможна?).
93. То же—по основанію, высотѣ и двумъ діагоналямъ (условіе возможности).
94. То же—по двумъ основаніямъ и двумъ діагоналямъ (условіе возможности).
95. Построить квадратъ по суммѣ стороны съ діагональю.
96. То же—по разности діагонали и стороны.
97. Построить параллелограммъ по двумъ діагоналямъ и высотѣ.
98. То же—по сторонѣ, суммѣ діагоналей и углу между ними.
99. Построить Д по двумъ сторонамъ и медіанѣ, проведенной къ третьей сторонѣ.
100. То же—по основанію, высотѣ и медіанѣ, проведенной къ боковой сторонѣ.
100,а. Построить прямоугольный А по гипотенузѣ и суммѣ катетовъ.
100, 6. То же — по гипотенузѣ и разности катетовъ.
КНИГА П.
ОКРУЖНОСТЬ.
ГЛАВА і.
Форма и положеніе окружности.
118. Опредѣленія. Окружностью (черт. 111) называется
замкнутая плоская линія, всѣ точки которой одинаково удалены
отъ одной и той же точки
С
(О), называемой центромъ.
Прямыя (ОА, ОВ, ОС...), соединяющія центръ съ точками окружности, называются радіусами.
Безконечная прямая (М№), проходящая черезъ какія-нибудь двѣ точки окружности, называется сѣкущею.
Отрѣзокъ прямой (ЕР), соединяющій двѣ какія-нибудь точки окружности, наз. хордою.
Черт. 111.
— 87 —
Всякая хорда (АВ), проходящая черезъ центръ, наз. діаметромъ.
Какая-нибудь часть окружности (напр., ЕтР) наз. дугою.
О хордѣ (ЕР), соединяющей концы какой-нпбудь дуги, говорятъ, что она стягиваетъ эту дугу.
Дуга обозначается иногда знакомъ напр., пишутъ такъ: >^ЕтР.
Часть плоскости, ограниченная окружностью, наз. кругомъ.
Часть круга (напр., часть СОВ, покрытая на чертежѣ штрихами), ограниченная дугою и двумя радіусами, проведенными къ концамъ дуги, наз. секторомъ.
Часть круга (напр., часть ЕтР), ограниченная дугою и стягивающею ее хордою, наз. сегментомъ.
Изъ этихъ опредѣленій слѣдуетъ:
1°, всѣ радіусы одной окружности равны между собою;
2°, всякій діаметръ равенъ суммѣ двухъ радіусовъ, и потому всѣ діаметры одной окружности равны между собою.
119. Точки внутри круга и точки внѣ его. Окружность раздѣляетъ всѣ точки плоскости, на которой она проведена, на 3 слѣдующія области:
1) точки, которыхъ разстоянія отъ центра больше радіуса; такова, напр., точка М (черт. 112), для которой разстояніе ОМ болѣе радіуса ОА;
Черт. 112.
2) точки, которыхъ разстоянія отъ центра равны радіусу (точки А,В,... черт. 112);
— 88 —
3) точки, которыхъ разстоянія отъ центра меньше радіуса; такова, напр., точка (черт. 112), для которой разстояніе ОН меньше радіуса ОВ.
Точки первой области лежатъ внѣ круга, точки второй области лежатъ на окружности и точки третьей области расположены внутри круга.
Слѣдующія предложенія мы принимаемъ за очевидныя:
1) отрѣзокъ прямой (п вообще всякой непрерывной линіи), соединяющій (черт. 113) какую-ппбудь внутреннюю точку А съ какою-нибудь внѣшнею точкою В, пересѣкается гдѣ-нибудь съ окружностью;
2) отрѣзокъ прямой, соединяющій любыя 2 внутреннія точки А и С (черт. 113), пе пересѣкается съ окружностію;
3) отрѣзокъ прямой, соединяющій 2 внѣшнія точки, иногда не пересѣкается (ВВ), иногда пересѣкается (ВЕ) съ окружностью.
120. Теорема. Прямая и окружность не могутъ имѣть болѣе двухъ общихъ точекъ.
_ Для доказательства предполо-
жимъ, что прямая 1ѴШ (черт. 114) / имѣетъ съ окружностью, которой
/ \\ центръ находится въ точкѣ О, трп
/ \\ общія точки А, В и С. Тогда
да .(А_______уд прямыя ОА, ОВ, ОС должны быть
А ВС равны между собою, какъ ра-
Черт 114 діусы, вслѣдствіе чего тр-ки ОАВ
и О АС будутъ равнобедренные, и, слѣд., /111=^2 и </1=^3; откуда: ^2=^3; но это певоз можно, такъ какъ Х.2, будучи внѣшнимъ по отношенію кт тр-нику ОВС, больше внутренняго, не смежнаго съ нимъ, угла 3 (45).
121. Слѣдствіе. Никакая часть окружности не можетъ совмѣститься съ прямой, потому что въ противномъ случаѣ окружность съ прямою имѣла бы болѣе двухъ общихъ точекъ.
Линія, которой никакая часть не можетъ совмѣститься съ прямой, наз. кривою линіей. Значитъ, окружность есть кривая линія.
— 89 —
122. Теорема. Черезъ три точки, не лежащія на одной прямой, можно провести окружность и притомъ только одну.
Черезъ три точки А, В и С (черт. 115), не лежащія на одной прямой, только тогда можно провести окружность, если существуетъ такая четвертая точка О, которая одинаково удалена отъ точекъ А, В и С. Докажемъ, что такая точка существуетъ
и притомъ только одна. Для этого примемъ во вниманіе, что всякая точка, одинаково удаленная отъ точекъ А и В, должна лежать на перпендикулярѣ М1Ѵ, проведенномъ къ сторонѣ АВ черезъ ея середину (63); точно также всякая точка, одинаково удаленная отъ точекъ В и С, должна лежать на перпендикулярѣ Рф, прове
денномъ къ сторонѣ ВС черезъ ея середпну. Значитъ, если существуетъ точка, одинаково удаленная отъ трехъ точекъ Л, В, иС то она должна лежать заразъ и на М1Я, и па Р($, что возможно только тогда, когда она совпадаетъ съ точкой пересѣченія этихъ
двухъ прямыхъ. Прямыя 2И2Ѵ и Р($ всегда пересѣкаются (83, 2°), такъ какъ онѣ перпендикулярны къ пересѣкающимся прямымъ АВ и ВС. Точка О ихъ пересѣченія и будетъ
точкой, одинаково удаленной отъ А, отъ В и отъ С; значитъ, если примемъ эту точку за центръ, а за радіусъ возьмемъ разстояніе О А (или ОВ, или ОС), то окружность пройдетъ черезъ точки А, В и С. Такъ какъ прямыя и Рф могутъ пересѣчься только въ одной точкѣ, то цептръ этой окружности можетъ быть только одинъ, и длина ея радіуса можетъ быть только
одна; значитъ, искомая окружность — единственная.
123. Слѣдствіе. Точка О (черт. 115), находясь на одинаковомъ разстояніи отъ А и отъ С, должна также лежать на перпендикулярѣ ВВ, проведенномъ къ сторонѣ АС черезъ ея середину. Такимъ образомъ:
— 90 —
три перпендикуляра къ сторонамъ треугольника, проведен
ные черезъ ихъ середины, пересѣкаются въ одной точкѣ.
124.Задача. Найти центръ данной окружности (черт. 116).
Взявъ на данной окружности какія-нибудь три точки А, В и С, проводятъ черезъ нихъ двѣ хорды, напр., АВ и СВ, и черезъ середины этихъ хордъ проводятъ къ нимъ перпендикуляры ИРЫ п Р($. Искомый центръ, будучи одинаково
удаленъ отъ А, В и С, долженъ лежать и на М1У, и на Р§\ слѣд.,
онъ находится въ пересѣченіи этихъ перпендикуляровъ, т.-е. въ точкѣ О.
ГЛАВА II.
Равенство и неравенство дугъ.
125. Теорема. Два круга одинаковаго радіуса равны (черт. 117.) Пусть О и Оі суть центры двухъ круговъ, которыхъ радіусы равны. Наложимъ кругъ О на кругъ Оі такъ, чтобы ихъ центры совпали. Тогда обѣ окружности совмѣстятся, такъ какъ въ противномъ случаѣ пхъ точки не одинаково отстояли бы отъ центра и, слѣд., радіусы были бы неравны.
126. Замѣчаніе. Вращая одинъ изъ совпавшихъ круговъ вокругъ общаго центра, мы не нарушимъ ихъ совмѣщенія. Изъ этого слѣдуетъ, что двѣ части одной окружности или двѣ части равныхъ окружностей могутъ быть наложены одна на другую такъ, что всѣ точки одной части окажутся лежащими на другой.
— 91 —
127. Опредѣленіе. Двѣ дуги одинаковаго радіуса счита ются равными, если онѣ при наложеніи могутъ быть совмѣ
щены. Положимъ, напр., что мы накладываемъ дугу АВ (черт. 118) па дугу СВ такъ, чтобы точка А упала въ точку С и дуга АВ пошла по дугѣ СВ (что возможно, какъ мы видѣли въ предыдущемъ замѣчаніи); если при этомъ концы В и В совпадутъ, то—АВ=^СВ; въ противномъ случаѣ дуги не равны, при чемъ та будетъ меньше, которая составитъ только часть другой.
Черт. 118.
Суммою нѣсколькихъ данныхъ дугъ одинаковаго радіуса наз. такая дуга того же радіуса, которая составлена изъ частей, соотвѣтственно равныхъ даннымъ дугамъ. Такъ, если отъ произвольной точкп М (черт. 118) окружности отложимъ часть М1Ѵ, равную АВ, и затѣмъ отъ точки № въ томъ же направленіи отложимъ часть НР, равную СВ, то дуга МР будетъ суммой дугъ АВ и СВ. Подобно этому можно составить сумму трехъ и болѣе Дугъ.
Изъ понятія о суммѣ дугъ одного и того же радіуса выводятся понятія объ ихъ разности, произведеніи и частномъ въ томъ же смыслѣ, какъ и для отрѣзковъ прямыхъ.
128. Теорема. Всякій діаметръ дѣлитъ окружность и кругъ пополамъ
(черт. 119).
Черт. 119.
Вообразимъ, что кругъ перегнутъ по
какому-нибудь діаметру АВ такъ, чтобы часть его АтВ упала на часть АпВ. Тогда всѣ точки дуги т совмѣстятся съ точками дуги п, потому что въ противномъ случаѣ точки одной дуги лежали бы ближе къ центру, чѣмъ точки другой дуги, что невозможно.
— 92 —
Такимъ образомъ, всякій діаметръ раздѣляетъ окружность на двѣ полуокружности, а кругъ—на два полу
круга.
129. Замѣчаніе. Всякая хорда СВ (черт. 119), не проходящая черезъ центръ, стягиваетъ двѣ неравныя дуги; одну, большую полуокружности, другую—меньшую ея. Когда говорятъ: «дуга, стягиваемая хордой», то обыкновенно разумѣютъ
ту пзъ двухъ дугъ, которая меньше полуокружности.
130. Теоремы. 1°. Діаметръ, перпендикулярный къ хордѣ,
Черт. 120.
дѣлитъ эту хорду и обѣ стягиваемыя ею дуги пополамъ.
2°. Дуги, заключенныя между параллельными хордами, равны.
1°. Пусть діаметръ АВ (черт. 120) перпендикуляренъ къ хордѣ СВ и ЕР || СВ; требуется доказать, что:
1°. СК = КВ,^СВ=^ВВ,^СА=^ВА.
2°. ~СЕ=~ВР.
Перегнемъ чертежъ по діаметру АВ
такъ, чтобы его лѣвая часть упала на правую. Тогда лѣвая полуокружность совмѣстится съ правою полуокружностью, перпендикуляръ КС пойдетъ по КВ и перпендикуляръ ЬЕ
пойдетъ по ЕР. Изъ этого слѣдуетъ, что точка С, представляющая
собою пересѣченіе полуокружности съ КС, упадетъ на В, а точка Е, представляющая собою пересѣченіе полуокружности съ ЪЕ, упадетъ на В; поэтому:
1°. СК=КВ-, ^ВС=~ВВ-, ~АС=~АВ.
2°. ^СЕ=^ВР.
Слѣдствія. 1°. Діаметръ (АВ), проведенный черезъ середину хорды (СВ), перпендикуляренъ къ этой хордѣ и дѣ
литъ дугу, стягиваемую ею, пополамъ.
2°. Діаметръ (АВ), проведенный черезъ середину дуги (СВВ), перпендикуляренъ къ хордѣ, стягивающей эту дугу, и дѣлитъ
ее пополамъ.
Оба эти предложенія (обратныя теоремѣ 1*) легко доказываются отъ противнаго.
Замѣчаніе. Изложенное доказательство убѣждаетъ насъ, что каждый діаметръкруга есть его ось симметріи.
— 93 —
131. Задача. Раздѣлить данную
дугу (АВ,
черт. 121) пополамъ.
Проведя хорду АВ, опускаемъ на нее перпендикуляръ изъ центра и продолжаемъ его до пересѣченія съ дугою. По доказанному въ предыдущей теоремѣ, дуга АВ раздѣлится этпмъ перпендикуляромъ пополамъ. Если же центръ неизвѣстенъ, тогда къ хордѣ АВ слѣдуетъ провести перпендикуляръ черезъ ея середину (§ 69, задача 6).
ГЛАВА III.
Зависимость между дугами, хордами и разстояніями хордъ отъ центра.
132. Теоремы. Въ одномъ кругѣ или въ равныхъ кругахъ: 1°, если дуги равны, то стягивающія ихъ хорды равны и
В
Черт. 122.
одинаково удалены отъ центра;
2°, если дуги не равны и притомъ каждая меньше полуокружности, то ббльшая изъ нихъ стягивается большею хордою, и эта большая хорда ближе къ центру.
1°. Пусть дуга АВ (черт. 122) равна дугѣ СВ; требуется доказать, что хорды АВ и СВ равны, а также равны перпендикуляры ОЕ и ОЕ, опущенные изъ центра на хорды. Повернемъ секторъ ОАВ вокругъ центра О въ направленіи, указанномъ стрѣлкою, на столько, чтобы радіусъ ОВ совпалъ съ ОС. Тогда дуга ВА пойдетъ по дугѣ СВ, и, вслѣдствіе ихъ равенства, эти дуги совмѣстятся.
Значитъ, хорда АВ совмѣстится съ хордою СВ (между двумя точками можно провести только одну прямую) и перпендикуляръ
— 94 —
ОЕ совпадетъ съ ОЕ (изъ одной точки можно опустить на прямую только одинъ перпендикуляръ), т.-е. АВ=СВ и ОЕ=ОЕ.
2°. Пусть дуга АВ (черт. 123) меньше дуги СВ, и притомъ обѣ дуги меньше полуокружности; требуется доказать, что хорда АВ меньше хорды СВ, а перпендикуляръ ОЕ больше перпендикуляра ОЕ.—Отдѣлимъ на дугѣ СВ е часть СК, равную АВ, и проведемъ вспомогательную хорду СК, которая, по доказанному, равна хордѣ АВ и р одинаково съ ней удалена отъ центра.
У тр-ковъ*) СОВ и СОК двѣ стороны одного равны двумъ сторонамъ другого (какъ радіусы), а углы, заключенные между этими сторонами, не равны; въ этомъ случаѣ, какъ мы Черт. 123. знаемъ (58), противъ большаго изъ
угловъ, т.-е. СОВ, должна лежать большая сторона; значитъ, СВ^>СК, и потому СВ>АВ.
Для доказательства того, что ОЕ^>ОЕ, проведемъ ОІА.СК и примемъ во вниманіе, что, по доказанному, ОЕ=ОЪ-, слѣд., намъ достаточно сравнить ОЕ съ ОЬ. Въ прямоугольномъ тр-кѣ ОЕМ (покрытомъ на чертежѣ штрихами) гипотенуза ОМ больше катета ОЕ-, но ОІ^>ОМ\ значитъ, и подавно, ОК>ОЕ и потому ОЕ>ОЕ.
Теорема, доказанная нами для одного круга, остается вѣрною и для. равныхъ круговъ, потому что такіе круги ничѣмъ, кромѣ своего положенія, другъ отъ друга не отличаются.
133. Обратныя теоремы. Такъ какъ въ предыдущемъ параграфѣ разсмотрѣны всевозможные взаимно исключающіе случаи относительно сравнительной величины двухъ дугъ одного радіуса, при чемъ получились взаимно исключающіе выводы относительно сравнительной величины хордъ и разстояній ихъ отъ центра, то обратныя предложенія должны бытьвѣрны(5І),аимепно: Въ одномъ кругѣ или въ равныхъ кругахъ: 1°, равныя хорды стягиваютъ равныя дуги и одинаково удалены отъ центра;
*) На чертежѣ 123-мъ надо провести радіусъ 00
— 95 —
2°, хорды, одинаково удаленныя отъ центраравныи стягиваютъ равныя дуги;
3°, изъ двухъ неравныхъ хордъ большая стягиваетъ ббльшую дугу и ближе къ центру;
4°, изъ двухъ хордъ, неодинаково удаленныхъ отъ центра, та, которая ближе къ центру, болѣе и стягиваетъ ббльшую дугу.
Эти предложенія легко доказываются отъ противнаго. Напр., для доказательства перваго изъ пихъ разсуждаемъ такъ: если бы данныя хорды стягивали неравныя дуги, то, согласно прямой теоремѣ, онѣ были бы не равны, что противорѣчитъ условію;
значитъ, равныя хорды должны стягивать равныя дуги, а если дуги равны, то, согласно прямой теоремѣ, стягивающія ихъ
хорды одинаково удалены отъ центра.
134. Теорема. Діаметръ есть наибольшая изъ хордъ.
Если соединимъ съ центромъ О концы какой-нибудь хорды, не проходящей черезъ центръ, напр., хорды АВ (чертежъ 124), то получимъ тр-къ АОВ, въ которомъ одна сторона есть эта хорда, а двѣ другія—радіусы. Но въ
тр-кѣ каждая сторона мепѣе суммы Черт. 124.
двухъ другихъ сторонъ; слѣд., хорда АВ
менѣе суммы двухъ радіусовъ; тогда какъ всякій діаметръ СВ равенъ суммѣ двухъ радіусовъ. Значитъ, діаметръ больше всякой хорды, не проходящей черезъ центръ. Но такъ какъ
діаметръ есть тоже хорда, то можно сказать, что діаметръ есть
наибольшая изъ хордъ.
ГЛАВА IV.
Свойства касательной.
136. Относительное положеніе прямой и окружности. Мы видѣли (120), что прямая и окружность не могутъ имѣть болѣе 2-хъ общихъ точекъ. Посмотримъ теперь,
— 96 —
О Л
7®---В
Е
Черт. 125.
при какихъ условіяхъ прямая съ окружностью можетъ имѣть 2 общія точки, 1 общую точку и ни одпой общей точки. Разсмотримъ слѣдующіе 3 случая:
1°. Разстояніе (ОС, черт. 125) центра (О) окружности отъ прямой (АВ) больше радіуса этой окружности. Тогда точка С прямой АВ. удалена отъ центра О больше, чѣмъ на радіусъ, п потому лежитъ внѣ круга. Всѣ остальныя точки прямой АВ удалены отъ О еще болѣе, чѣмъ точка С (59); значитъ, всѣ точки прямой АВ лежатъ внѣ круга, и потому эта прямая пе имѣетъ общихъ точекъ съ окружностью.
2®. Разстояніе (ОС, черт. 125) центра (О) окружности отъ прямой (АВ) меньше радіуса этой окружности. Въ этомъ случаѣ точка С лежитъ внутри круга. Но на прямой АВ, по обѣ стороны отъ точки С, можно найти такія точки Р и Е, которыя удалены отъ О болѣе, чѣмъ на радіусъ *), и которыя, слѣд., лежатъ внѣ круга. Но тогда каждый изъ двухъ отрѣзковъ: СБ и СЕ, соединяя внутреннюю точку съ внѣшней, долженъ пересѣчься съ окружностью. Слѣд., въ этомъ случаѣ прямая имѣетъ съ окружностью 2 общія точки.
3°. Разстояніе (ОС, черт. 125) центра (О) отъ прямой (АВ) равпо радіусу. Тогда точка С принадлежитъ и прямой, и окружности; всѣ же остальныя точки прямой удалены отъ О болѣе, чѣмъ точка С (59), и потому лежатъ впѣ круга. Значитъ, въ этомъ случаѣ прямая и окружность имѣютъ только одну общую точку, именно, точку С.
*) Если, напр., на прямой АВ отложимъ отъ точки С, по обѣ стороны отъ нея, отрѣзки, равные радіусу, то разстояніе ихъ концовъ до центра будутъ больше радіуса, такъ какъ гипотенуза больше катета.
- 97 —
136. Опредѣленіе. Прямая (АВ, черт. 126), имѣющая съ окружностью только одну общую точку (0, наз. касательною къ окружности; общая точка наз. въ этомъ случаѣ точкою р
касанія. ®
137. Теоремы. 1°. Если прямая / \
перпендикулярна къ радіусу въ концѣ / .п I
его, лежащемъ на окружности, то I и I
она есть касательная. \ /
2° (обратная). Если прямая каса-тельна къ окружности, то радіусъ, ч 126 проведенный въ точку касанія, перпендикуляренъ къ ней.
1°. Пусть О (черт. 127) есть центръ окружности, ОС какой-нибудь ея радіусъ и АВ прямая, перпендикулярная къ ОС и
проходящая черезъ С; требуется доказать, что эта прямая есть касатель- д пая.—Разстояніе прямой АВ отъ центра О равно перпендикуляру ОС; но, по условію, ОС есть радіусъ; значитъ, разстояніе прямой АВ отъ центра О равно радіусу; а въ этомъ случаѣ, какъ мы видѣли (135), прямая имѣетъ съ окруж
-----------В
/
/ /
/ /
о
Черт. 127.
ностью только одну общую точку; слѣд., АВ есть касательная.
2°. Пусть АВ (черт. 127) есть касательная и ОС радіусъ, проведенный въ точку касанія; требуется доказать, что ОСЛ.АВ. Предположимъ противное, т.-е. что радіусъ ОС не перпендикуляренъ къ АВ, а представляетъ собою наклонную къ этой прямой. Въ таномъ случаѣ какая-нибудь другая прямая, напр. ОСХ, будетъ перпендикуляромъ, опущеннымъ изъ центра О на касательную АВ (32). Такъ какъ перпендикуляръ короче наклонной (59), то ОСХ<ОС\ значитъ, тогда разстояніе прямой АВ отъ центра О, равное перпендикуляру ОСХ, будетъ меньше радіуса; а въ этомъ случаѣ, какъ мы видѣли (135), прямая должна имѣть съ окружностью 2 общія точки, а не одну, какъ данная
А. Киселевъ. Геометоіа. 7
— 98 —
касательная АВ. Слѣд., нельзя допустить, что радіусъ ОС не перпендикуляренъ къ АВ; значитъ, ОСЛ.АВ.
138. Теоремы. 1°. Если касательная параллельна хордѣ, то она дѣлитъ въ точкѣ касанія дугу, стягиваемую хордой, пополамъ.
Пусть прямая АВ (черт. 128) касается окружности въ точкѣ М и параллельна хордѣ СБ; требуется доказать, что ^СМ=~МБ.
Проведя черезъ точку касанія діаметръ ЕМ, будемъ имѣть:
ЕМЛ-АВ (137, 2°) и слѣд., ЕМ_1_СБ (82); поэтому >-'СМ=
~МБ (130, 1°).
2° (Обратная). Если касательная (ЛВ) проходитъ черезъ середину дуги (СП), то она параллельна хордѣ, стягивающей
эту дугу.
Дѣйствительно, эта касательная перпендикулярна къ діаметру (ЕМ), проведенному черезъ середину дуги, а такой діаметръ перпендикуляренъ къ хордѣ (130, слѣд. 2°); но два перпендикуляра къ одной и той же прямой должны быть параллельны.
139. Задача. Черезъ данную точку провести касательную къ данной окружности.
Если данная точка (напр., точка М, черт. 128) находится на окружности, то проводятъ черезъ нее радіусъ и черезъ конецъ радіуса перпендикулярную прямую. Эта прямая и будетъ искомой касательной (137, 1°). Другой касательной черезъ ту же точку окружности провести нельзя, такъ какъ касательная должна быть перпендикулярна къ радіусу въ концѣ его, лежащемъ на окружности, а двухъ различныхъ перпендикуляровъ къ одному и тому же радіусу черезъ одну
и ту же точку провести нельзя.
Разсмотримъ теперь случай, когда точка дана внѣ круга.
Пусть требуется (черт. 129) провести къ окружности центра О касательную черезъ точку А. Для этого изъ точки А, какъ центра, описываемъ дугу радіусомъ АО, а изъ точки О, какъ
— 99 —
центра, пересѣкаетъ эту дугу въ точкахъ В и С раствореніемъ
циркуля, равнымъ діаметру даннаго круга. Проведя затѣмъ
хорды ОВ и ОС, соединимъ точку А съ точками В и Е, въ которыхъ эти хорды пересѣкаются съ данною окружностью. Пря-
мыя АВ и АЕ и будутъ касательными къ окружности О. Дѣй-
ствительно, изъ построенія видно, равнобедренные (АО—АВ=АС) съ равными діаметру круга О. Такъ какъ ОВ и ОЕ суть радіусы, а радіусъ равенъ половинѣ діаметра, то В есть середина ОВ, а Е середина ОС; значитъ, прямыя АВ и АЕ суть медіаны, проведенныя къ основаніямъ равнобедренныхъ тр-ковъ, и потому перпендикулярны къ этимъ основаніямъ (39). Если же прямыя АВ и АЕ перпендикулярны къ радіусамъ ОВ и ОЕ въ ихъ концахъ, лежащихъ на окружности, то онѣ касательныя.
что тр-ки АОВ и АОС основаніями ОВ и ОС,
Черт. 129.
Замѣчаніе. Очевидно, что если данная точка лежитъ внутри круга, то черезъ нее нельзя провести касательной.
140. Слѣдствіе. Двѣ касательныя, проведенныя изъ одной точки къ окружности, равны и образуютъ равные углы съ прямою, соединяющею эту точку съ центромъ
Такъ, АВ=АЕ и ^ОАВ—/.ОАЕ (черт. 129), потому что прямоугольные тр-ки АОВ и АОЕ, имѣющіе общую гипоте
нузу АО и равные катеты ОВ и ОЕ (какъ радіусы), равны.
Само собою разумѣется, что здѣсь подъ словомъ «касательная» разумѣется собственно «отрѣзокъ касательной» отъ данной точки до точки касанія.
141. Задача.Провести касательную къ данной окружности параллельно данной прямой АВ (черт. 130).
— 100 —
Черезъ центръ О проведемъ МСА.АВ и черезъ точки В и въ которыхъ этотъ перпендикуляръ пересѣкается съ окружностью, проведемъ ЕЕ II АВ и Е1Е1 II АВ. Искомыя касательныя будутъ ЕЕ и Е^. Дѣйствительно, такъ какъ МСА.АВ и ЕЕ II АВ, а также и Е^ II АВ, то ЕЕ_\_ ОВ и Е^\\_ ОВц а прямая, перпендикулярная къ радіусу въ концѣ его, лежа
щемъ на окружности, есть касательная.
142. Задача. Къ двумъ окружностямъ провести общую касательную (черт. 131).
1°. Анализъ. Предположимъ, что задача рѣшена. Пусть АВ будетъ общая касательная, А и В точки касанія. Очевидно, что если мы найдемъ одну изъ этихъ точекъ, напр., А, то за-
жинѣ С; вслѣдствіе этого, если
тѣмъ легко найдемъ и другую. Проведемъ радіусы О А и О]В. Эти радіусы, будучи перпендикулярны къ общей касательной, параллельны между собою; поэтому если изъ Ог проведемъ ОгС II ВА, то тр-къ ОСОг будетъ прямоугольный при вер-опишемъ изъ О, какъ центра,
радіусомъ ОС окружность, то она будетъ касаться прямой ОгС въ точкѣ С. Радіусъ этой вспомогательной окружности извѣстенъ: онъ равенъ ОА—СА=ОА—ОГВ, т.-е. онъ равенъ разности радіусовъ данныхъ окружностей.
Построеніе. Обозначимъ радіусъ ббльшаго круга черезъ В и радіусъ меньшаго черезъ г. Опишемъ изъ центра О
окружность радіусомъ, равнымъ В—г; изъ Ог проводимъ къ этой окружности касательную ОгС (способомъ, указаннымъ въ предыдущей задачѣ § 139)* черезъ точку касанія С проводимъ радіусъ ОС и продолжаемъ его до встрѣчи съ данною окружностью въ точкѣ А. Наконецъ, изъ А проводимъ АВ параллельно СОг.
Доказательство (синтезъ). Такъ какъ О]С, по построенію, есть касательная въ точкѣ С къ окружности радіуса ОС, то 01СА.0С, и, значитъ, ОѴС±ОА. Такъ какъ АВ II СО1г
*) Если это возможно, т.-е. если центръ Оі окажется лежащимъ не внутри круга, описаннаго радіусомъ ОС=В—т.
— 101 —
то и АВА.ОА и потому АВ есть касательная къ данной окружности центра О (137). Остается доказать, что прямая АВ касается также и другой данной окружности. Для этого изъ центра Ох проведемъ ОіВЛ-АВ. Прямыя ОХВ и СА, будучи перпендикулярны къ АВ, должны быть параллельны; съ другой стороны, АВ || ОХС; слѣд., фигура О^САВ есть параллелограммъ; поэтому О1В=СА=ОА—ОС; но ОС=В—г; слѣд., ОіВ^В,—(В—г)—г. Значитъ, точка В принадлежитъ данной окружности центра Оь и прямая О^В есть радіусъ этой окружности. Такимъ образомъ, прямая АВ перпендикулярна къ радіусу ОгВ въ его концѣ, лежащемъ на окружности, а такая прямая есть касательная.
Совершенно такимъ же способомъ мы можемъ построить другую общую касательную А^ (черт. 131). Прямыя АВ и АіВі наз. внѣшними общими касательными.
Можно еще провести двѣ внутреннія касательныя слѣдующимъ образомъ.
2°. Анализъ. Предположимъ, что задача рѣшена (чертежъ 132). Пусть АВ будетъ искомая касательная. Проведемъ радіусы О А и ОгВ въ точки касанія А и В. Эти радіусы, будучи оба перпендикулярны къ общей касательной, параллельны между собою. Поэтому если изъ Ох проведемъ ОХС II ВА и продолжимъ ОА до точки С, то ОС будетъ перпендикуляренъ къ ОгС; вслѣдствіе этого окружность, описанная радіусомъ ОС изъ точки О, какъ центра, бу- Р
детъ касаться прямой ОХС въ точкѣ С. Радіусъ этой / вспомогательной окруж- / / / \
ности извѣстенъ: онъ ра- I \ /
венъ ОА + АС = ОА + О1В=В+г, т.-е. онъ ра
венъ суммѣ радіусовъ
данныхъ окружностей. Черт. 132.
Построеніе. Изъ О, какъ центра, описываемъ окружность радіусомъ, равнымъ суммѣ В+т; изъ Ох проводимъ къ этой окружности касательную ОХС*; точку касанія С соединяемъ съ
*) Если это возможно, т.-е. если центръ Ох окажется лежащимъ не внутри круга описаннаго радіусомъ ОС=Я-|-г.
— 102 —
О; наконецъ, черезъ точку А, въ которой ОС пересѣкается съ данной окружностью, проводимъ АВ II 01С.
Доказательство (синтезъ) остается то же самое, какъ и въ случаѣ 1°.
Подобнымъ же образомъ молено построить другую внутреннюю касательную А^^
Замѣчаніе. Не ко всякимъ двумъ окруяшостямъ можно провести общія касательныя; напр., если одна окружность леяситъ внутри другой, не имѣя съ ней ни одной общей точки, то очевидно, что къ такимъ окружностямъ нельзя провести ни внѣшнихъ, ни внутреннихъ общихъ касательныхъ; или, если окружности пересѣкаются, то очевидно, что къ нимъ нельзя провести внутреннихъ общихъ касательныхъ,
143. Общее опредѣленіе касательной. Пусть къ окружности центра О (черт. 133) проведены черезъ точку А касательная АТ и какая-нибудь сѣкущая АМ. Станемъ вращать эту сѣкущую вокругъ точки А такъ, чтобы другая точка пересѣченія В все ближе и ближе придвигалась къ А. Тогда д перпендикуляръ ОВ, опущен-
.........................................Т ный изъ центра на сѣкущую, /....................будетъ все болѣе и болѣе при-
/ / ближаться къ радіусу ОА, при-
I о ________/ чемъ уголъ АОВ, равный поло-
I I винѣ угла АОВ, можетъ сдѣ-
\ латься меньше всякаго малаго
X. угла. Уголъ МАТ, образован-
ный сѣкущею и касательною, Черт. 133. равенъ углу АОВ (вслѣдствіе
перпендикулярности ихъ сторонъ); поэтому при неограниченномъ приближеніи точки В къ А уголъ МАТ также можетъ быть сдѣланъ какъ угодно малъ. Это выражаютъ иными словами, такъ: касательная есть предѣльное положеніе, къ которому стр е мится сѣку щ а я, •ь проведенная черезъ
рі/ точку касанія, когда
- - вторая точка пере-
/ сѣченія пеограни-
А чепно приближается
Черт. 134. къ точкѣ касанія.
— 103 —
Это свойство принимаютъ за опредѣленіе касательной, когда рѣчь идетъ о какой угодно кривой. Такимъ образомъ, касательною къ кривой АВ (черт. 134) въ точкѣ ІИ н а з. предѣльное положеніе МТ, къ которому стремится сѣкущая М1Ѵ, когда точка пересѣченія Р неограниченно приближается къ М.
Опредѣляемая такимъ образомъ касательная можетъ имѣть съ кривою болѣе одной общей точки (какъ это видно на черт. 134).
ГЛАВА V.
Относительное положеніе окружностей.
144. Опредѣленіе. Если двѣ окружности имѣютъ только одну общую точку, то говорятъ, что онѣ касаются; если же двѣ окружности имѣютъ двѣ общія точки, то говорятъ, что онѣ пересѣкаются.
Трехъ общихъ точекъ двѣ несливающіяся окружности имѣть не могутъ, потому что въ противномъ случаѣ черезъ три точки можно было бы провести двѣ различныя окружности, что невозможно (122).
Будемъ называть линіей центровъ прямую,проходящую черезъ центры двухъ окружностей (напр., прямую ОО15 черт. 135).
145. Теорема. Если двѣ окружности имѣютъ общую точку по одну сторону отъ линіи центровъ, то онѣ имѣютъ общую точку и по другую сторону отъ этой линіи, т.-е. такія окружности пересѣкаются.
Пусть (черт. 135) двѣ окружности имѣютъ общую точку А, лежащую внѣ линіи центровъ ООі; требуется доказать, что эти окружности имѣютъ еще общую точку по другую сторону отъ прямой ООі.
Опустимъ изъ А на прямую ООі перпендикуляръ АВ и продолжимъ его на разстояніе ВАГ, равное АВ. Докажемъ
теперь, что точка Ах принадлежитъ обѣимъ окружностямъ.
— 104 —
Изъ построенія видно, что точки О и лежатъ на перпендикулярѣ, проведенномъ къ отрѣзку АА1г черезъ его середину. Изъ этого слѣдуетъ, что точка О одинаково удалена отъ А и (63, 2е); то же можно сказать и о точкѣ Ох; значитъ, обѣ окружности, при продолженіи ихъ, пройдутъ черезъ А^ Такимъ образомъ, окружности имѣютъ двѣ общія точки: точку А (по условію) и точку Аг (по доказанному); слѣд., онѣ пересѣкаются.
146. Слѣдствіе. Общая хорда (ЛЛЬ черт. 135) двухъ пересѣкающихся окружностей перпендикулярна къ линіи центровъ и дѣлится ею пополамъ.
147. Теорема. Если двѣ окружности имѣютъ общую точку на линіи ихъ центровъ, то онѣ касаются.
Пусть общая точка А двухъ окружностей лежитъ на линіи центровъ 00г (черт. 136 и 137). Требуется доказать, что такія окружности касаются, т.-е что онѣ не имѣютъ никакой другой общей точки.—Окружное™ не могутъ имѣть другой общей точки внѣ линіи центровъ, потому что въ противномъ случаѣ онѣ имѣли бы еще третью общую точку по другую сторону отъ линіи центровъ (145) и, слѣд., должны были бы слиться (122) Онѣ не могутъ имѣть другой общей точки п на линіи центровъ, такъ какъ на этой прямой, очевидно, нѣтъ другой точки, которая отъ обоихъ центровъ была бы удалена настолько же, какъ и точка А. Слѣд., окружности имѣютъ только одну общую точку, т -е онѣ касаются.
Черт. 136. Черт. 137.
148. Замѣчаніе. Касаніе двухъ окружностей наз. внѣшнимъ, если онѣ расположены одна внѣ другой (черт 136), и внутреннимъ, если одна изъ окружностей лежитъ внутри другой (черт. 137).
— 105 —
149. Теорема, (обратная предыдущей). Если двѣ окружности касаются, то точка касанія лежитъ на линіи центровъ.
Пусть двѣ окружности (черт. 136 и 137) касаются въ точкѣ А, т.-е имѣютъ только одну общую точку А; требуется доказать, что эта точка лежитъ на линіи центровъ.—Точка А не можетъ лежать внѣ линіи центровъ, потому что въ противномъ случаѣ окружности имѣли бы еще другую общую точку, что противорѣчитъ условію теоремы
150. Слѣдствіе. Двѣ касательныя окружности имѣютъ общую касательную въ точкѣ касанія, потому что если проведемъ черезъ точку касанія прямую (черт. 136 и 137), перпендикулярную къ радіусу О А, то эта прямая будетъ также перпендикулярна и къ радіусу 0^4*.
151. Различные случаи относительнаго положенія двухъ окружностей. Обозначимъ радіусы двухъ окружностей буквами В и и разстояніе между ихъ центрами буквою Л. Разсмотримъ, какова зависимость между
этими величинами въ различныхъ случаяхъ относительнаго положенія двухъ окружностей. Этихъ случаевъ можно указать слѣдующіе 5:
1°. Окружности лежатъ одна внѣ другой, не касаясь (черт. 138); въ этомъ случаѣ, очевидно,
2°. Окружности имѣютъ внѣшнее касаніе (черт. 139); тогда Л—ВА-В^ такъ какъ точка касанія лежитъ на линіи центровъ.
3°. Окружности пересѣка- Черт. 139.
ю т с я (черт. 140, 1° и 2°); тогда Л<ІВ -ННі и въ то же время й^>В—Вг, потому что въ тр-кѣ ОАОі сторона 00х, равная И, меньше суммы, но больше разности двухъ другихъ сторонъ, равныхъ радіусамъ В и Вх.
*) Окружности, касающіяся извнѣ, имѣютъ еще 2 общія внѣшнія касательныя,
— 106 —
4°. Окружности имѣютъ внутреннее касаніе (черт. 141); въ этомъ случаѣ "-х. —Вх, потому что точка касанія лежитъ
< -х\ па линіи центровъ.
[ А Наконецъ, 5°, одна окружность \П 1 лежитъ внутри другой, не к а -< 44--'у с а я с ь (черт. 142); тогда, очевидно,
и въ частномъ случаѣ й=О, когда центры обѣихъ окружностей сливаются (такія Черт. 141. окружностиназ.к о н ц е н т р и ч е скими).
Черт. 142.
152. Обратныя предложенія, такъ какъ разсмотрѣнные нами случаи расположенія двухъ окружностей таковы, что каждый изъ нихъ исключаетъ собою всѣ остальные, и случаи эти со
провождаются такими соотношеніями между разстояніемъ центровъ и величиною радіусовъ, которые тоже взаимно другъ друга исключаютъ, то обратныя предложенія должны быть вѣрны (51), а именно:
1° Если (ЕЖ+Ві, то окружности расположены одна внѣ другой, не касаясь.
2° Если й=В+Вх, то окружности касаются извнѣ.
3°. Если и въ то же время сС>В—Вх,
то окружности пересѣкаются.
4°. Если й=В—2?і, то окружности касаются извнутри.
5°. Если —Вх, то одна окружность ле
житъ внутри другой, не касаясь.
Всѣ эти предложенія легко доказываются отъ противнаго.
107 —
УПРАЖНЕНІЯ:
Найти геометрическія мѣста:
101. —точекъ, изъ которыхъ касательныя, проведенныя къ данной окружности, равны данной длинѣ.
102. —точекъ, изъ которыхъ данная окружность видна подъ даннымъ угломъ (т.-е. двѣ касательныя, проведенныя изъ каждой точки къ окружности, составляютъ между собою данный уголъ).
103. —центровъ окружностей, описанныхъ даннымъ радіусомъ и касающихся данной прямой.
104. —центровъ окружностей, касающихся данной окружности въ данной точкѣ.
105. —центровъ окружностей, описанныхъ даннымъ радіусомъ и касающихся данной окружности (два случая: касаніе внѣшнее и касаніе внутреннее).
106. Прямая данной длины движется параллельно самой себѣ такъ, что одинъ ея конецъ скользитъ по окружности. Найти геометрическое мѣсто, описанное другимъ концомъ.
107. Прямая данной длины движется такъ, что концы ея скользятъ по сторонамъ прямого угла. Найти геометрическое мѣсто, описываемое серединою этой прямой.
Доказать теоремы.
107,а. Въ кругѣ центра 0 проведена хорда АВ и продолжена на разстояніе ВС, равное радіусу. Черезъ точку С и центръ 0 проведена сѣкущая СВ (О вторая точка пересѣченія съ окружностью). Доказать, что уголъ АОВ равенъ утроенному углу АСВ.
108. Если черезъ центръ окружности и данную точку внѣ ея проведемъ сѣкущую, то часть ея, заключенная между данною точкою и ближайшею точкою пересѣченія, есть наименьшее разстояніе, а часть, заключенная между данною точкою и другою точкою пересѣченія, есть наибольшее разстояніе этой точки отъ окружности.
109. Кратчайшее разстояніе между двумя окружностями, лежащими одна внѣ другой, есть отрѣзокъ линіи центровъ, заключенный между окружностями.
110. Изъ всѣхъ хордъ, проведенныхъ въ окружности черезъ одну точку, наименьшая есть та, которая перпендикулярна къ радіусу, проходящему черезъ эту точку.
111. Если черезъ точку пересѣченія двухъ окружностей будемъ проводить сѣкущія, пе продолжая ихъ за окружности, то наибольшая изъ нихъ окажется та, которая параллельна линіи центровъ.
112. Если къ двумъ окружностямъ, касающимся извнѣ, провести три общія касательныя, то внутренняя изъ нихъ дѣлитъ двѣ другія въ точкахъ, одинаково удаленныхъ отъ точекъ касанія.
113. Всѣ хорды данной длины, проведенныя въ данной окружности, касаются нѣкоторой другой окружности.
— 108 —
114. Если черезъ одну изъ точекъ пересѣченія двухъ окружностей проведемъ діаметры въ каждой окружности, то прямая, соединяющая концы ихъ, пройдетъ черезъ другую точку пересѣченія.
114,а. Черезъ точку А окружности проведена хорда АВ и затѣмъ касательная въ точкѣ В; діаметръ, перпендикулярный къ радіусу 0А, встрѣчаетъ касательную и хорду соотвѣтственно въ точкахъ С и О. Доказать, что ВС = СВ.
114,Ь. Къ двумъ окружностямъ центровъ О и 01, касающимся извнѣ въ точкѣ А, проведена общая внѣшняя касательная ВС (В и С точки касанія); доказать, что уголъ ВАС есть прямой.
Задачи на построеніе.
115. Раздѣлить данную дугу на 4, 8, 16... равныхъ частей.
116. По суммѣ и разности дугъ найти эти дуги.
117. Изъ данной точки, какъ центра, описать такую окружность, которая раздѣлила бы данную окружность пополамъ.
118. На данной прямой найти точку, наименѣе удаленную отъ данной окружности.
119. Въ кругѣ дана хорда. Провести другую хорду, которая дѣлилась бы первою пополамъ и составляла бы съ нею данный уголъ.
120. Черезъ данную въ кругѣ точку провести хорду, которая дѣлилась бы этою точкою пополамъ.
121. Изъ точки, данной на сторонѣ угла, описать окружность, которая отъ другой стороны угла отсѣкала бы хорду данной длины.
122. Даннымъ радіусомъ описать окружность, которой центръ лежалъ бы на сторонѣ даннаго угла и которая отъ другой стороны его отсѣкала бы хорду данной длины.
123. Даннымъ радіусомъ описать окружность, которая касалась бы цанной прямой въ данной точкѣ.
124. Описать окружность, касательную къ сторонамъ даннаго угла, при чемъ одной изъ нихъ въ данной точкѣ.
125. Описать окружность, касающуюся трехъ сторонъ тр-ка.
126. Между двумя параллельными прямыми дана точка; провести окружность, проходящую черезъ эту точку и касающуюся данныхъ прямыхъ.
127. Провести къ данной окружности касательную подъ даннымъ угломъ къ данной прямой.
128. Изъ точки, данной внѣ круга, провести къ нему сѣкущую такъ, чтобы ея внутренняя часть равнялась данной длинѣ (изслѣдовать задачу).
129. Даннымъ радіусомъ описать окружность, проходящую черезъ данную точку и касательную къ данной прямой.
130. На данной прямой найти такую точку, чтобы касательныя, проведенныя изъ нея къ данной окружности, были данной длины.
131. Построить Д, зная одинъ уголъ и двѣ высоты, изъ которыхъ одна проведена изъ вершины даннаго угла.
— 109 —
132. Даны двѣ окружности; провести къ нимъ сѣкущую такъ, чтобы внутреннія части ея равнялись даннымъ прямымъ.
133. Даны двѣ точки; провести прямую такъ, чтобы перпендикуляры, опущенные на нее изъ этихъ точекъ, имѣли данныя длины.
134. Описать окружность, которая проходила бы черезъ данную точку и касалась бы данной окружности въ данной точкѣ.
135. Описать окружность, которая касалась бы двухъ данныхъ параллельныхъ прямыхъ и къ кругу, находящемуся между ними.
136. Даннымъ радіусомъ описать окружность, которая касалась бы даннаго круга и проходила бы черезъ данную точку.
137. Даннымъ радіусомъ описать окружность, которая касалась бы данной прямой и даннаго круга.
138. Даннымъ радіусомъ описать окружность, которая отъ сторонъ даннаго угла отсѣкала бы хорды данной длины.
139. Описать окружность, касающуюся даннаго круга въ данной точкѣ и данной прямой (2 рѣшенія).
140. Описать окружность, касающуюся данной прямой въ данной точкѣ и даннаго круга (2 рѣшенія).
141. Описать окружность, касающуюся двухъ данныхъ круговъ при чемъ одного изъ нихъ въ данной точкѣ (разсмотрѣвъ три случая: 1, искомый кругъ лежитъ внѣ данныхъ; 2, одинъ изъ данныхъ круговъ лежитъ внѣ искомаго, другой внутри; 3, оба данныхъ круга лежатъ внутри искомаго).
142. Описать окружность, касающуюся трехъ равныхъ круговъ извнѣ или внутри.
143. Въ даннный секторъ вписать окружность, касающуюся къ радіусамъ, ограничивающимъ секторъ, и къ дугѣ сектора.
144. Вписать въ данный кругъ три равные круга, которые касались бы попарно меледу собою и даннаго круга.
145. Черезъ точку внутри круга провести хорду такъ, чтобы разность ея отрѣзковъ равнялась данной длинѣ
146. Черезъ точку пересѣченія двухъ окружностей провести сѣкущую такъ, чтобы часть ея, заключенная внутри окружностей, равнялась данной длинѣ.
147. Изъ точки, данной внѣ круга, провести сѣкущую такъ, чтобы внѣшняя ея часть равнялась внутренней.
ГЛАВА VI.
Измѣреніе величинъ.
153. Общая мѣра. Общею мѣрою двухъ данныхъ отрѣзковъ прямой называется такой третій отрѣзокъ прямой, который въ каждомъ изъ данныхъ содержится цѣлое
— 110 —
число разъ безъ остатка. Такъ, если (черт. 143) М отрѣзокъ АМ содержится въ АВ и
। ] | [ |р въ СВ цѣлое число разъ (напр.,
5 разъ въ АВ и 3 раза въ СВ), то рі । । [д АМ есть общая мѣра АВ и СВ.
Подобно этому, можетъ быть Черт. 143. общая мѣра двухъ дугъ одина-
коваго радіуса, двухъ угловъ и вообще двухъ значеній одной
_ _А__
КГ Т~^|
Черт. 144.
и той же величины.
154. Нахожденіе наибольшей общей мѣры. Чтобы найти наибольшую общую мѣру двухъ отрѣзковъ прямой, употребляютъ способъ послѣдовательнаго отложенія, подобный тому послѣдовательному дѣленію, какимъ въ ариѳметикѣ находятъ общаго наибольшаго дѣлителя двухъ цѣлыхъ чиселъ. Этотъ способъ основывается на слѣдующихъ предложеніяхъ:
1°. Если меньшій изъ двухъ данныхъ отрѣзковъ (Л и В, черт. 144) содержится въ большемъ цѣлое число разъ безъ остатка, то наиб. общая мѣра такихъ отрѣзковъ есть меньшій изъ нихъ.
Пусть, напр., В содержится въ А ровно 3 раза; такъ какъ при этомъ, конечно, В содержится въ В ровно 1 разъ, то В есть общая мѣра отрѣзковъ А и В; съ другой стороны, эта мѣра есть и наибольшая, такъ какъ никакой отрѣзокъ, большій В, не можетъ содержаться въ В безъ остатка.
2°. Если меньшій изъ двухъ данныхъ отрѣзковъ (В, черт. 145) содержится въ б 6 л ь -ш е м ъ (въ А) цѣлое число разъ съ какимъ-нибудь остаткомъ (К), т о
А наиб. общая мѣра этихъ
отрѣзковъ должна быть К вмѣстѣ съ тѣмъ и наиб. Ь,В г общей мѣрой меньшаго
г ’ отрѣзка (В) и остатка (В).
Черт. 145. Пусть, напр., А=В+В+В+В.
— 111
Изъ этого равенства мы можемъ вывести слѣдующія два заключенія:
1) Всякій отрѣзокъ, содержащійся цѣлое число разъ безъ остатка въ В и въ В, содержится также безъ остатка и въ А; если, напр., какой-нибудь отрѣзокъ содержится въ В ровно 5 разъ и въ В содержится ровно 2 раза, то въ А онъ содержится 5+5+5+2, т.-е. 17 разъ безъ остатка.
2) Обратно: всякій отрѣзокъ, содержащійся цѣлое число разъ безъ остатка въ А и въ В, содержится также цѣлое число разъ безъ остатка и въ В; если, напр., какой-нибудь отрѣзокъ содержится въ А ровно 17 разъ и въ В ровно 5 разъ, то въ той части отрѣзка А, которая равна ЗВ, онъ содержится 15 разъ; слѣд., въ оставшейся части отрѣзка А, т.-е. въ В, онъ содержится 17—15, т.-е. 2 раза.
Такимъ образомъ у двухъ паръ отрѣзковъ: А и В В и В должны быть однѣ и тѣ же общія мѣры; поэтому и наибольшая общая мѣра у нихъ должна быть одна и та же.
Къ этимъ двумъ предложеніямъ надо еще добавить слѣдующую аксіому Архимеда (аксіому измѣренія).:
3) Какъ бы великъ ни былъ ббльшій отрѣзокъ (Л) и какъ бы малъ ни былъ меньшій отрѣзокъ (В), всегда, откладывая меньшій на большемъ послѣдовательно 1, 2, 3, ит. д. раза, мы дойдемъ до того, что послѣ нѣкотораго т-а г о отложенія или не получится никакого остатка, или получится остатокъ, меньшій меньшаго отрѣзка (В).
Примѣнимъ эти предложенія къ нахожденію наиб. общей мѣры данныхъ отрѣзковъ АВ и СВ (черт. 146). Для этого на большемъ отрѣзкѣ откла- Е
дываемъ меньшій (по- АІ 1 I 1 I ІВ мощью циркуля) столько разъ, сколько можно. С1 і НѲ
Если СБ уложится ВЪ АВ Черт. 146.
безъ остатка, то искомая мѣра, согласно предложенію 1-му, и есть СВ; если же этого не произойдетъ (какъ у насъ на чертежѣ), то, согласно предложенію 2-му, вопросъ приведется къ нахожденію наиб. общей мѣры двухъ меньшихъ отрѣзковъ,
— 112 —
именно СБ и перваго остатка ЕВ. Чтобы найти ее, поступаемъ по предыдущему, т.-е. откладываемъ ЕВ па СБ столько разъ, сколько можно. Если ЕВ уложится въ СБ безъ остатка, то искомая мѣра и будетъ ЕВ\ если же этого не произойдетъ (какъ у насъ на чертежѣ), то вопросъ приведется къ нахожденію наиб. общей мѣры двухъ меньшихъ отрѣзковъ, именно ЕВ и второго остатка ЕБ. Если, продолжая этотъ пріемъ далѣе, мы дойдемъ до того, что послѣ нѣкотораго отложенія уже не получится никакого остатка, то отрѣзокъ, который при этомъ откладывали (послѣдній изъ остатковъ), и будетъ искомая мѣра.
Чтобы удобнѣе вычислить, сколько разъ найденная общая наибольшая мѣра содержится въ данныхъ прямыхъ, выписываемъ рядъ равенствъ, получаемыхъ послѣ каждаго отложенія. Такъ, при нашемъ чертежѣ мы будемъ имѣть:
Послѣ 1-го отложенія......АВ—3 СБ-\-ЕВ
» 2-го » СБ=2 ЕВ-[-ЕБ
» 3-го » ЕВ—І ЕБ.
Переходя въ этихъ равенствахъ отъ нижняго къ верхнему, послѣдовательно находимъ:
ЕВ=І ЕБ- СБ=(І ЕБ).2\-ЕБ=9 ЕБ-АВ=(9 ЕП).3+4 ГО=31 ЕБ.
Подобно этому можно находить наиб. общую мѣру двухъ дугъ одинаковаго радіуса, двухъ угловъ и т. п.
Замѣчаніе. Найдя наибольшую общую мѣру, мы можемъ затѣмъ получить сколько угодно другихъ меньшихъ общихъ мѣръ; стоитъ только брать 1/2, 1/3, х/4 и т. д. наибольшей мѣры.
155. Соизмѣримыя и несоизмѣримыя длины. Можетъ случиться, что при нахожденіи общей мѣры мы никогда не дойдемъ до того, чтобы не получилось никакого остатка; тогда данныя прямыя пе будутъ имѣть общей мѣры.
Два отрѣзка прямой наз. соизмѣримыми, если они имѣютъ общую мѣру, и несоизмѣримыми, когда такой мѣры не существуетъ.
На практикѣ нѣтъ возможности убѣдиться въ существованіи несоизмѣримыхъ отрѣзковъ, потому что, продолжая послѣдовательное отложеніе, мы всегда дойдемъ до столь малаго
— 113 —
остатка, который въ предшествующемъ остаткѣ, повидимому, укладывается цѣлое число разъ. Быть можетъ, при этомъ и долженъ былъ бы получиться нѣкоторый остатокъ, но по причинѣ неточности инструментовъ (циркуля) и несовершенства нашихъ органовъ чувствъ (зрѣнія) мы не въ состояніи его замѣтить. Однако, можно доказать, что несоизмѣримые отрѣзки существуютъ. Приведемъ наиболѣе простой примѣръ такихъ отрѣзковъ.
156. Теорема. Если въ равнобедренномъ треугольникѣ уголъ при основаніи равенъ 2/&й, то боковая сторона его несоизмѣрима съ основаніемъ.
Пусть АВС равнобедренный тр-къ (черт. 147), у котораго каждый изъ угловъ А и С равенъ 2/5 д,\ требуется доказать, что боковая сторона АВ несоизмѣрима съ основаніемъ АС.
Прежде всего опредѣлимъ, которая изъ этихъ сторонъ больше. Для этого достаточно сравнить углы, противъ которыхъ лежатъ эти стороны. Такъ какъ, по условію, Л=С=2/5 сі, то В=2И— —2/5й—2/бй=<Ѵ; слѣД-’ В^>С; поэтому АС^>АВ.
Теперь найдемъ, сколько В
разъ въ АС можетъ уло-
житься АВ. Такъ какъ
АС<АВ+ВСкАВ=ВС, / V,
то АС<^2АВ; значитъ,
АВ въ АС можетъ уло- л 2 ]) р ъ
ЖИТЬСЯ ТОЛЬКО ОДИНЪ Чѳрт 147
разъ съ нѣкоторымъ
остаткомъ.
Такимъ образомъ, мы прежде всего замѣчаемъ слѣдующее свойство: если въ равнобедренномъ треугольникѣ уголъ при основаніи равенъ 2/5й, то боковая его сторона содержится въ основаніи только одинъ разъ и притомъ съ нѣкоторымъ остаткомъ.
Замѣтивъ это, приступимъ теперь къ послѣдовательному отложенію. Отложимъ на АС часть АТ), равную АВ-, тогда получимъ остатокъ ВС, который надо накладывать на АВ, пли, что все равно, на ВС. Чтобы узнать, сколько разъ ВС уложится
А. Киселевъ. Геометрія. ®
— 114 —
на ВС, соединимъ В съ О и разсмотримъ &ВВС. Найдемъ его углы. Такъ какъ ДЛВО равнобедренный, то его углы АВВ и АВВ равны; слѣд., каждый изъ нихъ равенъ 1/2(2й—Л)=1/2(2й— 2/5й)=4/5й. Н° Уголъ АВС, какъ мы прежде нашли, равенъ 6/5й; слѣд., ^.ВВС—6/5й—4/5й=2/бй. Такимъ образомъ, въ тр-кѣ ВВС есть два равныхъ угла при ВС\ слѣд., онъ равнобедренный, при чемъ каждый уголъ при его основаніи ВС равенъ 2/бй. Вслѣдствіе этого, по доказанному выше, боковая сторона его ВС (или ВВ) уложится въ основаніи ВС одинъ разъ съ нѣкоторымъ остаткомъ. Пусть этотъ остатокъ будетъ ЕС. Соединивъ Е съ В, мы снова получимъ равнобедренный тр-къ СВЕ, въ которомъ каждый уголъ при основаніи СВ равенъ 2/5й. Отложивъ ЕС (или ВЕ) па ВС (отъ точки В), мы снова получимъ равнобедренный тр-къ СЕЕ, у котораго каждый уголъ при основаніи СЕ равенъ 2/5й.
Такимъ образомъ, мы постоянно будемъ приходить къ равнобедренному тр-ку (все меньшему и меньшему) съ углами при основаніи, равными 2/5й; слѣд., мы никогда въ этомъ процессѣ не дойдемъ до конца. Значитъ, стороны АС и АВ не могутъ имѣть общей мѣры.
157. Приведемъ еще слѣдующій примѣръ несоизмѣримыхъ отрѣзковъ прямой.
Теорема. Діагональ квадрата несоизмѣрима съ его стороною.
Такъ какъ діагональ квадрата раздѣляетъ его на два равнобедренныхъ прямоугольныхъ тр-ка, то теорему эту можно высказать иными
словами такъ: гипотенуза рав-нобѳдренаго прямоугольнаго треугольника несоизмѣрима съ его катетомъ.
Предварительно докажемъ слѣдующее свойство такого тр-ка: если на гипотенузѣ (черт. 148) отложимъ часть АБ, равную катету, и проведемъ БЕ_1_АС, то образовавшійся при этомъ прямоугольный тр-къ БЕС б у-детъ равнобедренный, а отрѣзокъ ВЕ катета ВС окажется равнымъ отрѣзку БС гипотенузы. Чтобы убѣдиться въ Черт. 148.
этомъ, проведемъ прямую ВБ и разсмотримъ углы тр-ковъ БЕС и ВЕБ. Такъ какъ тр-къ АВС равнобедренный и прямоугольный, то /1 =1/8й; вслѣдствіе этого также равенъ 1/2Л; значитъ, Д1 = /2,
— 115 —
и потому СБ — БЕ. Въ тр-кѣ ВЕБ уголъ3 равенъ разности /_АВС— ^АВБ\ но / АВС = Ли ^АВБ^/^Л—214)=1/8(2й—*/2Л) =®/*й; слѣд., ^3 = Л—®/4Л = 1/4Л. Равнымъ образомъ, —^_АБВ = &—*/4Л
=г/4Л. Слѣд., ^3=^5 и потому ВЕ—БЕ; но БЕ = СБ\ значитъ, ВЕ=*СБ.
Замѣтивъ это свойство, станемъ отыскивать наибольшую общую мѣру сторонъ АС и АВ. Такъ какъ АС<.АВ-{-ВС, т.-е. АС<2АВ, то АВ отложится на АС только 1 разъ, причемъ получится нѣкоторый остатокъ Теперь надо этотъ остатокъ откладывать на АВ,
или—что все равно—на ВС. Для этого проведемъ БЕ_]_АС. Тогда по доказанному, ВЕ=БС и, слѣд., мы будемъ имѣть одно отложеніе остатка БС на катетѣ ВС. Остается теперь откладывать БС отъ точки Е къ С столько разъ, сколько можно. Но прямоугольный тр-къ БЕС, какъ мы видѣли, есть равнобедренный; значитъ, процессъ нахожденія общей мѣры гипотенузы АС и катета АВ даннаго равнобедреннаго тр-ка переходитъ теперь въ процессъ нахожденія общей мѣры гипотенузы ЕС и катета БС другого (меньшаго) равнобедреннаго тр-ка. Въ свою очередь, этотъ процессъ также сведется къ нахожденію общей мѣры гипотенузы и катета третьяго (еще меньшаго) равнобедреннаго тр-ка ит. д. безъ конца. Значитъ, діагональ квадрата и сторона его не могутъ имѣть общей мѣры.
158. Понятіе объ измѣреніи. Чтобы составить ясное представленіе о данной длинѣ, мы ее измѣряемъ при помощи другой, извѣстной намъ, длины, напр., посредствомъ метра. Эта извѣстная длина, съ которой мы сравниваемъ другія длины, паз. единицей длины.
При измѣреніи могутъ представиться два различныхъ случая: или измѣряемая длина соизмѣрима съ единицей, или несоизмѣрима съ ней.
1°. Измѣрить длину, соизмѣримую съ еди
ницей, значитъ узнать, сколько разъ въ
ней содержится единица или какая-ни-
будь доля единицы.
Пусть, напр., надо измѣрить (черт. 149) длину отрѣзка пря-
мой А при помощи единицы В, соизмѣримой съ А. Тогда находятъ ихъ общую мѣру и узнаютъ, сколько разъ она содержится въ В и Л. Если общей мѣрой окажется сама единица, В то результатъ измѣренія выразится цѣлымъ числомъ; такъ,
Черт. 149.
— 116 —
когда В содержится въ А три раза, то длина А равна 3 един. Если же общей мѣрой будетъ нѣкоторая доля В, то результатъ измѣренія выразится дробнымъ числомъ; такъ, если общая мѣра есть г/4 доля В и она содержится въ А девять разъ (какъ изображено на черт. 149), то длина А равна 9/і единицы.
Число, получившееся послѣ измѣренія длины А, наз. мѣрою этой длины; о немъ принято говорить, что оно измѣряетъ длину А въ единицѣ В. Числа цѣлыя и дробныя наз. соизмѣримыми (или раціональными) числами.
2°. Когда измѣряемая длина А несоизмѣрима съ единицею длины В, тогда при помощи соизмѣримыхъ чиселъ мы не можемъ получить точнаго результата измѣренія. Дѣйствительно, если предположимъ, что мы нашли точную мѣру длипы Л,папр., ?п
нашли, что Л=В.-’ТО это значило бы, что 1/п доля В содер-жится въ А ровно т разъ; тогда, значитъ, эта доля была бы общею мѣрою А и В, тогда какъ мы разсматриваемъ случай, когда эти длины не соизмѣримы.
Въ этомъ случаѣ при помощи соизмѣримыхъ чиселъ мы можемъ находить только приближенные результаты измѣренія, по съ какою угодно степенью точности. Пусть, напр., мы желаемъ найти приближенную мѣру длины А съ точностью до Это значитъ, что мы желаемъ найти число, которое измѣряло бы нѣкоторую соизмѣримую длину, различающуюся отъ данной несоизмѣримой длины А менѣе, чѣмъ на 1/10 долю единицы В. Для этого дѣлимъ единицу В на 10 равныхъ частей и одну такую
долю укладываемъ на А столько разъ, сколько молено. Пусть окажется, что 1/10 В содержится въ А 13 разъ (черт. 150), при чемъ получается остатокъ, меньшій 1/10 В. Тогда каждое изъ чиселъ:13/10 и 14/10 можно принять, какъ приближенную мѣру длины А, причемъ первое число будетъ съ недостаткомъ (такъ какъ 13/10 В<^Л), а второе—съ избыткомъ (такъ какъ »/)0 В>Л).
Черт. 150
— 117 -
Вообще, чтобы найти приближенныя мѣры длины А съ точностью до 1/„ единицы, дѣлятъ единицу В на п равныхъ частей и узнаютъ, сколько разъ 1/п доля единицы содержится въ А; если она содержится болѣе т разъ, но менѣе ?п+1 разъ *), то
т иі+1
числа — и —— будутъ приближенныя мѣры длины А съ точ
ностью до х/п, первое—съ недостаткомъ, второе—съ избыткомъ.
Замѣтимъ, что этимъ путемъ мы можемъ находить приближенные результаты измѣренія и тогда, когда измѣряемая длина А соизмѣрима съ единицей В; только въ этомъ случаѣ мы, если пожелаемъ, можемъ найти также и точный результатъ, тогда какъ въ случаѣ несоизмѣримости такого результата при помощи
однихъ соизмѣримыхъ чиселъ мы получить не можемъ.
За точную мѣру несоизмѣримой длины А принимаютъ нѣкоторое несоизмѣримое число, которое считается бблыпимъ всякаго соизмѣримаго числа, выражающаго приближенныя мѣры длины А съ недостаткомъ, и меньшимъ всякаго соизмѣримаго числа, выражающаго приближенныя мѣры длины А съ избыткомъ.
Сказанное объ измѣреніи длины прямой примѣнимо къ измѣ
ренію всякой иной величины, напр., дуги, угла и пр.
159. Отношеніе. Отношеніемъ одного от
рѣзка прямой (Л) къ другому отрѣзку прямой (В) наз. число, измѣряющее первый отрѣзокъ (Л), когда второй (В) принятъ за единицу.
Такъ, если отношеніе Л къ В есть число 23/4, то это значитъ, что число 23/4 измѣряетъ отрѣзокъ Л, когда отрѣзокъ В принятъ за единицу (другими словами—это значитъ, что В со
держится въ Л 2 раза, причемъ получается остатокъ, равный 3/4В).
Можно также сказать, что
отношеніемъ одного
отрѣзка прямой къ другому наз. число, на которое надо умножить второй отрѣзокъ, чтобы получить первый.
Такъ, если отношеніе Л къ В есть число 23/4, то это значитъ, что А=В . 23/4, т.-е. что Л получится, если В повторимъ слагаемымъ 2 раза и къ суммѣ еще добавимъ 3/4 В.
*) что всегда возможно, согласно аксіомѣ Архимеда (стр. 111).
— 118 —
Если разсматривается отношеніе отрѣзка А къ отрѣзку В, то А наз. предыдущимъ членомъ, а В послѣдующимъ членомъ.
Изъ опредѣленія слѣдуетъ, что нахожденіе отношенія отрѣзковъ А и В сводится къ измѣренію А, когда отрѣзокъ В принятъ за единицу. Поэтому мы можемъ здѣсь повторить все то, что раньше (158) говорили объ измѣреніи, а именно:
Если отрѣзки Л и В соизмѣримы, то отношеніе ихъ есть соизмѣримое число, цѣлое или дробное; если же эти отрѣзки несоизмѣримы, то при помощи соизмѣримыхъ чиселъ ихъ отношеніе можетъ быть выражено только приближенно, но съ какою угодно степенью точности. Такъ, если хотятъ найти отношеніе Л къ В съ точностью до 1/10, то дѣлятъ В на 10 равныхъ частей (черт. 150) и узнаютъ наибольшее содержаніе Ѵю В въ А; если окажется, напр., что 1/10 В содержится въ А болѣе 13, но менѣе 14 разъ, то числа 13/ю и 14/ю будутъ приближенныя значенія отношенія Л къ В съ точностью до 1/10, первое— съ недостаткомъ, а второе—съ избыткомъ.
Отношеніе отрѣзковъ Л къ В въ томъ случаѣ, когда эти отрѣзки несоизмѣримы, наз. также несоизмѣримымъ (такъ какъ оно представляетъ собою несоизмѣримое число).
Два отношенія считаются равный и, если они представляютъ собою одно и то же число; такъ, если отношеніе А къ В равно 9/4 и отношеніе Аг къ В± также равно 9/4, то эти отношенія равны между собою.
Въ случаѣ несоизмѣримыхъ отношеній равенство между ними узнается по слѣдующему признаку.
Два несоизмѣримыя отношенія равны, если ихъ приближенныя значенія, взятыя оба съ недостаткомъ, или оба съ избыткомъ, и вычисленныя съ одинаковою точностью, равны между собой при всякой степени точности*).
Сказанное объ отношеніи двухъ отрѣзковъ прямой можно повторить объ отношеніи двухъ угловъ, двухъ дугъ одинаковаго
*) Какъ извѣстно изъ алгебры (см. напр., § 200 Элем. алгебры А. Киселева) этотъ признакъ есть признакъ равенства самихъ несоизмѣримыхъ чиселъ.
119 —
радіуса и вообще объ отношеніи двухъ частныхъ значеній любой величины, доступной измѣренію.
Напомнимъ, что равенство 2-хъ отношеній наз. пропорціей.
160ѵ Свойство отношеній. Если отрѣзки А и В (черт. 151) измѣрены при помощи одной и той же единицы С, то отношеніе А къ В равно частному отъ дѣленія числа, измѣряющаго А, на число, измѣряющее В. Пусть, напр., отъ измѣренія отрѣзка А единицею С получилось число 7/2, а отъ измѣренія В тою же единицею С получилось число 5/3. Тогда по опредѣленію отношенія мы можемъ написать:
7 7
А 1-----1-----1----1—|
В I-----1-1
С I---1
Черт. 151.
5 5
в=с.5==з-с.
Чтобы найти теперь отношеніе А къ В, достаточно узнать, на какое число слѣдуетъ умножить 5/3 С, чтобы получить 7/2 С, или—что все равно—на какое число надо умножить 5/3 (какой-нибудь единицы), чтобы получить 7/3 (той же единицы). Такое число находится дѣленіемъ (согласно опредѣленію этого дѣйствія); значитъ:
7 б 21 1
отношеніе А къ В—- : -=
2 о 10 10
Вообще, если, измѣривъ отрѣзки А и В при помощи одной и той же единицы С, мы получимъ для А число т, а для В число п, то, повторивъ предыдущія разсужденія, найдемъ (каковы бы ни были числа т и п):
отношеніе А къ В=т:п.
120 —
Вслѣдствіе этого отношеніе А къ В принято обозначать помощью знаковъ дѣленія, а именно такъ:
А
А : В или — • х>
Здѣсь подъ буквами А и В, согласно указанному сейчасъ свойству отношенія, можно разумѣть и числа, измѣряющія отрѣзки Л и В въ какой-нибудь одной и той же единицѣ С.
16О2. Пропорція. Равенство двухъ отношеній составляетъ пропорцію. Если, напр., извѣстно, что отношеніе двухъ отрѣзковъ А и В равно отношенію двухъ другихъ отрѣзковъ Аг и Ві, то можно написать пропорцію:
А:В = А1:В1, А Аг
ИЛИ В^В/
Когда отрѣзки А, В, Аг и Вг измѣрены при помощи одной и той же единицы, то каждое изъ двухъ отношеній, составляющихъ пропорцію, можно замѣнить отношеніемъ чиселъ, измѣряющихъ отрѣзки. Послѣ замѣны получится числовая процорція, обладающая всѣми тѣми свойствами числовыхъ пропорцій, которыя были указаны въ ариѳметикѣ и алгебрѣ, напр.;
въ пропорціи произведеніе крайнихъ членовъ равно произведенію среднихъ;
въ пропорціи можно переставить средніе члены, крайніе члены и средніе съ крайними;
если въ пропорціи предыдущіе члены равны, то равны и послѣдующіе члены;
если въ пропорціи послѣдующіе члены равны, то равны и предыдущіе; и т. п.
— 121 -
ГЛАВА ѴП.
Измѣненіе угловъ помощью дугъ.
Центральный уголъ.
161. Опредѣленіе. Уголъ (АОВ, черт. 152), образованный двумя радіусами, наз. центральнымъ угломъ; о такомъ углѣ и дугѣ, заключенной между его сторонами, говорятъ, что они соотвѣтствуютъ другъ другу.
162. Теорема. Въ одномъ кругѣ или въ равныхъ кругахъ:
1°, если центральные углы равны, то и соотвѣтствующія имъ дуги равны;
2°, если центральные углы не равны, то
ббльшему ИЗЪ НИХЪ соотвѣтствуетъ бблЬ- Черт. 152. шая дуга.
Пусть (черт. 153) АОВ и СОВ два центральные угла, равные или неравные. Повернемъ секторъ АОВ вокругъ центра въ направленіи, указанномъ стрѣлкою, настолько, чтобы радіусъ О А сов- р ^7 мѣстился съ ОС. Тогда: 1°, если центральные углы равны, то радіусъ / \
ОВ совпадаетъ съ ОВ и, слѣд., дуга ді_________
АВ совмѣстится съ дугою СП; зна- I ® у Г
читъ, эти дуги будутъ равны; 2°, \ /
если же центральные углы неравны, X. У'
то радіусъ ОВ пойдетъ не по ОВ, а по какому-нибудь иному напра- Черт. 153.
вленію, напр., по ОЕ или по ОГ\ въ томъ и въ другомъ случаяхъ ббльшему углу, очевидно, соотвѣтствуетъ большая дуга.
Теорема, доказанная нами для одного круга, остается вѣрною для равныхъ круговъ, потому что такіе
— 122 —
круги ничѣмъ, кромѣ своего положенія, другъ отъ друга не отличаются.
163. Обратныя теоремы. Такъ какъ различные взаимно исключающіе случаи относительно равенства и неравенства двухъ центральныхъ угловъ сопровождаются взаимно исключающими выводами относительно равенства и неравенства соотвѣтствующихъ дугъ, то обратныя предложенія должны быть вѣрны (51), а именно:
Въ одномъ кругѣ или въ равныхъ кругахъ:
1°, если дуги равны, то и соотвѣтствующіе имъ центральные углы равны;
2°, если дуги не равны, то большей изъ нихъ соотвѣтствуетъ ббльшій центральный уголъ.
Доказательство отъ противнаго (или наложеніемъ) предоставляемъ самимъ учащимся.
164. Теорема. Въ одномъ кругѣ или въ равныхъ кругахъ центральные углы относятся, какъ соотвѣтствующія имъ дуги.
Пусть (черт. 154) АОВ и СОВ два центральные угла; требуется доказать, что
Х.АОВ : ЛСОВ=^АВ :^СВ.
1°. Допустимъ сначала, что дуги ™ АВ и СВ соизмѣримы, т.-е. что онѣ
; 7'7'>3 имѣютъ общую мѣру. Положимъ, ' '« • ' '/ \ что эта общая мѣра содержится т
/ \ разъ въ ДУ1"*5 АВ и п разъ въ СВ;
I I тогДа
\ АВ : СВ=т : п [1].
\ /
' ' V/ Соединивъ точки дѣленія дугъ съ центромъ, мы раздѣлимъ централь-
Черт. 1Б4. ные углы на равныя части (потому
что равнымъ дугамъ соотвѣтствуютъ равные центральные углы). Такъ какъ этихъ частей будетъ т въ углѣ АОВ и п въ углѣ СОВ, то
/_АОВ : Х.СОВ=т : п [2].
Сравнивая пропорціи [1] и [2], замѣчаемъ, что вторыя отношенія у нихъ равны; слѣд., равны и первыя отношенія, т.-е.
Х.АОВ : ЛСОВ=^АВ : ^СВ.
— 123 —
ЧИСЛО АОВ, но
Черт. 155.
разъ такъ тогда цѣлое
разъ какъ въ дугѣ АВ, и въ дугѣ СВ, и, зна-дуги эти имѣли бы общую именно дугу ЕР, что про-Та-
2°. Предположимъ теперь, что (черт. 156) дуги АВ и СВ несоизмѣримы. Тогда и соотвѣтствующіе имъ центральные углы будутъ также несоизмѣримы. Дѣйствительно, если бы эти углы имѣли какую-нибудь общую мѣру, напр., уголъ ЕОР, то это значило бы, что этотъ уголъ содержится цѣлое какъ въ углѣ
и въ углѣ СОВ-, дуга ЕР содержалась бы число такъ читъ, мѣру,
тиворѣчитъ предположенію.
кимъ образомъ, въ разсматриваемомъ случаѣ и отношеніе угловъ, и отношеніе дугъ оба несоизмѣримыя. Чтобы доказать равенство двухъ несоизмѣримыхъ отношеній, достаточно доказать равенство ихъ приближенныхъ значеній, вычисленныхъ съ произвольною, но одинаковою точностью (159). Найдемъ приближенное значеніе отношенія дугъ АВ и СВ съ точностью до 1/я. Для этого раздѣлимъ СВ на п равныхъ частей и одну часть отложимъ на АВ столько разъ, сколько можно. Пусть 1/„ доля СВ содержится въ АВ болѣе т разъ, но менѣе т+1 разъ; тогда
АВ т прибл. отношеніе ---ху = — (съ нед.).
Соединивъ точки дѣленія дугъ съ центромъ, мы раздѣлимъ уголъ СОВ на п такихъ равныхъ частей, какихъ въ углѣ АОВ содержится болѣе т, но менѣе ш+1; слѣд.:
X. АОВ т
прибл. отношеніе (съ нед.).
п
Сравнивая приближенныя отношенія угловъ и дугъ, видимъ, что они равны при всякомъ п; а такія несоизмѣримыя отношенія равны другъ другу.
165. Пропорціональныя величины. Двѣ зависящія другъ отъ друга величины наз. пропорціональными, если зависимость между ними состоитъ въ слѣдующемъ:
— 124 —
1°, каждому значенію одной величины соотвѣтствуетъ нѣкоторое значеніе другой величины и притомъ только одно;
2°, отношеніе двухъ какихъ бы то ни было значеній одной величины равно отношенію соотвѣтствующихъ значеній другой величины.
Изъ предыдущихъ теоремъ слѣдуетъ, что центральный уголъ пропорціоналенъ соотвѣтствующей ему дугѣ.
166. Измѣреніе угловъ. Измѣреніе угловъ сводится на измѣреніе соотвѣтствующихъ имъ дугъ слѣдующимъ образомъ.
За единицу угловъ берутъ уголъ, составляющій 1/90 часть прямого угла; эту единицу называютъ угловымъ градусомъ.
За единицу дугъ одинаковаго радіуса берутъ такую дугу того же радіуса, которая соотвѣтствуетъ центральному углу, \ /А
\ м
О Щ— В и Ір— Р
Черт. 156.
равному угловому градусу. Такая дуга наз. дуговымъ градусомъ. Такъ какъ прямому центральному углу соотвѣтствуетъ х/4 окружности, то угловому градусу соотвѣтствуетъ 1/90 четверти окружности; значитъ, дуговой градусъ есть 1/360 цѣлой окружности.
Пусть требуется (черт. 156) измѣрить какой-нибудь уголъ АОВ, т.-е. пайти отношеніе этого угла къ угловому градусу. Пусть этотъ градусъ будетъ уголъ М№. Опишемъ изъ вершинъ угловъ произвольнымъ, но одинаковымъ, радіусомъ дуги СВпЕР. Тогда углы АОВ и МЕР можно разсматривать, какъ углы центральные по отношенію къ тѣмъ равнымъ окружностямъ, которымъ принадлежатъ дуги СВ и ЕР. Вслѣдствіе этого (164): ^АОВ_^СВ ХМЁР~^ЕР'
— 125 —
Лѣвое отношеніе этой пропорціи есть число, измѣряющее уголъ АОВ въ угловыхъ градусахъ (159); правое отношеніе есть число, измѣряющее дугу СР въ дуговыхъ градусахъ. Слѣд., эту пропорцію можно высказать такъ:
Число, измѣряющее центральный уголъ въ угловыхъ градусахъ, равно числу, измѣряющему соотвѣтствующую дугу въ дуговыхъ градусахъ.
Для краткости эту фразу выражаютъ обыкновенно такъ:
У г о л ъ и з м ѣ р я е т с я соотвѣтствующей ему дугой.
При этомъ безразлично, какъ великъ взятый радіусъ дугъ ЕР и СВ, лишь бы только онъ былъ одинаковъ для обѣихъ этихъ дугъ (только при этомъ условіи углы пропорціональны дугамъ).
167. Подраздѣленіе градусовъ. Градусы угла или дуги подраздѣляются на 60 равныхъ частей, называемыхъ минутами (угловыми или дуговыми); минуту раздѣляютъ на 60 равныхъ частей, называемыхъ секундами (угловыми или дуговыми).
Изъ сказаннаго въ предыдущемъ параграфѣ слѣдуетъ, что въ углѣ содержится столько угловыхъ градусовъ, минутъ и секундъ, сколько въ соотвѣтствующей ему дугѣ заключается дуговыхъ градусовъ, минутъ и секундъ. Если, напр., въ дугѣ СВ (черт. 156) содержится 40 град. 25 мин. 13 секундъ (дуговыхъ), то и въ углѣ АОВ заключается 40 град. 25 мин. 13 сек. (угловыхъ); это выражаютъ сокращенно такъ:
2ІЛ0В=40о25'13",
обозначая значками (°), (') и (") соотвѣтственно градусы, минуты и секунды *).
168. Транспортиръ. Этотъ приборъ (черт. 157), употребляемый для измѣренія угловъ, представляетъ собою полукругъ, котораго дуга раздѣлена на 180 градусовъ. Чтобы
*) Употребительна также сотенная система мѣръ угловъ и дугъ; по ѳтой системѣ за градусъ дуги принимаютъ */100 четверти окружности (и, слѣд., за градусъ угла берутъ 1/100 прямого угла), минуту принимаютъ равной градуса, секунду—7іоо минуты.
— 126 —
измѣрить уголъ АОВ, накладываютъ на него приборъ такъ, чтобы центръ полукруга совпадалъ съ вершиною угла, а радіусъ ОМ совпадалъ со стороною АО. Тогда число градусовъ, содержащееся въ дугѣ, заключенной между сторонами угла АОВ, покажетъ
величину его. При помощи транспортира можно также начертить уголъ, содержащій данное число градусовъ.
Конечно, на такомъ приборѣ нѣтъ возможности отсчитывать не только секунды, но и минуты; измѣреніе и построеніе можно выполнять только приблизительно.
169. Выраженіе нѣкоторыхъ угловъ въ градусахъ. Такъ какъ прямой уголъ содержитъ 90°, то:
1°, сумма угловъ всякаго тр-ка равна 180°;
2°, сумма острыхъ угловъ прямоугольнаго тр-ка равна 90°; 3°, каждый уголъ равносторонняго тр-ка равенъ 60°;
4°, сумма угловъ выпуклаго мн-ка (89), имѣющаго п сторонъ, равна 180° (п—2);
5°, сумма внѣшнихъ угловъ выпуклаго мн-ка (90) равна 360°.
Вписанный уголъ.
170. Опредѣленіе. Уголъ, образованный двумя хордами, исходя щи ми изъ одной точки окружности, наз. вписаннымъ угломъ. Таковъ, напр., уголъ АВС (черт. 159). О вписанномъ углѣ принято говорить, что онъ опирается на дугу, заключенную между его сторонами. Такъ, уголъ АВС (черт. 159) опирается на дугу АБС.
171. Теорема. Вписанный уголъ измѣряется половиною дуги, на которую онъ опирается.
Эту теорему надо понимать такъ: внисанный уголъ содержитъ въ себѣ столько угловыхъ градусовъ, минутъ и секундъ, сколько дуговыхъ градусовъ, минутъ и секундъ заключается въ половинѣ дуги, на которую онъ опирается.
127 —
В
С
Черт. 158.
При доказательствѣ теоремы разсмотримъ особо три случая: 1°. Центръ О (черт. 158) лежитъ на сторонѣ вписаннаго угла АВС. — Проведя радіусъ АО, мы получимъ дЛВО, въ которомъ ОА=ОВ (какъ радіусы) и, слѣд., Х.АВО=Х.ВАО. По отношенію къ этому тр-ку уголъ АОС есть внѣшній; поэтому онъ равенъ суммѣ угловъ АВО и ВАО, или равенъ двойному углу АВО; значитъ, уголъ АВО равенъ половинѣ центральнаго угла АОС.
Но уголъ АОС измѣряется дугою АС, т.-е. онъ содержитъ въ себѣ столько угловыхъ градусовъ, минутъ и секундъ, сколько дуговыхъ градусовъ, минутъ и секундъ содержится въ дугѣ ЛС; слѣд., вписанный уголъ АВС измѣряется половиною дуги АС.
2°. Центръ О лежитъ между сторонами вписаннаго угла АВС (черт. 159).
Проведя діаметръ ВВ, мы раздѣлимъ уголъ АВС на два угла, изъ которыхъ, по доказанному въ первомъ случаѣ, одинъ измѣряется половиною дуги АВ, а другой—половиною дуги СВ; слѣд., уголъ АВС измѣряется суммою 1/2АВ+1/2ВС, а
эта сумма равна 1/2(АВ+ВС), т.-е. 1/2АС.
3°. Центръ О лежитъ внѣ вписаннаго угла АВС (черт. 160).
Проведя діаметръ ВВ, мы будемъ имѣть:
/.АВС=Х.АВВ—ЛСВВ.
Но углы АВВ и СВВ измѣряются, по доказанному, половинами дугъ АВ и СВ; слѣд., уголъ АВС измѣряется разностью 1/2ЛВ—гІ2СВ, а эта разность равна 1/2(АВ—СП), т.-е. ЧгАС.
— 128 —
172. Слѣдствіе 1-е. Всѣ вписанные углы, опирающіеся на одну и ту же дугу, равны между т собою (черт. 161), потому что ка-
ждый изъ нихъ измѣряется полови-/ \ \ ною одной и той же дуги. Если
величину одного изъ такихъ угловъ п і / \ /1 обозначимъ а, то можно сказать, что
^\\// сегментъ АтВ(покрытый на чертежѣ
АѴ Ув штрихами) вмѣщаетъ въсебѣ
\------' уголъ, равный а.
Черт 161 173. Слѣдствіе 2-е. Всякій впи-
санный уголъ, опирающійся на діаметръ, есть прямой (черт. 162), потому что каждый такой уголъ измѣряется половиною полуокружности и, слѣд., содержитъ 90°.
Черт. 162. Черт. 163.
174. Задача. Построить прямоугольный треугольникъ по гипотенузѣ АВ и катету АС (черт. 162).
На гипотенузѣ АВ, какъ на діаметрѣ, описываемъ полуокружность и изъ копца А проводимъ хорду АС, равную данному катету. Тр-никъ АСВ будетъ искомый (173).
Это построеніе можно, между прочимъ, примѣнить въ томъ случаѣ, когда (черт. 163) изъ данной точки А требуется провести касательную къ данной окружности О (см. § 139). Сединивъ А съ центромъ О, дѣлимъ отрѣзокъ АО пополамъ и изъ полученной середипы описываемъ окружность радіусомъ О^О\ черезъ А и точки В и Вх, въ которыхъ эта окружность пересѣкается съ данною окружностью, проводимъ прямыя АВ и АВГ. Эти прямыя и будутъ каса
— 129 —
тельными (137, 1°), такъ какъ углы ОБА и ОВіА (вписанные
во вспомогательную окружность и опирающіеся на ея діаметръ)—
прямые, и, значитъ, АВ_1_ОВ и
175. Задача. Изъ конца А (черт. 164) данной пря
мой АВ, не продолжая ея, возставить
К Ъ
ней перпендикуляръ.
Взявъ внѣ прямой произвольную точку О, опишемъ изъ нея окружность радіусомъ, равнымъ разстоянію между точками О и А; черезъ точку С, въ которой эта окружность пересѣкается съ прямой АВ, проведемъ діаметръ СВ и черезъ копецъ его В и точку А проведемъ прямую. Эта прямая и есть
Гч) д
Черт. 164.
В
искомый перпендикуляръ, потому что уголъ А прямой, такъ какъ онъ вписанный и опирается на діаметръ.
Уголъ, котораго вершина лежитъ внутри или внѣ круга.
167. Теоремы. 1°. Уголъ (АВС, черт. 165), вершина котораго лежитъ внутри круга, измѣряется полусуммою двухъ дугъ (АС и ВЕ), изъ которыхъ одна заключена между его сторонами, а другая—между продолженіями сторонъ.
2°. Уголъ (АВС, черт. 166), вершина котораго лежитъ внѣ круга и стороны пересѣкаются съ окружностью, измѣряется полуразностью двухъ дугъ (АС и ЕВ), заключенныхъ между
его сторонами.
Черт. 165. Черт. 166.
Проведя хорду АВ (на томъ и на другомъ чертежахъ), мы получимъ тр-къ АВВ (покрытый штрихами), относительно ко-
9
А. Киселевъ. Геометрія.
— 130 —
тораго разсматриваемый уголъ АВС служить внѣшнимъ, когда его вершина лежитъ внутри круга (черт. 165), и внутреннимъ, когда его вершина лежитъ внѣ круга (черт. 166). Поэтому
въ первомъ случаѣ: А^АВС=</_АБС-\-АІПАЕ-, во второмъ случаѣ: ^.АВС=^.АБС—^БАЕ.
Но углы АБС и БАЕ, какъ вписанные, измѣряются половинами дугъ АС и БЕ-, поэтому уголъ АВС измѣряется: въ первомъ случаѣ суммою 1/2АС-\-1/2БЕ, которая равна 1/2(АС-\-БЕ), а во второмъ случаѣ разностью ЧгАС—1/2ОВ, которая равна Х/2(ЛС— БЕ).
177. Слѣдствіе. Геометрическое мѣсто точекъ, изъ которыхъ данный отрѣзокъ прямой виденъ подъ даннымъ угломъ а, и которыя расположены по одну сторону отъ этого отрѣзка, есть дуга сегмента, вмѣщающаго уголъ а и построеннаго на данномъ отрѣзкѣ.
Пусть М (черт. 167) будетъ одна изъ Й точекъ, изъ которыхъ данный отрѣзокъ АВ виденъ подъ угломъ а, т.-е. допустимъ, что прямыя МА п МВ образуютъ уголъ а. Проведемъ черезъ три точки А, М и В окружность. Тогда часть этой окружности, именно дуга АтВ, будетъ искомымъ геометрическимъ мѣстомъ. Дѣйствительно, изъ каждой точки этой дуги прямая АВ видна подъ угломъ а, потому что всѣ вписанные углы, опирающіеся па АВ, равны углу Черт 167 АМВ, который есть а. Обратно: всякая точка, папр., Ы, изъ которой прямая АВ видна подъ угломъ а и которая расположена по ту же сторону отъ АВ, какъ и точка М, должна находиться на дугѣ сегмента АтВ, потому что, если бы такая точка лежала внутри или внѣ этого сегмента, то уголъ А1ѴВ не измѣрялся бы половиною дуги АпВ (176, 1° и 2°) и, слѣд., не былъ бы равенъ а.
По другую сторону отъ АВ существуютъ также точки, изъ которыхъ эта прямая видна подъ угломъ а; опѣ расположены
— 131 —
на дугѣ сегмента АрВ, равнаго сегменту АтВ, но расположеннаго по противоположную сторону отъ АВ.
Уголъ, котораго одна или обѣ стороны касаются окружности.
178. Теорема. Уголъ (АСВ, чертежи 168 и 169), составленный касательной и хордой, измѣряется половиною дуги, заключенной внутри его.
Черт. 169
Предположимъ сначала, что хорда СВ проходитъ черезъ центръ О, т.-е. что эта хорда есть діаметръ (черт. 168). Тогда уголъ АСВ—прямой (137, 2°) и, слѣд., равенъ 90°. Но и половина дуга СтВ также равна 90°, такъ какъ цѣлая дуга СтВ, составляя полуокружность, содержитъ 180°. Значитъ, теорема оправдывается въ этомъ частномъ случаѣ.
Теперь возьмемъ общій случай (черт. 169), когда хорда СВ не проходитъ черезъ центръ. Проведя тогда діаметръ СЕ, мы будемъ имѣть:
Ласв=/.асе—Лвсе.
Уголъ АСЕ, какъ составленный касательною и діаметромъ, измѣряется, по доказанному, половиною дуги СтЕ-, уголъ ВСЕ, какъ вписанный, измѣряется половиною дуги ВЕ-, слѣд., уголъ АСВ измѣряется разностью 1/2СтЕ—1/2ВЕ, т.-е. половиною дуги СтВ.
Подобнымъ же образомъ можно доказать, что тупой уголъ ВСВ (черт. 169), также составленный касательною и хордой, измѣряется половиною дуга СпЕВ-, разница въ дока
9*
— 132 —
зательствѣ будетъ только та, что этотъ уголъ надо разсматривать не какъ разность, а какъ сумму прямого угла ВСЕ и остраго ЕСВ.
179. Теорема. Уголъ (АВС, черт. 170), составленный касательной и сѣкущей, а также и уголъ (АВС, черт. 171), составленный двумя касательными, измѣряется полуразностыо двухъ дугъ, заключенныхъ между его сторонами.
Проведя (па томъ и па другомъ чертежахъ) хорду ВЕ, мы получимъ ДВЛЕ, относительно котораго уголъ СЕВ есть внѣшній; слѣд.,
/.В=/.СЕВ—^ВВЕ.
Но углы СЕВ и ВВЕ, по доказанному раньше, измѣряются половинами дугъ ЕтВ и ЕпЕ на первомъ чертежѣ и половинами дугъ ЕтВ и ЕпВ на второмъ чертежѣ; поэтому7 уголъ В измѣряется полуразностью этихъ дугъ.
180. Задача. На данномъ отрѣзкѣ прямой АВ построить сегментъ, вмѣщающій данный уголъ а (черт. 172).
Анализъ. Предположимъ, что задача рѣшена; пусть сегментъ АтВ будетъ такой, который вмѣщаетъ въ себѣ уголъ а, т.-е. такой, что всякій вписанный въ немъ уголъ АСВ равенъ а. Проведемъ вспомогательную прямую ЕР, касательную къ окружности въ точкѣ А. Тогда уголъ ВАЕ, составленный касательною и хордою, долженъ равняться вписанному углу АСВ, такъ какъ и тотъ, и другой уголъ измѣряются половиною дуги
— 133 —
АпВ. Примемъ теперь во вниманіе, что центръ О окружности долженъ лежать на перпендикулярѣ ВО, проведенномъ къ от- С _ - г
рѣзку АВ черезъ его середину, и въ то же время онъ долженъ X г“\ \
лежать и на перпендикулярѣ АО, / / 'ч і
возставленномъ къ касательной АЕ | / I
изъ точки касанія. Отсюда выво- р \ / / I \ /
димъ слѣдующее построеніе. I/ ’ \ /
Построеніе. При концѣ .„.ІВ—
отрѣзка АВ строимъ уголъ ВАЕ, & *
равный углу а; черезъ середину
АВ проводимъ перпендикуляръ ВО
и изъ точки А возставляемъ пер- черт. 172.
пендикуляръ къ АЕ. Пересѣченіе О этихъ двухъ перпендикуляровъ принимаемъ за центръ и радіусомъ ОА описываемъ окружность.
Доказательство. Сегментъ АтВ будетъ искомый, потому что всякій вписанный въ немъ уголъ измѣряется половиною дуги АпВ, а половина этой дуги измѣряетъ также и уголъ ВАЕ=а.
ГЛАВА VIII.
Вписанные и описанные многоугольники.
181. Опредѣленія. Если всѣ вершины многоугольника (АВСВЕ, черт. 173) лежатъ на окружности, то говорятъ, что что этотъ мн-къ вписанъ въ окружность, или что окружность описана около него.
Если всѣ стороны какого-нибудь многоугольника (МЕРО) касаются окружности, то говорятъ, что этотъ мн-къ описанъ около окружности, или что окружность в п и сана въ него.
— 134 —
182. Теоремы. 1°. Около всякаго треугольника можно описать окружность и притомъ только одну.
томъ только одну.
1°. Вершины А, В л
Черт. 174.
2°. Во всякій треугольникъ можно вписать окружность и при-
С всякаго тр-ка суть три точки, не лежащія па одной прямой; а черезъ такія точки, какъ мы видѣли (122), всегда можно провести окружность и притомъ только одну.
2°. Если возможна такая окружность, которая касалась бы всѣхъ сторонъ тр-ка АВС (черт. 174), то ея центръ долженъ быть точкой, одинаково удаленной отъ этихъ сторонъ. Докажемъ, что такая точка существуетъ. Геометрическое мѣсто точекъ, равно отстоящихъ отъ сторонъ АВ и АС, есть биссектрисса
АМ угла А (67); геометрическое мѣсто точекъ, равно отстоящихъ отъ сторонъ ВА и ВС, есть биссектрисса ВН угла В. Эти двѣ биссектриссы должны, очевидно, пересѣчься внутри треугольника, въ нѣкоторой точкѣ О. Эта точка и будетъ равно удаленной отъ всѣхъ сторонъ тр-ка, такъ какъ она находится на обоихъ геометрическихъ мѣстахъ. Итакъ, чтобы вписать кругъ въ тр-къ, дѣлимъ какіе-нибудь два угла его, напр., А и В, пополамъ и точку пересѣченія биссектриссъ беремъ за центръ. За радіусъ возьмемъ одинъ изъ перпендикуляровъ ОР, ОО, ОВ, опущенныхъ изъ центра на стороны тр-ка. Окружность коснется сторонъ въ точкахъ Р, ф, В, такъ какъ стороны въ этихъ точкахъ перпендикулярны къ радіусамъ въ ихъ концахъ, лежащихъ па окружности (137, 2°). Другой вписанной окружности не можетъ быть, такъ какъ двѣ биссектриссы пересѣкаются только въ одной точкѣ, а изъ одной точки на прямую можно опустить только одинъ перпендикуляръ.
183. Слѣдствіе. Точка О (черт. 174), находясь на одинаковомъ разстояніи отъ сторонъ АС и ВС, должна лежать на биссектриссѣ угла С (65); слѣд.,
— 136 —
биссектриссы трехъ угловъ треугольника сходятся въ одной точкѣ.
184. Внѣвписанныя окружности. Такъ называются окружности (черт. 175), которыя касаются одной стороны тр-ка и п р о -
д о л ж в н і й двухъ другихъ сторонъ (онѣ лежатъ внѣ тр-ка, вслѣдствіе чего и получили названіе в н ѣ в писанныхъ). Такихъ окружностей ддя всякаго треугольника можетъ быть три. Чтобы построить ихъ, проводятъ биссектриссы внѣшнихъ угловъ тр-ка АВС и точки ихъ пересѣченій берутъ за центры. Такъ, центромъ окружности, вписанной въ уголъ А, служитъ точка О, т.-е. пересѣченіе биссектриссъ ВО и СО внѣшнихъ угловъ, не смежныхъ съ А; радіусъ этой окружности есть перпендикуляръ,
опущенный изъ О на какую-либо
сторону треугольника.
185. Теоремы. 1°. Въ выпукломъ вписанномъ четыреугольникѣ сумма противоположныхъ угловъ равна двумъ прямымъ.
2°. Обратно: Если въ выпукломъ четыреугольникѣ сумма противоположныхъ угловъ равна двумъ прямымъ, то около него можно описать окружность.
1°. Пусть АВСВ (черт. 176) есть впи-
санный выпуклый четыреугольникъ; тре- В
буется доказать, что
,В4_-О=2й п А-}-С=2(і. [ / 'Х
Такъ какъ сумма всѣхъ 4-хъ угловъ V/ \ /
всякаго выпуклаго четыреугольника рав-на 4гі, то достаточно доказать только одно изъ требуемыхъ равенствъ. Дока-жемъ, напр., что В+Р=2й.—Углы В и I), Черт. 176. какъ вписанные, измѣряются: первый—половиною дуги АВС, второй—половиною дуги АВС-, слѣд., сумма В-\-В измѣряется суммою дугъ 1/2АВС-\-1І2АВС-,а. эта сумма равна 1І2(АВС+АВС), т.-е. равна половинѣ окружности; значитъ, В+П=180°=2й.
— 136 —
Чсрг. 177.
и АВС, т.-е. сумма рѣчитъ условію.
2°. Пусть АВВС (черт. 177) есть такой выпуклый четыреугольникъ, у котораго В-\-Б=2Л и, слѣд., ^+(7=2^.
Требуется доказать, что около такого четыреугольника можно описать окружность.—Черезъ какія-нибудь три его вершины, напр., черезъ А, В и С, проведемъ окружность (что всегда можно сдѣлать). Четвертая вершина Б должна находиться на этой окружности, потому что въ противномъ случаѣ вершина угла Б лежала бы или внутри круга, или внѣ его, и тогда этотъ уголъ не измѣрялся бы половиною дуги АВС (176, 1° и 2°) ; поэтому сумма В-\-Б не измѣрялась бы полусуммою дугъ АБС ]-Б не равнялась бы 2й, что противо-
186. Слѣдствія. 1°. Изъ всѣхъ параллелограммовъ только около прямоугольника (и, слѣд., около квадрата) можно описать окружность.
2°. Около трапеціи можно описать окружность только тогда, когда она равнобочная.
187. Замѣчаніе. Двѣ изложенныя теоремы о вписанномъ четыреугольникѣ (прямая и обратная) приводятъ насъ къ слѣдующему заключенію: для того, чтобы около выпуклаго четыреугольника можно было описать окружность, необходимо и достаточно чтобы сумма его противоположныхъ угловъ равнялась двумъ прямымъ. Дѣйствительно, это условіе необходимо, такъ какъ, согласно теоремѣ 1°, во всякомъ вписанномъ выпукломъ четыреугольникѣ сумма противоположныхъ угловъ равна 2й, и слѣд., безъ этого условія не можетъ существовать вписанный выпуклый четыреугольникъ; въ то же время это условіе и достаточно, такъ какъ, согласно теоремѣ 2°, если въ выпукломъ четыреугольникѣ сумма противоположныхъ угловъ равна 2й, то около такого четыреугольника можно описать окружность.
Замѣтимъ, что необходимость какого-нибудь признака еще не означаетъ его достаточности, равно какъ достаточность
— 137 —
какого-нибудь признака еще не влечетъ за собою его необходимости. Напр., для того, чтобы выпуклый четыреугольникъ былъ ромбомъ, необходимо, чтобы его діагонали были взаимно перпендикулярны (если есть ромбъ, то діагонали его взаимно перпендикулярны; значитъ, безъ перпендикулярности діагоналей ромбъ не существуетъ); однако этотъ признакъ не достаточенъ: нельзя утверждать, что если діагонали выпуклаго
Черт. 178.
четыреугольника взаимно перпендикулярны, то такой четыреугольникъ непремѣнно ромбъ (при перпендикулярности діагоналей выпуклый четыреугольникъ можетъ и не быть ромбомъ, черт. 178). Другой примѣръ: для того, чтобы двѣ дуги одной и той же окружности были равны, достаточно, чтобы онѣ заключались между параллельными хордами; однако это не необходимо, такъ какъ и безъ параллельности хордъ дуги могутъ оказаться равными (дуги АВ и СР, черт. 179).
Для того, чтобы быть увѣреннымъ, что нѣкоторый признакъ А необходимъ и достаточенъ для существованія нѣкотораго свойства В, надо отдѣльно доказать его необходимость (если есть В, то есть и Л) и его достаточность (если есть А, то есть и В).
188. Теорема. Въ описанномъ выпукломъ четыреугольникѣ суммы противоположныхъ сторонъ равны.
Пусть АВСБ (черт. 180) будетъ описанный выпуклый четыреугольникъ, т.-е стороны его касаются окружности; требуется доказать, что ЛВ+СВ= ВС-\-АВ.—Обозначимъ точки касанія черезъ М, 27, Р и Такъ какъ двѣ
Черт. 180.
— 138 —
касательныя, проведенныя изъ одной точки къ окружности, равны (140), то АМ=А$, ВМ=ВЯ, СХ=СР и БР=Р^ Слѣд,
АМ-\МВ+СР+РВ=А(^ВХ+ХС+(Д), т.-е. АВ+СВ=АВ+ВС
189. Обратная теорема. Если въ выпукломъ четыреугольникѣ равны суммы противоположныхъ сторонъ, то въ него можно вписать окружность.
Пусть АВСВ такой выпуклый четыреугольникъ (черт. 181), въ ко-
торомъ:
АВ + СВ = АВ + ВС.
въ него можно вписать окружность.—Проведемъ биссектриссы ВО и СО двухъ угловъ В и С. Эти прямыя должны пересѣчься, потому что сумма угловъ ѢТВО и КСО меньше (такъ какъ В-|-С<4й). Точка пересѣченія биссектриссъ должна быть одинаково удалена отъ сторонъ АВ, ВС и СВ; поэтому, если эту точку возьмемъ за центръ, а за радіусъ одинъ изъ трехъ равныхъ перпендикуляровъ ОМ, ОЕ, ОР, опущенныхъ изъ О на стороны угловъ В и С, то окружност коснется сторонъ АВ, ВС и СВ. Дока
жемъ, что она коснется и четвертой стороны АВ. Предположимъ противное, т.-е. что 4-я сторона АВ не касается проведенной окружности.
Тогда проведя изъ точки А касательную къ этой окружности, мы должны получить нѣкоторую прямую, не сливающуюся съ АВ. Пусть это будетъ прямая АЕ, расположенная ближе къ центру О, чѣмъ АВ. Тогда получится описанный выпуклый четыреугольникъ АВСЕ, въ которомъ, по доказанному выше, будемъ имѣть:
ВС + АЕ=АВ + СЕ.
Но по условію:
ВС + АВ = АВ + СВ.
Вычтя почленно первое равенство изъ второго, найдемъ:
АВ— АЕ = СВ— СЕ=ВЕ,
т.-е. разность двухъ сторонъ А АВЕ равна третьей сторонѣ ВЕ, что невозможно (52); значитъ, нельзя допустить, чтобы касательною къ нашей окружности была какая-нибудь прямая АЕ, лежащая ближе къ центру О, чѣмъ АВ. Такъ же можно доказать, что касательною не можетъ быть никакая прямая АЕХ, лежащая дальше отъ центра, чѣмъ АВ\ значитъ, АВ должна касаться окружности, т.-ѳ. въ четыреугольникъ АВСВ можно вписать окружность.
190. Слѣдствіе. Изъ всѣхъ параллелограмовъ только въ ромбъ (и, слѣд., въ квадратъ) можно вписать окружность.
— 139 —
191. Замѣчаніе. Двѣ изложенныя теоремы объ описанномъ четыреугольникѣ (прямая и обратная) приводятъ насъ къ слѣдующему заключенію: для того, чтобы въ выпуклый четыреугольникъ можно было вписать окружность, необходимо и достаточно чтобы у него были равны суммы противоположныхъ сторонъ.
ГЛАВА IX.
Четыре замѣчательныя точки въ треугольникѣ.
192. Центръ описаннаго и центръ вписаннаго круга.
Мы видѣли (123 и 183), что:
1°, три перпендикуляра къ сторонамъ треугольника, проведенные черезъ ихъ середины, сходятся въ одной точкѣ, которая есть центръ описаннаго круга;
2°, три биссектриссы угловъ треугольника сходятся въ одной тоннѣ, которая есть центръ вписаннаго круга.
Замѣтимъ (учащіеся сами могутъ убѣдиться въ этомъ), что центръ
вписаннаго круга всегда лежитъ внутри тр-ка, а центръ описаннаго
круга лежитъ внутри тр-ка только въ томъ случаѣ, когда тр-къ остроугольный; въ тупоугольномъ же тр-кѣ онъ лежитъ внѣ его, а въ прямо
угольномъ—на серединѣ гипотенузы.
Слѣдующія 2 теоремы указываютъ еще 2 замѣчательныя точки тр-ка: 3°, пересѣченіе высотъ и 4°, пересѣченіе медіанъ.
193. Теорема. Три высоты треугольника пересѣкаются въ одной тоннѣ.
Черезъ каждую вершину тр-ка АВС (черт. 182) проведемъ прямую, параллельную противоположной сторонѣ его. Тогда получимъ вспо-
могательный А А1В1С1, къ сторонамъ котораго высоты даннаго тр-ка перпендикулярны. Такъ какъ С1В = АС = ВА1 (какъ противоположныя стороны параллелограммо-мовъ), то точка В есть середина стороны А^і. Подобно этому, убѣдимся, что С есть середина А1В1 и А—середина В1С1. Такимъ образомъ,высоты АО, ВЕ и СЕ перпендикулярны къ сторонамъ тр-ка АіВіСі и проходятъ черезъ ихъ середины; а такіе перпендикуляры,
Черт. 182.
какъ мы знаемъ, пересѣкаются въ одной точкѣ.
Точка, въ которой пересѣкаются высоты треугольника, наз. ортоцентромъ, или точкою высотъ. Эта точка въ остроугольномъ тр-кѣ лежитъ внутри, въ тупоугольномъ—внѣ его, а въ прямоугольномъ—въ вершинѣ прямого угла.
— 140 —
194. Теорема. Три медіаны треугольника пересѣкаются въ одной точкѣ; эта точка отсѣкаетъ отъ каждой медіаны третью часть, считая отъ соотвѣтствующей стороны.
Возьмемъ въ тр-кѣ АВС (черт. 183) ® какія-нибудь двѣ медіаны, напр. АЕ
и ВО, пересѣкающіяся въ точкѣ О, и /С/ \ докажемъ, что
/ А ОВ=Ч3ВОи ОЕ=1/3АЕ.
У / Для этого, раздѣливъ О А и ОВ пополамъ
У у/У'І /' \ въ точкахъ Р и О, построимъ четыре-
\ угольникъ ОЕОР. Такъ какъ прямая РО А О_С соединяютъ середины двухъ сторонъ
Черт. 183. тр-ка АВО, то (115) РО || АВ и Р0=Ч2АВ.
Прямая ОЕ также соединяетъ середины двухъ сторонъ тр-ка АВС-, поэтому: ОЕ || АВ и ОЕ=1/3АВ. Отсюда выводимъ, что ОЕ || РО и ОЕ = РО-, слѣд., четыреугольникъ ОЕОР есть параллелограммъ (99, 2°), и лотому ОР — ОЕ и 00 = 00. Отсюда слѣдуетъ, что 0Е='І3АЕ и 00=Ч3ВО. Если теперь возьмемъ третью медіану съ одной изъ медіанъ АЕ или ВО, то также убѣдимся, что точка ихъ пересѣченія отсѣкаетъ отъ каждой изъ нихъ 1/3 часть, считая отъ соотвѣтствующей стороны; значитъ, третья медіана должна пересѣчься съ медіанами АЕ и ВО въ одной и той же точкѣ О.
Изъ физики извѣстно, что пересѣченіе медіанъ тр-ка есть его центръ тяжести; онъ всегда лежитъ внутри тр-ка.
УПРАЖНЕНІЯ.
Доказать теоремы:
148. Если двѣ окружности касаются, то всякая сѣкущая, проведенная черезъ точку касанія, отсѣкаетъ отъ окружностей двѣ противолежащія дуги одинаковаго числа градусовъ.
148, а. Отрѣзки двухъ равныхъ хордъ, пересѣкающихся въ одной окружности, соотвѣтственно равны.
148,Ь. Двѣ окружности пересѣкаются въ точкахъ А и В; черезъ А проведена сѣкущая, пересѣкающая окружности въ точкахъ С и О; доказать, что уголъ СВО есть величина постоянная для всякой сѣкущей.
149. Если черезъ точку касанія двухъ окружностей проведемъ двѣ сѣкущія и концы ихъ соединимъ хордами, то эти хорды параллельны.
150. Если черезъ точку касанія двухъ окружностей проведемъ внутри ихъ какую-либо сѣкущую, то касательныя, проведенныя черезъ концы этой сѣкущей, параллельны.
151. Если основанія высотъ тр-ка соединимъ прямыми, то получимъ новый тр-къ, для котораго высоты перваго тр-ка служатъ биссектрис-сами.
151,а. На окружности, описанной около равносторонняго тр-ка
— 141 —
АВС, взята произвольная точка М; доказать, что одна изъ прямыхъ: МА, МВ, МС равна суммѣ остальныхъ двухъ.
152. Если около тр-ка опишемъ окружность и изъ произвольной точки ея опустимъ перпендикуляры на стороны тр-ка, то ихъ основанія лежатъ на одной прямой (прямая Симпсона).
Задачи на построеніе.
153. На данной безконечной прямой найти точку, изъ которой другая данная конечная прямая была бы видна подъ даннымъ угломъ.
154. Построить Л по основанію, углу при вершинѣ и высотѣ.
155. Къ дугѣ даннаго сектора провести такую касательную, чтобы часть ея, заключенная между продолженными радіусами (ограничивающими секторъ), равнялась данной длинѣ (свести эту задачу на предыдущую).
156. Построить Л по основанію, углу при вершинѣ и медіанѣ, проведенной къ основанію.
157. Даны по величинѣ и положенію двѣ конечныя прямыя а и Ь, Найти такую точку, изъ которой прямая а была бы видна подъ даннымъ угломъ а, и прямая Ъ подъ даннымъ угломъ 0.
158. Въ тр-кѣ найти точку, изъ которой его стороны были бы видны подъ равными углами (указаніе: обратить вниманіе на то, что каждый изъ этихъ угловъ долженъ равняться
159. Построить Л по углу при вершинѣ, высотѣ и медіанѣ, проведенной къ основанію (указаніе: продолживъ медіану на равное разстояніе и соединивъ полученную точку съ концами основанія, разсмотрѣть образовавшійся параллелограмъ).
160. Построить Л. въ которомъ даны: основаніе, прилежащій къ нему уголъ и уголъ, составленный медіаною, проведенною изъ вершины даннаго угла, со стороною, къ которой эта медіана проведена.
161. Построить параллелограммъ по двумъ его діагоналямъ и одному углу.
162. Построить Л по основанію, углу при вершинѣ и суммѣ или разности двухъ другихъ сторонъ.
163. Построить четыреугольникъ по двумъ діагоналямъ, двумъ сосѣднимъ сторонамъ и углу, образованному остальными двумя сторонами.
164. Даны три точки А, В и С. Провести черезъ А такую прямую, чтобы разстояніе между перпендикулярами, опущенными на эту прямую изъ точекъ В и С, равнялась данной длинѣ.
165. Въ данный кругъ вписать Л. у котораго два угла даны.
166. Около даннаго круга описать Д, у котораго два угла даны.
167. Построить Л по радіусу описаннаго круга, углу при вершинѣ и высотѣ.
168. Вписать въ данный кругъ Д, у котораго извѣстны: сумма двухъ сторонъ и уголъ, противолежащій одной изъ этихъ сторонъ.
169. Вписать въ данный кругъ четыреугольникъ, котораго сторона и два угла, не прилежащіе къ этой сторонѣ, даны.
170. Въ данный ромбъ вписать кругъ.
— 142 —
171. Въ равностороннійДвписать три круга, которые попарно касаются другъ друга и изъ которыхъ каждый касается двухъ сторонъ тр-ка.
172. Построить четыреугольникъ, который можно было бы вписать въ окружность, по тремъ его сторонамъ и одной діагонали.
173. Построить ромбъ по даннымъ сторонѣ и радіусу вписаннаго круга
174. Около даннаго круга описать равнобедренный прямоугольный^.
175. Построить равнобедренный Д по основанію и радіусу вписаннаго круга.
176. Построить А по основанію и двумъ медіанамъ, исходящимъ изъ концовъ основанія.
177. То же—по тремъ медіанамъ.
178. Дана окружность и на ней три точки А, В и С. Вписать въ эту окружность такой Д, чтобы его биссектриссы, при продолженіи, встрѣчали окружность въ точкахъ А, В и С.
179. Та же задача, съ замѣною биссектриссъ тр-ка его высотами.
180. Дана окружность и на ней три точки М, $ и Р, въ которыхъ пересѣкаются съ окружностью (при продолженіи) высота, биссектрисса и медіана, исходящія изъ одной вершины вписаннаго тр-ка. Построить этотъ А.
181. На окружности даны двѣ точки А и В. Изъ этихъ точекъ провести двѣ параллельныя хорды, которыхъ сумма дана.
Задачи на вычисленіе.
182. Вычислить вписанный уголъ, опирающійся на дугу, равную Чіг части окружности.
183. Кругъ раздѣленъ на два сегмента хордою, дѣлящею окружность на части въ отношеніи 5 : 7. Вычислить углы, которые вмѣщаются этими сегментами.
184. Двѣ хорды пересѣкаются подъ угломъ въ 36°15'32". Вычислить въ градусахъ, минутахъ и секундахъ двѣ дуги, заключенныя между сторонами этого угла и ихъ продолженіями, если одна изъ этихъ дугъ относится къ другой, какъ 3 : 2.
185. Уголъ, составленный двумя касательными, проведенными изъ одной точки къ окружности, равенъ 25°15'. Вычислить дуги, заключенныя между точками касанія.
186. Вычислить уголъ, составленный касательною и хордою, если хорда дѣлитъ окружность на двѣ части, относящіяся, какъ 3 : 7.
187. Двѣ окружности одинаковаго радіуса пересѣкаются подъ угломъ въ 2/3Д; опредѣлить въ градусахъ меньшую изъ дугъ, заключающихся между точками пересѣченія.
Примѣчаніе. Угломъ двухъ пересѣкающихся дугъ наз. уголъ, составленный двумя касательными, проведенными къ этимъ дугамъ изъ точки пересѣченія.
188. Изъ одного конца діаметра проведена касательная, а изъ другого сѣкущая, которая съ касательною составляетъ уголъ въ 20°30'. Какъ велика меньшая изъ дугъ, заключенныхъ между касательною и сѣкущею?
— 143 —
КНИГА III
ПОДОБНЫЯ ФИГУРЫ.
ГЛАВА і
Подобіе треугольниковъ.
191. Сходственныя стороны. Въ этой главѣ намъ придется разсматривать такіе тр-ки или мн-ки, у которыхъ углы одного соотвѣтственно равны угламъ другого Условимся въ такихъ случаяхъ называть «сходственными» тѣ стороны этихъ тр-ковъ или мн-ковъ, которыя прилежатъ къ равнымъ угламъ (въ тр-кахъ такія стороны и противолежатъ равнымъ угламъ)
196. Лемма. Прямая (ВН, черт. 184), проведенная внутри треугольника (АВС) параллельно его сторонѣ (АС), отсѣкаетъ отъ него другой треугольникъ (БВЕ), у котораго: 1°, углы равны соотвѣтственно угламъ перваго треугольника и 2°, стороны пропорціональны сходственнымъ сторонамъ этого тре
угольника.
1° Углы тр-ковъ соотвѣтственно равны, такъ какъ уголъ В
у нихъ общій, а Б—А и Е=С, при параллельныхъ БЕ и АС и сѣкущихъ АВ и СВ.
2° Докажемъ теперь, что стороны тр-ка ЕВЕ пропорціональны сходственнымъ сторонамъ тр-ка АВС, т -е что
ВБ _ ВЕ_ БЕ ~АВ~~ВС~~~АС
какъ углы соотвѣтственные
Черт. 184.
Для этого разсмотримъ отдѣльно слѣдующіе два случая.
1°. Стороны АВ и БВ имѣютъ общую мѣру. Раздѣлимъ АВ на части, равныя этой общей мѣрѣ. Тогда ВБ
— 144 —
раздѣлится на цѣлое число такихъ частей. Пусть этихъ частей содержится т въ ВЛ и п въ АВ. Проведемъ изъ точекъ раздѣла рядъ прямыхъ, параллельныхъ АС, и другой рядъ прямыхъ, параллельныхъ ВС. Тогда ВЕ и ВС раздѣлятся на равныя части (113), которыхъ будетъ т въ ВЕ и п въ ВС. Точно такъ же БЕ раздѣлится на т равныхъ частей, а АС на п равныхъ частей, при чемъ части БЕ равны частямъ АС (какъ противоположныя стороны параллелограммовъ!Теперь очевидно, что
Слѣд.,
ВБ т ВЕ т БЕ т АВ п ’ ВС п ’ АС п
ВБ^ВЕБЕ АВ~ВС~^АС
2°. Стороны АВ и ВБ не имѣютъ общей мѣры (черт. 185).
Тогда стороны ВС и ВЕ, а также и стороны АС и БЕ, также не имѣютъ общей мѣры. Дѣйствительно, если допустимъ, что
Черт. 185.
дутъ имѣть общую мѣру,
стороны ВС и ВЕ (или АС и БЕ) имѣютъ какую-нибудь общую мѣру, то, раздѣливъ ВС (или АС) на части, равныя этой общей мѣрѣ, и проведя черезъ точки раздѣла рядъ параллельныхъ прямыхъ, какъ это мы дѣлали въ случаѣ 1-мъ, мы этими прямыми раздѣлимъ стороны АВ и ВБ также на равныя части; слѣд., тогда эти прямыя бу-что противорѣчитъ предположенію.
Значитъ, если стороны АВ и ВБ несоизмѣримы, то каждое изъ
трехъ отношеній:
ВБ ВЕ БЕ
ВА' ВС И АС
будетъ несоизмѣримое.
Найдемъ приближенное значеніе каждаго изъ нихъ съ точностью до х/н. Для этого раздѣлимъ АВ на п равныхъ частей и черезъ точки раздѣла проведемъ рядъ прямыхъ, параллель
— 146 —
ныхъ АС, и другой рядъ прямыхъ, параллельныхъ ВС. Тогда каждая изъ сторонъ ВС и АС раздѣлится также на п равныхъ частей (113). Предположимъ, что 1/п доля АВ содержится въ ВВ болѣе т разъ, но менѣе т+1 разъ; тогда, какъ видно изъ чертежа, гІ„ доля ВС содержится въ ВЕ также болѣе т, но менѣе т+1 разъ, и 1/п доля АС содержится въ ВЕ болѣе т, но менѣе т+1 разъ. Слѣд.:
ВР т ВЕ т ВЕ т
прибл. отн. — = —; прибл, отн. ~^.= —; прибл. отн. —7;= —•
* ВА п ВС п АС п
Отсюда слѣдуетъ, что приближенныя отношенія, вычисленныя съ произвольною, но одинаковою точностью, всегда равны другъ другу; а такія несоизмѣримыя отношенія мы условились считать равными (159); слѣд , и въ этомъ случаѣ можемъ написать:
ВР ВЕ ВЕ ВА~ВС~АС
197. Замѣчаніе. Доказанный рядъ равныхъ отношеній представляетъ собою три слѣдующія пропорціи:
ВЛ_ВВ ВВ_ВЕ, ВЕ_ВЕ ВА~~ ВС' ВА~ АС’ ВС~ Ад'
Примѣняя къ этимъ пропорціямъ свойства числовыхъ пропорцій, мы можемъ переставить въ нихъ средніе члены:
ВВ_ВА. ВВ_ВА. ВЕ_ВС ВЁ~ ВС' ВЁ~АС' ВЁ~ АС
Мы видимъ такимъ образомъ, что если въ треугольникахъ стороны пропорціональны, то отношеніе любыхъ двухъ сторонъ одного треугольника равно отношенію сходственныхъ сторонъ другоготреугольника.
198. Опредѣленіе. Два треугольника наз. подобными, если углы одного соотвѣтственно равны угламъ другого и стороны одного пропорціональны сходственнымъ сторонамъ другого.
А. Киселевъ. Геометрія. 10
— 146 —
Что такіе тр-ки возможны, показываетъ лемма предыдущаго параграфа, которую теперь можно высказать такъ: прямая, проведенная внутри треугольника параллельно какой-нибудь его сторонѣ, отсѣкаетъ отъ него подобный треугольникъ.
1ѲѲ. Теоремы (выражающія три признака подобія треугольниковъ). Два треугольника подобны:
1°, если два угла одного соотвѣтственно равны двумъ угламъ другого;
или 2°, если двѣ стороны одного пропорціональны двумъ сторонамъ другого, и углы, лежащіе между этими сторонами, равны;
пли 8°, если три стороны одного пропорціональны тремъ сторонамъ другого.
1°. Пусть АВС и А^Сі (черт. 186) будутъ два тр-ка, у которыхъ:
А=Аі, В=Ві и, слѣд., С=СѴ
Требуется доказать, что такіе тр-ки подобны.—Отложимъ на АВ часть ВВ, равную Л1В1 и проведемъ ВЕ II АС.
Тогда получимъ вспомогательный тр-къ ВВЕ который, со-
В
Черт. 186.
гласно предыдущей леммѣ, подобенъ тр-ку АВС. Съ другой стороны /\ВВЕ= /\АіВіСу. потому что у нихъ: ВВ=А1В1 (по построенію), В—Ві (по условію) и В=Аг (потому что
В=А и А=А1). Но если изъ двухъ равныхъ тр-ковъ одинъ подобенъ третьему, то и другой ему подобенъ; слѣд., Л Л1В1С1 подобенъ Д АВС.
2°. Пусть въ тр-кахъ АВС и А^^ дано (черт. 187):
В—Ві и
АВ ВС
%ВГВ&
[1]
— 147 —
Требуется доказать, снова часть ВВ, равную Лі#!, и проведемъ ВЕ—АС. Тогда получимъ вспомогательный Л ВВЕ, подобный Д АВС. Докажемъ, что онъ равенъ Д^ВА. Изъ подобія тр-ковъ АВС и ВВЕ слѣдуетъ:
что такіе тр-ки подобны.—Отложимъ
В
Черт. 187.
ЛВ _ ВС_АС ВВ~~ВЕ~ВЁ
Г2]
Сравнивая этотъ рядъ равныхъ отношеній съ даннымъ рядомъ [1], замѣчаемъ, что первыя отношенія обоихъ рядовъ одинаковы (ВВ—АіВі по построенію); слѣдовательно, остальныя отношенія этихъ рядовъ также равны, т.-е.
ВС _ ВС
В&~ВЁ'
Но если въ пропорціи предыдущіе члены равны, то должны быть равны и послѣдующіе члены; значитъ:
В^^ВЕ.
Теперь видимъ, что тр-ки ВВЕ и ЛХВА имѣютъ по равному углу (В—Ві), заключенному между равными сторонами; значитъ, эти тр-ки равны. Но Л ВВЕ подобенъ Л АВС\ поэтому и д И1В1С'1 подобенъ Д АВС.
3. Пусть въ тр-кахъ АВС и А^Сі (черт. 188) дано:
АВ _ ВС _ АС Г11
ЛВІ- ВА ~А1С1 1 1
Требуется доказать, что такіе тр-ки подобны.—Сдѣлавъ построеніе такое же, какъ и прежде, покажемъ, что &ВВЕ— =ДИ1В1С1. Изъ подобія тр-ковъ АВС и ВВЕ слѣдуетъ:
АВ_ВС_АС г . ВВ~~ВЁ~ВЁ Сравнивая этотъ рядъ съ даннымъ ря-
в
ю*
— 148 —
домъ [1], замѣчаемъ, что первыя отношенія у нихъ равны; слѣд., и остальныя отношенія равны, и потому
БС ВС „„
----=—; откуда; ВХСХ=ВЕ;
ВХСХ ВЕ
АС АС . „
и ------—; откуда: ЛХСХ=ВЕ.
ЛСі ВЕ
Теперь видимъ, что тр-ки ВВЕ и ЛХВХСХ имѣютъ по три соотвѣтственно равныхъ стороны; значитъ, они равны. Но одинъ изъ нихъ, именно ВВЕ, подобенъ Л АВС-, слѣд., и другой, т.-е. АіВуСі, подобенъ Л АВС.
200. Замѣчаніе о пріемѣ доказательства. Полезно обратить вниманіе на то, что пріемъ доказательства, употребленный нами въ трехъ предыдущихъ теоремахъ, одинъ и тотъ же, а именно: отложивъ на сторонѣ бблыпаго треугольника часть, равную сходственной сторонѣ меньшаго, и проведя прямую, параллельную другой сторонѣ, мы образуемъ вспомогательный тр-къ, подобный ббльшему данному. Послѣ этого, беря во вниманіе условія доказываемой теоремы и свойства подобныхъ тр-ковъ, мы обнаруживаемъ равенство вспомогательнаго тр-ка меньшему данному и, наконецъ, заключаемъ о подобіи данныхъ тр-ковъ.
201. Теоремы (выражающія еще 2 признака подобія треугольниковъ). Два треугольника подобны:
1°, если стороны одного соотвѣтственно параллельны сторонамъ другого;
или 2°, если стороны одного соотвѣтственно перпендикулярны къ сторонамъ другого.
Будемъ вести разсужденіе независимо отъ чертежа, при чемъ это разсужденіе отнесемъ одновременно къ обѣимъ теоремамъ.
Пусть стороны угловъ А, В, С нѣкотораго треугольника соотвѣтственно параллельны или перпендикулярны сторонамъ угловъ Аг, Ві, Сх другого треугольника. Тогда углы А и Лх или равны другъ другу, или составляютъ въ суммѣ два прямыхъ (85 и 86); то же самое можно сказать объ углахъ В и Вх, С и Сх. Чтобы доказать подобіе данныхъ тр-ковъ, достаточно убѣдиться, что какіе-нибудь два угла одного изъ нихъ равны со
— 149 —
отвѣтственно двумъ угламъ другого. Предположимъ, что этого нѣтъ. Тогда могутъ представиться слѣдующіе два случая:
1°. У треугольниковъ нѣтъ вовсе попарно равныхъ угловъ.
Тогда: Л+Лх=2й; В+Вх=2й; С+Сх=2й,
и, слѣд., сумма угловъ обоихъ треугольниковъ равна 6й. Такъ какъ это невозможно, то этотъ случай исключается.
2°. У треугольниковъ только одна пара равныхъ угловъ; напр., пусть Л=Л1. Тогда:
В+Вх=2гі; С+Сх=2й и, слѣд., В+Вх+С+Сх=4й,
и потому сумма всѣхъ угловъ обоихъ тр-ковъ больше 4й. Такъ какъ это невозможно, то и этотъ случай исключается.
Остается одно возможное допущеніе, что тр-ки имѣютъ двѣ пары равныхъ угловъ; но тогда онп подобны.
202. Теоремы (выражающія признаки подобія прямоугольныхъ треугольниковъ). Такъ какъ прямые углы всегда равны другъ другу, то на основаніи доказанныхъ признаковъ подобія треугольниковъ вообще мы можемъ утверждать, что
прямоугольные тр-ки подобны:
1°, если острый уголъ одного треугольника равенъ острому углу другого треугольника,
или 2°, если катеты одного треугольника пропорціональны катетамъ другого.
Укажемъ еще слѣдующій признакъ подобія прямоугольныхъ тр-ковъ, требующій особаго доказательства.
Теорема. Прямоугольные треугольники подобны, если гипотенуза и катетъ одного пропорціональны гипотенузѣ и катету другого.
Пусть АВС и А^С^ два тр-ка (черт. 189), у которыхъ углы В и Ві прямые и
ЛВ АС _
— 150 —
Требуется доказать, что такіе тр-ки подобны.—Для доказательства употребимъ тотъ же пріемъ, которымъ мы пользовались ранѣе (200). Отложимъ ВВ=А1В1 и проведемъ ВЕ || АС.
Тогда получимъ
АВ_АС ВВ~ВЁ
вспомогательный Л ВВЕ, подобный Л АВС (196). Докажемъ, что онъ равенъ Л АхВіСі. Изъ подобія трковъ АВС и ВВЕ слѣдуетъ:
[2]
Сравнивая эту пропорцію съ данной [1], находимъ, что первыя отношенія ихъ одинаковы; слѣд., равны и вторыя отно-
шенія, т.-е.
АС АС
вёГаы откуда:
ВЕ=А1С1.
если тр-ки
и
Черт. 190.
Теперь видимъ, что тр-ки ВВЕ и А^В^ имѣютъ по равной гипотенузѣ и равному катету; слѣд., они равны; а такъ какъ одинъ изъ нихъ подобенъ л АВС, то и другой ему подобенъ.
203. Теорема (выражающая свойство подобныхъ треугольниковъ). Въ подобныхъ треугольникахъ сходственныя стороны пропорціональны сходственнымъ высотамъ, т.-е. тѣмъ, которыя опущены на сходственныя стороны.
іВ^Сі (черт. 190) подобны, то прямоугольные тр-ки ВАВ и ВіАіВі также подобны (Л=ЛХ и В=В1)\ поэтому:
ВВ _ АВ _ ВгВі АгВг
ВС _ АС ~~в^сГа^с1'
— 151 —
Замѣчаніе. Можно также доказать, что въ подобныхъ тр-кахъ сходственныя стороны пропорціональны сходственнымъ медіанамъ, сходственнымъ бис-сектриссамъ, радіусамъ круговъ вписанныхъ и радіусамъ круговъ описанныхъ.
204. Задача. На данной сторонѣ (А^, черт. 191) построить тре- Р
угольникъ, подоб- /\ \ /
ный данному (АВС). / \ Ѵр
На данной сторонѣ стро- / \
имъ тр-къ, у котораго уголъ -У- -V- •-/ V-
А равенъ А и уголъ Сх /Д X /А
равенъ С. Этотъ тр-къ А С А, С«
подобенъ данному (199,1°). Черт. 191,
ГЛАВА II.
Подобіе многоугольниковъ.
205. Лемма. Если, разбивъ многоугольникъ АВСБЕ... (черт. 192) на треугольники М, Е,Р,..., мы построимъ на какой-нибудь конечной прямой А^Вг д Мг подобный д И, затѣмъ на сторонѣ его А^ построимъ ДЛ\, подобный д 27, далѣе па сторонѣ АхІ^ построимъ дРх, подобный д Р, и т. д., наблю
дая при этомъ, чтобы подобные треуголь-
ники были одинаково расположены, то мы
получимъ такой многоугольникъАіВіС^Е!...
у котораго: 1°, углы соотвѣтственно равны угламъ многоугольника
АВСЕЕ... и 2°, ст о р о-ны пропорціональны сходственнымъ сторонамъ этого
О
многоугольника. Черт. 192.
1°. Равенство угловъ мн-ковъ слѣдуетъ изъ равенства угловъ тр-ковъ; такъ, В=Ві и Е=Ег, какъ равные углы подобныхъ
— 152 —
тр-ковъ (М и Мг, Р и Рі), А=Аі, С=СЪ В=В1..., какъ суммы угловъ, соотвѣтственно равныхъ другъ другу.
2°. Пропорціональность сторонъ мн-ковъ слѣдуетъ изъ пропорціональности сторонъ подобныхъ тр-ковъ. Дѣйствительно, мы можемъ написать слѣдующіе ряды равныхъ отношеній:
АВ ВС АС
Изъ подобія М и Мг.. "А.В. ва АіСі
АС СВ АВ
Изъ подобія 27 и "А^ с^ АгВг'
АВ ВЕ ЕА
Изъ подобія Р и Рх... "‘А.В. ВіЕі
Разсматривая эти отношенія, замѣчаемъ, что послѣднее отношеніе 1-го ряда есть вмѣстѣ съ тѣмъ первое отношеніе 2-го ряда, а послѣднее отношеніе 2-го ряда есть вмѣстѣ съ тѣмъ первое отношеніе 3-го ряда; отсюда заключаемъ, что всѣ отношенія этихъ трехъ рядовъ равны между собою. Возьмемъ изъ нихъ только тѣ, въ которыя входятъ стороны данныхъ многоугольниковъ; тогда и получимъ пропорціональность сторонъ:
АВ _ ВС СВ _ ВЕ _ ЕА А^ВГ~ В^Г С&" В^Ёі~ Ё\АІ
Замѣчаніе. Изъ пропорціональности сторонъ двухъ мн-ковъ совершенно такъ же, какъ это было сдѣлано нами раньше для тр-ковъ (197) , можно вывести, что если въ мн-кахъ стороны пропорціональны, то отношеніе любыхъ двухъсторонъ одного мн-ка равно отношенію сходственныхъ сторонъ другого мн-ка.
206. Опредѣленіе. Два одноименныхъ*) многоугольника наз. подобными, если углы одного равны соотвѣтственно угламъ другого и стороны одного пропорціональны сходственнымъ сторонамъ другого.
Что такіе многоугольники возможны, показываетъ лемма предыдущаго параграфа, которую можно теперь высказать такъ: два многоугольника подобны, если они состоятъ изъ оди-
♦) Напр., два пятиугольника, два шестиугольника и т. д., вообще два многоугольника, имѣющіе одинаковое число угловъ.
— 153 —
лаковаго числа подобныхъ и одинаково расположенныхъ треугольниковъ.
207. Замѣчаніе. Для тр-ковъ, какъ мы видѣли (199), равенство угловъ влечетъ за собою пропорціональность сторонъ и, обратно, пропорціональность сторонъ влечетъ за собою равенство угловъ; вслѣдствіе этого для тр-ковъ одно равенство угловъ или одна пропорціональность сторонъ служитъ достаточнымъ признакомъ ихъ подобія. Для мн-ковъ же одного равенства угловъ или одной пропорціональности сторонъ еще не достаточно для ихъ подобія; напр., у квадрата и прямоугольника углы равны, но стороны не пропорціональны, у квадрата же и ромба стороны пропорціональны, а углы не равны.
Слѣдующія 2 теоремы выражаютъ главнѣйшія свойства подобныхъ многоугольниковъ.
208. Теорема. Подобные многоугольники (АВСВЕ и А^С^Е^ черт. 193) можно разложить на одинаковое число подобныхъ и одинаково расположенныхъ треугольниковъ.
Подобные многоугольники можно разложить на подобные
тр-ки различными способами. Укажемъ одинъ изъ нихъ.—
Возьмемъ внутри мн-ка АВСВЕ произвольную точку О и соединимъ ее со всѣми вершинами. Тогда мн-къ АВСВЕ разобьется на столько треугольниковъ,
С
Черс. 103.
сколько въ немъ сто
ронъ. Возьмемъ одинъ изъ нихъ, напр., АОЕ, (покрытый на
чертежѣ штрихами), и на сходственной сторонѣ АГЕГ другого многоугольника построимъ углы О^Еі и О^А^ соотвѣтственно угламъ ОАЕ и ОЕА-, точку пересѣченія соединимъ съ прочими вершинами мн-ка Л1В1С'1В1Е1. Тогда и этотъ мн-къ разобьется на то же число тр-ковъ. Докажемъ, что тр-ки перваго
многоугольника соотвѣтственно подобны тр-камъ второго многоугольника. &АОЕ подобенъ по построенію. Чтобы
154 —
доказать подобіе сосѣднихъ тр-ковъ АВО и ИрВ/?!, примемъ во вниманіе, что изъ подобія мн-ковъ, между прочимъ слѣдуетъ:
ВА АЕ
А=А1 И В^А~А^Ёі
и изъ подобія тр-ковъ АОЕ и А^^ выводимъ:
„ , АО АЕ
/.ОАЕ^^О^Ег п -- [2]
Изъ равенствъ [1] и [2] слѣдуетъ:
, , ВА АО
Л.ВАО=^.В1А1О1 и
Теперь видимъ, что тр-ки АВО п А1В1О1 имѣютъ по равному углу, заключенному между пропорціональными сторонами; значитъ, они подобны.
Совершенно такъ же докажемъ подобіе слѣдующихъ тр-ковъ ВСО и ВуСіОі, затѣмъ тр-ковъ СОВ и С^^ и т. п. При этомъ очевидно, что подобные тр-ки въ обоихъ мн-кахъ одинаково расположены.
Замѣчаніе. Точку О (черт. 193) мы можемъ взять и на какой-нибудь сторонѣ мн-ка, и въ вершинѣ любого угла его и даже внѣ мн-ка (въ послѣднемъ случаѣ получатся тр-ки, частью выступающіе за контуръ мн-ка).
2ОѲ. Теорема. Периметры подобныхъ многоугольниковъ относятся, какъ сходственныя стороны.
Пусть мн-ки АВС БЕ и А^С^Еі (черт. 193) подобны; тогда по опредѣленію:
АВ ВС СБ ВЕ ЕА
~А^В1~ В^Г С^Г В^Ёі~ ЁДі
Изъ алгебры извѣстно, что если имѣемъ рядъ равныхъ отношеній, то сумма всѣхъ предыдущихъ членовъ относится къ суммѣ всѣхъ послѣдующихъ, какъ какой-нибудь изъ предыдущихъ членовъ относится къ своему послѣдующему; поэтому:
АВ+ВС+СВ+ВЕ+ЕА АВ ВС АіВіА~ВіСіА~СіВі~{~ВіЕі-]~ЕіАі а^в^ В^Сі
— 156 —
Примѣръ. Если сторона одного многоугольника болѣе сходственной стороны другого многоугольника, подобнаго ему, въ 2 раза, 3 раза, 4 раза и т. д., то и периметръ перваго многоугольника болѣе периметра второго въ 2 раза, 3 раза, 4 раза и т. д.
210. Задача. На данной сторонѣ А& (черт. 192) построить многоугольникъ,подобный данному многоугольнику АВСЕЕ.
Разбивъ данный многоугольникъ на тр-ки М, Е, Р, строятъ, согласно леммѣ § 205, на данной сторонѣ А^ тр-къ подобный тр-ку М, затѣмъ на сторонѣ А^Сі—тр-къ Еъ подобный тр-ку Е, п т. д., наблюдая прп этомъ, чтобы тр-ки были одинаково расположены въ обѣихъ фигурахъ. Полученный такимъ образомъ мн-къ Вг Сі Еі подобенъ данному.
ГЛАВА III.
Фигуры, подобно расположенныя.
211. Опредѣленіе. Пусть намъ дано: какая-нибудь фигура Р (черт. 194), точка 8, которую мы назовемъ центромъ подобія, и отвлеченное число к, которое мы назовемъ отношеніемъ подобія. Возьмемъ въ фигурѣ Р произвольную точку А и черезъ нее изъ центра подобія $ проведемъ полупрямую 8 А. Найдемъ на этой полупрямой такую точку Аи чтобы отношеніе 8Аі : 8 А было равно д числу к (если к< 1, то точка Д п
расположится между 5 и А, V \
какъ у насъ на чертежѣ, ЕЧV.
если же к> 1, то точка бу-детъ лежать за точкой А). Возьмемъ какую-нибудь дру- I
гую точку В фигуры Р и сдѣ- Черт. 194.
лаемъ для нея то же построеніе, какое мы указали для т.-ѳ. черезъ В проведемъ изъ 5 полупрямую и на ней найдемъ такую точку Ви чтобы отношеніе 8Вг : 8В равнялось тому же числу к. Вообразимъ теперь, что, не измѣняя положенія точки 5 и величины числа к, мы для каждой точки фигуры Р находимъ указаннымъ путемъ соотвѣтствующую точку; тогда геометрическое мѣсто всѣхъ этихъ точекъ составитъ нѣкоторую новую фигуру Р±. Фигура Ри полученная такимъ образомъ, наз. фигурой, подобно расположенной съ фигурой Р относительно центра подобія 5 при данномъ отношеніи подобія к.
— 166 -
Полупрямыя 8Аи 8В!..., проводимыя изъ центра подобія черезъ различныя точки фигуры В, наз. лучами подобія; точки Л и А1г В и Вх и т. д. наз. сходственными точками фигуръ В и Вх-
Изъ сказаннаго слѣдуетъ, что если Вг есть фигура, подобно расположенная съ фигурой В относительно центра подобія В при отношеніи подобія к, то, обратно, В есть фигура, подобно расположённая съ фигурой Вг относительно того же центра подобія 8, но при отношеніи подобія равномъ не к, а обратному числу */к-
Подобно расположенную фигуру можно получить еще иначе. Вмѣсто того, чтобы точки Аг, В^.. сходственныя съ точками А, В... фигуры В, находить на лучахъ подобія (т.-е. по ту же сторону отъ центра подобія В, по которую отъ него расположены точки А, В...), можно брать ихъ на продолженіяхъ лучей подобія, по другую сторону отъ В. Тогда мы получимъ фигуру Рхх (черт. 194), которая тоже подобно расположена съ фигурой В относительно центра подобія В при томъ же отношеніи подобія к. Для отличія первое изъ указанныхъ нами подобій въ расположеніи наз. прямымъ, а второе—обратнымъ *).
212. Замѣчаніе. Фигуры Вг и Віг (черт. 194) равны между собою. Дѣйствительно, изъ равенствъ:
ВА1Х : ВА = к и ВАХ : 8А=к слѣдуетъ: ВАХХ = ВАХ; подобно этому ВВХХ = ВВХ и т. д. Поэтому, если секторъ 8АВ..., содержащій фигуру В, повернемъ въ плоскости вокругъ точки В на 180°, то точка Ах совмѣстится съ Ахх, точка Вх совмѣстится съ Вхх... и т. д.; значитъ, фигура Вх совмѣстится съ фигурой. Вц.
213. Теорема. Фигура, подобно расположенная съ отрѣзкомъ прямой (АВ. черт. 195), есть также отрѣзокъ прямой (АХВХ или 41ХВ1Х); этотъ отрѣзокъ параллеленъ первому и имѣ тъ съ нимъ одинаковое направленіе при прямомъ подобіи и противоположное при обратномъ; отношеніе этого отрѣзка къ первому равно отношенію подобія.
Будемъ говорить сначала только о прямомъ подобіи.
Найдемъ точки Ах и Вх, сходственныя съ концами А и В даннаго отрѣзка; эти точки должны лежать на лучахъ 8А и ВВ и удовлетворять равенствамъ <іѳ подобія. Соединивъ
♦) Подобіе въ расположеніи (прямое и обратное) наз. въ нѣкоторыхъ нашихъ руководствахъ (по образцу французскихъ) словомъ «г о м о т е-т і я», и фигуры, подобно расположенныя, наз. тогда «гомотетичными». Мы избѣгаемъ этихъ неблагозвучныхъ иностранныхъ названій.
— 167 —
Лх съ Вх прямой, докажемъ, что А^ || АВ и что ЛХВХ : АВ=к. Тр-ки ВЛХВХ и 8АВ Подобны, такъ какъ они имѣютъ по равному углу (при общей вершинѣ В), заключенному между пропорціональными сторонами. Изъ ихъ подобія слѣдуетъ, во 1, равенство угловъ и, слѣд., параллельность сторонъ ЛХВХ и ЛВ; во 2, пропорціональность сторонъ: ЛХВХ : ЛВ=ВЛХ : ВЛ=к.
Теперь докажемъ, что полученный нами отрѣзокъ ЛХВХ есть фигура, подобно расположенная съ отрѣзкомъ ЛВ. Для этого возьмемъ какую-нибудь точку М на ЛВ и проведемъ лучъ 8М; пусть Мг будетъ точка, въ которой этотъ лучъ пересѣкается съ ЛХВХ. Тр-ки ВЛХ2ИХ и 8АМ подобны, такъ какъ углы одного равны соотвѣтственно угламъ другого (вслѣдствіе параллельности сторонъ ЛХВХ и ЛВ). Изъ ихъ подобія слѣдуетъ: ВЛ/Х : 8М =ВЛх:ВЛ = к; значитъ, точка Л/х есть точка, сходственная съ М. Такимъ образомъ, какую бы точку М на ЛВ мы ни взяли, сходственная ей точка Л/х лежитъ на ЛХВХ. Вообразимъ теперь, что точка М перемѣщается по ЛВ отъ Л къ В; тогда сходственная ей точка будетъ перемѣщаться отъ Лх къ Вх, оставаясь постоянно на отрѣзкѣ ЛХВХ. Значитъ, этотъ отрѣзокъ и будетъ фигурой, подобно расположенной съ ЛВ.
То же самое можно повторить и для обратнаго подобія. При этомъ изъ чертежа непосредственно усматриваемъ, что направленіе отрѣзка ЛХВХ, получающагося при прямомъ подобіи, одинаково съ направленіемъ ЛВ, а направленіе отрѣзка Л1ХВХХ, получающагося при обратномъ подобіи, противоположно направленію ЛВ.
214. Теорема. Фигура подобно расположенная съ многоугольникомъ (ЛВСВ, черт. 196) есть также многоугольникъ (Л1ВХСХРХ или ЛцВцСцВц); этотъ многоугольникъ подобенъ первому, при чемъ отношеніе сторонъ его къ сходственнымъ сторонамъ перваго многоугольника равно отношенію подобія.
Согласно доказанному выше (213), фигура, подобно расположенная съ мн-комъ АВСВ, должна быть образована такими отрѣзками пря-
Черт. 196.
мыхъ, которые параллельны сторонамъ даннаго мн-ка и находятся къ нимъ въ отношеніи, равномъ отношенію подобія; слѣд., фигура ЛХВХСХВХ (и ЛХХВ1ХС1ХВХХ) есть мн-къ, у котораго стороны пропорціональны сторонамъ даннаго мн-ка. Съ другой стороны, такъ какъ отрѣзки ЛХВХ, ВХСХ... имѣютъ одинаковое направленіе съ отрѣз
— 158 —
ками АВ, ВС,..., а отрѣзки АиВх1, ВцС^,.... имѣютъ противоположное направленіе съ отрѣзками АВ, ВС,..., то (85) углы мн-ковъ А1В1С1В1 и АцВцСцВц равны соотвѣтственно угламъ мн-ка АВСВ-, значитъ, эти мн-ки подобны.
215. Замѣчаніе. Мы видимъ такимъ образомъ, что прямолинейныя фигуры, подобно расположенныя, оказываются вмѣстѣ съ тѣмъ и подобными (206). Поэтому фигуры эти наз. фигурами подобными и подобно расположенными.
216. Теорема. Фигура, подобно расположенная съ окружностью (центра О, черт. 197) есть также окружность; центръ (Ог или Ои) этой окружности лежитъ въ точкѣ, сходственной съ центромъ первой окружности; отношеніе радіуса этой окружности къ радіусу первой равно отношенію подобія.
Пусть В есть центръ подобія и к отношеніе подобія (на нашемъ чертежѣ мы взяли й=1/2)- Возьмемъ въ данной окружности вольный ОА и отрѣзокъ
добно расположенный съотрѣзкомъОЛ. По доказанному раньше (213) ОхЛх|[ О А иО^: ОА — к, т.-е. О1Л1 = ОЛ.й = Вк, ели буквою В обозначимъ радіусъ даннаго круга. Изъ послѣдняго равенства видно, что длина ОхЛх не измѣняется при измѣненіи положенія радіуса О А. Поэтому если станемъ вращать этотъ радіусъ вокругъ центра О, то подобно расположенный отрѣзокъ Ох^х будетъ вращаться вокругъ точки Ои при чемъ длина его не будетъ измѣняться; значитъ, точка А1 опишетъ при этомъ окружность, которой центръ есть и радіусъ Вх» Удовлетворяющій равенству: В1 = О1А1 = ОА.к = Вк. Такъ же докажемъ, что теорема остается вѣрной и при обратномъ подобіи (получается окружность центра Ои съ радіусомъ ОххЛи).
217. Теорема. Всякія двѣ окружности можно разсматривать, какъ подобно расположенныя относительно нѣкоторыхъ центровъ подобія.
произ-радіусъ построимъ Ох-^х, по-
Пусть (черт. 198) О и Ог будутъ центры двухъ окружностей и К и В, ихъ радіусы. Возьмемъ какіе-нибудь радіусы ОА и парал-
— 159 —
лельныѳ между собою, и черезъ концы ихъ А и 4Х проведемъ неограниченную прямую. Пусть точка пересѣченія этой прямой съ линіей центровъ будетъ Докажемъ, что эту точку можно разсматривать какъ центръ прямого подобія данныхъ окруя нютей. Изъ построенія видно, что
801_01Ах_ Кх 80 ОА~ В
Поэтому, если, взявъ за центръ прямого подобія точку 8 и за отношеніе подобія число к=В1 : Я, мы построимъ фигуру, подобно расположенную съ окружностью О, то, согласно предыдущей теоремѣ, эта фигура и будетъ окружность 0х. Значитъ, двѣ данныя окружности суть фигуры, подобно расположенныя относительно центра прямого подобія Я.
Такъ же убѣдимся, что если возьмемъ параллельные радіусы О А и 0х4п, которыхъ направленія противоположны, и черезъ концы ихъ А и 4ХХ проведемъ прямую, то эта прямая пересѣчетъ линію центровъ въ точкѣ 5Х, которую можно принять за центръ обратнаго подобія данныхъ окружностей.
Если радіусы В и Ях данныхъ окружностей будутъ равны, то прямая ААХ не пересѣчетъ линіи центровъ; въ этомъ случаѣ не существуетъ прямого подобія, а есть только обратное.
218. Замѣчаніе. Вообразимъ, что лучъ подобія 54 (черт. 198) все болѣе и болѣе отклоняется отъ линіи центровъ. Тогда точки А и В, въ которыхъ этотъ лучъ пересѣкается съ окружностью О, будутъ все болѣе и болѣе сближаться между собою; при этомъ и сходственныя имъ точки Аі и Вх будутъ также сближаться между собою, и въ тотъ моментъ, когда точки А и В сольются въ одну точку М, точки Ах и Вх также сольются въ одну точку М1г и тогда лучъ подобія сдѣлается общею внѣшнею касательною къ даннымъ окружностямъ. Такимь образомъ, общая внѣшняя касательная къ 2-мъ окружностямъ (если она существуетъ) проходитъ черезъ центръ 5 ихъ прямого подобія. Такъ же можно разъяснить, что общая внутренняя касательная къ 2-мъ окружностямъ (если опа существуетъ) проходитъ черезъ центръ 5Х ихъ обратнаго подобія. Добавленіе: «если она существуетъ» мы должны сдѣлать потому, что центры подобія 2-хъ окружностей существуютъ всегда (по крайней мѣрѣ обратнаго подобія), тогда какъ общія касательныя существуютъ не всегда (см. замѣчаніе къ задачѣ § 142).
Указанное свойство общихъ касательныхъ даетъ простой способъ ихъ построенія. Найдя центры 8 и 8г прямого и обратнаго подобія двухъ окружностей (посредствомъ проведенія параллельныхъ радіусовъ ОА, 0хАх и 0хАп, черт. 198), черезъ каждый изъ нихъ проводятъ касательныя къ одной изъ двухъ окружностей; эти касательныя должны касаться и другой окружности.
— 160 —
ГЛАВА IV.
Пусть стороны угла АВС
Черт. 199.
(или: ВВ : ВЕ=ВВХ : В1Е1;
Проводя вспомогательныя
Нѣкоторыя теоремы о пропорціональныхъ линіяхъ.
219. Теорема. Стороны угла, пересѣкаемыя рядомъ параллельныхъ прямыхъ, разсѣкаются ими на пропорціональныя части.
(черт. 199) разсѣкаются рядомъ параллельныхъ прямыхъ: В-Оі, ЕЕг, ЕЕ!... на части:
ВВ, ВЕ, ЕЕ...(сторонаВС);
ВВі, В^Е^ЕЕ!..(сторонаВЛ).
Требуется доказать, что части одной стороны пропорціональны соотвѣтствующимъ частямъ -Ддругой стороны, т.-е. что:
ВВ ВЕ ЕЕ
ВВі ВіЕі ЕіЕі
ВЕ : ЕЕ=В1Е1 : Е^; и т. д.) прямыя ВМ, ЕЕ..., параллель
ныя ВА, мы получимъ тр-ки ВВВЬ ВЕМ, ЕЕЕ..., которые всѣ подобны между собою, такъ какъ углы у нихъ соотвѣтственно равны (вслѣдствіе параллельности прямыхъ). Изъ ихъ подобія слѣдуетъ (197, замѣчаніе):
ВВ _ВЕ_ЕЕ_ ВВГ ВМ~~ЁЕ
Замѣнивъ въ этомъ ряду равныхъ отношеній отрѣзокъ ВМ на В^, отрѣзокъ ЕЕ на ЕіЕ^... (противоположныя стороны параллелограммовъ равны), мы получимъ то, что требовалось доказать.
220. Слѣдствіе. Двѣ прямыя (АВ и А^, черт. 200), пересѣкаемыя рядомъ параллельныхъ прямыхъ (ССЬ ВВі, ЕЕі...), разсѣкаются ими на пропорціональныя части.
— 161 —
Предположимъ сначала, что прямыя АВ и АУВХ не параллельны. Тогда онѣ обра- V/ Г/ в
зуютъ нѣкоторый уголъ. (і/ ІУ у /
Примѣняя къ этому углу А- / / / /
предыдущую теорему, мо- / / II
жемъ паписать: II II
СБ БЕ ЕЕ / / / / д
(части сторонъ угла, при- Черт. 200.
мыкающія къ его вершинѣ, мы отбрасываемъ).
Если теперь допустимъ, что АВ II то пропорціональность частей этихъ прямыхъ не нарушается и въ этомъ случаѣ, такъ какъ тогда соотвѣтственныя части не только пропорціональны, но и равны (СВ=С1В1, БЕ=Б1Е1 и т. д.).
221. Обратная теорема. Если на сторонахъ угла отложимъ отъ вершины пропорціональныя части, то прямыя, соединяющія соотвѣтственные концы ихъ, параллельны.
Пусть на сторонахъ угла АВС (черт. 201) отложены отъ вершины на сторонѣ ВС части: ВБ, БЕ....,
на сторонѣ ВА части: ВВл, БіЕ^..'
и пусть части одной стороны пропорціональны частямъ другой
стороны, т.-е.: ВБ БЕ
ВП1 БХЕХ
Требуется доказать, что г Предположимъ, что эти прямыя непараллельны. Тогда, проведя черезъ точку Е прямую, параллельную ББг (77), мы получимъ нѣкоторую линію, не сливающуюся съ ЕЕі, пусть это будетъ прямая ЕЕіг. Согласно предыдущей теоремѣ, мы будемъ имѣть:
ВБ БЕ
—> НО П(
БіЕц
ББг, ЕЕХ... параллельны.
Черт. 201. ВБ _ БЕ ВБг Оі7?і ’
А. Киселевъ. Геометрія.
1 I
— 162 —
Слѣд., Р1Е11=І)1Ь11, что при пашемъ предположеніи невозможно; значитъ, нельзя допустить, чтобы прямыя ВВХ и ЕЕХ были непараллельны; остается принять, что ВВг II ЕЕХ.
222. Теорема. Двѣ параллельныя прямыя (МЕ и МхЕг, черт. 202), пересѣкаемыя рядомъ прямыхъ (ОА, ОВ, ОС, ....), исходящихъ изъ одной и той же точки (О), разсѣкаются ими на пропорціональныя части.
Требуется доказать, что части: АВ, ВС, СВ,... прямой МЕпропорціональны частямъ А^, 7?А, СуРі... прямой М^.— Изъ подобія тр-ковъ ОАВ и ОА^ (196), затѣмъ тр-ковъ ОВС и ОВхСі выводимъ:
АВ ВО ВО ВС
АуВі ВіО* ВіО В&'
АВ ВС
ВА'
Подобнымъ же образомъ доказывается пропорціональность
и прочихъ частей.
223. Задача. Раздѣлить отрѣзокъ прямой АВ (черт. 203) на три части пропорціонально ряду т :п ’.р, гдѣ т, п и р суть данные отрѣзки прямой,
I—---1
т, п и р суть или данныя числа.
Проведя неограниченную прямую АС подъ произвольнымъ угломъ къ АВ, отложимъ на ней отъ точки А части, равныя В прямымъ т, п и р. Точку Е, составляющую конецъ р, соединяемъ съ В и черезъ точки отложенія проводимъ прямыя, параллельныя ВЕ. ТогдаЛВ раздѣлится въ точкахъ В и Е на части, пропорціональныя т:п:р (219). Если т, п и р означаютъ какія-нибудь числа, напр., 2, 5, 3, то построеніе выполняется такъ же, съ тою разницей, что на АС откладываются отрѣзки, равные 2, б и 3 произвольнымъ едини
цамъ длины.
— 163
Конечно, указанное построеніе примѣнимо къ дѣленію не
только на 3 части, но и на какое угодно иное число частей.
224. Задача. Къ тремъ даннымъ отрѣзкамъ
прямой а, Ъ и с найт ціональный (черт. 204), т.-е. найти такой отрѣзокъ прямой х, который удовлетворялъ бы пропорціи: а : Ъ= =с : х.—На сторонахъ произвольнаго угла АВС откладываемъ части: ВВ=а,ВЕ=Ъ, ВЕ=с. Соединивъ затѣмъ В и Р, проводимъ ЕС || БЕ. Отрѣзокъ ЕС будетъ искомый (219) *).
225. Задача. На безконечной прямой МЕ (черт. 205) найти точки,
и четвертый пропор-
которыхъ разстоянія
отъ двухъ данныхъ точекъ Ли В этой прямой относились бы, какъ т : п (ти п или данные
отрѣзки прямой, или данныя числа).
Черезъ А и В проводимъ какія-нибудь двѣ параллельныя прямыя и на нихъ откладываемъ АС—т и ВВ=ВЕ=п (если т и п числа, напр., т—3, п=2, то мы возьмемъ отрѣзокъ АС,
равный 3 какимъ-нибудь единицамъ длины, а отрѣзки ВВ и ВЕ, равные 2 такимъ же единицамъ). Затѣмъ проведемъ прямыя черезъ точку С и каждую изъ точекъ Е и В. Очевидно, каковы бы ни были т и п, прямая СЕ всегда пересѣчется съ Л/7Ѵ
т
*) Отрѣзокъ с можно откладывать, такъ же какъ и а, отъ вершины угла В; тогда и отрѣзокъ х отложится тоже отъ этой вершины. При такомъ построеніи пропорція а : Ь = с : х выводится изъ подобія тр-ковъ
И*
164 —
въ нѣкоторой точкѣ Р; прямая же СР пересѣчется съ ІЮТ' только въ томъ случаѣ, если т^п, причемъ точка пересѣченія О будетъ лежать направо отъ В, если т>п (какъ у насъ на чертежѣ), или налѣво отъ А, если т<Сп. Докажемъ, что точки В и О удовлетворяютъ требованію задачи. Дѣйствительно, изъ подобія треугольниковъ АСВ и ВВЕ, а затѣмъ изъ подобія тр-ковъ АСС и ВВС находимъ:
ВА : ВВ=АС : ВЕ=т : п СА : СВ=АС : ВВ=т : п.
Кромѣ этихъ двухъ точекъ на прямой МЫ нѣтъ ни одной точки удовлетворяющей требованію задачи. Дѣйствительно, если точку Р (черт. 206) передвинемъ ближе къ Л, то РА уменьшится, а РВ увеличится, потому отношеніе РА : РВ уменьшится; если же точку Р
А В .,
м к : г ' сі. " 14
Черт. 206.
перемѣстимъ ближе къ В, то РА увеличится, а РВ уменьшится, и потому отношеніе РА : РВ увеличится. Значитъ, между Ли В, кромѣ точки Р, не можетъ существовать никакой другой точки, разстоянія которой отъ Л и В относились бы между собою, какъ т : п.
Возьмемъ теперь какую-нибудь точку лежащую между В и О, и допустимъ, что
(7,4 : (7іВ = (7Л : 0В = т : п.
Чтобы доказать невозможность этой пропорціи, составимъ изъ нея слѣдующую производную пропорцію:
(ОхЛ—СхВ) : (?іВ=((7Л—ОВ) : 6В,
т.-е. АВ : в1В = АВ : (7В;
Откуда получимъ: 61В = 0В.
Такъ какъ это равенство невозможно, то значитъ, невозможна и допущенная нами пропорція, и потому нельзя допустить, чтобы между Л и С существовала какая-нибудь точка, удовлетворяющая требованіямъ задачи. Такъ же можно доказать, что никакая точка лежащая направо отъ О, не можетъ удовлетворить этимъ требованіямъ.
Наконецъ, если возьмемъ какую-нпбудь точку К, лежащую налѣво отъ Л, то для нея, очевидно, КА<_КВ, и потому отношеніе КА : КВ меньше 1 и, слѣд., оно не можетъ равняться отношенію
165 —
т : п, которое больше 1 при иг>п (если т<_п, то точка О будетъ находиться налѣво отъ А, а направо отъ В не будетъ ни одной точки, удовлетворяющей задачѣ).
Замѣчаніе. 1°. Когда т=п, существуетъ только одна точка (лежащая на серединѣ между Л и В), которая удовлетворяетъ требованію задачи, такъ какъ разстоянія какой-нибудь другой точки прямой отъ точекъ Л и В не могутъ быть равными.
2°. О точкахъ Г и (?, удовлетворяющихъ пропорціи РА : РВ—СгА : СВ=т : п, говорятъ, что онѣ дѣлятъ въ данномъ отношеніи т : п отрѣзокъ АВ (черт. 205) внутреннимъ и внѣшнимъ образомъ (точкаРвнутреннимъ, а точка (? внѣшнимъ); говорятъ также, что точки Р и (? дѣлятъ отрѣзокъ АВ гармонически.
226. Теорема. Биссектрисса любого угла треугольника, какъ внутренняго, такъ и внѣшняго, пересѣкаетъ противоположную сторону или ея продолженіе въ такой точкѣ, которой разстоянія отъ концовъ этой стороны пропорціональны соотвѣтственно другимъ сторонамъ треугольника.
Пусть (черт. 207) ВВ есть биссектрисса внутренняго, а ВВГ— биссектрисса внѣшняго угла тр-ка АВС. Требуется доказать, что точки Р и Рг дѣлятъ сторону АС внутреннимъ и внѣшнимъ образомъ на части, пропорціональныя сторонамъ ВА и ВС, т.-е., что:
ВА ВА ВгА ВА
ВС ВС' ВгС ВС
Черезъ вершину С проведемъ ЕЕі II АВ до пересѣченія съ обѣими биссектриссами (80,1°). Тр-ки АВВ и ВЕС подобны (углы при Р равны, какъ вертикальные, уг. 1=уг. 5, какъ углы внутр. накрестъ лежащіе при параллельныхъ); точно такъ же подобны тр-ки АВВг и СЕіВі. Изъ подобія ихъ находимъ:
ВА_ ВА ВгА_ ВА
~ПС ~ЕС В^С~СЁ'1
Чтобы перейти отъ этихъ пропорцій къ тѣмъ, которыя требуется доказать, достаточно убѣдиться, что ЕС=ВС и СЕ^ВС. Такъ
— 166 —
какъ уг. 2=уг. 1 (по условію) и уг. 5=уг. 1 (какъ внутренніе накрестъ лежащіе при параллельныхъ), то уг. 2=уг. б, и потому въ ДЕВС стороны ЕС и ВС равны; съ другой стороны, уг. 3=уг.4 (по условію) и уг.6=уг.4 (какъ углы внутр. накр. лежащіе
при параллельныхъ); значитъ у г. 3=уг. 6, и потому въ ДВСЕ! стороны СЕі и ВС равны. Замѣнивъ теперь въ пропорціяхъ [1 ] и [2] отрѣзки Е С и СЕг на ВС, получимъ тѣ пропорціи, которыя тре-
бовалось доказать.
Численный примѣръ. Пусть АВ=10, ВС=7 и АС—6. Тогда биссектриссы ВВ и ВВг опредѣляютъ точки В и ВІУ которыхъ разстоянія отъ А и С можно найти изъ пропорціи:
ВА _ 10 ВгА_ 10 ВС~7 И В^С~ 7‘ ВА+ВС 17 ВіА—В^С 3 откуда: =- и
6 _17 6 _ 3
т-’е’ йл“іо и 5м~іо;
60 о 60
значитъ: ВА= — — 3и В1Л= —— 20.
Замѣчаніе. Для биссектриссы внѣшняго угла тр-ка теорема не примѣнима въ томъ случаѣ, когда этотъ внѣшній уголъ лежитъ при вершинѣ равнобедреннаго тр-ка. Дѣйствительно, легко доказать, что въ этомъ случаѣ (если АВ=ВС, черт. 207) биссектрисса ВВі параллельна АС.
227. Обратная теорема. Если прямая, исходящая изъ вершины треугольника, пересѣкаетъ противоположную сторону (или ея продолженіе) въ такой точкѣ, которой разстоянія до концовъ этой стороны пропорціональны соотвѣтственно двумъ
— 167 —
другимъ сторонамъ, то она есть биссектрисса угла треуголь* ника (внутренняго или внѣшняго).
Пусть Б и Бі (черт. 208) двѣ точки, удовлетворяющія пропорціямъ:
БА_ ВА БгА_ ВА
йс“вс[1];
Требуется доказать, что прямыя ВБ и ВБі дѣлятъ пополамъ: первая внутренній, а вторая внѣшній уголъ тр-ка АВС.
Проведя черезъ точку С прямую ЕЕі II АВ, найдемъ изъ подобія треугольниковъ:
БА_ ВА БХА_ ВА
БС ~ ЕС БгС~ СЁг
Сравнивая пропорціи [3] съ [1] и [4] съ [2], находимъ: ЕС—ВС и СЕі=ВС.
Поэтому въ тр-кѣ ВЕС равны углы 2 и 5, а въ треугольникѣ ВЕгС равны углы 3 и 6; но уг. 5=уг. 1 (какъ внутренніе накр. лежащіе при пар.) и уг. 6=уг. 4 (по той же причинѣ); слѣд., уг. 2=уг. 1 и уг. 3=уг. 4, т.-е. ВБ и ВБХ суть биссектриссы.
228. Теорема. Геометрическое мѣсто точекъ, которыхъ разстоянія отъ двухъ данныхъ точекъ А и В находятся въ постоянномъ отношеніи т: п, есть окружность, когда т не равно п, и прямая, когда т=п.
Предположимъ сначала, что т не равно п. Тогда на безконечной прямой, проходящей черезъ А и В (черт. 209), можно найти двѣ точки принадлежащія искомому геометрическому мѣсту (225). Пусть это будутъ точки С и С1г т.-е.
СА : СВ — т : п и : (\В — т : п.
— 168 —
Предположимъ теперь, что существуетъ еще какая-нибудь точка М, не лежащая на прямой АВ и удовлетворяющая пропорціи:
МА : МВ = т : п.
Проведя СМ и МС±, мы должны заключить (227), что первая изъ етихъ прямыхъ есть биссектрисса угла АМВ, а вторая—биссектрисса угла ВМК; вслѣдствіе этого уголъ СМСі, составленный изъ двухъ
Черт. 209.
половинъ смѳж-ныхъ угловъ, долженъ быть прямой, а потому вершина его М лежитъ на окружности, описанной на СС1г какъ на діаметрѣ. Такимъ образомъ, мы доказали, что всякая точка М, принадлежащая искомому геометрическому мѣсту, лежитъ на окружности ССг. Теперь докажемъ обратное предложеніе, т.-е., что всякая
точка этой окружности принадлежитъ геометрическому мЬсту.
Пусть М есть произвольная точка этой окружности. Требуется доказать, что МА : МВ = т : п. Проведя черезъ В прямую ВЕ || АМ, будемъ имѣть слѣдующія пропорціи:
МА : ВЕ-С^А : С1В = »г : п; (1)
МА : ВЕ = СА : СВ = т : п. (2)
Откуда В В = В Е,,
т.-ѳ. точка В есть середина прямой ВЕ. Такъ какъ уголъ СМС1 вписанный и опирается на діаметръ, то онъ прямой; поэтому ^ВМЕ прямоугольный. Вслѣдствіе этого, если середину В гипотенузы ВЕ
примемъ за центръ и опишемъ окружность, то эта окружность пройдетъ черезъ М; значитъ, ВВ—МВ. Подставивъ теперь въ пропорцію (1) на мѣсто ВВ равную ей прямую МВ, будемъ имѣть:
МА : МВ — т : п.
Когда т = п, разсматриваемое геометрическое мѣсто, очевидно, обращается въ прямую, перпендикулярную къ отрѣзку АВ въ его серединѣ.
Замѣчаніе. Окружность, о которой говорится въ этой теоремѣ, извѣстна подъ названіемъ Аполлоніевой окружности (Аполлоні й— греческій геометръ, жившій за 2 вѣка до Р. Хр.).
— 169 —
ГЛАВА V.
Числовыя зависимости между элементами треугольника и нѣкоторыхъ другихъ фигуръ.
229. Теорема. Въ прямоугольномъ треугольникѣ перпендикуляръ, опущенный изъ вершины прямого угла на гипотенузу, есть средняя пропорціональная между отрѣзками гипотенузы, а каждый катетъ есть средняя пропорціональная между гипотенузой и прилежащимъ къ этому катету отрѣзкомъ.
Пусть АВ (черт. 210) есть перпендикуляръ, опущенный изъ вершины прямого угла А на гипотенузу ВС. Требуется доказать слѣдующія трп пропорціи:
ВВ АВ ВС АВ ВС АС
1° ---—----9° ---—------о° ----=-----
АВ ВС' ’ АВ ВВ' • АС ВС
Первую пропорцію мы до- д
кажемъ изъ подобія тр-ковъ
АВС и АВС, у которыхъ АВ X.
общая сторона. Эти тр-ки по- \
добны, потому что острые углы, \
обозначенные на чертежѣ однѣ- Щ
ми и тѣми же цыфрами, равны вслѣдствіе перпендикулярности Черт. 2іо.
ихъ сторонъ (86, 87). Возьмемъ въ /\АВВ тѣ стороны ВВ и АВ, которыя составляютъ первое отношеніе доказываемой пропорціи; сходственными сторонами въ /\АВС будутъ АВ и ВС\ поэтому;
ВВ : АВ=АВ : ВС.
Вторую пропорцію докажемъ изъ подобія тр-ковъ АВС и АВВ, у которыхъ АВ общая сторона. Эти тр-ки подобны, потому что они прямоугольные, и острый уголъ В у нихъ общій. Въ /\АВС возьмемъ тѣ стороны ВС и АВ, которыя составляютъ первое отношеніе доказываемой пропорціи; сходственными сторонами въ ДАВВ будутъ АВ и ВВ-, поэтому:
ВС : АВ=АВ : ВВ
Третью пропорцію докажемъ изъ подобія тр-ковъ АВС и АВС у которыхъ АС общая сторона. Эти тр-ки подобны, потому что они оба прямоугольные и имѣютъ общій острый уголъ С. Въ
— 170 —
Черт. 211.
/\АВС возьмемъ стороны ВС и АС; сходственными сторонами въ ДЛОС будутъ АС и ВС; поэтому:
ВС : АС=АС : ВС.
230. Слѣдствіе. Пусть А (черт. 211) есть произвольная точка окружности, описанной на діаметрѣ ВС. Соединивъ концы діаметра съ этою точкою, мы получимъ прямоугольный тр-къ АВС, у котораго гипотенуза есть діаметръ, а катеты суть хорды. Примѣняя доказанную выше теорему къ этому треугольнику, приходимъ къ слѣдующему заключенію:
Перпендикуляръ, опущенный изъ какой-либо точки окружности на діаметръ, есть средняя пропорціональная между отрѣзками діаметра, а хорда, соединяющая эту точку съ концомъ діаметра, есть средняя пропорціональная между діаметромъ и прилежащимъ къ хордѣ отрѣзкомъ его.
231. Задача. Построить среднюю пропорціональную междудвумяконечными прямыми а и Ъ.
Предыдущее слѣдствіе позволяетъ рѣшить эту задачу двоякимъ путемъ.
1°. На произвольной прямой (черт. 212) откладываемъ части АВ=а и ВС—Ъ; на АС, какъ па діаметрѣ, описываемъ полуокружность; изъ В возставляемъ до пересѣченія съ окружностью перпендикуляръ ВВ. Этотъ перпендикуляръ и есть искомая средняя пропорціональная между АВ и ВС.
прямой (черт. 213) откладываемъ отъ точки А части а и Ъ. На большей изъ этихъ частей описываемъ полуокружность. Проведя изъ конца меньшей части перпендикуляръ къ АВ до пересѣченія его съ окружностью въ точкѣ В, соединяемъ А съ В. Хорда
АВ есть средняя пропорціональная между а и Ъ.
2°. На произвольной
В
Черт. 213.
171
232. Теорема. Если стороны прямоугольнаго треугольника измѣрены одною единицею, то квадратъ числа, выражающаго гипотенузу, равенъ суммѣ квадратовъ чиселъ, выражающихъ катеты.
Пусть АВС (черт.214) есть прямоугольный треугольникъ и АБ перпендикуляръ, опущенный на гипотенузу изъ вершины прямого угла. Тогда, какъ было доказано (229),
ВС : АВ=АВ : ВБ и ВС : АС=АС : БС.
Когда стороны даннаго треугольника и отрѣзки гипотенузы выражены числами, то мы можемъ примѣнить къ этимъ пропорціямъ свойство числовыхъ пропорцій, по которому произведеніе среднихъ членовъ равно произведенію край
нихъ:
АВ2=ВС . ВБ и АС2=ВС . БС.
Сложивъ эти два равенства, получимъ то, что требовалось доказать:
АВ2+АС2=ВС(ВБ+ВС)=ВС . ВС=ВС2.
Эту теорему обыкновенно выражаютъ сокращенно такъ:
Квадратъ гипотенузы равенъ суммѣ квадратовъ катетовъ.
Примѣръ- Положимъ, что катеты,измѣренные какою-нибудь линейною единицею, выражаются числами 3 и 4; тогда гипотенуза въ той же единицѣ выразится числомъ х, удовлетворяющимъ уравненію: ®2=32+42=9+16=25; откуда: а;=]/25=5 *).
233. Численныя примѣненія. Пустьа,Ь,с,М'ис' (черт. 214) будутъ числа, выражающія въ одной и той же единицѣ стороны, высоту и отрѣзки гипотенузы прямоугольнаго гр-ка АВС. На основаніи предыдущихъ теоремъ мы можемъ вывести слѣдующія 5 уравненій, связывающія эти 6 чиселъ: с2=ас'; Ъ2—аЪ'\ к2—Ъ'с'‘, Ъ'-^-с'^а’ Ь2+с2=а2.
*) См. ниже § 323 о «Пиѳагоровыхъ» треугольникахъ.
— 172 —
Изъ этихъ уравненій только первыя четыре самостоятельны, а послѣднее составляетъ слѣдствіе двухъ первыхъ; вслѣдствіе этого уравненія позволяютъ по даннымъ двумъ изъ шести чиселъ находить остальныя четыре.
Для примѣра положимъ, что намъ даны отрѣзки гипотенузы: Ъ'=5 метрамъ и с'=7 метр.; тогда:
а=Ь'+с'=12; с=/ас'=/12 . 7=/84=9,165...
Ь=/аЬ'=/12 . 5 =/60=7,745...
Ъ=УѴс'=Ѵ5 . 7 =/35=5,916...
234. Слѣдствіе. Квадраты катетовъ относятся между собою, какъ прилежащіе отрѣзки гипотенузы. Дѣйствительно, изъ уравненій предыдущаго параграфа находимъ:
с2 : Ъ2=ас' : аЬ'=с' : Ъ'.
235. Замѣчаніе. Въ послѣдующихъ теоремахъ мы будемъ сокращенно говорить: «квадратъ стороны» вмѣсто: квадратъ числа, выражающаго сторону, или «произведеніе прямыхъ» вмѣсто: произведеніе чиселъ,выражающихъ прямыя. При этомъ будемъ подразумѣ-вать, что прямыя измѣрены одною и тою же единицею.
236. Теорема. Во всякомъ треугольникѣ квадратъ стороны, лежащей противъ остраго угла, равенъ суммѣ квадратовъ двухъ другихъ сторонъ безъ удвоеннаго произведенія какой-нибудь изъ этихъ сторонъ на отрѣзокъ ея отъ вершины остраго угла до высоты.
Пусть ВС есть сторона тр-ка АВС (черт. 215 или 216), лежащая противъ остраго угла А, и ВВ высота, опущенная на какую-либо изъ остальныхъ сторонъ, напр., на АС (или на продолженіе АС). Требуется доказать, что
ВС2=4В2+4С2—2АС . АВ.
Изъ прямоугольнаго тр-ка ВВС выводимъ:
ВС2=ВВ2+ВС2 [1]
— 173 —
Опредѣлимъ каждый изъ квадратовъ ВР2 и ВС2. Изъ прямоугольнаго тр-ка ВАВ находимъ величину ВВ2, а именно:
ВО2=ЛВ2—АВ2. [2]
Оь другой стороны: ВС=АС—АВ (черт. 215) или ВС=АВ—АС (черт. 216). Въ обоихъ случаяхъ для ВС2 получимъ одно и то же выраженіе:
ВС2=(АС—АВ)2=АС2—2АС . АВ+АВ2 | ВС2=(АВ—АС)2=АВ2—2АВ . АС+АС2 | 13 Ь
Теперь равенство [1] можно переписать такъ:
ВС2=АВ2—АВ^+АС2—2АС . АВ+АВ2.
Это равенство, послѣ уничтоженія подчеркнутыхъ членовъ —АВ2 и +АВ2, и есть то самое, которое требовалось доказать.
Замѣчаніе. Теорема эта остается вѣрною и тогда, когда уголъ С прямой; тогда отрѣзокъ СВ обратится въ нуль, т.-е. АС сдѣлается равною АВ, и мы будемъ имѣть:
ВС2=АВ2+АС2—2АС2=АВ2—АС2,
что согласуется съ теоремою о квадратѣ гипотенузы (232).
237. Теорема. Въ тупоугольномъ треугольникѣ квадратъ стороны, лежащей противъ тупого угла, равенъ суммѣ квадратовъ двухъ другихъ сторонъ, сложенной съ удвоеннымъ произведеніемъ какой-нибудь изъ этихъ сторонъ на отрѣзокъ ея продолженія отъ вершины тупого угла до высоты.
— 174 —
Пусть АВ есть сторона тр-ка АВС (черт. 217), лежащая противъ тупого угла, С и ВВ—высота, опущенная на какую-либо изъ остальныхъ сторонъ; требуется доказать, что
АВ2=АС2+ВС2+2АС . СВ.
Изъ прямоугольныхъ тр-ковъ АВВ СВВ выводимъ:
АВ2=ВВ2+АВ2-, [1]
ВВ2=ВС2—СВ2. [2]
Но АВ2=(АС+СВ)2=
=АС2+2АС . СВ+СВ2. [3] Замѣнивъ въ равенствѣ [1] ВВ2 АВ2 ихъ выраженіями изъ равенствъ [2] и [3], найдемъ:
АВ2—ВС2—СВ2+АС2+2АС . СВ+СВ2.
Такъ какъ подчеркнутые члены—СВ2 и +СВ2 взаимно уничтожаются, то это равенство и есть то, которое требовалось доказать.
238. Слѣдствіе. Изъ трехъ послѣднихъ теоремъ выводимъ, что квадратъ стороны треугольника равенъ, меньше или больше суммы квадратовъ другихъ сторонъ, смотря по тому, будетъ ли противолежащій уголъ прямой, острый или тупой; отсюда слѣдуетъ обратное предложеніе (51):
Уголъ треугольника окажется прямымъ, острымъ или тупымъ, смотря по тому, будетъ ли квадратъ противолежащей стороны равенъ, меньше или больше суммы квадратовъ другихъ сторонъ.
Примѣръ. Стороны тр-ка равны:
1) 5, 3, 4. Такъ какъ 52=32+42, то уголъ, лежащій противъ стороны 5, прямой.
2) 8, 4, 7. Такъ какъ 82<42+72, то уголъ, лежащій противъ стороны 8, острый.
3) 8, 4, 5. Такъ какъ 82>12+52, то уголъ, лежащій противъ стороны 8, тупой.
— 176 —
239. Теорема. Сумма квадратовъ діагоналей параллелограмма равна суммѣ квадратовъ его сторонъ.
Изъ вершинъ В и С (черт. 218) параллелограмма АВСВ опустимъ на основаніе АВ перпендикуляры ВЕ и СЕ. Тогда изъ тр-ковъ АВВ и АСВ находимъ:
ВВ2=АВ2-\-АВ2~2АВ . АЕ;
АС2=АВ2+СВ2+2АВ . ВЕ.
Черт. 218.
Прямоугольные тр-ки АВЕ и ВСЕ равны, такъ какъ они имѣютъ по равной гипотенузѣ и равному острому углу; поэтому АЕ=ВЕ. Замѣтивъ это, сложимъ два выведенныя выше равенства; тогда подчеркнутые члены взаимно уничтожатся, и мы получимъ:
вв2+ас2=ав2+ав2+ав2+св2=ав2-^-ав2а-+ВС2+СВ2.
240. Вычисленіе высотъ треугольника по его Сторонамъ. Если вершины тр-ка обозначены большими буквами А, В и С, то численныя величины сторонъ этого тр-ка обыкновенно обозначаютъ соотвѣтственными малыми буквами а, Ъ и с, причемъ буквою а обозначаютъ ту сторону, которая лежитъ противъ угла А, буквою Ь—ту сторону, которая лежитъ противъ угла В, и т. д. Численную величину высоты тр-ка обыкновенно обозначаютъ буквою к (первая буква французскаго
Черт. 219.
Черт. 220.
слова Ь а и I е и г—высота), сопровождаемою (внизу) одною изъ малыхъ буквъ: а, Ъ и с. Такъ, высота, опущенная на сторону
— 176 —
а, обозначается Ііа, высота, опущенная на сторону Ь, обозначается кь, и т. д.
Опредѣлимъ ка (черт. 219 и 220) въ зависимости отъ сторонъ тр-ка. Обозначимъ отрѣзки стороны а (продолженной въ случаѣ тупого угла С, черт. 220) такимъ образомъ: отрѣзокъ ВБ, прилежащій къ сторонѣ с, черезъ с', а отрѣзокъ БС, прилежащій къ сторонѣ Ъ, черезъ Ъ'. Пользуясь теоремою о квадратѣ стороны тр-ка, лежащей противъ остраго угла (236), можемъ написать: Ь2=а2+с2—2ас'.
Изъ этого уравненія находимъ отрѣзокъ с': а2+с2—Ь2
С = 2а ’
Послѣ этого изъ тр-ка АВБ опредѣляемъ высоту, какъ катетъ: а2+с2—Ь2\% 2а '
Такимъ же путемъ можно опредѣлить въ зависимости отъ сторонъ тр-ка численныя величины Ъь и кс высотъ, опущенныхъ на стороны Ъ и с.
241. Вычисленіе медіанъ треугольника по его сторонамъ. Численная величина медіаны тр-ка обыкновенно обозначается буквою т (начальной буквой слова ш е сі і а п е—средняя), сопровождаемою (вцизу) одною изъ маленькихъ буквъ а, Ъ и с въ зависимости отъ стороны тр-ка, къ которой проведена обозначаемая медіана. Опредѣлимъ величину іпа медіаны, проведенной къ сторонѣ а (черт. 221). Для этого продолжимъ медіану на разстояніе БЕ=АБ и соединимъ точку Е прямыми съ В и С. Тогда мы получимъ параллелограммъ АВЕС (101). Примѣнивъ къ нему теорему о суммѣ квадратовъ діагоналей (239), получимъ:
а2+(2та)2=2Ь24-2с2; откуда: 4ть2=2Ь2+2с2—а2
. 221.
*) Ниже, въ § 313, будетъ дана болѣе простая формула для высоты.
177 —
1 -------------
и, слѣд.: йі0= - |/2Ь2+2с2—а2.
а
Подобнымъ же образомъ можемъ найти величины и иі, медіань, проведенныхъ къ сторонамъ Ъ и с.
242. Теорема Птоломея. *) Произведеніе діагоналей вписаннаго выпуклаго четыреугольника равно суммѣ произведеній противоположныхъ сторонъ его.
Пусть АС и ВВ суть діагонали вписаннаго выпуклаго четыреугольника (черт. 222); требуется доказать, что
АС . ВВ=АВ . СВ+ВС . АВ, гдѣ подъ обозначеніями АС, ВВ и пр. разумѣются числа, измѣряющія діагонали и стороны въ одной и той же линейной единицѣ.
Черт. 222. Черт. 222а.
Построимъ уголъ ВАЕ, равный углу ВАС (меньшему изъ двухъ угловъ, на которые уголъ А дѣлится діагональю АС); пусть Е будетъ точка пересѣченія стороны этого угла съ діагональю ВВ. Тр-ки АВЕ и АВС (покрытые на чертежѣ штрихами) подобны, такъ какъ у пихъ углы В и С равны, какъ вписанные, опирающіеся на одну и ту же дугу АВ, а углы при общей вершинѣ А равны по построенію. Изъ подобія этихъ тр-ковъ выводимъ:
АВ : АС=ВЕ : СВ; откуда: АС . ВЕ=АВ . СВ.
Разсмотримъ теперь другую пару тр-ковъ, а именно: АВС и АЕВ (тр-ки эти на черт. 222,а покрыты штрихами). Они подобны,
*) Клавдій Птоломей извѣстный астрономъ, жившій въ Александріи во 2-мъ вѣкѣ по Р. Хр.
А. Киселевъ. Геометрія. 12
— 178 —
такъ какъ у нихъ углы ВАС и ВАЕ равны, какъ суммы соотвѣтственно равныхъ угловъ, а углы АСВ и АВВ равны, какъ вписанные, опирающіеся на одну и ту же дугу АВ. Изъ ихъ подобія слѣдуетъ:
ВС : ЕВ=АС : АВ- откуда АС . ЕВ=ВС . АВ.
Сложивъ полученныя два равенства, находимъ: АС(ВЕ+ЕВ)=АВ . СВ+ВС . АВ, т.-е. АС . ВВ=АВ . СВ+ВС . АВ.
Замѣчаніе. Подобнымъ же образомъ можно было бы до-
казать, что если выпуклый четыреугольникъ не вписанный, то въ немъ произведеніе діагоналей меньше суммы произве-
деній противоположныхъ сторонъ; поэтому теорема, обратная
Пголомеевой, вѣрна.
243- Задача. По данны мъ р а діу су В и дву мъ
хордамъ а и Ъ окружности вычислить длину
третьей хорды, которая стягиваетъ дугу,
равную: 1°, суммѣ дугъ, стягиваемыхъ
хордами а и Ъ, 2°,
Чорт. 223.
разности этихъ дугъ.
1°. Пусть хорда а (черт. 223) стягиваетъ дугу МЕ, а хорда Ъ—дугу ДОР; требуется вычислить хорду МР = х, которая стягиваетъ дугу МЕР, равную суммѣ дугъ МЕ и ЕР.—Проведя черезъ точку ДО, въ которой сходятся данныя хорды а и Ь, діаметръ ДОф, соединимъ ф прямыми съ точками М и Р. Тогда мы получимъ вписанный четыреугольникъ, у котораго діагоналями
служатъ: МР=х и Е(^=2В. Тр-ки СМЕ и (^ЕР прямоуголь
ные, первый при вершинѣ М, второй—при вершинѣ Р (173);
поэтому:
ДОд2—МДО2=/4В2—а2, р<і=Ѵ е^2—ер2=Ѵ4В2—ъ2.
Примѣнивъ теперь теорему Птоломея, получимъ уравненіе: 2В . х=ау+ 4В,2—Ъ2+Ъ^4В2—а2,
изъ котораго найдемъ х (раздѣливъ обѣ части уравненія на 27?).
— 179 —
. 224
2°. Пусть хорда а (черт. 224) стягиваетъ дугу М27, а хорда Ъ—дугу ^Р^, требуется вычислить хорду МР—х, которая стягиваетъ дугу, равную разности
Проведя снова черезъ точку М, въ которой сходятся 2 данныя хорды, діаметръ и соединивъ съ ІИ и Р, получимъ вписанный четыреугольникъ. Изъ прямоугольныхъ тр-ковъ и (<)РМ находимъ:
2Ѵ()2—>№=/ 4Й2—а2, и Р<2=Ѵ ЯО*—Р№=Ѵ 4В2—Ъ2.
Примѣнивъ теорему Птоломея, получимъ уравненіе: а/ 4В2—Ь2= 2 Вж+Ь/ 4 Я2—а2, изъ котораго опредѣлимъ х.
Замѣчаніе. Задачу эту можно высказать и такъ: п о двумъ даннымъ сторонамъ а и Ъ треугольника и радіусу В описанной около него окружности вычислить третью сторону этого треугольника. Задача эта вообще имѣетъ 2 рѣшенія, потому что прямыя а и Ъ могутъ быть отложены или по разныя стороны отъ діаметра 2*7^ (черт. 223), или по одну и ту же сторону отъ него (черт. 224). Если большая изъ двухъ данныхъ сторонъ равна 2В, то получается одно рѣшеніе, а если эта сторона превосходитъ 2В, то задача невозможна.
244. Теорема. Отношеніе діагоналей вписаі угольника равно отношенію суммы произведеній стс цахъ первой діагонали, въ суммѣ произведеній стор цахъ второй діагонали.
Обозначимъ численныя величины сторонъ вписаннаго выпуклаго четыреугольника АВСБ (черт. 225) буквами а, Ь, с и й и его діагоналей буквами х у. Докажемъ, что
х _ай + Ъс у аЬ+сА
Тр-ки АВВ и ВВС (покрытые штрихами) подобны, такъ какъ углы одного соотвѣтственно
12*
го выпуклаго четыре-іъ, сходящихся въ кон-I, сходящихся въ кон-
Черт. 225.
— 180 —
равны угламъ другого; по той же причинѣ подобны и тр-ки АБЕ и ЕВС. Изъ ихъ подобія выводимъ:
а АЕ ВЕ,
~~~БЕ~~СЕ' С‘1
А БЕ АЕ
Ь ~ СЕ~ ВЕ' И
Изъ втихъ пропорцій находимъ:
АЕ=— БЕ\ БЕ = 4~. СЕ. с Ь
Откуда: АЕ =-----Г-*"' =~іГ‘
' с \ о ) ос
_ аЛ / ай \
и, слѣд.: ® = АС = АЕ-\-СЕ=-^. СЕ+СЕ—1 + 1 ) СЕ.
т.-е. Х=^±Ѣ. СЕ. [3]
ос
Пользуясь тѣми же равенствами [1] и [2], получимъ: у=ВБ = ВЕ±БЕ =—. СЕ±—. СР=(—+-ь)- СР,-аЪ-\-сй
т.-е. У=~ьГ~‘ СР‘ М
Раздѣливъ равенство [3] на [4], получимъ ту пропорцію, которую требовалось доказать (Ъс и СЕ сократятся).
245. Вычисленіе діагоналей вписаннаго четыреугольника ПО его сторонамъ. Пользуясь теоремой Птоломея и теоремой объ отношеніи діагоналей вписаннаго четыреугольника, мы легко можемъ вычислить отдѣльно каждую его діагоналъ, если извѣстны всѣ стороны. Такъ, для чертежа 225-го мы будемъ имѣть:
х ай + Ьс ху^ас+ъа-,
Если эти 2 равенства почленно перемножимъ и затѣмъ почленно раздѣлимъ, то получимъ (по извлеченіи квадратнаго корня):
х—1/(ас + ЬЛ)(а<і+Ьс), у~Л/~(ас + Ъ(і) (аЬ+е<1)
V аЪ+сй ’ V аЛ + Ьс
Замѣтимъ для памяти, что въ числителѣ подкоренной величины первый множитель есть сумма произведеній противоположныхъ сторонъ, а второй—сумма произведеній сторонъ, сходящихся въ концахъ опредѣляемой діагонали, знаменатель же представляетъ сумму произведеній сторонъ, сходящихся въ концахъ другой діагонали*).
*) Въ предыдущихъ изданіяхъ этой книги (до 21-го) для вычисленія діагоналей вписаннаго четыреугольника указывался (въ § 214) иной способъ, независимый отъ теоремы Птоломея и отъ теоремы объ отношеніи діагоналей, при чемъ эти двѣ теоремы разсматривались, какъ простыя слѣдствія изъ формулъ, опредѣляющихъ діагонали. Въ перерабо-
— 181 —
246. Теорема. Если черезъ точку, взятую внутри круга, проведены какая-нибудь хорда и діаметръ, то произведеніе отрѣзковъ хорды равно произведенію отрѣзковъ діаметра.
Пусть черезъ точку М (черт. 226) проведена какая-нибудь хорда АВ и діаметръ СВ-, требуется доказать, что
МА . МВ=МС . МВ.
Проведя 2 вспомогательныя хорды АС и ВВ, мы получимъ два тр-ка АМС и МВВ (покрытые на чертежѣ штрихами), которые подобны, такъ какъ у нихъ углы Аи В равны, какъ вписанные, опирающіеся на
Черт. 226.
одну и ту же дугу ВС, и углы С и В равны какъ вписанные, опирающіеся на одну и ту же дугу АВ. Изъ подобія ихъ вы
водимъ:
МА : МВ=МС : МВ-, откуда: МА . МВ=МС . МВ.
247. Слѣдствіе. Если черезъ точку (М, черт. 226), взятую внутри круга, проведены нѣсколько хордъ (АВ, ЕЕ, КЬ...), то произведеніе отрѣзковъ каждой хорды есть число постоянное для всѣхъ этихъ хордъ, такъ какъ для каждой хорды это произведеніе равно произведенію отрѣзковъ діаметра СВ, проходящаго черезъ взятую точку М.
2°. Это постоянное число равно квадрату радіуса, уменьшенному па квадратъ разстоянія взятой точки отъ центра.
Дѣйствительно, обозначивъ радіусъ круга черезъ В, и разстояніе МО (черт. 226) черезъ Л, будемъ имѣть:
мс=в—а, мв=в+а-
слѣд.: ма . мв=мс. мв=(в—а)(в+а)=в2—а2.
тайномъ 21-мъ изданіи (и въ слѣдующихъ) въ числѣ многихъ другихъ измѣненій, мы сочли полезнымъ изложить классическое доказательство теоремы Птоломея, имѣющей весьма большое самостоятельное значеніе; но тогда вычисленіе діагоналей всего удобнѣе основывать, какъ это сдѣлано въ текстѣ, на теоремѣ Птоломея и теоремѣ § 244.
— 182 —
248. Теорема. Если изъ точки, взятой внѣ круга, проведены къ нему какая-нибудь сѣкущая и касательная, то произведеніе сѣкущей на ея внѣшнюю часть равно квадрату касательной (предполагается, что сѣкущая ограничена второю точкою пересѣченія, а касательная—точкою касанія).
Пусть изъ точки М (черт. 227), проведены какая-нибудь сѣкущая МА и касательная МС-, требуется доказать, что
Черт. 227.
МА . МВ=МС2.
Проведемъ вспомогательныя хорды АС и ВС; тогда получимъ два тр-ка МАС и МВС (покрытые на чертежѣ штрихами), которые подобны, потому что у нихъ уголъ М общій, и углы МСВ и САВ равны, такъ
какъ каждый изъ нихъ измѣряется половиною дуги ВС (178, 171). Возьмемъ въ &МАС стороны МА и МС\ сходственными сторонами въ Д.МВС будутъ МС и МВ\ поэтому
МА : МС=МС : МВ.
Откуда:
МА . МВ=МС2.
249. Слѣдствіе. 1°. Если изъ точки (М, черт. 227), взятой внѣ круга, проведены къ нему нѣсколько сѣкущихъ (МА, МВ, МЕ...), то произведеніе каждой сѣкущей на ея внѣшнюю часть есть число постоянное для всѣхъ этихъ сѣкущихъ, такъ какъ для каждой сѣкущей это произведеніе равно квадрату касательной (МС2), проведенной черезъ точку М.
2°. Это постоянное число равно квадрату разстоянія взятой точки отъ центра, уменьшенному па квадратъ радіуса.
— 183 —
Дѣйствительно, проведя радіусъ ОС, получимъ прямоугольный треугольникъ МСО, изъ котораго находимъ:
МС2=МО2~СО2=а2~В2.
250. Теорема. Произведеніе двухъ сторонъ треугольника равно произведенію діаметра круга, описаннаго около этого треугольника, на высоту его, опущенную на третью сторону.
Обозначивъ буквою В радіусъ круга, описаннаго около тр-ка АВС (черт. 228 и 229), докажемъ, что
Ьс=2В . ка.
Проведемъ діаметръ АВ и соединимъ В съ В. Тр-ки АВВ и АЕС подобны, потому что углы ВиЕ прямые и В—С, какъ углы вписанные, опирающіеся на одну и ту же дугу. Изъ подобія выводимъ:
с : ка=2В : Ь; откуда: Ьс=2В . ка.
251. Теорема. Произведеніе двухъ сторонъ треугольника равно квадрату биссектриссы угла, заключеннаго между этими сторонами, сложенному съ произведеніемъ отрѣзковъ третьей стороны.
Обозначивъ биссектриссу АО угла А (черт. 230) греческою буквою а, докажемъ, что Ъс=а2 + ВБ . БС. Продолжимъ АБ до пересѣченія съ окружностью въ точкѣ Е (эта точка лежитъ въ серединѣ
— 184 —
дуги ВС, такъ какъ углы ВАЕ и ЕАС равны). Тр-ки АВЕ и АВС
Черт. 230.
подобны, потому что углы при точкѣ А равны по условію и С = Е, какъ углы вписанные, опирающіеся на одну и ту же дугу. Изъ подобія ихъ слѣдуетъ:
с : а = АЕ : Ъ, откуда Ъс—л. АЕ
или 5с=а(а-|-РЕ)=а2-|-а . ВЕ.
Но а . ВЕ = ВВ . ВС (247, 1°).
Поэтому Ъс=а2 + ВВ . ВС. [2]
262. Вычисленіе биссектриссъ треугольника по его Сторонамъ. Изъ равенства [2| предыдущаго параграфа выводимъ: а3 = 6с— ВО . ВС.
Отрѣзки ВВ и ВС можно найти изъ пропорціи ВВ : ВС=с : Ъ (226); откуда:
ВВ+ВС Ъ + с ВВ+ВС Ъ+с
ВВ ~ с и ВС ~ Ь '
Замѣтивъ, что ВВ+ВС = а, получимъ:
Ъ+с 1>+с
Слѣд. а* = Ъс--??*?_ = Ъс Г(6+с)2—а2
(Ь+с)2 (Ы-с) '
Ъс
__-----(Ь-|-с + а) (&+с—а)].
(6±с)Ч ]
Это выраженіе можно упростить, если обозначимъ периметръ тр-ка, т.-е. а + 6-|-с, черезъ 2р; тогда 6 + с—а=2р—2а=2(р—а) и
2 _______
“ ~ 6+~еК
ГЛАВА VI.
Понятіе о приложеніи алгебры къ геометріи.
253. Задача. Данный отрѣзокъ прямой р а з-дѣлитьвъ средне мъи крайнемъ отношеніи. Эту задачу надо понимать такъ: раздѣлить данный отрѣзокъ прямой на такія двѣ части, чтобы бблыпая изъ нихъ была сред
— 186 —
нею пропорціональною между всѣмъ отрѣзкомъ и меньшею ея частью.
Задача будетъ рѣшена, если мы найдемъ одну изъ двухъ частей, на которыя требуется раздѣлить данный отрѣзокъ. Будемъ находить ббльшую часть, т.-е. ту, которая должна быть среднею пропорціональною между всей линіей и меньшею ея частью. Предположимъ сначала, что рѣчь идетъ не о построеніи этой части, а только объ ея вычисленіи. Тогда задача рѣшается алгебраически такъ: если число, измѣряющее въ какой-нибудь единицѣ длину даннаго отрѣзка, обозначимъ а, а число, измѣряющее въ той же единицѣ длину бблыпей его части, х, то число, измѣряющее длину другой части, выразится а—х, и, согласно требованію задачи, мы будемъ имѣть пропорцію:
а : х—х : (а—х);
откуда: х2=а(а—х)
или хг+ах—а2=0.
Рѣшивъ это квадратное уравненіе, находимъ:
І>=—®а+а2; ©г+л
Отбросивъ второе рѣшеніе, какъ отрицательное *), возьмемъ только первое положительное рѣшеніе, которое удобнѣе представить такъ:
Покажемъ прежде всего, что величина Хі меньше а.
♦) Не трудно было бы показать, что абсолютная величина этого отрицательнаго рѣшенія даетъ отвѣтъ на измѣненную задачу: данную прямую а продолжить на столько (на х), чтобы продолженіе было средней пропорціональной между а и а+х. Это будетъ тоже дѣленіе даннаго отрѣзка въ среднемъ и крайнемъ отношеніи; оно наз. внѣшнимъ въ отличіе отъ внутрен н яго, разсматриваемаго въ текстѣ.
— 186 —
Такъ какъ
отнявъ отъ обѣихъ частей этого неравенства по а, найдемъ, что
Отсюда заключаемъ, что задача всегда возможна и имѣетъ только одно рѣшеніе.
Если бы намъ удалось построить такую прямую, которой длипа численно выражается найденной выше формулой, то, нанеся эту длину на данную прямую, мы раздѣлили бы ее въ среднемъ и крайнемъ отношеніи. Итакъ, вопросъ сводится къ построенію найденной формулы.
Разсматривая отдѣльно выраженіе
/ѳ
2
+а2, мы замѣ-
чаемъ, что оно представляетъ собою длину гипотенузы такого
прямоугольнаго тр-ка, у котораго одинъ катетъ равенъ а, а другой а/2. Построивъ такой тр-къ, мы найдемъ прямую, вы-
/ѳ
ражаемую
формулой
2
+а2. Чтобы получить затѣмъ
длипу Хі, достаточно изъ гипотенузы построеннаго треугольника вычесть а/а.
Такимъ образомъ, построеніе можно выполнить такъ:
дѣлимъ (черт. 231) данный отрѣзокъ АВ пополамъ въ точкѣ С. Изъ конца В возставляемъ перпендикуляръ ВБ и откладываемъ на немъ ВБ=ВС. Соединивъ А съ Б прямою, получимъ прямоугольный тр-кь АВБ, у котораго катетъ АВ=а, а другой катетъ ВБ=а/2. Слѣд., его гипотенуза
АБ равна
/(Э
2
+а2.Чтобы вычесть изъ гипотенузы длину
«/г,
опишемъ изъ Б, какъ центра, дугу радіусомъ БВ=а[2. Тогда
отрѣзокъ АЕ будетъ равенъ
(1) 2^°2—2’ Т‘"е‘ бУдетъ Ра-
венъ жх. Отложивъ АЕ на АВ (отъ А до С), получимъ точку О,
— 187 —
въ которой отрѣзокъ АВ дѣлится въ среднемъ и крайнемъ отношеніи.
Замѣчаніе. Дѣленіе даннаго отрѣзка прямой въ среднемъ и крайнемъ отношеніи наз. также золотымъ дѣленіемъ.
254. Алгебраическій способъ рѣшенія геометрическихъ задачъ. Мы рѣшили предложенную задачу путемъ приложенія алгебры къ геометріи. Этотъ пріемъ состоитъ въ слѣдующемъ: сперва опредѣляютъ, какую прямую должно отыскать, чтобы можно было рѣшить задачу. Затѣмъ, обозначивъ численныя величины данныхъ прямыхъ буквами а, Ъ, с..., а искомой прямой—буквою х, составляютъ изъ условій задачи и извѣстныхъ теоремъ уравненіе, связывающее искомую прямую съ данными; полученное уравненіе рѣшаютъ по правиламъ алгебры. Найденную формулу изслѣдуютъ, т.-е. опредѣляютъ, при всякИхъ ли заданіяхъ это формула даетъ возможныя рѣшенія, или только при нѣкоторыхъ, и получается ли одно рѣшеніе или нѣсколько. Затѣмъ строятъ формулу, т.-е. находятъ построеніемъ такую прямую, которой численная величина выражается этой формулой.
Такимъ образомъ, алгебраическій пріемъ рѣшенія геометрическихъ задачъ состоитъ въ общемъ изъ слѣдующихъ 4-хъ частей: 1°, составленіе уравненія, 2°, рѣшеніе его, 3°, изслѣдованіе полученной формулы и 4°, построеніе ея.
Иногда задача приводится къ отысканію нѣсколькихъ прямыхъ линій. Тогда, обозначивъ численныя величины ихъ буквами х, у,..., стремятся составить столько уравненій, сколько неизвѣстныхъ.
255. Построеніе простѣйшихъ Формулъ. Укажемъ простѣйшія формулы, которыя можно построить посредствомъ циркуля и линейки; при этомъ будетъ предполагать, что буквы а, Ь, с... означаютъ величины данныхъ конечныхъ прямыхъ, а х величину искомой. Не останавливаясь на такихъ формулахъ:
а:=а+Ь+с, х—а—Ъ, х—2а, За..., построеніе которыхъ выполняется весьма просто, перейдемъ къ болѣе сложнымъ:
— 188 —
а а 2
1°. Формулы х=-, -,...х—-а,... и т. п. строятся посред-2 3 о
ствомъ дѣленія прямой а на равныя части (69,7; 114) и затѣмъ, если нужно, повтореніемъ одной части слагаемыхъ 2, 3... и т. д. раза.
аЪ
2°. Формула х=— представляетъ собою четвертую С
пропорціональную къ прямымъ с, а и Ь. Дѣйствительно, изъ этого равенства выводимъ:
сх=аЪ, откуда с : а=Ъ : х.
Слѣд., х найдется способомъ, указаннымъ нами (224) для построенія 4-й пропорціональной.
а2
3°. Формула х=— выражаетъ четвертую пропорціональную
къ прямымъ Ь, а и а, или какъ говорятъ, третью пропорціональную къ прямымъ Ь и а. Дѣйствительно, изъ даннаго равенства выводимъ:
Ъх=а2-, откуда Ъ : а=а : х.
Слѣд., х найдется тѣмъ же способомъ, какимъ отыскивается 4-я пропорціональная (только прямую а придется откладывать два раза) *).
4°. Формула х=Ѵ~аЪ выражаетъ среднюю пропорціональную между а и Ь. Дѣйствительно, изъ нея выводимъ:
х2=аЬ-, откуда а : х=х : Ъ.
Слѣд., х найдется способомъ, указаннымъ раньше для построенія средней пропорціональной (231).
5°. Формула х=Ѵа2-\-Ъ2 выражаетъ гипотенузу прямоугольнаго тр-ка, у котораго катеты суть « и Ъ-
♦) Можно также построить х, основываясь на теоремѣ § 229: отложимъ ВВ = а (см. черт. 210); проведемъ ВА_]_ВВ; отложимъ ВА — Ъ; соединимъ В съ А прямой; проведемъ АС_[_АВ. Тогда отрѣзокъ ВС и будетъ искомая линія, такъ какъ ВВ : ВА=ВА : ВС. Если а<5, то построеніе можно выполнитъ еще иначе, при помощи полуокружности (см. черт. 211), принявъ за діаметръ ВС отрѣзокъ Ь, а за хорду ВА отрѣзокъ а; тогда искомая линія будетъ ВВ.
— 189 —
6°. Формула х=Ѵай—Ь2 представляетъ катетъ прямо-угольнаго тр-ка, у котораго гипотенуза есть а, а другой катетъ Ь.
Построеніе всего удобнѣе выполнить такъ, какъ указано въ § 174.
Указанныя формулы можно считать основными. При помощи ихъ строятся болѣе сложныя формулы. Напр.:
аЪссІ
7°. х=~,—. Разобьемъ дробь на множителей такъ: с/д
аЪ с й аЬ
ж=—и положимъ, что—=к. Тогда й найдемъ, какъ е / 9 е
4-ю пропорціональную къ е, а и Ь. Найдя к, будемъ имѣть: ко й кс
х—-:' -' Положимъ, что Тогда I найдемъ, какъ 4-ю про-і 9 /
порціональную къ линіямъ /, к и с. Найдя I, будемъ имѣть Ш
х=-\ слѣд., х есть 4-я пропорціональная къ о, I и Н. д
Подобнымъ образомъ строятся также и формулы вида: аЬс...кІ ат
Х=а'Ь'с'...к' ИЛИ Х==
т.-е. такія формулы, въ которыхъ числитель и знаменатель представляютъ произведеніе липейныхь множителей (буквъ, означающихъ линіи), причемъ числитель содержитъ этихъ множителей па одинъ больше, чѣмъ знаменатель.
8°. х=аі/ Подведя а подъ знакъ радикала, получимъ:
Г 3
/2 „ Л 2
—а2— 1 / а.—а-
3 У 3
Отсюда видимъ, что х есть средняя пропорціональная между прямыми а и 2/3а.
9°. х=У а2-\-Ь2—с2+^2. Положимъ, что а2-\-Ъ2—к2. Тогда к найдется, какъ гипотенуза прямоугольнаго тр-ка, у котораго катеты суть аиЪ. Построивък, положимъ, что к2+<12=12. Тогда I найдется, какъ гипотенуза прямоугольнаго тр-ка, у котораго катеты суть к и Л. Построивъ I, будемъ имѣть: х—Ѵ і2-—с2. Слѣд., х есть катетъ такого тр-ка, у котораго гипотенуза I, а другой катетъ с.
— 190 —
10. х=а2И а2±Ьс. Если положимъ, что Ьс=й2, то найдемъ к, какъ среднюю пропорціональную между Ь и с. Тогда а2+ к2.
найдется, какъ было выше указано въ случаяхъ 5-мъ и 6-мъ.
11°. х=Ѵа*+Ь\ Положимъ, что
а* а2 а а аИ=Ъ*ѵ, отсюда: у=-=-
Изъ этого выраженія видно, что у найдется посредствомъ троекратнаго построенія 4-й пропроціональной. Построивъ у, будемъ имѣть:
Ж=ИЬ33/+Ь4= у/~Ѵъ\у+Ь)= у/~ ЪУЪ(у+Ъ).
Выраженіе V Ь(у+Ъ) представляетъ прямую, которая есть средняя пропорціональная между Ь и у+Ь. Пусть эта прямая будетъ к. Тогда ж=Ѵ Ьк\ значитъ, х найдется, какъ средняя пропорціональная между Ъ и к.
Ограничимся этими примѣрами. Замѣтимъ, что подробное разсмотрѣніе способовъ построенія алгебраическихъ формулъ приводитъ къ слѣдующему важному выводу:
помощью линейки и циркуля возможно строить только такія алгебраическія выраженія, которыя или вовсе не содержатъ радикаловъ, или же содержатъ только радикалы съ показателями 2, 4, 8..., т.-е. съ показателями, равными степени 2-хъ *).
УПРАЖНЕНІЯ.
Доказать теоремы.
189. Прямая, проведенная черезъ середины основаній трапеціи, проходитъ черезъ точку пересѣченія непараллельныхъ сторонъ и черезъ точку пересѣченія діагоналей.
_________ з
•) Напр., нельзя построить выраженіе 2аа, т.-е.—другими словами—нельзя только помощью циркуля и линейки рѣшить знаменитую съ древнихъ временъ задачу объ удвоеніи даннаго куба (со стороною а).
Объ однородности уравненій, получаемыхъ при рѣшеніи геометрическихъ задачъ, а также о построеніи корней квадратнаго уравненія см. ниже, §§ 342, 343.
— 191 —
189а. Если въ тр-кѣ изъ вершины угла, лежащаго между неравными сторонами, проведены биссектрисса и медіана, то первая меньше второй.
1896. Прямая, проходящая черезъ середину основанія равнобедреннаго тр-ка и ограниченная одною боковою стороною и продолженіемъ другой боковой стороны, больше основанія этого тр-ка.
190. Если два круга касаются извнѣ, то часть внѣшней общей касательной, ограниченная точками касанія, есть средняя пропорціональная между діаметрами круговъ.
190а. Доказать, что если А, В и С суть три послѣдовательныя точки прямой и М какая-нибудь точка внѣ прямой, то существуетъ соотношеніе (теорема Стюарта):
МА* . ВС+МС* . АВ— МВ* . АС = ВС . АВ .АС
(рѣшается при помощи теоремъ §§ 230 и 237).
1906. При помощи этого соотношенія найти выраженіе для биссек-триссъ тр-ка въ зависимости отъ его сторонъ (на основаніи § 226).
191. Сумма квадратовъ сторонъ треугольника равна утроенной суммѣ квадратовъ разстояній отъ точки пересѣченія медіанъ до вершинъ треугольника (§ 239).
192. Если въ прямоугольный тр-къ АВС вписать квадратъ ВЕЕС такъ, чтобы сторона СЕ лежала на гипотенузѣ ВС, то эта сторона есть средняя пропорціональная между отрѣзками гипотенузы ВС и ЕС.
193. Если двѣ конечныя прямыя АВ и СВ пересѣкаются (хотя бы и при продолженіи) въ точкѣ Е такъ, что
ЕВ . ЕА — ЕС . ЕВ,
то точки А, В, С и Р лежатъ на одной окружности (эта теорема обратна изложеннымъ въ §§ 247 и 249).
194. Дана окружность О и двѣ точки А и В внѣ круга. Черезъ эти точки проведены нѣсколько окружностей, пересѣкающихъ окружность О, или касающихся ея. Доказать, что всѣ хорды, соединяющія точки пересѣченія каждой изъ этихъ окружностей съ окружностью О, а также и общія касательныя, сходятся (при продолженіи) въ одной точкѣ, лежащей на продолженіи прямой АВ.
195. Основываясь на этомъ, вывести способъ построенія такой окружности, которая проходитъ черезъ 2 данныя точки А и В и касается данной окружности О.
196. Даны два какіе-нибудь круга на плоскости. Если два радіуса этихъ круговъ движутся, оставаясь постоянно параллельными, то прямая, проходящая черезъ концы ихъ, пересѣкаетъ линію центровъ всегда въ одной и той же точкѣ (эта точка наз. центромъ подобія двухъ круговъ).
197. Медіана тр-ка дѣлитъ пополамъ всѣ прямыя, проведенныя внутри тр-ка параллельно той сторонѣ, относительно которой взята медіана.
— 192 —
198. Даны три прямыя, исходящія изъ одной точки. Если по одной изъ нихъ движется какая-нибудь точка, то разстоянія ея отъ двухъ другихъ прямыхъ сохраняютъ всегда одно и то же отношеніе.
199. Если двѣ окружности концентрическія, то сумма квадратовъ разстояній всякой точки одной изъ нихъ отъ концовъ какого угодно діаметра другой есть величина постоянная (§ 239).
200. Если изъ трехъ вершинъ тр-ка и изъ точки пересѣченія его медіанъ опустимъ перпендикуляры на какую-нибудь внѣшнюю прямую, то послѣдній изъ 4-хъ перпендикуляровъ равенъ третьей части суммы первыхъ трехъ.
201. Если соединимъ прямыми основанія трехъ высотъ какого-нибудь тр-ка, то образовавшіеся при этомъ 3 тр-ка у вершинъ даннаго подобны ему. Вывести отсюда, что для тр-ка, имѣющаго сторонами прямыя, соединяющія основанія высотъ даннаго тр-ка, эти высоты служатъ биссектриссами.
202. Діаметръ АВ данной окружности продолженъ за точку В. Черезъ какую-нибудь точку С этого продолженія проведена неопредѣленная прямая СВ_1_АВ. Если произвольную точку М этого перпендикуляра соединимъ съ А, то (обозначивъ черезъ Аг вторую точку пересѣченія съ окружностью этой прямой) произведеніе АМ . АА± есть величина постоянная.
Найти геометрическія мѣста:
203. —серединъ всѣхъ хордъ, проходящихъ черезъ данную точку окружности.
204. —точекъ, дѣлящихъ въ одномъ и томъ же отношеніи т : п всѣ хорды, проходящія черезъ данную точку окружности.
205. —точекъ, которыхъ разстоянія отъ сторонъ даннаго угла имѣютъ одно и то же отношеніе т : п.
206. —точекъ, для которыхъ сумма квадратовъ разстояній отъ двухь данныхъ точекъ есть величина постоянная (§ 239).
207. —точекъ, для которыхъ разность квадратовъ разстояній отъ двухъ данныхъ точекъ есть величина постоянная.
208. —точекъ, изъ которыхъ касательныя, проведеннныя къ двумъ даннымъ окружностямъ, равны (это геометрическое мѣсто есть прямая^ перпендикулярная къ линіи центровъ; она назыв. радикальною осью двухъ круговъ).
209. —точекъ, дѣлящихъ въ данномъ отношеніи т : п всѣ прямыя, соединяющія точки окружности съ данною точкою О (лежащею внѣ или внутри круга).
210. Даны двѣ извнѣ касающіяся окружности. Черезъ точку касанія А проводятъ въ окружностяхъ двѣ перпендикулярныя хорды АВ и АС. Концы ихъ В и С соединяютъ прямой. Найти геометрическое мѣсто точекъ, дѣлящихъ ВС въ данномъ отношеніи т : п.
— 193 —
211. Данный уголъ вращается вокругъ своей вершины. На сторонахъ его, отъ вершины, откладываютъ перемѣнныя длины, но которыхъ отношеніе постоянно. Если конецъ одной стороны описываетъ данную по положенію прямую, то какую линію опишетъ другой конецъ?
Задачи на построеніе.
212. Черезъ точку, данную внутри или внѣ угла, провести прямую такъ, чтобы части ея, заключенныя между этой точкой и сторонами угла, имѣли данное отношеніе т ; п.
213. Найти въ треугольникѣ такую точку, чтобы перпендикуляры, опущенные изъ нея на стороны, находились въ данномъ отношеніи т : п : р (см. упражненіе 205).
214. Построить тр-къ по углу, одной изъ сторонъ, прилежащихъ къ нему, и по отношенію этой стороны къ третьей сторонѣ (сколько рѣшеній?).
215. То же—по углу при вершинѣ, основанію и отношенію его къ одной изъ боковыхъ сторонъ.
216. То же—по высотѣ, углу при вершинѣ и отношенію отрѣзковъ основанія.
217. То же—по углу при вершинѣ, основанію и данной на основаніи точкѣ, черезъ которую проходитъ биссектрисса угла при вершинѣ.
218. То же—по двумъ угламъ и суммѣ или разности основанія съ высотою.
219. Построить равнобедренный тр-къ по углу при вершинѣ и суммѣ основанія съ высотою.
220. Вписать въ даннный кругъ тр-къ, у котораго даны: основаніе и отношеніе двухъ другихъ сторонъ.
221. Вписать въ данный кругъ тр-къ, у котораго даны: основаніе и медіана относительно одной изъ неизвѣстныхъ сторонъ (см. упражненіе 203).
222. Вписать квадратъ въ дачный сегментъ такъ, чтобы одна его сторона лежала на хордѣ, а вершины противолежащихъ угловъ— на дугѣ.
223. Вписать квадратъ въ данный тр-къ такъ, чтобы одна сторона его лежала на основаніи тр-ка, а вершины противолежащихъ угловъ на боковыхъ сторонахъ тр-ка.
224. Въ данный треугольникъ вписать прямоугольникъ (см. пред. задачу), у котораго стороны относились бы, какъ т : п.
225. Около даннаго квадрата описать тр-къ, подобный данному.
226. Дана окружность и на ней двѣ точки 4 и В. Найти на этой окружности третью точку С, чтобы разстоянія ея отъ А и В находились въ данномъ отношеніи.
227. На данной прямой найти точку, которая одинаково была бы удалена отъ другой данной прямой и данной точки.
А. Киселевъ. Геометрія.
13
194 —
228. Построить тр-къ по двумъ сторонамъ и биссектриссѣ угла между ними (см. черт. 207. Сначала находимъ прямую БЕ изъ пропорціи АВ : ЕС (т.-е. ВС) = ВБ : БЕ\ затѣмъ строимъДВСЕ,....').
229. Построить прямую х, которая относилась бы къ данной прямой т, какъ а2 : &2(а и Ь данныя прямыя).
230. Найти внѣ даннаго круга такую точку, чтобы касательная, проведенная изъ нея къ этой окружности, была вдвое менѣе сѣкущей,
проведенной изъ той же точки черезъ центръ (приложеніемъ алгебры къ геометріи).
231. Черезъ данную внѣ круга точку провести такую сѣкущую, которая раздѣлилась бы этою окружностью въ данномъ отношеніи
(приложеніемъ алг. къ геом.).
282. Построить тр-къ по тремъ его высотамъ Лх, Л8 и Л3. (Предварительно изъ подобія прямоуг. тр-ковъ надо доказать, что высоты
обратно пропорціональны соотвѣтствующимъ сторо
намъ. Если стороны, на которыя опущены высоты Лх, к3 и Л8, обозначимъ соотвѣтственно черезъ 3^, х3 и х3, то
Я/Х • ~ ^2 •
, , , ^2__г, . ^1^2
Х2 ’ Х3—^3 • ^2 — ’ Л8 Л8
^1^2
откуда: хх : х3 : ж8 = Л8 : Лх : -т—
“з
Л । к3
Выраженіе —г— есть четвертая «з
пропорціональная къ к3, к3 и кг.
Построивъ ее (пусть это будетъ к), мы будемъ имѣть три прямыя: к2, к2 и к, которымъ искомыя стороны пропорціональны; значитъ,
тр-къ, имѣющій эти прямыя сторонами, подобенъ искомому,
и потому вопросъ приводится къ построенію такого тр-ка, который, будучи подобенъ данному имѣлъ бы данную высоту. Задача окажется невозможной, если по тремъ прямымъ Лх, к3 и к нельзя построить треугольникъ (52).
Задачи на вычисленіе.
233. По данному основанію а и высотѣ к остроугольнаго тр-ка вычислить сторону х квадрата, вписаннаго въ этотъ тр-къ такъ, чтобы одна сторона квадрата лежала на основаніи тр-ка, а двѣ вершины квадрата—на боковыхъ сторонахъ тр-ка.
234. Стороны тр-ка суть 10 ф., 12 ф. и 17 ф. Вычислить отрѣзки стороны, равной 17 ф., на которые она дѣлится биссектриссою противолежащаго угла.
235. Перпендикуляръ, опущенный изъ вершины прямого угла на гипотенузу, дѣлитъ ее на два отрѣзка т и п. Вычислить катеты.
236. Вычислить высоту тр-ка, опущенную на сторону, равную 20, если двѣ другія стороны суть 12 и 15.
237. Вычислить медіаны тр-ка, котораго стороны суть: а=5, &=7 и ₽=9.
— 195 —
238. Въ тр-кѣ АВС стороны суть: АВ=7, ВС = 15 и 4С=»10. Опредѣлить, какого вида уголъ А, и вычислить высоту, опущенную изъ вершины В.
239. Изъ точки внѣ круга проведены касательная а и сѣкущая. Вычислить длину сѣкущей, зная, что отношеніе внѣшней ея части къ внутренней равно т : п.
240. Къ двумъ кругамъ, которыхъ радіусы суть В и г, а разстояніе между центрами гі, проведена общая касательная. Опредѣлить вычисленіемъ положеніе точки пересѣченія этой касательной съ линіей центровъ,во 1-хъ, когда эта точка лежитъ по одну сторону отъ центровъ во 2-хъ, когда она расположена между ними.
ГЛАВА VII.
Правильные многоугольники.
256. Опредѣленія. Ломаная линія наз. правильной, если она удовлетворяетъ слѣдующимъ тремъ условіямъ:
1°, отрѣзки прямыхъ, составляющіе ее, равны; 2°, углы, составленные каждыми двумя сосѣдними отрѣзками, равны, и 3°, изъ каждыхъ трехъ послѣдовательныхъ отрѣзковъ первый и третій расположены по одну сторону отъ второго.
Таковы, напр., линіи АВСВЕ и ЕОНКЪ (черт. 232); но ле-маную МЕРфВ, нельзя назвать правильною, потому что она не удовлетворяетъ третьему условію.
Правильная ломаная можетъ быть выпуклой (34), какъ, напр., линія АВСВЕ (ломаную ЕОНКЬ нельзя назвать выпуклой).
Многоугольникъ наз. правильнымъ, если онъ ограниченъ правильною ломаною линіей, т.-е. если онъ имѣетъ равныя стороны и равные углы. Таковы, напр., квадратъ, равносторонній треугольникъ и многіе другіе.
13
— 196 —
Многоугольникъ, изображепныйна чертежѣ 233-мъ, есть в ы-п у к л ы й правильный пятиугольникъ; многоугольникъ чертежа 234-го также правильный пятиугольникъ, но не выпуклый
Черт. 233. Черт. 234.
(такъ называемы звѣздчатый). Мы будемъ разсматривать только выпуклые правильные мн-ки.
Послѣдующія теоремы показываютъ, что построеніе правильныхъ многоугольниковъ тѣсно связано съ раздѣленіемъ окружности на равныя части.
257. Теорема. Если окружность раздѣлена на нѣкоторое число равныхъ частей (бблыпее двухъ), то:
1°, соединивъ хордами каждыя двѣ сосѣднія точки дѣленія, получимъ правильный многоугольникъ (вписанный);
2°, проведя черезъ всѣ точки дѣленія касательныя до взаимнаго пересѣченія, получимъ правильный многоугольникъ (описанный).
Черт. 235. Черт. 236.
Пусть окружность (черт. 235) раздѣлена на нѣсколько равныхъ частей въ точкахъ А, В, С..., и черезъ эти точки проведены хорды АВ, ВС... и касательныя ММ, МР... Тогда:
— 197 —
1°. Вписанный многоугольникъ АВСВЕР правильный, потому что всѣ его стороны равны (какъ хорды, стягивающія равныя дуги) и всѣ углы равны (какъ вписанные, опирающіеся на равныя дуги).
2°. Чтобы доказать правильность описаннаго многоугольника МКР($В8, разсмотримъ тр-ки АМВ, БИС и т. д. У нихъ основанія АВ, ВС и т. д. равны; углы, прилежащіе къ этимъ основаніямъ, также равны, потому что каждый ивъ нихъ имѣетъ одинаковую мѣру (уголъ, составленный касательною и хордой, измѣряется половиною дуги, заключенной внутри его). Значитъ, всѣ эти тр-ки равнобедренные и равны между собою, а потому МК=КР... и М=К=... т.-е. мн-къ МКРСВ.8 правильный.
258. Замѣчаніе. Если возьмемъ середины дугъ АВ, ВС, СВ... (черт. 236), то получимъ точки, которыя дѣлятъ окружность на столько же равныхъ частей, на сколько она раздѣлена въ точкахъ А, В, С... Поэтому, если черезъ эти середины проведемъ касательныя до взаимнаго пересѣченія, то получимъ также правильный описанный многоугольникъ; стороны этого многоугольника параллельны сторонамъ вписаннаго мн-ка АВСВЕР (138, обратная теорема).
259. Теорема. Если многоугольникъ правильный, то
1°, около него можно описать окружность;
2°, въ него можно вписать окружность.
1°. Проведемъ окружность черезъ какія-нибудь три сосѣднія вершины А, В и С (черт. 237) правильнаго мн-ка АВСВЕ и докажемъ, что она пройдетъ черезъ слѣдующую четвертую вершину В. Опустимъ изъ центра О перпендикуляръ ОК на хорду ВС и соединимъ О съ А и В. Повернемъ четыреугольникъ АВКО вокругъ стороны ОК такъ, чтобы онъ упалъ на четыреугольникъ ОВСК. Тогда КВ пойдетъ по КС (вслѣдствіе равенства прямыхъ угловъ при точкѣ К), точка
В упадетъ въ С (такъ какъ хорда ВС дѣлится въ точкѣ К пополамъ), сторона ВА пойдетъ по СВ (вслѣдствіе равенства угловъ
— 198 —
В и С) и, наконецъ, точка А уп&р&ть въ В (вслѣдствіе равенства сторонъ ВА и СБ). Изъ этого слѣдуетъ, что О А совмѣстится съ ОВ, и, значитъ, точки И и В одинаково удалены отъ центра; поэтому вершина В должна лежать на окружности, проходящей черезъ А, В и С. Точно такъ же докажемъ, что эта окружность, проходя черезъ три сосѣднія вершины В, С и В, пройдетъ черезъ слѣдующую вершину Е ъ т. д.; значитъ, она пройдетъ черезъ всѣ вершины мн-ка.
2°. Изъ доказаннаго слѣдуетъ, что стороны правильнаго мн-ка всегда можно равсматривать, какъ равныя хорды одной окружности; но такія хорды одинаково удалены отъ центра; значитъ, всѣ перпендикуляры ОМ, опущенные изъ О на стороны многоугольника, равны между собою, и потому окружность, описанная радіусомъ ОМ изъ центра О, будетъ вписанной въ мн-къ АВСБЕ.
260. Слѣдствіе. Изъ предыдущаго видно, что двѣ окруж
ности: описанная около правильнаго мн-ка и вписанная въ него, имѣютъ одинъ и тотъ же центръ. Такъ какъ этотъ общій центръ одинаково удаленъ отъ всѣхъ вершинъ мн-ка, то онъ долженъ лежать на перпендикулярѣ, возставленномъ къ любой сторонѣ изъ ея середины, а будучи одинаково удаленъ отъ сторонъ каждаго угла, онъ долженъ находиться па его биссектриссѣ. По
этому,
чтобы найти ценг санной около п р а ві вписанной въ него, лить точку пересѣче куляровъ, возставле мн-ка изъ ихъ серед сектриссъ угловъ, ил пепдпкуляра съ бисс
261. Опредѣленія. Общі
р ъ окружности опи-ильнаго мн-ка, или достаточно опредѣ-нія двухъ перпенди-нныхъ къ сторонамъ инъ, или двухъ б и с-и одного такого пер-ектриссой.
ій центръ окружностей: опи-
санной около правильнаго мн-ка и вписанной въ него, наз. центромъ этого мн-ка, радіусъ описанной окружности наз. радіусомъ мн-ка, а радіусъ вписанной окружности—а п о-
ѳ е м о ю его.
Уголъ, составленный двумя радіусами, проведенными къ концамъ какой-нибудь стороны правильнаго мн-ка, наз. ц е н т
— 199 —
ральнымъ угломъ. Такихъ угловъ въ мн-кѣ столько, сколько сторонъ; всѣ они равны, какъ измѣряющіеся равными дугами.
Такъ какъ сумма всѣхъ центральныхъ угловъ равна 4й или 360°, то каждый изъ нихъ равенъ 4й : п или 360° : п, если п означаетъ число сторонъ мн-ка; такъ, центральный уголъ правильнаго 6-угольника равенъ 360 : 6=60°,—правильнаго 8-уголь-ника равенъ 360 : 8=45° и т. п.
262. Теорема. Правильные одноименные многоугольники подобны, и стороны ихъ относятся, какъ радіусы или апоѳемы.
1°. Чтобы доказать подобіе (черт. 238) правильныхъ одноименныхъ мн-ковъ АВСБЕЕ и Я1В1С'1В1Е1В1, достаточно обнаружить, что у нихъ углы равны и стороны пропорціональны.
Углы м-ковъ равны, такъ какъ каждый изъ нихъ содержитъ 180(п—2)
одно и то же число градусовъ, и именно---(169,4 ), если п
91»
означаетъ число сторонъ каждаго мн-ка. Такъ какъ АВ=ВС= =СБ=... и Л1В1=В1С1=С1В1=..., то очевидно, что:
АВ _ ВС _ СО _
АгВг ~ В^ ~ ’
т.-е. у такихъ мн-ковъ стороны пропорціональны.
Е______р
/у Е.---------------------Л
л К /Ю. 2е-
\ • 1 \ I \ / I \ /
\ * • X / \ * \ \у
у I V А, М. в.
А м В
Черт. 238.
2°. Пусть О и Оі (черт. 238) будутъ центры данныхъ мн-ковъ, ОА и ОіЛі ихъ радіусы, ОМ и ОгМі—апоѳемы. Тр-ки ОАВ и ОіАіВі подобны, такъ какъ углы одного соотвѣтственно равны угламъ другого. Изъ подобія ихъ слѣдуеъ (203):
АВ __ ОА ОМ
А іВі ОіАі ОіМі
— 200 —
263. Слѣдствіе. Такъ какъ периметры подобныхъ мн-ковъ относятся, какъ сходственныя стороны (209), то периметры правильныхъ одноименныхъ многоугольниковъ относятся, какъ радіусы или апоѳемы.
264. Симметрія правильныхъ многоугольниковъ. Проведемъ въ описанной окружности черезъ какую-нибудь вершину С правильнаго мн-ка (черт. 239, лѣвый) діаметръСЛ^, который раздѣлитъ окружность и многоугольникъ на двѣ части. Вообразимъ, что одна изъ этихъ частей (напр., лѣвая) повернута вокругъ діаметра СЕ,
Черт. 239.
какъ около оси, на столько, чтобы она упала на другую часть (на правую). Тогда одна полуокружность совмѣстится съ другою полуокружностью, дуга СВ совмѣстится съ дугою СВ (по равенству этихъ дугъ), дуга ВА совмѣстится съ дугою ВЕ (по той же причинѣ) и т. д.; слѣд., хорда ВС совпадетъ съ хордой СВ, хорда АВ съ хордой ВЕ и т. д. Такимъ образомъ, діаметръ описанной окружности, проведенный черезъ какую-нибудь вершину правильнаго многоугольника, служитъ осью симметріи этого многоугольника (вслѣдствіе чего каждая пара вершинъ, какъ В и В, А и Е и т. д., лежитъ на одномъ перпендикулярѣ къ діаметру СЕ, на равномъ отъ него разстояніи).
Проведемъ еще въ описанной окружности діаметръ МЕ (черт. 239, правый), перпендикулярный къ какой-нибудь сторонѣ СВ правильнаго мн-ка; этотъ діаметръ тоже раздѣлитъ окружность и многоугольникъ на двѣ части. Вращая одну изъ этихъ частей (лѣвую), вокругъ проведеннаго діаметра до тѣхъ поръ, пока она упадетъ на другую часть (правую), мы такъ же убѣдимся, что одна часть мн-ка совмѣстится съ другой частью. Значитъ, діаметръ описанной окружности, перпендикулярный къ сторонѣ правильнаго многоугольника, служитъ его осью симметріи (и, слѣд., каждая пара вершинъ, какъ В и Е, А и Р и т. д., лежитъ на одномъ перпендикулярѣ къ діаметру МЕ, на равномъ отъ него разстояніи).
Если число сторонъ мн-ка четное, то діаметръ, проведенный черезъ любую вершину мн-ка проходитъ также и черезъ противоположную вершину, и діаметръ, перпендикулярный къ любой сто
— 201 —
ронѣ мн-ка, перпендикуляренъ также и къ противоположной сторонѣ его; если же число сторонъ нечетное, то діаметръ, проходящій черезъ любую вершину, перпендикуляренъ къ противоположной сторонѣ, и обратно, діаметръ, перпендикулярный къ любой сторонѣ, проходитъ черезъ противоположную вершину. Отсюда слѣдуетъ, что во всякомъ правильномъ мн-кѣ есть столько осей симметріи, сколько въ недеъ сторонъ. Напр., въ правильномъ 6-угольникѣ есть 6 осей симметріи, именно: 3 оси, проходящія черезъ вершины, и 3 оси, пер
пендикулярныя къ сторонамъ; въ правильномъ 5-угольникѣ есть 5 осей симметріи; всѣ онѣ проходятъ черезъ вершины угловъ и въ то же время перпендикулярны къ сторонамъ.
Всякій правильный мн-къ четнаго числа сторонъ имѣетъ еще центръ симметріи (102), совпадающій съ центромъ мн-ка (черт. 240). Дѣйствительно, всякая прямая КБ, соединяющая 2 точки контура такого мн-ка и проходящая черезъ центръ О, дѣлится этою точкою пополамъ, какъ это видно изъ равенства тр-ковъ ОВК и ОЕЪ (покрытыхъ на чертежѣ штрихами).
Черт. 240.
265. Задача. Вписать въ ратъ и опредѣлить его мости отъ радіуса.
данный кругъ квад-
сторону въ зависи-
1°. Предположимъ, что АВ (черт. 241) есть сторона квадрата, вписаннаго въ данный кругъ О. Тогда дуга АВ должна равняться х/4 окружности и уголъ АОВ долженъ быть прямой. Поэтому для построенія вписаннаго квадрата (и слѣд., для раздѣленія окружности на 4 равныя части) достаточно провести два перпендикулярныхъ діаметра АС и ВВ и концы ихъ соединить хордами.
Черт. 241.
Вписанный четыреугольникъ АВСВ правильный, потому что
дуги АВ, ВС, СВ и ВА равны, какъ соотвѣтствующія равнымъ
центральнымъ угламъ.
2°. Изъ прямоугольнаго тр-ка АОВ находимъ:
АВ2=А02+В02, т.-е. АВ2=2АО2-
откуда АВ=А0Ѵг2.
— 202 —
Условимся всегда обозначать черезъ а численную величину стороны правильнаго вписаннаго мн-ка, имѣющаго п сторонъ, а черезъ В радіусъ описаннаго круга; тогда выведенное равенство изобразится такъ:
а4=Брг2?
266. Задача. Вписать въ данный кругъ правильный шестиугольникъ и опредѣлить его сторону въ зависимости отъ радіуса.
Предположимъ, чтоЛВ (черт. 242) есть сторона правильнаго вписан. шестиугольника. Тогда дуга ЛВ’должна быть 1Ів часть окружности и, слѣд., уголъ АОВ долженъ содержать 60°. Такъ какъ тр-къ АОВ равнобедренный (АО=ОВ), то углы А и В равны и каждый изъ нихъ содержитъ по 1/2 (180°—60°), т.-е. тоже по 60°. Такимъ образомъ, тр-къ АОВ оказывается равноугольнымъ и, слѣд., равностороннимъ, т.-е. АВ=АО=ОВ. Итакъ, сторона правильнаго вписаннаго шестиугольника равна радіусу, нами обозначенію, можно выразить такъ;
о6=В.
Отсюда возникаетъ весьма простой способъ построенія правильнаго вппс. шестиугольника (и дѣленія окружности на 6 равныхъ частей): давъ циркулю раствореніе, равное радіусу, откладываютъ этимъ раствореніемъ по окружности, одна за другою, равныя дуги и точки дѣленія соединяютъ хордами.
267. Задача. Вписать въ данный кругъ пра-в и л ь н ы й треугольникъ и о п р е дѣлить его сторону въ зависимости отъ радіуса.
1°. Чтобы раздѣлить окружность на 3 равныя части (черт. 243), дѣлятъ ее сначала на 6 равныхъ частей (какъ указано въ предыдущей задачѣ) и затѣмъ соединяютъ по двѣ части въ одну.
2°. Для опредѣленія стороны АВ проведемъ діаметръ ВВ и хорду АВ. Тр-къ АВВ прямоугольный при вершинѣ А; поэтому АВ=Ѵ ВВ2—АВ2. Но ВВ=2В
Черт. 242. что, по принятому
203 —
и АВ—В (потому что дуга АВ есть 1/ъ часть окружности и, слѣд., хорда АВ есть сторона правильнаго вписаннаго шестиугольника);
значитъ:
а3=ѴЗВ2=Б/з7
268. Задача. Вписать въ даппый кругъ правильный десятиугольникъ и опредѣлить его сторону въ зависимости отъ радіуса.
Предварительно докажемъ слѣдующее свойство правильнаго
десятиугольника.
Пусть хорда АВ (черт. 244) есть сторона такого многоугольника. Тогда уголъ АОВ равенъ 36°, а каждый изъ угловъ Ли В содержитъ по % (180°—36°), т.-е. по 72°. Раздѣлимъ уголъ А
пополамъ прямою АС. Каждый изъ угловъ, образовавшихся
при точкѣ А, равенъ 36°; слѣд., тр-къ АСО, имѣя два равные угла, есть равнобедренный, т.-е. АС=СО.Тр-къ АВС также равнобедренный, потому что В=72О; и С=180°—72°—36°=72°; слѣд., АВ= АС=СО. По свойству биссектриссы угла тр-ка (226) можемъ написать:
АО : АВ=ОС : СВ [1]
Черт. 244.
Замѣнивъ АО и АВ равными имъ прямыми ОВ и ОС, получимъ: ОВ : ОС=ОС : СВ, [2]
т.-е. радіусъ ОВ раздѣленъ въ точкѣ С въ среднемъ и крайнемъ отношеніи (253), при чемъ ОС есть его большая часть. Но ОС равна сторонѣ прав. впис. десятиугольника; значитъ:
сторона правильнаго вписаннаго десятиугольника равна ббльшей части радіуса, раздѣленнаго въ среднемъ и крайнемъ отношеніи.
Теперь задача рѣшается легко:
1°. Дѣлятъ радіусъ круга (напр., О А, черт. 245) въ среднемъ и крайнемъ отношеніи (253); затѣмъ, давъ циркулю раствореніе, равное
Черт. 245.
— 204 —
большей части радіуса, откладываютъ имъ по окружности дуги, одна за другою, и точки дѣленія соединяютъ хордами.
2°. Обозначивъ численную величину стороны правильнаго вписаннаго 10-угольника черезъ х, мы можемъ пропроцію [2] переписать такъ:
В. : х=х : (В—«), откуда х2-\-Вх—В2=о.
Рѣшивъ это квадратное уравненіе, найдемъ: р/5-1 х=а10=К------------------------.
2
269. Замѣчанія. 1°. Формулы, выведенныя нами въ предыдущихъ задачахъ для а4, а6, а3, а10, позволяютъ вычислить радіусъ описаннаго круга по данной сторонѣ правильнаго многоугольника. Такъ, изъ выраженія, опредѣляющаго а10, находимъ: 2а10 2а10 (}/ 54-1) 1 /.— \
=2“10 Ѵ^1 )
2°. Чтобы вписать въ данный кругъ правильный пятиугольникъ, дѣлятъ окружность на 10 равныхъ частей (какъ указано выше) и точки дѣленія соединяютъ черезъ одну хордами.
270. Задача. Вписать въ данный кругъ правильный пятиугольникъ.
Чтобы найти 1/15 окружности, достаточно изъ 1/6 ея части вычесть Ѵ10, какъ это видно изъ слѣдующаго равенства:
1 1_5 3 _ 2 _1 10 ~ 30 30~30—15
Поэтому если хорда АВ (черт. 246) равна радіусу, а хорда АС—большей части радіуса, раздѣленнаго въ среднемъ и крайнемъ отношеніи, то дуга СВ должна быть 1/15 окружности, а хорда СВ—сторона прав. впис. 15-уголыіика.
Вычисленіе стороны СВ можно выполнить, примѣняя теорему Птоломея (242) къ четыреугольнику АСВЛ, въ ко
Черт. 246.
— 205 —
торомъ ЛС = а10, СВ — а13, АБ—2В, АВ = ав = В, СБ = ']/Г4Н:‘—а102, ВБ = а3 (такъ какъ дуга ВБ равна ’/3 окружности).
Теорема Птоломея даетъ:
АВ . СБ = АБ . СВ + АС . ВБ,
т.-е. В~\Г 4ц2—«і02=2В . а15 + а10«3-
Подставивъ на мѣсто а10 и а3 ихъ выраженія, получимъ послѣ упроціеній:
271. Задача. По данному радіусу круга и сторонѣ правильнаго вписаннаго многоугольника вычислить сторону правиль-
наго одноименнаго описаннаго
много-
угольника.
Пусть АВСТ)... есть прав. вписанный мн-къ, а МЕР... одноименный прав. описанный (257). Такъ какъ стороны правильныхъ одноименныхъ мн-ковъ относятся, какъ ихъ радіусы или апоѳсмы (262), то:
МЕ : ЛВ=0В : ОЕ.
Черт. 247.
ОВ .АВ ОВ . ЛВ
Откуда: МЕ — ——— = —
ОЕ у ОВ2—ВЕ2
Обозначивъ численныя величины МЕ, АВ и ОВ соотвѣтственно черезъ Ьп, ап и В и замѣтивъ, что ВЕ—1^ ЛВ, будемъ имѣть:
4
Примѣръ. Вычислимъ сторону правильнаго описаннаго 10-угольника:
В°10 - 2В
4
«іо2
4В2—йі 02
2В
(/ 5—I)2 16—(/Г—I)2
— 206 —
= 2В1/ 2Д1/ (3-/[Х-бП)_„
V ЮЧ-зѴб г (5+Кб)(5— /б)
/5—2 Ѵб.
““б
272. Замѣчаніе. Формула, опредѣляющая Ьп, позволяетъ вычислить оп по даннымъ Ъп и В. Для этого стоитъ только рѣшить уравненіе, принимая а„ за неизвѣстное:
ѵ(в2~-^=лЧ2; Ьп2В2=ап
Оп
273. Задача. Удвоитьчисло сторонъ правиль-наго вписаннаго многоугольника.
Въ этомъ сокращенномъ выраженіи разумѣется собственно двѣ задачи: 1°, по дапному правильному впис. мн-ку п о-строить другой правильный С _ мн-къ, вписанный въ ту же ок-
""'Х. ружность и имѣющій вдвое болѣе сторонъ; 2°, вычислить сто-/х. В \ р о н у этого мн-ка по данной сто-
ронѣ перваго мн-ка и данному радіусу круга.
Черт. 248. 1°. Пусть АВ (черт. 248) есть
сторона прав. впис. мн-ка, имѣющаго п сторонъ и О центръ круга. Проведемъ ОС±_АВ и соединимъ. А съ С. Дуга АВ дѣлится въ точкѣ С пополамъ; слѣд., хорда АС есть сторона прав. впис. мн-ка, имѣющаго 2п сторонъ.
2°. Въ тр-кѣ АСО уголъ О всегда острый (такъ какъ дуга АСВ всегда меньше полуокружности и, слѣд., половина ея, дуга АС, меньше четверти окружности); поэтому (236): АС2—0А2+0С2—2ОС . ОВ.
т.-е. а2я2 =В2+В2— 2В . 0В=2В2—2В, . ОВ.
Изъ прямоугольнаго тр-ка АОВ опредѣлимъ катетъ ОВ-.
ОВ=і/ А02—АВ2=
о 2 В2—~ 4
— 207 —
слѣд.:
а2„=1 / 2В2—2й1/ В2——2
Г 4
Такова формула удвоенія числа сторонъ правильнаго вписан-нако многоугольника *).
Примѣръ. Вычислимъ сторону прав. впис. 12-угольника:
/ 1 /" л 2 / л Г
«12=1/ 2Я2—2й|/Я2—^- = 1/ 2В2—2В|/ 2-=
/1 Г о ---------. ---—
2В2—2В2 V — =1/2В2—В2 К 3 = В]/ 2— /з.
4 г Г
274. На сколько равныхъ частей можно дѣлить окружность помощью циркуля и линейки? Примѣняя указанные въ предыдущихъ задачахъ способы, мы можемъ помощью циркуля и линейки дѣлить окружность на такое число равныхъ частей (и слѣд., вписывать въ окружность правильные многоугольники съ такимъ числомъ сторонъ), которое заключается въ слѣдующихъ рядахъ:
3, 3.2, 3.2.2...вообще 3.2“
4, 4.2, 4.2.2...вообще 2“
5, 5.2, 5.2.2...вообще 5.2“
15, 15.2, 15.2.2...вообще 3.5.2"
Германскій математикъ Гауссъ (умершій въ 1855 г.) доказалъ, что посредствомъ циркуля и линейки можно дѣлить
окружность на такое число равныхъ частей, которое, будучи простымъ, выражается формулою 2" 4-1. Напр., можно раздѣлить окружность на 17 равныхъ частей и на 257 равныхъ частей, такъ какъ 17 и 257 суть простыя числа вида 2"4-1 (17=24-|-1, 257=284-1). Доказательство Гаусса выходитъ изъ предѣловъ элементарной математики.
Доказано также, что помощью линейки и циркуля окружность можно дѣлить на такое составное число равныхъ
♦) Сложные радикалы, получаемые изъ формулы удвоенія, могутъ быть преобразованы въ сумму или разность двухъ простыхъ радикаловъ (см. алгебра А. Киселева, § 238); напр., для а13 можно получить такое выраженіе: а12=1/2К(ѴЛ6—Ѵ2).
— 208 —
частей, которое, разложенное на простыхъ множителей, не содержитъ никакихъ иныхъ множителей, кромѣ множителей вида 2„4-1 при условіи, что эти множители всѣ различны, и множителя 2 въ какой угодно степени. Напр., въ окружность помощью цпркуля и линейки можно вписать правильный 170-угольникъ (170=2.5.17), но нельзя вписать правильный 9-угольникъ (хотя множитель 3 имѣетъ видъ 2И+1, но въ составѣ 9-и онъ повторяется).
На всякое иное число равныхъ частей окружность можетъ быть раздѣлена только приближенно.
275. Построеніе правильнаго многоугольника по данной сторонѣ. Для различныхъ правильныхъ многоугольниковъ существуютъ различные способы. Но можно указать слѣдующій общій способъ. Чертятъ окружность произвольнаго радіуса и вписываютъ въ пее правильный мн-къ съ такимъ числомъ сторонъ, которое должно быть у искомаго мн-ка; затѣмъ на данной сторонѣ строятъ мн-къ, подобный описанному (210).
УПРАЖНЕНІЯ.
241. Составить формулу для стороны правильнаго вписаннаго 24-угольника.
242. Составить формулы для сторонъ правильныхъ вписанныхъ 8-угольника и 16-угольника.
243. Исходя изъ формулы удвоенія, опредѣлить сторону правильнаго вписаннаго б-угольника.
244. Составить формулы для сторонъ правильныхъ описанныхъ треугольника и ціестиугольника.
245. Доказать, что если въ прав. б-угольникѣ проведемъ всѣ діагонали, то онѣ своими пересѣченіями образуютъ внутренній прав. 5-угольникъ.
246. Пусть АВ, ВС и СВ будутъ три послѣдовательныя стороны правильнаго мн-ка, имѣющаго центръ въ О. Если продолжимъ стороны АВ и СВ до рзаимнаго пересѣченія въ точкѣ Е, то четыреугольникъ ОАЕС можетъ быть вписанъ въ окружность.
247. Доказать, что: 1°, всякій вписанный равносторонній многоугольникъ есть правильный; 2°, равноугольный вписанный мн-къ есть правильный, когда число сторонъ его нечетное; 3°, всякій описанный равноугольный мн-къ есть правильный; 4°, описанный равносторонній мн-къ есть правильный, когда число сторонъ его нечетное.
— 209 —
248. Доказать, что двѣ діагонали правильнаго 5-угольника, не исходящія изъ одной вершины, пересѣкаются въ среднемъ и крайнемъ отношеніи.
249. На данной сторонѣ построить правильный 8-угольникъ.
250. На данной сторонѣ построить правильный 10-угольникъ.
251. Срѣзать отъ даннаго квадрата углы такъ, чтобы образовался правильный 8-угольникъ.
252. Въ данный квадратъ вписать равносторонній тр-къ, помѣщая одну изъ его вершинъ или въ вершинѣ квадрата, или въ серединѣ какой-либо стороны.
253. Вписать въ равносторонній тр-къ другой равносторонній треугольникъ, котораго стороны были бы перпендикулярны къ сторонамъ даннаго.
254. Построить углы: въ 18, въ 30, въ 75, въ 72 градуса.
КНИГА IV.
ВЫЧИСЛЕНІЕ ДЛИНЫ ОКРУЖНОСТИ И ЕЯ ЧАСТЕЙ.
ГЛАВА I.
Основныя свойства предѣловъ.
276. Величины постоянныя и перемѣнныя. Рѣшая какой-либо вопросъ, въ который входятъ нѣсколько величинъ, мы иногда предполагаемъ, что нѣкоторыя изъ этихъ величинъ сохраняютъ одно и то же неизмѣнное значеніе, тогда какъ другія способны принимать безчисленное множество различныхъ значеній. Первыя величины наз. постоянными, вторыя перемѣнными. Такъ, разсматривая зависимость между длиною хорды и ея разстояніемъ отъ центра, мы считаемъ радіусъ круга величиною постоянною, а длину хорды и ея разстояніе отъ центра—величинами перемѣнными.
Впрочемъ, нѣкоторыя величины являются постоянными не потому, что мы ихъ такими предполагаемъ, а вслѣдствіе своего основного свойства; такова, напр., сумма угловъ тр-ка, которая всегда равна 2д,.
Если величины выражены числами, то постоянной величинѣ соотвѣтствуетъ постоянное число, апере мѣнной величин ѣ—п еремѣпное число.
А. Киселевъ. Геометрія. 14
210 —
Черт. 249.
277. Перемѣнныя величины, стремящіяся къ нулю. Если перемѣнная величина (и перемѣнное число, измѣряющее ее), измѣняясь, дѣлается меньше любого даннаго значенія, какъ бы мало это значеніе ни было, и при дальнѣйшемъ измѣненіи постоянно остается меньше этого значенія, то говорятъ, что эта перемѣнная величина стремится къ нулю.
Напр., если черезъ какую-нибудь точку А окружности (черт. 249) проведемъ касатель-•—Т НуЮ и сѣкущую АМ и затѣмъ станемъ вращать сѣ-} кущую вокругъ точки касанія
/ такъ, чтобы вторая точка, пере-
' сѣченія В все ближе и ближе
Л придвигалась къ точкѣ А, то
при этомъ уголъ ТАМ, составленный касательною и сѣкущею, стремится къ нулю, по-
тому что, какъ мы это говорили прежде (143,) равный ему уголъ АОВ, составленный радіусомъ АО и перпендикуляромъ ОВ на хорду АВ, можетъ сдѣлаться меньше любого даннаго угла, напр. меньше угла въ 1', и, при дальнѣйшемъ сближеніи точекъ пересѣченія, постоянно остается меньше этого угла.
Точно такъ же центральный уголъ правильнаго многоугольника, котораго величина равна 4й/п, стремится къ нулю, если п, т.-е. число сторонъ этого мн-ка, неограниченно возрастаетъ; папр., при п=100 этотъ уголъ равенъ 0,04(2, при п=1000 онъ дѣлается 0,004<2 и т. д.
278. Перемѣнныя величины, увеличивающіяся безпредѣльно. Если перемѣнная величина (и перемѣнное число, измѣряющее ее), измѣняясь, дѣлается и остается больше любого даннаго значенія, какъ бы велико это значеніе ни было, то говорятъ, что она увеличивается безпредѣльно (или неограниченно) *).
*) Величины, увеличивающіяся безпредѣльно, принято въ математикѣ называть безконечно большими, а величины стремящіяся къ нулю, —б езконечно малыми. Въ этой книгѣ мы не будемъ однако употреблять этихъ терминовъ для избѣжанія нѣкоторой неясности представленія въ умѣ учащагося.
211 —
Напр., сумма угловъ выпуклаго многоугольника, равная 2сІ(п—2)=2<іп—4й, при неограниченномъ возрастаніи числа сторонъ увеличивается безпредѣльно; такъ, при п=100 она равна 196Л, при п=1000 она дѣлается 1996Й и т. д.
279. Перемѣнныя величины, стремящіяся къ предѣлу. Иногда случается, что перемѣнная величина, измѣняясь, стремится къ нѣкоторому предѣлу.
Предѣломъ перемѣнной величины наз. такая постоянная величина, къ которой перемѣнная приближается такъ, что разность между ними стремится къ нулю, т.-е. эта разность дѣлается и остается меньше любого даннаго значенія, какъ бы мало это значеніе ни было.
Приведемъ два примѣра перемѣнныхъ величинъ, стремящихся къ предѣламъ.
Черт. 250.
1°. Разсмотримъ (черт 250), процессъ измѣренія какой-нибудь длины А, несоизмѣримой съ единицею В Чтобъ измѣрить такую длину (158, 2°), мы дѣлимъ В на п равныхъ частей и одну изъ нихъ откладываемъ на А столько разъ, сколько можно. Тогда мы получаемъ соизмѣримую длину ЛІ5 которая меньше А; если же отложимъ х/я долю В еще одинъ разъ, то получимъ другую соизмѣримую длину А2, которая больше А; при этомъ каждая изъ разностей А—Лі и А2—А меньше 1/п доли В. Предположимъ теперь, что число п равныхъ частей, на которое мы дѣлимъ В, увеличивается неограниченно. Тогда длины Аг и А2 становятся перемѣнными, а длина А остается постоянной; такъ какъ г/п доля В при достаточномъ увеличеніи числа п можетъ быть сдѣлана меньше любой данной длины (напр., меньше миллиметра) и при дальнѣйшемъ увеличеніи п она постоянно остается меньше этой малой длины, то можно сказать, что перемѣнныя величины Аі и А2 стремятся при этомъ къ общему предѣлу А.
Изъ этого примѣра мы видимъ, что перемѣнная величина, приближаясь къ своему предѣлу, можетъ быть или меньше
14*
— 212 —
его, или больше; такъ, длина Лх постоянно меньше, чѣмъ А, а длина Л2, наоборотъ, всегда больше А.
2°. Сумма всѣхъ внутреннихъ угловъ выпуклаго многоугольника, имѣющаго п сторонъ, выражается, какъ извѣстно (89), формулой 2й(п—2); поэтому величина одного угла правильнаго п-угольника равна:
2й(п—2) 2Лп—4й 4й
—------=--------=2гі----.
п п п
Предположимъ, что число сторонъ многоугольника, т.-е. число п, неограниченно увеличивается; тогда, какъ видно изъ приведенной формулы, величина угла мн-ка, оставаясь всегда меньше 2й, все болѣе и болѣе приближается къ 2И такъ, что 4гі
разность между ними, равная —, дѣлается и остается меньше п
какого угодно угла. Поэтому можно сказать, что уголъ правильнаго мн-ка, при неограниченномъ увеличеніи числа его сторонъ, имѣетъ предѣлъ 2сІ.
280. Замѣчаніе. Если перемѣнная величина а, измѣняясь, остается постоянно бблыпей своего предѣла А, то ее можно разсматривать, какъ сумму А-}-х; если же перемѣнная величина а, измѣняясь, остается постоянно меньшей своего предѣла А, то ее можно разсматривать, какъ разность А—х; и въ томъ, и въ другомъ случаяхъ х означаетъ нѣкоторую положительную величину, которая, согласно опредѣленію предѣла, стремится къ нулю, когда перемѣнная величина а стремится къ своему предѣлу А.
281. Теорема. Если двѣ перемѣнныя величины, стремящіяся къ предѣламъ, при всѣхъ своихъ послѣдовательныхъ измѣненіяхъ остаются равными между собою, то равны и ихъ предѣлы.
Пусть а и Ъ двѣ перемѣнныя величины, а Ли В ихъ предѣлы; положимъ, что при всѣхъ послѣдовательныхъ измѣненіяхъ перемѣнныя величины а и Ъ всегда равны между собою; требуется доказать, что въ такомъ случаѣ и Л==В.
Предположимъ, что обѣ перемѣпныя величины а и Ъ, измѣняясь, остаются постоянно меньшими своихъ предѣловъ. Тогда
— 213 —
можно принять, что а=А—х и Ъ=В—у, гдѣ х и у нѣкоторыя положительныя величины, стремящіяся къ нулю. Такъ какъ, по условію, а=Ъ, то можно написать:
А—х=В—у.
Докажемъ, что это равенство возможно только тогда, когда А=В (и, слѣд., х=у). Перенеся въ этомъ равенствѣ постоянные члены въ одну часть, а перемѣнные въ другую, получимъ:
А—В=х—у.
Лѣвая часть послѣдняго равенства, представляя собою разность между постоянными величинами, должна равняться или нулю (если А=В), или нѣкоторой постоянной величинѣ. Правая часть того же равенства, представляя собой разность между такими перемѣнными величинами, которыя обѣ стремятся къ нулю, должна равняться или пулю (если х=у), или нѣкоторой перемѣнной величинѣ, стремящейся къ нулю. Такъ какъ постоянная величина не можетъ равняться перемѣнной величинѣ, то написанное равенство возможно только тогда, когда обѣ его части равны нулю, т.-е. только тогда, когда А=В (и х=у).
Подобнымъ же образомъ можно доказать, что А=В и въ томъ случаѣ, когда перемѣнныя а и Ъ остаются большими своихъ предѣловъ *).
282. Теорема. Если двѣ перемѣнныя величины, стремящіяся къ предѣламъ, при всѣхъ своихъ измѣненіяхъ сохраняютъ одно и то же отношеніе, то въ томъ же отношеніи находятся и ихъ предѣлы.
Пусть а и Ъ двѣ перемѣнныя величины, а Ли В ихъ предѣлы, и положимъ, что при всѣхъ измѣненіяхъ величины а и Ъ постоянно удовлетворяютъ пропрціи:
а : Ь—т : п, гдѣ т и п какія-нибудь постоянныя данныя числа. Требуется доказать, что въ такомъ слуачѣ и
А : В=т : п.
*) и даже въ томъ случаѣ, когда онѣ, измѣняясь, дѣлаются то меньшими, то большими своихъ предѣловъ.
— 214 —
Предположимъ снова, что обѣ перемѣнныя, измѣняясь, остаются меньшими своихъ предѣловъ; тогда можно принять, что а=А—х и Ъ=В—у, гдѣ вычитаемыя х и у суть нѣкоторыя положительныя величины, стремящіяся къ нулю. Подставивъ въ данную пропорцію на мѣсто а и Ь равныя имъ разности А—х и В—у, получимъ:
(Л—х) : (В—у)=т : п.
Откуда: (А—х) п=(В—у) т,
т.-е. Ап—пх—Вт—ту.
Такъ какъ величины х и у стремятся къ О, то и произведенія пх и ту стремятся къ О *); вслѣдствіе этого разности Ап—пх и Вт—ту представляютъ собою перемѣнныя величины, стремящіяся къ предѣламъ: первая разность—къ постоянной величинѣ Ап, а вторая разность—къ постоянной величинѣ Вт. Но если равны перемѣнныя, стремящіяся къ предѣламъ, то равны и ихъ предѣлы (281; значитъ:
Ап=Вт\ откуда: А : В—т : п.
283. Основное начало способа предѣловъ. Двѣ предыдущія теоремы составляютъ частные случаи слѣдующаго важнаго предложенія, которое мы примемъ безъ доказательства:
Если какое-либо равенство, содержащее перемѣнныя величины, стремящіяся къ предѣламъ, остается вѣрнымъ при всѣхъ измѣненіяхъ перемѣнныхъ, то оно остается вѣрнымъ и тогда, когда на мѣсто перемѣнныхъ подставимъ ихъ предѣлы.
Это предложеніе служитъ основаніемъ такъ называемому способу предѣловъ, которымъ иногда пользуются для доказательства нѣкоторыхъ геометрическихъ истинъ.
284. Понятіе О способѣ предѣловъ. Этотъ способъ состоитъ въ слѣдующемъ. Положимъ, что мы желаемъ
*) т.-е. каждое изъ этихъ произведеній дѣлается (и остается) меньше любого даннаго положительнаго числа, какъ бы мало это число ни было; напр., произведеніе пх дѣлается (и остается) меньше дроби 1-й милліонной, такъ какъ число х, измѣняясь, дѣлается (и остается) меньше Ѵп милліонной.
— 215 —
найти зависимость между нѣкоторыми постоянными величинами А и В, и допустимъ, что эту зависимость трудно (или даже невозможно) найти непосредственно. Тогда задаемся вопросомъ: нельзя ли величины Л и В разсматривать, какъ предѣлы нѣкоторыхъ перемѣнныхъ величинъ а и Ъ, и если возможно, то какова зависимость между а и Ъ? Положимъ, оказалось, что эта зависимость выражается равенствомъ:
а=ЗЪ2,
которое остается вѣрнымъ при всѣхъ измѣненіяхъ а и Ъ-, въ такомъ случаѣ можемъ принять, что это равенство остается вѣрнымъ и тогда, когда на мѣсто а и Ъ подставимъ ихъ предѣлы, т.-е., что и
л=зв2.
Такимъ образомъ, зависимость между Л и В мы найдемъ косвеннымъ путемъ, отыскавъ предварительно зависимость между перемѣнными.
Примѣненіе этого способа мы вскорѣ увидимъ.
ГЛАВА II.
Вычисленіе длины окружности.
285. Предварительное разъясненіе. Конечную прямую можно сравнивать съ другою конечною прямою, принятою за единицу, вслѣдствіе того, что прямыя линіи при наложеніи совмѣщаются. Дѣйствительно, только по этой причинѣ мы можемъ совершенно точно установить, какіе отрѣзі и прямыхъ считать равными и неравными, что такое сумма отрѣзковъ прямой, какой отрѣзокъ болѣе другого въ 2, 3, 4... раза и т. п. Точно такъ же дуги окружностей одинаковаго радіуса можно сравнивать между собою вслѣдствіе того, что такія дуги при наложеніи совмѣщаются. Но извѣстно, что никакая часть окружности (или другой кривой) не можетъ совмѣститься съ прямой (121); поэтому нельзя установить пу
— 216 —
темъ наложенія, какой криволинейный отрѣзокъ должно считать равнымъ данному прямолинейному отрѣзку, а слѣд., и то, какой криволинейный отрѣзокъ больше даннаго прямолинейнаго въ 2,3,4...раза.Такимъобразомъ,являетсянеобходимость опредѣлить, что мы разумѣемъ подъ длиною окружности (или части ея), когда сравниваемъ ее съ прямолинейнымъ отрѣзкомъ.
286. Опредѣленіе длины окружности и ея дуги. Впишемъ въ данную окружность (черт. 251) какой-нибудь выпуклый многоугольникъ АВСБЕЕ и найдемъ его р периметръ. Пусть это будетъ конечная
О прямая (черт. 252). Впишемъ въ ту же окружность какой-пибудь другой выпуклый мн-къ, у котораго стороны были бы меньше (и, слѣд., число сторонъ больше), чѣмъ у перваго мн-ка; найдемъ его периметръ; пусть это бу-Е детъ прямая Р2 (черт. 252). Впишемъ
далѣе въ нашу окружность третій мн-къ Черт. 251. , .
(онъ не указанъ на чертежѣ), у котораго стороны были бы еще меньше (и, слѣд., число сторонъ еще больше) и найдемъ его периметръ; пусть это будетъ прямая Р3. Вообра-
--------------------------------------------------1
р2|----------------------------------------------------1
ді-----------------------------------------------------1
!>-------------------------------------------------------
Ы----------------------------------------------------------1
Черт. 252.
зимъ теперь, что мы вписываемъ въ данную окружность все новые и новые мн-ки, у которыхъ стороны неограниченно уменьшаются, и каждый разъ находимъ ихъ периметры. Тогда мы получимъ безконечный рядъ периметровъ Р1( Р2, Р3, Р4....
— 217 —
Можно доказать *), что этотъ рядъ стремится къ опредѣленному предѣлу (напр., къ длинѣ Ь, черт. 252), не зависящему отъ того, по какому закону мы уменьшаемъ стороны вписанныхъ многоугольниковъ (и, слѣд., увеличиваемъ число ихъ сторонъ). Мы можемъ, напр., вписывать въ данную окружность мн-ки по такому закону: сначала впишемъ квадратъ (черт. 253); затѣмъ впишемъ правильный 8-угольникъ, далѣе правильный 16-угольникъ, потомъ 32-угольникъ и т. д., и т. д., все удваивая число сторонъ правильныхъ мн-ковъ. Можемъ
поступить и такъ: сначала впишемъ правильный 6-угольникъ (черт. 254), затѣмъ правильный 12-угольникъ, далѣе 24-уголь-никъ и т. д., и т. д., все удваивая число сторонъ мн-ковъ. Можемъ вписывать мн-ки и по какому угодно иному закону, причемъ вписываемые мн-ки могутъ быть и неправильные. Всегда окажется, что если только стороны вписаннаго выпуклаго мн-ка неограниченно уменьшаются, то периметръ его стремится къ одному и тому же предѣлу, опредѣленному для данной окружности. Этотъ предѣлъ принимается за длину окружности. Такимъ образомъ: за длину окружности принимаютъ предѣлъ, къ которому стремится периметръ вписаннаго въ эту окружность выпуклаго многоугольника, когда стороны его неограниченно уменьшаются.
') Доказательство помѣщено ниже, въ § 298.
— 218 —
Подобно этому за длину дуги (АВ, черт. 255) окруж-
ности (и вообще за длину какой-нибудь конечной кривой) принимаютъ предѣлъ, къ которому стремится периметръ ломаной линіи, вписанной въ эту дугу и имѣющей съ нею одни и тѣ же концы, когда стороны этой ломаной неограниченно уменьшаются.
287. Слѣдствія.
1°. Равныя дуги и равныя окружности имѣютъ одина-
ковыя длины.
Черт. 256.
Дѣйствительно, если дуги АВ и СВ (черт. 256) равны, то это значитъ, что онѣ при наложеніи совмѣщаются. Вслѣдствіе этого ломанныя линіи, вписываемыя въ нихъ, можно брать совершенно одинаковыми. Но тогда периметры этихъ ломаныхъ будутъ, конечно, стремиться къ одному и тому же предѣлу; а этотъ предѣлъ, согласно опредѣленію, и есть длина дуги какъ АВ, такъ и СВ.
То же самое можно повторить о равныхъ окружностяхъ.
2°. Длина суммы дугъ равна суммѣ длинъ этихъ дугъ.
Если дуга АВС (черт. 257) есть сумма двухъ дугъ АВ и ВС, то мы
можемъ вписывать ломаную линію въ дугу АВС такимъ образомъ, чтобы она всегда была составлена изъ двухъ ломаныхъ, сходящихся въ точкѣ В; тогда одна изъ нихъ будетъ вписана въ дугу АВ, а другая въ дугу ВС. При такомъ способѣ вписыванія, очевидно, предѣлъ периметра ломаной, вписаной въ дугу АВС, равенъ суммѣ предѣловъ периметровъ ломаныхъ, вписанныхъ въ дуги АВ и ВС; а это значитъ, что длина дуги АВС равна суммѣ длинъ дугъ АВ и ВС.
Въ частности, напр., длина цѣлой окружности, разложенной на нѣсколько дугъ, равна суммѣ длинъ всѣхъ этихъ дугъ.
288. Теорема. Длина дуги больше стягивающей ее хорды, но меньше всякой ломаной линіи, описанной около этой дуги и имѣющей съ нею одни и тѣ же концы.
— 219 —
1°. Пусть АСВ (черт. 258) есть дуга окружности, а АВ стягивающая ее хорда; требуется доказать, что длина дуги больше этой хорды.—Предположимъ, что въ дугу АСВ мы вписываемъ ломаныя линіи по такому закону: первая ломаная пусть будетъ какая угодно, напр., ломаная, со-
ставленная изъ 2-хъ хордъ АС и СВ- ____ -
вторая ломаная пусть будетъ АБСЕВ, Р
составленная изъ 4-хъ хордъ, при-
чемъ вершины первой ломаной, т.-е. и
точки А, С и В пусть входятъ также Черт. 258.
въ число вершинъ и второй ломаной.
Третья ломаная (не указана на чертежѣ) пусть будетъ такая, которая составлена изъ 8-ми хордъ, причемъ вершины второй ломаной, т.-е. точки А, В, С, Е и В, пусть входятъ также и въ число вершинъ третьей ломанной. Такимъ же образомъ вписывается четвертая ломаная, затѣмъ пятая и т. д. безъ конца. При такомъ законѣ вписыванія периметръ ломаной, съ каждымъ удвоеніемъ числа ея сторонъ, будетъ все возрастать (напр., АВ+ВС+СЕ+ЕЕ^>АС+СВ, такъ какъ АВ-\-БС^>АС и СЕ+ЕВ>СВ)-, вслѣдствіе этого предѣлъ, къ которому стремится этотъ периметръ, долженъ быть больше периметра первой ломаной, т.-е. суммы АС+СВ, и, значитъ, долженъ быть, и подавно, больше хорды АВ (53). Но предѣлъ, къ которому стремится периметръ вписанной ломанной линіи принимается за длину дуги АВ-, значитъ, эта длина больше хорды АВ.
2°. Пусть ломаная линія АСВ (черт. 259) описана около дуги АВ и имѣетъ съ этою дугою одни и тѣ же концы А и В; требуется доказать, что длина дуги С
меньше длины этой ломаной; дру- /X
гими словами, требуется доказать, что / X. предѣлъ В, къ которому стремится А,— -------
периметръ выпуклой ломаной ли-ніи вписанной въ дугу АВ, при неогра-
ничейномъ уменьшеніи ея сторонъ, Черт. 259.
меньше суммы АС-[-СВ, которую мы для краткости обозначимъ одною буквою 5. Для доказательства возьмемъ вспомогательную ломаную АтпВ, которая получится, если мы срѣжемъ уголъ С какимъ-нибудь отрѣзкомъ прямой тп, не пересѣкаю
— 220 —
щимся съ дугою АВ (что всегда возможно, если ломаная АСВ описана, т.-е. составлена изъ касательныхъ). Обозначимъ длину этой вспомогательной ломаной буквою 8^ Такъ какъ тп<^тС+Сп, то 8Х<^8. Докажемъ теперь, что предѣлъ Е не можетъ быть больше 8Х. Предположимъ противное, т.-е. что Е>8Х. Такъ какъ перемѣнная величина приближается къ своему предѣлу какъ угодно близко, то периметръ вписанной въ дугу АВ ломаной линіи, при достаточномъ уменьшеніи ея сторонъ, можетъ приблизиться къ своему предѣлу Е настолько близко, что разность между Е и этимъ периметромъ сдѣлается меньше постоянной разности Е—8Х; тогда, значитъ, периметръ вписанной ломанной сдѣлается больше 8Х. Но это невозможно, такъ какъ всякая выпуклая ломаная линія, вписанная въ дугу АВ, есть объемлемая по отношенію къ объемлющей ломаной АтпВ, и потому первая должна быть меньше второй (55). Слѣд., нельзя допустить, что значитъ, Е<8Х и такъ какъ 8Х<С8, то Ь<^8.
289. Замѣчаніе. Доказательство обѣихъ частей этой теоремы остается въ полной силѣ и тогда, когда дуга, о которой говорится въ теоремѣ, будетъ не дуга окружности, а часть какой-нибудь иной кривой, лишь бы только эта часть кривой была выпуклая, т.-е. такая, которая расположена по одну сторону отъ каждой своей касательной.
290. Слѣдствіе, вписанъ какой-нибудь описанъ какой-нибудь
Черт. 260.
О
Пусть въ данную окружность (черт. 260) выпуклый многоугольникъ АВСВ и многоугольникъ МШРС^В. Такъ какъ дуга АВ больше хорды АВ, дуга ВС больше хорды ВС и т. д., то длина окружности больше периметра вписаннаго многоугольника. Оь другой стрроны, такъ какъ дуга аЪ меньше описанной ломаной линіи аМ-\-МЪ, дуга Ьс меньше описанной ломаной линіи ЫІ+ІІс и т. д., то длина окружности меньше периметра описаннаго многоугольника.
Напр., длина окружности больше
периметра правильнаго вписаннаго шестиугольника и меньше
— 221 —
периметра описаннаго квадрата; значитъ, длина окружности больше 6-ти радіусовъ и меньше 8-ми радіусовъ (такъ какъ сторона правильнаго вписаннаго шестиугольника равна радіусу, а сторона описаннаго квадрата равна діаметру).
Для болѣе точнаго вычисленія длины окружности въ зависимости отъ радіуса докажемъ слѣдующую теорему.
291. Теорема. Длины окружностей относятся, какъ ихъ радіусы или діаметры.
Пусть Ви Ві (черт. 261) будутъ радіусы двухъ окружностей, а С и Сг ихъ длины; требуется доказать, что
С : (\=В : 7?і=27? :27?і.
Впишемъ въ дан-ныя окружности ка-кіе-нибудь правилъ- уу \\ уу
ные одноименные мно- и/ д К
гоугольники (напри- г--------У к * /I
мѣръ, шестиуголъ- \Х /и /г
ники) и затѣмъ во- 'ѵч //
образимъ, что число ихъ сторонъ одновре- Черт
менно неограниченно удваивается (т.-е. вмѣсто шестиугольниковъ берутся правильные вписанные 12-угольники, затѣмъ 24-угольники, 48-угольники и т. д. безъ конца). Обозначимъ перемѣнные периметры этихъ многоугольниковъ черезъ р и рѵ Тогда будемъ имѣть пропорцію (263):
Р : р1=В : Вр
Но если перемѣнныя величины сохраняютъ одно и то же отношеніе, то предѣлы ихъ находятся въ томъ же отношеніи (282); предѣлы же периметровъ р и Рі суть длины окружностей С и Сг;
значитъ:
С : С\=В : Ві.
Умноживъ оба члена второго отношенія на 2 (отчего отношеніе не измѣнится), получимъ:
С : (\=2В : 27?!.
292. Слѣдствія. 1°. Переставивъ въ послѣдней пропорціи средніе члены, получимъ:
С : 2В=Сг : 27?і,
— 222 —
т.-е. отношеніе одной окружности къ своему діаметру равно отношенію другой окружности къ своему діаметру; другими словами: отношеніе окружности къ своему діаметру есть число постоянное для всѣхъ окружностей.
Это постоянное число принято обозначать греческою буквою тс *).
2°. Зная радіусъ и отношеніе окружности къ своему діаметру, т.-е. число тс, мы можемъ вычислить длину окружности изъ равенства:
С : 2В=7С; откуда С=2В.,тс=В.2'ТС, т.-е. длина окружности равна произведенію ея діаметра на число те, или произведенію ея радіуса на удвоенное числок.
Чаще всего формулу для длины окружности пишутъ такъ: С=2иВ.
293. Понятіе о вычисленіи тс. Доказано, что отношеніе окружности къ діаметру пе можетъ быть выражено точно ни цѣлымъ, ни дробнымъ числомъ **). Но можно найти приближенное значеніе тс съ какою угодно точностью. Укажемъ одинъ изъ способовъ этого вычисленія.
Если радіусъ примемъ за единицу длины, то длина окружности выразится числомъ 2тс. Поэтому можно сказать, что тѵ есть длина полу окружности единичнаго радуіса. Чтобы вычислить полу окружность съ нѣкоторымъ приближеніемъ, находятъ полу периметры правильныхъ вписанныхъ мн-ковъ, которые получаютъ черезъ удвоеніе числа сторонъ какого-нибудь одного изъ нихъ, напр., шестиугольника. Для
*) Обозначеніе это введено, по всей вѣроятности, въ XVII столѣтіи. Буква к (пи) есть начальная буква греческаго слова леркрёргіа (окружность).
*♦) Отношеніе окружности къ діаметру есть число не только несоизмѣримое, но и трансцендентное, т.-е. такое, которое не можетъ служить корнемъ никакого алгебраическаго уравненія съ раціональными коэффиціентами (впервые это было доказано въ 1882 г. нѣмецкимъ математикомъ Ф. Линде-м а н о м ъ). Отсюда можно вывести заключеніе, что помощью циркуля и линейки нельзя рѣшить построеніемъ задачу о выпрямленіи окружности, т.-е. нельзя построить такой отрѣзокъ прямой, длина котораго въ точности равнялась бы длинѣ данной о кружности.
— 223 —
этого предварительно находятъ длины сторонъ этихъ мн-ковъ, а затѣмъ полу периметры. Обозначая, по принятому, черезъ а сторону правильнаго вписаннаго мн-ка, имѣющаго п сторонъ, будемъ имѣть:
а6=В=1.
Примѣняя формулу удвоенія, выведенную нами ранѣе (273): / а* а22„=2й2—2В1/ В2——”,
находимъ: а12=2—21/ 1—-—2—V3=0,26795... т 4
Послѣ этого, пользуясь тою же формулою, послѣдовательно вычисляемъ:
Положимъ, что мы прекратили удвоеніе на 96-угольникѣ. Чтобы получить его полупериметръ, надо сторону умножить на 48. Сдѣлавъ всѣ упрощенія и вычисленія, найдемъ (обозначая периметръ буквою р съ соотвѣтствующимъ знакомъ):
1
-р96 =3,1410319... а
Если полупериметръ 96-угольника примемъ за длину полуокружности, то, конечно, сдѣлаемъ нѣкоторую погрѣшность. Чтобы судить о величинѣ ея, вычислимъ еще полупериметръ правильнаго описаннаго 96-угольника Для этого воспользуемся формулою, дающею выраженіе для стороны описаннаго мн-ка по радіусу и сторонѣ вписаннаго (271):
1 48аэ6 2Р96
отсюда: -Р96 =--------= ——==,
1/1_____а 96 1/1_____а 96
У 4 У 4
гдѣ _Р96 означаетъ периметръ описаннаго 96-угольника. Под
— 224 —
ставивъ на мѣсто у2р96 и аэв найденныя прежде числа и сдѣлавъ вычисленія, найдемъ:
1
-Р96 =3,1427146... А
Полуокружность болѣе полупериметра вписаннаго, но меньше полупериметра описаннаго 96-угольника (290); поэтому она отличается отъ каждаго изъ этихъ полупериметровъ меньше, чѣмъ они разнятся между собою. Сравнивая два числа, найденныя для УгРэв и Уг^эв, замѣчаемъ, что у нихъ одинаковы цѣлыя, десятыя и сотыя доли; слѣд., разность между этими полупериметрами меньше у100. Поэтому, если положимъ, что тс=3,14, то получимъ приближенное значеніе тс съ точностью до 0,01, при чемъ это значеніе будетъ с ъ недостаткомъ, такъ какъ оно меньше у2р96 и> слѣд., подавно меньше полуокружности.
Если подобнымъ образомъ продолжимъ вычисленіе до полученія полу периметра мн-ка о 6144 сторонахъ, то получимъ слѣдующее число (съ недостаткомъ), точное до одной милліонной:
те=3,141 592.
Для практическихъ цѣлей достаточно запомнить три или четыре цыфры этого числа, а въ случаѣ особенной точности можно довольствоваться такимъ приближеннымъ значеніемъ (съ избыткомъ) числа тс, выраженнымъ 5-ю цыфрами:
77=3,1416.
Полезно также запомнить нѣсколько цыфръ числа
1
-=0,318 3098..., тг
часто встрѣчающагося при вычисленіяхъ.
294. Архимедово и Меціево отношенія. Архимедъ, знаменитый сиракузскій геометръ, жившій въ III вѣкѣ до Р. Хр., нашелъ для тс весьма простое число 22/7, т.-е. зу7. Это число нѣсколько болѣе тс и разнится отъ него менѣе, чѣмъ на 2 тысячныхъ.
Адріанъ Мецій, голландскій геометръ XVI столѣтія, далъ для отношенія окружности къ діаметру число 355/113, которое превосходитъ точное значеніе тѵ менѣе, чѣмъ на и о л у-
225 —
милліонную; его легко запомнить по слѣдующему правилу: написавъ по 2 раза первыя три нечетныя цыфры:
113 | 355,
слѣдуетъ послѣднія три взять числителемъ, а первыя знаменателемъ.
Ученые позднѣйшаго времени, пользуясь упрощенными способами (которые указываются высшей математикой), вычислили тс съ точностью, далеко превосходящею всякія практическія требованія (такъ, Ш е н к с ъ въ 1873 году нашелъ 707 десятичныхъ знаковъ числа тс *).
295. Длина дуги въ п°. Такъ какъ длина всей окруж-2тсВ тсВ
пости есть 2тсВ, то длина дуги въ 1° равна **);
360 180
слѣд., длина в дуги, содержащей п°, выразится такъ:
тсВп
180 ’
Если дуга выражена въ минутахъ (п) или въ секундахъ (п"), то длина ея опредѣлится формулами:
тсйп пИп
®1—180.60’ 511 ~ 180.60.60'
*) Для запоминанія довольно длиннаго ряда цыфръ, выражающихъ число к, можно пользоваться слѣдующимъ французскимъ двустишіемъ:
О и е У а і т е й Гаіге арргепдге
II п потЬге иѣііе аих ііоттев!
или слѣдующимъ русскимъ (придуманнымъ покойнымъ преподавателемъ Нижегородской гимназіи ШенроКом ъ):
Кто и шутя, и скоро пожелаетъ
Пи узнать число, ужъ знаетъ!
Если выписать въ рядъ числа буквъ, заключающихся въ каждомъ словѣ этихъ фразъ, то получимъ для к приближенное число (съ избыткомъ) 3,1415926536, вѣрное до одной половины десятибилліонной.
♦*) Цѣлую окружность можно разсматривать, какъ сумму 360 дугъ, равныхъ одному градусу; и такъ какъ длина суммы дугъ равна суммѣ длинъ этихъ дугъ (287, 2°), то дуга въ 1° должна имѣть длину, въ 360 разъ меньшую длины цѣлой окружности. Длина дуги въ п° есть сумма п дугъ въ 1°; поэтому она должна быть въ п разъ больше длины дуги въ 1°.
А. Киселевъ. Геометрія. 15
— 226 —
296. Задача 1-я. Вычислить съ точностью до 1 миллиметра радіусъ такой окружности, которой дуга, содержащая 81° 21'36", р а в н а 0,452 метра.
Обративъ 81° 21' 36" въ секунды, получимъ число 292896. пВ . 292896
Изъ уравненія: 0,452=—————
’ 180 . 60. 60
0.452 . 180 . 60 . 60 1
находимъ: В=------ ----=- = 0,318 (метра).
292896ТС ТС
Задача 2-я. Опредѣлить число градусовъ дуги, которой длина равна радіусу.
Замѣнивъ въ формулѣ, опредѣляющей длину дуги въ п°, величину в па В, получимъ уравненіе:
_ тсИп тсп
180 1
откуда: п=—=180. -=180.0,3183098
=57°,295764=57°17'44",8.
Теорема, служащая основаніемъ для опредѣленія длины окружности.
(См. § 286).
2Ѳ7. При доказательствѣ этой теоремы, мы будемъ основываться на слѣдующихъ почти очевидныхъ истинахъ:
1° Если перемѣнная величина, измѣняясь, все увеличивается, но при этомъ остается меньше нѣкоторой постоянной величины, то она имѣетъ предѣлъ.
2° Если перемѣнная величина, измѣняясь, все уменьшается, но при этомъ остается больше нѣкоторой постоянной величины, то она имѣетъ предѣлъ.
3° Если разность двухъ перемѣнныхъ величинъ стремится къ нулю, и одна изъ этихъ величинъ имѣетъ предѣлъ, то другая имѣетъ тотъ же предѣлъ.
2Ѳ8. Теорема. Периметръ выпуклаго многоугольника, вписаннаго въ окружность, стремится къ предѣлу, когда стороны этого многоугольника не* ограниченно уменьшаются (и, слѣд., число сторонъ неограниченно увеличивается); предѣлъ этототъ не зависитъ отъ закона, по которому стороны многоугольника уменьшаются.
Пусть АВС БЕ (черт. 262) есть какой-нибудь выпуклый многоугольникъ, вписанный въ данную окружность,
— 227 —
Проведемъ черезъ всѣ его
вершины касательныя къ окружности
до взаимнаго пересѣченія. Тогда получимъ описанный
мн-къ КЬМЕР. Условимся называть такой описанный мп-къ соотвѣтственнымъ для вписаннаго мн-ка АВСВЕ.
Доказательство наше будетъ состоять изъ слѣдующихъ трехъ частей:
1°. Пусть р есть периметръ какого угодно вписаннаго, а Р периметръ соотвѣтственнаго описаннаго мн-ка *). Докажемъ, что разность Р—р стремится къ 0, когда стороны вписан
Черт. 262.
наго мн-ка стремятся къ 0 по какому угодно закону. Для этого предварительно
найдемъ предѣлъ отношенія Р : р. Изъ вершинъ К, Ь, М, Е... опу
стимъ перпендикуляры на стороны вписаннаго многоугольника. Тогда Р = АЬ + ЬВ + ВМ + МС + СЕ + ЕВ + ОР + ...
р= АІ + ІВ+Вт + тС + Сп + пВ + Ор + ... (1)
Изъ алгебры извѣстно, **) что величина дроби: Р АЬ+ЬВ+ВМ +.......................
р~ АІ±ІВ + Вт +......
заключается между меньшею и ббльшею изъ дробей:
АЬ ЬВ ВМ
АГ ІВ' Вт' (2)
Докажемъ, что при неограниченномъ уменьшеніи сторонъ вписаннаго многоугольника каждая изъ этихъ дробей стремится къ пре-АЬ
дѣлу 1. Возьмемъ какую-нибудь одну изъ нихъ, напр. Изъ пря
моугольнаго тр—ка АІЛ (черт. 262) мы усматриваемъ, что
АЬ 1
АІ—АЬ соз А; откуда тг =-------
АІ соз А
Когда стороны вписаннаго многоугольника стремятся къ 0, уголъ А, составленный касательною АЬ и хордою АВ, также стремится къ О АЬ
(277); слѣд., соз А стремится при этомъ къ 1, и потому отношеніе
такжѳ имѣетъ предѣломъ 1. Такъ какъ это разсужденіе можно примѣнить кэ всякому тр—ку чертежа 262-го, то, значитъ, каждая дробь изъ ряда (2) имѣетъ предѣломъ 1.
Р
Отсюда слѣдуетъ, что и предѣлъ отношенія - также равенъ 1.
*) Не должно смѣшивать этихъ буквъ съ такими же, поставленными на черт. 262.
**) См., напр., «Элементарная алгебра» А. Киселева, § 264 (изд. 23-е и слѣд.).
15*
— 228 —
Доказавъ это, возьмемъ разность Р—р и представимъ ее такъ:
Р Р
/р \
Р—Р=Р{р~1 )
Отношеніе
стремится, по доказанному, къ 1; слѣд., разность
Р
—•—1 стремится къ 0; вслѣдствіе этого и произведеніе р
въ которомъ р есть величина конечная (такъ какъ периметръ любого
вписаннаго мн—ка всегда остается меньше периметра всякаго описаннаго), также стремится къ 0; значитъ, то же самое можно сказать о разности Р—р.
2°. Докажемъ теперь, что перимегръ вписаннаго мн—ка стремится къ предѣлу при слѣдующемъ частномъ законѣ вписыванія. Впишемъ въ кругъ правильный тр—къ; затѣмъ удвоимъ число сторонъ, т.-е. возьмемъ правильный вписанный 6-угольникъ; далѣе удвоимъ опять число сторонъ, т.-е. возьмемъ правильный 12-угольникъ; вообразимъ, что этотъ процессъ удвоенія идетъ безъ конца. Тогда периметры такихъ вписанныхъ многоугольниковъ, увеличиваясь съ каждымъ удвоеніемъ, все будутъ возрастать, оставаясь однако меньше периметра любого описаннаго мн—ка (напр., квадрата); вслѣдствіе этого периметръ вписаннаго мн—ка, стороны котораго стремятся къ 0 по этому частному закону, имѣетъ предѣлъ. Обозначимъ его черезъ Т. Тотъ же предѣлъ имѣетъ и периметръ соотвѣтственнаго описаннаго мн—ка, такъ какъ, по доказанному, разность между этими периметрами стремится къ 0.
3°. Докажемъ, наконецъ, что къ тому же предѣлу Т стремится периметръ вписаннаго мн—ка, стороны котораго уменьшаются по
какому угодно закону.
Пусть рг есть перемѣнный периметръ вписаннаго мн—ка, котораго стороны уменьшаются по произвольному закону, К р периметръ вписаннаго мн—ка, стороны котораго уменьшаются по указанному выше частному закону; положимъ еще, что и Р будутъ периметры соотвѣтственныхъ описанныхъ многоугольниковъ. По доказанному въ части 1° этого изложенія, разности:
Л— Рі и Р— р стремятся къ 0. Поэтому и сумма ихъ должна стремиться къ 0. Но эту сумму можно представить такъ:
(.Рі~Р)+(.Р—Рд-
Такъ какъ периметръ выпуклаго многоугольника меньше периметра всякаго другого многоугольника, объемлющаго его, то р<Рг и рх<Р; слѣд., обѣ разности Р±—р и Р—рг положительны; сумма же положительныхъ слагаемыхъ стремится къ 0 только тогда, когда каждое слагаемое стремится къ 0; слѣд., разности Рх—р и Р—р± стремятся къ О. Но величины р и Р имѣютъ общій предѣлъ Т; слѣд. (297, 3°), величины рх и Рх имѣютъ тотъ же предѣлъ Т.
— 229 —
Такимъ образомъ, предѣлъ периметра существуетъ и не зависитъ отъ закона, по которому стороны вписаннаго мн—ка уменьшаются.
Замѣчаніе. Примѣняя изложенное доказательство не къ цѣлой окружности, а къ какой-нибудь ея части, или вообще къ какой-нибудь конечной выпукло.# кривой (кривую не выпуклую можно разбить на выпуклыя части), мы можемъ доказать эту теорему по отношенію къ периметру ломаной линіи, вписанной въ эту конечную кривую.
УПРАЖНЕНІЯ.
255. Доказать, что въ двухъ кругахъ отношеніе центральныхъ угловъ, соотвѣтствующихъ дугамъ, имѣющимъ одинаковую длину равно обратному отношенію радіусовъ.
256. Какъ велика будетъ ошибка, если вмѣсто полуокружности возьмемъ сумму стороны правильнаго вписаннаго треугольника и стороны вписаннаго квадрата?
257. На окружности взята точка А и черезъ нее проведены: діаметръ АВ, сторона правильнаго вписаннаго 6-угольника АС и касательная МП. Изъ центра О опущенъ на АС перпендикуляръ и продолженъ до пересѣченія съ касательною въ точкѣ Р. Отъ этой точки отложена по касательной (черезъ точку А) прямая ВЕ, равная 3 радіусамъ. Точка Е соединена съ концомъ діаметра В. Опредѣлить, какъ велика погрѣшность, если прямую ВЕ возьмемъ за длину полуокружности *).
258. На діаметрѣ данной полуокружности построены двѣ равныя полуокружности и въ ту часть плоскости, которая заключена между тремя полуокружностями, вписанъ кругъ. Доказать, что діаметръ этого круга относится' къ діаметру равныхъ полуокружностей, какъ 2 : 3.
259. Вычислить въ градусахъ, минутахъ и секундахъ дугу, равную радіусу (рѣшеніе въ текстѣ, стр. 226).
260. Вычислить длину одного градуса земного экватора, принимая радіусъ земли въ 859 геогр. миль.
*) Доказано, что посредствомъ циркуля и линейки нѣтъ возможности построить такую конечную прямую, которая въ точности равнялась бы длинѣ окружности (задача о спрямленіи окружности невозможна, см. выноску къ § 293). Однако есть нѣсколько способовъ для приближеннаго спрямленія. Въ задачахъ 256 и 257 указаны два изъ этихъ способовъ. Послѣдній изъ нихъ, принадлежащій польскому іезуиту Коханскому (1683), замѣчателенъ тѣмъ, что можетъ быть выполненъ однимъ раствореніемъ циркуля.
230 —
КНИГА V.
ИЗМѢРЕНІЕ ПЛОЩАДЕЙ.
ГЛАВА I.
Площади многоугольниковъ.
2Ѳ9. Основныя допущенія о площадяхъ. Часть плоскости, заключенная внутри многоугольника или другой какой-нибудь плоской фигуры наз. площадью этой фи
гуры.
Площадь фигуры мы можемъ разсматривать, какъ величину особаго рода, если примемъ слѣдующія допущенія:
1°. Равныя фигуры (т.-е. такія, которыя могутъ быть
совмѣщены при наложеніи) имѣютъ равныя площади независимо отъ ихъ положенія въ пространствѣ.
2°. Площадь какой-нибудь фигуры (напр.,
Черт. 263.
изображенной на черт. 263), с о-стоящей изъ нѣсколькихъ частей (М, принимается за сумму площадей этихъ частей.
ЗОО. Слѣдствія. і°. П л о-щадьфигуры большепло-щади каждой ея части, такъ какъ сумма положительныхъ величинъ больше каждаго слагаемаго.
2°. Если фигура состоитъ изъ 2-хъ частей (черт. 263), то площадь каждой части разсматривается, какъ разность между площадью цѣлой фигуры и площадью другой ея части.
3°. Если фигуры (напр., изображенныя на черт. 264) состоятъ изъ одинаковаго числа частей (А, В...,), соотвѣтственно другъ другу равныхъ, то площади такихъ фигуръ, представляя собою суммы соотвѣтственно равныхъ слагаемыхъ,
считаются равными независимо отъ того, какъ расположены эти части относительно другъ друга.
— 231 - -
Черт. 204.
4°. Фигуры, площади которыхъ можно разсматривать, какъ разности площадей равныхъ фигуръ, имѣютъ одинаковыя площади. Мы вскорѣ встрѣтимъ такой случай (308).
Мы видимъ такимъ образомъ, что могутъ быть фигуры, которыя нельзя на
звать равными (такъ какъ онѣ пе могутъ быть совмѣщены), но которыя однако имѣютъ равныя площади; таковы, напр., прямоугольникъ, параллелограммъ и треугольникъ, изображенные на черт. 264
Фигуры, имѣющія равныя площади, называю т с я равновеликими.
Равныя фпгуры всегда равновелики, по равновеликія фигуры не всегда равны.
801. Замѣчанія. 1°. Относительно указанныхъ допущеній о площадяхъ возникаетъ слѣдующій важный вопросъ. Положимъ, что, разбивъ данную фигуру на нѣкоторое число частей произвольной формы, мы перемѣщаемъ эти части разнообразными способами (подобно тому, какъ на черт. 264-мъ перемѣщены части А и В); мы будемъ тогда получать различныя новыя фигуры. Не можетъ ли при этомъ получиться и такая фигура, которая, помѣщенная на начальную фигуру или на какую-нибудь изъ образовавшихся изъ нея новыхъ фигуръ, вся умѣстится внутри этой фигуры? Если бы это случилось, то мы имѣли бы тогда двѣ фигуры, которыя, съ одной стороны, состоя изъ одинаковаго числа попарно совмѣщающихся частей, должны считаться равновеликими; а съ другой стороны, та изъ нихъ, которая способна помѣститься внутри другой и, такимъ образомъ, можетъ составить часть этой другой, должна считаться меньшей изъ двухъ. Тогда указанныя допущенія о равенствѣ и неравенствѣ площадей теряли бы всякій смыслъ, такъ какъ, согласно этимъ допущеніямъ, двѣ площади могли бы одновременно считаться и равными, и неравными.
Впѳрвыѳ обратилъ вниманіе на этотъ вопросъ италіанскій математикъ Де-Цольтъ, который (въ 1881 г.) пытался доказать (но неудачно), что многоугольникъ никогда не можетъ оказаться равновеликимъ своей части (и, значитъ, предположенный нами случай невозможенъ). Это предложеніе Де-Цольта принималось сначала, какъ недоказуемый постулатъ равновеликости, но затѣмъ (въ концѣ XIX столѣтія) оно было строго доказано (С. Шату.
— 232
невскимъ, Гильбертомъ и др.). Мы опускаемъ эти доказательства по причинѣ ихъ сложности.
2°. Различаютъ равновеликость двухъ родовъ; одна изъ нихъ указана въ отдѣленіи 3° параграфа 300-го, другая—въ отдѣленіи 4° того же параграфа. Первую можно назвать равновеликостью «п о разложѳні ю», вторую—равновеликостью «по дополне-и і ю». Дѣйствительно, равновеликость 1-го рода можетъ быть высказана такъ: двѣ фигуры считаются равновеликими, если онѣ могутъ быть разложены на одинаковое число частей, соотвѣтственно другъ другу равныхъ, а равновеликость 2-го рода можетъ быть выражена такъ: двѣ фигуры считаются равновеликими, если ихъ можно дополнитъ равными другъ другу фигурами такимъ образомъ, что образовавшіяся суммы представляютъ собою тоже равныя фигуры. Примѣромъ равновеликости по
разложенію служатъ фигуры, указанныя на черт. 264; какъ примѣръ равновеликости по дополненію можно указать пар—мъ АВСБ и прям—къ АЕЕБ черт. 270-го. Дѣйствительно, обѣ эти фигуры даютъ одну и ту же трапецію АЕСБ, если пар—мъ дополнимъ тр—комъ АЕВ, а прям—къ дополнимъ тр—комъ БЕС, равнымъ /\АЕВ.
Для прямолинейныхъ фигуръ доказано, что равновеликость по дополненію есть вмѣстѣ съ тѣмъ и равновеликость по разложенію. Частный случай этой истины доказанъ нами въ § 309 помощью чертежа 273-го.
3°. Можно также доказать, что двѣ фигуры, равновеликія одной и той же третьей фигурѣ, равновелики и между собою. Мы принимаемъ эту истину безъ доказательства.
302. Единица площади. За единицу площади при измѣреніи ихъ обыкновенно берутъ площадь такого квадрата, у котораго сторона равна линейной единицѣ; таковы, напр., квадратный метръ, квадратный аршинъ и т. п.
Отношеніе двухъ квадратныхъ единицъ ____________ разныхъ названій
— - •• == равно второй сте-
=== ==== пени отношенія тѣхъ
- --" == линейныхъ единицъ,
__ ===== =====--------которыя служатъ сто-—— •--------------------- г--— ронами для этихъ
_... =_ - .. квадратиыхъедипицъ.
——-1 Такъ, отношеніе квадратной
Черт. 265. сажени къ квадр. аршину
— 233 —
ыхъ единицахъ данную
А
Черт. 266.
равно З2, т.-е. 9, что ясно видно изъ чертежа 265-го, на которомъ меньшій изъ двухъ квадратовъ изображаетъ квадратный аршинъ, а ббпыпій—квадратную сажень.
303. Понятіе О числѣ, измѣряющемъ площадь. Пояснимъ наглядно, что слѣдуетъ разумѣть подъ числомъ, измѣряющимъ въ квадратн площадь.
Проведемъ двѣ взаимноперпендикулярныя прямыя ДВ и 02) (черт. 266) и затѣмъ построимъ рядъ прямыхъ, параллельныхъ АВ, и другой рядъ прямыхъ, параллельныхъ С2), причемъ разстоянія между тѣми и другими прямыми возьмемъ одинаковыми, а именно равными какой-нибудь линейной единицѣ. Мы получимъ тогда сѣть квадратовъ, изъ которыхъ каждый представляетъ собою квадратную единицу. Вообразимъ, что на такую сѣть наложена та фигура, которой площадь мы
желаемъ измѣрить (напр., данный кругъ, какъ изображено на чертежѣ 266). Тогда по отношенію къ этой фигурѣ всѣ квадраты сѣти можно раздѣлить на три рода: 1) внѣшніе квадраты, которые расположены внѣ данной фигуры; 2) внутренніе квадраты, которые лежатъ внутри фигуры (они покрыты на чертежѣ двойными штрихами) и 3) тѣ квадраты, черезъ которые проходитъ контуръ фигуры и которые, слѣд., лежатъ частью внутри, частью внѣ данной фигуры (эти квадраты на чертежѣ покрыты простыми штрихами). Оставивъ безъ вниманія внѣшніе квадраты, сосчитаемъ отдѣльно квадраты 2-го и квадраты 3-го рода. Пусть первыхъ окажется т, а вторыхъ и. Тогда, очевидно, измѣряемая площадь больше т, но меньше тп-|-и квадр. единицъ. Числа т и т+п будутъ въ этомъ случаѣ приближенныя мѣры данной площади, первое число съ недостаткомъ а второе съ избыткомъ, причемъ погрѣшность меньше п квадр. ед. (меньше суммы тѣхъ квадратовъ, которые покрыты на нашемъ чертежѣ простыми штрихами).
Чтобы получить болѣе точные результаты измѣренія, уплотнимъ нашу сѣть квадратовъ, подраздѣливъ каждый изъ нихъ на болѣе мелкіе квадраты. Напр., раздѣлимъ стороны квадратовъ на 10 равныхъ частей и черезъ точки раздѣла проведемъ рядъ прямыхъ,
— 231
параллельныхъ АВ, и другой рядъ прямыхъ, параллельныхъ СВ. Мы разложимъ тогда каждый квадратъ сѣти на 100 мелкихъ квадратовъ, изъ которыхъ каждый составляетъ 1/100 часть квадратной единицы. Положимъ, что теперь всѣхъ внутреннихъ малыхъ квадратовъ будетъ т', а тѣхъ, которые пересѣкаются контуромъ фигуры, пусть т'
окажется и'. Тогда измѣряемая плоціадь будетъ болѣе урд’ но менѣе т' + п' Л
---100--квадратной единицы. Эти числа будутъ новыя приближенныя мѣры измѣряемой площади, первое съ недостаткомъ, второе съ из-п'
быткомъ, причемъ погрѣшность менѣе і^ квадр. един. Не трудно убѣдиться,что эта погрѣшность окажется менѣе прежней погрѣшности.
Дѣйствительно, отъ каждаго изъ тѣхъ квадратовъ чертежа 266-го, которые покрыты простыми штрихами, отойдутъ теперь, во 1, тѣ части, которыя составлены малыми квадратами, лежащими внѣ фигуры, и во 2, тѣ части, которыя составлены малыми квадратами, лежащими внутри фигуры. Для ясности мы на черт. 267-мъ изобразили въ увеличенномъ видѣ одинъ изъ квадратовъ, покрытыхъ на предыдущемъ чертежѣ простыми штрихами (именно, квадратъ, обозначенный буквою й), раздѣливъ его на 100 мелкихъ квадратовъ.
Черт. 267. Мы теперЬ ясно видимъ, что полоса, составленная изъ малыхъ квадратовъ, черезъ которые проходитъ контуръ фигуры (покрытая на черт. 267 простыми штрихами), значительно менѣе всего большого квадрата. Такъ какъ это справедливо для каждаго квадрата чертежа 266-го, покрытаго простыми штрихами, гі
то ясно, что погрѣшность, равная квадр. ед., менѣе погрѣшности, равной п квадр. ед.
Если подраздѣлимъ квадратную единицу на части еще болѣе мелкія, то, произведя указаннымъ путемъ измѣреніе, мы получимъ приближенныя мѣры площади еще съ меньшей погрѣшностью.
Иногда (напр., при измѣреніи площади прямоугольника, см. чертежъ 268), поступая описаннымъ способомъ, мы можемъ получить точную мѣру площади. Это будетъ тогда, когда контуръ данной фигуры представляетъ собою ломаную линію, которой стороны совпадаютъ съ частями прямыхъ линій, образующихъ сѣть квадратовъ; въ этомъ случаѣ, слѣд., не будетъ совсѣмъ квадратовъ, прорѣзываемыхъ контуромъ фигуры. Тогда число квадратовъ, лежащихъ внутри фигуры, составитъ точную мѣру измѣряемой площади. Во всѣхъ остальныхъ случаяхъ указанный пріемъ измѣренія даетъ только приближенные результаты, причемъ погрѣшность можетъ быть сдѣлана какъ угодно малой.
— 235 —
Представимъ себѣ, что какими-нибудь соображеніями мы нашли такое число @ (цѣлое, дробное или несоизмѣримое), которое оказывается ббльшимъ всякаго приближеннаго результата измѣренія, взятаго съ недостаткомъ, и меньшимъ всякаго приближеннаго результата измѣренія, взятаго съ избыткомъ; тогда такое число можетъ быть принято за точную мѣру измѣряемой площади.
Доказано, что такое число существуетъ для всякой площади и что оно не зависитъ отъ положенія тѣхъ прямыхъ АВ и СВ (черт. 266), параллельно которымъ проводятся линіи сѣти. *) Число это обладаетъ слѣдующими двумя свойствами: при одной и той же квадратной единицѣ 1) площадямъ равныхъ фигуръ (совмѣщающихся) соотвѣтствуютъ равныя числа, и 2) суммѣ площадей (399,2) соотвѣтствуетъ сумма чиселъ. Отсюда слѣдуетъ, что ббльшей площади соотвѣтствуетъ ббльшѳе число, равновеликимъ фигурамъ соотвѣтствуютъ равныя числа, и т. п.
304. Основаніе и высота. Измѣреніе площади только въ рѣдкихъ случаяхъ могло бы быть выполнено непосредственнымъ наложеніемъ квадратной единицы. Большею частью площади приходится измѣрять косвенно, посредствомъ измѣренія нѣкоторыхъ линій фпгуры.
Условимся одну изъ сторонъ треугольника или параллелограмма называть основаніемъ этпхъ фигуръ, а перпендикуляръ, опущенный на эту сторону изъ вершины тр-ка или изъ какой-ппбудь точки противоположной стороны параллелограмма, будемъ называть высотою.
Въ прямоугольникѣ за высоту можно взять сторону, перпендикулярную къ той, которая принята за основаніе.
Въ трапеціи основаніями называютъ обѣ параллельныя стороны, а высотою—общій перпендикуляръ между ними.
Основаніе и высота прямоугольника наз. его и з м ѣ ренія м п.
305. Теорема. Площадь прямоугольника равна произведенію его основанія на высоту.
*) См. \Ѵ, К 1 1 1 і п е ипд Ноѵѳзіасі I—НапбЬисЬ <іез таіііетаіізсііеп Впіеггісіиз, I Вапсі. 1910.
— 236 —
Это краткое предложеніе надо понимать такъ: число, выражающее площадь прямоугольника въ квадратныхъ единицахъ, равно произведенію чиселъ, выражающихъ основаніе и высоту его въ соотвѣтствующихъ линейныхъ единицахъ
При доказательствѣ разсмотримъ особо слѣдующіе три случая:
1°. Основаніеивысота, измѣренныя одной и той же единицей, выражаются цѣлыми
числами.
Пусть у даннаго прямоугольника (черт. 268) основаніе равно цѣлому числу Ъ линейныхъ единицъ, а высота—цѣлому числу к
треугольника, по сторонамъ даннаго
тѣхъ же единицъ. Раздѣливъ основаніе на Ъ и высоту на к равныхъ частей, проведемъ черезъ точки раздѣла рядъ прямыхъ, параллельныхъ высотѣ, и другой рядъ прямыхъ, параллельныхъ основанію. Отъ взаимнаго пересѣченія этихъ прямыхъ образуются нѣкоторые четыреугольники. Возьмемъ какой-нибудь одинъ изъ нихъ, напр., четыреугольникъ к (покрытый на чертежѣ штрихами). Такъ какъ стороны этого чепостроенію, параллельны соотвѣтствующимъ прямоугольника, то всѣ углы его прямые;
значитъ, четыреугольникъ к есть прямоугольникъ. Оь другой
стороны каждая сторона этого прямоугольника равна разстоянію между сосѣдними параллельными прямыми, т.-е. равна одной и той же линейной единицѣ. Значитъ, прямоугольникъ к представляетъ собою квадратъ, а именно ту квадратную единицу, которая соотвѣтствуетъ взятой линейной единицѣ (если, напр., основаніе и высота были измѣрены линейными сантиметрами, то квадратъ к есть квадратный сантиметръ). Такъ какъ сказанное объ одномъ четыреугольникѣ можетъ быть повторено о всякомъ другомъ, то, значитъ, проведеніемъ указанныхъ параллельныхъ прямыхъ мы разбиваемъ всю площадь даннаго прямоугольника на квадратныя единицы. Найдемъ ихъ число. Очевидно, что рядъ прямыхъ, параллельныхъ основанію, раздѣляетъ прямоугольникъ на столько равныхъ горизонтальныхъ полосъ, сколько
— 237 —
въ высотѣ содержится линейныхъ единицъ, т.-е. на к равныхъ полосъ. Съ другой стороны рядъ прямыхъ, параллельныхъ высотѣ, разбиваетъ каждую горизонтальную полосу на столько квадратныхъ единицъ, сколько въ основаніи содержится линейныхъ единицъ т.-е. на Ъ квадратныхъ единицъ. Значитъ, всѣхъ квадратныхъ единицъ окажется Ъ . к. Такимъ образомъ:
площадь прямоугольника —Ък,
т.-е. она равна произведенію основанія на высоту.
2°. Основаніе и высота, измѣренныя одною и тою же единицею, выражаются дробными числами.
Пусть у даннаго прямоугольника:
т р
основаніе=—лин. ед.: высота = —той же ед., п д
причемъ мы не исключаемъ и тотъ случай, когда какая-нибудь изъ этихъ дробей равна цѣлому числу.
Приведя дроби къ одинаковому знаменателю, получимъ:
тц рп
основаніе=—; высота =—• пд пд
Примемъ 1/ив долю линейной единицы за новую единицу длины. Тогда мы можемъ сказать, что основаніе содержитъ тд этихъ новыхъ единицъ, а высота рп тѣхъ же единицъ. Значитъ, по доказанному въ случаѣ 1°, площадь прямоугольника равна (тд) (рп) такихъ квадратныхъ единицъ, которыя соотвѣтствуютъ повой единицѣ длины. Но эта квадр. единица составляетъ 1/(яг)а часть квадр. единицы, соотвѣтствующей прежней линейной единицѣ (302); значитъ, площадь прямоугольника равна:
1 , . . . тарп тр т р
——.(т9) (рп)=—
(пд)а тгд2 пд п д
3°. Основаніе и высота (или только одно изъ этихъ измѣреній) несоизмѣримы съ единицей длины и, слѣд., выражаются несоизмѣримыми числами.
— 238 —
Черт. 269.
Пусть основаніе АВ прямоугольника АВСВ (черт. 269) выражается несоизмѣримымъ числомъ а и высота ВБ—несоизмѣримымъ числомъ р. Найдемъ приближенныя значенія этихъ чиселъ съ точностью до 1/п. Для этого па основаніи АВ, начиная отъ точки А, отложимъ ’/п долю линейной единицы столько разъ, сколько можно. Пусть окажется, что, отложивъ п такихъ долей, мы получимъ отрѣзокъ АВ^АВ, а отложивъ т+і долей, найдемъ отрѣзокъ АВ^>АВ. т ?п+1
Тогда дроби—и —— будутъ приближенныя значенія числа а, первая съ
недостаткомъ, вторая съ избыткомъ. Положимъ далѣе, что отложивъ г/п долю линейной единицы па высотѣ АБ (отъ точки А) р разъ, мы получимъ АВ1<^АВ, а отложивъ р+1 разъ, найдемъ р р+1
АВ2С>АВ; тогда дроби—и-^-будутъ приближенныя значенія числа р, первая съ недостаткомъ, вторая съ избыткомъ.Построимъ 2 вспомогательные прямоугольника АВ^С^ и АВ2С2В2. У каждаго изъ ппхъ основаніе и высота выражается дробными числами:
ЛВ,=—, ЛВ!=22±1; ЛПг=ВА
п п п п
Поэтому, согласно доказанному въ случаѣ 2°:
площ. АВ1С1В1= ~ п п
р+1
п
площади АВСВ,
площ. ЛВ2С2П2=----.
п
Такъ какъ площадь АВіС^ есть часть а эта послѣдняя есть часть площади АВ2С2В2, то
пл. ЛВіСіОх^пл. АВСЕ<^ал. ЛВ2С2О2, и потому:— . -<<числа, пзмѣр. пл. АВСВ<'-^І' $ п д п
Я
— 239 —
Это двойное неравенство остается вѣрнымъ при всякомъ значеніи п, т.-е. оно остается вѣрнымъ, съ какою бы точностью мы ни находили приближенныя значенія чиселъ а и р. Значитъ, мы можемъ сказать, что площадь АВСВ должна выражаться такимъ числомъ, которое больше произведенія любыхъ приближенныхъ значеній чиселъ а и р, если эти значенія взяты съ недостаткомъ, по меньше произведенія любыхъ ихъ приближенныхъ значеній, если эти значенія взяты съ избыткомъ. Такое число, какъ извѣстно пзъ алгебры, наз. произведеніемъ несоизмѣримыхъ чиселъ а и р. Слѣд.:
площ. АВСВ=а$,
т.-е. она и въ этомъ случаѣ равна произведенію основанія на высоту.
Это разсужденіе вполнѣ примѣнимо и къ тому случаю, когда только одно изъ измѣреній прямоугольника песоизмѣримо съ единицей длины.
ЗОв. Слѣдствіе. П л о щ а д и двухъ прямоугольниковъ, имѣющихъ равныя основанія, относятся, какъ ихъ высоты, а площади двухъ прямоугольниковъ, имѣющихъ равныя высоты, относятся, какъ ихъ основанія.
Дѣйствительно, если Ь, к и Р будутъ основаніе, высота и площадь одного прямоугольника, а Ъг, и Рг—основаніе, высота и площадь другого прямоугольника, то, по доказанному: Р=Ък и Р^Ъ^; слѣд.: Р:Рг—Ък Отсюда находимъ,
что если Ь=Ь15 то Р ; Рг=Аі -.ку, а если к—кг, то Р : Р^Ъ : Ъг.
307. Замѣчаніе. Въ послѣдующихъ теоремахъ мы будемъ сокращенно говорить: «площадь равна произведенію такихъ-то линій*, разумѣя подъ этимъ, что число, выражающее площадь въ квадратныхъ единицахъ, равно произведенію чиселъ, выражающихъ такія-то линіи въ соотвѣтствующихъ линейныхъ единицахъ.
— 240 —
308. Теорема. Площадь параллелограмма (АВСВ, черт. 270 и 271) равна произведенію основанія на высоту.
На основаніи АВ построимъ прямоугольникъ АЕРВ, у котораго сторона ЕР составляетъ продолженіе стороны ВС. Докажемъ, что площ. ЛВСТ)=площ. АЕРВ.—Изъ чертежей усматриваемъ, что
площ. АВСВ—площ. АЕСВ—площ. АЕВ и площ. АЕРВ—площ. АЕСВ—площ. ВРС.
Но прямоугольные тр-ки АЕВ и ВРС равны, потому что у нихъ: АЕ=ВР и АВ=ВС (какъ противоположныя стороны параллелограммовъ). Значитъ, равны и площади этихъ тр-ковъ. Поэтому площади АВСВ и АЕРВ представляютъ собою разности соотвѣтственно равныхъ площадей; вслѣдствіе этого (300, 4°):
площ. АВСВ=площ. АЕРВ.
Но пл. АЕРВ=Ыг, слѣд., и пл. АВСВ=Ък, причемъ Ъ можно разсматривать, какъ основаніе параллелограмма, и /і, какъ его высоту
Слѣдствіе. Параллелограммы съ равными основаніями и равными высотами равновелики.
309. Замѣчаніе. Параллелограммы, имѣющіе равныя основанія и равныя высоты, могутъ быть разложены на одинаковое число частей, попарно другъ другу равныхъ (конгруэнтныхъ). Для доказательства размѣстимъ параллелограммы такимъ образомъ, чтобы ихъ равныя основанія совпали. Тогда могутъ пред-
241
ставиться два случая: 1) когда верхнія стороны пар-мовъ имѣютъ какую-нибудь общую часть (черт. 272), и 2) когда такой общей части нѣтъ (черт. 273).
Разсмотримъ ѳти случаи отдѣльно.
1) Парал-мъ АВСБ прямою АЕ раздѣляется на 2 части: А АВЕ и трапеція АЕСБ-, другой парал-мъ прямою СБ разлагается на А БСЕ и ту же трапецію АЕСБ. Такъ какъ А АВЕ= А БСЕ, то значитъ, оба парал-ма составлены изъ попарно равныхъ частей.
2) Пусть К будетъ точка пересѣченія сторонъ АЕ и БС. Отложимъ на КС, начиная отъ К, части, равныя БК, столько разъ, сколько можно (на нашемъ чертежѣ отрѣзокъ КБ уложился на КС одинъ разъ до точки Е, причемъ получился остатокъ ЕС<_БК). Черезъ точки К и Е проведемъ прямыя, параллельныя АБ. Тогда пар-мъ АВСБ разложится на 3 пар-ма, изъ которыхъ два равны между собою; пар-мъ АЕЕБ также разложится на 3 пар-ма, изъ которыхъ два равны между собою. Проведя діагонали МЕ и затѣмъ Р8 || АЕ и ОВ || АВ, мы раздѣлимъ каждый изъ данныхъ пар-мовъ на 6 частей; не трудно видѣть, что части, обозначенныя на чертежѣ однѣми и тѣми же цыфрами, другъ другу равны.
310 Теорема. Площадь треугольника (АВС, черт. 274) равна половинѣ произведенія основанія на высоту.
Проведемъ ВЕ II АС и АЕ II ВС. Тогда получимъ пераллелограммъ АЕВС, котораго площадь, по доказанному, равна Ък. Но площадь ДЛВС составляетъ половину площади АЕВС; слѣд.:
І площ. АВС=—Ьк.
&
А. Киселевъ. Геометрія.
Черт. 274.
16
— 242 —
311. Слѣдствія. 1°. Треугольники съ равными основаніями
и равными высотами равновелики.
Черт. 275.
Если, напр., вершину В тр-ка АВС (черт. 275) будемъ перемѣщать по прямой, параллельной основанію АС, а основаніе оставимъ то же самое, то площадь тр-ка не будетъ измѣняться.
2°. Площадь прямоугольнаго тре-
угольника равна
Черт. 276.
половинѣ произведенія его катетовъ, потому что одинъ катетъ можно взять за основаніе, а другой за высоту.
Изъ черт. 276 непосредственно видно, что площадь такого тр-ка составляетъ половину площади прямоугольника, имѣющаго то же основаніе и ту же высоту.
2*. Площадь ромба равна половинѣ произведенія его діаго-
Черт. 277.
налей. Дѣйстіительно, если АВСВ (черт. 277) есть ромбъ, то его діагонали взаимно перпендикулярны. Поэтому:
пл. ДДВС=1/2 АС . ОВ.
пл. кАСВ^Аіъ АС . ОВ.
пл. АВСВ=Ч2 АС . (ОВ+ОВ)= =1/2 АС . ВВ.
4°. Площади треугольниковъ относятся, какъ произведенія основаній на высоты (множитель 1[і сокращается).
312. Замѣчаніе. Всякій треугольникъ разлагается на части, перемѣщеніемъ которыхъ можно образовать прямоугольникъ, имѣющій одинаковое съ треугольникомъ основаніе и высоту, вдвое меньшую высоты треугольника. Дѣйствительно, если въ тр-кѣ АВС (черт. 278)
— 243 —
Черт. 278.
черезъ середины Б и Е двухъ сторонъ (образующихъ съ третьей стороной острые углы) проведемъ прямую и на нее опустимъ перпендикуляръ ВР, то тр-къ АВС разобьется етими прямыми на 3 части, обозначенныя на чертежѣ цыфрами 1, 2 и 3. Повернувъ часть 1-ую вокругъ точки В на 180° (въ направленіи, указанномъ стрѣлкой), мы приведемъ ее въ положеніе АКБ; подобнымъ же образомъ часть 2-ю мы приведемъ въ положеніе СЬЕ. Тогда тр-къ АВС превратится въ прямоугольникъ АКЬС, у котораго основаніе то же самое, что и у тр-ка, а высота вдвое
меньше высоты тр-ка.
313. Теорема. Площадь & треугольника въ зависимости отъ его сторонъ а, Ъ и с выражается формулой:
Р(Р—а)(р—Ь)(р—с), гдѣ р есть полупериметръ треугольника, т.-ѳ.
Р^Са+Ы-с).
А
Пусть высота тр-ка АВС (черт. 279), опущенная на сторону
а, есть ка. Тогда:
5=-айв.
Чтобы найти высоту ка, возьмемъ уравненіе (236):
Ь2=а2-}-с2—2ас' и опредѣлимъ изъ него отрѣзокъ с’: , а2+с2—Ъ2
Изъ треугольника АВВ находимъ:
й =1/ с2— (аІ+с2 .ЬІ\2=— Ѵ±а2с2—(а2+с2—Ъ2)2. у \ 2а 1 2а
Преобразуемъ подкоренную величину такъ:
(2ас)2—(а2+с2—Ь2)2=(2ас+а2+с2—Ъ2)(2ас—а2—с2+Ь2) = =[(а2+с2+2ас)—Ь2][Ь2—(а2+с2—2ас)]= =[(а+с)2—Ь2][Ь2~ (а—с)2]= =(а+с+Ь)(а+с—Ь)(Ь+а—с)(Ь—а+с).
16'
— 244 —
Если положимъ, что а+Ъ+с=2р, то
а+с—Ь=(а+Ь4~с)—2Ь=2р—2Ь=2(р—Ь).
Подобно этому:
&+«—с=2(р—с);
&+с—а=2(р -а).
Поэтому подкоренную величину можно представить такъ:
16р(р—а)(р—Ь)(р—с).
2-1/ —————
Слѣд.: Лв=ТГ «)(Р—Ь)(р—с).
(ѵ
1 1/
Поэтому: 5=— ака= у р(р—а)(р—Ъ)(р—с).
а
Частный случай. Площадь равносторонняго треугольника со стороною а выражается слѣдующей формулой:
/ 1 \ а I — а ]
\ 2 /
4
814. Задача. Вычислить площадь треуголъ ни-к а АВС (черт. 280) по двумъ сторонамъ АВ и АС и углу А между ними.
Безъ помощи тригонометріи эта задача рѣшается только для нѣкоторыхъ частныхъ значеній угла А. Положимъ напр. что 4 = 18°. Тогда можно вычислить К въ зависимости отъ стороны АВ такимъ образомъ: продолживъ ВВ на разстояніе р БЕ=ВВ, соединимъ Е съ А. Тогда въ равнобедренномъ тр-кѣ АВЕ уголъ ВАЕ равенъ 36°. Изъ этого заключаемъ, что ВЕ, і н .Н і 1^ т.-е. двойная высота, есть сторона правиль-
Д [О наго 10-угольника, вписаннаго въ кругъ, I котораго радіусъ есть АВ. Поэтому ВЕ найдется по формулѣ, опредѣляющей сторону прав. вписан. 10-угольника ('68)
Черт. 280. Опредѣливъ высоту, найдемъ затѣмъ пло-
щадь тр-ка по формулѣ
Я=^40.Л.
Подобно этому задача рѣшается для
4=30°, 45°, 60°.
— 246 —
315. Теорема. Площадь трапеціи равна произведенію полусуммы основаній на высоту.
Черт. 281 Черт. 282.
Проведя въ трапеціи (черт. 281) АВСБ діагопаль АС, мы можемъ разсматривать ея площадь, какъ сумму площадей двухъ тр-ковъ САБ и АВС. Поэтому
111
площ. АВСБ=— АБ . к+~ВС . к=—(АБ+ВС)к.
316. Слѣдствіе. Если МК (черт. 281) есть средняя линія трапеціи, то, какъ извѣстно (117):
МХ==^-(АБ+ВС).
Поэтому площ. АВСБ=МК . к,
т.-е. площадь трапеціи равна произведенію средней линіи на высоту.
Это же можно видѣть и непосредственно изъ чертежа 282-го.
317. Теорема. Площадь всякаго описаннаго многоугольника равна произведенію периметра на половину радіуса.
Соединивъ центръ О (черт. 283) со всѣми вершинами описаннаго многоугольника, мы раздѣлимъ его на треугольники, въ которыхъ за основанія можно взять стороны многоугольника, а за высоту—радіусъ круга. Обозначивъ этотъ радіусъ черезъ В, будемъ имѣть:
1 площ. АОВ=АВВ-,
1 площ. А0Е=АЕВ; и т. д.
а
С
Черт. 283.
— 246 —
1 1
Слѣд., площ. АВСБЕ=(АВ+ВС+СБ+БЕ+ЕА) . ~В=Р . г В, А А
гдѣ буквою Р обозначенъ периметръ мп-ка.
318. Слѣдствіе. Площадь правильнаго многоугольника равна произведенію периметра на половину апоѳемы, потому что всякій прав. многоугольникъ можно разсматривать, какъ описанный около круга, у котораго радіусъ есть апоѳема.
319. Задача. Превратить многоугольникъ {АВСБЕ, черт. 284) въ равновеликій треуголъ-никъ.
Какою-нибудь діагональю АС М с. отсѣкаемъ отъ даннаго мн-ка
ДАВС. Черезъ ту вершину В этого тр-ка, которая лежитъ про-1 чВжЧЛ тивъ взят0Й діагонали, прово-
димъ прямую МЕ II АС. Затѣмъ /А Е продолжимъ одну изъ сторонъ || ЕА или БС, прилежащихъ къ
отсѣченному тр-ку, до пересѣче-Черт. 284. Н1-я съ ПрЯМ010 (на черТежѣ
продолжена сторона ЕА). Точку пересѣченія Е соединимъ съ С. Тр-ки СВ А и СЕ А равновелики (311, 1°), такъ какъ у нихъ общее основаніе АС, а вершины В и Е лежатъ на прямой, параллельной основанію. Если отъ даннаго многоугольника отдѣлимъ тр-къ СВА и вмѣсто него приложимъ равновеликій ему тр-къ СЕ А, то величина площади не измѣнится; слѣд., даннкй многоугольникъ равновеликъ многоугольнику ЕС БЕ, у котораго, очевидно, число угловъ на 1 меньше, чѣмъ у даннаго мн-ка. Такимъ же пріемомъ можно число угловъ полученнаго мн-ка уменьшить еще на 1 и продолжать такое послѣдовательное уменьшеніе до тѣхъ поръ, пока не получится треугольникъ (ЕСС на нашемъ чертежѣ).
320. Задача. Превратить данный многоуголь-никъ въ равновеликій квадратъ.
Сначала превращаютъ многоугольникъ въ равновеликій треугольникъ, а затѣмъ этотъ треугольникъ въ квадратъ. Пусть основаніе и высота треугольника будутъ Ъ и Н, а сторона иско
— 247 —
маго квадрата х. Тогда площадь перваго равна 1/2ЬТі, а второго я;2; слѣд.:
1 о 1
—Ък=х2, откуда —Ъ : х=х : к. а а
Изъ этой пропорціи видно, что х есть средняя пропорціональная между х/2 Ь и к. Значитъ, сторону квадрата можно построить способомъ, указаннымъ раньше (231) для нахожденія средней пропорціональной.
Замѣчаніе. Предварительное превращеніе даннаго многоугольника въ треугольникъ не всегда необходимо. Напр., если рѣчь идетъ о превращеніи къ квадратъ данной трапеціи, то достаточно найти среднюю пропорціональную между высотою трапеціи и ея среднею линіею и па полученной прямой построить квадратъ.
ГЛАВА II.
Теорема Пиѳагора и основанныя на ней задачи.
321. Теорема. Сумма площадей квадратовъ, построенныхъ на катетахъ прямоугольнаго треугольника, равна площади квадрата, построеннаго на гипотенузѣ.
Это предложеніе, извѣстное подъ названіемъ теоремы Пиѳагора (греческаго философа, жившаго въ VI вѣкѣ до Р. X.), имѣетъ многочисленныя доказательства. Приведемъ простѣйшія изъ нихъ.
Первое доказательство (Эвклида). Пусть АВС (черт. 285) прямоугольный треугольникъ, а ВВЕА, АГОС и ВСКН квадраты, построенные на его катетахъ н гипотенузѣ; требуется доказать, что сумма площадей двухъ первыхъ квадратовъ равна площади третьяго квадрата.
Проведемъ АМЛ.ВС. Тогда квадратъ ВСКН раздѣлится на два прямоугольника. Докажемъ, что пр-къ ВЬМН равновеликъ квадрату ВВЕА, а пр-кь ЪСКМ равновеликъ квадрату АЕСС.
— 248 —
Черт. 285.
Проведемъ вспомогательныя прямыя ВС п АН. Обратимъ вниманіе на два тр-ка, покрытые на чертежѣ штрихами. Тр-къ ВСВ, имѣющій основаніе ВВ, общее съ квадратомъ ВВЕА, а высоту равную высотѣ АВ этого квадрата, равновеликъ половинѣ его. Тр-къ АВН, имѣющій основаніе ВН, общее съ прямоугольникомъ ВЪМН, и высоту АР, равную высотѣ ВЬ этого прямоугольника, равновеликъ половинѣ его. Сравнивая эти два треугольника между собою, находимъ, что у нихъ ВВ=ВА и ВС=ВН (какъ стороны квадрата);
сверхъ того Х.ВВС—/1АВН, такъ какъ каждый изъ этихъ угловъ состоитъ изъ общей части АВС и прямого угла. Значитъ, тр-ки АВН п ВВС равны. Отсюда слѣдуетъ, что прямоугольникъ ВВМІІ равновеликъ квадрату ВВЕА.
Соединивъ О съ В и Л съ К, мы совершенно такъ же докажемъ, что прямоугольникъ ЬСКМ равновеликъ квадрату АГСС. Отсюда слѣдуетъ, что квадратъ ВСКН равновеликъ суммѣ квадратовъ ВВЕА и АГСС.
Второе доказательство. Пусть а, Ь и с означаютъ числа, выражающія гипотенузу и катеты прямоугольнаго треугольника въ одной и той же линейной единицѣ. Тогда, каю. мы видѣли раньше (232), между этими числами существуетъ такая зависимость:
а2=Ъ2+с\
Но а2, Ь2 и с2 суть числа, измѣряющія площади квадратовъ, которыхъ стороны а, Ъ и с; поэтому изъ написаннаго равенства слѣдуетъ, что площадь квадрата, построеннаго на гипотенузѣ, равна суммѣ площадей квадратовъ, построенныхъ на катетахъ.
— 249 —
Третье доказательство. Существуетъ много и такихъ доказательствъ, которыя показываютъ, на какія части надо разбить квадраты, построенные на катетахъ, чтобы перемѣщеніемъ этихъ частей образовать квадратъ, построенный на гипотенузѣ. Вотъ одно изъ такихъ доказательствъ.
Обозначимъ гипотенузу и катеты даннаго тр-ка соотвѣтственно буквами а, Ъ и с. Отложивъ на какой-нибудь прямой (черт. 286) АВ = Ъ и ВС=с, построимъ квадраты АВЕВ и ВЕНС. Площадь образовавшагося 6-угольника АВЕЕНС представляетъ собою сумму площадей квадратовъ, построенныхъ па катетахъ. Отложивъ еще АК=с (и, слѣд., КС = Ъ), проводимъ прямыя ВК и КН, которыя разложатъ шестиугольникъ на три части, обозначенныя на чертежѣ цыфрами 1, 2 и 3. Части 1-я и 3-я представляютъ собою прямоугольные тр-ки, равные данному. Повернемъ на 90° тр-къ 1-й вокругъ вершины В и тр-къ 3-й вокругъ вершины Н, какъ указано стрѣлками. Тогда эти части займутъ такія положенія, при которыхъ онѣ, вмѣстѣ съ оставшейся частью 2-й, образуютъ квадратъ, построенный на гипотенузѣ (предоставляемъ самимъ учащимся доказать это).
322. Задачи. 1°. Построить квадратъ, равновеликій суммѣ двухъ данныхъ квадр а-т о в ъ.
Строимъ прямоугольный треугольникъ, у котораго катетами были бы стороны данныхъ квадратовъ. Квадратъ, построенный на гипотенузѣ этого треугольника, равновеликъ суммѣ данныхъ квадратовъ.
2°. Построить квадратъ, равновеликій разности двухъ данныхъ квадратовъ.
Строимъ прямоугольный треугольникъ, у котораго піпоте-нузой была бы сторона •большаго изъ данныхъ квадратовъ, а катетомъ сторона меньшаго квадрата. Квадратъ, построенный на другомъ катетѣ этого треугольника, равновеликъ разности данныхъ квадратовъ.
— 260 —
3°. Построить квадратъ, котораго площадь относилась бы къ площади даннаго
квадрата, какъ т : п.
На произвольной прямой (черт. 287) откладываемъ АВ=т и ВС=п и на АС, какъ на діаметрѣ, описываемъ полуокружность. Изъ точки В возставляемъ перпендикуляръ ВВ до пересѣченія съ окружностью. Проведя хорды АБ и ВС, получимъ прямоугольный тр-къ, у котораго (234):
АВ2 : ВС2=АВ : ВС=т : п.
На катетѣ ВС этого треугольника отложимъ отрѣзокъ ВЕ, равный сторонѣ даннаго квадрата, и проведемъ ЕР II СА. Прямая ВЕ есть сторона искомаго квадрата, потому что
ВР АВ /'ВЕ\г /АВ\2
ВЁГІЮ' 0ТКуда: \вё) ~\ВС/ ’
слѣд.: ВР2 : ВЕ2=АВ2 : ВС2—т : п.
823. Пиѳагоровы треугольники. Такъ наз. прямоугольные тр-ки, у которыхъ стороны, измѣренныя одною и тою же единицей, выражаются цѣлыми числами. Такихъ тр-ковъ существуетъ безчисленное множество. Простѣйшій изъ нихъ есть тотъ (извѣстный еще съ глубокой древности), у котораго стороны выражаются числами: 3, 4 и б (3®+4г=5®). Доказано, что стороны пиѳагоровыхъ тр-ковъ могутъ быть выражены слѣдующими общими формулами:
х=2аЪ
катеты:
гипотенуза г=а2 4-Ь8,
гдѣ а и Ъ суть произвольныя цѣлыя числа, лишь бы было а>Ь.
ГЛАВА ІП.
Отношеніе площадей подобныхъ фигуръ.
324. Теорема. Площади двухъ треугольниковъ, имѣющихъ по равному углу, относятся, какъ произведенія сторонъ, заключающихъ эти углы.
— 251 —
Пусть (черт. 288) въ тр-кахъ АВС и А^В^ углы А и Яі равны. Проведя высоты ВР и В^, будетъ имѣть:
площ. АВС АС.ВР _ АС ВР .
Площ. А^В^С-і АіС/}»В]Рі А^Ві В^Р^
В
Черт. 288.
Тр-ки АВР и Л1В1Р1 подобны (А=А1 и Р=Рг); поэтому отношеніе ВР : ВхРх равно отношенію АВ : Я1В1; замѣнивъ первое вторымъ, получимъ:
площ, АВС _ АС АВ АС.АВ
площ. А^В^С^ -^іВі АіСі.АіВі
325. Замѣчаніе. Предлагаемъ самимъ учащимся доказать, что если у двухъ треугольниковъ АВС и (черт. 288)
углы А и Аг не равны, по составляютъ въ суммѣ 2й, то площади такихъ тр-ковъ также относятся, какъ произведенія сторонъ, заключающихъ углы А и Ах.
326. Теорема. Площади подобныхъ треугольниковъ или многоугольниковъ относятся, какъ квадраты сходственныхъ сторонъ.
1°. Если АВС и Л1В1С1 (черт. 288) два подобные треугольника, то углы одного равны соотвѣтственно угламъ другого; пусть А—Аі, В—Ві и С^Сі.Примѣняя къ нимъ предыдущую теорему, получимъ:
площ. АВС ____ АВ.АС _______ АВ АС
площ. А^Сі А1В1 . АгСі А^ А&
Но изъ подобія треугольниковъ слѣдуетъ:
АВ _ АС _ ВС .
А& — АіСі~ В&
— 262 —
Поэтому въ равенствѣ [1] мы можемъ каждое изъ отношеній АВ АС
— _ѵ замѣнить любымъ отношеніемъ ряда [2]; слѣд.:
площ. АВС / АВ \ 2_ ( АО \ 2_ / ВС \ 2
площ. Л1В1С1 Уа^Ві/ УАгСі/ Уб^)
_ АВ2 _ АС2 _ ВС2 ~ ЛіВ’і2 “ ла2 ~ в^с?
2°. Если АВСВЕ и АіВ^ВіЕі (черт. 289) два подобные многоугольника, то ихъ можно, какъ мы видѣли (208), разложить на одинаковое число подобныхъ и одинаково располо-
Чсрт. 289.
женныхъ тр-ковъ. Пусть эти тр-ки будутъ: АВО и А^О^ АОЕ и ЛіОіЕх и т. д. Согласно доказанному въ первой части этой теоремы, мы получимъ пропорцію:
площ. АОВ / АВ\2 площ. ВОС / ВС \2
------------= I-----;--------------=(-------) ; ит. д.
площ. А1О1В1 \ АіВі/ площ. В^С^ \ В^/
Но изъ подобія многоугольниковъ слѣдуетъ:
АВ _ ВС _ СВ А^В1~В^Сі~С^р'1
{ АВ\2 ( ВС \ 2 ( СВ \ 2 и потому:
площ. АОВ площ. ВОС площ. СОВ
Значитъ: -------ГТГН’ —------тТТГТГ =*----„ = • • •
площ. Л1О1В1 площ. ВіОхСх площ. 0$^
— 253 —
Откуда (по свойству равныхъ отношеній):
пл. ЯОВ+пл, ВОС +пл. СОР + пл. АВС РЕ АВ2 пл.Л1О1В1+пл.В1О1С1+пл.С'1О1І)1+... пл. А^СіЕ^ А^В^
327. Слѣдствіе. Площади правильныхъ одноименныхъ
многоугольниковъ относятся, какъ квадраты сторонъ, или квадраты радіусовъ, или квадраты апоѳемъ (262).
328. Задача. Раздѣлить данный треугольникъ на т равновеликихъ частей прямыми,
параллельными его сторонѣ.
Пусть, напр., требуется? раздѣлить тр-пикъ АВС (черт. 290) на 3 равновеликія части пря
мыми, пераллельпыми основанію АС. Предположимъ, что задача рѣшена, и что искомыя прямыя будутъ РЕ и ЕС. Очевидно, что если мы найдемъ отрѣзки ВЕ и ВС, то затѣмъ опредѣлятся и прямыя РЕ и ЕС. Тр-ки ВРЕ, ВЕСг и ВАС подобны; поэтому:
площ. ВРЕ ВЕ2 площ. ВАС ВС2
площ. ВЕСг ВО2
площ. ВАС ВС2
Но изъ требованій задачи видно, что: площ. ВРЕ 1 площ. ВЕСг 2 площ. ВАС 3 площ. ВАС 3 ’
Слѣд.: ВЕ2 1 ВС2 _ 2 ВС2 з 11 ВС2 3 '
Откуда: ВВ-] / _2_в<72=1/ вс У о Г 3 и ВС=і/-|-ВС2=’|/^-ВС.ВС.
Изъ этихъ выраженій видимъ, что ВЕ есть средняя пропорціональная между ВС и г/з а ЕСг есть средняя пропорціо-
— 254 —
нальпая между ВС и а/3 ВС (255, 4). Поэтому построеніе можно выполнить такъ: раздѣлимъ ВС на три равныя части въ точкахъ а и Ь; опишемъ на ВС полуокружность; изъ а и Ь возставимъ къ ВС перпендикуляры аН и ЪК. Хорды НВ и ВК будутъ искомыми средними пропорціональными: первая—между всѣмъ діаметромъ ВС и его третьею частью Ва, вторая—между ВС и ВЪ, т.-е. между ВС и 2/3 ВС (230). Остается отложить эти хорды на ВС отъ точки В- тогда получимъ искомыя точки Е и С.
Подобнымъ образомъ можно раздѣлить тр-къ на какое угодно иное число равновеликихъ частей.
ГЛАВА IV.
Площадь круга и его частей.
329. Лемма 1-я. При неограниченномъ удвоеніи числа сторонъ правильнаго многоугольника, вписаннаго въ окружность:
1°, сторона этого многоугольника стремится къ нулю;
2°, разность между радіусомъ окружности и апоѳемой многоугольника стремится къ нулю.
1°. Обозначимъ периметръ правильнаго вписаннаго многоугольника черезъ р, а число его сторонъ черезъ п; тогда длина одной стороны этого многоугольника выразится дробью р/п. При неограниченномъ удвоеніи числа сторонъ этого многоугольника знаменатель дроби */„ будетъ возрастать безпредѣльно, а числитель хотя и будетъ возрастать, по не безпредѣльно, такъ какъ периметръ всякаго вписаннаго выпуклаго многоугольника меньше периметра любого описаннаго многоугольника (напр., меньше описаннаго квадрата) *). Если же въ дроби знаменатель увеличивается безпредѣльно, а числитель хотя и увеличивается, но остается меньше нѣкоторой постоянной величины, то, какъ извѣстно изъ алгебры, эта дробь можетъ быть сдѣлана менѣе
*) Можно было бы сказать, что периметръ р не увеличивается безпредѣльно, потому что онъ остается всегда меньше длины окружности; но основаніе, приведенное въ текстѣ, удобнѣе, такъ какъ оно не предполагаетъ предварительнаго установленія понятія о длинѣ окружности.
— 255 —
любой данной положительной величины; значитъ, при неограниченномъ удвоеніи числа сторонъ вписаннаго правильнаго многоугольника сторона его, равная дроби р/п, стремится къ О.
2°. Пусть АВ (черт. 291) есть сто-
рона какого-нпбудь правильнаго вписаннаго многоугольника, ОА радіусъ и ОС апоѳема. Изъ тр-ка ОАС находимъ (52):
ОА—ОС<АС Л или ОА—ОС<— АВ,
т.-е. разность между радіусомъ и апоѳемою меньше половины стороны правильнаго многоугольника. Но при неограниченномъ удвоеніи числа
сторонъ правильнаго вписаннаго многоугольника сторона его, какъ мы видѣли, стремится къ нулю; поэтому разность между радіусомъ и апоѳемою и подавно стремится къ нулю.
230. Лемма 2-я. Разность между площадью правильнаго
многоугольника, описаннаго около круга, и площадью правильнаго одноименнаго многоугольника, вписаннаго въ тотъ же кругъ, при неограниченномъ удвоеніи числа сторонъ этихъ
многоугольниковъ, стремится къ нулю.
Впишемъ въ кругъ (черт. 292) п опишемъ около него по какому-
нибудь правильному мн-ку (па чертежѣ изображены 6-угольники).
Пусть В будетъ радіусъ круга, а— апоѳема вписаннаго мн-ка, д его площадь и О—площадь описаннаго мн-ка. Тогда (327):
О : д=В2 : а2.
Составимъ изъ этой пропорціи производную (разность членовъ перваго отношенія относится такъ къ предыдущему члену этого отношенія, какъ...):
В2—а2
а2
— 256 —
Откуда: (О—д)В2=^(В2—а2),
или (<2—^)В2=^(Т^+а)(I^-а).
При неограниченномъ удвоеніи числа сторонъ многоугольниковъ разность I?—а, по доказанному въ предыдущей леммѣ, стремится къ нулю, сомножитель уменьшается *), а сомножитель В+а всегда остается меньше В+В; вслѣдствіе этого правая часть послѣдняго равенства (слѣд., и лѣвая его часть), при неограниченномъ удвоеніи числа сторонъ мн-ковъ, стремится къ нулю. Но лѣвая часть равенстга, представляя собою произведеніе, въ которомъ множитель В®—число постоянное, можетъ стремиться къ нулю только тогда, когда его множимое стремится къ пулю; множимое же фи есть разность площадей правильныхъ многоугольниковъ, описаннаго и вписаннаго.
331. Замѣчаніе. Такимъ же путемъ мы можемъ доказать, что разность между периметромъ описаннаго и периметромъ одноименнаго вписаннаго правильнаго мн-ка, при неограниченномъ удвоеніи числа ихъ сторонъ, стремится къ нулю. Дѣйствительно, если Р и р будутъ периметры одноименныхъ правильныхъ мн-ковъ, описаннаго и вписаннаго, то (263):
Р : р = В : а.
Откуда: (Р—р) : Р=(В—а) : Е,
и, слѣд., (Р—р) В=(Е—а) Р.
При неограниченномъ удвоеніи числа сторонъ мн-ковъ правая часть послѣдняго равенства (слѣд., и его лѣвая часть) стремится къ нулю, такъ какъ множимое К—а, по доказанному, стремится къ нулю, а множитель Р уменьшается. Но лѣвая часть равенства, представляя собою произведеніе, въ которомъ множитель К—число постоянное, можетъ стремиться къ нулю только тогда, когда его множимое стремится къ нулю; а множимое и есть разность периметровъ Р и р.
332. Теорема. Площадь круга есть общій предѣлъ площадей правильныхъ вписанныхъ въ этотъ кругъ и описанныхъ около него многоугольниковъ при неограниченномъ удвоеніи числа ихъ сторонъ.
Пусть около круга, площадь котораго мы обозначимъ К, описанъ какой-нибудь правильный мн-къ и въ него вписанъ
*) такъ какъ при каждомъ удвоеніи числа сторонъ правильнаго описаннаго мн-ка отъ его угловъ срѣзываются небольшіе тр-ки, отчего, конечно, плоціадь мн-ка уменьшается.
— 257 —
одноименной правильный мн-къ (черт. 292). Обозначимъ площадь перваго а площадь второго д. Если станемъ удваивать число сторонъ этихъ мн-ковъ, то величины Цпц сдѣлаются перемѣнными, тогда какъ величина К останется неизмѣнной. Требуется доказать, что при неограниченномъ удвоеніи числа сторонъ мн-ковъ перемѣнныя величины С п д стремятся къ одному и тому же предѣлу, именно къ площади К.
Очевидно, что, каково бы ни было число сторонъ мн-ковъ, всегда $^>К^>д, и потому каждая изъ двухъ разностей: ф—К и К—д всегда меньше разности —д. Но при неограниченномъ удвоеніи числа сторонъ мн-ковъ разность —д, согласно леммѣ 2-й, стремится къ нулю; слѣд., при этомъ каждая изъ меньшихъ разностей: ф—К и К—д и подавно стремится къ нулю; а это, согласно опредѣленію предѣла, означаетъ, что
пред. §=К и пред. д=К.
333. Замѣчаніе. Можно также утверждать, что длина окружности есть общій предѣлъ периметровъ правильныхъ вписанныхъ въ эту окружность и описанныхъ около нея многоугольниковъ при неограниченномъ удвоеніи числа ихъ сторонъ. Дѣйствительно, изъ того обстоятельства, что разность Р—р стремится къ нулю (331), надо заключить, что перемѣнные периметры Р и р могутъ стремиться только къ одному и тому же предѣлу; но предѣлъ р есть то, что принимается за длину окружности; значитъ, и предѣлъ Р есть тоже длина окружности.
334. Теорема. Площадь круга равна произведенію длины окружности на половину радіуса.
Пусть I?, К и С означаютъ радіусъ, площадь и длину данной окружности, а д, р п а—площадь, периметръ и апоѳему какого-нибудь правильнаго вписаннаго многоугольника. Тогда можемъ написать (318):
1
д=р--а. [1]
Вообразимъ теперь, что число сторонъ вписаннаго многоугольника неограниченно удваивается. Тогда величины д, р и а дѣлаются перемѣнными, при чемъ первая имѣетъ предѣломъ площадь круга К, вторая—длину окружности С, а третья—радіусъ ея Н. Такъ какъ при этомъ равенство [1] остается постоянно
А. Киселевъ. Геометрія. 17
— 258 —
вѣрнымъ, то, согласно основному началу способа предѣловъ (283), оно останется вѣрнымъ и тогда, когда вмѣсто перемѣнныхъ подставимъ ихъ предѣлы; послѣ такой подстановки получимъ:
К=С.-П.
[2]
335. Слѣдствія. 1°. Площадь круга равна произведенію квадрата радіуса на число л (отношеніе окружности къ діаметру).
Дѣйствительно, подставивъ въ равенство [2] предыдущаго параграфа на мѣсто С произведеніе 2ігВ (292, 2), получимъ:
К=пП2.
2°. Площади круговъ относятся, какъ квадраты радіусовъ или діаметровъ.
Дѣйствительно, если К и Кг будутъ площади двухъ круговъ, а В и Д ихъ радіусы, то
Откуда:
К=ігВ2 и кі^2.
К ігй2 В2 4В2 (2В)2
Кі ісйі2 В,2 4ВХ2 (2ВХ)2
336. Задача I. Вычислить площадь круга, окружность котораго равна 2 метрамъ. Для этого предварительно находимъ радіусъ В изъ уравненія:
1
2тѵВ=2; откуда В=—=0,3183...
Затѣмъ опредѣляемъ площадь круга:
/ Л2 1
К=ісВ2=іг 1 — 1 =—=0,3183... квадр. метра.
іг/ іс
Задача 2. Превратить данный кругъ въ квадратъ (т.-е. построить квадратъ, равновеликій данному кругу).
Эта задача, извѣстная подъ названіемъ квадратуры круга, не можетъ быть рѣшена при помощи циркуля и ли
— 259 —
нейки. Дѣйствительно, если обозначимъ черезъ х сторону искомаго квадрата, а черезъ И радіусъ круга, то получимъ уравненіе:
ж=ігВ2; откуда: ъВ : х~х : В,
т.-е. х есть средняя пропорціональная между полуокружностью и радіусомъ. Слѣд., если извѣстна прямая, которая равна длинѣ полуокружности, то легко построить квадратъ, равновеликій данному кругу, и обратно: если извѣстна сторона квадрата, равновеликаго кругу, то можпо построить прямую, равную по длинѣ полуокружности. Но доказано, что помощью циркуля и линейки нельзя построить прямую, которая въ точности равнялась бы длинѣ полуокружности (см. выноску въ задачѣ № 257, стр. 229-я); слѣд , нельзя въ точности рѣшить задачу о превращеніи круга въ квадратъ. Приближенное же рѣшеніе можпо выполнить, если предварительно найти приближенную длину полуокружности и затѣмъ построить среднюю пропорціональную между этою длиною и радіусомъ.
337. Теорема. Площадь сектора равна произведенію его дуги на половину радіуса.
Пусть дуга ЛВ (черт. 293) сектора АОВ содержитъ п°. Оче-
видно, что площадь сектора, котораго дуга содержитъ 1°, составляетъ Ѵзео часть площади круга, т.-е. она равна
тсВ2
360*
Слѣд., площадь 8 сектора, котораго дуга содержитъ п°, равна
тгВ2п т^Вп В
8 360 І80 2
Черт. 203.
Т^Вп
Такъ какъ —— выражаетъ ІоО
длину дуги АВ, то, обозначивъ ее
черезъ $, получимъ:
5=8.
В
2
17
— 260 —
338. Задача. Вычислить площадь сегмента,
зная радіусъ
ключающееся
Черт. 294.
круга и число градусовъ, завъ дугѣ сегмента.
Чтобы получить площадь сегмента А8В, (черт. 294), достаточно изъ площади сектора АОВ вычесть площадь тр-ка АОВ, Проведя АС_\_ОВ, будемъ имѣть:
площадь сектора =-^ Вз;
площадь тр-ка=~2 ОВ.АС = ^ В. АС.
Слѣд., площ. сегмента В(«—АС).
Такимъ образомъ, вопросъ приводится къ вычисленію высоты АС. Геометрически (т.-ѳ. безъ помощи тригонометріи) ее можно вычислить только въ нѣкоторыхъ частныхъ случаяхъ слѣдующимъ способомъ.
Продолживъ АО до пересѣченія съ окружностью въ точкѣ О, мы увидимъ, что АС=СО и '~АВ = '^ВО\ значитъ, АС есть половина хорды, стягивающей дугу, вдвое ббльшую дуги сегмента. Отсюда заключаемъ, что если хорда, стягивающая двойную дугу, будетъ сторона такого правильнаго вписаннаго многоугольника, для котораго мы знаемъ формулу его стороны, то высота АС опредѣлится геометрически. Напр., пусть дуга сегмента содержитъ 60°. Тогда АО есть сторона правильнаго вписаннаго треугольника; значитъ, 4С=1/гВ)^3. Дуга АВ въ этомъ случаѣ равна х/в окружности, т.-е.
В; поэтому:
площ. сегмента = -^- 12^2^я—3)^3).
Замѣчаніе. Если хорда АВ есть сторона такого правильнаго вписаннаго п—угольника, которую мы можемъ вычислить по данному радіусу, то площадь сегмента можно найти также и по слѣдующей формулѣ:
пл. сѳгм. = —Іпл. круга—пл. прав. «-угольника I.
339. Теорема. Сумма площадей подобныхъ многоугольниковъ (или круговъ), построенныхъ на катетахъ прямоугольнаго треугольника, равна площади подобнаго многоугольника (или круга), построеннаго на гипотенузѣ, если катеты и гипотенуза служатъ сходственными сторонами этихъ многоугольниковъ (или діаметрами круговъ).
Пусть В и 8 будутъ площади подобныхъ фигуръ (или кру-
— 261 —
говъ), построенныхъ на катетахъ и гипотенузѣ прямоугольнаго тр-ка АБС (черт. 295). Тогда (326, 335, 2°)
АВ2 В_ВС2 ~8~АС*' ~8~АС*
Сложивъ эти равенства, найдемъ: <Э+В АВ2+ВС2.
8 АС2
Но АВ2+ВС2=АС2 (232;) поэтому:
340. Слѣдствіе. Если на сторонахъ прямоуголь
АВС (черт. 296) построимъ
наго треугольника
полукруги, расположивъ ихъ такъ, какъ указано на чертежѣ, то сумма площадей образовавшихся при этомъ фигуръ (луночекъ) М и 2Ѵ равна площади треугольника.
Дѣйствительно, сумма полукруговъ, построенныхъ на катетахъ, равна полу-кругу, построенному на гипотенузѣ; тч
если же отъ обѣихъ частей этого равен-ства отнимемъ сумму сегментовъ 1-го и 2-го, то получимъ:
М+У=площ. АВС. $
Фигуры М и 2Ѵ извѣ тны подъ назва-
ніемъ Гиппократовыхъ лу- Черт. 296.
ночекъ. *)
Когда треугольникъ равнобедренный, то обѣ луночки одинаковы
и каждая изъ нихъ равновелика половинѣ треугольника.
ГЛАВА V.
Соотношенія между сторонами треугольника и радіусами вписаннаго и описаннаго круговъ.
341. По теоремѣ § 250 мы имѣемъ: Ьс=2ЯЛо, гдѣ Ъ и с суть двѣ стороны треугольника, ка—высота, опущенная на третью сторону треугольника, и В—радіусъ описаннаго круга. Изъ этого равенства выводимъ:
Й-—•
Й-2ЛО
*) По имени греческаго геометра Гиппократа Хіосскаго, жившаго въ V вѣкѣ до Р. Хр.
— 262 —
Исключимъ изъ этой формулы высоту Ла; для этого умножимъ числителя и знаменателя дроби на а; тогда, замѣнивъ произведеніе Ъ,аа удвоенною площадью треугольника (которую обозначимъ 8), по-
лучимъ:
о аЬс аЪс
— 1 —- ' ІГ г" _ ...7. ~ — — — .
48 4 у р(р— а)(р— Ь)(р — с) гдѣ р=1/і(а+Ь + с).
Чтобы найти радіусъ г внутренняго вписаннаго круга (черт. 297), примемъ во вниманіе, что прямыя О А, ОВ и ОС раздѣляютъ данный тр-къ на три тр-ка, у которыхъ основаніями служатъ стороны даннаго тр-ка, а высотою—радіусъ т. Поэтому:
5=-^ аг+-^Ьг+±сг= г±(а + Ъ + с)=гр.
Отсюда:
Р г р
Радіусъ ро, внѣвписаннаго круга (черт. 298), касающагося сто роны а, можно опредѣлить изъ равенства:
Черт. 298.
пл. АВС=пл. АСО-У 4-пл. АВО—пл. ВОС, і , і 1 т.-е. ора+тг ера—2 «Ра-
Откуда:
28 _ 28 8
Р“ —а 2(р—а)~р-а
Подобно этому найдемъ: 8 8
Рь—и
Между четырьмя радіусами т, ро, рь, и ре существуютъ нѣкоторыя
зависимости. Укажемъ простѣйшую изъ нихъ:
1 Зр—а—Ъ—с Зр—2р_ р
К- 8 8 ~ 8
- + -Ра РЬ
р 1 1,1,11
Но-ст = —; слѣд., — +— V' 8 Г ' А Ра РЬ Ре
ДОБАВЛЕНІЕ.
Построеніе корней квадратнаго уравненія.
842. Объ однородности уравненій, получаемыхъ при рѣшеніи геометричеетихъ задачъ. Просматривая всѣ цѣлыя алгебраическія выраженія, найден
— 263 —
ныя въ геометріи для вычисленія различныхъ линій, мы замѣчаемъ, что всѣ они одного измѣренія, т.-е. всѣ содержатъ только одного буквеннаго множителя, выражающаго длину нѣкоторой линіи. Таковы, напр., выраженія:
Я/2?.. для стороны вписаннаго квадрата;
для стороны прав. впис. треугольника; 2иВ.... для длины окружности круга; и т. п.
(въ послѣдней формулѣ буква и означаетъ не линію, а отвлеченное число 3,14...; поэтому она не вліяетъ на измѣреніе выраженія).
Просматривая далѣе всѣ цѣлыя алгебраическія выраженія, найденныя въ геометріи для вычисленія площадей различныхъ фигуръ, мы замѣчаемъ, что всѣ они двухъ измѣреній, т.-е. всѣ содержатъ по 2 буквенныхъ множителя, выражающихъ длины нѣкоторыхъ линій. Таковы, напр., выраженія:
Ък... для площади прямоугольника;
1
-Ък... для площади треугольника;
-аѴз... для площади равност. треугольника; для площади круга, и т. п.
(Подобно этому, какъ мы впослѣдствіи узнаемъ изъ стереометріи, цѣлыя алгебраическія выраженія, служащія для вычисленія объемовъ, оказываются всѣ трехъ измѣреній, т.-е. содержатъ въ себѣ по 3 буквенныхъ множителя, выражающихъ длины нѣкоторыхъ линій).
Замѣтивъ это, примемъ во вниманіе, что всякое уравненіе есть равенство двухъ выраженій. Слѣд., въ геометрическомъ смыслѣ оно представляетъ собою или равенство линій, или равенство площадей (или равенство объемовъ), или же, наконецъ, равенство отношеній. Когда уравненіе, составленное при рѣшеніи геометрической задачи, выражаетъ равенство линій, обѣ его части должны быть одного измѣренія; когда оно выражаетъ равенство площадей, его части должны быть двухъ измѣреній, и т. д. Слѣд., во всѣхъ случаяхъ полученное уравненіе должно быть однороднымъ. Однородность не нарушится и
— 264 —
послѣ преобразованія уравненія, какъ не трудно видѣть, принявъ во вниманіе все то, что извѣстно намъ изъ алгебры о преобразованіи уравненій.
Сказанное, впрочемъ, вѣрно только при томъ условіи, если ниоднапзълиній, входящихъвъуравпеніе не принята за единицу. Въ противномъ случаѣ однородность нарушается. Напримѣръ, уравненіе я2=тсг2, выражающее равенство между площадями искомаго квадрата и даннаго круга, обращается въ неоднородное (я2=тс), когда радіусъ даннаго круга принятъ за 1.
343. Построеніе корней квадратнаго уравненія. Изъ сказаннаго слѣдуетъ, что если при рѣшеніи какой-нибудь геометрической задачи помощью алгебры мы получили уравненіе (при чемъ пи одна изъ линій, входящихъ въ уравненіе, не была принята за 1), то всѣ члены этого уравненія должны быть одинаковаго измѣренія. Поэтому, упростивъ квадратное уравненіе, мы всегда приведемъ его къ такому виду: я2±ря±аЬ=о, въ которомъ всѣ члены двухъ измѣреній (при чемъ буквы р, а и Ъ выражаютъ данныя положительныя длины, а буква х—искомую длину, положительную или отрицательную). Если предварительно построимъ (231) вспомогательную прямую д, представляющую собою среднюю геометрическую прямыхъ а и Ъ (т.-е. построимъ выраженіе то, замѣнивъ въ уравненіи
произведеніе аЪ на ц2, мы приведемъ его къ такому виду:
®2±раг±д2=о.
Сочетая различными способами знаки + и — передъ членами рх и д2, мы будемъ имѣть слѣдующіе 4 вида квадратныхъ уравненій:
1°. я2—ртЧд2=о; 3°. я2+ря+д2=о;
2°. я2—рх—д2=о; 4°. я2+ря—<^=о.
Нетрудно видѣть, что уравненія 3° и 4° получаются соотвѣтственно изъ уравненій 1° и 2° посредствомъ замѣны въ нихъ я на —я; значитъ, корни уравненій 3° и 4° суть корни соотвѣт
— 266 —
ственно уравненій 1° и 2°, только взятые съ противоположными знаками. Поэтому намъ достаточно указать построеніе корней только уравненій 1° и 2°.
1°. х2—рх} д2=о;
т.-е. ^Ц+]/
Предположимъ сначала, что
Тогда выраженіе
2
—д2 представляетъ собою
катетъ такого прямоуголь-
наго тр-ка, у котораго гипотенуза есть р/2, а другой катетъ равенъ д; вслѣдствіе этого построеніе всего проще можно вы
полнить такъ:
На какой-нибудь прямой АВ (черт. 299) беремъ произвольную точку С и возставляемъ изъ нея къ АВ перпендикуляръ, на которомъ откладываемъ СЛ=д. Изъ точки В, какъ центра, радіусомъ, равнымъ р/2, пересѣкаемъ
прямую АВ въ нѣкоторой точкѣ О; тогда, проведя прямую ОВ, мЫ получимъ прямоугольный тр-къ ОВС, у котораго
ос=Ѵ ов2—св2=|/ 92.
Остается теперь къ р/2 приложить ОС (тогда получимъ хО и отъ р/2 отнять ОС (тогда получимъ х^). Для этого раствореніемъ циркуля, равнымъ ОВ—р/2, откладываемъ на прямой АВ, въ обѣ стороны отъ точки О отрѣзки ОЕ и ОЕ-, тогда ЕС=Хі и СЕ=х2.
Если —=д, то ж1=ж2=—; если же -\д, то корни а?! игс2 А А А
будутъ мнимые.
— 266 —
Въ этомъ случаѣ корни всегда вещественные, при чемъ корень Хі положительный, а ж2 отрицательный. Такъ какъ выраженіе _ / / ®\2 , , -
I/ ( —] Н-д2 представляетъ собою гипотенузу прямоугольнаго V \2/
Р\2 , ,
—) +д2. Остается къ 2/
тр-ка, у котораго катеты равны р/а и д, то построеніе всего проще можно выполнить такъ:
Возставивъ изъ точки С перпендикуляръ къ АВ (черт. 300), отложимъ на немъ СП=д; на АВ отложимъ СО^^. Проведя прямую 01), мы получимъ прямоугольный тр-къ ОСВ, у котораго 00= Д/ОС24-СІ)2=
ОВ приложить ”/2 (тогда полу
чимъ жх) и отъ ОВ отпять ”/2 (тогда получимъ абсолютную величину жг).
УПРАЖНЕНІЯ.
Доказать теоремы:
261. Въ параллелограммѣ разстоянія какой-ниубдь точки діагонали отъ двухъ прилежащихъ сторонъ обратно пропорціональны этимъ сторонамъ.
262. Площадь трапеціи равна произведенію одной изъ непараллельныхъ сторонъ на перпендикуляръ, опущенный изъ средины другой непараллельной стороны на первую.
— 267 —
263. Два четыреугольника равновелики, если у нихъ равны соотвѣтственно діагонали и уголъ между ними.
264. Если площади двухъ треугольниковъ, прилежащихъ къ основаніямъ трапеціи и образуемыхъ пересѣченіемъ ея діагоналей, равны соотвѣтственно р® и ^2, то площадь всей трапеціи равна (р+з)®.
265. Площадь правильнаго вписаннаго шестиугольника равна 3/4 площади правильнаго описаннаго шестиугольника.
266. Въ четыреугольникѣ АВСП черезъ середину діагонали ВО проведена прямая, параллельная другой діагонали АС; эта прямая пересѣкаетъ сторону АП въ точкѣ Е. Доказать, что прямая СЕ дѣлитъ четыреугольникъ пополамъ.
267. Если медіаны треугольника взять за стороны другого треугольника, то площадь послѣдняго равна 3/4 площади перваго.
268. Въ кругѣ съ центромъ О проведена хорда АВ. На радіусѣ О А, какъ на діаметрѣ, описана окружность. Доказать, что площади двухъ сегментовъ, отсѣкаемыхъ хордою АВ отъ обоихъ круговъ, относятся, какъ 4:1.
Задачи на вычисленіе.
269. Вычислить площадь прямоугольной трапеціи, у которой одинъ изъ угловъ равенъ 60°, зная или оба основанія, или одно основаніе и высоту, или одно основаніе и боковую сторону, наклонную къ основанію.
270. Вычислить площадь равносторонняго треугольника, зная его высоту Л.
271. Даны основанія трапеціи В и Ь и ея высота Н. Вычислить высоту треугольника, образованнаго продолженіемъ непараллельныхъ сторонъ трапеціи до взаимнаго пересѣченія.
272. Составить формулу для площади правильнаго вписаннаго 12-угольника въ зависимости отъ радіуса круга.
273. Въ треугольникъ вписанъ другой треугольникъ, котораго вершины дѣлятъ пополамъ стороны перваго треугольника; въ другой треугольникъ вписанъ подобнымъ же образомъ третій тр-къ; въ третій—четвертый и т. д. безъ конца. Найти предѣлъ суммы площадей этихъ треугольниковъ.
274. Въ данномъ треугольникѣ извѣстны стороны а, Ь и с. Изъ серединъ этихъ сторонъ возставлены перпендикуляры х, у и г до взаимнаго пересѣченія въ центрѣ описаннаго круга. Найти въ зависимости отъ а, Ъ и с величины х, у и г и радіусъ В описаннаго круга. (Указаніе: пользуясь теоремою Птоломея (242), можно вывести уравненія: Ъг-}-су=аВ, сх+аг = ЪВ, ау+Ьх=с& и ах + Ъу + сг=28, гдѣ 8 есть площадь треугольника).
Задачи на построеніе.
275. Раздѣлить треугольникъ прямыми, проходящими черезъ его вершину, на три части, которыхъ площади относились бы, какъ т : п : р.
— 268 —
276. Раздѣлить пополамъ т-къ прямою, проходящею черезъ данную точку его стороны.
277. Найти внутри тр-ка такую точку, чтобы прямыя, соединяющія ее съ вершинами тр-ка, дѣлили его на три равновеликія части.
278. —то же—на три части въ отношеніи 2:3:4 (или вообще т : п : р).
279. Раздѣлить параллелограммъ на три равновеликія части прямыми, исходящими изъ вершины его.
280. Раздѣлить параллелограммъ на двѣ части въ отношеніи т : п прямою, проходящею черезъ данную точку.
281. Раздѣлить параллелограммъ на 3 равновеликія части прямыми, параллельными діагонали.
282. Раздѣлить площадь тр-ка въ среднемъ и крайнемъ отношеніи прямою, параллельною основанію.
283. Раздѣлить тр-къ на три равновеликія части прямыми, перпендикулярными къ основанію.
284. Раздѣлить кругъ на 2, на 3... равновеликія части концетри-ческими окружностями.
285. Раздѣлить пополамъ трапецію прямою, параллельною основаніямъ. (Указаніе: продолживъ непараллельныя стороны до взаимнаго пересѣченія, взять за неизвѣстную величину разстояніе конца искомой линіи до вершины тр-ка; составить пропорціи, исходя изъ площадей подобныхъ тр-ковъ...).
286. Данный прямоугольникъ превратить въ другой равновеликій прямоугольникъ съ даннымъ основаніемъ.
287. Построить квадратъ, равновеликій даннаго квадрата.
288. Превратить квадратъ въ равновеликій прямоугольникъ, у котораго сумма я или разность А двухъ смежныхъ сторонъ дана.
289. Построить кругъ, равновеликій кольцу, заключенному между двумя данными концетрическими окружностями.
290. Построить тр-къ, подобный одному и равновеликій другому изъ двухъ данныхъ тр-ковъ.
291. Данный тр-къ превратить въ равновеликій равносторонній (посредствомъ приложенія алгебры къ геометріи).
292. Въ данный кругъ вписать прямоугольникъ съ данною площадью т3 (посредствомъ приложенія алгебры къ геометріи).
293. Въ данный тр-къ вписать прямоугольникъ съ данною площадью т3 (приложеніемъ алгебры къ геометріи).
Числовыя задачи на разные отдѣлы планиметріи *).
294. Катеты прямоугольнаго тр-ка суть 3 ф. и 4 ф. Найти площадь круга, котораго окружность проходитъ черезъ середину меньшаго катета и касается гипотенузы въ ея серединѣ.
*) Взяты изъ «Сборника геометрическихъ задачъ для повторительнаго курса планиметріи», составилъ М. Попруженко, изданіе 3-е, исправленное и дополненное, Москва, 1905 г.
— 269 —
295. Точка касанія окружности, вписанной въ прямоугольный тр-къ, дѣлитъ гипотенузу на отрѣзки а и Ъ. Найти площадь тр-ка.
296. Катеты прямоугольнаго тр-ка суть Ъ и с. Найти биссектриссу прямого угла.
297. Радіусы двухъ концетрическихъ окружностей суть 15 см. и 8 см. На продолженномъ діаметрѣ взята точка на разстояніи 17 см. отъ общаго центра, и изъ нея проведены касательныя къ этимъ окружностямъ. Найти разстояніе точекъ касанія. (У казаніе: примѣнить теорему Птоломея).
298. Часть площади круга, заключенная между стороною вписаннаго квадрата и параллельною ей стороною правильнаго вписаннаго 6-угольника, равна 1/12 (л+зѴ 3—6) Найти сторону квадрата, равновеликаго данному кругу.
299. Въ ромбъ, который раздѣляется діагональю на два равносторонніе тр-ка, вписанъ кругъ. Найти сторону ромба въ зависимости отъ радіуса этого круга.
300. Въ тр-кѣ, котораго стороны суть 4 см., 5 см. и 6 см., проведены биссектриссы меньшаго угла и смежнаго съ нимъ внѣшняго угла. Найти отрѣзокъ противолежащей стороны, заключенный между этими биссектриссами.
301. Въ равностороннемъ тр-кѣ со стороною а вписана окружность, а изъ вершины тр-ка радіусомъ, равнымъ половинѣ его стороны, описана другая окружность. Найти площадь, общую обоимъ кругамъ.
302. Въ треугольникѣ двѣ стороны суть а и Ъ. Найти третью сторону и площадь, если уголъ между сторонами а и Ь равенъ 45°; 60°; 150°; 120°; 75°; 135°.
303. Длины двухъ параллельныхъ хордъ круга суть 30 д. и 16 д., а разстояніе между ними 7 д. Найти площадь круга.
304. Черезъ точку, удаленную отъ центра круга на длину діаметра, проведена такая сѣкущая, которая дѣлится окружностью пополамъ. Найти длину сѣкущей, если радіусъ круга равенъ
305. Въ кругѣ радіуса В проведена хорда, стягивающая дугу въ 108°. Найти ея длину.
306. На діаметрѣ полукруга радіуса В построенъ равносторонній тр-къ. Найти площадь той его части, которая лежитъ внѣ круга.
307. Найти радіусъ окружности, касательной къ сторонамъ а и Ь треугольника, и центръ которой лежитъ на третьей его сторонѣ с.
308. Къ двумъ извнѣ касающимся въ точкѣ А окружностямъ, радіусы которыхъ суть 3 см. и 1 см., проведена внѣшняя касательная ВС. Найти площадь фигуры АВС, ограниченной двумя дугами и касательной.
309. Полуокружность радіуса В раздѣлена на три равныя части и точки дѣленія соединены съ концомъ діаметра. Найти площадь, ограниченную двумя хордами и заключенною между ними дугою.
310. Стороны тр-ка АВС продолжены въ одномъ направленіи (сторона АВ за точку В, сторона ВС за точку С и сторона СА за
— 270 —
точку А) до точекъ Аг, Вг и С1г такъ что ААХ=ЗАВ, ВВ^ЗВС и СС1=ЗСЛ. Найти отношеніе площадей тр-ковъ АВС и 41В1С1.
311. Изъ вершины тр-ка проведена къ его основанію прямая, дѣлящая основаніе на два отрѣзка т и п. Найти длину этой прямой, если стороны тр-ка, прилежащія къ отрѣзкамъ т и п, суть а и Ъ.
312. Кругъ радіуса В обложенъ тремя равными кругами, касающимися даннаго и взаимно. Найти радіусъ одного изъ этихъ круговъ.
313. Опредѣлить высоту башни, если извѣстно, что нужно отойти на а метровъ отъ ея основанія, чтобы башня была видна подъ угломъ въ 30°.
314. По даннымъ хордамъ а и Ь, стягивающимъ двѣ дуги въ кругѣ единичнаго радіуса, найти хорду, стягивающую разность этихъ дугъ. (Указаніе: примѣнить теорему Птоломея).
315. Прямая, параллельная основаніямъ трапеціи, раздѣляетъ ее на двѣ части въ отношеніи 7 : 2 (считая отъ большаго основанія). Найти длину этой прямой, если основанія трапеціи суть 5 м. и 3 м.
316. Изъ точки, дѣлящей основаніе тр-ка въ отношеніи т : п, проведены прямыя, параллельныя двумъ другимъ сторонамъ. Найти отношеніе площади каждой изъ частей, на которыя раздѣлится тр-къ, къ площади всего тр-ка.
317. Изъ нѣкоторой точки внутри тр-ка на стороны его а, Ъ и с опущены перпендикуляры рг, р3. Найти отношеніе площади тр-ка, который образуется отъ соединенія основаній этихъ перпендикуляровъ, къ площади даннаго тр-ка. (У казаніе: см. § 325).
318. Вычислить діагонали трапеціи по четыремъ ея сторонамъ а, Ь, си й. (Указаніе: надо примѣнить къ діагонали теорему о квадратѣ стороны тр-ка).
319. Найти площадь трапеціи по четыремъ ея сторонамъ а, Ъ, с и й.
320. На противоположныхъ сторонахъ квадрата построены внутри его два равносторонніе тр-ка. Пересѣченіе сторонъ этихъ тр-ковъ опредѣляетъ нѣкоторый четыреугольникъ. Найти его видъ, стороны, углы и площадь, если сторона квадрата равна а.
321. Проведена окружность, касающаяся одной стороны прямого угла и пересѣкающая другую сторону въ точкахъ, отстоящихъ отъ вершины угла на 6 см. и 24 см. Вычислить радіусъ этой окружности и разстояніе точки касанія отъ вершины угла.
322. Вычислить площадь тр-ка по двумъ сторонамъ а и Ь и медіанѣ т относительно третьей стороны.
323. На общей хордѣ АВ построены (по одну сторону отъ АВ) два сегмента, изъ которыхъ одинъ вмѣщаетъ уголъ 135°, а другой 120°. Найти площадь луночки, заключенной между дугами сегментовъ.
324. На радіусахъ квадранта (четверти круга) внутри его построены два полукруга. Найти площадь той части квадранта, которая лежитъ внѣ полукруговъ, если радіусъ квадранта есть Я.
— 271 —
325. Въ прямоугольномъ тр-кѣ АВС опущенъ перпендикуляръ АВ на гипотенузу ВС. Зная радіусы гх и тя окружностей, вписанныхъ въ тр-ки АВО и АСВ, найти радіусъ г окружности, вписанной въ треугольникъ АВС.
326. На окружности радіуса Я отложены отъ точки А (по обѣ ея стороны) двѣ дуги: ЛС=30° и ЛВ=60°. Найти площадь тр-ка АВС.
СТЕРЕОМЕТРІЯ.
КНИГА I.
ПРЯМЫЯ ПЛОСКОСТИ.
ГЛАВА I.
Опредѣленіе положенія плоскости.
344. Опредѣленіе. Плоскостью (13) наз. поверхность, обладающая тѣмъ свойствомъ, что прямая, проходящая черезъ двѣ произвольныя точки этой поверхности, лежитъ на ней всѣми остальными своими точками. Возможность существованія такой поверхности принимается за аксіому.
Стереометріей, какъ мы говорили во введеніи (14), наз. часть геометріи, въ которой разсматриваются свойства такихъ фигуръ, которыхъ не всѣ части помѣщаются въ одной плоскости.
345. Аксіомы плоскости. Укажемъ слѣдующія свойства плоскости, которыя мы принимаемъ за очевидныя:
1°. Плоскость есть поверхность незамкнутая.
2°. Всякая плоскость дѣлитъ пространство на 2 части, изъ которыхъ одна расположена по одну сторону отъ плоскости, а другая по другую сторону отъ нея.
3°. Прямая, имѣющая съ плоскостью только одну общую точку, пересѣкаетъ плоскость, т.-е. изъ части пространства, лежащей по одну сторону отъ плоскости, переходитъ въ часть пространства, лежащую по другую ея сторону; такимъ образомъ, двѣ полупрямыя, на которыя раздѣляется эта прямая плоскостью, расположены по разныя стороны отъ плоскости.
— 272 —
4°. Отрѣзокъ прямой, соединяющій двѣ точки пространства, расположенныя по разныя стороны отъ плоскости, пересѣкаетъ эту плоскость, тогда какъ отрѣзокъ прямой, соединяющій двѣ точки, расположенныя по одну сторону плоскости, не пересѣкаетъ ее.
5°. Черезъ всякую прямую можно провести безчисленное множество плоскостей.
6°. Всякая прямая, проведенная на плоскости, раздѣляетъ ее на двѣ части (называемыя полуплоскостями).
7°. Плоскость можно вращать вокругъ любой прямой, лежащей на ней, при чемъ каждую изъ частей, на которыя плоскость дѣлится этою прямою, можно заставить пройти черезъ всякую
Черт. 301.
точку пространства.
846. Изображеніе и обозначеніе плоскости.
Плоскость изображается на чертежѣ въ видѣ нѣкоторой ея части, обыкновенно въ формѣ параллелограмма или прямоугольника (черт. 301). Обозначается плоскость большею частью одною или двумя буквами; такъ го
ворятъ: плоскость Р, плоскость М1Ѵ.
347. Теорема. Черезъ всякія три точки (Л, В и С, черт. 302), не лежащія на одной прямой, можно провести плоскость и притомъ только одну.
I 1°. Черезъ какія-нибудь двѣ
/ изъ трехъ данныхъ точекъ, —----------------------- напр., черезъ А и Б, проведемъ
/ / прямую и черезъ нее—произ-
/ вольную плоскость. Станемъ вра-
/ щать эту плоскость вокругъ пря-
0 ' мой АВ-, вращая, мы можемъ
Черт. 302. заставить ее пройти черезъ
точку С. Тогда будемъ имѣть плоскость, которая проходитъ черезъ три точки А, В и С.
Остается доказать, что такая плоскость можетъ быть только
одна.
2°. Предположимъ, что черезъ тѣ же три точки проведены двѣ плоскости. Обозначимъ одну черезъ Р, а другую черезъ Рх.
— 273 —
Докажемъ, что эти плоскости сливаются въ одну.—Предварительно замѣтимъ, что прямыя АВ, ВС и АС, проходящія черезъ каждую пару данныхъ точекъ, принадлежать обѣимъ плоско' стямъ, такъ какъ эти прямыя имѣютъ по двѣ общихъ точки и съ плоскостью Р, и съ плоскостью Рх. Возьмемъ теперь на плоскости Р какую-нибудь точку М и докажемъ, что эта точка принадлежитъ и другой плоскости Рх. Для этого па плоскости Р черезъ точку М проведемъ какую-нибудь прямую МР, пересѣкающую АВ и АС въ нѣкоторыхъ точкахъ Е и Р. Такъ какъ прямыя АВ и АС принадлежатъ и другой плоскости Рх, то точки ихъ Е и Р также принадлежатъ этой плоскости. Вслѣдствіе этого прямая МР, проходящая черезъ Е и Р, лежитъ вся въ плоскости Рх (по опредѣленію плоскости), а потому и ея точка М лежитъ въ этой плоскости. Такимъ образомъ, всякая точка М плоскости Р принадлежитъ и плоскости Рх; значитъ, эти плоскости сливаются.
348. Слѣдствія. 1°. Черезъ прямую и точку внѣ ея можно провести плоскость и притомъ только одну, потому что точка внѣ прямой вмѣстѣ съ какими-нибудь двумя точками этой прямой составляютъ три точки, черезъ которыя, по доказанному, можно провести плоскость и притомъ одну.
2°. Черезъ двѣ пересѣкающіяся прямыя можно провести плоскость и притомъ только одну, потому что, взявъ точку пересѣченія и еще по одной точкѣ на каждой прямой, мы будемъ имѣть три точки, черезъ которыя и т. д.
3°. Черезъ двѣ параллельныя прямыя можно провести плоскость и притомъ только одну, потому что паралелльныя прямыя, по опредѣленію, лежать въ одной плоскости; эта плоскость единственная, такъ какъ черезъ одну изъ параллельныхъ и какую-нибудь точку другой можно провести пе болѣе одной плоскости.
4°. Всякую часть плоскости можно наложить всѣми ея точками на другое мѣсто этой или другой плоскости, при чемъ накладываемую часть можно предварительно перевернуть другою стороною, потому что всегда возможно наложить одну плоскость на другую такъ, чтобы у нихъ совпали какія-нибудь три точки, не лежащія на одной прямой, а тогда совпадутъ и остальныя точки.
А. Киселевъ. Геометрія. 18
— 274 —
349. Теорема. Если двѣ плоскости имѣютъ общую точку, то онѣ имѣютъ и общую прямую, которая проходитъ черезъ эту точку и по которой плоскости пересѣкаются.
Пусть плоскость Р (черт. 303) имѣетъ точку А, общую съ другою плоскостью (^. Проведемъ на плоскости черезъ точку А какія-нибудь двѣ прямыя ВВ} и ССг. Если бы случилось, что одна изъ этихъ прямыхъ лежитъ и па плоскости Р, то плоскости имѣли бы общую прямую. Предположимъ, что этого нѣтъ; тогда обѣ эти прямыя пересѣкаютъ плоскость Р (345, 3°); слѣд., каждая изъ нихъ подраздѣлится плоскостью Р на двѣ полупрямыя, расположенныя по разныя стороны отъ этой пло-
скости. Возьмемъ па полупрямыхъ АС и АВ какія-нибудь точки Ри Рх и проведемъ прямую ББГ. Эта прямая, переходя изъ части пространства, лежащаго надъ плоскостью Р, въ часть пространства, лежащаго подъ плоскостью Р, пересѣчется съ плоскостью Р въ нѣкоторой точкѣ Е (345,4°). Такъ какъ, съ другой стороны, прямая ББг тлѣетъ съ плоскостью С двѣ общихъ точки (Б и Вх), то она принадлежитъ ей вся. Поэтому точка Е прямой ББг также принадлежитъ
плоскости (^. Итакъ, плоскости Ри имѣютъ двѣ общія точки Аи Е; значитъ, опѣ имѣютъ и общую прямую АЕ, проходящую
черезъ эти точки.
Что плоскости Ри $ пересѣкаются по прямой АЕ (а не касаются), слѣдуетъ изъ того, что прямыя ВВХ и ССХ, содержащіяся въ плоскости С, пересѣкаются съ Р.
350. Слѣдствіе. Пересѣченіе двухъ плоскостей всегда есть прямая линія.
Дѣйствительно, если плоскости пересѣкаются, то онѣ имѣютъ общую точку, но въ такомъ случаѣ онѣ имѣютъ и общую прямую.
— 276 —
Какой-нибудь еще общей точки, сверхъ точекъ этой прямой, плоскости имѣть не могутъ, такъ какъ въ противномъ случаѣ онѣ должны были бы слиться въ одну (348, 1°).
ГЛАВА II.
Перпендикуляръ къ плоскости и наклонныя къ ней.
351. Предварительное замѣчаніе. Возьмемъ ка-
кую-нибудь прямую АВ (черт. 304) двѣ произвольныя плоскости Р и ф; затѣмъ, взявъ на АВ какую-нибудь точку С, проведемъ на плоскостяхъ Р и С черезъ эту точку прямыя: СБА.АВ и СЕА.АВ. Черезъ двѣ пересѣкающіяся прямыя СБ и СЕ проведемъ плоскость В. Мы получимъ тогда такое расположеніе прямой (АВ) и плоскости (В), при которомъ эта прямая, пересѣкаясь съ плоскостью, оказывается перпендикулярной къ двумъ прямымъ (къ СБ и къ СЕ),
и проведемъ черезъ нее
Черт. 804.
проведеннымъ на этой плоскости черезъ точку пересѣченія.
Докажемъ теперь, что такое расположеніе прямой и плоскости
обладаетъ слѣдующимъ важнымъ свойствомъ.
352. Теорема. Если прямая (АА1г черт. 305), пересѣкающаяся съ плоскостью (Р), перпендикулярна къ двумъ прямымъ (СБ и ЕЕ), проведеннымъ на этой плоскости черезъ точку пересѣченія (В), то она перпендикулярна и ко всякой третьей прямой (МЕ), проведенной на плоскости черезъ ту же точку пересѣченія.
Отложимъ произвольной длины, но равные, отрѣзки ВА и ВАг и проведемъ на плоскости какую-нибудь прямую БЕ,
— 276 —
к угорая пересѣкала бы прямыя СБ, МЕ и ЕЕ. Точки пересѣченія В, и Е соединимъ съ точками А и Аг. Мы получимъ тогда нѣсколько тр-ковъ. Разсмотримъ ихъ въ такой послѣдовательности. Сначала возьмемъ тр-ки АЕБ и А^ЕБ; они равны, такъ какъ у нихъ: ЕБ общая сторона, АБ=А1Б1, какъ наклонныя къ прямой ААЪ одинаково удаленныя отъ основанія перпендикуляра ВВ; по той же причинѣ
Изъ равенства этихъ тр-ковъ слѣдуетъ, что ^.АБЕ=^.А1БЕ. Послѣ Черт 805 этого перейдемъ кь тр-камъ АБЕ
и ЛХВ^; они равны, такъ какъ у нихъ БЕ общая сторона, ЛВ=ЛХВ и Х.АБЕ=/_А1БЕ. Изъ равенства этихъ тр-ковъ выводимъ, что АЕ=АГЕ. Теперь возьмемъ тр-ки АВЕ и А1ВЕ-, они равны, такъ какъ имѣютъ соотвѣтственно равныя стороны. Изъ ихъ равенства выводимъ, что ^.АВЕ=ЛА1ВЕ- слѣд., АА^МЕ.
853. Опредѣленіе. Прямая наз. перпендикулярною къ плоскости, если она, пересѣкаясь съ этою плоскостью, образуетъ прямые углы со всѣми прямыми, проведенными на плоскости черезъ точку пересѣченія. Въ этоМъ случаѣ говорятъ также, что плоскость перпендикулярна къ прямой.
Прямая, пересѣкающаяся съ плоскостью, но не перпендикулярная къ ней, наз. наклонною. Точка пересѣченія прямой съ плоскостью наз. основаніемъ перпендикуляра или наклонной.
Возможность существованія перпендикулярной прямой къ плоскости составляетъ слѣдствіе предыдущей теоремы и предварительнаго разъясненія § 351-го.
354. Теорема. Если черезъ одну и ту же точку прямой проведемъ въ пространствѣ сколько угодно перпендикуляровъ къ этой прямой, то всѣ они лежатъ въ одной и той же плоскости (перпендикулярной ко взятой прямой).
— 277 —
Дана прямая АВ (черт. 306) и на ней точка В. Изъ этой точки
возставимъ въ пространствѣ прямой АВ. Для этого черезъ АВ проведемъ какія-нибудь плоскости Р, ф, В, 8... и на каждой изъ нихъ черезъ точку В проведемъ прямую, перпендикулярную къ АВ. Пусть это будутъ прямыя ВС, ВВ, ВЕ, ВЕ... Требуется доказать, что всѣ эти перпендикуляры лежатъ въ одной и той же плоскости,
нѣсколько перпендикуляровъ къ
перпендикулярной къ АВ. Для доказательства черезъ какія-нибудь два изъ нихъ, напр., черезъ ВС и ВБ, проведемъ плоскость
М, которая, согласно предыдущей теоремѣ, будетъ перпенди
кулярна къ АВ. Вообразимъ теперь, что какой-нибудь изъ прочихъ перпендикуляровъ, напр., ВЕ, проведенный въ пл. В, не лежитъ въ пл. М. Тогда пересѣченіе плоскостей Ви М должна быть нѣкоторая прямая, не сливающаяся съ ВЕ, и, слѣд., въ пл. В должны существовать 2 перпендикуляра къ АВ, проходящіе черезъ точку В: одинъ ВЕ, а другой—пересѣченіе плоскостей М и В (352); такъ какъ это невозможно, то нельзя допустить, чтобы какой-нибудь изъ проведенныхъ нами перпендикуляровъ не лежалъ въ пл. В; значитъ, всѣ они лежатъ въ этой плоскости,
которая, какъ мы говорили, перпендикулярна къ АВ.
355. Теорема. Черезъ всякую точку пространства можно провести плоскость, перпендикулярную къ данной прямой, и притомъ только одну.
Разсмотримъ отдѣльно 2 случая: когда точка лежитъ на данной прямой и когда она расположена внѣ этой прямой.
1°. Пусть С будетъ точка, взятая на данной прямой АВ (черт. 307). Проведемъ черезъ эту прямую какія-нибудь двѣ плоскости Р и ф и на нихъ возьмемъ прямыя СБ п СЕ, перпендикулярныя къ АВ. Черезъ этп двѣ пересѣкающіяся прямыя проведемъ плоскость В. Эта плоскость перпендикулярна къ АВ въ точкѣ С,
— 278 —
потому что двѣ ея прямыя СБ и СЕ перпендикулярны къ АС, и, слѣд., всякая третья прямая, проведенная на В черезъ точку С, также перпендикулярна къ АВ (352).
Для доказательства, что такая плоскость можетъ быть только одна, допустимъ, что черезъ точку С можно провести еще другую плоскость, перпендикулярную къ АВ. Обозначимъ ее Вг. Эта плоскость должна пересѣчься съ плоскостью Р по такой прямой, которая, во 1, проходитъ черезъ С и, во 2, перпендикулярна къ АВ. Но на плоскости Р существуетъ
только одна такая прямая, именно прямая СБ, которую мы раньше провели; значитъ, плоскость Вг должна пересѣчься съ Р по той же прямой СБ, по которой съ ней пересѣкается и пл. В, Такъ же убѣдимся, что пл. Вх должна пересѣчься съ пл. ф по той же прямой СЕ, по которой съ ней пересѣкается пл. В. Слѣд., пл. Вх должна проходить черезъ тѣ же пересѣкающіяся прямыя СБ п СЕ, черезъ которыя проведена нами ранѣе плоскость В. Но черезъ 2 пересѣкающіяся прямыя можно провести только
одну плоскость; значитъ, плоскости В и Вг должны слиться въ
одну.
2°. Пусть Б будетъ точка, взятая внѣ данной прямой АВ (черт. 307). Проведемъ черезъ Ни АВплоскость Ри черезъ АВеще какую-нибудь плоскость ф; на первой опустимъ на АВ изъ точки Б перпендикуляръ БС, а на второй возставимъ къ АВ изъ точки С перпендикуляръ СЕ. Плоскость В, проходящая черезъ БС и СЕ, и будетъ плоскостью, препендикулярною къ АВ и проведенною черезъ точку Б (352).
Предположимъ теперь, что черезъ точку Б можно провести еще другую плоскость Вх, перпендикулярную къ АВ. Эта плоскость должна пересѣчься съ пл. Р по такой прямой, которая, во 1, проходитъ черезъ Ни, во 2, перпендикулярна къ АВ. Но на пл. Р существуетъ только одна такая прямая, именно перпендикуляръ БС, который мы провели раньше; значитъ, пл. Вх
— 279 —
должна пересечься съ пл. Р по той же прямой ВС, по которой съ ней пересѣкается и пл. В. Но тогда съ пл. ф пл. Рх можетъ пересѣчься только по прямой СЕ, такъ какъ это—единственная прямая плоскости О, проходящая черезъ С и перпендикулярная къ АВ. Такимъ образомъ, пл. В^, проходя черезъ тѣ же двѣ пересѣкающіяся прямыя ВС и СЕ, черезъ которыя проведена пл. В,, должна слиться съ этою плоскостью.
356. Теорема. Черезъ всякую точку пространства можно провести перпендикуляръ къ данной плоскости и притомъ только одинъ.
Разсмотримъ отдѣльно 2 случая: когда точка, черезъ которую требуется провести перпендикуляръ къ данной плоскости, лежитъ на этой плоскости, н когда она расположена внѣ ея.
1°. Пусть точка О лежитъ на плоскости Р (черт. 308). Проведемъ черезъ нее на этой плоскости какую-нибудь прямую МЕ
и затѣмъ черезъ ту же точку О проведемъ плоскость О, перпендикулярную къ прямой МЕ, что, какъ мы видѣли (355, 1°), всегда возможно. Пусть плоскости Р и § пересѣкаются по прямой АВ. Въ плоскости ф проведемъ ОС-ЬАВ. Докажемъ, что полученная такимъ обра-
Черт. 308
зомъ прямая ОС есть перпендикуляръ къ плоскости Р. Такъ какъ прямая МЕ перпендикулярна къ пл. ф, то она перпендикулярна ко всякой прямой, проведенной на этой плоскости черезъ точку О; значитъ, ОСЛ-МЕ. Съ другой стороны, ОСЛ-АВ по построенію. Значитъ, прямая ОС перпендикулярна къ двумъ прямымъ, проведеннымъ на-пл. Р черезъ точку О; слѣд., она перпендикулярна къ пл. Р.
Предположимъ теперь, что кромѣ найденнаго нами перпендикуляра ОС существуетъ еще другой перпендикуляръ ОСХ (черт 309), проведенный къ пл. Р черезъ ту же точку О. Про
— 280 —
ведемъ черезъ прямыя ОС и ОСі плоскость (она не указана на чертежѣ); пусть эта плоскость пересѣчется съ пл. Р по прямой ОН.
Тогда углы СОН и С^ІІ должны оказаться оба прямые. Но это невозможно, такъ какъ одинъ изъ этихъ угловъ составляетъ часть другого. Значитъ, другого перпендикуляра черезъ точку О къ пл. Р провести нельзя.
2°. Пусть точка О лежитъ внѣ плоскости Р (черт. 310). Проведемъ па этой плоскости произ
вольную прямую и затѣмъ черезъ точку О проведемъ пло
скость ф, перпендикулярную къ прямой М1Я, что всегда возможно (355, 2°). Пусть плоскости Р и ф пересѣкаются по прямой
АВ. На пл. С проведемъ 0СА.АВ. Докажемъ, что полученная
такимъ образомъ прямая ОС есть
перпендпкуляръ къ пл. Р. Для этого достаточно показать, что эта прямая перпендикулярна къ какимъ-нибудь двумъ прямымъ, проведеннымъ на пл. Р черезъ точку С. Къ одной такой прямой, именно къ АВ, прямая ОС перпендикулярна по построенію. За другую прямую возьмемъ СП, соединяющую точку С съ какою-пибудь точкою И прямой М1Ѵ. Для доказательства, что ОС_1_СП, продолжимъ ОС на длину СОі—ОС и точки О и Оі соединимъ прямыми съ А и И. Такъ какьМ^Л-^,'^о М^ А.АОп МЯА_АОі,
значитъ, тр-ки ОАБ и ОіЛП прямоугольные при вершинѣ А.
У нихъ катетъ АБ общій и катеты АО и АОг равны, какь наклонныя, проведенныя на пл. ф изъ точки А къ прямой ооь при чемъ разстоянія ихъ основаній отъ основанія перпендикуляра АС (отрѣзки ОС и ОіС) равны. Изъ равенства этихъ тр-ковъ слѣдуетъ, что ОБ—ОіР. Перейдя теперь къ тр-камъ ОСИ и ОуСБ, видимъ,
что они равны, такъ какъ стороны одного равны соотвѣтственно
— 281
сторонамъ другого» Слѣд., Х.ССВ=Х.О1СВ и потому углы эти прямые. Такимъ образомъ, оказывается, что ОСА.СА и ОСА-СВ; значитъ, ОС_!_Р.
Допустимъ теперь, что кромѣ найденнаго нами перпендикуляра ОС можно опустить изъ точки О на пл. Р еще другой перпендикуляръ ОСг (черт. 311). Тогда, соединивъ точки С и прямой, мы получимъ тр-къ ОССГ, у котораго два угла (при вершинахъ С и Сі) прямые. Такъ какъ это
невозможно, то другого перпендикуляра изъ точки О на пл. Р опустить нельзя.
857. Сравнительная длина перпендикуляра и наклонныхъ. Когда изъ одной точки А (черт. 312) проведены къ плоскости перпендикуляръ АВ и наклонная АС, условимся называть проекціей наклонной на плоскость прямую ВС, проведенную между основаніями перпендикуляра и наклонной.
Теоремы. Если изъ одной и той же точки (А, черт. 312), взятой внѣ плоскости (Р), проведены къ этой плоскости перпендикуляръ (АВ) и какія-нибудь наклонныя (АС, АВ, АЕ...), то:
1°, перпендикуляръ короче всякой наклонной;
2°, двѣ наклонныя, имѣющія равныя проекціи, равны;
3°, изъ двухъ наклонныхъ та больше, которой проекція больше.
Вращая прямоугольные тр-ки АВС и АВВ вокругъ катета АВ, мы можемъ совмѣстить ихъ пло
Черт. 312.
скости съ плоскостью тр-ка АВЕ. Тогда всѣ наклонныя будутъ ле
жать въ одной плоскости съ перпендикуляромъ, и всѣ проекціи
— 282 —
расположатся на одной прямой. Такимъ образомъ, доказываемыя теоремы приводятся къ аналогичнымъ теоремамъ планиметріи (59, 1 и 2).
Замѣчаніе. Длина перпендикуляра, опущеннаго изъ точки А на пл. Р (черт. 312), принимается за мѣру разстоянія точки А отъ пл. Р.
358. Обратныя теоремы. Если изъ одной и той же точки, взятой внѣ плоскости, проведены къ этой плоскости перпендикуляръ и какія-нибудь наклонныя, то равныя наклонныя имѣютъ равныя проекціи, и изъ двухъ проекцій та больше, которая соотвѣтствуетъ ббльшей наклонной.
Доказательство (отъ противнаго) предоставляемъ самимъ учащимся.
359. Приведемъ еще слѣдующую теорему о перпендикулярахъ, которая понадобится намъ впослѣдствіи *).
Теорема. Прямая (РЕ, черт. 313), проведенная на плоскости (Р) черезъ основаніе наклонной (АС) перпендикулярно къ ея проекціи (ВС), перпендикулярна и къ самой наклонной.
Черт. 313.
Отложимъ произвольные, но равные, отрѣзки СР и СЕ и соединимъ точки А и В съ Р и Е. Тогда будемъ имѣть: ВВ=ВЕ, какъ наклонныя къ прямой РЕ, одинаково удаленныя отъ основанія перпендикуляра ВС; АВ=АЕ, какъ наклонныя къ плоскости Р, имѣющія равныя проекціи ВР и ВЕ. Вслѣдствіе этого Л АВЕ есть равнобедренный, и потому его медіана АС перпендикулярна къ основанію РЕ (39).
*) Въ нѣкоторыхъ курсахъ геометріи теорема эта (или нѣсколько измѣненная) носитъ названіе теоремы трехъ перпендикуляровъ. Дѣйствительно, въ ней говорится о связи, соединяющей слѣдующія 3 перпендикуляра: 1) АВ къ пл. Р, 2) ВС къ прямой ВЕ и 3) АС къ той же прямой ВЕ.
— 283 —
ГЛАВА III.
Параллельныя прямыя и плоскости.
Параллельныя прямыя.
860. Предварительное замѣчаніе. Двѣ прямыя могутъ быть расположены въ пространствѣ такъ, что черезъ
нихъ нельзя провести плоскости. Возьмемъ, папр., двѣ такія
прямыя АВ и ВЕ, изъ которыхъ одна пересѣкаетъ нѣкоторую плоскость Р, а другая лежитъ на ней, но не проходитъ черезъ точку пересѣченія С. Черезъ такія двѣ прямыя нельзя провести плоскости, потому что въ противномъ случаѣ черезъ прямую ВЕ и точку С проходили бы двѣ различныя
плоскости: одна Р, пересѣкающая прямую АВ, и другая, содержащая ее; а это невозможно (348, 1°).
Двѣ прямыя, не лежащія въ одной плоскости, конечно, не пересѣкаются, сколько бы ихъ ни продолжали; однако ихъ не называютъ параллельными, оставляя это названіе только для такихъ прямыхъ, которыя, находясь въ одной плоскости, не пересѣкаются, сколько бы ихъ ни продолжали.
Двѣ прямыя, не лежащія въ одной плоскости, наз. скрещивающимися.
Въ планиметріи мы видѣли (77 и 79), что черезъ всякую точку плоскости можно провести прямую, параллельную данной прямой, и притомъ только одну. То же самое можно сказать о всякой точкѣ пространства, потому что черезъ точку п данную прямую можно провести плоскость и только одну.
— 284 —
361. Теорема. Если плоскость (Р, черт. 315) пересѣкаетъ одну изъ параллельныхъ прямыхъ (ЛВ), то она пересѣкаетъ и другую (СВ).
Черт. 315.
Проведемъ черезъ АВ и СВ плоскость. Эта плоскость содержитъ въ себѣ ту точку В, въ которой прямая АВ пересѣкается съ Р; значитъ, эта плоскость пересѣкается съ Р по нѣкоторой прямой ВЕ (349). Эта прямая, находясь въ одной плоскости съ А В и СВ и пересѣкая одну изъ этихъ параллельныхъ, должна пересѣчь и другую (80) въ нѣкоторой точкѣ Г. Точка Р, находясь заразъ на прямой ВЕ и на прямой СВ, должна быть точкою пересѣченія плоскости Р съ прямой СВ.
362. Теорема. Если плоскость (Р, черт. 316) перпендику-
Черт. 316.
сѣчь СВ, потому что она, АВ, параллельную СВ.
лярна къ одной изъ параллельныхъ прямыхъ (ЛВ), то она перпендикулярна и къ другой (СП).
Предстоитъ доказать, что, во 1°, ил. Р пересѣкаетъ прямую СВ, а во 2°, эта прямая перпендикулярна къ какимъ-нибудь двумъ прямымъ, проведеннымт на плоскости Р черезъ основаніе СВ.
1°. Плоскость Р должна пере-по условію, пересѣкаетъ прямую
2°. Проведемъ черезъ ЛВ и СВ плоскость В и возьмемъ ея пересѣченіе ВВ съ плоскостью Р. Такъ какъ, по условію, ЛВ перпендикулярна къ Р, то ЛВХВВ; поэтому и СВА-ВВ (82). Проведемъ на плоскости Р прямую ВЕ, перпендикулярную къ ВВ, и возьмемъ какую-нпбудь наклонную МВ, для которой проекціей служить ВВ, Прямая ЕВ, будучи перпендикулярна къ проекціи ВВ, должна быть перпендикулярной и къ наклонной
— 285 —
МВ (359) и, слѣд., перпендикулярна къ плоскости В (352), значитъ, и къ прямой СВ. Такимъ образомъ, прямая СВ оказывается перпендикулярною къ двумъ прямымъ плоскости Р, именно къ ВВ и къ ВЕ\ слѣд., она перпендикулярна къ этой плоскости.
363. Обратная теорема. Если двѣ прямыя (АВ и СВ, черт. 317) перпендикулярны къ одной и той же плоскости (Р), то онѣ параллельны.
Предположимъ противное, т.-е. что прямыя АВ и СВ не параллельны. Проведемъ тогда черезъ точку В прямую, параллельную АВ. При нашемъ предположеніи это будетъ какая-нибудь прямая ВСі, не сливающаяся съ ВС. Согласно прямой теоремѣ, линія ВСг будетъ перпендикулярна къ пл. Р. Тогда, слѣд., мы будемъ имѣть два перпендикуляра къ пл. Р, проходящіе черезъ одну и ту же точку: ВС и ВСг. Такъ какъ это невозможно, то нельзя допустить, чтобы прямыя АВъСВ были непараллельны.
364. Теорема. Если двѣ прямыя (А и В, черт. 318) параллельны третьей прямой (С), то онѣ параллельны между собой.
Проведемъ плоскость Р, перпендикулярную къ С. Тогда А и В будутъ перпендикулярами къ этой плоскости (362), и, слѣд., А II В (363).
365. Теорема. Если двѣ прямыя (А и В, черт. 319) параллельны и черезъ каждую изъ нихъ проходитъ плоскость, то линія пересѣченія этихъ плоскостей (если она существуетъ) параллельна первымъ прямымъ.
— 286 —
Пусть черезъ прямую А проходитъ пл. Р и черезъ прямую В—пл. С, и пусть эти плоскости пересѣкаются по прямой СП;
требуется доказать, что СП IIА и СП II В.—Черезъ какую-нибудь точку Е линіи пересѣченія вообразимъ прямую Аг, параллельную А; тогда эта прямая должна быть также параллельна и В. Такъ какъ прямая Ах параллельна А и проходитъ черезъ точку Е, то Аг должна лежать въ плоскости, содержащей прямую А и точку Е, т.-е. въ пл. Р. Съ другой стороны, такъ какъ прямая Ах параллельна В и проходить черезъ
точку Е, то Аг должна лежать въ пл. (^. Если же прямая Аг лежитъ заразъ и въ пл. Р, и въ пл. С, то она должна совпадать съ линіей пересѣченія СП; значитъ, СП II А и СП II В.
Прямая и плоскость,
366. Опредѣленіе, въ этой плоскости, наз. не пересѣкаются,
параллельныя между собою.
Плоскость и прямая, не лежащая параллельными, если онѣ сколько бы ихъ ни продолжали.
Слѣдующія двѣ теоремы выражаютъ признаки параллельности прямой съ плоскостью.
367* Теорема 1. Если прямая (АВ, черт. 320) и плоскость (Р) перпендику
лярны къ одной и той же прямой (АС), то онѣ параллельны.
Предположимъ, что прямая АВ пересѣкается съ пл. Р въ нѣкоторой точкѣ М\ тогда, соединивъ прямой эту точку съ точкой С, въ которой пл. Р пересѣкается съ данной прямой, мы будемъ имѣть два перпендикуляра МС и МА на прямую АС изъ одной точки М, что невозможно; значитъ, АВ не пересѣкается съ Р, т.-е. АВ параллельна Р.
— 287 —
Черт. 821.
Теорема 2. Если прямая (АВ, черт. 321), параллельна какой-нибудь прямой (СВ), проведенной на плоскости (Р), то она параллельна самой плоскости.
Проведемъ черезъ АВ и СВ плоскость В, и предположимъ, что прямая АВ гдѣ-нибудь пересѣкается съ пл. Р. Тогда точка пересѣченія, находясь на прямой АВ, должна принадлежать также и пл. В, на которой лежитъ АВ-, въ то же время точка пересѣченія, конечно, должна принадлежать п
пл. Р. Значитъ, точка пересѣченія, находясь заразъ и на пл. В, и на пл. Р, должна лежать на прямой СВ, по которой пересѣкаются эти плоскости; слѣд., прямая АВ пересѣкается съ прямой СВ. Но это невозможно, такъ какъ, по условію, АВ II СВ. Значитъ, нельзя допустить, чтобы прямая АВ пересѣкалась Съ пл. Р, и потому АВ || Р.
Послѣдующія теоремы выражаютъ нѣкоторыя свойства прямой и плоскости, параллельныхъ
между собою.
368. Теорема. Если плоскость (Е, черт. 321) проходитъ черезъ прямую (АВ), параллельную другой плоскости (Р), и пересѣкаетъ эту плоскость, то линія пересѣченія (СВ) параллельна первой прямой (АВ).
Дѣйствительно, во 1-хъ, прямая СВ лежитъ въ одной плоскости съ АВ, во 2-хь, эта прямая не можетъ пересѣчься съ АВ, потому что въ противномъ случаѣ прямая АВ пересѣкалась бы
съ плоскостью Р, что невозможно.
369. Слѣдствіе. Если прямая (АВ, черт. 322), параллельна двумъ пересѣкающимся плоскостямъ (Р и ($), то она параллельна линіи ихъ пересѣченія (СВ).
Вообразимъ плоскость черезъ АВ и какую-нибудь точку М прямой СВ. Эта плоскость должна пересѣчься съ Р и § по прямымъ, параллельнымъ АВ и проходящимъ черезъ М. Но черезъ М можно
— 288 —
провести только одну прямую, параллельную АВ; значитъ, два пересѣченія воображаемой плоскости съ плоскостями Р ѵ $ должны слиться въ одну прямую. Эта прямая, находясь заразъ на пл. Р и на пл. (^, должна совпадать съ прямой СВ, по которой плоскости Р л () пересѣкаются; значитъ, СВ !І АВ.
370. Теорема. Всѣ точки пря-
М ЬІ мой (АВ, черт. 323), параллельной А плоскости (Р), одинаково удалены отъ
этой плоскости.
г---------------, Изъ какихъ-пибудь точекъ Л/ и А7
/-------------[—/ прямой АВ опустимъ на Р перпенди-
/Р Р / куляры МС и КВ. Такъ какъ эти
перпендикуляры параллельны (363), Черт. 823. то черезъ Нихъ можно провести плоскость. Эта плоскость пересѣкается съ Р по прямой СВ, параллельной АВ (368); поэтому фигура МЯВС есть параллелограммъ и слѣд., МС=^Б. Но длина перпендикуляра, опущеннаго изъ точки па плоскость, принимается за мѣру разстоянія этой точки отъ плоскости; значитъ, любыя точки М и Б прямой АВ одинаково удалены отъ пл. Р.
Параллельныя плоскости.
371. Опредѣленіе. Двѣ плоскости наз. параллельными, если онѣ не пересѣкаются, сколько
Черт. 324.
бы ихъ ни продолжали.
Слѣдующія двѣ теоремы выражаютъ признаки параллельности двухъ плоскостей.
372. Теорема 1. Если двѣ плоскости (Р и черт. 324) перпендикулярны къ одной и той же прямой (АВ), то онѣ параллельны.
Дѣйствительно, если бы плоскости Р и пересѣкались, то черезъ всякую точку ихъ пересѣченія проходили бы двѣ плоскости Р и 6, перпендикулярныя къ прямой АВ, что невозможно.
— 289 —
Теорема 2. Если двѣ пересѣкающіяся прямыя (АВ и АС, черт. 325) одной плоскости (Р) соотвѣтственно параллельны двумъ прямымъ (Л^ и АіСі) другой плоскости (ф), то эти плоскости параллельны.
Изъ точки А опустимъ на плоскость ф перпендикуляръ ААц и проведемъ прямыя ЛиВи и АиСп, соотвѣтственно параллельныя прямымъ АіВі и АіСі, эти прямыя также параллельны и линіямъ АВ и АС (364). Такъ какъ ЛЛц-кЛцВцИ АВ || ЯпВи то ААцЛ_АВ; такъ же доказывается, что ААцЛ-АС. Слѣд., прямая ААп перпендикулярна къ плоскости Р (352). Такимъ образомъ, плоскости Р
и С перпендикулярны къ одной и той же прямой ААи и потому параллельны.
Послѣдующія теоремы выражаютъ нѣкоторыя свойства параллельныхъ плоскостей.
373. Теорема. Если двѣ параллельныя плоскости (Р и С,
черт. 326) пересѣкаются третьею плоскостью (В), то линіи пересѣченія (АС и ВБ) параллельны.
Дѣйствительно, во 1-хъ, прямыя АС и ВВ находятся въ одной плоскости (В), во 2-хъ, онѣ не могутъ пересѣчься, такъ какъ въ противномъ случаѣ пересѣкались бы плоскости Р и <2, что противорѣчитъ условію.
374. Теоремы. 1°. Если пря-
Черт. 326.
мая пересѣкаетъ одну изъ параллельныхъ плоскостей, то она
пересѣкаетъ и другую.
2°. Если плоскость пересѣкаетъ одну изъ параллельныхъ плоскостей, то она пересѣкаетъ и другую.
1°. Пусть прямая АВ (черт. 327) пересѣкаетъ въ точкѣ В плоскость Р, параллельную (^. Соединимъ прямою точку В съ
А. Киселевъ. Геометрія.
19
— 290
какою-нибудь точкою плоскости О, и черезъ АВ и ВС проведемъ
плоскость (не указана на чертежѣ). Эта плоскость, содержа
Черт. 327.
въ себѣ точки В и С, пересѣкается съ Р и С по нѣкоторымъ прямымъ ВЕ и ЕН, которыя параллельны (373). Прямая АВ лежитъ въ одной плоскости съ ВЕ п ЕН и пересѣкаетъ одну изъ этихъ параллельныхъ; слѣд., какъ мы знаемъ изъ планиметріи (80, 1°), она пересѣчетъ и другую; значитъ, пересѣчетъ и плоскость ф.
2°. Пусть какая-нпбудь плоскость пересѣкаетъ плоскость Р (черт. 327), па
раллельную С. Тогда па ней можно взять прямую АВ, которая тоже пересѣкаетъ плоскость Р; по доказанному эта прямая пересѣкаетъ и плоскость ф; значитъ, съ этою плоскостью пере
сѣчется и та плоскость, въ которой взята АВ.
375. Теорема. Если прямая (АВ, черт. 328), перпендикулярна къ одной изъ параллельныхъ плоскостей (къ Р), то она перпендикулярна и къ другой (къ О).
Прямая АВ, пересѣкая одну изъ параллельныхъ плоскостей,
пересѣчетъ и другую въ нѣкоторой точкѣ Ві. Проведемъ черезъ
Черт. 328.
данной плоскости (О)
АВ какія-нибудь двѣ плоскости 7И и ІѴ, которыя пересѣкутся съ Р и ф по параллельнымъ прямымъ (373): одна по ВС и ВіСі, другая по ВВ и В^. Согласно условію, прямая АВ перпендикулярна къ ВС и ВВ, слѣд., она также перпендикулярна къ ВіСі и ВіВі, а потому перпендикулярна и къ плоскости (^.
376. Теорема. Черезъ всякую точку (В, черт. 328) пространства можно провести плоскость (Р), параллельную и притомъ только одну.
Всегда возможно изъ точки В опустить на пл. С перпендикуляръ ВВі и затѣмъ черезъ точку В провести пл. Р, перпендикулярную къ ВВі. Эта плоскость будетъ параллельна С (372,1°).
— 291 —
Другой плоскости, параллельной черезъ точку В провести нельзя, такъ какъ, если бы это было возможно, то тогда черезъ точку В проходили бы двѣ плоскости, перпендикулярныя къ ВВг (375), что невозможно.
377. Теорема. Отрѣзки параллельныхъ прямыхъ (АС и ВВ, черт. 329), заключенные между параллельными плоскостями (Р и О), равны.
Черезъ параллельныя прямыя АС и ВВ проведемъ плоскость В; она пересѣчетъ Р и ф по параллельнымъ прямымъ АВ и СВ-, слѣд., фигура АВСВ будетъ параллелограммъ, и потому АС=ВВ.
378. Слѣдствіе. Параллельныя плоскости вездѣ одинаково удалены одна отъ другой, потому что, если параллельныя прямыя АС и ВВ (черт. 329) будутъ перпендикулярны
къ Р, то онѣ также будутъ перпендикулярны къ ф и въ то же
время равны.
379. Теорема. Два угла (ВАС и В^С^ черт. 330) съ соотвѣтственно параллельными и одинаково направленными сторонами равны и лежатъ въ параллельныхъ плоскостяхъ(Р и О).
Что плоскости Р я $ параллельны, было доказано прежде (372, 2°); остается доказать, что углы А и Аг равны.—
Отложимъ АВ=А1В1, АС=А1С1 и проведемъ ААГ, ВВХ, ССГ,
ВС и ВіСі. Такъ какъ отрѣзки АВ и АхВі равны и параллельны, то фигура АВВіАі есть параллелограммъ (99, 2°); поэтому отрѣзки АА± и ВВг равны и параллельны. По той же причинѣ равны и параллельны отрѣзки ААГ и СС^, слѣд., ВВі II ССі и ВВ1=С'С'1. Поэтому ВС = ВіСі и Д АВС = Д А&Сі (по тремъ сторонамъ); значитъ, Х.А=Х.АѴ
19*
— 292 —
380. Теорема. Если двѣ прямыя (АВ и СО, черт. 331) пересѣкаются рядомъ параллельныхъ плоскостей (Р&,В...), то онѣ разсѣкаются этими плоскостями на пропорціональныя части.
Черт. 331
Пусть Е,Р,Н...будутъ точки пересѣченія прямой АВ съ плоскостями Р,ф, В... и К,Ь,М...—точки пересѣченія другой прямой СО съ тѣми же плоскостями; требуется доказать, что части ЕР, РН... одной прямой пропорціональны частямъ КО, ЬМ... другой прямой, т.-е. что
ЕР РН
КіГ ЬМ
Проведемъ черезъ точку Е прямую СгОу, параллельную СО, и черезъ двѣ пересѣкак.цГяся прямыя АВ и СуО-і вообразимъ плоскость. Прямыя ЬгР, М^Н..., по которымъ эта плоскость пересѣкается съ данными плоскостями, должны быть параллельны между собою (373); поэтому (219)
ЕР РН
Еі Ьі~Ь^М^"'
Но ЕЬ1 = КЬ, Ь1М1 = ЬМ,... (377); подставивъ въ полученный рядъ равныхъ отношеній отрѣзки КО, ЬМ... вмѣсто ЕЬ±, Ь^М^.., получимъ то, что требовалось доказать.
ГЛАВА IV.
Двугранные углы,
381. Опредѣленіе. Фигура, образованная двумя полу-
плоскостями (Ря$, черт. 332), исходящими изъ одной прямой (АВ) (вмѣстѣ съ частью пространства, ограниченной ими) наз. двуграннымъ угломъ.
Прямая АВ наз. ребромъ, а полуплоскости Р и —сторонами или гранями двуграннаго угла. Такой уголъ обозначается обыкновенно двумя буквами, поставленными у его
— 293
ребра (двугр. уголъ АВ). Но если при одномъ ребрѣ лежатъ нѣсколько двугранныхъ угловъ, то каждый изъ нихъ обозначаютъ 4-мя буквами, изъ которыхъ двѣ среднія стоятъ при ребрѣ, а двѣ крайнія у граней (напр., двугр. уголъ 8СБВ).
Если черезъ ребро {СБ, черт. 332) двуграннаго угла (РСБ8) проведемъ внутри его (т.-е. въ той части пространства, которая принадлежитъ углу) какія - нибудь полуплоскости (В, $...), то образовавшіеся при этомъ двугранные углы (ВСБ8, фСБВ...) разсматриваются, какъ части перваго двуграннаго
угла.
Если изъ произвольной точки Б ребра АВ (черт. 333) проведемъ на каждой грани по перпендикуляру къ ребру, то образованный ими уголъ СБЕ наз. линейнымъ угломъ двуграннаго. Величина линейнаго угла не зависитъ отъ положенія точки Б на ребрѣ. Такъ, линейные углы СБЕ и СхРхЕх равны, потому что ихъ стороны соотвѣтственно параллельны и одина
ково направлены.
Плоскость линейнаго угла перпендикулярна къ ребру, такъ какъ она содержитъ двѣ прямыя, перпендикулярныя къ нему (352).
382. Равенство и неравенство двугранныхъ угловъ. Два двугранные угла считаются равными, если они при вложеніи могутъ совмѣститься; въ противномъ случаѣ тотъ изъ угловъ считается меньшимъ, который можетъ составить часть другого угла.
Можно разсматривать сумму, разность, произведеніе и част
Черт. 333.
ное двугранныхъ угловъ въ томъ же смыслѣ, какъ и для угловъ планиметріи. Подобно этимъ угламъ двугранные углы могутъ быть смежные, прямые, вертикаль-
п ы е...
383 Теоремы. 1°. Равнымъ двуграннымъ угламъ соотвѣтствуютъ равные линейные углы.
2°. Ббльшему двугранному углу соотвѣтствуетъ ббльшій линейный уголъ.
— 294 —
Пусть РАВд и РМхВх^! (черт. 334) будутъ два двугранные угла. Вложимъ уголъ Л]Ві въ уголъ АВ такъ, чтобы ребро А^В^
Черт. 334.
совпало съ ребромъ АВ и грань съ гранью Р. Тогда, если эти двугранные углы равны, то грань совпадетъ съ ф; если же двугранные углы не равны, то грань не совпадетъ съ напр,, она займетъ нѣкоторое положеніе <2ц, если уголъ А^ будетъ меньше угла АВ.
Замѣтивъ это, возьмемъ на общемъ ребрѣ какую-нибудь точку В и проведемъ черезъ нее плоскость В, перпендикулярную къ ребру. Отъ пересѣченія этой плоскости съ гранями двугранныхъ угловъ получатся линейные углы. Ясно, что если двугранные углы совпадутъ, то у нихъ окажется одинъ и тотъ же линейный уголъ, именно СВВ-, если же двугранные углы не совпадутъ, если, напр., грань займетъ положеніе фи, то у большаго двуграннаго угла окажется большій линейный уголъ (именно: С'ВР>С'цВР).
384. Обратныя теоремы. 1°. Равнымъ линейнымъ угламъ соотвѣтствуютъ равные двугранные углы.
2°. Ббльшему линейному углу соотвѣтствуетъ большій двугранный уголъ.
Эти теоремы легко доказываются отъ противнаго (51).
385. Замѣчаніе. Мы принимаемъ за очевидное, что в ложе н і е одной фигуры въ другую, часто употребляемое въ стереометріи, всегда можетъ быть выполняемо въ такой послѣдовательности: во 1°, совмѣщаемъ какія-нибудь двѣ точки
— 295 —
фигуръ; во 2°, какія-нибудь двѣ полупрямыя, исходящія изъ совпавшихъ точекъ, й, въ 3°, какія-нибудь двѣ полуплоскости, исходящія изъ совпавшихъ прямыхъ. Совмѣстятся ли при
этомъ другіе элементы фигуръ, зависитъ отъ свойствъ ихъ.
386. Слѣдствія. 1°. Прямому двугранному углу соотвѣтствуетъ прямой линейный уголъ и обратно.
Пусть (черт. 335) двугранный уголъ РАВ(^ прямой. Это значитъ, что онъ равенъ смежному углу (^АВР},. Но въ такомъ случаѣ линейные углы СВЕ и
Черт. 335.
СЕЕі также равны; а такъ какъ они смежные, то каждый изъ нихъ долженъ
быть прямой. Обратно, если равны смежные линейные углы СВЕ
и СВЕІУ то равны и смежные двугранные углы, т.-е. каждый
изъ нихъ долженъ быть прямой.
2°. Прямые двугранные углы равны, потому что у нихъ равны линейные углы. По той же причинѣ:
3°. Вертикальные двугранные углы равны.
4°. Двугранные углы съ соотвѣтственно параллельными и
одинаково направленными гранями равны.
387. Теорема. Двугранные углы относятся, какъ ихъ линейные углы.
При доказательствѣ разсмотримъ особо два случая:
1°. Линейные углы СВВ и СіВхРх соизмѣримы (черт. 336). Пусть ихъ общая мѣра содержится въ первомъ углѣ т разъ, а во второмъ п разъ. Проведемъ рядъ плоскостей черезъ ребра и прямыя, дѣлящія линейные углы на части, равныя общей мѣрѣ; тогда мы раздѣлимъ уголъ АВ на т, а уголъ АІВ1 на
Черт. ззв.
— 296 —
п частей, которыя всѣ равны между собою (вслѣдствіе равенства линейныхъ угловъ). Поэтому:
X. СВВ т дв. уг. АВ т --------------- -—- =— • 2-СхВхД п дв.уг. АіВі п дв. уг. ЛВ 21 СВБ
°ТКУДа: дв. уг. Л1В1=^С1В1В1‘
2°. Линейные углы несоизмѣримы. Раздѣлимъ (черт. 336) уголъ С^В^ на п равныхъ частей. Пусть 1[п этого угла содержится въ углѣ СВВ болѣе т, но менѣе т+1 разъ. Тогда приближенное отношеніе угловъ СВВи съ точностью до 1/п (съ недост.), равно т/п. Проведя плоскости такъ же, какъ и въ первомъ случаѣ, найдемъ, что приближенное отношеніе двугранныхъ угловъ АВ и А^, съ точностью до 7» (съ недост.), также равно ”/„. Такимъ образомъ, приближенныя отношенія оказываются равными при всякомъ и; а въ этомъ случаѣ мы условились считать несоизмѣримыя отношенія равными.
388. Слѣдствіе. Если за единицу двугранныхъ угловъ возьмемъ такой уголъ, который соотвѣтствуетъ единицѣ линейныхъ угловъ, то можно сказать, что двугранный уголъ измѣряется его линейнымъ угломъ.
Перпендикулярныя плоскости.
389. Опредѣленіе. Двѣ плоскости наз. взаимно перпендикулярными, если, пересѣкаясь, онѣ образуютъ прямые двугранные углы. Возможность существованія такихъ плоскостей обнаруживается слѣдующей теоремой, указывающей признакъ перпендикулярности двухъ плоскостей.
390. Теорема. Если плоскость (Р, черт. 337) проходитъ черезъ перпендикуляръ (ЛВ) къ другой плоскости (ф), то она перпендикулярна къ этой плоскости.
— 297 —
На плоскости проведемъ ѢС±Л)Е. Тогда уг. АВС будетъ
линейнымъ угломъ двуграннаго угла РБЕф. Такъ какъ прямая АВ, по условію, перпендикулярна къ С, то АБА-ВС: значитъ, уг. АВС прямой, а потому и двугранный уголъ прямой (386), т.-е. пл. Р перпендикулярна къ ф.
Слѣдующія двѣ теоремы выражаютъ главнѣйшія свойства
перпендикулярныхъ плоскостей.
391. Теорема. Если двѣ плоскости (Р и <$, черт. 338) взаимно перпендикулярны и къ одной изъ нихъ (къ О) проведенъ перпендикуляръ (АВ), имѣющій общую точку (Л) съ другою плоскостью (съ Р), то онъ весь лежитъ въ этой плоскости.
Предположимъ, что АВ не лежитъ въ плоскости Р (какъ изображено у насъ на чертежѣ). Проведемъ на этой плоскости АСА-ВЕ, а па пл. С проведемъ СРА-ВЕ. Тогда уголъ АСР, какъ линейный уголъ прямого двуграннаго угла, будетъ прямой. Поэтому линія АС, образуя прямые углы съ ВЕ и СР, будетъ перпендикуляромъ къ пл.ф. Мы будемъ имѣть тогда 2 пер
пендикуляра, опущенные изъ одной и той же точки А на пл. ($,
именно АВ и АС. Такъ какъ это невозможно, то нельзя допустить, чтобы перпендикуляръ АВ не лежалъ въ пл. Р.
392. Слѣдствіе. Пересѣченіе (АВ, черт. 339) двухъ плоскостей (Р и <$), перпендикулярныхъ къ третьей плоскости (Е), есть перпендикуляръ къ этой плоскости.
Черт. 339.
Дѣйствительно, если черезъ какую-
— 296 —
ни будь точку А линіи пересѣченія вообразимъ перпендикуляръ къ пл. В, то этотъ перпендикуляръ, согласно предыдущей теоремѣ, долженъ лежать и въ пл. ф, и въ пл. Р; значитъ, онъ сольется съ АВ.
Уголъ двухъ скрещивающихся прямыхъ.
893. Мы видѣли (360), что въ пространствѣ могутъ быть взяты такія прямыя, которыя не пересѣкаются и въ то же время не параллельны, такъ какъ не лежатъ въ одной плоскости. Для
такпхъ скрещивающихся прямыхъ дадимъ слѣдующее Опредѣленіе. Угломъ двухъ скрещиваю-
щихся прямыхъ (АВ и СВ, черт. 340), которыхъ дано
положеніе и направленіе, наз.
Черт. 340.
уголъ (МОК), который получится, если изъ произвольной точки пространства (О) проведемъ полупрямыя (ОМ и О2Ѵ), соотвѣтственно параллельныя даннымъ прямымъ (АВ и СВ) и одинаково съ ними направленныя.
Величина угла МОМ не зависитъ отъ положенія точки О.
Въ самомъ дѣлѣ, если построимъ указаннымъ путемъ уголъ
при какой-пибудь другой точкѣ Оь то М0^=‘М101^1,
такъ какъ эти углы имѣютъ соотвѣтственно параллельныя и одинаково направленныя стороны (364 и 379).
Уголъ, образуемый прямой съ плоскостью.
394. Проекція прямой на плоскость. Мы говорили ранѣе (357), что когда изъ одной точки проведены къ плоскости перпендикуляръ и наклонная, то проекціей этой наклонной на плоскость наз. прямая, соединяющая основаніе
— 299 —
перпендикуляра съ основаніемъ наклонной. Дадимъ теперь болѣе общее опредѣленіе проекціи.
1°. Проекціей какой-нибудь точки на
плоскость (напр.,точкиМ на плоскость Р, черт. 341) н а з. основаніе (т) перпендикуляра, опущеннаго на эту плоскость изъ взятой точки.
2°. Проекціей какой-нибудь линіи на плоскость наз. геометрическое мѣсто проекцій всѣхъ точекъ эт
Черт. 341.
ой линіи.
Въ частности, если проектируемая линія есть прямая (напр., АВ, черт. 341), то проекція ея на плоскость (Р) есть также прямая. Въ самомъ дѣлѣ, если мы черезъ прямую АВ и перпендикуляръ Мт, опущенный па плоскость проекцій изъ какой-нибудь одной точки М этой прямой, проведемъ плоскость ф, то эта плоскость должна быть перпендикулярной къ пл. Р (390); поэтому перпендикуляръ, опущенный на пл. Р изъ любой точки прямой АВ (папр. изъ точки 27), долженъ лежать въ этой пл. ф (391) и, слѣд., проекціи всѣхъ точекъ прямой АВ должны лежать на прямой аЪ, по которой пересѣкаются плоскости Р и Такимъ образомъ, эта прямая аЪ представляетъ собою геометрическое мѣсто проекцій всѣхъ точекъ данной прямой АВ, и, слѣд., есть ея проекція.
Существуетъ, впрочемъ, одинъ частный случай, когда проекція прямой обращается въ точку; это бываетъ тогда, когда прямая перпендикулярна къ плоскости проекцій.
395. Уголъ прямой еъ плоскостью. У г л о мъ прямой (АВ, черт. 342) съ плоскостью (Р) въ томъ случаѣ, когда прямая наклонна къ плоскости, наз. уголъ (АВС), составленный этою прямою съ ея проекціей на плоскость.
— зоо —
Уголъ этотъ обладаетъ тѣмъ свойствомъ, что онъ есть наи
меньшій изъ всѣхъ угловъ, которые наклонная образуетъ
съ прямыми, проведенными на плоскости Р черезъ основаніе наклонной. Докажемъ, напр., что /.АВС меньше /.АВВ. Для этого отложимъ ВВ—ВС и соединимъ В съ А. У тр-ковъ АВС и АВВ двѣ стороны одного равны соотвѣтственно двумъ сторонамъ дру-
гого, но третьи стороны не равны
Черт. 342. а именно АВ>АС (357). Вслѣд-
ствіе этого /.АВВ больше /.АВС (58, 2°).
ГЛАВА V.
Многогранные углы.
396. Опредѣленіе. Возьмемъ нѣзколько угловъ (черт. 343): А8В, В8С, С8В..., которые, примыкая послѣдовательно одинъ къ другому, расположены въ одной плоскости вокругъ общей вершины Я. Повернемъ плоскость угла А8В
вокругъ общей стороны 8В такъ, чтобы эта плоскость составила нѣкоторый двугранный уголъ съ пл. В8С. Затѣмъ, не измѣняя получившагося двуграннаго угла, повернемъ его во
— 301 —
кругъ прямой 8С такъ, чтобы пл. В8С составила нѣкоторый двугранный уголъ съ пл. С8В. Продолжаемъ такое послѣдовательное вращеніе вокругъ каждой общей стороны. Если при этомъ послѣдняя сторона 8Г совмѣстится съ первою стороною &4, то образуется фигура (черт. 344), которая вмѣстѣ съ частью пространства, ограниченною плоскостями, называется многограннымъ угломъ. Углы А8В, В8С... наз. п л о с-скими углами или гранями, стороннихъ 8В... наз. ребрами, а общая вершина 5—вершиною многограннаго угла. Каждому ребру соотіѣгствуетъ свой двугранный уголъ; поэтому въ многогранномъ углѣ столько двугранныхъ угловъ и столько плоскихъ, сколько въ немъ всѣхъ реберъ. Наименьшее число граней въ многогранномъ углѣ три; такой уголъ наз. треграннымъ. Могутъ быть углы четыре-
•с
Черт. 345.
гранные, пятигранные и т. д.
Многогранный уголъ (черт. 344) обозначается или олною буквою 8, поставленною у вершины, или же рядомъ буквъ 8АВСВЕ, изъ которыхъ первая обозначаетъ вершину, а прочія —ребра по порядку ихъ расположенія.
Многогранный уголъ наз. выпуклымъ, если онъ весь расположенъ по одну сторону отъ каждой своей грани. Таковъ, напр., уголъ, изображенный на чертежѣ 344. Наоборотъ, уголъ па чертежѣ 345 нельзя назвать выпуклымъ, такъ какъ онъ расположенъ по обѣ стороны отъ грани А8В, или отъ грани В8С.
Если двѣ грани многограннаго угла пересѣчемъ плоскостью, то въ сѣченіи образуется многоугольникъ (аЪссІе, черт. 344 и 345). Въ выпукломъ углѣ этотъ многоугольникъ тоже выпуклый.
Мы будемъ разсматривать только выпуклые многогранные углы.
397. Теорема. Во всякомъ трегранномъ углѣ каждый плоскій уголъ меньше суммы двухъ другихъ плоскихъ угловъ.
Очевидно, теорема эта нуждается въ доказательствѣ только въ томъ случаѣ, когда она примѣняется къ плоскому углу,
— 302 —
наибольшему изъ трехъ. Пусть въ углѣ 8АВС (черт. 346) наибольшій изъ плоскихъ угловъ есть Л<8С.
Докажемъ, что даже этотъ наибольшій уголъ меньше суммы двухъ остальныхъ.
/ \ Отложимъ на углѣ А8С часть А8В, рав-
у ‘‘Л ную А8В. Проведемъ къ плоскости угла
/ » \ А8С какую-нибудь прямую АС, пересѣ-
Т : : тг \ кающую 8В въ нѣкоторой точкѣ В. Отло-/ ф \л жимъ 8В=8В. Соединивъ В съ Л и С,
П0ЛУчимъ ДЛСВ, въ которомъ:
® ' ЛО+ОС<ЛВ-|-ВС.
Черт. 346. Тр-ки А8В и А8В равны, такъ какъ они содержатъ по равному углу, заключенному между равными сторонами; слѣд., АВ—АВ. Поэтому въ выведенномъ неравенствѣ можно отбросить равныя части АВ и АВ, послѣ чего получимъ:
ВС<ВС.
Теперь замѣчаемъ, что у тр-ковъ 8СВи 8СВ двѣ стороны одного равны двумъ сторонамъ другого, а третьи стороны неравны; въ такомъ случаѣ противъ бблыпей изъ этихъ сторонъ лежитъ бблыпій уголъ (58, 2°); значитъ:
уголъ Сі8В<?угла С8В.
Приложивъ къ лѣвой части этого неравенства уголъ А8В, а къ правой равный ему уголъ А8В, получимъ неравенство, которое требовалось доказать:
уголъ Л5С<угл. С8В+уг. А8В.
Слѣдствіе. Отнявъ отъ обѣихъ частей послѣдняго неравенства по углу А8В или по углу С8В, получимъ:
уголъ А8С—уг. Л$Е<уг. С8В-, уголъ А8В—уг. С8Б<^уг. А8В.
Такъ какъ, кромѣ того, уголъ А8С, наибольшій изъ трехъ угловъ, конечно, больше разности двухъ другихъ угловъ, то заключаемъ:
Въ трегранномъ углѣ каждый плоскій уголъ больше разности двухъ другихъ угловъ.
— 303 —
398. Теорема. Во всякомъ выпукломъ многогранномъ углѣ сумма всѣхъ плоскихъ угловъ меньше 4гі.
Пересѣчемъ грани (черт. 347) выпуклаго угла 8АВСВЕ какою-нибудь плоскостью; отъ этого въ сѣченіи получимъ выпуклый п-у го льникъ АВСВЕ. Примѣняя теорему предыдущаго параграфа къ каждому изъ трегранныхъ угловъ, образовавшихся при точкахъ А, В, С, В и Е, находимъ: АВС<АВ8+8ВС- ВСВ<ВС8+ 8СВ,... Сложимъ почленно всѣ
эти неравенства. Тогда въ лѣвой части получимъ сумму всѣхъ угловъ многоугольника АВСВЕ, которая равна 2йп—4й (89), а въ правой—сумму угловъ тр-ковъ А8В, В8С... кромѣ тѣхъ угловъ, которые лежатъ при вершинѣ 8. Обозначивъ сумму этихъ послѣднихъ угловъ буквою х, мы получимъ послѣ сложенія: 2йп—4«’<^2йп—х
Откуда: ®<^4гі.
Равенство трехгранныхъ угловъ.
899. Дополнительный уголъ. Изъ вершины 8 (черт. 348) треграннаго угла 8 АВС возставимъ къ грани А8В перпендикуляръ^^.
направляя его въ ту сторону отъ этой грани, въ которой расположено противоположное ребро$0-Подобно этому проведемъ перпендикуляръ 8Аг къ грани В8С и 8Вг къ грани АЗС. Трегранный уголъ, у котораго ребрами служатъ полупрямыя 8Аг, 8Вг и 8Сг, наз. дополнительнымъ для угла 8АВС.
Замѣтимъ, что если для угла 8АВС дополнительнымъ угломъ
Черт. 348.
служитъ уголъ ЗА^іСі, то и наоборотъ: для уг. 8А1В1С1 дополнительнымъ угломъ будетъ 8АВС. Дѣйствительно, плоскость 8А1В1, проходя черезъ перпендикуляры къ плоскостямъ В8С и АЗС, перпендикулярна
— 304 —
къ нимъ обѣимъ, а слѣд., и къ линіи ихъ пересѣченія 8С-, значитъ, прямая 8С есть перпендикуляръ къ грани 8А1В1 и, кромѣ того, она расположена по ту же сторону отъ этой грани, по которую лежитъ противоположное ребро 8Сг. Подобно этому убѣдимся, что прямыя 8В и 8А соотвѣтственно перпендикулярны къ гранямъ ЗА^і и 5^x0, и расположены по ту сторону отъ нихъ, по которую лежатъ ребра 8ВХ и 8А±. Значитъ, углы 8АВС и 8А1В1С1 взаимно дополнительны.
400. Лемма 1. Если два трегранные угла взаимно дополнительны, то плоскіе углы одного служатъ дополненіемъ до 2Л къ противоположнымъ двуграннымъ угламъ другого.
Каждый плоскій уголъ одного изъ взаимно дополнительныхъ трегранныхъ угловъ образованъ двумя перпендикулярами,
возставленными къ гранямъ противоположнаго двуграннаго угла дру
гого треграннаго, изъ одной точки его ребра. Замѣтивъ это и принявъ
во вниманіе направленіе перпендикуляровъ, возьмемъ какой-нибудь
Черт. 349.
двугранный уголъ АВ (черт. 349) и изъ произвольной точки В его ребра возставимъ перпендикуляры: ВЕ къ грани АО и ВР къ грани АС, и затѣмъ черезъ ВЕ и ВР вообразимъ плоскость, которая должна быть перпендикулярна къ ребру АВ (390, 392). Пусть пересѣченія этой плоскости съ гранями угла АВ будутъ прямыя ВС и ВО. Тогда уголъ СВВ долженъ быть линейнымъ угломъ двуграннаго АВ. Такъ какъ стороны угла ЕВР соотвѣтственно перпендикулярны къ сторонамъ угла СВО, и эти углы неравны, то сумма ихъ равна 2й (86); что и требовалось доказать.
401. Лемма 2. Равнымъ треграннымъ угламъ соотвѣтствуютъ равные дополнительные углы и обратно.
Равные трегранные углы при вложеніи совмѣщаются; поэтому совмѣщаются и тѣ перпендикуляры, которые образуютъ ребра дополнительныхъ угловъ; значитъ, дополнительные углы также совмѣщаются.
Обратно: если совмѣщаются дополнительные углы, то совмѣщаются и данные углы.
402. Теоремы. Трегранные углы равны, если они имѣютъ:
1°, по равному двугранному углу, заключенному между двумя соотвѣтственно равными и одинаково расположенными плоскими углами;
или 2°, по равному плоскому углу, заключенному между двумя соотвѣтственно равными и одинаково расположенными двугранными углами;
или 3°, по три соотвѣтственно равныхъ и одинаково расположенныхъ плоскихъ угла;
или 4°, по три соотвѣтственно равныхъ и одинаково расположенныхъ двугранныхъ угла.
— 305 —
1°. Пусть 3 и 8} два трегранные угла (черт. 350), у которыхъ: ^А8В=^А181В1, ^А8С=^А181С1 и двугр. уг. АЗ = двугр. уг. А^З}. Вложимъ уголъ і5\ въ угОлъ 5 такъ, чтобы у нихъ совпали: точка 8} съ 8, прямая 8-іАі съ ЗА и плоскость А181В1 съ А8В. Тогда ребро 81В1 пойдетъ по 8В (по равенству угловъ А^^і и А8В), плоскость А181С1 пойдетъ по АЗС (по равенству двугранныхъ угловъ).
5 8.
Черт. 350.
и ребро 81С1—по 8С (по равенству угловъ А^ф и АЗС). Такимъ образомъ, трегранные углы совмѣстятся всѣми своими ребрами, значитъ, они будутъ равны.
2°. Второй признакъ доказывается вложеніемъ подобно первому.
Черт. 351.
3°. Пусть 8 к 8Г (черт. 351) два трегранные угла, у которыхъ плоскіе углы одного равны соотвѣтственно плоскимъ угламъ другого, и, кромѣ того, равные углы одинаково расположены.
О ложимъ на всѣхъ ребрахъ произвольные, но равные, отрѣзки 8А = 8В—8С=81А1 = ... и построимъ тр-ки АВС и А1В1С1. Изъ равенства тр-ковъ АВ8 и А1В181 находимъ: АВ = А1В1. Подобно этому изъ равенства другихъ боковыхъ тр-ковъ выводимъ: АС=А1С1 и ВС=В1С1. Слѣд., ААВС=/\А1В1С1. Опустимъ на плоскости этихъ тр-ковъ перпендикуляры 80 и З^. Такъ какъ наклонныя ЗА, 8В и 8С равны, то должны быть равны ихъ проекціи О А, ОВ и ОС; значитъ, точка О есть центръ круга, описаннаго около тр-ка АВС. Точно
А. Киселевъ. Геометрія.
— 306 —
такъ же точка 01 есть центръ круга, описаннаго около тр-ка Л1В1С1. У равныхъ тр-ковъ радіусы описанныхъ круговъ равны; значитъ, ОВ=О1В1. Поэтому ^ВВО — ВіВ^і (по гипотенузѣ и катету), и, слѣд., 08 = 018г. Вложимъ теперь фигуру 81А1В1С1 въ фигуру 8АВС такъ, чтобы равные тр-ки А^ВіС} и АВС совмѣстились; тогда совмѣстятся описанныя окружности, и, слѣд., ихъ центры 0х и О; вслѣдствіе этого перпендикуляръ 0181 пойдетъ по 08 и точка 8г упадетъ въ 8. Такимъ образомъ, трегранные углы совмѣстятся всѣми своими ребрами, значитъ, они равны.
4°. Четвертый признакъ легко доказывается при помощи дополнительныхъ угловъ. Если у двухъ трегранныхъ угловъ соотвѣтственно равны и одинаково расположены двугранные углы, то у дополнительныхъ угловъ соотвѣтственно равны и одинаково расположены плоскіе углы (400); слѣд., дополнительные углы равны; а если равны дополнительные, то равны и данные углы (401).
403. Симметричные многогранные углы. Какъ извѣстно, вертикальные углы равны, если рѣчь идетъ объ углахъ, образованныхъ прямыми или плоскостями.
Черт. 352.
Посмотримъ, примѣнима ли эта истина къ угламъ многограннымъ.
Продолжимъ (черт. 352) всѣ ребра угла 8АВСВЕ за вершину; тогда образуемъ другой многогранный уголъ 8 А1В1С1В1Е1, который можно назвать вертикальнымъ по отношенію къ первому углу. Не трудно видѣть, что у обоихъ угловъ равны соотвѣтственно и плоскіе углы, и двугранные; но тѣ и другіе расположены в ъ обратномъ порядкѣ. Дѣйствительно, если мы вообразимъ наблюдателя, который смотритъ извнѣ многограннаго угла на его вершину, то ребра 8 А, 8В, 8С, 8В, 8Е будутъ казаться ему расположенными противъ движенія часовой стрѣлки, тогда какъ, смотря на уголъ 5А1В1СХО1Е1, онъ
увидитъ ребра 54х, 8В1,... расположенными по движенію часовой стрѣлки.
Многогранные углы съ соотвѣтственно равными плоскими и двугранными углами, но расположенными въ обратномъ порядкѣ, вообще не могутъ совмѣститься при вложеніи; значить, они не равны. Такіе углы называются симметричными (относительно вершины 8).
— 307 —
КНИГА II.
МНОГОГРАННИКИ.
ГЛАВА I.
Свойства параллелепипеда и пирамиды.
404. Многогранникъ.Многогранникомъ наз. тѣло, ограниченное со всѣхъ сторонъ плоскостями. Многоугольники, образованные пересѣченіемъ этихъ плоскостей, наз. гранями, ихъ стороны—р е б р а м и, а вершины—в ерши-нами многогранника. Прямыя, соединяющія двѣ какія-нибудь вершины, не лежащія па одной грани, наз. діаго
налями многогранника.
Мы будемъ разсматривать только выпуклые многогран
ники, т.-е. такіе, которые расположены по одну сторону отъ
каждой своей грани.
Наименьшее число граней въ многогранникѣ четыре; такой многогранникъ получается отъ пересѣченія треграннаго угла
какою-нпбудь плоскостью.
405. Призма. Призмою наз. многогранникъ, у кото-
раго двѣ грани—равные многоугольники съ соотвѣтственно параллельными сторонами, а всѣ остальныя грани— параллелограммы.
Чтобы показать возможность существованія такого многогранника, возьмемъ (черт. 353) какой-нибудь многоугольникъ АВС БЕ и черезъ его вершины проведемъ рядъ параллельныхъ прямыхъ, не лежащихъ въ его плоскости. Взявъ затѣмъ на одной изъ этихъ прямыхъ произвольную точку А1г проведемъ черезъ нее плоскость, парал
Черт. 353.
лельную плоскости АВСБЕ-, черезъ каждыя двѣ послѣдова
тельныя параллельныя прямыя также проведемъ плоскости. Пересѣченіе всѣхъ этихъ плоскостей опредѣлитъ многогранникъ АВС БЕ ЛіВіСіРіЕі, удовлетворяющій опредѣленію
20*
— 308 —
призмы. Дѣйствительно, параллельныя плоскости АВСВЕ и Л1В1С1РіЕ1 пересѣкаются боковыми плоскостями по параллельнымъ прямымъ (373); поэтому фигуры АА^Е, ЕЕ^В и т. д.—параллелограммы. Съ другой стороны, у многоугольниковъ АВСВЕ и АіВіСіВіЕі равны соотвѣтственно стороны (какъ противоположныя стороны параллелограммовъ) и углы (какъ углы съ параллельными и одинаково направленными сторонами); слѣд., эти многоугольники равны.
Многоугольники АВСВЕ и А^С^Е^ лежащіе въ параллельныхъ плоскостяхъ, паз. основаніями призмы; перпендикуляръ ООХ, опущенный изъ какой-нибудь точки одного основанія на другое, наз. высотою призмы. Параллелограммы наз. боковыми гранями призмы, а ихъ стороны, соединяющія соотвѣтственныя вершины основаній,—б о -новыми ребрами. У призмы всѣ боковыя ребра равны, какъ отрѣзки параллельныхъ прямыхъ, заключенные между параллельными плоскостями.
Плоскость, проведенная черезъ какія-нибудь два боковыя ребра, не прилежащія къ одной боковой грани призмы (напр., черезъ ребра ААі и ССг, черт. 353), наз. діагональною
плоскостью.
Призма наз. прямою или наклонною, смотря по тому, будутъ ли ея боковыя ребра перпендикулярны или наклонны къ основаніямъ. У прямой призмы боковыя грани суть прямоугольники. За высоту такой призмы можно принять боко
вое ребро.
Прямая призма наз. правильною, если ея основанія правильные многоугольники. У такой призмы всѣ боковыя грани суть равные прямоугольники (черт. 354).
Призмы бываютъ: треугольныя, четыреугольныя и т. д., смотря по тому, лежитъ ли въ основаніи треугольникъ, четыреугольникъ и т. д.
406. Параллелепипедъ. Такъ называютъ призму, у которой основаніями служатъ параллелограммы (черт. 355).
— 309 —
Параллелепипеды могутъ быть прямые и наклонные. Прямой параллелепипедъ наз. прямоугольнымъ, если его основанія прямоугольники (черт. 356).
Изъ этихъ опредѣленій слѣдуетъ:
1°, у параллелепипеда всѣ шесть граней параллелограммы;
2°, у прямого параллелепипеда четыре боковыя грани прямоугольники, а два основанія—параллелограммы;
3°, у прямоугольнаго параллелепипеда всѣ шесть граней прямоугольники.
Черт. 355.
Черт. 356.
Три ребра прямоугольнаго параллелепипеда, сходящіяся въ одной вершинѣ, наз. его измѣреніями; одно изъ нихъ можно разсматривать, какъ длину, другое, какъ ширину, а третье, какъ высоту.
Прямоугольный параллелепипедъ, имѣющій равныя измѣренія, наз. кубомъ. У куба всѣ грани—квадраты.
Для краткости слово «параллелепипедъ» мы часто будемъ писать такъ: пар—дъ.
407. Пирамида. Пирамидою наз. многогранникъ, у котораго одна грань, называемая основаніемъ, есть какой-нибудь многоугольникъ, а всѣ остальныя грани, называемыя боковыми,—треугольники, имѣющіе общую вершину.
Чтобы получить пирамиду, достаточно какой-нибудь многогранный уголъ 5 (черт. 357) пересѣчь произвольною плоскостью АВСВ.
Общая вершина 8 боковыхъ треугольниковъ наз. вершиною пирамиды, а перпендикуляръ 80, опущенный изъ вершины на основаніе,—высотою ея.
— 310 —
Обыкновенно, обозначая пирамиду буквами, пишутъ сначала ту, которая поставлена у вершины, напр.: 8АВСБ (черт. 357).
Плоскость, проведенная черезъ вершину пирамиды и черезъ какую-пибудь діагональ основанія (напр., черезъ діагональ ВР, черт. 369), наз. діагональною плоскостью.
Пирамиды бываютъ: треугольныя, четыреугольныя и т. д., смотря по тому, лежитъ ли въ основаніи треугольникъ, четыреугольникъ, и т. д. Треугольная пирамида (черт. 358) наз. иначе тетраэдромъ; у такой пирамиды всѣ четыре грани тре
угольники.
Пирамида наз. правильною (черт. 359), если, во 1°, ея основаніе есть правильный многоугольникъ, и, во 2°, высота
проходитъ черезъ центръ этого многоугольника. Въ правиль
Черт. 360.
ной пирамидѣ всѣ боковыя ребра равны между собою (какъ наклонныя съ равными проекціями). Поэтому всѣ боковыя грани правильной пирамиды суть равные равнобедренные тр-ки. Высота 8М (черт. 359) какого-либо одного изъ этихъ тр-ковъ наз апоѳемою. Всѣ апо-ѳемы въ одной пирамидѣ равны.
408. Усѣченная пирамида. Отрѣзокъ пирамиды (черт. 360), заключенный между основаніемъ (АВСВЕ) и сѣкущею плоскостью (Л1В1(71Р1В1), па
— 311
раллельною основанію, наз. усѣченною пирамидою. Параллельные многоугольники наз. основаніями, а разстояніе между ними ООг—в ы с о т о ю. Усѣченная пирамида наз. правильною, если она составляетъ отрѣзокъ правильной пирамиды.
Равенство призмъ и пирамидъ.
409. Мы ограничимся указаніемъ только слѣдующаго признака равенства призмъ или пирамидъ.
Теорема. Двѣ призмы или двѣ пирамиды равны, если основаніе и боковая грань одной и основаніе и боковая грань другой соотвѣтственно равны, одинаково наклонены и одинаково расположены.
Пусть въ двухъ призмахъ (черт. 361) соотвѣтственно равны и одинаково расположены основанія и боковыя грани АО и А101 и, сверхъ того, равны двугранные углы АВ и А^В^ Вложимъ одну призму въ ДРУгую такъ, чтобы у нихъ совпали равныя основанія. Тогда, по ра-
Черт. 361.
Черт. 362.
венству двугранныхъ угловъ, грань АіТ)! пойдетъ по АО, а такъ какъ эти грани равны и одинаково расположены, то онѣ совпадутъ; но тогда совпадутъ и верхнія основанія (какъ параллельныя и равныя нижнимъ основаніямъ), т.-е. призмы совмѣстятся.
То же доказательство примѣняется и къ пирамидамъ (черт. 362)
312 —
Свойства граней и діагоналей параллелепипеда.
410. Теорема. Во всякомъ параллелепипедѣ противополож
ныя грани равны и параллельны.
Такъ, грани (черт. 363) ВВ^С и ААхВгВ параллельны, потому что двѣ пересѣкающіяся прямыя ВВі и ВхСі одной грани параллельны двумъ пересѣкающимся прямымъ ААг и А^! другой (372,2°); эти грани и равны, такъ какъ В^ = АіВц ВіВ = АХА (какъ противоположныя стороны параллелограммовъ) и /.ВВА = /.АА1В1 (379).
411. Теорема. Во всякомъ параллелепипедѣ всѣ четыре діагонали пересѣкаются въ одной точкѣ и дѣлятся въ ней пополамъ.
Возьмемъ (черт. 364) въ параллелепипедѣ какія-нибудь двѣ діагонали, напр., АСг и ВВі, и проведемъ вспомогательныя прямыя АВХ и ВС^ Такъ какъ ребра АВ и В^ соотвѣтственно равны и параллельны ребру ВС, то они равны и параллельны между собою; вслѣдствіе этого фигура АВС1В1 есть параллелограммъ (99,2°), въ которомъ прямыя СгА и ВВг—діагонали; а въ параллело
граммѣ діагонали пересѣкаются и дѣлятся въ точкѣ пересѣченія
пополамъ.
Возьмемъ теперь одну изъ этихъ діагоналей, напр., АСг, съ третьею діагональю, положимъ съ ВВг. Совершенно такъ же мы можемъ доказать, что онѣ пересѣкаются и дѣлятся въ точкѣ пересѣченія пополамъ. Слѣд., діагонали ВВ, и АСі и діагонали АСі и ВВХ (которыя мы раньше брали) пересѣкаются въ одной и той же точкѣ, именно въ срединѣ діагонали АСХ.
— 313 —
Наконецъ, взявъ эту же діагональ АСі съ четвертою діагональю АгС, мы такъ же докажемъ, что онѣ пересѣкаются и дѣлятся пополамъ. Значитъ, точка пересѣченія и этой пары діагоналей лежитъ въ срединѣ діагонали АСг. Такимъ образомъ, всѣ 4 діагонали пересѣкаются въ одной и той же точкѣ и дѣлятся этою точкою пополамъ.
412. Теорема. Въ прямоугольномъ параллелепипедѣ квадратъ любой діагонали равенъ суммѣ квадратовъ трехъ его измѣреній.
Пусть (черт. 365) прямая АСг есть какая-нибудь діагональ прямоугольнаго параллелепипеда. Проведя діагональ основанія АС, получимъ два тр-ка: АСіС и АСВ. Оба они прямоугольные; первый потому, что параллелепипедъ прямой, и, слѣд., ребро ССі перпендикулярно къ основанію; второй потому, что параллелепипедъ прямоугольный, значитъ, въ основаніи его
Черт. 365.
лежитъ прямоугольникъ. Изъ этихъ тр-ковъ находимъ: АС^АС^+ССі2 и АС*=АВ*+ВС*.
Слѣд., АС^АВЬ+ВСЧ-СС^АВ^+АВ^+ААі2.
413. Слѣдствіе. Въ прямоугольномъ параллелепипедѣ всѣ діагонали равны.
Свойства параллельныхъ сѣненій въ пирамидѣ.
414. Теоремы. Если пирамида (черт. 366) пересѣчена плоскостью, параллельною основанію, то:
1°, боковыя ребра и высота дѣлятся этою плоскостью на части пропорціональныя;
2°, въ сѣченіи получается многоугольникъ (аЬс&с), подобный основанію;
— 314 —
3°, площади сѣченія и основанія относятся, какъ квадраты
ихъ разстояній отъ вершины.
8
Черт. 366.
1°. Прямыя аЪ и АВ можно разсматривать, какъ пересѣченія двухъ параллельныхъ плоскостей (основанія и сѣкущей) третьею плоскостью А8В\ поэтому аЬ II АВ (373). По той же причинѣ Ъс II ВС, сЛ II СВ... и ат II АМ-, вслѣдствіе этого (219):
8а 8Ь 8с 8т
аА ЪВ сС тМ
2°. Изъ подобія тр-ковъ А8В и а8Ъ, затѣмъ В8С и Ъ8с и т. д. выводимъ:
АВ В8 В8 ВС АВ ВС
= ; =—; откуда: ------------ аЪ-----------------------------------Ъ8-Ъ8-Ъс аЪ-Ъс
ВС С8 С8 СВ ВС СВ
— —------• ---=---: откуда: —--------
Ъс с8 с8 ед, Ъс ссі
Такъ же докажемъ пропорціональность остальныхъ сторонъ мн-ковъ АВСВЕ и аЪсДе. Такъ какъ, сверхъ того, у этихъ мн-ковъ равны соотвѣтственные углы (какъ образованные параллельными и одинаково направленными сторонами), то они подобны.
3°. Площади подобныхъ многоугольниковъ относятся, какъ квадраты сходственныхъ сторонъ; поэтому:
площ. АВСВЕ_ ЛВ2_ / ЛВ\2
площ. аЪсде аЪ2 \ аЪ /
„ АВ А8 М8
аЬ а8 т8
о площ. АВСВЕ (М$\2 М82
Значитъ: --------------— I-- —-------•
площ. аЪсНе \ т8/ т82
415. Слѣдствіе. У правильной усѣченной пирамиды верхнее основаніе есть правильный многоугольникъ, а боковыя грани суть равныя и равнобочныя трапеціи (см. черт. 360).
Высота какой-нибудь изъ этихъ трапецій паз. апоѳемой правильной усѣченной пирамиды.
— 316 —
416. Теорема. Если двѣ пирамиды съ равными высотами разсѣчены на одинаковомъ разстояніи отъ вершины плоскостями, параллельными основаніямъ, то площади сѣченій пропорціональны площадямъ основаній.
Пусть (черт. 367) В и площади основаній двухъ пирамидъ, Н высота каждой изъ нихъ, Ъ и Ьх площади сѣченій плоскостями, параллельными основаніямъ и удаленными отъ вср-
Черт. 367.
шинъ на одно и то же разстояніе к. Согласно предыдущей
теоремѣ мы будемъ имѣть:
Ъ Ъ2 Ъі №
——— и —і=—.
В н2 вг н2
Откуда:
Ъ Ьі 'в~в1
ъ в
или —=— .
Ь1 Ві
417. Слѣдствіе. Если 5=^, то и Ь=Ьі, т.-е. если у двухъ пирамидъ съ равными высотами основанія равновелики, то равновелики и сѣченія, равноотстоящія отъ вершины.
ГЛАВА II.
Боковая поверхность призмы и пирамиды.
418. Теорема. Боковая поверхность призмы равна произведенію периметра перпендикулярнаго сѣченія на боковое ребро.
Перпендикулярнымъ сѣченіемъ (черт. 368) наз. многоугольникъ аЬс<1, получаемый отъ пересѣченія призмы
— 316 —
плоскостью, перпендикулярною къ боковымъ ребрамъ. Стороны этого многоугольника перпендикулярны къ ребрамъ (353).
Боковая пов
Черт. 368.
ерхность призмы представляетъ собою сумму площадей параллелограммовъ; въ каждомъ изъ нихъ за основаніе можно взять боковое ребро, а за высоту сторону перпендикулярнаго сѣненія. Поэтому:
Бок. пов. = ААг . аЪ + ВВі . Ъс + + ССг . сй + ББі . (Іа = (аЪ + Ъс + сй 4- сісі) . ААг.
419. Слѣдствіе. Боковая поверхность прямой призмы равна произведенію периметра основанія на высоту, потому что въ такой призмѣ за перпендикулярное сѣченіе можно взять само основаніе, а боковое ребро ея равно высотѣ.
420. Теорема. Боковая поверхность правильной пирамиды равна произведенію периметра основанія на половину апоѳемы.
Пусть (черт. 369) 8АВСВЕ есть правильная пирамида и
8М ея апоѳема. Боковая поверхность этой пирамиды есть сумма
8
Черт. 369.
площадей равныхъ равнобедренныхъ тр-ковъ. Площадь одного изъ нихъ, напр. А8В, равна АВ . 1/2 8М. Если всѣхъ тр-ковъ п, то боковая поверхность выразится АВ . 1/2 8М . п— =(АВ . п) . 1/2 8М, гдѣ АВ . п есть периметръ основанія, а 8М апоѳема.
421. Теорема. Боковая поверхность правильной усѣченной пирамиды равна произведенію полусуммы периметровъ обоихъ основаній на апоѳему.
Эта поверхность есть сумма площадей равныхъ трапецій. Площадь одной изъ нихъ, напр. АаЪВ (черт. 369), равна (ЛВ+
+«Ь) . Мт (315). Если число всѣхъ трапецій есть п, то
— 317 —
АВ+аЪ АВ.п+аЪ.п ,,
бок. пов.=------• Мт.п=-----------. Мт,
2 2
гдѣ АВ.п и аЪ.п суть периметры нижняго и верхняго основаній.
ЗАДАЧИ.
327. Высота прямой призмы, которой основаніе есть правильный треугольникъ, равна 12 метрамъ, сторона основанія 3 метр. Вычислить полную поверхность призмы.
328. Полная поверхность прямоугольнаго параллелепипеда равна 1714 кв. футовъ, а неравныя стороны основанія равны 25 ф. и 14 ф. Вычислить боковую поверхность и боковое ребро.
329. Въ прямоугольномъ параллелепипедѣ съ квадратнымъ основаніемъ и высотою Л проведена сѣкущая плоскость черезъ два противоположныя боковыя ребра. Вычислить полную поверхность параллелепипеда, зная, что площадь сѣченія равна 8.
330. Правильная шестиугольная пирамида имѣетъ сторону основанія а и высоту к. Вычислить боковое ребро, апоѳему, боковую поверхность и полную поверхность.
331. Вычислить полную поверхность и высоту треугольной пирамиды, у которой каждое ребро равно а.
332. Правильная шестиугольная пирамида, у которой высота 25 саптим., а сторона основанія 5 сант., разсѣчена плоскостью, параллельною основанію. Вычислить разстояніе этой плоскости отъ вершины пирамиды, зная, что площадь сѣченія = 2/з Ѵз квадр. сант.
333. Высота усѣченной пирамиды съ квадратнымъ основаніемъ равна к, сторона нижняго основанія а, а верхняго Ъ. Найти полную поверхность усѣченной пирамиды.
334. Высота усѣченной пирамиды равна 6, а площади основаній 18 и 8. Пирамида разсѣчена плоскостью, параллельною основаніямъ и дѣлящею высоту пополамъ. Вычислить площадь сѣченія.
318 —
ГЛАВА III.
Объемъ призмы и пирамиды.
422. Основныя допущенія объ объемахъ.
Часть пространства, занимаемая геометрическимъ тѣломъ, наз. объемомъ этого тѣла (если она разсматривается независимо отъ своей формы).
Объемъ тѣла мы можемъ разсматривать, какъ величину особаго рода, если примемъ слѣдующія допущенія объ объемахъ (аналогичныя допущеніямъ о площадяхъ, указанныхъ нами въ § 299):
1°. Равныя тѣла, т.-е. совмѣщающіяся при вложеніи, имѣютъ равные объемы, независимо отъ ихъ положенія въ пространствѣ.
2°.Объемъ какого-нибудь тѣла (напр., каждаго
параллелепипеда, изображеннаго
щ а г о изъ частей (Ри
Черт. 3/0.
на черт. 370), состоя-0, принимается за сумму объемовъ этихъ частей.
423. Слѣдствія. і°. Объемъ тѣла больше объемакаждой его части (сумма положительныхъ величинъ больше каждаго слагаемаго).
2°. Если какое-нибудь тѣло состоитъ изъ двухъ частей (черт. 370), то объемъ каждой части разсматривается, какъ разность между объемомъ всего тѣла и объемомъ другой
части.
3°. Если тѣла состоятъ изъ одинаковаго числа частей, соотвѣтственно другъ другу равныхъ (напр., два параллелепипеда, изображенные на черт. 370), то объемы этихъ тѣлъ, представляя собою суммы соотвѣтственно равныхъ слагаемыхъ, считаются равными, независимо отъ того, какъ расположены эти части въ пространствѣ.
— 319 —
4. Тѣла, объемы которыхъ можно разсматривать, какъ разности объемовъ равныхъ тѣлъ, имѣютъ одинаковые объемы; мы вскорѣ встрѣтимъ такой случай (428).
Мы видимъ такимъ образомъ, что могутъ быть тѣла, которыя нельзя назвать равными (такъ какъ они ие могутъ быть совмѣщены), но которые одпако имѣютъ равные объемы.
Тѣла, имѣющія равные объемы, мы будемъ называть равновеликими Таковы, напр , 2 параллелепипеда, изображенные на черт. 370-мъ
424. Единица объема. За единицу объемовъ, при измѣреніи ихъ, берутъ объемъ такого куба, у котораго каждое ребро равно линейной единицѣ Такъ, употребительны: куб. аршинъ, куб. метръ и т. д.
Отношеніе двухъ кубическихъ единицъ
разныхъ названій равно 3-ей степени отношенія тѣхъ линейныхъ единицъ, которыя служатъ ребрами для этихъ кубическихъ единицъ. Такъ, отношеніе куб. сажени къ куб. аршину равно З3, т.-е. 27-и,что ясно видно изъ черт. 371, на которомъ меньшій изъ двухъ
кубовъ изображаетъ куб. аршинъ, а бблыпій—куб. сажень.
425. Замѣчаніе. Относительно числа, измѣряющаго данный объемъ въ кубическихъ единицахъ, также можно сдѣлать разъясненіе, аналогичное тому, какое было нами приведено въ § 303 относительно числа, измѣряющаго данную площадь въ квадратныхъ единицахъ. Повторимъ вкратцѣ зто разъясненіе въ примѣненіи къ объемамъ.
Возьмемъ три взаимно перпендикулярныя прямыя (черт. 372): О А, ОВ и ОС и черезъ каждыя двѣ изъ нихъ проведемъ плоскость. Мы получимъ тогда 3 взаимно перпендикулярныя плоскости: АОС, СОВ и ВО А. Вообразимъ теперь 3 ряда параллельныхъ плоскостей: рядъ плоскостей, параллельныхъ пл. АОС, другой рядъ плоскостей, параллельныхъ пл. ВОА, и третій рядъ плоскостей, параллельныхъ плоскости ВОС- допустимъ, кромѣ того, что сосѣднія плоскости каждаго
— 320 —
Черт. 372.
ряда отстоятъ одна отъ другой на одно и то же разстояніе, равное какой-нибудь */* долѣ линейной единицы. Тогда отъ взаимнаго пересѣченія этихъ трехъ рядовъ плоскостей образуется пространственная сѣть кубовъ, изъ которыхъ каждый /1 V
представляетъ собоюII часть куб. еди-
ницы. Вообразимъ, что въ эту сѣть мы помѣстили то тѣло, объемъ котораго желаемъ измѣрить. Тогда всѣ кубы сѣти мы можемъ подраздѣлить на 3 рода: 1) кубы, которые расположены вполнѣ внутри тѣла, 2) кубы, которые нѣкоторою частью выступаютъ внѣ тѣла (которые, другими словами, пересѣкаются поверхностью тѣла), и 3) кубы, расположенные вполнѣ внѣ тѣла. Если кубовъ 1-го рода будетъ т, а 2-го рода п, то объемъ даннаго тѣла болѣе
т
т + «
но менѣе куб. ед. Значитъ, эти 2 числа будутъ приближенныя
мѣры даннаго объема съ точностью до^з куб. ед., первое число съ недостаткомъ, второе—съ избыткомъ. Уменьшая все болѣе и болѣе разстояніе между параллельными плоскостями, мы будемъ заполнять пространство все меньшими и меньшими кубами; и такъ же, какъ это мы раньше дѣлали для площадей, можно и здѣсь разъяснить, что по мѣрѣ уменьшенія кубовъ мы будемъ получать приближенные результаты измѣренія все съ ббльшею и ббльшею степенью точности; и если будетъ найдено такое число V (соизмѣримое или несоизмѣримое), которое окажется больше любого приближеннаго результата измѣренія, взятаго съ недостаткомъ, и меньше любого приближеннаго результата измѣренія, взятаго съ избыткомъ, то это число принимается за точную мѣру даннаго объема.
Доказано, что такое число существуетъ вообще для всякаго объема и что оно не зависитъ отъ выбора тѣхъ трехъ прямыхъ О А, ОВ и ОС (черт. 372), которыя были взяты для построенія пространственной сѣти кубовъ ♦). Число это обладаетъ слѣдующими двумя основными свойствами: при одной и той же кубической единицѣ 1) равнымъ тѣламъ (совмѣщающимся) соотвѣтствуютъ равныя числа, 2) суммѣ объемовъ (422, 2°) соотвѣтствуетъ сумма чиселъ. Отсюда уже слѣдуетъ, что ббльшему объему соотвѣтствуетъ ббльшее число, равновеликимъ тѣламъ соотвѣтствуютъ равныя числа, и т. п.
•)
<1ев
См. Н. К і 1 1 і п & ипй Ноѵезіай ѣ—Н а п й Ь и с Ь МаІЬѳтаѣізсЬѳп Опіеггісііів, I, 1910.
— 321 —
Объемъ прямоугольнаго параллелепипеда.
426. Теорема. Объемъ прямоугольнаго параллелепипеда равенъ произведенію трехъ его измѣреній.
Въ такомъ краткомъ выраженіи теорему эту надо понимать такъ: число, выражающее объемъ прямоугольнаго параллелепипеда въ кубической единицѣ, равно произведенію чиселъ, выражающихъ три его измѣренія въ соотвѣтствующей линейной единицѣ, т.-е. въ той едигицѣ, которая служитъ ребромъ куба, объемъ котораго принятъ за кубическую единицу. Такъ, если х есть число, выражающее объемъ прямоугольнаго параллелепипеда въ кубическихъ сантиметрахъ, и а, Ь и с числа, выражающія три его измѣренія въ линейныхъ сантиметрахъ, то теорема утверждаетъ, что х—аЬс.
При доказательствѣ разсмотримъ особо слѣдующіе три случая:
1°. Всѣ три измѣренія выражаются цѣлыми числами.
Пусть, напр., измѣренія будутъ (черт. 373): АВ=а, ВС=*Ъ
и ВБ=с, гдѣ а, Ъ и с какія-нибудь цѣлыя числа (напр., какъ
изображено у насъ на чертежѣ: а=4, Ь=2 и с=б).
Тогда основаніе параллелепипеда содержитъ аЪ такихъ квадратовъ, изъ которыхъ каждый представляетъ собою соотвѣтствующую квадратную единицу. На каждомъ изъ этихъ квадратовъ, очевидно, можно помѣстить по одной кубической единицѣ. Тогда получится слой (изображенный на чертежѣ), состоящій изъ аЪ куб. единицъ. Такъ какъ высота этого слоя равна 1 линейной единицѣ, а высота всего па
раллелепипеда содержитъ с такихъ единицъ, то внутри паралле-
А. Киселевъ. Геометрія.
21
— 322 —
лепипеда можно помѣстить с такихъ слоевъ. Слѣд., объемъ его равенъ аЪс куб. ед.
2°. Измѣренія (всѣ или нѣкоторыя) выражаются дробными числами.
Пусть измѣренія параллелепипеда будутъ:
т р г п д' 8
(причемъ нѣкоторыя изъ этихъ дробей могутъ равняться цѣлому числу).
Приведя дроби къ одинаковому знаменателю, будемъ имѣть: тдз рпз гпд
пдз пдз пдз
1
Примемъ долю линейной единицы за новую ^вспомога-тельную) единицу длины. Тогда въ этой новой единицѣ данныя измѣренія выразятся цѣлыми числами, а именно: тдз, рпз и гпд, и потому, по доказанному въ случаѣ 1°, объемъ параллелепипеда равенъ произведенію
(тдз) (рпз) (гпд), если измѣрять этотъ объемъ новой кубической единицей, соотвѣтствующей повой линейной единицѣ. Такихъ кубическихъ единицъ въ одной кубической единицѣ, соотвѣтствующей прежней линейной единицѣ, содержится (пдз)3-, значитъ, новая куби-
1
ческая единица составляетъ^^ прежней. Поэтому объемъ пар-да равенъ:
1 тдз рпз гпд
7--^ (?™) (т3)=~-- —• —=
іііибі • іьоо гіио ііио
т р г пдз
3°. Измѣренія (всѣ или нѣкоторыя) выражаются несоизмѣримыми числами.
Пусть у даннаго пар-да (черт. 374), который для краткости мы обозначимъ одною буквою измѣренія будутъ:
ЛВ=я; ЛС=р; ЛВ=у,
- 323 —
гдѣ а, р и у несоизмѣримыя числа (не исключается, впрочемъ, и случай, когда нѣкоторыя изъ этихъ чиселъ соизмѣримыя). Найдемъ приближенныя значенія этихъ чиселъ съ точностью до х/„. Для этого отложимъ 1/„ долю линейной единицы на измѣреніяхъ АВ, АС и АВ, начиная отъ точки А, столько разъ, сколько можно. Пусть окажется, что, отложивъ эту долю на АВ т разъ, мы получимъ отрѣзокъ АВ^АВ, а отложивъ эіу же долю т+1 разъ, получимъ отрѣ-
зокъ АВ2^>АВ. Тогда приближенныя значенія числа а съ точ-т т+1
ностыо до х/„ будутъ дроби — и---, первая съ недостаткомъ,
вторая съ избыткомъ. Пусть такимъ же образомъ окажется, Р р+1
что АСг=—и ЛС2=---------, при чемъ АСі<^АС<ІАС2,
п п
? ?4"1
и АВг= —, ЛП2—----------’ при чемъ АВ^АВ^АВ.^.
п п
Тогда приближенныя значенія будутъ:
т т+1
для числа а. . . .— > -5
п п
о ? Р+1.
для числа В. . . , ----»
г п п
9 «+1
для числа т.. . . —, --•
1 п п
Построимъ теперь 2 вспомогательные параллелепипеда: одинъ (обозначимъ его съ измѣреніями АВ±, АСг и АВ± и другой (обозначимъ, его фа) съ измѣреніями АВ2, АС2 и АВ2. Тогда, по доказанному въ случаѣ 2°, будемъ имѣть:
т р т+1 р+1 д+1
объемъ Оі =— •— — 5 объемъ Ог —-----•-----•----
п п п п п п
21*
— 324 —
Пусть число, выражающее искомый объемъ будетъ х.
Такъ какъ, очевидно, составляетъ часть ф, а ф составляетъ часть ф2, то:
об. Сі<об. $<об. фа;
т р д ?п+1 р+1 ^+1
слѣд., и —•— •— \ х <С------•----•---•
п п п п п п
Это двойное неравенство остается вѣрнымъ при всякой степени точности, съ которою мы находимъ приближенныя значенія чиселъ а, р и у. Значитъ, неравенство это мы можемъ высказать такъ: число, измѣряющее объемъ даннаго параллелепипеда, должно быть больше произведенія любыхъ приближенныхъ значеній чиселъ а, р п у, если эти значенія взяты съ недостаткомъ, но меньше произведенія любыхъ приближенныхъ значеній тѣхъ же чиселъ, если эти значенія взяты съ избыткомъ. Такое число, какъ извѣстно изъ алгебры, наз. произведеніемъ несоизмѣримыхъ чиселъ ару. Значитъ, и въ этомъ случаѣ объемъ ф=ару.
427. Слѣдствія. 1°. Пусть измѣренія прямоугольнаго параллелепппеда, служащія сторонами его основанія, выражаются числами а и Ь, а третье измѣреніе (высота)—числомъ с. Тогда, обозначая объемъ его въ соотвѣтствующихъ куб. единицахъ буквою V, можемъ написать:
Г’=аЬс=(аЬ)с.
Такъ какъ произведеніе аЬ выражаетъ площадь основанія, то можно сказать, что объемъ прямоугольнаго параллелепипеда равенъ произведенію площади основанія на высоту.
2°. Пусть а,Ь,с будутъ измѣренія одного прямоугольнаго парал-да, имѣющаго объемъ V, и —измѣренія другого
парал-да, котораго объемъ есть Ѵг. Тогда:
Ѵ=аЪс; Г’1=а1Ь1с1;
слѣд.: V : Ѵ!=(аЬс) : (аіЬіСі).
Отсюда видно, что если с=сх, то V : ^=(01») : (а^), а если аЬ=а1Ь1, то V : Р’1=с : сх; т.-е.:
— 326 —
объемы прямоугольныхъ параллелепипедовъ, имѣющихъ равныя высоты, относятся, налъ площади ихъ основаній;
объемы прямоугольныхъ параллелепипедовъ, имѣющихъ равныя площади основаній, относятся, какъ ихъ высоты.
3°. Объемъ куба равенъ 3-ей степени его ребра, такъ какъ при а=Ь=с произведеніе аЬс обращается въ а*.
Объемъ всякаго параллелепипеда.
428 Лемма. Наклонная призма равновелика такой прямой призмѣ, у которой основаніе равно перпендикулярному сѣченію наклонной призмы, а высота—ея боковому ребру.
Пусть дана наклонная призма АВСВЕ АуВ^іВ^ (черт. 375). Продолжимъ всѣ ея боковыя ребра и боковыя грани въ одномъ
направленіи, напр., внизъ. Возьмемъ на продолженіи одного какого-нибудь ребра произвольную точку а и проведемъ черезъ пее перпендикулярное сѣченіе аЪссІе. Зачѣмъ, отложивъ ааі=АА1, проведемъ черезъ аг перпендикулярное сѣченіе Такъ какъ плоско-
сти обоихъ сѣченій параллельны, то ЪЬГ= сСі= сИі= сеѵ= аах = ААг (377). Вслѣдствіе этого многогранникъ ахгі, у котораго за основанія приняты проведенныя нами сѣчепія, есть прямая призма, о которой говорится въ теоремѣ. Докажемъ, что даппая наклонная призма равновелика этой прямой. Для этого предварительно убѣдимся, что многогранники аВ и равны. Основанія ихъ аЪссІе и равны,
какъ основанія призмы ахй; съ другой стороны, приложивъ къ обѣимъ частямъ равенства АіА^а^ по одной и той же
прямой Ага, получимъ: аЛ=а1Л1; подобно этому:
сС^с^Сі и т. д. Вообразимъ теперь, что многогранникъ аВ
— 326 -
вложенъ въ такъ, чтобы основанія ихъ совпали; тогда
боковыя ребра, будучи перпендикулярны къ основаніямъ и соотвѣтственно равны, также совпадутъ; поэтому многогранникъ аВ совмѣстится съ с^В^, значитъ, эти тѣла равны.Теперь замѣтимъ, что если отъ цѣлаго многогранника ОіВ отнимемъ часть аВ, то получимъ прямую призму; а если отъ того же многогранника отнимемъ часть аіВг, то получимъ наклонную призму. Изъ этого слѣдуетъ, что эти двѣ призмы равновелики, такъ какъ объемы ихъ представляютъ собою разности объемовъ равныхъ тѣлъ (423,4°).
429. Теорема. Объемъ всякаго параллелепипеда равенъ произведенію площади основанія на высоту.
Ранѣе мы доказали эту теорему для параллелепипеда прямоугольнаго, теперь докажемъ ее для параллелепипеда прямого, а потомъ и наклоннаго.
Черт. 376.
1°. Пусть (черт. 376) АСі—прямое пар-дъ, т.-е. такой у котораго основаніе АВСВ какой-нибудь параллелограммъ, а всѣ боковыя грани — прямоугольники. Возьмемъ въ немъ за основаніе боковую грань АА^В-, тогда параллелепипедъ будетъ наклонный. Разсматривая его, какъ частный случай наклонной призмы, мы, на основаніи леммы
предыдущаго параграфа, можемъ утверждать, что этотъ пар-дъ равновеликъ такому прямому, у котораго основаніе есть перпендикулярное сѣченіе М1УР(д, а высота ВС. Четыреугольникъ А^Рф есть прямоугольникъ, потому что его углы служатъ линейными углами прямыхъ двугранныхъ угловъ; поэтому прямой пар-дъ, имѣющій это основаніе, долженъ быть прямоугольнымъ, и, слѣд., его объемъ равенъ произведенію трехъ его измѣреній, за которыя можно принять отрѣзки АНЯ, АІ$ и ВС. Такимъ образомъ:
Объемъ АСКАРА!. МЦ . ВС=МХ . (АЩ . ВС).
— 327 —
Произведеніе М(^ . ВС выражаетъ площадь параллелограмма
АВСВ1, поэтому:
Объемъ ЛСх=(площ. АВСБ) . іЮ=(плош. АВСВ) . ВВ^
2 . Пусть (черт. 377) АСі есть пар-дъ наклонный. Онъ равновеликъ такому прямому, у котораго основаніемъ служитъ перпен- д дикулярное сѣченіе (т.-е. перпендикулярное къ ребрамъ АВ, ВС...), а высотою ребро ВС. Но, по
Черт. 377.
доказанному, объемъ прямого параллелепипеда равенъ произведенію площади основанія на высоту; значитъ:
Объемъ ЛСх=(площ. МНР О). ВС.
Если В8 есть высота сѣченія то площадь
=Мф. В8; поэтому:
Объемъ . В8 . ВС .=(ВС . МО) . В8.
Произведеніе ВС . М§ выражаетъ площадь параллелограмма АВСВ; слѣд.:
Объемъ ДС1=(площ. АВСВ) . В8.
Остается теперь доказать, что отрѣзокъ В8 представляетъ собою высоту пар-да. Дѣйствительно, сѣченіе М^Р^, будучи перпендикулярно къ ребрамъ ВС, В^..., должно быть перпендикулярно къ гранямъ АВСВ, ВВхСіВ..., проходящимъ черезъ эти ребра (390). Поэтому, если мы изъ точки 5 возставимъ перпендикуляръ къ пл. АВСВ, то опъ долженъ лежать весь въ пл. М^Р^ (391) и, слѣд., долженъ слиться съ прямой 8В, лежащей въ этой плоскости и перпендикулярной къ М(^. Значитъ, отрѣзокъ 8В есть высота пар-да. Такимъ образомъ, объемъ и наклоннаго параллелепипеда равенъ произведенію площади основанія на высоту.
430. Слѣдствіе. Если У, В и Н суть числа, выражающія въ соотвѣтствующихъ единицахъ объемъ, площадь основанія и высоту какого ни на есть параллелепипеда, то можемъ
писать:
ѵ=вн.
— 328 —
Объемъ призмы.
431. Теорема. Объемъ всякой призмы равенъ произведенію площади основанія на высоту.
Сначала докажемъ эту теорему для треугольной призмы, а потомъ и для многоугольной.
]°. Проведемъ (черт. 378) черезъ ребро АА± треугольной призмы АВСАіВіСі плоскость, параллельную грани ВВ^С, а черезъ ребро ССг—плоскость, параллельную грани ААіВіВ\ затѣмъ продолжимъ плоскости обоихъ основаній призмы до пересѣченіпя съ ранѣе проведенными плоскостями. Тогда мы получимъ параллелепипедъ ВВГ, который діагональною плоскостью ААіСіС дѣлится на двѣ треугольныя призмы (изъ пихъ одна есть дапная). Докажемъ, что эти призмы равновелики. Для этого проведемъ перпендикулярное сѣченіе аМ. Въ сѣченіи получится парал-
лелограммъ, который діагональю ас дѣлится на два равные тр-ка. Данная призма равновелика такой прямой призмѣ, у которой основаніе есть Л аЪс, а высота—ребро ААг (428). Другая треугольная призма равновелика такой прямой, у которой основаніе есть Л а^с, а высота—ребро ААХ. Но двѣ прямыя призмы съ равными основаніями и равными высотами равны (потому что при вложеніи онѣ совмѣщаются); значитъ призмы АВСАіВ^х и АБСАіРіСг равновелики. Изъ этого слѣдуетъ, что объемъ дайной призмы составляетъ половину объема параллелепипеда ВВі, поэтому, обозначая высоту черезъ Н, получимъ (429):
(площ. АВСВ)Н Об. тр. призмы =------------=
3
площ. АВСВ =------о-----' П=(площ. АВС)Н.
— 329 —
2°. Проведемъ черезъ ребро ЛЛХ многоугольной призмы (черт. 379) діагональныя плоскости АА^С н АА^В. Тогда данная призма разсѣчется на нѣсколько треугольныхъ призмъ. Сумма объемовъ этихъ призмъ составляетъ искомый объемъ. Если обозначимъ площади ихъ основаній черезъ Ьх, Ь2, Ь3, а общую высоту черезъ Н, то получимъ:
Объемъ мн. призмы =Ъ1Н+Ъ2Н+Ъ3Н=(Ъ1+Ъ2+Ъ3')Н= =(площ. АВСВЕ)Н.
432. Слѣдствіе. Если V, В и Н будутъ числа, выражающія въ соотвѣтственныхъ единицахъ объемъ, площадь основанія и высоту призмы, то, по доказанному, можемъ писать: Ѵ=ВН.
Объемъ пирамиды.
433. Лемма. Треугольныя пирамиды съ равновеликими основаніями и равными высотами равновелики.
Черт. 380.
Пусть 5АВС и 8ХЛХВХСХ (черт. 380) будутъ треугольныя пирамиды, у которыхъ высоты одинаковы и основанія—равновеликіе тр-ки АВС и АіВіСг.
— 330 —
Раздѣлимъ (черт. 380) высоту каждой изъ этихъ пирамидъ на произвольное число п равныхъ частей и черезъ точки дѣленія проведемъ рядъ плоскостей, параллельныхъ основанію (на чертежѣ высота, а слѣд., и боковыя ребра, раздѣлены на 4 равныя части). Такъ какъ, по условію, основанія АВС и А^В-іС^ равновелики, то тр-ки, получившіеся въ сѣченіяхъ одной пирамиды, соотвѣтственно равновелики тр-камъ, получившимся въ сѣченіи другой пирамиды (417). Построимъ въ каждой пирамидѣ рядъ внутреннихъ призмъ такихъ, чтобы верхними основаніями у нпхъ были треугольники сѣченій, боковыя ребра были параллельными ребру 8А въ одной пирамидѣ и ребру 5х.4і въ другой, а высота каждой призмы равнялась бы 1/п высоты пирамиды. Такихъ призмъ въ каждой пирамидѣ будетъ п—1. Объемы призмъ пирамиды 5 обозначимъ по порядку, начиная отъ вершины, черезъ Рі,Р2,Рз---Ги—1> а объемы призмъ пирамиды 5Х, также по порядку отъ вершины, черезъ ді,Э2,9з,--9»-і-Тогда:
Рі=9і» Рг=9г, Рз—9з Рп—і~9п—1> потому что у каждой пары соотвѣтственныхъ призмъ основанія равновелики и высоты равны. Поэтому:
Рі +Рг +Рз+• • • і—9і+9г+9з+• • • 9п—і •
Предположимъ теперь, что число п равныхъ частей, на которыя мы дѣлимъ высоту пирамидъ, неограниченно возрастаетъ. Тогда обѣ части послѣдняго равенства сдѣтаются величинами перемѣнными. Докажемъ, что каждая изъ нихъ стремится въ предѣлѣ къ объему той пирамиды, въ которую призмы вписаны. Это достаточно доказать для какой-нибудь одной пирамиды, напр., для 8. Для этого построимъ въ ней еще рядъ призмъ, выходящихъ частью изъ пирамиды, такихъ, чтобы нижними основаніями ихъ служили треугольники сѣченій (и основаніе пирамиды), высоты были бы равны, попрежнему, 1/„ высоты пирамиды, а боковыя ребра параллельны тому же ребру 8А. Такихъ призмъ будетъ п. Обозначимъ ихъ объемы, начиная оть
— 331
вершины пирамиды, по порядку, черезъ р/, ра', р3',...р'п_і, р„ Не трудно видѣть, что
Р1'=Р1> Р/=Рз- Рз'=Рз.... Р'»-1=Р»-1-
Поэтому:
(Р1 +РзГ + • • • +р п-1 +Рі/)—(рі +Рз +Рз + • • • +Ри—1) —р'п-
Если объемъ пирамиды обозначимъ V, то очевидно:
Р1 +Р2* +Рз* + • • +Рм>Г>Р1 +Р2 + • • +Р»-1 •
Откуда: V— (Рі+р2+-..+р„-і)<р'я-
При неограниченномъ увеличеніи числа п объемъ призмы р„' стремится къ нулю (потому что высота ея стремится къ нулю, а основаніе не измѣняется); слѣд., разность V—(рх +р2+• • +Р«—і) и подавно стремится къ нулю; а это, по опредѣленію предѣла, означаетъ, что
7=пред. (Рі+ра+...+р^_і).
Такъ какъ это доказательство можно примѣнить ко всякой треугольной пирамидѣ, то можно утверждать, что Ѵц т.-е. объемъ пирамиды есть предѣлъ перемѣнной суммы ді+д2+-••+?«_____і-
Но если двѣ перемѣнныя величины, имѣющія предѣлы, всегда остаются равными, то равны и ихъ предѣлы (281); поэтому:
Ѵ=Ѵг *).
*) Проводя аналогію между площадями и объемами, можно было бы подумать, что равновеликость двухъ пирамидъ, о которыхъ говорится въ теоремѣ, можетъ быть сведена на равновеликость «по разложенію» (423, 3°), т.-е. что можно такія пирамиды разложить на одинаковое число частей, соотвѣтственно другъ другу равныхъ (конгруентныхъ). Однако, это не такъ. Въ 1900 году нѣмецкій математикъ Денъ (Оеііп) впервые строго доказалъ (его очень сложное доказательство было затѣмъ упрощено русскимъ математикомъ В. Каганом ъ), что двѣ пирамиды съ равновеликими основаніями и равными высотами вообще не могутъ быть разложены на конечное число соотвѣтственно конгруентныхъ частей. Болѣе того, доказано, что равновеликость такихъ пирамидъ не можетъ быть сведена даже и на равновеликость «по дополненію > (опредѣляемую въ § 423, 4°). Такимъ образомъ, способъ предѣловъ (какимъ мы пользовались въ текстѣ) есть единственный методъ доказательства равновеликости пирамидъ и вообще многогранниковъ.
— 332 —
434. Теорема. Объемъ всякой пирамиды равенъ произведенію площади основанія на треть высоты.
Сначала докажемъ эту теорему для пирамиды треугольной, а затѣмъ и мпогоугольпой.
1°. На основаніи треугольной пирамиды 8АВС (черт. 381) построимъ такую призму АВС БЕ 8, у которой высота равна высотѣ пирамиды, а одно боковое ребро совпадаетъ съ ребромъ 8В. Докажемъ, что объемъ пирамиды составляетъ третью часть объема этой призмы. Отдѣлимъ отъ призмы данную пирамиду. Тогда останется четыреугольная пирамида 8АБЕС (которая для ясности изображена отдѣльно). Проведемъ въ ней сѣкущую плоскость черезъ вершину 5 и діагональ основанія БС. Получившіяся отъ этого двѣ треугольныя ппрамиды имѣютъ общую вершину 5 н равныя основанія БЕС и БАС, лежащія въ одной плоскости; значитъ, согласно доказанной выше леммѣ, пирамиды 8БЕС и 8БАС равновелики. Сравнимъ одну изъ нихъ, именно 8БЕС, съ данной пирамидой. За основаніе пирамиды 8БЕС можно взять Д 8БЕ‘ тогда вершина ея будетъ въ точкѣ С, и высота равна высотѣ данной пирамиды. Такъ какъ А 8БЕ*= =ДАВС, то, согласно той же леммѣ, пирамиды С8БЕ и 8АВС
— 333 —
равновелики. Такимъ образомъ, сумма объемовъ трехъ пирамидъ, равновеликихъ данной, составляетъ объемъ призмы; слѣд :
1 (площ. АВС). Н Н
Об. 8АВС=—об.8ВЕАВС=----------------==(площ. АВС)~,
3 3 3
гдѣ Н означаетъ высоту пирамиды.
2°. Черезъ какуіо-ппбудь вершину Е (черт. 382) основанія многоугольной пирамиды 8АВСВЕ проведемъ діагонали ЕВ и ЕС. Затѣмъ черезъ ребро 8Е и каждую изъ этихъ діагоналей проведемъ сѣкущія плоскости. Тогда многоугольная пирамида разобьется на нѣсколько треугольныхъ, имѣющихъ высоту, общую съ данной пирамидой. Обозначивъ площади основаній треугольныхъ пирамидъ черезъ Ь2, Ъ3 и высоту черезъ Н, будемъ имѣть:
1 1 1
Объемъ 8АВСВЕ=-Ъ1Н+~Ь2Н+-Ъ3Н=
н и
<Ь1+Ь2+Ь3)—=(площ. АВСВЕ)г—.
3 3
435. Слѣдствіе. Если V, В и Н означаютъ числа, выражающія въ соотвѣтственныхъ единицахъ объемъ, площадь основанія и высоту какой угодно пирамиды, то
ѵ=~вн.
3
Объемъ усѣченной пирамиды и усѣченной призмы.
436. Теорема. Объемъ усѣченной пирамиды равенъ суммѣ объемовъ трехъ пирамидъ, имѣющихъ высоту, одинаковую съ высотою усѣченной пирамиды, а основаніями: одна—-нижнее основаніе усѣченной пирамиды, другая—верхнее основаніе этой пирамиды, а третья—среднее пропорціональное между ними.
— 334 —
Сначала докажемъ эту теорему для треугольной пира
миды, а потомъ и многоугольной.
1°. Пусть (черт. 383) АВСВЕР есть усѣченная треугольная пирамида. Отдѣлимъ отъ нея сѣкущею плоскостью АЕС треугольную пирамиду ЕАВС. Эта пирамида, имѣя основаніе АВС и вершину въ Е, удовлетворяетъ требованію теоремы. Оставшаяся часть есть четыреугольная пирамида ЕАВРС. Проведя въ пей сѣкущую плоскость черезъ точки Е, В и С, мы раздѣлимъ ее на двѣ треугольныя пирамиды ЕВРС и ЕАВС. Въ первой можно принять за основаніе Л ВЕР, т.-е. верхнее основаніе
усѣченной пирамиды, а за вершину точку С; слѣд., эта пирамида удовлетворяетъ требованію теоремы. Остается разсмотрѣть третью пирамиду ЕАВС. Превратимъ ее въ другую равновеликую пирамиду слѣдующимъ образомъ. Проведемъ прямую ЕК || ВА и точку К примемъ за вершину новой пирамиды, которой основаніемъ оставимъ тотъ же треугольникъ АВС. Пирамиды ЕАВС и КАВС іавновелики, потому что у нихъ общее основаніе АВС и высоты равны (такъ какъ вершины
лежатъ на прямой ЕК, параллельной АВ и, слѣд., параллельной плоскости основанія). Примемъ за вершину новой пирамиды точку В, а за основаніе Л АСК. Тогда высота ея будетъ равна высотѣ усѣченной пирамиды. Остается доказать, что основаніе АСК есть средняя пропорціональная величина между АВС и ВЕР, т.-е. что
площ. АВС площ. АСК
площ. АСК площ. ВЕР
— 335 —
У тр-ковъ АБС и АСК за основанія можно взять стороны АВ и АК-, тогда вершина у нихъ будетъ общая С, и слѣд., высоты окажутся одинаковы; поэтому:
площ. ЛВС АВ АВ , _
площ. АСК==АК~БЕ
(вмѣсто АК можно взять равный отрѣзокъ БЕ).
Треугольники АСК и БЕР имѣютъ по равному углу при вершинахъ А и Р; поэтому (324):
площ. АСК АС.АК АС
площ. БЕР БР.БЕ~ БР
(отрѣзки АК и БЕ, какъ равные, сокращаются).
Изъ подобія тр-ковъ АВС и БЕР слѣдуетъ, что правыя части равенствъ [1] и [2] равны; слѣд., равны и ихъ лѣвыя части, т.-е.
площ. АВС площ. АСК площ. АСК площ. БЕР
2°. Пусть (черт. 384) АЛ есть усѣченная пирамида, составляющая часть многоугольной пирамиды 8АБСБЕ. Превратимъ мн-къ А БСБЕ въ равновеликій тр-къ Р($В и, принявъ этотъ тр-къ за основаніе, по-
Черт. 384.
строимъ вспомогательную пирамиду
МР(№ съ такой же высо-
тою, какъ у пирамиды 5. Пересѣчемъ пирамиду М плоскостью,
— 336 —
параллельною основанію, на такомъ разстояніи отъ вершины, на какомъ въ пирамидѣ 5 проведена плоскость аЪссІе. Въ сѣченіи получится Л рдг, равновеликій мп-ку аЪссІе (417). Пирамиды 8АВСВЕ и МР(№ равновелики, такъ какъ у нихъ равновелики основанія и высоты равны; по той же причинѣ пирамиды ВаЬссІе и Мрдг тоже равновелики; отсюда слѣдуетъ, что усѣч. многоугольная пирамида Асі равновелика усѣч. треугольной пирамидѣ Рг; такъ какъ у этихъ двухъ усѣченныхъ пирамидъ основанія, и нижпее и верхнее, соотвѣтственно равновелики, а высоты равны, то теорема, доказанная для усѣченной треугольной пирамиды, остается примѣнимой и къ многоугольной.
437. Слѣдствіе. Пусть V, В, Ь и Н будутъ числа, выражающія въ соотвѣтствующихъ единицахъ объемъ, площадь нижняго основанія, площадь верхняго основанія и высоту усѣченной пирамиды; тогда:
ѵ=-вн+-ън+ - пѴ1Гь^~н (
3 3 3 3 \
в+ь+Ѵвь),
гдѣ VВЬ есть средняя пропорціональная величина между В и Ь.
438. Теорема. Объемъ треугольной призмы, усѣченной непараллельно основанію, равенъ суммѣ объемовъ трехъ пирамидъ, имѣющихъ общее основаніе съ усѣченной призмой, а вер* шины въ трехъ вершинахъ непа-Г раллельнаго сѣченія.
Пусть (черт. 385) АВСВЕР есть усѣченная треугольная призма, т.-е. такая, у которой плоскость ВЕР не параллель-н а основанію АВС. Проведя сѣкущую плоскость черезъ точки Е, А и С, мы отдѣлимъ одну изъ трехъ пирамидъ, указанныхъ въ С теоремѣ, именно пирамиду ЕАВС, имѣющую общее основаніе АВС съ усѣченной призмой и вершину Черт. 385. въ точкѣ Е. Проведемъ еще сѣ-
кущую плоскость черезъ точки Е.
— 337 —
О и С; тогда получимъ двѣ другія пирамиды: ЕВАС и ЕВЕС. Теорема будетъ доказана, если мы обнаружимъ, что эти пирамиды равновелики такимъ, у которыхъ основаніемъ служитъ Л АБС, а вершины лежатъ: одной въ В, другой въ Е. Дѣйствительно, пирамиды ЕВАС и ВАБС равновелики, потому что за основаніе ихъ можно взять общій тр-къ ВАС, и тогда вершины Е и В будутъ лежать на прямой ВЕ, параллельной плоскости основаній; пирамиды ЕВЕС и ЕАВС равновелики, потому что за основанія ихъ можно принять равновеликіе тр-ки: для первой СЕВ, для второй АЕС (311,1°), и тогда ихъ вершины Е и В будутъ лежать на прямой ВЕ, параллельной плоскости основаній.
439. Слѣдствіе. Пусть V, В, Лх, к2, к3 будутъ числа, выражающія въ соотвѣтствующихъ единицахъ объемъ, площадь основанія и высоты, опущенныя на основаніе изъ трехъ вершинъ непараллельнаго сѣченія; тогда:
111 Л.і4“/і24“^з
вк1+— Вк^-Вк^В- 8 -• ООО о
Когда призма прямая, высоты /іх, к2 и ка равны боковымъ ребрамъ ея.
ГЛАВА IV.
Подобіе многогранниковъ.
440. Опредѣленіе. Два многогранника наз. подобными, если они имѣютъ соотвѣтственно равные многогранные углы и соотвѣтственно подобныя грани. Соотвѣтственные элементы подобныхъ многогранниковъ наз. сходственными.
Изъ этого опредѣленія слѣдуетъ, что въ подобныхъ многогранникахъ:
1°. Двугранные углы соотвѣтственно равны и одинаково расположены, потому что многогранные углы равны.
2°. Сходственныя ребра пропорціональны, потому что въ каждыхъ двухъ подобныхъ граняхъ отношеніе сходственныхъ реберъ одно и то же, и въ каждомъ многогранникѣ сосѣднія грани имѣютъ по общему ребру.
Возможность существованія подобныхъ многогранниковъ доказывается слѣдующей теоремой.
А. Киселевъ. Геометрія. 22
338
441. Теорема. Если въ пирамидѣ (черт. 386) проведемъ сѣкущую плоскость
(АіВіСгПіЕі) параллельно основанію, то отсѣчемъ отъ нея другую пирамиду
(ВАіВіСіВіЕі), подобную
8
Черт. 386.
данной.
Такъ какъ АІВ11| АВ, ВХСХ || ВС и т. д. (373), то боковыя грани двухъ пирамидъ подобны; основанія ихъ также подобны (414). Остается доказать равенство многогранныхъ угловъ. Уголъ 8 у обѣихъ пирамидъ общій; трегранные углы Лх, В1г Сі... равны соотвѣтственно угламъ А, В, С..., потому что у каждой пары этихъ угловъ плоскіе углы соотвѣтственно равны и одинаково расположены (402, 3°).
442. Теорема. Двѣ призмы или двѣ пирамиды подобны, если основаніе и боковая грань одной и основаніе и боковая грань другой соотвѣтственно подобны, одинаково наклонены и одинаково расположены.
1°. Пусть у двухъ призмъ (черт. 387) соотвѣтственно подобны и оди-
Черт. 387.
наково расположены основанія АВСВЕ, аЪсЛе и грани ЛЛ1В1В, аа^Ъ (на чертежѣ онѣ покрыты штрихами) и, кромѣ того, равны двугранные углы АВ и аЪ. Для доказательства подобія этихъ призмъ, разсуждаемъ въ такой послѣдовательности. Трехгран-ные углы В и Ъ равны, потому что они имѣютъ по равному двугранному углу (ЛВ и аЬ), заключенному между двумя соотвѣт
ственно равными и одинаково расположенными плоскими углами (АЕС = аЪс и ЛВВх = а6Ьг); отсюда слѣдуетъ, что равны плоскіе углы ВгВС и ЪуЪс, а также и двугранные ВС и Ъс. Если же у двухъ параллелограммовъ ВВ^гС и ЬЬ1с1с имѣется по одному равному углу, то и остальные углы ихъ соотвѣтственно равны; такъ какъ, сверхъ того, ВС АВ
-у7=-^у(изъ подобія основаній)
ВВі АВ
и -уу — (изъ подобія бок. граней), ВС ВВі
то Ъс~ ЪЪі '
Значитъ, грани ВВ1С1С и 6Ь1с1с подобны. Переходя теперь къ треграннымъ угламъ С и с, совершенно такъ же убѣдимся, что они равны и что
— 339 —
8
Черт. 388.
грани и сс^й подобны. Такимъ образомъ, мы переберемъ всѣ
трегранные углы при основаніи и всѣ боковыя грани. Верхнія основанія А1В1С1О1Е1 и подобны, потому что они равны нижнимъ
основаніямъ; трегранные углы при верхнихъ основаніяхъ соотвѣтственно равны, потому что у нихъ равны и одинаково расположены плоскіе углы. Значитъ, разсматриваемыя призмы подобны.
2°. Пусть мы имѣемъ (черт. 388) двѣ пирамиды, у которыхъ соотвѣтственно подобны и одинаково расположены основанія АВСВЕ, аЪсЛе и боковыя грани 8АВ, ваЪ (на чертежѣ онѣ покрыты штрихами) и, кромѣ того, равны двугранные углы АВ и аЪ. Совершенно такъ, какъ это было сдѣлано для призмъ, мы докажемъ, что всѣ трегранные углы, прилежащіе къ основаніямъ, соотвѣтственно равны, и что всѣ
Тогда многогранные углы 8 и также будутъ равны, потому что, имѣя всѣ плоскіе и двугранные углы соотвѣтственно равные и одинаково расположенные, они при вложеніи одного въ другой совмѣщаются.
боковыя грани соотвѣтственно
443. Теорема. Подобные многогранники могутъ быть разложены на одинаковое число соотвѣтственно подобныхъ и одинаково расположенныхъ пирамидъ (черт. 389).
С
Черт. 389.
Указанное въ теоремѣ разложеніе можетъ быть выполнено различными способами. Мы поступимъ слѣдующимъ образомъ:
22*
— 340 —
Возьмемъ въ одномъ изъ данныхъ подобныхъ многогранниковъ вершину А какого-нибудь многограннаго угла. Возьмемъ далѣе всѣ тѣ грани многогранника, которыя не прилежатъ къ углу А. Въ нашемъ многогранникѣ такихъ граней четыре: ЕВКЕ, ВСНК, СВСН и ФОНКЪ. Каждую изъ этихъ граней примемъ за основаніе такой пирамиды, которой вершина лежала бы въ А. Тогда многогранникъ разобьется на пирамиды, сходящіяся вершинами въ точкѣ А. Въ другомъ многогранникѣ возьмемъ сходственную вершину 4, и тѣмъ же путемъ разложимъ его на одинаковое число пирамидъ. Докажемъ, что эти пирамиды соотвѣтственно подобны. И дѣйствительно, какую бы пару соотвѣтственныхъ пирамидъ мы ни взяли, легко найдемъ, что основаніе и грань одной пирамиды и основаніе и грань другой пирамиды соотвѣтственно подобны, одинаково наклонены и одинаково расположены. Напр., у пирамидъ АВЕЕК, А1В1Е1Е1К1 основанія ВЕЕК и В^Е^Е^К^ подобны, какъ сходственныя грани подобныхъ многогранниковъ, грани АВЕ и А1В1Е1 подобны, потому что подобные многоугольники АВСВЕ, А1В1С1В1Е1 разбиваются на соотвѣтственно подобные тр-ки; двугранные углы ВЕ, В1Е1 равны, какъ сходственные углы подобныхъ многогранниковъ. Изъ этого слѣдуетъ, что взятыя нами пирамиды подобны. То же самое можно сказать о другихъ пирамидахъ.
444. Теорема. Поверхности подобныхъ многогранниковъ относятся, какъ квадраты сходственныхъ реберъ.
Пусть Р1г Рг, Р3...Рп означаютъ площади отдѣльныхъ граней одного изъ подобныхъ многогранниковъ, а рх, р2, Рз---, рп площади сходственныхъ граней другого; положимъ еще, что Е и I будутъ длины двухъ какихъ-нибудь сходственныхъ реберъ. Тогда, вслѣдствіе подобія сходственныхъ граней и пропорціональности всѣхъ сходственныхъ реберъ, будемъ имѣть (326):
_Рі=Ь^.
Р1 I2 ’ Рз І3 ’ Рз Р рп * I3'
_ЕЪ
445. Теорема. Объемы подобныхъ многогранниковъ относятся, какъ кубы сходственныхъ реберъ.
1°. Сначала докажемъ теорему для подобныхъ пирамидъ. Пусть (черт. 390) пирамиды 8АВСВЕ и 81А1В1С1В1Е1 подобны. Вложимъ вторую пирамиду въ первую такъ, чтобы у нихъ совпали равные многогранные углы 8 и 5Х. Тогда основаніе
— 341 —
А1В1С1В1Е1 займетъ нѣкоторое положеніе аЪсЛе, причемъ стороны аЛ, Ъс,... соотвѣтственно параллельны сторонамъ АВ, ВС,... (вслѣдствіе равенства плоскихъ угловъ трегранныхъ А и Аг, В и Вг и т. д.); вслѣдствіе этого плоскость аЪсЛе параллельна АВСВЕ (372,2°). Пусть 80 и 8о—высоты двухъ пирамидъ. Тогда:
06. 8АВСВЕ = (плоці. АВСВЕ). »/, 80.
Слѣд. 06. 8аЪсйе—(площ. аЪсйе). */з 06. 8АВСВЕ_плаці. АВСВЕ 80
06. ЬаЬссІе площ. аЬс<іе 8о
Но площ. АВСВЕ 80* (414,3°)
площ. аЬсйе 8о3
Поэтому об. 8АВСВЕ_ 80* 8А3 (414,1°)
об. ВаЬсЛе 8о3 8а3~"’
2°. Теперь докажемъ теорему для двухъ какихъ угодно подобныхъ многогранниковъ, объемы которыхъ назовемъ V и ѵ. Разобьемъ ихъ на подобныя пирамиды (448). Пусть Ѵ1г Ѵг, Ѵ8... Ѵп и ѵ3, ѵа, ѵ3..лп будутъ объемы сходственныхъ пирамидъ, В и { длины какихъ-нибудь сходственныхъ реберъ. Тогда, согласно доказанному, будемъ имѣть:
12*—_3
I?! Р' Ѵ8 I3’ Іп I3
Откуда: Уі + ^г + --. + ^п_Ь3
Ѵі + ѵ3 + --.+ іп— I3’
т.-е. V В3
г= I3
446. Замѣчаніе. Въ стереометріи можно разсматривать ф и-гуры, подобно расположенныя, въ томъ же смыслѣ, какой былъ нами указанъ въ планиметріи (211 и слѣд.), причемъ и здѣсь, какъ и тамъ, подобіе въ расположеніи можетъ быть двоякое: прямое и обратное.
Не входя въ подробности этого разсмотрѣнія, замѣтимъ только слѣдующее важное различіе между подобіемъ въ расположеніи на плоскости и подобіемъ въ расположеніи въ пространствѣ 3-хъ измѣреній. Па плоскости, какъ мы видѣли (215), многоугольники, подобно расположенные, прямо или обратно, оказываются всегда подобными между собою; въ стереометріи же только при прямомъ подобіи въ расположеніи многогранники подобны между собою, при обратномъ же подобіи въ расположеніи многогранники вообще не подобны (примѣромъ могутъ служить симметричные многогранные углы, о которыхъ говорилось въ § 403).
ГЛАВА V.
Симметричныя фигуры.
447. Опредѣленія. Различаютъ три рода симметріи: относительно точки, относительно прямой и относительно плоскости.
— 342 —
Какъ мы уже говорили ранѣе (41), двѣ точки А и Аг (черт. 391) иаз. симметричными относительно точки О (центра симметрі и), если прямая ААг проходитъ черезъ точку О и дѣлится ею пополамъ.
Черт. 391. Черт. 392. Черт. 393.
Двѣ точки А и Аі (черт. 392) наз. симметричными относительно прямой ху (о с и симметріи) или (черт. 392) относительно плоскости Р (плоскости симметріи), если прямая ААг перпендикулярна къ ху или къ плоскости Р и дѣлится ими пополамъ.
Двѣ фигуры наз. симметричными относительно центра (черт. 394), оси (черт. 395), или плоскости (черт. 396), если каждой точкѣ одной
8
Черт. 394. Черт. 395. Черт. 396.
фигуры соотвѣтствуетъ симметричная точка другой. Симметричныя точки двухъ такихъ фигуръ наз. сходственными.
Легко видѣть, что двѣ фигуры, симметричныя относительно оси, равны. Въ этомъ убѣдимся, если по
— 343 —
вернемъ одну изъ фигуръ (черт. 395) вокругъ оси на 180°. Тогда
каждая точка А одной фигуры совпадетъ съ сходственной точкой Аг другой фигуры, и, слѣд., обѣ фигуры совмѣстятся.
448. Теорема. Фигуры, симметричныя съ одной и той же фигурой отно-
сительно различныхъ центровъ, равны между собою.
Д о к. Пусть фигуры Рі и Ри симметричны съ одной фигурой Р относительно центровъ О и 0г (черт. 397). Возьмемъ въ фигурѣ Р произвольную точку А и въ фигурахъ Рг и Р2 точки Аг и Аи, симметричныя съ А; затѣмъ проведемъ прямыя 001 и А1А11. Такъ какъ АО = Ах0 и АО1 = АІ1О1, то АМпІІ ООхи А1А11=2ОО1.
Такимъ образомъ, всѣ соотвѣтственныя точки фигуръ Рх и Р1Г (напр.,
Аг и 4П, и Вп, Сх и Сг1 и т. д.) лежатъ на разстояніяхъ, параллельныхъ прямой ОО1 и равныхъ 2ООХ. Поэтому, если перемѣстимъ фи
гуру Рг такъ, чтобы каждая ея точка описывала прямую, параллельную ООі и равную удвоенной этой линіи, то обѣ фигуры Рг и совмѣ
стятся; значитъ, онѣ равны.
449. Теорема. Если фигуры Р и Рг (черт. 398) симметричны относительно плоскости Р, то ихъ можно помѣстить такъ, что онѣ будутъ симметричны отно-
сительно любой точки О, взятой на этой плоскости; обратно, если фигуры Р и Ри симметричны относительно точки О, то ихъ можно помѣстить такъ, что онѣ будутъ симметричны относительно любой плоскости Р, проходящей черезъ эту точку О.
Д о к. Если фигуры Р и Рг симметричны относительно плоскости-Р, то прямая АА1} соединяющая какія-нибудь двѣ сходственныя
точки, перпендикулярна къ плоскости Р и дѣлится ею пополамъ; значитъ: 4а = Л1а. Если фигуры Р и Р1г симметричны относительно точки О, то прямая ААп, соединяющая двѣ сходственныя точки, про
— 344 —
ходитъ черезъ О и дѣлится этою точкою пополамъ; значитъ: АО=А11О. Замѣтивъ это, соединимъ Ах съ Ап и проведемъ ОМ перпендикулярно къ Р. Такъ какъ АО = АцО и Аа = А±а, то А14и||яО; слѣд., г'А11А1А=ХОаА = (1. Такъ какъ ОМ_]_Р и ААг_]_Р, то ОМ^АА^, изъ этого слѣдуетъ, что, во 1°, ОМ пересѣкается съ въ нѣкоторой точкѣ Ь, во 2°, Л А11ЪО=^_ А11А1А = Л, въ 3°, А1Ъ = А11Ъ (такъ какъ АцО = ОА). Если мы теперь повернемъ фигуры и Рг1 вокругъ оси ОМ на 180°, то точки Аг и Аи, а слѣд., и всѣ другія сходственныя точки, помѣняются мѣстами; значитъ, фигура Р± можетъ быть сдѣлана симметричною съ Р относительно точки О, а фигура Ргі можетъ быть сдѣлана симметричною съ Р относительно плоскости Р, что и требовалось доказать.
450. Слѣдствія. 1°. Фигуры, симметричныя съ одной и той же фигурой относительно различныхъ плоскостей, равны между собою, потому что эти фигуры всегда можно сдѣлать симметричными съ одной и той же фигурой относительно различныхъ центровъ, а такія фигуры, какъ мы видѣли (448), равны между собою.
2°. Если будемъ обращать вниманіе только на форму фигуры, а не на ея положеніе въ пространствѣ, то можемъ сказать, что данная фигура Р имѣетъ только единственную симметричную съ нею фигуру (относительно точки, или относительно плоскости, все равно), такъ какъ всѣ фигуры, симметричныя съ Р, равны между собою. Вслѣдствіе этого, при изслѣдованіи свойствъ симметричныхъ фигуръ, зависящихъ только отъ ихъ формы, мы можемъ по произволу разсматривать эти фигуры или какъ симметричныя относительно центра, или какъ симметричныя относительно плоскости.
451. Теоремы, выражающія свойства симметричныхъ фигуръ.
1°. Фигура, симметричная съ плоской фигурой, есть также плоская фигура, равная первой.
Это свойство сдѣлается очевиднымъ, если возьмемъ за плоскость симметріи плоскость данной фигуры; тогда симметричная фигура
сливается съ данной.
Въ частности, фигура, симметричная съ отрѣзкомъ прямой, есть равный отрѣзокъ прямой; фигура, симметричная съ угломъ, есть равный уголъ; фигура, симметричная съ плоскимъ многоугольникомъ, есть равный плоскій многоугольникъ; фигура, симметричная съ кругомъ, есть равный кругъ, и. т. п.
2°. Фигура, симметричная съ двуграннымъ угломъ (РАВ$, черт. 399), есть равный двугранный уголъ.
Это свойство сдѣлается очевиднымъ, если за плоскость симметріи возьмемъ биссектриссную плоскость В. Тогда фигура, симметричная съ гранью Р, будетъ другая грань и наоборотъ; слѣд., фи-
гура, симметричная съ угломъ РАВЦ, будетъ уголъ ЦАВР.
— 345 —
3°. Фигура, симметричная съ многограннымъ угломъ (8 А ВС БЕ, черт. 400),
есть многогранный уголъ, у котораго двугранные и плоскіе углы соотвѣтственно
равны двуграннымъ и плоскимъ угламъ перваго многограннаго угла, но расположены въ обратномъ порядкѣ.
Это свойство сдѣлается очевиднымъ, если возьмемъ за центръ симметріи вершину 8. Тогда получимъ два симметричные угла 8 АВС БЕ и 8А1В1С1В1Е1, у которыхъ двугранные и плоскіе углы соотвѣтственно равны, но расположены въ обратномъ порядкѣ (403).
Слѣдствіе. Симметричные многогранные углы вообще не равны, такъ какъ, вслѣдствіе обратнаго расположенія равныхъ двугранныхъ угловъ, они не могутъ совмѣститься. По той же причинѣ симметричные многогранники вообще не равны.
Черт. 400.
4°. Два симметричные многогранника равновелики.
Докажемъ сначала эту теорему для симметричныхъ пирамидъ (черт. 401) 8АВСБ и 8гАВСВ, которыя мы размѣстимъ такъ, чтобы плоскостью симметріи служило основаніе АВСИ. Такъ какъ точки 8 и симметричны относительно плоскости основанія, то высоты 80 и 8іР равны; вслѣдствіе этого пирамиды, имѣя общее основаніе и равныя высоты, равновелики.
Два какіе угодно симметричные многогранника всегда могутъ быть разложены на одинаковое число симметричныхъ пирамидъ; поэтому теорема вѣрна и для многогранниковъ произвольной формы.
Черт. 401.
ГЛАВА VI.
Понятіе о правильныхъ многогранникахъ.
452. Опредѣленіе. Многогранникъ наз. правильнымъ, если всѣ его грани суть равные правильные многоугольники и всѣ многогранные углы равны (таковъ, напр., кубъ).
Изъ этого опредѣленія слѣдуетъ,что въ правильныхъ многогранникахъ равны всѣ плоскіе углы, всѣ двугранные углы и всѣ ребра.
— 346 —
453. Какіе правильные многоугольники могутъ служить гранями правильныхъ многогранниковъ? Чтобы рѣшить этотъ вопросъ, примемъ во вниманіе, что въ многогранномъ углѣ наименьшее число граней три и что сумма всѣхъ плоскихъ угловъ выпуклаго мн-ка меньше 44 (398). Каждый уголъ правильнаго треугольника равенъ 2/34. Если повторимъ 2/34 слагаемымъ 3 раза, 4 раза и 5 разъ, то получимъ суммы, меньшія 44; а если повторимъ 2/34 слагаемымъ 6 разъ или болѣе, то получимъ въ суммѣ 44 или болѣе. Поэтому изъ плоскихъ угловъ, равныхъ угламъ правильнаго тр-ка, можно образовать выпуклые многогранные углы только трехъ видовъ: трегранные, четырегранные и пятигранные. Уголъ квадрата равенъ 4, а уголъ правильнаго пятиугольника равенъ в/64; повторяя эти углы слагаемымъ 3 раза, получаемъ суммы, меньшія 44, а повторяя ихъ 4 раза или болѣе, получаемъ 44 или болѣе. Поэтому изъ плоскихъ угловъ, равныхъ угламъ квадрата или правильнаго пятиугольника, можно образовать только трегранные углы. Уголъ правильнаго шестиугольника равенъ 1/34; поэтому изъ такихъ угловъ нельзя образовать даже треграннаго угла. Изъ угловъ правильныхъ многоугольниковъ, имѣющихъ болѣе 6-ти сторонъ, подавно, нельзя образовать никакого многограннаго угла.
454. Перечисленіе правильныхъ многогранниковъ. Изъ сказаннаго въ предыдущемъ параграфѣ слѣ-
Черт. 402. Черт. 403. Черт. 404.
дуетъ, что выпуклыхъ правильныхъ многогранниковъ не можетъ быть болѣе слѣдующихъ пяти *):
*) Ихъ не можетъ быть болѣе пяти, но существуютъ ли этИ пять, это предыдущими разсужденіями, конечно, не доказывается; мы опускаемъ это доказательство по причинѣ его сложности.
— 347 —
1°. Правильный четырегранникъ (или тетраэдръ), котораго поверхность составлена изъ 4-хъ правильныхъ тр-ковъ (черт. 402).
Черт. 405.
2°. Правильный восьмигранникъ (или октаэдръ), котораго поверхность составлена изъ 8-ми правильныхъ тр-ковъ (черт. 403).
3°. Правильный двадцатигранникъ (или икосаэдръ), образованный 20-ю правильными тр-ками (черт. 404).
4°. Правильный шестигранникъ (или экса-эдръ), образованный 6-ю квадратами (черт. 405). Онъ наз. иначе кубомъ.
5°. Правильный двѣнадцатигранникъ (или додекаэдръ), образованный 12-ю правильными пятиугольниками (черт. 406).
ЗАДАЧИ.
335, а. Ребро даннаго куба равно а. Найти ребро другого куба, котораго объемъ вдвое болѣе объема даннаго куба.
3 а м ѣ ч а н і е. Эта задача объ удвоеніи куба, извѣстная съ древнихъ временъ, легко рѣшается вычисленіемъ (именно: _______ з____
«=у 2а3 = йу 2 = я1,25992..), но построеніемъ (помощью циркуля и линейки) она рѣшена быть не можетъ, такъ какъ формула для неизвѣстнаго содержитъ радикалъ 3-й степени (см. конецъ § 225).
335. Вычислить поверхность и объемъ прямой призмы, у которой основаніе правильный тр-къ, вписанный въ кругъ радіуса г=2 метрамъ, а высота равна сторонѣ правильнаго 6-угольника, описаннаго около того же круга.
336. Опредѣлить поверхность и объемъ правильной 8-угольной призмы, у которой высота Л=6арш., а сторона основанія а =8 вершкамъ
— 348 —
337. Опредѣлить боковую поверхность и объемъ правильной шести* угольной пирамиды, у которой высота равна 1 метру, а апоѳема составляетъ съ высотою уголъ въ 30°.
338. Вычислить объемъ треугольной пирамиды, у которой каждое боковое ребро равно I, а стороны основанія суть а, Ь и с.
339. Данъ трегранный уголъ 8АВС, у котораго всѣ три плоскіе угла прямые. На его ребрахъ отложены длины: 8А = а, 8В = Ъ и 8С = с. Черезъ точки А, В и С проведена плоскость. Опредѣлить объемъ пирамиды 8АВС.
340. Высота пирамиды равна Л, а основаніе—правильный шестиугольникъ со стороною а. На какомъ разстояніи х отъ вершины пирамиды слѣдуетъ провести плоскость, параллельную основанію, чтобы объемъ образовавшейся усѣченной пирамиды равнялся V?
341. Опредѣлить объемъ правильнаго тетраэдра съ ребромъ а.
342. Опредѣлить объемъ правильнаго октаэдра съ ребромъ а.
343. Усѣченная пирамида, которой объемъ Ѵ = 1465 куб. сантим., имѣетъ основаніями правильные шестиугольники со сторонами: а=23 сант. и 6 = 17 сант. Вычислить высоту, этой пирамиды.
344. Объемъ V усѣченной пирамиды равенъ 10,5 куб. метра, высота 6=1^3 метр. и сторона а правильнаго шестиугольника, служащаго нижнимъ основаніемъ, равна 2 метр. Вычислить сторону правильнаго шестиугольника, служащаго верхнимъ основаніемъ.
345. Вычислить объемъ треугольной усѣченной призмы, у которой стороны основанія суть: а=7,5, 6=7 и с=6,5 и ребра, перпендикулярныя къ основанію, суть: к=2, і=3 и т=4.
346. На какомъ разстояніи отъ вершины 8 пирамиды 8АВС надо провести плоскость, параллельную основанію, чтобы отношеніе объемовъ частей, на которыя разсѣкается этою плоскостью пирамида, равнялось т?
347. Вычислить объемъ усѣченнаго параллелепипеда, у котораго основаніе есть В, а и суть длины перпендикуляровъ, опущенныхъ на плоскость нижняго основанія изъ двухъ вершинъ, лежащихъ на концахъ какой-нибудь діагонали верхняго основанія *).
348. Пирамида съ высотою Л раздѣлена плоскостями, паралелль-ными основанію, на три части въ отношеніи т : п : р. Опредѣлить разстоянія этихъ плоскостей до вершины пирамиды.
349. Сумма объемовъ двухъ подобныхъ многогранниковъ равна V, а отношеніе сходственныхъ реберъ равно т : п. Опредѣлить объемы ихъ.
350. Раздѣлить объемъ усѣченной пирамиды плоскостью, параллельною основаніямъ В и Ъ, на двѣ части въ отношеніи т : п.
*) Легко установить, что сумма А1+А8 равна суммѣ двухъ другихъ перпендикуляровъ, опущенныхъ на плоскость нижняго основанія изъ вершинъ, лежащихъ на концахъ другой діагонали верхняго основанія.
— 349 —
КНИГА III.
КРУГЛЫЯ ТЪЛА.
ГЛАВА I.
Цилиндръ и конусъ.
455. Поверхность вращенія. Поверхностью
вращенія наз. такая поверхность, которая получается отъ
вращенія какой-нибудь неизмѣняющейся линіи (МП, черт. 407), называемой образующей, вокругъ неподвижной прямой (АВ), называемой осью; при этомъ предполагается, что образующая (М1Х), при своемъ вращеніи, неизмѣнно связана съ осью (ЛВ).
Возьмемъ на образующей какую-нибудь точку Р и опустимъ изъ нея на ось перпендикуляръ РО. Очевидно, что при вращеніи не измѣняется ни длина этого перпен
дикуляра, ни величина угла АОР,
ни положеніе точки О. Поэтому каждая точка образующей
описываетъ окружность, которой плоскость перпендикулярна къ оси и центръ лежитъ на пересѣченіи этой плоскости съ осью. Отсюда слѣдуетъ, что плоскость, перпендикулярная къ оси, пересѣкаясь съ поверхностью вращенія, даетъ въ сѣченіи окружность.
Всякая сѣкущая плоскость, проходящая черезъ ось, наз. м е р и д і а-н а л ь н о ю плоскостью, а пересѣченіе ея съ поверхностью вращенія—м ери-д і а н о м ъ. Всѣ меридіаны равны между собою, потому что при вращеніи каждый изъ нихъ проходитъ черезъ
— 350 —
то положеніе, въ которомъ ранѣе былъ всякій другой меридіанъ.
456. Цилиндрическая поверхность. Цилиндрическою поверхностью наз. поверхность, производимая движеніемъ прямой (АВ, черт. 408); перемѣщающейся въ пространствѣ параллельно данному направленію и пересѣкающей при этомъ данную линію (М1Х). Прямая АВ наз. образующею, а линія ЛГУ направляющею.
в 457. Цилиндръ. Тѣло, ограниченное цилиндрическою поверхностью и двумя параллельными плоскостями, наз. цилиндромъ (черт. 409). Часть цилиндрической поверхности, заключенная
между плоскостями, паз. боковою поверхностью цилиндра, а части плоскостей, отсѣкаемыя этою поверхностью,—о снованіями цилиндра. Разстояніе между основаніями есть высота Черт. 409. цилиндра. Цилиндръ наз. прямымъ или наклоннымъ, смотря по тому, перпендикулярны или наклонны къ основаніямъ его образующія
параллельн
Прямой цилиндръ (черт. 410) наз круговымъ, если его основанія круги. Такой цилиндръ можно разсматривать, какъ тѣло вращенія, а именно, происходящее отъ вращенія прямоугольника САА^ вокругъ стороны 00], какъ оси; при этомъ сторона ААг описываетъ боковую поверхность, а стороны О А и ОхЛ]—-круги основаній. Всякая прямая ВС, параллельная РА, описываетъ также кругъ, перпендикулярный къ оси. Отсюда слѣдуетъ,что сѣченіе прямого кругового цилиндра плоскостью, ою основаніямъ, есть кругъ.
Въ элементарной геометріи разсматривается только прямой круговой цилиндръ; для краткости его называютъ просто цилиндромъ.
351
Иногда приходится разсматривать такія призмы, которыхъ основанія суть многоугольники, вписанные въ основанія цилиндра или описанпые около нихъ; такія призмы наз. вписанными въ цилиндръ или описанными около него.
458. Коническая поверхность. Коническою
поверхностью наз. поверхность, производимая движе
ніемъ прямой (АВ, черт. 411), перемѣщающейся въ простран
ствѣ такъ, что она при этомъ постоянно проходитъ черезъ не
подвижную точку (6) и пересѣкаетъ данную линію (іШ.
Прямая АВ наз. образующею, линія МЫ—п а п р а -
вляющею, а точка 5—в е р-шиною конической поверхности.
459. Конусъ. Тѣло, ограниченное коническою поверхностью и плоскостью, пересѣкающею всѣ образующія по одну сторону отъ вершины, наз. конусомъ (черт. 412). Часть конической поверхности, ограниченная этою плоскостью, наз. боковою поверхностью, а часть плоскости, отсѣкаемая боковою поверх
ностью,—о снованіемъ конуса. Перпендикуляръ, опущенный изъ вершины на основаніе, есть высота конуса.
Конусъ наз. прямымъ круговымъ, если его основаніе есть кругъ, а высота проходитъ черезъ центръ основанія (черт. 413). Такой конусъ можно разсматривать, какъ тѣло, происходящее отъ вращенія прямоугольнаго тр-ка 80Л вокругъ катета 80, какъ оси. При этомъ гипотенуза производитъ боковую поверхность, а катетъ О А—основаніе конуса. Всякая прямая ВОГ, параллельная АО, описываетъ при вращеніи кругъ, перпендикулярный къ оси. Отсюда слѣдуетъ, что сѣченіе пря-
— 352 —
Оі-
Черт. 413.
м о г о кругового конуса плоскостью, параллельною основанію, есть кругъ.
Въ элементарной геометріи разсматривается только прямой круговой конусъ, который для краткости наз. просто конусомъ.
Иногда приходится разсматривать такія пирамиды, которыхъ основанія суть многоугольники, вписанные въ основаніе конуса, или описанные около него, а А веріпипа совпадаетъ съ вершиною конуса. Такія пирамиды наз. вписанными въ конусъ пли описанными около него.
460. Усѣченный конусъ. Усѣченнымъ ко-
нусомъ (черт. 414) наз. часть полнаго конуса, заключенная между основаніемъ и сѣкущею плоскостью, параллельною основанію. Параллельные круги, ограничивающіе усѣченный конусъ, наз. основаніями его. Усѣченный конусъ можно разсматривать, какъ тѣло, происходящее отъ вращенія прямоугольной трапеціи ОАА^ вокругъ стороны 00и перпендикулярной къ основаніямъ трапеціи.
Поверхность цилиндра и конуса.
461. Опредѣленія. Боковыя поверхности цилиндра и конуса принадлежатъ къ поверхностямъ кривымъ, т.-е. къ такимъ, которыхъ никакая часть не можетъ совмѣститься съ плоскостью. Поэтому мы должны особо опредѣлить, что надо разумѣть подъ величиною боковой поверхности цилиндра или конуса, когда сравниваютъ эти поверхности съ плоскою единицею площади. Мы будемъ держаться слѣдующихъ опредѣленій.
— 353 —
1°. За величину боковой поверхности цилиндра принимаютъ предѣлъ, къ которому стремится боковая поверхность вписанной въ этотъ цилиндръ призмы, когда ея боковыя грани неограниченно уменьшаются (и, слѣд., число граней неограниченно увеличивается).
2°. За величину боковой поверхности конуса (полнаго или усѣченнаго) принимается предѣлъ, къ которому стремится боковая поверхность вписанной въ этотъ конусъ пирамиды (полной или усѣченной), когда ея боковыя грани неограниченно уменьшаются (и, слѣд., число граней неограниченно увеличивается)*).
462. Теорема. Боковая поверхность цилиндра равна произведенію окружности основанія на высоту.
Впишемъ въ пилпндръ (черт. 415) какую-нибудь призму. Обозначимъ буквами р и Н числа, выражающія въ соотвѣтствующихъ единицахъ периметръ основанія и высоту этой призмы. Тогда боко- Г Е вая поверхность ея выразится произведе- Д^і ніемъ рН. Предположимъ теперь, что боко- ।
выя грани вписанной призмы (слѣд., и і I
стороны вписаннаго многоугольника, слу- [ !
жащаго основаніемъ этой призмы) неогра- I ;
ниченно уменьшаются. Тогда периметръ р |
будетъ стремиться къ предѣлу, прини- у маемому за длину С окружности осно- д<^ ванія, а высота Н останется безъ измѣне- । нія; слѣд., боковая поверхность призмы, * равная всегда произведенію рН, будетъ стремиться къ предѣлу СН. Этотъ предѣлъ и принимается за величину боковой поверхности цилиндра. Обозначивъ ее буквой 5, можемъ написать:
8=СІІ.
463. Слѣдствія. і°. Если В означаетъ радіусъ основанія цилиндра, то С=2кВ; поэтому боковая поверхность цилиндра выразится:
8=2ъВН.
*) Въ теоріи предѣловъ доказывается, что эти предѣлы суціе* ствуютъ и что они не зависятъ отъ закона, по которому боковыя грани уменьшаются.
А. Киселевъ. Геометрія.
23
— 364 —
2°. Чтобы получить полную поверхность цилиндра, достаточно приложить къ боковой поверхности сумму площадей двухъ основаній; поэтому, обозначая пол-8 ную поверхность черезъ Т, будемъ имѣть:
АТ=2тсВН-ЬтсВ2+'гсВ2=27гВ(Н-ЬВ).
464. Теорема. Боковая поверхность конуса равна произведенію окружности основанія на половину образующей.
Для простоты доказательства впишемъ 0 въ конусъ (черт. 416) не какую-нибудь пирамиду, а правильную, и обозначимъ т 416 буквами р и I числа, выражающія въ соотвѣтствующихъ единицахъ периметръ основанія и апоѳему этой пирамиды. Тогда боковая поверхность ея выразится произведеніемъ г/2 рі. Предположимъ теперь, что боковыя грани вписанной пирамиды (слѣд., и стороны вписаннаго многоугольника служащаго основаніемъ этой пирамиды) неограниченно уменьшаются. Тогда периметръ р будетъ стремиться къ предѣлу, принимаемому за длину С окружности основанія, а апоѳема I будетъ имѣть предѣломъ образующую конуса (такъ какъ изъ тр-ка 8АК слѣдуетъ, что —8К<АК)-, значитъ, если образующую конуса обозначимъ буквою Ь, то боковая поверхность вписанной пирамиды, постоянно равная 1/2рІ, будетъ стремиться къ предѣлу Этотъ предѣлъ и принимается за величину боковой поверхности конуса. Обозначивъ ее буквою 8, можемъ написать:
1 1 8=-СЬ = С.-Е.
465. Слѣдствія. 1°. Такъ какъ С—2кЛ, то боковая поверхность конуса выразится:
1 5=—. 2тсВП=тсВП.
2°. Полную поверхность конуса получимъ, если къ боковой поверхности приложимъ площадь основанія; поэтому:
Т =тг ЛЬ +кП2 =тс Н(П+В).
— 355 —
466. Теорема. Боковая поверхность усѣченнаго конуса равна произведенію полусуммы окружностей основаній на обра-
зующую.
Для простоты доказательства впишемъ въ усѣченный конусъ (черт. 417) не какую-пибудь усѣченную пирамиду, а правильную, и обозначимъ буквами р, Рі и I числа, выражающія периметръ нижняго, периметръ верхняго основаній и апоѳему этой пирамиды. Тогда боковая поверхность ея выразится произведеніемъ
1
~г(.р+Рі)1-а
Черт. 417.
При неограниченномъ уменьшеніи боковыхъ граней вписанной пирамиды периметры р и рг стремятся къ предѣламъ, принимаемымъ за длины С п Сг окружностей основаній, а апоѳема I, какъ не трудно видѣть, имѣетъ предѣломъ образующую Ь усѣченнаго конуса. Слѣд., боковая поверхность вписанной пирамиды стремится къ предѣлу, равному 1/2(С+С1)Ь. Этотъ предѣлъ и принимается за величину боковой поверхности усѣченнаго конуса. Обозначивъ ее буквой 5, будемъ имѣть:
„ 1
(С+СУЬ.
а
467. Слѣдствія. і°. Если В и Вг означаютъ радіусы окружностей нижняго и верхняго основаній, то боковая поверхность усѣченнаго конуса выразится:
8=± (ЯкВ+Ш^В^В+ВДЪ. а
2°. Проведемъ въ трапеціи ОО^А (черт. 417), отъ вращенія которой получается усѣченный конусъ, среднюю линію ВС (117). Тогда получимъ:
ВС=| (ОА +ОМ а 4
Откуда: В-\-Вл=2ВС.
Слѣд., 5=2тсВС.П,
— 366 —
т.-е. боковая поверхность усѣченнаго конуса равна произведенію окружности средняго сѣченія на образующую.
3°. Полная поверхность Т усѣченнаго конуса выразится такъ:
Т=тс(В2+В12+ВЫ-В1П).
468. Замѣчаніе. Въ предыдущихъ теоремахъ боковыя поверхности цилиндра и конуса разсматривались, какъ предѣлы боковыхъ поверхностей вписанныхъ призмъ или пирамидъ. Если бы, подобно тому, какъ мы это дѣлали при доказательствѣ этихъ теоремъ, мы стали находить предѣлы описанныхъ призмъ или пирамидъ, то нашли бы, что эти предѣлы тѣ же самые, какъ и для вписанныхъ призмъ или пирамидъ. Вслѣдствіе этого боковыя поверхности цилиндра и конуса можно разсматривать, какъ общій предѣлъ боковыхъ поверхностей призмъ или пирамидъ, какъ вписанныхъ, такъ и описанныхъ.
469- Развертка цилиндра И конуса. Впишемъ въ цилиндръ (черт. 418) какую-нибудь призму и затѣмъ вообразимъ, что боковая ея поверхность разрѣзана вдоль какого-нибудь бокового ребра. Очевидно, что, вращая ея грани вокругъ реберъ, мы можемъ развернуть эту поверхность въ одну плоскость, безъ разрыва и безъ складокъ. Тогда получится то, что наз. разверткою боковой поверхности призмы. Она представляетъ собою прямоугольникъ КЬМіі, составленный изъ столькихъ прямоугольниковъ, сколько въ призмѣ боковыхъ граней. Основаніе его равно периметру основанія призмы, а высота КК есть высота призмы.
Черт. 418.
Вообразимъ теперь, что боковыя грани вписанной призмы неограниченно уменьшаются; тогда ея развертка будетъ все удлиняться, приближаясь къ предѣльному прямоугольнику КРфЛ’, у кото
— 367 —
раго основаніе равно длинѣ окружности основанія цилиндра, а высота есть высота цилиндра. Этотъ прямоугольникъ наз. разверткою боковой поверхности цилиндра.
Подобно этому вообразимъ, что въ конусъ вписана какая-нибудь пирамида (черт. 419). Мы можемъ разрѣзать ея боковую поверхность
Черт. 419.
по одному изъ реберъ, и затѣмъ, повертывая грани вокругъ реберъ, получить ея развертку въ видѣ многоугольнаго сектора 8КЬ, составленнаго изъ столькихъ равнобедренныхъ тр-ковъ, сколько въ пирамидѣ боковыхъ граней. Прямыя 8К, 8а, 8Ь... равны боковому ребру пирамиды (или образующей конуса), а длина ломаной КаЪ.,.Ь равна периметру основанія пирамиды. При неограниченномъ уменьшеніи боковыхъ граней вписанной пирамиды развертка ея увеличивается, приближаясь къ предѣльному сектору 8КМ, у котораго дуга КМ равна окружности основанія, а радіусъ 8К—образующей конуса. Этотъ секторъ наз. разверткою боковой поверхности конуса.
Подобно этому можно получить развертку боковой поверхности усѣченнаго конуса (черт. 419) въ видѣ части кругового кольца КМ^Р.
Легко видѣть что боковая поверхность цилиндра или конуса равна площади соотвѣтствующей развертки.
Объемы цилиндра и конуса.
470. Лемма. 1. Объемъ цилиндра есть общій предѣлъ объемовъ правильныхъ вписанныхъ и описанныхъ призмъ при неограниченномъ удвоеніи числа ихъ боковыхъ граней.
Впишемъ въ цилиндръ и опишемъ около него по какой-нибудь правильной одноименной призмѣ. Обозначимъ объемъ, площадь основанія и высоту соотвѣтственно: для цилиндра—V, В, Н. для вписанной призмы—Вг, Н и для описанной призмы— Ѵ2, В2, Н. Тогда будемъ имѣть (431):
72=В2Н; Ѵ^ВуН.
Откуда: Ѵ2—Ѵг=(В2—Вг)Н.
— 368 —
При неограниченномъ удвоеніи числа боковыхъ граней призмъ разность В2—Вг стремится къ нулю (330), а множитель Н есть число постоянное; поэтому правая часть послѣдняго равенства, а слѣд., и его лѣвая часть, стремится къ нулю. Объемъ цилиндра, очевидно, больше объема вписанной призмы, но меньше объема описанной; поэтому каждая изъ разностей V—и Ѵ2—V меньше разности Ѵ2—Ѵі, но послѣдняя, по доказанному, стремится къ нулю; слѣд., и первыя стремятся къ нулю; а это, по опредѣленію предѣла, означаетъ, что
7=п р е д. 7і=п р е д. Ѵ2.
471. Лемма. 2. Объемъ конуса полнаго и усѣченнаго есть общій предѣлъ объемовъ правильныхъ вписанныхъ и описанныхъ пирамидъ при неограниченномъ удвоеніи числа ихъ боковыхъ граней.
1°. Впишемъ въ конусъ и опишемъ около него по какой-нибудь правильной одноименной пирамидѣ. Употребляя тѣ же обозначенія, какъ и въ предыдущемъ параграфѣ, будемъ имѣть (434):
О о
„ „ 1
Откуда: Ѵ2— Ѵ^-Ц^—В^.
О
Изъ этого равенства такъ же, какъ и въ предыдущей леммѣ, заключаемъ, что разность Ѵ2—Ѵг стремится къ нулю, когда число боковыхъ граней вписанной и описапной пирамиды неограниченно удваивается; а такъ какъ каждая изъ разностей: Ѵ2—V и V—іѴ1 меньше Ѵ2—Ѵъ то эти разности и подавно стремятся къ нулю; а это значитъ, что
Г=пред. Иі=пред. Ѵ2.
2°. Вообразимъ, что усѣченный конусъ дополненъ до полнаго конуса (черт. 420). Впишемъ въ этотъ полный конусъ и опишемъ около него по какой-нибудь правильной одноименной пирамидѣ. Части этихъ пирамидъ, заключенныя между пло
— 369 —
скостями нижняго и верхняго пирамиды, одна—вписанная въ описанная около него. Обозначимъ объемы конуса, пирамиды вписанной и пирамиды описанной соотвѣтственно буквами:
для полныхъ . ... V, Ѵ1} Ѵ2;
для усѣченныхъ . . . ѵ, ѵ1г ѵ2.
Изъ чертежа непосредственно усматриваемъ, что разности объемовъ:
ѵ2—ѵ и ѵ—г?!
основаній, будутъ усѣченныя усѣченный конусъ и другая,
Черт. 420.
составляютъ нѣкоторыя части разностей объемовъ:
Ѵ2—Ѵ и V— 7і;
поэтому первыя разности меньше вторыхъ. Но при неограниченномъ удвоеніи числа боковыхъ грапей пирамидъ каждая изъ разностей: Ѵ2—V и V—Ѵг стремится, какъ мы видѣли, къ нулю; слѣд., каждая изъ меньшихъ разностей ѵ2—ѵ и ѵ— стремится при этомъ и подавно къ нулю. Изъ этого слѣдуетъ, что
пред. ѵ1=пред. ѵ2=ѵ.
Замѣчаніе. Въ доказанныхъ двухъ леммахъ вписанныя и описанныя призмы и пирамиды предполагаются правильными только ради простоты доказательства; содержаніе этихъ леммъ остается въ полной силѣ и тогда, когда призмы и пирамиды будутъ неправильныя, лишь бы боковыя грани ихъ неограниченно уменьшались.
472. Теоремы. 1°. Объемъ цилиндра равенъ произведенію площади основанія на высоту.
2°. Объемъ конуса равенъ произведенію площади основанія на треть высоты.
— 360 —
Впишемъ въ цилиндръ какую-нибудь правильную призму, а въ конусъ какую-нибудь правильную пирамиду; тогда, употребляя прежнія обозначенія, будемъ имѣть:
для призмы .... Р’1=В1Н;
1 для пирамиды .. Р'1=—ВгН.
о
Эти равенства остаются вѣрными, сколько бы мы ни удваивали числа боковыхъ граней призмы и пирамиды; поэтому они останутся вѣрными и тогда, когда на мѣсто перемѣнныхъ подставимъ ихъ предѣлы (283); слѣд.:
для цилиндра .... Ѵ=ВН\
1
для копуса......Ѵ=—ВП.
О
473. Слѣдствіе. Если радіусъ основанія цилиндра или конуса обозначимъ черезъ В, то В=,кВ2; поэтому:
1
06. цил. Ѵ—~В2Н; об. кон. V— ~-ъВ,2Н.
О
474. Теорема. Объемъ усѣченнаго конуса равенъ суммѣ объемовъ трехъ конусовъ, имѣющихъ одинаковую высоту съ усѣченнымъ конусомъ, а основаніями: одинъ—нижнее основаніе этого конуса, другой—верхнее, третій—среднее пропорціональное между ними.
По доказанному раньше, объемъ усѣченнаго конуса есть общій предѣлъ объемовъ правильныхъ вписанныхъ и описанныхъ усѣченныхъ пирамидъ. Но объемъ Ѵг правильной вписанной усѣченной пирамиды, которой высота есть Н, а площади основаній Вх и Ьх, выражается равенствомъ (437):
Илщв^+УВА). о
Въ предѣлѣ, при неограниченномъ удвоеніи числа боковыхъ граней вписанной пирамиды, это равенство даетъ:
7=4н(В + ь+Квёо,
О
гдѣ V есть объемъ, В и Ъ площади основаній и Н высота усѣченнаго конуса.
— 361 —
475. Слѣдствіе. Если В и г означаютъ радіусы нижняго и верхняго основаній усѣченнаго конуса, то В=тсВ2, Ъ=тѵгй и поэтому:
1
Об. ус. конуса Г=—7гН(В2+г2+Вг).
О
476. Замѣчаніе. Объемъ усѣченнаго конуса можно найти и независимо отъ свойствъ предѣловъ слѣдующимъ образомъ. На верхнемъ основаніи усѣченнаго конуса (черт. 421) помѣстимъ такой малый конусъ (съ высотою Л), чтобы усѣченный конусъ превратился въ полный. Тогда объемъ V усѣченнаго конуса можно разсматривать, какъ разность объемовъ полнаго конуса и дополнительнаго. Поэтому:
Ѵ=-|«Я2( Я + Л V ^*г2к = 4 ~ ГК2Н+(К2-г2)к
Изъ
подобія тр-ковъ находимъ:
Я И 4- к Н—г
— !—; откуда:-------
т Л г
Н к ’
слѣд., к =
Слѣд., Ѵ = |кГя2Я + (Я2 — т2)к 1 =-^ к[я2Н+(Я+г)гЯ
Подобные цилиндры и конусы.
477. Опредѣленіе. Два цилиндра или конуса наз. подоб
ными, если они произошли отъ вращенія подобныхъ прямоугольниковъ или треугольниковъ вокругъ сходственныхъ сторонъ.
362 —
Обозначимъ (черт. 422 и 423) черезъ й и Лх высоты двухъ подобныхъ цилиндровъ или конусовъ, черезъ г и гх радіусы ихъ основаній и черезъ I и I] образующія; тогда, согласно опредѣленію, будемъ имѣть:
_г_= Гх Лх І!
Откуда по свойству равныхъ отношеній выводимъ: г + к г г+1 г
= — и .
= — и ---------- —
Ъ+'*1 ГХ 7Х +І! ГХ
478. Теорема. Боковыя и полныя поверхности подобныхъ цилиндровъ или конусовъ относятся, какъ квадраты радіусовъ или высотъ, а объемы—какъ кубы радіусовъ или высотъ.
Обозначимъ черезъ 8, Т и V соотвѣтственно боковую поверхность, полную поверхность и объемъ одного цилиндра или конуса, а черезъ 8Х, Тх и Рх тѣ же величины для другого цилиндра или конуса, подобнаго первому. Тогда будемъ имѣть.
Для цилиндровъ.
8 2-кгк _ тк _ г к к* .
8Х 2^т^ г1к1 гх йх гх2~ Лх2’ Т___ 2пг(г+А) _ г г+к _ г2 _ Л2 .
Т,~ 2г.гх(гх+Лі)_ тх 'тх+Лх- гх2~ А,2’
V к 2Л г2 к_
Ѵх пгх2Лх гх2 кі гх® Лх®
Для конусовъ.
8 _ -кгі _ г _ г _ ^а-\ Ча~ V’
Т _ г.г(т+1) _ г г+1 _ г _ к .
2’1~ "П(’гі + ?х) “ гх ’ тх2 “ Лх2’
V _ Ѵз* 2І» __ г к _ т®_ Л® Ч&т&Г гх2 ' ЬГ гх®~ Л,® -
ГЛАВА II.
Шаръ
Сѣченіе шара плоскостью.
479. Опредѣленіе. Тѣло, происходящее отъ вращенія полукруга вокругъ діаметра, ограничивающаго его, наз. шаромъ, а поверхность, образуемая при этомъ полуокружностью, наз. шаровою или сферическою по
— 363 —
верхностью. Эта поверхность есть геометрическое мѣсто точекъ, одинаково удаленныхъ отъ одной и той же точки, называемой центромъ шара.
Прямая, соединяющая центръ съ какою-нибудь точкою поверхности, наз. радіусомъ, а прямая, соединяющая двѣ точки поверхности и проходящая черезъ центръ, наз. діаметромъ шара. Всѣ радіусы одного шара равны между собою, а діаметръ равенъ двумъ радіусамъ.
Два шара одинаковаго радіуса равны, потому что при вложеніи они совмѣщаются.
480. Теорема. Всякое сѣченіе шара плоскостью есть кругъ.
1°. Предположимъ сначала, что (черт. 424) сѣкупая плоскость АВ проходитъ черезъ центръ О шара. Всѣ точки линіи пересѣченія, при-надлежа шаровой поверхности, одинаково />>—р-^М\
удалены отъ точки О, лежащей въ сѣкущей рР плоскости; слѣд., сѣченіе есть кругъ. у4-— }
2°. Положимъ теперь, что сѣкущая пло- х. ! У скоть СВ не проходитъ черезъ центръ.
Опустимъ на нее пзъ центра перпенди- Черт. 424. куляръ ОК и возьмемъ на линіи пересѣченія какую-нибудь точку М. Соединивъ ее съ О и К, получимъ прямоугольный тр-къ МОК, изъ котораго находимъ:
МК=ѴОМ2—ОК2. [1].
Такъ какъ длины ОМ и ОК не измѣняются при измѣненіи положенія точки М на линіи пересѣченія, то разстояніе МК есть величина постоянная; значитъ, линія пересѣченія есть окружность, которой центръ есть точка К.
481. Слѣдствіе. Пусть В, г и Ц означаютъ: радіусъ шара, радіусъ круга сѣченія и разстояніе сѣкущей плоскости отъ центра; тогда равенство [1] приметъ видъ:
Г=/В2—^2.
Изъ этой формулы выводимъ:
1°. Наибольшій радіусъ сѣченія получается при й=0, т.-е. когда сѣкущая плоскость проходитъ черезъ центръ шара.
— 364 —
Въ этомъ случаѣ г=В. Кругъ, получаемый въ этомъ случаѣ, наз. большимъ кругомъ.
2°. Наименьшій радіусъ сѣченія получается при (1=В. Въ этомъ случаѣ т=0, т.-е. кругъ сѣченія обращается въ точку.
3°. Сѣченія, равноотстоящія отъ центра шара, равны.
4°. Изъ двухъ сѣченій, не одинаково удаленныхъ отъ центра шара, то больше, которое ближе къ центру.
Свойства большихъ круговъ.
482. Теорема. Всякій большой кругъ дѣлитъ шаръ и его
поверхность пополамъ.
Вообразимъ, что мы разрѣзали шаръ (черт. 425) по какому-нибудь большому кругу и, перевернувъ верхнюю часть шара, вложили ее въ нижнюю такъ, чтобы у нихъ совпали круглыя основанія. Тогда всѣ точки одной части шаровой поверхности совмѣстятся съ точками другой части, потому что тѣ и другія одинаково удалены отъ общаго центра. Изъ этого слѣдуетъ, что большой кругъ дѣ-
Черт 425. литъ шаръ и его поверхность пополамъ.
483. Теорема. Черезъ всякія двѣ точки шаровой поверхности, не лежащія на концахъ одного діаметра, можно провести
только одну окружность большого круга.
Пусть на шаровой поверхности (черт. 426), имѣющей
центръ О, взяты какія-нибудь двѣ точки, напр., С и 27, не лежащія на одной прямой съ точкой О. Тогда черезъ точки С, О и 27 можно провести плоскость. Эта плоскость, проходя черезъ центръ О, дастъ въ пересѣченіи съ шаровою поверхностью окружность большого круга.
Другой окружности большого круга черезъ тѣ же двѣ точки С и провести
нельзя. Дѣйствительно, всякая окружность большого круга
— 366 —
должна, по опредѣленію, лежать въ плоскости, проходящей черезъ центръ О шара; слѣд., если бы черезъ С и можно было провести еще другую окружность большого круга, то тогда выходило бы, что черезъ 3 точки С^иО, не лежащія на одной прямой, можно провести 2 различныя плоскости, что невозможно.
Замѣчаніе. Всякія двѣ точки шаровой поверхности могутъ быть соединены двумя дугами большого круга, составляющими въ суммѣ окружность большого круга (такъ, точки С и черт. 426, соединяются дугою С^ и дугою СМБ^ и сумма этихъ дугъ составляетъ окружность большого круга).
Если взятыя двѣ точки не лежатъ на концахъ одного діаметра, то одна изъ этихъ дугъ меньше полуокружности, а другая больше.
484. Теорема. Окружности двухъ большихъ круговъ пересѣкаются пополамъ.
Дѣйствительно, центръ О (черт. 426), находясь на плоскостяхъ обоихъ большихъ круговъ, долженъ лежать на прямой МЫ, по которой эти круги пересѣкаются; значитъ, прямая МК есть діаметръ того и другого круга, а діаметръ дѣлитъ
окружность пополамъ.
485. Теорема. Кратчайшее разстояніе на шаровой поверхности между двумя ея точками есть дуга большого круга (меньшая полуокружности), прове
денная между ними.
Пусть т (черт. 427) есть дуга большого круга, проведенная на шаровой поверхности между двумя ея точками А и В, а « какая-нибудь линія, проведенная на шаровой поверхности между тѣми же точками. Докажемъ, что з длиннѣе иі. Возьмемъ на кривой з произвольную точку гі и соединимъ ее съ А и В дугами большого круга. Проведя радіусы ОА, Ой и ОВ, примемъ ихъ за ребра треграннаго угла. Въ этомъ углѣ, какъ во всякомъ трегранномъ (397), сумма плоскихъ угловъ АОй и йОВ больше
третьяго плоскаго угла АОВ. Но эти углы измѣряются дугами Ай, йВ и АВ, проведенными изъ вершины угловъ однимъ и тѣмъ же радіусомъ; слѣд., сумма дугъ Ай и йВ больше дуги АВ. Возьмемъ теперь на кривой 8 промежуточныя точки е и / и проведемъ дуги большого
— 366 —
круга черезъ каждыя двѣ сосѣднія точки: А, е, Л, / и В (дуги эти на чертежѣ не указаны). Такъ же, какъ и прежде, убѣдимся, что Ае + еИ> Ай и гі/+/В>йВ; значитъ, сумма 4е + ей + й/+/В больше АЛ+ЛВ, а потому подавно больше дуги т. Вообразимъ теперь, что число промежуточныхъ точекъ, взятыхъ на кривой 8, неограниченно увеличивается, и между каждыми двумя сосѣдними точками постоянно проводятся дуги большихъ круговъ; тогда линія, составленная изъ этихъ дугъ, все увеличивается, и постоянно остается больше дуги т; значитъ, и предѣлъ*), къ которому она стремится, долженъ быть больше т; а этотъ предѣлъ принимается ва длину дуги з.
Плоскость, касательная къ шару.
486. Опредѣленіе. Плоскость, имѣющая съ шаровою поверхностью только одну общую точку, наз. касательною плоскостью.
Возможность существованія такой плоскости доказывается слѣдующей теоремой.
Теорема. Плоскость (Р, черт. 428), перпендикулярная къ радіусу (ОЛ) въ концѣ его, лежащемъ на поверхности шара, есть касательная.
Черт. 428.
Возьмемъ на плоскости Р произвольную точку В и соединимъ ее съ центромъ О. Такъ какъ ОВ наклонная, а ОА перпендикуляръ къ Р, то ОВ>ОА. Поэтому точка В не можетъ лежать на шаровой поверхности; слѣд., у плоскости Р есть только одна общая точка А съ шаровою поверхностью; значитъ, эта плоскость касательная.
487. Обратная теорема. Касательная плоскость (Р, черт. 428) перпендикулярна къ радіусу (ОА), проведенному въ точку касанія.
*) Мы принимаемъ безъ доказательства, что предѣлъ кривой АеЛ/В, составленной изъ дугъ большихъ круговъ, существуетъ, и что онъ не зависитъ отъ закона, по которому увеличивается число точекъ на кривой з.
— 367 —
Такъ какъ, по опредѣленію, точка А есть единственная общая у плоскости съ шаровою поверхностью, то всякая другая точка плоскости лежитъ внѣ шаровой поверхности и, слѣд., дальше отстоитъ отъ центра, чѣмъ А; такимъ образомъ, прямая ОА есть кратчайшее разстояніе точки О отъ плоскости Р, т.-е. ОА есть перпендикуляръ къ Р.
Поверхность шара и его частей.
Черт. 429.
488. Опредѣленія. 1°. Часть шаровой поверхности (черт. 429), отсѣкаемая отъ нея какою-нибудь плоскостью (ЛЛі), наз. сегментною поверхностью.
Окружность ААг есть основаніе, а отрѣзокъ КМ радіуса, перпендикулярнаго къ плоскости сѣченія, есть высота сегментной поверхности.
Часть шаровой поверхности, заключенная между двумя параллельными сѣкущими плоскостями (ААг и ВВі, черт. 429), наз. шаровымъ поясомъ или зоною.
Окружности сѣченій ААг и ВВг наз. основаніями, а разстояніе КЪ между параллельными плоскостями— высотою пояса.
Шаровой поясъ и сегментную поверхность можно разсматривать, какъ поверхности вращенія: въ окружность МАВК, вращаясь вокругъ
ваетъ шаровую поверхность, часть ея АВ опишетъ поясъ, а часть МА—сегментную поверхность.
Для нахожденія величины шаровой поверхности и ея частей мы должны предварительно доказать слѣдующую вспомогательную истину.
489. Лемма. Боковая поверхность каждаго изъ трехъ тѣлъ: конуса, усѣченнаго конуса и цилиндра равна произведенію
то время, какъ полудіаметра МК, описы-
— 368 —
высоты тѣла на длину окружности, у которой радіусъ есть перпендикуляръ, возставленный къ образующей изъ ея середины до пересѣченія съ осью.
1°. Пусть конусъ образуется (черт. 430) вращеніемъ тр-ка АВС вокругъ катета АС. Если В есть сере-
А дина образующей АВ, то (464):
С ®ок- пов- конуса =2тсВС.ЛІ) [1]
У
< Проведя ВЕА.АВ, получимъ два по-
/ добныхъ тр-ка АВС и АВЕ (они прямо-
Г угольные и имѣютъ общій уголъ Л);
изъ ихъ подобія выводимъ:
ц ВС:ЕВ=АС:АВ-,
I откуда: ВС.АВ=ЕВ.АС.
Черт. 430.
Поэтому равенство [1] можно написать
такъ:
Боков. пов. конуса=2тсЕІ).ЛС. Что и требовалось доказать. 2°. Пусть усѣченный конусъ (черт. 431) производится вра-
і
Черт. 431.
щеніемъ трапеціи АВСВ вокругъ стороны АВ. Проведя среднюю линію ЕЕ, будемъ имѣть (467, 2°):
Боков. пов. ус. конуса =2пЕЕ.ВС [2] Проведемъ ЕСА-ВС и ВН II АВ-, тогда получимъ два подобныхъ тр-ка ЕЕС и ВСН (стороны одного перпендикулярны къ сторонамъ другого); изъ ихъ подобія выводимъ:
ЕЕ : ВН=ЕС: ВС.
Откуда: ЕЕ . ВС=ВН . ЕС=АВ . ЕС.
Поэтому равенство [2] можно написать такъ:
Бок. пов. усѣч. конуса=2тсЕ<7 . АВ. Что и треб. доказать.
3°. Теорема остается вѣрной и въ примѣненіи къ цилиндру, такъ какъ окружность, о которой говорится въ теоремѣ, равна окружности основанія цилиндра.
— 369 —
490. Опредѣленіе. За величину поверхности шарового пояса, образуемаго вращеніемъ (черт. 432) д
какой-нибудь части (ВЕ) полуокружности
(АСЕ) вокругъ діаметра (АЕ), принимаютъ /7 предѣлъ, къ которому стремится поверх- —----------
ность, образуемая вращеніемъ вокругъ того же [ д
діаметра вписанной ломаной ли- I _ ніи (ВСЪЕ), когда ея стороны неограни-
ченно уменьшаются *).
Это опредѣленіе распространяется и на
сегментную поверхность, и на шаровую по- черт. 432. верхность; въ послѣднемъ случаѣ ломаная линія вписывается въ пѣлую полуокружность.
491. Теоремы. 1°. Сегментная поверхность равна произведенію ея высоты на окружность большого круга.
2°. Поверхность шарового пояса равна произведенію его высоты на окружность большого круга.
1°. Для бблыпей простоты разсужденія мы впишемъ въ дугу АЕ (черт. 433), производящую при вращеніи сегментную
поверхность, не какую-нибудь ломаную линію, а правильную
АСЪЕЕ съ произвольнымъ числомъ сторонъ.
Поверхность, получающаяся отъ вращенія этой ломаной, состоитъ изъ частей, образуемыхъ сторонами АС, СЪ, ЪЕ.... Эти части представляютъ собою боковыя поверхности или полнаго конуса (сть вращенія АС), или усѣченнаго конуса (отъ вращенія СЪ, ЕЕ...), или цилиндра (отъ вращенія ЪЕ, если ЪЕ || АВ). Поэтому мы можемъ примѣнить къ нимъ лемму § 489-го. При этомъ замѣтимъ, что перпендикуляры, возставленные изъ серединъ образую
Чѳрт. 433.
*) Въ теоріи предѣловъ доказывается, что этотъ предѣлъ существуетъ и что онъ не зависитъ Отъ закона, по которому стороны ломаной неограниченно уменьшаются.
Л. Киселевъ. Геометрія. 24
— 370 —
щихъ до пересѣченія съ осью, равны апоѳемѣ ломаной линіи. Обозначивъ эту апоѳему черезъ а, получимъ:
поверхн. АС=Ас 2тса;
поверхп. СТ)=сй.2тса;
поверхн. І)Е=йе.2тса;
Сложивъ эти равенства почленно, найдемъ:
поверхн. АСВЕЕ=А[.2ка.
При неограниченномъ удвоеніи числа сторонъ вписанной ломаной апоѳема а стремится къ предѣлу, равному радіусу шара В, а прямая А/ остается безъ измѣненія; слѣд.:
предѣлъ поверхности АСВЕЕ=А/.2т;В.
Но предѣлъ поверхности АСВЕЕ принимаютъ за величину сегментной поверхности, а прямая А/ есть высота Н поверхности; поэтому:
сегментная поверхность =Н.2ъВ=2кВН.
2°. Предположимъ, что правильная ломаная линія, о которой мы сейчасъ говорили, вписана не въ дугу АЕ, образующую при вращеніи сегментную поверхность, а въ какую-нибудь дугу СЕ, образующую шаровой поясъ. Это измѣненіе, какъ легко видѣть, нисколько не повліяетъ на ходъ разсужденій, изложенныхъ въ части 1° этого доказательства, поэтому и выводъ останется тотъ же, т.-е. что
поверхность шарового пояса=Н.2тгІ?=2тс2Ш,
гдѣ буквою Н обозначена высота с/ шарового пояса.
492. Замѣчаніе. Пусть около дуги АЕ (черт. 434) описана правильная ломаная линія АіСіРіЕіЕі, стороны которой параллельны сторонамъ правильной вписанной ломаной линіи АСВЕЕ. Поверхность, получаемая вращеніемъ вокругъ діаметра АВ этой описанной ломаной, также состоитъ изъ частей, къ которымъ мы можемъ примѣнить лемму § 489. Тогда, замѣтивъ, что перпендикуляры, возставленные изъ серединъ образующихъ
А,
Черт. 434.
— 371 —
до пересѣченія съ осью, будутъ теперь всѣ равны радіусу В круга, мы получимъ:
поверхность Л1С1П1Е1Г1=Лі/і. 2тсВ.
При неограниченномъ удвоеніи числа сторонъ вписанной и описанной ломаныхъ линій отрѣзокъ діаметра Ах{х стремится, какъ не трудно видѣть, *) къ предѣлу Л/, т.-е. къ высотѣ Н сегментной поверхности; поэтому:
пред. поверхп. Л1С1П1Е1Е1=Н . 2і:В=пред. поверхн. АСБЕР.
Такимъ образомъ, сегментную поверхность можно разсматривать, какъ общій предѣлъ поверхностей, образуемыхъ вращеніемъ правильныхъ ломаныхъ линій, какъ вписанныхъ, такъ и описанныхъ.
То же самое можно повторить о поверхности шарового пояса.
493. Теорема. Поверхность шара равна произведенію окружности большого круга на діаметръ;
или поверхность шара равна учетверенной площади большого круга.
Поверхность шара, производимую вращеніемъ полуокружности АБВ (черт. 433), можно разсматривать, какъ сумму поверхностей, образуемыхъ вращеніемъ дугъ АБ и БВ. Поэтому, согласно предыдущей теоремѣ, можемъ написать:
пов. шара=2тсВЛЛ-2ігЕ.йВ=2‘ісІ?(Лй-ЬйВ)=
=2ігВ.2В=4'гсВ2.
*) Для этого достаточно показать, что отрѣзки ААХ и РРХ (а слѣд., и отрѣзокъ Ні<.РРі) стремятся къ О. Изъ чертежа усматриваемъ (219);
ААг_В—а РРА_В—а ѵА а и оР а
Отсюда (принимая во вниманіе, что ОА=0Р=В) находимъ:
АА^У^-РР^ а 1
Такъ какъ разность В—а стремится къ О, величина В постоянна, а апоѳема а увеличивается, то изъ послѣдней формулы видно, что отрѣзки ААг и РРХ стремятся къ О.
— 372 —
494. Слѣдствіе. Поверхности шаровъ относятся, какъ квадраты радіусовъ или діаметровъ, потому что, обозначая черезъ Н и Д радіусы, а черезъ 5 и поверхности двухъ шаровъ, будемъ имѣть:
5 : 51=4ігВ2 : 4тсВ12=В2 : ВХ2=(2В)2 : (2ВД*.
Объемъ шара и его частей.
495. Опредѣленія. Тѣло, получаемое отъ вращенія
(черт. 435) кругового сектора (СОТУ) вокругъ діаметра (АВ), не пересѣкающаго его площади, наз. ш а-ровымъ секторомъ; это тѣло ограничено боковыми поверхностями двухъ конусовъ и поверхностью шарового пояса; послѣдняя поверхность наз. основаніемъ шарового сектора. Въ частномъ случаѣ одинъ изъ радіусовъ кругового сектора можетъ совпадать съ осью вращенія; напр., секторъ АОС, вращаясь вокругъ АО, производитъ шаровой сек
торъ ОСАСі, ограниченный боковою поверхностью конуса и
сегментною поверхностью.
Для нахожденія объема шарового сектора и цѣлаго шара мы должны предварительно доказать слѣдующую лемму.
Черт. 436.
496. Лемма. Если тр-къ ЛВС (черт. 436) вращается вокругъ оси ху, которая лежитъ въ плоскости тр-ка и проходитъ черезъ его вершину А, но не пересѣкаетъ его площади, то объемъ тѣла, получаемаго при этомъ вращеніи, равенъ произведенію поверхности, образуемой противоположною стороною ВС, на одну треть высоты И, опущенной на эту сторону.
При доказательствѣ разсмотримъ три случая.
1°. Ось совпадаетъ со сторо-
- 373 —
не парал
М
вою АВ (черт. 437). Въ этомъ случаѣ искомый объемъ равенъ суммѣ объемовъ двухъ конусовъ, получаемыхъ вращеніемъ прямоугольныхъ тр-ковъ ВСВ и ВС А. Первый объемъ равенъ 1/3т:СВ2. ВВ, а второй—Ѵ&^СТ)2 . ВА-, поэтому:
об. АВС =-^СВ2(ВВ+ВА)=-^СВ.СВ.ВА. 3 3
Произведеніе СВ . ВА равно ВС . к, такъ какъ каждое изъ этихъ произведеній выражаетъ двойную площадь тр-ка АВС-, поэтому:
об. АВС =-ъСВ.ВС.к. 3
Но произведеніе тгСВ. ВС равно боковой поверхности конуса ВВС-, значитъ:
об. ЛВС=(пов. ВС).^-к.
2°. Ось не совпадаетъ съ АВ и л е л ь н а ВС (черт. 438). Въ этомъ случаѣ искомый объемъ равенъ разности объемовъ, производимыхъ вращеніемъ тр-ковъ АМС и АМВ. По доказанному въ первомъ случаѣ, объемъ АМС—1/^ (пов. МС), а объемъ АМВ= 1/Зк (пов. МВ)-, слѣд.:
об. АВС=^к (пов. МС—пов. МВ)
=~^1 (пов. ВС).
3е. Ось параллельна сторонѣ ВС (черт. 439). Тогда искомый объемъ равенъ объему ВЕВС безъ суммы объемовъ АЕВ и АСВ-, первый изъ нихъ равенъ пВС2 . ЕВ, второй—1/3т:ЕВ2 . ЕА и третій—у&ВС2. АВ. Принявъ теперь во вниманіе, что ЕВ=ВС, получимъ:
объемъ АВС=ъВС2[ЕВ—1(ЕЛ+ЛІ))]=
3
1 9
^тгВС\ЕВ— ± ЕВ) = -т.ВС2. ЕВ.
3 3
— 374
Произведеніе 2г ГС . ЕГ выражаетъ боковую поверхность цилиндра, производимаго стороною ВС\ поэтому:
Черт 439. брать иногда ихъ
Об. ЛВС=(пов. ВС)1РС=(пов. ВС)-Ъ. 3 3
Замѣчаніе. На нашихъ чертежахъ мы брали тр-къ остроугольный. Доказательство нѣсколько измѣнится (въ случаяхъ 1° и 3°), если тр-къ будетъ тупоугольный (при вершинѣ А или В въ случаѣ 1° и при вершинѣ В или С въ случаѣ 3°).Разница въ доказательствѣ будетъ та, что вмѣсто суммы объемовъ придется разность. Предлагаемъ учащимся самимъ
разобрать эти случаи.
497. Теорема. Объемъ шарового сектора равенъ произведенію поверхности его основанія на треть радіуса.
Пусть шаровой секторъ производится вращеніемъ вокругъ діаметра ЕР (черт. 440) сектора АОБ. Доказательство расположимъ въ слѣдующей послѣдовательности:
1°. Впишемъ въ дугу АБ правильную ломаную линію АВСБ
Черт. 440.
съ произвольнымъ числомъ сторонъ и затѣмъ, продолживъ конечные радіусы О А и ОБ, опишемъ около дуги АБ правильную ломаную АіВ^іБі, стороны которой параллельны сторонамъ вписанной ломаной. Многоугольные секторы ОАВСБ и ОАіВіСіБ! произведутъ при вращеніи нѣкоторыя тѣла, объемы которыхъ обозначимъ: перваго черезъ Ѵг, а второго черезъ Ѵг. Докажемъ прежде всего, что при неограниченномъ удвоеніи числа сторонъ обѣихъ ломаныхъ линій разность Ѵ2—Гі стремится къ О.
Объемъ Ѵ\ есть сумма объемовъ, полу
чаемыхъ вращеніемъ тр-ковъ ОАВ, ОВС, ОСБ вокругъ оси ЕР\ объемъ есть сумма объемовъ, получаемыхъ вращеніемъ вокругъ той же оси тр-ковъ ОА1В1, ОВгСъ ОС^. Примѣнимъ
— 375 —
къ этимъ объемамъ лемму предыдущаго §, при чемъ замѣтимъ, что высоты первыхъ тр-ковъ равны апоѳемѣ а вписанной ломаной, а высоты вторыхъ тр-ковъ равны радіусу В шара. Согласно этой леммѣ будемъ имѣть:
7і=пов. (АВ)- +пов. (ВС)-+пов. (СВ)- = 3 3 8
=(пов. АВСВ)?-'
У2=пов. (ЛА)-Н-пов. (В^-Н-пов. (С^К)-^ 3 3 3
=(пов. А&СМ-. 3
Вообразимъ теперь, что число сторонъ обѣихъ ломаныхъ линій неограниченно удваивается. При этомъ условіи поверхности АВСВ и ЛіВіСіВі стремятся къ общему предѣлу, именно къ поверхности шарового пояса АБ (492), а апоѳема а имѣетъ предѣломъ радіусъ В; слѣд., объемы Ѵ\ и Ѵ2 стремятся при этомъ къ общему предѣлу, именно къ произведе-Л
нію (пов. АВ). —. Но тогда, значитъ, каждый изъ перемѣнныхъ 3
объемовъ и Ѵ2 приближается къ одной и той же постоянной величинѣ какъ угодно близко; это возможно только тогда, когда разность между этими перемѣнными стремится къ О.
2°. Обозначимъ буквою V объемъ шарового сектора ОАВ. Очевидно, что Ѵ>Ѵ\ и Ѵ<^Ѵ2; значитъ, каждая изъ разностей Ѵ2—V и Ѵ—Ѵі меньше разности Ѵ2—Но эта разность, какъ мы видѣли, при неограниченномъ удвоеніи числа сторонъ ломанныхъ стремится къ О; слѣд., разности Ѵ2—V и V— и подавно при этомъ стремятся къ О. Отсюда заключаемъ, что постоянная величина V есть общій предѣлъ перемѣнныхъ объемовъ Ѵ2 и Ур Но этотъ общій предѣлъ, какъ мы нашли, есть 7?
произведеніе (пов. АБ)—- значитъ:
3
7=(пов. АВ) .
3
— 376 —
Замѣчаніе. Теорема и ея доказательство не зависятъ отъ того, будетъ ли одинъ изъ радіусовъ кругового сектора совпадать съ осью вращенія или нѣтъ.
498. Теорема. Объемъ шара равняется произведенію его поверхности на треть радіуса.
Разбпвъ полукругъ АВСБ (черт. 441), производящій шаръ, на какіе-нибудь круговые секторы АОВ, ВОС, СОВ, мы замѣтимъ, что объемъ шара можно разсматривать, какъ сумму объемовъ шаровыхъ секторовъ, производимыхъ вращеніемъ этихъ круговыхъ. Такъ какъ, согласно предыдущей теоремѣ:
объемъ ЛОВ=(пов. АВ)1!3В, объемъ ВОС=(пов. ВСУ/3ІІ, объемъ СОВ=(пов. СВр/зВ, то объемъ шара=(пов. ЛВ+пов. ВС+пов. СВ)1/3В=
—(пов. АВСВУ/зВ.
489. Слѣдствіе 1-е. Обозначимъ высоту шарового пояса или сегментной поверхности черезъ II, радіусъ шара черезъ В, а діаметръ черезъ В; тогда поверхность пояса или сегментной поверхности выразится, какъ мы видѣли (491), формулой 2тсВН, а поверхность шара (493) формулой 4т:В2; поэтому:
об. шарового сектора=2ігВН . 1/3В=2/3тсВ2Н;
об. шара=4тсВ2. 1/3В=4/3,й:В3=4/3'п/ — Ѵ^/.ісВ3. \ 2 /
Отсюда видно, что объемы шаровъ относятся, какъ кубы ихъ радіусовъ или діаметровъ.
Слѣдствіе 2-е. Поверхность и объемъ шара составляютъ 2/3 соотвѣтственно поверхности и объема цилиндра, описаннаго около шара.
Дѣйствительно, у цилипдра, описаннаго около шара, радіусъ основанія равепъ радіусу шара, а высота равна діаметру шара; поэтому для такого цилиндра:
полная поверхность=2иВ . 2В+2,гсВ2=6тсВ2;
объемъ =тсВ22В=2ігК3.
— 377 —
(АСС1г черт. 442),
Отсюда видно, что 2/3 полной поверхности этого цилиндра равны 4тс7?2, т.-е. равны поверхпотси шара, а 2/3 объема цилиндра составляютъ Ч^В3, т.-е. объемъ шара *).
500. Опредѣленіе. Часть ша] отсѣкаемая отъ него какою-нибудь плоскостью (ССі), наз. шаровымъ сегментомъ. Кругъ сѣченія наз. основаніемъ сегмента, а отрѣзокъ Ат радіуса, перпенидкулярнаго къ основанію,—в ы с о т о ю сегмента.
Часть шара, заключенная между двумя параллельными сѣкущими плоскостями (ССХ и наз. шаровымъ слоемъ. Круги паралелль-пыхъ сѣченій наз. основаніями между ними—его высотою.
Оба эти тѣла можно разсматривать, какъ происходящія отъ вращенія вокругъ діаметра АВ части круга АтС, или части СтпБ.
Черт. 442. слоя, а разстояніе тп
501. Теорема. Объемъ шарового сегмента равенъ объему цилиндра, у котораго радіусъ основанія есть высота сегмента, а высота равна радіусу шара, уменьшенному на треть высоты сегмента,
т.-е. Ѵ=гЛІ\В—ЧгЯ), Д
гдѣ Н есть высота сегмента, а В радіусъ шара.
Объемъ шарового сегмента, получаемаго вращеніемъ вокругъ діаметра АБ (черт. 443) части круга АСВ, найдется, если изъ объема шарового сектора, получаемаго вращеніемъ кругового сектора АОВ, вычтемъ объемъ конуса, получаемаго вращеніемъ
Черт. 443.
*) Это предложеніе было доказано Архимедомъ (въ III вѣкѣ до Р. Хр.). Архимедъ выразилъ желаніе, чтобы чертежъ этой теоремы былъ изображенъ на его гробницѣ, что и было исполнено римскимъ военачальникомъ Марцелломъ (Ф. К э д ж о р и—Исторія элементарной математики).
— 378 —
тр-ка СОВ. Первый изъ нихъ равенъ 2/3т:В,2Н, а второй Ѵз ъСВ2. СО. Такъ какъ СВ есть средняя пропорціональная между АС и СБ, то СВ2=Щ2В—И); поэтому СВ2. СО= Щ2В.—ІГ) (В—Н)=2В2Н—ВН2—2ВН2+Н3=2В,2Н—ЗНВ2+Н5-
9 1
слѣд., об. АВВ1=об. ОВАВі—об.ОВВ1=-'кЕ2Н—-^СВ2.СО= 3 3
= 1тсВ2Н+тсВН2— -тАР = г.Н2(П—-1Г).
3 з 3 3
502. Теорема. Объемъ шарового слоя равенъ объему шара, имѣющаго діаметромъ высоту слоя, сложенному съ полусуммою объемовъ двухъ цилиндровъ, у которыхъ высота равна высотѣ слоя, а основанія: у одного нижнее, у другого верхнее основаніе слоя,
т.-е. Г = -^ігЯ3+^г(г1‘+^)Я,
гдѣ Н есть высота слоя, а г, и г2 радіусы основаній слоя.
Предварительно найдемъ объемъ, получаемый вращеніемъ вокругъ діаметра АР (черт. 444) кругового сегмента ВС (покрытаго на чертежѣ штрихами). Этотъ объемъ есть разность между объемомъ шарового сектора ОВС и объемомъ тѣла, получаемаго вращеніемъ тр-ка ОВС. Первый равенъ */3пВ2Н, 1 1
а второй=(пов. ВС)п^ОЕ= (рпОЕ.Ну^-ОЕ = О о
2
= -^пОЕ2Н. Слѣд., объемъ отъ вращенія сег-О
мента выразится такъ:
2 2 2 1 1
тт«Я(В2— ОЕ2)=~кН . СЕ^-ъг.Н . -гВС^-^пВС» . Н. О О О ** V
Чтобы получить объемъ слоя, достаточно къ найденному объему приложить объемъ усѣченнаго конуса ВВхС^-, поэтому объемъ слоя выразится такъ:
^пВС2 . Я4-|к(Саг4-ВЬг4-Са . ВЪ) И =~кІІ(ВС2+2Са2 +
2ВЪ*+2Са . ВЪ).
Проведя ВБ_]_Са, будемъ имѣть:
ВС2=ВО2 + СО2 = Н2+(Са—ВЪ)2 = П2 + Са2 + ВЬ2~2Са . ВЬ.
Подставивъ это выраженіе въ предыдущую формулу, найдемъ:
об. слоя — ^пП(Н*+ЗСа2+ЗВЪ*) =-^г.Н3 + -2к(Са2 + ВЪ2)Н
— 379 —
или, обозначая Са черезъ гг, а ВЪ черезъ га: об. сегм.=-^яЯ3 4"2’к(г1г+г1г)Н.
Положивъ въ этой формулѣ г2=0, получимъ другое выраженіе для объема шарового сегмента:
об. сегм.=-^ігНа + тгп *Н, О ха
т.-е. объемъ шарового сегмента равенъ объему шара, имѣющаго діаметромъ высоту сегмента, сложенному съ половиною объема цилиндра, у котораго радіусъ основанія есть радіусъ основанія сегмента и высота равна высотѣ сегмента.
ЗАДАЧИ.
353. Объемъ цилиндра, у котораго высота вдвое болѣе діаметра, равенъ 1 куб. метру. Вычислить его высоту.
354. Діаметръ основанія цилиндра = 16 сант., а полная поверхность его содержитъ 1546 квадр. сант. Вычислить высоту этого цилиндра.
355. Найти вѣсъ желѣзной цилиндрической трубки, которой внутренній діаметръ =17 сант., внѣшній діаметръ = 18 сант., а длина = =74 сант.; удѣльный вѣсъ желѣза 7,7.
356. Въ сосудъ, имѣющій форму конуса, обращеннаго вершиною внизъ, вливаютъ 345 граммовъ ртути. Зная, что уголъ при вершинѣ конуса равенъ 60°, а уд. вѣсъ ртути 13,596, вычислить высоту, до которой налита въ сосудѣ ртуть.
357. Вычислить боковую поверхность и объемъ усѣченнаго конуса, у котораго радіусы основаній суть 27 и 18 сант., а образующая 21 сант.
358. На какомъ разстояніи отъ центра шара, котораго радіусъ равенъ 2,425 метра, слѣдуетъ провести сѣкущую плоскость, чтобы отношеніе поверхности меньшаго сегмента къ боковой поверхности конуса, имѣющаго общее съ сегментомъ основаніе, а вершину въ центрѣ шара, равнялось 7 : 4.
359. Найти объемъ тѣла, происходящаго отъ вращенія правильнаго 6-угольника со стороною а вокругъ одной изъ своихъ сторонъ.
360. Вычислить радіусъ шара, описаннаго около куба, котораго ребро равно 1 метру.
361. Желѣзный пустой шаръ, котораго внѣшній радіусъ равенъ 0, 154 метра, плаваетъ въ водѣ, погружаясь въ нее на половину. Вычислить толщину оболочки этого шара, зная, что. уд. вѣсъ желѣза равенъ 7,7.
362. Вычислить объемъ тѣла, происходящаго отъ вращенія правильнаго треугольника со стороной а вокругъ оси, проходящей черезъ его вершину и параллельной противоположной сторонѣ.
363. Данъ равносторонній А АВС со стороною а; на ВС строятъ квадратъ ВСВЕ, располагая его въ противоположную сторону отъ
— 380 —
треугольника. Вычислить объемъ тѣла, происходящаго отъ вращенія б-угольника АВЕВС вокругъ стороны АВ.
364. Данъ квадратъ АВСВ со стороною а. Черезъ вершину А проводятъ прямую АВ, перпендикулярную къ діагонали АС, и вращаютъ квадратъ вокругъ АВ. Вычислить поверхность, образуемую контуромъ квадрата, и объемъ, образуемый площадью квадрата.
265. Данъ правильный 6-угольникъ АВСБЕР со стороною а. Черезъ вершину А проводятъ прямую АВ, перпендикулярную къ радіусу ОА, и вращаютъ 6-угольникъ вокругъ АВ. Вычислить поверхность, образуемую контуромъ, и объемъ, образуемый площадью прав. 6-угольника.
366. Въ шарѣ, котораго радіусъ равенъ 2, просверлено цилиндрическое отверстіе вдоль его діаметра. Вычислить объемъ оставшейся части, если радіусъ цилиндрическаго отверстія равенъ 1.
— 381 —
ПРИЛОЖЕНІЕ.
Главнѣйшіе методы рѣшенія геометрическихъ задачъ иа построеніе.
1. Методъ геометрическихъ Мѣстъ , извѣстный еціѳ со временъ Платона (IV вѣка до Р. Хр.), состоитъ въ слѣдующемъ. Положимъ, что рѣшеніе предложенной задачи сводится къ нахожденію нѣкоторой точки, которая должна удовлетворять извѣстнымъ условіямъ. Отбросимъ изъ этихъ условій какое-нибудь одно; тогда задача сдѣлается неопредѣленною, т.-ѳ. ей можетъ удовлетворять безчисленное множество точекъ. Эти точки составятъ нѣкоторое геометрическое мѣсто. Построимъ его, если это окажется возможнымъ. Затѣмъ примемъ во вниманіе отброшенное нами условіе и откинемъ какое-нибудь другое; тогда задача будетъ снова удовлетворяться безчисленнымъ множествомъ точекъ, которыя составятъ новое геометрическое мѣсто. Построимъ его, если это возможно. Искомая точка, удовлетворяя всѣмъ условіямъ, должна лежать на обоихъ геометрическихъ мѣстахъ, т.-е. она должна находиться въ ихъ пересѣченіи. Задача окажется возможной или невозможной, смотря по тому, пересѣкаются или нѣтъ найденныя геометрическія мѣста; и задача будетъ имѣть столько рѣшеній, сколько окажется точекъ пересѣченія.
Приведемъ на этотъ методъ одинъ примѣръ, который вмѣстѣ съ тѣмъ
покажетъ намъ, какъ иногда приходится вводить въ чертежъ вспомога-
тельныя линіи съ цѣлью принять во вниманіе всѣ данныя условія задачи.
Задача.
Построить
треугольникъ по основа-
нію а, углу при вершинѣ А сторонъ.
Пусть АВС будетъ искомый Д. Чтобы принять во вниманіе данную сумму боковыхъ сторонъ, продолжимъ ВА и отложимъ ВМ=з. Проведя МС, получимъ вспомогательный тр-къВМС. Если мы построимъ этотъ тр-къ, то затѣмъ легко построимъ и тр-къ АВС. Построеніе тр-ка ВМС сводится къ нахожденію точки М. Замѣтивъ, что тр-къ АМС равнобедренный (АМ=АС) и, слѣд., ^.М=1/2А (такъ какъ
М^.С = А), мы видимъ, что точка М должна удовлетворять двумъ условіямъ: 1) она удалена отъ В на
и суммѣ $ боковыхъ
Черт. 445.
разстояніе з, 2) изъ нея данная конечная прямая ВС видна подъ угломъ, равнымъ ЧъА. Отбросивъ второе условіе, мы получимъ безчисленное множество точекъ М, лежащихъ на окружности, описанной
— 382 —
изъ В радіусомъ, равнымъ в. Отбросивъ первое условіе, мы получимъ также безчисленное множество точекъ ЛГ, лежащихъ на дугѣ сегмента, построеннаго на ВС и вмѣщающаго уголъ, равный 1/ЯА. Такимъ образомъ, нахожденіе точки ІИ сводится къ построенію двухъ геометрич-скихъ мѣстъ, изъ которыхъ каждое мы построить умѣемъ. Задача окажется невозможною, если эти геометрическія мѣста не будутъ имѣть общихъ точекъ; задача будетъ имѣть одно или два рѣшенія, смотря по тому, касаются ли, или же пересѣкаются эти мѣста (на нашемъ чертежѣ дуга сегмента пересѣкается съ окружностью; вслѣдствіе этого получаются два тр-ка АВС и АіВС, удовлетворяющіе условіямъ задачи).
Иногда задача сводится не къ опредѣленію точки, а къ нахожденію прямой, удовлетворяющей нѣсколькимъ условіямъ. Если отбросимъ одно изъ нихъ, то получимъ безчисленное множество прямыхъ; при этомъ можетъ случиться, что эти прямыя опредѣляютъ нѣкоторую линію (напр., всѣ онѣ будутъ касательными къ нѣкоторой окружности). Отбросивъ другое условіе и принявъ во вниманіе то, которое было откинуто ранѣе, мы получимъ снова безчисленное множество прямыхъ, которыя, быть-можетъ, опредѣлятъ нѣкоторую другую линію. Построивъ, если возможно, эти двѣ линіи, мы затѣмъ легко найдемъ и искомую прямую. Пусть, напр., намъ предложена задача: провести сѣкущую къ двумъ даннымъ окружностямъ О и Оі такъ, чтобы части сѣкущей, заключенныя внутри окружностей, равнялись соотвѣтственно даннымъ длинамъ а и ах. Если возьмемъ только одно условіе, напр., чтобы часть сѣкущей, лежащая внутри круга О, равнялась а, то получимъ безчисленное множество сѣкущихъ, которыя всѣ должны быть одинаково удалены отъ центра этого круга (такъ какъ равныя хорды одинаково удалены отъ центра). Поэтому, если въ кругѣ О гдѣ-нибудь построимъ хорду, равную а, и затѣмъ радіусомъ, равнымъ разстоянію этой хорды отъ центра, опишемъ окружность, концентрическую съ О, то всѣ сѣкущія, о которыхъ идетъ рѣчь, должны касаться этой вспомогательной окружности; подобнымъ образомъ, принявъ во вниманіе только второе условіе, мы увидимъ, что искомая сѣкущая должна касаться второй вспомогательной окружности, концентрической съ 01. Значитъ, вопросъ приводится къ построенію общей касательной къ двумъ окружностямъ.
Кромѣ тѣхъ геометрическихъ мѣстъ, которыя указаны въ текстѣ (этой книги (§§ 67, 112, 177 , 228), полезно замѣтить еще слѣдующія доказательство предоставляемъ самимъ учащимся):
1°. Геометрическое мѣсто точекъ, дѣлящихъ въ данномъ отношеніи отрѣзки параллельныхъ прямыхъ, заключенные между сторонами даннаго угла, есть прямая, проходящая черезъ вершину угла и какую* нибудь одну изъ этихъ точекъ.
2°. Геометрическое мѣсто точекъ, которыхъ разстоянія отъ сторонъ даннаго угла находятся въ данномъ отношеніи, состоитъ изъ двухъ
— 383 —
прямыхъ, проходящихъ черезъ вершину угла, и изъ которыхъ одна лежитъ внутри угла, а другая внѣ его.
3°. Геометрическое мѣсто точекъ, дѣлящихъ въ данномъ отношеніи всѣ равныя хорды данной окружности, есть окружность, концентрическая съ данною.
4°. Геометрическое мѣсто точекъ, изъ которыхъ касательныя, проведенныя къ данной окружности, имѣютъ данную длину, есть окружность, концентрическая съ данной.
5°. Геометрическое мѣсто точекъ, квадраты разстояній которыхъ отъ двухъ данныхъ точекъ А н В имѣютъ постоянную сумму, есть окружность, которой центръ лежитъ въ серединѣ прямой АВ (доказательство основывается на теор мЬ § 239).
6°. Геометрическое мѣсто точекъ, квадраты разстояній которыхъ отъ двухъ данныхъ точекъ А и В имѣютъ постоянную разность, есть прямая, перпендикулярная къ прямой АВ.
1°. Геометрическое мѣсто точекъ, сумма разстояній которыхъ отъ сторонъ даннаго угла постоянна, есть лежащій внутри угла отрѣзокъ прямой, отсѣкающей отъ угла равнобедренній тр-къ. Продолженія этого отрѣзка (въ обѣ стороны) представляютъ геометрическое мѣсто точекъ, которыхъ разность разстояній отъ сторонъ угла постоянна.
8°. Геометрическое мѣсто точекъ, дѣлящихъ въ данномъ отношеніи хорды, проведенныя изъ одной точки А данной окружности, есть окружность, касательная къ данной въ точкѣ А.
Послѣднее геометрическое мѣсто составляетъ частный случай слѣдующаго болѣе общаго (см. §§ 211—218):
9°. Если изъ данной точки О (черт. 446) къ различнымъ точкамъ А Ах, какой-нибудь фигуры Р проведемъ прямыя ОА, 0Ах, ОАц.. и на каждой изъ нихъ отложимъ части Оа, 0аи 0аіг... такія, что
Оа : ОА — Оа! : ОА1 = Оа11 : 0Аи = ...,
то геометрическое мѣсто точекъ а, а1г ап... есть фигура /, подобная фигурѣ Р и одинаково съ ней расположенная относительно точки О.
Такимъ образомъ, если фигура Р есть прямая, то и / есть прямая, параллельная Р; если Р есть многоугольникъ, то и / есть многоугольникъ, подобный Р и одинаково съ нимъ расположенный; если Р есть окружность, то и / есть окружность.
Черт. 446.
— 384 —
Когда пропорціональныя части Оа, 0аи 0аи... откладываются на продолженіяхъ линій О А, 0А1... (за точку О), то получается тоже подобная фигура, но расположенная обратно относительно точки О.
Точка О въ этихъ случаяхъ наз. центромъ подобія фигуръ Р и /, точки А и а, Аг и аг и т. д. наз. сходственными точками, а прямыя О А, ОА1...—л учами подобія.
2. Методъ подобія. Онъ состоитъ въ томъ, что, пользуясь нѣкоторыми данными задачи, строятъ сначала фигуру, подобную искомой, а затѣмъ переходятъ къ послѣдней. Этотъ методъ особенно удобенъ тогда, когда только одна данная величина есть длина, а всѣ прочія суть или углы, или отношенія линій; таковы, напр., задачи:
Построить треугольникъ по данному углу, сторонѣ и отношенію двухъ другихъ сторонъ, или по двумъ угламъ и длинѣ нѣкоторой прямой (высотѣ, медіанѣ, биссектриссѣ и т. п.).
Построить квадратъ по данной суммѣ или разности между діагональю и стороною, и т. п.
Въ этихъ задачахъ положеніе искомой фигуры остается произвольнымъ; но во многихъ вопросахъ требуется построить фигуру, которой положеніе относительно данныхъ точекъ или линій вполнѣ опредѣлено. При этомъ можетъ случиться, что, отрѣшившись отъ какого-нибудь одного изъ условій положенія и оставивъ всѣ остальныя, мы получимъ безчисленное множество фигуръ, подобныхъ искомой. Въ такомъ случаѣ методъ подобія можетъ быть употребленъ съ пользою. Приведемъ примѣръ.
Задача. Въ данный уголъ АВС вписать окружность, которая проходила бы черезъ данную внутри угла точку Л/ (черт. 447).
Отбросимъ на время требованіе, чтобы окружность проходила черезъ точку М. Тогда вопросу удовлетворяетъ безчисленное множество окружностей, которыхъ центры лежатъ на биссектриссѣ ВВ. Построимъ одну изъ такихъ окружностей, напр., ту, которой центръ
— 385 —
есть о. Возьмемъ на ней точку т, сходственную точкѣ М, т.-е. лежащую на лучѣ подобія МВ, и проведемъ радіусъ то. Если теперь построимъ МО || тпо, то точка О будетъ центромъ искомаго круга. Дѣйствительно, проведя къ сторонѣ АВ перпендикуляры ОМ и оп, мы получимъ подобные тр-ки МВО и тВо, МВО и пВо, изъ которыхъ будемъ имѣть: МО : то = ВО : Во МО : по = ВО : Во
Откуда: МО : то = МО : по.
Но иіо = по; слѣд., и МО = МО, т.-ѳ. окружность, описанная изъ центра О радіусомъ ОМ, касается стороны АВ; а такъ какъ ея центръ лежитъ на биссектриссѣ угла, то она касается и стороны ВС.
Если за сходственную точку возьмемъ другую точку т1 пересѣченія луча МВ съ окружностью о, то найдемъ другой центръ 0х искомаго круга. Слѣд., задача допускаетъ два рѣшенія.
3. Методъ параллельнаго перенесенія. Весьма часто бываетъ полезно перемѣстить нѣкоторыя части данной или искомой фи-
гуры въ другое положеніе, при которомъ легче обнаружить зависимость между данными элементами и искомыми. Существуютъ различ-
ные пріемы такого перемѣщенія, лельное перенесеніе.
Задача. Построить чет тежъ 448), зная всѣ его соединяющую середи: сторонъ АВ и СВ.
Разсмотримъ сначала п а р а л-
ы реугольникъ АВСВ (чѳр-стороны и прямую ЕР, и ы противоположныхъ
Чтобы сблизить между собою данныя линіи, перенесемъ парал
лельно самимъ себѣ стороны АВ и ВС въ положенія ЕВ1п ЕС±. Тогда
прямая ВВХ будетъ равна и параллельна АЕ, а прямая ССі равна и параллельна ЕВ; но такъ какъ АЕ~ЕВ, то ВВХ = СХС и ВВ± || СС^
Вслѣдствіе этого тр-ки ВВ±Р и СС1Р будутъ равны (такъ какъ у нихъ: ВВ1 = СС1, ВР—СР и / ВгВР = / РСС]); значитъ, / ВХРВ = / СРСг, и потому линія В1РС1 должна быть прямая, т.-е. фигура ЕВ-іРСі окажется треугольникомъ. Въ этомъ тр-кѣ извѣстны двѣ стороны (,ЕВі = АВ и ЕСг= ВС) и медіана ЕР, проведенная къ третьей сторонѣ. По этимъ даннымъ легко построить треуголь
никъ (если продолжимъ медіану ЕР за точку Р на длину, равную ей, и полученную точку соединимъ съ Вх и Сх, то получимъ параллело-
граммъ, у котораго извѣстны стороны и одна діагональ).
Найдя А ВВХСХ, строимъ затѣмъ тр-ки В^ВР и СгСР, а затѣмъ и весь четыреугольникъ АВСВ.
А. Киселевъ. Геометрія.
25
— 386 —
Замѣтимъ, что иногда бываетъ полезно перенести параллельно данному направленію цѣлую фигуру, напр., окружность. Въ этомъ случаѣ всѣ точки перемѣщаемой фигуры описываютъ параллельныя и равныя прямыя (см., напр.. задачу 383, стр. 388>.
4. Методъ вращенія вокругъ ТОЧКИ. Для уясненія этого особеннаго вида перенесенія приведемъ слѣдующій примѣръ:
Задача. Даны по положенію точка С (черт. 449) » » ' идвѣбезконѳчныяпря-
мыя а и Ъ. Построить ' ""Дді треугольникъ АВС, ко -
. р / I тораго одна вершина
| ' т- .X была бы въ С, адвѣ д р у -
I / і гія лежали бы па пря-
\ і I /> м ы х ъ а и Ъ, и который,
„ ! V і кромѣ того, былъ бы
а —1—* п
I А и подобенъ данному тре-
угольнику (не помѣщенному Черт. 449. на чертежѣ).
Пусть задача рѣшена. Замѣтивъ,
что углы искомаго тр-ка даны, обозначимъ одинъ изъ нихъ, который находится при точкѣ С, черезъ ш. Повернемъ всю фигуру вокругъ точки С въ направленіи, указанномъ стрѣлкою, на уголъ ш и найдемъ положеніе, которое займетъ послѣ вращенія прямая а. Для этого достаточно опустить на а перпендикуляръ СО, затѣмъ повернуть его на уголъ <о въ положеніе СОѴ и провести черезъ Ог прямую аъ перпендикулярную къ С0±. Прямая и будетъ то положеніе, которое займетъ послѣ вращенія прямая а. Такъ какъ при вращеніи всѣ части фигуры повертываются на одинъ и тотъ же уголъ, то СА, послѣ вращенія, пойдетъ по СВ, вслѣдствіе этого точка А упадетъ въ т.-ѳ. въ точку пересѣченія СВ съ аг. Такъ какъ отношеніе СА къ СВ или, все равно, отношеніе САг къ СВ дано (пусть это будетъ т : п), то теперь вопросъ сведенъ къ тому, чтобы черезъ точку С провести такую прямую СА1г которая пересѣкалась бы съ прямыми Ь и аг въ точкахъ В и А, удовлетворяющихъ пропорціи;
САі ; СВ = т : п.
Чтобы провести такую прямую, достаточно раздѣлить СОХ въ нѣкоторой точкѣ х такъ, чтобы : Сх — т : п, и черезъ точку дѣленія провести прямую, параллельную а.^, пересѣченіе этой прямой съ Ъ опредѣлитъ точку В.
5. Методъ вращенія вокругъ прямой (или методъ симметріи). Иногда пріемъ построенія легко обнаруживается, если перегнемъ часть чертежа вокругъ нѣкоторой прямой такъ, чтобы эта часть заняла симметричное положеніе по другую сторону отъ этой прямой. Приведемъ примѣръ.
— 387 —
Задача. На безконечной прямой АВ (черт. 450) найти точку х, чтобы сумма ѳя разстояній отъ данныхъ точекъ М и была наименьшая.
Если, перегнувъ чертежъ вокругъ АВ, приведемъ точку М въ симметричное относительно АВ положеніе М1г то разстояніе точки М отъ какой угодно точки прямой АВ сдѣлается равнымъ разстоянію точки Мг отъ той же точки прямой АВ. Поэтому суммы Мх+х^
... равны соотвѣтственно суммамъ Мх^-І-а:#, +
но изъ послѣднихъ суммъ наименьшая будетъ та, при которой линія окажется прямою. Отсюда становится яснымъ пріемъ построенія.
То же самое построеніе рѣшаетъ и другую задачу: на прямой АВ найти такую точку х, чтобы прямыя хМ и хХ, проведенныя отъ нея къ даннымъ точкамъ М и Р!, составляли съ АВ равные углы.
в. Методъ обратности. Иногда бываетъ полезно, такъ сказать, перевернуть задачу, т.-е. данныя условія задачи взять за искомыя и наоборотъ. Примѣромъ служитъ слѣдующая задача.
Задача. Въ данный треугольникъ АВС вписать
другой треугольникъ, у котораго стороны были бы параллельны сторонамъ другого даннаго треугольника МНР.
Перевернемъ вопросъ; опишемъ около тр-ка МНР другой тр-къ АхВіСх, у котораго стороны были бы параллельны сторонамъ тр-ка АВС (что, конечно, легко выполнить). Тогда мы получимъ фигуру, подобную искомой; раздѣливъ затѣмъ какую-нибудь сторону тр-ка АВС на двѣ части, пропорціональныя отрѣзкамъ сходственной стороны тр-ка 41В1С1, мы получимъ одну изъ вершинъ искомаго тр-ка.
7. Алгебраическій методъ. Сущность этого метода, а также и примѣры задачъ, рѣшаемыхъ имъ, были указаны ранѣе (§§ 254, 255, 342, 343 и задачи №№ 230, 231, 285, 288, 289, 290, 291, 292, 293).
Примѣры задачъ, рѣшаемыхъ этими методами.
1°. Методъ геометрическихъ мѣстъ.
367. Построить четыреугольникъ АВСВ, около котораго можно было бы описать окружность, зная его стороны АВ и ВС, діагональ АС и уголъ между діагоналями.
368. Построить треугольникъ по основанію, углу при вершинѣ и суммѣ или разности квадратовъ двухъ другихъ сторонъ (напр., осно
— 388 —
ваніе а, уголъ при вершинѣ А и сумма квадратовъ боковыхъ сторонъ к3).
369. Около равносторонняго треугольника описать квадратъ такъ, чтобы обѣ фигуры имѣли общую вершину.
370. Найти точку, изъ которой три отрѣзка данной прямой АВ, ВС и СВ были бы видны подъ равными углами.
371. Внутри тр-ка найти такую точку, которой разстоянія до сторонъ тр-ка относились бы между собою, какъ 6:3:2.
372. Найти точку, изъ которой три данные круга были бы видны подъ равными углами (указаніе: надо сначала найти гѳометр. мѣсто точекъ, изъ которыхъ два данные круга видны подъ равными углами).
373. Дана окружность и какія-нибудь двѣ прямыя. Найти на окружности такую точку, чтобы сумма ея разстояній отъ этихъ прямыхъ была наименьшая.
374. Превратить данный тр-къ въ другой равновеликій тр-къ съ даннымъ основаніемъ и съ даннымъ угломъ при вершинѣ.
375. Въ данной окружности провести двѣ хорды данной длины такъ, чтобы онѣ пересѣкались подъ даннымъ угломъ и одна изъ нихъ проходила черезъ данную точку.
2°. Методъ подобія.
376. Построить тр-къ по углу при вершинѣ, высотѣ и отношенію отрѣзковъ, на которые основаніе дѣлится высотою.
377. Вписать квадратъ: 1, въ данный тр-къ; 2, въ данный секторъ; 3, въ данный сегментъ.
378. Черезъ данную точку провести прямую такимъ образомъ, чтобы три данныя прямыя, исходящія изъ одной точки, отсѣкали отъ искомой прямой отрѣзки, находящіеся въ данномъ отношеніи.
379. Черезъ данную точку А окружности провести хорду АВ, которая пересѣкалась бы съ данною хордою ВС въ такой точкѣ Е, чтобы прямыя ВЕ и ВС находились въ данномъ отношеніи.
380. Провести внутри тр-ка прямую, параллельную основанію, такъ, чтобы эта прямая была средней пропорціональной между отрѣзками одной боковой стороны.
381. Построить равнобедренный тр-къ, зная его боковую сторону и сумму высоты съ основаніемъ.
382. На данной прямой найти такую точку, чтобы ея разстоянія отъ данной точки и другой данной прямой находились въ данномъ отношеніи.
3°. Методъ параллельнаго перенесенія.
383. Между двумя данными окружностями провести прямую данной длины а параллельно данной прямой М1Ѵ.
(Указаніе: надо одинъ кругъ приблизить къ другому, перенеся его параллельно прямой МК на разстояніе «).
— 389 —
384. Въ кругѣ даны двѣ хорды АВ и СВ. Найти на окружности такую точку х, чтобы прямыя хА и хВ отсѣкали отъ хорды СО отрѣзокъ, равный данной длинѣ (методъ парал. перенесенія и геом. мѣстъ).
385. Въ данномъ тр-кѣ АВС найти такія точки: х на сторонѣ АВ и у на сторонѣ ВС, чтобы прямая ху была данной длины и, кромѣ того, отношеніе Ах : Су было бы данное (парал. перенесеніе и методъ подобія).
386. Построить трапецію по одному ея углу, двумъ діагоналямъ и средней линіи.
387. Построить четыреугольникъ по тремъ сторонамъ а, Ъ, с и двумъ угламъ а и 0, прилежащимъ къ неизвѣстной сторонѣ.
388. Къ двумъ даннымъ кругамъ провести общую сѣкущую, параллельную данной прямой, такъ, чтобы сумма или разность хордъ, опредѣляемыхъ точками пересѣченій, была равна данной длинѣ.
389. Съ корабля видны два маяка, положеніе которыхъ на картѣ извѣстны, подъ даннымъ угломъ. Когда корабль, прошелъ извѣстную длину въ данномъ направленіи, тѣ же самые маяки видны подъ другимъ даннымъ угломъ. Опредѣлить на картѣ мѣсто корабля (геом. мѣсто и параллельное перенесеніе).
4°. Методъ вращенія вокругъ точки.
390. Построить тр-къ, подобный данному тр-ку, такъ, чтобы одна его вершина лежала въ данной точкѣ А, а двѣ другія вершины находились бы на данныхъ окружностяхъ О и 0г (одна на 0, другая на 00-
391. Данъ кругъ и внѣ его двѣ точки А и В; провести къ кругу касательную такъ, чтобы разстоянія точки А до этой касательной и до перпендикуляра, опущеннаго изъ В на касательную, были въ даномъ отношеніи.
(Указаніе: надо повернуть вокругъ точки А на 90° прямоугольный тр-къ, у котораго гипотенуза есть АВ, а одинъ катетъ—разстояніе точки А до перпендикуляра, опущеннаго на касательную изъ точки В. Эту же задачу можпо рѣшить при помощи одновременнаго пользованія методомъ подобія и методомъ гсометр. мѣстъ).
392. Построить тр-къ, котораго стороны были бы пропорціональны числамъ 3, 4 и 5, и котораго вершины лежали бы на трехъ данныхъ параллельныхъ прямыхъ.
5°. Методъ вращенія вокругъ прямой.
393. Построить по четыремъ сторонамъ четыреугольникъ АВСО, зная, что его діагональ АС дѣлитъ уголъ А пополамъ.
394. Конечная прямая АВ пересѣчена въ точкѣ С прямой 2И2Ѵ; найти на ЛІЛГ такую точку, изъ которой отрѣзки АС и ВС видны подъ равными углами (эту задачу можно также рѣшить методомъ геометр. мѣстъ).
395. Построить квадратъ, двѣ противоположныя вершины кото
— 390 —
раго находились бы на двухъ данныхъ окружностяхъ, а двѣ другія на данной прямой, расположенной между окружностями.
396. На прямоугольномъ бильярдѣ дано положеніе двухъ шаровъ А и В. Въ какомъ направленіи надо толкнуть шаръ А, чтобы онъ, отразившись послѣдовательно отъ всѣхъ четырехъ бортовъ, ударилъ затѣмъ шаръ В?
397. Данъ уголъ и внутри его точка. Построить тр-къ наименьшаго периметра такой, чтобы одна его вершина лежала въ данной точкѣ, а двѣ другія на сторонахъ угла.
398. Рѣшить методомъ симметріи задачу, которая выше (стр. 384) была рѣшена методомъ подобія: въ данный уголъ вписать окружность, которая проходила бы черезъ точку, данную внутри угла.
6°. Методъ обратности.
399. Въ данный секторъ вписать тр-къ, равный данному тр-ку.
400. Построить тр-къ, равный данному тр-ку, такъ, чтобы его вершины лежали на трехъ данныхъ прямыхъ, исходящихъ изъ одной точки.
401. Построить тр-къ, подобный данному тр-ку, такъ, чтобы его вершины лежали на трехъ данныхъ концентрическихъ окружностяхъ.
402. Въ данный тр-къ вписать тр-къ, подобный другому данному тр-ку, такъ, чтобы одна изъ его вершинъ лежала въ точкѣ, данной на основаніи.
ОГЛАВЛЕНІЕ.
Цыфры означаютъ номера страницъ.
Предисловіе III—XII.
Введеніе. Математическія предложенія, I.—Прямая линія, плоскость. Понятіе о геометріи, 8.
ПЛАНИМЕТРІЯ.
КНИГА I. ПРЯМАЯ ЛИНІЯ.
Глава I. Углы. Предварительныя понятія, 9.—Свойства прямого угла, 12.—Свойства смежныхъ и вертикальныхъ угловъ, 17.
Упражненія, 23.
Глава II. Треугольники и многоугольники. Понятіе о многоугольникѣ и треугольникѣ, 24.—Свойства равнобедреннаго треугольника, 27.— Признаки равенства треугольниковъ, 29.—Соотношенія между углами и сторонами треугольника, 32.—Сравнительная длина объемлющихъ и объемлемыхъ ломаныхъ линій, 36.—Треугольники съ двумя соотвѣтственно равными сторонами, 40.
Глава III. Перпендикуляры и наклонныя,—41 Равенство прямоугольныхъ треугольниковъ, 43.
Глава IV. Свойство перпендикуляра къ серединѣ прямой и свойство биссек-триссы угла, 44.
Глава V. Основныя задачи на построеніе, 47.
Упражненія, 53.
Глава VI. Параллельныя прямыя. Основныя теоремы, 55.—Углы съ соотвѣтственно параллельными или перпендикулярными сторонами, 64. Сумма угловъ треугольника и многоугольника, 66.—О постулатѣ параллельныхъ линій, 68.
Глава VII. Параллелограммы и трапеціи. Главнѣйшія свойства параллелограммовъ вообще, 72.—Особыя формы параллелограммовъ: прямоугольникъ, ромбъ и квадратъ, 76.—Нѣкоторыя теоремы, основанныя на свойствахъ параллелограмма, 79.—Опредѣленіе и свойства трапеціи, 82.
Упражненія, 83.
КНИГА II. ОКРУЖНОСТЬ.
Глава I. Форма и положеніе окружности, 86.
Глава II. Равенство и неравенство дугъ, 90.
Глава III. Зависимость между дугами, хордами и разстояніями хордъ отъ центра, 93.
— 392 —
Глава IV. Свойства касательной, 95. Основныя задачи на проведеніе касательной, 98 и слѣд.
Глава V. Относительное положеніе окружностей, 103.
Упражненія, 107.
Глава VI. Измѣреніе величинъ. 109.
Глава VII. Измѣреніе угловъ помощью дугъ, 121.
Глава VIII. Вписанные и описанные многоугольники, 133.
Глава IX. Четыре замѣчательныя точки въ треугольникѣ, 139.
Упражненія, 140.
КНИГА III. ПОДОБНЫЯ ФИГУРЫ.
Глава I. Подобіе треугольниковъ, 143.
Глава II. Подобіе многоугольниковъ, 151.
Глава III. Фигуры, подобно расположенныя, 155.
Глава IV. Нѣкоторыя теоремы о пропорціональныхъ линіяхъ, 160.
Глава V. Числовыя зависимости между элементами треугольника и нѣкоторыхъ другихъ фигуръ, 169.
Глава VI. Понятіе о приложеніи алгебры къ геометріи, 183.
Упражненія, 190.
Глава VII. Правильные многоугольники, 195.
Упражненія, 208.
КНИГА IV. ВЫЧИСЛЕНІЕ ДЛИНЫ ОКРУЖНОСТИ И ЕЯ ЧАСТЕЙ.
Глава I. Основныя свойства предѣловъ, 209.
Глава II. Вычисленіе длины окружности, 215.
Упражненія, 229.
КНИГА V. ИЗМѢРЕНІЕ ПЛОЩАДЕЙ.
Глава I. Площади многоугольниковъ, 230.
Глава II. Теорема Пиѳагора и основанныя на ней задачи, 247.
Глава III. Отношеніе площадей подобныхъ фигуръ, 250.
Глава IV. Площадь круга и его частей, 254.
Глава V. Соотношеніе между сторонами треугольника и радіусами вписаннаго и описаннаго круговъ, 261.
Добавленіе.
Построеніе корней квадратнаго уравненія, 262.
Упражненія, 266.
Числовыя задачи на разные отдѣлы планиметріи, 268.
— 393 —
СТЕРЕОМЕТРІЯ.
КНИГА I. ПРЯМЫЯ И ПЛОСКОСТИ.
Глава I. Опредѣленіе положенія плоскости, 271.
Глава II. Перпендикуляръ и наклонныя къ плоскости, 275.
Глава III. Параллельныя прямыя и плоскости. Параллельныя прямыя, 283.—Прямыя, параллельныя плоскости, 286,—Параллельныя плоскости, 288.
Глава IV. Двугранные углы, 292.—Перпендикулярныя плоскости, 296.— Уголъ двухъ скрещивающихся прямыхъ, 298.—Уголъ, образуемый прямой съ плоскостью, 298.
Глава V. Многогранные углы, 300.—Равенство трегранныхъ угловъ, 303.
КНИГА II. МНОГОГРАННИКИ.
Глава I. Свойства параллелепипеда и пирамиды.Опредѣленія, 307. — Равенство призмъ и пирамидъ, 311.—Свойства граней и діагоналей параллелепипеда, 312.—Свойства параллельныхъ сѣченій въ пирамидѣ, 313.
Глава II. Боковая поверхность призмы и пирамиды, 315.
Задачи, 317.
Глава III. Объемъ призмы и пирамиды. Опредѣленія, 318. — Объемъ прямоугольнаго параллелепипеда, 320.—Объемъ всякаго параллелепипеда, 325.—Объемъ призмы, 328.—Объемъ пирамиды, 329.—Объемъ усѣченной пирамиды и усѣченной призмы, 333.
Глава IV. Подобіе многогранниковъ, 337.
Глава V. Симметричныя фигуры, 341.
Глава VI. Понятіе о правильныхъ многогранникахъ, 345.
Задачи, 347.
КНИГА III. КРУГЛЫЯ ТБЛА.
Глава I. Цилиндръ и конусъ. Опредѣленія, 349.—Поверхность цилиндра и конуса, 352.—Объемъ цилиндра и конуса, 357.—Подобные цилиндры и конусы, 361.
Глава II. Шаръ. Сѣченіе шара плоскостью, 362.—Свойства большихъ круговъ, 364.—Плоскость, касательная къ шару, 366.—Поверхность шара и его частей, 367.—Объемъ шара и его частей, 372.
Задачи, 379.
Приложеніе. Главнѣйшіе методы рѣшенія геометрическихъ задачъ на построеніе, 381. Примѣры задачъ, рѣшаемыхъ этими методами, 387.