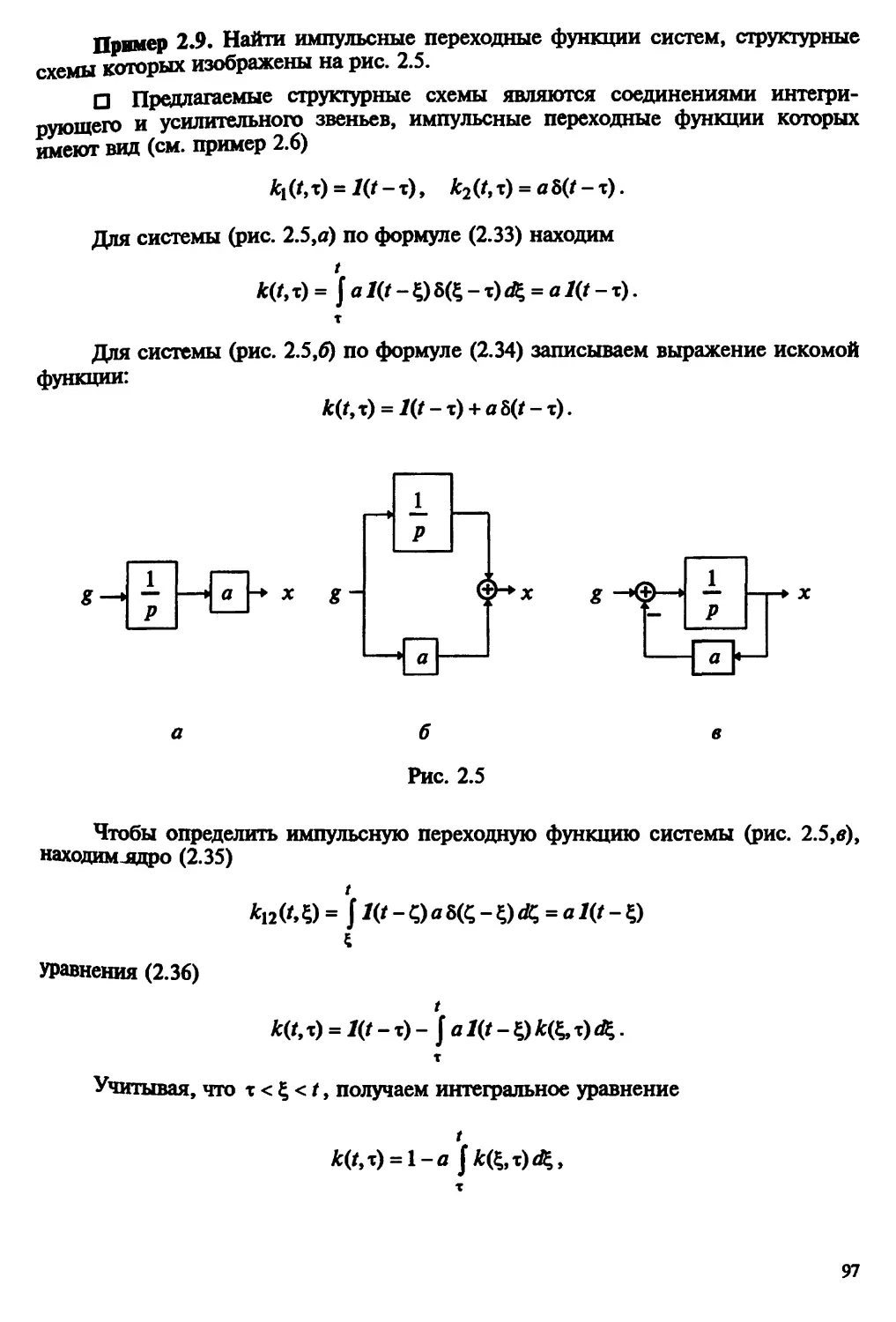
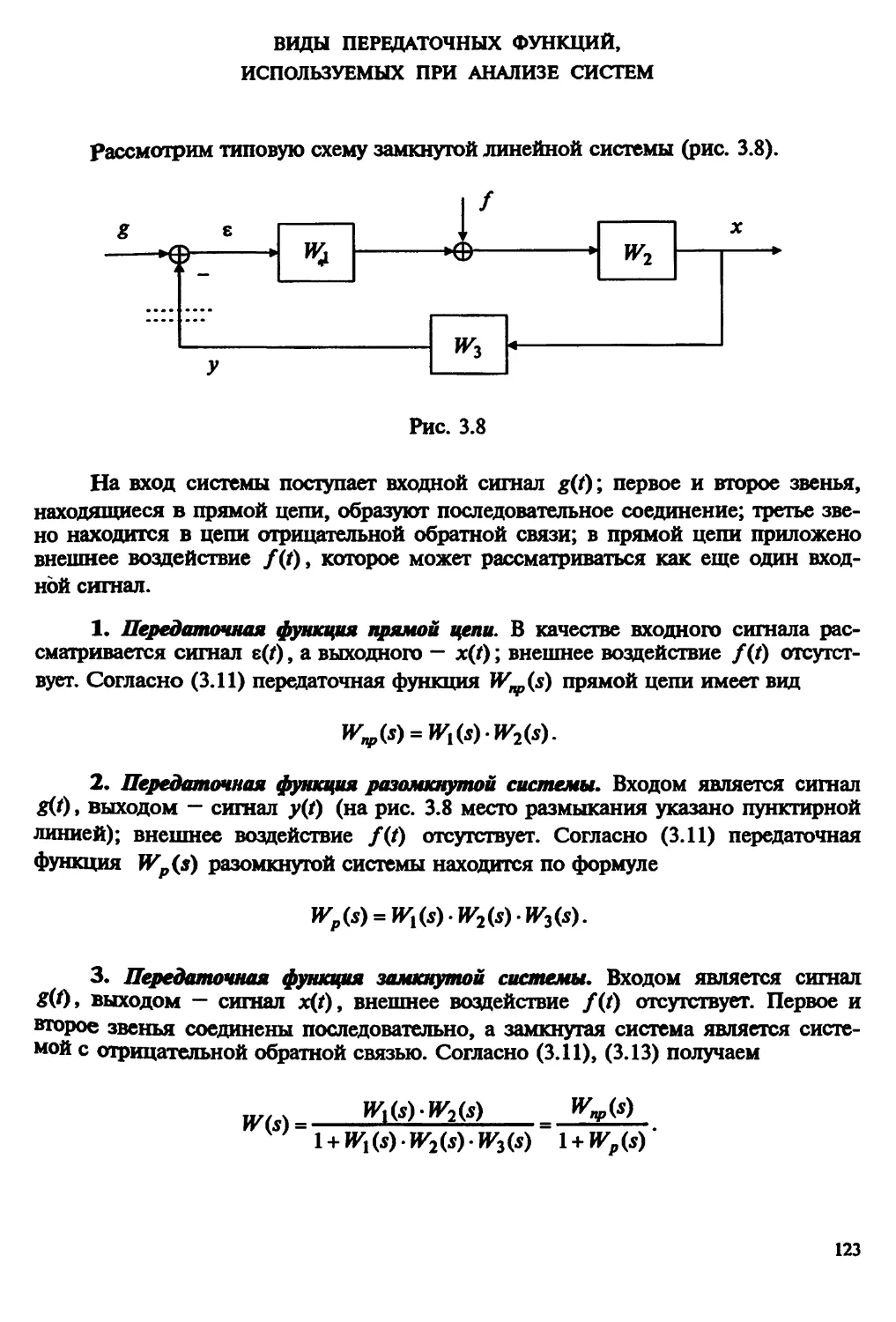
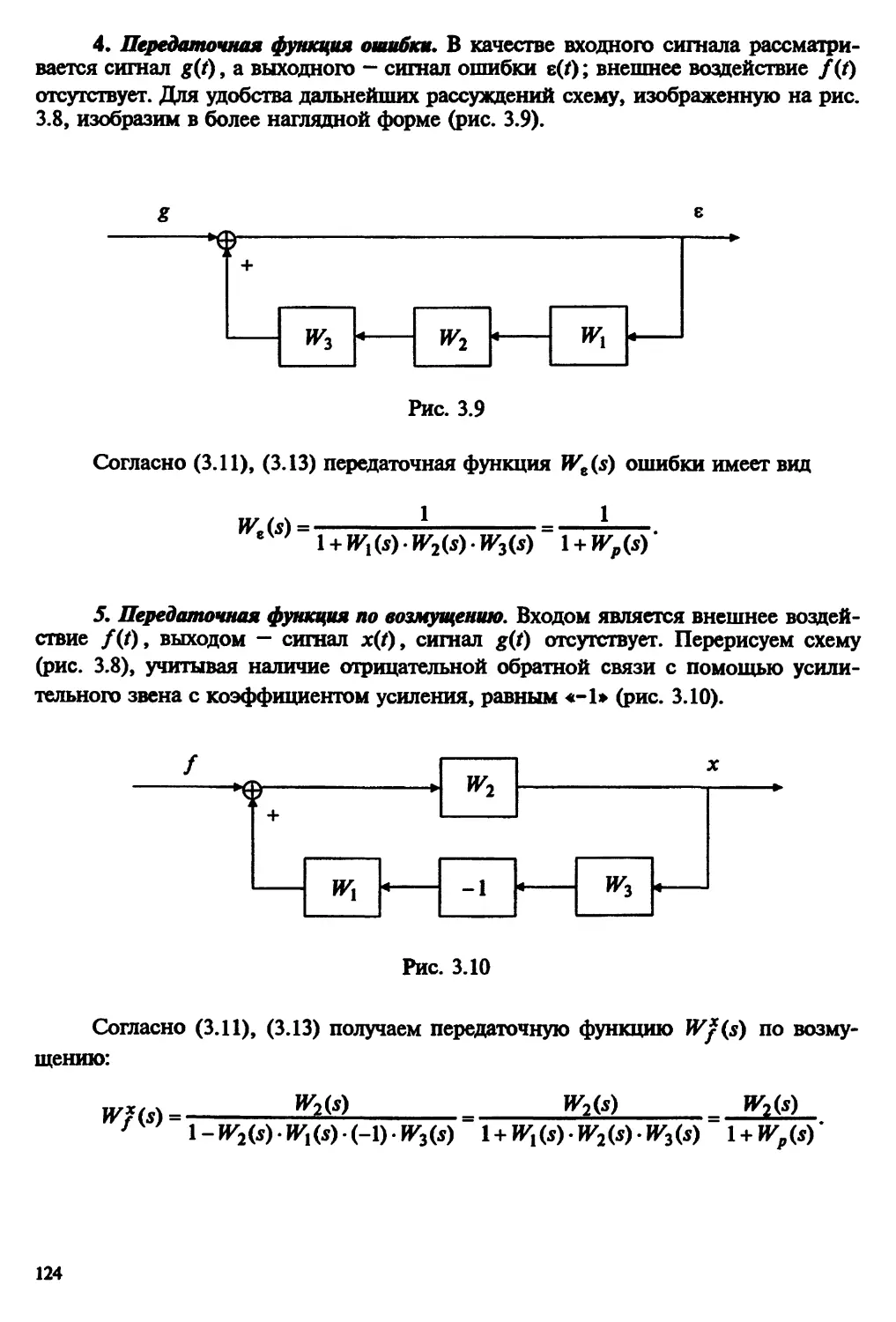
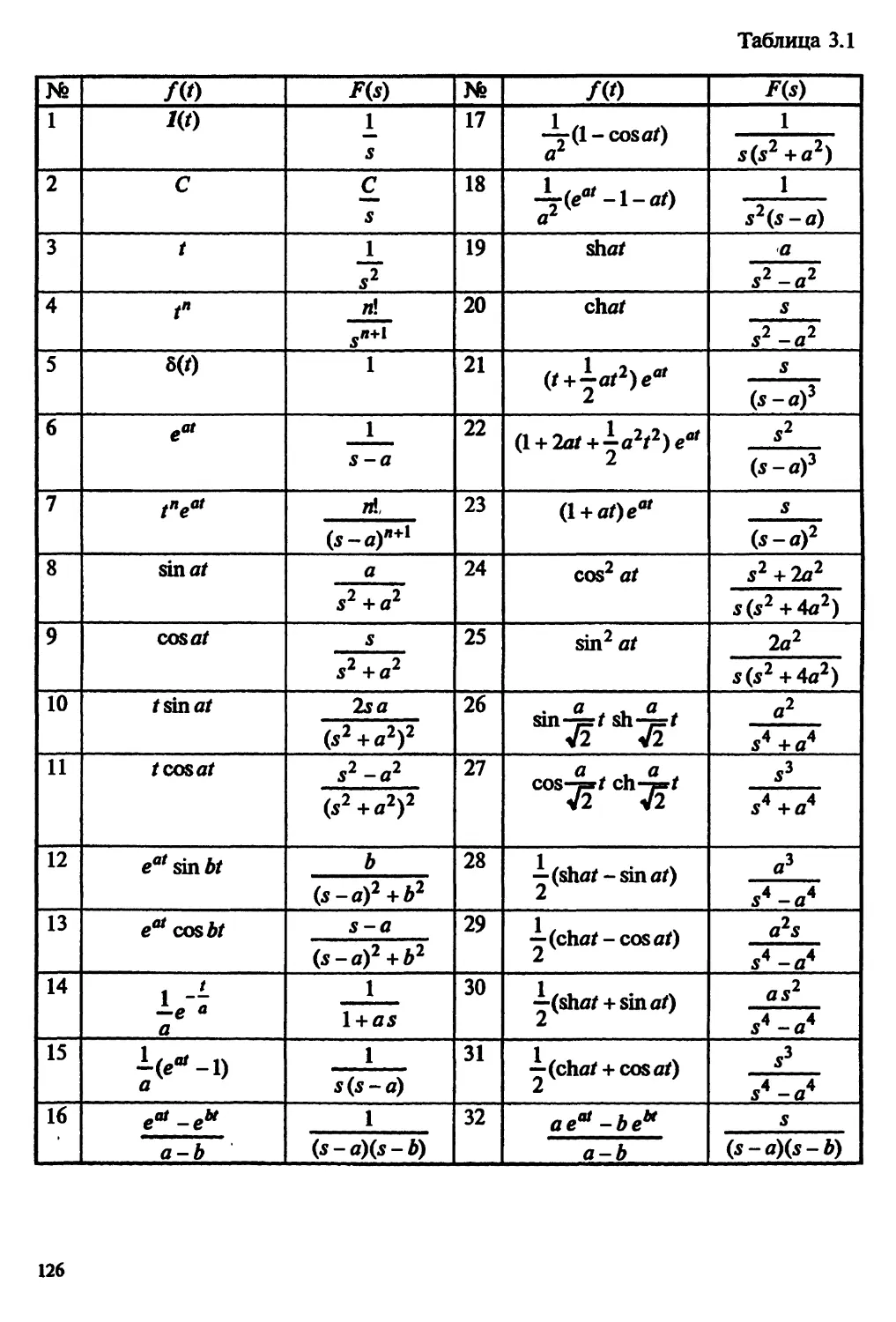
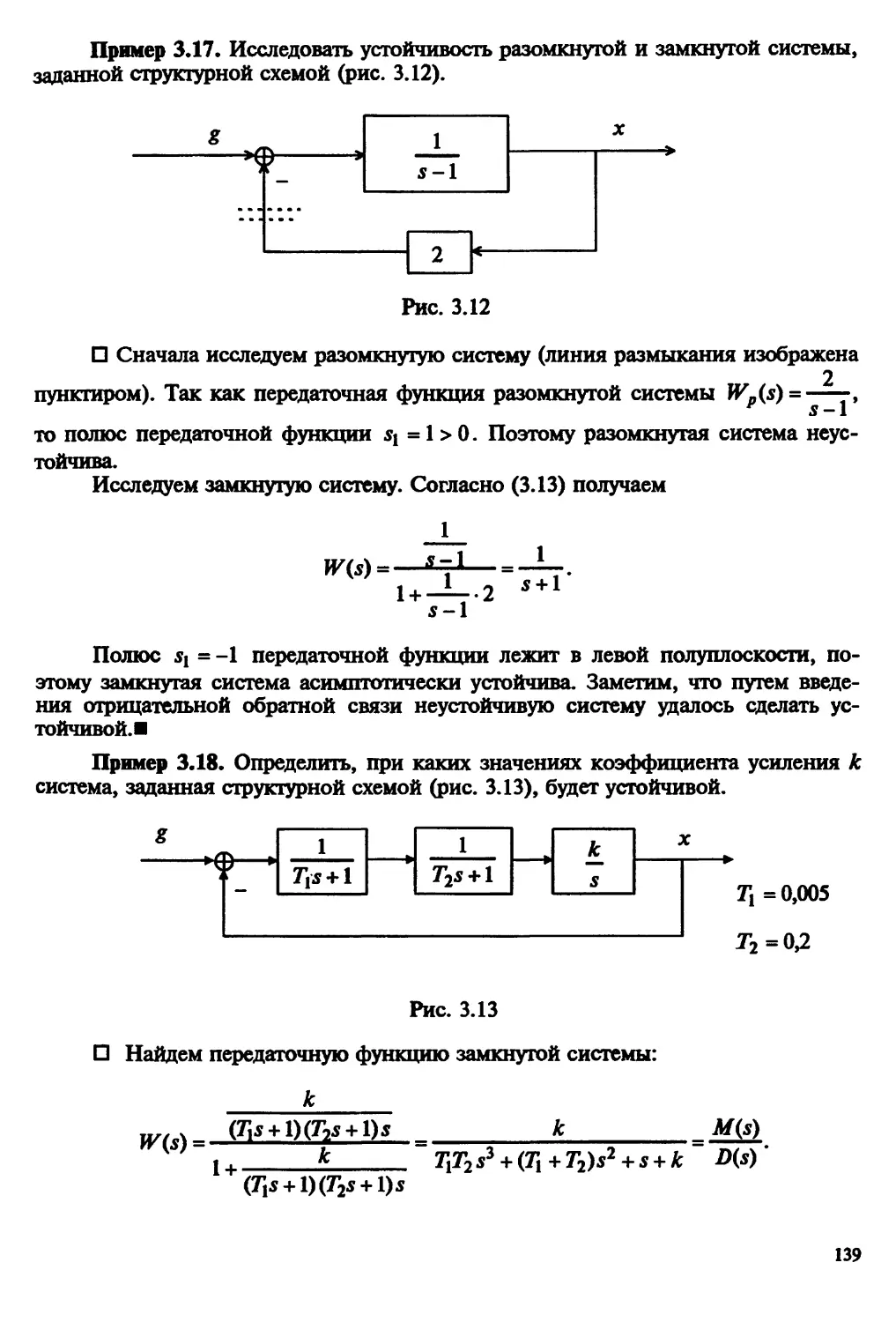
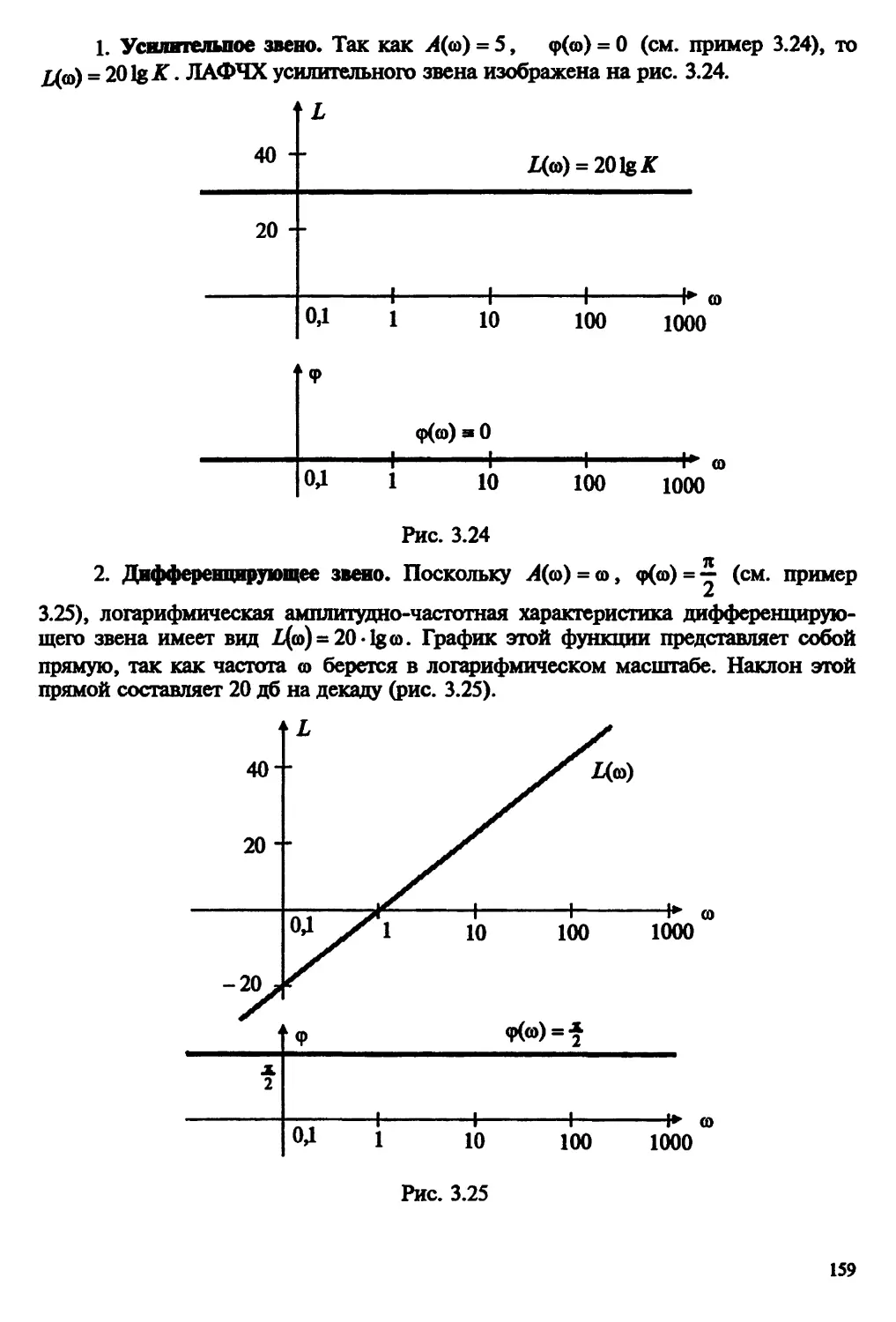
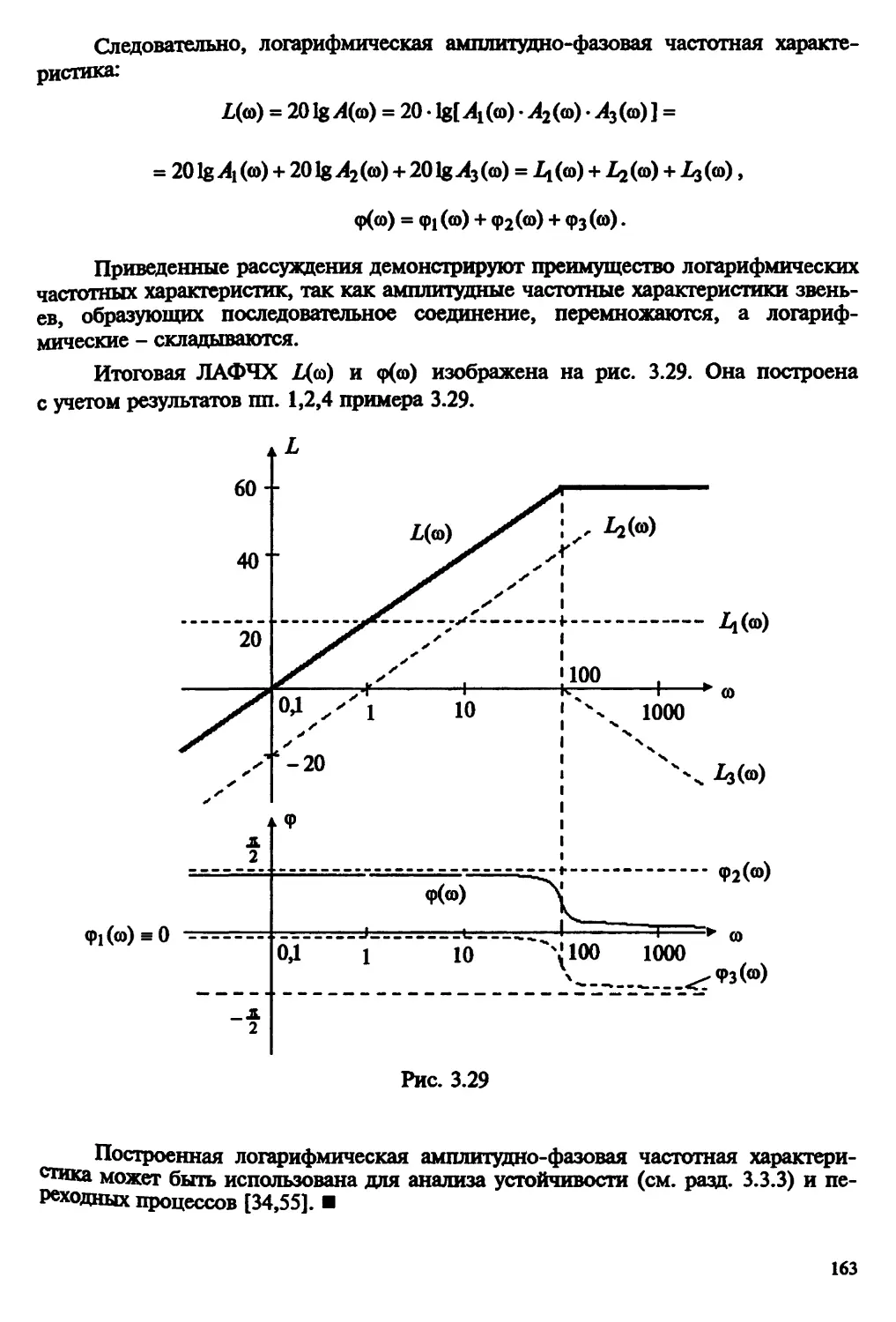
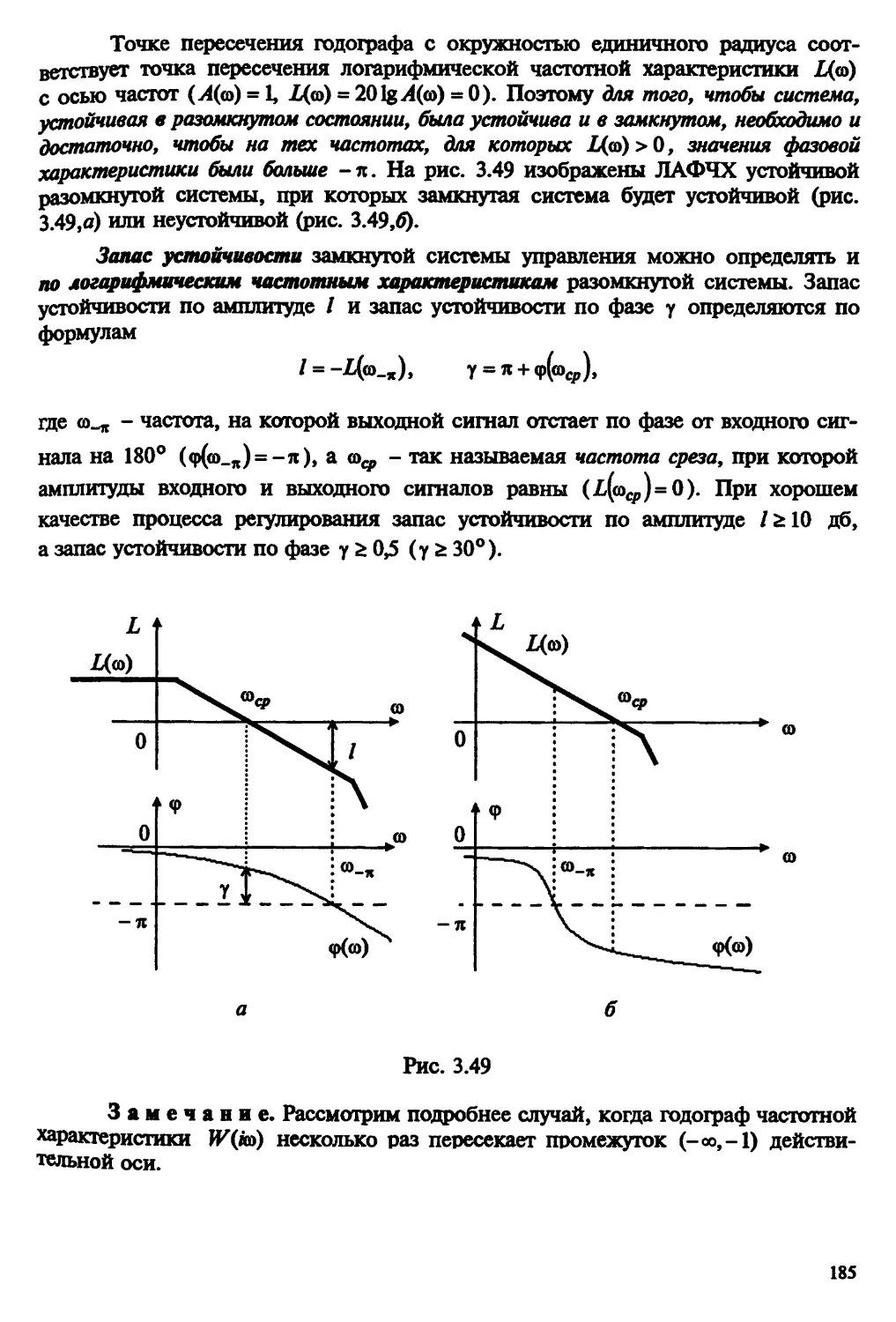
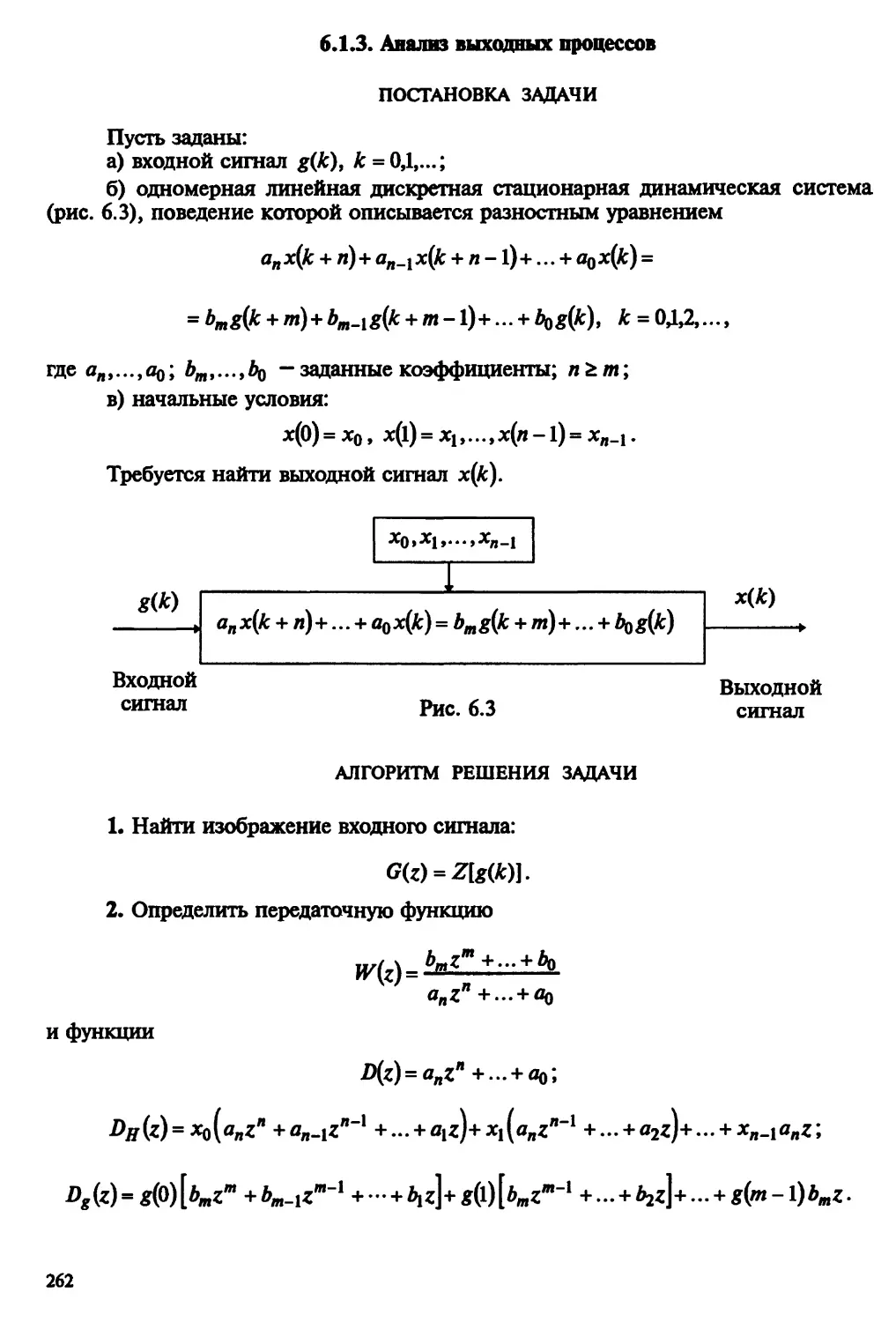
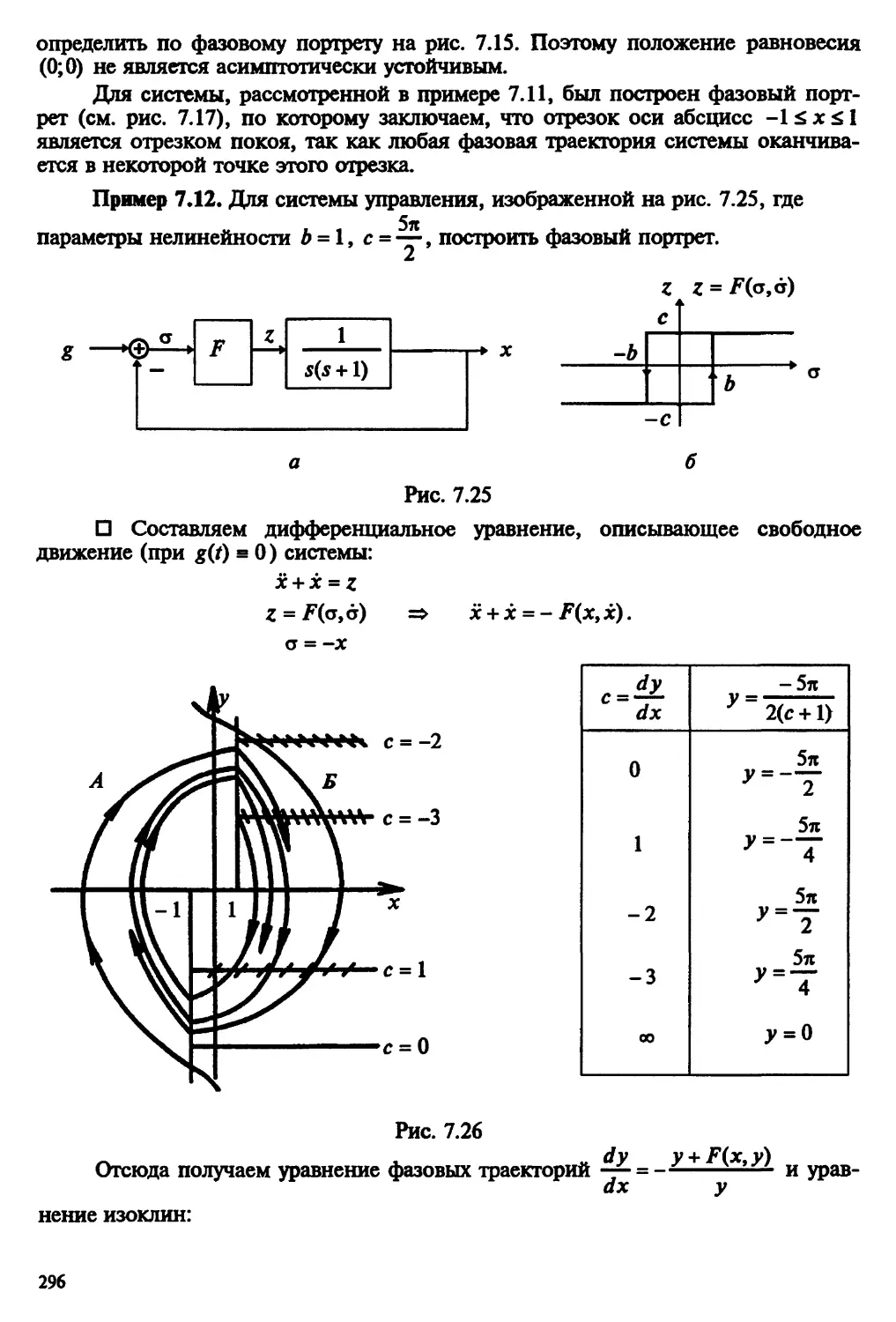
Теория управления в примерах и задач - Пантелеев А.В., Бортаковский А.С.

Автор: Пантелеев А.В. Бортаковский А.С.
Теги: исследование операций алгебра системы управления
ISBN: 5-06-004136-0
Год: 2003
Похожие
Методы оптимизации в примерах и задачах
Синергетическая теория управления
Прикладная теория оптимального управления. Оптимизация, оценка и управление.
Современная теория систем управления.
Текст
                    ПРИКЛАДНАЯ МАТЕМАТИКА
для ВТУЗов
А. В. Пантелеев
А.С. Бортаковский
ТЕОРИЯ
УПРАВЛЕНИЯ
В ПРИМЕРАХ
И ЗАДАЧАХ
Рекомендовано Учебно-методическим объединением
высших учебных заведений Российской Федерации
по образованию в области авиации, ракетостроения
и космоса в качестве учебного пособия для студентов
высших технических учебных заведений
Москва
«Высшая школа»
2003

УДК 519.8
ББК 22.14
П16
Рецензенты:
кафедра «Теория динамических систем»
Московского государственного университета им. М.В. Ломоносова
(зав. кафедрой академик РАН Д.В. Аносов);
д-р техн. наук, проф. В.Н. Баранов
(Московский авиационный институт
(государственный технический университет)
Пантелеев, А.В.
П16 Теория управления в примерах и задачах: Учеб. посо-
бие/А.В. Пантелеев, А.С. Бортаковский. — М.: Высш. шк., 2003.—
583 с: ил.
I8ВN 5-06-004136-0
Изложены методы решения задач описания, анализа и синтеза линейных и
нелинейных систем управления. Приведены примеры решения задач анализа выходных
процессов, устойчивости, управляемости и наблюдаемости линейных непрерывных
систем с использованием всех четырех форм математического описания систем:
дифференциальными уравнениями, переходными функциями, интегральными и
спектральными преобразованиями. Рассмотрены методы описания и анализа дискретных
линейных систем с помощью разностных уравнений и 2-преобразования. Описаны
алгоритмы исследования нелинейных систем управления методами фазовой
плоскости, гармонической и статистической линеаризации. Изложены задачи синтеза
оптимальных непрерывных, дискретных, непрерывно-дискретных детерминированных и
стохастических систем, задачи совместного оценивания и управления.
Для студентов, аспирантов технических вузов и университетов, изучающих
теорию управления и регулирования.
УДК 519.8
ББК 22.14
18ВК 5-06-004136-0 С ФГУП «Издательство «Высшая школа», 2003
Оригинал-макет данного издания является собственностью издательства «Высшая
школа», и его репродуцирование (воспроизведение) любым способом без согласия
издательства запрещается.

ОГЛАВЛЕНИЕ
Предисловие 9
Введение Ю
Часть I. ЛИНЕЙНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ 16
Глава 1. Описание и анализ непрерывных линейных систем с помощью
дифференциальных уравнений 16
1.1. Одномерные системы при детерминированных воздействиях 16
1.1.1. Описание сигналов и систем 16
1.1.2. Связь структурной схемы с дифференциальным уравнением 22
1.1.3. Дифференциальные уравнения соединений 25
1.1.4. Связь вход-выход 30
1.1.5. Анализ выходных процессов 33
1.2. Многомерные системы при детерминированных воздействиях 40
1.2.1. Описание сигналов и систем 40
1.2.2. Уравнения состояния и выхода соединений 42
1.2.3. Связи вход-состояние и вход-выход 47
1.2.4. Анализ выходных процессов 49
1.3. Линейные системы при случайных воздействиях 59
1.3.1. Описание сигналов и систем „ 59
1.3.2. Связи вход-выход 61
1.3.3. Анализ выходных процессов 63
1.4. Устойчивость, управляемость и наблюдаемость линейных
стационарных систем ¦ 67
1.4.1. Анализ устойчивости 67
1.4.2. Анализ управляемости и наблюдаемости 73
Глава 2. Описание и анализ непрерывных линейных систем с помощью
переходных функций 79
2.1. Одномерные системы при детерминированных воздействиях 79
2.1.1. Описание сигналов и систем 79
2.1.2. Связи вход-выход 80
2.1.3. Нахождение переходных функций 83
2.1.4. Импульсные переходные функции соединений 95
2.1.5. Анализ выходных процессов 98
2.2. Многомерные системы при детерминированных воздействиях 101
2.2.1. Описание сигналов и систем 101
2.2.2. Связи вход-состояние и вход-выход 102
2.2.3. Нахождение импульсных переходных функций 102
2.2.4. Анализ выходных процессов 103
2.3. Линейные системы при случайных воздействиях 107
2.3.1. Описание сигналов и систем 107
2.3.2. Связи вход-выход 107
2.3.3. Анализ выходных процессов 109
3

Глава 3. Описание и анализ непрерывных линейных систем с помощью
интегральных преобразований 114
3.1. Одномерные стационарные системы при детерминированных
воздействиях. Применение преобразования Лапласа 114
3.1.1. Описание сигналов и систем 114
3.1.2. Связь вход-выход 116
3.1.3. Передаточные функции соединений 117
3.1.4. Анализ выходных процессов 125
3.1.5. Анализ устойчивости 138
3.1.6. Анализ чувствительности 140
3.2. Многомерные стационарные системы при детерминированных
воздействиях. Применение преобразования Лапласа. 143
3.2.1. Описание сигналов и систем 143
3.2.2. Связи вход-состояние и вход-выход 144
3.2.3. Анализ выходных процессов 144
3.3. Одномерные стационарные системы. Применение преобразования
Фурье , 151
3.3.1. Описание сигналов и систем 151
3.3.2. Анализ выходных процессов при случайных воздействиях 164
3.3.3. Анализ устойчивости 169
Глава 4. Описание и анализ пепрерывных линейных систем с помощью
спектральных преобразований 194
4.1. Одномерные системы при детерминированных воздействиях 194
4.1.1. Описание сигналов и систем 194
4.1.2. Связь вход-выход 201
4.1.3. Двумерные нестационарные передаточные функции
соединений 202
4.1.4. Анализ выходных процессов 204
4.2. Одномерные системы при случайных воздействиях 211
4.2.1. Описание сигналов и систем 211
4.2.2. Связи вход-выход 211
4.2.3. Анализ выходных процессов 213
Глава 5. Описание и анализ дискретных линейных систем с помощью
разностных уравнений 218
5.1. Одномерные системы при детерминированных воздействиях 218
5.1.1. Описание сигналов и систем 218
5.1.2. Связь вход-выход 219
5.1.3. Анализ выходных процессов 222
5.2. Многомерные системы при детерминированных воздействиях 230
5.2.1. Описание сигналов и систем 230
5.2.2. Связи вход-состояние и вход-выход 230
5.2.3. Анализ выходных процессов 235

5.3. Одномерные системы при случайных воздействиях 241
5.3.1. Описание сигналов и систем 241
5.3.2. Связи вход-выход 241
5.3.3. Анализ выходных процессов 243
Глава 6. Описание и анализ дискретных линейных систем с помощью
2- преобразования 257
6.1. Одномерные стационарные системы при детерминированных
воздействиях 257
6.1.1. Описание сигналов и систем 257
6.1.2. Связь вход-выход 261
6.1.3. Анализ выходных процессов 262
6.2. Многомерные стационарные системы при детерминированных
воздействиях 267
6.2.1. Описание сигналов и систем 267
6.2.2. Связи вход-состояние и вход-выход 267
6.2.3. Анализ выходных процессов 268
Часть П. НЕЛИНЕЙНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ 275
Глава 7. Формы математического описания нелинейных систем управления 275
7.1. Описание нелинейных систем дифференциальными уравнениями 275
7.2. Нелинейные системы с одним нелинейным элементом 277
7.3. Описание нелинейных систем стохастическими дифференциальными
уравнениями 281
7.4. Поведение нелинейных систем на фазовой плоскости 286
Глава 8. Методы анализа нелинейных систем управления 301
8.1. Анализ выходных процессов методом линеаризации 301
8.1.1. Постановка задачи 301
8.1.2. Линеаризация нелинейных систем 301
8.1.3. Алгоритм анализа выходных процессов 304
8.2. Анализ автоколебаний методом гармонической линеаризации 307
8.2.1. Постановка задачи 307
8.2.2. Гармоническая линеаризация нелинейных элементов 308
8.2.3. Алгоритм анализа автоколебаний 312
8.3. Анализ абсолютной устойчивости 318
8.3.1. Постановка задачи 318
8.3.2. Условия абсолютной устойчивости 318
8.3.3. Алгоритм анализа абсолютной устойчивости 320
8.4. Анализ выходных процессов при случайных воздействиях методом
статистической линеаризации 325
8.4.1. Постановка задачи 325
8.4.2. Статистическая линеаризация нелинейных элементов 325
8.4.3. Алгоритм анализа выходных процессов 328

Часть Ш. ОПТИМАЛЬНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
334
Глава 9. Синтез оптимальных непрерывных детерминированных систем 334
9.1. Нахождение оптимального программного управления 334
9.1.1. Постановка задачи 334
9.1.2. Принцип максимума 336
9.1.3. Оптимальное управление линейными системами 364
9.2. Нахождение оптимального управления с полной обратной связью 366
9.2.1. Постановка задачи 366
9.2.2. Уравнение Беллмана 367
9.2.3. Синтез оптимальных линейных регуляторов 379
9.3. Нахождение оптимального управления с неполной обратной связью.... 388
9.3.1. Постановка задачи 388
9.3.2. Соотношения для нахождения оптимального управления 390
Глава 10. Синтез оптимальных непрерывных стохастических систем 402
10.1. Нахождение оптимального программного управления 402
10.1.1. Постановка задачи... 402
10.1.2. Стохастический принцип максимума 403
10.1.3. Оптимальное управление линейными системами 404
10.2. Нахождение оптимального управления с полной обратной связью 408
10.2.1. Постановка задачи 408
10.2.2. Уравнение Беллмана 409
10.2.3. Синтез оптимальных линейных регуляторов 412
10.3. Нахождение оптимального управления с неполной обратной связью... 415
10.3.1. Постановка задачи 415
10.3.2. Соотношения для нахождения оптимального управления 417
Глава 11. Синтез непрерывных линейных систем совместного оценивания
и управления 428
11.1. Оптимальное управление линейными непрерывными стохастическими
системами с накоплением информации о состоянии 428
11.1.1. Постановка задачи 428
11.1.2. Теорема разделения 429
11.1.3. Синтез оптимальных линейных регуляторов 429
11.2. Управление линейными непрерывными детерминированными
системами с накоплением информации о состоянии 433
11.2.1. Постановка задачи 433
11.2.2. Синтез наблюдателей состояния 435
11.2.3. Синтез линейных регуляторов 437
Глава 12. Синтез оптимальных дискретных детерминированных систем 440
12.1. Нахождение оптимального программного управления 440
12.1.1. Постановка задачи 440
12.1.2. Дискретный принцип максимума 441
с

12.2. Нахождение оптимального управления с полной обратной связью 452
12.2.1. Постановка задачи 452
12.2.2. Уравнение Беллмана 453
12.2.3. Синтез оптимальных линейных регуляторов 455
Глава 13. Синтез оптимальных дискретных стохастических систем 461
13.1. Нахождение оптимального программного управления 461
13.1.1. Постановка задачи 461
13.1.2. Стохастический дискретный принцип максимума 462
13.1.3. Оптимальное управление линейными системами 463
13.2. Нахождение оптимального управления с полной обратной связью 464
13.2.1. Постановка задачи 464
13.2.2. Уравнение Беллмана 465
13.2.3. Синтез оптимальных линейных регуляторов 466
Глава 14. Синтез дискретных линейных систем совместного оценивания
и управления 473
14.1. Оптимальное управление линейными дискретными стохастическими
системами с накоплением информации о состоянии 473
14.1.1. Постановка задачи 473
14.1.2. Теорема разделения 474
14.1.3. Синтез оптимальных линейных регуляторов 475
14.2. Управление линейными дискретными детерминированными
системами с накоплением информации о состоянии 478
14.2.1. Постановка задачи 478
14.2.2. Синтез наблюдателей состояния 480
14.2.3. Синтез линейных регуляторов 482
Глава 15. Синтез оптимальных непрерывно-дискретных детерминированных
систем 487
15.1. Нахождение оптимального программного управления 487
15.1.1. Постановка задачи 487
15.1.2. Необходимые условия оптимальности 488
15.2. Нахождение оптимального управления с полной обратной связью 491
15.2.1. Постановка задачи 491
15.2.2. Соотношения для нахождения оптимального управления 492
15.2.3. Синтез оптимальных линейных регуляторов 495
Глава 16. Оптимальное управление пучками траекторий 501
16.1. Описание математической модели движения пучков 501
16.2. Нахождение оптимального гарантирующего управления 502
16.2.1. Постановка задачи 502
16.2.2. Необходимые условия оптимальности 503
16.2.3. Синтез оптимальных линейных регуляторов 508
7

16.3. Нахождение оптимального в среднем управления 514
16.3.1. Постановка задачи 514
16.3.2. Необходимые условия оптимальности 515
16.3.3. Синтез оптимальных линейных регуляторов 517
Глава 17. Синтез оптимальных непрерывных систем по минимаксному
критерию 521
17.1. Нахождение оптимального программного управления 521
17.1.1. Постановка задачи 521
17.1.2. Необходимые условия оптимальности 523
17.2. Нахождение оптимального позиционного управления 527
17.2.1. Постановка задачи 527
17.2.2. Уравнение Айзекса 528
17.2.3. Синтез оптимальных линейных регуляторов 531
Глава 18. Синтез оптимальных логико-динамических систем 535
18.1. Описание математической модели логико-динамической системы 535
18.2. Нахождение оптимального управления с полной обратной связью 536
18.2.1. Постановка задачи 536
18.2.2. Достаточные условия оптимальности 537
18.3. Нахождение оптимального программного управления 540
18.3.1. Постановка задачи 540
18.3.2. Соотношения для нахождения оптимального управления 540
18.4. Синтез автоматной части логико-динамической системы 543
18.4.1. Постановка задачи 543
18.4.2. Необходимые условия оптимальности... 544
18.4.3. Достаточные условия оптимальности 547
Глава 19. Синтез оптимальных непрерывных детерминированных систем
с дискретным управлением 549
19.1. Нахождение оптимального дискретного программного управления 549
19.1.1. Постановка задачи 549
19.1.2. Соотношения для нахождения оптимального управления 550
19.2. Нахождение оптимального дискретного управления с полной
обратной связью 559
19.2.1. Постановка задачи 559
19.2.2. Соотношения для нахождения оптимального управления 560
19.3. Нахождение оптимального дискретного управления с неполной
обратной связью 564
19.3.1. Постановка задачи 564
19.3.2. Соотношения для нахождения оптимального управления 565
Ответы 572
Литература 581

ПРЕДИСЛОВИЕ
Нашему учителю, профессору
Виктору Владимировичу Семенову
посвящается
Книга включает методы решения задач описания, анализа и синтеза
линейных и нелинейных непрерывных, дискретных и непрерывно-дискретных
систем управления. Она состоит из трех частей, которые охватывают основные
разделы курса 'Теория автоматического управления", читаемого на факультете
"Прикладная математика и физика" Московского авиационного института.
Первая часть содержит методики и примеры решения задач анализа
выходных процессов, устойчивости, чувствительности, управляемости и
наблюдаемости линейных систем управления. При этом используются все известные
формы математического описания непрерывных систем: дифференциальными
уравнениями, переходными функциями, интегральными и спектральными
преобразованиями, а также две формы описания дискретных систем: разностными
уравнениями и2- преобразованием.
Вторая часть посвящена исследованию нелинейных систем управления,
описываемых дифференциальными и разностными уравнениями, а также
структурными схемами с одним нелинейным элементом. Рассматриваются задачи
анализа выходных процессов при детерминированных и случайных воздействиях
методами линеаризации в окрестности опорной траектории и статистической
линеаризации, анализа автоколебаний методом гармонической линеаризации и
анализа абсолютной устойчивости.
В третьей части нашли отражение методики решения задач оптимального
управления детерминированными и стохастическими системами при различной
информированности о векторе состояния, а также алгоритмы синтеза систем
совместного оценивания и управления.
Данная книга является обобщением ранее изданных учебных пособий [30,
35,36,48,49] и содержит результаты, приведенные в монографиях и учебниках
авторов [30,37,39,40,51-53]. Вопросы анализа линейных систем управления
с помощью дифференциальных уравнений более подробно изложены в [40],
решение задач синтеза оптимальных непрерывных систем при неполной
информации, дискретных, непрерывно-дискретных и логико-динамических систем
описано в [36].
Изложение построено по единой схеме, включающей краткое описание
основных элементов постановок задач, алгоритмы решения и подробный анализ
типовых и нетиповых примеров. Предлагаются задачи для самостоятельного
решения, в том числе зависящие от параметров т — номера учебной группы и п
- номера студента по списку группы.
Книга может быть использована как для изучения под руководством
преподавателя, так и при самостоятельном освоении курса, поскольку содержит весь
необходимый теоретический материал и большое количество детально
разобранных примеров и задач.
9

ВВЕДЕНИЕ
В.1. Основные понятия и определения
Система управления (СУ) - совокупность управляющего устройства (УУ) и
объекта управления (ОУ), действия которой направлены на достижение
некоторого результата — цели управления (рис. В.1).
Целью управления могут быть: поддержание заданной высоты полета
самолета, подъем самолета на заданную высоту по желаемой траектории, сближение
самолета с мишенью, обеспечивающее минимальный промах и др.
:
УУ
ОУ
СУ:
Рис. В.1
Управляющее устройство реализует следующие функции:
а) сбор информации;
б) переработку информации;
в) передачу информации;
г) выработку команд управления.
Функциональная схема системы управления, каждому блоку которой
соответствует определенное функциональное назначение, изображена на рис. В.2.
Информация
о желаемом
движении
объекта
Устройство
переработки
информации
Исполнительное
устройство
Объект
управления
УУ
Источник информации
о текущем положении
объекта
Рис. В.2
В зависимости от предметной области функциональная схема системы
управления наполняется конкретным содержанием. Например, на рис. В.З
приведены схемы систем управления углом тангажа самолета, производством товара,
процессом обучения.
10

Датчик
угла
Усилитель
Ы ДвигательМРедуктор
Рулевая Ы Летательный
машинка[ | аппарат
Товар
Спрос
Переработка
информации
т
Производственное
задание
ГТпр>ттпгъ^р>1л«р> и.
.Ц Производство
1 товара
Модель требуемых
знаний
Сравнение
1 ;
1
Методика
обучения
Сознание
Модель текущих
знаний
Знания
Рис. В.З
Общим принципом формирования систем управления является принцип
обратной связи: управление объектом осуществляется на основе получения
информации о желаемом и текущем движениях объекта и их сравнении для нахождения
ошибки и выработки такого управляющего воздействия, чтобы ошибка с течением
времени стремилась к нулю и выполнялась конечная цель управления.
В.2. Классиф]
систем управления по виду их математической модели
Математическая модель системы управления — это пара "оператор системы
и модель внешних воздействий". Оператором системы называется закон, в
соответствии с которым система преобразует внешнее (входное) воздействие # в
выходной сигнал х (рис. В.4).
Я
Внешнее
воздействие
(входной сигнал)
Оператор
системы
Выходной
сигнал
Рис. В.4
и

По виду оператора системы управления делятся на:
а) линейные и нелинейные;
б) непрерывные, дискретные, непрерывно-дискретные;
в) нестационарные и стационарные;
г) детерминированные и стохастические;
д) одномерные и многомерные;
е) с сосредоточенными и с распределенными параметрами.
Внешние воздействия делятся на:
а) непрерывные (функции непрерывного аргумента) и дискретные (функции
дискретного аргумента);
б) детерминированные и случайные;
в) одномерные и многомерные.
Чтобы классифицировать конкретную систему, нужно указать на шесть
классов, к которым принадлежит оператор системы, и на три класса, к которым
принадлежат внешние воздействия. Например, она может оказаться линейной
непрерывно-дискретной нестационарной детерминированной одномерной с
сосредоточенными параметрами при непрерывных случайных одномерных
внешних воздействиях.
Поясним названия классов операторов на примере описания систем
дифференциальными или разностными уравнениями. Линейные системы
описываются линейными дифференциальными уравнениями, нелинейные —
нелинейными дифференциальными уравнениями. Непрерывные системы описываются
дифференциальными уравнениями; дискретные — разностными; непрерывно-
дискретные — дифференциально-разностными уравнениями. Нестационарные
системы описываются уравнениями с переменными коэффициентами,
стационарные — уравнениями с постоянными коэффициентами. Детерминированные
системы описываются уравнениями, коэффициенты которых являются
детерминированными величинами или функциями времени, стохастические —
стохастическими уравнениями. Одномерные системы имеют один вход и один выход,
многомерные системы имеют суммарное число входов и выходов, большее двух.
Наконец, системы с сосредоточенными параметрами описываются
обыкновенными дифференциальными уравнениями, с распределенными параметрами —
уравнениями в частных производных.
В.З. Классификация задач расчета систем управления
Задачи расчета систем управления делятся на три группы.
1. Задачи анализа: по заданному входному воздействию и оператору
системы исследовать закон изменения выходного сигнала (рис. В.5,а).
2. Задачи синтеза: по желаемому выходу найти входной сигнал и оператор
системы (неопределенные параметры оператора) (рис. Ъ.5,б).
3. Задачи идентификации: по входному и выходному сигналам определить
оператор системы (рис. В.5,в).
? ?
Вход
Оператор
системы
Выход Вход
Оператор
системы
Выход Вход
Оператор
системы
Выход
б
Рис. В.5
12

Данное учебное пособие включает методы решения задач описания,
анализа и синтеза линейных и нелинейных непрерывных, дискретных и непрерывно-
дискретных систем управления. Оно состоит из трех частей.
Первая часть содержит методики и примеры решения задач анализа
линейных систем управления. При этом используются все известные формы
математического описания непрерывных систем: дифференциальными уравнениями,
переходными функциями, интегральными и спектральными преобразованиями, а
также две формы описания дискретных систем: разностными уравнениями и2-
преобразованием.
Задачи анализа линейных систем:
а) анализ выходных процессов (основная задача анализа);
б) анализ устойчивости;
в) анализ чувствительности;
г) анализ управляемости;
д) анализ наблюдаемости.
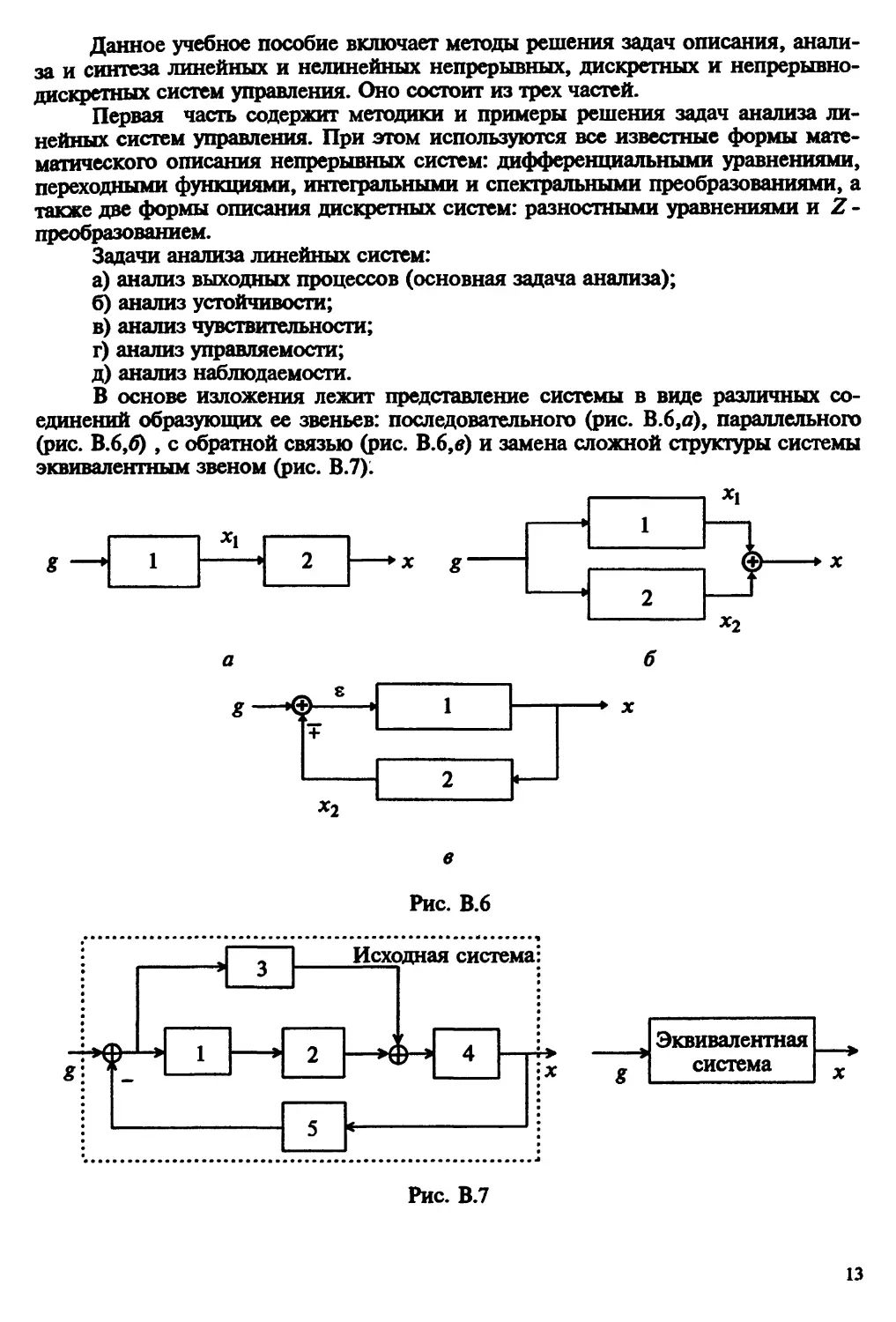
В основе изложения лежит представление системы в виде различных
соединений образующих ее звеньев: последовательного (рис. В.6,о), параллельного
(рис. В.6,ф , с обратной связью (рис. В.6,*) и замена сложной структуры системы
эквивалентным звеном (рис. В.7).
*1
*1
1
э-
-> X
*2
*Ф
*2
-> X
8\
Л 3
в
Рис. В.6
Исходная система:
¦Н 1 Н 2 —>$-*\ 4
5 К-
Эквивалентная
система
Рис. В.7
13

Вторая часть пособия посвящена исследованию нелинейных систем
управления, описываемых дифференциальными и разностными уравнениями, а также
структурными схемами с одним нелинейным элементом (рис. В.8).
Рассматриваются задачи анализа выходных процессов при детерминированных и случайных
воздействиях методами линеаризации в окрестности опорной траектории и
статистической линеаризации, анализа автоколебаний методом гармонической
линеаризации и анализа абсолютной устойчивости.
КЭ—ч
Нелинейный
элемент
Линейная часть
системы
Рис. В.8
В третьей части нашли отражение методики решения задач оптимального
управления детерминированными и стохастическими системами при различной
информированности о векторе состояния, а также алгоритмы синтеза систем
совместного оценивания и управления. Типовая схема оптимальной системы
изображена на рис. В.9. Каждая постановка задачи синтеза оптимального
управления включает математическое описание всех блоков, образующих систему
управления.
Краевые
условия
Внешние
воздействия
Погрешности
измерений, помехи!
Модель объекта
управления
Промежуток времени
функционирования
Управляющее
воздействие
Состояние
Модель измерительной!
системы
Измерение
Ограничения
на состояние
и управление
Алгоритм управления
х
Цель управления
Рис. В.9
14

Постановка задачи синтеза оптимальной динамической системы содержит
следующие основные элементы.
1. Модель объекта управления. Обычно описывается уравнением состояния,
отражающим применение известных законов физики и техники, например
стохастическим или обыкновенным дифференциальным уравнением, уравнением
с частными производными, разностным, дифференциально-разностным
уравнением. Параметры модели задаются либо статистическими характеристиками,
либо множествами возможных значений. Состояние модели может задаваться,
например, вектором, объединяющим характерные изменяющиеся параметры
объекта, или функцией, описывающей поведение модели в пространстве и времени.
2. Краевые {начальные и конечные) условия. Они могут быть
детерминированными, случайными (определяться своими статистическими
характеристиками) или описываться множествами возможных значений.
3. Внешние воздействия. Как правило, описываются статистическими
характеристиками или множествами возможных значений.
4. Промежуток времени функционирования системы. Может быть заданным
конечным или бесконечным, случайным, оптимизируемым и т.д.
5. Ограничения на состояние и управление. Они обычно задаются
множествами их допустимых значений.
6. Модель измерительной системы. Описывается, например, функциями или
операторами состояния, стохастическими дифференциальными уравнениями.
Входом модели является состояние, а выходом — значение измерений.
7. Погрешности измерения, помехи. Как правило, описываются
статистическими характеристиками или множествами возможных значений.
8. Алгоритм управления. Определяется характер использования информации
об измерении, способ выработки и приложения управляющих воздействий.
Алгоритм управления вырабатывает управляющее воздействие по получаемой
информации об измерениях.
9. Цель управления. Как правило, цель управления описывается некоторым
критерием качества и отражает требования, предъявляемые проектировщиком к
оптимальной системе (наилучшей с точки зрения выбранного критерия).
Третья часть учебного пособия посвящена изложению не только
классических, но и новых результатов в области синтеза оптимальных систем с
неполной информацией о состоянии, непрерывно-дискретных и логико-
динамических систем.
Данная книга является обобщением ранее изданных учебных пособий [30,
35-36,49] и содержит результаты, приведенные в монографиях [37,51-531.
Вопросы анализа линейных систем управления с помощью дифференциальных
уравнений и интегральных преобразований более подробно изложены в [39,40].

Часть I. ЛИНЕЙНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Глава 1. ОПИСАНИЕ И АНАЛИЗ НЕПРЕРЫВНЫХ
ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
1.1. ОДНОМЕРНЫЕ СИСТЕМЫ ПРИ ДЕТЕРМИНИРОВАННЫХ
ВОЗДЕЙСТВИЯХ
1.1.1. Описание сигналов и систем
1. Описание сигналов. Сигналы, действующие в системах управления, во
временной области описываются различными функциями, в том числе
обобщенными. Выделяют два типовых сигнала: импульсное воздействие, которое
описывается дельта-функцией б(/ - т), и единичную ступенчатую функцию /(* - т).
1. Дельта-функция (асимметричная) определяется формулой [20]
//<0«(/-т)А«
Дт + 0), т€[а,*),
@, т€(-оо,а)Щ*, + оо),
справедливой для любой кусочно-непрерывной функции /(/).
Аналогично определяются производные дельта-функции:
(_1)*/<*>(т + 0), т€[а,5),
A1)
\ №*№{*-*)* =
0, т€(-со,д)Щ*, + оо),
где /@ — любая функция, имеющая кусочно-непрерывную производную
соответствующего порядка.
2. Единичная ступенчатая функция
Д'-т)
[1, />т,
A.2)
Момент т соответствует моменту приложения входного воздействия к
системе управления (рис. 1.1).
Типовые сигналы связаны
соотношением
*('-*)
/б(т!-т)Ж1 = /(/-т),
Рис. 1.1
т.е. дельта-функцию 6(/ - т) можно считать
производной от единичной ступенчатой
функции 7(/ - т).
16

2. Описание систем. Непрерывные процессы, протекающие в системах
управления, могут быть описаны обыкновенными дифференциальными
уравнениями с соответствующими начальными условиями. Тоща, если известен
входной сигнал, выходной сигнал определяется б результате решения задачи
Коши для обыкновенного дифференциального уравнения.
Одномерная линейная непрерывная нестационарная система управления
описывается дифференциальным уравнением
М0^^+.-+^@«@-*«@^^+...+М0«(в A.3)
с начальными условиями
*('о) = *6, *(Г0) = *о,..., х(л-1)^о) = 4Л")' A-4)
где $(/) — входной сигнал; *(/) — выходной сигнал; / — время; ал(О»—»0о(О»
6л,(/),...,4>@ — коэффициенты левой и правой частей уравнения; п и т —
порядки старших производных выходного и входного сигналов соответственно;
/0 — момент начала функционирования системы.
Если коэффициенты уравнения постоянны, система называется линейной
стационарной:
ап2^+..- + *ох@ = Ьт2-^ + .-. + Ь08(*)- A.5)
В операторной форме уравнение A.3) имеет вид
ПЬАхЮ-ЗЦрАя®,
ще р = — — символ, обозначающий операцию дифференцирования; 1)(р,*),
ш
М(р,$ — дифференциальные операторы левой и правой частей уравнения A.3):
ДОМ) = *л@рй+...+*1@р+ *<)('), М(р,*) = 1ъ@ря+--*Шр + Ш-
Уравнение A.5) в операторной форме имеет вид
Я(р)х(*) = МШ(*)> A6)
где /)(р) = алрл+...+д1р + а0 , М(р) = Ътрт+...+ Ъур + Ьп .
Из операторной формы уравнения следует способ изображения
стационарной системы на структурных схемах (рис. 1.2).
р(р)
Рис. 1.2
17

Сложные системы управления, как правило, состоят из элементарных и
типовых звеньев.
1. Усилительное злено (рис. 1.3,д) описывается уравнением
(Ь7)
где К(*) — коэффициент усиления. Если звено стационарное, то К(г) = К = соп$1.
Примеры усилительных звеньев:
а) трансформатор (рис. 1.3,6), где выходное напряжение связано с входным
соотношением: 11выхA)« КЦ^);
б) редуктор (рис. 1.3,*), где угловые скорости выходного и входного вала
связаны через соотношение чисел зубьев шестерен:
а>2 =—«>1 = АГ(/)<»1,
п2
КA) = К=2^.
п2
•и-
*(он *<о
]-**> "«^11
«I
Ю2
1
ит,
5
Рис. 1.3
2. Диффереюцчуют/к звено (рис. 1.4) описывается уравнением
*(') =
я2
A.8)
Выходной сигнал равен производной входного сигнала. Уравнение A.8) в
операторной форме имеет вид х(/) = р&A).
*(»
-СП-
*<» *(')-
2.
р
х«)
:\..*
Я
\*м
Рис. 1.4 Рис. 1.5
3. Интегрирующее звено (рис. 1.5,а) описывается уравнением
Л
¦*(>).
A9)
18

Выходной сигнал получается в результате интегрирования входного. В
операторной форме уравнение A.9) имеет вид
/>*(') = *(') или х@ = -*@.
Р
Для примера рассмотрим процесс изменения угловой скорости о» диска
с моментом инерции / под действием управляющего момента внешних сил М
из состояния покоя (рис. 1.5,6).
Уравнение вращательного движения: /—=М, а>(/о) = 0. Отсюда имеем
До) М М ,« ЛЧ
—=—, а если положить х = со, # в — > получаем уравнение A.9).
ш / /
4. ^емо чистого запаздывания описывается уравнением х@ = &('-?)> гДе
у — величина запаздывания выходного сигнала относительно входного.
5. Апериодическое звено (рис. 1.6,я) описывается уравнением
^+*(,) = *@,
A.10)
где Т — действительное положительное число, называемое постоянной времени.
Операторная форма записи уравнения A.10) имеет вид
G> + 1) *(/) = *(/).
В качестве примера рассмотрим схему с заданным сопротивлением Я и
емкостью С (рис. 1.6,6). В начальный момент времени емкость не заряжена.
*(')-
7> + 1
*@ Ц
Г = /?С
Рис. 1.6
Требуется составить дифференциальное уравнение, описывающее
изменение выходного напряжения при условии подачи на вход постоянного
напряжения единичной величины.
Запишем уравнение второго закона Кирхгофа, соотношение, связывающее
ток и напряжение на емкости, и начальные условия:
19

Отсюда следует
/ = с—***-,
яс^^+и~*ю=и«ю>
Используя обозначения Г = КС, х = ^вых , # = ^ , получаем уравнение
вида A.10). Если #(/) = #«@ = /(/), то решение этого линейного неоднородного
дифференциального уравнения имеет вид
На рис. 1.6, в изображены входной и выходной (заметим, что он
непериодический) сигналы.
6. Колебательное звено (рис. 1.7,а) описывается уравнением
Г2<^ + 24ГМ> + Х(,) = Я(,),
(Ы1)
где Т > 0 — постоянная времени; § — коэффициент демпфирования, \ % \ < 1.
Для примера рассмотрим схему с известными параметрами Я, Ь, С (рис.
1.7,6). В начальный момент времени ток в цепи отсутствует, а емкость не
заряжена. Требуется составить дифференциальное уравнение, описывающее
изменение выходного напряжения.
8('Ц
1
Т2р2 + 2$Тр + 1
>х(*) V,
а б в
Рис. 1.7
Запишем уравнение второго закона Кирхгофа, соотношение, связывающее
ток и напряжение на емкости, и начальные условия:
1^ + /Л + ^ш=^
"«а@)=0,
/=с^-
Л
/@) = 0.
20

Отсюда получаем
По сравнению с A.11) здесь Г = 71с, $ = -71/7" > ^«*=х» и*х = &-
График типовой реакции рассматриваемой схемы на единичное ступенчатое
входное напряжение при комплексных корнях характеристического уравнения
с отрицательной вещественной частью и нулевых начальных условиях изображен
на рис. 1.7,*.
7. Неустойчивое апериодическое звено (рис. 1.8,а) описывается уравнением
где Г > 0 — число, называемое постоянной времени.
8. Неустойчивое колебательное звено (рис. 1.8,6) описывается уравнением
где Т > О — постоянная времени; В, — коэффициент демпфирования.
9. Дифференцирующее звено первого порядка (рис. 1.8,*) описывается
уравнением
где Г— постоянная времени.
10. Дифференцирующее звено второго порядка (рис. 1.8,г) описывается
уравнением
40 = Г>^+24гМЦ*@.
Л2 Л
Гр-1
Г2р2+2$7>-1
* *
—> —
7> + 1
Т2р2+1^Тр + \
Рис. 1.8
Замечание» Первые четыре звена называются элементарными, так
как они не могут быть представлены через другие звенья.
21

1.1.2. Связь структурной схемы с дифференциальным уравнением
1. Построение структурной схемы по дифференциальному уравнению.
Структурные схемы строятся с помощью элементарных, типовых звеньев и
сумматоров, описывающих преобразование сигналов. Они служат одним из
языков описания систем управления. По структурным схемам, как правило,
находится эквивалентный оператор системы управления, а затем решаются
различные задачи анализа.
АЛГОРИТМ ПОСТРОЕНИЯ СТРУКТУРНОЙ СХЕМЫ
1. Выразить член со старшей производной из дифференциального
уравнения A.3) и представить полученное соотношение с помощью сумматора,
дифференцирующих и усилительных звеньев.
2. Все низшие производные получить как сигналы на соответствующих
выходах последовательно соединенных интегрирующих звеньев.
3. Начальные условия A.4) представить как постоянные во времени
воздействия, приложенные на выходах интегрирующих звеньев.
Пример 1.1. Построить структурную схему системы, описываемой
дифференциальным уравнением
4х-3х + х = 2#
с начальными условиями х@) = Хо, х@)=хо.
? Выразим из уравнения член со старшей производной:
4дс = 2# + 3х-х.
Изобразим схему получения сигнала 45с (рис. 1.9). С помощью
усилительного звена с коэффициентом усиления 1/4 получим сигнал х. Построим теперь
прямую цепь схемы, последовательно преобразовывая сигнал х
интегрирующими звеньями. Добавляя на выходах интегрирующих звеньев соответствующие
начальные условия, получаем часть прямой цепи схемы, в которой присутствуют
выходной сигнал х и его производные х, х. Изображаем сумматор, выходным
сигналом которого служит 4х. На этом сумматоре нужно реализовать равенство
4х = 2# + 3х-х
*о
*о
Г11
4
X
1
^
^
э
)
ц&
Р\УП
Рис. 1.9

Для этого добавляем к прямой цепи соединение дифференцирующего и
усилительного звеньев, которые из входного сигнала # позволяют получить
нужный сигнал 2# на входе сумматора. Сигналы х и Зх подаем на сумматор с
соответствующим знаком, используя обратные связи. Таким образом, получаем
структурную схему (рис. 1.9), соответствующую заданному дифференциальному
уравнению.»
Пример 1.2. Построить структурную схему системы, описываемой
дифференциальным уравнением
5х + /х + /2х = # + 2#
с начальными условиями х@) = Хо, *@) = хо, х@) = х$.
О Выразим из уравнения член со старшей производной:
5'х=8 + 2х-1х-12х.
Согласно алгоритму получим структурную схему системы (рис. 1.10)Л
п
5
X
*
1И-
-Ж
рЧЬгп
*0 х0 х0
Рис. 1.10
Пример 1.3. Построить структурную схему системы, описываемой
дифференциальным уравнением
х + х + х = #.
? Выразим из уравнения член со старшей производной:
х=#-х-х
и с помощью алгоритма получим схему (рис. !.!!).¦
*—-1
х0
| р 1
Рис. 1.11
23

2. Составление дифференциального уравнения по структурной схеме. Для
записи дифференциального уравнения следует обозначить на схеме все
промежуточные сигналы, записать уравнения для каждого звена и для каждого сумматора
и из полученной системы дифференциальных и алгебраических уравнений
исключить промежуточные переменные кроме входного и выходного сигналов.
Пример 1.4. Составить дифференциальное уравнение по структурной схеме,
изображенной на рис. 1.12.
B)
р
-> X
Рис. 1.12
П Составим уравнения элементов схемы:
Отсюда
1)<х = -е; 2)е = *-х.
Р
х=—(х-х), рх = х-х, (р + 1)х = $.
Р
Дифференциальное уравнение системы имеет вид
х(/) + х@ =*(/),
что совпадает с A.10) при Т = 1, т.е. система, состоящая из интегрирующего
звена, замкнутого отрицательной обратной связью, является апериодическим
звеном."
Пример 1.5. Составить дифференциальное уравнение по структурной схеме,
представленной на рис. 1.13.
C)8
О)
Р(р+1)
B) 2
Рис. 1.13
П Составим уравнения элементов схемы:
24

1) х- , в ; 2) ? = 2х; 3) е=*-?.
1>0> + 1)
Отсюда
(/>2+/0* = 3(*-у) = 3(*-2х) = 3*-6х.
Переходя от операторной формы записи дифференциального уравнения
к обычной, получаем
х + х + вх = 3# .¦
1.1.3. Дифференциальные уравнения соединений
Рассмотрим три вида соединений двух звеньев: последовательное,
параллельное и с обратной связью (рис. 1.14).
А(р>0ч-а#1(а0«
*1
Н *>2(Р>*)х = М2(р,*)х{
А0>>0*1=^1(Р,0*
*1
Н А<А0*2-в^2(А'>*
Ф *
*2
ч
6
? *
*г
А(Л<)х = Л/,(р,0е
Ог{р,*)х2=М2{р,{)х
X
Рис. 1.14
ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ: заданы дифференциальные уравнения звена 1
и звена 2 в операторной форме. Требуется найти дифференциальное уравнение
соединения в операторной форме:
Щр,0х = М(р,*)8.
A.12)
25

Для решения задачи применим метод уравнивающих операторов [50].
1. Последовательное соединение (см. рис. 1.14,я). Пусть заданы
дифференциальные уравнения звеньев 1 и 2 в операторной форме:
A.13)
О2(р,0х = М20к0х1.
Для нахождения дифференциального уравнения последовательного
соединения умножим первое уравнение в A.13) слева на некоторый
дифференциальный оператор 11\{рЛ), а второе уравнение на 112(р^) • Получим:
&• А]*-& •"*]*.
Выберем уравнивающие операторы V\и 1/2 так, чтобы выполнялось
равенство
С/1*А8^2*^2- A14>
Тогда
р2^2]х = р1*М1]^9 A.15)
ще, сравнивая с A.12),
2>0>,0 = */2*А, М{рЛ = Щ*Мх.
Пусть порядки операторов А» А» М\9М2,11\, 1?2 равны ль л2, л^, л^,
V, ц соответственно. Тоща из A.14) следует равенство порядков операторов
в левой и правой части: щ+ч^щ+р. Поэтому можно выбрать V - т2, ц = щ
и искать уравнивающие операторы, в виде
щьл=2>доУ, ^2^0=^моУ. (Мб)
/-о /-о
Общее число неизвестных коэффициентов в A.16) равно щ+пь + 2, а
число уравнений, получающихся в результате приравнивания коэффициентов
при одинаковых степенях р в правой и левой части A.14) составит щ+щ+1.
Один коэффициент в процессе решения выбирается произвольно, например
ау@ = 1.
При перемножении операторов применяется правило
4*4-Е^пМ2^г. <1Л7>
>о АР* Г-
где операторы Аи А2 имеют порядок соответственно т, п .
Если т = 1, то формула A.17) имеет вид
А1*А2=А1А2+4Аа2Р. A.18)
ар
26

При действии оператора р на функцию, зависящую от аргумента X,
производится дифференцирование, например: р-1 = 0, />-/ = 1, р*2=2*>
ряп/=*со8/ итд. Для избежания ошибок коэффициенты дифференциальных
операторов, равные 1, следует писать явно. Например:
р*1 = р-1 + 1-1-р = р9
р*1 = р^ + 1*{-р = 1 + 1-р,
(Р + 0*($И11• р +1) = (р + /)($ш* р +1) +1 • (зтГ• р +1)/? =
= $т/ р2 + Г + A + со8/ + /$т/)р.
Пример 1.6. Заданы дифференциальные уравнения звеньев
(*2+$т*р)х1=*2г,
(гх = $т^рхг.
Требуется найти дифференциальное уравнение последовательного
соединения этих звеньев.
? Сравнивая с A.13), имеем Д = г1 + 8т / • р, ^ = Г2, /J = *3,
АГ2 = 8и1 * • Р • Порядки уравнивающих операторов V = т2 = 1, ц = «1 = 1 и,
следовательно, они имеют вид Щ = ао + с^р, G2 « ро + $\Р • Записываем левую и
правую части равенства A.14), применяя правила A.17),A.18):
Щ*1)х =(а0+а!р)*(/2 +8Ш/р) =
= а0/2 + а\РX2 + а0 81П/• р + а.\рвт*р + а\12р + а{ 8Ш/• р2 =
= а0/2 + 2а^ + а08т/• р + с^ со8/ •р + а^2/> + а! 8т/• р2;
1/2*М2 =(Ро +р1Р)*(8ш//>) = ро8т/р + р1р8т/-р + р1 8т/р2 =
= Р081П/р + р1 С08//> + р! 81П*/>2.
Приравнивая коэффициенты при одинаковых степенях р , получаем
р2: а18т/ = р181п/,
р1: а08т/ + а1со8/ + а1/2 =р0$ш* + р1 соз/,
р°: а0/2+20^ = 0.
2 /2 2
Положим ау = ^ = 1. Тогда р! =1, а0 = —, Ро = — •
/ 81П/ /
27

Найдем операторы искомого дифференциального уравнения A.15):
2) = [/2*2J=: [— -+Ь/> */3= — 2/2+1/?/3+1*3/> =
2 2 [яп/ / ) яп/
= - 2/2+1.3/2 + /3р = /2+ — + /3/?;
ЯП/ ЯП/
Отсюда /2 + + 6^ = 6^а искомое дифференциальное уравнение
^ яп/ )
имеет ввд /Зх(/) + /2 + -г— х(/) = /2$(/) или / х(/) + 1 + -?— х(/) = *(/) .¦
^ яп/^ ^ вт!)
2. Параллельное соединение (см. рис. 1.14,6). Пусть заданы
дифференциальные уравнения звеньев 1 и 2 в операторной форме:
А(А0х1=14(р,*)*,
А(Р.0*4-АГ2(р,1)Л
Х = Х!+Х2.
Из второго и третьего уравнений получаем
Вг(РМ* -*\\- АОМ)* - Ыр,*)*\ = М2(Р>*)8-
Исключим X} из первого и последнего уравнений. Для этого умножим их
слева на уравнивающие операторы Щ(р,*) и #20М) соответственно. Находим
р2 * 2J]* - [1/2 ¦ 2J]*1 = Р2 ¦ М2}&.
Выберем уравнивающие операторы V\и XI2 так, чтобы выполнялось
равенство
(/!*А=[/2*2J- A.19)
Тогда получаем дифференциальное уравнение параллельного соединения
а операторы уравнения A.12) равны
2) = 172*02» М = [1/2*М2]+[171*М1]. A.20)
При этом у = л2, \1 = щ.
28

Пример 1.7. Заданы дифференциальные уравнения звеньев 1 и 2 :
Ср + 1)х,=$,
Требуется найти дифференциальное уравнение параллельного соединения
этих звеньев.
? Сравнивая с общей постановкой задачи, имеем А « р +1, М{ = 1,
2J-р, Л/2=1. Порядки уравнивающих операторов у = л2-1, цв^=1»
поэтому ^«схо + а^, ^2=Эо + Р1Р-
Запишем соотношение A.19):
(ао+а1р)*A-р + 1) = аоР + а0+а1р1/? + а1р1 + а1р2 + а1р =
= а0р + а0 + ахр2 + а^ = (р0 + р1/>)*A /О = Ро/> + Ф\Р' * * /> + Р1/>2 =
Приравнивая коэффициенты при одинаковых степенях р , имеем
а1 =Рь ао+«1 ^Ро» ао-0:=> <*1 =ау =1, ${ =1, а0 = 0, р0 =1.
Тогда можно записать дифференциальные операторы параллельного
соединения в виде A.20):
В = 1Г2*02=A + 1 •/>)*A-р) = 1-р + 1 р-1р + 1р2=р2+р;
а само уравнение - в форме
(р2+р)х = Bр + 1)х или х(/) + х@ = 2^@+ *(/)•¦
3. Соединение с обратной связью (см. рис. 1.14,*). Пусть заданы
дифференциальные уравнения звеньев 1 и 2 в операторной форме, а обратная связь
отрицательная:
АО'.Ох-ОД'.')'.
е = *-х2.
Подставляя третье уравнение в первое, получаем
1>1(р,0х = М1(р,*)8-М1(р,*)х2.
Исключим х2 из второго и полученного уравнений. Для этого умножим их
слева на уравнивающие операторы 11\(рЛ) и 172(р,0 соответственно. Находим
[^¦А]х = [^1*М1]^-[^1^1]х2,
[1/2*П2]х2=р2*М2]х.
29

Выберем уравнивающие операторы 1/х и 1/2 так, чтобы выполнялось
равенство
^¦^=^2*2J. A.21)
Тогда получаем дифференциальное уравнение соединения с отрицательной
обратной связью:
а операторы дифференциального уравнения A.12) равны
2) = [#1*А]+[#2*^2Ь М=11х*Мх. A.22)
При этом V = «2, ц = т\.
Пример 1.8. Заданы дифференциальные уравнения звеньев 1 и 2:
0> + 1)х = е,
рх2=х.
Требуется найти дифференциальное уравнение соединения с
отрицательной обратной связью.
О Сравнивая с общей постановкой задачи, имеем 2>}=/? + 1, М{=1,
#2 = р, М2 = 1. Порядки уравнивающих операторов V = л2 = 1, ц = /»1=0,
поэтому С^-ао+ош», #2=Ро-
Выпишем равенство A.21) с применением A.17),A.18):
(ао+а1р)*1 = а01 + а1р.1 + а1-1р = ао+а1р = ро*/? = РоР-
Отсюда а0 = 0, Ро = а1 • При ау = а{ = 1 имеем а0 = 0, р0 = 1.
Операторы искомого дифференциального уравнения:
П = [1/1*П1]+[1/2*М2] = Aр)*Aр + 1) + (\*1) =
= 1рЛр + 1-рЛ + (р + 1)р + 1 = р2+р + 1;
М = Щ*Мх=(\р)*\ = \рЛ + р = р.
Поэтому дифференциальное уравнение соединения с обратной связью имеет вид
(р2+р + 1)х = рз или х@ + *@ + *@ = *(').¦
1.1.4. Связь вход-выход
Рассмотрим систему, описываемую дифференциальным уравнением
«л(Ох(л)@+...+ло@^@ = ^@^(т)@+...+^@^0; A.23)
с начальными условиями
х(*о) = *б . *('о) = *о..... *Р-Ч*Ь) = >4Г1) • A24)
Требуется по заданному входному сигналу и начальным условиям найти
выходной сигнал.
30

Для линейных систем справедлив принцип суперпозиции: эффект,
вызываемый суммой нескольких воздействий, равен сумме эффектов каждого из
воздействий в отдельности. Поэтому выходной сигнал линейной системы
представляется в виде суммы свободного и вынужденного движений:
*@ = *с«)+ *,«*('). A.25)
Свободное движение хс(*) происходит при отсутствии внешнего
воздействия ($(/) = 0) вследствие ненулевых начальных условий. Оно является решением
однородного дифференциального уравнения, соответствующего исходному
уравнению системы:
*„(>) *(й)(') +... + *о@ *<>) - 0 A.26)
с начальными условиями A.24). В случае, когда начальные условия нулевые,
свободное движение в системе отсутствует (хс(/) = 0).
Вынужденное движение хвым@ происходит вследствие внешнего
воздействия #@ при нулевых начальных условиях. Оно является решением
неоднородного уравнения A.23) при нулевых начальных условиях. Вынужденное движение
хвын(() отлично от нуля только после приложения внешнего воздействия.
Подчеркивая эту причинно-следственную связь, вынужденное движение системы
при внешнем воздействии, отличном от нуля при />/0> будем обозначать
х9ын@' *(* ~ 'о)» гДе *(' - 'о) ~ единичная ступенчатая функция A.2).
Выходной сигнал системы будет иметь вид
*(') = *с@ + хвым@ - /(/ - /0), A.27)
где функции хс(/), хеьш(() можно считать п раз непрерывно
дифференцируемыми.
Замечания.
1. Общее решение однородного уравнения A.26) находится по формуле
ло@ = ^Ф1@ + ... + слФй@, A.28)
где <?!,...,<*, — произвольные постоянные; Ф1@»-"»ФЛ@ "фундаментальная
система решений уравнения A.26).
Если система A.23) стационарная, т.е. описывается уравнением
^х<л>@ + ... + ^дс@ = ^^(,,,)@ + ... + А)^@
с постоянными коэффициентами, то сначала определяются корни Хь...,\п
характеристического уравнения:
ап Хп + ап_х Xй +... + оо = 0. A.29)
Если корни действительные разные, то A.28) имеет вид
ХоО-С!**1' +с2ех*' +... + слеХ"'. A.30)
31

Бели среди корней есть кратный действительный корень X^ кратности к ,
то ему соответствует следующая составляющая общего решения:
х0№-(с1+С2*+... + ск<к-1)е}ь''9 A.31)
где си...,ск — произвольные постоянные.
Паре комплексных сопряженных корней а^ ± ру- / соответствует решение
*о;@ - **' '(с1 о™*]' + с2 ял р/), A.32)
а паре комплексных сопряженных корней кратности к —
*<у@ = еау'[(с1 + с2/+...+с***-1)со$р/ + (</1 +42*к..-мЬ'*~1)япр;'] , A.33)
где си...,скУ </!,...,</*— произвольные постоянные.
2. Частное решение неоднородного уравнения»''A.23) находится методом
вариации произвольных постоянных или методом подбора [40]. В частном
случае, когда система описывается уравнением
айх<й>@ + ... + оох(/) = *@, ^) = [^@со8р/ + />/@8Юр^]^г,
где ЯдA)> ^/(О" многочлены степеней ди/ соответственно, а, р — заданные
числа, частное решение ищется в форме
^@ = ^[0т@со8р/ + Гт@8Шр/]./5, A.34)
в которой /и = шах (я,/) > 0т@>^«@ "" многочлены степени /и с
неопределенными коэффициентами; показатель степени 5 определяется следующим образом:
Г 0, если число (а + ф) не совпадает ни с одним из корней
I характеристического уравнения,
I &, если число (а + /р) совпадает с корнем характеристического уравнения
[ кратности к.
3. Методика решения задачи анализа выходных процессов для
стационарных систем с помощью перехода от начальных условий к начальным значениям
изложена в разд. 3.1.4.
4. По реакции системы на входное воздействие в виде единичной
ступенчатой функции можно определить основные показатели качества переходных
процессов (рис. 1.15):
а) статическое отклонение хф = Ит *(/);
б) максимальное отклонение х^^;
в) время переходного процесса Тр — наименьшее время, после которого
выполняется условие | хA) - хф\ < Л, где А — заданная величина;
г) перерегулирование а = -ш§2 — • 100%, если х^ ф 0;
д) число колебаний выходного сигнала за время переходного процесса.
32

Рис. 1.15
Система управления удовлетворяет требуемому качеству, если все
показатели качества не превышают заранее заданных значений.
1.1.5. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть известны:
а) входной сигнал $(/);
б) система, описываемая дифференциальным уравнением
«л(')х(л)@+...+*<>(')*(') = М')*(т)<0+...+МО *(');
в) начальные условия:
Требуется найти выходной сигнал *(/).
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти свободное движение, решив однородное дифференциальное
уравнение A.26) с заданными начальными условиями A.24).
2. Найти вынужденное движение, решив неоднородное дифференциальное
уравнение A.23) с нулевыми начальными условиями.
3. Определить выходной сигнал как сумму свободного и вынужденного
движений.
Пример 1.9. Найти реакцию системы, описываемой дифференциальным
уравнением
Тх@ + х(*) = 8(<), Т>0,
на входной сигнал $(/) = /(/) при нулевых начальных условиях.
33

П 1. Найдем свободное движение. Так как начальные условия нулевые,
свободное движение отсутствует, т.е. хс@ » 0.
2. Найдем вынужденное движение как решение уравнения Тх(*) + х@ = 1
при условии х@) = 0:
а) общее решение однородного уравнения
Гх@ + х(/) = 0.
Характеристическое уравнение ГХ + 1 = 0 имеет корень Х = ——. Согласно A.30)
общее решение однородного уравнения имеет вид х0A) = Се т;
б) частное решение неоднородного уравнения: *„(/) = 1;
в) общее решение неоднородного уравнения:
х@ = Хо@ + хя@ = Се ^+1;
г) из начального условия х@) = С +1 = 0 следует С = -1 . Окончательно
получаем х^у,(/) = 1-в г.
3. Выходной сигнал определяется вынужденным движением
Реакция апериодического звена на единичное ступенчатое воздействие
изображена на рис. 1.6, в.ш
Пример 1.10. Найти реакцию колебательного звена, описываемого
дифференциальным уравнением
Зх@ + 1/Зх@ + х@ = *@,
на входное воздействие #(/) = /@ при нулевых начальных условиях (здесь
Т = Л9 $ = 0,5).
? 1. Найдем свободное движение. Так как начальные условия нулевые,
свободное движение отсутствует, т.е. хс@ « 0.
2. Найдем вынужденное движение, которое является решением
неоднородного дифференциального уравнения Зх(/) + </Зх@+ *(/) = 1 при нулевых
начальных условиях х@) = 0, х@) = 0:
а) общее решение однородного уравнения:
ЗхХ0 + Лх(/) + х(*) = 0.
Характеристическое уравнение ЗХ2 + 4ъ\ + 1 = 0 имеет корни
34

Согласно A.32) общее решение однородного уравнения имеет ввд
хь(/) = ва/(с1со8р/ + с28Шр/) = в б [с1со8- + с2зш-1;
б) частное решение неоднородного уравнения: хй(/) = А. В результате
подстановки в неоднородное уравнение имеем А « 1 = хм(/);
в) общее решение неоднородного уравнения:
*@ = *о@+ *„(') = * 6 исо8^ + с281пЛ + 1;
г) из начальных условий
х@) = с, +1 = О,
*@) = -^с1+^ = 0
получаем С1 = -1, с2 = —— > а вынужденное движение
*<**(') = * б 1-сов--—8Ш-1 + 1.
3. Выходной сигнал определяется вынужденным движением:
*@ = *<»ш@ = «"| -соз^-^впД +1, * * 0. ¦
I 2 3 2^
Пример 1.11. Найти свободное и вынужденное движения, а также
выходной сигнал системы, описываемой дифференциальным уравнением
х(/) + х@ = *(*),
с начальным условием х@) = 0,5 при входном сигнале $(/) = /(/).
? 1. Определяем свободное движение как решение однородного
дифференциального уравнения х@ + х(/) = 0 при начальном условии х@) = 0,5.
Характеристическое уравнение X +1 — 0 имеет корень Х = -1. Согласно
A.30) общее решение однородного уравнения имеет вид х0@ = С^"/. Из
начального условия получаем х@) = С = 0,5, и окончательно свободное движение
хс(/)=±<г'.
2. Находим вынужденное движение как решение неоднородного
дифференциального уравнения х@ + х@ = 1 при начальном условии х@)« 0:
а) общее решение однородного уравнения имеет вид хб(/) = Се (см. п.1);
35

б) частное решение неоднородного уравнения ищется в виде: хнA) = А.
В результате подстановки в неоднородное уравнение имеем А = 1, хнA) = 1;
в) общее решение неоднородного уравнения:
г) из начального условия х@) = С +1 = 0 следует С = -1. Тогда
вынужденное движение
*,««(') = -«"'+ 1.
3. Выходной сигнал определяется по формуле A.25):
х(*)=±е-'-е-' +1 = 1-1*-', г*0.И
Пример 1.12. Найти свободное и вынужденное движения, а также
выходной сигнал системы, описываемой дифференциальным уравнением
х@-Зх(/) + 2х@ = *@,
с начальными условиями х@) = 1, х@) = 3 при входном сигнале
[о, /*о.
П 1. Определяем свободное движение как решение однородного
дифференциального уравнения х(/) - Зх(/) + 2х(/) = 0 при начальных условиях х@) = 1,
х@) = 3.
Характеристическое уравнение Х2-ЗХ + 2 = 0 имеет два корня: Х!=1,
Х2=2.
Согласно A.30) получаем общее решение однородного уравнения:
х0@ = с1е'+с2е2/.
Из начальных условий
Х@) = С!+С2=1,
х@) = с{ + 2с2 = 3.
имеем сх = -1, с2 = 2, а свободное движение
хс(<) = -е'+2е2*.
2. Находим вынужденное движение как решение неоднородного
дифференциального уравнения х@ - Зх(/) + 2х(Г) = 2е3/ при условиях х@) = 0, х@) = 0:
а) общее решение однородного уравнения получено в п.1:
х0(*) = с1е< +с2е2*;
б) частное решение неоднородного уравнения хнA) = Аеу. Подставляя в
неоднородное уравнение, имеем: 9е*'А - 9Ае*' + 2Аеъ* = 2ег*. Отсюда А = 1,
*«@ = е3';
36

в) общее решение неоднородного уравнения:
х(Г) = *о@ + *•<*> - с1е' + Vй + *3'»
г) подставляя в начальные условия, получаем:
х@) = С!+с2+1 = 0,
х@) = С! +2с2+3 = 0.
Отсюда С1 = 1, с2 = -2, а вынужденное движение
3. Выходной сигнал определяется по формуле A.25):
х(*) = -е'+2е2'+е'-2е2*+ег( =е3', 1*0. ¦
Пример 1.13. Найти свободное и вынужденное движения, а также
выходной сигнал системы, описываемой уравнением
х@ + 4х(/) = *@
с начальными условиями х@) = 1, х@) = -1 при входном сигнале
*О)-сов2М@-
П 1. Определяем свободное движение как решение однородного
дифференциального уравнения х(/) + 4х(/) = 0 при начальных условиях х@) = 1,
х@) = -1.
Характеристическое уравнение 7? + 4 = 0 имеет два комплексных
сопряженных корня Хх%2 = ±2/ (а = 0, р = 2). Согласно A.32) получаем общее решение
однородного уравнения:
Хо@ = С{ С08 2/ + С2 81П2Л
Из начальных условий
х@) = с1=*1,
х@) = (-2с{ зш 2/ + 2с2 со» 2/) |/ш0= 2с2 - -1
имеем сх = 1, с2 = —-, а свободное движение
хс@ = соз2/ —-81П 2/.
2. Находим вынужденное движение как решение неоднородного
дифференциального уравнения х(/) + 4х(/) = со$2/ при нулевых начальных условиях
*@) = 0, х@) = 0:
а) общее решение однородного уравнения получено в п.1:
хо@ = С1 со8 2г + с2$ш2/;
37

б) поскольку параметры правой части сс = 0, р = 2,# = 0, а число а + ф = 2/
совпадает с корнем характеристического уравнения кратности к-\, то
5 = 1, т - О и частное решение неоднородного уравнения ищется в форме A.34):
х|Д/) = /(Лсо$2/ + Дяп2/).
Последовательно дифференцируя, имеем
Хн @ = А С08 Ъ + В 81П 2/ + / (-2Л 81П 2/ + 25 С08 2/) =
= (А + 25/) со82/ + E - 2Л/) 8ш2/,
х„ (/) = 25 сое 2/ - 2(Л + 25*) 8Ш 2Г - 2Л 8т 2/ +
+ 2E - 2АО сое 2/ = D5 - 4АО со8 2Г - D А + 4Л) 8т 2/.
Подставляя в неоднородное уравнение, получаем
D5 - 4 АО сев 2/ - D А + 45/) 8т 2/ + 4/( А со8 2/ + 5 8т 2/) = со8 2/
или
45со82/-4Л8т2/ = со82/.
Приравнивая коэффициенты при одинаковых функциях от (, находим
45 = 1, -4Л = 0.
Отсюда А = 0, 5 = — и х„(/)= — 8т2/;
4 4
в) общее решение неоднородного уравнения:
*@ = *о@ + **(') = с1 со$2/ + с2 8т2/ + --8т2/;
4
г) используя нулевые начальные условия, получаем:
х@) = С1=0,
х@) = 2с2=0.
Отсюда вынужденное движение хвын (/) = — 81п 2/.
4
3. Выходной сигнал
х@ = хс@ + хвьш@ = со82/—-8т2/+^8т2/ , /^О.И
Пример 1.14. Найти свободное и вынужденное движения, а также
выходной сигнал системы, описываемой уравнением.
х@-3х@ + 3х@-х@ = *@
с начальными условиями х@) = 0, х@) = 0, х@) = 2 при входном сигнале
*(Г) = *'./(*).
38

а 1. Определяем свободное движение как решение однородного
дифференциального уравнения х@-Зх(/) + Зх@-*(/) = 0 при начальных условиях
х@)в0,х@) = 0,дс@) = 2.
Характеристическое уравнение X3 - ЪУ? + ЗА, -1 = (X -1K = 0 имеет один
корень Х = 3 кратности к = 3. Согласно A.31) получаем общее решение
однородного уравнения:
хо(*) = (с1+с2* + сг*2)е'.
Из начальных условий последовательно получаем
Х@) = с,=0,
хф) = [(с2+2с30е' +(с2* + с3*2)е')\м=с2=0,
х@) = [2сге* + 2сг*е* + 2сг*е* + с3Л?'] |,.0 = 2с3 = 2
имеем с\ = с2 = 0, с3 = 1, а свободное движение хсA) = /V.
2. Находим вынужденное движение как решение неоднородного
дифференциального уравнения
х(/) - Ъх@ + 3х@ - х@ = в'
с нулевыми начальными условиями х@) = 0, х@) = 0, х@) = О :
а) общее решение однородного уравнения получено в п.1:
*о@ = (с1+С2> + оз'2)е';
б) поскольку параметры правой части ос = 1, р = 0, д = 0,а число а + /р = 1
совпадает с корнем Х = 1 характеристического уравнения кратности к = 3, то
5 = 0, т = 0 и частное решение ищется в форме A.34):
хвЮшЛМ.
Последовательно дифференцируя, имеем
хн(*) = МBе'+А*ге', хм(<) = 6А*2е(+6А*е* + А?г\
3ся@ = А > V + 9А / V + \%А 1г1 +6Ае(.
Подставляя в неоднородное уравнение, получаем
А / V + 9А /V + 18Л ^е^ +6Ае* - 18Л /V - 18Л и? -
- ЗЛ / V + 9Л / V + ЗА /V - Л /V = г1
или 6Ле'=ег.
Отсюда 6А = 1, Л = ± и хн(*) = *-е(.
6 6
39

в) общее решение неоднородного уравнения:
г) используя нулевые начальные условия, последовательно получаем
х@) = сх ш 0, х@) = с2 = 0, х@) = 2с3 = 0.
Отсюда вынужденное движение х^Ц) = -т-е'.
6
3. Выходной сигнал
л
х(/) = хс@ + х«„@ = '2е'+—е', Г^О.и
1.2. МНОГОМЕРНЫЕ СИСТЕМЫ ПРИ ДЕТЕРМИНИРОВАННЫХ
ВОЗДЕЙСТВИЯХ
1.2.1. Описание сигналов и систем
1. Описание сигналов. Входные, выходные и промежуточные
детерминированные сигналы в многомерных системах представляются вектор-функциями
времени, например:
Гл«1
*(')=
(МО}
У«) =
{*Л0) Ш0)
где $(*) - г-мерный входной, а уA) — ^-мерный выходной сигналы. В качестве
компонент входного сигнала #@ могут использоваться единичные ступенчатые
функции A.2) и дельта-функции A.1).
2. Описание систем. Многомерные линейные нестационарные системы в
отличие от одномерных имеют г входов и к выходов (рис. 1.16). Они описываются
уравнениями состояния вида
х@ = ДО *(') + *(')*(» A.35)
с начальными условиями
и уравнениями выхода
*('о) = *о
A.36)
A.37)
40

где х - л-мерный вектор состояния; & - г-мерный вектор входных воздействий
(управлений); у - ^-мерный вектор выхода (вектор измерений); х0 "~ начальное
состояние, I - время; *о " начальный момент времени (момент подачи входного
воздействия); А®, В{1), С(/) - матрицы размера (пхп), (лхг), (кхп)
соответственно.
Л »
л ,>ч'>::>С.
*г ,
"*С* ,>.**
*' .
*' ,
*" .
...V*** ***.•"•••
**.¦••*. !'ч*"
»•''** '*•'.
л .
Л .
у*.
Вход
Состояние
Рис. 1.16
Выход
Многомерную систему можно рассматривать как совокупность г к
одномерных систем, каждая из которых связывает один из г входов с одним из
к выходов. Если г = 1 и к = 1, система является одномерной. Если матрицы
Л(/), 2?(;), С(/) не зависят от времени ( , система называется многомерной
стационарной.
Пример 1.15. Записать уравнения состояния и выхода многомерной
системы:
*1=*2+*1>
х2 = -х1+2х2-3^1,
У\=*2
в матричной форме.
? Определяем размерности сигналов: л = 2, г = 1, # = 1 и записываем
соответствующие уравнения:
жо т са)
Пример 1.16. Записать уравнения состояния и выхода многомерной
системы:
х1=х1-/х2+2^1+^2, У\ =х{+2х2,
Х2=Х2+ГХз+$2>
у2=-х2+3х3
Х3 = 81П / X! + 2х2 + ЗХз + ^1,
в матричной форме.
О Определяем размерности сигналов: л = 3, г = 2, А: = 2 и записываем
соответствующие уравнения:
41

6
*2
Л,
=
г 1
0
^81П/
-/ 0)
1 А
2 3)
I '
г2
1*з,
+
'2 \У
0 1
,1 0)
О- Й-С -¦ 3
*1
*2
1*з
мы:
Ж0 ва) сц)
Пример 1.17. Записать уравнения состояния и выхода многомерной систе-
х + 2х + г = 2#ь ух=х-2г,
г-х + 3г = $2> ^2=^
в матричной форме.
? Обозначим X! « х, х2 = х, х3 » г, х4 - х3. Тогда уравнения можно
переписать в виде
XI = Х2,
Х2=-2х2-хз + 2^ь
*3 в*4»
х4=х2-Зхз+^2»
или в матричной форме (л = 4, г = 2, к = 2):
^ =Х!-2Х3,
*2=*2
</
Л
*1
*2
*3
к*4>
/
\
0 1 0 0>
0-2-10
0 0 0 1
10 1 -3 0
АA)
*1
*2
Кх4)
'0 0^
2 0
0 0
10 I)
и
ВA)
(я) (я)шA ° -2 °1
Ы' Ы [0 1 0 0)
*1
*2
*3
к*4.
С(/)
1.2.2. Уравнения состояния н выхода соединений
Как следует из разд. 1.2.1, многомерная система, описываемая
уравнениями состояния и выхода, полностью характеризуется набором трех матриц: А, В,
С. Здесь и далее аргумент / для сокращения записи опущен. Две многомерные
системы могут образовывать три типа соединений: параллельное,
последовательное и с обратной связью, изображенные на рис. 1.17,а-в.
Предполагается, что обе системы, образующие соединения, описываются
в пространстве состояний соотношениями:
хх=Ахх1+Вх&\ у1 =Схх1,
A.38)
Х2~А2Х2+В282, У2=С2Х2,
A.39)
42

где х1, Я1 у У1 ~" векторы состояния, входного сигнала и выхода первой системы
размерности щ,гькх соответственно; х2, $2, у2 - векторы состояния,
входного сигнала и выхода второй системы, размерности которых п2уГ2Ук2
соответственно.
*'=*г
8 —|
й2-х 1
5 а
Л1
>б
а
йА
у'
»
1
\льВ1,С1 |-
^2>^2»^2 Г
а
<\ала
\Аг>&1>Сг
9
лЛ
1 уХ
®->у = у1+у2
-|у2 *'=*-
1
У у = Г
У=*2
4»^1»^1
5
^2»^2>^2
-*у = у2
* *
Л,Я,С
\ * У
г
Рис. 1.17
Требуется заменить соединение эквивалентной системой, описываемой
уравнениями A.35), A.37) и изображенной на рис. 1.17, г, в которой п9 г, к —
размерности векторов состояния х, входного сигнала # и выхода у.
1. Параллельное соединение (рис. 1.17, а). Условия соединения:
у = у1+у2, к = к{=к2, 8 = 81=82, г = гх = г2.
Перепишем соотношения A.38), A.39) с учетом того, что у = у1 +у2:
и и и а.-к»)
жо *го сц)
Полагая дс = (х1, дс2) ,л = й1+л2 и сравнивая с A.35), A.37), получаем
матрицы
-к :)• "(й- с=(с' с*>
43

эквивалентной системы размера (щ + п2) х (щ + п2), (п\ + п2) х г\, ^ х ^ + л2)
соответственно.
Пример 1.18. Системы, образующие параллельное соединение,
описываются уравнениями:
первая система:
Ш-. дан-, за- "-<°"й)'
4@ *|0 С!A)
где щ = 1, ^ - 2, *1 = 1;
вторая система:
*\ = *?+*1 -2*2, У? -Зое?,
где /12=1,/!г=2,А:2=1, Л2@ = 1, *2@ = A -2),С2@ = 3.
Требуется записать уравнение эквивалентной системы.
а Условия соединения к{ = к2 =1> г{= г2 = 2 выполняются. Согласно
A.40) эквивалентная система имеет вид
/-и >
1
г2
1хз>
=
г1 1 (Г|
-1 2 0
,0 0 1)
1 1
Г2
1*з >
/
+
V
(г -4
и и
А«) ВA)
где л = щ + п2 = 3, г = /} = гц ш 2, Л = к\ = Л2 = !•'
у = @ 1 3)
С@
'XI
*2
ч*з>/
2. Последовательное соединение (рис. 1.17,6). Условие соединения &2=ух9
Г2 = кх. В первом соотношении A.39) учтем, что #2 = у1 = С^х1, а из сравнения
рис. 1.17,6и 1.17,г, получаем: у = у2, к = к2, & = 81, г = /\. Эквивалентная
система имеет вид
#ИД №(*)»• '¦• «й-
A-41)
и и и
А(() В{1) СО)
Полагая х-1*1,*2) , п = щ+п2 и сравнивая с A.35), A.37), получаем
матрицы
44

эквивалентной системы размера (щ + п2) х (п{ + л2), (щ + л2) х г\, *2 х (Й1 + л2)
соответственно.
Пример 1.19. Системы, образующие последовательное соединение,
описываются уравнениями:
первая система:
""«¦А Й)-(Л)*
где л, = 1, п = и *1 - 2, 4@ -1. *<0 = 1. <?,(/) = ГД1;
вторая система:
л2(о в2а) с2(о
ще л2 в 2, г2 = 2, #2 = 1.
Требуется записать уравнения эквивалентной системы.
П Условие соединения г2 = к\ = 2 выполняется. Согласно A.41)
эквивалентная система имеет вид
Л
где /! = /*!+л2=3, г = /-!=!, * = *2=1, * = *{.¦
3. Соединение с обратной связью (рис. 1.17, в). Условия соединения:
Я =8±у29 х2 =у1у г = г{=к2, ъ = к\. В первом соотношении A.38) положим
Я = 8±у2 =#±С2х2, а в первом уравнении A.39) &2=Схх{. Сравнивая рис.
1.17, в и 1.17, г, получаем у = у1. Эквивалентная система имеет вид
1 !
*2
1*з >
=
' 1 0 <П
-1 1 -1
[17 -1 0^
\Х2
1*3,
¦Ю*
и и
АЦ)
т
? = (<> 1 -1)
<хз)
и
С«)
АA)
«о
С@
A.42)
45

Полагая х = (хх х2\ , п = щ+п2 и сравнивая с A.35), A.37), получаем
матрицы
ЧД Т)' -в)- с-<с-°>
эквивалентной системы размера (щ + л2) х («1 + п2), («1 + п2) *г{, ^ х («! + п2)
соответственно. Знак «плюс» - для положительной, а знак «минус» — для
отрицательной обратной связи.
Пример 1.20. Системы, образующие соединение с отрицательной обратной
связью, описываются уравнениями:
первая система:
МО
с,@
где «1=2, /1=1, *1 =2;
вторая система:
ЙК Ш Эй)- --о 45-
2?2@
С2@
где л2 = 2, /2 = 2, *2 = 1.
Требуется записать уравнения эквивалентной системы.
? Условия соединения г2 = кц = 2, /\ = &2 = 1 выполняются. Согласно
A.42) эквивалентная система имеет вид
1
Г2
Г3
1*4 >
=
г 1 -1-3 6^
-1 2 1 -2
13 0 1
,-2 -1 1 <0
(хЛ
г2
Г3
1*4,
+
г3>
-1
0
1о]
и и
МЯ
т
(УЛA 3 0 <Г|
Ьг) 1-2 -1 0 (^
*2
*3
^*4
с(о
где л = щ + «2 = 4, г = /^ = к2 = 1, к-к\-Ъ\
46

1.2.3. Связи вход-состояние и вход-выход
Рассмотрим многомерную линейную систему, описываемую уравнениями
состояния м выхода:
*0 = С(/)х@.
Для линейных систем справедлив примут суперпозиции: эффект,
вызываемый суммой нескольких воздействий, равен сумме эффектов от каждого из
воздействий в отдельности. Закон изменения вектора состояния линейной системы
представляется в виде суммы свободного и вынужденного движений:
х@ = хсA) + хвын(*) . Аналогичное соотношение справедливо и для вектора
выхода: у(*) = Ус(*У + УеынЦ) в силу связи A.37).
Свободное движение хс(/) (ус@) происходит при отсутствии внешнего
воздействия (#@ « 0) вследствие ненулевых начальных условий A.36). Оно
определяется решением однородной системы уравнений, соответствующей исходному
уравнению состояния A.35):
хЦ) = АЦ)хЦ) A.43)
с начальными условиями х(@) = хц. Если начальные условия нулевые, свободное
движение в системе отсутствует, т.е. хс(/) а 0.
Вынужденное движение хвынA) (УдеДО) ~~ это реакция системы на внешнее
воздействие $(/) при нулевых начальных условиях. Оно определяется решением
неоднородного уравнения A.35) при нулевых начальных условиях.
Для многомерных нестационарных систем, описываемых соотношениями
A.35)—A.37), законы изменения векторов состояния и выхода определяются по
формулам
х@ = ФС'о)*о + {ф(>>тJХт)*(т)А, A.44)
*0 = С@*@ = С(/)Ф(Мо)*о +С@/ф(*,тJ>(т)*(т)А, A.45)
Где Ф(/,т) — переходная матрица, или матрица Коти, являющаяся решением
уравнения
^^=Ж/)Ф(*,т) A.46)
ох
с начальным условием
Ф(т,т) = Я. A.47)
Первые слагаемые в A.44), A.45) описывают свободное движение, а вторые
"~ вынужденное.
47

Формулы A.43)—A.46) следуют из общего алгоритма решения линейных
систем обыкновенных дифференциальных уравнений [40], включающего три
этапа.
Первый этап. Решается однородная система дифференциальных уравнений
х@ = Л@*@,
соответствующая исходной неоднородной системе
х@ = Л@*(') + *@*@.
Ее общее решение записывается в форме
х0@ = Ф(Ос = Ес/ф/@,
/-1
где с = (с!,...,сл)г — вектор произвольных постоянных, <р(/) = (фь...,фл) —
фундаментальная матрица, Ф1 (/),...,ф„@ - линейно независимые решения однородной
системы. Каждый столбец <р/(/) фундаментальной матрицы удовлетворяет
однородной системе, т.е. справедливы равенства ф/@ = Ж0ф/@> ' = 1,—,л или
<К0 = Ж')Ф@.
Второй этап. Ищется общее решение неоднородной системы методом
вариации произвольных постоянных:
х(/) = Ф@с@,
ще вектор-функция с@ = (с{ (/),...,сл(/))г подлежит определению.
Подставляя х@ в неоднородную систему, получаем
мм*)+ф(Ос(о=жоф(Ос(о+т*ю.
С учетом ф(/) = Л(/)ф@ имеем
Ф@с@ = *(')*(>) или с(/) = ф-1@^@^@.
Обратная матрица ф_1@ существует, поскольку ёе1ф(/)*0 как определитель
Вронского. Интегрируя последнее соотношение, находим
с@=/ф(тI?(т)^(т)Л + с6,
где со — вектор произвольных постоянных. В результате искомое общее решение
имеет вид
I
Третий этап. Ищется частное решение неоднородной системы,
удовлетворяющее начальным условиям х(/0) = *о:
х(*о) = у(*о) со = хо.
48

Отсюда со = ф Со) *о и
х@ = ф(Оф(^о)^о + /ф@ф_1(т) *(*)*(*)*•
Обозначая Ф(/,х) = ф(/)ф(^)» получаем формулу A.44). При Г = т получаем
начальное условие A.47). Умножая уравнение ф(/) = Ж0ф@ справа на матрицу
ф-^т), имеем ^(Оф-1^) = ^@ - фОф'Ч*), т.е. уравнение A.46).
ЗФ(Г,т) Ф(Г,т)
Замечание. Для многомерных стационарных систем, описываемых
уравнениями
т-ЛхЮ + ВМ, A.48)
х@) = дсо, A.49)
М0 = Сх(/), A.50)
законы изменения вектора состояния и вектора выхода находятся по формулам
х@ = Ф@*о + /Ф('-т)**(т)Л, A51)
о
ЯО = Сх(/) = СФ(/)хо+С/Ф(Г-тJ?я(т)Л, A.52)
о
где Ф(ц) = Ф(/ - т) - переходная матрица стационарной системы, зависящая от
разности / - т = т|. В данном случае решение уравнения A.46) имеет вид
Ф(/, т) = <И('-Т> = Ф(/ - х) = Ф(л).
1.2.4. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть известны:
а) входной сигнал $(*) (см. разд. 1.2.1);
б) система, описываемая уравнениями состояния и выхода
х(<) = А(*)х(*) + В(*)8(*), *(*о) = *о,
><0 = С@х@;
в) вектор начальных состояний хо (см. разд. 1.2.1).
Требуется найти законы изменения вектора состояния хA) и вектора
выхода у(Г).
49

Замечание. Если система образована соединениями подсистем, то
она заменяется эквивалентной системой так, как показано в разд. 1.2.2.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти переходную матрицу (одним из трех способов, рассмотренных
далее).
2. Используя соотношения A.44), A.45) или A.51), A.52) в зависимости от
типа системы, определить законы изменения векторов состояния и выхода.
Рассмотрим различные способы нахождения переходной матрицы.
Первый способ. Если фундаментальная матрица <р(/) = (<р| (/),..., Фл @) >
столбцы которой образуют фундаментальную систему решений однородной
системы дифференциальных уравнений A.43), известна, то переходная матрица
находится по формуле
Ф(Г,х) = ф@ф(т). A.53)
Замечание. Общее решение однородной системы A.43) можно
записать в виде
*о@ = с{ фКО +... + сн <ря@, A.54)
где С},...,сл — произвольные постоянные.
Для стационарных систем следует выполнить действия:
1. Найти корни характеристического уравнения
|Л-ХД|=0, A.55)
где Е - единичная матрица.
2. Выписать выражение общего решения A.54) для каждой компоненты
вектора х , следуя известным правилам в зависимости от типа корней (см. разд.
1.1.4). При этом произвольные постоянные в выражениях различны.
3. Полученные выражения подставить в однородную систему. Во многих
случаях достаточно подставить в первые п -1 уравнений системы, что облегчает
решение задачи.
4. Приравнять коэффициенты при одинаковых функциях аргумента I и
решить полученную систему уравнений.
5. Выписать общее решение, зависящее от п произвольных постоянных
в форме A.54). В результате находится фуццаментальная матрица, а по формуле
A.53) — переходная.
Пример 1.21. Найти переходную матрицу системы, описываемой
дифференциальными уравнениями
х1=х1+2х2,
х2 =4х1+Зх2 + #.
50

П Составим матрицу системы Л = I I. Используем приведенный выше
II — X 2 1
л \ = ®> Х2-4Х-5 = 0
действительные разные: Х1 =5, Х2 = -1.
2. Запишем выражения общего решения для каждой компоненты:
х1(/) = С1е5/+С2е-г,
х2@ = В1е5'+В2е-'.
3. Подставим полученные соотношения а первое уравнение системы:
5С{ еи -С2е-( =С{ е5'+С2е~(+2Вхе5' +2^<г'.
4. Приравняв коэффициенты при е5{ и е~*, получим
4^=2*,, *-2С„
или
— 2С2 = 22>2, В2 =—С2.
5. Из пп. 2, 4 имеем
®Н$Ъ№Н$\
Ф1@ Ф2@
Отсюда
«»-& -"¦)• -'«Ч(С3
и по формуле A.53)
Пример 1.22. Найти переходную матрицу системы, описываемой
дифференциальными уравнениями
х2=-х1-2х2+в.
51

а Составим матрицу системы Л = ( 1. Используем приведенный
выше алгоритм.
1-Х 1 I о
1 = 0» X +2Х + 1 = 0
" "¦* /» в ЛI
действительный кратный: X = -1, к = 2.
2. Выражения общего решения для каждой компоненты имеют вид
*1@ = (С1+С2Г)е-',
3. Подставим полученные соотношения в первое уравнение системы:
С2в"' - (С{ + С20 <Г' = (^ + В20 е'(.
4. Приравняв коэффициенты при е~* и /е_/, получим
^2 ~ ^1 - В\,
- С2 = Я2.
5. Из пп. 2, 4 имеем
ЫОГиЪ-СОе-'-С^е-') 1{-е-') + %"<-*-')
и и
Ф10) Ф2<0
Отсюда находится фундаментальная матрица
ф@-
и по формуле A.53)
= Гв-<г-т)+(г_т)е-0-т) (,_т)е-<»-*) ^| (е-п+це-п ле-п ^
( -('-*)«~('~т) е-('-т)-(Г-т)е-('-т);Л -лв-1 в-ч-чв-*/
В случае нестационарных систем для определения фундаментальной
матрицы можно воспользоваться следующим приемом, позволяющим уменьшить
порядок системы, если известно ее решение ф] - (фц--фЯ1) и фЛ)@ * 0 при I > т.
52

Тогда вектор-функции ф^ = (щд.--9пд) > Я = 2,3,..,л, образующие вместе
с функцией Ф1</) фундаментальную систему решений для A.43), можно найти по
формулам
Ф1? = ^Ф11 + *1$>
где
Фл-1,? = д*Фл-1Д + *п-1,я у Я = 2,3,...,/!,
Фл? = &?Фл1»
••¦^И4"^*'
A.56)
а функции 1зд(*) = (*\д>->*п-11д) > я = 2$9...9п являются линейно независимыми
решениями системы (л -1) порядка
Ф/>1
л-1
5=1
Фл1
1и> Р = 1,...,Л-1.
A.57)
Пример 1.23. Найти переходную матрицу системы, описываемой
дифференциальными уравнениями
П Для определения переходной матрицы Ф(/,т) нужно найти два
линейно независимых решения заданной системы. Первое решение будем искать с
помощью рядов, представляя функции х^/), х2@ в виде
Л1-0 Л1=0
Подставив эти функции в систему, предварительно умножив первое
уравнение на Г (/2 +1), а второе - на /2(/2 +1), имеем
X Г(/2 +1)/**,, Г* = |]B/2 + 1)ат г* - X Г3*т /«,
Л1«1 Л!«0 т»0
2 'V +1)т*т <-> = § <Ь<и " I '*«'М-
Л!«1 Л1=0 Л!«0
Приравнивая коэффициенты при одинаковых степенях /, получаем
53

а0 =0, ах =а{>
а2 +2яо = 2«2»
аг + 2а{ =3а$+аи
а0=0,а{ -Ао = 0э
а4-^ = 3^ + ^,
дт + 2а«-2 - Ьт-Ъ в 0" - 2)ат-2 - ***/»> *т " Ьт-\ - 0» - 0^я-1 + (т - 3)^.3,
/И = 5,6,... .
Данной системе уравнений удовлетворяют коэффициенты:
а0 = 0,а1=1,дда = 0,т = 2Д...; 4> = 1»4* = 0,01-1,2,3,... •
Таким образом, вектор-функция (*, 1)г является решением системы.
Обозначим это решение <рхA) = (/, 1)г. Так как <р2\(*) = 1*0 при всех /, можно
понизить порядок системы. Согласно A.56) второе решение
Ф2@ = (Ф12@»Ф22@)Г ищется в виде
Ф12<0 = 3@ Фц@+ *('), Ф22@'-в@ф21(*);
где 3@= Г—7
1
*@<#, а *(/) — решение системы A.57), которая
Ф21(>) /2(/2+1)
в данном случае состоит из одного уравнения (п -1 = 1):
;@ = [4^-*Н^4-
|_*(/2+1) Ф21@/2(Г2+1)
«М-
Подставляя Фц@ = * и ф21@ = 1 > получаем уравнение
/2 + 1
решение которого находится с помощью разделения переменных, т.е.
— = — аЧ. В результате г(/) = *2 + 1. Тогда $(/)= Г-гЛ =— и> следователь-
* /2 +1 Ч2 /
но, Ф12@ = — * + /2+1 = *2, Ф22@ = ~.
По найденным решениям ф]@ и ф2@ составляем фундаментальную
матрицу
Ф@ =
По формуле A.53) имеем
1
1 Л
и чг'ГО—?4
*2+1
- г1
и -о
«*',*)=
т2+1
1 -I
г.
- х2
Г *A + *т) /т(т-/Л
т(т2+1) т2 + 1
/-т т(/т + 1)
[х/(х2+1) /(т2+1>;
54

Второй способ. Применение теоремы разложения Сильвестра [60].
Переходная матрица стационарной системы определяется по формуле
Ф(Л) = ^Л=1
м
вМ
1-1 Х/-Лу
A.58)
где X/ - собственные значения матрицы Л (здесь предполагается, что они
различны), а Е - единичная матрица.
Пример 1.24. Найти законы изменения векторов состояния и выхода
многомерной системы:
хх = *1+2*2+$, у = хх+х2
х2=2х1+х2,
[0, /*0.
с начальными условиями х{@) = 1, х2@) = -1 при входном сигнале
П 1. Перепишем уравнения системы в матричной форме:
2. Найдем переходную матрицу. Для этого определим собственные
значения матрицы А. Получим
1-Х 2 I о
2 1-хИ A-Х>2-4 = °-
Отсюда XI « 3, Х2 в -1. По формуле A.58) имеем
^ 3-(-1) +в (-1)-3 4в 12 2) 4е 1,2 -2)
=±Гв3,,+в~ч е3ц-е~п)
2[в3»-в"" е3*+е-*)'
3. По формулам A.51), A.52) найдем законы изменения векторов
состояния и выхода:
«ГЛ-1 (•*¦•"" в3'-е"'1П11гИ")+«"('") ез<г-,).е-«-,)Ул
*'" 2[е* -е"' е3' + е"'Д-0 2 ^ [е*'"* -<Г<'-> е*'-*> + *"<'-> Д0^ * "
55

¦м-
ХСA)
1 зг 1 -г
г3'-г
и 2 4
и
1 з» 3 _,
1 3/ 1 / 3 _,
.4 2 4
1 Зг 1 -<
г -г
Г -/ -»1 П Зг 1 -I 1 Зг 1 « 1 -Л 1 Зг 1 /
-[. »..»]+|_^._. '+Г^_-е'+-е ']-^-тЛ
Пример 1.25. Найти законы изменения векторов состояния и выхода
многомерной системы:
Л = *2.
*1=-*2+*Ь
*2=*1+*2>
с начальными условиями Х|@) = -1, х2@) = 0 при входном сигнале
,1
/2, *>0, /л_/1, *>0,
*м уравнения системы в матричной фс
П 1. Перепишем уравнения системы в матричной форме:
2. Найдем переходную матрицу. Для этого определим собственные
значения матрицы А. Получим
|"Х "!| = 0, Х2+1 = 0.
Отсюда X! = /, X 2 ~ -*• По формуле A.58) имеем
(со&х\ -$1птЛ е*ц+е-'п е*п-е-'п
= . ,таккак со8Т1 = , 81пл = гт .
^8ШТ1 С08Т]; 2 Ъ
56

3. По формулам A.51), A.52) найдем законы изменения векторов
состояния и выхода:
/х (со&1 -$шЛ(-П 'г(со8(/-т) -$ш(/-тЛA (Л/^
_ Л-соеА Г-1 + 2 ил/ + сое Л М + 2вшЛ
~1-ап/У 12-2со$* + 8ш*; 12-2со8*,Г
Г° 1^-совЛ ГО ПМ + 2яп/ + со8Л
^"и оЖ-Я1ШЛ1 0,5А2-2со8* + 8ш/,1~
( '**{ V р-2со8/ + 8шЛ / 2-2со8Г >|
Ус® Уеьш@
Третий способ. Использование теоремы Кели-Гамильтона [60].
Рассмотрим два случая ее применения.
1. В случае различных собственных значений матрицы А :
Ф(л) = г0^ + М+...+ гй_1^л-1 =Я(А), A.59)
где п — число строк матрицы А; Ап~1 - (л -1) -я степень матрицы А;
коэффициенты го, /},...,г„_1 многочлена К(Х) находятся из системы уравнений
ех" = Д(Х,) = г0 + г{ X, +... + /•„_! X/*-1, / = 1,..., л. A.60)
2. В случае кратных собственных значений матрицы А формула A.59) также
справедлива. Корню X/ кратности ц в системе /I уравнений A.60) соответствуют
соотношения
</*еХп </*Д(Х) 1 . Л1 , П,1Ч
Пример 1.26. Найти переходную матрицу системы, если матрица А
в уравнении состояния имеет вид А = [ I (см. пример 1.24).
а Собственные значения матрицы А. \х = 3, Х2 =-1 различны, л = 2.
Поэтому составим систему уравнений A.60):
е-п=/Ъ+1(-1).
57

Отсюда г0 =-т[в3п +Зе"п]» П =т[в3п ¦в]- По Ф^РМУ^ A59> имеем
Результат совпадает с полученным ранее.И
Пример 1.27. Найти законы изменения векторов состояния и выхода
многомерной системы:
х2=-х1-2х2, у2=^1
с начальными условиями хх@) = 1, х2@) = -1 при входном сигаале
Г-1, />0,
П 1. Перепишем уравнения системы в матричной форме:
и и и
жо т см
где л = 2, г = 1, Л = 2.
2. Найдем переходную матрицу. Для этого определим собственные
значения матрицы А. Получим
I. } ЛШЬ Х2+2Х + 1-0.
|-1 -2-Х|
Отсюда Хх = Х2 = -1 (корень действительный кратный). По формуле A.61) имеем
4еХц «/(гр+^Х)
т.е.
|Х = Х,'
</Х Л
Отсюда /& = е"ц + т]е"п, /! = х\е~п. По формуле A.59) получаем
58

3. По формулам A.51), A.52) найдем законы изменения векторов
состояния и выхода:
*')=[ -** е"'-ИМ оЧ -«-Ф-('-т) в-<'-)-(г-т)в-<'->ЛоГ
_ ( е-') (V + 2*"' - 2) [V + Зе"' - 2\
~ (_в-^ + [ 1 _ в"' - иг* ) \\ - 2е-* - 1е~')
[ е-' ) {-2 + ге-^+^е-^) [-2+ 3<Г'+*"'/"
Ус(<) УеьшЮ
1.3. ЛИНЕЙНЫЕ СИСТЕМЫ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
1.3.1. Описание сигналов и систем
1. Описание сигналов. Сигналы в системах управления, подверженных
случайным воздействиям, являются случайными процессами. В качестве их
характеристик обычно используются:
математическое ожидание:
т;(*) = М[О@]= /«</,*>*. (Ь62)
к*
где М — операция вычисления математического ожидания; (?(/) — вектор
входного сигнала; /К', я) — плотность вероятности случайного процесса <7@;
ковариационная функция [44]:
^(/1^2) = ^г{[^1)-^(/1)][G(/2)-т^(/2)]г}, A.63)
где *! и /2 ~ два момента времени. Ковариационная функция удовлетворяет
условию ^(*1,/2)-ОД.4)-
При 4 = /2 ковариационная функция представляет собой ковариационную
матрицу |^(г) = /^(*,/), на главной диагонали которой находятся дисперсии каж-
Дой компоненты вектора 6A):
59

А@ = Ял@ - М{[С,(*) - тл®]2}. A.64)
Частным случаем случайных процессов является белый шум N@,
имеющий нулевое математическое ожидание и ковариационную функцию
ЛлК'1,>2) = ^о('1M(>1 -*г), 065)
где 8^х) _ интенсивность шума, симметрическая неотрицательно определенная
матрица; 5D - /2) ~~ симметричная дельта-функция, определяемая условием
/Л05(/-т)Л =
а
О, тб(-оо, а) II (*, + «>),
/(т), хе(а,Ь), 6
0,5/(а), т = а, * ' '
0,5/(А), т = *
для любой непрерывной в точке т функции /(/).
Стационарные случайные процессы имеют постоянные по времени
математические ожидания, а их ковариационные функции зависят от разности своих
аргументов ^ - *2 = Л. Поэтому последние можно рассматривать как функции
одного аргумента:
^(/1Л)-^(/,-/2) = ^(п). A67)
Дисперсия стационарного процесса постоянна и равна В = /^@).
Например, стационарный белый шум имеет нулевое математическое ожидание и
ковариационную функцию
*и(*ъ*г) = ЗьЫЧ-Ч) или ЛЛг(л) = ^о8(п), A.68)
ще 5о — постоянная матрица интенсивности шума.
2. Описание систем. Линейные системы при наличии случайных
воздействий в пространстве состояний описываются стохастическими
дифференциальными уравнениями, которые могут быть записаны в различных формах.
Первый способ. Система описывается уравнением
4%& = АA) ХЦ) + В@ G@, Х(*0) = *0, A.69)
где АA), Д@ - матрицы размера (лхл), (лхг); G@ - г-мерный случайный
процесс с математическим ожиданием т^(г) и ковариационной функцией
&х(*и*2) = $о(*0 Ш\ -*г)> Хо ~ л-мерный случайный вектор, характеризующий
начальное состояние системы. Если т^(/) = 0, сигнал (?(/) совпадает с белым
шумом ТУХ*).
60

Второй способ. Система описывается уравнением
где 0@ -~ г-мерный винеровский случайный процесс, удовлетворяющий условиям:
О(*о) - О, М{О@) = 0 для всех г > /0, вектор 0@ для любых I > /0 распределен
по гауссовскому закону, процесс является однородным с независимыми
приращениями. Его ковариационная функция К8(*и*2) = $о™Ы*1>*21 &яш 80 = Е,
винеровский случайный процесс называется стандартным.
13.2. Связи вход-выход
Если система задана уравнением A.69), то закон изменения
математического ожидания вектора состояния имеет вид
тх($шАA)тхЮ + В@тжЮ, тх(*0) = то. A.71)
Закон изменения ковариационной матрицы вектора состояния:
Ах@ = А@ Кх@ + ЯхA) АТA) + В@ $о(<)Вт«), Кх(*0) = /%. A.72)
Ковариационная функция определяется по формуле
где ОД,/2) ~ переходная матрица, удовлетворяющая уравнению
дФ('\''2)=А(*})*('1,'г), <Н^2)-Е. A.74)
д*\
Если система задана уравнением A.70), то в A.71) следует положить
т8@ я 0, а в A.72) подставить 50@ «*$о-
Уравнение A.71) получается из A.69) путем нахождения математического
ожидания левой и правой частей.
Поясним соотношения A.72),A.73). Применим формулу Коши A.44) для
уравнения A.71):
г
^х@ = Ф(/,/0)/яо+ $Ф(*,х)В(х)т;(х)ат. A.75)
<ь
Обозначим
РХ(') = М[Х(*)ХТ(*)], Рц@ = ЩХ(*)От@), Р^О-МЮЫХТЦ)]
и определим ковариационную матрицу
61

КхA) = М{[ХA)-тх@][ХA)-тхA)}Т) = М[ХA)ХA)т]-М[ХA)тхтA))-
A.76)
- М[тх(() хТA)] + тх(()тхт(() = Рх{1) - тх({) т/(().
Выведем уравнение, описывающее изменение Рх{1). С учетом A.69)
получаем
РхA) = Щ Х({) ХТЦ)\ + ЩХ«) ХтA)] ш
= АA)ЩХ{1)ХТЩ+ВA)ЩС@ХТЩ+ЩХ(()ХТЩАТ@+ЩХ@СТЩВТA) =
= до РхA)+Д/) Р^@+/>Х(<МГ(<)+/>„« Лг@-
Найдем РчA) с учетом формулы A.44) и того, что Х0 и G@ не коррели-
рованы (Дзд =0):
^@ = Д#[ АГA)<7Г@] - ЩФ(ШХо О7® + / Ф(*,тJ»(т)<7(т)<7г@*] =
= Ф(*,*о)«о и/@+ |ф(/,т)В(т)^<?(т)<?т@]Л.
"о
Определим взаимную ковариационную функцию
^(^|>*2) = Л/{[^1)-'их(г1)][^2)-т,(^)]7'} =
= Л/ЬЩ)*?7^)} - тх(A)т/(B) - тх^)т/A2) + т»(/,)«/(/2) =
-'*('1.«1)-Я«х('1)«ГГ(«1)-
Используем полученное соотношение:
Д/[G(т)(?г@] = ^(т,0 = «ь(г)«/@ + Л,(х,0 =
= тг(т)от/@ + .ЗД8(* - <)•
Тогда
62

Используя A.74) и A.75), имеем
Рч@ - «ж@»/<0+1^(^0^@^0@ = тх@т/@ + ^@^о@.
Аналогично можно показать, что
Поэтому
Ъ<0 = **@««Г@+|*@*г@-
>яA) = Л@ *<@ + />*@ЛГ@ + ВЦ)т8«)тхтЦ) +
Продифференцировав A.76), с учетом A.75) и РХЦ) = ВхЦ) + тхA)тхтA),
+ тх(От/(/)*г@ + ЖО^о(ОЛГ@
[ров
получим уравнение A.72):
Д*@ = Рх -тх(*)тхТ(*)-тх(*)тхТ(*) =
= Д/)Рх@ + Рх(ОЛг@ + Я@*оМ^^
-ЛЮщи)т/@-ттяЮт/Ю-тхМщтЮ^^
= Ж0**@ + Ж0тх(/)т/@ + 4г(/МгD + щЮт/ЮЛ7® + Щ*Ш0*Т«>"
-ЖО*,<О»*Г<О-'М0*ЬГ<^^^
1.3.3. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть известны:
а) входной сигнал, заданный своими статистическими характеристиками
ю*@, ^(/1,/2) или *,(/);
б) система, описываемая одним из уравнений A.69) или A.70);
в) математическое ожидание щ и ковариационная матрица В$ гауссов-
ского закона распределения начального состояния Х0.
Требуется найти статистические характеристики случайного процесса
*@: поведение математического ожидания щЦ) и ковариационной матрицы
Д*@, а также ковариационную функцию Ях(*1,*2)-
63

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Решая уравнение A.71), найти закон изменения математического
ожидания выходного сигнала щЦ).
2. Решая уравнение A.72), определить закон изменения ковариационной
матрицы ЯхA).
3. Найти переходную матрицу, удовлетворяющую уравнению A.74), и
ковариационную функцию по формуле A.73).
Пример 1.28. Дано уравнение
*(/) = -*(/) + <?(/), *@) = *0,
где /1^@ = 1, А^иЬ) = &(*\ -*г)- Начальное состояние Х$ характеризуется
параметрами щ = 0 и Во = 0.
Требуется найти щЦ), ЯхA), ЯхAи12)-
П 1. Так как А(*) = -1, В(() = 1, уравнение A.71) имеет вид
тх(*) = -тх@ + 1, /11,@) = щ = 0.
Его решение: щЦ) = 1 - е~1.
2. Так как »У0(/) = 1, уравнение A.72) принимает форму
Ях@ = -2ЯХA) +1 , Ях @) = Яо = 0.
1 _?*
Его решение: Дх@ = --A -е ").
3. Найдем переходную матрицу Ф(^,/2) системы, удовлетворяющую
уравнению A.74):
Отсюда Ф(/1,/2) = е"('|_'2).
Ковариационная функция определяется по формуле A.73):
Д*('ь<2) =
Пример 1.29. Дано уравнение
ЯЧ0 = '*('),*(<>) = *0.
Начальное состояние Х0 характеризуется параметрами щ = \ и Во = 10.
Требуется найти %(*), Дх@» ДхСь^)-
П 1. Так как А(*) = /, ВA) = 0, уравнение A.71) имеет вид
тхA) = 1тхA), ^@) = щ = 1 .
Его решение: тх(*) = е2.
64

2. Уравнение A.72) принимает ввд Кх@ = 2/Ях@, Ях@) = Д> -10.
Его решение: Дх (*) = 10 е .
3. Найдем переходную матрицу Ф(/1,/2) системы, удовлетворяющую урав-
г2-/2
нению A.74): ^'^^П^,^), Ф(>2,/2) = 1. Отсюда Ф(*,,*2) = « 2 •
Ковариационная функция определяется по формуле A.73):
Я*('1>'2) = 1
е * 10Л НъН. те адл)ш10.^
10 Л 2 , ^^
Пример 1.30. Дана система уравнений
Х{@ = Х2@, ^@) = ^,
^2@ = С?@, *2@) = *20>
тде О@ — стационарный белый шум с интенсивностью 50 = 1 (так называемый
стандартный белый шум).
Начальное состояние Х0 = (Хго, Х^O описывается гауссовским законом
распределения с т^ = I I и Во = I I.
Требуется найти математическое ожидание тх({) и ковариационную
матрицу Лх@.
П Так как Л@ = I I и В@ = I I, уравнения A.71), A.72) имеют ввд
^@ = 1о о)^0, ^@) = ^ = у,
те тх = х' ; Л_ = _*" *12 . Перепишем их в координатной форме:
\тХ1) {К^ ЯХа)
тХ1Ц) = щ1Ц), тя,@) = 1; я^ГО-0, да*2@) = 2;
Лхп@ = 2ЛЧ2(/), ЛГ|1@) = 2; ^(О-Лчв», *г|2@) = 1;
Л*Ю-1. 4^@) = 3.
65

Их решение определяет законы изменения математического ожидания и
ковариационной матрицы выходного сигнала:
л1ц(!)-2* + 19 /иХ2(/) = 2;
ЯЧ1<0-ЗГ2+|г3+2Г + 2, Л^М-р+а + 1, КХ22(*) = * + ЗМ
Пример 1.31. Дана система уравнений
*1<0 = -*!« + *2@, *1@) = *10,
*2(/) = -2*2@ + 2G@, *2@) = *20,
вде G@ - входной сигнал с /и^(/) = 1, Лу(*1,/2) = ОД - /2) •
Начальное состояние Х0 - (ЛГ10, Х^)т характеризуется
"*-C и *-(о ?)¦
Требуется найти математическое ожидание щA) и ковариационную
матрицу ЛЛ0.
П Так как Л(/) = (~ 1 и #@ = (9), уравнения A.71), A.72) имеют
вид
^«-("о ЛН+*»(~/ ЛИЗ*40 2)> *<»-*-С Э-
или
*ч @ = -«ч @ + «х2 @, «х, @) = 0; тх, @ = -2т,, @ + 2, иц @) = 1;
^,@—2^,@ + 2^@, Лх,,@) = 0; АХ12@ = -ЗА,12@ + Лхн@, Лг12@) = 0;
ДХ22@ = -4ЛХг@ + 4, ЛХп@) = 1.
Их решение определяет законы изменения математического ожидания и
ковариационной матрицы выходного сигнала:
«,,@ = 1-6-', да*2@ = 1;
Дч,М-}-«-2' ¦у*"*. Лх12@ =}A-«-3'), Лхи@-1. ¦
66

14 УСТОЙЧИВОСТЬ, УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ
ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ
1.4.1. Анализ устойчивости
1. Одномерные системы. При изучении различных форм математического
описания систем управления большое внимание уделяется алгоритмам решения
основной задачи анализа — задачи анализа выходных процессов, т.е. получению
количественных характеристик процессов, происходящих в системах. В данном
разделе рассмотренные выше системные характеристики используются для
выяснения качественных особенностей поведения систем управления.
ПОСТАНОВКА ЗАДАЧИ
Рассмотрим одномерную стационарную систему управления, поведение
которой описывается дифференциальным уравнением
алх<л>@+...+ а0*<') = &т*(да)@+...+ *о*<0 A.77)
с начальными условиями
*('<>) = *<ь *0о) = *о.-. х(л-1>(/0) = х<л-1),
где #@ и хA) - входной и выходной сигналы; /0 ~~ начальный момент времени.
В соответствии с представлением A.25) выходного сигнала системы в виде
суммы свободного и вынужденного движений: х@ = хс(/) + хвынA) вводятся
следующие понятия устойчивости системы.
Система управления называется устойчивой по начальным данным
{асимптотически устойчивой), если при ненулевых ограниченных начальных
условиях свободное движение хс(/) ограничено при всех /е[/0,+оо) и
Иш хс@ = 0.
Система управления называется устойчивой по входу, если при любом
ограниченном воздействии #(/) реакция системы хвынA) является ограниченной
в любой момент времени / € [/0,+оо).
Более краткий термин — устойчивая система управления — употребляется,
если система устойчива и по входу, и по начальным данным.
Требуется определить, является ли система устойчивой.
КРИТЕРИИ УСТОЙЧИВОСТИ
1* Для устойчивости системы A.77) по начальным данным необходимо и
достаточно, чтобы корни X/ характеристического уравнения
а„ Хл + дя_! Хл_1 +... + % = О A.78)
имели отрицательные действительные части: КеХ/ < О, / = 1,...,л, т.е.
располагались елевой полуплоскости комплексной плоскости (рис. 1.18).
67

11ШКнёК1!11!!!:>!111!111У
Н11Н11111ИИ111ИИНШ11И1И11Ш11ИШ1
1т X
Правая полуплоскость
КеХ>0
КеХ
Рис. 1.18
2. Для проверки отрицательности действительных частей корней
характеристического уравнения A.78) можно использовать критерий Рауса-Гурвица.
Для устойчивости системы A.77) по начальным данным необходимо и
достаточно, чтобы при ап>0 угловые миноры А/ матрицы
0}
<*п-1
О
О
ап-г *л-5
ап-2 ап-А
ап-\ ап-Ъ
ап ап-2
О
О
О
«0^
A.79)
были положительны: А/ > 0, / = 1,...,л, где ^ - а1
л-1
^п-1 ап-гЛтд
V Ощ ап_2)
При заполнении квадратной порядка п матрицы A.79) отсутствующие
в уравнении A.78) коэффициенты ап_( и а1 при / > п заменяются нулями.
3. Если система устойчива по начальным данным и порядок т
дифференциального оператора М(р) = Ьтрт+...+ &о правой части уравнения A.77) не больше
порядка п дифференциального оператора В(р) = апрп+...+а0 левой части, т.е. тип, то
система A.77) устойчива по входу [42].
Необходимое условие устойчивости. Если система A.77) устойчива, то все
коэффициенты характеристического уравнения A.78) имеют одинаковые знаки.
Замечания.
1. Первый критерий устойчивости называется прямым, а второй —
косвенным, так как в этом случае процедура анализа устойчивости не требует
нахождения корней уравнения A.78).
2. Коэффициент ап в уравнении A.78) всегда можно сделать
положительным, например, умножая уравнение на (-1).
68

3. Анализ устойчивости элементарных и типовых звеньев систем
управления (см. разд. 1.1.1) можно также выполнить, пользуясь определениями и
сформулированными критериями. Устойчивыми являются усилительное,
апериодическое (при Т>0) и колебательное (при Г > 0, 0 < 5 < 1) звенья.
Дифференцирующее звено не устойчиво по входу, а интегрирующее звено не устойчиво и
по входу, и по начальным данным.
4. Критерий асимптотической устойчивости является результатом анализа
выражения A.28), определяющего свободное движение, и A.30)—A.33).
Пример 1.Э2. Исследовать устойчивость системы, описываемой
дифференциальным уравнением (апериодическое звено A.10))
Зх + х = &.
? Характеристическое уравнение ЗХ +1 = 0 имеет отрицательный корень
Х =—. Кроме того, порядок (т = 0) правой части уравнения меньше порядка
(/1 = 1) левой части. Согласно первому и третьему критериям система
устойчива. ¦
Пример 1.33. Исследовать устойчивость системы, описываемой
дифференциальным уравнением
4х-х = $.
П Характеристическое уравнение 4Х -1 = 0 имеет положительный корень
X =—. Согласно первому критерию система не является устойчивой.»
4
Пример 1.34. Исследовать устойчивость системы, описываемой
дифференциальным уравнением (колебательное звено A.11))
х + 2х + х = &.
? Характеристическое уравнение Х2 + 2Х + 1 = 0 имеет отрицательный
(кратный) корень X = -1. Кроме того, порядок (/и = 0) правой части уравнения
меньше порядка (л = 2) левой части. Согласно первому и третьему критериям
система устойчивей
Пример 1.35. Исследовать устойчивость системы, описываемой
дифференциальным уравнением
х + 2х - х = #.
? Характеристическое уравнение X2 + 2Х -1 = 0 имеет два корня:
^1 --1 + 1/2 >0, Х2 =-1-1/2 <0, один из которых положительный. Согласно
первому критерию система не является устойчивой.»
Пример 1.36. Исследовать устойчивость системы, описываемой
дифференциальным уравнением
х + 2х + Зх + Ах = #.
П Здесь аг = 1, а2 = 2, ах = 3, а0 = 4. Необходимое условие устойчивости
выполняется. Составим матрицу A.79):
69

B
1
1о
4
3
2
°1
0
Л)
Вычисляем угловые миноры:
А!=2>0, А2 =
2 4
1 3
= 2>0, А3 =
2 4 0
1 3 0
0 2 4
= 4А2=8>0.
Они положительны, следовательно, по второму критерию заключаем, что
система является устойчивой по начальным данным. Кроме того, порядок (/и = 0)
правой части уравнения меньше порядка (/1 = 2) левой части. Согласно третьему
критерию система устойчива и по входу, т.е. является устойчивой.¦
Пример 1.37. При каких значениях параметра к система, описываемая
дифференциальным уравнением
хD) + 4хC) + 2хB) +3х + кх = х,
будет устойчивой.
? Здесь а4 = 1, а3 = 4, а2 = 2, а{=39 а0 = к. Необходимое условие
устойчивости выполняется, если к > 0. Составим матрицу A.79):
Г4 3 0 О")
1 2 к 0
0 4 3 0*
1о 1 2 *;
Для удовлетворения всех условий критерия Рауса—Гурвица должны выполняться
следующие неравенства:
14 3 0[
1 2 к\
А{ =4>0,
Л И 3 С А л
2= 1 2| 3 =
0 4 3
= 15- 16Л: >0, Д4=*Д3 >0.
15
Отсюда 0 < к < —. Кроме того, порядок (т = 0) правой части уравнения меньше
16
порядка (л = 4) левой части. Согласно второму и третьему критериям система
устойчива при 0 < к <—М
16
Пример 1.38. Найти все положительные значения коэффициента усиления
к , при которых система, заданная структурной схемой (рис. 1.19), будет
устойчивой.
Я
>е 8
*^
1
Р2 + Р + 2
Рис.
1
Р + 1
1.19
—>
к
70

? По структурной схеме составляем дифференциальное уравнение (см.
разд. 1.1.2). Уравнения элементов системы в операторной форме A.6) имеют вид
к
(р + 1)(р2+р + 2)
Исключая 6, получаем уравнение
'х + 2х + 3х + (к + 2)х = к&.
Составляем матрицу A.79):
B к + 2 0 ^
13 О
1о 2 к + 2)
и вычисляем ее угловые миноры:
А!=2>0, Д2=4-*, А3 = А2(^ + 2).
Из условия их положительности заключаем, что при всех к е (О,4) система будет
устойчива по начальным данным. Так как порядок (/1 = 3) дифференциального
оператора левой части больше порядка (т = 0) дифференциального оператора
правой части, то при к е @,4) система будет устойчива и по входу. ¦
2. Многомерные системы. Аналогично одномерным системам рассмотрим
качественное поведение многомерных систем, описываемых уравнениями
состояния.
ПОСТАНОВКА ЗАДАЧИ
Рассматривается линейная многомерная стационарная система,
описываемая уравнением состояния A.35):
х(/) = Лх@+ **(/), *@) = х<), A80)
где х - /1-мерный вектор состояния; # — г -мерный вектор входных воздействий;
^ — время; начальный момент времени /0 = 0; х0 — начальное состояние; Л, В —
матрицы размера (л х п), (л х г) соответственно.
Система A.80) называется асимптотически устойчивой, если ее свободное
движение хс(/) (при #@ = 0) ограничено при ограниченных начальных
состояниях *о и выполняется условие
Шп||хс@|| = 0. A.81)
КРИТЕРИИ УСТОЙЧИВОСТИ
1. Для асимптотической устойчивости системы A.80) необходимо и
достаточно, чтобы корни X,- характеристического уравнения
Ы(А-ХЕ) = 0 A.82)
имели отрицательные действительные части: КеХ/ < 0, / = 1,...,л, т.е.
располагались в левой полуплоскости комплексной плоскости (см. рис. 1.18).
71

2. Для проверки отрицательности действительных частей корней
характеристического уравнения A.82), которое записывается в форме A.78), можно
использовать критерий Рауса—Гурвица.
Необходимое условие устойчивости. Если система A.80) асимптотически
устойчива, то все коэффициенты характеристического уравнения A.82) имеют
одинаковые знаки.
Пример 1.39. Исследовать устойчивость системы, описываемой
дифференциальными уравнениями
х1=х1+2х2,
х2 = 4х{ + Зх2 + Д.
П Здесь А = I I. Характеристическое уравнение ^ 1 = 0 или
\4 3; | 4 3-Х|
X2 - 4Х - 5 = 0 имеет действительные корни разных знаков: X! = 5 > 0,
А, 2 = -1 < 0. Согласно первому критерию система не является устойчивой. ¦
Пример 1.40. Исследовать устойчивость системы, описываемой
дифференциальными уравнениями
*1 = *2>
х2 = -х1-2х2 + д.
-с ')¦
П Здесь А = . Характеристическое уравнение
-х 1 =о
-1 -2-Х
или X2 + 2Х +1 = 0 имеет отрицательный корень (кратности 2): Х^ = -1.
Согласно первому критерию система является устойчивой.в
Пример 1.41. Исследовать устойчивость системы, описываемой
дифференциальными уравнениями
*1=-*2+*ь
*2=*1+*2-
? Перепишем уравнения системы в матричной форме:
ЛИП! о]ы + [о Ли}
А В
Найдем корни характеристического уравнения. Получим
Отсюда X1 = /, Х2=-/. Действительная часть корней равна нулю. Согласно
первому критерию система не является устойчивой."
72

Пример 1.42. При каких положительных значениях параметра а система,
описываемая дифференциальными уравнениями
хх =-ах{+819
х2=(а-2)х3+81+82,
хг=-х2-2ах3-г2%
будет устойчивой?
? Составляем характеристическое уравнение A.82):
йеЦА-ХЕ) =
-а-Х
О
О
О О
-X а-2
-1 -2а-Х
= -(Х + я)(Х2+2дХ + а-2) =
= -Х3-ЗаХ2+(-2д2-а + 2)Х-а2 + 2а = 0.
Его корни: Хх=-а, Х2 =-а-4а2 -а + 2, Х3 =-а + 4^-а + 2 действительные.
При а > 0 корни X! и Х2 отрицательны. Из неравенства X з < 0 находим, что
а > 2. Следовательно, рассматриваемая система устойчива при а > 2.
Проверим этот вывод при а = 3, используя критерий Рауса-Гурвица.
Характеристическое уравнение имеет вид -Х3-9Х2-19Х-3 = 0. Умножая его на
(-1), получаем коэффициенты: аъ = 1, а2 = 9, ах = 19, а0 = 3. Составляем мат-
(9 3 0^
Затем вычисляем ее угловые миноры: А! = 9 > 0,
рицу A.79):
1 19 О
Ч> 9 Ъ)
А 2 = 168 > 0, А з = 504 > 0. Согласно второму критерию система устойчива.
Проверим результат при а = 1. Характеристическое уравнение имеет вид
-X3 - ЗХ2 - X +1 = 0. Так как коэффициенты этого уравнения имеют разные
знаки, то согласно необходимому условию система не является устойчивой. ¦
1.4.2. Анализ управляемости и наблюдаемости
ПОСТАНОВКА ЗАДАЧИ
Дана линейная многомерная стационарная система управления, поведение
которой описывается уравнениями состояния и выхода:
х(*) = Ах«) + Ви«), х(/о) = х0,
№ = Сх«),
A.83)
где х — л-мерный вектор состояния; и - г-мерный вектор управления, и еЯг;
* "¦ время, / б[/0,/1] - промежуток времени функционирования системы; у — к-
мерный вектор выхода; А, В, С - матрицы размера (л х л), (л х г), (кхп) соот-
ветственно; *о - начальное состояние.
73

Система A.83) называется вполне управляемой по состоянию, если выбором
управляющего воздействия !/(/) на промежутке времени [/о>4] можно перевести
систему из любого начального состояния х(/0) в произвольное заранее заданное
конечное состояние х(({).
Система A.83) называется вполне управляемой по выходу, если выбором
управляющего воздействия !/(/) на промежутке времени [/о,^] можно перевести
систему из любого начального состояния х0@ в такое конечное состояние, при
котором обеспечивается заранее заданное произвольное значение выхода у({{).
Система A.83) называется вполне наблюдаемой, если по реакции у@ на
выходе системы на промежутке времени [/о>^] при заданном управляющем
воздействии и(/) можно определить начальное состояние х(/0).
Постановка задачи формулируется следующим образом.
Пусть известны матрицы А, В, С системы A.83). Требуется определить,
является ли система вполне управляемой и наблюдаемой.
КРИТЕРИИ УПРАВЛЯЕМОСТИ И НАБЛЮДАЕМОСТИ
Критерий управляемости по состоянию. Доя того чтобы система A.83) была
вполне управляемой по состоянию, необходимо и достаточно, чтобы ранг матрицы
управляемости по состоянию
IV = [В ЛВ А2В .. АП-ХВ)
равнялся размерности вектора состояния:
тщ1У = п. A.84)
Критерий управляемости по выходу. Для того чтобы система A.83) была
вполне управляемой по выходу, необходимо и достаточно, чтобы ранг матрицы
управляемости по выходу
Р = (СВ САВ СА2В ... СА"-1В)
равнялся размерности вектора выхода:
тгп&Р = к. A.85)
Критерий наблюдаемости. Для того чтобы система была вполне
наблюдаемой, необходимо и достаточно, чтобы ранг матрицы наблюдаемости
0 = (СТ АТСТ (АТJСТ .. (АТ)"-1СТ)
равнялся размерности вектора состояния:
гапее = л. A.86)
74

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. В уравнениях состояния и выхода выделить матрицы А, В, С.
2. Составить матрицу IV управляемости по состоянию, матрицу Р
управляемости по выходу и матрицу наблюдаемости й-
3. Подсчитать ранги матриц и сделать вывод об управляемости и
наблюдаемости на основе соответствующего критерия.
Замечание. Если линейная стационарная система управления
описывается соотношениями
ап х(й>(/) +... + до х = *(>) , у@ = х«),
то, вводя обозначения хх = х, х2 = х,..., хп = х*л_1), и = #, их можно
записать в эквивалентной форме:
и, у = A 0 ••• 0)х.
х\
х2
\хп)
_
' 0
0
_к
^ ап
1
0
_.*!-
«л
0
1
_^1
<*п
0 ^
0
ДЛ-1
ап )
1 !
Г2
1 •
Ч*л,
+
'СП
0
\_\
<ап)
А ВС
Пример 1.43. Исследовать управляемость и наблюдаемость системы:
хх = *2»
х2=и,
П 1. В уравнениях состояния и выхода выделим матрицы А, В, С:
^=(о 3* *=С)'с-& °>'й=2' г=1> *я1-
2. Составляем матрицы управляемости и наблюдаемости:
Ж = B> АВ)^ Л), Р = (СД С42>)=@ 1), в-(С ^СГ) = (^ Д.
3. Определяем ранги матриц: гап8ЙК = 2 = л, гавд Р = 1 = &, гап80 = 2 = л.
Согласно критериям управляемости A.84),A.85) и наблюдаемости A.86) система
вполне управляема по состоянию и по выходу, а также вполне наблюдаема. ¦
Пример 1.44. Исследовать управляемость и наблюдаемость системы:
хг = -Зх{ + 5х2 + и,
±2=2*,+2и, У-*-*г-
П 1. В уравнениях состояния и выхода выделим матрицы А, В, С:
л=И о)* ^Ы'с=A _1)'л=2, г=1, *=1-
75

2. Составляем матрицы управляемости и наблюдаемости:
К=(В АВ)-^ "§, Р = (СВ СЛВМ-1 5), <2 = (ст АТСТ) = [^ ).
3. Определяем ранги матриц: гапяИ' = 2 = п, пищ /> = 1 = к, пищС? = 1 * л.
Согласно критериям управляемости A.84),A.85) и наблюдаемости A.86) система
вполне управляема по состоянию и по выходу, но не является вполне
наблюдаемой.»
Пример 1.45. Исследовать управляемость и наблюдаемость системы:
Хг=Х2+и,
х2=-х{-2х2-и,
Ух=х19
У2=ХХ+Х2.
П 1. В уравнениях состояния и выхода выделим матрицы А, В, С:
ч°, $¦ '-о. ч: з- •-»¦ »'• *-»¦
2. Составляем матрицы управляемости и наблюдаемости:
г.A щ.{\ -'),мс» сщ.§ -]),<,.{€* лгсг),^; \ ;д.
3. Определяем ранга матриц: гапяЖ = 1 ф п , пищ Р = 1*к, пищ С? = 2 = л.
Согласно критериям управляемости A.84),A.85) и наблюдаемости A.86) система
не является вполне управляемой по состоянию и по выходу, но вполне наблю-
даема.и
Пример 1.46. Исследовать управляемость и наблюдаемость системы:
*1 =х2-и,
х2 =5х\ + 2*з + и, у = -2x1 + х2.
х3 = -2х1 -2х3 -и,
О 1. В уравнениях состояния и выхода выделим матрицы А, В, С:
А =
@ 1 0'
5 0 2
1-2 0 -г
, в=
'-ъ
1
<-ъ
, С = (-2 1 0), л = 3, г = 1, * = 1.
2. Составляем матрицы управляемости и наблюдаемости:
(-1 1 -Я
1У = (в АВ А2В) =
1 -7 13
-1 4 -«У
, Р = (СВ С4Д С42л)=C -9 27),
е=(сг лгсг (лгJсг) =
Г-2 5 -1*
1-2 5
1о 2 -в;
76

3. Определяем ранги матриц: тап&1У = 2 * л, пищ Р = 1 = к, гап&(? = 2 *п.
Согласно критериям управляемости A.84),A.85) и наблюдаемости A.86) система
не является вполне управляемой по состоянию и вполне наблюдаемой, но
является вполне управляемой по выходу.и
Пример 1.47. Исследовать управляемость и наблюдаемость системы:
2х-4х + х = &.
? 1. Согласно замечанию к алгоритму перепишем систему в
эквивалентной форме и в полученных уравнениях состояния и выхода выделим матрицы
А, В, С:
Но,* 9- 43'с=A о)'л=2' г=1> *-!-
2. Составляем матрицы управляемости и наблюдаемости:
Г-(в Л8)-(„° ";'). '-(С* СЛ*)-@ ОД,
«-(*• ЛГ)-(о 3-
3. Определяем ранги матриц: гап8)^ = 2 = л, гап8Р = 1 = &, гап8(? = 2 = л.
Согласно критериям управляемости A.84),A.85) и наблюдаемости A.86) система
вполне управляема по состоянию, по выходу и вполне наблюдаема. ¦
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.1. Составить дифференциальные уравнения, описывающие процессы
в схемах, изображенных на рис. 1.20,а-* и записать эти уравнения в операторной
форме.
—*А I-
I/-
В | | ' "—&1 1—х—• °1 г11 I |—о
± 1_и - 1 1е* с 1 1—0
а б в
Рис. 1.20
1.2. По дифференциальным уравнениям, описывающим звенья, составить
дифференциальные уравнения их соединений:
а) последовательного соединения: рхх = &, рх = хх;
б) параллельного соединения: рхх = #, рх2 = &;
в) соединения с отрицательной обратной связью: рх = е, рд^ = х.
1.3. Составить дифференциальное уравнение параллельного соединения
Двух звеньев: л/вс^*! =$, ^х2=р^У х = хх+х2.
77

1.4. Составить дифференциальное уравнение последовательного соедине-
1 .
ния двух звеньев: — хх + хх = #, тх + х = хх.
1.5. Составить дифференциальные уравнения, описывающие динамические
системы, структурные схемы которых изображены на рис. 1.21, а-в.
чз-
р
к=т; а=ш
1
71р + 1
>
1
Т2р + 1
1
Р
'¦"¦*¦%¦ т>-ш
К
к
\
1
р
Ц
т
1
I2
1 р.
к-« Т-^-.Ь.Щ
Рис. 1.21
1.6. Используя элементарные звенья, изобразить структурные схемы,
соответствующие следующим дифференциальным уравнениям:
а) х(/) + #(/) + /2х@ = *@ + 31п/.*(/), Хо = 1, х0 = 2;
б) Зс@ + лх(/) + тлл:@ + /пх@ = т2^@ + ^@, х<> = 0, х<>=л, х0 = тп.
1.7. Найти свободное, вынужденное движения и выходной сигаал системы,
описываемой дифференциальным Уравнением:
х@ + B-л)х@-2лх@ = *@, х@) = л,х@) = 0, *@ = { '' '>0
[о, /^о.
1.8. Найти законы изменения векторов состояния и выхода многомерной
системы:
*1 =(л + 2)х1 + х2+#1, у = хх+2х2,
Х2=(-2п-Ъ)хх-4х2+&г,
с начальными условиями х^О) = 2, х2@) = 0 при входном сигнале
ЛA)~К /*о, *2(') = {о, **о.
78

Глава 2. ОПИСАНИЕ И АНАЛИЗ НЕПРЕРЫВНЫХ
ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПЕРЕХОДНЫХ
ФУНКЦИЙ
2.1. ОДНОМЕРНЫЕ СИСТЕМЫ ПРИ ДЕТЕРМИНИРОВАННЫХ
ВОЗДЕЙСТВИЯХ
2.1.1. Описание сигналов и систем
1. Описание сигналов. Для описания сигналов используются функции
времени (см. разд. 1.1.1). Выделяют два специальных сигнала: импульсное
воздействие в виде дельта-функции A.1) и единичную ступенчатую функцию A.2). Им
соответствуют две системные характеристики: импульсная переходная и
единичная переходная функции.
2. Описание систем. Рассматривается поведение линейной одномерной
нестационарной системы управления, описываемой дифференциальным уравнени-
ем
«л(Ох(|,)@ + ... + «о(Ох(/)-*т@^(т)@ + ... + *о@^) B.1)
с начальными условиями
*('о) = *<ь *(>о) = *<ь- *{п-Х\Ч) = 4"* B-2)
где #@ и х(/) - входной и выходной сигналы; пит — порядки старших
производных выходного и входного сигналов соответственно; ал (/),..., #о@>
&т@>—»М0 ~" коэффициенты, зависящие от времени / ; *о ~ начальный
момент времени (как правило, момент подачи входного сигнала).
Импульсной переходной (весовой) функцией линейной системы называется
реакция &(/,т) системы на воздействие в виде дельта-функции $(/) = 5(/-т) при
нулевых начальных условиях. Мгновенное значение &(*,т) импульсной
переходной функции зависит от момента / наблюдения реакции системы и от момента
т приложения импульсного воздействия (рис. 2.1,а). Импульсная переходная
функция к((9х)9 рассматриваемая как функция аргумента ( при фиксированном
значении т , называется нормальной импульсной реакцией системы (рис. 2.2). При
фиксированном значении / функция &(/,т) аргумента т называется сопряженной
импульсной реакцией.
л5(/-т)
,8(/-т)
*('-т)
'о х
Рис. 2.1
79

Единичной переходной функцией линейной системы называется реакция
Л(/,т) системы на воздействие в виде единичной ступенчатой функции
#@ = 7(/ - т) при нулевых начальных условиях.
Замечания.
1. Поскольку следствие - появление ненулевого выходного сигнала —
не может опережать по времени причину - приложение входного воздействия —
переходные функции удовлетворяют условию физической реализуемости (рис. 2.2):
к(*,х) = 0 при / йт; Л(/,т) = 0 при / й т. B.3)
Нормальная импульсная
реакция
Сопряженная импульсная
реакция
/ = т
Рис. 2.2
2. Для линейных стационарных систем, описываемых уравнением
ап *<">(/) +... +4, *(/) = Ьт *<*>(/) + ...+*ь №,
B.4)
где а„ ,...,йо, Ат,...,^) — постоянные коэффициенты, мгновенное значение к(*,т)
импульсной переходной функции зависит только от промежутка времени
т\ = / - т, прошедшего после приложения импульсного воздействия (рис.2.1,6):
к(*,т) = кЦ-т) или к(*,т) = к(х\), т\ = / -т.
Единичная переходная функция Л(/,т) стационарной системы также
зависит только от разности своих аргументов:
Л(/,т) = Л(/ - т) или Л(/,т) = к(т\), л = ' - *.
2.1.2. Связи вход-выход
Пусть импульсная переходная функция к(*,х) системы B.1) известна.
Получим формулу, позволяющую находить реакцию *(/) системы B.1) на
воздействие #(/) при нулевых начальных условиях.
80

По определению импульсная переходная функция &(/,т), рассматриваемая
как функция аргумента / (нормальная импульсная реакция), является решением
дифференциального уравнения B.1) при воздействии #(/)=б(*-т), где т -
фиксированный момент приложения дельта-функции:
в.«^^+...+^)^)-^)^^+... + ^)в(г-т), B.5)
с нулевыми начальными условиями
*ми-».^и-° ^Ик-«-
Умножим обе части уравнения B.5) на функцию #(т) и проинтегрируем по
х (*о**<+со):
=**(<O^^
Поменяем порядок операций дифференцирования и интегрирования, так
как они выполняются по разным аргументам:
-ио^7«(х)8(/-т)*+-"+ль(гO«(т)8(/-т)*-
*' 'о <Ь
Используя определение дельта-функции, имеем
*ю-^7*&т>«<т>*+-"+*<о7^*мо* - *1-»*м»+-+«ь»^)-
Заметим, что правая часть полученного уравнения совпадает с правой
частью уравнения B.1). Следовательно, решение х(/) уравнения B.5) имеет вид
х(/) = 7*М*М*.
'о
Учитывая условие физической реализуемости (к(*,т) = 0 при /^т),
интервал интегрирования можно уменьшить:
*(/)= }*(/,т)*(т)А. B.6)
'о
81

Формула B.6) - это связь вход-выход, которую устанавливает импульсная
переходная функция. Реакция х(г) представляет собой вынужденное движение
системы, т.е. решение уравнения B.1) с нулевыми начальными условиями:
х(/0) = 0,х(/0) = 0,..., х<л-1>(/0) = 0.
Рассмотрим случай стационарной системы, которая описывается
уравнением B.4) с постоянными коэффициентами. Свойства такой системы, разумеется,
не меняются с течением времени. Поэтому в качестве начального момента
времени /0 выбирают равный нулю. С учетом свойства &(/,т) = кЦ-т) стационарной
системы формула B.6) связи вход-выход принимает вид
*(/) = } *(' - т)*(т) А = ) *Ш> " *)* • B.7)
о о
Связь B.6) показывает, что реакция системы в момент времени /
определяется входным сигналом не только в этот момент времени, но и- во все
прошлые моменты.
Памятью системы называется отрезок времени, отсчитываемый от
настоящего момента времени / в прошлое, за пределами которого значения
входного сигнала практически не влияют на значение выходного сигнала в момент /.
Память системы определяется сопряженной импульсной реакцией. Пусть,
например, две системы имеют импульсные переходные функции ^(/,т) и &2(/,т),
причем сопряженные импульсные реакции при фиксированном / имеют вид,
изображенный на рис. 2.3. Тогда можно сказать, что память у первой системы
меньше, чем у второй.
<*2<'.*>
Рис. 2.3
Поясним, почему импульсная переходная функция также называется
весовой. Для этого запишем приближенное равенство для выходного сигнала,
заменив интеграл в B.6) интегральной суммой. Разбивая отрезок интегрирования
точками т*=/0+&-Дт, к = 0,1,...,т, на т интервалов длиной Дт = ~ ° ,
поде
лучаем
Величина к(*,хк) определяет, с каким весом входит значение входного
сигнала &(тк) в реакцию *(/). В этом смысле импульсную переходную функцию
называют весовой функцией системы.
82

2.1.3. Нахождение переходных функций
НАХОЖДЕНИЕ ПЕРЕХОДНЫХ ФУНКЦИЙ
ПО УКОРОЧЕННОМУ ДИФФЕРЕНЦИАЛЬНОМУ УРАВНЕНИЮ
Рассмотрим случай, когда система управления описывается укороченным
дифференциальным уравнением:
*л@*(л)@+.. + ^(')*<0 = *@.
B.8)
Импульсную переходную функцию ОДт) системы B.8) можно искать
несколькими способами.
Первый способ. Будем искать импульсную переходную функцию по
определению как вынужденное движение х(г) системы под воздействием в виде дельта-
функции $(г) = 8(/-т) Щ>и нулевых начальных условиях. Найдем это решение
х(/) неоднородного уравнения при / > т методом вариации произвольных
постоянных. Пусть Ф1(')»Ф2@»-"»Фл@ "" Фундаментальная система решений
однородного уравнения. Тогда частное решение неоднородного уравнения будет иметь
вид [40]:
*(') = <*С0ф1(')+ •+ *«('Ы'). B-9)
где функции С1@,...,ся(/) удовлетворяют системе уравнений
Ф1@ - Ф«@ ]
1*Мю - фНсо]
т*ЬД
*„(>)
/^п^
чЬ
B.10)
Отсюда по правилу Крамера находим
сМ вл@А@ • ¦•¦-"•
где д(/) - определитель матрицы системы B.10), дД/) — определитель матрицы,
получающейся из матрицы системы заменой /-го столбца столбцом свободных
членов. Интегрируя, получаем
п' I вя(в)д(в) ап(х)А(хУ
,(в)д(в) а„(т)д(т)'
т.е. функции С/(() не зависят от I. По формуле B.9) имеем
B.11)
B.12)
83

Упростим полученное выражение. Для этого разложим определитель дДт)
по / -му столбцу. Все элементы этого столбца нулевые, за исключением
последнего, равного единице. Поэтому в разложении получим только алгебраическое
дополнение ненулевого элемента / -го столбца. Это алгебраическое дополнение
совпадает с алгебраическим дополнением элемента <р/'(/) определителя д(/).
Поэтому сумму в B.12) можно представить как разложение по последней строке
следующего определителя:
Ф1@
Ч>'\Ь)
фН>(т)
фЛ')
Фл(*)
ф'я@
Ф„(')
-ЕМт)ф,{г).
/-1
Подставляя сумму в B.12), окончательно получаем
*М-
*ш(*Ы*)
Ф(й-2)(х)
Ф1(>)
Фя@
ФиМ
Ф^-Ч)
ф„(>)
при ^>x.
B.13)
Последовательно (л-1) раз меняя местами строки: л-ю с (л-1)-ой, (л-1)-ю с
(л - 2)-ой и т.д., переместим последнюю строку на место первой. Тогда формула
B.13) примет вид [50]:
дл ИГ1
Ф1(')
К®
ф!(»)
Фл(>)
Фя(»)
Фя@
„(«^(х) ... ^(х)
при г>т.
B.14)
Заметим, что при ^йx согласно условию физической реализуемости
*(*,т) = 0.
Итак, если известна фундаментальная система ф1(/),ф2(/),...,ф„(*) решений
уравнения B.8), то импульсная переходная функция #(/,т) при / > т
определяется по формуле B.13) (или B.14)), где д(т) — определитель Вронского:
Ф1(*) «• ФлМ
ф!@ ... ф'л@
д(т) =
#%) ... &%)
B.15)
84

Пример 2.1. Найти импульсную переходную функцию системы,
описываемой дифференциальным уравнением
</*+1M@-2/*<0 + 2х<0-*(!).
? Однородное уравнение (/2 +1) хA) - 2(хA) + 2х(/) = 0 имеет частное
решение ф]@ ='. Общее решение <р(/) этого уравнения находим по формуле
Остроградского — Лиувилля [40]:
Ф1 Ф
= с2е
ЪИ)
или
.д.
Ф1
«2@
, где с2 =соп51.
|Ф1 ф| " л1фи
Подставляя в последнее равенство коэффициенты уравнения а{({) = -21,
я2@ = /2 +1 и частное решение ф! = /, получаем
фЮ«<*(/2-1) + С1/.
Следовательно, фундаментальная система решений однородного уравнения
состоит из двух линейно независимых частных решений: ф^/) = /, ф2@ = *
По формуле B.13) находим искомую системную характеристику:
-1.
1гA т\ - -
(х2
4-1)
х2-1
/2-1
х х2
1 :
и 1
(/-х)A + хр
(т2 + 1J
при />х.1
Второй способ. При выводе формулы B.13), когда импульсную переходную
функцию искали методом вариации произвольных постоянных, было показано
(см. формулу B.11)), что функции С1(/),...сл(*) не зависят от времени /
наблюдения выходного сигнала, а определяются в момент времени х приложения
импульсного воздействия. Отсюда следует, что импульсная переходная функция
&(/,х) является вырожденной функцией своих аргументов:
А:(г,х)=с1(х)Ф1@+... + сй(х)фл@
и может быть найдена как частное решение однородного уравнения при
некоторых специально подобранных начальных условиях в момент времени г = х.
Начальными значениями импульсной переходной функции и ее
производных называются правосторонние пределы этих функций при I -> х + 0. По
формуле B.13) находим
&*¦»
Г»т+0
Ч(*)д(*)
Ф1(т)
фК*)
фИ*)
Ф<;>(х)
Фл(*)
ф'я@
фУЧт)
85

При у = 0,1,...,л-2 правая часть равна нулю, так как в определителе будет
две одинаковых строки. При у = л-1 в правой части получаем определитель
Вронского B.15), который сокращается с определителем л(т), стоящим в
знаменателе. Таким образом, начальные значения импульсной переходной функции
определяются равенством
О, у = 0,1,...,л-2,
|^>ио=
1 ,„ , B.16)
——, у = л-1.
Заметим, что в отличие от нулевых начальных условий начальные значения
импульсной переходной функции отличны от нуля.
Таким образом, импульсная переходная функция &(/,т) является решением
однородного дифференциального уравнения
ал@*(л)@ + ... + *о(')*@ = О
при ненулевых начальных значениях B.16).
Пример 2.2. Определить импульсную переходную функцию системы,
описываемой дифференциальным уравнением
/х@ + A + 2/)х(/) = *(*).
? Здесь л = 1, ах(() = /, а0(/) = 1 + Ъ. Найдем общее решение однородного
по-
уравнения ^к(^) + A + 20^@ = 0. Разделяя переменные — = -|2 + -|Л ,
лучаем решение &(/,с) = -е~2'. Начальное значение B.16) для рассматриваемой
системы имеет вид
Следовательно, -е~2х =-. Отсюда с(т) = е2т . Подставляя выражение для с(х) в
т т
общее решение, находим искомую функцию:
*(/,т) = ±«Г2('-т) при ^>xМ
Третий способ. Найдем связь между переходными функциями к((,х) и Л(/,т)
системы. По определению переходная функция Л(/,т) есть реакция системы на
воздействие в виде единичной ступенчатой функции #(/) = /(* - т) при нулевых
начальных условиях. Подставляя этот входной сигнал в связь вход-выход B.6),
получаем
'о
86

Учитывая, что 1D-т) = 0 при Ч^х, уменьшим интервал интегрирования
й(/,т) =)*(/,$) <^. B.17)
Дифференцируя по аргументу т , получаем
*(,,т) = -^-Л(/,т). B.18)
ох
формулы B.17) и B.18) связывают переходные функции системы, позволяя
выражать одну системную характеристику через другую.
Имея в виду связь B.18), можно предложить следующий способ
нахождения импульсной переходной функции системы B.8): сначала найти единичную
переходную функцию Л(/,т) системы как решение неоднородного уравнения
в,@т*(^) + ... + ^@*(/,х) = 1 B.19)
при нулевых начальных условиях
а затем, используя связь B.18), найти импульсную переходную функцию.
Пример 2.3. Найти переходные функции Л(/,т) и ОДт) системы,
описываемой дифференциальным уравнением
(/2+1)х(/)-2/х@ + 2х@ = *(/).
? Единичная переходная функция Н((9х) является решением уравнения
(^ +1) А(/) - Ъ Н@ + 2 Л(/) = 1
при нулевых начальных условиях
Соответствующее однородное уравнение (/2 +1) Л(/) - 2/ Л@ + 2 Л@ = О
имеет два линейно независимых частных решения <Р1(/) = '> Ф2(') = '2-1 (°м.
пример 2.1). Следовательно, общее решение однородного уравнения имеет вид
ф(/)-^/ + е2(/2-1).
1^е ^1, С2 — произвольные постоянные.
Так как функция Л^(/) = — является частным решением неоднородного
Уравнения (/2 +1) А"@ - 2/ Л@ + 2 Л(/) = 1, то общее решение неоднородного
уравнения имеет вид
87

-> 1
Л(*,с1,с2) = с1/ + с2(Г-1) + -.
Из начальных условий
С1Т + с2(т2-1)+- = 0,
С\ +2с2т = 0,
77\- С2(т)=^+1)
шение, определяем единичную переходную функцию:
находим с\(х)=-^—, с2(т) = —-——. Подставляя эти выражения в общее ре-
и+ ч ** г-1 1
*&*) =—= +—; + - при />т
т2+1 2(т2+1) 2
и импульсную переходную функцию системы:
1/. ч д ^и ч (*-т)A + т/)
Щ,х) = -—Л(/,т) = ч " , при / > т.!
5х (т2+1J
НАХОЖДЕНИЕ ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ ФУНКЦИИ
ПО ДИФФЕРЕНЦИАЛЬНОМУ УРАВНЕНИЮ ОБЩЕГО ВИДА
Рассмотрим теперь систему управления, описываемую линейным
дифференциальным уравнением B.1). Предположим, что известна импульсная
переходная функция А^(/,т), соответствующая укороченному уравнению B.8). Тогда
импульсную переходную функцию к({,х) системы B.1) можно найти как
реакцию системы B.8) на воздействие
*@=ио 8(и)(' - х>+...+ш б(* - х).
Используя связь вход-выход B.6), получаем
^,т)=|^5)кEM(т%-т) + ... + ^)^-т)к. B.21)
Последовательно находим интегралы, используя определение дельта-
функции и ее производных (см. разд. 1.1.1):
I
I
1коШЛ)&Чъ-*Н=(-1Г^М<,*МI

Подставляя эти выражения в B.21), получаем
Таким образом, нахождение импульсной переходной функции к(*,т) по
дифференциальному уравнению общего вида B.1) проводится в два этапа.
1. Определяется импульсная переходная функция А^(/,т) системы,
описываемой укороченным дифференциальным уравнением B.8). Это можно сделать
одним из трех рассмотренных выше способов.
2. Находится искомая импульсная переходная функция по формуле
А:(/,х)=(-1Г-^Г[^(г,х)Ат(х)] + ...+ Ло(/,т)^(т) при />т. B.22)
Пример 2.4. Найти импульсную переходную функцию системы,
описываемой дифференциальным уравнением
(/2+1)х@-2/х(/) + 2х@ = (/2 + 1)^@ + ^).
П Для укороченного дифференциального уравнения (см. пример 2.3)
импульсная переходная функция Л^(/,т) имеет вид
. и ч (*-т)A + т/)
(т2+1J
Подставляя это выражение в формулу B.22), получаем искомую функцию:
(/-т)A + т*)
Л(/,т)=-|7[/:о(^)^1(т)]+Ло(/,т)бо(х)= -|-
(ЦШ^(т2 + 1)
+ " (х2+1J
(х2+1)
(Г-т)A + /т)A + 2т) 1 + 2/т-*2 ти
= - г + ; ПРИ 1>ХМ
(т2+1J т2+1
Пример 2.5. Найти импульсную переходную функцию системы,
описываемой дифференциальным уравнением
/2дс(/)-2/х@ + 2х@ = Ы.*(/)+у*@.
П Однородное уравнение А:(/)-2/х(Г) + 2х@ = 0 является уравнением
Эйлера [40], которое имеет частные решения вида <р(/) = /Л Подставляя х = ^
в однородное уравнение, получаем
?К]-\)^-2-21]^-х + 2/'=0 => УО-1)-2у + 2 = 0 =>
У2-Зу + 2 = 0 => Л =1, У2=2.
89

Следовательно, функции Ф1@ = * и Фг@ = « являются решениями
(линейно независимыми) однородного уравнения. По формуле B.13) находим
импульсную переходную функцию *о('»т) укороченного уравнения:
М*,т)=-
X X
I *2
X X*
1 2х
/2х-/х2 (I Л /
х2Bх2-х2) 1Т Мх2
Искомую импульсную переходную функцию &(/,х) системы получаем по
формуле B.22):
Л(/'т)=-^[G-7Iпт]+G-7)т=71птC'-2т)щ,и
*>т.Ш
НАХОЖДЕНИЕ ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ ФУНКЦИИ
СТАЦИОНАРНОЙ СИСТЕМЫ
Рассмотрим особенности нахождения импульсной переходной функции
стационарной системы управления, описываемой уравнением B.4):
ап х<й>@ +... +4, *(') = Ьт *<*>(/) +... +^ *(/).
В первую очередь найдем связи между переходными функциями
стационарной системы B.4). Для этого в формулах B.17) и B.18) учтем, что переходные
функции &(/,х) и Л(/,х) стационарной системы зависят только от разности
аргументов т! = /-х, т.е. к(г()=кA-х) и Л(п)=Л(/-х). Подставим эти функции
в B.17):
После замены С, = *-% переменной интегрирования, получаем
*(п)-)*(«)*.
о
Формула B.18) для стационарной системы принимает вид
B.23)
B.24)
Теперь определим связи переходных функций Н(х\) и к(ц) системы B.4)
с переходными функциями Но(х\) и *о(л) стационарной системы, описываемой
укороченным дифференциальным уравнением
ап *<">(/) +... + ао х(() = ^@. B.25)
90

Подставляя в B.22) *(*,т) = *(п), *о(/,т) = *о(п), Л = '-*> и учитывая, что
коэффициенты АвЛ»-» *« " постоянны, получаем
*(л) = *т 4т)(л) +... + Ьо Мл) при Т] > 0. B.26)
Используя связь B.23), проинтегрируем обе части равенства B.26) в
пределах от 0 до я • Получим равенство
Л(л) = Ьт 4т)(т\) + .. + Ьо МЛ) при Л > 0. B.27)
Опираясь на полученные связи, можно предложить два способа
нахождения импульсной переходной функции стационарной системы.
Первый способ. Для уравнения B.4) сравнительно просто находится
фундаментальная система решений однородного уравнения. Поэтому наиболее
удобный способ поиска импульсной переходной функции к(т\) = к(*-х) состоит
в следующем.
1. По корням Х!,...,ХЛ характеристического уравнения ап Хп +... + а0 =0
определить фундаментальную систему решений Ф1 (/)>..> Фл('). При этом каждому
действительному корню X кратности р соответствует р линейно независимых
решений е™,1ех<,...91р~1еи, а каждой паре Х = а±/р комплексных сопряженных
корней кратности р отвечают 2р линейно независимых решений
ва/япр/,...,/'"!ва/8тр/; ваГсо8рГ,...,//,-1ва/со8рл
2. Определив п линейно независимых решений Ф1@,—,ФЛ@ однородного
уравнения, получить импульсную переходную функцию Мл) системы,
описываемой укороченным дифференциальным уравнением B.25) по формуле B.13),
которая для уравнения B.25) имеет вид
ф1@) ... Фл@)
Ф1@) •• ф'„@)
Мл)=-
1
ф|й-2)@)
Ф1(Л)
ф(Г2)@)
Фл(л)
А =
Ф1@)
ф!@)
Ф„@)
ф'„@)
№"-» ... флл-!>@)|
B.28)
3. Найти импульсную переходную функцию к(ц) системы B.4), учитывая
ее связь B.26) с импульсной переходной функцией к0(х\) соответствующего
укороченного дифференциального уравнения:
да
Замечание. Если система управления описывается уравнением ви-
алх<л>@ + ... + Лох(/) = *т@^(т)@ + ... + ^)@^),
B.29)
Ще коэффициенты в левой части уравнения не зависят от времени, а в правой
части — зависят, импульсную переходную функцию А^(/,т) укороченного уравне-
91

ния B.25) можно найти по формуле B.28), т.е. как для стационарных систем.
При этом она оказывается функцией разности аргументов:
М^т) = *о(/-т) = Мл).
Искомая импульсная переходная функция к(*9х) нестационарной системы
находится по формуле, следующей из B.22):
^,т) = (-1Г-|^[^(/-х)Ьт(т)] + ...+ ^(^х)^(т) при ^>x. B.30)
дхт
Пример 2.6. Найти импульсные переходные функции элементарных и
типовых звеньев систем управления.
? Усилительное звено (см. рис. 1.3,д). Подставляя в уравнение A.7)
входной сигнал $(/) = 5(/ - х), получаем к(*> х) = КA) 5(/ - т).
Дифференцирующее звено (см. рис. 1.4). Подставляя в уравнение A.8)
входной сигнал #@ = 5(* - т), получаем к(*9 х) = 6(/ - т).
Интегрирующее звено (см. рис. 1.5,а) . Дифференциальное уравнение A.9)
при #@ - 5(/ - х) имеет решение &(/,т) = /(/ - т).
Апериодическое звено (см. рис. 1.6,а). Запишем для уравнения системы A.10)
задачу Коши B.8), B.9):
однородное уравнение: Т—#(/,т) + А:(/,т) = 0,
Ы
начальное значение импульсной переходной функции: *('»*) |/шт+0 =—•
Общее решение однородного уравнения имеет вид к(^х) = се т. Из
начального условия получаем выражение для параметра с:
-- 1 1 -
Окончательно получаем
*(',*) = уГ* т при/>т.
Как видим, найденная импульсная переходная функция зависит только от разно-
1 -я
ста /-т,т.е. к(т\) = —е т, т! = /-т.
Колебательное звено (см. рис. 1.7,а). Составляем характеристическое
уравнение для дифференциального уравнения A.11) : Г2Х2 + 27Ч;Х + 1 = 0. При
5 е (-1,1) это уравнение имеет два комплексных сопряженных корня
42 ^(-^мГь!1),
92

поэтому фундаментальную систему решений образуют функции
ф1 (/) = е~ы 81П Ы, ф2@ = е~а* соз со/,
17
5
где а = ^' @ = "
'1-в'
По формуле B.28) находим импульсную переходную
функцию колебательного звена:
к(ч) =
1
Т2
0
1 1
е~ац вимоц е~ап созю т\ \
0 ,|
о -а |
Г2«>
--ап
8ШС0Я-
Пример 2.7. Найти импульсную переходную функцию системы,
описываемой дифференциальным уравнением
Зс -дс(/) + 4х(/)-4х@ = зт/.^@ + сое/ ^@.
? Сначала находим фундаментальную систему решений однородного
уравнения
Зс-х(/) + 4х@-4х(/) = 0.
Для этого решаем соответствующее характеристическое уравнение
Х3-Х2+4Х-4 = 0 => (Х-1)(Х2 + 4) = 0 => X! =1, Х^з =±2/\
Полученным корням отвечают три линейно независимых решения:
Ф1@ = *', Ф2@ = со8 2/, Фз@ = зт2/,
которые образуют фундаментальную систему решений. По формуле B.28)
находим импульсную переходную функцию *о(/ - т) для укороченного уравнения:
*о(л) =
ец со$2ц 81п2я
1 1 0
1 0 2
1 -4 0
= 0,2*л -0,2со82г1 -0,18т2т1, г\ = /-т.
Наконец, по формуле B.30) с учетом замечания для систем, описываемых
Уравнением B.29), находим импульсную переходную функцию к(*,т) системы:
*(/,т) = -—{[о,2е'~х - 0,2соз2(/ - т) - 0,181П 2(/ - т) 1 8т т}+
дх 11
+ [0,2 е'~х - 0,2 соз 2(/ - т) - 0,1 зш 2(/ - т) ] соз х =
= [о,2е'~т+0,4зш2(/-т)-0,2соз2(/-т)]8Ц1т при ^>xМ
93

Второй способ. Если требуется найти переходные функции к(г\) и к(т\)
стационарной системы B.4), то следует выполнить следующие действия.
1. Решить задачу Коши:
ай^>(л)+...+ аоМл) = 1,
Лб@) = Л6@) = ... = ^л-1)@) = 0
для единичной переходной функции /^(л) системы, описываемой укороченным
дифференциальным уравнением.
2. Найти единичную переходную функцию к(т\) системы B.4), используя ее
связь B.27) с функцией Ло(л)'
*Л> = ^4№л>+••• + ** *><Л>-
3. Найти импульсную переходную функцию к(т\) системы по формуле
B.24):
Пример 2.8. Найти переходные функции А(л) и к(т\) системы,
описываемой дифференциальным уравнением
Г*(/) + *@ = **('),
ще Г и Ь — положительные числа.
П 1. Решаем задачу Коши B.18) :
ГМл) + Мл) = 1,М0) = 0.
Ее решение Ио(т\) = 1 - е т - единичная переходная функция системы,
описываемой укороченным дифференциальным уравнением Г *(/) + *(/) = $(/), т.е.
единичная переходная функция апериодического звена A.10).
2. Находим единичную переходную функцию данной системы по формуле
BЛ9):
п(ч) = Ьа-е~Т).
3. Дифференцируя к(г\), определяем искомую импульсную переходную
функцию:
а -Я-
*(Л) = |* т.
При Ь = 1 результат совпадает с полученным в примере 2.6 для апериодического
звена.»
94

2.1.4. Импульсные переходные функции соединений
Для определения импульсной переходной функции по структурной схеме
нужно сначала найти импульсные переходные функции отдельных звеньев
системы, а затем получить переходные функции соединений этих звеньев. При этом
полезно использовать ранее найденные (см. разд. 2.1.3) импульсные переходные
функции элементарных и типовых звеньев систем управления.
Рассмотрим три типа соединений (рис. 2.4, а—в). Пусть известны
импульсные переходные функции к^т) и к2(*,т) соответствующих звеньев. Требуется
найти импульсную переходную функцию к(*,%) соединения.
*!(',*)
*1
кг(*,-с)
X
я
№,%)
к2«,х)
*1
г X
} "
*2
уС
*ч
8
?* 1
х2
кх«,т)
*2<'.т>
X
'" >
кхЦл) V
б
*1 ^ч х
/У*
*!</,*>
т
Ь&т)
Рис. 2.4
Последовательное соединение звеньев (рис.2.4,а). Запишем связь вход-выход
Для второго звена:
*(')=|М>>Ю*1(*)^. B.32)
к
Если на вход системы подать сигнал $(/) = б(/ - т), то на выходах звеньев получим
по определению сигналы х1(/) = А:1(г,т) и х(/) = #(/,т). Подставляя эти функции в
B-32), находим
к(их)=\к2(и$к&х)а%.
95

Учитывая условие физической реализуемости (к{(^х) = 0 при ^т),
получаем импульсную переходную функцию последовательного соединения
к(^)=\к2(^)кх(^т)^. B.33)
т
Параллельное соединение звеньев (рис.2.4,б). Подадим на вход соединения
сигнал $(/) = б(* - т). Тоща на выходе первого звена получим сигнал хД/) = кх(^х)9
на выходе второго звена — сигнал х2(*) = *2('»т)> а на выходе соединения —
сигнал х(/) = *(/,т). Учитывая, что х(г) = х1(/)+х2(/), получаем формулу для
импульсной переходной функции параллельного соединения:
к^х) = к1(^х)+к2^х). B.34)
Соединение с обратной связью (рис.2.4,*). Заметим, что выходной сигнал
х(/) получается в результате прохождения сигнала ошибки е(/) = #(/) Т х2(/) через
первое звено с импульсной переходной функцией к^х). Так как для линейных
систем справедлив принцип суперпозиции, это эквивалентно независимому
прохождению сигналов #(/) и х2(/) через первое звено и последующему сложению
результатов с соответствующим знаком. Следовательно, структурную схему
рассматриваемого соединения можно заменить эквивалентной схемой (рис.2.4,г).
Обозначим через к{2((,х) импульсную переходную функцию
последовательного соединения звеньев в цепи обратной связи. По формуле B.33) находим,
что
*12^) = /*|(«)*2М*. B.35)
т
Тогда, используя связь вход-выход для цепи обратной связи, получаем
Подав на вход соединения сигнал #(/) = б(/-т), на выходе первого звена
появится сигнал х1(/) = /:1(/,т), а на выходе соединения - искомая переходная
функция х(/) = к(*,х). Подставим эти сигналы в равенство х(/) = х^/)* у(*):
к(*,х) = к1(*,х)* /*п('.«)*М*-
Учитывая условие физической реализуемости (&(^,т) = 0 при %йх),
окончательно получаем
*(г,х) = *|(г,т)т /к12(<,$к(Ьх)а\. B.36)
т
Знак «плюс» выбирается для положительной обратной связи, а «минус» — для
отрицательной. Как видим, для нахождения импульсной переходной функции
соединения с обратной связью нужно решить интегральное уравнение Вольтерра
второго рода B.36) с ядром B.35).
96

Пример 2.9. Найти импульсные переходные функции систем, структурные
схемы которых изображены на рис. 2.5.
а Предлагаемые структурные схемы являются соединениями
интегрирующего и усилительного звеньев, импульсные переходные функции которых
имеют вид (см. пример 2.6)
*1(',т) = /(*-т), к2(*,т) = аЬ(*-х).
Для системы (рис. 2.5,а) по формуле B.33) находим
*(/,т)=/*/(/-§) 5(§-т)^ = а/(/-т).
т
Для системы (рис. 2.5,6) по формуле B.34) записываем выражение искомой
функции:
*(/,т) = /(/-т) + а6(/-т).
<-ЕНв*
х 8
1 1
Т_о_Г
&
1 а \*—
Рис. 2.5
Чтобы определить импульсную переходную функцию системы (рис. 2.5,*),
находющвдро B.35)
Уравнения B.36)
/
*(/,т) = 7(/-т)-/*/(/-$)*&т)^.
т
Учитывая, что т < ^ < ', получаем интегральное уравнение
*(/,т) = 1-*/*Й,т)<й;,
97

которое эквивалентно задаче Коши:
Решение этой задачи имеет вид кA,т) = е"а^~хК Поэтому для импульсной
переходной функции, учитывая условие физической реализуемости, можно записать
выражение
к(*,т) = е-а«-хI(*-т)М
2.1.5. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Основная задача анализа системы управления состоит в нахождении
реакции системы на заданное воздействие. Пусть система управления задана
структурной схемой, дифференциальным уравнением или известна ее импульсная
переходная функция. На вход системы, начиная с момента времени /0, подается
заданный входной сигнал
потребуется найти выходной сигнал *(/) при нулевых начальных условиях:
х(/о) = 0,х(/0) = 0,...,^л-1>(^о) = 0.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти импульсную переходную функцию системы, если она не задана.
Это можно сделать двумя способами. Если система задана дифференциальным
уравнением, то ее импульсную переходную функцию находим с помощью
методов, изложенных в разд. 2.1.3. Если система задана структурной схемой, то
нужно либо по схеме составить соответствующее дифференциальное уравнение (см.
разд. 1.1.2), а затем по уравнению найти импульсную переходную функцию, либо
по известным импульсным переходным функциям отдельных звеньев,
составляющих систему, найти импульсную переходную функцию всей системы,
используя формулы для соединений (см. разд. 2.1.4).
2. Определить закон изменения выходного сигнала по формуле B.6) или
B.7) в зависимости от типа системы.
Пример 2.10. Найти реакции системы, структурная схема которой
изображена на рис. 2.6, на воздействия
при нулевых начальных условиях.
98

1
Т
Рис. 2.6
? 1. Составляем дифференциальное уравнение по структурной схеме
(см. разд.1.1.2). Уравнения элементов схемы в операторной форме имеют вид
1
х = — 6,
Р
Исключая е, получаем
Трх + х = &,
т.е. система описывается дифференциальным уравнением Т хA) + хA) = %(*).
Такое уравнение соответствует апериодическому звену (см. разд.1.1.1).
Импульсная переходная функция апериодического звена была найдена в примере 2.6:
1 --
2. По формуле B.6) определяем реакции системы на заданные воздействия:
б) *(/)=,[-* т $<К=1±е ^-«Х-Г-ГО-е т)м
о ^ о ^
Пример 2.11. Найти реакции системы, описываемой дифференциальным
Уравнением
/*(/) +A +20 х@ = *@,
на воздействия
а)*(/) = /(*-3); б)*@
при нулевых начальных условиях.
= (е',/>1,
10,^1
99

? 1. Импульсная переходная функция системы была найдена при
решении примера 2.2:
*<г,т) Л «***>, />т.
2. По формуле B.6) находим реакции системы на заданные воздействия:
з
а) х@ = } ±*2<-<>А ш±<Х-е2^), / > 3;
б) *(/) = / !«*" V* = ±-(е* - ег~ь), * > 1Л
Пример 2.12. Найти реакцию системы, описываемой дифференциальным
уравнением
х(/)-Зх@ + 2х@ = *@-*@,
на воздействие #(/) = е3'/(/) при нулевых начальных условиях.
? 1. Характеристическое уравнение Х2-ЗХ + 2 = 0, соответствующее
однородному дифференциальному уравнению х':-Зх + 2х = 0, имеет корни Х{=\у
Х2 = 2. Поэтому фундаментальная система решений однородного уравнения
имеет вид <р{@ = е*, <р2@ = е7*. Так как данная система управления
стационарная, то импульсную переходную функцию для укороченного дифференциального
уравнения находим по формуле B.28):
*о(л) =
1 1
е* е2х*
1 1
1 2
.«^-«ч
Теперь по формуле B.26) определяем импульсную переходную функцию
рассматриваемой системы:
*(л) = Мл)-*о(л) = е2п.
2. По формуле B.7) вычисляем искомую реакцию системы:
х(Г) = }л*'-»«/-0«*вв* |<ГЧ = *3' -в* •¦
о о
100

2.2. МНОГОМЕРНЫЕ СИСТЕМЫ ПРИ ДЕТЕРМИНИРОВАННЫХ
ВОЗДЕЙСТВИЯХ
2.2.1. Описание сигналов и систем
1. Описание сигналов. Сигналы, действующие в системе, описываются
функциями времени (см. разд. 1.2.1). Среди них выделяют два типовых сигнала:
импульсное воздействие в виде дельта-функции 6(Г-т) и единичную
ступенчатую функцию 1(/-т).
2. Описание систем. Многомерные нестационарные системы описываются
уравнениями состояния A.34) и выхода A.36):
B.37)
Я0=с@х(г),
ще х — п -мерный вектор состояния; # — г-мерный вектор входных
воздействий; у - А:-мерный вектор выхода; / - время; Л(()9 ВЦ), С(/) - матрицы
размера (лхл), (лхг), (Ьл) соответственно.
Преобразование сигналов в системе отражено на рис. 1.16.
Закон изменения 1-й координаты вектора состояния при воздействии
8^) = 5(/ - т) нау-м входе, нулевых воздействиях на остальных входах и нулевых
начальных условиях называется импульсной переходной функцией по состоянию
*/*(',*), / = 1,...,л;./ = 1,...,г.
Закон изменения р-й координаты вектора выхода при воздействии
#Д0 = 5(/ - т) на/-м входе, нулевых воздействиях на остальных входах и нулевых
начальных условиях называется импульсной переходной функцией по еыходу
Ц^), р = 1,...,*;У = 1,...,г.
Импульсные переходные функции по состоянию и выходу представляются
матрицами *х(/,т) = || Х$</,т) ||> *у(/,т)=| **//,т) | размера (лхг), (кхг)
соответственно. Как и в случае одномерных систем (см. разд. 2.1.1), импульсные
переходные функции удовлетворяют условию физической реализуемости:
АГ*(/,т)=* О при /йт, КУЦ,%) = О при /йх,
а для стационарных систем, описываемых уравнениями
х@ = Л*@ + 2**@,
Х0-СхA),
зависят только от разности 1-х = ц своих аргументов:
Кх(*,х) = Кх(* - х) = Кх(х\), КУ«,х) = КУЦ - т) = К'Ы.
101

2.2.2. Связи вход-состояние и вход-выход
Импульсные переходные функции позволяют определить законы
изменения векторов состояния и выхода при нулевых начальных условиях, т.е.
вынужденное движение системы.
Для многомерных нестационарных систем, описываемых соотношениями
B.37), они находятся по формулам
х@= )кх(*,т)8(т)а\, у@= *\КЧи%Ж%)*9 B.38)
к к
где /о — момент начала функционирования системы (возможен случай /0 = -оо).
Для многомерных стационарных систем законы изменения векторов
состояния и выхода находятся по формулам
*(/) = \К*(*-тЫ%)*=\Кх(Ъ)&-Ъ)Л%
о о B39)
о о
Связи B.38), B.39) вход-состояние и вход-выход являются обобщением на
многомерный случай формул B.6), B.7). Как уже отмечалось (см. разд. 1.2.1),
многомерную линейную систему, имеющую г входов и к выходов, можно
рассматривать как совокупность г • к одномерных систем, каждая из которых
связывает один из г входов с одним из к выходов. Реакция #@ на / -м выходе,
согласно принципа суперпозиции, равна сумме реакций от каждого входа в
отдельности:
Записав эту формулу в матричном виде, получим связь B.38).
2.2.3. Нахождение импульсных переходных функций
Сравнивая B.38) с A.44) при нулевых начальных условиях, получаем
формулы для нахождения импульсных переходных функций:
Кх{г9х) = Ф(/,т)*(т), К* (их) = С@ Ф(/,т)*(т), B.40)
где Ф(*,т)— переходная матрица.
Для стационарных систем имеем
КХЬ\) = Ф(т\)В9 КУ(ц) = СФ(ч)В. B.41)
Замечание. Импульсные переходные функции 7^(/,т), связывающие
У-й вход (У = 1,...,г) с /-М выходом (/ = !,...,&), можно искать, используя
алгоритмы для одномерных систем, рассмотренные в разд. 2.1.3 и 2.1.4.
102

Пример 2.13. Найти импульсную переходную функцию системы,
структурная схема которой изображена на рис. 2.7, а.
Р
-* У
*2
X
—ФЧа I
а
-1
р П
Рис. 2.7
П Рассматриваемая система имеет два входа (г = 2) и один выход (к = \),
поэтому импульсная переходная функция имеет вид
*^т) = (*>(/,т) КУ2Ц9х)\
При отсутствии входного сигнала #2 (й@ = 0) структурная схема данной
системы является соединением с отрицательной обратной связью (см. рис. 2.4,*).
Импульсная переходная функция такой системы была найдена в примере 2.9:
*й(*,т) = <Гв('-т) при/>т.
При отсутствии сигнала & (&(/)» 0) структурную схему системы можно
представить в виде, изображенном на рис. 2.7,6. Составим дифференциальное
уравнение, описывающее систему (см. разд. 1.1.2):
а
У = —е,
Р
е = *2+>'-
Отсюда у + ау = -а&2 или — у + у = -#2. Как следует из примера 2.8, импульсная
переходная функция такой системы: К{2(*,т) = -ае"л(/"т), так как Т = —, * = -1.
юм, искомая импульсная переходная фу]
**(/,т) = (<Г°<'-т> -а<Гл('-т>) при*>т.
Таким образом, искомая импульсная переходная функция многомерной
системы имеет вид
2.2.4. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть заданы:
а) входной сигнал $(/);
б) система, описываемая уравнениями состояния и выхода B.37);
в) нулевые начальные условия.
Требуется найти законы изменения вектора состояния х(/) и вектора
выхода^).
юз

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти переходную матрицу (одним из трех способов, рассмотренных
в разд. 1.2.4).
2. Найти импульсные переходные функции по формулам B.40) или B.41).
3. Определить законы изменения векторов состояния и выхода системы по
формулам B.38) или B.39).
Пример 2.14. Найти законы изменения векторов состояния и выхода
многомерной системы:
хх = х1+2х2 + &,
ДС2=2Х!+Х2,
с нулевыми начальными условиями х1@) = 0, х2@) = 0 при входном сигнале
*(/) = *'/(*).
? 1. Перепишем уравнения системы в матричной форме:
А В С
и найдем переходную матрицу (см. результат примера 1.24):
<ы \-1( е*+е~п в3"-е-")
2. По формулам B.41) найдем импульсные переходные функции:
д ™-2(у-_<.-•> езп+е-п^@^-2[езп_в-п^•
3. По формулам B.39) определим законы изменения векторов состояния и
выхода:
уA) = \ е*'" V* = ±(е* - в') .¦
104

Пример 2.15. Найти законы изменения векторов состояния и выхода
многомерной системы:
*2=*1+Й. У2 = Хх+-Х2
при нулевых начальных условиях х{@) = О, х2@) = 0 и входном сигнале с
компонентами й(/) = 2 • /(/), ^(О = *(')•
П 1. Перепишем уравнения системы в матричной форме:
*ин:-.')ик;п(:)- к; а:)
А В С
и найдем переходную матрицу (см. пример 1.25):
Гсозл -зштП
^ 81ПТ1 С08Ц )
2. По формулам B.41) определим импульсные переходные функции :
[ ЯПТ) С08Т1 ДО 1^ [ 8ШТ] С08Т1 У
Ку(\(® 1 ^(СОЗЛ -80111^1 0)_Г 81ПТ1 С08Т1 ^
^ 1 0,5 ^ 8и1Л со8Л ДО 1 ) \ со8л + 0,58тт1 0,5со8Т1-8тг1 )'
3. По формулам B.39) найдем законы изменения векторов состояния и
выхода системы:
Х(*)= Г { «ЯР-*) -81п^"т) }B)<к = ( 28Ш/ + С08/-1 ^
Д8т(/-т) со8(/-т)Д1; B-2со8/ + 8т/ у
уЦ) = \{ 8т(/-т) С08(/-т) Уг^ . B-2сов/ + 8ш/^
I \ С08(/- т) + 0^8Ш(/ -X) 0,5С08(/ - т) -81П(/ -т) )[\) ~{ 2^81П/ /
Пример 2.16. Найти законы изменения векторов состояния и выхода
многомерной системы:
2*2+1 *2 „з л
7(р7Г)Х1'771Х2+( +1)Л§ Я@-*1+'**.
яри нулевых начальных условиях и входном сигнале с компонентами
*1@-'8(*_2), «(О-^А'-г).
105

? 1. Как следует из примера 1.23, переходная матрица системы имеет вид
Ф(',т) =
х2+1
\1 *
и -^
( /A + *т) *т(т-0 "|
т(т2+1) т2+1
/-т т(*т + 1)
I, т/(т2+1) /(т2+1);
2. Так как в рассматриваемой системе
Ч';' /¦.)• С*К! -'О'
то, используя B.40), получаем
**</,т) = Ф(Г,тJ>(т) =
С 1A+ (х) 1х(х-1) ^
т(т2+1) т2+1
Г-т т(/т + 1)
1,т/(т2+1) /<х2+1) ^
*A + 1т) 1т(х-1)Л
Гт3+т 0 )_
( 0 х2+1)
КЦ(,х) = С(/)Ф(>,тJ>(т) = Г | _'2 )
( Н1 + *х) (х(х-1) ~]
х(х2+1) т2+1
1-х хAх + 1)
^ т/(х2 + 1> 1(х2+1))
(т3+т 0 )_
I 0 х2 + 1)
( 12х + 2(-х Кх2-Bх + хЛ
[ 13х + (х -(Зх-(х )'
3. По формулам B.38) найдем законы изменения векторов состояния и
выхода:
»(*A + *т) 1х(х-Г))
2 I ( I
20 5
к 5 + 4 г 5 )
( хЦх-2) \
,л \{г2х + Ъ-х Ъх2-Bх + х}( хЪ(х-2))
*>'1{ А + * -Л-/* Дт2/(*-2)Г =
Г 0Д5>6 + 0.25/4 + 8>2 -8,8/-8 "I и
[ -0,25>7 -0.25/5 +8/3 +8/ /
106

23. ЛИНЕЙНЫЕ СИСТЕМЫ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
2.3.1. Описание сигналов и систем
1. Описание сигналов. Для описания сигналов используются моментные
характеристики: математическое ожидание и ковариационная функция (см. разд.
1.3.1). В качестве типового входного сигнала применяется белый шум.
2. Описание систем. Поведение одномерных систем управления описывается
дифференциальным уравнением
МО^ПГ+... + ао(')*@ = М0^^ +... + МОЖО > B.42)
где G@ и Х(?) — входной и выходной сигналы; пит — порядки старших
производных выходного и входного сигналов соответственно; дл(/),...,До@>
6да@,..»А)@ " коэффициенты, зависящие от времени г.
Входное воздействие подается на систему в момент / = /0 = 0.
Начальные условия считаются нулевыми, поэтому параметры
распределения вектора Х@): т0=09 Д> = 0 — соответственно начальные математическое
ожидание и дисперсия.
2.3.2. Связи вход-выход
Реакция Х(*) системы на воздействие (?(/) определяется связью вход-выход
B.6):
ХЦ) = / к(и т)<7(т) А. B.43)
к
Усредняя левую и правую части этого равенства по множеству реализаций
случайных сигналов ЛГ(/), G(/) и учитывая, что импульсная переходная функция
является детерминированной характеристикой, получаем
тх(*)=М[Х{<)] = м\ \к(ихH(х)<к = \к(ит)М[б(х)]<к= /*(/,т)т,(т)А,
где &(/,т) — импульсная переходная функция системы; /и^@, щ(*) ~~
математические ожидания входного и выходного сигналов соответственно.
Следовательно, закон изменения математического ожидания выходного сигнала имеет вид
тх(*)=1к(*,-с)т;(т)ат. B.44)
о
Получим теперь выражение для ковариационной функции выходного
сигнала. Для этого рассмотрим центрированные сигналы
107

которые, как это следует из B.43), связаны соотношением
Х(*)=)к(*,х)в(х)ах.
Образуем произведение
Шк^)к(^ч)кь)^1 }^2,т2)^(т2)Л2 = ) )к(^х{)к^Х2)Ь{х{H{х2)а\1а\2
8 Щи*\№\)*4 ]к({29х2H(х2)ах2 =]}
*> *> <6 Ь
и найдем математическое ожидание левой и правой частей:
Лх('1^2)=^1№)]= } }^1^1)^2^2)^(х1Их2)]л1Л2 =
= } ]*ки*\)Ы$ъъ)&жЬ\.*г)*ч Л2,
'о 'о
где /^(/ь/2) и 1?х('1,'2) "* ковариационные функции входного и выходного
сигналов соответственно. Отсюда следует, что ковариационная функция выходного
сигнала определяется по формуле
\\
Л*('ь>2)= ) )Щ,хх)кЦъх2)К8{хих2)ах2ахх. B.45)
Дисперсия Вх(*) выходного сигнала для любого момента времени /^/0
находится, если в формуле B.45) положить 4 = /2 = /:
2)х@= \ \к(ихх)к(их2)К^иЧ)<Ь2<Ь\ • B.46)
о о
Если входной сигнал является стационарным белым шумом с
ковариационной функцией А;('ь'2) = 8ф(Ч - *2), формулы B.45), B.46) имеют вид
Д*('ь'2) =
»$0 } к(*1,х2)к(*2,х2)ах2, 4 * *2>
До/*('ь*1>*<'2.*1>*ь <2*'ь
B.47)
2)х(/) = 50/А:2(/,т)Л.
108

2.3.3. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть заданы:
а) входной сигнал G(Г), заданный своими статистическими
характеристиками т8@> &г(*ь*гУ>
б) система, описываемая дифференциальным уравнением B.42);
в) нулевые начальные условия (при /о = 0): щ=09 Д> = 0.
Требуется найти статистические характеристики выходного сигнала:
/Ях('), Д*('1>'2)-
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти импульсную переходную функцию системы (см. разд. 2.1.3).
2. По формуле B.44) определить закон изменения математического
ожидания выходного сигнала.
3. По формулам B.45), B.46) найти ковариационную функцию и
дисперсию выходного сигнала.
Пример 2.17. Для системы, описываемой уравнением
*<0+2ЛГ(о»е@,
где /и^(/)»0, А;D,*2) = 5D -^)» найти тх(/), 2)х@, &Х(Ч>*2) ПРИ нулевых
начальных условиях.
? 1. Найдем импульсную переходную функцию системы (см. разд. 2.1.3).
Единичная переходная функция системы удовлетворяет уравнению
Л(л) + 2Мл) = 1, А@) = 0.
Отсюда Л(л)=тA-е~2п), а импульсная переходная функция к(г\) = к(г\) = е~2п
или *(/,т) = е('~т), так как т\ = X - т.
2. По формуле B.44) с учетом /и^(/) з 0 имеем тх{$) = 0.
3. Из B.46), B.47) следует
е-Ч<-г)
**('ь<2) =
о 4
о
'-±0-^>;
4
1.-ад+«)[.^-1],^*/1.
I 4
Заметим, что входной сигнал - стационарный белый шум, а выходной
сигнал в силу стационарности и устойчивости системы становится стационарным
при г-> -ко. Тогда
109

Шп 4,@-7;
Г-ич» 4
Ш Дж(*„*2) = /Шп 1[в-ЭД-*> -в-ЭД^] = 7еч = 2),(т0,
ГДе Ц = /1-/2, *1 **2-И
Пример 2.18. Для системы, описываемой уравнением
*(/) + *(') = <?('),
где /и^(/) = 2, 1^(Мг)м*~2**('1-'2)» найти щЦ), 1>х@> АхСь'г) при нулевых
начальных условиях щ = 0, Д> =0.
О 1. Импульсная переходная функция системы находится аналогично
предыдущему примеру. кA, т) - е"(г~т).
2. По формуле B.44) получаем
/и,
:@=/2*-('-т)А = 2в-('-т>
= 2A-*"').
3. По формуле B.46) определяем дисперсию
I I
^>х@= //в"(Г"Т,)е"(Г"Т2)еТ|8^1 -т2)А2Л1 =
00
о о
По формуле B.45) находим ковариационную функцию
Ях(^2)-))е'(A-Х1)е^-^е-2^(хх -т2)А2*1 =
00
|в-(г,-т|)е-(г2-т1)в-2т1Л1> /а^^
1*1*"
*-<''+ч /,^2,
<4+'2)
, ЬЫХ.
110

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
2.1. Найти импульсные переходные функции стационарных систем,
описываемых уравнениями:
а) х@ + л*@ = *(');
б) *@+^±*@+*(/) = п№+*@;
л
в) х@ + л2х@ = *(') + C0 - л)*@.
2.2. Найти переходные функции л(/,т), к(*,%) нестационарных систем,
описываемых уравнениями:
а) 2/2х@+ *(') =-*(>);
б)/х@-*@ = '2со$'*@;
в)^0 + (' + 1)*@ = зЛг'*@.
2.3. Построить графики нормальной (при т = 10) и сопряженной (при
г = 0) импульсных реакций системы, описываемой уравнением
*@ + -у^-*<'> = *<'>•
г + л
2.4. Найти импульсные переходные функции систем, описываемых
дифференциальными уравнениями, если известно частное решение <р@
соответствующего однородного уравнения:
а) х@-7*@ + 4*<'> = *<'>' Ф<'> = '2;
б) *2т -1 х(о+х«=/2#о+з/2^о, <р(о=л
2.5. Найти импульсные переходные функции систем, описываемых
дифференциальными уравнениями:
а) дс@ + Ъп х@ + 2л2х@ = /т*@ + *@;
б) х@ + 2л х@ + (л2 + Л12)х@ = ял / ^@ + со8 / • $@;
в) х@ + Bл + т) х@ + лBл! + л) х@ + тл2х@ = *"$@ + 'т*@ + *@;
г) /2х@ + (л - /и +1)/ х@ - тл х@ « /Л"т^(/) + *@;
Д) /Зх@ + (л + 3)Г2х@ + л/х@ - л х@ = КО + *т^@ + е**^).
2.6. Найти импульсные переходные функции систем, заданных
структурными схемами (см. рис. 1.21,д-*).
2.7. Найти импульсные переходные функции соединений двух звеньев,
если известны импульсные переходные функции этих звеньев:
а) последовательное соединение: Д^(/,т)-е л+1, А^(/,т) = т/(/-т);
Г-т
б) параллельное соединение: ^(/,т) = е л+1, А^т) = т • 1(/-т);
в) соединение с отрицательной обратной связью:
*1(',т)-с ^,^(/,т) = л|1(Г-х).
Ш

2.8. Найти импульсные переходные функции систем, описываемых
дифференциальными уравнениями, и реакции х(/) систем на соответствующее
детерминированное воздействие #(/) при нулевых начальных условиях:
а) /1п/х(/)-2х(/) = 1п/*@, &(*) = (п\п* + т*2 ]п2 *) 1(/-т);
б) B> + 1)х(/)-2х@ = 4/*(/), ^) = B/ + 1)л/(/-т);
в) /х(/)-/х(/) = *'*(/), *(/) = 1п (/*)•/(*-т).
2.9. Построить график выходного сигнала х(/) для систем, структурные
схемы которых изображены на рис. 1.21,а—в, если на вход системы при нулевых
начальных условиях подается сигнал #(/) = Ш • /(/ - т).
2.10. Найти реакции систем на воздействие $(/) при нулевых начальных
условиях:
а) х(*) + (п + т)х(*) + тпх(*) = *8(*) + 8(*)> яЮ-тЛМ;
б) х(/) + л2х(>) = *(') +'*('), *(/) = //(/-/и);
в) /2х(/) + (/| + 1)/х@-2л2х(/) = /я(/)-/|^@, *@ = 'т*(>-1).
2.11. Найти импульсные переходные функции многомерных систем,
описываемых следующими уравнениями состояния и выхода:
х1=х2 + *л+т*1,
а) ± - ШЕг п-т-\ _ .*п-тл
х* ^Г ! / 2 *2'
и=*1;
X! = 2/»! + (т - 2л)х2 + &,
б) х2 = пхх + (т - л)х2 + /2#2,
Л = *1+*2;
X! = (л + т)х! + ах2 - л Хз + / &,
Х2=*Х1+ЛХ2-^Хз+^2>
В) . ,з вшИЮ;*0'
х3=тх1+дх2+Г^3»
У\=хх-Мх2, у2=*хх-*2хг.
2.12. Найти импульсные переходные функции многомерных систем,
заданных структурными схемами на рис. 2.8,а—е.
2.13. Для систем управления, уравнения состояния и выхода которых
заданы в задаче 2.11, найти при нулевых начальных условиях реакции на
воздействия:
а) для системы «а»: д(/) = гл1(/ - 2), $2(/) = /т/(/ - 2);
б) для системы «б»: &(/) - лб(г), #2@ = /и//^);
в) для системы «в»: &(*) = *лб(*), $2(г) = л • /(/ - 2), #3(') - т' • *(')•
112

2.14. Для систем управления, структурные схемы которых изображены на
рис. 2.8, определить реакции при нулевых начальных условиях на воздействия:
а) для схемы рис. 2.8,а : &(/) = /л5@, *2@ = т - ДО, *3@ = *" • ДО;
б) для схемы рис. 2.8,0: & A) = /и/л5@, $2@ = т. Щ;
в) для схемы рис. 2.8,*: д @ = ШтЩ, ^2@ = т • Щ, *з@ = «"'МО •
А
4-г4^1
¦X
1л
а = т; *--
*1
*2
к^ 1
\
\,_
\г
у
л_
/
•\2/ *
2.
а
Ь
%
У\
У2
а = т; *.-
Ф > ДЪ
из

Глава 3. ОПИСАНИЕ И АНАЛИЗ НЕПРЕРЫВНЫХ
ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ИНТЕГРАЛЬНЫХ
ПРЕОБРАЗОВАНИЙ
3.1. ОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ ПРИ
ДЕТЕРМИНИРОВАННЫХ ВОЗДЕЙСТВИЯХ. ПРИМЕНЕНИЕ
ПРЕОБРАЗОВАНИЙ ЛАПЛАСА
3.1.1. Описание сигналов и систем
1. Описание сигналов. Для описания сигналов используется преобразование
Лапласа:
(?(*) = ДЛЯ] = ]*Ю«-*А, C.1)
о
где #@ — сигнал (оригинал); 0(з) — его изображение по Лапласу [39].
2. Описание систем. Рассматриваются линейные одномерные стационарные
системы управления, описываемые дифференциальным уравнением
ап *<">(/) +... + аох«) = *т*(да)(/) +... + ^*@, C.2)
где #(/) и х(() — входной и выходной сигналы; тип- порядки старших
производных входного и выходного сигналов соответственно; ал,...,а0, Ьт9...9Ь0 -
коэффициенты, не зависящие от времени.
Импульсная переходная функция &(/,т) стационарной системы является
функцией разности своих аргументов &(/,т) = к(г\), ц = г - т (см. разд. 2.1.1).
Передаточной функцией \У(з) стационарной линейной системы называется
преобразование Лапласа импульсной переходной функции к(ц):
Щз) = Цк(ц)) = } те'* ац. C.3)
о
Передаточная функция является функцией комплексного переменного 5.
По дифференциальному уравнению системы передаточная функция
находится следующим образом:
щ8)=МШ
В(Р)
ЬтЗт + ... + ^5 + ^ ^
р=з апзп +... + а15 + а0
где /)(/?) = апрп+..лахр + а$\ М(р) = Ьтрт+...+ 1\р + Ь$ — дифференциальные
операторы левой и правой части уравнения C.2).
Корни числителя передаточной функции, удовлетворяющие уравнению
М(з) = 0, называются нулями передаточной функции. Корни знаменателя
передаточной функции, удовлетворяющие уравнению #($) = 0, называются полюсами
передаточной функции.
114

При выводе формулы C.4Х предполагается, что на вход системы,
описываемой уравнением C.2), подается сигаал в(х\) = 5(т0 при нулевых начальных
условиях. Поэтому выходом системы является импульсная переходная функция
*(Л): '
ап *<л)(п) +... + ао *(ц) = Ьт б^л) +... + ^ 5(л),
Применим преобразование Лапласа к левой и правой частям уравнения,
используя свойства:
а) линейности:
где /1(л),...,/я(л) -оригиналы; с{,...,сп -числа;
б) дифференцирования оригинала:
Дх(л)@] = зпХ(з) - зп~1х0 -... - 5 х<л-2) - 4я,
где Х(з) = Цх(*)], а х@) = *<>, х@) - х<>,..., х(л_1)@) = х^п) - начальные условия.
При нулевых начальных условиях справедливо равенство Дх(л)(/)] = зпХ(з),
например, Ц *(/)(л)] = ^Х[А:(тО] - *' ^E), / = 1,...,л;
в) преобразования дельта-функции и ее производных:
Д5(т,)] = 1, Д5<»(л)] = «Л У = 1,...,т.
В результате получаем
ап Ц*(л)(л)] +... + ОоД*(Л)] = *тД8<«>(Л)] +... + *04$(л)]
или
)ГE)(Д|15Л+... + ао) = *т5т+... + Ао.
Отсюда следует связь C.4) передаточной функции с дифференциальным
уравнением.
Пользуясь формулой C.4) и уравнениями A.7)—A.11) можно получить
передаточные функции элементарных и типовых звеньев:
а) усилительного: IV (з) = К;
б) дифференцирующего: Щз) = з;
в) интегрирующего: Щз) = -;
г) апериодического: Щз) =
д) колебательного: IV (з) = -
Тз + 1'
1
7,2^+2$7,$ + 1
115

е) неустойчивого апериодического: Ж($) =
Т$-\
1
ж) неустойчивого колебательного 1У(з) = „ „ ,
Т252+2$Т5-1
з) дифференцирующего первого порядка: №($) = Г$ +1;
и) дифференцирующего второго порядка: ЖE) = Г252+2^Г$ + 1 ;
к) чистого запаздывания: \У(з) = в"Т5.
3.1.2. Связи вход-выход
Выходной сигнал представляется в виде суммы свободного и вынужденного
движений с помощью формулы, следующей из A.27) при *о=0:
«)=^)+ио«ад, (з.5)
где функции хс@, хвын{{) — п раз непрерывно дифференцируемы.
Обозначим Х(з) = Цх«)]> Хс(з) = Дхс(/)], Хвыи(з) = Цх^Ц)./(/)] - изо-
бражения по Лапласу выходного сигнала, свободного и вынужденного движения
соответственно.
С использованием свойств преобразования Лапласа получаем:
Цх?Ч*)] = 5пХс(з) - Ло-... - 5 х<"-2> - х<?-{), C.6)
Щхвынт*)}™]-*"*,^).
Из C.6) и C.5) имеем
Дх<л>(*)] = зп[ХсE) + Х^з)} -5л-2Хо -...- 5х<л> - 4Я'1)• C.7)
При п = О из C.5) и C.6) следует, что ЛХ$) = Хс(з) + Хвын(з). Поэтому
Дх(л)(/)] = ЛГ(*)-*"-!дсь -...-5х<л-2) -х^.
Выполним преобразование Лапласа от левой и правой частей
дифференциального уравнения C.2):
алх<л>@ + ... + аох@ = *т Ы<)Щ}т) + ... + ^*(')*@,
используя C.7) и свойство Д{#@*@}(т) 1 = *Л1 &(*)•
В результате получаем
ДДлх<л>(/) + ... + а0х@] = 2>E)^E)-1)||E),
116

где 2)($) = ал$л+...+ 0О; М(з) = Ьтзт+...+ Ьо;
2)Я($) = Х0(Д1 + Д2$+...+ ал5Л~1) + *о(л2 + д3 $+...+ Ял 5Л)+...
.+Х<Я-2)(ДЯ.1 +ДЯ5) + Х^-1)ДЛ = ^"^„Хо + ^^^Хо+Д^Хо]^..
...+[*„ хь0 + *„-! х0(л-2)+...+д2 х0 + ах х0]. C.8)
Окончательно имеем:
2)E)^ГE)-2)ЯE) = ЛГE)GE)
или с учетом C.3):
Х(з) = Хс(!) + Х^(*) = ^+^С(!)=&& + Щ!)С(*). C.9)
Если начальные условия нулевые, то /)„($) = 0 и выходной сигнал
совпадает с вынужденным движением:
ХE) = ЩзH(з). C.10)
Из C.10) следует эквивалентное определение передаточной функции как
отношения изображения по Лапласу выходного сигнала к изображению входного
сигнала при нулевых начальных условиях.
3.1.3. Передаточные функции соединений
НАХОЖДЕНИЕ ПЕРВДАТОЧНОЙ ФУНКЦИИ ПО СТРУКТУРНОЙ СХЕМЕ
Если система представляет собой соединение звеньев, то передаточная
функция системы определяется с помощью формул:
для последовательного соединения (см. рис. 3.1,а):
Щз) = ЩE)ЩE); C.11)
для параллельного соединения (см. рис. 3.1,ф:
Щя)шЦ\(а) + яг2(яу9 C.12)
для соединения с обратной связью (см. рис. 3.1,в):
ВДе знак «плюс» для отрицательной обратной связи, а «минус» — для
положительной; Щ(з), 1У2(з) — передаточные функции первого и второго звеньев.
117

0(з)
*!<*)
*1<*)
Щ(°)
Х(8)
0(в)
щи)
4 и^
(*)
ВД
т
Х2(*)
С(*)
Е(з)
Х2(!)
Щ(*)
ХE)
Щ(!!)
в
Рис. 3.1
С целью получения формулы C.11) следует воспользоваться связью вход-
выход C.10) для первого и второго звеньев (см. рис. 3.1,в):
Х1(з) = Щ(зH(з),
Х(з) = ^2(з)Х1(з).
Отсюда следует формула для нахождения передаточной функции
последовательного соединения:
Х(!) = Щ(*IУ2(з)С(з).
Для доказательства формулы C.12) следует воспользоваться связью вход-
выход C.10) для первого и второго звеньев, а также записать уравнение
сумматора (см. рис. 3.1, б):
Х1(8) = Щ($)С($),
Х2E) = Щ($HE),
Х(и) = Х1E) + Х2E).
Отсюда следует формула для нахождения передаточной функции
параллельного соединения:
Х(х) = [Ц^) + Щ($)]С(з).
118

С целью получения формулы C.13) необходимо воспользоваться связью
вход-выход для обоих звеньев и записать уравнение сумматора (см. рис. 3.1,в):
*(*) = Щ(.з)Е(з),
Х2(з) = Щ(з)Х(з),
Е(з) = С(з)*Х2(з).
Отсюда Х(з) = Щ(з)[С(з)*1Г2(з)Х(з)] = Щ(з)С(з)*И^ИДООД и
Х(з) =
Щ(*)
\±Щ{з)Щ(в)
0(з).
*Ч»>
Пример 3.1. По передаточным функциям звеньев найти передаточные
функции систем, заданных структурными схемами (рис. 3.2,а-в).
х 8
¦$: \Щ} г
-¦ х
Г
1 Щ
I—1 ^3 гФН ж*1
I—ЛРП—I
а
¦+ х
Рис. 3.2
О На рис. 3.2,а звенья 1 и 2 соединены последовательно, а 3 и 4 —
параллельно, сама схема является соединением с обратной связью, поэтому
1Пз)-
Шь.
Ь^ИЪОГз+ИЪ)
На рис. 3.2,5 параллельное соединение звеньев 3 и 4 соединено
последовательно со звеньями 2 и 5, поэтому
ЖE) =
т
\ + 1У11У50У3+}УлIУ2
119

На рис. 3.2,9 звенья 3 и 4 образуют соединение с обратной связью:
Щз) =
IV.
1УхA + Щ1Ул)
1 + 1^3^4
НАХОЖДЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ В СИСТЕМАХ
С НЕСКОЛЬКИМИ ВХОДАМИ
Если в системе несколько входов, передаточная функция по
фиксированному входу ищется при нулевых входных сигаалах, кроме данного. При этом для
удобства рекомендуется перестроить структурную схему.
Пример 3.2. Для системы с двумя входами #(/) и /(/) и одним выходом
*(/), заданной структурной схемой, изображенной на рис 3.3,д, найти
передаточные функции.
\щ
щ\
Рис. 3.3
а Положим /(/) г 0. Тоща передаточная функция по входу #(/) будет
щу2
ЦТ (с\= "^
Положим #(/) в 0 и перестроим схему (рис. 3.3,6). Усилительное звено
с коэффициентом усиления К = -1 введено в силу отрицательной обратной
связи на сумматоре в схеме на рис. 3.3,а.
В результате имеем
Пример 3.3. Для системы с двумя входами #(/) и /@ и одним выходом
х@, заданной структурной схемой, изображенной на рис. 3.4,а, найти
передаточные функции.
О Положим /@ з 0. Тогда передаточная функция по входу $(/) будет
ЦГ-Л1—
ум- >1+^^= &*а .
1, »|Уа 1 + ЩЩ+ЩЩ
120

т
к
-*х
а >
г
11/
 |
1 щ\
щ
-1
* X
Рис. 3.4
Положим #@а0 и перестроим схему (рис. 3.4,6). Отсюда передаточная
функция по входу /(/):
^¦^у,^л
НАХОЖДЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ МЕТОДОМ ПРЕОБРАЗОВАНИЯ
СТРУКТУРНЫХ СХЕМ
В некоторых задачах связи между звеньями таковы, что не позволяют
найти передаточные функции системы с использованием формул для типовых
соединений. В этом случае требуется преобразовать схему к виду, допускающему
применение формул. Приведем два способа такого преобразования:
Первый способ. Перенос сумматора через линейное звено (рис. 3.5,а -
перенос вперед; рис. 3.5,5 - перенос назад).
Второй способ. Перенос точки разветвления через линейное звено (рис.
3.6,а - перенос вперед; рис. 3.6,5 — перенос назад).
Изображенные на рис. 3.5 и рис. 3.6 слева и справа схемы эквивалентны.
>Ф-
Н IV
| IV
| IV
\(л
л
N ь
Г
* X
IV
ф > х
У
к^р4
* 1
IV
1 1
IV Г
б
Рис. 3.5
121

\У
IV
_1_
IV
Н IV
-> х
. У
IV |
\У
X
У
б
Рис. 3.6
Пример 3.4. Найти передаточную функцию системы, заданной структурной
схемой, изображенной на рис. 3.7,а.
П Необходимо перенести первый сумматор вперед через звенья 1, 2,
второй сумматор вперед через звено 2, а последнюю точку разветвления назад через
звено 4 (результат преобразований показан на рис. 3.7, б). Передаточная функ-
ция системы имеет вид Ж($) = Щ Щ
\-{Цгл+Щ-ЩЦГ2\УА)Щ
Т\ 1
г
щ
%г
ч
сч
} >
щ
щ
~™*\\
122
б
Рис. 3.7

ВИДЫ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ,
ИСПОЛЬЗУЕМЫХ ПРИ АНАЛИЗЕ СИСТЕМ
рассмотрим типовую схему замкнутой линейной системы (рис. 3.8).
* е
К
4
7
^
У
Ъ
1
»Цу
V
г
'3
Щ
X
Рис. 3.8
На вход системы поступает входной сигнал #@; первое и второе звенья,
находящиеся в прямой цепи, образуют последовательное соединение; третье
звено находится в цепи отрицательной обратной связи; в прямой цепи приложено
внешнее воздействие /(/), которое может рассматриваться как еще один
входной сигнал.
1. Передаточная функция прямой цепи. В качестве входного сигнала
рассматривается сигнал е(/), а выходного — х@; внешнее воздействие /(/)
отсутствует. Согласно C.11) передаточная функция 1У^(з) прямой цепи имеет вид
2. Передаточная функция разомкнутой системы. Входом является сигнал
#@, выходом — сигнал >>(/) (на рис. 3.8 место размыкания указано пунктирной
линией); внепгаее воздействие /(/) отсутствует. Согласно C.11) передаточная
функция №р{з) разомкнутой системы находится по формуле
3. Передаточная функция замкнутой системы. Входом является сигнал
$@» выходом — сигнал *(/), внешнее воздействие /(Г) отсутствует. Первое и
второе звенья соединены последовательно, а замкнутая система является
системой с отрицательной обратной связью. Согласно C.11), C.13) получаем
123

4. Передаточная функция ошибки. В качестве входного сигнала
рассматривается сигнал $@, а выходного - сигнал ошибки е(/); внешнее воздействие /(/)
отсутствует. Для удобства дальнейших рассуждений схему, изображенную на рис.
3.8, изобразим в более наглядной форме (рис. 3.9).
Я
ч
+
щ
щ
Щ
8
Рис. 3.9
Согласно C.11), C.13) передаточная функция \Уг(з) ошибки имеет вид
1 1
*;(*)=
\ + Щ(з) \У2{з)ЦГъ(з) \ + \УЛзУ
5. Передаточная функция по возмущению. Входом является внешнее
воздействие /(/)» выходом — сигнал хA), сигнал #(/) отсутствует. Перерисуем схему
(рис. 3.8), учитывая наличие отрицательной обратной связи с помощью
усилительного звена с коэффициентом усиления, равным «-1» (рис. 3.10).
/
ч
+
^1
Щ
-1
Щ
X
Рис. 3.10
Согласно C.11), C.13) получаем передаточную функцию И^/Су) по
возмущению:
И7(Ф
Щ(з)
\-Щ{з) ЩE)(-1) \Уг(8) \ + Щ(з) Щ(*)ЩE) 1 + ^E)*
*2<*)
124

3.1.4. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть известны:
а) входной сигнал $(*), * > 0, вде $(/) - т раз непрерывно
дифференцируемая функция на промежутке @, + оо) функция ограниченного роста [39];
б) линейная стационарная система, описываемая уравнением C.2);
в) начальные условия
х@) = хо, *@) = *о,..., ^(О) - х<>-».
Требуется найти выходной сигнал хA).
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти изображение входного сигнала по формуле C.1):
2. Получить передаточную функцию 1УE) системы одним из методов,
рассмотренных в разд. 3.1.1 и 3.1.3, и, если начальные условия ненулевые, 2)($) и
Вн(з) - по формулам C.4),C.8):
ап$п + ... + Д15 + д0
А,(*) = *о(*1 +а25+...+ ап5п-1)+ х0(а2+агз+...+ ап $л~2)+...
••. +$-*(**-!+*ш?) + *^1}ая.
3. Определить изображение по Лапласу выходного сигнала по формуле
C.9):
Л& У х \*) '
4. Найти выходной сигнал, используя обратное преобразование Лапласа:
| С+/00
х@ = 1Г1[Х(*)) = ^ рГE)влЛ = хеЦ) + х^СО.
С—/оо
Интегрирование ведется по прямой Кея = с в области аналитичности функции
Как правило, при выполнении пп. 1 и 4 применяются таблица
преобразования Лапласа и его свойства. Приведем часть таблицы, используемой в
примера (табл. 3.1), вде /(/) - оригинал, а Р{8) - соответствующее изображение.
125

Таблица 3.1
|№
1
2
3
4
5
6
7
18
9
110
1 И
12
13
14
15
16
Л0
/<о
С
/
гп
6@
е«
1пеа<
8ша(
со$о/
/зта/
/со$а/
еа*Ш1Ы
е^со&Ы
!(««'-1)
а-&
Л*)
^
5
с:
5
1
*2
1
1
5-а
тА,
E-а)й+1
а
*2+а2
5
з2+а2
Ъа
(у2+а2J
52-а2
(*2+а2J
Ь
(з-аJ+Ь2
8-а
(з-аJ+Ъ2
1
1 + Я5
1
$($-а)
1
(*-а)<5-*)
N0
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
ДО
-="A - соза/)
от
а1
$Ьа/
сЬа/
(, + 1а,2)е"
A + 2а/ + ^а2/2)ввГ
2
A + д/)воГ
соз2а/
яп2 аХ
1^ 1/2
—(8На/-япаО
—(сЬаГ-созаО
—(8Ьа/ + 5шаО
—(сЬаГ + созаО
аеш-Ьеы
а-Ь
Ш 1
1
зE2+а2)
1
з2E-а)
а 1
*2-а2
5 1
*2-а2
& 1
E-еK
*2
(* -аK |
5 1
E-аJ
з2+2д2
*(*2+4«2)
2а2
хE2+4а2)
а2
*4+а4
*3
54+а4
а3
? -а4
А
И -о4
а*2 1
*4 -а4
53
*4-*4
я 1
<*-«&<*г*и
126

[ЕЕ
ГзГ
гаг
ГзГ
ГзГ
ГзГ
П38
|39
40
41
42
43
[44
|45~
|4Г
иг
ИГ
Г /(О
(с-Ь)еш +(а-с)еы +(Ь-а)е"
(а-Ь)(а-с)(с-Ь)
Г д(Ъ-с)еш +Ь(с-а)еы +с(а-Ь)е(*
(а-Ь)(Ь-с)(а-с)
а2(Ь с)е"+Ь2(с-а)еы+с2(а-Ь)ес'
(а-Ъ)ф-с)(а-с)
\ а$тЫ-Ь§та1
а2-Ь2
со&Ы-со&а!
а2-Ь2
а$ша1-ЬяпЬ1
а2-Ь2
а2со5а( -Ь2 со&Ы
а2-Ь2
ЬвЬа1-а&Ш
а2-Ъ2
сЪа^ - сЬЫ
а2-Ь2
а зНд/ - Ь зЫ>Г
а2-Ъ2
а2сЪа*-Ь2сШ
а2-Ъ2
. 1 . ,
/—япд/
а
а
1-со$а/ $шд/
2
1-сЬд/+—&Ьа*
2
1 *2со8д/-а2со8^/
а2-Ь2
. Ь2&иИ-а2<ЗаЫ
+ а2-Ь2
Продолжение табл. 3.1
| _ *(А I
1
(8-а)(8-Ь)(8-с) 1
5 1
E-а)(з-Ь)E-с) 1
52
(з-а)(з-Ь)(з-с) |
аЬ
E2+02)(!2+Ь2)
Р
| (р2+в2)(р2+*2) 1
1 °2
E2+а2)E2+Ь2)
*3
(*2+о2)($2+Ь2)
аЬ
{з2-а2)(з2-Ь2)
5 1
<*2-а2)<*2-*2)
з2
{в2-а2){з2-Ь2)
$Ъ
($2-а2)(з2-Ь2)
а2
з2(з2+а2)
а2
Л*1-*2)
а*
з(з2+а2J
о4
ф2-а2J
а2Ь2
з(з2+а2)(з2+Ь2)
а2Ь2
р{р2-а2)(р2-Ь2) \
127

Продолжение табл. 3.1
I50
г1
52
г (81П Си - а1 С08 а1)
2а3
/8111 а/
2а
—(зта/ + а/со8 я/)
2а
1 ~~~1
(,2+а^
5 1
{?2+а2У
**
{?+ а»? |
Пример 3.5. Найти реакцию усилительного звена с коэффициентом
усиления К = 5 на линейное воздействие #(/) = /, / > 0 при нулевых начальных
условиях.
? 1. Найдем изображение входного сигнала (по формуле 3 табл. 3.1):
2. Получим передаточную функцию: 1У(з) = 5.
3. Определим изображение по Лапласу выходного сигнала: Х(з) - —.
4. Найдем выходной сигнал: *(/) = 5/, / > О.и
Пример З.б. Найти реакцию системы, описываемой дифференциальным
уравнением х(/) = 4#(/), на входной сигнал #(/) = 8тЗ/ при нулевых начальных
условиях.
? 1. Найдем изображение входного сигнала (по формуле 8 табл. 3.1):
3
0(з) =
з2+9
2. Получим передаточную функцию: Щз) =
М(р)
В(Р)
3. Определим изображение по Лапласу выходного сигнала:
Х(з)=± 3 4 45
з'з2+9 35 3E2+9)'
4. Найдем выходной сигнал: х@ = — A - сое 3/). ¦
Пример 3.7. Найти реакцию системы, описываемой дифференциальным
уравнением *(/) + *(/) = $(/), на входные сигналы а@в'@ и ^@ = 5@ при
нулевых начальных условиях.
? 1. Найдем изображения входных сигналов (по формулам 1 и 5 табл. 3.1):
<?!(*)=-, 02(з) = 1.
8
128

2. Получим передаточную функцию:
1
р + 1
р=з
5 + 1
3. Определим изображения по Лапласу выходных сигналов:
*1(*)=—г*"' х2^) =—7*
5+1 5 5+1
4. Найдем выходные сигналы:
*!(/) = 1-е"', х2(*) = е-*М
Пример 3.8. Найти реакцию системы, описываемой дифференциальным
уравнением х(() + х(() = $(() с начальным условием х@)=—, на входной сигнал
*(/) = *(').
П 1. Найдем изображение входного сигнала: 0(з) = —.
5
2. Получим передаточную функцию:
р + 1
1 М(з) л/ х - л , ч 1
/>=5 5 + 1 1/E) 2
так как п = 1, «1=1.
3. Определим изображение по Лапласу выходного сигнала:
гп _ 1 1
{3) 2E+ 1) +5E + 1)'
4. Найдем выходной сигнал:
х@ = \е-' +1-^ = 1-1в-г.1
2^- Хло' 2
Пример 3.9. Найти реакцию системы, описываемой дифференциальным
уравнением
х(/)-3*@ + 2х@ = *@
с начальными условиями х@) = 1, х@) = 3, на входной сигнал #(/) = 2ег*1(().
2
О 1. Найдем изображение входного сигнала: 0E) = .
5-3
2. Получим передаточную функцию:
цг(ш)ш 1_| = 1 ШШ
р2-Зр + 2\Р = з 52-35 + 2 Щз)'
129

/)($) = з2 - Ъ8 + 2 , Вн E) = *о («1 + Д2$) + *О02 - 1 • (-3 + 5) + 3 • 1 = 5.
3. Определим изображение по Лапласу выходного сигнала:
5 2 5 2
Х(з)ш
52-35 + 2 E2-3$ + 2)E-3) <5-1)E-2) E-1)E-2)E-3)
_1 2 1 2_ 1
5-1 5-2 5-1 5-2 5-3/
Хе(з) Х^з)
4. Найдем выходной сигнал:
х(/) = ге''+2е2'+е' -Ь2* +ег'. = е*. ¦
Пример ЗЛО. Найти реакцию системы, описываемой дифференциальным
уравнением
х@-Зх@ + 2х@ = я<0-*<0
с начальными условиями х@) = 1, х@) = 3, на входной сигнал #(/) = е3г1@.
? 1. Найдем изображение входного сигнала: 0(з) = -.
5-3
2. Получим передаточную функцию:
угA) Р-1 I 5-1 ^E)
р2-Зр + 2|Р = * 52-35 + 2 2>(*Г
ДE> = 52 - 35 + 2 , ВнE) = Хо(Д! + 02*) + *0*2 = 1 • (-3 + 5) + 3 • 1 = 5.
3. Определим изображение по Лапласу выходного сигнала:
5 5-1 5 5-1
*E) =
52-35 + 2 E2-35 + 2)E-3) E-№-2) <5 - 1)<5 - 2)E - 3)
_1 2_ _1 1_
5-1 5-2 5-3 5-2/
4. Найдем выходной сигнал:
х(*) = 2^^ + е^^ = е3' +еь -е'м
Пример 3.11. Найти реакцию системы, описываемой уравнением
х(/)+4х(/) = *@
с начальными условиями х@) = 1, х@) = -1, на входной сигнал #(/) = соз 2/ • /(*).
130

а 1. Найдем изображение входного сигнала:
52+4'
2. Получим передаточную функцию:
81 +4
и функции 2)($) = $2+4, Пм(з) = х0(а1 + а2$)+*о*2 = 1@ + 1$)-Ы = $-1.
3. Определим изображение по Лапласу выходного сигнала:
„/ч 5-1 5 5 1 3
52+4 E2+4)> 52+4 52+4 .^а+4I'
4. По формулам 8-10 табл. 3.1 найдем выходной сигнал:
х(/) = со$2/—-ял2/+ 4-81П2/ . ¦
2 ,4
*(') *~ (О
Пример 3.12. Найти реакцию системы, описываемой уравнением
*(/)-3*(/)+Зх@-х(>) = *@
с начальными условиями х@) = 0, х@) = 0, 5с@) = 2 при входном сигнале
м-1-т-
П 1. Найдем изображение входного сигнала: G(у) = —-.
5-1
2. Получим передаточную функцию:
и функции /)E)=E-1M, Д,($) = х0(а, +о2* + вЗ'$2)+^о@2+0з*)+*оаз =2.
3. Определим изображение выходного сигнала
„/ч 2 1 2! 1
(.-IK (*-!)« (.-IK 6 E_1L-
4. По формуле 7 из табл. 3.1 найдем выходной сигнал:
х(/)=Л?'+±>3е'.в
131

Замечание. Для решения задач анализа выходных процессов
стационарных линейных систем (см. разд. 1.1.4) методами теории
дифференциальных уравнений следует рассматривать правую часть уравнения C.2) на интервале
@, + оо), т.е. после момента приложения входного воздействия. При этом
начальные условия выходного сигнала и его производных должны быть
заменены эквивалентными начальными значениями х(+0) ,...,х(л)(+0).
Действительно, с одной стороны, из C.8), C.9) следует
адад-/)йE) = Щ(?E),
а с другой стороны, применяя преобразование Лапласа к уравнению C.4), где
процесс рассматривается после момента приложения входного воздействия,
получаем
Щ5)ХE)-Вн+E) = МEHE)-ПГE), C.14)
где 2)я+E) = хD0)(а1 +а2з+ ...+апзп~1) + х(+0)(а2 +а35+ — +ап5"~2) +• ••
... + х(л)(+0)(ал_1 +ап5) + х(п~1)(Ща„, т.е. /)„+($) совпадает по форме записи с
ДДя), где вместо начальных условий используются соответствующие начальные
значения (пока неизвестные). Функция /)/($) определяется аналогично Вн(з):
ВГ(А = 5т~1Ьт8(Щ + ^-2[^(+0) + ^.^(+0)]+...+[^(да-1)D0) +...+ ^(+0)] ,
где #(+0), ^(+0) ,...,^^т_1)(+0) ~ значения пределов справа входного сигнала и его
производных.
Из сравнения C.9), C.14) следует уравнение
А,+(*) = АЛ*) + Л/<*) (ЗЛ5)
или в подробной записи:
5я ап х(Щ + зп-2[ап х(+0) + ал_1 х(+0)] + ... + [ал х(л-1)(+0) + ... + а2 МЩ + ц 4+0I =
= 5п 1апХо+зп 2[апх0+ап_1х0] + ... + [апхр 1) +... + а2х0 +а{ Хо ]+ C.16)
Приравнивая коэффициенты при одинаковых степенях 5 , из C.16) можно
получить систему для определения начальных значений.
Приведем методику решения задачи анализа выходных процессов путем
сведения к задаче Коши с начальными значениями.
1. Составить уравнение C.16) и найти начальные значения
х(+0), х(+0),...,х(я-1)(+0).
2. Записать уравнение системы на интервале @, + «>) совместно с
начальными значениями.
132

3. Решить полученную в результате задачу Коши и найти выходной сигнал
Пример 3.13. Решить пример 3.10, используя методику решения задачи
анализа выходных процессов путем сведения к задаче Коши с начальными
значениями.
? 1. Из условия задачи следует: а2=1, ах=-39 а0 = 2, л = 2, ^=1,
&, = -1, т-1, хь = 1, *о = 3, *(+0)= Шп е3'=1.
Составим уравнение C.16):
5х(+0) + [1х(+0) + (-3).х(+0)] = 51 + [ЬЗ + (-3).1] + 11.
Приравняв коэффициенты при одинаковых степенях 5 , получим искомые
начальные значения: х(+0) = 1, х(+0) = Зх(+0) + 1 = 4.
2. Запишем дифференциальное уравнение системы, справедливое на
интервале @, + оо), подставив заданный сигнал в правую часть, совместно с
найденными начальными значениями:
х(/)-Зх(/) + 2х(/) = 2е3',
х(+0) = 1, х(+0) = 4.
3. Общее решение однородного уравнения (см. разд. 1.1.4) имеет вид
а частное решение неоднородного уравнения хя(/) = е3*. Получаем общее
решение неоднородного уравнения:
*(') = *о<» + **(') - Схе2< + С2е( + е*.
Из начальных значений имеем
х(+0) = С,+С2+1 = 1,
х(+0) = 2С,+С2+3 = 4.
Отсюда ^«1, С2 =-1, а выходной сигнал х@ = е* + еъ - е* М
Пример 3.14. Найти реакцию системы, описываемой уравнением
3с@ + 6х(/) +11х(/) + 6х@ = *(/) + 5*@ + 6^@
с начальными условиями х@) = 1, х@)--3, х@) = 9, на входной сигнал
*@ = /@.
О Решим задачу двумя способами.
Первый способ. Воспользуемся преобразованием Лапласа.
1. Найдем изображение по Лапласу входного сигнала: С(з) = -.
133

2. Получим передаточную функцию по формуле C.4):
щз) = *+** + '
52+55 + 6 <5 + 2)E + 3) МE).
/.=5 53 + вз2 +115 + 6 (^ + 0(* + 2)E + 3) 2)E) '
/г+6/г+11р + 6
2)E) = 53+б52+115 + 6 = E + 1)E + 2)E + 3);
Вн(8) = 52Х<) + 5[Хо + 6*б] + Хо + 6*6 + 11х0 = 52 + 35 + 2 = E + 1)E + 2) .
3. Определим изображение по Лапласу выходного сигнала:
Х() E+1)E + 2) E + 2)E + 3) 1_ 1 1
1; E + 1)E + 2)E + 3) E + 1)E + 2)E + 3) 5 5 + 3 5E + 1)*
4. Найдем выходной сигнал: х@ = е~3' +1 - е~*.
Второй способ. Применим методику решения задачи анализа выходных
процессов путем сведения к задаче Коши с начальными значениями.
1. Составим уравнение C.16):
52х(+0) + 5 [ х(+0) + 6 х(+0) ] + [ х(+0) + 6 х(+0) +11 х(+0) ] =
= 52+5[-3 + б1] + [9-18 + 11] + 511 + [Ь0 + 51].
Приравнивая коэффициенты при одинаковых степенях 5, имеем
х(+0) = 1, х(+0) + 6х(+0) = 4, х(+0) + 6х(+0) +11х(+0) = 7.
Отсюда х(+0) = 1, х(+0) = -2, х(+0) = 8.
2. Запишем дифференциальное уравнение, справедливое на @;+оо),
подставляя #@ = 1@, совместно с полученными начальными значениями:
х@ + 6х@ +11х@ + 6х(/) = 6,
х(+0) = 1, х(+0) = -2, х(+0) = 8.
3. Общее решение однородного уравнения имеет вид:
х0@ = Схе + С2е-2' + С3е-г*.
Частное решение неоднородного уравнения хж(/) = 1. Поэтому общее
решение неоднородного уравнения: х(/) = х0(/) + х„(/) = Схе~1 + С2е~2' + С3вг +1.
Из начальных значений получаем
х(+0) = Сх + С2 + С3 +1 = 1,
х(+0) = -С!-2С2-ЗСз=-2,
х(+0) = С1+4С2+9С3 =8.
Отсюда Сх = -1, С2 = 0, С3=1 и х(/) = е~3/ +1 -е~1 - искомая реакция
системы.»
134

ОПРЕДЕЛЕНИЕ НАЧАЛЬНЫХ И УСТАНОВИВШИХСЯ ЗНАЧЕНИЙ
ВЫХОДНЫХ ПРОЦЕССОВ
Начальные и установившиеся значения реакции динамической системы
можно получить по изображению выходного сигнала, не находя его оригинала.
Действительно, согласно свойствам преобразования Лапласа имеем:
для установившегося значения выходного сигнала х(/)
ху = Шп х(/) = Шп 5Х(з)
/->+00
*-*0
и его производных.
5-+О
5 З2 5*
* = 1,2,...;
для начальных значений выходного сигнала х(/) и его производных.
х(+0) = Шп х@ = Шп 8Х(з),
/-++0 д-+оо
х(*>(+0) = Шп х(*>(/) = Шп зк+г
/-> + 0 5-*00
*<*)-
х(+0) х(+0)
Лк-\)
(+0)
* 8*
где при вычислении пределов считается, что Ке$ > 0.
,* = и,...,
Пример 3.15. Найти начальные и установившиеся значения выходного
сигнала х(/) и его производных х(/), х(/) для системы, рассмотренной в примере
3.14.
? Изображение Х(з) выходного сигнала системы имеет вид
*(,)«-!т+- 1
52 + 25 + 3
5 + 3 5E + 1) 5E + 1)E + 3)
Находим установившиеся значения:
Г V/ Ч 1- 52+25 + 3 ,
дг-и»1»[лгц-2ь-41-и»4/<2^^-11-°-
' «0 [ '' 5 д2] ,_*(, [$(* + 1)(* + 3) X]
135

Определяем последовательно начальные значения:
52 + 25 + 3
х(+0) = Пт 5 Х(з) = Ит 5
5_*« 5-*00 $($ + 1)($ + 3)
= 1,
•/ лч г гГУ/ ч *(+°I г гГ л2+25 + 3 11 г -2л2 .
х(+0)= Ьт *2 ЛГ(*)—*—- = ]шзг\—————— = Ит— = -2,
I 5 з2 \ *-*• [5E + 1)E + 3) 5 52]
х(+0) = Ит 53 ЛГ($)
5-*00
Результаты совпадают с найденными ранее. ¦
ОСОБЕННОСТИ АНАЛИЗА ВЫХОДНЫХ ПРОЦЕССОВ
АСТАТИЧЕСКИХ СИСТЕМ
Рассмотрим поведение замкнутой системы с отрицательной обратной
связью (рис. 3.11).
я ^ 8
— т
с-¦
^р(^)
X
Рис. 3.11
Если передаточная функция разомкнутой системы представила в виде
.У*
где 1ш1^0('5) = ^<0О> то при ^*° система называется астатической к-го
порядка, а при к = 0 — статической. Передаточная функция астатической
системы к -го порядка астатизма имеет полюс к-то порядка в начале координат.
Передаточная функция статической системы не имеет полюса в начале координат.
Исследуем установившееся движение еуст =Ите(/) под воздействием вход-
/ч **
ного сигнала вида #(г) = — ,у = 0,1,2,... Для решения задачи используем преобра-
зование*Лапласа.
1. Найдем изображение входного сигнала (табл. 3.1):
^Чй]"^- '-"*-
136

2. Найдем передаточную функцию ошибки (см. разд. 3.1.3)
3. Определим изображение ошибки, используя связь вход-выход
«к
^--"•^¦ттш-т*-
4. Найдем установившуюся ошибку
5к+\
гжт = Ит 8Е(з)= Ит т ; •
Исследуем полученное решение при различных значениях порядка
астатизма к.
1. Пусть к = О, т.е. рассматривается статическая система.
При У = 0 (#@ = 1@) получаем
е^ = 1ш1 = 9*0.
*" *-о
[1 + »>о(*)]* 1 + Л
Следовательно, статическая система при воздействии в виде единичной
ступенчатой функции имеет ненулевую установившуюся ошибку.
При у = 1 (#@ = /) находим е™ = Ит
ут' *-<> г,АигШ.2
[1 + ЗД]*2
/2
при } = 2 ($(/) = —) имеем е™ = Ит = оо и т.д.
2 ^ '-°[1 + »Кв(,)]в3
Полученные результаты свидетельствуют о том, что ошибка при линейном
и квадратичном входном воздействии (аналогично для более старших степеней)
неограниченно возрастает.
2. Пусть к =1, т.е. рассматривается астатическая система первого порядка
астатизма.
При у = 0 получаем: густ = Ит = Ит —ттггг = °>
82 1
при 7 = 1 имеем густ = Ит = — *0,
"°[1 + Щ(з)]з2 А
а при у = 2 б_т = Ит - = оо и т.д.
137

Следовательно, при воздействии в виде единичной ступенчатой функции
установившаяся ошибка равна нулю, а при воздействии в виде линейной
функции не равна нулю. Если на вход астатической системы первого порядка аста-
тизма подать квадратичный сигнал, то ошибка неограниченно возрастает.
Аналогично можно показать, что при порядке астатизма к = 2
установившаяся ошибка при воздействии в виде единичной ступенчатой и линейной
функции равна нулю, а в виде квадратичной функции не равна нулю.
На основании проведенного анализа можно сделать вывод о том, что чем
выше порядок астатизма, тем выше максимальная степень сигналов,
обрабатываемых замкнутой системой с нулевой установившейся ошибкой.
3.1.5. Анализ устойчивости
ПОСТАНОВКА ЗАДАЧИ
Рассматривается одномерная линейная стационарная система,
описываемая передаточной функцией
ап-зп+... + ао *>(з)
Требуется определить, является ли система асимптотически устойчивой
(см. разд. 1.4.1).
КРИТЕРИЙ УСТОЙЧИВОСТИ
При решении поставленной задачи используется, что корни
характеристического многочлена /)($) = <*„ -$и +... + ао ( или, что то же самое, корни
характеристического уравнения апХп +... + а0 =0) являются полюсами
передаточной функции. В общем случае характеристический многочлен имеет п кор-
ней 5\,..«, 5ц.
Для асимптотической устойчивости одномерной линейной стационарной
системы необходимо и достаточно, чтобы все полюсы передаточной функции имели
отрицательные действительные части: Ке^<0, / = 1,...,л, т.е. располагались,
в левой полуплоскости комплексной плоскости (см. рис. 1.18).
Пример 3.16. Исследовать устойчивость системы, заданной передаточной
функцией ЦГ{8)=— — .
E2+5 + 5)E + 3)
? Найдем полюсы передаточной функции, т.е. корни характеристического
многочлена: В(з)-(з2 +я + 5)-($ + 3) = 0. Получаем 5и =-1±2|, 53 =-3. Так как
все полюсы лежат в левой полуплоскости, то исследуемая система является
асимптотически усгойчивой.я
138

Пример 3.17. Исследовать устойчивость разомкнутой и замкнутой системы,
заданной структурной схемой (рис. 3.12).
Ч
...
ГЧ
?7~
¦>
1
5-1
2
X
>
Рис. 3.12
П Сначала исследуем разомкнутую систему (линия размыкания изображена
2
пунктиром). Так как передаточная функция разомкнутой системы \УЛз) = —-,
5-1
то полюс передаточной функции 5! = 1 > 0. Поэтому разомкнутая система
неустойчива.
Исследуем замкнутую систему. Согласно C.13) получаем
1
1
1 + _!_.2 * + 1
5-1
Полюс 5! = -1 передаточной функции лежит в левой полуплоскости,
поэтому замкнутая система асимптотически устойчива. Заметим, что путем
введения отрицательной обратной связи неустойчивую систему удалось сделать
устойчивой. ¦
Пример 3.18. Определить, при каких значениях коэффициента усиления к
система, заданная структурной схемой (рис. 3.13), будет устойчивой.
*
шА
т\
7 *
1
1
715 + 1
>
1
Г25 + 1
—*
5
X
71=0,005
т2 = од
Рис. 3.13
П Найдем передаточную функцию замкнутой системы:
к
Щ;)- СПд + ШГц + О*
1 +
(Г!5 + 1)(Г25 + 1M
М(з)
Т{Г2 53 + G; + Т2M2 + 5 + к Я(з)
139

Выделим характеристический многочлен
*3 . /7! _^Т-\*2 .
Р(з) = Т1Т2з' +(Т1+Т2M1 + 1 з+ к
«ь
и применим критерий Рауса-Гурвица:
Тх+Т2 к О
Тх Т2 1 О
О Тх+Т2 *
А1=Г1+Г2>0,
А2=(Т1+Т2)-Т1Т2к>0,
Дз=*Д2 >0.
Отсюда находим, что при 0<к< 1 ? = ' =205 система является
*1*2 0,001
устойчивой.»
3.1.6. Анализ чувствительности
ПОСТАНОВКА ЗАДАЧИ
Рассматривается линейная стационарная система, заданная структурной
схемой с изменяемыми параметрами.
Способность динамических характеристик системы меняться при малом
изменении параметров называется чувствительностью.
Требуется установить степень чувствительности системы к изменению
выбранных параметров.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Выбрать изменяемый параметр и исследуемую характеристику. С
использованием связи вход-выход составить формулу, отражающую их
взаимозависимость.
2. Малым изменениям параметров придать смысл вариаций относительно
заранее заданных значений.
3. Найти зависимость вариации исследуемой характеристики от вариации
изменяемого параметра - функцию чувствительности. Провести качественный
анализ полученной зависимости.
Пример 3.19. Дана система, описываемая структурной схемой (рис. 3.14).
^/1
1
в
э
к —
У
г
ЩE)
'егулято!
>
Ш*)
Щ(з)
Объект
X
Регулятор
Рис. 3.14
140

Передаточные функции объекта и регуляторов имеют вид
где к\ и к2 ~ коэффициенты усиления регуляторов, а к0 — изменяемый
параметр.
Требуется исследовать влияние вариации параметра к$ прямой цепи на
изображение выходного сигнала системы.
? Согласно постановке задачи, изменяемым параметром является к0, а
исследуемой характеристикой - выходной сигнал. Используем связь вход-выход:
1+^E)^0E)^2E)
У,E)-*6-УроE)
1 + й^E)^.ЖооE).Ж2E) 1;"
2. Придадим малым изменениям параметра к0 смысл вариаций 5/^.
3. Найдем связь вариаций Ьк$ с вариациями выходного сигнала:
окц
И + ЩЮ-ко-ЯпЮ-ЪЮ?
.^.8Аь= ШЛШ ед.«,.
Учитывая вид передаточных функций регуляторов, получаем:
аад- Ь-ЩЫ-ЩО -.<г(,).8*0.
[1 + *, .^10E) ко }УооE)к2 Ф20E)]2
При к2-+оо вариация выходного сигнала ЬХ(з)-+0, т.е. при увеличении
коэффициента усиления к2 влияние вариации Ьк0 изменяемого параметра к$
уменьшается. Заметим, что влияние коэффициента кх аналогично. При
отсутствии цепи обратной связи описанное свойство не выполняется.
На основании проведенных рассуждений можно сформулировать
характерное свойство соединения с обратной связью: обратная связь компенсирует
влияние вариации параметров прямой цепи на выход системыМ
141

Пример 3.20. Дана система, описываемая структурной схемой (рис. 3.15).
/
«
-Ф
Щ(А
-Ф
^о(*)
Регулятор
Объект
Щ(з)
Регулятор
Рис. 3.15
Передаточные функции регуляторов имеют вид Щ(з) = кх Що(з),
Щ(з) = к21^20(*)» гДе *1 и *2 ~" коэффициенты усиления.
Требуется исследовать влияние внешнего возмущения / на изображение
выходного сигнала системы.
П 1. Согласно постановке задачи изменяемым параметром является /,
а исследуемой характеристикой — выходной сигнал. Используя связь вход-выход
с применением передаточной функции по возмущению при отсутствии сигнала
# (см. рис. 3.10), имеем:
Х(з) =
^о(*)
\ + Щ(з)Щ(з)\У2(з)
И*).
2. Придадим малым изменениям внешнего возмущения / смысл вариаций
5/ (при использовании преобразования Лапласа ЪР).
3. Найдем связь вариаций внешнего возмущения с вариациями выходного
сигнала:
и<А-±\ 5МЙ р(зIьр = Ь&
(з)Щ(з)
ЬР =
^о(^)
1 + »ГО«-*|-»Г1о(*)-*2-»Г20(*)
•ЪР.
При к2 ->« вариация выходного сигнала ЬХ(з) ->0, т.е. при увеличении
коэффициента усиления к2 уменьшается влияние изменений внешнего
возмущения. Заметим, что влияние коэффициента к\ аналогично. При отсутствии
цепи обратной связи описанное свойство не выполняется.
На основании проведенных рассуждений можно сформулировать еще одно
характерное свойство соединения с обратной связью (первое свойство
сформулировано и доказано при решении примера 3.19): в замкнутой системе
подавляется влияние внешних возмущений, действующих в прямой цепиМ
142

3.2. МНОГОМЕРНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
ПРИ ДЕТЕРМИНИРОВАННЫХ ВОЗДЕЙСТВИЯХ.
ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
3.2.1. Описание сигналов и систем
1. Описание сигналов. Используется преобразование Лапласа сигнала #@ •
в(з) = Хк@] = ] *<««"**, C.17)
о
где $@ - г-мерная вектор-функция; 0{з) - ее изображение по Лапласу.
2. Описание систем. Рассматриваются линейные стационарные многомерные
системы, описываемые уравнениями ,A.35)—A.37):
х(/) = Лх@ + Я*@, *@) = *о; ЯО = Сх(/), C.18)
где х — л-мерный вектор состояния; # — г-мерный вектор входных
воздействий; у — ^-мерный вектор выхода; х$ — начальное состояние; / — время, г0 = 0 -
начальный момент времени; А, В, С — матрицы размера (лх л), (пх г), (кхп)
соответственно.
Как следует из разд. 2.2.1, импульсные переходные функции по состоянию
и выходу стационарной системы являются функциями разности *-х = ц своих
аргументов:
Кх(*,х) = Кх(* - т) = Кх(гд, КУ(*,т) = КУЦ - х) = **(л).
Передаточной функцией \Ух(з) стационарной линейной многомерной
системы по состоянию называется преобразование Лапласа импульсной переходной
функции по состоянию:
ЦГх(з) = 4*Г*(Т1)]=] Кх(ц) е-*<Ь\. C.19)
о
Передаточной функцией \Уу(з) стационарной линейной многомерной
системы по выходу называется преобразование Лапласа импульсной переходной
функции по выходу:
фУ(8) = 1\ку (я)] - ] КУ (я) е-**ац. C.20)
о
Передаточные функции 1Ух(з)9 1Уу(з) представляются матрицами размера
(лхг), (к у. г) соответственно, элементы которых являются функциями
комплексного переменного 5. Они могут быть найдены по формулам
\Ух(з) = [зЕ - А\1В, ЦГУ{з) = С[зЕ -А]~1В. C.21)
143

Замечание. Сравнивая C.21) с B.41), получаем еще один способ
нахождения переходной матрицы (см. разд. 1.2.З.):
Ф(тд = Г1{[яЕ-ЛУ1}9 C.22)
где Vх - обратное преобразование Лапласа.
3.2.2. Связи вход-состояние и вход-выход
Применяя преобразование Лапласа к левой и правой частям уравнений
состояния и выхода C.18), имеем
зХ(з) - х0 = А Х(з) + В 0(з), У (з) = С Х(з),
где Х(з) = 1{х@], У (з) = Х[у@] • 0(з) = Х[#(/)] — изображения По Лапласу
векторов состояния, выхода и входа. Отсюда
Х(з) = [зЕ - А]~1х0 + [зЕ - А]~1ВО(з),
У(з) = С[зЕ- А]~1х0 + С[зЕ-А]~1ВО(з). C.23)
Учитывая C.21), получаем искомые связи вход-состояние и вход-выход:
Х(з) = [зЕ - А]~1х0 + IVх (з) 0(з),
У(з) = С[зЕ- А]~1х0 + Фу (з) 0(з). C.24)
Первые слагаемые в C.24) представляют собой изображения по Лапласу
свободного движения, а вторые — вынужденного (см. разд. 1.1.4).
3.2.3. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть известны:
а) входной сигнал #@;
б) линейная стационарная многомерная система, описываемая
уравнениями C.18);
в) начальные условия х@) = х$.
Требуется найти законы изменения вектора состояния х(/) и вектора
выхода уA).
144.

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти изображение входного сигнала: 0(з) = Ь[^@] •
2. Найти матрицы [яЕ-А], С[зЕ-А]~1 и передаточные функции по
формулам
\УХE) = [5Е-А]-1В,
ЦГу(з) = С[5Е-А]-1В.
3. Используя связи вход-состояние и вход-выход, найти изображение
по Лапласу законов изменения векторов состояния и выхода:
Х(з) = [зЕ-А]-1х0 + IVх (з) 0(з),
ад) х^и)
У (*) = С[зЕ-АУ1х0 + ЦТ у E) 0(&).
4. Найти законы изменения векторов состояния и выхода с помощью
обратного преобразования Лапласа:
ха) = Ь'1[ХE)] = хс@^хвын@9
При выполнении пп. 1 и 4 применяются табл. 3.1 преобразования Лапласа и его
свойства.
Пример 3.21. Найти законы изменения векторов состояния и выхода
многомерной системы:
хг =х1+2х2+8, У = хг+Х2,
х2 = 2хх+х2,
с начальными условиями ^@) = 1, х2@) = -1 при входном сигнале #(/) = е'1A).
П Перепишем уравнения системы в матричной форме:
и и и
А В С
1. Найдем изображение входного сигнала: 0(з) = —-.
145

2. Получим передаточные функции:
5-1
E-3)E + 1) E-3)E + 1)
2 *-1
1(*-3)С* + 1) E-3X5 + 1),)
С\*Е-АГ1=A ^-^-(-^ -1-).
Г_5-1 ч
E-3X5 + 1)
2
^E-3X5+1);
^E)-с[5^-^Г^=A О^-^Г'^-тгз-
3. Определим изображения законов изменения векторов состояния и выхо-
Х(з) =
5-1
E-3)E + 1) E-3)E + 1)
2 5-1
и^-3)E + 1) E-3X5 + 1);
(-.)¦
5-1
(*-3)E + 1)
2
и*-з)E+1);
1
5-1
1 ^
5 + 1
-1
и+и
1
E-3)E + 1)
2
и*-3)E + 1)<5-1);
( 1 
5 + 1
-1
и + 1
ХсE)
1
+ 4
1
1
5-3 5+1
1 2 } 1
1,5-3 5-1 5 + 1
и
уп_( 1 1 VII 1 11 1
№ и-3 5-ЗД-О 5-3*5-1 2E-3) 2E-1)'
4. Находим искомые законы изменения векторов состояния и выхода:
х(*\-(е")Л( '*-«"' )-Г 0.2^+0,7^-' )
^ [-е-')+4{е*-2е1 +е-1)(оа5е* -0,5е' -0,75*"',)'
*с(') *«ы»@
у@ = Х-'[1гE)] = 04в3'-0^в'.

Заметим, что по формуле C.22) можно найти переходную матрицу:
'' 5-1 2
ФЫ> = 1Г1[№-АУ1}шГ1
= 1Г
1 1
- + -
1
E-3)E + 1) E-3)E + 1)
2 5-1
[и*-3)(* + 1) E-3)E + 1^
1 ^
2E-3) 2E + 1) 2E-3) 2E + 1)
1 1 1 1
(,2E-3) 2E + 1) 2E-3)+ 2E + 1),!
Результат совпадает с полученным в примере 1.24. ¦
Пример 3.22. Найти законы изменения векторов состояния и выхода
многомерной системы
*1=-*2+*Ь У1=Х2,
*2=*1+*2> Уг=Хх+0ЛХ2
с начальными условиями х1@) = -1, х2@) = 0 при входном сигнале
Л@-2.«0,Л@ = «0.
П Перепишем уравнения системы в матричной форме:
А
в
1. Определим изображение входного сигнала: С(з) =
2. Получим передаточные функции:
с
BЛ
8
I
К 8 )
-1 
52+1 52+1
52+1 52+и
с[8Е-аГ^х $№-*Т1-
52+1 52+1
5 + 04 0,55-1
и2+1 82+1^
яг'(АшЬе-аГ1ВшЬв-лГ1§ °} =
-1 
52+1 52+1
1 5
и2+1 52+и
147

^М-с^-лГ1*-^ $&-*% ?) =
52+1 52+1
5 + 0,5 0,55-1
и2+1 52+1>/
3. Найдем изображения законов изменения векторов состояния и выхода:
*<*)-
-1 ^
52+1
-1
52+1 52+1
1 5
52+1 52+1>1
25-1
(»'>
5 -1 ^
52 + 1 52+1
1 5
52+1 52+и
5<52+1)
2 + 5
\52+1) ^5E2+1);
-52+25-1
5E2+1)
I *(*2 + 0 )
Г-1 2 ^
' 52+1
2 25_
5 52+1)
Г(з)>
' 1 5
52+1 52+1
5 + 0,5 0,55-1
и2+1 з2 + \)
52+1 52+1
5 + 0,5 0,55-1
и2+1 52+и
( 2 )
ф2+1)
4-25
и*2+1)]
V
2 25
* 52+1
2 1.
52+1 82+\)
4. Находим искомые законы изменения векторов состояния и выхода:
/л г-1Гу/ ч1 Г-008^ М + 2вН1* + СОвЛ М + 2ЯПЛ
хс(/)
Л)-1Г»[к»1-Г,2.-2в"'1.
,у/ 1 ч п (,2яп/-со8{/

Заметим, что по формуле C.22) можно найти переходную матрицу:
ФA0-Г!{(Л-Л1"!}-Г
5 -1 ^
52+1 52+1
и2+1 52+1
ГС08Т1 -81ПТ1
'}
Результаты совпадают с полученными в примере 1.25. ¦
Пример 3.23. Найти законы изменения векторов состояния и выхода
многомерной системы
*2=-*1-2*2> У2=х1
с начальными условиями х{@) = 1, х2@) = -1 при входном сигаале #(г) = -/(/).
О Перепишем уравнения состояния и выхода в матричной форме
1
43 н<:
1. Найдем изображение входного сигнала: С(з) = —.
2. Получим передаточные функции:
( 5 + 2
1 я
I E + 1J (* + 1?)
<Ьв-аГш^ ^[*е-аГ =
1 1
5 + 1 5 + 1
5 + 2 1
( 5 + 2 ^
г*Ь)-Ье-лГв-Ьв-аТ1Р\-
1
I Ь + 1?)
щг'Ц-сЬв-лГвш^ ^-4-^)-
1 ^
5 + 1
5 + 2
{<? + !?)
149

3. Найдем изображения законов изменения векторов состояния и выхода:
щ=
1
5 + 2
A + 1? (* + 1?
1 л
I (. + 1J (* + 1)Ч
( 5 + 2
(АНШ-Э-
I Ь + 1?)
5 + 1
1_
к 5 + 1
хе{*)
5 + 2
5E + 1J
1
[ 5E + 1^ )
5 + 1
1_
5 + 1
1
E + 1J 5E + 1J
1
5E + 1J
УE) =
5 + 1 5 + 1
5 + 2 1
Ш
( 1 ^*
»
К^!J;
1,5 + 1
5E + 1)
5 + 2
= 1 1 | +
5 + 1
5E + 1)
1 2
ч E+1J 5E+1^
Представим слагаемое
в виде
1
. = ¦1 -^-+- С
5E + 1J ~"""~ 5E + 1J * 5 + 1 (у +1J '
где А, В, С — неопределенные коэффициенты.
Умножая на общий знаменатель, находим А(з + 1J +2?$($ + 1)+С$ = 1.
При 5 = -1, 5 = 0, 5 = 1 последовательно получаем С = -1, Л = 1, 2? = -1:
1 1 1 1
5E + 1J 5 5 + 1 E + 1J*
4. По формулам 2, 6, 7, 23 табл. 3.1 найдем законы изменения векторов
состояния и выхода:
*(А-( е~* \А-*е-* -2 + 2е-* +Ие-'Л_(-2 + Ъе-* +1е~'Л
Х[и-[-е-*У{ 1-е-'-*е-< ){ 1-2е-'-*е-< )9
*М
*ы*(')
*'Н«-'Н-'«"'-2+^-4^
ш
~^Ж
150

3.3. ОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ.
ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
33.1. Описание сигналов и систем
1. Описание сигналов. Для описания детерминированных сигналов
используется преобразование Фурье:
0(*)ш1[ю]ш /^Ое-^Л, C.25)
-во
где #@ ~ сигнал; <7(а>) — его изображение по Фурье.
В качестве моделей случайных сигналов рассматриваются стационарные
одномерные случайные процессы (см. разд. 1.3.1), например О@, которые имеют
постоянные математические ожидания /и^(Г) = сопзГ, а их ковариационные
функции зависят от разности аргументов ^ - /2 = *1 и поэтому являются
функциями одной переменной:
^М)-^1-<2)-^(л).
Дисперсия стационарного случайного процесса получается при *\=*2> т- е- ПР"
х\ = 0: 2)^@ = 1^@) = сопя.
Примером стационарных случайных процессов является стационарный
белый шум, имеющий нулевое математическое ожидание и ковариационную
функцию Д;(л) = <?0 6(л), ще 50 - интенсивность белого шума.
С помощью интегрального преобразования Фурье можно получить
характеристики стационарных случайных процессов, эквивалентные моментным
функциям (см. разд. 1.3.1).
Спектральной плотностью называется преобразование Фурье
ковариационной функции стационарного случайного процесса:
^(ш) = /^(Л)]= /^(лК*"»!. C.26)
-«о
Эта функция частоты о» в силу четности функции /^(л) является четной.
Переход от спектральной плотности к ковариационной функции выполняется с
помощью обратного преобразования Фурье:
*,<*) =^ ]^(«)в^УЬ. C.27)
—«о
При т] = 0 в силу четности 5^(а>) получаем формулу для вычисления
дисперсии:
1)^=^@)=^- /|У,(ю)Ж> = -/^(ю)<&>. C.28)
151

2. Описание систем. Рассматриваются линейные одномерные стационарные
системы управления, описываемые обыкновенным дифференциальным
уравнением
ап *<">(/) +... + ао *(/) = Ьт *<*>@ +... + Ьо М, C.29)
где #(/) и х(/) - входной и выходной сигналы; пит — порядки старших
производных выходного и входного сигналов соответственно; д0,...,дл, Ь0,...9Ьт —
постоянные коэффициенты. Если к системе приложен случайный входной
сигнал, то на выходе также получается случайный сигнал. Для обозначения
случайных сигналов будем использовать прописные буквы (?(/), ЛГ(/).
Учтем, что для стационарных систем импульсная переходная функция
кA,х) является функцией разности *-т = т! своих аргументов: кA,т) = к(г\) 9
причем к(т\) = 0 при т] < 0 (см. разд. 2.1.1).
Частотной характеристикой Ж(/ш) стационарной линейной системы
называется преобразование Фурье импульсной переходной функции:
ЩЬ) = Г[к(Ц)]=]к(т])е-<**ач.
о
C.30)
цией:
Существует связь между частотной характеристикой и передаточной функ-
Щко) = Щ5)
5*=/й)
C.31)
Частотная характеристика является комплекснозначной функцией
вещественного аргумента ш — частоты, изменяющейся в промежутке от 0 до +оо, и
может быть представлена в показательной, тригонометрической и
алгебраической формах:
IV (/©) = А(<о) е/ф<<0) = А(а>). [ соз <р(«>) + / зт <р(«>) ] = (/(©) + / К(<о), C.32)
где А((о), ф(со) — амплитудная и фазовая частотные характеристики; 1/(а>),
К(со) — вещественная и мнимая частотные характеристики; Л(ео) = | IV(т) |,
Ф(©) = аг8 Щ/ю) , Щ©) = КеЖ(ло), У(ъ) = \тЩт) :
А(ъ) = 4и2{<й) + У2(<ъ) , <р(а)) =
агс1§
агс1&
агс!8
1^2)
^(*>)
Г(о>)
^(*>)
(/(©)> 0, Г(а>)*0,
+ *, G(«>)<0, К(ю)^0,
-я, (/(©)<0, К(а>)<0,
|, Щ«,) = 0, Г(со)>0,
-^ #(а>) = 0, К(со)<0.
152

Заметим, что в начале координат ап$ \У(т) не определен.
Частотная характеристика IV(т) изображается годографом в координатах
1/9 V или в полярных координатах А, <р, называемым амплитудно-фазовой
частотной характеристикой (рис. 3.16).
Рис. 3.16
Методика нахождения частотных характеристик состоит в следующем:
1. По дифференциальному уравнению системы найти передаточную
функцию Щз).
2. Найти частотную характеристику Щт) по формуле связи C.31).
3. Определить вещественную и мнимую, а также амплитудную и фазовую
частотные характеристики по формулам C.32).
Установим физический смысл частотной характеристики. Для этого в
формуле C.30) произведем замену переменных: т! = /-т. Отсюда следует, что
а\\ = -А, а значениям ц = 0, ц = +оо соответствуют т = / и т = -оо:
Щю>) = } Ш • е-^ац = - / *(/ - т) • е-^^ах =
о г
= \к(<-т)-е-'<*(-х)а\ = е-ш \ к(* - т). е,с>тЛ.
-00 —00
Используя C.32) и формулу Эйлера е/в>т = созшт + /япсот, получаем
Щш>) • еш = А(<о) • е/ф<в>). еш = А(<о). «'I**-* 1 =
I
= |А:(/-т)[со8©т + /81па)х]Л
-00
или
I
А(<в) • {соз[ф(ш) + ш/]+/8Ш [ф(ш) + ©/]}= I кA - т) • [созсот + /81П сот ]Л.
153

Приравнивая действительные и мнимые части, имеем
I
>4(ю)-со5[ф(со) + со/]= ^(/-фсозштА,
-00
/
Л(<о)-яп[ф(о)) + а)/]= |А:(/-т)-япо>тЛ.
-00
Из полученных соотношений следует, что если на вход стационарной
линейной системы продолжительное время (бесконечно долго) действует
гармонический сигнал частоты со, то наблюдаемый выходной сигнал будет тоже
гармоническим с той же частотой. Амплитуда его отличается в Л(со) раз, а фаза —
на величину <р(а>).
Приведенный анализ служит основой для экспериментального нахождения
частотной характеристики. При этом на вход динамической системы при
помощи генератора подается гармонический входной сигнал ^(() = А{ $тШ. На
выходе измеряются амплитуда и фаза гармонического сигнала *(/) = А2 • $т(ы + <р),
а затем вычисляется отношение амплитуд выходного и входного сигналов
Лу
А((о) = -*-. Повторяя описанную процедуру при различных значениях частоты
со € [0,+ оо), можно построить годограф частотной характеристики (рис. 3.17).
Генератор гармонических
сигналов
#(/) = 481П0>/
Система
х(/) = Л2 31п(се
>' + ф)
со
СО!
<02
А(<о) = &
А(<о2)
ф(со)
ф(С01)
ф(С02)
Логарифмической амплитудной частотной характеристикой (ЛАЧХ)
называется функция
1(а>)=20.1я| 1Г(/©)| = 2О1яЛ(с0). C.33)
Она вместе с фазовой частотной характеристикой <р(ю) служит для описания
стационарной системы. Частотная характеристика выражается через ЛАЧХ по
формуле
154

1Г(к>) = е0'051**) 1п1О+/ф(<0)
Пара Ц(о) и <р(ш) называется логарифмической амплитудно-фазовой
частотной характеристикой системы (ЛАФЧХ). При графическом изображении
ЛАФЧХ используют акустические единицы измерения. Говорят, что частоты щ
и ©2 Двух гармонических сигналов ^) = А{ мп^^ + щ) и х(*)=А2 -зш^' + Фг)
отличаются на декаду, если —2-= 10 (соответственно 1в—^-= 1)- Отношение
мощностей сигналов измеряется в децибелах (дб): 1 децибел равен 0,1 бела
A б =10 дб). Один бел соответствует увеличению мощности гармонического
сигнала в 10 раз, 2 б - изменению мощности в 100 раз, и т.д. Амплитудная
частотная характеристика А(<о) равна отношению амплитуд выходного и
входного сигналов Л(ю) = --2-, а мощность сигнала пропорциональна квадрату его ам-
А
плитуды. Поэтому для выражения в белах отношения мощностей сигналов
следует вычислить десятичный логарифм от квадрата амплитудной характеристики:
1*[4о)Р=2М")-
Умножив эту величину на 10, получим ее выражение в децибелах. Поэтому в
правой части C.33) имеется множитель 20. Один децибел соответствует
изменению амплитуды колебаний в 2^/7о»1Д22 раз, т.е. является сравнительно
небольшой величиной.
Логарифмическая амплитудно-фазовая частотная характеристика строится
в прямоугольной системе координат. По оси абсцисс откладывается частота о
в логарифмическом масштабе. По оси ординат - равномерная шкала децибел.
Ось абсцисс проходит через нуль на оси ординат, что соответствует значению
А((о) = 1 (амплитуды входного и выходного сигналов равны). Нуль на оси абсцисс
(со = 0) - это бесконечно удаленная точка ( Шп 1ясо = -оо). Поэтому ось ординат
о>-»+0
проводится через произвольную точку на оси абсцисс, так чтобы справа от оси
ординат оказалась интересующая нас часть графика логарифмической частотной
характеристики.
Пример 3.24. Построить частотные характеристики усилительного звена
A.7) с коэффициентом усиления К = 5.
? Уравнение звена: х(/) = 5#(/).
1. По уравнению найдем передаточную функцию: Ж($) = 5.
2. Найдем частотную характеристику по формуле C.31): Ж(/со) = 5.
3. Используя формулы C.32), имеем:
Л(©) = 5, ф(со) = 0, 17(со) = 5, Г(©) = 0.
Полученные частотные характеристики изображены на рис. 3.18.И
155

А
5
Л(а>) = 5
<р(а>) = 0
Рис. 3.18
04*») = 5 |
V
Пример 3.25. Построить частотные характеристики дифференцирующего
звена A.8).
? Дифференциальное уравнение звена: *(/) = #(Г) •
1. По дифференциальному уравнению найдем передаточную функцию:
Щ5) = 5.
'т
2. Найдем частотную характеристику по формуле C.31): Щт) = ко = со е 2.
3. Используя формулы C.32), имеем:
Ф<«>-|, #(«>) = 0, К(со) = со.
Л(со) = со,
Полученные частотные характеристики изображены на рис. 3.19Л
\Щю>)
КП
со = 0
V
A9).
Рис. 3.19
Пример 3.26. Построить частотные характеристики интегрирующего звена
? Дифференциальное уравнение звена: х(/) = #(?).
1. По дифференциальному уравнению найдем передаточную функцию:
1
ЖE)=-.
2. Найдем частотную характеристику по формуле C.31):
/со со со
156

3. Используя формулы C.32), имеем:
Л(*)=-, Ф(«>) = ~, ^(*) = 0, К(ш) = -1.
со 2 со
Полученные частотные характеристики изображены на рис. 3.20.1
А 4 Ф ¦ У*
= +00
G
ЩЬ)
Рис. 3.20
Пример 3.27. Построить частотные характеристики системы, описываемой
дифференциальным уравнением 2хA) + х(() = 2#@.
а Дифференциальное уравнение звена в операторной форме:
B/> + 1)х = 2*.
1. По дифференциальному уравнению найдем передаточную функцию:
2
Щз) =
25 + 1
2. Найдем частотную характеристику по формуле C.31):
ИЧи>)=-
•-/-
4<*>
2/00 + 1 1 + 4со2 1 + 4ю2
3. Используя формулы C.32), имеем:
Л(св) = ] * + "?'а- у 2 0> Ф(«>)--агс182а>; У^—^-; ^(«)—ТТ«
|A + 4со2J ^1 + 4со2 1 + 4со2 1 + 4со2
Заметим, что [#(ю)-112+К2(ю) = 1.
Искомые частотные характеристики изображены на рис. 3.21.¦
ф
0
я
2
Рис. 3.21
со
V
0
@ в +00
<о
V0.
27 G
Щйв)
157

Пример 3.28. Построить амплитудно-фазовую частотную характеристику
системы, заданной структурной схемой (рис. 3.22).
1
5 + 1
1
5 + 2
зП
5
Рис. 3.22
П 1. Найдем передаточную функцию системы:
1
И^) = 3 » + Р» + Э = ^ \ .
^ , 1 53+352+35
E + 1)E + 2)
2. Получим частотную характеристику и выделим ее действительную и
мнимую части:
3 9 . 3C-о2)
Щю>) =
- /ю3 - 3<о2 + 3/а> 9а>2 + C - а>2J 9а>3 + <оC - а>2J !
G(а>) = --
9 „, , 3C-о2)
— —, К(а>) = т-* *-т-гг
о2+C-а>2J 9а>3+а>C-а>2J
Амплитудно-фазовая частотная характеристика изображена на рис. 3.23.1
V
-1 -*
Щк»)
<0 = +00
V
Рис. 3.23
Пример 3.29. Построить логарифмические амплитудно-фазовые частотные
характеристики усилительного, дифференцирующего, интегрирующего,
апериодического и колебательного звеньев.
П Используем C.33) и результаты решения примеров 3.24—3.27.
158

1. Усилительное звено. Так как А((о) = 5, <р(со) = 0 (см. пример 3.24), то
дш) = 201я К. ЛАФЧХ усилительного звена изображена на рис. 3.24.
М
40 +
20 +
0,1
од
Дсо) = 201я*
10
ф(со)а0
Н
10
100
100
со
1000
—К со
1000
Рис. 3.24
2. Дифференцирующее звено. Поскольку Л(со) = со, <р(со)= — (см. пример
3.25), логарифмическая амшштудно-частотная характеристика
дифференцирующего звена имеет вид 1(со) = 20-1§со. График этой функции представляет собой
прямую, так как частота со берется в логарифмическом масштабе. Наклон этой
прямой составляет 20 дб на декаду (рис. 3.25).
4* со
1000
*> со
100 1000
Рис. 3.25
159

3. Интегрирующее звепо. Поскольку А(а>) = —, <р(а>) = —— (см. пример 3.26),
а> 2
логарифмическая амплитудно-частотная характеристика интегрирующего звена
имеет ввд Хг(со)= 201^— = -20 1яю. График этой функции представляет собой
@
прямую, наклон которой равен - 20 дб/дек (рис. 3.26).
Ь
2
од
10
100
1000
Ф(ю) = -*
Рис. 3.26
4. Апериодическое звепо. Так как передаточная функция апериодического
звена ЦГ(з)=— , а частотная характеристика 1У(т) = \У(з)
1
= «о
1-7Ь
ге
-/ап*87Ь
A + Г«))A-7Ь) ^1 + 2*т2
фазовая частотная характеристика имеет вид:
77ю + 1
то логарифмическая
амплитудного^ 201я
^Тг5^
г = -201я^1 + 7'2о>2э <р(а)) = -агс18 7Ь.
где Т
постоянная времени. Для построения графика можно рассмотреть два
промежутка изменения частоты. Обозначим через ©0 = ¦— так называемую
сопрягающую частоту. Если а>«а>0, то 1{а>)*0. Если а>»а>0» т°
1^а>)»-20187Ь = -20 1яГ-20 1яа> (график - прямая, имеющая наклон
-20 дб/дек). На рис. 3.27 изображен приближенный график ЛАЧХ - ломаная
из двух звеньев, а также точный график - пунктирной линией. Наибольшее
отклонение этих графиков, равное 20 *]я^2» 3,01 дб , достигается на сопрягающей
частоте.
160

на Щз) =
Рис. 3.27
5. Колебательное звено. Так как передаточная функция колебательного зве-
1
Г252 + 2§Г5 + 1'
а частотная характеристика Ж(ко) = ЖE)
\5 = 1
/алЗД
2$Го
Х(ш) = 201^
1/A-Г2а>2J+B§Га>J
1-г2©2, то логарифмическая амплитудно-фазовая
= -20181(A-^2<о2J+B§Г©J,
<р(а>) = -а1Х%
2$7Ь
где Т - постоянная времени, % - коэффициент демпфирования. Для построения
графика этой функции рассмотрим два промежутка изменения частоты.
Обозначим через а>о="^ сопрягающую частоту. Если а>«а>0, то 1,(а>)»0. Если
о»со0, то 1(а>)*20-18Г2а>2 = -40]&Т-40-]&<а (график - прямая, имеющая
наклон - 40 дб/дек). На рис. 3.28 изображен приближенный график ЛАЧХ -
ломаная из двух звеньев. Точный график отличается от приближенного, причем
наибольшее отклонение АЬ достигается на частоте сопряжения: А1г = 20-1вB§).
Эта величина зависит от коэффициента демпфирования. На рис. 3.28
пунктирными линиями изображены точные графики ЛАЧХ для разных коэффициентов
Демпфирования. ¦
161

5 = 0,05
¦»> оо
5 = 0,2
Рис. 3.28
Пример 3.30. Построить логарифмическую амплитудно-фазовую частотную
характеристику системы с передаточной функцией
Щз) =
105
0,015 + 1
П Представим передаточную функцию системы в форме произведения
передаточных функций образующих ее звеньев:
Щз) =
Юз
0,015 + 1
где ^E) = 10, Щ{з) = $9 Щ(з)=-
-1Г1(*)'1Гг(')-1Гъ(*)*
1
. Первое звено - усилительное, второе
- дифференцирующее, а третье - апериодическое с сопрягающей частотой
©о = тгт7 = ЮО • О™ образуют последовательное соединение. Используя
показательную форму записи C.32), частотную характеристику системы можно записал»
в виде
ЩЬ) = Лх(со). е'*(ф) • А2(<») • е'ъ<ф) • Аг(а) • «'*<•> =
ж5
162

Следовательно, логарифмическая амплитудно-фазовая частотная
характеристика:
Да>) = 201« А(а) = 20 • ^[^(ю) • Л2(а>) • Л3(а>)] =
= 201е4(о>) + 20]&А2(&) + 2018^3(ш) = ^(ю) + /^(ю) + 1з(а>),
<р(а>) = ф! (а>) + <р2(а>) + Фз (со).
Приведенные рассуждения демонстрируют преимущество логарифмических
частотных характеристик, так как амплитудные частотные характеристики
звеньев, образующих последовательное соединение, перемножаются, а
логарифмические - складываются.
Итоговая ЛАФЧХ Дсо) и ф(ю) изображена на рис. 3.29. Она построена
с учетом результатов пп. 1,2,4 примера 3.29.
Ф1(<о) = 0
Рис. 3.29
Построенная логарифмическая амплитудно-фазовая частотная
характеристика может быть использована для анализа устойчивости (см. разд. 3.3.3) и
переходных процессов [34,55]. ¦
163

3.3.2. Анализ выходных процессов при случайных воздействиях
ПОСТАНОВКА ЗАДАЧИ
Пусть известны:
а) входной стационарный случайный сигнал (?(/) с известными
математическим ожиданием т8 и ковариационной функцией /^(л);
б) линейная стационарная система, описываемая дифференциальным
уравнением C.29). Она должна быть устойчивой (см. разд. 1.4.1).
Требуется найти математическое ожидание тх, ковариационную функцию
Ях(ц) и дисперсию Вх выходного сигнала Х{г) в стационарном режиме (при
/->+00 ).
связи вход-выход
Рассматривается линейная стационарная система, описываемая уравнением
ап .*<">(/) +... + *о Х«) = Ьт -0^A) +... + Ьо .<?(/).
Так как система устойчива, то в стационарном режиме при /-++00
сигналы практически не изменяются. Применяя операцию нахождения
математического ожидания к левой и правой частям уравнения с учетом т8 = соп&,
получаем связь между математическими ожиданиями входного и выходного сигналов:
во • ?пх = ^о • т^ или тх = —^- • т^.
Установим связь между спектральными плотностями сигналов на входе и
выходе. Для этого используем B.32), учитывая, что к(*,х) = кA -т) в силу
стационарности системы и Л;(т1,Т2) = А;(т1 -Т2>, так как входной сигнал
стационарный:
О О
= )<Ь\ \*{*\ -ч)Шг -Х2)-Лх(х, -т2)Л2.
о о
Обозначим х\-^ -*2> % = *\ -*ь Х = ^2~т2- Тогда <й; = -<&!, &1 = -<кг и
лх(/2+л^2)= / * }*(*) *(х)-лх(л+х-0*.
о о
Поскольку система устойчива, то при /->+«> выходной сигнал является
стационарным случайным процессом. Следовательно, его ковариационная
функция зависит от разности аргументов:
164

о о
Применим преобразование Фурье C.26):
5х(<о) = ,Р1Лж(тО] = ]^]*Й)*(х))л,A1 + Х-5)в-'в,,А1^ =
0 0 -со
= ) <Ц • т ¦ е-"* ) *(х) • */юх4с ] Пй (П + X - О ¦ *-"*»*-*>*! ¦
0 0-оо
Согласно C.30), C.26) получаем
о
Учтем также, что {ОД-е^^-^Чь)-^-*»)» где Ж*(*о) и Ж(«>)
о
связаны как комплексные сопряженные выражения. В результате находим
искомую связь
^(ю) = Щю>)• IV*(ко)• ^(ю) =| *Г(ко) |2 ^(со).
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти спектральную плотность входного сигнала ^(ю) по формуле
C.26). Так как функция 1^01) четная, т.е. Д;(-л) = Л;(л), то может быть
использована эквивалентная формула косинус-преобразования Фурье:
5^(а>) = 2 |^(л)со8(©т1)Аь C.34)
о
2. Определить частотную характеристику системы \У(кь) (см. разд. 3.3.1).
3. Найти математическое ожидание выходного сигнала в стационарном
режиме
тх=—/и^. C.35)
°о
4. Вычислить спектральную плотность выходного сигнала по формуле
«$х(«>) = IЩ**) |2 $,<©). C.36)
165

5. Найти ковариационную функцию Ях(ц) и дисперсию Вх выходного
сигнала по формулам C.27), C.28). Здесь иногда полезным оказывается
представление спектральной плотности в виде
$х (©) = $х (Ь) + 5^ (- ю>). C.37)
Тогда, заменяя ко = 5 и применяя обратное преобразование Лапласа, имеем
М\1ГЧРХ(А}, Л* О,
гМ,~1г1йг<-*>], л<о.
C.38)
Пример 3.31. Найти спектральную плотность стационарного белого шума
с интенсивностью Зо.
П Так как ЯЕ(г\) = $о &(л) > используя C.26), получаем
51(ш)-]лЬв(л)«"*и,А| = ^о-"
-00
Пример 3.32. Найти спектральную плотность сигнала, ковариационная
функция которого
'1-М. М<1.
О, |л1^1.
П По формуле C.34) имеем
*У^(а>) = 21^(г1)со8(а>г1)**п = 2 | A -т0со8(а>л)<Ь] =
о о
— ГA-л)</($ша>т1):
СО л
о
A — "П) 81П СОТ]
1 V
+ ] 81П СОЛ дх\
О О
= —A-СО8С0).!
Пример 3.33. Для стационарного случайного процесса со спектральной
плотностью
* [0, | со
|*а>я
1>©я»
где со/7 > 0, найти ковариационную функцию и дисперсию.
П В силу четности заданной функции 3^(оо) по формулеC.27) имеем
1 со « со | оо
Я^(х\)=— $ 5,^(со)вЙ1>11^со=— |5^(со)со8сог1*/со + /— |^(ш)зшсот1 </со =
= — *У* (СО) С08 С0Т|Д(О= — I ЛСО5С0Г| ОО = Ч = 81ПС0яЛ^
71 Т1
7СТ1
166

п =»@)=Цт^аЯП=^Шп^Д = ^
Пример 3.34. Определить дисперсию и ковариационную функцию
выходного сигнала системы, описываемой дифференциальным уравнением
Т ХA) + Х(*) = К6(*)> на вход которой подается белый шум с математическим
ожиданием т8 и интенсивностью 5<).
? 1. Ковариационная функция входного сигнала Я^(ц) = 50 5A]). Из
примера 3.31 следует, что 5^(ю) = *$о-
2. Найдем частотную характеристику системы, используя C.31):
Щш>) =
Щр)
К
рш5шь Тр +1
рш5шк> Тип +1
3. По формуле C.35) с учетом того, что а0 = 1, Ь$ = К, получаем
то
ТПХ = ~~ ТПт = К.Ша .
4. Вычисляем спектральную плотность выходного сигнала. Так как
|ж(^|2Н7^тГ=|^7р'=Т^Ь-'
с / ч К1 „ 50К2 ( 1 1 ^
5. По формуле C.37) 8Х(Ь) =
5п*2
2A+ 7Ь)
, а из C.38) следует, что
я^ь-ЧШ--^^^
Учитывая четность Д^ОО, получаем
г-1
$о*2 1
2Т 1
*$о*
2Г
2 _а
с гг! _1д1 с »г2
При Г = 1, Х-1, ^0-1> «*=1: *х«1. ^(п)^. />,-|л
Пример 3.35. Дана система (рис. 3.30) с IVр(з) =—, на вход которой посту-
N =Ы
пает сигнал с ковариационной функцией 1^(т0 =— е т ,К = 3, Г = 2, # = 10
и /и^ - 2.
167

Требуется найти математическое ожидание тх и дисперсию Вх выходного
сигнала в стационарном режиме.
*<^
км
- х
Рис. 3.30
П 1. Используя результат примера 3.34, определяем спектральную
плотность входного сигнала:
N
* 1 + Г2©2
2. Получим частотную характеристику. Для этого найдем передаточную
функцию по формуле для соединения с отрицательной обратной связью (см.
разд. 3.1.2):
1 К К + 8
Соответствующее дифференциальное уравнение в операторной форме имеет вид
(р + К)Х = К & или х + Кх = К&. По формуле C.31)
Щш) =
К + з
К + /а>
3. Так как а0 = К, Ьц = К, по формуле C.35) получаем тх = — 2 = 2.
4. Найдем спектральную плотность выходного сигнала. Так как
|ИЧ*о)|2=
5. По формуле C.28)
К2+<о2
, ТО $х(<й) =
К2
N
К2+а>2 1 + Г2©2'
1 ЛТФ^
</<0
п $ Т2и*+(Х + Т2К2)тг+К
Пользуясь таблицами интегралов, имеем
ах п
г ах я
I ахА+2Ьх2 + с 2^2с(Ь + ^ж) '
где а
= Т2,Ь =
\ + Т2К2
о 15
, с = К*. Следовательно, Вх = —.
168

3.3.3. Анализ устойчивости
ПОСТАНОВКА ЗАДАЧИ
Пусть дана линейная одномерная стационарная система управления,
описываемая структурной схемой, изображенной на рис. 3.31,а или 331,6, с
известной передаточной функцией Ж(з).
Требуется исследовать, является ли система устойчивой (см. разд. 1.4.1).
ЧАСТОТНЫЕ МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ
Анализ устойчивости линейных стационарных систем управления удобно
проводить на основе двух частотных критериев. Критерий Михайлова
применяется для систем (рис. 3.31,а) с известной частотной характеристикой Ж(/а>), а
критерий Найквиста - Михайлова позволяет судить об устойчивости замкнутой
системы (рис. 3.31,6) по частотной характеристике И'(мо) разомкнутой системы.
Щз)
-Ф
Щз)
Рис. 3.31
Методика применения частотных критериев использует следующее
построение. Пусть задана функция % = /($) комплексного переменного 5,
аналитическая на всей комплексной плоскости, за исключением конечного числа
изолированных полюсов. Если для каждого действительного значения со из
промежутка [0; + оо) определен аргумент комплексного числа /(/со) , то можно
вычислить приращение А Аде /(ко) функции Аде/(/оо) при изменении частоты со
от 0 до + оо . Если же при некоторых значениях со из промежутка [ 0; + оо)
функция Аде/(/со) не определена, т.е. /(/©) = О или /(/со) = <х>, то промежуток
[0; + оо) следует разбить на интервалы, исключив недопустимые значения со,
вычислить величину приращения ААде/(/со) на каждом интервале, а затем
полученные величины приращений сложить. Описанная процедура легко выполняется,
если построить годограф функции /(/со) при изменении частоты со от 0 до
+ <» . Тогда приращение ААде/(ш>) находится как величина <р угла поворота
радиус-вектора, конец которого перемещается по годографу функции /(/со) при
возрастании частоты от 0 до + оо :
Ф = Д Аде /(/со).
О^ах+оо
C.39)
169

В этом случае говорят, что годограф /(ко) охватывает точку г = 0 на угол
<р. При вычислении величины <р поворот радиус-вектора против часовой стрелки
считается положительным, а по часовой стрелке - отрицательным. Если годограф
/(ко) проходит через начало координат г = 0 или бесконечно удаленную точку
г = оо, то его следует разбить на участки, исключив указанные точки, вычислить
величину ф угла поворота радиус-вектора для каждого участка годографа, а затем
полученные величины сложить. На рис. 3.32 показаны примеры вычисления
величины C.39) по годографу /(ко).
->+00
-)-
-6
>•>
^
Ф = Ч>1 +Ч>2
/Ф2 \
^ ) ¦
^-^7
Рис. 3.32
Рассмотрим теперь в качестве функции /(з) характеристический
многочлен В(з) = ап8п + алЧ зп~х +... + % с действительными коэффициентами
а0,Д!,...,ал. Если многочлен В(з) имеет Л корней, лежащих в левой
полуплоскости (Ке$ < 0), П корней - в правой полуплоскости (Ке$ > 0) и Н корней - на
мнимой оси (Яе5 = 0), то справедлива формула
А А1Е Д(ко)=^(Л-П).
О^ОХ+00 2
C.40)
Сумма неотрицательных целых чисел Л, П, Н по основной теореме
алгебры равна степени п многочлена И(з):
л^Л+П+Я.
C.41)
Поясним формулу C.40). Так как характеристический многочлен имеет п
корней, то его можно представить в виде
П(з) = апзп+ап_1зп +>.. + во =ап (з-зг) (з-з2).-.(з-5п).
170

Положим $ = /со и воспользуемся показательной формой представления
комплексного числа:
2)(/а>) = А(а>) • е,ф<*) = ап ^(©). «'*<•> - Л2(а>) • в/ф2<*> •... - Лп(ю). е/ф"(а>) -
Поэтому Агв 2)(/со) = <р(а>) = ф^со) + ФгОо) +... + Ф„(а>),
я
ААк2)(ш))= ]Г ААгв (ио-$/).
а>е[0,+оо) ув1 о>е[0,+оо)
Если корень 8] лежит в левой полуплоскости, то при изменении частоты со
от 0 до + оо аргумент изменяется на ¦- (рис. 3.33,а).
т л»
> +00
со = 0
*/'
•5'
Т со —> +оо
^>
X
со = 0
а! +<Х2 =
Рис. 3.33
Паре комплексных сопряженных корней соответствует изменение
аргумента, равное п (рис. 3.33,6). Если корни расположены в правой полуплоскости,
величина изменения аргумента отличается знаком. Следовательно, имеем
ААгс#(/со) = — »Л——-П= — '(Л-П). Для устойчивости (по начальным данным)
а>е[0,+оо) 2 2 2
необходимо и достаточно (см. разд. 1.4.1), чтобы все корни характеристического
многочлена лежали в левой полуплоскости. Положив П = 0, Н = О и учитывая
C.41), получаем А Апг 2)(/со) = — • Л = ¦- • п.
о>е[0,+оо) 2 2
1. Критерий Михайлова. Этот критерий позволяет сделать вывод об
устойчивости системы по годографу характеристического многочлена.
Утверждение. Для устойчивости (по начальным данным) линейной
стационарной системы (см. рис.3.31,а), описываемой передаточной функцией
**Ч$) = _) = -а ——— , необходимо и достаточно, чтобы годограф харак-
Щ8) ал5л+... + во
пуристического многочлена 2)(ко) при изменении частоты со от О до +оо,
охватывал начало координат на угол <р = ~л, где п - порядок характеристического
многочлена.
171

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Определить порядок п знаменателя 2)($) передаточной функции IV(з)
системы.
2. Построить на комплексной плоскости годограф многочлена 2)(ко) при
изменении частоты ю от 0 до + оо .
3. Вычислить величину <р угла, на который годограф охватывает начало
координат (точку г = 0):
Ф = А А1В #(ко).
4. Проверить выполнение условия ср = — л. Если условие выполнено, то
система устойчива по начальным данным. Если, кроме того, порядок т
числителя передаточной функции не больше порядка п ее знаменателя, то система
устойчива и по входу. Если годограф характеристического многочлена проходит
через начало координат, то говорят, что система находится на границе
устойчивости (оставаясь неустойчивой).
°1
0
/
(
к
2)(/а>)
/*~Ч Р
ю = 0
Ф = -2
б
Рис. 3.34
На рис. 3.34 приведены различные случаи применения критерия при
л = 3, />(ю) = Ке2)(/а)), (?((©) = 1т/)(/©). Годограф, изображенный на рис. 3.34,а,
соответствует устойчивой системе, годографы, изображенные на рис. 3.34,6-* -
неустойчивой.
Замечание. Существуют эквивалентные формулировки критерия
Михайлова.
1. Для устойчивости линейной стационарной системы по начальным данным
необходимо и достаточно, чтобы годограф характеристического многочлена,
начинаясь на положительной части действительной оси, проходил против часовой
стрелки последовательно п квадрантов.
На рис. 3.35 приведены примеры годографов характеристических
многочленов устойчивых систем.
172

/1 = 2
2. Для устойчивости линейной стационарной системы по начальным данным
необходимо и достаточно, чтобы нули действительной Р(ы) и мнимой С(со) частей
характеристического многочлена чередовались, а их общее число равнялось п.
Рис. 3.36
На рис. 3.36 изображены графики действительной и мнимой частей
характеристического многочлена, соответствующие устойчивой системе при п = 3.
Пример 3.36* Найти все положительные значения коэффициента усиления
К, при которых устойчива система (рис. 3.37).
1 1
| 52+5 + 2
1
5 + 1
К
Рис. 3.37
а Передаточная функция замкнутой системы имеет вид
173

Щз) =
К
53+252+Зз + К + 2'
1. Знаменатель этой функции является многочленом 3-й степени, т.е. /1 = 3.
2. Построим годограф этого многочлена, используя значения
/)(/©) = К + 2 - 2со2 + /соC - со2) при некоторых характерных частотах со (рис.
3.38).
3. Как видим, при К = 4 годограф проходит через начало координат, а при
К е @; 4) годограф проходит последовательно через /, //, /// квадранты,
охватывая точку г = 0 на угол <р = —. При ^еD;оо) годограф проходит через /,
IV, /// квадранты, а <р = —-. Таким образом, при всех К е @; 4) система будет
устойчивой.
> 1т/)(/©)
К = 2
1/2 4 6 8 Яе/>(/со)
* = 4
©
0
га
3
+ 00
/)(/©) 1
А- + 2
К-4
ЛГ-16-18/
— 00 — I 00
Рис. 3.38
Воспользуемся альтернативной формулировкой критерия Михайлова.
Найдем корни действительной и мнимой частей характеристического многочлена:
/>(©) = * + 2-2©2=0,
О(©) = ©C-©2) = 0.
Из второго уравнения получаем щ = 0, ©2 = 7з (корень ъг=-4ъ не при-
надлежит промежутку [0,+ оо)). Из первого уравнения следует © = Л —-
вне чередования корней будет выполнено, если
1. Уело-
[»<^<л.
или
*>0,
-2<к<49
к>0.
Отсюда получаем, что при 0 < к < 4 система будет устойчивой.!
174

Пример 3.37. Является ли устойчивой система, описываемая
дифференциальным уравнением 2х(/) + *(/) = 2$(/) ?
О 1. Передаточная функция системы
Щз) =
25 + Г
поэтому Д($) = 2$ + 1, л = 1.
2. На рис. 3.39,а изображен годограф 2>(ш>) = 1 + /2а> , так как Ке2)(ш>) = 1,
1т Д(*а>) = 2ю.
1т/)(/©)
я
Ф=2
/
1
<
2)(ю>)
ю = 0
Ке2)
Л(ю>)
/-9
1т/>(*»)
^! ^
-3
ф = я
2
Ке/)(/ш)
ш
0
1
Л
+ 00
2)(ю>) 1
0
-3 + 2/
-9
—оо —/оо
Рис. 3.39
3,4. Очевидно, при изменении со от 0 до + оо угол ф = — , что
удовлетворяет условию ф =—л при п = 1. Поэтому система устойчива. ¦
Пример 3.38. Исследовать на устойчивость систему, заданную структурной
схемой (см. рис. 3.22).
П 1.Передаточная функция замкнутой системы имеет вид (см. пример 3.28)
и*)=-
зг + 3$2 + 35
2. Годограф характеристического многочлена изображен на рис. 3.39,5, так
как Щ>) = -3<о2 + АоC-о>2).
3,4. Угол ф = Л Аф />(&>)= я *-~л при л = 3. Поэтому система не является
03а>«*> 2
Устойчивой. ¦
175

Пример 3.39. Исследовать устойчивость системы с передаточной функцией
80
Щз) =
0,01 *3 + 0,52 з2 +75 + 80*
? 1. Знаменатель передаточной функции является многочленом третьей
степени, т.е. л = 3.
2. Построим годограф характеристического многочлена
2)A<о) = В(з)\ 3 = /ш = -0,01 /ю3 -0,52а>2 +7/© + 80 =
= 80 - 0,52<о2 + / G© - 0,01 а>3),
Р(»)
<?(»)
вычислив действительную Р(<о) и мнимую 0(а>) части при различных значениях
частоты о (рис. 3.40,а) и графики действительной и мнимой частей
характеристического многочлена (рис. 3.40,6).
со
/>(©)
0(<о)
0
80
0
4
71,7
27,4
8
46,7
50,9
12
5,1
66,7
16
-53,1
71,0
20
-128
60
24
-219,5
29,8
28
-327,7
-23,5
32
- 452,5
- 103,7
+ оо 1
-00 1
-00
Л 0
Рис. 3.40
3. Очевидно, годограф проходит последовательно через I, II, III
квадранты, охватывая точку г = 0 на угол <р = —. Одновременно корни действительной
и мнимой частей характеристического многочлена чередуются, а их общее число
равно трем,
4. Согласно критерию Михайлова система является устойчивой. ¦
176

Пример 3.40. Определить, при каком положительном значении
коэффициента усиления к система, описываемая передаточной функцией
Щз)= кик
аА84 + а$5г + а2з2 + а\$ +1 + к
будет на границе устойчивости, если ^ = 0,01; Ьц = 1; аА = 0,01; аъ = 0,2; а2 = 5.
? Система находится на границе устойчивости, если годограф
характеристического многочлена Д/со) проходит через начало координат, т.е. справедливы
условия Р(ю) = 0, й(а>) = 0.
Так как
В(ко) = а4<о4 -а^кй? -а2<й2 +ахЬ + \ + к =
= (*4 ®>4 - а2 <а2 +1 + к + т(а\ - а$®?),
то условия принимают вид
а4<а4 -а2<о2 +1 + к = 0,
со (д1 -а$®2) = 0.
Из второго уравнения получаем щ =0, со2 = Л » ^з =~^ • При а>! из
первого уравнения находим к--\ (не удовлетворяется условие к>0)9 при со2
частота изменяется от 0 до + оо. Таким образом, при к = ккр= 224 система будет
находиться на границе устойчивости."
2. Критерий Найквиста-Михайлова. Рассматривается система управления
(см. рис. 3.31, б)у замкнутая отрицательной единичной обратной связью.
Передаточная функция разомкнутой системы имеет вид
ГпшШшЬС±=±Ь., C.42)
Щз) ал5л+... + во
причем многочлены М(з) и 2)($) не имеют общих корней и порядок т
числителя C.42) не больше порядка п знаменателя.
Пусть передаточная функция C.42) имеет П полюсов (с учетом их
кратности), лежащих в правой полуплоскости, и Н полюсов, лежащих на мнимой оси.
В этом случае (при П + Н > 0) разомкнутая система неустойчива.
Требуется исследовать устойчивость замкнутой системы по годографу
частотной характеристики й^(/со) разомкнутой системы.
177

Для решения задачи найдем передаточную функцию замкнутой системы
(с отрицательной единичной обратной связью):
ш гл_ у»> _ д<*> _ м&
Ж*)
Характеристический многочлен замкнутой системы имеет вид
2)E) + А/E) = Д5)|1+-|^1 = 2)E).[1 + ^E)].
Воспользуемся критерием Михайлова:
А АГ8 [Д(/ю) + Л/(/ю)] = А Аг8 [Д(«о) • A + Щ/ю))] = А Агв Д(Ь) + А Аге [1 + Щш>)].
О&0<+оо 0^«к+оо О^ох+оо О^ах+оо
По формуле C.40) ДАгв 2)(/а>) =— (Л-П). Поскольку при т^п степень
О^ак+оо 2
многочлена 2)(ко) + Л/(ио) определяется числом л, то критерий устойчивости
имеет вид А Аг& [2)(ш>) + Л/(ш>)] = — * л. Отсюда находим
О^ох-ню 2
АА18[1 + Щ«0)] = ^и-^(Л-П).
Так как Л = л-П-Я, то окончательно получаем
ААг8[1 + )Г(«о)] = ^л-^.(/1-П-Я-П) = ^.BП + Я).
0^со<+оо 2 2 2
Заметим, что при т> п степень многочлена 2)(/со) + АГ(ко) равна т , тогда
критерий устойчивости принимает форму ДАг8[/)(ю) + Л/(&>)] = "/и и
о^ск-к» 2
ААг8[1 + )Г(ю))] = ^.т-^.(Л-П) = ^.т-^.(т-П-Я-П) =
0^ак+со 2 2 2 2
= |(т-л + 2П + Я).
Утверждение. Для устойчивости замкнутой системы необходимо и
достаточно, чтобы годограф частотной характеристики \У(ю>) разомкнутой системы
при изменении частоты ю от 0 до + <х> охватывал точку г = -1 + /0 ял угол
^BП + Я):
А Аг$ A + Щш>)) = -^BП + Я). C.43)
О^ахоо 2
178

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти передаточную функцию И^я) разомкнутой системы. Определить
количество корней знаменателя передаточной функции \У(з), лежащих в правой
полуплоскости (П) и на мнимой оси (Я).
2. Построить на комплексной плоскости годограф функции IV (ил) при
изменении частоты со от 0 до +оо.
3. Подсчитать величину <р угла, на который построенный годограф
охватывает точку г = -1 + /0. Для этого нужно построить вектор с началом в
критической точке -1 + /О, конец которого перемещается по годографу IV (т), и
вычислить величину угла, на который поворачивается вектор при изменении частоты
со от 0 до +оо.
4. Проверить выполнение условия <р = —¦ BП + Н). Если условие
выполняется, то система устойчива, в противном случае - неустойчива.
Замечания.
1. Критерий Найквиста-Михайлова представляет собой необходимое и
достаточное условие устойчивости замкнутой системы как по входу, так и по
начальным данным. В приведенной формулировке критерий применим, если
разомкнутая система строго физически реализуема, т.е. когда порядок числителя
передаточной функции Ж($) не больше порядка знаменателя. Если разомкнутая
система не является строго физически реализуемой, т.е. т > п, то замкнутая
система будет физически реализуемой и для ее устойчивости необходимо и
достаточно выполнения условия
А А1Е а + Ж(/со))=^(т-л + 2П + Я). C.44)
0^е><+оо 2
2. Рассмотрим особенности применения критерия Найквиста-Михайлова
для различных разомкнутых систем.
А. Если разомкнутая система устойчива (П = 0 и # = О, т.е. все корни
характеристического уравнения /)($) = 0 имеют отрицательные действительные
части), то для устойчивости замкнутой системы необходимо и достаточно, чтобы
годограф частотной характеристики И^/со) при изменении частоты со от 0 до
+ оо не охватывал критическую точку -1 + /О (рис. 3.41, а), т.е.
А А1Е A + Ж(ю>)) = 0.
0^в)<+оо
Б. Если передаточная функция Ж($) разомкнутой системы имеет полюсы,
лежащие на мнимой оси, то годограф частотной характеристики Ж(/со) будет
достигать бесконечно удаленной точки. В этом случае, как было указано выше,
следует разбить годограф на непрерывные участки, вычислить величину
приращения аргумента C.43) на каждом участке, а затем сложить найденные
величины (рис. 3.41,6).
179

<р = 0
ю = 1 + 0..
->+С0
Рис. 3.41
Пример 3.41. Исследовать устойчивость замкнутых систем (рис. 3.42) при
всех положительных значениях параметров К и Т.
8 ф
К
Тз + 1
-¦ х
¦Ф
К
Тз-1
->х
Рис. 3.42
П 1. Записываем для разомкнутых систем передаточные функции и
определяем количество полюсов, лежащих на мнимой оси и в правой полуплоскости:
/5 + 1
б)^E) = ~-г, Я = 0, П = 1.
/5-1
2. Строим годографы частотных характеристик (рис. 3.43).
Ф = 0
-1
1Я> = +°° К
(О, К<1,
' [п, К > 1
*>1 .*<1
И^ио)
© = ОЛ -1 ^-Л
Щш>)
К
<0 = +оо
180
Рис. 3.43

3, 4. Для системы "а" при любом положительном значении К годограф не
охватывает критическую точку -1 + /0, т.е. ф = 0. Поэтому равенство C.43) будет
выполняться и замкнутая система будет устойчивой при всех К > 0.
Для системы "б" возможны два случая. Если А^ е @; 1), то годограф
частотной характеристики не охватывает критической точки -1 + /0, т.е. <р = 0, и
равенство C.43) не выполняется: А Агв A + Ж(«о)) = 0 * л. Следовательно, сис-
тема неустойчива. Если А" > 1, то годограф будет охватывать точку -1 + /0 на
угол ф « я. Следовательно, система "б" устойчива при всех К е A;оо). ¦
Пример 3.42. Разомкнутая система имеет передаточную функцию
5 + 1
цгE) = — . Будет ли устойчива замкнутая система?
з2 +1
П 1. Данная передаточная функция имеет два чисто мнимых полюса
*1 = /, 52 = -/, т.е. Н = 2 и П = 0.
2. По годографу (рис. 3.44) частотной характеристики определяем величину
А Агв A + Ж(ло)) = ф! +ф2 =т+"Г = я-
о*о<+<» 4 4
3, 4. Сравнивая ее с величиной ф = — BП + Н) = п, убеждаемся, что
критерий Найквиста-Михайлова выполняется. Следовательно, замкнутая система
будет устойчивой. ¦
ф = ф| +Ф2 = Я
ш
0
2
1-0
1+0
2
+ 00
ИЧ«*>) = -—т
1-аГ
1 1
4 2.
+ оо + /оо
—оо —/оо
1 2.
"з-Г
-0-/0 |
о = 1 + 0
Рис. 3.44
Пример 3.43. Будет ли устойчивой замкнутая система, если разомкнутая
система имеет передаточную функцию IV (з) =
52+2
5-1
181

П Так как разомкнутая система не является строго физически
реализуемой, то по ее передаточной функции определяем значения параметров, входящих
в правую часть формулы C.44): /и = 2, л = 1, П«1, # = 0. По годографу (рис.
3.45) частотной характеристики определяем величину А Агз A + 1У(кв))=—.
О^ох-к» 2
Так как для найденных величин равенство C.44) выполняется, делаем вывод
о том, что замкнутая система будет устойчивой. ¦
3*
-2 -1
Щт)
©->+00
о
0
1
2
+ 00
1 + ю2
-2
11.
-21
0
2 4.
1 + /оо
Рис. 3.45
Замечание. Для астатических систем с порядком астатизма (см.
разд. 3.1.4), равным к, можно использовать эквивалентную
формулировку критерия Найквиста-Михайлова. Согласно определению передаточная
функция ЦГр(з) = —«-*¦ астатической системы имеет полюс в начале координат.
5*
Кратность полюса 5 = 0 равна порядку астатизма к, поскольку ЖоФ) * О •
Обозначим Н - количество отличных от нуля полюсов \Ур(8), расположенных на
мнимой оси, т.е. Н = Н-к. Применяя C.43), получаем
А Агё A + )Гр(^))=^BП + Я) = ^BП + » + Л)=^BП + ») + ^
0*©<оо '22 22
или
Ф = А А18A + ^(/а>))-^ = ^BП + »).
Чтобы вычислить величину угла <р, следует построить годограф частотной
характеристики 1Ур(иь) при изменении частоты от 0 до +оо, а затем дополнить
его дугой бесконечно большого радиуса, начинающейся на положительной части
действительной оси и проходящей по часовой стрелке (в отрицательном
направлении) к квадрантов. Угол <р вычисляется как угол, на который дополненный
годограф охватывает точку г = -1 + /0.
182

АЛГОРИТМ АНАЛИЗА УСТОЙЧИВОСТИ АСТАТИЧЕСКИХ СИСТЕМ
1. Построить годограф частотной характеристики 1Ур(кь) разомкнутой
системы при Ю€@,+ оо).
2. Дополнить годограф дугой бесконечно большого радиуса, начинающейся
на положительной части действительной оси и проходящей по часовой стрелке
к квадрантов (с центральным углом, равным -*-¦).
3. Подсчитать величину угла <р, на который дополненный годограф
охватывает точку г = -1 + /0.
4. Проверить выполнение условия <р =—BП + #). Если условие
выполняется, то замкнутая система устойчива, в противном случае — неустойчива.
Пример 3.44. Даны годографы частотной характеристики разомкнутой сие»
темы, заданной следующими параметрами:
а) П = 0,# * 19к = 1 (рис. 3.46,0),
б) П = 0,# а 1,* »1 (рис. 3.46,6),
в) П = 0,# = %к = 2 (рис. 3.47).
Требуется исследовать устойчивость замкнутой системы.
Рис. 3.46
Рис. 3.47
О Применим алгоритм анализа устойчивости для случаев "а" и "б".
1,2. На рис. 3.46,а и рис. 3.46,5 изображены годографы частотной
характеристики \Ур{ий) при порядке астатизма & = 1, дополненные дугой бесконечно
большого радиуса с центральным углом, равным -—.
3. Подсчитаем величину угла <р, на который эти годографы охватывают
точку г = -1 + /0. в первом случае (рис. 3.4б,а) ф = 0, а во втором случае (рис.
3.46,6) ф = -2и.
183

4. Так как П = 0,# = 1, к = 1,то # = 0 и ф = ~BП + #) = 0. Поэтому в
первом случае замкнутая система устойчива, а во втором — нет.
Рассмотрим случай "в".
1, 2. На рис. 3.47 изображен годограф частотной характеристики #р(ш>)
при порядке астатизма к = 2, дополненный дугой бесконечно большого радиуса
с центральным углом, равным - п.
3. Подсчитаем угол, на который дополненный годограф охватывает точку
* = -1 + /0: <р = 0.
4. Так как П = 0,# = 2,* = 2, то Я = Н-к = 0 и ^BП + #) = 0. Поэтому
замкнутая система устойчива.»
НАХОЖДЕНИЕ ЗАПАСОВ УСТОЙЧИВОСТИ
Из критерия Найквиста-Михайлова следует, что для устойчивости
замкнутой системы, устойчивой в разомкнутом состоянии, необходимо и достаточно,
чтобы годограф частотной характеристики разомкнутой системы при изменении
частоты со от 0 до +оо не охватывал критическую точку -1 + /0.
Запас I устойчивости замкнутой системы по модулю определяется
расстоянием от критической точки -1 + /0 до точки пересечения годографа ^(/со)
с действительной осью. Запас у устойчивости замкнутой системы по фазе
определяется аргументом точки пересечения годографа \Ур{ии) с окружностью
единичного радиуса (рис. 3.48,а). На практике, задавая / и у, можно выделить
запретную область, которую не должен пересекать годограф (рис. 3.48,6).
V
ФРЫ
+ 11
+ V
»^(*о)
Рис. 3.48
Используемый здесь критерий устойчивости можно переформулировать
следующим образом. Для устойчивости замкнутой системы, устойчивой в
разомкнутом состоянии, необходимо и достаточно, чтобы всем точкам годографа
частотной характеристики разомкнутой системы до его пересечения с
окружностью единичного радиуса соответствовали значения фазовой характеристики <р(со),
большие - п.
184

Точке пересечения годографа с окружностью единичного радиуса
соответствует точка пересечения логарифмической частотной характеристики До)
с осью частот (Л(ю) = 1, До) = 20\%А(а>) = 0). Поэтому для того, чтобы система,
устойчивая в разомкнутом состоянии, была устойчива и в замкнутом, необходимо и
достаточно, чтобы на тех частотах, для которых Дю)>0, значения фазовой
характеристики были больше -я. На рис. 3.49 изображены ЛАФЧХ устойчивой
разомкнутой системы, при которых замкнутая система будет устойчивой (рис.
3.49,а) или неустойчивой (рис. 3.49,6).
Запас устойчивости замкнутой системы управления можно определять и
по логарифмическим частотным характеристикам разомкнутой системы. Запас
устойчивости по амплитуде / и запас устойчивости по фазе у определяются по
формулам
/ = -1(©_х), у = * + ф(юсД
где ©-^ - частота, на которой выходной сигнал отстает по фазе от входного
сигнала на 180° (<р(ю_п) = -я), аш9- так называемая частота среза, при которой
амплитуды входного и выходного сигналов равны (Дсоср)=0). При хорошем
качестве процесса регулирования запас устойчивости по амплитуде /^10 дб,
а запас устойчивости по фазе у ^ 0,5 (у 2:30°).
Ь |
Д<о)
0
0
-71
к
"Ч
}ч>
ч>
\1
у 1"\:ь
^
@
к'
гю
«>-*
р(<о)
а> 0
Рис. 3.49
Замечание. Рассмотрим подробнее случай, когда годограф частотной
характеристики 1У(ко) несколько раз пересекает промежуток (-оо,-1)
действительной оси.
185

Переход годографа частотной характеристики Щио) при возрастании
частоты ю через промежуток (-оо,-1) действительной оси из верхней
полуплоскости в нижнюю называется положительным переходом, а из нижней
полуплоскости в верхнюю - отрицательным. Тогда критерий формулируется следующим
образом. Для того чтобы система, устойчивая в разомкнутом состоянии, была
устойчива и в замкнутом, необходимо и достаточно, чтобы число положительных
переходов совпадало с числом отрицательных (рис. 3.50,а).
Так как в точках перехода логарифмическая амплитудная характеристика
Ц<а) положительна (Л(<о)>1, Дю) = 201§/1(ш) >0) , а фазовая характеристика
ф(со) пересекает прямую <р = -я снизу вверх (при положительном переходе) или
сверху вниз (при отрицательном переходе), то критерий устойчивости
применительно к логарифмическим частотным характеристикам принимает следующую
форму. Для того чтобы система, устойчивая в разомкнутом состоянии, была
устойчива и в замкнутом, необходимо и достаточно, чтобы при тех значения
частоты (о, для которых Дсо)>0, разность между числом положительных и
отрицательных переходов фазовой характеристики <р(а>) через прямую <р = -я была равна
нулю (рис. 3.50,6).
Да>)>0
Рис. 3.50
Пример 3.45. Исследовать устойчивость замкнутой системы C.31,6) по
логарифмической амплитудно-фазовой частотной характеристике, если
передаточная функция разомкнутой системы
ио-
10
(Ю5 + 1)E + 1)@Д5 + 1)
? Разомкнутая система, очевидно, устойчива, так как все полюсы
передаточной функции 51 = -0Д; 82 --1,$з =-Ю находятся в левой полуплоскости
(см. разд. 3.1.5). Передаточная функция разомкнутой системы может быть пред-
186

ставлена как эквивалентная передаточная функция четырех звеньев, образующих
последовательное соединение: одного усилительного с коэффициентом усиления
^_до (Щ(з) = 10) и трех апериодических с постоянными времени
Г,=10;Г2=1;7'з=0Д (ЩE) = -±-, ЩЮ*-^, ^4<*) = од77Г>- Каадому
апериодическому звену соответствует своя частота среза: щ2 = ОД, со0з = 1»
©04 = 10. Используя результаты примеров 3.29, 3.30, построим логарифмическую
амплитудную Да>) и фазовую <р(а>) частотную характеристики
последовательного соединения, складывая характеристики /,/(©),срДш), / = 1,...,4, образующих
его звеньев соответственно (на рис. 3.51 они изображены пунктиром).
92(<о) %|фз(о)) | \Ф4(«)
Рис. 3.51
Поскольку на тех частотах, для которых Дю) > 0, значения фазовой
характеристики не превосходят - п, согласно сформулированному выше критерию
система, устойчивая в разомкнутом состоянии, будет устойчива и в замкнутом.
Запасы устойчивости /,у по амплитуде и фазе отмечены на рис. 3.51. ¦
187

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
3.1. Найти передаточную функцию системы, структурная схема которой
изображена на рис. 3.52, если звенья этой системы заданы следующим образом:
¦шаг
Рис. 3.52
а) звено 1 описывается дифференциальным уравнением
у+у+у=ё+е ;
звено 2 имеет импульсную переходную функцию #2(/,т) = е™~х';
звено 3 - интегрирующее;
б) звено 1 - апериодическое с постоянной времени Т = —;
п
звено 2 имеет импульсную переходную функцию к2(*,т) = л/(г - т);
звено 3 - усилительное с коэффициентом усиления, равным 3.
3.2. Найти передаточные функции систем, структурные схемы которых
изображены на рис. 2А9а-в.
3.3. По передаточным функциям звеньев найти передаточные функции
соединений, представленных на рис. 3.53,а-г.
-Ч иъ Кг1®-—\ щ I
\щ\—*&-
А ж4|—'
"** е
8
/ ¦
к^Т\ ш
¦¦"НИ/ ¦
/
>VI/ •
Й"
~^г\
{щ_
"| ^3
©-^
х 8
№
и®—.
\Г'
К
Рис. 3.53
188

3.4. Определить передаточную функцию корректирующего контура
1Укк(з), обеспечивающего получение системы (рис. 3.54,о,б), инвариантной
к возмущению %. Построить амплитудно-фазовую характеристику Ткк(ш>).
8—*©-
1
(Г,*+ 1X725 +1X7^ + 1)
г—{ У«г Н
5 + 1 1И + 1 ¦
I,
*->®
0,2^ + 1
Т 10,55 + 1
I—П^Г
5
Рис, 3.54
3.5. Найти передаточные функции по состоянию и выходу для систем,
заданных уравнениями
а) х{ = лх1+х2+$1, х2=х{+пх2, у = х{+х2;
б) Х1=-Х1+ЛХ2+^1, Х2=-ПХ1-Х2+82> У = Х\-*2>
в) хх ш2пхг +(т-2п)х2 + д, х2 = их! + (л-т)х2 + #2> ;У = *1+*2;
г)х!=х2, х2=х3, х3 = -лх3 + $, Д'1=х1+тх2, ;к2 = х2;
д) *! ={т + п)хх + ах2-лх3+#1, х2 -&С1 + лх2 - &с3 + 2#2,
х3 = тх!+ах2+3$3, ^ «X! +х2, у2 =хх -2х3, а =
т
100'
10
3.6. Найти реакции систем (рис. 3.55,а-*) на единичное ступенчатое
воздействие при нулевых начальных условиях.
3.7. Найти установившееся значение ху = Нт х@ реакции системы
(Рис. 3.56,а,ф на воздействие $(/) = -гу*кЩ-
189

'~~*ф\
5 + 11
-* х *
—*®—1
Ь + 1
гч
^
ч
1
3
<
1
5 + 1
Рис. 3.55
8 -
./
—К:
л
^
Ч
к
75 + 1
*.
1 1
•У 1
1 1
5 1
^
75 + 1
1
3 \
[П
б
Рис. 3.56
3.8. Найти свободное и вынужденное движения системы, описываемой
дифференциальным уравнением
а) 5с + 3х + 2х = л$, *о = 1, х<) = 0, $(/) = /и/(/);
б) 5с + (л+ 1)х + лх = /!$ + $, хо=л, Хо = /и, $@ = ';
в) х + л2х = $, Хо=л, *о=т, $(/) = 31п(л0;
г) Зс-(л + 3)х + B + Зл)х-2лх = /и#, Хо = 0, х0 =1, х<) = 2, #(/) = /и/.
3.9. Найти выходные сигналы систем, структурные схемы которых
изображены на рис. 2.4,0-*, если на все их входы поданы единичные ступенчатые
сигналы, а начальные состояния систем - нулевые.
190

ЗЛО. Определить установившуюся ошибку гу следящей системы (рис. 3.57)
ей1
при воздействии на нее полезного сигнала $@="Г-*@ и постоянного
возмущения М.
М
^ 5 + 1
1^1 г252
->х
Рис. 3.57
3.11. Построить амплитудно-фазовые частотные характеристики систем,
структурные схемы которых изображены на рис. 1.21, а-в.
3.12. Построить амплитудно-фазовые частотные характеристики систем,
структурные схемы которых изображены на рис. 3.55,д-* и 3.56,аД
5 + 1
3.13. На систему с передаточной функцией ]РК($) = — продолжи-
з* +5 + 6
тельное время действует сигнал #@ = /ияп(лО- Найти вынужденное движение
системы в установившемся режиме.
3.14. Определить спектральную плотность процесса с ковариационной
функцией 1^(п)=Л"|1Ы.
3.15. Дана система с единичной отрицательной обратной связью.
Разомкнутая система имеет передаточную функцию ЖЛя) =-т=—т\ • **а вход замкнутой
$Gз +1)
системы поступает белый шум с интенсивностью «V Найти дисперсию
выходного сигнала в стационарном режиме.
3.16. Используя критерий Михайлова, найти все положительные значения
коэффициента усиления к, при которых устойчивы системы, изображенные на
рис. 3.58,аД
—»ф->| к I—й
1
71$+ 1
1
Т2з + \
-+х Г,=±; 72=1
п тп
Т\ 1
г
к
1
Тх$ + \
1
Т25 + 1
1
Т3з + 1
б
Рис. 3.58
- х 7!=±; 72=-
п т
Г,=-
т + п
191

3.17. Используя критерий Найквиста, найти все положительные значения
коэффициента усиления к, при которых устойчивы системы, изображенные на
рис. 3.58,аД
3.18. Найти все положительные значения коэффициента усиления к, при
которых системы, изображенные на рис. 3.59,а-*, будут устойчивы.
8—>©
G1р + 1)(Г2р + 1)GзР + 1)
/I
7з =
1000
$~*ф
(Т^р + ЩТ.р + Х)
>х 7^, = ОД;
А: А: = 3*
Г-—* / -1-
1 0' л_1'
*,(Ч» + 1)
Р
_*2_
—
Р
к\к2
+ х т = 1;
#! &2 = т; Ты = —
Рис. 3.59
3.19. Для системы, описываемой дифференциальными уравнениями, на
вход которой поступает случайный сигаал G@ с известным математическим
ожиданием /и^(/) и ковариационной функцией /^(/ь/2)> найти законы
изменения математического ожидания щЦ) и ковариационной функции Ях(гь^2)
выходного сигнала:
Г0 0^
2<х
а) *,(/) = -*,<*) + ДГ2@, *2(*) = -Ы1+Ш, щ=(°),Е0 =
о о Ш
тхA) = 1, Дг(*„/2) = б(*, -*2), а =-!-;
/1 + 1
б) *(*) = -*(>) + <?(*), щ = 1, ^ = 0, т$A) = 2, Я^ьЬ) = е'^, - /2);
192

в) *(*)—2ДГA)+ <?(*), то=0, /% = 0, т^@ = 0, ^(/ь/2)-в(/1-'2)-
3.20. Исследовать устойчивость, управляемость и наблюдаемость
следующих многомерных систем:
а) *!=-*!+$, У = хх-х2, б) х1=х2+я, У = х{+х2,
х2=-х2+$; х2=хг+8;
в) х1=х2-&, у = -2х{+х2,
х2=5х{+2х3+8,
хг = -2х1-2хъ-8.
3.21. Исследовать устойчивость многомерных систем:
а) *!=2х1-д^ + *1, б) х{=-х1+ах2 + Ьхг+81,
х2=Зх{-2х3+82,
х2=-ах{-х2+ахг+82,
1
/! + Г
1_
т + 1'
Хз=5х1-4х2+^1+^2; *з=-^1-я*2-*з+*з;
в) хх =ах1+Ьх2+8г,
1
1
с = -
т + 1
*2 = -&*1+<*2+*2» а = —^-, 6=- _
л + 1 т + 1 /1 + 1
3.22. При помощи преобразования Лапласа найти свободное, вынужденное
движение и выходной сигнал системы, описываемой дифференциальным
уравнением:
а) х(/) + B-л)х@-2лх@ = *(/), х@) = л,х@) = 0, *(/) =
б) дс@ + 2л х(/) + (л2 +1) х@ = *(/), х@) = л, х@) = 0, *(') -
пе~4', />0,
0, /^0;
<Гл/81П/, Г>0,
0, / < 0.
3.23. При помощи преобразования Лапласа найти законы изменения
векторов состояния и выхода многомерной системы:
х{ =(л + 2)х!+х2+Я1, у = х{+2х2,
х2 = (-2л - 8) х{ - 4х2+$2,
с начальными условиями х^О) = 2, х2@) = 0 при входном сигнале
гл, />0,
й@ =
0, /^0,
*2@
Г 2, />0,
[0, /<0.
193

Глава 4. ОПИСАНИЕ И АНАЛИЗ НЕПРЕРЫВНЫХ
ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ СПЕКТРАЛЬНЫХ
ПРЕОБРАЗОВАНИЙ
4.1. ОДНОМЕРНЫЕ СИСТЕМЫ ПРИ ДЕТЕРМИНИРОВАННЫХ
ВОЗДЕЙСТВИЯХ
4.1.1. Описание сигналов и систем
Представление процессов радами является довольно универсальной
формой их описания. Эту форму можно рассматривать как промежуточную между
описанием процессов во временной области и интегральными
преобразованиями. К первому способу эта форма тяготеет в тех случаях, когда оперируют
собственно рядом как функцией времени; ко второму - когда коэффициенты рада
отрывают от ряда и во всех вычислительных операциях используют лишь
совокупность этих коэффициентов. Последний подход привел к формированию
спектральной формы описания процессов [51—53]. В этой форме временные
процессы рассматриваются на конечных, в общем случае нестационарных, интервалах
времени. Спектральный метод расчета систем управления, являясь
аналитическим, в то же время хорошо приспособлен к применению цифровых
вычислительных машин, так как решение задач сводится к алгебраическим
операциям с матрицами. Практическое использование спектрального метода
обеспечено развитой библиотекой стандартных программ.
Для описания сигналов используются базисные системы функций.
Базисная система в общем случае комплексных функций
{/?(/,/,е),/ = 0,1,...}, определенная на отрезке [0,/], называется ортонормирован-
ной, если все функции этой системы удовлетворяют условию
/рЧ/,',6)р(М6)Л = {*' 1=]: D.1)
где в - текущее время, 0^6^/; р*(/,/,в) - комплексная сопряженная
функция; / — правый конец отрезка времени, на котором решается задача анализа.
Широкое применение нашли следующие базисные системы функций:
нестационарные полиномы Лежандра:
кШ) = 1Щ±%1ис2г> / = 0Д,... , D.2)
где/л=(-1)^С/+лС/-*;
*0,,,в)=-^, р(и,в) = 1[Г^-1), Ъю-Щ*-^.
Р&*.*)-Щ20^-30^ + 12^-11 и т. д.;
194

нестационарные косинусоиды:
С(/,г,е) =
-рг, I ш О,
/-сое—в, / = 1,2,...,
D.3)
с(о,/,в)=-^, с(ив)=Лсоз^, са*9е)={1*л&9
СC,/,в) = Лсо8^ и т. д.;
а также функции Уолша и другие [51-53].
1. Описание сигналов. Нестационарной спектральной
(НСХ) функции #F) по заданному ортонормированному базису
Ы'»'»в)»'; = 0Д,..} называется функция
<?(/,') = ^@I = Ь*(/,',в)*(в)<*), / = <Ц,2,....
/> ' о
D.4)
Она представляется бесконечной матрицей-столбцом
0(*) =
р
0@,*)
GA,0
вB,*)
а при численных расчетах - конечной матрицей-столбцом.
Индекс базисной системы пишется под знаком спектральной
характеристики, указывая, относительно какой базисной функции она определена.
Для перехода от спектральных характеристик к функциям времени,
используется формула обращения:
*(в) = з-1[С«)] = 2 <?(/,') Р(*,',е), о * в * и D.5)
2. Описание систем. Рассматривается поведение нестационарной линейной
системы, описываемой дифференциальным уравнением
«л(в)х<л>(в) + ... + ао(в)х(в) = Ада@)^>@) + ... + А)(в)^(в),
D.6)
ВДе ВФ) — входной сигнал; х(в) — выходной сигнал; пит — порядки старших
производных выходного и входного сигналов; алF),...,а0F); 0тФ)^-ОоФ) -
коэффициенты, зависящие от времени 6. Система исследуется на отрезке времени
[О,/], правый конец / которого может быть подвижен или задан.
195

Двумерной нестационарной передаточной функцией У С, О (ДНПФ)
рр*
линейной системы D.6) называется двумерная нестационарная спеюральная
характеристика импульсной переходной функции
1ГШМ-1Я Гр*(Л,Г,в)р(/,/,т)А:(в,т)Л, /г,/ = 0ДД.., D.7)
»* о о
где {/К'»'» 6),/ = 0,1,...} - базисная система.
ДНПФ представляется бесконечной матрицей
рК@,0,/,0 Щ0Х*Л Щ0А*Л А
»кAА/,о щш,*) »гад/,о ...
|0Ч2,<Ш) Щ2Х*Л Щ2,2,*,*) ...
где /г — номер строки, / — номер столбца. Если длина / интервала времени
фиксирована, матрица ДНПФ является числовой. При численных расчетах ДНПФ
представляется в виде конечных квадратных матриц.
Замечания.
1. В определении D.7) можно учесть условие физической реализуемости
B.3):
ЩН,и<) = /Л $ /(Л,/,в)р(/,/,т)А:(в,т)Л.
РР 0 0
2. Элементы матриц ДНПФ физически реальных систем обладают
свойством: их модули стремятся к нулю при росте дискретных аргументов Ли/.
ДНПФ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
1. Усилительное звено. Поскольку импульсная переходная функция
усилительного звена имеет вид к(9,х) = а@M(в), где а(в)- коэффициент усиления (см.
пример 2.6), то
А(к,Ш)= Г/(М,6)р(/,/,6)а(е)<Й.
рр о
Если дF) =* а = соп$1, то двумерная нестационарная передаточная функция
усилительного звена представляется в форме
4(/,/) = аЯ
рр
в силу ортонормированности базисной системы функций.
196

2. Интегрирующее звено. Импульсная переходная функция интегрирующего
звена имеет вид &F,т) = 1F-т) (см. пример 2.6). При применении полиномов
Лежандра по формуле D.7) получаем соответствующую двумерную
нестационарную передаточную функцию интегрирующего звена:
Гл1(''') = '
рр
' 1
2
1
21/з
0
0
сл,0
^ ...
1
2Л
0
1
21/15
0
спЛ
0
1
21/15
0
1
21/35
спЛ
0
0
1_
21/35
0
сп%г •
\
.. с0>„ ...
.. с1?л ...
.. с2,л ...
• *3,л -
• <Чл ...
)
где ся>й_! = -сл_1л =
2^4^Т
» сл,л-* -.С*-М = °> * = 0,2,3,..., л.
При использовании нестационарных косинусоид имеем:
Р-\*,1) = <
се
Г I
2
21/2
я2
0
21/2
9я2
сл,0
21/2
я2
0
4
Зя2
0
слд
0
4
Зя2
0
4
5я2
Сп,2
241
9я2 *
0
4
5я2 '
0
сл,3 .
\
.. С0>л ...
•• с1,л •••;
.. с2,л ...
•• сз,л ...
•- <Чл -
где
_ П + (-1У"']У2.
с0,л ~ с0,л ~ 2 2 ' л»л ~ '
_ - 2[1 + (-1)*»'1 4 12 _ ,
197

3. Дифференцирующее звено. Импульсная переходная функция
дифференцирующего звена имеет вид &F,т) =—^-—— (см. пример 2.6). При применении
ев
полиномов Лежандра по формуле D.7) имеем
Л«><>=7
РР
1 4ъ 4ъ 4п
-Л з VI? Ш
4ь -4ъ 5 1/35
-«/7 Ш -435 7
сл,0 спЛ сп,2 сл,3
сп%п
где се^к = V Bл +1) Bл - 2к +1), сл_м = (-1)* V Bл - 2к +1) Bл +1) .
При применении нестационарных косинусоид получаем
где
се X
VI 2 -^ 2
Г2 * 2 -|
л 2 т 2
ся,0 сл,1 си,2 ся,3
Со,я=(-1)л1/2; е^-Л; сял=2,
сп,п-к = ~сп-к%п ~
2[(-1)*(л-*J-л2]
(л-*J-л2
с0,л
С2,л
С3,л
* = 1,2,...,л-1.
СВОЙСТВА СПЕКТРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ
1. Линейность. Если сигнал хF) представляется в виде линейной комби-
п
нации хF) = ^а^^Ъ), где ау- постоянные коэффициенты, то
^(в)]=Хау^[х;(в)].
198

2. Дифференцирование оригинала:
</х(е)
= Р (',')*('),
рр
где Р(',0— двумерная нестационарная передаточная функция дифференцирую-
Р (Л, /, /, 0 = Я 5<в-т) , Л, / = 0,1,...; ДГ@ - нестационарная
яр* дрЧ о9 ] />
яр
щего звена:
спектральная характеристика сигнала х(9).
3. Интегрирование оригинала:
/х(т)Л
>-1/
др *
/ в
где Р ~1 (Л, /, /, 0 = «У [ 7F - т) ] = Г Л9 Г р* (Л, /, в) />(/, /, в) Л - двумерная нестацио-
ЛР* » 0 0
нарная передаточная функция интегрирующего звена; Х(*) — нестационарная
р
спектральная характеристика сигнала хF).
4. Умножение функций времени. Если сигнал х(9) представляется в виде
произведения двух функций: дс(9) = Х!(в)х2(в), то
ще
аде)] = *(М = ^ ад/,/,/)лг2(/,о,
Р Р I рр* р
Х{(к,Ш) = ^[х1(вM(9-т)]= Г/(Л,/,9)р(/,/,е)х1F)Л.
ЯР
ЯР
НАХОЖДЕНИЕ ДВУМЕРНОЙ НЕСТАЦИОНАРНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
ПО ДИФФЕРЕНЦИАЛЬНОМУ УРАВНЕНИЮ
Установим связь ДНПФ с дифференциальным уравнением D.6),
описывающим систему. Согласно определению импульсная переходная функция
удовлетворяют уравнению
*л(в)^|^
Применим к левой и правой частям спектральное преобразование с учетом
свойств 5-функции:
Д99

а«(е>тт/^/>т)/:(е'т)А+-+ао(еI^/>т)/:(е'т)Л=
«в о о
т г
=^(в>^1^^т>6(е-т>л+--+^(е)^(/'/'тN(е-т)Л=
«в 0 о
Введем обозначение #(/,/,6) = Г/?(/,/,т)&(е,т)Л - нестационарная сопряжен-
р о
моя передаточная функция.
Тогда последнее уравнение перепишется в форме
1«ие)^я(и,в)=|;^(в)^г^.
Применим спектральное преобразование к левой и правой частям с учетом
свойств линейности и умножения функций:
<** Я(/,/,в)
в*(в)-
<1&*
рр* р
<1&К р
, к = \,...,п;
ькт
<1крA,1,в)
ВкA,1M
рр' Р
I*
, # = 0,1,..,/я,
где Л* (/,/), ДЛ (/, 0 ~ двумерные нестащюнарные передаточные функции неста-
рр* рр*
ционарных усилительных звеньев.
Согласно свойству дифференцирования оригинала
4-^ #(/,/,6I = Р\A.Ъ$НA919В)],
р\ёЪК р \ рр* р1р ^
р\ав*
-р*(/,04р('.'.в)].
Заметим, что согласно определениям D.1),D.7)
4я(/,г,вI- г г/(*,/,вIких)*(^т)ЛА - »;(*, ио,
Ф0", ', е)] = Г р (А, г, е) />(/, *, в) <й = \
р о [0, А*/.
200

В результате получаем
2 Ак«ЛРк{и)ЦГ(!Л= X ВкЫ)Р\«Л
к=0рр* РР" РР* к=0РР* Рр
или
1-1 г
Ап«,*)Рп(*9*) + ... + Ао(*,*)
.рр* рр рр*
Вт(*,0Ру,*) + ... + В0Aу1)
рр* рр рр*
РР*
Используя свойство (А • В)~х = В'1 • А~1, преобразуем выражение
1-1
Ап(*,*)Ру,*) + ... + Ао(<><)
РР
* ДО
1рр* рр* рр
\-1
рр*
Окончательно получаем
рр* рр*
Ап(*,*) + ... + А0(*,*)Р-Ч*,*)
рр* рр* рр
вт(и)ру,*)+... + в0(*,*)
1 1рр* рр рр*
D.8)
4.1.2. Связь вход-выход
Найдем связь вход-выход, устанавливаемую двумерной нестационарной
передаточной функцией при нулевых начальных условиях. Воспользуемся
формулой B.6) с учетом D.5) и условия физической реализуемости (&F,т) = 0 при
9<т):
*(в) = I *(в,т)*(т)Л =| ЩтJ<г(/,0/К/,/,т)Л.
о о /
Применим спектральное преобразование и формулу D.7):
/
о
«)] = Г/(Л,/,в)х(в)Л = Х(к,о = X [[/(М,е)/>(/,/,т)Щт)ла(?(/,/) =
р л р I а р
' 00
В итоге получаем
I рр* р
р рр* р
D.9)
201

4.1.3. Двумерные нестационарные нередаточные функции соединений
Если система представляет собой соединение звеньев, то для нахождения
ДНПФ системы применяются следующие соотношения:
для последовательного соединения (см. рис. 4.1, а):
рр* рр* Рр*
для параллельного соединения (рис. 4.1, б):
рр рр* рр*
для соединения с обратной связью (рис. 4.1, в):
D.10)
DЛ1)
иу.0 = и^С'ИЯ ± Ж2(/,0 И^ОГ = [Л ± ^(/,0 ж2(/,0Г ^(',0, D.12)
рр рР* рР* рр* рР* рР* рР*
где знак «плюс» — для отрицательной, а знак «минус» — для положительной
обратной связи; ^(/.ОэИЪ&О "" двумерные нестационарные передаточные функ-
* *
рр рр
ции первого и второго звеньев соответственно.
*1@
р
G@
р
рр*
*1<0
р
РР*
Х@
р
рр'
"Ч *
*@
—>
Х2Ю
р
G@
р
^
3
ДО
Х,A)
*
*
рр
Рис. 4.1
Х@
р
>
202

Действительно, для последовательного соединения с учетом связи
имеем
р рр* р
ДО = ^20,0*10).
Исключая Х{ (/), получаем формулу D.10):
ДО = ^20,0*10,О<?0).
' рр* рр* .р
РР*
Заметим, что матрицы в формуле D.10) могут быть не перестановочны.
Для параллельного соединения справедливо:
^1@ = ^10,0^@,
р рр* р
^@ = ^20,0^@,
р рр* р
*0) = *10) + *20).
Р р р
Отсюда следует формула D.11):
^@ = 1^10,0 + ^20,0
Р рр* рр*
<70,О-
р
щи)
рр*
Для соединения с обратной связью имеем
р рР* р
р р р
^2@ = ^20,0^@.
р рр* р
Тогда
до - щам ^0,0^^20,0^@
р рр* \^р рр* р
\Е±ЩA,()Щ(*,{)
=сдоем? щыти,*) х(о,
рр> р рр* рр* р
Р »»• Р

Отсюда следует вторая из формул D.12):
1-1
р V рр* рр* ] рр* *
Получим эквивалентную формулу. Для этого умножим уравнение
Х{*)~Щ{и*)Е{1) слева на И^ (/,/):
р рр* р рр*
ЩЫ)ХЦ) = Щ(*,*)Щ(*,*)Е(*),
рр* р рр* рр* р
р р рр* р
Отсюда
р р рр* рр* р
и, следовательно, имеем
Поэтому
р V рр* рр* ]р
ЕЮ = \е±ПГ2{*.01Г1(*9<А G@
р I рр* рр* ] р
Х(Ъ=Щ(ЩЕ±Щ{и)Щ{Ш вЦ).
р рр* V рр* рр* \ р
Отсюда следует первая из формул D.12).
4.1.4. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть известны:
а) входной сигнал $F);
б) система, заданная в одной из возможных форм математического
описания (см. гл. 1-3);
в) нулевые начальные условия.
Требуется найти выходной сигнал хF).
204

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
Перед решением задачи анализа задается длина / отрезка [0,/] и система
базисных функций (здесь предлагается использовать либо систему полиномов
Лежандра, либо систему нестационарных косинусоид).
1. Найти спектральную характеристику С(*) входного сигнала $F).
р
2. Определить ДНПФ №(*,*) системы одним из двух способов: по диффе-
рр*
ренциальному уравнению или по структурной схеме.
Первый способ. Если задано дифференциальное уравнение D.6), то ДНПФ
определяется по формуле D.8):
и<4/,/) = р-уАлп{^)+..лМ^)р-чЩ |в^Орул+.-.+ ыи) 1,
РР* РР* [рр* рр* РР* ] 1рр* РР* рр* \
ще ЛД/,0, В *(*,*) - ДНПФ усилительных звеньев аДб),*, (в); Р (/,/), Р~1(и О
рр* рР* рр* рр*
- ДНПФ дифференцирующего и интегрирующего звеньев.
Если система стационарная, т.е. а1 (в) = а1 = сопз*, АД6) = Ь^ в сопз1,
имеем 4 (/,/) = а{Е9 2*у(/,0 = Ъ^Е, где Е - единичная матрица.
рр* рр*
Второй способ. Нахождение ДНПФ по структурной схеме.
Если система состоит из звеньев и их соединений, то для нахождения
ДНПФ системы применяются соотношенияD.10)—D.12). ДНПФ элементарных
звеньев берутся из таблиц [51]-[53].
3. Вычислить спектральную характеристику выходного сигнала по формуле
D.9):
ХЦ)=1УШH«).
р рр* р
4. Определить выходной сигнал по формуле обращения D.5):
х(в) = $-1[Х@] = 2 *(/,') Р(Ш), 0 й в <; и
р р у Р
Замечание.
1. При практических расчетах используются базисные системы с конечным
числом функций, т.е. 1р(/,*,в),/ = 0Д,...,ЛГ}. Тогда бесконечные матрицы
заменяются конечными соответствующих размеров. Число N называется масштабом
усечения.
2. Решение одной и той же задачи с применением разных базисных систем
или одной базисной системы с разным масштабом усечения является одним из
эффективных способов контроля достоверности и точности результата.
Пример 4.1. Определить реакцию интегрирующего звена A.9) на единичное
ступенчатое входное воздействие #F) = 1F) при нулевых начальных условиях.
П Решим задачу двумя способами с применением различных систем
базисных функций.
205

Первый способ. Выберем / = 1 и систему нестационарных полиномов
Лежандра D.2).
1.. Найдем спектральную характеристику входного сигнала:
'о о /7
?аО-][1-Аив)Л-][1.Д(^-1)Л = 0,...,
«0 =
р
о
О
ч:/
2. Используем ДНПФ интегрирующего звена, определенную относительно
полиномов Лежандра:
рр рр
< I
2
1
2Л
0
1_
2у/з
0
1
2^5
\_
2Л5
О
3. Найдем спектральную характеристику выходного сигнала при / = 1:
' 1 —1- ч
2 2Л
р
1
2^15
1
2^5
т
0
0
^:>
—
2
1
2Л
0
1
4. Определим выходной сигнал по формуле обращения:
т = Е*(/,')р(/,',е) = ± • 1+Д- Л Bв -1) = е.
/ Р * 2*3
Второй способ. Выберем / = 1 и систему нестационарных косинусоид D.3).
1. Найдем спектральную характеристику входного сигнала:
' ' 1 I-
<?(<>,/)= |ьс(о,/,е)<й= |1--4гвв»// = 1»
с о о V'
206

0A,() = } 1-СA,(,9)*= ) 1 Лсо8^Л = /|^п7
= 0,...,
0@ =
С
'о
о
о
2. Используем ДНПФ интегрирующего звена, определенную относительно
нестационарных косинусоид:
1 2Л Л
^(/,0 = ^-4^0 = ^
ее ос
2 я2
2Л
я
0
3712
Зя2
3. Найдем спектральную характеристику выходного сигнала при I = 1:
1 2Л Л
*(') =
2
2Л
' я2
0
я*
0
~3я2
Зя2
2Л
' я2
0
4. Определим выходной сигнал по формуле обращения:
х(е) = ^лх/,0С(/,/,е) = ^.1+и
Пример 4.2. Определить реакцию интегрирующего звена на линейное
входное воздействие #F) = в • 1F) при нулевых начальных условиях.
О Выберем / = 1 и систему нестационарных полиномов Лежандра.
1, 2. Воспользуемся результатом примера 4.1:
' 1 ^
р
2Л
0
рр рр
207

3. Найдем спектральную характеристику выходного сигнала:
*(') =
р
2
1
2у1ъ
О
1_
2Л
О
1
2^15
1
2^5
О
\
V
( 1 )
2
1
' 2Л
0
ч : )
( П
й\
12
Л
60
1о;
4. Определим выходной сигнал по формуле обращения:
х(в) = 1.1 + ^ЛBв-1) + ^ЛFв2-бе + 1) = ^-.И
Пример 4.3. Определить реакцию стационарного усилительного звена A.7)
с коэффициентом усиления К на линейное воздействие #(9) = в • 1F) при
нулевых начальных условиях.
?1.Найдем спектральную характеристику входного сигнала (см.пример 4.2):
' 1 ^
«о-
р
2Л
0
2. ДНПФ усилительного звена: Ж(/, /) = КЕ.
рр
3. Найдем спектральную характеристику выходного сигнала:
( К\
р р
2
К
2Л
0
4. Определим выходной сигнал по формуле обращения:
хF) = —+ -4= ЛB9-1) = КвМ
2 2Л
Пример 4.4. Определить реакцию системы, изображенной на рис. 1.12,
на единичное ступенчатое входное воздействие #F) = 1F) при нулевых
начальных условиях.
П Найдем приближенное решение задачи двумя способами с
применением различных систем базисных функций, задав масштаб усечения N = 1.
208

Первый способ. Выберем 1 = 1 и систему нестационарных полиномов
Лежандра.
1. Пользуясь результатом примера 4.1, имеем
1
р \})
2. Воспользуемся формулой для соединения с обратной связью:
рр рр рр
где матрица двумерной нестационарной передаточной функции имеет размер
Bx2):
рр
' 1
2
1
,2Л
Ц
2 Л
0
)
( -
2
1
Ьл
=
1 л
2Л
1
)
г 7
19
6
,19Л
-1
г 1
2
1
,2Л
6_^
19Л
1
19 )
•
-—1
2 Л
0
)
( 12 6 >
19 19Л
6 18
1 19Л 19 ,
р
19
6
иэЛ;
3. Найдем спектральную характеристику выходного сигнала:
' 1_ 6_^ ( 1 ^
19 19Л Н
и*/з 19 ;
4. Найдем выходной сигнал по формуле обращения:
х@) = — .1 + -^=гЛBе-1) = ~ + — в.
19 19Л 19 19
Графики приближенного и точного решения хточн(&) = 1 -е~в изображены
на рис. 4.2.
+ е
Рис. 4.2
209

Второй способ. Выберем / = 1 и систему нестационарных косинусоид.
1. Пользуясь результатом примера 4.1, найдем спектральную
характеристику входного сигнала С(?)
2. Чтобы найти ДНПФ, воспользуемся формулой для соединения с
обратной связью: Иг(/1/) = Р~!(/,/)[2? + р-1(/,/)]~|, где матрица двумерной нестацио-
се се ее
нарной передаточной функции интегрирующего звена имеет размер Bx2):
ее
I 2Л1
2 -2
„2
Л
О
2
2 я
ъП
„2
2ЛУ1
2
2*2
2*2
Г*2+16 4Л1
.2
Зя2+16
2*2
2Л
„2
_8_
4 о
8Л
Зя2 + 16
Г *2+16
3*2+16 Зя2+1б
4Л 16
1 2Л1
2Л 3
п2 2 )
I Зя2+16 Зя2 + 1б;
3. Найдем спектральную характеристику выходного сигнала:
*<0 =
с
( п2 +16 8Л
Зя2+1б Зя2+16
4Л 16
I Зя2+1б Зя2+1б;
( я2+16 1
3*2+1б
4Л
I Зя2 + ^
4. Найдем выходной сигнал по формуле обращения:
хF)= * +1б.1+ ~4^ Лсо8яег0,567-0,175со8яе.
3*2+1б 3*2+16
Графики приближенного и точного решений изображены на рис. 4.3.
Точность расчета может быть существенно повышена при увеличении размерности
матриц. ¦
*@)
Рис. 4.3
210

4.2. ОДНОМЕРНЫЕ СИСТЕМЫ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
4.2.1. Описание сигналов и систем
1. Описание сигналов. Для описания случайных процессов используются
спектральные характеристики их моментных функций.
Первой нестационарной спектральной плотностью случайного процесса
называется нестационарная спектральная характеристика его математического
ожидания (см. формулу A.62)):
1Зя(М-1рт0Л*)тж(в)А9 / = 0Д,2,.... D.13)
р о
Второй нестационарной спектральной плотностью случайного процесса
<7@) называется двумерная нестационарная спектральная характеристика его
ковариационной (корреляционной) функции (см. формулу A.63)):
^(Л,/^,0=/^1/р*(Л,/,в1)р(/,/,е2)^(в1,е2)Л2, м-ода.... <4Л4>
рр* о о
Первая нестационарная спектральная плотность представляется
бесконечной матрицей-столбцом, вторая - бесконечной матрицей.
Математическое ожидание и ковариационная функция определяются по
спектральным плотностям с помощью формул обращения:
Vе) - Е ^СО/К/Лв), 0 * в * 1;
' р
^(вьв2) = ЕЕ^(^|^'/)^^^в1)^*(/»^в2)> 0*6!*/, 0<;е2*Л D.15)
н / „•
Вторая нестационарная спектральная плотность стационарного белого
шума с учетом D.15) и формулы A.68) его ковариационной функции имеет вид
8жМ = 8ъЕ, D.16)
рр*
где «У0 — интенсивность шума; Е - единичная матрица.
2. Описание систем. Для описания линейных нестационарных систем
управления, как правило, используется ДНПФ (см. разд. 4.1.1), определенная
относительно некоторой базисной системы функций.
4.2.2. Связи вход-выход
Установим связи между спектральными характеристиками моментных
функций входного и выходного сигналов системы, описываемой
дифференциальным уравнением
211

ал(в)^я>(в) + ... + ао(в)ДГ(в) = ^(в)G^>(в) + ... + ^(в)G(в).
Воспользуемся связью вход-выход D.9):
*<О-»Г<МH<О
р рр* р
и найдем математическое ожидание правой и левой частей.
Учтем, что
\
/р*(Л,/,в)х(в)Л
- |р*(А,/,е)А/[х(в)]<*)= |р*(Л,/,в)тхF)Л= ^х(/,/).
о о *
р
Аналогичные преобразования выполним с правой частью. Поэтому имеет
место соотношение
р / рр* р
или
^хМ-И^МI*,». DЛ7)
р *>* Р
Далее представим входной и выходной сигналы в форме
^(в) = т^(в) + ^(в), х(в) = тх(в) + хС1(в).
Применим спектральное преобразование к левой и правой частям,
используя свойство линейности:
0@ = ^(О + ВД), ЛГ<0« ^хЮ + ^М-
' р р р р р
Поэтому
П 1М1* П ЯЯ* в
ЯР
= и;(*,о<7«0).
или
Аналогично имеем
212

Перемножим два последних равенства, учитывая, что
р*р рр*
/> / V Ц РР* РР Р Р-
Находя математическое ожидание с учетом D.14), получаем:
ЗсЛио=Ц ж(л, у,/,о^;(/,ц,/,о^^,ц,/,о
РР* V Ц ЛР* »* „•
ИЛИ
рр* *• ,/• РР*
где >Г+(/,/) = ЙР*(/,0 — матрица, эрмитово сопряженная с 7Р (/,/)• Если
др* 1_др* ] яр*
в качестве базисных систем используются действительные функции, то эрмитово
сопряженная матрица совпадает с транспонированной.
4.2.3. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть известны:
а) математическое ожидание т^F) и ковариационная функция ^F1,е2)
входного сигнала С?(в);
б) линейная нестационарная система, заданная в одной из известных форм
математического описания;
в) нулевые начальные условия.
Требуется найти математическое ожидание /к*F), ковариационную
функцию Дк(б1,62) и дисперсию #хF) выходного сигнала ЛГ(в).
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
Перед решением выбирается длина отрезка [0,/] и система базисных
функций.
1. Найти первую спектральную плотность входного сигнала ^(О-
р,
I
1$жA.Ъ-1р*AЛВ)тж(В)Л9 / = 0,1,2,....
р о
2. Найти вторую спектральную плотность входного сигнала 5^(/,/):
рр*
I I
%№.*.*) = \<&х /р*(Л,/,в1)р(/,/,в2)^(в1,в2)^92, /*,/ = 0,1,2,....
рр* о о
213

3. Определить двумерную нестационарную передаточную функцию Ж(*,0
рр*
системы (см. разд. 4.1.1 и 4.1.3).
4. Найти первую и вторую спектральные плотности выходного сигнала:
р рр* Р
^0 = ^(М)^(',0^+(','),
рр* рр рр* рр
где И'+(/,0 = IV* (/,*) - матрица, эрмитово сопряженная с IV(/,/).
рр* 1рр* ^ рр'
5. Найти математическое ожидание /ИхF) и ковариационную функцию
/2ХF1N2) выходного сигнала Х(&) по формулам обращения:
«х») = Е ^Л №> '• е>> ° ^ е *';
Лх(в1^2) = Х2^(Л>/^^)^Л>^в1)^*(/^>в2)> °*01 *'> 0^в2^/.
Л 1 Др*
Положив 9 = в! = в2, найти дисперсию Вх(в) = 1^F,6).
Пример 4.5. На вход системы, описываемой уравнением
*(в) = <7(в), *@) = 0,
поступает белый шум с математическим ожиданием т^(в) = 0 и ковариационной
функцией 1^(б1,е2) = 5F} - 62).
Требуется найти математическое ожидание, ковариационную функцию и
дисперсию выходного сигнала.
П Найдем приближенное решение задачи двумя способами, применяя
различные системы базисных функций с масштабом усечения N = 1.
Первый способ. Выберем / = 1 и базисную систему нестационарных
полиномов Лежандра D.2).
1. Так как /и^F) = 0, то по формуле D.13) имеем ^@ = 0.
р
2. Согласно D.16) 5^(/,/) = Е, так как ^0 = 1 •
рр
3. Поскольку N = 1, производим усечение матриц до размера B х 2) (см.
пример 4.2):
214

рр
( I
2
ил
1 ^
2 Л
О
4. По формуле D.17) с учетом п.1 получаем ^(О = 0, а по формуле D.18)
р
¦с з-
Г 1
2
1
ил
1 ^
2 Л
О
2 2Л
' 1 _Ц|
3 4Л
1 _1_
ил 12 ^
5. По формулам обращения при / = 1: /^(в) г О
1
4Л
Лх(в1,в2) = | + ^ЛBв1 -1) + ^=гЛBе2 -1) + ^3Bв1 -1)Bв2 -1) =
"Е + 0А;
2)х(е) = /Мб,е) = ^+б2
Второй способ. Выберем / = 1 и базисную систему нестационарных
косинусоид D.3).
1. Так как /и^(в) ¦ 0, то по формуле D.13) имеем !^@ = 0.
с
2. Согласно D.16) *У^(/,0 = Е, так как ^0 в 1-
ее
3. Поскольку N = 1, производим усечение матриц до размера Bx2):
се
1
2ЛЛ
V Я
2 71
2Л
,2
(см. пример 4.2).
4. По формуле D.17) с учетом п.1 получаем Х8ХA) = 0, а по формуле D.18):
с
1 2Л)
¦Г1 °1-1 2
I П 1 I I О -/о
¦**(',') =
ОС
2 я
2Л ,
\ я*
1_
2Л
,2
2^
2
V я
Гя4+32 _ Л1
_2
4я
Л 8
я4 )
215

5. По формулам обращения при г = 1: /ИхF) = 0,
Лх(еье2) = ^—1- —72СО8Я0! Л С08яв2+ —С08 710^087192 =
4я л2 л2 я
32 + я* 2 2 8
= г Г-СО87101 Г-СО8 7Г02 +—Т-СО8 7Г0! С08я62,
4я 71 Я Я
/>х(в) = Лг(в,в) = ^^ ^С08яе + 4-С082яв.И
4я я я
Пример 4.6. На вход системы, изображенной на рис. 1.12, поступает
стационарный сигнал с математическим ожиданием т8(в) = \ и ковариационной
функцией /^Fье2) = 5(в! -62). Начальные условия нулевые.
Требуется найти математическое ожидание, ковариационную функцию и
дисперсию выходного сигнала.
О Выберем / = 1 и базисную систему нестационарных полиномов Лежан-
дра D.2), полагая N -1.
1. По формуле D.13) с учетом D.3) получим
у-0-
2. Согласно D.16) »5^(/, /) = Е, так как *У0 = 1.
№
3. Поскольку N = 1, производим усечение матриц до размера B ж 2) и,
воспользовавшись результатом примера 4.4, имеем
рр
< 7
19
6
а9Л
6 ч
19Л
1
19 )
4. Находим первую и вторую спектральные плотности выходного сигнала:
Г 7_ 6_ч ( ]_ \
1с (ЛА 19 19Л A)_\ 19
ЫЛ 19 ; ЬэЛ)
7_
19
119Л
6 Ч
19Л
_1_
19
С 3-
G 6 ]
19 19Л
6 1
1 19Л 19 )
1
361
1Л )
216

5. По формулам обращения получаем математическое ожидание,
ковариационную функцию и дисперсию выходного сигнала:
м'(9L1+1^!ЛBе-1L+§е'
Лж(в1,в2) = ^-[ 61 + 36B6! -1) + 36B92 -1) +13 • 3B9, - 1)Bв2 -1I =
зы
= т^гA56е^г - 6 в! - 6 в2 + 28),
361
Лх(е) = ЛхF,6) = ^A5бв2 -126 + 28).
При увеличении размеров матриц точность расчетов существенно
улучшается."
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
4.1. Найти двумерную нестационарную передаточную функцию системы,
если известна ее импульсная переходная функция:
а) *(е,т) = (л + 1M(в-т);
б)*F,т) = (/1 + 1IF-т);
в)*(е,т) = ^(/1 + 1IF-т).
6
В качестве базисной системы функций использовать нестационарные полиномы
Лежандра. Масштаб усечения спектральных характеристик взять равным 3.
4.2. Найти двумерную нестационарную передаточную функцию системы,
структурная схема которой изображена на рис. 3.29,а—в.
4.3. Найти реакцию нестационарной системы, описываемой уравнением
6хF) - х(в) = 6#F), на воздействие #(9) = 61F) при нулевых начальных условиях.
В качестве базисной системы функций использовать нестационарные полиномы
Лежандра, ортонормированные на отрезке [0,/]. Масштаб усечения
спектральных характеристик взять равным 3.
4.4. Найти реакцию системы, описываемой уравнением хF) + 4х(9) = 3#F),
на воздействие #F) = созб • 1F) при нулевых начальных условиях. В качестве
базисной системы функций использовать нестационарные косинусоиды
ортонормированные на отрезке [0,я]. Масштаб усечения спектральных характеристик
взять равным 3.
4.5. Определить спектральную плотность выходного сигнала, если на вход
системы, структурная схема которой изображена на рис. 3.29,а-в, поступает
белый шум с интенсивностью *У0 =100/я + п •
217

Глава 5. ОПИСАНИЕ И АНАЛИЗ ДИСКРЕТНЫХ ЛИНЕЙНЫХ
СИСТЕМ С ПОМОЩЬЮ РАЗНОСТНЫХ УРАВНЕНИЙ
5.1. ОДНОМЕРНЫЕ СИСТЕМЫ ПРИ ДЕТЕРМИНИРОВАННЫХ
ВОЗДЕЙСТВИЯХ
5.1.1. Описание сигналов и систем
1. Описание сигналов. Сигналы в дискретных динамических системах
описываются последовательностями: {&(к), к = к0,ко + 1,...},{*(&), к = к^уко +1,...},
где к0 — начальный момент дискретного времени к.
2. Описание систем. Дискретная система преобразует входной сигнал в
выходной при заданных начальных условиях (рис. 5.1). Математические модели
таких систем описываются разностными уравнениями.
А
1 • . • .
_1_ * к 1
I > л
>
Входной 1
сигнал
Начальные условия
^
Дискретная
динамическая
система
X*
• •
•
> к
^
Выходной
сигнал
Рис. 5.1
В общем случае одномерная линейная дискретная нестационарная система
описывается линейным разностным уравнением
ап(к)х(к + л)+а„-\(к)х(к + п -1)+... + а0(к)х{к) =
=и%(^+^)+^-1(%(^+^-о+...+м%(^ *=*о,*о+1,..., EЛ)
с начальными условиями
х(к0) = х0, х(к0+\) = х1,..., х(к0+п-1) = хп_и
E2)
где $(к) — входной сигнал; х(к) - выходной сигнал; к - дискретное время;
ал(#),...,йо(Л:); Ат (*),..., Дь(#) - коэффициенты левой и правой частей,
зависящие от времени к; п и т — заданные числа, п^т.
Примером рассматриваемой математической модели может служить
уравнение
х(* + 1) = A +а) *(*) + *(*), к = 0,1,2,...,
х@) = х0,
218

описывающее состояние х(к) балансового счета в банке в начале каждого к-то
месяца. Здесь а - месячная процентная ставка, хо - начальный капитал,
1с — дискретное время, %(к) — сумма взносов и изъятых денег в течение к-то
месяца. Предполагается, что величина капитала вычисляется ежемесячно на
основании баланса на начало месяца. В результате может быть получена
последовательность х(к)>к = 0Х— В данном уравнении входным сигналом можно
считать &(к) — сумму взносов и изъятых денег в течение к -го месяца, а
выходным х(к) — состояние балансового счета.
Замечания.
1. Если ап(к)*0, а0(к)^09 уравнение E.1) называется уравнением л-го
порядка. Его решение определяется п начальными условиями (рис. 5.2).
*о
*«-1
х(ко + л)
*о| *о+1 к0+п-1 ко+п к
Рис. 5.2
2. Одномерная линейная дискретная стационарная система описывается
разностным уравнением
ап х(к + п)+ап_\ х(к + п -1)+... + а$ х(к) =
E.3)
= Ьт8(к + т)+Ьт_18(к + т-1)+... + Ь0х(к), * = 0,1,2,...,
с начальными условиями
х@) = х0, х(\) = хь..., х(п -1) = хп_х, E.4)
ВДе ал,...,Оо; ЬтУ...,^ - постоянные коэффициенты.
5.1.2. Связь вход-выход
Для линейных дискретных систем, как и для непрерывных, справедлив
принцип суперпозиции (см. разд. 1.1.3). Выходной сигнал системы
представляется в ввде суммы свободного и вынужденного движений:
х(к) = хс(к)+хвын(к).
219

Свободное движение хс(к) происходит при отсутствии внешнего
воздействия (#(&) ¦ 0) вследствие ненулевых начальных условий. Оно определяется
решением однородного уравнения, соответствующего исходному уравнению E.1):
ап(к)х(к + п)+... + а0{к)х(к) = 0,
с начальными условиями
*(*о) = *о> *(*о +1) - *1.-. х(к0 + л -1) = хп_{.
В случае, когда начальные условия нулевые, свободное движение
отсутствует (хс(к) = 0).
Вынужденное движение х^^к) — это реакция системы на внешнее
воздействие при нулевых начальных условиях. Оно определяется решением
неоднородного уравнения E.1) при нулевых начальных условиях.
Замечания.
1. Общее решение однородного уравнения записывается в форме:
где С\9...,Сп — произвольные постоянные; щ(к\...,уп(к) — элементы
фундаментальной системы решений, образуемой п линейно независимыми решениями
однородного уравнения, удовлетворяющими условию
Ф1&)) Ф1(*0+1) - Ф1^0+Л-1)
Фг(*о) Ф2(*6+0 •* Ф2(*о+ч-1)
Ф#,(*о) Фл(*о+0 - Фл(*о+л-1)
*0.
2. Процедура нахождения свободного движения для стационарных систем
E.3),E.4) сводится к решению соответствующего однородного уравнения
(*(*) = 0)
ап х(к + п) +... + ах х(к +1)+ д0 х(к) = 0
с начальными условиями
х@) = *о, *(*) = *!,.«, х(п -1) = хп_{
и содержит три этапа.
Первый этап. Составить характеристическое уравнение
апХп+ап_1\п-1+... + а0=0
и найти его корни: Хь..., Хл.
220

Второй этап. В зависимости от типа корней выписать общее решение
однородного уравнения (четыре случая).
Если корни действительные разные, общее решение записывается в форме
х(к) = С,Х,* + С2Х2к +... + СпХпк, E.5)
где Си..., Сп - произвольные постоянные.
Паре а ± /р комплексных сопряженных корней соответствует компонента
х(к) = гк [Сх созф* + С2 ап ук ], E.6)
где г - модуль числа X = а + / р, а ф - аргумент, определяемые по формулам
г = ^2+Р2,
аОД-В-, а>0, р>0,
а
агс18 — + *, а<0, Э>0,
а
|, а-0, р>0.
Действительному корню X^ кратности т соответствует следующая
составляющая общего решения:
х(к)-(с1+С2*+...+ Сщ*-1).х/, E.7)
а паре комплексных сопряженных корней кратности т:
х(к) = гк[(с1 +С2к+...+Сткт-х )со&<рк+(вх + В2к+...+ Вткт~{ )&тук), E.8)
где Сь...,Ст; Ви...,Вт - произвольные постоянные.
Третий этап. Найти произвольные постоянные с помощью начальных
условий.
3. Методика нахождения вынужденного движения содержит четыре этапа.
Первый этап. Найти общее решение однородного уравнения.
Второй этап. Найти частное решение неоднородного уравнения. В общем
случае применяется метод вариации произвольных постоянных, а в частном
случае, когда система описывается уравнением
ап х(к + п)+... + ах х(к + 1)+Оо х(к) = 8(к), $(*) = г*[1^(Л:)со8ф/; + Р^к) зтук],
ще Кд(к)уР1(к) — многочлены степени д и / соответственно, ги<р- заданные
действительные числа, — метод подбора. Тогда частное решение ищется в форме
*«(*) = гк[Bр(к)со&ц>к + Тр(к)яп <рк ]. к3, E.9)
в которой /> = тах{д;/}; Bр(к)9Тр(к) - многочлены переменной к степени р
с неопределенными коэффициентами; число 5 находится следующим образом:
221

О, если число г(со8 <р + / 8т <р) не совпадает
5 = ¦{ ни с одним из корней характеристического уравнения,
т, если число г(со$ ф + / $ш <р) совпадает с корнем кратности т •
Коэффициенты многочленов Ор(к),Тр(к) находятся из тождества, которое
получается при подстановке E.9) в E.1).
Третий этап. Найти общее решение неоднородного уравнения как сумму
общего решения однородного уравнения и частного решения неоднородного
уравнения.
Четвертый этап. Определить произвольные постоянные из нулевых
начальных условий.
4. Одномерная дискретная стационарная система может быть задана
структурной схемой. Основными элементами структурных схем являются
усилительное звено, сумматор и звено задержки. Выходной сигнал усилительного звена
равен входному сигналу, умноженному на некоторый коэффициент усиления К.
Сумматор осуществляет операцию алгебраического суммирования входных
сигналов. Выходной сигнал звена задержки запаздывает по отношению к входному
сигналу на один шаг дискретного времени, т.е. если входной сигнал равен х(к),
то выходным будет х(к-\). Построение структурной схемы по разностному
уравнению осуществляется также как для дифференциального. Если
стационарная система описывается укороченным уравнением
апх(к + п)+ап_1х(к + п-1)+... + а0х(к)=8(к), к = 0,1, 2,...,
то для построения структурной схемы следует выразить апх(к + п). Сигнал
х(к + п), получаемый из апх(к + п) путем умножения на —, подается на звено
задержки, поэтому на его выходе получается х(к + п-1). Для получения х{к)
требуется п последовательно соединенных звеньев задержки. Обратные связи
в схеме определяются выражением для а„ х(к + п).
5.1.3. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть известны:
а) входной сигнал {в(к), к = кц,ко +1,...};
б) дискретная динамическая система, описываемая разностным уравнением
ап х(к + п)+ап_{ х(к + п -1) +... + а^ х(к) =
= Ьт8(к + т)+Ьт_1х(к + т-1) + ... + Ь08{к), к = 0,1, 2,...;
в) начальные условия.
Требуется найти выходной сигнал {х(к)> к = ко,к0 +1,...}.
222

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти свободное движениехс(к).
2. Найти вынужденное движениехвыя(А:).
3. Определить выходной сигнал как сумму свободного и вынужденного
движений: х(к) = хс(к) + х^к).
Пример 5.1. Найти свободное движение дискретной системы, описываемой
уравнением
4х(к + 2)+4х{к +1)- Зх{к) = &(к)
с начальными условиями х@) = 8, хA) - -6.
П Применим описанную в разд. 5.1.2 методику нахождения свободного
движения:
а) составим характеристическое уравнение 4Х2+4Х-3 = 0 и найдем его
-4±^6 + 48 -4±8
корни: Хи= - —-—;
3 1
б) так как корни XI = —г, Х2 =— действительные разные, то согласно E.5)
общее решение имеет вид: ^(^) = С1[--г + С2 —1 ;
в) произвольные постоянные находятся из начальных условий:
х@) = С!+С2=8,
хA) = -|с1+±С2=-6.
Отсюда С{ = 5,С2 = 3 и свободное движение хс(к) = 5 • -—] + 3 •[ — 1 . ¦
Пример 5.2. Найти свободное движение дискретной системы, описываемой
уравнением
х(к + 2)+ 2х(к +1)+ 4х(к) = *(*)
с начальными условиями х@) = 3, хA) = 0.
? Применим описанную в разд. 5.1.2 методику нахождения свободного
Движения:
223

а) составим характеристическое уравнение Х2+2Х + 4 = 0 и найдем его
корни: Х^2 = -1 ± 4ъ I;
б) так как корни Х},Х2 - комплексные разные, то согласно E.6) общее
решение имеет вид
х(к) = 2к(сх со&—к + С2 зт^*1,
поскольку а = -1; р = ^3, г = ^а2 + р2 = 2
Ф = агс1§~ + п = агс1§ (- 7з)+ п = —- + я = —;
в) произвольные постоянные находится из начальных условий:
х@) = С1=3,
хA) = 2|-±С1+^С2
= 0.
Отсюда Сх=\ С2=4ъ и искомое свободное движение
хс(к)=2к -Гз сову* + Л ап^*! ¦
Пример 5.3. Найти свободное движение дискретной системы, описываемой
уравнением
х(к + 3)- Зх(* + 2)+ Ъх(к +1)- х{к) = &(к)
с начальными условиями х@) = 1, хA) = 4, хB) = 9.
а Применим описанную в разд. 5.1.2 методику нахождения свободного
движения:
а) составим характеристическое уравнение Х3-ЗХ2+ЗХ-1 = 0 и найдем
его корни: (X -1K = 0, X = 1;
б) так как корень Х1 = 1 действительный кратности т = 3, то согласно E.7)
общее решение имеет вид
х(к) = (с1+С2к + Сгк2)\к = СХ+С2к + Сък2\
в) произвольные постоянные находятся из начальных условий:
224

х@) = С1=1,
хA) = С1+С2+С3=4,
хB) = С1+2С2+4С3=9.
Отсюда С\ = 1,С2 = 2,С3 = 1 и свободное движение хс(к) = 1 + 2к + к2, ш
Пример 5.4. Найти свободное движение дискретной системы, описываемой
уравнением
4х(к + 5)- 4х{к + 4)+4х{к + 3)- 4х(к + 2)+х(* +1)- х(к) = *(*)
с начальными условиями х@) = 5, хA) = 1, хB) = -4, хC) = 1 + ^, хD) = 5.
Составить структурную схему.
П Применим описанную в разд. 5.1.2 методику нахождения свободного
движения:
а) составим характеристическое уравнение 4Х5 -4Х4 +4Х3 -4А,2 +Х-1=0
и для нахождения его корней разложим на множители: (к -1) • B X2 +1) = 0;
Л
б) так как корень Х1 = 1 — действительный, а Х^ъ - ±"^Г/ ~" паРа ком"
плексных сопряженных корней кратности т = 2, то согласно E.5) и E.8) общее
решение имеет вид
<к)
= С3 1* +Ш) [(С, +С2к)со$1к + (В1 +Л2*)Й11|*|,
Л 42 п
поскольку а = 0; р = — ;г =—, <р = - ;
в) произвольные постоянные находятся из начальных условий:
х@) = С3+С,=5,
*A) = С3+;у.(*1+*2) = 1.
хB) = С3-±(С1+2С2) = -4,
хC) = С3 -—(^ + ЗД2) = 1 + 41,
4
*D) = С3+±(С,+4С2) = 5.
4
225

Отсюда Сх =4, С2 = 3, С3 = 1, В{ = 2, В2=-2 и искомое свободное движение
хс(к)=1к+{<2]
{Щ ГD + ЗА:)со8-А: + B-2А:)ш1^А:1.
Составим структурную схему (рис. 5.3), пользуясь п.4 замечаний. Выразим
член 4х(к + 5) из уравнения:
4х{к + 5) = 8(к) + 4х(к + 4)-4х{к + 3)+4х(к + 2)-х(к + \)+х{к).
Реализуем полученное равенство на сумматоре. Для нахождения сигаала х(к + 5)
используем усилительное звено с коэффициентом усиления К=—. Сигаал
4
х(к + 5) подается на пять последовательно соединенных звеньев задержки C3). В
результате получается выходной сигнал х(к). Коэффициенты усиления обратных
связей определяются уравнением для 4х(к + 5)). ¦
*<*)
7
/-
/1
11
4х(к + 5)
тч
р^
\
1
_4_
"¦ —п^Ч
| н г
+ 4)
1
и±1
4
х(к
+
3)
"»|Зо
х(к
4
+ 2) дс(* + 1) х(к)
*К>о|
Рис. 5.3
Пример 5.5. Найти свободное движение дискретной системы, описываемой
уравнением
х(к + 2)- 5х{к +1)+6х{к) = *(*)+ 2*(* +1)
с начальными условиями х@) = 1, х(\) = 2.
П Применим описанную в разд. 5.1.2 методику нахождения свободного
движения:
а) составим характеристическое уравнение Х2-5Х + 6-0 и найдем его
корни X! = 2, Х2 = 3;
б) поскольку корни действительные разные, то согласно E.5) общее
решение однородного уравнения х(к + 2)-5х(к + 1)+6 = 0 имеет вид:
х(к) = С12к+С2'*к;
226

в) найдем произвольные постоянные Сх и С2 из начальных условий:
х@)=С1+С2=1,
д:A)=2С1+ЗС2=2.
Отсюда С2 = 0, Сх = 1 и свободное движение хс(к) = 2* .¦
Пример 5.6. Найти реакцию дискретной системы, описываемой уравнением
х(к + 2)-5х(к +1)+6ф) = &(к)
на входной сигнал $(&) в 1 при начальных условиях х@) = 1, х(\) = 2.
? 1. Свободное движение системы хс(к) = 2к найдено в примере 5.5 и
является решением однородного уравнения х(к + 2) - 5 х(к +1) + 6 х(к) = 0 с
начальными условиями х@) = 1, х(\) = 2.
2. Найдем вынужденное движение согласно изложенной в разд. 5.1.2
методике:
а) общее решение однородного уравнения х(к) = С\ • 2* + С2 • 3* найдено в
примере 5.5;
б) найдем частное решение неоднородного уравнения. Для этого
определим параметры правой части $(&)=1: г = 1, <р = 0, /^(А:)=1,Р/(/:) = 0;^ = 0. Число
I = 1 не совпадает с корнями 2 и 3 характеристиче-
5 = 0, так как г
СО$ф + 181Пф
ского уравнения, поэтому согласно E.9) хн(к)=1к • Л . Подставляя в
неоднородное уравнение, имеем А-5А + 6А = 1, т.е. Л=— и *„(/:) = —;
в) составим общее решение неоднородного уравнения:
х(к) = С1-2к+С2-Зк+±;
г) определим произвольные постоянные Сх и С2 из нулевых начальных
условий:
х@) = С1+С2Д = 0,
хA) = 2С!+ЗС2+- = 0.
Отсюда С2 -I, С, =-1 и а^Л*)—2* +±-3* + ±
3. Найдем выходной сигнал как сумму свободного и вынужденного
движений:
*ю- ^ 4-2*+тз*-44'3*
хЛк)
2 2 2 2
хвын'^/
227

Пример 5.7. Найти реакцию дискретной динамической системы,
описываемой уравнением
х(к + 1)-2х(к) = 2в(к)
на входной сигнал %(к) = к при х@) = 0.
? Находим вынужденное движение (поскольку начальные условия
нулевые, то свободное движение отсутствует, т.е. хс(к) в 0) как решение
неоднородного уравнения при нулевых начальных условиях:
х(к + 1)-2х(к) = 2к, х@) = 0.
Используем методику нахождения вынужденного движения:
а) определим общее решение однородного уравнения х(к +1) - 2х(к) = 0.
Характеристическое уравнение X - 2 = 0 имеет действительный корень X} = 2,
поэтому общее решение х(к) = С{ X* = С\ 2*;
б) найдем частное решение неоднородного уравнения методом подбора,
анализируя параметры правой части 2%(к) = 2к: ф = 0, Яд(к) = 2к, # = 1 ,г = 1.
Число 5 = 0, так как г(соз ф + / зт ф) = 1 не совпадает с корнем X] = 2, поэтому
частное решение ищется в форме:
хм(к) = 1к[ак + Ь] = ак + Ь.
Подставляя в неоднородное уравнение, получаем:
а(к + 1) + Ь-2ак-2Ь = 2к.
ак+а
Приравнивая коэффициенты при одинаковых степенях к, имеем
а-Ь = 0, -а = 2 или д = -2,& = -2. В результате хм(к) = -2к-2;
в) составим общее решение неоднородного уравнения как сумму общего
решения однородного уравнения и частного решения неоднородного уравнения:
х(к) = Сг2к-2к-2;
г) найдем произвольную постоянную Сх из нулевых начальных условий:
х@) = С!20-2.0-2 = ^-2 = 0, С! =2.
В результате получаем вынужденное движение:
хпм(к) = 2 2к -2к-2 = 2Bк -к-\).ш
Пример 5.8. Найти реакцию дискретной динамической системы
х(к + 2) - 2х(к +1) + х(к) = 2&(к)
на входной сигнал &(к) = 2к при х@) = 1, хA) = 0.
П 1. Находим свободное движение как решение однородного уравнения
х(к + 2) - 2х(к +1) + х(к) = 0 с начальными условиями х@) = 1, хA) = 0:
228

а) составим характеристическое уравнение X2 - 2Х +1 = (X -1J = О и
найдем его корни;
б) поскольку корень Х{=1 действительный кратности т = 2, то согласно
E.7) общее решение однородного уравнения имеет вид
х0(к) = (С, +С2к) Хк{ = С{ + С2к;
в) определим произвольные постоянные Сх и С2 из начальных условий'
х0@) = С1=1,
х0A)=С1+С2=0.
Отсюда Сх = 1, С2=-1 и свободное движение хс(к) = 1 - к М
2. Найдем вынужденное движение как решение неоднородного уравнения
с нулевыми начальными условиями:
х(к + 2)-2х(к + 1) + х(к) = 22к, х@) = 0, хA) = 0:
а) общее решение однородного уравнения найдено в п.1:
х0(к) = С1+С2к;
б) найдем частное решение неоднородного уравнения методом подбора.
Анализируя параметры правой части 2%(к) = 2 • 2*, имеем: <р = 0,Яд(к) = 2, д = 0,
г = 2. Число г(со$ф + /8Шф) = 2 не совпадает с корнем X! =1, поэтому 5 = 0 и
решение ищется в форме: хн(к) = Л2к. Подставляя в неоднородное уравнение,
получаем:
Л-2'+2-2у*.2'+1+у*.2*=2.2*.
Сокращая на 2*, имеем А22-4А + А = 2 или А = 2. В результате хн(к) = 2• 2*;
в) составим общее решение неоднородного уравнения как сумму общего
решения однородного уравнения и частного решения неоднородного уравнения:
х{к) = Сх+С2к + 2 2к\
г) найдем произвольные постоянные Сх и С2 из нулевых начальных
условий:
х@) = С!+2 = 0,
х(\) = С{+С2 +4 = 0.
Отсюда С! =-2, С2=-Сх -4 = -2 и хвын(к) = -2-2к + 2-2к.
3. Найдем выходной сигнал как сумму свободного и вынужденного
движений:
х (к) = хс(к) + хвын(к) = 1-к-2-2к + 2 2к=-\-Зк + 2 2кМ
229

5.2. МНОГОМЕРНЫЕ СИСТЕМЫ ПРИ ДЕТЕРМИНИРОВАННЫХ
ВОЗДЕЙСТВИЯХ
5.2.1. Описание сигналов и систем
1. Описание сигналов. Сигналы представляются последовательностями
векторов, зависящих от дискретного времени:
т-
*(*) =
{хп(к))
№-
2. Описание систем. Многомерная линейная нестационарная система
описывается уравнением состояния
х(к + \)=А(к)х(к)+В(кМк) , * = *о,*о+1,..
с начальными условиями
*(*о)=*о =
*10
*20
и уравнением выхода
№ = С(к)х(к),
E.10)
E.11)
E.12)
где х — л-мерный вектор состояния; $ — г-мерный вектор входных
воздействий (управлений); у — 5-мерный вектор выхода; А(к),В(к),С(к) — матрицы
размера (л х л), (лх г), E х п) соответственно; к0 — начальный момент времени
(момент подачи входного воздействия).
Замечания.
1. Многомерная система описывается набором из трех матриц:
А(к)9В(к),С(к).
2. Если матрицы А(к), В(к), С(к) не зависят от дискретного времени,
система называется стационарной. Тогда уравнения E.10)—E.12) принимают вид:
х(к + 1)=Ах{к)+В8(к),к = 0,1,...', х@) = х0; E.13)
у(к) = Сх{к).
5.2.2. Связи вход-состояние и вход-выход
Для многомерных линейных дискретных систем, как и для непрерывных,
справедлив принцип суперпозиции:
х(к) = хс(к) + х^к), у(к) = ус(к) + у^к),
230

где свободное движение хс(к),ус(к) является решением однородной системы
при отсутствии внешнего воздействия, а вынужденное движение хмм(к)9увынAс)
- решением неоднородной системы с нулевыми начальными условиями.
Рассмотрим процедуры нахождения свободного и вынужденного движений
дискретной системы, описываемой уравнением состояния:
х{к +1) = А{к)х{к) + В(к)г{к), х{ко) = х0 . E.14)
Нахождение свободного движения ( при ^) = 0) связано с решением
однородной системы уравнений:
х(к +1) = А(к)х{к), к = к0, ко +1,....
Выписывая эту зависимость последовательно при к = к09к = к0+\9
к = ко+2 и т.д., имеем
х(к0 +1) = А(к0)х{к0) = А(ко)х0,
х(к0 + 2) = А(ко + 1)х(*о +1) = А(к0 +1) А(ко)х0,
х(к)=А(к-1)А(к-2)-.А(к0)хо = ПЛ@*о • EЛ5)
1-Ао
Соотношение E.15) определяет свободное движение в текущий момент
времени к по начальному состоянию х$.
Получим общую формулу для нахождения решения неоднородной системы
E.14) с учетом E.15). Для этого запишем уравнение E.14) последовательно при
* = *оД = *о+1, Ь^о+2ит.д.
В результате имеем
х{к0 +1)=А(ко)х^+В(коЫк0),
х{к0+2)=А{к0+1)х{ко+1)+В(к0 +1)*(*о +1) =
= А{ко + 1)Л(*о)*о + 4*о + 1JК*оЫ*о)+ В(к0 + 1)*(*0 +1),
*-1 *-2
Х(к)= гМ0*о +1
'=*6 У-*б|>7+1
*-1
ГМ')
\В0Ш+В(к-1Мк-1)-
свободное движение
E.16)
= Ф(*,*о)*о, + ЁФ(*.У' + 1)Л0')*0').
свободное движение /~*0
вынужденное движение
231

гае Ф(&,&о) — переходная матрица, определяемая соотношением
Ф(*.*о) = {
А(к-1)А(к-2)-А(ко), *>*0+1>
Е, * = Ао-
Переходная матрица удовлетворяет уравнению
Ф(* + 1,*о) = А(к)ф(к,ко), к* ко,
E.17)
Ф(*о,*о)=.Е.
Замечания.
1. Для стационарных систем, описываемых уравнениями
х{к + 1)=Ах{к)+В«(к), х@)=х0, * = 0A,2,...,
у{к) = Сх{к),
переходная матрица зависит от разности аргументов: Ф(к,к0) = Ак~к" = ф(к -ко).
Связи вход-состояние и вход-выход принимают вид:
х{к)=Ак *0 + 1 Акч~х в^^^)=ф^к)xо+к^IФ(к-^-^)вю)
Ф® >"° Ф]^м) **
Ак)=Сх(к) = САкх0 + %1С Ак~'-1 В еО).
2. Одномерная система
а„(к)х(к + п)+ ап_,(*)х(* + п -1)+... + «о(*)*(*)= *о(*)
может быть представлена с помощью эквивалентной многомерной системы.
Действительно, используя обозначения
*,(*)=*(*), х2{к)=х{к + 1),..., хп{к)=х(к + п-1),
получаем
х,(* + 1) = *2(*)>
х2(к + 1) = х3(к),
E.18)
232

или
' 0 10..
0 0 1..
0 0 0..
1 «„(*)
0 ,
0
«„(*) )
,*(*) =
' 0 >
0
к<*>;
х(* + 1)=4Ф(*)+*(*)>где А(к) =
3. Для решения неоднородной системы можно использовать метод
вариации произвольных постоянных. Рассмотрим этапы его применения для решения
системы
х(к + 1)=А{к)х(к)+В{к)х{к), * = *ь,*о+1,...; *(*о) = *о-
Первый этап. Решается однородная система (при &(к) г 0)
х(к + 1) = А(к)х(к).
Ее общее решение имеет вид:
л
хь(*)-ф(*).С = 2с/Ф/(*).
/=1
где С!,...,СЛ — произвольные постоянные; ф(#) =
E.19)
Фц(*) Ф12<*) ••• Ф1л(*)
Ф21<^) Ф22(^) •• Ф2л(*)
^ФЛ1(^) Фл2(*) - Флл(*),/
фундаментальная матрица, составленная из линейно независимых решений
Ф/(#) = (ф1/(&),...,Фм(к))Т, / = 1,...,л однородной системы, т.е. для любого
номера / справедливо ф,(А: + 1)=Л(А:)ф/(А:) или
ф(* + 1) = Л(*)ф(*Ь E20)
Второй этап. Ищется общее решение неоднородной системы в виде
х(*) = ф(*)С(*), E.21)
где С(к) = (Сх(к),...,Сп(к))Т - столбец функций, подлежащих определению.
Подставим E.21) в неоднородную систему:
ф + \)С{к +1)= А(к)ц>(к)С(к)+ В{к)з(к).
Вычитая из обеих частей у(к + 1)С(к), получаем:
ц>(к + \)С(к + 1)-ф(А: + \)С{к) = А(к)ф)С(к)+ В{к)&{к)-у{к + \)С{к),
Ф^'+1)
233

так как столбцы фундаментальной матрицы у(к) удовлетворяют однородному
уравнению E.20). В результате имеем
ф(* + 1)АС(к)=Л(к)^к),
где АС(к) = С(к + \)-С(к) — конечная разность первого порядка, или
АС(к) = ц{к + 1)-1В(кJ(к).
Выпишем полученное выражение при к = #о, к$ +1,..., к -1:
С{к)-С(к-1) = <р-1(к)В(к-1)8(к-1),
С(*о + 2)-С(*о +1) = ф-1(*0 + 2)Я(*0 + 1)*(*о +«,
С(Лб +1)-С(*о) = дгЧ*,) + 1JК*о)*(*о).
Суммируя, получаем
Ф)= 2!ф-!(/ + 1)Л(/)«(/)+С(*о).
После подстановки в E.21) имеем
д<*)-ф(к)С(*о)+ф(*) Е ф"|(/ + 1)Л(/)в(/).
При А: = /^ должно выполняться начальное условие х(/^) = ф(#о)С(#о) = хо»
поэтому С(*о)-ф(Л0)х0 и
*(*) = ф(*)ф-1(*о)*о + Е<Р(^Ф",0 + 1)^)^(/)-
7=*»
Сравнивая с E.16), обозначим переходную матрицу
Ф(*,у + 1) = ф(А;)ф-1(/ + 1) E.22)
— переходная матрица. Тогда связь вход-состояние имеет вид
*(*)=ф(*,*о)хо + 1ф(*>;+1)я(/Ш-
^#Г ^ ^ ¦
234

С учетом уравнения у(к) = С(к)х(к), получаем связь вход-выход:
у{к) = С{к)Ф{к,к0)х0 + к^С(к)ф(к9] + 1)В(;)80У
УеынФ)
4. Отметим важные свойства переходной матрицы:
1) ф(*2>*1)ф(*ь*о)=ф(*2,*о)-
Действительно, согласно п.З справедливо Ф(^2>^1) = ф(^2)ф~1(^1)>
ф(*ь*о) = ф(*1)ф~1(*о)-
Поэтому ф(А:2,^)ф(А:1,Ло) = ф(^2)ф~1(^1)ф(^1)ф(^о)= Ф(^2»^о);
Е
2) Ф(^1,^2) = Ф_1(^2»^1)- В соответствии с правилом [А • В]~1 = В~1 • А~{
имеем ф-1(/:2Д1)=[ф(^2)ф(^1)]=ф(^)ф(^2) = Ф(^1^2).
5. Если начальные условия нулевые, связи вход-состояние и вход-выход
можно переписать в форме
где 1Гх(*,у) = Ф(*,./ + 1)Л(/)э Ку(к,Д = С(к)ф(кл' + 1)В(;) - переходные функции
многомерной системы по состоянию и выходу.
5.2.3. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть известны:
а) входной сигнал #(&) = I I;
б) система, описываемая уравнениями состояния и выхода
х(* +1) = А(к)х(к)+В(к)х(к), к = ко, ко +1,...
у(к) = С{к)х{к);
в) начальные условия
*(*о)=*0= :-
Требуется найти законы изменения вектора состояния и вектора выхода.
235

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти переходную матрицу (одним из двух способов, рассмотренных
далее).
2. Используя соотношения E.16) или E.18) в зависимости от типа системы,
определить законы изменения векторов состояния и выхода.
Переходную матрицу нестационарной системы можно найти по формуле
E.22).
Для нахождения переходной матрицы Ф(к)=Ак стационарной системы
можно воспользоваться теоремой Кели-Гамильтона о том, что
характеристический многочлен матрицы является ее аннулирующим многочленом.
Разделив Хк на характеристический многочлен Р(х) - йеХ (А - ХЕ) матрицы
А, получаем
Хк=Р(хH(х) + К(х), E.23)
где 0(х) — частное, а Я(х) — остаток, причем остаток — это многочлен степени
меньше, чем размерность п матрицы А, имеющий вид
Д(Ь) = гп-\ Ь"~1 + Ъ-2 *л + - + 1 х + го • E-24)
Подставив в E.23) вместо X матрицу А приходим к равенству
Ак=Я{Л)9 E.25)
так как по теореме Кели-Гамильтона Р(А) = 0. Таким образом, для нахождения
переходной матрицы Ф(к) = Ак нужно подобрать коэффициенты г0,/),...,/*„_!
многочлена E.24). Это можно сделать, подставляя в E.23) корни
характеристического уравнения. Заметим, что в E.23) вместо характеристического многочлена
можно использовать минимальный многочлен матрицы. При этом остаток Я(х)
может иметь меньший порядок.
В случае простых различных корней характеристического уравнения,
подставляя корень X/ в E.23), получаем Хк = Л(Х/), так как />(Х/) = 0, т.е.
х)=Л(Х/) = гл.1ХГ1+гл.2ХГ2+... + г1Х/+г0, / = 1,...,л . E.26)
Если X/ — действительный корень характеристического уравнения
кратности ц, то, учитывая, что
Р(к,) = 0, Р'(Х,) = 0,..., рО-0(х,.) = 0,
из E.23), последовательно дифференцируя, получаем
, У = ОД ц-1. E.27)
вии>-)
Это система ц линейных уравнений относительно коэффициентов г0уг1у...9гп,{
многочлена Я(х). Если Х1>2 = а±р/ — пара комплексных сопряженных корней
236

кратности ц, то из E.27) получаем систему 2ц уравнений, приравнивая
действительные и мнимые части.
Таким образом, из E.25) следует, что переходная матрица Ф(к) линейной
стационарной системы имеет вид
ф(к) = /•„_! АпЛ +... + г{ А + г0 Е, E.28)
где коэффициенты /ь»гь—,^-1 многочлена, зависящие от дискретного времени
к, находятся из E.26),E.27).
Пример 5.9. Найти законы изменения векторов состояния и выхода
многомерной динамической системы:
при входном сигнале %(к) = 3* и начальных условиях хх @) = 3, х2@) = 0.
? Уравнения состояния и выхода имеют вид E.13) с матрицами
соответственно.
1. Найдем переходную матрицу. Составим характеристическое уравнение
для матрицы А:
= 0 о Х2-Х-2 = 0.
Оно имеет два простых корня X! =-1 и Х2 =2 (кратность ц = 1). Поскольку
п « 2, то согласно E.24) имеем
д(х) = гх X + го.
Записывая для каждого корня равенство E.26), получаем систему двух
линейных уравнений с двумя неизвестными г0, гх:
-1+го=(-1)*,
2/1+г0=2*.
Отсюда находим коэффициенты г0 =-B* +2-(-1)*), г{ =-B* -(-1)*).
Из равенства E.28) определяем переходную матрицу
1-Х -1
-2 X
237

После упрощений получаем
Отсюда
ФМЛГ 2*+1+(-1)* -2*+ИЧ
"*'-з(-2*+1+2-(-1Г 2*+2-(-1)к/
2. Используя переходную матрицу, запишем формулу E.18) связи вход-
состояние для х0 = и $(&) = 3*:
Х{К} з[-2*+1+2.(-1)* 2*+2-(-1)к; Н +
* V IГ 2*"' + (" 1)*"У " 2*"М + (" 1)*";"' 1Г 1 ) V
Д 3 (- 2*"^ + 2 - (-1^-* 2*"» + 2 • (-1)*-'/1-1,1
х(А)_Г 2-2*+(-1)* УЫГ 2*-^'.У )
к-\ к-\
По формуле ак -Ьк =(а-Ь) ^ а*"^1 *; вычисляем ^ г*"-' >3^ = 3* -2*.
у=о у-о
Подставляя сумму в выражение для х(к), окончательно получаем
х(к) = { И?+2*+Э* ]
Х^ [2-(-1)*-2*-3*/
Выход системы находим по формуле E.18):
Пример 5.10. Найти законы изменения векторов состояния и выхода
многомерной динамической системы:
х1{к + 1) = 4х1(к)-х2(к)+ф),
х2(к + 1) = х1(к)+2х2(к),
у{к) = -х1(к)+х2(к)
3 9
при входном сигнале ^(к) = 1 и начальных условиях хх @) = —, х2 @) =—.
4 4
? Уравнения состояния и выхода имеют вид E.13) с матрицами
238

-С -/)• -й- с=(-"
соответственно.
1. Найдем переходную матрицу. Составим характеристическое уравнение
для матрицы Л:
4"Х ~1 =0 <=> Х2-бХ + 9 = 0.
I 1 2-Х|
Характеристическое уравнение имеет один корень X! = 3 (кратность ц = 2). Как
и в предыдущем примере согласно E.24) имеем
Л(Х) = /\ Х + г0.
Записывая для этого корня систему E.27), получаем
Зп +г0=Зк ,
гх=к-Ък.
Отсюда находим коэффициенты Г\ = к • 3*~1, г0 = 3* - А: • 3*.
Из равенства E.28) определяем переходную матрицу
Ф(*) = ,И + г0* = *.3*->D -1^C*_*.з*)^ 0).
После упрощений получаем
Ф(*)=Г3*+*-3*~! -к'ък'1 1
Ч) { *.з*-' зк-к-зк-*у
реходную мат]
состояние для дсо = ' 1 и е{к) = 1:
Х(ки(зк+к*к-1 -*-3* и°-751+
т ( *-з*-' ъ'-к-з*-1)^)*
кт!{зк->-1+(к-]-\).ък-)-2 -(к.^¦-^).зк-^-2 )П)
Р>{ {к-]-\)Ък-1-2 Зк-'-1-(к-]-1).Зк-'-2)\0)
2. Используя переходную матрицу, запишем формулу E.18) связи вход-
Отсюда
л).( °.753* -о»5*-3* 1+у Г3*-' +(*-У-1)-з*-^ 1 E 29)
4*' [ 2,25-3* -0,5*. Зк) + &[ (к-;-1)-Зк^-2 | E29)
239

Для упрощения используем формулу суммы к членов геометрической
прогрессии
л 2 к-\ 0*~1
1 + Я + Я +... + Я = л .
д-1
к-\ з* -1
При $ = 3 получаем ^ 3* '~х =— . Чтобы вычислить сумму
у-о 3 -!
у=0 И!=0
продифференцируем равенство E.30). Тогда имеем
Подставляя в это равенство 9 = 3, находим
E.30)
2 ю-з'"-^— ^1.
т=0 4
Учитывая результаты суммирования, упрощаем E.29):
«ю-
4 2
4 2
^ ^з*-1 2*.з'-1-з'+1
—+ 5
2*. З* -3*+1
<=>
о х{к) =
Выход системы находим по формуле E.18):
Я*) = (-1 1)
3 3* 3 4
2.3*-1*.3*Д ,
з 4;
з*_1*.з*-1 Л
2.3*-±*.3*Д
= 3*Д.
240

5.3. ОДНОМЕРНЫЕ СИСТЕМЫ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
5.3.1. Описание сигналов и систем
1. Описание сигналов. Сигналы в дискретных системах, подверженных
случайным воздействиям, являются случайными последовательностями. В
качестве их характеристик обычно используются моменты:
— математическое ожидание.
тг(к) = М[0(к)], E.31)
где С(к)— г-мерный входной сигнал, М — операция вычисления
математического ожидания;
- ковариационная функция.
Л,(/,У) = «* {0{!)МЛ} = М{ [(?@-т1@][(?(Л-»1(Л]ГЬ E.32)
где 19] — дискретные моменты времени.
При I = У = к ковариационная функция представляет собой
ковариационную матрицу К8(к) = Я^(к9к), на главной диагонали которой находятся
дисперсии соответствующих компонент вектора С(к).
2. Описание систем. Линейные дискретные системы при наличии
случайных воздействий описываются разностными уравнениями
Х(к + 1) = А(к)Х(к) + В(к)в(к), * = *о,*о+1,...; *(*о) = *0, E.33)
где 0(к) — г -мерная случайная последовательность с математическим
ожиданием т3(к) и ковариационной функцией /^ (/,./); А(к),В(к) — матрицы размера
(лхл),(/1хг) соответственно; Х0 — л-мерный случайный вектор,
характеризующий начальное состояние системы. Предполагается, что Х0 и С{к) не
коррелированны, т.е. справедливо условие М[Х0 0Т(к)] = 0.
5.3.2. Связи вход-выход
Рассмотрим динамическую систему, описываемую разностным уравнением
Х(к +1) = А(к) Х(к) + В(к) 0(к);к = ко,ко+1,...; ЛГ(^) = Х0,
где входной сигнал С(к) задан статистическими характеристиками:
математическим ожиданием щ(к) и ковариационной функцией
^ (/,./) = 1^@ 5(/ - У), где 5(/ - У) = ] ' . . ; начальное состояние Х0 характе-
ризуется гауссовским законом распределения с математическим ожиданием щ,
ковариационной матрицей Во.
241

Закон изменения математического ожидания вектора состояния имеет вид
тх(к +1) = А(к) тх(к) + В(к) т&(к)у т(к0) = т^. E.34)
Закон изменения ковариационной матрицы вектора состояния:
Кх(к +1) = А(к) Кх(к) А(к)Т + В(к) Я8(к) В(к)т, Кх(ко) = Во. E.35)
Ковариационная функция определяется по формуле
^'Чадф'с/.о. /*л E36)
ще Ф(/,у) — переходная матрица.
Действительно, осредним левую и правую части уравнения E.33) с учетом
линейности операции вычисления математического ожидания. В результате
получим уравнение
тх(к +1) = А(к) тх(к) + В(к) тё(к), т(к0) = т^,
описывающее изменение математического ожидания выходного сигнала.
Вычитая из E.33) уравнение E.34), имеем
Х(к +1) - тх(к +1) = А(к) [Х(к) - тх(к)] + В(к) [0(к) - т^к)\.
Используя свойство (А • В)Т =ВТ Ат ,из последнего уравнения находим
[Х(к + 1)-тх(к + 1)]т = [Х(к)-тх(к)]тА(к)т +[0(к)-т;(к)]т В(к)т.
Найдем математическое ожидание от произведения левых и правых частей
двух последних уравнений с учетом E.32):
М{[Х(к +1) - тх(к +1)] [Х(к +1) - тх(к +1)]7*} =
= А(к) М{[Х(к) - тх(к)] [Х(к) - тх(*)]г} Л(*)Г +
+ В(к) М{[0(к) - тЛк)] [0(к) - тЛк)\Т) В(к)т +
« ~—. - '
+ А(к) М{[Х(к)-тх(к)) [в(к)-т,(к)]Т} В(к)т +
+ В(к) М{[0(к) - т,(к)] [Х(к) - тх(*)]г} А(к)Т.
242

Поскольку ХЦ) зависит от 0@ только при / < ), то Яц(к) = Яр(к) = 0 и
окончательно получаем
Ях(к +1) = А(к) Ях(к) А(к)т + В(к) К8(к) В(к)т, Дх(*о) = *6 •
Найдем ковариационную функцию ЛХ(/,У) при / * у:
ЯхЦ9Л^соу{ХA)9Хи)} = соу{Ф(и)Х(])+ § Ф(/,р + 1I?(р).G(р), Х0)} =
= ф(/,У)соу{^0),лго)} = Ф(/,ллха), /*у.
Аналогично получаем ЛХ(|,У) = Дх@ ФГ(У,/), / ^ У. В итоге имеем
соотношение E.36).
5.3.3. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть известны:
а) входной сигнал С(к), заданный своими статистическими
характеристиками: математическим ожиданием тп8(к) и ковариационной функцией
Л,(/,Л = Л*(/N(/ - У), где 5(/ - у) =
б) динамическая система, описываемая разностным уравнением
Х(к + 1) = А(к)Х(к) + В(кH(к); * = *о,*0+1,...; Х(ко) = Х0;
в) математическое ожидание щ, ковариационная матрица Я$ гауссовского
закона распределения начального состояния Х0. Начальное состояние и
входной сигнал не коррелированны.
Требуется найти статистические характеристики выходного сигнала Х(к):
законы изменения математического ожидания тпх(к) и ковариационной матрицы
Ях(к), а также ковариационную функцию ЛХ(/,У).
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Решая уравнение E.34), найти закон изменения математического
ожидания выходного сигнала тх(к).
2. Решая уравнение E.35), определить закон изменения ковариационной
матрицы Ях(к).
3. Найти ковариационную функцию по формуле E.36).
1, '-У.
О, /*У
243

Пример 5.11. Дана динамическая система, описываемая уравнением
Х{к +1) = ±Х(к) + ЪО(к), к = ОД,...; *(<>) = Х0,
где входной сигнал 0(к) задан математическим ожиданием т^{к) = 4 и
ковариационной функцией ^(/,У) = 55(/-у), начальное состояние характеризуется
математическим ожиданием щ = 1 и ковариацией /^ = 2.
Требуется найти законы изменения математического ожидания тх(к)9
ковариационной матрицы Кх(к) и ковариационную функцию Лх(/,у), а также
исследовать установившийся режим при А: -> +оо.
а 1. Составим уравнение E.34):
тх(к +1) =—тх(к) + 3• т^(/г) =—тх(А?) +12, тх@) = то " 1>
так как Л(*) = |, Д(*) = 3, /и^*) = 4, /^(*) = 5.
Найдем его решение, следуя алгоритму решения линейных разностных
уравнений:
а) получим общее решение однородного уравнения:
тх(к + 1)--тх(к) = 0.
Заметим, что корень X = — характеристического уравнения X -— « О
удовлетворяет условию | х| < 1, процесс устойчив (см. разд. 5.4.1), а общее решение
имеет ввд тх(к) « с\ ¦- , где с - произвольная постоянная.
б) частное решение неоднородного уравнения ищем в ввде тх(к) = А.
Подставляя, получаем А = --А +12, следовательно, А = 24;
в) общее решение неоднородного уравнения записывается в виде суммы
общего решения однородного уравнения и частного решения неоднородного
уравнения:
"*(*) = <{±] +24;
г) найдем частное решение, удовлетворяющее начальному условию:
244

Отсюда получаем с = -23. Тогда закон изменения математического
ожидания выходного сигнала:
тх(*) = -2зД1 +24.
При к ->+оо имеем тх(+оо) = 24. Заметим, что этот же результат можно
получить, переходя к пределу при к-++*> в исходном уравнении, т.е.
1
Т
2. Составим уравнение E.35):
/ях(+«>) =-тх(+оо) +12.
Лх(Аг + 1)=^Лх(А:)^ + 3.5.3=4лх(А:) + 45; Лх@) = /^,=2.
2 2 4
Решая аналогично п.2, получаем закон изменения ковариационной
матрицы выходного сигнала:
ДХ(*) = -58Д1 +60.
При #-*+оо имеем Лх(+со) = 60. Этот же результат можно найти из
исходного уравнения, переходя к пределу при к -> +оо, т.е.
Дх(+оо)=1лх(+оо) + 45.
3. Найдем ковариационную функцию по формуле E.36). Поскольку по
формуле E.21) Ф&Л^яКОдгЧУ), где <р</> = Г — I - элемент фундаментальной
системы решений однородного уравнения х(к + 1)=—х(к)9 то
^'•ЧШ)~ЧСУ)-огсюда
Кх«,/) = <Н1,ЛКхи)={$' У)|-58.^У +б0| =
СМ)
= -58-^ +60-^ при/5у.1
245

Пример 5.12. Дана динамическая система, описываемая уравнением
Х{к +1) = | Х(к) + кв(к), к = 0,1,..., ЛГ@) = Х0,
где входной сигнал задан математическим ожиданием т8(к) = 0 и
ковариационной функцией Л^A,./) = 5(/-у), начальное состояние Х0 характеризуется
параметрами щ =0, Ло =0.
Требуется найти законы изменения математического ожидания и
ковариационной матрицы.
? 1. Составим уравнение E.34):
тх(к + 1) =—тх(к) + к 0, тх(Ъ) = щ =0,
так как А(к) = —, В(к) = к, т^(к) = 0. Очевидно, тх(к) = 0, т.е. математическое
Ях(к + 1)=±Ях(к)± + кЛк=±Ях(к) + к2, Ях@) = Яо=0,
2
ожвдание выходного сигнала не изменяется.
2. Составим уравнение E.35):
1-Ях(к)- + к1.к=±-° "-\^ъ*
2 *ч '2 4
так как А(к) = ^, В(к) = к, Я^(к) = 1.
Общее решение однородного уравнения имеет вид (см. п.1. примера 5.11):
Частное решение неоднородного уравнения ищется в форме E.9):
Ях:(к) = ак2+Ьк + с,
так как г = 1, <р = 0, д = 2 и поэтому р = 2, 5 = 0. Подставляя в уравнение, находим
а(к + 1J+Ь(к + 1) + с = -ак2+±Ьк + -с + к2,
4 4 4
а к2 + 2а к + а + Ь к + А + с = — а к2 +—А А: + — с + #2.
4 4 4
Приравнивая коэффициенты при одинаковых степенях к, имеем:
а=— д + 1, 2а + о = —о, д+о+с=— с.
4 4 4
л_ 4 , 32 80 „„,,. 4,2 32, 80
Отсюда а=— * = -— с = — и Д;(#)=ТА: -—*+—•
3 9 27 х 3 9 27
Общее решение неоднородного уравнения:
Ях(к) = Д2С*> + «,"<*) = с(±) +|*2 -у *+§•
246

Найдем частное решение, удовлетворяющее начальному условию:
80 _
+ 27-
*х@) = С + | = 0. Отсюда С = -§ и Лх(*) = -|.A) *±*-%к
Пример 5.13. Дана динамическая система, описываемая уравнениями
Х1(к + 1) = аХ1(к) + Х2(к),
Х2(к + 1) = ЬХ2(к) + С(к),
где входной сигнал С(к) задан математическим ожиданием т^(к) = 0 и
ковариационной функцией Л^(/,Л = 8('-Д начальное состояние Х0 характеризуется
математическим ожиданием щ = и ковариационной матрицей Во = .
Требуется найти ковариационную матрицу в установившемся режиме при
? В данной задаче А = Г М, Я = К 1. **(*) = 1.
Найдем корни характеристического уравнения:
\а-Х 1
\А-\Е\ =
0 Ь-ХГ°9 <«-Х)(*-Х)-0, А,!-*, Х2=А.
Условие устойчивости системы (см. разд., 5.4.2) имеет вид:
|Х!|-|в|<1, |Х2|-|*|<1.
Запишем уравнение E.25):
Й&8 *:Г,Н К « 3-ГО-* * —
или в координатной форме
ЛХп(А: + 1) = а2ЛХ11(А;) + 2аЛх.2(А:) + ЛХ22(А:), ЛХп@) = 0,
ЯХп(к + 1) = аЬЯХп(к) + ЬЯХ22(к), ЛХ12@) = 0,
ь2
Переходя к пределу при к -* +оо, получаем систему уравнений,
описывающих установившийся режим:
КХ12(к + 1) = Ь*КХп(к) + 1, ЛХ22@) = 0.
пределу при к -* +оо, получаем си
йся режим:
^(+«>) = ^хп(+«>) + 2лЛХп(+оо) + /гхм(+оо),
ях12(+«>) = <'ЬКХ12(+<») + Ь
ЯХп(+со) = Ь2ЯХ22(+^) + 1.
1Х*И К ' ~ " "*11 ^ ' т *"* "*12 Ч ' Т *22
Отсюда
1-62' х'2' ;"A-*2)A-в*)' *|Л '~A-«2)A-А2)<1-«*)'
247

5.4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ
ДИСКРЕТНЫХ СИСТЕМ
5.4.1. Анализ устойчивости одномерных систем
ПОСТАНОВКА ЗАДАЧИ
Пусть заданы:
а) одномерная линейная дискретная стационарная динамическая система,
поведение которой описывается разностным уравнением:
апх(к + п) + ап_1х(к + п-1)+... + а0х(к) = Ьт8(к + т)+
к = 0,1,2,... ;
б) начальные условия:
х@) = х0, *A) = *!,..., х(п-1)=хп_1.
Линейная дискретная стационарная система называется асимптотически
устойчивой, если при ненулевых ограниченных начальных условиях свободное
движение хс(к) (при &(к) = 0) ограничено при всех к = 0,1,2,... и выполняется
условие хс(к)^0 при к->+со .
Требуется исследовать, является ли динамическая система асимптотически
устойчивой.
КРИТЕРИЙ УСТОЙЧИВОСТИ
Для асимптотической устойчивости линейной одномерной стационарной
дискретной динамической системы необходимо и достаточно, чтобы корни X;
характеристического уравнения
апХп + ап^Хп~1 +... + До = 0 E.37)
были по модулю меньше единицы: |Х/1 < 1; / = 1,..., п.
Это означает, что все корни должны располагаться внутри круга
единичного радиуса с центром в начале координат (рис. 5.4).
248

4 \тХ
Рис. 5.4
КеХ
Замечание. Нахождение корней характеристического уравнения, как
правило, связано с большими вычислительными трудностями. Как и для
непрерывных динамических систем, в качестве косвенного критерия устойчивости
можно использовать критерий Рауса-Гурвица (см. разд. 1.4.1). Для этого следует
выполнить конформное отображение плоскости комплексного переменного X на
плоскость комплексного переменного IV таким образом, чтобы окружность
|х| = 1 перешла в мнимую ось, а внутренность .круга |х| < 1 отобразилась на левую
полуплоскость Яеи><0. Такое отображение выполняется с помощью дробно-
линейного преобразования: X = .
1-м>
Пример 5.14. Исследовать устойчивость дискретных динамических систем,
описываемых уравнениями:
а) Ъх(к + 1)+ х{к) = *(*) ; б) 4х(к +1)-х(к) = *(*) ;
в) х(к + 1)+ 2х(к) = &(к) ; г) х(к + 2)+ 2х(к + 1)+ х(к) = $(*) ;
д) х(к + 2)+±х(к) = 8(к) ; е) х(к + 2)-х(к + 1)+±-х(к)= *(*) ;
4 2
ж) х(к + 3)-1-х(к + 2)+-х(к)=8(к); з)х(к + 3)+2х(к + 2)+2х(к + 1)= $(*).
2 4
? а) Характеристическое уравнение ЗХ + 1 = 0 имеет корень Х\
Г,
лежащий внутри круга единичного радиуса, так как ^^ = - < 1. Согласно критерию
система асимптотически устойчива.
249

б) Характеристическое уравнение 4Х -1 = О имеет корень X! =—, лежащий
внутри круга единичного радиуса , так как |Х}| = — <1. Согласно критерию сие-
4
тема асимптотически устойчива.
в) Характеристическое уравнение X + 2 = 0 имеет корень X! = -2, не
лежащий внутри круга единичного радиуса, так как \кх\ = 2 > 1. Согласно критерию
система не является асимптотически устойчивой.
г) Характеристическое уравнение X2 + 2Х +1 = 0 имеет корни X! = Х2 = -1,
лежащие на границе круга единичного радиуса. Согласно критерию система не
является асимптотически устойчивой.
д) Характеристическое уравнение X2 +—= О имеет корни Х1 = —, Х2 = -—,
4 2 2
лежащие внутри круга единичного радиуса. Согласно критерию система является
асимптотически устойчивой.
е) Характеристическое уравнение Х2-Х + —= 0 имеет корни X! =—A + /),
Х2=—A-/), лежащие внутри круга единичного радиуса, так как
/г
\^\\ = |^2| = "Г" < 1 • Следовательно, система асимптотически устойчивая.
ж) Характеристическое уравнение X3—гХ2+-- = 0 имеет корни X! = —-,
2 4 2
^2 ="гA + 0» *»з =тA-0» лежащие внутри круга единичного радиуса, так как
1 45,
\Ь\\ = Т < Ъ |*2| = |^з| = "Г" < 1 • Система асимптотически устойчивая.
Решим задачу с помощью критерия Рауса-Гурвица. Для этого сделаем
замену X = в характеристическом уравнении:
Г1 + мЛ3 1Г1 + мЛ2 1 Л
250

1 + Зи> + Зиг + иг — + т^ -т^ + т^ +т~т^ + т^ ~т^
2 2
4 4
4
а-*»3
= 0.
5 3 17 2 7 3 л
В результате получим — иг +—иг +—и»+— = 0 или после умножения на 4 :
4 4 4 4
5и>3+17и>2+7и> + 3 = 0.
Составим матрицу и вычислим угловые миноры:
Г17 3 (Г|
5 7 0
0 17 3
, Л1=17>0, Д2=104>0, А3 = 3104 = 312>0.
Так как все угловые миноры положительны, система асимптотически
устойчивая.
з) Характеристическое уравнение X3 + 2Х2 + 2Х = 0 имеет корни ^1=0,
Х2 = -1 + /, Х3 = -1 -/, первый лежит внутри круга единичного радиуса, а Х2, Х3
лежат вне круга, так как |х2| = |х3| = 42 > 1. Согласно критерию система не
является асимптотически устойчивой.
Решим задачу с помощью критерия Рауса-Гурвица. Для этого сделаем
1 + и>
замену X = в характеристическом уравнении:
Г1-K+2Г1-J+21-=о,
и-*7 \1-*>) 1-й*
1 + Зи> + Зи>2 + и»3 + 2 - 2и>2 + 2и> - 2и>3 + 2 - 2и> - 2и>2 + 2и>3
A-й»K
В результате получим и»3 - и>2 + Зи> + 5 = 0 .
Составим матрицу и вычислим угловые миноры:
= 0.
Г-1 5 0^
1 3 0
0-15
А! =-1<0, А2=-8<0, Д3=-40<0.
Так как не все угловые миноры положительны (они отрицательны),
система не является асимптотически устойчивой. ¦
251

Пример 5.15. Найти свободное движение и исследовать устойчивость
дискретной системы
х(к + 2) - Ъх(к +1) - 10х(к) = 0, х@) = 3, хA) = -1.
П Характеристическое уравнение X2 - ЗА, -10 = 0 имеет действительные,
различные корни: X! = -2, Х2 = 5. Согласно E.5) имеем
х(*) = С,(-2)*+С25*.
Найдем постоянные С{ и С2 из начальных условий
х@) = С1+С2=3,
хA) = -2С1+5С2=-1.
Отсюда С1=—-, С2=— и свободное движение
7 7
^(А)=^(-2)*+|5*=И(-2)*+15*+1.
Так как \Х\\ > 1, |Х2| > 1, согласно критерию система не является
асимптотически устойчивой. ¦
Пример 5.16. Найти свободное движение и исследовать устойчивость
дискретной системы
х(к + 2)-Лх(к + \) + х(к) = 0, *@)=1,хA)=^.
? Характеристическое уравнение Х2-^ЗХ + 1 = 0 имеет пару комплексных
4Ъ 1
сопряженных корней Х^2 = — ±--1. Поэтому согласно формуле E.6) получаем
/г «
общее решение в виде х(к) = Сх соз-^А; + С2 зт-^к, поскольку а = —, р = —,
6 6 2 2
1 ¦ Я *
г = 1, <р = агс*8— = ^.
Найдем постоянные Сх и С2 из начальных условий
*@) = с1=±,
хA)=—С1+-С2=т.
1 41
Отсюда С* = —, С2 = —- и свободное движение
2 2
1 я, УЗ. я, . п п, п . п, . я(# +1)
-соз-гА: +—ЯП—/: = яп— соз—/: + соз— зт—Л: = зш—*--—-.
2626 66 66 6
Так как [х^ = |х2| = 1, согласно критерию система не является
асимптотически устойчивой.*!
252

5.4.2. Анализ устойчивости многомерных систем
ПОСТАНОВКА ЗАДАЧИ
Пусть заданы:
а) многомерная линейная дискретная стационарная динамическая система,
поведение которой описывается уравнением состояния:
х(к + 1) = Ах(к)+В8(к), * = 0,1,...;
б) начальное условие:
*@) = *о,
где *о - начальное состояние.
Многомерная линейная стационарная дискретная динамическая система
называется асимптотически устойчивой, если ее свободное движение хс(к),
к = 0,1,2,... (при &(к)*0) ограничено при ограниченных начальных состояниях
х0 и выполняется условие
б *с(*)|| -* 0 Щ>и к -> -ко ,
где |дс| —какая-либо норма вектора х, например, Цх|| = Л 2]х/2 .
Требуется исследовать, является ли динамическая система асимптотически
устойчивой.
КРИТЕРИЙ УСТОЙЧИВОСТИ
Для асимптотической устойчивости многомерной линейной стационарной
дискретной динамической системы необходимо и достаточно, чтобы корни X,
характеристического уравнения
й&(А-ХЕ) = 0 E.38)
были по модулю меньше единицы: |Х;|<1, /=1,...,л.
Это означает, что все корни Х{ должны располагаться внутри круга
единичного радиуса с центром в начале координат (см. рис. 5.4).
253

Очевидно, как и для одномерных динамических систем, для анализа
устойчивости многомерных систем можно применять критерий Рауса-Гурвица.
Пример 5.17. Исследовать устойчивость дискретных динамических систем,
описываемых уравнениями состояния:
а)х,(* + 1) = -дс2(*)+й(*).
х2(к + 1) = *,(*)+ 82(к);
б)х1(к + 1)=-±х2(к)+г1{к))
х2(к + 1)=Х1(к)-х2(к)-81(к);
в)х1(к + 1)=х1(к)+2х2(к),
х2(к + 1) = 4Х1{к)+Зх2(к)+ц{к).
О а) Здесь А = . Найдем корни характеристического уравнения
-С о')-
де1(Л-ХЕ) = 0: = 0, или X2 +1 = 0. Отсюда ХХ =/, Х2 = -/. Так как
1^11 = |^г|*= 1 > те- корни не лежат внутри круга единичного радиуса (они лежат на
его границе), то система не является асимптотически устойчивой.
б) Здесь А =
и -О
Найдем корни характеристического уравнения
1 -1-Х
= 0, или Х2+Х+- = 0. Отсюда X! = -(-1 + /), Х2 =-(-1-/). Так
как |Х1| = |х2| = — < 1, то система является асимптотически устойчивой.
] хш
Используем критерий Рауса-ГУрвица. Для этого сделаем замену X =
1-и>
П + иЛ2 1 + м> 1
в характеристическом уравнении: + + —= 0 . В результате получаем
\1-\у) 1-1? 2
\ + 2м + \у2 + 1-м>2 +--м> + -м>2 - -
=-2 2— = о или -г^2+>у + - = 0.
A-м>J 2 2
254

Составим матрицу и вычислим угловые миноры:
1^
, А1=1>0, А2=->0.
Так как все угловые миноры положительны, система асимптотически
устойчивая.
в) Здесь А = . Найдем корни характеристического уравнения
1 / ? = 0 или Х2-4Х-5 = 0.
Отсюда Х( =5, Х2 =-1. Так как корни не лежат внутри круга единичного
радиуса, система не является асимптотически устойчивой. ¦
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
5.1. Исследовать устойчивость дискретной системы, описываемой
разностным уравнением
х(к + 2)--х(к + 1) + -
п 4
A + п2)
{ * )
**) = *(*).
52. Исследовать устойчивость, найти свободное движение, вьшужденное
движение и выходной сигнал дискретной системы
х(к +1) + (л + 2)х(к) = «(к), х@) = л, 8(к) = л к.
5.3. Исследовать устойчивость, найти свободное движение, вынужденное
движение и выходной сигнал дискретной системы
х(к + 2) - (л + 5) х(к +1) + Dл + 4) х(*) = *(*),
х@)
"й-
хA) = 3, 8(к) = 2.
5.4. Исследовать устойчивость, найти свободное движение, вынужденное
движение и выходной сигнал дискретной системы
х,(* + 1)=х2(*),
хг{к +1) = - Dл + 4) х, (к)+(л + 5) х2{к)+*(*);
Х*)-а*(*)-*»(*).
*1<0) = [|], х2@) = 3; *(*) = 2.
255

5.5. Исследовать устойчивость, найти свободное движение системы
х(к + 2) -х(к + 1) + х(к) = в(к),
х@) = 1,хA) = 2.
5.6. Исследовать устойчивость, найти свободное движение системы
х(к + 2) - Л х(к +1) + х(к) = $(*);
1 Л
*@)=^,хA)=^-.
5.7. Исследовать устойчивость, найти свободное движение системы
х(к + 2) - Ъх(к +1) - 10х(*) = *(*);
х@) = 3,хA) = -1.
5.8. Найти выходной сигнал дискретной системы
х(к + 2) + 4х(к + 1) + Зх(к) = г(к), *(*) = 1,
х@) = 1,хA) = 1.
5.9. Найти выходной сигнал дискретной системы
х(к + 2) - 5х(к +1) + 6х(*) = 8(к), *(*) = 2 • 4*,
х@)=2,хA)=1.
5.10. Найти выходной сигнал дискретной системы
х(к + 2)-4х(к + 1)+4х(к)=8(к), *(*) = 3*,
х@) = х0, х(\) = х1.
5.11. Найти выходной сигнал дискретной системы
х(к + 3)-Зх(к + 2) + Зх(к + 1)-х{к) = 8(к), ё(к) = 2к,
х@) = 0,хA) = 0,хB)=1.
5.12. Дана динамическая система, описываемая уравнением
*(* + 1) Л *(*) + <?(*), * = 0,1,...; Х@) = Х0,
где входной сигнал С(к) задан математическим ожиданием /Ид(/:) = 0 и
ковариационной функцией ^(/,У) = 5(/-У), начальное состояние характеризуется
математическим ожиданием щ = 0 и ковариацией Я0 = 0.
Требуется найти законы изменения математического ожидания тх(к),
ковариационной матрицы Ях(к) и ковариационную функцию Ях(/,./), а также
статистические характеристики в установившемся режиме при к -> +оо.
256

Глава 6. ОПИСАНИЕ И АНАЛИЗ ДИСКРЕТНЫХ
ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ
2 -ПРЕОБРАЗОВАНИЯ
6.1. ОДНОМЕРНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ ПРИ
ДЕТЕРМИНИРОВАННЫХ ВОЗДЕЙСТВИЯХ
6.1.1. Описание сигналов и систем
1. Описание сигналов. Для описания сигналов и систем будем использовать
I -преобразование. Приведем основные определения [39].
Оригиналом называется последовательность {/(к), к = 0,1,...},
удовлетворяющая условию | /{к)\ < Меак, где М и о — положительные постоянные (рис.
6.1).
/@)
/A)
/B)
/D)
/О) I /E)
Рис. 6.1
Изображением последовательности {/(к), к = 0,1,...} называется функция
Р(%) комплексного переменного г , определяемая равенством
*Ю-2
т
F.1)
*=о г
Совокупность всех оригиналов называется пространством оригиналов,
а совокупность всех изображений — пространством изображений.
Переход F.1), определяющий изображение Р{{) по оригиналу
{/(&), А: = ОД,...}, называется 2-преобразованием:
*Ю-2Ш.
F.2)
Оригинал находится по изображению с помощью обратного
2-преобразования:
/{к) = 2-1[Р{г)\ = ±г§РAIк-Ч1, * = 0,1,... ,
F.3)
ВДв С— контур, внутри которого лежат все особые точки функции Р(г).
257

СВОЙСТВА Я-ПРЕОБРАЗОВАНИЯ
Пусть /•(*) = 2Г[/(*)].
1. Линейность. Для любых постоянных с,-, / = 1,...,/и, справедливо
г[с1/1(А:)+...+ ст/т(А:)] = с1/1(^)+...+ ст^т(г),
F.4)
ще {/!(*), к = 0,1,...},...,{/т(А:), * = 0,1,...} -оригиналы, а /1(^),...,^т(г) - их
изображения.
2. Запаздывание (формула запаздывания):
2[/{к-\)]=1-1Р{1),
2{/(к-п)] = г-пР{г), /1 = 1,2,...,
где /(к - я) = 0 при к - п < 0 (рис. 6.2).
F.5)
F.6)
/
4
2"
0
1
/<*)
1 :
г :
1.
5 4 *
/
4
2
0
к
1 1
Г(*-1)
1]
> 3 4
——*
1
4
2
о!
1
а*
4
п
-п)
/1 + 1
А:
Рис. 6.2
3. Опережение (формула опережения):
*[/(* + !)]=* И*)-/@)],
*[/(* + ")]=*М*)- г"/@)- г"-7A) - ••• - г/(л -1)
4. Дифференцирование изображения:
2[к/(к)]—г
4Р_
F.7)
F.8)
F.9)
5. Умножение изображений. Сверткой оригиналов {/(к), А = 0,1,...} и
{$(&), А: = 0Д,...} называется сумма ^/(/)-$(А:-/). Свертке оригиналов соответ-
1=0
ствует произведение изображений:
258

№/®-&-Л-*<*)¦<№, F.10)
и-о
где <?(*)= 4*(*)]-
6. Теоремы о предельных значениях. Если Р{г) = 2\/(к)], то
/A)=ШпгИг)-/@)], F.11)
/B)= Нтг'^Ь/Ю-ЛО-г] ИТ-Д-
где I стремится к бесконечности вдоль произвольного пути.
Если Шп /(к) существует, то
Шп /(к) = Шп {г - \)Р{г) . F.12)
*-»+«
*-м-со г_>1
2. Описание систем. Рассматривается одномерная линейная дискретная
стационарная система, описываемая разностным уравнением
ап х{к + л)+ан_г х(* + п -1)+... + д0 *(*) = F 13)
= ^т^(А: + т)+Ат_1^(А: + т-1)+... + ^)^(/:), /: = 0,1, 2,...,
с начальными условиями
д:@) = х0, хA) = хь..., х(/1-1) = хл_ь F.14)
где ал,...,ао; Ьт,...,Ь^ - заданные постоянные коэффициенты; $(/:) — входной
сигнал.
Передаточной функцией 1У(%) линейной стационарной дискретной
системы называется функция
у(е)- ^+- + дь FЛ5)
Передаточная функция является функцией комплексного переменного г.
При решении задач анализа дискретных систем предполагается, что
сигналы принадлежат пространству оригиналов. Для нахождения их изображений и
Решения обратной задачи используется табл. 6.1.
259

Таблица 6.1
[73Г
\Г~
12
3
4
15
6
7
8
9
10
/<*)
1
(-0*
*
к2
как~1
С?ак
ак
(к + 1)ок
/<0) = 0,/(*)=Д
/@) = 0,/(*)=-^-
к
т
г
1-1
г
г
(г-1J
г(г+0
(г-1K
г
(г-*J
атг
(г-а)т+1
г
г-а
гг
(г-вJ
ЧЬ
1
№
и
12
13
14
15
16
17
18
19
20
/(*)
к(к-\)
2
к(к-1)--(к-т+1)
япДр
совАр
ак$тк$
ак совк$
-0*яп(*-1)Р
д*$Ь*р
аксЫф
т 1
а |
г 1
(г-1?
7. 1
<*-1)т+1
гзшр 1
г2-2гсозр + 1 1
г(г-созр)
г2-2гсс$р + 1
огзтр 1
22-2агсо$р + а2
г (г-асовр)
г2-2агс<кр + а2
2 8ш р (* - 2асо51Р) 1
12-2а*со$р + а2
аг&Ьр 1
г2-2агсЬр + д2 1
г(г-асьр)
*2-2агсЬр + а2
260

6.1.2. Связь вход-выход
Предположим, что входной сигнал х(к),к = 0,1,... и выходной сигнал
х(к), к » 0,1,... принадлежат пространству оригиналов: СA)-2\^к)]9Х(г) = 2[х(к)].
Для решения поставленной задачи применим 2 -преобразование к левой и
правой частям уравнения F.13) с учетом формулы опережения F.8):
2[х(к + п)] = 1пХ&)-1пх0-...-гхн_19
2и{к^т)]^1тО{г)-1т^)-...-г^(т-\).
Применяя свойство линейности, получаем
[ап1п +... + а0)х&)-х0(ап1п +ап_хг*-1 +... + д^)-
-*@)к*да +^_1гщ-1+...+^]-^)^-и... + ^]-...-^-1I^.
Обозначим
Из равенства 2)(гЩг) = АГ(г)G(г) + 2)я(г)-2)^(г) находим изображение
выходного сигнала:
Ще функция ЩА = --^2. = "Е* +- + 0) является передаточной функцией.
Искомый выходной сигнал х(А:) определяется с помощью обратного
2 -преобразования.
Замечание. Первое слагаемое в F.16) описывает свободное движение
(при ненулевых начальных условиях и нулевом входном сигнале), а второе и
тРетье - вынужденное (под действием входного сигнала при нулевых начальных
Условиях). Если начальные условия нулевые, выходной сигнал определяется
вынужденным движением. При т = 0 функция 2ЭДО=0.
261

6.1.3. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть заданы:
а) входной сигнал %(к), к = ОД,...;
б) одномерная линейная дискретная стационарная динамическая система
(рис. 6.3), поведение которой описывается разностным уравнением
апх(к + п)+ап_хх(к + п -1)+... + а0х(к) =
= Ьт8(к + т)+Ьт_18(к + т-1)+... + Ь08(к), * = 0Д,2,...,
где ал,...,ао; Ат,...,й& - заданные коэффициенты; л^/и;
в) начальные условия:
х@)=х0, хA)=х1,...,д:(/1-1) = д:11_1.
Требуется найти выходной сигнал х(к).
8(к)
апх(к + п)+... + аох(к) = Ьт&{к + т)+... + Ьоф)
х(к)
Входной Выходной
сигнал Рис. 6.3 сигнал
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти изображение входного сигнала:
2. Определить передаточную функцию
апгп +...+Оо
и функции
2)(г)=вяг"+...+ао;
Я#(г)=*о(влг'1 +ол_,г'1 +...+а1г)+>:,(влг" +...+а2г)+- + *и-1вяг;
^(г)=*@)кгм +Ьт_1га-1 +•••+«**]+«Мк*"-1 +...+**]+...+*(«-!)*„*.
262

3. Найти изображение выходного сигнала:
ад=^иг).<*>-3$.
Хе{1) *«,(*)
4. Найти выходной сигнал, используя обратное ^-преобразование:
х(к) = Г^ад] = хс(к) + хвын(к).
Пример 6.1. Найти реакцию дискретной динамической системы,
описываемой уравнением х(к + 1)-2х(к) = 2^(к)9 на входной сигнал &{к) = к при
х@) = х0=0.
П 1. Найдем изображение входного сигнала по формуле 3 из табл. 6.1:
функци
VIJ'
2. Определим передаточную функцию:
2
*-2'
Поскольку х0=0ит = 0,то 2)#(*) = 0 и 08{г) = 0.
3. Найдем 2 -преобразование выходного сигнала:
*(*) = Т^-7-^=2.
г-2 (г_1J [г-2 (г_1J «-1]
4. Найдем выходной сигнал по формулам 1, 3, 7 из табл. 6.1 :
х(*)=2.[2*-*-1]. ¦
Пример 6.2. Найти реакцию дискретной динамической системы,
описываемой уравнением х(к + 2)-2х(к + 1)+х(к)=28(к), на входной сигнал &(к)=2к
при х@)=хA) = 0.
П 1. Найдем изображение входного сигнала по формуле 7 из табл. 6.1:
2. Определим передаточную функцию:
и^(г)=—1 -2—.
г2-2г + 1 (г-1J
263

Поскольку х0 = XI = 0 и т = 0, то Ви(г) = 0 и />г(г) = 0.
3. Найдем 2 -преобразование выходного сигнала:
2г г
*(*)=
(г-1J *-2'
4. Найдем обратное 2 -преобразование путем деления числителя на
знаменатель:
*(*>-7 §7 Т = -1 Г = 2*-2+8*-3 + 22*-4+... .
(г-^-г) г3-4г2+5*-2
С учетом F.1) имеем х@) = хA) = 0, хB) = 2, хC) = 8, хD) = 22, .... ¦
Пример 6.3. Найти реакцию дискретной динамической системы,
описываемой уравнением х(к + 2)-5х(к + \)+6х(к)= ^(к), на входной сигнал &(к) = 1
при начальных условиях х@) = 1, х(\) = 2.
П 1. Найдем изображение входного сигнала:
2. Определим передаточную функцию:
-Г-5* + 6
и функцию
Д#(г) = х0(*2*2+Я1*)+*1*2* = 1A -*2-5*)+2.1-* = *2-3*.
Поскольку т = О, то В8(%) = 0.
3. Найдем 2 -преобразование выходного сигнала:
12-Ът. . 1 г
ХМ-
г2-5* + 6 ^2-5г + 6 г-1
г I г | 1 _г 5_+1 *
г-2 (г-1)(г-2)и-3) *-2 2^-1 г-2 2г-3/
Хю *™о)
4. Найдем выходной сигнал по формулам 1, 3, 7 из табл. 6.1 :
х(к)= 2к +--2* +-3* =^ + 1-3^. ¦
&) ^ , 2 , 2 2
264

Пример 6.4. Найти реакцию дискретной динамической системы,
описываемой уравнением х{к + 2) - Зх(к +1) + 2х(к) = 2&(к +1) - 2&(к), на входной
сигнал &(к) = \ ' , ~ при начальных условиях х@) = хA) = 0.
П 1. Найдем изображение входного сигнала. По определению получаем
<?(*) = !.
2. Определим передаточную функцию:
п-к) 2г~2 - 2(г~° —
^ г2-Зг + 2 (*-1)(«-2) 1-2
и функции
Л(г) = г2-3* + 2; ^(г) = *@)й,г = 2г, ля(г) = 0.
3. Найдем ^-преобразование выходного сигнала:
«-2 *2-3* + 2
4. Найдем выходной сигнал.
Представим Х(г) в виде
Отсюда по формулам F.5), 1 и 7 из табл. 6.1 получаем
х(*)=2.2*-2-2*+2 = 2-2*, к*\
и х@) = 0 , так как согласно F.11) хF)= ]ип Х(%) = 0. Окончательный ответ:
х(к) = 2-2к9к>0.т
Пример 6.5. Найти реакцию дискретной динамической системы,
описываемой уравнением х(к + 2) - 5х(к +1) + 6х(к) = &(к +1) - 3&(к), на входной сигнал
&{к) ш 1, при начальных условиях х@) = 1, хA) = 2.
? 1. Найдем изображение входного сигнала:
_1
I-
2. Определим передаточную функцию:
в{г)=2[1)=^-х.
V -51 + 6 г-2
и Функции
265

/>(*) = г2 - 5* + 6, Я# (г) = г2 - Зг (см. пример 6.3),
Лж(*)-*@)А1* = Ы-« = *.
3. Найдем 2^ -преобразование выходного сигнала:
1-2 1-2 1-Х 1-2 г-Ъ'
4. Найдем выходной сигнал по формулам 1 и 7 из табл. 6.1 :
х(к)= 2* + 3*-1 + 2*-3*=3-2*-1-3*. ¦
Пример б.б. Найти реакцию дискретной динамической системы,
описываемой уравнением х(к + 2)-5х(к + 1)+6х{к) = ^(к + 2)-3^(к + 1)+2^(к)9 на
входной сигнал &(к) = 1, при начальных условиях х@) = 1, хA) = 2.
П 1. Найдем изображение входного сигнала:
1-1
2. Определим передаточную функцию:
И;) ^-Зг + 2 (г-1Щ-2) ;-1
^г' г*_5г+6 (г_2)(«-з) г-3'
^>я(г)=г2-3г (см. пример 6.3), 2)(г)=г2-5г+6,
Л«(*)=гф)^2 + *,* ]+ *A)*гг = г2 - Зг+г = г2 - 2?.
3. Найдем 2 -преобразование выходного сигнала:
г | г г ^ г
г-2 г-З г-3 г-2'
4. Найдем выходной сигнал: х(к) = 2*. ¦
266

6.2. МНОГОМЕРНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
ПРИ ДЕТЕРМИНИРОВАННЫХ ВОЗДЕЙСТВИЯХ
6.2.1. Описание сигналов и систем
1. Описание сигналов. Используется г -преобразование вектор-функции
%(к), зависящей от дискретного времени:
<?(*) = *[*(*)],
где &(к) — г- мерный сигнал; 0(к) - г-мерный вектор его изображений.
2. Описание систем. Рассмотрим линейные стационарные многомерные
системы, описываемые уравнениями состояния и выхода:
х(к + \) = Ах(к) + В8(к)9к = 0,\,...; х@) = х0; F.17)
у{к) = Сх{к). F.18)
Аналогично непрерывным системам вводятся в рассмотрение дискретные
передаточные функции по состоянию и выходу.
Передаточной функцией IVх (г) стационарной линейной многомерной
системы по состоянию называется функция
Гх&) = (гЕ-А)-1В. F.19)
Передаточной функцией IV у(?) стационарной линейной многомерной
системы по выходу называется функция
ЦГу&) = СAЕ-А)-1В = СЦ'х{!). F.20)
Передаточные функции IVх (г) и IVу (г) представляются матрицами размера
(л х г), (/и х г) соответственно, элементы которых являются функциями
комплексного переменного г..
6.2.2. Связи вход-состояние и вход-выход
Предположим, что входной и выходной сигналы, а также закон изменения
вектора состояния принадлежат пространству оригиналов.
Применим к левой и правой частям уравнения состояния F.17)
^-преобразование с учетом формулы опережения F.7) и обозначений
*(г) = 4х(*)], <?(*) = *[*(*)]:
1Х{г)-1Хъ=АХA)+ВО{1).
267

Тогда получим
Выражая ЛГ(г), получаем
ХA) = (гЕ-А)-11ХпЦгЕ-АГ1В6{1)9 F.21)
где Е - единичная матрица.
Из уравнения выхода F.18) следует У (г) = С Х(%) , т.е.
У(*) = С(&-АГхгъ. + С(гВ-АГхВ.(К$я. F.22)
тюУ{г) = 2\у{к)].
Первые слагаемые в полученных связях вход-состояние F.21) и вход-выход
F.22) описывают свободное движение (при ненулевых начальных условиях и
нулевом входном сигнале), а вторые - вынужденное (под действием входного
сигнала при нулевых начальных условиях).
6.2.3. Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть заданы:
[*Щ
а) входной сигнал &(к) = I I;
б) многомерная линейная дискретная стационарная система (рис. 6.4),
поведение которой описывается уравнением состояния
х{к + \)=Ах(к)+Вз(к)
и уравнением выхода
у(к) = Сх(к),
где х— л-мерный вектор состояния, у — т-мерный вектор выхода; А,В,С~
матрицы размера (яхл), (пхг), (ихп) соответственно;
в) начальное условие
*@) = хо,
где хо = {хю,...9хмУ ~ начальное состояние.
Требуется найти законы изменения векторов состояния х(к) и выхода
№¦
268

*0
$(к)
Входной
сигнал
1
Гх{к + \) = Ах(к)+Вг(к)
х(к + 1)
Задержка
х(к)
»
у(д=с4к)\
Вектор
состояния
Рис. 6.4
У{к)
Выходной
сигнал
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти изображение входного сигнала:
<?(*) = 2Ш].
2. Найти матрицы (гЕ-А)'1, СAЕ-А)"{ и передаточные функции:
ЯГ*Ь)шЬЕ-АТ1В, 1УУ&) = СAЕ-А)-1В.
3. Определить изображение законов изменения векторов состояния
и выхода:
УA)=С(гЕ-АТ11Ч+\УУAУбA) .
УМ
Г«ш(Э
4. Найти законы изменения векторов состояния и выхода, используя
обратное ^-преобразование:
х(к)=2-{[Хк)) = хс(к) + хвын(к),
Лк)=2-1[УЬ)] = ус(к) + Упш(к).
Пример 6.7. Найти законы изменения векторов состояния и выхода
многомерной динамической системы:
при входном сигнале в{к) « 3* и начальных условиях х8 (ЭД **$. х2 @) » 0.
269

П 1. Найдем изображение входного сигнала:
2. Найдем передаточные функции. Так как А = \ , В = \ 1
С = A 1), Хо= 0,то
да:
""«-«--^-тЫл «"-X1.)-
3. Определим изображение законов изменения векторов состояния и выхо-
+ Ь-2)Ь
=&)-
з*2
(г + 1)(г-2)т(г-2)(г-3)
6* г
I, (г+1)(г-2) (г-2)(г-зу
4. Найдем законы изменения векторов состояния и выхода:

г+1 г-г г-г *-з
2—ь—2—5-+- г
г+1
г-2 г-1 г-Ъ )
Для дробей г—— и г нужно использовать формулы 2 , 7 из табл. 6.1
~ г+1 г-2
и, в силу наличия множителя г, формулу F.7). Получаем
I, * + 1 *-2 *-3 )
Отсюда по формулам F.7) и 7 из табл. 6.1 имеем
хШ_Г-(-1)*+1+2*+1-2*+зП_[ (-1)*+2*+3* ] Я*)=3.(-1)*
^ Ч 2-(-1)*-2*-3* ] [2.<-1)*-2*-3*;' ^М1Г'
Результат совпадает с полученным в примере 5.9. ¦
Пример 6.8. Найти законы изменения векторов состояния и выхода
многомерной динамической системы:
х1{к + 1) = 4х1(к)-х2(к)+8(к),
х2(к + 1) = Х1(к)+2х2(к),
у(к) = -Х1{к)+х2(к)
3 9
при входном сигаале &{к)= 1 и начальных условиях ^(О)* —, х2@) =—.
4 4
? 1. Найдем изображение входного сигнала:
2. Найдем передаточные функции. Так как Л = к , Я = I,
(*" 1 0> *о = о > получаем
271

-^[-Ь-з) и-з,]-^-! 0:
3. Определим изображение законов изменения векторов состояния и
выхода:
™-1М'? .-«)«
4
9
(г-зJ
2 _зз
и* а)
Ну
1 (г-2\ г
1 )г-1
(г-зJ(г-1)
*Дг)
(.(М^^
*«.»(«)
з г2
15
4 (г-3J 4 (г_зJ
9 г2 33 г
И (г-3J 4 (г_3)Ч
2г
(г-З)^-!) (г-ЗJ^-!)
г-з
4
и;
г 1 ^ г _з г г
I г-ъ)г-\ 2^-2 (г-1)(г-3)*
4. Найдем законы изменения векторов состояния и выхода.
Воспользуемся разложениями:
1
1111
+ —•
(*-1)(г-3) 2 1-Х 2 1-У
1111 11
¦ + Т-- Г + -Г-
(*-3J(*-1) 4 *-3 2 (г-3J 4 1-Х
272

Тогда
*(г) =
Г 1 1 * , * '2
Гз <2 15 г ]
4 (г-зJ 4 (г-зJ
9 г2 33 г
[4 (г-3J 4 (г-зJ]
. 1 . г . 1 г
1 4'**-з" 2 (г-зJ  "«-Г 2 г-3
[ 4г-з 2'(г_зJ 4*г-
+
* 1 _5_1
(г-3J 2 г-1
*«.<«>
1' 2 г-3 2 г-1 2 г-3'
г-з 2 г-1 2 г-
По формулам 1, 7, 8 из табл. 6.1 и F.7) получаем
*(*)=
<1(* + 1)з*-^*3*-^
2^+^-^аз*-1
И 4 .
Г-^3**1 +|(*+1>з*+Н3* -*3* -т!
_13*+1*з*-,+1
4 2 4
Aкгк Дз* -4*з* -^з* Д*з* Дз* -1 Дз* -±з*1
4 44 42 242 3'
4з* +±*з* +±-Д*з* Дз* -±1*з*
4 6 4 4 4 4
Г з*4м*-1 Л
2.3*4*3*4,
3 А)
я*)-тз*44з*-э*4-
2 2
Результат
совпадает с полученным в примере 5.10.
273

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
6.1. Используя 2-преобразование, найти свободное движение,
вынужденное движение и выходной сигнал дискретной системы
х(к + 1) + (п + 2)х(к) = г(к), *@) = л, &(к) = пк.
6.2. Используя 2-преобразование, найти свободное движение,
вынужденное движение и выходной сигнал дискретной системы
х(к + 2)-(п + 5)х(к + 1) + Dп + 4)х(к) = 8(Ь), х@) = Г^1, хA) = 3, *(*) = 2.
6.3. Используя 2-преобразование, найти свободное движение,
вынужденное движение и выходной сигнал дискретной системы
х1(к + \)=х2(к)9 *1@) = [|], Лк) = Х1(к)-х2(к),
Хг{к + 1) = -Dп + 4)Х1(к)+(п + 5)х2{к)+8(к); х2@) = 3, *(*) = 2.
6.4. Используя 2-преобразование, найти свободное движение системы
х(к + 2)-х(к + 1) + х(к) = 8(к), х@) = 1, хA) = 2.
6.5. Используя 2-преобразование, найти свободное движение системы
х(к + 2) - Дх(к +1) + х(к) = *(*); х@) = ±, хA) = ^.
6.6. Используя 2-преобразование, найти свободное движение системы
х(к + 2) - Зх(* +1) - 10х(*) = &(к); х@) = 3, хA) = -1.
6.7. Используя 2-преобразование, найти выходной сигнал системы
х(к + 2) + 4х(к + 1) + Зх(к) = х(к), х@) = 1, хA) = 1, *(*) = 1.
6.8. Используя 2-преобразование, найти выходной сигнал системы
х(к + 2)-5х(к + 1)+6х{к) = в(к), х@)=2, хA)=1, #) = 2.4*.
6.9. Используя 2-преобразование, найти выходной сигнал системы
х(к + 2)-4х(к + \)+4х{к) = 2(к)> х@)=х0, хA)=хь *(*) = 3*,
6.10. Используя 2-преобразование, найти выходной сигнал системы
х(к + 3)- Зх(* + 2)+ Зх(* + 1)- х(к) = *(*), г(к) = 2к,
х@) = 0,хA) = 0,хB)=1.
274

Часть П. НЕЛИНЕЙНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Глава 7. ФОРМЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ
НЕЛИНЕЙНЫХ СИСТЕМ УПРАВЛЕНИЯ
7.1. ОПИСАНИЕ НЕЛИНЕЙНЫХ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫМИ
УРАВНЕНИЯМИ
Для решения задач анализа и синтеза системы управления прежде всего
необходимо построить ее математическую модель, которая характеризует связь
выходных сигналов системы, описывающих поведение системы, с входными
сигналами, отражающими приложенные к системе воздействия. В системах
управления движением, как правило, выходными сигналами являются изменяющиеся
во времени координаты пространственного положения объекта управления
(обобщенные координаты), а также компоненты вектора скорости движения
(обобщенные скорости). Входные сигналы порождаются действующими на
объект управляющими и возмущающими силами.
Для описания поведения нелинейных систем используются общие теоремы
динамики или уравнения Лагранжа второго рода. Преобразовав эти
дифференциальные уравнения второго порядка к системе уравнений первого порядка,
разрешенных относительно производных обобщенных координат и обобщенных
скоростей, получим уравнение движения системы управления:
^^ = /|Й*1@,...,хя@.А@,...,*«М), */('о) = *,о, |'-1,...,л, G.1)
где *!(/),...,х„@ — выходные сигналы; &\@,...,8тA) -~ входные сигналы
системы управления, /0 — момент начала движения, х/0 - начальные значения
выходных сигналов.
Вектор-функцию х(/) = (хх (/),..., х„ A))Т, удовлетворяющую уравнениям
G.1), называют траекторией движения, а ее мгновенное значение при
фиксированном времени / — состоянием системы управления в данный момент времени.
Вектор-функцию #(/) = (^ (/),..., #т@)Г называют внешним воздействием
(возмущением, управлением). Поскольку система уравнений G.1) описывает
эволюцию состояния системы управления, то уравнения G.1) или их векторную
запись
*@ = Ж*@,*@), *(>о) = *<ъ G.2)
называют также уравнениями состояния системы управления.
Пример 7.1. Составить систему уравнений, описывающую процесс
торможения летательного аппарата (ЛА) в атмосфере планеты.
? Составим уравнения движения центра масс летательного аппарата,
совершающего пассивный полет в атмосфере Марса. В качестве координат
состояния аппарата примем скорость V и высоту Н полета, а также угол в наклона
траектории к линии местного горизонта (рис. 7.1).
275

На аппарат действуют следующие силы: X - аэродинамическое
сопротивление, Х = -схру25ЯА; У - подъемная сила, У = -суру2«УЛА; т^м - сила гра-
витационного притяжения планеты. Здесь р — плотность атмосферы; сХ9 су —
аэродинамические коэффициенты; 5да ~ характерная площадь ЛА; т — масса
ЛА; &м - ускорение свободного падения на Марсе.
Рис. 7.1
Согласно второму закону Ньютона
та- X + У + т%м.
Проецируя части этого уравнения на оси хил скоростной системы координат,
получаем касательное ах и нормальное а„ ускорения:
г
V у
щег - радиус кривизны траектории в точке А.
Учитывая, что угол поворота вектора скорости V относительно
фиксированного направления ОМ (рис. 7.1) равен разности 6-ф, а скорость ф враще-
V V
ния отрезка О А равна ——-сое 6, преобразовываем отношение —, выражая
скорость и радиус кривизны через дифференциал дуги Ж:
V Л$ й /л ч </е </ф А V л
— = . . (в-ф) = — 7^ = 6—-—-со$в.
г #Л* г/ йг йг Я + Н
Следовательно, для нормального ускорения будем иметь
. V2 У
а губ--—-созв = засове.
Я + Н т
276

Подставляя теперь в уравнение выражения для динамических сил, разрешаем их
относительно уи б. Добавляя к двум уравнениям кинематическую связь для к,
получаем
^ 1 2 ' . Л
7Гв~:гр х~** '
—г 1Р^ЛФ —+-^ъ> G3)
йк
Здесь ах — баллистический параметр аппарата, ах = * ЛА ; /^ — эффектив-
т
с«
ное аэродинамическое качество аппарата, А:^ « кб со8ус (А;5 = — "~ балансиро-
сх
вочное качество аппарата; ус — угол крена).
Ускорение свободного падения &м зависит от высоты полета:
где $0 ~" ускорение свободного падения на поверхности планеты (при к = 0), а
Я — радиус планеты.
Плотность атмосферы р также зависит от высоты. Однако в отличие от
ускорения &м(к) вид функции р = р(й) можно выбрать на основе имеющейся
информации об атмосфере по-разному. Для атмосферы Земли можно использовать
модель стандартной атмосферы. Для менее изученных планет можно принять
экспоненциальную модель:р(Л) = р0<Грл, в которой плотность р0 атмосферы на
поверхности планеты и показатель р уменьшения плотности с ростом высоты
выбираются исследователем.
Управлением (входным сигналом) в системе G.3) служит эффективное
аэродинамическое качество Д^С)» которое можно изменять, разворачивая аппарат
вдоль продольной оси (т.е. меняя угол крена ус), что, конечно, влияет на
траекторию полета.
Отметим в заключение, что в данной модели плоского движения
летательного аппарата планета считается сферической, вращение планеты и ее
атмосферы не учитывается.»
7.2. НЕЛИНЕЙНЫЕ СИСТЕМЫ С ОДНИМ НЕЛИНЕЙНЫМ
ЭЛЕМЕНТОМ
Для исследования линейных систем управления были разработаны удобные
Формы математического описания и эффективные методы анализа. Применение
этих методов для нелинейных систем общего вида невозможно. Однако среди
нелинейных систем можно выделить такой класс систем управления, для
которых разработанный аппарат применим с незначительными изменениями. Это
класс систем управления с одним нелинейным;
277

Структурные схемы замкнутой и разомкнутой системы с одним
нелинейным элементом (звеном) изображены на рис. 7.2,7.3, где # - входной сигнал,
х - выходной сигнал, а, г - промежуточные сигналы, /"(а), Р(&) -функции,
устанавливающие связь вход-выход нелинейного элемента, 1У(з) — передаточная
функция линейной части разомкнутой системы. Заметим, что входной сигнал
в общем случае может быть как детерминированным, так и случайным.
-Ф
/4°)
Щз)
т
Щв)
Рис. 7.2
Рис. 7.3
Нелинейный элемент задается функцией г = ?(<*) > которая значению а(/)
входного сигнала ставит в соответствие значение *(/) выходного сигнала звена:
г(/) = ^(а@). Встречаются также звенья, в которых значение ф) выходного
сигнала зависит не только от значения а(/) входного сигнала, но и от скорости
а@ его изменения. В этом случае нелинейный элемент задается функцией
* = /*(а,а).
Широкое применение на практике получили нелинейные элементы с
негладкой характеристикой Р(о). Приведем примеры типовых нелинейных звеньев.
1. Релейный элемент (рис. 7.4).
2. Релейный элемент с зоной нечувствительности (рис. 7.5).
3. Элемент с зоной нечувствительности (рис. 7.6).
4. Элемент с петлей гистерезиса (рис. 7.7) имеет зону неоднозначности, т.е.
выходной сигнал г(/) зависит при о(/) е[-Ь;Ь] от знака скорости (возрастания
или убывания) входного сигнала.
5. Элемент с зонами нечувствительности и неоднозначности (рис. 7.8).
Другие типовые нелинейные элементы приведены в [54,55] (см. также
приложение в [14]).
Для негладких характеристик г = В(р) обычно отмечают наличие
следующих характерных зон:
зоны нечувствительности, если имеется промежуток значений входного
сигнала а, при которых выходной сигнал г - Р(о) равен нулю;
участков насыщения, если имеются промежутки (конечные или
бесконечные) значений а, на которых функция Г(а) постоянна;
зоны неоднозначности, если имеются промежутки значений а, на которых
выходной сигнал может принимать различные значения в зависимости от
некоторых параметров или от знака скорости а изменения входного сигнала;
участков линейности, если на некоторых промежутках функция /*(<*)
является линейной.
278

с
г = Р(о)
-с
т=
Су а>0,
О, <т = 0,
-с, а>0.
г г = /Г(а)
Рис. 7.4
с*
т-с
Да) =
с, а > Ь,
О, -*:$а**,
-с, а<-&.
* = Яа)
-*
г = /*(а,а)
-*1
Рис. 7.5
с (о - Ь), а > Ь9
Г(а) « <{ О, - 6 * а * $,
с (а + 6), а < -6,
фа = с.
Рис. 7.6
Да,6) =
С, СТОИЛИ
-с, а^-Ь или
Г-*<а<*1
1 иа<0 у
{-Ь < а ^ *1
{ иа>0 }'
Рис. 7.7
279

-Ь-гЬ
I = *Х<т,а)
Д<т,а) =
гЪ Ь
-с
с, <у^Ь или
{гЬ<а <Ь)
и а < О у
О,-гЬйойгЬ или
/* < а < А]
и а > О
или
- с, а ^ -Ь или
0<г<1.
Рис. 7.8
Линейная часть системы задается передаточной функцией
У(,)-**"*"**>
ал5л+... + До
или эквивалентным дифференциальным уравнением
Г- А < а < -/#1
1 и а<0 }'
{- & < а < -л&1
и а>0 }'
гС«),
а„ **"'(') +.- + «о *М = *да ««(О + -. + *Ь *Ю.
G.4)
G.5)
связывающим входной г@ и выходной х@ сигналы системы.
Наличие нелинейного звена придает системе управления свойства,
присущие только нелинейным системам (например, автоколебания, рассмотренные в
гл.8). С другой стороны, поскольку нелинейный элемент один, то для упрощения
анализа той или иной особенности поведения системы его можно заменить тем
или иным эквивалентным линейным звеном. При этом необходимо использовать
различные методы линеаризации, описанные в гл. 8.
Пример 7.2. Составить уравнения состояния системы управления,
структурная схема которой изображена на рис. 7.9, где к, Г, ^ - параметры
колебательного звена (см. разд. 1.1.1).
ь^Г) к
*1Я/
т
По)
—»
к
Т2з2+ 2§7Ь + 1
Рис. 7.9
П В прямой цепи системы управления последовательно включены
колебательное звено и нелинейное звено с характеристикой г = /*(<*). Сигналы #, а,
г, х связаны уравнениями
Т2х + 2ЬТх + х = к1,
280

Исключая из этих уравнений промежуточные переменные а и г,
получаем
Т2х + 1Х>Тх + х = кГ(в-х). G.6)
Обозначив выходной сигнал х и скорость х его изменения через х{ и х2>
приведем уравнение G.6) к системе дифференциальных уравнений первого
порядка вида G.1):
которые являются уравнениями состояния динамической системы,
представленной на рис. 7.9.И
7.3. ОПИСАНИЕ НЕЛИНЕЙНЫХ СИСТЕМ СТОХАСТИЧЕСКИМИ
ДИФФЕРЕНЦИАЛЬНЫМИ УРАВНЕНИЯМИ
Поведение нелинейных систем при случайных входных воздействиях
формально может быть описано стохастическим дифференциальным уравнением
1Ш = /(/, Х@) + а(/, Х«)) С«), G.7)
ах
где X — л-мерный вектор состояния, /(/,*), ст(/,х) — соответственно векторная
(л х 1) и матричная (л х к) функции; 0(г) — ^-мерный стандартный гауссовский
белый шум, удовлетворяющий условиям М[С(()] = О, М[0A{HТA2)] = 5(*1 -*т)•
Начальные условия задаются в виде
*<Го) = *о, G.8)
где Х0 — либо известный вектор, либо векторная случайная величина с
известной плотностью вероятности.
Чтобы придать G.7) строгий смысл, это уравнение сначала переписывают в
дифференциальной форме:
ОХ = /(/, Х@) Л + а(Г, Х@) <*Щ*), G.9)
где Ж(г) — ^-мерный стандартный винеровский случайный процесс [22],
удовлетворяющий условиям: Щ*о) = °» М[Щ*)] = ® для всех ^>^^у вектор ЩО для
любых * > *0 распределен по гауссовскому закону, процесс является однородным
с независимыми приращениями. Ковариационная функция стандартного вине-
ровского процесса Л^(/1,^2) = ^т1п(Г1,/2), а производная формально равна
стандартному белому шуму: 0A) = ——.
о/
281

Затем уравнение записывается в интегральной форме:
*(/)-*(«,)+ {/(т,*(т))*+ \а(хуХ(х))(!Щх)9 G.10)
где первый интеграл представляет собой среднеквадратический интеграл, а
второй — стохастический интеграл.
Наиболее часто применяется стохастический интеграл Ито, который
определяется как предел сходящихся в среднеквадратическом смысле интегральных
сумм:
где /0 = *о < т1 <•• • < *и = * "" такая последовательность точек разбиения
интервала интегрирования [/о,*] на Участей, что А = тах (х/ - тм) -> 0 при N -> +оо.
1=1,...,#
Так же применяются интеграл Стратоновича и более общий в -интеграл
[22].
Уравнение G.10), в котором используется интеграл Ито, называется
интегральным уравнением Ито, а уравнение G.9) - стохастическим
дифференциальным уравнением Ито.
Случайный процесс ЛГ(/), удовлетворяющий уравнению G.10), в котором
интегралы представляют собой среднеквадратические пределы соответствующих
интегральных сумм, называется средним квадратическим решением
стохастического дифференциального уравнения [22].
Обычные правила дифференцирования здесь в общем случае не
применимы. Для нахождения решений стохастических дифференциальных уравнений
используется формула дифференцирования Ито.
Если <р(/,х) ~ непрерывно дифференцируемая по / и дважды непрерывно
дифференцируемая по х функция, то
<Ар(', *(')) =
'езМШ^ЁяМШ^^х^
Ы { дх )
^У'а^ G.11)
*2,
до (Гф
где —х и —*г — вектор частных производных первого порядка и матрица част-
дх дх2
ных производных второго порядка функций <р(/,х) соответственно; (г — след
матрицы.
Если в G.9) л = 1,/(/,х) = 0,о(/,х)э1, т.е. <ОГC = <ЛГ@, а ф(/,х) = ф(х),
то
^1М) «Лл + ЙШдк», G.12)
2 ах2 <?х
282

С помощью формул G.11) и G.12) можно найти точное решение некоторых
стохастических дифференциальных уравнений. В общем случае применяются
оделенные методы решения, изложенные в [30].
При решении проблем анализа и синтеза систем управления удобно
исходную стохастическую задачу свести к соответствующей детерминированной
задаче. Для этого рассмотрим уравнение G.9) на некотором промежутке времени
Т = ['о>'11 и предположим, что:
а) функции Мих), / = 1,...,п; <х|7(/,х), / = 1,...,л, У = 1,...,# кусочно
непрерывны по / для всех х € В";
б) для любых /€ Т функции /}(/,*) еС1(Яп), / = 1,...,л и имеют
ограниченные первые производные по х; функции <*ц(*,х)еС2(Яп), / = 1,...,л,
] = 1,..., А: и имеют ограниченные первые и вторые производные по х;
в) существует сх = сопЛ > 0 такая, что
ХХМ^^у^Ы!2 V(/,x)€ГxЛ^ ЪеЯп,
к
где аи (/, х) = ^ аи (/, х) • ау- / (/, х).
/-1
Тогда решение стохастического дифференциального уравнения G.9)
существует, единственно и является непрерывным марковским процессом. Если
плотность вероятности этого процесса р(*,х)еС1*2(ТхЯп), где С1*2(ТхЯп) —
пространство непрерывных функций вместе с производными р{"х> Р\>х>
Ы дх(
д2р(*,х) . , . , ^ „
——-—,1 = 1,..., п, ] = 1,..., п, то она удовлетворяет уравнению Фоккера-Планка-
ОХ\ ОХ г
Колмогорова [22,30,31,58]:
= АиУ[р(*,х)] Ч(*,х)еТхЯп
с начальным условием
р{*о>х) = Ро(х)>
где /?о(х) — начальная плотность вероятности, характеризующая начальное
состояние Х0; Ли(>[] - дифференциальный оператор, Д/,х) = (/!(/,х),...,/л(/,х))г
- вектор сяоса; а(/,х) - матрица диффузии.
В задаче анализа выходных процессов требуется по заданным начальной
плотности вероятности р0(х) , вектору сноса /(*,х) и матрице диффузии а(/,х)
найти закон изменения плотности вероятности р(/,х). Решая уравнение Фокке-
Ра-Планка-Колмогорова (ФПК), являющееся уравнением в частных производ-
283

ных параболического типа, одним из аналитических или численных методов [30],
можно получить наиболее полную информацию о поведении динамической
системы. По плотности вероятности находятся любые статистические
характеристики процесса ХA). Уравнение ФПК наряду с исходным стохастическим
дифференциальным уравнением G.9) служит математической моделью системы
управления.
Пример 73. Доказать, что ХЦ) = еЖ(/) является решением уравнения
<!Х = -Х(*)А + Х(*)<!Щ0
с начальным условием Х@) = 1.
? Положим ф(х) = ех и применим формулу G.12):
<*р(*@) = ±ет<Н + ех®<ПГЮ = |фШ/)) А + <?(Х(*)) <1Щ*).
При / = 0 Х@) = е^@) = 1, так как Ж@) = 0. Поэтому случайный процесс
Х{() = е^(г) - решение уравнения.и
Пример 7.4. Доказать, что ХЦ) = е 2 является решением уравнения
0Х = ХЮAЩЪ, ЛГ@) = 1.
П Положим <р(/,х) = в 2 и применим формулу G.11) при /(/,*) = 0,
<*,*) = 1:
1 *<0-х 1 *<0-г ДГС0--
4р(*,ЛГ@)-[-±е 2 +^е *]А + е *ЛГ(П = <#>Х№Л1Г®.
При / = 0 ЛГ@) = 1, так как ЩО) = 0. Таким образом, функция ЛГ(/) = е 2
удовлетворяет уравнению.»
Пример 7.5. Доказать, что ХA) = 1 +-"Т"^ является решением уравнения
ахш^А+^Щагу), х@) = \.
4
П Положим <р(х) = 11+^1 и применим формулу G.12):
При / = 0 АХ0) = 1, так как 0^@) = 0. Таким образом, функция
Х($) = 1 + * удовлетворяет уравнению."
284

Пример 7.6. Решить уравнение
1де р > 0 — параметр.
1 + х
О Положим<р(х) = 1п- . Поэтому
дф) 0 а<р(х) 2 а2<р(х) 4х
а/ ' дх 1-х2' ах2 A-х2J'
По формуле G.12) имеем
т 1 [1-АГ2(/)] 2 [1-Х2(/)]2 ] [1-*2(/I
= [-2р2Лг(/) + 2р2Лг@]Л + 2рЛГ = 2р^)Г@.
Отсюда ф(ЛГ@) -ф(АГ@)) = 2р1Г@ и
ь1±^^1±^^ = ы[1^@]>[1^@)]=2р^(/)<
1-ЛГ(/) 1-*@) [1-ЛГ(/)Ы1-ЛГ@)] Р Ч'
Искомое решение имеет вид ХЦ) = ^ е ^ ~|, где 2Г@) = ^^ .¦
ст2
Пример 7.7. Доказать, что ,ДГ(/) = АГ0ехр[F I + а1УA)] является
решением уравнения
дХ = Ъ Х(№ + а *(') 4Щ*), *@) = АГ0,
где Л, а —параметры.
ст2
? Положим ф9х) = Х0схр[(Ь—~)/ + ох]. По формуле G.11) при
/(/,*) г 0, о(/,х) = 1 получаем
<**/, Х«)) = |(* -^)Х0 ехрЬ ~) Г + аЛГ(о1+|^о^2ехри-^)/ + а^@||л +
+ сХ0ехр №-^)/ + аА'@и^=^ф(/,Аг(/))Л + аф(/,;!Г@)^^@,
что и требовалось доказать.
При / = 0 АХ0) = *0, так как Щ0) = 0. Таким образом, функция
2
Я"@ = ДГ0 ехр[(Ь ) / + а1УA)] удовлетворяет уравнению.¦
285

7.4. ПОВЕДЕНИЕ НЕЛИНЕЙНЫХ СИСТЕМ
НА ФАЗОВОЙ ПЛОСКОСТИ
Для исследования свободного движения автономных систем, описываемых
дифференциальным уравнением второго порядка
х@ = /(х@,х@), G.13)
где /(х,х) - кусочно-непрерывная функция, применяется метод фазовой
плоскости.
Перепишем уравнение G.13) в виде системы двух уравнений первого
порядка:
G.14)
Поскольку время / входит неявно в уравнение движения (рассматриваемая
система автономна), то его легко исключить, поделив второе уравнение системы
G.14) на первое. Получим уравнение фазовых траекторий системы G.13):
&..Д&А, G.15)
ах у
которое связывает положение х и скорость движения у = х системы G.13).
Решение у = у(х) уравнения G.15) называется фазовой траекторией, а производная
-у- - фазовой скоростью.
ах
Заметим, что для нахождения свободного движения х(() нужно решать
уравнение G.13) второго порядка с начальными условиями х(/0) = х0, х(/0) = *0.
Фазовая траектория у = у(х) определяется как решение уравнения G.15) первого
порядка при начальном условии у(х0) = х0.
Графики фазовых траекторий строятся на фазовой плоскости в
координатах х и у = х. Изменению положения системы G.13) с течением времени
соответствует движение изображающей точки (*(/), *@) по фазовой траектории. Тем
самым анализ свободного движения сводится к построению фазовых траекторий
системы G.13), которые показывают ее поведение на фазовой плоскости.
АЛГОРИТМ ПОСТРОЕНИЯ ФАЗОВОЙ ТРАЕКТОРИИ
1. Составить дифференциальное уравнение свободного движения системы
*@ = /(*('),*(')),
если система управления задана структурной схемой или описана каким-либо
другим способом [30].
2. Записать уравнение фазовых траекторий
А У Ах, у)
их у
286

и начальное условие в виде у(*о) = хь-
3. Получить фазовую траекторию у = у(х)9 решая задачу Коши,
поставленную в п.2. ^
4. Построить график зависимости у = у(х) на фазовой плоскости (в
координатах х и у). Указать (стрелкой) направление движения по фазовой
траектории, которое происходит в сторону увеличения координаты х при у > 0 и в
сторону уменьшения абсциссы при у < 0. Отметим, что ось абсцисс фазовые
траектории пересекают вертикально.
Пример 7.8. Для системы управления, структурная схема которой
изображена на рис. 7.10, при начальных условиях х@) = 1, х@) = 0 построить фазовую
траекторию.
_ а
э—¦
1
з2
Рис. 7.10
Рис. 7.11
? 1. По структурной схеме (рис. 7.10) составляем дифференциальное
уравнение. Сигналы #, а, х связаны соотношениями х = о? а = $-х.
Следовательно, свободное движение при (#@ г 0) описывается уравнением х = -х.
2. Записываем уравнение фазовых траекторий и начальное условие
?—. *0-о.
их у
G.16)
3. Разделяя переменные в уравнении G.16) и интегрируя, получаем
Из общего интеграла х2 +у2 -с2 = 0 уравнения G.16) выделяем
2^ = _*1 ±
2 2 + 2
частный интеграл х2 + у2 -1 = 0, удовлетворяющий начальному условию.
4. Частный интеграл в неявном виде задает фазовую траекторию, график
которой представляет собой окружность. На рис. 7.11 изображена искомая
фазовая траектория и указано направление движения по ней, соответствующее
изменению положения х(/) и скорости х(/) рассматриваемой системы с течением
времени. Как видим, данная система управления при отсутствии внешних воз-
Действий совершает незатухающие (так как фазовая траектория — замкнутая
линия) колебаниям
Замечание. Если в системе присутствуют нелинейные элементы,
имеющие релейный характер, или элементы с зоной нечувствительности либо
с зоной неоднозначности (см. разд. 7.2), то фазовую плоскость следует разбить
84 области и для каждой области записать соответствующее уравнение фазовых
Траекторий. Затем необходимо построить фазовую траекторию в области, содер-
287

жащей начальную точку (хо,Хо). Если фазовая траектория, исходящая из точки
(*о»*о), достигает границы, отделяющей начальную область от соседней, то
следует найти координаты (хьХ!) точки ее пересечения с границей. Эти
координаты используются в качестве начальных условий для решения уравнения фазовых
траекторий, соответствующего соседней области.
Таким образом, построение фазовой траектории для рассматриваемых
систем начинается с области, содержащей начальную точку (х<),хо) и продолжается
последовательно, переходя от области к области. Отметим, что на границе
областей фазовая траектория непрерывна, а фазовая скорость —*- может терпеть
разах
рыв.
Пример 7.9. Для системы управления, структурная схема которой
изображена на рис.7.12, при начальных условиях х@) = 4, х@) = 0 построить фазовую
траекторию.
х
Я —Ф
1
1
-2 -1
-1
т
1 2
Рис. 7.12
? По структурной схеме (рис. 7.12) составляем дифференциальное
уравнение свободного движения (#@ з0):
х = г,
I = /*(а,сг),
а = -х,
х = ^(-х,-х).
Поскольку функция Р нечетная, то уравнение движения можно записать
так: х = -Г(х,х) • Тогда уравнение фазовых траекторий будет иметь вид
йу Г(х,у)
их у
Данная система содержит релейный элемент Г с зоной
нечувствительности и с зоной неоднозначности. Разделим фазовую плоскость на три области
Л, Б, В (рис. 7.13), в каждой из которых функция Г(х9у) принимает одно из
значений: -1,0, 1.
Запишем уравнения фазовых траекторий:
для области А: —— = —; для области Б: -~ = 0; для области В: —*- = —.
ах у их ах у
Начальная точка »УD; 0) лежит в области В, поэтому сначала решаем задачу
Коши —ь- = —, уD) = 0 для этой области.
их у
288

А
"*\
А
М\
~^
1
у|«
Г-1 :
_-Уб
Б
Ыт.
~т\
|ЛГ
ч
\\Г
У ¦
к
В
В
\р
Тб
Рис. 7.13
Интегрируя уравнение, получаем семейство парабол ¦=~ = -х + с, из которого
у2
выбираем параболу х = 4--^--, проходящую через начальную точку »УD;0).
Устанавливаем направление движения изображающей точки по данной параболе и
отбрасываем одну из ее ветвей (ветвь при у > 0), так как движение по этой ветви
могло быть только до начального момента времени. Оставшаяся ветвь параболы
достигает границы (х = 1; у < 0) области В в точке К(\;-4в) и попадает в
область Б. Составляем задачу Коши для области Б:
^ = 0, уA) = -<[б.
Как видим, в области Б фазовая скорость не меняется и фазовая траектория
является прямой: у(х) = -^6. Границу (х = -2; у < 0) области Б эта прямая
пересекает в точке Д-2; - Тб). Далее последовательно получаем:
дуга ЬМ\ х = ^--5; М(-\\ 2^2);
дуга А/#: у = 2^2; NB; 2^2);
дугаМ>: * = 6-^; />F;0).
Фазовая траектория системы изображена на рис. 7.13.
289

ПОСТРОЕНИЕ ФАЗОВОГО ПОРТРЕТА МЕТОДОМ ИЗОКЛИН
Для получения полного представления о поведении автономной системы
второго порядка, в частности для анализа устойчивости, необходимо изобразить
на фазовой плоскости все характерные фазовые траектории системы, т.е.
построить фазовый портрет системы управления. Для приближенного построения
фазового портрета удобно использовать метод изоклин, не требующий
интегрирования уравнения G.13) фазовых траекторий.
Метод состоит из двух этапов:
1. На фазовой плоскости строим систему изоклин — линий с одинаковым
наклоном фазовых траекторий. Уравнение изоклин имеет вид
^Л = С9 G.17)
У
где параметр с равен тангенсу угла наклона фазовой траектории и может
принимать любые действительные значения. На каждой изоклине (при конкретном
йу
значении с) штрихами наносим направление (-г- = с) прохождения фазовой
ёх
траектории.
2. По изоклинам строим (приближенно) фазовые траектории. Например,
на рис. 7.14 имеются две изоклины с нанесенными на них направлениями
фазовой скорости. Из точки А проводим две прямые: ЛВ с наклоном сх и АО с
наклоном с2. Выбираем на отрезке ВВ середину - точку Е. Проводим прямую
АЕ, считая, что отрезок ЛЕ приближенно совпадает с фазовой траекторией,
проходящей через точку А
При наличии в системе управления нелинейных элементов с разрывными
характеристиками фазовая плоскость разбивается на части, в каждой из которых
строится свой портрет, при этом учитывается, что на границе областей фазовые
траектории непрерывны, а фазовые скорости могут иметь разрыв.
Рис. 7.14
Рис. 7.15
Пример 7.10. Для системы управления, структурная схема которой
изображена на рис. 7.10, построить фазовый портрет.
X X
П Уравнение изоклин для этой системы имеет вид: — = с или у = —,
У с
что следует из уравнения G.17). Таким образом, семейство изоклин представляет
собой пучок прямых, проходящих через начало координат.
290

йу
Заметим, что направление фазовой траектории тт^ = с перпендикулярно изокли-
не у__2Е.р Поэтому фазовые траектории являются окружностями. Фазовый
с
портрет рассматриваемой системы изображен на рис. 7.15. ¦
Пример 7.11. Для системы управления, структурная схема которой
изображена на рис. 7.16, построить фазовый портрет.
П Составляем уравнение фазовых траекторий:
х + х = Г(о),
* = 0,
=> х = -х-Г(х) => ^ = -1-^>.
ах у
(Ъ ° >
ш >
Г
1
—>
1
5
—>
1
5 + 1
7. \
1
-1
-1
1
Рис. 7.16
с = -0,5 -чч*
с = 0
с = 1 -*
с = -2
с = -1,5 ^
Г(х)
Уравнение изоклин имеет вид -1 — = с. Поскольку система управле-
У
ния содержит релейный элемент Г с зоной нечувствительности, то фазовую
плоскость разбиваем на три области А, Б, В (рис. 7.17), в которых функция
Р(х>у) принимает постоянные значения:-!; 0 ; 1.
291

Запишем уравнения изоклин: для области А: у-—-; для области А
с + 1
у = . В области Б уравнение изоклин имеет вид с = -1, что свидетельст-
с + 1
вует о том, что все фазовые траектории в этой полосе являются прямыми ли-
ниями с наклоном ~--\. В области Л строим семейство изоклин, выбирая
ах
значения параметра с так, чтобы изоклины равномерно заполняли эту область.
Наносим штрихами направления прохождения фазовых траекторий и затем
строим приближенно фазовые траектории, указывая на них направление
движения изображающей точки. В области В картина фазовых траекторий
симметрична построенной в области Л . Фазовый портрет системы изображен на рис. 7.17.И
ОСОБЫЕ ТОЧКИ И ОСОБЫЕ ЛИНИИ ФАЗОВОГО ПОРТРЕТА
Анализ поведения автономной системы второго порядка сводится к
построению ее фазового портрета, по которому можно проследить эволюцию
свободного движения системы из любого положения. Фазовые траектории системы
G.13) могут быть трех типов:
а) точка (х0,0), если уравнение G.13) имеет решение х(Оэ*о
(у(/) = х(Г) г 0). Такая точка фазовой плоскости называется положением
равновесия системы. Если в любой окрестности положения равновесия имеется хотя бы
одна фазовая траектория, уходящая от него при / -> -к©, то точка равновесия
является неустойчивой. Если же все фазовые траектории в окрестности точки
равновесия неограниченно приближаются к ней при / -> -к», то данное положение
равновесия называется асимптотически устойчивым;
б) замкнутая кривая (траектория), если уравнение G.13) имеет
периодическое решение;
в) незамкнутая кривая, которая соответствует непериодическому решению
уравнения G.13);
Для анализа поведения системы достаточно выяснить качественную
картину разбиения фазовой плоскости на характерные области с однотипными
траекториями. Поэтому нужно выяснить расположение не всех фазовых кривых, а
лишь некоторых особых траекторий.
Приведем имеющуюся классификацию особых точек и особых линий
фазового портрета. Особые точки — это точки равновесия системы, которые
определяются из системы уравнений:
/СздО-0. G18)
у = 0.
В особых точках скорость х@ и ускорение х@ равны нулю, а фазовая скорость
—• системы не определена. Если функция /(х,у) гладкая в окрестности особой
ах
точки, то поведение системы в этой окрестности положений равновесия
совпадает с поведением линеаризованной системы (см. разд. 8.1). Линеаризуем
уравнение G.13) около опорного режима *(/) = х0 = соп$1. Получим
5*-Л(ДСо,0Nх-/х(хо,0Mх = 0.
292

Корни Х{, Х2 характеристического уравнения
*2-Л(^>0)Х-/х(хо,0) = 0
определяют поведение фазовых траекторий линеаризованной системы в
окрестности особой точки. Имеются четыре типа особых точек: фокус, узел, седло и
1. Особая точка называется фокусом, если корни Х{, Х2 комплексные
сопряженные. Фокус является устойчивой точкой равновесия (рис. 7.18,я), если
корни имеют отрицательные вещественные части и неустойчивой (рис. 7.18,6) в
противном случае.
уЬ
ф-Г Р^т^т
>*
ИД^
Рис. 7,18
2. Особая точка называется узлом, если корни X}, Х2 действительные
одного знака. Причем узел является устойчивым (рис. 7.19,6), если оба корня
отрицательны, и неустойчивым (рис. 7.19,д), если оба корня неотрицательны.
*»
Рис. 7.19
293

3. Особая точка называется седлом, если корни X! , Х2 действительные
разных знаков. Седло - неустойчивая точка равновесия (рис. 7.20).
Рис. 7.20
4. Особая точка называется центром (рис. 7.21), если корни Х{ , Х2 чисто
мнимые.
е&
Рис. 7.21
На рис. 7.18-7.21 изображены фазовые траектории (оси координат х, у) и
соответствующие им траектории движения (оси координат ^, х)9
характеризующие поведение системы в окрестности особой точки. На рис. 7.19-7.20
соответствующие траектории обозначены одинаковыми цифрами.
Рис. 7.22
Для систем, содержащих нелинейный элемент с зоной нечувствительности,
на фазовом портрете возникает особый отрезок (рис. 7.22), состоящий из точек
294

равновесия. Если все эти точки равновесия устойчивые, то особый отрезок
называют отрезком покоя рассматриваемой системы.
Кроме особых точек, следует указать особые линии фазового портрета:
предельные циклы и сепаратрисы.
Предельным циклом называется замкнутая фазовая кривая, в окрестности
которой все фазовые траектории неограниченно приближаются к этой замкнутой
КрИВОЙ При / -» +<Х> ИЛИ При / -» -оо .
Предельный цикл может быть устойчивым (рис. 7.23,а), если любая
изображающая точка (х(/),Я0) в его окрестности приближается к циклу при
/ _> +оо; неустойчивым (рис. 7.23,6), если все изображающие точки в окрестности
цикла приближаются к нему при / -* -оо, и полуустойчивым (рис. 7.23,6?).
Рис. 7.23
Сепаратрисой называют фазовую траекторию, стремящуюся (при /->±оо)
к некоторому положению равновесия, в любой окрестности которой имеются
траектории, вначале приближающиеся к этому положению равновесия, а затем
удаляющиеся от него. Например, сепаратрисами являются четыре луча,
пересекающиеся в особой точке типа седло (см. рис. 7.20) и служащие асимптотами для
других фазовых траекторий.
Точки равновесия, предельные циклы и сепаратрисы определяют
качественную картину поведения остальных фазовых траекторий. Например, на рис.
7.24 особые точки типа центр разделяются сепаратрисами.
Рис. 7.24
Для системы управления, рассмотренной в примере 7.8, было получено
Уравнение G.16) фазовых траекторий. Единственная особая точка х = 0, у = 0 на
Фазовой плоскости для этой системы является центром, что сразу же можно
295

определить по фазовому портрету на рис. 7.15. Поэтому положение равновесия
@;0) не является асимптотически устойчивым.
Для системы, рассмотренной в примере 7.11, был построен фазовый
портрет (см. рис. 7.17), по которому заключаем, что отрезок оси абсцисс -1^х^1
является отрезком покоя, так как любая фазовая траектория системы
оканчивается в некоторой точке этого отрезка.
Пример 7.12. Для системы управления, изображенной на рис. 7.25, где
параметры нелинейности Ь = 1, с- — 9 построить фазовый портрет.
><Т> ст 1
т-
1
р
1
—»
1
5E + 1)
-V А.
г
-Ъ
-с
1 = Г(а,6)
^
ъ
а б
Рис. 7.25
? Составляем дифференциальное уравнение, описывающее свободное
движение (при #@ = 0) системы:
х + х = г
1 = Р(а,6) => х + х = -Г(х,х).
а = -х
у****е*1 с = -2
их
0
1
-2
-3
00
-5я
У~ 2(с + \)
5я
5я
>--
5я
у=т
5я
* = 0
Рис. 7.26
Отсюда получаем уравнение фазовых траекторий
йу у + Р(х,у)
их у
нение изоклин:
и урав-
296

у + Р(х,у) Р(*>У)
±-Ш- = -с или у = —^-~.
у с + 1
Разделим фазовую плоскость на две области: А и Б, в которых функция
Г(х,у) принимает постоянные значения: ——, — (рис. 7.26). Запишем
уравнение изоклин: для области А: у =—- -; для области Б: у = -
2(с + 1)' ' ' 2(с + 1)'
Построим изоклины и фазовые траектории в области Б, а затем
симметрично относительно начала координат в области А
Приближенное построение фазового портрета позволяет обнаружить
особую линию - предельный цикл, которому соответствует замкнутая фазовая
траектория. Найдем время, за которое изображающая точка проходит предельный
^/у у + с
цикл один раз. Для этого проинтегрируем уравнение -*- = фазовых траек-
ах у
торий в области Б и получим общее решение: х = с )п(у + с)-у + а9 где а —
произвольная постоянная. Найдем значение произвольной постоянной, предполагая,
что фазовая траектория начинается в точке A;уо):
1 = с1п(у0+с)-у0+а => а = у0+1-с]п(у0+с).
Следовательно, фазовая траектория определяется равенством:
у + с
х = с1п— +Уо-у + 1. Найденная фазовая траектория выходит из области Б,
Уо+с
пересекая прямую х = -1 в точке (-1;у{). Так как траектории в области А
симметричны траекториям в области Б относительно начала координат, то для того,
чтобы траектория, начинающаяся в точке A;у0)> была замкнутой, достаточно,
чтобы она оканчивалась в области Б в точке (-1;-Уо). Поэтому значение у0
С — Уп
должно удовлетворять уравнению с1п——+2д*>+2 = 0. Решая приближенно
с + Уо
это уравнение при с =—, получаем у0 «5,13.
Определим теперь время в прохождения изображающей точки от
положения A;?о) Д° положения (—1;—у0). Для этого проинтегрируем уравнение
у + у - -с при начальном условии у@) = у0. Получим у = (у0+ с)е~* - с. В мо-
С — Уп
мент / = 9 должно выполняться равенство у(в) = ~Уо => 6 = -1п——. Под-
с + Уо
ставляя найденное выше значение у0 * 5ДЗ, определяем 9 « 1,56. Следовательно,
весь предельный цикл изображающая точка проходит за время 26 * ЗД2. По
фазовому портрету заключаем, что предельный цикл является устойчивым.и
Заметим, что предельные циклы и сепаратрисы могут не быть фазовыми
траекториями, но в любой окрестности этих линий обязательно проходят
интегральные кривые уравнения фазовых траекторий. Рассмотрим теперь пример,
который показывает существование особых движений системы, не подчиняющихся
Уравнению фазовых траекторий.
297

Пример 7.13. Для системы управления, изображенной на рис. 7.27,
построить фазовый портрет.
г 1 = Р(р)
8
-> х
1
-1
а б
Рис. 7.27
П Составим уравнение свободного движения системы:
Х = У,
V = г, => х = -Р(х + х)
1 = Г(а), а = $-х-у, # = 0
*/у Р(х + у)
и уравнение фазовых траекторий: -*- = —-—^. Разделим фазовую плоскость
ах у
на две области: А и Б, в которых функция /* принимает постоянные значения:
-1 или 1 (рис. 7.28).
Ук
Рис. 7.28
Запишем уравнения фазовых траекторий: для области А: -~ =—; для области Б:
ах у
йу 1 ^
— = —. Следовательно, фазовые траектории системы представляют собой па-
у2 у2
раболы: для области А х = ~ + а; для области Б: х = а--^--, где а -
произвольная постоянная.
На линии у = -х переключения релейного звена отметим две точки:
СA;-1) и />(-!; 1), которые разбивают ее на три части. В точках, лежащих на
298

прямой переключения вне отрезка СИ, происходит переход изображающей
точки с параболы одного семейства (например, соответствующей области А) на
параболу другого семейства (соответствующую области Б). При этом фазовая
траектория остается непрерывной, хотя фазовая скорость терпит разрыв. В каждой
точке отрезка СБ встречаются две фазовые траектории, поэтому, попав на
отрезок СВ, изображающая точка не может его покинуть и будет скользить по нему
к началу координат. С другой стороны, точное движение по линии
переключения невозможно, так как оно может иметь место лишь при мгновенном
срабатывании релейного элемента. Из-за немгновенного действия реле возникает
высокочастотный режим следующих друг за другом переключений, которому
соответствуют высокочастотные колебания изображающей точки вокруг линии
переключения. Такое движение нелинейных систем называется скользящим
режимом*
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
7.1. Составить дифференциальное уравнение, описывающее поведение
системы, структурная схема которой изображена на рис. 7.29, а—в. Характеристика
нелинейного элемента г = Р(а) показана на следующих рисунках:
а) на рис. 7.4 (релейный элемент), где с = л +1;
б) на рис. 7.5 (релейный элемент с зоной нечувствительности), где
с = л + 1, Ь-т + \\
в) на рис. 7.6 (элемент с зоной нечувствительности), где с = л +1, Ь = т + 1;
г) на рис. 7.7 (элемент с петлей гистерезиса), где с = л +1, Ь = т + 1;
д) на рис. 7.8 (элемент с зонами нечувствительности и неоднозначности),
где с = л +1, 6 = /и +1.
*—К§>
Н к
1
5(Тз + 1)
-* X
Т = -
1
л + 1
Я—¦©¦
е\
[_
Р
г
—»
1
5
г—1
1
Тз + 1
х Т=-
л + 1
5^
Ж
Р
1
к
»
1
(Г,* + 1)G2+1)
¦ X
Тх =¦
Ъ =
1
л + 1'
1
/и + 1
Рис. 7.29
299

7.2. Составить уравнения состояния систем, структурные схемы которых
изображены на рис. 7.30, д-*. Характеристика нелинейного элемента г = /"(а)
показана на следующих рисунках:
а) на рис. 7.4 (релейный элемент), ще с = л +1;
б) на рис. 7.5 (релейный элемент с зоной нечувствительности), где
с = л + 1, Ъ = т + \\
в) на рис. 7.6 (элементс зоной нечувствительности), где с = л +1, Ь = т + \;
г) на рис. 7.7 (элемент с петлей гистерезиса), гдес = л + 1,А = т + 1;
д) на рис. 7.8 (элемент с зонами нечувствительности и неоднозначности),
гдес = л + 1,Д = /и + 1.
в 1 71 =
я-КЭ—уч~"*Ф~~1
1
715 + 1
1
5(Т28+\)
1
л + Г
к25
Т2 =
1
Л1 + 1'
&1 = т + л;
А:2 = л
?"~*Ф"~1 *
Гр
>
1
G15 + 1)(Г2+1)(Г3+1)
7\ =
л + 1 *
1
2 = Г>
171 + 1
Л1 + 1
л + 1
Т2
1 1 1 1* 1
ХЛ—Г| 1 1 5(Г2$2+247Ь + 1) 1 |
1 1
г=-
л + 1
Рис. 7.30
7.3. Для систем, заданных в задаче 7.1, составить уравнение фазовых
траекторий.
7.4. Для систем, заданных в задаче 7.1, методом изоклин построить
фазовые портреты.
300

Глава 8. МЕТОДЫ АНАЛИЗА НЕЛИНЕЙНЫХ СИСТЕМ
УПРАВЛЕНИЯ
8.1. АНАЛИЗ ВЫХОДНЫХ ПРОЦЕССОВ МЕТОДОМ ЛИНЕАРИЗАЦИИ
8.1.1. Постановка задачи
Основная задача анализа выходных процессов нелинейной
детерминированной системы управления G.1) состоит в нахождении выходного сигнала *(/)
(траектории движения) на отрезке времени ( е[@^{] по заданному на этом
отрезке входному сигналу #(/) и начальному состоянию дс(/0) = х0. Как и в случае
линейных систем, движение системы при отсутствии внешних воздействий
(#@ = 0) называют свободным движением, а при наличии ненулевых воздействий
(#@ * 0) — вынужденным. Однако в отличие от линейных систем, в которых
выполняется принцип суперпозиции, движение нелинейной системы нельзя
представить в виде суммы свободного и вынужденного движений.
Для решения задачи анализа обычно используются численные или
численно-аналитические методы решения систем дифференциальных уравнений,
поскольку аналитическое решение этих нелинейных уравнений удается найти
крайне редко.
Применение широко развитых методов анализа линейных систем к
данному классу задач является весьма привлекательным и становится возможным
после процедуры линеаризации уравнений G.1).
8.1.2. Линеаризация нелинейных систем
Предположим, что задана опорная траектория х*(/), являющаяся
решением уравнения
*(>) = /(',*(>),*(») (8.1)
при некотором входном сигнале #(/) = #*@ и начальном условии х(/0) = х$, т.е.
*Ч0 = /(',*Ч0,**М>. **('о) = *о. (8.2)
Здесь все обозначения совпадают с используемыми в разд. 7.1.
Поведение х(() нелинейной системы в окрестности опорной траектории
может быть представлено с помощью отклонений (вариаций) &с(/) от опорной
траектории:
х@ = х*@ + &с('). (8.3)
Подставляя (8.3) в (8.1), имеем
**(*) + 5х(/) = /(*,*•(/) + а*),**» + **(')), (8.4)
301

где 6#(/) — вариация внешних воздействий, 5#(/) = $(*)-**(*)• Раскладывая
функцию / в ряд Тейлора в окрестности опорной траектории, ограничиваясь
членами только первого порядка (линейными членами) и вычитая (8.2) из (8.4),
получаем, что вариации &с(/) описываются уже системой линейных уравнений:
5х@ = /ЯЛ**<1).**@)«*М + /*(',** <0,**<0) **('), §*('о) - *(>о) "*о, <85)
где /х, /е - матрицы частных производных вектор-функции /(/,*,$) по соот-
— — *Ш <<Ш - - - «
/: = 1,...,т.
Поэтому дальнейший анализ нелинейной системы (8.1) в окрестности
опорного режима проводится методами анализа линейных систем,
применяемыми к уравнениям в вариациях (8.5). Такой прием приближенной замены
нелинейной системы линейной называется линеаризацией уравнений движения (8.1)
относительно опорной траектории.
Замечание. Аналогичная процедура линеаризации применима и для
систем, описываемых уравнениями /1-го порядка. Рассмотрим ее на примере
системы, описываемой дифференциальным уравнением второго порядка:
Р{х,х,х,х,8) = 09 (8.6)
где Р - нелинейная функция своих аргументов.
Предполагается, что задана опорная траектория **(/), которая получается
в результате решения уравнения (8.6) с начальными условиями
х*('о) = *о> *('о) = *о и известным входным сигналом Я*(')» те-
Обозначим Дх(/) = *(/)-**(/), 4&@ = *@~**@ "~ отклонения от опорного
режима, где *(/) — решение уравнения (8.6) с начальными условиями
х('о) = *о> *('о) = *0 Я входным сигналом $(/) (рис. 8.1).
Для проведения линеаризации разложим функцию Р в ряд Тейлора в
окрестности опорной траектории, ограничиваясь членами только первого порядка
(линейными членами):
Знак * отражает факт, что все производные подсчитываются на опорной
траектории. Первый член обращается в нуль, так как опорная траектория **(/)
удовлетворяет уравнению (8.6).
Введем обозначения:
302

Тогда последнее соотношение можно переписать в форме
с начальными условиями
Д*('о) = *о-*<ь Дх(/о) = *о-*о-
Его решение определяет отклонение Ах(/) от опорной траектории (см. рис. 8.1).
Х\ Ддс@ = х@-**(') .
*о
*0
'о
*^
х@
*
Рис. 8.1
Пример 8.1. Линеаризовать систему, описываемую дифференциальным
уравнением
^ = Зс + х2 + япх + ех-1 + $2-$ = 0
с начальными условиями х@) = х0, *(9) = *о> *@) = *о относительно опорной
траектории х*(/) = 0, я*@аО-
П Найдем коэффициенты разложения функции Г в ряд Тейлора:
Отсюда получим дифференциальное уравнение линеаризованной системы:
Дх@) = хо-х*@) = Дх0,
Лх@) = х0-х*@) = Лх0,
Ах@) = дс0-^@) = Дх0.
Ее структурная схема изображена на рис. 1.1 \М
303

8.1.3. Алгоритм анализа выходных процессов
В задаче анализа (см. разд. 8.1.1) требуется найти выходной сигнал *(/),
^ъ<>^<^\, системы по входному сигналу #@ и начальному состоянию х(/0) = хо.
Для этого нужно выполнить следующие операции:
1. Задать начальное состояние *5» опорный входной сигнал &*(/) и найти
опорную траекторию х*@, удовлетворяющую уравнению (8.2).
2. Определить отклонения начального состояния 6х(/0) = х0 - *о и
входного сигнала 5#@ = #(/) - #*(/).
3. Записать уравнение (8.5) для вариации &с(/) и найти его решение при
начальных условиях &с(/0) = 5х0 и сигнале 6#(/), полученных в п. 2.
4. Найти выходной сигнал *(/) нелинейной системы по формуле (8.3).
Полученное приближенное решение х(/) отличается от точного решения
уравнения (8.1) на величину, имеющую второй порядок малости по сравнению
с|&с0|и||б*(/)||= шах |5*(/)|.
Пример 8.2. Для летательного аппарата (ЛА), совершающего спуск на
поверхность Луны:
а) составить систему уравнений, описывающих вертикальное движение ЛА
на этапе реактивной мягкой посадки;
б) определить траекторию движения на отрезке времени [0,4], если
реактивный двигатель включается на полную тягу в момент времени гв е [0,^];
в) линеаризовать уравнения движения относительно найденной
траектории;
г) исследовать поведение системы в окрестности опорной траектории при
малых отклонениях начальной массы ЛА.
? а) Рассмотрим движение летательного аппарата на заключительном
этапе спуска на поверхность Луны — этапе реактивной мягкой посадки.
Вертикальное движение аппарата происходит под действием двух сил: гравитационного
притяжения и тяги реактивного двигателя. Записывая второй закон Ньютона,
получаем уравнение
ту = -т %д + кТ и,
где тп — масса аппарата; V — вертикальная скорость; %л — ускорение свободного
падения; кти — сила тяги реактивного двигателя, которая пропорциональна
секундному расходу топлива !/(/) {кт — коэффициент пропорциональности).
Выражая из этого уравнения ускорение т> и добавляя уравнения изменения
высоты полета к и массы аппарата /и, получаем систему уравнений движения ЛА:
тп
304

Начальными условиями для данной системы являются масса то, скорость
у0 и высота До в момент времени г = 0 начала вертикального спуска. Входным
сигналом (управлением) служит закон и(/) изменения секундного расхода
топлива. Функция и({) ограничена: 0 ^ и(/) ^ итах, где итах — максимальный (для
реактивного двигателя) секундный расход топлива. Выходными сигналами системы
считаем зависимости массы, скорости и высоты полета от времени.
б) Найдем выходные сигналы /и@, у(/), к((), если заданы начальные
условия:
/и@) = /Яо, у@) = у0, Л@) = Ао
и релейный закон управления
где /д ¦" момент включения двигателя; 1\ — момент окончания процесса
управления.
Рассмотрим два участка траектории движения. На первом участке — до
включения двигателя — происходит свободное падение аппарата, масса которого
не меняется. Интегрируя уравнения движения при и(() ¦ О, находим
На втором участке - после включения двигателя — на аппарат действует
постоянная сила тяги, а масса аппарата изменяется. Обозначим: х = (-(в -
время работы двигателя; у(т) = у(/) - ^(/), Л(т) = Н(() - к$) — отклонения
скорости и высоты полета при включенном двигателе от соответствующих величин
при свободном падении. Тогда с помощью уравнений движения получим
уравнения для введенных переменных:
ду ду й , ч кТ ду кт
Ок ОН Л .. .. _ йН _
""л(А-А') = у-У1 = у =» "у'
Начальные условия при т = 0 (что соответствует моменту времени / = /д) для
отклонений V и к - нулевые:
Интегрируя полученные уравнения при нулевых начальных условиях, находим
о т ^^о^
305

к = ГуА = - Г ктщ — \<к = ктт + -Е-—1п — .
Следовательно, после включения двигателя выходные сигналы системы
имеют вид
т{^) = щ-(^-^в)итяX9
2 Щ \ Щ )
Найденная траектория движения является решением поставленной задачи
анализа.
в) Теперь выполним линеаризацию уравнений движения ЛА. Полученную
траекторию и заданное релейное управление примем в качестве опорного
режима. Обозначим через 51/, 5т, 5у, Ьк отклонения (вариации) входного и
выходных сигналов относительно опорного режима. Система уравнений в
вариациях имеет вид
—5/и = -51/,
йг
±дУ=к^ди^иЬт9
<?* т щ2
4-5Л = 5у.
Л
Заметим, что малые вариации управления Ьи для рассматриваемой модели
должны удовлетворять ограничениям: 5и(/) ^ 0 при ^ < 1В и Ьи{$) <> О при 1>(в>
что отвечает выбранному опорному режиму и имеющимся ограничениям на
управление.
г) Пусть начальная масса ЛА отличается от заданного (номинального)
значения щ на величину Ъщ. Найдем приближенное решение уравнений
движения, используя систему уравнений в вариациях, составленную в предыдущем
пункте. Так как управление в рассматриваемом случае не отличается от опорного
управления, то 5«@ = 0, 0й / < 4. На первом участке траектории — до
включения двигателя (*<1В , и = 0) - уравнения в вариациях имеют вид
4-&и = 0, 4-$у = 0, ^Ьк = Ьу.
й1 йх йг
Решая эти уравнения с начальными условиями 5т@) = 6то, 6у@) = 0,
Щ0) = 0, получаем 5т@ = 5то, 5у(/) = 0, 5Л(/) = 0, Ъ<^<^^в.
На втором участке траектории — после включения двигателя (/^*д,
и = итях) — уравнения в вариациях имеют вид
306

—6/11 = 0, —6у = —^итах5т, —,
-5.6/11 = 0, — 6у = —^итах6т, ^"8Л = 5у, ^Ш^.
Решая эти уравнения с начальными условиями 6/и(/д) = 5/ив, 6у(^) = 0,
6Л(Ы = 0, получаем
т{щ т(*
6т(/) = Ьто, 6у(/) = *г| — -— бто,
6Л(/) = кТ\
I. "*> итах V *"<> У]
^ / ^ Г,.
Таким образом, получим приближенное решение уравнений движения:
т@ + *1иь, К0 + 6у@, Л@ + 6Л@,
где /и@, ></), Л(/) — опорная траектория, найденная в п."б". ¦
8.2. АНАЛИЗ АВТОКОЛЕБАНИЙ МЕТОДОМ ГАРМОНИЧЕСКОЙ
ЛИНЕАРИЗАЦИИ
8.2.1. Постановка задачи
Рассматривается замкнутая система с одним нелинейным элементом (см.
рис. 7.2). Изучается свободное движение системы, т.е. движение при ненулевых
начальных условиях в отсутствии входного сигнала (&(/) г 0).
При отсутствии внешних воздействий свободное движение линейной
системы может быть периодическим, если корни характеристического уравнения
чисто мнимые. Однако практически такие движения не реализуются, так как
малейшее изменение параметров системы приводит к тому, что колебания
становятся либо затухающими, либо расходящимися, поскольку появляются
отрицательные или положительные действительные части у корней характеристического
уравнения.
В отличие от линейных систем в нелинейных системах управления при
отсутствии внешних воздействий возможны устойчивые периодические движения,
которые принято называть автоколебаниями.
На фазовой плоскости автоколебаниям соответствует устойчивый
предельный цикл (см. рис. 7.23,а), где х, у = х — выходной сигнал и его производная.
Пусть известны:
а) характеристика Г(а) нелинейного элемента;
б) передаточная функция }У(з) линейной части системы (см. рис. 7.2),
имеющая вид G.4).
Требуется определить:
а) возможны ли в системе автоколебания?
б) параметры автоколебаний: амплитуду ап и частоту со^ предельного
ВДкла, если ответ на первый вопрос положительный.
Анализ периодических движений систем управления с одним нелинейным
элементом будем проводить методом гармонической линеаризации ее
единственного нелинейного звена.
307

8.2.2. Гармоническая линеаризация нелинейных элементов
Рассмотрим нелинейный элемент с характеристикой г = Р(<у), на вход
которого подается гармонический сигнал а(/) = а яп со/ с амплитудой а > О и
частотой со > 0. Выходной сигнал г(/) = Г(а $т со/) нелинейного звена будет
периодическим, но не гармоническим. Разложение в рад Фурье этого сигнала
имеет вид
*@ = Яо(а) + 4(а) я $1П со/ + дх(а) а со$ со/ +... ,
где
0(а) = — Г,Р(аш1\|/)8ш\|/</1|/,
1 2п
д\(а) =— [Да8ш\|/)со8\|/Л|/.
1Г/Т •
О
(8.7)
2я
Предположим, что:
— постоянная составляющая д0(а) сигнала отсутствует (для нечетной
характеристики Г(а) это всегда выполняется);
— линейная часть системы (устойчивая) обладает свойствами фильтра
низких частот [30,42]: | IV (т) |»| IV (Пая) | при к > 1, поэтому учет высших
гармоник не является существенным (гипотеза фильтра).
Тогда приближенное выражение выходного сигнала будет иметь вид
г(/) = д(а) а 8т со/ + д\ (а) а со8 со/.
Такой же выходной сигнал можно получить, подав гармонический сигнал
а(/) = а8шсо/ на вход линейного звена с передаточной функцией
Ун(<*,5) = д(а)+Щ±-!-5. Частотная характеристика \Ун(а9т) этого эквивалент-
со
ного звена зависит только от амплитуды а и не зависит от частоты со:
ад-^м
= д(а) + 1дх(а). (8.8)
.г»/со
Функцию №я(а) называют комплексным коэффициентом усиления
нелинейного элемента, а коэффициенты д(а) и д\(а) - коэффициентами
гармонической линеаризации.
Таким образом, нелинейный элемент г = ^(а) может быть заменен
линейным, частотная характеристика которого зависит от амплитуды входного сигнала.
Этот прием получил название гармонической линеаризации нелинейностей.
308

Пример 8.3. Найти комплексные коэффициенты усиления нелинейных
звеньев, характеристики которых изображены на рис. 8.2.
1 +
-1
-И
-1
-1
-* а
Рис. 8.2
О Построим диаграмму (рис. 8.3) преобразования сигнала а = а яп у
релейным звеном с зоной нечувствительности (рис. 8.2,а). Поскольку выходной
сигнал г(н/) является нечетной функцией, то коэффициент ^(а) равен нулю.
Ч
11
-1
п п + уо 2я
—1——• гт_^ «»^
Уо я -уо
V
а = а 81П \|/
Рис. 8.3
Коэффициент д(а) находим по формуле (8.7):
д(а) = — Г ^(а 8ии|/)81пшЛ}/ = — Гяп\|/*Л|/ =
Ж/Т * ЧГ/7 *
па
па
щ
4 4 Г 1
= —со8\|/0 =—Л1—г при а>1,
яд 7X01 а2
. 1
Уо = агсз1п—.
а
309

Таким образом, комплексный коэффициент усиления (8.8) для данного
«>1,
паЦ а2
элемента имеет вид IVн (а) =
[О, а й 1.
Построим диаграмму (рис. 8.4) преобразования сигнала а = а$ш \|/ для
элемента (рис. 8.2,6) с петлей гистерезиса. По формулам (8.7), в которых отрезок
интегрирования можно взять любым, лишь бы его длина была равна 2л,
находим коэффициенты гармонической линеаризации:
г = /Ча)
1
-Г
а = а зш у
Ч>0
я + \|/0
2*
2я+^ур
Рис. 8.4
| 4*0+2* |
0(а)=— Г /7(я8туMтч/<Л}/= —
па * па
| 81П \|/ </ц/ - Г 81П\|/^Д(/
I. чч> ч»о+*
4 4 Г Г
= —созуо =—«I1—т ПРИ а>1»
яа яа I а1
Ч»о+2л
1 Ч'оу" I
Я\(<*)=— [ Г(а$т\у)со&уа\у =—
па ^ яа
Ч»0
4*0+11
. Ч*о
. 1
у о =агс81П—;
а
щ+2я
Г СО81у0\у~ Гс08\|/Оу
4*0+*
4.4
= 8Ш\|/0 = 7 при а>1.
яа па2
Подставляя эти коэффициенты в (8.8), находим комплексный коэффици-
D Г Г • 4 1
—«|1—г-1—г, а>1,
ент усиления
[0, а<1.
Для типовых нелинейных элементов комплексные коэффициенты усиления
приведены в табл. 8.1 и [14,34].
310

Таблица 8.1
Нелинейный элемент
Коэффициенты гармонической линеаризации
№
Ь/п
Название
Графики
аналитическое
задание
Я(а)
01 (*)
Релейный
элемент
Рис. 7.4
= —
па
Релейный
элемент
с зоной

нечувствительности
Рис. 7.5
па I а2
4 = 0 , а<Ь
Элемент
с зоной

нечувствительности
Рис. 7.6
2с( . Ь
д = с агсзш— +
п \ а
4 = 0 , а<Ь
а^Ь ;
Элемент
с петлей
гистерезиса
Рис. 7,7
Ас \л Ь2
па 1 а2
4= — 1/1—т> а*ь>
4 = 0 , а <&
Я\ = т,а>Ь;
па1
41 = 0 , а < 6
Элемент
с зонами

нечувствительности
и
неоднозначности
Рис. 7.8
2с
4= —
710
4 = 0 , а<Ь
_ 2с6A-г)
41 = 5—»
•мг
а^Ь;
41 = 0 , а <Ь
311

8.2.3. Алгоритм анализа автоколебаний
С помощью гармонической линеаризации нелинейного элемента система,
представленная на рис. 7.2, приводится к виду, изображенному на рис. 8.5.
* Ф-^Ч **<«.*>
Щ*)
-> X
Рис. 8.5
Применяя преобразование Фурье (см. разд.3.3) к линеаризованной системе
(рис. 8.5), получаем:
ЛГ(а>) = ^(с)Ж(/соI(о>),
2(о>) = <?(©)-*(©).
Эти уравнения связывают изображения Х(а>), Х(со), (?(©) сигналов х, а,
# и частотные характеристики IVн (а) и Ж(/со) звеньев системы. При
отсутствии внешних воздействий ($(/) = 0) получим соотношение
[1 + Цгн(а)Щко)]1,(<й) = 0,
которое выполняется для периодического (не равного нулю) сигнала а(/)
B(со) * 0) только тогда, когда амплитуда а и частота со удовлетворяют
уравнению гармонического баланса:
ЯГн(а)ЩЬ) ш-\.
(8.9)
Это уравнение можно рассматривать как условие наличия чисто мнимого
корня /со характеристического уравнения линеаризованной системы, что
связано, как отмечалось выше, с существованием периодических движений линейных
систем.
Уравнение (8.9) гармонического баланса можно записать с учетом (8.8)
в виде системы двух уравнений относительно двух неизвестных а и со:
Я(а) Ке IV (т) - дх (а) 1т IV (/со) = -1,
ах (а) Ке Щ/со) + д(а) 1т IV(ю>) - 0,
(8.10)
где ?(а) и 01 (а) — коэффициенты гармонической линеаризации нелинейного
элемента.
Применяются также и другие формы записи уравнения (8.9):
^я(*) = -777тт; ЩЬ)-МИ{а)9т>Мн{а)ш-- 1
1Г(/а>)'
ИЪ(«>
312

При решении задач удобно пользоваться следующей графоаналитической
схемой (диаграммой Гольдфарба).
1. Построить годограф Ж(/со) при соб[0;+оо).
2. Построить годограф Мн(а) = —
1
при аб[0; + оо).
Гн(а)
3. Найти значения частоты со я и амплитуды ап периодического
движения, соответствующие точкам пересечения годографов (решить уравнение (8.9)
или систему (8.10)).
4. Если при движении по годографу Мн(а) = —
1
.„ . -, соответствующем
увеличению амплитуды а от значения ап, окажемся в точке, которая не будет
охватываться годографом Щ/со) (рис. 8.6, точка 2), то амплитуде ап будут
соответствовать устойчивые автоколебания, а в противном случае (рис. 8.6, точка 1)
- неустойчивые.
V
:+00
а = 0
со = 0
Рис. 8.6
Замечания.
1. Метод гармонической линеаризации является приближенным. Поэтому
отсутствие решений уравнения (8.9) гармонического баланса означает, что
используемый метод не позволяет выделить периодических движений у
исследуемой системы.
2. После нахождения частоты периодического движения следует проверить
выполнение гипотезы фильтра: | IV(юп) \»\ \У(Ис<йП) \ при к > 1.
Пример 8.4. Исследовать систему (рис. 8.7) на наличие автоколебаний.
? 1. Строим годограф частотной характеристики линейной части
разомкнутой системы при © е [0;+оо) (рис. 8.8):
ЩЬ) =
(/соK + 3 (/соJ + /со - Зсо2 +1 (со - со3 )
-I-
3A-о2)
3(-Зсо2-/(<о-<о3))_ 9
9©4+со2A-<о2J " 9а>2 + A-а>2J ' 9а>3 +соA-со2J
313

>ф-
Яст)
X3 +3х2 +Х
*| *-^<а)
1
-1
Рис. 8.7
2. Коэффициенты гармонической линеаризации релейного звена имеют
вид (п.1 табл. 8.1):
4
710
Строим годограф функции
Мн(а) =
при ае[0;+оо) (рис. 8.8).
-1
7Ш
д(а) + 1д1(а) 4
ЖГ*(*) -1
ш
0
0,5
1
2
+ 00
^<*>)
-9
-3,2
-1
-0,2
0
К(ш)
— 00
-1,6
0
од
0
Рис. 8.8
3. Находим амплитуду ап и частоту о>#, соответствующие точке
пересечения годографов Ми (а) и Щио), решая уравнение гармонического баланса
ИЧ/а>) = Л/я(а):
--/
, 3A-(Р2)
яа
9<о2+A-«>2J 9а>3+а>A-а>2J 4
Приравнивая действительные и мнимые части, получаем:
314

па 3A-ср2) _0
9со2+A-<о2J 4' 9оо3+соA-<о2J
Из второго уравнения следует со = ±1 (со = -1 не подходит, так как
4
со <= [0,+°о)), поэтому соП = 1. Из первого уравнения находим аП = —.
4. По диаграмме Голвдфарба (рис. 8.8) определяем, что найденным
значениям параметров соответствуют устойчивые автоколебания, так как при
увеличении а (а>ап) точка, движущаяся по годографу Мн(а), не охватывается
годографом Ж(/со). ¦
Пример 8.5. Исследовать систему (см. рис. 7.25) на наличие автоколебаний,
где параметры нелинейности Ь = 1; с = —.
П 1. Частотная характеристика линейной части системы имеет вид
1
И^/оо) =
ф + 1)
|$ = /со <,:52 +5
- со2 - /со
5 = №> / СО - СО СО - (/со)
-<р(со + /) , -1 / ,
~©2(©2+1)~1 + со2 соA + со2)'
Строим годограф ^(/со) при соб[0;+оо) (рис. 8.9).
2. Находим комплексный коэффициент усиления нелинейного элемента
с петлей гистерезиса (п.4 табл. 8.1):
и.обратную характеристику Мн(а) = -
Гн(°)
*ж /ч а2 а2(Уд2-1+/) \(ГГ~7 Л
10(^7-/) 10(а2-1-/2) 10 И ^
Построим годограф Мн{а) при ае[0;+оо) (рис. 8.9).
3. Найдем параметры автоколебаний. Для этого составим уравнение
гармонического баланса Мн(а) ¦= ^(ио):
ЮЧ У 1 + оэ2 соA + а>2)
315

МН(а)
'а> = 0
СО
0
0,5
1
2
+ 00
Щ<»)
-1
-0,8
2
_1
5
0
УМ
— 00
-1,6
—1
2
—ь
10
0
Рис. 8.9
НИИ
Приравнивая действительные и мнимые части, получаем систему уравне-
^^-
1
1
1
10
1 + со2
Ю 00A + со2)*
Из второго уравнения со3 + со -10 = 0 определяем частоту <ьп = 2 автоколебаний.
Заметим, что других действительных корней это уравнение не имеет. Подставляя
найденную частоту в первое уравнение системы, определяем амплитуду
автоколебаний: ап - ыЪ. При частоте сод = 2 период колебаний —2- = я, что примерно
соя
совпадает со временем 2&«ЗД2 одного прохождения изображающей точкой
предельного цикла, которое найдено в примере 7.12.
4. Как видим (рис. 8.9), годографы пересекаются в одной точке, которой
ссютветствуют устойчивые автоколебания, так как при увеличении а (а>ап)
окажемся в точке, которая не охватывается годографом И^/со). ¦
Пример 8.6. Исследовать систему (рис. 8.7) на наличие автоколебаний, если
в качестве нелинейного элемента используется релейный элемент с зоной
нечувствительности (рис. 7.5) и параметрами Ь = 1, с = я.
? 1. Строим годограф частотной характеристики линейной части
разомкнутой системы при со € [0;+оо) с учетом п.1 примера 8.3 (рис. 8.10,а):
04*») = —
--!
3A-о2)
2+A-со2J 9а>3+юA-со2J
2. Находим комплексный коэффициент усиления (п.2 табл. 8.1):
™ 1 а2 па2
и обратную характеристику Мд(а) = -
И'я(а)
316

Мн(а) = -
па"
4с у с
Определим значение а, обеспечивающее максимальную величину Л/#(а).
Для этого применим необходимое условие безусловного экстремума:
21Ш-4с^а2-Ь2-па24с- **
йа
1^Т2
16с V-*2)
= 0
или 8яас(д2-А2)-4тш3с = 0, 2(а2-Ь2) = а2. Отсюда а2 =2Ь2 и а* =Ль
(значение а = -42Ь не подходит, так как а ^ Ь).
Вычислим значение обратной характеристики при а = а* - 42Ь:
п2Ь2 пЬ
Мн(а') = -
АсЬ
2с'
Для заданной нелинейности (Ь = 1,с = п) находим а* -42, Л/#(д*) = -—.
Построим годограф Мн(а) = -
4^а2-\
(рис. 8.10,а).
3. Очевидно, точка пересечения построенных годографов имеет
координаты {/ = -1, Г = 0. По годографу частотной характеристики Ж(/со) находим
частоту автоколебаний (см. рис. 8.8): <оП = 1. Амплитуду определяем из условия
Мн(а) = Т— = -1.
4^-1
Отсюда а2=4^а2-\, о4=1б(а2-1), а4 -16а2 +16 = 0, а2 =8 ±4^3.
Следовательно, получаем два решения:
ах =4*-44ъ =1,035 и а2 = V 8 + 4^3 = 3,863.
© = 0
1 я
1,01
1Д
к/2
2
3
^я(*)
-1,8
-0,66
-0,5
-0,577
-0,795
317

4. Для наглядности изобразим условно график (рис. 8.10,а) , отражая факт
наличия двух "берегов" у годографа Мн(а) (рис. 8.10,6). При увеличении а от 1
до а* = 4т. изображающая точка двигается вправо, а при а > а* = у2 - влево
вдоль действительной оси. Тогда очевидно, что годографы IV(т) и Мн(а)
пересекаются в одной точке при двух разных значениях амплитуды: ах и а2. Так как
при а > ах точка охватывается годографом частотной характеристики IV {т), то
первому пересечению соответствует неустойчивое периодическое решение.
Второе пересечение определяет устойчивые автоколебания с параметрами
®п =1>ап =02=1г8 + 4^3 , так как при а > а2 точка не охватывается годографом
ИЧ/о>).и
8.3. АНАЛИЗ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ
8.3.1. Постановка задачи
Рассматривается замкнутая система с одним нелинейным элементом (см.
рис. 7.2). Изучается свободное движение системы, т.е. движение при ненулевых
начальных условиях в отсутствии входного сигнала (#@ = 0).
Система называется асимптотически устойчивой, если при ненулевых
ограниченных начальных условиях свободное движение х(/) ограничено при
г б[0;+ оо) и Ит х(/) = 0. Если окажется, что это свойство выполняется для лю-
/->+00
бых нелинейных элементов из некоторого класса, то устойчивость называется
абсолютной.
8.3.2. Условия абсолютной устойчивости
Утверждение 8.1 (достаточные условия абсолютной устойчивости, теорема
В.М. Попова). Пусть выполняются условия:
1) все полюсы передаточной функции линейной части системы имеют
отрицательные действительные части (т.е. линейная часть разомкнутой системы
устойчива);
2) характеристика нелинейного элемента принадлежит сектору [0;&], т.е.
/40) = 0, 0^^^-йк при всех а*0; (8.11)
а
3) существует действительное число # такое, что при всех со е[0;+оо)
выполняется неравенство
Ке[A + /©0)Щ/©)]+~->О. (8.12)
Тогда при любых ограниченных начальных отклонениях от нулевого значения
функция а@ остается ограниченной при * > 0 и о(/) -> 0 при / -»-ко (т.е. система
будет асимптотически устойчивой, так как из ограниченности о(() следует,
ограниченность х@, а из стремления а@ к нулю следует, что х(/) -> 0 при X -> -ко.
Доказательство этого утверждения приведено в [45].
318

1-ка
;1г = /Ча)
Рис. 8.10
Заметим, что условие (8.11) принадлежности характеристики сектору [0;к]
означает, что график функции г = РF) лежит между осью абсцисс и прямой
1-ка (рис. 8.10). При этом конкретный вид функции в формулировке критерия
не играет никакой роли. Можно сказать, что рассматривается сразу целый класс
систем с различными нелинейными элементами, характеристики которых
принадлежат сектору [0;к], и критерий определяет абсолютную устойчивость
указанного класса. В частности, в данный класс входят и линейные системы,
получающиеся заменой нелинейного элемента усилительным звеном с
коэффициентом усиления, не превышающим к.
Утверждение 8.2 (необходимые условия устойчивости). Если система (см.
рис. 7.2) с нелинейной характеристикой Г(о), принадлежащей сектору [0;к],
асимптотически устойчива, то:
1) линейная часть разомкнутой системы — устойчива (т.е. полюсы
передаточной функции №(8) лежат в левой полуплоскости (Ке$ < 0));
2) годограф модифицированной частотной характеристики
Щю>) = Ке Ф(Ь) + «о 1т Щш>)
Ы)
(8.13)
действи-
линейной части системы при со е@;+оо) не пересекает луча
тельной оси.
Приведем также условие абсолютной устойчивости для часто
встречающегося случая, когда передаточная функция \У($) имеет один нулевой полюс, а
нелинейный элемент Г(а) имеет зону нечувствительности [42].
Утверждение 8.3. Пусть все полюсы передаточной функции 1У(з) линейной
части системы лежат в левой полуплоскости (Ке$<0), за исключением одного,
Ровного нулю, причем Итз}УE)>0. Пусть, кроме того, характеристика РF)
нелинейного элемента удовлетворяет условиям: РF) = 0 при о^ ^ а ^ а2;
319

0<ГF)йк(а-а2) при о>о2', ^(а-а^ </*(а) <0 при а<а{ ; причем
да О
|[Лег-^(аI*/а = оо, \[РF)-кв]а*а = со(т.е. график функции % = Г(о) не при-
О -00
ближается "плотно" к границе секторов, изображенных на рис. 8.11).
Тогда, если существует такое действительное число д>0, что — неявля-
о
ется полюсом IV(з), и для всех со € [0,+оо) выполняется неравенство
Ке[A + /ю$)^(/а>)] + -^>0,
к
(8.14)
то при любых ограниченных начальных условиях процессы в системе останутся
ограниченными и а@ при I -> +а> стремится к одной из точек отрезка покоя [а1;а2].
г = Да)
г = к(о-с1)
Рис. 8.11
8.3.3. Алгоритм анализа абсолютной устойчивости
1. Найти все полюсы передаточной функции IV(з) линейной части
системы и проверить, имеют ли все из них отрицательные действительные части. Если
хотя бы один полюс не лежит в левой полуплоскости (КекО), необходимое
условие абсолютной устойчивости (п.1 утверждения 8.2) не выполняется и
система не является абсолютно устойчивой.
2. Найти параметр к (лучше наименьший из возможных),
удовлетворяющий условию (8.11) в п.2 утверждения 8.1.
3. Проверить выполнение условия (8.12) п.З утверждения 8.1.
Если все три проверенных условия выполняются, то система является
абсолютно устойчивой.
320

Для решения задач удобно использовать геометрическую интерпретацию
условий абсолютной устойчивости [42,45]:
1. Построим годограф модифицированной частотной характеристики
*Г(/со), определяемой выражением (8.13).
2. Построив годограф, получим одну из трех возможных ситуаций:
а) годограф Ж(ио) пересекает луч -°°;-т' действительной оси (рис.
8.12,а) — в этом случае абсолютной устойчивости нет;
б) годограф Ж(ко) не пересекает луча -«^-тч и можно провести прямую
Попова, проходящую через точку (-т;01 и лежащую левее годографа (рис.
8.12,6), — в этом случае система абсолютна устойчива;
в) годограф не пересекает луча -°°;-"Г действительной оси и провести
прямую Попова нельзя (рис. 8.12,в) — в этом случае никакого заключения об
абсолютной устойчивости мы сделать не можем.
Прямая Попова 1
Пример 8.7. Исследовать устойчивость нелинейной системы, структурная
схема которой изображена на рис. 8.13, если нелинейная характеристика имеет
следующий вид:
а) для элемента, описываемого соотношением: Г(о) = — (а + 8т а);
а-2, а>2,
б) для элемента с зоной нечувствительности: Г(а) = <
О, -2^а^2,
а + 2, а < -2;
[ 1, а>0,
в) для релейного элемента: Г(а) = \ 0, а = 0,
-1, а<0.
321

•тст >
1
Ш
г
1
52 + 5 + 1
—>
Рис. 8.13
1
5 + 1
П 1. Находим передаточную функцию \У(з) линейной части разомкнутой
системы, которая представляет собой последовательное соединение
колебательного и апериодического звеньев:
1
Щз) =
($2+* + !)($+ 1)
Линейная часть системы устойчива, так как корни знаменателя передаточной
функции №(з): ^1 = -1, $2,3 = т^— имеют отрицательные действительные
части.
2. Определим теперь сектор [0,к], которому принадлежат характеристики
рассматриваемых нелинейных элементов. Для нечетной функции г=-(а + «та)
имеем при а^О оценку — (а + $та)^а, поэтому (в случае "а") можно взять
к = 1. Для элемента с зоной нечувствительности (случай "б") величина к также
равна 1. Для релейного элемента (случай "в") следует положить к = +оо.
3. Частотную характеристику
*Г(/со) = Щз)
= 1 1-2<о2-/<оB-<о2)
*Ыа> A - со2 + /со) A + /со) A - со2 + со4) A + со2)
подставим в неравенство (8.12):
^A + /ш?)[1-2со2-1соB-со2)] | 1 ^
A-со2+со4)A + со2) к
(8.15)
Выделяя действительную часть и умножая на положительный знаменатель
дроби, получаем
1-2ю2+дсо2B-со2) + ^A + со6)>0.
Для неотрицательной переменной X = со2 полученное неравенство имеет вид
322

^Х3-^Х2+2Х(^-1) + 1+^->0. (8.16)
к к
Критерий Попова будет выполняться, если найдется число д, для которого
неравенство (8.16) окажется справедливым при всех X ^ 0.
Запишем неравенство (8.16) при к = 1 (случаи "а* и "б"):
Х3-$Х2+2Х(я-1) + 2>0.
При д = 2 многочлен, стоящий в левой части неравенства, будет монотонно
возрастать для всех X б(-оо;+оо). Поскольку при X = 0 многочлен положителен, то
при X ^ 0 он будет принимать только положительные значения. Таким образом,
системы с нелинейностями "а" и "б" будут устойчивыми.
Для к = +оо неравенство (8.16) примет вид
-дк2+2\(д-\) + 1>0. (8.17)
Для положительных значений д неравенство не будет выполняться при
больших значениях X. Если же ?<0, то минимальное значение квадратного
трехчлена в (8.17) достигается при X = ^— > 0 и это значение отрицательно:
_,B^+Ж^I+1=к^1+1=11^±1<о.
д2 Я Я Я
Таким образом, ни при каких значениях д неравенство (8.17) не будет
справедливым при всех X ^ 0, т.е. критерий Попова для рассматриваемой системы с
релейным элементом (случай "в") не выполняется.
Покажем, что в данном случае система неустойчива. Действительно,
необходимое условие устойчивости выполняется, если годограф модифицированной
частотной характеристики.(8.13)
#Ют1^-§г&=р. (8.18)
1 + юб 1 + юб
при со €@;+оо) не пересекает луча |-оо;—— действительной оси. Годограф
Функции (8.18) пересекает действительную ось в точке 1 при со = 0 и в точке
—г при 0 = 1/2 (рис. 8.14). Поэтому рассматриваемая система неустойчива для
всех нелинейных элементов, характеристики которых не принадлежат сектору
[0; 3]. В частности, система с релейным элементом (случай "в"), характеристика
которого принадлежит сектору [0; + оо), будет неустойчивой. При этом, так как
годограф \У(их>) пересекает луч (-<»;0], необходимое условие устойчивости не
выполняется. ¦
323

ш
0
2
4г
+ 00
&(ш>)
1
2.
"Г
1
~3
0
Рис. 8.14
Пример 8.8. Исследовать абсолютную устойчивость системы, структурная
схема (рис. 8.15,а) которой включает релейный элемент с зоной
нечувствительности (рис. 8.15,*) или элемент с зонами нечувствительности,
линейности и насыщения (рис. 8.15,6).
^
П<у)
3E + 1)
-2
* = *(«)
1 2
¦*<т
-1
г = /Ха)
1
-1
в
О Передаточная функция Щз) =
Рис. 8.15
1
линейной части системы удовле-
5E + 1)
творяет условиям утверждения 8.3, так как один полюс равен нулю (зг = 0), а
другой лежит в левой полуплоскости (з2 = -1), причем Ит зЩз) = 1 > 0. Срав-
нивая характеристики нелинейных элементов с характеристикой, изображенной
на рис. 8.11, определяем значения величин: а! = -1, а2 = 1, к = 1 для первого
элемента (рис. 8.15,E) и к = +оо для второго элемента (рис. 8.15,*).
Запишем неравенство (8.14): Ке . ^1Ш?Ч + — > 0. Выделяя действительную
иоA + /а>) к
часть,
>, получаем -*—2"+Т>0- Невидно, что при д > 1 последнее неравенство
1 + оэ
выполняется при всех <о и любых к>0. Таким образом, точки отрезка покоя
[<*ьв2] = [-1;1] являются устойчивыми положениями равновесия для системы
(рис. 8.15,я) с любым из рассматриваемых нелинейных элементов.*
324

8.4. АНАЛИЗ ВЫХОДНЫХ ПРОЦЕССОВ ПРИ СЛУЧАЙНЫХ
ВОЗДЕЙСТВИЯХ МЕТОДОМ СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ
8.4.1. Постановка задачи
Рассматривается разомкнутая система с одним нелинейным элементом (см.
рис. 7.3).
Пусть известны:
а) нелинейный элемент с однозначной нечетной характеристикой Г(&);
б) передаточная функция Ж($) линейной части системы, имеющая вид
G.4); предполагается, что линейная часть системы устойчива;
в) входной стационарный сигнал с математическим ожиданием т% = соп&
и ковариационной функцией /^(л)> который действует на систему
продолжительное время.
Требуется найти математическое ожидание щ и ковариационную
функцию Ях(г\) выходного сигнала в стационарном режиме (при / -* +оо).
Точное исследование нелинейных систем при случайных воздействиях
значительно сложнее, чем исследование линейных систем, так как нелинейные
элементы обычно существенно искажают входной сигнал. Например, распределение
(одномерное) реакции релейного звена будет дискретным для любого входного
сигнала, в том числе и для сигналов с непрерывным распределением. Поэтому
в практике расчетов нелинейных систем управления применяются
приближенные методы, к которым относится рассматриваемый ниже метод статистической
линеаризации.
8.4.2. Статистическая линеаризация нелинейных элементов
Пусть на вход нелинейного звена (рис. 8.16,а) с однозначной
характеристикой г = Г(&) поступает случайный сигнал #@. Выделяя в сигналах #@ и
о о
г@ = ^($@) средние /и^@, /^@ и центрированные $(/), г@ составляющие,
получаем
*@ = тгЦ) +1@, *@ = тг«) + г@. (8.19)
В соответствии с представлением (8.19) преобразование входного сигнала
#@ в выходной сигнал г(') нелинейным звеном (рис. 8.1б,а) заменим двумя
преобразованиями (рис.8.16,6): нелинейным по математическому ожиданию и
линейным по центрированной составляющей. При такой замене получим
отличный от г(/) выходной сигнал
?@ = /11,@ + к{ 1@ = Щт;«)) + кх 1@. (8.20)
Для нечетных характеристик г = ^(#) нелинейное преобразование
"Н. @ = /^(^(О) заменяют, в свою очередь, линейным /иг@ = #от*@- В этом
325

случае выходной сигнал ?(/) = к$ т^(Г) + к\ я@ получается в результате
преобразований средней и центрированной составляющих входного сигнала #@ двумя
усилительными звеньями (рис. 8.16,*), коэффициенты усиления к$, кх которых
называют коэффициентами статистической линеаризации.
ш9-
А
ГB)
Щт^Г"]™*
*1 Н*1*
ТП9
к^тп^
*1 Н*1*
а б в
Рис. 8.16
Выбор коэффициентов статистической линеаризации делают по-разному
в зависимости от требований к статистической эквивалентности линейных
звеньев исходному нелинейному звену. Обычно используют один из следующих двух
способов.
Первый способ обеспечивает равенство математических ожиданий и
дисперсий сигналов *(/) и ?@:
Лг@ = Л?(') = М[т - т?@]2 = М[т - ко т,(/)]2 = М\кх I (/)]2 = #/>,<|).
Отсюда получаем
*о@ =
1 () Ко'
(8.21)
где /)^(/), 2>г@ — дисперсии входного и выходного сигналов.
При втором способе линеаризации минимизируется математическое
ожидание квадрата ошибки: / = МI (г@ - ?@J -> пил. С учетом представления
?(') = *0 *!!,(/)+ *1^@ ИМееМ /-^|[«@-*0^@-*1в@]2|-
Применим необходимое условие безусловного экстремума:
5*о I
Ш)-котЙA)-к1еA)](
^ = 2М\ [г@-*о «,(>Ь*1 *<'»• <-*«>[-0
-тг@I = 0,
326

или
| тгЦ) - ко т8Ц) - кх МШ\} ¦ (-«,@) = 0.
-МШЫт^кот^ОМШ^к.М^Ш]2}
Поскольку М[х(*)] = 0, м\ [$(/)]21 = 2)^@, получаем
[ = 0.
*«-*$. фю-*ШШ. (8.22)
Коэффициент ^1 можно взять либо равным А^1*, либо равным к^, либо
равным их полусумме. Коэффициент &о выражается одинаково в обоих случаях
(8.21), (8.22). Заметим, что коэффициенты статистической линеаризации зависят
от распределения (одномерного) входного сигнала #(/). Эта зависимость может
быть указана явно, если в формулы (8.21), (8.22) подставить выражения
400
«с@- /ОДА'.;)*.
-оо
Дг@ = 7*2(*>1#,#> * " и?<0. (8-23)
—00
+оо
Л/[г@*@1 = | Г(а) (* -ж,(М) /К'.*)*.
-00
П*е Р('»#) ~~ плотность распределения #(/). При нормальном законе
распределения #@, который задается параметрами /л^@ и 2)^(/), коэффициенты
линеаризации (8.21), (8.22) будут функциями этих параметров *о = *о0и*@»2^(/)) >
*1=*!(т,(/),2),(/)).
Пример 8.9. Найти коэффициенты статистической линеаризации релейного
элемента с характеристикой г = я&п#, если на его вход подается случайный
сигнал #(/), имеющий нормальное распределение.
П Для плотности нормального распределения р(*> #) = г 2/>*('*
V 2*0,@
находим в соответствии с (8.23)
+оо ( т И\ \
1иг@= \ Я8П*Ж*)* = 2ФМ^ I,
327

Лг@ = \ (818П«Jр(Г,«)*-т|@ = 1-4Ф
-00
»$(»
-7 (*-*!«))*<.«)*- /С*-*х@IК',*)*-^^« 2/>х@.
/ъГ
1 хг-Т
где Ф(х)=-^=г |е 2 <&с - функция Лапласа, а о^ =^Щ- Подставляя найден-
ные выражения в (8.21) и (8.22), получаем искомые коэффициенты:
*о(» =
«,@
Ф
Г 111,@
КМ/
2^@
(8.24)
8.4.3. Алгоритм анализа выходных процессов
В результате статистической линеаризации нелинейного элемента исходная
система (рис. 7.3) заменяется статистически эквивалентной (рис. 8.17).
т9
к^т^
Щз)
^1 Г ^
Рис. 8.17
Математическое ожидание и центрированная составляющая преобразуются
двумя последовательно соединенными линейными звеньями с передаточными
функциями #о ЙЧ$) и кх №(з) соответственно. Поэтому формулы C.35), C.36),
устанавливающие связи вход-выход, принимают вид
тх=ко ^-тя = к0 ЩО)т6, 8х(р) = | кх 1Г(/а>)|2^(©).
Для решения задачи анализа выходных процессов нужно выполнить
следующие операции.
328

1. Найти коэффициенты к$, кх статистической линеаризации по формулам
(8.21) или (8.22) с учетом (8.23).
2. Определить математическое ожидание выходного сигнала в
стационарном режиме:
тх=к0Щ0)тё. (8.25)
3. Найти спектральную плотность входного сигнала 5^ (со) по формуле
преобразования Фурье:
+00
.?»= /^(цу-^А, . (8.26)
-00
4. Определить спектральную плотность выходного сигнала по формуле
Зх(<о) = | кх Щио) \2$г(<о) . (8.27)
5. Найти ковариационную функцию выходного сигнала в стационарном
режиме по формуле обратного преобразования Фурье:
, +00
Пример 8.10. Для разомкнутой системы (см. рис. 7.3) с нелинейной
характеристикой /*(&) = ЭДП* и передаточной функцией }У(з) = найти матема-
5 + 1
тическое ожидание и ковариационную функцию выходного сигнала (в
стационарном режиме), если на вход системы поступает нормально распределенный
сигнал #@ с математическим ожиданием те = 1 и ковариационной функцией
Л*<л) = е-|п|.
П 1. Подставляя математическое ожидание т% = 1 и дисперсию
2>2 = 1^@) = 1 в формулы (8.24), получаем
ко = 2ФA), *<*> =1/1-4Ф2A), к\2) =1/Х
2. Находим математическое ожидание выходного сигнала по формуле
(8.25): тх = 2ФA) ЩО) т8 = 2ФA), так как ЩО) = 1.
3. Находим спектральную плотность входного сигнала по формуле (8.26):
-00 0 -00 О
е1| (!-/«)
A-/о>)
0 в-ц<1+Л»)
+
-A + /©)
1 1
- + •
1 - /со 1 + /со 1.
329

4. Находим спектральную плотность выходного сигнала по формуле (8.27),
взяв к{ =кР = Л—:
I пе
Лх(а>):
7гв 11 + ш> I 1 + ©2 явA + ©2J
5. Выполняя обратное преобразование Фурье, получаем искомую
ковариационную функцию выходного сигнала. При т\ > О по формуле (8.28) находим
*,(Л) =т-7 -—~ге^ Л»ш± гее [—Ц-е" =
2я _*, Яв A + 0,2J пе г=, [ A + ^2J ^
Яв »-»!^4(*-0 (* + ') ] "в »-><[(« +/J (д + /K ]
яе [4 4/] яв
При вычислении несобственного интеграла с помощью вычетов
использована формула D.33) из [39], а для нахождения вычета в полюсе я = / второго
порядка, лежащем в верхней полуплоскости, — формула D.22) из [39].
Учитывая четность ковариационной функции, окончательно получаем
Лх(л) = 1(|л| + 1)еЧпИ.«
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
8.1. Нелинейная система задана дифференциальным уравнением:
а) 81ПХ + хс = *-#2 + #;
б) ххп +Х8тд;-агс18хл +#с2 +е* = 0;
в) Х&х-]п*пх + пхп =/#-1п$;
г) зЬ х + 2х2х - 2лх2 = й? - к2-
Составить структурную схему нелинейной системы. Линеаризовать систему
относительно соответствующего опорного режима:
а)х*@ = л>,*'@ = л;
б) х*@ = 1, **(') = >1п^;
г) х*Ц) = Ш29 ^*@ = яп/.
Построить структурную схему линеаризованной системы.
330

8.2. Для систем, заданных в задаче 8.1, найти отклонение выходного
сигнала от опорного режима при нулевом начальном отклонении состояния и
соответствующем отклонении входного сигнала:
а) Л**@-л + 1;
б) 4?*С)-л1 + 1;
в) Дг*(/) = л + /;
г) Л#*@ = 'и + л.
8.3. В окрестности положений равновесия исследовать поведение фазовых
траекторий систем:
а)х = йх2-х;
б) х = п2х - хъ;
\ •• 2 3 4
в) х = /иг - п х*.
8.4. Найти коэффициенты гармонической линеаризации следующих
нелинейных звеньев:
а) релейного элемента (см. рис. 7.4);
б) релейного элемента с зоной нечувствительности (см. рис. 7.5);
в) элемента с зоной нечувствительности (см. рис. 7.6);
г) элемента с петлей гистерезиса (см. рис. 7.7);
д) элемента с зонами нечувствительности и неоднозначности (см. рис. 7.8).
Параметры нелинейных элементов: с = л +1, Ь = т + \.
8.5. Вывести уравнение гармонического баланса, используя для
линеаризованной системы критерий Найквиста.
8.6. Для системы, структурная схема которой изображена на рис. 8.18,
показать наличие автоколебаний, найти их амплитуду ап и частоту <оп.
8
*
¦ч
?
*1
7^ + 1
а
'+
{ту
1
кг
з(Т2з +1)
X
Рис. 8.18
Вычислить амплитудные частотные характеристики линейной части системы для
частот ©/у и Зю/7, найти их отношение. Численные значения параметров ли-
л + 1,
100 '
т +1
Т2 = . Характеристика не-
нейных звеньев: к{ =л + 2; к2 =/и + 5; Т{ =
линейного элемента г = Р(а) показана на следующих рисунках:
а) на рис. 7.4 (релейный элемент);
б) на рис. 7.5 (релейный элемент с зоной нечувствительности);
в) на рис. 7.6 (элемент с зоной нечувствительности);
г) на рис. 7.7 (элемент с петлей гистерезиса);
д) на рис. 7.8 (элемент с зонами нечувствительности и неоднозначности).
Параметры нелинейных элементов: с = л +1, 6 = т +1.
331

8.7. При каких положительных значениях коэффициента усиления ку
в системах, структурные схемы которых изображены на рис. 8.19,я—*, возможны
автоколебания? При наличии автоколебаний исследовать их устойчивость и
найти амплитуду и частоту устойчивых автоколебаний.
В качестве нелинейного звена взять один из следующих элементов:
а) релейный элемент (см. рис. 7.4);
б) релейный элемент с зоной нечувствительности (см. рис. 7.5);
в) элемент с зоной нечувствительности (см. рис. 7.6);
г) элемент с петлей гистерезиса (см. рис. 7.7);
д) элемент с зонами нечувствительности и неоднозначности (см. рис. 7.8).
Параметры нелинейных элементов: с = л +1, Ь = т + \.
-Ф
^
<^г0-
5(Т{5 + 1)(Т25 + 1)
71 =
72 =
1
л + Г
1
/и + 1
8 ,т°.Г71г.
*Х | ' \ р
ку
а(Т2а2 + 2^Тх + 1)
в
Рис. 8.19
* , Тш
5 =
1
/1 + Г
1
т + 1
8.8. Определить сектор [(У,к], которому принадлежат характеристики
следующих нелинейных элементов:
а) релейный элемент (см. рис. 7.4);
б) релейный элемент с зоной нечувствительности (см. рис. 7.5);
в) элемент с зоной нечувствительности (см. рис. 7.6).
Параметры нелинейных элементов: с = л +1, Ь = т + 1.
8.9. При каких положительных значениях параметра а будет устойчива
система, структурная схема которой изображена на рис. 7.2, если передаточная
функция линейной части системы имеет вид
332

Щ5)-(Т5 + 1)E + \)' Т~п + 1'
а в качестве нелинейного звена взят один из следующих нелинейных элементов:
а) релейный элемент (см. рис. 7.4);
б) релейный элемент с зоной нечувствительности (см. рис. 7.5);
в) элемент с зоной нечувствительности (см. рис. 7.6).
Параметры нелинейных элементов: с = л +1, Ь-т + 1.
8.10. При каких положительных значениях параметра а будет устойчива
система, структурная схема которой изображена на рис. 7.2, если передаточная
функция линейной части системы имеет вид
Щ3)= 1 , Г=-Ц-,
(Н + 1)(*2+* + 1) п + 1
а в качестве нелинейного звена взят один из следующих нелинейных элементов:
а) релейный элемент (см. рис. 7.4);
б) релейный элемент с зоной нечувствительности (см. рис. 7.5);
в) элемент с зоной нечувствительности (см. рис. 7.6).
Параметры нелинейных элементов: с = л +1, Ь = т + \.
8.11. Найти коэффициенты статистической линеаризации при нормально
распределенном входном сигнале следующих нелинейных звеньев:
а) релейного элемента (см. рис. 7.4), вде с = п +1;
б) релейного элемента с зоной нечувствительности (см. рис. 7.5), где
с = л + 1, Ъ = т + \\
в) элемента с зоной нечувствительности (см. рис. 7.6), где с = л + 1,
Ь = т + \.
8.12. Методом статистической линеаризации найти математическое
ожидание и ковариационную функцию выходного сигнала (в стационарном режиме)
последовательных соединений одного из нелинейных звеньев, заданных в задаче
8.11, и апериодического звена с постоянной времени Т = . На вход соеди-
л + 1
нения поступает нормально распределенный сигнал #(/) с математическим
ожиданием /1^@ = 1 и ковариационной функцией Я^(х\) = е~'п'.
8.13. Методом статистической линеаризации найти математическое
ожидание и ковариационную функцию выходного сигнала (в стационарном режиме)
для прямых цепей систем, структурные схемы которых изображены на рис.
8.18,0,*, если на вход нелинейного элемента подается нормально распределенный
сигнал $(/) и ковариационной функцией 1^(т1) = е~'п'. В качестве нелинейного
звена взять один из следующих элементов:
а) релейный элемент (см. рис. 7.4), где с = п +1;
б) релейный элемент с зоной нечувствительности (см. рис. 7.5), где
с*и + 1, Ь = т + 1;
в) элемент с зоной нечувствительности (см. рис. 7.6), где с = л+1,
**/и + 1.
ззз

Часть III. ОПТИМАЛЬНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Глава 9. СИНТЕЗ ОПТИМАЛЬНЫХ НЕПРЕРЫВНЫХ
ДЕТЕРМИНИРОВАННЫХ СИСТЕМ
9.1. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО ПРОГРАММНОГО УПРАВЛЕНИЯ
9.1.1. Постановка задачи
Пусть поведение модели объекта управления описывается обыкновенным
дифференциальным уравнением
*@ = /(/,*@,и@), (9.1)
где х — вектор состояния системы, х = {хх,...,хп)Т еЯп; и — вектор управления,
и = (щ9...9ид)Т е1/ сЛ?, V — некоторое заданное множество допустимых
значений управления; / — время, 1еТ = [@,({] — промежуток времени
функционирования системы; /(/,*, и) - непрерывная вместе со своими частными
производными вектор-функция, /(/,х,1/) = (/1(/,х,1/),...,/й(/,х,1/))г, Д/,х,1/):ГхЛлхG->Дй;
Яп — л-мерное евклидово пространство.
Момент начала процесса /0 задан, а момент окончания процесса *,
определяется первым моментом достижения точкой (/,*(/)) некоторой заданной
поверхности Г с Яп+{:
Г = {(*1,х)\Г1(*их) = 0,1 = 1,...,1; ^€(/о,+оо), хеЯп}9 (9.2)
т.е. в момент *{ должны выполняться условия
Г/(/1,Х(/!)) = 0, 1 = 1,...,/,
где 0 ^ / й п +1, при / = п +1 множество Г представлено точкой в пространстве
Яп+{, функции Г/(/ьх) — непрерывно дифференцируемы; система векторов
(дГ!^^ ^^ линейно независима Ч(*их) е /Г+1.
I 0*1 эхп а/! ;
Начальное условие х(@) = х$ задает начальное состояние системы.
Предполагается, что при управлении используется информация только
о времени, т.е. система управления в данном случае является разомкнутой по
состоянию и рассматривается так называемое программное управление (рис. 9.1).
334

Множество допустимых управлений Щ образуют кусочно-непрерывные
функции !/(•) со значениями в множестве I/. В точках разрыва значение
управления определяется как предел справа.
Определим множество допустимых процессов &Aо,х$) как множество
троек й - D,х0,и0), которые включают момент окончания процесса Гь
траекторию *(•) и управление «(•) (где V/ € Т: *(/) € Кп, */(/) е V, функции *(•)
непрерывны и кусочно-дифференцируемы, а «(•) е 2У0 кусочно-непрерывны),
удовлетворяющие уравнению (9.1) с начальным условием х(/0) = х0 почти всюду на
множестве Т и условию (9.2).
х«)
«о
1 х(/0) = х0
^ = /(/,*@,|/@)
ш
*
Рис. 9.1
На множестве 4?(*0>х0) определим функционал качества управления
/(</) = )/°(*,х(*)М'))<1' + т,х(<1)), (9.3)
где /°(*,х,и), /'(^х) - заданные непрерывно дифференцируемые функции.
Требуется найти такую тройку й* = Й',х*(•),!/*(•)) € #(/о»*о)> ч*10
/(О- ппп /(</). (9.4)
Задача (9.4) с функционалом (9.3) называется задачей Вальца; если в
функционале (9.3) функция ^(/ьх)нО (отсутствует так называемый терминальный
член) — задачей Лагранжа; если /°A,х,и) = 0 (отсутствует интегральный член) —
задачей Майера.
Искомые функции х*() и г/*() называются соответственно оптимальной
траекторией и оптимальным управлением, а ({ — оптимальным моментом
окончания процесса.
Замечание. Если любое допустимое управление и() е 0/о
порождает единственную тройку </е #(/0,Хо), то задача (9.4) может быть записана
в эквивалентной форме:
/('о,*<ъ«*())= шш /(<Ь,хь.и0).
и()еи0
335

9.1.2. Принцип максимума
Необходимым условием экстремума функционала в задаче (9.4) является
принцип максимума [3,5,6,8,11,25,27,35,57].
Утверждение. Пусть на тройке </* = (*{,х*(•),!/*(•)) € Щ^9х0) достигается
минимум функционала (9.3). Тогда существует такая вектор-функция
Ч'@ = (Ч'1@,.-.,УЛ@O\ что:
1) в каждой точке непрерывности управления и*(/) функция
Я(/, \|/A), х* (/), и) достигает максимума по управлению, т. е.
тах#(^(/),х*@,и) = Я(/, уМ.ЛО У<0>,
где #(/,у,х,и)= ][>; /у(*,х,и)-/°(*,х,и);
2) выполняется условие трансверсальности
б^-Ж/Г)-*! + ]>;('Г)-&Су =0 (9.5)
7-1
/|р</ любых Ы{ и Ьx^, удовлетворяющих системе
аг,(/Г,х*<гГ))-о, / = 1,...,/,
Г/(/Г,хЖ))-0, / = 1,...,/,
гае Я(/П = ЯЙ*,у(/Г),х*(/1*),и*(/Г)), /'(/Г) = Ж»**Ю) > л вариации
определяются следующим образом:
то=«**.,•«» -_^Ж>) 5, + ±Ш*Ш^,
3) функции х*(),ч/(*) удовлетворяют системе уравнений
*'(/) = **(^),*-@,«Ч0).^(^-(^„-(о), *;<,„) = *„,., , = !,...,«,
МЙ^О.хЖ-Ж, , = 1 й. (9.б)
336

Используемые в формулировке утверждения функции ц/1 (/)»•.-,М'л@ назы-
ваются вспомогательными переменными, #(/,у,х,1/) - гамильтонианом, а
система (9.6) — системой канонических уравнении
Замечания.
1. В частном случае задания множества Г, когда момент времени ({ задан и
фиксировано к координат хп,...,хк1 вектора х^), т.е. *1=Т{, х](*х) = Хд,
у = 1,...,&; О^к^п, / = & + 1, функции Г^(^^,x) имеют вид
ГуЙ,х) = х7-ху1 =0, 7 = 1,..., к;
Гл+1(/1,х) = /1-Г1=0.
Здесь при к = п правый конец траектории фиксирован, а при к = 0 свободен.
Отсюда следует, что &су- =0, ] = 1,...,*; Ых =0.
Решаемая задача с фиксированным временем окончания записывается
в форме
/<</)= )[/Ч/,х@,|/@)Л + ^(х(/1))^тш.
к
Решением згой задачи является пара (х*(),и*()): оптимальные траектория
и управление.
2. В случае, когда начальное состояние и момент начала процесса /0 не ^
даны, а определяются вместе с конечными состояниями соотношениями
Г/(/0,х(/0)^1,х(/1)) = 0, / = 1,...,/,
терминальный член функционала может задаваться в виде разности
Р\(*\>х(Н)) ~ ^о('<ъ*('о)) • Тогда решаемая задача записывается в форме
'1
Д<0 = ] /°(',х(/),1/(/))Л + /К/,,*/,)) - /ЪСо^Со)) "> ПШ1,
а условия трансверсальности имеют вид
при ЬГМ,хЧ*о),*1,хЧ**1)) = 0, / = 1,...,/;
Г|(/0*,^(^о)^Г,х*(^)) = 0 , / = 1,...,/.
Решением задачи в этом случае является четверка (*о,'Г»х*(•),*/*(•)),
включающая оптимальные моменты начала и окончания процесса, траекторию и
Управление.
Щ(ф-ЩфЫ0 + ^^о)^Ло =0 <97>
337

3. В общем случае гамильтониан следует записывать в форме
я
а при решении задачи рассматривать два случая: у0@ = ° и Уо@*0 •
Приведенное утверждение соответствует второму случаю, когда полагают ч/0@ = -1 •
4. Если на управление нет ограничений, т.е. (/ = ЯЯ , то максимум
гамильтониана ищется с помощью необходимых и достаточных условий
безусловного экстремума.
5. Если модель объекта управления описывается линейным
дифференциальным уравнением, а функционал квадратичный, принцип максимума является
необходимым и достаточным условием оптимальности в задаче (9.4).
АЛГОРИТМ ПРИМЕНЕНИЯ ПРИНЦИПА МАКСИМУМА
л
1. Составить гамильтониан: #(/,у,х,и) = 2)ч^ /Д/,х,ы)-/0(/,х,1/).
2. Найти структуру оптимального управления !/*(/) = 1/*(/,у@,*@) из
условия максимума гамильтониана по управлению.
3. Составить систему канонических уравнений (9.6) с заданными в задаче
условиями.
4. Из условий трансверсальности (9.5) или (9.7) получить недостающие
краевые условия для уравнений составленной системы.
5. Решить двухточечную краевую задачу для системы канонических
уравнений, полученную в п. 3, с учетом результатов пп. 2 и 4. В итоге определяется
тройка (*Г,х*0,и*(•)), на которой может достигаться экстремум функционала.
В соответствии с пп. 1, 2 замечаний к формулировке принципа максимума
решениями задачи в зависимости от постановки могут бьггь также пара
(х'(),1/*0) или четверка (&*Г,*•(•)• »*(•»•
Пример 9.1. Даны модель объекта управления
х(/) = «@, *@) = 0, *A) = |,
где хеК; иеК; /б[0;1], и функционал
1
/= |[м2@ + х2C№-»тш.
о
Требуется найти оптимальную пару (х*(•)•«*(•))» на которой достигается
минимум функционала.
П Сравнивая с общей постановкой задачи, имеем: /(/,х,ы) = 1/,
/°(/,х,1/) = 1/2+х2, Щ9х)ш09 Г1(/1,х(/1)) = ^1-1 = 0, Г2(/1,х(/1)) = хA)-| = 0.
Решается задача Лагранжа.
1. Составляем гамильтониан: НA, у, х, и) = у и - и2 - х2.
338

2. Находим максимум гамильтониана по управлению. Так как ограничения
на управление отсутствуют, можно применить необходимые условия
безусловного экстремума -2-Щ*М*),х(*)>и) = у(*)-Ь* = 0- Отсюда и*@=^- Найден-
ди 2
ное управление обеспечивает максимум функции Я(/,\|/(/),х@,ы) по
управлению, так как удовлетворяются достаточные условия экстремума
-4-#(/,у@,*@,и) = -2<0.
ди2
3. Выписываем уравнения системы (9.6):
т^ита)шШ9 х@) = 0, хA) = ±,
у@ = -^-Щ*М<),х(*)М')) = 2х@.
ох
4. Проверяем условия трансверсальности (9.5). Так как /,(/1,х)аО, то
6^ = 0 и [-Я(/1)-8/1+\|;(/1)-8х]
= 0. Поскольку /!=1 и х(*{) = ~ заданы,
4-1 2
то 5/! =0, 5х = 0. Поэтому условия трансверсальности выполняются.
5. Решаем полученную двухточечную краевую задачу:
х(/)=-^, х@) = 0, хA)=±,
*@ = 2х(/).
^_ */.ч е(е*+е~') ,/Л е(е*-е~~*) ш
Отсюда находится искомая пара: I/ (Л = —*—- х (/) = —*—= -. ¦
2(е2-1) 2(е2-1)
Пример 9.2. Даны модель объекта управления
*@ = х@ + |/@, *<0>-0,
где х е Л; и € Л; / € [0;1], и функционал
1
/= |ы2(/)Л-ХA)^1ШП.
о
Требуется найти оптимальную пару (х*(), */*(•)), на которой достигается
минимум функционала.
О Сравнивая с общей постановкой задачи, имеем: /(/, х, и) = х + и,
/ (',х,ы) = 1/2, ОД» *) = -*» Ц(/1,х(/1)) = /1-1 = 0. Решается задача Больца.
1. Составляем гамильтониан: Я(*, у, х, и) = у • (х + и) - и2.
339

2.Находим максимум гамильтониана по управлению (см. п.2 примера 9.1):
^-Я(/,ч<0,^),и) = у@-2и=0. Отсюда и'(() = ^ и ¦^тЩ1М(),х@,и)=-2<0.
ди 2 ди*
3. Выписываем уравнения системы (9.6) с учетом результата п.2:
<7Х
4. Проверяем условие трансверсальности в форме (9.5). Так как
%*) = -*! то &Р = -8х и [-&с-Я(/1)8/1 +^Й)8х] =0. Поскольку *г = 1,
то Ы{ = 0. Ограничений на х(^) не наложено, поэтому вариация &с
произвольна. В результате имеем [ ^(^) -1 ] • &с
= 0 и, следовательно, ц/A) -1 = 0.
5. Решаем полученную двухточечную краевую задачу.
т-хЮ+3&, х@) = 0,
ф(/) = -М/@, М/A) = 1.
Из второго уравнения с конечным условием имеем \|/@ = е1 . Поэтому
оптимальное управление и*A)=—е1~'. Решая первое уравнение системы с начальным
условием, получаем оптимальную траекторию х*(/) = «—[в1+/ -*1"']. ¦
4
Пример 9.3. Даны модель объекта управления
*1@ = *2<», *!@) = 1, Х!B) = 0,
*2(') = и@, х2@) = 1, х2B) = 0,
где х = (х{,х2)т € Л2, и € К, г € [0; 2], и функционал
12г ,
/=1||/2(/)Л-*|ШП.
2 о
Требуется найти оптимальную пару (х*(•),!/*(•)), на которой достигается
минимум функционала.
П Сравнивая с общей постановкой задачи, имеем
340

Мих,и) = х2, /2(*,х,и) = и, /°(/,х,и) = |и2, Щ,х) = 0, Г1(/1,х(/1)) = /1-2 = 0,
Г2('1,*Й)) = ^B) = 0, Г^х^)) = х2B) = 0.
Решается задача Лагранжа.
1. Составляем гамильтониан: #(/,у,х,и) = у{ х2 + у2 и""Т*
2. Находим максимум гамильтониана по управлению. Так как ограничения
на управление отсутствуют, можно применить необходимые условия
безусловного экстремума:
^Я(/,#,х(/),и) = У2(/)-и = 0.
си
Отсюда и*(*) = у2@- Найденное управление обеспечивает максимум функции
#(/,ц/(/),л:(/),и) по управлению, так как удовлетворяются достаточные условия
а
2
экстремума —-#(Г,\|/(/),х@,и) = -1 < 0.
Ъиг
3. Выписываем уравнения системы (9.6):
*1@ = *2(/), *1<0) = 1, Х!B) = 0,
х2@ = |/@ = М/2@, х2@) = 1, х2B) = 0,
*10) = ~Н«М*)М*)М0) = 0,
а*!
*2@ = -т-*(*> ч>@,*@,и@) = -мчС).
ах2
4. Проверяем условия трансверсальности (9.5). Так как РЦ\,х) ¦ 0, а 4 = 2,
Х!B) = 0, х2B) = 0, т.е. заданы, то ЬГ = 0, 5^=0, 8х1=0, &с2=0.
Следовательно, условия трансверсальности выполняются.
5. Решаем полученную в п.З двухточечную краевую задачу:
4*1@ = соп& = С,, у2@ = -С^ + С29
Из краевых условий находим С1,С2,С3,С4:
Х!@) = С4=1, х1B) = -|с1+2С2+2С3+С4=0,
х2@) = С3 = 1, х2B) = -2С! + 2С2 + С3 = 0.
341

п
Отсюда Сх = -3, С2 =-- и искомая пара (х*() = (х,*(),х2*())г,и*()) , где
2 4 2 2 2
Пример 9.4. Даны модель объекта управления
Х!@ = х2@,
3 е _1
с краевыми условиями Х!@) = 2, х2@) = —г, Х!A) = —, х2A) = -е 1 и
функционал
1
/= |ц2(/)<й->тш.
о
Требуется найти оптимальное программное управление «*(•) и
соответствующую траекторию х*().
П Здесь х = (хих2)т е Я2, ие11 = К, X е [0;1], /°(/,х,и) = и2, Щ,х) э О,
/1(/,х,1/) = х2, /2(*,х,1/) = х1+1/, Г1(/1,х(/1)) = /1-1 = 0, Г2(/1,х(/1)) = х1A)-^ = 0,
Гз(^1, хA{)) = х2A) + е~1 = О. Решается задача Лагранжа.
1. Составляем гамильтониан
Я(/, у, х, и) = ц/1Х2 + \|/2(х! + и) - и2.
2. Находим максимум гамильтониана по управлению:
^-Я(Ми(/),х(/),1/) = м/2(/) - 2и = 0.
си
Отсюда «'(О -*?& и -^НЦМО.хЮ.и) = -2<0.
3. Выписываем уравнения системы (9.6) с учетом результата п.2:
*1@ = *2<'), *1@) = 2, х,а)-|,
х2@=х,@+^, х2@) = -|, х2<1) = -*-',
дхх
дх2
342

4. Проверяем условия трансверсальности (9.5). Так как /Й,х)аО, то
Поскольку значения ^=1, ^A)= —, х2A) = -е~! заданы, ™> 5*1=0, 8х!=0,
&с2 » 0. Поэтому условия трансверсальности выполняются.
5. Решаем записанную в п.З двухточечную краевую задачу. Из двух
последних уравнений получаем
*1<0 = -*2<0-^1@.
Общее решение этого уравнения имеет вид
ух(() = Схе'+С2е-<9
вде С\ и С2 — произвольные постоянные.
Тогда из третьего уравнения системы у2(/) = -4*1@ = -^ в' + С2 е~г.
Запишем первые два уравнения системы:
*1<0 = *2«),
Отсюда х1@ = х2(/) = дс1@-^+^е-/или х,(/)-х1@ = -^г+^г.
Найдем общее решение полученного неоднородного уравнения:
а) общее решение однородного уравнения х{(()-хг@ = 0:
*1о@ = С3г'+С4<Г';
б) частное решение неоднородного уравнения ищем в виде (см. разд. 1.1.4):
х1м(*) = А1е* +В*е~*.
Тоща х1мЦ) = Ае* +А %е1 + Ве~1 -Вг е'*9
хи(*) - Ые' +А%е1 -2Ве'* + ВХе~*.
Подставляя в неоднородное уравнение, получаем:
2Ае( + А*е* -2Ве~* +В<е~' -А1е1 -ВХе~* = -^»-е' +&е~'.
2 2
Приравнивая коэффициенты при одинаковых функциях /, имеем
343

2Л = _а -2В=&, или А = -&, *—&.
С С
В результате х1я(/) = —-*-/е' 2-/в_/;
4 4
в) общее решение неоднородного уравнения
4 4
Из первого уравнения системы имеем
*2@ = *1<0 = сз*' -С* --^е' Ае' -^е"' -Ае"'.
4 4 4 4
Для нахождения коэффициентов С( С4 используем краевые условия:
х,@) = С3+С4=2,
х2@) = Сз-С4-^-^. = -|,
4 4 2
х2A) = С3е-С4е-1 -^е-^е-^е'1 +^.<Г1 —в.
4 4 4 4
Получаем Сх = 2, С2 = 4, С3 = С4 = 1. В результате найдена искомая пара:
оптимальная траектория х*(/) = (х? @?*2@/ > гДе
и оптимальное управление и* @ = -ег + 2е~*. ¦
Пример 9.5. Даны модель объекта управления
*1<0-*2М.
х2@ = -*!(')+ «('), М*1,
с начальными условиями х^О) = 0, х2@) = 0 и функционал
/ = Х2Bя)^ПШ1.
Требуется найти оптимальное программное управление !/*(•) и
соответствующую ему траекторию х*().
344

? Здесь х = (хих2)т еЯ2, /б[0;27с], на управление наложено
ограничение |и|*1, т.е. 1/е(/ = [-1;1], /°(/,х,1/) = 0, Щ,х) = х29 М*,х9и) = х2,
/2A,х,и) = -хх + и, Г^!,хй)) = ^ - 2я = 0. Решается задача Майера.
1. Составляем гамильтониан Щ*,у,х,и) = у1 -х2 +у2 [-Х\ +и].
2. Находим максимум гамильтониана по управлению. Так как имеются
ограничения на управление, требуется найти условный максимум гамильтониана
по управлению. В данной задаче гамильтониан линеен по и на заданном отрезке
изменения управления [-1; 1], поэтому оптимальное управление имеет вид
«•(/) = а18тах#(/,м,@,*(/),!/) = Ьадп УгЮ>
т.е. является релейным. Величина управления определяется знаком функции
у2(/).
3. Выписываем канонические уравнения (9.6) принципа максимума:
*!(') = *2('Ь ^1@) = 0,
Х2@ = -Х1@ + И*@ = -Х1(/) + 81ЙПМ/2@, Х2@) = 0,
ОХ\
Ы0 = -^Щ<М0,х(О,«*@) = - ч^М-
4. Проверяем условия трансверсальности (9.5):
= 0,
>1
Г!«=2я
где ЬГ = —* 5*1 + 2—* в*/ = 8х2. Группируя члены, получаем
-ЯBяM/! +\|/1Bя)8х1 + [1 + у2Bя)]&с2 =0.
Момент окончания 4 задан, поэтому 6^ = 0. Так как правый конец свободен, то
вариации 5^, Ьх2 считаются произвольными. Чтобы равенство выполнялось для
любых вариаций, необходимо, чтобы щBп) = 0, у2Bл) = -1.
5. Решаем двухточечную краевую задачу с учетом пп. 2 и 4:
*1@ = *2<0, х1(°) = 0; *2@ = -*1@ + Я8П\|/2@, *2@) = 0;
4/1@ = ^2@, М/1Bя) = 0; у2(/) = -х|/1@, х|/2Bя) =-1.
345

Имеем: \|/!(/) = -8т/, угЮ^-соз/, и*@ = 8Щп(-со80 = -Я8Д(со8/). Найденное
оптимальное управление и* @ на отрезке [0,2л] имеет две точки переключения
и, следовательно, три промежутка знакопостоянства:
1)при 0**<-у, и*@ = -1, Х1*@ = со8/-1, Х2@ = -яп^;
2)при-у^/<-22_, и*(/) = 1, х1*@ = со8/-2»п/ + 1, Х2@ = -зт/-2со8/;
3)при — й*й2п, «*(*)«-1, Х1(<) = со&*-4$т*-1$
х5(/) = -8Ш*-4С08*.
Минимальное значение функционала равно х^2*) = -4. ¦
Пример 9.6. Даны модель объекта управления
х@ = и@, х@) = 1,
где х € К; к € Д; / е [0; 4], и функционал
1 ч
I = - 11/2(/)Л + 4х(/1)-»тт.
2 о
Задано конечное условие: х(^) = 4 -1.
Требуется найти оптимальную тройку (^*,х*(•),«*())> на которой
достигается минимум функционала.
? Сравнивая с общей постановкой задачи, имеем: /°(*,х,1/)=—1/2,
РA\,х) = 4х, /(/,х,и) = и, Г^х^)) «^-х^)-1 = 0. Решается задача Больца.
1. Составляем гамильтониан: #(*, у, х, и) = у • и -—и2.
2.Находим максимум гамильтониана по управлению:
-2-Щ(М*),х(!),и) = Ч(*)-и=0. Отсюда н'@ = У@ и -^7Я(^'),*@,и) = -1<0.
он Э»г
3. Выписываем уравнения системы (9.6) с учетом результата п. 2:
ЗО-н'Ю-Ув). *@) = 1,
Ч#) = -^-Я(/,ч/@,х(/),«'@) = 0.
<7Х
4. Проверяем условия трансверсальности (9.5) с учетом условия
Г1Й,х(/1)) = /1-х(/1)-1 = 0. Имеем ЬГ = 4&х, бГ^ьх^))^ -&с = 0 и,
следовательно, 45х-#(/1)б/1 + ^(^)бос = 0, ^-х^)-!=0, 5/!-8х = 0, где
346

ЯЛ) = Я(Г1,Ч#1>,*(/1),И*('1» = М) • УЙ) -^Л) = |^2('1). ДЛЯ ЛЮбЫХ &С
имеем [4-|м/2(/1) + м/(^I&с = 0, а отсюда 4-|у2(/1) + ч'('1) = 0.
5. Решаем краевую задачу:
х|/(/) = 0, 4--М/2(/1) + М/(/1) = 0, /!-дс(/1)-1 = 0.
Получаем: и* (*) = \\гA) = С = сотнХ, х(/) = С/ + 1. Для определения постоянной
С при / = *1 решаем систему уравнений:
4_1с2+С = 0, /1-С/1-2 = 0.
2 2
Отсюда С = -2, *! = — или С = 4, ^ = —. Второе решение не подходит, так как
?! должно бьпъ положительно. Таким образом, искомая тройка имеет вид:
2
оптимальный момент окончания $ = —, оптимальное управление */*(/) =-2,
оптимальная траектория **(/) = -2 * +1. ¦
Пример 9.7. Даны модель объекта управления
где х € /?; I/ € Я; / € [0; /,], и функционал
Требуется найти оптимальную тройку (*Г,х*()>ы*()), на которой
достигается минимум функционала.
? Сравнивая с общей постановкой задачи, имеем: /°(*,х,и)=— и2,
Р{*и*) = — (*\ -1J+—х2, /(/,х, 1/) = и. Решается задача Больца.
1 ^
1. Составляем гамильтониан: Я(/, у, х, и) = у • и - -• и .
2. Находим максимум гамильтониана по управлению. Так как ограничения
н* управление отсутствуют, можно применить необходимые условия безуслов-
ного экстремума — Я(/, \|/(/), *(/),и) - Ч>@ - и = 0. Отсюда и* (/) = \|/(/). Найден-
ди
ное управление обеспечивает максимум функции Я(*,\|/@>*(/),и) по управле-
347

юно, так как удовлетворяются достаточные условия экстремума
3. Выписываем уравнения системы (9.6):
хA) = и'A) = уA), х@) = зЛ,
ч.@ = -^-Я(г)Ч,@,х@,и@) = 0.
ОХ
4. Проверяем условия трансверсальности (9.5). Имеем
ЪР = (/1 -1) • 6/1 + х • 6х и, следовательно, (*{ -1N/1 + х(*\ )&с - #('1 У&Н + у(*1 )&* = О
или
[М/(/1) + х(/1)].6х + [/1-1-Я(/,)]б/1=0.
Так как х(/!)и /! не заданы, то 8х и 6/) произвольны. Поэтому из условия
трансверсальности следует у(/1) = - х(/1), /| -1 - НЦХ) = 0.
5. Решаем краевую задачу:
*М-У<0, *<0) = 31/2,
*@ = 0, уй) = -*</,), /! -1 -ЯЙ) = 0.
Отсюда \|/(/) = сопЛ = С1!, х(/) = С{ / + С2, х@) = С2 = 3^2.
Тогда
М/(/1) = С1=-х(/1) = -С1/1-31/2,
/1-1-М/2(/1) + |М/2(/1) = 0 или <{-1-1с?=0.
—ъ4т. 9
Из первого уравнения С^ = . Поэтому /1-1 — = 0 или
1 + *1 A + 4)
/13+/12-/1-10 = 0, (/, -2)(/,2 + 3/1+5) = 0.
Полученное уравнение имеет один действительный корень 1{ = 2. Отсюда
С?! = -42 ив результате получаем искомую тройку
/Г =2, х*(/) = -^2/ + 3^, !**(/) =-VI ¦
Пример 9.8. Даны модель объекта управления
*!(/) = х2(/),
*2<0 = и@.
где х = (хь х2)г е Л2, и € Л, / е [0; 1], и функционал
348

1 1 1
/ = / «2(/)Д-^Х12@) + ^х2A) -> 1ШП.
о 2 , 2
19
Задано граничное условие: ^A) + х2A) = —.
о
Требуется найти оптимальную пару (х*(),1/*0), на которой достигается
минимум функционала.
? Сравнивая с общей постановкой задачи (9.4), имеем
/°(*,*,и) - и2, А(*,х,и) = х2, /2(/,х,и) = и, ШМ'х)) = /1-1 = 0
Г2(Г1,х(/1)) = х1A) + х2A)-^ = 0, /о(/о,х(/0))=1х?@), /^х^))-±х22A).
Решается задача Лагранжа.
1. Составляем гамильтониан:
#(/,\|/,Х,1/) = У! -Х2+у2 1/-1/2.
2. Находим максимум гамильтониана по управлению:
^-#(/,Ч,@,*@,и) = Ч/2(') - 2и = 0.
Отсюда н*@ -**^ и -2тЯ(/,ч>(О.х@.||) = -2<0.
3. Выписываем уравнения системы (9.6) с учетом результата п.2:
*,(>) = *2@> ДГ1A) + х2A)=^)
*1«=- -г-щ*мъ.*юмт=о,
У2@ = - Т^-#(*,Ч/(/),х@,и(')) = "ЧПО-
ах2
4. Записываем условия трансверсальности (9.7). Поскольку ^=1 и /0=0
заданы, то 8/0 =0, 5*! = 0, а, следовательно, 5ху/1 = &с,(*1) = &ху A),
&с^=^у(^о) = ^у@),7 = 1,2. Так как /ЬСо.*)-^*'» ^Й-*)"^» то
^о(^о) = х1@).5х1@), 6/1(/1) = х2A)&с2A).
349

В результате имеем
х2A)-8х2A)-ЯA):6^ + Ч/,A)-5х1A) + у2A)-8х2A)-х1@)&с1@) +
+ Я@)-8Г0-Ч'1@)-5х1@)-ч»2@)&с2@) = -[дс1@) + Ч;1@)].8х1@)-ч»2@)-8х2@) +
+ 4/1A)8*1A) + 4/2A)8*2A) + *2A)8х2A) = 0,
Г2('1,*(>1)) = *1A) + *2<1) -^ = 0, 8Г2(/,,х(*,)) = &С1A) + 8х2A) = О,
Так как начальные условия не заданы, то вариации 5Х|@) и 8х2@)
произвольны. Отсюда
Ч/2@) = 0, ч»,@) = -*,(<>),
4чA)8х,A) + ч-2AMх2A) + х2A)8х2A) = 0,
6х,A) + 8х2A) = 0, х,A) + х2A)=-^.
Поэтому получаем 5х|A) = -8х2A) и [ч'2A) + х2A)-Ч'1A)]-8х2A) = 0.
В силу произвольности &с2A) получаем равенство у2A) + х2A) - 44A) = 0.
5. Решаем краевую задачу:
*!(') = *2('), Х1A) + Х2A)^,
*«>-*&.
У!@ = 0, Ч»1@) = -ДС,@))
ф2@ = -ч»1@, Ч»2@) = 0, у2A) + х2A)-4чA) = 0.
Отсюда
4-1@ = 0,, ч»2@ = -С,г + С2,
*2(,) = -^+& Х2(,) = _а,2+^1+Сз>
М1) = Х2«), Х,@ = -%-13 +^- + С3/+'С4.
12 4
350

Используя краевые условия, получаем
Ч>2<0) = С2 = 0, щ@) = С, = -*!(<>) = -С4,
м/2а)+^а)-м/1а)=-с1+с2-^+%+с3-с1=о,
4 2
^1 ^2 п п С\ С2 гу 19
-п+-4-+с>+с<-Т+-±+с>-Т-
9
В результате находим Сх=\9 С2=0, С3=—, С4=-1 и искомую пару.
4
оптимальную траекторию х*(*)в(*Г(').*2@Г , где х1^ = "То+7г~1,
/2 9 /
х5(г) = —7"+т> и оптимальное управление и*@ = —-. ¦
Пример 9.9. Найти оптимальное по быстродействию управление,
соответствующие ему траекторию и время, затрачиваемое на переход из состояния
Х(@) = 0, х2@) = -4 в начало координат для модели объекта управления,
описываемой системой дифференциальных уравнений
*1<0-*2<*).
*2(>) = "(')>
где х = (хьх2)Т, \и\$1.
П Сформулируем проблему в форме задачи минимизации функционала
т
I = | Л -> пнп,
о
где момент окончания процесса управления Г не задан и подлежит определению.
В данном примере /{(*,х,и) = х2, /2(/,х,и) = ы и /°(/,х,и) = 1, РAХ,х) = 0,
*1 = Т, ЦСГ.хСГ)) = ^(Г) = 0, Г2(Г, х(Г)) = х2(Т) = 0. Решается задача Лагранжа.
Требуется найти оптимальное программное управление !/*(•),
соответствующую ему траекторию х*() и время Т.
1. Составляем гамильтониан: ^Г(/,\|/,х,и) = 1^ • х2 +у2 • ы -1.
2. Находим условный максимум гамильтониана по управлению
(аналогично п.2. примера 9.5):
и*@ = агвтах#(/,уф,*@,ы) = 1 • 8ЩП Ч>2@.
М*1
351

3. Выписываем канонические уравнения (9.6) принципа максимума:
*!(>) = *г('), *,@) = 0, *1СО = 0,
х2@ = и*@ = яда «МО, х2@) = - 4, х2(Г) = 0,
ф(г) д Щ(М(),х((),и'(()) 0>
Э Х2
4. Проверяем условия трансверсальности (9.5):
= 0,
>1
4=Г
где 6/г = 0. Так как момент окончания Т не задан, а х^Г) и х2(Г) заданы, то
вариация 5^ произвольна, а б*! =0, 8х2 =0. Поэтому из условия
трансверсальности следует Н(Т) = Н(ТМТ),х(Т),и(Т)) = 0.
5. Решаем двухточечную краевую задачу с учетом пп. 2 и 4:
*1<0-*2<0, *!(<>) = 0, Х!(Г) = 0,
х2@ = з18ПМ/2@, х2@) = -4, х2(Г) = 0,
\|/2@ = -М/1@,
Я(Г,м,(Г),х(Г),1/(Г)) = 0.
Решая два уравнения для вспомогательных переменных, получаем
щЦ) = С{ = сошЛ, у2@ = -С! / + С2,
|/*@ = Ь 318П (-С! Г + С2).
Так как линейная функция меняет знак не более одного раза, то
оптимальное управление является кусочно-постоянной функцией, имеющей не более
двух интервалов знакопостоянства. На одном интервале 1/@ = 1, а на другом
«@—1.
Построим фазовый портрет. Уравнение фазовых траекторий системы
*1@ = *2<О.
Х2@ = 1/@ = СОП51
352

имеет вид -г^- = —. Отсюда <ЫХ =— дх7 или х% = —^- + С. На рис. 9.2,а,#
дх2 и и 2и
изображены два возможных семейства парабол. По траекториям, проходящим
через начало координат, движение происходит на последнем интервале знакопо-
стоянства управления. Результирующий фазовый портрет и искомая оптимальная
траектория, соответствующая заданным начальным условиям, представлены на
рис. 9.2,*.
На первом участке оптимальной траектории до линии переключения
и*@ = 1, а на втором ы*(/) = -1.
Найдем время Т = Т1 + т2, затрачиваемое на переход из точки х0 = @, - 4)т
в начало координат. Здесь х{ - время движения с управлением «*(/) = 1 до точки
переключения, т2 - время движения с управлением и* @ = -1.
и<0--1
Рис. 9.2
На первом участке х1A) = х2(*)> х2@ = ы*@ = 1, откуда х2@ = ' + Сь
*1@= —+ С1/ + С2. При / = 0 имеем х2@) = С1=-4, х{{0) = С2=0, поэтому
*1@=у-4/,х2(/) = /-4.
На втором участке х1(/) = х2@> *г@ = и*@ = -1» откуда х2(*) = -* + С{,
,2
хх@ = —— + С?! / + С2. В конечный момент времени Т = х{ + т2 траектория
должна попасть в начало координат:
х1(т1+т2) = -(т1+2Т2) + С1(т1+т2) + С2=0,
Х2(Т! +Т2) = -(Т! + Т2) + С{ =0,
из чего следует Сх =т1+т2, С2=-(т1+Т2) .
353

В силу непрерывности траектории при (= т{9 имеем
*,(т,)=^-4т, =-^ + (т, +т2)х, -<И±Е221,
*2(т1) = х1 -4 =-XI +Т! +Т2.
В результате получаем т2 = *1 -4, х\-8т1 +8 = 0 и т! = 4 + 2^2, так как
т2 ^ 0. Поэтому т2 = 2^2 и Т = 4 + 4VI. Решение задачи найдено.
Рассмотрим одну модификацию рассмотренной постановки задачи. Если
модель объекта управления описывается системой дифференциальных уравнений
*1@ = *2<>)-Р,
х2(/) = |/@,
где р - заданное действительное число, то методика решения задачи не
изменяется. Оптимальное управление является кусочно-постоянной функцией,
имеющей не более двух интервалов знакопостоянства: на одном интервале 1/@ = 1, а
на другом 1/@ = -1. Уравнения фазовых траекторий получаются при 1/@ = соп$1:
#- = ^А Лсх=^^Лс2
сЬс2 и и
или, интегрируя,
Рис. 9.3
На рис. 9.3, а,б изображены соответствующие фазовые траектории при
и@ = 1 и и@ = -1, а на рис. 9.3,* — результирующий фазовый портрет с
характерными оптимальными фазовыми траекториями. ¦
354

Пример 9.10. Требуется найти оптимальное программное управление и*(),
соответствующую ему траекторию х*() и время Г, затрачиваемое на переход из
состояния XI @) = 12, х2@) = 0 в начало координат для модели объекта
управления, описываемой системой дифференциальных уравнений
*!(') = *2@,
*2@ = «@,
где х = (х!, х2)г, | и \ й 1, минимизирующее функционал
т
1= /A+ |и@|)А->пш1.
о
? В данном примере /1(*,х,ы) = х2, /2(/,х,и) = 1/ и /°(/,х,ы) = 1 + |ы|,
ОД»*)- °> Г1(Г,хG)) = х1G,) = 0, Г2(Г,хG')) = Х2GТ) = 0. Решается задача
Лагранжа.
Требуется найти оптимальное программное управление «*(•),
соответствующую ему траекторию х*() и время Т.
1. Составляем гамильтониан: #(/,ц/,х,1/) = ^ • х2 + \|/2 • и -1 -| и |.
2. Находим условный максимум гамильтониана по управлению:
**(') =
-1, \|/2@<-1,
0, -1^м/2@^1,
1, У2@>1-
3. Выписываем канонические уравнения (9.6) принципа максимума:
*1@ = *2М, *,@) = 12, х1(Т) = 09
*2(» = **('), *2«>) = 0, х2(Г) = 0,
у.1(/) = _ая(/>уи@,х@,^@)=0>
ах!
Э х2
4. Проверяем условия трансверсальности (9.5):
= 0,
[а*-Я(/1)*1 + 5>/'1>-«*у]
где 8/? = о.
г,-г
355

Так как момент окончания Г не задан, а х,(Г) и х2(Т) заданы, то
вариация 5/| произвольна, а бл^ =0, &с2 =0. Поэтому из условия трансверсальности
следует ЩТ) = #(Г, уСО, х(Т), и(Т)) = 0.
5. Решаем двухточечную краевую задачу с учетом пп. 2 и 4. Интегрируя
уравнения для вспомогательных переменных, получаем
у!(/) = Сх = СОП51, \|/2@ = - С{ X + С2 .
Поскольку в конечный момент времени и*(Т)*09 иначе нарушилось бы
условие Н(Т) = 0, то | \|/2(Г) I> 1. Рассмотрим случай 4^G*) > 1 • Случай
у2(Т) < -1 аналогичен и, как показывает анализ, для заданных начальных
состояний не реализуется. Линейная функция у2Ц) = -Сх * + С2 принимает
значения 1 и -1 не более чем в двух точках. Поэтому оптимальное управление имеет
не более двух переключений, т.е.
[-1, 0^/<Т1,
1/*@ = ]0, Т1*/<1Т2,
11, т2<*<Г,
где Х|, т2 — моменты первого и второго переключения управления:
О^Т! <Т2 йТ.
Найдем траектории, соответствующие такому трехпозиционному релейному
управлению.
При 0^/<ть и*@ = -1:
*!(') = *2('Ь *2(') = -1.
Отсюда Х1@ = 12- —, х2@ = -*. При / = *! получаем конечное состояние
(*и»*21)Г на первом участке постоянства управления: Хц =*1(т1) = 12-~,
хг\ = *2(т1) = -т1- Э10 конечное состояние служит начальным состоянием для
второго участка.
При ъхШ^х2, и*@ = 0:
*1<0-*2<0,
*2@ = 0,
откуда XI@ = хп + х21. (/-хг), х2@ = х2!.
При / = т2 получаем конечное состояние (*12,*22)Г системы на втором
участке постоянства управления: *п = *1 (т2) = *11 + *21(т2 ~х\)»
*22 = *2(т2)-*21- Это конечное состояние служит начальным состоянием для
третьего участка.
При т2й*йТ, «*@ = 1:
*1@-^@.
х2@ = 1.
356

Отсюда Х1@а*12+*д('-*2) + 22; , х2@ = Х22+/-т2, аде х12=х1(т2),
х?2 = х2(хг) * Учитывая, что конечное состояние известно, имеем
х1(Г) = х12+х22(Г-т2)+(ГТ2) =0, х2(Г) = х22+Г-т2=0.
Обозначим через 62 = Г-т2 длительность интервала времени, на котором
управление ы*(/) = 1, а через б! = Г - Т! длительность интервала времени после
первого переключения управления со значения -1 на значение 0. Тоада
последние уравнения можно записать в форме
в 2
Х12+х22е2+-|- = 0, х^+в^О.
Таким образом, можно сделать вывод о том, что второе переключение
управления происходит, если точка (Х12,х22)г принадлежит ветви параболы
хх = —х2 на фазовой плоскости Оххх2 при х2 ^0 (рис. 9.5 на стр. 377).
Линейная функция у2@ = -С|/ + С2 принимает значения -1 при / = Т! =Т-вх и 1
при / = т2=Г-62. Следовательно, она имеет вид \р2(/) = 1+ "х2\ в ко-
Т2-Т!
нечный момент времени Г, учитывая, что и*(Г)«1, из условия п.4 получаем
2 (Т — т ^
1+_Ь 1—1-1 = 0, откуда 2(Г-т2) = т2 -тх , или, заменяя х\9 т2 через 6^
т2~т1
в2: 262 =в! -62,т.е. 9! -362.
Выразим теперь х12, х22 через хп, х21:
*12 =*11 +^21^2-^1) = ^11 + ^21 (®1 -02>» *22 в *21 -
Учитывая равенства в1=362, х22=-в2, х12=-х|2, для координат точки
(хпрс21)г получаем соотношение
Х11+2Х21 02=-Х?1 => Ч1-2д^1»1х|1 =» Х,|-|х&.
Теперь можно сделать вывод о том, что первое переключение управления
происходит, если точка {хП9х2\)Т попадает на ветвь параболы хх =—х2 на фазовой
плоскости Оххх2 при х2 ^0. Подставляя выражения для хи, х21 в X! =— х2 ,
находим первый момент переключения:
357

*п-*!<*!> = 12-^-|<-т,J => Зх?=12,
откуда т! = 2, так как отрицательный корень отбрасывается. Первое
переключение происходит, когда Хц = 10, х21 = -2. Найдем момент т2 второго
переключения управления. При г = т2:
*12=|*22> х12=10-2(т2-2) = 2, *22=-2,
откуда т2 = 6. Второе переключение происходит , когда х!2 = 2, хм = -2, а
момент окончания процесса находится из соотношения: х22+Г-т2=0 =>
Т = т2 - х22 = 6 + 2 = 8. Минимальное значение функционала вычисляем по
найденному оптимальному управлению:
о 2 6 8
тт/= |A + |и*@|)*= /2Л+/1Л+|2Л = 12.
Пример 9.11. Даны модель объекта управления
х@ = и@, х@) = 0,
где х € К, | и |^ 1, / € [0; Т], и функционал
т
1= \ 1х@ + и2A)\& -+ пил,
о
где Г— заданный параметр.
Требуется найти оптимальную пару (х*(•),!/*(•)), на которой достигается
минимум функционала при Т = 1 и Г = 3.
П Сравнивая с общей постановкой задачи, имеем /(/,х,и) = 1/,
/°(*,х,и) = х + и2, ^Й.х) в 0, Г*!(*!,*(*!)) = 4 - Г = 0. Решается задача Лагранжа.
1. Составляем гамильтониан: #(/, у, х, и) = у • и - х - и2.
2. Находим максимум /Г(/,\|/@,х(/),ы) по управлению. При этом решается
задача поиска наибольшего значения квадратного трехчлена на отрезке [-1;1]
допустимых значений управления. В результате получаем структуру
оптимального управления:
-1 ^й<-1
2
«•@-1^. -1^11.
358

3. Выписываем уравнения системы (9.6):
ЗД-«*@. х(О) = 0,
До) = -Л-НAМ')М')У@) -1-
ох
4. Проверяем условия трансверсальности (9.5): для ^(/ьх)»0 имеем
$/• = 0 и
Так как 4 =Г задано, то Г(/ьх(/)) = /1 -Г = 0 и 6/} =0. Ограничений на
х(^) не наложено, поэтому вариация &с произвольна. Следовательно,
у(Г)&с = 0 и \|/(Г) = 0.
5. Решаем краевую задачу с учетом результатов пп.2,4:
*Ю-и*<0. *(<>) = 0;
\|/(/) = 1, ^(Л = 0 (при Г = 1 или Г = 3).
Получаем \|/@ = ' + С и у(Г) = Т + С = 0. Поэтому у(*) = *-Т.
Рассмотрим два случая:
а) пусть Г = 1. Тогда уA) = 1-1. Так как р^Ы —^-|<1 ДЛЯ всех / на
отрезке времени [0;1], то 1/*(*)=^-^ = —^— — оптимальное управление. При
Г2 /
этом **(/) = --—— — оптимальная траектория;
4 2
б) пусть Г = 3. Тогда \|/(/) = /-3. На промежутке времени [0;1)
—г- = —-<-1 и оптимальное управление и*(/) = -1, а на отрезке [1;3]
чЧ0| |'-зк, */Л у@ '-з „ ,
—^—I = I———I^ 1 и и (/)=-ш- = —-. Поэтому на первом участке (при
^ I I 2 | 2 2
' € №1)) оптимальная траектория х'A) удовлетворяет условиям
*@ = -1 , *@) = 0,
т.е. х?(*) = -/, а на втором участке
*(')=-^, *0)—1,
т.е. х'@=-^-Н+1.
4 2 4
359

Пример 9.12. Даны модель объекта управления
*!</) = *2@,
*2@ = "(», \и^)\<29
краевые условия х{ @) + хх A) = 0, х2 @) + х2 A) = 0, и функционал
1
/= |х1(/)Л^тт.
о
Требуется найти оптимальное программное управление ит() и
соответствующую ему траекторию **(•).
? Сравнивая с общей постановкой задачи, имеем х = (х{,х2)Т е К2;
/€[0;1]; на управление наложено ограничение |и|^2 , т.е. и е I/ = [-2; 2];
/°(/,*,и) = *1, Щ,х)ш0, /1(*,х,и) = х2, М*,х,и) = и,
Г1(/о.«(^о).^.^1))-^1-1 = 0, Г2(/0,д:(/о),/1,д:(/1)) = х1@) + д:1A) = 0,
Г3(/0)^0)^Ь^1)) = ^2@) + ^2@ = 0-
1. Составляем гамильтониан: #(/, у, х, и) = У1 • х2 + у2 • и - х{.
2. Находим максимум #(/,у,х,и) по управлению (см. п.2 примера 9.5):
и*(/) = агетах#(/,у(/),*(/),и) = 2 • зщп \|/2(/).
3. Выписываем канонические уравнения принципа максимума (9.6):
*1@ = *2@, х1@) + х1A) = 0,
х2(/) = */*(/) = 2 81вп м/2@, *2@) + х2A) = 0;
*1<0 = " -^#(/,1К0,*(/),и*@) = 1•
м>2(') = -т^-Я(/,м/(/),х@,и*@) = - ^1@-
<7Х2
4. Проверяем условия трансверсальности (9.7). Так как /г(/1,х)э0, то
6^ = 0. Моменты начала и окончания процесса управления фиксированы
(/0 =0, /1=1), поэтому их вариации равны нулю F/0 =0,5/1 =0), а»
следовательно, 5*у ^ = Ьx^ (/!) = &су A), &су-^ = Ьx^ (/0) = Ьx^ @), у = 1,2. Учитывая эти
равенства, записываем условие трансверсальности:
щA) &х{{\) + у2A) **2<Х)-ЩФ) «*!«>)-чг2@> &х2@) = 0.
360

Начальное и конечное состояние объекта управления связаны
ограничениями:
Г2(/0,^о)^ь^1)) = ^@) + ^A) = 0,
Г30Ь»*('о).'ь*('1)) = *2@) + *г0) - 0,
варьируя которые, находим связи между вариациями переменных хг и х2 в
начальный и конечный моменты времени:
8Г2(/0,^0),/1,х(/1)) = &х1@) + 5х1A)«0,
8Гз(Г0,^о),/1,х(/1)) = бх2@) + 5х2A) = 0.
Подставляя 5x^0) = -5x^1) и &с2@) = -6х2A) в условие трансверсальности,
получаем
[У1A) + М/1@)]5х1A) + [М/2A) + м,2@)]6х2A) = 0.
Здесь вариации 8x1A) и 8х2A) уже не связаны ограничениями (могут принимать
любые значения), поэтому для вьшолнения равенства необходимо и достаточно,
чтобы вспомогательные переменные удовлетворяли двум условиям:
М/1A) + ^@) = 0, 1|/2A) + Ч/2@) = 0.
5. Решаем краевую задачу с учетом пп.2,4:
*1<О-*2<0, х1@) + х1A) = 0;
х,@ = 2. 8щп м/2@, *2@) + х2A) = 0;
44@ = 1, У1A) + У1@) = 0;
Уг@ = -^1@> М/2A) +м/2@) = 0.
Интегрируя два последних уравнения и учитывая граничные условия, получаем:
Щ(*) = * + Сх, М/1A)-ьМ/1@) = 1 + 2С1 =0, С{=-± => 1М') = '-|;
4*2@ = -|'2+! + С2, м/2A) + М'2@) = 2С2=0 => м;2@ = -|/2+^.
Так как при г е @Ц) у2(/) > 0, то оптимальное управление имеет вид и*@ = 2.
Теперь оптимальная траектория находится как решение первых двух
дифференциальных уравнений с соответствующими граничными условиями:
хГ<0-/2-/, *5<0-2Г-1.и
361

Пример 9.13. Даны модель объекта управления
*1<0 = *г('), *1@) = 1,
х2@ = и@, *2@) = 0, х2A) = -1,
где х = (хьх2)т € К2, I/ € [-2; 1], / € [0;1], и функционал
1
о
Требуется найти оптимальную пару (х* (•)»«*(•))» на которой достигается
минимум функционала.
О Сравнивая с общей постановкой задачи, имеем Л(*,х,и) = х2,
/г(*,х,и) = и, /°(/,х,1/) = хь ^(/ьх)-0, Г1(/1,х(/1)) = Г1-1 = 0,
Г2(Н>Х(*\)) = х2A) +1 = 0. Решается задача Лагранжа.
1. Составляем гамильтониан: #(/,\|/,х,ы) = чм • х2 + \|/2 • и - х{.
2. Находим максимум гамильтониана по управлению. В результате поиска
условного экстремума на множестве V = [-2; 1], получаем:
¦•«¦и:
у2@>0;
у2(/)<0.
3. Выписываем уравнения системы (9.6):
*1@ = *2('), *,@) = 1,
х2@ = и('), х2@) = 0, х2A)=-1,
Ф1@ = - -р-Я(*.ч»<0,л#),»(О) = 1,
Фг(') = - -^-Я((М0,х(()М0) = - чмС).
ах2
4. Проверяем условия трансверсальности (9.5). Так как /г(^,х) = 0, /| =1,
х2A) = -1, то 6/' = 0, 8х2=0, 8^=0. Отсюда у|A)-&С1=0 и, следовательно,
у 1A) = 0, поскольку вариация 8Х} произвольна.
5. Решаем полученную двухточечную краевую задачу:
*»-Ц ««<»: *@,=0' "*>-¦
*1@-1. М/!A) = 0,
362

Отсюда \С1(/) = ' + Сь щA) = 1 + Сг=0, С, =-1. Поэтому щ{1) = 1-1,
л \
уф = 1 + С2. Найдем корни уравнения м/2@ = —г« +/ + С2 =0:
,..-1±^;з^-1Тупщ-.
Если С2 < —, то действительных корней нет и у2(') < 0- Тогда и*@ = -2
и х2@ = -2, х2@ = -2^ + С3, х2@) = 0, С3=0. Но при этом х2A) = -2^-1, т.е.
краевые условия не выполняются.
Если С2>0, то 4*2@ > 0 при *€[0;1]. Тогда и*@ = 1 и ЭД/)-1»
Х2(/) = / + С4, х2@) = 0, С4 = 0. Но при этом х2A) = 1 * -1, т.е. краевые условия
также не выполняются.
Если -—<С2<0, то ц/2@<0 и и*@ = -2 при /е[0;т), а при *б(т;1]
УгО > 0 и и*(/) = 1, где х — некоторый момент времени (момент переключения
управления). Тогда на промежутке [0;т] имеем х2@ = -2, х2(/) = -2/ + С5,
х2@) = С$ = 0, х2@ = -2г. На промежутке [т; 1] получаем х2@ = 1, х2@ = * + Сб,
х2A) = 1 + Сб=-1,С6=-2, х2@ = /-2.
Так как функция х2(*) непрерывна, то момент т определяется из условия
2
^2(т) = _2т = т-2,т.е. т = —. Поэтому
*2*(>) =
-2/, 0*/*у,
/-2, !*/*!,
«40-
-2, 0*Г<|,
1, |*/*1.
Найдем X! * (/). Поскольку хх (/) = х2 (/) = -2 / при / € 0; — ,
^1@ = -/2+С7,л:1@) = С7=1, Х1(!) = -'2+1.
При ^||;1| имеем х1(/) = х2@ = ^2, х1[|)=|-
В результате
то
Отсюда
Х1*<0 =
1->2,
О*/*}'
1,2
1Т<2-2<4 Ь-
363

9.1.3. Оптимальное управление линейными системами
Пусть система (9.1), описывающая поведение модели объекта управления,
имеет вид
х@ = Ж0*@+ *(')"(>), (9.8)
где А{1),ВЦ) — матрицы размера (лхл),(лх^соответственно, элементы
которых непрерывны; на управление ограничений не наложено, т.е. и еС1 = № у
г € Т = [/о,^] ~~ промежуток времени функционирования системы, моменты
начала процесса /0 и окончания процесса 4 заданы, правый конец траектории хA{)
свободен.
Начальное условие дс(/0) -х0еВп задано и определяет начальное состояние.
Пусть функционал качества управления (9.3) квадратичный:
/-тН*Г<'>*Ю*0 + иг<0^ (9.9)
где 5@, Л - неотрицательно определенные симметрические матрицы размера
(л х л), а (?(/) - положительно определенная симметрическая матрица размера
Требуется найти пару й* =(**(•),«*(•))» на которой достигается минимум
функционала (9.9).
Сравнивая (9.8), (9.9) с общей постановкой задачи (9.1), (9.3), имеем:
/(*,х,и) = А(*)х + В(*)и, /°(*,х,1/) Л[хТ$Юх + иТ№и], Г(х)=±[хтЛх\
Применяя для решения задачи общую методику, учитываем известные
правила и обозначения:
1.1М*Цлг; 2. д(хТАх) = Ах + Атх; 3. (АВ)Т =ВТАТ.
дх дх
Воспользуемся алгоритмом, изложенным в разд. 9.1.2.
1. Составляем гамильтониан:
Я(/,м/,х,1/) = М/г[Д/)х + 1?@|/]-|[хг^(/)х + 1/гО@«/].
2. Находим максимум гамильтониана по управлению. Так как ограничения
на управление отсутствуют, можно применить необходимые условия
безусловного экстремума:
дН«,уУ),хЮ,и)шВт у@_б(/)и = 0.
ди
Отсюда находим
«•<0-<Г|Ю*г(/)Ч'(О. (9л0>
364

Найденное управление обеспечивает максимум функции Я(/,\|/(/),х(/),и) по
управлению, так как удовлетворяются достаточные условия максимума
я Н(*.тп,х{)>и) р^ ^ в силу положительной определенности матрицы
ди2
ОМ-
3. Выписываем уравнения системы (9.6) с учетом (9.10) и правил 1-3:
х(/) = Л@*@ + В(*H-1(*)Вт(*) у(|), х(*0) = х0;
ч/@ = -Ж0м/@ + ^@х@.
4. Используем условия трансверсальности в форме (9.5). Так как 4 задано,
а состояние хD) свободно, то 64 = 0, а 5х - произвольно. Находим вариацию
1 т \дР1? т
функции Г(х)=-г[хлАх]: 6^= — 8х = дгЛ6х. Поэтому условие (9.5)
принимает вид [хгD)Л + 1угD)]бх = 0. В силу произвольности 6х и правила 3:
у(/1) = -Лх(/1).
5. Двухточечная краевая задача принципа максимума будет иметь вид
х(/) = А(<) х@ + тОГх®Вт(П м/@, х(*0) = х0;
ф@ = -Ж0м/@+^@х@, м/D) = -лхD); (9.11)
|/*@=е-!@^г@у@.
Таким образом, задача нахождения оптимального программного
управления линейной системой с квадратичным критерием качества сводится к
решению двухточечной краевой задачи для системы линейных дифференциальных
уравнений.
Пример 9.14. Для задачи
х(/) = -х@ + и@, х@) = хо,
1=\\и2«)* + ±-х\\)->тт
20' 2
требуется найти оптимальную пару (х* (•),«*(•)), на которой достигается минимум
функционала.
П Сравнивая постановку задачи с (9.8), (9.9), получаем АA) - -1; ВA) = 1;
Щ = 0; ()(/) = 1; л = 1, /0 = 0; 4 = 1. Тогда система (9.11) имеет ввд
х(/) = -х@ + чК0, ^@) = хо;
Ф@ = М/@, м/A) = -хA);
365

Отсюда получаем
Ч,@ = СУ, у(\) = С{е = -хA), х@ = С2е-/+|с1е/, х@) = С2 +±СХ = х0,
2 1-Зе2 1-Зе2
а искомая пара:
х.(,)=*о(*'-з;2-'>, «-@=^4.-
1-Зв2 1-Зе2
9.2. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
С ПОЛНОЙ ОБРАТНОЙ СВЯЗЬЮ
9.2.1. Постановка задачи
Пусть поведение модели объекта управления описывается обыкновенным
дифференциальным уравнением
*@ = /(',*@,и@), (9.12)
где х — вектор состояния системы, хеКп; и — вектор управления, ие1/ ^ К9;
I/ — некоторое заданное множество допустимых значений управления,
1еТ = [*0,1{] — промежуток времени функционирования системы, моменты
начала процесса /0 и окончания процесса 4 заданы, /(/,х,и):Гх Яп х1/ -> Яп;
Яп - л-мерное евклидово пространство.
Начальное условие х(/0) = х0 еВ", где начальное состояние х0 заранее не
задано и может быть произвольным.
Определим множество допустимых процессов ОСо»**)) как множество пар
<* = (*(•)>«(•))> которые включают траекторию х() и управление и() (где
V/ еГ: х(/) бЛл,!/(/) €#, функции х(») непрерывны и
кусочно-дифференцируемы, а и() кусочно-непрерывны), удовлетворяющие уравнению (9.12) с
начальным условием х(/0) = х© почти всюду на Т.
На множестве Ю(/0,Хо) определим функционал качества управления
Д<0 = } /°(/,х@,и@)Л + /Чхй)), (9.13)
А)
где /°(*,х,и), ^(х) — заданные непрерывно дифференцируемые функции.
Предполагается, что при управлении используется информация о времени
г и векторе состояния х.
Множество 1Ап допустимых управлений с полной обратной связью
(позиционных управлений) образуют функции «(/,х): Т х Кп -+И, которые для лю-
366

бых начальных состояний порождают ссчлветствующие пары
</ = (*(•),*/(•)) €ОДь*о), где программные управления и0 е%» а
ЪеТ и@ = «(',*<>)).
Применяемое в каждый момент времени / € Т управление имеет вид
управления с полной обратной связью по вектору состояния (рис. 9.4).
\х({0) = ХоеЯп
= /(*,х@М0)
и@-«(',х@)
и(/,х)
- х(/)
Рис. 9.4
Требуется найти такую функцию «*(/,*) €ЖЛ, что
(9Л4)
где^ = (х*(),«*0 = «'(^0)).
Функция ит((,х)е$/п называется оптимальным управлением с полной
обратной связью. Для любого начального состояния Хо из множества Яп она
порождает соответствующую оптимальную пару, т.е. оптимальную траекторию
х*() и оптимальное программное управление «*(•).
9.2.2. Уравнение Беллмана
Достаточным условием минимума функционала (9.13) является уравнение
Беллмана для непрерывных детерминированных систем [5,6,8,13,19,22,58].
Обозначим: 0 = (/<ь*1)хДл; С|д@ - множество функций у(*>х):@~**'
непрерывно дифференцируемых по / и х.
Утверждение (достаточные условия оптимальности в задаче (9.14)).
Если существует функция <р(/,х) бС1Д@, удовлетворяющая уравнению Беллмана
с граничным условием
шах
иеЦ
{^+1^У*,ж,«)-/Ч*,«>} = 0 У(/,*)еО, (9-15)
<К*,,х) = -/•(*) VX6Д^
367

и управление и*A,х) еип, удовлетворяющее условию
•Ч/,х)-а18111мB;^^/|Йх,«)-А//х,«)к
ие1/ [Д дХ( \
то и*A,х) является оптимальным управлением с полной обратной связью.
При этом минимальное значение функционала (9.13)
лап /(</) =-<р('о>*о) Vxо€Л^ (9.16)
АЛГОРИТМ СИНТЕЗА ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
С ПОЛНОЙ ОБРАТНОЙ СВЯЗЬЮ
1. Записать уравнение Беллмана (9.15) с граничным условием.
2. Найти структуру оптимального управления с полной обратной связью
в результате поиска максимума в (9.15) по управлению. Искомое управление
«*('>*) обычно выражается через производные функции <р(/,х).
3. Подставить полученное выражение для управления в уравнение (9.15).
Проблема сводится к решению нелинейного дифференциального уравнения
с частными производными первого порядка.
4. Найти решение полученного уравнения и явный вид искомого
управления.
Замечания.
1. Уравнение Беллмана применяется и при негладких функциях <р(/,х).
Обоснование этого получено в работах В.Г.Болтянского, М.М.Хрусталева,
У.Флеминга, А.И. Субботина и др.
2. Величина функции ф(/,х) определяется так называемыми оставшимися
потерями на управление:
у(*,х) = - шп 1@) Ч(*,х) € С
</е-0(/,х)
3. Если положить Ф*(/,х) = -ф(/,х), то, используя равенство:
тах/(д:) = -тт [-/(*)], можно переписать уравнение Беллмана и граничное
условие (9.15) в эквивалентной форме:
тш
иеЦ
\ дуБ(*9х) ^д<р*(/,х) г,л ч ,0/. ч
[ Ы м дх(
= 0, уБ(^х) = Р(х). (9.17)
При этом минимальное значение функционала (9.13)
тт 1@) = ф5(*0,*о) Ух0 € Яп. (9.18)
</е.0(/о»*о)
4. Рассмотрим более общий случай. Предположим, что поведение модели
объекта управления описывается обыкновенным дифференциальным уравнением
(9.1). Момент начала процесса задан, а момент ^ окончания процесса
определяется первым моментом достижения точкой (/,*(/)) некоторой поверхности Г,
заданной соотношениями (9.2). На множестве допустимых процессов Ю(^ухо)
368

задан функционал (9.3). Обозначим ОсЛй+1 — множество точек (/,*), из
которых можно достигнуть терминального множества Г по некоторой траектории,
соответствующей допустимому управлению; (?(*о)- сечение множества О при
фиксированном * = *о • Начальное состояние х$ заранее не задано и может быть
произвольным в множестве 0(/0).
Множество %/„ допустимых управлений с полной обратной связью
(позиционных управлений) образуют функции иA,х):ТхЯп ->и, которые для
любых начальных состояний Хоеб('о) порождают соответствующие тройки
</ = D,х(-)»и('))€-&(/о»хб)> гДе программные управления и()еЖо> а
УГеГ и@ = «(',*('))•
Требуется найти такую функцию »*(*,*) е 2/п, что
7(<Г) = тш /(</) Ухо € С('о), (9.19)
где^=(/Г,х*0,и*0 = «Ч^())).
Функция и*(*)х)е%/п называется оптимальным управлением с полной
обратной связью. Для любого начального состояния х0 из множества б(/0) она
порождает соответствующую оптимальную тройку, т.е. оптимальную траекторию
**(•), оптимальное программное управление и*(), оптимальный момент
окончания процесса $.
Введем в рассмотрение множество Ф функций <р(/, х): С -> Я,
непрерывно дифференцируемых всюду, за исключением конечного числа сечений б при
фиксированных / [13,22].
Утверждение (достаточные условия оптимальности в задаче (9.19)).
Если существует функция <р(*,х) е Ф, удовлетворяющая уравнению Беллмана с
граничными условиями
иеЦ { дг ^ ЬХ{ \ (9
20)
фих) = -Г(*19х) Ч(*г,х)еГ,
и управление и*A,х) е 2/п, удовлетворяющее условию
|/Ч/,х) = а15тах{|;^^//(/,х,1/)-/()(/,х,1/)}, (9.21)
ие1/ [ы\ дХ( \
то и (/, х) является оптимальным управлением с полной обратной связью в задаче
(9.19). При этом минимальное значение функционала
ПШ1 /(*/) = -ф(/<ь*0) V(/о,Xо)€0.
369

Пример 9.15. Даны модель объекта управления
ще хе К, иеК, / е [0; 1], и функционал
/(</) = ± / и2<0<* Д х2A) -». пил.
2о
Требуется найти оптимальное управление «*(Г,х).
П Сравнивая с общей постановкой задачи, имеем: /(*,х,ы) = 1/,
/° (*, х, и) = — и2, ^(х) = — х2. Решается задача Больца.
1. Выписываем уравнение Беллмана и граничное условие (9.15):
Гдф(/,х) а<р(/,х) 1 21 л
1 аг ах 2
^+^ =0> ф(и)=_^2.
2. Находим структуру оптимального управления из условия максимума
выражения в фигурных скобках. Применяя необходимое условие безусловного
д{} а<р(;,х) л ¦„ ч а<р(/,х)
экстремума: —ц = ^х ' -и = 0, получаем к (*,х) = ^ .
аи ах дх
3. Подставляем полученное выражение для управления в уравнение
Беллмана:
4. Будем искать решение уравнения в виде <р(/,х)=—К2(*)х2, ще А^О -
неизвестная функция. Подставляя в п.З и приравнивая коэффициенты при х2
-> 1
нулю, получаем ^2@ = -^г@» ЛГ2A) = —1. Отсюда К2(*)=—г, а искомое
оптимальное управление с обратной связью и*(их) = ЯГ2(/)х = —-.
Покажем, что оптимальное управление »*(/,х) с обратной связью
порождает оптимальные пары (х* (•),«*(•)) для любого начального условия.
Действительно, пусть управление »*(/,х) используется в схеме, изображенной на рис.
9.4. Тогда запишем уравнение, описывающее поведение замкнутой системы:
Х = 7Г2' х@) = х°* °гсюда х^"^2"°, «*@ = «*а,х*@) = 772^0^-
370

=: —^-. Таким образом, для любого х0 можно получить соответствующую пару:
оптимальную траекторию и оптимальное управление.
Применим принцип максимума для непосредственного определения
оптимального программного управления и соответствующей траектории:
а) составляем гамильтониан: Я(/, у, х, и) = у • и -—и2;
б) находим безусловный максимум #(/,у(/),х(/),1/) по управлению:
г^.^^.«).^.,.0>01В№,.ст.^,^^,д<о,щ)..1<о;
ди ди2
1 2
в) проверяем условия трансверсальности (9.5). Так как Р(х)=—х , то
&Г = х&х и [х(/1Nх-Я(/1>5/1+\|/(/1)8х]/|Ш1=0. Поскольку /1=1, то /1-1 = 0 и
8/! =0. Ограничений на х(^) не наложено, поэтому вариация &с произвольна.
В результате имеем [(ч/('1) + *('1)M*Ь1«1=0 и, следовательно, уA) + хA) = 0, т.е.
уA) = -хA);
г) выписываем уравнения системы (9.6) с учетом результата пп. "б", ив"'
х(*) = и*@ = У(*)> х@) = х0;
х.@ = _ая(/,М;(/)>х(/)>ц)=0> м/A) = _хA);
ох
д) решаем полученную двухточечную краевую задачу. В результате имеем
у(/) = соп81 = -хA) = !/*(/), х(/) = -хA)/ + х0. При / = 1: хA) = -хA) + х<>, отсюда
хA) = ^. и, следовательно, х*(/) = **&-*) , «•(/)«-^. Заметим, что для лю-
бого начального состояния х© оба подхода (уравнение Беллмана и принцип
максимума) дают один и тот же результат. ¦
Пример 9.16. Даны модель объекта управления в форме
*1 (') = "('),
Х2(/) = Х1(/),
и квадратичный функционал
2
2
/=^/1/2(/)Л + 1[х12B) + х2^2)]^тт.
о
Здесь хеЯ2, иеЯ, /е[0;2], /°(/,х,1/) = ||/2, Г(х) = ^[хх2 +х22], Л(/,х,1/)-«,
Ы*,х,и) = х1.
371

А. Требуется найти оптимальное управление «*(/,*).
П 1. Для рассматриваемой задачи уравнение (9.15) имеет вид
тах
и
[дф,х) + д?«,х)и+дф,х) 1ц2
\ Ы дх{ дх2 2
\ = 0, фB,х) = -1х12-|х22.
2. Дифференцируя по управлению и приравнивая производную нулю, на-
ходим структуру оптимального управления: и (/,х) = —¦"—-.
дх{
3. Подставим полученное выражение для управления в уравнение:
\2
ду(*,х) | 1 [а<р(;,х)| | дф,х)х
ы г\ дх{ ] дх2 г
ы
4. Будем искать решение этого уравнения в виде
ф,х)=±Ки(<)х? +К12(*)х1х2+±К22(*)х$,
где КГц (/), ^12@» КГ22@ — неизвестные функции. Подставляя <р(*,х) в
уравнение и граничное условие, приравнивая затем члены при одинаковых степенях хх
и х2 нулю, получаем
Кхх = -2КГ12 - К{I, Кп= -К22 - КХ2КХI, К22 = -КХ2,
*пB) = -1, *12B) = 0, *22B) = -1.
Решение системы имеет вид
Ч12±4B^!^01( Кп(() -6B-0D-0
12C-/) + B-/KF-/) 12C-0 + B-03(б-0
Ги@. =«2^
12C-0+ B-/) F-0
а оптимальное управление с полной обратной связью
.•Лх).Г„A)Ч .^(Ох,^!12^^-^^^-^^2-^4^)^. .
11 ! 12C-0 + B-03F-0
Б. Требуется найти оптимальное программное управление и*() для
начального условия х(/0) = х0.
О Применим условия принципа максимума для данной задачи.
1 7
1. Составляем гамильтониан: #(/,у,х,и) = у{ • и + у2 • X! -—и •
372

2. Находим безусловный максимум функции Я(/,у@,х(/),и) по управле-
аЖ^@,х(/),И) = м<1@_и=0 Поэтому Н.(,) = Ч,1(,).
3. Выписываем соотношения (9.6):
Х1«) = и*(*) = щ(*), Х!@) = Х10, ^@-4@, ^2@) = Х20,
ф1(/) = -У2@, ч>2@ = 0.
1 5 1 5
4. Проверяем условия трансверсальности (9.5). Так как ^(х) =,гх1 +т*2 »
то 5^ = х^! + х26х2 и
[х^ + х28х2 -Щ*хM^ + у^) 5х! + \|/2Й)ах2] /1ж2 = 0.
Так как ^ =2 , то ^ -2 = 0 и 5^ =0. Ограничений на х\(^)9 х2A\) не
наложено, поэтому вариации &сь &с2 произвольны. В результате имеем
[У1B) + х1B)]8х1+[М/2B) + х2B)]5х2=0
и, следовательно, 1И1B) = -Х!B), У2B) = -х2B).
5. Записываем двухточечную краевую задачу:
*!(*)-«*(*)-гМ*). ^@) = х10; ^@-ЧA)> *2(<>) = *2о;
*1@-^И2@. М/!B) = -Х!B); м/2@ = 0, м/2B) = -х2B).
Ее решение:
у1@ = -х1B)-х2B).B-0, У2@ = -^B),
Х1«-*1(?)-C-0 + ^B)-B-02,
х2@ = х2B)-х1B)<2-^4-^-х2B)^.
Из последних двух соотношений при / = 0 получаем
х1B) = "Х<°х^; х2B) = 4*10+3*И.
Тогда оптимальное программное управление имеет вид
*(п *ю + 6x20 B - 0Dх10 + Зх20)
*' 21 7
Подстановкой найденной оптимальной траектории х*@ в управление
* (*,х) можно показать, что для заданногд начального условия х0 =(х10,Х2о)Г
оптимальное управление и*(их) с полной обратной связью порождает
оптимальное программное управление */*(•). ¦
373

Пример 9.17. Дана модель объекта управления
х@ = и@,
гдехбД, ке[-1;1], ^[О,^].
Требуется найти оптимальное управление в*(/,х) с обратной связью,
переводящее объект из любого начального состояния в начало координат за
наименьшее время, т.е. обеспечивающее минимум функционала
1=\<Н Ух@)еЛ.
о
? Сравнивая с общей постановкой задачи, имеем: /(/,х,и) = и,
/°(*,х,и) = 1, РЦ\,х)¦ 0. Решается задача Лагранжа или, с учетом смысла
функционала, задача быстродействия.с конечным условием х(Ц) = 0.
1. Выписываем уравнение Беллмана и граничное условие (9.20) в форме,
аналогичной (9.17):
Так как все траектории системы должны попасть в точку х = 0 при 1 = 1\, то
граничное условие определено только в этой точке.
2. Находим структуру оптимального управления из условия минимума
Зу*(/,х)
дх
3. Подставляем полученное выражение для управления в уравнение
Беллмана:
выражения в фигурных скобках: и*(/,х) = - зщп-
дуБ(их)
дУ(<,х)
дх
+ 1 = 0, ф/?(/1,0) = 0.
4. Функция <р5(/,х) = |х| является решением уравнения, так как
удовлетворяет ему в двух областях: при х > 0 и при х < 0, в чем можно легко убедиться
прямой подстановкой. Граничное условие также выполняется при х = 0.
Искомое оптимальное управление имеет вид
Г-1, х>0,
«*(',*) =
0, х = 0,
1, х<0,
а минимальное значение функционала для произвольного начального состояния
хо определяется по формуле
^(х0)= пш! /(</) = Ф*('<ъ*оН*о| УхобЛ.и
<*е©0Ь,Хо)
374

Пример 9.18. Дана модель объекта управления в виде
*1<О-*2@.
*2@ = «('),
гдехеЛ2, 1/б[-1;1],/€[0,^].
Требуется найти оптимальное управление и*(/,х) с обратной связью,
переводящее объект из любого начального состояния в начало координат за
наименьшее время, т.е. обеспечивающее минимум функционала
/=/Л Ух@)еД.
о
? Сравнивая с общей постановкой задачи, имеем: /1 (*, х, и) = х2,
/2(*,х,и) = и,/°(*,х,и) = 1,ГA1,х)*0, х(*х) = ф ОO*. Решается задача Лагранжа.
1. Для рассматриваемой задачи записываем уравнение Беллмана и
граничное условие (9.20) в форме, аналогичной (9.17):
\дуБ(*,х) а<р*(/,х) дуБ{их) Л г, Б/. лч л
щш 1 у\>/+ г ^» ' х + уч>/ц+11=0, фл(/ь0) = 0.
|«р11 ы дхх 2 дх2 \
Так как все траектории системы должны попасть в точку х = @,0)г при / = ^, то
граничное условие определено только в этой точке.
2. Находим структуру оптимального управления из условия минимума
выражения в фигурных скобках: «*(*,х) = -а&п у *' '.
дх2
3. Подставляем полученное выражение для управления в уравнение
Беллмана:
д9Б((,х) дуБЦ,х)
+ Хо —
Ы дхх 2
д<рБ(*,х)\
дх2
+ 1 = 0, ф^О) = 0.
4. Функция
Ф* (>,*) =
х2 + /4х7 + 2хУ, X! > --х2|х2|,
|*2|. ХХ=--Х2\х2\,
-х2 + /-4x7 + 2x1, X! <--х2|х2|
Удовлетворяет граничному условию и уравнению в трех характерных областях,
в чем можно убедиться подстановкой.
375

Искомое оптимальное управление с полной обратной связью имеет вид
[-.. Ч»-1*Ы.
«*(/, X) = | - 81®П Х2, Х{ = -~Х2 \х2\,
где ^ = —х2 \х2\ — уравнение линии переключения оптимального управления.
Вычисляя, например, при х{ > —гх2 \х2\ производные функции Беллмана:
^Ф*(/,х) = 0, ^-ф*<г,х) =
дХ* ' 4*Хх+2х1 ' аХ2
а .^»^и ??2_
Ф*(*,х) = 1 +
/^
,+2х|
замечаем, что ф5(/,*)>0, т.е. и*(;,х) = -81дп у 1' '=-1. Подставляя
а Х2 а Х2
выражения в левую часть уравнения Беллмана, получаем
эти
Эф*(/,х) аФ*(;,х)
+ Хо —
а/ а^ 2
аф5(/,х)
>о +
/4х7+2х|
¦х2-
1 +
ах2
2хо
/4x7+2x1
+ 1 =
+ 1 = 0.
Следовательно, в области X! >—-х2|х2| полученные функции ф5(*,х) и «*(/,х)
являются решением задачи. В других областях проверка выполняется
аналогично. Траектории оптимальной системы и управление для фиксированного
начального состояния совпадают с найденными в примере 9.9. ¦
Пример 9.19. Даны модель объекта управления в виде
*1<0 = *2<О.
х2@ = "@,
ще х = (хьх2)г € К2, ие [-1; 1], и функционал
/={A + ||<0|)<&->
потребуется найти оптимальное управление «*(/,х) с обратной связью,
переводящее объект из любого начального состояния в начало координат.
376

О Сравнивая с общей постановкой задачи, имеем: /\Ц,х,и) = х2,
}2{их,и) = и9 /0(/Ли)-1 + |«|, Щ,х) = 09х(Н) = @ 0)г. Решается задача
Лагранжа.
1. Для рассматриваемой задачи записываем уравнение Беллмана и
граничное условие (9.20):
Так как все траектории системы должны попасть в точку х = @,0)т при / ~ *1 > то
граничное условие определено только в этой точке.
2. Находим структуру оптимального управления:
«*(',*) =
афО^х)
дх2
дх2
_ дф,х)
дх2
3. Как показывает анализ оптимального программного управления,
проведенный ранее для данной задачи (см. пример 9.10), оптимальное управление
может принимать только три значения: -1, 0, 1. Области постоянства
оптимального управления и найденная в примере 9.10 оптимальная траектория
изображены на рис. 9.5. Решение задачи ищется в трех областях А, В, С и на кривой у:
^-|х Х1>Х?-'|х2ЫЬ В = \Х \-Х2-^Х2\х2\*Х{<Х%-1х2\х2\\,
С = \х\хх < -х\ --*2|х2| |, у = \х\х{ = -—х2|дг2| I.
*\=-\*г
хх=\х\
Рис. 9.5
377

4. Функция
Ф* (',*) =
-2*2-1/12X1+6*2, *€Д
2х2-^-12х1+бх|, хеС,
-2Ы,
Х€у
удовлетворяет граничному условию и уравнению в трех характерных областях и
на кривой у, в чем можно убедиться подстановкой. Искомое оптимальное
управление с полной обратной связью имеет вид
-1, х € А,
|0, хеВ, ш
1, хеС,
(-8Ц5ПХ2, хеу.
«*(',*) =
Пример 9.20. Даны модель объекта управления
х(/) = и@*<0,
где х€ Я, ие К, X е [О,^], значение ^ задано, и функционал
«1
/(</) = р I «2@^ + а1п2х(/1)->тт, а>0, р>0.
Требуется найти оптимальное управление и*(/,х).
О Сравнивая с общей постановкой задачи, имеем: /(/,х,ы) = 1/х,
/°(/,х,1/) = ры2, ^(х) = сс1п2 х. Решается задача Больца.
1. Для рассматриваемой задачи записываем уравнение Беллмана и
граничное условие (9.15):
тах
иеЯ
{^+^«х-Р«>} = 0, «М)-«Ы»
2. Находим структуру оптимального управления из условия максимума
выражения в фигурных скобках. Применяя необходимое условие безусловного
экстремума, получаем:
378

3. Подставляем полученное выражение для управления в уравнение Белл-
мана:
аФ(*,х) х2(дч>(*,х)J 2
4. Будем искать решение уравнения в виде
<р(*,х) = ф(/).1п2х,
где Ф@ - неизвестная функция. Подставляя Ф(/, х) = Ф(/) • 1п2 х в уравнение и
граничное условие и приравнивая нулю коэффициенты перед 1п2 х, получаем
Ф(/)Дф2(/) = 0, Ф^-а.
Отсюда находим функцию Ф(*) = ^ , затем функцию
Р + а(*1-0
„л \- <*р1п2х
Ф1Г»*)- в + а(^ _л и искомое оптимальное управление с обратной связью
и* &х) а1пх ш
р + а^-О'
9.2.3. Синтез оптимальных линейных регуляторов
Пусть уравнение (9.12), описывающее поведение модели объекта
управления, имеет вид
*(') - ЛЦ) х(*) + ВЦ) иЦ), (9.22)
где АЦ), ВЦ) - матрицы размеров (лх л), (лх$) соответственно, элементы
которых непрерывны; на управление ограничений не наложено, т.е. ие[/ = Я«.
Пусть функционал качества управления (9.13) квадратичный:
1 '' Г
1 ш7 11хГ«^@«@ + иг@0@и@]л+ххг(/1)А х(/0, (9.23)
% 2
/ ^ ' ~~ неотрицательно определенные симметрические матрицы размера
Л а д(/) - положительно определенная симметрическая матрица (?х #).
связью1^5^^^ НаЙТИ оптимальное Управление !**(*, х) с полной обратной
Сравнивая (9.22), (9.23) с (9.12), (9.13), имеем:
'ЬъЧ-АЮх + Щйи, /\*,х,и)Л[хТтх + иТа«)и1 Г(х)ЛХтАх.
379

Далее используем известные правила и обозначения:
1.^=/; 2.У&&шЛх + Лтх; 3. (АВ)Т =ВТАТ;
дх дх
4. хтАх зе 0 <=> А + Ат = 0; 5. ХхЛ = ^ан — след матрицы Л .
/=1
Из (9.15) получаем уравнение Беллмана для рассматриваемой задачи:
пт|^^+[^^]Г[жох+2»(о«]4[л(')^)+«ге(Ои]1=о,
<К*1,х) = -^хтАх. (9.24)
Отсюда
и*(/,:с) = аг8тах
2&*>] 2»@«-^игО@и
Найдем максимум по управлению в последнем выражении, используя
необходимые условия экстремума и правила 1—3. Дифференцируя выражение
в квадратных скобках по и и приравнивая результат нулю, получаем структуру
оптимального управления
и (их) = 0-1(ОЛГ(')аф(',Х). (9.25)
дх
Решение уравнения (9.24) ищется в виде
М,х) = ±хтК2«)х, (9.26)
где К2A) ~ неизвестная симметрическая матрица (лх л).
Подставляя (9.26) в уравнение (9.24) и приравнивая нулю квадратичные
формы с использованием правила 4, получаем:
К2^) = -Ат@К2@-К2^)А@-К2@В@О-1@Вти)К2@ + 3@,
(9.27)
*2(/,) = -Л.
Решая уравнение Риккшпи (9.27), находим матрицу К2@ и явный вид
оптимального управления (9.25) с полной обратной связью
иЦ,х) = д-хЦ)Вт«)К2Ц)х. (9.28)
Минимальная величина функционала вычисляется по формуле
пил 1@)--ч(йо9хо)ш-\х[Кг(Ь)хо Vxо€Л^
</сЕ.е>0Ь,ло) 2
380

Синтезированная оптимальная система с полной обратной связью
изображена на рис. 96.
Ы'о) = *оеЛл
*! ^-Л<0*<0 + *<0и*<О
«•@ = ¦•('.*»>
«*(',*) = ог1{ЪВ'№2(Ях у
•+ *(')
Рис. 9.6
Замечания.
1. Если обозначить />(/) = -К2($, то соотношения (9.27), (9.28), следующие
из (9.17) при ф*(*,ж) = -хтР{()х, имеют вид
Р@ = -Ат(*)Р(<)-Р(*)А(*) + Р(*)В№-1(*)Вт(<)Р@-$(*), Щ) = Л, (9.29)
••(/.х) = - СЧО^Ю/ЧО* = "ЯОх, *<1) = 0-1{ОВтЮР(й9 (9.30)
2. Если ^ =+», матрицы А, В, *У, С не зависят от /, система является
вполне управляемой (см. разд. 1.4.2), то оптимальный регулятор в задаче
х@ = А х(/) + *1/@, х@) = х0,
/=1 |[хг@5,х@ + иг@еи@]л^тт,
определяется соотношением [25]:
и*(х) = -()-1ВтРх = -Рх, Р = 0'1ВтР9
(9.31)
где Р - положительно определенная симметрическая матрица, удовлетворяющая
алгебраическому уравнению Риккати
-АТР-РА + РВB-1ВТР-5 = 0.
(9.32)
Решение этого уравнения, удовлетворяющее критерию Сильвестра, единственно.
Можно показать [25], что замкнутая система, описываемая уравнением
хЮт[л-В(Г1Втр]хЮ9 *@) = х0,
является асимптотически устойчивой, т.е. *(/) -> 0 при /->+».
381

Данная проблема получила название задачи Летова-Калмана
аналитического конструирования оптимальных регуляторов.
3. Для уменьшения вычислительных трудностей при решении уравнения
Риккати можно использовать уравнение относительно матрицы Р~1 (О. Так как
РA) • Р~1@ = Е, то после дифференцирования получим
Р@ • Р~х (О + />@ • Р-1 @ = 0 или Р-1 @ = -Р @ • Р@ • Р~г @.
С учетом (9.29) имеем
Р @ = А(*) /> @ + Р~1 (г) Лг@ - Д@ О @ Яг@ + Р @ 5X0 ^_1 @,
(9.33)
/>-1(/1) = л-1.
После нахождения Р@ определяются матрицы Р@ и
^@ = б @ДГ @^@ > а также управление »* (/, х) = - ДО *.
4. Существует альтернативный подход к проблеме синтеза оптимальных
линейных регуляторов, предложенный А.А. Красовским: аналитическое
конструирование по критерию обобщенной работы. Основное отличие от задачи
в классической постановке заключается в применении полуопределенного
функционала
То.Р. =7 НхГМ*<О*О + «Л0<Х01<О + Ч^^ (9.34)
где функция ч/(/,х) определяется только после получения решения задачи. Такой
подход обосновывается тем, что лишь в отдельных случаях удачного выбора
коэффициентов 5@,6@>Л первое найденное решение при классическом подходе
удовлетворяет требованиям практики. Чаще после нахождения первого решения
и моделирования синтезированной системы приходится корректировать
минимизируемый функционал и вновь находить решение. Применение критерия
обобщенной работы облегчает однократное решение задачи.
Можно показать, что оптимальное по критерию обобщенной работы
управление имеет вид
»'Лх)-(Г1@*г@2^,
ох
где <рG,х)— решение линейного уравнения в частных производных
д* дх 2 (9.35)
Ч(*1,х) = --хтАх.
382

При этом функция \|/(/,х), доопределяющая функционал, находится по
формуле
у ох ) ох
Для доказательства следует выписать уравнение Беллмана для задачи
оптимизации функционала обобщенной работы и убедиться, что функция <р(/,х)
является его решением. Решение уравнения (9.35) ищется в форме
ф(^х)=—хтК2(*)х, где К2A) - неизвестная симметрическая матрица (лхл).
Подставляя в (9.35) и используя правило 4, получаем
К2A) = -ЛТ®К2@-К2@А@ + $У). *2(/,) = -Л. (9.36)
Это уравнение в отличие от уравнения (9.27) является линейным,
поскольку нелинейный член К2Ц)ВЦ)ОГх(()Вт(()К2A) в нем отсутствует.
Структура оптимального регулятора имеет вид
и&х) = <ГхЦ)Вт№2Ц)х (9.37)
и совпадает с (9.28).
Неопределенный член функционала (9.34) находится по формуле
Ч/(*,х) = хтК2(<)В(*)B-1(')Вт(*)К2(<)х. (9.38)
Пример 9.21. Для задачи
*@ = -х@ + и@, *@) = *о>
/=1 /|/2@Л + ^Х2A)-^Ш1П
20
требуется найти оптимальное управление «*(/,*).
П Сравнивая постановку задачи с (9.22), (9.23), имеем: Л(/) = -1, ВЦ) = 1,
0@ = 1, 8A) = 0, Л = 1, /0 = 0, /1=1. Тогда уравнение (9.27) примет вид
К2«) = 2К2-К}, *2A) = -1.
Находя его решение К2A)= г-т-, по формуле (9.28) получаем оптимальное
Управление и* (*,х)= **
1-Зе2*'
Найдем траектории и управление, порождаемые управлением и*(?,х) для
Различных начальных состояний. Уравнение модели объекта с учетом
оптимального управления с полной обратной связью имеет вид
383

х@ = -*(*)+, 2*УЪ> *(°) = *о-
\-Ъе2'м
е1 -Зе2~*
Эта задача Коши имеет решение х*@ = *о 5~» следовательно, для
1-Зе2
А/Л 2х0е'
оптимального программного управления получаем выражение и*@ =—*—=¦.
1-Зе2
Заметим, что оно совпадает с управлением, найденным с помощью принципа
максимума в примере 9.14. ¦
Пример 9.22. Для задачи
х{ (/) = «(/),
*2(') = *1@,
1 о 2
требуется найти оптимальное управление с полной обратной связью.
? Сравнивая с (9.22), (9.23), имеем
-р. »-@.«-. ....*.(; д.»...,.,.
а искомая симметрическая матрица К^{$) = п 12 , где #12 = К2\ •
^Л21 л22>/
Тогда из (9.27) следует
Кп(*) = -2Кп-К?и *„B) = -1,
^12 О = ~^22 ~ К\ 1 ^12» ^12 B) = 0 ,
*22@ = -*122, ^22B) = .
Решение системы и оптимальное управление с полной обратной связью
совпадает с результатом п. А примера 9.16. ¦
Пример 9.23. Для задачи
*1<0 = *2<О.
*2(') = "@,
/=1 |[х12@ + 2х|@ + и2@]л^1тп
2 о
384

требуется найти оптимальное управление и*(х) с полной обратной связью.
О Сравнивая с общей постановкой задачи, имеем
Чо ;> -о- «-• *-с. з-
а искомая симметрическая матрица Р = I |! 12 , где />12 = Р21 •
Составим алгебраическое уравнение Риккати (9.32) с учетом
симметричности матрицы Р и выпишем структуру регулятора (9.31):
и*(х) = -Р21х1-Р22х2,
/Й-1-0,
_^11 + ^12^22 =0»
-2Р12+/&-2 = 0.
Условию положительной определенности матрицы Р удовлетворяет
решение Рп = 2, Р12 = ^21 = 1, Р22 = 2. Отсюда следует, что оптимальный регулятор
и*(х) = -хх -2х2. ш
Пример 9.24. Для задачи
*1<0-**<*).
/ = ^|/2@Л+|хг(Г)Лх(Г)-.тш, Л = (^1 ^,
требуется найти оптимальное управление и*(гух) с полной обратной связью.
О Сравнивая с общей постановкой задачи, имеем
А~§ ^Ч?Н = 1'Чо ^-М-г.ад-о.
Запишем уравнение (9.33) для К(() = Р~1A), учитывая, что матрица КA) -
симметрическая:
(*и *12) = Г° П№1 '12)+С'и *пуо <П(О <Л
1*12 *У 10 0А*п *п) 1*12 Кп)\\ 0) {О I)'
К{Т) =
г 1 ^
— о
\2)
385

или поэлементно в развернутой форме
Кп =2АГ12,
К\2 = ^22»
К^ = -1,
А»!
*12(Г) = 0,
^2200 = ^2 = 7"~
А,2
Отсюда
^11@=-2^ + ^(Г-02+^=у + ^2+^1,
^22(/) = G,-0 + ^2=^ + ^2»
где т = Т - * - время, оставшееся до конца процесса управления.
х4 х3
Определитель матрицы КA) равен Д =—+</2— н-*/^^^-
Тогда
*>-*-».(* *}•
где
Р /Л т + </* Р /Л т2+2</2т р т3+3</2т2+34
В результате
«•('.*)—(Г1@*Г@Л0*—/Ь@*1 -*аЮ*г =
-—2Г"Х' з! *2'ш
Пример 9.25. Для задачи
х@ = и@,
/=1/1/2@Л+|х2A)^1ШП
найти оптимальное управление по критерию обобщенной работы.
? В данной задаче А(*) = 0, В(*) = 1, $(/) = 0, 0@ = 1, Л = 1, /0 = 0, 4 = 1.
Тогда уравнение (9.36) принимает вид К2@ = 0,^2@ = -Ь Отсюда #2@а-1 и
согласно (9.37) и*(/,х) = -х. С учетом (9.38) находим \|/(/,х) = х2 и выписываем
функционал (9.34) обобщенной работы
386

1о.Р.=\ /[в2(о+*2ю]*+^*2а).
20
Заметим, что решение задачи синтеза регулятора в классической
постановке приведено в примере 9.7.
Если искать минимум сформированного функционала обобщенной работы,
то с учетом (9.27), (9.28) получаем ОДО-'^гЮ+^гОK"-*- Отсюда
Х2@ ¦ -1 и и*(/,х) = -х, т.е. найденное управление действительно обеспечивает
минимум функционала обобщенной работы. ¦
Пример 9.26. Для задачи
х@ = -х(/) + */@,
1
/ = 1/|/2@А + ^х2A)->тт
2о
требуется найти оптимальное управление по критерию обобщенной работы.
? Поскольку АЦ) = -1, В(Г) = 1, 8Ц) - 0, 0@ = 1, Л = 1, /0 = 0> *\ = 1. то
уравнение (9.36) принимает вид ^2@ = 2^@,^2A) = -1. Отсюда К2(*) = -е2'~2
и и*(/,х) = -в2/~2х. Функционал обобщенной работы имеет вид
2 о 2
Пример 9.27. Для задачи
*1<0 = "('),
*2@-«|@.
1 2 1
/ = М|/2@Л + ^[х12B) + х22B)]-.тш
1 о ^
требуется найти оптимальное управление по критерию обобщенной работы.
Уравнение (9.36) имеет вид
(*„</) *12(о,| Го 1у*„(о к12ц))(кп(() к12Щ(о о) го <л
1*12@ Хц@) 1° <>Д*12<') *и<01 ЦГиМ *пШ1 0) {О О)'
или поэлементно в развернутой форме
387

*ц@—2ЛГ,2@. ЛГ„С9—1.
КпЦ)=-КпЦ), *12B) = 0,
^22@ = 0, *22B) = -1.
Решение системы: КцЦ) = -1,Ки(() = (-2,Кп(() = -12 +41-5, &
оптимальное управление
И'(^) = A О)^2;^ /_-12][^] = (-/2+4Г-5)х1+(/-2)х2.
Заметим, что используемые уравнения значительно проще выписанных
в примерах 9.16 и 9.22.И
9.3. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ С НЕПОЛНОЙ
ОБРАТНОЙ СВЯЗЬЮ
9.3.1. Постановка задачи
Пусть поведение модели объекта управления описывается обыкновенным
дифференциальным уравнением
^ = /(/,хЮ,и@), х(*0) = х0, (939)
где х — вектор состояния системы, х-{хх,х2)Т еЯп9 х1 = (х!,...,хт)г,
х2 = (хда+1,...,хл)г, Ойтпйп (предположим, что о компонентах вектора х1 €Ят
известна текущая информация, а о компонентах вектора х2 € Яп"т она
отсутствует); и — вектор управления, и е V с Я9, V ~ некоторое заданное множество;
/ -время, ^€Г' = [/0,/1] = ги{г0}11{/1}, Т'- промежуток времени
функционирования системы, моменты времени ?0 и Ч заданы, внешние воздействия на
объект управления отсутствуют, /(*,х,и):Т'*Яп хЦ -+ Яп - непрерывно
дифференцируемая вектор-функция.
Обозначим: В = Яп,В{ = Ят,В2 = Яп~т; 0 = (*0,*1)хЯп, 0' = ['<ь>1]х *"•
Начальные условия х(/0) заданы множеством О с Яп, размерность которого
равна т, т.е.
х(/0) € О = {х| х2 = у0(х1), х1еЯт= Вх }, (9.40)
где ущ{х1), } = т + 1,...,л, - заданные непрерывно дифференцируемые функции;
0 <> т <. л.
388

При /я = 0 множество О является точкой, а при т - п совпадает с
множеством Яп. Условия на вектор состояния на правом конце промежутка времени
Т' не заданы.
Предполагается, что при управлении используется информация только
о времени / и о компонентах вектора х1, т.е. управление !/(/) , применяемое в
каждый момент времени ^еТ', имеет вид управления иA) = и((,х{A)) с неполной
обратной связью по вектору состояния (рис. 9.7).
!/(/) = И&хЧО)
1 х(@) = х0 <
еП
^ = /(',*@,и<'))
и((,х1)
Л
*ч
х(/) = (хЧ0,^@)
*1@ = (*1@,...,*т@)'
0<т</1
Рис. 9.7
Множество допустимых управлений 2/т с неполной обратной связью
образуют функции ю(/,х!): Т'хВ{ ->1/ такие, что функции М*,х,иA,х1)), / = 1,...,л,
определены на С', непрерывны вместе с частными производными по х,
кусочно-непрерывны по /. При этом управление и(/) = в(/,х1@) кусочно-непрерывно
по /, а в точках разрыва значение управления определяется как предел справа.
Определим множество допустимых процессов Ю(*0)х$) как множество пар
<* = (*(),"(•))> удовлетворяющих уравнению (9.39) с начальным условием (9.40)
почти всюду на 7", где У*еТ' х(/)е Кп9и(*)е 1/9 функции х() непрерывны и
кусочно-дифференцируемы, а и() кусочно-непрерывны.
На множестве #(/0,х<)) определим функционал качества управления
где / A,х,и),Р(х) — заданные непрерывно дифференцируемые функции.
Требуется найти такую функцию в*(/,х!) € ит, что
(9.41)
/(О- ппп Щ) Ух0€О,
(9.42)
гД^*=(Л.),и*() = «*(,х1-(.)).
389

Функция и*(*ух{)ее/т называется оптимальной синтезирующей функцией
на множестве О. Для каждого начального условия из множества О она
порождает оптимальную пару, т.е. оптимальную траекторию х*() и оптимальное
программное управление «*(•). Предполагается, что минимум в (9.42) и функция
и*(*,х1) существуют.
Подчеркнем, что число используемых в управлении координат вектора
состояния совпадает с размерностью множества начальных условий О. При
т = 0 множество О является точкой х$у для которой ищется оптимальное
программное управление !/*(/), а при т = п множество О совпадает с п -мерным
пространством состояний и ищется оптимальное управление «*(*,х) с полной
обратной связью по вектору состояния.
9.3.2. Соотношения для нахождения оптимального управления
В [30,35,37] доказаны достаточные условия оптимальности управления
в задаче (9.42) и выведены соотношения для определения оптимальной
синтезирующей функции на множестве П. Для этого требуется решить систему из
2(л-/и) + 1 уравнений в частных производных первого порядка с 2(п-т) + 1
краевыми условиями на концах промежутка 7":
д( & дх,
^=-1ЧУ'"'/К',*|,/(',*'),«,(/,*'))+
1 м
}»>('о.*') = Уо]{х1), }=т + 1,...,я,
ЭУ/С,*1) дН\1,х\у{г,х1)) .
* = — , I = т + 1,...,п,
Ы дх] '
ЧМ*1>* ) / -. ]=т + \,...,п,
дх]
ЩAУ)= ± ^(х''/(/1'*1))у>1,«')-^(«',/(/|,х1)),
(9.43)
где
390

„( \ ^ эщ*,х1) ,,л ч л ^ аУу(/,х!) ^
/=1 **/ у-м+1 /=1 ^*/
у=т+1
Минимальное значение функционала (9.41) можно вычислить по формуле:
,гшп № = -Щ1ь.4)- X ^о,4) •*<>;, Vxо€п. (9.44)
АЛГОРИТМ ПРИМЕНЕНИЯ ОПТИМАЛЬНЫХ СИНТЕЗИРУЮЩИХ ФУНКЦИЙ
Первый этап — нахождение оптимальной синтезирующей функции и*((,х1).
1. Для рассматриваемой постановки задачи записать систему (9.43).
2. Найти максимум функции НA9х19у*A9х1),и) по управлению. В
результате определяется структура оптимальной синтезирующей функции «* (/,**),
зависящая от функций Ж(/, х1), у^ (/, х1) и их производных.
3. Полученные выражения подставить в систему (9.43).
4. В результате решения системы определить явный вид функций
у(/, х1), 1У(*, х1), у^ (/, х1) и оптимальной синтезирующей функции и * (/, х1),
структура которой найдена в п.2. Получено решение задачи (9.42).
5. Определить минимальное значение функционала качества управления по
формуле (9.44).
Второй этап — применение оптимальной синтезирующей функции и*A,х1)
для управления детерминированной системой (9.39) (нахождение решения задачи
для фиксированного начального условия из множества О).
1. Задать начальное состояние х(/0) € О.
2. Решить уравнение (9.39) совместно с найденной на предыдущем этапе
оптимальной синтезирующей функцией и*((,х1) для начального условия
х(*0)е&. В результате определяется пара д* =(х*(-),«*(•) = **(>хх*(•))), т.е.
оптимальная траектория и оптимальное управление. Этот процесс
функционирования оптимальной системы с неполной обратной связью отражается структурной
схемой, изображенной на рис. 9.7.
3. Перейти к п.1 данного этапа для задания нового начального состояния.
Замечания.
1. В предельных случаях информированности о векторе состояния (им
соответствуют различные способы задания множества начальных условий О)
система (9.43) преобразуется к соотношениям принципа максимума и уравнению
Беллмана соответственно.
391

При /я = 0 множество П является точкой х(/0) = *о и ищется оптимальное
программное управление «*(•). Соотношения (9.43) для общего случая
преобразуются к соответствующим принципу максимума:
*>) = /,(',**(').«*(')), х'A0) = хор ] = \ л,
(9.45)
где
Н((,х,и)= 2 у/0 //',*.«)-/°(',*,и);
7=1
#'(*,х*(/)) = тахЯ(^х*@,и) = Ж',*' @, «*(')) •
Функция Ж(/) определяется как решение уравнения
^•=-ячлх'(о) + 1ая'1^,@)х;(о
с конечным условием
После решения системы (9.45) можно проинтегрировать уравнение для
функции \У{) и вычислить минимальное значение функционала по формуле
шш /(Ю = -^)-2>/'о)*о;.
Если /и = л, то множество С1-Кп и ищется оптимальное управление
и*(*,х) с полной обратной связью. Система (9.43) для общего случая
преобразует к уравнению Беллмана (9.15), где ф9 х) - Ж(/, х).
2. Рассмотрим более общую задачу с подвижным правым концом
траекторий. Пусть в отличие от задачи (9.42), где момент 1{ окончания процесса
управления считается заданным, а правый конец траектории хAх) - свободным,
время окончания процесса управления определяется первым моментом достижения
точкой (/,*(/)) некоторой заданной поверхности Г с Кп+{:
Г = {(/1,х)|Г/(/1,х) = 0,/ = 1,...,/; М(/0,+оо), хеКп}, (9.46)
где 1^/^/1 + 1, при / = п +1 множество Г представлено точкой в пространстве
Яп+1\ функции Г/D,х) — непрерывно дифференцируемы; система векторов
392

(дг,(*},х19 дг^.х) дг^.х)) / = 1 л линейно независима у(/ьХ)€ЛЛ+1.
[ дхх дхп д*х )
Бели число т используемых в управлении координат задано, то I йп-т + 1, т.е.
размерность множества Г не меньше размерности множества начальных
условий.
Множество допустимых процессов #(/0,*о)> как в задачах (9.4),(9.19),
определяется как множество троек */ = (/!,х(), */(•)), которые включают момент
окончания процесса /ь траекторию х(-) и управление и(«) (ще У/еГ:
х@еЛл, и(*)е1/, функции х() непрерывны и кусочно-дифференцируемы,
а !/(•) € #о кусочно-непрерывны), удовлетворяющие уравнению (9.39) с
начальным условием х(/0) = х0 почти всюду на множестве 7" и условию (9.46).
На множестве ^(/0,х0) определим функционал качества управления
/(</) = } /°(/,х@,«@)Л + Л*1.*('1»,
где /°(/,х,1/),7г(/1,х) - заданные непрерывно дифференцируемые функции.
Требуется найти такую функцию «*(/, х1)еМт9 что
ЦП - гат Ц4) Ух0 € П, (9.47)
где ^ -(гГ,х*0. «*(•)-¦Ч-.х|*(-))) •
В [30,35,37] показано, что для нахождения оптимального управления
с неполной обратной связью требуется решить систему:
ду)(ихх) * ду)(*9х1) 1.1.1
а г /в1 ах,
+ /^(/,х1,/(/,х1),в*(Лх1)), у = т + 1,...,л, У(/,х!) е й,х,,
у;^о,х1) = ^оу(^1),Уг=^ + и,»; Vx1 е^, (/<>),
\дЩ*,Х1) " дН'Ц,х\у*{ихХ)) .„ к гг/. 1 V. 1ч Л л
т^1 Г^" Е ' "у^их1) + Н(*,х\у (*,х1)9и)\ = 0,
и€и [ °% у=т+1 °х} )
*уА*>*1) эд'Сх'.у'С*1)) , т+1 „
—*Г^ , у = т + 1,...,л,
а/ аху
393

(9.48)
ИЧ'1,*')+ I ^(/„х,)у;(*„х,) + /-(/1>х1)/(^1,х1)) = 0>
./=я>+1
Г/(/1,Х,,/(/„Х1)) = 0, 1 = 1,...,/,
5Г1(Г„х,)/а,,х1)) = 0, 1 = 1,...,/,
Я'СЛ/С*1)) = тахЩ(,х1,у'A,х1),и).
где
5^ =8^ьх'>/(Г„х')) = Д^»*1./^.*1))^ + ^ ^,,х',/(,„х'))
д11 >т+1 Эху
Я(*„х') = НЦих\уЦих*),и(*ьх1)),
я(/,х,1/) = 5; —^-^м*>х,и)+ Ехг1 —* /}(*.*.«)+
/=1 *х/ У=т+1 1-1 *х/
У=т+1
С с Лл+1 — множество точек (/,х), из которых можно достигнуть терминального
множества Г по некоторой траектории, соответствующей допустимому кусочно-
непрерывному управлению (при этом Лег б(/0), 0(*о) ~ сечение множества О
при фиксированном ^ = ^^^ йх\(^) — проекция множества (?(/0) на Вх)\ 0{х\ —
проекция множества О на пространство [/о>+°°)* В\.
В частном случае, когда момент ^ фиксирован, а правый конец
траектории свободен, система (9.48) совпадает с (9.43). При т = п из (9.48) следует
уравнение Беллмана (9.20), а при т = 0 — соотношения принципа максимума.
Еще одна форма записи системы (9.48) для данной задачи изложена в [37].
3. Решение задачи синтеза оптимальных линейных регуляторов с неполной
обратной связью изложено в [36,37].
394

Пример 9.28. Даны модель объекта управления в форме
*1<0 = и<*),
и квадратичный функционал
2
2
1Л\и^)^Л[х{2B) + х22B)\^тт.
о 2
Начальные условия заданы множеством П:
4
х(*0)еП = {х\х2=--х19 ххеЯ}.
Требуется найти оптимальную синтезирующую функцию и*A,х{) на
множестве О.
? Здесь х€Д2, иеЯ, Г€[0;2], /°(/,х,и) =|и2, ^(х) = ^[х,2 + х22],
/\(*,х,и) = и, /2(*,х,и) = х{.
Выпишем систему (9.43) для данной задачи, учитывая, что
1 7 4
х1 =хи х1 = х2, Уо(х{) = --хи <р(*,х) = Щ*,х{) + уA,х1)х2,
#G,Х,И) = ^И+--^ИХ2+1|/(/,Х1)Х, --И2,
0 XI О XI ^
#'(Х *1, Ж *1)) = тах Н(и хх, у(г, хх)9и).
и
Она имеет вид
дЩихх) дЩ*,хх) .„ , , „ , 1 *2/, ч л
77""^ + —ТТ^» Лх^ + ^х,).^--» 2(^,л:1) = 0,
ОТ ОХх 1
01 ОХ\
——— = ^ и \*>х\) + х\> УК^х1) = -—х1.
Используя необходимые условия экстремума для нахождения максимума
по управлению и, определим структуру оптимального управления:
395

¦„ ч дЩ^хх) ду(ихх) „ ч
ОХх ОХх
Будем искать неизвестные функции, входящие в записанную выше
систему, в виде
Щ*,хг) = |ЛГ2@ X!2 + *,(/) х, + *0@,
где Уо@>У1D>^о@>^1@>'2@>^@>^@ ~ Функции, подлежащие определению.
Тогда получим
и*(^,Xx) = К2Xx+Кx+N^(у0+уxXx).
Здесь и далее аргументы функций для краткости опущены.
Подставляя Ж*1>> Щ*>Хх), чК'>*1)» «*('»*!> в систему и приравнивая
члены при одинаковых степенях хх нулю, получаем
Л+Л№+^И>>-0, Уо@) = 0,
Л+Л*2-1 + Л2^-0, л@) = -|,
Ч/ = -^2у0 - * *ь УB) = -у0B),
й = -К2М-ухМ29 МB)=-ухB),
Л:2+*22+2^-^=0, *2B) =-1 + ^B),
*1+*1*2+1г-ИЛЛГ2-0, *!<?> = ЛB)Л<2),
^0+|^2"}^2=0' *о<2) = -|*2B).
Решение данной системы имеет вид
Уо«) = *о@ « *!(') = 4*0 - *(» - о, ух@ = -B~(з^^ **М = "EТ7)-
С использованием связи х2 = Ж^) определим явный вид искомой
оптимальной синтезирующей функции и выражение для вычисления минимального
значения функционала качества:
396

Ч>(*0,х) = Щ0,х1) + уф,х1)х2=-±х?=- ппп /(</) УхеО.
Оптимальное программное управление и оптимальное управление с полной
обратной связью найдено в примере 9.16. С учетом полученных в п. А примера
9.16 соотношений, можно показать, что соответствующая функция <р(/,х) при
/. ч /л ч 23х? + 24Х|Х2+9х|
г = /0 = 0 имеет вид <р(*<ьх) = <р@,х) = ¦ ^-* «-.
4
На множестве О, где х2 = -—хх, находим
Ф@,х1,^о(х1)) = -7х12="^ Ш* Л*) У*€Я,
т.е. управления и*(*,х) и и*(',*1) для начальных условий из множества а
обеспечивают одно и то же минимальное значение функционала качества
управления."
Пример 9.29. Даны модель объекта управления
*!(/) = х2@,
*2<>) = "('),
и функционал
1 о 1
Начальные условия заданы множеством О размерности т = \:
х(/0)€О = |х х2=-тх1, х^Лк
Конечные условия определены соотношениями:
Г1(/ь*(/1)) = ххB) + х2B) = 0, Ш,х(*1)) = /1-2 = 0.
Требуется найти оптимальную синтезирующую функцию »*(/,*,) на
множестве п.
ПЗдесьх = (х1,х2O'€Л2, 1/€Л,/е[0;2], /\их,и)Ли2, Лх) = |х|,
/1(/,Х,1/) = Х2, /2(/,Х,1/) = 1/, X1 = ХЬ X2 = Х2, Уъ(хХ) = --ХХ.
Выпишем систему (9.48) для данной задачи с учетом того, что
д Х| G X} х
Тогда, используя необходимые условия экстремума для нахождения макси-
мУма по управлению и , найдем структуру оптимального управления:
397

и*(*,хх) = агвтахЯ(/, хь/(/, хх)уи) = у(*,х{).
и
В результате получим
«2йа1..в^а1ЖХ1)+.-(/,Х1), *о,*,)=-|*..
01 ОХ\ х
а/ эх, п' ' ах, '
*2,х,)8х2 - ЛB,х,)8/, + Ч/B,х,)8х2 =0,
Щ2,х,) + уB,х,) • *2,х,) + ±у2B,х,) = О,
Г1(/1,х„^,,х1)) = х1 +Я2,Х!) = 0, ГгЙ.хьу^.х,))-/, -2 = 0,
8Г1(*1,Х1,уD»х|)) = 8х2 = О, 8Г2(/, х,,;к(/,,х,)) = 8/, = 0.
Будем искать неизвестные функции, входящие в эту систему, в виде
Ж*1>-й(<)*1, Щ/,х,)=-|*2@х,2, Ч/(/,лг1) = ЛГ@лг1,
где У1A),К2((),Щ1) — функции, подлежащие определению.
Подставив последние соотношения в выписанную систему и приравк
члены при одинаковых степенях х(, получим двухточечную краевую задачу:
Л--*? + *, л@) = -|, ЛB) = -1,
К2 = 2ЛГЛ2-ЛГ2, *2B) = -Л2B)-2ЛГB)ЛB) = -1 + 2ЛГB),
// = -2ЛГу,-^2.
Ее решение имеет вид
10-6/+ /2 A0-6/ +ГJ 10-6/ +Г
2
а искомая оптимальная синтезирующая функция в*(*,*1) = -хр¦
10 - 6/ + /2
398

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
9.1. Для задачи
х(/) = и@, *@) = *0,
1'гГ.,2
1 = ± \[и2(*) +хЩл^тт
найти: а) оптимальное программное управление и * (•) и оптимальную
траекторию х * (•), применяя принцип максимума; б) оптимальное управление «*('»*)
с полной обратной связью.
9.2. Для задачи
**<*)-«20). ^2@) = О,
' = / [«?(') +  (')] Л + X! A) -> ПШ1
о
найти оптимальное программное управление и*(«) и оптимальную траекторию
х*().
9.3. Для задачи
*1<0-*!<О + И<<).
о
найти оптимальный регулятор и*(х).
9.4. Для задачи
х2(г) = -х2@,
х(/) = Зх(/) + 1/@, х@) = хь,
7 4 / [и2@ + 7х2(о]л + |х2A) -> лип
20 2
найти оптимальное управление и*(/,х) с полной обратной связью.
399

9.5. Для задачи
х(/) = -Зх@ + 2и@, *@) = дсб,
" \ I Iй2® + 10*2<')]Л + \х2Ы "> Ш1П
/
4 о
найти оптимальное управление и*(*,х) с полной обратной связью.
9.6. Для задачи
х(*) = ах(*) + Ьи(*), х@) = *о,
/= |[е!/2@ + 5,х2@]л + Лх2(Г)^тт, Й>0, 5^0, Л*0,
о
найти оптимальное управление »*(/,х) с полной обратной связью.
9.7. Для задачи
*!(') = *2@,
*2@ = "('),
о
найти оптимальный регулятор «*(х).
9.8. Для задачи
*1@ = *2('),
х2(г) = М0,
/=Д / [^(О + ^^ + е!/2^)]^^!!!^, О>0, ^ *0,.У2*0,
2 о
найти оптимальный регулятор и*(х).
9.9. Для задачи
*!(') = *2@, ^@) = 0, д*A>-1,
х2@ = и@, х2@) = 0, х2A) = 0,
1
/= |1/2@Л->ПШ1
0
найти оптимальное программное управление г/ * (•) и оптимальную траекторию
хЧ).
400

9.10. Для задачи быстродействия
*1@ = *2('), *!@) = 0, х{A) = Ь,
*2@ = "('), х2@) = 0, х2A) = 0,
1и(*)\* а, 0<$/^7\ д>0,
т
I = |Л -> пнп
о
найти оптимальное программное управление и * (•) и оптимальную траекторию
*ч>.
9.11. Для задачи быстродействия
^@ = ^2@, ^1@) = 0, х1A) = 6,
ЪЮ-иЮ. х2@) = 0, х2A) = 0,
г
| и2@ Л = а (изопериметприческое ограничение), а > 0,
о
г
/ = |А -> пил
о
найти оптимальное программное управление и * (•) и оптимальную траекторию
*Ч>.
Указание, вводя дополнительную переменную, замените изопериметриче-
ское ограничение условиями
*з@ = @, *з@) = 0, х3(Г) = а.
9.12. Для задачи
х(г) = - п х(Г) + и@, х@) = п -10,5;
/ = "/ [-и2@ + х2(о1л-+тш,
где п - некоторое натуральное число, найти оптимальное программное
управление и * () и оптимальную траекторию х * (•).
9.13. Найти оптимальное по быстродействию управление !/*(•),
соответствующую ему траекторию х * (•) системы:
х1(*) = х2(<) + п-10$9
х2(/) = и(/), |«#I*1, 0*/<;7\
и время Г, затрачиваемое на переход из начального состояния х{@) = п,
*г@) = 1 в начало координат. Здесь п - номер студента по списку.
401

Глава 10. СИНТЕЗ ОПТИМАЛЬНЫХ НЕПРЕРЫВНЫХ
СТОХАСТИЧЕСКИХ СИСТЕМ
10.1. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО ПРОГРАММНОГО УПРАВЛЕНИЯ
10.1.1. Постановка задачи
Пусть поведение модели объекта управления описывается стохастическим
дифференциальным уравнением Ито [44,58]:
Ж = Я*9ХЮМтЛ + Ы?,т,«Ю)ЛГ, Х(*0) = Х0, A0.1)
где X — вектор состояния системы, X еВ"; и — вектор управления, и е V с В?,
V — некоторое заданное множество допустимых значений управления;
( еТ = [Г0уГг] — промежуток времени функционирования системы, моменты
времени Г0 и 1Х заданы; \УA) - ^-мерный стандартный винеровский случайный
процесс, не зависящий от Х0 (второй член в уравнении A0.1) характеризует
случайные внешние воздействия на объект); /(/,дс,ы):Г х Вп х V -> Вп, а(/,х,и) —
матричная функция размера (л х к). Обозначим: В = Вп, О = (*о,*\) * Яп •
Начальное состояние Х0 определяется плотностью вероятности
р(*о,х) = р0(х)еР, A0.2)
где Р = | /?(х) | р(х) € С2(В), \р(х)<Ы = 1, р(х) 2> 0 Ух е Б I, С*(#) - множество
к - раз непрерывно дифференцируемых на В функций.
Предполагается, что при управлении используется информация только
о времени /, т.е. система управления в данном случае является разомкнутой по
состоянию и рассматривается так называемое программное управление и({).
Множество допустимых управлений Щ образуют функции и():Т -+ V
такие, что функции /;и('\*,х) = /1(*,хМ*)), о$)(*,х) = ои(*,х,и(*)), / = 1,....л,
} = 1,...,&, удовлетворяют условиям (см. разд. 7.3), при которых решение
уравнения A0.1) существует, единственно и является непрерывным марковским
процессом. Если плотность вероятности этого процесса рA,х) еС1*2@)9 то она
удовлетворяет уравнению Фоккера-Планка-Колмогорова [22,30,31,58]:
ОI ,-„10 Х\ 2. |=| *_| 0X1 ОX^
= А^[р{1,х)] У(*,х)€е A0.3)
402

с начальным условием A0.2). Здесь А"®[] - дифференциальный оператор,
С1,2@) ~~ пространство функций рG,х), непрерывных на (? вместе с частными
др(*,х) др(*,х) д2р(*,х) ,. , . , ч
производными-^-^, V , /;*' (/ = 1,....л; у = 1,...,л),
г 0Г 0X1 ОХ1ОХ^
к
аи(*,х,и) = ^ <*//(',*,«)<*;/С*, и).
/=1
Обозначим через &о(*о,Ро(х)) множество пар </0 = (р(у),«О)» где функции
р(у) €С1,2@, «(•) еЩ и удовлетворяют уравнению A0.3) с начальным условием
A0.2).
Определим на множестве 4Ь('о> А>(*)) функционал качества управления
'D>) = }//°(/,х,иA))Жх)А*+ ^(х)/#ь*)А =
- А#| )/°(Г,т«<0)Л + ПЩ)) I (Ю.4)
где М— знак математического ожидания; непрерывные функции
/°(*,х9и):Т х ВхЦ -> Я, Г(х):В-+Я удовлетворяют условию полиномиального
роста: Ч(*,х,и)еТхВх1/ \/°(*,х,и)\ йс{ A + |х|+|и|)*, \ Г(х)\ йс{A+\ х\)°*; сьс2
— некоторые постоянные.
Требуется найти такой элемент </о = (Р*(>),"*(•)) €€>0(*о,/>о(*))' что
'Ю- гшп /(</<)). (Ю.5)
4>е/*>('о.А>(*))
10.1.2. Стохастический принцип максимума
Утверждение. Если элемент </© =(Р*(»),«*(•)) €Фо('о»Ро(*)) удовлетворяет
условию A0.5), то выполняются соотношения стохастического принципа
максимума:
арУ = ли()[/> * ('>*)]. /> * (>о>*) = л(*).
ОТ
^^ = -А"%(>,дс)] + /°(',*>«*@), <р((их) = -Р(х), (Ю.б)
ОТ
и*A) = агатах Г
«",
,«1 ^Х,
п п *Ъп
41Е1^^(^.»)-/0(^,«)
11=\]=\дх1дх]
р*(*,х)ах,
403

где Аи()[ф(/,*)] = Х^^^^^ - сопря-
женный дифференциальный оператор.
В результате решения краевой задачи A0.6) может быть найдено
оптимальное программное управление и * (•).
Минимальное значение функционала A0.4) вычисляется по формуле
пил /(</<)) = - \<?(*о,х)Ро(х)ах.
4>еОоОЬ,А>(*)) д
Замечание. Если использовать понятие обобщенного решения
дифференциальных уравнений, то ограничения на функции, входящие в A0.1)-
A0.3), можно ослабить. При этом соотношения для нахождения оптимального
управления остаются справедливыми.
10.1.3. Оптимальное управление линейными системами
Пусть уравнение A0.1) имеет вид
4Х = [А@Х® + В@иЩА + С@4ЦГ9 A0.7)
где Л@, В(*)9 С@ — матрицы размеров (лхл), (пхд), (пхк) соответственно,
элементы которых непрерывны; на управление ограничений не наложено, т.е.
Пусть начальная плотность вероятности A0.2) — гауссовская с
математическим ожиданием щ и ковариационной матрицей В0. Функционал качества
управления A0.4) квадратичный
/=1}/[х^(Ох + 1/гО@|/]р(/,х)ЛЛ+^[хгЛх]/К/,,х)^ =
1ьв 1в
= М
|)[лгг@5@^@ + иг(/H@|/@]Л+|[^гЙ)ллг(/1)]
, (Ю.8)
где 5@, Л - неотрицательно определенные симметрические матрицы размера
(л х л), а 0(/) - положительно определенная симметрическая матрица {дха).
Сравнивая A0.7), A0.8) с A0.1), A0.4), имеем:
/(/,*,!/) = А(*)х + ВA)и; а(*,х,и) = С«)СТ Ц);
/\*,х,и)Л[хт$Юх + итО(*)и\, Г(х) = ^[/Лх].
404

Система A0.6) для определения оптимального программного управления
и *() преобразуется к виду
Р*((о,х) = Ро(х),
^=_^^^М(г)х+^)и<@]_1№|С(ОсГ(/)^о|+
+±[хт$«)х + и*(»т0A)и'A)],
1 т
Ч>(*1,х) = --[х'Ах],
и*@ = а1вт^|\^^)г2^^ (Ю.9)
д2р(*,х) д2ц>(*,х)
где V- оператор градиента ; 1г - след матрицы; — ' ,— ' - матрицы
дх2 дх2
вторых производных.
Функция ф(/,х) ищется в виде
<р(/,х) = ±хтК2(*)х + КхтЦ)х + К0(<), A0.10)
ще АГ2@ - симметрическая матрица размера (лхл), КХЦ) - вектор (лх1),
^о@ ~" скалярная функция, подлежащие определению.
Пользуясь правилами матричных операций (см. разд. 9.2.3), запишем
выражение, определяющее структуру оптимального управления:
и I 2 ) и
где т(г) = | хр*(?,х) дх — математическое ожидание.
в
Так как на управление ограничений не наложено, воспользуемся
необходимым и достаточным условиями безусловного максимума:
ди
405

Отсюда
и^) = а~^)ВтШ^ЫУК^)]. A0.11)
Так как )* ** = -б(*)> а 6@ ~ положительно определенная
матрица, то достаточное условие максимума функции #(/,р*(/,х),и) по
управлению выполняется.
Далее, умножая первое уравнение в системе A0.9) на х, интегрируя по
частям по множеству В с учетом A0.11), получаем уравнение, описывающее
изменение математического ожидания:
т = [/|@+5(/)е-1@1?г@^2@]^ + ^)е@^Г@^1@. т{^) = щ. A0.12)
Подставляя A0.10), A0.11) в уравнение и граничное условие для функции
<р(/,х), входящие в A0.9), и приравнивая члены с одинаковыми степенями х
нулю , получаем
К2 = -АТК2 -К2А + 5, К2(*{) = -Л,
Кх = -АТКХ -К2В0ГхВтКх -К2ВОГхВтК2тп, К{(*{) = 0, A0.13)
К0 =| \ттК2ВОГхВтК2т-КхВОГхВтКх -1т(сСтК2)]9 К0(*х) = 0.
Здесь аргумент / для краткости опущен.
Решая систему A0.13), можно найти оптимальное программное управление
и * (•) и вычислить минимальное значение функционала A0.8):
гщп ч/(^) = -Ы/0,*)^
= -^щтК2(^)щ -|*г[*2(/0)^ ]-Кхт(*0)щ -*0('о).
Замечание. Полагая \у(*)= К2(*)т(*)+ Кх(*), систему A0.11)-A0.13)
можно записать в эквивалентной форме:
т = Л('М')+ ВкHГх1$)ВТ{$№)9 п^0) = щ,
«•М-о-1»^)^).
406

Пример 10.1. В задаче
ах = и(/)л+<№, *(о)- х0,
1 = \\\и2<[)р(их)ах* + ±\х2р(\,х)<Ь^тпт,
10К 1К
где хеЯ, /е[0;1], иеК, л% = 1, Д>=1, требуется найти оптимальное
программное управление и * (•).
? В поставленной задаче .4@-0, 4@-1, С@ = 1, дУ@ = О, 0@ = 1,
Л - \9 /0 = 0, 4 = 1. Выпишем условия A0.11)—A0.13):
тп = *2(/)/и(/) + к\ (')> »@) = 1;
*2 = о, *2A) = -1;
X, =-^22@т(/)-^(/)^2(О, ^1A) = 0;
*о =±[К}(*)тЦ*)-КН')-К2(<)}, *оA)-0.
Сначала интегрируем три последних уравнения:
а затем находим оптимальный закон изменения математического ожидания и
оптимальное программное управление:
«*@=1-|, «•«—!.
Минимальное значение функционала определяется по формуле
^^Й)(-))/№) = ^Г^2(°)т° Ч***2^*6 Ь'1Г@)«Ь "'о@)-
=1 1-1 2.1
2 + 2 2 + 4Ш4*
Такой же результат получается при использовании эквивалентной формы
записи условий стохастического принципа максимума:
т = у(<), /и@) = 1;
* = 0, чДО—«ДО; 1/*@ = м/@"
407

10.2. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
С ПОЛНОЙ ОБРАТНОЙ СВЯЗЬЮ
10.2.1. Постановка задачи
Пусть поведение модели объекта управления описывается стохастическим
дифференциальным уравнением Ито A0.1), а начальное состояние Х0
определяется плотностью вероятности A0.2).
Предположим, что о компонентах вектора состояния X известна полная
текущая информация, т.е. управление и((), применяемое в каждый момент
времени (еТ, имеет вид управления с полной обратной связью: и(() = и((9ХA))
(рис. 10.1).
,*('о) = *о
то
А йХ = /(/, *(*), и@) Л + а(/, *(/),«(!)) Ш
и«) = и(*,Х«))
»(/,х)
- Х@
Рис. 10.1
Множество допустимых управлений с полной обратной связью 2/п образуют
функции и(*,х):ТхВ->Ц такие, что для всех / = 1,...,л; ] = \,...,к функции
/"®(/, х) = /у (/, х, «(/, х)), а"]} (Г, х) = а/у (/, х, и(/, х)) удовлетворяют условиям (см.
разд. 7.3), при которых решение уравнения A0.1) существует, единственно и
является непрерывным марковским процессом. Если плотность вероятности этого
процесса рA,х) еС1^@)9 то она удовлетворяет уравнению Фоккера-Планка-
Колмогорова A0.3) с начальным условием A0.2).
Обозначим через 0л(*о»А)(х)) множество пар йп = (/>(-,-)>*(*»*))> гДе функции
/?(-,) еС1,2@, «(•,) е$/п и удовлетворяет уравнению A0.3) с начальным
условием A0.2).
Определим на множестве &„Aо>Ро(х)) функционал качества управления
'&)= )\/%хМихЫ,х)<Ьс*+ \Р(х)р{*х,х)<Ьс, A0.14)
%в в
где функции /°(/,х,и), /*(х) удовлетворяют условию полиномиального роста
(см. разд. 10.1.1)
Требуется найти такой элемент A„=(р*(,),«*(•,)) €Юп(/0,Ро(*)) > что
408

/(</;)= 1шп /(</„). A0.15)
функция и * (у) € ип называется оптимальным управлением с полной
обратной связью.
10.2.2. Уравнение Беллмана
Для определения оптимального управления с полной обратной связью
служит уравнение Беллмана для непрерывных стохастических систем
[6,19,45,39,58,61].
Утверждение. Если существует функция <р(/,х) бС1,2(С), удовлетворяющая
уравнению Беллмана и граничному условию
тах
\ д<Ж,х) ^Эф(/,х)./ ч 14г^д2у(*,х) и ч -ол \| л
V(/,д:NС?,
A0.16)
^Ьх) = -Г(х) ЧхеВ,
и управление и * (у) € Чп, удовлетворяющее условию
я2
и *(*,х) = адетах
/-1 дх1 *^ш^^-^дx^°x^ ]
то и* (/,х) является оптимальным управлением с полной обратной связью.
к
Здесь, как и ранее, используется обозначение д|у(/,х,и) = ^а,/ (/, х,и)• ау/(/,х,и).
/«1
Уравнение A0.16) является нелинейным дифференциальным уравнением
с частным производными второго порядка. Структура управления определяется
в результате максимизации выражения в фигурных скобках по управлению.
Минимальное значение функционала A0.14) вычисляется по формуле
пил 7(с!п)=-1<?(<0,х)р0(х)ах. A0.17)
4|«0ЯОЬ.А>(*)) д
Оно достигается для любой начальной плотности вероятности Ро(х). В этом
заключается основное преимущество управления с обратной связью. При
решети задачи достаточно определить только оптимальное управление и*(/,х),
а затем его можно использовать для получения оптимальных пар
"я в(Р*(у),**(у)) еЮп при любых начальных данных. Если плотность
вероятности дельтаобразная: Ро(х) = Ь(х-х0), то минимум функционала достигается
Для любого начального состояния хо-
409

АЛГОРИТМ СИНТЕЗА ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
С ПОЛНОЙ ОБРАТНОЙ СВЯЗЬЮ
1. Записать уравнение Беллмана A0.16) с граничным условием.
2. Найти структуру оптимального управления с полной обратной связью
в результате поиска максимума в A0.16) по управлению. Искомое управление
и * (/,х) обычно выражается через производные функции <р(/,х).
3. Подставить полученные выражения для управления в уравнение A0.16).
Проблема сводится к решению нелинейного дифференциального уравнения
с частными производными второго порядка.
4. Найти решение полученного уравнения и явный вид искомого
управления.
Замечание. Если обозначить <р*(/,х) = -<р(/,х), то уравнение
Беллмана A0.16) и A0.17) с учетом равенства тах/(х) = -тт(-/(х)) можно
переписать в эквивалентной форме [ 6, 19, 31, 58, 61 ]:
У(/,х)€Й, A0.18)
Ф*('1,х) = /(х) ЧхеВ,
пип /&)- Г Ф*(*0,*)/*(*)<**. (Ю.19)
</яе©я(*>,Л(*)) ^
Пример 10.2. Дана модель объекта управления
4Х = иЦ)А + Д-01Г9 ЛГ@) = ЛГ0,
тдрХеК, |ы|^#тах» /е[0;Г]; а, Т, ^Ш - заданные положительные
числа.
Требуется найти оптимальное управление и *(/,*) с полной обратной
связью, обеспечивающее минимальное значение функционала
/Л\х2р(Т,х)<!х.
*я
П Сравнивая с общей постановкой задачи, имеем: /((,хуи) = и,
о(/,х,1/) = 1^, /°(гЛц)-0, ?{х) = ±х2.
1. Выписываем уравнение Беллмана и граничное условие A0.18):
И**—! ы дх 2 ах2 / 2
410

2. Находим структуру оптимального управления из условия минимума
выражения в фигурных скобках: и * (/, х) = - Gтах 81$п
3. Подставляем найденное выражение для управления в уравнение Беллма-
на:
2 дхл 2
4. Решение уравнения является четной по х функцией и при х > О может
быть записано в форме [61]
Ч>Ч*,х)= 1\^у2р(*,х-у)+ху{у)р(*,х + у)]<Ьг,
где
л -> \ --Л Ь-&--/)«у-.]21
чЬ>) = ^-е-*")-±уе-*У, «3»..
Искомое оптимальное управление с обратной связью: и * (/,*) = -^/тах 8цо1х. ¦
Пример 10.3. Дана модель объекта управления
М = [ А х(*) + и(*))(Ь+ &<!№, Х@) = Х0,
где X € К, | и | ^ 1, * € [0;Г]; а, Г — заданные положительные числа. Начальная
плотность вероятности гауссовская с математическим ожиданием щ = 2 и
дисперсией /^ = 3.
Требуется найти оптимальное управление «*(/,*) с полной обратной
связью, обеспечивающее минимальное значение функционала
/= \хр(Тух)<1х.
к
П Сравнивая с общей постановкой задачи, имеем: /(*,х,и) = Ах + и9
<К*,х,и) = &9 /°(/,*,1/) = 0, Г(х) = х.
1. Выписываем уравнение Беллмана и граничное условие A0.16):
1«1*1 [ Ы дх 2 дх2 I
д<рБ((,х)
дх
д9БA,х) „
д<РВ((,х)
дх
411

2. Находим структуру оптимального управления из условия максимума
выражения в фигурных скобках:, и * (/, х) = явп ] г.
3. Подставляем найденное выражение в уравнение Беллмана:
Ы I дх I дх 2 дх2
4. Решение уравнения находим в виде <рA,х)= К^х + К0(*), где К\{1),
К0(() — неизвестные функции. Подставляя в уравнение и приравнивая
коэффициенты при одинаковых степенях х, получаем
АГ1=-,М, *,(Г) = -1;
К0 = -|*,|, К0{Т) = 0; и *({,х) = $&1 *,(*)•
Отсюда А-,(/) = -е^<г-'>, К^)-^™-\\, и*A,х) = -1.
Минимальное значение функционала вычисляется по формуле A0.17):
шп ..Ж)— \ч®,х)р()(хLх = -\±2[еЛТ-\\-еЛТщ\ =
= 2еАТ+Ц1-еАТ].ш
10.2.3. Синтез оптимальных линейных регуляторов
Уравнение Беллмана A0.16) для задачи управления линейной системой
A0.7) с функционалом A0.8) имеет вид
д
тах
-1[хг5@х + нгО@и]} = 0, <Жьх) = -±хтКх. A0.20)
птимального управления
(^)г^)-т"г<*)"
Отсюда находится структура оптимального управления
чг
и*(*,х) = агатах
A0.21)
Решение уравнения A0.20) ищется в виде
<р{*9х)ЛхтК2(*)х + К0(*), A0.22)
412

где скалярная функция ЛГ0(/) и симметрическая матрица К2(() размера (пхп)
подлежат определению.
Подставляя A0.22) в A0.21), получаем
и * (/, х) = 0Г1{$)Вт{$)К2{()х. A0.23)
Подставляя A0.22), A0.23) в A0.20) и приравнивая квадратичную форму и
свободный член нулю, имеем
к2Ц) = -АТЦ)К2Ю - К2Ц)АЦ) - *2<ОЛМ<Г!М*Г<0 К2Ц) + 3@, К2(<{) = -Л.,
A0.24)
К0(*) = -±<х{С«)Ст(ОК2(*)}, К0{*{) = 0.
Первое уравнение в A0.24) является уравнением Риккшпи. Решая систему
A0.24), можно получить оптимальное управление A0.23) с полной обратной
связью и минимальную величину функционала A0.8) по формуле A0.17):
^^ф)I^*)-- \Ф&.*Ы*)Л--м{±хтК2(*0)х + *0(/о)} =
Замечание. Сравнивая A0.23), A0.24) с (9.28), (9.27), можно
сделать вывод о совпадении оптимального управления с полной обратной связью
для стохастических и детерминированных линейных систем с квадратичным
функционалом.
Пример 10.4. Для задачи
4Х = и(*)(И + <НУ9 Х@) = Х09
1 1 1
^оя 1 к
где х еК, г е[0;1], и еК, ^ = 1, Д>=1, требуется найти оптимальное
управление и *(/,*) с полной обратной связью.
О В поставленной задаче Л(/) = 0, В(*) = 1, С(/) = 1, $@ = 0, 0@ = 1,
Л-1,^о = 0,/1=1. Выпишем соотношения A0.23),A0.24):
АГ2=-*22(/), *2A) = -1;
^о-—*^)' ^оA) = 0; и*(*,х)=К2(*)х.
413

Отсюда К2(*) = —г, ^о@-—0 , а искомое оптимальное управление
с полной обратной связью и * (/, х) = —-.
Минимальное значение функционала определяется по формуле
<,. А(*>/ю=-Ьг^°ь> 4и^(оК}-а(оL+г1т=1±г1-
Заметим, что оно меньше минимального значения функционала,
обеспечиваемого с помощью оптимального программного управления (см. пример 10.1). ¦
Пример 10.5. Для задачи
AХ = [АХ(*)+Ви(*)]A* + С<1П', Х@) = Х0,
т
1 = \\\\зх2+ди\их)\Ж,х)&сй^тот,
где хеЯ, /€[0,74, иеЯ9 Т, 5, б - заданные положительные числа; А, В,
С - заданные числа, требуется найти оптимальное управление «*(*,*) с полной
обратной связью.
? В поставленной задаче АЦ) = А, В(() = В, С(/) = С, 5X0 = 5, 0@ = О,
Л = 0, /0=°» *1=7\ Выпишем соотношения A0.23),A0.24):
К2=-2АК2(*)-&№ + 3, К2(Т) = 0;
*о=-\с2К2(*), *0(Г) = 0;
«*М = |*2(фс.
Отсюда получаем:
„„ з\е-Ыт-<)-\\
ок-А + Ь + АуЪР-')] » С
414

10.3. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
С НЕПОЛНОЙ ОБРАТНОЙ СВЯЗЬЮ
10.3.1. Постановка задачи
Поведение модели объекта управления описывается стохастическим
дифференциальным уравнением Ито:
йХ = /(иХЦ),иЦ))й + аЦ,ХЦ),иЦ))<1ЦГ, Х(*0) = *<ь (Ю.25)
где X — вектор состояния системы, X = (ХХ,Х2)Т еКп9 X = (Х\,...,Хт) ,
Х2=(Хт+\,...,Хп)Т, 0^тип; и - вектор управления, 1/€*7сД*, V -
некоторое заданное множество, *еТ = [*0,*{), Т - промежуток времени
функционирования системы, моменты времени /0 и *\ заданы.
Предполагается, что о компонентах вектора Xх е Кт текущая информация
известна, а о компонентах вектора X2 е Яп~т отсутствует. Обозначим: В = Кп,
Вг=Кт, В2=Яп-т,B = (*0,*1)хКп.
Начальное состояние Х0 определяется плотностью вероятности
р(*о,х) = р0(х)еР Ухе В,
A0.26)
где Р = \р(х)\р(х)еС2(В),\р(х)ах = 1,р(х)±0 ЧхеВ>> Ск(В)- множество
к-раз непрерывно дифференцируемых на В функций.
Предполагается, что при управлении используется информация только
о времени * и о компонентах вектора Xх, т.е. управление, применяемое
в каждый момент времени (еТ, имеет вид управления с неполной обратной
связью и@ = в(/,ЛГ1@) (рис 10.2).
Х(*0) = Х0
Щ')
йХ = Д*,Х(*),и(<))<!* + о(*,Х(*)М<))<ПГ
Х(*) = (ХХ«),Х2«))
и(*) = и(*,Хх(*))
иЦ,хх)
ХХЦ) = (*,(/),..., Хт{1))Т
0*тп<п
Рис. 10.2
Число т, О^т^п, определяется условиями информированности. При
т а л имеется информация о всех координатах вектора X, т.е. система (рис. 10.2)
415

будет системой с полной обратной связью, а при т = 0 — системой, разомкнутой
по состоянию. В последнем случае рассматривается так называемое программное
управление и(/).
Множество допустимых управлений с неполной обратной связью %/т
образуют функции и(-,):ТхВх -*(/ такие, что для всех / = 1,...,л;У = 1,...,Л:
функции //и('Ч^*) = //(',*>«('» я1)), а//()(/,х) = а/у(/,х,1г(/,х1)) удовлетворяют
условиям (см. разд. 7.3), при которых решение уравнения A0.25) существует,
единственно и является непрерывным марковским процессом. Если плотность
вероятности этого процесса р(*,х)еС1>2@), то он удовлетворяет уравнению
Фоккера-Планка-Колмогорова
д * М дх1 1 Ы\ )т\ ОХ1 дХ)
= Аии\р(*,х)], У(/,х)€0 A0.27)
с начальным условием A0.26). Здесь Аи^[] — дифференциальный оператор,
к
аи (и х, и) = ]Г <т/7 (/, х, и) аЛ (/, х, и).
/=1
Обозначим через #„,(*о><Ро(*)) множество пар </«=(/>(•,•)»*(•»•))» где
функции р(-,)€С1*2@, «(-,-) €^да и удовлетворяют уравнению A0.27)
с начальным условием A0.26).
Определим на множестве #да(*о»Ро(х)) функционал качества управления
Шт) = } / /\*,р(Г,х)М*,х1))ахЛ + 1?(р(*19х)), A0.28)
где/°(/,р,1/):ТхЯ+х[/-+К, ^ОК)):Р-» Л - заданные непрерывные функция
и функционал, К+ = [0,оо], р(х) = р(/,х) при фиксированном /.
Задача 1. Требуется найти такой элемент ^/да* = (/>*(•,),»*(•,))е^т(/0,Д)(х)),
что
Одновременно рассмотрим более общую задачу нахождения так
называемых оптимальных синтезирующих функций вида
и*(ихх\р()).ТхВххР->11, являющихся функциями от *,х* и функционалами
от плотности вероятности. Предполагается, что кавдая из них (при
фиксированном т) для заданной начальной плотности вероятности порождает
управление «*(-,-)е6Гм, т.е. если имеется решение р*(*,х) уравнения A0.27)
совместно с и-«'(Л*1 ;/<•)) Для произвольной начальной плотности
вероятности р(*0,х)еР,то «*(*,х1;р*(.)) = и*(/,х1).
416

Задача 2. Требуется найти такую синтезирующую функцию и*A,х1 ;/>(•)),
что
Лр*«>х),и*«,х1;р*(<>))) = , пил /(</„) ^Ро(х)еР. A0.30)
Таким образом, проведена редукция исходной стохастической задачи
к детерминированной задаче управления решением уравнения с частными
производными A0.27), что отражено на рис. 10.3.
Р('о,
II
ОТ
Р(*>х)
и(т,х1) = и(*,х1;р(т,))
и{их\р())
Рис. 10.3
Здесь роль новой модели объекта управления играет уравнение A0.27), а
состояние описывается функцией рA,х). При решении задачи 2 следует иметь в
виду наличие двух уровней определения управления системой A0.25).
Управление на схеме (рис. 10.3) для каждой начальной плотности вероятности
р(/0,х) порождает оптимальное управление и*(г,х1) в задаче 1, которое затем
используется в схеме (рис. 10.2) для управления траекториями исходной системы.
10.3.2. Соотношения для нахождения оптимального управления
В [30,37] доказаны достаточные условия оптимальности управления
в задачах 1 и 2 и выведены соотношения для его определения.
Утверждение (достаточные условия оптимальности в задаче 2).
Если существуют функция *У(/,р())бЕ и управление и*(г,х1;р()),
удовлетворяющие уравнению и граничному условию
т*,РЫ)
Ы
+ 1
*1
тах
/М*м§а]'м-/Ч'Н
Лс1
<&'=0, A0.31)
Ч((,р(х))еТхРу
Щ,Р(х)) = -Р(р(х)) Чр(х)еР, A0.32)
"о выполняется условие A0.30).
417

Здесь Л»и[<р(/,хI - сопряженный оператор, \Лр(/,х) € С1»2 (б)
/-1 **/ 1Ы\]=\дх1дх]
а —1»А*Л _ вариационная (функциональная) производная, Е- класс функций,
5р(х)
непрерывных на ГхР, непрерывно дифференцируемых по / и имеющих
непрерывную вариационную производную по р(х), принадлежащую С1,2 (О).
Приведем краткие сведения о вариационных производных.
Пусть дана функция $(*,р(-)):ТхР->Я, которая является функцией
аргумента I и функционалом по плотности вероятности. Рассмотрим ее
значение на функции />(•) +5/К)> где вариация бр(-) равна нулю всюду, кроме
некоторой окрестности А(х) точки х множества ВсЯп.
Вариационной производной функционала <?(/,/?(•)) по функции р() в точке
х называется предел:
Д(*> Д(х)
те«Д(х)-»0
если он существует, не зависит от вида 5р(), от закона, по которому / Ьр(В)а^
стремится к нулю, и способа стягивания к нулю тез А(х).
Вариационная производная является функционалом от /?(•) и функцией
от х. Если 5,(/,р(-))= /я(',$)РЙ)<й; — линейный функционал, где а(/,У -
известная функция, то
^^ = *,*). A0.33)
5р(х)
Замечания.
1. Если /и = 0 (текущая информация о векторе состояния отсутствует), то
решается задача поиска оптимальной синтезирующей функции
и*A\р()):Т*Р ^>11, порождающей на решениях уравнения A0.27)
оптимальные программные управления */*(/) для каждой начальной плотности
вероятности р(*о,х) еР.Из A0.31), A0.32) следует уравнение Р. Мортенсенаг.
д8(ир{х))
\ {^и[5^0)]/<х) - /вй**).и) } ах = 0, A0.34)
Щ,р(х)) = -Г(р(х)). A0.35)
418

2. Если т = п (имеется полная текущая информация о векторе состояния),
то соотношения A0.31), A0.32) записываются в виде
д*<>*х)К /пшхЫ^ A0.36)
Щ,р(х)) = -1?(р(х)).
A0.37)
Решение данной задачи определяет оптимальную синтезирующую функцию
и*A,х;р(-)):ТхКп хР^>17, порождающую для каждой начальной плотности
вероятности р(*ц,х) соответствующее оптимальное управление «*(/,х) с полной
обратной связью.
Как и показано в [30,37], для нахождения оптимального управления
и * (*,хг) (решения задачи 1) требуется решить систему уравнений:
^=-1^^(^'в*(/'х'))р*(''хI411^гк(^>в*(^,))х
~ Щх) ' *'1>х) м^Г"' A0,38>
и*(/,х!) = агатах Г
иеЦ
Ь
я л л2Л
^д<р(*,х) ,ЙЛ ч 1^^ а>(/,х)
/-1 О Х{ 2/-1у=1 **/**;
х«/
Ще
аи(*,х,и)]р*(*,х)-/°(*,р*(<,х),и) \<Ьс2,
Я(/,Р(Г,Х),1Г*(/,Х1))= {
Х^^/,(^,«*(',*1)) +
^•лх)-/0^*^),.*^1))!*.
1^-\^ш\оx^дx^
Затем можно решить уравнение
ЛЕЧО
Щ'г) = -1ч«1,х)р*(*1,х)<Ьс-Г(р*(*1,х))
419

и подсчитать минимум функционала A0.28) по формуле
пил ,№„) = -1фо,х)р0(х)сЬ-Щ*0).
Замечания.
1. Соотношения A0.38) получены путем применения необходимых условий
экстремума. Поэтому если найдено решение системы A0.38), то это еще не
означает, что пара йт * оптимальна.
вид
2. Если функционал A0.28) линеен по плотности вероятности, т.е. имеет
н
Шт)= }|/°Лх,1Г(/,Х1))Жх)^Л+ \Р(Х)РЦЬХ)(ЬС =
Ц>В В
= м\ )/*A,Х®М*.ХЧМ* + Г(т)) [. (Ю.39)
и ]
где непрерывные функции /0(*,х$и):Т*Вх1/-+ Я1,Г(х):В-+ Я удовлетворяют
условию полиномиального роста (см. разд. 10.1.1), оптимальное управление
и * (/, х1) можно найти из системы
т |=1 дх§ 2 м ув, дх1 дх]
хр*(',х)]=Аии\р*(*,х)], Р*(*о,х) = Ро(х)>
д<р(*,х) ^Э<р(/,х) г,л й/, кч 1ААд2<р(Г,х) /, */, 1чч
а Г м 0Х, *Ы}ш\0*10Х]
+ /0(^х,1г*а,х1)) = -Аи(>[ф(/,х)] + /0(/,х,1г*(^х1)), Ф(/1,х) = -/'(х),
*/, к гГ^5Ф('»*Ъ/, ч 1^Лд2ф(',х) /.
-/°(*,х,и)]р*«,х2\х1)<1х2,
|/>*(/,х)<&2
где р * (Г, х2 | хх) — условная плотность вероятности.
A0.40)
г,х,ы)-
420

Минимум функционала A0.39) можно вычислить по формуле
гаш /(<!„) = -1ф0,х)р0(х)ах. A0.41)
Если т = 0 (текущая информация о векторе состояния отсутствует),
система A0.40) принимает форму стохастического принципа максимума для
нахождения оптимального программного управления */*(/):
дР\(''Х)=А*>\р*(',х)], />*(/0.*>-Л<*>.
^^ = -Л^[ф(/,х)] + /0(/,х,1/*(/)), фх,х) = -Г(х),
ОХ
«бР ^ [м ах, 2,_,мах,дх]
-/0«,х,и)]р*(.*,х)<Ь,
ще А^М/.х)]-2;М^Л(/Л1,»(<))+1|;^^!!^в (/ЛИ»@) -
/=1 дхв *Ы\)=\°Х1°Х]
сопряженный дифференциальный оператор.
Если т = п (имеется полная информация о векторе состояния), то
соотношения для общего случая преобразуются в уравнение Беллмана для
стохастических систем для определения оптимального управления и*((9х)
с полной обратной связью:
Сдф&х) АЭф&хЬ,, . 1ААд2<р(>,*) ы ч
-/°(*,х,и) 1=0 У(/,х)е(?, <р(*их) = -Г(х) ЧхеВ.
3. Решение задачи синтеза оптимальных линейных регуляторов при
неполной информации о состоянии приведено в [36,37].
4. Задача нахождения оптимального управления с незаданным временем
окончания процесса может быть решена в двух постановках [30,37].
Если решается задача поиска наилучшего момента окончания процесса, то
на множестве троек йт, включающих момент гх окончания процесса, плотность
вероятности рA,х) и управление «(^х1), определяется функционал
Щт)= ) I /\*,р(*,х)М*,х1))<Ь<*< + т,Р('ьх))-
тах
и
421

В этом случае к системе A0.38) добавляется условие
я«Г.1>'(/Г.х).«*«Г,*'))-^(<Г'|>'(/Г,х)).
Во второй постановке задачи момент окончания процесса является
случайным. Поведение модели системы управления описывается уравнением
A0.25) с начальным условием, определяемым A0.26), и задано открытое
множество В с Яп с компактным замыканием В' = В II дВ, где дВ - кусочно-
гладкая граница.
Обозначим: 0 = (*о,Тх)хВ, где момент времени 7]>/0 задан,
Г = Фо,Т1]хдВ)[}({1\}хВ) ; #1,2*2 ~ проекции множества В соответственно на
Ят, Яп~т. Моментом окончания процесса считается первый момент *е[1ъ,Т\],
когда точка (*,Х(()) достигает множества Г. Функционал качества имеет вид
/(*«)-А#| )/°(*,ХЮМ*ХШ* + т.Х{*1)) I.
Как показано в [30,37] , искомое оптимальное управление и * A,х{) можно
найти в результате решения системы
01 »=1 °х1 11.\ у-1 °х1 °х]
хр*((,х)]=Аи1)\р*A,х)) У(Г,х)€0; Р*A0,х) = Ро(х) ЧхеВ;
^ = -±^/^иЧ^))-\±±^ои((,х,и*((,Х1)) +
д( /-1 °х1 '/-1>1 ЩОХ]
+ /°((,х,и*A,х1)) = -Аи()№,х)] + /(>({,х,и*«,х{)), Ч((,х)е<2,
фьх) = -Р{х), У(/,,х)€Г, A0.42)
и*(/,х') = а18тах
IV Ы\ дх1 *Ы\]=\°Х1°Х]
/р*(',*)<**2
*2
Данная система совпадает с необходимыми условиями экстремума,
полученными У. Флемингом.
422

Пример 10.6. Для задачи
ОХ = иA)Л + ЛУ, Х@) = Х0.
^ = -^[«@Жх)]Д^^, р@,х) = р0(Х),
Ы ох 2 дх
1 ! 1
2 од 2 я
где хеЯ, /б[0,1], иеК,т = 09 требуется найти оптимальное программное
управление и * (.) для различных начальных плотностей вероятности Ро(х).
? 1. Находим оптимальную синтезирующую функцию и*((;р()) (решение
задачи 2).
Соотношения A0.34), A0.35) для данной задачи имеют вид
у ^ " =тах
Ы и л
, Г аГб^,р@I 1 д2 Гад/,*-))] 1 21^^
3(\,р(х)) = -\\х2р(х)<1х.
1 к
Так как ограничения на управление отсутствуют, то используя
необходимые условия экстремума, можно найти структуру оптимального
управления: и^Г,р(.))= \ ±\Щ!^]р(х)<1х.
я
Будем искать решение в форме
12
, (Ю.43)
*?(',/>())= \\\к2Ц)х2 +К1(<)х + К0(о]р(х)<1х+±Що\ \хр{х)сЬ
где К2((), К\(()9 Ао@» #@ ~ неизвестные функции.
Введем обозначения: т= \хр(х)<Ы, 2)= ^х2р(х)дх. Тогда по формуле
я я
A0.33) имеем
5У/Р(;))=7^2@х2 + К1(*)х + К0(*) + Щ1)хт,
Ьр(х) 2
=№]-«*¦*.»¦*»- ЗРИ-*»-<->
Подставляя A0.43), A0.44) в уравнение и приравнивая члены при
одинаковых степенях переменных т, И, получим систему:
423

*2=0, К2(\) = -1;
Кх + КХК2 + Шх = О, КхA) = 0;
2^0+^+^2=0, ^0A) = 0;
Лг + *22+ЛГ2+2М:2=0, #A) = 0.
Здесь аргументы неизвестных функций для краткости опущены.
Решение: ЛГ2@—1, ^@-0, *0(')=^> *<'>=7Г?
Поэтому оптимальная синтезирующая функция имеет вид
\хр(х)<Ьс
иЧг,Р(')) = *2@т + К1@ + Щ0т=-^=« /2 . A0.45)
2. Предположим, что начальной плотности вероятности р@,х)
соответствует математическое ожидание щ. Тогда из уравнения модели объекта
и A0.45) следует уравнение — = —Ц-, /и@) = щ.
Таким образом, для различных то оптимальная синтезирующая функция
A0.45) порождает соответствующие пары функций (решения задачи 1):
т«) = щ[\-^, 1/(/) = »*(/;т(/)) = -^.
3. Найдем решение задачи 1 вторым способом. Для этого используем
систему A0.11)-A0.13):
и * @ = (Г1<0*г<0№<')»М + *1<0Ь
т = [А@ + В@О-1@ВТ^)К2@]т + В^)О-1а)ВТ@К{@, т(/0) = то,
К2 = -АТК2 -К2А + 8, К2ЦХ) = -Л,
Кх = -АтКх -К2В(ГхВтКх-К2В<ГхВтК2т, КХЦХ) = Ъ,
К0 =[тТК2ВО'1ВТК2т-КхВО-хВТКх -1т{ССтК2}]/2, К0(*х)-0,
Для данного примера она имеет вид
тп = К2т + Кх, /и@) = щ\ !/*(/) = К2Ц)тЦ) + *,(/),
К2=0, *2A) = -1; Кх=-КхК2-К22т, ^A) = 0;
К0 = ± [*22т2(/) - *!2 - *2], *00) = 0.
424

Отсюда Х2(<)—1, ^1@=-2й^, *о(') = ^|~7 + 1Ч1+1Г' "'
следовательно, т * (/) = щ 1 - — , !/*(/) = —-^~ ~ оптимальный закон изменения
математического ожидания и оптимальное программное управление.
Полученный результат подтверждает свойство оптимальной синтезирующей
функции и*(*,р(')) порождать соответствующие оптимальные управления и*(«)
для каждой начальной плотности вероятности.и
Пример 10.7. Решить задачу:
-|2
\хр(\,хLх-\ I ->пцп,
1 = и\и2«)р«,х)<Ьс<Ь-
^оя
я
где хеЯ, *б[0,1], иеК, /и = 0.
П Смысл задачи заключается в определении управления, обеспечивающего
наименьшее отклонение конечного значения математического ожидания от
единицы при одновременной минимизации затрат на управление. Найдем
оптимальную синтезирующую функцию «*(/,/?(•)). Уравнение A0.34) и условие
A0.35) для данной задачи имеют вид
у'^у " =тах
Ы и я
$A,р(х)) = - /хр(х)<&-1 -Мхр(х)Л +2\хр(х)(Ьс-\. A0.46)
Так как ограничения на управление отсутствуют, используя необходимые
условия экстремума, получаем структуру оптимального управления:
Будем искать решение в форме
[п2
\хр(х)<Ьс\ +К1(*Iхр(х)<Ьс + К0«) =
я ] я
Лк2Ц)т2 +К{(*)т + К0(*), A0.47)
^е ^г@, К\(()9 ^о(') ~" неизвестные функции.
425

Сравнивая A0.47) и A0.46), получаем, что при / = 4 = 1
*2A) = -2, *1A) = 2, К0A) = -\. A0.48)
Тоща
дх
Щ^У) -ЪЮтх + Хг®** (Ю.49)
[ М*) ] 2К; П'' дх2[ Ьр(х) \
Подставляя A0.49), A0.47) в A0.46) и приравнивая члены при одинаковых
степенях т нулю, получаем систему
К2 -2К2 + К22 =0, К2A) = -2;
К1+КгК2-К1=09 К{A) = 2;
2*0+*12=0, *оA) = -1.
Ее решение: К2Ц)=- |г—тг, ЛЦ0-- ^^"^^
2 1-ехрB/-2) ' 1-2ехрB-2/)
Поэтому оптимальная синтезирующая функция имеет вид
2ехрA-/)
1г*(/;рО) = ^2@т + ^@=-; Т^^гт-
1 - ехрB/ - 2) 1 - 2ехрB - 2/)
Предположим, что начальной плотности вероятности р@,х) соответствует
математическое ожидание щ. Тоща с учетом полученного результата следует
уравнение, описывающее изменение математического ожидания
1 + 2ехрB/-2) 2ехр(/-1) т/т_т
т-2ехрB/-2)т(/)-1-2ехрB-2/)' "^-"о*
Отсюда
т(/) = A-2е2) + [1-2ехрB-20]Bгто-1)
2[1-2*2]ехрA-0
Подставляя последнее равенство в оптимальную синтезирующую функцию,
для каждого начального математического .ожидания можно получить
соответствующее оптимальное программное управление и * (/) .¦
426

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
10.1. Для задачи
<1Х = и{*)<Н + Ш9 т@) = щ,
р-ЛгЦ}И)+1Г2A)]*]
->ПЦП,
найти: а) оптимальное программное управление и * (/);
б) оптимальное управление и*((,х) с полной обратной связью.
10.2. Для задачи
4Х&) = [ ДГ2(/)+ щ @1 А + </1Г, щ@) = 1,
<ОГ2@ = «2@* + ацг> т2$) = 0»
= а/|1|[цЧ0^22@]*4^AJ}-
> тш,
применяя стохастический принцип максимума, найти оптимальное программное
управление «*(/)•
10.3. Для задачи
ЛГ@ = [ЗЛГ@+^0]* + ^
/ = 1г|1 / [«/2(г)+7Аг2(/)]Л+^Аг2AI -> пил,
12о 2 ]
найти оптимальное управление и*((,х) с полной обратной связью.
10.4. Для задачи
^@ = [-ЗЛГ@+2|/@]Л + ^/Ж,
/ = м\Х \ [и2(*)+\0Х2{*)]й+±Х2Щ -+ пил,
найти оптимальное управление и *(*>х) с полной обратной связью.
10.5. Для задачи
/ = Л/{±|[1Н*@+ДГ*@]л}^т1п, Т-1+Щ
Найти: а) оптимальное программное управление и *(/);
б) оптимальное управление и *(*,*) с полной обратной связью.
427

Глава 11. СИНТЕЗ НЕПРЕРЫВНЫХ ЛИНЕЙНЫХ СИСТЕМ
СОВМЕСТНОГО ОЦЕНИВАНИЯ И УПРАВЛЕНИЯ
11.1. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЛИНЕЙНЫМИ НЕПРЕРЫВНЫМИ
СТОХАСТИЧЕСКИМИ СИСТЕМАМИ С НАКОПЛЕНИЕМ
ИНФОРМАЦИИ О СОСТОЯНИИ
11.1.1. Постановка задачи
Пусть модели объекта управления и измерений описываются
стохастическими дифференциальными уравнениями Ито [22]:
йХ = [А(*) Х(*) + В(*) 1/@] Л + оманги Х(*0) = Х0,
йУ = С(/) ХA) <Н + а2@ Шъ ПЧ) = 0,
где X — вектор состояния, X е В"; У — вектор измерений, У еВт; время
/ еГ = [/0,^], моменты времени /0, ^ начала и окончания процесса заданы;
матрицы АA), ВA), С(/), СУ1<0» <*2@ имеют размеры (лхл), (лх^), (тхп),
(пхк), (их/) соответственно, а их элементы непрерывны на Г; на управление
ограничений не наложено, иеВч\ И^СО» ^@ "" независимые стандартные
винеровские случайные процессы.
Начальное состояние Х0 определено гауссовской плотностью вероятности
с математическим ожиданием щ и ковариационной матрицей />о. Начальное
значение вектора измерений равно нулю.
Обозначим: У^ ={У(т), /0 <т</}, 4A) = а1@<т1г@, Л2@ = а2(/)а2г@.
Предположим, что при управлении в момент времени / используется
информация У/0 о всех измерениях, производимых на промежутке времени ['о,'Ь
Множество допустимых управлений образуют функции 1/@ = и(*уУ/0),
зависящие от предыдущих измерений, причем V/ € Т 1/@ е В?, при которых система
A1.1) имеет единственное решение (Х(*)9УA)) [58].
Зададим функционал качества управления в форме
/ = АГи)уГг(/)*<0*(^ A1.2)
где »У@, Л - неотрицательно определенные симметрические матрицы размера
(лхл), 0@ ~- положительно определенная симметрическая матрица размера
(Я х а), Л/ - знак математического ожидания, которое вычисляется как по
начальным условиям, так и по реализациям случайного процесса ХA).
Требуется найти управление «*(/,У^) из множества допустимых,
обеспечивающее минимум функционала A1.2).
428

11.1.2. Теорема разделения
Утверждение. Оптимальное управление «*(/,У^) в задаче, сформулированной
в разд. 11.1.1, имеет вид
и а) = иЦ,У*к) = 0-\ЪВТ№г(ШЪ, A1.3)
где ХA) = М{Х(*)\У*} — оценка вектора состояния модели объекта управления
по результатам наблюдений, удовлетворяющая уравнению
^ = [ЖО^@ + Ж0иЧО]Л+^@[^0-С@^)Л], х«о) = щ; (ПА)
К2({) - симметрическая матрица коэффициентов усиления оптимального
регулятора, удовлетворяющая уравнению
х2@--^г@^2@-^2(^0-^2@«0О"Ч0Лг@^2@ + *@,
(И.5)
18Г(/) — матрица коэффициентов усиления фильтра размера (пхт), определяемая
по формуле
К(*) = Г(*)СТ №?(*), A1.6)
Г(*) = М{[Х(*)-Х(*)][Х(()-Х(*)]Т} - ковариационная матрица ошибки
оценивания, удовлетворяющая уравнению
Г = АГ + ГАТ -ГСТК51СГ+Я1, Г(/0) = 2>о. A17)
Доказательство утверждения (теоремы разделения) приведено, например
в [6,9,15,18,29,45,58]. Оптимальное управление A1.3) с накоплением информации
является функционалом измерений, так как в силу A1.4) оценка вектора ХA)
зависит от У^.
Здесь уравнения A1.4),A1.6),A1.7) являются уравнениями фильтра Калма-
нау обеспечивающего нахождение оптимальной оценки вектора состояния
модели объекта управления с минимальной нормой ковариационной матрицы
ошибки оценивания. Соотношения A1.4),A1.5) соответствуют случаю определения
оптимального управления линейной детерминированной системой при полной
информации о векторе состояния. Задачи синтеза оптимального управления и
фильтра можно в данном случае решить независимо.
11.1.3. Синтез оптимальных линейных регуляторов
АЛГОРИТМ НАХОЖДЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
1. Решить проблему синтеза оптимального детерминированного линейного
Рехулятора в соответствии с алгоритмом, изложенным в разд. 9.2.3, для задачи
429

х = АA) х@ + ВA)!/(/), х(/0) = х0,
/ =4 } [хг@^@д<0+»г@(К0и@]*+7[*гЙ)А^1)] -* т1п-
2. Синтезировать оптимальный линейный фильтр в соответствии с
уравнениями A1.4),A1.6),(П.7).
3. Согласно теореме разделения выписать оптимальное управление с
накоплением информации по формуле A1.3).
Полученная структура оптимальной системы с накоплением информации,
где по измерениям производится оценка вектора состояния и ее использование в
управлении, изображена на рис. 11.1.
1 >
!**> 1
^1@
ОХ = [А(*)Х(*) + В(*)и\*))A* + щ(*)AЩ
Модель объекта управления
Ци'A)=0Г1«)ВТ№2(()ХA)
|Щ>) = 0
[ ^2«)
ёУ = СA)ЛГЮ<* + а2@^^2@
Модель измерений
I Х(^) = щ
"*@
аХ = [А(*)Х(*) + Д@ и* (/)] Л + КA) [ йГ - С(*)ХA) (ПУТ
Оптимальный регулятор
Оптимальный фильтр
Рис. 11.1
Пример 11.1. Пусть модели объекта управления и измерений имеют вид
аХ = иA)<1* + (!Цги Х@) = Х0,
4У = ХA)<Н + <№2у У@) = 0,
где начальное состояние Х0 определено гауссовской плотностью вероятности
с математическим ожиданием од = 1 и дисперсией 2>о = 2. Функционал качества
управления задан в форме
/ = Л/
[1|1/2@лД^Г2AI.
Требуется найти управление и*(/,Уо) из множества допустимых,
обеспечивающее минимум функционала.
? Сравнивая с A1.1),A1.2), имеем А(*) = 0, Д(/) = 1, С@ = 1, ^@ = 1»
а2@ = 1, ^@ = 0, 6@ = 1, Л = 1, /0 = 0, Н =1, *<0-1, Л2<0 = 1.
430

Выпишем соотношения A1.3)—A1.7):
и(*) = «*(/,У0') = *2<0*<0.
аХ = и*A)А + КAI4ГЦ)-Х(*)А], *@) = 1,
К2 = -К\, *2A) = -1, *(/) = ДО,
Г = -Г2+1, Г@) = 2.
ра и оптимального фильтра имеют вид
^ = 1/Ч/)Л + ^^[*У(/)-*(/)А], 1@)-1- ¦
3-е"*
Пример 11.2. Пусть модели объекта управления и измерений имеют вид
AХ = [-Х(*) + и(*)]А + Д<11Уи *@) = ЛГ0,
4Г = Х(*)А + </1Г2, У@) = О,
где начальное состояние Х0 определено гауссовской плотностью вероятности
с математическим ожиданием щ = 2 и дисперсией 2>о = 5. Функционал качества
управления задан в форме
1 = М\
||][[31г2(о+и2@]*+^2аI
Требуется найти управление а*(/,У0') из множества допустимых,
обеспечивающее минимум функционала.
? Сравнивая с (ИЛ), A1.2), имеем Л(/) = -1, 4@-1» С(/) = 1,
°1@ = 1/з, а2@ = 1,Я@ = 3, 0@ = 1, Л = 1,/0 = 0,/1=1, 1м@ = 3, Л2@ = 1.
Выпишем соотношения A1.3)-A1.7):
1/ЧО = «*(^о') = *2@*@,
^ = [-^(/) + 1/*(/)]Л + ^(/)[^@-^(/)Л], *@) = 2,
*2=2*2-*22+3, *2A) = -1, *(/) = Л0,
Г = -2Г-Г2+3, Г@) = 5.
л 2 + Зе-4*
'отсюда ЛГ2(/) = -1, д/) _ а соотношения для оптимального регулятора
2-е'
и оптимального фильтра имеют вид
431

И*A)-«*(/,У0'>—*Ю.
аХш-2ХЮА+223±^.[4Г(П-Х(п&]9 *@) = 2. ¦
2-е~™
Пример 11.3. Пусть модели объекта управления и измерений имеют вид
<ЙГ = 1/@Л, Х@) = Х0,
й? = ХA)А + а2 4Щ, У@) = 0,
где начальное состояние Х0 определено гауссовской плотностью вероятности
с математическим ожццанием щ и дисперсией 2>о. Функционал качества
управления задан в форме
/-1#Д/||2(|)Л+1ЛГ2(Г)}.
2о
Требуется найти управление и*(/,Уо) из множества допустимых,
обеспечивающее минимум функционала.
? Сравнивая с A1.1),A1.2), имеем Л@ = О, ВA) = 1, С@ = 1, ^@ = 0,
а2(/) = а2, 5X0 = 0, 0@ = 1, Л = 1, /0 = 0, ^=Г, ^(/) = 0, Д2@ = а1 = Д2.
Выпишем соотношения A1.3)—A1.7):
1/Ч0 = «Ч^0') = *2@*@,
аХ = и*A)А + КШ4У(Ъ-ША]9 Х@) = щ,
К2=-К1 *2A) = -1, К(*)=2р->
ЛО-1^. Д0) = Д0*.
Отсюда К2(*)=—^Г"Т> ДО =—^ г , а соотношения для оптимального регу-
^-Т-^ Я2+Во*
лятора и оптимального фильтра имеют вид
*-Г-1 К2+Щ*
432

11.2. УПРАВЛЕНИЕ ЛИНЕЙНЫМИ НЕПРЕРЫВНЫМИ
ДЕТЕРМИНИРОВАННЫМИ СИСТЕМАМИ
С НАКОПЛЕНИЕМ ИНФОРМАЦИИ О СОСТОЯНИИ
11.2.1. Постановка задачи
Пусть модель объекта управления описывается уравнением
х@ = А(*) хЦ) + ВЦ) 1/@, х(*0) = х0, A1.8)
а модель измерений — соотношением
у@ = С@*@, A1.9)
где х - вектор состояния, х е Яп; у — вектор измерений, у еЯт; г — время,
*еТ = [*о,1\] , моменты времени /0» *\ заданы, Л@, 2?@, С@ — матрицы
размера (пхп), (пха), (тхп) соответственно, элементы которых непрерывны; на
управление ограничений не наложено, т.е. и е Яя; размерность вектора
измерений не больше размерности вектора состояния (т<п).
Начальное состояние произвольное: х$ еЯп. Вместе с тем предполагается,
что имеется некоторая точка х$, в окрестности которой расположены
возможные начальные состояния. Обычно это предположение используется для учета
реальных условий функционирования системы управления.
Пусть функционал качества управления квадратичный:
/ю-7}[*гмад*о+иг<о^ <11Л°)
где *?(/), Л — неотрицательно определенные симметрические матрицы размера
(п х п), а 0@ - положительно определенная симметрическая матрица ($ х а).
Известно (см. разд.9.2.3), что оптимальная синтезирующая функция и*(*,х)
с полной обратной связью имеет вид
иЦ,х) = 0-\ЪВТ№2(!)х, A1.11)
где симметрическая матрица К2(*) определяется из уравнения
К2«) = -АтA) *2@ - *2('М@ - К2«)В(*H-1(*)Вт(*) К2@ + 5@,
(И.12)
*2('1) = -Л.
Замечание. Если обозначить Р@ = -Кг(*)> то соотношения A1.12),
A111) для синтеза оптимального линейного регулятора принимают форму
433

Нп=-лтмт-тт+тв{погЧъвт(йР®-8{ъ>
(П.13)
/>(*!> = Л,
и (их) = -ОгЧ0ВтЮРЮх~-Р(()х, т-ОГ1ЮВтЦ)т. (И-14)
В законах управления A1.11),A1.14) предполагается, что в каждый момент
времени известна информация о всех координатах вектора х. Как следует из
разд. 9.2.1, оптимальная синтезирующая функция A1.11) порождает оптимальные
пары (х*(-),и*(-)) для любых начальных состояний. Однако в рассматриваемой
задаче вектор х не доступен для использования в управлении, а измеряется
вектор у, информация о котором накапливается.
Требуется найти управление «(',1^), зависящее от всех доступных
к текущему моменту времени измерений У* = {у(т), *0 ^тй*} так, чтобы
свойства синтезируемой системы были близки к соответствующему случаю полной
информации о состоянии.
Идея решения состоит в получении оценки х(/) вектора состояния х(/)
в текущий момент времени / по результатам измерений У* и использовании
этой оценки в управлении A1.11) вместо *(/)• Тоща, чем точнее оценка х(/),
тем ближе синтезированная система по своим свойствам к оптимальной при
полной информации о состоянии. Структура такой субоптимальной системы
изображена на рис. 11.2. В детерминированных системах процесс получения
оценок вектора состояния по измерениям иноща называется восстановлением
или наблюдением, а устройства, позволяющие решить задачу наблюдения, —
наблюдателями. Рассмотрим задачу синтеза наблюдателей.
*0б)
^=Л(/)х@ + *(/)и*@
Х(Г)
>> = С(/)х@
у@
Модель объекта управления
Модель измерений
|*оь) = *ь
Ч **(') = <2-1(*)ВТ(*)К2(*)х(/)
«40
Накопление информации и выработка
оценки вектора х
Оптимальный регулятор
Наблюдатель состояния
Рис. 11.2
434

11.2.2. Синтез наблюдателей состояния
НАБЛЮДАТЕЛИ ПОЛНОГО ПОРЯДКА
Рассмотрим задачу синтеза наблюдателя полного порядка. Если т = п и
матрица С(/) не вырождена V/ € Т, то вектор состояния х(/) может быть
найден из A1.9) по формуле х@ = С-1@^@« В этом случае ошибка оценки вектора
х равна нулю и синтезируемая система совпадает с оптимальной при полной
информации о состоянии. Для всех начальных состояний обеспечивается
минимум функционала A1.10).
В общем случае предположим, что сигнал уA) поступает на вход
устройства, оценивающего вектор состояния *(/), которое описывается линейным
дифференциальным уравнением
^ = 1X0*0 +Л(О|<0 + «О*О, *(«,)-*2, (И.15)
где /)(/), Я(/), К(() — неизвестные матрицы размера (лхп), (лхд), (лхт)
соответственно. Здесь в начальном условии учтена априорная информация о
системе. Обозначим через е@ = *(/) - х(/) ошибку оценивания и получим
дифференциальное уравнение, описывающее ее изменение. Для этого вычтем из
уравнения A1.8) уравнение A1.15). Учитывая A1.9), получаем
^^=лц) Х(о - /)(о но+[т - тт «ко - «о сю *ю.
Если принять Я(/) = 2?@, /)(/) = Л(/) - ЛГ@ С@, то уравнение для ошибки
оценивания будет иметь вид
^ = И@ - К{1) С(/)] 6@, е(*0) = хЦо) - х5. A1Л6)
Вид ошибки оценивания е(/) полностью определяется свойствами матрицы
А({) - К(() С(/) и величиной начальной ошибки е(/0) •
Неизвестная матрица КA) должна быть выбрана такой, чтобы ошибка
достаточно быстро убывала (стремилась к нулю при г -> +оо). Если все матрицы не
зависят от времени, то для этого требуется, чтобы действительные части
собственных значений матрицы А - КС были отрицательными.
Уравнение оценивающего (наблюдающего) устройства с учетом A1.15) и
найденных матриц имеет вид
^ = А@%0 + В(<)и(<) + К(*)-[у(*)-С(*J(*)], х(/0) = *о. (И.17)
Структура оценивающего устройства совпадает с конструкцией фильтра
Калмана, но здесь имеется произвол в задании матрицы К($). Оценка зависит от
вс^х измерений до момента X, т.е. является функционалом У1. Следовательно,
435

управление A1.11), использующее вместо вектора х его оценку, а именно
и* (О = С (О Вт (О К2 (О *@, также зависит от У^, что и требовалось.
Оценивающее устройство имеет порядок п по числу координат вектора
оценок, удовлетворяющего дифференциальному уравнению A1.17). Если
начальное состояние х(/0) совпадает с х5 , то, как следует из A1.16), е@ = 0,
х@ в х@. Иначе только при правильном задании матрицы К(*) получаем, что
*(/) -> *(/) при / -> +оо.
НАБЛЮДАТЕЛИ НИЗКОГО ПОРЯДКА
Для стационарных систем, для которых уравнения A1.8),A1.9) имеют вид
*(/) = Ах«) + В 1/@, Я0 = Сх(<), A1.18)
а матрица С имеет ранг /и, можно построить наблюдающее устройство порядка
п-тп. При этом предполагается, что система является вполне наблюдаемой (см.
разд. 1.4.2).
Для построения наблюдателя следует расширить вектор измерений у с
помощью вектора г до размерности п :
где 6 — неизвестная матрица размера (л - /и) х л. Тогда, если матрица I
размера (л х /|) невырожденная, можно вычислить значения вектора состояния по
формуле
Так как измерения г в модели отсутствуют, их предлагается заменить оценкой
I, удовлетворяющей уравнению
^ = 2) 2@+ #и@+ *><*), 2(>о) = <г*о, (ПЛ9)
где матрицы И, Н, К должны выбираться из условия стремления ошибки
оценивания к нулю, т.е. е@ = г@ - 2@ -> 0 •
Получим уравнение, описывающее ошибку:
± = ^_^ = 0^*1 = ОАх-П2 + (СВ--Н)и-Ку.
<?* йг йг йг йг *
Так как у = Сх, % = Ох, 2 = *-е,то
436

^. = Пг + (СА-Па-КС)х + FВ-Н)и.
Бели действительные части собственных значений матрицы 2) отрицательные и
выполняются условия:
ОА-ПО-КС = 0, вВ-Н = 0, A1.20)
то ошибка оценивания е@ стремится к нулю при г -> +оо.
Обычно на практике задают матрицы 2), К и находят неизвестные
матрицы Я, О из условий A1.20). Для существования решения в A1.20) требуется,
чтобы собственные значения матриц Л и 2) были различными.
Зная *(/) и у(*), оценка вектора х вычисляется по формуле
'-Ш8Э-
*"-Ы ^. (.1.21)
Порядок оценивающего устройства (оно называется наблюдателем Люен-
бергера), описываемого соотношениями A1.19)—A1.21), равен (п-т) по числу
координат вектора г, удовлетворяющего уравнению A1.19). Синтезируемый
наблюдатель низкого порядка с найденными матрицами 2), Н, К, О может быть
помещен в соответствующий блок схемы, изображенной на рис. 11.2.
11.2.3. Синтез линейных регуляторов
АЛГОРИТМ НАХОЖДЕНИЯ УПРАВЛЕНИЯ
1. Синтезировать оптимальный линейный регулятор с помощью
соотношений A1.11),A1.12).
2. Синтезировать наблюдатель полного или низкого порядка согласно
указаниям, данным в разд. 11.2.2.
3. Получить управление, используемое в системе, изображенной на рис.
11.2:
и(*,У1) = 0-1(*)ВТ«)К2«)х«).
Пример 11.4. Пусть модели объекта управления и измерений, а также
функционал качества управления заданы в форме
*1@ = и@, У(*) = х2(*)>
*2@ = *!('),
/=1/|/2@Л+^[х12B)+х22B)]->гшп.
Требуется найти управление с накоплением информации о состоянии.
О Перепишем модель в матричной форме:
437

ю с общей постановкой задачи имеем
А'Ц о)> '"О' С = (° »>' -*• -I. -8-Е
т.е. по сравнению с общей постановкой задачи имеем
1. Оптимальный линейный регулятор найден в примере 9.16:
•,,* уч [12 + 4B-0аE-0]Х1+6B-0D-0*1
0 (*,Х1,Х2) = '—= *-.
12C-0 + B-/KF-/)
2. Рассмотрим два способа построения оценивающего устройства.
А. Для синтеза оценивающего устройства второго порядка A1.17) зададим
матрицу К = I I. При этом матрица А - КС = I I имеет кратные
собственные значения X! = X 2 = -1. Тогда, выписывая A1.17), получаем
^- = Зс1(/) + 2[ЯО-х2(/)], х2@) = 1.
Б. Для синтеза оценивающего устройства первого порядка A1.19)—A1.21)
зададим /) = -1, К = 1. Искомую матрицу С = (д $2) и число Я определим из
A1.20):
(й 0) + (Л й)-@ 1) = 0, Л-Я-0.
Отсюда ^ = -1, #2 = 1, Я = -1, и из A1.19), A1.21) находим
^—*@-«@ + *0, *@) = (-1 0(|) = °.
т.е. х1(/) = М0-г@, х2(/) = ^/).
3. Получаемые с помощью наблюдателей оценки используются вместо
соответствующих координат вектора х в оптимальном управлении, полученном в
п.1, т.е.
и(иП) = «-«Д<0Л@) = ^ + 4B-0>E-0]*,(,) + 6B-,)D-,)^) „
12C-/)+ B-0 F-0
438

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
11.1. Для задачи
ЛГ@»[3^@ + 11@№ + 44/^1, /я& = 2, 2)^ = 3,
4У = Х(г)<Н + <т29 7@) = 0,
1 = М\
^][[«2@ + 7ЛГ2(/IЛ+^ЛГ2а)
тш
найти управление л*(/,Уо) из множества допустимых, обеспечивающее минимум
функционала.
11.2. Для задачи
4Х(*) = 1-ЪХЦ) + 2иЦ)\И + 4<1Щ9 щ = 3, /)? = 4,
</Г = ЛГ@Л + ^2, ПО) = 0,
/ = А/Д/[1/2(/)+ 10Лг2@^ + ^2A)|^тт
найти управление и*(/,У0') из множества допустимых, обеспечивающее минимум
функционала.
11.3. Для задачи
ЛМИ-^М + ^А + я^, ^=2 + [?]' ^^й*
4У = пХ{ЪА + 4п<ПГ29 У@) = 0,
найти управление 1г*(/,Уо) из множества допустимых, обеспечивающее минимум
функционала.
11.4. Для задачи
^@ = Х1(О + Х2(/),хГ=1 + И, ><0 = *1@ + Л*2('),
*2(') = /"/('), х;=2 + И,
Обуется найти управление с накоплением информации о состоянии.
439

Глава 12. СИНТЕЗ ОПТИМАЛЬНЫХ ДИСКРЕТНЫХ
ДЕТЕРМИНИРОВАННЫХ СИСТЕМ
12.1. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО ПРОГРАММНОГО УПРАВЛЕНИЯ
12.1.1. Постановка задачи
Пусть поведение модели объекта управления описывается разностным
уравнением
х(к + 1)=/{к,х{к\и{к)), * = 0,1,...,#-1, A2.1)
где х — вектор состояния системы, хеКп; и — вектор управления,
ие1/(к)^Яя, 1/(к) — некоторое замкнутое выпуклое множество допустимых
значений управления; к - дискретное время, &еГ = [0,1,...#-1], число шагов
N задано, /(к9х,и):ТхЯпх1/(к)->Кп - непрерывно дифференцируемая вектор-
функция, /(к,х,и)=(/1(к,х,и\...Лп(к,х,и))г.
Начальное состояние системы A2.1) задано
*@) = х0. A2.2)
Конечное состояние х(#) должно удовлетворять условию:
гДх(#)) = 0, / = 1,...,/, A2.3)
где 0^/<л, функции Г,(х) - непрерывно дифференцируемы; система векторов
{аг/(х(^))/ах1,...,аг/(х(^))/ахй}, / = 1,...,/, линейно независима Ух^)еКп.
Предполагается что при управлении используется информация только
о дискретном времени к, т.е. применяется так называемое программное
управление (рис. 12.1).
и(к)
"(к)
Р
х(к + 1) = /(к,х(к)Мк))
х(к + 1)
Задержка
х(к)
Рис. 12.1
Последовательность векторов и@),иA),...,1/GУ-1) называется управлением
«(•), а последовательность х@),хA),...,л:(#), определяемая уравнением A2.1)
с начальным условием A2.2) и управлением !/(•) , — траекторией х().
440

Множество допустимых управлений Ж0 образуют управления и(), при
которых для заданных начальных условий A2.2) траектория системы A2.1)
удовлетворяет условию A2.3), причем и(к)е1/(к)9 & = 0,1,...,#-1.
Определим множество допустимых процессов Ю(Оух0) как множество пар
</ = (*(•), «(•))» включающих траекторию х() и управление 1/0€^о,
удовлетворяющих уравнению A2.1) с начальным условием х@)=хо и конечным условием
A2.3).
На множестве Ю@,х$) определим функционал качества управления
*№-^/*&Ф\Ф))+*№)). A2.4)
где /°(к9х9и)9 Г(х) — заданные непрерывно дифференцируемые функции.
Требуется найти такую пару ё*= (**(•),и*())€ ^@,*о)> что
/(^*)=1шп/(</). A2.5)
</е*>@,*о)
Задача A2.5) с функционалом A2.4) называется задачей Больца.
Если в функционале A2.4) функция ^(х(#))=0 (отсутствует так
называемый терминальный член), она называется задачей Лагранжа, а если
/°(к9х(к\и(к))зО (отсутствует "интегральный" член) — задачей Майера.
Искомые элементы пары й* траектория **(•)= {х<),х*A),...,х*(#)| и
управление и*() ={и*@),м*A),...,и*(#-1)} называются соответственно оптимальной
траекторией и оптимальным управлением.
12.1.2. Дискретный принцип максимума
Необходимым условием экстремума функционала в задаче A2.5) при
некоторых дополнительных предположениях (см. п.4 замечаний на стр. 443) является
дискретный принцип максимума [7, 43, 57].
Утверждение. Пусть на паре а1*=[х*(:\и*(:)]€Ю@,х0) достигается минимум
Функционала. Тогда существуют не равные нулю одновременно вектор-столбцы
*(*И*1D".>%(*)Г> * = 1,...,ЛГ, такие, что:
1) при каждом к = 0X^.9N-\ функция Н[к9хУ(к + \)9х*(к\и) достигает
максимума по управлению, т.е.
н(к9Ч{к + \\х\к\и\к))=т^н{кМЬ +1**44"), A2.6)
где
иеЦ(к)
Н(к9^9х9и)^^ /}(*,*, 1/)-/°(*,*,и);
/=1
441

2) функции **(•), ф() удовлетворяют системе уравнений
х){к + \)=ф,х\к\и{к% *;@)=*о,, ^ = ^,...,п, * = 0,1 ЛГ-1,
Ч#)т°&&*№&*Йш у.1 и, кт1 ЛГ-1, A2.7)
ах,
Гу(х*(^))=0, / = 1,...,/;
3) выполняется условие трансверсальности
при любых Ьx^(N), удовлетворяющих системе
Г,(**(Л0)=О, / = 1,...,/,
бГ^МЦ, / = 1,...,/;
где вариации определяются следующим образом:
A2.8)
5Г,1
м
ах,
В формулировке утверждения система A2.7) называется системой
канонических уравнений, функция Н(к9Ч*,х,и) — гамильтонианом, а
^(/:),...,хРл(/:), & = 1,...,ЛГ- вспомогательными переменными.
Замечания.
1. Если в решаемой задаче ограничения A2.3) на правом конце траектории
отсутствуют, то условие трансверсальности A2.8)
I
№1
ЭХ: Л '
&с,(#)=0
в силу произвольности вариации &ху(ЛГ) приобретает вид
дх.
A2.9)
442

2. Если в функционале A2.4) Г(х(М))шО и отсутствуют ограничения A2.3),
хо условие A2.8) в силу произвольности вариации &сД#) принимает форму
3. Если 1/(к)=Яд, то для нахождения максимума в A2.6) может быть
использовано необходимое условие безусловного экстремума
ЭЯН* + 1КЫ=0> * = 0Д N-1, / = 1,...,,. A2.11)
дЩ
с проверкой соответствующих достаточных условий.
4. Утверждение справедливо, если множество 1/(к) выпукло, а
гамильтониан является вогнутой функцией по и. Дискретный принцип, максимума
применим для систем с выпуклой вектограммой [57].
Вектограммой управляемой системы A2.1) в точке {к9х(к)) называется
множество /(к,х,1/(к)) значений функций /(к9х9и) при фиксированных к и х,
когда управление и принимает все возможные значения из 1/(к):
/{к9х9Щк))= У /&х.«).
и € (/(к)
В общем случае дискретных систем необходимые условия экстремума не
совпадают с дискретным принципом максимума и изложены в [7, 10, 43, 57]. По
сравнению с приведенным утверждением в них условие A2.6) заменяется
условием:
±дН^к + 1^кУ^1и1-иПф0, * = 0,1 N-1,
для всех иеЦ(к), т.е. гамильтониан достигает в точке и*(к) либо наибольшего
значения на множестве (/(*), либо и* (к) является стационарной точкой
(локальным минимумом или максимумом, седловой точкой).
АЛГОРИТМ ПРИМЕНЕНИЯ ДИСКРЕТНОГО ПРИНЦИПА МАКСИМУМА
1. Составить гамильтониан
Н(к9Ч>9х9и)=% ^/'Хк9х9и)-/0{к9х9и).
2. Найти структуру оптимального управления из условия максимума
гамильтониана по управлению:
н(кМк + 1\х\к\и\к))=т^к)Н{кМк + 1\х*{к\и).
443

3. Составить систему канонических уравнений с заданными в задаче
условиями:
х)(к + \)=ф,х\к\и{к% *;@)=Хоу, ; = 1,...,л, * = 0,1,...,#-1,
чДО-И^ + »*>К(*)), , = 1,...,Л, * = !,...,*-!, A2.12)
Г,(х*(*))=0, / = 1,...,/.
4. Из условия трансверсальности A2.8) или их следствий A2.9), A2.10)
в частных случаях постановки задачи определить недостающие краевые условия
для уравнений системы A2.12).
5. Решить полученную краевую задачу. В итоге определяется пара
(х*(-), !/*(•)) на которой может достигаться минимум функционала A2.4).
Пример 12.1. Даны модель объекта управления
х(к + 1)=х(к)+и(к)9 х@)=2, А: = 0,1,
ще хеЯ; иеК, и функционал
1=%[и2(к) + х2(к)]^> тт.
Требуется найти оптимальную пару (**(•), «*(•)), на которой достигается
минимум функционала.
П Сравнивая с общей постановкой задачи, имеем:
/(к,х,и)=х + и, /°(к9х,и)=и2 + х2, Г(х)=09 1/(к)=К, ЛГ = 2. Решается задача
Лагранжа.
1. Составляем гамильтониан
Н(к,Ч,х,и)=Ч'(х + и)-(и2+х2).
2. Находим максимум гамильтониана по управлению. Так как ограничения
на управление отсутствуют, можно применить необходимые условия
безусловного экстремума A2.11):
ди
Отсюда и*(к)= \ К Найденное управление обеспечивает максимум функций
Н(к,Ч*(к + 1\х(к\и) по управлению, так как удовлетворяются достаточные
условия экстремума:

3, 4. С учетом A2.10) составляем краевую задачу A2.12):
х\к + 1)=х\к)+?^, /@)=2,
ч(к)=Ч>{к + 1)-2х*{к), Ч/B)=0.
5. Решение краевой задачи: х*@)=2, и*@)=-\9 х*A) = 1, и*A)*0,^A)=-2,
х* B) = 1,4/B)=0 дает искомую пару: оптимальную траекторию **(•)= {2,1,1} и
оптимальное управление */*(•)= {-1,0 }.¦
Пример 12.2. Даны модель объекта управления
х{(к + 1)=х{(к)+и(к),
х2(к + \)=2х1(к)+х2(к), * = 0Д,
с начальными условиями х1@)=2, х2@)=1, и функционал
Требуется найти оптимальное программное управление !**(•) и
соответствующую ему траекторию **(•).
П Здесь х = (хх, х2 )т е Я2, на управление ограничений не наложено,
/°(к,х9и)Л[и2+х?+х}], Г(х)=0, N = 2, /{(к,х,и)=хх+и, /2(к,х,и)=2х{ + х2,
правый конец траектории свободен. Решается задача Лагранжа.
1. Составляем гамильтониан
Н(к,Ч,х,и)=Чх [хг + и]+Ч2[2х{ + х2]-±[и2 + *? +х| ].
2. Находим максимум гамильтониана по управлению (см. п.2 примера 12.1):
Отсюда и-(к)=Ч{к + 1). Приэтом ^^*;^Ш„1<0,
в и2
3. 4. С учетом A2.10) составляем краевую задачу A2.12):
х,*(* + 1)= *,*(*)+<Г,(* + 1), х,*@)=2, * = 0,1,
х№ + 1)-2х№)+х;(*). *;@)=1, А; = 0,1,
Ч',(*)=Ч',(* + 1)+2Ч'2(А: + 1)-х,*(А:), Ч-,B)=0, *-1,
*2(*)=Ч,2(* + 1)-^(*). Ч,2B)=0, *-1.
445

5. Решение краевой задачи:
*Г@)=2, *2@)=1, «»=-1, х1A)=1, хК1)=5,1/*A)=0,
М1)=-Ъ ^2A)=-5; хГB)=1, х;B)=7, ^B) = 0, Ч>2B)=0
дает искомую пару, оптимальную траекторию х1*()={2,1,1}, *2(-)={1,5,7} и
оптимальное управление и*() = {-1,0}.и
Пример 12.3. Даны модель объекта управления
х1(/: + 1)=х1(/:)+1/(А:),
х2(к + 1)=2х1(к)+х2(к), * = 0Д,
с начальными условиями Х}@)=2, х2@)=1, и функционал
/=ТХ [«2М+*12(к)+^(к)]+Х,B)^11Й11.
Требуется найти оптимальное программное управление !/*(•) и
соответствующую ему траекторию х*().
П Здесь х = (х1,х2У е К2, на управление ограничений не наложено,
/°(к,х9и)=-[и2 +х? +х}\ Г{х)=хи # = 2, А{к,х,и)=х{ +и, /2(к,х,и)=2х1 +х2,
правый конец траектории свободен. Решается задача Больца.
1. Гамильтониан совпадает с полученным в п.1 примера 12.2.
2. Находим структуру оптимального управления: и*(к)=Ч?х(к + 1) (см.
пример 12.2)
3. 4. С учетом A2.9) составляем краевую задачу A2.12):
х;(к + 1)вх^)+Ч',(к + 1), Х1@)=2,
х5(к + 1)-2х;(к)+д5(к), х^@)=1,
^1(Л)=^(^ + 1) + 24'2(А: + 1)-х1», ^B)=-1,
ЧЪЮ-^+ !)-**(*). ^2B)=0.
5. Решение краевой задачи:
х?@)-2; х5@)-1; «*@)—|; хДО-0,5; дДО-5; «'(О— 1;
^A)=-1,5; У2A) —5; х,*B)=-0,5; Х2B)=6; ^B) = -1, ч>2B)=0
дает искомую пару: оптимальную траекторию Х!*()={2;0,5;-0,5}, Х20= {1,5,6} и
оптимальное управление «*(•) = ] —;-1 1.И
446

Пример 12.4. Даны модель объекта управления
х1(А: + 1)=х1(А:)+1/(А:), |«|*1,
х2(к +1) = 2хх (к) + х2(к), к = ОД
с начальными условиями *!(()) = 2, х2@)=1, и функционал
/ = хгB)+х2B)-* тш.
Требуется найти оптимальное программное управление !/*(•) и
соответствующую ему траекторию х*().
? Здесь х = (хьх2)г еЯ2, управление входит в правую часть разностного
уравнения линейно и ограничено по модулю: \и\й1, иеЦ(к)=[-1,1]9/°(к,х,и)*0,
Г{х)=Х1 + х2, N = 2, Мк,х,и)=Х1+и, /2(к,х,и)=2х{ + х2, правый конец
траектории свободен. Решается задача Майера.
1. Составляем гамильтониан:
Я(А:,^,х,и)=^1[х1+и]+^2[2х1+х2].
2. Так как имеются ограничения на управление, находим условный
максимум гамильтониана по управлению. В данной задаче гамильтониан линеен по и
на заданном отрезке изменения управления [-1,1], поэтому структура
оптимального управления имеет вид:
и*(к)= яътахН(к,Ч(к + 1),х(к),и)=яяп Чх(к +1).
3,4. С учетом A2.9) составляем краевую задачу A2.12):
х\(к + \)=х\{к)+ яйпЧ^ + О, х,»=2,
х2(к + 1)= 2х;(*)+ х*2(к), х2@)=1,
Ч>1(к)=Ч1(к + 1) + 2Ч'2{к + 1)9 ^1B)=-1,
^)-^ + 1). ^2B)=-1.
5. Решаем краевую задачу. При этом воспользуемся тем, что решение
уравнений для вспомогательных переменных не зависит от решений остальных
уравнений. Решение
*Г@)=2, х;@)=1, и*@)=-1; *ГA)=1, *2*A)=5, и*»—1,
*1A) = -3, ^2A)=-1; хГB) = 0, х2B) = 7, ^B)=-1, У2B)=-1
дает искомую пару: оптимальную траекторию х1*()={2,1,0}, х2()={1,5,7} и
оптимальное управление м*()={-1, - !}.¦
447

Пример 12.5. Даны модель объекта управления
х,(А: + 1)=х,(А:)+и(А:),
х2(к + 1)=2х1{к)+х2{к), |и|*1, * = 0,1,
с начальными условиями х^О^З, х2@) = 1, и функционал
/=1[х,2B)+х22B)]->тт.
Требуется найти оптимальное программное управление !/*(•) и
соответствующую ему траекторию х*().
? Здесь х = (х1>х2)т еЛ2, управление входит в правую часть разностного
уравнения линейно и ограничено по модулю:
|и|<Л, ие1/(к) = [-1,1], /°(к9х,и) = 0,
Г{х)=-[х?+х$]9 N = 2, /1(А:,х,1/)=х1+1/, /2(к,х,и) = 2х{ + х2,
правый конец траектории свободен. Решается задача Майера. Отличие от
примера 12.4. заключается только в форме терминального члена функционала, что при
решении задачи отражается в краевых условиях на Ч^ТУ).
1. Гамильтониан совпадает с полученным в п.1 примера 12.4.
2. Находим структуру оптимального управления:
и*(к)= агв тах Н{к,ч{к + 1^D«)=8р 4{(к +1).
3. 4. С учетом A2.9) составляем краевую задачу A2.12):
х\(к + \)=х1(к)+я&14{{к +1), Х!*@)=3,
х2(к +1)=2*Г(*)+ хт2(к), х2@)= 1,
^(А:)=4'1(А: + 1)+24'2(А: + 1), ^B)=-х1B)9
Ъ(Ь)=Ъ(Ь + 1)> ^2B)=-х;B).
5. Решаем краевую задачу. В отличие от примера 12.4 в силу краевых
условий решение уравнений для вспомогательных переменных зависит от решения
уравнений для определения траекторий. Вычисляем х{ (^\х2(^):
х1*B) = х1*@)+8щп[-х1*B)-2х^B)]+8щп[-х1*B)],
*гB) = 4х;@)+ х;@)+ 28щп [- хГB)- 2x^B)].
448

Подставляя начальные условия, заключаем, что х{(?) > О и х2{2) > 0.
Отсюда получаем 1/*@)=818п[-Х1*B)-2х2B)]=-1, 1/*A)=81$п[-Х1B)]=-1 и
*Г@)=3,*;@) = 1, и@)=-1; *ГA)=2, х'2(\)=7, и*A)=-1,
^A) —23, ^2A) = -П; ^ГB) = 1, Х2B)=11, ^B) = -1, Ч>2B) = -\1.
Искомая пара: оптимальная траектория *1*()={3,2,1}, Х2()={1,7,11} и
оптимальное управление и*(•) = {-1, - 1}.и
Пример 12.6. Даны модель объекта управления
х1(А: + 1)=х1(А:)+и(А:),
х2(к + \)=2хх(к)+х2{к), * = 0,1,
с начальными условиями х,@) = 2, х2@)=1,
граничным условием Г(хB)) = хх B) + 2х2 B) - 4 = О
и функционал / = - ]Г [ы2(А:)+х*(к)+х\(к)\ -> пап.
2*=0
Требуется найти оптимальное программное управление и*() и
соответствующую ему траекторию х*().
? Здесь х=(*!, х2)г е Я2, на управление ограничений не наложено,
/°(к,х,и)=^[и2 +х? +х%\, *(х)=0, # = 2, /{{к9х9и)=х1+и9/2{к9х9и)=2х1+хъ
правый конец траектории в отличие от примера 12.2 должен удовлетворять
граничному условию Г(х(#)) = г(хB)) = хг B)+2х2 B) - 4 = 0. Решается задача
Лагранжа.
1. Гамильтониан совпадает с полученным в п.1 примера 12.2.
2. Находим структуру оптимального управления: и*(к)= ^(к +1).
3. Составляем краевую задачу A2.12):
х^ + О^М+Ч^-И), *;@)=2,
х*2{к + 1)= 2х\{к)+ х2{к)9 х2@)= 1,
Ч>1{к)=Ч'1(к + \)+2Ч>2(к + 1)-х;(к),
Ч2{к)=Ч2{к + \)-х*2{к),
г(х*B))=х1{2)+2х2{2)-4 = 0.
449

4. Из условия A2.8) следует:
Ч',B)8х,B)+ *2B)8х2B)=О
при любых 6*! B), 5х2 B), удовлетворяющих связи 8х1B) + 28х2B)=0.
Следовательно, 2Ч,,B)=Ч'2B). Обозначим У, B)=ц, тогда »Р2B)=2ц.
5. Решаем краевую задачу:
*,'(* + 0= *Г(*)+ Ъ(к +1), *Г@)=2,
х2(А: + 1)=2х1,(А:)+х2(*), *5@)-1.
Ч^-Ч^ + О+И^ + О-чСк), «Р,B)=ц,
Ч2(к)=ъ(к + 1)-хШ *2B)=2ц,
г(х*B))=хГB)+2х2B)-4 = 0.
Вычисляем х,'B\ х2B)- Имеем х,*B)=2 + ч/,A)+ц, х2B)=9 + 2Ч',A), где
кР1A)=-1 + -ц. Воспользовавшись краевым условием на Х1*B),х2B), находим
22 «, л\ 82
Ц = -^, откуда «Р,A) = - — .
Решение краевой задачи: XI* @) = 2, х^ @)=1, и* @)=-—; х^ A) = ,
х2A)=5, «*(!)=-§, *1A)=-|. ^A)=-^;
*?»-§. ^*B)=|, ЧЙ-§. *2B)=-|
дает
*,ч Г. 28 501
искомую пару: оптимальную траекторию XI (•) = < 2, -—, - — >,
*2(*)Н Ъ*»^ г и оптимальное управление и (•)=< -—,- — }>.¦
Пример 12.7. Даны модель объекта управления
Х!(А: + 1)=Х1(А:)+2и(/:),
х2(к + \)=-х?{к)+х2(к)+и2(к), \и\й5, * = 0,1,
с начальными условиями х^О^З, х2@)=0 и функционал
/ = -х2B)->тт.
450

Требуется найти оптимальное программное управление //*(•) и
соответствующую ему траекторию х*(). Показать, что оптимальное управление не
удовлетворяет дискретному принципу максимума.
? Здесь х = (х1,х2)г еЛ2, управление входит в правую часть разностного
уравнения линейно и ограничено по модулю:
|и|<;5, и €(/(*)= [-5,5], /°(к,х,и)=0,
Г(х)=-х2, N = 2, /1(А:,х,1/)=х1+2«, /2(к,х,и)=-х? +х2 +и2,
правый конец траектории свободен. Решается задача Майера.
Найдем оптимальное управление, непосредственно минимизируя
функционал
/ = -*2B)=х?(^
= [3 + 2«@)]2+9-1/2@)-1/2A) = 3[2 + 1/@)]2 +6-1/2A)
по переменным иF\ 1/A).
С учетом ограничения |и|^5 получаем 1/*@)=-2, 1/*A)=±5, тт/ = -19.
Искомые пары: оптимальная траектория *,*(•)= {3,-1,9}, х^() ={0,-5,19} и
оптимальное управление //*(•)={-2,5} или оптимальная траектория
х{(•) = {3, -1, -11}, х2 (•)={0, - 5,19} и оптимальное управление и* (•)={- 2, - 5}.
Заметим, что гектограмма управляемой системы не является выпуклой, но
все-таки применим дискретный принцип максимума.
Составляем гамильтониан:
Н{к,Ч,х,и)=Чх [х! +2|/]+4/2[-х? +х2 +ы2 ].
С учетом A2.9) составляем краевую задачу A2.12):
х;(* + 1)=хГ(*)+2//*(*), *;@)=3,
х;{к + 1)=-х{(кJ +х*2(к)+[и(к)]\ х2@)=0,
Ч1(й=Ч& + 1)-2х№)ч2& + 1). *,B)=0,
ЧЪЮ-Ч^ + О, ^2B)-1.
Для пары Х!*()={3,-1,9}, х2()= {0,-5,19}, //*(•)={-2,5} решение имеет
вид ^A) = 2, 4^@=1. При к = 0 на оптимальном управлении и*@)=-2
гамильтониан # = 2 • C + 2//)- 9 + и2= и2 + Аи-3 достигает по переменной и своего
наименьшего, а не наибольшего, значения, т.е. условие A2.6) не выполняется. При
этом справедливо дН\$,ч{&х*(р\иЩ/ди = Ъ, поэтому необходимое условие
оптимальности выполняется (см. п.4 замечаний на стр. 443).и
451

12.2. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ С ПОЛНОЙ
ОБРАТНОЙ СВЯЗЬЮ
12.2.1. Постановка задачи
Пусть поведение модели объекта управления описывается разностным
уравнением
х(к + \)=/{к,х(к\и(к))9 * = 0,1,...,ЛГ-1, A2.13)
где х - вектор состояния системы, хеКп; и - вектор управления,
ие17(к)^Яя, 1/(к) — некоторое заданное множество допустимых значений
управления; к - дискретное время, #€7* = [0Д,.,.,#-1], число шагов N задано,
/(к,х,и):ТхКп х 1/(к)->Кп — непрерывная вектор-функция.
Начальное состояние системы A2.13)
х@)=ХоеЯп A2.14)
заранее не задано и может быть любым.
Предполагается, что при управлении используется информация о времени к
и о векторе состояния х(к).
Множество 2/п допустимых управлений с полной обратной связью образуют
функции и(к,х):ТхКп -»*/(/;), которые на траекториях системы A2.13) для
различных начальных состояний A2.14) порождают соответствующие допустимые
программные управления !/(•)еЯ/0, где УкеТ и(к)=и(к,х(к))е 1/(к).
Применяемое в каждый дискретный момент времени кеТ управление
имеет вид управления с полной обратной связью по вектору состояния (рис. 12.2).
:
х@)еД'
1
х(к + 1) = /(к,х(к)Мк))
и(к)
= и(к,х(к))
х(к +1)
и(к ^
¦*\1У,
Задержка
х(к)
х(к)
Рис. 12.2
Определим множество допустимых процессов 0@, хо) как множество пар
*/ = (*(•), и()), включающих траекторию х() и управление и{)е&09
удовлетворяющих уравнению A2.13) с начальным условием х@)= дс<).
452

На множестве #@, *о) определим функционал качества управления:
№=Ъ/ЧЫкШ)+ГШ)> A2.15)
*-о
где /°(к9х9и)9 Г(х) - заданные непрерывные функции.
Требуется найти такую функцию и*(к,х)е&п9 что
где/^х'аиЧЬ^^'О))-
Функция и*(к9х)е&п называется оптимальным управлением с полной
обратной связью. Для каждого начального состояния х0 из множества Кп она
порождает соответствующую оптимальную пару, т.е. оптимальную траекторию
х*() и оптимальное программное управление ы*()е &$.
12.2.2. Уравнение Беллмана
Утверждение [19, 23, 43]. Оптимальное управление и*(к9х)е0/п определяется
в результате решения уравнения Беллмана для дискретных детерминированных
систем:
В(к,х)= Л [/°{к,х,и)+В(к + \,/(к,х,и))] ЧхеК", к = 0,1,...,#-1,A2.17)
с граничным условием
В{Ы9х) = Р(х) ЧхеК", A2.18)
где В(к9х) - функция Беллмана;
и\к9х)=гт%п^[/°(к9х9и)+В(к^\9/(к9х9и))] ЧхеЯп9 * = 0,1,...,ЛГ-1. A2.19)
При этом минимальное значение функционала A2.15)
тш /(</)= Д@,х0) ЧхоеК". A2.20)
Таким образом, значение функции Беллмана 2*@,х0) определяет
минимальную величину функционала для любого начального состояния. С другой
стороны, значение функции Беллмана совпадает со значением так называемых
текущих потерь на управление В(к9 х)= пип Ш) Ух € Яп.
Структура оптимального управления с полной обратной связью
определяется в результате поиска минимума в A2.19) по управлению.
453

Пример 12.8. Даны модель объекта управления
х(к + \)=[х(к)+и(к)?, * = 0,1,
где х € Я, и е Я, и функционал
1
I.
*«0
'(<0=Е [х2(*)ч^(*)]+хB)^1шп.
Требуется найти оптимальное управление и*(к,х).
П Сравнивая с общей постановкой задачи, имеем /(к,х9и)=[х + ир9
/°(к,х, и)=х2 + и2, ^(х)=х. Решается задача Больца.
1. Выписываем уравнение Беллмана A2.17) с граничными условием A2.18):
В(к,х)=пил {х2 + и2 + В^ + 1,[х + и]2)} VхеЛ, * = 0,1,
ДB,х)=х УхеД.
2. Решаем уравнение Беллмана в обратном времени.
При к = \ имеем
ДA,х)=гшп {х2+1/2+[х + 1/]2} Ухе Д.
Найдем структуру оптимального управления из условия минимума
выражения в фигурных скобках. Дифференцируя по управлению и приравнивая резуль-
татнулю, получаем и*A,х)=—х. Функция Беллмана #A,х)=--х2.
При к = 0 имеем
^@,х)=тт|х2+1/2+|[х + 1/]41 Ухе Я.
Дифференцируя по управлению и приравнивая результат нулю, получаем
и + 3[х + и]3=0.
Уравнение имеет единственный действительный корень «*@,х)=-х + а(х),
где
{х Гх2 1~| I х Гх21
1/3
Минимальная величина функционала находится по формуле A2.20):
тт/ = ^@,хо)=2х^-2хоа(хо) + а2(х0)+-а4(хо) Ух0еД.И
454

12.2.3. Синтез оптимальных линейных регуляторов
ПОСТАНОВКА ЗАДАЧИ
Пусть математическая модель объекта упраеления описывается разностным
уравнением
х(к + 1)=А(к)х(к)+В(к)и(к)9 к = 0,1,...,ЛГ -1, A2.21)
с начальным условием
*@)=Хо, <12-22)
а функционал качества управления имеет вид
1=^[хТ(кM(к)х(к)+иТ(кH{№ A2.23)
где *?(&), Л — неотрицательно определенные симметрические матрицы размера
(лхл), а 0(к) - положительно определенная симметрическая матрица (дх$г).
Требуется найти управление и*(к,х) с полной обратной связью,
минимизирующее функционал A2.23).
СООТНОШЕНИЯ ДЛЯ НАХОЖДЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Поставленная задача является частным случаем общей постановки задачи,
где следует положить
/{к9х,и)=А{к)х + В(к) и, /°{к,х,и)=хт5(к)х + ит <2{к)и9 Г{х)=хтЛх.
Тогда уравнение Беллмана и граничное условие A2.17), A2.18) принимают
вид
^,х) = т1п[хг^)х + 1/гфI/ + ^ + 1,4А:)х + Б(А:I/)] ЧхеК", *=0,1,...,АГ-1,
A2.24)
В(М9х)=хт\х Ухе/Г.
Предлагается искать функцию Беллмана В(кух) в виде квадратичной формы
В(к,х)=хтР(к)х, A2.25)
где Р(к) — неизвестная неотрицательно определенная симметрическая матрица
размера (лхл).
Подставляя A2.25) в A2.24), получаем утверждение.
455

Утверждение [19, 30]. В задаче A2.21)—A2.23) оптимальное управление
определяется соотношением
и\к9х)=-Цк)х9 * = 0,1,...,#-1, A2.26)
где Цк) — матрица коэффициентов усиления регулятора размера (# х п)
^)=[0(^)+^Г(^)^ + 0^)]^Г(^)^ + 0^)> * = 0,1,...„/\Г-1, A2.27)
а матрица Р(к) размера (п х п) удовлетворяет уравнению
Р(к)=3(к)+ЬТ(кH(кI(к)+[А(^ + 1)[А(к)-В(к)Ь{кI
* = #-1,...,1,0,
A2.28)
Р(ЛГ)=Л.
Минимальная величина функционала определяется по формуле
тт/ = х^Р@)х0 V хо € Кп. A2.29)
Замечания.
1. Как следует из раздела 12.2.1, для каждого начального состояния х0 е Яп
оптимальный линейный регулятор порождает оптимальное программное
управление и*()еЩ и оптимальную траекторию х*(). Структурная схема этой
системы изображена на рис. 12.3.
х@) € Яп
х(к +1) = А(к) х(к) + В(к) и(к)
х(к + 1)
Задержка
х(к)
и(к) = и(к9х(к))
и(к9х) = -Цк)х
х(к)
Рис. 12.3
2. Если в поставленной задаче матрицы А, В, 3,B постоянны, а время
функционирования системы не ограничено (# =+<х>), то соотношения A2.21) -
A2.23) принимают форму
х{к +1)= А х(к)+ В и(к)9 к = 0,1,..., х@)=х0,
7 =2 [хТ(кMх(к)+иТ(кHи(к)\ -^тт.
456

Тогда оптимальный регулятор будет иметь вид [36]
и{х)=-Ьх, A2.30)
где Ь — постоянная матрица коэффициентов усиления регулятора размера (д х п)
и необходимая для ее определения постоянная матрица Р размера (л х п)
удовлетворяют соотношениям
1 = [0 + ВтРв]~1ВтРА9
1 } A2.31)
Р = 8 + 17Р1 + [А-В1$Р[А-В1].
Если матрицы «У, б положительно определены, то искомая матрица Р
также положительно определена.
АЛГОРИТМ НАХОЖДЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
1. Составить систему A2.27), A2.28).
2. Определить матрицы Р(к\ Цк).
3. Построить оптимальный регулятор и* (к, х) = - Ь(к)х.
4. Определить значение функционала на оптимальном управлении по
формуле A2.29).
Пример 12.9. Даны модель объекта управления
х(к + 1)=х(к)+и(к), х@)=х0, к = 0,1,
где хеЯ, иеЯ,и функционал
1(<!)=Ъ1и2(к)+х2(к)]^тт.
ы>
Требуется найти оптимальный регулятор и*(к, х) и оптимальную траекторию
для х0=2.
? Решается задача Лагранжа, А(к) = 1, В(к) = 1,8(к) = 1, B(к) = 1, А = 0.
1. Составляем уравнения A2.27), A2.28):
1(к)=[1 + Р(к + \)]-1Р(к + 1),
Р(к)=1 + 1?{к)+[1-1(к)]2Р{к + \\ * = 0,1; />B)=0.
3 1
2. Получаем решение уравнений: />A)=1, 1A)=0, Р@)=-, 1@)=-.
3. Находим оптимальный регулятор: и* @, х)=-—х, и* A, х)=0.
4. Определяем оптимальное значение функционала: пил / =—х2@).
457

Найдем оптимальное управление и оптимальную траекторию для
начального условия х@)=2. Для этого решим уравнение объекта совместно с
оптимальным регулятором. Имеем
**@)=2, **A)=1, *'B)=1; «•@)=«*@>х*@))=-|х-@)=-1,«*A)=0,
что совпадает с результатами примера 12.1, полученными при использовании
дискретного принципа максимума."
Пример 12.10. Даны модель объекта управления
х(к + 1)=х(к) + и(к), х@)=х0, * = <>Л,
где хеЯ, иеЯ,п функционал
/(</)=х2B)-»пип.
Требуется найти оптимальный регулятор и*(к9х).
П Решается задача Майера.
1. Решаем уравнения A2.27), A2.28):
Ь(к)=\9 * = 0,1; Р(к)=0, * = 0,1; />B)=1.
2. Находим оптимальный регулятор: и*(к, х)=- х, к = 0,1.
3. Получаем оптимальное значение функционала: пип / = 0.и
Пример 12.11. Даны модель объекта управления
х(к + 1)=х(к)+и(к), х@)=х0, * = °Л,
где хеЯ, иеЯ,и функционал
/(<0=Е [х2(к)+и2{к)\+х2{2)->тт.
Требуется найти оптимальный регулятор и*(к9х).
П Решается задача Больца.
1. Составляем уравнения A2.27), A2.28):
Ь{к)=[1 + Р{к + 1)]-1Р(к + 1),
Р{к)=1 + 12(к)+[\-1{к)]2Р(к + \), * = 0,1; />B) = 1.
2. Получаем решение уравнений:
РB)=1, ^1)=|, 1A)=1 Р@)Л, 1@)=|.
3. Находим оптимальный регулятор: и* @, х) = — х, и* A, х) = -—х.
о
4. Определяем оптимальное значение функционала: пип / =—х2@). ¦
458

Пример 12.12. Даны модель объекта управления
х(к + 1)=х(к)+и{к), х@)=Хо, *=0,1...,
тдрхеЯ9 и € Я, и функционал
^)=1И^)+^)]-^П1Ш.
Требуется найти оптимальный регулятор и*(х).
П Особенность задачи заключается в том, что время функционирования
системы не ограничено (N -+оо).
1. Составляем уравнения A2.31), которые являются алгебраическими:
1=—^-, Р = 1 + 12+[1-1,]2Р,где Ь,Р -числа.
1+^5 1-^5
2. Получаем решение уравнений. Из двух решений: /> =—-— и Р=—-—
выбираем положительное, которому соответствует величина
1 + Л
3 + ^5
3. Находим оптимальный регулятор A2.30): »*(х)= «х, &=0Д,..
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
12.1. Для задачи
х1(к + 1)=х2(к)+и{к), хх{0)=\, к = 0Х
х2{к + \)=-хх{к)+х2(к), х2@)=1, * = 0Д,
применяя дискретный принцип максимума, найти оптимальное управление и
оптимальную траекторию.
12.2. В задаче 1 заменить функционал на
'~1 И*)+*?Ю+*1Ю]+*?С2)+*2<2) ^шш
гкш0
и найти оптимальное управление и оптимальную траекторию.
459

12.3. Для задачи
х1{к + 1)=х1(к)+х2(к)+щ(к), х{@)=\9 * = 0Д;
х2(к + 1)=х2{к)+х%(к)+и2{к)9 х2@)=-1, * = 0,1,
Ы*1, ' = 1,2,
/ = Х!B)+ Х2B) -> 1ШП
найти оптимальные программное управление и траекторию.
12.4. Для задачи
хх(к +1)=хх(к)+ х2(к)+щ{к), хх@)=-1, к = 0,1;
х2(к + 1)=х2(к)+х}(к)+и2{к\ х2@)=1, * = 0,1,
Ы*1, / = 1,2,
найти оптимальные программное управление и траекторию.
12.5. Для задачи
х^к + ^хМ+хМ+ик),
х2(к + 1)=-Х1(к)+х2(к), * = 0,1,
^= Е [«2(*)+*?(*)+*2(*)] -> тт
найти оптимальный регулятор «*(&,х).
12.6. Для задачи
хх(к + 1)=и(к),
х2(А: + 1)=-х1(А:)+х2(А:), * = 0,1,
' = X [(*)+ *?(*) ]+ *2B) -> тт.
найти оптимальный регулятор и*(кух).
12.7. Для задачи
х(* + 1Ил + 1)х(*)+1|(*), * = 0Д,2, х@) = 1 + [|1
/-2 [(л + 1)и2(*)+х2(*) ]+лх2C) -»тш
найти оптимальный регулятор и*(к,х), оптимальные программное управление и
соответствующую траекторию.
460

Глава 13. СИНТЕЗ ОПТИМАЛЬНЫХ ДИСКРЕТНЫХ
СТОХАСТИЧЕСКИХ СИСТЕМ
13.1. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО ПРОГРАММНОГО УПРАВЛЕНИЯ
13.1.1. Постановка задачи
Пусть поведение модели объекта управления описывается уравнением
Х(к +1)« /(к,Х(к),и(к),Щк)), к = 0,1,...,# -1, A3.1)
вде ЛГ- вектор состояния системы, ХеКп,Кп - л-мерное евклидово
пространство; и - вектор управления, и е 1/(к) е Я9 у Щк) — некоторое заданное
выпуклое множество допустимых значений управления; к — дискретное время,
*еГ = [0Д,...эЛГ-1], число шагов N задано; /(к,х,и,п):ТхКпх1!(к)хКт -+Яп
- непрерывно дифференцируемая вектор-функция; 1У(к), # = 0,1,...,#-1,—
т -мерный случайный вектор с известным законом распределения,
описывающий случайные внешние воздействия на объект управления.
Начальное состояние системы A3.1)
*@) = *о
A3.2)
является случайным вектором с заданным законом распределения.
Предполагается, что при управлении используется информация только
о дискретном времени к, т.е. применяется так называемое программное
управление (рис. 13.1).
«(*)
и(к)
1 Х0 1 Щк)
Х(к + \) = Г(к,Х(к),и(к),Щк))
*(* + 1)
Задержка
Х(к)
Рис. 13.1
Множество допустимых управлений 0/о
 = МО),1/A),...,1/(^-1)}, ще ЧкеТ и(к)еЦ(к).
Определим функционал качества управления
I /°(к,
*«0
образуют управления
Х(к)Мк)) + Г(Х№)
\.
A3.3)
461

где /°(к,х,и), Г(х) - заданные непрерывно дифференцируемые функции, М -
знак математического ожидания, причем осреднение производится по множеству
реализаций случайного процесса Х(к)9 порожденного случайными векторами
Х@) и №(к), # = 0Д,...,#-1 при допустимом управлении и()е
Потребуется найти управление !/*(•) еЩ, обеспечивающее минимум
функционала A3.3).
Искомое управление и*(-)е$/0 называется оптимальным программным
управлением.
13.1.2. Стохастический дискретный принцип максимума
Утверждение. Пусть на управлении и*()е$/$ достигается минимум
функционала A3.3). Тогда выполняются условия:
1) при каждом к = ЪХ—>Н-I
м\н(к,Пк + 1)>Щ)>иЧЬ),ЩЬ))]= тах М[Н(к,Ч>(к + 1),Х{к),и>Щк))], A3.4)
где
Щк,Ч,Х,и,Ю = ^МКХ,и,ЦГ)-/\к,Х,иУ,
2) функции Х()9Ч*(-) удовлетворяют системе
ъ(к) = аЛ(№+1),хЮ,иЧк),Щк))г кш1 „_и у = 1> Л)
дХI
A3.5)
дЧ!)
* = 0,1 N-1, ^т1ш...,н;
*,«)) = *0;, Т/*)--*^^, У-1 "• A3.6)
Замечания.
1. Система уравнений A3.5) называется системой канонических уравнений,
функция Н{к,хУьХ9и9Цг) — гамильтонианом, а Ч^(/:),...,^„(й), # = 1,...,#, —
вспомогательными переменными.
2. Утверждение справедливо, если гамильтониан является вогнутой
функцией по и, а несобственные интегралы в выражении для нахождения
Л/[#(#, Ч/(А: +1), Х(к), и(к)91У(к))] равномерно сходятся при всех к = 0,1,..., N -1.
462

13.1.3. Оптимальное управление линейными системами
ПОСТАНОВКА ЗАДАЧИ
Пусть поведение модели объекта управления описывается уравнением
Х(к + 1) = А(к)Х(к) + В(к)и(к) + Щк), * = 0,1,...,ЛГ-1, Х@) = Х0, A3.7)
где все обозначения совпадают с обозначениями разд. 13.1.1, иеЯд, А(к)9В(к)
- матрицы размера (лх п) и (лх#), а IV(к) — последовательность взаимно
независимых гауссовских случайных п -мерных векторов, некоррелированных с Х0 и
удовлетворяющих условиям:
[0, к*п.
Здесь предполагается, что Ях(к) — симметрическая неотрицательно
определенная матрица размера (пхп).
Начальное состояние Х@) = Х0 определено гауссовской плотностью
вероятности с математическим ожиданием щ и ковариационной матрицей И$.
Функционал качества управления имеет вид
1 = М\ Х' [*Г (*)*(*) Х(к) + иТ(к) 0(к) и(к) + ХТ(Ю Л Х(Ю ] 1, A3.8)
где 5(к), А — неотрицательно определенные симметрические матрицы размера
(/|хл), а B(к) — положительно определенная симметрическая матрица (дхд);
М- знак математического ожидания.
Требуется найти оптимальное программное управление и*()е2У0,
минимизирующее функционал A3.8).
СООТНОШЕНИЯ ДЛЯ НАХОЖДЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Известно [9,18,29], что при заданном управлении математическое
ожидание т(к) и ковариационная матрица К(к) удовлетворяют уравнениям:
т(к +1) = А(к) т(к) + В(к) и(к), /и@) = щ,
Я(к +1) = А(к) Я(к) АТ(к) + Л, (к), Я@) = П§,
а
м[хт (к) 5(к) Х(к)] = тт(к) 5(к) т(к) + !г {5(к) Я(к)}. A3.10)
С учетом A3.9), A3.10) функционал A3.8) можно записать в форме
/ = т0г5г@)т0+1г{5'@J)одс}+ Ё [тТ(к)$(к)т(к) + 1т{$(к)Я(к) }]+
A3.9)
*«1
+ тг(АГ)Лт(ЛГ) + 1г{лЛ(^)}+ ^ ит(кH(к)и{к).
*-0
A3.11)
463

Из A3.8), A3.9) следует, что программное управление влияет только на
изменение математического ожидания и, следовательно, только на величину
соответствующих членов в A3.11). Поэтому в поставленной задаче оптимальное
программное управление будет таким же, как оптимальное программное
управление в следующей детерминированной задаче, решение которой может быть
получено с помощью применения дискретного принципа максимума (см. разд.
12.1.2):
т(к +1) = А(к) т(к) + В(к) и(к), /и@) = щ,
Пример 13.1. Даны модель объекта управления
Х(к +1) = Х(к) + и(к) + Щк), к = 0,1,
где Л' € Л, и € Л, /*1(&) = 1, /и@) = 2, Д? = 2, и функционал
/ = ля
[х[|/2(А:) + ^2(А:)])-.тт.
Требуется найти оптимальное программное управление и*().
П Перейдем к эквивалентной детерминированной задаче A3.12):
т(к +1) = т(к) + и(к), т@) = 2, к = 0,1,
/=2[и2<*)+т2<*)]^™п-
Ее решение: т*@) = 2, и*@) = -1; т*A) = 1, и'A) = 0, т*B) = 1, т.е.
оптимальное программное управление и*() = {-1,0} (см. пример 12.1).И
13.2. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ С ПОЛНОЙ
ОБРАТНОЙ СВЯЗЬЮ
13.2.1. Постановка задачи
Пусть поведение модели объекта управления описывается уравнением
Х(к +1) = Дк,Х(к)9и(к), Щк)), к = 0,1,...,# -1, A3.13)
где X — вектор состояния системы, X е Яп; и — вектор управления,
ие1/(к)сЯ99 1/(к) — некоторое заданное замкнутое множество допустимых
значений управления; к — дискретное время, &€Г = [0,1,...,#-1], число шагов
N задано; /(к,х,и,1У):ТхЯп х1/(к)хЯт -+ Яп - непрерывно
дифференцируемая вектор-функция; №(к), & = 0,1,...,#-1 — т-мерный случайный вектор
с известным законом распределения, описывающий случайные внешние
воздействия на объект управления.
464

Начальное состояние системы A3.13)
Х@) = Х0еЯп
A3Л4)
является случайным вектором с заданным законом распределения.
Предполагается, что при управлении используется информация о времени
Но векторе состояния Х(к).
Множество допустимых управлений с полной обратной связью ип образуют
функции и(к,х):ТхЯп ->1/(к), которые на траекториях системы A3.13) для
различных начальных условий A3.14) порождают соответствующие программные
управления ы(-), где Ук е Т и(к) = и(к,Х(к)) е Щк).
Применяемое в каждый дискретный момент времени кеТ управление
имеет вид управления с полной обратной связью по вектору состояния (рис. 13.2).
\Х@)еЯп I
04*)
Х(к + \) = /(к,Х(к)Мк),Щк))
Х(к + 1)
Задержка
Х(к)
и(к) = и(к,Х(к))
и(к,х)
Х(к)
Рис. 13.2
Определим функционал качества управления:.
Г N-
/ = Л/
%/°(к,Х(к)Мк)) + Г(Х(М))\,
A3.15)
где /°(к,х,и), Г(х) — заданные непрерывно дифференцируемые функции, М
— знак математического ожидания, причем осреднение производится по
множеству реализаций случайного процесса Х(к), порожденного случайными
векторами Х@) и Щк), * = 0,1,...,#-1 и допустимым управлением и(к) = и(к,х(к)).
Требуется найти допустимое управление с обратной связью и*(к,х)е&п,
обеспечивающее минимум функционала A3.15).
Функция и*(к,х)е$/п называется оптимальным управлением с полной
I связью.
13.2.2. Уравнение Беллмана
Утверждение [18]. Оптимальное управление и*(к,х)е2/п определяется
решением уравнения Беллмана для дискретных стохастических систем:
465

В(к9х) = гшп {/°(к9х9и) + М[В(к + 19/(к9х9и9Щк)))\х9и]\ ЧхеЯп9 A3.16)
ие[/(ку
* = 0Д Л^-1,
с граничным условием
В(М9х) = Г(х) ЧхеК», A3.17)
где В(к, х) — функция Беллмана, М — знак условного математического ожидания,
и*(М) = а!В попЛ/\к,х,и) + М[В(к + 1,/(к9х9и9Щк)))\х,и]} Чх е Яп9
ие1/(ку
* = 0,1,...,#-1.
При этом минимальное значение функционала A3.15)
1ШП/ = Л/[Я@,ЛГ0)]. A3.18)
Структура оптимального управления с полной обратной связью
определяется в результате поиска минимума в A3.16) по управлению.
13.2.3. Синтез оптимальных линейных регуляторов
ПОСТАНОВКА ЗАДАЧИ
Пусть математическая модель объекта управления описывается уравнением
Х(к +1) = А(к)Х(к) + В(к)и(к) + Щк)9 к = ОД,...,N -1, Х@) = Х0, A3.19)
где все обозначения совпадают с обозначениями разд. 13.1.3, иеЯя9 А(к)9 В(к)
— матрицы размера (л х п) и (л х а), а \У{к) — последовательность взаимно
независимых гауссовских случайных л-мерных векторов, некоррелированных с Х0 и
удовлетворяющих условиям:
М[Щк)]ш 0, м[щк)ЦгТ(п)]= ЯДОв*; 5*, = |^ * " *
Здесь предполагается, что /?}(&) — симметрическая неотрицательно
определенная матрица размера (пхп).
Начальное состояние Х$ определено известной гауссовской плотностью
вероятности с математическим ожиданием щ и ковариационной матрицей 2>о •
Множество допустимых управлений с полной обратной связью образуют
функции и(к9х)ей/П9 причем Ук = 0,1,...,N -1 и(к) - и(к9х(к)) е К9.
Функционал качества управления имеет вид
1 = М\ % [*Т(ЬK(Ь) *(*) + ит(кH(к) и(к) ]+ Хт (ЛГ) Л Х(Ю 1, A3.20)
466

где <?(&), Л — неотрицательно определенные симметрические матрицы размера
(лхл), а 0(к) — положительно определенная симметрическая матрица размера
(д*Я)> М - знак математического ожидания;
Требуется найти управление и*(к,х) с полной обратной связью,
минимизирующее функционал A3.20).
СООТНОШЕНИЯ ДЛЯ НАХОЖДЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Поставленная задача является частным случаем общей постановки задачи,
сформулированной в разд. 13.2.1, где следует положить
/(к, Ху и, IV) = А(к) X + В(к) и + №,
/°(к,Х,и) = ХтЗ{к)Х + ит0{к)и, Г(Х) = ХТАХ.
Тогда уравнение Беллмана A3.16) и условие A3.17) принимают вид
В(к, х) = тт [хТ$(к) х + ит0(к) и + М{В(к +1, А(к) х + В(к) и + Щк)) \х,и}]
УХ€/Г,* = 0,1,...,#-1,
A3.21)
В№,х) = хтАх УХ€/*Л.
Предлагается искать функцию Беллмана В(к9х) в виде
В(к9 х) = хтР(к) х + К0(к), A3.22)
где Р(к) — неотрицательно определенная неизвестная симметрическая матрица
размера (пхп), К$(к) — неизвестная функция.
Подставляя A3.22) в A3.21), приходим к утверждению [18].
Утверждение. В задаче A3.19) — A3.20) оптимальное управление определяется
соотношением
и*(к,х) = - Д*)х, к = 0,1,...,# -1, A3.23)
где Цк) — матрица коэффициентов усиления регулятора размера (д х п)
Цк) = [0(к) + ВТ(к)Р(к + 1)В(к)]~1ВТ(к)Р(к + 1)А(к), к = 0,1,...,#-1, A3.24)
а матрица Р(к) размера (п х п) удовлетворяет уравнению
Р(к) = $(к) + ЬТ(к) 0(к) Цк) + [ А(к) - В(к) Цк) У Р(к +1) [ А(к) - В(к) Цк) ],
* = #-1,...,1,0,
A3.25)
Р(Ю = А.
467

Минимальная величина функционала определяется по формуле A3.18)
тт1 = т0ТРф)т0 + 1г{р@)Щ }+ ^1г{Р(А: + 1)Ях(к)}. A3.26)
Замечали я.
1. В выражении A3.24) обратная матрица существует.
2. Если в фунюшонале A3.20) Л = 0, то граничное условие в A3.25) имеет
вид Р(ЛГ) = 0.
3. Оптимальный стохастический линейный регулятор совпадает с
оптимальным регулятором для соответствующей детерминированной задачи:
х(к +1) = А(к)х(к) + В(к)и(к)9 к = 0,1,...,N -1, х@) = Хо,
/= X [хт(кK(к)х(к) + ит(кH(к)и(к)]+хт(ЮАх(Ю^тт,
*-о
решение которой дано в разд. 12.2.3.
АЛГОРИТМ НАХОЖДЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
1. Составить систему A3.24), A3.25).
2. Определить матрицы Р(к), Цк).
3. Построить оптимальный регулятор и*(к,х) = - Цк)х.
4. Определить значение функционала на оптимальном управлении по
формуле A3.26).
Пример 13.2. Даны модель объекта управления
Х(к +1) = Х(к) + и(к) + Щк), Х@) = Х0, к = 0,1,
где X е Я, ие Я, Ях(к) = 1, т$ = 1, И$ - 2, и функционал
1 = м\ X [и2М + **<*> ]} ^ пип.
Требуется найти оптимальный регулятор и*(к,х).
П Согласно п.З замечаний запишем соответствующую детерминированную
задачу
х(к + 1) = х(к) + и(к), х@) = Хо, к = 0,1,
'= %[и2{к) + х2(к)]-+тт.
*«0
468

Для этой задачи оптимальный регулятор имеет вид (см. пример 12.9)
«*@,х) = -|х, «*A,х) = 0.
Минимальное значение функционала находится по формуле A3.26)
3
Так как Р@) = -,/>A) = 1,РB) = 0 (см. пример 12.9), щ=1, ^=2,
лип/ = — •¦
Пример 13.3. Даны модель объекта управления
Х(к + 1) = Х(к) + и(к) + Щк), Х@) = Х0, к = 0,1,2,
гцеХеК, иеЯ, Я{(к) = 19 и функционал
/ = м№[иНк) + ХНк)]+Х\3)\.
>ПШ1.
Начальное состояние задано параметрами щ = 1, 2>о = 2.
Требуется найти оптимальный регулятор и*(к9х).
П 1. Составляем уравнения A3.24), A3.25):
Цк) = [\ + Р(к + 1)]-{Р(к + 1)9
Р(к) = 1 + 1?(к) + [1 - Цк) ]2Р(к + 1), к = 0,1,2; РC) = 1.
3 1
2. Получаем решение уравнений : РC) = 1, РB) = -, 1B) = -,
РA) = |, Д1) = |, ^@) = ^, Д0) = ^-
3. Строим оптимальный регулятор:
«*@,х) = --|х, «*A,х) = -|х, «*B,х) = -±х.
4. Находим минимальное значение функционала по формуле A3.26):
т1п/ = ^^+§^о+/>A)Л1@) + />B)Л1A) + />C)Л1B) =
21 42 8 3 1163
~13 + 13 + 5 + 2 130 '
таккакто=1, 2#=2, ^)»1.1

Пример 13.4. Даны модель объекта управления
Х1(к + \) = Х1(к) + Х2(к) + и(к) + Щ(к), * = 0,1 ,
Х2(к + \) = Х2(к) + и(к) + 1У2(к),
где X еЯ29 иеК, Я{ (к) = Е, и функционал
1 = М\ X 1<*) + Х*№ + ^22(^) ]+ *12B) + ^22BI "> ШШ.
Требуется найти оптимальный регулятор.
П Согласно п.З замечаний перейдем к соответствующей
детерминированной задаче
х{ (к + \) = х{ (к) + х2 (к) + и(к), А: = 0,1 ,
х2(к + \) = х2(к) + и(к) ,
/ = Е \и\к) + х{2(к) + х22(*) ]+ хг2B) + х22B) -> шш,
гдеД*)^ | ), *(*) = ( [.], 5»)-А-( ; ?).
1. Выписываем соотношения A2.27), A2.28) или A3.24), A3.25):
Д*) = |1 + A 1)Л* + 1>A)} A 1)Л* + 1)(^ []. *-0Д,
¦-С :)¦
*=0,1,
РB) =
2. Получаем решение: 1A)
¦A !)•
/40 =
Г5 1
3 3
I 1
3 3
, ДО) = @,4; 0,8).
3. Оптимальный регулятор A2.26) или A3.23) имеет вид
«*@,х) = -0,4X! -0,8х2 , в*A,х) = -|х1 -1*2-«
470

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕ0ИЯ
13.1. Для задачи
Хх(к +1) = Х{(к) + Х2(к) + и(к) + Щк), тгФ) = I
Х2(к +1) = -Хх(к) + Х2(к) + Щк), т2@) *Ъ к = ОД,
/ = мЦ 2 [и2**) + ЛГ^*) + ЛГ22(Л:) ]+ ^2B) + ;Г22B)[ "> "^
найти оптимальное программное управление !/*(•).
13.2. Для задачи
Хх (к + \) = Хх (к) + и(к) + Ж(*),
Х2(к +1) = 2^ (А:) + Х2(к) + Ж(*), А: = ОД,
т!@) = 2, т2@) = 1,
I 2 *-0 ]
тт
найти оптимальное программное управление !/*(•).
13.3. Для задачи
Х1(к + 1) = Х1(к) + Х2(к) + и(к) + Щ(к),
Х2(к +1) = -Х{ (А:) + ВД) + Щ(к), к = ОД,
'-"{Х [^а') + ^2(^^22(^)]1-
тш
найти оптимальный регулятор и*{к9х).
13.4. Для задачи
Х{(к +1) = */(*) + Щ(к), к = ОД,
*2(* +1) = -^(А:) + *2(*) + \У2(к)9 к = ОД,
/ = Л/] У \и2(к) + ЛГ,2(*) 1+ *22BI -> тш
г{1о[(^) + ^12^)]+^22B)}
найти оптимальный регулятор и*(А:,х).
13.5. Для задач
Хх(к +1) = -2*,(*) + ЛГ2(*) + Щ{к),
Х2(к +1) = ^(А:) + и(к) + ИЪ(*), * = ОД,
471

а) / = м12 [и2(к) + Х22(к)]+ Х{2B) + Х22B)\
б) / = м\ X [|/2(*)]+ ^2B) + 2*22BI
в) / = Л/{^[|/2(А:) + ^12(А:)]1
пип;
г(к) + Х1\к)\\-*тт\
найти оптимальные регуляторы и*(к,х).
13.6. Для задач
Хх(к +1) = ЛГ^А:) + 2Х2(к) + ^(*),
*2(* +1) = -2ХХ (к) + *2(*) + и(к) + 1Г2(А:), А: = ОД,
а) / = м\2 [и2(А;) + 2Хх2(к) + *22(*) ]+ Хх2B)\ -+ гшп;
б) / = м\ 2 [и2(*)]+ ЛГ12BI -» тт;
в) / = Л/| X [и2(*) + Хх2(к) ] 1 ^ тт;
найти оптимальные регуляторы и*(к,х).
13.7. Для задачи
Хх(к +1) = Х{(к) + ЛГ2(*) + и(к) + ^(А:),
ЛГ2(* +1) = -Х{ (А:) + *2(*) + 1У2(к)9 к = ОД,
и-о
>Ш1П
найти оптимальный регулятор и*(к9х).
13.8. Для задачи
Х(к + 1) = (п + \)Х(к) + и(к), /по=1 + Г^1,
/ = Л/
Х[(л + 1)и2(^) + ^2(^)] + л^2C)|^тт
найти оптимальное программное управление и*() и оптимальный регулятор
ит(к,х).
472

Глава 14. СИНТЕЗ ДИСКРЕТНЫХ ЛИНЕЙНЫХ СИСТЕМ
СОВМЕСТНОГО ОЦЕНИВАНИЯ И УПРАВЛЕНИЯ
14.1. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЛИНЕЙНЫМИ ДИСКРЕТНЫМИ
СТОХАСТИЧЕСКИМИ СИСТЕМАМИ С НАКОПЛЕНИЕМ
ИНФОРМАЦИИ О СОСТОЯНИИ
14.1.1. Постановка задачи
Пусть модели объекта управления и измерений описываются уравнениями:
Х(к +1) = А(к) Х(к) + В(к) и(к) + Щк), к = 0,1,...,N -1, Х@) = Х0,
(ИЛ)
У (к) = С(к)Х(к) + У (к), к = 0,1,..., N -1,
где X — вектор состояния, X еЯп; У — вектор измерений, У е Ят; АA), ВA),
С(/) — матрицы размера (пхп), (йх^), (тхп) соответственно, на управление
ограничений не наложено, т.е. иеЯя; IV(к), У (к) — последовательности
взаимно независимых гауссовских случайных л- и т-мерных векторов,
некоррелированных с Х0 и удовлетворяющих условиям:
М[Щк)] = 0, М[У(к)] = 0, М[ ЩкIУТ(п)] = Я{(к)Ькп;
М[ У(к)Ут(п)) = Я2(к)Ькп; М[ Щк) Ут(п)] = 0, 5*, = } ^ * = *
[ 0, к * п.
Здесь предполагается, что Ях(к) — симметрическая неотрицательно
определенная матрица (пхп), Я2(к) - симметрическая положительно определенная
матрица (тхт); М - знак математического ожидания.
Начальное состояние Х0 определено известной гауссовской плотностью
вероятности с математическим ожиданием т$ и ковариационной матрицей 2>о .
Обозначим У0к ={Уф),У(\),...,У(к)} - вектор, содержащий информацию
о всех измерениях, проводимых с начала процесса.
Множество допустимых управлений образуют функции и(к) = и(к,У0к),
зависящие от предыдущих измерений, причем Чк = 0,1,..., N -1 и(к) е Я9.
Функционал качества управления имеет вид
<Г = м\ 1^1ХТ(кK(к)Х(к) + иТ(кH(к)и(к)] + 1ХТ(М)АХ(Ю] 1, A4.2)
473

где 8(к), Л - неотрицательно определенные симметрические матрицы размера
(л х п), а 0(к) — положительно определенная симметрическая матрица (д х #).
Требуется найти управление в*(А:,У0*) из множества допустимых,
обеспечивающее минимум функционала A4.2).
14.1.2. Теорема разделения
Утверждение [18]. Оптимальное управление и*(к9У0к) в задаче,
сформулированной в разд. 14.1.1, имеет вид
и (к) = и (к,У0к) = -Цк)Х(к), к = 0,1,...,ЛГ -1, A4.3)
где Х(к) = М{ Х(к) \ Уо } "~ апостериорная оценка вектора состояния модели
объекта управления по результатам наблюдений, удовлетворяющая уравнению
Х(к) = Х(к) + К(к)[У(к)-С(к)Х(к)\, *-1,...,*-1, Х@) = то; A4.4)
Х(к) — априорная оценка вектора состояния Х(к) до проведения измерения
У (к):
Х(к +1) = А(к)Х(к) + В(к)и*(к), к = 0,1,...,# - 2, Х@) = /Ио ; A4.5)
К(к) — матрица коэффициентов усиления фильтра A4.4) размера (лх/и),
которая определяется по формуле
К{к) = Т(к)СТ(к)[С(к)Т(к)Ст(к) + Я2(к)]~1, к = 1,...,N -1; A4.6)
Г(Л) = Л/{[ЛГ(А:)-^(А:)][А'(А:)- Х(к)]т) - ковариационная матрица ошибки
г(к) = ЛГ(^) - ЛГ(А:) априорной оценки Х(к)
Г(* + 1) = А(к)Г(к)Ат(к) + Я1(к), к = 0Д,...,#-2, Г@) = 2H'; A4.7)
Г(^) = Л/{[АГ(^)-^)]Щ^)-ЛА:)]7'} - ковариационная матрица ошибки
Л А
е(А;) = Х(к) - Х(к) апостериорной оценки Х(к) после проведения измерения У (к),
Г(к) = Т(к) -Т(к) Ст(к) [С(к)Т(к)Ст(к) + Я2(к)Г1С(к)Т(к), к = 1,..., N -1;
A4.8)
Г@) = 2HХ,
474

Цк) — матрица коэффициентов усиления регулятора A4.3) размера (? х п),
Цк) = [B(к) + ВТ(к)Р(к + 1)В(к)]~1ВТ(к)Р(к + \)А(к), к = N-1,...Д,0, A4.9)
Р(к) — матрица размера (пхп), которая удовлетворяет уравнению
Р(к) = ^(А:) +1? (к) B(к) Цк) + [ А(к) - *(*) ДА:) )Т Р(к +1)[ Л(*) - В(к)Цк) ],
* = #-1,...Д,0,
A4.10)
Р(ЛГ) = Л.
Минимальное значение функционала A4.2) определяется по формуле
тт/ = тоГ/>@)то+1г[/>@)/)^]+ ]^1г[ />(/: +1) ^(А:) ] +
*-о
+ Х1^{тIГ(А:)[1?г(/:)/>(/: + 1I?(А:) + е(А:)]Д/:)}. A4.11)
Первые два слагаемых характеризуют влияние неопределенности задания
начальных условий, третье — внешних воздействий на объект, четвертое —
погрешностей оценивания.
Доказательство утверждения (теоремы разделения или стохастической
эквивалентности) приведено, например, в [9, 18]. Оптимальное управление A4.3)
с накоплением информации является функционалом измерений, так как в силу
A4.4) оценка Х(к) вектора Х(к) зависит от У0К.
Уравнения A4.4)—A4.8) являются уравнениями фильтра Калмана для
дискретных линейных систем, обеспечивающего нахождение оптимальной оценки
вектора состояния модели объекта управления с минимальной нормой
ковариационной матрицы ошибки оценивания. Соотношения A4.9), A4.10)
соответствуют случаю определения оптимального управления линейной дискретной
детерминированной системой при полной информации о векторе состояния,
который рассмотрен в разд. 12.2.3.
Задачи синтеза оптимального управления и оптимальной фильтрации
можно в данном случае решить независимо (раздельно).
14.1.3. Синтез оптимальных линейных регуляторов
АЛГОРИТМ НАХОЖДЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
1. Решить проблему синтеза оптимального детерминированного
дискретного линейного регулятора с помощью соотношений A4.9),A4.10), используя
алгоритм, изложенный в разд. 12.2.3, для задачи
х(к + \) = А(к)х(к) + В(к)и(к), * = 0,1,...,#-1; х@) = Хо,
7 = Ё [*Т(к)**(*)*(*) + иТ(к)С(*)"(*) ]+ [хТ(Х)Лх(Ю ]^тш.
*-о
475

2. Синтезировать оптимальный дискретный линейный фильтр
в соответствии с уравнениями A4.4)—A4.8).
3. Согласно теореме разделения получить оптимальное управление
с накоплением информации по формуле A4.3).
4. Найти минимальную величину функционала по формуле A4.11).
Структура оптимальной системы с накоплением информации
о состоянии, где по измерениям производится оценка вектора состояния,
используемая в управлении, изображена на рис. 14.1.
*@)
Модель объекта
!*(* + !)
У(к)
Задержка
Х(к)
Модель измерений
У(к)
и*(к)
и'(к) = -Цк)Х(к)
Х(к)
Х@) = то
и(к)
Накопление информации
и выработка оценки вектора Х(к)
Оптимальный регулятор
Оптимальный фильтр
Рис. 14.1
Пример 14.1. Даны модель объекта управления
Х(к +1) = Х(к) + и(к) + Щк), к = 0,1,2; Х@) = Х0,
где ХеК\ иеК, Я{(к) = 1;
модель измерений У (к) = Х(к) + У(к), где У е Я, Я2(к) = 1,
и функционал качества управления
= м||;[|/2(А:) + ^2(А:)]+ЛГ2C)|.
гаш.
Начальное состояние задано параметрами щ = 1, Щ = 2.
Требуется найти оптимальный регулятор с накоплением информации
о состоянии.
? Сравнивая с общим случаем, имеем А(к) = 1, В(к) = 1, С(к) = 1,
<2(к) = 1, 5(к) = 1, Л = 1, N = 3.
1. Находим оптимальный линейный регулятор для соответствующей
детерминированной задачи
х(к + 1) = х(к) + */(*), * = 0,1,2; х@) = Хо,
/ = X \и2(к) + х2(к) ]+ х2C) -> тт.
*«о
476

Составляем уравнения A4.9), A4.10) (см. также пример 13.2).
Цк) = [\ + Р(к + 1)]-{Р(к + 1),
Р(к) = \ + 12(к) + [1-Цк)]2Р(к + 1), * = 0,1,2; РC) = 1.
3 1
Получаем решение уравнений: РC) = 1, РB) =—, Д2) = —,
«1)-|, Д1)=|, *Р>-^. Ц0)=Тз'
Оптимальный линейный детерминированный регулятор A2.28)
определяется соотношениями:
»*@,х) = -—х, «*A,х) = --х, в*B,х) = --х.
2. Синтезируем оптимальный линейный фильтр. Уравнение A4.6)—A4.8)
имеют вид
К(к) = г(к)[г(к) + 1У19 * = 1,2,
Г(* + 1) = Г(*) + 1, Аг = 0,1; Т@) = Щ=2,
г(к)=Т(к)-Т(к)[г(к) + \У1Т(к), *-и; г@) = д0*=2.
Решение: ГA) = 3, ГA)Л, ГB)Л, ГB) = -^, К(\)Л, КB)=1-.
4 4 И 4 11
3. Согласно теореме разделения оптимальное управление с накоплением
информации находим по формуле A4.3) с учетом результатов п.1:
иф) = -^ 3с@) = -^, и\\) = -|хХ1), и*B) = -|хB).
Уравнения блоков, входящих в замкнутую схему, изображенную на рис.
14.1, имеют вид
Х(к +1) = Х(к) + и {к) + Щк), к = 0,1,2; Х@) = *„,
У(к) = Х(к) + У(к), к = 1,2,
*(^1) = *(*) +*/*(*), * = 0Д; *@) = то=1,
*(*) = *(*) + *(ЖШ-*(*)], * = 1,2; *@) = /По=1,
*A)Л, К<Я-1.
477

4. Минимальное значение функционала находим по формуле A4.11):
тю/=^1и02+^1)ьх + Л1)Л1@) + Л2)Л1A) + ДЗ)Л1B) +
+ Г@)Д0)[РA) + 1]Д0) + ГA)Д1)[РB) + 11Д1) + ГB)Д2)[РC) + 1]Д2) =
21 42 8 3 , „ 8 Г8 Л 8
=Тз + 1з+Г2+1+2-Тз[?+1]-П+
3 ЗГЗ Л 3 7 1 г, л 1 68117 ,1ППО
14.2. УПРАВЛЕНИЕ ЛИНЕЙНЫМИ ДИСКРЕТНЫМИ
ДЕТЕРМИНИРОВАННЫМИ СИСТЕМАМИ
С НАКОПЛЕНИЕМ ИНФОРМАЦИИ О СОСТОЯНИИ
14.2.1. Постановка задачи
Пусть модель объекта управления описывается уравнением
х(к +1) = А(к) х(к) + В(к) и(к), к = ОД,..., N -1, х@) = Хо, A4.12)
а модель измерений — соотношением
у(к) = С(к)х(к), * = 0,1,...,#-1, A4.13)
где х — вектор состояния, хеКп; у — вектор измерений, уеЯт, тип; А(к),
В(к), С(к) — матрицы размера (пхп), (пхд), (тхп) соответственно; на
управление ограничений не наложено, т.е. и е Кд.
Начальное состояние произвольное: х@) е Яп.
Вместе с тем предполагается, что имеется некоторая точка х$ , в
окрестности которой находятся начальные состояния. На практике эта точка
фактически локализует область функционирования системы и задается из технических
соображений.
Пусть функционал качества управления квадратичный:
Iв Е [хТ(к)$(к)х(к) + иТ(к)д(к)и(к)] + [хТ(М)Ах№)], A4.14)
где 5(к), Л - неотрицательно определенные симметрические матрицы размера
(лхл), а B(к) — положительно определенная симметрическая матрица размера
(дхд).
478

Известно (см. разд. 12.2.3), что оптимальное управление и (к9х) с полной
обратной связью имеет вид
и*(к,х) = -Цк)х9 * = 0,1,...,ЛГ-1, A4.15)
где Цк) — матрица коэффициентов усиления регулятора размера (дхп)
Цк) = [0(к) + Вт(к)Р(к + \)В(к)]-1Вт(к)Р(к + 1)А(к), А: = ЛГ- 1,...Д,0, A4.16)
а матрица Р(к) размера (л х п) удовлетворяет уравнению
Р(к) = 5(к) + Ьт (к) (}(к) Цк) + \Л(к) - В(к) Цк) ]т Р(к +1) [А(к) - В(к) Цк) ],
* = #-1,...4,0,
A4.17)
Р(ЛГ) = Л.
Соотношения A4.15)—A4.17) справедливы, если в каждый момент времени
известна информация о всех координатах вектора х(к). Как следует из
утверждения, приведенного в разд. 12.2.3, оптимальное управление и*(к9х) с полной
обратной связью порожцает оптимальные пары (**(•)» и* (•)) для любых начальных
состояний.
Однако в рассматриваемой задаче вектор х(к) не доступен для
использования в управлении, а измеряется вектор у(к), информация о котором
накапливается.
Требуется найти управление и(к,У0к), зависящее от всех доступных
к текущему моменту времени измерений У0* ={уФ)>УA)>—>У(к)} так, чтобы
свойства синтезированной системы были близки к достижимым в случае полной
информации о состоянии.
х@)
х(к + 1)
г-Н *(* +1) = Л(к)х(к) + В(к) и(к)\
Задержка
х(к)
у(к) = С(к)х(к)
У(к)
Модель объекта управления
Модель измерений
х@) = *5
иЧк)
«•(*)
и'(к) = -Цк)х(к)
х(к)
Накопление информации
и выработка оценки вектора х(к)
Оптимальный регулятор
Наблюдатель состояния
Рис. 14.2
479

Идея решения состоит в получении оценки х(к) вектора состояния х(к)
в текущий момент времени к по результатам измерений У0к и использовании
этой оценки в управлении A4.15) вместо х(к). Тоща, чем точнее оценка х(к),
тем ближе синтезированная система по своим свойствам к оптимальной при
полной информации о состоянии. Структура такой системы изображена на рис.
14.2.
В детерминированных системах процесс получения оценок вектора
состояния по измерениям называется восстановлением или наблюдением, а
соответствующее устройство — наблюдателем. Задача синтеза управляемой системы
сводится к задаче синтеза наблюдателя.
14.2.2. Синтез наблюдателей состояния
НАБЛЮДАТЕЛИ ПОЛНОГО ПОРЯДКА
Рассмотрим задачу синтеза наблюдателей полного порядка, в которых для
получения оценки требуется решить разностные уравнения, число которых
совпадает с размерностью вектора состояния.
Если т = п и матрица С(к) не вырождена для & = 0,1,...,#-1, то вектор
состояния может быть найден из A4.13) по формуле х(к)« С (А:) у(к). В этом
случае ошибка оценки вектора х равна нулю и синтезируемая система совпадает
с оптимальной при полной информации о состоянии. Для всех начальных
состояний обеспечивается минимум функционала A4.14).
В общем случае предположим, что вектор у(к) поступает на вход
устройства, оценивающего вектор состояния х(к), которое описывается разностным
уравнением
х(к + 1) = В(к)х(к) + Н(к)и(к) + К(к)у(к), х@) = Хо , A4.18)
где /)(*), Щк), К(к) - неизвестные матрицы размера (пхп), (пхд), (пхт)
соответственно. Здесь в начальном условии учтена априорная информация о
системе.
Обозначим через е(к) = х(к) - х(к) ошибку оценивания и получим
уравнение, описывающее ее изменение. Для этого вычтем из уравнения A4.12)
уравнение A4.18) с учетом A4.13):
х(к +1) - х(к +1) = А(к) х(к) - И(к) х(к) + [ В(к) - Н(к) ] и(к) - К (к) С(к) х(к).
Если принять Н(к) = В(к), В(к) = А(к)-К(к)С(к), уравнение для ошибки
оценивания имеет вид
е(к +1) = [А(к) - К(к) С(к) ] е(к), е@) = х@) - х*0. A4.19)
Вид ошибки оценивания г(к) полностью определяется свойствами
матрицы А(к) -К(к)С(к) и величиной начальной ошибки е@).
480

Уравнение оценивающего (наблюдающего) устройства с учетом A4.18) и
найденных матриц имеет вид
х(к +1) = А(к) х(к) + В(к) и(к) + К(к)[у(к) -С(к) х(к)], х@) = х*0. A4.20)
Структура оценивающего устройства совпадает с конструкцией фильтра
Калмана, но здесь имеется произвол в задании матрицы К(к). Оценка зависит
от всех измерений до момента к, т.е. является функцией от У0 •
Поэтому управление A4.15), использующее вместо х его оценку х,
а именно: и* (к) = -Цк)х(к) также зависит от У0к, что и требовалось.
Оценивающее устройство имеет порядок п по числу координат вектора
оценок, удовлетворяющего разностному уравнению A4.20).
Если начальное состояние х@) совпадает с Хо, то, как следует из A4.19),
е(*) = 0 и х(к) = х(к). Правильным выбором матрицы К(к) можно добиться
уменьшения ошибки: х(к) -* х(к) при А:->+«>. Например, если все матрицы
в A4.12)—A4.14) не зависят от к , удобно задавать матрицу коэффициентов
наблюдателя К так, чтобы собственные значения матрицы А-КС равнялись
нулю.
Тогда йе1(ХЕ-(А-КС))**Хп, и по теореме Кели-Гамильтона
(А-КС)" =0. Из A4.19) получаем е(п) = (А-КС)пф) = 0, т.е. любое начальное
значение ошибки уменьшается до нуля самое большое за п шагов.
НАБЛЮДАТЕЛИ НИЗКОГО ПОРЯДКА
Рассмотрим задачу синтеза наблюдателей низкого порядка, в которых для
определения оценки требуется решить разностные уравнения, число которых
меньше размерности вектора состояния и равно (п-т).
Пусть модель объекта управления описывается уравнением
х(к + 1) = Ах(к) + Ви(к), к = 0,1,...,#-1, х@) = х0, A4.21)
а модель измерений — соотношением
у(к) = Сх(к)9 * = 0,1,...,#-1, A4.22)
где х - вектор состояния, хеКп\ у - вектор измерений, уеКт, тип; А, В,
С - матрицы размера (лхл), (пха), (т х л) соответственно, не зависящие от
к; на управление ограничений не наложено, т.е. иеЯ9.
Предполагается, что система вполне наблюдаема, т.е. выполнено условие
ъщ\СТАТСТ...(АТ)п-1СТ | = л.
Недостатком структуры A4.20) наблюдателя полного порядка является
зависимость оценки х(к +1) только от измерений до„ момента к, т.е.
независимость от измерения у(к +1). Этого недостатка лишена следующая структура:
481

х(к + 1) = Ах(к) + Ви(к),
A4.23)
х(к + 1) = Ах(к) + Ви(к) + К[у(к + 1)-Сх(к + \)]> х@) = х5,
где К — неизвестная матрица размера (л х /и). Здесь в начальном условии учтена
априорная информация о системе.
Подставляя первое уравнение во второе, из A4.23) получаем
х(к + \) = [Е-КС).[Ах(к) + Ви(к)] + Ку(к + 1), х@) = *5. A4.24)
Обозначим через е(к) = х(к) - х(к) ошибку оценивания и получим
уравнение, описывающее ее изменение. Для этого вычтем из уравнения A4.21)
уравнение A4.24) с учетом A4.22). В результате имеем
г(к +1) = [А - КС А] г(к), е@) - х@) - *5- A4.25)
При этом
у(к + 1)-Сх(к + 1) = Сг(к + 1) = [СА-СКСА]г(к) = [Е-СК]САг(к).
Если гапяС = т, то выберем матрицу Ктак, чтобы
Е-СК = 0. A4.26)
Тогда у(к + 1)-С х(к +1), что можно считать условием точного
восстановления.
Из системы A4.24) можно исключить т уравнений и понизить порядок
наблюдателя. Структура системы управления с использованием управления
A4.15) и оценивающего (наблюдающего) устройства A4.24) изображена на рис.
14.2.
14.2.3. Синтез линейных регуляторов
АЛГОРИТМ НАХОЖДЕНИЯ УПРАВЛЕНИЯ
1. Синтезировать оптимальный линейный регулятор с помощью
соотношений A4.15)—A4.17), используя алгоритм, изложенный в разд. 12.2.3.
2. Синтезировать наблюдатель полного или низкого порядка.
3. Получить искомое управление с накоплением информации о состоянии
и\к) = -Щ)х(к),
используемое в схеме на рис 14.2.
482

Пример 14.2. Для задачи
х,(* + 1) = х,(*) + х2(*) + И(*),
х2(* + 1) = х2(*) + и(*),
**) = х,(*)-х2(*), кшО,\;
I = X [н2(*) + х12(А:) + х22(*)) + х12B) + х22B) -> гшп
*-о
требуется найти оптимальный регулятор с накоплением информации, если
известно, что х5 = A,1)г.
? Сравнивая с общим случаем, имеем
Ж*)=(о I)'**>"(!)• ^^"(о !).Й(*) = 1.ОД = A -1).
1. Синтезируем оптимальный регулятор.
Выпишем соотношения A2.29), A2.30) или A4.16), A4.17) (см. также
пример 13.4):
Д*) = |1 + A 1)Р(* + 1)Г|11 A 1)Р(* + 1)^ |), *«0,1,
*»-(; ;)+^(*)д*)+{^;)-(;) д*)}г/>(Л+1){(; з-^к»}.*-^
¦Р. 3-
, ДО) = @,4; 0,8).
РB)
3 3
1 5
Решая их, находим: Д1) = I - — I, РA) ¦¦
3 Ъ)
Оптимальный регулятор A2.28) или A4.15) имеет вид
«*@,х).,-0,4х, -0,8х2 , «*A,х) = -|х, -|х2.
2. Синтезируем наблюдатель.
Наблюдатель полного порядка определяется уравнением A4.20):
Получим матрицу:
-*-(; ш» -"-к г:э-
16»
483

При этом собственные значения матрицы А - КС определяются из условия
|1-^-Х 1 + *, I
I -К2 1 + ^2-х|
Характеристическое уравнение имеет вид
Х2+Х(-2-К2+К1) + \-К1 + 2*2=0.
Согласно разд. 14.2.2 требуется, чтобы собственные значения равнялись
нулю. Отсюда получаем: -2-К2+К{ =0> \-К\ + 2К2 = 0. Следовательно,
КХ=Ъ, К2=\.
Наблюдатель полного порядка имеет вид
** + 1) = *1<*) + й<*> + 1<*) + 3^ х1@) = х51=1,
х2(А:+1) = х2(А:) + и(А:) + [х1(/:)-Х2(А:)-х1(А:) + Х2(А:)], х2@) = х*02 =1.
Наблюдатель низкого порядка определяется уравнением A4.24):
**+,)=(-~^ !)М!)н(*)+й)**+1)
или
х1(к + 1) = A-К0х1(к) + х2(к) + и(к) + К1у(к + \),
х2{к +1) = -К2 х{ (к) + х2(к) + и(к) + К2 у(к +1).
Условие A4.26) имеет вид
Е-СК = \-{\ -1) 1^0 = 1-*,+*2=0.
Вычитая из первого уравнения наблюдателя второе с учетом связи:
1 - К{ = -К2 или ^-^=1, получаем
х1(к + 1)-*2(к + 1) = (К1-К2)у(к + \) = у(к + \).
Отсюда х2(к + \) = х\(к + \)-у(к + 1).
Подставляя последнее соотношение в первое уравнение наблюдателя,
имеем
х1(к + 1) = A-К0х{(к) + х1(к)-у(к) + и(к) + К1у(к + \) =
= B-К1)х1(к) + и(к) + К1у(к + 1)-у(к).
Следуя рекомендациям, изложенным в разд. 14.2.2, зададим К{ так, чтобы
собственное значение равнялось нулю: 2 - К\ - А, = 0. Отсюда К\ = 2.
484

В результате наблюдатель низкого порядка имеет вид
$х{к + \) = и(к) + 2у(к + \)-у(к), Зсх@) = х*ох=1,
й<* + 1> = *1<* + 1>-** + 1>. *2@) = *52=1.
Он имеет порядок л - /и = 1, так как для определения оценки требуется
решать только одно (первое) разностное уравнение.
3. Получим искомое управление с накоплением информации. Для этого
в структуре оптимального регулятора, полученного в п.1, вектор состояния
заменим его оценкой, вырабатываемой наблюдателями полного или низкого порядка:
|/*@) = - 0,4^@) - 0,8х2@), 1/*A) = -|х1A) -|х2A) .¦
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
14.1. Для задачи
хх(к +1) = хх(к) + кх2(к) + ки(к),
х2(к + \) = х2(к) + ки(к),
у(к) = хх(к)-х2(к), * = 0,1;
где к > 0, синтезировать наблюдатели полного и низкого порядка.
14.2. Для задачи
X! (к +1) = хх (к) + к х2(к) + к и(к),
х2(к + \) = х2(к) + ки(к),
№ = хх(к), * = 0Д;
Где к > 0, синтезировать наблюдатели полного и низкого порядка.
14.3. Для задач
хх (к +1) = хх (к) + х2(к) + и(к),
х2(к + \) = х2(к) + и(к),
№) = х2(к), к = 0,1;
а) /= %и2(к) + хх2B) + х22B)-+тт;
б) /=2>2(*) + х22B)^пцп;
кшО
в) / = Е [ и2(к) + хх2(к) + х22(*)] + ^B) -> тш;
*=о
найти регуляторы с накоплением информации.
485

14.4. Для задач
хх(к + 1) = х1(к) + х2(к),
х2(к + 1) = хх(к) + и(к),
Лк) = х1(к) + х2(к), * = 0Д;
а) /- X [и2(А:) + х12№) + х22№)] + х12B) + х22B)^1Шп;
б) /- ^и\к) + хх\2) + х2\г)^тт\
в) /=2[и2№) + х12№)] + ^22B)-*тт
найти регуляторы с накоплением информации.
14.5. Для задачи
х1(А: + 1)^лх1(А:)+Х2(А:), 4\ + 7 »
х2(к + \)~хх{к) + {* + Ъи{к). ^02-2 + И,
Хк) = (п+1)Х1(к)+х2(к), к = 0*,2;
*«о
найти регулятор с накоплением информации.
14.6. Для задачи
Х(к + \) = {п + \)Х(к) + и(к) + Щк), щ «[§] + !> А*=||] + 1,
У(к)~(п + 1)Х(к) + У(к), к = 0Л,2; АХ=Я2=\9
найти оптимальный регулятор с накоплением информации.
486

Глава 15. СИНТЕЗ ОПТИМАЛЬНЫХ
НЕПРЕРЫВНО-ДИСКРЕТНЫХ ДЕТЕРМИНИРОВАННЫХ
СИСТЕМ
15.1. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО ПРОГРАММНОГО
УПРАВЛЕНИЯ
15.1.1. Постановка задачи
Пусть поведение модели объекта управления описывается совокупностью
дифференциальных и разностных уравнений
*(') = /(',Д#).?('*).«D). '* * * < '*+1 >
A5.1)
гае х,у — векторы состояния непрерывной и дискретной частей системы
соответственно, хеЯп,уеЯт; щу — векторы управления непрерывной и
дискретной частями соответственно, ие VсЯ9,у еУ ^Я*9 I/ н V - заданные
множества допустимых значений управления; / — время, *еТ = [*091#); Т~~
промежуток времени функционирования системы, на котором выделены моменты
/*, А; = 0Д,...,ЛГ-1, разбивающие множество Т на непересекающиеся
полуинтервалы Тк=[*к,*м)9 * = 0,...,#-1; /(*,х,у,и):ТхЯп хЯт х1Г-+Яп,
&(и х, у, у) : Т х Яп х Ят х V -» Ят - непрерывно дифференцируемые вектор-
функции; х(*м) = хA# -0).
Предполагается, что множество достижимости \)&(*к+\>х9у9у) выпукло
для любых х,у и * = 0,1,...,Л"-1.
Начальное состояние системы A5.1) задано
х(/0) = хо € Я\ Я/0) = Уо € В". A5.2)
Конечное состояние (х(*н),у(*н)) системы произвольно.
Предполагается, что при управлении используется информация только
о текущем времени, т.е. рассматривается так называемое программное управление.
Множество допустимых управлений 2/0 образуют кусочно-непрерывные
функции и():Т-+1/, */(*) = и(* + 0), и последовательности уй«М4))м,
К^)бК,Л = 1,...,^.
Определим множество допустимых процессов &(*о,х0>у0) как множество
четверок </ = (*(•), ><),и(),у()), включающих траекторию х() непрерывной
части, последовательность Я*) = {)>('* И^-о " траекторию дискретной части,
Управление (и()9у())е&о, удовлетворяющих уравнению A5.1) с начальным
Условием A5.2).
487

На множестве &((о,х0,у0) определим функционал качества управления:
+ Р(хA„),у((„)),
A5.3)
где /*(их,у,и),&*(их,у,у),Р(х,у) - заданные непрерывно дифференцируемые
функции.
Требуется найти процесс й* = (х*(),у*(•)»«*(•),V*())е 0(*о,хо,уо), на
котором достигается минимум функционала A5.3):
/(</¦)= тт /(</). A5.4)
</е!?0Ь,Яо,И))
Искомые элементы */*: траектория х*(), У*() = 0'о>>;*(^)>"»У*(^)} и
управление и*О, V*(•) = {у*A\),...,у*(/#)} называются соответственно оллш-
мальной траекторией и оптимальным управлением.
15.1.2. Необходимые условия оптимальности
Утверждение [36]. Пусть на допустимом процессе
ё* = (х * (•), у * (•), и * (•), V * (•)) € .0(/о, *о, уо) достигается минимум функционала
A5.3). Тогда существуют вектор-функции ЧЧО^О^О» •»х*'л@)Г и
л@ = (щ(*),- -»Лт@)Г» удовлетворяющие уравнениям
Т,-^ = — , 1-1,...,/!, Г€2*,
дх,-
* = 0,1,...,#-1,
ш„ т ш/, V ^Яд(^ьл(^1),х*(^1)>У*(^)>у*(^1)) . ,
0Х/
A5.5)
Л/СО = * - > у = 1,...,т, /€Ул,
т ^Яд(^ьг1(^1),х*(^1),У*(^),У*(^1)) . -
Лу('*+1 "°)= 77 » У =1,...,Л1
с условиями
488

дх1
A5.6)
Лу(^) = Г » у=1,...,т,
такие, что в каждой точке непрерывности управления и* (О и при всех
[с = ОД,..., N -= 1 выполняются условия
где
и * (I) = а1втах#н(/,т* * (*),У* С*),"), '« П.
У*(^+1) = а1втахЯд(^+1,л(/*+1),х*(/л+1),у*(^),у),
М
т
У=1
A5.7)
A5.8)
- гамильтонианы непрерывной и дискретной частей системы A5.1)
с функционалом A5.3).
Соотношения A5.1), A5.2), A5.5)—A5.7) представляют собой краевую
задачу для 2(п + т) уравнений.
АЛГОРИТМ ПРИМЕНЕНИЯ НЕОБХОДИМЫХ УСЛОВИЙ ОПТИМАЛЬНОСТИ
1. Составить гамильтонианы A5.8).
2. Найти структуру оптимального управления из условия A5.7) максимума
по управлению гамильтонианов непрерывной и дискретной частей системы.
3. Составить краевую задачу A5.1), A5.2), A5.5), A5.6).
4. Решить полученную в п. 3 краевую задачу. В итоге определяется четверка
(х*(),У*()>и*(),у*())б^(/0,х0,^0), на которой может достигаться минимум
функционала A5.3).
Пример 15.1. Даны модель объекта управления
*(') = *('*)+ «('), *еТк; х@) = 1,
*'*+1> = *('*+!>+ у('*+1>, А: = 0,1; ^@) = 1,
гдехеД; иеЛ, у еЛ; уе Д,/€Г = [0,2), То = [ОД), Тг = [1,2), N = 2, /0 = 0, /1=1,
1г = 2, и функционал
489

+|[х2B) + ^2B)]->тш.
Требуется найти оптимальный процесс (х*(),у*(),и*(-),у*()), на
котором достигается минимум функционала.
П Сравнивая с общей постановкой задачи, имеем
/(/, х, у, и) = у + и, /°(/, х, у, и) = -и2,
^,х,у,у)*х + у, *°(*,х,у,у)=~у2, Ях,у)=|[х2 +у2].
1. Составляем гамильтонианы A5.8):
Нн№,х,у,и) = Ч >[у + и\-±и2, Яд(*лъЗДу)*л-[х + у]-|у2.
2. Согласно A5.7) находим максимум гамильтониана по управлению. Так
как ограничения на управление отсутствуют, можно применить необходимые
условия безусловного экстремума:
ДЯна,У@,«*@,у*(/.),и)_
0И
а Дд('*+1.п('*+1).* * (^|),у * С*).у)
ау
=ч('*+1)-у = о.
Отсюда и*(*)= 440, *€7*,* = 0Д; у*('*+1)-Л0*+!),* = °Д-
Найденное управление обеспечивает максимум гамильтонианов, так как
удовлетворяются достаточные условия экстремума
32Ян«,Ч'«),х»@,У*&),и) 1 ^0>
дУ2
3. Выписываем краевую задачу A5.1), A5.2), A5.5), A5.6):
*(') = .*'* ) + «(>), *еТк; х@) = 1,
*@ = 0, ЧЧ***1 -0)-»РС**+|> + п(***1); ТО)—*©,
т|(/) = - Ч»(/), Ч('*+1 - 0) = 0, * = 0,1; г,B) - - уB).
490

4. Находим решение краевой задачи, обозначая С = 4/B - 0) = -хB) - у{2):
* = 1, 1**<2: У@ = С, л(/) = СB-0, "*(') = <?, у*B) = -Д<2),
* = 0, 0*/<1: У@ = 2С, л@ = 2СA-/), 1/*(/) = 2С, у*A) = С.
Решая уравнения движения с найденным управлением, получаем
* = 0, 0*/<1: х@-1 + A + 2С)/, ><1) = 2+ЗС,
*«1, 1**<2: х@ = 2A + 2С)/-2С, ;*2) = 4A + 2С) - 2С - ><2).
Положив / = 2, имеем хB) = 4 + 6С, уB) = 2 + ЗС. Постоянную С
3
определяем из условия С = -хB) -уB) = -6 -9С, откуда С = —-.
Таким образом, оптимальный процесс имеет вид
0**<1,
х*(')<
1
^
5»
6 2/
[5 5'
= ¦
б
'
3
.'
0**<1,
**(!) = },
У*B)=19
у*Ф = -|, ^B) = -|,
а минимальное значение функционала пип / « —. |
15,2, НАХОЖДЕНИЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ С ПОЛНОЙ
ОБРАТНОЙ СВЯЗЬЮ
15.2.1. Постановка задачи
Пусть поведение модели объекта управления описывается системой
х@ = /(/,хA)»*'*),«@). *к * * < '**ь
Я<*+1) -«(^ь^ы)»М)>И^1))< *-0А....ЛГ-1,
Где все обозначения совпадают с обозначениями, принятыми в разд. 15.1.
Ванильное состояние
х(г0) - *о € Дя, д#0)в Уо « *т>
заранее не задано и может быть любым.
A5.9)
A5.10)
491

Предполагается, что при управлении используется информация о текущем
времени и о векторе состояния (х,у).
Множество допустимых управлений с полной обратной связью $/п образуют
функции и(*,х,у):ТхЯпхЯт -+и и К/,х,^):{/, /^(хЛлхЛт-»К, которые
на траекториях системы A5.9) для различных начальных состояний A5.10)
порождают допустимые процессы й = (х{),у()9и()9у())е4?A0,х0,у0) (см. разд.
15.1).
Требуется найти такие функции (и * (/, х, у), у * (/, х, у)) е 2/п, что
7^*) = ,>п /Ю ^х^еЛ-хЛ*, A5.11)
где</* = (хЧ), У*(), "Ч) = «Ч,*Ч),Д'*()), ^О^М'О.Д'Ч))).
Пара (и*(*,х,у),у*A,х,у))е1/п называется оптимальным управлением
с полной обратной связью. Для каждого начального состояния (х0,у0) из
множества Я" х Ят это управление порождает соответствующую оптимальную
четверку, т.е. оптимальную траекторию (х * (•), у * (•)) и оптимальное
программное управление (и*(),у*())е1/0. При этом и* (О = »*(*,*(/),></*))
У/бГь V • (ГА+1) - Г * С/Л+1,Х(/Л+1),>Ч/*)), *=0,1,...,#-1.
15.2.2. Соотношения для нахождения оптимального управления
Утверждение [36]. Если существуют функция у(*,х,у):ТхЯп хЯт -> Я,
кусочно-непрерывная по I на Т при фиксированных х>у, причем
ф(*,х,у) = ф(/ + 0,х,у), частные производные которой по переменным I и х
существуют и непрерывны на ТхЯ" хЯт за исключением конечного числа значений
г е Г, и управление (и * (/, х, у), у * (/, х, у)) е ип, удовлетворяющие условиям:
тах
ФмЛу) = -Г(х,у) У(х,у) € Яп х /Г, A5.12)
ф('*+1 " 0, *> У) = тах {ф(/л+1,х,*(/*+1,х, у, V)) - $°(**+,,*,У, V) }, * = 0,...,N -1,
ие1/ [Д ЭХ,- ]
у(х,у)€/глх/гт,
то управление (и * (/, х, у), у * (/, х, у)) с полной обратной связью оптимально.
492

Условия A5.12). представляют собой задачу Коши для уравнения
с частными производными первого порядка относительно функции ф,х,у).
Минимальное значение функционала A5.3) определяется по формуле
гшп /(</) =-ф(/<ь*<ъ;Но) Ч(х0,Уо)еЯпхЯт- A5.13)
г/е*?0Ь,Ло,Д))
АЛГОРИТМ НАХОЖДЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
1. Составить систему A5.12).
2. Найти структуру оптимального управления из условий максимума
по управлению.
3. Подставить найденные выражения в систему A5.12).
4. Найти решение полученной системы и явный вид искомого управления.
Пример 15.2. Даны модель объекта управления
*(') = *('*) +"(О, '€7*; *@) = 1>
><^+1) = ^+1) + у(^+,), * = 0,1; у@) = 1,
где хеК, иеК, уеЯ, /еЛ, / € Т = [0,2), Г0 = [0,1), Тг = [1,2), N = 2,10=0,
1Х = 1, г2 = 2, и функционал
4ы
}и2@Л + У2(^+1)
1Ь
+ 1;[х2B) + у2B)]^>гтп.
Требуется найти оптимальное управление (и*(*,х,у),у*A,х,у)) с полной
обратной связью.
П Сравнивая с общей постановкой задачи, имеем
/(*,х,у, и) = у + и, /°(*,х,у,и)=-и2, &(их,у,у) = х +V,
&\<>х,у,у) =|у2, Г(х,у) =±[х2 +у2].
1. Выписываем систему A5.12):
^\^^,^ЬАь + и)Ли г\ = 0> ^х,у) = -^-\у\
и I 01 ОХ 2. ) 11
Ф(^+1-0,х,у) = тах|<р(^+1,х,х + у)--у21, * = 0,1.
2. Находим структуру оптимального управления из условия максимума
выражения в фигурных скобках по управлению. Применяя необходимое условие
^Условного экстремума, получаем
493

ОХ ОУ
3. Подставляем найденные выражения для оптимального управления
в уравнение и условие перехода к следующему полуинтервалу:
,х,у) дЫ*,х,у) 1ГЭф(*,х,уI Л /^ ч 1 2 1 2
ф('*+1 -0,х,^) = ф(^+1,х,х + у*(^+1,л,у))-|[у*(^+1,х,у)]2, * = 0,1.
4. Решение уравнения ищем в виде
<&,х,у)Лк«)х2 + Ц0ху + 1л#(*)у2,
где КA),Щ)9МA) — неизвестные функции времени.
Подставляя в п.З и приравнивая коэффициенты при одинаковых степенях
х,у, получаем
*(/) = -*2, *B) = -1; АГ@ = -I2 - 21, Л/B) = -1; ДО = -КЬ-К, Д2) = 0,
ш*(*лу)тК(Ъх + ЦПу9 *еТк9
Д'*+1-0) = 0, А/(^+1-0) = 0, А = 0,1,
Решая систему, имеем
при /е[1,2):
*@=-Цг, ДО =44. А/(/) = /-4+: 4
,_|> ^"-^-1> "^- 3 9</-§)'
«*(/,х,у) = Х + B:^, г»B,х,у) = -Ь
при / € [ОД):
*(')=-г-г, ДО=44. Л/@ = *-т+; 4
494

Минимальное значение функционала определяется по формуле A5.13)
с учетом структуры функции ф,х,у):
4се0(О,дь,Я)) 10 5 10
Например, при Хо = у0 = 1 тт/ = -.
Оптимальное управление Aг*(/,х,,у),1»*(/,х,у)) с полной обратной связью
порождает оптимальные четверки (х * (-),у * (•), и * (•), V * (•)) для любых начальных
состояний. Например, для начальных условий, совпадающих с заданными в
примере 15.1, запишем уравнения, описывающие поведение системы с обратной
связью в*(/,х,^),р*(/,х,у):
при ге[ОД): х(/) = уф)+Щ+^'^\ х@) = 1,
уA) = хA) -|хA) = ±х<1), уф) = 1;
4 4
*2) = хB)-±хB)=±;сB).
Отсюда получаем:
при/е[ОД): х@-1-|, и *(/) = «*(>, *@,:К0)) = -|,
|.*A,хA),Я0)) = -|, *1)-±.
при {е [1,2): *0)=|-у, «*@ = «*(',*@,;К1)) = -|>
г*B,хB),Я1)) = -|, *2)=|,
что совпадает с результатами примера 15.1. Аналогичная закономерность
справедлива и для других начальных состояний.ш
15.2.3. Синтез оптимальных линейных регуляторов
ПОСТАНОВКА ЗАДАЧИ
Пусть система A5.9), описывающая поведение модели объекта управления,
имеет вид
НО = МЛ *<0+В{1) и@+Р«) у{гк), /к*К(к+и
^+|) = С*+1^*) + 1L+1у(^+,) + Gа+,х(Г4+,), * = 0Д ЛГ-1, A5.14)
*(<<>) = *о> Я*о) = УО'
495

где АЦ)9ВЦ)9РЦ) — матрицы размера (лхл), (пха), (пхт) соответственно,
элементы которых непрерывны; Ск+\9Вк+\9Ок+1 - матрицы размера (тхт)9
(тхз), (тхп) соответственно; на управление ограничений не наложено, т. е.
ие1/ = Я<1, уеУ = Я5.
Пусть функционал качества управления A5.3) имеет вид
N-1
'=1
*«0
7[7*Г<'>^'>*'>+^
*2
+}^+1) Рм ^+1)+хг(^+1)^+1 у{гк) + ±хг(/*+1)л*+1 х(^+1)}+
+ 1хг(^)Л^+1х(^)+|/(^)^+1у(^) + хг(^)^+1у(^), A5.15)
где 5(*)>&к+\>^к+\ — неотрицательно определенные симметрические матрицы
размера (пхп)9 (тхт)9 (пхп) соответственно; (?(/),РЛ+1 — положительно
определенные матрицы размера {дха)9 (зхз) соответственно; Ф@,^+1 —
матрицы размера (п х т).
Требуется найти оптимальное управление (и * (/, х, у), * * (*> х9 >0) € &п
с полной обратной связью, минимизирующее функционал A5.15).
СООТНОШЕНИЯ ДЛЯ НАХОЖДЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Сравнивая A5.14), A5.15) с A5.9), A5.3), имеем
/(и х, У, и) = А(*) х + В(() и + /*(/) у9 /°(/, х, у, и) = ±[хТ$(*) х + иТB(*) и}+ хгФ(/)я
*('*+ь*>:и^) = Ск+1 у + Пк+х У + Ск+1 х9
8°(*к+\>х,у,у) = -утЯк+1 у+-утРк+1 у + хг^+1 у+-хгЛ*+1 х;
**(*,:и) =^^гл^+1 х+-угл^+1 у + хтч„+{ у.
Функция <р(/,х,>0, входящая в A5.12), ищется в виде
ф9х9у) ЛхтКЦ)х + хтЬ(г)у + ±утМЦ)у9 A5.16)
где К(г)9ЬЦ)9МA) — неизвестные матрицы размера (пхп), (пхт), (тхт)
соответственно, причем К(*),МA) — симметрические. Подставляя A5.16)
496

в A5.12) и приравнивая нулю соответствующие билинейные формы, получаем
структуру оптимального управления:
и * (*,*,;К'*)) = <2-1A)Вт(()[К(*)х + ДО*('*)]> >* *' < '*+ь.
У*(*к*1,х(*ш),Л(к)) = 1Рк+1-1>1+1Щ1к+1I>шГ11>к+1х A5.17)
уравнения для нахождения матриц КA),Щ)9МЦ) из A5.16):
^ЛГ1 + 1Г^ + 1:*(Г!ЯГХ-Ф = 0, /* *'<**+ь A5.18)
М + Р7!, + !?> +17 В 0-1ВтЬ = 0,
условия перехода к следующему полуинтервалу:
*('*+1 -0) = К + М + От1т + ОтМС - Л + [X + <7гЖГ]2) [Р - ВтМВ]~1 ВТ[ЬТ + ^С],
Д^+1-0) = 1,С + ^гМС-^ + [1 + GгМ]2)[/>-/)гМ2)Г12)гМС, A5.19)
Щ'к+1 " 0) = СГЖ7 - Л + СгМВ [Р - ВтМВ]-{ ВТМС,
конечные условия:
К(Ь)т-Лы, Д/лг) = -^+ь М«„) = -Я„+1. A5.20)
В правых частях выражения A5.19) для вычисления
К(*к+\ -0), Ц*ы _°)> ^('*+1 ~°) матрицы КA),Ц]09М(й берутся в момент
/ = '*+ь а матрицы Р,К,Ч*,К,С,В90 имеют индексы А: + 1.
АЛГОРИТМ НАХОЖДЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
1. Из конечного условия A5.20) найти матрицы К(*к+\),Ц*к+\)>М(*к+1)
при & = #-1.
2.По формуле A5.19) вычислить матрицы К(*к+{ -0), Д/*+1 -0), М(*к+{ -0).
3. Решить систему уравнений A5.18) справа налево от момента / = ^к+x -0
До 1 = ;к с конечными условиями, найденными в п.2. В результате находятся
матрицы К@9Ц*),М(*).
497

4. Выполнить пп.2,3 для * = #-2,#-3,...Д,0. В результате находятся
матрицы КA),ЦЦ,МA) на всех полуинтервалах Тк.
5. Подставляя нашейные матрицы К((),Щ),М(() в A5.17), получить
искомое оптимальное управление с обратной связью.
Минимальное значение функционала A5.15) находится по формуле A5.13)
с учетом A5.16):
пин Ш) = -Фо>Ъ>Уо) = -\4К('о)Ъ-4ШУо-\уоМ('о)Уо- 05.21)
Пример 15.3. В задаче
х = У\{*к) + иA), х@) = х0$ /**/</*+1,
й(^1)вЙЙ). У1@) = У\0,
У2«к+1) - V(^+1), У2@) = ^20, * = ОД,
/ = ^ /1/2@Л + ^2A) + ^2B) + ^Х2B)^1ШП
2 0 2 2 2
требуется найти оптимальное управление с полной обратной связью.
П Сравнивая постановку задачи с A5.14), A5.15), имеем
/1 = 1, т = 2, /1@ = 0; «0-1; /*@ = A 0), 5@ = 0; 6@ = 1; Ф@ = 0;
д1=д2=д3=0, />!=/>2=1; ^=^=^3=0; /0=0; /1*1, /2=2; с = Р М,
2> = Н, ^ = 0; Л!=Л2=0, Л3=1.
Запишем выражения A5.17)—A5.20) для нахождения скалярной функции
*@, вектор-функции Д0 = (А@, ^@), матрицы М(*) = " " и
оптимального регулятора:
К + К2=0, Ц+К + К1л=0, 12+^12=0,
ЛГ11+211+112=0, Мп +12+^12=0» АГ22+^2=0»
^(^-о)-^^)^/>(У , А('*+1-о) = о,
1-Л*22(**+1)
498

1-Л*22М*+1)
Мц(*м -0) = А/,2(^+, -0) = 0, *=0,1,
м22(^, -о) = а/„(^1)+ У*;»>
1-Л/22('*+1)
ЛГB) = -1, 1,B) = 12B) = 0) А/„B) = А/12B) = А/22B) = 0,
«*(>,*, *'*)) = ЛГ(Одс + Щ*)У1(*к) + Ш »('*).
км. ,У1 \-МпЦм)
Согласно приведенномуалгоритму синтеза получаем
1. При I = 2: *B) = -1, .6,B) = 1^B) = 0, А/„B) = А/12B) = Ми{2) = 0.
2. При Г = 2-0, к = \:
КB-0) = -1, 1,B-0) = 12B-0) = 0, А/пB-0) = А/,2B-0) = А/22B-0) = 0.
3. При 1 & г < 2, * = 1:
*(') = —> *|(') = 7г|, 12@- о, л/12@ = л/22М = о,
^и@ = '-1 + ~, и*((,х,№ = -^х + 1-±У1A), р*B,х,У) = 0.
4. При I = 1:
*A) = -|, 40) = -|, ^гA) = 0, А/„A) = -|, А/,2A) = А/22A) = 0.
5. При / = 1-0, * = 0:
АГA-0) = -1, 1,A-0) = 0, 12A-0) = -!,
А/„A -0) = А/12A -0) = 0, А/22A -0) = -±.
499

6. При 0 * / < 1, * = 0:
г»-^. АЮ-^, ^@=^3,
Л/ц@-' + 1+73з, АГ12@ = -^, А/и@=7Гз.
Минимальное значение функционала находится по формуле A5.21):
тт !((!) =-ф,х0,у0)=-х02+-х0[у10+у20} + -[у10+у2о]2.
</е#@,льл>) 6 3 6
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
15.1. Найти оптимальное программное управление и оптимальную
траекторию в задаче
*@ = >>('*)+ "('), **Т; х@) = 4,
*'*+!>-*'*+!>+ ***+!), *-0А У@) = 0,
иеК, \у(*к+х)\й!9 Л: = ОД; /0=0, /1=1, /2=2,
'41
}|/2(/)Л + у2(^+1)
ь*
1 1
+ — ДГB)->1ШП.
2
15.2. Решить задачу 1 при х@) -1.
15.3. Найти.оптимальное управление с полной обратной связью в задаче
^2(^+1) = >^2(^) + ^(^+1), у2@) = у2о, * = 0,1;
2
/=1 |и2(/)Л+1у2A)+|у2B)+1х2B)+1Л2B) _> пйп
500

Глава 16. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ПУЧКАМИ
ТРАЕКТОРИЙ
16.1. ОПИСАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДВИЖЕНИЯ ПУЧКОВ
Траектория движения детерминированной системы определяется
начальным состоянием, параметрами системы и действующими на нее в процессе
движения управляющими сигналами. В тех случаях, когда точные значения
параметров или начальное положение системы неизвестны, возникает необходимость
описания всех траекторий движения, исходящих из допустимых начальных
состояний при всех возможных значениях параметров. Совокупность этих
траекторий образует пучок траекторий движения.
Для описания поведения модели системы управления в условиях
неопределенности используются дифференциальные уравнения с параметром
Х@в/('.*@.И@.в). *е<*; Х(*0) = 3, 5€0,
где х — вектор состояния системы, х е Яп; и — вектор управления, X — время,
аеКк— вектор параметров, зеЯп - начальное состояние системы. Точные
значения а и 8 неизвестны, но множества а и о их возможных значений
считаются заданными.
Расширив вектор состояния компонентами хл+1 = а{,...,хп+к = ак и добавив
к уравнениям движения уравнения хл+1 =0,...,хп+к = 0, можно исключить в
модели параметры а и считать, что пучок траекторий порождается только
неопределенностью начального состояния х(/0) € а х ос.
Предполагая, что указанное исключение параметров сделано, будем
рассматривать модель объекта управления, поведение которого описывается
обыкновенным дифференциальным уравнением
х(из) = /«,х(*,з),и(')) > х(*0,з) = зео, A6.1)
где и - вектор управления, ие1/ ^Яя, G- заданное множество допустимых
значений управления; г — время, / € Т = [/0,^] — промежуток времени
функционирования системы, моменты начала процесса *о и Ч заданы, 5 — начальное
состояние системы, зеосЯ", а - заданное компактное множество допусти-
*ьа начальных состояний, х(*,з)— значение вектора состояния х е Яп в момент
времени /, соответствующее фиксированному начальному состоянию 5 и
управлению ы(.); /(/,*, и):ТхЯпх1/-» Яп - непрерывная вместе со своими частными
производными вектор-функция, Яп — л-мерное евклидово пространство.
Правый конец траектории свободен.
Предполагается, что при управлении используется информация только
° времени /, т.е. рассматривается так называемое программное управление.
501

Множество допустимых управлений Щ образуют кусочно-непрерывные
функции 1/() со значениями в множестве I/.
Для каждого допустимого управления и()е 2/0 имеется совокупность
решений хA,з) уравнения A6.1) для различных фиксированных начальных
состояний 5 € о. Объединение этих решений: Ух(*,5) называется пучком (ансамблем)
траекторий системы A6.1), порожденным управлением !/(•) и множеством о
[23,30,33,36].
Критерий качества управления пучком может быть задан разными
способами. Наиболее часто встречаются две конструкции, соответствующие задачам
синтеза оптимального гарантирующего управления и оптимального в среднем
управления. Эти варианты постановки задачи рассматриваются в разд. 16.2 и
16.3.
16.2. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО ГАРАНТИРУЮЩЕГО
УПРАВЛЕНИЯ
16.2.1. Постановка задачи
На траекториях системы A6.1) определим функционал качества управления
/(*,*()) = ) /°(/,х(Г,5),1/@)Л + ^<Д#1, *», A6.2)
где /°A,х,и), Г(х) — заданные непрерывно дифференцируемые функции.
Качество управления и() е Щ пучком траекторий оценивается
максимальным значением функционала A6.2):
/г(|/()) = тах/E,1/0). A6.3)
При фиксированном управлении величина /г(г/()) равна значению функционала
A6.2), полученному для наихудшей траектории в пучке при самом
неблагоприятном выборе начального условия 5. Эта величина является гарантирующей
оценкой в том смысле, что при любом другом выборе параметра лее значение
/E,1/()) будет не больше, чем /г («(-))•
Требуется найти допустимое управление */*(•) € *У0, на котором достигается
минимум функционала A6.3):
/г(|/*())= пгёп тах/E,1/0). A6.4)
и()еи0 зео
Такое управление и*() называется оптимальным гарантирующим.
502

16.2.2. Необходимые условия оптимальности
Утверждение [ 36 ]. Пусть и*() - оптимальное гарантирующее управление, а
\\х(,5) ~ соответствующий этому управлению пучок траекторий, описываемых
хЦ,з) = Д/,х(М),1/*(/)), 1*Т, A6.5)
х(Г0,5) = 5€а. A6.6)
Тогда существует скалярная функция <р(*,з) и вектор-функция
Ч(*,8) = (ч^ (/,$),...^„(М)^, удовлетворяющие уравнениям
ф(/,5) = -/0(^х(/,5),1/*@), 'еТ, зеа,
фуй5)--аЯ(/'У^д)'д<^д,^д)>> 7 = 1,..,*, 06.7)
дх]
с условиями
<№Ь8) = Г{х(Ч,з)), зео,
ЧА*1,з) = -дГ(х(Н'3)), } = \>^п, A6.8)
дх]
такие, что в каждой точке непрерывности управления и * (*) выполняется
соотношение
1ШП { #(/,ЧЧ/,5),х(/,5),1/) - Я(Г,^(/,5),Х(^,5),1/ * @) } * 0 VI/ € *7, A6.9)
5еа*
где Щ^9х9и) = ]Г У, ./^*,х,и)-/°(*,х,и) -гамильтониан,
о* = | 5* е а | ф(/о,$*) = тах <р(/<ь*) [ - совокупность точек глобальных максимумов
функции ф(/0,$) на множестве а.
Соотношения A6.5)—A6.9) представляют собой краевую задачу для
системы Bл +1) обыкновенных дифференциальных уравнений с параметром $.
Замечание. Условие A6.9) можно записать в виде
и*@ = а1втах ппп {Я(г9У№5)>х(^,5)911)-Я(г9^(/,«)9х(М)9м*A))}. A6.10)
При решении практических задач, чтобы упростить нахождение структуры
оптимального гарантирующего управления из условия A6.9), допустимо предположе-
503

ние о том, что множество а * точек глобальных максимумов функции ф('о>з)
состоит из конечного числа элементов: о* - {^1,...,5*). В этом случае необходимые
условия оптимальности формулируются следующим образом.
Утверждение. Пусть и * (•) — оптимальное гарантирующее управление и
имеются к траекторий х1@ = х(/, я1),..., х*(/) = хA,зк), удовлетворяющих уравнению
*(^ = Ж*(М'),и*@), *еТ, A6.11)
х(*о,5!) = 5* еа, 1 = 1,...,*, A6.12)
на которых функционал A6.2) достигает наибольшего значения:
1(81,и * О) =... = 7(*\и * О) = тах/E,1/ * (•)). A6.13)
Тогда существуют числа \{,...,\к:
2>,-1 06.14)
/«1
и вектор-функции У1 (/) = *Р(/,51),...,Ч**(/) = Ч*(/,5*), удовлетворяющие уравнениям
ф1 ая(/,^@,хЧО,«*@)> ,. = 1 4 у.и ,шГ Aб15)
а^
с условиями
^М) — дПХл]{Ч)\ / = 1,...,*, У = 1,...,/1, A6.16)
такие, что в точке непрерывности управления и * (/) выполняется соотношение
|/*(/) = аг8тах ^ Х/Я^Ч*'@, *'('),"). A6.17)
Замечание. Оптимальное гарантирующее управление и*г(/,х)
с полной обратной связью совпадает с оптимальным управлением и*(*,х) для
функционала A6.2). Действительно, управление «*(/,х), как отмечалось в разд.
9.2.2, порождает оптимальные траектории для каждого начального состояния
х(/0) € Яп, в том числе и для каждого состояния х(Г0) = 5 из заданного
множества асКп, т.е. 1E,и*(*,х))й1E9и(*,х)) для всех зеа и любого управления
«(/, х) € Жл. Следовательно,
1Т(и * (г,х)) = тах /($,» * (/,х)) ^ тах /($,«(*, х))
504

и оптимальное управление «*(/,*) с полной обратной связью является
оптимальным гарантирующим управлением для любого пучка траекторий системы
A6.1).
Пример 16.1. Даны модель объекта управления
*(/,*) = !/(*), х@) = $, 5еа = [0,1],
где х е Л; | и|^ 1; / €[0,1], и функционал
/г(«0) = тах -х2A,5) -» тт.
0***1 2
Требуется найти оптимальное гарантирующее программное управление и* (•).
П Сравнивая с общей постановкой задачи, имеем: /(*,х,и) = и,
/°(/,х,и) = 0,Ях) = |х2.
1. Составляем гамильтониан: Я^Ч^х,!/) = Ч(г,з) и.
2. Записываем уравнения системы A6.5)—A6.9) с учетом A6.10):
Х(/,5) = Ы*@, Х@,5) = 5,
ф(Г,5) = 0, фЛ*) = ~*2A,5), 0 <; зй 1, A6.18)
*(*,*) = 0, т*) = -*A,*),
и*@ = а18тах гат^,5)[й-и*(/)].
|и|*1 5еа
3. Ищем функции х(/,$), ф(/,$), Ч*(*,з) в виде многочленов, зависящих от
параметра *:
х(/,5) = Х0@ + Х!(/M, ф(/,5) = Фо+Ф!* + Ф2*2, ЧЧ*,*) = ^0 +^1».
где коэффициенты Ф0, Ф19 Ф2, Ч^» Ч^ берутся не зависящими от /, так как
функции ф(/,5), Ч*(М) в силу A6.18) не меняются со временем.
Подставляя эти многочлены в A6.18) и приравнивая коэффициенты при
одинаковых степенях *, получаем
Х0@ = и*('), Х0@) = 0; Х!@ = 0, Х,@) = 1,
Фо=!*о2A), Ф^ХоШХ^!), Ф2=|х?A), Ч'о=-Х0A), У,—Х!A>.
Следовательно, Х^О = 1, и тогда
*(/,*) = 5 + Х0@, ф(/,5)=|х2A) + Х0AM + ^2, ЧЧ/,5) = -Х0A)-*. A6.19)
505

о* =
Функция я>@,$) достигает наибольшего значения по переменной 5 на концах
промежутка [0,1]. Поэтому
{0}, <р@,0)><р@Д),
{0,1}, <р@,0) = ф@Д),
{1}, <р@,0)<ф@Д),
{0}, 1 + 2Х0A)<0,
{0;1}, 1 + 2Х0A) = 0, A6.20)
{1}, 1 + 2Х0A)>0.
а с учетом A6.19)
о* =
Проверим каждый из указанных в A6.20) случаев.
Если о* = {0}, то из A6.18) следует:
!/*(/) = 318 шах Ч/(/,0)[1/-и*(/)] = 818П^(/,0),
или с учетом A6.19): */*(/) = - здп Х0A).
Интегрируя уравнение Х0@ = -8ф&Х0A), получаем, что
Х0@ = -^-авп Х0A). При / = 1 имеем равенство Х0A) = -я$п Х0A). Следова»
теяьно, ХоA) = 0, что противоречит первому условию в A6.20). Аналогичное
противоречие имеет место и в случае о* = {1}.
Рассмотрим случай а* = {ОД}, коада в пучке траекторий имеются две
наихудших. Для этого случая Х0A) = ™, Ч?(/,0) = —, Ч/(/Д) = —г. При этом
а функция Хо@ = —г удовлетворяет уравнению Х0@ = — с нулевым
начальным условием.
В результате находим искомое оптимальное гарантирующее управление
г/*(;) = —?, а минимальное значение функционала вычисляется по функции
Ф@,5): /г(«*()) = Ф@,0) = ф@Д)=-|.в
Пример 16.2. Даны модель объекта управления
*!(/,$) * Х2(*,5), Х,@,5) = 5€О = [ОД],
*2<М) = "('), *2@,5) = 0
506

и функционал
/(*,«<))=7К<<>л+7*?<и),
2о
Л*(и(')) = шах /E,1/0) ->
потребуется найти оптимальное гарантирующее программное управление //*(•).
аЗдесьх = (х1,х2)геЛ2, >б[0,1], иеЯ, /°(*,х,1/) = |1/2, Р(х) = |*12. Так
как функционал /E,1/0) является выпуклой функцией параметра 5 при любом
допустимом управлении, то из пучка траекторий достаточно выделить две
траектории х!@ = *('»0) и х2@ = *(*Д), соответствующие крайним значениям
параметра 5 е[0,1]. Для нахождения искомого управления используем систему
уравнений A6.11)-( 16.17).
1 ->
1. Составляем гамильтониан: Щ*,Ч,х,и) = ЧГ\(*9з)х2 + Ч*2(/, 5)и-—и .
2. Находим структуру оптимального управления из A6.17):
«*(/) = а^тах^^
= Х, *](>)+Х2У22@, A6.21)
так как X) + Х2 = 1.
3. Записываем краевую задачу A6.11), A6.12), A6.15), A6.16):
*!(') = *2(>)> *!(<) = ^1^1@+ ^(г), х|@) = 0, х!@) = 0;
*/(о=о, едо—уЧсо, т/ю—*1о>. ^1о)=о,
*?<0 = *2@. ^@ = ^@ + 4^2@, *?@)-1, *|@) = 0,
*12@ = 0, *22@ = -У,2@, ^12A) = -*?0>, ^22A) = 0.
Решая полученную систему, имеем
*№)=-аь ^(О = «!('-»> *12Ю—«2. ^('ЬМ'-!),
гдеа^х/а), а2=дс,2A).
Управление A6.21) имеет вид
и * @ = (Х^ + Х2а2) (/ ~1), A6.22)
507

а траектории:
*2(>) = *2@ = \^\*\ + *-2«2) И - 2<).
х}@ = |(Х,а1+Х2а2)(г3-3/2),
*?(') = 1+-|(Я.1ос1 + Х2а2)(/3 - 3B).
При / = 1 получаем систему уравнений относительно а1 = х{A), а2 = х*A):
«1=-з[х«а1+х2а2]. C + Л,)а,+Л2а2=0,
- ИЛИ
а2=1-}[Х,а1+Х2а2] ^ а,+C + Х2) а2 =3 .
Добавляя условие A6.13): /(О,и*0) = /A,и*0) или |(а1J = |(а2J, а
также A6.14), получаем систему алгебраических уравнений
(З + Х^сц + Х2а2 =0,
А.1<Х1 + C + Х2)а2 =3,
(счJ=(а2>2,
X! +Х2 =1.
Из первых двух уравнений следует, что с^ =—2-, <х2 = —Ц—. Подставляя эти
4 4
выражения в последние два уравнения и решая их, получаем X! =-1, Х2 =2,
а! =-«-, а2 =—. Тогда из A6.22) находим искомое оптимальное гарантирующее
управление и *(/) = —(/-1) и, затем, минимальное значение функционала
гшп/г(«())=/г(и*(.)) = |.«
16.2.3. Синтез оптимальных линейных регуляторов
ПОСТАНОВКА ЗАДАЧИ
Пусть система A6.1), описывающая поведение модели объекта управления,
имеет вид
х«,з) = /1@ х(и$) + В(<)!/(/), A6.23)
где А(*), ВЦ) - матрицы размера (лхй), (лх^) соответственно. На допустимые
значения управления и@ ограничений не наложено, т.е. I/ = Я9.
508

Пусть функционал качества управления A6.2) изолированной траекторией
пучка квадратичный:
где 5A), л ~ неотрицательно определенные симметрические матрицы размера
(лхл); 0@ "" положительно определенная симметрическая матрица размера
{Я*4I х(*>5) ~~ траектория системы A6.23), исходящая из начального состояния
х(*о>*) = 5 • Зависимость матриц А, В,5, 0 от времени V непрерывная.' .
Качество управления пучком траекторий оценивается функционалом
A6.3):
М'о^о.иО)* = шах/(/0, *,«(•)),
зеоо
A6.25)
где а0 — множество возможных начальных состояний объекта управления. „
Пусть I - система компактных подмножеств Яп пространства состояний
объекта управления. Обозначим через. а@ сечение пучка траекторий в момент
времени /: о@ = [х е Кп \ х = *(*,$), 5 € а(/0)}.
Предположим, что в процессе управления пучком, траекторий в каждый
момент времени г используется информация о множестве о@ возможных
в данный момент времени состояний системы A6.23), т.е. управление строится
по принципу обратной связи: и@ = й(/,о@)>' € Т '(рис. 16.1)!
Множество И допустимых позиционных управлений пучком траекторий
образуют функции и: Т х I -> Кя, которые для каждого множества а0 из
Е'порождают такой пучок о@» <*(/0) = ао» что управление и@ = »(*, ст@)» ' «Т, является
допустимым управлением из &0.
Требуется найти такую функцию ш*Г(*96)еи9 которая'для каждого
множества а из 2 порождает оптимальное гарантирующее программное
управление и*(), минимизирующее функционал A6.25):
М'<ь<*<ь«*г) = Л-('(ь<*<ьи*(•))- тЬ тах/(/0,5,!/(•)),
где и*@ = «*гМ0). /€Г,для всех а0€Е.
1
*('о>*)
^^¦ = А(()х((,з) + В(()и(()
) = «Г/.
стГ/»
и(/,ог)
а</)
Рис. 16.1
509

НАХОЖДЕНИЕ ОПТИМАЛЬНОГО ГАРАНТИРУЮЩЕГО УПРАВЛЕНИЯ
Утверждение [36]. Оптимальное гарантирующее позиционное управление
«*г ('><К0) пучком траекторий линейной системы A6.23) с критерием качества
A6.24) имеет вид
«*г СМ')) = «*г (/,хг@) = О-Ч0^@Ф@хг@, A6.26)
где хг@ — оценка вектора возможных состояний системы, которая выбирается из
выпуклой оболочки со о{() множества о@ по формуле
хг@ = агатах тш (хгФ@ х + (х - х)тЧ«) (х - х)}. A6.27)
Х€СОО</) Х€аЮ
Здесь Ф@ — симметрическая порядка п матрица коэффициентов усиления
оптимального регулятора (см. разд. 9.2.3), удовлетворяющая уравнению
оКО--^(/)Ф@-<1КОДО-Ф@5@0"ЧО^г(ОФ@ + ^@, ф(>1) = -л; A6.28)
*Р(*) — симметрическая порядка п матрица, удовлетворяющая уравнению
Ф@ = -АТ(*)П0-ЧЧ'МЮ+Ф@ЯЮСГЧ')*Г@ФA), уй) = о. A6.29)
Из условий A6.26), A6.27) следует, что оптимальное позиционное
управление 0*г зависит от множества о@ как сложная функция и*Г =ш*Г(*>хГ),
хг=хг(/,о(/)).
Для нахождение этого управления достаточно:
1) решить уравнения A6.8), A6.29);
2) из условия A6.27) определить вектор хг(/,о), который играет роль
оценки состояния системы (сравнить с разд. 3.1.2);
3) найти оптимальное гарантирующее управление в виде линейного
регулятора A6.26).
Замечания.
1. В результате решения уравнений A6.28), A6.29) определяются матрицы
Ф@ и Ф(/) квадратичной функции
Р(/,х,х) = -|хгФ@х-1(:с-х)гЧ'@(х-х). A6.30)
С помощью этой функции условие A6.27) можно записать в виде
хг = агвтш тах р(*,х,х). A6.31)
хесоо(/) ХесЮ
В начальный момент времени значение функции Р((о,х0,х0) равно
значению Л'<ьх<ь"@) функционала A6.24), вычисленного на управлении к(»)>
510

рое является оптимальным для траектории, исходящей из начального состояния
х0. Если оценка х совпадает с вектором х, то функция р(*,х,х) оказывается
равной функции Беллмана <рБ(/,х), в частности:
Р('о>*<ь*о) = ФБ('<ь*о) = Я?"?, /('<ъ*о>"())-
2. Если система подмножеств 2 состоит из центрально симметричных
подмножеств пространства состояний ^ ив множестве со а найдется точка
хг(а), удовлетворяющая условию [36]:
УЮхгМ-СОД+ «*))-4°),
где г(о) — центр симметрии множества обЕ, то в качестве оценки хг(г)
в управлении A6.26) нужно брать именно эту точку, т.е. хг(/) = хг(о(/)).
Действительно, при выборе оценки точка максимума по х функции A6.30)
совпадает с центром симметрии множества о, что из соображений симметрии
обеспечивает выполнение условия A6.27).
Пример 16.3. Найти оптимальное гарантирующее управление системой:
х,@ = х2(/), «(Осе Л,
х2(/)«и@, 0*/*1,
с квадратичным критерием /= —|ы2(/)А+—*20)> если множество а0 возмож-
ных начальных состояний ограничено эллипсом:
М^1-^10J+2А)(^1-г10)(^2-^20) + Й)(х2~«20J^и Ц>>0, %С0>Ь^.
Используя найденное позиционное управление, найти оптимальное
гарантирующее программное управление, если множество <т0 является кругом:
Х!2 + (х2-1J^2.
? Сравнивая с постановкой задачи A6.23), A6.24), имеем
н: I)- '-о- '-• «-¦ ч: о)-
Записываем уравнения A6.28), A6.29):
Фи ~Ч>12 ж°* Ф12+911-ФПФ22 1Ь^> Ф22 + 2ф12~Ф22 -°>
«11©—1, Ф120) = °> ФяФ-О,
фц +ф122 =0, ф12 +УП +ФПФ22 *°» *22 +2\|/12 +ФИ2 *0,
«пГО-тоГО-УиСО-О.
511

Решая эти уравнения, получаем
1 х х2
Ф11 @ = -^> Ф12@ = Ф21<0 = "-> Ф22<0 = "у >
х3 х4 х5
Ч>11 (О = -—• 4*12@ = 4*21@ = -^. 4*22@ = -^.
где х = 1-/, 6 = 1 +—.
Функция A6.30) для данного примера имеет вид
1 X3 А А X3 А А 5
р(/,х,х)=-(х! + хх2J -—(х{ +хх2)(*1 +тх2)+—(^ + хх2J, A6.32)
«*г (*,а@) = «*Г (/Л@)-О"!@*Г»Ф@хг«-
= Ф12@ *1 @ + Ф22@ *2@ = *1@ -^*2<0• A6.33)
О О
Так как множество о0 возможных начальных состояний является эллипсом
(точнее частью плоскости 0Х]Х2, ограниченной эллипсом), то при любом
допустимом программном управлении множество а@ возможных состояний в момент
г является эллипсом:
а@ (*1" *1@J + 2»(Г) (X! - гШ (х2 - *2@) + с@ (х2 - г2@J * 1,
где ^@, г2@ "~ координаты центра эллипса а(/), удовлетворяющие
уравнениям:
^1@ = ^2@, *1('о) = *10>
г2@ = «С). ^о) = ^2о»
а коэффициенты а, Ь, с изменяются со временем:
а@ = 0, *@ = -«@, с(/) = -2^@,
с@) = йо, *@) = ^, с@) = «),
т.е. а@ = «о, &@ = *о-*о'> с(/) = с0 -2*0' +До'2-
Для оптимальности управления »*г (/,х@) нужно выбрать оценки х{, х2
так, чтобы выполнялось условие A6.31). Квадратичная функция A6.32) достигает
своего наибольшего значения на границе множества о(У). Решая задачу
максимизации функции р(/,х,х) по х = (Х(,х2) при условии
*(*1 -1\J+2Ь(хх -*1)(х2 -г2) + с(х2 -12J =1,
512

получаем, что максимум функции может достигаться в двух точках А и В,
координаты которых
Х\А = *1 +
Х\В = 1\ -
Х(с-Ьх)
д '
Х(с-Ьх)
Х2А = *2 +
Х2В =*2-
Х(ах-Ь)
А '
Х(ах-Ь)
где Х =
70(с~6тJ+2*(с-*т)(*т-*) + с(вт-*J
, А = ас-Ь2
Минимизируя по х наибольшее из двух значений функции A6.32) в точках
А и В, получаем, что искомые оценки A6.31) должны удовлетворять условию
*1-**2 =
1\ +т*2 +
Х(ах2 -2Ьх + с)
, *1+**2>
тгХ(ах2-21п + с)
ЗД
A6.34)
38(^1 +тг2) , , .т3А,(ат2-2*г + с)
^ ' I «1 +Т^ I * ^ '
Х(ат2-26т + с) т3Х(дт2-2^г + с)
Получим теперь конкретный вид оптимального гарантирующего
программного управления !/*(•) для случая, когда множество а0 является кругом
1 + Н
*1 +(лЪ-1J*2. В этом случае я(/)=т> *@в-Г. сО=—т—, г1о=°> *20=1-
Из условия A6.34) получаем х{ -хх2 =—- * \* • Следовательно, можно
положить *Ю--2Ц&. *,Ю-2&&.
Тогда оптимальное гарантирующее управление будет иметь вид
т
гДе ^1,^2"" координаты центра эллипса а@.
Центр множества о@ описывается уравнениями
*1@-*2<0. г,@) = 0,
-г
Приводим эту систему к одному уравнению второго порядка:
513

решения которого ищем в виде гх = х*, х = 1-л Подставляя гх = х* в уравнение,
%-к 2кхк~^
получаем Щ-1)х*~2 =——+ . Следовательно, к(к-\) = -3 + Зк. Отсюда
т2 т
к = 1 или & = 3, а *1 = х или ^ = х3 - частные решения уравнения. Общее
решение имеет вид 1ХA) = Схт + С2тг. Отсюда %2(*) = -Сх -ЗС2х2, где С1э С2 —
произвольные постоянные. Выбираем произвольные постоянные так, чтобы
выполнялись начальные условия при / - 0 (или х = 1): ^(О) = Сх + С2 = 0,
г2@) = - Сх - ЗС2 = 1. Следовательно, Сх =—, С2 = —-. Таким образом, находим
траекторию центра множества о@:
Подставляя координаты центра эллипса в позиционное управление и*г (/,а@),
получаем оптимальное гарантирующее программное управление :
*/*(/) = -Зх = 3/-ЗЛ
16.3. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО В СРЕДНЕМ УПРАВЛЕНИЯ
163.1. Постановка задачи
Пусть на траекториях системы A6.1) задан функционал качества управления
A6.2). Качество управления и() е 2/0 пучком траекторий оценивается
функционалом
/,("(•)) = IФ) /<*,иО> *, A6.35)
а
где ф): а -» К - измеримая функция, принимающая только неотрицательные
значения, множество а возможных начальных состояний предполагается
измеримым.
При фиксированном управлении величина * представляет собой
\Ф)Ж
среднее взвешенное с весом ф) значение функционала A6.2). Величина
| ф)Ж обычно отбрасывается, так как не зависит от управления или считается
о
равной единице, т.е. весовая функция нормируется.
Требуется найти допустимое управление и*() е Щ, на котором
достигается минимум функционала A6.35):
514

/с(" * О) = пйп Г р<*)/<*,«(•))&. A6.36)
О
Такое управление и * (•) называется оптимальным в среднем.
163.2. Необходимые условия оптимальности
Утверждение [36]. Пусть и*() — оптимальное в среднем управление, а
М *(¦,$) ~~ соответствующий этому управлению пучок траекторий, описываемый
уравнением
Х(Г,5) = /(*,Д«,*),«*@), ^Г, A6.37)
х(*0,$) = $€о. A6.38)
Тогда существует вектор-функция ЧЧ/,$) = (Ч^ (/,$),..., Ч*л(/,$))г, удовлетворяющая
уравнениям
у^,)-^^^3»^^»), ,€Г,,У«1,..,„, A6.39)
Эху
с условиями
У/(ГьД) —а^У>,Д)), *€<т, У = 1,...,л, A6.40)
0Х;
для которой в каждой точке непрерывности управления и * (/) выполняется
соотношение
и * (/) = а1В шах Г р(*) #(/,т *),*(',*), и) Ж, A6.41)
а
л
где Я(/,У,х,и)=^ Ч*^*,$)/^*,х,и)-/0(*,х,и) -гамильтониан.
М
Соотношения A6.37)—A6.41) представляют собой краевую задачу для
системы 2/1 обыкновенных дифференциальных уравнений с параметром 5.
Методика решения этой задачи отличается от изложенной в разд. 9.1.2 только наличием
параметра 5 и условием A6.41) вместо максимума гамильтониана.
Замечание. Оптимальное в среднем управление и*с(/,х) с
полной обратной связью совпадает с оптимальным управлением «*(*,х)для
функционала A6.2). Действительно, как отмечалось в разд. 9.2, управление к*(/,х)
порождает оптимальные траектории для каждого начального состояния
*(*о)€ Яп, в том числе и для каждого состояния х(/о)-5 из заданного
множества асЯл, т.е. 7($,1г*(/,х))^/($,«(/, х)) для всех зеа и любого управления
и(их)еип. Следовательно,
515

/с(«*(/,*)) = /р(*)/(«.и¦ (*,*))& <; \рШеъ«('.х))А
а о
и оптимальное управление »*(/,*) с полной обратной связью является
оптимальным в среднем управлением для любого пучка траекторий системы A6.1).
Пример 16.4. Даны модель объекта управления
*,(*,*) = х2(*,5), ^(О,*) = 5 € а = [0,1],
Х2(*,5) = 1/@, Х2@,5) = 0
и функционал
/СИ))=//(^И())Л^1ШП,
а
1 ! 1
где /E,и()) = ^1/2@Л+^х12A,5).
Требуется найти оптимальное в среднем программное управление.
Р(*) = 1
П Здесь х = (хих2)теЯ29 /€[0,1], иеЯ, /°(*,х,а) = ±и2, Р(х)=±хх2,
1. Составляем гамильтониан: Я(/, Ч^х, и) = Ч^ (/, 5) х2 + Ч*2 (*, $) и - — и2.
2. Находим структуру оптимального управления из A6.41):
1/*@ = аплпах| /Гу1(/,*)х2(/,5) + У2Л»)«-|«2]* =/^ ('>*)<&.A6.42)
3. Записываем краевую задачу A6.37)—A6.40):
х\(*>з) = Х2(*,з)> *2(М) = |/*@, х1@,5) = $ео = [0,\], х2@,5) = 0,
Ф^-О, *2(^5) = -^(/,5), ^1A,5) = -Х1A,5), ^2A,5) = 0. A6.43)
Очевидно, что функция х2(*9з) не зависит от 5, а функция Ч*\A,5) не
зависит от /. Поэтому будем искать неизвестные функции в A6.43) в виде
х1(^5) = 5 + Л'|@, х2A9з) = Х2A). Подставляя в A6.43), получаем
Х{(*) = Х2(*), *2(/) = 1/*(Г), *!«>) = 0, *2@) = 0. A6.44)
Из остальных уравнений в A6.43) следует, что
4^,5) = -С-5, ^2(/,5) = (С + 5)(/-1),
где С = -^A). Управление A6.42) имеет вид
516"

»*(<)-/(С + *)(/-1)Л«Гс + |)</-1). A6.45)
Решая A6.44) совместно с A6.45), получаем
При / = 1 имеем А'1A) = --[с+--|. Отсюда С = -^ A) = —. Тогда из A6.45)
получаем искомое оптимальное в среднем программное управление:
3
и *(/)=—(/_ 1) 9 а также минимальное значение функционала:
4
1ШП/С(|/0) = /С(|/*0)=-|."
16.3.3. Синтез оптимальных линейных регуляторов
ПОСТАНОВКА ЗАДАЧИ
Пусть система A6.1), описывающая поведение модели объекта управления,
имеет вид A6.23). На допустимые значения управления и(/) ограничений не
наложено, т.е. (/ = Яд.
Пусть функционал A6.2) качества управления изолированной траекторией
пучка квадратичный A6.24).
Качество управления пучком траекторий оценивается функционалом A6.3):
/с('о,°о>"())= {/('о,*,**))*, A6.46)
где а0 - множество возможных начальных состояний объекта управления.
Пусть 2 — система измеримых подмножеств Кп пространства состояний
объекта управления. Множество М допустимых позиционных управлений
пучком траекторий образуют функции и: Т х Е -> Я9, которые для каждого
множества <т0 из Е порождают такой пучок а@, в('о) = ао> что управление
"(О = »(/,а(/)), / е Т, является допустимым программным управлением из 2/0.
Требуется найти такую функцию «*с(/,а)еЖ, которая для каждого
множества а из Е порождает оптимальное в среднем программное управление
"* О, минимизирующее функционал A6.46):
/сDь <*<)>« *с) = 'с('(ь<*0,«*(•)) = Я?1п. Г А'о. *.«<•)) Ж,
и( )е#о *
где и»@ = в *с AМ()), (€ Г, для всех о0 « *•
517

НАХОЖДЕНИЕ ОПТИМАЛЬНОГО В СРЕДНЕМ УПРАВЛЕНИЯ
Утверждение [36]. Оптимальное в среднем позиционное управление
и*с (/,<?(/)) пучком траекторий линейной системы A6.23) с критерием качества
A6.24) имеет вид
и *с (*М0) = «*с <>,*с(») - 0-1(*)ВТ«)Ф«)хс(*), A6.47)
где хс({) — оценка вектора состояния системы, которая выбирается из выпуклой
оболочки со а(/) множества а(/) по формуле
*с(')= агатах / [хТФ(*)х + (х-х)ТЧ'(*)(х-х)]е1х. A6.48)
хесоо@ ^
Здесь Ф@ — симметрическая порядка п матрица коэффициентов усиления
оптимального регулятора (см. разд. 9.2.3), удовлетворяющая уравнению A6.28);
4/@ — симметрическая порядка п матрица, удовлетворяющая уравнению A6.29).
Из условий A6.47), A6.48) следует, что оптимальное управление и *с
зависит от множества а@ как сложная функция и*с =и*с (*,хс) > *с = *с('»а@) •
Замечание. Из условий A6.47), A6.48) следует, что оптимальное
в среднем управление пучком траекторий линейной системы с квадратичным
критерием качества совпадает с оптимальным управлением изолированной
траекторией, которую описывает с течением времени геометрический центр тяжести
множества возможных в текущий момент времени состояний системы [33,36]:
\х<Ьс
*с(/)=^г—. A6.49)
I ах
Для нахождения этого управления достаточно:
1) решить уравнения A6.28), A6.29);
2) из условия A6.48) (или A6.49)) определить вектор хс(/,а), который
играет роль оценки состояния системы;
3) найти оптимальное в среднем управление в виде линейного регулятора
A6.47).
Пример 16.5. Найти оптимальное в среднем позиционное управление сие-
темой
*2(') = и@, 0*/*1,
с квадратичным критерием качества
/=1/|/2(/)Л+1х12A),
* о *
если множество сг0 возможных начальных состояний ограничено эллипсом:
^(*1-*10J+^(*1-Ы(*2-*20) + С0(*2-г20J*1, % > 0 , *0 С0 > Ь$.
518

? Уравнение A6.28) для данной задачи было решено в примере 16.4.
Поэтому оптимальное в среднем управление имеет вид
«•с(/,о@) = -|«1«-у«2М.
где *1(')> *2@ ~" координаты центра эллипса о(/)- Найдем конкретный вид
оптимального в среднем программного управления и*с(»), если множество а0
является кругом: Х!2+(х2-1J^2.
В этом случае координаты ^, *2 центра множества о(/) удовлетворяют
уравнениям
*<О«*20). ^1@) = О,
«2@—^«-Т*». ^2@) = 1,
О О
Для функции ^(/) имеем уравнение второго порядка
«10> - -7&1« + **1«). *@) = 0, «@) = 1.
функция %(*) = х, х = 1 - /, является частным решением этого уравнения.
Общее решение будем искать в виде 1\(*) = ту(*). Относительно функции
( х3 1
у(Г) получаем уравнение %у-\ 2 У = 0. Интегрируя, получаем
х3 х2
у^)-Сх +С,2|"~т1- Следовательно, ^ = С1Х-С2 +С2 —, г2 =-^1 -С2—.
Находим значения произвольных постоянных Сь С2, удовлетворяющие
начальным условиям при / = 0 (х = 1):
г1@) = С1-С2+|с2=0, г2@) = -С1-1с2=1.
5 3
Следовательно, С{ = -~; С2 =---. Таким образом, траектория, которую описы-
8 4
вает центр множества о@, имеет вид
/л 3 5т *3 /.ч 5 3*2
*(')=Г7' *2(') = 8+ — *
Подставляя эти выражения в позиционное управление и *с, получаем
оптимальное в среднем программное управление
4 4
519

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
16.1. Найти оптимальное гарантирующее позиционное управление
и *г (/,ст) пучком траекторий в задаче
х = и, 1/(/)еЛ, 0*/<11,
1 о ^
если известно, что множество а возможных состояний в каждый момент
времени является отрезком. Найти оптимальное гарантирующее программное
управление и *г @, если множество возможных начальных состояний является отрезком
[0,1].
16.2. Найти оптимальное гарантирующее позиционное управление
»*г('»а) системой
хх = и, и(/) € Я,
х2=*ь 0 ^/^2,
1 2 1
с критерием качества / = —|и2@<# + т*22B)> если известно, что в каждый
2 о 2
момент времени множество а возможных состояний системы является
некоторым отрезком АВ на плоскости Ох{х2. Найти оптимальное гарантирующее
программное управление, если множество возможных начальных состояний является
отрезком оси Охх: а(/0) = {(*ь*2) € Я2 | 0 ^ хх й 2, х2 = 0 }.
16.3. Решить задачу 2, если в каждый момент времени множество
возможных начальных состояний системы является треугольником ЛВС на плоскости
0*1*2-
16.4. Найти оптимальное гарантирующее позиционное управление
и\ (/,а) системой
хх = и, и(/) € Л,
*2=*1> 0 ^/^2,
с критерием качества /= — | и2(/)Л+—*12B)+—Х2B)> если известно, что
2 0 2 2
в каждый момент времени множество а возможных состояний системы является
некоторым отрезком на плоскости Оххх2.
16.5. В условиях задачи 1 найти соответственно оптимальное в среднем
позиционное управление »*с(/,а) и оптимальное в среднем программное
управление и *с (/).
16.6. В условиях задачи 2 найти соответственно оптимальное в среднем
позиционное «*с (/,а) и программное и*с (/) управления.
16.7. В условиях задачи 3 найти соответственно оптимальное в среднем
позиционное и*с (*,ст) управление.
16.8. В условиях задачи 4 найти соответственно оптимальное в среднем
позиционное и *с (/,а) управление.
520

Глава 17. СИНТЕЗ ОПТИМАЛЬНЫХ НЕПРЕРЫВНЫХ
СИСТЕМ ПО МИНИМАКСНОМУ КРИТЕРИЮ
17.1. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО ПРОГРАММНОГО УПРАВЛЕНИЯ
17.1.1. Постановка задачи
Пусть поведение модели объекта управления описывается обыкновенным
дифференциальным уравнением
*@ = Д',*@,и@^@), *('о) = *о, A7Л)
где х - вектор состояния системы, х = (хь..,хпУ еКп, и - вектор управления
первого игрока (оперирующей стороны), ие1/ дЛ*; V — вектор управления
второго игрока (противника), уеУ сЛг;/ - время, ^€Г = [/0,^] — промежуток
времени функционирования системы, моменты /0 начала и Ц окончания процесса
управления фиксированы; /(*,*, ы,у):ТхЯ"х(/хУ->Кп — непрерывно
дифференцируемая вектор-функция / = (/х,...,/^.
Движение системы A7.1) происходит под управлением двух сторон (или
двух игроков). Первая оперирующая сторона (первый игрок) воздействует на
систему, задавая управление и, вторая оперирующая сторона (второй игрок)
влияет на систему, выбирая управление V.
Предполагается, что при выборе управления каждый из игроков
располагает информацией только о времени /, т.е. рассматриваются так называемые
программные стратегии управления.
Множества допустимых программных управлений и0, ^ образуют
кусочно-непрерывные на Т функции «(•), у(-) со значениями в множествах I/, V
соответственно. Элементы множеств й<0, 0^ будем называть программными
управлениями первого и второго игроков соответственно. Предполагаем, что
каждой паре (и(),у()) допустимых управлений и() е &0, у(-) е <К0 отвечает
единственная непрерывная кусочно-дифференцируемая функция х: Т -+ К",
удовлетворяющая почти всюду на Т уравнению движения A7.1) при начальном
условии хA0) = х0. Эту траекторию движения будем обозначать
х@ = х(г, /0, Хо, и(), у(-)). Заметим, что для существования единственного решения
уравнения A7.1) достаточно выполнения ограничения:
||/(/,х,и,у)||^СA + ||х||) У(/,х,1/,у)€ГхД"х#хК.
На множестве допустимых управлений #о х ^о зададим функционал
качества управления:
<0
521

где /°(/,х,1/,у), Г(х) - заданные непрерывно дифференцируемые функции, а
*(/) = х(*;*о,Хо,и{\у(-)) - траектория движения, соответствующая управлениям */(•)
иЧ).
При выборе управлений игроки руководствуются противоположными
целями. Цель первого игрока — минимизировать критерий качества A7.2), цель
второго — максимизировать его. В соответствии с терминологией, принятой в
теории игр [32], функционал A7.2) называют платой игры, т.е. первый игрок
платит второму /(*/(•),у()) условных единиц. Первый игрок стремится найти
допустимое управление */*(•), минимизирующее плату игры при самом
неблагоприятном для себя выборе стратегии V * (•) вторым игроком (противником):
/,(«*()) = ^ /,(»()), A7.3)
где /1 (*<(•)) — гарантированная плата первого игрока второму при выборе
управления !/(•):
Второй игрок преследует противоположную цель, т.е. ищет допустимое
управление, максимизирующее показатель
где /2 04)) — гарантированная оплата второго игрока, которую он получает при
выборе управления у{):
Ш))=да/(«(Н))-
Показатели 1Х и /2 гарантированных результатов игроков связаны
неравенством [21,32]:
пэд! 1Х (*/(.)) = пэд! тах /(ЧН)) * ^^7(«(^())= та^/2(у(.)).
Предполагается, что имеет место точное равенство
пт^ тах 7A/(^0)= тах^/(и(^0). A7.5)
В этом случае говорят, что игра имеет седловую точку.
Требуется найти допустимые управления «*(•) и у*(«), удовлетворяющие
условию
7(Н*(>М0) = дао^ахп/(^Ч))%Гпда/(«(Н)). 07.6)
т.е. доставляющие минимакс (и максимин) функционалу A7.2).
Искомые функции г/ * (•) и V * (•) будем называть оптимальными
программными управлениями, а значение 1(и * (•), V * (•)) в A7.6) - ценой игры.
522

17.1.2. Необходимые условия оптимальности
Утверждение [12]. Пусть пара («*(•)»?*(•)) допустимых управлений
удовлетворяет условию A7.6), а х * (•) — соответствующая этим управлениям
траектория движения системы A7.1). Тогда существует вектор-функция
Ч/(/) = (ч/1(гХ...,Ч'л(/))г, удовлетворяющая уравнениям
ФД» = -а*М4**D"*DУ*(')), / = 1>..>й, ,.Г. A7.7)
дх,
с условиями
Ш)--*&Ь&. 1-й.». A7.8)
дХ;
такая, что в каждой точке непрерывности функций и * (/) и V * (/) выполняется
условие
тах тт Н1$,Щ,х * (^н,у) = НЬЩх * (&« * DV * (/)) =
нес/ УвК
= тт тахя(/,Ч>Dх*(/),1/,у), A7.9)
V е К к € (/
где
Н(*,Ч,х,и,у)=% ^Л(/,х,1/,у)-/°(/,х,1/,у) A7.10)
/-1
— гамильтониан системы, Ч^/) — вектор вспомогательных переменных.
Соотношения A7.1), A7.7)—A7.9) представляют собой двухточечную
краевую задачу для нахождения оптимальных управлений и оптимальной траектории.
Эта задача аналогична рассмотренной в разд. 9.1.
АЛГОРИТМ ПРИМЕНЕНИЯ НЕОБХОДИМЫХ УСЛОВИЙ ОПТИМАЛЬНОСТИ
1. Составить гамильтониан A7.10).
2. Найти структуру оптимальных управлений и*,у* из условия A7.9), т.е.
выразить управления как функции вектора вспомогательных переменных и
вектора состояния х:
«*(>)= и*Ы').**(')), у^у^М'),*'®)- A7.11)
3. Составить систему канонических уравнений
т-^4®'*®''®**®-/&.*•№&
эчл
у*@), / = 1,.,л; A7.12)
^Мш-№^^х*^и^>^ / = 1 п
дх,
523

4. Дополнить систему A7.12) краевыми условиями
**Ы-*Ь. %М = ~дГ{Х*^> '-и*- A7.13)
дх1
5. Решить двухточечную краевую задачу A7.12), A7.13). В результате
определяется траектория х*@ и функция Ч/(/), подставляя которые в A7.11),
получаем управления и * (/) и V * (/). На этих управлениях может достигаться мини-
макс (максимин) A7.6) функционала A7.2).
Замечания.
1. Условие A7.5) существования седловой точки дифференциальной игры
отвечает ситуации равновесия, при которой информированность каждого из
игроков не имеет ценности. Первый игрок может до начала игры сообщить
противнику свое управление и * (•) и при этом результат игры не изменится. Такая
ситуация складывается далеко не во всех случаях (см. пример 17.1).
2. Условие существования седловой точки гамильтониана Н по
допустимым значениям управлений и и V выполняется, когда, например, переменные и
и V входят в уравнение движения раздельно, т.е. функции / и /° представимы
в виде:
/(',*,«, V) = /%х,и)+ /*(/,*, у), /°{*,х,и,у) = /01(',*,«)+ /02(',*,у).
Пример 17.1. Показать, что условие A7.5) существования седловой точки
не выполняется для следующей игры:
х«) = [*(/)- у(*)]2, *@) = 0,
0<$и(/)<;1, 0<;у(/)<;1, 0</<1,
/(и(.Ы.)) = *A).
? Рассмотрим два варианта информированности игроков. В первом случае
— минорантная игра [32] — первый игрок сообщает заранее свою стратегию
управления второму игроку, который на основании этой информации выбирает
свою стратегию управления. Такая игра, вообще говоря, не выгодна первому
игроку. Во втором случае — мажорантная игра [32] - происходит все наоборот, т.е.
второй игрок заранее (до начала игры) сообщает первому свою стратегию
управления, что выгодно для первого игрока.
Подсчитаем значение платы первого игрока в результате этих двух
вариантов разыгрывания. Критерий качества управления можно представить в виде
/ = хA)=/[|/(/)-у@]2Л. A7.14)
о
Если второй сообщит первому до начала игры свое управление у(), то
первый игрок возьмет управление и(/)=у(/), 0^/^1, и получит нулевое значение
показателя качества. Следовательно,
/2(У())=1^|./(«(Н)) = 0
для любого управления у() € Го •
524

Наоборот, если первый игрок сообщит заранее второму свое управление
Г1, 0*1/@<0,5
и(), то второй игрок выберет управление у(/) = \ и получит выиг-
[0, 0,5<;и@*1
рыш не меньше, чем 0,25. Следовательно,
1М)) = г^*(«(;Ы))±<>&
для любого управления !/(•) € 2/0.
Таким образом, в рассматриваемой игре условие A7.5) не выполняется:
0 = тах тт /(и(), у()) < тт тах 1(и{\ у(-)) = 0,25 ,
т.е. предварительная информация о намерениях противника имеет существенное
значение. ¦
Пример 17.2. Даны модель объекта управления
*(/)*= и(/)-у@, х@) = *о,
где х € Я, иеЯ, уеЯ, г € [0,1],и функционал
/=1[4)-^)]л4^)-
о 1
Требуется найти оптимальные управления и*(), у*() и
соответствующую им траекторию **(•), на которых достигается минимакс функционала.
П Сравнивая данный пример с общей постановкой задачи, имеем
/(/,Х,И,У) = 1/-У, /°(/,Х,1/,у)=1/2-2у2, Г(Х)=±Х2,
1. Составляем гамильтониан: Н = ^(и - у) - (и2 - 2у2).
2. Находим минимакс гамильтониана по переменным и и V. Так как
ограничения на управление отсутствуют, можно использовать следующие
необходимые условия экстремума:
^=*(*)-2« = о =* «*@=^;
Найденные управления отвечают седловой точке гамильтониана, так как
матрица производных второго порядка (матрица Гессе)
<»"Н-„2 9
является знаконеопределенной.
525

3. Записываем уравнения системы A7.12):
2 4
Ф(/) = 0.
4. Добавляем к системе дифференциальных уравнений краевые условия
х@) = *о, Щ--&Ш--4).
ОХ
5. Решаем полученную в пп. 3,4 краевую задачу. Так как функция Ч/(/)
постоянна, то ч/(/)и -хA). Интегрируя уравнение движения, находим
При / = 1 определяем конечное состояние:
хA)=Хо-^ => *)-<*.
Таким образом, находим искомые оптимальные управления
«*(о=-^. »•«—а,
соответствующую этим управлениям траекторию: **(')= 1-т*о и ченУ игры
Пример 17.3. Даны модель объекта управления
х@=«(/)-у(/), *@)-2.
| «(/) | ^ 2, |у(г)|$1, 05/51,
и функционал
Требуется найти оптимальные программные управления игроков.
? Сравнивая условия примера с общей постановкой задачи, имеем
х2
/(/,Х,1/,У)=1/-У, /°(',*,^) = 0, *Х*)=—,
[/ = [-2,2], К = [-1,1], /0=0, /1-1.
1. Составляем гамильтониан: Н = Ч/(и - у).
2. Находим структуру оптимальных управлений игроков из условия A7.9).
Если Ч/(/)<0, то ы*(/) = -2, у*(/) = -1. Если Ч/(/)>0, то и*(/)=2, у*(/)=1.
Следовательно, и * (/) = 2 8щп Ч/(/), V * (/) = я$п ч/(/).
526

3. Записываем уравнения системы A7.12):
х(/) = я8пЧ'(/),
Ч>(/) = 0.
4. Краевые условия для уравнений п. 3 имеют вид
х@) = 2, ч/A) = -*A).
5. Решаем полученную в пп 3,4 краевую задачу. Если хA)>0, то Ч/(/)<0,
и*(/) = -2, у*@ = -1,*(/)=2-*.
Если хA)<0,тоЧ/(/)>0, и*(г)=2, у*(/)=1, х(/) = 2 + /.
Из двух траекторий х(/) = 2±/ выбираем траекторию х*(/) = 2-/, так как
х*A) = 1>0.
Таким образом, получаем оптимальные программные управления игроков
и*(/) = -2, у*(/) = -1; оптимальную траекторию х*(/)=2-/ и минимаксное
(максиминное) значение цены игры /*=—.¦
17.2. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО ПОЗИЦИОННОГО УПРАВЛЕНИЯ
17.2.1. Постановка задачи
Пусть поведение модели объекта управления описывается обыкновенным
дифференциальным уравнением
*@ = Ж*('),и@,ЧО), A7.15)
где х - вектор состояния системы, х = (хь..,хпУ еЯп, и — вектор управления
первого игрока (оперирующей стороны), ие1/ ^Яд; V - вектор управления
второго игрока (противника), уеУ^Яг; г - время, ^€7, = [/'0,/1]- промежуток
времени функционирования системы, моменты /0 начала и 4 окончания процесса
управления фиксированы; /(/,х,и,у):ТхЯп х[/хУ -+ Яп - непрерывно
дифференцируемая вектор-функция / = (/ь».,Л)Г'
Начальное условие х(/0) = х0 еЯп заранее не задано.
Предполагается, что при выборе управления каждый из игроков использует
информацию о времени * и векторе состояния, т.е. рассматриваются так
называемые позиционные управления или управления с полной обратной связью.
Множества 2/п, <Уп допустимых управлений с полной обратной связью
первого и второго игроков соответственно образуют функции »(/,х): ТхЯп ->Gи
*(*>х) '-ТхЯп -+У, которые для любых начальных условий х(/0)« х<) порождают
траекторию х(») системы A7.15) и допустимые программные управления
4)е &ъ, у{) € *о такие, что и(*) = »(',х(/)), у(/) = ?(/,х(/)) для всех г € Т.
527

Качество позиционных управлений оценивается функционалом
'(«, ")= }/°М*М'Ы0)* + *ОД'1)). A7.16)
где /°(/,х,1/,у), ^(х) — заданные непрерывно дифференцируемые функции.
Каждой паре (и,у)е&пх<Гп допустимых позиционных управлений « = «(/,х),
у = у(*,х) функционал A7.16) ставит в соответствие значение /(и, у), которое
вычисляется по программным управлениям иA) = к(/,х(/)), у(/) = у(/,х(/)), / € Г, и
траектории х(/) = х(/; /0,м(),у()), порожденными позиционными управлениями.
Требуется найти такие функции »*(/,х)еЖ11 и у*(/,х)б(Кл, что
/(»*, V *) = пип тах /(«, у) = тах тт /(», у) A7.17)
при любых начальных условиях.
Функции и * (/, х) е й<л, р * (/, х) € (Кл называются оптимальными
позиционными управлениями или оптимальными управлениями с полной обратной связью.
Замечани е. Траектории движения системы A7.15) для негладких
управлений к*(/,х) и )>*(/,х), определяются в результате пошаговой процедуры
[21] следующим образом. Промежуток времени Т разбивается на малые
подынтервалы Р/,/,+1] длиной е, на каждом из которых управления игроков считаются
постоянными. Предел получаемых при кусочно-постоянных управлениях
решений A7.15), когда е->+0, принимается за траекторию движения системы
A7.15), соответствующую позиционным управлениям »*(/,х) и у*(/,х).
17.2.2. Уравнение Айзекса
Достаточным условием минимакса (максимина) функционала A7.16)
является уравнение Айзекса для непрерывных детерминированных систем [1,21].
Утверждение [21]. Если существует функция <р(*,х), непрерывная вместе
со своими частными производными первого порядка, удовлетворяющая уравнению
Айзекса с граничным условием
тш тах {М^ + уМ^ /^и, у)- /%х,и,у)\ =
I ОХ /=1 аХ/ )
= тах тт
ивЦ усУ
<р(/1,х) = -/'(х) УхбЛл, A7.18)
и управления и * (*, х), V * (/, х), удовлетворяющие условиям
528

#(/,Фх(/,х),х,«*(/,х),у*(/,х)) = шах ттН(*,ч>х(*,х\х9и,у) =
ие1/ V е V
= тт тах#(/,фх(/,х),х,и,у), A7.19)
где
то дифференциальная игра A7.15)-A7.17) имеет седловую точку A7.17), а
управления являются оптимальными управлениями с полной обратной связью, при этом
цена игры определяется равенством /(в*, V *) = - фС*о,х0).
При решении задачи синтеза оптимального управления на основе
достаточных условий в первую очередь определяется структура управлений «*(/,х),
?*(/,*) из условия A7.19) минимакса (максимина) функции #(/,фх,х,и,у) по
переменным и и V. Искомые управления выражаются через производные
функции ф(/,х). После подстановки найденных выражений в A7.18) задача сводится к
решению дифференциального уравнения с частными производными первого
порядка. В результате решения определяется функция ф(/,х), по которой
окончательно находятся оптимальные управления игроков.
Пример 17.4. Для задачи
х(/)=и(/)-у(/),
|и@|<12, |т{/)|*1, 0*/<11,
/ = 1х2AЬгэд1 шах
требуется найти оптимальные позиционные управления и * (/,х), V * (/,х).
П Сравнивая условия примера с общей постановкой задачи, имеем
/(/,х,и,у) = 1/-у, /°(/9дс;«,у)-09 Г(х) = ^х29
(/ = [-2,2], Г = [-1,1], /0=0, /1-1.
1. Записываем уравнение Айзекса и граничное условие A7.18):
„ах гм (М^+М*1(и_уI =
. а*, „ах /12^+М^(н_у)} = 0,
|у]*1 \и\*2 \ Ы дХ У )
ч>М=-±*2.
529

2. Находим структуру оптимальных управлений игроков (см. пример 17.3):
«*(/,х)=2-я$п<рх(*,х), р*(*,х) = &\щч>х(*,х).
3. Подставляем эти выражения в уравнение Айзекса:
фД'»*)+| Фх(',*) 1 = 0, фA,х) = -- х2.
4. Разобьем плоскость переменных /, х на три области А, Б, В, где
производная фх(/,х) больше, меньше или равна нулю соответственно. В области А9 где
Фх(/,х) > 0, уравнение имеет решение
В области Б, где фх(*,х) < 0, решение уравнения имеет вид
ф(/,х) = -1(х + /-1J.
Найдем теперь границы указанных областей (см. рис 17.1):
А: фх(/,х) = -х-/ + 1>0 => х</-1, 0^/^1;
Б: фх(/,х) = -х-/ + 1<0 => 1-/<х, 0^/^1.
X '
1
о"
-1
ч. Б и* = -2, у* = -1
^\* = 1-г
и* = 0, у* = 0 ^^
^х-/-1
<^А "* = 2, у* = 1
1
/
Рис. 17.1
В области #, где /-1:^x^1-/, 0^/^1, производные функции ф(/,х)
равны нулю. Следовательно, она постоянна и равна нулю, так как из граничного
условия имеем ф(/,0) = 0. Таким образом, функция ф(*,х), удовлетворяющая
уравнению Айзекса, и оптимальные управления игроков имеют вид
530

фМ=
-г(* + 1-02> х<*-1, 0<1/*1,
О, Г-1*х*1-/, 0***1,
-гС^ + ^-1J» !-/<*, 0*/*1,
'М-
2, х</-1, 0***1,
О, /-1*х*1-/, 0*/*1,
-2Э 1-/<х, 0 ***1;
'М-
[1, х<г-\, 0*/*1,
О, /-1*х*1-/, 0***1,
-1, 1-*<х, 0***1;
В области В управления и * и V * можно выбирать произвольно среди
допустимых значений. В указанных выше формулах взято нулевое значение. Если в
области В взять другие значения управлений, то результат от этого не изменится.
Заметим, что для начального состояния х@)= 2 оптимальные управления и
траектория совпадают с найденными в примере 17.3Л
17.2.3. Синтез оптимальных линейных ре1уляторов
Пусть система A7.15) описывающая поведение модели объекта управления,
имеет вид
х(*) = Л(*) х(*)+ ВЦ) «(*)+ С(*) !</), A7.20)
где Л(*), 2?(*), С(*) - матрицы размера (лхл), (лхд), (лхг) соответственно.
На допустимые значения управлений и(*), у(*) ограничений не наложено.
Пусть функционал качества управления A7.16) квадратичный:
/М = ±)И/M^ A7.21)
Ч 1
Ще *У(*), л - симметрические матрицы размера (л х л); (?(*), G@ -
положительно определенные симметрические матрицы размера (# х ц) и (г х г)
соответственно.
Требуется найти оптимальные позиционные управления «*(*,х),
**(*,х) игроков.
Сравнивая задачу A7.20), A7.21) с общей постановкой задачи A7.15) -
A7.16), имеем
/(/,х,и, у) = А$)х + *(*)*/ + С(*)у ,
/О(/,X,II,V)=^[xГ^)x + I/^е@«-VГG@V], ^)ЛХГЛХ.
531

Функция Я(/,фх,х,и,у) в уравнении Айзекса A7.18) для рассматриваемой
задачи имеет вид
Я(^фx,X,«,V) = [^^^^И0x + #)« + С@V]-^[xГ^)x + «^•О@«-VГ^)V].
Найдем выражения для оптимальных управлений из условия A7.19)
достижения функцией Я(/,фх,х,и,у) седловой точки. При каждом фиксированном
значении V она достигает максимум по аргументу и, если
и*(*,х) = (}-1(*)Вт{*)?2&&. A7.22)
дх
Минимум функции Я(/,фх,х,!/,у) по аргументу V при фиксированном
значении и достигается, если
**М- -<?"!(') С7» &&*!. A7.23)
дх
Решение уравнения A7.18) ищется в виде
ф(г,х)-1хгФ(г)х, A7.24)
где Ф(/) — неизвестная симметрическая матрица размера (пхп).
Подставляя A7.22), A7.23), A7.24) в уравнение и граничное условие
A7.18), получаем
Щ = -Ат(*)Щ-ФA)А(й-<1%)В№
0@ =-Л. A7.25)
Решая задачу Коши A7.25) для матричного уравнения Риккати, можно
найти матрицу <!>(/), а затем функцию A7.24) и оптимальные управления
с полной обратной связью
• •&*) = (Г1@*ГС') Ф(')*> у*(/,х) = -G-1(/)Сг(/)ф(/)х. A7.26)
Минимаксное (максиминное) значение критерия качества A7.21)
вычисляется по формуле
1ЭД1 тах/(и(.), у(-))= -ф('о>*о) = - ^ *оГФ('о)*о
для любого начального состояния х0 е Яп.
Пример 17.5. Для задачи
х2(/) = и(/)-у@,
требуется найти оптимальные управления с полной обратной связью.
532

П Сравнивая данный пример с общей постановкой задачи A7.20), A7.21),
имеем
л = 2, $ = 1, г = 1, 6 = 1, G = 2, *ь-0, 4-1,
Функция <р(/,х) ищется в виде A7.24) :
<рМ-М»» *121х-7»П««?+»12«*1«2+^22@*|.
2 \^Ф12 Ф22У 2 2
Записывая уравнение и граничное условие A7.25) для данной задачи, полу-
Фи =~тФ12» ФиA) = -1>
Я>12 =-фЦ -ТФ12Ф22» Ф12@ = 0»
ф22 =~2ф12 -ТФ22» Ф22(!) = 0-
Решая эти уравнения, находим
гдед@ = 1-^-.
О
Следовательно, матрица Ф(/) в A7.24) имеет вид
ф(')=-^)A-, а-й-
а оптимальные позиционные управления игроков
и * (/,*) = @ 1)ф(/)х = -^ [х, + A - 0х2],
**(',*) = -(<> -0,5)ф@* = -^[х, +A-г)«а].
Минимаксное (максиминное) значение функционала качества вычисляется
Для любых начальных состояний хх @) = хH, х2(*)= х20 по формуле
гостах/(и(-М)) = тахпэдг/(и(И)) = -<р@,х1о,х2о)=-(х,0 + х^М
533

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
17.1. Найти оптимальные позиционные управления и минимаксное
значение критерия качества в задаче
х@ = «(>)-Ч0+л, |«(/)|*2я1, |у(г)|*Я1, 0***1,
/4*2A)^12№
где т, п — заданные положительные величины.
17.2. Найти оптимальные программные управления игроков, оптимальную
траекторию и минимаксное значение критерия качества в задаче
х®шахк)+Ь14)+у(й9 *@)=1, К')!*"*, |у@|*л, 0***1,
где а, А, т, л - заданные положительные величины.
17.3. Найти оптимальные программные управления игроков, оптимальную
траекторию и минимаксное значение критерия качества в задаче
х@ = A-')«(')+*('). 4>) = /я + л,
|и(/)|*т, №)|*я, 05<51,
/ = х2A)^п|птах,
где /и, л — заданные положительные величины.
17.4. Найти оптимальные управления (программное и позиционное) в
задаче
х(') = *(')+«('Ь><>)> *@) = *6>
Й')-Я0+*С0-*('). Я0)-*ь
и(г)€Л, у(г)бЛ, 0*/*1,
17.5. Найти оптимальные позиционные управления и цену игры в задаче
х1(/) = лх2(/),
х2(/) = ти@-у@,
и(/)€/?, у(*)еК, 0*/*1,
534

Глава и. СИНТЕЗ ОПТИМАЛЬНЫХ
ЛОГИКО-ДИНАМИЧЕСКИХ СИСТЕМ
18.1. ОПИСАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
ЛОГИКО-ДИНАМИЧЕСКОЙ СИСТЕМЫ
Поведение модели детерминированной логико-динамической системы (ЛДС)
описывается соотношениями
х(/) = /(/,х@,;К'),и@), A8.1)
у(*)еУ(*,х('Ш-<>)), A8.2)
где х, у — векторы состояния динамической и логической частей ЛДС,
х = (хи...,хп)Т еЯп, у = (у\,...9ут)Т е2м\ и - вектор управления, ие1/^Яя;
( - время, *еТ = [/о>4] ~" промежуток времени функционирования системы,
моменты /0 начала и 4 окончания процесса управления заданы;
/С»х,у,и):ТхКпх2т х1/-+Яп - непрерывно дифференцируемая вектор-
функция / = (/ь...,/„)г; множество У(*,х,у) задает совокупность тех состояний
логической части ЛДС, в которые возможен переход из состояния у при
заданном в текущий момент времени I положении х динамической части ЛДС.
Возможность мгновенного изменения состояний логической части ЛДС делает
необходимым принятие следующих ограничений относительно многозначного
отображения У. Для любой непрерывной функции хA) отображение
1->УЦ9хA)9у) считаем непрерывным справа, т.е. У(г + 0,х(/ + 0),у) = У(/,х(/),у).
Кроме того, чтобы исключить многократные переключения логического блока
в фиксированный момент времени полагаем, что У(/,х,у)еУ(/,х,>0 для всех
УбГ(/,х,>0.
Математическая модель движения ЛДС A8.1), A8.2) служит для описания
многорежимных систем автоматического управления технологическими
процессами и движущимися объектами. В частности, соотношениями A8.1), A8.2)
описывается движение летательных аппаратов, управляемых с помощью бортовых
вычислительных комплексов. В этом случае включение A8.2) описывает
вычислительный комплекс как автомат с памятью. В отличие от непрерывно-
дискретных систем (см. разд. 15), где изменение дискретной части системы
происходит в тактовые заранее заданные моменты времени, логическая часть ЛДС
может изменять состояние в произвольные заранее не заданные моменты
времени в зависимости от текущего состояния динамической части ЛДС и
предшествующего состояния логической части ЛДС. Для описания работы логической
части ЛДС могут быть использованы и другие модели [36]. Если выбор
последующего состояния логической части не зависит от ее предшествующего
состояния, т.е. когда многозначное отображение У(*,х,у) не зависит от у, модель
A8.1), A8.2) соответствует описанию системы с переменной структурой, а
включение A8.2) характеризует работу автомата без памяти.
535

18.2. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ С ПОЛНОЙ
ОБРАТНОЙ СВЯЗЬЮ
18.2.1. Постановка задачи
Пусть поведение логико-динамической системы управления описывается
соотношениями A8.1), A8.2) с начальными условиями
х(*о) = хо,у(*о-0) = Уо- A8.3)
Множество &((о,х0,у0) допустимых процессов образуют тройки
(*(•), у(-), !/(•)), в которых управление и():Т ->17 — кусочно-непрерывная
функция; траектория динамической части ЛДС *(•) :Т -> Яп — непрерывная кусочно-
дифференцируемая функция; траектория (последовательность состояний)
логической части ЛДС у():Т->2т — непрерывная справа функция, имеющая
конечное число точек разрыва первого рода. Функции *(/), уA), ы(/)
удовлетворяют соотношениям A8.1), A8.2) и начальным условиям A8.3).
На множестве 0Aо,хъ9уо) задан функционал качества управления
/= }/°<',*О,*0,|#>>* + Х *\^)М1-0)М*)) + Г(х(Н),У('1)), A8.4)
где /°A,х,у,и), ^(х,^) - заданные непрерывно дифференцируемые функции, а
8°A,х9у9и) - заданная ограниченная функция. Суммирование в выражении
A8.4) производится по всем точкам х разрыва функции >>(/).
Множество и допустимых позиционных управлений динамической частью
системы образуют функции и(*,х,у): Т х Яп х 2т -> I/, а множество У
допустимых позиционных конструкций логической части системы состоит из функций
у(*,х,у): Тх Яп х 2т -+ 2т.
Предполагаем, что каждая допустимая пара (у,й)еУх0/ для любого
начального состояния (хо>Уо) порождает допустимый процесс
(*(¦),*•),«(•»е0(*о,хо,Уо), где и(/) = в(/,х@,у@), *0 = .К',*@,:К'-0)) при
всех 1$Т. Применяемое в каждый момент времени 1еТ управление
«(/,*(/), у(/)) и конструкция у(*,х(*),у(*-0)) имеют вид управления с полной
обратной связью по векторам состояний динамической и логической частей ЛДС.
Требуется найти такие функции и* е и и у* е V> которые для каждого
начального условия порождали бы допустимый процесс й* = (х * (-),у * (•),!/ * (•)),
минимизирующий функционал A8.4):
/(</*)= ппп /(</).
Функции и*A,х,у) и у*(*,х,у) называются оптимальным позиционным
управлением динамической частью ЛДС и оптимальной позиционной конструкцией
логической части ЛДС соответственно.
536

18.2.2. Достаточные условия оптимальности
Утверждение [36]. Если существует функция у(*9х9у):ТхКп *2т -+Я —
кусочно-непрерывная по * при фиксированных х и у, непрерывная по х при
фиксированных * и у, частные производные <р,, <рх которой непрерывны на всей области
определения, за исключением конечного числа значений 1еТ, а также функции
и*е& и у* еР, удовлетворяющие условиям
<р(*1,х,у) = -Г(х,у),
ф - 0,х,у) = ф(/,х,у * (*,х,у)) - ^(их,у9у * (/, х,у)),
Ч>Л*,х,у) + #(*,<рх(/,х,.к * (их,у)),х,у * (/,х,>0,« * (/,х,у)) = 0, A8.5)
У*{*,х9у) = т тах #(*,фх(/,х,у),х,у,»*(*,х,;у)),
и * (г,х9у) = а18тах#(/,<рх(/,х,у * (/,х,^)),х,^ * (*,х,у),и),
то функции и*((,х,у) и у*A,х,у) являются оптимальным управлением
динамической частью ЛДС и оптимальной конструкцией логической части ЛДС
соответственно.
В соотношениях A8.5) обозначены:
Н(*,<рх,х,у,и) = %д*'Лу) М*9х,у,и) - Л'ЛЛ»)
/=1 дх1
- гамильтониан системы A8.1) с функционалом A8.4); Ут(*,х,у) - множество
точек, в которых функция V -* [у(*9х9у)^80A,х9у,у)\ достигает своего
наибольшего значения на У(*9х9у):
У*(*,х,у) = Агь тах (ф(/,х,у)-^°(/,х,^,у) ).
уеУA,х,у)
Замечания.
1. Соотношения A8.5) представляют собой задачу Коши для
дифференциального уравнения с частными производными первого порядка относительно
функции ф(/,х,у), которая может иметь разрывы первого рода по аргументу /.
Управление «*(/,х,>0 и конструкция у*(*9х9у)9 удовлетворяющие условиям
A8.5), являются позиционными (с полной обратной связью).
2. Соотношения A8.5) можно записать в форме, аналогичной уравнению
Беллмана:
тах тах {ф,(/,х,у) -#(/,фх(/,х, у),х,у,ы)} = 0,
ие1/ УеГ'и,х,у)
Ф(/ -0,х,;у) = тах {Ф(/,х,у) - *0(Г.х»У.«) }, A8.6)
уеУ{1,х,уу
у(*1,х9у) = -Г(х9у).
537

Первое уравнение описывает изменение функции <р(*,х,у) всюду, за
исключением точек разрыва, второе уравнение указывает величину скачка этой
функции в точках разрыва, третье соотношение — краевое условие.
3. Наименьшее значение функционала A8.4) находится по формуле
тш 7(Ю = -ф(Го-0,х<ьИ>). <1817>
Пример 18.1. Найти оптимальное позиционное управление и * (*,хуу) и
оптимальную позиционную конструкцию у*A>хуу) логической части, а также
наименьшее значение функционала качества в задаче
хГО-иЮ + УС), *@) = *о, *о€Д,
у«)еУ(уA-0)), А-0) = у0, Уо €Н,0Д},
|и(/)|*1, У(у) = {уе2:\у\ф\}, 0*Г*1,
/*х2A)-><1)->1ШП .
13 Сравнивая данный пример с общей постановкой задачи, имеем
/(/,*,!/,V) « и + у, /°(/,*,!/,V) = 0 , «°(*,Х,?, V) * 0 , Р(Х,У) = X2 - У ,
Г0-0, Г!-1, 17-[-1,11. УA)*Г(-1) = {-1,0,1}, Г@) = {0}.
Логическая часть системы в начальный момент времени может находиться
в трех состояниях: ± 1 или 0. Если у0«0, то, согласно ограничению
|><0|*|у('-0)|, получаем, что ^*(г,х,0) = 0. В этом случае остается
синтезировать оптимальное управление и*(/,х,0) динамической частью системы, решая
следующую задачу оптимального управления (см. разд. 9.2):
х@ = «@,
|и@|*1,О*/*1,
/ * Х2A) -* 1ШП .
Применяя достаточные условия, находим функцию ф(/,х,0) и оптимальное
управление:
-(х + 1-02, х**-1, [1, х<;/-1,
<р(/,х,0)*] 0, *-1<х<1-*, и*(Г,х,0)«
-(х + /-1J, 1-/<1х;
0, /-1^x51-/,
-1, 1-/*х.
Рассмотрим теперь случай, когда начальное состояние логической части
ЛДС отлично от нуля: у$=±1. Соотношения A8.6) для данного примера имеют
вид
538

тах {ф,(*,х,у) + фх(*,х,у)A/ + у)} = 0,
.01*1 Уе1Г(у)
ф(*-0,х,>0 = тах ф(/,х,у),
уеУ{у)
ф(Г,,х,у) = ^-х2.
Если >> = ±1, то в конечный момент времени функция ф(;,х,у) имеет
скачок
фA-0,х,у)= тах {у-х2 }=1-х2,
У*Г(У)
т.е. у*A,х,у) = а!8 тах {у-х2 }«1 при у = ±1.
уеУ(у)
Из условия максимизации по переменным и и V определяем
«* = $ц$Пф*(*,х,у), у* = адпфх(г,х,у). Решаем теперь уравнение Ф/+2|фх| = 0
с граничным условием фA - 0,х,у) = 1 - х2. Для этого разбиваем плоскость
переменных (/,х) на три области А, Б, В (см. рис. 18.1), где фх >0, фх -0, фх <0
соответственно. В каждой из областей получаем решения:
Рис. 18.1
Областью 2A-*)**, 0^^<1:
Ф(/,х,±1) = 1-[х-2A-0]2> »*(ГЛ±1)—1, у * (/,х, ± 1) =-1;
Область^: -2A-/)*х*2A-0> 0*Г<1:
ф(Г,х,±1) = 1, в*(/,х,±1)-0, у*(*,х9±1) = \;
Область А х^2A-/), 0^/<1:
ф(/,х,±1) = 1-[х + 2A-/)]2, «*(/,х,±1)-1, ;*(/,*±1)-1.
Полученные функции являются искомыми для рассматриваемой задачи
в случае, когда Уо*0.ш
539

18.3. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО ПРОГРАММНОГО
УПРАВЛЕНИЯ
18.3.1. Постановка задачи
Пусть поведение модели ЛДС описывается соотношениями A8.1), A8.2)
с начальными условиями A8.3). На множестве допустимых процессов
&(*о>хо,Уо) задан функционал A8.4).
Требуется найти оптимальный процесс */* = (х*(•),)>*(•)>и*(•)),
минимизирующий функционал A8.4):
/(</*)= тш 1@).
Функции х*() и !/*(•) называются оптимальной траекторией и
оптимальным программным управлением динамической частью ЛДС; функция у * (•)
называется оптимальной программной конструкцией логической части ЛДС.
18.3.2. Соотношения для нахождения оптимального управления
Применяя достаточные условия оптимальности ЛДС для функции
1=1
где 4A, у) и у(*,у) — кусочно-дифференцируемые по / функции, получаем
следующие соотношения [36]:
х*(/) = /(/,х*@,у*@,и*@), **('о) = *о;
У,(>, V * (Г,?)) + П',у * (*,У))[ А*,х * (/),у * (*,у),и * (иу)) - /(их * @,у * (О," * (*)>]-
- /°С* * @,V * (*,>>),« * Ц,у)) = 0, у(<иу) = -/*(х * (^у),
%(*,* * (*>У)) + Нх(ич(*,у * СдО),* * @, V * (*,;и),и * С?)) = 0,
у(* - о,у) = У(/, V * (/,^)) - &\их * (о,*у * (/,^)),
Ч(*-0,у) = Ч(*,у*(*,У))-*0х(',х*(<),У,у*(',У)), A8.8)
^*@ = У*(/,у*(/-0)), и*@ = и*(',:И*('-0)),
и * (/,у) = а18тахЯ(/,^(/,V * (иу)),х * @,у * (/,у),и)
540

V * (/,?) = агатах {у,(/, V) + У(/, у)[/(/,х * @. у,и • (/,?)) -
уеГ*(/,х*(Г),у)
- /(их * @,У * @," * @) ] - /°(',* * @. V.» * (/,?)) (,
У*(/,х*A),й= Агатах (у(^)-*0(>,**@,:^)}.
увГ(/,х*@,У)
АЛГОРИТМ НАХОЖДЕНИЯ ОПТИМАЛЬНОГО ПРОГРАММНОГО УПРАВЛЕНИЯ
1. Составить гамильтониан
Щ*,Ч',х,у9и) = %Ч>, М'>х,у,и)-/°«,х,у,и).
ы\
2. Найти структуры оптимального управления динамической частью ЛДС и
оптимальной конструкции логической части ЛДС:
и*(*,у) = а1&тэхЩиП<,У),х*(<),У*(*),и),
V * </,у) = агатах {у,(г,у) + ЧЧ*, у)[/(/,ж * @, у,и * (Г,у)) -
У€Г*(Г,Х*@,У)
- /(/,*• ю, * * <о,« • @I - /°(>,х * @^,1/ * (/.у»},
Г •<'.*•(*),)» = Агатах {у<Г,у)-*о</,х*@,*у)}.
У€Г(/,Х*(Г),У)
3. Записать систему A8.8) дифференциальных уравнений для функций
х * @, у(*,у) у Ч?(*,У) и ограничений на скачки функций у(*,у), Ч?(*,у).
4. Добавить к уравнениям, полученным в п.п. 3,4, краевые условия
х * (*Ь) = *о. УЙ.Й - -Пх * (/1),й, чЧ'ьЙ = -Рх(х * й)^).
5. Решить краевую задачу, полученную в пЗ, 4. В результате получаем
траекторию х*(/) и вспомогательные функции у(*,у), Ч?A,у), по которым
окончательно определяем управление !/*(/) и конструкцию у*@ логической
части ЛДС.
Пример 18.2. Найти оптимальное программное управление и оптимальную
программную конструкцию логической части системы, а также наименьшее
значение функционала качества в задаче
х@ = "@ + Я0, х@) = 5,
у(*)еУ(у(*-0)), у(-0) = \,
|и@|*1. Г(у)-{уе2:\у\*\у\}9 0*/*1,
1 = х2(Х)-у(Х)->тш.
541

П 1. Составляем гамильтониан Н = Ч*(и + у).
2. Находим структуру оптимального управления и*(*9у) = яд1Ч'A,у).
Записываем соотношения для нахождения оптимальной конструкции логической
части:
увГ*(у)
У*(у) = Ац щах у(/,у).
уеУ(у)
3. Записываем систему уравнений A8.8):
Уг+^[1/*(/)+У-И*@->'*@] = 0,
%(*,У) = 0, у(/ - О,?) - у(/, V * (>,>0), У(/ - 0,у) = У(/, V * (/,?)).
4. Записываем краевые условия:
х@) = 5, П1,У) = -2х*A), уA,у) = у-(х*A)J.
5. Решаем краевую задачу п.З, 4. Замечаем, что функция ХР(/,^) постоянна
и ^(/,у) = -2х*A). Так как х*(/)>0 при всех /б[0,1], то и*(/,>0 = -1. Найдем
уA - 09у) из соотношения
уA-0,у) = П1|ах[у-(х*A)J] => УA -О,*) = 1 -(х*(I)J .
Как видим, функция уA-0,>0 не зависит от у, поэтому множество У *(у) ее
точек максимума совпадает со всем множеством У (у), а
г-о.,-11' I''"-
[о, *=<>.
Следовательно, у*A,у) = §щх1Ч*(*,у) = -1 при 0^/^1; V*A,,у) = 1. Подставляя
и*иу*в уравнение движения, получаем
х*(/) = -2 => х*(/) = 5-2/, 0<;/*1.
Таким образом, найдены оптимальная траектория и оптимальное
управление динамической частью системы:
х*(/) = 5-2/, и*@ = -1, 0*/*1,
оптимальная программная конструкция логической части:
*•(*)—1. 0*/*1, >>*A) = 8,
а также минимальное значение функционала качества:
пш1/ = [х*A)]2-^*A) = 8.и
542

18.4. СИНТЕЗ АВТОМАТНОЙ ЧАСТИ ЛОГИКО-ДИНАМИЧЕСКОЙ
СИСТЕМЫ
18.4.1. Постановка задачи
Пусть поведение детерминированной ЛДС описывается.соотношениями
х@ = /(/,х@,Я0), 08.9)
Я/)бУ(/,х@,></-0)), A8.10)
где х, у — векторы состояния динамической и логической частей ЛДС,
хеХсЯп, уеУ ^Кт\ / - время, 1еТ ^[Ь,^] - промежуток времени
функционирования системы; /A,х,у):ТхХ*У-+Яп непрерывная вместе со своими
частными производными вектор-функция. Многозначное отображение У(*,х,у)
является непрерывным справа
У(/ + 0^дс(г + 0),й-У(/,дсA),Л
и удовлетворяет условию
У(*,х,у)=>У(<,х,у) ЧуеУ(*,х,у)9 A8.11)
т.е. в множество У(*,х9у) включаются все состояния м>бУ(/,х,у), в которые
можно попасть из состояния уеУ(*9х9у). Условие A8.11) не исключает
возможности появления скользящего режима со счетным числом переключений
логического состояния, которые происходят, однако, в различные моменты времени.
Допустимыми процессами считаются пары (*(•), Н))> гДе у0 ~ непрерывная
справа кусочно-постоянная функция, х(») — непрерывная кусочно-гладкая
функция, причем пара функций (*(•),}>(•)) удовлетворяет при всех ^еТ рекуррентному
включению A8.10) и почти всюду на Т — уравнению A8.9) с начальными
условиями
*(>о)=*о; Я'о-о)=:и>. <18Л2>
Каждой допустимой функции у(*)9 задающей эволюцию состояний логической
части системы, отвечает единственное решение х(() задачи Коши A8.9), A8.12).
Функция *(/) — определяет траекторию динамической части ЛДС.
На допустимых процессах (траекториях) системы A8.9), A8.10) задан
функционал
/(х(-).И-»- ^г(^1).^1»+^/0(г^г).у(г»Л + 5; *°(^«(т),^-0).^)). A8-13)
где функции Р(х9у)9 /°(*,х9у)9 8°(*,х,у,у) - непрерывно дифференцируемы по
всем аргументам. Суммирование в A8.13) ведется по всем точкам т разрыва
функции у{).
Требуется найти допустимый процесс (х{\у{))9 минимизирующий
функционал A8.13).
543

Сформулированная задача имеет следующий смысл. Управление
динамической частью ЛДС осуществляется только путем выбора того или иного
состояния логической части ЛДС. Можно считать, что выбором состояния
логической части ЛДС определяется тот или иной тип траектории движения
динамической части ЛДС. Поэтому задача состоит в конструировании (нахождении)
траектории движения из конечного числа типовых траекторий. Функция у($)
определяет конструкцию траектории х(г) динамической части ЛДС, поскольку
функция ЯО указывает последовательность, в которой сменяются типовые
траектории, а также продолжительность движения по каждой типовой траектории. В
этом смысле решение поставленной задачи (функцию у{)) можно назвать
оптимальной программной конструкцией автоматной (логической) части ЛДС,
поскольку она зависит только от времени.
Заметим, что в отличие от классической задачи оптимального управления
(см. разд. 9) на значения у(*) допустимых функций >>(•), играющих в данной
задаче роль управления, наложены ограничения, зависящие от выбора
предшествующих значений у{*-0). Это ограничение, вообще говоря, не позволяет
использовать игольчатые вариации управления при выводе необходимых условий
оптимальности, как, например, в принципе максимума. Поэтому
рассматриваются два типа вариаций. Во-первых малые вариации 5у(/) при фиксированных
моментах х переключения логического блока. Вариации этого типа изображены на
рис. 18.2, где взяты два момента переключения логического блока. Полужирными
стрелками на рисунке обозначено опорное управление (функция у{*)), а
обычными — управление у([) + йуA). Во втором случае вариация у(?) происходит
только за счет изменения моментов переключения автоматной части ЛДС.
Моменты переключения т получают приращение т + 5т. Вариации этого типа
изображены на рис. 18.3.
У '
'о
с
_^|
^"^'
V
1
Т2
1
—#ь'
1
н
(
у '
«0
г
1
— к^ 1 ^
1
V
»!.!
Гятт^^\ р|
ъ
*-'
ш^^\
к
(
Рис. 18.2
Рис. 18.3
18.4.2. Необходимые условия оптимальности
Утверждение 1. Пусть допустимый процесс (*(•),}>(•)) удовлетворяет
соотношениям A8.9)-A8.12). Пусть непрерывные справа кусочно-гладкие на [/0; 1{]
функции ч/(/) и у(/) при всех ^е[@;^], за исключением точек т разрыва функции у{),
удовлетворяют уравнениям
Ц()=-ну[(), у(/,) = -^[/,1,
A8.14)
544

а в каждой точке х (х € [^; 1{\)
1у(т-0) = ч,(т)-*°[т], A8.15)
у(т-0) = -4И,
где
Н = Н(*,у,х,у)=% V/ •/Д/ЛуЬЛ/.х.Л A816)
М
— гамильтониан динамической части ЛДС.
7Ъгда, если конструкция у{) минимизирует функционал A8.13), то для любых
допустимых вариаций Ьу(х)
Е(у(х)-^°м)-8Ях)^0, A8.17)
т
где суммирование проводится по всем точкам т разрыва функции у().
Здесь аргумент [/] означает, что функция вычислена на данном допусти-
мом процессе (*(•), ?()) > например, НХЩ = —-Я(/, у(/), хD у(/)).
а х
Утверждение 2. Пусть допустимый процесс (*(•),Я*)) удовлетворяет
соотношениям A8.9)-A8.12). Пусть кусочно-гладкая на [^о;^] функция у(/) л/и/ всех
* е Йь ^Ь 5Д исключением точек х разрыва функции у{), удовлетворяют
уравнениям A8.14), а * каждой точке х (т € Г) — условию A8.15).
7Ъгда, если конструкция у() минимизирует функционал A8.13), то * каждой
точке х разрыва функции у{) выполняются неравенства
Я(*ч<т),а<тЫт))-Я(т,^
A8.18)
Пример 18.3. Найти оптимальную программную конструкцию ЯО
автоматной части ЛДС, а также наименьшее значение функционала качества в
задаче:
*@ = ;К0, *@) = 0, 0*/<;1,
у(/)€{±1}, у(-0) = 1,
/=/|дс@|Л+^Х1^)-^-0)|^ти1.
О Эи т
О Составим гамильтониан A8.16): Н = \^(() у-\х\. Запишем уравнения
A8.14), A8.15):
#) = Я8пх@, ^A) = 0, м/(х-0) = м/(т).
545

Последнее условие обеспечивает непрерывность функции у(/). Так как
функция 8°(*,х,у,у)= 8°(у,у) = \у-у\ не зависит от / и х, то из неравенств
A8.18) следует, что в момент т переключения логического блока выполняется
условие
Я(т,м/(т),х(х^(^))-Я(т,м/(х),хD><т-0)) = 0 =>^(т) [у(х)-у(х-0)] = 0 =>м/(т) = 0.
Это условие позволяет определить оптимальную последовательность
т! < т2 <... < т# переключений логической части ЛДС. В самом деле, пусть хк,
т*+1 "" Две соседних точки разрыва функции у(*). Тогда у(хк) = у(хк+\) = 0 •
Заметим, что у = 1 или \|/ = -1. Поэтому на промежутке [хк; хк+х] функция ц/(/)
представляет собой двухзвенную ломаную, изображенную на рис.18.4 сплошной или
пунктирной линией. Причем звенья ломаной равны по длине, т.е. изменение
производной \|/ происходит в середине отрезка. Значит, функция х(/) обращается
в нуль в середине промежутка [хк; хк+х] (см. рис.18.5). Отсюда следует, что
оптимальная траектория является ломаной с равными звеньями:
*(ч) = -*(*2)> *Ы = -*(*з)>..м х(т*) = -хA),
а моменты переключений следуют через равные промежутки времени:
2*-1
4 =
2ЛГ + 1
, * = 1,2,...,#.
V
Ч
У **+1
V
Рис.18;4
Рис.18.5
Теперь осталось определить оптимальное количество переключений.
Вычислим значения функционала качества для N = 0,1,2,3:
/.=}¦
/.-•!¦=-
31
6 50 150*
2 10 + 50 50' 3 14 + 50 350'
При дальнейшем увеличении количества переключений N последовательность
1н монотонно возрастает. Наилучшее значение /2 = 0,18 достигается при двух
переключениях, когда программная конструкция автоматной части имеет вид
у(*) = 1 при 0*/<0,2; у(*) = -1 при 0,2^/<0,6; Я0 = 1 Щ»* 0,6*/*1Л
546

18.4.3. Достаточные условия оптимальности
Пусть поведение детерминированной ЛДС описывается соотношениями
A8.9),A8.10). Множество У допустимых позиционных конструкций логической
(автоматной) части ЛДС образуют такие функции у(*,х,у):ТхКпхКт ->Ят,
которые для любого начального состояния (хо; у0) порождают допустимый
процесс DЫ-))>где К/) = уМ^></-0)) при всех /€Г.
Требуется найти такую функцию у*еР, которая для каждого начального
условия A8.12) порождала бы допустимый процесс (х*(),у *(•)),
минимизирующий функционал A8.13). Функция у*(*,х,у) называется оптимальной
позиционной конструкцией логической (автоматной) части ЛДС.
Утверждение. Если существует функция у({9х,у):ТхКп хКт ->К —
кусочно-непрерывная по / при фиксированных х и у, непрерывная по х при
фиксированных 1 и у, частные производные ф,, <рх которой непрерывны на всей области
определения, за исключением конечного числа значений *еТ, а также функция
у* € У, удовлетворяющие условиям
<!<*\,х,у) = -Г(х,у),
Ф(' - 0,х9у) = ф(/,х,у * (/,х,>0) - 8°(*,х9у9у * (их,у)), A8.19)
Ф,(*,х,;к) + #(/,Фх(/,х,у * (*,х,у)),х,у * (*,х,у)) = 0,
у*(*,х,у) = яъ тах #(/,фх(/,х,у),х,у),
уеУ*(Г,х,у)
то функция у * ((,х,у) является оптимальной конструкцией логической части ЛДС.
В соотношениях A8.19) обозначены:
Я(/>Фх>х>у) = |]аф(Г>х>:к)//^х>у)>/0(Г>х>у)
М дХ1
- гамильтониан системы A8.9) с функционалом A8.13); У*(г9х,у) - множество
точек, в которых функция V -> ( ф(/,х,у) - 8°A,х,у,у)) достигает своего
наибольшего значения на У(*,х,у):
У*(/,х,у) = А18 тах (ф</,дс,у)-*°(/,х,Лу) ).
Замечания.
1. Соотношения A8.19) следуют из A8.5), так как задача синтеза
автоматной части ЛДС является частным случаем общей задачи, рассмотренной в
разд. 18.2.
2. Методика применения достаточных условий аналогична рассмотренной
в разд. 18.2.
547

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
18.1. Найти оптимальную позиционную конструкцию логической части
ЛДС в задаче
Ш I ПК У = Ъ
18.2. Найти оптимальное программное управление и оптимальную
программную конструкцию логической части системы, а также наименьшее
значение функционала качества в задаче
х(/) = 1/@ + Я0, *@) = 4,5; 0*/*1, |и(/)|*1,
*/)€Г(/,х@,;К'-0)), Я-0) = 0,
™*о) = 1{0'~1}' х>4'
Пит 1@,-1,-3}, х*4,
У(/,х,-1) = {-1}, У(/,х,-3) = {-3},
/=-гх2A)->тт.
2
18.3. При всех положительных значениях X найти оптимальную
программную конструкцию автоматной части логико-динамической системы, а также
наименьшее значение функционала качества в задаче
х@ = ;К0, *@) = 0, 0*/*1,
*0€{±1}, Я-0) = 1,
1=1\х(<)\<!* + \%\у(т)-у(х-0)\^тт .
0 х
548

Глава 19. СИНТЕЗ ОПТИМАЛЬНЫХ НЕПРЕРЫВНЫХ
ДЕТЕРМИНИРОВАННЫХ СИСТЕМ С ДИСКРЕТНЫМ
УПРАВЛЕНИЕМ
19.1. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО ДИСКРЕТНОГО
ПРОГРАММНОГО УПРАВЛЕНИЯ
19.1.1. Постановка задачи
Пусть поведение модели объекта управления описывается обыкновенным
дифференциальным уравнением
*@ = /(',*('),"('*)), *еТк=[*к,*к+1), * = 0,1,...,*-1, A9.1)
где х - вектор состояния, х е Кп\ и - вектор управления, и е V с Я9, I/ -
некоторое заданное множество допустимых значений управления;
/ еТ = [/о,*ц) -промежуток времени функционирования системы. Моменты
времени /0, *#, а также разбиение множества Т на полуинтервалы Тк = [**,'*+1)>
где *к <(к+1,А: = 0Д,...1АГ-1 заданы. В каждый момент 1к траектория непрерывна
слева: х($к) = х(*к -0).
Обозначим Г = ик)кш0 "" множество точек, в которых задается управление.
Предположим, что начальное состояние задано: х(/0) = х$ еЯп.
Предполагается, что при управлении используется информация только
о текущем дискретном времени, т.е. рассматривается дискретное программное
управление.
Множество допустимых дискретных программных управлений 2/0 образуют
последовательности: и() = {и(*к)}к~ъ, иAк) е V.
Определим множество допустимых процессов 1?(^9х0) как множество пар
<? = (*(•)>и()), где функции !/(•) принадлежат множеству допустимых управлений
#о> Функции х() непрерывны и кусочно-дифференцируемы на Т, и
удовлетворяют уравнению A9.1).
На множестве ^(/0,х0) определим функционал качества управления
/(<0= Е 1ТММЪМ*к))Л + *.к(х(Ь)МШ + Л*('*))> A9.2)
Аг-0 гк
где /°(/,х,1/), #*(х,ы),А: = 0,...,#-1; ^(х)- заданные непрерывно
дифференцируемые функции, х(/#) = х(*х - 0).
Требуется найти такую пару й* € #(/о»*о)» на которой достигается
минимум функционала A9.2), т.е.
/(О - пш1 /A0- A9.3)
549

19.1.2. Соотношения для нахождения оптимального управления
Из системы уравнений, полученной для общего случая задачи синтеза
оптимального управления при неполной дискретной информации о состоянии (см.
систему A9.24) в разделе 19.3.2), следует система для нахождения оптимального
дискретного программного управления и*(-):
^(,„-о)У) = -^-°'у», ; = !,...,„,
дХ{
ты -<Ы = ЕаЛх(^"°>У))х/^ -0,у)-/Хх(^ -0,у)),
7-1 дх]
МЛ'**) аЯ(/,У(/,у),х(/,у),у)
ы
дх,
, ]ш\9.„9пъ
У(/,у)€Г*х#, * = 0,1,...,ЛГ-1,
дЩ*,у)
д
М) гг/, «,/, ч /, ч ч ^ ЭЯ(/,ЧЧ?,У),х(/,У),У) ы ч
^ = Я(Г,У(/,У),Х(/,У), V) - ]Г ' */('»У)>
т*к -о,у)=т*км*к))+%ч('кМ'к))ъ(<к)-
7-1
7-1
A9.4)
«('*) = агатах
>1
,иI, * = 1,...,ЛГ-1,
и(<о) = ^и*^\ Щк>») + Ё'Р/ОЬ.и) *6; -*о(*о>и)
^ = /(и^),У), ЧA,у)еТкх1/, * = 0Д,...,ЛГ-1,
*('*,у) = *('*) = *('* -0,1/(^_!)), * = 1,...,7У-1,
ще Яр.Ч'.х.у)- %Ч>^,у)/^,х,у)-/°(*,х,у).
7-1
550

Пример 19.1. Даны модель объекта управления
*(')=¦ «@), х@)-хо,
где х е К, и е К, / € Т0 = [0,1), и функционал
/=^2@)+^х2A)-»пш1.
Требуется найти оптимальное дискретное программное управление.
О Для данного случая система A9.4) имеет вид
УA-0,у) = -хA-0,у), »Ч1-0,у)=|х2A-0,у),
*(',у) = 0, -1Г(Г,у) = ч/(г,у)у,
1/*@) = ахвпшх | Щ0,и) + ^@,1/)х0 -±иА,
Х(*,У)=:У, Х@,У) = Хо,
где Я(/,Ч/,х,у) = ч/(/,у)у.
Из этой системы следует. х(/, у) « хо + V /, 4/A - 0, у) = - (х0 + у),
ЧЧ', у) = -(*<>+у), ^A-0,у)=|(хо+уJ, ^(/,у) = (хо + у)у.
В результате имеем решение: Ж(/,у) = (х0 +у)у/ + — (х$2 -у2) и искомое
оптимальное управление
|/*@) = а1Вшах||(хо2 -и2)-(*о + «)х0 -}} = -^.
Оптимальная траектория: х*(') = х(/,ы*@)) = ^ .¦
Пример 19.2. Даны модель объекта управления
х@ = -х(/) + 1/(Г*), * - 0,...,ЛГ -1, х@) = х0,
где х € Я, и е К, г е Т «[0,1), и функционал
1 л^-1 '*¦» „ 1 -.
Требуется найти оптимальное дискретное программное управление.
П Здесь &к ш 0, /°(/, х, и) = -и2, Р(х) = -х2. Рассмотрим два случая.
551

1. N = 1 (один полуинтервал управления), Т = То= [0,1).
Для данного случая система A9.4) имеет вид
#(*,Ч',х,у) = Ч'(>,у)[-х + у]-|у2,
ЧЧ1-0,у) = -дсA-0,у), Щ1-0,у)-ух2A-0,у),
*(/,у) = «?(/, у),
-Ж(*,у) = ЧЧ*,у)у-|у2,
и,@) = аг8тах{Щ0,н) + Ч'@,и)х0},
и
Х(/, V) = - Х(/, V) + V, Х@, V) = Хо .
Из этой системы следует: х(/, у) ¦ [хо - у] е"' + у,
хA-0,у) = [х0-у]в-1+у, ЧЧ/,у) = С!е'.
При/ = 1: гРA-0,у) = С1в = -хA-0,у) = -{[х0-у]в+у}. Отсюда
у(/,у) = -{[х0 -у\е~2 +уе~1)е\ Щ*,у) = {[хо -у]«Г2 +ув_1}вгу + ^у2.
Решение последнего уравнения имеет вид
Щ*,у) = {[х0 -у]в +У*-1}*' у+^у2/ + С2.
При / = 1:
ЖA-0,у) = [х0-у]ув-1+у2+|у2+С2=|х2A-0,у)=|{[х0-у]в-1+у}2.
Отсюда определяется коэффициент С2, а искомое оптимальное управление
находится из условия:
и*@) = ах$тах{Щ0,и) + Ч'@,и)хо} = э1%тж\[хо-и}и
и и [ 2 ч
+ и }2 --и2 -[х0 -и]*/*-1 -{[х0 -и]е'2 +ие~1}х01.
Применяя необходимое условие экстремума, имеем
2г2-2г + 1
552

2. N = 2 (два полуинтервала управления), Т0 = [0;0,5), Т\ = [ОД 1).
Для данного случая система A9.4) имеет вид
#(*,У,х,у) = У(/,у)[-х + у]-«|у2, ЧЧ1-0,у) = -хA-0,у),
ИЧ1-0,г) = !*2A-0,г),
Ф(*, V) = У(/, V), - *Г(/, V) = У(/, V) V -|у2,
*(/,у) = -х(/,у) + у, х@,у) = х0, /еГ*, А: = 0,1,
и* @,5) = щ = агг тах {)Г@,5; и) + ^@,5; и) х@,5; и)},
и
и*@) = ио = агк тах (ИЧМН'ИМ) *о },
Ч'@,5-0;у) = ч'@,5;и1),
Щ0.5 - 0; у) = Щ0& щ) + «Р@,5; и,) х@,5; у) - «Р@,5; н,) х@,5; у) = Щ0& щ),
х(ОАу) = х@M-0;ио).
Из системы уравнений получаем:
хA,у) = {[*<, -у0]+[у0 -У1]в°-5}е-' + у, ,
хA-0,у) = [*о -У0]е-1 +[у0 -У^е-0,5 +у, ,
х@& у) = [хо - у0] е-°* + у0, ЧЧ>, у) = С, в',
где у0 _ значение управления на полуинтервале Т0, а VI — на полуинтервале 71.
При / = 1:
Ч'A-0,у) = С,в = -хA-0,у) = -{[дсо-Уо]в-,+[Уо-У1]в-0,5+^ }.
Отсюда Ч/(*,у) = -{[хо -у0]в +[у0 -у^в'5 +у, в-1}е'.
Для * € 7*1 имеем
Щ*,у) = -ЧЧ*,у)у, + ±у,2 = {[хо -у0)е-2 +[у0 -у^е-5 +у, е}^ е' +±у,2.
Решение этого уравнения:
»Ч>>у) = {[хо -у0]е-2 +[у0 -у,] в-5 +У! в-^у, в' +1у,2Г + С2.
553

При Г = 1:
^A-0,V) = {[х0 -у0]е'1 + [у0 -У1] е'** +ух}ух +±у,2 +С2 =
= 1х2A-0,у)=|{[х0 -Уо]^1 + [у0 -у1]<Г0'5 +^ }2.
Отсюда определяется коэффициент С2, а оптимальное управление на
полуинтервале Тх находится из условия
ы*@,5) - щ = ахв тах { ^@Д и) + 440,5; и) х@Д и)} =
= агатах \ [х^ -у0] ив,5 +[у0 -и] ие~1 + и2е~0* +—И2 —и2 +
и I 4 2
+ Т{[*о -^о] в + [П> -и]в*5 +и} -{[*о -у0] не'1 +[у0 -и] ив-0*5 + </2}-
-{[хо -*0]<Г1'5 + № -и]* + *"^5}{[*о -У0]е-** +у0}}.
Применяя необходимое условие экстремума по и и производя сокращения,
получаем
2х0[в°'5-1] + 2Уо[1-2в0'5+в] = 1/1[4в1-2в0'5-Зв1'5]. A9.5)
Для / € 7о имеем
Ж(/,у) = -ЧЧ/,у) у0 +|у^ = {[хо -у0]*-2 +[у0 -»|]в-у +И1 ^ }у0 е' +|у^ .
Решение этого уравнения:
Щ*^) = {[хо -у0]е +[у0 -1/1]<Г1'5 +1/! в-^цв' +^02* + С3.
При * = 0,5:
Ж@,5 - ^у) = {[*о - у0] у0 е"!<5 + N - «11У0 в + «! у0 е-°* }+1у# + С3 =
= Ж@Д|/1) = [х0-у0]и1е^+[у0-1/1]|/1е-и1/?е-^+1|/12-1|/12 +
4 2
+>2 {[*о "уо1«_1 +[уо -Ц1 е-0*5 +«/! }2 -{[х© -у0] щ е~1 +[у0 -щ]щ <Г0'5 +И? }.

Отсюда определяется коэффициент С3, а оптимальное управление на
первом полуинтервале находится из условия
ы*@) = щ - агатах {Щ0,и) + Ч*@,и) х0 }= альтах \[х0 -и] ие~2 +
и и
+ [и-щ] ие*5 + щ ие~х + [х0 - и] щ в,5 + [и - щ] щ е"х + и} е*5 +
+ Iй* ~1Ы* + *2 ^ ""'** +[и/11 в"°'5 +и1} "(^ "и1 и1 е~Х +
+ [и-1/1]и1в,5 +ип-[хо -I/] 1/в*5 -[и-щ] ие~х -щ ив,5 -—и2 -
' 4
-{[*о -ы]*~2 +[и-щ]в»5 +!/! в-1}^ }.
Применяя необходимое условие экстремума по и , получаем
2хо[в0»5-1] = 21/1[-в1»5+2в-в0»5] + и0[-в2+4в0'5-2в-2]. A9.6)
Полагая в A9.5) V = щ и решая совместно с A9.6), находим
2П-е0»51
1/*@,5) - Ц - — ?/' ~*] Л< Х0 .
A9.7)
Решение данного примера можно получить путем представления
минимизируемого функционала через неизвестные управления г/*@), и* @,5) или г/0, I/]
в силу установленной зависимости х(/,у) от параметров управления и
применения необходимых условий экстремума получающейся при этом функции. ¦
Пример 19.3. Даны модель объекта управления
х@ = х@ + !/(/*), * = 0,...,ЛГ -1; х@) = 0,
где х € Д, и е К, г € Т = [0,1), /* = А: А/, А/ = —, и функционал
N
1= ^и2(/*)Д/-хA)-»1шп.
Требуется найти оптимальное дискретное программное управление.
? Здесь **(х,1/) = 1/2(/*)Д/, /°(/,х,и)=0, ^(х) = -х.
555

Для данного случая система A9.4) имеет вид
#(/,Ч',х,у) = Ч'(*,у)[х + у]>
дх
Щ1_0,у) = дР(х('« ~°>У))хA„ -0,у)-Р(хAы -0,у)) = 0,
дх
ф(/> у) _ .МШММ = _ч>(,,у), A9.8)
Эх
- И>(/,у) = НA,П^),х^У),У)-дтМ1'^'Х(('У)'У) х((,у) = У(*,у) [х(Г,у) +
+ К'*I - «Р^.у) х(Г, у) = «?(',у) у(^), * = 0.....ЛГ -1,
Щ(к -0,у) = пик {Щ*к,и) + Ч(*к,и) хAк,и)-и2Цк)Ы-Ч{1к "<>>*) хAк -0,у)},
П<к -0,у) = Ч>(*кУ(<к)), * = 1,...,ЛГ-1,
и'(*к) = аг8тах{и'(ГА,и) + Ч'(/А,и)х(^>и)-а2(^)А^}, * = 1,...,ЛГ-1,
и*@) = агв тах [щО, и) + ^(О, и) хф, и) - и2@) М},
х(*,у) = -хA,у) + у((к), к = 0,1 N -1,
*('*+!. V) = *('*+1 -0,и*(/*)), А: = 0Д.....ЛГ-1,
х@,у) = хо=0.
Из этой системы следует:
а) УA-0,у) = 1; Ф(/,у)—ЧЧ'.у); ОД-О^у)-ОД, «*('*)). * = 1 N-I.
Поэтому 4A, у) = в1"', Г е [ОД).
б) х(Г,у) = -х(*,у) + у(>*), * = 0Д,...,#-1,
*0*+1.»>-*('*+1 -<>,«*('*))> * = 0Д ЛГ-1,
х@,у) = Хо=0.
556

Отсюда х(/, V) = С е* - у{$к).
При / = 0: 0 = С -у@), поэтому х(/,у) = у@) [е' -1], * е [О, А/).
При Г = А/: и@) [вА' -1] = С еы - у(А/), поэтому
х(/,у) = уЩ)[е'-" -1] + и@)[е( -е'-" ], / € [Д/,2Д/).
При/ = 2А/: 1/(А/)[вА/-1] + 1/@)[в2л/«вл/] = Се2д/-уBА0,
х(/,у) = уBА/)[вг-2Д/-1] + 1/(А/)[^"А/ -^-^1 + 1/@)[«'-в'""], /б[2Д/,ЗД/).
Аналогично при / = ЗА/:
*(', V) = у(ЗАГ) \е1-гы -1 ] + иBД/) [е'-2" -е'* ] + и(А/) [«'"" - в'* ] +
+1/@) [ е' - е*-" ], / € [ЗА/, 4Д/).
По индукции получаем общую формулу:
к0)[е'-1], /€[0,А/)
х(/ V) = \ к-Л
ЫШ)[е'-ш -1]+% иAА*)[е'-ш -е'-(и»" ], * е [Ш, (к + 1)А/),
I /-о
* = 1,...,ЛГ-1.
в) - ЙГ(/, у) = в1"' у, Щ\ - 0, V) = 0,
Щ*к-Ъ,у) = т2х{цгЦк,и) + ех-** дс(^эи)-и2А/-в!^ х(/*-0,у)}.
Решение имеет вид
Ж(/,у) = ув1"/+С. A9.9)
При / -1 = N А/ имеем: 0 = V [(# -1) А/] + С, поэтому
^(^-ЖЛГ-ОЛ'Не0-!], /€[(#-1)Д/,ЛГД/).
При / = СЛГ-1)Д/:
ИЧ(# - 1)Д/ - 0, V) = шах {«[(ЛГ - 1)А/] [ е1'^^ -1 ] + е1"^-!)* {и[(^ _ 1)д,] х
х[во _1] + Н^и(ш){е{Ы-т-ш _е^-'^-('+1L']}-и2[(ЛГ-1)Д^ДГ-
/-0
- е1-^-х)ы х[(# - \)Ы - 0, V) (. A9.10)
557

Применяя необходимое условие экстремума, имеем
в1-(ЛМ)д/ _!_ 2ц[(# - 1)Д/] А/ = 0.
Поэтому
Л-(ЛМ)Д/1
и[(ЛГ-1)Д*] = - — 1-, /€[(ЛГ-1)А/, ММ). A9.11)
2ДГ
Выпишем A9.9) при / = (# -1)ДГ с учетом A9.10),A9.11):
Щф - 1)Д/ - О, V) = — [ вМЛМ)" -1 ]2 + в1-(^-1)Д/ ^(^ _ 2)А/] х
4Д*
х[е(М-1-Н+1>6й _^-1-^+2-1)А/ЬвИ^-1)А/ ^ __ 2)д/] [в<ЛМ-*+2)Д/ _ ц =
= в1-(ЛГ-1)А/ у[(#-2)Д/] + С.
Отсюда для / € [(# - 2)Д/, (# - 1)А/):
Ж(Г,и) = и[(ЛГ - 2)Д*] [е1-' - «МАГ-О* ] + -±- [вМ"-0" -1 ]2.
4Д*
При / = (#-2)Д/:
Ж((ЛГ - 2)Д/ - О, V) = тах (и[(М - 2)Д/] [е1-<"-2>д/ - «М*-1>" ] +
и 1
+ 4Д/ [ еЫ*~1)А' "! I2 + е1"*"^ {*<* - 2)Д/] [ е° -1 ] +
+ 2и('Л')[е("-2-')д/ -в<^-3>АГ]}-и2[(^-2)Д/] Д/-
1-0
- в»-<"-2)л/ {т1(* - 3)Д*] [еА/ -1] ^ «(/ДО [в(^-0Д/ _в<*-/-3)дг) ] |}
/=0
Используя необходимое условие экстремума, получаем
в1-("-2)А/ _ в1-(ЛГ-1)А/ _ ад^ _ 2)д,, д, = 0
Поэтому
-1-(ЛГ-2)Д/ Л-(#-1)Д/
и[(М-2)М\=1 ^ , *€[(ЛГ-2)Д*,(ЛГ-1)Д0.
По индукции получаем формулу для определения оптимального
дискретного программного управления
4Ш] = - - , /е[*Д/,(* + 1)Д/), к = 0,...,ЛГ-1. ¦ A9.12)
2 А/
558

19.2. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО ДИСКРЕТНОГО
УПРАВЛЕНИЯ С ПОЛНОЙ ОБРАТНОЙ СВЯЗЬЮ
19.2.1. Постановка задачи
Пусть поведение модели объекта управления описывается обыкновенным
дифференциальным уравнением
*(') = /(',*('),"('*))> '«П =['*.'*+!>. * = 0,1,...,ЛГ-1, A9.13)
где х — вектор состояния, х е Яп; и — вектор управления, и е I/ с Я9, Ц—
некоторое заданное множество допустимых значений управления; /еГ = [/0,^) ~~
промежуток времени функционирования системы. Моменты времени *о>'#> а
также разбиение множества Т на полуинтервалы 7* =[/*,/*+!), где 1к<*к+\>
А; = 0,1,...,#-1 заданы. В каждый момент гк траектория непрерывна слева:
х(/*) = х(/*-0).
Обозначим Г = {*к}%~$ "" множество точек, в которых задается управление.
Предположим, что начальное состояние не фиксировано и может быть
любым: х(/0) = х0 еЯп.
Предполагается, что при управлении используется информация о
дискретном времени и векторе состояния в заданные дискретные моменты, т.е.
рассматривается дискретное управление с полной обратной связью.
Множество допустимых дискретных программных управлений 2/0 образуют
последовательности: и() = {иAк)}%^, и(*к)е1/.
Определим множество допустимых процессов Ю(^,х$) как множество пар
<? = (*(')> "О), где функции !/(•) принадлежат множеству допустимых управлений
#о, функции х() непрерывны и кусочно-дифференцируемы на Г, и
удовлетворяют уравнению 09.13).
На множестве Ю(*0,х0) определим функционал качества управления
N-1 '*¦; л
Ш)= I [ }/°(/.Д<0.и(/*))* + Л(«(/*).и(/*))] + ^(«(^)Х A9.14)
*-° <*
где/°(/,х,1/), 8ь(х,и), # = 0,...,#-1; Г(х) - заданные непрерывные функции.
Множество ип допустимых дискретных управлений с полной обратной
связью образуют функции: иAк,х):ГхЯп -» G, которые порождают допустимые
дискретные программные управления для каждого начального состояния
х(*0) € Я», где и(.) = {*/(/*) = шЦк9хШк)) }^Го ^ и0.
Требуется найти такую функцию «*(/*,*) е &п , что
/(</*)= пил /(</) Чх0еЯ\ A9.15)
559

где й* = (х*0, и*() = [и*(**) = **('* 1*('*))Ь-о ]"" результат решения уравнения
A9.13) с управлением и*((к,х) е &п и начальным условием х0 € Яп.
Искомая функция и*((к,х) называется оптимальным дискретным
управлением с полной обратной связью. Для любого начального состояния оно порождает
оптимальную пару й* € .0(*о»*о)-
19.2.2. Соотношения для нахождения оптимального управления
Из системы уравнений, полученной для общего случая задачи синтеза
оптимального управления при неполной дискретной информации о состоянии (см.
систему A9.24) в разд. 19.3.2), следуют соотношения для определения
оптимального дискретного управления с полной обратной связью «*(/*, х):Гх Яп ->11:
Щ*„-0,х,у) = -Г(х),
-^^=^ У(,,х,^х/Гх<7,
Ы /=1 Эх,
* = 0Д...,ЛГ-1,
^(^-0,х,у) = Щ^,х,1/(/ьх))-^(х,1/(^,х)), * = 1,...,ЛГ-1, A9.16)
и(^,х) = а1втах{Ж(/л,х,1/)-^(х,1/)}, & = 0,1,...,#-1.
Пример 19.4. Даны модель объекта управления
х@ = «@), х@) = х0,
где х € Я, и е Я, / е Г0 = [ОД), и функционал
/=^1/2@)+^х2A)-»тш.
2 2
Требуется найти оптимальное дискретное управление с полной обратной
связью и*(/^,х).
П Система A9.16) имеет вид
_8У(иу).аУ^у)У[ Щ1-0,х,у) = -1х2, A9.17)
д/ дх 2
К@, X) = Э1Х1ШХ | »Ч0, X, И) -|и2|.
560

Будем искать ее решение в виде
тих9у)Лк2(иу)х2^кх(иу)х^к{,(иу).
Подставляя последнее выражение в A9.17) и приравнивая нулю члены при
одинаковых степенях х, получаем
*2(*,у) = 0, *2A-0,у) = -1,
Кх(*,у) = -К2(*,у)у, ^A-0,у) = 0,
*0('.у) = -*,(/,у) V, *0A-0,у) = 0.
Решение этой системы:
*2(/,у) = -1, ^(/,у) = у(/-1), *0('^) = -±у2(*-1J.
Поэтому искомое оптимальное управление с полной обратной связью имеет вид
«*@,х) .а^тах \-^2 -их--и1 --и11 = -у.
Полученное оптимальное управление с полной обратной связью для
каждого начального условия х0 е Я порождает соответствующее оптимальное
дискретное программное управление, найденное в примере 19.1.И
Пример 19.5. Даны модель объекта управления
х@ = х@ + и(^), к = 0,...,# -1; х@) = 0,
где*€Д, иеЯ, /€Г = [0,1), *к=кМ, А/ = —, и функционал
N
/ = 2 1/2(/А:)АГ- хA) -> тт.
Требуется найти оптимальное дискретное управление с полной обратной связью.
? Здесь**(х,1/) = 1/2(^)Д/, /°(/,х,1/)^0, Г(х) = -х.
Система A9.16) имеет вид
дЩ*,х,у) дЩ*,х,у)г , и,п Л ч ^
7 = 7 [х + у], *кA-0,х,у) = х,
Э/ дх
Щ*к -0,х,у) = тах{и^,х,1/)-1/2(^)Д/ }, * = 1,...,#-1,
и
и(*к,х) = э1$тах{щ*к,х9и)-и2(*к)А*}, * = 0,..,#-1.
561

Будем искать ее решение в виде
Щ*,х, у)=|ад у) х2+ад V) х+ад V).
Подставляя последнее выражение в систему и приравнивая нулю члены
при одинаковых степенях х, получаем
ад V) = -2К2(г,у), *2A -0,у) = О,
аду) = ~аду)-аду)у, ^A-0,у) = 1,
*<>(', V) = -аду) V, *0<1 -О, V) = 0.
Решение этой системы: К2(*,у) = Се"ъ, Кх(иу) = Се~', *<>(*,у) = уе1"' + С,
а с учетом конечных условий
аду)=о, аду)=е'-', аду)-у[«!-'-1], /€[(лг-1)ди).
Отсюда Ж(/,х,у) = в1"гд: + у[в1-/-1], *е[(#- 1)Д/, 1).
При / = (#-1)Д/:
»Ч(ЛГ- 1)Д/-0,х,у) = тах {вИ#-1)д/ х + ^_ 1)д/] [е^ _ц_ц2^м ^Х)д,] д,}
Применяя необходимое условие экстремума, имеем
е" -1-2и[(М-\)А*]А* = 0.
Отсюда
и[(^-1)А/]=^-^, /€[(^-1)А/,1).
Тогда Ж((#-1)Д/-0,х,у) = е^х+—[еА'-1]2.
Поэтому ЛГ1((ЛГ-1)А/-0,у) = еА/> ЛГ0((^-1)А^-0^)=-^-[^-1]2.
4А/
При / е [(ЛГ - 2)Д/, (# - 1)А/):
Кх(*,у) = Се-'9 е" =Св-("-1)А/, С = е, аду) = е1"',
аду^уе'-'+С, -^-[е^-П^уе^+С,
4А/
*о('> V) = V [в1"' - в" ] +-1- [е" -1]2.
562

Поэтому Щ*,х,у) = е1-' х + у[е1~' -ем]+^-[еы -I]2.
При / = (ЛГ-2)А/:
Ж((^-2)АГ-0,х,у)«тах(в2^х + и1(^-2)А/][в2л/-вд/]-1/2[(ЛГ-2)АГ]АГ +
и
¦«г1*"*
Применяя необходимое условие экстремума, получаем
е2* _е* _ 2и[(М - 2)Д/] А/ = 0.
Отсюда
и[(ЛГ-2)А*] = € ~е". X €[(ЛГ-2)Д*. (# - 1)А0.
2Д/
Поступая аналогично, имеем
^((^-2)А/-0,х,у) = ^х+-Ь[еА/-1]2+-17[е2д/-вА/]2.
4Д/ 4Д/
При * е [(ЛГ - 3)Д*, (ЛГ - 2)Д/):
/Г1(Г,у) = Се-', в24,=Св-(ЛГ-2L', С = е, ЛГ,(Г,у) = е,-')
*0(<^) =уе1"' +С, -^-[е" -I]2 +^-[в2л/ -е4гJ=У^' +С,
4Д* 4А/
*о</,у) = у[*,-'-*2"] + ^[г"-1]2+^[*24'-вА']2.
4А/ 4Д/
Поэтому
1-Г ^ . « г „1-/ „2Д/ 1 ^ * г ЛД/ _ п2 ^ 1 г Л2Д/ _ ЛД/ л2
Щ*,х,у) = е1-'х + у[е1~' -е™]+^[е" -I]2 +-?--[е2" -е")
4Д/ 4Д/
При / = (#-3)ДГ:
Ж((ЛГ-3)ДГ-0,х,у)==тах{е3*х + 1^
4Д*1 4ДГ '
Применяя необходимое условие экстремума, имеем
е3" -е2**- 2«[(# - 3)А/] А/ = 0.
5<

Отсюда
|/[(ЛГ-3)А/] = * ^ , /€ [(*-3)Д/, (*-2)Д/).
По индукции получаем формулу для определения оптимального
дискретного управления
л-ш _л-<*+1)л/
и[*Д*] = - г2 , *е[Ш,(к + 1)Ы), * = 0,...,#-1.
2А/
Заметим, что в данной задаче оптимальное дискретное управление с
полной обратной связью не зависит от х и совпадают с дискретным программным
управлением (см. пример 19.3).И
19.3. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО ДИСКРЕТНОГО УПРАВЛЕНИЯ
С НЕПОЛНОЙ ОБРАТНОЙ СВЯЗЬЮ
19.3.1. Постановка задачи
Пусть поведение модели объекта управления описывается обыкновенным
дифференциальным уравнением
*@ = /(>,*<'),"<>*)), *еТкш[ым), * = 0,1,...,АГ-1, A9.18)
где х - вектор состояния, х е Кп; и — вектор управления, и € 17 с Я9, V —
некоторое заданное множество допустимых значений управления; 1 € Т = [/<)>'#) ~~
прамеокуток времени функционирования системы. Моменты времени *о,*н, а
также разбиение множества Т на полуинтервалы 7*=Йь'*+1)> гДе
*к <**+ь & = 0,1,...,АГ-1 заданы. В каждый момент 1к траектория непрерывна
слева: х(*к) = х(*к -0).
Предположим, что начальные состояния принадлежат множеству
&'• *('о) = *о €ЙдЛл, а модель измерений описывается соотношениями
*('*) = *('*,х<'*)Х * = ОД,...,* -1, A9.19)
где геКт - вектор измерений, Ой тип; функции Лу(/,х)бС1(ГхЛл),
] - 1,...,/и ; Г = {^}^о " множество моментов времени, в которых производятся
измерения.
Множество допустимых дискретных программных управлений 2/0 образуют
последовательности: и() = {и('*)}ь."о »и(*к)е V-
Определим множество допустимых процессов Ю(^9х^) как множество пар
*/ = (х(-), !/(•)), где функции !/(•) принадлежат множеству допустимых управлений
564

#0> функции х() непрерывны и кусочно-дифференцируемы на Г,и
удовлетворяют уравнению A9.18).
На множестве Ю(^9х^) определим функционал качества управления
Д<0= Е1 [ 7/°Л^0,|</*))Л + Ы«('*).иD))] + '(«(^)). A9.20)
*-о ^
где /°(/,х,и), #*(х,1/), & = 0,...,#-1; ^(х) — заданные непрерывно
дифференцируемые функции.
Множество Мт допустимых дискретных управлений с неполной обратной
связью образуют функции «(/*,*): Гх Дт -»G, которые порождают допустимые
пары <? = (х(-), и(-))е Ю(*0)х0) для каждого начального состояния х0еС19
причем и(*к) = и(*к,*(/*)) = «С*>*('*. х(/*))) для всех к = ОД,...,N -1.
Требуется найти такое дискретное управление с неполной обратной связью
и*(^,г)€^,что
/(</*) = тш /(</) УхоеО, A9.21)
где </* = (х*(), и*(.))€.0(/о,хо) ~" результат решения уравнения A9.18) с
управлением «*('*>?)€ &т и начальным состоянием д^ей.
Искомая функция «*('*»*) называется оптимальной синтезирующей
функцией на множестве О {оптимальным дискретным управлением с неполной
обратной связью).
19.3.2. Соотношения для нахождения оптимального управления
В [36,37] сформулированы и доказаны достаточные условия оптимальности
искомого управления. При этом предполагается, что:
1) пищ л/дН(*'х) =т Ч((,х)еГхЯп9
причем базисный минор располагается в первых т столбцах. Число т и
размерность вектора измерения совпадают;
2) множество О определяется соотношением х2=у0{х1)9 где
*1=(х1,...,хт)г, *2=(хт+1,...,хл)г, х = (х*,х2); Уо^М^т + Ъ.^п, -
заданные непрерывно дифференцируемые функции, т.е. размерность множества О
равна т;
3) существует вектор-функция у(*,х1) :ТхЯт -> Яп~т, удовлетворяющая
системе
+ /]&х\у{их\иЦкМк1Хк{их1)))\ } = т +1,...,л; У(/,х') е Тк х Ят, A9.22)
565

У^'о>х1) = Уо^х1), у = /и + 1,...,/1, A9.23)
где х*(/,х') = х«к; &\у(<,х1)), х(*к) = х(*к; **).
Заметим, что решение системы A9.22), A9.23) позволяет описать
множество возможных состояний в момент г с помощью связи:
х2=у(*9х1) У(*,х1)еТкхКт. Если х(/) - решение уравнения A9.18), имеем:
х2@ = Ж*Ч0) **еТк.
Предполагается, что размерность множества, описываемого соотношением
х2 = у(ихх\ остается постоянной и равной т при всех / е Тк;
4) гапе ?*'(',*) УЙх^бГхЯ",
а(хь...,хт)
гдеЛ,(/,х1) = Л(/,х,,Жх1)).
Из условий 1-4 следует, что имеется взаимно однозначное соответствие
между х1 и г V/ € Г на многообразии, описываемом системой A9.22),A9.23),
*('* у *(>*)) = «(>* > *(>*, х1 (гк), ><'*, х1 [$к)))) = «'('* > х1 (*к)). Поэтому будем
рассматривать эквивалентную проблему нахождения оптимального управления в форме
иAк,х1):ГхЯт ->1/, так как векторы г и х1 \#еГ содержат одну и ту же
информацию о векторе состояния системы A9.18).
При выполнении этих условий в [36,37] получена следующая система
уравнений для нахождения оптимальной синтезирующей функции «*(/*,*) бЖт на
множестве О:
—*—Г. = "Е—Н /1(*,х1,уЧ*,х1,у),у) + /^*,х1,ууA9х1,у),у),
01 ы1 0Х/
) = /и + 1,...,/г, V(/,x1,V) еТкхКтх1/9 к = 0,1,...,# -1,
УуСо,*1^) = Уо](х1), ) = т + 1,...,л,
^(^,х1,у) = ^,х1) = ^(/Л -О^в^ь^^х'"'^ -0,х!)))),
У;(/ЛГ-0,х1,у) = -а/Г(Х >УУ('*-°>х >у)\ у = т + 1,...,л, У(х1,у)еЛтх(/,
Эху
щ*м-а.**.у)- Е а^'*Ч'*~0>*1>у))у)(^-о,х',у)-г&уци-о,х\у)),
у-т+1 0*у
аЧ^&Ду) ЭЯ(/,х|,у,г(/,х|>у),у)
а/ аху
-, у = т +1,...,л,
566

Ч(*,х\у)еТкхЯтх1Г, * = 0Д,...,ЛГ-1,
И^-0,х1,у) = Ж(/ъх1,«(/*,х1))+ 2 ^к^Ки^х^у^х1)-
- Е ^уС* -О,*1^)*)^ -09х\у)-ь(хКу(*к,х1)9ш%9х*))9 A9.24)
У-т+1
У(х!,V) € Ят х 1/,Л: = 1,...,ЛГ -1,
.1 „(* ~1\ „V* ~Ь
эх,
и(/*,г) -иЦк,Ы?к.х1 ,УИк,х1))) = *'(>*,*') = 318пш: {щ**,*'.и) +
+ Е,Р/('*,«1.и)^(<'*,ж,)-Л(*,.><<'*.«1).и)}, *-1,...,ЛГ-1,
У-лн-1
«('<»*) = «Со»^»*1»^*1))) = 313тах Цо^1»") +
У-т+1
ще
« як/// *Л
Я(/,х,у) = 5] //(/,х,у) +
У=т+1 /-1 ох1 У-т+1
В случаях отсутствия дискретной информации о векторе состояния или
наличии полной информации система уравнений A9.24) преобразуется
соответственно к A9.8) или A9.16).
Пример 19.6. Даны модель объекта управления
*1<0 = и@,
*2<0 = *!(')
и функционал
/ = «2@) + |[х?B) + х22B)] -> шп,
где х/B) = х/B-0),/ = 1,2.
567

Здесь х = (хих2)т ей2, иеК, /€ Т = Т0 =[0,2), # = 1, 80(х,и) = и2,
Пх)Л[х1+х1\.
Рассмотрим частные случаи информированности о состоянии.
А. /11 = 0, множество начальных условий О задано точкой
*(*о) = *о=(-3,4)г.
Требуется найти оптимальное дискретное программное управление и*().
П Применим соотношения A9.8) для данной задачи:
Я(/,Ч^,Х, V) - Ч>,(/, V) V + У2(/,V) ХЬ
Х\(*>У) = у> ^1@, V) = Х10 - -3,
*2& у) = *1 Л у)» х2@»у) = *20 = 4,
Ф1(/,у) = -Ч>2(/,у), 41B-0,V) --Х|B-(Ьу),
*2(/,у) = 0, ^2B-0,у) = -х2B-0,у),
1/*@) = аггтах{ж@,и)-^1@,1/)-3 + 4/2@,и).4-1/2},
Щ2-0,у) = -|[х,2B-0>у) + х|B-0,уI,
- Щ1,У) = *,(*, V) V + Ч»2(*,У) Х,(/,у) - Т2(/, V) Х,(Г, V) = «?,(/, У> V .
Отсюда получаем
Ч'1(*,у) = -х1B-0>у) + х2B-0,у)[/-2], Ч'2(Г,у) = -Х2B-0,у),
у[<-И2
*1(>^) = х,B-0,у) + у[Г-2], х2(*,у) = х2B-0,у) + х,B-0,у)[Г-21 + -
Из последних двух соотношений при / = 0 имеем
-3 = х,B-0,у)-2у, 4 = х2B-0,у)-2х1B-0,у) + 2у,
следовательно, Х1B-0,у) = 2у-3; Х2B-0,у) = 2у-2.
Поэтому
аду) = 3-2у + [2у-2][*-2], «Р2^у) = 2-2у,
Щ2-0,у)=±[2у-2]2+±[2у-3]2,
-РК(Г,у)-{[3-2»] + [2у-2][Г-2]}у.
568

Тогда
Щ^у)=|[2у-2]2+|[2у-3]2+[2у-3][/-2]у-|[2у-2][/-2]2,
а оптимальное программное управление определяется из условия
1/^0) = агатах |-&/+-у + [2-2|/].4-[-6и + 7]3-1/2|.
Так как на управление ограничений не наложено, применяя необходимое
условие экстремума, получаем: 2 - 2и = 0 и и*@) = 1.
Б. Начальные условия заданы множеством О размерности т = 1:
х(/0) е П = | х | х2 = у0(хх) = —*1, *1 € Я \.
Требуется найти оптимальную синтезирующую функцию »*@,Х!) на
множестве О.
? Будем искать функции, входящие в A9.24), в виде
Ж*1, V) = Уо(*9 V) + Л(/, У)ХЬ ЧГЦ,Хи V) = У&у) + Щ*,У)ХЬ
Щ*,*1>У) = |^2^ V) X? + *!(*, V) X! + К0(*,у) ,
где ?ь(',у), л(/,у), К0(*,у), КгA9у), К2(*,у), Ч^у), #(/,у) - неизвестные
функции.
Тогда получим
#(/,Х, V) = [*2(/, V) X! + *!</,V)] V + ЛГ(/,у) Х2 V + [У(/, V) + ЛГ(/,У) X! ] Х2 ,
Л)('.*> + Л('.*)*1 =-^(/,у) У + Х! ,
4
И>@,у) + и@,у)х1 =-з"Х|'
^B-0,у) + ЛГB-0,у)х1=-^оB-0,у)-у1B-0,у)х1,
*(*, V) + NA, V) ХХ = - #(/, V) V .
Отсюда
Л0.*> = -*('.*>*. ^о@^) = 0,
Л('.у)-1, И<0,у) = -|,
*('^) = -ЛГ(/,у)у, ^B-0,у) = -^0B-0,у),
569

^(*,у) = 0, ЛГB-0,у) = -ЛB-0,у).
Из двух первых уравнений имеем
Уо(',у) = УоB-0,у)-У1B-0,у)у[{-2]-^уЦ-2]2,
Л(',у)-лB-0,у) + [/-2|,
2 2
где, полагая * = 0, получаем УоB-0,у) = —у, лB-0,у) =—, а из оставшихся
соотношений
ту) = -|у+|у['-2], ЛГ(/,у) = -|.
Вьшишем аналог второго и четвертого соотношения из A9.24):
1аГ2B-0,у) х? +*,B-0,у) х, + *0B-0,у) = ±у§B -0, у) +
+ УоB-0,у) у,B-0,у) х, +1Л2B-0,у) х? -±х,2,.
|лГ2(<,у)х2 +*,(', у) *1 + *0('^) + *2(*,у)ух, +*,(*,у)у + Ч'(*,у)х1 + ЛГ(*,у)х,2 =0.
Отсюда имеем
*2(',у) = -уЛГ(',у), ЛГ2B-0,у) = -1 + Л2B-0,у),
^,(Г>у) = -ЛГ2(/,у)у-Ч'(Г>у), АГ,B-0,у) = ЛB-0,у)^B-0,у),
*0(>,у) = -*.(>,У) у, *0B-0,у) =|^B-0,у) .
Решение имеет вид
*2<>^) = -| + |[*-2], ЛГ1(/,у)=|у+уу[*-21-у[Г-2]2(
ВД^=|у2-|у2[/-2]-|±у2[/-2]2+|у2[*-2]3.
Искомая оптимальная синтезирующая функция:
н*@,х,) = 318тах \\к2@,и) х,2 + ЛГ,@,и) х, + АТ0@,н)-1^0,н) х, -
и 12 3
570

--#@,1/) х? -и2| = а1втах|-—х? -6их{ -4и2 +- ихх +-Х? -и2|.
Применяя необходимое условие экстремума, находим
«*@,х,) = -|*,.
Сравнивая найденное управление с результатом, полученным в п. А ,
можно сделать вывод, что для начального состояния х0 =(-3,4)т еС1 управление
»*@,Х!) порождает соответствующее оптимальное дискретное программное
управлением
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
19.1. Для задачи
х(/) = х@ + и@), х@) = Хо, хеЯ,иеЯ,*еТ0=[ОЛ
/=1|/2@) + 1х2A)-»пш1,
а) найти оптимальное дискретное программное управление и*();
б) найти оптимальное дискретное управление с полной обратной связью
19.2. В задаче
х(/) = 1/(/*), *-0Д х@) = Хо, Х€ Д иеЯ, N = 2; Т0 =[0,1), ТХ =[1,2),
/=тЕ(^)+^2B)^пип,
2 Я 2'
а) найти оптимальное дискретное программное управление и*(«);
б) найти оптимальное дискретное управление с полной обратной связью
и«к,х).
19.3. В задаче
х@ = х@+ «(**)> * = 0Д; х@) = Хо, хеК, иеЯ^ = 2; Т0 = [0;0,5), Т{ =[0,5; 1),
а) найти оптимальное дискретное программное управление */*(•);
б) найти оптимальное дискретное управление с полной обратной связью
571

ОТВЕТЫ
Глава 1
1.1. а) ЯСбпа + Жж =Цвх; G> + 2)х = $, где Т = КС. 1.2. а) р2х = *.
1.3. (/28т/р + 2/2)х = [-/3р2+A-^3со8/ + 2/2)р + со8/ + /38т/ + 2/2со8/]^.
1.4. Ъс = (ф +1)# при л = 0 . 1.5. [а^р3 +а2р2 + а{р + а0\х = \р2 +1р + Ц&, где
а3 =81П/, Д2 =1 + 2с08/ + /8Ш/, й\ = 1 + / +/81П/+ *С08Г - 81П/, 0О =/ + С08/, Щ>И
л = 1, т = 0. 1.6. а) (р + \)х = р& при т = 1, л = 100.
Глава!
2.1. а) *(/-т) = вТ-'/(/-х) при л = 1. 2.2. а) И(*,т) = \---$А1(*-%),
*(/,т) = -^т=Д'-т). 2.3. а) *(/,0) = . 1 7@, Щт) = ^т2 + 1 1(-т) при
л = 1. 2.4. а) *(;,т) = ' C* Гт ^(/-т). 2.5. а) *(/,т) = 2в2(т-'>/(/-т) при л - 1,
2т4
/и = 0. 2.6. а) *(/,т) = -ет~'/(/-т) при л = 100, /и = 1.
2.7. а) *(/,т) = A-^-')/(/-т) при л = 0, /и = 1. 2.8. а) *(/,т) = -!^/(/-т),
х@=-Н2-1Iп2/./(/-т) при л = 0, /и = 1.2.9. а) х@ = 100A - /ДО - т) при
л = 100, тп = 1. 2.10. а) х@ = [0,75 - 0,5<г' + в'@,5/ - 0,25)]/@ при л = 0, тп = 1.
Дг-т),*^т) = [0 1^1|./(/-т) при л = 0,
1 ^
2.11. а) Кх«,т) =
0 -
т )
тп = 0. 2.12. а) ЛГХ(/, т) = (8т(/ - т) соз(/ - т) - 8т(/ - т)) • /(/ - т) при л = 10,
т = 0.2.13. а) у^)^Нъ2\п^^ +4У/(/-2) при л = 0, /и = 0.
2.14. а) х@ = (со8/-1)-1@ при л = 10, т = 0.
572

Глава 3
3.1. а) Щх)=-7—г-±т • 3<2-а> У<йш[-Г Г гЧ "Ри
я-10. «-0. ЗА а) щ5)=Ж±±Ш1±]Ш2.. 3.4. а) ^„М—±г при
1 + *г 2*^3 5 + *
/1 = 1. 3.5. а) цг*(,) = ^- «у , ^E)=^±1 при /1 = 0.
3.6. а) х(/) = 1-в^*[сов^+^яп^/|Щ/). 3.7. а) ху = к при л = 0.
3.8. а) хс@ = B<г'-в-2')./@, х,ы,Д0 = 0,5 при /1 = 1, /и = 1.
3.9. а) х@ = B-2со8/ + 81п/I@ при л = 10, т = 0. 3.10. еу=дГ2+Л/.
3.13. хй(/) = 8шA/з/ + -|) при /1 = 1/3, т = <|/з. 3.14. ^(<в)= ?^,.
о ог + ц^
3.18. *< 122,21 при л = 100. 3.19. а) тх(/) = [1 *'],
3.15. Дх=4*
* 2
*« /^ [Ф('ь'2>Д*<'2>. '1**2, Г^Л„ .V («*"* (/1-/2)«/2"/,1
= ГФ(/ь/2)Лх(^2), '1**2,
;
неуправляема; не наблюдаема. 3.21. а) неустойчива.
Глава 4
4.1. а) Щ*,*)-.
(\ 0
0 1
1о о
°1
0
V
при
л = 1. 4.2. а) Щ*,*) = Р~2[Я + Р'х + Р] !.
Глава Ъ
5.5. хс(А:) = со8— + Ляп—, * = 0,1,... . 5.6. хс(^) = 8ш^-^, А: = 0,1,...
3 3 6
1
16
1 7,
5.7. хс(к) =у5*+1 +у(-2)*. 5.8. х(*)-| +^ИГ "^(-3)* .
5.9.х(*) = 4* + 6 • 2* -5. 3*. 5.10. х(к) = 3* -2* + х0(* +1J* + (^ -4х0 - \)к • 2*.
573

5.11. х(к) = 2к-\-к. 5.12. тх(к) = 0; Дх(*) = | Ь-ф . *,(+«>) =|,
Глава 6
6.4. хс(А;) = со8~+Л8т^, * = 0Д,... . 6.5. х(.(А:) = 8т-2%^) * = 0Д
3 3 6
6.6. хс(к)Л5к* +^(-2)*. 6.7. *(*) =1Д(-1)* -|(-3)* .
6.8.х(*) = 4* +6-2* -5-3*. 6.9. х(к) = Ък -2* + х0(к + \Jк +(хх -4*о -\)к-2к-1.
6.10. х(к) = 2к-\-к.
Глава!
7.1. а) Тх + х = кГ(^-х). 7.2. б) Х1=х2, *2=*з» х3 =-5х3 - &х2 - 4хг +
+4Л*(*-х))при л = 1,т = 1. 7.3.б)^ = ^(у + Щх,^)).
сЫ Ту
Глава %
8.1. а) Дх + /Лх + Дх = А& + 2ОД при л = 1. 8.2. б) Ддс = 0 при л = 1, т = 1.
4с
8.3. а) @,0) - центр; A,0) - седло. 8.4. а) д(а) =—; л(а) = 0. 8.6. а)
па
со/т = 39,6 с; аП = 0Д1 при л = /и = 0, с = 1. 8.7. а) устойчивые автоколебания с
1 Ау* ПГ Т
параметрами <ап = . ; ап =—ку 1 2 возможны (в системе на рис. 8.17,
у^Гг я 71+72
б) при всех положительных значениях ку. 8.8. а) сектор [0;+оо). 8.9. а) при всех
а е@;+оо) система неустойчива при л = 0. 8.10. а) при всех а е@;+оо) система
неустойчива при л = 0. 8.11. а) ^ =—Ф|^-|, к[Х) =— /1-4Ф2[^М,
кФ=Ь_е *Ы ,щеФ(х)= -±=\е *А.
1г2яа^ 42ъ 0
574

Глава 9
е'+в2"'
е'-е2"'
1-е
2-2/
9.1.а)*«@-*Ь/ 2 , «*(')=*<>' 2 ; б)и*A,х) =
1 + е2 1 + е1 1 + е* а
9Л. *Г<')=^-^-^ х1«) = *±-1, иГ@—|, «2@ = *-^--
9.3. в'(*) = -A+Л)*. 9.4. и,а,х) = 3с8/8х. 9.5. «'(*,х) = -л
| = -дс.
»^ ./. ч * и/.ч п/Л (а + Р)(Лт-о + Р) + р-а-(Лг-д-Р)а@
9.6. и (Л*) = --Р(фс, где ^т' ^Лг_д/р_(^.0-р)а(<) '
«*(*) = е-2«г-'), р = 1рД, г = 4- 9.1. н*(х) = -(*, + ^2).
9.8. «*(*) =-|(*12х1+АГ22х2), ще ^г»}^, *и =}/}К* + 2гДо]-
9.9. и*@ = 7-б*. хГ@ = 3/2-|/3, дОД-бГ-;/2.
«¦ ¦•»-{^;««г "¦•,''-
а/2 -{
, 0йК*и
-•^-+С,/ + С2, <1***Г,
«&«-{*' „ ^'^ где с*-«г. с2=*-^, /,=1 г-аД-
24' [-а* + С1,*1***Г, 1 2 2*2 Та
-/и^; б) «*(/,*) =
1-е
2-2/
1 + е
2-2*
Глава 10
10.1. а) т*(/) = ^±^/По, «•0-^4"'
1 + е2 1 + е2
10.2. ^Сг)-уГ^-~-Л + 1. *2@ = |[4-'1 «?»—|. «5-|('-1).
10.3. д*(/,х)=3в8г8х. 10.4. «*(/,х) = ~х.
/кою 11
11.1. и*®шш\*9Г{)т-7\**^ %Я, 4У-[з1(г)+11*<01* +
1 + Зе
8-2е*0'
+ ^ [дТ(/)-*@<ЙЬ *@) = 2.
-юг
1 + е
11.2. 1/*@«**(/,1Ъ')--*(<), ** = -4&/ + ^ + ^"^ [ДГ@ - *(/)*?], *@) = 3.
6-е
-ЮГ
575

Глава 12
12.1. х,*@)=1, х2*@) = 1, н*@)=-3/4, х,*A)=1/4, х^A) = 0,
н*A)=-1, х,*B)=-1, х$B)=-1/4.
12.2. х,'@) = 1, Х2@)=1, «*@)=-3/4, х,*A)=1/4, х^О,
и*A)=0, х,*B)=0, хф)—1/4.
12.3. хГ@)=1, хг@)—1, ыГ@) = -1, «2'@)=-1, х,*A)=-1,Х2A)=-1,
«ГA) = -1, @—1, х;B)=-3, ХгB)=-1.
12.4. хГ@)=-1,х2*@)=1, иГ@)—1, ОД—1/2. х^)—1, ^A)=-1/2,
и,*A)=-1, И2*A)=-1/2,хГB)—5/2, ХгB)=-3/4.
12.5. н*@,х)=-A/2)[х,+х2], в*A,х)=0, пип/=-х,20-х10х20+-х|0.
12.6. и*@,х)=--х, +-х2, и*A,*)=0, тт/=-х2о--х10Х2о +у *и>-
Глава 13
13.1. т,*@) = 1, т2*@) = 1, и*@) = -1,54; /я,'A) = 0,46; т2'A) = 0,
и*A) = -0Д4; т,*B) = 0,07; т2'B) = -0,46.
13.2. «,*(•) = {2,1,1}, т2*() = {1,5,7}, «'(•) = {-1,0}.
13.3. «'(О,х) = -A /2)[х, + х2], «'A,х) = 0.
13.4. в'@,х) = -A/3)х, +A/3)х2, и*A,х) = 0.
13.5. а) «•@,х) = -2х,+B/3)х2, в'A,х) = -A/2)х1:
б) и'@,х) = -E/2)х, + х2, и*A,х) = -B/3)х,;
в)и'@,х)=0, и'A,х) = 0.
13.6. а) «*@,х) = D/3)х,-C/2)х2, «*A,х) = 0;
б) в'@,х) = F/5)х,-(8/5)х2, «*A,х) = 0;
в)«*@,х) = 0, в'A,х) = 0.
13.7. и'@,х) = - х, -A/3)х2, и*A,х) = 0.
Глава 14
14.1. Коэффициенты усиления наблюдателя полного порядка: К{ =2 + 1/Н,
Кг = \1Н; низкого порядка: Кх = 1 + 1/А, К2=\/Н.
14.2. Коэффициенты усиления наблюдателя полного порядка: К{ = 2,
К2=1/к; низкого порядка: К{ = 1, АГ2 = 1/Л.
143. а) И*@) = -B/3)х,@) _A/3)*2@), и*A) = -B/3)х,A)-0/3)х2A);
576

б) и*@) = -A/3)х,@)-A/3)х2@), и,A) = -A/2)х,A);
в) и,@) = -D/5)х,@)-(^5)х2@), и*A) = -A/2)х,A)-A/2)х2A).
Коэффициенты наблюдателя полного порядка: К\=2, К2=\.
Коэффициенты наблюдателя низкого порядка: ДГ] = 1, АГ2 = 1.
14.4. а) и,@) = -Зс1@)-A/3)х2@), «*A) = -ф)щ(\)\
б) н*@) = -х,@)-A/2)х2@), н*A) = -0/2)х,A);
в)и*@) = 0,«*A) = -A/2)х,A).
Коэффициенты наблюдателя полного порядка: К\ = 1, К2 = 0.
Коэффициенты наблюдателя низкого порядка: К{ =0, К2 =1.
Глава 15
'* *' |5-2Г, 1й1<2, у*A) = -1, у*B) = 0, тю/ = 1.
\1-*, !<:/<
15.3.
1, 0*/<1, у*0) = -1, У*B) = -1, и*@ = 0, 0**<2,
-и 1<:/<;
1 . 1-* ,ЛЧ 1 ,Л, 1
2, у*A)--1, у*B) = 0, тт/=0.
Глава 16
16.1. в *г </,о) = и *г (/,хХа)) = -^,
в, р(',о,оMР(Г,*>а),
*(',«)
=М
^оУл0' «',*,*) >РО,М) и р</,*,*)>р<Ла,А),
2A-0
*, р(/А*) *№,«,*),
«>,*,*) = -—^(х2+A-0(*-*J), «*г (/) = —.
16.2. « *г (*,о) = и*г (/,*•(*)) = -7^7(^1 + *г).
3 + г"

ге,а)|
о-ЛВ
(хи^иУ, №,А,А)*№,В,А),
^7~(Ял +хи> хгл +хгв)Т> №,А,А) > №,В,А) и №,В,В) > р((,А,В),
Ы>*гвУ> №,В,В)<>№,А,В),
х^аI.шс='
где М!,х,х) =———{-3(хх1+х2У-(х(х1 -х,) + х2 -х2? )'.
2C+ т }
х = 2-Г, и*г@ = -|B-/).
16.3. Функции и *г (/,ст) и Р(*,х,х) такие же, как и в задаче 16.2;
[А, &г,А,Л)<.№,В,А) и №,А,А)*№,С,А),
&м, №,А,А)>#1,В,А) и №,Л,&АВ)>№С,&М),
хлвс, №,А,А)>№,В,А) и №,А,хав)>№,С,хав),
где х,^ — любое решение уравнения:
(Я-Л)г[(Ф + Ч0С8 + Л)-2«Гх] = 0;
хавс~ любое решение системы уравнений:
{(В-А)т[(Ф + Ч)(В + А)-УГх] = 0,
\(С-А)т[(Ф + Ч>)(С + А)-2Ух] = 0;
№,х,2)ш1хтфA) х+1(х-2)Тч>@ (х-2),
<но
< ;)•
ЧЧ0=}ф('), т = 2-/, 5 = 1 + у.
Остальные формулы для нахождения оценки х(*,а) получаются из указанных
циклической заменой вершин треугольника: А-+В -*С -+ А.
16.4. ,*г('.о)-В-гЛЙ(о))—^^2.,
*(',°)
а=ЛЯ
1ч»-'(Ф + Ч0(Л + 2>), Ы,А,А)>№,В,А) и «*,2>,2>)>Э(>,Л,10,
2>, №,В,В)*Ю,А,В),
где р(/,х,Зс)=1хгФ(/)х+1(х-х)гЧ'@(х-х), •(*)-—[ ^' *1 ],
578

*(,)„
A + т2)Д-Д' тА-4"
тА--
Чг,
-3 4 3
, т = 2-*, Д = 1 + т + у + ^-; Д' = 1 + т2+у,
д* = 2т + т2, Д" = 2 + 2т.
16.5. «*с(/,о) = «*с(>,х(о)) = -^, ^.^)|в-М]=^; «*с@ = -|.
16.6. ••с«;о).В*с(/,5(о))—-^т^+5,), х(*,с)| = ^,
3 + т ю«л* 2
гяет = 2-/; н*с(/) = -^й.
16.7. Функция и *с (<>о) такая же, как и в задаче 16.6,
*/, ч1 Л + Д + С
16.8. Функция «*с ('><?) такая же, как функция «*г(*,а) в задаче 16.4,
А + В
*(',*)(
а-ЛД
17.1. »*(*,х) =
Глава 17
2/и, х<(п + т)(*-1\ ОйГйХ,
О, (л + т)(/-1)*х*(л-т)(/-1^ 0***1,
-2т, (л-/и)(/-1)<х, 0*/*1;
/я, х<(л + т)(/-1), 0***1,
О, (л + /и)(/-1)*х*(л-т)(/-1), 0*/*1,
-/и, (л-т)(/-1)<х, 0*/*1;
— (хо н-т + лJ, Хо<-л-/и,
О, -л-т*х0 *от-л,
— (хо+л-тJ, п-пкхц.
17.2. 1/*(*) = -т, у*(/) = л, х*@ = г*'+^^A-е*'),
!* = е« + «*-Л|
т>'
17.3. и*(/) = -т, у*(г) = л, х*(/) = л + т + (л-т)/ + ^-,
17.4. 1/*(/) = 1/(/,х) = -1, у*(*) = у(*,х) = 1, тттах/= х©+Уо-
579

17.5. и.(,,х) = -^(*1+Лтх2); „*(,,х) = -21(х1 + л,*2), 7> 3(х,Ф + нх^
А 6 + 2п*[т* -1)
где
т=1_,, д=1+л!к^1!
18.1. у*(Г,х,1) = 1, ?*(',*,<>) =
/логш18
О, х >*(/),
1, хй&),
где г@ =
8(Г-1) ' 2^ ^Х*
18.2. !/*(/) = -1, >>*(') =
1ШП / = 2.
О, 0 ^ / < 0,5,
-3, 0,5*/*1,
**(') =
4,5-/, 0^/<0,5,
6-4/, 0,5^/^1,
18.3. Оптимальная программная конструкция у*@ представляет собой
функцию принимающую попеременно значения 1 или (-1), моменты переклю-
2к-\
чения т*= —-—-, А: = 1,2,..., #, где N - количество переключений, опреде-
2N + 1
ляемое по величине X из неравенства
1 , 1
; при этом
2D(ЛГ + 1J-1) 2DЛГ2-1)
наименьшее значение /# функционала качества вычисляется по формуле
/* =
1
2B^ + 1)
+ 2ХЛГ.
Глава 19
19.1. а)и*@) = *о вA ,в) ; б) д*@,х) = х вA „в) .
°[(е-1J+1]' Кв-1J+1]
19.2. а)|/*@) = 1/*A) = -|хо; б) «*@,х) = -±х; «*A,х) = -|х.
19.3. а)|/*@) = Хо (/2"° ; и*№ = х0 А(*~*2) Х ;
[в2 -2*2 +2в-2в2 +2] [е2 -2е2 + 2е-2е2 +2]
1 2 1
б) 1/*@,х) = х <** "° х ; 1/-@,5;х) = х (** \е) .
[*2-2<?2+2е-2е2+2]
[е-2е*+2]
580

ЛИТЕРАТУРА
1. Айзеке Р. Дифференциальные игры.— М.: Мир, 1967.
2. Алексеев В.М., Галеев Э.М., Тихомиров В.М. Сборник задач по
оптимизации. — М.: Наука, 1984.
3. Алексеев В.М., Тихомиров В.М., Фомин СВ. Оптимальное управление. -
М.: Наука, 1979.
4. Аркин В.И., Евстигнеев КВ. Вероятностные модели управления и
экономической динамики. — М.: Наука, 1979.
5. Атанс М, Фалб П. Оптимальное управление. — М.: Машиностроение,
1968.
6. Афанасьев В.Н., Колмановский В.Б., Носов В.Р. Математическая теория
конструирования систем управления. — М.: Высшая школа, 1989.
7. Болтянский В.Г. Оптимальное управление дискретными системами. - М.:
Наука, 1973.
8. Брайсон А., Хо-Ю-Ши. Прикладная теория оптимального управления. —
М.: Наука, 1972.
9. Браммер К, Зиффлинг Г. Фильтр Калмана-Бьюси. - М.: Наука, 1982.
10. Васильев Ф.П. Лекции по методам решения экстремальных задач. — М.:
Изд-во МГУ, 1974.
11. Габасов Р., Кириллова Ф.М. Принцип максимума в теории оптимального
управления. — Минск: Наука и техника, 1974.
12. Гаврилов В.М. Оптимальное управление в конфликтных ситуациях. -
М.: Сов. Радио, 1969.
13. Гурман В.И. Принцип расширения в задачах управления. - М.: Наука,
1985.
14. Задачник по теории автоматического управления / Под ред. АС.
Шаталова. — М.: Энергия,1974.
15. Иванов ВЛ, Фалдин Н.В. Теория оптимальных систем автоматического
управления. - М.: Наука,1981.
16. Казаков И.Е. Статистические методы проектирования систем
управления. — М.: Машиностроение, 1969.
17. Казаков И.Е., Гладков Д.И. Методы оптимизации стохастических
систем. - М.: Наука,1987.
18. Квакернаак X., Сиван Р. Линейные оптимальные системы управления.
- М.: Мир,1977.
19. Колосов Т.Е. Синтез оптимальных автоматических систем при случайных
возмущениях. - М.: Наука,1981.
20. Корн Г., Корн Т. Справочник по математике. — М.: Наука, 1977.
581

21. Красовский Н.Н., Субботин АН. Позиционные дифференциальные игры.
- М.: Наука,1974.
22. Кротов В.Ф., Гурман В.И. Методы и задачи оптимального управления. -
М.: Наука,1973.
23. Куржанский А.Б. Управление и наблюдение в условиях
неопределенности. - М.: Наука, 1973.
24. Лебедев АА, Красильщиков М.Н., Малышев В.В. Оптимальное
управление движением космических летательных аппаратов. — М: Машиностроение,
1974.
25. ЛетовАМ. Динамика полета и управление. — М.: Наука, 1973.
26. Малышев В.В., Кибзун А.И. Анализ и синтез высокоточного управления
летательными аппаратами. — М.: Машиностроение, 1987.
27. Математическая теория оптимальных процессов / Л.С. Понтрягин,
В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. - М.: Наука, 1983.
28. Матросов В.М. Метод векторных функций Ляпунова: анализ
динамических свойств нелинейных систем. - М.: Наука,2001.
29. Медич Дж. Статистически оптимальные линейные оценки и
управление. - М.: Энергия, 1973.
30. Методы описания, анализа и синтеза нелинейных систем управления
/ В.В. Семенов, А.В. Пантелеев, Е.А. Руденко, А.С. Бортаковский. — М.: Изд-во
МАИД993.
31. Методы оптимизации в статистических задачах управления / А.М. Бат-
ков и др. — М.: Машиностроение, 1974.
32. Нейман Дж., Моргенштерн О. Теория игр и экономическое поведение. —
М.: Наука, 1970.
33. Овсянников ДА. Математические методы управления пучками. — М.:
ЛГУ, 1980.
34. Основы автоматического регулирования / Под ред. В.В. Солодовникова.
- М.: Машгиз,1954.
35. Пантелеев А.В. Вариационное исчисление в примерах и задачах. — М.:
Изд-во МАИ, 2000.
36. Пантелеев А.В., Бортаковский А.С., Летова ТА. Оптимальное
управление в примерах и задачах. — М.: Изд-во МАИ, 1996.
37. Пантелеев А.В., Семенов В.В. Синтез оптимальных систем управления
при неполной информации. - М.: Изд-во МАИ, 1992.
38. Пантелеев А.В., Летова ТА. Методы оптимизации в примерах и задачах.
- М.: Высшая школа, 2002.
39. Пантелеев А.В., Якимова А.С. Теория функций комплексного
переменного и операционное исчисление в примерах и задачах. — М.: Высшая школа,
2001.
40. Пантелеев А.В., Якимова АС, Босов А.В. Обыкновенные
дифференциальные уравнения в примерах и задачах. — М.: Высшая школа, 2001.
41. Параев Ю.И. Введение в статистическую динамику процессов
управления и фильтрации. — М.: Сов. Радио, 1976.
582

42. Первозванский АЛ Курс теории автоматического управления. - М.:
Наука, 1986.
43. Пропой А.И. Элементы теории оптимальных дискретных систем. — М.:
Наука, 1973.
44. Пугачев В.С., Синицын И.Н. Стохастические дифференциальные
системы. - М.: Наука, 1985.
45. Ройтенберг Я.Н. Автоматическое управление. — М.: Наука, 1978.
46. Сборник задач по теории автоматического регулирования и управления
/ Под ред. В.А. Бессекерского. — М.: Наука, 1978.
47. Сейдж Э.П., Уайт Ч.С. Оптимальное управление системами. - М.:
Радио и связь, 1982.
48. Семенов В.В. Формы математического описания линейных систем. —
М.: Изд-во МАИ, 1980.
49. Семенов В.В., Пантелеев А.В., Бортаковский АС Математическая теория
управления в примерах и задачах. - М.: Изд-во МАИ, 1997.
50. Солодов А.В., Петров Ф.С Линейные автоматические системы с
переменными параметрами. — М.: Наука, 1971.
51. Солодовников В.В., Семенов В.В. Спектральная теория нестационарных
систем управления. - М.: Наука, 1974.
52. Солодовников В.В., Семенов В.В. Спектральный метод расчета
нестационарных систем управления летательными аппаратами. — М.: Машиностроение,
1975.
53. Солодовников В.В., Семенов В.В., Пешелъ М., Недо Д. Расчет систем
управления на ЦВМ: спектральный и интерполяционный методы. - М.:
Машиностроение, 1979.
54. Теория автоматического управления. Ч. 2. — Теория нелинейных и
специальных систем автоматического управления / Под ред. А.А. Воронова. — М.:
Высшая школа, 1986.
55. Техническая кибернетика. Теория автоматического регулирования. Т.1/
Под ред. В.В. Солодовникова. — М.: Машиностроение, кн.1,2, 1967, кн.З, ч.1,2,
1969.
56. Ту Ю. Современная теория управления. - М.: Машиностроение, 1971.
57. Федоренко Р.П. Приближенное решение задач оптимального
управления. - М.: Наука, 1978.
58. Флеминг У, Ришел Р. Оптимальное управление детерминированными и
стохастическими системами. - М.: Мир, 1978.
59. Цирлин А.М., Балакирев В.С, Дудников КГ. Вариационные методы
оптимизации управляемых объектов. — М.: Энергия, 1976.
60. Чаки Ф. Современная теория управления. — М.: Мир, 1975.
61. Черноусько ФЛ., Колмановский В.Б. Оптимальное управление при
случайных возмущениях. - М.: Наука, 1978.
62. Черноусько Ф.Л., Меликян А.А. Игровые задачи управления и поиска. —
М.: Наука, 1978.

Учебное издание
Пантелеев Андрей Владимирович,
Бортаковский Александр Сергеевич
ТЕОРИЯ УПРАВЛЕНИЯ
В ПРИМЕРАХ И ЗАДАЧАХ
Художник В.А. Казак
Технический редактор Л.Л. Овчинникова
Корректор Н.Е. Жданова
Лицензия ИД № 06236 от 09.11.2001
Изд. № РЕНТ-13. Подл, в печать 20.09.2002. Формат 60x90 У16
Бум. офсетная. Гарнитура «Тайме». Печать офсетная
Объем: 36,5 усл. печ. л., 37,0 усл. кр.-отт.
Тираж 6000 экз. Заказ № 2742
ФГУП «Издательство «Высшая школа», 127994, Москва, ГСП-4,
Неглинная ул., 29/14
Тел. @95) 200-04-56
Е-таИ: ин~о@у-8Ько1а.ги пИр://шшш.у-8пко1а.ги
Отдел реализации: @95) 200-07-69, 200-59-39, факс @95) 200-03-01
Е-таП: $а1е$@у-$Ько1а.ш
Отдел «Книга-почтой»: @95) 200-33-36. Е-таИ: Ъоокро81@у-8пко1а.ги
Отпечатано во ФГУП ИПК «Ульяновский Дом печати»
432980, г. Ульяновск, ул. Гончарова, 14