Автор: Пантелеев А.В. Бортаковский А.С.
Теги: алгебра математика линейная алгебра математический анализ издательство высшая школа
ISBN: 5-06-004138-7
Год: 2005
Текст
4
ПРИКЛАДНАЯ МАТЕМАТИКА
для ВТУЗов
А.С. Бортаковский А.В. Пантелеев
ЛИНЕЙНАЯ
АЛГЕБРА
В ПРИМЕРАХ
И ЗАДАЧАХ
О
ПРИКЛАДНАЯ МАТЕМАТИКА
для ВТУЗов
А.С. Бортаковский
А.В. Пантелеев
ЛИНЕЙНАЯ
АЛГЕБРА
В ПРИМЕРАХ
И ЗАДАЧАХ
Рекомендовано Учебно-методическим объединением
высших учебных заведений Российской Федерации
по образованию в области авиации, ракетостроения
и космоса в качестве учебного пособия для студентов
высших технических учебных заведений
Москва
«Высшая школа»
2005
УДК 512
ББК 22.143
Б 82
Рецензенты:
кафедра «Прикладная математика» Московского государственного
технического университета гражданской авиации (зав. кафедрой
д-р техн, наук, проф. В.Л. Кузнецов);
д-р физ.-мат. наук, проф. А.Н. Сиротин Московский авиационный
институт (государственный технический университет)
Бортаковский, А.С.
Б 82 Линейная алгебра в примерах и задачах: Учеб. пособие/А.С. Бор-
таковский, А.В. Пантелеев. — М.: Высш, шк., 2005. —591 с.: ил.
ISBN 5-06-004138-7
Изложены основные понятия, теоремы и методы решения задач по всем разделам
курса: матрицы и определители, системы линейных алгебраических уравнений, функ-
циональные матрицы и функции векторного аргумента, многочленные матрицы н фун-
кции от матриц, линейные пространства и линейные отображения, численные методы.
В каждом разделе кратко изложены основные теоретические сведения, приведе-
ны решения типовых примеров и задачи для самостоятельного решения с ответами.
Для студентов технических вузов.
УДК 512
ББК 22.143
ISBN 5-06-004138-7 © ФГУП «Издательство «Высшая школа», 2005
Оригинал-макет данного издания является собственностью издательства «Высшая
школа», и его репродуцирование (воспроизведение) любым способом без согласия издатель-
ства запрещается.
ОГЛАВЛЕНИЕ
Предисловие....................................................8
Введение.......................................................9
В.1. Множества и операции над ними...........................9
В-2. Основные алгебраические структуры......................11
В.2.1. Арифметические операции и их свойства............11
В.2.2. Бинарные операции и их свойства..................15
В.2.3. Группы, кольца, поля.............................18
В.З. Поле комплексных чисел.................................25
В.4. Кольцо многочленов................................... 29
В.5. Аксиоматические построения и логические рассуждения....38
Глава 1. Матрицы и действия над ними..........................46
1.1. Числовые матрицы.......................................46
1.2. Линейные операции над матрицами...................... 48
1.2.1. Сложение матриц..................................48
1.2.2. Умножение матрицы на число.......................49
1.3. Умножение матриц.......................................50
1.3.1. Определение произведения матриц..................50
1.3.2. Свойства умножения матриц...................... 54
1.3.3. Умножение матриц на столбцы и строки единичной
матрицы.................................................57
1.3.4. Степень матрицы..................................59
1.4. Транспонирование и сопряжение матриц...................62
1.4.1. Транспонирование матриц..........................62
1.4.2. Сопряжение матриц................................65
1.4.3. След матрицы.....................................68
1.5. Блочные (клеточные) матрицы............................70
1.5.1. Блочные матрицы и операции над ними..............70
1.5.2. Кронекеровские произведение и сумма матриц.......74
1.6. Элементарные преобразования матриц.....................75
1.6.1. Метод Гаусса приведения матрицы к ступенчатому виду.75
1.6.2. Элементарные преобразования как умножения матриц.83
1.6.3. Нахождение элементарных преобразующих матриц.....91
Глава 2. Определители.........................................99
2.1. Индуктивное определение................................99
2.2. Формула разложения определителя по элементам строки
(столбца)..................................................102
2.3. Свойства определителей................................104
2.3.1. Основные свойства определителей.................104
2.3.2. Формула полного разложения определителя.........108
з
2.3.3. Формула Лапласа..................................11и
2.3.4. Определитель произведения матриц.................И2
2.4. Методы вычисления определителей........................П5
2.4.1. Применение элементарных преобразований..........115
2.4.2. Метод рекуррентных уравнений....................121
Глава 3. Ранг матрицы........................................128
3.1. Линейная зависимость и линейная независимость строк
(столбцов) матрицы.........................................128
3.2. Ранг матрицы..........................................131
3.2.1. Базисный минор матрицы..........................131
3.2.2. Теоремы о базисном миноре и о ранге матрицы.....133
3.3. Методы вычисления ранга матрицы.......................138
3.3.1. Метод окаймляющих миноров.......................138
3.3.2. Метод Гаусса....................................140
3.4. Ранг системы столбцов (строк).........................143
Глава 4. Обратная матрица....................................149
4.1. Определение, существование и единственность обратной
матрицы....................................................149
4.2. Свойства обратной матрицы.............................151
4.3. Способы нахождения обратной матрицы...................153
4.4. Матричные уравнения...................................160
4.5. Полуобратная и псевдообратная матрицы.................162
4.5.1. Односторонние обратные матрицы..................162
4.5.2. Полуобратная матрица............................164
4.5.3. Псевдообратная матрица..........................170
Глава 5. Системы линейных алгебраических уравнений...........185
5.1. Основные понятия и определения........................185
5.2. Правило Крамера.......................................187
5.3. Условие совместности системы линейных уравнений.......189
5.4. Метод Гаусса решения системы линейных уравнений.......190
5.5. Структура общего решения однородной системы...........194
5.6. Структура общего решения неоднородной системы.........200
5.7. Применение полуобратных матриц........................203
5.8. Псевдорешения системы линейных уравнений..............209
Глава 6. Функциональные матрицы и функции векторного
аргумента....................................................218
6.1. Функциональные матрицы скалярного аргумента...........218
6.2. Производные скалярной функции по векторному аргументу..222
4
6.3. Производные векторной функции по векторному аргументу....224
6.4. Производные матричной функции по векторному аргументу....230
6.5. Линейные и квадратичные формы.........................231
6.5.1. Преобразования форм при линейной замене переменных.235
6.5.2. Приведение квадратичной формы к каноническому виду.238
6.5.3. Закон инерции вещественных квадратичных форм.......248
6.5.4. Знакоопределенность вещественных квадратичных форм .... 251
6.5.5. Применение форм к исследованию функций на экстремум .. 254
Глава 7. Многочленные матрицы и функции от матриц............261
7.1. Многочленные матрицы (А. -матрицы)....................261
7.1.1. Определение многочленных матриц (А-матриц)......261
7.1.2. Операции над А.-матрицами.......................262
7.1.3. Элементарные преобразования А.-матриц...........271
7.1.4. Инвариантные множители А.-матрицы...............279
7.2. Характеристические матрицы и многочлены...............282
7.2.1. Собственные векторы и собственные значения матрицы.282
7.2.2. Подобие числовых матриц.........................291
7.2.3. Характеристический многочлен матрицы............298
7.2.4. Теорема Гамильтона - Кэли. Минимальный многочлен
матрицы.............................................. 300
7.3. Жорданова форма матрицы...............................306
7.3.1. Элементарные делители матрицы...................306
7.3.2. Жордановы клетки и матрицы......................309
7.3.3. Приведение матрицы к жордановой форме...........316
7.3.4. Многочлены от матриц............................331
7.3.5. Применение многочленов от матриц для решения систем
линейных рекуррентных уравнений с постоянными
коэффициентами.........................................342
7.4. Функции от матриц.....................................346
7.4.1. Функции, определенные на спектре матрицы........347
7.4.2. Определение и свойства функций от матриц .......348
7.4.3. Способы нахождения функций от матриц ...........349
7.4.4. Свойства функций от матриц......................354
7.4.5. Применение функций от матриц для решения систем
линейных дифференциальных уравнений с постоянными
коэффициентами.........................................356
Глава 8. Линейные пространства...............................364
8.1. Определение и примеры линейных пространств............364
8.1.1. Аксиомы линейного пространства..................364
8.1.2. Простейшие следствия аксиом.....................365
8.1.3. Примеры линейных пространств....................366
5
8.2. Линейная зависимость и линейная независимость векторов.....370
8.2.1. Понятие линейной зависимости и линейной
независимости векторов..................................370
8.2.2. Свойства линейно зависимых и линейно независимых
векторов.................................................372
8.2.3. Аффинные, неотрицательные и выпуклые комбинации
векторов................................................373
8.3. Размерность и базис линейного пространства.................376
8.3.1. Определения размерности и базиса..................376
8.3.2. Примеры базисов линейных пространств..............379
8.4. Координаты и преобразования координат...................383
8.4.1. Координаты векторов в данном базисе...............383
8.4.2. Линейные операции в координатной форме............383
8.4.3. Преобразование координат вектора при замене базиса...385
8.4.4. Свойства матрицы перехода от одного базиса к другому.387
8.5. Изоморфизм линейных пространств.........................389
8.6. Подпространства линейного пространства..................391
8.6.1. Определение линейного подпространства.............391
8.6.2. Примеры линейных подпространств...................392
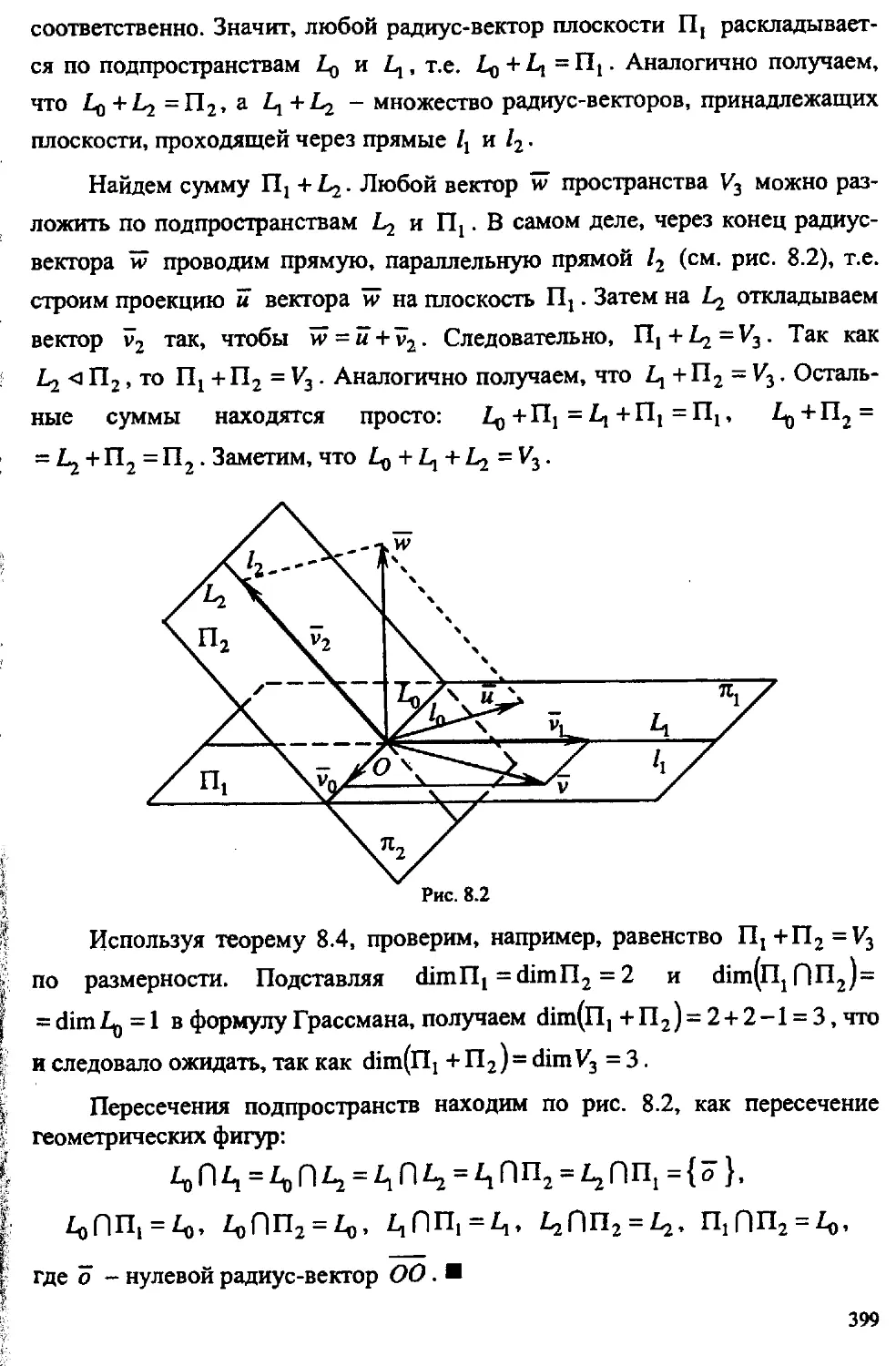
8.6.3. Пересечение и сумма подпространств................395
8.6.4. Прямая сумма подпространств.......................400
8.6.5. Способы описания подпространств...................403
8.7. Линейные многообразия...................................419
8.7.1. Определение линейного многообразия................419
8.7.2. Свойства линейных многообразий....................420
8.7.3. Способы описания линейных многообразий............421
8.8. Евклидовы пространства..................................426
8.8.1. Определение евклидова пространства................426
8.8.2. Примеры евклидовых пространств....................428
8.8.3. Длина вектора. Угол между векторами...............430
8.8.4. Ортогональные векторы и их свойства...............433
8.8.5. Процесс ортогонализации Грама - Шмидта............434
8.8.6. Ортогональный и ортонормированный базисы..........437
8.8.7. Ортогональные дополнения .........................443
8.8.8. Задача о перпендикуляре...........................447
8.8.9. Унитарные пространства............................453
Глава 9. Линейные отображения и операторы......................459
9.1. Линейные отображения....................................459
9.1.1. Определение линейных отображений..................459
9.1.2. Примеры линейных отображений......................460
9.1.3. Свойства линейных отображений.....................462
9.1.4. Матрица линейного отображения.....................464
9.1.5. Ядро и образ линейного отображения................467
6
9.2. Линейные преобразования (операторы)......................471
9.2.1. Определение и примеры линейных преобразований......471
9.2.2. Матрицы линейного преобразования в разных базисах..475
9.2.3. Алгебра линейных операторов........................476
9.3. Инвариантные подпространства.............................478
9.3.1. Определение и примеры инвариантных подпространств..478
9.3.2. Свойства инвариантных подпространств...............480
9.4. Собственные векторы линейного преобразования.............482
9.4.1. Собственные векторы и собственные значения.........482
9.4.2. Примеры собственных векторов.......................487
9.4.3. Свойства собственных векторов......................489
9.5. Канонический вид линейного преобразования................494
9.5.1. Приведение линейного преобразования к диагональному
виду.....................................................494
9.5.2. Приведение линейного преобразования к каноническому
виду.....................................................496
9.6. Линейные преобразования евклидовых пространств...........513
9.6.1. Ортогональные преобразования.......................513
9.6.2. Сопряженные преобразования.........................522
9.6.3. Самосопряженные преобразования.....................523
9.6.4. Приведение квадратичной формы к главным осям.......528
9.6.5. Линейные преобразования унитарных пространств......532
Глава 10. Численные методы линейной алгебры.....................539
10.1. Основные положения. Нормы матриц........................539
10.2. Прямые методы решения систем линейных алгебраических
уравнений................................................... 545
10.2.1. Численные схемы реализации метода Гаусса.........545
10.2.2. Метод прогонки...................................550
10.2.3. Метод LU -разложения.............................555
10.2.4. Метод квадратных корней..........................561
10.3. Итерационные методы решения систем линейных
алгебраических уравнений......................................564
10.3.1. Метод простых итераций...........................564
10.3.2. Метод Зейделя....................................570
10.4. Итерационный метод Шульца нахождения обратной матрицы...575
10.5. Методы решения задач о собственных значениях
и собственных векторах матрицы................................578
10.5.1. Метод итераций...................................579
10.5.2. Метод вращений...................................582
Литература....................................................590
ПРЕДИСЛОВИЕ
Книга включает теоретические основы и методы решения задач линей-
ной алгебры и охватывает основные разделы курса, читаемого на факультете
"Прикладная математика и физика" Московского авиационного института.
Курс линейной алгебры во Втузе читается первокурсникам в двух ва-
риантах: сокращенном (для инженерных специальностей) и достаточно пол-
ном (для специальности "Прикладная математика"). Как правило, в других
математических дисциплинах (дифференциальные уравнения, оптимизация,
теория вероятностей и математическая статистика, численные методы и т.п.)
приходится возвращаться к некоторым разделам линейной алгебры, допол-
няя базовый курс теми или иными сведениями.
Несмотря на то что курс линейной алгебры во всех технических уни-
верситетах имеет примерно одинаковый объем и традиционное содержание,
его изложение в разных вузах существенно отличается. Причина заключает-
ся в том, что курс имеет две составляющие: алгебраическую и геометриче-
скую. Поэтому в зависимости от предпочтений преподавателя и от уровня
подготовки студентов построение курса может быть различным: "более ал-
гебраическим", либо "более геометрическим". Это обстоятельство учитыва-
лось при написании пособия. Некоторые понятия (собственные векторы,
жорданова форма матрицы, квадратичные формы) освещаются с разных то-
чек зрения. Например, собственные векторы матрицы вводятся "алгебраиче-
ски" в разд.7, в разд. 9 они изучаются с геометрической точки зрения, а в
разд. 10 обсуждаются вычислительные особенности их нахождения.
Существующие учебные пособия либо не охватывают соответствую-
щие программы курсов линейной алгебры, либо написаны труднодоступным
для вчерашних школьников языком. Авторы ставили перед собой задачу на-
писать доступное для широкой студенческой аудитории пособие, где все
теоретические положения подкрепляются подробным разбором типовых
примеров. Особое внимание уделялось описанию методик решения рас-
сматриваемых задач.
Изложение построено по единой схеме, включая описание элементов
постановок задач, алгоритмы решения и подробный анализ типовых приме-
ров. Предлагаются задачи для самостоятельного решения, в том числе зави-
сящие от параметров т - номера учебной группы и п - номера студента по
списку группы.
Данное пособие входит в серию книг "Прикладная математика в при-
мерах и задачах", составляя с ними единый учебно-методический комплекс.
ВВЕДЕНИЕ
Изложение начнем с важных математических понятий: множеств, опе-
раций, основных алгебраических структур. Приводимые во введении сведе-
ния, определения и свойства часто имеют предварительный (ознакомитель-
ный) характер. Некоторые "тонкие" моменты и вопросы здесь не рассматри-
ваются.
ВЛ. МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ
Понятие множества, элемента и принадлежности элемента множеству
являются первичными (неопределяемыми через другие) понятиями матема-
тики. Для интуитивного понимания множества достаточно считать, что
множество - это совокупность определенных и различимых между собой
объектов (элементов), мыслимая как единое целое (Г.Кантор).
Множества принято обозначать прописными буквами А, В , С,... и
т.п., а их элементы - строчными буквами а, b, с,... и т.п. Если а является
элементом множества А , то пишут а 6 А (читается: а принадлежит
множеству А ). Если же а не принадлежит множеству А , то пишут a g А .
Два множества называются равными, если они состоят из одних и тех
же элементов. Равенство А = В означает, что одно и то же множество обо-
значено разными буквами А и В .
Множества могут быть заданы перечислением своих элементов. При
этом составляющие множество элементы указываются в фигурных скобках.
Например, запись А - { а, Ь, с } означает, что множество А состоит из эле-
ментов а, b, с. Порядок, в котором перечисляются элементы множества,
не играет никакой роли, например, { а, Ь, с } = { с, а, b } = { Ь, а, с }.
Чаще множество задается указанием характеристического свойства,
которое формулируется в виде высказывания (утверждения) Р(х), которое в
зависимости от значений параметра х может быть либо истинным, либо
ложным. Тогда
Х={х:Р(х)}
- обозначает множество X , состоящее из таких элементов х, для которых
высказывание Р(х) истинно (утверждение Р(х) верное). Например,
{х: х- родитель человека, читающего эту фразу }=
= { отец читателя, мать читателя };
{х:а <х<(>}=[а,б];
{ прямоугольник : прямоугольник с равными сторонами }=
= { ромб : ромб с равными диагоналями } - множество квадратов.
9
Для формулировки характеристических свойств, а также других ут-
верждений и высказываний, применяются сокращения: символ V (квантор
общности) заменяет слова "для любого", "для каждого", "для всех"; символ
3 (квантор существования) читается как слово "существует". Например,
V числа х 3 натуральное число п такое, что х < п (аксиома Архи-
меда);
V треугольника 3 окружность, проходящая через все его вершины.
Множество, не содержащее ни одного элемента, называется пустым и
обозначается символом 0 . Если каждый элемент множества А принадле-
жит множеству В , то говорят, что А является подмножеством В , и пи-
шут А с В (А содержится в В) или В О А (В содержит А ). Пустое мно-
жество 0 считается подмножеством каждого множества. Если А произ-
вольное множество, то 0С А и А С А .
Если все рассматриваемые в ходе рассуждения множества являются
подмножествами некоторого множества U , то это множество U называет-
ся универсальным для данного рассуждения.
Пример В.1. Сколько подмножеств имеет множество А = {1,2,3 } ?
□ Множество А состоит из трех элементов (чисел). Запишем все его
подмножества: пустое множество - 0; одноэлементные подмножества -
{1}, {2}, { 3 }; двухэлементные подмножества - {1,2}, {2,3 }, {1,3};
само множество А — {1,2,3 }. Всего 8 подмножеств.
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Для наглядного представления операций над множествами используют
диаграммы Эйлера - Венна. Универсальное множество U изображают в
виде прямоугольника, а его подмножества - в виде эллипсов (рис. В.1,а).
Пусть даны два множества А и В .
Объединением множеств А и В называется множество A(JB, со-
стоящее из элементов, принадлежащих хотя бы одному из множеств А и В
(рис. В. 1,6):
AljB = {x:xeA или хе В }.
Пересечением множеств А и В называется множество АП В, со-
стоящее из элементов, принадлежащих как множеству А , так и множеству
В (рис. В.1,в):
АПВ = {х:хеА и хе в}.
Разностью (относительным дополнением) множеств А и В назы-
вается множество А \ В , состоящее из элементов множества А , не принад-
лежащих множеству В (рис. В. 1,г):
А\В = {х:хеА ихйВ}.
10
Симметрической разностью множеств А п В называется множество
ЛДВ, состоящее из элементов, принадлежащих только одному из двух мно-
жеств А или В и не принадлежащих другому (рис. В.1,Э):
АА5 = (лив)\(АПв).
Абсолютным дополнением множества А называется множество А
всех элементов, которые не принадлежат множеству А (рис. В.1,е):
~A=U\A.
д
Рис. В.1
Пример В.2. Пусть Л = {1, 2,3 } и В = { 2,3,4 }. Найти объединение
A U В, пересечение А Г) В, разности А\Вп В\А,а также симметрическую
разность ЛАВ.
□ По определению получаем: A U В = {1, 2,3,4 }; АГ)В = {2,3};
Л\В = {1}; В\А ={4 }; ЛДВ-{1,4}.И
В.2. ОСНОВНЫЕ АЛГЕБРАИЧЕСКИЕ СТРУКТУРЫ
В.2.1. Арифметические операции и их свойства
Первоначальными понятиями в алгебре являются числа и действия над
ними. В курсе арифметики и алгебры средней школы вводятся множества
натуральных чисел - N ; целых чисел - Z ; рациональных чисел - Q ; ирра-
циональных чисел; действительных чисел - В , а также четыре арифметиче-
ских действия: сложение, вычитание, умножение и деление.
И
Напомним обозначения:
№ {1,2,3,4,5,... } - множество натуральных чисел;
Z = { • ,~3, - 2, -1,0,1,2,3,... } - множество целых чисел;
Q = < — :те Z;ne N> - множество рациональных чисел.
[ п J
Рациональным называют число, которое можно представить (хотя бы одним
способом) в виде отношения целого числа к натуральному, при этом дроби
тк , тк т ,
вида--, где хе N, считаются равными: --= — (основное свойство дро-
пк пк п
би). Любое рациональное число можно представить в виде конечной или
бесконечной периодической десятичной дроби.
Множество R действительных (вещественных) чисел образовано чис-
лами, которые представимы в виде конечных или бесконечных десятичных
дробей. Оно включает перечисленные выше множества
AfcZcfic/?-
Для множества иррациональных чисел специального обозначения не вводят,
так как это множество - есть разность R \ Q. По определению это действи-
тельные числа, которые не являются рациональными.
Остановимся подробнее на свойствах арифметических операций, так
как законы арифметики распространяются и на другие математические объ-
екты.
Каждая из арифметических операций производится над двумя числами,
т.е. имеется два операнда, а сама операция называется бинарной. Для сло-
жения или умножения порядок, в котором берутся слагаемые или множите-
ли, не важен. Для вычитания и деления чисел нужно указывать, которое из
двух чисел уменьшаемое (делимое), а которое - вычитаемое (делитель), т.е.
пара чисел должна быть упорядочена.
СЛОЖЕНИЕ И УМНОЖЕНИЕ
Для сложения и умножения чисел выполняются следующие свойства
(законы):
1) сложение чисел коммутативно’ a + b = b + a -,
2) сложение чисел ассоциативно: a + (b + c)~ (a+b)+c;
3) умножение чисел коммутативно: аЬ = Ьа;
4) умножение чисел ассоциативно: a(bc)=(ab)c;
5) сложение и умножение связаны законом дистрибутивности:
(а + b)c - ас + Ьс.
12
Законы коммутативности и ассоциативности сложения чисел позволя-
ют не обращать внимания на порядок слагаемых (не расставляя скобок). По-
этому в алгебре суммы или произведения большого числа однотипных сла-
гаемых (имеющих один и тот же вид и отличающихся только индексами)
п
записывают при помощи знака суммы. Символ , вслед за которым за-
1=1
писано некоторое выражение, содержащее индекс i, означает сумму таких
п
выражений для всех значений индекса от 1 до п, т.е. а, + а2 + ... + ап = У'.Щ
1=1
(читается: "сумма а, по i от 1 до п "). Индекс I называется индексом сум-
мирования. В качестве индекса суммирования может быть использована
любая буква. Суммирование по двум индексам записывается в виде:
т п
Пц + а12+... + а1п + а21 + а22 + ... + а2„ + ... + ат1 + ат2 + ... + а„„ = .
1=1 ;=1
Приведем правила обращения со знаком суммы.
1. Индекс суммирования может быть изменен, т.е.
п п
1=1 >1
2. Множитель, не зависящий от индекса суммирования, можно выне-
сти за знак суммы:
п п
i=l 1=1
3. Порядок суммирования можно изменить:
т п пт
,=1 j=l j=l 1=1
Законы коммутативности и ассоциативности умножения чисел позво-
ляют не обращать внимания на порядок множителей (не расставляя скобок).
Поэтому произведения большого числа однотипных множителей (имеющих
один и тот же вад и отличающихся только индексами) записывают при по-
п
мощи знака произведения. Символ П , вслед за которым записано некото-
рое выражение, содержащее индекс i, означает произведение таких выра-
п
жений для всех значений индекса от 1 до п, т.е. а{ -а2 •... ап = П а, (чита-
i=I
ется: "произведение а, по i от 1 до п"). Индекс i называется индексом
умножения. В качестве индекса умножения может быть использована
13
1
любая буква. Нахождение произведения по двум индексам записывается в
виде:
Я] ] • я,2 ... я1л а21 а22 ... а2п ... • ат] ат2 ... атл = П П яу.
Правила обращения со знаком произведения.
1. Индекс умножения может быть изменен, т.е.
п п
П я = П я;.
<=1 7=1 '
2. Множитель, не зависящий от индекса умножения, можно вынести
за знак произведения'.
П (Хя )=Л." П а..
/=1 '
3. Порядок умножения можно изменить:
т п пт
П П а - = П П а,7.
<=1 7=1 1 j=l '=1 1
Замечание В.1. Начальное значение индексов суммирования или
умножения может отличаться от единицы, например:
а) для любых целых чисел т и п (т < п):
п
^Га1=ат+ат+1+... + а„ (п-т + 1 слагаемых);
1=т
П я, = ат ат+1 .аП (п-т + 1 множителей);
б) для любого натурального п:
п i п п
Z 24 =аЧ +а21 +а22 + - + «„! +ап2 +•••«„» =2 2aV •
/=1 /=1 7=1 <=7
ВЫЧИТАНИЕ И ДЕЛЕНИЕ
Вычитание и деление чисел вводятся как операции, обратные по отно-
шению к сложению и умножению. Например, разностью а - Ь чисел а и b
называют такое число d, что b + d = a. Вычитание чисел можно
определить (эквивалентным образом) по-другому, подчеркивая особую роль
числа нуль. В самом деле, нуль обладает важным свойством: для любого
числа я имеет место равенство я + 0 = я . Поэтому для любого числа я
(целого, рационального, действительного) имеется противоположное число
(-я) (соответственно целое, рациональное, действительное) такое,
что я + (-я) = 0.
14
Теперь разность а -Ь можно определить, как сумму числа а с числом, про-
тивоположным Ь :
а - b = а + (-/>).
Аналогичным образом вводится операция деления. Особую роль здесь
играет число 1 (единица): для любого числа а справедливо равенство
а 1 = а . Для любого числа а (рационального, действительного), отличного
ГО
от нуля, имеется обратное число — (соответственно рациональное, дейст-
ва )
вительное) такое, что а-| — | = 1. Поэтому операцию деления чисел а и Ь
\а )
можно определить, как умножение числа а на число, обратное к b :
, ГО
а: b = а- — .
В отличие от сложения и умножения операции вычитания и деления
чисел не удовлетворяют законам коммутативности и ассоциативности. Бо-
лее того, если сложение или умножение двух любых натуральных чисел да-
ет натуральное число, то при их вычитании или делении может получиться
и не натуральное число. Поэтому говорят, что вычитание и деление не опре-
делены на множестве натуральных чисел (имея в виду, что они не выполня-
ются для всех натуральных чисел). В этом смысле операция деления на
отличное от нуля число не определена также и на множестве целых чисел,
так как частное от деления двух целых чисел не обязательно является
целым.
В.2.2. Бинарные операции и их свойства
Определим теперь понятие алгебраической операции, обобщающее
арифметические действия. Пару чисел называют упорядоченной, если ука-
зано, какое число в этой паре является первым, а какое - вторым. Например,
в упорядоченной паре (a, b) число а - первое, число b - второе.
Будем говорить, что на множестве М определена бинарная алгебраи-
ческая операция (обозначим ее символом *), если каждой упорядоченной
паре (a, Ь) элементов Этого множества ставится в соответствие единствен-
ный элемент с = а * b из этого же множества М .
Например, на множестве натуральных чисел определены операции
сложения и умножения, так как сумма двух натуральных чисел (или их про-
изведение) является натуральным числом. Нетрудно заметить, что операции
сложения и умножения определены также на множествах целых, рациональ-
ных, действительных чисел.
15
Определим основные свойства (или законы) алгебраических операций.
Пусть на множестве М определена алгебраическая операция *. Говорят,
что эта операция:
1) коммутативна, если а * b = b * а;
2) ассоциативна, если а * (b * с) = (а * b)* с ;
для любых элементов а, b , с из М .
Операции сложения и умножения подчиняются законам коммутатив-
ности и ассоциативности на любом из множеств TV, Z , Q, R Приведем
примеры некоммутативных или неассоциативных операций.
Пример В.З. Доказать, что
а) операция вычитания на множестве целых чисел не является комму-
тативной и не является ассоциативной;
б) операция "вычитания по модулю": а06 = | а-б|, определенная на
множестве целых чисел является коммутативной, но не является ассоциа-
тивной;
в) операция "умножения на модуль": а ®Ь = а • | b |, определенная на
множестве целых чисел, не является коммутативной, но ассоциативна.
□ а) Для опровержения какого-либо свойства достаточно привести
контрпример:
1-2*2-1;
1-(2-3)*(1-2)-3.
Первое неравенство показывает некоммутативность вычитания, второе -
неассоциатив ность;
б) для любых целых чисел а и b справедливо равенство
<706 = | a-b | = | b-a\=b®a.
Следовательно, операция 0 - коммутативна. Но эта операция не является
ассоциативной, так как
1®(203) = 11-| 2-3 || = 0*2 = || 1-2 |-з| = (102)03;
в) для любых целых чисел а, b и с справедливо равенство
а®(б®с) = а - | 6-| с | | = а | b | • | с | = (а- |б| )-| с| = (а®б)®с.
Следовательно, операция ® - ассоциативна. Но эта операция не является
коммутативной, так как это свойство не выполняется, например, для чисел 1
и(-2):
1®(-2) = 1-|-2 | *(-2)-| 11 =(-2)®1.
Итак, на каждом из множеств N, Z, Q, R определены две
алгебраические операции - сложение и умножение, которые обладают
свойствами коммутативности и ассоциативности.
16
Для алгебраической операции можно определить обратную операцию.
Пусть на множестве М определена операция * и выполняются два усло-
вия:
1) в М существует нейтральный элемент 0 такой, что
а*0 = 0*а=а для любого а е М ;
2) для любого а е М существует обратный элемент a~l е М такой,
что а * я-1 = * а = 0 .
Тогда для любой пары (а, Ь) можно определить операцию а + Ь, по-
ложив
a~b = a*tTx.
В самом деле, элемент d = а + Ь = а*Ь 1 принадлежит М , поскольку
а е М , b~l е М , а операция * определена на М . Тем самым определена
операция ч-, которую можно считать обратной по отношению к операции *.
Покажем, что для сложения эти два условия выполняются на множест-
вах Z , Q, R , поэтому на этих множествах определена обратная операция -
операция вычитания. В самом деле, в каждом из множеств Z, Q, R для
операции сложения имеется "нейтральный элемент" - нуль: я + 0 = 0 + а = а
для любого а. Кроме того, для любого числа а существует "обратный эле-
мент" - противоположное число (-а): а+ (-а) =(-«) +а = 0, причем про-
тивоположное число (-а) принадлежит тому же множеству, что и а. Оста-
лось определить разность чисел а - b = а + (- b), как сумму а с числом, про-
тивоположным b. Как видим, условия 1 и 2 позволяют определить опера-
цию вычитания. Заметим, что операцию вычитания нельзя считать опреде-
ленной на множестве натуральных чисел, так как в этом множестве нет нуля
(а также и противоположных чисел). Разность некоторых натуральных чисел
может оказаться натуральным числом, если уменьшаемое больше вычитае-
мого. В остальных случаях разность отрицательна или равна нулю, т.е. не
принадлежит множеству натуральных чисел.
Исследуем, на каких множествах можно определить операцию деле-
ния. Сначала рассмотрим множества Q, R . Операция умножения, опреде-
ленная на этих множествах, удовлетворяет условиям 1 и 2. Действительно,
существует "нейтральный" для операции умножения элемент - единица:
а 1 = 1 • а = а . Кроме того, для каждого числа а, отличного от нуля, сущест-
1 ГН
вует "обратный элемент" - число —: а — = 1. Следовательно, на множе-
а \aj
2 - 4549
17
ствах Q\{0} и Л\{О } можно определить частное a:b = a-( — как про-
изведение числа а на число, обратное к b, т.е. операцию деления, обрат-
ную умножению.
На множествах натуральных ( N) и целых (Z) чисел результат деле-
ния может не оказаться натуральным или целым числом соответственно.
В этих множествах не у каждого элемента, отличного от нуля, существует
обратный, принадлежащий тому же множеству, т.е. не выполняется усло-
вие 2. Следовательно, операция деления не определена на множествах N и
Z.
Таким образом, вычитание определено на множествах Z , Q, R , а де-
ление - на множествах б\{о}и Я\{0}.
В.2.3. Группы, кольца, поля
ГРУППА
Множество G с алгебраической операцией * называется группой,
если выполняются следующие условия:
1) операция * в Gассоциативна: a*(b*c) = (a*b)*c Va,b,c€G;
2) в G существует нейтральный элемент 0:а*0 = 0*д=а Va € G;
3) для каждого элемента а е G существует обратный ему элемент
а’'еб: а*а-1 =а-1 *а =0.
Если операция * коммутативна, то группа называется коммутатив-
ной, или абелевой. В противном случае группа называется некоммутатив-
ной.
Относительно операции сложения группами являются множества Z,
Q, R . Относительно операции умножения группами являются множества
0\{о}и/?\{о} отличных от нуля рациональных и действительных чисел,
поскольку для нуля не существует обратного элемента. Все эти группы
коммутативные.
В группах по сложению нейтральный элемент 0 называют нулевым
(или просто нулем), а обратный элемент а-1 - противоположным (-а). В
группах по умножению нейтральный элемент 0 называют единичным (или
просто единицей) и обозначают е, для обратного элемента а-1 название и
обозначение сохраняется.
Пример В.4. Доказать, что множество {О }, состоящее из одного числа
нуль, образует коммутативную группу по сложению.
18
□ Действительно, операция сложения определена на указанном мно-
жестве, так как 0 + 0 = 0. Из этого равенства следует, что этот единственный
элемент множества служит нулевым (нейтральным) элементом, а также про-
тивоположным (обратным) для себя. Ассоциативность сложения очевидна:
(0 + 0)+0 = 0 + (0+ О). Следовательно, все (три) условия в определении груп-
пы выполняются. Учитывая коммутативность сложения, заключаем, что рас-
сматриваемое множество - коммутативная группа.
Пример В.5. Доказать, что множество { + 1,-1}, состоящее из двух
чисел, образует коммутативную группу по умножению.
□ Действительно, операция умножения определена на указанном мно-
жестве, так как
(+1)(+1) = +1, (+!)•(-!) = (-1)-(+1) = -1, (-1)-(-1)=+1. (В.1)
Следовательно, произведение элементов есть элемент того же множества.
Ассоциативность умножения очевидна. Из равенств (В.1) следует, что суще-
ствует единичный элемент е = +1. Кроме того, каждый элемент имеет об-
ратный: (+1)-1 = +1, (-1)1 =-1 Таким образом, все (три) условия в опре-
делении группы выполняются. Из (В.1) следует, что умножение коммута-
тивно, поэтому данная группа коммутативная.
кольцо
Множество К , на котором заданы две операции - сложение (+) и ум-
ножение (), называется кольцом, если выполняются следующие условия:
1) относительно операции сложения множество К - коммутативная
группа, т.е.
а) операция сложения коммутативна:
a + b = b + a VacK,VbeK-,
б) операция сложения ассоциативна:
a + (b + с)= (a + b)+c VaG К , VZ>G К , VcG К ;
в) существует нулевой элемент 6 : a + Q = Q + a = a Vae К ;
г) для каждого элемента a G К существует противоположный ему
элемент (-а) G К: а + (-а) = (-а) + а = 0;
2) операция умножения в множестве К ассоциативна:
a-(b-c) = (a-b)-c VaG К , \fb& К , VcG К ;
3) операции сложения и умножения связаны законами дистрибутивно-
сти:
(а + Ь) с = а-c + b-c и с (a + b) = с а + c-b Vae К , VbG К , VcG К .
2*
19
Если операция умножения коммутативна: а • b = b а, то кольцо назы-
вается коммутативным, в противном случае кольцо называется некомму-
тативным. Если для операции умножения существует единичный элемент
е: ае = еа = а,то говорят, что кольцо К - есть кольцо с единицей.
Кольцами являются множества целых, рациональных, действительных
чисел, причем все они - коммутативные кольца с единицей. Примеры дру-
гих колец, в том числе и некоммутативных, встретятся в дальнейшем. Как
видим, кольцо — это множество, в котором определены три операции', сло-
жение, умножение и вычитание.
Рассмотрим подробнее законы дистрибутивности. Пусть на множестве
К заданы две операции Фи®. Операция ® называется дистрибутивной
слева относительно операции Ф , если для любых а , b , с из К
с ® (а ф />) = (с ® а) Ф (с ® &),
и дистрибутивной справа относительно операции Ф , если
Если операция ® коммутативна, то дистрибутивность слева операции
® относительно операции Ф влечет дистрибутивность справа, так как
(a®Z>)®c = с®(аФЬ) = (с®а)ф(с®£)= (а®с)ф(б®с).
В этом случае говорят, что операция ® дистрибутивна относительно опе-
рации Ф. Например, операция умножения чисел дистрибутивна (слева и
справа) относительно операции сложения чисел. Следующий пример пока-
зывает, что имеются операции с "односторонней" дистрибутивностью.
Пример В.6. Рассмотрим множество Л+ положительных действитель-
ных чисел. На этом множестве определим две операции: умножения (а b) и
возведения в положительную степень (а 1Ь = аь). Доказать, что операция
Т возведения в степень дистрибутивна справа относительно умножения, но
не дистрибутивна слева.
□ В самом деле, для любых положительных действительных чисел а,
b, с справедливы равенства
(a-b)Tс = [а-Ь^ -ас Ьс = (аТс)-
Следовательно, операция Т дистрибутивна справа относительно операции
умножения чисел. Дистрибутивность Т слева относительно умножения оп-
ровергается примером
2 Т (3-2)= 23'2 = 2б = 64^ 32 = 23-22 = (2 ? з)-(2 Т 2).
Пример В.7. Доказать, что множество чисел вида
т + п>[2,
где т и п - целые числа, является кольцом.
20
(В.2)
□ Действительно, операции сложения и умножения определены на
рассматриваемом множестве, так как сумма и произведение двух чисел вида
(В.2) имеют тоже самое представление:
(otj + л1л/2)+(/п2 + л2з/2)=(от1 +zn2)+(n1 +n2}*/2 ;
(otj +^^/2}- {m2 + п2-/2^= {mpn2 +2л1п2)+(/и1п2 + m2nl)y[2 .
Числа (otj+ot^, («i+n2), {mlm2 +2ntn2), (отр^ + от^), очевидно, целые
для любых целых тх, т2, , п2. Законы коммутативности, ассоциативно-
сти и дистрибутивности не нуждаются в проверке, так как речь идет о сло-
жении и умножении действительных чисел. Нулевым элементом служит
число в = 0 + Ол/2 . Для каждого числа т + njl противоположным элемен-
том является число (- от)+ (- п , так как
(от + лV2)+ ((-от)+ (- л)>/2 )= (от - от)+ (л - л)>/2 = 0 + д/2 .
Таким образом, рассматриваемое множество удовлетворяет всем условиям
определения кольца.
ПОЛЕ
Множество П, на котором заданы две операции: сложение (+) и ум-
ножение (), называется полем, если выполняются следующие условия:
1) П - коммутативное кольцо с единицей (е Ф 9);
2) для каждого элемента а е П, отличного от нулевого (а * 0 ), суще-
ствует обратный элемент а-1 е П : а • а-1 - е.
Как видим, поле - это множество, в котором определены четыре опе-
рации: сложение, умножение, вычитание и деление. Полями, например,
являются множества рациональных и действительных чисел.
Пример В.8. На множестве М3 = { 0,1,2 } трех целых чисел определим
две операции:
"сложение по модулю 3" — остаток от деления суммы а + b на 3 (обо-
з
значим через а+Ь)~,
"умножение по модулю 3" - остаток от деления произведения ab на 3
з
(обозначим через а • b ).
Доказать, что множество М2 является полем относительно введенных
операций.
□ В этом примере остаток от деления целого числа а на 3 будем обо-
значать через {а}3. Напомним простые свойства деления целых чисел с ос-
татком:
21
- остаток от деления на 3 суммы не изменится, если слагаемое (или не-
сколько слагаемых) заменить его остатком при делении на 3:
{а+/>}3 ={а+{/>}3}3;
- остаток от деления на 3 произведения не изменится, если множитель
(или несколько множителей) заменить его остатком при делении на 3:
{afe}3 ={а-{/>}3}3.
Рассматриваемые в примере операции "сложения по модулю 3" и "ум-
ножения по модулю 3" можно представить в виде
3 3 г
a + b = {a + b}3 и ab = {aZ>}3,
а указанные свойства остатков записать так
3 3 3 Зг
a + b = a+{b}3, ab-a{b}3.
Перейдем теперь к решению задачи. Отметим, что введенные операции
3 3
а+b и а-b определены на М3. Составим таблицы "сложения по модулю
3" и "умножения по модулю 3" (рис.В.2). Как видим, результаты этих опера-
ций принадлежат М3. Следовательно, операции действительно определены
на М з.
Таблица- "сложения
3
по модулю 3" (а +Ь )
Хь а 0 1 2
0 0 1 2
1 1 2 0
2 2 0 1
Таблица"умножения
з
по модулю 3" ( а - b )
а 0 1 2
0 0 0 0
1 0 1 2
2 0 2 1
Рис. В.2
Покажем, что множество М3 является коммутативным кольцом с еди-
ницей. В самом деле, операция "сложения по модулю 3" коммутативна и ас-
социативна. Это следует из коммутативности и ассоциативности сложения
чисел. Действительно, из равенства a +b = b + а следует, что
3 3
a+b = {a + b}3={b + a}3=b+a .
Коммутативность доказана. Заметим, впрочем, что коммутативность "сло-
жения по модулю 3" видна непосредственно по таблице (см. рис.В.2): сла-
гаемые а и b в таблице можно поменять местами, при этом таблица не
изменится.
Из равенства a + (b + c)=(a + b)+c следует, что
22
з/ 3 \ / з Аз
а+ /> + с = {а + {/> + с}3}3 = {а + Ь + с}3 = {{а + />}3 + с}3 = а + £ +с
Ассоциативность "сложения по модулю 3" доказана.
Нулевым элементом б служит число 0. По таблице "сложения по мо-
дулю 3" определяем, что для каждого элемента а из Л/3 имеется противо-
положный элемент (-а): (-О) = 0 ; (-1) = 2; (~2) = 1.
Действительно, по таблице "сложения по модулю 3" получаем
3 3 3 3 3 3
0+(-0) = 0 + 0 = 0; 1+(-1) = 1+2 = 0 ; 2+(-2)= 2 + 1 = 0;
Итак, множество Л/3 относительно операции "сложения по модулю 3” явля-
ется коммутативной группой.
> Операция "умножение по модулю 3" ассоциативна и коммутативна,
что следует из ассоциативности и коммутативности умножения целых чи-
сел, а также свойств остатков:
з/ з А ( з Аз
a lb-c = {a-{b-c}3}3 = {а-6-с}3 = {{a-Z>}3-с}3 = а-b -с;
з з
а b = {a - b}3 ={b a}3 = b а .
Проверим дистрибутивность:
V з А
а • 6 +с = {а -{t + с}3}3 = {a -(b + c)}3 = {ai> + ac}3 =
/з Аз/ з A
- W3 + 1ас}з J3 = «- ^+ «- C .
Следовательно, операция "умножения по модулю 3" дистрибутивна слева
относительно операции "сложения по модулю 3". Дистрибутивность справа
можно не проверять, так как обе операции коммутативны.
Единичным элементом служит число 1 (что видно по таблице "умно-
жения по модулю 3"). Следовательно, М3 - коммутативное кольцо с едини-
цей.
Осталось показать существование обратных элементов. Для любого
аеМ3, отличного от нуля, существует обратный элемент а-1: 1-1=1;
1 3 -1 3
2 = 2. В самом деле, по таблице "умножения по модулю 3": 1-1 = 1-1 = 1
3 -1 3
и 2-2 =2-2 = 1. Таким образом, множество М3 с введенными операциями
является полем.
Замечание В.2. Можно доказать, что числовое множество
Мр ={б, 1, 2.р-1 } с операциями "сложения по модулю р" и "умноже-
ния по модулю р " является полем для любого простого числа р.
23
Пример В.9. Доказать, что множество чисел вида
P + q4i, (В.З)
где р и q - рациональные числа, является полем.
□ Действительно, операции сложения и умножения определены на
рассматриваемом множестве, так как сумма и произведение двух чисел вида
(В.З) имеют тоже самое представление:
(pi+q\'/2)+(p2+^2'^)=(Pi + Pz)+(qt + q2^;
(pi + <71 ^2 )• (р2 + q24i}= (Plp2 + 2ад2)+ {Plq2 + p2q{ )^2 .
Числа (a + p2), (<71+?г)' (P1P2 + ’ (Р\Я2 +РгЯ\)' очевидно, рацио-
нальные для любых рациональных р{, р2, qt, q2. Законы коммутативно-
сти, ассоциативности и дистрибутивности не нуждаются в проверке, так как
речь идет о сложении и умножении действительных чисел. Нулевым эле-
ментом служит число 0 = 0 + Ол/2 Для каждого числа р + qj2 противопо-
ложным элементом является число (-р) + (~з)Т2 , так как
(р + qjl)+ ((- р)+ (- 9)^/2)= (р - р)+ (q ~q)j2 = 0 + 0>/2 .
Единичным элементом служит число е =1+0^2 . В самом деле, для любого
числа р + q-j2 имеет место равенство:
(р + ^л/2 ) (1 + 0л/2^)= (1+-О-ч/з")-(р + ^->/2^)= p + q-^2
Таким образом, рассматриваемое множество является коммутативным коль-
цом с единицей (е 0). Осталось показать, что любое число р + q-$2, от-
личное от нулевого элемента 0 = 0 + Ол/2 , имеет обратный. В самом деле,
учитывая, что
1 = Р~д^2 = р_____________д
p + qji [p + q42){p-qj2} р2 ~2q2 р2 ~2q2
определим обратный элемент равенством
р — 2q р — 2q
Тогда
[p + qy!2}\p + q41^ = [p+q-j2^ -(p + qjl^
= (р + gV2)/— Р--------V= 1 + 0^ = е
Чр ~2.q2 р2-2q2 J
Заметим, что знаменатель р2 — 2q2 отличен от нуля для любых рациональ-
ных чисел р и q, не равных нулю одновременно. Действительно, равенство
24
2 = 2q2 равносильно равенству | р | = | q | ^2 , а это означает, что л/2 -
рациональное число. Поскольку число V? - иррациональное, значит
р2 _ 2q2 0 , т.е. обратный элемент существует для любого р + q^2 * 9.
Так как рассматриваемое множество является коммутативным кольцом
с единицей и каждый элемент, отличный от нуля, имеет обратный, то оно
является полем.
В.З. ПОЛЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Рассмотрим важнейший пример числового поля - поле комплексных
чисел.
Комплексным числом называется выражение вида х + yi, где х и у -
действительные числа, a i - символ, называемый мнимой единицей. Числа
х и у называются соответственно действительной и мнимой частями
комплексного числа z = х + yi и обозначаются
х = Re (х + yi)- Re z , у = Im (х +yi)= Im z (В-4)
Если мнимая часть равна нулю (у = 0), то число х + Oi считается совпа-
дающим с действительным числом х. Если действительная часть равна ну-
лю (х - 0), то число 0 + yi называется чисто мнимым и обозначается про-
сто yi.
Два комплексных числа xt + yxi и х2 + y2i называются равными, если
равны их действительные и мнимые части соответственно:
f X] = х2 ,
х^у^хг+угг <=> { _
(Л “ У1
Множество комплексных чисел обозначается символом С. Определим
Иа этом множестве арифметические операции.
СЛОЖЕНИЕ И ВЫЧИТАНИЕ
<чг,
'W.
*> Суммой Z[ + z2 комплексных чисел zt - Xj + у,/ и z2 = х2 + y2i назы-
вается комплексное число
I z = Zi + z2=(x1+x2) + (yI + y2)i. (В.5)
даз этого определения и свойств операции сложения действительных чисел
Следует, что:
ж а) операция сложения комплексных чисел коммутативна;
I zt + z2 = z2 + Z] VZ] G С, Vz2 g С ;
f 25
I
б) операция сложения комплексных чисел ассоциативна:
Zi + (z2 + z3) = (zi + z2)+ z3 Vzj e C , Vz2 e C , Vz3e C;
в) существует нулевой элемент 0 = 0 + 0 г: z + 0 = 0 + z = z VzeC', ну-
левой элемент обозначается просто символом нуль 0 = 0 + 0/';
г) для каждого комплексного числа z = х + yi существует противопо-
ложный ему элемент (- г) = (- х) + (- у) i: z + (-z) = (~z) + z = 0 -
Из последнего свойства следует, что на множестве комплексных чисел
определена операция вычитания (обратная к сложению). Разностью чисел
zl = Xj + У]/ и z2 = х2 + у2/ называется комплексное число
z = z1-z2 = (x1-x2)+(y1-y2)/ •
УМНОЖЕНИЕ И ДЕЛЕНИЕ
Произведением z^2 комплексных чисел zx = х( + yti и z2=x2 + y2i
называется комплексное число
Z = ZjZ2 = (х,х2 - у,у2)+ (xjy2 + х2у{) / . (В.6)
В частности,
// = (0 +1/)-(0 + 1/)= (0 0-1-1)+(0-1 + 01)/ = -1 + 0/=-1, т.е. /-/ = -1.
Правую часть формулы (В.6) можно получить, если перемножить выраже-
ния (х, + У]/) и (х2 + у2/), как двучлены, и учесть равенство / • / = -1.
Из определения (В.6) и свойств операции умножения действительных
чисел следует, что:
а) операция умножения комплексных чисел коммутативна:
zrz2 = z2zi Vz] е С , Vz2 е С;
б) операция умножения комплексных чисел ассоциативна:
zi(z2zs)= (ziz2) z3 VZ1eC, Vz2eC, Vz3gC;
в) существует единичный элемент е = 1 + 0/: ze = ez = z \/z&C\ еди-
ничный элемент обозначается просто символом единица: 1 = 1 + 0/;
г) для каждого комплексного числа z = х + у/, отличного от нуля, су-
ществует обратный ему элемент
такой, что zz 1 = z *z = 1. В самом деле, знаменатель дробей отличен от ну-
ля, так как равенство х2 + у2 =0 означает, что х = 0 и у = 0, т.е.
Z = 0 + 0/ = 0. Следовательно, для z * 0 правая часть определена. Проверим
равенство zz-1 =1. Используя определение (В.6) и равенство //=-1, по-
лучаем:
26
+....~-У
1 . ,.2 v2 , 2
1±£+-^+^=1+о;=1.
.2,2 JI , ,,2
Из последнего свойства следует, что на множестве отличных от нуля ком-
плексных чисел определена операция деления (обратная к умножению).
Частным двух чисел zt = Xj + y\i и z2-x2 + y2i называется ком-
плексное число
Z1 _ *1*2 + У1У2 УЛ~Х1У2
Z 2 2 о й 1
2 2 х2 + У 2 х2 + У2
Правую часть формулы (В.7) можно получить, если умножить числитель и
с zi
знаменатель дроби — на число х2 - y2i.
Z2
Операции сложения и умножения связаны законом дистрибутивности:
(Zj + z2)• z3 = zt z3 + z2 • z3 Vzje C , Vz2e C, Vz3eC.
Таким образом, множество С комплексных чисел является полем.
Пример В.10. Пусть Zj = 2 -t- i, z2 = 1 + 2i. Вычислить z3 + z2, zt - z2 ,
(В.7)
Z1
,ZiZ2, —•
Z2
□ По определению операций получаем
Z[ +z2 = (2 + i) + (l+ 2i) = 3 + 3i; Zj - z2 = (2 + i)-(l+ 2i) = l-i;
z,z2 = (2 + O’(1 + 2') = 2 + 4/ + i + 2i2 = 2-2 + 5i = 5i;
zi 2 + i (2 + i)-(l-2i) 2 + i-4i-2i2 _4-3i
---~--------------r—7---г =--------------—------— U,O “ U,Of .
z2 l + 2z (l + 2i)(l-2i) 1-4;2 5
При нахождении произведения и частного использовалось равенство
i2 =-1.
СОПРЯЖЕННЫЕ ЧИСЛА
Комплексные числа называются сопряженными, если у них равны
действительные части, а мнимые - противоположны по знаку. Число, со-
пряженное числу z = х + yi, обозначается z = х - yi.
Из определения следует, что сумма и произведение сопряженных чи-
сел - есть числа действительные:
z + z = (х + уг)+2х = 2Re z ;
z • z = (x + yi) • (x- yi) = x2 + y2.
Используя правила арифметических операций для комплексных чисел,
можно установить справедливость свойств операции комплексного сопря-
жения:
27
1) zl±z2 = z]±z2;
2) z, z2 = z, z2, в частности: z” = (z)" Vn 6 TV;
\z2 J z2
Пример B.ll. Решить уравнение z2 - 2z + 5 = 0.
□ Пусть z = x + yi - корень уравнения. Тогда
(x + yz)2-2(x + yz)+5 = 0 о х2 + 2xyi-y2-2x-2yi + 5-0
или (x2-у2-2x + 5)+(2xy-2y)z = 0.
Приравнивая нулю действительную и мнимую части, получаем
х2-у2-2х + 5 = 0, 1х2-у2-2х + 5 = 0,
7 о <
2ху-2у = 0, (х-1)у = 0.
Из второго уравнения следует, что х = 1 (случай у = 0 не подходит, так как
уравнение х2 - 2х + 5 = 0 не имеет действительных корней). Подставляя
х = 1 в первое уравнение, получаем у2 =4 о у = ±2. Таким образом,
уравнение имеет два комплексных сопряженных корня zi2 = 1 ± 2/ .
Замечания В.З.
1. Квадратное уравнение az2+bz + c = Q с действительными коэффи-
циентами и отрицательным дискриминантом D = Ь2 - 4ас < 0 имеет два
-b + h[-D
комплексных сопряженных корня z} 2 =-------.
2. Равенство (В.7) можно получить, умножая числитель и знаменатель
дроби — на число z2, сопряженное числу z2 (см. пример В. 10).
z2
3. Из свойств операции комплексного сопряжения следует, что
для любого многочлена pn(z)= a„zn+a„_lzn~l + ... + a]Z + a0 степени n
с действительными коэффициентами ап, a„_t,..., , а0 .
4. Рассмотренные ранее числовые поля удовлетворяют включениям
Q a. R с С, т.е. поле комплексных чисел содержит поле действительных
чисел, которое, в свою очередь, содержит поле рациональных чисел.
28
В.4. КОЛЬЦО МНОГОЧЛЕНОВ
Многочленом степени п от переменной х называется выражение
вида
р(х) = апхп + а„_1хл’1 +... + д1Х + д0 , (В-8)
где а„,...,а1,а0 - рациональные, действительные или комплексные числа
(коэффициенты многочлена), ап — старший коэффициент (а„^0).
Каждое слагаемое akxk в (В.8) называют членом многочлена, в частности,
а„хп — старший член, а0 — свободный член. Степень многочлена п — це-
лое неотрицательное число (обозначается degp(x)). Многочлен нулевой
степени ( и = 0) - это одночлен аох° - а0 (просто число). Если в выраже-
нии (В.8) все коэффициенты равны нулю, то получается нулевой многочлен.
Два многочлена р(х) и q(x) считаются равными (тождественно
равными), если равны их коэффициенты при одинаковых степенях пере-
менной х, т.е. когда они состоят из одинаковых членов, за исключением
членов с нулевыми коэффициентами. Из этого определения следует, что при
записи многочлена, в случае необходимости, можно добавить члены с ко-
эффициентами, равными нулю. Например,
х3 +2х = х3 + 0-х2 +2х + 0.
Пусть даны два многочлена
р(х) = а„хл + а„_1х”*1 + ... + а1х + а0, ап *0;
q(x) = Ьтхт + йт_1х'л-1 +... + А]Х + Ьо, Ьт * 0.
Суммой многочленов р(х) и q{x) называется многочлен
p(x) + q(x) = cX +cJ_lxv'1 + ... + с,х + с0,
коэффициенты которого получаются сложением соответствующих коэффи-
циентов многочленов р(х) и q(x):
с^ч+Ь, / = 0,1,...,*, (В.9)
где k = тах{ и; /и} - наибольшее из чисел пит, причем в формуле (В.9)
ап+1 = ап+2 = -=am=Q при п < т или Ат+1 = Ьт+2 =... = йп = о при п > т.
Заметим, что при сложении многочленов степень суммы не превосходит
тах{ п; т} - наибольшей из степеней слагаемых, т.е. может оказаться мень-
ше.
Произведением многочленов р(х) и q(x) называется многочлен
р(х) q(x) = dn+mxn+m + dn+m_iXn'm~x + ... + dtx + d0,
коэффициенты которого вычисляются по формулам
29
d„+m=anbm, d„+m_{ = anbm_} + an_lbm d2 = a2b0 +atbt + aob2,
d} = a0*i +«i*o- ^o=«o*o-
т.е. коэффициент dk при xk равен сумме произведений таких коэффициен-
тов а; и bj многочленов р(х) и q(x), что i + j = k. Из равенства
d„+m ~ anbm следует, что dn^m # 0, т.е. степень произведения многочленов
равна сумме степеней многочленов-множителей:
deg (р(х) q(x)) = deg р(х)+ deg q(x).
Пример В.12. Даны многочлены р(х)=2х2 +5 , q(x) = -2x2 + 3х . Най-
ти их сумму и произведение.
□ Допишем недостающие члены с нулевыми коэффициентами
р(х)= 2х2 + 0-Х + 5 , q(x)- -2х2 + Зх + 0 .
Теперь согласно определениям суммы и произведения многочленов, полу-
чаем
р(х) + q(x) = (2х2 + 0• х + 5)+ (-2х2 + Зх + о)= 0 • х2 + Зх + 5 = Зх + 5 ;
p(x)q(x) = fax2 +0х + 5)(-2х2 +3х + о)=
= 2(-2)х4+(2-3 + 0-(-2))х3+(2-0 + 0-3 + 5-(-2))х2+(0-0 + 5-3)х + 5-0 =
= -4х4 + 6х3 -10х2 +15х .
Степень суммы оказалась меньше степеней слагаемых, а степень произведе-
ния равна сумме степеней слагаемых. Заметим, что введенные операции
сложения и умножения многочленов совпадают с обычными правилами
сложения и умножения в элементарной алгебре.
Обозначим через Р множество многочленов переменной х. Если рас-
сматриваются многочлены с рациональными (действительными, комплекс-
ными) коэффициентами, то говорят, что Р - множество многочленов над
полем рациональных (действительных, комплексных) чисел. На множестве
Р определены две алгебраические операции - сложение и умножение мно-
гочленов. Покажем, что множество многочленов представляет собой кольцо.
В самом деле, коммутативность и ассоциативность сложения многочленов
вытекают из коммутативности и ассоциативности сложения чисел, так как
складываются соответствующие коэффициенты многочленов. Роль нулевого
элемента играет число нуль, рассматриваемое как одночлен. Для произволь-
ного многочлена р(х) = апхп +аП_1х"~] + ... + 0^ + 00 противоположным бу-
дет многочлен
?(*)=-«„*" - «„-I*"’1 -«ix-ao,
30
так как р(х)+^(х)=О. Поэтому определена операция вычитания много-
членов, обратная к сложению. Следовательно, относительно операции сло-
жения рассматриваемое множество Р является коммутативной” группой.
Умножение многочленов коммутативно. Это следует, в частности, из
того, что в определении произведения р(х)?(х) коэффициенты многочле-
нов р(х) и q(x) используются равноправным образом (формулы не изме-
нятся, если букву а заменить на b, а букву b - на а). Операция умноже-
ния многочленов ассоциативна. Действительно, пусть даны многочлены
р(х)=а„х" + ап_1х"~1 +... + а]х + а0, ап #0;
Xх) = bmxm + bm_}xm~' + ... + blx + b0, bm*0.
r(x)=CsXS +CS_}XS~' + ... + С]Х + С0, Cj *0.
Вычислим по определению
р(х)[Хх)г(х)] = (а»х'' +- + а1х + ао)[ VX+I +- + (^С0 +^0с1)Х + &0С0 ] =
= ^mcsxn+m+s + - + [%со +о0(б|Со + Ьос})]х + аоЬосо;
[р(х)Хх)]г(х) = [ anbmx"+m +... + (alb0 + aQb})x + aQb0]{csxs +... + с1х + с0)^
= a„bmc5xn*m+s + + [(аД + aQby )с0 + aoboc}]х + aobocQ .
Сравнивая коэффициенты, заключаем, что р(*) [<?(*) г(*)]= [р(х)'?(х)]г(х),
т.е. умножение многочленов ассоциативно.
Осталось убедиться в дистрибутивности, причем в силу коммутативно-
сти умножения многочленов, достаточно проверить, например, дистрибу-
тивность слева:
Xх) [<?(х)+ Кх)] = Xх) Хх)+ р(х) г(х) •
Найдем коэффициент при хк в левой и правой частях этого равенства:
соак-> (^j С])+... + др+ ск) в левой части;
(akb0 + ak_}b} + ... + aQbk')+(akcQ +ak_fy + ... + аоск) - в правой части.
Как видим, коэффициенты равны. Следовательно, операции сложения и ум-
ножения многочленов подчиняются закону дистрибутивности.
Заметим еще, что в множестве Р имеется единичный элемент е(х) = 1
- многочлен нулевой степени, поскольку для произвольного многочлена
р(х) = апх" + а„_1хя~1 +... + а1х + я0 выполняется равенство
р(х)е(х)= е(х) р(х)= р(х).
Таким образом, множество Р многочленов относительно введенных
операций представляет собой коммутативное кольцо с единицей.
31
Замечания В.4.
1. В качестве коэффициентов многочлена обычно рассматриваются ра-
циональные, действительные или комплексные числа, т.е. элементы число-
вых полей. Это обстоятельство существенным образом используется при
доказательстве свойств операций сложения и умножения многочленов, так
как для сложения и умножения коэффициентов многочленов - элементов
числовых полей - законы коммутативности, ассоциативности и дистрибу-
тивности имеют место. Можно рассмотреть множество многочленов с це-
лыми коэффициентами. Это множество с введенными операциями сложения
и умножения многочленов также является кольцом. Но, например, много-
члены с натуральными коэффициентами кольцо не образуют.
2. Операция деления многочленов, обратная умножению, не всегда вы-
полнима, т.е. кольцо многочленов не является полем. Например, любой мно-
гочлен ненулевой степени не имеет обратного, так как при умножении его
на любой другой многочлен произведение не будет равно 1.
3. Свойства кольца многочленов во многом аналогичны свойствам це-
лых чисел, известным из курса арифметики и алгебры. Например, операция
деления целых чисел с остатком, понятие делителя, свойства простых чисел
переносятся на многочлены.
ДЕЛИМОСТЬ МНОГОЧЛЕНОВ
Деление с остатком. Для произвольных многочленов р(х) и <?(х)^0 из
кольца Р существуют многочлены з(х) и г(х) из того же кольца Р, что
р(х) = 5(х)<?(х) + г(х), (В. 10)
причем степень многочлена г(х) меньше степени многочлена <?(х) или же
г(х) = 0. Многочлен s(x) называется частным {неполным частным), а
многочлен г(х) - остатком от деления р(х) на <?(х).
Частное и остаток при делении многочленов определяются однознач-
но. При этом можно использовать обычный алгоритм "деления многочленов
уголком".
Замечание В.5. Если р(х) и q(x) - многочлены с рациональными,
действительными или комплексными коэффициентами, то частное s(x) и
остаток г(х) будут многочленами с рациональными, действительными или
комплексными коэффициентами соответственно.
Если остаток от деления многочлена р(х)^0 на многочлен <?(х)^0
равен нулю, то говорят, что р(х) делится {делится без остатка) на <?(х):
32
p(x) = j(x)<7(x).
При этом многочлен </(х) называют делителем многочлена р(х).
Многочлен d(x)*0 называется общим делителем отличных от нуля
многочленов р(х) и q(x), если каждый из них делится на d(x) без остатка.
Общий делитель максимальной степени называется наибольшим общим
делителем. Так как каждый многочлен делится на любое отличное от нуля
число, то наибольший общий делитель существует. В крайнем случае, это
будет многочлен нулевой степени (просто число). Для однозначности опре-
деления наибольшего общего делителя обычно дополнительно требуют,
чтобы его старший коэффициент был равен единице. Тогда можно утвер-
ждать, что для любых ненулевых многочленов существует единственный
наибольший общий делитель. Понятия общего делителя и наибольшего об-
щего делителя распространяются на любое конечное число многочленов.
Как и в случае с целыми числами, наибольший общий делитель многочле-
нов можно найти, применяя алгоритм Евклида [30].
Если р(х) = апхп + ап_1х"-1 +... + а1х + а0 есть некоторый многочлен, а
с — некоторое число, то число р(с) = апсп + an_lcn~1 -t-.-. + ajC + ao, получен-
ное подстановкой в выражение р(х) вместо переменной х числа с, называ-
ется значением многочлена р(х) при х = с. Если р(с) = 0, то число с
называется корнем многочлена р[х).
Понятие корня тесно связано с делимостью многочленов. В самом де-
ле, при делении многочлена р(х) на линейный двучлен q(x)=x-c в пред-
ставлении (В.10) получаем остаток г(х) нулевой степени, т. е. число г:
p(x) = i(x)-(x-c) + r.
Подставляя х = с , имеем г = р(с), т.е. остаток от деления многочлена
р(х) на линейный двучлен (х—с) равен значению р(с) многочлена р(х) при
х = с {теорема Безу). Поэтому число с является корнем многочлена р(х)
тогда и только тогда, когда р(х) делится на (х-с).
Может оказаться, что многочлен р(х) делится на (х - с/ , где нату-
ральное число к больше 1, т.е. p(x) = (x-c)S(x), причем многочлен j(x)
не делится на (х-с), т.е. s(c)* 0. В этом случае говорят, что с - кратный
корень, а показатель к называют кратностью корня с. При k = 1 корень
с называют простым. Например, многочлен р(х)=(х-1)(х-2)"(х-3)5
имеет простой корень х = 1 (кратности 1), двойной корень х = 2 (кратности
2)и корень х = 3 кратности 5.
3-4549
33
ПРОИЗВОДНАЯ МНОГОЧЛЕНА
Производной (первой производной) многочлена
р(х) = а„х" + . + ajX + а0
называется многочлен
/(*) = ла„х'’’1 + (п -1) ал_1х',“2 +... + а1.
Второй производной р"{х) многочлена р(х) называется многочлен
р"(х) = (р'(х)) и т.д., производной к-го порядка р^к\х} называется произ-
водная от многочлена р^”’\х) - производной (к -1) -го порядка:
Понятие производной многочлена формально отличается от определе-
ния, принятого в математическом анализе [19,25], где многочлен р(х) рас-
сматривается как функция аргумента х. Однако, как видим, оба определе-
ния дают одно и то же выражение для производной. Поэтому свойства и
правила дифференцирования, известные из математического анализа, вы-
полняются и для рассматриваемого понятия производной многочлена. В ча-
стности, многочлен р(х) = апхп + «„^х"-1 +... + а}х + а0 можно представить
в виде
р(х)=р(с)+^р/(с)(х-с)+^-р"(с)(х-с)2+... + ^-р(',)(с)(х-с)п, (В.11)
1! 2! п!
так как остаточный член в формуле Тейлора равен нулю [19,25].
Если многочлен имеет корень с кратности к, т.е.
p(x)=(x-c^s(x),
то для его производной
р\х)= [(х-с)* s(x) ] = Л(х-с/-15(х)+(х-с)* /(х)
корень с имеет кратность k -1; для второй производной р"{х) = ^р'(х^) -
кратность к-1 и т.д. В частности, простой корень (кратности k = 1)
многочлена не является корнем его производной.
Из формулы (В.11) следует справедливость утверждения: для того
чтобы число с являлось корнем кратности к многочлена р(х), необходимо
и достаточно, чтобы выполнялись следующие условия:
р(с)=0, р'(с)=0,..., р(*'1)(с) = 0, p(i)(c)*0. (В.12)
Пример В.13. Определить кратности корней Xj = 1 и х2 = 2 многочле-
на р(х)= х5-2х4+2х3-12х2+ 21х-10 .
34
□ Найдем первую и вторую производные
р'(х) = 5х4 - 8х3 + 6хг - 24х + 21, р"(х) = 20х3 -24х2 + 12х - 24.
Так как р'(1) = 0 и р"(1) = -16*0, то корень хх - двойной (кратности
кх = 2 ). Так как р'(2)= 13 * 0, то корень х2 - простой (кратности к2 -1 )•
ОСНОВНАЯ ТЕОРЕМА АЛГЕБРЫ И ЕЕ СЛЕДСТВИЯ
Теорема [26,30] (основная теорема алгебры). Всякий многочлен, сте-
пень которого не меньше единицы, имеет хотя бы один корень, в общем
случае комплексный.
Следствие 1. Любой многочлен p{z) = at,zn+an_lzn~l+... + a1z + a0
степени п > 1 с комплексными коэффициентами а0 , ах , ап * 0
можно представить в виде произведения линейных двучленов:
anzn + an_xzn~x +... + axz + a0=an(z-zx')k'{z-z1f1 •... • (z - z,)*’ , (В. 13)
где zx,z2,---,zs - корни многочлена кратности kx,k2,...,ks соответствен-
но, причем kx + к2+... + к5 =п. Другими словами, многочлен п-й степени
имеет ровно п корней, если каждый корень считать столько раз, какова
его кратность.
Следствие 2. Если многочлены p[z} и q(z}, степени которых не пре-
восходят п, имеют равные значения более чем при п различных значениях
переменной z, то эти многочлены равны: p(z) = q(z).
В самом деле, по условию многочлен [p(z)-q(z)] имеет более, чем п
корней, хотя его степень меньше или равна п, что противоречит следст-
вию 1 из основной теоремы алгебры. Следовательно, это многочлен нулевой
степени p(z)~ q(z)= а0. Так как он имеет корни, то а0 = 0. Следовательно,
p(z)-?(z)=0,t.e. p(z) = ?(z).
Это следствие позволяет рассматривать многочлен р(х) не как фор-
мальное выражение вида (В.8), а как функцию переменной х, поскольку ра-
венство многочленов р(х) = q(x), определенное выше как равенство коэф-
фициентов при одинаковых степенях х, совпадает (в силу следствия 2) с
понятием равенства р(х) = q(x) двух функций при всех значениях х.
Рассмотрим многочлен р(х) = апхп + ал_1х" 1 +... + п1х + п0 с действи-
тельными коэффициентами а0 ,ах,...,ап_х ,ап * 0. Разложение (В. 13) для
этого многочлена имеет вид
р(х) = пл(х-х1)<:|(х-х2У:2 -...-(х-х,)*' ,
где Х|, х2,..., Xj - корни многочлена (может быть комплексные).
3»
35
Если комплексное число с является корнем этого многочлена, т.е.
р(с) = апсп + ап_хсп~{ +... + ахс + а0 = 0,
то сопряженное число с также является его корнем, т.е. р(с) = О. Это
вытекает из равенства р(с)- р(с) (см. разд. В.З). Поскольку числа с и с
являются корнями многочлена, то он делится (без остатка) на произведение
(х-с)(х-с)=х2 -(с + с)х + сс.
Так как сумма (с+с) и произведение сс сопряженных чисел являются дей-
ствительными числами (см. разд. В.З), то правая часть последнего равенства
есть квадратный трехчлен с действительными коэффициентами. Причем, ес-
ли с * с , то дискриминант этого квадратного трехчлена отрицательный (см.
разд. В.З).
Следствие 3. Если комплексное (но не действительное) число с - ко-
рень многочлена р(х) с действительными коэффициентами, то сопряжен-
ное число с является его корнем той же кратности.
В самом деле, если с - корень кратности к, то для него выполняются
условия (В. 12)
р(с) = 0, р'(с) = 0,..., //*-|\с) = 0, р^(с)*0.
Из условий р(с)= р(с)=0, р'(с)= р'(с) = 0, ..., р^-1\с)=0,
/>(?)=/>(0)^0 следует, что с - корень той же кратности к.
Следствие 4. Всякий многочлен р[х) = апхп +ап_{хп~х + ... + ахх + ай
с действительными коэффициентами представляется в виде произведения
линейных двучленов и квадратных трехчленов (с отрицательными дискри-
минантами):
апх" + ап-\х"~' + - + V + а0 = а„(х - Х| )* • (х -х2•... • (х - xs•
(х2+р1х + ^)"1 (x2+p2x + q2p -... (х2+р,.х + <7,.)'‘', (В.14)
где Х|,х2,...,х5 — действительные корни кратности k\,k2,...,ks, причем
кх +к2 +... + ks+2ml +2т2 + ... + 2тг =п.
Следствие 5. Многочлен нечетной степени с действительными коэф-
фициентами всегда имеет хотя бы один действительный корень.
Многочлен четной степени с действительными коэффициентами
может не иметь действительных корней (при этом в разложении (В.14) от-
сутствуют линейные двучлены (х - X!), (х - х2),..., (х - xs)).
36
Пример В.14. Многочлен р(х)=х5 -2х4 + 2х3 -12х2 + 21х-10
а) представить в виде (В.14);
б) представить в виде (В. 13).
□ Данный многочлен имеет двойной корень х, = 1 и простой корень
х2 = 2 (см. пример В. 13). Поэтому его можно представить в виде
Хх) = (х-1)2(х-2)9(х).
Разделим многочлен р(х) на многочлен (х -1)2 (х - 2) = х3 - 4х2 + 5х - 2
"уголком":
х5-2х4 +2х3- 12х2 +21Х-10 | х3-4х2+5х-2
х5 - 4х4 + 5х3 - 2х2 х2 + 2х + 5
2х4-Зх3 -10х2 +21Х-10
2х4 -8х3 + 10х2 -4х
5х3 -20х2 +25х-10
5х3 - 20х2 +25х-10
О
Следовательно, р(х)=(х-1)2(х-2)(х2+ 2х + б). Это разложение имеет вид
(В.14), поскольку дискриминант О = 4-20 = -16 квадратного трехчлена
х2 +2х + 5 отрицательный, что и требовалось в п. "а";
б) разложим квадратный трехчлен х2 + 2х + 5 на линейные множители,
что возможно над полем комплексных чисел:
х2 +2х + 5 = (x-x3)(x-x4) = (x + 1-2j)(x + 1 + 2z),
так как уравнение х2 + 2х + 5 = 0 имеет два комплексных корня
Тогда разложение (В. 13) для данного многочлена принимает вид
р(х)=(х-1)2(х-2)(х+1-2/)(х + 1 + 2/).
Согласно следствию 1, многочлен имеет один двойной корень (xt = 1), один
простой действительный корень ( х2 = 2) и пару простых сопряженных кор-
ней (х3 4 =-1±2т), т.е. всего 5 корней (с учетом их кратности).
37
В.5. АКСИОМАТИЧЕСКИЕ ПОСТРОЕНИЯ И ЛОГИЧЕСКИЕ
РАССУЖДЕНИЯ
При построении математической теории обычно применяется аксио-
матический подход, при котором сначала определяются основные объекты
и основные отношения между ними, которые формулируются в виде аксиом
- утверждений, принимаемых без доказательств. Используя основные объ-
екты и отношения, вводятся новые понятия, изучаются свойства, формули-
руются теоремы. При этом требуется, чтобы каждое новое утверждение
(теорема, лемма и т.п.) доказывалось на основе аксиом или ранее доказан-
ных теорем.
ВЫСКАЗЫВАНИЯ И ПРЕДИКАТЫ
Рассмотрим логическую конструкцию математических утверждений
(теорем, предложений, лемм). Формулировки теорем содержат высказыва-
ния. Напомним, что под высказыванием понимается языковое предложение,
о котором имеет смысл говорить, что оно истинно или ложно. Высказыва-
ниями, например, являются предложения: "дважды два - четыре", "диагона-
ли прямоугольника равны", "сборная Бразилии не была чемпионом мира по
футболу", "Москва - столица Франции". Первые два высказывания - истин-
ны, третье и четвертое - ложны. Предложения: "пойдем на лекцию", "когда
закончится этот фильм" высказываниями не являются. Высказывание может
принимать только одно из двух истинностных значений: "истина", "ложь".
Отрицанием высказывания А называется высказывание, которое ис-
тинно, если А ложно, и ложно, когда А истинно. Отрицание А обознача-
ется через -1А и читается как "не А ".
Пусть А и В два высказывания. Из них можно составить новые вы-
сказывания. Рассмотрим четыре высказывания:
высказывание " А и В " называется конъюнкцией высказываний А и
В (обозначается A&Z?);
высказывание " А или В " называется дизъюнкцией высказываний А
и В (обозначается A v В);
высказывание "из А следует В " (или " А влечет В ") называется им-
пликацией высказываний А и В (обозначается А => В); высказывание А
называется посылкой импликации, высказывание В - заключением-,
высказывание " А эквивалентно В " называется эквиваленцией выска-
зываний А и В (обозначается А ~ В или А <=> В).
Конъюнкция А&В - это высказывание, которое истинно тогда и
только тогда, когда истинны оба высказывания А и В одновременно.
Дизъюнкция A v В - это высказывание, которое ложно тогда и только
тогда, когда ложны оба высказывания А и В одновременно.
38
Импликация А => В - это высказывание, которое ложно тогда и толь-
ко тогда, когда А истинно, а В ложно. В самом деле, высказывания "из ис-
тины следует истина", "из лжи следует ложь", "из лжи следует истина" есте-
ственно считать истинными (из неверного условия можно получить любое
заключение), а высказывание "из истины следует ложь" следует признать
ложным.
Эквиваленция А ~ В - это высказывание, которое истинно тогда и
только тогда, когда истинностные значения высказываний А и В совпада-
ют. Действительно, высказывания "истина эквивалентна истине", "ложь эк-
вивалентна лжи" естественно считать истинными, а высказывания "истина
эквивалентна лжи", "ложь эквивалентна истине" - ложными.
Рассмотрим предложения, зависящие от параметра. Например, " х > 0",
"у и z близнецы". При подстановке вместо х некоторого числа, а вместо
у и z - имен конкретных людей, получаем высказывания, истинные или
ложные. Такие предложения называются предикатами. На основе предика-
тов можно составить более общие предложения, чем при помощи высказы-
ваний. При этом используются кванторы общности и существования. Пусть
д(х) - некоторое предложение, зависящее от параметра х, которое для
каждого значения х из множества X либо истинно, либо ложно. Тогда вы-
ражение УхеХ а(х) читается "для любого х из X А(х)это высказы-
вание, которое истинно, если для каждого элемента х из множества X вы-
сказывание д(х) истинно, и ложно - в противном случае. Выражение
Зхб X Д(х) читается "существует такой х из X, что А(х)" или "сущест-
вует такой х из X , для которого д(х)" - это высказывание, которое истин-
но, если в множестве X существует такой элемент х, для которого а(х)
истинно, и ложно - в противном случае. Если хотят подчеркнуть, что суще-
ствует единственный элемент х, для которого А(х) истинно, то применяют
символ 3!, например, 3!хе X д(х) читается "существует единственный
элемент х из множества X , что д(х)".
ЛОГИЧЕСКИЕ КОНСТРУКЦИИ ТЕОРЕМ
Пусть А и В два высказывания. Теоремы обычно имеют логическую
конструкцию одного из двух видов:
А В или А <=> В .
В импликации А => В, применительно к теоремам, высказывание А
называют условием теоремы, а В - заключением теоремы. Формулиров-
ку теоремы А => В можно читать, как "из А следует В ", "А влечет В ",
"если А , то В "," В необходимо для А "," А достаточно для В ".
39
Не всякое необходимое условие является достаточным и не всякое дос-
таточное условие является необходимым, т.е. из справедливости теоремы
А => В не всегда следует справедливость теоремы В => А . Например, в
евклидовой геометрии справедливо утверждение "если две прямые пересе-
каются, то они лежат в одной плоскости", но неверно утверждение "если
прямые лежат в одной плоскости, то они пересекаются".
С каждой теоремой вида А => В можно связать еще по крайней мере
три теоремы: обратную, противоположную, обратно-противоположную.
Обратной к теореме А => В называется теорема В => А , в которой
условие и заключение по сравнению с исходной теоремой меняются места-
ми. В этом контексте теорему А => В называют прямой теоремой.
Противоположной к теореме А => В называется теорема А=> —> В ,
в которой условие А и заключение В исходной теоремы заменяются их от-
рицаниями.
Обратно-противоположной к теореме А => В называется теорема
—। В => —। А , в которой условие и заключение исходной теоремы заменяются
их отрицаниями и меняются местами.
Из истинности теоремы А => В не всегда следует истинность обратной
и противоположной, но всегда следует справедливость обратно-противопо-
ложной. Например, справедлива теорема "если натуральное число оканчива-
ется цифрой 2, то его квадрат оканчивается цифрой 4". Обратная теорема
"если квадрат натурального числа оканчивается цифрой 4, то само число
оканчивается цифрой 2" не справедлива (контрпример: 82 = 64). Противо-
положная теорема "если натуральное число не оканчивается на 2, то его
квадрат не оканчивается на 4" также не справедлива (тот же контрпример).
Обратно-противоположная теорема "если квадрат натурального числа не
оканчивается на 4, то само число не оканчивается на 2" справедлива.
Формулировку теоремы А <=> В можно читать, как " А эквивалентно
В ", "из А следует В , и наоборот, из В следует А ", "если А , то В , и на-
оборот, если В , то А ", " А необходимо и достаточно для В ", " В необхо-
димо и достаточно для А ", "А тогда и только тогда, когда В ". Теоремы с
такими формулировками называют критериями. Заметим, что теорема
А <=> В эквивалентна конъюнкции (А => в)&(в => А), т.е. верны прямая и
обратная теоремы одновременно.
Довольно широко встречаются теоремы существования и единствен-
ности. Их конструкции включают квантор существования:
А => Э х в(х) — "если А , то найдется х, что в{х)
А => Э! х в(х) - "если А , то существует единственный х, что в(х)".
40
Многие теоремы формулируются с применением квантора общности (так
называемые общезначимые теоремы), например,
Vx А(х) => В - "для любого х А(х) влечет В ".
Пример В.15. Даны высказывания:
А - "треугольник является прямоугольным";
В = "сумма квадратов двух сторон треугольника равна квадрату треть-
ей стороны";
С = "на небе есть тучи
D = "идет дождь ".
Сформулировать теоремы: А => В; В=> A; —iA=>—iB’, -1В => -1А ;
А «5; С=>£>; £>=> С ; -.С =>-. £>; -,D=>-,C; C&D
и установить истинность или ложность каждой из них.
□ Составим из высказываний формулировки указанных теорем:
1) А => В : если треугольник является прямоугольным, то сумма квад-
ратов двух его сторон равна квадрату третьей стороны;
2) В => А: если сумма квадратов двух сторон треугольника равна
квадрату третьей стороны, то треугольник является прямоугольным;
3) -п А => —1В : если треугольник не является прямоугольным, то сумма
квадратов двух сторон треугольника не равна квадрату третьей стороны;
4) -п В => —1А : если сумма квадратов двух сторон треугольника не
равна квадрату третьей стороны, то треугольник не является прямоуголь-
ным;
5) А В : для того чтобы треугольник был прямоугольным, необхо-
димо и достаточно, чтобы сумма квадратов двух его сторон равнялась квад-
рату третьей стороны;
6) С=> D : если на небе тучи, то идет дождь;
7) D => С : если идет дождь, то на небе тучи;
8) -IС => —1D: если на небе нет туч, то дождь не идет;
9) -п D => -1С: если дождь не идет, то на небе нет туч;
10) С <=> D: на небе есть тучи тогда и только тогда, когда идет дождь.
Теоремы 1, 2, 3,4, 5,7, 8 справедливы, а теоремы 6, 9, 10 не верны.
МЕТОДЫ ДОКАЗАТЕЛЬСТВ ТЕОРЕМ
Доказательство математического утверждения, как правило, представ-
ляет собой цепочку правильных рассуждений, использующих аксиомы и
теоремы, справедливость которых установлена ранее. Рассуждение называ-
ется правильным, если из истинности всех посылок следует истинность за-
ключения. Пусть высказывания А], А2,..., Ап - посылки, а высказывание В
41
- заключение. Рассуждение проводится по схеме ----------, т.е. из пред-
В
положений Ах,А2^....Ап следует заключение В . Это рассуждение является
правильным, если формула (Aj & А2 &...& А„)=> В тождественно-истинная,
т.е. истинна для любых истинностных значений входящих в нее высказыва-
ний А,, А2,..., А„,В .
Правильным рассуждениям соответствуют, например, схемы:
А=>В, А
----—------правило вывода (modus ponensy,
А => В, В => С
---------------правило силлогизма',
А=>С
A=>B,—iB
----—------правило контрапозиции.
По первой и третьей схемам построены следующие рассуждения:
если натуральное число п делится на 4, то оно четное. Число п делит-
ся на 4. Следовательно, число п четное;
если натуральное число п делится на 4, то оно четное. Число п нечет-
ное. Следовательно, число п не делится на 4.
Оба рассуждения правильные для любых натуральных чисел п . В са-
мом деле, даже при п = 1, несмотря на кажущуюся противоречивость, имеем
правильное рассуждение: "если число 1 делится на 4, то оно четное. Число 1
делится на 4. Следовательно, число 1 четное", поскольку из ложных посы-
лок можно делать какие угодно заключения.
„ А => В, В
Рассмотрим пример рассуждения по схеме----------:
А
если натуральное число п делится на 4, то оно четное. Число п чет-
ное. Следовательно, число п делится на 4.
При и = 6 и п = 8 соответственно получаем:
если натуральное число 6 делится на 4, то оно четное. Число 6 четное.
Следовательно, число 6 делится на 4;
если натуральное число 8 делится на 4, то оно четное. Число 8 четное.
Следовательно, число 8 делится на 4.
Оба рассуждения неправильные, хотя заключение второго рассуждения
. „ А=> В, В
истинно (число 8 действительно делится на 4), т.е. схема-------не со-
А
ответствует правильным рассуждениям.
Часто вместо доказательства теоремы вида А => В доказывают истин-
ность некоторого другого утверждения, эквивалентного исходному. Такие
42
формы доказательства называют косвенными. Одним из них является спо-
соб доказательства от противного. Чтобы доказать истинность высказы-
вания А => В предполагаем, что это утверждение ложно. Исходя из такого
предположения, приходим к противоречию, а именно доказываем, что неко-
торое утверждение выполняется и не выполняется одновременно. Отсюда
делается вывод о том, что предположение неверно, а исходное высказыва-
ние истинно.
Пользуясь описанным способом, докажем утверждение:
если п нечетное число, то и число п2 - нечетное.
Предположим противное, т.е. пусть имеется такое нечетное число п, что
число п2 - четное. Тогда, с одной стороны, разность п2-п будет нечетным
числом, а с другой стороны, число п2 -n = n(n-i) заведомо четное, как
произведение двух последовательных целых чисел. Получено противоречие,
а именно: число п —п является четным и нечетным одновременно. Это до-
казывает, что сделанное предположение неверно и, следовательно, исходное
утверждение справедливо.
Рассмотренная схема доказательства от противного не единственная.
Применяются также другие схемы доказательства от противного:
Еще одна схема косвенного доказательства (по закону контрапозиции)
основана на эквивалентности двух утверждений А => В и —i В => -i А. В
самом деле, эти утверждения либо оба истинны, либо оба ложны. Например,
высказывания "если идет дождь, то на небе есть тучи" и "если на небе нет
туч, то не идет дождь" оба истинны, а высказывания "если на небе есть тучи,
то идет дождь" и "если не идет дождь, то на небе нет туч" оба ложны.
Во многих задачах нужно доказать справедливость некоторого утвер-
ждения (формулы) для любого натурального числа п. Непосредственная
проверка таких утверждений для каждого значения п невозможна, посколь-
ку множество натуральных чисел бесконечно. Для доказательства таких ут-
верждений (формул) применяется метод математической индукции, суть
которого заключается в следующем. Пусть требуется доказать истинность
высказывания а(и) для всех ne N - Для этого достаточно доказать два
утверждения:
1) высказывание А (и) истинно для и = 1. Эта часть доказательства на-
зывается базой индукции',
2) для любого натурального к из того, что высказывание истинно для
п = к (индукционное предположение) следует, что оно истинно и для сле-
43
дующего числа и = Л + 1,т.е. а(л)=> А(Л + 1). Эта часть доказательства на-
зывается индукционным шагом.
Если п.1, 2 доказаны, можно сделать вывод об истинности высказыва-
ния А (и) для любого натурального п .
В самом деле, если высказывание А(1) истинно (см. п.1), то высказы-
вание А(2) тоже истинно (см. п.2 при п = 1). Поскольку А(2) истинно, то
а(з) тоже истинно (см. п.2 при и = 2) и т.д. Таким образом можно дойти до
любого натурального числа п, убеждаясь в справедливости А (л) .
Замечание В.6. В ряде случаев бывает необходимо доказать спра-
ведливость некоторого утверждения А(и) не для всех натуральных п, а
лишь для п > р , т.е. начиная с некоторого фиксированного числа р. Тогда
метод математической индукции модифицируется следующим образом:
1) база индукции: доказать истинность А(р);
2) индукционный шаг: доказать а(а)=> А(Л + 1) для любого фиксиро-
ванного к> р.
Из п.1, 2 следует, что утверждение а(и) верно для всех натуральных п > р .
Пример ВЛ6. Доказать справедливость равенства
1+3+5+...+(2л-1) = п2
для любого натурального п.
□ Обозначим сумму первых п нечетных чисел через
Sn = 1 + 2 + ... + (2и-1). Требуется доказать утверждение Л(п): "равенство
Sn =п2 верно для любого ие N ". Доказательство проведем по индукции.
1) Поскольку = 1 = I2, то при п -1 равенство Sn = п2 верное, т.е.
высказывание А(1) истинно. База индукции доказана.
2) Пусть к - любое натуральное число. Выполним индукционный шаг
а(&)=> А(£+ 1). Предположив, что утверждение А(и) истинно при п-к,
т.е. Sk =к2, докажем, что утверждение а(и) истинно для следующего на-
турального числа п = к +1, т.е. 5i+1 = (к +1)2 . Действительно,
Sk+i = 1 + 3 + 5 + ... + (24:-1) + [2(Л +1)-1] = Sk + 2к +1 = к2 + 2к +1 = (к +1)2.
' £
Поэтому а(&)=> A(fc + 1) и на основании метода математической индукции
заключаем, что высказывание а(и) истинно для любого натурального п,
т.е. формула Sn = п2 верна для любого и 6 W.
44
Пример В.17. Перестановкой из п чисел называется набор первых п
натуральных чисел, взятых в некотором порядке. Доказать, что количество
различных перестановок равно и!. Выражение л! (читается " п факториал")
равно и!= 1-2-3-...-(н-1)-и . Две перестановки ,х2,...,/„) и (Д,Л.Л) из
п чисел считаются равными, если j, = Д д2 = = jn, а в случае на-
рушения хотя бы одного из равенств перестановки считаются различными.
□ Проведем доказательство методом математической индукции.
1) Для п = 1 имеется всего одна перестановка (1), т.е. 1!=1 и утвер-
ждение верно.
2) Предположим, что для любого к количество перестановок равно к\.
Докажем, что количество перестановок из (£ + 1) чисел равно (Л 4-1).' - В
самом деле, зафиксируем число (£ + 1) на любом месте в перестановке из
(к +1) чисел, а первые к натуральных чисел разместим на оставшихся к
местах. Количество таких перестановок равно количеству перестановок из
к чисел, т.е. к\ по индуктивному предположению. Так как число (£ + 1)
можно было поставить на любое из (к +1) мест в перестановке, заключаем,
что количество различных перестановок из (fc + 1) чисел равно
(к +1)-(к 1) = (к +1)1. Таким образом, предположив, что утверждение верно
для п = к, удалось доказать, что оно верно для п = к +1.
Из пунктов 1 и 2 следует, что утверждение верно для любого нату-
рального числа п.
Замечание В.7. Формальные методы вывода теорем, использую-
щие многочисленные схемы правильных рассуждений, изучаются в матема-
тической логике [27]. Как правило, эти методы порождают лишь новые
формулировки теорем, отражающих старое содержание. Поэтому для разви-
тия математической теории они малоэффективны. Однако, законы матема-
тической логики и схемы правильных рассуждений, должны обязательно
соблюдаться при изучении любой математической проблемы.
ГЛАВА 1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
1.1. ЧИСЛОВЫЕ МАТРИЦЫ
Рассмотрим важные математические объекты - матрицы.
Матрицей размеров тхп называется совокупность т-п чисел, рас-
положенных в виде прямоугольной таблицы из т строк и п столбцов:
'аи а12
А = а21 а22 • а1п или А = (ац), i = l,..,/n ; j = 1,..,л
<ат1 &т2 • атп j
Числа, составляющие матрицу, называются элементами матрицы', -
элемент матрицы, стоящий на пересечении i -й строки и j -го столбца мат-
рицы. Всюду далее предполагаются, что элементы матриц являются дейст-
вительными числами, если не оговорено противное.
Пример 1.1. Определить размеры матриц
р 0 4 2^
1^3 6 8 1J’
с = (1 2 3), d =
□ Матрица А имеет размеры 3x2, а матрица В — 2x4, с - 1x3,
d - 2x1 .
Две матрицы А и В называются равными (А- В), если они имеют
одинаковые размеры (тхп) и равные соответствующие элементы:
а,, = Ьц , i = ; j = 1,..,п .
ТИПЫ МАТРИЦ
В общем случае матрицу (размеров иг Хи) называют прямоугольной.
В частности, если матрица состоит из одного столбца (и = 1) или одной
строки (т = 1), то она называется матрицей-столбцом или матрицей-
строкой (либо просто столбцом или строкой) соответственно. Матрицы-
строки или матрицы-столбцы часто обозначают строчными буквами (в при-
мере 1.1: с - строка, d - столбец). Матрица размеров 1x1 - это просто
число (единственный элемент матрицы).
Если у матрицы количество строк (т) равно количеству столбцов (п),
то матрицу называют квадратной (п-го порядка). Элементы
ан ,а22>-- ’алл образуют главную диагональ квадратной матрицы (ей соот-
ветствует штриховая линия на рис. 1.1, соединяющая левый верхний угол
46
матрицы (элемент аи) с правым
нижним углом (элемент ат)). Диа-
гональ, соединяющая левый ниж-
ний угол (элемент ап1) с правым
верхним углом (элемент а1п), на-
зывается побочной.
Побочная диагональ
Главная диагональ
Рис. 1.1
Квадратная матрица вида
О
а22
, у которой все
I о 0 ... апп)
элементы, стоящие вне главной диагонали, равны нулю, называется диаго-
нальной и обозначается diag(all,ат}. Частным случаем диагональ-
ной матрицы служит квадратная матрица
(1 0 .
0"
0
1,0 0
которая называется единичной (и -го порядка) и обозначается Е (или Еп).
Диагональная
Верхняя
треугольная
Рнс. 1.2
Нижняя
треугольная
Если все элементы квадратной матрицы, расположенные ниже (выше)
главной диагонали, равны нулю, то матрицу называют верхней треугольной
(нижней треугольной). На рис. 1.2 изображены диагональная и треуголь-
ные матрицы (здесь и далее будем полагать, что в частях матрицы, помечен-
ных символом О, все элементы равны нулю, а в частях, помеченных симво-
лом * и линиями, элементы матрицы могут быть произвольными). Заметим,
что диагональная матрица, в частности единичная, является одновременно
верхней и нижней треугольной.
Матрица, все элементы которой равны нулю, называется нулевой.
47
Пример 1.2. Определить типь i матриц
(0 0 оА (1 2 Г
/0 01 0 01 fl 0
0 jJ’ '1 в = 0 ) 4 5 0 9, '1 С = 0 J О' , Я °J У 0 0 oj О' Е = 1° 1
F = 0 1 0 > G = 2 3 0 , н = 0 2 0
<0 0 и 4 5 6> 0
□ Матрица А - прямоугольная размеров 2x3, нулевая; матрица В -
верхняя треугольная третьего порядка; С - нижняя треугольная второго по-
рядка; D - квадратная второго порядка, нулевая; Е - единичная второго
порядка; F - единичная третьего порядка; G - нижняя треугольная третье-
го порядка; Н - диагональная третьего порядка.
1.2. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ
1.2.1. Сложение матриц
Пусть A = (atj) и В = (Ьц) - матрицы одинаковых размеров тхл.
Матрица С = (су) тех же размеров тхи называется суммой матриц А и
В, если ее элементы равны сумме соответствующих элементов матриц
АиВ: Су=ау+Ьу, j = l,..,n. Сумма матриц обозначается
С = А + В . Операция сложения матриц определена только для матриц оди-
наковых размеров и выполняется поэлементно:
41 ап -• а. 1л [Ч ^12
а21 а22 а2п + ^21 ^22 " Ь2п
<aml ат2 атп; ^т2 •• ь тп у
а12 +Ь 12 “ а1п
а21+&21
а22+^22 •" а2п+^2п
aml + fynl
о__ + b„„
mz mz тп тп У
Из определения следует, что складывать можно только матрицы оди-
наковых размеров. Нельзя, например, найти суммы вида
fl 2А |ЗА ,, (ЗА
+ или (1 2)+ .
1з 4J 16J ' ' 14J
48
Пример 1.3. Найти сумму двух матриц А = 3 4 ,
'О
В= 1
.0
Г
о
0,
15 6J
□ Складывая соответствующие элементы матриц, получаем
'1 2' 'о Г '1 + 0 2+Г '1 3'
с = 3 4 + 1 0 = 3+1 4+0 - 4 4
.5 6, <0 0, ч5+0 6 + 0у <5 6,
(3x2) (3x2) (3x2)
Г1 2^
1.2.2. Умножение матрицы на число
Произведением матрицы А = (а^) на число X называется матрица
С = (сц) тех же размеров, что и матрица А , каждый элемент которой равен
произведению числа X на соответствующий элемент матрицы А :
с,у=Ха,у, z = l,...,zn; j = l,...,n.
Произведение обозначается ХА или АХ. Операция умножения матрицы на
число выполняется поэлементно:
%1 а12 ’ • а1п" Хав Xaj2
X а21 а22 ‘ а2п = Ха2] X^22 ^а1п
^ml ат2 ’ атп> Лаш1 ^am2 ’ атп ,
Умножить на число можно любую матрицу, при этом каждый ее элемент
умножается на это число.
fl 2>
Пример 1.4. Найти произведение матрицы А = 3
4 на число 2.
□ Умножая на 2 каждый элемент матрицы А , получаем
р 2) '1-2 2-2У '2
С = 2А = А-2 = 2- 3 4 = 3-2 4-2 = 6 8 .
<5 6J [5-2 6-2) J0 12,
Матрица (-1)-А называется противоположной матрице А и обозна-
чается (- А). Сумма матриц В и (- А) называется разностью и обозначает-
ся В - А. Для нахождения разности матриц В - А следует из элементов мат-
рицы В вычесть соответствующие элементы матрицы А . Вычитать можно
только матрицы одинаковых размеров.
4 - 4549
49
Пример 1.5. Даны матрицы А = 3 4 ,
5 6,
'0 Г
В - 1 0 . Найти разности
О О,
В —А и А —В.
□ Вычитая друг из друга соответствующие элементы, находим
В — А =
'0-1
1-3
.0-5
0-4
0-6,
-2 -4
-5 -6,
'1-0 2-1> (1 П
3-1 4-0
^5-0 6-0,
А — В =
2 4
5 6
СВОЙСТВА ЛИНЕЙНЫХ ОПЕРАЦИЙ
Операции сложения матриц и умножения матрицы на число называют-
ся линейными операциями над матрицами. Непосредственно из опреде-
лений вытекают следующие свойства линейных операций.
Для любых матриц А, В, С одинаковых размеров и любых чисел а,
Р справедливы равенства:
1. А+В = Я + А (коммутативность сложения);
2. (А + В)+С = А + (в+С) (ассоциативность сложения);
3. существует нулевая матрица О (тех же размеров, что и А ): А+О = А;
4. существует матрица (- а) , противоположная матрице А : А + (- А) = О;
5. а(А + в) = аА+аВ \
6. (а + Р)А = аА + РА;
7. (ар)А = а(РА);
8. 1-А = А.
Замечание 1.1. Свойства 5 и 6 определяют законы дистрибутив-
ности: умножение матрицы на число дистрибутивно по отношению к сло-
жению матриц (свойство 5); умножение матрицы на число дистрибутивно
по отношению к сложению чисел (свойство 6).
1.3. УМНОЖЕНИЕ МАТРИЦ
1.3.1. Определение произведения матриц
Пусть даны матрицы А-(а,у) размеров тхр и В = (/>,-,) размеров
рхп. Матрицу С размеров тхп, элементы с^ которой вычисляются по
формуле
су =anbij +ai2b2j +--- + atpbpj > i = 1.-.,лп ; j = ;
50
называют произведением матриц А и В и обозначают С = АВ . Операция
умножения матрицы А на матрицу В определена только для согласован-
ных матриц, у которых число столбцов матрицы А равно числу строк мат-
рицы В :
С = А В .
глхл тхр рхп
Рассмотрим подробнее процедуру нахождения произведения матриц.
Чтобы получить элемент , стоящий на пересечении i -й строки и j -го
столбца матрицы С, следует выделить i -ю строку матрицы А и j -й стол-
бец матрицы В (рис. 1.3). Они содержат одинаковое число элементов, так
как матрицы А и В согласованы. Затем найти сумму попарных произведе-
ний соответствующих элементов: первый элемент i -й строки умножается
на первый элемент j -го столбца, второй элемент i -й строки умножается на
второй элемент j -го столбца и т.д., а результаты перемножений складыва-
ются.
Рис. 1.3
В произведении А • В матрицу А называют левым множителем для В
и говорят об умножении матрицы В на матрицу А слева. Аналогично мат-
рицу В называют правым множителем для А и говорят об умножении мат-
рицы А на матрицу В справа.
р (Г
, В = 0 1 . Вычислить
J ь
fl 2 1
Пример 1.6. Даны матрицы А =
произведения АВ и ВА.
□ Используя правило умножения, получаем
"1 (Г
О 1
J J
fl 2 1
А • В =
ни — to 1 2
2x3 3x2 '
''1-1 + 2-0 + 1-1
JM + 1-0+2-1
10+2-1+1 Г
0-0+11 + 21,
'2 3^
ч2 3)
2x2 ?
51
'1 o'
В A = О 1
3x2 2x3 M 1
1 2
О 1
1
2
'1 1 + 0-0
01 + 1-0
J-l + 1-0
1-2 + 01
0-2 + 11
1-2 + 11
11 + 0-2'
0-1 + 1-2
1-1 + 1-2,
'1 2 1'
О 1 2
J 3 3J
3x3
Оба произведения A В и В • А определены, но являются матрицами разных
размеров, т.е. АВ * ВА.
(12 11
Пример 1.7. Даны матрицы А =) I,
\хз)
/> = (1 2 3).
Найти произведения Ах, bx, xb.
□ Используя правило умножения, получаем
fl
А • х =
2x3 3x1 х®
1-Xj +2-х2 + 1-х3 ] jx1+2x2+x3
O-xj + 1-х2 + 2-х3 J х2+2х3
2d
b • х =(1 2 3)- х2 =(1-Xj+2-x2+3-x3) = Xj+2х2+Зх3;
1*3 3x1 1Х1
Пример 1.8. Даны матрицы
0
1
0 = 1 . Вычислить произведения АВ, BA, АЕ, ЕА, ВО, ОВ.
□ Все матрицы квадратные второго порядка. Следовательно, все про-
изведения будут квадратными матрицами того же порядка. Используя пра-
вило умножения, получаем
АВ =
f°
4J I1
BA
А-Е =
°1 Г1
1J\з
Г1
4J 1°
0]_р-0 + 2-1 1-0 + 2-р_Г2 2'
lJ~^3-0 + 4-l 30+4-lJ-^4 4?
2> f0-l+0-3 0-2+0-4'l_f0 О'
4j-(<l-l + l-3 1-2+1-4;-|<4 6
О'! р-1 + 2-0 l-O+2-lAp 2'
lJ-b-l + 4-0 3-0+4-1J-(з 4,
1
3
0
1
52
ВО
ЕА
О ОА
1 1)
О
О
OW1 2Д р-1 + 0-3 1-2+0-4W1 2\
JI3 4J loi + l-З 0-2 + 1-4,)ДЗ 4/
oWo °\ о в-[° 0>| (° °)_f° 0
oj~[о oj’ До оД1 рДо °.
Замечание 1.2. Непосредственным вычислением можно доказать
основное свойство единичной матрицы:
АЕ_ = ЕтА = А
П т
для любой матрицы А размеров тхп.
Пример 1.9. Найти произведения АВ и В -А :
а)А = (1 2 3), В = Ч' 5 ; 6) Л = [;
<6>
-4 -Г
"2 L
, в = (1 3).
□ а) Произведением А • В является число:
6П
= (1-4 + 2-5 + 3-б) = (32) =32,
'-ixTJ
А-В = (1 2 З)- 5
к
3x1
а произведением В V ВА= 5 Л 4 - квадрата (i 2 3)= ая матрица третьего порядка: '4-1 4-2 4-ЗА (4 8 12' 5-1 5-2 5-3 = 5 10 15 к6-1 6-2 6-3J (б 12 18,
1x3
3x1 3x3
Очевидно, что A-В* В-А\
1 2W-1 ЗДр-(-1) + 2-1 1-3 + 2-1W 1 5\
3 1J\1 м1з-(-1) + 1-1 3-3+1-1)Д-2 lOj’
2x2 ' 2x2 ' " 2x2
Г-1 3W1 2ДГ(-1)-1 + 3-3 (~1)-2 + 3 1W8 П
VI 1J\з ijy 11+1-3 1-2 + 1-1 Дд 3)
2x2 2x2 2x2
53
Оба произведения - это квадратные матрицы одного и того же порядка, но
А-В*В-А;
в)
_Гб 1) Г—4 — 1) Гб-(—4) + 1-(—2) 6 (-1) + 1-1Л Г-26 -5)
Л'В=\2 1J (-2 1 J“|<2-(-4) + l-(-2) 2-(-l) + l-lJ"(-10 “J’
2x2 2x2 2x2
Г-4 -П Гб 1) Г(-4)-6 + (-1)-2 (-4)-1 + (-1)-1) (-26 -5)
(-2 1 J V2 1J ( (-2)-6 + 1-2 (-2)1 + 11 ) (-10 -1J
2x2 2x2 2x2
Результаты умножения совпадают, т.е. А-В = В-А;
г) произведение А В не может быть найдено, так как число столбцов
матрицы А (три) не равно числу строк матрицы В (одна). При этом гово-
рят, что нельзя умножить матрицу А на матрицу В справа. В то же время
можно умножить матрицу А на матрицу В слева:
Г 3 2 Г1
В А = (\ 3)- [ = (1-3 + 3 0 1-2 + 3-1 1-1 + 3-2) = (3 5 7).
1x2 > , < 1x3
2x3
1.3.2. Свойства умножения матриц
Пусть X - любое число, А , В , С - произвольные матрицы, для кото-
рых определены операции умножения и сложения, записанные в левых час-
тях следующих равенств. Тогда определены операции, указанные в правых
частях, и справедливы равенства:
1. (АВ)С = А(ВС);
2. Л(В + С)= АВ + АС;
3. (А + В)С = АС + ВС ;
4. Х(ЛВ) = (М)В.
(ассоциативность умножения матриц)
(дистрибутивность умножения)
(дистрибутивность умножения)
Пример 1.10. Продемонстрировать справедливость свойств 1, 2, если
Г1 2'
I3
г 5 6
5“17 8
С = Р °
10 2
□ Проверим свойство 1: (А В) С = А (В С).
, \ ГГ1 2>1
4J
5 б\
7 8J
1 0) <19 22) (1 0W19 44
0 2Г143 50) [о 2 I“143 100
54
x-(*-c)=Q
2 А 175 6W1 о\
4J [? 8j\0 2)
1 2W5 12ЛГ19 44
3 4Д7 16j \43 100
Проверим свойство 2: А (В + С) = АВ + АС.
л-(в+с)=
2
4
6> Г1 о\
8J+1° 2J
1 2W6 б)_(20 26'
3 4Д7 10j(,46 58
fl
AB + AC=\
3
2W5 6> p 2> p 0)_fl9 22^ p 4> <20 26Л
4J I7 8J + l3 4J 1° 2J I43 50J + l3 8 J I46 58J
Замечания 1.3.
1. В общем случае умножение матриц не является коммутативным.
Произведение зависит от перестановки множителей, т.е. А-В * В-А. Во-
первых, размеры матриц А и В могут быть такими, что произведение АВ
определено, а произведение ВА - не существует и наоборот (в примере 1.7
найдено произведение Ах, а произведение хА не определено; в примере
1.9, г найдено произведение В- А, а произведение А В не определено). Во-
вторых, если оба произведения АВ и ВА определены, результаты могут
оказаться матрицами разных размеров (см. пример 1.6 и 1.9, а). Если матри-
цы А и В квадратные одного порядка, то произведения АВ и ВА будут
также квадратными матрицами того же порядка. Даже при этих условиях
умножение матриц не коммутативно (см. пример 1.8 и 1.9,6, где
А-В* В-А). С другой стороны, в примере 1.8 АЕ= Е-А = А и
ВО = ОВ = 0 ,ав примере 1.9, в А- В = В- А, т.е. существуют квадратные
матрицы, произведение которых не зависит от перестановки множителей.
Матрицы А и В называются перестановочными, если
А-В = ВА.
Перестановочными могут быть только квадратные матрицы одного и того
же порядка. В частности, например, можно показать, что диагональные мат-
рицы одного и того же порядка перестановочны.
2. Для любой квадратной матрицы А порядка п справедливы сле-
дующие равенства
А-Е = Е-А = А,
где Е - единичная матрица порядка п. Другими словами, единичная мат-
рица перестановочна с любой квадратной матрицей того же порядка.
3. Для любой матрицы А справедливы равенства
А-О = О и ОА = О,
где О - нулевые матрицы соответствующих порядков, т.е. нулевая квадрат-
ная матрица перестановочна с любой квадратной матрицей того же порядка.
55
4. Множество квадратных матриц одного и того же порядка п > 1 с
операциями сложения матриц и умножения матриц на число представляет
собой некоммутативное кольцо с единицей. Кольцо не является коммута-
тивным, так как операция умножения квадратных матриц порядка п > 1 не
коммутативна. Единичным элементом кольца служит единичная матрица.
5. Заметим, что сумма и произведение диагональных (верхних тре-
угольных, нижних треугольных) матриц одного и того же порядка являются
диагональными (верхними треугольными, нижними треугольными) матри-
цами. Следовательно, операции сложения и умножения матриц определены
на множествах диагональных (верхних треугольных, нижних треугольных)
матриц одного и того же порядка. Поэтому каждое из указанных множеств
является кольцом с единицей, причем кольцо диагональных матриц комму-
тативное.
Пример 1.11. Найти матрицы, перестановочные с матрицей
А =
10 1J
□ Для выполнения равенства АВ = ВА искомая матрица В должна
(х у
быть квадратной второго порядка. Пусть она имеет вид В =
I Z w
и удов-
летворяет равенству
р 1
О 1
X у ]_[ X у 1 [ 1 1
z wj wj ^0 1у
После умножения получаем в левой и правой частях равенства квад-
ратные матрицы второго порядка:
fx + Z У+мЛ f х х + у'
z w J ^z z + wj
Записывая равенство соответствующих элементов этих матриц, полу-
чаем систему уравнений
z = z,
y+w-x+y,
w= z + w.
Из первого уравнения следует, что z = 0, а из третьего: х = w. Следо-
вательно, искомые матрицы имеют вид
5 =
1°
где х, у - параметры, принимающие любые действительные значения.
56
1.3.3. Умножение матриц на столбцы и строки единичной матрицы
Рассмотрим два типа преобразований квадратной матрицы А п -го по-
рядка при помощи умножения на строки и столбцы единичной матрицы.
Обозначим j -й столбец и i -ю строку единичной матрицы п -го по-
т
рядка через и соответственно:
1. Найдем произведения
Г«и
Как видим, в результате умножения матрицы А справа на Столбец еj выде-
ляется j -й столбец матрицы А , а при умножении слева на строку е[ полу-
чаем i -ю строку матрицы А . Элемент atj матрицы А может быть получен
как произведение
е[Ае}-=(0 1 О) «л
^лл,
57
Пример 1.12. Даны матрицы
Д 2 3'
А = 4 5 6
J 8 9,
ef=(l О О),
е2 =
Гоа
1
<0,
Вычислить Ае2 , е[ А , е[Ае2 .
□ Перемножая матрицы, получаем:
ei Ае2 = С1
О 0) 4
В результате умножений из данной матрицы А выделены 2-й столбец,
первая строка, элемент а12 = 2.
2. Умножая справа матрицу А сначала на столбец , а затем на строку
т
получаем квадратную матрицу п -го порядка, в которой все элементы
равны нулю, за исключением элементов j -го столбца, который совпадает с
j -м столбцом матрицы А :
При помощи умножения на строки ej и столбцы можно, например,
заменить j -й столбец матрицы A i -м столбцом матрицы В (квадратной
п -го порядка):
А - + ВеД .
58
Вычислить Ае2ёу , Ве}е2 , А - Ае2е2 + BeYe2 .
□ Выполняя действия, получаем:
"9 8 7' Г9' '0 9 О'
Ве{е2 = 6 5 4 0 (0 1 0) = 6 (0 1 о)= 0 6 0
<3 2 1, .3, ч0 3 0,
(1 2
Л - Ае2е? + Ве^т = 45
'1 9 3'
4 6 6
J 3 9,
I7 8
В результате 2-й столбец матрицы Л заменен 1-м столбцом матрицы В .
1.3.4. Степень матрицы
Для любой квадратной матрицы А (п -го порядка) определено произ-
ведение А А (матрицы А на себя). Поэтому можно говорить о целой неот-
рицательной степени матрицы, определяя последовательно
А° = Е, А1 = А, А2 = А-А, А3 = А2 -А,.... Ат = Ат~1 А__
Заметим, что степени А* и А1 одной и той же матрицы А
перестановочны А* А1 = А1 • Ак :
Ак -А1 =(А-А-...-А)-(А-А-...-А)=А-А-...-А = А*+; ;
'—I—'—?
А1 Ак = (А-Аа)-(a-а- ..-а) = АА-...-А = Ak+l.
Поэтому справедливы обычные свойства степеней:
Ак А1 = А1 Ак = Ak+I,
(Ак]‘= Ак1,
с натуральными показателями.
59
МНОГОЧЛЕНЫ ОТ МАТРИЦ
При помощи операций возведения в степень, сложения матриц и ум-
ножения матрицы на число можно получать многочлены от матриц. Пусть
рт(х) = а0+а1х + а2х2+... + атхт - многочлен (степени т) переменной х,
А - квадратная матрица л -го порядка. Выражение вида
Рт(А) = ао £ + а1А + а2А2 + ••• + атАт
А0
называется многочленом от матрицы А. Многочлен Рт(А) является
квадратной матрицей л -го порядка.
з fl 2^1
Пример 1.14. Найти А , если А = I I.
□ По определению степени матрицы получаем
з fl 2? fl 2V1 2^ fl 2^ f3 4Л fl 2^ f7 10^
A = = • • = • =
VI 1J V 1J V1 1) U 1J <2 3) Vl 1J 15 7 J
, f 2
Пример 1.15. Найти/(A), если f(x) = x~—5x + 3, A=l
-1
3
□ Используем определение многочлена от матрицы:
' 2 -Г| (2 -С f 2 -Г) fl 0^
-5- +3-
-з з) V-з з) V-3 з) fo ij
(7 -5W10 -5^ f3 0}f0 0^
Д-15 12J V-15 l5J + l° 3J~ 1°
fA 1"|
Пример 1.16. Найти A" , если A -1 j, «G JV.
□ По определению степени матрицы последовательно находим:
A2 fX fX 2Л1
До aJ\o aJ [о a2J;
V 2A\fA n = fx3 ЗА2'
k0 А2 До A J [о A\
Предполагаем, что A" =
A" nA"
0 A"
Докажем эту формулу по индукции
(см. разд. В.5).
Действительно, при п = 1 формула верна. Теперь, предполагая, что для
любого натурального л формула верна, докажем ее справедливость для
(л +1). В самом деле,
60
,л+1_.л Л-(Х‘ nX-’WX iWr1 (л + 1)А"1
= л До X- J\о хД о X”' )'
„ . ГА" nA"-1"!
Следовательно, А = I I для любого натурального п .
Из перестановочности степеней одной и той же матрицы следует, что
многочлены от одной и той же матрицы перестановочны. Действительно,
если p(x) = aQ+axx + a2x2 +... + атхт и q(x) =b0 +bxx + b2x2 +... + bnxn, то
т п
/=0 j=0
7=01=0 д=о J\j=o /
= ?(а)-р(а),
что и требовалось показать.
Со степенью матрицы связаны следующие определения, характери-
зующие ее свойства. Квадратная матрица А называется
- идемпотентной, если А2 = А ;
- инволютивной, если А2 = Е;
- периодической, если Ak = Е при некотором натуральном к (число
к называется периодом матрицы А );
- нильпотентной, если Ак - О при некотором натуральном к (число
к называется показателем нильпотентности матрицы А ).
Пример 1.17. Даны матрицы:
"-26 -18 -27Л "-53 -36 -54> "0 1 О'
А = 21 15 21 , В = 42 29 42 , 7 = 0 0 1
J2 8 13 J <24 16 25, <о 0 0,
Показать, что матрица А - идемпотентная, В - инволютивная (периодиче-
ская), J - нильпотентная. Найти многочлены Р(а), р(в), Р(у) от этих
матриц, если Р(х) = х2 + 2х + 3.
□ Находим степени матриц
Г-26 -18 -27^ Г-26
21
12
А2
15
8
21
13
21
12
-18
15
8
-27^ Г-26 -18
21
13
21
12
15
8
-27'
21
13 .
= А;
61
в2 =
(-53 -36 -54" 42 • '-53 -36 -54" — Г1 0
42 29 42 29 42
<24 16 25, 24 16 25 J <0
1 0 а 1 (Г (С 0 р
J2 = С 0 1 с 0 1 С 0 0
<с 0 0 0 о, 5 0 0>
'0 0 Р '0 1 '0 0 0
J3 = J2- J 0 0 0 0 0 1 0 0 0
<° 0 о> <0 0 3, <0 0 0
О
1
= 0.
О
О
О
1
= Е;
Следовательно, матрица А - идемпотентная, В - инволютивная (периоди-
ческая с периодом 2), J - нильпотентная (с показателем 3).
По определению находим многочлены
'-75 -54 -8Р
р(а) = А2 + 2А + ЗЕ = А + 2А + ЗЕ = 3 (А + Е) = 63 48 63
<36 24 42,
'-102 -72 -108'
Р(в)=В2+2В + ЗЕ= Е + 2В + ЗЕ = 2В + 4Е = 84 62 84 ;
< 48 32 54 ,
'0 0 1W0 2 О'] (3 0 О' Гз 2 Р
P(j)= J2 +2J + 3E= 000 + 002 + 0 3 0 = 0 3 2 .
чо о oj (о 0 oj ^0 0 3, [о о з,
1.4. ТРАНСПОНИРОВАНИЕ И СОПРЯЖЕНИЕ МАТРИЦ
1.4.1. Транспонирование матриц
Для любой матрицы
а11 а12 а1п
а21 <2 22 "'а2п
А -
к.ат\ ат2"'атп^
транспонированной матрицей называется матрица
62
all a2l
#12 #22 **’#
И1Л ^2n &mn j
получающаяся из матрицы А заменой строк столбцами, а столбцов - стро-
ками. Чтобы по данной матрице А получить матрицу Ат, нужно первую
строку матрицы А записать как первый столбец матрицы Аг , вторую стро-
ку матрица А записать как второй столбец матрицы Аг и т.д. Эта операция
называется транспонированием матрицы А .
Квадратная матрица называется симметрической, если
АТ = А,
И кососимметрической, если
АТ = -А .
У симметрической матрицы элементы, расположенные симметрично отно-
сительно главной диагонали, равны между собой. У кососимметрической
матрицы элементы, расположенные симметрично относительно главной
диагонали, имеют противоположные знаки, а все диагональные элементы
равны нулю.
СВОЙСТВА ОПЕРАЦИИ ТРАНСПОНИРОВАНИЯ
Пусть Л - любое число, А , В - произвольные матрицы, для которых
определены операции умножения и сложения, записанные в левых частях
следующих равенств. Тогда определены операции, указанные в правых час-
тях, и справедливы равенства:
1. (ЛЛ)Г=Л-ДТ ;
2. (А + В)т =Ат +Вт-,
3. (А-В)т = Вт-Ат ;
4,(а^=А.
Пример 1.18. Найти Ат , Вт , Ст, если
□ Согласно определению, при транспонировании первая строка мат-
рицы А является первым столбцом матрицы Ат, вторая строка - вторым
столбцом:
63
Аналогично находим
'1 o'
2 1
13 2J
(3x2)
-4 5 '
О -6
6 0 ,
fl
(7=4
<3
4 5'
2 6
6 з,
Так как Вт = -В , то матрица В - кососимметрическая. Поскольку Ст = С,
то матрица С - симметрическая.
Пример 1.19. Продемонстрировать справедливость свойств 1, 2, 3, 4,
если
, „ (1 2) (5 6
1=2, А = , В =
13 41 17 8
□ Продемонстрируем свойство 1: (ЛА)г = Л • Ат. Вычисляя левую и
(2-А)г=[Д*
т П
2-AT = 2-
3
правую части, получаем равные матрицы:
2У|Г_р 47_f2 б'»
4/ ~[б 8J ~ [4 8/
27 fl 3^1 f2 6^1
4J 4) I/ 8 J
Продемонстрируем свойство 2: (А + В)г = Ат + Вт. Вычисляя левую и
правую части, получаем равные матрицы:
(А + 5)г
1 2^| f5 6Y
3 4j + |<7 8J
f6 8 7
[10 12J
6 lO'j
8 12/
1 27 f5 67_fl 3^1 f5 7^_f6 10A
3 4) +(J 8j “(2 4у+[б 12y
Продемонстрируем свойство 3: (,А-В)Т =Bt At . Вычисляя левую и
правую части, получаем равные матрицы:
(А-ВГ
Вт
Ат =
1 24] (5
3 4j\7
f5 б7
I7 8J
б7Г_р9 227 _f19 43s]
8J ”[43 50j ”[22 50/
27_f5 7W1 3A_fl9 43^
4J “|б 8j\2 4j(22 50/
1
з
64
Продемонстрируем свойство 4: ) — А. Вычисляя левую часть, по-
дучаем правую:
иМ12 -1з =р2=л..
V 7 И 4 |2 4 1з 4
V / 4 7 4 7
Пример 1.20. Пусть А - произвольная матрица размеров тХи, В —
любая квадратная п -го порядка. Доказать, что матрицы ААТ , АТА, В + Вт
_ симметрические, а матрица В-Вт - кососимметрическая.
□ По свойствам 3,4 получаем:
(аАт]Т =(ат]Т АТ=:ААТ-
(ата)т = ат(ат)т=ата.
По свойствам 2,4 имеем:
[в + Вт)Т =ВТ +(вт)Т =ВТ +В = В + ВТ ;
(в-вт)т = вт ~(вт)т =вт-в = -(в-вт).
1.4.2. Сопряжение матриц
Пусть А — матрица размеров тхп, элементы которой являются ком-
Тллексными числами аа -аы +РИ' (комплексная матрица). Сопряженной
матрицей А* называется матрица размеров пхт, получаемая из матрицы
А в результате транспонирования и замены каждого элемента транспони-
рованной матрицы АТ комплексным сопряженным.
Квадратная матрица А называется эрмитовой, если А* = А .
Пример 1.21. Даны матрицы
fl i 1 + А f 2/ 1+iM ( 1 3-2Л
, B = > c =
1^2/ 2-3/ 0 ) (j-/ 2 + 3iJ ^3 + 2i 2 )
Найти сопряженные матрицы A*, В*, С*
О Найдем транспонированные матрицы:
АТ
' 1 2i А
i 2—31
J + 1 0 J
( 2i 1-М
Ц + i 2 + 3iJ’
Сг =
1
3-21
3+2/
2
Заменим
все элементы сопряженными:
"S-4549
65
-2i'
2 + 3/
О ,
. (-2/ 1 + i) t { 1 3-2/
в = , с =
11—I 2-3/1 I 3+2/ 2
Заметим, что матрица С - эрмитова, так как С* = С.
СВОЙСТВА ОПЕРАЦИИ СОПРЯЖЕНИЯ МАТРИЦ
1. (Ла)*=Л-А*;
2. (А + В)* = А* + В*;
3. (A-В)* =В*-А*;
4. (а*) = А,
где А, В - произвольные матрицы, для которых определены соответст-
вующие операции, Л = а + 0/ - любое комплексное число, X = а - 0/ - со-
пряженное к Л число.
Пример 1,22. Продемонстрировать справедливость свойств 1, 2, 3, 4,
□ 1. Вычисляем и сравниваем левую и правую части равенства 1:
(М) - ,
11-2/ 1
-i-i2 1 + 2/ + /2
J-/-2/2 1 + i
( i-i2 1 + /-2/2^_р + « 3+p
\Д-2/ + /2 1-/ , [-2/ 1 —ij
2. Вычисляем и сравниваем левую и правую части равенства 2:
( -i 1+р Г 2/ 1+iVf / 2 + 2р* Г —i 2+3/
' Jj-2/ 1 2 + 3/J ”|2-3i 3 + 3/J -[2-2/ 3-3/
„» _» ( i 1 + 2/Л (- 2/ 1 + i ( - i 2 + ЗГ
A +B = + =
1,1- i 1 ) 2-3/J 1^2-2/ 3-3/J
66
3. Вычисляем и сравниваем левую и правую части равенства 3:
Г 1 + '^ Г 2i 1 + z
|j-2i 1 2 + 3iJ
- i 2i + (1 + i)-(1 -i) - z(l + i)+ (1 + i). (2 + 3i) V
(l-2i)-2i + l-(l-i) (l-2i).(l + i)+l.(2 + 3i)J
_ ( 4 4i _ Л 4 5 _ j >
^5 + z 5 + 2iJ 4i 5 — 2iJ
D... f~2i l + i Y i 1 + 21Л
(j-i 2-31Д1-1 1 J
f -2i-i + (l + i)-(l-i) -2i• (1 + 2z) + (1 + /)• 1 > f 4 S-i")
“Ц1—i)/ + (2—3i)(l-0 (l-i)-(l + 2i)+(2-3i)-lJ“[-4i 5-2iJ'
4. Вычисляем левую часть равенства 4 и сравниваем ее с правой
частью:
Замечания 1.4.
1. Если все элементы матрицы А действительные числа {действи-
тельная матрица), то сопряженная матрица совпадает с транспонирован-
ной, т.е. А* = АТ .
2. Всякую комплексную матрицу С (с элементами ca=au+bui)
можно представить в виде
С = A + Bi,
где А = Re С и В = Im С - действительная и мнимая части матрицы С
(с элементами аи = Re си и ba = Im си соответственно). При этом сопря-
женную матрицу можно представить в виде С* = АТ - BTi.
3. Всякую эрмитову матрицу С можно представить в виде С = А + Bi,
где А = Re С - действительная симметрическая матрица (Ат = А ), а
В = Im С — действительная кососимметрическая матрица (Вт = -В). В са-
мом деле, из равенства С* = С, учитывая п. 2, следует, что
АТ - Втi = A + Bi. Равенство действительных частей дает Ат = А , а равен-
ство мнимых частей влечет Вт = -В .
Пример 1.23. Пусть А - комплексная матрица размеров тхп. Дока-
зать, что матрицы АА*, А*А - эрмитовы т -го и п -го порядков соответст-
венно.
□ Используя свойства 3, 4, получаем:
(аА*)*=[а* ]*А*=АА*;
(а*а)* = а‘[а* ]* = л’а,
что и требовалось доказать.
Замечания 1.5.
1. Эрмитова матрица с действительными элементами является симмет-
рической.
2. Элементы эрмитовой матрицы, стоящие на главной диагонали, дей-
ствительны (например, матрица С в примере 1.21).
1.4.3. След матрицы
Следом квадратной матрицы называется сумма ее элементов, стоящих
на главной диагонали. След квадратной матрицы А п -го порядка обознача-
ется
Ц А = ^аи .
i=i
Для любых квадратных матриц А , В , С п -го порядка и столбцов х,
у размеров лх1 справедливы следующие свойства:
1. tr(A + B)=tr A + tr В;
2. tr А = tr АТ ;
3. tr(ATB)=tr(BTA)=ti(ABT)=tr(BAT);
4. tr (х уг )=хг у ;
5. ц(аххг)=хгАх.
6. tr (АВС) = tr (ВСА)= tr (CAB).
7. =tr(A5T).
i=i j=i
Замечание 1.6. След матрицы также обозначается sp А .
68
fl 2А [5 61
Пример 1.24. Даны квадратные матрицы А= , В = н
13 4) V °)
столбцы х =
. Продемонстрировать справедливость свойств 1,
2,3,4,5,7.
□ 1. trA = l + 4= 5, tr/? = 5 + 8 = 13, trA + trB = 18,
'6 8^
JO 12J
tr(A + B)=tr
= 18;
f3 1
xry = (l 2) 1 = 1-3 + 2-4 = 11;
22 / -r\
7. =1-5+ 2-6 + 3-7 + 4-8 = 70 =tr(ABr).
r=i ;=i
69
1.5. БЛОЧНЫЕ (КЛЕТОЧНЫЕ) МАТРИЦЫ
1.5.1. Блочные матрицы и операции над ними
Числовая матрица А размеров тхп, разделенная горизонтальными и
вертикальными линиями на блоки (клетки), которые представляют собой
матрицы, называется блочной (клеточной) матрицей. Элементами блочной
матрицы А являются матрицы Ау размеров т,ХПу, i = 1,2,...,р,
j = 1,2,...,q , причем /щ +w2 + ... + тр = т и гц + л2 +... + «9 =п.
Операции с блочными матрицами выполняются по тем же правилам,
что и с числовыми матрицами. Если числовые матрицы А и В равных раз-
меров одинаково разбиты на блоки А = (а^-) и В = {By), то их сумму
С = А + В можно аналогичным образом разбить на блоки С = (С(у), причем
для каждого блока Су = Ay + By . Если блочную матрицу А = (Ау) умно-
жить на число, то получим матрицу АА = АА = (АА/;- ). При транспонирова-
нии блочной матрицы транспонированию подлежит блочная структура и все
ее блоки, например
Ат =|А1
<А1
Аг
Аг
А1
/Г2
А1
АТ
Л22}
Аг | „
--- и В =
A22j
"1 1
2 1
.3 0
#11
#21
#12
#22
А =
4
5
6
_ Г Al
\ Aai
0>
2
1
Пример 1.25. Даны блочные матрицы
2 3
3 4
4 5
Найти матрицы С = А +В, D = 5B, Вт .
□ Матрицы А и В имеют блоки одинаковых размеров: блоки А], и
Вн имеют размер!.! от, х^ =1x2 ; блоки А12 и В12 - тх Хп2 = 1X1; блоки
А21 и В21 - тп2Хл1=2х2; блоки
А22 и В22 - ^xn2=2xl. Матрица
С = А + В будет иметь такие же по
размерам блоки С = --
VQ1
12
22/
• Для
каждого блока находим
Cii=Ai+#n=(2 3)+(1
4); С12 - А12 + В12 - (4) + (о) - (4);
(3 4) (2
Qi - А1 + #21 д 5HI3
1 1-1 5
оГЬ
51 Г51 Г24! Г7
’ ^*22 ” ^27 ^22 — I "И “
5) 22 22 22 1б) 11) 17
70
Следовательно, матрица С будет следующая
4^ ,
7 =f~
7 ^21
С12^
Сгг J
С =
г3 4
5 5
7 5
Матрица D = 5B будет иметь блоки тех же размеров, что и В :
DH =5ВП =5 (1 1) = (5 5); О12 = 5В12 =5-(0)=(0);
(2 Р (10 5) (2У flO'l
О21 - 5В21 = 5 "[15 oj; П22=5В22=5\1? 4J
Поэтому матрица D будет иметь вид
D = f 5 5 0^ _fAi ^12
10 5 J5 0 10 5,
k^21 ^22 j
Используя правило транспонирования блочных матриц, получаем
Вт =
2 3"
1 О
2
Рассмотрим теперь операцию умножения блочных матриц А и В .
Блочные матрицы А к В называются согласованными, если разбиение
матрицы А = (а11с ) на блоки по столбцам совпадает с разбиением матрицы
по строкам, т.е. блоки Ajk имеют размеры m, х рк , а блоки By -
pkxnj (к = 1,2,...,з). У согласованных блочных матриц блоки Alk и By
являются согласованными матрицами.
Произведением С = А-В согласованных блочных матриц А и В на-
зывается блочная матрица С = (С(у), блоки которой вычисляются по сле-
дующей формуле
Cjj = + A'2^2j +--- + ^is^sj •
Это означает, что блочные матрицы, разделенные на блоки надлежащим об-
разом, можно перемножать обычным способом. Чтобы получить блок Су
произведения, надо выделить i -ю строку блоков матрицы А и j -й столбец
блоков матрицы В . Затем найти сумму попарных произведений соответст-
вующих блоков: первый блок i -й строки блоков умножается на первый
блок j -го столбца блоков, второй блок i -й строки блоков умножается на
второй блок J -го столбца и т.д., а результаты умножений складываются.
71
Пример 1.26. Даны блочные матрицы
4^
5
6
'2 з
3 4
.4 5
Ai
Ai
Аг | „
--- и В =
Аг/
(Г
2
1.
ГА1
Iai
Аг"1
А =
2 1
3 О
Найти произведение С = АВ.
□ Матрица А разбита на блоки: Аи размеров т}хр} = 1x2; Л12 -
т1хр2 =1x1; А21 - m2Xpl=2x2; А22 - т2хр2-2х1. Матрица В раз-
бита на блоки: Вн размеров р]Хи1=2х2; В12 - р{хп2=2х1-, В21 -
р2 X nj =1x2; В22 - р2 х п2 = 1X1. Блочные матрицы А и В согласованы.
Матрица А разбита по столбцам на два и один (считая слева), матрица В
разбита по строкам на две и одну (считая сверху). Поэтому произведение
АВ определено. Матрица С = АВ будет иметь блоки С =------------. Для
kQi ^22)
каждого блока находим
Cn = AiAi + AiAi =(2 3)Q ^+(4)-(3 0) = (8 5)+(12 0)=(20 5);
С12 = А1Аг + АгАг=(2 3)- +(4)-(1)=(б)+(4)=(10);
. J
c2i - AiAi+ АгА1
'з
Л
4
5
+ , (з о)=
/
11 7^ р5
14 9/Ь8
°)_f26 7^
oJ-(32 9J
(3 4W0') f5) ,. (5
С-22 ~ Al Аг + Аг®гг ~ . -И - + L. Н1)~ + ,
14 51\2J 16) (10) (6
'13А
20 5
26 7
32 9
Следовательно, матрица С будет иметь вид
КГ
13
16,
Gi
c2i
Замечания 1.7.
1. Операции сложения, умножения на число и произведения блочных
матриц выполняются по тем же правилам, что и для обычных матриц, толь-
ко вместо элементов в формулах используются блоки.
72
2. Выполняя операции над блочными матрицами, всегда можно их рас-
сматривать как числовые, и проводить указанные операции по обычным
правилам для числовых матриц. При этом результат операций (числовая
матрица) будет один и тот же. Действия с блочными матрицами предпочти-
тельнее, чем с числовыми, в том случае, когда в результате вычислений тре-
буется искать не всю матрицу, а только ее часть - блок.
3. Матрица, у которой большинство элементов отличны от нуля, назы-
вается плотной матрицей. Матрица, большинство элементов которой -
нули, называется разреженной матрицей. Для разреженных матриц, по-
давляющее количество элементов которых равно нулю, полезно выделять
нулевые блоки с целью уменьшения вычислительных операций.
□ Разобьем данные матрицы на блоки размеров 2x2:
А =
1 0 0 1 0 0 0 0
1 2 3 4 1 0 0 к
Е С I о Со
'1 0 0 1 1 О'1 0 1
0 0 д 0 5 6 7 8,
Е Е
О D
01 (О
- единичная, О =
1) 10
°1
О - нуле-
АВ =
Е I <?VE I Е
С ЕДО D
fl 21 (5 61 (1
где С = , D = , Е =
I3 4J I7 8J <0
вая. Запишем сначала произведение блочных матриц
ЕЕ + ОО EE + O-D
СЕ + ЕО CE + ED) I^ClC+D/
Следовательно, вместо умножения матриц А и В достаточно определить
только один блок, сложив матрицы С и D :
21 (5
+
4 U
(1
C+D =
3
б|-1 6
8 Г110
8
12
Е
Е
Осталось записать результат
АВ —
р 0 1 0> р 0 1 0)
0 1 0 1 0 10 1
1 2 6 8 12 6 8
I3 4 10 12J b 4 ю 12J
73
1.5.2. Кронекеровские произведение и сумма матриц
Пусть даны матрицы А = Ц,) и В размеров т х п и р х q соответст-
венно. Числовая матрица размеров mp-x.nq, составленная из блоков ауВ :
а\\' В аы-В
А®В =
- атп-В)
называется (правым) кронекеровским произведением матриц А к В (или
(правым) прямым произведением матриц).
Пусть А и В квадратные матрицы п -го и т -го порядков соответст-
венно. Кронекеровской суммой матриц А и В называется квадратная мат-
рица тп -го порядка
А® В = (Ет®А)+(В®Еп),
где Ет, Еп - единичные матрицы соответствующих порядков.
Пример 1.28. Даны матрицы
Л1 2> fl 0 2^1 Л5 б¥
л = , в= , с=
<3 4J ^0 2 3J м
Найти кронекеровское произведение А®В и кронекеровскую сумму
А®С .
□ По определению находим
А®В = 1- '1 0 2х] J) 2 з] fl 0 2¥ 2- ^0 2 3j fl 0 2 2 0 4' _ 0 2 3 0 4 6 ” 3 0 6 4 0 8 ’ [o 6 9 0 8 12,
"о ~ о fl 0 2) 4- 1° 2 3JJ
а®с=(е®а)+(с®е)=
fl
0-
1^3
(I
1 -
^3
о
1
о
1
о¥
1J
'1
з
о
.0
0 6 ОНб
5 0 6 3
0 8 0 7
7 0 8J [о
2 6 О'
9 0 6
0 9 2
7 3 12,
74
1.6. ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ МАТРИЦ
Элементарными преобразованиями матрицы называются следующие
ее преобразования:
I. Перестановка двух столбцов {строк) матрицы.
II. Умножение всех элементов одного столбца {строки) матрицы на одно и
то же число, отличное от нуля.
III. Прибавление к элементам одного столбца {строки) соответствующих
элементов другого столбца {строки), умноженных на одно и то же чис-
ло.
Матрица В, полученная из исходной матрицы А конечным числом
элементарных преобразований, называется эквивалентной. Это
обозначается А~В.
Элементарные преобразования применяются для упрощения матриц,
что будет в дальнейшем использоваться для решения разных задач.
1.6.1. Метод Гаусса приведения матрицы к ступенчатому виду
Покажем, как при помощи элементарных преобразований можно при-
вести матрицу к ступен чатому виду (рис. 1.4). Здесь высота каждой "сту-
пеньки" составляет одну строку, символом 1 (единицей) обозначены еди-
ничные элементы матрицы, символом * - обозначены элементы с произ-
вольными значениями, остальные элементы матрицы нулевые. К ступенча-
тому виду можно привести любую матрицу, причем достаточно использо-
вать только элементарные преобразования строк матрицы.
'0 ••• 0 | 1 * * ••• * 0 ••• 0 о| 1 * ... ♦ * *...*#* ... * *-..***...*
0 ••• 0 0 0 0 ••• 0 I ♦ ♦
0 ••• 0 0 0 0 ••• 0 0 ••• 0 0 0 0 - 0 чо 0 0 0 0 ••• о ••• ; * * ... * 0 0-0 |1 * * 0 0 - 0 0 0 -0 0 0 ••• 0 0 0 0,
Рис. 1.4
75
Чтобы привести матрицу к ступенчатому виду (рис. 1.4), нужно вы-
полнить следующие действия.
1. В первом столбце выбрать элемент, отличный от нуля (ведущий
элемент). Строку с ведущим элементом (ведущая строка), если она не пер-
вая, переставить на место первой строки (преобразование I типа). Если в
первом столбце нет ведущего (все элементы равны нулю), то исключаем
этот столбец, и продолжаем поиск ведущего элемента в оставшейся части
матрицы. Преобразования заканчиваются, если исключены все столбцы или
в оставшейся части матрицы все элементы нулевые.
2. Разделить все элементы ведущей строки на ведущий элемент (пре-
образование II типа). Если ведущая строка последняя, то на этом преобразо-
вания следует закончить.
3. К каждой строке, расположенной ниже ведущей, прибавить веду-
щую строку, умноженную соответственно на такое число, чтобы элементы,
стоящие под ведущим оказались равными нулю (преобразование III типа).
4. Исключив из рассмотрения строку и столбец, на пересечении кото-
рых стоит ведущий элемент, перейти к пункту 1, в котором все описанные
действия применяются к оставшейся части матрицы.
Пример 1.29. Привести к ступенчатому виду матрицы
□ В первом столбце матрицы А выбираем ведущий элемент
ап = 3*0. Делим все элементы первой строки на ап =3 (или, что то же
1 1
самое, умножаем на — = —):
а,. 3
0 9 > Г1 3"|
2 4 J\2 4J
Прибавим ко второй строке первую, умноженную на (-2):
'1 3^ (-2) |[ 1 3
<2 4J ^-1 Ч0]-2/
Первый столбец и первую строку исключаем из рассмотрения. В оставшейся
части матрицы имеется один элемент (-2), который выбираем в качестве
ведущего. Разделив последнюю строку на ведущий элемент, получаем мат-
рицу ступенчатого вида
76
Ced) "(Ч-ц)-
Преобразования закончены, так как ведущая строка последняя. Заметим, что
получившаяся матрица является верхней треугольной.
В первом столбце матрицы В выбираем ведущий элемент &21 —2^0.
Меняем местами строки, ставя ведущую строку на место первой, и делим
элементы ведущей строки на ведущий элемент 2 :
0 2 3\ 43 4 6^ Г|1 2 3]
2 4 6ЦО 2 3 J~[ о] 2 3 Г
Пункт 3 алгоритма делать не надо, так как под ведущим элементом стоит
нуль. Исключаем из рассмотрения первую строку и первый столбец. В ос-
тавшейся части ведущий элемент - число 2. Разделив ведущую строку (вто-
рую) на 2, получаем ступенчатый вид:
В~
1 2 3
о ГЛ 3
1 П1 2 3 * * *
;(о|1 1,5 /
Преобразования закончены, так как ведущая строка последняя.
В первом столбце матрицы С выбираем ведущий элемент сп = 2^0.
Первая строка - ведущая. Делим ее элементы на сн = 2. Получаем
ш4
3 5
1
3
6
С =
7 \
2Л
5
7>
Ко второй и третьей строкам прибавим первую, умноженную на (-3) и на
(- 6) соответственно:
fl] 2^ (-3) С-6)
3 5^
<6 7Г
]1 2 '
о]-1
<0
Обратим внимание на то, что полученная матрица еще не является матрицей
ступенчатого вида, так как вторую ступеньку образуют две строки (2-я и
3-я) матрицы. Исключив 1-ю строку и 1-й столбец, ищем в оставшейся части
ведущий элемент. Это элемент (-1 ) Делим вторую строку на (-1), а затем
к третьей строке прибавляем ведущую (вторую), умноженную на 5:
77
Г 1 2 р 2 >
0 -1 Л» 0 1 (5)
-5 У <0 -5 J ^1
Исключим из рассмотрения вторую строку и второй столбец. Поскольку ис-
ключены все столбцы, дальнейшие преобразования невозможны. Получен-
ный вид - ступенчатый.
Замечания 1.8.
1. Говорят, что матрица имеет ступенчатый вид также и в случае, когда
на месте ведущих элементов (обозначенных на рис. 1.4 единицей) стоят лю-
бые отличные от нуля числа.
2. Считается, что нулевая матрица имеет ступенчатый вид.
Пример 1.30. Привести к ступенчатому виду матрицу
'О 1 1 1 1 Г
, 0 112 3 2
А —
0 2 2 1 2 1
0 4 4 4 6 4,
□ Первый столбец матрицы А - нулевой. Исключаем его из рассмот-
рения и исследуем оставшуюся часть (последние 5 столбцов):
0 1 1 1 1 Г
0 112 3 2
0 2 2 1 2 1
0 4 4 4 6 4,
Берем в качестве ведущего элемент а12 = 1. Прибавляем ко второй строке
первую, умноженную на (-1); к третьей строке - первую, умноженную на
(-2); к четвертой строке - первую, умноженную на (-4). Тем самым "об-
нуляются" все элементы второго столбца, расположенные ниже ведущего
элемента:
'0 [Т] 1 1 1 (-1) (- 2) (-4) fo| 1 1 1 1 р
0 112 3 2 1 0 0 0 1 2 1
А-
0 2 2 12 1 0 0 0 -1 0 -1
10 4 4 4 6 4 —— ч0 0 0 0 2 0,
78
Полученная матрица не имеет ступенчатого вида, так как одна из ступенек
имеет высоту в три строки. Продолжаем преобразования. Первую строку и
второй столбец исключаем из рассмотрения. Поскольку первый столбец в
оставшейся части матрицы нулевой, исключаем его. Теперь оставшаяся
часть матрицы - это матрица (размеров 3x3), образованная элементами,
расположенными в последних трех строках и трех столбцах полученной
матрицы. В качестве ведущего элемента выбираем аи = 1. К третьей строке
прибавляем вторую. Получаем матрицу
''oil 1 1 Г
ООО Г~Г~] 2 1 (1)
0 0 0 -1 0 -1 -*-*
.0 О 0 0 2 0,
f 01 1 11 1 Р
0 ° 0 I1 2 1
0 0 0 0 2 0
.0 0 0 0 2 0,
Вторую строку и четвертый столбец исключаем из рассмотрения. Берем
элемент а35 = 2 в качестве ведущего. Делим третью строку на число 2 (ум-
ножаем на 0,5 ):
'0 1 1
0 0 0
0 0 0
.0 0 0
1 1 Г
1 2 1
о ПЛ о
(0,5)
0 2 0J
'0|11 1 1 Г
0 0 0| 1 2 1
0 0 0 0~| 1 0
.0 0 0 0 2 0,
К четвертой строке прибавляем третью, умноженную на (-2):
'0 1
0 0
0 0
.0 0
1 1 1 Р
0 12 1
0 °Ш0 (-2)
0 0 2 oj-*—।
'01 1 1 1 1 Р
0 0 01 1 2 1
0 0 0 0~| 1 0
.0 0 0 0 0 0,
Третью строку и четвертый столбец исключаем из рассмотрения. Поскольку
в оставшейся части матрицы все элементы (один) нулевые, преобразования
закончены. Матрица приведена к ступенчатому виду (см. рис. 1.4).
Замечание 1.9. Продолжая выполнять элементарные преобразова-
ния над строками матрицы, можно упростить ступенчатый вид, а именно
привести матрицу к упрощенному виду (рис. 1.5).
79
г0 01 1 о * * 0 ••• 0 о] 1 ♦ ♦ Z * * * * О О * * * * О о
о о о о о о 1 * ... ♦ о ♦ ••• *
о ••• о о о о о о - о о о о — о .0 0 0 0 0 0 : • ’ . • 0 ♦ • • • ♦ 0 0 0 | 1 * ••• * 0 0 0 0 0 0 0 0 0 0 0 — 0,
Рис. 1.5
Здесь символом 1 обозначены элементы матрицы, равные единице, симво-
лом * - обозначены элементы с произвольными значениями, остальные
элементы матрицы нулевые. Заметим, что в каждом столбце с единицей ос-
тальные элементы равны нулю.
Пример 1.31. Привести к упрощенному виду матрицу
"О 1 1 1 1 Р
'0 0 0 1 2 1
А =
0 0 0 0 1 0
.0 О О О О О,
□ Матрица имеет ступенчатый вид. Прибавим к первой строке третью,
умноженную на (-1), а ко второй строке третью, умноженную на (-2):
"О 1 1 1 О Г
0 0 0 1 0 1
0 0 0 0 1 0
.0 О О О О О,
Теперь к первой строке прибавим вторую, умноженную на (-1). Получим
матрицу упрощенного вида (см. рис. 1.5):
"01110
0 0 0 1 0
0 0 0 0 1
.0 0 0 0 0
1 (-D
о
О,
"О | 1 1 000"
О О о 11 О 1
ООО о| 1 о
.0 0 0 0 0 0,
80
Замечание 1.10. При помощи элементарных преобразований
(строк и столбцов) любую матрицу можно привести к простейшему виду
(рис. 1.6).
Г1 0 0 О'
0 ••• 1 0 О (Ег О')
О 0 0 О О)
0 - 0 0 0J
4 'тхп
Рис. 1.6
Левый верхний угол матрицы представляет собой единичную матрицу по-
рядка г (0< г < min{m; п}), а остальные элементы равны нулю. Считается,
что нулевая матрица уже имеет простейший вид (при г = 0).
61 2 ЗЛ
Пример 1.32. Привести матрицу А -1 I к простейшему виду.
□ В качестве ведущего элемента возьмем ап =1. Ко второй строке
прибавим первую, умноженную на (- 2):
12J 2 ЗЛ (-2) Г1 2 3"|
2 4 5J—е—। ~ 1^0 О -1J'
Ко второму столбцу прибавим первый, умноженный на (- 2), а к третьему —
первый, умноженный на (-3):
02 3>|
Го о -ij
(_2>_1
(-3) —
10 0'
О О -1,
Умножим все элементы последнего столбца на (-1) и переставим его на ме-
I.
сто второго:
1 0 О')
О О -1J
(-D
10 0
О 1 О
в-4549
81
Таким образом, исходная матрица А при помощи элементарных пре-
образований приведена к простейшему виду (см. рис. 1.6).
Подчеркнем следующие свойства элементарных преобразований.
Теорема 1.1 (о приведении матрицы к ступенчатому виду). Любую
матрицу при помощи элементарных преобразований ее строк можно при-
вести к ступенчатому (или даже упрощенному) виду.
Следствие (о приведении матрицы к простейшему виду). Любую
матрицу при помощи элементарных преобразований ее строк и столбцов
можно привести к простейшему виду.
Замечания 1.11.
1. Преобразования, обратные к элементарным, являются элементар-
ными. В самом деле, если в матрице поменяли местами два столбца (преоб-
разование I типа), то исходную матрицу можно получить, еще раз поменяв
местами эти столбцы. Если столбец матрицы умножили на число А. О
(преобразование П типа), то для получения исходной матрицы надо этот
столбец умножить на обратное число — * 0. Если к i -му столбцу матрицы
А.
прибавили j -й столбец, умноженный на число А, то для получения исход-
ной матрицы достаточно к i -му столбцу матрицы прибавить j -й столбец,
умноженный на противоположное число (- А.).
2. В теореме 1.1 говорится о приведении матрицы к ступенчатому (уп-
рощенному) виду при помощи элементарных преобразований только ее
строк, не используя преобразования ее столбцов. Чтобы привести произ-
вольную матрицу к простейшему виду (следствие теоремы 1.1), нужно ис-
пользовать преобразования и строк, и столбцов матрицы.
3. Рассмотрим следующую модификацию п.З метода Гаусса. Ведущий
элемент, выбранный в п.1 метода Гаусса, определяет ведущую строку и ве-
дущий столбец матрицы (он находится на их пересечении). Делим все эле-
менты ведущей строки на ведущий элемент (см. п.2 метода Гаусса). Прибав-
ляя ведущую строку, умноженную на соответствующие числа, к остальным
строкам матрицы (аналогично п.З метода Гаусса), делаем равными нулю все
элементы ведущего столбца, за исключением ведущего элемента. Затем,
прибавляя полученный ведущий столбец, умноженный на соответствующие
числа, к остальным столбцам матрицы, делаем равными нулю все элементы
ведущей строки, за исключением ведущего элемента. При этом получаем
ведущие строку и столбец, все элементы которых равны нулю, за исключе-
нием ведущего элемента, равного единице.
Модифицированный таким образом метод Гаусса называется методом
Гаусса-Жордана. Его применение позволяет сразу получить простейший
вид матрицы, минуя ее ступенчатый вид.
82
1.6,2. Элементарные преобразования как умножения матриц
Квадратную матрицу, полученную из единичной при помощи конечно-
го числа элементарных преобразований, будем называть элементарной.
Покажем, что элементарные преобразования можно представить как про-
цесс умножения данной матрицы на элементарные матрицы.
I. Перестановка двух столбцов {строк) матрицы. Пусть дана матрица
А размеров тХп. Для перестановки двух столбцов (г -го и у-го) данной
матрицы достаточно умножить ее справа на квадратную матрицу 5zn п -го
порядка вида
fl ... О 0 О’)
О
О •••
О 1 О
1 О О
(1.1)
|0 ... о ••• О 1J
1 I j п
Эта матрица получена из единичной матрицы п -го порядка при помощи пе-
рестановки i -го и j -го столбцов.
Чтобы поменять местами две строки (i -ю и j -ю) данной матрицы А ,
достаточно умножить ее слева на элементарную матрицу Sf т -го порядка
вида
Г1 • 0 • 0 • (Г 1
0 • - 0 • • 1 • • 0 i
5,Л = (1-2)
0 • 1 • 0 0 j
<0 • • 0 • • 0 • • L т
Эта матрица получена из единичной матрицы т -го порядка при помощи
Перестановки i -й и j -й строк.
б«
83
<12 3
Пример 1.33. Дана матрица А = 2
4'
6
7.
. Показать, что умноже-
ние данной матрицы слева на матрицу Sj = О
О'
1
0.
приводит к переста-
4 5
5 6
10
0
О
1
новке 2-й и 3-й строк матрицы А , а умножение данной матрицы А справа
"1 0 0 О'
0 0 0 1
на матрицу S2 - 0 0 10 приводит к перестановке 2-го и 4-го столб-
о о О '
цов.
□ Матрица А имеет размеры 3x4, т.е. т = 3, п = 4. Матрица по-
лучена из единичной матрицы третьего порядка при помощи перестановки
2-й и 3-й строк. Находим произведение матрицы А на матрицу 51 слева:
(1 О OY1 2 3 4^1
SrA= 0 0 1
1 о,
'1
3
2 3 4'
5 6 7
4 5 6у
2 4 5 6
<3 5 6 7>
Сравнивая результат с исходной матрицей А , замечаем, что 2-я и 3-я строки
поменялись местами.
Матрица S2 получена из единичной матрицы четвертого порядка при
помощи перестановки 2-го и 4-го столбцов. Умножим матрицу А справа на
52:
1
2
3
4^
О
О
О
2А
4
3
as2 =
о
1
О
О
4
2
2
6
5
4
5
6
О
1
о
О
О
6
5
3
7
7
3
5
6
О
1
О
Сравнивая результат с исходной матрицей А, замечаем, что 2-й и 4-й
столбцы поменялись местами.
II. Умножение всех элементов одного столбца (строки) матрицы на
одно и то же число, отличное от нуля. Пусть дана матрица А размеров
тхп. Для умножения всех элементов одного столбца (i -го) данной матри-
цы на одно и то же число Л, отличное от нуля, достаточно умножить мат-
рицу А справа на элементарную матрицу:
84
1
О ОЗ
(1.3)
Эта квадратная матрица и-го порядка получена из единичной матрицы
п -го порядка умножением i -го столбца на число Л.
Чтобы умножить все элементы i -й строки данной матрицы на одно и
то же число Л, отличное от нуля, достаточно умножить матрицу А слева на
элементарную матрицу вида:
(1-4)
Эта квадратная матрица т-го порядка получена из единичной матрицы
т -го порядка умножением i -й строки на число Л.
fl
Пример 1.34. Дана матрица А = I
<2
данной матрицы слева на матрицу 5] = I
элементов I-й строки матрицы А на число 2; умножение матрицы А справа
2 33
I. Показать, что умножение
03
I приводит к умножению всех
на матрицу S2 - О
.0
О О'
1 О
О 3,
приводит к умножению 3-го столбца матрицы
А на число 3.
□ Матрица А имеет размеры 2x3, т.е. т-2, п = 3. Матрица S, по-
лучена из единичной матрицы второго порядка умножением первой строки
на число 2. Матрица S2 получена из единичной матрицы третьего порядка
умножением 3-го столбца на число 3. Находим произведения:
Г 2 OW1 2 33 f2 4 63
[о 1J\2 3 4J (^2 3 4/
85
A S2 =
1 2 3)
2 3 4J
'1 О О'
О 1 О
ч0 0 3,
1 2 9^|
2 3 12J’
что и требовалось показать.
III. Прибавление к элементам одного столбца (строки) соответст-
вующих элементов другого столбца (строки), умноженных на одно и то же
число. Пусть дана матрица А размеров тхп. Чтобы прибавить к одному
столбцу (i -му) соответствующие элементы другого столбца (j -го), умно-
женные на одно и то же число А, достаточно умножить матрицу А справа
на элементарную матрицу вида:
fl О 0 О')
0 ••• 1 0 0
О X ••• 1 О
(1.5)
^0 0 0 1J
1 i J п
Эта квадратная матрица п -го порядка получена из единичной матрицы
п -го порядка в результате прибавления к i -му столбцу соответствующих
элементов j -го столбца, умноженных на число Л.
Чтобы прибавить к одной строке (i -й) соответствующие элементы
другой строки ( j -й), умноженные на одно и то же число Л, достаточно ум-
ножить матрицу А слева на элементарную матрицу вида:
fl ... о ••• 0 0>1
(1-6)
Эта квадратная матрица т -го порядка получена из единичной матрицы
т -го порядка прибавлением к элементам i -й строки соответствующих эле-
ментов j -й строки, умноженных на число Л.
86
fl 2 3^
Пример 1.35. Дана матрица А = Показать, что умножение
<2 3 4J
с ( 1 оА ,
данной матрицы слева на матрицу = I I приводит к прибавлению к
элементам второй строки соответствующих элементов первой строки, ум-
ноженных на (- 2).
□ Матрица А имеет размеры 2x3, т.е. т = 2, и = 3. Матрица по-
лучена из единичной матрицы второго порядка путем прибавления к эле-
ментам 2-й строки соответствующих элементов 1-й строки, умноженных на
число (- 2). Находим произведение:
fl О') f 1 2 3W1 2 3 А
1 1,-2 1J 1,2 3 4J [о -1 -2/
что и требовалось показать.
Приведение матрицы к ступенчатому виду (методом Гаусса) или к
простейшему виду (методом Гаусса-Жордана) сводится к последовательно-
му умножению данной матрицы на элементарные матрицы.
„ ? 1 2 ЗА
Пример 1.36. Привести матрицу А = I I к пРосте”шемУ ВИДУ
при помощи умножения на элементарные матрицы.
□ При помощи элементарных преобразований эта матрица в приме-
ре 1.32 была приведена к простейшему виду. Запишем последовательность
преобразований, представляя их как умножения на матрицы специального
вида.
На первом шаге ко второй строке прибавляли первую, умноженную на
(-2). Этому преобразованию соответствует умножение матрицы А слева
на матрицу Sj °) (см. пример 1.35):
f i 0W1 2 зА fi 2 з>
с .л _I I 1 = 1
1 1,-2 1Д2 4 5J 1,0 О -1/
Затем ко второму столбцу прибавили первый, умноженный на (-2), а
к третьему - первый, умноженный на (- 3). Эти действия соответствуют по-
следовательному умножению данной матрицы справа на матрицы
52 = '1 -2 О' 0 1 0 о b S II '1 0 -3' 0 1 0 .0 0 1,
Матрица S2 получена из единичной матрицы третьего порядка путем при-
бавления к элементам 2-го столбца соответствующих элементов 1-го столб-
87
ца, умноженных на число (- 2). Матрица S3 получена из единичной матри-
цы третьего порядка путем прибавления к элементам 3-го столбца соответ-
ствующих элементов 1-го столбца, умноженных на число (-3). Находим
произведения
5, A -S2 - L
2 3
-2 ОЛ
О 3
О -1J’
о о"!
О -1/
Последний шаг - умножение последнего столбца на (-1) и перестановка его
на место второго. Этим действиям соответствует последовательное умноже-
ние преобразуемой матрицы справа на матрицы
'10 0' '1 0 О'
S4 = 0 1 0 > $5 - 0 0 1
<0 0 Ч 0 1 0,
Матрица S4 получена из единичной матрицы третьего порядка путем ум-
ножения элементов 3-го столбца на число (-1)- Матрица S5 получена из
единичной матрицы третьего порядка при помощи перестановки 2-го и 3-го
столбцов. Находим произведения
fl О
Si ' А S2 * • Sa —
1 10 0
s1 a-s2-s3-s4 s5 =
0
1
0’
0
1
0
Таким образом, исходная матрица А с помощью умножения на элементар-
ные матрицы приведена к простейшему виду (см. рис. 1.6).И
'0 1 1 1 1 1
0 1 1 2 3 2
Пример 1.37. Привести матрицу А = 0 2 2 1 2 1
.0 4 4 4 6 4
к ступенчатому виду при помощи умножения на элементарные матрицы.
88
□ При помощи элементарных преобразований эта матрица в приме-
ре 1.30 была приведена к ступенчатому виду, причем преобразования вы-
полнялись только над ее строками. Запишем последовательность преобразо-
ваний, представляя их как умножения матрицы А слева на элементарные
матрицы. Первое преобразование - прибавление ко второй строке первой,
умноженной на (-1), - соответствует умножению матрицы А слева на мат-
рицу
5,=
( 1
-1
О
. О
о о О'
1 о о
О 1 о
о о 1>
Действительно,
S,A =
-1
О
О
О
1
О
О
О
О
1
О
О'
О
О
1.
'О
О
О
.0
1
1
2
4
1
1
2
4
1 1 П <о 1 1 1 1
232 00012
1 2 1 “ 0 2 2 1 2
4 6 4) Ц) 4 4 4 6
Г
1
1
4,
слева на матрицу
Второе преобразование - прибавление к третьей строке первой, умноженной
на (-2), что соответствует умножению матрицы
52 -
О
-2
О
о
1
о
о
О
О
1
о
О'
о
о
1.
Третье преобразование - прибавление к четвертой строке первой, умножен-
ной на (-4), что соответствует умножению матрицы S2SjA слева на мат-
рицу
fl 0 О О'
89
Действительно,
1 1 1 Г
0 12 1
0-10-1
0 0 2 0,
Далее были использованы следующие преобразования: к третьей строке
прибавляли вторую; умножили третью строку на 0,5; к четвертой строке
прибавили третью, умноженную на (- 2). Этим преобразованиям соответст-
вует умножение матрицы $3$2$1А слева на матрицы:
'1 0 0 0' '1 0 0 0) fl 0 0 О'
0 10 0 0 1 0 0 0 1 0 0
54 = ; 0 110 S< = 5 0 ; $6 = 0 03 0 0 0 1 0
.0 0 0 1, .0 0 0 1J (о 0 -2 1,
Действительно, выполняя умножения, получаем ступенчатый вид
'011111'
0 0 0 1 2 1
cSaS-jS'iSi А — .
0 0 0 0 1 0
0 0 0 0 0 0,
Указанные ранее свойства элементарных преобразований можно пере-
формулировать следующим образом:
1. Для любой матрицы А существуют набор таких элементарных
матриц Sj, S2,..., Sp вида (1.2), (1.4), (1.6), что матрица
Sp—S2Sl-A
будет иметь ступенчатый или даже упрощенный вид. В частности, если
матрица А - квадратная, то матрица Sp-...-S2-SfA будет верхней тре-
угольной.
2. Для любой матрицы А существуют набор таких элементарных
матриц S2,..., Sp, s{,...,s' вида (1.1)-(1.6), что матрица
Sp-—,S2-S1-ASl-S2-...-Sq
будет иметь простейший вид.
Так как произведение элементарных матриц является элементарной
матрицей, то последнее свойство можно сформулировать следующим обра-
зом.
Теорема 1.2 (о приведении матрицы к простейшему виду). Для лю-
бой матрицы А размеров тхп существуют такие элементарные матри-
90
цы S и Т m-го и п -го порядков соответственно, что матрица
A = S-A-T имеет простейший вид (см. рис. 1.6):
(F П\
A = SAT= (1-7)
\о)'
где 0 < г < min{ т, п }. Матрицы S и Т будем называть элементарными
преобразующими матрицами.
1.6.3. Нахождение элементарных преобразующих матриц
Для приведения матрицы А к простейшему виду (1.7) и нахождения
элементарных преобразующих матриц 5 и Т нужно выполнить следующие
действия.
1. Приписав к матрице А (размеров тх.п) справа и снизу единичные
матрицы Ет и Еп соответственно, составить блочную матрицу:
Элементы правого нижнего блока этой матрицы можно не указывать, так
как они не участвуют в дальнейших преобразованиях, либо считать их рав-
ными нулю.
2. При помощи элементарных преобразований, выполняемых над стро-
ками и столбцами блочной матрицы, привести ее левый верхний блок А к
простейшему виду (1.7). При этом блочная матрица преобразуется к виду
слева на матрицу
где Л - матрица простейшего вида, а 5 и Т - искомые преобразующие
матрицы, связанные с матрицей А равенством (1.7).
Действительно, элементарные преобразования (указанные в п.2 алго-
ритма) относятся к первым т строкам и первым п столбцам блочной мат-
рицы (1.8). Этим преобразованиям соответствует умножение матрицы (1.8)
5 СН (Г I О
-----и справа на матрицу ~~ ——
О\Еп) Ет
, где символом О
обозначены нулевые матрицы соответствующих размеров. Выполняя умно-
жение блочных матриц (см. разд. 1.5.1), получаем
'S ОЛ
J W &т)
'S-А I ГТ I ОА Г$-А-Т
~Еп [ Г j Oj ’
Эта матрица совпадает с (1.9), если Л-5А-Т. Другими словами, если в
результате п.2 алгоритма левый верхний блок А матрицы (1.8) приведен к
91
простейшему виду Л, то в других блоках матрицы (1.9) получаем искомые
преобразующие матрицы S и Г.
f 1 -1 2 ОЛ
Пример 1.38. Привести матрицу А = -1 2 -3 1
к простейшему
^0 1 -1 1J
виду. Найти элементарные преобразующие матрицы S и Т, удовлетво-
ряющие равенству (1.7).
□ Припишем к матрице А справа и снизу единичные матрицы соот-
ветствующих размеров
-1 2 0 1 О О'
2 -31010
1 -11001
ООО
1 0 0
0 1 0
0 0 1 ,
Возьмем в качестве ведущего элемент =1*0. Ко второй строке приба-
вим первую:
' 1 -1 2 0 -12-31 0 1-11 1 0 О' 0 1 0 0 0 1 - '1-12 0 0 1-11 0 1-11 1 0 О' 1 1 0 0 0 1
10 0 0 0 10 0 0 0 10 ^0 0 0 1 У 10 0 0 0 10 0 0 0 10 J) 0 0 1 >
Ко второму столбцу прибавим первый, к третьему - первый, умноженный на
(-2):
'1-12 0 0 1-11 0 1-11 1 0 0^ 1 1 0 0 0 1 '10 0 0 0 1-11 0 1-11 1 0 о" 1 1 0 0 0 1
10 0 0 0 10 0 0 0 10 J) 0 0 1 11-20 0 10 0 0 0 10 0 0 0 1 7
92
Теперь возьмем в качестве ведущего элемент <я22 = 1*0. К третьей строке
прибавим вторую, умноженную на (-1):
"10 0 0 0 1-11 0 1-11 1 0 0> 1 1 0 0 0 1 "10 0 0 0 1-11 0 0 0 0 1 0 О' 1 1 0 -1 -1 1
11-20 0 10 0 0 0 10 ЧО 0 0 1 11-20 0 10 0 0 0 10 ч0 о 0 1 J
К третьему столбцу прибавим второй, а к четвертому столбцу - второй, ум-
ноженный на ( -1):
'10 0 0 0 1-11 0 0 0 0 1 0 О' 1 1 0 -1 -1 1 "10 0 0 0 10 0 0 0 0 0 1 0 О' 1 1 0 -1-11 z
11-20 0 10 0 0 0 10 0 0 0 1 11-1-1 0 11-1 0 0 10 0 0 0 1 ( Л j "(г >
В результате преобразований на месте исходной матрицы А получена мат-
рица
"1 0 0 0'
Л =0 1 о о
0 0 0 0,
о
о
о
простейшего вида (1.7), а на месте единичных матриц - элементарные пре-
образующие матрицы
fl 0 0)
fl 1 -1 -П
S= 1 1 о
<-1 -1 L
0 11-1
0 0 10
0 0 b
Проверим равенство Л = 5 - А • Т, вычисляя произведение
fl 1
fi о 0W1 -1 2 0^1
93
-1
1
О
2
-1
О
1
1
О
О
-1
1
1
о
-Г
-1
о
1.
О'
о
О.
находятся неодно-
О
О
О
1
О
о
о
о
1
о
О
О
О
и
т
о
о
о
что и требовалось показать.
Замечания 1.12.
1. Элементарные преобразующие матрицы S
значно, так как зависят от выбранной последовательности преобразований.
2. Если требуется найти одну из элементарных преобразующих мат-
риц, например, 5, то достаточно применить рассмотренный выше алгоритм
к матрице (А | Ет). Выполняя элементарные преобразования над строками
матрицы (А | Ет) и над первыми ее столбцами, входящими в левый блок,
получим матрицу (л | S), где Л - матрица простейшего вида, aS- иско-
мая матрица. Если требуется найти одну матрицу Т, то выполняем преобра-
зования матрицы
Л')
3. Учитывая свойство 1 элементарных преобразований (см. разд. 1.6.2),
теорему 1.1 можно сформулировать следующим образом: для любой матри-
цы А размеров глуп существует такая элементарная матрица S т -го
порядка, что матрица SA имеет упрощенный вид (см. рис. 1.5).
Для нахождения матрицы S нужно составить блочную матрицу
(л | Ет), затем при помощи элементарных преобразований, выполняемых
только над строками матрицы (А | Ет), привести ее левый блок А к упро-
щенному виду. При этом блочная матрица преобразуется к виду (л | S), где
Л - матрица упрощенного вида (см. рис. 1.5), aS- искомая элементарная
матрица.
4. Диагональная матрица является элементарной.
Пример 1.39. Найти элементарную преобразующую матрицу S, при-
водящую матрицу А = -1
. О
-1
2
1
□ Припишем к матрице А
2 О'
-3 1
справа единичную матрицу 3-го порядка.
к упрощенному виду (см. рис. 1.5).
(Л |Е)= -1
10
-1 2 0 1 0 0'
2-31010
1 -110 0 1,
94
Элементарными преобразованиями строк блочной матрицы приводим ее ле-
вый лок к упрощенному виду. Для этого ко второй строке прибавляем пер-
вую. Затем к третьей строке прибавляем вторую, умноженную на (-1), а к
первой строке прибавляем вторую. В результате преобразований получаем:
о
о
1
1-12 0
(А | Е}~ 0 1 -11
0 1-11
1
1
О
О
1
О
о
1 I
0 1-11
оооо
2
1
-1
1
1 о| = (Л|$).
-1
1
Левый блок Л матрицы (Л | S) имеет упрощенный вид, а правый блок -
искомая матрица S. Проверим равенство Л = SA , вычисляя произведение
SA =
'2
1
-1
1
1
-1
1
-1
О
-1
2
1
2
-3
-1
1 0 1
О 1 -1
ООО
Матрица SA действительно имеет упрощенный вид.
1
1
О,
О
О
1
О
1
1
Задачи для самостоятельного решения
1.1. Даны матрицы А =
4
2 3
5 6
1 О
О 1
1
Найти А + В, 2А, А-ЗВ, Ат,
ABT,tr(ABT).
fl
Ответ’. А + В =
15
3 31 <2 4
, 24 =
5 Т 18 10
6 I
12Г
А-ЗВ =
1 -I
1 5
3'
3 ’
Ат =
2
3
4
5
6
т |2
, А-Вт =
5
4 1 т
, Ъ(А-ВТ)=\2.
10/ ’
(3
1.2. Даны матрицы А = $
-2
-4
(3
'*"2
41
5’С"3
2
-3
-4
-5
2'
1 ,
3,
'2 5 б'
£)= 1 2 5 , F = (l 2 3),
Д 3 2.
G =
Г 2
-1 , Н =
О .
-5
5
<-16
1
-3
1
-II
1
-4
4
-15
-Р
4
-3
14,
95
'1 -2 3 4s
11 О 3 4
5 4 3 0
22 2 9 8,
"5 2 -2 3'
6 4-35
9, 2 -3 4
/ 6 -4 7,
"2 22 2 '
-1 -5 3 11
16 24 8 -8
8 16 О -16у
Найти АВ, CD, FG , GF , HQ, SK .
'1 5 -5'
(5 2^1
Ответ АВ = . CD = 3 10 0 . F G-0,
I7 °/
? 9 -7,
'1 0 0 0'
2 4 6
0 2 0 0
GF = -1 -2 -3 , HQ = , S-K=O
0 0 3 0
0 0 0
/ J) 0 0 4у
г2 3 -Р ( 1 2 Г
1.3. Даны матрицы А = -1 1 0 , в = 3 1 2 . Найти АВ-ВА
2 3 1 1,
и АТВ + В. '-2 -1 9 ' 6 6 2 '
Ответ: АВ-ВА = -2 -6 3 , АТ В + В-- 9 10 9
-8 -9 8, L-1 -2
'0 1 0 0^
0 0 1 0 Гз
1.4. Даны матрицы А = 0 0 0 1 ^1
о 0 0 0,
Ответ: А5-О, В3 = 35 го'!
20 15 Г
Г
2,
Найти А5,В3.
а
с
1.5. Найти все матрицы
второго порядка, квадрат которых ра-
вен нулевой матрице.
Ответ:
а
<с
b
-а
, где а2 +Ьс = О.
96
(а Ь\
1.6. Найти все матрицы I I второго порядка, квадрат которых ра-
вен единичной матрице.
(a b 'I ,
Ответ: +E или , где a +fec = l
(c -a)
fl
1.7. Найти все матрицы, перестановочные с матрицей
Ответ'.
a 2b 1 t „
, где а,об R .
3b а + ЗЬ
'3
1.8. Найти все матрицы, перестановочные с матрицей О
О
О'
1
3.
Ответ:
а b с'
О а b , где a,b,c& R.
ООа.
(2 -1Y
1.9. Доказать, что а) I \
f1 °)
(О I I n~ четное,
3 _ 2 I n~ Учетное;
fcosa -sina
б) .
Iosina cosa J
° Y
0
l" fees па
I I sin па
- sin nd.
cos «а
в)
о
Л2
Кк
о
%
о
о
О
О
О
О
2
4
1
3
О
••• X
О
О
2 I j. „ .» .
. Наити A , i-A.
3/J
f— 2 + i 2i A
’ , А = 15 + 2/ -ЗГ
[1 + 2/
1.10. Дана матрица А = I
'1-2/ 2+5/
2 -3/
Ответ: А* -
1.11. Вычислить /(А), если /(х) - х2 2х + 1, А =
О 1
Ответ: f(A) = О.
2 - 4549
97
1.12. Привести матрицы
Ч 0 4 -Г Г3 2 4 4 5
2 1 11 2 7 5 9 8 9
а) 11 4 56 5 ; б) 5 3 7 9 4
<2 -1 5 "б, 6 5 7 5 -5
-У
5 2
3 4
9 -2
4 3'
5 1
2 9,
к ступенчатому виду. Ступенчатый вид определяется неоднозначно.
Ответ'.
О
4
1
1
1
-1
-1
а)
;б)
-1
-11
41
-7
-2
-2
-8
-1
-7
О
о
1
3
4
о
1
6
9
2
2
о
о
о
о
о
о
1
; в)
о
1
3
О
О
О
О
1
о
о
о
о
о
о
о
о
о
о
1.13. Даны блочные матрицы
2
1
(1 2
А =
10 3
(2 1)
5 =----- . С =
11 OJ
2)
-1
О 1
1 О
1
О
2
1 О 2
3 4 1
О =
1 2
О 1
О
О
О
1
2
1
2
1 О
1
1
1
3
Пользуясь правилом умножения блочных матриц, найти А В, С • D . Вы-
полнить проверку, перемножая матрицы, как числовые.
Г4 1
Ответ: А-5 =
13 О
со=
(3 3 4 5 3 91
3 2 6 14 2 1 2 7 8 5 6 Ч
. Найти кронекеровское
(12) (5
1.14. Даны матрицы А = , В =
13 4J 17
произведение А® В И кронекеровскую сумму АФЕ3.
"2 2 0 0 0 0>
"5 6 10 12^ 3 5 0 0 0 0
7 8 14 16 Л 0 0 2 2 0 0
Ответ: А® В —- , А Ф £3 =
15 18 20 24 0 0 3 5 0 0
.21 24 28 32J 0 0 0 0 2 2
—\ V) m 0 0 0 О >
ГЛАВА 2. ОПРЕДЕЛИТЕЛИ
2.1. ИНДУКТИВНОЕ ОПРЕДЕЛЕНИЕ
Пусть А - квадратная матрица порядка п. Определитель (детерми-
нант) квадратной матрицы А - это число det А, которое ставится в соот-
ветствие матрице и вычисляется по ее элементам согласно следующим пра-
вилам.
1. Определителем матрицы А = (ди) порядка п = 1 называется единст-
венный элемент этой матрицы: det(an )= atl.
«п
2. Определителем матрицы А =
<«л!
«1л
: порядка п > 1 называ-
ния,
ется число
det А = (-1)1+1а11Л/11 +(-1)1+2а12М12+... + (-1)1+"а1„Л/1п , (2.1)
где - определитель квадратной матрицы порядка и -1, полученной из
А вычеркиванием первой строки и j -го столбца.
Определитель матрицы обозначают, заключая матрицу в "прямые"
скобки:
detA = | А| =
«11 а1п
«л1 ••• «ил
Имея в виду это обозначение, для краткости говорят о порядке определите-
ля, строках или столбцах определителя, элементах определителя, опус-
кая при этом слово "матрица". Например, первая строка определителя п -го
порядка - это первая строка an,ai2 квадратной матрицы n-го по-
рядка.
Индуктивное определение позволяет вычислить определитель любого
порядка. По второму правилу (т.е. по формуле (2.1)) нахождение определи-
теля п -го порядка сводится к вычислению п определителей ( п -1 )-го по-
рядка. Нахождение каждого определителя ( и -1 )-го порядка сводится к вы-
числению п-1 определителя (п-2)-го порядка и т.д., пока не получим и2
определителей 1-го порядка, которые находим по первому правилу. Конеч-
но, такая процедура неудобна из-за своей громоздкости, но вполне реали-
зуема и может быть принята в качестве определения.
Квадратную матрицу, определитель которой равен нулю, называют
вырожденной (особой), в противном случае - невырожденной (неособой).
т
99
Получим формулы вычисления определителей второго и третьего по-
рядков. По определению при п = 2
" “>2 =(-1)1+1а11Л/11+(-1У+2й12Л/12.
«21 «22
При вычеркивании первой строки и одного столбца по-
лучаем матрицу, содержащую один элемент, поэтому
Л/ц = det(a22) = а22 , Л/12 =det(a21) = a21.
Подставляя эти значения в правую часть, получаем
формулу вычисления определителя второго порядка
ап
«21
«12
«22
_«11«22 «12«21 ’
(2.2)
Определитель второго порядка равен разности произведения элементов,
стоящих на главной диагонали, и произведения элементов, стоящих на по-
бочной диагонали (см. схему на рис. 2.1).
Для определителя третьего порядка имеем
аи а12 «13
«21 а22 «23
«31 «32 а33
= + (-1У+2а12^12 + (rif+3ai3M13.
При вычеркивании первой строки и одного столбца получаем опреде-
лители квадратных матриц второго порядка:
Мп =
а22
«32
«23
а33
«21
«31
«23
азз
М13 =
«21
«31
а22
а32
М12 -
Эти определители второго порядка записываем по формуле (2.2) и получаем
формулу вычисления определителя третьего порядка
а11 а12 й13 а22
«21 а22 а23 = «1Г а32
«31 а32 а33
а23 «21
«12 '
«33 «31
а23 + ап- а21 а22
«33 а31 а32
~«11(«22«33 а23а32)~а12(а21а33 «23«31)+ а1з(«21«32 ~«22«31)~
(2.3)
~а11а22а33 + «12 «23 «31 + «13 «21 «32 «13 «22 «31 а12 а21 а33 ~ а11 а23 а32 •
а б
Рис. 2.2
100
Определитель (2.3) представляет собой сумму шести слагаемых, каждое из
которых есть произведение трех элементов определителя, стоящих в разных
строках и разных столбцах. Причем три слагаемых берутся со знаком плюс,
а три других - со знаком минус.
Для запоминания формулы (2.3) используется правило треугольников-.
надо сложить три произведения трех элементов, стоящих на главной диаго-
нали и в вершинах двух треугольников, имеющих сторону, параллельную
главной диагонали (рис. 2.2,а), и вычесть три произведения элементов,
стоящих на побочной диагонали и в вершинах двух треугольников, имею-
щих сторону, параллельную побочной диагонали (рис. 2.2,6).
Рис. 2.3
Можно также пользоваться схемой вычисления, изображенной на
рис. 2.3 (правило Саррюса): к матрице приписать справа первый и второй
столбцы, вычислить произведения элементов, стоящих на каждой из указан-
ных шести прямых, а затем найти алгебраическую сумму этих произведе-
ний, при этом произведение элементов на
прямых, параллельных главной диагонали,
берутся со знаком плюс, а произведение
элементов на прямых, параллельных побоч-
ной диагонали, - со знаком минус (согласно
обозначениям на рис. 2.3).
Итак, получены формулы для вычис-
ления определителей второго и третьего порядков. Можно продолжить вы-
числения по формуле (2.1) для и>3 и получить формулы для вычисления
определителей четвертого, пятого и т.д. порядков. Следовательно, индук-
тивное определение позволяет вычислить определитель любого порядка.
Другое дело, что формулы будут громоздкими и неудобными при практиче-
ских вычислениях. Поэтому определители высокого порядка (четвертого и
более), как правило, вычисляют на основании свойств определителей.
Пример 2.1. Вычислить определители
1 2 3
5 4 6
7 -8 -9
1
3
2
4
□ По формулам (2.2) и (2.3) находим
1
5
7
2 3
4 6
-8 -9
= 1-4-(-9)+2-6-7 + 3-5-(-8)-3-4-7-2-5-(-9)-1-6-(-8)=
= -36 +84-120-84 + 90 + 48 =-18.
101
2.2. ФОРМУЛА РАЗЛОЖЕНИЯ ОПРЕДЕЛИТЕЛЯ
ПО ЭЛЕМЕНТАМ СТРОКИ (СТОЛБЦА)
Пусть дана квадратная матрица А порядка п.
Дополнительным минором Му элемента называется определитель
матрицы порядка п-1, полученной из матрицы А вычеркиванием i -й
строки и j -го столбца.
Алгебраическим дополнением Ау элемента ау матрицы А называет-
ся дополнительный минор Му этого элемента, умноженный на (-1)’+7 :
Ay Му.
Теорема 2.1 (формула разложения определителя по элементам
строки (столбца)). Определитель матрицы А равен сумме произведений
элементов произвольной строки (столбца) на их алгебраические дополне-
ния:
det А = £ (-1)'+* alk М,к =^а,кА,к
4=1 4=1
det А = £(- tf+J akjMkj = £ akjAkj
4=1 4=1
Замечания 2.1.
1. Доказательство формулы проводится методом математической ин-
дукции [4].
2. При индуктивном определении (2.1) фактически использована фор-
мула разложения определителя по элементам первой строки.
(разложение по i -й строке);
(разложение по j -му столбцу).
Теперь разложим определитель третьего порядка по последнему столбцу:
О
det А = -5 •
2
О
-1
— —5 ( О - Ли + 3 /ijj + 0 • А^у )= —5 • 3 •
2 1
-1 2
2
О
102
Определитель второго порядка вычисляем по формуле (2.2):
det А = 15-
2
-1
= 15-(2-2-(-1)-1)= 15-5 = 75 .
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ ТРЕУГОЛЬНОГО ВИДА
Применим формулу разложения для нахождения определителя верхней
треугольной матрицы
ап а12 а\п
Д _ 0 а22 ••• а2п
; - •
о 0 ... ап„
Разложим определитель по последней строке (по п -й строке):
Ад ~ 0 ’ + - + 0 ' л-1 + апп ’ = апп (~ ^пп = апп^пп >
где - дополнительный минор элемента ат. Обозначим Мт = Д„_].
Тогда Д„ = алл-Дл_1. Заметим, что при вычеркивании последней строки и
последнего столбца определителя Дп , получаем определитель Д„_] верхней
треугольной матрицы такого же вида, как Дл, но (н-1 )-го порядка. Раскла-
дывая определитель Дл_, по последней строке ( (и -1) -й строке), получаем
Ад-i = an-i л-i Ал-2 • Продолжая аналогичным образом и учитывая, что
Дн = ан, приходим к формуле
Дд ~ апп Ад-1 = апп ‘ал-1 л-1 ‘ Дд-2 — — ~ апп 'ап-\п-1 ••'711 »
т.е. определитель верхней треугольной матрицы равен произведению эле-
ментов, стоящих на главной диагонали.
Замечания 2.2.
I. Определитель нижней треугольной матрицы равен произведению
элементов, стоящих на главной диагонали.
2. Определитель единичной матрицы равен 1.
3. Определитель матрицы треугольного вида будем называть опреде-
лителем треугольного вида. Как показано выше, определитель треугольного
вида (определитель верхней или нижней треугольной матрицы, в частности,
диагональной) равен произведению элементов, стоящих на главной диаго-
нали.
103
2.3. СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
2.3.1. Основные свойства определителей
1. Для любой квадратной матрицы det А = det(/l7 ), т.е. при транспо-
нировании определитель не изменяется. Из этого свойства следует, что
столбцы и строки определителя "равноправны": любое свойство, верное для
столбцов, будет верным для строк.
2. Если в определителе один из столбцов нулевой (все элементы
столбца равны нулю), то определитель равен нулю'. det(... о...) = 0 .
3. При перестановке двух столбцов определитель меняет знак на про-
тивоположный (свойство антисимметричности)'.
det(... aj ... ak ...)= -det(... ak ... Oj ...).
4. Если в определителе имеется два одинаковых столбца, то он равен
нулю'.
det(... Oj ... ak ...)= О при Oj = ak .
5. Если определитель имеет два пропорциональных столбца, то он ра-
вен нулю'.
det(... aj ... ak ...)= О при = "kak .
6. При умножении всех элементов одного столбца определителя на
число определитель умножается на это число'.
det(a,... X • aj ... «„)= X• det(a, ... ау ... а„).
7. Если j -й столбец определителя представляется в виде суммы двух
столбцов Oj + bj, то определитель равен сумме двух определителей, у ко-
торых j -ми столбцами являются Oj и bj соответственно, а остальные
столбцы одинаковы'.
det(...ay +bj ...)= det(...<7у... )+det(...Z>y ...).
8. Определитель линеен по любому столбцу:
det(.. .а • + Р • 6у...) = а det (.. ,<7у...)+Р • det(.. .bj...).
9. Определитель не изменится, если к элементам одного столбца при-
бавить соответствующие элементы другого столбца, умноженные на одно
и тоже число:
det(...а} + k-ak ...ak ...)= det(...ay ...ak ...).
10. Сумма произведений элементов какого-либо столбца определителя
на алгебраические дополнения соответствующих элементов другого столб-
ца равна нулю:
iaki'Akj=0 при i*j.
k = l
104
Замечания 2.3.
1. Первое свойство определителя доказывается по индукции [4]. Дока-
зательства остальных свойств проводятся с использованием формулы раз-
ложения определителя по элементам столбца. Например, для доказательства
второго свойства достаточно разложить определитель по элементам нулево-
го столбца (предположим, что j -й столбец нулевой, т.е. akj = О
к = \, 2,...,п'):
det^=S^A =E °Л=0-
*=1 Л=1
Для доказательства свойства 10 нужно прочитать формулу разложения
определителя справа налево, а именно, сумму произведений элементов i -го
столбца на алгебраические дополнения элементов J -го столбца представить
как разложение по у -му столбцу определителя
п
@ki * ^kj ~
к-\
«11
«„1
"• «1п
" апп
у которого на месте элементов j -го столбца стоят соответствующие эле-
менты i -го столбца. Согласно четвертому свойству такой определитель ра-
вен нулю.
2. Из первого свойства следует, что все свойства 2-10, сформулиро-
ванные для столбцов определителя, будут справедливы и для его строк.
3. По формулам разложения определителя по элементам строки (столб-
ца) и свойству 10 заключаем, что
И
' Akj ~
t=l
0, i* j,
det A, i = j,
n
Y^k'djk =
t=l
o, ' * j,
det A, i = j.
(2-4)
4. Пусть A - квадратная матрица. Квадратная матрица А+ того же по-
рядка, что и А , называется присоединенной по отношению к А , если каж-
дый ее элемент а* равен алгебраическому дополнению элемента aJt мат-
рицы А : «у = Ajt. Иными словами, для нахождения присоединенной мат-
рицы следует:
а) заменить каждый элемент матрицы А = j его алгебраическим до-
полнением А^ =(-1),+7Л/у, при этом получим матрицу (-4,,);
б) найти присоединенную матрицу А+, транспонируя матрицу (яу).
105
Из формул (2.4) следует, что АА+ = А+ А = det А- Е, где Е — единич-
ная матрица того же порядка, что и А .
fl 2^
Пример 2.3. Дана матрица А = . Сравнить определитель матри-
13 4 J
цы А с определителями матриц
Аг;
f1 2'l п+зл 2+4^
f3A 4А/ 3 4 J
□ Определитель матрицы А был найден в примере 2.1: det А = -2. По
формуле (2.2) вычисляем определители остальных матриц:
3
4
det(AT)= *
= 1-4-3-2 =-2 = det А ,
что соответствует свойству 1;
2
4
1
3
det В =
= 2-3-l-4 = 2 = -detA,
что соответствует свойству 3, так как матрица В получена из матрицы А
перестановкой 1-го и 2-го столбцов;
3 4
detC = 1 2 = 3-2-41 = 2 = -detA,
что соответствует свойству 3, так как матрица С получена из матрицы А
перестановкой 1-й и 2-й строк;
1 2
ЗА 4А
= l-4A-2-3A = -2A = AdetA,
что соответствует свойству 6, так как матрица D получена из матрицы А
умножением элементов 2-й строки на число Л;
det F =
1 + ЗА 2 + 4А
3 4
= (l + 3A)-4-(2 + 4A)-3 = -2 = detA,
что соответствует свойству 9, так как матрица F получена из матрицы А
прибавлением к элементам первой строки соответствующих элементов вто-
рой строки, умноженных на Л.
fl 2 3 А
Пример 2.4. Дана матрица А = 5 4
6 . Найти присоединенную
-8 -9)
матрицу А+ и вычислить произведения АА+ и А+А .
□ Найдем алгебраические дополнения всех элементов матрицы А :
106
Ли=ИЖ 4 -8 6 -9 = 12, Л12=(-1)1 + 2 5 7 - 6 -9 = 87,
Аз=И1+3- 5 7 4 -8 = -68, а21=(-1)2+1 2 ’ -8 3 =-6 -9
a22 = (-i)2+2- 1 7 3 -9 = -30, М-1)2+3 1 ' 7 2 -8 = 22,
АзИ-Г- 2 4 3 6 0, А32=И3+2 1 ' 5 3 6 = 9,
Лзз=(-1Г- 1 5 2 4 -6.
Составим присоединенную матрицу, транспонируя матрицу (см, п.4
J \ "12 87 -68' т ' 12 -6 0 '
замечаний 2.3), т.е. А+=Цу) = -6 -30 22 — 87 -30 9
.° 9 ~6 , -68 22 -6,
Вычислим произведения
"1 2 3 W 12 -6 0 > Л-18 0 0 '
АА+ = 5 4 6 87 -30 9 = 0 -18 0
<7 -8 -9, к-68 22 < 0 0 -18,
' 12 -6 0 ' р 2 3 ' "-18 0 0 '
А+А = 87 -30 9 5 4 6 = 0 -18 0
-68 22 ~6> 7 -8 "9> . о 0 -18,
что соответствует п.4 замечаний 2.3, так как det А — -18 (см. пример 2.1).
Пример 2.5. Найти определитель блочно-диагональной матрицы
А О
От Е
, где А - произвольная квадратная матрица, Е - единичная, а О
— нулевая матрица соответствующего порядка, От — транспонированная.
□ Разложим определитель по последнему столбцу. Так как в этом
столбце все элементы нулевые, за исключением последнего, равного 1, по-
лучим определитель такого же вида, что и исходный, но меньшего порядка.
Раскладывая полученный определитель по последнему столбцу, уменьшаем
его порядок. Продолжая таким же образом, получаем определитель матри-
О
Е
цы А . Следовательно,
А
От
= det А
107
2.3.2. Формула полного разложения определителя
Разложим определитель п -го порядка по первой строке (согласно оп-
ределению)
det А = «и «21 «12 ’ «22 ‘ • «1л • «2л =«п(-Г- «22 «2л +
«л! «л2 ’ ' «лл «л2 апп
+ а12(-1У+2- «21 «23 ’ •• «2л + ...+ «[„(-! 1+л «21 «2п-1
«Л1 «лЗ ' «лл «Л1 «пл-1
Продолжая раскладывать каждый из полученных определителей по первой
строке, получаем формулу полного разложения определителя-.
detX = ..• (2-5)
(д./г. -А)
Каждое слагаемое - это произведение а1у-а27 --anj п элементов опреде-
лителя, взятых из разных строк и разных столбцов: из первой строки взят
один элемент , стоящий в jt -м столбце; из второй строки - элемент
a2j2 , стоящий в j2-M столбце, причем j2 * и т.д., из последней строки -
элемент , стоящий в j„ -м столбце, причем * Л, Л * Л > -• Л * Л-1
Упорядоченный набор (j],j2>—>7П) неравных между собой первых п нату-
ральных чисел называется перестановкой (см. пример В. 17). Например,
имеется 6 перестановок из первых трех натуральных чисел: (1, 2,3), (1,3, 2),
(2,1,3), (2,3,1), (3,1, 2), (3, 2,1). Перестановка (1, 2,3,...,и) называется
тождественной. Суммирование в (2.5) проводится по всем перестановкам
(л>72>•••’Л) из п чисел. Всего в правой части (2.5) имеется п! слагаемых
(по количеству различных перестановок). Определим знак, стоящий перед
каждым произведением аг^а22г Заметим, что при разложении опре-
делителя первое слагаемое имеет вид
а\ 1(-1)1+1 • «22 (~ 1)1+‘ ••• •«„«(- Г)1+1 = «11«22 • «лл «
т.е. произведение а1}а22-...-апп элементов на главной диагонали определи-
теля входит в сумму со знаком плюс. Этому произведению соответствует
тождественная перестановка (1, 2,3,...,п) номеров столбцов. Произведению
соответствует перестановка (д, Jz' --Jn) номеров столбцов.
108
Если столбцы определителя переставить так, чтобы эти элементы оказались
на главной диагонали, то перед их произведением оказался бы знак плюс.
Поскольку при перестановке двух столбцов определитель меняет знак на
противоположный, то перед произведением а, а-, -а нужно поста-
Ul nJn '
вить коэффициент .где u(jl,j2......ул) - соответствующее ко-
личество перестановок столбцов определителя. Это число равно количеству
транспозиций - перемен местами двух чисел в перестановке - необходи-
мых для приведения перестановки (j\, j2к тождественной. Напри-
мер, для определителя 3 -го порядка (п = 3) найдем знак, с которым в пра-
вую часть (2.5) входит произведение а13а22а31. Этому произведению соот-
ветствует перестановка (Д, J2, У3) = (3,2,1). Поменяем местами 1-е и 3-е
числа, получим тождественную перестановку (1,2,3). Следовательно,
о(3,2,1) = 1, т.е. перед произведением ai3a22a31 стоит коэффициент
(-1)1 = -1, что и указано в формуле (2.3).
Пример 2.6. Доказать, что определитель п -го порядка "с большим ну-
левым углом" равен нулю, т.е.
О 0 au+i
б 0
am+ll ” am+lk am+lk+l
anl ” ank ank+\
к
□ Рассмотрим произведение
хотя бы один множитель равен нулю, то и произведение будет равным ну-
лю. Поэтому из первой строки надо брать элемент ац , стоящий в столбце
j\>k, из второй строки - элемент a2j2, стоящий в столбце j2 > к и
j2 * у), и т.д. из т -й строки - элемент ат]~ , стоящий в столбце jm > к ,
Но выбрать т разных столбцов из (п-к)
столбцов невозможно при п - к < т. Поэтому хотя бы один из множителей в
ах^а2^ будет равным нулю. Таким образом, каждое слагаемое в
правой части (2.5) для данного определителя равно нулю, т.е. сумма равна
нулю.
ат
>т
@тл
&т+1 п
апп
= 0 при к +т>п .
>а2; — а„: в правой части (2.5). Если
109
2.3.3. Формула Лапласа
Теорема Лапласа [1,10,42] обобщает формулу разложения определите-
ля по элементам строки (столбца).
Пусть А - квадратная матрица п -го порядка. Выберем в матрице А
к строк (1<к<п) с номерами z] ,i2,...,ik (1< z) < i2 < ...< ik < и) и к
столбцов с номерами jr, j2,..., jk (1 < j{< j2 < — < jk^n).
Минором к -го порядка матрицы А называется определитель
матРиць1 "го порядка, образованной элементами, стоящими на
пересечении выбранных к строк и к столбцов матрицы А . Обозначая ми-
норы, номера выбранных строк будем указывать верхними индексами,
а выбранных столбцов - нижними.
Алгебраическим дополнением минора называется
умноженный на (-1)'1 +,i+-+'z+A+h+-+J* определитель матрицы (и-&)-го по-
рядка, полученной из матрицы А вычеркиванием выбранных к строк и к
столбцов.
Формула Лапласа разложения определителя. Определитель матри-
цы А равен сумме произведений миноров к -го порядка, расположенных в
выбранных к строках (столбцах), на их алгебраические дополнения:
det А = (разложение по к строкам);
detA= А ЛА Л (разложение по к столбцам).
1<(| <i2 <...<<*
Пример 2.7. Вычислить по формуле Лапласа определитель
1 0 3 4
0 3 0 1
det А = 3 0 1 2
4 1 2 3
□ Выберем в матрице А первые две строки (z] = 1, z2 = 2 ). В этих
строках расположены 6 миноров, которые получаются при произвольном
выборе двух столбцов: 12 1 0 Л/.1,2 = = 3; 12 0 3 ла12 = 1 3 Л = 0; Л/.1? 0 0 14 1 “ 0 4 = 1; 1
ПО
Найдем алгебраические дополнения этих миноров
й=(-1Г*м- *
^=(-1)Н2Н+3
ЛЙ=(-1ГМ’< ’ ‘ »-2;
Вычислим определитель, используя формулу разложения по двум
строкам:
detA = 3-(-l)+O-2 + l(-l)+(-9)-l + (-12)-(-2)+3-3 = 2O.
Используем теперь формулу разложения по столбцам. Выберем, на-
пример, 1-й и 4-й столбцы (ji = 1, j2 =4). Находим миноры, расположен-
ные в этих столбцах, и их алгебраические дополнения
^(-if2^4. л<4=(_1)1+4+1+4. А* =(-1)2+4+1+4- 0 1 1 2 3 0 0 1 0 3 0 1 = -1; а£=(-1У+3+М' = 3; А243 =(-1)2+3+1+4 - = 0; аДМ-!)3^4- 3 0 1 2 0 3 1 2 0 3 3 0 ЧЭ С*', Ох 1 1 1 11 11 11
Вычисляем определитель, используя формулу разложения по двум
столбцам:
det А = 1-(-1)+(-10)-(-б)+(-13)-3 + (-3)(-3)+(-4)-0+1-(-9)=20.
Замечания 2.4.
1. Дополнительный минор элемента a.j (см. разд.2.2) является мино-
ром (л-1)-го порядка, т.е. Ji’J+i.Sr
2. Если А и С квадратные матрицы, В, О матрицы соответствую-
щих размеров, причем О — нулевая, то определитель блочно-треугольной
матрицы находится по формуле
111
А В
О С
=И-1С1-
Действительно, применяя формулу Лапласа к столбцам, в которых
расположена матрица А, получим одно слагаемое | А |-| С |. Остальные
миноры в этих столбцах равны нулю, так как содержат нулевую строку.
2.3.4. Определитель произведения матриц
Теорема 2.2 (об определителе произведения матриц). Пусть А и В
- квадратные матрицы одного и того же порядка. Тогда
det(AB) = detA -det В, (2.6)
т.е. определитель произведения матриц равен произведению их определите-
лей.
Доказательство теоремы проводится в три этапа. Во-первых, теорема
справедлива, если один из сомножителей имеет простейший вид (см.
рис. 1.6). Пусть, например, матрица А квадратная л-го порядка имеет про-
стейший вид: А = —
I О
О'
О,
. Если г<п, то в произведении АВ последние
(л-г) строк будут нулевыми. Тогда по свойствам 1,2 определителей:
det(/lZ?) = 0 и det А = 0 , т.е. равенство (2.6) верно. Если же г = л, то А = Еп
- единичная матрица. Тогда det(HS) = det(£nfi)= det В = det Еп -det В, т.е.
равенство (2.6) справедливо. Аналогично рассматривается случай, когда
матрица В имеет простейший вид.
Второй этап - доказательство формулы (2.6) для элементарных матриц.
Если матрица В элементарная вида (1.1), (1.3) или (1.5), то ее определитель
равен (-1), X или 1 соответственно, а произведение АВ есть элементарное
преобразование столбцов матрицы А . По свойствам 1, 3, 6 или 9 определи-
телей убеждаемся в справедливости (2.6). Аналогично рассматривается слу-
чай, когда матрица А -элементарная вида (1.2), (1.4), (1.6).
Третий этап - доказательство формулы (2.6) для произвольных квад-
ратных матриц п -го порядка. По теореме 1.2 любую квадратную матрицу
можно представить в виде произведения простейшей (она является элемен-
тарной (см. разд. 1.6.2)) и элементарных преобразующих матриц:
А = SA -ЛА ТА и В = SB- АВТВ . Тогда, используя результат первых двух
этапов, можно записать
det (АВ) = det (SaAaTa SBABTB) = det SA det Aa det TA det SB det AB det TB =
= det (SA -Aa -Tx) det (SB -AB • TB) = det Я det В,
что и требовалось доказать.
112
(1
Л =
1з
Следовательно, det(/l.S) =
Пример 2.8. Найти определитель произведения матриц
4 Д' ’}
4j I4 5/
□ Находим определители данных матриц второго порядка (см. при-
мер 2.1): det А = -2, det В = -7 . По теореме об определителе произведения
матриц получаем det(AB) - det А det В = (- 2) (- 7) = 14 . Вычислим этот же
определитель, находя произведение матриц:
fl
АВ =
(3
9
19
2 if1 3Vf9 13
4Д4 5J U9 29
13
29
= 9-29-13-19 = 14. Результат совпадает
с полученным ранее.
Пример 2.9. Найти определитель матрицы
D =
1
3
О
о
о
2
4
О
О
О
У
2
4
-8
z
3
6
-9
и
v
w
1
5
7
на блоки:
А В}
□ Разобьем данную матрицу D
D = -
О
fl 2^
где А =
3 4
\ U V W]
, я= , <9 =
у z J
01 (1
О , С= 5
О
2
4
-8
3 '
6
-9.
справедливости этого
Представим блочную матрицу как произведение (в
представления можно убедиться, найдя произведение по правилам умноже-
ния блочных матриц)
( А В\
£> =------
О С,
6‘j
~с V
А От'
о Е-, ,
О
О
О
О
7
В
От
д
о
где Е2, Е3 - единичные матрицы соответствующих порядков. Применяя
результат примера 2.5, имеем
Л |ОГ
О Е3
= detC = | С |.
= det А = | А |,
8 - 4549
113
Е2
Матрица I —
Д')
К J
- треугольная (все элементы на главной диагонали рав-
ны единице), поэтому
Е2 В
О Е3
По теореме об определителе произве-
дения получаем
в
К
А В = Е2
О С ~ ~о
от
с
О Е3
о
Подставляя в правую часть определители |л| = -2, |С| = -18 (см. при-
мер 2.1), получаем | D | = 36.
Пример 2.10. Дана квадратная матрица А и-го порядка. Найти опре-
делитель det А+ присоединенной матрицы.
□ Согласно п.4 замечаний 2.3
АА+ = rdet А 0 0 det Л • - 0 ' • 0
( о 0 det Л,
Определитель диагональной матрицы в правой части равен (det л)". Следо-
вательно, по теореме об определителе произведения имеем равенство
det(/4А+ )= det А • det А + = (det Л)" .
Отсюда находим det А+ = (det л)"-1.
Замечание 2.5. Обобщением теоремы 2.2 служит формула Бине-
Коши [5,10], выражающая определитель произведения прямоугольных мат-
риц А и В размеров m х п и п х пг соответственно ( m < п ):
где в правой части вычисляется сумма произведений всевозможных мино-
ров m -го порядка матрицы А на соответствующие миноры того же порядка
матрицы В.
Пример 2.11. Используя формулу Бине-Коши, вычислить определи-
/ Ч (1 2>1
<1 2 ЗЛ
тель произведения матриц А = , В= 2 0 .
1 V [3
114
□ По формуле (2.7) получаем
1
О
det(/lZ?) =
2 12 13
12 0 + 0 2
1 2 2
+
3 1 1
3 2 0
2 3 1
= Ь(-4)+2-(-5)+Ь2 = -12.
2
3
2
0
1
Найдем произведение матриц = Р
тельно, det(>4fi) =
14 5
8
14
8
$ I. Следова-
2)
- -12. Результаты вычислений совпадают.
2
3
2
2.4. МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ
2.4.1. Применение элементарных преобразований
При вычислении определителей высокого порядка (больше 3-го) опре-
деление, как правило, не используется, так как это приводит к громоздким
выражениям и требует большого количества арифметических операций. Го-
раздо эффективнее использовать свойства определителей. Наиболее важны-
ми для вычисления определителей являются свойства 3, 6, 9. Эти свойства
можно назвать элементарными преобразованиями определителя, что со-
ответствует элементарным преобразованиям матрицы (см. разд. 1.6).
I. Перестановка двух столбцов (строк) определителя приводит к изме-
нению его знака на противоположный.
II. Умножение всех элементов одного столбца (строки) определителя на
одно и то же число, отличное от нуля, приводит к умножению опре-
делителя на это число.
III. Прибавление к элементам одного столбца (строки) определителя
соответствующих элементов другого столбца, умноженных на одно и
то же число, не изменяет определитель.
При помощи элементарных преобразований можно упростить опреде-
литель, т.е. привести его к виду, удобному для вычислений.
МЕТОД ПРИВЕДЕНИЯ К ТРЕУГОЛЬНОМУ ВИДУ
При помощи элементарных преобразований любую матрицу можно
привести к верхнему (или нижнему) треугольному виду (см. метод Гаусса в
разд. 1.6.1). Отсюда следует, что любой определитель, используя перечис-
ленные выше элементарные преобразования, можно привести к треугольно-
му виду, а затем вычислить согласно п.З замечаний 2.2.
8*
115
Итак, метод состоит из двух шагов.
1. При помощи элементарных преобразований привести определитель
к треугольному виду.
2. Вычислить определитель треугольного вида, перемножая его эле-
менты, стоящие на главной диагонали.
Пример 2.12. Вычислить определитель
1 2 3 4
2 3 4 1
det А = 3 4 1 2
4 1 2 3
приводя его к треугольному виду.
□ 1. При помощи элементарных преобразований приведем матрицу к
треугольному виду. Взяв элемент <2ц =1 первой строки в качестве ведуще-
го, все остальные элементы первого столбца сделаем равными нулю. Для
этого ко второй строке прибавим первую, умноженную на (-2), к третьей
строке прибавим первую, умноженную на (-3), а к четвертой строке приба-
вим- первую, умноженную на ( -4):
1 2 3 4 1 2 3 4
2 3 4 1 0 -1 -2 -7
3 4 1 2 0 -2 -8 -10
4 1 2 3 0 -7 -10 -13
Заметим, что при использовании этих элементарных преобразований III
типа определитель не изменяется.
Умножим элементы второй строки на (-1), а элементы третьей строки
— на 0,5, при этом, чтобы не нарушить равенство, надо полученный опреде-
литель разделить на (-1)- 0,5 = -0,5, т.е. умножить на (-2):
1 2 3 4 1 2 3 4
0 -1 -2 -7 = -2- 0 1 2 7
0 -2 -8 -10 0 -1 -4 -5
0 -7 -10 -13 0 -7 -10 -13
В полученной матрице нужно сделать равными нулю элементы а32 =-1 и
а42 = -7 второго столбца, стоящие ниже главной диагонали. Для этого бе-
рем в качестве ведущего элемента агг -1 и прибавляем к третьей и четвер-
той строкам вторую строку, умноженную на 1 и на 7 соответственно:
116
1 2 3 4 1 2 3 4
0 1 2 7 0 1 2 7
-2- 0 -1 — 4 -5 = -2- 0 0 -2 2
0 -7 -10 -13 0 0 4 36
Осталось сделать равным нулю элемент а43. К четвертой строке прибавим
третью, умноженную -2- на 2 (определи- 12 3 4 0 12 7 0 0-22 0 0 4 36 гель п] = —2- эи этом не изме 12 3 4 0 12 7 0 0-22 0 0 0 40 чится):
Получили определитель треугольного вида.
2. Вычислим определитель верхней треугольной матрицы, перемножая
элементы, стоящие на главной диагонали:
12 3 4
0 12 7
det А = —2 = -2 1 1 (-2)-40 = 160.И
0 0-22
0 0 0 40
МЕТОД ПОНИЖЕНИЯ ПОРЯДКА
Этот метод также основан на элементарных преобразованиях опреде-
лителя.
1. При помощи элементарного преобразования Ш типа нужно в одном
столбце (или одной строке) сделать равными нулю все элементы, за исклю-
чением одного.
2. Разложить определитель по этому столбцу (строке) и получить опре-
делитель меньшего порядка, чем исходный. Если его порядок больше 1, то
следует перейти к п. 1, иначе вычисления закончить.
Пример 2.13. Вычислить определитель
10 3 4
0 3 0 1
detA- 3 0 12
4 12 3
методом понижения порядка.
□ 1. В качестве ведущего элемента возьмем аи = 1, а все остальные
элементы второй строки при помощи элементарных преобразований сдела-
117
ем равными нулю. Для этого ко второму столбцу прибавим четвертый, ум-
ноженный на (-3):
10 3 4 0 3 0 1 3 0 12 4 12 3 1 -12 3 4 0 0 0 1 3-612 4-823
2. Разложим определитель по второй строке
1 -12 3 4 0 0 0 1 3-612 4-823 = 1-(-1)2+4- 1 -12 3 3 -6 1 4-8 2
Получили определитель третьего порядка.
Вынесем за знак определителя множитель (2) из второго столбца
(точнее все элементы второго столбца умножим на 0,5 , а получившийся оп-
ределитель умножим на 2):
1 -12 3 3 -6 1 4-8 2 = 2- 1 -6 3 3 -3 1 4-4 2
Прибавим ко второму столбцу первый
1 -6 3 1 -5
2- 3 -3 1 = 2- 3 0
4-4 2 4 0
3
1
2
Полученный определитель разложим по второму столбцу
1 -5 3
2-301 =2-(-5)-(-1)1+2-
4 0 2
3 1
4 2
3 1
4 2
= 10-
Получили определитель 2-го порядка.
Прибавим ко второй строке первую, умноженную на (-2)
10-
= 10-
3 1
-2 0
3 1
4 2
Разложим определитель по второй строке и заменим определитель первого
порядка единственным его элементом
10-
3
-2
= 1О-(-2)-(-1)2+1 -1 = 20.
Результат совпадает с полученным в примере 2.7.
118
МЕТОД ИЗМЕНЕНИЯ ВСЕХ ЭЛЕМЕНТОВ ОПРЕДЕЛИТЕЛЯ
При вычислении определителей бывает полезно изменить все его эле-
менты, умножив их на одно и то же число, не равное нулю, либо прибавить
к каждому элементу одно и то же число. Найдем формулы изменения опре-
делителя при этих преобразованиях.
Пусть дана квадратная матрица А п -го порядка. Из свойства 6 следу-
ет, что при умножении всех элементов определителя п -го порядка на число
1*0 определитель умножается на число А" : det(AA) = A" det А .
Рассмотрим теперь определитель матрицы В, элементы которой
by = а,у + х получены из соответствующих элементов матрицы А
прибавлением числа х:
detB =
ап + х
а]2 +х
<*п1+х ап2+х
а1п+х
ат + х
Применяя свойство 7 к первому столбцу этого определителя, получаем сум-
му определителей
det В -
а11 а12+х
flni аП2+х
а1я +х
апп+х
а12+х
ап2+х
а]п+х
апп+х
X
То же свойство применяем к каждому определителю ("раскладывая" второй
столбец) и т.д. В итоге получим сумму 2” определителей и-го порядка,
причем определители, имеющие по два и более столбцов из элементов, рав-
ных х, равны нулю (по свойству 4). Поэтому в сумме остаются только
(л +1) слагаемых: определитель матрицы А и п определителей вида
aii
а1 j-l х а1 J+1
а1п
ЙИ1
ап j-l Х ап j+l
отличающихся от определителя матрицы А только j -м столбцом. Раскла-
дывая этот определитель по j -му столбцу, получаем сумму алгебраических
дополнений элементов этого столбца, умноженную на х:
п
Dj = x'^Aij
i=l
Следовательно, сумма всех таких определителей Dj (j = 1,2,...,и) равна
сумме алгебраических дополнений всех элементов матрицы А , умноженной
на х:
119
Окончательно получаем, что при увеличении всех элементов опреде-
лителя на число х, определитель увеличивается на сумму всех алгебраиче-
ских дополнений, умноженную на число х :
аи+х ' а1п+Х а11 • •• Я1П
ат+х • апп+х ап\ • ” апп i=l >1
Пример 2.14. Вычислит е> определитель аг х х х х а2 х х х х а2 х
□ Рассмотрим опр det А = едели at - л 0 0 хх х ап гель диагональной ма г 0 0 а2— х 0 0 а3 - х • • 1Трицы А 0 0 0
0 0 0 ап~х
Искомый определитель Dn получается прибавлением к каждому элементу
определителя матрицы А числа х. Поэтому
D„=detA + x-^^Atf.
/=1 j=i
Определитель диагональной матрицы А равен произведению диаго-
нальных элементов: det А = (aj ~х)(а2 -х)-... -(ап -х). Осталось вычислить
сумму алгебраических дополнений всех элементов матрицы А . Заметим,
что алгебраическое дополнение недиагонального элемента равно нулю
(Ау = 0 при i* j, так как дополнительный минор содержит нулевой стол-
бец). Дополнительный минор диагонального элемента - это определитель
диагональной матрицы, т.е. Aii=(al-x)-...-(ai_1-x)(ai+l-x)-...-(an-x).
Поэтому
D« =(fli-x)(a2-х}-...\а„- х} +
120
+ *'Z(fli ~x)••• (а<-1 ~x)(a,+1-x)-x).
i=l
2.4.2. Метод рекуррентных уравнений
Этот метод заключается в том, что исходный определитель Дп и -го
порядка выражается через определители Д„Ч,ДП_2,...,Д того же вида,
но меньшего порядка. Получается рекуррентное уравнение
Решая это уравнение, находим формулу, выражающую определитель Дп
через определители Д^До.-.-.Дт и порядок и:
Дп-^(п,Д1,Д2,...,Ди).
В последнюю формулу подставляем определители Д1,Д2,...,Дт невысоко-
го (т < п) порядка, которые нетрудно вычислить каким-либо другим спосо-
бом.
Замечание 2.6. Рекуррентным уравнением называется равенство
вида хл =y(n,xn_1,...,xn_m)= 0, выражающее и-й член хп искомой число-
вой последовательности {хп } через т ее предыдущих членов
xn_j ,xn_2,...,xn_m. Методы решения таких уравнений рассматриваются в
разд.7.3.5.
Пример 2.15. Вычислить определитель и -го порядка
3 2 0 0 0
-2 3 2 0 0
0-2 3 0 0
0 0 0 ••• 3 2
0 0 0 ••• -2 3
□ Разложим определитель по первой строке
3 2 •• • 0 0 -2 2 - • 0 0
-2 3 . 0 0 0 3 - • 0 0
АП=3(-1У+1- : • • + 2(-1У+2-
0 0 - • 3 2 0 0 - • 3 2
0 0 •• • -2 3 0 0 •• • -2 3
121
Первый из полученных определителей (п-1)-го порядка обозначим An_]
так как он имеет такой же вид, что и Дп . Разложив последний определитель
по первому столбцу, получим определитель того же вида, что и Дп , но
(п - 2 )-го порядка
-2 2 0 • • 0
0 3 2 0
Д^ЗД^-2- 0 -2 3 • • 0
0 0 0 • 3
3 2 • • 0
-2 3 • 0
0 0 • 3
Следовательно, искомый определитель удовлетворяет рекуррентному урав-
нению
А„ =3-A„_j +4-Д„_2 .
Решение этого уравнения будем искать в виде Дп = а • (-1)” + Ь • 4", где а и
b - неизвестные коэффициенты. Заметим, что эта формула дает решение
рекуррентного уравнения при любых коэффициентах а и b . В самом деле,
подставляя Дп=а-(-1)” +fe-4" в уравнение, получаем тождество
а(-1)” + b-4n = 3-[а-(-1)”’1 +fe-4n_1]+4-[a-(-l)n"2+fe-4n’2] фф
« а-(-1)л+fe-4” =-За-(-1)”+ —-fe-4n+4а-(-1)”+—•fc-4'1 фф
4 4
ФФ а-(-1)”+fc-4” =а-(-1)”+fe-4” .
Подберем теперь коэффициенты а и b в формуле Дп = а • (-1)" + Ь • 4я так,
чтобы при п -1 и п - 2 она давала правильные результаты, т.е.
+Ь-41 =3; Д2 =а-(-1)2+£>-42 = =13.
Решая систему уравнений
f —а + 4Ь = 3,
1 получаем а = —, [ а +16/> = 13, 4 , b = —. Следовательно, искомый определитель равен ДП=|(-1)Я+|4Я=|[(-1)Л+4Я+1 ].
122
Пример 2.16. Вычислить определитель Вандермонда
где Xj, х2 .., хп - действительные числа.
□ Рассмотрим определитель
1 1
который отличается от определителя Вандермонда последним столбцом, но
совпадает с ним при х = хп: Дп (хп) - Дп . Раскладывая определитель Дп (х)
по последнему столбцу, получаем многочлен (п -1 )-й степени действитель-
ной переменной х:
Дп(х) = ап-1ХЛ 1+- + а1х + а0,
где старший коэффициент an_: равен алгебраическому дополнению элемен-
та х"-1: an_j - (-1)”+пДп_1 = Дп_1, т.е. определителю Д„_[ - определителю
Вандермонда (n-l)-ro порядка. Заметим, что при х = х( определитель
Дп(х) равен нулю, так как от имеет два одинаковых столбца (свойство 4).
Следовательно, Х[ - корень многочлена Дп(х). То же самое можно сказать
про числа х2 ,х3,...,хп_1. Все они являются корнями многочлена Д„(х).
Следовательно, этот многочлен имеет вид (см, следствие 4 основной теоре-
мы алгебры в разд. В.4): Дп(х) = Дп_! •(х-х1)(х-х2)-...-(х-хп_1). Подстав-
ляя в это равенство х = хп и учитывая, что Д„ (х„) = Дл , получаем рекур-
рентное уравнение
= Д„-1' к - xj)(xn -х2)-...• (х„ -хпЧ).
Записывая аналогичным образом Дп_р Д„-2 ...... Д2 и учитывая, что Д] =1,
получаем
Д„ = (х2 - Х1) ‘ (х3 - X, ) (х3 - х2)- - (х„ - х,) (хп - х2 )•... • (х„ - xn_t).
Таким образом, определитель Вандермонда равен произведению всех разно-
стей х, - х; при 1 < j < i < п : Дп - < Г?.<л(х< ~ xj) •
123
Задачи для самостоятельного решения
2.1. Найти определители второго порядка:
а+b а—Ь sin а - cos a a2 ab
а) ; б) ; в) »
а-b а+Ь cos a sin a ab b2
sina cosa sina + sin0 cos0 + cosa
г) д)
sin0 cos0 cos0-cosa sina-sinp
Ответ: a) 4ab; б) 1; в) 0; г) sin(a-0); д) 0.
2.2. Вычислить определители третьего порядка:
321 2 -1 3 210 3 -2 1
а) 2 5 3 ; б) -2 3 2 ; в) 1 0 3 ; г) -2 1 3 ;
342 025 05 -1 20 -2
1 0 1 2 4 6 2 0 5
д) 2 1 3 ; е) 5 12 19 ; ж) 1 3 16 .
5 0 -1 3 9 17 0 -1 10
Ответ: а) -3; 6)0; в) -29; г) -12; д) -6 ; е) 8; ж) 87.
2.3. Найти определители третьего порядка:
а)
а
-1
а
б) 0
1
0
-Ь
в) b
г) х
1 а
а 1
— 1 а
1
b
b
b
0
а
с
b
с
а
с
а
b
а
х
X X
Ь х
X с
Ответ: а) 4а; б) -2Ь2; в) ЗаЬс-а3-Ь3-с3;
г)2х3 ~(a+b + c)x2 + abc.
2.4. Не вычисляя определителей, указать, почему они равны нулю:
а) 0 0
б) 2
1 17
2 15
3 9
в) О
г)
sin2 a
sin2 Р
. 2
sin у
2
cos a
COS2p
cos2 у
cos 2a
cos 20
cos2y
0 1
1 2
2
О
3
1
3
О
1
1 2
2 4
2 3
Ответ: а) есть нулевая строка; б) имеются два одинаковых столбца;
в) первые две строки пропорциональны; г) если из второго столбца вычесть
первый, то в определителе будут два одинаковых столбца.
124
2.5. Вычислить определители | АВ | и | ВА | произведений матриц
(1 2 А (-1 3^1
А = I I, В = I I, применяя теорему 2.2. Сделать проверку, вычис-
ляя сначала произведения АВ и ВА, а затем определители | АВ | и | ВА |.
1
3
<1 5| (8
Ответ: АВ = Л , ВА =
1-2 101 (4
, det АВ = 20 = (-5)- (-4) = det ВА .
det A det В
2.6. Показать, что определитель
аг
6 sin А
с sin А
b sin А
1
cos А
с sin А
cos А
1
равен нулю,
если а, b , с - стороны треугольника; А - величина угла, противолежаще-
го стороне а.
Указание: разложить определитель, вынести общий множитель sin2 а,
применить теорему косинусов.
2.7. Вычислить определители при помощи элементарных преобразова-
ний:
1111 0 111
1-111 _ I 0 1 1
а) ; б)
'11-11 1101
111-1 1110
Указание: а) вычесть первую строку из всех строк; б) вычесть послед-
нюю строку из всех строк и разложить определитель по первому столбцу.
Ответ: а) -8; б) -3.
2.8. Найти определители четвертого и пятого порядков:
а)
112 3
12 3 1
2 3 6 4
3 5 9 4
б)
2 + а 1 а а
2 + Ь 2 b а
2 + с 3 с а
2 + d 4 d а
125
1 -1 3 -2 4 1 2 0 0 0
0 3 2 0 1 3 2 3 0 0
в) 0 0 4 -1 -1 г) 0 4 3 4 0
0 6 4 2 3 0 0 5 4 5
1 -1 3 — 2 5 0 0 0 6 5
Ответ: а) - -1; б) 0; в) 24; г) 640.
2.9 . Вычислить определители 111-1 1 И -ГО ПО эядка: 1 1 1 1
0 2 2 • 2 2 2 1 • 1 1
а) 0 0 3 • • 3 3 ; б) 3 3 • • 1 1
0 0 0 • • п-1 п-1 п-1 п-1 • 1 1
п п п п 2л п п • п 1
в) 0 11-1 10 1-1 110-1 ♦
1 1 1 ••• о
О 1 о ••• о
О О 1 ••• о
д)
О О О 1
1 о о ••• о
г) е) 1 п и ••• и и 2 и и и и 3 ••• и и и п ••• и 0 1 0 - 0 0 1- ООО-. 12 3- 0 D 1 п
Указание', а) представить определитель в виде суммы двух определите-
лей (первый из них получается вычитанием п из последней строки);
б) привести к треугольному виду, вычитая из второй строки удвоенную пер-
вую, из третьей - утроенную первую и т.д.; в) все столбцы прибавить к пер-
вому, а затем первую строку вычесть из всех остальных; г) вычесть послед-
нюю строку из всех предыдущих; д, е) разложить по первому столбцу.
Ответ: а) п'. ; б) (-1)пЧ(п-1)!; в) (-1)"-1 (и-1); г)(-1)п-1п!;
д) (~1)п+‘; е) (-1)л+1.
126
2.10. Вычислить определитель п -го порядка, элементы которого
1
aiy=max{i,/}: Д„ =
и
2 3
2 3
3 3
п п
п
п
п
п
Указание: вычесть первую строку из всех строк, разложить по послед-
нему столбцу, воспользоваться п.З замечаний 2.2.
Ответ: =(-1)"+1и.
2.11. Вычислить определитель и -го порядка, элементы которого
1 1 1 • 1
1 2 2 • • 2
ay=min{i,j}: Д„ = 1 2 3 - • 3
1 2 3 • п
Указание: вычесть первую строку из всех строк, разложить по первому
столбцу и получить рекуррентное уравнение Дл =Дя-р
Ответ: Дя=1-
2.12. Вычислить определители и -го порядка:
0 11-11 1 1 1 ••• 1 1
1 1 0 0 0 1 1 0 ••• 0 0
10 1—00 0 1 1 ••• 0 0
а) д« = ; б) дя =
10 0-10 0 0 0 — 1 0
10 0 — 01 0 0 0 - 1 1
Указание: а) разложить по последней строке, получить сумму двух оп-
ределителей, один из которых равен An4, другой определитель разложить
по последнему столбцу, после чего решить рекуррентное уравнение
Д„ = Дп_] -1; б) разложить по последней строке, получить сумму двух оп-
ределителей, один из которых равен An_j, другой определитель разложить
по последнему столбцу, после чего решить рекуррентное уравнение
ДЯ=Д„_,
Ответ: а) Дп = -(и -1); б) Д„ =
ГЛАВА 3. РАНГ МАТРИЦЫ
3.1 ЛИНЕЙНАЯ ЗАВИСИМОСТЬ И ЛИНЕЙНАЯ
НЕЗАВИСИМОСТЬ СТРОК (СТОЛБЦОВ) МАТРИЦЫ
В гл.1, были введены операции умножения матриц на число и сложе-
ния матриц, в частности, для матриц-столбцов (иХ1) и матриц-строк (1хи).
Матрицы-столбцы (матрицы-строки) будем называть далее просто столбца-
ми (соответственно строками) и обозначать в этой главе прописными бук-
вами. При помощи этих операций можно составлять некоторые алгебраиче-
ские выражения. Напомним, что равными считаются столбцы одинаковых
размеров с равными соответствующими элементами.
Столбец А называется линейной комбинацией столбцов Ai,A2,...,Ak
одинаковых размеров, если
A = a1A1+a2A2+... + ajlAj(., (3.1)
где а2,а2,...,ак - некоторые числа. В этом случае говорят, что столбец
А разложен по столбцам Аг, А2 Ак, а числа щ,а2,...,а.к называют
коэффициентами разложения. Линейная комбинация А = 0А1 +
+ 0 • /^ +... + 0 • At с нулевыми коэффициентами называется тривиальной.
Если столбцы в (3.1) имеют вид
то матричному равенству (3.1) соответствуют поэлементные равенства
а,- = ОС] -а(1 +а2 а;2 + — + «* ' Дд > i = 1,—•
Аналогично формулируется определение линейной комбинации строк
одинаковых размеров.
Набор столбцов Aj,A2,...,Ak одинаковых размеров называется сис-
темой столбцов.
Система из к столбцов А1У А2,..., Ак называется линейно зависимой.
если существуют такие числа аг,а2,...,ак, не все равные нулю одновре-
менно, что
oqA +a2A2 +... + aiXi =о. (3.2)
Здесь и далее символом о обозначается нулевой столбец соответствующих
размеров.
Система из к столбцов А1,А2,...,Ак называется линейно независи-
мой, если равенство (3.2) возможно только при otj = a2 =... = ак = 0, т.е.
128
i когда линейная комбинация в левой части (3.2) тривиальная. Аналогичные
В определения формулируются и для строк (матриц-строк).
F Замечания 3.1.
[ 1. Один столбец Аг тоже образует систему: при А1-о - линейно
> зависимую, а при А, * о линейно независимую.
I 2. Любая часть системы столбцов называется подсистемой.
1 Пример 3.1. Используя определение, установить линейную зависи-
I мость или линейную независимость систем столбцов
| ГУ Г2) ГС Го>
I. а) А = I I, А2 — i б) А] — , А2 — •
I 1 l°J l2J
I ГУ ' Г2)
□ а) Столбцы A] = и A2 = линейно зависимы, так как можно
О IО1
л.' \ / \ /
составить нетривиальную линейную комбинацию, например, с коэффициен-
ту Т2) ?0Л
тами (Xj = 2 ,а2 =-1, которая равна нулевому столбцу: 2-1 1-1-1 q I = l I •
ГУ Го)
б) Столбцы Aj = I I и А2 = I 2 I линейно независимы, так как равенст-
Т1) ТО) ТО) fl-ai=O
во ом + а, = , равносильное системе , оказывается вер-
\oj \2J |2-a2=0
ным только при aj = a2 = 0 .
СВОЙСТВА ЛИНЕЙНО ЗАВИСИМЫХ И ЛИНЕЙНО НЕЗАВИСИМЫХ СТОЛБЦОВ
Понятия линейной зависимости и линейной независимости определя-
ются для строк и столбцов одинаково. Поэтому свойства, связанные с этими
понятиями, сформулированные для столбцов, разумеется, справедливы и
для строк.
1. Если в систему столбцов входит нулевой столбец, то она линейно
зависима.
2. Если в системе столбцов имеется два равных столбца, то она ли-
нейно зависима.
3. Если в системе столбцов имеется два пропорциональных столбца
( А/ = кАj), то она линейно зависима.
4. Система из к >1 столбцов линейно зависима тогда и только тогда,
когда хотя бы один из столбцов есть линейная комбинация остальных.
5. Любые столбцы, входящие в линейно независимую систему, образу-
ют линейно независимую подсистему.
6. Система столбцов, содержащая линейно зависимую подсистему,
линейно зависима.
9 - 4549 1 29
7. Если система столбцов Ар А2,..., Ак —линейно независима, а после
присоединения к ней столбца А — оказывается линейно зависимой, то
столбец А можно разложить по столбцам At, А2......Ак, и притом един-
ственным образом, т.е. коэффициенты разложения находятся однозначно.
Докажем, например, последнее свойство. Так как система столбцов
Aj, А2,..., Ак , А линейно зависима, то существуют числа а,, а2,..., , а не
все равные 0, что cq А] + а2А2 +... + ак Ак + аА = о. В этом равенстве а 0.
В самом деле, если а = 0, то oCjA, + а2А2 +... + а.кАк = о. Значит, нетриви-
альная линейная комбинация столбцов А], А2,..., Ак равна нулевому столб-
цу, что противоречит линейной независимости системы А,, А2,..., Ак. Сле-
довательно, а*0 и тогда A = -—Aj—А^ , т.е. столбец А есть ли-
се а
нейная комбинация столбцов А1,А2,...,Ак. Осталось показать единствен-
ность такого представления. Предположим противное. Пусть имеется два
разложения А = cqА2 ч-.-. + а^А^ и А = Р]А] ч-.-. + Р^А^, причем не все коэф-
фициенты разложений соответственно равны между собой (например,
cq *Р]). Тогда из равенства се1А1 +...+акАк =Р1А1 +... + Р^А^ получаем
(«1 -Р1М1 +- + (at -PtK =о .
Следовательно, линейная комбинация столбцов А], А2,..., At равна нулево-
му столбцу. Так как не все ее коэффициенты равны нулю (по крайней мере
oct - Pj Ф 0), то эта комбинация нетривиальная, что противоречит условию
линейной независимости столбцов Ах,А2,...,Ак. Полученное противоречие
подтверждает единственность разложения.
Пример 3.2. Доказать, что два ненулевых столбца А1 и А2 линейно
зависимы тогда и только тогда, когда они пропорциональны, т.е. А] = ХА2.
□ В самом деле, если столбцы At и А2 линейно зависимы, то сущест-
вуют такие числа cq, а2, не равные нулю одновременно, что
ci] At + а2А2 = о. Причем в этом равенстве cq Ф 0. Действительно, предпо-
ложив, что ОС] = 0, получим противоречие ос2А2 = о, поскольку ос2 0 и
столбец А2 - ненулевой. Значит, cq 0. Поэтому найдется число А. = -^2.
«1
такое, что А] = АА2 . Необходимость доказана.
Наоборот, если А]=АА2, то 1А1ч-(-А,)-А2 =о. Получили нетриви-
альную линейную комбинацию столбцов, равную нулевому столбцу. Зна-
чит, столбцы линейно зависимы.
130
Пример 3.3. Рассмотреть всевозможные системы, образованные из
столбцов
Исследовать каждую систему на линейную зависимость.
□ Рассмотрим пять систем, содержащих по одному столбцу. Согласно
п.1 замечаний 3.1: системы А2, А3, Д4, А5, линейно независимы, а систе-
ма, состоящая из одного нулевого столбца At, линейно зависима.
Рассмотрим системы, содержащие по два столбца:
- каждая из четырех систем А], А2; Aj, А3; Aj, А4 и Aj, А3 линейно
зависима, так как содержит нулевой столбец At (свойство 1);
- система А2 , А3 линейно зависима, так как столбцы пропорциональны
(свойство 3): Aj = 2 • А2;
- каждая из пяти систем А2, А4; А2, А5; А3, А4 ; А3, А5 и А4, А5 ли-
нейно независима, так как столбцы непропорциональные (см. утверждение
примера 3.2);
Рассмотрим системы, содержащие три столбца:
- каждая из шести систем А{, А2, А3; Аг, А2, А4; At, А2, Д5; А,, А3, А4
Aj, А3, As и Aj, А4, А5 линейно зависима, так как содержит нулевой столбец
Aj (свойство 1);
- системы А2, А3, А4; А2, А3; А5 линейно зависимы, так как содержат
линейно зависимую подсистему А2, А3 (свойство 6);
- системы А2, А4, Aj и А3, А4, Л5 линейно зависимы, так как послед-
ний столбец линейно выражается через остальные (свойство 4):
Aj = 2- А2 + Д4 и А3 = Аз + А4 соответственно.
Наконец, системы из четырех или из пяти столбцов линейно зависимы
(по свойству 6).
3.2. РАНГ МАТРИЦЫ
3.2.1. Базисный минор матрицы
Пусть А - матрица размеров техн, а к - натуральное число, не пре-
восходящее тип: к< min{ т; п }. Минором к -го порядка матрицы А
Называется определитель матрицы к -го порядка, образованной элементами,
стоящими на пересечении произвольно выбранных к строк и к столбцов
9« 131
матрицы А - Обозначая миноры, номера выбранных строк будем указывать
верхними индексами, а выбранных столбцов - нижними, располагая их по
возрастанию.
Пример 3.4. Записать миноры разных порядков матрицы
'1 2 1 О'
А= 0 2 2 3
VI 4 3 3)
□ Матрица А имеет размеры 3x4. Она имеет: 12 миноров 1-го по-
рядка, например, минор =det(a32) = 4 ; 18 миноров 2-го порядка, напри-
2 1
2 2
12 '
мер, 2з =
= 2; 4 минора 3-го порядка, например,
В матрице А размеров тпхл минор г-го порядка называется базис-
ным, если он отличен от нуля, а все миноры (г+ 1)-го порядка равны нулю
или их вообще не существует.
Рангом матрицы называется порядок базисного минора. В нулевой
матрице базисного минора нет. Поэтому ранг нулевой матрицы, по опреде-
лению полагают равным нулю. Ранг матрицы А обозначается rg А.
Пример 3.5. Найти все базисные миноры и ранг матрицы
'1 2 2 0'
А= 0 2 2 3
О О О О,
□ Все миноры третьего порядка данной матрицы равны нулю, так как
у этих определителей третья строка нулевая. Поэтому базисным может быть
только минор второго порядка, расположенный в первых двух строках мат-
рицы. Перебирая 6 возможных миноров, отбираем отличные от нуля
2 О
2 3
1 2
О 2
1 О
О 3
•х12 _ .И2 _
Л* 12 -Л»13 -
»ж 12 _ as 12 _
Af 24 - Л? 34 ~
и =
. Каждый из этих
пяти миноров является базисным. Следовательно, ранг матрицы равен 2.
Замечания 3.2.
1. Если в матрице все миноры k -го порядка равны нулю, то равны ну-
лю и миноры более высокого порядка. Действительно, раскладывая минор
132
(& + 1)-го порядка по любой строке, получаем сумму произведений элемен-
тов этой строки на миноры к -го порядка, а они равны нулю.
2. Ранг матрицы равен наибольшему порядку отличного от нуля мино-
ра этой матрицы.
3. Если квадратная матрица невырожденная, то ее ранг равен ее поряд-
ку. Если квадратная матрица вырожденная, то ее ранг меньше ее порядка.
4. Для ранга применяются также обозначения Rg А, rang А, rank А .
5. Ранг блочной матрицы определяется как ранг обычной (числовой)
матрицы, т.е. не обращая внимания на ее блочную структуру. При этом ранг
блочной матрицы не меньше рангов ее блоков: rg (А | В)>rgA и
rg (А | в)> rg В, поскольку все миноры матрицы А (или В) являются так-
же минорами блочной матрицы (А | в).
3.2.2. Теоремы о базисном миноре и о ранге матрицы
Рассмотрим основные теоремы, выражающие свойства линейной зави-
симости и линейной независимости столбцов (строк) матрицы.
Теорема 3.1 (о базисном миноре). В произвольной матрице А каж-
дый столбец (строка) является линейной комбинацией столбцов (строк),
в которых расположен базисный минор.
Действительно, без ограничения общности предполагаем, что в матри-
s це А размеров тхп базисный минор расположен в первых г строках и
? первых г столбцах. Рассмотрим определитель
«11 • «1<- а1к
о = • •
«,1 • • агг агк
«51 ’ а,г <hk
, который получен приписыванием к базисному минору матрицы А соответ-
ствующих элементов s -й строки и к -го столбца. Отметим, что при любых
1<1<ти1<Кл этот определитель равен нулю. Если s < г или к < г, то
определитель D содержит две одинаковых строки или два одинаковых
, столбца. Если же s>rnk>r, то определитель D равен нулю, так как яв-
ляется минором (г + 1)-го порядка. Раскладывая определитель по последней
строке, получаем
asl + — + dsr '&r+ir + ask '^r+lr+l
где Dr+lj - алгебраические дополнения элементов последней строки. Заме-
тим, что Dr+1 г+1 * 0, так как это базисный минор. Поэтому
133
^=^га.51+- + Ча№ где Ху=--——, j = 1,2,..., г.
иг+\ г+1
Записывая последнее равенство для j = 1,2,..., т , получаем
т.е. к -й столбец (при любом 1 < к < п) есть линейная комбинация столбцов
базисного минора, что и требовалось доказать.
Теорема о базисном миноре служит для доказательства следующих
важных теорем [4].
Теорема 3.2 (необходимое и достаточное условие равенства нулю
определителя). Для того чтобы определитель был равен нулю необходимо
и достаточно, чтобы один из его столбцов (одна из его строк) был линей-
ной комбинацией остальных столбцов (строк).
В самом деле, необходимость следует из теоремы о базисном миноре.
Если определитель квадратной матрицы л-го порядка равен нулю, то ее
ранг меньше п, т.е. хотя бы один столбец не входит в базисный минор. То-
гда этот выбранный столбец по теореме 3.1 является линейной комбинацией
столбцов, в которых расположен базисный минор. Добавляя, при необходи-
мости, к этой комбинации другие столбцы с нулевыми коэффициентами,
получаем, что выбранный столбец есть линейная комбинация остальных
столбцов матрицы. Достаточность следует из свойств определителя. Если,
например, последний столбец А„ определителя det(/4] А2 Ап) ли-
нейно выражается через остальные
= А.| •/<| + Л,2 • Л2 +...+ Хя_! An_t,
то прибавляя к Ап столбец А}, умноженный на (-Xj, затем столбец А2,
умноженный на (-Х2), и т.д. столбец Ап_х, умноженный на полу-
чим определитель det(/4( ••• Ля_] о) с нулевым столбцом, который равен
нулю (свойство 2 определителя).
Теорема 3.3 (об инвариантности ранга при элементарных преобра-
зованиях). При элементарных преобразованиях столбцов (строк) матрицы
ее ранг не меняется.
Действительно, пусть rg А = г. Предположим, что в результате одного
элементарного преобразования столбцов матрицы А получили матрицу А'.
Если было выполнено преобразование I типа (перестановка двух столбцов),
то любой минор (г + 1)-го порядка матрицы А' либо равен соответствую-
щему минору (г + 1)-го порядка матрицы А , либо отличается от него зна-
ком (свойство 3 определителя). Если было выполнено преобразование II ти-
134
па (умножение столбца на число А * 0), то любой минор (г + 1)-го порядка
матрицы А' либо равен соответствующему минору (г + 1)-го порядка мат-
рицы А , либо отличается от него множителем А * 0 (свойство 6 определи-
теля). Если было выполнено преобразование III типа (прибавление к одному
столбцу другого столбца, умноженного на число А), то любой минор (г +1)-
го порядка матрицы А' либо равен соответствующему минору (г+ 1)-го по-
рядка матрицы А (свойство 9 определителя), либо равен сумме двух мино-
ров (г + 1)-го порядка матрицы А (свойство 8 определителя). Поэтому при
элементарном преобразовании любого типа все миноры (г + 1)-го порядка
матрицы А! равны нулю, так как равны нулю все миноры (г+ 1)-го порядка
матрицы А . Таким образом, доказано, что при элементарных преобразова-
ниях столбцов ранг матрицы не может увеличиться. Так как преобразования,
обратные к элементарным, являются элементарными (см. п.1 замечаний
1.11), то ранг матрицы при элементарных преобразованиях столбцов не мо-
жет и уменьшиться, т.е. не изменяется. Аналогично доказывается, что ранг
матрицы не изменяется при элементарных преобразованиях строк.
Следствие 1. Если одна строка (столбец) матрицы является линейной
комбинацией других ее строк (столбцов), то эту строку (столбец) можно
вычеркнуть из матрицы, не изменив при этом ее ранга.
Действительно, такую строку при помощи элементарных преобразова-
ний можно сделать нулевой, а нулевая строка не может входить в базисный
минор.
Следствие 2. Если матрица приведена к простейшему виду (1.7), то
rg Л = rg Л = г .
Действительно, матрица простейшего вида (1.7) имеет базисный минор
г -го порядка.
Следствие 3. Любая невырожденная квадратная матрица является
элементарной, другими словами, любая невырожденная квадратная мат-
рица эквивалентна единичной матрице того же порядка.
Действительно, если А - невырожденная квадратная матрица п -го по-
рядка, то rg А = п (см. п.З замечаний 3.2). Поэтому, приводя элементарными
преобразованиями матрицу А к простейшему виду (1,7), получим единич-
ную матрицу А = Еп, так как rg А - rg Л = п (см. следствие 2). Следователь-
но, матрица А эквивалентна единичной матрице Еп и может быть получена
из нее в результате конечного числа элементарных преобразований. Это
означает, что матрица А элементарная.
Теорема 3.4 (о ранге матрицы). Ранг матрицы равен максимальному
числу линейно независимых строк этой матрицы.
135
В самом деле, пусть rg А = г . Тогда в матрице А имеется г линейно
независимых строк. Это строки, в которых расположен базисный минор. Ес-
ли бы они были линейно зависимы, то этот минор был бы равен нулю по
теореме 3.2, а ранг матрицы А не равнялся бы г. Покажем, что г - макси-
мальное число линейно независимых строк, т.е. любые р строк линейно за-
висимы при р>г. Действительно, образуем из этих р строк матрицу В.
Поскольку матрица В - это часть матрицы А , то rg В < rg А = г < р . Зна-
чит, хотя бы одна строка матрицы В не входит в базисный минор этой мат-
рицы. Тогда по теореме о базисном миноре она равна линейной комбинации
строк, в которых расположен базисный минор. Следовательно, строки мат-
рицы В линейно зависимы. Таким образом, в матрице А не более, чем г
линейно независимых строк.
Следствие 1. Максимальное число линейно независимых строк в мат-
рице равно максимальному числу линейно независимых столбцов:
rgA = rgAr.
Это утверждение вытекает из теоремы 3.4, если ее применить к стро-
кам транспонированной матрицы и учесть, что при транспонировании ми-
норы не изменяются (свойство 1 определителя).
Следствие 2. При элементарных преобразованиях строк матрицы ли-
нейная зависимость (или линейная независимость) любой системы столб-
цов этой матрицы сохраняется.
В самом деле, выберем любые к столбцов данной матрицы А и соста-
вим из них матрицу В. Пусть в результате элементарных преобразований
строк матрицы А была получена матрица А', а в результате тех же преоб-
разований строк матрицы В была получена матрица В'. По теореме 3.3
rg В' = rg В. Следовательно, если столбцы матрицы В были линейно неза-
висимы, т.е. к = rg В (см. следствие 1), то и столбцы матрицы В' также ли-
нейно независимы, так как k = rgB'. Если столбцы матрицы В были ли-
нейно зависимы (к > rg В), то и столбцы матрицы В' также линейно зави-
симы (к > rg В'). Следовательно, для любых столбцов матрицы А линейная
зависимость или линейная независимость сохраняется при элементарных
преобразованиях строк.
Замечания 3.3.
1. В силу следствия 1 теоремы 3.4 свойство столбцов, указанное в
следствии 2, справедливо и для любой системы строк матрицы, если эле-
ментарные преобразования выполняются только над ее столбцами.
2. Следствие 3 теоремы 3.3 можно уточнить следующим образом: лю-
бую невырожденную квадратную матрицу, используя элементарные преоб-
разования только ее строк {либо только ее столбцов), можно привести к
единичной матрице того же порядка.
136
В самом деле, используя только элементарные преобразования строк,
любую матрицу А можно привести к упрощенному виду Л (рис. 1.5) (см.
теорему 1.1). Поскольку матрица А невырожденная (det/1*0), то ее
столбцы линейно независимы. Значит, столбцы матрицы Л также линейно
независимы (следствие 2 теоремы 3.4). Поэтому упрощенный вид Л невы-
рожденной матрицы А совпадает с ее простейшим видом (рис. 1.6) и пред-
ставляет собой единичную матрицу Л = Е (см. следствие 3 теоремы 3.3).
Таким образом, преобразовывая только строки невырожденной матрицы, ее
можно привести к единичной. Аналогичные рассуждения справедливы и для
элементарных преобразований столбцов невырожденной матрицы.
Теорема 3.5 (о ранге произведения матриц). Ранг произведения мат-
риц не превышает ранга множителей'. rg(AB)< min{ rg A, rg В }.
В самом деле, пусть матрицы А и В имеют размеры тх р и рхп.
Припишем к матрице А матрицу С = АВ: (А | С). Разумеется, что
rg С < rg(Л | С), так как С - это часть матрицы (А | С) (см. п.5 замеча-
ний 3.2). Заметим, что каждый столбец Cj, согласно операции умножения
матриц, является линейной комбинацией столбцов At, А2 ,..., Ар матрицы
Л = (я, - Ар\.
Cj = A}-b}j+A2-b2j+... + Ap- bpj, j = \, 2,...,п.
Такой столбец можно вычеркнуть из матрицы (я | С), при этом ее ранг не
изменится (следствие 1 теоремы 3.3). Вычеркивая все столбцы матрицы С,
получаем: rg(/l | с) = rg Я . Отсюда, rg С <rg (А | С) = rg А. Аналогично
можно доказать, что одновременно выполняется условие rg С < rg В, и сде-
лать вывод о справедливости теоремы.
Следствие. Если А невырожденная квадратная матрица, то
rg(AB) = rgB и rg(CA)=rgC, т. е. ранг матрицы не изменяется при ум-
ножении ее слева или справа на невырожденную квадратную матрицу.
Теорема 3.6 (о ранге суммы матриц). Ранг суммы матриц не превы-
шает суммы рангов слагаемых'. rg(^ + B)^rg^ + rgB.
Действительно, составим матрицу (А + В | А | в). Заметим, что каж-
дый столбец матрицы А + В есть линейная комбинация столбцов матриц А
и В . Поэтому rg(/4 + B | А | B)=rg(A | В). Учитывая, что количество ли-
нейно независимых столбцов в матрице (Я | в) не превосходит rg А + rg В,
a ^(я + в) < rg^ + В | Я | в) (см. п.5 замечаний 3.2), получаем доказывае-
мое неравенство.
137
3.3. МЕТОДЫ ВЫЧИСЛЕНИЯ РАНГА МАТРИЦЫ
3.3.1. Метод окаймляющих миноров
Находить ранг матрицы по определению - вычисляя миноры всех по-
рядков - очень трудоемкая операция. Следующий алгоритм позволяет
уменьшить число рассматриваемых миноров.
Пусть дана матрица А размеров тхп. Будем говорить, что минор
^j'ji i + О‘го П0РяДка окаймляет (содержит в себе) минор
к -го порядка. При описании метода индексы выбранных строк и столбцов,
в которых располагается минор, будем указывать, не упорядочивая их по
возрастанию. При этом рассматриваемый минор и минор с упорядоченными
индексами равны по абсолютной величине и, быть может, отличаются по
знаку, но это для метода окаймляющих миноров не имеет никакого значе-
ния, поскольку нас интересует только ответ на вопрос: равен минор нулю
или нет.
1. Выбираем строку и столбец у) так, чтобы минор 1-го порядка
= aitjt был не равен нулю. Если это возможно, то rg А > 1, иначе про-
цесс завершается и rg А = 0 .
2. Окаймляем минор * 0, добавляя к выбранным -ой строке и
у) -му столбцу еще строку i2 * /] и столбец у2 у) так, чтобы минор
Af''‘j =
hh
й, i
Ч 71
Я, ,
‘2JI
о, I
'1/2
й, ,
'2/2
0 . Если это возможно, то rg А > 2, иначе процесс за-
вершается и rg А = 2 .
3. Окаймляем минор * 0, добавляя к выбранным ранее строкам и
столбцам новую строку /3 и новый столбец у3 так, чтобы получить минор
* 0 ’ Если это удалось, то rg А > 3 , иначе процесс завершается и
rg А = 3 .
Продолжаем процесс окаймления, пока он не завершится. Пусть най-
ден минор г -го порядка * 0, т.е. rg А > г . Однако, все миноры
(г + 1)-го порядка, окаймляющие его, равны нулю =0 или не
существуют (при г = т или г = п). Тогда процесс завершается и rg А = г.
138
Пример 3.6. Методом окаймляющих миноров найти ранги матриц
ООА (3 9^ (0 2 3
, Л = , 5 =
00/ 12 4/ 1^2 4 6
'10 2 13'
2 0 112
3 0 3 2 5
□ Матрица 0. 1. В этой матрице нет отличных от нуля миноров пер-
вого порядка, так как все ее элементы равны нулю. Поэтому rg О = 0 .
Матрица А . 1. Выбираем первую строку (Zj = 1) и первый столбец
(у'] =1) матрицы А, на пересечении которых стоит ненулевой элемент
Я] । = 3 * 0 . Получили минор = 3 * 0 . Следовательно, rg А > 1.
2. Добавляем к выбранным строке и столбцу еще одну строку i2 = 2 и
еще один столбец j2 = 2. Получаем отличный от нуля минор второго по-
3 9
2 4
рядка М\2 = det А -
= -6*0. Следовательно, rg A > 2.
3. Поскольку исчерпаны все строки и все столбцы матрицы А, мино-
ров, окаймляющих М\2 * 0, нет. Следовательно, rg А = 2 .
Матрица 5.1. Выбираем первую строку и второй столбец матрицы
В , на пересечении которых стоит ненулевой элемент =2*0. Получили
минор М12 = 2 * 0 . Следовательно, rg В > 1.
2. Добавляем к уже выбранным вторую строку и третий столбец. По-
2 3
4 6
лучаем минор второго порядка
Л/’23 =
= 0 . Выбор оказался неудач-
ным, так как получили нулевой минор. Вместо третьего столбца возьмем
первый. Тогда получим отличный от нуля минор второго порядка
2 0
4 2
= 4*0. Следовательно, rg В > 2 .
3. Все строки матрицы В исчерпаны. Миноров третьего порядка нет.
Поэтому rg В = 2.
Матрица С. 1. Выбираем первую строку (i, =1) и первый столбец
(Д=1) матрицы С, на пересечении которых стоит ненулевой элемент
। = 1*0. Получили минор М, =1*0. Следовательно, rg С > 1 .
2. Добавляем к выбранным строке и столбцу еще одну строку i2 = 2 и
г 12 1 0
еще один столбец j2 = 2. Получили минор второго порядка Л/, 2 = .
Выбор второго столбца оказался неудачным, так как получили минор, рав-
139
ный нулю. Возьмем вместо второго третий столбец (j2 = 3). Получим ми-
нор Л/,12 =
= -3*0. Следовательно, rg С > 2.
3. Окаймляем минор * 0. Имеется три окаймляющих минора
Л/123 = м134 1 2 2 1 1 1 = 0, Л/123 = Л7135 - 1 2 2 1 3 2 = 0, Л/123 = '"132 1 2 2 1 0 0 = 0
3 3 2 3 3 5 3 3 0
Три определителя равны нулю, так как третья строка равна сумме первых
двух строк. Следовательно, нельзя найти отличный от нуля окаймляющий
минор 3-го порядка, т.е. ранг матрицы С равен 2.
Замечание 3.4. Метод окаймляющих миноров позволяет умень-
шить по сравнению с определением количество рассматриваемых миноров.
Если в матрице размеров тхп выбран минор г-го порядка
(г < min{ т, п }), то количество окаймляющих его миноров (г + 1)-го поряд-
ка равно —г), а общее количество миноров (г + 1)-го порядка го-
раздо больше.
3.3.2. Метод Гаусса
Пусть дана матрица А размеров тхп. Для нахождения ее ранга нуж-
но выполнить следующие действия.
1. Привести матрицу к ступенчатому виду (см. метод Гаусса в
разд. 1.6.1).
2. В полученной матрице вычислить количество г ненулевых строк.
Это число равно рангу матрицы А .
Замечания 3.5.
1. Обоснованием этого метода служит следствие 2 теоремы 3.4. Базис-
ным минором в матрице ступенчатого вида (см. рис. 1.4) является минор
1 * ... *
О 1 *
0 0-1
составленный из столбцов, содержащих единичные элементы (в начале каж-
дой "ступеньки"). Этот определитель треугольного вида отличен от нуля
(равен 1), а любой его окаймляющий минор (если такой найдется) равен ну-
лю, так как содержит нулевую строку.
140
2. Метод Гаусса для нахождения ранга произвольной матрицы наибо-
лее экономичен, так как требует меньше вычислений, чем другие методы.
Конечно, для матриц какого-либо специального вида (блочных, разрежен-
ных и т.п.) можно предложить более эффективные методы.
(О 0)
Пример3.7. Методом Гаусса найти ранги матриц 0 = 1 q I’
II 53 3? 4k 'О to II 53 o' 4k NJ o\ w Q II '1 0 2 1 3' 2 0 112 k3 0 3 2 5, , D = '1 2 3' 0 0 0 2 1 3 1 1 2 <3 2 5,
□ Матрица 0.1. Нулевая матрица уже имеет ступенчатый вид (см. п.2
замечаний 1.8).
2. Количество ненулевых строк равно нулю. Следовательно, rg О = 0.
Матрица А . 1. Приводим матрицу А к ступенчатому виду (см. при-
мер 1.29):
А
2. В этой матрице две ненулевые строки. Следовательно, rg А = 2.
Матрица В.1. Приводим матрицу
мер 1.29):
В к ступенчатому виду (см. при-
1 2
Oil
2. В этой матрице две ненулевые строки. Следовательно, rg В = 2.
Матрица С. 1. Приводим матрицу С к ступенчатому виду. Взяв в ка-
честве ведущего элемента an = 1, делаем равными нулю остальные элемен-
ты первого столбца: ко второй строке прибавляем первую, умноженную на
(- 2), к третьей строке - первую, умноженную на (- 3). Получаем матрицу
1
2
3
о
о
о
2
1
3
1
1
2
3
2
5
1
О
О
о
о
о
2
-3
-3
1
-1
-1
3 '
-4 ,
-4.
У которой имеются две равные строки. По следствию 1 теоремы 3.3 одну из
равных строк вычеркиваем:
141
10 2 1 3 'l
0 0-3-1 -4J
Получили матрицу ступенчатого вида (см. п. 1 замечаний 1.8).
2. В этой матрице две ненулевые строки. Следовательно, rg С = 2 .
Матрица D . 1. Приводим матрицу D к ступенчатому виду. Вычерк-
нув предварительно нулевую строку, берем в качестве ведущего элемента
Д]! = 1, и делаем равными нулю остальные элементы первого столбца:
Последние три строки матрицы пропорциональны. По следствию 1 теоре-
мы 3.3 две из них можно вычеркнуть:
12 3)
0 -1 -1/
Получили матрицу ступенчатого вида (см. п.1 замечаний 1.8).
2. В этой матрице две ненулевые строки. Следовательно, rg D = 2.
Заметим, что rg С =rg D, так как D = CT (см. следствие 1 теоремы 3.4).
0) (0 0) (0 1
0) 0 11 11 1
. Най-
Пример 3.8. Даны матрицы А =
ти ранги матриц: А + В; А + С ; АВ ; АС .
□ По определению имеем rg Д = 1, rg В = 1, rg С = 2 . Находим суммы
и произведения данных матриц, а также их ранги:
11
д+с =
(о
(1
д-в =
о
О'
0,
О') (°
ОНО
0
+
11
(1
д-с =
0
О'
0.
О'
1.
11-11
1Г 1
°1-1 °
1 J-lo
(Г
1.
, rg (д + в) = 2, т.е. rg (д + в) = rg Д + rg В ;
j, rg(A + C) = l,T.e. rg(A + c)<rgA + rgC;
О'
О,
1'
0.
, rg (дв) = 0, т.е. rg (дв)< min{ rg Д, rg В };
, rg(ДС) = 1,т.е. rg(дс)= min{rg A,rgC}.
(1
д + в =
о
0) (О
+
О о
1
о
о
1
1
1
0
0
Полученные результаты иллюстрируют справедливость теорем 3.5, 3.6.
142
3.4. РАНГ СИСТЕМЫ СТОЛБЦОВ (СТРОК)
Пусть дана система столбцов А, ,А2,..., Ап размеров mxl. Рангом
системы столбцов называется максимальное число линейно независимых
столбцов этой системы и обозначается rg(A1,A2,—,An). Максимальной
линейно независимой подсистемой столбцов (или базой системы столб-
цов [36]) называется линейно независимая подсистема, состоящая из
Tg(Al,A2,.-.,An) столбцов. Максимальность здесь понимается в том смысле,
что любое большее количество столбцов данной системы образует линейно
зависимую подсистему.
Для нахождения максимальной линейно независимой подсистемы
столбцов надо выполнить следующие действия.
1. Составить из данных столбцов матрицу А = (А] А2...Ал) размеров
тхп.
2. Найти базисный минор этой матрицы.
3. Столбцы, в которых расположен базисный минор, образуют иско-
мую подсистему (т.е. базу данной системы столбцов).
Замечания 3.6.
1. Ранг системы столбцов равен рангу матрицы, составленной из этих
столбцов: rg(A1,A2,...,A„) = rg(A1 А2 ••• Ап).
2. У системы столбцов может быть несколько максимальных линейно
независимых подсистем, но все они состоят из одинакового количества
столбцов.
3. Столбцы, в которых расположен базисный минор матрицы
А =(А[ А2 ... Ап), можно найти методом Гаусса. Для этого приводим матри-
цу А к ступенчатому виду, используя только преобразования ее строк (см.
п.2 замечаний 1.11). В матрице ступенчатого вида выбираем базисный ми-
нор (см. п.1 замечаний 3.5). Столбцы, в которых расположен базисный ми-
нор матрицы А , совпадают (по номерам) со столбцами, в которых располо-
жен базисный минор матрицы ступенчатого вида (см. следствие 2 теоре-
мы 3.4 о ранге матрицы).
4. Пусть дана система строк А,, А2 Ал размеров Ixm. Рангом сис-
темы строк называется максимальное число линейно независимых строк
этой системы. Для нахождения максимальной линейно независимой
подсистемы строк нужно составить из этих строк матрицу и найти ее ба-
зисный минор (например, используя только элементарные преобразования
ее столбцов). Строки, в которых расположен базисный минор, образуют ис-
комую подсистему. Другим путем решения задачи является ее сведение к
нахождению максимальной линейно независимой системы столбцов
А[Г , А2 ,..., Aj (см. следствие 1 теоремы 3.4 о ранге матрицы).
143
Пример 3.9. Дана система столбцов
2^1
1
А, = о , А2 = 1 , А3 = 2 , А4 = 2 , As = 4
5
2
3
1
10.
Найти ранг системы и максимальную линейно независимую подсистему
столбцов.
□ 1. Составляем из данных столбцов матрицу
(О 1 2
1
А = (Д А2 А3 А4 А5)= 0 12 2 4
0 1 2
3 5
2. Находим базисный минор этой матрицы. Для этого приводим ее к
ступенчатому виду, преобразовывая только строки:
<0
о
.0
2
2
2
1
2
3
1
1
1
4
5
А =
'о
о
О
3^| Г О
1
2
1
1
о
3
1
о
2
0
0
1
о
о
1
О
О
2
О
О
1
1
2
О
О
1
1
О 1
Следовательно,
М
= 1*0- базисный минор этой матрицы (один
из них) и rg А = 2. Второй и четвертый столбцы преобразованной матрицы
линейно независимы. Так как преобразования выполнялись только над стро-
ками, то второй и четвертый столбцы исходной матрицы
А = (А] А2 А3 А4 А5) также линейно независимы (см. следствие 2 теоре-
мы 3.4). Поэтому ранг системы столбцов равен 2. Следовательно, А2 , А4 -
максимальная линейно независимая подсистема системы столбцов
А], А2, А3, А4, А5 . В примере 3.3 были найдены и другие максимальные ли-
нейно независимые подсистемы, каждая из которых состоит из двух столб-
цов.
Пример 3.10. Дана система строк
А1=(1 2 3), А2=(2 3 1), А3 = (1 3 1),А4=(2 2 3).
Найти ранг и максимальную линейно независимую подсистему строк.
□ 1. Составляем из данных строк матрицу
Л1 2 ЗА
12 2 3J
2. Преобразуем матрицу, используя элементарные преобразования ее
столбцов:
144
о'
о
-7
7,
Хотя это не ступенчатый вид, нетрудно заметить, что минор м}2з = 7*0-
базисный (один из них) и rg А = 3. Поэтому ранг данной системы строк ра-
вен 3. Первые три строки преобразованной матрицы линейно независимы.
Так как преобразовывались только столбцы матрицы, делаем вывод, что
первые три строки исходной матрицы также линейно независимы (см. п.1
замечаний 3.3). Поэтому Л,, Аг, Л3 - максимальная линейно независимая
подсистема строк данной системы.
Задачи для самостоятельного решения
3.1. По определению найти базисный минор и вычислить ранг матри-
цы:
<0 О') '1 -П f 1 o'l
а) 5) J ; в) ’> г)
-2J 0 1J
fl 1 1> <1 2 3 4 \ '1 0
е) 2 2 3 ; ж) 2 4 6 8 ; з) 0 0
<3 3 4, 3 6 9 12 7 .2 0
% 0 ... о 0 о"
о Х2 ... 0 0 ••• 0
и) 0 0 0 0 , где X,- * 0
0 0 ... о 0 0
<° 0 ... 0 0 0,
Ответ:
0
0
0
0
0
0
о
о
1)
о j ’
'о
;д) 0
.1
5^
о
11.
i = 1, 2,
а) базисного минора нет, rg = 0; б) М} = 1, rg = 1;
в) M^ = l, rg = 2; г) =1, rg = l; д) M?23 = -l; rg = 2;
о
1
о
о
о
о
е) Л1‘23=1, rg = 2; ж) м} = 1, rg = l; з) = *
5
И
= 1, rg = 2;
10 - 4549
145
и) Л/|‘^ ’гг =^^2 rg = r. В случаях б), е), ж) базисные миноры опре-
деляются неоднозначно.
3.2. Вычислить ранги матриц, приводя их к ступенчатому виду (мето-
дом Гаусса):
'1 2 3 4'
а) А = 1 2 5 6 ; б)
6 13 16,
10 4 -Г
2 1 11 2
11 4 56 5
J2 -1 5 -6,
0 2
25 31 17 43' -1 -4
75 94 53 132
А- ; в) А = 3 1
75 94 54 134 о с
<25 32 20 48, и 2 □ 3
24 19 36 72 -38'
49 40 73 147 -80
л) А =
73 59 98 219 -118
-4'
5
7 ;
-10
0 ,
Ответ: а) А - 0
10
2
0
О
17 43'
2 3
1 2
0 °,
fl 2 1 3 -4>
0 -29 12 0 58
Д) А ~ 0 0 -11 0 0
<о 0 0 0 0
ределяется неоднозначно.
rgA = 3. Ступенчатый вид матрицы оп-
3.3. Вычислите ранг матрицы методом окаймляющих миноров
(1 0 2 О'
'1 2 3 4' ; б) А = 4 3 1 2
а) А = 1 2 5 6 6 3 5 2
з 6 13 16
<5 3 3 2,
146
Указания-, а) можно рассмотреть цепочку окаймляющих миноров:
М\ *0, МЦ =
б) можно
рассмотреть
.,12 _
Л/]2 -
.,124_
^123 “
#0,
.,123 _
^123 “
3
5
13
= 0, м}” =
цепочку окаймляющих
= 0, м}“ =
= 0, М& =
= 0.
3
5
13
миноров:
= 0,
4
6
16
= 0;
М} *0,
1 3
1 5
* о, м}™ =
1
1
3
2
2
6
1
1
3
1
4
о
3
1
4
6
о
3
3
2
1
5
1
4
6
о
3
3
о
2
2
1
4
5
о
3
3
2
1
3
1
4
5
0
3
3
0
2
2
Ответ: a) rg А = 2; б) rg А = 2.
3.4. При каждом действительном значении параметра вычислить ранг
матрицы:
I Е
а) А = 1
г) А =
Указания:
в)
1
е
1
е
Е2
Е"-1
цепочку окаймляющих
рассмотреть
миноров М, =1*0,
-1
Af^ = l*O, м™ =
2 -1
1 10
= ЗЛ-9, М{Ц =
-6
= -Л + 3;
1
1
1
1 Л
2
5
1
1
2
1
2
5
1
г) вычислить определитель, используя формулу для определителя Вандер-
Л“1
монда (см. пример 2.16 при Xj = 1 ,х2 = Е ,...,хп =е
det А = (е'-1 - е' 1) = Ц е'-1 (е'"' -1).
ISii jin liii jin
Уравнение detA = O имеет три действительных корня Е = 0, Е = ±1. Рас-
смотреть три случая:
ю*
147
1
1
О
при
£ = 0 получаем А =
при
€ = 1 получаем А =
О •
1 ••
1 ••
при
€ = —1 получаем А =
1
-1
1
1 •••'
,т.е. rgA = 2.
1
1
1
1
1
1
1
Ответ: a) rgA = 2 Veg/?; б) rgA = 2 VXg/?; в) rgA = 2 при
Л = 3, rgA = 3 при Л.^3; г) rgA = 2 при Е = 0, rgA = l при е = 1, rgA = 2
при е = -1, rgA = « при е*0 и е^±1.
3.5. В данной системе столбцов найти все максимальные линейно неза-
висимые подсистемы:
ные миноры; б) составить матрицу А = (А! А2 А3
и найти ее базис-
А4), убедиться в том,
что rgA = 4.
Ответ: а) любые два столбца образуют максимальную линейно неза-
висимую подсистему данной системы столбцов; б) искомая подсистема
совпадает со всей системой А(, А2, А3, А4, так как данная система столбцов
линейно независимая.
ГЛАВА 4. ОБРАТНАЯ МАТРИЦА
4.1. ОПРЕДЕЛЕНИЕ, СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ
ОБРАТНОЙ МАТРИЦЫ
Рассмотрим проблему определения операции, обратной умножению
матриц.
Пусть А - квадратная матрица порядка п . Матрица А”1, удовлетво-
ряющая вместе с заданной матрицей А равенствам:
А-1 А = АА~1 = Е,
называется обратной. Матрицу А называют обратимой, если для нее су-
ществует обратная, в противном случае - необратимой.
Из определения следует, что если обратная матрица А-1 существует,
то она квадратная того же порядка, что и А . Однако не для всякой квадрат-
ной матрицы существует обратная. Если определитель матрицы А равен
нулю (det А - 0), то для нее не существует обратной. В самом деле, приме-
няя теорему об определителе произведения матриц для единичной матрицы
Е = А-1 А получаем противоречие
det Е - det(A-1 - а)= det А-1 • det А = det А-1 0 = 0,
так как определитель единичной матрицы равен 1. Оказывается, что отличие
от нуля определителя квадратной матрицы является единственным условием
существования обратной матрицы. Напомним, что квадратную матрицу, оп-
ределитель которой равен нулю, называют вырожденной (особой), в про-
тивном случае - невырожденной (неособой).
Теорема 4.1 (о существовании и единственности обратной матри-
(“и —
цы). Квадратная матрица А =
, определитель которой от-
^an\ '' ‘ апп,
личен от нуля, имеет обратную матрицу и притом только одну.
ГА1 А1 . А 1 ЛЛ1
А’1- 1 • Аг Аг • Аг = —^— А det А
det А <Ал Ал • Ал лл У
А21 ... АЛ1
•• Аг
(4-1)
Аг
- матрица, транспонированная для матри-
^2п • j
Цы, составленной из алгебраических дополнений элементов матрицы А .
149
Матрица А* называется присоединенной матрицей по отношению к мат-
рице А (см. п.4 замечаний 2.3).
В самом деле, матрица —5— А+ существует при условии det Л * 0 .
det Л
Надо показать, что она обратная к А , т.е. удовлетворяет двум условиям:
1) А-1 —— -А+ | = £;
( det A J
2) f——Л+|-Л = £.
det A J
Докажем первое равенство. Согласно п.4 замечаний 2.3, из свойств опреде-
лителя следует, что АА+ =detA-E. Поэтому
А •[ —-— Л+ I = —-— АА* = —-— det А £ = £ ,
V det A J det A det А
что и требовалось показать. Аналогично доказывается второе равенство.
Следовательно, при условии det/l^O матрица А имеет обратную
А~1=-——-А*.
det Л
Единственность обратной матрицы докажем от противного. Пусть
кроме матрицы А~1 существует еще одна обратная матрица В (В * А~1)
такая, что АВ = Е. Умножая обе части этого равенства слева на матрицу
А~1, получаем А~'АВ = А~1Е. Отсюда В = А~1, что противоречит предпо-
Е
ложению В * А"1. Следовательно, обратная матрица единственная.
Замечания 4.1.
1. Из определения следует, что матрицы А и Л-1 перестановочны.
2. Матрица, обратная к невырожденной диагональной, является тоже
диагональной:
1 1 _L
rl I a22 ann ,
[ diag(an, а22,..., = diag —,
3. Матрица, обратная к невырожденной нижней (верхней) треугольной,
является нижней (верхней) треугольной.
4. Элементарные матрицы имеют обратные, которые также являются
элементарными (см. п.1 замечаний 1.11).
150
4.2. СВОЙСТВА ОБРАТНОЙ МАТРИЦЫ
Операция обращения матрицы обладает следующими свойствами:
1. (Л-’У1 = Л;
2. (АВ)~' =В-'А~';
3. кГ=(и-Г;
4. det А~' = —-— ;
det Л
5. Е"' = Е,
если имеют смысл операции, указанные в равенствах 1 - 4.
Докажем свойство 2: если произведение АВ невырожденных квадрат-
ных матриц одного и того же порядка имеет обратную матри1{у, то
(ав)~х = в~'а~' .
Действительно, определитель произведения матриц АВ не равен ну-
лю, так как det(.45) = det А det В , где det А * 0, det В * 0. Следовательно,
обратная матрица (АВ)~1 существует и единственна. Покажем по определе-
нию, что матрица 5-1Л-1 является обратной по отношению к матрице АВ.
Действительно:
(АВ)• (в~'А'1 )= А а~' = АА~' = Е '>
Е
(в-1 А ’ )• (ав) = В-1 (л^л)- в = В~'В = Е.
Е
Из единственности обратной матрицы следует равенство (лв)-1 = В~{ А~х.
Второе свойство доказано. Аналогично доказываются и остальные свойст-
ва [4].
Замечания 4.2.
1. Для комплексной матрицы справедливо равенство, аналогичное
свойству 3:
где * - операция сопряжения матриц (см. разд. 1.4.2).
2. Операция обращения матриц позволяет определить целую отрица-
тельную степень матрицы. Для невырожденной матрицы Л и любого нату-
рального числа п определим Л_я=(л-1) .
J51
ОРТОГОНАЛЬНЫЕ И УНИТАРНЫЕ МАТРИЦЫ
Действительная квадратная невырожденная матрица А называется
ортогональной, если А-1 = АТ. Из определения следуют основные свойства
ортогональной матрицы А .
1. АТА = Е = ААТ.
2. | det А | --1 - модуль определителя ортогональной матрицы равен
единице.
3. Матрица А-1 (или, что то же самое Аг) является ортогональной.
4. Произведение ортогональных матриц одного и того же порядка яв-
ляется ортогональной матрицей.
Докажем последнее свойство. Пусть А и В - ортогональные матрицы
одного и того же порядка. Тогда по свойствам операций обращения и транс-
понирования матриц имеем
(А5)-1 = 5-1А-1 = ВТ Ат = (АВ)Г.
Следовательно, произведение АВ есть ортогональная матрица.
(cosa -sina^
Пример 4.1. Доказать, что матрица А = является орто-
^sina cos a j
тональной.
□ Найдем произведения
4А7' = 'cosa -sina' ksina cos a , 'cosa sina' k-sina cos a, = 'о -? О
АТА = ' cos a -sin a sin a' cos a, 'cos a - sin c? ksina cosa, О — О
Следовательно, по определению Ат = A-1. Вычислим определитель матри-
цы А : det А = cos a sin a -sin a cos a = cos2 a + sin2 a = 1 (см. свойство 2).
Комплексная квадратная невырожденная матрица А называется
унитарной, если А-1 - А*. Следующие свойства унитарной матрицы А
аналогичны свойствам ортогональной матрицы.
1. АА* =Е = А*А.
2. | det А | = 1 - модуль определителя унитарной матрицы равен еди-
нице.
3. Матрица А~1 является унитарной.
4. Произведение двух унитарных матриц одного и того же порядка яв-
ляется унитарной матрицей.
152
4.3. СПОСОБЫ НАХОЖДЕНИЯ ОБРАТНОЙ МАТРИЦЫ
Пусть дана квадратная матрица А. Требуется найти обратную мат-
рицу А~1.
Первый способ. В теореме 4.1 существования и единственности обрат-
ной матрицы указан один из способов ее нахождения.
1. Вычислить определитель det А данной матрицы. Если detA=O, то
обратной матрицы не существует (матрица А вырожденная).
2. Составить матрицу из алгебраических дополнений
A.. =(-iy+J Му элементов матрицы А.
3. Транспонируя матрицу (а^.), получить присоединенную матрицу
4. Найти обратную матрицу (4.1), разделив все элементы присоединен-
ной матрицы на определитель det А: А-1 = —-— А+.
det А
Второй способ. Для нахождения обратной матрицы можно использо-
вать элементарные преобразования.
1. Составить блочную матрицу (А | Е), приписав к данной матрице А
единичную матрицу того же порядка.
2. При помощи элементарных преобразований, выполняемых над стро-
ками матрицы (а | Е), привести ее левый блок А к простейшему виду Л
(1.7). При этом блочная матрица приводится к виду (Л | S), где S - квад-
ратная матрица, полученная в результате преобразований из единичной мат-
рицы Е.
3. Если Л = Е, то блок S равен обратной матрице, т.е. S = А-1. Если
Л * Е , то матрица А не имеет обратной.
В самом деле, при помощи элементарных преобразований строк мат-
рицы (а | Е) можно привести ее левый блок А к упрощенному виду Л
(см. рис. 1.5). При этом блочная матрица (а | Е) преобразуется к виду
(Л | S), где 5 - элементарная матрица, удовлетворяющая равенству
Л = SA . Если матрица А невырожденная, то согласно п.2 замечаний 3.3 ее
упрощенный вид совпадает с единичной матрицей Л = Е. Тогда из равенст-
ва Е = Л = SA следует, что S = А-1. Если же матрица А вырожденная, то ее
упрощенный вид Л отличается от единичной матрицы, а матрица А не
имеет обратной.
Замечания 4.3.
[ а b ]
1. Для невырожденных квадратных матриц Л= второго поряд-
ке “)
ка можно указать простое правило нахождения обратной матрицы, следую-
щее из первого способа:
а) поменять местами элементы на главной диагонали;
б) изменить знаки у элементов побочной диагонали;
в) поделить полученную матрицу на
В результате получим обратную матрицу
Л''-----1- И
ad - be I - с
определитель det А = ad —be.
(4-2)
Действительно, следуя первому способу, имеем:
_ /.\ ( d
-b
I. det А = ad - be;
2.
3. A
-b} , 1
; 4. А 1 =
а I
-b
ad-be а )
2. Второй способ нахождения обратной матрицы при помощи элемен-
тарных преобразований данной матрицы может быть реализован следую-
щим образом (см. п.2 замечаний 1.12).
1. Составить блочную матрицу — ,
приписав к данной матрице А
а
а
d
— c
единичную матрицу того же порядка.
2. При помощи элементарных преобразований над столбцами привести
блочную матрицу к виду — . В полученной матрице блок Т равен обрат-
\Т )
ной матрице, т.е. Т = А~1.
(1 2 ]
Пример 4.2. Дана матрица А = I I. Найти обратную.
□ Первый способ. 1. Находим определитель det Л =
1 2
1 4
этому матрица А невырожденная и, следовательно, имеет обратную.
2. Составляем матрицу из алгебраических дополнений:
= 2*0. По-
154
3. Транспонируя матрицу получаем присоединенную матрицу
-2
1
4. Разделив все элементы присоединенной матрицы на определитель
det А = 2, находим обратную матрицу: А~'
Сделаем проверку
' 2
1
к 2
О
1
-п
1 (4 2
2\-1 1Дч
х
2 7
Используя правило, указанное в п.1 замечаний 4.3, для матрицы
'1 2Wa b'
J 4J d;
получаем А
1 ( d
det АI - с
1
2 У
„ .„—ill
Заметим, что det л = — =-.
2 det Л
Второй способ. 1. Составляем блочную матрицу
(Я | Е) =
1 2
1 4
1 °)
0 1)
2. Элементарными преобразованиями над строками приводим ее к про-
стейшему виду (е | Л”1). Ко второй строке прибавляем первую строку, ум-
ноженную на ( -1):
, , , 2 1 0W1 2 1 (П
4 0 J~[0 2 -1 1/
Теперь к первой строке прибавим вторую, умноженную на (-1):
'12 1 0Н1 0 2 -Г1
ч0 2 -1 1До 2-1 1 )'
Для получения в левом
строку на 2:
'1
<0
блоке единичной матрицы надо разделить вторую
0 2 -Г '1 0 2 -1
2 -1 1, | о 2 2
А'1
' 2
I 2
В правом блоке получили обратную матрицу
-Г
1
2 J
155
fl 2 С
Пример 4.3. Дана матрица А = О 1 О
^0 2 2)
Найти обратную.
□ Первый способ. 1. Находим определитель матрицы det А = 2.
2. Находим алгебраические дополнения данной матрицы:
= -2;А22=(-1)2+2-
и составляем из них матрицу
I’1
О '
-2
3. Транспонируя матрицу (/t), получаем
присоединенную матрицу
-2 -Г
2 О
-2 L
4. Разделив все элементы присоединенной матрицы на определитель
det А = 2, получим обратную матрицу: А' -1 __ d 2 1 etA р А+ 2 '1 0 0 -1 1 -1 р 2 0 1 2 7
'1 -1
0
Проверим равенство А *А = Е : 0 1 0 0 1 0 = 0 1 0
0 -1 к 2 / 2 2 |о 0
Второй способ. 1. Составим блочную матрицу (А | Е), приписав к мат-
рице А единичную матрицу того же порядка:
'1 2 1
(А | Е)= 0 1 О
.0 2 2
1 0 О'
0 1 0
0 0 1,
2. Элементарными преобразованиями над строками приводим ее к виду
156
'12 11
0 10 0
к0 2 2 0
'10 11
0 10 0
0 0 10
О 0W1 о
10-01
о 1J |о о
-2
1
-1
11-2 0''
0 0 10
2 0-2 1;
-1
1
-1
.ХА
2
о
1
2 7
В правом блоке получаем обратную матрицу А-1 =0 1
Л
2
О
1
2 J
О -1
ОБРАЩЕНИЕ БЛОЧНЫХ МАТРИЦ
Пусть квадратная невырожденная матрица Q (т+п)-го порядка раз-
бита на блоки
(А В)
О =-------,
(,С DJ
где А — невырожденная квадратная матрица т -го порядка, а В, С, D -
произвольные матрицы размеров тхп, пхт, пхп соответственно.
Обратная матрица Q существует и находится по формуле Фробениуса
[Ю]:
! _ (А-1 + A~xBNCA~l
-NCA'1
-A~lBN
(4.3)
где N = [d~CA~1 в] 1. Эта формула сводит обращение матрицы (т + л)-го
порядка к обращению двух матриц А и N меньшего порядка (т и п соот-
ветственно).
Если предположить, что матрица D - невырожденная (вместо матри-
цы А), то формула имеет вид:
е-1 = Г м -MBD~X 'I 9
-D~lCM D~l +D~lCMBD'\
где М = (а - BD~xc] ' - квадратная матрица т -го порядка.
Наконец, если обе матрицы А и D невырожденные, то
Q~l =( M -MBD~X> M -a~1bn} (4.4)
~D'XCM N J -NCA~l N J
157
где, как и ранее, М =(a-BD~1c) ’, N = {р-СА ’в) * - квадратные мат-
рицы порядков т и п соответственно.
Доказательство формул (4.3), (4.4) сводится к умножению блочных
матриц (см. разд. 1.5.1).
Пример 4.4. Найти обратную для блочной матрицы
О 1
-1 О
О 1
1 2
f 1 -1
-1 2
О
. 2
Q =
2
О
□ Матрица А - невырожденная второго порядка. Применяя правило
(4.2), последовательно находим:
"I 2 7 "[1 J'
"О 2V2 2\
ч2 oJtl V И 2J’
. (О 1^1 (2 2V 0 1^1 (О П Г-2
D-CA ЧВ =
Ц 2) ^4 2Д-1 Oj ^1 2) — 2
у = (d-ca^b)-1 =—Г 2
v ' -H-3
A'lB =
'0
-1
(2
Jl3
A~lBNCA~l =
-3V2 2W-4
-1Д4 2j \-2
2)1] _i (-2
; A-1 + A-1 BNCA 1 =
0 (-1
"2 -1Y2 2W0 2^
ч3 -2Д4 2j^-2 2)
Г-2 3 -4 3 А
-1 1 -1 1
По формуле (4.3) имеем Q 1 = 0 -2 2 -1
< 2 ~2 3 -2J
Учитывая, что матрица D в данной блочной матрице Q является не-
вырожденной, обратную матрицу Q 1
можно найти по формуле (4.4). Вы-
'2 f|
J J
П Г-1
числяем левый верхний блок матрицы
Q~l (остальные блоки такие же как
формуле (4.3):
। ( 1
A-BD~lC =
_11-(0
2 JI-1 °Л1
1W0 2)_( 1 -1) Г 0 2
О)!2 0 " 1-1 2 J~l-2 4
158
Г1 -31 ( . \-i (1 -31 (-2 3
= ; M={A-BD~lc) =
I1 ~2) V I1 ~2J I"1 к
Результаты вычислений по формулам (4.3) и (4.4) совпадают.
Замечание 4.4. Если определитель Д =
разбит на четыре
блока, где матрицы А и D - квадратные, то справедливы формулы [10]:
Д = |А|| D-CA~'b\ при|АрО;
Д=| А-5О-1с||о| при|ОрО.
В частном случае, когда все четыре матрицы А , В, С, D квадратные
одного и того же порядка, справедливы формулы Шура:
Д = | AD-ACA~'B^ при|А|?*0;
Д = | AD-BD~lCD\ npH|DpO.
Если матрицы А и С перестановочны (АС = СА ), то Д = | AD-СВ |, а ес-
ли матрицы С и D перестановочны, то Д = | AD - ВС |.
Докажем, например, формулу Д = | а|- О-СА-1В . Пусть А и D -
квадратные матрицы т -го и п -го порядков соответственно, причем
А
* 0. Составим блочную матрицу S =
Ет
-СА~1
О1
, где О - нулевая
О I
— в результате прибавления ко второй ее строке блоков
Еп)
матрица размеров тхп. Матрицу S можно рассматривать как элементар-
ную блочную матрицу, так как она получена из единичной блочной матрицы
( Ет
F =1 ——
^т+п I фГ
первой строки блоков, умноженных на матрицу (-СА-1). Умножим блоч-
(А В
ную матрицу I — —
слева на матрицу S :
( Ет О1 В1 U_| в
(-С4-' EJ 1с dJ И d-ca~'b
Найдем определители матриц в левой и правой частях этого равенства. Оп-
ределитель матрицы S равен единице, так как это нижняя треугольная чи-
словая матрица с единицами на главной диагонали (см. п.1 замечаний 2.2).
Определитель матрицы в правой части равен | Aj-I D-CA~lB , так как это
159
блочно-треугольная матрица (см. п.2 замечаний 2.4). По теореме 2.2 об оп-
ределителе произведения матриц получаем доказываемую формулу
А В
С D
О
-СА~' Е„
А
От
В
d-ca-'b
<=> 1-Д = | А | | D-CA-'B |.
4.4. МАТРИЧНЫЕ УРАВНЕНИЯ
Рассмотрим матричное уравнение вида
АХ = В,
(4.5)
где А и В - данные матрицы, имеющие одинаковое количество строк,
причем матрица А квадратная. Требуется найти матрицу X, удовлетво-
ряющую уравнению (4.5).
Теорема 4.2 (о существовании и единственности решения матрич-
ного уравнения (4.5)). Если определитель матрицы А отличен от нуля, то
матричное уравнение (4.5) имеет единственное решение X = А~1 В.
В самом деле, подставляя X - А~1В в левую часть равенства (4.5), по-
лучаем ^(я-1д)= АА~1 В = В , т.е. правую часть этого равенства.
Е
Заметим, что решением матричного уравнения АХ = Е служит обрат-
ная матрица X = Л-1.
Рассмотрим также матричное уравнение вида
YA = В , (4.6)
где А и В - данные матрицы, имеющие одинаковое количество столбцов,
причем матрица А квадратная. Требуется найти матрицу У, удовлетво-
ряющую уравнению (4.6).
Теорема 4.3 (о существовании и единственности решения матрич-
ного уравнения (4.6)). Если определитель матрицы А отличен от нуля, то
уравнение (4.6) имеет единственное решение Y = ВА~1.
Заметим, что матрица X является как бы "левым" частным от "деле-
ния" матрицы В на матрицу А , поскольку матрица X в (4.5) умножается
на А слева, а матрица Y - "правым" частным, так как матрица Y в (4.6)
умножается на А справа.
Пример 4.5. Даны матрицы А =
Решить уравнения: а) АХ = В ;
( 2
б)
□ Обратная матрица А 1
2 ]
, в =
4
YA = B-
3 Ч С =
4 6)
3
5
в) YA = C.
2'
4
6,
была найдена в примере 4.2.
1
2
2
2 У
160
а) Решение уравнения АХ = В находим, умножая обе его части слева
на А~1: Х = А~1В = _±
-Г
1
2 У
1 3 5'
2 4 6>
'О 2 4'
1 ± 1
к2 2 2/
б) Уравнение не имеет решений, так как матрицы А и В имеют раз-
ное количество столбцов (2*3).
в) Решение уравнения YA = С находим, умножая обе его части справа
'1 2' ' 2 -С '1 0 '
на А"1: У = СА~' = 3 4 _ 1 х = 4 -1 .
<5 6, к 2 2 ) -2>
Пример 4.6. Решить уравнение: ВХ + 2Х - Е, где В =
□ Преобразуя левую часть уравнения:
ВХ + 2Х = ВХ + 2ЕХ = (В + 2Е)Х,
приведем его к виду (4.1)
АХ = Е, где А = В + 2Е -
'1
2
2
2
4
Следовательно, X = А~ХЕ = А~1. Обратная матрица найдена в примере 4.2:
А 1 = , ! . Значит, X = А 1
2 J
' 2 -Г|
_1 1
к 2 2 J
Пример 4.7. Решить уравнение АХВ = С , где
А =
1 21
1 4
1
О
о
2
1
2
3 5
4 6
С =
О ,
2.
2
□ Обратные матрицы А~1 =
-1
В~1 = О
1 -1
1
О -1
были
и
2
О
2
2
2 ;
найдены в примерах 4.2, 4.3 соответственно. Решение уравнения находим по
формуле X = А 1СВ
-1
1
-1
1
О
о
2
2
2
о
3
4
5
6
2
2 7
1
О
О
Го
2J
1
-1
Го -2 2
т °
\2
2
4
2
о
2
И -4549
161
Г1 21 Г1 о
Пример 4.8. Решить уравнение АХ = В, где А = I I, В = I
□ Определитель матрицы А равен нулю, следовательно, обратная
матрица не существует. Поэтому нельзя использовать формулу X = А 1В.
Будем искать элементы матрицы X =
'а
b'
. Подставляя в уравнение, по-
лучаем
1 (а
2 [с
&W1
dJIjZ oj
Находим произведение, а затем приравниваем соответствующие элементы
матриц в левой и правой частях уравнения:
( а+ 2с b + 2d fl (А а+ 2с = 1,
12а + 4с 2b + 4dJ (2 0) ** b+2d=0.
Здесь, учитывая пропорциональность уравнений, в системе оставлены толь-
ко два уравнения из четырех. Выразим неизвестные а и Ь :
а = 1 — 2с,
b = -2d.
Следовательно, решение матричного уравнения имеет вид
fl—2с -2d\
X = , где параметры с и d могут принимать любые значе-
k с )
ния. Таким образом, данное матричное уравнение имеет бесконечное мно-
жество решений.
4.5. ПОЛУОБРАТНАЯ И ПСЕВДООБРАТНАЯ МАТРИЦЫ
Как следует из теоремы 4.1, невырожденная квадратная матрица имеет
обратную матрицу и притом только одну. Рассмотрим проблему "обраще-
ния" вырожденных и неквадратных матриц.
4.5.1. Односторонние обратные матрицы
Пусть А произвольная матрица размеров тхп. Матрица разме-
ров пхт называется правой обратной матрицей для матрицы А, если
АА~? -Ет . Матрица AJ1 размеров пхт называется левой обратной для
матрицы А , если А~1А = Еп. Каждую из этих матриц называют односто-
ронней обратной.
Обратная матрица А-1 согласно определению АА~1 =Е = А-1 А явля-
ется левой и правой обратной одновременно. Наоборот, если для матрицы
А существуют левая обратная и правая обратная матрицы, то из равенств
162
л;1 = а;’(аа^) = а^аа"1 = = а;'р
Е„ Е'
следует, что они совпадают между собой и с обратной матрицей:
AJ^A^A"1.
Непосредственное применение односторонних обратных матриц за-
труднительно, так как произвольная матрица может не иметь ни левой, ни
правой обратной. Поэтому эти матрицы не решают полностью проблему
"обращения" вырожденных и неквадратных матриц.
Рассмотрим другой подход к "обращению" матриц, связанный с эле-
ментарными преобразованиями матриц.
СКЕЛЕТНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
При помощи элементарных преобразований (см. теорему 1.2) любую
ненулевую матрицу А размеров тхп можно привести к простейшему виду
(1.7):
А = SAT, (4.7)
где S и Т - элементарные преобразующие матрицы порядков тип соот-
ветственно, а А - матрица размеров тхп простейшего вида (см. рис. 1.6):
А =
О
О'
О,
(4-8)
В (4.8) матрица Ег - единичная г -го порядка (г = rg А, 1 < г < min{т;п }),
О - нулевые матрицы соответствующих размеров.
Матрицы S и Т получены из единичных матриц Ет и Еп при помо-
щи элементарных преобразований над строками или столбцами соответст-
венно (см. разд. 1.6.3). Согласно п. 4 замечаний 4.1, элементарные матрицы
имеют обратные, которые также являются элементарными. Следовательно,
обратные матрицы S-1 и Т-1 существуют и являются элементарными.
Поэтому равенство (4.7) можно записать так:
А = 5-1ЛТ-1. (4.9)
Используя представление (4.8), получаем
| О)-ТЛ=ВС.
I О О (OJ ------------
4 7 у_______i с
в
Таким образом, любую ненулевую матрицу А размеров тхп можно
представить в виде произведения
А = ВС ; В = S~l
Jo/
C = (Er | О)?"1, (4.10)
и*
163
где В и С - матрицы размеров тхг и гхп соответственно, причем
г = rg А. Представление ненулевой матрицы в виде произведения матриц
(4.10) называется скелетным разложением матрицы [10]. Матрицы В и С
в разложении определяются неоднозначно. Они зависят от выбранной по-
следовательности элементарных преобразований (см. п.1 замечаний 1.12).
Нетрудно показать, что матрицы В и С в (4.10) имеют левую обрат-
ную и правую обратную соответственно:
5;’=(Er |V)S;
(4-11)
где U и V произвольные матрицы размеров (л-г)хг и
гх(т-г).
В самом деле, вычисляя произведения
С р \ ( р Л
= (Ег | V)^ = (Ег | = Ег,
получаем единичные матрицы.
Таким образом, любую ненулевую матрицу можно представить в виде
произведения (4.10) двух матриц, каждая из которых имеет одностороннюю
обратную (4.11).
4.5.2. Полуобратная матрица
Пусть А - произвольная матрица размеров тхп. Матрица А-4 раз-
меров пХт называется полуобратной для матрицы А , если выполняется
условие [40]:
АА”’1А = А. (4.12)
Если, кроме того, выполняется условие
А^АА^’=аЛ (4.13)
то матрицу А-’1 называют взаимной полуобратной. Далее будут рассмат-
риваться только взаимные полуобратные матрицы, поэтому термин взаим-
ные будем опускать для краткости.
Заметим, что если матрица А имеет обратную А-1, то она также явля-
ется и полуобратной (а-11 = А-1), так как условия (4.12) и (4.13) для обрат-
ной матрицы выполняются:
АА^А = ЕА = А и А"1 АА"1 = ЕА'1 = А'1.
Е Е
Замечание 4.5. Из определения следует, что
164
В самом деле, находя сопряженные матрицы (см. разд. 1.4.2) для обеих час-
тей равенств (4.12), (4.13), получаем
а*(а^а* = аг, (а^а*(а^ =(а^.
Следовательно, матрица (а~- полуобратная к сопряженной матрице А*.
АЛГОРИТМ НАХОЖДЕНИЯ ПОЛУОБРАТНОЙ МАТРИЦЫ
Пусть дана ненулевая матрица А размеров тхп. Для нахождения по-
луобратной А-11 нужно выполнить следующие действия.
1. Составить блочную матрицу
А
А
, приписывая к матрице А
слева и снизу единичные матрицы соответствующих размеров. Правый
нижний блок этой матрицы может быть произвольным, так как не участвует
в дальнейших преобразованиях.
2. Элементарными преобразованиями над первыми т строками и пер-
(Л. S
выми п столбцами привести блочную матрицу к виду I —
матрица размеров тхп простейшего вида (4.8), г = rg А.
3. Записать полуобратную матрицу
, где Л -
А~'1=Т-
(4.14)
где U и V - произвольные матрицы размеров (л-г)хг и гх(т-г) соот-
ветственно.
В первых двух пунктах алгоритма фактически находится скелетное
разложение (4.10) матрицы А :
/ р \
А = ВС; B = S~1- -^J, С = (ЕГ | д) Т~\
не вычисляя, однако, самих множителей В и С. Учитывая (4.11), матрицу
(4.14) можно представить в виде
А-1=С^В;1. (4.15)
Докажем, что матрица (4.15) является полуобратной. Нужно проверить ра-
венства (4.12) и (4.13). Подставляя матрицы А = ВС и А-11 - С~? • В~1
в (4.12) и (4.13), убеждаемся в справедливости этих равенств
АА^А = ВС С;' в;1 ВС = ВС = А-,
165
а^'аа-11 = С"1 вЛвс^в;1 - с;Х = а-1 .
Следовательно, матрица (4.15) (или, что то же самое, (4.14)) является полу,
обратной.
Замечания 4.6.
1. Из алгоритма следует, что любая матрица А имеет хотя бы одну по-
луобратную матрицу. Если матрица А обратима, то обратная матрица A-11
как следует из (4.12), является полуобратной, т.е. А-11 = А-1. Если исходная
матрица А нулевая размеров тхп, то любая матрица А-11 размеров пхт
удовлетворяет условию (4.12), т.е. является полуобратной (но не взаимной
полуобратной). Взаимная полуобратная матрица А-11 для нулевой матрицы
А это нулевая матрица размеров пхт.
2. Первые два пункта алгоритма совпадают с алгоритмом нахождения
элементарных преобразующих матриц (см. разд. 1.6.3).
3. Полуобратная матрица (4.14) определена неоднозначно. Элементы
матриц U и V можно выбрать произвольным образом. Справедливо и об-
ратное утверждение [40]: любая взаимная полуобратная матрица А-11 для
ненулевой матрицы А может быть записана в виде (4.14), (4.15). Ничего
плохого в этой неоднозначности нет. Более того, в зависимости от приложе-
ния, выбирая надлежащим образом матрицы U и V , можно придать полу-
обратной матрице дополнительные свойства.
4. Если поставлена задача нахождения хотя бы одной полуобратной
матрицы, то проще всего в формуле (4.14) взять матрицы U и V нулевыми.
Тогда в п.З алгоритма получим полуобратную матрицу
AJl=T-AT-S, (4.16)
где А - матрица простейшего вида (4.8), полученная в п.2 алгоритма.
5. Если строки или столбцы матрицы А (размеров тхп) линейно не-
зависимы, то в формуле (4.14) отсутствует блок V или блок U
соответственно:
А-11 -Т-(Еп | V)-S при г = п.
А=Т- -S при г =
и
Если г = т = п, то А - невырожденная квадратная матрица, которая имеет
обратную и А-11 = А-1.
' 1 -1 2 0
Пример 4.9. Для матрицы А=-1 2 -3 1 найти полуобратную.
to 1 -1 1J
□ 1, 2. Первые два пункта алгоритма выполнены при решении приме-
ра 1.29, где получены матрицы
166
л =
'1 0 0 0'
0 10 0
о о о о,
( 1 О О')
S = 1 1 о
1-1 -1 1,
'1 1 -1 -Г
0 11-1
0 0 10
,о о о ь
удовлетворяющие равенству Л = SAT. Осталось выполнить п.З алгоритма.
3. Найдем хотя бы одну полуобратную матрицу, воспользовавшись
формулой (4.16):
'l 1
О 1
О О
О О
О'
О
О
о>
'1
1
-1
О
1
-1
О'
О
1,
'2
1
О
ч0
1
1
О
о
Нетрудно проверить, что эта матрица полуобратная:
О'
о
о
О,
-1
2
1
2
-3
-1
О'
1
1,
Найдем множество всех полуобратных матриц по формуле (4.14). Оп-
РОДелим размеры матриц U и V . Так как т-3, п = 4 и г = rg А = 2 , то
167
матрица U имеет размеры 2x2, а V - 2x1. Обозначим элементы этих
матриц через
(a b'
U Iе J’
Запишем полуобратную матрицу (4.14)
I S
У =
u
, (Е,}
А^=т\ —
О
1
5
t
' 1 О О'
1 1 О
Г1 ’I h
5
t
При любых значениях параметров полученная матрица будет полуоб-
ратной. Возьмем, например, следующие значения параметров: а - —; Ь = 0 ;
с = —; d=—; j = — ; t = —. Тогда получим полуобратная матрицу
Проверка условий (4.12), (4.13) делается так же, как в первом варианте.
Пример 4.10. Используя полуобратную матрицу, решить уравнение
fl 2^ Г1 oS
АХ = В, где А = , В =
1^2 4) ^2 0)
□ Определитель матрицы А равен нулю, следовательно, обратная
матрица не существует. Пусть матрица А-11 полуобратная для А . Уравне-
ние АХ = В запишем, используя равенство (4.12):
АА^АХ = В.
Заменяя в левой части произведение АХ матрицей В , получаем
АА~'1В = В.
Отсюда следует, что матрица А^В является одним из решений уравнения
АХ = В , т.е. X = А^1В . Получим это решение, используя алгоритм нахож-
дения полуобратной матрицы.
168
1. Составим блочную матрицу
U и V. Так как т = п = 2 и г = 1, то
/и-г) = 1х1.
и d : U = (с),
3. Определим размеры матриц
матрица U имеет размеры (л-г)хг = 1x1, матрица V - rx(i
Обозначим единственные элементы этих матриц через с
V = (</). По формуле (4.14) запишем полуобратную матрицу:
1
-2
0
1
А~^=Т-
1-2с
1 - 2c - 2d + 4cd d - 2cd
c - 2cd cd
Умножая ее справа на матрицу В , получаем решение уравнения
1-2с О
с О
Х=А~"В =
1 — 2с — 2d + 4cd d — 2cd
с — 2cd cd
'1 О'
.2 О,
Таким образом, для любого значения параметра с полученная матрица бу-
дет решением уравнения. Заметим, что
шения этого уравнения:
в примере 4.8 были найдены все ре-
(1-2с
Х =
-2d
d
где параметры с и d могут принимать любые значения. Сравнивая эту мат-
рицу с полученной при помощи полуобратной матрицы, видим, что найдены
не все решения уравнения, а лишь соответствующие нулевому значению па-
раметра d.
169
4.5.3. Псевдообратная матрица
Обратная матрица в отличие от полуобратной имеет в силу определе-
ния очевидные свойства:
(аА'1)‘ = АА'1 и (а-1 а)* = А'1 А,
так как единичная матрица Е = АА-1 = А-1 А, разумеется, эрмитова (см.
разд. 1.4.2). В определении полуобратной матрицы имеется некоторый про-
извол (см. п.З замечаний 4.6), которым можно воспользоваться так, чтобы
полуобратная матрица обладала аналогичными свойствами.
Пусть А - произвольная матрица размеров тхп. Полуобратная мат-
рица А'1 размеров пхт называется псевдообратной для матрицы А [35],
если матрицы АА'1 и А“*А эрмитовы, т.е. псевдообратная матрица А"1
определяется четырьмя условиями
АА~*А = А; А~1АА~1=А~1; (4.17)
(АА'1)’ = АА'1; (а^а)* = А'1 А. (4.18)
Покажем, что псевдообратная матрица А'1 существует для любой
матрицы А . Действительно, если А = О - нулевая матрица размеров тхп,
то А'1 = ОТ - нулевая размеров пхт, что следует из равенств (4.17).
Пусть матрица А — ненулевая. Тогда матрица А'1, удовлетворяющая
равенствам (4.17), имеет вид (4.14):
lv)’s- (4-19)
Покажем, что выбором матриц U и V в формуле (4.19) можно получить
матрицу, удовлетворяющую условиям (4.18). В самом деле, запишем ске-
летное разложение (4.10) матрицы А :
А = 5"1Л7”1 =5'1Г^Ц-^1т"1 =S-1-f—l-(Er I
\О О) {О) ' г ' '
Найдем произведение
АА'1 =5'1-| —|-(Ег | О)-72Ц1| —|-(£г I V)-S =
Ч / Е„ \ J
= I I V)-5 = S'1-^V)-S =
E,
s.
Подставим его в первое из равенств (4.18):
170
V
о
s
l о
V)
— -S.
О)
Используя свойства операции сопряжения, а также п. 1 замечаний 4.2, полу-
чаем
Умножая обе части равенства на матрицу S слева и на матрицу 5* справа,
приходим к равенству
Е,
V'
Подставим в это равенство матрицу SS*, предварительно разбив ее на бло-
ки SS* =[—
и прямоугольными матрицами S2 и S3 размеров rx(m-r) и (т-г)хг со-
ответственно. Выполняя умножение блочных матриц, получаем
— с квадратными матрицами St и S4 порядков г и \rn-r)
$4j
5з
О] J St+S2V
Р+54У
S2 + VS/I
О ,
Si+VS3
о
$2
54
Равенство полученных блочных матриц обеспечивается условием
v = -x2x;1,
поскольку 53 = S2, = 5*, S4 = 5* в силу эрмитовости матрицы SS*, а
(Хд1)* =(54]Г1 (см. п. 1 замечаний 4.2).
Аналогичным образом можно показать, что второе из равенств (4.18)
выполняется, если положить
и=-т41т3,
где Т3, Т4 - блоки размеров (л-г)хг и (л-г)х(п-г) матрицы
(
7’7’-р
Таким образом, для любой матрицы существует псевдообратная
матрица и притом только одна [10].
т4
Er VA (Sj
О
о
53
О
о
О
о
171
Замечания 4.7.
1. Если матрица А обратимая, то обратная матрица А 1, как следует
из п.1 замечаний 4.6, совпадает с псевдообратной, т.е. А"1 = А~1.
2. Из невырожденности матриц S и Т следует, что при любом раз-
биении эрмитовых матриц
SS*
Si
S3 S4
A)
на квадратные блоки , S4, TJ, T4, существуют обратные матрицы 5j1,
S4l, 7J-1, Tf1 (см. п.4 замечаний 8.12).
3. Имеются другие определения псевдообратной матрицы [3,10,35],
равносильные приведенному выше. Например, в [3]
А'1 = 1нп(а*А+е2-е)~ А* = limА*-(а*А + е2-eY .
е-хг ' е-х) ' '
4. В общем случае (ав)~1 * В'1 • А'1.
СВОЙСТВА ПСЕВДООБРАТНОЙ МАТРИЦЫ
Операция псевдообращения матриц обладает следующими свойствами:
1.(л-'У=л;
хкГМл-П
3. А'1 = (а*а)"1 А* = а'(аа‘У ;
4. (ААЧУ = АА~‘;
5. (а^а)2 = А'1 А.
Эти свойства доказываются по определению (4.17), (4.18). Докажем,
например, свойство 3 (первое равенство). По определению псевдообратной
матрицы имеем:
(а* а)-’А*
А- (а*а)'1 А*
Следовательно, А =
(а’а^а*
= (а*а)г,.(а’а).(а-а)'1а*
= (а*а)‘1а*.
. Тогда по свойству 1: А*1 = (а’аГ 1 А*.
СПОСОБЫ НАХОЖДЕНИЯ ПСЕВДООБРАТНОЙ МАТРИЦЫ
Пусть дана ненулевая матрица А размеров тхп. Требуется найти
псевдообратную матрицу А'1.
172
Первый способ. Для нахождения псевдообратной матрицы (4.19) нуж-
но выполнить следующие действия.
( А
1. Составить блочную матрицу —
Е 1
—— , приписывая к матрице А
слева и снизу единичные матрицы соответствующих размеров. Правый
нижний блок этой матрицы может быть произвольным, так как не участвует
в дальнейших преобразованиях.
2. Элементарными преобразованиями над первыми т строками и пер-
выми п столбцами привести блочную матрицу к виду —-------, где Л -
матрица размеров тхп простейшего вида (4.8), т.е. Л =
o'!
— , в кото-
°)
рой Ег - единичная матрица г-го порядка (1< г <min{ т\п }), О - нуле-
вые матрицы соответствующих размеров.
3. Найти произведения 55*, Т*Т и представить их в виде блочных
матриц
, ( S, 5,') . (Т,
SS = ——- , тт= — — ,
(J’j T4J
выделяя блоки S2, S4, Т3, Т4 размеров rx(m-r),
(n-r)xr, (n-r)x(n-r) соответственно.
4. Вычислить матрицы
(/=-7717’3, У = -525;1.
(4.20)
(т - г)х (т - г),
5. Получить псевдообратную матрицу
A-‘=T ^ (Ег | V)-S. (4.21)
Замечание 4.8. Если г = m или г = п в (4.20) будут отсутствовать
блоки S2, S4 или Т3 , Т4, так как в формуле (4.21) будут отсутствовать блоки
V или U соответственно (см. п.5 замечаний 4.6). В частных случаях, когда
строки матрицы А линейно независимы (г = m) или столбцы матрицы А
линейно независимы ( г = п), псевдообратную матрицу А~1 можно найти
проще, чем описанным выше способом (см. далее частные случаи нахожде-
ния псевдообратной матрицы).
Второй способ. Для нахождения псевдообратной матрицы используем
скелетное разложение (4.10).
1, 2. Выполнить два первых пункта, указанных в первом способе. По-
лучим матрицы S , Т и Л, удовлетворяющие условию
A. = SAT,
173
где 5, Т - элементарные преобразующие матрицы порядков m и п соот-
(Ег О'! „ _
ветственно’ Л= —--------- матрица простейшего вида; £, - единичная
О)
г -го порядка (1 < г < tnin{ m; п }), О - нулевые матрицы соответствующих
размеров.
3. Найти обратные матрицы £ 1 и Т 1
4. Записать матрицы В = £ 1
и С = (Ег | Ь)-Т 1. Матрица В со-
ставлена из первых г столбцов матрицы 5 1, а матрица С - из первых г
-г-1
строк матрицы Т
5. Получить псевдообратную матрицу по формуле
Л'1 =С*(сС*)Г1(в*в)'1В*. (4.22)
Докажем, что второй способ дает ту же псевдообратную матрицу, что и
первый. В самом деле, имея в виду скелетное разложение матицы А :
(£ \
А = ВС; £ = £"’. -Г I С = (ЕГ | О)Т~',
найдем произведение
Обращая блочную матрицу ££* =
1^2
по формуле Фробениуса (4.4),
имеем
5, кГ_ М
-S?S3M
-MS2S?
" у
где М = - £2£4 '£3 j , # = ^£4.Подставляя ($£*) и выпол-
няя умножение блочных матриц в квадратных скобках, имеем
м -ms2s;'
-s;'s3m N
(в'в)"' b*s-'= М~' (Ег | О)
= (м | -MS2S;')=(Er | -ВД')=(£Г | Г).
Таким образом, (Er | E)S = (b*b] ' 5*,где l/ = -S2S^'.
174
для U = ’7^.
Аналогично показывается, что Т-
Поэтому формулы (4.22) и (4.21) дают одну и ту же псевдообратную матри-
цу.
fl -1 2 ОА
Пример 4.11. Для матрицы Л= -1 2 -3 1 найти псевдообрат-
(0 1 -1 А)
ную.
□ Первый способ. 1, 2. Первые два пункта алгоритма выполнены при
решении примера 1.38, где получены матрицы
fl о
Л= 0 1
0 О'
о о
0 °,
' 1
S= 1
-1
О О'
1 о
Ч 1 -1 -1'
0 11-1
0 0 10
.0 0 0 1 ,
^0 0
удовлетворяющие равенству А = SA Т. Следовательно, г = rg Л = rg Л = 2 .
3. Найдем произведения
1
1
-1
О
1
-1
-1
-1
1
-1 -2
-1
-2
3
1
1
-1
-1
О
1
1
-1
О
о
1
о
О'
О
О
1.
'1
О
о
.0
1
1
О
О
-I
о
1
1 1 1 2 -1 -1 0 -2
-1 0 -1 -2 3 0 0 3
55'
О
О
1
О
О
1
1
1
1
2
0
г’г=
о
Следовательно, S2
-1
0 1 (3
, 74 =
-21 4 0
О
3
4. Находим произведения
. 1Гз oV-i o')
и = ~ТГ1Т,=— II п
9[о 311-1 -2J
/ = -525;'
з
2 •
о
2 ’
з
•5 =
5. По формуле (4.21) получим псевдообратную матрицу
Л'1
175
'\ 1
О 1
о о
<° 0
-1
1
1
о
-iVi о)
-I О
'1
О
к
О
1
-1
О'1
о
b
2
о
2
з/
Псевдообратная матрица найдена.
Второй способ. 1, 2. Первые два пункта алгоритма выполнены при ре-
шении примера 1.38.
3. Найдем обратные матрицы
( 1 °
5-1 = 1 1
-1 -1
oY1 р о o'
О =-110
1J 1 L
7”’
'1 1
О 1
о о
ч° 0
4. Запишем матрицы
2 О'
-1 1
1 О
О L
C = (Er I о)-?”1 =
Ч
-1
о)р o'
о о_2
1До о,
Ч
-1
<0
О'
1
р
О О') О
о oj о
.0
-1
1
о
о
2 О'
-1 1 _р -1 2 О')
1 0 “[о 1 -11)
0
5. Псевдообратную матрицу получим по формуле (4.22). Для этого
сначала найдем произведения и обратные матрицы
о
1
1
176
( 1 O')
,[1-12
CC =
I о 1 -1
10
1
-1
3
2_ ’
3/
а затем псевдообратную матрицу
( 1
A~' =С*(сС'У(в*вУ В* =
\°
1 J
1 2
9 9
1 1 ’
' 9 9
1 5
9 9 J
что совпадает с полученным ранее результатом.
Третий способ. Для последовательного нахождения строк псевдооб-
ратной матрицы используется метод Грееилля.
Пусть ак — к -й столбец матрицы А (\< к<п); Ак - матрица, обра-
зованная первыми к столбцами матрицы A (At =at, А„ = А); Ак1 - соот-
ветствующие псевдообратные матрицы (к = 1,2,..., п); Ьк - последняя строка
в матрице Ак1 (Л = 1,2,.о - как и ранее, нулевой столбец.
1. Положить к = 1. Если Д] * о, найти Л('’ = aj~l = —J— а*.
aiai
Если Д] = о, то А{~] = оТ .
2. Положить к = к +1. Найти:
a) dk = Ак11 • ак;
б) ск = ак - Ak_\dk ;
в) если ск * о, то Ьк = ск 1 = (скск) ск ;
если ск = о, то Ьк = (1 + dkdk ) dk Aklt;
г) Вк = Aklt -dkbk ;
i (вЛ
д) 4~‘= ? •
V>k )
3. Если к = п, процесс завершить: Л'1 = Л^1. Иначе перейти к п.2.
12 -4549
177
fl -1 (H
Пример 4.12. Для матрицы А =
1
-1
найти псевдообратную
V0 -1 1
методом Гревилля.
□ Так как данная матрица действительная, операция сопряжения сов-
падает с операцией транспонирования.
1. Положим к = 1. Так как первый столбец at =(1 -1 2 0)г ненуле-
вой, то -1 2 0)=(1 -± | о).
21. Положим к - к +1 = 2.
в) так как с2 * о, то
31. Так как Л = 2^л = 3,то перейдем к п.2.
2 2. Положим к = к +1 = 3.
178
a) d3 — A2 a3 —
Az
з
з
1
3
Г О Л
( 1 -1A C o'!
6) c3 = a3 - A2d3 =
0
1
-1
1
-i
2
<0
1
'o'
1
-1
<1 /
'O'
0
О
.oJ
в) так как c3 = о, то
З2. Так как к = 3 - п , то процесс завершен и A~l = А31.
ЧАСТНЫЕ СЛУЧАИ НАХОЖДЕНИЯ ПСЕВДООБРАТНОЙ МАТРИЦЫ
1. Если матрица А = (а, () - число, то
—, ап*0,
аи
0 ,
А
ап=0-
2. Если матрица А диагональная A = diag(all,a22, -,ann), то псевдо-
обратная матрицы также диагональная
( 1
—, а,,*0,
а„ " 1 = 1,2,...,п.
0, а„=0,
3. Если столбцы матрицы А линейно независимы, то
а-’^а’аГ’а*.
[аП’ а22’—’ апп )’ г^е аи
(4.23)
(4-24)
12*
179
4. Если строки матрицы А линейно независимы, то
А~1 = А* (ДА*)’1. (4.25)
Пример 4.13. Для матриц
'1
5 = (1 2 3), С = 1
О'
1
ъ
найти псевдообратные.
Матрица А - диагональная. По формуле (4.23) находим
А4
'1 О О'
О | О
<° 0 °,
Для матрицы-строки В по формуле (4.25) получаем
Столбцы матрицы С линейно независимы. По формуле (4.24) имеем
°1
1
1
2 -2| Г1 1
—2 3 J I0 1
1 Ч-Р
1 Ju
2
2
О
1
1
1
О
Найдем матрицу С первым способом.
1. Составляем блочную матрицу
1
-1
С Е3
1
1_
1
О
о
1
о
1
О'
о
1
□
С
1 1 1
О 1 1
1
1
О
1
1
О
2
2
1
О
о
о
1
о
1
1
2. Приводим блок С к простейшему виду
с \Е3
е2
Ч о 1 1 1 1 1 0 О' 0 1 0 0 0 1
1 0 1
1 0 0 1 0 1 1 0 о' -1 1 0 -1 0 1
1 0 0 1
1 0 0 1 0 0 1 0 О' -1 1 0 0 -1 1
1 0 0 1
180
Получили матрицы Т - Е2, S = -1
. О
О О'
О . Ранг матрицы С равен коли-
1.
1
-1
честву ненулевых строк, т.е. г = rg С = 2 = п, Ег = Е2.
3. Находим произведения
SS
1
-1
О
о
1
-1
-1
1
О
-1
1
1 -1
-1__2_
О -1
О '
-1
2 .
fi
S3
^2
о
1
О
О
• ( 1
т г =
1о
О] / X
1 Ка-
В матрице Т*Т блоки Т2, Т3, Т4 отсутствуют (см. замечание 4.8).
4. Из-за отсутствия блоков Т3, Т4 вычислять матрицу U не нужно.
Го')
1-1
Находим только матрицу V = -S2S4
V / 42/
5. Находим псевдообратную матрицу по формуле (4.21), учитывая от-
сутствие матрицы U (см. п.5 замечаний 4.6):
1 7.1 I 1 0W1
с~х=т-е2-(е2 v)-S=I •
I 0 1JI о
O']
2/
-1
о
о
1
-1
О'
О
1
1
2.
-1
О
о
1
-1
О"
О
1.
1
-1
1 О О
О 1
о
1
1 О
О 1
0
0
2
2
Результаты обоих способов нахождения матрицы С'1 совпадают.
ПСЕВДООБРАЩЕНИЕ БЛОЧНЫХ МАТРИЦ
Пусть дана блочная матрица
(А
М= —— ,
Iе D)
где А - квадратная невырожденная матрица г -го порядка
г = rg А = rg М .
Тогда псевдообратная матрица М~х является блочной матрицей и
ходится по формуле [10]
и
на-
181
м~'
(а'а+с'с) '(л* I с’).
(4.26)
Пример 4.14. Для блочной матрицы
М = -1 2
2 О'
-3 1
-1 L
А
С
<В
D
( 1 -1
1° 1
найти псевдообратную.
□ Заметим, что rg А = 2 = rg Л/. Последовательно вычисляем
(лл’ + вв’)’1 =
-1V 1
2 Д-1
-Р| ( 2
2 Д-З
0V2
До
2 -ЗД 4 -6'
-3 5 Д-6 10,
"6 Д 1 _ 1 (5 3'
-9 15J "з|з 2,
-1V 1
2 Jt-1
(л’л+с’с) ' =
' 1
Н
Ip 1V6 ДД5 8'
Д iJv3 2ДЦ9 5,
По формуле (4.26) имеем
I I
-1 2
2 -3
0 1
Л/’1
1(15
9 I 9
-1
2
' 1 -Г
ОД -1___2_ р
1J~9 2 -3 [4
.°
1
1 5)
что совпадает с результатом примера 4.11.
182
Задачи для самостоятельного решения
4.1. Найти матрицы, обратные к данным:
а)
5
7 h6)
2
О
О
О
3
О
О
о
4
в)
'3 2
О 1
.0 О
1
1
г)
2
1
2
1
3
3
1
Д)
"2
3
.1
7
9
5
3^1
4 ; е)
3.
3
4
2
О
-2
2
5
ж)
'3
1
5
2
3
3
2'
1
4.
Г7
Ответ: а) I
3
б)
2
О
о
О
з
О
О
О
V
г)
8
-1
-5
-1
О
1
1
3
Д)
з
5
3
-2
2
-1
1
з
з
1
в)
з
О
О
_ 2
7
1
О
3
-1
1
;е)
7
4
3
2
2
_9
4
_ 5
2
-1
5
4
3.
2 J
' 1
7
ж)
5
_J2
. 5
_ 2
7
2
7
1
7
7
5
7
7 У
4.2. Доказать, что матрицы ортогональные:
а)
cos a sin а ]
; б)
sin а -cosal
15
2
15
2
2
15
14
15
_ 1
3
з
з
2
3
4.3. Решить матричные уравнения:
. О 2>
а)
3 4
3 5|-
5 9J’
б) 3
3
2
2
-1
— 4
О
10
10
-3
2
7
О'
7
8.
-1 2
<3 -2^
в) X =| ।,
15 -4, 1-5 6
183
[0-1] [2 1] [1 2
г) АХ+2Х=В + СХ .где А= ’ *= 9 i ’ С= n л
\ A kz у \ А у к kz
(0 -1А (2 1А fl 2А
д) ХА + 2Х = В +ХС ,гд,е А= ’ *= 9 i ’С= п Л
\ A \J 1 \ Z> А у \ \J kz у
Го
1 2 1
е) 2 1 3 X = 1
1 3 1
з) Г 4 5
2 1
2 =(5
4.
5);
г) уравнение
,1 "ЗА -1
D = A + 2E-C = \ , D=-
1 2 J
Указания:
к виду XD = B, D = А + 2Е-С =
Ответ: а)
Х=\ 1
I 2
г) Но
1А (0,6
; д) Х =
о) 1о,6
ж) Г 2
.1
и)
'О
1
.1
14 16
9 10
О'
2
1.
преобразовать к виду DX = В,
if2 зА
у! 1 1 ’ Д) УРавнение преобразовать
П=1(2 3
51-1 1
-6
-28
-21
-4
-5
мА
; е) X =
1,4 J
-19 -23 ; в) X =
-13
'-6
1
4
-17
-2
-4
-2
1
1
1
1
О
2
О
2
1
1
3
3
1
1
О
2
з
1
2
, D
Х =
3
5
1
5
-1
ж)У= -2
. 1
0
2
4
и) X = |
3
0
О
4.4. Найти матрицы, псевдообратные для данных матриц:
О О
а)
;б)
о о
л
2
1 2
3 О
4 2
Г
1
2,
(° 0] (°
Ответ: а) ; б) ,
lo oj
' —4 14 10
-1 „ 1 -23 34 11
1 ; г) 186 68 -52 16
°, -6 9
ГЛАВА 5. СИСТЕМЫ ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
5.1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Системой т линейных алгебраических уравнений с п неизвестны-
ми называется система уравнений вида
а11х1 + а12Х2 +'" + а1пхл = ^1>
a2IXj + а22х2 + • • + а2пхп = Ь2,
+ ат2х2 +- + атпхп = Ьт
Числа а,у, i = l,...,m, j = l,...,n называются коэффициентами системы-,
by ,b2,...,bm- свободными членами, Ху,х2,...,хп - неизвестными. Коли-
чество т уравнений в системе может быть меньше, больше или равно числу
п неизвестных.
Решением системы называется упорядоченная совокупность п чисел
(ap^,....^) такая, что после замены неизвестных Ху,х2,...,хп соответ-
ственно числами aj,a2,...,a„ каждое уравнение системы превращается в
верное числовое равенство. Система называется совместной, если она име-
ет хотя бы одно решение. Если система не имеет ни одного решения, то она
называется несовместной.
Система (5.1) называется однородной, если все свободные члены рав-
ны нулю:
<*n*i +а12х2 + — + а1пхп = 0,
a2tXy + а22х2 -I I- а2пхп =0,
ат1х1 + ат2х2 *" атпхп 0 •
В отличие от однородной, систему общего вида (5.1) называют неоднород-
ной.
Систему (5.1) принято записывать в матричной форме. Для этого из ко-
эффициентов системы составляем матрицу системы
кат1 ’ ‘' атп ,
свободные члены записываем в столбец свободных членов
185
а неизвестные - в столбец неизвестных
Матричная запись неоднородной системы уравнений (5.1) имеет вид
Ах = Ь, (5.3)
а однородной:
Ах = о,
(5.4)
где символ о в правой части обозначает нулевой столбец размеров mxl.
Матричную запись (5.3) системы уравнений можно представить в эк-
вивалентной форме
( «1
Тогда решение системы представляется столбцом х =
равенству
и удовлетворяет
(5-5)
т.е. столбец свободных членов является линейной комбинацией столбцов
матрицы системы.
Относительно системы уравнений нас интересуют ответы на следую-
щие вопросы:
1. Совместна система или нет?
2. Если система совместна, то имеет ли она единственное решение или
нет?
3. Если решение единственное, то как его найти?
4. Если система имеет бесконечно много решений, то какова структура
множества решений?
5. Как в бесконечном множестве решений системы определить одно
решение, наилучшее с практической точки зрения?
6. Если система несовместна, то как определить ее приближенное ре-
шение?
186
5.2. ПРАВИЛО КРАМЕРА
Рассмотрим случай, когда число т уравнений равно числу п неиз-
вестных (т = п ), т.е. систему
апХ1+--- + а1плп=^,
(5.6)
ani*i+”- + annxn=6n,
где матрица системы - квадратная п -го порядка:
ап а12 •• а1п
fl21 а22 а2п
ап2 ••• ат>
Ее определитель обозначим
ап а12 ’ ” а1„
Д = det А = а21 а22 ’ ’ а2п
ani ап2 ' апп
Теорема 5.1 (правило Крамера). Если определитель Д матрицы сис-
темы п линейных уравнений с п неизвестными отличен от нуля, то сис-
тема имеет единственное решение, которое находится по формулам
х,= —, i = l
‘ Д
где Aj — определитель матрицы, полученной из матрицы системы заменой
i -го столбца столбцом свободных членов, т.е.
п,
а11 ... аи-1 *1 а1|+1 " а1п
а21 ... а2!-1 62 а21+1 ‘ " а2п
аЛ1 ... «п г-1 Ьп апМ ’ апп
как
В самом деле, рассмотрим систему (5.6)
Ах = Ь (см. разд. 4.4). Так как определитель Д матрицы А отличен от нуля,
по теореме 4.2 заключаем, что матричное уравнение Ах = b имеет единст-
венное решение:
матричное уравнение
х = А~1Ь,
187
где A~l = — А+ - обратная матрица (см. теорему 4.1). Запишем i -й элемент
Д
столбца х, учитывая, что в i -й строке присоединенной матрицы А+ стоят
алгебраические дополнения i -го столбца матрицы А :
х, = —(АцЬ^ + A2ib2 + ...+ Anlbn).
Заметим, что в скобках записано разложение определителя Д, по i -му
д,
столбцу, т.е. х( = —, что и требовалось доказать.
Д
Замечания 5.1.
1. На практике при больших п правило Крамера не применяется, так
как вычисление (и +1) определителя л -го порядка требует большого числа
арифметических операций. Поэтому применяются более экономичные алго-
ритмы (см. разд. 10.2, 10.3). Обычно, правило Крамера используется, когда
нужно найти только несколько неизвестных (например, одну) среди многих.
В теоретических исследованиях правило Крамера незаменимо и использует-
ся весьма продуктивно.
2. Если Д = 0 и хотя бы один определитель Д, * 0, то система несо-
вместна. Если Д = Д| = ... = Д„ = 0, то возможны два случая: либо система
несовместна, либо имеет бесконечно много решений.
Пример 5.1. Решить систему линейных уравнений
2Х' + 2х2 + х3 = 9,
х( + х2 = 3,
2х2 + х3 = 7.
г2
□ Составим матрицу системы А = 1
.0
2
1
2
Г
О . Вычислим ее определи-
1
2 1
1 0
2 1
= 2 + 2-2 = 2. Так как определитель отличен от нуля,
система имеет единственное решение (см. теорему 5.1). Находим определи-
тели Д, и неизвестные х, (i = 1, 2,3):
9 2 1
3 1 0
7 2 1
Д,=
2
= 9 + 6- 7- 6 = 2, х. = — = 1;
2
188
2 2
1 1
О 2
9
3
7
д3 =
= 14 + 18-12-14 = 6,
5.3. УСЛОВИЕ СОВМЕСТНОСТИ СИСТЕМЫ ЛИНЕЙНЫХ
УРАВНЕНИЙ
Рассмотрим систему (5.3) т линейных уравнений с п неизвестными.
Составим блочную матрицу, приписав к матрице А справа столбец свобод-
ных членов. Получим расширенную матрицу системы:
(5.7)
Эта матрица содержит всю информацию о системе уравнений, за исключе-
нием обозначений неизвестных.
Теорема 5.2 (теорема Кронекера-Капелли). Система Ах = Ь совме-
стна тогда и только тогда, когда ранг матрицы системы равен рангу
расширенной матрицы: rg А = rg(/l | b).
Необходимость следует из равенства (5.5) и следствия 1 теоремы 3.3.
Если система имеет решение, то столбец свободных членов есть линейная
комбинация столбцов матрицы системы. Поэтому при вычеркивании столб-
ца b из расширенной матрицы (А | b) ее ранг не изменяется. Следователь-
но, rg(/l 12>)=rg А .
Для доказательства достаточности нужно использовать теорему о ба-
зисном миноре. Из равенства rg А - rg (а | b) следует, что базисный минор
матрицы А является базисным минором расширенной матрицы (А | б). По-
этому столбец Ь является линейной комбинацией столбцов базисного ми-
нора матрицы А , а, значит, и всех столбцов матрицы А. Следовательно,
существуют числа а, ,а2,...,а„, удовлетворяющие условию (5.5), т.е. сис-
тема совместна.
Замечание 5.2. Теорема Кронекера-Капелли дает лишь критерий
существования решения системы, но не указывает способа отыскания этого
решения.
189
Пример 5.2. Имеет ли система
х, + 2х3 + х4 = 1,
2х1 + х2 + х4 = 0,
Зх! + х2 + 2х3 + 2х4 = 2
решения?
□ Составим матрицу системы и расширенную матрицу системы
Ранг матрицы А равен 2, так как она имеет не равные нулю миноры второго
порядка и третья строка этой матрицы равна сумме первых двух строк. Сле-
довательно, третью строку можно вычеркнуть (см. следствие 1 теоремы 3.3),
при этом ранг матрицы не изменится. Ранг расширенной матрицы равен
трем, так как она имеет не равный нулю минор третьего порядка, например,
минор, составленный из первого, второго и последнего столбцов расширен-
ной матрицы
О 1
1 О
1 2
1*123 2
^*125 z
= 2 + 2-3 = 1*0.
Следовательно, rg А Ф rg(A | б). Поэтому система несовместна (не имеет
решений).
5.4. МЕТОД ГАУССА РЕШЕНИЯ СИСТЕМЫ
ЛИНЕЙНЫХ УРАВНЕНИЙ
Пусть дана система (5.3) т линейных уравнений с п неизвестными.
Для ее решения нужно выполнить следующие действия.
1. Составить расширенную матрицу (5.7) системы:
(А | Ь) =
<hn
атп
2. Используя элементарные преобразования над строками матрицы
(А | b), привести ее к ступенчатому виду (см. разд. 1.6.1). Если базисный
минор матрицы А расположен в первых г строках и г столбцах, получится
следующий вид:
190
1 а12 •• а1г а1п *1
0 1 а2г а2п ^2
ib.) <3-; II 0 0-1 ат Я'
0 0-0 ••• 0 br+l
0 0 — 0 — 0 0
(5.8)
3. Выяснить, совместна система или нет. Для этого определить ранги
матриц А и (А | b):
rg А = rg А = г - число ненулевых строк в матрице А ;
rg(A | i>)=rg(A | b
г +1, если Z>r+1 # 0,
г, если br+l =0.
Если rg А * rg(A | b) (при 6г+1 # 0), то система не имеет решений.
Процесс решения завершен. Если rg А = rg(A | b) (при br+l = 0), то система
совместна. Процесс решения продолжается.
4. Для совместной системы (rg A = rg(A | b)= г) привести матрицу
(а | б) к упрощенному виду (см. разд. 1.6.1). Для этого при помощи эле-
ментарных преобразований над строками добиваемся того, чтобы в каждом
столбце, входящем в базисный минор, все элементы были равны нулю, за
исключением одного, равного единице. Если базисный минор матрицы А
расположен в первых г строках и первых г столбцах, то матрица приво-
дится к упрощенному виду:
'1 0 0 1 • • 0 0 «1г+1 / а2г+1 - «1'л ••• «2л Z>2
(А' 1 У) = 0 0 • 1 агг+1 - < b'r (5-9)
0 0 • 0 0 ... о 0
0 0 0 ... о °,
Первые четыре пункта составляют прямой ход метода Гаусса. В результате
прямого хода исходная система существенно упрощается (имеет вид
А'х = Ь'):
191
*1 +a'lr+1xr+i + ... + a'lnx„ -b{,
(5.10)
xr + a'rr+lxr+1 + ... + a'rnx„ = b'r .
5. По упрощенному виду (5.9) разделяем все неизвестные хг,х2,...,хп
на базисные и свободные. Неизвестные, которым соответствуют столбцы,
входящие в базисный минор, называются базисными переменными, ос-
тальные неизвестные - свободными переменными. Для системы (5.10) ба-
зисными переменными являются х1,х2,...,хг, свободными переменными -
xr+i,xr+2 ,...,х„ . Выражаем в (5.10) базисные переменные через свободные:
Х1 = ^1 ~ а1 г+1хг+1 _ ~ а1 пхп •
• (5.11)
— br — ar r+iXr+j —... — arnxn .
Если ранг г матрицы системы равен числу п неизвестных
(т = rg А = п ), то левый блок матрицы (5.9) будет представлен единичной
матрицей Еп :
"1 0 0
(а'и= ° 5 ; ° ь\ •
0 0 - 1 Ъ'П/
Все неизвестные хх,х2,...,хп будут базисными и формула (5.11) будет оп-
ределять единственное решение системы
*1 = Ь{,
х2 — Ь2,
(5-12)
хп =ЬП-
Если ранг матрицы системы меньше числа неизвестных (rg А < п), то
система имеет бесконечно много решений, задаваемых формулой (5.11), ко-
торая обладает следующими свойствами:
- при любых значениях свободных переменных хг+1 ,хг+2 ,...,хп по
формуле (5.11) получаются такие значения базисных переменных, что упо-
рядоченный набор чисел х1,х2,...,х„ является решением системы (5.3);
- любое решение х1,х2,...,хп системы (5.3) удовлетворяет равенствам
(5.П).
Равенства (5.11), выражающие базисные переменные через свободные,
называются общим решением системы (5.3). Решение системы, получаю-
192
щееся по формуле (5.11) при задании конкретных значений свободных пе-
ременных, называется частным решением системы (5.3).
Процесс решения совместной системы (5-3) заканчивается получением
формулы (5.11) общего решения (в частности, определением единственного
решения (5.12)).
Содержание п.5 алгоритма составляет обратный ход метода Гаусса.
Пример 5.3. Решить систему линейных уравнений
х{ + х2 + 2х3 + х4 =1,
- 2xt + Зх2 + х4 = 0,
3х1 + 4х2 + 2х3 + 2х4 = 1 -
□ 1. Составим расширенную матрицу системы
112 1
(А | &)= 2 3 0 1
3 4 2 2
Г
о
2. Используя элементарные преобразования над строками матрицы
(А | b), приводим ее к ступенчатому виду. Берем в качестве ведущего эле-
мента ап=1*0. Ко второй строке прибавим первую, умноженную на
(- 2), а к третьей - первую, умноженную на (- 3):
1 1
(А | b)= 2 3
3 4
2 1 0 1 2 2 о "112 1 01-4-1 0 1 -4 -1 Г -2 -2 7
Ведущий элемент а22 = 1 # 0. К третьей строке прибавим вторую, умножен-
ную на (-1):
Расширенная матрица системы приведена к ступенчатому виду.
3. Определяем ранги матриц: rg A = rg(A | t>)=2. Согласно теоре-
ме 5.2, система совместна.
4. Приводим матрицу к упрощенному виду. Выбираем в качестве ба-
зисного минора М\2 К первой строке прибавляем вторую, умноженную на
(-1):
13-4549
193
1 1
О 1
О О
5. Переменные х.
3 1
2
-4
О
1
-1
О
1
-2
О
6
-4
О
2
-1 -2 =(Л’|&')-
О
1
О
О
О
1
О
о
- базисные, а
общее решение системы, используя (5.11):
- свободные. Записываем
X] = 3 - 6х3 - 2х4 ,
х2 = -2 + 4х3 + х4 .
Система имеет бесконечно много решений. Найдем частное решение. На-
пример, для х3 = х4 = 0 получаем X] = 3, х2 = -2. Следовательно, столбец
х = (3 -2 0 0) г - частное решение системы.
5.5. СТРУКТУРА ОБЩЕГО РЕШЕНИЯ ОДНОРОДНОЙ
СИСТЕМЫ
Однородная система линейных уравнений
ДцХ,+д12х2+•• +д1пхп =0,
а21х]+а22х2+- + а2„х„=0,
или Ах = о
ат1х1 +ат2х2+- + атпхп = ° >
всегда совместна, так как имеет тривиальное решение Xj = х2 -... = х„ = О
(х = о). Если ранг матрицы системы равен количеству неизвестных
(rg А = п), то тривиальное решение единственное. Предположим, что
г = rg А < п . Тогда однородная система имеет бесконечно много решений.
Заметим, что расширенная матрица (А | о) однородной системы при эле-
ментарных преобразованиях строк приводится к упрощенному виду (л' | о),
т.е. Ь[ = Ь2 =... = Ь'Г= 0. Поэтому из (5.11) получаем общее решение
однородной системы-.
X] = — Д] г+1ХГ+] —... — Д] пхп,
: (5.13)
Хг = ~ &гг+\Хг+\ ~ ••• ~ агпХп
Получим другую форму записи решений однородной системы, которая
раскрывает структуру множества решений. Для этого подчеркнем следую-
щие свойства.
194
СВОЙСТВА РЕШЕНИЙ ОДНОРОДНОЙ СИСТЕМЫ
1. Если столбцы <pj, ф2,..., ф^ ~ решения однородной системы уравне-
ний, то любая их линейная комбинация оц -ф| + сс2 -ф2 + ... + а4 -фл также
является решением однородной системы.
В самом деле, из равенств A<pt = о, А(р2 =о А(рк = о следует, что
А (а, - ср! +а2 -ф2 + ... + аА ф4)=а)Дф1 +а2Лф2 + ... + аЛЛф* = о,
т.е. линейная комбинация решений является решением однородной системы.
2. Если ранг матрицы однородной системы равен г, то система име-
ет (п - г) линейно независимых решений.
Действительно, по формулам (5.13) общего решения однородной сис-
темы найдем (п-r) частных решений <pj ,<р2 ,...,<рп_г, придавая свободным
переменным следующие стандартные наборы значений (всякий раз пола-
гая, что одна из свободных переменных равна единице, а остальные - равны
нулю):
1) хг+] =1,хг+2 =0,...,хя =0: Ф]=(-а1'г+1 •" -<r+1 1 0 •" о)Г;
2) хг+1 =0,xr+2 = 1,...,хл =0: Ф2=(~<+2 -а'гг+2 0 1 о)Г;
хг+1=0,хг+2 =0,...,хл=1: Фя_г=(-<
Получим (л-г) решений
о ° О"
агг+1 ~а'гг+2
Ф1 = 1 . Ф2 = 0 > -> Ф„-г
0 1
о
о
I 0 J к 0 J
I 1 J
которые линейно независимы. В самом деле, если из этих столбцов соста-
вить матрицу, то последние (л - г) ее строк образуют единичную матрицу.
Следовательно, минор, расположенный в последних (л - г) строках не равен
нулю (он равен единице), т.е. является базисным. Поэтому ранг матрицы бу-
дет равен (л-г). Значит, все столбцы этой матрицы линейно независимы
(см. теорему 3.4).
Любая совокупность (л-г) линейно независимых решений
Ф; ,ф2 ,...,фя_г однородной системы называется фундаментальной систе-
мой (совокупностью) решений.
,3. 195
Заметим, что фундаментальная система решений определяется неодно-
значно. Однородная система может иметь разные фундаментальные систе-
мы решений, состоящие из одного и того же количества (п-r) линейно не-
зависимых решений.
Теорема 5.3 (об общем решении однородной системы). Если
Ф1. Ч>2.<9п-г ~ фундаментальная система решений однородной системы
уравнений (5.4), то столбец
х = С1-ф1+С2ф2 + -- + С„_гф„_г (5.14)
при любых значениях произвольных постоянных С], С2..., Сп_г также
является решением системы (5.4), и, наоборот, для каждого решения х
этой системы найдутся такие значения произвольных постоянных Сг,
С2..., Сп_Г, при которых это решение х удовлетворяет равенству (5.14).
Прямое утверждение теоремы следует из свойства 1 решений однород-
ной системы. Докажем обратное утверждение о том, что любое решение х
можно представить в виде (5.14). Для этого составим матрицу Н , приписав
к столбцам фундаментальной системы решений столбец х :
' Ф11 Ф1л-г *1 '
Я=(Ф1
Фг1
Фг+11
Фгл-
Фг+1и
ч Фл1 " Флл-г хп ,
Найдем ранг этой матрицы. Так как первые (n-г) столбцов линейно неза-
висимы, то rg Я >п-г. Так как каждый из столбцов матрицы Н является
решением системы А’х = о , то по первой формуле из (5.13) получаем
<р, = -а,' ,Ф , -...-а' <р ,
vln-r Ir+l^r+ln-r 1«тяп_г>
X] = - П1г+1Хг+] - ,..-а1ях„ .
Следовательно, первая строка матрицы Н является линейной комбинацией
последних (п - г) строк этой матрицы.
По второй формуле из (5.13) получим, что вторая строка матрицы Н
является линейной комбинацией последних (п-r) строк этой матрицы, и
т.д. По г -й формуле из (5.13) получим, что г -я строка матрицы Н является
линейной комбинацией последних (и-г) строк этой матрицы. Значит, пер-
вые г строк матрицы Н можно вычеркнуть и при этом ранг матрицы не
196
изменится (см. следствие 1 теоремы 3.3). Следовательно, rg Н <п-г, так
как после вычеркивания в матрице Н будет всего (и-г) строк. Таким об-
разом, rg Н - п - г . Значит, есть базисный минор матрицы Н , который
расположен в первых (и - г) ее столбцах, а столбец х не входит в этот ба-
зисный минор. Тогда по теореме 3.1 (о базисном миноре) найдутся такие
числа Cj, С2,..., С„_г, что
х = С1-ф1+С2-ф2+-. + Си_гфя_г.
Обратное утверждение доказано.
АЛГОРИТМ РЕШЕНИЯ ОДНОРОДНОЙ СИСТЕМЫ
1-5. Выполнить первые 5 пунктов алгоритма Гаусса (см. разд. 5.4). При
этом не требуется выяснять совместность системы, так как любая однород-
ная система имеет решение (п.З метода Гаусса следует пропустить). Полу-
чить формулы (5.11) общего решения, которые для однородной системы бу-
дут иметь вид (5.13).
Если ранг г матрицы системы равен числу и неизвестных
(г = rg А - п), то система имеет единственное тривиальное решение х - о и
процесс решения заканчивается.
Если ранг матрицы системы меньше числа неизвестных (rg А < п), то
система имеет бесконечно много решений. Структуру множества решений
находим в следующих пунктах алгоритма.
6. Найти фундаментальную систему ф, ,ф2 ,...,фя_г решений однород-
ной системы. Для этого подставить в (5.13) последовательно (n-г) стан-
дартных наборов значений свободных переменных, в которых все свобод-
ные переменные равны нулю, кроме одной, равной единице (см. свойство 2
решений однородной системы).
7. Записать общее решение однородной системы по формуле (5.14).
Замечания 5.3.
1. В п.6 алгоритма вместо стандартного набора значений свободных
переменных можно использовать и другие наборы значений, лишь бы они
обеспечивали линейную независимость получаемых частных решений од-
нородной системы.
2. Матрица Ф = (ф] ф2 Фл_г), столбцы которой образуют фун-
даментальную систему решений однородной системы, называется фунда-
ментальной. Используя фундаментальную матрицу, общее решение (5.14)
однородной системы можно записать в виде
х = Фс,
гдес = (С) ••• Сп_г )г - столбец произвольных постоянных.
197
3. Если базисный минор матрицы А расположен в левом верхнем углу
(в первых г строках и первых г столбцах), то упрощенный вид расширен-
ной матрицы (5.9) однородной системы можно представить в виде блочной
матрицы
"1 0 • 0 1 - • 0 а1г+1 • 0 а2г+1
(А' | У)= 0 0 • " 1 агг+1
0 0 • 0 0
о о 0 0
Тогда блочная матрица ф = [ r) I размеров пх(п-г) является фун-
I En-r J
даментальной. В этом можно убедиться, используя стандартные наборы
значений свободных переменных. Применение блочных матриц может слу-
жить вторым способом нахождения фундаментальной системы решений.
Пример 5.4. Найти фундаментальную систему решений и общее реше-
ние однородной системы
л, + х2 + 2х3 + х4 = 0,
2xj + Зх2 + х4 — 0,
3xt + 4х2 + 2х3 + 2х4 = 0.
□ 1. Составляем расширенную матрицу системы
О'
(А | о)= 2 3 0 1 0.
0
112 1
^3 4 2 2
2-4. Используя элементарные преобразования над строками матрицы
(А | о), приводим ее к ступенчатому, а затем и к упрощенному виду (см.
решение примера 5.3):
(1 0 6
(А'|о)= 0 1 -4
ООО
Пункт 3 метода Гаусса пропускаем.
2 О"
-1 0
0 °,
5. Переменные Xj, х2 - базисные, а х3, х4 - свободные. Записываем
формулу (5.13) общего решения однородной системы
198
fxj =-6х3-2х4,
1 *2=4х3+х4.
6. Находим фундаментальную систему решений. Так как п = 4 и
г = rg А = 2, надо подобрать п - г = 2 линейно независимых решения. Под-
ставляем в систему стандартные наборы значений свободных переменных:
1) если х3 = 1, х4 = 0, то X] = - 6, х2 = 4;
2) если х3 = 0, х4 = 1, то Xj = -2 , х2 = 1.
В результате получили фундаментальную систему решений
7. Записываем общее решение однородной системы по формуле (5.14):
Заметим, что фундаментальную систему решений можно получить,
взяв иные наборы значений свободных переменных. Например, х3 = 1,
х4 = 2 и х3 = 2, х4 = 3 . Тогда получим другую фундаментальную систему
решений
и общее решение системы
Несмотря на различия, обе формулы задают одно и то же множество реше-
ний.
199
5.6. СТРУКТУРА ОБЩЕГО РЕШЕНИЯ НЕОДНОРОДНОЙ
СИСТЕМЫ
В разд. 5.4 была выведена формула (5.11) общего решения системы
линейных уравнений. Получим другую форму записи, отражающую струк-
туру множества решений.
Рассмотрим неоднородную систему
Ах = Ь
и соответствующую ей однородную систему
Ах = о.
Между решениями этих систем имеются связи, выражающиеся следующими
свойствами.
СВОЙСТВА РЕШЕНИЙ НЕОДНОРОДНОЙ СИСТЕМЫ
1. Разность двух решений х и у неоднородной системы есть решение
однородной системы.
Действительно, из равенств Ах = Ь и Ay = Ь следует, что
А^х-у}-Ах-Ay-b-b-о.
2. Пусть хн - решение неоднородной системы. Тогда любое решение
х неоднородной системы можно представить в виде
х = хн+х°
»
где х° - решение однородной системы.
В самом деле, для любого решения х неоднородной системы разность
х-хн по свойству 1 является решением однородной системы, т.е.
х° = х-хн - решение однородной системы.
Теорема 5.4 (о структуре общего решения неоднородной системы).
Пусть хн - решение неоднородной системы, a <Pj, <р2.(рп_г - фунда-
ментальная система решений соответствующей однородной системы
уравнений. Тогда столбец
х = хн+С1(р1+С2(р2+--- + Сп_г-<рп_г (5.15)
при любых значениях произвольных постоянных Q, С2..., Сп_г является
решением неоднородной системы, и, наоборот, для каждого решения х
этой системы найдутся такие значения произвольных постоянных С,,
С2..., Сп_г, при которых это решение х удовлетворяет равенству (5.15).
Говорят, что общее решение неоднородной системы есть сумма част-
ного решения неоднородной системы и общего решения соответствующей
однородной системы:
200
х ~ х ( fi ' Ф1 + ^2 ' фд + '" Сп-Г ' Фл-г '
частное решение общее решение однородной системы
неоднородной системы
Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.
АЛГОРИТМ РЕШЕНИЯ НЕОДНОРОДНОЙ СИСТЕМЫ
1-5. Выполнить первые 5 пунктов метода Гаусса решения системы
уравнений (см. разд.5.4) и получить формулу общего решения неоднород-
ной системы вида (5.11).
6. Найти частное решение хн неоднородной системы, положив в
(5.11) все свободные переменные равными нулю.
7. Записав формулы (5.13) общего решения соответствующей однород-
ной системы, составить фундаментальную систему <рх ,ср2 ,--->Фл-г ее реше-
ний. Для этого подставить в (5.13) последовательно (и-г) стандартных на-
боров значений свободных переменных, в которых все переменные равны
нулю, за исключением одной, равной единице.
8. Записать общее решение неоднородной системы по формуле (5.15).
Замечания 5.4.
1. Используя фундаментальную матрицу Ф однородной системы
Ах = о , решение неоднородной системы Ах = b можно представить в виде
х-хн +Ф с,
где хн - частное решение неоднородной системы, a с = (С, Сп_г)Т-
столбец произвольных постоянных.
2. Если базисный минор матрицы А расположен в левом верхнем углу
(в первых г строках и первых г столбцах), то упрощенный вид расширен-
ной матрицы (5.9) неоднородной системы можно представить в виде блоч-
ной матрицы
'1 0 ••
О 1
О
^0 0
0 <+1 - а1п
0 а2г+1 - а2л
1 <+1 - а'т
о о - о
0 0-0
201
Тогда блочная матрица Ф = —J/*1"— оказывается фундаментальной (см.
I Еп-г )
н ( Ь'^ )
п.З замечаний 5.3), а столбец х — ---
неоднородной системы (в этом можно убедиться, подставляя в (5.11) нуле-
вой набор свободных переменных). Используя блочные матрицы, общее ре-
шение (5.15) неоднородной системы можно представить в виде
x = x"+0-c = f-^->
где c = (Q Cn_r) - столбец произвольных постоянных. Получен-
ную формулу можно считать вторым способом решения неоднородной сис-
темы.
является частным решением
~АГ.
Е
(5.16)
Пример 5.5. Найти структуру (5.15) общего решения неоднородной
системы
2х1 + 3х2 + х4 = 0,
3xr + 4х2 + 2xj + 2х4 = 1.
□ 1-5. Первые 5 пунктов метода Гаусса выполнены при решении при-
мера 5.3, где получены формулы общего решения неоднородной системы:
f = 3-6х3 -2х4 ,
[х2 = -2+4х3 + х4 .
Переменные Xj, х2 - базисные, а х3, х4 - свободные.
6. Полагая х3 = 0, х4 = 0, получаем частное решение неоднородной
системы хн = (3 - 2 0 of.
7. Находим фундаментальную систему решений однородной системы
(см. пример 5.4):
Ф,= (-6 4 1 Of, ф2=(-2 1 0 if.
8. Записываем по формуле (5.15) общее решение неоднородной сис-
темы
IJ
х = х +С1-ф1+С2’(Р2 =
Искомая структура множества решений найдена.
202
Получим формулу общего решения вторым способом, используя п.2
замечаний 5.4. При решении примера 5.3 расширенная матрица системы бы-
ла приведена к упрощенному виду. Разбиваем ее на блоки:
3 '
(д | b)~ 0 1 -4 -1 -2
О
'1 0 0 1 6 2 -4 -1 3 A z -2 = ^2x2 ^2x1
I и О ° J
[о 0 0 0
10 6 2
0 0 0 0
Записываем частное решение неоднородной системы
хн =( Ьг*х
V°(n-r)xl
^2x1
°2х1,
—2
О
О
и составляем фундаментальную матрицу:
Г-6
4
1
О
ф —I ^'х(л~г) | — I ^2x2
I Еп-г ) \ ^2
х = хн +Ф-
с.
-2"
1
О
1 .
= (<Р1 ф2).
По формуле (5.16) получаем общее решение неоднородной системы, кото-
рое преобразуем к виду (5.15):
которое совпадает с ранее полученным.
5.7. ПРИМЕНЕНИЕ ПОЛУОБРАТНЫХ МАТРИЦ
Получим решение системы линейных уравнений при помощи полуоб-
ратной матрицы (см. разд.4.5.2).
Требуется решить неоднородную систему линейных уравнений
Ах = Ь, (5.17)
где А - произвольная матрица размеров тхп. Если матрица системы ну-
левая (А = О), то система либо несовместна (при Ь * о), либо имеет беско-
нечное множество решений (при Ъ = о любой подходящий по размерам
столбец х является решением). Далее рассматриваем случай ненулевой
матрицы А.
Пусть А-11 - матрица, полуобратная к матрице системы. Используя
определение (4.12) полуобратной матрицы, запишем (5.17) в виде
203
AA^Ax = b.
(5-18)
Если х - решение системы (5.17), то подставляя Ах-b в левую часть
(5.18), приходим к равенству
АА"ЛЬ=Ь. (5.19)
Преобразуем (5.19) следующим образом:
(Ет~ AA~i\b = o. (5.20)
Следовательно, условие (5.20) - необходимое для совместности системы
уравнений (5.17). Из равенств (5.17), (5.19) также следует, что столбец
х = А~лЬ (5.21)
является решением системы (5.17). Значит, условие (5.20) - это необходимое
и достаточное условие совместности системы (5.17).
Поскольку полуобратная матрица определена неоднозначно (см. п.З
замечаний 4.5), то формула (5.21) фактически задает множество решений
системы (5.17). Преобразуем (5.21) так, чтобы была видна структура этого
множества, в частности, выясним количество независимых параметров,
входящих в (5.15).
Возьмем фиксированную полуобратную матрицу (4.16):
0^
5 ,
1 — т Г Е.
А^1 =T/^S=T- —
4 О О
(5.22)
где Т, S - элементарные матрицы порядков п и m соответственно, Л -
матрица простейшего вида, эквивалентная матрице А (Л = 5АТ и
А = 5’1Л7”1), r = rgA.
Преобразуем матрицу Em-AA'~'i в левой части (5.20), подставив вы-
ражение (5.22) и А = S~'AT~l:
Em - АА-11 = Em - S-'AT^ -TrfS = S’1 Em -
S=S
-1-
10
о '
^т-Г/
s.
Образуем матрицу Y размеров (m - r)x m из последних (m - г) строк
матрицы S:
T = (<9 | £m_r)5. (5.23)
При помощи этой матрицы равенство (5.20) принимает вид S 1х¥Ь = о . Ум-
ножая обе его части слева на невырожденную матрицу 5 , получаем
Vb^o. (5.24)
Условие (5.24) необходимо и достаточно для совместности системы (5.17).
Система (5.24) содержит (m-г) числовых равенств. При r = m матрица
нулевая и система (5.17) совместна.
Используя полуобратную матрицу (5.22), по формуле (5.21) получаем
частное решение неоднородной системы
204
хн = =
I О
Найдем теперь общее решение однородной системы. Составим матри-
цу Ф размера п х (л - г) из последних (п - г) столбцов матрицы Т :
ф = 7’.| —(5.25)
Заметим, что эти столбцы линейно независимы, так как матрица Т невыро-
жденная (rg Т = и ). Кроме того, они являются решениями однородной сис-
темы, так как справедливо:
АФ = 5"1Л7"1т[ — | = 5'^
(о
Следовательно, матрица Ф = (срj • • • <рл_г) - фундаментальная, ее столбцы
образуют фундаментальную систему решений однородной системы. По тео-
реме 5.4 общее решение системы (5.17) можно представить в виде
н +х° = АТ'б + Ф с = Т [—
I О
О] , (О }
— -5-^ + Г----- с
о {Еп_г
(5.26)
где с = (Cj • • Сп_г )Т - столбец произвольных постоянных.
Таким образом, справедливы следующие утверждения.
Теорема 5.5 (о совместности неоднородной системы и о структуре
ее общего решения). Неоднородная система (5.17) совместна тогда и
только тогда, когда столбец свободных членов является решением одно-
родной системы (5.24). Если система (5.17) совместна, то ее общее реше-
ние имеет вид (5.26).
АЛГОРИТМ ПРИМЕНЕНИЯ ПОЛУОБРАТНОЙ МАТРИЦЫ
Нахождение решения системы (5.17) в виде (5.26) сводится к следую-
щим действиям (рассматривается случай, когда матрица системы ненуле-
вая).
1. Привести матрицу А системы (5.17) к простейшему виду (см.
разд. 1.6.З.): А = SAT . При этом находятся элементарные преобразующие
матрицы S и Т, а также ранг г = rg А > 1.
2. Проверить условие (5.24) совместности системы. При г = т система
совместна. Если г < т , то составить матрицу Ч7 = (<Э | Em_r) 5 и проверить
условие 'Yb = о. Если условие выполняется, то система совместна. В про-
тивном случае система несовместна и процесс решения заканчивается.
3. Найти частное решение неоднородной системы по формуле
205
XH =AJlb=T-
4. Составить фундаментальную матрицу Ф = Т • -
5. Записать общее решение системы (5.17) в виде (5.26)
х = хн +Фс ,
где с = (Cj • • Сл_г )т - столбец произвольных постоянных.
Замечания 5.5.
1. Формула (5.25) определяет третий способ нахождения фундамен-
тальной матрицы.
2. Положив хн =о в формуле (5.26), получаем структуру общего ре-
шения однородной системы
х = Ф • с = 71------ • с
гдес = (С! Сп_г У - столбец произвольных постоянных.
3. Теорема 5.5 равносильна альтернативе Фредгольма (4].
Пример 5.6. Решить систему уравнений
%! + х2 + 2х3 + х4 = 1,
2хг + Зх2 + х4 = 0,
3xj + 4х2 + 2х3 + 2х4 = 1
представив ее решения в виде (5.26).
□ 1. К матрице А системы приписываем справа и снизу единичные
матрицы порядков т = 3 и п-4 соответственно:
2
О
2
Элементарными преобразованиями приводим матрицу А к простейшему
виду. Взяв ведущий элемент ан = 1, делаем равными нулю остальные эле-
менты в первой строке и в первом столбце блока А :
206
А *4 '1 1 2 1 01-4-1 01-4-1 1 0 О' -2 1 0 -3 0 1 - '10 0 0 01-4-1 01-4-1 1 0 0 -2 1 0 -3 0 1
— ~ 1 0 0 0 '0100 0 0 1 0 ч0 0 0 1 7 1 -1 -2 -1 0 10 0 0 0 10 0 0 0 1
Взяв в полученной матрице ведущий элемент а2г = 1, делаем равными нулю
остальные элементы во второй строке и во втором столбце блока А :
'1 0 0 0 1 0 О') fl 0 0 0 1 0 О' 01-4-1-210 0100-210 П 1 А 1 Q Л 1 ЛЛПП 111
( А
_ 1 1 Э 1 11 — А 0
1а Прост Л = 5 гейши АТ = 0 0 <0 й вид '1 0 0 1 1 0 0 1 0 0 натрин 0 О' 0 0 0 0 14 1 0 0 0 1 0 1 ) (0 0 0 1 , ы А получен, следовательно, , х fi -1 -6 fl 0 О'] 0 14 1 , S = -2 1 0 , Т= , г = 2 0 0 10 -1 -1 1 v 7 (О 0 0 1 J
1^0 0 0 °,
2. Проверяем условие совместности (5.24). Так как г = 2 < 3 = т,
то составляем матрицу Т = (<? | Em_r) S, выделяя последнюю строку мат-
рицы S:
О
Т = (0 0 | 1) -2
-1
О
1
-1
1
Записываем условие 'УЬ = о:
(-1
-1
= 0. Условие выполняется,
значит, система совместна.
3. Находим частное решение неоднородной системы
207
И (Ег
хн =Т- -7
I О
-1
1
о
о
О
О
О
О>
-2
-1
-1
1
о
о
о
1
-1
-6
4
1
о
оУС
о
1
-2'
1
О
1 .
"1 0 0 1 °v 0
0 0 0 0 ojv
-1
1
о
о
о
о
о
о
-2
-1
О
1 О
-1 1
-2
О
оур
о
1.
( 3 '
-2
О
. О .
О
О
О
О
О
О
о
о
1
о
о
о
( О )
4. Записываем фундаментальную матрицу Ф = Т- - , составляя ее
из последних п-г = 4-2 = 2
• 1
о
о
о
столбцов матрицы Т:
ф=г.[_2_
-1
1
о
о
-6
4
1
О
-2
1
о
1
"О О
О О
1 О
.0 1
Столбцы этой матрицы образуют фундаментальную систему решений одно-
родной системы.
5. Записываем общее решение системы в виде (5.26)
Пример 5.7. Проверить совместность системы уравнений
4
1
О
1
о
2xj + 3x2 + х4 = 0,
3xj + 4х2 + 2х3 + 2х4 = 2,
используя условие (5.24).
□ Данная система отличается от решаемой в примере 5.6 свободным
членом третьего уравнения. При решении примера 5.6 были получены мат-
рица
5 =
1 О О'
-2 1 О
-1 -1 1
208
и ранг г ~2 матрицы системы. Так как m-r = 3-2 = l, то в матрицу 4х
следует включить только одну последнюю строку матрицы 5, т.е.
Т = (-1 -1 1). Вычислим левую часть (5.24):
'¥b = (-l -1 1) 0 =1.
Л
Следовательно, условие ИЬ-о не выполняется, т.е. система несовместна.
Тот же вывод получен в примере 5.2 по теореме 5.2 Кронекера-Капелли.
5.8. ПСЕВДОРЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Как показано выше, система т линейных алгебраических уравнений
с п неизвестными
Ах = b
(5.27)
может иметь единственное решение, бесконечно много решений или вообще
не иметь решений. Все эти случаи встречаются на практике. В частности,
несовместной системе отвечает противоречивая ситуация, сложившаяся при
математическом описании реальных объектов или процессов. Разумеется,
что несовместная система не имеет решения в привычном понимании. По-
этому возникает необходимость изменить само понятие решения так, чтобы
любая система линейных уравнений имела бы единственное в некотором
смысле "решение".
Для дальнейших рассуждений нам потребуется количественная харак-
теристика для "измерения" и "сравнения" между собой матриц-столбцов.
Для этого каждому столбцу поставим в соответствие неотрицательное дей-
ствительное число.
Модулем (нормой) столбца x = Gq х2 хп)Т называется неотри-
цательное число
I x\=Jxi+x% + ... + Х* .
Заметим, что величина е(х)=| Ах-/>| характеризует погрешность ре-
шения системы. Если величина е(х) велика, то столбец х - плохое прибли-
женное решение. Если погрешность е(х) мала, то столбец х — хорошее
приближенное решение. Если же х является решением системы (в привыч-
ном понимании), то е(х) = 0.
Псевдорешением системы линейных уравнений (5.27) называется наи-
меньший по модулю столбец х среди всех столбцов х, минимизирующих
величину | Ах-b |.
14 — 4549 209
Как показано в [3,27], любая система имеет единственное псевдоре-
шение
х = А~1Ь, (5.28)
где матрица А'1 — псевдообратная для матрицы системы (см. разд. 4.5.3).
Понятие псевдорешения позволяет обойти не только факт неединст-
венности, но и факт несуществования решений. Если система несовместна,
то псевдорешение х обеспечивает наименьшую величину погрешности
е(х). Если система совместна, то псевдорешение х является ее решением,
т.е. е(х) = 0, причем наименьшим по модулю.
АЛГОРИТМ НАХОЖДЕНИЯ ПСЕВДОРЕШЕНИЯ НЕОДНОРОДНОЙ СИСТЕМЫ
1. Найти псевдообратную матрицу А"1 одним из способов, рассмот-
ренных в разд.4.5.3.
2. Найти псевдорешение х = А"1 b .
Пример 5.8. Найти псевдорешение системы
Xi + х2 + 2х3 + х4 = 1,
• 2Xj + 3X2 + *4=0,
3xj + 4х2 + 2х3 + 2х4 = 1.
□ 1. Найдем псевдообратную матрицу. При решении примера 5.6 мат-
рица системы была приведена к простейшему виду
A = SAT = '1 0 0 1 0 О' 0 0 z ч (1 -1 -6 -2^ Г1 о о> 0 14 1 , S= -2 1 0 , Т = , г = 2 0 0 10 -1 -1 1 4 7 ^0 0 0 1 J
0 0 0J
По матрицам S и Т находим псевдообратную матрицу (см. первый
способ в разд. 4.5.3). Вычисляем произведения SS , Т Т и разбиваем их на
блоки
SS*
' 1
-1
-6
-2
f 1
-2
^-1
0 0
1 0
4 1
1 0
0V1 -1 -6
0 0 14
0 0 0 1
iJto о о
-2Л (1 -1 -6 -2>|
1 -1 2 10 3 т2
0 -6 10 53 16 Из
1J 1-2 3 16 6)
Вычисляем матрицы
210
и =-т;'т3=-
1 ( 6
62 [-16
V = -S254-1
-16Y-6 10Д_1_Г4 -12)
53 Д-2 3 J 62^10 1 J
По формуле (4.21) вычисляем псевдообратную матрицу
'1 -1
О 1
о о
<° 0
А-1 =Т
-6
4
1
О
-2Y62
О
1
-1
О'
О
Г1
1 1
62 3
О
О
10
-1
1
О
о
-6
4
1
О
1 О
О 4
1 Дю
О '
62
-12
1 ,
3
О
О
3
О О'
1 о
-1 L
Г1 -1
1
186
О
О
1
О
(о о
-6
4
1
О
-2Y186 О
1 0 186
О 12 -36
1Лзо 3
62 '
-62
16
9 ,
[ 1
-2
-1
О О'
1 о =
-1 1J
Г1 -1
1 0 1
186 О О
^0 О
-6
4
1
О
-г'!
о
1
1
124 -62 62 ' '-4 14 10'
-310 248 -62 1 -23 34 11
68 -52 16 "186 68 -52 16
15 -6 9 , <15 -6 9
2. Находим псевдорешение
—4 14
-23 34
68 -52
к 15 -6
х = A~'b-——
186
10'
11
16
9,
/Т
о
Л
1
186
Г6'
-12 =J_
84 31
<24,
Г 1 '
-2
14
<4>
Покажем, что это решение минимальное по модулю по сравнению со
всеми остальными решениями системы. Действительно, в примере 5.5 было
Найдено общее решение рассматриваемой системы
14*
211
Модуль этого столбца имеет выражение
| х |=^(з - 6 q - 2 q )2 + (- 2+4 q + q )2 + q2 + с22.
Вместо минимизации модуля будем искать минимум его квадрата, чтобы
избавиться от квадратного корня. Эти задачи, разумеется, эквивалентны, так
как точки минимума неотрицательной функции и ее квадрата совпадают.
Итак, будем искать минимум функции
/(q, q)=| х |2 =(3-6q -2 q)2 +(-2+4q ч-q)2 +q2 +q2,
зависящей от двух переменных (см. [32], а также разд. 6.5.5).
Для нахождения стационарных точек приравниваем частные производ-
ные первого порядка нулю (применяем необходимое условие экстремума):
= 2(3 - 6q -2 q)(- б)+2(- 2+4 q+q)(4)+2 q = о,
^ = 2(3-6q-2q)(-2)+2(-2+4q+q)+2q=o.
Упрощая уравнения, получаем систему
53q+i6q =26,
i6q+6q = 8,
которую решаем, например, по правилу Крамера:
26 16
А] _ 8____6 _ 28 _ 14
А “ 53 16 ~ 62 ~31 ’
16 6
53 26
А2 16 8
А 53 16
16 6
8 4
62 31
Поскольку угловые миноры матрицы Гессе
положительные:
Д]=53>0, А2 =53-6-162 > 0, найденная стационарная
(14 4
точка —; —
<31 31
является точкой минимума.
Следовательно, наименьший модуль среди всех решений системы име-
ет решение
212
Пример 5.9. Найти псевдорешение системы
X] - х2 = 6,
- X] + 2х2 + х3 = 9,
2Х| - Зх2 - х3 = -9,
х2 + х3 = 18.
□ Нетрудно заметить, что эта система несовместна (сложив второе и
третье уравнения, получим уравнение х1 — х2=0, которое противоречит
первому уравнению системы). Составим матрицу системы
Г 1 -1 О'
Л. 2 1 .
2 -3 -1
<0 1 1,
1. Псевдообратная матрица для матрицы А была найдена в примере
4.12:
2. По формуле (5.28) получаем псевдорешение
'9"
4
Л
Покажем, что это решение минимизирует погрешность
е(х) -1 Ах - b |.
Для этого найдем минимум квадрата этой функции (см. пример 5.8)
е2(х) = | Ах-b |2 =(х| -х2 -б)2 +(—Х| + 2х2 +х3 -9)2 +
+ (2Х] -Зх2 -х3 +9)2 +(х2 +х3-18)2 .
Приравнивая к нулю частные производные по переменным Х], х2, х3,
получаем после упрощений систему уравнений
213
2jq -3x2 — x3 = -7,
- 3xj + 5x2 + 2x3 = 19,
— Xj + 2x2 + x3 =12.
Методом Гаусса (см. разд. 5.4) находим общее решение этой системы
Xj = 22-х3,
х2 =!7-х3,
(5.29)
где х3 - свободная переменная. Следовательно, функция е(х) имеет беско-
нечно много стационарных точек, на которых достигается ее наименьшее
значение. Заметим, что найденное псевдорешение х принадлежит этому
множеству. Покажем теперь, что х - это наименьший по модулю элемент
множества (5.29). Для этого составим функцию, равную квадрату модуля
решения х = (22-х3 17-х3 х3У:
Дх3)=| х |2 = (22 - х3 )2 + (17 - х3 f + х32.
Найдем точку минимума этой функции одной переменной:
f\x3)= 2(22-Хз)(-1)+2(17-х3)(-1)+ 2х3 =0 => х3=13.
Поскольку функция выпуклая, наименьшее по модулю решение (5.29) полу-
чается при х3=13. Это решение совпадает с найденным ранее
псевдорешением х = (9 4 13)г.
Задачи для самостоятельного решения
5.1. Решить системы уравнений по правилу Крамера:
х( + 2х2 + х3=4, Xj+x2 + x3=2, 2xj-4х2+Зх3 =1,
а) • Зх] -5х2 + Зх3 = 1, б) 3х1 + 2х2 + 2х3 = 1, в) х1~2х2 + 4х3 = 3,
2xJ+7х2-Xj =8; 4х,+3х2+3Xj =4; ЗХ]-х2+5х3 = 2;
„ г Г2 2 -1 1УхЛГ4^
х.+2х,-х=2, х, +2х, + 2х. =9,
ч ' 2 3 3 4 3 -1 2 х2 6
г) 2х. -Зх, + 2х, = 2, д) 2х. + х, - 2х, = 0, е) = * 2 3 1 2 3 8 5 -3 4 х3 12
Зх, +х„ + х, =8; 2х.-2х„+х =0;
2? о? 1 СП СП —/ п 4
Указания: б) Д = О, Д2 * 0; д) Д = -27
е) Д = 2; Д,=2; Д2=2; Д3=-2; Д4 = -2;
Aj=-27, Д2=-54, Д3 = -54;
Ответ: a) xt = х2 = х3 = 1; б) нет решений; в) Xj = -1, х2 = 0, х3 = 1;
г) Xj = 1, х2 = 2, х3 = 3; д) Xj = 1, х2 = 2, х3 = 2; е) х3 = 1; х2 = Г, х3 = ~1 '>
214
5.2. Решить системы уравнений методом Гаусса:
'ЗХ]+2х2+х3=5,
х( + Зх2 + 5х3 + 7х4 + 9х5 = 1,
в)] Xi+x2-x3=O,
4Xj - х2 + 5х3 = 3;
Xi + 2х2 - х3 = 2,
2xj "" х2 + х3 2,
Xj - х2 + 2х3 = 5,
г) 2xi “ 2х2 - х3 = -5,
3Xj + х2 - 2х3 — 2;
3xj - Зх2 + х3 = 0;
Xi-x2 + x3-x4=0, Х!+х2-2х3+х4 = 1, ЗХ] +х2 -Зх3 + х4 = 2; Указания: е) - 6х, +3х2 + 2х3 +3х4 + 4х5 = 5, 4xj + 2х2 + х3 + 2х4 + Зх5 = 4, 4xj + 2х2 + Зх3 + 2х4 + х5 = 0, 2xi + х2 + 7х3 + Зх4 + 2х5 = 1.
a) (A |Z>) = '3 2 1 1 1 -1 о '1 0 1 1 -1 -4 С Г 5 - rg (А | />) = 3 = = rg А = п;
6) rg (А | b ; г) (А | b) = ? -1 5 l = 3*2 = rg '1 -1 2 2 -2 -1 V А ; 5' -5 В 0 0 1 ) rg (а I ь) "1 -1 2 0 0 1 г = 3 5' 3 rg А = и; '1 -1 0 0 0 1 -f 3 »
rg(A|Z>) = Ответ 3 -3 1 2 = rg А < и = п: a) Xj 0 , = 3. = -1 ♦ 1° х2 0 = 3 0 , х 0 з = 2 ООО б) сис °, тем. 1 несовместна;
1=х2 = х3 =1; г *1 = = - 1 + х 2 ’ хз = 3, х2 е R ; д) X] = 0,5 + О,5х3
х3еЯ, х4еЯ; е) х2 = -2х,+1,5х3, х4=-1-3,5х3,
4 х2 = 0,5 + 1,5х3 - х4,
; ** = 2 + х,, х. е R,
! Ж 31
- ЮТся неоднозначно.
х, g R. В п. г, д, е формулы общего решения определя-
э I
5.3. Найти фундаментальную систему решений и записать структуру
общего решения:
н Xj-х2 + х3-х4 =0,
t •) • Xj + х2 - 2х3 + х4 = 0,
, Зх. + х9 - Зх, + х. = 0;
1 2 3 4
б)
х. + 2х, + 4х, - Зх. = 0,
1 I 3 4
ЗХ| +5х2 + 6х3 -4х4 = 0,
4х. + 5х, -2х, + Зх. = 0,
12 3 4
Зх. + 8х, + 24х, - 19х. = О
12 3 4
215
решений определяется неоднозначно.
5.4. Найти фундаментальную матрицу системы уравнений:
2xj - Зх2 + 5х3 + 7х4 = 0,
б) • 4Xj - 6х2 + 2х3 + Зх4 = 0, в) •
2Х] - Зх2 -11х3 - 15х4 = 0;
система
5х. + 24х, - 7х, - х = О
а) ) 1 2 34
I - х, - 2х2 + 7х3 + Зх4 = О
Х1 + Х2 О ’
Xj -х2 =0.
Ответ: а) Ф =
41
-2
1
. О
-1
о
1
3
2
О
О
О
-22
16
; в) фундаментальной
; б)
Ф =
матрицы нет. В п. а, б фундаментальная матрица определяется неоднознач-
но.
5.5. Составить однородную систему уравнений, для которой данная
матрица является фундаментальной:
а) Ф =
4
2
.1
б) Ф =
1
о
2
1
О
1
3
2
1
О
Указания: матрица А искомой системы уравнений Ах = о является
фундаментальной для системы Фгх = о.
2х. + Зх2 - х3 = 0,
„ Системы уравнений
х,+2х,-х. =0.
1 2 4
Ответ: a) Xj - хг - х3 = 0; б) •
определяются неоднозначно.
5.6. Дана фундаментальная система <р3 = (1 2 3)г, <р2 = (3 2 1)Т
некоторой однородной системы Ах = о, А * О. Являются ли решениями
этой системы столбцы: а) х = (4 5 6)4 б) х = (2 3 5)г ?
Указание: использовать формулу (5.14).
Ответ: а) да; б) нет.
216
5.7. Известны три решения (1 2 З)7, (3 2 1)г, (2 3 1)г некото-
рой неоднородной системы уравнений Ах = Ь, А * О. Являются ли реше-
ниями этой системы столбцы: а) х = (4 4 - 2)Т ; б) х = (2 3 5)Г ?
Указание: использовать формулу (5.15).
Ответ: а) да; б) нет.
5.8. При каждом значении параметра X решить однородную систему
уравнений (а~ХЕ)х = о , где А = 2
4
1
5
4
-1
-2
-1
Указание-. А-ХЕ =
4-Х
2
4
1
5-Х
4
-1
-2
-1-Х
, det(A-Xf) = (г-ХХЛ-З^О
при X = 2 и X = 3; если X = 2, то
А-Х£ =
-2
-3
'2
О
.0
-1
О
; если
Х = 3,то А-ХЕ = 2
.4
-2
-4
Ответ: при X = 2 :
х = С\ 2 ; при Х = 3:
; если
1
2
4
О
О
1
О
о
О
О
2
2
4
1
3
4
1
2
О
1
О
2
О
1
4
Х^2 и Х^3,то х = о.
5.9. При всех со решить систему уравнений Ах = о, где
1 1'
со со2
со2 со?
Г1
Указание: det А = -(со-1)2со(со+2)=0 при со = 0, со =-2, со = 1.
Ответ: при со = О
х = Q 1
Г-С
'-Г
+С2 о
; при остальных значениях со
х = о.
ГЛАВА 6. ФУНКЦИОНАЛЬНЫЕ МАТРИЦЫ И
ФУНКЦИИ ВЕКТОРНОГО АРГУМЕНТА
В этом разделе рассматриваются функциональные матрицы, элемента-
ми которых являются функции. Основные понятия математического анализа
[19,25,43] в применении к функциональным матрицам нас будут интересо-
вать с алгебраической точки зрения, а именно с точки зрения использования
матричной алгебры (см. гл.1, 2). Рассматриваются операции дифференциро-
вания и интегрирования функциональных матриц, правила их применения и
матричная форма записи этих операций. Вопросы существования и свойства
соответствующих производных и интегралов, изучаемые в курсе математи-
ческого анализа [19,25,43], здесь не рассматриваются.
6.1. ФУНКЦИОНАЛЬНЫЕ МАТРИЦЫ
СКАЛЯРНОГО АРГУМЕНТА
Функциональной матрицей скалярного аргумента t называется мат-
рица, элементы которой являются функциями независимой переменной t:
А(г)=
А.10 -
При фиксированном значении t функциональная матрица становится чи-
словой. Поэтому все операции, введенные для числовых матриц (см. гл. 1-4),
полностью переносятся на функциональные.
Рассмотрим некоторые понятия математического анализа в примене-
нии к функциональным матрицам.
1. Пределом функциональной матрицы A(t) при стремлении пере-
менной t к значению t0 называется матрица А(г0), элементами которой
служат соответствующие пределы элементов матрицы А(г), если они суще-
ствуют, т.е.
А(г0)= lim А(г) =
<-»/0
liman (г)
limaml(r)
- limaln(/)'
- lima^r)
Другими словами, предел матрицы определяется "поэлементно" как матри-
ца, составленная из пределов соответствующих элементов.
218
2. Производной функциональной матрицы А(г) по независимой пе-
dA(t)
ременной t называется матрица ——, элементами которой служат
dt
производные соответствующих элементов матрицы А(г), т.е.
^11(0 ... daln{t)
dA(t) _ Ф dt
dt daml(t) ... da^t)
dt dt '
Другими словами, производная матрицы определяется "поэлементно" как
матрица, составленная из производных соответствующих элементов. В ча-
стности, производная столбца ) = (х,(t) хп(t)f есть столбец
dx(t)
dt
fdxjf)'
dt
dxn(t)
< dt >
Нетрудно проверить справедливость правил дифференцирования:
1. Производная суммы матриц A(t) и B(t) равна сумме производных
этих матриц:
2. Постоянный числовой множитель можно вынести за знак
дифференцирования:
dtx dt
3. Производная произведения матриц A(t) и B(t) находится по фор-
муле
В частности,
^(лМ-в(г))=^в(г)+л(>)^.
at at at
<*k(*)-y(Q] = dxT(t) zx xTtt\dy(f).
dt dt dt ’
= dA(t) / л лд dx(t)
dt dt dt ’
219
где x(t), y(t) - столбцы одинаковых размеров, A{t), С — матрицы соот-
ветствующих размеров, причем матрица С числовая.
4. Производная обратной матрицы (если она существует) вычисляет-
ся по формуле
dt dt
В самом деле, дифференцируя тождество Л“'(/)л(/)= Е по правилу 3,
'(0 \ J-l(\dA^t) Z1 У
получаем ----— A(t)+A (z;—— = О, так как производная постоянной
dt dt
матрицы (Е) равна нулевой матрице. Умножая последнее равенство на
Л-1(?) справа, выражаем искомую производную. 1
5. Производная определителя квадратной матрицы A(t) ( п -го поряд-
ка) вычисляется по формуле
^(det4))=XZ40—= trP+^~У
dt ” dt I dt J
где 4y(z) - алгебраическое дополнение элемента a^t) матрицы A(t) ;
A+(t) - присоединенная матрица.
Действительно, так как det Л-а^Ад + ai2Ai2 +... + ainAin, то частная
производная --(det л)= Ац . Поэтому полная производная вычисляется по
дау
формуле = =
3. Определенным интегралом от функциональной матрицы A(t)
в пределах от t0 до называется матрица р1(г)Л, элементами которой
*0
служат интегралы от соответствующих элементов матрицы A(t):
'i
jA(t)dt =
’ fai„(()dt
fami(t)dt
т.е. интеграл от матрицы определяется "поэлементно".
220
Пример 6.1. Найти производную произведения матрицы J(Z) = I
на столбец x(z) = (sinz cos?)7.
□ По правилу дифференцирования произведения получаем
О OVsinz'l (1 1V cos/ ( cos/-sin/
I + 1=1
О IJ^coszJ гд-sin/J ^2cosZ-Zsinz
Сделаем проверку, выполняя дифференцирование после вычисления произ-
ведения матриц:
Результаты совпадают.
Функциональные матрицы применяются, например, для матричной
записи систем разностных и дифференциальных уравнений [31,34].
Система п линейных разностных (рекуррентных) уравнений с п неиз-
вестными имеет вид
xt (к +1) = О], (к) х, (Л) +... + а („ (Л) хп (k) + f (к), х, (к0) = Х10 ,
хп^ + 1)=а„](л)х1(л)+... + а„„(л)х„(л)+/„(л), хл(Л0)=хи0 ,
где к - дискретное время, к = к0, к0 +1,...; к0 - начальный момент дис-
кретного времени; х10,...,хл0 - начальные значения переменных
Х](л)..хл(&). Используя функциональные и числовые матрицы
систему можно записать в матричной форме:
х(к +1)= A(k)x(k)+f(k),
Система п линейных обыкновенных дифференциальных уравнений
с п неизвестными имеет вид
= Ч10 X!(z)+... + а1л0x„(z)+ / (z), Х](,о) = Xio ,
= ал1 (/) xt(z) +... + апп(z) х„(z) + fn (z), x„(z0) = xn0 ,
221
где t - время, t0 - начальный момент времени; х10,...,хл0 - начальные зна-
чения переменных xn(t). Используя функциональные и числовые
матрицы
то
систему можно записать в матричной форме:
^ = А(т)х(г)+/(т), х(?0)=х0.
Хо= :
Применение матриц не ограничивается записью систем. Решение этих
систем уравнений находится с использованием функций от матриц (см.
разд.7.4.5,7.5.4).
6.2. ПРОИЗВОДНЫЕ СКАЛЯРНОЙ ФУНКЦИИ
ПО ВЕКТОРНОМУ АРГУМЕНТУ
Рассмотрим скалярную (числовую) функцию нескольких переменных
/(х!,х2..хл). Упорядоченный набор переменных х1,х2,...,хп будем назы-
вать векторным аргументом этой функции и обозначать х. Первый диф-
ференциал функции f{x}~ /(хрх2,..., хп) имеет вид [19,25,43]:
J/(x) = -^^dx, + ^^dx2 + ... + -^^dx„.
vXj CXn
части можно представить как произведение строки
<dxl'
: , либо как произведение
dx„ .
(6.1)
Сумму в правой
#(x)_fdf(x)
dx
Эх]
df(x)}
—— на столбец ах =
J
, г е- df(x) f df (х)АГ , ( х df(x) т df(x)
строки dx на столбец —' : df (х) - — dx = dx -'.
dxT I dx ) dx dxT
Матрица-строка
или матрица-столбец
dxT
определяют производную скалярной функции по векторному аргу-
менту {градиент скалярной функции). Двойственность определения отно-
сится только к форме записи, поскольку векторный аргумент функции мож-
но считать столбцом (в этом случае дифференциал dx - столбец) или пони-
мать как строку. В любом случае для первого дифференциала получаем од-
но и то же выражение (6.1).
222
Второй дифференциал функции f(x) = f(xl,x2,.-,xn) имеет вид
dxt dXj .
(6.2)
Эх.2
ах,ахи
Обозначим через —=г-^ =
dxTdx
д2
матрицу частных
дхпдх1
дхп
производных второго порядка (матрицу Гессе). Тогда правую часть (6.2)
можно записать в виде произведения
dxTdx
Замечания 6.1.
1. Для записи производных можно использовать символические векто-
ры (столбцы или строки):
[—
... -Q vr=^-= ’? .
dx (^Эх, дх„) dxT д
Л,
При этом дифференцирование функции формально записывается как умно-
жение функции на символический вектор производных. Например, градиент
функции есть произведение вектора V на функцию /(х):
V/ =
дхп,
, а матрица
Гессе есть произведение символической
А
матрицы
а2
ах,2
а2
а2
Эх. Эх
1 п
ЭхиЭх,
а2
*Хп
на функцию /(х).
2. Определитель матрицы Гессе называется гессианом.
3. Свойства градиента функции и матрицы Гессе используются в мето-
дах поиска экстремума функции [32].
223
Пример 6.2. Найти первую и вторую производные сложной функции
g(t) = /(x(t)) = /(х] (гхп(t)), применяя матричные обозначения.
□ Находим производные функции g(t), заменяя суммирование опера-
циями умножения соответствующих матриц:
dg(t) _ydf(x(t)) dxfr) _df(x(t)) dx(t)
dt Эх dt dx dt
^/(4)) dxfc) ! df(x(t)) d2x(t)
dt J dxTdx dt dx dt2
Сравним матричную форму записи этих производных с производными
в случае скалярной функции x(t):
dg(t} = df(x(t)) dx(t) d2g(t) = df(x(t)) d2x(t) + d2f(x(t}) f
dt dx dt dt2 dx dt2 dx2 I dt J
Выражения для первой производной совпадают, а для второй производной -
отличаются незначительно, причем полное совпадение будет, если учесть,
что хт - х для скалярной величины х.
6.3. ПРОИЗВОДНЫЕ ВЕКТОРНОЙ ФУНКЦИИ
ПО ВЕКТОРНОМУ АРГУМЕНТУ
/itxp.-.xj
Пусть задан столбец f(x)-
функций нескольких пере-
^(xi-.-xJ,
менных (говорят, что задана вектор-функция векторного аргумента).
Первый дифференциал вектор-функции имеет вид [19,25,43]:
224
Обозначим через
'dfAx)
df(x) _
Л Ут(х}
Эх,
1
УМ'
дх„
dfm(x)
матрицу частных произ-
водных первого порядка заданных функций (матрицу Якоби). Тогда вы-
ражение для первого дифференциала можно записать в виде
\ df(x\ df(x)
df[x) = -^-L-Ldx,T.e. - - производная вектор-функции векторного ар-
dx dx
гумента.
Как и в случае с аргументом х, упорядоченный набор функций можно
считать не матрицей-столбцом, а матрицей-строкой (/(х))г . Этот случай
сводится к предыдущему, учитывая, что операции дифференцирования и
транспонирования можно выполнять в любом порядке, так как d(fT)= (df)T
(здесь и далее аргумент х для упрощения записи опущен). Поэтому из ра-
df f df^
венства df = — dx получаем dfT = (dx)r — - (dx; —=-, где
dx {dx J dx
dfT
jjr
'd/~i(x) dfm\x)
дхг дх{
d/i(x) ... 5/т(х)
Эх„ дх„
- транспонированная матрица Якоби вектор-функции /(х).
Заметим, что из равенства d(/r)=(rf/)r следует правило транспони-
dfT
рования производных вектор-функции: —~ =
dx
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ ПО ВЕКТОРНОМУ АРГУМЕНТУ
Векторный аргумент х, его приращение dx считаем матрицами-
столбцами размеров иХ1.
1. Первый дифференциал скалярной функции f(x) имеет вид:
dx dxT
df (df
гое —= -------
dx ^6^X]
df ] i j. df (df
-d— - градиент функции, a -d— = -d-
dxn) dx {.dx.
15 - 4549
225
2. Второй дифференциал скалярной функции fix') имеет вид
г ,Т d2f J d2f(x)
d2f =dxr —-—dx, где —=
dxT dx dx dx
э2/(х)
dx2
d2/(x)
dx dx,
n J
э2/(х)
dx2
п
- матрица Гессе.
3. Первый дифференциал вектор-функции {матрицы-столбца)
имеет вид'.
df df(x)
df =——dx,где —=
dx dx
d/i(x)
Эх!
d/i(x)
dxn
— матрица Якоби.
Эх.
К
Первый дифференциал матрицы-строки'. d(fT}= dxT .
4. В частном случае, когда f(x)= х, получаем
dx „ dx1 „
— = Е, —=r=E,
dx dxT
где Е - единичная матрица п -го порядка.
5. Числовую матрицу С (соответствующих размеров) можно выно-
сить за знак производной'.
4/7) _#гс
dx dx ’ dxT dxT
Последняя формула следует из правила транспонирования производных:
d(fTc)=(d(c*fN=С СТ ^\=df_c
dxT dx > t dx) dxT
6. Производные суммы, разности и произведения вектор-функций и(х)
и v(x) одинаковых размеров тх 1:
d(u + v) _ du dv d(u-v) _du _dv
dx dx dx’ dx dx dx'
226
d\uTv) т du T dv д(игт) duT dvT
—i---‘ = v— + u —; —* —* = —rv + ——u .
dx dx dx dxT dx1 dx'
Докажем, например, последнее равенство. Найдем частную производ-
ную скалярной функции uTv по переменной Xj :
m
=z
д(мгу)
dxj
dut
dZVi
+«i
dvj
dxi.
ui
dy
dxj
itdxj
Тогда первый дифференциал функции uTv имеет вид
Запишем это выражение, используя матричные обозначения
dum' <dvl
d[uTv)=(dx1 • ’ dxn) dxj dxj V + dxt
dux ^x„ dxn J™, dvt dxn
= dx
dvm'
Сравнивая полученное выражение с
dxT
, приходим к равен-
</(игу) duT dvT
ству —> ——— v4-----—и , что и требовалось доказать.
dxT dxT dxT
7. Производная сложной функции
z(y(x)), где
z = z(y)=
Ч(уГ
dz(y(x)) dz(y(x)) dy(x)
, вычисляется no формуле'. ----------— --------*— или,
dx dy dx
dz dz dy
опуская аргументы, — —-------.
dx dy dx
Действительно, запишем первый дифференциал векгор-функции:
dz(x}= — dy = — — dx. Заметим, что матрицы Якоби в правой части фор-
dy dy dx
15*
227
dz dy
мулы согласованы: матрица — имеет размеры кхт, матрица — - тхп.
dy dx
Найдем, используя обычные правила дифференцирования, частную произ-
3z,(y(x)) A dzt дук „
водную ——- /,—- В правой части стоит произведение i -и
dyk dxj
dz . „ dy .
строки матрицы — на j -и столбец матрицы —, что и требовалось пока-
dy dx
ЗХ:
зать.
Использование матричных обозначений позволяет записывать и при-
менять правила дифференцирования по векторному аргументу аналогично
правилам дифференцирования в скалярном случае. Например, правило 7
дифференцирования сложной вектор-функции формально совпадает с
с dz dz dy
обычным цепным правилом — -----------— дифференцирования скалярной
dx dy dx
сложной функции одной переменной. Разумеется, что формальное совпаде-
ние правил становится фактическим в скалярном случае, когда все матрицы
имеют размеры 1x1.
Пример 6.3. Применяя правила дифференцирования по векторному ар-
гументу, найти производные следующих функций:
а) стх; б) хтс; в) Ах; г) хтА ; д) хт Ах,
где А - квадратная числовая матрица п -го порядка; х, с - столбцы разме-
ров и Х1, причем столбец с числовой.
□ а) Вынося постоянный множитель (матрицу-строку) ст по правилу
. dicrx) т dx -г т
5 и учитывая правило 4, получаем: —1--L = с — -с Е = с .
dx dx
б) Учитывая, что величина хтс скалярная, т.е. хтс
с х, по-
лучаем —1‘ i-------L - с1 . Заметим, что ' _ ' - - ' = с.
dx dx dxT dxT
. rr , , d(Ax} .dx
в) I Io правилам 4 и 5 находим: —5—- - A— = AE = A.
dx dx
. rr . c dxr
г) По правилам 4 и 5 находим: ' = —— А = ЕА = А.
dxT dxT
д) Представляя скалярное выражение хтАх как произведение строки
хт на столбец Ах, по правилу 6 (где ит = хт, v Ах) получаем
228
4» , (лЛ- * + г = xrАт dx + хгл Л =
dx dx dx dx dx
+4
либо с учетом правила транспонирования производных
,, ,,“ и АХ/ ,т . —
Учитывая результат п. б , имеем —Ч--< = А + А .
dx dx
Замечания 6.2.
1. В некоторых областях прикладной математики, например, в методах
оптимизации и теории управления [31,32,41], часто используются другие со-
глашения, совпадающие с изложенными с точностью до операции транспо-
нирования. Производная — (градиент функции /(х)) считается матри-
dx
цей-столбцом, а производная —- матрицей-строкой:
dx
df(x) _ д*1 df(x)_''df df'
dx Э/ ' dxr ЭхПу
эГ
к "7
Тогда соответствующие формулы дифференцирования, аналогичные
полученным в примере 6.3, имеют вид [41]:
rf(crx) _ б/(хгс) _ rf(xrc) _ d(crx) _ ?г .
dx dx ’ dxT dxT
d(Ax)_A_ d(xTA)_A
dxT ' dx '
2, Если матрица Якоби квадратная (m = п ), то ее определитель называ-
ется якобианом.
3. След матрицы Якоби (при m = п ) определяет дивергенцию
dx
d^i
вектор-функции /(х) векторного аргумента х.
229
6.4. ПРОИЗВОДНЫЕ МАТРИЧНОЙ ФУНКЦИИ
ПО ВЕКТОРНОМУ АРГУМЕНТУ
Рассмотрим функциональную матрицу А(х) , элементами которой слу-
жат функции (х) векторного аргумента х . Дифференциал этой функции
имеет вид
°Xi
ЭА(х) _ .
где —-— - частная производная матрицы по одной переменной (см.
Эх,
разд. 6.1). Совокупность частных производных (градиент функциональной
да. W
матрицы) представляет объект, элементы которого —-— нумеруются
Эх*
тремя индексами: номер строки, номер столбца и номер переменной диффе-
ренцирования. Поэтому заменить операцию суммирования в правой части
формулы операцией умножения матриц в данном случае не представляется
возможным. Необходимо вводить другие объекты - тензоры и операции над
ними [4,11,46]. Поясним формальную сторону получения удобных формул
дифференцирования на примере функциональных матриц. Примем следую-
щие правила индексирования:
1) элементы матрицы А = (а^) обозначаются a‘j, где i - номер строки,
a j - номер столбца. В частности, х = (х') - матрица-столбец (или просто
столбец), а У = (у;) - матрица-строка (или просто строка);
2) частную производную функции F(x) (скалярной, векторной или
матричной) по переменной х' будем обозначать, приписывая нижний ин-
dF
деке i в скобках: —r =
Эх' U
3) если в произведении одинаковые индексы встречаются сверху и
снизу, то по ним производится суммирование (хотя знак суммы не указыва-
ется). Например, если А = (я у) - матрица размеров тхп, х = (х;) - столбец
размеров их1, у = (у,.) - строка размеров 1х/л, то
« m m n
a‘jxJ== XX» * a‘ixiyi=-
7=1 (=1 1=1 7=1
т.е. a‘jXJ - i -й элемент столбца Ах, а^у, - j -й элемент строки уА, a'jX^yj
- число уАх.
230
Применяя эти соглашения, запишем дифференциалы:
- скалярной функции: df — f^dx', d2f = f^yix'dx1;
-вектор-функции /=(/') (функции-столбца): df‘ = f(j)dxJ’
- функциональной матрицы F = (/j): dfj = fj(k)dxk
dfj
частная производная первого порядка элемента функциональной матри-
цы F по переменной хк.
Одним из преимуществ принятых соглашений является получение
простого вида формул. Другие преимущества раскрываются и используются
в тензорном анализе [4,11,42,46].
6.5. ЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
Рассмотрим скалярную (числовую) функцию f(x)~ /(хр х2>> хп)
векторного аргумента jc = (jq ••• х„)г, которая каждому значению век-
торного аргумента х, т.е. каждому числовому столбцу размеров лх1, ста-
вит в соответствие число (значение скалярной функции).
Наиболее простыми функциями векторного аргумента являются мно-
гочлены.
Многочленом первой степени от п переменных хг,...,хп называется
выражение вида р1(х)=с1х1 + с2х2+... + слхл+с0, где числа CQ.q,...,^ -
коэффициенты многочлена (предполагается, что среди коэффициентов
с1,...,сп есть отличные от нуля); коэффициент с0 называется свободным
членом. Многочлен первой степени называется однородным, если
р1(Ах)=Ар1(х) для любого числа X. Нетрудно показать, что многочлен
P1W будет однородным тогда и только тогда, когда отсутствует свободный
член(с0 =0).
Линейной формой переменных х{,...,хп называется однородный
многочлен первой степени
п
g(x)=^c‘x‘' (6.3)
/=1
где коэффициенты с1,...,сп многочлена (6.3) называются коэффициента-
ми линейной формы. Составляя из коэффициентов матрицу-строку
с = (q • • • сп) {строка коэффициентов линейной формы), а из перемен-
231
ных — матрицу-столбец х = (jq • • хп )Г , линейную форму можно записать
в виде
g(x) = cx. (6.4)
Многочленом второй степени ох п переменных jq называется
Л Л л
выражение вида р2(х)= + с0, где числа ay, bit с0 -
>=1 j=i i=i
коэффициенты многочлена-, а у - старшие коэффициенты (или коэффи-
циенты квадратичных членов), bt - коэффициенты линейных членов,
с0 - свободный член. У многочлена второй степени не все старшие коэффи-
циенты а,у равны нулю одновременно. Многочлен второй степени называ-
ется однородным, если р2(Ах) = А2р2(х). Нетрудно показать, что многочлен
р2(х) будет однородным тогда и только тогда, когда отсутствуют линейные
члены и свободный член (bi = b2 =... = Ьп = 0, с0 = 0).
Квадратичной формой переменных jq,..., х„ называется однородный
многочлен второй степени
’ <6-5)
<=1 j=i
коэффициенты которого удовлетворяют условиям симметричности
ay =ajt i = l,...,n, j = Это условие не ограничивает общности, так
как сумму двух подобных членов аух^, + a^Xt с неравными коэффициен-
тами ау Ф a jj (при i # j) всегда можно заменить суммой а'х,ху- + a',XyXf с
, t ау+ан
равными коэффициентами, положив ау = . Приводя подобные
члены, квадратичную форму (6.5) можно представить в виде
9(х)=днх12 + 2a12.qx2 +... + 2д1лх1хл +д22х2 +2д23х2х3 +... + аллхл.
Это вид квадратичной формы с приведенными подобными членами.
Симметрическая матрица А = [ау), составленная из коэффициентов
квадратичной формы (6.5), называется матрицей квадратичной формы.
Определитель этой матрицы называется дискриминантом, а ее ранг - ран-
гом квадратичной формы. Квадратичная форма называется вырожденной,
если ее матрица вырожденная (rg А < п), в противном случае, когда матри-
ца невырожденная (rg А = п), квадратичная форма называется невырож-
денной.
232
Составляя из переменных матрицу-столбец х = (х1 хл)г, квадра-
тичную форму можно записать в виде
q(x)=xTAx. (6-6)
Чтобы получить матрицу А квадратичной формы (6.6), нужно:
1) записать квадратичную форму в виде (6.5), разбив удвоенные произ-
ведения на сумму двух одинаковых слагаемых;
2) из коэффициентов в (6.5) составить матрицу квадратичной формы.
Коэффициенты у отсутствующих членов считаются равными нулю.
Чтобы составить матрицу квадратичной формы с приведенными по-
добными членами, нужно на главной диагонали матрицы поставить коэф-
фициенты при квадратах переменных, а элементы, симметричные главной
диагонали, взять равными половине соответствующих коэффициентов у
произведений разных переменных.
Пример 6.4. Составить матрицу квадратичной формы, найти ее дис-
криминант и ранг: q(x) - xf + 2х3х2 + Зх2х3 + 4xj.
□ Приведем данную квадратичную форму к виду (6.5):
q(x) = х2 + XjX2 + 0 • Х]Х3 + х2х{ + 0 - х2 + 1,5х2х3 + 0 х3хх + 1,5х3х2 + 4х3.
Получили коэффициенты ан = 1; al2 = а21 = 1; а13 - а31 = 0; а22 = 0,
д23 = азг = 1’5 > азз = Следовательно, матрица квадратичной формы имеет
вид
fl 1 (Н
А= 1 О
ч0 1,5
1,5
4,
Сравнивая эту матрицу с коэффициентами заданной первоначально формы
q(x)=xi + 2х3х2 + Зх2х3 + 4х3 , отмечаем, что на главной диагонали стоят ко-
эффициенты при квадратах переменных, а элементы, симметричные относи-
тельно главной диагонали, равны половине соответствующих коэффициен-
тов у произведений разных переменных. Вычисляем дискриминант и ранг
квадратичной формы det А = -6,25, rg А = 3 (так как определитель матрицы
не равен нулю).
Пример 6.5. Записать линейную и квадратичную формы
a) g(xj, х2, х3) = Xj-2х2+Зх3; б) q(xl,x2,x3)-x^ +2xjX2 + 3х2 + 4xtx3 + х3
в матричном виде как функции векторного аргумента х = (jq х2 х3 )т и
найти их производные первого и второго порядков.
□ а) Запишем линейную форму g(x) в матричном виде:
233
— 2л2 + Зх3 = (1 - 2 3)
х2 = с х,
где с- О ~2 3) - строка коэффициентов линейной формы. Находим
/ \ d2 2
градиент -£- = с = (1 -2 3) и матрицу Гессе —= О, где О - нулевая
dx dx1 dx
матрица 3-го порядка (см. разд. 1.1).
б) По заданной квадратичной форме q(x) = xf + 2xlx2 + Зх2 + 4xtx3 + х3
с приведенными подобными членами составляем ее матрицу, записывая ко-
эффициенты 1,3,1 при квадратах xf , х2, х3 переменных на главную диа-
гональ: ап = 1, а22 = 3, а33 = 1, а половины соответствующих коэффициен-
тов при произведениях 2х{х2, 4xjX3 - симметрично главной диагонали:
а12 = а21 = 1, а13 = а31 = 2. Коэффициенты у отсутствующих членов (х2х3,
х3х2) заменяем нулями: а23 =а32 = 0. Получаем матричную форму записи
данной квадратичной формы
1 1 2>
Xi + 2х3х2 + Зх2 + 4Х]Х3 + х3
Х2
*2
,т
^2 0 lJ(x3J
где А - матрица квадратичной формы. Находим градиент функции q(x) и
матрицу Гессе (см. разд. 6.2)
= (2xi + 2х2 + 4х3 2х! + 6х2
4х1+2х3) = 2(х1 х2
х3) 1 3
.2 0
0 = 2хтА,
1.
<12<1 _2
dxTdx
= 2А.
1 1
1 3
2 О
0
1
Вычислим дискриминант и ранг данной квадратичной формы:
rg А = 3.
det А = -10,
Замечания 6.3.
1. Важным примером линейной формы служит первый дифференциал
скалярной функции /(х) векторного аргумента х (см. разд. 6.2):
dftx^Y^dx^^dx,
rj dx, dx
234
где дифференциалы dxldxn являются переменными линейной формы,
градиент - , вычисленный при некотором фиксированном значении ар-
dx
гумента, является строкой коэффициентов линейной формы, а дифференци-
ал векторного аргумента dx = (dxl • dxn У служит столбцом переменных
линейной формы.
2. Важным примером квадратичной формы служит второй дифферен-
циал скалярной функции векторного аргумента (см. разд. 6.3):
d2f^=±t
;=i ;=1
Э2/(*)
Эх,Эх,
dXjdXj = dxT
dx7dx
где дифференциалы dxt ,...,dxn являются переменными квадратичной фор-
r
мы, матрица Гессе ——д—-, вычисленная при некотором фиксированном
dx‘dx
значении аргумента, является матрицей квадратичной формы, а дифферен-
циал векторного аргумента dx = {dxY dxnJ служит столбцом перемен-
ных квадратичной формы. При этом дискриминант квадратичной формы ра-
вен гессиану скалярной функции, вычисленному при некотором значении
векторного аргумента х.
3. Как и в случае с многочленами одной переменной (см. разд. В.4)
многочлены нескольких переменных можно рассматривать либо как функ-
ции, применяя к ним понятия математического анализа, либо как алгебраи-
ческие выражения определенного вида (см. разд.В.4), над которыми можно
производить некоторые действия по указанным правилам. Например, ли-
нейная форма (6.3) или квадратичная форма (6.5) определены как многочле-
ны, т.е. выражения некоторого вида. При этом можно не указывать область
значений переменных, равенство двух многочленов понимать как равенство
их степеней и соответствующих коэффициентов и т.п. В то же время, ли-
нейную и квадратичную формы можно рассматривать как скалярные функ-
ции векторного аргумента. При этом необходимо указывать область опреде-
ления, равенство двух функций понимать как равенство их значений при
каждом значении аргумента и т.п. Каждый из двух подходов полезен для
выяснения тех или иных свойств многочленов, и в силу основной теоремы
алгебры оба подхода по существу совпадают (см. разд. В.4).
6.5.1. Преобразования форм при линейной замене переменных
Рассмотрим, как меняются коэффициенты линейной и квадратичной
форм при линейной замене переменных.
235
Пусть переменные Х],...,хл (условно называемые старыми) заменя-
ются на переменные у1,...,у„ (условно называемые новыми) по формулам
\ = 511У1+ --+Wn .
(6-7)
хп = хп1У1+~ + хтУп .
где Sy - некоторые числа (i = l,...,n, j = !,...,»). В (6.7) каждая старая пере-
менная является линейной формой новых переменных. Такая замена
переменных называется линейной. Составим из коэффициентов Sy
линейных форм (6.7) квадратную матрицу линейной замены переменных
S = (j4y). Тогда формулы (6.7) можно записать в виде
x = Sy. (6.8)
Линейная замена (6.8) называется невырожденной, если определитель мат-
рицы 5 отличен от нуля.
СВОЙСТВА ЛИНЕЙНЫХ НЕВЫРОЖДЕННЫХ ЗАМЕН ПЕРЕМЕННЫХ
1. Если х = Sy - линейная невырожденная замена переменных, то об-
ратная замена у = S~xx, выражающая новые переменные (ур..., уп) через
старые (Xj,..., хп), является также линейной и невырожденной.
2. Если x = Sy и y = Tz — линейные невырожденные замены перемен-
ных, то замена х = STz является также линейной и невырожденной.
Получим формулу изменения коэффициентов линейной формы при
линейной невырожденной замене переменных. Подставляя выражение
(6.8) в линейную форму g(x)=cx, получаем снова линейную форму
g(Sy) = cSy = c'y, коэффициенты с' = (с, ••• с„) которой связаны с коэф-
фициентами с = (q • •• сп) заданной формы (6.4) равенством
c=cS. (6.9)
Пример 6.6. Получить формулы преобразования первого дифферен-
циала скалярной функции при линейной невырожденной замене векторного
аргумента.
□ Пусть /(х) - скалярная функция векторного аргумента
х = (xj • • • х„ )Т. Первый дифференциал
,, уч df j df
df=y zf~dXi= — dx
Эх, dx
является линейной формой дифференциалов dxt,...,dxn независимых пере-
менных (см. п. 1 замечаний 6.3).
236
Рассмотрим сложную функцию /(х(у)), где x(y) = Sy - линейная за-
мена векторного аргумента. Учитывая, что матрица Якоби — = 5 и
dy
dy = S~xdx (так как y-S *х), найдем первый дифференциал сложной
функции /(х(у)):
df =^Ldy = ^^-dy = ^l — dy = —SS~xdx = —dx.
dy dy dx dy dx' ’ dx
Таким образом, форма первого дифференциала не изменяется при линейной
замене аргумента. Это частный случай известного свойства инвариантности
формы первого дифференциала [19,25,43].
Получим формулу изменения матрицы квадратичной формы (6.6)
при линейной невырожденной замене переменных. Подставляя (6.8) в
(6.6), получаем
<](Sy)=(Sy)T ASy = yrSrA Sy = yTA'y,
т.е. квадратичную форму q(y)= yT A'y , матрица которой связана с матрицей
заданной квадратичной формы равенством
A' = STAS. (6.10)
Пример 6.7. Найти второй дифференциал сложной функции
z(y)=/My)). где х(у) = Sy, в окрестности некоторого фиксированного
значения векторного аргумента у0, если известны матрица Гессе, вычис-
ленная при x - x0 = Sy0, и матрица S линейной замены переменных:
<l2fM ( 1] s=p 2]
dxTdx v 1J v -V
□ Второй дифференциал скалярной функции f(x)
----— dxjdxj - dx1 —=г-£ dx
dxjdx j dxTdx
является квадратичной формой дифференциалов dxl,...,dxn независимых
переменных (см. п.2 замечаний 6.3), причем матрица Гессе является матри-
цей этой квадратичной формы. При линейной замене переменных матрица
Гессе функции z(y) преобразуется по закону (6.10), т.е.
d2z(y0)_sT d2f(xo) 1'
dyTdy dxTdx v
1 1V1 2W4 10A
1 1Д1 sJ-^lO 25/
Следовательно, искомый дифференциал имеет вид
, , .(4 10 V dyi'l . , 2 ,
d2z = (dyl dy2) - 4dyt + 20dy,dy2 + 25dy2.
I 1U 2Э JI «72 J
237
6.5.2. Приведение квадратичной формы к каноническому виду
Говорят, что квадратичная форма имеет канонический вид, если ее
матрица диагональная, другими словами, в квадратичной форме имеются
только члены с квадратами переменных, а все попарные произведения раз-
личных переменных отсутствуют (соответствующие коэффициенты равны
нулю):
?(у) = \у2 + ^2У2 +- + ^пУп =yrAy. (6.П)
где Л = diagtynД2,...,А.Я) - диагональная матрица, для которой условие
симметричности матрицы квадратичной формы, разумеется, выполняется.
Задача приведения квадратичной формы к каноническому виду форму-
лируется следующим образом. Для данной квадратичной формы (6.5) требу-
ется найти такую линейную невырожденную замену переменных (6.8), при
которой квадратичная форма принимает канонический вид (6.11). Как пока-
зывает следующая теорема, эта задача всегда разрешима. Заметим, что на
практике нередко бывает достаточно определить только канонический вид
квадратичной формы, не указывая замены переменных.
Теорема 6.1 (о приведении квадратичной формы к каноническому
виду). Любая квадратичная форма может быть приведена к каноническо-
му виду при помощи некоторой линейной невырожденной замены перемен-
ных.
Конструктивное доказательство этой теоремы составляет содержание
метода Лагранжа приведения квадратичной формы к каноническому виду.
МЕТОД ЛАГРАНЖА
Для приведения квадратичной формы п переменных
?(х)=а11х12 + 2a12*l*2 +-+2alnJClJCn + а22Х2 + 2а23х2Х3 +- + ашхп
к каноническому виду нужно выполнить следующие действия.
1. Выбрать такую переменную (ведущую), которая входит в квадратич-
ную форму во второй и в первой степени одновременно (если в квадратич-
ной форме есть член с квадратом переменной и с произведением этой пере-
менной на другую переменную), и перейти к п.2.
Если в квадратичной форме нет ведущих переменных, то выбрать пару
переменных, произведение которых входит в квадратичную форму с отлич-
ным от нуля коэффициентом, и перейти к п.З.
Если в квадратичной форме отсутствуют произведения различных пе-
ременных, то никаких преобразований делать не надо, так как она уже имеет
канонический вид.
2. По ведущей переменной выделить полный квадрат: собрать в квад-
ратичной форме все члены с ведущей переменной, дополнить сумму этих
членов до полного квадрата (разумеется, добавленные члены нужно также и
238
вычесть, чтобы не изменилась сумма). Получим сумму полного квадрата не-
которой линейной формы (в которую входит ведущая переменная) и квадра-
тичной формы, в которую ведущая переменная не входит. Сделать замену
переменных: линейную форму, содержащую ведущую переменную, принять
за одну из новых переменных, а все старые переменные, за исключением ве-
дущей, принять за соответствующие новые. Продолжить преобразования
с п.1.
3. Выбранную пару переменных заменить на разность и сумму двух
новых переменных, а остальные старые переменные принять за соответст-
вующие новые переменные. При этом произведение пары выбранных пере-
менных преобразуется к разности квадратов двух новых переменных, т.е. в
новой квадратичной форме q(y) будут квадраты переменных с отличными
от нуля коэффициентами. Продолжить преобразования новой квадратичной
формы с п.1.
Идея метода Лагранжа состоит в том, что прием, используемый в п.2
(выделение полного квадрата), исключает одну переменную из числа веду-
щих. Например, если переменная х, - ведущая (т.е. ап Ф 0 и хотя бы один
из коэффициентов а!2 ,а13 ,...,а1л отличен от нуля), то выделяем полный
квадрат по переменной х1 (собираем все члены с и дополняем их сумму
до полного квадрата):
а12 а1п '
—х2 + ... + —хл +
«11 «11 ,
\2
^-х2+... + ^-х„
«11 «11 J
q(x)=au xf+2xi
~ап
^-х2+..
,«п
+ — хп
«11
+ а22х! + 2а23х2х3 +... + аллхл2.
Выражение, стоящее в квадратных скобках, есть полный квадрат. Поэтому
?(*1. Х2...хп
\ ^12
)=«и х^-12.
Х2+... + -^-Хл
«11 «11
+ ?1(х2,-,хп),
z \2
где 91(х2,...,хп)=а22х^ + 2а23х2х3 + ... + аллх2-ап -^-х2+...+-^-хл
к«и «и J
квадратичная форма, в которую не входит ведущая переменная Xj;
Л19 О]- ,
Xj +-^л2 - линейная форма, содержащая ведущую перемен-
«11 «и
а]л
ную Х|. Обозначим У1 = х1 +---х2+...+—х„, у2=х2,..., у„=х„, или,
«п «и
что то же самое, сделаем линейную замену переменных:
239
al1 “11
Х2=У2’ (6.12)
хп=Уп-
Тогда данная квадратичная форма преобразуется к виду
?(У1 ,У2 >> Уп) = Я] 1Т12 + ?! (у2 ,-,Уп)-
Заметим, что в результате этого преобразования все члены, содержа-
щие ведущую переменную х, в первой и второй степени, заменены квадра-
том одной новой переменной у,. В дальнейших преобразованиях перемен-
ная yt уже никогда не будет ведущей.
Многократно применяя этот прием, исключаем одну за другой все ве-
дущие переменные, получая тем самым канонический вид квадратичной
формы. Однако выделение полного квадрата невозможно, если в квадратич-
ной форме вообще отсутствуют члены с квадратами переменных. В этом
случае применяется способ, описанный в п.З, который порождает члены с
квадратами переменных.
Например, в п. 1 выделена пара переменных xt и х2, произведение ко-
торых входит в квадратичную форму с отличным от нуля коэффициентом
( а12 * 0). Тогда нужно сделать замену переменных
Х2=У1+У2’
хз=У3’ (6.13)
. Хп=Уп-
При этом получим новую квадратичную форму q(y), в которой появятся
квадраты новых переменных с отличными от нуля коэффициентами, так как
в результате замены член 2а12х}х2 преобразуется к виду
2°12Л1*2 = -Т2)(у! +ъ)= 2а12^|2 ~2апУ22 ’
а других членов с у\ в новой квадратичной форме не будет.
Заметим, что при помощи метода Лагранжа не только находится кано-
нический вид, но и определяется искомая невырожденная замена перемен-
ных. В самом деле, замены переменных (6.12), (6.13), которые производятся
в п.2, 3 алгоритма, это линейные замены с матрицами
240
«1/ '1 -1 0 • • o'
«11 1 1 0 0
0 , s2 = 0 0 1 • 0 (6.14)
1 , 0 0 1,
Определители матриц отличны от нуля (detS'1 = 1, det S2 = 2 ). Следователь-
но, эти замены переменных невырожденные. Выполняя п.2, 3 алгоритма,
можно определить матрицы используемых замен переменных. В результате
их перемножения (в порядке нахождения) получается матрица искомой за-
мены (согласно свойству 2 линейных замен переменных из разд. 6.5.1).
Пример 6.8. Привести квадратичную форму
</(х) = х,2 + 2ххх2 -2х1х3 + х2 -х2х3 +х3
к каноническому виду.
□ I1. В данную квадратичную форму переменная X] входит в первой и
второй степенях одновременно. Выбираем ее в качестве ведущей.
21. По ведущей переменной (Xj) выделяем полный квадрат:
q(x) = Xj +2xjX2 -2xtx3 +х2 -х2х3 +х33 = [х2 +2х|(х2 -х3)+(х2 -х3)2]-
-(х2 - хз)2 + х2 ~Х2Х3 + х3 = (х1 + х2 -Х3)2 +х2х3.
Обозначим ух = Xj + х2 - х3, у2 = х2, у3 = х3, Тогда получим новую квад-
ратичную форму д(у1,У2>Уз)=У} +УзУз- Продолжим преобразования, пере-
ходя к п. 1 алгоритма.
I2. В квадратичной форме д(у\,У2^Уз)=У\ + У2У3 нет ведущих пере-
менных, поскольку каждая переменная входит в форму либо во второй сте-
пени, либо в первой, но не в первой и второй степенях одновременно. Одна-
ко имеется произведение у2у3 разных переменных. Переходим к п.З алго-
ритма.
З1. Заменяем выбранную пару переменных у2 = z2 - х3, у3 = z2 + х3.
Оставшуюся старую переменную у{ принимаем за соответствующую новую
yt = X]. Получаем квадратичную форму
9 (х,, Х2, Х3) = X2 + (х2 - Z3 ) (х2 + Х3) = х2 + X2 - X2 .
Переходим к п. 1 алгоритма.
I3. В квадратичной форме ^(х1,х2,х3)= х2 +xj-x3 нет ведущих пе-
ременных (все переменные входят в форму во второй степени), кроме того,
нет произведений различных переменных. Следовательно, квадратичная
форма имеет канонический виде диагональной матрицей Л = rf/ag(l, 1, — l).
I6 — 4549 241
Найдем теперь невырожденную линейную замену переменных, приво-
дящую данную форму к каноническому виду. В п. 21 и 3* решения выпол-
нялись замены х = ^у и y-S2z с матрицами
'1 -1 1'
51 = 0 1 О
[о о 1,
S2= О
О'
-1
о
1
1
1°
Следовательно, матрица S искомой замены х = Sz находится как произве-
дение
'1
S = StS2 = о
.0
-1
1
о
1V1 о
Г1
-1 = 0
1J [о
О 2'
1 -1
О О 1
w 1
Получим матрицу Л квадратичной формы, приведенной к каноническому
виду по формуле (6.10): Л = STAS , где А - матрица заданной квадратичной
формы (см. примеры 6.4, 6.5). Имеем
"1 0 О' '1 1-1' '10 2' '10 О'
A = STAS = 0 1 1 1 1 -7 0 1 -1 0 1 0
? -1 L (-1 -1 1 J ч° 1 L ЧО 0 -1,
т.е. Л = diag{\, 1, -1), что соответствует найденному каноническому виду.
Замечания 6.4.
1. Канонический вид квадратичной формы определен неоднозначно,
так как зависит от последовательности выбора ведущих переменных. Сде-
лав, например, замену переменных у; = а;г; (1 = 1,..., л) в (6.11), получим
другую квадратичную форму, которая тоже имеет канонический вид.
2. Элементы матрицы невырожденной линейной замены переменных,
приводящей квадратичную форму к каноническому виду, вычисляются при
помощи арифметических операций по коэффициентам квадратичной фор-
мы. Поэтому, если коэффициенты квадратичной формы рациональные, дей-
ствительные, комплексные, то и коэффициенты линейной замены рацио-
нальные, действительные, комплексные соответственно.
МЕТОД ЯКОБИ
Рассмотрим еще один метод приведения квадратичной формы к кано-
ническому виду, который учитывает особенности преобразования (6.10)
матрицы квадратичной формы при линейной замене переменных.
Две квадратные матрицы А и А' одного и того же порядка называют-
ся конгруэнтными [39], если существует такая невырожденная матрица $ ,
что А' = STAS . Конгруэнтными, например, являются матрицы квадратич-
242
ных форм, получающиеся при невырожденной замене переменных (6.8), так
как они связаны равенством (6.10).
Напомним, что главными минорами квадратной матрицы называются
миноры, составленные из ее элементов, стоящих на пересечении строк и
столбцов с одинаковыми номерами. Например, - главный минор
к -го порядка (1 < ^ < i2 <... < i* < и, 1 < к < п) квадратной матрицы п -го
порядка. Угловыми минорами квадратной матрицы А (п -го порядка) на-
зываются следующие главные миноры
^=М{=ап,^М\^
fl21
Я12
а22
Д = М™~п = detA,
п 12...п ’
.= Л&
12 к
где угловой минор Ак -Mi2"k
к -го порядка составлен из элементов мат-
рицы А, стоящих на пересечении первых к строк и первых к столбцов
матрицы А, т.е.
41 | а12 - flin
fl21 а22 '' ‘ а2п
а . а ~ ••• а
\ л! л2 лл
СВОЙСТВА КОНГРУЭНТНЫХ МАТРИЦ
1. Конгруэнтные матрицы имеют равные ранги.
В самом деле, ранг произведения матрицы А на невырожденную мат-
рицу $ и Sr равен рангу матрицы А (см. следствие теоремы 3.5).
2. Матрица, конгруэнтная симметрической матрице, также является
симметрической.
Действительно, если А = АГ и A' = STAS, то
(а')т ={stasJ ^stat(stJ =StAS = A'.
3. Определители действительных конгруэнтных матриц имеют оди-
наковые знаки. В частности, если А' = ST AS и det S = 1, то det А' = det А .
В самом деле, из равенства А = S AS и свойства 1 определителя (см.
]зазд. 2.3.1) следует, что det А' = det ST det А • det S = det A • (det S )2, т.е. знаки
величин det А' и det А совпадают. Если же det S = 1, то det A' = det A .
4. Если квадратные матрицы А и А' связаны соотношением
A' =ST AS, где матрица S - верхняя треугольная с единицами на главной
диагонали
16*
243
fl
10
то все угловые миноры матриц А
обозначаются любые числа.
* ... и?
1 ... *
0 ••• 1,
(6.15)
и А' равны, где в (6.15) звездочкой (*)
Действительно, разобьем квадратные матрицы А, S и А' на блоки,
выделив в каждой квадратный блок в первых к строках и первых к столб-
цах:
0V4
I *
( ЧТ
A' = STAS = ±
*
*11 о *
Ак$к *
* * ^ *
Здесь О - нулевые матрицы соответствующих размеров, а звездочкой (*)
обозначаются блоки соответствующих размеров, значения элементов кото-
рых для доказательства не существенны и могут быть любыми. Получили,
что А'к - Sk AkSk Учитывая, что det Sk = 1 для любого к = 1,..., п, по свойст-
ву 3 имеем А'к = det Ак - det Sk det A* det Sk = det Ak = Ak, т.е. угловые мино-
ры A'k и Ak матриц А' и А равны для любого Jt = l,...,n.
Замечания 6.5.
1. Линейная невырожденная замена переменных не изменяет ранга
квадратичной формы. Это следует из свойства 1 конгруэнтных матриц.
2. Ранг квадратичной формы равен количеству отличных от нуля ко-
эффициентов Л1,Л2,...,ЛЯ в ее каноническом виде (6.11). Действительно,
согласно предыдущему пункту rg А = rg Д, но ранг диагональной матрицы
A = diag(X1,Z,2,...,An) равен количеству ненулевых ее элементов (см.
разд.3.3.2).
Теорема 6.2 (теорема Якоби о каноническом виде квадратичной
п п
формы). Если квадратичная форма ^(х) = У, = хТ Ах имеет ранг
i=i ;=1
г = rg А и ее угловые миноры отличны от нуля-.
а11 а12
а21 а22
то ее можно привести к каноническому виду
§(у) = Х1у,2+Х2у2 +...+Хгу2, где X,=y*-,i = l......г,Д0=1,
Д] -ап #0 , Д2 -
#0,..., Д = м£'*0,
(6.16)
(6.17)
/-I
при помощи линейной замены переменных x = Sy с верхней треугольной
матрицей S вида (6.15).
244
Действительно, применяя метод Лагранжа, выбираем первую перемен-
ную X] в качестве ведущей (А! =ан * 0) и выделяем по ней полный квад-
рат. Другими словами, делаем линейную замену переменных (6.12). Этой
замене соответствует матрица St в (6.14), которая является верхней тре-
угольной вида (6.15). Получим квадратичную форму с матрицей
0 0
A’ = S^ASi = 0 а22 *
0 * *
где звездочкой (*) обозначены некоторые элементы матрицы А'. Заметим,
что матрица Sj - верхняя Треугольная с единицами на главной диагонали.
Тогда по свойству 4 конгруэнтных матриц, получаем Д2 = Д2 =>
. , , Д-
Д2 = апа22 = Д^и- Отсюда а22=—-*Q. Значит, вторую переменную
Д1
можно взять в качестве ведущей и выделить по ней полный квадрат. Для
этого делаем линейную замену переменных с матрицей вида (6.15) и т.д.
Условия (6.16) обеспечивают возможность применения п.2 метода Лагранжа
г раз. В результате описанных действий получается канонический вид
(6.17). Формулы (6.17) для вычисления X; следуют из свойства 4 конгру-
энтных матриц. Так как угловые миноры матриц А и A = diag(X1,X2,..„Xn)
соответственно равны (по свойству 4 конгруэнтных матриц), то
Д. = Х., Д, = Х.Х, ,..., Д„ = Х.Х9 -...Х. Отсюда
1 1 Л ЛГ • Л 9* 9
X. =д., х2=-\..., хг=-^-.
1 1 2 Д1 дг_,
Остальные угловые миноры равны нулю Дг+1 =... = Дп, так как rg А = г.
Таким образом, для нахождения канонического вида квадратичной
формы методом Якоби необходимо выполнить следующие действия.
1. Составить матрицу А (п -го порядка) квадратичной формы.
2. Найти первые г отличных от нуля угловых миноров матрицы квад-
ратичной формы. Если Д| Ф 0, Д2 # 0,..., Д„ * 0, то перейти к п.З, положив
г = п. Если Д, = аи = 0, то процесс закончить, так как метод Якоби непри-
меним. Если #0,Д2 #0,...,Дг 0 и Дг+1 = 0, где 0<г<п-1,то найти
отличный от нуля минор (г+ 1)-порядка, окаймляющий минор Дг # 0 . Если
такого минора нет, то перейти к п.З, иначе процесс закончить, так как метод
Якоби неприменим.
3. Записать искомый канонический вид (6.17) квадратичной формы
245
я(у) = -^У1 +^У2Уг^ где до=1-
До Д] ДгЧ
Замечания 6.6.
1. Алгоритм метода Якоби можно модифицировать, дополнив его пе-
ренумерацией переменных. Например, замена х,- на х; и, одновременно,
Xj на х, (короче, перенумерация х, <-> х;) приводит к перестановке i -й и
j -й строк, а также i -го и j -го столбцов матрицы квадратичной формы. Та-
кая замена является линейной невырожденной и не нарушает симметрично-
сти матрицы квадратичной формы. При помощи таких двойных перестано-
вок можно любой главный минор симметрической матрицы переместить в
левый верхний угол, т.е. сделать его угловым. Например, для матрицы
ГО 1>
А = I I квадратичной формы метод Якоби неприменим, так как
Д1=а11=0. Перенумеровав переменные х1<->х2, получаем матрицу
А' = ^ qJ, для которой условия (6.16) применимости метода Якоби вы-
полняются.
2. При выполнении условий теоремы 6.2 метод Лагранжа (последова-
тельного выделения полных квадратов) соответствует методу Гаусса приве-
дения матрицы А к ступенчатому виду [10].
3. При выполнении условий теоремы 6.2 для нахождения матрицы S
линейной замены переменных, приводящей квадратичную форму к канони-
ческому виду, нужно выполнить следующие действия:
1. Составить блочную матрицу (а | Е), приписав к матрице А квадра-
тичной формы единичную матрицу тех же размеров.
2. Привести левый блок А к ступенчатому виду А' при помощи эле-
ментарных преобразований III типа строк блочной матрицы (а | Е). В ре-
зультате получить блочную матрицу (а' | $г), где S - искомая матрица за-
мены переменных. Элементы главной диагонали матрицы А' равны коэф-
фициентам в квадратичной форме (6.17):
^•1 = ап ’^2 ~ а22 ~агг-
Пример 6.9. Привести квадратичную форму
<?(х) = xj2 + 2xjX2 - 2Х]Х3 + х2 - х2х3 + х3
к каноническому виду методом Якоби.
□ 1. Составляем матрицу квадратичной формы (см. пример 6.8):
246
А= 1
-1
i -Г
1 4
4 1
2. Вычисляем угловые миноры Д, = 1 # 0, Д2 =
= 0. Получили
г = 1 < п. Ищем отличный от нуля минор 2-го порядка, окаймляющий минор
Д]. Например, М™ -
1
.1
2
= — # 0. Следовательно, метод Якоби для
рассматриваемой формы применить нельзя.
Воспользуемся перенумерацией переменных (см. п.1 замечаний 6.6).
Сделаем замену xt <-> х3, т.е. меняем местами 1-ю и 3-ю строки и 1-й и 3-й
столбцы матрицы А. Получим матрицу
1
А' =
2
-1
! Применяем для нее метод Якоби.
-1
1
1
2
1
1
2'. Вычисляем угловые миноры Д^ = 1 0,
1
J.
2
=^0,
4
Д2 _
2
1
Д3 = det А’ - —- # 0. Найдено г = 3 = п отличных от нуля угловых миноров.
4
3'. Записываем искомый канонический вид ?(у)= у? +—у2 Уз , так
4 3
, Д1 , Д'9 3 , д3 1
как X. =—т* = 1, X, =—7- = — , X, =-у- = —
1 до 2 д; 4 3 Д' 3
Этот вид отличается от полученного в примере 6.8, что соответствует п.1
замечаний 6.4.
Пример 6.10. Найти матрицу линейной замены переменных, приводя-
щей квадратичную форму д(х) = х3 - х,х2 - 2xjX3 + х2 + 2х2х3 + х3 к кано-
ническому виду.
1
□ Составим матрицу квадратичной формы А =
1 1
-1
(см. пример 6.9 после перенумерации переменных х, ох3). Применяем к
этой матрице алгоритм, описанный в п.З замечаний 6.6.
247
I. Составляем блочную матрицу
-1 1
О о"
1 О
0 h
2. Элементарными преобразованиями III типа, выполняемыми над
строками блочной матрицы, приводим ее левый блок к ступенчатому виду:
(А | Е)~ О
О
Следовательно, искомая матрица 5=0
1
2
1
О
2 \
з
_2
3
, а коэффициенты квадра-
тичной формы q(y)= У!2 +—~У2 ~ — Уз > имеющей канонический вид, являют-
4 3
ся элементами главной диагонали матрицы А' = О
з.
4
О
, что совпада-
1 О
1 О
О
V
(1
О
к
ет с результатом примера 6.9. Нетрудно
Т ( 3 l')
STAS = A = diag\ 1,-,-- .
I 4 3j
проверить равенство
6.5.3. Закон инерции вещественных квадратичных форм
Рассмотрим вещественные (действительные) квадратичные формы, ко-
эффициенты которых являются действительными числами, а переменные
принимают действительные значения. Любую вещественную форму
q(x) = хт Ах можно привести к каноническому виду
0(у) = АчУ12+*2У2+--- + М« (6.18)
при помощи линейной невырожденной замены переменных х = Sy с дейст-
вительной матрицей 5 (см. теорему 6.1 и п.2 замечаний 6.4). Коэффициен-
ты X,, Х2 ,..., Хл квадратичной формы являются действительными числами.
Количество положительных (отрицательных) коэффициентов в кано-
ническом виде (6.18) называется положительным {отрицательным) ин-
дексом квадратичной формы, а разность положительного и отрицательного
индексов называется сигнатурой квадратичной формы. В примере 6.10
квадратичная форма была приведена к каноническому виду
248
<j(y)= У\ +^"У2 ~~зУз • положительный индекс р = 2 , отрицательный ин-
декс равен 1, а сигнатура а = 2 -1 = 1.
Замечания 6.7.
1. Согласно п.2 замечаний 6.5 количество ненулевых коэффициентов в
(6.18) равно рангу r = rgA квадратичной формы. Перенумеруем перемен-
ные так, чтобы в сумме (6.18) первыми были р слагаемых с положитель-
ными коэффициентами, затем (г-р) слагаемых с отрицательными коэффи-
циентами, а остальные слагаемые с нулевыми коэффициентами. Всего будет
г отличных от нуля слагаемых (Х(* 0 , i = 1,...,г). Если сделать невырож-
денную замену переменных
Zt , i > г.
то получим нормальный вид квадратичной формы
?(z) = z2 + Z2 + - + г2р -Zp+1 -Zp+2 --~zr< (6.19)
в котором коэффициенты равны либо единице, либо минус единице (пере-
менные zr+1,...,zn входят с нулевыми коэффициентами).
2. Из четырех величин: ранга, положительного и отрицательного ин-
дексов и сигнатуры, достаточно знать любые две, чтобы вычислить осталь-
ные. Например, если известны ранг г и положительный индекс р (см.
форму (6.19)), то отрицательный индекс равен (r-р), а сигнатура
в = р-(г-р) = 2р-г.
Теорема 6.3 (закон инерции квадратичных форм). Ранг, положи-
тельный и отрицательный индексы, а также сигнатура вещественной
квадратичной формы не зависят от действительной невырожденной ли-
нейной замены переменных, приводящей квадратичную форму к канониче-
скому виду.
Из теоремы 6.3 следует, что два канонических вида одной и той же
квадратичной формы имеют:
а) одинаковое количество ненулевых слагаемых (которое определяется
рангом квадратичной формы);
б) одинаковое количество слагаемых одного знака.
В самом деле, пусть квадратичная форма q(x) = хТ Ах ранга г приве-
дена к нормальному виду (6.19)
= у1 + у\ + - + Ут - Ут+1 -Ут+2~ - - У г .
невырожденной заменой переменных х = Ту , а невырожденной заменой пе-
ременных x = Sz - к другому нормальному виду:
249
ZZ( \ 2 2 2 2 2 2
(z) — Z] + Z2 + + Zp ~ Zp+i ~ Zp+2~ ~ Zr i
причем число г = rg А в этих формулах одно и то же (см. п.1 замечаний 6.5).
Докажем, что положительные индексы т и р равны. Предположим про-
тивное. Пусть р > т. Поскольку замены переменных невырожденные, то
Т~1х = у и S-Ix = z. Рассматривая последние равенства как неоднородные
системы уравнений относительно неизвестных X], х2 ,..., хп, подберем такое
ее решение х°, чтобы выполнялись условия у, = 0,...,ут =0,
zp+i =0,...,z„ = 0. Для этого составим однородную систему, выбрав пер-
вые т уравнений из системы Т-1х = у и последние (n-р) уравнений сис-
темы S-Ix = z:
'{Ет |о)т-1х = О,
Получили однородную систему (m + n-p) уравнений с п неизвестными.
Так как р>т, то число уравнений меньше количества неизвестных. По-
этому система имеет нетривиальное решение х° * о (см. разд.5.5). Вычис-
лим значение квадратичной формы для этого столбца х° значений пере-
менных. Для ненулевых столбцов
уО=г-1Ло=(0 ... q ?т+1 ... yJ,
т
... z„ о of.
п-р
получаем
ч(хО)=д(у°)=-у1+1-..--у2г<0 и q(x0)=q(z°)= Z? +... + Zp >0,
т.е. <j(x°)<0 и q(x°)>0 одновременно, чего не может быть. Заметим, что
при т = 0 и р = п оба неравенства выполняются для любого ненулевого
вектора х°. Следовательно, предположение р>т приводит к противоре-
чию. К аналогичному противоречию приводит предположение р<т . Зна-
чит, р = т. Другими словами, положительный индекс квадратичной формы
не зависит от способа ее приведения к каноническому виду. Ранг формы
также не зависит от выбора невырожденной замены переменных. В силу п.2
замечаний 6.7 делаем аналогичный вывод для отрицательного индекса и
сигнатуры.
250
6.5.4. Знакоопределенность вещественных квадратичных форм
Вещественная квадратичная форма q(x) = хт Ах называется положи-
тельно [отрицательно) определенной, если ^(х) > 0 (q(x\< 0) для любых
х Ф о . Положительно и отрицательно определенные квадратичные формы
называются определенными [знакоопределенными). Если неравенство
q(x) > 0 (q(x) < 0) выполняется для любых значений х, то квадратичная
форма называется неотрицательно [неположительно) определенной. В
этом случае говорят, что квадратичная форма полу определенная. Если же
квадратичная форма принимает как положительные, так и отрицательные
значения, то она называется неопределенной [знакопеременной). Опреде-
ленность, полуопределенность и неопределенность квадратичных форм обо-
значается неравенствами <?(х)>0, q(x)<0, g(x)>0, <?(х)<0 ,q(x) <0 соот-
ветственно.
Поскольку каждой вещественной квадратичной форме соответствует
ее матрица, то эта терминология переносится на действительные симметри-
ческие матрицы. Например, симметрическая матрица А называется поло-
жительно определенной, если такой является квадратичная форма хТ Ах.
Определенность, полуопределенность и неопределенность симметрической
матрицы обозначаются неравенствами Д > 0, А<0, А > 0, А < О и А < О
соответственно.
Пример 6.11. Исследовать знакоопределенность квадратичных форм
a) q{xx, х2) = х? - 2х,х2 + 2х2 ; б) q(xt, х2) = х2; в) q(xY, х2) = 2xjx2 .
□ а) Выделим полный квадрат по переменной Xj:
^(xj,x2)= -х2)2 +х2 > О для любого х * о . Следовательно, данная форма
положительно определенная.
б) Квадратичная форма q(xy,x2)~ х2 не является положительно опре-
деленной, так как q(l, о) = 0 для х = (1 0)г *о. В силу неравенства
^(х1,х2)= х2 > 0 эта форма неотрицательно определенная.
в) Квадратичная форма ^(х1,х2) = 2х(х2 неопределенная, так как она
может принимать как положительные, так и отрицательные значения. На-
Цример, q(l-, 1) = 2 > 0 , ^(1; -1) = -2 < 0.
Замечания 6.8.
1. Положительно определенная квадратичная форма приводится к нор-
мальному виду (6.19)
q(z)=z? + z2+...+ z2.
251
т.е. р = г - <з - п - положительный индекс (р), ранг (г) и сигнатура (а)
равны количеству (п) ее переменных. Отрицательный индекс равен нулю.
Согласно теореме 6.3, они не изменяются при невырожденной замене пере-
менных.
2. Дискриминант положительно определенной квадратичной формы
больше нуля, т.е. det А > 0 .
Действительно, матрица нормального вида положительно определен-
ной квадратичной формы - единичная (см. п.1). Следовательно, матрица А
положительно определенной квадратичной формы конгруэнтна единичной
матрице Е = STAS . Следовательно, det A (det S’)2 = 1, т.е. det А > 0 .
3. Неотрицательно определенная квадратичная форма приводится к
нормальному виду (6.19)
g(z)=z2 +Z2 + ...+ Z2,
т.е. р = г = а <п - положительный индекс (р), ранг (г) и сигнатура (ст)
равны, но меньше количества переменных. Отрицательный индекс равен
нулю.
4. Для отрицательно (неположительно) определенных квадратичных
форм справедливы утверждения аналогичные п.1-3, так как знаки форм
<?(х) и [ - q(x) ] противоположные.
Теорема 6.4 (критерий Сильвестра). Для того чтобы вещественная
квадратичная форма q(x) = xTAx была положительно определенной, необ-
ходимо и достаточно, чтобы все угловые миноры ее матрицы были поло-
жительны'.
Д| — [ > 0 , Д2 —
«11
«21
«12
«22
>0,..., Д =det?l>0.
п
(6.20)
Для отрицательной определенности квадратичной формы необходимо
и достаточно, чтобы знаки угловых миноров ее матрицы чередовались, на-
чиная с отрицательного:
Д] =аИ <0, Д2 =
«и
«21
£2i п
12 >0
«22
(-1)" Дл = (-1)" det ?1 > 0. (6.21)
В самом деле, рассмотрим первое утверждение теоремы (о положи-
тельной определенности). Достаточность условий (6.20) следует из теоре-
мы 6.3 (теоремы Якоби), так как при выполнении этих неравенств квадра-
тичная форма приводится к каноническому виду
252
с положительными коэффициентами при квадратах переменных (До = 1).
Ясно, что q(y) > 0 для всех у * о , т.е. q(x) = q{s~}x)> 0 для всех х * о .
Для доказательства необходимости рассмотрим квадратичную форму
qk(xi,...,xk) = q(xl,...,xkfi,...,O) переменных Xj.-.-.x* (1<Л<л). Матрица
Ак этой формы представляет собой левый верхний блок матрицы
данной квадратичной формы (звездочкой (*), как обычно, обо-
значены блоки, не существенные для рассуждений). Из положительной оп-
ределенности q(x) следует положительная определенность формы
qk(xl,...,xk). Тогда из п.2 замечаний 6.8 следует, что detJA.>0, но
ДА = det Ак - угловой минор к -го порядка матрицы А. Таким образом,
Д* > 0 для 1 < к < п, что и требовалось доказать. Второе утверждение сво-
дится к первому, если рассмотреть квадратичную форму [ - q(x) ] (см. п.4
замечаний 6.8).
Теорема 6.5 (критерий полуопределенности квадратичной формы).
Для того чтобы квадратичная форма q{x)-xTAx была неотрицательно
определенной, необходимо и достаточно, чтобы все главные миноры ее
матрицы были неотрицательны.
Для неположительной определенности квадратичной формы необхо-
димо и достаточно, чтобы все главные миноры ее матрицы удовлетворяли
условиям:
>0 (6.22)
' z J\ Jl— Jk
для 1 <ij <i2 <...<ik <n , 1 < j, < j2 <...< jk ^n, l<k <n .
Условия (6.22) означают, что главные миноры четного порядка должны
быть неотрицательны, а нечетного порядка - неположительны. Для доказа-
тельства [10] теоремы используется критерий Сильвестра.
Пример 6.12. Выяснить знакоопределенность квадратичных форм с
матрицами
□ Матрица А - положительно определенная (А > 0), так как ее угло-
вые миноры положительны Д] = Д2 = 1 > 0. Следовательно, квадратичная
форма <?(х) = хГАх = х2 + 2xjX2 + 2х2 положительно определенная (см. тео-
рему 6.4). Этот вывод подтверждается выделением полных квадратов:
<?(х)= (xj +х2)2 +х2, т.е. квадратичная форма знакоопределенная.
253
Матрица В не является положительно или отрицательно определен-
ной, так как ее угловые миноры не удовлетворяют критерию Сильвестра:
Д1=-1<0, Д2=0. Проверим условия (6.22): =(-1)1Д1 =1 >0,
(-1)1 Л/2 = (-1)'(-1) = 1 > 0, (- 1)2Л/'2 = (- 1)2Д2 = 0 Условия выполняются,
значит, матрица В является неположительно определенной (В < 0 ). Следо-
вательно, квадратичная форма q{x) = хт Вх неположительно определенная.
Этот вывод подтверждается выделением полного квадрата:
q(x) = xrBx = -xf +2x^2-х2 = -(х, -х2^ , т.е. для всех х, у которых
X] = х2 , справедливо равенство <?(х) = 0, а для остальных х выполняется
неравенство q(x)< 0.
Матрица С не является положительно или отрицательно определен-
ной, так как ее угловые миноры не удовлетворяют критерию Сильвестра:
Aj = 0, Д2 = -1 < 0, Д3 = 1 > 0 . Кроме того, эти миноры не удовлетворяют
критерию полуопределенности (см. теорему 6.5). Следовательно, матрица
С неопределенная (С <0). Тогда и квадратичная форма
<?(х) = хтСх = 2Х]Х2 - х3 неопределенная. Действительно, выпишем
главные миноры первого порядка: м' = 0, М2 = 0 ,М3 = -1;
главные миноры второго порядка: Л/'2 = -1, М™ = 0, Л/22 = 0;
главный минор третьего порядка: = 1.
Так как среди них есть хотя бы один отрицательный, то квадратичная форма
не является неотрицательно определенной. Поскольку среди главных мино-
ров четного порядка есть отрицательный (среди главных миноров нечетного
порядка есть положительный), то квадратичная форма не является неполо-
жительно определенной. Нетрудно заметить, что при Xj = х2 - 0, х3 =1
<?(^) = -1 < 0, а при X! = х2 = 1, х3 = 0 <у(х) = 2 > 0, т.е. квадратичная форма
принимает как положительные, так и отрицательные значения, следователь-
но, является знакопеременной (неопределенной).
6.5.5. Применение форм к исследованию функций на экстремум
Рассмотрим скалярную (числовую) функцию /(x) = /(xj, х2,..., хп)
векторного аргумента х = (х, • • • х„ )г, которая каждому действительному
значению векторного аргумента х (т.е. каждому действительному числово-
му столбцу размеров их1) из области определения функции/(х), ставит в
соответствие действительное число (значение скалярной функции). В этом
254
разделе значение векторного аргумента х будем называть также точкой в
области определения функции [32].
Напомним необходимые и достаточные условия локального безуслов-
ного экстремума функции [32]. Точка х* называется точкой локального
минимума (максимума) функции /(х), если существует такая окрестность
точки х*, целиком лежащая в области определения функции, что для любой
точки х из этой окрестности выполняется условие /(х*)< /(х) (соответст-
венно Дх’)> /(х)). Точки минимума или максимума называются точками
экстремума.
Необходимые условия первого порядка. Если х* является точкой
экстремума дифференцируемой функции /(х), то ее первый дифференци-
ал, вычисленный в этой точке х*, есть равная нулю линейная форма
df(x*)=Q. (6.23)
Точки, удовлетворяющие условию (6.23), называются стационарными
точками дифференцируемой функции /(х).
Необходимые условия второго порядка. Если стационарная точка
х* является точкой минимума (максимума) дважды дифференцируемой
функции f(x), то ее второй дифференциал есть неотрицательно (неполо-
жительно) определенная квадратичная форма-.
d2f\x*\>Q (соответственно t/2/(x*J<0). (6.24)
Заметим, что порядок условий определяется порядком используемых
Производных, первый дифференциал df{x) является линейной формой, а
второй дифференциал - квадратичной формой (см. п.1, 2 замечаний 6.3) от-
носительно переменных dxl,...,dxn. Матрицу-строку коэффициентов ли-
dflx]
нейной формы (6.23) определяет градиент ——
dx
квадратичной формы (6.24) - матрица Гессе —-—
dx dx
-1—£, а матрицу
dx
—, вычис-
dxTdx
ленные в стационарной точке х*.
Достаточные условия экстремума функции. Для того чтобы ста-
ционарная точка х* дважды дифференцируемой функции f(x) была точ-
кой минимума (максимума), достаточно, чтобы ее второй дифференциал
был положительно (отрицательно) определенной квадратичной формой:
«/2/(х*)>0 (соответственно d2/(x‘)<0). (6.25)
255
Используя матричные записи первого и второго дифференциалов ска-
лярной функции (см. разд.6.2), условия (6.23)-(6.25) можно представить в
виде равносильных соотношений:
#(х*)=0 «• ^И = ог; (6.26)
dx
d2f(x')>0 « (6.27)
' ' dxTdx
</2/(x‘)<0 (6.28)
' ' dxT dx
J2/(x*)>0 « ^>0, (6-29)
v ' dxTdx
d2f[x*)<0 « ^XL)<0, (6.30)
' ' dxTdx
где oT - нулевая строка размеров lx и.
Для нахождения точек локального экстремума функции нужно выпол-
нить следующие действия.
1. Записать необходимые условия первого порядка (6.26):
dx
и найти стационарные точки х* в результате решения получающейся сис-
темы п уравнений, в общем случае нелинейной.
2. Для каждой найденной стационарной точки проверить выполнение
достаточных условий (6.29) или (6.30) с помощью критерия Сильвестра
(теорема 6.4). Если они выполняются, то на основании (6.29) или (6.30) сде-
лать вывод о том, что в исследуемой точке достигается локальный минимум
или максимум функции соответственно. Если достаточные условия не вы-
полняются, проверить необходимые условия второго порядка (6.27) или
(6.28) с помощью теоремы 6.5. В случае их невыполнения сделать заключе-
ние об отсутствии экстремума в рассматриваемой точке, а в случае выпол-
нения (6.27) или (6.28) сделать вывод о том, что в рассматриваемой точке
может быть минимум или максимум соответственно, однако, условия второ-
го порядка этого не гарантируют. В этом случае требуется продолжение ис-
следований, например, с учетом дифференциалов более высокого порядка.
Пример 6.13. Найти точки локального экстремума функции
/(х) = 3xf + х4 - 5х2 - 2х2 х2 + хj.
□ 1. Найдем градиент функции и запишем необходимые условия экс-
тремума первого порядка (6.26):
256
Ш = (|5^ + 4^-15^-4^
ИЛ I ОЛш иЛл I
Отсюда получаем систему уравнений
15х4 + 4xf - 15х2 - 4х,х2 = 0,
- lx? + 2х2 = 0.
2
Подставляя х2 = Xj в первое уравнение, получаем
15х4-15х2 = 15х2(х2-1)=0 . Следовательно, Х[=0, либо Х!=±1. Таким
образом, найдены три стационарных точки х° = (0 , х1 = (1 1)г,
х2 = (-1 1)Г, которые могут быть точками экстремума функции.
2. Для проверки условий (6.27)-(6.30) находим матрицу Гессе
э2/(*Г
ЭХ]Эх2
э2/(х)
Эх2 ;
d2f(x)_ Эх2
dxT dx Э2/(х)
Эх2Эх]
60Х]3 +12х2 - 3Oxj - 4х2 - 4xj
. -ч 2 ,
в каждой стационарной точке:
d2/(x°) _р <Г| Л2/(х1)< 38 -4^1
dx7dx .0 2j dx dx \~4 2 J
<*2/(х2)_Г~22 4"|
dxT dx V 4 2J
0 0 j
° 2J
Исследуем точку x°. Так как Д( = 0, Д2 = 0, согласно критерию Силь-
вестра (6.20), (6.21), достаточные условия не выполняются. Для проверки
необходимых условий второго порядка вычислим главные миноры: первого
порядка Л/* =0,Л/2 =2; второго порядка Л/'2 =0. Так как все главные
миноры неотрицательные, то квадратичная форма J2/(x°) и матрица
являются неотрицательно определенными (по теореме 6.5). Соглас-
но (6.27) точка х° может быть точкой минимума. Поскольку один минор
Л/2 = 2 нечетного порядка положителен, то квадратичная форма согласно
(6.22) не является неположительно определенной. Следовательно, необхо-
димое условие (6.28) второго порядка не выполняется, поэтому точка х° не
может быть точкой максимума. Продолжим исследование поведения функ-
ции в окрестности точки х°. Покажем, что в любой сколь угодно малой ок-
рестности точки х° найдется точка х, для которой /(х)<0 = /(х°), т.е.
значение функции меньше, чем в исследуемой точке. Действительно, поло-
17 -4549
257
жив х2=0, имеем /(х,, о)= Зх, + х* -5х2 = -х3(5-х, -Зх2). При любых
малых положительных значениях х, выражение в скобках положительно
(примерно равно 5), поэтому /(х,,0)<0. Следовательно, точка х° не явля-
ется точкой минимума (по определению). Так как в точке х° нет ни мини-
мума, ни максимума, то она не является точкой экстремума.
Исследуем точку х1. Так как Д, = 38 > 0, Д2 = 60 > 0, т.е. угловые ми-
норы матрицы Гессе положительные, то по критерию Сильвестра (6.20)
.2/1) (38 -4х)
квадратичная форма a f\x ) и матрица I I положительно опреде-
ленные. Это означает, что достаточное условие минимума (6.29) выполняет-
ся. Следовательно, точка х1 является точкой минимума.
Исследуем точку х2. Так как Д, =-22<0, Д2 =-60<0, то критерий
Сильвестра и, следовательно, достаточные условия экстремума не выпол-
няются. Проверим необходимые условия второго порядка. Находим главные
миноры матрицы Гессе. Главные миноры первого порядка:
Л/, = -22,М2 = 2, главный минор второго порядка = -60. Поскольку
среди них есть отрицательные, то квадратичная форма J2/(x2) и матрица
не могут быть неотрицательно определенными. Поэтому точка
2
является точкой минимума. Так как главный минор = — 60 чет-
(-22
I 4
х2 не
ного порядка отрицательный, то квадратичная форма J2/(x2) и матрица
Гессе не могут быть неположительно определенными. Поэтому точка х2 не
является точкой максимума. Следовательно, в точке х2 нет экстремума.
Задачи для самостоятельного решения
6.1. Найти градиент и матрицу Гессе скалярной функции векторного
аргумента х = (х, х2 х3 У:
a) f(x) = х, - х3; б) /(х) = х2 + х2 + х2 + 2х2х3; в) /(х) = х3 + х2 + х,х2х3.
Ответ; а) ^Ы = (1 0 -1);
dx dxT dx
df(\ 2 ( \ f2 0 0>
6) - J - = (2х, 2х,+2х, 2х, +2х2); — = 0 2 2;
dx 1 2 3 3 2/ dxTdx Л „
258
. df(x) L 2 o \ J2/(x)_ 1 n
e) - (Зх, + 2x, + x2x3 XjX3 XjXj); хз 0
I X2 Xl
xl
6.2. Найти матрицу Якоби и якобиан вектор-функции векторного аргу-
мента:
а) /(*)=
Л^Х2
5"Х2>
б) /(х)=
S^COSXj'
х2 sinXj
з
Ответ: а) dx I, ' X2 Xj' J "lJ 3 df(x) dx = X2 1 X1 -1 = -xl-x2-,
df(x)_ <-x2sinxI cosx^ 4f(x)
б) dx X2 COSXj < o sinXj 0 и 1> 9 dx -X2.
6.3. Доказать, что вектор-функция
решением системы рекуррентных уравнений
( 1 —Л (1 А (\\
’(‘ + |)=(-2 О НН-1)’ ’ ^°) = [о/
6.4. Доказать, что вектор-функция х(/)=
Зе3'
Зе3'
является решени-
является
ем системы дифференциальных уравнений
dx(f) fl 2^1
~dt V2 lJ
x(0)=
<2J
4).
6.5. Записать линейную и квадратичную формы
g (xt, х2, х3) = 2Xj + х2 - Зх3, д(х,, х2, х3) = 2х3 - 4XjX2 + х2 + 6х2х3 - х3
в матричном виде. to 1 to о
Ответ: g(x)=(2 1 -3)х; ^(х)=хг -2 1 3 < о 3 -1? X
17*
259
6.6. Привести вещественные квадратичные формы к нормальному виду
методом Лагранжа. Указать ранг (г), положительный индекс (р) и сигна-
туру (о):
a) q(x) = х2 + х2 + Зх2 + 4xtx2 + 2xtx3 + 2х2х3;
6) q(x) = х2 - 2х2 + х2 + 2xtx2 + 4xtx3 + 2х2х3;
в) q(x) = х2 - Зх2 - 2xjX2 + 2xjX3 - 6х2х3.
Ответ: a) q(y) = У\ +Уг~Уз' г = ^' Р = 2, о = 1;
б) я(у)=У1-у1~у1 . г = 3, р = 1, о = -1;
в) <7(у)=У?~У2’ г=2> Р = 1> 0 = 0 •
6.7. Привести вещественные квадратичные формы, указанные в задаче
6.6, к каноническому виду методом Якоби.
Ответ: а)
ч(у)= yf -bl^yj-.
В) д(у)=у2-2у2.
6.8. Найти линейную невырожденную замену переменных, приводя-
щую вещественную квадратичную форму к нормальному виду:
a) q(x) - х(х2 + XjX3 + х2х3;
б) q(x) = х2 + 5х2 - 4х2 + 2xjx2 - 4Х]Х3.
Ответ: а) х1 = у1 + у2 + у3, х2 = -у2-у3, х3 = у3;
1 5
б> х1 = У1~,У2+-7Уз’
£ О
1 1
1
*з=^з-
Замена пе-
ременных определяется неоднозначно.
6.9. Исследовать на экстремум следующие функции:
а) /(х)=х2+х2; б) /(х) = х2-х2; в) /(х)=-х2 -х2 -х2 -X! +х1х2 + 2х3 ;
г) /(х)= х2 + х2 + х2 + х2х3 -Зх1 + 6х2 + 2.
Ответ: а) х* = (о 0)г - точка минимума функции;
б) нет экстремума;
в)х*=(—| 1^ - точка максимума функции;
г) х* = (1 -4 2)г - точка минимума функции.
ГЛАВА 7. МНОГОЧЛЕННЫЕ МАТРИЦЫ
И ФУНКЦИИ ОТ МАТРИЦ
7.1. МНОГОЧЛЕННЫЕ МАТРИЦЫ (А-МАТРИЦЫ)
7.1.1. Определение многочленных матриц (А -матриц)
Многочленной матрицей (или А -матрицей) называется матрица,
элементами которой являются многочлены переменной А. Многочленные
матрицы являются частным случаем функциональных (см. разд.6.1). Далее
будут рассматриваться только квадратные А -матрицы п -го порядка:
(7-1)
Элементы А -матрицы - это многочлены вида
Д(7(А)=^)Ат +йМАт-1 + ...+$Х + а^,
где а^,...,а^ - коэффициенты; т - степень многочлена (в общем случае
разная для разных элементов матрицы).
Случай, когда все элементы А-матрицы тождественно равны нулю,
сводится к числовой нулевой матрице. Поэтому нулевые А -матрицы далее
не рассматриваются.
Любую А -матрицу и -го порядка можно представить в виде многочле-
на с матричными коэффициентами:
А(А) = AmAm + Am_1A"”1 +...+АА + Ao, (7.2)
где A^,, Ат_!,..., А|, Ад - числовые квадратные матрицы и -го порядка, мат-
рица А„, Ф О - старший коэффициент, матрица Ад - свободный член, не-
отрицательное целое число т - степень многочлена (7.2). Заметим, что
степень т многочлена (7.2) равна наибольшей из степеней элементов
А-матрицы (7.1). Многочлен (7.2) называется регулярным, если определи-
тель старшего коэффициента не равен нулю: det Ат Ф 0.
Две А -матрицы А(А) и jE?(A) называются равными (А$) = 5(A)), если
они имеют одинаковый порядок (п) и равные соответствующие элементы:
^(А)=^(А) i = 1, .,п ; j = 1,...,п.
Пример 7.1. Представить А-матрицу а(Х)=
А3-2А2
JA3+4
А2 +А + 2^
5А2 + 6 J
в виде многочлена с матричными коэффициентами.
261
□ Данная А-матрица 2-го порядка (л = 2), наибольшая из степеней
многочленов-элементов матрицы равна 3 (т = 3). Применяя линейные опе-
рации над матрицами, получаем
fx3-2A2 А2+А + 2) fl 0) . f-2 П , fO Q fO 2)
, , = -л+ -A + -A +
^3A3+4 5A2+6 ) <3 Oj fO 5J (0 Oj I4 6 j
A2 Xj Xq
Полученный многочлен не является регулярным, так как определитель
, fl (Р|
старшего коэффициента равен нулю: det = 0 .
Замечания 7.1.
1. Учитывая представление А -матриц в виде многочленов (7.2) с мат-
ричными коэффициентами, можно показать, что "к-матрицы /1(х) и В(х)
равны тогда и только тогда, когда они имеют одинаковый порядок (л),
одинаковую степень (/и) и равные матричные коэффициенты при одинако-
вых степенях А.
2. Еще один критерий равенства А-матриц нетрудно получить, вспо-
миная следствие 2 основной теоремы алгебры (см. разд. В.4): X-матрицы
Л(А) и В(Х), степень которых не превосходит т, равны тогда и только
тогда, когда равны числовые матрицы А(\)= В^.,) при (лг + 1) различных
значениях А1,А2,...,АИ),Ав1+| переменной А.
7.1.2. Операции иад А -матрицами
Все операции, определенные для числовых матриц (см. гл. 1), перено-
сятся на А -матрицы.
СЛОЖЕНИЕ А-МАТРИЦ
Пусть л(а) и В(а) - А -матрицы л -го порядка:
Л(А)=Л Ат + Л ,Aw“1+...+ /tA+/l0, А *О,
' ' т т-1 1 0 ’ т ’ (7 3)
в(а)=5/А/+В(_1А/’1+... + Д1А + В0, Bt*O.
Суммой А -матриц л(а) и в(а) называется матрица С(а) л-го по-
рядка, элементы которой вычисляются по формуле:
су W = ау(А)+б,7(а), i = l,...,л , j=l,..„п .
262
При этом сумма Л(Х)+ 7?(х) может быть представлена в виде многочлена с
матричными коэффициентами, степень которого не превосходит наиболь-
шей из степеней слагаемых:
/1(х)+5(х)=(Л+5А)Х* + ... + (Л1+В1)Х + (л0+50), (7-4)
где к = тах{ т,1 }, Л. =О при i >т , В.=О при j >1
УМНОЖЕНИЕ X -МАТРИЦЫ НА МНОГОЧЛЕН
Произведением р(х)-л(х) X -матрицы л(х) на многочлен р(х) на-
зывается X-матрица С(х) того же порядка, что и л(х), элементы которой
вычисляются по формуле
суМ= ' = 1., j = 1> -
Произведение матрицы (7.2) на многочлен р(х)= Рк/к + ...+ + р0,
рк*Ъ можно представить в виде многочлена с матричными коэффициен-
тами
р(х)-Л(х)=рА 4Х'"+* + {РкАт^+Рк_}Ат)кт+к~х +...+ Р0-Л, (7.5)
степень которого равна сумме степеней множителей.
В частном случае, когда многочлен р(х) тождественно равен постоян-
ной р0, получаем операцию умножения X -матрицы на число.
Операция вычитания '/.-матриц /1(х) и 2?(х) определяется как сло-
жение матрицы Л(х) с матрицей (—1)-2?(х):
л(х)- в(х) = л(х)+(-1). в(х).
Линейные операции (сложение, вычитание, умножение на число, ум-
ножение на многочлен) с X-матрицами обладают теми же свойствами, что и
линейные операции с числовыми матрицами (см. разд. 1.2).
УМНОЖЕНИЕ X-МАТРИЦ
Пусть л(х) и в(к) - X -матрицы п -го порядка (7.3). Матрицу С(х)
того же порядка, элементы которой вычисляются по формуле
= (*•)+• • + i = 1,.,« , 7=1,-.Л ,
называют произведением к-матриц л(х) и 2?(х) и обозначают
С(х)= zf(x)-Z?(x). Произведение Х-матриц можно представить в виде мно-
гочлена с матричными коэффициентами, степень которого не превышает
суммы степеней множителей:
Л(х).Д(Х)= AmB, Xm+l +(AmBl_l+Am^Bl)km+l-' +...+ А0В0. (7.6)
263
ТРАНСПОНИРОВАНИЕ А,-МАТРИЦ
Транспонированной для X -матрицы А(Х) называется X-матрица
С(х), элементы которой вычисляются по формуле
= 1 = 1,-,и, j = l
Она обозначается АГ(Х).
Транспонируя выражение А(Х) = AmXm + А^Д"1-1 +...+АД + Ад, полу-
чаем представление транспонированной X -матрицы в виде многочлена
Ar(X)=A^Xm + А^_Дт 1+... + А17Д + ДД
j
Пример 7.2. Даны X -матрицы Л(Х) = I
И .
( 1 21
SW-U 3
и многочлен р(Х) = 2Х + 3. Найти А(Х)+в(Х), р(Х)в(Х), д(Х)в(Х), в(Х)д(Х)
и АГ(Х).
□ Запишем данные X -матрицы 2-го порядка (и = 2) как многочлены
(степени т = 2 и Z = 1 соответственно) с матричными коэффициентами:
т2 Г° Ст Г’1 1
X + Х +
(1 0 1-2 3
А(Х) = Р2"1 X + 1W
V ' (Д-2 3 J I'
Мх + 2
Найдем по определению сумму и представим ее как многочлен с матричны-
ми коэффициентами
а(х)+в(х)=^2_'1
1
О
О
О
— Л2Х2 + АД + Ад;
2] (0 0), (1 2)
— Л + — 2?i Л + Вл .
XJ 11 1J 12 0 1 0
X +1
3
1 2
X + 2 X
X2 х + з
2Х Х + З
'1 о
.0 о
X2
'О
.2
Х2-1 + 1 Х + 1 + 2'
X—2+Х+2 3+Х j
О 3"
О з/
1
Тот же результат получаем по формуле (7.4), где А: = шах{ 2; 1 } = 2:
А(Х) + /?(Х) — Д2Х2 + (а, + ) X + (Ад + Bq )=
'-1 П Г1 2^1
-2 з) + (2 oj
О 3^
О ЗГ
1
О
О
О
X2
О
1
1
О
Г
О,
О
о
Го oV
1 JJ
x2+f° 1
2 1
х+
Заметим, что
степеней слагаемых.
степень суммы (равная двум) не превышает наибольшей из
264
Найдем по определению произведение р(Л)в(Л) и представим его
в виде многочлена с матричными коэффициентами
р(Х).в(Х)=(2Л + 3)[ 1 2U <2\3)1 , <2^3>'2^
V 7 \Х + 2 A.J Ц2Х + 3)(Х + 2) (2X + 3)-XJ
( 2Х + 3 4Х + 6 А ГО 0\, (2 4\ (3 6^1
^2Х2 + 7Х + 6 2X2 + 3Xj ^2 2) <7 3) 1,6 0)
Тот же результат получаем по формуле (7.5), где к=1, т = 1, Pi =2,
Ро=3-
р(х)- в(Х) = (р,Х + р0) (^Х + Во) = рД Л2 + (piB0 + p0Bi)Л + р0В0 =
О
2
Х + 3-
1 2'
.2 0?
°>+р 4)
2 \7 3
Заметим, что степень произведения равна сумме степеней множителей.
Найдем по определению произведение А(Х)в(Х) и представим его в
виде многочлена с матричными коэффициентами:
А(х)в(х)=
'х2-1
Л-2
X + 1V 1 2"
3 J (Х + 2 X,
<[к2-1)-1 + (к + 1)-(Х + 2)
(Х-2)-1+3-(Х + 2)
(х2-l)-2 + (X + l)-X'j
(Х-2)-2 + 3-Х )
'2Х2 + ЗХ + 1 ЗХ2+Х-2^_Г2 3\2ГЗ /1 -2^
, 4Х + 4 5Х-4 J <0 Oj \4 5) \4 -4)
Тот же результат получается по формуле (7.6). Заметим, что в данном случае
произведение X -матриц имеет степень меньше, чем сумма степеней множи-
телей: 2 <2 + 1.
Найдем по определению произведение В(Х)л(Х) и представим его в
виде многочлена с матричными коэффициентами:
Га.2-1
^Х-2
X +1
3
1(х2-1)+2-(Х-2) 1-(Х + 1)+2-3
JX + 2)-(x2-1)+Х-(Х-2) (Х + 2)-(Х + 1)+Х-Зу
265
' X2+2X-5 X + 7 "j
чХ3 + 3X2-3X-2 X2 + 6X + 2j
i\ I'5
A +
6) 1-2
+ 7
2
В данном случае степень произведения оказалась равной сумме степеней
множителей.
лг(х)=
Найдем транспонированную Л-матрицу
0i2-i х+1У
Х-2 3 .
Х2-1 Х-2
Х + 1 3 }
Замечания 7.2.
1. Произведение многочленов (7.5) с матричными коэффициентами в
отличие от произведения обычных многочленов может иметь степень мень-
ше, чем сумма степеней множителей (см. пример 7.2). Действительно, стар-
ший коэффициент A^i произведения (7.6) может быть равен нулю, даже
если матрицы Ат и В1 ненулевые. Если хотя бы один из множителей - ре-
гулярный многочлен, то степень произведения равна сумме степеней мно-
жителей. В самом деле, если матрицы Ат и В/ - ненулевые и, кроме того,
det Ат * 0, то произведение AmBt * О.
2. Как и у числовых матриц, произведение X -матриц некоммутативно,
т.е. а(Х)в(Х)в(Х)а(Х) (см. пример 7.2).
ОПРЕДЕЛИТЕЛЬ А-МАТРИЦ
Для нахождения определителя X -матрицы используются те же правила
и свойства, что и для числовых матриц, поскольку X -матрица при фиксиро-
ванном значении X становится числовой. Заметим, что определитель
X-матрицы, ее миноры и алгебраические дополнения представляют собой
многочлены переменной X. Рангом X-матрицы называется максимальный
порядок минора, не равного тождественно нулю, т.е. rg А(Х)= г , если в мат-
рице А(Х) имеется отличный от нуля минор г-го порядка, а все миноры
большего порядка тождественно равны нулю или не существуют.
Присоединенная X-матрица А+(Х), транспонированная для матрицы,
составленной из алгебраических дополнений элементов матрицы А(Х),
представляет собой X -матрицу, причем, как и ранее, справедливо равенство
А(Х)А+ (X) = А+ (Х)А(Х) = det А(Х)• Е, (7.7)
где Е - единичная матрица того же порядка, что и матрица а(Х) .
266
Действительно, докажем, что А(Х)А+(Х) = det А(Х)-Е, используя п.2
замечаний 7.1. Пусть степени левой и правой частей не превосходят т.
Возьмем (т + 1) различных чисел Для любого из них
имеет место равенство
A(X/)A+(X/)=detA(Xf)-E, i = 1,...,т,т + 1,
справедливое для числовых матриц (см. п.4 замечаний 2.3). Следовательно,
А.-матрицы в левой и правой частях доказываемого равенства совпадают.
Аналогично можно доказать равенство А+(Х)а(Х) = det А(Х)- Е.
ОБРАЩЕНИЕ Л-МАТРИЦ
Обратной для квадратной X-матрицы А(Х) называется X-матрица
А-1 (X), если
а(Х)а-‘(Х)=Ач(Х)а(Х)=Е, (7.8)
где Е - единичная матрица того же порядка, что и матрица А(Х).
Необходимым и достаточным условием существования обратной
X-матрицы А-1(Х) является условие det А(Х) = const * 0, т.е. определитель
обращаемой X -матрицы должен быть отличным от нуля многочленом нуле-
вой степени (постоянной). Необходимость следует из (7.8). Действительно,
по теореме 2.2 об определителе произведения матриц имеем
detA(X)-detA-1(X) = 1, т.е. произведение двух многочленов (определителей
X -матриц) равно многочлену нулевой степени. Значит, оба множителя - по-
стоянны (многочлены нулевой степени), поэтому detA(X)=J, где Д#0.
Достаточность условия detA(X)=d *0 следует из теоремы 4.1 существова-
ния и единственности обратной матрицы. Формула
действительно определяет X-матрицу. В этом можно убедиться прямой
подстановкой в (7.8) с учетом (7.7).
Матрица А(Х), для которой существует обратная А-1(Х), называется
обратимой.
. ( 1
Пример7.3. Для X-матрицы А(Х)= .
+ 1 л
□ Вычислим определитель данной матрицы
detA(X) =
найти обратную.
1 Х-1
Х+1 X2
= Х2
267
Находим обратную X-матрицу (по правилу п.1 замечаний 4.3):
A-'(X) = f ~Л + 1 .
V ’ I-Л-1 1 )
Сделаем проверку:
\Л “Г 1 Л J ' X2 t-X-1 -Х + Р 1 J \о
Л-(Л)Л(1)=Г f -у1' — Л — 1 1 ' 1 +1 Х-Р X2, -Г1 "to
Соотношения (7.8), определяющие обратную матрицу, выполняются.
ДЕЛИМОСТЬ Л-МАТРИЦ
О
1
Рассматривая X-матрицы как многочлены (7.2) с матричными коэф-
фициентами, можно ввести операцию деления многочлена на многочлен с
остатком. Нам потребуется операция деления X-матрицы на линейный дву-
член вида (А-ХЕ), где А - числовая матрица.
Теорема 7.1 (о делимости X-матриц на линейный двучлен). Любую
X -матрицу Р(Х) = PmXm +...+P{k + Ро можно разделить слева на линейный
двучлен (A-Хе), где А - числовая матрица того же порядка, что и Р(Х),
т.е. существуют единственные X -матрица !2лев(Х) и числовая матрица
К лев такие, что Р(Х) = (А-ХЕ)-Сл„(Л)+Елев, где £лев(Л) - левое част-
ное, RMe - левый остаток.
Доказательство этого утверждения проводится как для обычных
многочленов, только при умножении нельзя изменять порядок множителей
(в силу некоммутативное™ произведения матриц).
Аналогично определяется деление X-матрицы Р(Х) справа на
(А - ХЕ): Р(Х)=Qnp (X)- (А - ХЕ)+ Rnp . Частные и остатки при делении слева
и справа в общем случае не совпадают: <2лев(Х)* Qnp(X), Rxea *Rnp. При
делении с остатком левое частное <2лев(А) умножается слева на двучлен
(А-ХЕ), а правое частное (2П/,(Х)- справа.
Многочлен с матричными коэффициентами можно записать двумя
способами
P(X) = PmXm+... + P1X + P0 и P(X)=XmPm+... + XP1 + P0,
которые, разумеется, при любом значении X дают один и тот же результат.
Если же вместо переменной X подставить числовую квадратную матри-
268
цу А того же порядка, что и Р(Х), то получим, в общем случае, разные
матрицы:
Рпр(А)=РтАт +... + Р1А + Р0 и Рлев(А)=А'"Рот+... + АР1 + Р0,
которые называются, соответственно, правым и левым значениями много-
члена Р(Х) при подстановке матрицы А вместо X. При вычислении право-
го значения /^>(а) матричные коэффициенты многочлена умножаются
справа на матрицу А , а при вычислении левого значения Рлм(а) - слева.
Подставляя в равенства
Р(Х)=ечр(Х)(А-ХЕ)+/?ч, и Р(Х)=(А-Х£)-2л„(Х)+Ялев
вместо переменной X матрицу А , получаем P„p(a) = R„p и Рлм(а) = Rnee.
Теорема 7.2 (обобщенная теорема Безу). Остаток от деления
X -матрицы Р(Х) слева (справа) на линейный двучлен (А-KE) равен левому
значению Ржв(А) (соответственно, правому значению Р„р(а)).
^2 + 1 X ‘
2 Х-1
Пример 7.4. Разделить X-матрицу р(Х)=
на матрицу
/ , \ (12)
(А-ХЕ), где A=l I.
□ Запишем X -матрицу Р(Х) как многочлен второй степени с матрич-
ными коэффициентами:
Р(Х)=
10) ,
= р2х2 + рх+р0.
2 -1) 2 10
X2 + 1 X Ц1 о
2 X-1J (.О 0
Разделим Р(Х) слева на (A-Хе), повторяя, по существу, алгоритм де-
ления "уголком" (см. пример В. 14 в разд. В.4). Прибавляя к Р(Х) многочлен
(а-хе)р2х, получаем X -матрицу первой степени:
Р2Х2 + РД + PQ + (А - ХЕ)Р2Х = (fl + АР2 )• X + Ро =
0 А (1 А , fl 0
I — I I ’X+1
-1J ^3 1J 1^2 -1
этому линейному двучлену выражение
О пр 2V1 О
О 1 г 3 olio о
•х2 +
0 1
1
2
Продолжая процесс, прибавим к
(A-XE)pW. В результате получим числовую матрицу (остаток):
1 2 V1 '
3 ОДЗ 11“
о
Р® X + ро + (А - XE)pW = ро + АР® = Q °
Итак, Р(Х)+(А - ХЕ)Р2Х + (А - Хе)р/^ = R . Отсюда
3)
= /?.
2J
5
269
р(Х) = (А-Х£)-елев(Х)+Р_,
гда <2ли(Х)=-Р2Х-/](1) = -^ о]’Х“(з ;]-левое~^=-
(8 3>1
= - левый остаток.
I5 2J
Разделим Р(Х) справа на (A-Хе). Прибавляя к Р(Х) многочлен
р2(а-хе)х, получаем X -матрицу первой степени Р^к + Ро, где
О . Затем к многочлену Рр^Х + PQ прибавляем
/^(а-хе) и получаем числовую матрицу R (остаток), равную Ро + рДа .
Выполнив эти действия, имеем
P(k)=Qnp(X)-(A-kE)+Rnp,
pi(2) = p1+p2a =
Rnp = pa + P}2]A =
где G„(^) = -P2^-^ = -f1 |Х-Г 3
2 1 (О oj pl
fll 2^1
5 J - правый остаток.
Для проверки полученных результатов воспользуемся теоремой 7.2.
Вычислим Рлм(а) и Р„р(а), подставив вместо переменной X матрицу А :
правое частное, а
О
7
3
РМ =
о
0^1 р 2> Го
о) (з б]+(о
01 2
а2 +
0J
р р
Лз
/ \ 7 f 1 О
РлМ = А 1
л“' ’ (00
1 г') fo 1
з о
2^1 р (Г
бДо 0.
0 Г
0 1/
1
2 -1
С (
+
1)
О
-1
21 (
+
OJ I
+ А-
Р
(1 0
А +
р
1 °'|-Р1
Ч5
1 0
2 “I
_р 3"
“Ь 2.
-1
-Rnee
О 1
1
2
Замечания 73.
1. Выясним связь операции транспонирования с вычислением правых и
левых значений X -матрицы. Пусть
P(M= V+-+PlX + P0 и Рг(Х)=РигХт+... + Р1гХ+Рог.
Подставляя в эти многочлены вместо аргумента X матрицы А и Аг , най-
дем значения
РдМ = АтРт +... + АР{ + Ро, (аг )=/£(аг)"+... + рТАТ + Рог.
270
Транспонируя матрицу Р,га(л), получаем
[p«.w 7 - <(*")'
Следовательно, [ Р,„(л)]г = Р^(лг).
2. Если X-матрица Р(Х) симметрическая: Р(Х)= РГ(Х), то
[ РлеАА) ]Г ~ Если, кроме того, матрица А симметрическая, то ле-
вое и правое значения Л -матрицы совпадают: Рже(А)= ЛДа)
3. Если р(х) - обратимая Л-матрица, то ее остаток от деления на ли-
нейный двучлен (А-ХЕ) также обратимая числовая матрица. В самом деле,
пусть P(X)=QjX)(A-XE) + Rnp, где Rnp = Рпр (а) - правое значение мно-
гочлена р(Х) при подстановке матрицы А вместо Л. Умножив Р(Х) справа
на Р"1 (X), получим E = Qnp(X)(A-XE)p~l(X)+ RnpP~l(X). Подставим вместо
X матрицу А : Е - RnpP„p{A) = R„pR^p Следовательно, правый остаток Rnp
- обратимая числовая матрица. Для левого остатка аналогично получаем
Рл1(ЛХев = R»eeR»ee = Е ’ те- Rm» ~ обратимая числовая матрица.
7.1.3. Элементарные преобразования X -матриц
Элементарными преобразованиями X-матрицы называются следую-
щие ее преобразования:
I. Перестановка двух столбцов (строк) матрицы.
II. Умножение всех элементов одного столбца (строки) матрицы на одно и
то же число, отличное от нуля.
III. Прибавление к элементам одного столбца (строки) соответствующих
элементов другого столбца (строки), умноженных на один и тот же
многочлен р(Х).
Матрица в(Х), полученная из исходной матрицы а(Х) конечным чис-
лом элементарных преобразований, называется эквивалентной. Это обо-
значается а(х)~в(х).
Напомним, что многочлен </(х)^0 называется общим делителем от-
личных от нуля многочленов р(Х) и <?(Х), если каждый из них делится на
flf(x) без остатка (см. разд. В.4). Общий делитель максимальной степени (со
старшим коэффициентом, равным единице) называется наибольшим общим
делителем. У любых ненулевых многочленов существует единственный
наибольший общий делитель (см. разд. В.4). Понятия общего делителя и
наибольшего общего делителя распространяются на любое конечное число
271
многочленов. В частности, если один из многочленов тождественно равен
единице, то он является наибольшим общим делителем.
При помощи элементарных преобразований X -матрицу можно привес-
ти к диагональному виду. Алгоритм повторяет в общих чертах метод Гаусса
(см. разд. 1.6.1), но имеются некоторые отличия при выборе ведущего эле-
мента.
АЛГОРИТМ ПРИВЕДЕНИЯ X-МАТРИЦЫ К ДИАГОНАЛЬНОМУ ВИДУ
1. В X -матрице выбрать отличный от нуля элемент наименьшей степе-
ни {ведущий элемент). Если имеется несколько элементов наименьшей сте-
пени, то среди них выбирается любой. Переставить (при необходимости) два
столбца и две строки так, чтобы ведущая строка и ведущий столбец, на
пересечении которых стоит ведущий элемент, оказались на месте первой
строки и первого столбца (преобразование I типа). Ведущий элемент при
этом окажется в левом верхнем углу рассматриваемой матрицы.
Если все элементы ведущего столбца и ведущей строки, за исключени-
ем ведущего элемента, равны нулю, то этот столбец и эту строку следует ис-
ключить из рассмотрения и продолжить поиск ведущего элемента в остав-
шейся части матрицы. Преобразования заканчиваются, если исключены все
столбцы и строки, или в оставшейся части матрицы все элементы нулевые,
или в оставшейся части матрицы имеется только один элемент.
Если все элементы ведущего столбца и ведущей строки делятся без ос-
татка на ведущий элемент, то перейти к п. 3.
Если не все элементы ведущего столбца и ведущей строки делятся на
ведущий элемент, то степень ведущего элемента нужно понизить, переходя
к п.2.
2. Если в первом столбце имеется элемент а;1(Х), который не делится
на ведущий элемент ап(Х)^0, то представить этот элемент в виде
адМ = р(А.)ап(Х)+г(Х), где остаток г(Х) / 0 и степень г(Х) меньше, чем
степень многочлена ап(Х). Прибавить к /-й строке первую строку, умно-
женную на многочлен (~р(Х)), при этом получить на месте элемента а;1(Х)
многочлен г(Х). Перейти к выбору ведущего элемента, т.е. к п.1. Поступить
аналогично, если в первой строке есть элемент, который не делится на ве-
дущий (использовать то же представление и преобразование столбцов).
3. К каждой строке, расположенной ниже ведущей, прибавить веду-
щую строку, умноженную соответственно на такой многочлен, чтобы эле-
менты, стоящие под ведущим оказались равными нулю (преобразование III
типа). Аналогично, к каждому столбцу, расположенному правее ведущего
прибавить ведущий столбец, умноженный соответственно на такой много-
член, чтобы элементы, стоящие правее ведущего, оказались равными нулю
(преобразование III типа).
272
4. Исключив из рассмотрения строку и столбец, на пересечении кото-
рых стоит ведущий элемент, перейти к п.1, в котором все описанные дейст-
вия применить к оставшейся части матрицы.
Пример 7.5. Привести Л -матрицы
А(Л) =
Л Л2 -Л
Л2 + Л — А +1
, В(Л) =
Л
Л2-2Л + 1
A2+2A + 4^
О ,
Гх
, с(л)= о
.о
1
л
о
О'
1
л>
к диагональному виду.
□ Матрица А . 1. Наименьшую степень имеет элемент (Л) = Л . Вы-
бираем его в качестве ведущего. Все элементы ведущего (первого) столбца и
ведущей (первой) строки делятся на ведущий элемент. Поэтому переходим к
п.З алгоритма.
3. Ко второй строке прибавим первую, умноженную на (-Л-1):
А(Л) =
Х+л
Л2-Л\(Л Л2-Л 'l (л л2-л'
-A + 1J [о -А + 1 + (-А-1)(л2-л)] |о -Л3 + 1,
Ко второму столбцу прибавим первый, умноженный на (1 - Л):
л л2-л\Гл о А
О -A3 + 1J [о -A3 + 1J"
4. Исключим из рассмотрения первый столбец и первую строку.
Оставшаяся часть матрицы состоит из одного элемента. Преобразова-
ния закончены, матрица приведена к диагональному виду.
Матрица В. I1. В качестве ведущего элемента выбираем /?|1(Л) = Л.
Первый столбец и первая строка матрицы - ведущие. Так как элемент
621(Л)=(Л-1)2 не делится на ведущий без остатка, то переходим к п.2 алго-
А(Л)~
ритма.
2. Разделим многочлен (>21 (Л) = Л2 - 2Л +1 на Ьг j (Л) = А :
Л2-2Л + 1 = (Л-2)-Л+1.
Прибавим ко второй строке первую, умноженную на (-Л + 2):
"А Л2+2А + 4Ч
,1 -Л3+ 8 ,
Л Л2 + 2Л + 4
Л2-2Л + 1 0
Возвращаемся к п. 1.
1 2 . Выбираем элемент наименьшей степени (единицу) в качестве ве-
дущего. Меняем местами первую и вторую строки:
1 -Л3+8
Л Л2 + 2Л + 4.
5(Л) =
5(A) ~
18 - 4549
273
Все элементы ведущего (первого) столбца и ведущей (первой) строки делят-
ся на ведущий элемент. Поэтому переходим к п.З алгоритма.
3. Прибавляем ко второй строке первую, умноженную на (-Х), а затем
ко второму столбцу прибавляем первый, умноженный на (х3 - в) :
-х3 + в Wi о
X4 + X2 — 6Х + 4, (О Л4 + X2 — 6Х + 4
4. Исключаем из рассмотрения первую строку и первый столбец мат-
рицы. Переходим к п. 1 алгоритма.
13. Поскольку в оставшейся части матрицы имеется только один эле-
мент, то преобразования надо закончить - матрица 2?(Х) приведена к диаго-
нальному виду.
Матрица С. I1. Выбираем в качестве ведущего элемент с12(Х)= 1 наи-
меньшей степени. Меняем местами первый и второй столбцы:
fX 1 (Л
с(х)=
О X 1
<° 0 \
'1 X О'
X 0 1
<о о х,
Все элементы ведущего (первого) столбца и ведущей (первой) строки делят-
ся на ведущий элемент. Поэтому переходим к п.З алгоритма.
З1. Ко второй строке прибавляем первую, умноженную на (-Х), а за-
тем ко второму столбцу прибавляем первый, умноженный на (-Х):
'1 к °1 '1 X О' '1 0 О'
с(х)~ X 0 1 ~ 0 -X2 1 - 0 -X2 1 .
.о о о 0 X, 0 0
41. Исключаем первую строку и первый столбец из рассмотрения и
переходим к п.1.
1 2. В оставшейся части матрицы выбираем ненулевой элемент наи-
меньшей степени, который равен единице. Меняем местами второй и третий
столбцы:
'1 0
С(Х)~ 0 -X2
0 0
oWi о о'
1 - О 1 -X2
XJ (о X 0 >
Все элементы ведущей (второй) строки и ведущего (второго) столбца делят-
ся на ведущий элемент (на 1). Поэтому переходим к п.З алгоритма.
3 2 . К третьей строке прибавляем вторую, умноженную на (-Х), а за-
тем к третьему столбцу прибавляем второй, умноженный на X2:
274
4 2. Исключаем второй столбец и вторую строку из рассмотрения. Пе-
реходим к п. 1 алгоритма.
13. Так как в оставшейся части матрицы имеется единственный эле-
мент, преобразования заканчиваются, матрица приведена к диагональному
виду.
Замечания 7.4.
1. Диагональный вид Л-матрицы - не единственный. Он зависит от
выбранной последовательности элементарных преобразований. Напомним,
что простейший вид числовой матрицы определяется единственным обра-
зом, несмотря на разные последовательности используемых элементарных
преобразований. Для А -матриц можно уточнить понятие диагонального ви-
да так, чтобы оно отвечало условию единственности. Нормальным диаго-
нальным видом Л -матриц п -го порядка называется диагональная матрица
^(Л) 0 0 ••• (Л
0 •• ег(М 0 ... о (7.9)
0 0 0 ... о
< 0 0 0 ... 0,
у которой все многочлены, стоящие на главной диагонали, имеют старшие
коэффициенты, равные единице; причем многочлен г2(Х) делится на ^(Л),
е3(Л) делится на е2(Л) и т.д. ег(Л) делится на Количество г нену-
левых многочленов больше нуля, так как рассматриваются ненулевые
Л -матрицы, и не превосходит порядка матрицы, т.е. 1 < г < п.
2. Чтобы привести Л-матрицу к нормальному диагональному виду,
нужно сначала привести матрицу к диагональному виду:
Элемент а'ц (Л) выбираем в качестве ведущего (если старший коэффи-
циент этого многочлена не равен единице, то разделить на него многочлен).
Если среди диагональных элементов есть элемент, например, а'и(Х), кото-
рый не делится на ведущий элемент, степень ведущего элемента можно по-
низить. Для этого прибавляем i -й столбец к ведущему (первому) столбцу, а
затем переходим к п. 2 алгоритма приведения Л -матрицы к диагональному
виду.
18*
275
Если все диагональные элементы делятся на то, исключив пер-
вую строку и первый столбец, следует продолжить преобразования с остав-
шейся частью диагональной матрицы. Преобразования заканчиваются, если
в диагональной матрице остался один ненулевой элемент.
3. Алгоритм приведения Л -матрицы к нормальному диагональному
виду отличается от соответствующего алгоритма приведения числовой мат-
рицы к простейшему виду выбором ведущего элемента. Необходимо, чтобы
ведущий элемент оказался делителем всех элементов ведущей строки и ве-
дущего столбца (либо всех диагональных элементов, если Л-матрица диа-
гональная). Для этого метод Гаусса дополняется приемами понижения сте-
пени ведущего элемента. Действительно, понижая степень многочлена, обя-
зательно получим многочлен, на который делятся другие. В крайнем случае,
получим многочлен нулевой степени (отличную от нуля постоянную вели-
чину), на который делятся все многочлены.
4. Для Л-матриц, как и для числовых, преобразования, обратные к
элементарным, являются элементарными.
5. Элементарные преобразования числовых матриц можно представить
как умножение на элементарные матрицы (см разд. 1.6.2). Аналогичным об-
разом, X -матрицу, полученную из единичной матрицы при помощи конеч-
ного числа элементарных преобразований, назовем элементарной
X -матрицей. Тогда совокупность элементарных преобразований, приво-
дящих матрицу к нормальному диагональному виду, можно представить как
умножение данной X-матрицы слева и справа на элементарные матрицы.
Другими словами, справедливо утверждение: для любой X -матрицы д(Х)
п -го порядка существуют такие элементарные преобразующие матрицы
5(Л) и т(Л) п -го порядка, что матрица
(7-10)
имеет простейший вид (7.9): Л(Х) = diag(el(k),..., ег(Х), 0,...,0). Согласно п.4
элементарные матрицы имеют обратные, поэтому (7.10) равносильно равен-
ству д(Х) = 5-1(Х)л(Х)7'-1(Х). Для нахождения элементарных матриц 5(х)
и Г(Х) нужно (см. разд. 1.6.3), приписав к данной матрице А(Х) справа и
снизу единичные матрицы, составить блочную матрицу
Е\
— . Эле-
I Е
менты правого нижнего блока этой матрицы можно не указывать, так как
они не участвуют в дальнейших преобразованиях. Затем при помощи эле-
ментарных преобразований, выполняемых над строками и столбцами блоч-
ной матрицы, привести ее левый верхний блок А(Х) к нормальному диаго-
нальному виду (7.9). При этом блочная матрица преобразуется к виду
276
л(х) ад
Ж] )
, где л(Х) - матрица простейшего вида (7.9), эквивалентная
матрице д(Х), а 5(Х) и Т'(Х) - искомые преобразующие матрицы, связан-
ные с матрицей д(Х) равенством (7.10).
6. Если Л-матрицы д(Х) и Z?(X) эквивалентны, то существуют такие
обратимые Л-матрицы 5(Х) и г(Х),что В(Х) = В(Х)д(Х)т(Х).
Пример 7.6. Привести X -матрицы
О'
1
к нормальному диагональному виду. Для матрицы А(Х) найти элементар-
ные преобразующие X-матрицы S(X) и 7'(Х), приводящие ее к виду (7.9).
□ Матрица / . Приписываем к матрице А(Х) справа и снизу единич-
E'j
Е
нальному виду (см. пример 7.5):
( X х2-х 1 o'] Гх X2- -X 1 o'
р(х) ЕЛ Л.2 + Л — Л +1 0 1 0 -X3 + l -X-l 1
Iе ) 1 0 1 0
1 0 1 7 lo /
|х К2-Х 1 о' rx 0 1 o']
0 - Х3 + 1 -Х-1 1 0 -X3 + l -X -1 1
1 0 1 1-X
1о 1 / 1
Полученный диагональный вид не является нормальным, так как двучлен
(- X3 +1) не делится на X. Продолжаем преобразования согласно п.2 заме-
чаний 7.4. Прибавляем к первому столбцу второй. Затем, согласно п.2 алго-
ритма приведения X -матрицы к диагональному виду, разделим многочлен
(-Х3 +1) на X: - X3 +1 = (- Х2)х +1 и получим частное р(Х) =-X2. Прибав-
ляем ко второй строке первую, умноженную на — р(Х) = X2:
277
А(Х) ' к -Х3+1 0 -X3 + 1 1 О' -Х-1 1 ' X 0 1 -Х3 + 1 1 О' Х2-Х-1 1
Е 2-Х 1-Х 2-Х 1-Х
t 1 1 7 1 1
Теперь ведущий элемент равен единице. Поэтому меняем местами первую и
вторую строки, а затем ко второй строке прибавляем первую, умноженную
на (-Х):
1 -X3
X о
Х2-Х-1 1
1 о
2-Х
1
1-Х
1
1
о
2-Х
О
-Х3 + 1
X4-X
1-Х
1
Х2-Х-1 1
—X3 + X2 + X +1 — X
Прибавляя ко второму столбцу первый, умноженный на (х3 -1), получаем
1 0 Х2-Х-1 1
0 х4-х —X3 + X2 + X +1 —X
2-Х -Х4+2Х3-1
1 X3
(л(х) s(x)'
"w)T '
Матрица Л(Х)
\ Г1 о
Л( )"(о X4-X
из соответствующих блоков
М-ХДД lJг(х)=
приведена к нормальному диагональному виду (7.9), где
. Элементарные преобразующие Л-матрицы выписываем
2-Х
1
-Х4+2Х3-1
X3
Проверим равенство (7.10), умножив матрицу л(Х) на элементарные
преобразующие X-матрицы S(X) и т(Х):
S(Z)4(X)7-(X) = [ ДД ‘ 2
\ Л тЛ +Л + 1 “ЛИЛ + л
Х2-Х
-Х + 1
2-Х -Х4 + 2Х3-1
1 X3
X
( Х2-Х-1 1
X3 + X2 + X +1 — X
X
-X3 +Х2 +Х + 1
х4-х
-хб+х5+х4+х3-х2-х
-11 0
До х4-х
= Л(Х).
278
Равенство выполняется. Заметим, что полученные матрицы 5(Х) и Т(Х) об-
ратимы, так как det 5(Х) = -1, det т(Х) = 1.
Матрица В . Приводим матрицу к диагональному виду (см. при-
мер 7.5):
1 О
О Х4+Х2-бХ + 4
Этот вид является нормальным, поскольку многочлен
е2 (А) - Л4 + X2 - 6Х + 4 делится на многочлен (X) = 1.
Матрица С. Приводим матрицу С(Х) к диагональному виду (см. при-
мер 7.5):
В(Л)~
Этот вид является нормальным, так как многочлен е3(Х) = Х3 делится на
е2(Х) = 1,а е2(Х) = 1 делится на е1(Х) = 1.
7.1.4. Инвариантные множители Л -матрицы
Пусть А(Х) - Л -матрица п -го порядка. Любой минор этой матрицы
представляет собой многочлен переменной Л. Напомним, что рангом
Л -матрицы называется максимальный порядок минора, не равного тождест-
венно нулю, т.е. rg А(Х) = г, если в матрице А(Х) имеется отличный от нуля
минор г -го порядка, а все миноры большего порядка тождественно равны
нулю или не существуют.
Обозначим через dk (X) наибольший общий делитель миноров к -го
порядка Л -матрицы А(Х). Для определенности будем считать, что старшие
коэффициенты многочленов dk (X) равны единице. Заметим, что в совокуп-
ности многочленов
...
где г = rg Л(Х), каждый последующий многочлен делится на предыдущий.
В самом деле, разложив любой минор к -го порядка по строке, полу-
чим сумму миноров (&-1)-го порядка, взятых с некоторыми коэффициен-
тами. Так как каждый минор (Л-1)-го порядка делится на d*_i(X), то и вся
сумма будет делиться на dk_fy}. Следовательно, любой минор к -го поряд-
279
ка делится на dk_1(k). Поэтому и наибольший общий делитель dk(k) также
делится на ^^(Х).
Многочлены
е,(Х) = </,(Х), «2(Л) = ^ <7Л1)
называются инвариантными множителями Л-матрицы А(Х). Здесь г -
ранг Л-матрицы А(Х).
Теорема 7.3 (об инвариантных множителях). При элементарных
преобразованиях X -матрицы ее инвариантные множители не изменяются.
Достаточно показать, что при элементарных преобразованиях не изме-
няются многочлены di{k),d2{k],...,dr(k). Это доказательство почти до-
словно повторяет доказательство теоремы 3.3. В самом деле, при одном
элементарном преобразовании (I, II или III типа) матрицы А(Х) любой ее
минор к -го порядка либо не изменится, либо поменяет знак на противопо-
ложный, либо совпадет с другим минором к -го порядка, либо окажется
равным сумме двух миноров к -го порядка (взятых с некоторыми множите-
лями). Ни одно из этих действий не может изменить наибольшего общего
делителя dkty). Отсюда следует, что и отношения (7.11) наибольших общих
делителей не изменяются.
Следствие 1. Ранг X -матрицы не изменяется при элементарных пре-
образованиях столбцов (строк).
Следствие 2. Инвариантные множители X -матрицы полностью оп-
ределяют ее нормальный диагональный вид, т.е. многочлены е,(Х),
i = l,...,г, в (7.9) совпадают с инвариантными множителями (7.11)
X -матрицы.
В самом деле, все миноры первого порядка матрицы (7.9), т.е. элемен-
ты этой матрицы, делятся на е^Х). Поэтому dx (X) = ej (X). Все миноры вто-
рого порядка матрицы (7.9) делятся на произведение е,(Х)е2(Х). Следова-
тельно, = ei(X) e2(X) и т.д. Рассматривая миноры г-го порядка полу-
чаем, что dr(k)= е1(Х)-е2(Х)-...-ег(Х). Отсюда следуют равенства (7.11). По
теореме 7.3 все эквивалентные X-матрицы имеют одни и те же инвариант-
ные множители, которые, как мы только что убедились, полностью опреде-
ляют нормальный диагональный вид X -матрицы.
Следствие 3. Эквивалентные X -матрицы приводятся к одному и то-
му же нормальному диагональному виду.
280
СПОСОБЫ НАХОЖДЕНИЯ ИНВАРИАНТНЫХ МНОЖИТЕЛЕЙ
Первый способ. Привести А-матрицу к нормальному диагональному
виду (7.9): diagfafa),..., ег(к), Ненулевые многочлены, стоящие на
главной диагонали, являются искомыми инвариантными множителями.
Второй способ.
1. Найти наибольший общий делитель d{(k) миноров 1-го порядка
А-матрицы (т.е. ее элементов); найти наибольший общий делитель
миноров 2-го порядка и т.д. Процесс завершить, если все миноры некоторо-
го порядка (г +1) либо тождественно равны нулю, либо не существуют.
2. Найти инвариантные множители по формулам (7.11).
Пример 7.7. Найти инвариантные множители матриц
А-1
О
А-1
О
О
А-2
'А
О
<0
А =
° 1
A-1J ’
В =
1
А
О
(Р
1
□ Матрица А . Первый способ. Матрица А имеет нормальный диаго-
нальный вид. Поэтому е](А) = А-1 и е2(А) = А-1.
Второй способ. 1. Запишем ненулевые миноры первого порядка мат-
рицы А . Они равны А -1. Следовательно, их наибольший общий делитель
</,(А) = А -1. Минор второго порядка этой матрицы единственный и равен
(А -1)2. Следовательно, d2(A) = “ 1/ •
2. По определению (7.11) находим инвариантные множители:
e,(X)=rf,(x).X-l. е2(Х)=^.^-Х-1.
Матрица В . Второй способ. 1. Диагональный вид матрицы В не яв-
ляется нормальным, поскольку двучлен (А - 2) не делится на двучлен (А -1)
(без остатка). Запишем ненулевые миноры первого порядка: А-1, А-2.
Наибольший общий делитель этих многочленов равен единице, т.е.
</;(А)= 1. Матрица В имеет единственный минор второго порядка, поэтому
</2(А)=(А-1)(А-2).
2. По формулам (7.11) находим инвариантные множители:
«,(X)-J,(X)-1. е2(Х) = ^ = ^^^ = (Х-1)(Х-2).
Матрица С. Первый способ. Матрица с(А) была приведена к нор-
мальному диагональному виду (см. пример 7.6): С(А) ~ diag^., 1, А3), поэтому
е](А)=1, е2(А) = 1, е3(А) = А3.
281
7.2. ХАРАКТЕРИСТИЧЕСКИЕ МАТРИЦЫ И МНОГОЧЛЕНЫ
Пусть А - числовая квадратная матрица п -го порядка. Матрица
А-Л.Е называется характеристической для А, а ее определитель
Дд (А) = det(A — АЕ) характеристическим многочленом матрицы А :
аи
А-кЕ =
I ат
Характеристическая матрица - это А -матрица. Ее можно представить в
виде регулярного многочлена первой степени с матричными коэффициента-
ми. Нетрудно заметить, что степень характеристического многочлена равна
порядку п характеристической матрицы.
7.2.1. Собственные векторы и собственные значения матрицы
Пусть А - числовая квадратная матрица п -го порядка. Ненулевой
столбец х =
, удовлетворяющий условию
Ах = Ах,
(7.13)
называется собственным вектором матрицы А. Число А в равенстве
(7.13) называется собственным значением матрицы А . Говорят, что собст-
венный вектор х соответствует (принадлежит) собственному значению
А.
Поставим задачу нахождения собственных значений и собственных
векторов матрицы. Определение (7.13) можно записать в виде
(а-АЕ)х = о ,
где Е - единичная матрица n-го порядка. Таким образом, условие (7.13)
представляет собой однородную систему п линейных алгебраических урав-
нений с п неизвестными jq, х2 ,. -, хп :
(ан-А)*]+а12 х2+ ... + ain хп =0,
а21 Ч + (а22 ~ М Лг+ • • •+ а2п хп = 0» ...
. «п1 Ч+ап2 ^2+••• + («/« =0.
Поскольку нас интересуют только нетривиальные решения (х о) од-
нородной системы, то определитель матрицы системы должен быть равен
нулю:
282
В противном случае по теореме 5.1 система имеет единственное тривиаль-
ное решение. Таким образом, задача нахождения собственных значений
матрицы свелась к решению уравнения (7.15), т.е. к отысканию корней ха-
рактеристического многочлена ДЛ(Л)= det(A-Afi) матрицы А . Уравнение
ДЛ(Л)=0 называется характеристическим уравнением матрицы А . Так
как характеристический многочлен имеет и -ю степень, то характеристиче-
ское уравнение - это алгебраическое уравнение л-го порядка. Согласно
следствию 1 основной теоремы алгебры (см. разд. В.4), характеристический
многочлен можно представить в виде
Ax(A) = det(A-X£) = nn(A-A1)n-(A-X2)nj -... - (Л-X*,
где - корни многочлена кратности nltn2,...,nt соответствен-
но, причем «j +«2 + ... + nt = п. Другими словами, характеристический мно-
гочлен имеет п корней, если каждый корень считать столько раз, какова его
кратность.
Теорема 7.4 (о собственных значениях матрицы). Все корни харак-
теристического многочлена (характеристического уравнения (7-15)) и
только они являются собственными значениями матрицы.
Действительно, если число Л - собственное значение матрицы А , ко-
торому соответствует собственный вектор х*о, то однородная система
(7.14) имеет нетривиальное решение, следовательно, матрица системы вы-
рожденная, т.е. число Л удовлетворяет характеристическому уравнению
(7.15). Наоборот, если Л - корень характеристического многочлена, то оп-
ределитель (7.15) матрицы однородной системы (7.14) равен нулю, т.е.
rg(A-XE) < п. В этом случае система имеет бесконечное множество реше-
ний (см. теорему 5.3), включая ненулевые решения. Поэтому найдется стол-
бец х о, удовлетворяющий условию (7.14). Значит, Л - собственное зна-
чение матрицы А.
СВОЙСТВА СОБСТВЕННЫХ ВЕКТОРОВ
Пусть А - квадратная матрица п -го порядка.
1, Собственные векторы, соответствующие различным собственным
значениям, линейно независимы.
283
В самом деле, пусть 5! и s2 - собственные векторы, соответствующие
собственным значениям X, и Х2, причем X, * Х2. Составим произвольную
линейную комбинацию этих векторов и приравняем ее нулевому столбцу:
а,5|+а252 =о. (7.16)
Надо показать, что это равенство возможно только в тривиальном случае,
когда cq = а2 = 0 . Действительно, умножая обе части на матрицу А и под-
ставляя As, = X* j* и As2 = ^2s2 > имеем
+ a2s2) = o <7 a,As,+a2As2 =o о сцХ^ + a2X2s2 =o .
Прибавляя к последнему равенству равенство (7.16), умноженное на (- Х2),
получаем
сцХ^-a1X2s1 =о о aJXj-А-2)$! =о .
Так как Sj * о и X] * Х2, делаем вывод, что сц = 0. Тогда из (7.16) следует,
что и а2 = 0 (поскольку s2 * о ). Таким образом, собственные векторы 5, и
s2 линейно независимы. Доказательство для любого конечного числа соб-
ственных векторов проводится по индукции.
2. Ненулевая линейная комбинация собственных векторов, соответ-
ствующих одному собственному значению, является собственным векто-
ром, соответствующим тому же собственному значению.
Действительно, если собственному значению X соответствуют собст-
венные векторы s1 ,...,sk, то из равенств As, = 7^,, i = следует, что
вектор j = +... + 0*5* также собственный, поскольку:
As = ^(a^! + ... + a*s*) = c^X^i +... + a*Xs* = X^S] + ... + a*s*) = Xs .
3. Пусть (A - X£)+ - присоединенная матрица для характеристиче-
ской матрицы (А-ХЕ). Если Хо - собственное значение матрицы А, то
любой ненулевой столбец матрицы (А - Хо£)+ является собственным век-
тором, соответствующим собственному значению Хо .
В самом деле, применяя формулу (7.7) имеем (Л-Х£)(Я-Х£)+=
= Д^(х)-£ . Подставляя корень Хо, получаем (Л-ХОЕ)(Л-ХО£)* = О. Ес-
ли s - ненулевой столбец матрицы (Я - Х0£У, то (Я-Х0£)-5=о о
As = Xos . Значит, s - собственный вектор матрицы А .
Замечания 7.5.
1. По основной теореме алгебры (см. разд. В.4) характеристическое
уравнение имеет п в общем случае комплексных корней (с учетом их крат-
ностей). Поэтому собственные значения и собственные векторы имеются у
любой квадратной матрицы. Причем собственные значения матрицы опре-
284
деляются однозначно (с учетом их кратности), а собственные векторы - не-
однозначно.
2. Чтобы из множества собственных векторов выделить максимальную
линейно независимую систему собственных векторов, нужно для всех раз-
личных собственных значений записать одну за другой системы
линейно независимых собственных векторов, в частности, одну за другой
фундаментальные системы решений однородных систем
(Л-А[Е)х=о, (Л-А.2£)х = о,..., [А-^кЕ)х = о.
Полученная система собственных векторов будет линейно независимой в
силу свойства 1 собственных векторов.
3. Совокупность всех собственных значений матрицы (с учетом их
кратностей) называют ее спектром.
4. Спектр матрицы называется простым, если собственные значения
матрицы попарно различные (все корни характеристического уравнения
простые).
5. Для простого корня Л = А.о характеристического уравнения соответ-
ствующий собственный вектор можно найти, раскладывая определитель
матрицы (Л-А.0Е) по одной из строк. Тогда ненулевой вектор, компоненты
которого равны алгебраическим дополнениям элементов одной из строк
матрицы (А - Aqe), является собственным вектором.
НАХОЖДЕНИЕ СОБСТВЕННЫХ ВЕКТОРОВ И СОБСТВЕННЫХ
ЗНАЧЕНИЙ МАТРИЦЫ
Для нахождения собственных векторов и собственных значений квад-
ратной матрицы А п -го порядка надо выполнить следующие действия.
1. Составить характеристический многочлен матрицы
АА (А.) = det(A - Л£).
2. Найти все различные корни А.,,...,^ характеристического уравне-
ния Д^(а.) = О (кратности П],п2,...,пк (+ п2 +... + пк-п) корней опреде-
лять не нужно).
3. Для корня л = найти фундаментальную систему (р, ,<р2 > --,9л-г
решений однородной системы уравнений
(Л L А]Е)х = о ,
где г = rg (Д-XjE). Для этого можно использовать либо алгоритм решения
однородной системы (см. разд. 5.5), либо один из способов нахождения
фундаментальной матрицы (см. п.З замечаний 5.3, п.1 замечаний 5.5).
4. Записать линейно независимые собственные векторы матрицы А,
отвечающие собственному значению А.]:
=C’1cpl, s2=C2(p2,..., sn_r=C„_r(p„_r, (7.17)
285
где С) ,C2,. -,C„_r - отличные от нуля произвольные постоянные. Сово-
купность всех собственных векторов, отвечающих собственному значению
At, образуют ненулевые столбцы вида s = + C2(p2 +-- + C„_r(p„_r. Здесь
и далее собственные векторы матрицы будем обозначать буквой s .
Повторить п.З, 4 для остальных собственных значений А2 А*.
Л1 -2Л fl -44!
риц: А = , В = , С =
(з 8 ) Ц 1 )
Пример 7.8. Найти собственные значения и собственные векторы мат-
1 1 р
111.
1 1 I
□ Матрица 4.1. Составляем характеристический многочлен матрицы
ДЛ(Л) =
-2
8-А
= (1-А)(8-А)+6 = А2-9А + 8 + 6 = А2-9А + 14.
2. Решаем характеристическое уравнение:
А2-9А + 14 = 0 => А| = 2 , А2 = 7 .
3*. Для корня А, = 2 составляем однородную систему уравнений
(A —AjZij-T^o:
'1-2 -2WxjW0A
3 8-2J x2J 40j
-1 -2WxA foA
3 6 J ^x2 J l^oj
Решаем эту систему методом Гаусса, приводя расширенную матрицу систе-
мы к упрощенному виду
-1 -2 СП р 2 ОА р 2 О
з 6 о)~1з б oj~lo О О
Ранг матрицы системы равен 1 (г = 1), число неизвестных п = 2, следова-
тельно, фундаментальная система решений состоит из п - г = 1 решения.
Выражаем базисную переменную Xj через свободную: х, = -2х2. Полагая
х2 = 1, получаем решение
<-2А
4*. Записываем собственные векторы, соответствующие собственному
значению А1 = 2: =Ct <р1, где Q - отличная от нуля произвольная по-
стоянная.
Заметим, что, согласно п.5 замечаний 7.5, в качестве собственного век-
тора можно выбрать вектор, составленный из алгебраических дополнений
286
Н
элементов второй строки матрицы I
-2"| Г 2 )
, т.е. . Умножив этот
6 J 1-1J
столбец на (-1), получим (р1.
З2. Для корня А2 = 7 составляем
(А -А2£)х = о :
р-7 -2
I 3 8-7
однородную систему уравнений
-6 -2
3 1
1-1°
1°
Решаем эту систему методом Гаусса, приводя расширенную матрицу систе-
мы к упрощенному виду
Л-6 -2 О'
3 1
-6
1
-2 О
1 з
-6 -2 О
1 (г = 1), число неизвестных
п = 2, следова-
Ранг матрицы системы равен
тельно, фундаментальная система решений состоит из п - г = 1 решения.
Выражаем базисную переменную Х[ через свободную: xt = —| х2. Полагая
х2 -1, получаем решение
з
42 . Записываем собственные векторы, соответствующие собственному
значению А2 = 7: s2 = С2 (р2, где С2 - отличная от нуля произвольная по-
стоянная.
Заметим, что, согласно п.5 замечаний 7.5, в качестве собственного век-
тора можно выбрать вектор, составленный из алгебраических дополнений
(-6 -2^ ( И
, т.е. . Поделив его на
3 1 J 1-3J
ф2 =
элементов первой строки матрицы
(- з), получим (р2 .
Матрица В . 1. Составляем характеристический многочлен матрицы
1-А — 4
1 1-А
дв(х)-
= (1-А)2+4 = А2-2А + 1 +4 = А2 -2А+ 5 .
2. Решаем характеристическое уравнение:
А2-2А + 5 = 0 => Aj =1 + 2/, А2 =1-2/.
З1. Для корня А] =1 + 2/ составляем однородную систему уравнений
0
о
О
О
о
1
о
О
з
О О
287
1 -(1 + 2z) -4 fX] pp fx1'l _fO
1 l-(14-2i)J\x2J~l^oj [ 1 -2iJ ^x2J~^0
Решаем эту систему методом Гаусса, приводя расширенную матрицу систе-
мы к упрощенному виду
-2/ -4 ОН 1 -2г О') р -21 О
1 -2/ о] l-2i -4 О) IO О О
Ранг матрицы системы равен 1 (г = 1), число неизвестных п = 2, следова-
тельно, фундаментальная система решений состоит из и - г = 1 решения.
Выражаем базисную переменную Xj через свободную: xl = 2ix2 Полагая
х2 = 1, получаем решение
2i
1
41. Записываем собственные векторы, соответствующие собственному
значению Xj = 1 + 2i: Sj = Q (pt, где Ct - отличная от нуля произвольная
постоянная.
Заметим, что, согласно п.5 замечаний 7.5, в качестве собственного век-
тора можно выбрать вектор, составленный из алгебраических дополнений
(-21 - 4 'j (- 2гЛ
элементов первой строки матрицы , т.е. . Умножив этот
1^1 - 2zJ \ 1 /
столбец на (-1), получим (pj.
З2. Для корня Л2 — 1 — 2i составляем однородную систему уравнений
(В-Л2Е)х = о:
Г1-(1-2г) -4 f рр
( 1 l-(l-2z)J\xJ "W
2z
1
-4
2z
Решаем эту систему методом Гаусса, приводя расширенную матрицу систе-
мы к упрощенному виду
'2i -4 (Г\ Г1 21 (Г| <1 21 О
1 2г oj~^2z -4 0j[0 О О
Ранг матрицы системы равен 1 (г = 1), число неизвестных п = 2, следова-
тельно, фундаментальная система решений состоит из и - г = 1 решения.
Выражаем базисную переменную Х[ через свободную: Xj = -2ix2. Полагая
х2 = 1, получаем решение
<-2Л
Фг= ,
288
4 2 . Записываем собственные векторы, соответствующие собственному
значению Х2 = l — 2z: s2 = Q Фг > где С2 ~ отличная от нуля произвольная
постоянная.
Заметим, что, согласно п.5 замечаний 7.5, в качестве собственного век-
тора можно выбрать вектор, составленный из алгебраических дополнений
f2z -zTl Г 2М
элементов первой строки матрицы , т.е. . Умножив его на
1 2/ J V
(-1), получим (р2 .
Матрица С. 1. Составляем характеристический многочлен матрицы
1-Х
дс(х)=| С-ХЕ) =
1
1-Х
1
1
1
1-Х
= (1-х)3 + 2 - з(1 -X) = -X3 + ЗХ2.
2. Решаем характеристическое уравнение:
-Х3+ЗХ2=0 => Х,=3,Х2=0.
Х3 = 3 составляем однородную систему уравнений
З1. Для корня
(C-XjE)x = o
р-з
1
. 1
1
1-3
1
1
1-3
х2
или
- 2х] + х2 + х3 = 0,
X] - 2х2 + х3 = 0,
Х[ + х2 — 2х3 = 0.
о
о
элементы выделены
Решаем эту систему методом Гаусса, приводя расширенную матрицу систе-
мы к упрощенному виду (ведущие
вом):
полужирным курси-
1 1
0 3
0 -3
-2
1
1
-2
-3
3
1
-2
1
-2
-1
О
1
-2
1
1
1
-2
-2
1
1
О'
о
0.
-1
-1
о
О'
о
О
1
1
— 2
О
О
О
о
о
о
о
о
о
О
О
1
1
О
1
О
о
о
1
о
(г - 2), число неизвестных
и = 3 , следова-
Ранг матрицы системы равен 2
тельно, фундаментальная система решений состоит из и - г = 1 решения.
Выражаем базисные переменные X], х2 через свободную х3:
' 1-^2 *3 ’
и, полагая х3 = 1, получаем решение
19 - 4549
289
9 =
1
41. Все собственные векторы, соответствующие собственному значе-
нию Xj = 3, вычисляются по формуле 5 = С( - <р, где Q - отличная от нуля
произвольная постоянная.
Заметим, что, согласно п.5 замечаний 7.5, в качестве собственного век-
тора можно выбрать вектор, составленный из алгебраических дополнений
'-2 1 1 ' Гз'
элементов первой строки матрицы 1 -2 1 , т.е. 3 , так как
. 1 1 "2, Л
Разделив его на 3, получим (р .
З2. Для собственного значения Л2 = О
имеем однородную систему
Сх - о. Решаем ее методом Гаусса:
'1 1
(С | о)= 1 1
I1 1
1 оН1
10-0
1 Oj b
1 1 o'
ООО
ООО,
Ранг матрицы системы равен единице (г -1), следовательно, фундамен-
тальная система решений состоит из двух решений (и - г = 2). Базисную пе-
ременную X] выражаем через свободные: х( = -х2-х3. Задавая стандарт-
ные наборы свободных переменных х2 -1, х3 = 0 и х2 = 0, х3 = 1, получаем
два решения
42. Записываем множество собственных векторов, соответствующих
собственному значению Х2 = 0: 5 = + С2ф2, где С,, С2 - произволь-
ные постоянные, не равные нулю одновременно. В частности, при С] = 0,
С2 = -1 получаем = (1 0 -1)г ; при С{ = -1, С2 =0 : s2 =(1 -1 0)г.
Присоединяя к этим собственным векторам собственный вектор
$3 = (1 1 1)Г , соответствующий собственному значению \ = 3 (см. п. 41
290
при С, = 1), находим три линейно независимых собственных вектора мат-
рицы С :
Заметим, что для корня Х2 = 0 собственный вектор нельзя найти, при-
меняя п.5 замечаний 7.5, так как алгебраическое дополнение каждого эле-
мента матрицы А равно нулю.
7.2.2. Подобие числовых матриц
Квадратные матрицы А и В п -го порядка называются подобными,
если существует такая невырожденная матрица S (det 5 Ф 0), что
В = 5-1А5.
Преобразование матрицы А по формуле 5-1А5 называется преобразова-
нием подобия, а матрица S - преобразующей.
СВОЙСТВА ПОДОБНЫХ МАТРИЦ
1. Каждая квадратная матрица подобна самой себе: А = Е [АЕ .
2. Если матрица В подобна матрице А, то и А подобна В :
B = S~lAS «=> А=Т~1ВТ при T = S~l.
3. Если матрица А подобна матрице В, а В подобна С, то А
подобна С :
A = S~lBS
В = Т~ХСГ
=> А = Р~хВР,где P = TS.
4. Подобие является частным случаем эквивалентных преобразований.
5. В случае ортогональности преобразующей матрицы (см. разд. 4.2)
подобные матрицы являются конгруэнтными (см. разд. 6.5.2).
Поясним свойства 4, 5. Напомним, что эквивалентные матрицы (см.
разд. 1.6.2) связаны соотношением В = SAT, где S и Т - невырожденные
(элементарные) матрицы. Если Т = S”1, то получаем преобразование подо-
бия В = SAS~X <=> A = S-IBS. Если же матрица 5 ортогональная
(5'1 — ST), то подобные матрицы, связанные равенством B-S~XAS , ока-
зываются конгруэнтными, так как В = STAS.
19*
291
Подобные матрицы возникают во многих алгебраических задачах при
замене переменных. Например, при решении системы уравнений Ах = Ь
с невырожденной квадратной матрицей А можно сделать линейную замену
неизвестных: ввести столбец у - новых неизвестных (х = S у) и новый
столбец свободных членов с (b = Sc ), для которых система уравнений бу-
дет выглядеть так
ASy=Sc или S~lASy=c.
Матрица S~l AS = Л полученной системы подобна матрице исходной сис-
темы. Например, если в результате преобразования подобия полученная
матрица Л имеет диагональный вид: Л = Ла^(Л1,...,Лл), то решение систе-
мы Лу = с находится просто:
С;
У‘=Т
i = l,...,и, после чего нетрудно вы-
числить и решение исходной системы х = S у.
ПРИВЕДЕНИЕ МАТРИЦЫ К ДИАГОНАЛЬНОМУ ВИДУ
Рассмотрим задачу приведения квадратной матрицы А к диагональ-
ному виду Л = diag{kx, Х2,...,Х„) при помощи преобразования подобия.
Теорема 7.5 (о приведении матрицы к диагональному виду). Для
того чтобы квадратная матрица А п -го порядка приводилась к диаго-
нальному виду A = S 'AS, необходимо и достаточно, чтобы она имела п
линейно независимых собственных векторов.
Действительно, запишем равенство Л = S lAS в виде SA = AS , т.е.
= AS
$пп у
или (jj s„)a = A(ji ••• s„), где Sj -столбцы матрицы S . От-
сюда получаем систему уравнений для столбцов s, матрицы S :
As,=X,s,-, (7-18)
Поэтому, если матрицу А можно привести преобразованием подобия к диа-
гональному виду Л = S-1AS , то для столбцов матрицы S выполняются ра-
венства (7.18), т.е. столбцы st являются собственными векторами матрицы
А , причем они линейно независимы, так как матрица S невырожденная.
Необходимость доказана. Пусть, наоборот, матрица А имеет п линейно не-
зависимых собственных векторов j,, удовлетворяющих (7.18). Тогда, соста-
вив из них матрицу S , получим для нее равенство SA = AS , равносильное
(7.18). Учитывая, что матрица S невырожденная (из-за линейной независи-
292
мости ее столбцов), получаем A = S *А5 , т.е. матрица А подобна диаго-
нальной. Достаточность доказана.
Следствие 1. Если матрица имеет простой спектр, то она приводит-
ся к диагональному виду.
Действительно, в этом случае по свойству 1 собственных векторов все
собственные векторы будут линейно независимы.
Следствие 2. Если матрица А приводится к диагональному виду
A = S~XAS = Ла^(А1,А2,...,Ал), то числа А1,А2,..., Ал (среди которых мо-
гут быть равные) являются собственным значениями матрицы А, а
столбцы jj,..., sn преобразующей матрицы S = (s\ ••• sn) являются со-
ответствующими собственными векторами матрицы А.
Следствие 3. Если jj,..., sn - линейно независимые собственные век-
торы матрицы А, соответствующие ее собственным значениям
А1#А2,..., Ал {среди которых могут быть равные), то матрица А приво-
дится к диагональному виду Л = S~{AS = diag(kt, А2,...,АЛ) при помощи пре-
образующей матрицы ••• sn), составленной из собственных век-
торов.
Чтобы привести квадратную матрицу А (л -го порядка) к диагональ-
ному виду при помощи преобразования подобия Л = S~lAS и найти преоб-
разующую матрицу S , нужно выполнить следующие действия.
1. Найти л линейно независимых собственных векторов s1,...,sn мат-
рицы А (при этом использовать алгоритм в разд. 7.2.1 с учетом п.2 замеча-
ний 7.5).
2. Из собственных векторов j, ,...,sn составить преобразующую мат-
рицу 5= ••• зл) (см. следствие 3 теоремы 7.5).
3. По собственным значениям матрицы А составить матрицу
Л = diag(ki, А2,...,Ал) - диагональный вид матрицы А. Иначе матрицу Л
можно найти, выполняя преобразование подобия Л = S~iAS.
Пример 7.9. Привести данные матрицы к диагональному виду
(1 -Д') f 4 Д')
В= , С =
11 1J 1-1 О
fl -2
А =
I3 8
и найти соответствующие преобразующие матрицы.
□ Матрица А . 1. Собственные векторы и собственные значения этой
матрицы были найдены в примере 7.8. Для собственных значений Aj = 2 и
А2 = 7 возьмем соответствующие собственные векторы (полагая -1,
С2=3):
293
Эти столбцы линейно независимы (по свойству 1 собственных векторов).
2. Составляем из собственных векторов преобразующую матрицу
3. Находим диагональный вид Л матрицы А , выполняя преобразова-
ние подобия:
Л = S-1AS =
'-2 -Г] Y1
< 1 з Д 3
-2V-2 -Л
3j
На главной диагонали (согласно следствию 2 теоремы 7.5) стоят собствен-
ные значения матрицы А.
Преобразующую матрицу можно было составить по-другому:
, , \ -2А
S =(s2 . Тогда в результате преобразования подобия полу-
чили бы диагональную матрицу Л' = (S') 1 AS' = diagij, 2).
Матрица В. 1. Собственные векторы и собственные значения этой
матрицы были найдены в примере 7.8. Для собственных значений 1, = 1 + 2i
и Х2 = 1 - 2i возьмем соответствующие собственные векторы (полагая
q =1, С2=1):
— 2i
1
*1 =
Г2Л
Gp"
Эти столбцы линейно независимы, поэтому матрицу В можно привести к
диагональному виду.
2. Составляем из собственных векторов преобразующую матрицу
/ ч Г2/
1
-2i
1
Л
Выполняем преобразование подобия
if1
4-i
2i
2i
-4V2Z
1 A1
-2/") 71
1 J I1
-4Y2'
1 А1
-2i
1
-2i
1
1 Г 1
4t[-l
2/V-4+2/
2/JI 1 + 2/
-4-2Л
1-2/ J
. -1 Г 2*
Л = 5 *В5 =
1
1
294
1 Г—8 + 4i 0 (1+2/ О
4x1 О 8 + 4zJ I О 1-2г
На главной диагонали матрицы Л стоят (согласно следствию 2 теоремы 7.5)
собственные значения матрицы В .
Матрица С . Найдем собственные векторы матрицы С , используя ал-
горитм, изложенный в разд.7.2.1.
1. Составляем характеристический многочлен
ДС(Л.)-
4-Л
-1
= Л.2-4А + 4 = (А-2)2.
2. Решаем характеристическое уравнение (Л. - 2)2 = 0 => Л = 2.
3. Для собственного значения Л. = 2 составляем однородную систему
уравнений (С-2Е)х = о, которую решаем методом Гаусса. Приводим
расширенную матрицу системы к упрощенному виду
(С-2-Е | о) =
"2 4
-1 -2
оЛ < 1 2 О W1 2
-2 oj\o О
О
О
Ранг матрицы равен единице (г = 1), количество неизвестных п = 2. Поэто-
му фундаментальная система решений содержит п - г -1 решение. Выража-
ем базисную переменную х1 через свободную: Xj = -2х2 Полагая х2 = 1,
находим решение <pj =
4. Все собственные векторы, соответствующие собственному значению
Л = 2, имеют вид
j — Qcpi — Q
, где - произвольная постоянная,
отличная от нуля.
Как видим, матрица С второго порядка имеет только один линейно
независимый собственный вектор, поэтому ее нельзя привести к диагональ-
ному виду при помощи преобразования подобия.
fl 1
Пример 7.10. Привести матрицу 4=111
Ц I 1J
к диагональному виду и
найти соответствующую преобразующую матрицу. Найти выражение для
степени Ат с натуральным показателем те N.
□ 1. Собственные векторы и собственные значения этой матрицы были
найдены в примере 7.8. Выберем три линейно независимых собственных
вектора (см. пример 7.8):
295
5, = О
-1
-1
о
s3 =
*2 =
1
1
рицу S , при помощи которой матрица А
Векторы j] и 52 соответствуют собственному значению X = 0, вектор 53 -
собственному значению X = 3.
2, 3. Составляем из этих собственных векторов преобразующую мат-
приводится к диагональному виду
'о о о
A = S~}AS = ООО
0 0 3
о
-1
1
-1
о
1
1
5 =
Найдем т -ю степень матрицы А , учитывая, что А = SAS 1:
Ат = (w1= SAS~lSAS~'-...SAS~\ = 5Лт5ч.
т
Нетрудно получить степень Ат диагональной матрицы, так как произведе-
ние диагональных матриц является диагональной матрицей:
о
о
о
о
о
о
Ат
о
о
зт
Следовательно,
О
О
О
о
о
о
Ат = SAmS
ч
о
-1
1
-1
о
1Уо
1
1
о У 1
о
зт
о
-1
1
-1
о
^т
зт
-1
-1
-1
2
-1
2'
-1
-1.
зт
зт
зт
зт
зт
зт
зт
зт
= 3'
о
о
о
о
о
1
1
1
1
3
1
1
1
1
1
1
1
СВЯЗЬ ПОДОБИЯ ЧИСЛОВЫХ МАТРИЦ с
ХАРАКТЕРИСТИЧЕСКИХ
ЭКВИВАЛЕНТНОСТЬЮ
МАТРИЦ
их
Получим необходимое и достаточное условие подобия числовых квад-
ратных матриц А и В и -го порядка. Напомним, что с этими числовыми
матрицами связаны Х-матрицы (а-Хе) и (B-Хе), которые называются
характеристическими. Две Х-матрицы называются эквивалентными, если
одна из них получена из другой при помощи элементарных преобразований
(см. разд.7.1.3). Согласно п.6 замечаний 7.4, если Х-матрицы А(Х) и в(х)
296
эквивалентны, то существуют такие обратимые Л-матрицы 5(Л) и Т(к),
что в(Л)=5(Х)а(Х)т(Л).
Теорема 7.6 (критерий подобия числовых матриц). Для того чтобы
числовые матрицы А и В были подобными необходимо и достаточно,
чтобы их характеристические Л -матрицы (A-Хе) и (B-ХЕ) были экви-
валентны.
В самом деле, если числовые матрицы подобны, т.е. В = S-' AS , то
В-ХЕ = SHA5-XS~lES = S~1(A-XE)S.
Значит, характеристические матрицы эквивалентны, так как числовую мат-
рицу S можно считать частным случаем X-матрицы, а невырожденная чи-
словая матрица является элементарной (следствие 3 теоремы 3.3). Необхо-
димость доказана.
Для доказательства достаточности запишем условие эквивалентности
Л-матриц (A-Ле) и (B-ХЕ):
b-xe=s(x)(a-xe)t(x).
Перепишем равенство в виде
5Ч(Х)(В-ЛЕ) = (А-Х£)Т(Х). (7.19)
Разделим Л-матрицу S~l(X) слева на (А —ХЕ), а Л-матрицу Т(Х) справа на
(В-ХЕ):
S~l(X)=(A-XE)Sl(x)+S0- 7'(Х) = Т1(Х)(В-АЕ)+7'о. (7.20)
Здесь остатки и - обратимые числовые матрицы, так как 3~1(х) и
Т(Х) - обратимые Л-матрицы (см. п.З замечаний 7.3). Подставим выраже-
ния (7.20) в (7.19):
[(А - ХЕ) S^X)+ So ] (В - ХЕ) = (А - ХЕ) [TJX) (в - ХЕ)+То ].
Преобразуем равенство
(А - ХЕ) [S, (А) - Т\ (X)] (В - ХЕ) = (А - ХЕ) То - So (В - ХЕ).
Отсюда следует, что Sl(X) = Tl(X), в противном случае равенство ложное,
так как степень многочлена в левой части не менее второй, а в правой части
- не более первой. При Sl(X) = Tl(X) получаем
S0(B-XE) = (a-XE)T0. (7.21)
Сравнивая это равенство с (7.19), делаем вывод, что Л-матрицы 5-l(x) и
Т(Х) в (7.19) можно заменить числовыми матрицами SQ и То. Приравнивая
в (7.21) коэффициенты при одинаковых степенях X, находим
SQ=T0 и AT0=S0B. (7.22)
Следовательно, В = Sq'ASq , т.е. матрицы А и В подобны.
297
Следствие. Если матрицы А и В подобны, т.е. В = 50*AS0, то в ка-
честве преобразующей матрицы So можно взять матрицу
S0=S^B)=Tnp(B) ~ левое или правое значения соответствующих
Л, -матриц из равенства
B-XE = S(X)(A-kE)T(k). (7.23)
В самом деле, из доказательства теоремы следует, что Л-матрицы в
(7.23) можно заменить числовыми матрицами:
В-Л.Е = Sq1(a-A.E)T0 ,
где преобразующая матрица То согласно (7.20) равна правому остатку при
делении Т(к) на (B-ХЕ), который по теореме Безу равен правому значе-
нию Тпр(в). Учитывая (7.22), получаем SQ =TQ = Т (в). Равенство
So=[$U*)]_1 доказывается аналогично на основании теоремы Безу [10].
7.2.3. Характеристический многочлен матрицы
Напомним, что характеристическим многочленом квадратной матрицы
А (л-го порядка) называется многочлен Ax(X) = det(A-XE). Степень ха-
рактеристического многочлена совпадает с порядком матрицы А . Рассмот-
рим другие свойства характеристического многочлена.
1. Характеристический многочлен квадратной матрицы А п -го по-
рядка может быть представлен в виде
ДлМ=(-№~ V‘(^2)n2 - --(Х-А.*)"‘, (7.24)
где Хн Х2X* - корни характеристического многочлена (собственные
значения матрицы А) кратности п{, п2,..., пк соответственно, причем
пг >1,п2 >1,...,л4 >1 и пг + л2 +... + пк =п .
Действительно, указанное разложение (7.24) имеет любой многочлен
степени л (см. следствие 3 основной теоремы алгебры в разд. В.4). Старший
коэффициент ап = (-1)" характеристического многочлена вычисляется, раз-
лагая определитель det(A-XE).
2. Характеристический многочлен квадратной матрицы А п -го по-
рядка может быть представлен в виде произведения инвариантных мно-
жителей (см. разд.7.1.4) характеристической матрицы (А - ХЕ):
Да W = (" 1)" М*2 М' М • (7-25)
В самом деле, характеристическая матрица имеет нормальный диаго-
нальный вид (7.9): diag^e^k), е,(Х),...,еи(Х)), так как rg(A-XE) = n.
298
Наибольший общий делитель d„(A) (старший коэффициент которого равен
единице) единственного минора п -го порядка матрицы (А-АЕ) отличается
от определителя det(A-AE) только множителем (~1)п,т.е. характеристиче-
ский многочлен Дл(А) = (-1)"dn(k). Подставляя </я(А) = е1(А)е2(А)-...-ея(А)
(см. следствие 2 теоремы 7.3), получаем (7.25).
3. Характеристические многочлены подобных матриц совпадают.
В самом деле, пусть матрицы А и В подобны, т.е. существует такая
матрица 5 , что В = S~lAS . Преобразуем характеристический многочлен
матрицы В по теореме 2.2 (об определителе произведения матриц) с учетом
свойства 4 обратной матрицы (см. разд.4.2):
AB(A) = det(B -АЕ) = det(s-1A5 -S~lkEs)= det [ S~1(A-XE)S ] =
= det(s~1}-det(A-XE)-detS =—-—det(A-AfJ-detS = Да(А),
det S
что и требовалось показать.
4. Характеристический многочлен матрицы А п -го порядка имеет
вид
дл(1)=(-л)л+(-л)л-1-1га+...+(-аг<
1S/| <i2 <...«* in
+ (- А) • £ M\' + det A. (7.26)
is/, «2
Минор k -го порядка , составленный из элементов матрицы, стоя-
щих на пересечении одноименных строк и столбцов, называется главным
минором. В формуле (7.26) коэффициент при (-А)п~* равен сумме главных
миноров к -го порядка, в частности, след матрицы tr А = ап + а22 + — + апП -
это сумма главных миноров 1-го порядка, определитель матрицы - это глав-
ный минор п -го порядка.
Поясним формулу (7.26). Пусть at - i -й столбец матрицы А , е, - i -й
столбец единичной матрицы Еп. В этих обозначениях запишем характери-
стический многочлен матрицы
ДА(Х) = | А-АЕ | = | О]-Ав] п2-Ае2 ап-кел\.
Представим этот определитель в виде суммы определителей, используя его
линейность по каждому столбцу (см. свойство 8 в разд. 2.3.1). Получим
Дл(А) = |а1-Ае1 а2-Ае2 ••• ая-А^„| = |Л1 а2 ••• <г„| +
+ (-А)• {|е, а2 - an|+|flt g2 Д„|+-+|Д1 Д2 - |}+
в каждом определителе один столбец единичной матрицы
299
+ (-Л)2 • {|е, е2 а3 | + -+ | Д; ••• е„х е„ |}+- +
в каждом определителе два столбца единичной матрицы
+ (-Х)Л'1-{|е1 е2 е3 aJ + .-. + l^ ••• еп_х ej}+...+
у у '
в каждом определителе \п-\)столбцов единичной матрицы
+ (“М"‘|е1 е2 «3 еп|-
Разлагая определители, стоящие в фигурных скобках, по столбцам единич-
ной матрицы, получаем главные миноры матрицы А , например:
| q е2 а3 ап | = М34.'.'.п > |е1 а2 е3 еп\ = М2=а22-
Таким образом, коэффициент при (-А)"-* равен сумме главных миноров
k -го порядка матрицы А .
5. Подобные матрицы имеют: равные определители, равные следы,
равные суммы главных миноров одного и того же порядка, совпадающие
спектры.
В самом деле, подобные матрицы имеют равные характеристические
многочлены (по свойству 3). У равных многочленов - одинаковые корни
(т.е. спектры подобных матриц совпадают), а также равные соответствую-
щие коэффициенты в (7.26), которые по свойству 4 выражаются через глав-
ные миноры матриц.
6. Определитель матрицы равен произведению ее собственных значе-
ний (с учетом их кратности).
Действительно, характеристический многочлен можно разложить на
множители (см. следствие 1 основной теоремы алгебры в разд. В.4 и (7.24)):
а,(а)=(-1)л(а-а1).(л-а2).....(х-ал),
где А1(А2,...,АЯ - корни многочлена (быть может, совпадающие). Отсюда
Дл(о)=А1А2 •...-Ап. С другой стороны, по определению получаем
A4(o) = det(A-AE)|x=o=det А . Следовательно, det А = —-А„ .
7.2.4. Теорема Гамильтона-Кэли. Минимальный многочлен матрицы
Многочлен р(А) переменной А называется аннулирующим для квад-
ратной матрицы А , если при подстановке в многочлен матрицы А вместо
переменной X получаем нулевую матрицу, т.е. р(д) = О.
Напомним, что для любой квадратной матрицы А многочлен
Ax(A) = det(A -АЕ) называется характеристическим.
300
Теорема 7.7 (теорема Гамильтоиа-Кэли). Характеристический мно-
гочлен матрицы является аннулирующим для нее, т.е. Дл(а) = О .
В самом деле, обозначим через (А-ХЕ)+ матрицу, присоединенную к
характеристической матрице (A-Хе). Тогда из (7.7) следует
(а-Хе)-(А-Хе)+=ДЛ(Х)Е и (а-Хе)+-(А-Хе) = Дл(Х)е. (7.27)
Правые части этих равенств можно рассматривать как многочлены с мат-
ричными коэффициентами (каждый коэффициент характеристического мно-
гочлена умножается на единичную матрицу). Из (7.27) следует, что
X-матрица ДЛ(Х)Е делится на (а-Хе) слева и справа без остатка, т.е. ос-
таток равен нулевой матрице. По обобщенной теореме Безу (теорема 7.2)
остаток равен левому и правому значениям многочлена Дл(х)е при подста-
новке матрицы А вместо X. Отсюда получаем Дл(а)Е = О, т.е. Дл(а)=(Э,
что и требовалось доказать.
Пример 7.11. Показать, что характеристический многочлен матрицы
fl 1 С
А= 1 1 1
является для нее аннулирующим.
v 1 и
□ Находим характеристический многочлен матрицы (см. пример 7.8)
Дл(Х) = 6с1(а-Хе) = 1
1 1
1-Х 1
1 1-Х
= (1-Х)3 + 2-3(1-Х) = ЗХ2-X3.
Подставляя вместо переменной X матрицу А , получаем
''l 1
дл(а)=за2-а3 =3- 1 1
Ь 1
Г 2 1 г 3 "3 3 з' X 40 40
1 - 1 1 1 = 3- 3 3 3 - 9 9 9 = 0,
1) J 1 ,3 3 3, ? 9 9,
что и требовалось показать.
Теорема Гамильтона-Кэли говорит о том, что для квадратной матрицы
А п -го порядка всегда найдется аннулирующий многочлен п -й степени
(характеристический многочлен имеет п -ю степень). Возникает вопрос о
существовании аннулирующего многочлена меньшей степени.
Минимальным многочленом матрицы А называется ее аннулирую-
щий многочлен наименьшей степени (со старшим коэффициентом, равным
единице). Минимальный многочлен будем обозначать цл(Х).
301
СВОЙСТВА МИНИМАЛЬНОГО МНОГОЧЛЕНА
1. Любой аннулирующий многочлен матрицы делится на минимальный
многочлен (без остатка). В частности, характеристический многочлен де-
лится на минимальный многочлен.
Действительно, предположим противное, пусть аннулирующий много-
член р(Х) делится на минимальный многочлен цл(Х) с остатком:
р(Х)=<?(Х).цл(Х)+г(Х),
причем степень остатка г(Х) меньше степени делителя цл(Х). Тогда, под-
ставляя вместо X матрицу А, получаем г(а)=О, так как р(А)=О и
цл(а) = О. Следовательно, г(Х) - аннулирующий многочлен, степень кото-
рого меньше, чем степень минимального многочлена, что противоречит оп-
ределению минимального многочлена. Таким образом, предположение ока-
залось ложным, т.е. любой аннулирующий многочлен делится на минималь-
ный (без остатка). Поскольку по теореме Гамильтона-Кэли характеристиче-
ский многочлен является аннулирующим, то он также делится на мини-
мальный многочлен.
2. Для каждой квадратной матрицы А минимальный многочлен един-
ственный.
В самом деле, если бы существовали два минимальных многочлена, то
они имели бы одну и ту же степень и делились бы друг на друга, т.е. отли-
чались бы только постоянным множителем. Однако, старшие коэффициенты
этих многочленов равны единице, поэтому такие многочлены совпадают.
3. Все собственные значения матрицы являются корнями минимально-
го многочлена.
Действительно, из равенства р.л(л) = <9 следует, что X-матрица
Мл(Х)-Е делится (например, слева) на характеристическую матрицу
(А-ХЕ),т.е. рл(Х)-Е = (а-ХЕ)-3(Х), где 5(X) - некоторая X-матрица (ле-
вое частное). Найдем определитель левой и правой частей последнего ра-
венства с учетом теоремы 2.2 и п.З замечаний 2.2:
[Мл(Х)]п = AA(X)-det5(X). (7.28)
Подставляя в равенство (7.28) любой корень Х(, i = l,...,n характеристиче-
ского многочлена, получаем [цл (Х;)]п =0, т.е. ЛЛ(Х() = О, что и требова-
лось показать.
4. Если характеристический многочлен имеет вид (7.24), то мини-
мальный многочлен этой матрицы можно представить в форме
- (7-29)
где l< mt 1 < те2 -п2 ит.д., причем пц + т2 + + mk =т<п.
Это утверждение следует из свойства 3.
302
5. Минимальный многочлен матрицы А находится по формуле
dn-&) '
(7.30)
где dn_l(k') - наибольший общий делитель миноров (н-1)-го порядка ха-
рактеристической матрицы (А-ХЕ).
Действительно, по свойству 1 характеристический многочлен ДЛ(Х)
делится на минимальный многочлен, т.е. Да^)^-!)"где р(Х)
- некоторый многочлен со старшим коэффициентом, равным единице. Ум-
ножив обе части равенства рл(х)-Е = (а-ХЕ\ 5(Х) (см. свойство 3) на
(-1)"р(Х), получим в левой части характеристический многочлен, умно-
женный на единичную матрицу:
ДЛ(Х)- Е = (-1)"(А-ХЕ)- р(Х)$(Х).
Сравним это равенство с (7.27):
Дл(Х)-Е = (А-Хе)-(а-ХЕ)+. (7.31)
При делении X-матрицы ДЛ(Х)-Е слева на характеристическую матрицу
(А - ХЕ) частные (левые) должны совпадать в силу единственности деления.
Поэтому
(-1)" р(Х)-5(Х) = (А-ХЕ)+,
т.е. многочлен р(Х) - делитель всех элементов присоединенной матрицы.
Заметим, что степень многочлена р(Х) должна быть максимальной, так как
минимальный многочлен рл(Х) имеет наименьшую возможную степень, а
сумма степеней этих двух многочленов в силу равенства
Дд(Х) = (-1)"р(Х)-цл(Х) фиксирована и равна п . Поэтому многочлен р(Х)
— это наибольший общий делитель элементов присоединенной матрицы
(А-ХЕ)+. Так как элементы присоединенной матрицы пропорциональны
минорам (п -1) -го порядка характеристической матрицы, то р(Х) = dn_} (X).
Таким образом, ДЛ(Х)= (-1)п4/л_1(Х) рЛ(Х), откуда следует формула
(7.30).
6. Минимальный многочлен матрицы А совпадает с последним инва-
риантным множителем еп(Х) характеристической матрицы (А-Хе).
В самом деле, наибольший общий делитель <7„(Х) единственного ми-
нора л-го порядка характеристической матрицы (а-ХЕ) отличается от оп-
ределителя этой матрицы множителем (-1)", т.е. ДЛ(Х) = (-1)Л*/„(Х). Под-
ставляя это выражение в (7.30), получаем
303
ц (х)=L1L-(0—=AM =
V ’ dn-M л ’
СПОСОБЫ НАХОЖДЕНИЯ МИНИМАЛЬНОГО МНОГОЧЛЕНА МАТРИЦЫ
Пусть А - квадратная матрица п -го порядка. Требуется найти ее ми-
нимальный многочлен.
Первый способ.
1. Составить характеристическую матрицу (Я-ХЕ).
2. Привести ее к нормальному диагональному виду
(А-ХЕ)- diag{ex{k\ е2(х),..., е,(х)).
Последний инвариантный множитель е„(х) является минимальным много-
членом матрицы А (по свойству 6).
Второй способ.
1. Составить характеристическую матрицу (А - ХЕ).
2. Найти характеристический многочлен (х) = det(/l - ХЕ).
3. Найти наибольший общий делитель ^„^(х) миноров (и-1)-го по-
рядка X-матрицы (/(-ХЕ).
4. По формуле (7.30) получить минимальный многочлен.
р
Пример 7.12. Найти минимальный многочлен матрицы А = 1
1 f
1 1
1 V
Используя минимальный многочлен, найти степень Ат с натуральным по-
казателем те N.
□ Первый способ. 1. Составляем характеристическую матрицу
'1-Х 1 1 '
Л-ХЕ = 1 1-Х 1 1 1
(7.32)
2. Приводим эту X -матрицу к нормальному диагональному виду. По-
меняем местами первую и третью строки. Выберем в качестве ведущего
элемента единицу, оказавшуюся в левом верхнем углу матрицы. При помо-
щи ведущего элемента делаем равными нулю остальные элементы первой
строки и первого столбца:
'1-Х 1 1 > ' 1 1 1-Х> '1 0 0 '
Л-ХЕ = 1 1-Х 1 — 1 1-Х 1 0 -X X
. 1 1 ;-х 1.1, .0 X 2Х-Х2,
304
Берем в качестве ведущего элемент (-Х) и делаем равными нулю все ос-
тальные элементы второй строки и второго столбца. Затем умножаем вто-
рую и третью строки на (-1), чтобы старшие коэффициенты диагональных
элементов оказались равными единице. Получим нормальный диагональный
вид:
° 'j р
X ~ О
2х-х2; l^o
Г1 О
А-кЕ~ О -X
к0 X
о
-X
о
° ") р
о - о
3X-X2J 1^0
о о '
X о
о х2-зх?
Минимальный многочлен матрицы р.А (х) = е3 (х) = X2 - ЗХ.
Второй способ. 1. Составляем характеристическую матрицу (7.32).
2. Находим характеристический многочлен Ал(х) = ЗХ2-Х3 (см. при-
мер 7.11).
3. Находим миноры второго порядка характеристической матрицы
(Л-Х£). Ограничимся минорами, расположенными в первых двух строках:
м,12
1-Х 1
1 1-Х
= Х2-2Х, Л/’2
1-Х 1
1 1
= -Х, Л/’2 =
1 1
1-Х 1
= Х.
Выражения для остальных миноров совпадают с найденными. Наибольший
общий делитель многочленов Х2-2Х, (-Х), X равен Х,т.е. =
(-1Р(зх.2 -X3)
4. По формуле (7.30) получаем: цА (х) = ‘ = X2 - ЗХ.
Для проверки вычислим
'1 1 1Y р
рА(А) = А2-ЗА= 111 -3-1
V 1 J V
1 Р f3
11 = 3
1 и ь
Действительно, минимальный многочлен цл(х)
3>1 Р
3 -3- 1
Ь
1 f
1 1 =0.
1 I
является аннулирующим,
т.е. цл(/1)= О. Заметим, что для матрицы А минимальный и характеристи-
3
3
3
ческий многочлены отличаются только множителем (-Х).
Найдем теперь степень Ат матрицы А . Для этого рассмотрим много-
член X"1. Разделим его на минимальный многочлен ц^(х). Остаток от деле-
ния (многочлен степени не выше первой) представим в виде аХ + Р. Полу-
чим
Xм =Х^)(^2 -Зх)+аХ +р,
где р(х) - частное, а (аХ + р) - остаток. Найдем коэффициенты аир,
подставляя в равенство корни минимального многочлена:
при X = 0 имеем: О'" = р(х)- 0 + а • 0 + Р ;
20 - 4549
305
при X = 3 имеем: З"1 - р(Х)-0 + се-3 + р.
Следовательно, а - З"1-1,0 = 0. Поэтому Xм = р(Х) (х2 - ЗХ)+ 3m-1X. Теперь
подставим вместо переменной Л матрицу А :
Ат = р(д) (а2 - 3 • а)+ Зт-1 • А = р(а)-О + Зт-1 • А = З"1-1
'1
1
Г
1
1
1
1
Результат совпадает с полученным в примере 7.10.
7.3. ЖОРДАНОВА ФОРМА МАТРИЦЫ
Рассматривается задача упрощения квадратной матрицы при помощи
преобразования подобия. Наиболее простой вид квадратной матрицы - диа-
гональный. Для диагональных матриц легко решаются многие типовые за-
дачи линейной алгебры, например, обращение матриц, решение системы
уравнений, нахождение многочлена от матрицы и т.п. Однако, как показано
в разд.7.2.2, не всякая квадратная матрица подобна диагональной. Поэтому
возникает необходимость приведения матрицы к такому виду, пусть даже не
диагональному, чтобы при решении типовых задач линейной алгебры не
возникало значительных трудностей.
7.3.1. Элементарные делители матрицы
Пусть А - числовая квадратная матрица п -го порядка. Характеристи-
ческая матрица (А-ХЕ) приводится (элементарными преобразованиями) к
нормальному диагональному виду Аа^(е1(Х),...,еп(Х)), где е,(Х) - инвари-
антные множители матрицы (А-ХЕ) (см. разд. 7.1.3, 7.1.4). Характеристи-
ческий многочлен согласно свойству 2 можно представить в виде (7.25):
AaW=(-1)" ei(X)e2(X)-...-e„(X).
Разложим каждый из многочленов е, (X) на линейные множители
е1(х)=(х-х,Г (х-х2^-....(х-х,Г‘,
e2(x) = (X-Xj--(X-X2^-...-(X-Xt)i’‘,
..... (7.33)
e„-1(M = (^-^)Z’-(X-X2^-...-(X-Xj‘.
еп(Х)=(Х-Х1Г--(Х-Х2)^....-(Х-Х4Г“.
Здесь Х[ ,Х2 .....Х^ - различные собственные значения матрицы А ; показа-
тели степеней, удовлетворяют неравенствам 0 < а, < />, <... < Z, S mi
306
(i = ), так как каждый последующий инвариантный множитель делится
на предыдущий. Некоторые из множителей (Х-Х;)7 в (7.33) могут иметь
нулевую степень, т.е. быть равными единице. Исключение составляют мно-
жители (Х-Х,)"' минимального многочлена (7.29) (цЛ(Х)= е„(Х) по свой-
ству 6) , для которых согласно свойству 4 все показатели степеней больше
или равны единицы (mi > 1, i = 1,...,к).
Учитывая, что характеристический многочлен (7.24) равен произведе-
нию инвариантных множителей (с коэффициентом (-1)"):
АЛ(Х) = (-1)Л(Х-Х1)"1 *(Х-Х2^ -...-(X-Xj* =(-1Ге1(Х)-е2(Х).....ея(Х),
? получаем, что а,+/>,+... + /,+т, = и,- (i = l,...,X) и nt +п2 +...+пк = п , т.е.
I сумма степеней всех инвариантных множителей равна порядку квадратной
матрицы А .
s Каждый отличный от единицы многочлен вида (Х-Х,)7, указанный в
; разложениях (7.33) инвариантных множителей, называется элементарным
делителем характеристической матрицы (А-кЕ) (или просто элемен-
i тарным делителем матрицы А ).
» По формулам (7.33) можно составить таблицу элементарных делите-
5 лей:
Г (x-x,r, (Х-Х,/-, ... , (X-XJ-, (х-х^’,
г (х-х2Г\ (х-х2У2. (х-х2)\ (х-х2г,
[ ........................ (7.34)
; (x-xtr, (X-Xj‘,... , (x-xj*, (х-х>.
СОСТАВЛЕНИЕ ТАБЛИЦЫ ЭЛЕМЕНТАРНЫХ ДЕЛИТЕЛЕЙ
ПО ТАБЛИЦЕ ИНВАРИАНТНЫХ МНОЖИТЕЛЕЙ
( Для составления таблицы (7.34) элементарных делителей по таблице
(7.33) инвариантных множителей нужно:
? а) в первый столбец таблицы (7.34) записать элементарные делители
| последнего инвариантного множителя еп(Х) из таблицы (7.33);
I б) во второй столбец (7.34) записать элементарные делители предпо-
|следнего инвариантного множителя e„_j(X) из таблицы (7.33) так, чтобы в
J i-Й строке (7.34) были степени одного и того же двучлена (Х-Х;), и т.д.
В последний столбец (7.34) записать элементарные делители первого инва-
|риантного множителя е,(Х) из таблицы (7.33) так, чтобы в i -й строке (7.34)
L были степени одного и того же двучлена (X - X,).
20* 307
Элементы, тождественно равные единице, не являются элементарными
делителями и в таблицу (7.34) не заносятся. Поэтому в каждой строке таб-
лицы может быть разное количество элементарных делителей, точнее, в ка-
ждом последующем столбце количество делителей не больше, чем в преды-
дущем. В каждой строке таблицы (7.34) стоят делители (Х-Х,/, относя-
щиеся к одному собственному значению X,. Поскольку собственные значе-
ния Л.],...,!* могут быть упорядочены по-разному, то и строки таблицы
(7.34) можно переставлять. Это не будет в дальнейшем иметь существенного
значения.
СОСТАВЛЕНИЕ ТАБЛИЦЫ ИНВАРИАНТНЫХ МНОЖИТЕЛЕЙ
ПО ТАБЛИЦЕ ЭЛЕМЕНТАРНЫХ ДЕЛИТЕЛЕЙ
По таблице (7.34) элементарных делителей можно восстановить табли-
цу (7.33) инвариантных множителей. Для этого нужно:
а) перемножая элементарные делители первого столбца таблицы (7.34),
получить последний инвариантный множитель е„(х) в таблице (7.33);
б) перемножая элементарные делители второго столбца таблицы (7.34),
получить предпоследний инвариантный множитель в таблице (7.33)
и т.д. Исчерпав столбцы таблицы (7.34), дописываем недостающие инвари-
антные множители, полагая их равными единице (количество инвариантных
множителей равно сумме степеней всех элементарных делителей, т.е. по-
рядку матрицы).
Заметим, что, составляя таблицу (7.33) по таблице (7.34), можно пере-
ставлять строки таблицы (7.34), так как это не приведет к изменению табли-
цы (7.33). Столбцы таблицы (7.34) переставлять нельзя.
Согласно теореме 7.3, эквивалентные характеристические матрицы
(А-ХЕ) и (B-ХЕ) имеют одинаковые инвариантные множители (7.33). То-
гда они имеют и одинаковые элементарные делители (7.34). Следовательно,
критерий подобия числовых матриц (теорему 7.6) можно сформулировать
следующим образом.
Теорема 7.8 (критерий подобия матриц). Числовые матрицы подоб-
ны тогда и только тогда, когда они имеют одинаковые элементарные де-
лители.
Таким образом, нахождение подобных матриц связано с умением со-
ставлять матрицы, элементарные делители которых совпадают с заданной
таблицей (7.34).
308
7.3.2. Жордановы клетки и матрицы
Квадратную матрицу (г -го порядка) вида
ро 1 0 • • О'
0 Ч 1 • • 0
л(
0 0 0 • • 1
.° 0 0 • ^о,
(7-35)
называют жорданоеой клеткой г -го порядка, соответствующей собствен-
ному значению Л.о . Все элементы на главной диагонали этой верхней тре-
угольной матрицы равны Хо , элементы над главной диагональю равны еди-
нице, а остальные элементы равны нулю.
Найдем элементарные делители жордановой клетки. Для этого соста-
вим характеристическую матрицу
%-Х 1 0 0 Хо-Х 1 0 ' 0
Jr(X0)-XE = 0 0 Хо ~ Л. 1
0 0 0 Л-0 —
и найдем наибольшие общие делители <7,(^) миноров i -го порядка. Среди
ненулевых миноров первого порядка есть минор, равный единице (М\ = 1).
Рассматривая его как многочлен нулевой степени, заключаем, что наиболь-
ший общий делитель миноров первого порядка должен быть также много-
членом нулевой степени, т.е. dt (х) = 1. Среди миноров второго порядка
также имеется минор, равный единице:
1
Хо — А.
О
1
М'23 =
, следовательно,
<72(х)~1 и т.д. Минор (r-l)-ro порядка Л/23"''-1 имеет нижний треуголь-
ный вид с единичными элементами на главной диагонали, т.е. Л/2з"гг~1 =1.
Поэтому 4/r_j(A.) = l. Минор г-го порядка, т.е. определитель характеристи-
ческой матрицы, равен (Х0-Л.)г, поэтому dr(x) = (Х-ХОУ. По формулам
(7.11) находим инвариантные множители: е](Л.)=е2(х)=... = ег1(х) = 1,
er(k) = (k-X0Y. Следовательно, жорданова клетка (7.35) имеет всего один
элементарный делитель (Х-Х0)г. Поэтому характеристическая матрица
приводится к нормальному диагональному виду (7.9):
309
(/г(х0)-хе)~ ^g(i,...,i,(x-x0)f).
(7.36)
Заметим, что характеристический многочлен Ау,(х0) = (х0-х/ имеет един-
ственный корень Хо кратности г, т.е. Хо - собственное значение матрицы
(7.35).
Рассмотрим теперь блочно-диагональную матрицу
J=diag(jr(\\Л2(\))=
Z,(xi)
о
(7.37)
О
где Jri(Aj) и Jrj(X2) - жордановы клетки, а О - нулевые матрицы соответ-
ствующих размеров. Для определенности считаем, что rl>r2. Характери-
стическая матрица (j-ХЕ) также имеет блочно-диагональный вид. С по-
мощью элементарных преобразований каждого блока матрица (/-ХЕ),
учитывая (7.36), приводится к диагональному виду
(j - ХЕ) - JMg(l,...,l,(X-X1)\ 1,..., 1, (X - Х2)г’).
Если Х^Хг.то rf1(X) = ... = dr+rj_1(X) = l, <1+г2(Х) = (Х-Х1)г>(Х-Х2^ .
Тогда e1(X) = ... = ez.i+rj_1(X)=l, еп+Г2(Х) = (Х-Х1)Г‘-(Х-Х2)Г2 Следователь-
но, матрица (7.37) имеет два элементарных делителя (Х-Х1)г‘ и (Х-Х2)Г;!.
Если Х1=Х2, то ^(Х)=... = <1+Г2_2(Х) = 1, ^Г1+Г2_1(Х) = (Х-Х1)Г2,
• Тогда eiW=-=.
ег1+г2(^)=(^~^1)Г‘ • Следовательно, матрица (7.37) имеет два элементарных
делителя (Х-Х1)г‘ и (X-Xj)'2 .
Таким образом, элементарные делители блочно-диагональной матрицы
(7.37) получаются объединением элементарных делителей каждого блока.
Жордановой матрицей называют блочно-диагональную матрицу, на
диагонали которой стоят жордановы клетки:
J-diag[j^ (Xj), (xj.., (Xt)j
(7.38)
310
Здесь О - нулевые матрицы соответствующих размеров. Среди собствен-
ных значений Ап А2,...,А* могут быть равные, размеры q, г2. гк жор-
дановых клеток (всех или некоторых) тоже могут совпадать. Жорданова
матрица - почти диагональная. На ее главной диагонали стоят собственные
значения, некоторые элементы над главной диагональю равны единице, ос-
тальные элементы нулевые. Про матрицу (7.38) говорят, что она имеет нор-
мальную жорданову форму (или просто жорданову форму}.
Элементарные делители жордановой матрицы (7.38)
(a-aJ-, (а-а2)г’....(х-^У*
получаются в результате объединения элементарных делителей жордановых
клеток.
СОСТАВЛЕНИЕ ЖОРДАНОВОЙ МАТРИЦЫ ПО ТАБЛИЦЕ ЭЛЕМЕНТАРНЫХ
ДЕЛИТЕЛЕЙ
Чтобы составить по таблице (7.34) элементарных делителей
соответствующую жорданову матрицу, нужно:
а) для первой строки (А-А]/"1 .(А-А,/1 .(А-А^1 эле-
ментарных делителей в (7.34) записать жордановы клетки
•^т1 (^1)’ Д (^1 )’ ••> Л, (^1 )> ^а{ (^1);
б) для второй строки (А-А2У"2 ,(А-А2/2 .....(А-АгУ2 ,(А—А2)“2 эле-
ментарных делителей в (7.34) записать жордановы клетки
и т.д. Получив полный набор жордановых клеток (количество которых сов-
падает с количеством элементарных делителей в таблице (7.34)), составить
из них блочно-диагональную матрицу вида (7.38). Порядок, в котором нуж-
но располагать жордановы клетки на диагонали, строго не регламентирован.
Поэтому-для одной и той же таблицы (7.34) можно получить разные жорда-
новы матрицы, отличающиеся только перестановкой жордановых клеток.
СОСТАВЛЕНИЕ ТАБЛИЦЫ ЭЛЕМЕНТАРНЫХ ДЕЛИТЕЛЕЙ ПО ЖОРДАНОВОЙ
МАТРИЦЕ
Чтобы по жордановой матрице (7.38) составить таблицу (7.34) ее эле-
ментарных делителей, нужно:
а) выбрать в жордановой матрице все жордановы клетки, соответст-
вующие собственному значению А]; составить для каждой клетки элемен-
тарный делитель, а затем записать эти элементарные делители в порядке
убывания степеней в первую строку таблицы (7.34), например, для жордано-
вых клеток Jrmi(A1),J,i(AI).где тх>1х>...>Ьх>ах>Л,
311
записать строку (X - Xj )m‘ , (X - Л| У1 .., (X - X] У' , (X - X] У' элементарных
делителей;
б) выбрать в жордановой матрице все жордановы клетки, соответст-
вующие собственному значению Х2, составить для каждой клетки элемен-
тарный делитель, а затем записать эти элементарные делители в порядке
убывания степеней во вторую строку таблицы (7.34) и т.д., пока не исчер-
паются все собственные значения данной жордановой матрицы. Порядок, в
котором выбираются собственные значения жордановой матрицы, точно не
устанавливается. Поэтому для одной жордановой матрицы можно получить
разные таблицы элементарных делителей, которые будут отличаться только
перестановкой строк. Ранее (см. разд. 7.3.1) отмечалось, что перестановка
строк таблицы (7.34) не влияет на составление таблицы (7.33) инвариантных
множителей.
Замечания 7.6.
1. Диагональная матрица имеет жорданову форму:
diag^ ,...,kn)=diag(jt (X]),..., Л(Х„)),
в которой все жордановы клетки первого порядка.
2. Хотя жорданова матрица в общем случае не диагональная, для нее
достаточно просто решаются типовые задачи линейной алгебры. Например,
для неоднородной системы уравнений Jx = b с невырожденной матрицей
J = Jп (Хо) можно сразу записать решение:
г _ ьп г _ г
хп -Т“ ’ xn-i - 2 ----Г •
Ло л0 Ао
3. Для решения тех или иных задач линейной алгебры используются
различные простые виды квадратных матриц, которые обычно называют
нормальными, или каноническими формами, например, первая и вторая ес-
тественные формы матрицы [10], вещественная жорданова форма [42]. Мат-
рицу (7.38) называют также канонической формой.
Пример 7.13. Найти элементарные делители и инвариантные множи-
тели жордановых матриц
А Г1 0 0 0> f\ 1 0 1 0 0 o' 0 . Г* Ч 1 0 1 0 0 0 0
0 2 0 0
а; А — 0 .0 0 0 3 1 0 3, ; о) d — 0 0 1 0 , В) С — 0 0 <° 0 1 1 0 к
to 0 0 2,
□ Матрица А = diag^l), ^(2), /2(з)) состоит из трех жордановых
клеток с разными собственными значениями X] = 1, Х2 = 2, Х3 = 3. Для
каждого собственного значения запишем жорданову клетку и соответст-
вующий элементарный делитель:
312
Л] =1 => 7](1) => (Л-1);
Л2=2 7,(2) => (Л-2);
Л3 =3 => /2(3) => (Л-3)2
Получили таблицу элементарных делителей, которая состоит из одного
столбца. По этой таблице составляем инвариантные множители (количество
которых равно порядку матрицы А ). Записываем (см. разд.7.3.1) последний
инвариантный множитель е4(Л)=(Л-з)2(Л-1)(Л-2), перемножая элемен-
тарные делители первого столбца. Поскольку исчерпаны все элементарные
делители (второго столбца в таблице нет), то остальные инвариантные мно-
жители полагаем равными единице: е3 (Л) = е2(Л) = ег (Л) = 1.
Матрица В = diag(j2(l\ Л(1), -Л (2)) состоит из трех жордановых кле-
ток, соответствующих двум разным собственным значениям Л1 = 1, Л2 ~ 2 •
Для каждого собственного значения записываем соответствующие жордано-
вы клетки и элементарные делители:
Л]=1 => А(1),Л(1) => (Л-1)2, (Л-1);
Л2=2 => Л(2) => (Л-2).
Получили таблицу элементарных делителей, которая состоит из двух столб-
цов. По этой таблице составляем инвариантные множители (количество ко-
торых равно порядку матрицы В). Записываем (см. разд.7.3.1) последний
инвариантный множитель е4(Л)= (Л-1)2(Л-2), перемножая элементарные
делители первого столбца. Записываем предпоследний инвариантный мно-
житель е3(Л) = (Л-1) по второму столбцу таблицы. Поскольку исчерпаны
все элементарные делители (третьего столбца в таблице нет), то остальные
инвариантные множители полагаем равными единице: е2(Л)= е[(Л) = 1.
Матрица С = diag(j 2(1\ /2(1)) состоит из двух одинаковых жордано-
вых клеток, соответствующих одному собственному значению Л! = 1. Для
этого собственного значения записываем жордановы клетки и соответст-
вующие элементарные делители:
Л,=1 => л(1).л(1) => (л-1)2, (Л-1)2.
Получили таблицу элементарных делителей, которая состоит из двух столб-
цов. По этой таблице составляем инвариантные множители (количество ко-
торых равно порядку матрицы С). Записываем (см. разд.7.3.1) последний
инвариантный множитель е4(Л) = (Л-1)2 по первому столбцу таблицы. За-
писываем предпоследний инвариантный множитель е3(Л)=(Л-1)2 по вто-
рому столбцу таблицы. Поскольку исчерпаны все элементарные делители
313
(третьего столбца в таблице нет), то остальные инвариантные множители
полагаем равными единице: е2(Х) = е1(Х)= 1.
Пример 7.14. По инвариантным множителям найти жорданову матри-
цу:
а) матрица А : е1(А) = е2(Х) = е3(А)= 1, е4(Л)=(Л-1)(Л-2)(Л-3)(Л-4);
б) матрица В : е!(Л)=е2(Л)=1, е3(Л)= (Л-1), е4(Л)= (Л-1)3;
в) матрица С : (X) = 1, е2(Л)=(Л-1), е3(Л)=(Л-1), е4(Л) = (Л-1)2.
□ Для матрицы А составляем таблицу (7.34) элементарных делителей
(см. разд.7.3.1). В первый столбец таблицы записываем элементарные дели-
тели последнего инвариантного множителя:
(*-з),
(Л-4).
Остальные элементарные делители равны единице и в таблицу не заносятся.
Составляем по таблице элементарных делителей жорданову матрицу. Для
каждого элементарного делителя записываем соответствующую жорданову
клетку: /1(1), Л (2), /Дз), (4). Располагая эти клетки на главной диаго-
нали блочной матрицы, получаем искомую жорданову матрицу:
Для матрицы В составляем таблицу (7.34) элементарных делителей
(см. разд.7.3.1). В первый столбец таблицы записываем единственный эле-
ментарный делитель последнего инвариантного множителя е4(Л), во второй
столбец - предпоследнего инвариантного множителя е3(Л):
(Л-1)3, (Л-1).
Инвариантные множители е1(Л)=е2(Л)=1 не содержат элементарных дели-
телей, отличных от единицы, и поэтому в таблицу не записываются. Состав-
ляем по таблице элементарных делителей жорданову матрицу. Для каждого
элементарного делителя записываем соответствующую жорданову клетку:
/3(1), /Д1). Располагая эти клетки на главной диагонали блочной матрицы,
получаем искомую жорданову матрицу:
314
rl 1 О СТ
0 110
0 0 10
ч0 о О I 1у
Для матрицы С составляем таблицу (7.34) элементарных делителей
(см. разд.7.3.1). В первый столбец таблицы записываем единственный эле-
ментарный делитель последнего инвариантного множителя е4(Л), во второй
столбец - предпоследнего инвариантного множителя е3(Л), в третий стол-
бец- е2(Л):
Инвариантный множитель ex(X) = 1 не содержит элементарных делителей,
отличных от единицы, и поэтому в таблицу не записывается. Составляем по
таблице элементарных делителей жорданову матрицу. Для каждого элемен-
тарного делителя записываем соответствующую жорданову клетку: /2(1),
/J1), /1(1). Располагая эти клетки на главной диагонали блочной матрицы,
получаем искомую жорданову матрицу:
1 1 о 1 0 0 0 0
0 0 1 0
0 0 0 1
Теорема 7.9 (о приведении матрицы к нормальной жордановой
форме). Любая квадратная матрица подобна жордановой матрице. Две
жордановы матрицы подобны тогда и только тогда, когда они составле-
ны из одинаковых жордановых клеток и отличаются друг от друга лишь
расположением клеток на главной диагонали, другими словами, любую
квадратную матрицу при помощи преобразования подобия можно привес-
ти к нормальной жордановой форме и притом единственной (с точностью
до перестановок жордановых клеток).
В самом деле, для любой квадратной матрицы А можно найти элемен-
тарные делители, т.е. составить таблицу (7.34). По элементарным делителям
можно составить соответствующую жорданову матрицу J А . При этом мат-
рицы А и J А будут иметь одинаковые элементарные делители, что являет-
ся критерием их подобия (см. теорему 7.8 в разд.7.3.1). Значит, найдется не-
вырожденная преобразующая матрица 5 такая, что J А = S~lAS . Заметим,
что жорданова форма JА матрицы А определяется по ее элементарным де-
лителям единственным образом с точностью до перестановок жордановых
клеток.
315
7.3.3. Приведение матрицы к жордановой форме
Задача приведения матрицы к жордановой форме формулируется сле-
дующим образом. Требуется привести квадратную матрицу А к жордано-
вой форме J А при помощи преобразования подобия: J А -S~l AS , т.е.
найти жорданову форму JA квадратной матрицы А (первый этап);
найти преобразующую матрицу S (второй этап), для которой
JA = S-1 AS . (7.39)
В некоторых прикладных и теоретических задачах достаточно опреде-
лить только жорданову форму матрицы, т.е. ограничиться первым этапом.
Однако чаще кроме жордановой формы JA матрицы А требуется также
найти и преобразующую матрицу S , т.е. выполнить оба этапа.
НАХОЖДЕНИЕ ЖОРДАНОВОЙ ФОРМЫ МАТРИЦЫ
Для нахождения жордановой формы JА квадратной матрицы А нуж-
но выполнить следующие действия.
1. Составить характеристическую матрицу (А — Ле).
2. Найти ее инвариантные множители (7.33) одним из способов, рас-
смотренных в разд. 7.1.4.
3. По инвариантным множителям (7.33) составить таблицу (7.34) эле-
ментарных делителей (см. разд. 7.3.1).
4. По элементарным делителям составить жорданову форму J А (см.
разд.7.3.2).
НАХОЖДЕНИЕ ПРЕОБРАЗУЮЩЕЙ МАТРИЦЫ
Рассмотрим два способа нахождения преобразующей матрицы.
Первый способ. Если жорданова форма J А матрицы А известна, то
для нахождения преобразующей матрицы S нужно выполнить следующие
действия.
1. Составить матричное уравнение SJ А = AS относительно неизвест-
ной матрицы S, которое равносильно однородной системе п2 линейных
уравнении с п неизвестными элементами s,j матрицы S .
2. Найти такое частное решение этой системы уравнений, для которого
det S Ф 0.
Второй способ. Для нахождения преобразующей матрицы S можно
использовать следствие теоремы 7.7.
316
1. Составить блочную А-матрицу (А-кЕ | Е), приписав к характери-
стической матрице (А-ZE) единичную матрицу того же порядка. При по-
мощи элементарных преобразований, выполняемых над строками и столб-
цами блочной матрицы, привести ее левый блок к нормальному диагональ-
ному виду (7.9). При этом блочная матрица преобразуется к виду
(л(А) | 5Л(А)), где Л(А) = Jia^(e1(A),...,en(A)) - матрица нормального диаго-
нального вида, эквивалентная матрице (а-АЕ), а 5Л(Л) - некоторая эле-
ментарная Л-матрица.
2. Составить блочную Л-матрицу (/Л-ЛЕ | E), приписав к характе-
ристической матрице (/Л-АЕ) единичную матрицу того же порядка. При
помощи элементарных преобразований, выполняемых над строками и
столбцами блочной матрицы, привести ее левый блок к нормальному диаго-
нальному виду (7.9). При этом блочная матрица преобразуется к виду
(Л(Л)| 5у(Л)),где Л(А) = diag(e^\...,en(X)) — такая же матрица, что ив п.1,
a Sy(A) - некоторая элементарная Л-матрица.
3. Найти Л-матрицу S(A) = SJ*(A)Sa(A).
4. Вычислить левое значение 5лев(/Л) при замене переменной А мат-
рицей JA (см. разд. 7.1.3).
5. Найти преобразующую матрицу S, обращая матрицу 5лев(/Л):
Действительно, при помощи элементарных преобразований характери-
стические матрицы (A-Аг) и (/л-АЕ) приводятся к одному и тому же
нормальному диагональному виду Л(А):
5у(А)(/л-Ае)7’/(А) = Л(А)=5л(А)(А-Ае)7’л(а).
Отсюда JA - А.Е = Sj1 (Л) SA (А) (А - АЕ) Та (А) 7}-1 (А.), т.е.
ул-ае=$(а)(а-ае)т(а),
где s(A) = SJ‘(A)sa(A), Т(А) = 7’л(А)7’/'1(А). Согласно следствию теоремы
£
; 7.6, преобразующая числовая матрица S = [S Iee(7A)] 1, т.е. S - это матрица,
обратная к левому значению Л-матрицы 5ле„(/л) при подстановке вместо
• А. матрицы JА.
I Замечания 7.7.
1. Несмотря на простоту, первый способ мало пригоден из-за большого
( объема вычислений. Количество решаемых уравнений - и2.
| 2. Второй способ позволяет полностью решить задачу приведения мат-
[ рицы к жордановой форме. Выполняя п.1, находим нормальный диагональ-
317
ный вид Л(Л)= 4/105(6! (Л),...,ел(Л)) характеристической матрицы (А-ЛЕ),и,
как следствие, ее инвариантные множители еДЛ),..., ел(Л). Тогда выполняя
п.З, 4 алгоритма нахождения жордановой формы, получим жорданову фор-
му J А матрицы А. Далее выполняем п.2, 3 второго способа и находим
преобразующую матрицу.
3. В п.1, 2 второго способа X-матрицы, стоящие в левых блоках мат-
риц (А-ЛЕ | Е) и (jA -ХЕ | Е) , приводятся к нормальному диагональному
виду при помощи элементарных преобразований над строками и над
столбцами (см. разд.7.1.3). При этом правые блоки этих матриц
"учитывают" только преобразования строк, в отличие от алгоритма,
описанного в п.5 замечаний 7.4.
4. Преобразующая матрица S в (7.39) определяется неоднозначно. В
самом деле, если S — преобразующая матрица, а М - невырожденная мат-
рица, перестановочная с А (АЛ/ = МА), то матрица Т = MS будет также
преобразующей. Действительно, матрица Т - обратимая и
T~lAT = S~lM~'AMS = S~lM~lMAS - S~XAS - JA .
Первый способ нахождения преобразующей матрицы, вообще говоря, по-
зволяет найти все такие матрицы, перебирая в п.2 подходящие частные ре-
шения однородной системы. Второй способ позволяет найти одну преобра-
зующую матрицу из этого множества. Как правило, на практике достаточно
найти хотя бы одну преобразующую матрицу.
5. Задачу приведения матрицы к диагональному виду (см. разд.7.2.2)
можно считать частным случаем задачи приведения матрицы к жордановой
форме. Если квадратная матрица А л -го порядка имеет п линейно незави-
симых собственных векторов, то, как это следует из теоремы 7.5, ее жорда-
нова форма J А является диагональной матрицей (с собственными значе-
ниями на главной диагонали), а преобразующая матрица 5 может быть со-
ставлена из л линейно независимых собственных векторов матрицы А .
Пример 7.15. Привести к жордановой форме следующие матрицы:
□ Матрица А . Первый этап - нахождение жордановой формы матри-
цы А.
4-Л 4
-1 -л)
1. Составляем характеристическую матрицу А-ЛЕ =
2. Инвариантные множители будем искать по формуле (7.11) (см. вто-
рой способ в разд.7.1.4). Записываем миноры 1-го порядка: Л/1=4-Л,
318
M\=4, Ml=-X. Находим наибольший общий делитель этих
многочленов: 1. Минор второго порядка равен определителю харак-
теристической матрицы М^2 =
4-Х 4
-1 -X
= (X - 2)2. Следовательно,
</2(Х) = (Л~2)2 Таким образом, по формуле (7.11) получаем
|е1(Л)=4(Л)=1, е2(Х)=^ = (Х-2)2.
“1W
3. По инвариантным множителям составляем таблицу (7.34) элемен-
тарных делителей. Так как собственное значение матрицы единственное
(Xj = 2), то таблица (7.34) состоит из одной строки (и одного столбца):
(Х-2)2.
4. Единственному элементарному делителю (Х-2)2 соответствует од-
на жорданова клетка 2-го порядка, образующая жорданову форму мат-
рицы А :
Л-Р *).
А 1^0 2)
Второй этап - нахождение преобразующей матрицы. Воспользуемся
первым способом.
1. Составляем матричное уравнение SJA - AS :
х у') (2 l') Г 4 4^ (х у')
z wl lo 2J 1-1 о) lz w)
Перемножая матрицы, получаем однородную систему уравнений относи-
fx у
тельно элементов искомой матрицы S =
I z w
2x = 4x + 4z,
2z = -х,
х+2у = 4y + 4w,
z + 2w = -y,
2x+4z = 0,
x + 2z = 0,
x-2y-4w = 0,
у + z + 2w = 0.
2. Решаем эту систему (см. разд.5.5, 5.6). Расширенную матрицу систе-
мы приводим к ступенчатому, а затем к упрощенному виду:
319
, (2 01
где А = I I. Находим фундаментальную матрицу Ф
п.З замечаний 5.3) и общее решение (см. разд.5.5):
(согласно правилу
(~А‘
Ф =----
1£2
где Q, С2 - произвольные постоянные.
Следовательно, любая преобразующая матрица имеет вид
-2С/
SJX У|=Г2С’
U WJ I С1 -2 J
где С,, С2 - произвольные постоянные, но Сх Ф 0, так как матрица S не-
вырожденная: det 5 = -2CiC2 + С2 + 2С1С2 = С2 Ф 0. Например, при С, - -1,
Г2 С
С2 - 0 получаем 5 = 1 I.
Используем второй способ нахождения преобразующей матрицы.
/ Л I \ I X 4
1. Составляем блочную матрицу: (А-ХЕ | £j=l X О 1Г
При помощи элементарных преобразований, выполняемых над строками и
над столбцами этой блочной матрицы, приводим левый блок к нормальному
диагональному виду. Меняем местами строки и умножаем первую строку на
(-1). Выбрав ведущий элемент, равный единице, делаем равными нулю ос-
тальные элементы в первом столбце и в первой строке левого блока:
0 -И
1 О
4-Х 4
-1
1 0
0) 1^0 (Х-2)2 1 4-Xj
1 0W 1 X 0 -1
-X О 1J~^4-X 4 1
, . fO -1 >
Следовательно, 5Л(Х) =
V 4-XJ
2. Составляем блочную матрицу и приводим левый блок этой матрицы
к нормальному диагональному виду (jA~kE | е)=^
1 2-Х 1 О'
2-Х 0
1 Х-2 1 0
0 1) ^2-Х 0
=
1Х-2 11
2-Х
О
О
1
2-Х
1
1
О
О
1
О'
1
0 lj~|o (Х-2)2 Х-2 1
320
3. Обращаем матрицу S/(A): S/(X)
Находим X-матрицу S(X) = SJ*(X)SA(X) =
которая оказалась независящей от Л.
4. Так как X-матрица S(X) оказалась числовой, то 5лев(/д) = [
detS7(X) Л ~ 1 ^2-Х 1J’
1 о Wo -1 Wo -С
2-Х 1 J\1 4-Xj Д1 2 J’
5. Находим преобразующую матрицу
S = k (j )?‘=f0 '=(2 1
I леД аЛ I t 2 I I х 0
V Z К >
Такой же результат, как частный случай, был получен первым способом.
^"Матрица В . Будем искать преобразующую матрицу 5 вторым спосо-
бом. При этом попутно найдем и жорданову форму Jв матрицы В (см. п.2
замечаний 7.7).
1. Составляем блочную матрицу:
'1-Х
(В-ХЕ | Е)= О
-1
О
1-Х
-1
1 1 О О'
-10 10
1-Х 0 0 1,
Выполняя элементарные преобразования над строками и над столбцами
этой блочной матрицы, приводим левый блок к нормальному диагонально-
му виду. Меняем местами первую и третью строки и умножаем первую
строку на (-1). Выбрав ведущий элемент, равный единице, делаем равными
нулю остальные элементы в первом столбце и в первой строке левого блока:
'1-Х 0 1 1 0 О' ' -1 -1 1-Х о о Г
0 1-Х -1 0 10- 0 1-Х -1 0 1 0 —
-1 -1 1-Х 0 0 1, J-X 0 1 1 0 0,
г 1 1 Х-1 с о -А '10 0 0 0 -Г
— 0 1-Х -1 с >10- 0 1-Х -1 0 1 0
<1 -X 0 11 0 0 J J) Х-1 (X-1)2+1 1 0 L-X,
Меняем местами второй и третий столбцы и умножаем вторую строку на
(-1). Выбрав ведущий элемент, равный единице, делаем равными нулю ос-
тальные элементы во втором столбце и во второй строке левого блока:
"1 О
О 1-Х
О Х-1
О
-1
(Х-1)2 + 1
оо -О fi
0 1 0-0
1 О 1-xJ fo
О ООО
-1 1-Х О 1
(X-lf + l х-1 1 о
-г
о
1-Х,
21 -4549
321
о
о
1
'10 0 0
О 1 Х-1 о
/) (Х-1)2 + 1 Х-1 1
о
-1
о
-И fi о о
0-01 о
1-Xj 1^0 О (1-Х)3
О -1 '
-1 о
(Х-1)2 + 1 1-Х,
Умножая третий столбец на (-1), получаем нормальную диагональную
форму характеристической матрицы и матрицу SB(X):
В-КЕ-
'10 0 '
О 1 О
ч0 О (Х-1)3,
Го о -1
= Л(Х),
SB(X)= о
1
-1
Х2-2Х + 2
О
1-Л,
Находим жорданову форму Jв матрицы В (см. п.2 замечаний 7.7). По
инвариантным множителям е1(Х)=е2(Х) = 1,е3(Х)=(Х-1)3 составляем таб-
лицу элементарных делителей. Таблица состоит из одного делителя (Х-1)3,
которому соответствует одна жорданова клетка 3-го
порядка (для собствен-
ного значения Xj = Х2 = Х3 = 1):
<1 1 ОА
J В ~ 0 1 1 0
2. Составляем блочную м: прицу Г1-Х 1 0 1
(JB-XE|E) = 0 1 -X 1 0
< 0 0 -X 0
О О'1
1 О
0 L
Приводим левый блок этой матрицы к нормальному диагональному виду.
Меняем местами столбцы левого блока
'1-Х 1
О 1-Х
. О о
о
1
1-Х
1 о оЛ f 1
О 1 О - 1-Х
О О 1J [ о
о
1
1-Х
1-Х 1 О О'
О 0 10
О 0 0 1,
Выбираем ведущий элемент, равный единице, в левом верхнем углу. Делаем
в левом блоке равными нулю все элементы ведущей (первой) строки и ве-
дущего (первого) столбца, за исключением ведущего элемента:
' 1
1-Х
< 0
О
1
1-Х
1-Х 1
о о
о о
о оЛ f1 о
10-0 1
О 1J (о 1-Х
О 1 О О'
-(Х-1)2 Х-1 1 о
О 0 0 1,
Выбираем ведущий элемент, равный единице, на пересечении второго
столбца и второй строки. К третьей строке прибавляем вторую, умножен-
ную на (X -1), а затем к третьему столбцу прибавляем второй, умноженный
322
на (X -1)2, и, наконец, умножаем третий столбец на (-1). В результате по-
лучим р 0 0 1 0 О'! А 0 0 1 0 О'!
0 1 -(Х-1)2 X- -110- -01 о Х-1 1 0 .
1° 1- X 0 с 0 h J) 0 (Х-1)3 (Х-1)2 Х-1
1 0 О’)
Следовательно, S/(X) = Х-1 1 0 , л(Х)=Ла#(1,1,(Х-
!(* -1)2 Х-1
3. Обращаем матрицу 5У(Х):
( 1 0 o'!
s;4x)= 1 5* detSy(X) 5 * 7 (Х)= 1-х 1 ч 0 1-Х 0 . 1,
Находим X-матрицу $(Х) =
< 1 0 °) (0 0 -i'l <0 0 -1 'I
s(x)= 1-Х 1 0 0 -1 0=0 -1 Х-1 .
0 1-Х 1J J (X-l)2 + l 1-XJ (1 х2-х+ 1 1-xJ
4. Представляем 1-матрицу s(X) в виде многочлена с матричными
коэффициентами, ставя переменную X перед коэффициентами:
s(x)=x2 '0 0 o' ООО 0 1 0, +х 'о о o' Д о о — о + "0 0 -1' 0 -1 -1 .1 1 1J
Подставляем вместо аргумента X матрицу Jв :
'1 1 О' 2 'о 0 О'! '1
^(^)= 0 1 1 0 0 0 + 0
0 L .° 1 °J ?
'1 2 р р) 0 0^ '0 )
= 0 1 2 - 0 0 0 + 0 - 1
.0 0 1 0 1 0 о - 1
1 1 0 г 0 -1 О' 1 1 + L '0 0 с 0 0 1 <0 -1 - о о -Г 0 -1 -1 1 1 1 >' + 7 ( 1 "о 0 0 -1 <1 1 1 О' 0 -1 1 0 -р -1 1, =
5. Обращая полученную матрицу, находим преобразующую
'о 1 о V1
0 0-1
11 0 ,
'-1
1
о
о Г
о о
-1 о,
21*
323
Сделаем проверку, сравнивая левую и правую части равенства SJв = BS :
SJB =
О
О О
-1 О
-1
1
-1
1
о
-1
BS =
о
-1
о
1
-1
-1
1
о
о
-1
-1
1
-1
о
-1
1
о
П Г1
о
о
1
о
1
1
о
о
1
1
1
о
о
1
о
1
о
матрицы С (см. п.2 за-
Следовательно, равенство верное.
Матрица С. Применяем второй способ нахождения преобразующей
матрицы, попутно определяя жорданову форму
мечаний 7.7).
1. Составляем блочную матрицу:
(с-ХЕ I Е)= 1
1
1
1-Х
1
1
1
1-Х
1
о
о
о о
1 о
О 1
Элементарными преобразованиями приводим левый ее блок к нормальному
диагональному виду (см. пример 7.12). Меняем местами первый и третий
столбцы, выбираем первую строку и первый столбец в качестве ведущих и
делаем равными нулю все элементы выбранной строки (в пределах левого
блока) и выбранного столбца, за исключением ведущего элемента:
1 О О'
-1 1 о
Х-1 О 1
О
X
2Х-Х2
о
-X
X
1
1-Х
1
1-Х
1
1
о o'! fi
1 о
0 к
Умножаем второй столбец на (-1), выбираем ведущими вторую строку и
второй столбец, делаем равными нулю соответствующие элементы этой
строки и столбца:
1
1-Х
о
X
-X
о
X
2Х-Х2
1
-1
Х-1
о o'!
1
о
о
о
зх-х2
1
-1
Х-2
О'
о
1.
1
О
о
О
О
О
О
о
1
1
о
о
о
X
о
о
1
1
Умножим третий столбец на (-1), чтобы старший коэффициент многочлена
был равен единице. Итак, получили матрицу 5С(Х) =
о
1
1
О'
О и нор-
b
(с-хе)~
-1
Х-2
мальный диагональный вид характеристической матрицы
~ diag(l, X, Х(Х - 3)). Составляем таблицу (7.33) инвариантных множителей:
324
е,(Х) = 1;
е2(Х) = Х;
е3(Х)=Х(Х-3).
Составляем таблицу (7.34) элементарных делителей:
X, X,
х-з.
Каждому из трех делителей соответствует жорданова клетка 1-го порядка
(для собственных значений XL =Х2 =0, Х3 =3), т.е. жорданова форма мат-
рицы С - диагональная матрица:
(О О
jc = j/^(j1(o),j1(o),j1(3))= О О
о"
о
1° 0
2. Составляем блочную матрицу
-X
(jc-xe|e)= о
1°
О 0 10 0"
-X О 010
О 3-Х О О 1^
Левый блок этой матрицы имеет диагональный вид, который не является
нормальным, так как (3-Х) не делится на (-Х). Прибавляем к первому
столбцу третий, к третьей строке прибавляем первую, умноженную на (-1),
меняем местами первую и третью строки:
-X
(jc-Xe|e)~ о
(з-х
О 0 10
-X О О 1
о 3-Х о о
о"
о -
-X о
О -X
3-Х -1
10-0
О 1J [-Х
О 3-Х -1 о Г
-X О 010
о 0 i о о,
О 1
о о
Разделим первый столбец на 3, возьмем ведущий элемент, стоящий в левом
верхнем углу, и сделаем равными нулю соответствующие элементы:
' 1
О
_ л.
к 3
О
-X
О
3-Х -1
о о
О 1
i'i Г1
0-0
oj [о
о о
-X О
о x-f
-1
о
о 1'
1 о
о
1
о
325
Умножив второй столбец на (-1), а третью строку на (- 3), получим в левом
блоке нормальный диагональный вид Л(Х) = гйа#(1,X, X2 -ЗХ), а в правом
блоке матрицу
( -1
(X) -
3. Обращаем матрицу 5У(Х):
^х-з
О 1 '
1 О
О -X,
s;‘(x)=
—к—-5;(х)=--
detS7(X) м 3
'-X
о
чз-х
з
0=0
-1 1-—
V I1 з
п
з
О
_ _1_
37
О
о
3
о
О
1
о
Находим X-матрицу 5(Х)= S/1(X)SC(X):
(2_ 2Х _1 __1\
3 3 3 3
-1 1 О
_5_2Х _1 _1
\3 3 3 37
4. Представляем X-матрицу S(X) в виде многочлена с матричными ко-
эффициентами, помещая переменную X перед коэффициентами:
Подставляем вместо аргумента X матрицу Jc :
'О 0 0 0 o' 0 (_2 3 0 0 0 o' 0 + ' 2 3 -1 _1 3 1 T° 7 2 3 -1 _1 3 1 3 0
to 0 V __2 k 3 0 0 7 _5 I 3 3 1 3j 1 k 3 1 3 -1 37
5. Обращая полученную матрицу, находим преобразующую
' 2. _1 _1> -1 ' 1 o -Г
3 3 3
5 = -1 1 0 = 1 1 -1
_1 -2 -1 4
k 3 3 з) <
Сделаем проверку, вычислив матрицу С = SJCS 1:
(1 0 -l') fo 0 O'] <2 3 _± 3 _1\ 4
c = 1 1 -1 0 0 0 -1 1 0 =
1-2 -1 -J lo 0 3j k 3 1 3 -1 з)
326
' 1
1
-2
О -Г
1 -1
-1 -1,
'О О (Р
ООО
-1 -1 -1,
'1 1 г
= 111
J 1 I
Заметим, что в примере 7.10 эта матрица была приведена к диагональ-
ному виду. Поэтому, согласно п.5 замечаний 7.7, ее жорданова форма явля-
ется диагональной, а преобразующая матрица составляется из линейно неза-
висимых собственных векторов:
(О О ОА
(1 1 п
Jc= О О
О
5 = О
^0 О
-1 1
О I
Эта матрица 5 отличается от найденной вторым способом. Но она тоже яв-
ляется преобразующей (проверка равенства JA = S~lAS была фактически
выполнена в примере 7.10).
Матрица D. Применяем второй способ нахождения преобразующей
матрицы 5, попутно определяя жорданову форму JD матрицы D (см. п.2
замечаний 7.7).
1. Составляем блочную матрицу:
(D-ЛЕ | Ё)=
'-2-Л
-2
1
5
5-Х
-1
-3 1
-3 о
-Л о
о о4
1 о
О L
Элементарными преобразованиями приводим левый ее блок к нормальному
диагональному виду. Взяв элемент, равный единице, в качестве ведущего,
делаем равными нулю все элементы ведущего (первого) столбца и ведущей
(третьей) строки (в пределах левого блока):
Ъ 3-Л -3-2Л-Л2 1 0 Л + 2"
(D-ЛЕ | Е)~ 0 3-Л -3-2Л 0 1 2
1 0 0 0 0 1 У
К первой строке прибавляем вторую, умноженную на (-1), затем к третьему
столбцу прибавляем второй, умноженный на (-2):
N <3 | О 1 СП 1 О | о СП О — 1 -1 Л 0 1 2 0 0 1 ** "о 0 -Л2 0 3-Л -9 1 0 0 к 1 -1 Л? 0 1 2 0 0 1 У
Ко второму столбцу прибавляем третий, умноженный на ~, а затем к пер-
вой строке прибавляем вторую, умноженную на (—у):
327
о
о
1
£1^1
9
О
о
-X2 1
-9 О
О О
\ /
-1 А О
1 2 ~ О
О 1 1
Ха(х-з)
9
О
О
О 1 -1-f х-^
-9 0 1 2
ООО 1
Меняем местами второй и третий столбцы, затем умножим первую строку
на 9, второй столбец разделим на (-9):
О 0 -^21 1
0-9 0 01
10 000
9Х-2Х2 '
9
2
Го
О Х2(Х-3) 9 -9-Х2 9Х-2Х2>
10 0 1 2
0 0 0 0 1
- О
1 1
Меняем местами первую и третью строки, после чего получим в левом бло-
ке нормальный диагональный вид характеристической матрицы (£>-Хе), а
в правом блоке - матрицу SD(X):
1 '
2
9Х-2Х\
Составляем таблицу (7.33) инвариантных множителей:
г1(х) = 1;
е2(Х)=1;
е3(Х) = Х2(Х-3).
Составляем таблицу (7.34) элементарных делителей:
X2,
х-з.
Делителю X2 соответствует жорданова клетка 2-го порядка, а делителю
(Х-З) - жорданова клетка 1-го порядка, т.е. жорданова форма матрицы D
имеет вид:
JD=diag{j2{o\jx(3))= О
2. Составляем блочную матрицу:
(Jd-XE|e) = О
1
-X
3-Х
1
о
о
1
о
о
О'
о
о
1
о
О'
о
О о
О
о
о
о
Приводим левый блок этой матрицы к нормальному диагональному виду.
Выбираем единицу в качестве ведущего элемента и делаем равными нулю
328
соответствующие элементы левого блока, а затем меняем местами первый и
второй столбцы:
(JD-kE I е)--Л2
О
о
о
3-Л
о 0^1 fl
1 о
О 1
О
-к2
О
О
О
3-Л
(Г
о
1.
Полученный диагональный вид не является нормальным, так
(-Л2). Поэтому прибавляем ко второму столбцу третий, умно-
(-1), а затем ко второй строке прибавляем третью, умноженную
делится на
женный на
на (Л + 3):
о
-л2
Л-3
О
О
3-Л
О О4) fl
1 О
О 1
О О
О -9 9-Л2
О Л-3 3-Л
как
не
1
О
О
1
к
о
О
О
1
к
о
О
1
О
О
О
1
Л
о
1
к
о
О
1
О
о '
Л + 3
1 ,
Разделив второй столбец на (-9), получим элемент, равный единице, кото-
рый принимаем за ведущий, и делаем равными нулю соответствующие эле-
менты второй строки и второго столбца:
1
О
О
о о
1 9-Л2
V 3-Л
о
Л+3
1
1
Л
х(х-з)
9
о
1
х-з
9
О
Л+3
V
9 .
1 О
Л 1
О о
1
О
О
О
1
О
о
о
9
Умножив третью строку на (-9), получим в левом блоке нормальный диа-
гональный вид характеристической матрицы (jD -ЛЕ)-diag(l, 1,Л2(Л-3)),
1
Л
зл-л2
3. Обращаем матрицу 57(Л):
а в правом блоке - матрицу Sj (Л)=
О
1
3-Л
О '
Л+3
-Л2.
С-«(Л)=—1 5;(л)=4
7 v ’ detS/Л) 1 -9
-9
9Л
О
О
-л2
Л-3
-Л-3
1
Находим Л-матрицу 5(Л) = 571(Л)-5О(Л):
'-9
9к
О
о
-л2
Л-3
О
-Л-3
1 Д9
о
1
-9-Л2
1 л
2
9Л-2Л\
О
329
9
О О -9 '
-9Л-27 Л3 + 2Х2 + 9Л + 27 2А?-5Л2-18Л
9 -Л2+Л-12 -2Л.2 + 11Л-6>
4. Представляем А.-матрицу S(X) в виде многочлена с матричными
коэффициентами, помещая переменную Л перед коэффициентами:
Л3 (°
$(Л) =-----о
Л3
О
-9
О
О
1
О
о '
-18
И .
О'
2
О,
О
О
О
' О
-27
. 9
Л2
9
О
2
-1
О
27
-12
О
-5
-2
-9
О
-6
Л
9
9
О
О
9
1
9
Подставляем вместо аргумента X матрицу JD. Учитывая, что
D
1
о
о
"О
О
.0
О'
о ,
3,
О'
о ,
9,
"0
О
О
О'
О
27
2 _
D ~
о
о
о
О
О
О
3 _
D ~
о
о
о
получаем
лев
о
о
-9
О
О
-18
-9
о
о
-is') ( о
о
33
-27
9
О
27
-12
-9
О
-6
9
О
о
о
9
О
3
Ч -1 з'
= 3-30
-1 2 -1,
5. Обращая полученную матрицу, находим преобразующую
Ч -1 3^1 1
S= 3 -3 о
Г1 2 -1,
'3 5 9'
3 2 .9
-1 о,
Сделаем проверку, вычислив матрицу D = SJDS~l:
1
9
'3 5 9'
3 2 9
.з -1 о,
'О 1
О о
<° 0
°1 (1
О • 3
3JI-1
-1
-3
2
з'
о
ч
330
'о 3 27"
О 3 27
<0 3 О,
' 1
3
-1
-1
-3
2
ЗА Г-2 5
О = -2 5
-У U -1
-3"
-3
О,
Получили заданную матрицу D .
7.3.4. Многочлены от матриц
Напомним определение многочлена от матрицы (см. разд. 1.3.4). Пусть
заданы многочлен (степени т) переменной Л:
/(*) = атХ” + +... + aik + а0, (7.40)
А - квадратная матрица п -го порядка. Выражение вида
/(А)= атАт + am_1Am~l+...+aiA + a0E (7.41)
называется многочленом от матрицы А .
При больших значениях тип вычисление выражения (7.41) затруд-
нительно из-за операции возведения матрицы в натуральную степень. По-
этому требуется найти другие, эквивалентные определению (7.41), формы
записи и алгоритмы эффективного вычисления многочлена от матрицы. Для
упрощения (7.41) имеются две возможности. Во-первых, можно упростить
матрицу А так, чтобы многочлен (7.40) от упрощенной матрицы уже вы-
числялся сравнительно просто. Например, выражение (7.41) легко вычисля-
ется, если матрица А диагональная. Во-вторых, можно понизить степень т
многочлена, тогда самая трудоемкая операция - возведение матрицы в сте-
пень - упрощается.
ИСПОЛЬЗОВАНИЕ ЖОРДАНОВОЙ ФОРМЫ МАТРИЦЫ
Использование жордановой формы для нахождения многочлена от
матрицы основано на трех свойствах.
1. Многочлены от подобных матриц подобны.
Действительно, пусть при помощи преобразования подобия матрица
А приведена к жордановой форме J А: J А = S~XAS. Подставим
А = S JAS~l в правую часть (7.41):
/(А) - am(sJAS-'J” + (sJAS~l )"' +... + aJsJAS~l)+ a0E .
Учитывая, что = SJAS~l SJAS~l ,.. SJAS~l =5 JAS~l для любого
к множителей J А
натурального к, получаем
/(А)= s(amJ% + am_lJA~l +... + a,JA + пое)S-1 = S f(jA)S~'.
331
Таким образом, многочлены /(а) и /(/Л) подобны (с той же самой
преобразующей матрицей 5):
A = SJaS~1 => f(A)=Sf(JA)S~l.
2. Многочлен от блочно-диагональной матрицы является блочно-
диагональной матрицей.
„ (А, О}
Пусть А = I — — I, где и Л2 - квадратные матрицы, а О - нуле-
вые матрицы соответствующих размеров. Для блочно-диагональных матриц
справедливы равенства (они следуют из операций над блочными матрицами
(см. разд.1.5.1)):
о'
О А2) (о а^
аЛ*-(а*А1*
акА о
, где к& N.
Поэтому /(а)=
f/(A)
I о
о 1
Ж)/
Для большего числа блоков доказательство
о '
аналогичное.
3. Многочлен (7.41) от жордановой клетки Jr(k0) имеет вид
(7.42)
О О
Это верхняя треугольная матрица г -го порядка, на главной диагонали кото-
рой стоят значения функции /(Z.) в точке А,о , над диагональю - значения
первой производной в этой же точке и т.д., т.е. коэффициенты ряда Тейлора
[19,25,44] для функции /(Л).
Действительно, разложим многочлен (7.40) по формуле Тейлора в ок-
рестности точки Л = Ло :
/М=Ж)+^Ж)(^-^о)+^/%)(^-^о)2+--+-к:/(т)(Хо)(Х-ХоГ.
1! 2! т!
Остаточный член в данном случае равен нулю, так как все производные бо-
лее высокого порядка, чем т, тождественно равны нулю. При вычислении
/(Л(А-о)) линейный двучлен (Х-Хо) заменяется матрицей
332
у которой элементы над главной диагональю равны единице, а остальные
элементы равны нулю, т.е. I = (0 ех ег ••• ег-Х), где et - i-й столбец
единичной матрицы г -го порядка.
Можно показать, что при возведении в степень единичные элементы
матрицы I смещаются вверх:
I2 =(0 0 ех е2 ег_2),13 = (р 0 0 е, ег_3) и т.д.,
причем 1к - нулевая матрица при к > г. Подставляя эти матрицы в форму-
лу Тейлора, получаем
/(A)-/(A0)E+lr(Z0)-7+l/^0).Z2+... + ^/W(Z0)./m.
1! 2! т!
Складывая матрицы в правой части, получаем квадратную матрицу г -го по-
рядка, у которой элементы главной диагонали равны /(Хо), элементы над
главной диагональю равны ~ /'(Ло) и т.д., т.е. матрицу вида (7.42).
Пример 7.16. Найти многочлен /(Л.)=Х2 +Х + 1 от матриц
'2 1 О' "2 1 О' f2 1 О'
а) А = 0 2 1 , б) В = 0 2 0 , в) С = 0 2 0
0 0 2> 0 2, <° о з,
□ а) Матрица А - это жорданова клетка 3-го порядка, соответствую-
щая собственному значению 2: А = 73(2). Находим значения функции и ее
производных в точке Л = 2: /(2)=7, /'(2) = 5, /"(2)=2. Составляем мат-
рицу вида (7.42), учитывая, что г = 3:
333
/(2)
/(A)=/(j3(2)) =
Г(2) Г(2У
1! 2!
/(2)
0 /(2)
'7 5
0 7
<0 0
f
5
7,
б) Матрица В имеет жорданову форму В = diag(j2(2), (2)), т.е. явля-
ется блочно-диагональной. По свойству 2 многочлен от матрицы В являет-
ся блочно-диагональной матрицей. Записываем многочлен /(X) от каждой
жордановой клетки по формуле (7.42):
/(А(2))= . /(А(2))=/(2)=7.
О
Здесь число 7 рассматривается как квадратная матрица 1-го порядка. Со-
ставляем из этих квадратных матриц искомую блочно-диагональную
матрицу
f(B) = diag
. х (1 5 0^
(7 5) )
1(7) = 0 7 0 .
^0 1) V ' -----—
О 7J
в) Матрица С имеет жорданову форму С = diag{j2(?.\ /Дз)), т.е. явля-
ется блочно-диагональной. Записываем многочлен /(1) от каждой жорда-
новой клетки по формуле (7.42):
/(Л (2)) = ^ /(А(3))=/(3)=13.
Составляем из этих квадратных матриц искомую блочно-диагональную
матрицу
ПЕРВЫЙ СПОСОБ НАХОЖДЕНИЯ МНОГОЧЛЕНА ОТ МАТРИЦЫ
1. Привести матрицу А к жордановой форме J А = S~lAS , т.е. опреде-
лить жорданову форму JA и преобразующую матрицу 5 .
2. Составить блочно-диагональную матрицу /(/д), размещая на ее
диагонали многочлены от жордановых клеток (7.42).
3. Найти многочлен от матрицы А по формуле /(а)=5 f(jA)S~l.
334
Пример 7.17. Найти многочлен /(Х) = Хт (при т > 1) от матриц:
( 4
А =
1-1
В = 0 1-1
-1 -1 1,
'1 1 Г
с= 1 1 1
J 1 b
'—2 5 -3'
-2 5 -3
J -1 о>
4
О
Г1 о 1 >
□ Матрица А . 1. Жорданова форма J А и преобразующая матрица 5
были найдены в примере 7.15:
(2 1^ f 2 1А . ГО -1)
^0 2) l“l Oj I1 2 J
2. Жорданова форма JA состоит из одной жордановой клетки
= J2(2) 2-го порядка, соответствующей собственному значению X = 2.
Найдем значения функции /(Х)=Хт и ее производной = при
Л = 2: /(2) = 2т, f'(2) = m2m 1. Запишем многочлен от жордановой формы
(блочно-диагональную матрицу с одним блоком):
т2т~1
2т
2m+1
3. Найдем многочлен от матрицы А :
2т m2'”-1W0 -Г|_Г2 1\рп2т’1
О 2т ) (j 2 Jl-1 I 2m
= Г(т + 1)2и m2m+x
[-m2”-1 -(m-l)2mJ
Матрица В . 1 Жорданова форма JB и преобразующая матрица 5
были найдены в примере 7.15:
'1 1 (Г| Г-1 0 1Л Го 1 О'
JB = 0 1 1 , 5= 1 0 0, $*’= 0 0 -1 .
<° 0 J [о -1 о] [1 1 0,
2. Жорданова форма Jв состоит из одной жордановой клетки
/в=/з(1) 3-го порядка, соответствующей собственному значению Л = 1.
Найдем значения функции /(Л) и ее производных /'(Л), /"(X) при Х = 1:
/(1) = 1, /'(!)=ш, Г(1) = т(т -1). Запишем многочлен от жордановой фор-
мы (г =3):
3. Найдем многочлен от матрицы В :
335
Г1
Лв)= 1
. о
О
о
-1
ml
О5
-1
О ,
1 Му"'
1- 2
m(m-l
2~
-т
। + т\т
2
-т
-т
1
Матрица С. 1. Жорданова форма Jc
были найдены в примере 7.15:
преобразующая матрица 5
'О О О'
Jc = 0 0 0 ,
0 0 3
( 1
1
-2
о
1
-1
-1
-1
(1
S~l = -1
к 3
_1
3
1
3
1
о
о
1
о
о
т
1
О
2
т
1
m
и
S =
О
О
1
1
о
1
з
О
2. Жорданова форма Jc состоит
рядка Jc = diag(jx(о), Jj(о), J, (з)), соответствующих собственным значени-
ям Х = 0 и X = 3. Найдем значения функции /(Х)=Хт при Х = 0 и Х = 3:
/(о) = 0, /(з) = Зт. Запишем многочлен от жордановой формы:
из трех жордановых клеток 1-го по-
Го
О
О
3«
о
о
3. Найдем многочлен от матрицы С :
( 1
/(с)= 1
-2
о
1
-1
-1
-1
О VI
о
зт
3
-1
з зУ
3«-1
3^-1
3т-1
Зт~1
Зт~1
Зт~1
3тЧ
3«-1
= 3'
Результат совпадает с найденным в примерах 7.10, 7.12.
Матрица D. 1. Жорданова форма
были найдены в примере 7.15:
JD и преобразующая матрица S
'О 1 О'
JD= О О 0 ;
0 0 3,
5
2
-1
9'
9
0.
5"‘ =
3
-1
-1
-3
2
3'
О
-1,
5 = -
9
о
о
о
о
о
о
з
1
з
О
з
3
3
1
1
1
1
1
1
1
336
2. Жорданова форма JD состоит из двух жордановых клеток 2-го и
1-го порядков JD = diag(j2(o), -Л(з)), соответствующих собственным значе-
ниям X = О и X = 3. Найдем значения функции /(о) - 0, /(3)-- Зт и произ-
водной /'(о) = 0 (так как т > 1). Запишем многочлен от жордановой формы
f(jD)=diag(f(j2(o)\f(jl(3)))= '0 0 0 0' 0 0 0 3"\
3. Найде :m многочлен от матрицы D : '3 5 9WO 0 0W1 -1 3 ' 1 2 -P
/(o>4- 3 2 9 00 0-3 -3 ч3 -1 OJ (o 0 3m) (-1 2 0 = 3m - 1 2 -1 3 0 0,
ИСПОЛЬЗОВАНИЕ АННУЛИРУЮЩИХ МНОГОЧЛЕНОВ
Для понижения степени многочлена (7.41) можно использовать анну-
лирующие многочлены матрицы А, например, ее характеристический
ДЛ(Х) = det(A-XE) или минимальный HaW многочлены.
Обозначим через v степень минимального многочлена
цА(Х) = (Х-Х1)т‘ -(х-х^ •...•(*-ЛУ"*
Заметим, что v не превосходит порядка п матрицы А (или, что то же са-
мое, степени п характеристического многочлена ДА(Х)), т.е.
V = mt + ... + тк < п. Разделим заданный многочлен (7.40) на минимальный:
/(Х)=9(Х)цА(Х)+г(Х). (7.43)
Здесь <?(Х) - частное, а г(Х) - остаток, степень которого меньше v :
г(Х) = rv_1Xv~1 + rv_2Xv ~2 +... + rtX + г0. (7.44)
Подставив в (7.43) вместо переменной Л матрицу А , получим:
/(л) = г(А), (7.45)
поскольку минимальный многочлен является аннулирующим (цА(л)=О).
Таким образом, вместо вычисления многочлена (7.41) степени т мож-
но вычислить многочлен (7.44), степень которого меньше v . Коэффициенты
г0, И...., rv_j многочлена (7.44) находятся следующим образом.
Если все корни минимального многочлена простые, то, подставляя ко-
рень в (7.43), получаем /(Х;) = г(Х;), так как ЦА(Х;) = 0, т.е.
/(* J= 'v-AT* + rv-2A72 +- + 'i\ +'•(), j = l.-,V .
22 - 4549
337
Если Л j - корень минимального многочлена кратности , учитывая,
что цЛ(Л?) = О, Цд(Ху) = О,...,Ц^,у ^(х?)=О (см. (В.12) в разд. В.4), из
(7.43), последовательно дифференцируя, получаем
Записывая равенства (7.46) для каждого корня минимального многочлена,
получим совместную систему v линейных уравнений с v неизвестными
ro > Г1 rv-i •
ВТОРОЙ СПОСОБ НАХОЖДЕНИЯ МНОГОЧЛЕНА ОТ МАТРИЦЫ
1. Найти минимальный многочлен цЛ(А) матрицы А одним из спосо-
бов, рассмотренных в разд.7.2.4. Определить его степень v и записать мно-
гочлен (7.44) с неопределенными коэффициентами r0, qrv-1 :
r(X)=rv_]A. '+rv_2XV 2+... + Г]Л + .
2. Для каждого корня (кратности ) минимального многочлена
по формулам (7.46) составить уравнений. Все уравнения объединить в
одну систему.
3. Решить составленную систему, т.е. найти коэффициенты
r0, qrv_( многочлена г(Л.).
4. По формуле (7.45) найти многочлен от матрицы:
/(а)= г(а) = rv_1Av"1 + rv_2Av~2 +... + zj А + r0E.
Замечания 7.8.
1. Вместо минимального многочлена можно использовать характери-
стический многочлен матрицы, который также является аннулирующим (см.
теорему 7.7 Гамильтона-Кэли в разд.7.2.4). При этом в п.1,2 алгоритма ми-
нимальный многочлен заменяется характеристическим, степень которого
равна п .
2. В первом способе нахождения многочлена от матрицы используются
все инвариантные множители, так как нужно получить жорданову форму.
Во втором способе требуется только один последний инвариантный множи-
тель, который совпадает с минимальным многочленом. Можно сказать, что
жорданова форма матрицы излишне информативна для решения поставлен-
ной задачи.
338
Пример 7.18. Найти (вторым способом) многочлен
/(Х) = Г
(при
т > 1) от матриц:
fl 0 1 '
; В= 0 1 -1
-1 -1 1,
"1 1 Г
<7=111
<1 1 к
(-2 5 -3>
D= -2 5 -3
J "I О,
□ Матрица А . 1. Для матрицы А в примере 7.15 были найдены инва-
риантные множители. Минимальный многочлен совпадает с последним ин-
вариантным множителем (см. свойство 6 в разд.7.2.4). Поэтому
цл(Л) = е2(Л)=(Л-2)2. Степень v минимального многочлена равна двум.
Значит, многочлен (7.44) линейный: г(Л) = rjk + г0.
2. Для двойного корня Л = Л1=2 (т1=2) составляем уравнения (7.46):
/(2)=г(2),
df(k)
dk
_ dr(k)
Х=2 dk
2m=r1-2 + r0,
m2'"4 = г,.
Х=2
3. Решая систему, получаем q = т2т~1
г(к)—т2т~1-к + (1
4. Находим многочлен от матрицы А :
4 4Ъ1_т)2'"Р 0И('и+1)2'п т2И+1
-1 (J [б 1J I -т2т~1 -(т-1)2т
> го
/(А)=г(А) = т2‘
Матрица В . 1. Инвариантные множители характеристической матри-
цы (В-ЛЕ) найдены в примере 7.15. Минимальный многочлен равен по-
следнему инвариантному множителю: цв(Л)=е3(Л)=(Л-1)3. Степень v
минимального многочлена равна 3. Значит, многочлен (7.44) - это квадрат-
ный трехчлен: г(Л) = г2Л2 + zjX + г0.
2. Для тройного корня Л = Л1=1 (т1=3) составляем уравнения (7.46):
df(k) _ dr(k)
d^ x=i dk Х=1
d2f(k) __ d2r(k)
dk X=1 dk x=]
r=r2-l2+zj-l + r0,
m I”1-1 - 2r2 • 1 + »j,
т(т-1)-Г~2 =2r2.
22*
339
_ га т -11 /
3. Решая систему, получаем г2=—г\=т\
w-l) ,2 / , (w-l)(w-2)
---’--К + т{т-2)Х + ±---------
2--2
2 'l
-2
1
-1
2
-2
Г° 2
4. Вычисляя В2 -
и г(Х)=
( О
1
-2
, записываем искомый многочлен:
/(я)=г(в) = »
-1
2
-2
' О
1
.-2
2 1 f 1
-2 +m(2-w)- О
1
О'
О
1.
« тут
2~
— т
I’1
m(m-l)
2
-т
О
1
-1
1
-1
1
2
О
О
О
1
О
т
- т
1
Матрица С. 1. Минимальный многочлен найден в примере 7.15.
цс(х) = Х(Х -3). Степень v многочлена равна 2. Следовательно, многочлен
(7.44) имеет первую степень: r(x) = г, X + г0 .
2. Для каждого простого корня X = Xt = 0 и Х = Х2=3 записываем пер-
вое равенство из (7.46):
/(0) = r(0), |0т=г1.0 + го,
Z(3)=r(3), |зт = Г|-3+г0 .
3. Решая систему, получаем = Зт 1, г0 = 0 и г(х) = З7"*1 X.
4. Находим многочлен от матрицы С :
А 1 f
/(c) = r(c) = 3m’1C = 3m'1 • 111.
Ь 1 I
Найдем /(с), используя характеристический многочлен вместо ми-
нимального. Согласно п.1 замечаний 7.8, выполняем все действия второго
способа, заменяя минимальный многочлен характеристическим.
1. Найдем характеристический многочлен матрицы С (см. при-
мер 7.11): Ас (X) = X2 (з - X). Это многочлен 3-й степени. Поэтому многочлен
(7.44) будет 2-ой степени: r(x) = r2X2 + zjX + г0.
2. Для двойного корня X = 0 записываем два уравнения из (7.46), а для
простого корня X = 3 одно:
340
/(0) = r(0),
#(x) _
z=o x=o
/(3) = r(3),
O'" =r2 -02 +zi O+ro ,
m - O'"-1 = 2r2 -0 + rj ,
3m =r2-32+q-3 + r0 .
3. Решая систему, получаем r2=3'"2, и =r0 =0 и r(A.) = 3m 2A.2.
"3 3
4. Вычисляя C2 = 3 3
3'
3 , записываем искомый многочлен:
Поскольку степень характеристического многочлена больше степени
минимального многочлена (3 > 2 ), его применение менее эффективно.
Матрица D . 1. Инвариантные множители характеристической матри-
цы (z>-A.£) найдены в примере 7.15. Минимальный многочлен равен по-
следнему инвариантному множителю: piD(A.) = e3(A) = А?(А.-3). Степень v
минимального многочлена равна 3. Значит, многочлен (7.44) - это квадрат-
ный трехчлен: r(A.) = r2A.2 + А. + rQ.
2. Для двойного корня А. = А.[ = 0 (т1 = 2) записываем первые два ра-
венства (7.46), а для простого корня А. = А.2 = 3 ( zm2 = 1) - первое равенство
из (7.46). Получаем систему трех уравнений относительно коэффициентов
квадратного трехчлена г (А.):
#(*) = dr(x)
х=о х=о
Z(3) = r(3),
О'" = г2 • О2 + ?i 0 + г0 ,
- т О'"-1 = 1гг • 0 + Г] ,
3'"=г2-32 + г]-3 + г0.
3. Решая систему, получаем г2 = Зт 2, г, = г0 = 0 и r(A.) = Зт 2 А.2.
4. Находим многочлен от матрицы D:
'-2 5 -3? Г-1 2 -1"
/(£>)= г(£>) = 3"”2£>2 =Зт-2 • -2 5 -3 = Зт • -1 2 -1
I1 -1 0 ) [ 0 0 0 ,
341
Эта формула справедлива при т > 1, так как при т = 1 или т = 0 в системе
для нахождения коэффициентов многочлена г(л) появляются неопределен-
ные выражения (0°). Впрочем, для этих показателей степени (т = 1, т - 0)
многочлен /(о) легко находится по определению £>'=£>, D° = Е.
Все результаты совпадают с полученными в примере 7.17.
7.3.5. Применение многочленов от матриц для решения систем
линейных рекуррентных уравнений с постоянными коэффициентами
Рассмотрим систему линейных рекуррентных уравнений
x1(fc + l)=a11x](^)+aI2x2(fc)+... + alnx„(t)+/1(^),
(7.47)
х„ (Л +1) = ап} х, (Л) + ал2х2 (*)+... + аппх„ (к) + fn (к),
где а,у - коэффициенты системы, / (к) - заданные, а х, (л) - неизвестные
функции дискретного аргумента к, к = к0,к0 + 1, £0 + 2,.... При описании
дискретных динамических систем [31] аргумент к в (7.47) называют дис-
кретным временем.
Систему (7.47) можно записать в матричном виде:
х(А: + 1)=Лх(л)+/(л), (7.48)
где А - квадратная матрица (п -го порядка) коэффициентов системы рекур-
рентных уравнений, f(k) = {f\(k) /„(к))1 - столбец заданных функций,
а х(к)=(х}(к) хп(к))Т - столбец неизвестных.
Решением системы (TAi) называется последовательность столбцов
{х(А:))“=Ао , при подстановке которых в (7.48) получаются верные равенства
для всех к = kQ, к0 +1, к0 + 2,....
Поставим задачу нахождения решения системы (7.48), удовлетворяю-
щего начальным условиям
х(^0)=х0, (7.49)
гдех0=(х]0 хп0У - заданный столбец.
Рассмотрим сначала однородную систему (f(k) s о) с постоянными
коэффициентами
х(к + 1)= Ах(к), к =к0, к0 +1, к0 +2,.... (7-50)
Записывая (7.50) для к = к0,к0 +1Д0 +2,..., последовательно получаем
х(к0 +1)= Ах{к0), х(к0 +2)= Ах(к0 + 1) = А2х[к0) и т.д. Следовательно, реше-
ние однородной системы (7.50), удовлетворяющее начальным условиям
(7.49), имеет вид:
342
х(к) = Ак k°xQ, k - к0, к0 +1, k0 +2,.... (7-51)
Получим теперь решение системы (7.48). Учитывая (7.49), запишем
(7.48) для к = к0, к0 +1, к0 + 2,...:
х(ко + 0= Лх(*о)+ Лк0)= Ахо + Ж)>
х(*о + 2)= Ах(к0 +1)+ f(kQ +1) = А • [ Ах0 + f(kQ) ]+ f(kQ +1)=
= ЛЧ+Л/(£0)+/(£0+1),
х(А) = Ах(к -1)+ f(k -1) = А + f(k -1)+ Af(k - 2)+... + )
и т.д. Следовательно, решение системы (7.48) имеет вид
x{k}=Ak~k°xQ/fs-j-'f(jY (7-52)
j=k0
Первое слагаемое в (7.52) - решение однородной системы (7.50) с началь-
ными условиями (7.49), второе слагаемое - решение системы (7.48) с нуле-
выми начальными условиями (т.е. при х(&0)=о ).
АЛГОРИТМ РЕШЕНИЯ СИСТЕМЫ РЕКУРРЕНТНЫХ УРАВНЕНИЙ
Для нахождения решения системы (7.48) с начальными условиями
(7.49) требуется выполнить следующие действия.
1. Найти выражение для степени матрицы Ак одним из способов, рас-
смотренных в п.7.3.4.
2. Записать по формуле (7.52) искомое решение.
Замечания 7.9.
1. Линейное рекуррентное уравнение с постоянными коэффициентами:
а„х(к + п)+ a„_lX{k + п -1)+... + аох(к) = f0(k)
может быть сведено к эквивалентной системе рекуррентных уравнений вида
(7.47). Действительно, используя обозначения
Х\(к) = х(к), х2(к)=х(к + 1.), ..., хп(к) = х(к + п-\),
получаем
Х1(£ + 1)=х2(*),
х_,(* + 1)= *„(*),
а а« а
Л П П
343
или в матричной форме (7.48): х(к +1)= Ах(к}+ f(k} с матрицами А и
Ак}-
' 0 1 0 ••• 0 Г 0 >
0 0 1-0
А = > Ак}- 0
0 0 0 1 /о(^)
а0 а\ а1 ап-1
ч ап ап ап ап > < ап J
2. Применение других методов для решения систем рекуррентных
уравнений рассмотрено в [31].
Пример 7.19. Найти решение рекуррентного уравнения
х(Х + 2)-Зх(Х + 1)-4х(х)= О
с начальными условиями х(1)=3, х(2) = 13.
□ В соответствии с п.1 замечаний 7.11 составим систему уравнений
Г х,(Л + 1) = х2(А:),
[х2 (Л +1) = 4х[ (к) + Зх2 (к),
где Х|(х)=х(х), х2(х) = х(Х + 1). Требуется найти решение этой системы,
удовлетворяющее начальным условиям: х, (1) = 3, х2 (1) = 13 .
(О 1] к
1. Составим матрицу системы А = | I и найдем ее степень А , ис-
пользуя второй способ в разд.7.3.4. Характеристический многочлен
АлМ=
-X 1
4 3-Х
= X2 - ЗХ - 4 имеет вторую степень и два простых корня:
X, =-1, Х2 = 4. Поэтому многочлен (7.44) - линейный: г(х) = г1Х + г0. Для
его коэффициентов записываем систему (7.46):
М-1)=г(-1), |(-1)>=Г|.(_|)+Го,
I /(4)-Н«). 4*=Г[-4 + г0.
Отсюда Г] =
j[4‘-(-I)* ]. 4> = j[4‘+4'
(-1)* ]. Таким образом,
Ак =г(л)=г1Л + г0£ = |[4*-(-1)* ]-Л + |[4*+4-(-1)* ]£ =
= lf 4*+4-(-1)* 4*-(-1)*'
5[4*+,-4(-1)* 4‘+I+(-!)*/
344
2. По формуле (7.52) записываем решение системы (учитывая, что
*о=1> /G>0):
ГхДЛ^^Гд*-' + 4-(-1)*-1 4*-’ -(-1)*-'V 3 Л
Д(*)у 5^ 4*-4-(-l/_1 4*+(-1)*“' Д13/
Нас интересует только первый элемент этого столбца:
Решение совпадает с найденным в примере 2.15 (см. разд. 2.4.2).
Пример 7.20. Найти решение системы рекуррентных уравнений:
X] (к +1) = -2xj (Л) + 5х2 (к) - Зх3 {к) + к,
< x2(A: + l) = -2x](^)+5x2(^)-3x3(A)+3t,
(7.53)
с начальными условиями X] (о) = 1, х2 (о) = 2, х3 (о) = 1.
□ Запишем систему в матричной форме (7.48):
х(к +1) = Dx{k)+ f(k), где D = - 2
и начальные условия х(0)=хо=(1 2 if.
1. Выражение для степени матрицы D
5
5
-1
-3"| Г к
-3 , /(*)= 3'
0
-к
найдено в примерах 7.17 и 7.18:
£>* = 3*
-1
-1
О
2. Выражение, полученное для
пример 7.18). Поэтому для к = 0; 1
Найдем х(1), х(2) непосредственно из системы (7.53)
-Г
-1 при Л = 2,3,....
°,
Dk, справедливо только при к > 1 (см.
формулу (7.52) нельзя использовать.
2
2
О
к
'-2 5 -3' Т '5'
x(l)=Dx(0)+/(0)= -2 5 -3 2 Н F 3° = 6
J -1 °, Л <-1,
-2 5 -3' '5' '24'
x(2)=Dx(l)+/(l) = -2 5 -3 • 6 ь З1 = 26
1 -1 0, ,-1, <-1,
Далее записываем искомое решение
(7.52) слагаемые с D° = Е и D} = D :
для Л = 3,4,..., выделяя в формуле
345
x(Zr) = DkxQ + E f(k -1)+ D f{k - 2)+ X Dk-^f{j) =
J=o
5
5
-1
-3
-3
0
' k-2 '
з*-2
.-Л + 2,
к-3 '-1 2 -Г ' j 2-3*+2Л-3 + 5-3*-2 к-3 '2'
-1 2 -1 V = 2-3*+3*-1+Л-2 + 5-3*-2 + Хз*-1 2
7=0 .0 0 °, ~ Л -З*-2 -1 к > 7=0 А
В последней сумме слагаемые не зависят от индекса суммирования, т.е. это
сумма (к-2} одинаковых слагаемых. Поэтому, приводя подобные члены,
получаем
х(А) =
"гл-з+гз-з*-2"
Л-2 + 26-3*-2
-1-3*-2
2(Л-2)-3*-1
+ 2(Л-2)-3*-1
О
2Л-3+ (бЛ +11)-3*-2>
Л-2 + (бЛ + 14)-3*-2
-1-3*-2
Таким образом, решением заданной системы является последовательность
столбцов:
( 24Л
2к -3 + (бЛ + 11)-3*-2'
х(1)= 6 , х(2)= 26 , х(л) = Л-2 + (бЛ + 14)-3*-2
-1-3*-2
1-2.
где к >3.
7.4. ФУНКЦИИ ОТ МАТРИЦ
Пусть А - числовая квадратная матрица и /(х) - скалярная функция
переменной 1. В этом разделе понятие функции распространяется на мат-
ричные значения аргумента. Если /(Х) - многочлен, то задача нахождения
многочлена /(л), получающегося при подстановке матрицы А вместо пе-
ременной X, была решена в разд.7.3.4. Требуется определить, что следует
понимать под выражением /(л) для достаточно произвольной функции
/(х). Разумеется, что определение функции от матрицы, когда функция яв-
ляется многочленом, должно совпадать с определением многочлена от мат-
рицы (см. разд. 1.3.4, 7.3.4).
346
7.4.1. Функции, определенные на спектре матрицы
Напомним, что спектром квадратной матрицы А называется совокуп-
ность всех ее собственных значений (корней характеристического много-
члена). Все собственные значения являются также корнями минимального
многочлена (см. свойство 3 минимального многочлена в разд. 7.2.4):
ЦЛ(Х)=(Х-X,/"- (Х-Х2^ •...•(*-**)'"* , (7.54)
где А.] - корень кратности т}, Х2 - корень кратности т2 и т.д. Степень v
минимального многочлена не превосходит порядка п матрицы А:
v = т} + т2 + ...+ тк <п .
Говорят, что скалярная функция /(х) переменной X определена на
спектре матрицы А , если для функции /(х) определены значения
А),/'(X,),...,/""^(Xj, i = l, 2,...,*, (7.55)
т.е. функция /(х) определена в окрестности каждой точки X = X,-
(i = 1, 2,...,* ) вместе со своими производными до указанного порядка. Сово-
купность (7.55) значений функции и ее производных будем обозначать
Ж).
Две функции /(х) и g(x) называются равными на спектре матрицы
А, если
Ж = Ж, Ж) = Ж,-., /('B'“’)(Xl)=g(m-’l)(xJ, /=1,2,...,*. (7.56)
Эти равенства будем записывать в форме /(Л^ ) = g(AA ).
Теорема 7.10 (основное свойство многочленов от матриц). Если
f (X) и g(x) - многочлены, то
Ж)=Ж) О /W=g(x), (7.57)
т.е. многочлены, равные на спектре матрицы, имеют равные матричные
значения, и наоборот, если равны матричные значения многочленов, то рав-
ны их значения на спектре матрицы. Другими словами, значения
многочлена на спектре матрицы полностью определяют его значение /(л)
От матрицы А .
В самом деле, пусть /(л)= g(^), тогда разность о’(х) = /(x)-g(x) яв-
ляется аннулирующим многочленом: ог(л) = О . Разделим его на минималь-
ный многочлен с/(х) = д(а) ц^(х) (свойство 1 в разд.7.2.4). Из (7.54) следу-
ет, что число X,- является корнем многочлена с/(х), причем его кратность
больше или равна /л,-. Тогда (см. (В. 12) в разд. В.4):
rf(X,) = 0, cZ'(xJ = 0</'"н)(Х()=0,/ = 1,2,...,*,
347
что равносильно (7.56). Следовательно, /(ЛЛ)=#(ЛЛ). Достаточность до-
казана. Для доказательства необходимости нужно все рассуждения провести
в обратном порядке, либо вернуться ко второму способу нахождения много-
члена от матрицы в разд.7.3.4: в системе (7.46), которая позволяет найти ко-
эффициенты искомого многочлена, левые части уравнений являются значе-
ниями многочлена /(X) на спектре матрицы А .
7.4.2. Определение и свойства функций от матриц
Основное свойство (7.57), справедливое для многочленов, переносится
на произвольные функции и фактически берется за основу определения
функции от матрицы.
Пусть /(X) - произвольная функция, определенная на спектре матри-
цы А . Значение /(а) функции /(X) от матрицы А определяется равен-
ством
/(А)=я(А), (7.58)
где g(X) - любой многочлен, принимающий на спектре матрицы А те же
значения, что /(X): /(Лл)= я(лл).
Поскольку функции от матриц определяются через многочлены, то на
них переносятся свойства многочленов от матриц, рассмотренные в
разд.7.3.4.
1. Функции от подобных матриц подобны.
2. Функция от блочно-диагональной матрицы является блочно-
диагональной матрицей, т.е. если матрица А имеет вид A = diag(Al,...,Ak),
где Al,...,Ak некоторые квадратные матрицы, то
М = diagif^f(Ak)).
3. Функция /(X) от жордановой клетки 7г(Х0) имеет вид
7м у/М ••
/(лМ)= о /к) • (7.59)
. ° ° • fM ,
Это верхняя треугольная матрица г -го порядка, на главной диагонали кото-
рой стоят значения функции /(X) в точке Хо, над диагональю - значения
первой производной в этой же точке и т.д., т.е. коэффициенты формулы
Тейлора для функции /(X).
348
ТАЗ. Способы нахождения функций от матриц
Из определения функции от матрицы следует, что первый и второй
способы нахождения многочлена от матрицы, рассмотренные в разд.7.3.4,
пригодны и для любой функции, определенной на спектре матрицы. Поэто-
му они могут считаться первым и вторым способами нахождения функ-
ции от матрицы. Далее излагается третий {интерполяционный) способ
решения этой же задачи.
(4 4
Пример 7.21. Найти функцию /(Л,)=ех от матрицы А = 1
□ Первый способ (см. разд.7.3.4). 1. Жорданова форма JА и преобра-
зующая матрица S были найдены в примере 7.15:
(2 1) „ (2 1) (О -Г|
J. = ,S= , S 1 =
А ^0 2J 1~1 Oj U 2 J
2. Жорданова форма JA состоит из одной жордановой клетки
Л=Л(2) 2-го порядка, соответствующей собственному значению Л = 2.
Найдем значение функции /(2) = е2 и ее производной /'(2)=е2. Запишем
функцию от жордановой формы (7.59):
3. Найдем функцию от матрицы А :
/х а / X -1 (2 1Л , Л1 1Л fO
f(A)=eA =S f(jA}S *= -L J’ ,
v ' A> ^-10 (0 1J ^1
4
-1
Второй способ (см. разд.7.3.4). 1. Минимальный многочлен матрицы
А найден в примере 7.18: цЛ(Х)=е2(^)=(^-2)2- Степень V минимального
многочлена равна 2. Значит, многочлен (7.44) линейный: г(Л)= r\k + г0 .
2. Для двойного корня X = Х] = 2 (wij = 2 ) составляем уравнения (7.46):
/(2)=г(2),
Г(2)=/(2),
e2=q-2 + r0,
е2 = г..
3. Решая систему, получаем гх ~е2 , г0=-е2 и г(Х)=е2Х-е2.
4. Находим функцию от матрицы А :
! \ А / \ 2 ( 3 4 4>| 2 Г1 0^1 , ( 3 4 А
/(а) = ел = г(а) = е2 • _ -е • =е2'1
М ’ ^-1 Oj (0 1J ^-1 -1J
Полученные разными способами результаты, разумеется, совпадают.
349
ИНТЕРПОЛЯЦИОННЫЙ СПОСОБ НАХОЖДЕНИЯ ФУНКЦИИ ОТ МАТРИЦЫ
Рассмотрим сначала частный случай, когда все корни минимального
многочлена простые: цл(х)=(Х-Х|)(Х-Х2)-...-(А.-Xv). В этом случае зна-
чения функции на спектре матрицы А — это совокупность значений функ-
ции /(М в точках X,, Х2V /(A^)={/(Xt),/(X2),...,/(Xv)}. Обозна-
чим через г(х) интерполяционный многочлен Лагранжа [8,21,39]:
для которого r(X,)= /(X,), i = . Тогда
(х. _ Х|)..... (х. - X). (х. - Х/+](х,. - xv)
Таким образом, для нахождения функции /(х) от матрицы А в случае
простых корней минимального многочлена, нужно выполнить следующие
действия.
1. Найти минимальный многочлен цл(х) одним из способов, рассмот-
ренных в разд. 7.2.4. Убедиться в том, что все корни Х]Д2 ,---Av мини-
мального многочлена простые.
2. Вычислить значения /(Х,),/(Х2),...,/(Xv) функции на спектре
матрицы А и составить по формуле (7.60) интерполяционный многочлен
Лагранжа г(х).
3. Найти значение функции от матрицы /(л) = г(я).
Пример 7.22. Найти функцию /(1)= ех от матрицы С = 1
1
Г
1
1.
1
1
1
□ Интерполяционный способ (случай простых корней). 1. Минималь-
ный многочлен найден в примере 7.12: цс (А.) = Х(Х - з). Все его корни
X] =0, Х2 =3 простые.
2. Находим значения функции на спектре матрицы /(о)= 1, /(з)= е3.
Составляем по формуле (7.60) интерполяционный многочлен Лагранжа:
м Х-3 , Х-0 з е3-1
’ 0-3 3-0 3
3. Находим функцию от матрицы С :
350
/(б?) = ес = r(c) =
'1 1 P
1 1 1
J 1 I
'1 0 0"
+ 010
10 0 1J
e3-l
3-l
e3-l
<?3+2
e3-l
e3-f
e3 -1
e3+2
7
Рассмотрим общий случай, когда минимальный многочлен (7.54)
Цу4(х)=(х-х1)т' (х-ХзУ"2
имеет кратные корни'. Х1 - корень кратности , Х2 - корень кратности
т2 и т.д. Степень v минимального многочлена не превосходит порядка и
матрицы А : v = тх + т2 +... + тк < п .
Многочлен г(х) степени меньшей, чем v, удовлетворяющий
условиям:
АМ4 /'(Х,)=г'(Х,),..., /=1,2,...Л,
называется интерполяционным многочленом Лагранжа-Сильвестра для
функции /(х), определенной на спектре матрицы А .
Многочлен Лагранжа-Сильвестра однозначно определяется значения-
ми функции на спектре матрицы и находится по формуле [10]:
г(*)=£Ьо + /;I(x-x,)+...+^(_1(x-x/)m'-1 W)> (7.61)
1=1
где у,(х) - многочлен, равный отношению минимального многочлена и со-
/. \ Ц Л (^")
ответствующего элементарного делителя: y,(AJ=----а выражение в
квадратных скобках равно сумме первых mi членов разложения функции
,7 = 0,1,...,т,-1;
i = l.к.
Замечания 7.10.
1. Если минимальный многочлен имеет один корень (кратности v):
Hx(l) = (X-X1)v, то многочлен Лагранжа-Сильвестра совпадает с много-
членом Тейлора [19,25,43]. Действительно, в этом случае к = 1, m}=v,
Vi(x) = l, поэтому формула (7.61) принимает вид
’ что совпадает с первыми v членами ряда Тейлора.
1 dj Г /(X) '
у! rfk'Lv/M.
/(х)
— \ . по формуле Тейлора, т.е. г„
w)
351
2. Если все корни минимального многочлена простые:
p^(x) = (X-X1)(X-X2)-...-(X-Xjt), тогда v = k, т{ = т2 = ... = тк =1,
y/.(X)=(X-X1)-...(X-X/_1)-(x-X.+1)-...-(X-Xjt), поэтому формула (7.61)
принимает вид (7.60), т.е. многочлен Лагранжа-Сильвестра совпадает с мно-
гочленом Лагранжа.
3. В [10] рассматриваются также и другие способы нахождения функ-
ции от матрицы.
Для нахождения функции /(х) от матрицы А при наличии кратных
корней минимального многочлена нужно выполнить следующие действия.
1. Найти минимальный многочлен матрицы А :
ц^(х)=(х-х1)и--(х-х2^....(х-х*)и*
одним из способов, рассмотренных в разд. 7.2.4.
2. Для каждого корня X, кратности т, (i = 1,2,..., к) найти многочлен
......... и вычислить коэффициенты г, разложения функции
/л л уИ.-.J
у(х)
—в точке X, по формуле Тейлора:
и
= 1 ,±_\ ~
у! <Д/[ч'<(х)
, j = 0,1,..., mi -I;
3. Составить по формуле (7.61) интерполяционный многочлен г(х)
Лагранжа-Сильвестра.
4. Найти значение функции от матрицы /(л) = г(а).
Пример 7.23. Найти функцию /(х)=е'~ от матрицы
D =
-2
1
5
5
-1
-3
0
□ Интерполяционный способ (случай кратных корней). 1. Минималь-
ный многочлен найден в примере7.15: цо(х) = е3(х)=Х2(Х-3). Корень
X, = 0 - двойной, а Х2 = 3 - простой, т.е. количество различных корней
к = 2 , кратности корней т} = 2, т2 = 1.
2. Для двойного корня X] =0 находим многочлен
(х)
\|/] (х) = ° у = X - 3 и соответствующие коэффициенты
352
rf Г еМ
<Л(Х-3 J
х=о
1 1
х=о
Ге^-3)-ех>)
I № J
х=о
Для простого корня Х2 =3 находим многочлен q/2(l) =
Но(М_
Х-3
и коэф-
фициент г2 0 =
9 '
1=3
4
9'
3. Составляем по формуле (7.61) интерполяционный многочлен Ла-
гранжа - Сильвестра:
'W = ho + ri 1 (х ~ \)]’ Vi М+'го ’ Vz W =
4. Находим функцию от матрицы D :
f(D)=eD
= r(D) = -----D1
v > 9
п с *3-4
+ D + Е =---
9
-9
-9
О
18
18
О
-9'
-9
О
"-2
-2
. 1
5
5
-1
-3'
-3
о
О'
О
1
З-е3
2-е3
1
2е3-3
2е3-2
-1
l-eJ
1-е3
1
О
О
О
1
О
Проверим полученный результат, используя первый способ нахожде-
ния функции от матрицы.
1. В примере 7.15 были найдены жорданова форма матрицы D и пре-
образующая матрица S:
'О 1 О'
JD= 0 0 0 ;
О 0 3.
9
'3 5 9'
3 2 9;
<з -1 о,
<1
S~‘= 3
Г1
-1 3 '
-3 о
2 -L
2. Жорданова форма J D состоит из двух жордановых клеток 2-го и
1-го порядков JD = J/ag(j2(o), Jx (з)), соответствующих собственным значе-
ниям X = О и X = 3. Найдем значения функции на спектре матрицы:
/(О) = 1, /'(о) = 1 и /(з) = е3. Запишем функцию от жордановой формы
/(уо)=^(/(у2(0Й/(л(з)))=
'11 О'
О 1 о
<0 0 <
3. Найдем функцию от матрицы D :
23 - 4549
353
/(D) = eD=S/(jD)5-1=|
"3
3
.3
5 91 f1 1
2 9 0 1
-1 oj |o 0
O'
0
' 1
3
-1
-1 3 '
-3 0
2 -1,
'з-e3 2e3-3 l-e3>
2 —e3 2e3-2 1-e3
1 -1 1
\ /
Результаты, полученные разными способами, совпадают.
7.4.4. Свойства функций от матриц
Многие свойства функций скалярного аргумента распространяются на
функции от матриц [10]. Рассмотрим некоторые из них.
1. Если функция /(X) разлагается в степенной ряд [19,25,33,43]
/М=£л(Х-Х0)*, (7.62)
к=0
сходящийся в круге | X — Хо | < R, то для любой матрицы А, собственные
значения которой лежат внутри круга сходимости, справедливо разложе-
ние
ео
(7.63)
*=о
Здесь предел последовательности матриц (частичных сумм ряда) понимает-
ся поэлементно (см. разд. 6.1), как совокупность пределов элементов матри-
цы. Напомним, что (a -Xqe)° = Е.
В самом деле, степенной ряд можно почленно дифференцировать лю-
бое число раз внутри круга сходимости. Поэтому функция /(X) определена
на спектре любой матрицы, собственные значения которой лежат внутри
круга сходимости.
Из свойства 1 следуют, например, разложения в ряд (7.62) при
еА = Е +—А + —А2 +... + —Ак +...;
1! 2! к\
cosA = Е——А2 + — А4 + ... + (—Г А21 +...;
2! 4! (2к !
354
A2k+l
sinA=lA_±43+ , (-1/
1! 3! (2fc + l)!
справедливые для любой квадратной матрицы А .
2. Если функция /(X) разлагается в степенной ряд, а собственные
значения функциональной матрицы At при всех t лежат внутри круга схо-
димости этого ряда, то определена сложная функция f(At), производная
которой находится по формуле-.
df(At)_A 4f(At)
dt dk
В самом деле, подставим в ряд (7.62) вместо X матрицу At:
4=0
Найдем производную этой функции (см. разд.7.1.1). Учитывая, что много-
члены от одной и той же матрицы перестановочны (см. разд. 1.2.7), по пра-
вилу 3 дифференцирования произведения матриц (см. разд.7.1.1) получаем
dt dt dt
= a(az - хое)+(az - хое)а=2A(Az -Хое),
= .(лz_хое)+(At-Х0Е)2 =
dt dt dt
= 2A(Az -Хо£)2 + (At -Х0Е)2 A =3A(Az -Х0£)2 и т.д.,
т.е. ib~^~ = ^At ~ ‘ Поэтому
“ 4=1
Сравнивая полученный ряд с производной = У'кс. (X - Хо )*~‘ ряда
аХ t=1
(7.62) при подстановке вместо X матрицы At, приходим к доказываемому
равенству.
Пример 7.24. Используя разложение в степенной ряд, найти функцию
Г-2 5 —3^
5 -3 .
и -1 °>
□ Запишем степенной ряд (7.63)
f(D) = eD , где D = -2
23*
355
-2
5 -3
eD=E +—D + — D2 +... + — Dk +
к!
1!
2!
-2
-3
2!
-1
-1
27
3!
-1
-1
-1
-3
-1
-2
-3
-1
-1
Учитывая разложение
е3 =1 + 2.+
1!
-3
Г-1
eD =
-2
-3
-1
-С
-1
-1
Зк
к\
9 27
2! 3!
3*
-1
-1
-1
Зк
к\
9
— + ...+—+..., получаем
2! к\
-1
З-е3
2-е3
-3+2е3
-2 + 2е3
l-eJ
1-е3
9
О
1
5
6
1
1
О
О
о
О
1
О
5
2
2
О
О
5
6
1
2
2
О
О
О
2
2
О
1
О
1
О
2
2
О
О
О
О
О
2
2
-1
1
1
О
О
1
О
-1
1
Результат совпадает с полученным в примере 7.23.
7.4.5. Применение функций от матриц для решения систем линейных
дифференциальных уравнений с постоянными коэффициентами
Рассмотрим систему линейных дифференциальных уравнений с посто-
янными коэффициентами
= ацХ1(г)+<212*2 (')+- + а1»Л.0+ Л0 •
at
= ал1*10 + ая2*2 0 + • + Ялл *л 0 + /л 0 -
где ау - коэффициенты системы, f^t) - заданные, а х( (г) - неизвестные
функции аргумента г, fe [г0; + «). При описании непрерывных динамиче-
ских систем [31] аргумент t обозначает время.
Систему (7.64) можно записать в матричном виде:
^ = Ax(t)+f(t), (7.65)
at
356
где А - квадратная матрица и-го порядка, /(?) = (/1(?) “ - стол-
бец заданных функций, а х(г)=(хх (г) х„(t))Г - столбец неизвестных.
Решением системы (7.65) называют столбец х(г)=(х1(г) хл(г))г
дифференцируемых функций, при подстановке которых в (7.65) получаются
верные равенства, тождественно выполняющиеся при t G [t0; + °°).
Поставим задачу нахождения решения системы (7.65), удовлетворяю-
щего начальным условиям
4'о)=*Ь» С7-66)
гдех0=(х10 хп0)г-заданныйстолбец.
Как известно [10,31,34,39], решение системы (7.65) с начальными ус-
ловиями (7.66) имеет вид:
х(г) = еА^ха + j Л'~х)/(т)<*г. (7.67)
В самом деле, найдем производную функции (7.67). Применяя правило
Лейбница
d \ ^Э/(г,т), / i \\dv / (\\^и
dti) «(*) dt dt dt
и свойство 2 функций от матриц (см. разд.7.4.4), получаем
= Аел('_'°)хо + f AeA^~^f(r)dT+ f(t)-Ax(t) + f(t),
dt }
{0
т.е. x(r) является решением системы (7.65). При г = г0 формула (7.67) дает
x(r0) = е°Хо = Ех0 - х0, где О - нулевая, а Е - единичная матрицы. Равен-
ство е° = Е следует, например, из разложения в ряд функции еА (см. свой-
ство 1 в разд.7.4.4). Следовательно, решение (7.67) удовлетворяет и началь-
ным условиям (7.66).
Поэтому для нахождения решения нужно выполнить следующие дей-
ствия.
1. Найти выражение для функции еА‘ одним из способов, рассмотрен-
ных в разд.7.4.3.
2. Записать искомое решение по формуле (7.67).
Замечания 7.11.
1. Нахождение функции /(А.) от функциональной матрицы At облег-
чается, если учитывать, что собственные значения Х,(г) матрицы At про-
357
порциональны собственным значениям матрицы A: = Дейст-
вительно, характеристический многочлен матрицы At имеет вид
Дл,(А.)= det(/4z-X£)= det
= tn-detf A-—E | = г"д/- I•
I t J {tj
Поэтому, если число - корень характеристического многочлена матрицы
Л : ДЛ(А,)=О , то число X = - корень многочлена Дл,(х), причем той же
кратности. Такая же связь между корнями минимальных многочленов
и если Х; - корень минимального многочлена то Х = А; -
корень минимального многочлена р.А1 (а).
2. Решение линейного дифференциального уравнения с постоянными
коэффициентами a„x^(/)+... + a1x'(z) + aox(t) = b0(t) сводится к решению
системы вида (7.64), получающейся после замены X](r) = x(z),
x2(z)=x'(r),..., x„(z) = x(n’1)(z).
3. Другие методы решения систем линейных дифференциальных урав-
нений рассматриваются в [31,34]. В частности, для нахождения функции
можно использовать следующий способ. Найти п линейно незави-
симых решений ф]0,...,фл(?) однородной системы ^^ = Лх(0 и соста-
dt
вить из этих столбцов фундаментальную матрицу ф(?) = (ф1 (z) ••• фп0)
системы (7.65). В силу линейной независимости столбцов ф1(/),...,фя(/) оп-
ределитель фундаментальной матрицы (определитель Вронского) отличен
от нуля: бе1ф(/)^о для z>z0. Поэтому определена обратная матрица
Ф ’*(z). Как показано в [31,34], функция еА^' (называемая матрицей
Коши, или переходной матрицей) может быть найдена по формуле
И'-т) = ф(?)ф-‘(т).
Пример 7.25. Найти решение системы дифференциальных уравнений
= 4х] (z) + 4х2 (z) + 4,
dt <\
^гй=-х,И-2,
dt 7
удовлетворяющее начальным условиям X] (б) = 1, х2 (б) = 2 .
358
f4 4)
□ 1. Составим матрицу А коэффициентов системы: Л = 1 I и
функцию /(?) = Найдем выражение для функции ек от матрицы
X = At (т.е. функции еА>), используя второй способ нахождения функции от
матрицы (см. разд. 7.3.4, 7.4.3). Минимальный многочлен рл(х)=(Х-2)2
матрицы А был найден в примере 7.18. Согласно п.1 замечаний 7.11, мини-
мальный многочлен матрицы At имеет вид цЛ/(х) = (Х-2/)2. Степень v
минимального многочлена равна 2. Значит, многочлен (7.44) линейный:
г(х) = г, X + г0 . Для двойного корня X = Xj = 2г (т{ = 2) составляем уравне-
ния (7.46) (см. пример 7.21):
е2г = rt -2t+ r0
Решая систему, получаем i\=e2‘, г0=е2'(1-2/) и г(х)=е2<Х + е2,(1-2/).
Находим функцию от матрицы At:
ч (4 4\ „, . (1 (Л fl + 2t At 'I
eAl = r(At) = r.At + rr.E = e2‘ -/ + e2,(l-2/)- =e •
v ’ 1 0 <-i oj 1° V I 1-2/J
2. По формуле (7.67) записываем искомое решение (t0 = 0):
21
4/ V Г
1-2/Дг,
4(/-т) у 4 А
1_2(г_т)Д_2;т
fi+юЛ
I
I2-5')
<2-5/)
if 4Ъ('-)
2l“2J
U-o
= е
Задачи для самостоятельного решения
7.1. Представить Х-матрицы в виде многочленов с матричными коэф-
“ Л. Л,
J , фициентами: а) 2 ; б)
о о"| 2 f-1
х2 +
10 У
Ответ: а)
\2+1 X
. I X2-
1^; б) [1 °
2) 1о 1
1о о
о
-1
359
7.2. Найти левое Рм(а) и правое Р„р(а) значения А-матрицы
rW=f"J
X. ™
X'j
2XJ
при подстановке матрицы А =
fl I4!
вместо
Ь 3J
С -1 "А С1 ? А
Ответ-. Р (д)= ; Р (д) =
левХ / gl пр\ / I J I
7.3. Найти частное (левое <2лев(Х) и правое Qnp(k)) и остаток (левый
R
лев
и правый
при делении Л-матрицы
Х"|
, на
2Х J
К Л
X-матрицу (А-ХЕ), где A=Q
, . ( О
Ответ-. О (Х) =
VjK’v ' 1^-3-Х
-Г1 21
ир-17 ЮГ
3 ЗА
9 8J’
( 1 -Р|
)“(-1_Х -3/
' х3-х
чХ2+5Х
мальному диагональному виду.
V (х О 'I fx о >
(^0 X(X + 2)J (j) Х(Х2-10Х-3/J
7.4. Привести X-матрицы:
f-X
а) X2
х I-
2Х)’
б)
2Х2>|
ЗХ J
к нор-
7.5. Найти собственные значения и соответствующие собственные век-
торы матриц:
Го
” 1
-21
-3 ’
Г 5 -2) Г1 -1)
б) ; в) ;
1-2 8 J 11 -11
|2
е) 4
-1
О
-1
2
О
-1
1
-1
(О
Г)Ь
1'
-1 :
0.
f 2
1
-2
-1
О
1
2
2
-1
О
I о
; л> L
1 у
-2 ’
8
; «)
-1 ; з)
1 .
1
2
; и)
Ответ', a) Xt = -1,
Г1! Л г2] Г 1 1
-2, ; б) Х.=4, , Х,=9, ;
W Ч1/ 4~2J
в) X =Х, =0, I |; г) X = i, ( \ |, X- =-i, | М; д) X. =Х, =-1, | \ |;
U/ i-d Id 1-iJ
360
е)
(2
Л3
Х^О, Х2=1О, Qj; ж) Х1=Х2=1,(1 1 о)г, (-1 О 1)Т,
= 3, (-1 1 о)г; з) Х,=1, (1 1 1)г, Х2=-1, (1 -3 -5)Т, Х3=2,
О 1)г; и) Xj=l, (О 2 1)г, Х2=«, (2 2 j-l)7, Х3=-«,
2 -i -1)г. Собственные векторы матриц определяются неоднозначно.
7.6. Привести матрицы к диагональному виду при помощи преобразо-
вания подобия (найти диагональный вид Л и преобразующую матрицу S):
'1 0 3'
а) 2 1 2 ; б)
.3 0 1
Ответ:
а)
1 ; в)
1.
'о
о
3
.-1
0
о
4
-1
1
о
о
о
о'
1
о
0.
г)
-1
1
-1
1
-1
1
1
-1
1
-1
1
-1
1
A = difl$(-2;1;4), S = О
-1
З"
4 ;б)
3.
1
-1
О
1
о
-1
О')
; в) A = diag(i
Г) Л = diag(0‘, 0; 0; 4), S =
о
1
1
о
о
о
1
1
1
-1
1
-1
. Преобразующая матрица опреде-
"0 1
1 0
2 2
1
о
1
о
0
S =
1
2
1
О
о
S =
о
о
1
1
о
0
О
1
1
<ъ
ляется неоднозначно.
множители характеристической матрицы
7.7. Найти инвариантные
(A-Ле), характеристический (АД(Л)) и минимальный (ЦД(Х)) многочлены,
а также жорданову форму JA матрицы А :
а)
' 0 1 О'
А= -4 4 0 ; б)
.-2 1 2.
'12 -6 -2
А= 18 -9 -3 ; в)
.18 -9 -3,
1
-2
О
-1
-3
-6
-3
-4
о
о
1
о
3
13
3
8
А =
361
Ответ: a) et(X) = l, е2(Х) = Х-2, е3(Х) = (Х-2)2, ДЛ(Х) = (2-Х)3,
рл(Х) = (Х-2)2, JA=diag(j2(2),Jl(2))-, б) ei(A)=l, е2(Х) = Х, е3(Х) = Х2,
да(Х) = -Х\ Ма(Х) = Х2, JA=diag(j2(o\ У1(о)); в) <?i(X) = l, е2(Х)=1,
е3(Х)=Х-1, е4(Х) = (Х-1Л Дд(Х)= (Х-1)4, рл (X) = (X -1)3,
JA = diag{j. Жорданова форма определяется неоднозначно.
7.8. Привести матрицы к жордановой форме при помощи преобразова-
ния подобия (найти жорданову матрицу J и преобразующую матрицу S ):
"о 3 3 '9 -6 -2А "о 1 -1 Г
-1 2 -1 1
а) -1 8 6 ; б) 18 -12 -3 ; в) -1 1 1 0
<2 -14 -10, ч18 -9 -1 1 0
Ответ: a) J = diag^J^O), J2(-l)), S= 1
I"1
3'
1
О,
92
6
б) J = Jia5(j2(-3),JI(-3)), 138 -3
-1
138
f0 0 1
в) j=diag(j2(l\j2(l)), S =
(J 0 0
-3'
-10
Жорданова форма и преобразующая матрица определяются неоднозначно.
7.9. Найти еА для матриц: а) А =
4 2
; б) 6 4
.5 3
-5
-9
-7
Ответ: а)
. Г Зе — 1 е
— 1^
; б) Зе е + 3
0 J
^Зе-1 е + 1
-Зе + Г
-Зе-3
-Зе ,
Г
1
о
1
362
7.10. Найти решение системы дифференциальных уравнений
dr,(r) ,,
^>-=-х1(,)-2х2(г).
удовлетворяющее начальным условиям х((о) = 3, х2(о) = 1.
Ответ:
/ \ [ в 1 + 3te 1 + 2
7.11. Найти решение системы дифференциальных уравнений
dr, (г) .,
—^ = х.(г)+1,
dr '
удовлетворяющее начальным условиям х|(о)=-1, х2(о) = О.
, . (-l + 2sinr
Ответ: х(г) =
I 2-2cosr
7.12. Найти формулы общих членов последовательностей {xt}, { yt),
|zA}, {“*}’ {v*}’ удовлетворяющих системе рекуррентных уравне-
ний:
р
Г xt+1 =mxJt+nyJt+/izJt,
«• Ум=тУк+^к,
о iZk+l = mZi’, v *=0x2,...;
,5 uk+l=nuk+(n + m)wk,
1 vt+i=”vt’
и'*+1=ли'*’
<: *+1
с начальными условиями х0=1, yQ=m, z0=n, uQ=n + m, v0=n-m,
Z^=mn. Здесь m - номер студенческой группы, п - номер студента по
Списку группы.
ГЛАВА 8. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
8.1. ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ ЛИНЕЙНЫХ ПРОСТРАНСТВ
8.1.1. Аксиомы линейного пространства
Линейным (векторным) пространством называется множество V
произвольных элементов, называемых векторами, в котором определены
операции сложения векторов и умножения вектора на число, т.е. любым
двум векторам и и v поставлен в соответствие вектор u + v, называемый
суммой векторов и и v, любому вектору v и любому числу А. из поля
действительных чисел R поставлен в соответствие вектор Av, называемый
произведением вектора v на число А; так что выполняются следующие
условия:
1. u+v=v+u \fu,veV (коммутативность сложения);
2. m + (v + h')=(u + v)+m’ \fu, v, weV (ассоциативность сложения);
3. существует такой элемент о е V , называемый нулевым вектором,
что v+o-v Vv е К ;
4. для каждого вектора v существует такой вектор (- v) е V, называе-
мый противоположным вектору v , что v + (- v) = о ;
5. А(и + v) = Хи + Av Vu, v е V, VA е R;
6. (A + p)v = Av + pv Vv е К , VA, peR;
7. A(pv) = (Ар) v Vv e V , VA, p e R ;
8. l-v = v \/veV.
Условия 1-8 называются аксиомами линейного пространства. Знак равен-
ства, поставленный между векторами, означает, что в левой и правой частях
равенства представлен один и тот же элемент множества V . Такие векторы
называются равными.
В определении линейного пространства операция умножения вектора
на число введена для действительных чисел. Такое пространство называют
линейным пространством над полем действительных (вещественных)
чисел, или, короче, вещественным линейным пространством. Если в оп-
ределении вместо поля R действительных чисел взять поле комплексных
чисел, то получим линейное пространство над полем комплексных чисел,
или, короче, комплексное линейное пространство. В качестве числового
поля можно выбрать и поле Q рациональных чисел, при этом получим ли-
нейное пространство над полем рациональных чисел. Далее, если не огово-
рено противное, будут рассматриваться вещественные линейные простран-
ства. В некоторых случаях для краткости будем говорить о пространстве,
364
опуская слово линейное, так как все пространства, рассматриваемые ниже -
линейные.
Замечания 8.1.
1. Аксиомы 1—4 показывают, что линейное пространство является
коммутативной группой относительно операции сложения (см. разд. В.2.3).
2. Аксиомы 5 и 6 определяют дистрибутивность операции умноже-
ния вектора на число по отношению к операции сложения векторов (ак-
сиома 5) или к операции сложения чисел (аксиома 6). Аксиома 7, иногда
называемая законом ассоциативности умножения на число, выражает
связь двух разных операций: умножения вектора на число и умножения чи-
сел. Свойство, определяемое аксиомой 8, называется унитарностью опера-
ции умножения вектора на число.
3. Линейное пространство - это непустое множество, так как обяза-
тельно содержит нулевой вектор.
4. Операции сложения векторов и умножения вектора на число назы-
ваются линейными операциями над векторами.
5. Разностью векторов и и v называется сумма вектора и с проти-
воположным вектором (- v) и обозначается: и - v = и + (- v).
6. Два ненулевых вектора и и v называются коллинеарными (про-
порциональными), если существует такое число X, что v = Хи. Понятие
коллинеарности распространяется на любое конечное число векторов. Нуле-
вой вектор о считается коллинеарным с любым вектором.
8.1.2. Простейшие следствия аксиом
1. В линейном пространстве существует единственный нулевой вектор.
2. В линейном пространстве для любого вектора v е V существует
единственный противоположный вектор (-v)e V .
3. Произведение произвольного вектора пространства на число нуль
равно нулевому вектору, т.е. 0v = o VveK.
4. Произведение нулевого вектора на любое число равно нулевому век-
тору, т.е Хо = о для любого числа X.
5. Вектор, противоположный данному вектору, равен произведению
данного вектора на число (-1), т.е. (- v) = (-1) v Vv е V .
6. В выражениях вида а + й + ... + z (сумма конечного числа векторов)
или а₽•... со v (произведение вектора на конечное число множителей)
можно расставлять скобки в любом порядке, либо вообще не указывать.
Докажем, например, первые два свойства. Единственность нулевого
вектора. Если о и о' - два нулевых вектора, то по аксиоме 3 получаем два
равенства: о' + о = о или о + о' = о , левые части которых равны по аксио-
ме 1. Следовательно, равны и правые части, т.е. о = о'. Единственность про-
365
тивоположного вектора. Если вектор v G V имеет два противоположных
вектора (-v) и (-v) , то по аксиомам 2, 3,4 получаем их равенство:
(“”) =(-”) +v + (->J= (-v) +v+(-v)= (-v).
О о
Остальные свойства доказываются аналогично.
8.1.3. Примеры линейных пространств
1. Обозначим {о } - множество, содержащее один нулевой вектор, с
операциями о+о = о и Хо = о. Для указанных операций аксиомы 1-8 вы-
полняются. Следовательно, множество { о } является линейным пространст-
вом над любым числовым полем. Это линейное пространство называется
нулевым.
2. Обозначим Vt, V2 , V3 - множества векторов (направленных отрез-
ков) на прямой, на плоскости, в пространстве соответственно с обычными
операциями сложения векторов и умножения векторов на число. Выполне-
ние аксиом 1-8 линейного пространства следует из курса элементарной гео-
метрии. Следовательно, множества У,, V2 , У3 являются вещественными ли-
нейными пространствами. Вместо свободных векторов можно рассмотреть
соответствующие множества радиус-векторов. Например, множество векто-
ров на плоскости, имеющих общее начало, т.е. отложенных от одной фикси-
рованной точки плоскости, является вещественным линейным пространст-
вом. Множество радиус-векторов единичной длины не образует линейное
пространство, так как для любого из этих векторов сумма v + v не принад-
лежит рассматриваемому множеству.
3. Обозначим R" - множество матриц-столбцов размеров лх1 с опе-
рациями сложения матриц и умножения матриц на число. Аксиомы 1-8 ли-
нейного пространства для этого множества выполняются (см. разд. 1.2). Ну-
левым вектором в этом множестве служит нулевой столбец о = (0 0)т .
Следовательно, множество R" является вещественным линейным простран-
ством. Аналогично, множество С" столбцов размеров nxl с комплексными
элементами является комплексным линейным пространством. Множество
матриц-столбцов с неотрицательными действительными элементами, напро-
тив, не является линейным пространством, так как не содержит
противоположных векторов.
4. Обозначим {Дх = о} - множество решений однородной системы
Ах = о линейных алгебраических уравнений с п неизвестными (где А -
действительная матрица системы), рассматриваемое как множество столб-
цов размеров лх1 с операциями сложения матриц и умножения матриц на
366
число. Заметим, что эти операции действительно определены на множестве
{Ах = о}. Из свойства 1 решений однородной системы (см. разд. 5.5) следу-
ет, что сумма двух решений однородной системы и произведение ее реше-
ния на число также являются решениями однородной системы, т.е. принад-
лежат множеству {Лх = о}. Аксиомы линейного пространства для столбцов
выполняются (см. п.З в примерах линейных пространств). Поэтому множе-
ство решений однородной системы является вещественным линейным про-
странством.
Множество {Ах = b} решений неоднородной системы Ах = b , Ь * о,
напротив, не является линейным пространством, хотя бы потому, что не со-
держит нулевого элемента (х = о не является решением неоднородной сис-
темы).
5. Обозначим Мтхл - множество матриц размеров тхп с операциями
сложения матриц и умножения матриц на число. Аксиомы 1-8 линейного
пространства для этого множества выполняются (см. разд. 1.2). Нулевым
вектором является нулевая матрица О соответствующих размеров. Следо-
вательно, множество Мявляется линейным пространством.
6. Обозначим Р(с) - множество многочленов одной переменной с
комплексными коэффициентами (см. разд. В.4). Операции сложения много-
членов и умножения многочлена на число, рассматриваемое как многочлен
нулевой степени, определены и удовлетворяют аксиомам 1-8 (в частности,
нулевым вектором является многочлен, тождественно равный нулю). По-
этому множество /*(с) является линейным пространством над полем ком-
плексных чисел. Множество /*(/?) многочленов с действительными коэф-
фициентами также является линейным пространством (но, разумеется, над
полем действительных чисел). Множество P„(r) многочленов степени не
выше, чем п, с действительными коэффициентами также является вещест-
венным линейным пространством. Заметим, что операция сложения много-
членов определена на этом множестве, так как степень суммы многочленов
не превышает степеней слагаемых (см. разд. В.4).
Множество многочленов степени п не является линейным простран-
ством, так как сумма таких многочленов может оказаться многочленом
меньшей степени, не принадлежащим рассматриваемому множеству. Мно-
жество всех многочленов степени не выше, чем п, с положительными ко-
эффициентами также не является линейным пространством, поскольку при
умножении такого многочлена на отрицательное число получим многочлен,
не принадлежащий этому множеству.
7. Обозначим С(т?) - множество действительных функций, определен-
ных и непрерывных на R . Сумма (/ + #) функций f, g и произведение
X/ функции f на действительное число к определяются равенствами:
367
(/ + g) (*) = /(*) + g(x). (V) (*) = • f(x) для всех xe R . Эти операции дей-
ствительно определены на c(r), так как сумма непрерывных функций и
произведение непрерывной функции на число являются непрерывными
функциями, т.е. элементами C(r). Проверим выполнение аксиом линейного
пространства. Из коммутативности сложения действительных чисел следует
справедливость равенства f(x)+g(x) = g(x)+f(x) для любого хе R. По-
этому f + g = g + f , т.е. аксиома 1 выполняется. Аксиома 2 следует анало-
гично из ассоциативности сложения. Нулевым вектором служит функция
о(х), тождественно равная нулю, которая, разумеется, является непрерыв-
ной. Для любой функции f выполняется равенство /(х)+о(х) = /(х), т.е.
справедлива аксиома 3. Противоположным вектором для вектора f будет
функция (- /) (х) = -/(х). Тогда f + (-/) = о (аксиома 4 выполняется). Ак-
сиомы 5, 6 следуют из дистрибутивности операций сложения и умножения
действительных чисел, а аксиома 7 - из ассоциативности умножения чисел.
Последняя аксиома выполняется, так как умножение на единицу не изменя-
ет функцию: 1/(х) = /(х) для любого хе R, т.е. 1-/ = f. Таким образом,
рассматриваемое множество C(r) с введенными операциями является ве-
щественным линейным пространством. Аналогично доказывается, что
C!(r), C2(r),..., Cm(R),... - множества функций, имеющих непрерывные
производные первого, второго .и т.д. порядков соответственно, также явля-
ются линейными пространствами.
Обозначим Tu(r) - множество тригонометрических двучленов (часто-
ты со 0) с действительными коэффициентами, т.е. множество функций ви-
да f (г)=a sin tot + b cos tor, где ae R , be R. Сумма таких двучленов и про-
изведение двучлена на действительное число являются тригонометрическим
двучленом. Аксиомы линейного пространства для рассматриваемого множе-
ства выполняются (так как tJ^R)c.C(R)). Поэтому множество Тш(д) с
обычными для функций операциями сложения и умножения на число явля-
ется вещественным линейным пространством. Нулевым элементом служит
двучлен o(t) - 0 • sin tor + 0 costnt, тождественно равный нулю.
Множество действительных функций, определенных и монотонных на
R, не является линейным пространством, так как разность двух монотон-
ных функций может оказаться немонотонной функцией.
8. Обозначим Rx - множество действительных функций, определен-
ных на множестве X, с операциями: (/ + #)(х) = /(х)+ #(х),
(Л/) (х) = Л. • /(х) Vx6 X . Оно является вещественным линейным простран-
ством (доказательство такое же, как в предыдущем примере). При этом
368
множество X может быть выбрано произвольно. В частности, если
X ={1,2,....и }, то f(x) - упорядоченный набор чисел Л,’•••’Л > гДе
ft - /(')’ 1 ~ • Такой набор можно считать матрицей-столбцом разме-
ров лх1, т.е. множество Л^1,2.совпадает с множеством Л" (см. п.З
примеров линейных пространств). Если X = N (напомним, что N — множе-
ство натуральных чисел), то получаем линейное пространство RN - множе-
ство числовых последовательностей { /(г) . В частности, множество схо-
дящихся числовых последовательностей также образует линейное простран-
ство, так как сумма двух сходящихся последовательностей сходится, и при
умножении всех членов сходящейся последовательности на число получаем
сходящуюся последовательность. Напротив, множество расходящихся по-
следовательностей не является линейным пространством, так как, например,
сумма расходящихся последовательностей может иметь предел.
9. Обозначим R+ - множество положительных действительных чисел,
в котором сумма а © b и произведение X * а (обозначения в этом примере
отличаются от обычных) определены равенствами: a®b-ab, Л*а=а\
другими словами, сумма элементов понимается как произведение чисел, а
умножение элемента на число - как возведение в степень. Обе операции
действительно определены на множестве 7?+, так как произведение положи-
тельных чисел есть положительное число и любая действительная степень
положительного числа есть положительное число. Проверим справедли-
вость аксиом. Равенства
a®b = ab = ba = b®a, a®(b®c) = a[bc) = tab} c = [a®b}®c
показывают, что аксиомы 1, 2 выполняются. Нулевым вектором данного
множества является единица, так как а®1 = а-1 = а, т.е. о = 1. Противопо-
1
ложным для а вектором является вектор —, который определен, так как
а
а * 0. В самом деле, а© — = а — -1 = о . Проверим выполнение аксиом 5, 6,
а а
7,8:
5) к*(а®Ь)=(а-ЬУ =akbx =к*а®к*Ь-,
6) (Л + ц)*а = аХ+и =</-ац =Л*л®ц*а ;
7) к*(И*а) = (а>1| = а^=(Х-Ц>а ;
8) 1*а =а1 =а .
Все аксиомы выполняются. Следовательно, рассматриваемое множество яв-
ляется вещественным линейным пространством.
24 - 4549
369
10. Пусть V — вещественное линейное пространство. Рассмотрим
множество определенных на V линейных скалярных функций, т.е. функций
f: V —> R , принимающих действительные значения и удовлетворяющих
условиям:
f(u + v) = f(u)+f(v) Xfu,veV (аддитивность)-,
f(kv )=Xf(v) VveV,VXe7? (однородность).
Линейные операции над линейными функциями задаются также, как в п.8
примеров линейных пространств. Сумма f + g и произведение X/ опреде-
ляются равенствами:
(/ + ^Х”) = /(>’)+Н”) VpgV; (W) = A/(v) VvgV.VAg/?.
Выполнение аксиом линейного пространства подтверждается также, как в
п.8. Поэтому множество линейных функций, определенных на линейном
пространстве V , является линейным пространством. Это пространство на-
зывается сопряженным к пространству V и обозначается V . Его элемен-
ты называют ковекторами.
Например, множество линейных форм п переменных (см. разд. 6.5),
рассматриваемых как множество скалярных функций векторного аргумента,
является линейным пространством, сопряженным к пространству /?" .
8.2. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ И ЛИНЕЙНАЯ
НЕЗАВИСИМОСТЬ ВЕКТОРОВ
8.2.1. Понятие линейной зависимости и линейной независимости
векторов
Для элементов линейного пространства были введены операции умно-
жения вектора на число (из некоторого числового поля) и сложения векто-
ров. При помощи этих операций можно составлять алгебраические выраже-
ния.
Вектор v называется линейной комбинацией векторов Vj, v2,..., vk,
если
v = a1vl + а2р2 +...+atpt, (8.1)
где а( ,a2,...,at - некоторые числа. В этом случае говорят, что вектор v
разложен по векторам vx,v2,...,vk (вектор v линейно выражается че-
рез векторы V! ,v2,...,vk), а числа cq ,a2,...,at называют коэффициен-
тами разложения. Линейная комбинация с нулевыми коэффициентами
v = 0• + 0• v2 +... + 0 vk называется тривиальной.
Набор векторов >q ,v2,...,vk из V называется системой векторов, а
любая часть системы векторов - подсистемой.
370
Система из к векторов v1 ,v2,...,vk называется линейно зависимой,
если существуют такие числа al,a2,—,ctk > не все равные нулю одновре-
менно, что справедливо равенство
+ a2v2+... + а*у* =о, (8.2)
т.е. линейная комбинация является нулевым вектором.
Система из к векторов Vj ,v2 ,...,vk называется линейно независимой,
если равенство (8.2) возможно только при 0Ц = а2 = ... = ак = 0, т.е. когда
линейная комбинация в левой части (8.2) тривиальная.
Замечания 8.2.
1. Один вектор V] тоже образует систему: при у, = о - линейно зави-
симую, а при У| Ф о - линейно независимую.
2. Понятия линейной зависимости и линейной независимости для век-
торов определяются также, как для столбцов (см. разд. 3.1). Поэтому все
свойства, рассмотренные в разд. 3.1, переносятся на векторы. Применение
свойств, доказанных для векторов, к столбцам, можно делать без обоснова-
ния, так как множество столбцов является линейным пространством (см. п. 3
в разд. 8.1.З.).
3. Рангом системы векторов у(,у2,...,vk называется максимальное
число линейно независимых векторов этой системы и обозначается
rg(y1,y2>...,vj.
Пример 8.1. Установить необходимые и достаточные условия линей-
ной зависимости двух, трех, четырех ненулевых векторов пространства V3,
где V3 - множество векторов (направленных отрезков) пространства (см. п.2
i вразд.8.1.3).
: □ Из элементарной геометрии известно, что два ненулевых вектора а
• и Ь коллинеарны (а || b ) тогда и только тогда, когда существует такое чис-
ло X, что а = ХЬ. Это равенство можно представить в виде
• 1а+(-Х)Ь=0,т.е. в виде нетривиальной линейной комбинации векторов
j а и b , равной нулевому вектору. Следовательно, условие коллинеарности
t необходимо и достаточно для линейной зависимости двух ненулевых векто-
| ров.
; Рассмотрим три ненулевых вектора а, b и с. Они компланарны
; (принадлежат или параллельны одной плоскости) тогда и только тогда, ко-
гда один из них может быть разложен по другим, т.е. когда существуют та-
? кие числа аир, что с =aa + pi . Записав это равенство в виде равной
: нулевому вектору нетривиальной линейной комбинации:
371
24*
а-а+Р-6+(-1)'С = 0,
делаем вывод, что три ненулевых вектора пространства линейно зависимы
тогда и только тогда, когда они компланарны.
Покажем, что любые четыре ненулевых вектора а , b , с , d линейно
зависимы. Если три вектора а , b , с компланарны, то с=а а+Р &. От-
сюда получаем равенство a a+P-fe+(-l) c+O J =0, т.е. векторы а , b ,
с, d линейно зависимы. Если же векторы а , Ь , с не компланарны, то
вектор d может быть разложен по ним, т.е. представлен в виде
d = аа+рЬ+у-с, где a, 0, у - некоторые числа. Отсюда получаем ра-
венство: aa+p-fe+yc+(-1)J =0. Значит, векторы a, b, с, d линей-
но зависимы.
8.2.2. Свойства линейно зависимых и линейно независимых векторов
1. Если в систему векторов входит нулевой вектор, то она линейно за-
висима.
2. Если в системе векторов имеется два равных вектора, то она ли-
нейно зависима.
3. Если в системе векторов имеется два пропорциональных (коллине-
арных) вектора ( у, = Ху;- ), то она линейно зависима.
4. Система из к >1 векторов линейно зависима тогда и только тогда,
когда хотя бы один из векторов есть линейная комбинация остальных.
5. Любые векторы, входящие в линейно независимую систему, образу-
ют линейно независимую подсистему.
6. Система векторов, содержащая линейно зависимую подсистему,
линейно зависима.
7. Если система векторов v,, у2,..., vt —линейно независима, а после
присоединения к ней вектора у - оказывается линейно зависимой, то век-
тор у можно разложить по векторам vl,v2,...,vt и притом единствен-
ным образом, т.е. коэффициенты разложения (8.1) находятся однозначно.
8. Пусть каждый вектор системы и} ,и2,...,и1 может быть разло-
k
жен по векторам системы ypyj,...^, т.е. и, =\,а,-,у ,, i=A,...,l (гово-
>=1
рят, что система векторов щ ,и2,...,и1 линейно выражается через сис-
тему векторов У] ,v2,...,vk). Тогда, если l> к, то система векторов
и1,и2,...,и1 - линейно зависима.
372
Докажем, например, последнее свойство. Составим линейную комби-
нацию векторов и1,м2, -.,н; с коэффициентами x1,x2,...,xJ и приравняем
ее нулевому вектору:
^х;и,=о. (8.3)
1=1
Надо показать, что эта линейная комбинация может быть нетривиальной,
т.е. среди коэффициентов х,, / = , можно взять числа, не равные нулю.
Действительно, подставим в линейную комбинацию (8.3) разложения векто-
ров Uj по векторам системы Pj, v2 , > vk '
° = ui = VJ = vi
1=1 <=1 y=l y=lki=l >
Чтобы это равенство выполнялось, достаточно потребовать, чтобы
I
У^а^х, = 0, j=l,...,к. Таким образом, получили однородную систему
1=1
Ах-о линейных уравнений с неизвестными х, ,х2,...,X/. Матрица
А = (aj,) системы имеет размеры kxl, т.е. количество уравнений (к) мень-
ше количества (I) неизвестных, так как 1>к . Поэтому rg А < к < I, т.е.
система имеет бесконечно много решений, в том числе и ненулевых (см.
разд.5.5). Таким образом, линейная комбинация в (8.3) может быть нетриви-
альной, т.е. система векторов иг, и2.., ut линейно зависима.
8.2.3. Аффинные, неотрицательные н выпуклые комбинации векторов
Пусть дана система векторов Pj,v2,...,vk вещественного линейного
пространства V (т.е. над полем R ). Множество линейных комбинаций век-
торов у,, v2,..., называется их линейной оболочкой и обозначается:
Lwi(v1,v2,...,yt)={v: у = (XjVj +<x2v2 + ... + akvk; а.е/?, / = 1,.
Векторы У],у2,...,у* называются образующими линейной оболочки
Lin(Vi,v2,...,vk).
Линейная комбинация векторов У] ,у2,...,уд называется аффинной,
если сумма ее коэффициентов равна единице. Множество аффинных комби-
наций векторов У] ,y2,...,yt называется их аффинной оболочкой и обозна-
чается:
1, а( G R, i = l,...,k .
373
Линейная комбинация векторов v1 ,v1,...,vk называется неотрица-
тельной, если все ее коэффициенты — неотрицательные числа. Множество
неотрицательных комбинаций векторов называется их кониче-
ской оболочкой и обозначается:
Co«(v1,v2,...,vt)={ v: v = a1v1 + а2У2 + ... + a*yt; af^0, i = l,...,£}•
Линейная комбинация векторов Vj , y2,...,yt называется выпуклой, ес-
ли все ее коэффициенты - неотрицательные числа, а их сумма равна едини-
це. Множество выпуклых комбинаций векторов у1 , y2,...,yt называется их
выпуклой оболочкой и обозначается:
к
v = a1v1+a2v2+...+a*vt; ^« =1, a, >0, i = l,
i=l
,k
Аналогично определению образующих линейной оболочки, векторы
У], у2 ,..., уt называют образующими множеств A#(ppv2 vj,
Con (v1,v2,...,vt), Солу(урУ2,...,УА) соответственно.
Понятия линейной, аффинной, конической и выпуклой оболочек, оп-
ределенные для конечной системы векторов, можно обобщить.
Линейной оболочкой непустого подмножества М линейного про-
странства V (MeV ,М^0) называется множество всевозможных ли-
нейных комбинаций векторов из М:
Ле N, у. е М, a(. е R, i = 1,..
k к
Аналогично определяются аффинная, коническая и выпуклая обо-
лочки непустого подмножества М:
Если множество М пустое (М - 0 ), то по определению считается, что
Un(M}-Aff(M} = Соп(М) = Conv(M) = {о }.
Из определений следуют включения:
М с Сот (М) с Aff(M)clin(M), М ее Сот (М) с Соп(М )с£лп(м) ;
и равенство Сот(М) = Con (М) П Aff(M).
374
Пример 8.2. В пространстве V2 радиус-векторов на плоскости (см. п.2
в разд.8.1.3) даны два неколлинеарных вектора а =ОА и b = ОВ (рис.8.1).
Найти Lin(a, fe), Aff[a,fe), Сол(а,b), Conv{a,b).
□ Lin{a, b). Любой радиус-вектор с = ОС плоскости можно разло-
жить по двум неколлинеарным векторам этой плоскости, т.е. представить в
виде линейной комбинации с =а а + pfe , где ае R и ре R. Следователь-
но, множество всевозможных линейных комбинаций векторов а и b сов-
падает со всем пространством V2 радиус-векторов на плоскости, т.е.
Lin(a, b) = V2.
Affifi, b). Заметим, что точка С - конец вектора ОС = аОА + $ОВ
при условии а + Р = 1 принадлежит прямой АВ, так как (при а = 1 - р)
ос=оа+р-(ов-оа)=оа+р-ав,
т.е. радиус-вектор ОС получается в результате прибавления к вектору ОА
некоторого вектора, параллельного прямой АВ. Следовательно, Aff{a, b) -
множество радиус-векторов, концы которых лежат на прямой, проходящей
через точки А и В (см. рис.8.1).
Соп\а,Ь). При умножении вектора на положительное число его на-
правление не изменяется. Поэтому вектор ОС = а-ОА + $ ОВ при а>0,
Р > 0 можно рассматривать как сумму двух векторов, принадлежащих лу-
чам ОА и ОВ соответственно. По правилу сложения векторов заключаем,
Что радиус-вектор ОС лежит либо между этими лучами, либо на одном из
них. Следовательно, множество Соп(а, b) образуют радиус-векторы, концы
которых принадлежат углу АОВ (заштрихованное множество на рис. 8.1).
375
Conv\a,b). Конец радиус-вектора ОС = ос• ОА + Р ОВ при а + р = 1,
а > 0, Р > 0 принадлежит прямой АВ и углу АОВ одновременно. Следо-
вательно, точка С принадлежит отрезку АВ. Поэтому Conv(a,b) - множе-
ство радиус-векторов, концы которых принадлежат отрезку АВ
(см. рис.8.1). Этот вывод соответствует указанному выше равенству
Conv{M) = Con(M )f\Aff(M).U
Замечания 8.3.
1. Свойство 7 линейно зависимых и линейно независимых векторов
можно сформулировать (без указания единственности разложения) следую-
щим образом: если система векторов Pj, v2,..., vk линейно независима, а по-
сле присоединения к ней вектора v - оказывается линейно зависимой, то
вектор ve Lin(v1,p2,...,vjl).
2. Свойство 8 линейно зависимых и линейно независимых векторов
можно сформулировать так: если каждый вектор системы ,m2,...,uz при-
надлежит линейной оболочке Lin(vl,v2,—,vk) и />к , то система векторов
, и2 И/ - линейно зависима.
3. Свойства аффинных оболочек будут рассматриваться в разд.8.7.
Свойства конических и выпуклых оболочек относятся к выпуклому анализу
и применяются в теории оптимизации [32].
4. В некоторых источниках для линейной оболочки векторов использу-
ется обозначение Spanlyv...,vk).
8.3. РАЗМЕРНОСТЬ И БАЗИС ЛИНЕЙНОГО ПРОСТРАНСТВА
8.3.1. Определения размерности и базиса
Линейное пространство V называется п -мерным, если в нем сущест-
вует система из п линейно независимых векторов, а любая система из
большего количества векторов линейно зависима. Число п называется раз-
мерностью (числом измерений) линейного пространства V и обозначается
dimV . Другими словами, размерность пространства - это максимальное
число линейно независимых векторов этого пространства. Если такое число
существует, то пространство называется конечномерным. Если же для лю-
бого натурального числа п в пространстве V найдется система, состоящая
из п линейно независимых векторов, то такое пространство называют бес-
конечномерным (записывают: dimV =°°). Далее, если не оговорено про-
тивное, будут рассматриваться конечномерные пространства.
Базисом л-мерного линейного пространства называется упорядочен-
ная совокупность п линейно независимых векторов (базисных векторов).
376
Теорема 8.1 (о разложении вектора по базису). Если е(,е2,...,е„ -
базис п -мерного линейного пространства V, то любой вектор v е V мо-
жет быть представлен в виде линейной комбинации базисных векторов:
v = + v2e2 +... + vnen (8.4)
и притом единственным образом, т.е. коэффициенты v1,v2,...,v„ опреде-
ляются однозначно. Другими словами, любой вектор пространства может
быть разложен по базису и притом единственным образом.
Действительно, размерность пространства V равна п. Система векто-
ров Cj ,е2 ,- .,еп линейно независима (это базис). После присоединения к ба-
зису любого вектора v, получаем линейно зависимую систему
el,e2,...,en,v (так как это система состоит из (л + 1) векторов л-мерного
пространства). По свойству 7 линейно зависимых и линейно независимых
векторов (см. разд.8.2.2) получаем заключение теоремы.
Следствие 1. Если ei,e2,...,en - базис пространства V, то
V = Lin(ei,e2,...,en ), т.е. линейное пространство является линейной оболоч-
кой базисных векторов.
В самом деле, для доказательства равенства V = Ып(е},е2,...,е„) двух
множеств достаточно показать, что включения V с Lin(el,e2,...,en) и
Lin(e1,e2,...,en)dV выполняются одновременно. Действительно, с одной
стороны, любая линейная комбинация векторов линейного пространства
принадлежит самому линейному пространству, т.е. Lin(el,e2,...,en)c. V. С
другой стороны, любой вектор пространства по теореме 8.1 можно предста-
вить в виде линейной комбинации базисных векторов, т.е.
V с Lin(et,е2,...,еп). Отсюда следует равенство рассматриваемых множеств.
Следствие 2.Если elte2,...,en —линейно независимая система векто-
ров линейного пространства V и любой вектор veV может быть пред-
ставлен в виде линейной комбинации (8.4): v = viei +v2e2 + ...+vnen, то про-
странство V имеет размерность п, а система е1,е2,...,еп является его
базисом.
В самом деле, в пространстве V имеется система п линейно незави-
симых векторов, а любая система «j ,u2,...,uk из большего количества век-
торов (к > п) линейно зависима (по свойству 8 в разд.8.2.2), поскольку каж-
дый вектор из этой системы линейно выражается через векторы
е, ,е2 ,...,еп. Значит, dimV = п и е} ,е2 ,...,е„- базис V .
Теорема 8.2 (о дополнении системы векторов до базиса). Всякую ли-
нейно независимую систему к векторов п -мерного линейного пространст-
ва (1 <к <п)можно дополнить до базиса пространства.
377
В самом деле, пусть е, ,е2 ,-,ек - линейно независимая система век-
торов и -мерного пространства V (\<к < и). Рассмотрим линейную обо-
лочку этих векторов: Lk = Ып{е],е2,...,ек\ Любой вектор v е Lk образует с
векторами е{, е2.., ек линейно зависимую систему et ,e2,...,ek,v, так как
вектор v линейно выражается через остальные (см. свойство 4 в разд.8.2.2).
Поскольку в л-мерном пространстве существует п линейно независимых
векторов, то Lk # V и существует вектор ei+] е V, который не принадлежит
Lk. Дополняя этим вектором линейно независимую систему е{,е2,...,ек,
получаем систему векторов ех,е2,...,ек,ек+х, которая также линейно неза-
висимая. Действительно, если бы она оказалась линейно зависимой, то из
п.1 замечаний 8.3 следовало, что et+1 e Ып{ех,е2,...,ек) = Lk, а это противо-
речит условию ек+х i Lk . Итак, система векторов ех, е2,..., ек, ек+х линейно
независимая. Значит, первоначальную систему векторов удалось дополнить
одним вектором без нарушения линейной независимости. Продолжаем ана-
логично. Рассмотрим линейную оболочку этих векторов:
=^«(е1>е2. -.^,е*+1)- Если Z*+1=K, то ех ,е2,...,ек,ек+х - базис и
теорема доказана. Если Lk+X *V, то дополняем систему ех ,е2,...,ек ,ек+х
вектором ек+2 g Lk+X и т.д. Процесс дополнения обязательно закончится, так
как пространство V конечномерное. В результате получим равенство
V = Ln = Lin(ex,...,ek,...,e„), из которого следует, что ех ,...,ек ,...,еп - базис
пространства V . Теорема доказана.
Замечания 8.4.
1. Базис линейного пространства определяется неоднозначно. Напри-
мер, если ех,е2,...,е„ - базис пространства V, то система векторов Хе]э
Хе2 ,...,Хеп при любом также является базисом V. Количество ба-
зисных векторов в разных базисах одного и того же конечномерного про-
странства, разумеется, одно и то же, так как это количество равно размерно-
сти пространства.
2. В некоторых пространствах, часто встречающихся в приложениях,
один из возможных базисов, наиболее удобный с практической точки зре-
ния, называют стандартным.
3. Теорема 8.1 позволяет говорить, что базис - это полная система
элементов линейного пространства, в том смысле, что любой вектор про-
странства линейно выражается через базисные векторы.
4. Если множество L является линейной оболочкой Lin(yx, v2,..., v*) ,
то векторы v,, v2,..., vk называют образующими множества Z. Следст-
вие 1 теоремы 8.1 в силу равенства V = Ып(е1,е2,...,еп) позволяет говорить,
378
что базис - это минимальная система образующих линейного пространства
V, так как нельзя уменьшить количество образующих (удалить хотя бы
один вектор из набора et ,е2 ,...,е„) без нарушения равенства
V = Ып(е},е2...е„).
5. Теорема 8.2 позволяет говорить, что базис - это максимальная ли-
нейно независимая система векторов линейного пространства, так как базис
- это линейно независимая система векторов, и ее нельзя дополнить каким-
либо вектором без потери линейной независимости.
6. Следствие 2 теоремы 8.1 удобно применять для нахождения базиса и
размерности линейного пространства. В некоторых учебниках оно берется
за определение базиса, а именно: линейно независимая система ех, е2
векторов линейного пространства называется базисом, если любой вектор
пространства линейно выражается через векторы е1,е2,...,еп. Количест-
во базисных векторов определяет размерность пространства. Разумеется,
что эти определения эквивалентны приведенным выше.
8.3.2. Примеры базисов линейных пространств
Укажем размерность и базис для примеров линейных пространств, рас-
смотренных в разд.8.1.3.
1. Нулевое линейное пространство {о } не содержит линейно незави-
симых векторов. Поэтому размерность этого пространства полагают равной
нулю: dim{ о } = 0 . Это пространство не имеет базиса.
2. Пространства VX,V2, V2 имеют размерности 1, 2, 3 соответственно.
Действительно, любой ненулевой вектор пространства Vy образует линейно
независимую систему (см. п.1, замечаний 8.2), а любые два ненулевых век-
тора пространства Vx коллинеарны, т.е. линейно зависимы (см. пример 8.1).
Следовательно, dim Vy = 1, а базисом пространства VA является любой нену-
левой вектор. Аналогично доказывается, что dim V2 = 2 и dim К = 3 . Бази-
сом пространства И2 служат любые два неколлинеарных вектора, взятые в
определенном порядке (один из них считается первым базисным вектором,
другой - вторым). Базисом пространства И3 являются любые три некомпла-
нарных (не лежащих в одной или параллельных плоскостях) вектора, взятые
в определенном порядке. Стандартным базисом в Vx является единичный
вектор i на прямой. Стандартным базисом в /2 считается базис i , j, со-
стоящий из двух взаимно перпендикулярных единичных векторов плоско-
сти. Стандартным базисом в пространстве И3 считается базис / , j, к , со-
379
ставленный из трех единичных попарно перпендикулярных векторов, обра-
зующих правую тройку.
3. Пространство R" содержит не более, чем п , линейно независимых
векторов. В самом деле, возьмем к столбцов из Rn и составим из них мат-
рицу размеров пхк . Если к > п, то столбцы линейно зависимы по теореме
3.4 о ранге матрицы. Следовательно, dim7?n<«. В пространстве R" не-
трудно найти п линейно независимых столбцов. Например, столбцы еди-
ничной матрицы
линейно независимы. Следовательно, dim/?" = п . Пространство 7?" называ-
ется п-мерным вещественным арифметическим пространством. Ука-
занный набор векторов считается стандартным базисом пространства R".
Аналогично доказывается, что dim С" = п , поэтому пространство С" назы-
вают п -мерным комплексным арифметическим пространством.
4. Напомним, что любое решение однородной системы Ах-о можно
представить в виде х = Ct(pj + С2ф2 +•+ C„_r(p„_r, где г = rg А, a (pj, <р2
ф„_г - фундаментальная система решений (см. разд. 5.5). Следовательно,
{Ах = о}=Ей(ф1,ф2,..., Ф„_г), т.е. базисом пространства {Лх = о} решений
однородной системы служит ее фундаментальная система решений, а раз-
мерность пространства dim { Ах - о }=л-г, где п — количество неизвест-
ных, а г - ранг матрицы системы.
5. В пространстве Af2x3 матриц размеров 2x3 можно выбрать 6 мат-
риц:
fl О О') fO 1 О) (О О
(ООО/2 (0 0 о) (о о oj
(о о o') (ООО) (о о o')
(1 О О) 5 (0 1 0J (0 0 1J
которые линейно независимы. Действительно, их линейная комбинация
(а, а2 а,')
cq-ei+а2-е2 + а3е3 + а4-е4+а5-е:5+а6-е6= (8.5)
(а4 а5 а6 J
равна нулевой матрице только в тривиальном случае а, =а2 = ... = а6 =0-
Прочитав равенство (8.5) справа налево, заключаем, что любая матрица из
Л/2х3 линейным образом выражается через выбранные 6 матриц, т.е.
380
Af2x3 - Lin(e},e2,...,e6). Следовательно, dimM2x3 - 2• 3 - 6, а матрицы ,
e2,..., e6 являются базисом (стандартным) этого пространства. Аналогично
доказывается, что dim Л/mxn = тп.
6. Для любого натурального п в пространстве Р(с) многочленов с
комплексными коэффициентами можно найти п линейно независимых эле-
ментов. Например, многочлены et = 1, е2 = z, е3 = z2,..., еп= znl линейно
независимы, так как их линейная комбинация
ах q + а2 е2 +... + ап • еп = + a2z +... + anz"-1
равна нулевому многочлену (o(z) = 0) только в тривиальном случае
а1 =а2 ~ — = ап = 0 • Поскольку эта система многочленов линейно незави-
сима при любом натуральном п, пространство Р(с) бесконечномерное.
Аналогично делаем вывод о бесконечной размерности пространства p(r)
многочленов с действительными коэффициентами. Пространство Рп(р)
многочленов степени не выше, чем п, конечномерное. Действительно, век-
торы «1=1, е2=х, е3=х2,..., ея+1=х" образуют базис (стандартный) это-
го пространства, так как они линейно независимы и любой многочлен из
Рп(к) можно представить в виде линейной комбинации этих векторов:
апхп +... + агх + а0 = а0 • et + - е2 +... + ап • е„+1.
Следовательно, dim Рп (/?) = п +1.
7. Пространство с(7?) непрерывных функций является бесконечно-
мерным. Действительно, для любого натурального п многочлены
1,х ,х2,...,х"-1, рассматриваемые как непрерывные функции, образуют ли-
нейно независимые системы (см. предыдущий пример).
В пространстве тригонометрических двучленов (частоты со^О)
С действительными коэффициентами базис образуют одночлены
ej(f) = sincor, e2(r) = cos<Br. Они линейно независимы, так как тождествен-
ное равенство a sin ом+ b cos он sO возможно только в тривиальном случае
(а = b = 0). Любая функция вида f (t)=a sin сог + fe cos (0/ линейно выража-
ется через базисные: f(t) = а (г)+b е2 (t).
8. Пространство Rx действительных функций, определенных на мно-
жестве X , в зависимости от области определения X может быть конечно-
мерным или бесконечномерным. Если X - конечное множество, то про-
странство Rx конечномерное (например, X ={ 1,2, ...,п }). Если X - бес-
конечное множество, то пространство Rx бесконечномерное (например,
Пространство RN последовательностей).
381
9. В пространстве R+ любое положительное число et, не равное еди-
нице, может служить базисом. Возьмем, например, число е, = 2. Любое по-
ложительное число г можно выразить через е1, т.е. представить в виде
а, • е1: г = 2log2 r = log 2 r*2 = al*el, где cq - log2 г. Следовательно, размер-
ность этого пространства равна 1, а число ех - 2 является базисом.
10. Пусть е{ ,е2,...,еп — базис вещественного линейного пространства
V . Определим на V линейные скалярные функции ,е2 ,--,еп , положив:
I \ Р’ ' = л
[0, i*j.
При этом, в силу линейности функции е. , для произвольного вектора
” =v1e1 +v2e2 +...+vnen получаем £,(v)=^v;E1(eJ=v/.
j=i
Итак, определены п элементов (ковекторов) е,, е2.........еп сопряженно-
го пространства V*. Докажем, что , е2 ,..., еп - базис V*.
Во-первых, покажем, что система е1,е2,...,еп линейно независима. В
самом деле, возьмем линейную комбинацию этих ковекторов
(ot^ +... + an£n)(i’) = a1£1(v)+... + an£n(v) и приравняем ее нулевой функции
o(v) (где o(v) = 0 VveV): aI£1(v)+... + a„£n(v) = o(v) = 0 VveV. Под-
ставляя в это равенство v=e(, < = 1...п, получаем Ct] = а2 =...-ая = 0 .
Следовательно, система элементов е1,е2,...,еп пространства V* линейно
независима, так как равенство + ... + a„cn = о возможно только в триви-
альном случае.
Во-вторых, докажем, что любую линейную функцию f &V* можно
представить в виде линейной комбинации ковекторов е1,е2,...,еп. Дейст-
вительно, для любого вектора v = vleI + v2e2 +... + vnen в силу линейности
функции f получаем:
/(v)=/(vie1+... + vnen) = v1/(e1)+... + v„/(en)=/(e,)£I(v)+... + /(en)£n(>>) =
= (/(ei) £1 + - + f(en )еп)(р)= (P^i +... + ) (г),
т.е. функция f представлена в виде линейной комбинации
f = (31£1 +... + Р„£„ функций е1,е2,...,еп (числа =/(е,) - коэффициенты
линейной комбинации). Следовательно, система ковекторов в, ,е2 ,...,еп яв-
ляется базисом сопряженного пространства V* и dimV* =dimV (для ко-
нечномерного пространства V).
382
8.4. КООРДИНАТЫ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ
8.4.1. Координаты векторов в данном базисе
Пусть в] ,е2 - базис линейного пространства V . Каждый вектор
veV можно разложить по базису (см. теорему 8.1), т.е. представить в виде
v = v1el+v2e2+... + v„en, причем коэффициенты vltv2,..., v„ в разложении
определяются однозначно. Эти коэффициенты У],у2,...,уя называются
координатами вектора v в базисе е1уе2,...,еп (или относительно базиса
е1 ,е2 ). Координаты v1,v2,...,vn вектора v - это упорядоченный на-
бор чисел, который представляется в виде матрицы-столбца
v = (vj vn)r и называется координатным столбцом вектора v (в
данном базисе). Вектор и его координатный столбец обозначаются одной и
той же буквой полужирной или светлой соответственно.
Если базис (как упорядоченный набор векторов) представить в виде
символической матрицы-строки (е) = (ер...,е„)= (е, ••• е„), то разложение
вектора v по базису (е) можно записать следующим образом:
v = vlel+v2e2+... + vnen=(ei - е„)
(8.6)
Здесь умножение символической матрицы-строки (е) на числовую матрицу-
столбец v производится по правилам умножения матриц (см. разд. 1.3.1).
При необходимости, если речь идет о разных базисах, у координатного
столбца указывается обозначение базиса, относительно которого получены
координаты, например, v - координатный столбец вектора v в базисе
(е) = (е1,...,еп).
Из теоремы 8.1 следует, что равные векторы имеют равные соответ-
ствующие координаты (в одном и том же базисе), и наоборот, если коор-
динаты векторов (в одном и том же базисе) соответственно равны, то
равны и сами векторы.
8.4.2. Линейные операции в координатной форме
Пусть ег,е2еп - базис линейного пространства V , векторы и и v
Имеют в этом базисе координаты и = («; ••• ип)Т и v = (vj v„)r соот-
s ветственно, т.е.
и = и1е1 + и2е2 +... + unen, v = + v2e2 +... + vnen.
(8.7)
Складывая эти равенства, получаем
« + v = (w1 +vj)e| + (w2 +v2)e2 + ... + (u„+v„)e„ ,
т.е. при сложении векторов их координаты складываются.
Умножая второе равенство в (8.7) на число X, получаем
Xv = (Xv1)e1 + (Xv2)e2 + ... + (Xv„)e„,
т.е. при умножении вектора на число все его координаты умножаются на
это число.
Другими словами, сумма векторов u + v имеет координаты u + v, а
произведение Хг имеет координаты Xv. Разумеется, что все координаты
получены в одном базисе (е)= (е1,...,е„).
Замечания 8.5.
1. Нетрудно показать, что координатный столбец линейной комбина-
ции a-a + 0-A + ... + <o-z векторов a,b,...,z равен линейной комбинации
a-a + pZ> + ... + (Bz координатных столбцов a,b,...,z этих векторов.
2. Если система векторов линейно зависима (линейно независима), то
их координатные столбцы, полученные относительно одного базиса, обра-
зуют линейно зависимую (соответственно, линейно независимую) систему.
Это следует из равносильности равенств aa + pft + ... + a>z = o и
a a + Р • Ь +... + <o-z = o. Например, если в этих равенствах не все коэффици-
енты равны нулю, т.е. система векторов a,b,...,z и система a,b,...,z их
координатных столбцов линейно зависимы одновременно.
3. Все свойства линейной зависимости и линейной независимости век-
торов (см. разд. 8.2.2) переносятся без изменений на их координатные
столбцы, полученные в одном и том же базисе. И наоборот, свойства, сфор-
мулированные в разд.3.1 для матриц-столбцов, переносятся на векторы, если
матрицы-столбцы считать их координатными столбцами.
4. Выбрав в п -мерном вещественном линейном пространстве V неко-
торый базис, можно установить взаимно однозначное соответствие: каж-
дому вектору поставить в соответствие его координатный столбец (в вы-
бранном базисе), и наоборот, каждому координатному столбцу поставить в
соответствие вектор. Другими словами, любой фиксированный базис
п -мерного вещественного линейного пространства позволяет установить
взаимно однозначное соответствие между всеми векторами вещественно-
го пространства V и всеми столбцами п -мерного арифметического про-
странства R" . Это соответствие обозначается И <->/?". Для п -мерного
комплексного линейного пространства V аналогичное взаимно однозначное
соответствие устанавливается с пространством Сп.
384
8.4.3. Преобразование координат вектора при замене базиса
Пусть заданы два базиса пространства V: (е)= (е},е2,...,е„) и
(е')=(е{,е2,...,еп). Базис (е) будем условно называть "старым", а базис (е') -
"новым". Пусть известны разложения каждого вектора нового базиса по ста-
рому базису:
е. =5.. е, +S... +... + S . е , г=1, 2,...,п . (8.8)
I 1г 1 2i 2 ш п ’ ’ ’ ’ v z
Записывая по столбцам координаты векторов (е[,е2,...,е'п) в базисе (е), со-
ставляем матрицу:
511 '" Лл
(8.9)
Ч^л1 ‘ ’ snn ,
Квадратная матрица 5, составленная из координатных столбцов векторов
нового базиса (е') в старом базисе (е), называется матрицей перехода от
старого базиса к новому. При помощи матрицы перехода (8.9) формулы
(8.8) можно записать в виде:
(е[ ” en)=(ei " ел)'$ или, короче, (e‘)=(e)-S. (8.10)
Умножение символической матрицы-строки (е) на матрицу перехода 5 в
(8.10) производится по правилам умножения матриц (см. разд. 1.3.1).
Пусть в базисе (е) вектор v имеет координаты v} ,v2,...,vn, ав базисе
(е') - координаты V; , v'2 ,..., v'n, т.е.
v = у]в1 + v2e2 +... + Vne„ = v[e'} + v'2e2 +... + v'„e’n
или, короче, v = (e) v = (e') v'. Подставляя в правую часть последнего равен-
ства выражение (8.10), получаем v = (е) v = (е) Sv- два разложения вектора
v в одном и том же базисе (е). Коэффициенты этих разложений должны
совпадать (по теореме 8.1), так как это координаты одного и того же вектора
в одном базисе. Поэтому
v = S v или, что то же самое,
W И
snn J\Vnj
(8.11)
Формула (8.11) устанавливает связь координат вектора в разных бази-
сах: координатный столбец вектора в старом базисе получается в резуль-
тате умножения матрицы перехода на координатный столбец вектора в
новом базисе.
Пример 8.3. В пространстве Р2(в} многочленов степени не выше вто-
рой даны две системы многочленов:
Й-4549 385
е, =1,е2 =х,е3 = х2 и f\ = (x + l)2,/2 = (x-l)2,/3 = x2.
Доказать, что каждая система является базисом пространства Р2(я). Найти
матрицу S перехода от базиса (е) к базису (/). Определить координаты
квадратного трехчлена р = х2 -х + 1 относительно базисов (е) и (/).
□ Система многочленов ех = 1, е2 = х, е3 = х2 является стандартным
базисом пространства Р2(я) (см- п-6 в примерах базисов в разд. 8.3.2). До-
кажем, что система = (х +1)2, /2 = (х -1)2, /3 = х2 является базисом. По-
ступим следующим образом. Найдем координатные столбцы f{, f2, f3 этих
многочленов в стандартном базисе. Раскладывая по базису (е), получаем
/j = (х+1)2 = х2+ 2х + 1 = 1-е,+2-е2+1-е3, т.е. /] =(1 2 1)г ;
/2=(jf-l)2=x2-2x+l = be1-2-e2+l-e3,T.e./2 = (l -2 if;
/3 =х2 =O ej+0-е2+1-е3,т.е. /3 =(0 0 if.
fl 1
Составим из этих столбцов матрицу 5=2 - 2
О'
О . Ранг этой матрицы ра-
U 1
вен 3, так как det S = - 4 * 0 . Следовательно, столбцы , f2, f3 линейно
независимы, тогда и многочлены /1,/2,/3 линейно независимы (см. п.2
замечаний 8.5). Итак, многочлены /1,/2,/з являются базисом пространст-
ва Р2(р), а матрица 5 - искомая матрица перехода от базиса (е) к базису
(/). Осталось найти координаты многочлена р = х2-х + 1 в этих базисах.
Раскладывая р по базисам, находим
р = х2-х + 1 = 1е1-1е2 + 1е3, т.е. р=(1 -1 if;
2 . (х + 1)2 + 3(х-1)2 1 . 3 , _ , ( 1 3 nV
р = х -х + 1 = --i-----~=~fi +7/2+O/3, Т.е. р = (| | 0J .
4 4 4 (/)
Проверим результат, вычисляя р по формуле (8.11):
Результаты совпадают.
386
8.4.4. Свойства матрицы перехода от одного базиса к другому
1. Пусть имеются три базиса (е), (/), (g) пространства V и извест-
ны матрицы перехода: S от базиса (е) к базису (/); S от (f) к
<«)-»(/) (/)-»(«)
(g); S от (е) к (g). Тогда
(8.12)
(*)->(«) (')->(/) (/Me)
Действительно, запишем связь (8.10) для данных базисов:
(/)=(< = s (g) = (e)- 5
(«)-»(/) </)-»(g) («>-»
Подставляя первое выражение во второе равенство, получаем
(g)=(е)- S • S Сравнивая с третьим равенством, приходим к (8.12).
(«)->(/) (/)->(«)
2. Если S -матрица перехода от базиса (е) к базису (/), то матри-
ца S обратима и обратная матрица 5-1 является матрицей перехода от
базиса (/) к базису (е). Координаты вектора v в базисах (е) и (/) связа-
ны формулами:
, , (31 (11 (11 (-
базиса: Л =1 f2 =1 j I и gi =1 2 I, g2=l t
v = S v , v =S
(«) (/) (/)
В самом деле, пусть Т - матрица перехода от базиса (/) к базису (е).
Учитывая, что матрица перехода от базиса (е) к базису (е) — единичная,
применяем свойство 1 к трем базисам (е),(/),(е): E = ST. Для трех бази-
сов (/),(е),(/) аналогично получаем: E = TS . Следовательно, Т = S~l (см.
разд. 4.1).
3. Всякая обратимая квадратная матрица п -го порядка может слу-
жить матрицей перехода от одного базиса п-мерного линейного про-
странства к другому базису.
Пример 8.4. В двумерном арифметическом пространстве R2 даны два
. Найти матрицу S пе-
(/Ня)
рехода от базиса (/) к базису (g) и координаты вектора v =Р
в каждом
из базисов.
(11 (01 ,
□ Рассмотрим стандартный базис et =1 1,е2 =1 I пространства R
(см. п.З в разд. 8.3.2). Находим координаты векторов , f2, gt, g2 в стан-
дартном базисе. Раскладываем вектор /,:
25»
387
(3) fl) fO) f3)
Л42]=зи и=3'е,+2е2,теЛ=и’
В стандартном базисе (е) пространства R2 координатный столбец Д
совпадает с вектором ft. Для других векторов аналогично получаем
fl) fl) f-1)
f2 = 111, gj = I 2 I > g2 -1 j I • Из координатных столбцов составим
матрицы перехода (8.9) от стандартного базиса (е) к данным базисам (/) и
(g)-
1 -1
2 1
S
-I3 м
(еН/)"(2 V (*Нг)
По свойству 1 матриц перехода имеем S' = S • S .По свойству 2:
(/Hr) (/He)(e)->U)
S = S 1 . Поэтому
(/Не) (•)->(/)
-1 Гз 1) 1 Г1
S = S”1 S =
(/Hr) (еН/ИНг) (2 1J (2
-2
5
-1
4
1 -1
2 1
-1
3
В стандартном базисе (е) пространства R2 координатный
'6)
$ I совпадает с вектором v . Найдем координаты этого вектора в бази-
се (/) (по свойству 2 матрицы перехода):
'3 1Y* f6) f 1 -Г) Гб) f-зЛ
ч2 1J \9j~l-2 3 15 J'
В самом деле, справедливо разложение
6) (3) Г1
= -3 +15
9) 12J 11
-1) ( 1
1 0-2
столбец
V =
v = S 1 v —
(/) (<Н/) (е)
v =
= -3/1+15./2.
Найдем координаты вектора v в базисе (g) двумя способами:
-1 ("I
V = S ‘ V =
(«) (/Не)(/) 14
-2) 7-3
5 J 115
-I 5
31-4
2'
-1.
-3|_Г5
15 J 1-1
11(61_( 5
1Д 9 J —1
v -- S 1 v =[
U) («НМ |2
-П [б) И 1
1 J U” з[-2
Полученный результат подтверждает разложение:
ГбЛ fl) . ,f-l) . .
V = L =5L И-1) 1 =5
388
«1
и2 <->v2
8.5. ИЗОМОРФИЗМ ЛИНЕЙНЫХ ПРОСТРАНСТВ
Говорят, что между элементами двух множеств U и V установлено
взаимно однозначное соответствие, если указано правило, которое каж-
дому элементу u&U сопоставляет один и только один элемент vе V , при-
чем каждый элемент vG V оказывается сопоставленным одному и только
одному элементу и е И . Взаимно однозначное соответствие будем обозна-
чать U <-> V , а соответствующие элементы: и <-> v.
Два линейных пространства V и V называются изоморфными, если
между их элементами можно установить такое взаимно однозначное соот-
ветствие, что выполняются условия:
1) сумме векторов пространства V соответствует сумма соответст-
вующих векторов пространства V:
=> («j +и2)<-> (pi +р2);
2) произведению числа на вектор пространства V соответствует про-
изведение того же числа на соответствующий вектор пространства V :
и <-> v => Хи <-> Xv .
Другими словами, изоморфизм - это взаимно однозначное соответст-
вие, сохраняющее линейные операции.
Пример 8.5. Установить между пространствами U = R и V = R вза-
имно однозначное соответствие, которое
а) является изоморфизмом; б) не является изоморфизмом.
□ а) Поставим в соответствие каждому числу ие R число vg R по
правилу: v = 2и . Тогда каждое число ve R отвечает одному числу и = v.
Следовательно, правило v = 2и устанавливает взаимно однозначное
соответствие Д < >R. Если <-> V! и u2e v2, т.е. = 2и{ и v2 - 2иг,
То («j+и2)<-> (vj + v2), так как v, + v2 - 2ut + 2v2 = 2(uj + и2). Если u<->v,
Т.е. v = 2и , то Хи <-> Xv для любого действительного числа X, так как
Xv = Х-(2и)= 2(Хи). Следовательно, соответствие у = 2и сохраняет линей-
ные операции, т.е. является изоморфизмом.
б) Рассмотрим взаимно однозначное соответствие R<———>R, уста-
' < а
навливаемое формулой v = и (число v оказывается сопоставленным числу
и = Vv ). Это соответствие не является изоморфизмом, так как не сохраняет
Нинейные операции. Например, если и <-> v, т.е. v = и3 ‘ то (2и)3 - 8и3 = 8v .
Значит, 2и 8v, что противоречит условию Хи <-> Xv для X = 2 .
389
Замечания 8.6.
1. При изоморфизме линейных пространств U и V :
- их нулевые элементы соответствуют друг другу (ov <-> ov );
- противоположные элементы соответствуют друг другу.
Это следует из определения, если в условии 2 положить X = О или X = -1.
2. Линейной комбинации векторов пространства U соответствует ли-
нейная комбинация соответствующих векторов пространства V .
3. Линейно независимой (линейно зависимой) системе векторов про-
странства U соответствует линейно независимая (линейно зависимая) сис-
тема векторов пространства V . Действительно, из п.1,2 следует, что равен-
ства AjM, + ... + Хпип =ov и Х,^ + ... + X„vn -ov равносильны. Если не все ко-
эффициенты Хр-.-.Х,, равны нулю, то обе системы ut,u2,...,un и
Vj ,v2 линейно зависимы, в противном случае, обе системы линейно
независимы.
4. Любое п -мерное линейное вещественное пространство V изоморф-
но п -мерному арифметическому пространству Rn, а п -мерное комплекс-
ное пространство изоморфно С".
Это следует из п.4 замечаний 8.5, где установлено взаимно однознач-
ное соответствие V <-> Rn между векторами и координатными столбцами.
Линейные операции с векторами в координатной форме (см. разд.8.4.2) по-
казывают, что это взаимно однозначное соответствие является изоморфиз-
мом.
5. Если пространство U изоморфно пространству V , а V изоморфно
пространству W , то пространства U и W также изоморфны.
В самом деле, имея взаимно однозначные соответствия U «-> V и
V <-» W, поставим в соответствие вектору и такой вектор и», что
и «-> v <-> и». Такое "сквозное" соответствие U 4-+W будет взаимно одно-
значным, сохраняющим линейные операции.
Теорема 8.3 (об изоморфизме линейных пространств). Два конечно-
мерных линейных пространства (над одним и тем же числовым полем)
изоморфны тогда и только тогда, когда они имеют одну и ту же размер-
ность.
Действительно, если пространства изоморфны (U «-> V ), то базису
uI,u2,...,un пространства V соответствует линейно независимая система
векторов Vj.Vj,...,пространства V (см. п.З замечаний 8.6), которую в
случае необходимости можно дополнить до базиса пространства V (см.
теорему 8.2). Следовательно, dimt/ <dimV . Аналогично получаем проти-
воположное неравенство dimU > dimV. Таким образом, dim U = dimV (не-
обходимость доказана). Достаточность следует из п.4,5 замечаний 8.6. Дей-
390
ствительно, пусть U и V определены над полем R и dim U = dimV = п .
Тогда, выбрав любые базисы в пространствах U и V , установим изомор-
физмы U Rn и V Rn, если U и V - вещественные пространства. Ес-
ли пространства U и V определены над полем С комплексных чисел, то
U Сп и V Сп . В обоих случаях, согласно п.5 замечаний 8.6, простран-
ства U и У изоморфны. Теорема доказана.
Следствие. Изучение конечномерных линейных пространств сводится
к изучению арифметических пространств той же размерности.
8.6. ПОДПРОСТРАНСТВА ЛИНЕЙНОГО ПРОСТРАНСТВА
8.6.1. Определение линейного подпространства
Непустое подмножество L линейного пространства V называется
линейным подпространством пространства V , если
1) и + ve L V и, ve L (подпространство замкнуто по отношению к
операции сложения)-,
2) Xve L V v е Z, и любого числа А (подпространство замкнуто по
отношению к операции умножения вектора на число).
Для указания линейного подпространства будем использовать обозна-
чение L < V , а слово "линейное" опускать для краткости.
Замечании 8.7.
1. Условия 1, 2 в определении можно заменить одним условием:
Аи + цг е L Vu,vtL и любых чисел Аир.. Разумеется, что здесь и в оп-
ределении речь идет о произвольных числах из того числового поля, над ко-
торым определено пространство V (см. разд.8.1.1).
2. В любом линейном пространстве V имеются два линейных подпро-
странства:
а) само пространство V , т.е. V < V ;
б) нулевое подпространство { о }, состоящее из одного нулевого век-
тора пространства V, т.е. {о}<У. Эти подпространства называются
несобственными, а все остальные - собственными.
3. Любое подпространство L линейного пространства V является его
подмножеством: L<V => L с V , но не всякое подмножество М сV яв-
ляется линейным подпространством, так как оно может оказаться незамкну-
тым по отношению к линейным операциям.
4. Подпространство L линейного пространства V само является ли-
нейным пространством с теми же операциями сложения векторов и умно-
жения вектора на число, что и в пространстве V , поскольку для них выпол-
391
няются аксиомы 1-8 (см. разд.8.1). Поэтому можно говорить о размерности
подпространства, его базисе и т.п.
5. Размерность любого подпространства L линейного пространства
V не превосходит размерности пространства V : dimL< dimV . Если же
размерность подпространства L<V равна размерности конечномерного
пространства V (dimL = dimV ), то подпространство совпадает с самим
пространством-. L = V.
Это следует из теоремы 8.2 (о дополнении системы векторов до бази-
са). Действительно, взяв базис подпространства L, будем дополнять его до
базиса пространства V . Если это возможно, то dimL< dimV . Если нельзя
дополнить, т.е. базис подпространства L является базисом пространства V ,
то dimL = dimV . Учитывая, что пространство есть линейная оболочка ба-
зиса (см. следствие 1 теоремы 8.1), получаем L = V .
6. Для любого подмножества М линейного пространства V линей-
ная оболочка Ып(м) является подпространством V и М С Ып(м) < V .
В самом деле, если М = 0 (пустое множество), то по определению
Ып(м) = { о }, т.е. является нулевым подпространством и 0c{o}<V.
Пусть М *0 . Нужно доказать, что множество Ып(м) замкнуто по отно-
шению к операциям сложения его элементов и умножения его элементов на
число. Напомним, что элементами линейной оболочки Ып(м) служат ли-
нейные комбинации векторов из М . Так как линейная комбинация линей-
ных комбинаций векторов является их линейной комбинацией, то, учитывая
п.1, делаем вывод, что Ып{м} является подпространством V, т.е.
Lin(M) < V . Включение М а Ып{м) - очевидное, так как любой вектор
v е М можно представить как линейную комбинацию 1-у , т.е. как элемент
множества 1лп(М).
7. Линейная оболочка Lin(L) подпространства L<V совпадает с
подпространством L,m.e. Lin(L) = L.
Действительно, так как линейное подпространство L содержит все-
возможные линейные комбинации своих векторов, то Lm(L)cL. Противо-
положное включение (L с Li«(L)) следует из п.6. Значит, Lin(L}-L .
8.6.2. Примеры линейных подпространств
Укажем некоторые подпространства линейных пространств, примеры
которых рассматривались в разд. 8.1.3. Перечислить все подпространства
линейного пространства невозможно, за исключением тривиальных случаев.
1. Пространство {о }, состоящее из одного нулевого вектора простран-
ства V , является подпространством, т.е. { о }< V .
392
2. Пусть, как и ранее, Ц, V2 , V3 - множества векторов (направленных
отрезков) на прямой, на плоскости, в пространстве соответственно. Если
прямая принадлежит плоскости, то Ц < V2 < Vj • Напротив, множество еди-
ничных векторов не является линейным подпространством, так как при ум-
ножении вектора на число, не равное единице, получаем вектор, не принад-
лежащий множеству.
3. В л -мерном арифметическом пространстве Rn рассмотрим множе-
ство L "полунулевых" столбцов вида x = (*i ••• *т 0 ••• 0)Т с по-
следними (л-m) элементами, равными нулю. Сумма "полунулевых" столб-
цов является столбцом того же вида, т.е. операция сложения замкнута в L.
Умножение "полунулевого" столбца на число дает "полунулевой" столбец,
т.е. операция умножения на число замкнута в L. Поэтому L < R" , причем
dim L = т . Напротив, подмножество ненулевых столбцов /?" не является
линейным подпространством, так как при умножении на нуль получается
нулевой столбец, который не принадлежит рассматриваемому множеству.
Примеры других подпространств Rn приводятся в следующем пункте.
4. Пространство {Лх = о} решений однородной системы уравнений с п
неизвестными является подпространством п -мерного арифметического
Пространства R”. Размерность этого подпространства определяется матри-
t Цей системы:
| dim{4x = o}= n-rg А .
(Множество {Ах = b} решений неоднородной системы (при b * о) не
Является подпространством Rn, так как сумма двух решений неоднородной
Системы не будет решением той же системы.
5. В пространстве МпХп квадратных матриц порядка п рассмотрим
г Два подмножества: множество симметрических матриц и множество
Илхл кососимметрических матриц (см. разд. 1.4.1). Сумма симметрических
матриц является симметрической матрицей, т.е. операция сложения замкну-
; Та в М. Умножение симметрической матрицы на число также не нару-
шает симметричность, т.е. операция умножения матрицы на число замкнута
в М™. Следовательно, множество симметрических матриц является под-
пространством пространства квадратных матриц, т.е Л/„“” <Мпхп. Нетруд-
? Но найти размерность этого подпространства. Стандартный базис образуют
п матриц с единственным ненулевым (равным единице) элементом на глав-
ной диагонали: а„ =1 i =!,...,«, а также матрицы с двумя ненулевыми (рав-
ными единице) элементами, симметричными относительно главной диаго-
393
1 О
о L
нали: а^=а^=1, i = j = i,» + л - Всего в базисе будет
л + (л-1)+... + 2 + 1= п-п +1) матриц. Следовательно, dimМ.
2 2
Аналогично получаем, что < Л/пхп и dim М„°сп - —
Множество вырожденных квадратных матриц л -го порядка не являет-
ся подпространством Л/пХп, так как сумма двух вырожденных матриц мо-
жет оказаться невырожденной матрицей, например, в пространстве М :
1 Го ОА
о о]\о 1J
6. В пространстве многочленов P(r) с действительными коэффициен-
тами можно указать естественную цепочку подпространств
Р0(я)< P2(r)<... < P„(r)<...< P(r) •
Множество четных многочленов (р(- х) = р(х)) является линейным подпро-
странством P(r), так как сумма четных многочленов и произведение четно-
го многочлена на число будут четными многочленами. Множество нечетных
многочленов ( р(- х) = -р(х)) также является линейным пространством.
Множество многочленов, имеющих действительные корни, не является ли-
нейным подпространством, так как при сложении таких двух многочленов
может получиться многочлен, который не имеет действительных корней,
например, (х2 - х)+ (х +1) = х2 +1.
7. В пространстве С(й) можно указать естественную цепочку подпро-
странств: с(я)>С1(й)>С2(я)>...>С'"(я)>... . Многочлены из Р(я)
можно рассматривать как функции, определенные на R . Так как многочлен
является непрерывной функцией вместе со своими производными любого
порядка, можно записать: p(r)<C(r) и Рл(/?)< Cm(/?) Vm,neN. Про-
странство тригонометрических двучленов Тш(/?) является подпространст-
вом Ст(/?), так как производные любого порядка функции
/(z)=asin(oz + Z>coscor непрерывны, т.е. Тш(л)<Ст(я) V те N . Множест-
во непрерывных периодических функций не является подпространством
C{R), так как сумма двух периодических функций может оказаться непе-
риодической функцией, например, sin t + sin(ra).
Многочисленные примеры линейных подпространств имеются в за-
дачниках [16,17,36,38].
394
8.6.3. Пересечение и сумма подпространств
Пусть Lj и L2 - подпространства линейного пространства V .
Пересечением подпространств Lt и L, называется множество
LiDL2 векторов, каждый из которых принадлежит и одновременно,
> т.е. пересечение подпространств определяется как обычное пересечение
двух множеств.
Алгебраической суммой подпространств L, « L, называется мно-
жество векторов вида Vj + v2 , где Vj е , v2 е £2 Алгебраическая сумма
(короче просто сумма) подпространств обозначается :
Л, + £2 = {v G V :v = Vj + v2, v, е L], v2 e }.
Представление вектора v e £j +в виде v = Vj + v2, где Vi e £j, v2 e £2,
называется разложением вектора v no подпространствам ЦнЪ.
Замечания 8.8.
1. Пересечение подпространств является подпространством. Поэтому
' понятия размерности, базиса и т.п. применяются к пересечениям.
2. Сумма подпространств является подпространством. Поэтому поня-
> тия размерности, базиса и т.п. применяются к суммам.
| Действительно, нужно показать замкнутость линейных операций в
| множестве Ц + £j. Пусть два вектора и и v принадлежат сумме £, + £j,
г т.е. каждый из них раскладывается по подпространствам:
I « = «!+м2, и,е £], и2б £3; v = v1+»>2, v2g£2.
I Найдем сумму: и + v = (и(+«2)+(vi+»’2) = (и1 + »’1)+(и2 + »’2). Так как
г в] + Vjе Z,, а и2 + v2£ £2 , то u + ve 1^ + 1^. Следовательно, множество
£ц + £2 замкнуто по отношению к операции сложения. Найдем произведе-
ние: Xv = Х(^! + v2)=Xv1 +Xv2. Так как е £j, a Xv2e £2, то kve 1^ + 1^.
i Следовательно, множество l^+L^ замкнуто по отношению к операции ум-
, ножения на число. Таким образом, £, + £2 - линейное подпространство.
। 3. Операция пересечения определена на множестве всех подпро-
странств линейного пространства V . Она является коммутативной и ассо-
циативной. Пересечение любого семейства подпространств V является ли-
нейным подпространством, причем скобки в выражении 11П£2Г1...Г1£4...
можно расставлять произвольно или вообще не ставить.
4. Минимальным линейным подпространством, содержащим под-
I Множество М конечномерного линейного пространства Указывается
‘ пересечение всех подпространств £ < V , содержащих М , т.е. П £ •
MtzLoV
Если М = 0 , то указанное пересечение совпадает с нулевым подпростран-
395
ством {о }, поскольку оно содержится в любом из подпространств L <1V .
Если М - линейное подпространство V (М <1V), то указанное пересече-
ние совпадает с М, поскольку Л/ содержится в каждом из пересекаемых
подпространств (и является одним из них: М с М < V ).
Минимальное свойство линейной оболочки: линейная оболочка
Ып(м) любого подмножества М конечномерного линейного пространст-
ва V является минимальным линейным подпространством, содержащим
М, т.е. Ып(м)= A L.
M<zL<V
Действительно, обозначим П = П L. Надо доказать равенство двух
множеств: Ып{м}= П . Так как М с Цп(м)< V (см. п.6 замечаний 8.7), то
П с£/и(л/). Докажем включение £/л(Л/)сП. Произвольный элемент
к
v е Ып(м) имеет вид v = '^k(vi, где v,- еЛГ ,i = . Пусть L - любое
<=1
подпространство, содержащее М (М a: L <V). Оно содержит все векторы
у,, i = и любую их линейную комбинацию (см. п.7 замечаний 8.7), в
частности, вектор v . Поэтому вектор v принадлежит любому подпростран-
ству L, содержащему М . Значит, v принадлежит пересечению П таких
подпространств. Таким образом, £/п(Л/)сП. Из двух включений
П с Lin(M) и Ип[м} с П следует равенство 1лп(м) = П .
5. Операция сложения подпространств определена на множестве всех
подпространств линейного пространства V . Она является коммутативной и
ассоциативной. Поэтому в суммах £( + £2 + ... + Lk конечного числа подпро-
странств скобки можно расставлять произвольно или вообще не ставить.
6. Можно определить объединение Lr U £2 подпространств £, и L2,
как множество векторов, каждый из которых принадлежит пространству L,
или пространству £2 (или обоим подпространствам). Однако, объединение
подпространств в общем случае не является подпространством (оно будет
подпространством только при дополнительном условии Lx с. £2 или
£2 с £]).
7. Сумма подпространств £, + £2 совпадает с линейной оболочкой их
объединения 1^+1^= Lin(L^ U £j). Действительно, включение
Li + LqC. Linfa U£2) следует из определения. Любой элемент множества
+ £2 имеет вид vl+v2, т.е. представляет собой линейную комбинацию
двух векторов из множества £, U Докажем противоположное включение
£/«(£, U £2) с £] + £2. Любой элемент и» е £/«(£, (J Lq) имеет вид
396
k
tv = У h'V;, где Vj e Z( U L2. Разобьем эту сумму на две, относя к первой
i=i
сумме все слагаемые , у которых р,- 61^ . Остальные слагаемые соста-
вят вторую сумму: tv = Х,р; + Х(.р(. = tvj + tv2. Первая сумма - это не-
|=1.к (=1....к
v.eij
который вектор w, е Ц, вторая сумма - это некоторый вектор tv2 e L2.
Следовательно, tv = tvj + tv2 е Lx + L2. Значит, Lin(L} U Z2)a Zj + Z2. Полу-
ченные два включения говорят о равенстве рассматриваемых множеств.
Теорема 8.4 (о размерности суммы подпространств). Если L, и 1г
подпространства конечномерного линейного пространства V, то размер-
ность суммы подпространств равна сумме их размерностей без размерно-
сти их пересечения {формула Грассмана):
dim(Z] + Z2)=dimZ] + dimZ2 -dim^ C1Z2). (8.13)
В самом деле, пусть (е) = (ер..., е^) - базис пересечения Zj PlZ2
(dim(zq П bj) = 5). Дополним его упорядоченным набором (е') = (е'+1,..., )
векторов до базиса (е),(е') подпространства Z, (dimZ, =т{) и упорядо-
ченным набором (e'') = (e"+i, векторов до базиса (е),(е") подпро-
странства Zj (dimZj = т2). Такое дополнение возможно по теореме 8.2. Из
указанных трех наборов векторов составим упорядоченный набор
(е), (е'), (е") векторов. Покажем, что эти векторы являются образующими
пространства 1^+1^. Действительно, любой вектор v этого пространства
представляется в виде линейной комбинации векторов из упорядоченного
набора (е),(е'),(е"):
5 mt з т2
” = Р] + v2 = £а,- е, + Ya'i e'i+ & е> + •
i=l i=i+l i°l i= >1
”1 v2
Следовательно, Zj + L2 = Lin((e\ (e'\ («")) - Докажем, что образующие
(e),(e')>(e ) линейно независимы и поэтому они являются базисом про-
странства Zj + Z2. Действительно, составим линейную комбинацию этих
векторов и приравняем ее нулевому вектору:
у ^2
Ха<- ei + SР' e>i + e'i=° (8-14)
1=1 i=j+l i= »1
»| w2
397
Первые две суммы обозначим w1 - это некоторый вектор из L], последнюю
сумму обозначим w2 - это некоторый вектор из 1^. Равенство (8.14):
w, + м>2 =о означает, что вектор w2 = принадлежит также и простран-
ству L]. Значит, w2 е L] Г12^. Раскладывая этот вектор по базису (е), нахо-
дим w2 = У 5,е,. Учитывая разложение этого вектора в (8.14), получаем
1=1
5 m2 S т1
w2 = = £Yi< <=> £з,е,. - = о.
1=1 i’ej+1 i=l i-s+l
Последнее равенство можно рассматривать, как разложение нулевого векто-
ра по базису (е),(е") подпространства 1^. Все коэффициенты такого раз-
ложения нулевые: 8j = ... = 35 =0 и у5+1 = — = ут2 = 0. Подставляя у, =0 в
s т,
(8.14), получаем У а,е, + У,Р,е,- = о Это возможно только в тривиальном
1=1 i=s+l
случае al=... = as=0 и Pi+i = ... = Pm] =0, так как система векторов
(е).(е') линейно независима (это базис подпространства L]). Таким обра-
зом, равенство (8.14) выполняется только в тривиальном случае, когда все
коэффициенты равны нулю одновременно. Следовательно, совокупность
векторов (е), (е'), (е") линейно независима, т.е. является базисом простран-
ства L] + L2 • Подсчитаем размерность суммы подпространств:
din^Lj +£2) = 5 + (/и1 -s)+(m2 — s) = ml +гп2 -s^dimZ, -t-dimZ^ —dirr^Z, ClZ^),
что и требовалось доказать.
Пример 8.6. В пространстве V3 радиус-векторов с общим началом в
точке О заданы подпространства: Lq , Ц и 1^ - три множества радиус-
векторов, принадлежащих пересекающимся в точке О прямым lQ, Zj и 12
соответственно; П( и П2 - два множества радиус-векторов, принадлежа-
щих пересекающимся плоскостям и л2 соответственно; прямая при-
надлежит плоскости JUj, прямая 12 принадлежит плоскости л2, плоскости
л, и л2 пересекаются по прямой /0 (рис. 8.2). Найти суммы и пересечения
каждых двух из указанных пяти подпространств.
□ Найдем сумму Lq + Z,. Складывая два вектора, принадлежащих Lq
и Z, соответственно, получаем вектор, принадлежащий плоскости П1. На-
оборот, любой вектор v (см. рис.8.2), принадлежащий П], можно предста-
вить в виде v0 + vj, построив проекции v0 и v( вектора v на прямые /0 и
398
соответственно. Значит, любой радиус-вектор плоскости П, раскладывает-
ся по подпространствам Lq и Ц, т.е. L^+Ц =11,. Аналогично получаем,
что Ц + Ц =П2, а + Ц _ множество радиус-векторов, принадлежащих
плоскости, проходящей через прямые и Z2.
Найдем сумму П] + 1^. Любой вектор w пространства V3 можно раз-
ложить по подпространствам и П1. В самом деле, через конец радиус-
вектора vv проводим прямую, параллельную прямой 12 (см. рис. 8.2), т.е.
строим проекцию й вектора ю на плоскость IIj. Затем на откладываем
вектор v2 так, чтобы w = m + v2. Следовательно, П1 + Г2=У3. Так как
Ц < П2, то Пг + П2 = V3. Аналогично получаем, что Ц + П2 = У3. Осталь-
ные суммы находятся просто: +П] = L,+П1 = П1, Ц+П2 =
= 1^ + П2 -П2. Заметим, что Lq + L3 + L1=V3.
Используя теорему 8.4, проверим, например, равенство ГЦ +П2 = V3
по размерности. Подставляя (ИтЩ =dimn2 = 2 и dim(n]nn2)=
= dim = 1 в формулу Грассмана, получаем dim(n, + П2) = 2 + 2-1 = 3, что
и следовало ожидать, так как dim^ +n2) = dimV3 =3.
Пересечения подпространств находим по рис. 8.2, как пересечение
геометрических фигур:
1ц)Г)Ц = Гц)ПГ2 = ЦПЦ = Г1 ГШ2 = ЦПП; — {о },
цпп1 = ц, Л)ПП2 = Ц, ЦПП^Ц, п1пп2 = ц,
где о - нулевой радиус-вектор ОО.
399
8.6.4. Прямая сумма подпространств
Алгебраическая сумма подпространств I, и линейного простран-
ства V называется прямой суммой, если пересечение подпространств со-
стоит из одного нулевого вектора. Прямая сумма подпространств обознача-
ется Ll®L2 и обладает следующим свойством: если V = 1^® L^, то для
каждого вектора v G V существует единственное представление в виде
v = vl+v2, г&е Fi е А, v2 е А •
Действительно, если предположить противное, а именно существова-
ние двух разных разложений: г = v1 +v2 = и», +и'2, где VpifjElj,
v2,H'2eL2, то получим противоречие: из равенства
V[ - Wj = - v2 следует, что ненулевой вектор v1 - и»] Ф о принадлежит
обоим подпространствам А и А одновременно, значит, принадлежит их
пересечению, а по определению их пересечение состоит из одного нулевого
вектора.
ПРИЗНАКИ ПРЯМЫХ СУММ ПОДПРОСТРАНСТВ
Сумма V = 1^ +1^ является прямой суммой, если'.
— существует вектор г G V, который однозначно представляется в
виде v -vl+v2, где Vj G А > F2 е А >
- базис пространства V является объединением базисов подпро-
странств А м А>’
- справедливо равенство dimV = dim А + dim А •
Замечания 8.9.
1. Понятие прямой суммы распространяется на любое конечное число
слагаемых. Сумма V =А®А®—®А называется прямой суммой под-
пространств, если пересечение каждого из них с суммой остальных равно
одному нулевому вектору: А П (А + — + А-1 + А+1 + — + А)= { ° } •
2. Свойства и признаки, указанные для прямой суммы двух подпро-
странств, справедливы и для любого конечного числа слагаемых. Отметим
еще одно свойство: если eY,e2,...,en - базис пространства V, то
V = Lin(el)®... ф Ып[еп).
Пример 8.7. В примере 8.6 найдены алгебраические суммы подпро-
странств. Какие суммы являются прямыми?
□ Так как L® П А = ° , то сумма 1$ Ф— прямая. Аналогично полу-
чаем, что суммы Lq®!^, 1^®!^, П! Ф А» А®п2. А®А®А ~ пря-
400
мые. Остальные суммы подпространств, найденные в примере 8.6, не явля-
ются прямыми: Lfl+rij, Ло+П2, Lj+nj, Т^ + П2, + П2, поскольку их
пересечение содержит не только нулевой вектор. Например, пересечение
ПП2 = Lg *{о }.
АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ ПОДПРОСТРАНСТВ
Пусть L — подпространство конечномерного линейного пространства
V . Подпространство L+ < V называется алгебраическим дополнением
подпространства L в пространстве V , если V = L®L+. Говорят, что L+
дополняет (алгебраически) подпространство L до V .
Рассмотрим свойства алгебраических дополнений.
1. Для любого подпространства L<V существует алгебраическое
дополнение L+ < V.
Действительно, если L-{o }, то L+ = V . Если L = V , то L+ ={о }. В
остальных случаях базис el,e2,...,es подпространства L можно дополнить
по теореме 8.2 до базиса в] ,...,es ,ej+1 ,...,ед пространства V. Тогда
L+ - Lin(es+1,...,en). В примере 8.7 получено равенство У3=£1®П2, т.е.
подпространства £, и П2 дополняют друг друга до всего пространства.
2. Базис любого подпространства L < V дополняется базисом алгеб-
|' раического дополнения Д <V до базиса всего пространства.
13. Алгебраическое дополнение L+ подпространства L<V, кроме слу-
чаев L = { о } или L = V, определяется неоднозначно.
В примере 8.7 дополнением плоскости П2 в пространстве У3 служит
множество радиус-векторов, принадлежащих любой прямой, пересекающей
плоскость П2 в точке О, в частности, подпространство £,.
4. Для любого подпространства L<V : L+ ® (l+ У = V .
• Это равенство следует непосредственно из определения. Заметим, что
равенство L = (b+ У в силу неоднозначности определения алгебраического
дополнения, вообще говоря, не справедливо.
5. Если Lj и 1^ - подпространства пространства V , то пересечение
; их алгебраических дополнений является алгебраическим дополнением суммы
' подпространств, и, наоборот, сумма алгебраических дополнений является
алгебраическим дополнением пересечения подпространств-.
(L1+L2)®(zq+n^)=V и (LinL2)®(l1++^)=V. (8.15)
t 26 - 4549 401
Заметим, что равенства + Zj)+ = Zf Л L2 и (Z] |~| )+ = + ZJ в СИЛУ
неоднозначности определения алгебраического дополнения, вообще говоря,
не справедливы.
Докажем последнее свойство. Как при доказательстве теоремы 8.4 по-
строим базис суммы подпространств из трех наборов (е),(е'),(е") векторов:
Lj+L2= Lin((e), (е'), (е")). Дополним теперь этот базис (по теореме 8.2) век-
торами (/)= (/] ,•,/*) до базиса (е), (е'), (е"), (/) пространства V . Так как
(е),(е') базис Lx, то по свойству 2 алгебраических дополнений заключаем,
что (е"), (/) - базис Ц . Аналогично получаем, что (е'), (/) - базис 1^, .
Следовательно, (/) - базис пересечения Q L2. Таким образом, базис все-
го пространства V получается объединением базиса суммы Ц +1^ и базиса
пересечения Zj" Cl Д: (е) (е') (е") (/) . Используя признак 2 прямой суммы
Л+/'2
подпространств, получаем (Z, + ) © (zf Г1Д )= V . Равенство
(£] nz2)®(z]+ +д)=И следует аналогично из структуры (е) (е')(е")(/)
базиса пространства V.
ЛИНЕЙНАЯ ЗАВИСИМОСТЬ И ЛИНЕЙНАЯ НЕЗАВИСИМОСТЬ ВЕКТОРОВ
НАД ПОДПРОСТРАНСТВОМ
Говорят, что система векторов vl,...,vk пространства V линейно за-
висима над подпространством L<V, если существует нетривиальная ли-
нейная комбинация этих векторов, принадлежащая подпространству Z, т.е.
найдутся такие числа at,..., ак , не равные нулю одновременно, что
ai V1 +<Х2 V2 +-+а* vk е Z •
Если последнее включение возможно только в тривиальном случае, т.е при
at = a2 =... = ак = 0 , то векторы .., vk называют линейно независимы-
ми над подпространством L.
Понятие линейной зависимости или независимости над подпростран-
ством обобщает обычное, рассмотренное ранее (см. разд. 8.2.1), понятие ли-
нейной зависимости или независимости векторов, и совпадает с ним, если в
качестве подпространства Z < V взять нулевое Z = {о }.
Следующие свойства прямых сумм подпространств можно сформули-
ровать при помощи понятия линейной зависимости и линейной независимо-
сти над подпространством.
402
1. Если пространство V представлено в виде прямой суммы подпро-
странств V = L^® L2, то любая линейно независимая система векторов
подпространства Lx будет линейно независимой над подпространством
Z2.
2. Базисом алгебраического дополнения I? подпространства L<V
является максимальная совокупность векторов пространства V, линейно
независимая над подпространством L (см. свойство 2 алгебраических до-
полнений подпространств).
Пусть имеется цепочка подпространств L < М < V. Подпространство
L+ Q М называется алгебраическим дополнением подпространства L
относительно подпространства М (или относительным дополнением
L до подпространства М). Базисом относительного дополнения £+ А Л/
служит максимальная система векторов М, линейно независимая над L.
8.6.5. Способы описания подпространств
Рассмотрим два важных способа описания линейных подпространств,
которые условно будем называть внутренним и внешним. В первом (внут-
реннем) способе используется понятие линейной оболочки векторов (см.
разд.8.2.3), когда все элементы подпространства выражаются через некото-
рые его элементы (образующие). При втором (внешнем) способе применя-
ются однородные системы уравнений (см. разд.5.5). В этом случае подпро-
странство описывается как пересечение некоторых содержащих его мно-
жеств. Для каждого способа описания подпространств укажем методики на-
хождения размерностей, базисов, алгебраических дополнений, пересечений
и сумм подпространств.
Любое п -мерное вещественное линейное пространство И изоморфно
(см. разд. 8.5) «-мерному арифметическому пространству Л" . Чтобы уста-
новить изоморфизм F <->/?", достаточно выбрать в пространстве V базис и
каждому вектору поставить в соответствие его координатный столбец. По-
этому в данном разделе будем рассматривать описание подпространств п -
мерного арифметического пространства R” .
Первый (внутренний) способ. Пусть в пространстве Rn заданы столб-
цы ах,а2,...,ак . Напомним (см. разд. 3.4), что для систем столбцов
ах,а2,...,ак были определены понятия базы (максимальной линейно неза-
висимой подсистемы столбцов) и ранга (максимального числа линейно не-
зависимых столбцов системы), а также методы их нахождения.
Рассматривая линейную оболочку L = Ып(ах,а2,...,ак) столбцов
ах, а2,..., ак как линейное подпространство R", заключаем, что база систе-
26*
403
мы столбцов является базисом этого подпространства, а ранг системы
столбцов равен размерности подпространства dimL = rg (арО^,...,^).
Поэтому для нахождения размерности и базиса подпространства
L = 1лп{а1,а2,...,ак) нужно выполнить следующие действия (см. п.З замеча-
ний 3.6 в разд.3.4):
составить из данных столбцов матрицу A = (at ак) размеров
пхк;
привести ее к ступенчатому виду А' (1.4), используя элементарные
преобразования строк;
определить размерность и базис подпространства L = 1лп(а1,а2,...,ак)-.
- количество ненулевых строк в матрице А' равняется размерности
подпространства, т.е. dimL = rg А = rg (ара2,...,а4)= rg А',
- столбцы матрицы А', содержащие единичные элементы (в начале
каждой "ступеньки"), определяют номера линейно независимых столбцов
матрицы А , т.е. искомый базис.
Таким образом, если подпространство L<Ra задано своими обра-
зующими alta2 ,-,ак : L = Ып^а^а^... ,ак), то его размерность равна рангу
системы столбцов alta2,...,ak, т.е. dimL=rg(a1,a2,...,at), а базисом L
служит максимальная линейно независимая подсистема образующих.
Второй {внешний) способ. Пусть подпространство L<Rn задано как
множество L = { Ах = о } решений однородной системы Ах = о т уравне-
ний с п неизвестными. Множество решений системы уравнений можно рас-
сматривать как пересечение т подпространств где Lt - мно-
жество решений i -го уравнения системы (i = 1,...,т). Напомним, что любое
решение однородной системы представляется в виде линейной комбинации
элементов фундаментальной системы решений (см. разд. 5.5). Поэтому раз-
мерность пространства dimL = «-rgA, а базисом L служит фундамен-
тальная система решений однородной системы Ах = о . Способы нахожде-
ния фундаментальной системы решений рассмотрены в разд. 5.5,5.6.
ПЕРЕХОД ОТ ОДНОГО СПОСОБА ОПИСАНИЯ К ДРУГОМУ
Переход от внутреннего описания к внешнему. Пусть подпространство
задано линейной оболочкой столбцов ах,а2,...,ак: L = Ып(а1,а2,...,ак).
Требуется составить такую однородную систему Тх = о уравнений, множе-
ство решений которой совпадает с L, т.е. L = { Тх = о }. Для этого нужно
выполнить следующие действия.
404
Ег О']
О | о/
1. Из данных столбцов составить матрицу А = (л] ак) размеров
(лхЛ), а затем блочную матрицу (А | Е), приписав к матрице А единич-
ную матрицу Е п -го порядка.
2. Элементарными преобразованиями над строками блочной матрицы и
первыми к ее столбцами привести матрицу (А | Е) к виду (л ] 5), где Л -
простейший вид матрицы А (см. рис. 1.6 в разд. 1.6.1): Л =
3. Из последних (л —г) строк матрицы S составить матрицу 'Р:
Т = (О|ЕИ_Г)5.
4. Записать искомую систему уравнений Тх = о.
Поясним содержание алгоритма. Заданное подпространство L состоит
из линейных комбинаций данных векторов, т.е. все его элементы имеют вид
х = Р1а1 + ... + Рд.а*.. Решаемую задачу можно сформулировать так: для каких
векторов х найдутся такие числа Р1 ,...,Pt, чтобы выполнялось равенство
х = р1а1+... + Р^а* . Другими словами, при каких х неоднородная система
АР = х (л уравнений с к неизвестными P = (Pi ••• Pt)Т) имеет решения?
Используя необходимое и достаточное условие (5.24) совместности систе-
мы, получаем равенство Ч*х = о . Заметим, что решение поставленной задачи
неоднозначно, так как существует много однородных систем, имеющих од-
но и то же множество решений.
Пример 8.8. Подпространство L < Я4 задано линейной оболочкой
столбцов aY = (1 1 1 1)т, а2 = (1 2 1 3)г, а3 = (3 4 3 5^. Составить
систему уравнений, определяющую подпространство L.
□ 1. Составляем матрицу А = (aj аг
а3) и блочную матрицу:
(а | Е4)=
1
2
1
3
3
4
3
5
1
О
О
О
О
1
О
О
О
О
1
О
О
о
о
1
1
1
1
2. Приводим левый блок к простейшему виду. Вычитаем первую стро-
ку из остальных, а затем к четвертой строке прибавляем вторую, умножен-
ную на (-2):
О О О'
1 О О
О 1 О
-2 О 1,
405
Преобразовываем столбцы левого блока: ко второму столбцу прибавим пер-
вый, умноженный на (-1), к третьему столбцу прибавим первый, умножен-
ный на (-3), а затем второй, умноженный на (-1). Эти преобразования не
изменяют правый блок полученной матрицы. Находим простейший вид Л
матрицы А и матри! (1 1 3) 0 1 1 А- ООО <° 0 °J НУ S: '1 0 0 1 О' 0 =л
0 0 ч0 0 0 оу
(1 О О СА
-1 1 О
-1 0 1
1 -2 0
0
0
; г = rg А = 2 .
3. Из последних п-г = 4-2 = 2 строк матрицы S составляем матрицу
„,(-10 10)
Чг = искомой системы.
11 -201)
4. Записываем систему уравнений Тх = о :
- X] + х3 = 0,
х1 - 2х2 + х4 = 0.
Заданные в условии примера столбцы а1, а2, а3 являются решениями полу-
ченной системы, в чем можно убедиться при их подстановке в систему
уравнений вместо х.
Переход от внешнего описания к внутреннему. Пусть подпространство
L задано как множество решений однородной системы т уравнений с п
неизвестными: L = {Ax = o}. Требуется найти размерность к и базис
<₽!,...,этого подпространства, т.е. представить его в виде линейной обо-
лочки L = . Для этого нужно выполнить следующие действия.
1. Найти фундаментальную систему ф! ,...,ф„_г решений однородной
системы Ах = о (г = rg А). Искомая размерность к = п-r (см. п.4 в разд.
8.3.2).
2. Представить заданное пространство как линейную оболочку
£ = Ьл(ф1,...,фи_г).
Первый пункт алгоритма удобно выполнять следующим образом:
_ М)
- составить блочную матрицу — , приписав к матрице А единичную
J
матрицу Е п -го порядка;
- элементарными преобразованиями над столбцами блочной матрицы
и строками верхнего блока А привести матрицу
простейший вид матрицы А (см. рис. 1.6 в разд. 1.6.1): Л =
। , Л ,
— к виду — , где Л -
Ег | СА
о 1оГ
406
- из последних (п — г) столбцов матрицы Т составить фундаменталь-
но
ную матрицу Ф : Ф = Т • ---- (см. формулу (5.25)).
\En-r J
Столбцы фундаментальной матрицы Ф = (ф1 фп_г) составляют иско-
мую фундаментальную систему решений.
Заметим, что решение поставленной задачи неоднозначно, так как су-
ществует много базисов одного и того же линейного подпространства.
Пример 8.9. Найти размерность и базис подпространства L < Л4, за-
данного системой уравнений
х1 + х2 + 2*3 + х4 = 0,
2х, + Зх2 + х4 = 0,
ЗХ] + 4х2 + 2х3 + 2х4 = 0.
□ 1. Фундаментальная матрица для этой системы была найдена в при-
мере 5.6 (/л = 3, п = 4, г = rg А = 2):
4
1
О
Ф = (<Р1 Фг)~
-2'
1
О
1 .
Ее столбцы ф!, ф2 образуют фундаментальную систему решений. Размер-
ность подпространства L равна к = п - г = 2, dim L = 2.
2. Столбцы Ф1, ф2 являются искомым базисом, так как они линейно
независимы(rg Ф = 2 ) и L = Lin^,^)•
НАХОЖДЕНИЕ АЛГЕБРАИЧЕСКОГО ДОПОЛНЕНИЯ ПОДПРОСТРАНСТВА
Для заданного подпространства L < Rn требуется найти алгебраиче-
ское дополнение L+, т.е. такое подпространство L+ <Rn, что Rn = L®I?
(см. разд.8.6.4).
В зависимости от способа описания подпространства L, используем
одно из следующих двух утверждений.
1. Если подпространство L<Rn задано как линейная оболочка
L = Ltn(alt...,ak) столбцов матрицы А = (а] ••• ак], то множество ре-
шений однородной системы АТх = о является его алгебраическим дополне-
нием L+ <Rn, т.е.
L= Lin(alt...,ak) => L+={azx = o). (8.16)
407
2. Если подпространство L< R" задано как множество решений од-
нородной системы Ах = о т уравнений с п неизвестными, то линейная
оболочка столбцов а^,...,аТт транспонированной матрицы
АТ - (а[ а^ j является его алгебраическим дополнением L+ < R", т.е.
£ = {Ах = о) => L+= Lin{ay (8.17)
где a] — i -й столбец матрицы АТ .
Разумеется, в (8.16) и (8.17) указано одно из возможных алгебраиче-
ских дополнений подпространства L (см. свойство 3 алгебраических до-
полнений в разд. 8.6.4).
Докажем сначала справедливость (8.16) в одномерном случае {k = 1), а
потом в общем. Пусть L = Lin{a) - одномерное подпространство R",
а = (а1 • • • а„ )г - ненулевой столбец. Найдем алгебраическое дополнение
подпространства L. Рассмотрим уравнение аТх~о в координатной форме:
а^! + ... + аяхя =0. Множество |агх = о j решений однородной системы,
состоящей из одного уравнения, образует подпространство L' размерности
(и-1) (см. п.4. разд.8.6.1). Найдем пересечение L^L'. Подставляя элемент
х = Ла линейной оболочки L в уравнение атх = о, получаем
4(“1)2 +(а2)2 + - +(ал)2 ]=°,
что возможно только при X = 0, так как а * о . Следовательно, элемент х
из L принадлежит подпространству L' только тогда, когда х - нулевой
столбец, т.е. L A L' - {о }. Учитывая, что dimL + dim L' = п, заключаем, что
L' - алгебраическое дополнение подпространства L в R":
£ © L' = R" .Таким образом,
Lin(a)®[aTx = o }=Л". (8.18)
Учитывая (8.18), докажем (8.16) в общем случае (£>1). Представим
£ = ввиде суммы £ = Ц +... + Lk, где £,=£/«(<3,), 1 = 1,...,£.Из
(8.15) следует, что (Zq + ... +£^)®(Д R" Согласно (8.18), множе-
ство £+ =|(а.)гх = о | решений однородной системы, состоящей из одного
уравнения, дополняет £, до всего пространства R". Пересечение множеств
решений отдельных уравнений дает, разумеется, множество
Zq+ П...П£* ={агх = о | решений системы этих уравнений. Поэтому
(Zq + ... 4" кк )®|ягх = о }=/?”, что и требовалось доказать. Утверждение
(8.17) доказывается аналогично, используя (8.18).
408
Пример 8.10. Найти алгебраическое дополнение подпространства
L = (t +1)3] в пространстве P3(r) многочленов не более, чем 3-й
степени (здесь в отличие от п.4 примеров подпространств в разд.8.1.2 неза-
висимая переменная многочленов обозначена через t).
□ Сначала нужно переформулировать задачу для арифметического
пространства (см. следствие теоремы 8.3 об изоморфизме конечномерных
пространств). Для этого возьмем в P3(R) стандартный базис
e1(r) = l,e2(r) = r ,е3(г) = г2 ,е4(г) = ? (см. п.6 в разд. 8.3.2). Пространство
P3(r) изоморфно Л4. Найдем координаты многочленов Л](г)=(г —1)2 и
а2 (/) = (/ +1)3 в стандартном базисе. Раскладывая а} (г) по базису, получаем:
ai(f)=(f-1)2=1-2f + f2 =1 ^i(z)+(-2) ^(f)+1 гз(/)+0 еЖ)>
т.е. многочлену соответствует координатный столбец
а, =(1 -2 1 0)г - элемент пространства R4. Аналогично получаем ко-
ординатный столбец а2 = (1 3 3 if для многочлена а2 (?).
Таким образом, исходная задача сводится к следующей: требуется най-
ти алгебраическое дополнение подпространства L = Linia^ а2) в простран-
стве /?4 . Используя правило (8.16), получаем, что L+ - это множество ре-
т т / \т0~21 0^
шений системы А х = о, где А = (л а?) = , т.е. системы
\ 1 х/ I 1 О Т 1 I
Xj - 2х2 + х3 = 0,
X] + Зх2 + Зх3 + х4 = 0.
Решаем ее методом Гаусса. Приводим матрицу системы к упрощенному ви-
ду, прибавляя ко второй строке первую, умноженную на (-1), поделив вто-
рую строку на 5, а затем прибавив ее, умноженную на 2, к первой:
т <1 -2 1 0W1 -2 1 OW1 0 1,8 0,4^
А =
1^1 3 3 1J I/) 5 2 1J (/) 1 0,4 0,2)
Базисные переменные xt,x2, свободные - х3,х4. Выражаем базисные пе-
ременные через свободные: Xj = -1,8 х3 - 0,4 х4; х2 = - 0,4 х3 - 0,2 х4. Нахо-
дим фундаментальную систему решений (см. разд.5.3). Подставляя стан-
дартные наборы свободных переменных (х3 = 1, х4 = 0 и х3 = 0, х4 = 1), по-
лучаем решения: ф!=(-1,8 -0,4 1 0)т, <р2=(-0,4 -0,2 0 1)7 , кото-
рые образуют фундаментальную систему решений и являются базисом ал-
гебраического дополнения L+ = Lirfa, <р2). Полученный результат перено-
409
сим в пространство многочленов. По координатному столбцу ф] находим
многочлен
ф1 (z) = -1,8 • (z) - 0,4 • ег (г)+1 • е3 (t) + 0 е4 (z) = -1,8 - 0,4z + z2.
Аналогично получаем cp2(z)=-0,4-0,2z + Z3. Искомое алгебраическое до-
полнение имеет вид L+ = Lzn((-1,8 - 0,4z + z2), (- 0,4 - 0,2z +t3)).
Проверим равенство L П L+ = { о }. Для этого приравняем между собой
линейные комбинации многочленов a1(z),a2(0 и Ф1(*)»Фг(*):
а(1 —z)2 + p(l + z)3 = y(-l,8-0,4z + z2)+5(-0,4-0,2z + z3).
Преобразовывая, получаем
(Р - б) • z3 + (а + ЗР - у) • z2 + (-2а + ЗР+0,4у + 0,25) z + а + Р + 1,8у + 0,45 = 0.
Чтобы это равенство выполнялось тождественно, все его коэффициенты
должны быть равны нулю:
р-5 = 0, f ° 1 0 -П Г°1
а + ЗР~у = О, 1 3 -1 0 р 0
-2а+ зр + 0,4у +0,25 = 0, -2 3 0,4 0,2 Y 0
а+ Р + 1,8у+0,45 = 0, 1 1 1,8 0.4 j W
в
Ранг матрицы В этой системы равен 4 (находится, например, методом Га-
усса). Поэтому однородная система имеет только нулевое решение
а = Р = у = 5 = 0 (см. разд. 5.5). Таким образом, равенство L A L+ = { о } вы-
полняется.
НАХОЖДЕНИЕ АЛГЕБРАИЧЕСКОЙ СУММЫ ПОДПРОСТРАНСТВ
Для заданных подпространств А и В пространства Rn требуется
найти размерность и базис их алгебраической суммы А + В. Рассмотрим
методику решения этой задачи для двух случаев описания подпространств.
Пусть подпространства заданы линейными оболочками своих обра-
зующих (внутреннее описание): А - Lin[ai,...,aki) и В - . Тогда,
приписывая к образующим ai,...,aki одного подпространства образующие
,- ;Ьк1 другого подпространства, получаем образующие суммы подпро-
странств А и В:
► => А + В =Lin[al,...,aki,bl,...,bkj), (8.19)
поскольку любой вектор ve А + В имеет вид
А = 1лп\ах,...,ак
В = Lin\bi„..,bk
410
V = а1Д1+-+atifljfc[ + ЗА +...+р^2 .
A v2E В
Базис суммы А + В = ZJn^ap...,^ , ) можно найти как максимальную
подсистему линейно независимых столбцов (см. разд. 3.4).
Пусть подпространства заданы как множества решений однородных
систем уравнений (внешнее описание): А = {Ах = о} и В = { Вх - о }. Тогда,
переходя к внутреннему описанию, сводим задачу к предыдущему случаю, а
именно нужно выполнить следующие действия:
1) для каждой однородной системы Ах = о и Вх = о найти фундамен-
тальные системы решений (pj ,...,(рл_^ и \|/1 ,...,\|/п_Г(| соответственно. При
этом получим А = ) и В = Lin^,..., 1|Хи_Гв ), где rA=rgA,
f
/s = rgB;
f «•
2) по правилу (8.19) найти сумму А + В = 1лл((р1,...,фя_Гл,ч/1,...,ч/п_Гв).
г
, Пример 8.11. Найти размерность и базис алгебраической суммы
VA + B подпространств А, В < Л4, если подпространство А задано систе-
мой уравнений
Xj + х2 + 2х3 + х4 = 0,
• 2xj + Зх2 + х4 = 0,
3xj + 4х2 + 2х3 + 2х4 - 0,
подпространство В - линейной оболочкой своих образующих:
Г В = £й(^,^2), =(-4 3 1 -lf,Z>2=(l 1 1 if.
к □ Образующие подпространства А были найдены в примере 8.9:
нА = Lin(a1,a2), где ^=(-6 4 1 of, а2=(-2 1 0 if. По правилу
^8.19) получаем А+В = Lin(al,a2,b1,b2). Найдем базис этого подпростран-
(^ЯВа как максимальную линейно независимую подсистему столбцов (см.
разд.3.4). Составляем из этих столбцов матрицу и приводим ее методом Га-
*усса к ступенчатому виду:
' н
'-6 -2
4 1
1 О
<0 1
— 4 1') fl
4
-6
о 1 1W1 о 1
1 3 1 0 1-1
-2-41 0-22
1 -1 1J [о 1 -1
1 '
-3
7
3 1
1 1
-1 1J 10
411
'1 О 1
О 1 -1
ООО
J) о о
1'
-3
1
О,
Первый, второй и четвертый столбцы полученной матрицы линейно незави-
симы. Значит, соответствующие столбцы аг, а2, Ь2 исходной матрицы так-
же линейно независимы (так как выполнялись элементарные преобразова-
ния только над строками). Поэтому они являются базисом А+В и
dim(A + B) = 3.
НАХОЖДЕНИЕ ПЕРЕСЕЧЕНИЯ ПОДПРОСТРАНСТВ
Для заданных подпространств А и В пространства Л" требуется
найти размерность и базис их пересечения А Г] В. Рассмотрим методику
решения этой задачи для двух случаев описания подпространств.
Пусть подпространства заданы как множества решений однородных
систем уравнений (внешнее описание): А = {Ах = о} и В = { Вх = о }. Тогда,
приписывая к системе Ах = о, задающей одно подпространство, систему
Вх = о, задающую другое подпространство, получаем систему
Ах = о
Вх = о
определяющую пересечение подпространств:
А-{Ах-о}1 А в = | ГЛЪ = О | (8.20)
в={вх=о}] Цв;
Базисом пересечения служит ее фундаментальная система решений.
Пусть подпространства А и В пространства Яп заданы линейными
оболочками своих образующих (внутреннее описание): А = ) и
В = Lin[bx,...,bk^). Переходя от внутреннего описания подпространств к
внешнему, можно свести задачу к предыдущему случаю. Однако удобнее
сделать иначе [36]. Пересечению АП В принадлежат только такие хе Л",
которые можно представить как равные между собой линейные комбинации
столбцов at,...,ati и столбцов bt,...,Ъкг соответственно:
х = щ ах+... + акакх =р1^+...+р^2. (8.21)
Представим второе равенство в (8.21) в матричном виде Аа = ВР, где
А = (а] ак ), В = (й> ••• Ьк1) - матрицы, составленные из данных
412
столбцов, a = (aj ••• oqj, Р = (Р] - столбцы коэффициентов
линейных комбинаций. Равенство Aa = ВР можно рассматривать как одно-
родную систему Аа-ВР = о п уравнений с (к1+к2) неизвестными а и р.
Каждому решению этой системы соответствует вектор х = Аа - ВР, при-
надлежащий пересечению А Г) В. Однако, на практике удобнее вместо сис-
темы Аа-ВР = о рассматривать однородную систему Aa+BP = o, реше-
ния которой обладают теми же свойствами (тогда вектор х = Аа = -ВР при-
надлежит пересечению А П В).
Поэтому для нахождения пересечения подпространств
А = Lin{al,...,ak), В = ) и базиса пересечения нужно выполнить
следующие действия.
1. Составить блочную матрицу (А | В) коэффициентов однородной
системы уравнений Аа + ВР = о, где матрицы A =
В - •• • Ькг) образованы из заданных столбцов.
2. Для однородной системы с матрицей (а | В) найти фундаменталь-
ную матрицу Ф (одним из способов, рассмотренных в разд. 5.5, 5.6). Мат-
рица Ф имеет размеры (ij + i2)x(b+^2 ~г)’где r = rg(A | В).
3. Из первых кх строк матрицы Ф составить матрицу Фа:
Фа=[в(-1 | О)Ф • Столбцы матрицы Фа = (<Р1 <Pt1+t2-г) содержат ис-
комые коэффициенты а = (cq • •• линейных комбинаций (8.21).
4. Записать пересечение А Г1В как линейную оболочку столбцов мат-
рицы АФа: АПЛ = 1»»(а<р1,...,А<Р4|+*1_г).
5. Найти базис пересечения как максимальную линейно независимую
подсистему образующих Афр..., АфА)+*2_г (см. разд.3.4 и первый (внутрен-
ний) способ описания подпространств в п.8.6.5).
Пример 8.12. Найти размерности и базисы суммы А+В и пересече-
ния А П В подпространств А, В < Я4, если они заданы линейными оболоч-
ками своих образующих: А = Ып(ах,а2,а3), В = где
«1 = т 1 1 . а2 = 'Г -1 1 > а3 = т 3 1 А Т 2 0 <2> . ъ2 - Т 2 1 А . Ьз = А 1 3 Л
□ Найдем базис и размерность суммы А + В. Составим из данных
столбцов блочную матрицу
413
Элементарными преобразованиями над строками приведем ее к ступенчато-
му виду (см. п.1 замечаний 1.8):
'1 1 1 113^ '1 1 1 113'
(А 1 в)~ 0-2 2 1 1 -2 0-2 2 1 1 -2 _(д' I д'
ООО -10 0 ООО -10 0 -И 1 а
J) -2 2 1 1 -2, /) 0 0 0 0 0 ,
По ступенчатому виду определяем, что первый, второй и четвертый столбцы
линейно независимы. Следовательно, из 6 образующих , а2, а3, , Ь2, Ь3
подпространства А + В максимальную линейно независимую подсистему
составляют столбцы at, а2, bt (в этих столбцах расположен базисный минор
матрицы). Следовательно, эти столбцы служат базисом суммы:
А + В = L/n(a1,a2,i1) и dim(A + B)=3. По ступенчатому виду матрицы
(А | В) можно также определить размерности подпространств. В блоке А'
две ненулевых строки, следовательно, dimA = rg A = rg А' = 2. Ненулевые
строки блока В' линейно независимы, следовательно,
dim В = rg В = rg В' = 3.
Найдем базис и размерность пересечения А А В (к{=к2=3,
г = rg(A | В) = 3).
1. Первый пункт алгоритма выполнен выше: матрица (А | в) однород-
ной системы Aa + вр = о приведена к ступенчатому виду (а' | В').
2. Находим фундаментальную систему решений (используя алгоритм,
описанный в разд. 5.5). Приводим матрицу (А' | В') системы к упрощенно-
му виду:
'1 1 1 113' 10 2 О to /
0-2 2 1 1 -2 0 1 -1 0 1
(а в')= 2
0 0 0 -10 0 0 0 0 1 0 0
0 0 0 0 0 0 , J) 0 0 0 0 0,
Базисные переменные: av, а2
Pt; остальные переменные - свободные.
Выражаем базисные переменные через свободные:
3
ai ~ ~2аз ~^2~ 2Р3 ’
414
а, =а, +—6,-6,; Р, = 0. Придавая свободным переменным наборы зна-
.£ J 1 х ’ J X
чений (а3 = 1, р2 = 0, Р3 = 0; а3 - 0 , Р2 = 2, Р3 = 0 и а3 = 0, Р2 = 0,
Р3 = 1), получаем линейно независимые решения <pt = (- 2 4 1 О О 0)г ,
<р2=(-3 1 О 0 2 0)7,(р3
ная матрица имеет вид
-1
О О О 1)т, т.е. фундаменталь-
'-2
1
1
О
О
. О
-3
1
о
о
2
О
-2"
-1
О
О
О
1 .
3. Из первых трех строк (= 3) матрицы Ф
составляем матрицу
Фа
'-2
1
. 1
-3
1
О
-2'
-1
О '
ф =
4. Вычисляем произведение
на
1
1
1
этой
1
-1
1
-1
-2
1
1
-3
1
о
-2'
-1
О .
о
о
о
о
-3
-1
-3
-1
Столбцы
А QB = Lin(o,c,,c.
с2=(-3 -1 -3 -if.
5. Найдем базис пересечения А Г) В. Для этого матрицу АФа приво-
дим к ступенчатому виду
О
О
О
О
матрицы
>, L], 1*2 ), ГДС О
АФа
-2
-4
-2
-4
образующими пересечения
являются
- нулевой столбец, с(=(-2 -4 -2 -4f,
-2
-4
-2
-4
-1
-3
-1
ГО
О
О
.0
2
О
О
О
3'
5
О
0.
о
о
о
о
2
1
О
О,
3
1
3
последние
1
О
О
О
два столбца матрицы
с2 являются ба-
По ступенчатому виду определяем, что
АФа линейно независимы. Следовательно, два столбца Cj
зисом пересечения AflB = Zin(ct,c2) и dim(A |"|Zf)= 2 .
415
Проверим размерность пересечения подпространств, которую вычис-
лим, используя формулу (8.13):
dim(A П В) = dim А + dim В - dim(A + В) = 2 + 3- 3 = 2,
что совпадает с найденной ранее размерностью.
Пример 8.13. Найти размерности и базисы пересечения А А В и сум-
мы А+В подпространств А, В < /?4, если они заданы однородными систе-
мами уравнений:
Xi + х2 + 2х3 + х4 = 0,
А: 2xj + Зх2 + х4 ~ 0,
Зх] + 4х2 + 2х3 + 2х4 = 0,
2xt + Зх2 + х3 + 2х4 = 0,
Xj + 2х2 + 2х4 = 0.
В:
□ Обозначим матрицы данных систем через А и В соответственно.
По правилу (8.20) пересечение А А В описывается однородной системой
|Ах = о „
< . Найдем базис пересечения - фундаментальную систему решении
[Вх = о
этой однородной системы уравнений. Составляем матрицу системы
— и
bJ
приводим ее к ступенчатому виду (см. рис. 1.4 в разд. 1.6.1), а затем к упро-
щенному виду:
р 1 2 А (1 1 2 Р р 1 2 Р Р 1 2 Р
2 3 0 1 0 1-4-1 0 1-4-1 0 1-4-1
pf) 3 4 2 2 0 1-4-1 0 0 0 0 0 0 1 1
l^BJ 1110 0 0-1-1 0 0-1-1 0 0 0 0
2 3 12 0 1-30 0 0 1 1 0 0 0 0
J 2 ° 2, 01-2 lz 1 0 0 2 2у 0 0 0 0,
р 0 6 2 р 0 0-4^
0 1-4-1 0 10 3
0 0 1 1 0 0 11
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
J) 0 0 0 0 0 0 0 J
Базисные переменные: xt, х2, х3, свободная переменная - х4 . Выражаем ба-
зисные переменные через свободную: Xj = 4х4 ; х2 = - Зх4; х3 = - х4. Фун-
даментальная система содержит одно решение <pt = (4 -3 -1 1)т, кото-
416
рое получаем, задавая хл = 1. Следовательно, А Г) В = Lin(<p() и
dim(Ane) = l.
Найдем теперь сумму А + В . Фундаментальная система решений од-
нородной системы Ах = о была найдена в примере 8.9. Следовательно,
А = Ып(а1,а2), где аг=(-6 4 1 Of, а2=(-2 1 0 if, dimA =2.
Найдем фундаментальную систему решений однородной системы Вх = о.
Для этого приводим матрицу системы к ступенчатому виду, а затем к упро-
щенному:
'1 1
В= 2 3
Г1 1 1
2-01-1
2) [о 1 -1
Г1 1
2-01
2) [о 0
1
-1
0
2-01
о) [о о
2 -2'
-1 2
0 0 >
1
1
О
оА fi о
Базисные переменные: х1,х2, свободные переменные: х3,х4 . Выражаем ба-
зисные переменные через свободные: = -2х3 + 2х4; х2 = х3 - 2х4. Фунда-
ментальная система состоит из двух решений = (- 2 1 1 of,
/>2 = (2 -2 0 if, которые находим, придавая свободным переменным
стандартные наборы значений (х3 = 1, х4 = 0 и х3 = 0, х4 = 1). Следователь-
но, В = Lin(bi,b2) и dimB = 2.
По правилу (8.19) находим сумму А + В = Чтобы оп-
ределить базис, составим из столбцов аг, а2, bt, b2 матрицу и приведем ее к
ступенчатому виду:
-6 -2 -2 2' '1 0 1 0 ' '1 0 1 О' Г1 0 1 О'
4 1 1 -2 0 1 -3 -2 0 1 -3 -2 0 1 -3 -2
1 0 1 0 0 -2 4 2 0 0 -2 -2 0 0 1 1
<0 1 0 1, 0 1 0 <0 0 3 3 , <0 0 0 о,
Первые три столбца линейно независимы. Следовательно,
А + В = Lin^a^a^bt) Hdim(A + B)=3.
Проверим размерность суммы подпространств. По формуле (8.13) по-
лучаем
dim(A + В) = dim А +dim В - dim(A Пв) = 2 + 2-1 = 3,
что совпадает с найденной ранее размерностью.
НАХОЖДЕНИЕ ОТНОСИТЕЛЬНЫХ АЛГЕБРАИЧЕСКИХ ДОПОЛНЕНИЙ
Пусть дана цепочка подпространств А < В < R" . Требуется найти от-
носительное дополнение А+Г1В подпространства А до подпространст-
ва В.
27 - 4549 417
Рассмотрим случай внешнего описания подпространств - как мно-
жеств решений однородных систем уравнений: А = {Ах = о} и
/} = {Ях = о}. Согласно (8.17) базис пространства А+ образуют линейно
независимые столбцы транспонированной матрицы Аг . Тогда относитель-
ное дополнение А+ Г) В составляют такие векторы х = Ату, которые удов-
летворяют системе Вх = о. Если обозначить через Ф фундаментальную
матрицу системы ВАТу = о, то линейно независимые столбцы матрицы
АтФ являются максимальной системой векторов подпространства В, ли-
нейно независимой над А, т.е. базисом относительного дополнения.
На практике нахождение базиса А+ ft В удобнее производить, исполь-
зуя ступенчатые виды матриц А и В , согласно следующей методике.
1. Привести матрицы А и В при помощи элементарных преобразова-
ний строк к ступенчатому виду и удалить нулевые строки. В результате по-
лучим матрицы (л)ст и (в)ст модифицированного ступенчатого вида
(строки каждой из этих матриц линейно независимые).
2. Найти фундаментальную матрицу Ф однородной системы уравне-
ний {В^^а/^у = о (одним из способов, рассмотренных в разд. 5.5, 5.7).
3. Вычислить матрицу (л)^Ф Ее столбцы образуют искомый базис
A+ftB.
Рассмотрим случай внутреннего описания подпространства А как ли-
нейной оболочки своих образующих: А = Linfa,..., at\ Согласно (8.16)
множество решений системы уравнений Агх = о (матрица Я = (а1 ак)
составлена из образующих) является алгебраическим дополнением А+ . То-
гда множество решений системы
А Тх = о,
Вх = о,
является относительным дополнением А+ ftB, а ее фундаментальная сис-
тема решений - базисом относительного дополнения.
Замечание 8.10. Способы описания подпространств комплексного
линейного пространства, а также методы решения типовых задач аналогич-
ны рассмотренным. В отличие от вещественного арифметического про-
странства Rn вместо операции транспонирования матрицы в комплексном
арифметическом пространстве С" нужно использовать операцию сопряже-
ния матрицы (см. разд. 1.4.2).
418
8.7. ЛИНЕЙНЫЕ МНОГООБРАЗИЯ
8.7.1. Определение линейного многообразия
Пусть L подпространство линейного пространства V , a v0 е V - не-
который вектор. Множество векторов v е V, представимых в виде
v = v0 + /, где I е £, называется линейным многообразием, проходящим
через вектор v0 параллельно подпространству L, и обозначается
v0+£ = {v0+/:/e£). (8.22)
Говорят также, что линейное многообразие получено параллельным сдви-
гом подпространства L на вектор v0, а подпространство £ называют
однородной частью линейного многообразия v0 + £. Размерностью ли-
нейного многообразия называют размерность его однородной части, т.е.
dim£.B и-мерном линейном пространстве (п-1)-мерное линейное много-
образие называется гиперплоскостью. Обратим внимание на то, что раз-
мерность многообразия равна максимальному числу линейно независимых
векторов не самого многообразия, а его однородной части.
ПРИМЕРЫ ЛИНЕЙНЫХ МНОГООБРАЗИЙ
1. Любое подпространство £<Г является линейным многообразием
о + £, где о е V - нулевой вектор.
2. В пространстве И3 (радиус-векторов с общим началом в точке О)
рассмотрим плоскость L, проходящую через точку О (рис.8.3) и плоскость
П , проходящую через конец вектора с параллельно плоскости £ .
Рис. 8.3
Любой вектор ё, конец которого принадлежит плоскости П, можно пред-
ставить в виде ё = с + d , где d - вектор, принадлежащий плоскости £ .
27*
419
Следовательно, множество радиус-векторов, концы которых принадлежат
плоскости П , это линейное многообразие с + L. Его размерность равна 2,
так как dim/, = 2 (базисом L являются любые два не коллинеарных вектора,
принадлежащие L, например, векторы а и Ь ). Заметим, что вектор с в
многообразии c + L можно заменить любым радиус-вектором g, конец ко-
торого принадлежит плоскости П , т.е. с + L = g + L.
8.7.2. Свойства линейных многообразий
1. Линейное многообразие, параллельное линейному подпространству
L<V, однозначно определяется любым своим вектором, другими словами,
если w е v + L ,то w + L = v + L .
2. Непустое пересечение линейных многообразий является линейным
многообразием, другими словами, если v е (v, + )A (v2 + L2), то
(vi + A)H(v2 + £2) = р + £] A L2 , т.е. однородная часть пересечения совпада-
ет с пересечением однородных частей многообразий, а вектор, определяю-
щий сдвиг - это любой вектор пересечения многообразий.
3. Любое г -мерное линейное многообразие можно представить как
аффинную оболочку (см. разд. 8.2.3) не более, чем (г + 1) векторов.
В самом деле, пусть v0+L - г -мерное линейное многообразие, т.е.
dimZ = r. Выберем базис ех,...,ег подпространства L и образуем г век-
торов V] = v0 + е,,..., vr = v0 + ег линейного многообразия v0 + L . Покажем,
что v0 +L = Л#(р0,Р],...,рг). Действительно, любой вектор vev0 + £ мож-
но представить в виде v = v0 +<Mi + . +arer. Преобразуем это выражение,
подставляя е, = v,- - v0, i = l,...,r:
v = v0 4-a^Vi - v0)+... + ar(v/. - v0) = (l-cq - ...-ar)v0 ч-cqv] + ... + arvr.
Получили аффинную комбинацию векторов v0,Vj,...,vr, так как сумма ко-
эффициентов равна единице. Следовательно, v0 + L сЛ#(г0,г„...,гг).
Пусть теперь v е 4^(v0,V],...,vr). Тогда v = a0v0 + a1v1 +... + arvr,
причем a0 -юц +...+ar =1. Подставляя a0 =1-0] -,..-ar, получаем:
v = (l-a] ~...-ar)v0 + a,v1 + ... + a/.v/. =
= v0 + «!(vj - v0)+... + ar(vr - v0) = v0 + ajCj +... + arer,
т.е. v e v0 + L . Следовательно, Aff(y0, v,,..., vr)c v0 + L.
Из двух включений получаем равенство v0 + L = Aff(y0,vx,...,vr).
420
Из доказательства следует, что
Aff(y0,v},...,vr) = v0+ Lin(v} -v0,v2-v0,...,vr-v0). (8.23)
4. Аффинная оболочка непустого подмножества конечномерного про-
странства является линейным многообразием.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ЛИНЕЙНЫХ МНОГООБРАЗИЙ
Линейные многообразия обобщают обычные объекты стереометрии -
прямые и плоскости. Следующие признаки и определения обобщают из-
вестные стереометрические свойства, характеризующие взаимное располо-
жение прямых и плоскостей. Геометрическая терминология естественно
применяется для многообразий. Говорят, что одно линейное многообразие
лежит в другом, если первое многообразие является подмножеством вто-
рого. Пересечение или объединение линейных многообразий понимается
как пересечение или объединение множеств векторов. Говорят, что линей-
ные многообразия не пересекаются, если у них нет общих векторов, т.е. пе-
ресечение этих множеств пусто.
Приведем признаки включения и равенства (совпадения) линейных
многообразий:
1) линейное многообразие V]+Zq лежит в линейном многообразии
t>2 + Z,2 тогда и только тогда, когда —Vj е L2 и < L2;
2) линейные многообразия Vj + Zq и v2 + L2 совпадают тогда и толь-
ко тогда, когда Zq = L2 и v2 - Vj е L2.
Два непересекающихся линейных многообразия v, + Zq и v2 + Z2
называются параллельными, если одно из подпространств L{ или Z2
лежит в другом: < Z2 или L2 < Lx (иными словами, если одна из
однородных частей содержится в другой).
Два непересекающихся линейных многообразия V] + Zq и v2 + Z2 на-
зываются скрещивающимися, если пересечение подпространств Zt и Z2
есть нулевой вектор: Zq П Z2 = о.
8.7.3. Способы описания линейных многообразий
В разд. 8.6.5 для линейных подпространств рассматривались два спо-
соба описания: внутренний (при помощи линейных оболочек) и внешний
(при помощи однородной системы уравнений). Свойства 3, 4 определяют
внутреннее описание линейных многообразий при помощи аффинных обо-
лочек векторов. Внешнее описание линейных многообразий задается неод-
нородной системой линейных уравнений. Действительно, множество
{ Ах = Ь } решений будем рассматривать как подмножество п -мерного
421
арифметического пространства R" . Структура общего решения неоднород-
ной системы была найдена в разд. 5.6:
х = хн +С, -ф! +С2 ф2 + — + C„_r
где хн - частное решение неоднородной системы, ,ф2,..., Ф„_г - фунда-
ментальная система решений соответствующей однородной системы
Ах = о ; С], С2..., Сп_г - произвольные постоянные, г = rg А - ранг матри-
цы системы. Как показано в разд.8.6.5, множество { Ах-о } решений одно-
родной системы является линейным подпространством R", а именно
{ Ах = о }= Е/л(ф],...,фл_г). Следовательно, множество = решений
неоднородной системы является линейным многообразием в R" :
{ Ax = b }-хн + Linfa,.г). (8.24)
В частности, множество решений одного уравнения
йцХ] + ... + а1лх„ =6, с ненулевыми коэффициентами (хотя бы один коэффи-
циент при неизвестных отличен от нуля), представляет собой гиперпло-
скость, т.е. линейное многообразие размерности (л-1), так как размер-
ность (л-r) его однородной части { Лх = о } = Е/л(ф1,...,фл_г) равна (л-1),
поскольку г = 1. Поэтому множество решений системы т линейных урав-
нений можно представить как пересечение т гиперплоскостей. По свойству
2 пересечение линейных многообразий есть линейное многообразие.
Равенство (8.24) определяет переход от внешнего описания линейного
многообразия (левая часть) к внутреннему описанию (правая часть). Рас-
смотрим обратный переход: от внутреннего описания к внешнему.
Пусть дано линейное многообразие а0 + 11п(а1г...,ак). Требуется соста-
вить неоднородную систему уравнений, множество решений которой совпа-
дало бы с заданным многообразием. Учитывая, что разность двух решений
неоднородной системы является решением однородной системы (см.
разд.5.6), используем переход от внутреннего описания линейного подпро-
странства к внешнему (см. разд. 8.6.5). Для нахождения неоднородной сис-
темы нужно выполнить следующие действия.
1. Из данных столбцов составить матрицу
J=(ai-a0 а2-л0 - ак~ао)
размеров (лхЛ), а затем блочную матрицу (л | Е), приписав к матрице А
единичную матрицу Е л -го порядка.
2. Элементарными преобразованиями над строками блочной матрицы и
первыми к ее столбцами привести матрицу (а | Е) к виду (A | S), где А -
£г О
~0~0
, г = rg А .
простейший вид матрицы А (см. разд. 1.6.1): А =
422
3. Из последних (п-r) строк матрицы 5 составить матрицу Т:
Т = (О | E„_r)S .
4. Записать искомую систему уравнений в форме Тх = Ч'ад.
Пример 8.14. Многообразие А задано аффинной оболочкой векторов
Л = Л^(а0, aj, а2, а3), где а0 =
Составить систему неоднородных уравнений, задающую это же многообра-
зие.
□ Согласно (8.23), зададим линейное многообразие в форме
а0 + L‘n(ai ~а0> а2 ~а0’ a3 ~ао)~
1. Из данных столбцов составляем матрицу
А = («] - а0 а2-а0 а3 - а0), а затем блочную матрицу
(Л | Е) =
1
1
1
1
1
1
2
1
1
О
о
о
о
1
о
о
о
о
1
о
О'
о
о
1.
1
о
1
2. Элементарными преобразованиями над строками блочной матрицы и
над ее первыми тремя столбцами приводим левый блок к простейшему виду.
Прибавляем ко второй и последней строке первую, умноженную на (-1),
затем меняем местами вторую и третью строки:
(Л I Е)~
1
О
О
О
1
о
1
о
1
о
2
о
1
-1
о
-1
о
1
о
о
О
О
1
О
О
О
О
1
р
о
о
.0
1
1
О
О
1
2
о
о
1
о
-1
-1
о
о
1
о
о
1
о
о
О'
о
о
Прибавим ко второму и третьему столбцам первый, умноженный на (-1), а
затем к третьему столбцу - второй, умноженный на (-2). При этом в левом
блоке получим простейший вид А матрицы Л (ее ранг г = rg Л = 2), а пра-
вый блок матрицы не изменится:
Л ~А =
о
1
о
о
О'
о
о
О.
о
-1
-1
о
о
1
о
о
1
о
о
о
о
о
1
О
О
О
5 =
423
3. Из последних п-г = 4- 2 = 2 строк матрицы 5 составляем матрицу
(-1 1 0 0^1
Т =
^-1 0 0 1J
4. Записываем искомую систему уравнений в форме Тх = Та0:
|-Х1+Х2=1, и
[-Х] + х4 = 1.
Пример 8.15. Найти размерность пересечения многообразий А и В,
если А - многообразие, заданное в примере 8.14 аффинной оболочкой век-
торов, а многообразие B = {Bx = b} - множество решений неоднородной
системы
X] + х2 + 2х3 + х4 = 1,
2xt +3х2 +х4 = 0,
3xj + 4х2 + 2х3 + 2х4 = 1.
□ В примере 8.14 найдена система неоднородных уравнений, описы-
( 1 [ - х, + х2 = 1,
вающая многообразие А = { Ах = a |: ! Составляя из систем
X] + х4 = 1.
Ах = а и Вх = Ь одну систему, получаем внешнее описание пересечения
_ [ Ах = а 1
многообразий: А П В = { >. Найдем множество решении этой систе-
[ Вх = b J
мы. Составляем матрицу системы и приводим ее к ступенчатому виду:
'-1 1 0 0 В р -1 0 0 -А <1-10 0 -Г ч -1 0 0 1 1 0 -1 0 1 0 0 1 0 -1 0
=1 1211-0221 2-0023 2- В b 7 23010 05012 0006 2 <3 422 1Jl<0 7 22 4 J ^0 0 2 9 4,
'1-10 0 0 10-1 -р 0 '1-10 0 0 10-1 -р 0
0 0 1 1,5 0 0 0 6 ч0 0 0 6 1 2 2, 0 0 1 1,5 0 0 0 1 ^0 0 0 0 1 1 0J
Система имеет единственное решение х = (-у | у . Следовательно,
пересечение многообразий состоит из одного вектора. Поскольку однород-
ная часть пересечения представлена нулевым пространством, то
dim (^4 П в) = dim {о } = 0.
424
Пример 8.16. Исследовать взаимное расположение многообразий А,
В и С, если А - многообразие, заданное в примере 8.14 аффинной обо-
лочкой векторов, В - многообразие, заданное в примере 8.15 неоднородной
системой уравнений, а многообразие С = с0 + Ып(сх) - проходит через век-
тор с0 = (1 0 0 0)г параллельно линейной оболочке вектора
с,=(1 1 1 1)г.
□ В примере 8.15 показано, что многообразия А и В пересекаются и
лпя=М.*=(4 i 1
Найдем пересечения многообразия С с многообразиями А и В. Лю-
бой вектор из С имеет вид с = (1 +1 t t t)T, где параметр teR. Подста-
вим выражения для координат этого вектора в системы, описывающие мно-
гообразия А и В (система для многообразия Л получена в примере 8.14):
(l + z)+z + 2z + / = l,
2(1 + /)+ 3t+t = О,
3(1 + r)+4r + 2t + 2t = 1.
Каждая из систем несовместна. Следовательно, многообразие С не пересе-
кает многообразий А и В .
Найдем пересечение однородной части С с однородными частями А
и В . Однородная часть С задана линейной оболочкой Ып(сх). Однород-
ную часть А находим по правилу (8.23):
А = Aff(a0, ах,а2, а3)=а0+Ып(а]-а0, а2-а0, а3 -а0).
Так как а2 -а0 = (1 1 1 1)г = С;, то справедливо включение
Lin(cx)= Lin(a2~ aQ)с: /./«(я] - а0, а2 - aQ, а3 - а0 ).
Поскольку однородная часть многообразия С содержится в однородной
части многообразия А, то, согласно определению, многообразия А и С
параллельны.
~(l + z)+/ = l
~(1+?)+/==1
Однородную часть В определяем, используя структуру общего реше-
ния неоднородной системы (она была найдена при решении примера 5.5):
. В = хн + Ып(<?х, <р2). Найдем пересечение подпространств Ып(сх), кх = 1 и
I ф2), к2 =2. Для этого (см. алгоритм нахождения пересечения под-
425
пространств в разд. 8.6.5) составляем матрицу (q | <р, ср2) и приводим ее к
ступенчатому виду
(с> 1 Ф1 Ф2) = р 1 1 -6 -2> 4 1 1 0 0 1 , р 1 1 0 1 > 4 1 1 0 -6 -2, р 0 0 <0 0 1 > 4 0 1 -1 -6 -3, р 0 0 <0 о Г 1 0 0 1 0 °,
Поскольку г =rg(c] | cpj <р2)=3, то размерность пересечения равна нулю:
£i+£2-r = l + 2-3 = 0. Так как /./«(с^ПА^ср],ф2)= {о } и многообразия
В и С не пересекаются, то они скрещивающиеся.
8.8. ЕВКЛИДОВЫ ПРОСТРАНСТВА
8.8.1. Определение евклидова пространства
Вещественное линейное пространство Е называется евклидовым, ес-
ли каждой паре элементов и, v этого пространства поставлено в соответст-
вие действительное число (и, v), называемое скалярным произведением,
причем это соответствие удовлетворяет следующим условиям:
1. (и, v) = (v, и) V и, v е Е ;
2. (и+ v, w)=(«, w)+(v, н>) V «, v, weE;
3. (Х -и, v)=X -(«, v) V», ve£,VXe/?;
4. (v,v)>0 tf v*e и (v,v)=0 => v=o.
В скалярном произведении (и, v) вектор и - первый, а вектор v - второй
сомножители. Скалярное произведение (v, v) вектора v на себя называется
скалярным квадратом. Условия 1-4 называются аксиомами скалярного
произведения. Аксиома 1 определяет симметричность скалярного произ-
ведения, аксиомы 2 и 3 - аддитивность и однородность по первому
сомножителю, аксиома 4 - неотрицательность скалярного квадрата
(v,v).
Линейные операции над векторами евклидова пространства удовлетво-
ряют аксиомам 1-8 линейного пространства, а операция скалярного умно-
жения векторов удовлетворяет аксиомам 1-4 скалярного произведения.
Можно сказать, что евклидово пространство - это вещественное линейное
пространство со скалярным произведением. Поскольку евклидово простран-
ство является линейным пространством, на него переносятся все понятия,
определенные для линейного пространства, в частности, понятия размерно-
сти и базиса.
426
ПРОСТЕЙШИЕ СЛЕДСТВИЯ ИЗ АКСИОМ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
1. Аксиомы 2 и 3 скалярного произведения можно заменить одним ус-
ловием линейности скалярного произведения по первому сомножителю:
(а и + р- v, h>)= а (и, н’)+ р (р, ip) V и, р, н> е Е , V а, Р е R .
2. Условие линейности скалярного произведения по первому сомножи-
телю в силу симметричности (аксиома 1) справедливо и для второго сомно-
жителя, т.е. скалярное произведение линейно по любому сомножителю.
3. Линейность скалярного произведения по любому сомножителю рас-
пространяется на линейные комбинации векторов:
/ \
т п т п i \
V=1 ;=1 J i-l /=1
для любых векторов и(, v - и действительных чисел at , Р7 , i =
4. Если хотя бы один сомножитель - нулевой вектор, то скалярное про-
изведение равно нулю:
(р, о) = (<?, р) = О V v е Е .
Действительно, представим нулевой вектор в виде о = 0 и , где и -
произвольный вектор из Е . Тогда из аксиомы 3 получаем:
(о, р) = (о • и, р) = 0 (и, р) = 0.
НЕРАВЕНСТВО КОШИ-БУНЯКОВСКОГО
Для любых векторов и и р евклидова пространства Е выполняется
неравенство Коши-Буняковского:
(и, р)2 < (и, «)• (р, р) . (8.25)
В самом деле, для любого действительного числа X и любых векторов
и и р справедливо неравенство:
0< (и-Хр, и -Хр)= Х2(р, р)-2Х(«, р)+(и, «).
। Следовательно, дискриминант квадратного трехчлена (переменной X) не
i больше нуля, т.е. 4 • («, р)2 - 4 (и, «) (р, р) < 0. Отсюда следует (8.25). Заме-
| тим, что равенство нулю дискриминанта возможно только в случае сущест-
i вования такого корня X, для которого (и-А.р, и-Хр) = 0. Это условие рав-
носильно коллинеарности векторов и и р : и = А. р . Напомним, что ненуле-
: вые векторы и и v называются коллинеарными, если существует такое
число X, что и = X р . Нулевой вектор считается коллинеарным любому
вектору. Неравенство Коши-Буняковского выполняется как равенство толь-
' ко для коллинеарных векторов и как строгое неравенство для неколлинеар-
, НЫХ.
427
8.8.2. Примеры евклидовых пространств
Определяя для элементов линейного пространства операцию скалярно-
го произведения, получаем евклидово пространство. Если скалярное произ-
ведение можно ввести разными способами в одном и том же линейном про-
странстве, то и получаемые евклидовы пространства будут разными. Приве-
дем примеры евклидовых пространств, соответствующих рассмотренным в
разд.8.1.3 примерам линейных пространств.
1. В нулевом линейном пространстве {о } скалярное произведение
можно определить единственным способом, положив (о, о) = 0 . Аксиомы
скалярного произведения при этом выполняются.
2. В пространствах И], И2, И3 векторы (свободные или радиус-
векторы) рассматриваются как направленные отрезки. В курсе элементарной
геометрии вводятся понятия длины вектора и величины угла между векто-
рами, а затем определяется скалярное произведение: (w, v) = | й |-| v |-созф .
Аксиомы 1-4 для этого скалярного произведения выполняются. Поэтому
пространства , V2, V3 являются евклидовыми. Неравенство Коши-Буня-
. . I (й, v) I
ковского в этом пространстве означает, что costp =, _ . _, < 1. Геомет-
I « |-| v |
рический смысл: длина проекции не превосходит длины наклонной (катет
короче гипотенузы).
3. В пространстве Rn скалярное произведение столбцов
x = (x] ••• xj и j = ••• у „У можно задать формулой:
(х, у) = хт Ау = £ £ayXiyj , (8.26)
1=1 >1
где А - квадратная симметрическая положительно определенная матрица
п -го порядка (см. разд.6.6.3). Проверим выполнение аксиом 1-4. Аксиома 1
(симметричность) выполняется в силу симметричности матрицы А:
(х, у)= хгАу = утАгх = угАх = (у, х), поскольку число при транспонирова-
нии не изменяется, т.е. хтАу = утАтх. Свойство линейности по первому
сомножителю (см. п.1 простейших следствий из аксиом) для (8.26)
выполняется: (ах + $у,г)=(ах + $уУ Az = ахт Az+ $ут Az = a(x,z)+p(y,z).
Значит, выполняются аксиомы 2 и 3. Аксиома 4 также выполняется, так как
квадратичная форма (х,х)=хгАх положительно определенная (см.
разд. 6.5.4). Таким образом, пространство R" со скалярным произведением
(8.26) является евклидовым пространством. В частности, если в качестве
матрицы А взять единичную матрицу, формула (8.26) примет вид:
428
(х, у)=хту = х]У1 + х2у2+... + х„у„ . (8.27)
Это скалярное произведение считается стандартным в пространстве R".
Неравенство (8.25) Коши-Буняковского в «-мерном арифметическом про-
странстве R" со скалярным произведением (8.27) трансформируется
в неравенство Коши:
{\Ух+х2У2+- + хпуУ ^(xf+х2+...+х2)-(у2 +j2+... + y2).
Приведем примеры формул, которые не задают скалярного произведе-
ния в R2:
(х, у) = | х1 | • | у{ | +1 х2 | • | у2 | - аксиомы 1, 4 выполняются, а аксиомы
2, 3 - нет;
(х, У)= х2-у2 - аксиомы 1, 2, 3 выполняются, а аксиома 4 - нет.
4. Пространство {Лх = о} решений однородной системы Ах = о линей-
ных уравнений со скалярным произведением (8.27) является евклидовым
пространством.
5. В пространстве С [a, ft] действительных функций, определенных и
непрерывных на данном промежутке [а, б], скалярное произведение можно
задать формулой:
ь
(f,g)=$f(x)g(x)dx. (8.28)
а
В самом деле, аксиомы 1, 2, 3 для (8.28) выполняются в силу свойств
определенного интеграла. Проверим выполнение аксиомы 4. Для ненулевой
ь
функции /(х): (/,/)= {[Л(х)]2 dx > 0, так как, если в какой-нибудь точке
а
х0 е (а, Ъ) функция /(х0)^ 0, то в силу непрерывности она отлична от нуля
в некоторой окрестности точки х0, целиком лежащей в интервале (a, Ь).
Поэтому интеграл от (/(х)]2 в этой окрестности больше нуля.
Таким образом, пространство С [а, £>] со скалярным произведением
(8.28) является евклидовым. Скалярное произведение (8.28) считается стан-
дартным в пространстве С [а, £>]. Для разрывных функций формула (8.28) не
определяет скалярного произведения, так как нарушается аксиома 4. Нера-
венство (8.25) Коши-Буняковского в пространстве С [a, ft] со скалярным
произведением (8.28) трансформируется в неравенство Шварца:
(ь У ь ь
J7(x) ?(*)<& f/2(x) dx- j g2(x)dx.
/а a
429
6. В пространстве P(r) многочленов с действительными коэффициен-
тами скалярное произведение можно задать формулой (8.28), так как много-
члены являются непрерывными функциями.
В пространстве Рп (/?) многочленов степени не выше, чем п, зададим
скалярное произведение многочленов р(х)=<тпхп+... + <7|Х + <70 и
^(х)= Ьпх" +... + Ь\Х + Ь0 формулой:
(р, <?) = апЬп + - + «1*1 + «о*о • (8-29)
Выражение в правой части (8.29) симметрично для коэффициентов двух
многочленов, поэтому аксиома 1 выполняется. Аксиомы 2, 3 следуют из ли-
нейности выражения по коэффициентам каждого многочлена. Проверим ак-
сиому 4. Запишем скалярный квадрат (р, р)=«„ +... + «]2 +«о ^0 . Заметим,
что (р, р) = 0 только при ап =... = at = а0 = 0, т.е. в случае нулевого много-
члена р(х) = 0 . Следовательно, формула (8.29) задает скалярное произведе-
ние в пространстве Рп (/?).
В пространстве Р3(/?) определим произведение формулой:
(Л ч)= р(0<7(1)+ р(2)<7(2)+ Х3)<т(3)- (8.30)
В силу симметричности и линейности правой части (8.30) по значениям
многочленов, заключаем, что аксиомы 1-3 выполняются. Проверим выпол-
нение аксиомы 4. Приравняв скалярный квадрат нулю, получаем
U р)=[ ХОР +[X2)f +[Х3)Г = °-
Это возможно только при р(1) = р(2) - р(з) = 0 . Из этих трех равенств не
следует, однако, что многочлен р(х) нулевой. Например, ненулевой много-
член р(х)=(х-1)(х-2)(х-3) удовлетворяет трем равенствам. Следова-
тельно, в пространстве Р3(к) формула (8.30) не задает скалярного произве-
дения. Напротив, в пространстве Р2(л) формула (8.30) определяет скаляр-
ное произведение. Так как из равенств р(1) = р(2) = р(з)=0 следует, что
многочлен степени не выше второй тождественно равен нулю (см. разд.
В.4).
8.8.3. Длина вектора. Угол между векторами
Длиной (нормой) вектора v в евклидовом пространстве Е называет-
ся число | V | = J (v, v).
Имея в виду обозначение, длину | v | называют также модулем векто-
ра. Рассматривается арифметическое значение квадратного корня, которое
определено для любого вектора из-за неотрицательности подкоренного вы-
430
ражения (аксиома 4). Поэтому каждый вектор имеет положительную длину,
за исключением нулевого, длина которого равна нулю: | о | = 0.
Углом между ненулевыми векторами и и v евклидова пространства
Е называется число
(«, v) (и>v)
<р = arccos , т.е. cos ф = . . . и 0 < ф 2 к.
И'М l"Hvl
Представив неравенство Коши-Буняковского (8.25) в виде
|(«,у)|<|И|-| v|,
можно сделать вывод, что абсолютное значение выражения .—г не
I " II v I
превосходит единицы, т.е. величина угла определена для любой пары нену-
левых векторов. Заметим, что угол между коллинеарными векторами равен
нулю или л.
Длина вектора и угол между векторами называются основными мет-
рическими понятиями [42].
Из неравенства Коши-Буняковского (8.25) следует неравенство тре-
угольника:
||«|-|v||<|« + v|<|«| + |v|.
Докажем последнее неравенство. Применяя оценку (и, v)< | и |-[ v |,
получаем
| и + v |2 = (и + v, и + v) = («, и)+ 2(«, v) + (v, v)<
<|«|2+2-|«|-|vI + M2=(|"| + M)2 ’
т.е. | u + v |2 ^(| и | + | v | У о |« + v|<|h| + |v|.
Пример 8.17. Даны векторы евклидовых пространств:
ГП (О’) 1
а) х = I I, у = I I _ элементы пространства R со скалярным произ-
ведением (8.27): (х, у) = Х]У[ + х2у2;
ГП Го") 2
б)х = 11,у = 11- элементы пространства R со скалярным произ-
(2 1
ведением (8.26): (х, у) = хг
+ Х]У2 + х2_У, + х2у2;
431
в) /(x) = sinx, g(x) = cosx - элементы пространства С [-л, л] соска-
Я
лярным произведением (8.28): (/,#)= |f(x)g(x)dx-,
-п
г) р(х) = х2 -2х + 1, q(x) = x + 2 - элементы пространства P2(R) со
скалярным произведением (8.29): (р, q} = a2b2 + аД +по^о >
д) р(х) = х2 -2х + 1, q(x) = x + 2 - элементы пространства Р2(л) со
скалярным произведением (8.30): (р, q)= p(l)-g(l)+ p(2)-q(2) + р(з)-д(з).
В каждом пространстве найти длины двух данных векторов и угол ме-
жду ними.
□ а) Находим скалярные произведения: (х, х) = 1-1 + 00 = 1;
(х, у) = 1-0 + 01 = 0; (у, у) = 0-0+1-1 = 1. Следовательно, | х | = л/1 = 1,
Л" 0 7С
I у I =vl =1, <p = arccos— = arccosO=—.
11 1-1 2
б) Находим скалярные произведения: (х,х) = 2-1-1 + 1-0 + 0-1 + 0-0 = 2;
(х,у)=2-1-0 + 1-1 + 00+0-1 = 1; (у, у) = 2-0-0 + 0-1 + 1-0 + 1-1 = 1. Следова-
I 1 I । /7 , 1 з/2 л
тельно, j х | = V2 , | у ] = VI = 1, <р = arccos^— = arccos-^-=—.
в) Находим скалярные произведения:
" 1" 1Л 1
(sinx,sinx)= Jsin2xd5c = — J(l-cos2x)dr = — I x-sin2x = л;
-n -n ' -я
Я j я j
(sinx,cosx) = | sinxcosxdr = — |sin2xdr =—cos2x| =0;
' ' J 2 J 4
-It -It
I J f J
^cosx,cosx) = Jcos2xdr = — J(l + cos2x)tfx = —I x +—sin2x
-it -it ' •
л
= л;
-Л
Следовательно, | sinx | = 4^> | cosx | = -ул , (p = arccos-7=—== = —
ул-ул 2
г) Находим скалярные произведения: (р, р)=1-1 + (-2)-(-2) + 1-1 = 6;
(p,q) = 10+(-2) l + l-2 = 0; (q,q)=0 0 + l l + 2-2=5. Следовательно,
0
| р\=4б, | ?|=Т5 , ф =
arccos
Тб-л/5
« л
= arccosO = —
2
432
д) Находим скалярные произведения: (р, р) = 00 + 11 + 4-4 = 17;
(p,g) = 0-3 + l-4 + 4-5 = 24; (g,g)=3-3 + 4-4 + 5-5 = 5O. Следовательно,
I р I = Vr7, I а I = ->/50 = 5V2 , <р = arccos—. arccos^2^=.
11 11 V17-5V2 5V34
8.8.4. Ортогональные векторы и их свойства
Два вектора и и у евклидова пространства называются ортогональ-
ными (перпендикулярными), если их скалярное произведение равно нулю:
(u,v) = 0.
Система векторов называется ортогональной, если все ее
векторы попарно ортогональны, т.е. (v(, vy) = 0 при i* j. Система векторов
vi,v2,...,vk называется ортонормированной, если все ее векторы попарно
ортогональны и длина (норма) каждого вектора системы равна единице, т.е.
/ \ fl, i = J,
IV., V . I=(
'* 11 [О, i*j.
Говорят, что вектор v ортогонален (перпендикулярен) множеству
М , если он ортогонален каждому вектору из М . Ортогональность векторов
Обозначается знаком перпендикуляра (± ).
СВОЙСТВА ОРТОГОНАЛЬНЫХ ВЕКТОРОВ
1. Нулевой вектор ортогонален каждому вектору пространства.
2. Взаимно ортогональные ненулевые векторы линейно независимы.
В самом деле, пусть векторы v1,v2,...,vi попарно ортогональны. Со-
ставим из них линейную комбинацию и приравняем ее нулевому вектору:
=о.
Умножим обе части равенства скалярно на вектор У]:
Xi (у,, Vj)+Л2 (v,, v2)+...+(у,, vt) = (у,, о).
О 0 0
Следовательно, Л] -| vt |2 = 0. Так как v1 Ф о , то Л, = 0. Аналогично дока-
зываем, что Л2 =... = = 0, т.е рассматриваемая линейная комбинация три-
виальная. Значит, ортогональная система векторов Vj,v2,...,vk линейно
независима.
3. Если сумма взаимно ортогональных векторов равна нулевому век-
fnopy, то каждое из слагаемых равно нулевому вектору.
28 _ 4549
433
4. Если вектор и ортогонален каждому вектору системы
vx,v2,...,vk, то он также ортогонален и любой их линейной комбинации.
Другими словами, если и ± V,, i = l,...k ,то и ± 1лп{ух,..., vk).
5. Если вектор и ортогонален подмножеству М евклидова про-
странства, то он ортогонален и линейной оболочке этого подмножества,
т.е. и ± М => иА.1лп(м).
6. Если V;, i>2 >•> vk ~ ортогональная система векторов, то
| v,+v2+... + vt |2 =| Vj |2+|v2 |2+... + | vk |2.
Это утверждение является обобщением теоремы Пифагора.
8.8.5. Процесс ортогонализации Грама-Шмидта
Рассмотрим следующую задачу. Дана линейно независимая система
v1,v2,...,vjl векторов конечномерного евклидова пространства. Требуется
построить ортогональную систему wl,w2,...,wk векторов того же про-
странства так, чтобы совпадали линейные оболочки:
£й(и»], н-2.**)= Lin(v1, v2.vk).
Решение задачи находится при помощи процесса ортогонализации
(Грама - Шмидта), выполняемого за к шагов.
1. ПОЛОЖИТЬ Н»] = Vj.
(v2, н»,)
2. Наити w2 = v2-a2i •н’1, где а21 = 4-^—Ч.
„ тт „ (р3, Н’1) (v3, w2)
3. Наити w3 = v3 -а3и’, -а32w2, где а3. = 4-^—Ч-, а32 = 4-;
(h-pH-i) (и'г.и’г)
и т.д.
*-i (v И’-)
к) Найти wk=vk~y'akiwi,ne aki=y^—Ц, i = l........к-1.
ы к.
Поясним процесс ортогонализации. Искомый на втором шаге вектор
w2 представлен в виде линейной комбинации w2 = v2 — а • н»,. Коэффициент
а подберем так, чтобы обеспечить ортогональность векторов w2 и .
Приравняем нулю скалярное произведение этих векторов
(h'2,h’1) = (v2, Wj)-а-(n»i, н’1)=0. Отсюда получаем, что а = а21 (см. п.2 ал-
горитма). Подбор коэффициентов а,, на j -м шаге алгоритма делается так,
чтобы искомый вектор Wj был ортогонален всем ранее найденным векто-
рам н»!, h»2 ,..., Н’у_1 .
434
Замечания 8.11.
1. Векторы, найденные в процессе ортогонализации, обладают сле-
дующими свойствами:
a) Wj ± Lin^....’•’/-J, j = 2,...,к ;
б) Lin(n’1)=Lin(v1), j = 2,...,k.
Первое свойство следует из свойства 4 ортогональных векторов (см.
разд. 8.8.4). Второе свойство следует из того, что каждый вектор системы
н’1, ...,Wj линейно выражается через векторы ...,vj, и наоборот.
2. В процессе ортогонализации любой вектор можно заменить на
коллинеарный ему ненулевой вектор X-Wj. При этом свойства, перечис-
ленные в п.1, не нарушаются.
3. Если система vI,v2,...,vJt векторов линейно зависима, то в процессе
ортогонализации будем получать (на некоторых шагах) нулевые векторы.
Действительно, если подсистема v1,v2,...,i>7 линейно зависима, то
Vjе Lin[wl,...,Wj_t). Тогда вектор Wj = vf одновременно удовле-
1=1
творяет двум условиям Wj ± Ьл(н’1,...,н’7_1) и Unfa.....................’•’/-J- Значит,
это нулевой вектор Wj = о.
Поэтому в данном случае формулы вычисления коэффициентов <ху( на
j -м шаге следует записывать в виде:
О,
В остальном процесс ортогонализации остается неизменным.
4. Процесс ортогонализации можно дополнить процессом нормировки,
разделив каждый вектор ортогональной системы н’), н»2,..., на его
длину:
в: Г < =1,—,к.
HI
В результате получим ортонормированную систему е, ,е2 ,...,ек , отвечаю-
щую условию Lin(el,...,ek) = Lin(yl,...,vk). Если исходная система векторов
является линейно зависимой, то среди векторов ортогональной системы
*1, н»2 ,..., wk будут нулевые. Чтобы получить ортонормированную систе-
му, нулевые векторы следует исключить, а остальные векторы нормировать.
28*
435
Пример 8.18. Даны системы векторов евклидовых пространств:
Г1Л p'l (o')
а) х = I I, у = I Q I, z = I I ~ элементы пространства к со скаляр-
<2 l')
ным произведением (8.26): (х, у) = хг1 ly = 2xtyj + xty2 + x2yj + х2у2;
б) pi(x)=l, р2(х)=х, р3(х)=х2 - элементы пространства с[-1;1] со
1
скалярным произведением (8.28): (/, g)- J/(х) g(x)dx.
Провести ортогонализацию данных векторов.
□ а) Заметим, что система векторов х, у , z линейно зависимая, так
как х и у пропорциональны, поэтому используем процесс ортогонализа-
ции Грама - Шмидта с учетом п.З замечаний 8.11.
1. Полагаем и = х.
„ „ (у,и) 2-2-1 + 1-0 + 0-2 + 00 4
2. Вычисляем а91 =-)-( =-----------------=—
21 (и,u) 2-11 + 10+01+0-0 2
(2А ГП ГОЛ
v = y-a9i-u = -2- = .
loJ loj loj
2 и находим
Получили нулевой вектор.
„ о (г.и) 2 0 1 + 0 0 + 1 1 + 1-0 1
3. Вычисляем <ХЧ| = -;-г =-------------------= —
(и,и) 2-1-1 + 1-0 + 0-1 + 0-0 2
гласно п.З замечаний 8.11, так как v = о , и находим
а32 =0 со-
у =
,°1 1 Pi n ( °) (41
w= z-a,, -- = 2 •
31 32 (1J 2 (Oj V 1 J
Проверим условие ортогональности (и, w) = 2 • 1 • (-j-)+1 1 + 0• (у)+ 0-1 = 0.
Для получения ортонормированной системы исключаем нулевой век-
тор v = о , а остальные нормируем (см. п.4 замечаний 8.11):
2 ;
1 Р
и =—=•
V2 (0
0J
Таким образом, для системы
нальная система из трех векторов
_1_ [-0,5
'oj I 1 .
*=M
трех векторов х, у , z построена ортого-
и , v, w и ортонормированная система из
И' =
V2
'г
. 1
и —
436
двух векторов й, w. Линейные оболочки этих трех систем совпадают между
собой (и со всем пространством R2).
6) 1. Полагаем ^(х) = р1(х) = 1.
2. Вычисляем а21
С1
Jll dx
:2 = 0
и на-
ходим ?2(х)=х-0-1 = х.
3. Вычисляем Ct,, = - [ х2 • 1 dx :2 = —х3| :2- — -—- — ,
31 та» Ц J 3 11 323
32 та Ц J
1 зР „
—х =0 и находим
3 1-1
Чз(*)=х2-а3{-1-а32-х = х2-^.
Получили ортогональные многочлены ^(х) = 1, q2(x) = x,
q3 (х) = х2 - у. Выполним нормировку: | qt (х) | - ^(qt (х), qt (х)) = ^2 ;
| ^(4 |=7(?2(4 (4)=’ | ?3(4 |=7W4 ^W)=;
*w'kbriW=^‘’^; ’г(х)=ьЬ|’2(х)=т1х;
Получили ортонормированные многочлены (см. многочлены Лежандра
[8,25,42]).
8.8.6. Ортогональный и ортонормированный базисы
Так как евклидово пространство является линейным, на него перено-
сятся все понятия и свойства, относящиеся к линейному пространству, в ча-
стности, понятия базиса и размерности.
Базис евклидова пространства называется ортогональным,
если все образующие его векторы попарно ортогональны, т.е.
(е,,е2)=0 при i# j, i = l,...,n, j = l,...,n.
Базис et,...,en евклидова пространства называется ортонормирован-
ным, если его векторы попарно ортогональны и длина каждого из них равна
единице:
437
(е.,«.)=< ’ i = l,...,n, j = l,...,n. (8.31)
' ‘ 1 [ 0, i * j,
Теорема 8.5. В конечномерном евклидовом пространстве любую сис-
тему ортогональных (рртонормированных) векторов можно дополнить до
ортогонального (ортонормированного) базиса.
В самом деле, по теореме 8.2 любую систему линейно независимых
векторов, в частности, ортогональную (ортонормированную), можно допол-
нить до базиса. Применяя к этому базису процесс ортогонализации (см.
разд. 8.8.5), получаем ортогональный базис. Нормируя векторы этого базиса
(см. п.4 замечаний 8.11), получаем ортонормированный базис.
ВЫРАЖЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ЧЕРЕЗ КООРДИНАТЫ
СОМНОЖИТЕЛЕЙ
Пусть - базис евклидова пространства, в котором векторы х
и у имеют координаты х!,...,хл и у!,...,ул соответственно, т.е.
х = ххе{ + ...+ хпеп, у = у^ + ...+ упеп .
Выразим скалярное произведение, используя следствие 3 из аксиом скаляр-
ного произведения (см. разд. 8.8.1):
(х,у)=(х1е1 + ...+хлел, у^ +...+ улел) = ^^х,уу(е,.,еу).
i=i j=i
Преобразуем это выражение, используя операции с матрицами:
(х, y) = xrG(e1,...,e„)y, (8.32)
где х = (х] ••• хпУ , у = (у] ••• ул)Г - координатные столбцы векторов
х и у, а о(е1,...,ел) - квадратная симметрическая матрица, составленная
из скалярных произведений
G(e!,...,en) =
(8.33)
- (en,e„),
которая называется матрицей Грама системы векторов е1,...,еп.
ПРЕИМУЩЕСТВА ОРТОНОРМИРОВАННОГО БАЗИСА
Для ортонормированного базиса ех,...,еп формула (8.32) упрощается,
так как из условия (8.31) следует, что матрица Грама G^,...,^) ортонор-
мированной системы е1,...,еп равна единичной матрице: G(e1,...,e„)= Е .
438
1. В ортонормированием базисе скалярное произведение век-
торов х и у находится по формуле: (x,j) = xIy1+х2у2+... + хпу„, где
Хр..., х„ - координаты вектора х, а у(.уп - координаты вектора у .
2. В ортонормированном базисе е1,...,е„ длина вектора х вычисля-
ется по формуле | х | = д/х2 + х2 +... + х2 , где х1,...,хп - координаты век-
тора х.
3. Координаты х1,...,хп вектора х относительно ортонормирован-
ного базиса е1,...,е„ находятся при помощи скалярного произведения по
формулам: Xj = (х, et),..., хи = (х, еп).
В самом деле, умножая обе части равенства х = х^, + ... + хлел на ej,
получаем (х,е1) = х1(е1,е1)+х2(е2,₽]) + ...+хл(ел,ел), т.е. Ана-
i о ' о
логично доказываются остальные формулы.
ИЗМЕНЕНИЕ МАТРИЦЫ ГРАМА ПРИ ПЕРЕХОДЕ ОТ ОДНОГО БАЗИСА
К ДРУГОМУ
Пусть (е) = (е, ел) и - два базиса евклидова про-
странства Е, a S - матрица перехода от базиса (е) к базису (/):
(/)=(е) S . Требуется найти связь матриц Грама систем векторов (е) и (/).
По формуле (8.32) вычислим скалярное произведение векторов х и у
в разных базисах:
(х’3,)=йГс(е.....................
где х , х и у , у - координатные столбцы векторов х и у в соответст-
(«) (/) (е) (/)
вующих базисах. Подставляя в последнее равенство связи х = S х ,
(«) (/)
у = S у , получаем тождество
(«) (/)
.....................
Отсюда следует формула изменения матрицы Грама при переходе от од-
ного базиса к другому:
0(/1...fn}=STG(ev...,en}s.
Записав это равенство для ортонормированных базисов (е) и (/), по-
лучаем E = STES, так как матрицы Грама ортонормированных базисов
единичные: с(е|,...,ел)=б(/1,...,/я)= Е. Поэтому матрица S перехода от
439
одного ортонормированного базиса к другому является ортогональной:
5“‘ = ST (см. разд. 4.2).
СВОЙСТВА ОПРЕДЕЛИТЕЛЯ ГРАМА
Определитель матрицы (8.33) называется определителем Грама. Рас-
смотрим свойства этого определителя.
1. Критерий Грама линейной зависимости векторов: система векторов
Vj,..., vk линейно зависима тогда и только тогда, когда определитель Гра-
ма этой системы равен нулю.
Действительно, если система , v2,. ->vt линейно зависима, то суще-
ствуют такие числа Х],..., xt, не равные нулю одновременно, что
х, vl+... + xt vk=o.
Умножая это равенство скалярно на Vj, затем на v2 и т-д- на vk > получаем
однородную систему уравнений G(v1,v2,...,vJt)x = о , которая имеет нетри-
виальное решение х = (^ ••• хк )г. Следовательно, ее определитель равен
нулю (см. разд.5.5). Необходимость доказана. Достаточность доказывается,
проводя рассуждения в обратном порядке.
Следствие. Если какой-либо главный минор матрицы Грама равен ну-
лю, то и определитель Грама равен нулю.
Главный минор матрицы Грама системы v],v2,...,vi представляет со-
бой определитель Грама подсистемы векторов. Если подсистема линейно
зависима, то и вся система линейно зависима (см. разд.8.2.2).
2. Определитель Грама detG(v],..., vA) не изменяется в процессе орто-
гонализации системы векторов Vj,..., vk. Другими словами, если в процессе
ортогонализации векторов V],.... vk получены векторы witw2,...,wk, то
det G(v,, v2,..., vk ) = detG(wj, w2,..., wk) = (w,, Wj)• (w2, w2)•...• (»*, wk).
Действительно, в процессе ортогонализации (см. разд. 8.8.5) по векто-
рам Vj, v2,..., vk последовательно строятся векторы
k-l
wi=vi- w2 = v2-a21w1,..., wk=vk-Yiakjwj.
j=i
После первого шага определитель Грама не изменяется
det G(v,, v2,..., vk ) = det G^, v2,..., vk ).
Выполним с определителем detG^j,v2,...,vt) следующие преобразования.
Прибавим ко второй строке первую, умноженную на число (- a2,), а затем
ко второму столбцу прибавим первый, умноженный на (-а2]). Получим
440
определитель dett?^, v2-a21H’1,...,vi)=detG(H’],H’2,v3,...,vJt). Так как при
этих преобразованиях определитель не изменяется (см. разд. 2.3), то
detG(v1,v2,...,vJ=detG(H>1>v2,...,vJ=detG(H-1,H-2,v3,...,vJ.
Значит, после второго шага в процессе ортогонализации определитель не
изменяется. Продолжая аналогично, получаем после к шагов:
det G(v] , v2,..., vk) = det G(h'1, h>2 ,..., wk).
Вычислим правую часть этого равенства. Матрица О(н’1,н'2,...,н'4) Грама
ортогональной системы Wj, н>2,..., юк векторов является диагональной, так
как (м»;, и’у) = 0 при г* j. Поэтому ее определитель равен произведению
элементов, стоящих на главной диагонали:
det G(h>, , w2,..„ wk )= (и-!, w, )• , и-;, )•...• (wk, wk).
3. Определитель Грама любой системы Vj,v2,..., vk векторов удовле-
творяет двойному неравенству
( 0<detG(v1,v2,...,vJ<(v1,v1)(v2,v2)-...-(vi,vi).
Докажем неотрицательность определителя Грама. Если система
Vj, v2,..., vk линейно зависима, то определитель равен нулю (по свойству 1).
Если же система Vj,v2,...,vt линейно независима, то, выполнив процесс
ортогонализации, получим ненулевые векторы , w2 ,..., wk , для которых
Vno свойству 2:
detG(v1,v2,...,vt)=detG(w1,w2,...,M’*)=| |2-| н-2 |2 -...-| wk |2 >0.
• Оценим теперь скалярный квадрат (vy , vyJ. Выполняя процесс ортого-
нализации, имеем v7 = Wj + а71и’1 + ... + а77_]н'7_1. Отсюда
v7)=(h-7, wj\
Г = 1
Следовательно, по свойству 2:
(vi>vi)(v2>v2)—(vt>vJt)-(M’l,M'1)(H’2,H’2)"(H’t,M'i) = detG:(H’1,H’2,...,H'i).
Замечания 8.12.
ы 1. Матрица Грама любой системы векторов является неотрицательно
определенной (см. разд. 6.6.3), так как все ее главные миноры также являют-
ся определителями Грама соответствующих подсистем векторов и неотри-
цательны в силу свойства 3.
2. Матрица Грама любой линейно независимой системы векторов явля-
Стся положительно определенной, так как все ее угловые миноры положи-
тельны (в силу свойств 1,3), поскольку являются определителями Грама ли-
нейно независимых подсистем векторов.
§ 3. Определитель квадратной матрицы А (п -го порядка) удовлетворяет
। Неравенству Адамара:
441
(detAy^nfe+a^+.-.+afJ.
1=1
Действительно, обозначив alt...,an столбцы матрицы А, элементы
матрицы АтА можно представить как скалярные произведения (8.27):
(а/,ау)=(а,)гау. Тогда АгA = G(a1,..., ап) - матрица Грама системы
векторов пространства R". По свойству 3, теореме 2.2 и свойству
1 определителя (см. разд.2.3.1) получаем доказываемое неравенство:
(det А)2 - det А • det А = det Ат det А = det(Ar а)=
=detc(fli.ая)Ф1 Г=£J(flA+а^+-+а.2«)-
4. Если А - невырожденная квадратная матрица, то любой главный
минор матрицы АТА положителен. Это следует из п.2, учитывая представ-
ление произведения АтА = ап) как матрицы Грама системы линейно
независимых векторов ах,...,ап - столбцов матрицы А (см. п.З).
ИЗОМОРФИЗМ ЕВКЛИДОВЫХ ПРОСТРАНСТВ
Два евклидовых пространства Е и Е' называются изоморфными
(Е Е' ), если они изоморфны как линейные пространства (см. разд.8.5) и
скалярные произведения соответствующих векторов равны:
(и, *)=(»', И ,
где (-, ) и (•, •) - скалярные произведения в пространствах Е и Е' соответ-
ственно.
Напомним, что для изоморфизма конечномерных линейных про-
странств необходимо и достаточно, чтобы их размерности совпадали (см.
теорему 8.3). Покажем, что это условие достаточно для изоморфизма евкли-
довых пространств (необходимость следует из определения). Как и при до-
казательстве теоремы 8.3, установим изоморфизм п -мерного евклидова
пространства Е с вещественным арифметическим пространством R" со
скалярным произведением (8.27). В самом деле, взяв в пространстве Е ка-
кой-нибудь ортонормированный базис = поставим в соответ-
ствие каждому вектору хе Е его координатный столбец хе Rn (х <-эх).
Это взаимно однозначное соответствие устанавливает изоморфизм линей-
ных пространств: Е Rn . В ортонормированием базисе скалярное произ-
ведение векторов х и у пространства Е находится по формуле
и <-> и
V <-> у'
442
(х, у)= + х2у2 +• .. + хпуп (см. п.1 преимуществ ортонормированного ба-
зиса). Такое же выражение дает скалярное произведение (8.27) координат-
ных столбцов х и у, т.е. скалярные произведения соответствующих эле-
ментов равны (х,у)=х1у1 + х2у2 +••• + х„у„ = хту . Следовательно, евклидо-
вы пространства Е и R" изоморфны.
Таким образом, изучение конечномерных евклидовых пространств
может быть сведено к исследованию вещественного арифметического про-
странства Rn со стандартным скалярным произведением (8.27).
8.8.7. Ортогональные дополнения
Ортогональным дополнением непустого подмножества М евклидова
пространства Е называется множество векторов, ортогональных каждому
вектору из М . Ортогональное дополнение обозначается
Af1 ={у : (у, н>) = 0, VweA/}.
Рассмотрим примеры ортогональных дополнений.
1. Ортогональным дополнением нулевого подпространства {о}<Е
служит все пространство Е : { о }х = Е. Ортогональным дополнением всего
пространства является его нулевое подпространство Z?1 = { о }.
2. Пусть в пространстве V3 радиус-векторов (с началом в точке О) за-
даны три взаимно перпендикулярных радиус-вектора ОА , ОБ и ОС. Тогда
ортогональным дополнением вектора ОА является множество радиус-
векторов на плоскости, содержащей векторы ОБ и ОС, точнее,
{оА J1 = Lin{pB, Ос). Ортогональным дополнением векторов ОА и ОБ
служит множество радиус-векторов на прямой, содержащей вектор ОС:
{оА, ОБ }Х = Tin (ос). Ортогональным дополнение трех заданных векторов
служит нулевой радиус-вектор: {оА, ОБ, ОС J*- = {оо }.
3. В пространстве P2(r) многочленов степени не выше второй со ска-
лярным произведением (8.29) (см. п.6 в разд.8.8.2) задано подмножество
— многочленов нулевой степени. Найдем ортогональное дополнение
этого подмножества. Для этого приравняем нулю скалярное произведение
многочлена р2(х) = ах2+Ьх + с на постоянный многочлен Р0(х) = d:
(р2(х), р0(х)) = «- O+Z>-O + c- rf = O. Поскольку величина d произвольная,
то с - 0. Следовательно, ортогональным дополнением подмножества Pq(r)
является множество многочленов из P2(r) с нулевым свободным членом.
443
СВОЙСТВА ОРТОГОНАЛЬНОГО ДОПОЛНЕНИЯ
Рассмотрим свойства ортогональных дополнений подмножеств
п -мерного евклидова пространства Е .
1. Ортогональное дополнением1' непустого подмножества МсЕ
является линейным подпространством, т.е. М1 <Е, и справедливо вклю-
чение М с (л/1)1.
В самом деле, множество Л/1 замкнуто по отношению к операциям
сложения векторов и умножения вектора на число, так как сумма двух век-
торов, ортогональных М , ортогональна М , и произведение вектора, орто-
гонального М , на любое число является вектором, ортогональным М . Jlp-
кажем включение Л/с (л/1 . Пусть we М, тогда (w, v)=0 для любого
вектора v е ML. Но это означает, что н> е .
2. Пересечение любого непустого подмножества МсЕ со своим ор-
тогональным дополнением есть нулевой вектор'. Л/АЛ/1={о}.
Действительно, только нулевой вектор ортогонален самому себе.
3. Если L - подпространство Е (L< Е), то E = L®Ll.
Действительно, возьмем в L ортогональный базис (е) = («],...,ек). До-
полним его векторами (/) = (/*+],••.,/„) до ортогонального базиса (е),(/)
всего пространства Е . Тогда произвольный вектор we Е можно предста-
вить в виде суммы
к п
w = w. е. + У w. f. = и + v ,
,=1 j=k+i
где ueL,a vgZ,1, так как (у,е^= и'Д/,.,0 для i = 1,Следо-
=4+1
вательно, любой вектор пространства Е раскладывается по подпространст-
вам L и Z.1, т.е. Е -L + Ll . Эта алгебраическая сумма является прямой
суммой по свойству 2, поскольку LL = {о }. Следовательно, Е = L® Ll .
4. Если L< Е, то dim!.1 = dim£-dimZ,.
5. Если L - подпространство Е, то L = (z.1)1.
Из первого свойства следует включение L с (ь1)1. Докажем, что
(l1)1 cL. Действительно, пусть н>е(/,±У’. По свойству 3: w = u + v, где
444
ueL, velL. Найдем скалярное произведение (w, v)= (и + v, v) =
о
= (и, v)+(v, v)= (v, v). Следовательно, (v, v)=0, и согласно аксиоме 4 ска-
о
лярного произведения (см. разд. 8.8.1) v = o, поэтому и> = и + г =
= и + о = ие L. Значит, (//"У <=£,. Из двух включений Гс^У" и
с£ следует равенство 1 = (1±У.
6. Если L}<E и L2<E, то
(Li + L2y-=I^LL2 и (£1ПЬ2)1 = ^+^.
Последние свойства аналогичны свойствам алгебраических дополне-
ний (см. разд. 8.6.4).
НАХОЖДЕНИЕ ОРТОГОНАЛЬНОГО ДОПОЛНЕНИЯ ПОДПРОСТРАНСТВА
В разд. 8.6.5 для описания подпространств линейных пространств ис-
пользовались два способа описания (внешний и внутренний). Рассмотрим
применение этих способов описания для нахождения ортогональных допол-
нений подпространств. Учитывая изоморфизм евклидовых пространств, бу-
дем рассматривать арифметическое пространство R" со скалярным
произведением (8.27).
Для заданного подпространства L<R" требуется найти его ортого-
нальное дополнение Ll . В зависимости от способа описания подпростран-
ства L используем одно из следующих двух утверждений.
1. Если подпространство L<R" задано как линейная оболочка
L = Lin(ax,...,ak) столбцов матрицы A = (at ak), то множество ре-
шений однородной системы АТх = о является его ортогональным дополне-
нием Е*~ <Rn, т.е.
£ = Ljn(a|,...,at) => Z,1 = {агх = о |. (8.34)
2. Если подпространство L<R" задано как множество решений од-
нородной системы Ах-о т уравнений с п неизвестными, то линейная
оболочка столбцов а^,...,а^ транспонированной матрицы
АТ =[а^ а^) является его ортогональным дополнением <Rn , т.е.
L = {Ax = o} => Z,1 = Lin(af,...,a*), (8.35)
где a] -i -й столбец матрицы АТ .
445
Докажем, например, первое утверждение. Линейное однородное урав-
нение aaxt + ai2x2 +... + а^хп = 0 можно записать при помощи скалярного
произведения (а(,х) = 0, так как (ai,x) = (al)Tх по формуле (8.27). Тогда
множество {(а., х)=о } решений одного уравнения совпадает с множеством
векторов, ортогональных at. Поэтому множество {Атх = о } совпадает
с множеством векторов, ортогональных каждому из векторов ах,..., ак , зна-
чит, и их линейной оболочке L = Lin(ax.ак) (см. свойство 4 в разд. 8.8.4).
Таким образом, L1 = { Атх = о }.
Замечания 8.13.
1. В отличие от алгебраического дополнения L+ подпространства
L < Е (см. разд. 8.6.4) ортогональное дополнение L1 находится однознач-
но.
2. Ортогональное дополнение Ll подпространства L < Е в силу свой-
ства 3 является также и алгебраическим дополнением. Это обстоятельство
учитывалось при нахождении алгебраических дополнений при помощи ут-
верждений (8.16) и (8.17), которые по существу совпадают с утверждениями
(8.34) и (8.35).
Пример 8.19. В примере 8.10 для линейного подпространства
L-Lin^t-l)2,(t + 1)3) пространства многочленов не более, чем 3-й
степени, было найдено алгебраическое дополнение
L+ = Lin((-1,8-0,4г + г2),(-0,4-0,2f+r3)). Доказать, что это алгебраическое
дополнение является ортогональным дополнением подпространства L евк-
лидова пространства P3(r) со скалярным произведением (8.29).
□ Для решения задачи достаточно показать, что образующие подпро-
странства L:
P!(f)=(f-1)2 = 0-г3 + 1-Г2 +(—2)-г+1; p,(t) = (t + 1)3 =l-r3 + 3-r2 + 3-/ + 1
ортогональны образующим алгебраического дополнения L+ :
91(f)=0-?+l f2+(-0,4) f + (-l,8), <?2(f)= 1-f3+0 f2+(-0,2) f+ (-0,4).
По формуле (8.29) находим
(aW^iW)=00 + 1-1 + (-2)-(-0,4)+1(-1,8) = 0;
(р1(4?2Ю)=01 + 10 + (-2М-0,2)+1(-0,4) = 0;
(p2(W)H O + 31 + 3-(-0,4)+1 (-l,8) = 0;
(p2(492(0) = ll+3-O+3(-O,2)+l(-O,4) = O.
Следовательно, L1 = L+.
446
8.8.8. Задача о перпендикуляре $
Й
Пусть L - подпространство конечномерного евклидова пространств?
Е . Для любого вектора v е Е (по свойству 3 ортогонального Д°полненйв
существует единственное разложение:
v=l + h, где le L, he . (8,зб)
Вектор I называется ортогональной проекцией вектора v на подпростран-
ство L, а вектор h - ортогональной составляющей вектора v относи-
тельно подпространства L. По аналогии с привычными терминами курса
элементарной геометрии ортогональную составляющую h называют пер-
пендикуляром, опущенным из конца вектора v на подпространство L.
Из-за ортогональности составляющих I и h разложение (8.36) называют
ортогональным.
Задача о перпендикуляре ставится следующим образом. В п -мерном
евклидовом пространстве заданы вектор vе Е и подпространство L<E.
Требуется найти ортогональную проекцию leL вектора у и его ортого-
нальную составляющую (перпендикуляр) h е Ll , т.е. представить заданный
вектор v в виде (8.36).
Для решения задачи о перпендикуляре нужно выполнить следующие
действия.
1. Взять любой базис е1,...,ег подпространства L (полагаем, что
dim L = г < п).
2. Составить неоднородную систему
'(е1,е1)41 + (е1,е2)-/2+...+(ерег)/г = (врк),
« •
.(er^l)Zl +k’^)’Z2 + • + k’₽r)Zr =(er’’’)
г уравнений с г неизвестными /1,...,Zr.
3. Решить систему, составленную в п.2.
4. Найти ортогональную проекцию I = el + ...+lr er, а затем - орто-
гональную составляющую (перпендикуляр) h = v-l.
Поясним алгоритм решения. Разложив ортогональную проекцию
I = ll-e1+...+lr er по базису подпространства, запишем ортогональную со-
ставляющую (перпендикуляр): h = v - I = v -11е1-ег. Затем найдем
скалярные произведения {h,ej), i = l,...,r, умножая последнее равенство по-
следовательно на е,,...,^. Учитывая, что (h,e() = 0, i = l,...,r, получаем
систему из п.2 алгоритма. Заметим, что матрица полученной системы - это
матрица Грама G(el,...,er) линейно независимой системы векторов (базиса)
447
et,...,er. По свойству 1 определителя Грама detG(e1;...,er)* 0, значит, рас-
сматриваемая система имеет единственное решение.
Пример 8.20. В пространстве Л4 со стандартным скалярным произве-
дением (8.27) заданы: вектор v = (-3 2 0 о)г и подпространство L -
множество решений однородной системы
х, + х2 + 2х3 + х4 = 0,
- 2х, + Зх2 + х4 = 0,
Зх| + 4х2 + 2х3 + 2х4 = 0.
Требуется найти ортогональную проекцию I е L и ортогональную состав-
ляющую heLL вектора v относительно подпространства L .
□ 1. Базис подпространства был найден в примере 8.9: L = £,т(ср1,ф2 ),
гдеф]=(-6 4 I 0)г,<р2=(-2 1 0 1)г.
2. Вычисляем скалярные произведения
(ф1>ф])=(-б)2 +42 +12 +02 =53; (ф1,ф2) = (-б) (-2)+41 + Ь0 + 01 = 16;
(ф2>Фг)=(-2)2+12+02+12 =6; (ф„ v)=(-6)(-3) + 4-2 + 1 0 + 0 0 = 26 ;
(ф2> v)=(-2) (-3)+l -2 + 0-0 + l-0 = 8, (ф2,ф|)=(ф,,ф2)=16
и составляем неоднородную систему
53 /, +16 /2 =26,
16/,+6Z2 =8.
3. Решаем систему по правилу Крамера (см. разд.5.2):
/ 26-6-16-8 28 _ 14 ; 53-8-16-26 _ 8 4
1 ~ 53-6-16-16 “ 62 “ 31 ’ 2 " 53-6-16-16 ~ 62 ” 31 ’
4. Находим ортогональную проекцию и ортогональную составляющую
/=" -6> 4 4 + — '-2> 1 '-92> 60 ; Л = -з> 2 __1_ '-92^ 60 __1_ '-Г 2
31 1 31 0 ~31 14 0 31 14 "31 -14
< 1 , < 4 , <0, < 4 J <~4>
Проверим ортогональность составляющих:
(/, A)=-p-((-92)-(-l) + 60-2 + 14-(-14) + 4-(-4))=0.
Замечания 8.14.
1. Из теоремы Пифагора | v |2 = 1112 +| h |2 следуют неравенства:
| / | < [ v |, | h [ < | v |. Равенства возможны только тогда, когда v е L или
v ± L соответственно. В остальных случаях неравенства строгие, т.е. полу-
чаем утверждения, знакомые читателю из курса геометрии: 111 < | v | - про-
448
екция меньше наклонной, | Л | < | v | - перпендикуляр есть кратчайшее рас-
стояние от конца вектора v до подпространства L.
2. Для одномерного подпространства L = Ып(е) составляющую I е L в
разложении (8.36) называют ортогональной проекцией на ось, задаваемую
вектором е (или на направление, задаваемое вектором е ). Если ось зада-
ется единичным вектором (| е | = 1), то длина ортогональной проекции равна
/ = |/| = (Ле).
3. Если в подпространстве L взять ортонормированный базис
ех,...,ег, то квадрат длины вектора I можно вычислить по формуле
| / |2 = /2 + /2 + ... + Z2, где Ц = (l, е,), i = l,...,r. Тогда из неравенства (см. п.1)
| / | < | v | следует:
У/2 < | v |2 (неравенство Бесселя),
» |=1
т.е. квадрат длины вектора не меньше суммы квадратов длин его проекций
йа любые г взаимно ортогональных направлений.
4. В процессе ортогонализации системы векторов v} ,v2,...,vk на каж-
дом шаге фактически решается задача о перпендикуляре. Например, на j -м
шаге находится ортогональная составляющая Wj вектора Vj относительно
подпространства Lin(wl,..., ) (см. п. 1 замечаний 8.11).
5. В приложениях приходится также рассматривать задачу о перпенди-
куляре не для подпространства, а для многообразия. Пусть в п -мерном евк-
лидовом пространстве заданы вектор v е Е и многообразие v0 + L
(рис. 8.4, а). Требуется найти разложение v = т + Л , где т е v0 + L, he L1 .
; 29 — 4549 449
Здесь h - перпендикуляр, опущенный из конца вектора v на многообразие
у0 + L. Заметим, что составляющие т и h в общем случае не ортого-
нальны.
Поставленная задача сводится к задаче нахождения ортогональной
проекции I = т - v0 и ортогональной составляющей h вектора v - v0 отно-
сительно подпространства L (см. рис. 8.4, 6). Найдя ортогональное разло-
жение v - v0 = I+h , можно получить и искомое разложение v = т +h , где
т = I + у0 .
Пример 8.21. В пространстве /?4 со стандартным скалярным произве-
дением (8.27) задано линейное многообразие М ={Ax = b} - множество
решений неоднородной системы:
xt + х2 + 2х3 + х4 = 1,
• 2xj + Зх2 + х4 = 0,
3х1 + 4х2 + 2х3 + 2х4 = 1.
Требуется найти разложение нулевого вектора o = m + h, где те М , а
вектор Л перпендикулярен однородной части многообразия М .
□ В примере 5.5 была получена структура общего решения заданной
неоднородной системы уравнений
'-6'
4
1
. О ,
LJ
х = х +Cj ф, +С2 ф2 =
-2
О
О
1
О
1
2
где Q, С2 - произвольные постоянные. Отсюда следует (см. решение при-
мера 8.16), что многообразие М можно представить в виде М =хн +L, где
L - { Ах = о } - множество решений соответствующей однородной системы.
Учитывая п.5 замечаний 8.14 ( v0 =хн, v = о), сформулируем задачу о пер-
пендикуляре: для вектора v- v0 - о-хн = (-3 2 0 0^ найти ортого-
нальную проекцию I и ортогональную составляющую h относительно
подпространства L = { Ах = о }. Эта задача была решена в примере 8.20. По-
этому осталось записать искомые составляющие т и h нулевого вектора
o-m + h:
m = l+xH = —
31
h= —
31
-14
-4J
2
450
Равенство m--h в данном случае может служить для контроля вычисле-
ний. Обратим внимание, что составляющая т является решением неодно-
родной системы уравнений. Причем это решение "ближайшее" к нулевому
вектору, т.е. имеет наименьшую длину. Такие решения в разд. 5.8 называ-
лись псевдорешениями. Поэтому полученная в данном примере составляю-
щая т совпадает с псевдорешением, найденным в примере 5.8.
МЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛИТЕЛЯ ГРАМА
Пусть V],v2,...,vt — линейно независимая система векторов «-мер-
ного евклидова пространства (к < п ). Определим по индукции понятие
многомерного объема. Обозначим через h. - перпендикуляр, опущенный
из конца вектора на подпространство Lin(v1,...,V;_1), J = 2,...,k.
Обозначим
V#Vi “ | vi | ~ одномерный объем - длина вектора Vj;
V#yliF ‘I Аг | = | ’’i Н ^2 | - двумерный объем - площадь параллело-
грамма, построенного на векторах Vj, р2 ;
’| | = | ’’i I I Аг Н *з | ~ трехмерный объем - объем па-
раллелепипеда, построенного на векторах V], v2, v3;
.....= %.......ft i | hk |=| Vj |-| h2 |.....|hk | - -мерный объем - объем
< параллелепипеда, построенного на векторах vl,v2,...,vk.
Проводя ортогонализацию системы векторов vt,v2,...,vk , получаем,
согласно п.4 замечаний 8.14, перпендикуляры Aj = vl,h2,...,hk. Тогда по
свойству 2 определителя Грама имеем
' V#,,.... =|й1|2 |й2|2-.-|Л* |2=detG(v1,..„vi), (8.37)
т.е. определитель Грама векторов vY,v2,...,vk равен квадрату к-мерного
объема параллелепипеда, построенного на этих векторах. В этом заключа-
ется геометрический смысл определителя Грама.
Расстоянием от конца вектора v до подпространства L называ-
ется наименьшее значение длин векторов (v -1), где / е L, т.е.
d = min I v-l I.
leL 1 1
Аналогично определяется расстояние от конца вектора до многообразия.
Углом между ненулевым вектором v и подпространством L назы-
вается наименьший угол между вектором v и ненулевыми векторами
подпространства, т.е.
29«
451
f (v’O |
Ф = mini arccos.- , , ' .
te4 H-I'IJ
Аналогично определяется угол между вектором и многообразием, как угол
между вектором и однородной частью многообразия.
Из неравенств п.1 замечаний 8.14 следует, что
1) расстояние от конца вектора v до подпространства L равно длине
перпендикуляра, опущенного из конца вектора v на подпространство L,
т.е. d = | h |;
2) угол между ненулевым вектором v и подпространством L равен
углу между вектором v и его ортогональной проекцией на подпространство
L.
Для нахождения расстояний и углов можно использовать формулу
(8.37).
Пусть задан вектор v и подпространство L = Un(ely...,er), причем
векторы е1г...,ег линейно независимы. Тогда У#е е „=1#^ е | й|, где
h — ортогональная составляющая вектора v относительно подпространства
V
L. Отсюда, I h | ---1...’’ . Используя (8.37) для вычисления объемов, по-
V#«,..
лучаем, что длина | h | ортогональной составляющей (расстояние от конца
вектора v до подпространства L = Lin(el,...,er)) находится по формуле
(838)
1 1 j detG(el,...,er)
а угол ф между ненулевым вектором v и подпространством находится по
формуле
ф = arcsin
й
v
(8.39)
Пример 8.22. В пространстве Я4 со стандартным скалярным произве-
дением (8.27) заданы: вектор v = (-3 2 0 0)г и подпространство L -
множество решений однородной системы:
Xj + х2 + 2х3 + х4 = 0,
2х, +3х2 +х4 =0,
ЗХ] + 4х2 + 2х3 + 2х4 = 0.
Требуется найти расстояние | h | от конца вектора v до подпространства L
и угол между вектором v и подпространством L.
452
□ Базис подпространства был найден в примере 8.9: £ = 1лп(ф1,ф2),
где ф!=(-6 4 1 of, <Pj = (—2 1 0 if. Составляем определители
Грама ((v, v)=| v |2 = (- З)2 + 22 + О2 + О2 = 13, остальные скалярные произве-
дения векторов найдены в примере 8.20):
53
26
det G(<pp ф2, v)= 16 6 8 =14,
detG(<Pi,<p2)=
26
53 16
16 6
= 62.
Тогда 1*1-^-^.
найдены ортогональная проекция Z = (-^p ji зР и °Ртогональная
составляющая h = ^f. Вычисляя длину вектора h, получаем
й I = - Результаты совпадают.
8.8.9. Унитарные пространства
Комплексное линейное пространство V называется унитарным (или
эрмитовым), если каждой паре элементов и, v этого пространства постав-
лено в соответствие комплексное число (и, у), называемое скалярным про-
изведением, причем это соответствие удовлетворяет следующим условиям:
1. (и, у) = (у,и) Vn,yet7;
2. (u + v, w) = (u, >у)+(у, и») Vu,v,weU;
3. (А-и,у)=Х-(и,у) X/и, ve U , V А.е С;
4. (y,y)>0 Vy*o и (у,у)=0 => у=о.
Условия 1-4 называются аксиомами скалярного произведения (в ком-
плексном линейном пространстве). По аксиоме 1 комплексные числа (и, у)
и (у, и) сопряженные, а скалярный квадрат (у, у)= (у, у) - действительное
число, причем неотрицательное (по аксиоме 4).
Из аксиом 1 и 3 следует правило вынесения числового множителя от
второго сомножителя скалярного произведения:
(п,А-у) = А(в,у).
Из аксиом 1-3 следует общая формула
453
т п т п . \
Ya‘ui' = Р;(“>•’ vj)
ч<=1 j=l J 1=1 ;=1
для любых векторов и,, Vj и комплексных чисел а(,(3?, i = L,...,m;
J=1....п.
Для унитарных пространств также, как для евклидовых, вводятся поня-
тия длины (нормы, модуля) вектора, ортогональности векторов, ортогональ-
ного и ортонормированного базисов, процесса ортогонализации, ортого-
нального дополнения, изоморфизма. В частности, любое и -мерное унитар-
ное пространство изоморфно комплексному арифметическому пространству
Сп со стандартным скалярным произведением
(х, у) = хТ у = X!У1 + х2у2 +... + хпуп,
где х = (Х1 ••• х„)г,у = (у1 уп)т.
Задачи для самостоятельного решения
8.1. Выяснить, является ли линейным пространством данное множест-
во радиус-векторов с обычными операциями сложения векторов и умноже-
ния вектора на число:
а) множество радиус-векторов, параллельных данной прямой;
б) множество радиус-векторов, перпендикулярных данной прямой;
в) множество радиус-векторов, параллельных данной плоскости;
г) множество радиус-векторов, перпендикулярных данной плоскости;
д) множество единичных радиус-векторов;
е) множество радиус-векторов, образующих с данной прямой угол ве-
личиной 45’.
Ответ: а) да; б) да; в) да; г) да; д) нет; е) нет.
8.2. Выяснить, является ли линейным пространством данное множест-
во функций, определенных на R , с обычными операциями сложения функ-
ций и умножения функции на число ((/ + ^/х) = f(x)+g(x),
(WXx) = WW):
а) множество четных функций (/(-х) = /(х));
б) множество нечетных функций (/(-х)= ~/(х));
в) множество периодических функций (с разными периодами);
г) множество периодических функций (с одним и тем же периодом);
д) множество возрастающих функций;
е) множество ограниченных функций;
ж) множество функций, разрывных в нуле.
Ответ: а) да; б) да; в) нет; г) да; д) нет; е) да; ж) нет.
454
8.3. Выяснить, является ли линейным пространством данное множест-
во матриц с обычными операциями сложения матриц и умножения матрицы
на число:
а) множество диагональных матриц порядка п ;
б) множество верхних треугольных матриц порядка п ;
в) множество треугольных матриц порядка п ;
г) множество вырожденных квадратных матриц порядка п;
д) множество невырожденных квадратных матриц порядка п .
Ответ: а) да; б) да; в) нет; г) нет; д) нет.
8.4. Найти размерность и базис следующих линейных пространств:
а) пространство четных многочленов степени не выше 2п;
б) пространство нечетных многочленов степени не выше 2n +1;
в) пространство тригонометрических многочленов (не выше п -го по-
рядка), т.е. функций вида f(t) = а0 + ах cos t+bx sin t+...+an cos nt+bn sin nt.
Ответ: а) размерность: n + 1; базис: 1, x2,..., x2"; б) размерность:
n + Г, базис: x, x3,..., x2n+1; в) размерность: 2n+l; базис: 1, cost, sint,
cos2t, sin2t,..., cos nt, sin nt. Искомые базисы определены неоднозначно.
8.5. Доказать, что в заданном линейном пространстве система (е) век-
торов образует базис. Разложить вектор v по данному базису:
—2 6Л ( i'
6) пространство С : = U’e2“ , V = W 1 -3j:
'П '2> Г14>
в) пространство R3: ех - 1 ,е2 = 1 ,е3 = 2 , v= 9
и 16,
г) пространство Р2 многочленов степени не выше второй: е1(х) = х + 1,
е2(х)=х2-1, е3(х) = х-1, v(x) = 2x2.
Ответ: a) v = 2 е{ +3 е2; б) v = 2i-e] + (-1)-е2;
в) v -1-е1+2-е2+Зе3; г) v = 1-Cj +2-е2 + (-1)е3.
8.6. Найти матрицу 5 перехода от базиса (/) к базису (g):
а) fl “[2/ uJ’ **Ч-2/ *2Ч6Г
455
б) /, = 2 , /2 =
.1,
'2"
3
.3,
'3'
/з= 7
1
*1 = 1
.4.
f 1 '
• = 1
Ответ: a) S ~
-6
10
13 I; б) 5 =
-20 J
'-27
9
. 4
-71 -4Г
20 9
12 8 J
8.7. Найти размерности и базисы подпространств А и В, их суммы
А+В и пересечения АПЛ, если подпространства заданы линейными обо-
лочками своих образующих А = Lin(a{,a2,a3), В = Lin{bl, b2, b3):
Ответ: a) dimA = 2, базис: aJy a2; dimB = 2, базис: bltb2;
dim(A + B) = 2, базис: a(, a2 ; dim(A П В) = 2, базис: bl,b2;
6) dim A = 2, базис: alta2; dimB = 2, базис: bl,b2\ dim(A + B) = 3,
базис: apa2 ; dim(AnB) = l, базис: (3 5 1)г;
в) dimA - 3, базис: al,a2,a3; dimB - 2, базис: bt, b2 ; dim(A + B) = 3 ,
базис: al,a2,a3', dim(AHB) = 2, базис: b},b2. Искомые базисы определя-
ются неоднозначно.
8.8. Найти размерности подпространств А и В, их суммы А + В и
пересечения АПВ , если подпространства заданы как множества решений
однородных систем линейных уравнений А = { Ах = о }, В = { Вх = о }:
f 1 1 2 1Л fl 2 -1 ЗЛ
а)А = , В= ;
^2 2 3 2/ ^2 4 -2 6J
456
„ (2 -1-3 8 ]
б)А = , В =
13 2-1 -2J
'3
-1
2
-9
3
-6
1
-2
1
4
1
Ответ: a) dimA = 2, dimB = 3, dim(A + B) = 4, dim(Anu) = l;
6) dimA = 2, dimB = 2, dim(A+ B)= 3, dim(ADB) = l.
8.9. В линейном пространстве R4 co стандартным скалярным произве-
дением (х,у) = хТу дана система векторов ^=(2 1 3 -
а2 = (7 4 3 - 3)г, а3 = (1 1 - 6 о)г, д4 = (5 7 7 8)т. Применяя
процесс ортогонализации, найти соответствующую ортогональную систему
векторов.
Ответ: (2 1 3 — 1)г, (3 2 -3 -1)г, (1 5 1 К))7. Искомая
система определена неоднозначно.
8.10. Подпространство L<E задано линейной оболочкой своих обра-
зующих L - Lin(aга2,а3,а4), которые в ортонормированием базисе
(е)= (е},е2,е3,е4,е5) имеют координатные столбцы а} = (1 0 1 -1 2)г,
а2=(1 0 1 -1 -2)г,а3 =(1 0 3 0 0)г,а4=(0 0 2 1 б)Т.
Найти:
а) размерность и ортогональный базис подпространства L;
б) размерность и ортогональный базис ортогонального дополнения
£х.
Ответ: a) dimL = 3, ортогональный базис: -eY +е3 -е4 + 2-е5 ,
Ь, = 2-е. + 2-е,-2-е.-3-е,, А, =-е, +5-е, +4-е4; б) dimL1 = 2, ортого-
нальный базис: Ь.-Зе, +е--е. + 2-е., Ь,--3-е, +14-е, +е,-2-е,. Ис-
4 123 4 3 1 2 3 4
комые базисы определены неоднозначно.
8.11. Линейное подпространство L<R4 задано как множество
L = { Ах - о } решений однородной системы линейных уравнений с матри-
(2 1 3 -П
цей А= 3 2
<3 1
0 - 2 . Найти систему уравнений, задающую ортогональ-
9 -У
ное дополнение L1.
Ответ: ортогональное дополнение задается системой
бХ] -9х2 -х3 = 0,
х, + х. = 0.
2 4
Искомая система определена неоднозначно.
457
8.12. Найти ортогональную проекцию / и ортогональную составляю-
щую h вектора v относительно подпространства L < Л4 :
a) L = Ь1п(а},а2,а3), = (1 1 1 1)г, а2=(1 2 2 -1)Г,
а3=(1 0 0 зУ,у = (4 -1 -3 4f;
3
б) L = {Ax = o }, А= 3 2 2 1
, v = (7 —4 -1 2f.
2 2 -9j
Ответ- а)/ = (1 -1 -1 5)7, h = (3 0 -2 -1/;
6)Z = (5 -5 -2 -1)7',й = (2 1 1 З)1.
8.13. Найти расстояние от конца вектора v = (4 2 -5 1У до много-
образия, заданного в пространстве Л4 системой линейных уравнений
2xj - 2х2 + х3 + 2х4 = 9,
2х. -4х, + 2х. + Зх. = 12.
12 3 4
Ответ: 5.
8.14. Найти угол между вектором v = (2 2 1 1)г и подпространст-
вом L < Л4 , L - Lin(a{,a2), а{ =(3 4 -4 -1У,а2=(о 1 -1 2У .
Л л
Ответ:
3
8.15. В пространстве Р2 многочленов степени не выше второй скаляр-
ное произведение задано одной из формул:
(р(х), <?(х)) = п р(0) ^(0)+ т р(1)- ^(1)+ (30 - «)• p(2) q(2);
(Я4 <?(х)) = jp(x)q(x)dx .
Требуется найти:
а) ортонормированный базис, применяя процесс ортогонализации к
стандартному базису: 1, х, х2;
б) ортогональную проекцию элемента /(х)=х2 + тх + п пространства
Р2 на подпространство Р} - многочленов степени не выше первой. Здесь т
- номер учебной группы, п - номер студента по списку группы (и < 30).
ГЛАВА 9. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ И
ОПЕРАТОРЫ
9.1. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
9.1.1. Определение линейных отображений
Напомним основные определения [19,25,43], связанные с понятием
отображения (функции, оператора).
Пусть V и W - заданные множества. Говорят, что на множестве V
определено отображение (функция) f, если каждому элементу v е V по-
ставлен в соответствие единственный элемент /(v) множества W . Такое
соответствие называют также отображением множества V в множест-
во W и обозначают f: V -> IV, или V ——> W . Если отображение f
элементу v е V ставит в соответствие элемент w е IV, т.е. w = f(y), то
элемент w называется образом v, а элемент v - прообразом w.
Два отображения f :V ->W и g:V -+IV называются равными, если
/(v)=g(v) VveK.
Отображение f: V -> W называется:
инъективным, если разным элементам множества V соответствуют
разные образы: v, * v2 => )*/(v2);
сюръективным, если для каждого элемента из множества IV имеется
хотя бы один прообраз: Vw elV 3 v е К : w = f(y);
биективным (взаимно однозначным), если оно инъективно и сюръек-
тивно одновременно.
Сюръективное отображение называется также отображением мно-
жества V на множество W .
Композицией отображений g.U —>V и /: К ->IV называется ото-
бражение f о g : U -> W, определяемое равенством (/о g)(u) -
Отображение : V -> V называется тождественным, если каждому
элементу множества V ставится в соответствие этот же элемент: £у (v) = v
VveK.
Отображение : IV -> V называется обратным для отображения
f-.V^W, если f~' Of = $y-.V -+V и /о/’1 = -W-+W. Отображе-
ние f называется обратимым, если для него существует обратное отобра-
459
жение. Необходимым и достаточным условием обратимости является усло-
вие биективности (взаимной однозначности) отображения.
Пусть V и W - линейные пространства (над одним и тем же число-
вым полем). Отображение о?: V —» W называется линейным, если
1. o^(v] + v2)=c4(v1)+o^(p2) VvjeV, Vv2gV ;
2. o?(A v)=A of(v) VveV и любого числа А (из данного числового
поля).
Условие 1 называется аддитивностью отображения, а условие 2 - од-
нородностью. Пространство V называется пространством прообразов, а
пространство W - пространством образов.
Замечания 9.1.
1. Линейное отображение d: V —> W нулевому элементу Оу про-
странства V ставит в соответствие нулевой элемент ow пространства W .
2. Условия аддитивности и однородности можно заменить одним усло-
вием линейности отображения:
+X2v2) = X1o?(vI)+X2ef(v2) VvjeV, Vv2eV
и любых чисел А, и Л2 из данного числового поля.
3. При линейном отображении образ линейной комбинации является
линейной комбинацией образов:
к 1=1 ) 1=1
4. Взаимно однозначное линейное отображение является изоморфиз-
мом (см. разд. 8.5).
9.1.2. Примеры линейных отображений
1. Обозначим 0:V —- нулевое отображение, которое ставит в со-
ответствие любому вектору v е V нулевой элемент ow пространства W .
Условия аддитивности и однородности такого отображения, разумеется, вы-
полняются. Это отображение не является инъективным (разным прообразам
Vj и v2 соответствует один и тот же образ ow ), не является сюръективным
(из всех векторов пространства W только у нулевого имеется прообраз).
Поэтому нулевое отображение не является биективным и, следовательно,
обратимым.
2. Пусть в п -мерном линейном пространстве V задан базис et ,...,е„ .
Обозначим аг:У —> Rn отображение, которое ставит в соответствие каждо-
му вектору v его координатный столбец v = (vj • • • vn )г относительно за-
460
данного базиса. Такое отображение является линейным, так как при сложе-
нии векторов в одном и том же базисе их координаты складываются, а при
умножении вектора на число - координаты вектора умножаются на это чис-
ло (см. разд. 8.4.2). Это отображение является инъективным (разные векто-
ры имеют разные координаты (в одном и том же базисе)), является сюръек-
, тивным (для любого столбца v = (v, v„)T е Rn существует прообраз
v = Vi«i + ...+v„e„). Поэтому отображение зе биективное и, следовательно,
обратимое. Напротив, отображение, которое каждому вектору veV ставит
в соответствие столбец v = (vj + l vn +1)7^ е Rn не является линейным,
так как образом нулевого вектора оу£? служит столбец (1 1)г#о,
отличный от нулевого.
3. Пусть в л-мерном евклидовом пространстве Е задан ненулевой
/ \ \€ V)
вектор ее Е . Обозначим пр (v)= \ * . - алгебраическое значение проек-
н
ции вектора veE на направление, задаваемое вектором е . Тогда отобра-
жение пре :Е —>R будет линейным, так как скалярное произведение линей-
но по второму сомножителю (см. разд. 8.8.1). Это отображение не является
инъективным (разные векторы могут иметь одну и ту же проекцию), являет-
ся сюръективным (для любого действительного числа X, задающего вели-
Х-е
чину проекции, найдется прообраз, например вектор т—г). Поэтому ото-
н
бражение не является биективным и, следовательно, обратимым. Отображе-
ние Е —> R, которое каждому вектору г е Е ставит в соответствие его дли-
ну | v | е R не является линейным, поскольку не выполняется, например, ус-
ловие однородности: I Ал» | * X | г | для отрицательных X.
4. Пусть /’„(/?) и Pn_i(7?) - пространства многочленов с действитель-
ными коэффициентами степени не выше п или (л-1) соответственно. Обо-
значим через ©(р(х))= производную многочлена р(х)б Р„(??). Тогда
dx
отображение (оператор дифференцирования) ©: Р„(я)—» Pn-i(R) ставит в
соответствие каждому многочлену р(х)е Р„(/?) его производную, т.е. мно-
гочлен из пространства Этот оператор линейный, так как производ-
ная суммы равна сумме производных, а производная произведения функции
на число равна произведению производной на это число [19,25,43]. Опера-
тор дифференцирования не является инъективным (два многочлена, отли-
чающиеся свободными членами имеют одну и ту же производную), является
461
сюръективным (для любого многочлена рп_{ (х) имеется прообраз - много-
член из множества первообразных |pn_1(x)t£r + C, где С - произвольная
постоянная). Поэтому оператор дифференцирования не является биектив-
ным и, следовательно, обратимым. Оператор интегриро вания
7: > Рп(к), который многочлену pn-1(x)e Рп_1(К) ставит в соответ-
X
ствие многочлен ря(х) = | , также является линейным (см. свойства
о
интеграла в [19,25,43]). Этот оператор является инъективным (из равенства
образов, дифференцируя по верхнему пределу интегрирования, получаем
равенство прообразов), не является сюръективным (многочлен с отличным
от нуля свободным членом не имеет прообраза). Поэтому оператор интегри-
рования не является биективным и, следовательно, обратимым.
9.1.3. Свойства линейных отображений
Пусть сА: V —> W - линейное отображение.
1. Если векторы г1я..., vk линейно зависимы, то их образы также ли-
нейно зависимы.
Действительно, если нетривиальная линейная комбинация равна нуле-
вому вектору: + ... + ltvt =ov , то, применяя к обеим частям отображе-
ние еА , в силу его линейности с учетом п.1,3 замечаний 9.1, получаем
+^i<A(vi)=ofy,
т.е. равную нулевому вектору нетривиальную линейную комбинацию обра-
зов заданных векторов. Значит, образы ^(г,),...,^^) заданных векторов
линейно зависимы.
2. Пусть cA .V —> W - сюръективное отображение пространства V
на пространство W и векторы пространства W образуют ли-
нейно независимую систему. Тогда в пространстве V существует такая
линейно независимая система векторов Гр..., , что )= ж(., i = .
Действительно, в силу сюръективности отображения у векторов
найдутся прообразы Vj,...,^. Если система vt,...,vt линейно
зависима, то и система Ж],..., w* была бы линейно зависимой (по свойству
1). Поэтому найденная система прообразов линейно независимая.
3. При линейном сюръективном отображении <А :V —>W конечно-
мерного пространства размерность пространства образов не превосходит
размерности пространства прообразов, т.е. dimW < dimV.
В самом деле, в пространстве образов W нет линейно независимой
системы из большего, чем dimV , количества векторов. Если бы такая сис-
462
тема векторов была, то прообразы этих векторов были бы линейно незави-
симы (по свойству 2). Но в пространстве V не может быть линейно незави-
симой системы из большего, чем dimV , количества векторов.
4. Композиция линейных отображений является линейным отображе-
нием.
Действительно, пусть С = о А - композиция линейных отображений
A.U —э V и j8: V -> W . Тогда отображение С аддитивно:
C(u] +и2)= + u2)=J8(A(u1 + и2))= ^В(А(и1)+A(u2)) =
= &(А (ux)) + (u2)) = c(u:) + c(u2).
Однородность отображения С доказывается аналогично.
5. Если линейное отображение A:V —>W обратимое (взаимно одно-
значное), то обратное отображение A~l: W —»V -линейное.
Докажем, например, аддитивность обратного отображения
’(ж!+ H'2)=d>f 1(н'1)+с>/ Чм'г).
Обозначим v = A ’(wj+ef Ни'г) Тогда в силу линейности , получаем
c^(v)=of(e>f 1(wl)+A 1(ж2))=о/(о/"1(ж1))+с^(э/ l(w2))=
= (А о A~l\Wl )+ (а о A^W, )= (ж, ) + (ж2)= Ж, + w2.
Следовательно, с^-1^ + m>2)=v-A ’(wj+of ’(м'г)» что и требовалось
доказать. Однородность обратного отображения доказывается аналогично.
6. Линейное отображение конечномерного пространства однозначно
задается образами базисных векторов.
В самом деле, пусть ei,...,en - базис пространства V, a Д -
произвольная система векторов пространства W . Докажем, что существует
единственное линейное отображение А: V —> W , удовлетворяющее услови-
ям ctf(e,)=ft, i =.
Вассмотрим отображение Ул,/ , где v1,...,vM - координаты
i=l
вектора v в заданном базисе: v = +... + vnen. Это отображение удовле-
творяет заданным условиям, так как ctf(e,) = fi. Покажем, что оно аддитив-
ное и однородное:
I п _Л _п п
A(u + v) = A\ +v()«i = £(«, +V/)Z =£«, ft fi=A(u) + A(v)-,
A{kv) = A )e, = )Z = vi f = X
v=i
463
Существование доказано. Единственность докажем от противного. Пусть ив
- еще одно линейное отображение, удовлетворяющее условиям j8(e() = /(,
i = 1,...,л . Для любого вектора v = Vje, +...+ vaea имеем
•®(V) = V‘e‘ j = Z ) = i
Следовательно, - еб.
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ЛИНЕЙНЫМИ ОТОБРАЖЕНИЯМИ
Суммой отображений ef: V —>W и J8: V —» РИ называется отобра-
жение (c>f + J8): V —>W , определяемое равенством (ctf + ^)(v)=af(v)+JB(v)
для всех v G V .
Произведением отображения сА: V —> W на число А называется
отображение (1 • сА): V —> W , определяемое равенством (1 • d\v) = А • <Л(у)
для всех v G V .
Нетрудно доказать, что сумма линейных отображений и произведение
линейного отображения на число являются линейными отображениями.
9.1.4. Матрица линейного отображения
Пусть of: V —> W - линейное отображение п -мерного пространства
V в т -мерное пространство W . Зафиксируем в пространстве V произ-
вольный базис (е) = (е1,...,еп), а в пространстве W базис (/)= (Л,—,/т).
Линейное отображение однозначно задается образами базисных векторов
(см. свойство 6). Разложим образы c^(e(), i = l,...,n, базисных векторов (е)
по базису (/):
т
' , = 1’ ’Л‘
/=1
Из координатных столбцов векторов ,...,с#(еп) относительно базиса
(/) составим матрицу размеров тХп:
41 ••• ain'
(9-1)
Она называется матрицей линейного отображения в базисах (е) и
(/). Матрицу отображения обозначают также А , чтобы подчеркнуть ее
зависимость от выбранных базисов.
464
При помощи матрицы отображения найдем координаты образа
w = c^(v) по координатам прообраза v . Пусть v = (vt vn)т - коорди-
натный столбец вектора v , a w = (н^ - • • wmY ~ координатный столбец
вектора и» , т.е. v = + ... + vnen и w = +...+ wmfm. Тогда
w=crf(v) = £vjCrf(e,.) =
i=i <=i j=i
В силу единственности разложения вектора w по базису (/) получаем
Используя матричные операции, связь координат можно записать в виде
w = Av,
(9.2)
где А - матрица (9.1) отображения сА .
Таким образом, для каждого линейного отображения п -мерного про-
странства V в т -мерное пространство W {с фиксированными базисами
(е) и (/) соответственно) определена единственная матрица (9.1) этого
отображения, и наоборот, любая числовая матрица размеров тхп являет-
ся матрицей некоторого линейного отображения п -мерного пространства
V в т -мерное пространство W .
Для нахождения матрицы отображения c#: V -» W нужно выполнить
следующие действия:
1) зафиксировать базисы (е) = (вр.-.е,,) и (У) = (Уп—,Ут) пространств
V и W ;
2) найти образ с^(е,) первого базисного вектора и разложить его по
базису (/). Полученные координаты записать в первый столбец матрицы
(9.1) отображения еА ;
3) найти образ of(e2) второго базисного вектора и разложить его по
базису (у). Полученные координаты записать во второй столбец матрицы
(9.1) отображения и т.д. В последний столбец матрицы (9.1) записать коор-
динаты образа of(en) последнего базисного вектора.
Найдем матрицы отображений, рассмотренных в разд.9.1.2.
1. Матрица нулевого отображения O:V—>W нулевая относительно
любых базисов пространств V и W , так как образ любого базисного векто-
30 - 4549
465
ра равен нулевому вектору ow , координаты которого равны нулю (относи-
тельно любого базиса пространства W ).
2. Пусть в л-мерном линейном пространстве V задан базис е} ,...,еп.
Рассмотрим отображение ее: И —> R", которое ставит в соответствие каждо-
му вектору v = +... + vnen его координатный столбец v = (v, ••• v„)T
относительно заданного базиса. В пространстве R" выберем стандартный
базис е{ ,...,еп (см. п.З в разд. 8.3.2). Напомним, что в стандартном базисе
координатный столбец вектора х = (х, • • • х„ )т совпадает с самим столб-
цом х, так как
Поэтому образ «(ej первого базисного вектора имеет координатный
столбец = (1 0 - • 0)г, совпадающий с первым базисным вектором
е, еЛ". Образ ге(е2)=е2 и т.д. Составляя из этих столбцов матрицу ото-
бражения аг: V -> R”, получаем единичную матрицу Е п -го порядка.
3. В и -мерном евклидовом пространстве Е возьмем ортонормирован-
ный базис еп . В качестве базиса одномерного линейного пространства
R возьмем единицу. Рассмотрим отображение npej :Е —> R, где
прГ| (v) = (в], у) - алгебраическое значение проекции вектора v на направ-
ление, задаваемое вектором е1. Тогда матрица отображения пр4| имеет вид
(1 0 О), так как npei(e1) = (e1,e1)=l, а пре (е/)=(е1,е/)= 0 для i1.
4. Взяв в пространствах /’„(я) и Pn-\(R.) стандартные базисы (см. п.6 в
разд.8.3.2), находим образы базисных векторов (первые производные мно-
гочленов):
©(1)=0 = 0-1 + 0х + 0х2 +... + 0-Х"’1;
©(х)=1 = 11 + Ох + О-х2+...+ 0-Х"-1;
©(х2)=2х = 0-1 + 2-х + 0-х2+... + 0-хл-1;
©(х")= п х"-1 =0-1 + 0-х + 0-х2 + ...+ л-х"-1.
Записывая найденные координаты по столбцам матрицы отображения, по-
лучаем матрицу размеров п х (и +1):
466
Го 1 о (А
1^0 о
2 ••• О
О И,
СВОЙСТВА МАТРИЦ ЛИНЕЙНЫХ ОТОБРАЖЕНИЙ
При фиксированных базисах линейных пространств:
1) матрица суммы линейных отображений равна сумме их матриц-,
2) матрица произведения линейного отображения на число равна про-
изведению матрицы отображения на то же самое число-,
3) матрица обратного отображения является обратной для матрицы
отображения;
4) матрица композиции С = $ ° еА отображений равна произведению
матриц отображений: С = ВА .
Докажем, например, последнее свойство. Пусть в линейных простран-
ствах V, W, U фиксированы базисы (е), (/),(#) соответственно. Отобра-
жения сА :V -+W, —> t7, а также их композиция С = з8 ° еА, имеют
матрицы А, В, С относительно соответствующих базисов. Для коорди-
натных столбцов v, w, и векторов р е V, н> = of (v), и = JB(h’) = C(v) запи-
шем связи (9.2): w=Av, u-Bw, u = Cv. Тогда Cv = Bw-BAv для коор-
динатного столбца v произвольного вектора veV. Отсюда следует, что
С = ВА.
9.1.5. Ядро и образ линейного отображения
Ядром линейного отображения сА :V -+W называется множество
таких векторов ре К, что of(p) = o(F, т.е. множество векторов из V , кото-
рые отображаются в нулевой вектор пространства W . Ядро отображения
сА : V -> W обозначается:
Ker of = { v:veK,of(p)=oH,).
Образом линейного отображения cA :V называется множество
образов of(p) всех векторов v из V . Образ отображения of: V -> W обо-
значается 1т Л или of (и):
1т еА = cA(v)= { w.w = eA(v\ VveK}.
Заметим, что символ 1т еА следует отличать от Imz - мнимой части ком-
плексного числа.
30*
467
ПРИМЕРЫ ЯДЕР И ОБРАЗОВ ЛИНЕЙНЫХ ОТОБРАЖЕНИЙ
1. Ядром нулевого отображения О: V является все пространство
V , а образом служит один нулевой вектор, т.е. Кег О = V , Im О = {ow }.
2. Рассмотрим отображение ге: V —> R", которое ставит в соответствие
каждому вектору v п -мерного линейного пространства V его координат-
ный столбец v = (vj ••• v„)r относительно заданного базиса et,...,e„.
Ядром этого отображения является нулевой вектор оу пространства V, по-
скольку только этот вектор имеет нулевой координатный столбец
аг(ог) = оеЛ". Образ преобразования аг совпадает со всем пространством
R", так как это преобразование сюръективно (любой столбец из Л" являет-
ся координатным столбцом некоторого вектора пространства V).
3. Рассмотрим отображение пре :£->/?, которое каждому вектору v
«-мерного евклидова пространства Е ставит в соответствие алгебраиче-
ское значение npe(v)=(e, v) его проекции на Направление, задаваемое еди-
ничным вектором е . Ядром этого преобразования является ортогональное
дополнение {е j1 - множество векторов, ортогональных е . Образом явля-
ется все множество действительных чисел R .
4. Рассмотрим отображение ©: P„(r)-> P„^(R), которое каждому
многочлену степени не выше и ставит в соответствие его производную.
Ядром этого отображения является множество P0(r) многочленов нулевой
степени, а образом - все пространство P„_\(r).
СВОЙСТВА ЯДРА И ОБРАЗА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ
1. Ядро любого линейного отображения -+W является подпро-
странством'. {оу ]< Кег еЛ <V.
В соответствии с определением (см. разд. 8.6.1) требуется доказать, что
множество Кег сА является непустым и замкнутым относительно операций
сложения векторов и умножения вектора на число. В самом деле, из одно-
родности отображения следует, что
<Я(оу) = с/1 (О - v) = 0 • сА(v) = ow,
т.е. нулевой вектор оу отображается в нулевой вектор ow . Следовательно,
ядро любого линейного отображения не является пустым и содержит, по
крайней мере, нулевой элемент: оу е Кег <Я . Покажем, что множество
Кег чА замкнуто по отношению к операциям сложения векторов и умноже-
ния вектора на число. Действительно:
468
v. fzKereA =>of(v. )=ou, 1 , 4 Z x , x
=>
=> v1 + v2 e Ker <A;
v e Ker cA => of(v)= ow => o?(X- v) = Xof(v) = ^-°w = ow => X-v e Ker eA .
Следовательно, множество Ker eA является линейным подпространством
пространства V .
2. Образ любого линейного отображения eA:V —>W является под-
пространством'. Im с4 < W.
В самом деле, докажем, например, замкнутость множества 1т Л по
отношению к операции умножения вектора на число. Если w е 1т сА, то
существует вектор v е V такой, что м> = сА(у). Тогда
сА(X • v) = X • <Л(у) = X н>, т.е. X • w е 1т .
Поскольку ядро и образ линейного отображения являются линейными
подпространствами (свойства 1 и 2), можно говорить об их размерностях.
Дефектом линейного отображения называется размерность его ядра:
d = dim (Ker cd), а рангом линейного отображения - размерность его об-
раза: rg сА = г = dim (im <А).
3. Ранг линейного отображения равен рангу его матрицы (определен-
ной относительно любых базисов).
В самом деле, если е1,...,еп любой базис пространства V, то
Im сА = Ып(аА(е}},...,<Л(еп)). Поэтому максимальное число линейно незави-
симых векторов системы с>>?(е1),...,с^(ея) (ранг системы векторов) равно
максимальному числу линейно независимых столбцов матрицы А отобра-
жения, т.е. рангу матрицы: dim(/m сА) = rg А = rg сА .
4. Линейное отображение A:V-^W инъективно тогда и только то-
гда, когда Кег сА = {ок ], другими словами, когда дефект отображения
равен нулю: d = dim (Кег <А)=0.
Действительно, образом нулевого вектора ov служит нулевой вектор
ow . Поэтому, если отображение инъективно, то ядро содержит только ну-
левой вектор Оу, иначе два разных вектора имели бы один и тот же образ
ow . Обратно, при условии Кег сА = {оу } разные векторы Vj # v2 не могут
иметь одинаковые образы c>>f(v1)= c^(v2), так как в этом случае из равенств
<A(vl)-cA(v2) = cA(vI -у2) = о>у следует, что ненулевой вектор
(vj -v2)eKer сА (приходим к противоречию).
469
5. Линейное отображение cd: V —» W сюръективно тогда и только
тогда, когда Im cd=NV, другими словами, когда ранг отображения равен
размерности пространства образов: г = dim (lm cd) = dim W .
6. Линейное отображение Л: V —э W биективно (значит, обратимо)
тогда и только тогда, когда Кег cd = { ov } и Imcd = W одновременно.
Теорема 9.1 (о размерностях ядра и образа). Сумма размерностей
ядра и образа любого линейного отображения eA:V —> W равна размерно-
сти пространства прообразов:
dim {Ker сА)+ dim (7m сА) = dimV . (9.3)
Действительно, пусть d = dim (Ker cd), dimV = n. Выберем в подпро-
странстве Ker cA <V базис e1,...,ed и дополним его векторами ed+1 ,...,еп
до базиса е1,...,еп всего пространства V. Покажем, что векторы
ctf(ed+1),...,ctf(en) образуют базис подпространства Im cd <W.
Во-первых, Im сА = Lin(cd(ed+l),...,cd(en)), так как образ любого векто-
ра v = +...+vded +vd+1ed+l +... + vne„ линейно выражается через векторы
(Л П ! X d 1 \ П /\" /\
i=l ) 1=1 1=1 '—* ' i=d+l i=d+l
°w
Во-вторых, образующие c#(erf+1 ),..., cd (e„) линейно независимы. Если
п
их линейная комбинация равна нулевому вектору: ow =
i=d+l
(п А п
У'К, е. , то вектор принадлежит ядру (его образ - нулевой
i=d+l J i=d+l
вектор). Однако, по построению этот вектор принадлежит алгебраическому
дополнению (Ker cd)+ . Учитывая, что Ker cd П {Ker cd)+ = { о? }, заклю-
п
чаем: е. =оу . Получили разложение нулевого вектора по линейно не-
i-d+{
зависимой системе ed+1,...,en векторов, значит, все коэффициенты 1, =0.
Поэтому равенство = ow справедливо только для тривиальной
i=d+l
линейной комбинации, т.е. система векторов cd(ed+l),...,cd(en') линейно не-
зависимая.
470
Таким образом, векторы <A(ed+1)...cf(e„) образуют базис подпро-
странства Im <А = Lin(erf(ed+1),..., cf(en)), а его размерность определяется ко-
личеством базисных векторов, т.е. dim(/m cf) = и -d , что равносильно (9.3).
Следствие. Линейное отображение cA:V —>W биективно (значит,
обратимо) тогда и только тогда, когда обратима его матрица {опреде-
ленная относительно любых базисов).
Действительно, для обратимости преобразования сА: V —> W (см.
свойство 6) его матрица А (размеров тХп) должна удовлетворять услови-
ям (см. свойства 3,4,5):
rg А = rg cf = dim(/m о?) = dimW - т, d = dim(Xer <А) = 0.
Тогда по теореме 9.1 заключаем, что т - n-d - п, т.е. матрица А - квад-
ратная и -го порядка и невырожденная (rg А = п ), что и требовалось дока-
зать.
Обратимые линейные отображения называются также невырожден-
ными (имея в виду невырожденность их матрицы).
9.2. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ (ОПЕРАТОРЫ)
9.2.1. Определение и примеры линейных преобразований
Линейным преобразованием {линейным оператором) линейного про-
странства V называется линейное отображение cA:V —>V пространства V
в себя.
Поскольку линейное преобразование является частным случаем ли-
нейного отображения, к нему применимы все понятия и свойства, рассмот-
ренные для отображений: инъективность, сюръективность, биективность,
обратимость, ядро, образ, дефект, ранг и т.д.
Матрицей линейного преобразования cA.V —^V в базисе ei,...,en
пространства V называется квадратная матрица А , составленная из ко-
ординатных столбцов образов базисных векторов <Л(е1),...,<А(еП), найден-
ных относительно базиса ег,..., еп.
Матрица биективного линейного преобразования обратима, т.е. невы-
рождена. Поэтому биективное (обратимое) преобразование называют также
невырожденным.
ПРИМЕРЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ
1. Обозначим O:V-^V - нулевое преобразование «-мерного про-
странства V , которое ставит в соответствие любому вектору v е V нулевой
элемент о пространства V . Это преобразование не является инъективным,
сюръективным, биективным, обратимым. Матрица нулевого преобразования
471
(в любом базисе) нулевая, ядро преобразования Кег О = V , образ преобра-
зования 1т О = {о }, дефект d =п, ранг г = 0.
2. Обозначим £: V —> V - тождественное преобразование и -мерного
пространства V , которое ставит в соответствие каждому вектору v е V этот
же вектор &(у) = v . Это преобразование является инъективным, сюръектив-
ным, биективным, обратимым. Матрица тождественного преобразования (в
любом базисе) единичная л-го порядка, ядро преобразования Кег@ = {о },
образ преобразования Im $ = V , дефект d = 0, ранг г = п .
3. Обозначим Zo : V -> V - центральную симметрию п -мерного
пространства V (относительно нулевого вектора о), т.е. преобразование,
которое каждому вектору ставит в соответствие противоположный ему век-
тор: Z0(y) = -v . Это преобразование линейное, инъективное, сюръективное,
биективное, обратимое. Матрица преобразования противоположна единич-
ной (в любом базисе): Zo =-Е ; ядро преобразования KerZg = {о }, образ
преобразования Im Zg = V , дефект d -0, ранг г = п.
4. Обозначим : V V - гомотетию п -мерного пространства V
(с коэффициентом Л), т.е. преобразование, которое каждому вектору ставит
в соответствие коллинеарный ему вектор: 9f^(y)=k-v. Это преобразование
линейное. При А. Ф 0 оно инъективное, сюръективное, биективное, обрати-
мое. Матрица преобразования пропорциональна единичной (в любом бази-
се): 7/^ =Х Е, ядро преобразования KertH^ ={<'}, образ преобразования
Im = V , дефект d =0, ранг г = п. При А = 0: Wo =0 (см. п.1); при
А = 1: Wj = £ (см. п.2); при А = -1: Wj.j) -- Zo (см. п.З).
5. Рассмотрим линейное пространство
j V2 радиус-векторов (с общим началом в точке
J v м о), принадлежащих одной плоскости (рис.
уьг— р 9.1). Обозначим Jllf:V2—^V2 - поворот во-
\ круг точки О (на угол ф в положительном
\ Ф
I > Г направлении (против часовой стрелки)). Это
преобразование линейное, инъективное,
Рис 9 1 сюръективное, биективное, обратимое. Най-
дем матрицу поворота в стандартном орто-
нормированием базисе /, j. Раскладывая образы = / = Л (j) ба-
зисных векторов по базису, получаем
|' = СО5ф1 +5тф-у ,
/ = -81Пф-« +СО5ф- j .
472
Составляем матрицу (9.1) преобразования, записывая найденные координа-
ты образов по столбцам:
coscp - sin <р
sincp coscp
Ядро преобразования Кег Я - { о }, образ преобразования 1т = V2 , де-
фект d=0, ранг г = 2. При <р = 2л£, keZ: ^?2jbt =£ (см- п-2)1 ПРИ
<р = л+2пк, ке Z: ЯП+2П1Ь = 20 (см. п.З).
6. Обозначим ©: Рл(я)—» Рп(я) - оператор дифференцирования, кото-
рый каждому многочлену степени не выше п ставит в соответствие его
производную, рассматриваемую как многочлен степени не выше п:
©Ш) = р'(х). Это преобразование линейное, неинъективное, несюръек-
тивное, небиективное, необратимое. Квадратная матрица ((и +1) -го порядка)
преобразования в стандартном базисе имеет вид
(О 1 0 О'
О 0 2 ••• О
©= : : :
О 0 0 п
J) О О О,
Ядро преобразования Кег © = Р0(я) - пространство многочленов нулевой
степени, образ Im ^) = РпХ{р] - пространство многочленов степени не вы-
ше (и -1), дефект d = 1, ранг г = п, dim Рп (я) = n +1.
Рассмотрим преобразование © :Тш(я)—>Тш(я) линейного пространст-
ва тригонометрических многочленов (частоты (0*0) с действительными
коэффициентами: Тш(р)= Lin(sma>t, cos(Of), т.е. Тш(я) - множество функ-
ций вида f(t)=asinojf + tcosojf, где аеЯ, be Я (см. п.7 в разд.8.1.3). За-
метим, что это множество является двумерным вещественным линейным
пространством (см. п.7 в разд.8.3.2). Стандартный базис пространства Ta(R)
образуют функции е{ (г) = sin (Of, е2 (t)- cos (Of, поскольку они линейно неза-
висимы (тождественное равенство нулю a sin (Of + Z>cos(Of = 0 возможно
только в тривиальном случае a=b = Q). При дифференцировании функции
/(f) получаем функцию /'(()=-£? (О sin (Of-I-а (0 cos (Of того же вида. Следо-
вательно, преобразование ©:Гш(я)—>Гш(я) определено. Это преобразова-
ние линейное, инъективное, сюръективное, биективное, обратимое. Найдем
матрицу преобразования в стандартном базисе ej(f) = sin(Of, e2(f) = cos(Of.
Раскладывая образы базисных векторов, получаем
473
©(e,) = cocos<oz = Osincor + cocoscoz‘,
©(e2) = -co • sin at = - co sin at + 0 cos co?.
Составляем матрицу (9.1) преобразования, записывая найденные координа-
ГО -со4)
ты образов по столбцам: D = . Ядро преобразования
° J
Кег © = { о(с)} - нулевое подпространство, образ /да © = 7^(7?), дефект
d = 0 , ранг г - 2, o(t) = 0 sin at + 0 • cos at.
Аналогичными свойствами обладает преобразование
©: Та(с)-+ ТО(С), где Тш(с) = Lin(sin at, cosat) - множество функций вида
asincoz + fecoscor с комплексными коэффициентами аеС и fee С. Множе-
ство Тш(с) является двумерным комплексным линейным пространством.
7. Пусть линейное пространство разлагается в прямую сумму подпро-
странств V = Ll®L2. Обозначим : V —> V - оператор проектирова-
ния на подпространство Ц параллельно подпространству Ь2, который
каждому вектору v -vI +v2, где Vj е Z,, v2 e L2, ставит в соответствие его
составляющую (проекцию) V] е Z,, т.е. n£i(vt + v2)= vi (рис.9.2). Это пре-
образование линейное. При L^V оно неинъективное, несюръективное,
небиективное, необратимое. Ядро преобразования Кег П£ = L2, образ пре-
образования 1т П£ = Zj, дефект d = dimZ2, ранг г = dim 7^. При Z] = V :
Пи = £; при Z2 = V : П(в} = О.
Рис. 9.2 Рис. 9.3
8. Пусть линейное пространство разлагается в прямую сумму подпро-
странств V = Lj®L2. Обозначим ZLi : V —> V - оператор отражения в
подпространстве Z] параллельно подпространству L2 (или преобразо-
вание симметрии относительно подпространства Z] параллельно под-
474
пространству L2), который каждому вектору v = v, + v2, где v, е Z,,
v2e£2, ставит в соответствие вектор (vj-v2), т.е. ZL (v, + v2) = v,-v2
(рис. 9.3). Это преобразование линейное, инъективное, сюръективное, биек-
тивное, обратимое. Ядро преобразования KerZL = {о), образ преобразо-
вания Im ZL = V , дефект d = 0, ранг г = dim V . При L{ = V : Zv = Е .
9.2.2. Матрицы линейного преобразования в разных базисах
Найдем связь матриц одного и того же линейного преобразования в
разных базисах.
Пусть в базисе (е)= (ej,...,en) преобразование cA:V -+V имеет мат-
рицу А, а в базисе (/)= (/j - матрицу А . Если S - матрица пере-
хода от базиса (е) к базису (/), то
A=S~lAS. (9.4)
(/) (е)
Докажем формулу (9.4). Пусть векторы v и w в базисах (е) и (/)
имеют координатные столбцы v , v и w, w соответственно. Если
М (/) (<)’(/)
w = то по формуле (9.2) имеем
w = A- v , w = А v .
W WW (/) (/)(/)
Подставляя в первое равенство связи координат векторов в разных базисах
(см. разд. 8.4.3) v = S • v , w = S• w , получаем S w = A-S- v или, учи-
P (e) (/) (e) (/)’ (/) Й (/)
тывая обратимость матрицы S : w = S-1 -А-S- v . Сравнивая последнее pa-
(/) (e) (/)
венство c w = A • v , убеждаемся в справедливости (9.4).
(/) (/)(/)
Замечания 9.2.
1. Матрицы линейного преобразования в разных базисах оказываются
подобными (см. разд. 7.2.2). И наоборот, любые две подобные матрицы яв-
ляются матрицами некоторого линейного преобразования, найденными от-
носительно разных базисов.
2. Для матриц преобразований справедливы свойства, рассмотренные в
разд. 9.1.4. В частности, при фиксированном базисе матрица суммы преоб-
разований равна сумме их матриц, матрица произведения преобразования на
число равна произведению матрицы преобразования на это же число, мат-
рица композиции преобразований равна произведению матриц преобразова-
ний, матрица обратного преобразования является обратной для матрицы об-
ратимого преобразования.
475
9.2.3. Алгебра линейных операторов
Рассмотрим множество £?(v) - линейных преобразований (операто-
ров) и -мерного линейного пространства V . Напомним, что два преобразо-
вания A :V —>У и j6:V—>У называются равными, если ef(v)=J8(v)
VpgV .
На множестве £(v) определены две линейные операции: сложение
еобразований и умножение преобразования на число, поскольку в резуль-
тате этих операций получается линейное преобразование (см. разд. 9.1.3).
Нетрудно показать, что эти операции удовлетворяют условиям:
1. А+£=£+А
2. of+ (Я + С) = (с^ + «)+С Vof,J6,Ce£(v);
3. существует нулевое преобразование Ое £(у) такое, что А+ 0 = А
\fAe £(v);
4. для каждого преобразования of существует противоположное
преобразование (- of) = (-1) • А такое, что of + (- А) - О ;
5. X-(of + ЗВ)-ХА+A-J8 Vof, £?(у) и любого числа Л;
6. (A+g)of=A-of+р-А VAg£(v) и любых чисел Л, ц;
7. X(p. of)=(X|x) of Vofe£(v) и любых чисел Л, р ;
8. l of = of Vofe£(v).
В условиях 5-7 говорится о числах из того же числового поля, над которым
определено линейное пространство V .
Условия 1-8 повторяют аксиомы линейного пространства (см. разд.
8.1.1). Поэтому множество £(v) с линейными операциями является линей-
ным пространством. Если пространство V вещественное (комплексное), то
и пространство й(У) вещественное (комплексное).
Найдем размерность пространства £(У). При фиксированном базисе
имеется взаимно однозначное соответствие между линейными преобразова-
ниями и их матрицами, причем это соответствие сохраняет линейные опера-
ции (см. п.2 замечаний 9.2). Следовательно, пространство £(У) изоморфно
пространству М- квадратных матриц и -го порядка (см. п.5 в разд.8.3.2).
Размерность пространства равна л2. По теореме 8.3 (см. разд.8.5):
dim £(у)=dim Мпкп =п2, т.е. dim £(v)=(dimVJ2 -
Кроме линейных операций в множестве £(у) определена операция
умножения элементов. Произведением преобразований А и 38 назовем их
композицию, т.е. А 38 = А ° 38 - В результате композиции линейных преоб-
476
разований получается линейное преобразование. Операция умножения
удовлетворяет следующим условиям:
1. df(£C)=&£)С
2. с^(^ + с)=^В + с^С Ve#,$,Cc£(v);
3. (^ + ^В)С = ^С + £С V<^,jB,Ce£(y);
4. существует тождественное преобразование £ такое, что
= <Л Шс£(у).
Первое условие выражает ассоциативность операции умножения, ус-
ловия 2 и 3 - законы дистрибутивности, условие 4 - существование ней-
трального элемента (см. разд. В.2.2, В.2.3). Множество £?(v) с операциями
сложения и умножения элементов является кольцом с единицей (вообще го-
воря, некоммутативное, так как в общем случае еЛ £ * Я <Л).
Операции умножения преобразований и произведения преобразования
на число (из заданного числового поля) удовлетворяют условию:
5. (X-rf)j8 = ef(A-J8)=A-(rf Я).
Линейное пространство, которое является кольцом, удовлетворяющим
условию 5, называется алгеброй. Поэтому множество £(v) называют
алгеброй линейных операторов (преобразований).
МНОГОЧЛЕНЫ ОТ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
В алгебре £(v) можно определить целую неотрицательную степень
оператора of: V —> V , полагая по определению
<d°=£, еЛг=<Я = of"-Iof.
Пусть р(к) = атХп + ... + ajX + a0 - многочлен переменной X. Много-
членом р(^1) от линейного преобразования of называется преобразова-
ние р{с4} = атеЛт+... + а^+О(^.
Многочлен />(Х) = атХт+... + а]Х + а0 называется аннулирующим для
линейного преобразования , если р(<#)=0 - нулевое преобразование.
Заметим, что у каждого линейного преобразования :V —>V и-мерного
линейного пространства V существует аннулирующий многочлен степени
не выше и2. Действительно, система из (п2+1) элементов £,е£ ,...,е£"
линейного пространства £(v) линейно зависима (так как dim £(v) = л2).
Поэтому существуют такие числа a0,aj,...,a г, не все равные нулю одно-
временно, что апг<£п +. . + «1^ + а0& = О.
477
Следовательно, многочлен р(А.) = ал1Л" +...+а1Л + а0 - аннулирующий для
преобразования сЯ.
Замечания 9.3.
1. При фиксированном базисе каждому преобразованию (оператору)
можно сопоставить его матрицу. Свойства линейных операций 1-8, запи-
санные для матриц преобразований, повторяют свойства линейных опера-
ций с матрицами (см. разд. 1.2.2), а свойствам 1-5 произведения операторов
отвечают свойства операции умножения матриц (см. разд. 1.3.2).
2, При фиксированном базисе многочлен р(е£) от линейного преобра-
зования <Я имеет матрицу р(А) = атАт +... + а1А + а0Е, где А - матрица
преобразования еЯ в том же базисе. Поэтому свойства многочленов от мат-
риц (разд. 7.3.4) переносятся на многочлены от линейного преобразования.
В частности, многочлены от одного преобразования перестановочны (см.
разд. 1.3.2):
3. Функции от матриц (см. разд. 7.4) определяются при помощи много-
членов от матриц. Поэтому можно определить функции от линейных преоб-
разований.
9.3. ИНВАРИАНТНЫЕ ПОДПРОСТРАНСТВА
9.3.1. Определение и примеры инвариантных подпространств
Пусть еЯ: V —> V - линейное преобразование линейного пространства
V . Линейное подпространство L < V называется инвариантным относи-
тельно преобразования еЯ, если образ любого вектора из L принадлежит
подпространству L, т.е. c4(v)e L V ve L. Другими словами, инвариант-
ное подпространство L включает свой образ сЯ(ь): c4(l)cL. Нулевое
подпространство { о } и все пространство V являются инвариантными под-
пространствами для любого линейного преобразования cf: V —> V .
Пусть L - инвариантное подпространство относительно преобразова-
ния еЯ: V V . Линейный оператор еЯ: L —> L, рассматриваемый как ли-
нейное преобразование пространства L в себя, называется сужением (ог-
раничением) линейного преобразования еЯ: V —> V на инвариантное
подпространство L<V и обозначается <ЯL :L—>L, или еЯ|£ :L —> L.
478
Для всех векторов ve L выполняется равенство £(v) = cf(v), т.е. V ve L
образы, порождаемые оператором и его сужением сА L, совпадают.
ПРИМЕРЫ ИНВАРИАНТНЫХ ПОДПРОСТРАНСТВ
Рассмотрим инвариантные подпространства линейных преобразова-
ний, определенных в разд. 9.2.1.
1. Для нулевого преобразования 0:V—>V любое подпространство
L<V является инвариантным, так как 0(l) = {o }с£. Сужение нулевого
преобразования 0L : L —> L является нулевым преобразованием.
2. Для тождественного преобразования £: V —> V любое подпростран-
ство L<V является инвариантным, так как £(b)=L. Сужение тождест-
венного преобразования ££ : L —> L является тождественным преобразова-
нием.
3. Для центральной симметрии Z„ : V —> V любое подпространство
L<iV является инвариантным, так как Z0(l)=L. Сужение центральной
симметрии Z0\l :L—> L является центральной симметрией.
4. Для гомотетии любое подпространство L<V является
инвариантным, так как flx(L)=L (при Л*0). Сужение гомотетии
J/x|£ : L—> L является гомотетией.
5. Для поворота : V2 —> V2 плоскости (при ср * -лк, к е Z ) имеются
два инвариантных подпространства: нулевое { о } и вся плоскость V2. Дру-
гих инвариантных подпространств нет.
6. Для оператора дифференцирования ©: Рл(л)—» Рл(л) каждое из
подпространств {о(х) }< Р0(я)< ... < Рл(я) является инвариантным,
так как при дифференцировании степень многочлена уменьшается.
7. Рассмотрим оператор Пд : V —> V проектирования на подпростран-
ство Д параллельно подпространству . Здесь V - Ц® 1^,
(v] + v2 )= для v = Vj + v2, V] е L], v2 е 1^. Для этого оператора под-
пространства Д и L, инвариантные, так как П£| (£,)=£] и
С Lj. Сужение оператора проектирования на подпространст-
во Lj является тождественным
преобразованием П£|
= £, а сужение на
подпространство 1^ - нулевым
1^=0.
479
8. Рассмотрим оператор Z£| : V —> V отражения в подпространстве Z,
параллельно подпространству L2. Здесь К = ® £2, 2£| (v] + v2) = Vj - v2
для v = v, + v2, V] e , v2 e L2. Для этого оператора подпространства £, и
L2 инвариантные, так как Z£[ (£])=£] и 2£(£2)=£2. Сужение оператора
отражения на подпространство Z] является тождественным преобразовани-
ем Z£| j = £, а сужение на подпространство Ь2 - центральной симметрией
|£j = Zo, так как И£_ (v2 )= - v2.
9. В пространстве У2 радиус-векторов пространства, отложенных от
фиксированной точки О, рассмотрим поворот на угол <р * пк , к е Z , вокруг
оси I, заданной радиус-вектором I . Подпространство L-Lin^ инвари-
антно относительно этого преобразования, так как любой вектор, принадле-
жащий L, не изменяется в результате поворота, т.е. отображается в себя.
Подпространство П = Z,1 - радиус-векторов, принадлежащих плоскости,
перпендикулярной оси вращения, также инвариантное, так как в результате
поворота все эти радиус-векторы остаются в той же плоскости.
9.3.2. Свойства инвариантных подпространств
1. Если L — инвариантное подпространство относительно обрати-
мого линейного преобразования <А .V —> С, то его сужение еЛL :L-t L
также обратимое линейное преобразование.
2. Для любого линейного преобразования :V —>V ядро Кег сА и об-
раз 1т о? являются инвариантными подпространствами, так как
<A(Ker crf)= {о }< Кег Д и ed(lm ctf)< 1т сА .
3. Если L — инвариантное подпространство относительно линейного
преобразования еА :V —> К, то L - инвариантно относительно любой на-
туральной степени этого преобразования, причем
cZT(z)<... W(z)<£(l) = L.
В самом деле, каждое из указанных множеств является линейным под-
пространством, так как это образы сужений линейных операторов, напри-
мер, c^'”(z)= Ли (<з?£)т . Докажем, например, включение e^2(z)< o?(z).
Для любого wec^2(l) существует вектор veo?(/,)<iZ, что и> = сг?(р).
Следовательно, и» е e?(z).
480
4. Если L - инвариантное подпространство относительно линейного
преобразования :У —> И, то L - инвариантно относительно любого
многочлена от этого преобразования.
Теорема 9.2 (о матрицах оператора и его сужения на инвариантное
подпространство). Пусть :У -*У - линейное преобразование
п -мерного пространства V, a L — подпространство, инвариантное от-
носительно преобразования . Тогда существует базис (<?) = (е},...,еп)
пространства V, в котором матрица А преобразования Л имеет нуле-
вой угол:
(В
Л=-------,
1^0 D)
где В - матрица сужения £ преобразования <А на подпространство L,
О - нулевая матрица размеров (л ~/)х/, I = dim£. И наоборот, если в не-
котором базисе (е) матрица А преобразования сА имеет нулевой угол
(нулевую матрицу О размеров {п-1)к1), то преобразование имеет
I -мерное инвариантное подпространство.
В самом деле, возьмем базис е} подпространства L и дополним
его векторами е[+{ ,...,еп до базиса ,...,еп всего пространства У . Раскла-
дывая образы первых / базисных векторов по этому базису, получаем
<^к)=а1Л +• + anei +Оем +- + О еп ’
так как с/(е,)е£, z = l,...,/. Следовательно, последние («-/) элементов
первых I столбцов матрицы А преобразования равны нулю. Обратное
утверждение доказывается, проводя аналогичные рассуждения в обратном
порядке.
Следствие. Если п -мерное пространство V представлено в виде пря-
мой суммы ненулевых инвариантных относительно преобразования сА
подпространств
V = 1^ ®...®Li,
то существует базис, в котором матрица преобразования имеет блочно-
диагональный вид
где At - матрица сужения сА L преобразования на подпространство
1 = 1,...,*.
31 -4549
481
Например, рассмотрим операторы проектирования :V —и от-
ражения 2^ :V -+V (см. п.7, 8 в разд. 9.3.1). Объединяя базисы подпро-
странств Lj и Lz, получаем базис пространства V = ® L,, в котором
матрицы преобразований имеют блочно-диагональный вид
„ (Е О'] (Е О']
[О О) (О -EJ
9.4. СОБСТВЕННЫЕ ВЕКТОРЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
9.4.1. Собственные векторы и собственные значения
Пусть of : V —э V - линейное преобразование и -мерного линейного
пространства V. Ненулевой вектор s линейного пространства V,
удовлетворяющий условию
«f(s)=As, (9.5)
называется собственным вектором линейного преобразования еА . Число
А в равенстве (9.5) называется собственным значением преобразования
<А. Говорят, что собственный вектор соответствует (принадлежит)
собственному значению А. Если пространство V вещественное (ком-
плексное), то собственное значение А - действительное (комплексное) чис-
ло.
Множество всех собственных значений линейного преобразования на-
зывается его спектром.
Поясним геометрический смысл собственных векторов. Ненулевой
вектор s является собственным для преобразования еА, если его образ
ef(s) коллинеарен прообразу s. Другими словами, если s - собственный
вектор, то преобразование сА имеет одномерное инвариантное подпро-
странство Lin(s). Справедливо и обратное утверждение.
В самом деле, пусть собственный вектор s соответствует некоторому
собственному значению А. Любой вектор v из Lin(s) имеет вид v = as, где
a - любое число из заданного поля. Найдем образ этого вектора
<А(у) = <?f(as) = acsf(s)= aXsе Lin(s).
Следовательно, о?(у)е Lin(s) для любого вектора veLin(s), т.е. подпро-
странство Lines') инвариантно относительно преобразования <А. Размер-
ность подпространства Lin{s) равна единице, так как s*o по определению.
Обратное утверждение доказывается, проводя рассуждения в обратном
порядке.
482
СВЯЗЬ СОБСТВЕННЫХ ВЕКТОРОВ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ И
СОБСТВЕННЫХ ВЕКТОРОВ ЕГО МАТРИЦЫ
В разд. 7.2.1 рассматривались собственные векторы и собственные
значения матрицы. Напомним, что собственным вектором квадратной мат-
рицы А п-го порядка называется ненулевой числовой столбец
j = (з1 • • sn )г, удовлетворяющий условию (7.13):
Aj = Ал . (9.6)
Число А в (9.6) называется собственным значением матрицы А . При этом
считалось, что собственное значение А и числа / = 1,...,п, принадлежат
полю комплексных чисел.
Эти понятия связаны с собственными векторами и собственными зна-
чениями линейного преобразования.
Теорема 9.3 (о собственных векторах линейного преобразования н
его матрицы). Пусть еА: V —э V - линейное преобразование п -мерного ли-
нейного пространства V с базисом е1,...,еп. Тогда собственное значение
А и координатный столбец s собственного вектора s преобразования <А
являются собственным значением и собственным вектором матрицы А
(см. разд. 7.2.1) этого преобразования, определенной относительно базиса
т.е.
<sf(s) = As => Aj = A-j,
где s = slel+...+snen, J = (j[ ••• sn)Т . Обратное утверждение справедли-
во при дополнительных условиях: если столбец s - (sl sn)T и число А
являются собственным вектором и собственным значением матрицы А,
причем числа sl,..., $п,А принадлежат тому же числовому полю, над ко-
торым определено линейное пространство V, то вектор s = + ... + snen
и число А являются собственным вектором и собственным значением ли-
нейного преобразования сА: V —с матрицей А в базисе е1,...,еп.
В самом деле, условие (9.5) в координатной форме имеет вид (9.6), что
совпадает с определением (7.13) собственного вектора матрицы. Наоборот,
из равенства (9.6) следует равенство (9.5) при условии, что векторы
s = jjtfj +... + inen и A s определены, т.е. числа j,,...,^, А принадлежат
тому же числовому полю, над которым определено линейное пространство.
Напомним, что нахождение собственных значений матрицы сводится
к решению ее характеристического уравнения Дд(А) = 0, где
Ax(A) = det(A-Af) - характеристический многочлен матрицы А . Для ли-
нейного преобразования введем аналогичные понятия.
Характеристическим многочленом линейного преобразования
cA:V —>V п -мерного линейного пространства называется характеристиче-
31»
483
ский многочлен Дс4(х)= det(/l - А.Е) матрицы А этого преобразования,
найденной относительно любого базиса пространства V .
Уравнение Ды?(к)=0 называется характеристическим уравнением
линейного преобразования.
Преобразование - ХЕ называется характеристическим для линей-
ного преобразования с4: И —> И .
Замечания 9.4.
1. Характеристический многочлен линейного преобразования не зави-
сит от базиса, в котором найдена матрица преобразования.
В самом деле, матрицы А и А линейного преобразования в бази-
(е) (/)
сах (£) = (₽!,...,£„) и (/) = (/[,...,/„) являются, согласно (9.4), подобными:
A = S~X AS , где S - матрица перехода от базиса (е) к базису (/). Как по-
(/) (е)
казано в разд. 7.2.3, характеристические многочлены подобных матриц сов-
падают (см. свойство 3). Поэтому для характеристического многочлена пре-
образования сА[ можно использовать обозначение Д^(^), не указывая мат-
рицу этого преобразования.
2. Из теоремы 9.3 следует, что любой комплексный (действительный,
рациональный) корень характеристического уравнения является собствен-
ным значением линейного преобразования : V -> V линейного простран-
ства V, определенного над полем комплексных (действительных, рацио-
нальных) чисел.
3. Из теоремы 9.3 следует, что любое линейное преобразование ком-
плексного линейного пространства имеет одномерное инвариантное под-
пространство, так как это преобразование имеет собственное значение
(см. п.2), а следовательно, и собственные векторы. Таким подпространством
является, например, линейная оболочка любого собственного вектора.
У преобразования вещественного линейного пространства одномерных ин-
вариантных подпространств может и не быть, если все корни характеристи-
ческого уравнения комплексные (но не действительные).
Теорема 9.4 (об инвариантных подпространствах линейного пре-
образования вещественного пространства). У всякого линейного преобра-
зования вещественного линейного пространства существует одномерное
или двумерное инвариантное подпространство.
Действительно, составим матрицу А линейного преобразования
с4: V V п -мерного вещественного линейного пространства V в произ-
вольном базисе е,,..., еп . Элементы этой матрицы - действительные числа.
Следовательно, характеристический многочлен Acrf(x)=det(^-XE) - это
многочлен степени п с действительными коэффициентами. Согласно след-
ствиям 3, 4 основной теоремы алгебры (см. разд. В.4), такой многочлен мо-
484
жет иметь действительные корни и пары комплексных сопряженных корней.
Если jX = X - действительный корень характеристического уравнения,
то и соответствующий собственный вектор 5 = ^ ••• зпУ матрицы А
также действительный. Поэтому он определяет собственный вектор
s = $1«1 + ... + з„е„ линейного преобразования (см. теорему 9.3). В этом слу-
чае существует одномерное инвариантное относительно подпространст-
во Lin(s) (см. геометрический смысл собственных векторов).
Если Х = а±0г - пара комплексных сопряженных корней (Р^О), то
собственный вектор s о матрицы А также с комплексными элементами:
5 = (x1+y1i ••• хп+уя/)г. Его можно представить в виде s = x + yi, где
х, у - действительные столбцы. Равенство (9.6) при этом будет иметь вид
А • (х+yi) - (а + pi)- (х + yi).
Выделяя действительную и мнимую части, получаем систему
Лх = ах-ру, (97)
Ау = Рх + ау.
Покажем, что столбцы х и у линейно независимы. Рассмотрим два случая.
Если х = о, то из первого уравнения (9.7) следует, что у = о, так как р 0.
Тогда 5 = о, что противоречит условию 5 * о. Предположим, что х ф о и
столбцы х и у пропорциональны, т.е. существует такое действительное
число у , что у = ух . Тогда из системы (9.7) получаем
Лх = (а-ру)х,
уЛх = (р + ау)х.
Прибавляя ко второму уравнению первое, умноженное на (-у), приходим к
равенству [(р + ау)-у(а-0у)]х = о. Так как хфо, то выражение в квад-
ратных скобках равно нулю, т.е. (р + ау)-у(а-Ру) = р(1 + у2]=0. Поскольку
Р 0, то у2 = -1. Этого не может быть, так как у - действительное число.
Получили противоречие. Таким образом, столбцы х и у линейно незави-
симы.
Рассмотрим подпространство Ып(х, у), где х = х]^] +... + хпеп,
у = у1е1+... + упеп. Это подпространство двумерное, так как векторы х,у
линейно независимы (как показано выше, их координатные столбцы х, у
линейно независимы). Из (9.7) следует, что
c4(x) = ax-0j,
c^(y)=Px + aj,
485
т.е. образ любого вектора, принадлежащего Lin(x, у), также принадлежит
Lin(x, у). Следовательно, Lin(x, у) - двумерное подпространство, инвари-
антное относительно преобразования of , что и требовалось доказать.
НАХОЖДЕНИЕ СОБСТВЕННЫХ ВЕКТОРОВ И СОБСТВЕННЫХ ЗНАЧЕНИЙ
ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
Для нахождения собственных векторов и собственных значений ли-
нейного преобразования сА: V —» V вещественного линейного пространства
V следует выполнить следующие действия.
1. Выбрать произвольный базис е1,...,е„ линейного пространства V и
найти в этом базисе матрицу А преобразования еА .
2. Составить характеристический многочлен преобразования еА :
Дс4(А) = det(A-АЕ).
3. Найти все различные действительные корни А],...,А4 характери-
стического уравнения Д^(А) = 0. Комплексные (но не действительные) кор-
ни характеристического уравнения следует отбросить (см. п.2, замечаний
9.4).
4. Для корня А = А] найти фундаментальную систему ф, ,ф2 ,...,фп_г
решений однородной системы уравнений
(a-AjE)x = o ,
где г = rg (А - А,Е). Для этого можно использовать либо алгоритм решения
однородной системы (см. разд. 5.5), либо один из способов нахождения
фундаментальной матрицы (см. п.З замечаний 5.3, п.1 замечаний 5.5).
5. Записать линейно независимые собственные векторы преобразова-
ния of , отвечающие собственному значению :
51=фне1+... + фл1еп,
«2=Ф12е,+...+Фл2ея,
sn-r =<Pi„-r ei+- + (Pnn-ren-
Для нахождения совокупности всех собственных векторов, отвечаю-
щих собственному значению А,, образовать ненулевые линейные комбина-
ции
s = C]S| + C2s2 +... + Cn_rsn_r,
где CjCn_r - произвольные постоянные, не равные нулю одновременно.
Повторить п.4, 5 для остальных собственных значений А2,..., At.
Для нахождения собственных векторов линейного преобразования
комплексного линейного пространства нужно в п.З определить все корни
486
характеристического уравнения и, не отбрасывая комплексные корни, вы-
полнить для них п.4,5.
9.4.2. Примеры собственных векторов
1. Для нулевого преобразования О: V —э V любой ненулевой вектор
SGV является собственным, соответствующим нулевому собственному
значению А. = 0, так как 0(s)=0-s VsgV.
2. Для тождественного преобразования £: V —эV любой ненулевой
вектор s G V является собственным, соответствующим единичному собст-
венному значению Л = 1, так как £(s) = 1 • s Vs G V .
3. Для центральной симметрии ZO.V —любой ненулевой вектор
s 6 V является собственным, соответствующим собственному значению
Х = -1,таккак 2e(s)=(-l)-s VsgV.
4. Для гомотетии : V —э V любой ненулевой вектор s G V является
собственным, соответствующим собственному значению А. (коэффициенту
гомотетии), так как (s) = Л s Vs G V .
5. Для поворота : V2 —» V2 плоскости (при ф * тск, к G Z) собствен-
ных векторов нет, так как при повороте на угол, не кратный тг, образ каждо-
го ненулевого вектора неколлинеарен прообразу. Здесь рассматривается по-
ворот вещественной плоскости, т.е. двумерного векторного пространства
над полем действительных чисел.
6. Для оператора дифференцирования £>: Д, (/?)-» Рп(я) любой нену-
левой многочлен нулевой степени (не равный тождественно нулю) является
собственным вектором, соответствующим нулевому собственному значе-
нию А. - 0, так как £>($(*))=0- s(x) V s(x)=const. Любой многочлен нену-
левой степени не является собственным вектором, так как многочлен не
пропорционален своей производной: £>(s(x))=s'(x)* A.s(x), поскольку они
имеют разные степени.
7. Рассмотрим оператор :V —» V проектирования на подпростран-
ство £, параллельно подпространству L2 . Здесь V = Ц ® L2,
(v, + v2)=fi для f = f! + f 2, Fi G Л > v26^2 - Для этого оператора любой
ненулевой вектор vj G является собственным, соответствующим собст-
венному значению А. = 1, так как (v1) = l v1, а любой ненулевой вектор
v2 G L2 является собственным, соответствующим собственному значению
А. = 0, так как П^(р2) = 0-р2- Другие векторы не являются собственными,
487
так как равенство (v, + v2) — vi = ^•(*’1 + ) возможно либо при Vj =о,
либо при v2 ~ ° •
8. Рассмотрим оператор Z^ :V —>V отражения в подпространстве
параллельно подпространству Ь2. Здесь V = L] ФL,, ZLi(vl+v2)=vi-v2
для v = V] + v2, Vj G L], v2 G Lj. Для этого оператора любой ненулевой век-
тор Vj G является собственным, соответствующим собственному значе-
нию А. = 1, так как Z^ (v1) = 1 - , а любой ненулевой вектор v2 G L2 являет-
ся собственным, соответствующим собственному значению А. = -1, так как
2^(v2)=(-l)-v2. Другие векторы не являются собственными, так как ра-
венство Zti(vI +v2)=Vi -v2 = A.(v] + v2) возможно либо при 1^=0, либо
при v2 = о.
9. В пространстве V3 радиус-векторов пространства, отложенных от
фиксированной точки О, рассмотрим поворот на угол ф Ф пк , к G Z , вокруг
оси I, заданной радиус-вектором I . Любой ненулевой вектор, коллинеар-
ный вектору I, является собственным, отвечающим собственному значению
А. = 1. Других собственных векторов у этого преобразования нет.
Пример 9.1. Найти собственные значения и собственные векторы опе-
ратора дифференцирования ©:?] —>7] (см. п.6 в разд. 9.2.1), преобразую-
щего пространство тригонометрических многочленов (частоты (0 = 1):
а) с действительными коэффициентами Tt = 7](7?) = Linfsint, cost);
б) с комплексными коэффициентами 7] =Т,(с)= Lin(sint, cost).
□ 1. Выберем стандартный базис q(t)=sinz, <?2(z) = cosz и составим в
этом базисе матрицу D оператора ©:
fO -Й
D =
V 0)
2. Составим характеристический многочлен преобразования ©
-А. -1
1 -А.
= А.2
3. Характеристическое уравнение А.2+1 = 0 имеет комплексные со-
пряженные корни А.] = i, А.2 = -i. Действительных корней нет, поэтому
преобразование © вещественного пространства 7] (/?) (случай (а)) не имеет
собственных значений, а следовательно, и собственных векторов. Преобра-
зование © комплексного пространства 7j(c) (случай (б)) имеет комплекс-
ные собственные значения А.(, А.2.
488
41. Для корня Л] = i находим фундаментальную систему (Pj решений
однородной системы уравнений (d - AjE) х = о :
Г - i -1V jq 'j f O')
1 -i J l^x2 J \oj
Приведем матрицу системы к ступенчатому виду, умножая первое уравне-
ние на i и вычитая его из второго уравнения:
(- i -fl fl -fl fl - А
-J~|o °J
Выражаем базисную переменную Xj через свободную: x{=ix2. Полагая
х2 = 1, получаем х1 = i, т.е. ф] = (i 1)г.
51. Записываем собственный вектор, отвечающий собственному зна-
чению A.J =i: jj(t)=i-sinr + l-cosr . Совокупность всех собственных векто-
ров, отвечающих собственному значению Aj = i, образуют ненулевые функ-
ции, пропорциональные 5,(/).
42. Для корня А2 - -I аналогично находим фундаментальную систему
(состоящую из одного вектора) ф2 = (- i 1)г решений однородной системы
уравнений (z>-A2£’)x = o:
fi -1 Vxj f (У)
Ц i J kx2 J
52. Записываем собственный вектор, отвечающий собственному зна-
чению А2 = -i: 52(t) = -i - sin t +1 cos/. Совокупность всех собственных век-
торов, отвечающих собственному значению Л2 = -/, образуют ненулевые
функции, пропорциональные s2(t).
9.4.3. Свойства собственных векторов
1. Собственные векторы линейного преобразования, принадлежащие
различным собственным значениям, линейно независимы.
Аналогичное утверждение было доказано для собственных векторов
матрицы (см. свойство 1 в разд. 7.2.1).
2. Все собственные векторы линейного преобразования cA'.V —»V ,
принадлежащие одному собственному значению, совместно с нулевым век-
тором образуют линейное подпространство, инвариантное относительно
489
преобразования с4. Такое линейное подпространство называется собст-
венным для преобразования с/1.
В самом деле, условие (9.5) можно записать в виде (ef-X-£)(s) = o,
где £: V —> V - тождественное преобразование. Множество векторов s,
удовлетворяющих последнему равенству, составляет ядро линейного преоб-
разования (о?-Х £), т.е. является линейным подпространством
Кег (с4-Х-$)< V (собственное подпространство, отвечающее собственно-
му значению X). Покажем, что это подпространство инвариантно относи-
тельно преобразования Л . Действительно, любой вектор Ker (<sf -Л£)
в силу равенств (of - X £)(s) = о <=> of (s) = X - s отображается в коллинеар-
ный ему вектор X s , также принадлежащий Ker —X • £).
3. Для собственного значения X линейного преобразования : V —э V
существует цепочка инвариантных подпространств
{о}<К{<К1<...<К^ <V, (9.8)
где К{ = Кег К*= Кег -Х-£)2.... К™ = Кег -Х-^)"1;
т - некоторое натуральное число (т<п = dimV ).
Все перечисленные в цепочке (9.8) множества К* , к =1,...,т , являют-
ся линейными подпространствами по свойству ядра линейного преобразова-
ния. Каждое из подпространств К* инвариантно относительно преобразо-
вания , поскольку для любого вектора vg Кк его образ w =еА(у)& Кк,
так как в силу перестановочности многочленов от одного и того же линей-
ного преобразования (см. п.2 замечаний 9.3)
(of - X • (w) = (of - X • of (v)=of (of - X • (v)=of (o) = о ,
так как (of-X-^)*(i') = o V v G К* согласно определения ядра.
Докажем включение К[<К£. Если vgK{, то , при
этом очевидно, что (of-X•$)-(of-X-$)(i') = (of-X-£)(o) = o, т.е. veK%.
Остальные включения доказываются аналогично.
Из цепочки (9.8) "расширяющихся" подпространств следует, что их
размерности не убывают
О<dimК{ <dimK2 <...<dimK™ <dimV ,
поэтому в силу конечномерности пространства V существует такое т, что
dimК"' = dimK™+1, т.е. К™ = K™+i. Покажем, что дальнейшего "увеличе-
ния" подпространств нет, т.е. К™ = K™+1 = ... = К™*к для любого натураль-
ного к . Предположим противное. Пусть К™ = К™+} и для некоторого к > 1
490
пространства не совпадают: К™+к AT™+i+1, т.е. существует вектор
реАГ™+*+1, который не принадлежит пространству К™+к. Обозначим
w = (сА . Тогда, с одной стороны, н'еАГ™+1, так как
(с4-А-^)™+1(н’) = (с^г-Л-₽)™+/:+1(р) = о, поскольку veK™+k+1. С другой
стороны, w g К™, так как (сА-k^'f(<w) = (cA-Х-^Уп+к(у')^о , поскольку
v g К™+к. Следовательно, и» е К™+1 и и» g К” одновременно, что противо-
речит предположению К™ - К™+1.
Таким образом, в цепочке (9.8) размерности пространств К-к,
к = , возрастают. Поэтому т < п = dimV .
Корневым подпространством линейного преобразования сА для соб-
ственного значения Л называется линейное подпространство
К™ -Кег (tff-Л-$)™ с наименьшим натуральным показателем т, для ко-
торого
4. Если Л — собственное значение линейного преобразования
<A.V —> V , то пространство V можно представить в виде прямой суммы
V = К™ ® L, где К™ — корневое подпространство, a L = 1т{аА-Л-^)™ —
инвариантное относительно <Л подпространство, в котором нет собст-
венных векторов, принадлежащих собственному значению X.
В самом деле, покажем, что пересечение этих подпространств есть ну-
левой вектор: АГ™П£ = {о }. Выберем вектор we К™Г1£. Так как вектор
•и» е L, то существует такой вектор v е V , что w =(сА . Поскольку
we АГ™, то (c^-A^)™(w) = o. Тогда («/-Л^)2т(г)= (С?/-Л^)т(и') = о . Сле-
довательно, вектор v е К2™, но К^т = К™, так как К™ - корневое подпро-
странство. Значит, V&K™ => w-(еА-к^У‘(у) = о , т.е. АГ™ [~|£ = {о }. По
теореме 9.1 о размерности ядра и образа получаем, что
dim АГ™ + dimL = dimV. Следовательно, пространство V можно предста-
вить в виде прямой суммы подпространств V = К™ ® L (см. признаки пря-
мых сумм подпространств в разд.8.6.4).
Докажем, что в L нет собственных векторов, принадлежащих собст-
венному значению Л. Действительно, пусть s - собственный вектор, соот-
ветствующий собственному значению Л. Тогда seK{ ив силу (9.8)
s е АГ™. Подпространство L имеет с АГ™ только один общий вектор (нуле-
491
вой). Поэтому s g L, так как sto. Инвариантность подпространства L
следует из перестановочности операторов с4 и (с4-Л(см. п.2 замеча-
ний 9.3). В самом деле, для любого вектора w & L существует прообраз
v eV : и’ = (с4-Л-^),п(р). Поэтому в силу перестановочности операторов
c4(»p) = c^(o?-X-^)m(p) = (C7?-X-₽)mc^(p)eL,
поскольку c4(v)eV и L = Im(e/f . Таким образом, инвариантность
подпространства L доказана, так как е#(н»)е L V we L.
Теорема 9.5 (о разложении пространства в сумму корневых под-
пространств). Если все различные корни klt...,Xk характеристического
уравнения линейного преобразования dl: V —> V являются его собственны-
ми значениями, то пространство V можно разложить в прямую сумму
инвариантных (корневых) подпространств:
V =К"‘ , (9.9)
где К"1 =Кег(^-Х.-^ — корневое подпространство, соответствую-
щее собственному значению i = 1,..., к .
В самом деле, по свойству 4 можно "отщепить" корневое подпростран-
ство К™' , т.е. представить пространство V в виде прямой суммы инвари-
антных подпространств V = © Ц, причем в Ц нет собственных векто-
ров, принадлежащих собственному значению Xj. В пространстве Ц опре-
делено сужение : 1^ 1^ преобразования с4 . Применяя свойство 4 к
сужению , аналогичным образом можно "отщепить" корневое
подпространство К™* , т.е. представить пространство Ц в виде прямой
суммы инвариантных подпространств: Ц = К™* © . Этот процесс следует
продолжить до тех пор, пока не исчерпаются все корни характеристического
уравнения.
Следствие. Если все различные корни Xj,..., характеристического
уравнения линейного преобразования df: V V являются его собственны-
ми значениями, то существует базис пространства V, в котором матри-
ца А линейного преобразования имеет блочно-диагональный вид
A = diag(Al..Ак),
где Aj,..., Ак — матрицы сужений с4: K-J —> K~f ‘
i = 1,...,к, преобразо-
вания с4 на корневые подпространства.
492
Согласно следствию из теоремы 9.2, такой базис можно получить,
записывая последовательно базисы корневых подпространств (9.9).
АЛГЕБРАИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ КРАТНОСТИ СОБСТВЕННЫХ
ЗНАЧЕНИЙ
Алгебраической кратностью собственного значения Л] линейного
преобразования df: V V называется кратность корня А = А( характери-
стического многочлена А(А) (или, что то же самое, кратность корня ха-
рактеристического уравнения (А) = 0).
Геометрической кратностью собственного значения А1 линейного
преобразования df: V —> V называется размерность собственного подпро-
странства = Ker {df -X, •₽), соответствующего этому собственному
значению.
Теорема 9.6 (о кратностях собственных значений). Геометрическая
кратность собственного значения не превосходит его алгебраической
кратности.
Представим пространство V в виде прямой суммы V = К® L (см.
свойство 4) и обозначим г = dimК™' . Выбрав базис пространства К™' , до-
полним его до базиса всего пространства. В этом базисе, согласно следст-
вию теоремы 9.5, матрица А преобразования df будет иметь блочно-
диагональный вид A = diag(Al, А2), где квадратная матрица А] порядка г
является матрицей сужения с4 преобразования df на подпространство
К"' , а матрица А2 является матрицей сужения dfL. Характеристический
многочлен матрицы А имеет вид (см. определитель блочно-диагональной
матрицы в разд. 2.3.4)
det(A-A£') = det(A1 -A£')-det(A2 -ХЕ) = Ptfi,)- р2(Х),
где pt(A), р2(А) - многочлены степеней г и (л-г) соответственно. Так как
сужение сА не имеет собственных значений, отличных от Аи то
р1(А) = (-1)г(А-А1)г, в силу того, что Pj(\)=O и основной теоремы алгеб-
ры. Поскольку сужение сАL не имеет собственных векторов, принадлежа-
щих собственному значению Ар то p2(Aj) Ф 0. Следовательно, г -
алгебраическая кратность собственного значения Ар Тогда утверждение
теоремы следует из включения (9.8): dimX^ <dimXp, так как К^ < X”1.
493
9.5. КАНОНИЧЕСКИЙ ВИД ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
Матрица линейного преобразования : V -> V п -мерного линейного
пространства определяется относительно его базиса. Выбирая разные бази-
сы, получаем разные матрицы одного и того же преобразования. Поэтому
возникает задача приведения линейного преобразования к каноническому
виду, требуется найти такой базис пространства V , в котором матрица пре-
образования имеет наиболее простой вид. Упрощение матрицы преобразо-
вания позволяет выяснить его структуру, представить в виде композиции
простых преобразований. Например, если в некотором базисе матрица пре-
образования оказывается диагональной, то с геометрической точки зрения
это преобразование сводится к гомотетиям вдоль каждого из направлений
базисных векторов. Кроме того, приведение преобразований к каноническо-
му виду позволяет сравнивать различные преобразования. Все преобразова-
ния, которые имеют одинаковый канонический вид, эквивалентны, так как
обладают одинаковыми свойствами.
В разд. 7.2.2 и 7.3 была рассмотрены задачи приведения матрицы к
диагональному виду и к жордановой нормальной форме при помощи преоб-
разования подобия. В этом разделе аналогичные задачи рассматриваются
для линейного преобразования.
9.5.1. Приведение линейного преобразования к диагональному виду
Говорят, что линейное преобразование <df-.V —и-мерного линей-
ного пространства V приводится к диагональному виду, если существует
базис, в котором матрица А преобразования диагональная, т.е.
А = diag{kx, Х2,—Ли), где ,..., - некоторые числа, среди которых мо-
гут быть равные. Если преобразование с4 приводится к диагональному ви-
ду, то оно называется диагонализируемым.
В разделе 7.2.2 было сформулировано необходимое и достаточное ус-
ловие приводимости матрицы к диагональному виду. Переформулируем это
условие для линейного преобразования: линейное преобразование
cA.V —» Г приводится к диагональному виду тогда и только тогда, когда в
пространстве V существует базис из собственных векторов.
Действительно, предположим, что в базисе 5, ,...,sn матрица преобра-
О
зования имеет диагональный вид А = diag[kx,...,'kn') =
. Найдем
О
образ Умножая матрицу А на координатный столбец
.^=(1 0 ••• О)7 базисного вектора Sj =1S] +0 s2 +... + О sn , получаем
494
Asl =^-1s1. Значит, c^(s1)=X]s1, т.е. вектор S| является собственным, а пре-
образование Л действует в подпространстве Lin{s^) как гомотетия (с ко-
эффициентом Xj). Аналогичный вывод можно сделать и про другие базис-
ные векторы. Следовательно, базис пространства состоит из собственных
векторов 5] ,...,sn. Необходимость доказана. Достаточность доказывается
путем приведения тех же рассуждений, но в обратном порядке.
Критерий диагонализируемости линейного преобразования можно
сформулировать иначе.
Теорема 9.7 (о диагонализируемости линейного преобразования).
Для того чтобы линейное преобразование приводилось к диагональному ви-
ду, необходимо и достаточно, чтобы все корни характеристического мно-
гочлена являлись собственными значениями преобразования и геометриче-
ская кратность каждого собственного значения была равна его алгебраи-
ческой кратности.
Достаточность следует из теорем 9.5 и 9.6. Действительно, если для
каждого из различных собственных значений геометрическая
кратность равна алгебраической кратности, то dimJf} = dim К™'т.е.
для всех i = l,...,k. Поэтому в равенстве (9.9) корневые подпро-
странства можно заменить собственными:
Выбрав в каждом собственном подпространстве базис и объединив все эти
базисы в единую систему, получим базис всего пространства, составленный
из собственных векторов. Достаточность доказана. Необходимость доказы-
вается путем приведения тех же рассуждений, но в обратном порядке.
В разд. 7.2.2 было доказано, что существование п линейно независи-
мых собственных векторов необходимо и достаточно для диагонализируе-
мости матрицы при помощи преобразования подобия (см. теорему 5.7). Тео-
рема 9.7 дает более тонкое условие диагонализируемости матрицы линейно-
го преобразования. В разд. 7.2.2 отмечалось также, что не всякую матрицу
можно привести к диагональному виду при помощи преобразования подо-
бия (см. пример 7.9). Аналогичный вывод справедлив и для линейного пре-
образования.
Следствие 1. Если характеристическое уравнение линейного преобра-
зования комплексного (вещественного) пространства имеет п попарно
различных комплексных (действительных) корней (короче говоря, преобра-
зование имеет простой спектр), то это преобразование приводится к диа-
гональному виду.
Действительно, в этом случае алгебраическая и геометрическая крат-
ности каждого собственного значения равны единице.
495
Следствие 2. Если сумма размерностей всех собственных подпро-
странств линейного преобразования df: V —» V равна размерности линей-
ного пространства V, то линейное преобразование приводится к диаго-
нальному виду.
Пример 9.2. Линейное преобразование с4 : V —> V в базисе ег, е2, е3
fl 1 Г|
имеет матрицу А = 1 1
1 . Привести это преобразование к диагонально-
11 1 V
му виду, т.е. найти базис , s2, s3, в котором матрица преобразования име-
ет диагональный вид, и найти эту диагональную матрицу.
□ Задача сводится к нахождению собственных векторов и собствен-
ных значений преобразования. Применяем для их нахождения алгоритм,
рассмотренный в разд. 9.4.1.
1. Выбираем базис е1,е2,е3, в котором задана матрица преобразова-
ния.
2-5. Собственные значения и собственные векторы этой матрицы, а
также ее диагональный вид были найдены в примере 7.10:
X, =х2 =о,хз =3, 5,=(1 О -if, J2 = (l -1 of, 53=(1 1 if,
diag(0,0,3).
Осталось по координатным столбцам sl,s2, s3 записать искомый базис
=1-е1 +0-е2 + (-1)-е3 =ег-е3; s2=e[-e2-, s3 = et +е2 + е3.
9.5.2. Приведение линейного преобразования к каноническому виду
Говорят, что линейное преобразование с4:V —>V «-мерного линей-
ного пространства V приводится к каноническому виду, если существует
базис, в котором матрица А преобразования имеет нормальную жорданову
форму (см. разд.7.3). Такой базис называется жордановым.
Напомним, что жордановой клеткой г-го порядка, соответствующей
собственному значению Л, называют квадратную матрицу г-го порядка
(7.35): 'Л 1 0 (Г 0 Л 1 ••• 0
Л(Л)= i i \ ••. i . 0 0 0 1 ООО (9.10)
Жордановой матрицей называют блочно-диагональную матрицу вида (7.38):
496
о
о
(9.11)
на диагонали которой стоят жордановы клетки (9.10), причем среди собст-
венных значений Хр-.-.Х^ могут быть равные, порядки Гр...,г4 жордано-
вых клеток (всех или некоторых) могут совпадать.
СУЩЕСТВОВАНИЕ И СТРУКТУРА ЖОРДАНОВА БАЗИСА
Пусть преобразование df: V —> V имеет собственный вектор s , соот-
ветствующий собственному значению X. Вектор s^, удовлетворяющий ус-
ловию <s>f(s^^)=Xs^ + s, называется присоединенным вектором 1-го по-
рядка. Вектор в®, удовлетворяющий условию cp?(s^)=Xs^ + s^, называ-
ется присоединенным вектором 2-го порядка и т.д. Присоединенный век-
тор р-го порядка определяется соотношением c^s^j^Xs^ + s^-1),
где - присоединенный вектор (р-1)-го порядка.
Определение присоединенных векторов можно записать эквивалент-
ным образом, используя преобразование J8 = c4-X£ (характеристическое
преобразование для преобразования еЛ): вектор является присоеди-
ненным р-го порядка, если JBp(s^)=s, где s - собственный вектор
преобразования с4 .
Действительно, при р = 1 из условия Jb(s^)=s получаем
(<rf-X^)(s^)=s, т.е. ctf^’^Xs^ + s . При р = 2 из условия J82(s(2))=s
имеем (f^-X^)2(s(2))=(f^-X^)[(c^-X^)(f(2))]=J. Отсюда -X^)(s(2))=
= s^, т.е. с#(у(2))=Х$(2)+ и т.д. Заметим, что присоединенный вектор
s(p) р -го порядка по определению удовлетворяет одновременно двум усло-
виям:
J8p(s(p))*o и ^+1(s(/,))=o,
так как собственный вектор s ненулевой, а
£P+i (s(p))=j8(s) = ) = о , поскольку tf?(s) = Xs .
Необходимость рассмотрения присоединенных векторов объясняется
следующим свойством: жорданов базис состоит из собственных и присое-
497
32 - 4549
диненных векторов линейного преобразования, взятых в определенном по-
рядке.
Предположим, что в базисе е1,^2,...,ел пространства V матрица А
преобразования с4: V —» V имеет жорданову форму (9.11). Рассмотрим пре-
образование первых г, базисных векторов (г, - порядок первой жордановой
клетки Jr (Xj в (9.11)). Умножая координатный столбец е, = (1 0 ••• 0)г
базисного вектора et на матрицу А с учетом (9.10), получаем Ае^Х^,
т.е. о?(е1)=Х1ег Следовательно, вектор е{ - собственный. Умножая матри-
цу А на координатный столбец е2=(о 1 ••• 0)г базисного вектора е2,
получаем Аег = Xte2 + ег, т.е. <s?(e2)=X1e2+ е,. Следовательно, е2 - присое-
диненный вектор (1-го порядка). Аналогично заключаем, что векторы
е3,...,ег также присоединенные (от второго до (rj-l)-ro порядков соот-
ветственно). Для других жордановых клеток выводы аналогичные.
Таким образом, жорданов базис составляют собственные и присоеди-
ненные векторы, взятые в следующем порядке (базисные векторы
е, ,е2,...,еп удобно обозначить иначе):
spsj2\...,s2,................sk,s^,s|2\...,(9.12)
где s( ,s2,...,st — собственные векторы, а остальные векторы - соответст-
венно присоединенные к ним, rl+r2+... + rk=n. Каждой из к жордановых
клеток в (9.11) отвечает одна группа векторов в (9.12). Количество собст-
венных векторов в (9.12) равно количеству жордановых клеток в (9.11). Пе-
рестановке групп векторов в базисе (9.12) соответствует перестановка жор-
дановых клеток в (9.11), при этом форма матрицы остается жордановой.
Докажем существование жорданова базиса для преобразования
Л: V —э V п -мерного линейного пространства V при условии, что все
корни характеристического уравнения являются собственными значениями
преобразования с4 .
Сначала рассмотрим случай, когда преобразование cfl имеет единст-
венное собственное значение X. В этом случае в прямой сумме (9.9) имеет-
ся одно слагаемое V = К" (см. теорему 9.5), а цепочка (9.8) инвариантных
подпространств имеет вид
498
где Kg =Ker (cA-'k-g'f = Ker !RP, p = am- наименьшее нату-
ральное число, при котором Kg = Kg+l. Здесь, как и ранее, = -
характеристическое преобразование для преобразования е? .
Каждое подпространство Kg, р = 2,...,т, состоит из собственных
векторов (которые образуют собственное подпространство К^) и присое-
диненных векторов первого, второго и т.д. до (р—1)-го порядка включи-
тельно. Действительно, присоединенный вектор s^p~1^ определяется равен-
ством J8p_I(s^-1’)=s, где s - собственный вектор. Тогда
= j8(s) = o , т.е. s^p~^eKg.
Будем строить базис корневого подпространства Kg следующим об-
разом. Так как Kg~l не совпадает с Kg, то существует максимальная ли-
нейно независимая над подпространством Kg~l<Kg система
присоединенных векторов (т-1)-го порядка (которая дополняет
любой базис подпространства Kg~l до базиса подпространства Kg,
кт =dimK™-dimК’™"1). Напомним, что векторы называ-
ются линейно независимыми над подпространством Kg~l < Kg, если любая
нетривиальная линейная комбинация этих векторов не принадлежит
Kg~x (см. разд. 8.6.4).
Векторы являются присоединенными (т-2)-го
порядка, принадлежат Kg~x и линейно независимы над подпространством
Kg~2 < Kg~l [42]. Дополним их присоединенными векторами
...,sjm"2) (т-2)-го порядка (кт_{ =dimA'£1-1 -dimX’™'2-кт) до макси-
мальной линейно независимой над подпространством Kg"1 < Kg^ систе-
мы Применяя к этим векторам пре-
образование j8 , получаем линейно независимые над подпространством
д-т-З < Кт-2 векгоры ),..., ).
Дополняем их векторами до максимальной линейно
независимой над подпространством Kg~3 < Kg~г системы. Продолжая ана-
логично, приходим к следующей таблице базисов:
32* 499
(9-13)
В таблице базисов (9.13) указаны следующие базисы:
в последней строке - базис собственного подпространства ;
в двух последних строках - базис подпространства ЛГ2 и т.д.;
вся таблица - базис корневого подпространства К™.
По таблице (9.13) составим базис корневого подпространства. Записы-
ваем векторы, стоящие в первом столбце, один за другим снизу вверх, начи-
ная с собственного вектора:
К ним приписываем в таком же порядке векторы, стоящие во втором столб-
це, и т.д. Получим жорданов базис корневого подпространства, состоящий
из собственных и присоединенных векторов, взятых в определенном поряд-
ке, как это указано в (9.12). Все клетки жордановой формы (9.11) соответст-
вуют собственному значению X. Каждому из первых кт столбцов таблицы
(9.13) соответствует жорданова клетка m-го порядка, каждому из кт_х сле-
дующих столбцов соответствует жорданова клетка (m-l)-ro порядка и т.д.
Общее число жордановых клеток равно количеству собственных векторов в
последней строке таблицы (9.13).
Таким образом, доказано существование жорданова базиса в случае
единственного собственного значения.
Рассмотрим теперь случай, когда имеется несколько различных собст-
венных значений Хр...Д*. В этом случае по теореме 9.5 пространство раз-
лагается в прямую сумму инвариантных (корневых) подпространств
V = К™' ®...®К™1. При объединении жордановых базисов корневых под-
пространств получаем жорданов базис всего пространства. Таким образом,
справедливо следующее утверждение.
Теорема 9.8 (о приведении линейного преобразования к канониче-
скому виду). Если все корни характеристического уравнения являются соб-
ственными значениями преобразования, то это преобразование приводится
к каноническому виду, т.е. существует базис пространства, в котором
матрица преобразования имеет жорданову форму.
500
Из теоремы следует, что любое линейное преобразование комплексно-
го линейного пространства приводится к каноническому виду, а преобразо-
вание вещественного линейного пространства приводится к каноническому
виду только тогда, когда все корни характеристического уравнения действи-
тельные.
Замечания 9.5.
1. По таблице (9.13) нетрудно выразить количество кр жордановых
клеток порядка р через ранги преобразований rp =rg (с?/-Л£)₽, учитывая,
что dimAjP = п-гр. Количество кт жордановых клеток порядка т равно
количеству векторов в первой строке таблицы (9.13):
к = dim КТ1 -dimK,”-1 =(и-г )-(и-г ,)=г ,-г . Количество к .
жордановых клеток порядка (ш-1) равно количеству векторов
s(m-2), 5(т-г) в0 BTOpOg строке таблицы (9.13): kml = dim АГ”-1 -
— dimКТ1 2 — к —{п — г .)— (и — г (г . — г )= г 0—2г . + г .
Л т \ т—1/ \ т-2/ \ т-1 т/ т-2 т-1 т
Продолжая вычисления аналогичным образом, получаем следующий
результат: количество кр жордановых клеток порядка р находится по
формуле
kP = rp-i ~ 2гР + г₽+1 ’ Р = 1’ ’m ’ (9Л4)
где rp =rg , г0 -п ; т — наименьшее натуральное число, при ко-
тором гт^=гт.
2. Число т в (9.14) равно кратности корня Л минимального много-
члена матрицы А линейного преобразования [10].
3. Из п.1 следует единственность жордановой формы матрицы линей-
ного преобразования (с точностью до перестановок жордановых клеток), так
как состав жордановых клеток (количество и порядки) полностью определя-
ется по размерностям инвариантных подпространств (9.8), (9.9). От выбора
базиса зависит расположение жордановых клеток на главной диагонали мат-
рицы (9.11). Поэтому жордановы формы, отличающиеся перестановкой
жордановых клеток, считаются одинаковыми.
МЕТОДИКА ПРИВЕДЕНИЯ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
К КАНОНИЧЕСКОМУ ВИДУ
Задача приведения линейного преобразования к каноническому виду
формулируется следующим образом. Требуется найти базис п -мерного ли-
501
нейного пространства V , в котором матрица линейного преобразования
ctf :V —>V имеет жорданову форму JА , т.е.
- найти жорданову форму J А матрицы А преобразования (первый этап);
- найти жорданов базис (второй этап).
НАХОЖДЕНИЕ ЖОРДАНОВОЙ ФОРМЫ МАТРИЦЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
Для нахождения жордановой формы JА матрицы линейного преобра-
зования нужно выполнить следующие действия.
1. Выбрать произвольный базис et ,...,еп линейного пространства V и
найти в этом базисе матрицу А преобразования .
2. Составить характеристический многочлен преобразования <Л :
Arf (А) = det(A - Ае) .
3. Найти все различные корни Ар-.-.А^ характеристического уравне-
ния (А) = 0 и их алгебраические кратности п1,...,п1(.
4. Для корня А = Aj кратности п} найти ранги матриц
rp=rgBp, /> = 1,...,^,
где В = А - AjE, а т^ - наименьшее натуральное число (т^ < ), при кото-
ром rm+1=rm . Ранг матрицы Вр можно найти одним из способов, равг
смотренных в разд 3.3. Если в дальнейшем предполагается искать жорданов
базис, то для нахождения ранга лучше использовать метод Гаусса (разд.
3.3.2), приводя матрицу Вр элементарными преобразованиями строк к мо-
дифицированному ступенчатому виду (в₽Д. Он получается в результате
вычеркивания нулевых строк из матрицы ступенчатого вида (см. разд. 1.6.1).
5. Определить количество кр жордановых клеток JДА,) порядка р:
к = r ,-2г + г„.1, р = 1,...,т.,
р р-1 р р+1 ’ г л
где r0 = п (см. п. 1 замечаний 9.5).
Повторить п.4, 5 для остальных собственных значений А2А* •
6. Составить искомую матрицу J А блочно-диагонального вида (9.11)»
располагая найденные жордановы клетки на главной диагонали.
НАХОЖДЕНИЕ ЖОРДАНОВА БАЗИСА
Пусть в базисе (е) = (ep...,en) линейного пространства V преобразова-
ние eA.V -эV имеет матрицу А . Требуется найти матрицу перехода S от
502
базиса (е) к жорданову базису (s)= (sp.(s) = (e)-5 (см. разд.8.4.3).
Предполагаем, что жорданова форма J А матрицы А известна.
1. Для собственного значения Xj (алгебраической кратности zij) найти
характеристическую матрицу В = А-Х1Е и по жордановой форме JA оп-
ределить наибольший порядок т1 жордановых клеток, соответствующих
собственному значению Xj.
2. Привести матрицы Вр, р = к модифицированному ступен-
чатому виду (вр (он получается в результате удаления нулевых строк из
матрицы ступенчатого вида (см. разд. 1.6.1)).
3. Найти фундаментальную матрицу Фт однородной системы
уравнений
и составить матрицу = (вт‘ -1 ^Фт • Если Вт' - нулевая матрица, то
1 , так как в этом случае Фщ - единичная матрица.
Вычислить матрицу , найти фундаментальную матрицу Фт ч
однородной системы уравнений
и составить матрицу BS^m' Если однородная
система не имеет фундаментальной матрицы (система имеет только триви-
альное решение), то = BS^m,~^.
Вычислить матрицу В8^т> 2\ найти фундаментальную матрицу Фт _2
однородной системы уравнений
и составить матрицу 2^|(в'П| 3^.Фт _2^. Если фундамен-
тальная матрица Фщ _2 не существует, то 5^т'-3) = дд^-2).
503
Продолжить аналогичным образом построение матриц
^(з) ^(2)
Вычислить матрицу BS^, найти фундаментальную матрицу Ф2 од-
нородной системы уравнений
( (в2} 'I
и составить матрицу (BS^2^| (в)с*Ф2)- Если фундаментальная матрица
Ф2 не существует, то = BS^.
Вычислить матрицу BS^\ найти фундаментальную матрицу Ф] одно-
родной системы уравнений
и составить матрицу 5^ = (Ф] j. Если фундаментальная матрица Ф1
не существует, то .
Если = 1, то 5^°^ = Ф!, где Ф, - фундаментальная матрица одно-
родной системы уравнений (/?)стх = о .
4. Из столбцов полученных матриц
... |b2jW.„B2jW|
= |&(г) ...
(9.15)
s(mi-2)=| $('Я1"2)...$('",_2) I,
составить первые и, столбцов искомой матрицы S, записывая первые
столбцы матриц затем вторые столбцы этих
матриц и т.д.
Выполнить п.1-4 для остальных собственных значений Л.2 , по-
лучая следующие n2,...,n/i столбцов искомой матрицы S соответственно
(при этом тх заменяется на т2тк).
504
Данный алгоритм использует метод нахождения относительных алгеб-
раических дополнений, рассмотренный в разд. 8.6.5.
Замечания 9.6.
1. Для нахождения матрицы S перехода к жорданову базису можно
использовать также способы, рассмотренные в разд. 7.3.3.
2. Вместо модифицированного ступенчатого вида (в/’).т матрицы Вр ,
р = 1,...,/«], можно использовать любую максимальную линейно независи-
мую систему строк матрицы Вр .
3. Жорданов базис и, следовательно, матрица S, определяются неод-
нозначно.
4. Для вещественных матриц операция сопряжения, обозначенная звез-
дочкой (*), соответствует операции транспонирования.
Пример 9.3. Линейное преобразование еА: V -> V в базисе
'1 -1 1 -Р
-33-54
6], е2, е2, е4 имеет матрицу А = 8-43-4 . Привести это преоб-
J5 -10 11 -11,
разование к каноническому виду, т.е. найти базис s^,s2,s2,s^, в котором
матрица преобразования имеет жорданову форму, и найти эту жорданову
матрицу.
□ Первый этап. Найдем жорданову форму J А матрицы преобразова-
ния.
1. Выбираем базис , е2, е3, е4, в котором задана матрица преобразо-
вания ( п = dimH = 4).
2. Составляем характеристический многочлен преобразования <А
1-Х -1 1 -1
(х) = det(у4 - ХЕ) = -3 3-Х -5 4 8 -4 3-Х -4 15 -10 11 -11-Х = (Х + 1)3 4
3. Находим корни характеристического уравнения (Х + 1)4 =0 и их ал-
гебраические кратности: Xj = -1 - единственный корень кратности = 4 .
4. Для корня X] = — 1 кратности ^=4 находим ранги матриц
В = А -(-1)-Е = А + Е , В2, В?, В4 Выполняя элементарные преобразова-
ния над строками матриц, приводим матрицы к ступенчатому виду:
505
' 2 -1 1
-3 4 -5
8-4 4
J5 -10 11
f 2
-3
8
<15
-1 1
4 -5
-4 4
-10 11
1 -P
0 0
о 0
о 0,
'2 -1 1 -Г 3 '0 0 0 0'
-34-54 0 0 0 0
д3 = — = 0
8-44-4 0 0 0 0
<15 -10 11 -10, ч0 0 0 0,
r2 = rg В2 = 1, r3 = rg В3 - 0, Wj = 3, так
как
Отсюда г, = rg В = 2 ,
r4=° = r3.
5. Определяем количество kt жордановых клеток J,(-l) 1-го порядка:
кг = rQ - 2rt + гг - 4 - 2 • 2 +1 = 1, где г0 = п = 4. Следовательно, в жордановой
форме JА имеется одна клетка jJ-l).
Определяем количество к2 жордановых клеток J2(-l) ^~го порядка:
к2 = Fj - 2г2 + г3 = 2 - 2 1 + 0 = 0. Следовательно, в жордановой форме JА
нет клеток J2(-l).
Определяем количество к3 жордановых клеток ^3(~1) 3-го порядка:
к3 = r2 - 2r3 + r4 = 1 - 2 • 0 + 0 = 1. Следовательно, в жордановой форме JА
имеется одна клетка J3(-1).
6. Составляем искомую матрицу J А блочно-диагонального вида (9.11),
располагая найденные жордановы клетки на главной диагонали:
Г-1 1 о О'
JA = diag(j3(-l\J1(-l))= 0 -1 1 0 0-1 0 0
ч0 0 0 -1J
Второй этап. Найдем жорданов базис.
1. Для собственного значения \ =-1 кратности л(=4 по жордановой
форме JA определяем максимальный порядок = 3 жордановых клеток,
506
соответствующих собственному значению = -1. Составляем матрицу
B = A-(—l)-E.
2. Приводим матрицы В , В2, В3 к модифицированному ступенчато-
му виду (см. п.4 первого этапа)
(В)ст=[о ~5 -7 (Л^=(2 -1 1 -1)> В3 = °-
3. Так как матрица В3 = О, то S® = (т?2)ст - (2
-1 1 -1)Г.
Вычисляем В$(2) =
' 2 -1 1 -pm ' 7 '
-3 4 -5 4 -1 -19
8 -4 4 -4 1 28
J5 -10 11 -10, Я, <6i,
Находим фундаментальную матрицу Ф2 однородной системы уравне-
ний
х = о:
"2 -1 1 -1
7 -19 28 61
I
-3
4
-3
5
-7
5J
'6
о
12 -17^р
-7 14
= о.
кЛ27
Поскольку определитель матрицы системы не равен нулю, система имеет
только нулевое решение. Поэтому фундаментальная матрица не существует
и, следовательно, = BS^ - (7 -19 28 61)Г.
' 2 -1 1 -Г ' 7 ' 'О'
А) -3 4 -5 4 -19 7
Вычисляем 7 = 8 -4 4 -4 28 — 0 , находим фун-
J5 -10 И -10, <61,
даментальную матрицу Ф( однородной системы уравнений
'1 -3
0 5
4
-7
0
-3'
5
'2
л3
Хл
'О'
0
Я
10 4
0 1 0
,0 0 7
-6'
-1
-10,
'О'
о
Я
507
Фундаментальная матрица содержит один столбец Ф] = (2 7 10 7)г
(здесь вместо стандартного значения х4 = 1 свободной переменной положи-
ли х4 = 7 для получения целочисленных значений).
( 0
Составляем матрицу 5^°^ = (55^1 Ф]
2'
7
10
7,
1-7
составляем искомую
4. Из столбцов полученных матриц , S^,
матрицу S:
' 0 2> ' 7 > ' 0 7 2 2'
7 7 , S(1) = -19 , 5(2) = -1 => 5 = 7 -19 -1 7
0 10 28 1 0 28 1 10
k-7 7/ <61, <—ь I'7 61 -1 7,
записывая сначала первые столбцы матриц S^2\ а затем второй
столбец матрицы
Нетрудно проверить, что матрица 5 удовлетворяет равенству
SJА = AS , т.е. является матрицей перехода к жорданову базису (s) = (е) S :
st =7-е2-7-е4; s2 =7-et+(-19)-е2+28е}+61-е4; s3=2-e1~e2+e3~e4;
s. = 2 - е. + 7 • е. +10 • е, + 7 е..
4 12 3 4
Пример 9.4. Линейное преобразование еА : V -> V в базисе et, е2, е3,
е4,е5 имеет матрицу
'1 0 0 1 -Р
0 1 -2 3 -3
А = 0 0 -1 2 -2
1 -1 1 0 1
-1 1 -1 2 ,
Привести это преобразование к каноническому виду, т.е. найти базис
S,, s2, s3, $4, $5, в котором матрица преобразования имеет жорданову фор-
му, и найти эту жорданову матрицу.
□ Первый этап. Найдем жорданову форму JA матрицы преобразова-
ния.
1. Выбираем базис , е2, е3, е4, е5, в котором задана матрица преоб-
разования (п = dim V - 5 ).
508
2. Составляем характеристический многочлен преобразования сА
1-Х 0 0 1-1
0 1-Х -2 3 -3
(X) = det (А - ХЕ) = 0 0 -1-Х 2 -2 = (x-i)4(-i-x)
1-1 1 -X 1
1-1 1-1 2-Х
3. Находим корни характеристического уравнения (Х-1)4(-1-Х)=0 и
их алгебраические кратности: \ =1 (кратность и, =4), Х2 =-1 (кратность
и2 =1)-
41. Для корня X] = 1 кратности пх = 4 находим ранги матриц
В = А-'к1Е = А-IE, В2, В3, В4 . Выполняя элементарные преобразова-
ния над строками матриц, приводим матрицы к ступенчатому виду:
'0 0 0 1 -Г '1 -1 С 0 О'
0 0-2 3 -3 0 0 0 0
В = 0 0-2 2 — 2 0 0 С 1 -1 9
1 -1 1 1 0 0 С 0 0
J -1 1 1, ^0 0 с ° °,
"0 0 0 1 -1' '0 0 0 0 О' '0 0 1 -1 1'
0 0- -2 3 -3 0 0 4 -4 4 0 0 0 0 0
В2 = 0 0 - -2 2 -2 = 0 0 4 -4 4 0 0 0 0 0
1 -1 1 -1 1 0 0 0 0 0 0 0 0 0 0
J -1 1 -1 1 <° 0 0 0 °> 0 0 ч 0 0 0,
'0 0 с 1 -Р 3 '0 0 0 0 0 'о 0 1 -1 1
0 0- 2 3-3 0 0 8 8-8 0 0 0 0 0
В3 = 0 0- 2 2-2 = 0 0 8 8 -8 0 0 0 0 0
1 -1 -1 1 0 0 0 0 0 0 0 0 0 0
ч1 -1 -1 1 , 0 0 0 0 0 , 0 0 0 0
Отсюда 5 = rg в = 3, r2 = rg В 2 - 1, тх = 2 < и,, так как r3=rgB3=l = r2
51. Определяем количество кх жордановых клеток J,(l) 1-го порядка:
к{ ~ гй -2г, + гг = 5-2-3 + 1 = 0, где г0=и = 5. Следовательно, клеток 1-го
порядка, соответствующих собственному значению Л., = 1, нет.
509
Определяем количество к2 жордановых клеток /2(1) 2-го порядка:
к2 = /j - 1гг + г3 = 3 - 2 • 1 +1 = 2 . Следовательно, в жордановой форме J А
имеются две клетки J2(l).
4 2 . Для простого корня Х2 = -1 (кратность п2 =1) находим ранг мат-
рицы В = А-Х2Е = А + Е. Выполняя элементарные преобразования над
строками матрицы, приводим ее к ступенчатому виду:
'2 0 0 1 -1> '1 0 0 0 0^
0 2 -2 3 -3 01-100
В = 0 0 0 2 -2 0 0 0 1 0
1-11 1 1 0 0 0 0 1
J -1 1 -1 3 , ч0 0 0 0 0,
Отсюда Tj — rg В — 4, а так как r2 - rg В2 = 4 , то т2 - п2 = 1.
52. Определяем количество к{ жордановых клеток 1-го поряд-
ка: = г0 -2г( +г2 =5-2-4+ 4 = 1, где г0=п=5, г2 = = 4 . Следователь-
но, в жордановой форме JA имеется одна клетка Jl (-1).
6. Составляем искомую матрицу JA блочно-диагонального вида (9.11),
располагая найденные жордановы клетки на главной диагонали:
Р 1 0 0 °1
0 1 0 0 0
JA=diag(j2(l),J2(lp,(-l)) = 0 0 1 1 0
0 0 0 1 0
[о 0 0 0
Второй этап. Найдем жорданов базис.
I1. Для собственного значения \ = 1 кратности zij = 4 по жордановой
форме JA определяем максимальный порядок - 2 жордановых клеток,
соответствующих собственному значению /Ц = 1. Составляем матрицу
В = А -1 • Е (см. п. 4* первого этапа).
21. Приводим матрицы В
и В2 к модифицированному ступенчатому
виду (см. п. 41 первого этапа)
(5)ст
'1-10 0
0 0 10
J) О О 1
О'
О
ч
(В2)СТ=(О 0 1 -1 1).
510
З1. Находим фундаментальную матрицу Ф2 однородной системы
уравнений [в2\т(в)‘тх = о:
0 О'1
-1 0 0 *1
0 1-11) 0 1 0 Х2 = 0
0 0 1 X-
К
<0 0 -1,
Выражая базисную переменную х2 через свободные (хг, х3), получаем
х2 =0 Х]+2-х3. Для Xj = 1,х3 = 0 находим х2=О,для Х]=0,х3=1 нахо-
z ЧТ
(1 О 0Y
дим х, = 2. Отсюда Ф, = . Составляем матрицу
* z I Л О 1 J
' 1 0 О' ' 1 О'
-10 0 '1 О' -1 0
s®=(b)* ф2 = 0 1 0 0 2 = 0 2
0 0 1 0 1, 0 1
<0 0 -к <0 Ч
Находим фундаментальную матрицу Ф1 однородной системы уравне-
НИИ
х = о:
'О'
О
о
о
Я
Ранг матрицы системы равен числу неизвестных, поэтому система имеет
только тривиальное решение. Следовательно, матрица Ф1 отсутствует.
fol (1) [0 0 0 2 2 j
Составляем матрицу 5' 1 - BSV ’ =1 _
^2 2 0 0 0;
41. Из столбцов полученных матриц 8^, 8^ составляем первые
= 4 столбца искомой матрицы 5 :
511
'0 2> 0 2 0 0 2 0 <2 0, , = ' 1 О' -1 0 0 2 0 1 .о -К => S = '0120*' 0-120* 0 0 0 2 * 2 0 0 1 * 2 0 0-1 *,
записывая сначала первые столбцы матриц S®, S^, а затем вторые. Неиз-
вестные пока элементы матрицы 5 обозначены звездочкой (*).
I2. Для собственного значения Х2 = -1 кратности И] = 1 по жордано-
вой форме J А определяем порядок тг = 1 единственной жордановой клет-
ки соответствующей собственному значению А.2=-1. Составляем
матрицу В = А + Е (см. п. 42 первого этапа).
22. Приводим матрицу В к модифицированному ступенчатому виду
(см. п. 42 первого этапа)
'1 0 0 0 0
01—100
0 0 0 1 0’
J) 0 0 0 1,
З2. Находим фундаментальную матрицу 0! однородной системы
уравнений
© о о о ы '0>
X-
0 1 -1 0 0 2 0
(В1тл: = о <=> X,
х /СТ 0 0 0 1 0 J 0
X О О о о 1—- Х4 <Х5> Я
Полагая х3 = 1, находим значения базисных переменных xt = 0, х2 = 1,
х4 =х5 = 0. Следовательно, S® =Ф1 = (0 110 0)г.
42. Полученный столбец записываем в матрицу, найденную в п. 41:
'0 1
0 -1
2 О О'
2 0 1
О 2 1
О 1 О
О -1 0?
5 = 0
0
2 О
<2 0
512
Матрица перехода от базиса (е) к жорданову базису (s) найдена. С ее
помощью находим жорданов базис (s)=(e)S: sl=2-ei+2e5;
s2 = l-в] +(-1) е2; s3 - 2-Cj + 2-е2 ; s4 = 2е3 +1-е4 +(-1)-е5;
s5 =1е2 + 1е3.
9.6. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ ЕВКЛИДОВЫХ
ПРОСТРАНСТВ
Рассмотрим линейное преобразование of: Е —> Е п -мерного евклидо-
ва пространства Е . Напомним, что евклидово пространство является веще-
ственным линейным пространством со скалярным произведением (см.
разд.8.8). Поэтому все понятия и свойства линейных преобразований веще-
ственных линейных пространств полностью переносятся на линейные пре-
образования евклидовых пространств. Наличие скалярного произведения
позволяет определить важные свойства таких преобразований.
9.6.1. Ортогональные преобразования
Преобразование сА: Е —э Е п -мерного евклидова пространства Е на-
зывается ортогональным, если оно сохраняет скалярное произведение век-
торов, т.е.
(of(v), cA(w)) = (v,H’) V v, w&E. (9.16)
Из определения следуют простейшие свойства: при ортогональном
преобразовании не изменяются длины векторов, а также углы между век-
торами, поскольку | of(v)|2 =(of(v),c>f(v)) = (v,v) = | v |2
и для ненулевых
векторов cos ср -
(т.н») (cA(v),cA(w))
|р| M=WIWI
Перейдем к изучению других свойств ортогональных преобразований.
СВОЙСТВА ОРТОГОНАЛЬНЫХ ПРЕОБРАЗОВАНИЙ
1. Ортогональное преобразование — линейное.
В определении намеренно не говорится о линейности преобразования
сА , поскольку она следует из (9.16). Действительно, выберем в Е ортонор-
мированный базис (е)= (е1,...,еп). Тогда векторы cf(ej,...,cf(en) также об-
разуют ортонормированный базис пространства Е , так как по определению
(“»(’,) <4^))=(г,..,)={ о (9.17)
33 -4549
513
Найдем координаты образа of (у) произвольного вектора
v = Vjg] +... + vnen в базисе of(ej),...,of(en). Так как (of(y),of(ej) =
= (v, ej= v,., i = l,...,n, получаем
of(y)= v1of(e1)+...+ vnof(en). (9.18)
Найдем образ произведения вектора v на число X
of (X • у )=(Х^ )of (е,)+...+(Xv„ )of (en )=X (v,of (^)+...+vndt(en))=X • dt(y).
Следовательно, преобразование <Л - однородное. Аддитивность доказыва-
ется аналогично.
2. Линейное преобразование ортогонально тогда и только тогда, ко-
гда оно отображает ортонормированный базис в ортонормированный.
Необходимость следует из (9.17). Докажем достаточность. Пусть
е1,...,еп и of(e1),...,of(e ) - ортонормированные базисы пространства Е.
В силу линейности преобразования для любого вектора v = +...+удел
справедливо (9.18). Поэтому
л лл / \ ( п п '
=Ev<M'i=YYviwj\ei'ejr ’Ewa-
<=i »=i>i <<=i j=i j
что и требовалось доказать.
3. Линейное преобразование <Л :Е Е ортогонально тогда и только
тогда, когда его матрица А в любом ортонормированном базисе является
ортогональной, т.е. АТ = А’1.
В самом деле, пусть в ортонормированном базисе (e)=(er...,en) орто-
гональное преобразование <Л имеет матрицу А . Найдем произведение об-
разов ^{е)=^аьек и 4;)=Zv(
*=1 i=i
Согласно (9.17) имеем
базисных векторов (см. разд. 9.3.2).
Последнюю сумму можно рассматривать как произведение элементов / -й
строки транспонированной матрицы АГ на соответствующие элементы
j -го столбца матрицы А . Поэтому Ат А = Е, тогда и AAr = Е. Следова-
тельно, Аг = А-1. Для доказательства достаточности проводим рассуждения
в обратном порядке и приходим к заключению, что преобразование of
514
(с ортогональной матрицей А ) отображает один ортонормированный базис
в другой. По свойству 2 такое преобразование ортогональное.
4. Ортогональное преобразование обратимо, т.е. инъективно и сюръ-
ективно-. КегсА = { о }, Im <А = Е . Это следует из свойств ядра и образа
линейного отображения (см. разд. 9.1.5).
5. Корни характеристического уравнения ортогонального преобразо-
вания по модулю равны единице {собственные значения равны +1 или —1).
Действительно, пусть А - матрица ортогонального преобразования в
ортонормированием базисе. Характеристическое уравнение имеет действи-
тельные коэффициенты, так как матрица А действительная. Если
Ij 2 = а ± Pi - пара комплексных сопряженных корней характеристического
уравнения, то найдется ненулевой столбец z (с комплексными элементами),
для которого Az = Лг. Выполняя комплексное сопряжение и транспониро-
вание обеих частей равенства, получаем z*A* = Лг* (см. разд. 1.4.2). Пере-
множим оба равенства: z*A*Az = ЛЛг*г- Так как А* = АТ = А~1, то
z*z = AXz*z - Для ненулевого столбца (z*o) z*z*O и, следовательно,
ЛЛ = 1112 = 1. Поэтому для собственных значений, которые являются дей-
ствительными числами, получаем Л = ±1.
6. Определитель матрицы ортогонального преобразования равен +1
или -1. Это свойство следует из равенства AAr = Е, так как
(detA)2 = detAdetAr = det(AAr)=detE = l => detA = ±l.
Ортогональное преобразование of называется собственным, если
det А = 1 и несобственным, если det А = -1.
7. Пусть L — инвариантное относительно ортогонального преобразо-
вания сА .Е —ьЕ подпространство Е . Тогда его ортогональное дополне-
ние LL также инвариантно по отношению к преобразованию сА .
По свойству 4 ортогональное преобразование сАL :L-> L (сужение
преобразования сА.Е-ьЕ на инвариантное подпространство L <1Е) обра-
тимо. Поэтому для любого we L найдется прообраз ve L : w=of(v). То-
гда для любого ue L1 имеем (cf(«),w) = (cf(u),cf(v))=(«, v) = 0, т.е.
of(u)e L1. Следовательно, подпространство L1 < Е инвариантно относи-
тельно преобразования сА , т.е. Ll и даже L1 в силу обра-
тимости еА.
8. Пусть Л = а ± pi - пара комплексных сопряженных корней (р Ф 0)
характеристического многочлена ортогонального преобразования
сА :Е Е. Тогда существует такая пара равных по длине ортогональных
векторов х и у, что
33*
515
<9J9<
[ c#(y) = 0x + ay.
В самом деле, в теореме 9.4 доказано существование линейно незави-
симых векторов х и у , удовлетворяющих системе (9.19), которая в коор-
динатной форме имеет вид (9.7). Матрица сужения ЛL L^>L преоб-
разования e/J на двумерное инвариантное подпространство L = Ып(х,у)
относительно базиса х, у имеет вид AL =
а 0>
. Она составлена из ко-
-0 al
ординатных столбцов векторов crf(x), of (у) в базисе х ,у , т.е. из коэффи-
циентов разложений (9.19) этих векторов по базису.
Докажем ортогональность векторов хну. Находим скалярные про-
изведения, учитывая (9.19) и ортогональность преобразования:
| х |2 = (dt(x\с4(х)) = а2| х |2 -2а0(х,у)+02| у |2,
(x,y) = (of(x), с#(у)) = а0| х|2 + (а2-02)(х,у)-а0| у |2.
Подставляя а2 -1 - 02 (см. свойство 5) и сокращая на 0*0, получаем сис-
тему уравнений
p(l/y|2-|x|2k2a(x’J')=0-
-a(| у |2-| х |2)-20(х,у) = О
относительно двух неизвестных (| у |2 -| х |2 ) и (х,у). Определитель мат-
рицы системы
0 -2a
-a -20
= -2(a2 + 02 )= -2 * 0, следовательно, система
имеет только тривиальное решение: | у |2 -| х |2 = 0, (х,у) = 0, т.е. векторы
х и у имеют равные длины и перпендикулярны.
КАНОНИЧЕСКИЙ ВИД ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ
Рассмотрим инвариантные подпространства ортогонального преобра-
зования. По теореме 9.4 линейное преобразование вещественного простран-
ства имеет одномерное или двумерное инвариантное подпространство. Вы-
ясним геометрический смысл сужения ортогонального преобразования на
инвариантное подпространство.
1. Пусть L - одномерное инвариантное подпространство с базисом е{.
Тогда, - собственный вектор преобразования: с^(е1) = Л€1. По свойству 5
А = ±1. Следовательно, ортогональное преобразование Л : L—> L одно-
516
мерного пространства - это либо тождественное преобразование cd(el) = el,
либо отражение (симметрия) cd(el) = -e[.
2. Пусть L - двумерное инвариантное подпространство с ортонорми-
рованным базисом е., е,. Запишем для матрицы А = ортогонально-
\с d)
го преобразования cd: L -> L равенство Ат = А-1:
(a o') 1 (d —
I b dj det Al-c a }
а-Х b
b —а— X
По свойству 6 для собственного преобразования det А = 1, поэтому d - а ,
c = -b, det А = а2 +Ь2 =1, т.е. а = соаф и 6 = sin<p, где ф - некоторый
угол. Следовательно, матрица собственного ортогонального преобразования
двумерного пространства совпадает с матрицей поворота на угол (- ф) (см.
(сояф вшф^
п.5 в разд.9.2.1): А = к = . Для несобственного преобразо-
v ^-8Шф созфу
вания detA = —1 (см. свойство 6), поэтому d = -a, c — by detA =
2 2 [ Н Ь |
= —a —b =-1. Матрица А = имеет два действительных собствен-
~а)
ных значения (Xj=l, 12=-1), так как det(A-XE) =
= X2-a2-b2 = X2 -1. Поэтому несобственное ортогональное преобразова-
ние имеет два одномерных инвариантных подпространства (см. п.1).
Получим канонический вид преобразования. Пусть L - одномерное
или двумерное инвариантное подпространство для ортогонального преобра-
зования cd .Е -*Е. Представим пространство в виде прямой суммы
Е = L®L!l . Выберем в L ортонормированный базис и дополним его до ор-
тонормированного базиса всего пространства. В этом базисе матрица А
преобразования будет иметь блочно-диагональный вид А - diag\AL, Ах ],
где А£ - матрица сужения cd L преобразования cd на L, а А х - матрица
сужения ctf х преобразования cd на L1. Согласно п.1, 2: Ад=(1) или
, х ( СО5ф 5Шф^
А, = (-1) при dim L -1, либо А, = R = при dim L = 2.
L ' ’ L V ^-ЯПф СОБф^ H
Следовательно, в матрице А = diag[AL, А ±) ортогонального преобразования
блок Al имеет один из указанных трех видов. Поскольку подпространство
517
L1 инвариантно относительно ортогонального преобразования с/7 (см.
свойство 7), то к матрице A L применимы те же выводы, что и к матрице
А . Таким образом, справедливо следующее утверждение.
Теорема 9.9 (о каноническом виде ортогонального преобразова-
ния). Для каждого ортогонального преобразования Л : Е —> Е п -мерного
евклидова пространства Е существует ортонормированный базис, в ко-
тором матрица преобразования имеет канонический вид:
Г±1
о
Д= 11 R • (9.20)
О
Rm
к ъ;
На главной диагонали матрицы стоят либо числа 1 или (—1), либо блоки
(cos<p sin ср'j
вида R = , а остальные элементы матрицы равны нулю.
ф sin ср coscpj
Базис (s) = (s1,...,sn), в котором матрица преобразования имеет вид
(9.20), называется каноническим. Заметим, что канонический базис опреде-
ляется неоднозначно.
ПРИВЕДЕНИЕ ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ К КАНОНИЧЕСКОМУ
ВИДУ
Задача приведения ортогонального преобразования к каноническому
виду формулируется следующим образом: требуется найти базис (канони-
ческий), в котором матрица ортогонального преобразования имеет канони-
ческий вид (9.20). Для приведения ортогонального преобразования к кано-
ническому виду нужно выполнить следующие действия.
Нахождение канонического вида ортогонального преобразования (пер-
вый этап).
1. Выбрать базис е1,...,е пространства Е и найти матрицу А преоб-
разования в этом базисе.
1. Составить характеристическое уравнение det(A-XE’) = O и найти
различные его корни А.*,..., А.* (а также их алгебраические кратности).
3. Записать блочно-диагональную матрицу (9.20) канонического вида
ортогонального преобразования:
каждый действительный корень Д кратности п} поместить на главной
диагонали п{ раз;
518
для каждой пары X = а ± Pi комплексных сопряженных корней крат-
(а Р^|
ности т записать т блоков вида R = „ (см. доказательство свой-
ф aj
ства 8 ортогональных преобразований).
Нахождение канонического базиса (второй этап).
4. Для действительного корня Xj кратности zij найти фундаменталь-
ную систему х1,...,хл решений однородной системы (а-Х1Е)х = о. Ли-
нейно независимую систему х. ,...,х векторов (пространства Rn) ортого-
нализировать и нормировать (см. разд. 8.8.5). Получим векторы 5],..., .
5. Для пары X = a±Pi комплексных сопряженных корней кратности
т найти фундаментальную систему Z1,---,Zm решений однородной систе-
мы (A-(a + Pi)E)z = o. Выделяя действительные х^. = Re zy и мнимые час-
ти у. =Imz;., j = 1,—,т > комплексных столбцов г,,..., zm, получить т пар
ортогональных векторов Xj.Jj ;х2,у2;...;хт,ут (пространства /?"). Эту
систему векторов ортогонализировать и нормировать. Получим 2т векто-
ров 3!,...,32т.
6. Выполнить п.4 или п.5 для всех различных корней характеристиче-
ского уравнения. Получаемые в результате группы столбцов последователь-
но записать в матрицу 5 перехода от базиса е1,...,еп к искомому канони-
ческому базису slt...,sn: (s) = (e)S. Матрица 5-1А5 преобразования Л
будет иметь канонический вид (9.20), полученный в п.З.
Замечания 9.7.
1. Собственные векторы ортогональной матрицы, принадлежащие раз-
личным собственным значениям, ортогональны [10,43].
2. Из п. 1 следует, что для получения ортонормированного базиса дос-
таточно ортонормировать отдельно каждую группу векторов, получаемых в
п.4 или п.5 алгоритма, причем по свойству 8 столбцы х., у. в п.5 будут ор-
тогональными.
3. Матрицу вида (9.20) можно представить в виде произведения мат-
риц, каждая из которых есть либо матрица Jiag(l,...,l,-1,1,...,1) простого
отражения относительно гиперплоскости, либо матрица
, 1,...,1] простого вращения двумерной плоскости. Поэтому
любое ортогональное преобразование можно представить в виде компози-
ции простых отражений и простых вращений.
519
Пример 9.5. Ортогональное преобразование : V —»V в базисе
е1>е2’ез
имеет матрицу
. Привести это преобразование
к каноническому виду, т.е. найти базис Sj, s2 , s3, в котором матрица преоб-
разования имеет канонический вид (9.20).
□ Первый этап. Нахождение канонического вида преобразования.
1. Выбираем базис е{ ,е2<ез, в котором задана матрица преобразова-
ния.
2. Составляем характеристическое уравнение
Уравнение имеет три простых (кратности 1) корня: один действительный
Г“ г~
^-i -1 и пару комплексных сопряженных 'k23-^+~i, а=у, Р = -у--
3. Записываем искомый канонический вид (9.20), указывая на главной
диагонали действительный корень = 1 и блок
< 2
A = diag 1,
(»)
Второй этап. Нахождение канонического базиса. Найдем матрицу 5
перехода от данного базиса , е2, е3 к каноническому.
4. Для действительного корня X] кратности 1 находим фундаменталь-
ную систему решений однородной системы (А-Х1Е)х = о . Приводим мат-
рицу системы к упрощенному виду:
Следовательно, фундаментальная
система содержит одно решение
х = (1 1 1)г. Нормируя это решение (поделив координаты на норму
| х | = 712 + I2 +12 = т/з), получаем столбец
г _(4з_ 4з_ Л/
1 3 3 3 J
520
5. Для пары комплексных сопряженных корней Л2 3 = находим
фундаментальную систему решений однородной системы (a-X2E)z = o .
Приводим матрицу системы к упрощенному виду
Следовательно, фундаментальная система содержит одно решение. Полагая
z3 = 1, получаем z=l—y-i ~з+2г И ' ВВД6™6*1 действительную
и мнимую части x = Rez = (-y —| 1)Г, y = Imz=^-Jy & 0^ .Нор-
мируя столбцы (поделив координаты вектора х на его длину
| х j = + (-‘I’)2 +12 = > а координаты вектора у - на |y|=Jy-),
получаем
_ Уб пУ
S2 6 6 3 J ' S3 { 2 2 ) '
6. Записываем полученные в п.4, 5 столбцы 51, s2, s3 в искомую мат-
рицу перехода
.ТП
2
Л
2
. Проверим равенство
5 А = AS (рав-
(»)
О
носильное А = S-1 AS ), находя произведения
(*)
Результаты совпадают.
521
9.6.2. Сопряженные преобразования
Пусть <А : Е —> Е - линейное преобразование п -мерного евклидова
пространства Е . Преобразование еЯ*: Е —> Е называется сопряженным
преобразованию сА , если для любых векторов х и у из пространства Е
выполняется равенство
(4),у)=(хЛ’Ь)). (9.21)
СВОЙСТВА СОПРЯЖЕННОГО ПРЕОБРАЗОВАНИЯ
1. Сопряженное преобразование — линейное.
Докажем, например, однородность: е?*(Лу) = Ло£*(у) VAe/?. Пусть
(е) = (ef ,-.,еп) - ортонормированный базис пространства Е . Тогда
(ер cZr*(Ay))= Ау)=А у)=А (ер еА* (у ))= (ер W*(.y)),
т.е. первые координаты векторов с/Г*(Ау) и Ао?*(у) равны. Аналогично по-
казывается, что равны и остальные координаты этих векторов. Значит, это
равные векторы. Аддитивность сопряженного преобразования доказывается
аналогично.
2. Для каждого линейного преобразования существует единственное
сопряженное преобразование, причем матрица сопряженного преобразова-
ния (в любом ортонормированном базисе) является транспонированной по
отношению к матрице данного преобразования (в том же базисе).
Пусть в ортонормированном базисе (е)= (е1,...,ел) преобразование сА
имеет матрицу А . Рассмотрим преобразование сА', которое в данном бази-
се имеет матрицу АТ . Для координатных столбцов х, у любых векторов
х , у имеем равенство (Ах,у)= хт Ату = {х,Ату) (см. (8.27) в разд.8.8.2).
Следовательно, (сА(х\ у) = (х, сА'(у)), т.е. согласно (9.21) преобразование
сА' - сопряженное: еА' = еА*. Итак, сопряженное преобразование существу-
ет и его матрица в любом ортонормированном базисе является транспони-
рованной Ат по отношению к матрице данного преобразования. Отсюда
также следует единственность, так как транспонированная матрица нахо-
дится однозначно.
3. Если L — подпространство, инвариантное относительно линейного
преобразования сА ’.Е —> Е , то его ортогональное дополнение L1 является
инвариантным подпространством относительно сопряженного преобразо-
вания сА*. Действительно, покажем, что образ cZf*(y) любого вектора
у е L1 ортогонален любому вектору х& L , т.е. с^*(у)е L1. Учитывая, что
522
cZF(x)g L, по определению (9.21) получаем (x, cZf*(y))=(of(x), y) = 0, что и
требовалось доказать.
Замечания 9.8.
1. Из второго свойства следует, что на сопряженные преобразования
переносятся свойства транспонированных матриц (см. разд. 1.4.1). В частно-
сти: (cZf*)*=cZf, (of®)* = JB’cZf*, а также (cZf-1) = (c?f*) ' Для обратимого
преобразования.
2. Матрица А* сопряженного преобразования of* в произвольном
(неортонормированном) базисе связана с матрицей А преобразования of
следующей формулой
A* =G~'ATG,
где G - матрица Грама данного базиса.
3. Условие ортогональности преобразования of (см. свойство 2) мож-
но представить в виде of* = с/Г1.
9.6.3. Самосопряженные преобразования
Линейное преобразование of :Е —» Е п -мерного евклидова простран-
ства Е называется самосопряженным, если оно является сопряженным
самому себе, а именно of * = of , т.е. (of (х), у) = (х, of (у)) для любых векто-
ров х и у из пространства Е .
Например, самосопряженными преобразованиями являются нулевое
преобразование О и тождественное £.
СВОЙСТВА САМОСОПРЯЖЕННОГО ПРЕОБРАЗОВАНИЯ
1. Матрица А самосопряженного преобразования в любом ортонор-
мированном базисе является симметрической (АТ = А), и наоборот, если в
каком-либо ортонормированном базисе матрица преобразования симмет-
рическая, то это преобразование самосопряженное.
2. Все корни характеристического уравнения самосопряженного пре-
образования действительные.
В самом деле, предположим противное, а именно существование пары
комплексных сопряженных корней А. = а ± |3i, |3 * 0. По теореме 9.4 преоб-
разование имеет двумерное инвариантное подпространство с линейно неза-
висимыми образующими х и у , удовлетворяющими системе (9.19), кото-
рая следует из (9.7):
of(x)= ах -ру,
of(y) = px + ay.
Найдем скалярные произведения:
523
Mx), y) = ct(x, у)—Р| у |2, (x,cZf(y))=P| x|2 + ct(x, y).
Левые части равенств совпадают из-за самосопряженности преобразования
<sf . Значит, равны и правые части: а (х, у)—Р | у |2 = Р | х |2 + ос (х, j). От-
сюда p(|x|2+|j|2)=0. Поскольку Р * 0, то х-у = о, что противоречит
линейной независимости хну.
3. Собственные векторы, принадлежащие различным собственным
значениям самосопряженного преобразования, ортогональны.
Действительно, пусть cZf(x) = A1x и cZf(y) = A2y , At *А2.Тогда
(с^(х),у) = А,(х,у) и (х,«?(у)) = А2(х,у).
Так как (cZf(x), у) = (х, cZf(y)), то А^х, у) = А2(х, у) <=> (А1-А2)(х, у)=0.
Отсюда (х, у)=0, так как А( А2. Значит, собственные векторы х и у ор-
тогональны.
4. Если L — подпространство, инвариантное относительно самосо-
пряженного преобразования сЯ :Е —> Е, то его ортогональное дополнение
L1 также инвариантно относительно преобразования .
Это следует из свойства 3 сопряженных преобразований (см.
разд. 9.6.2).
Теорема 9.10 (о диагонализируемости самосопряженного преобра-
зования). Для всякого самосопряженного преобразования сЛ :Е —> Е
п -мерного евклидова пространства Е существует ортонормированный
базис (из собственных векторов), в котором матрица преобразования име-
ет диагональный вид
А = <йа^(А1.Ап), (9.22)
где Ар..., А — собственные значения преобразования с/1, повторенные
в соответствии с их кратностью.
Диагональный вид (9.22) называется также каноническим видом само-
сопряженного преобразования, а базис, в котором матрица имеет вид (9.22),
- каноническим.
Для доказательства теоремы 9.10 нужно показать, что если существует
ортонормированный базис пространства Е , состоящий из собственных век-
торов преобразования, тогда оно приводится к диагональному виду (см.
разд. 9.5.1). Действительно, для собственного значения А] найдем единич-
ный собственный вектор s1. Представим пространство в виде прямой сум-
мы Е - L] ® , где Lj = Lin(s{) - одномерное инвариантное подпростран-
ство. Сужение преобразования (по свойству 4) на инвариантное подпро-
странство является самосопряженным. Поэтому в 1^ можно найти од-
524
номерное инвариантное подпространство L2 = Lin(s2), где s2 - собствен-
ный вектор, перпендикулярный . Продолжая аналогичным образом, полу-
чим Е =1^ ®...®Ln , где Lj - одномерное инвариантное подпро-
странство, причем базис Sj ,...,sn.из собственных векторов ортогональный,
а после нормировки - ортонормированный.
ПОЛОЖИТЕЛЬНЫЕ И НЕОТРИЦАТЕЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
Самосопряженное преобразование называется положительным
(неотрицательным), если (cZf(x),x)>0 для любого ненулевого вектора
хе Е (соответственно (cZf(x),x)>0 для любого вектора хе Е ).
Эти понятия связаны с положительностью (неотрицательностью) сим-
метрических матриц и квадратичных форм (см. разд. 6.5.4). Действительно,
запишем неравенство (cZf(x),x)>0 в координатной форме (в ортонормиро-
ванном базисе). Учитывая, что (c/f(x),x) = (Ax,x) = хТАтх = хтАх, получаем
хтАх>0 для любого столбца хе Rn, что совпадает с определением неот-
рицательности квадратичной формы хтАх .
Отметим следующие свойства положительных и неотрицательных
преобразований.
1. Преобразование сА положительно (неотрицательно) тогда и
только тогда, когда все его собственные значения положительные (неот-
рицательные).
2. Для любого неотрицательного (положительного) преобразования
существует такое единственное неотрицательное (положительное)
преобразование £ , что J82 = <Д.
Действительно, в каноническом базисе (s) = (sI,...,sn) матрица преоб-
разования Д имеет диагональный вид (9.22). Преобразование определя-
ем его матрицей в базисе (s), полагая В = diag(jk^. Тогда В2 = А .
3. Преобразования и ДД* являются самосопряженными неот-
рицательными (положительными) для любого (невырожденного) преобра-
зования <А.
Теорема 9.11 (о разложении невырожденного линейного преобра-
зования). Любое невырожденное линейное преобразование :Е —» Е
п -мерного евклидова пространства Е можно представить в виде компо-
зиции положительного самосопряженного преобразования и ортогонально-
го преобразования.
Действительно, рассмотрим самосопряженное положительное преобра-
зование © = (см. свойство 3). Для него существует такое положи-
525
тельное самосопряженное преобразование $ , что £) = <£<£' = <£'* «S' (свойст-
во?). Рассмотрим преобразование 5В = сД 6’~'. Это преобразование ортого-
нальное (см. п.З замечаний 9.8), так как
© © £ £
Следовательно, сА = <£8 - композиция положительного самосопряженного и
ортогонального преобразований.
Замечания 9.9.
1. Из теоремы 9.10 следует, что для любой действительной симметри-
ческой матрицы А существует диагональная матрица Л = diagfa,...,^)
(с собственными числами матрицы А на главной диагонали) и ортогональ-
ная матрица S (ST = 5-1), что Л = STAS .
2. Всякое обратимое самосопряженное преобразование можно пред-
ставить как композицию растяжений (с коэффициентами, равными собст-
венным числам Х.],...,А.я) вдоль взаимно перпендикулярных направлений
(задаваемых ортонормированным базисом sy,...,sn из собственных векто-
ров). Растяжение с отрицательным коэффициентом А.] < 0 понимается как
композиция зеркального отражения и растяжения с коэффициентом | Л.j |.
3. Теорема 9.11 справедлива для любого линейного преобразования,
если условие положительности самосопряженного преобразования заменить
условием его неотрицательности.
4. Геометрический смысл теоремы 9.11 следующий: любое невырож-
денное линейное преобразование можно представить как композицию пре-
образований, каждое из которых есть либо простое отражение (относитель-
но гиперплоскости), либо простой поворот (двумерной плоскости), либо
растяжение вдоль взаимно перпендикулярных направлений.
ПРИВЕДЕНИЕ САМОСОПРЯЖЕННОГО ПРЕОБРАЗОВАНИЯ
К ДИАГОНАЛЬНОМУ ВИДУ
Пусть в некотором ортонормированном базисе (е) = (е1,...,еп) самосо-
пряженное преобразование сД :Е -> Е имеет матрицу А . Требуется найти
базис (s)= в котором матрица преобразования имеет диагональ-
ный вид (9.22). Для решения задачи нужно выполнить следующие действия.
Нахождение диагонального вида матрицы самосопряженного преобра-
зования (первый этап).
1. Составить характеристическое уравнение det(j-A.£') = O, найти его
корни Л.,,..., kk и их алгебраические кратности п1пк, п}+... + пк=п .
526
2. Составить искомую диагональную матрицу (9.22):
A. = diag( А.2,...,А,2,..., А^.-.А.* ).
"1 Я2
Нахождение матрицы S перехода от данного базиса (е) к канониче-
скому базису (s) (второй этап).
3. Для корня А.] кратности п} найти фундаментальную систему
Ф]фя решений однородной системы (л -Х}Е)х = о . Столбцы ф1,..., фя
ортогонализировать и нормировать. Получим л, столбцов .
4. Записать полученные столбцы Tj ,...,тя в первые столбцов мат-
рицы S.
Выполнить п.З, 4 для остальных собственных значений Л2,..., А.* , до-
бавляя полученные столбцы в матрицу S. В результате получим искомую
матрицу перехода: (s) = (e)S .
Пример 9.6. Самосопряженное преобразование cZ?: Е —> Е в ортонор-
fi 1 о
мированном базисе , е2, е3 имеет матрицу А = 1 1
1 . Привести это
I
U 1
преобразование к диагональному виду, т.е. найти ортонормированный базис
Sj, s2, s3, в котором матрица преобразования имеет диагональный вид
(9.22), и найти эту диагональную матрицу.
□ Первый этап. Находим диагональный вид матрицы преобразования.
1. При решении примера 9.2 были найдены корни характеристического
уравнения А^ = 0 (кратности п} = 2) и А.2 = 3 (кратности n2 = 1).
2. Составляем искомую диагональную матрицу Л = diag{b, 0,3).
Нахождение матрицы S перехода к каноническому базису (второй
этап).
З1. Для собственного значения A.J = 0 в примере 9.2 была найдена
фундаментальная система решений ф, = (1 0 - if, Ф2=(1 -1 Of. Ор-
тогонализируем их, используя метод Грама-Шмидта (см. разд.8.8.5). Поло-
жим Vi=<Pi=(l 0 -if, ф2=ф2-аф]. Коэффициент а выбираем из
условия ортогональности (ф], ф2) = 0:
' 1 '
О
(1 0 -1)
= 1(1-а)+0-(-1)+(-1)а = 0
1-а-2 = 0.
527
Следовательно, а = 0,5 и \|/2=(0,5 _1 0,5 )г. Нормируем столбцы
(|V1| = V2,|v2| = 7|):
Полученные столбцы записываем в искомую матрицу
* . Звездочкой обозначены неизвестные пока элементы
матрицы.
З2. Для собственного значения Х2 =3 фундаментальная система ре-
шений содержит одно решение <р3 = (1 1 1)Г (см. пример 9.2). Нормируя
к (4з Л Уз/
этот столбец, получаем $3 = -у- -у- -у I .
42. Полученный столбец дописываем в матрицу, полученную в п. 4*,
(£ А
2 6 3
s= о -4 4-
/2 Уб /з
I 2 6 3 J
Матрица перехода к каноническому базису найдена.
9.6.4. Приведение квадратичной формы к главным осям
В разд. 6.5.3 была рассмотрена задача приведения вещественной квад-
ратичной формы
?(*)= = x?Ax (9’23)
i=i j=i
п переменных х ,...,х к каноническому виду (6.18)
£(y) = A1y2+X2y22+... + V2 (9.24)
при помощи невырожденной линейной замены переменных х = Sy Для ре-
шения этой задачи использовался метод Лагранжа (см. разд.6.5.2).
Рассмотрим другой подход к решению. Линейную невырожденную за-
мену переменных х = Sy с ортогональной матрицей S (S~l = ST) будем на-
528
зывать ортогональной заменой переменных (или ортогональным преоб-
разованием переменных).
Сформулируем задачу приведения квадратичной формы к главным
осям-, требуется найти ортогональную замену переменных х = Sy
(S-1 = ST), приводящую квадратичную форму (9.23) к каноническому виду
(9.24).
Для решения используем следующий геометрический смысл задачи.
Будем считать переменные х1,...,хп координатами вектора х п -мерного
евклидова пространства Е в ортонормированном базисе (е)= (е1,...,еп), а
матрицу А квадратичной формы (9.23) - матрицей некоторого линейного
преобразования eti'.E —> Е в том же базисе. Причем это преобразование
самосопряженное, так как его матрица симметрическая: АТ = А. Квадра-
тичную форму (9.23) можно представить в виде скалярного произведения
?(х)=(о?(х),х)=(х, вф)).
Ортогональной замене переменных х = Sy соответствует переход от одного
ортонормированного базиса к другому. Действительно, пусть S - матрица
перехода от ортонормированного базиса (е) к ортонормированному базису
(s)= (sp...,sn), т.е. (s) = (e)s и S-' = ST. Тогда координаты х вектора х в
базисе (е) и координаты у того же вектора в базисе (s) связаны формулой
(8.11): x = Sy.
Таким образом, задача приведения квадратичной формы к главным
осям может быть сформулирована так: требуется найти в пространстве Е
такой базис, в котором матрица самосопряженного преобразования d име-
ет диагональный вид. Эта задача была решена в разд. 9.6.3. По теореме 9.10
нужно выбрать ортонормированный базис из собственных векторов самосо-
пряженного преобразования. При этом матрица перехода 5 к каноническо-
му базису оказывается ортогональной: ST = 54 .
Сформулируем этот результат для квадратичной формы.
Теорема 9.12 (о приведении квадратичной формы к главным
осям). Вещественная квадратичная форма (9.23) при помощи ортогональ-
ного преобразования переменных х = Sy может быть приведена к канони-
ческому виду (9.24), где Л1.- собственные значения матрицы А.
Следствие. Квадратичная форма (9.23) является положительно опре-
деленной (неотрицательно определенной) тогда и только тогда, когда все
собственные значения ее матрицы положительны (неотрицательны).
Замечания 9.10.
1. При линейной невырожденной замене переменных матрица квадра-
тичной формы изменяется по формуле (6.10): А'= ST AS . Для ортогональ-
34 - 4549
529
ной матрицы 5 эта формула принимает вид А' = S~lAS, который совпадает
с формулой (9.4) изменения матрицы линейного преобразования при замене
базиса.
2. Для нахождения канонического вида (9.24) достаточно определить
все корни Aj ,...,ЛЛ (среди которых могут быть равные) характеристическо-
го уравнения det(A - кЕ) = 0.
3. Следствие теоремы 9.12 можно использовать для анализа знакоопре-
деленности квадратичной формы:
если все собственные значения положительные (отрицательные), то
квадратичная форма положительно (отрицательно) определенная;
если все собственные значения неотрицательные (неположительные),
то квадратичная форма неотрицательно (неположительно) определенная;
если имеются собственные значения разных знаков, то квадратичная
форма неопределенная (знакопеременная).
4. Результаты, сформулированные в п.З замечаний, могут быть исполь-
зованы для проверки достаточных и необходимых условий второго порядка
в задаче поиска безусловного экстремума функций (см. разд. 6.5.5). Для это-
d2f(x)
го следует наити собственные значения Л,,...,Л матрицы Гессе —в
1 " dxTdx
каждой из стационарных точек х* функции /(х) = /(х1,...,хл).
Если все собственные значения положительные: Х(. >0, i = l,...,n, то
в точке х* локальный минимум;
если все собственные значения отрицательные: \<0, i = l,...,n, то
в точке х* локальный максимум;
если все собственные значения неотрицательные: к*. >0, i = l,...,n , то
в точке х* может быть локальный минимум;
если все собственные значения неположительные: <0, i = 1,...,и, то
в точке х* может быть локальный максимум;
если собственные значения , i - 1,...,л, разных знаков, то в точке х*
нет экстремума;
если все собственные значения нулевые: Х(. = 0, i = , то требуется
дополнительное исследование.
5. Задача приведения квадратичной формы к главным осям решается
при помощи алгоритма, рассмотренного в разд. 9.6.3. При этом находится
диагональный вид матрицы квадратичной формы и ортогональная матрица
S замены переменных х = Sy, приводящей квадратичную форму к канони-
ческому виду (к главным осям).
530
Пример 9.7. Выяснить знакоопределенность квадратичной формы
q(x) = х2 + 2х{х2 + 2xjX3 + х2 + 2х2х3 + х2
и найти ортогональную замену переменных х = Sy, приводящую квадра-
тичную форму к каноническому виду (к главным осям).
Л
□ Составляем матрицу квадратичной формы: А = 1
1 Г
1 1 . В приме-
1 I
ре 9.6 были найдены собственные значения этой матрицы: = Л2 = 0,
Л3 = 3. Все собственные значения неотрицательные, поэтому квадратичная
форма является неотрицательно определенной (см. п.4 замечаний 9.10).
В примере 9.6 была найдена ортогональная матрица
приводящая матрицу А к диагональному виду Л = diag(0,0,3). Записываем
искомую ортогональную замену переменных х = Sy:
X -—V +—v + —у х = —— у +—у • х =-—у +—у +—у
1 2 Ч б “2 3 •'З ’ 2 3 3 “з ’ 3 2 “1 6 У2 3 “З
и квадратичную форму в каноническом виде: (у) = Зу 2 .
Пример 9.8. Найти точки локального экстремума функции
/(х) = Зх3 + х* - 5х3 - 2х2х2 + х2 .
□ В п.1, примера 6.13 найден градиент функции, а из необходимого
условия экстремума первого порядка три стационарные точки: х° = (о о)г,
х‘=(1 1)Г,х2=(-1 1)Г.
Матрица Гессе имеет вид
df (х) (60х3 + 12х2 - ЗОх, - 4х, - 4х.
dx7dx ч - 4xJ 2 ,
Найдем собственные значения матрицы Гессе в каждой стационарной точке:
#(x°)_f° О') #(х')_Г 38 -4^ df(x2)r~22 4^1
dxTdx [б 2j’ dxTdx [-4 2 J’ dx7 dx [ 4 2j
и воспользуемся п.4 замечаний 9.10.
34*
531
О ( \Г [ 'J V I
В точке х =(0 0) матрица Гессе имеет вид .Из уравнения
-X
0
О
2-Х
= 0 находим X] = 0, Х2 = 2. Так как все собственные значения
неотрицательные, то в точке х° может быть локальный минимум и для
окончательного вывода требуется дополнительное исследование (см. при-
мер 6.13).
f 38 — 4^|
В точке х1 =(l if матрица Гессе имеет вид I I. Из уравнения
38-Х -4
-4 2-Х
= 0, или Х2-40Х + 60 = 0 получаем X] 2 = 20 +V340 . По-
скольку все собственные значения положительные, то в точке х1 локальный
минимум функции.
2 / V <-22
В точке х =(-1 1) матрица Гессе имеет вид
\ 4 2
. Из уравне-
ния
-22-Х
4
4
2-Х
= 0,или Х2 + 2ОХ-6О = О получаем X]2 = -10 +V160 .
Поскольку собственные значения имеют разные знаки, то в точке х2 нет
экстремума.
9.6.5. Линейные преобразования унитарных пространств
Рассмотрим линейные преобразования конечномерных унитарных
пространств, т.е. комплексных линейных пространств со скалярным произ-
ведением (см. разд. 8.8.9). Заметим, что в отличие от линейных преобразо-
ваний вещественных пространств любое линейное преобразование ком-
плексного пространства всегда имеет собственные значения и собственные
векторы, которые совпадают с собственными значениями и собственными
векторами матрицы этого преобразования, определенной относительно лю-
бого базиса.
СОПРЯЖЕННЫЕ ПРЕОБРАЗОВАНИЯ
Пусть сА : U -> U - линейное преобразование п -мерного унитарного
пространства U . Преобразование :U ->U называется сопряженным
преобразованию , если для любых векторов х и у из пространства U
выполняется равенство
532
И(4 y) = (x,ctf'(/)).
Определения сопряженных преобразований унитарных и евклидовых
пространств совпадают. Поэтому они имеют аналогичные свойства
(см. разд.9.6.2).
1. Сопряженное преобразование - линейное.
2. Для каждого линейного преобразования существует единственное
сопряженное преобразование, причем матрица сопряженного преобразова-
ния является сопряженной по отношению к матрице данного преобразова-
ния. Другими словами, если А - матрица преобразования <Д (определенная
относительно ортонормированного базиса), то сопряженная матрица А* яв-
ляется матрицей сопряженного преобразования (определенной относи-
тельно того же базиса).
3. Если L — подпространство, инвариантное относительно линейного
преобразования <Д '.U -yU, то его ортогональное дополнение Z1 является
инвариантным подпространством относительно сопряженного преобразо-
вания <Д*.
ЭРМИТОВО ПРЕОБРАЗОВАНИЕ
Линейное преобразование cA’.U -> V п -мерного унитарного про-
странства U называется эрмитовым, если оно является сопряженным са-
мому себе, а именно Д* , т.е. {уА(х\ у) = (х, с^(у)) для любых векторов
х и у из пространства U .
Определение эрмитова преобразования аналогично определению само-
сопряженного преобразования евклидова пространства. Поэтому они имеют
аналогичные свойства (см. разд.9.6.3).
1. Матрица А эрмитова преобразования в любом ортонормирован-
ном базисе является эрмитовой (А* = А), и наоборот, если в каком-либо
ортонормированном базисе матрица преобразования эрмитова, то это
преобразование является эрмитовым.
2. Все корни характеристического уравнения эрмитова преобразова-
ния действительные.
3. Собственные векторы, принадлежащие различным собственным
значениям эрмитова преобразования, ортогональны.
4. Если L - подпространство, инвариантное относительно эрмитова
преобразования <Д :U -yU, то его ортогональное дополнение L1 также
инвариантно относительно преобразования .
533
УНИТАРНОЕ ПРЕОБРАЗОВАНИЕ
Преобразование :U -+U п -мерного унитарного пространства U
называется унитарным (изометрическим), если оно сохраняет скалярное
произведение векторов, т.е.
(c^(v),c#(h')) = (v,w) V v, weU.
Унитарное преобразование аналогично ортогональному преобразова-
нию евклидова пространства и обладает соответствующими свойствами (см.
свойства ортогонального преобразования в разд.9.6.1).
1. Унитарное преобразование - линейное.
2, Линейное преобразование унитарно тогда и только тогда, когда
оно отображает ортонормированный базис в ортонормированный.
3. Линейное преобразование -^U унитарно тогда и только то-
гда, когда его матрица А в любом ортонормированном базисе является
унитарной, т.е. А* = А-1.
4. Унитарное преобразование обратимо.
5. Все собственные значения унитарного преобразования по модулю
равны единице.
6. Определитель матрицы унитарного преобразования по модулю ра-
вен единице.
7. Пусть L - инвариантное относительно унитарного преобразова-
ния cA:U U подпространство U . Тогда его ортогональное дополнение
L1 также инвариантно по отношению к преобразованию .
НОРМАЛЬНОЕ ПРЕОБРАЗОВАНИЕ
Линейное преобразование сА: U —> U п -мерного унитарного про-
странства U называется нормальным, если оно перестановочно со своим
сопряженным, т.е. сАсА* = <Л*еА.
Эрмитовы и унитарные преобразования являются нормальными, так
как из равенства сА = еА* следует, что <Л<Л* = сАсА - сА*<Л , а из равенства
с#-1 — сА* следует, что сА<Л* = $ = <Л~1<Л = <Л*сА .
Нормальное преобразование обладает следующими свойствами [10].
1. Каждый собственный вектор нормального преобразования
<Л .и -+U является также собственным вектором сопряженного преоб-
разования еА*.
2. Пусть L - подпространство, инвариантное относительно нор-
мального преобразования Л '.U —>U. Тогда его ортогональное дополнение
L1 также инвариантно по отношению к преобразованию сА .
534
Теорема 9.13 (о диагоиализируемости нормального преобразова-
ния). Для всякого нормального преобразования cA:V -^U п -мерного уни-
тарного пространства U существует ортонормированный базис (из соб-
ственных векторов), в котором матрица преобразования имеет диагональ-
ный вид
h = diag[kx.А„), (9.25)
где Ар..., Ап — собственные значения преобразования , повторенные
в соответствии с их кратностью.
Следствие 1. Унитарное преобразование приводится к диагональному
виду (9.25) с собственными значениями Ар..., Ад, по модулю равными еди-
нице.
Следствие 2. Эрмитово преобразование приводится к диагональному
виду (9.25) с вещественными собственными значениями Ар..., Ап.
Методика приведения нормального преобразования к диагональному
виду аналогична методике приведения самосопряженного преобразования к
диагональному виду (см. разд.9.6.3).
Задачи для самостоятельного решения
9.1. Выяснить, является ли заданное преобразование пространства У2
радиус-векторов на координатной плоскости Оху инъективным, сюръек-
тивным, биективным, обратимым, линейным (для линейного преобразова-
ния найти ядро, образ, дефект, ранг):
л
а) поворот плоскости вокруг начала координат на угол <р = —;
б) поворот плоскости вокруг точки а(1; 1) на угол Ф = “»
в) параллельный перенос на ненулевой вектор а : v —> v + а ;
г) симметрия относительно прямой, проходящей через начало коорди-
нат;
д) симметрия относительно прямой, не проходящей через начало коор-
динат;
е) ортогональное проектирование на данную прямую, проходящую че-
рез начало координат;
ж) ортогональное проектирование на прямую, не проходящую через
начало координат.
Ответ-, а,г) преобразование инъективное, сюръективное, биективное,
обратимое, линейное, ядро: { 0 }, образ: V2 , дефект: 0; ранг: 2; б,в,д) преоб-
разование инъективное, сюръективное, биективное, обратимое, не является
линейным; е) преобразование неинъективное, несюръективное, небиектив-
535
ное, необратимое, линейное, ядро - множество радиус-векторов, перпенди-
кулярных данной прямой; образ - множество радиус-векторов, принадле-
жащих данной прямой; дефект: 1; ранг: 1; ж) преобразование неинъектив-
ное, несюръективное, небиективное, необратимое, не является линейным.
9.2. Найти ядро и образ линейного преобразования <Л : R3 —> Л3, кото-
Г 0 1 Г
рое в стандартном базисе пространства R3 имеет матрицу А = 1 10.
-1 0 1
Указать, является ли преобразование инъективным, сюръективным, биек-
тивным, обратимым.
Ответ: Ker = Lzn((l -1 1)г), 1тсЛ = 1лп^0 -1 1)г,(1 1 0)г),
преобразование неинъективное, несюръективное, небиективное, необрати-
мое.
2 2 ГП I2
9.3. Линейное преобразование : R —> R в базисе а2 = I I, п2 ~ I g
(3 S''
имеет матрицу А = I ,
, Г3) Г4') f4 б')
се =1 1 1,&2 =1 2 I имеет матрицу
а линейное преобразование J8: R2 —> R2 в бази-
. Найти матрицу преобразо-
вания ef + Я в базисе Ьх, Ь2.
Ответ:
' 44
-29,5
44
-25
9.4. Линейное преобразование вещественного пространства задано в
некотором базисе матрицей: а, б, в, г из примера 7.5. Привести преобразова-
ние к диагональному виду путем перехода к новому базису, т.е. найти диа-
гональный вид А матрицы преобразования и матрицу 5 перехода к новому
базису.
7-1 0") (2 П (4 0А (2 1
Ответ: а) А = 1 , S = ;б)А = , S = ;
1^0 -2) (j 1) 1^0 9) 1^1 -2)
в, г) привести к диагональному виду нельзя. В п.а, б матрица S определяет-
ся неоднозначно.
9.5. Линейное преобразование комплексного пространства задано в не-
котором базисе матрицей: а, б, в, г из примера 7.6. Привести преобразование
к диагональному виду путем перехода к новому базису, т.е. найти диаго-
нальный вид А матрицы преобразования и матрицу S перехода к новому
базису.
Ответ: см. ответы к примеру 7.6.
9.6. Линейное преобразование задано в некотором базисе матрицей: а,
б, в из примера 7.8. Привести преобразование к каноническому виду, т.е.
найти жорданову форму J матрицы преобразования и матрицу S перехода
к жорданову базису.
Ответ: см. ответы к примеру 7.8.
9.7. Ортогональное преобразование задано в некотором ортонормиро-
ванном базисе матрицей:
Г i 3 2 3 _1> 3 ( ± 2 х 2 2 Г 3 4 1 4 4
а) А = 2 3 3 2 3 ; б) А = х 2 2 41 2 ; в) А = £ 4 3. 4 Уб 4
2 2 41 _41 г\ А _А 1
1 3 3 3 J 1 2 2 0 I4 4 2 J
Привести преобразование к каноническому виду, т.е. найти матрицу А пре-
(*)
образования в каноническом базисе и матрицу S перехода к каноническому
базису.
Ответ: а) А = О
w о
'1
б) А= О
О
О
-1
9.8. Для линейного преобразования пространства V2 радиус-векторов
на координатной плоскости Оху :
а) проектирование на ось Ох параллельно прямой у = х;
б) отражение относительно оси Ох параллельно прямой у = х;
в) поворот вокруг начала координат на угол (р
найти соответствующее сопряженное преобразование.
Ответ: а) проектирование на прямую у = -х параллельно оси Оу ;
б) отражение относительно прямой у = —х параллельно оси Оу ;
в) поворот на угол (- <р).
537
9.9. Привести квадратичную форму к главным осям, т.е. найти канони-
ческий вид д(у) квадратичной формы и матрицу S соответствующей орто-
гональной замены переменных х = Sy:
а) д(х) = 2х(х2 ; б) д(х) = Зх2 + Зх2 + 4Х]Х2 + 4хрс3 - 2х2х3 .
Ответ: а) д(у) = у2 -у2, S= \
2
2
б) д(у) = ~2у2+4у2+4у2, S =
2
О
5
9.10. Пусть V - конечномерное линейное пространство над полем
действительных чисел; £ - тождественное преобразование: ₽(v) = v,
V v е V; О - нулевое преобразование: о(х)=о Xf v е V.
а) Считая, что dim V = 2 , при всех действительных значениях а найти
преобразование X: V —> V , удовлетворяющее уравнению
тХ2 + пХ + а£ = О,
где т - номер учебной группы, п - номер студента по списку учебной
группы.
б) При каких значениях р и д существует преобразование %: V -> V ,
удовлетворяющее уравнению
X2+pX + q& = 0 ?
Найти общий вид и выяснить геометрический смысл преобразования X в
случаях его существования. Первоначально рассмотреть случай dim К = 2 .
ГЛАВА 10. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ
АЛГЕБРЫ
10.1. ОСНОВНЫЕ ПОЛОЖЕНИЯ. НОРМЫ МАТРИЦ
Классическим средством изучения математических моделей и исследо-
ваний на их основе свойств реальных объектов являются аналитические
методы, позволяющие получать точные решения в виде математических
формул. Эти методы дают наиболее полную информацию о решении задачи,
и они до настоящего времени не утратили своего значения. Однако, к сожа-
лению, класс задач, для которого они могут использоваться, весьма ограни-
чен. Поэтому решение, как правило, осуществляется численными методами.
Численные методы - это методы приближенного решения задач при-
кладной математики, основанные на реализации алгоритмов, соответствую-
щих математическим моделям. Наука, изучающая численные методы, назы-
вается также численным анализом, или вычислительной математикой.
Численные методы, в отличие от аналитических, дают не общие, а частные
решения. При этом требуется выполнить достаточное количество арифмети-
ческих и логических действий над числовыми и логическими массивами.
В численном анализе используются два класса численных методов:
1. Прямые методы, позволяющие найти решение за определенное
число операций.
2. Итерационные методы, основанные на использовании повторяю-
щегося (циклического) процесса и позволяющие получить решение в ре-
зультате последовательных приближений. Операции, входящие в повто-
ряющийся процесс, составляют итерацию.
Решения, получаемые численными методами, в силу их приближенно-
сти содержат некоторые погрешности. Рассмотрим их источники и типы.
Один из типов погрешностей обусловлен неадекватностью выбран-
ной математической модели исходной физической. Эта неадекватность в
большей или меньшей степени присуща всем приближенно решаемым зада-
чам. Данная погрешность является неустранимой. Неточность (неопреде-
ленность) задания исходных данных приводит также к неустранимым по-
грешностям.
Если мы устраним неопределенность в исходных данных и найдем ре-
шение с помощью какого-либо численного метода, то получим результат, не
в точности соответствующий исходным данным в силу погрешности чис-
ленного метода. В компьютере все числа представляются в конечном виде,
и поэтому при использовании вычислительного алгоритма реализуются
ошибки арифметических и других операций над числами, а также ошибки
округления.
Дадим некоторые понятия из теории погрешностей вычислительных
действий над приближенными величинами.
539
Пусть х - точное, но, как правило, неизвестное значение некоторой
величины, а т - ее известное приближенное значение.
Абсолютной погрешностью приближения х называется разность
Д х = х - х (в общем случае Д х имеет размерность величины х).
Относительная погрешность приближения х обозначается 8 и вы-
Дх л
ражается отношением 8 = :—г ( 8 - безразмерная величина, х 0). Часто
И
величина 8 вычисляется в процентах, и тогда она умножается на сто.
Так как величина х, как правило, неизвестна, а погрешность необхо-
димо определять, то в рассмотрение вводится предельная абсолютная по-
грешность Д(х):
Дх = | х - х | < Д(х) .
Раскрывая в этом неравенстве модуль, получаем соотношение, задающее
отрезок, которому принадлежит точное значение: х - Д(х) < х < х + Д(х).
Таким образом, величина х находится в Д-окрестности (дельта-
окрестности), определяемой величинами х и Д(х) .
Предельная относительная погрешность приближения
Д(х)
определяется отношением 8(х) = . А. .
Такие погрешности оцениваются при рассмотрении численных мето-
дов. Эти оценки могут производиться до выполнения вычислений (априор-
ные оценки) и после них (апостериорные оценки).
Как правило, численный алгоритм решения задачи завершается, если
погрешность меньше заданной заранее величины.
При решении многих практических задач необходимо как-то ’’изме-
рять” матрицы, чтобы говорить, что одна матрица больше другой. Правило,
по которому матрице (в частности, матрице-столбцу) ставится в соответст-
вие некоторое неотрицательное число, имеющее смысл меры, определяет
понятие норма.
Нормой матрицы-столбца
называется функция ||х||, удов-
летворяющая следующим аксиомам:
I. ||х|| > 0 для любого столбца х, причем ]|х]| = 0 в том и только в том
случае, если х - нулевой столбец;
540
2. ||ах|| - |а| - ||х|| для любого действительного числа а;
3. ||х + ^|| <||х||+||у|| для любых двух столбцов хи у размеров (их1).
Аксиома 3 называется неравенством треугольника.
Примером нормы матрицы-столбца может быть семейство норм
К<=1 7
где при любом целом положительном р определяется функция, удовлетво-
ряющая условиям 1-3.
Приведем часто используемые нормы матриц-столбцов.
1. || х [j] = шах |х, | - максимум среди модулей элементов столбца;
п
2. IIх IL = 22 Iх'I - сУмма модулей элементов столбца;
/=1
| п
3. || х ||3 = I ^х? - квадратный корень из суммы квадратов элементов.
I <=1
Последняя норма называется евклидовой, так как совпадает с модулем
столбца (длиной вектора), т.е. || х ||3 = |х| = 7хгх .
Замечания 10.1.
1. Можно показать [8], что справедливы следующие соотношения
НХН2 s Из - llxlli ’ а также Из " 11х112 ’ И " Из •
2. Норма может быть использована при анализе сходимости последо-
вательностей матриц-столбцов.
Последовательность матриц-столбцов |х(1),...,х^\...} сходится
к столбцу х„, если lim = х,г для всех / = 1,...,и. Для того чтобы после-
довательность |x^1),...,x(i\... j сходилась к столбцу х., необходимо и доста-
точно, чтобы lim ||х<*> - хф|| = 0 .
3. Для определения псевдорешений систем линейных алгебраических
уравнений в разд. 5.8 использовалась евклидова норма || х ||3.
4. Нормы позволяют оценить скорость сходимости последовательно-
стей. Рассмотрим последовательность [х(/г)|, сходящуюся к х.. Предполо-
жим, что все ее элементы различны и ни один из них не совпадает с х..
Наиболее эффективный способ оценивания скорости сходимости состоит в
541
сопоставлении расстояния ||х(*+|)-х,|| между х(*+1) и х, с расстоянием
||х<*> - х.|| между xw и х,.
Последовательность {х^} называется сходящейся с порядком р,
если р - максимальное число, для которого
||x(i+,)-xJI
0< lim ----------<оо .
||XW -х<||/’
Поскольку величина р определяется предельными свойствами {x(i)|,
она называется асимптотической скоростью сходимости.
Если последовательность jx^' j - сходящаяся с порядком р, то число
называется асимптотическим параметром ошибки. Если р = 1, с < 1 , то
сходимость линейная, если р = 2 - квадратичная, если р = 3 - кубиче-
ская и т.д. Если р > 1 или р = 1, с - 0 , то сходимость сверхлинейная. Ли-
нейная сходимость является синонимом сходимости со скоростью геомет-
рической прогрессии. Сверхлинейная сходимость является более быстрой,
чем определяемая любой геометрической прогрессией.
Пример 10.1. Вычислить нормы столбца х = (1 -2 3 -4f .
□ |х|, = max |xj =тах{|1|,|-2|,|3|,|-4| }= 4 ;
1=1
IIx Из = JJ? = Vl2+(-2)2+32+(-4)2 = Тзо .
I <=i
Заметим, что свойство ||x||2 > ||x||3 > ||x||, очевидно, выполняется.И
Пусть А - произвольная матрица размеров (тхп).
Нормой матрицы А называется функция ||л||, удовлетворяющая сле-
дующим аксиомам:
1) || А || > 0 для любой матрицы Л, причем || А || - 0 в том и только
в том случае, если А - нулевая матрица;
2) || аА || = | а | || А || для любого действительного числа а;
542
3) ||Я + 5||<|И|+||В|| для любых двух матриц А и В размеров (тхп)
(неравенство треугольника)',
4) ||Л-В||<|И|-||В|| для любых двух матриц, у которых определено
произведение.
Матричные нормы удобно определять через нормы матриц-столбцов.
Для этого, задавшись какой-нибудь нормой для матриц-столбцов, рассмат-
риваются значения ||Лх|| при всевозможных х, удовлетворяющих условию
||х|| = 1. Максимальное из этих значений, которое найдется всегда, берется в
качестве нормы матрицы А : ||Л|| = max ||Лх||. Такую матричную норму на-
М-|
зывают индуцированной.
Заметим, что в качестве определения индуцированной матричной нор-
II и ||Ях||
мы часто используется выражение Л = sup-jj—п-, характеризующее мак-
х#о ||х||
симальную величину, на которую преобразование, описываемое матрицей
А, может растянуть любой ненулевой вектор в заданной норме (см.
разд.9.6).
Наиболее употребительными являются следующие формулы для вы-
числения значений норм матриц с действительными элементами.
п
1) || A Uj = max |ау | - максимум суммы модулей элементов в строке;
' У=1
п
2) II= тах£ | а,у|- максимум суммы модулей элементов в столбце;
J i=i
з) 114 = J).m31i(ArA) - квадратный корень из максимального собствен-
ного значения kmax(AT А) матрицы АгА (см. разд. 7.2.1);
Inn
4) || А ||4 = I ау — квадратный корень из суммы квадратов элемен-
V 1=1 ;=1
тов.
Заметим, что вычисление нормы ||л||3 = Xma]i(ATА) связано с весьма
трудоемкими операциями. Поскольку справедливо неравенство
. inn
II л ||3=< || я ц4 = I
I <-1 7=1
543
то норма || А ||4 часто используется в оценках вместо || А ||3. Норма || А ||4
возникает, если матрице А поставить в соответствие ’’длинный столбец”:
(aii,a2l,...,aml,a12,a22,...,am2,....,amt)r и применить норму ||х||3.
Пример 10.2. Вычислить нормы матриц
а) А = ' 1 -2 3 л 4 5-6 -7 8 9 j ; б) В = "10 0 0 1 0 <0 0 1
□ а) |4 =max{|l|+|-2|+|3(; |4| + |5|+|-4 |-7| +|8|+|9|}=
= max {6,15,24 } = 24;
I42=„»x{|i|+|4H-4 |-2|+М*Н;
= max{12,15,18} = 18 ;
||Л||4 = 71 + 4 + 9+16 + 25 + 36 + 49 + 64 + 81 = 7285 ;
б) И=И2=ь ||в||4=-Л+1+1 = 7з.и
Норма матриц может быть использована при анализе сходимости раз-
личных численных процедур. Пусть имеется последовательность матриц
{а(1),...,А(4),...} размеров (тхп). Матрица А называется пределом
последовательности матриц , если lima,^ =ай для всех
jt—>«• ' J
i = l,...,m; j = . Это обозначается lim Aw - A.
k—>°°
Для сходимости последовательности матриц {a(I),..., A(i),...) к мат-
рице А необходимо и достаточно, чтобы lim Aw - А =0 . При этом по-
к-^*3 н II
следовательность, составленная из норм матриц А^, сходится к норме мат-
рицы А , т.е. hm ||aw|| = ||а|| .
Отметим некоторые свойства предела матриц.
Если limA(i:)=A, lim В^ = В, то:
к—>°° к—>°°
1) limL(/:)±5(/:)|= А±В; 2) 1йп1а(*’ • Bw]= А-В ;
к—к—
3) lim [а®]"1 = А*1; 4) lim СА(к) = СА, lim A(k}D = AD,
it—>«. к—
где считается, что все операции определены.
544
10.2. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
10.2.1. Численные схемы реализации метода Гаусса
Рассмотрим частный случай изучаемой в гл. 5 проблемы - задачу на-
хождения решения системы линейных алгебраических уравнений
«пх1 + а12х2+-- + а1пх„ =ЪХ,
«21х1+«22х2+ — + «2лхл =Ь2,
или Ах = Ь,
(Ю.1)
anixi + ап2х2 + "'+ атхл = Ь,
«п
"• «1л
где А =
- квадратная матрица n-го порядка;
annj
Ь =
\.ап\
%"
: - столбцы размеров (nxl). Это означает, что число уравнений сов-
Ь.
падает с числом неизвестных, т.е. т = п . Предполагается, что выполняется
условие detA = |а| # 0. Тогда по теореме 5.1 решение системы (10.1) суще-
ствует и единственно.
Согласно изложенному в разд. 5.4, метод Гаусса содержит две сово-
купности операций, которые условно названы прямым ходом и обратным
ходом.
Прямой ход состоит в исключении элементов, расположенных ниже
элементов, соответствующих главной диагонали матрицы А . При этом мат-
рица А с помощью элементарных преобразований преобразуется к верхней
треугольной, а расширенная матрица (А | Ь) - к трапециевидной:
'«и «12 ’ • «1п / 1 «12 ’ • «1,
(А|Ь) = «21 «22 ’ ' а2п h2 0 1 • «2п
Л» «л2 0 k 0 • • 1
- \
^2
= (Яр).
ь.
Заметим, что в отличие от общего подхода здесь не требуется приво-
дить расширенную матрицу к упрощенному виду. Считается, что для реали-
зации эффективных численных процедур достаточно свести проблему к ре-
шению системы с треугольной матрицей коэффициентов.
Обратный ход состоит в решении системы А х = b .
35-4549
545
АЛГОРИТМ
1. Прямой ход.
а) Положить номер шага к = 1. Переобозначить все элементы расши-
ренной матрицы (Л| Ь) через а^0), i = l,...,n; j = 1,...,п + 1;
б) Выбрать ведущий элемент одним из двух способов.
Первый способ (схема единственного деления). Выбрать в качестве ве-
дущего элемента * 0.
Второй способ (схема с выбором ведущего элемента). На к -м шаге
сначала переставить (л-А+1) оставшихся уравнений так, чтобы наиболь-
ший по модулю коэффициент при переменной хк попал на главную диаго-
наль, а затем выбрать в качестве ведущего элемента а^-1).
в) каждый элемент строки, в которой находится ведущий элемент, по-
(кУ *j 1 1
делить на него: al/ = „ , / = ],...,« +1;
V у/*-1)
акк
г) элементы строк, находящихся ниже строки с ведущим элементом,
подсчитать по правилу прямоугольника, схематически показанного на
рис. 10.1 (исключить элементы, стоящие ниже ведущего элемента).
Рис. 10.1
i = k + l,...,n-,
j = к,...,п + 1.
Поясним алгоритм исключения на рис. 10.1. Пусть рассчитывается
значение на к-м шаге. Следует соединить элемент с ведущим
элементом а^-1). Получена одна из диагоналей прямоугольника. Вторую
диагональ образует соединение элементов a-*-1) и . Для нахождения
значения из его текущего значения а^-1) вычитается произведение
элементов и , деленное на ведущий элемент;
д) если к ф п , то перейти к п."б", где вместо к положить к + 1.
Если к = п , завершить прямой ход. Получена расширенная трапецие-
видная матрица из элементов а\р , соответствующая (A |6).
546
2. Обратный ход. Составить систему
Ах = Ь
и решить ее, начиная с последнего уравнения.
Замечания 10.2.
1. Схема единственного деления имеет ограничение, связанное с тем,
что ведущие элементы должны быть отличны от нуля. Одновременно жела-
тельно, чтобы они не были малыми по модулю, поскольку тогда погрешно-
сти при соответствующем делении будут большими. С этой точки зрения
схема с выбором ведущего элемента является более предпочтительной.
2. По окончании прямого хода может быть вычислен определитель
матрицы А путем перемножения ведущих элементов.
3. В расчетных формулах все элементы расширенной матрицы обозна-
чаются одним символом " а ", так как они преобразуются по единым прави-
лам.
4. Понятие нормы квадратной невырожденной матрицы позволяет ис-
следовать влияние малых изменений правой части и элементов матрицы на
решение систем линейных уравнений. Положительное число
cond Л = ||л||-|]л-1| называется числом обусловленности матрицы. Суще-
ствует и более общее определение числа обусловленности, применимое к
вырожденным матрицам: cond А =
Чем больше число обуслов-
ленности, тем сильнее ошибка в исходных данных сказывается на решении
линейной системы. Если число cond А велико, система считается плохо
обусловленной, т.е. решение системы может существенно изменяться даже
при малых изменениях элементов матрицы А и столбца свободных членов
Ь.
Пример 10.3. Найти число обусловленности матрицы системы
+10х2 =йр
ЮОХ] +1001х2 =1101.
Решить систему при Ь{ =11 и Ь} =11,01, сравнить близость полученных ре-
шений.
□ По
формуле (4.2) для матрицы А =
100 1001
получаем
. (1001 -10) I
Л*=1 iqq 1 • Тогда || А К, = max 2, |а„| = max {11; 1101} = 1101,
35'
547
|| A 1 Uj = max{ 1011; 101} = 1011. В результате cond A = ||a||||A *||=
= 11011011 = 1113111. Очевидно, число обусловленности матрицы системы
достаточно велико, поэтому система является плохо обусловленной.
При ^=11 система имеет единственное решение хг = 1, х2 = 1. а при
by = 11,01, единственное решение xY = 11,01; х2 = 0. Несмотря на малое раз-
личие в исходных данных: Д^ = (11 -11,011 = 0,01, полученные решения от-
II fl) fll,01)||
личаются существенно: Ах = 111 1-1 =10,01, т.е. погрешность Ах
решения в 1001 раз больше погрешности Afy правой части системы.
Таким образом, решение плохо обусловленной системы может сущест-
венно изменяться даже при малых изменениях исходных данных.
Пример 10.4. Решить систему линейных алгебраических уравнений
2xt +х2 + 4х3 = 16,
3Xj +2х2 + х3 = 10,
х3 +3х2 +Зх3 = 16
методом Гаусса (схема единственного деления).
□ 1. Прямой ход. Запишем расширенную матрицу и реализуем прямой
ход с помощью описанных преобразовании:
'2 1 4 16'
*=1
(А|6) = 3 2 1 10 —> 0
J з 3 16,
'1 1
Jt=3 2
—> 0 1
0 0
1 2 8 ' Jt=2 '1 j. 7 2
1 -5 -14 —> 0 1 -10
4 1 8 0 0 26
2 >
2 8 "
/ 1 «V 1
-10 - -28 = (A PJ.
1 3
*=з
-28 ->
78
Согласно п.2 замечаний 10.2 определитель матрицы системы равен
произведению ведущих элементов: det А = 2 — • 26 = 26.
2. Обратный ход. По матрице (а | b) составим систему уравнений
( 1 1
1 - 2 2 <хЛ ( 8 A Xj+-x2 + 2x3 =8,
0 1 -10 • х2 = -28 или х2-10х3=-28,
0 0 1 W к 3 J хз=3.
А
548
Решая эту систему, начиная с последнего уравнения, находим: х3 = 3,
х2 = 2, Xj = 1 .
Пример 10.5. Методом Гаусса с выбором ведущего элемента по столб-
цам решить систему:
-3xj + 2,099х2 + 6х3 = 3,901;
Юх! -7х2 +0х3 = 7;
5xj —х2 +5х3 =6.
□ 1. Прямой ход. Реализуем поиск ведущего элемента по правилу: на
к -м шаге переставляются (п - к +1) оставшихся уравнений так, чтобы наи-
больший по модулю коэффициент при хк попал на главную диагональ:
г-3 2,099 6 3,90 Г *1 (10 -7 0 7 '
(ф) = 10 -7 0 7 -3 2,099 6 3,901
<5 -15 6, 1 5 -15 6 ,
"1 -0,7 0 0,7 4 '1 -0,7 0 0,7
Jt=l
—> 0 - 0,001 6 6,001 *1 0 2,5 5 2,5
2,5 5 2,5 , 0 -0,001 6 6,001
*=2
'1 -0,7 0 0,7 ' (1 -0,7 0 0,7"]
к=2 0 1 2 1 *=з -> 0 1 2 1 =(л|б
0 6,002 6,002, 1° 0 1 и
Согласно п.2 замечаний
10.2 определитель матрицы системы равен
произведению ведущих элементов: det А = 10 • 2,5 • 6,002 = 150,05.
2. Обратный ход. По матрице U | b I составим систему уравнений:
'1 -0,7 0" '0,7'
0 1 2 *2 = 1 или
0 < 1 ,
Х[ -0,7х2 = 0,7,
х2 +2х3 = 1,
х3 =1.
А b
Решая ее, последовательно получаем: х3 = 1, х2 - -1, X! = 0 .
Пример 10.6. Решить систему уравнений
xt - х2 + х3 - 4х4 - -2 ,
8xj - х2 - х3 + 2х4 =11,
X] + 6х2 - 2х3 - 2х4 = -7
методом Гаусса единственного деления.
□ 1. Прямой ход.
549
(Л\Ь) =
2
8
<1
-1
1
О
О
-1
1
-1
6
1
_2
7
22
3
40
3
1
-5
-I
-2
-4
3
13
_57
3
-2"
2
11
-L
k=i
к=4
-4
1
2
-2
-2'
2
13
-19
-1
1
О
О
I
_ 7
7
1
О
Ч
О
О
О
-4
3
39
22
1
О
О
О
-1
1
О
о
-2'
2
39
22
1
-1
3
7
7
1
-7
-9
-3
1
_ 7,
з
1
О
— 4
9
34
2
-4
3
39
22
2614
66
-2
6
27
-5
-2 '
2
39
22
2814
66 J
к=2
о
о
о
О
о
о
2. Обратный ход. По матрице (-4 | Z>) составим систему уравнений:
+^х =
3 + 22 4 22 ’
Х4 = 1 .
Отсюда х4=1, х3 =||--||х4 =0, х2 =2 + |х3-Зх4 =-1,
Х| = -2 + х2 - х3 + 4х4 = 1.
В результате получено решение: х, = (1 -1 О 1)г .
10.2.2. Метод прогонки
Метод применяется в случае, когда матрица А - трехдиагональная.
Сформулируем общую постановку задачи.
Дана система линейных алгебраических уравнений с трехдиагональной
матрицей А . Развернутая запись этой системы имеет вид
аЛ-1 + у,х(+1 = ^> а1 = Уп ‘(Ю.2)
которому соответствует расширенная матрица
550
'-Pi Yi 0 0 • 0 0
а2 "Р2 Y2 0 • - 0 0 б2
0 аз ~Рз Уз • 0 0 5з
ч 0 0 • ап -₽п
Здесь первое и последнее уравнения, содержащие по два слагаемых,
знак минус (-) при коэффициенте р, взят для более удобного представления
расчетных формул метода.
Требуется найти решение х. = (х,1х.2 х.п)г системы (10.2) методом
исключения Гаусса.
Если к (10.2) применить алгоритм прямого хода метода Гаусса, то вме-
сто исходной расширенной матрицы получится трапециевидная:
( 1 -Д 0 0 ••• 0 0^
0 I -р2 0 - о q2
0 0 1 -Р3 - 0 Q3 .
.0 0 0 0 - 1 Qn>
Учитывая, что последний столбец в этой матрице соответствует правой час-
ти, и переходя к системе, включающей неизвестные, получаем рекуррент-
ную формулу:
х, = /’х,+1 + !2( , / = 1,...,и-1. (10.3)
Соотношение (10.3) есть формула для обратного хода, а формулы для
коэффициентов P^Q,, которые называются прогоночными, определяются
из (10.2), (10.3). Запишем (10.3) для индекса /-1: х,_! = Д_1х/ +Q^\ и
подставим в (10.2). Получим
(Р^Л + б,.,) - р/х, + у(х,+1 = 8,.
Приводя эту формулу к виду (10.3) и сравнивая, получаем рекуррент-
ные соотношения для P^Q,:
Yi q _ aiQi-l
(Ю.4)
i =1.
Определение прогоночных коэффициентов по формулам (10.4) соот-
ветствует прямому ходу метода прогонки.
Обратный ход метода прогонки начинается с вычисления х„. Для
этого используется последнее уравнение, коэффициенты которого опреде-
лены в прямом ходе, и последнее уравнение исходной системы:
Xn-1 = ^п-1Хи + Qn-l ’
551
a. х . - В x + 0-x =6 .
П Л~1 "И п и + 1 п
Тогда определяется хп:
х„ = g"£-,i.~A = q ; т.е. х = Q . (10.5)
Остальные значения неизвестных находятся по рекуррентной формуле
(ЮЗ).
АЛГОРИТМ
Прямой ход.
1. Вычислить Рх =—; Qi ---1- (в (10.4) подставить а! = 0).
₽1 31
2. Вычислить прогоночные коэффициенты: P2,Q2‘, P^Qj,—\ Pn.vQn-\
по формулам (10.4).
Обратный ход.
1. Найти х„ = а^п-1- ~-5-^.
₽я-<хЛ-.
2. Значения хп_1>хп_2,...,х1 определить по формуле (Ю.З):
х„-1 = Р„_1х„ + 2„_!, х„_2 = Р„_2х„_1 + Q„_2 ,..., X! = Рхх2 + Q,.
Замечания 10.3.
1. Аналогичный подход используется для решения систем линейных
алгебраических уравнений с пятидиагональными матрицами.
2. Алгоритм метода прогонки называется корректным, если для всех
i = l,...,n, —а..Р._^ ^0 , и устойчивым, если |Pf| <1, i = l,...,n~l.
3. Достаточным условием корректности и устойчивости прогонки яв-
ляется условие преобладания диагональных элементов в матрице А, в
которой а( *0 и у, *0 (/ = 2,3,...,п-1):
| Р/|-| а/| + Ь< | <10-6)
и в (10.6) имеет место строгое неравенство хотя бы при одном i.
4. Алгоритм метода прогонки является экономичным и требует для
своей реализации количество операций, пропорциональное п.
Пример 10.7. Дана система линейных алгебраических уравнений
с трехдиагональной матрицей А (и = 4):
5х, + Зх2 = 8,
Зх] + 6х2 + х3 = 10,
х2 + 4х3 - 2х4 = 3,
х3 - Зх4 = -2
(оц =0, у4 = 0). Решить эту систему методом прогонки.
552
□ Данная система удовлетворяет условию преобладания диагональных
элементов (10.3): в первом уравнении 5 > 3, во втором уравнении 6 > 3 + 1;
в третьем уравнении 4 > 1 + 2, в четвертом уравнении 3 > 1. Далее выполня-
ем прямой и обратный ход, учитывая, что расширенная матрица имеет вид
<5 3 0 0 8 '
3 6 1 0 10
014-2 3
/) 0 1 -3 -2,
Прямой ход. Вычислим прогоночные коэффициенты:
1 ₽! -5 5’ р, -5 5’
8
р _ У2 ______1__________5 _ _ a20i ^2 _ 5________ 26
21’ 2~42-^i _6_3/_з)”21'
I 5; I 5J
Подчеркнем, что Pj = -5; р2 = -6; р3 = -4; Р4 = 3 , так как в (10.2)
во втором слагаемом взят знак “минус”:
1.26_3
Р ~2 Q -Л^~5з_ 21 _37
3 Рз-“Л -4-1/-79’ 3 Рз-^ -4-1/- _Г| 79
I 21) I 21)
Обратный ход:
37
а,£Л-5, 7<э - 42 37
Г -П = 4^3----1 = --12--- = 1‘ Г =Рг 4-0 =---1-1-— = 1-
42
79
5 26 3 8
х2 ~ ?2хз +^2~~~21^+'21~^ Х{~ ^Хг + ^’ У’+"5 ~
Подстановкой решения xt = (1 1 1 1)г в исходную систему
убеждаемся, что задача решена верно. Для данного примера р. -а.Р^ *0 ,
i = 1,2,3,4 ; |р | < 1, i = 1,2,3, т.е. метод прогонки оказался корректным и ус-
тойчивым (см. п.З замечаний 10.3).
Для наглядности представления информации исходные данные и ре-
зультаты расчетов поместим в табл. 10.1, где в первых четырех колонках со-
держатся исходные данные, а в последних трех - полученные результаты.
3 3 4
79 79
₽4 а4Р3 3_!
553
Таблица 10.1
i ai 3/ У, 8« Р< Qi Xi
1 0 -5 3 8 -3/5 8/5 1
2 3 -6 1 10 -5/21 26/21 1
3 1 -4 -2 3 42/79 37/79 1
4 1 3 0 -2 - 1 1
Пример 10.8. Дана система линейных алгебраических уравнений с
трехдиагональной матрицей А :
Xj + 2х2 = 5 ,
2хг - х2 + х3 = 3 ,
х2 - х3 + х4 = 3 ,
х3 + х4 = 7 .
Решить систему методом прогонки.
□ Результаты расчетов в прямом и обратном ходе занесены в
табл. 10.2.
Таблица 10.2
i а/ 3/ Y; 8/ Pi Q xi
1 0 -1 2 5 -2 5 1
2 2 1 1 3 1/5 7/5 2
3 1 1 1 3 5/4 -2 3
4 1 -1 0 7 - 4 4
В результате получено решение: х, = (1 2 3 4)г. Заметим, что ус-
ловие преобладания диагональных элементов в данном примере не выпол-
нено, но алгоритм метода прогонки позволил получить точное решение. При
этом обратим внимание на небольшой порядок системы и отсутствие по-
грешностей вычислений.
Пример 10.9. Решить методом прогонки систему уравнений
2х] + х2 = 4,
2xj +3х2 -х3 =9,
x2 -x3 + 3x4 = 12,
x3~*4 =“4-
2 10 0 4
2 3-10 9
□ Расширенная матрица системы имеет вид 0 1-13 12
0 0 1-1 -4
554
Прямой ход. Вычислим прогоночные коэффициенты:
p=2i.=_L = -1
1 ₽1 -2 2’
Р2=—12—=------
02 _з_2.Г_2
I 2/
а=-^-±=2,
1 01 -2
_a2fl-82 2-2-9
2 ₽2-а2^1 _3_2.f_l
I 2
5
2 ’
Р,=-^- = -^- = 6;
03~а3^2 1-1 —
2
„ . 1-—12
a=S&zSl=^_=-l9.
0з а3Р2 i-i.J-
2
Обратный ход:
а46з~54 _1-(~19)-(-4)
Р4-а4Р3 1-1-6
Лз = Р3х4 + 23 = 6-3-19 = -1,
= 3 = х4,
х2 =Р2х3+С2 =|(-1)+-| = 2, хг =P1x2 + Gi =-у-2 + 2 = 1.
Результаты расчетов приведены в табл. 10.3.
Таблица 10.3
i а,- 0/ Y; 5, Pi а xi
1 0 — 2 1 4 - 1/2 2 1
2 2 -3 -1 9 1/2 5/2 2
3 1 1 3 12 6 - 19 - 1
4 1 1 0 -4 - 3 3
Получено решение системы: х„ = (1 2 -1 3)г .
10.23. Метод LU -разложения
Рассмотрим ещё один метод решения задачи (10.1). Метод опирается
на возможность представления квадратной матрицы А системы в виде про-
изведения двух треугольных матриц:
A = LU, (10.7)
где L- нижняя, a U - верхняя треугольные матрицы,
Ai 0 • 0 ' '1 «12 • «12
L = ^21 ^22 ' 0 , и = 0 1 u2n
^n2 ' ’ Am, .0 0 • 1 ,
С учётом (10.7) система Ах = Ь представляется в форме
555
LUx = b. (10.8)
Решение системы (10.8) сводится к последовательному решению двух
простых систем с треугольными матрицами. В итоге процедура решения со-
стоит из двух этапов.
Прямой ход. Произведение U х обозначим через у . В результате ре-
шения системы (,
Ly = b
находится вектор у.
Обратный ход. В результате решения системы
Ux = y
находится решение задачи - столбец х.
В силу треугольное™ матриц L и U решения обеих систем находятся
рекуррентно (как в обратном ходе метода Гаусса).
Из общего вида элемента произведения А = LU, а также структуры
матриц L и U следуют формулы для определения элементов этих матриц:
./-1
~ &ij ~ hsusj> * — У»
J=1
(Ю.9)
1 ( 'l
иу ~ ", ау ~ lisusj ’
< j=l J
' < j.
Результат представления матрицы А в виде произведения двух тре-
угольных матриц (операции факторизации) удобно хранить в одной мат-
рице следующей структуры:
^п\ ^п2 ^пЗ *” ^пп у
Вычисления на к -м шаге метода LU -разложения удобно производить,
пользуясь двумя схемами, изображенными на рис. 10.2.
Замечания 10.4.
1. Всякую квадратную матрицу Л, имеющую отличные от нуля угловые
миноры Д, =аи *0, Д2 =
ап
а21
ап
12 *0,
а22
Д„ = |Л | * 0 , можно предста-
вить в виде LU - разложения, причем это разложение будет единствен-
556
ным [8]. Это условие выполняется для матриц с преобладанием диагональ-
п
ных элементов, у которых |аа| > |а,,|, ‘ - 1,2,...,п.
7=1
7*<
2. В результате прямого хода может быть вычислен определитель мат-
рицы А по свойствам определителя произведения матриц (теорема 2.2) и
определителя треугольных матриц: deM = detZ-det(/ = /и /22 •••/,„, (см.
разд. 2.2).
АЛГОРИТМ
1. Выполнить операцию факторизации исходной матрицы А, приме-
няя схемы (рис. 10.2) или формулы (10.9), и получить матрицы L и U .
2. Решить систему Ly = b.
3. Решить систему Ux = y.
^ik~aik ^JisUsk
5=1
к-й столбец нижней
треугольной матрицы
к-я строка верхней
треугольной матрицы
Рис. 10.2
Пример 10.10. Решить систему линейных алгебраических уравнений
2х1 +х2 + 4х3 = 16,
Зх] +2х2 + х3 = 10,
х, +3х2 +Зх3 = 16
методом LU -разложения.
557
□ 1. Выполним операцию факторизации:
1 4'
2~Т
1 1.
3
при к = 1
при к = 2
0,5 [-J0
2,5 26
'2 0,5 х2 '
3 0,5-10
<Г/2,5/ [3~?
^21 = а21 = 3 1 /31 = а31 = 1;
_* -ПС -1 -4-о
и12 -^а12-0,5 , «13-“а13-~-2,
/22 = а22 ~^2\и\2 = 2-3-0,5 = 0,5 ;
^32 ~ аз2 _^31М12 = 3-1-0,5 = 2,5 ;
«2з = ~—(«23 -^21u13) = Tt(1-3-2) = -10;
‘22 и>-)
^зз = «зз _^31И13 _^32м23 = 3-1-2-2,5-(-10) = 26.
(2 ,0,5, -2^1
к=1
3; 2
/ 3
А1 = ai 1 = 2;
1
,z 2
1
к=2
при к = 3
В результате получены две треугольные матрицы:
L =
U~
'1 0,5
О
.0
1
0
2
-10
1
определитель
матрицы
'2 0 О'
3 0,5 0 ,
J 2,5 26,
Согласно п.2 замечаний 10.4,
в результате перемножения диагональных элементов
deU = 2-0,5-26 = 26
2. Решим систему Ly = b :
Л
У2
А находится
матрицы L:
'2 0 0
3 0,5 О
J 2,5 26) ^у3/
L
'16
10
Т
или
2у, =16,
Зл + 0,5-у2 = Ю,
Отсюда л = 8, у2 = (10—3 - З)- 2 = -28 , у3
16-8 + 70
26
3. Решим систему U х = у:
0
0
0,5
1
О
2 '
-10
1 .
Х2
-28
3
или
X] + 0,5х2 + 2х3 = 8,
х2 -10х3 - -28,
х3 = 3.
и
У
Отсюда х3=3, х2 =-28 + 10-3 = 2, х, =8-2 3-0,5-2 = 1. Получен
ответ: х, = (1 2 3)Г .
558
Пример 10.11. Решить систему линейных алгебраических уравнений
Зх, - х2 = 5 ,
-2х1 + х2 +х3 = 0,
2Х) - х2 + 4х3 =15.
методом LU -разложения.
□ 1. Выполним операцию факторизации:
при к = 1
к=3
>
А1-ап_3; /21=а21--2; Z3i — <731 — 2;
"12
£12_ = _1
'и 3
'п
при к = 2
^22-а22~^21 “12"! 2---^, /32 — 0^2 ^31 "12 “
U23 > (а23 ^21и1з)~х( 2) о)-3,
*22 3
зри к = 3
^33 а33 ^31 "13 ^32М23-4-2-0 3-
= 5.
2. Решим систему L у = b:
ЗУ!=5,
-2у,+^- = 0,
3
559
Отсюда yt = j, y2 = 10 > Уз - 3 •
3. Решим систему U х = у:
или
х2 + Зх3 = 10,
х3 =3.
Отсюда х3 = 3, х2 = 1, xi ~ 2.
Пример 10.12. Решить систему линейных алгебраических уравнений
2х] + х2 = 4,
2xj + Зх2 - х3 = 9,
х2 - х3 + Зх4 = 12,
х3-х4 =-4
методом LU - разложения.
□ 1. Выполним процедуру факторизации:
'2
2
0
<0
10 О'
3 -1 о
1 -1 3
0 1 -1,
2—0 О
2 1/
к=з 2 2 - + О
---> / 2 /
/ 1 г
О ,1 -6
/ / 2А---
х,о о' 1 I-1J
_1_
2
2
1
О
( 1 'l
2—0 О
2 / /
2 ...О
/У,-/. Д'" _
O><1Z>-1 3
чо о 1 ПТ
о о
к=3
В результате получаем
(2 О О
^0 О
О
j_
2
1
£
2
т
2
1
О
-6
5,
О'
О
О
5,
(7=0 1
О О
<° 0
О
2
1
О
О
о
-6
1 >
2
-_>2
О
560
при Z: = 1 Zjj = 2 , Z21 = 2, Z3|=0, Z41=0,
k]7=— -1= —, и,3=— 0 = 0, «|4= — -0 = 0;
12 2 2 2 2
при k = 2 /22 =3-2~ = 2, Z32=l-0-y = l, /42 = 0 — 0 •—• = 0,
“23 =|(-l-2 °)=- p “24 =y(0-2-0)=0;
при£ = 3 Z, =-l—] = - — , / =l-0-0-0-[-—1 = 1,
33 L 2 J 2 43 1.2J
и34 = -L(3-00-10) = -6;
2
приЛ = 4 /44 =-l-(0 0 + 0 0 + l(-6))=5.
2. Решим систему Ly = b -.
'2 0 0 0' (4 '
2 2 0 0 У1 9
0 1 -1 0 Уз 12
<° ° 1 5> <~4>
или
2^=4,
2^ + 2у, =9,
^2-^з=12>
У3 +5у4 =~4.
5
У1 =2> Уг = Уз =~19, У4 =3‘
Отсюда
Отсюда получаем: х4 = 3 , л3 = -1, х2 = 2, = 1 или х* = (1 2 -1 з/ .
10.2.4. Метод квадратных корней
При решении систем линейных алгебраических уравнений с симмет-
рическими матрицами можно сократить объем вычислений почти вдвое.
Пусть А - симметрическая квадратная матрица системы Ах = b по-
рядка п . Решим задачу ее представления в виде
36 - 4549 561
где U = '“п 0 A = UT U,
“12 •" “1л' “22 " “2л , ит = '“п “12 0 - “22 " 0 ' 0
0 •" “лл, <“1л “2л " “лл,
Находя произведение UT U, составим систему п(п + 1) —-— уравнении
относительно неизвестных элементов матрицы U :
'«п о
«12 «22
«12
«22
«1л"
«2л
<«1и «2п
«2л
Система имеет следующий вид:
2
«Ц—«Ц, «11 “12 ~ «12 ’ “11 “1л “ «1л >
иЛЛ
пп /
2 2
“12 +«22 = «22 ’ “12“1л +«22“2л ~ а2п >
“1л+«2л+- + «лл «лл ’
Из первой строки системы находим
I—
“n=V«ii> uij ~ ’ 7 = 2,...,и.
“и
Из второй строки определяем
I Y a2j~ul2ulj . _
«22 — У «22 «12» U2j---------------’ J — 3,...,И И Т.Д.
“22
| п-1
Из последней строки имеем ит = .
1 к=1
Таким образом, элементы матрицы U находятся из соотношений
un=Jaii-Xuki ’ ' =
I *=1
(10.10)
<-1
«у-£«И«*?
“у =----—------, 7 = 2,...,п; j>i; «/y=0,j<i.
“«•
562
При осуществлении UTU -разложения симметрической матрицы могут
возникать ситуации, когда «„ = 0 при некотором i или подкоренное выра-
жение отрицательно. Для симметрических положительно определенных
матриц (см. разд.9.6.3) разложение выполнимо [8].
Если матрица А представима в форме UTU , то система Ах = b имеет
вид UTU х = Ь. Решение этой системы сводится к последовательному реше-
нию двух систем с треугольными матрицами. В итоге процедура решения
состоит их двух этапов.
Прямой ход. Произведение Ux обозначается через у. В результате
решения системы UTу = Ь находится столбец у .
Обратный ход. В результате решения системы Ux- у находится ре-
шение задачи - столбец х.
АЛГОРИТМ
1. Представить матрицу А в форме А = UTU , используя (10.10).
2. Решить систему UTу -Ь п найти у .
3. Решить систему Ux = у и найти х.
Пример 10.13. Найти решение системы
2xj +х2 +4х3 =16,
%1 + х2 + Зх3 = 12,
4xt + Зх2 + 14х3 = 52
методом квадратных корней.
□ 1. Представим матрицу А в форме A = UTU , используя (10.10):
I гу “12 1 “в 4
при i = l получаем = Jau = V2 , и12 =------= ~7=> “в ~----= ~7=;
“и V2 “п V2
при i = 2 имеем
°23 3 Tz"~rZ
к=\ v2 V2 rz
“2з =----—---------------j----=*2;
“22 —
4i
w33 = Ja33 _ ~ Va33— “13 _“23 = V14-8 —2 = 2.
I k=l
при
36*
563
Таким образом, получили
О
О
О
2
2. Решим систему UT у = b :
О
Л
fi
Уг
Г16'
12
<52,
или
V2y,=16,
^+i*=12’
^Л+з/2у2+2у3=52.
о
о
2
Отсюда у] = -5Д = 8>/2 , уг =м4^~У\ , у3 =————- = 6.
<2 2
3. Решим систему Ux = у.
или
Утх. + -у^х, +-^х, = 85/2,
1 V2 2 Л 3
А=х. + >/2х, = 4^2,
V2 2 3
2х3 = 6.
В результате получаем решение задачи х3 = 3, х2 = 8 - 2х3 = 2,
16-12-2
10.3. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
10.3.1. Метод простых итераций
Альтернативой прямым методам, рассмотренным в разд. 10.2, являют-
ся итерационные методы, основанные на многократном уточнении х(0), за-
данного приближенного решения системы Ах = Ь. Верхним индексом в
скобках здесь и далее по тексту обозначается номер итерации (совокупно-
сти повторяющихся действий).
Реализация простейшего итерационного метода - метода простых ите-
раций - состоит в выполнении следующих процедур.
1. Исходная задача А х = b преобразуется к равносильному виду:
х = ах + р, (10.11)
564
где а - квадратная матрица порядка п; 0 - столбец. Это преобразование
может быть выполнено различными путями, но для обеспечения сходимости
итераций (см. процедуру 2) нужно добиться выполнения условия ||а|| < 1.
2. Столбец 0 принимается в качестве начального приближения х(0) = 0
и далее многократно выполняются действия по уточнению решения, соглас-
но рекуррентному соотношению
х(*+1) =ах(*)+0, * = 0,1,... (10.12)
или в развернутом виде
*1(*+0 = а1Iх}*’ +012*2*’ +- + а1П4*’ +₽1 >
*2*+0 = а21Х1*’ +“22*2*’ +-" + а2пХп*) +02 ,
ХпМ) = аи1х1*’ +ал2*2*’ +- + аПл*л*> + ₽л
3. Итерации прерываются при выполнении условия
|х(*+1>_х(*)||<е, (10.13)
где е > 0 - заданная точность, которую необходимо достигнуть при реше-
нии задачи.
Замечания 10.5.
1. Процесс (10.12) называется параллельным итерированием, так как
для вычисления (к +1) -го приближения всех неизвестных учитываются вы-
численные ранее их к -е приближения.
2. Начальное приближение х(0) может выбираться произвольно или из
некоторых соображений. При этом может использоваться априорная ин-
формация о решении или просто “грубая” прикидка.
При выполнении итераций (любых) возникают следующие вопросы:
а) сходится ли процесс (10.12), т.е. имеет ли место xw-+x, при
к оо, где х, - точное решение?
б) если сходимость есть, то какова ее скорость?
в) какова погрешность найденного решения х(*+1), т.е. чему равна нор-
ма разности ||х“> - х,|| ?
Ответ на вопросы о сходимости дают следующие две теоремы.
Теорема 10.1 (о достаточном условии сходимости метода простых
итераций). Метод простых итераций, реализующийся в процессе последо-
вательных приближений (10.12), сходится к единственному решению ис-
ходной системы Ах = Ъ при любом начальном приближении х(0) со скоро-
565
стью не медленнее геометрической прогрессии, если какая-либо норма мат-
рицы а меньше единицы, т.е. ||а||^ <1 (5 е {1,2,3}).
Замечания 10.6.
1. Условие теоремы 10.1, как достаточное, предъявляет завышенные
требования к матрице а, и потому иногда сходимость будет, если даже
НФ’-
2. Сходящийся процесс обладает свойством самоисправляемости, т.е.
отдельная ошибка в вычислениях не отразится на окончательном результате,
так как ошибочное приближение можно рассматривать, как новое началь-
ное.
3. Условия сходимости выполняются, если в матрице А диагональные
элементы преобладают, т.е.
К| 2:|ал| +... + |a,j-i| +|«,;,+1| + - + |а'И|> * = , (10.14)
и хотя бы для одного i неравенство строгое. Другими словами, модули диа-
гональных коэффициентов в каждом уравнении системы больше суммы мо-
дулей недиагональных коэффициентов (свободные члены не рассматрива-
ются).
4. Чем меньше величина нормы || а ||, тем быстрее сходимость метода.
Теорема 10.2 (о необходимом и достаточном условии сходимости
метода простых итераций). Для сходимости метода простых итераций
(10.12) при любых хт и р необходимо и достаточно, чтобы собственные
значения матрицы а были по модулю меньше единицы, т.е.
|\(а)|<1, г = 1,...,п.
Замечание 10.7. Хотя теорема 10.2 дает более общие условия сходи-
мости метода простых итераций, чем теорема 10.1, однако ею воспользо-
ваться сложнее, так как нужно предварительно вычислить границы собст-
венных значений матрицы а или сами собственные значения (см.
разд. 7.2.1).
Преобразование системы Ах = b к виду х = ах + р с матрицей а, удов-
летворяющей условиям сходимости, может быть выполнено несколькими
способами. Приведем способы, используемые наиболее часто.
1. Уравнения, входящие в систему Ах = Ъ , переставляются так, чтобы
выполнялось условие (10.14) преобладания диагональных элементов (для
той же цели можно использовать другие элементарные преобразования). За-
тем первое уравнение разрешается относительно х1, второе - относительно
х2 и т.д. При этом получается матрица а с нулевыми диагональными эле-
ментами.
Например, система
566
-2,8Х| + х2 + 4х3 =60,
10xj -х2 + 8х3 =10,
- xt + 2х2 - 0,6х3 = 20
с помощью перестановки уравнений приводится к виду
10х1 — х2 + 8х3 = 10,
-х, +2х2 -0,6х3 =20,
- 2,8xt + х2 + 4х3 = 60,
где |10| >|-1| + |8|, |2| > |—1| +1—0,б|, |4|>|-2,8|+|1|, т.е. диагональные эле-
менты преобладают.
Выражая X] из первого уравнения, х2 - из второго, а х3 - из третьего,
получаем систему вида х = ах + 0 ;
' 0 од Xj =O‘Xj +0,1х2 -0,8х3 +1, х2 = 0,5х] + 0х2 +О,Зх3 +10, х3 = 0,7xj -0,25х2 + 0-х3 +15,
-0,8' Г г
где а = 0,5 0 0,3 , 0= 10 . Заметим, что
.0,7 -0,25 0 ,
Н = max {0,9;0,8; 0,95}=0,95 <1,
т.е. условие теоремы 10.1 выполнено.
Проиллюстрируем применение других элементарных преобразований.
Так, система
4х1 + х2 +9х3 = -7,
Зх;+8х2-7х3 =-6,
X] + х2 - 8х3 = 7
путем сложения первого и третьего уравнений и вычитания из второго урав-
нения третьего уравнения преобразуется к виду
5х, + 2х2 + х3 =0,
2х1 +7х2 +х3 = -13,
X] + х2 - 8х3 = 7
с преобладанием диагональных элементов.
2. Уравнения преобразуются так, чтобы выполнялось условие преобла-
дания диагональных элементов, но при этом коэффициенты а„- не обяза-
тельно равнялись нулю.
Например, систему
1,02 X! -0,15 х2 =2,7,
можно записать в форме
0,8xj+1,05х2 =4
567
х, = -0,02х, + О,15х2 +2,7,
х2 = -0,8Х] -О,О5х2 +4,
для которой ||сх||j = тах {0,17; 0,85 } = 0,85 < 1.
3. Если det 4*0, систему Ах = Ь следует умножить на матрицу
D- A~l -Е, где {еу } - матрица с малыми по модулю элементами. Тогда
получается система (A~l-e)Ax = Db или А~'Ах-еАх = Db, которую
можно записать в форме х = ах + 0, где а = гА, $ = Db. Если
|Еу|, i,J = !,...,« достаточно малы, условие сходимости выполняется.
АЛГОРИТМ
1. Преобразовать систему Ах = b к виду х - ах + 0 одним из описан-
ных способов.
2. Задать начальное приближение решения х^0) произвольно или по-
ложить х<°> = 0, а также малое положительное число £ (точность). Поло-
жить к - 0.
3. Вычислить следующее приближение х<*+1) по формуле
х<*+’> =ах<*> + 0.
4. Если выполнено условие ||x(i+1)-x(i)|| < s, процесс завершить и в
качестве приближенного решения задачи принять х„ = х<*+1). Иначе поло-
жить к = к +1 и перейти к п.З.
Пример 10.14. Методом простых итераций с точностью s = 0,01 ре-
шить систему линейных алгебраических уравнений:
2Х] +2х2 + 10х3 = 14,
1 Oxj + х2 + х3 = 12,
2Х] +10х2 +х3 =13.
□ 1. Так как |2| < |2|+|10|, |1| <|10| + |1|, |1| <|2|+|10|, условие (5.41) не
выполняется. Переставим уравнения так, чтобы выполнялось условие пре-
обладания диагональных элементов:
10Х| +х2 +х3 = 12,
2х; +10х2 + х3 =13,
2Х] + 2х2 +10х3 =14.
568
Получаем |10| > |l| + |i|, |10| > |2| + |1|, |10| > |2| + |2|. Выразим из первого урав-
нения X!, из второго х2, из третьего х3:
Х| = - 0,1 • х2 - 0,1 х3 +1,2, ' 0 -0,1 -0,Г '1,2''
х2 =-0,2-Х|-0,1-х3 +1,3, а = -0,2 0 -0,1 ; Р = 1,3
х3 = -0,2-Х] -0,2-х2 +1,4; -0,2 -0,2 0J Л4,
Заметим, что ||а|| = max {0,2; 0,3; 0,4 } = 0,4 < 1, следовательно, условие схо-
димости (теорема 10.1) выполнено.
2. Зададим х<0) = р = 1,3
.1,4
. В поставленной задаче
Е = 0,01 .
3. Выполним расчеты по формуле (10.12):
' 0 -0,1 -0,Г (xf^ '1,2'
х(*+0 = -0,2 0 -0,1 х<*> + 1,3
-0,2 -0,2 °, х(*) 1 3 J J>4J
А: = 0,1,...
х<*+1> = -0,1х^ -0,hf ’ +1,2;
х<*+1) = -О,2х1(*)-О,1х^)+1,3; А = 0,1,...
x<t+l)=-0,2x,w-0,2xW+l,4;
до выполнения условия окончания и результаты занесем в табл. 10.4.
Таблица 10.4
к Х(к} X(t) х3 |pt)-X(*-1)||i
0 1,2000 1,3000 1,4000 —
I 0,9300 0,9200 0,900 0,5
2 1,0180 1,0240 1,0300 0,13
3 0,9946 0,9934 0,9916 0,0384
4 1,0015 1,0020 1,0024 0,0108
5 0,9996 0,9995 0,9993 0,0027 < £
4. Расчет закончен, поскольку выполнено условие окончания
||x(*+1)-x(t)|| = 0,0027 <е.
Приближенное решение задачи: х. = (0,9996 0,9995 0,9993)г . Оче-
видно, точное решение: х, = (1 1 1)Г.
Приведем результаты расчетов для другого начального приближения
х(0)=(1,2 0 0)г и в = 0,001 (табл. 10.5).
569
Таблица 10.5
к -Г Х(к} а2 х<*> Аз xW-x**-') 1
0 1,2000 0 0 —
1 1,2000 1,0600 1,1600 1,1600
2 0,9780 0,9440 0,9480 0,2220
3 1,0108 1,0096 1,0156 0,0676
4 0,9975 0,9963 0,9959 0,0133
5 1,0008 0,0009 1,0012 0,0053
6 09998 0,9997 0,9997 0,0015
7 1,0001 1,0001 1,0001 0,0004 < Е
Приближенное решение задачи: х. = (1,0001 1,0001 1,0001)г.И
10.3.2. Метод Зейделя
Этот метод является модификацией метода простых итераций и в неко-
торых случаях приводит к более быстрой сходимости.
Итерации по методу Зейделя отличаются от простых итераций (10.12)
тем, что при нахождении / -й компоненты (k +1) -го приближения сразу ис-
пользуются уже найденные компоненты (к +1) -го приближения с меньши-
ми номерами 1,2,...,/-!. При рассмотрении развернутой формы системы
итерационный процесс записывается в виде
.(*+!)_„ r(k) г(к) (к) (к)
1 ~ а11х1 +а12х2 +а13х3 +- + а1пхп
+а х(<г)
В каждое последующее уравнение подставляются значения неизвест-
(10.15)
+ Рп
ных, полученных из предыдущих уравнений, что показано в записи (10.15)
стрелками.
Теорема 10.3 (о достаточном условии сходимости метода Зейделя).
Если для системы х = ах + 0 какая-либо норма матрицы а меньше
единицы, т.е. ||а||^ <1 (se{ 1,2,3}), то процесс последовательных прибли-
жений (10.15) сходится к единственному решению исходной системы
Ах = Ь при любом начальном приближении х<0).
570
Записывая (10.15) в матричной форме, получаем
х(*+|) = Lx(/r+1)+(/xw+p, (10.16)
где L, U являются разложениями матрицы а:
' 0 0 0 О' 41 «12 «13 °1л'
а21 0 0 0 0 а22 а23 а2„
L = «31 «32 0 ” 0 , и = 0 0 «зз «з„
ч«л1 а„2 а„3 - 0, . 0 0 0 - «лл,
Преобразуя (10.16) к виду х = ах+р, получаем матричную форму ите-
рационного процесса метода Зейделя:
х(*+,) =(£_£)-1[/х(*)+(£-£)-1р. (10.17)
Тогда достаточное, а также необходимое и достаточное условия схо-
димости будут соответственно такими (см. теоремы 10.1 и 10.2):
||а|| = || (Е - A)”' UI < 1, | X, (а) | = | X, ((Е - х)-11/)| < 1.
Замечания 10.8.
1. Для обеспечения сходимости метода Зейделя требуется преобразо-
вать систему Ах = Ь к виду х = ах + Р с преобладанием диагональных эле-
ментов в матрице а (см. метод простых итераций).
2. Процесс (10.15) называется последовательным итерированием, так
как на каждой итерации полученные из предыдущих уравнений значения
подставляются в последующие. Как правило, метод Зейделя обеспечивает
лучшую сходимость, чем метод простых итераций (за счет накопления ин-
формации, полученной при решении предыдущих уравнений). Метод Зейде-
ля может сходиться, если расходится метод простых итераций, и наоборот.
3. При расчетах на ЭВМ удобнее пользоваться формулой (10.16).
4. Преимуществом метода Зейделя, как и метода простых итераций,
является его самоисправляемость.
5. Метод Зейделя имеет преимущества перед методом простых итера-
ций, так как он всегда сходится для нормальных систем линейных алгебраи-
ческих уравнений, т.е. таких систем, в которых матрица А является сим-
метрической и положительно определенной (см. разд. 6.5.4). Систему ли-
нейных алгебраических уравнений с невырожденной матрицей А всегда
можно преобразовать к нормальной, если ее умножить слева на матрицу
АТ (матрица АтА - симметрическая). Система АтАх = АТЬ является Нор-
мальной.
571
АЛГОРИТМ
I. Преобразовать систему Ах = b к виду х = ах + р одним из описан-
ных способов.
2. Задать начальное приближение решения х^ произвольно или по-
ложить х(0) = Р, а также малое положительное число е (точность). Поло-
жить к = 0.
3. Произвести расчеты по формуле (10.15) или (10.16) и найти х(*+1).
4. Если выполнено условие окончания ||х(/г+1)-х(^||<е, процесс за-
вершить и в качестве приближенного решения задачи принять х, = х<*+1).
Иначе положить к = к +1 и перейти к п.З.
Пример 10.15. Методом Зейделя с точностью £ = 0,001 решить
систему линейных алгебраических уравнений:
2Х] + 2х2 + 10х3 = 14,
10Х| + х2 +х3 = 12,
2х} + 10х2 + х3 = 13.
□ 1. Приведем систему Ах = Ь к виду х = ах+Р (см. пример 10.14):
X] = -0,1х2-0,1х3 +1,2, ( 0 -0,1 -0,Г
х2 =-0,2.х,-0,1-х3+1,3, а= -0,2 0 -0,1
х3 =-0,2-х1-0,2х2+1,4; t-0’2 “°’2 °,
'1,2'
Р= 1,3
.1,4.
Так как ||а|| = max { 0,2; 0,3; 0,4} = 0,4 < 1, условие сходимости выполняется.
2. Зададим х<0) = (1,2 0 0)г . В поставленной задаче е = 0,001.
3. Выполним расчеты по формуле (10.15):
х<*+1) =-0,1х^) -0,1х^ +1,2;
х^+,) =-0,2хр+1)-0,1x^+1,3; Л = 0,1,...
х^^-О^’-О^^+М;
и результаты занесем в табл. 10.6.
Таблица 10.6
к х<*> X(t) х2 г(*>
0 1,2000 0 0 —
1 1,2000 1,0600 0,9480 1,0600
2 0,9992 1,0054 0,9991 0,1008
3 0,9996 1,0002 1,0000 0,0052
4 1,0000 1,0000 1,0000 0,0004 < Е
572
Очевидно, найденное решение х, = (1 1 1)г является точным.
4. Расчет завершен, поскольку выполнено условие окончания
||х(*+1>_х(*)|| = 0,0004 <е.И
Пример 10.16. Методом Зейделя с точностью е = 0,005 решить систе-
му линейных алгебраических уравнений:
4Xj — х2 +Xj = 4,
X] +6х2 +2х3 =9,
-X] -2х2 +5х3 = 2.
□ 1. Так как [4| >|-1|+|1|, |б| > |l| +|2|, |5| >|-1|+|-2|, в данной систе-
ме диагональные элементы преобладают. Выразим из первого уравнения xt,
из второго х2, из третьего х3:
3 = 4Х2"4*3+1’
*2 =-6Х1 ~ зхз + ~>
:з= ixi +i хг +i>
2. Зададим х(0) = (о 0 0)г . В поставленной задаче е = 0,005 .
3. Выполним расчеты по формулам (10.15):
.(*+1)_1г(*) _!„(*) . г
1 4 2 4 3
х(**«)=_±х(*+>)_1х(*)+2; А = о,1,...
Z 0 1 J Z
.(*+1) . 2_.(*+1) , 2.
'3 5 1 5 2 5 ’
и результаты занесем в табл. 10.7.
Таблица 10.7
к х<‘> X(t) х2 х(*) Xj
0 0 0 0 —
1 1,0000 1,3333 1,1333 1,3333
2 1,0500 0,9473 0,9889 0,3860
3 0,9896 1,0050 0,9999 0,0604
4 1,0010 0,9999 1,0000 0,0114
5 1,0000 1,0000 1,0000 0,0010 < Е
Очевидно, найденное решение х. = (1 1 1)г является точным.
4. Расчет завершен, поскольку условие
Цх^+О _ ХМ)|| = 0,001 < е выполнено.И
окончания
573
Пример 10.17. Решить систему
X] -х2 +Х3 -4х4 = -2 ,
2Х( + х2 - 5х3 + х4 = 2,
8Х] - х2 - х3 + 2х4 =11,
х( +6х2 -2х3 - 2х4 = -7
методами простых итераций и Зейделя.
□ 1. Переставляя уравнения местами, преобразуем систему к виду с
преобладанием диагональных элементов:
8х. ~х, -х, + 2х. =11,
12 3 4 ’
X) + 6х2 -2х3 -2х4 = -7,
2х( +х2 -5х3 + х4 = 2,
X] —х2 +х3 -4х4 = —2 .
Так как |8|>|_1|+|_1|+|2|, |6|>|V|-2|+|-2|, |-5|>|2|+|1|+|1|,
|-4|>|1|+|-1|+|1|, то условие преобладания диагональных элементов вы-
полняется.
2. Выразим из первого уравнения х,, из второго х2 , из третьего х3, а
из четвертого х4 :
«*3~4Х4+Т’
Х2 = -^Х| + 3 Х3 + jx4 ,
Х3 = -X, + JX2 + уХ4 --,
Х4 ~ 4Х1 “ 4Х2 +4Х3 + 2 '
3. Зададим начальное приближение х^ = (0 0 1 2)г и е = 0,001.
Расчеты методом простых итераций выполним по следующим форму-
лам (результаты приведены в табл. 10.8, где А = |х(4) - )•’
х(М-1х(*)+1х(*)_1х(*) + 11
Л1 - 8 2 8 3 4 4 8 ’
x(*+0__ix(*)+ix(*)+ixU)_z
х2 6Л| т з Л3 т 3 Л4 6 ,
х(*+1) - 2 (*) I (t) 1 (к) _ 2
Л3 “51 5 2 т 5 4 5 ’
х(*+0 _ JLX(*) _1ХЮ +1М +1
л4 “ 4 1 4 2 4 3 2 ’
Расчеты методом Зейделя выполним по формулам (результаты приве-
дены в табл. 10.9):
X(M_1X(*)+1XW_1X(*)+JLL
Л1 8 2 + 8 3 4 Х4 Т 8 ’
Таблица 10.8
к х/> Х(к} х2 Х(к) х3 XW л4 А
0 0 0 1 2 —
1 1 -0,1667 0 0,75 1,25
2 1,1667 - 1,0833 0,1166 0,7916 0,9166
3 1,0562 - 1,0583 0,0083 1,0916 0,3000
4 0,9708 -0,9760 0,02916 1,0307 0,0854
5 0,9889 - 0,9752 - 0,0007 0,9940 0,0367
6 1,0045 - 1,0021 0,0030 0,9933 0,0269
7 1,0018 -1,0019 0,00006 1,0025 0,009
8 0,9992 -0,9995 0,0008 1,0009 0,0024
9 0,99994 - 0,9993 -0,00004 0,99986 0,00104
10 1,0001 - 1,0000 0,00009 0,99979 0,0007
Таблица 10.9
к 0 1 2 3 4 5 6 7
X 1 0 1 1,1458 1,0052 1,0059 1,0004 1,00025 1,0002
X 2 0 -0,3333 -0,9409 -0,9713 -0,9967 -0,9988 -0,9998 -0,9999
хз 1 0,3333 0,0534 0,0148 0,0026 0,00067 0,000125 0,00003
X 4 2 0,9166 1,0351 0,9978 1,0013 0,99995 1,00005 0,99999
д - 1,083 0,6075 0,1406 0,0254 0,0055 0,0011 0,00023
Методом простых итераций получено приближенное решение
х(10) =(1,0001 -1,0000 0,00009 0,99979/ за 10 итераций, а методом Зей-
деля: х(7) = (1,0002 -0,9999 0,00003 0,99999/ за 7 итераций. Точное
решение: х, = (1 -1 0 1/. Очевидно, метод Зейделя сошелся за меньшее
число итераций.И
10.4. ИТЕРАЦИОННЫЙ МЕТОД ШУЛЬЦА НАХОЖДЕНИЯ
ОБРАТНОЙ МАТРИЦЫ
Пусть дана квадратная невырожденная матрица А порядка п. Будем
искать обратную матрицу Л-1 в результате последовательных приближе-
ний, обозначая эти приближения ,...,U^k\... . Отклонение (невяз-
575
ку) текущего приближения от искомой обратной матрицы предлагается оце-
нивать величиной > где = Е- A-Uik). Равенство невязки нулю
означает, что текущее приближение совпадает с обратной матрицей.
АЛГОРИТМ
1. Положить <1 = 0. Задать Z7(0) - начальное приближение обратной
матрицы; е - малое положительное число; т - порядок метода.
2. Вычислить = E-A-U^.
3. Вычислить • Если ||'FW|| < Е, процесс завершить и положить
Л-1 = . Иначе перейти к п.4.
4. Найти следующее приближение
(10.18)
положить к = к +1 и перейти к п.2.
Теорема 10.4 (о сходимости итерационного метода Шульца). Пусть
квадратные матрицы А и [7(0) таковы, что матрица (7(0) имеет обрат-
ную и ||т(0)|| < 1 • Тогда существует обратная матрица А-1 и к ней схо-
дится последовательность матриц определяемая итерационным
процессом (10.18).
Замечания 10.9.
1. Заданием параметра т можно получать различные итерационные
процедуры, обладающие ( т +1 )-м порядком сходимости. Обычно полагают
т = 1 или т = 2 . Очевидно, чем больше т, тем больше порядок сходимо-
сти метода, однако при т = 2 обеспечивается минимум вычислительных за-
трат, требующихся для обращения матриц с заданной точностью методами
семейства (10.18).
2. Для выбора начального приближения 1/(0) существуют следующие
рекомендации. Если А - симметрическая положительно определенная мат-
рица и ее спектральный радиус р(А)<0 (см. разд. 10.5), то С/(0) -аЕ, где
( 2^
ае 0;—J. Если А - произвольная невырожденная матрица и спектраль-
ный радиус р(ааг)< 0, то (7(0> = аАТ , где ае ’ ^днако надо иметь в
576
виду, что при этом может не удовлетворяться условие
||'Р(0)||<1. Поэтому
лучше задавать матрицу <7(0) так, чтобы это условие выполнялось. Тогда
алгоритм достаточно быстро сходится к искомому решению задачи.
Пример 10.18. Дана матрица А = 0
.0
1 0 . Найти обратную матрицу
2 2,
итерационным методом Шульца.
□ 1. Положим к = 0, е = 0,01; m = 1. Зададим начальное приближение
и™ = "0,6 -0,5 -0,4^ 0,1 0,6 0,2 0,1 -0,5 0,5 у ( 0,1 -0 2 -0,5'
2. Вычислим Т® = Е- А -0,1 0,4 — 0,4 -0,2 -0,2 -0.4,
3. Так как р’(0) = 0,933 <1, то выполняется условие теоремы 10.4.
Поскольку Ьр(0) = 0,933 > Е = 0,01, перейдем к п.4.
4. Найдем
=ит
' 0,87
-0,03
-0,74
0,78
^-0,04 -0,82
-0,44'
-0,05
0,35 >
ит
Положим к = 1 и перейдем к п.2. Далее процесс продолжается. Приведем
результаты на последующих итерациях:
Т(1) =E-A-Um = "0,23 0,03 0 0,22 0,19' 0,05 , ||'Р(1)|| =0,572 >Е = 0,01;
0,14 0,08 0,4 J
u(2)=uw- [е+т <»]= " 0,986 -0,938 -0,488^ -0,021 0,948 -0,037 ч-0,025 -0,972 0,441 ? i
"0,08 0,015 0,12 '
Ч,(2) =Е-А-ит = 0,021 0,052 0,037 , ||’Р<2)|| = 0,269 >Е = 0,01;
0,091 0,05 0,191, II 114
37 - 4549
577
' 1,001 -0,996 -0,497
/<3>=t/<2>.[E + T(2) -6,029x10-3 0,995 -6,715х10-3 -1,002 -0,011 0,487
/ 0,017 7,942x10’3 о,озз'
Т(3) =E-A-U{3) = 6,029хЮ-3 4,878хЮ’3 0,025 0,013 0,011 0,049,
И = 0,07 >е = 0,01; 4
' 1 -1 -0,5 '
[у'4’ =(7<3).[£' + 'р(3)]= -4,246x10-4 1 -8,109x10-4
ч-4,63х10"4 -1 0,499 ,
1,192x10-3 6,192 x1g-4 2,276х10-3>
Т(4) =E-A-UW = 4,246x10’4 2,244х10-4 8,109хЮ-4
1,775 хЮ-3 к 9,259x10-4 3,391 х10-3
= 4,836х 10 3 < е = 0,01, процесс завершается и в качест-
Поскольку
ве приближенного решения задачи принимается А 1 = . Найденный ре-
зультат практически совпадает с полученным в примере 4.3.
10.5. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ О СОБСТВЕННЫХ
ЗНАЧЕНИЯХ И СОБСТВЕННЫХ ВЕКТОРАХ МАТРИЦЫ
Пусть задана квадратная матрица А порядка п. Напомним, что числа
X] Д2,...,А.л , являющиеся решениями характеристического уравнения:
|я-а.е| = о,
называются характеристическими (собственными) значениями матрицы
А , а соответствующие каждому Х.,г = 1..п, ненулевые векторы X', удов-
летворяющие системе
АХ‘ = \Х‘ или =0, г = 1,2,...,п,
называются собственными векторами.
Различают полную и частичную проблему собственных значений,
когда необходимо найти весь спектр (все собственные значения) и все ли-
нейно независимые собственные векторы либо часть спектра, например:
р(И) = тах|А.(.(Л)| и тт|Х(.(Л)|. Величина р(Я) называется спектралъ-
1 i
ным радиусом.
578
10.5.1. Метод итераций
Для решения частичной проблемы собственных значений и собствен-
ных векторов в практических расчетах часто используется метод итераций
(степенной метод). На его основе можно определить приближенно собст-
венные значения матрицы А и спектральный радиус p(J) = max | Х;(Я)|.
Пусть матрица А имеет п линейно независимых собственных векто-
ров X' ,i = 1,...,п, и собственные значения матрицы А таковы, что
р(Л) = |Х](Л)|>|Х2(Л)|>...>|Хл(Л)|.
АЛГОРИТМ
1. Выбрать произвольное начальное (нулевое) приближение собствен-
ного вектора (второй индекс в скобках здесь и ниже указывает номер
приближения, а первый индекс без скобок соответствует номеру собствен-
ного значения). Положить к - 0.
ХК1)
2. Найти .¥1(1) = /LV1(0>, Х^0 где 1 - любой номер 1<1<и,и
xi
положить к = 1.
3. Вычислить = AXW.
x1(i+,)
4. Найти Х(*+1) = , где x!(*+I\ xl(t) - соответствующие коорди-
х‘( } ‘
наты векторов и Х,(4). При этом может быть использована любая
координата с номером i, 1 < i < п.
5. Если Д - |х(*+1) - X^J < е, процесс завершить и положить X] = Х(*+1),
р(л) = | Xt |. Если Д > е , положить к = к +1 и перейти к п.З.
Замечания 10.10.
1. Процесс последовательных приближений
^*(1) = ^ЦО), %К2) = ^1(1) = Л2^1(0)
X™ = = А Ак-'Х1т = АкХ'(0\...
сходится, т.е. при Х->оо вектор Х1^ стремится к собственному вектору
X1.
2. Вместо применяемой в п.4 алгоритма формулы для )Sk+r> можно
взять среднее арифметическое соответствующих отношений для разных ко-
ординат.
3. Метод может использоваться и в случае, если наибольшее по моду-
лю собственное значение матрицы А является кратным, т.е.
М* 579
Xt = X2 = ... = XJ, и |Л1|>|ЛА.| при£>$.
4. При неудачном выборе начального приближения Х1(0) предел от-
xK*+i)
ношения может не существовать. В этом случае следует задать дру-
гое начальное приближение.
5. Рассмотренный итерационный процесс для Xj сходится линейно
Х2
с параметром с =-*- и может быть очень медленным.
6. Используя Xj, можно определить следующее значение Х2 по фор-
муле
rK*+D_i ГК*)
_xi Aixi
2 ч-№>-У Л4-1)
X( Aj X.
(i = l,2,...,n). Эта формула дает грубые значения
для Х2, так как значение Х1 является приближенным. Если модули всех
собственных значений различны, то на основе последней формулы можно
вычислять и остальные X (j = 3,4,...,л) .
7. После проведения нескольких итераций рекомендуется “гасить” рас-
тущие компоненты получающегося собственного вектора. Это осуществля-
ли*)
ется нормировкой вектора, например, по формуле
Пример 10.19. Для матрицы А = 1 4
найти спектральный
радиус степенным методом с точностью е = 0,1.
приближение собственного вектора
□ 1. Выбирается начальное
Х<°> = (1 1 1)т. Положим к = 0.
<5
2. Найдем Х1(1) = АХ|(0) = 1
.2
положим к = 1.
3. Вычислим
Х1(2) =АХ1(1) = 1 4 1
2 1 3
x1(I) Я
id) _Д1________-2-8
А1 1(0) t 8’
58
38
40
1
4
1
1
2
1
2
1
3
2^ m
1
3
1
1
g
6
6
5 I 2
8
6
6
580
го
4. Найдем Л(2) = = — = 7,25.
1 х*(1) 8
5. Так как |л(2) = 0,75 > е , то процесс необходимо продолжить.
Результаты вычислений удобно представить в виде табл. 10.10.
Таблица 10.10
к г1(*) •*1 ГЦ*) Л2 J(t) л3 А® А^-А^1’
0 1 1 1 — —
1 8 6 6 8 —
2 58 38 40 7,25 0,75
3 408 250 274 7,034 0,116
4 2838 1682 1888 6,9559 0,078 < Е
Точность по достигнута на четвертой итерации. Таким образом,
в качестве приближенного значения Л] берется 6,9559, а в качестве собст-
венного вектора принимается X1 = (2838 1682 1888)г .
Так как собственный вектор определяется с точностью до постоянного
множителя, то X1 лучше пронормировать, т.е. поделить все его компоненты
на величину нормы. Для рассматриваемого примера получим
х1 =—!—
2838
2838' ' 1,000
1682 0,5927
1888, 0,6652
Согласно замечаниям, в качестве собственного значения Л, матрицы
/(4) 2838
А можно взять не только отношение -------------------= 6,9559, но и
X(3> 408
.1(4)
2____
.1(3)
'2
1682 x\w 1888 , „
= 6,7280; — = ~ 6,8905, а также их среднее арифмети-
6,9559 + 6,728+6,8905 ЛОСО1 _
---------------------- 0,03 о 1 .
ческое
3
Пример 10.20. Найти максимальное по модулю собственное значение
(2 -1 Г
матрицы А = -1 2 -1 и соответствующий собственный вектор.
<0 0 з]
□ 1. Зададим начальное приближение Х1(0) =(1 -1 1)3 * * * 7 и е = 0,0001.
581
Выполним расчеты согласно методике (табл. 10.11).
Таблица 10.11
it Х«к> у1(*) х2
0 1 - 1 1 — —
1 4 -4 1 4 —
2 13 - 13 1 3,25 0,75
3 40 -40 1 3,0769 0,17307
4 121 -121 1 3,025 0,0519
5 364 -364 1 3,00826 0,01673
б 1093 -1093 1 3,002747 0,005512
7 3280 -3280 1 3,000914 0,00183
8 9841 -9841 1 3,000304 0,000609
9 29524 -29524 1 3,000101 0,000202
10 88573 -88573 1 3,000034 0,000067
В результате получено собственное значение X] = 3,00003 и собствен-
ный вектор %’= (88573 -88573 l)r или после нормировки X1 =
= —!— (88573 -88573 1)г=(1 -1 0,0000113У.
88573 v / к /
10.5.2. Метод вращений
Метод используется для решения полной проблемы собственных зна-
чений симметрической матрицы и основан на преобразовании подобия ис-
ходной матрицы А е Rn*n с помощью ортогональной матрицы Н (см.
разд. 9.6.4).
Напомним, что две матрицы А и А^ называются подобными, если
Л(/) = Н-'АН или А = НА^Н~' , где Н - невырожденная матрица.
В методе вращений в качестве Н берется ортогональная матрица,
такая, что ННТ = НтН = Е , т.е. Нт = . В силу свойства ортогонально-
го преобразования евклидова норма исходной матрицы А не меняется. Для
преобразованной матрицы А^ сохраняется ее след и собственные значения
п п
х<: trA=Хаи = X\oo=tr?1(‘)
<=1 1=1
При реализации метода вращений преобразование подобия применяет-
ся к исходной матрице А многократно:
Л(*+|) =[н(к)\'А^Н^ = A(k)Hw, Л =0,1......... (10.19)
Формула (10.19) определяет итерационный процесс, где начальное
приближение = А . На к -й итерации для некоторого выбираемого при
582
решении задачи недиагонального элемента * j, определяется орто-
гональная матрица Н^к\ приводящая этот элемент пЬ+1) (а также и а^+1>)
к нулю. При этом на каждой итерации в качестве выбирается наиболь-
ший по модулю. Матрица Н(к\ называемая матрицей вращения Якоби,
зависит от угла <pw и имеет вид
'1 - 0 0 0 0 0 0 • •• o'
0 1 0 0 - 0 0 0 ••• 0
0 0 cos<p(Zr) 0 0 -sin <p(Zr) 0 ••• 0 i -я строка
0 ••• 0 0 1 0 0 0 ... 0
Н<‘’ = 0 ••• 0 0 0 1 0 0 ... 0
0 ••• 0 sin <p(i) 0 0 cos <p(i) 0 ... о j -я строка
0 0 0 0 - 0 0 1 ... 0
0 0 0 0 - 0 0 0
Ф Ф
z -й столбец J -й столбец
В данной ортогональной матрице элементы на главной диагонали еди-
ничные, кроме = cos <р^ и = cos , а остальные элементы нуле-
вые, за исключением =-sin =sin (pw (Л„ - элементы матри-
цы Н).
Угол поворота q/*) определяется по формуле
2a(t) _ 1
tg2<pw = ‘J =Pk~, <pw =-arctgPt, (10.20)
au ~aii 7
где |2<p(Zr)| <y, i < j выбирается в верхней треугольной наддиагональ-
ной части матрицы А ).
В процессе итераций сумма квадратов всех недиагональных элементов
при возрастании к уменьшается, так что a(A(k+v>) <а(А^).
Однако элементы , приведенные к нулю на к-й итерации, на после-
583
дующей итерации немного возрастают. При к —> °° получается монотонно
убывающая ограниченная снизу нулем последовательность
а(А(1))>а(А(2,)>••>a(Aw)---. Поэтому a(A(i>)->0 при к—Это и
означает сходимость метода. При этом A(i> —> Л = diag(kv..., кп).
АЛГОРИТМ
1. Положить к = О, А(0) = А и задать е > 0.
2. Выделить в верхней треугольной наддиагональной части матрицы
A(i) максимальный по модулю элемент аУ\ i< j.
Если < е для всех i * j, процесс завершить. Собственные значе-
ния определяются по формуле X(.(Aw)=a<*\ i = l,....л.
Собственные векторы X' находятся как i -е столбцы матрицы, полу-
чающейся в результате перемножения:
vk ={х',х2,х3,...,хп).
Если > е ’ процесс продолжается.
1
3. Найти угол поворота по формуле <p(i) = — arctg - -—
2
« л
4. Составить матрицу вращения
5. Вычислить очередное приближение А(*+1) = (я w
Положить к = к +1 и перейти к п.2.
Замечания 10.11.
1. Используя обозначение Рк =
можно в п.З алгоритма вы-
числять элементы матрицы вращения по формулам
sin <p(Zr) = sign Рк
cos <р =
2. Контроль правильности выполнения действий по каждому повороту
осуществляется путем проверки сохранения следа преобразуемой матрицы.
3. При п = 2 для решения задачи требуется одна итерация.
584
Пример 10.21. Для матрицы А = I I методом вращений найти соб-
ственные значения и собственные векторы.
□ 1. Положим к = О, А<0)=А = | |,е = 1О’10.
I1 3J
2°. Выше главной диагонали имеется только один элемент
3°. Находим угол поворота матрицы по формуле (10.20), используя в
расчетах 11 цифр после запятой в соответствии с заданной точностью:
2а.. э
tg2<p<0)=——=—=-2;
ай-а.. 2-3
sincp<0> =-0,52573111212; coscp<0) =0,85065080835.
4°. Сформируем матрицу вращения:
Я(0) =
coscp(0)
ksin ф(0)
-sincp(0)W 0,85065080835 0,52573111212)
cos<p(0) I ~<-0,525731 И212 0,85065080835J
5°. Выполним первую итерацию:
А(1)=(Н(О))ГА(О)Н(О) =
0,85065080835 - 0,52573111212) 0,85065080835 0,52573111212
0,52573111212 0,85065080835 J <-0,52573111212 0,85065080835
1,38196601125 - 4,04620781325-Ю’12'
k-4,04587474634-IO”12 3,61803398874
Очевидно, след матрицы с заданной точностью сохраняется, т.е.
2 2
^а^ = У^а^ = 5 . Положим к = 1 и перейдем к п.2.
1=1 i=i
21. Максимальный по модулю наддиагональный элемент
|ар| = 4,04620781325-10”12 <е = 1О’10. Для решения задачи (подчеркнем,
что п = 2) с принятой точностью потребовалась одна итерация, полученную
матрицу можно считать диагональной. Найдены следующие собственные
значения и собственные векторы: = 1,38196601125 ; Л2 = 3,61803398874 ;
1 _( 0,85065080835
<-0,52573111212,
_(0,52573111212
<0,85065080835
585
Пример 10.22. Найти собственные значения и собственные векторы
<5 1 2>
матрицы
4
1
V
□ 1. Положим к = 0, А(0) = А, Е = 0,001.
2°. Выделим максимальный по модулю элемент в наддиагональной
части: - 2. Так как а]3 = 2 > е = 0,001, то процесс продолжается.
3°. Находим угол поворота:
1 2 1 д 1
ф(0) =—arctg- = -arctg— = -arctg2 = 0,553574,
2 «11 ~«33 2 5-3 2
sin (p(0) = 0,52573; cos <p(0) = 0,85065.
4°. Сформируем матрицу вращения:
'0,85065 0 -0,52573х
Н<°> = 0 1 0
0,52573 0 0,85065 ,
5°. Выполним первую итерацию:
' 6,236 1,376 2,33 Ю"6'
А(1) = (//«» f АтНт = 1,376 4 0,325
2,33-Ю-6 к 0,325 1,764 У
Положим к =1 и перейдем к п.2.
21. Максимальный по модулю наддиагональный элемент -1,376.
Так как > е, процесс продолжается.
З1. Найдем угол поворота:
Ф(1) =—arctg =larctg 2'?’376 =1 arctg 1,230769 = 0,444239 ,
2 afP-4’ 2 Б 6,236-4 2
5Шф(1) = 0,429770, созф(1) = 0,902937 .
(0,902937
41. Сформируем матрицу вращения: Hw = 0,429770
-0,429770 0"
0,902937 0
0 1>
51. Выполним вторую итерацию:
586
д(2)
= (Я(1))ГА(1)Я(1) =
6,891
2,238-10"4
0,14
2,238-10-4 0,14
3,345 0,293
0,293 1,764
Положим к = 2 и перейдем к п.2.
22. Максимальный по модулю
42) = 0,293>е.
наддиагональный элемент
З2. Найдем угол поворота:
<р(2) =larctg-^'-^-- =-arctg-.2'0,293 =-arctgO,370651= 0,177476,
2 ag -азз 2 3,345-1,764 2
sin ф(2) = 0,1765460; coscp<2) = 0,9842924 .
42. Сформируем матрицу вращения '10 0 ' Н(2) = 0 0,9842924 - 0,1765460 . J) 0,1765460 0,9842924 ? 5 2 Выполним третью итерацию: <6,891 0,025 0,138 >
л(3)=(я(2)ул(2)я(2)= ад25 3398 зз75.10-7 k 0,138 3,375-10“7 1,711 Положим к = 3 и перейдем к п.2.
23. Максимальный по модулю наддиагональный а™ = 0,138 > £ . З3. Найдем угол поворота: элемент
<p(3) =—arctg 13 =—arctg—2 °’138— =—arctg0,05328 = 0,026615,
2 a™-a™ 2 5 6,891-1,711 2
sin <p(3) = 0,026611; cos cp(3) = 0,999646.
43. Сформируем матрицу вращения:
<0,999646 0 - 0,02661 Pl
Я(3) =01 0
1^0,026611 0 0,999646 J
53. Выполним четвертую итерацию:
587
л(4)
= (п<3))ГА'3)Н®
6,895
0,025
8,406-IO'6
к
0,025 8,406 •Ю'6
3,398 - 6,649-10"4
-6,649 IO”4 1,707
Положим к = 4 и перейдем к п.2.
24. Так как = 0,025 > Е, процесс повторяется.
З4. Найдем угол поворота
ф(4) =-iarctg
2-а(4)
х «12
aw-aw
«11 «22
1 2-0,025
=—arete—————
2 6,895-3,398
= 0,0071484,
sin <р(4) = 0,0071483; cos ф(4) = 0,9999744.
44. Сформируем матрицу вращения:
"0,9999744 - 0,0071483 О'
Н(4)= 0,0071483 0,9999744 0 < 0 0 1, 54 . Выполним пятую итерацию: f 6,895 4,774-10~7 3,653-10”6 '
л(5)=(я(4)ул(4)я(4)= 4774.10-7 3,398 3,653-10”6 - 6,649 Ю”4 X. -6,649 10~4 1,707 /
Положим к = 5 и перейдем к п.2.
25 . Так как наибольший по модулю наддиагональный элемент удовле
творяет условию |- 6,649 • 10”'4| < е = 0,001, процесс завершается.
Собственные значения: = 6,895, = 3,398
А3 = = 1,707. Для нахождения собственных векторов вычислим
V5 отсюда X (4) _ , х "0,753 -0,458 -0,473" 0,432 0,886 -0,171 , 0,497 - 0,076 0,864,
0,753" 0,432 к0,497, 1 , х2 / "-0,458 0,886 с 0,076 -0,517" з _ "-0,473" -0,171 , 0,864 , "-0,5474" или после нормиров
ки X1 = 0,5737 , X2 = 1 , х3 = -0,1979 .
0,660, С 0,0858, 1 ,
4ЯЙ
Задачи для самостоятельного решения
10.1. Дана система с трехдиагональной матрицей А :
2х, +х2 =2,+‘з‘”’
^+3х2 +Хз =v+2'”’
- 2х, + Зх, + х. = 1,
2 3 4
х3-2х4 =-|+|-и,
где п - номер студента по списку учебной группы.
Требуется:
а) убедиться, что матрица этой системы удовлетворяет условию преоб-
ладания диагональных элементов;
б) решить систему методом прогонки;
в) подстановкой полученного решения в исходную систему убедиться
в правильности результата.
10.2. Методом простых итераций и методом Зейделя решить с точно-
стью е = 0,001 систему линейных алгебраических уравнений Ах = b , где
А =
5 1 1
2 6-1
2 3 10
'11 + 0,8-п
13 + 0,9-и
18-0,5-п
Ь =
п - номер студента по списку учебной группы.
10.3. Для следующих матриц с точностью е = 0,01 определить методом
вращения собственные значения и собственные векторы. Методом итераций
найти спектральный радиус.
'2,1 1 1,Г '2,4 1 1,4' '1,3 0,4 0,5'
а) 1 2,6 1,1 ; б) 1 2,3 1,4 ; в) 0,4 1,3 0,3
J.1 1,1 3,1, J.4 1,4 3,4, 0,5 0,3 1,3,
Шульца.
10.4. Методом квадратных корней, методом Гаусса, LU -разложения,
методом простых итераций и методом Зейделя решить систему
'16 -8 -4 0 V Г-8'
-8 13 -4 -3 Х2 7
-4 -4 9 0 хз 6
-3 0 3J Л, l-з,
Найти определитель матрицы системы и обратную матрицу методом
ЛИТЕРАТУРА
1. Александров П.С. Лекции по аналитической геометрии. - М.: Наука,
1968.
2. Александров П.С. Курс аналитической геометрии и линейной алгебры. -
М.: Наука, 1979.
3. Алберт А. Регрессия, псевдоинверсия и рекуррентное оценивание. - М.:
Наука, 1977.
4. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. -
М.: Наука, 1984.
5. Беллман Р. Введение в теорию матриц. - М.: Наука, 1969.
6. Бугров Я.С, Никольский С.М. Элементы линейной алгебры и аналити-
ческой геометрии. - М.: Наука, 1980.
7. Бутузов В.Ф., Крутицкая Н.Ч., Шишкин А.А. Линейная алгебра в во-
просах и задачах. - М.: Физматлит, 2001.
8. Вержбицкий В.М. Основы численных методов. - М.: Высшая школа,
2002.
9. Воеводин В.В. Линейная алгебра,- М.: Наука, 1980.
10. Гонтмахер Ф.Р. Теория матриц- М.: Наука, 1988.
11. Гельфанд И.М. Лекции по линейной алгебре. - М.: Наука, 1971.
12. Глаголева Р.Я., Осипова В.А. Методы линейной алгебры и их приложе-
ния к инженерным задачам. -М.: МАИ, 1981.
13. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в уп-
ражнениях и задачах: Учебное пособие для студентов втузов. В 2-х ч. 4.1. -
М.: Высшая школа, 1986.
14. Ефимов И.В. Квадратичные формы и матрицы. -М.: Наука, 1967.
15. Ефимов Н.В. Краткий курс аналитической геометрии. - М.: Физматгиз,
1962.
16. Задачник-практикум по аналитической геометрии и высшей алгебре:
Учебное пособие / Волков В.А., Ефимова Т.А., Райнес А.А., Шмидт Р.А. -
Л.: Изд-во ЛГУ, 1986.
17. Икрамов Х.Д. Задачник по линейной алгебре. - М.: Наука, 1975.
18. Ильин В.А., Позняк Э.Г Линейная алгебра. - М.: Наука, 1984.
19. Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ. -
М.: Наука, 1979.
20. Канатников А.Н., Крищенко А.П. Линейная алгебра. - М.: Изд-во
МГТУ, 2001.
21. Киреев В.И., Пантелеев А.В. Численные методы в примерах и зада-
чах,- М.: Высшая школа, 2004.
22. КлетеникД.В. Сборник задач по аналитической геометрии. - М.: Нау-
ка, 1964.
23. Кострикин А.И. Введение в алгебру. Основы алгебры. - М.: Физмат-
лит, 1994.
590
24. Кочетков ЕС., Осокин А.В. Начала линейной алгебры: Учебное посо-
бие. - М.: МАИ, 1999.
25. Кудрявцев Л.Д. Курс математического анализа: Учебник. - М.: Высшая
школа, 1988.
26. Курош А.Г. Курс высшей алгебры. - М.: Наука,1965.
27. Ланкастер П. Теория матриц. - М.: Наука, 1988.
28. Нефедов В.Н., Осипова В.А. Курс дискретной математики. - М.: Изд-во
МАИ, 1992.
29. Общий курс высшей математики для экономистов: Учебник / Под ред.
В.И. Ермакова. — М.: ИНФРА-М, 2003.
30. Окунев Л.Я. Высшая алгебра. - М.: Просвещение, 1966.
31. Пантелеев А.В., Бортаковский А.С. Теория управления в примерах и
задачах. - М.: Высшая школа, 2003.
32. Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и зада-
чах. - М.: Высшая школа, 2002.
33. Пантелеев А.В., Якимова А.С. Теория функций комплексного пере-
менного и операционное исчисление в примерах и задачах. - М.: Высшая
школа, 2001.
34. Пантелеев А.В., Якимова А.С., Босов А.В. Обыкновенные дифференци-
альные уравнения в примерах и задачах. - М.: Высшая школа, 2001.
35. Прасолов В.В. Задачи и теоремы линейной алгебры. - М.: Наука, 1996.
36. Проскуряков И.В. Сборник задач по линейной алгебре. - М.: Наука,
1978.
37. Пугачев В.С. Лекции по функциональному анализу. - М.: Изд-во МАИ,
1996.
38. Сборник задач по математике для втузов. Линейная алгебра и основы
математического анализа / Под ред. А.В. Ефимова, Б.П. Демидовича. - М.:
Наука, 1981.
39. Сигорский В.П. Математический аппарат инженера. - Киев: Техника,
1975.
40. Соболев С.Л. Введение в теорию кубатурных формул. - М.: Наука,
1974.
41. Чаки Ф. Современная теория управления. - М.: Мир, 1975.
42. Шилов Г.Е. Математический анализ (конечномерные линейные про-
странства). - М.: Наука, 1969.
43. Шилов Г.Е. Математический анализ (функции нескольких веществен-
ных переменных). - М.: Наука, 1972.
44. Шипачев В.С. Основы высшей математики. - М.: Высшая школа, 1994.
45. Фаддеев Д.К, Соминский И.С. Сборник задач по высшей алгебре. - М.:
1977.
46. Федорчук В.В. Курс аналитической геометрии и линейной алгебры:
Учебное пособие. - М.: Изд-во МГУ, 1990.