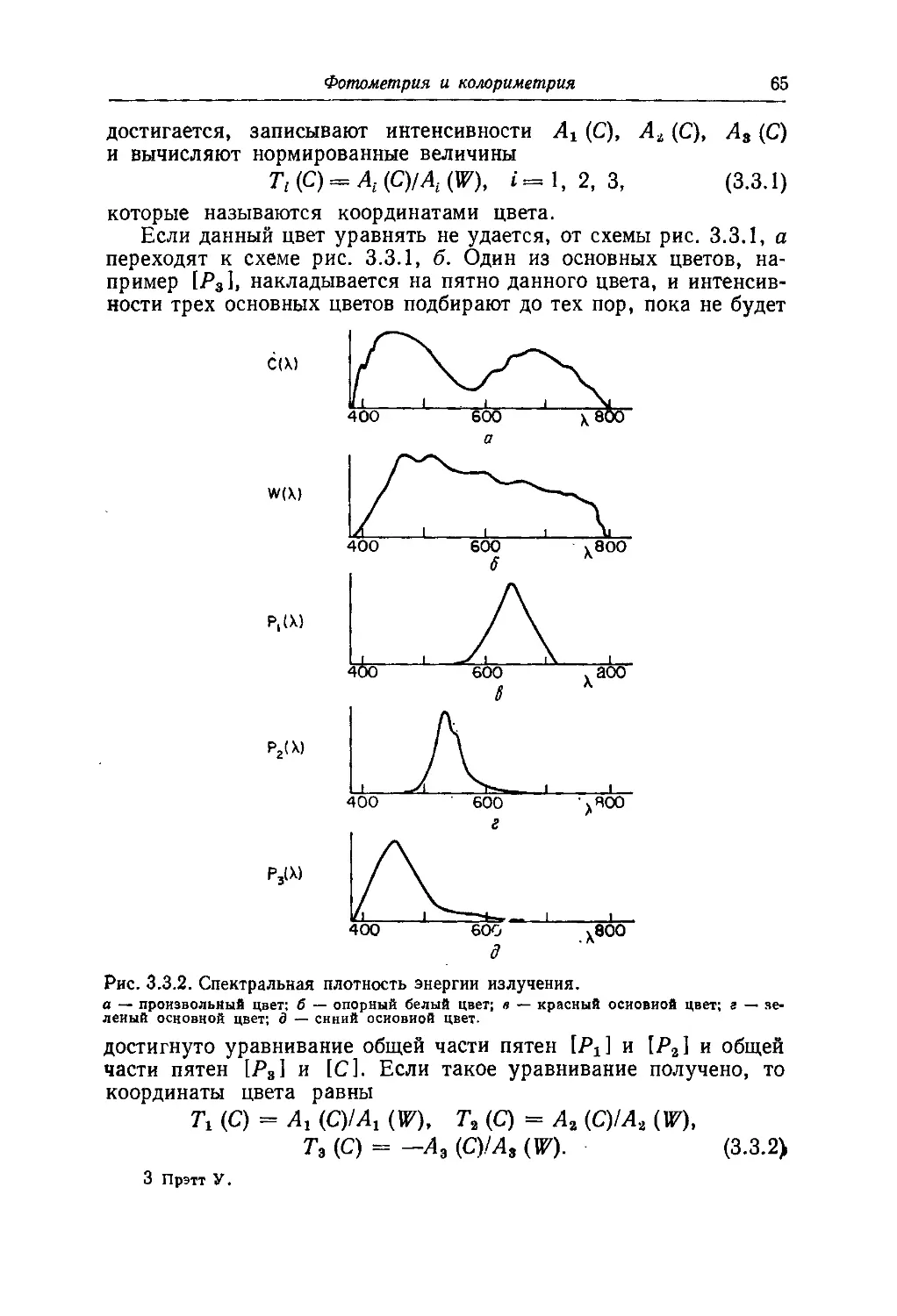
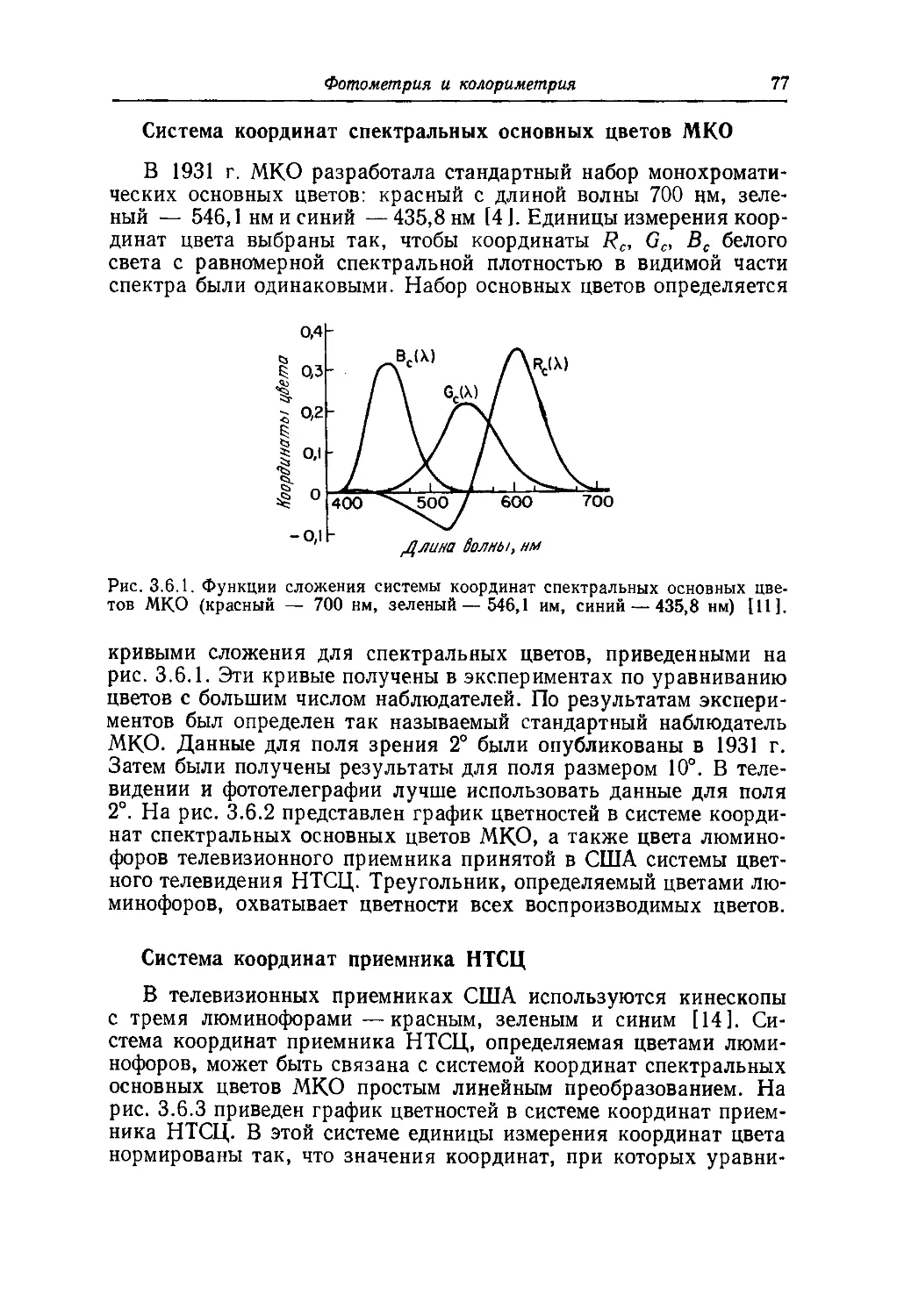
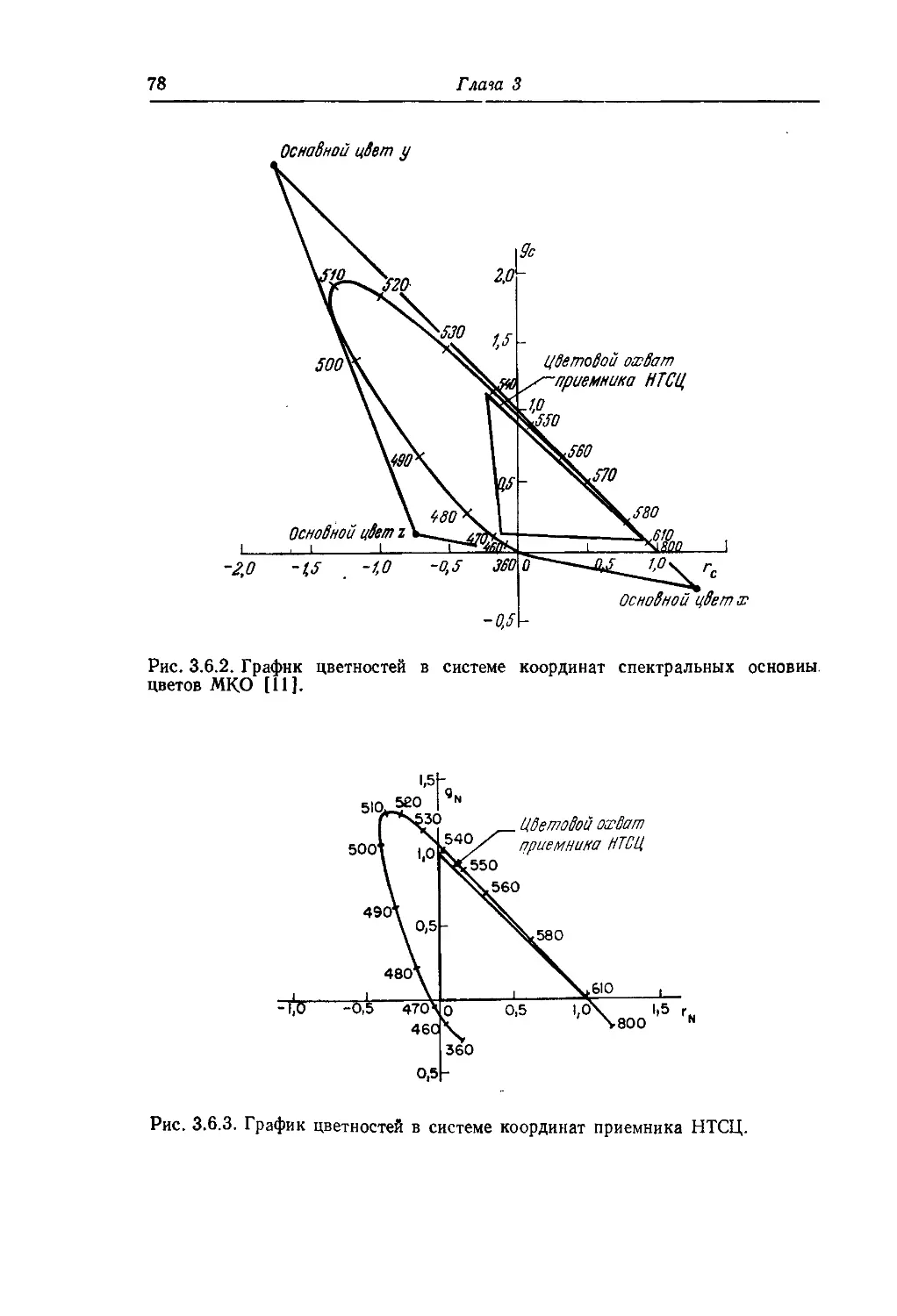
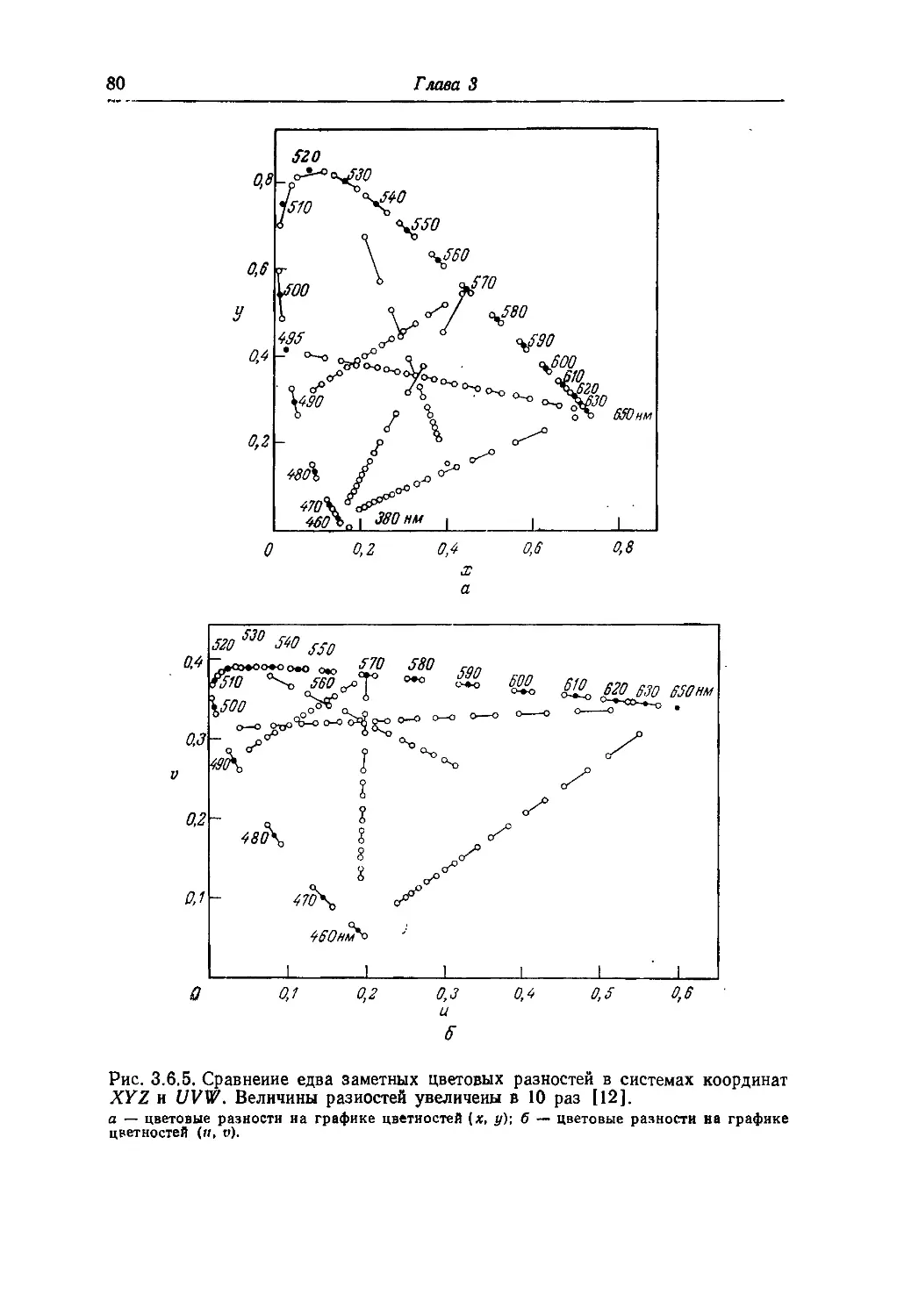
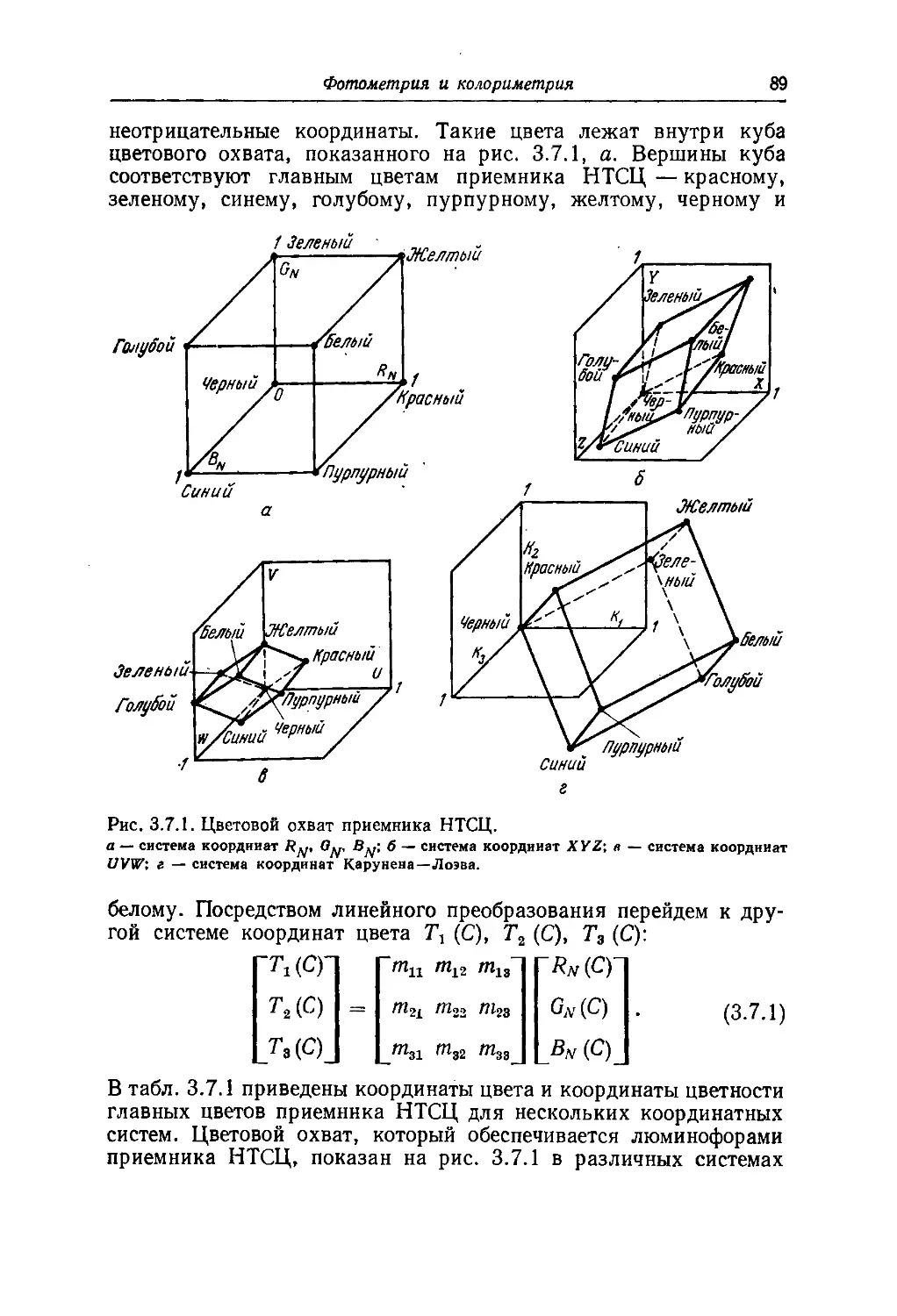
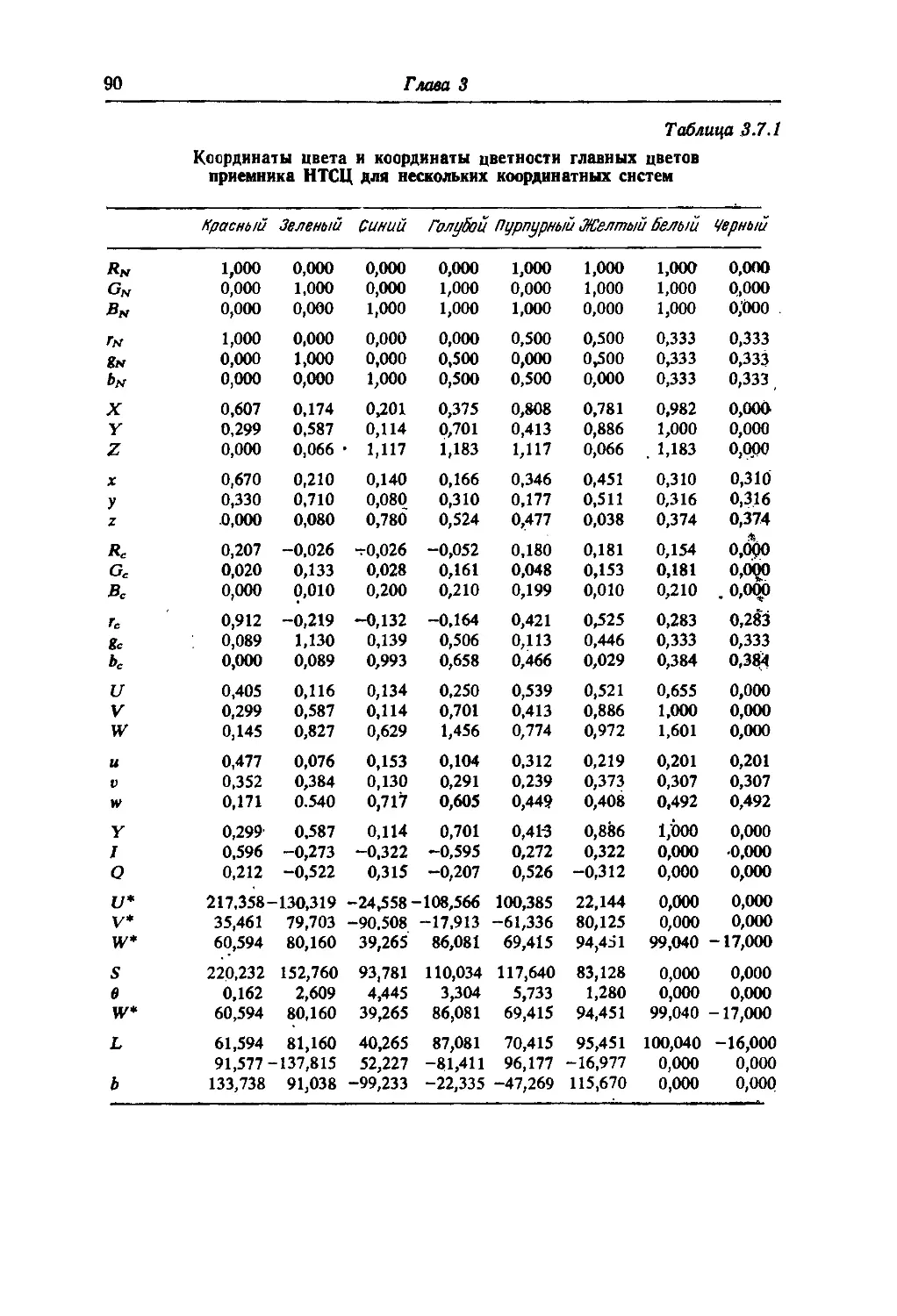
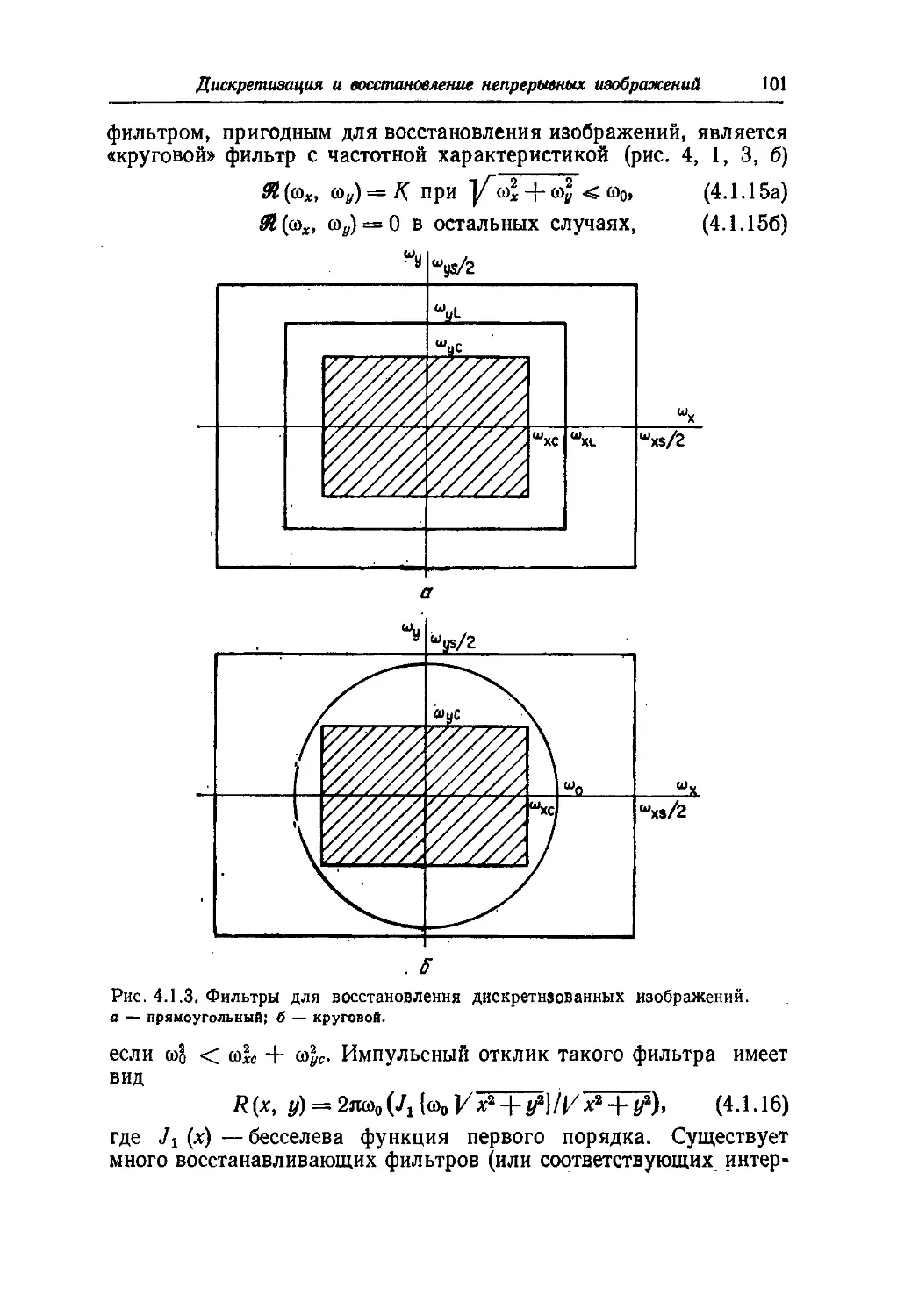
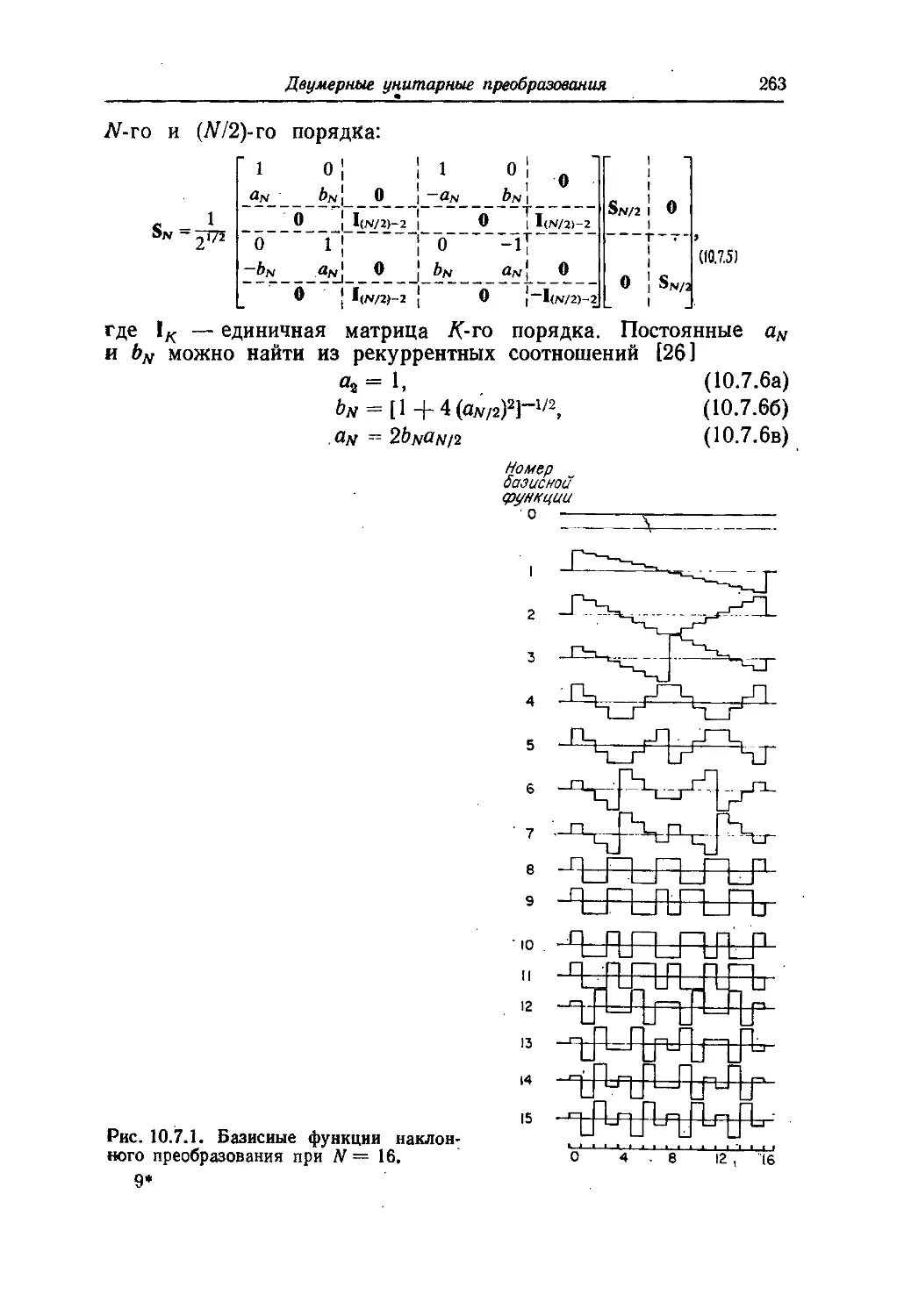
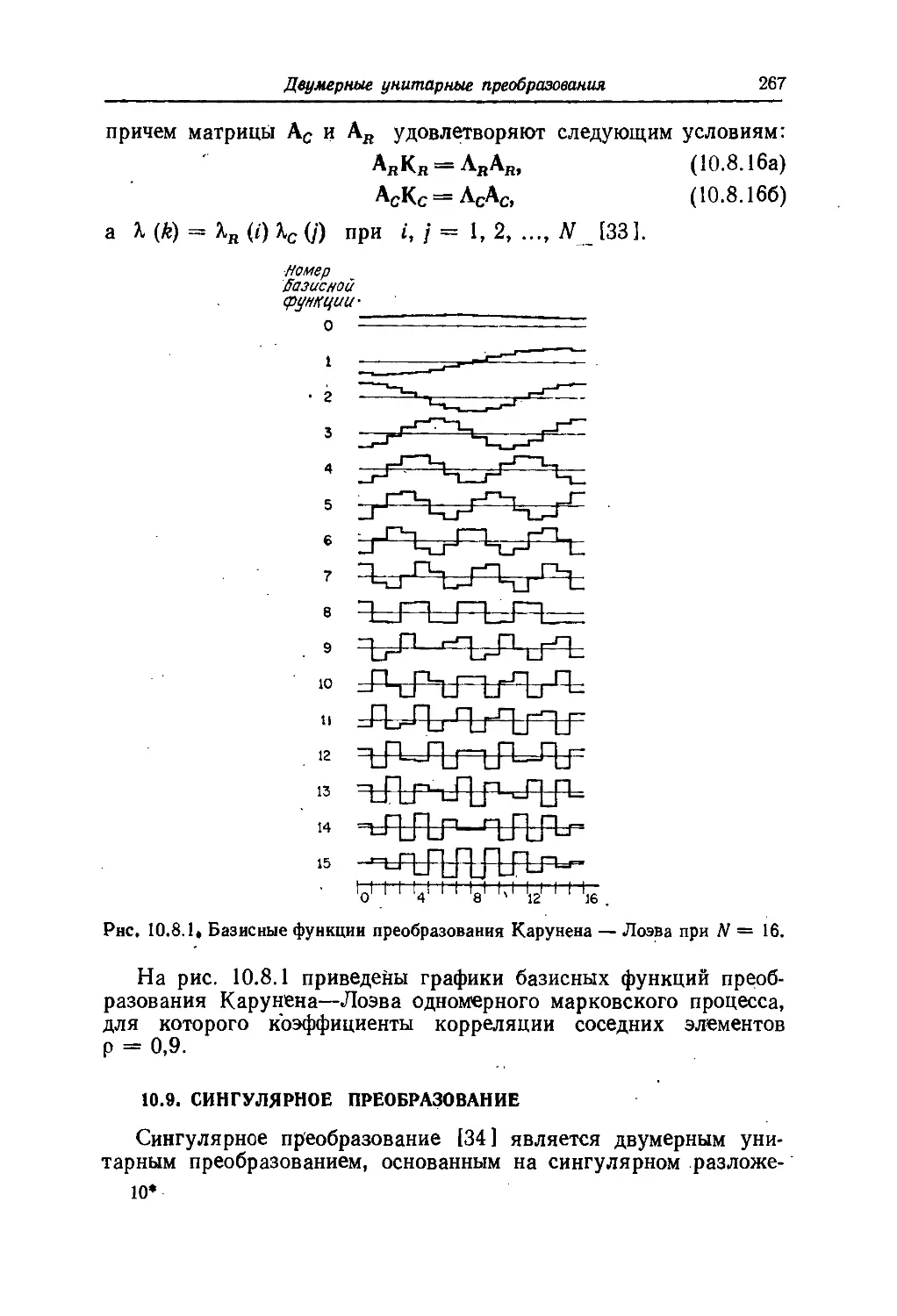
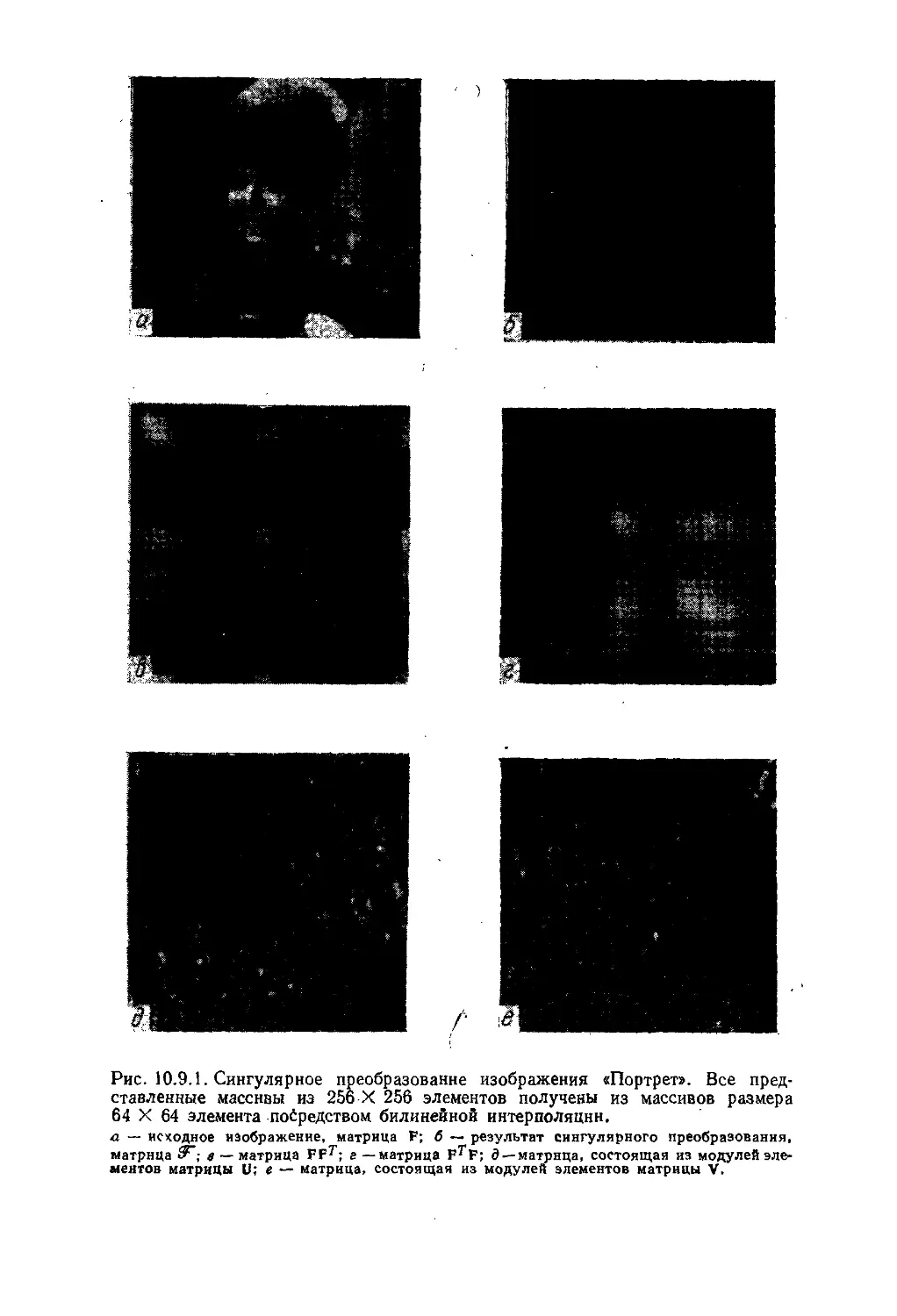
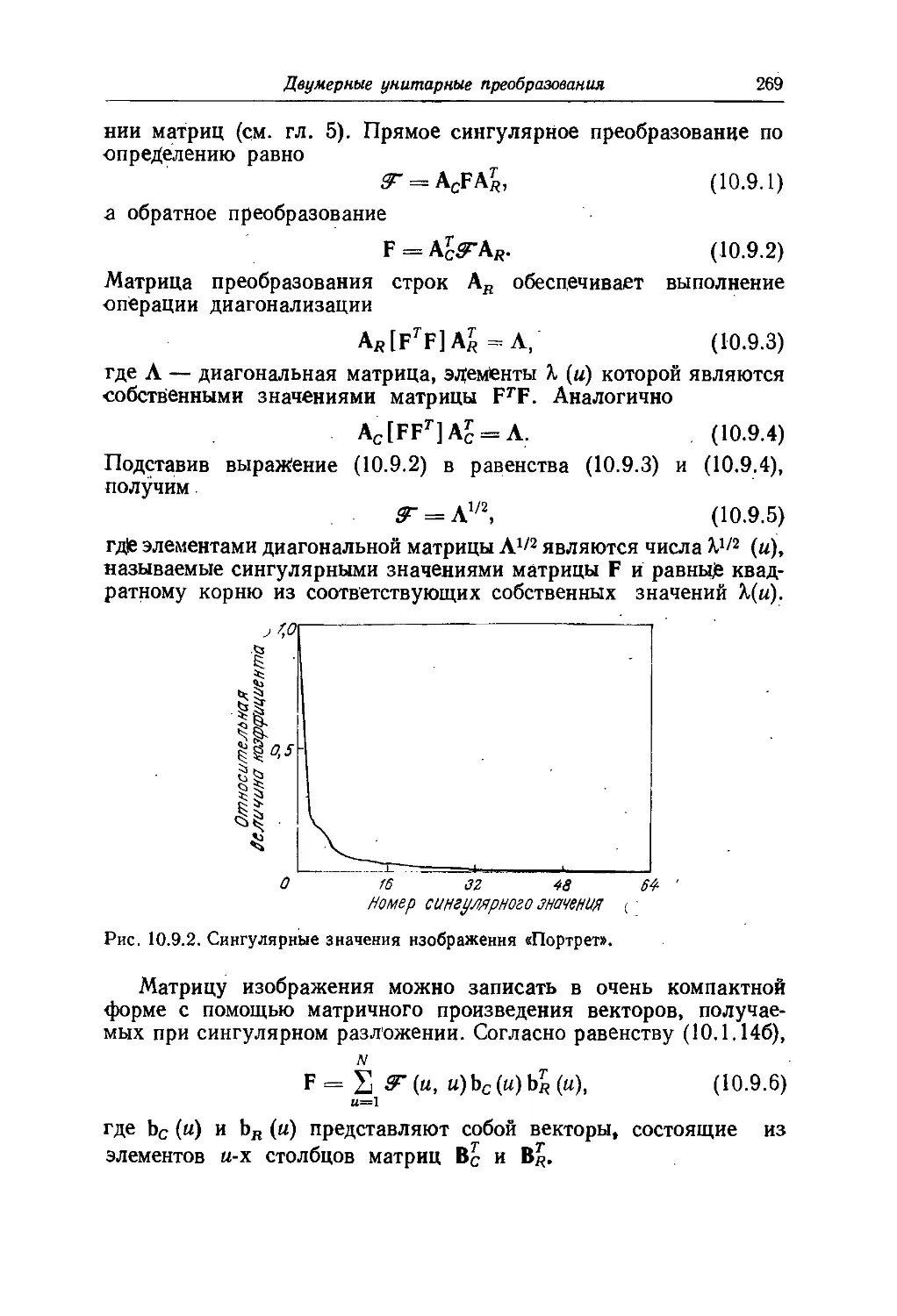
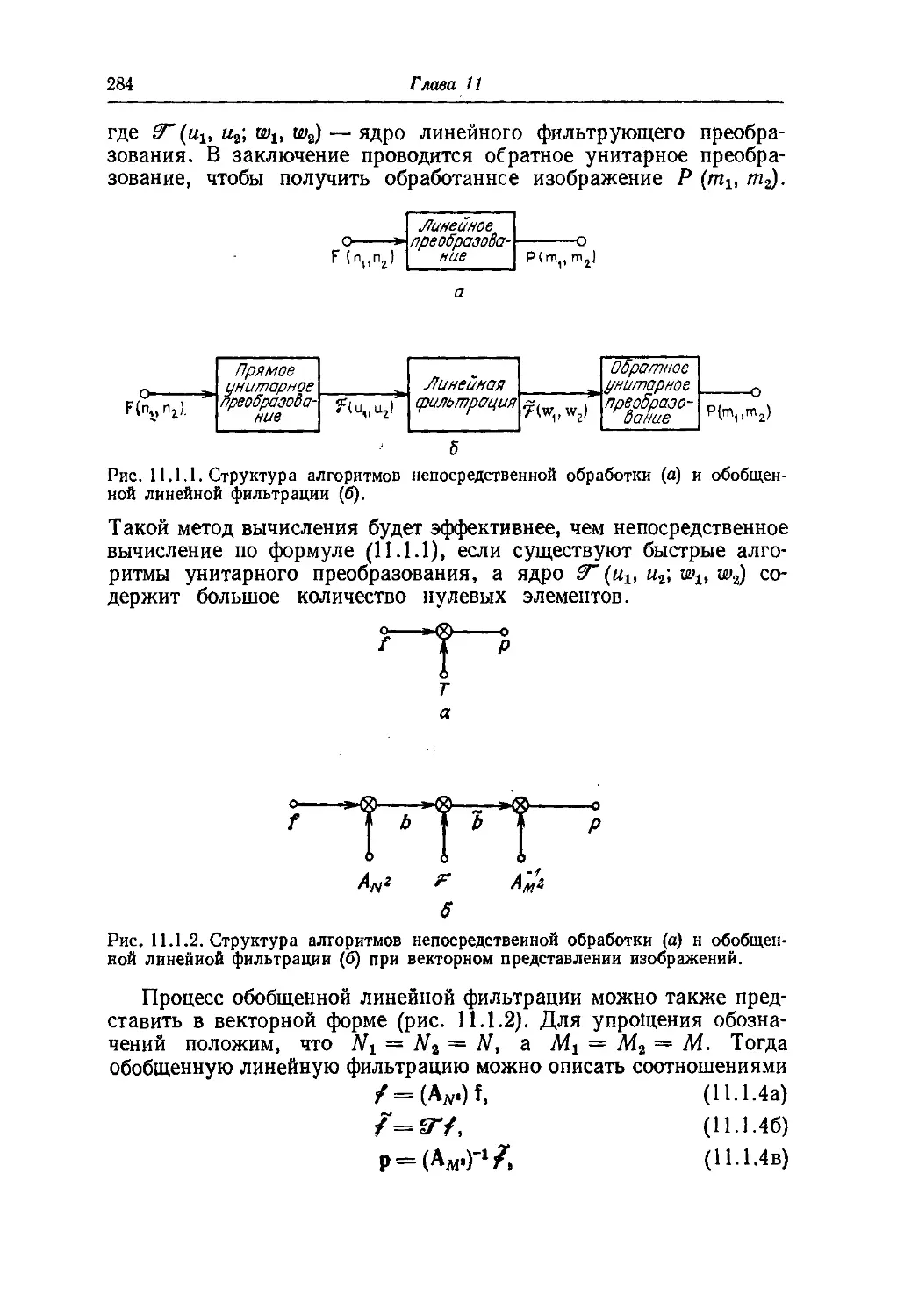
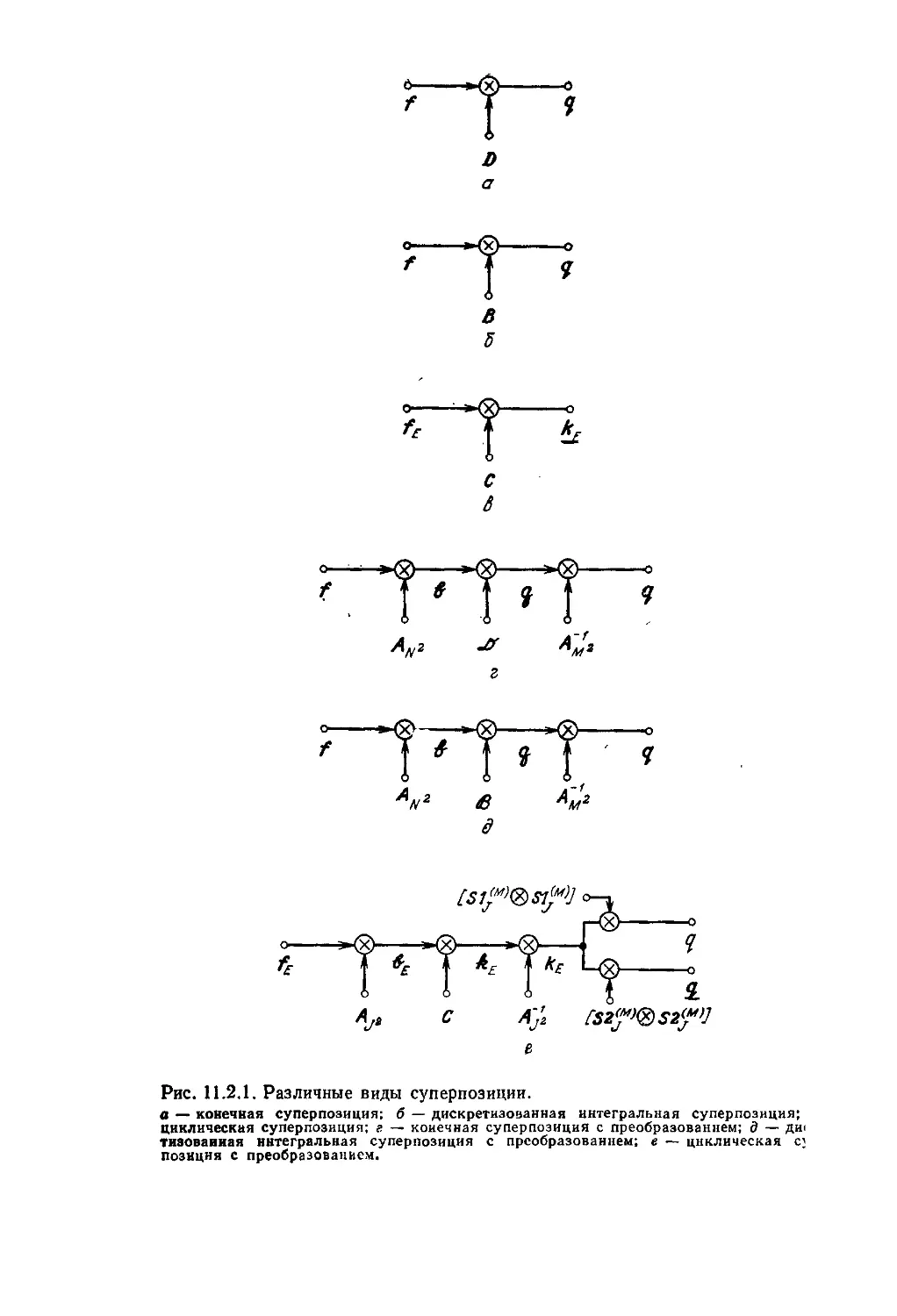
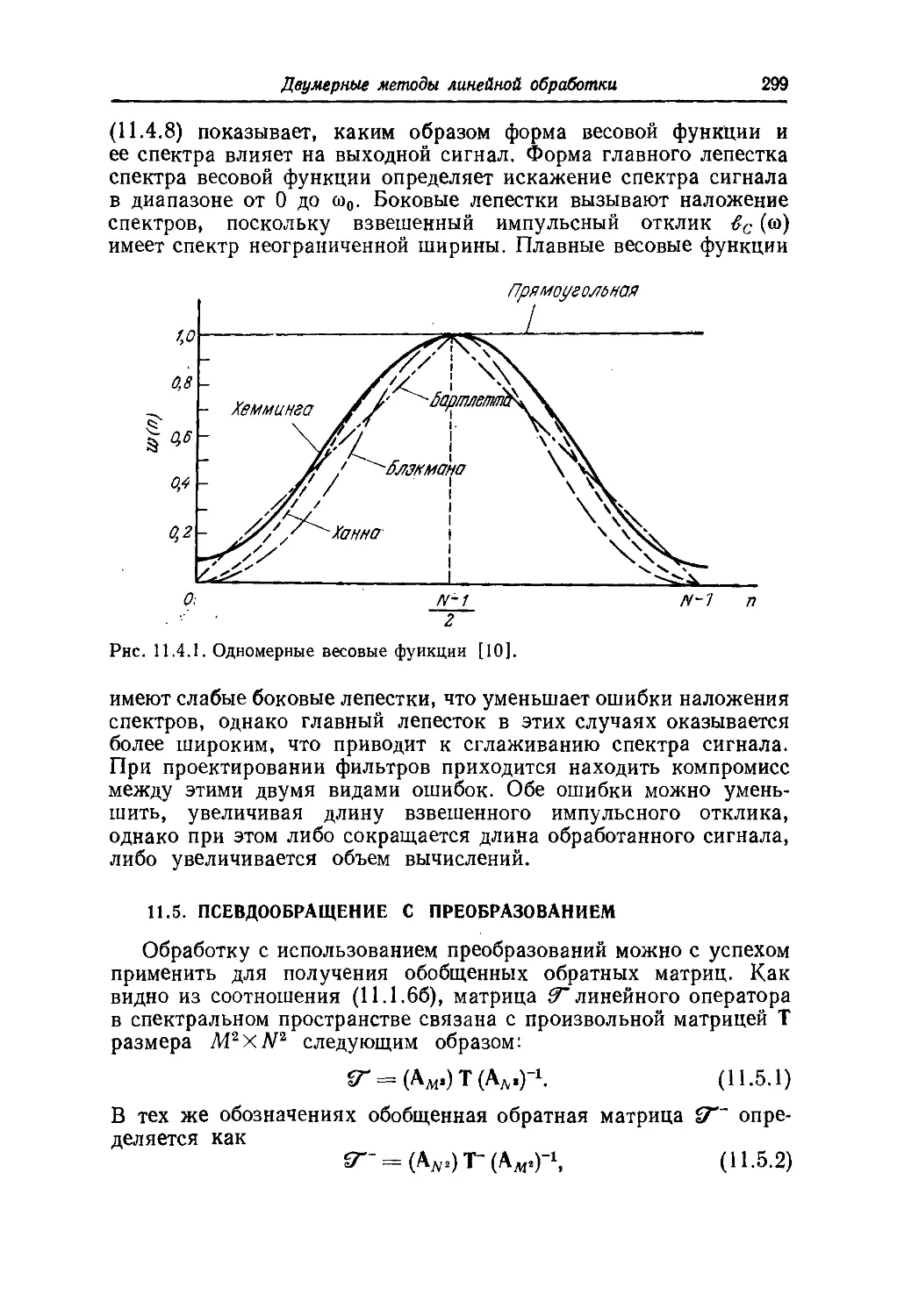
Текст
DIGITAL
IMAGE
PROCESSING
William K. Pratt
Professor of Electrical Engineering
Image Processing Institute
University of Southern California
Los Angeles, California
A W1LEY-1NTERSC1ENCE PUBLICATION
JOHN WILEY AND SONS
NEW YORK/CH1CHESTER/I3R1SBANE/TORC
1978
У. Прэтт
ЦИФРОВАЯ
ОБРАБОТКА
ИЗОБРАЖЕНИЙ
В 2-х книгах
1
Перевод с английского
под редакцией
канд. техн. наук Д. С. ЛЕБЕДЕВА
ИЗДАТЕЛЬСТВО «МИР»
МОСКВА 1982
ББК 32.94
П85
УДК 621.372.542
Прэтт У.
П85 Цифровая обработка изображений: Пер. с англ.—М.:
Мир, 1982.— Кн.1—312 с, ил.
Монография крупного американского специалиста в области обработкн
изображений, который с 1971 по 1980 г. возглавлял Институт обработкн изобра-
изображений при Южнокалифорннйском университете в Лос-Анджелесе; наиболее пол-
полная по данной области знания.
В русском переводе монография выпускается в двух книгах. Книга 1 посвя-
посвящена вопросам математического представления непрерывных н дискретных нзо-
нзображений. Подробно рассмотрены двумерные преобразования, в том числе пре-
преобразования Фурье, Адамара и Карунена— Лоэва.
Предназначена для специалистов, имеющих дело с обработкой нзображе-
нзображений, а также для студентов, изучающих методы цифровой обработкн изображений.
Редакция литературы по новой технике
Copyright © 1978 by John Wiley & Sons, Inc.
All rights reserved. Authorized translation from
English language edition published by John
Wiley & Sons, Inc.
© Перевод на русский язык, «Мир», 1982
ПРЕДИСЛОВИЕ К ПЕРЕВОДУ
Цифровая обработка изображений представляет собой само-
самостоятельную область знания, которая быстро развивается во
многих странах, в том числе и в Советском Союзе. Отечественной
промышленностью выпускаются устройства ввода и регистрации
изображений, дисплеи, графопостроители, специализированные
процессоры и другое оборудование. Созданы мощные центры циф-
цифровой обработки изображений для исследования природных
ресурсов и охраны окружающей среды, работают многочислен-
многочисленные цифровые установки для медицинской диагностики, в том
числе томографические.
С обработкой изображений приходится иметь дело специали-
специалистам различного профиля, причем большинство из них закомятся
с этим предметом самостоятельно. В связи с этим возникает не-
необходимость в соответствующих учебных пособиях. По цифровой
обработке изображений и смежным вопросам опубликовано много
работ, но, как правило, они посвящены отдельным аспектам об-
обработки изображений, что, естественно, затрудняет выбор лите-
литературы. .
Монография Прэтта, несомненно, окажется полезной для
советских специалистов, ;кйк*;„з!1ако'мых с методами обработки
изображений, так и для новичков. Она выгодно отличается от
других книг на эту тему "полнотой' охвата материала. В ней рас-
рассматривается большинство известных методов и алгоритмов об-
обработки изображений. Однако цифровая обработка изображений —
предмет настолько обширный и разнородный, что уместить его
в одну книгу совершенно невозможно. Так, в монографии не на-
нашли отражения некоторые вопросы, отмеченные в предисловии
автора, недостаточно полно рассмотрены статистические методы
обработки изображений, которые в последние годы успешно
применяются для улучшения и анализа изображений. Мы сочли
целесообразным привести список статей и книг, опубликованных
после выхода данной монографии в свет. В этот же список включены
основные работы советских авторов, большой вклад которых в об-
обработку изображений отражен в монографии совершенно недо-
недостаточно.
Предисловие к переводу
При переводе возникли большие терминологические трудно-
трудности. Хотя не все решения, принятые редактором перевода и пе-
переводчиками, можно считать бесспорными, проделанная ими ра-
работа будет несомненно способствовать развитию и упорядочению
терминологии в области цифровой обработки изображений.
Перевод выполнен В. П. Андреевым (гл. 17—20), А. Л. Зай-
Зайцевым (гл. 4, 6, 7, 9, 10, 11), канд. техн. наук Д. С. Лебедевым
(гл. 1—3), канд. техн. наук В. Г. Поляковым (гл. 21—24),
Н. Н. Тетекиным (гл. 5, 8) и канд. техн. наук В. А. Хлеборо-
довым (гл. 12—16).
Чл.-корр. АН СССР
В. И. Сифоров
ПРЕДИСЛОВИЕ
За последнее десятилетие область применения цифровой об-
обработки изображений значительно расширилась. Этому способ-
способствовало повышение скорости работы, а также уменьшение стои-
стоимости и размеров цифровых вычислительных машин и техниче-
технических средств обработки сигналов. Методы обработки изображений
уже играют значительную роль в научных исследованиях, про-
промышленности, медицине, космических исследованиях и информа-
информационных системах. Примерами применения этих методов могут
служить цифровая передача изображений с космических кораб-
кораблей, видеотелефонная связь по телефонным каналам, повышение
четкости изображений, создаваемых электронным микроскопом,
коррекция искажений изображений, принимаемых из космоса,
автоматический анализ характера местности, исследование при-
природных ресурсов по фотоснимкам, передаваемым со спутников
Земли, формирование и улучшение качества биологических и
медицинских изображений, включая рентгенограммы, термограм-
термограммы и изображения-радиоизотопной диагностики, автоматическое
составление карт по аэрофотоснимкам, обнаружение дефектов в де-
деталях машин с помощью промышленных рентгенограмм. Нет
сомнения, что со временем методы обработки изображений най-
найдут еще более широкое применение в медицине, во многих слу-
случаях облегчая врачу постановку диагноза, и в технике. Дей-
Действия робота, наделенного «зрением», будут основываться на ав-
автоматическом анализе сцен. Эффективные методы кодирования
изображений, по-видимому, позволят в будущем создать инди-
индивидуальные каналы двусторонней телевизионной связи как лич-
личного, так и служебного пользования.
Эта книга предназначается в качестве руководства по курсу
«Цифровая обработка изображений» для студентов и аспирантов,
специализирующихся в области электронной и вычислительной
техники, и может быть также использована в качестве справочного
пособия научными работниками и инженерами, связанными с ис-
исследованиями и практическими разработками в области обработки
изображений. Цифровая обработка изображений — предмет ши-
широкого профиля, охватывающий вопросы физики, физиологии,
электронной и вычислительной техники, математики. Предпола-
Предисловие
гается, что читатель имеет подготовку в какой-либо из этих обла-
областей в объеме программы технического вуза. Весьма желательно
(но не обязательно) знакомство с теорией линейных систем,
векторной алгеброй, теорией вероятностей и теорией случайных
процессов.
Книга разделена на шесть частей. Часть 1, состоящая из трех
глав, посвящена непрерывным изображениям. Здесь дано мате-
математическое представление непрерывного изображения, описаны
психофизические свойства зрения человека и рассмотрены вопросы
фотометрии и колориметрии. В части 2 приведены методы дискрети-
дискретизации и квантования, вопросы математического описания дискрет-
дискретных изображений и выбора критериев для оценки качества изоб-
изображения. В части 3 обсуждаются методы двумерной обработки
сигналов. Рассматриваются обобщенные линейные операторы,
операторы псевдообращения, суперпозиции и свертки, а также опе-
операторы унитарных преобразований, в частности преобразований
Фурье, Адамара и Карунена—Лоэва. В заключительной главе
части 3 проводится сравнительный анализ линейных методов
фильтрации, основанных на непосредственном вычислении сверт-
свертки, выполнении преобразования Фурье и рекурсивной фильт-
фильтрации.
В части 4 описываются методы улучшения и реставрации изоб-
изображений. Для улучшения изображений используются операции,
в результате которых изображение становится субъективно бо-
более приемлемым для зрительного восприятия либо облегчается
визуальный или машинный анализ изображения. Задача рестав-
реставрации состоит в том, чтобы повысить верность изображения,
скорректировав искажения. В части 5 основное внимание сосре-
сосредоточено на вопросах анализа сцен и интерпретации изображений.
Рассматриваются задачи выделения и измерения признаков,
обнаружения объектов, совмещения изображений, символического
описания изображений, а также системы понимания изображений.
Часть 6 посвящена вопросам кодирования изображений, осуще-
осуществляемого с целью сокращения количества двоичных единиц,
затрачиваемых на описание одноцветных и цветных изображений
в системах передачи и запоминания изображений.
Хотя монография охватывает чрезвычайно широкий круг
вопросов, многие темы, относящиеся к области обработки изобра-
изображений, пришлось опустить из-за ограниченного объема книги.
Среди них наиболее важными являются распознавание и класси-
классификация образов, цифровая голография и томография. Библио-
Библиография по этим вопросам дана в приложении 1.
У. К- Прэтт
Малибу, Калифорния
январь, 1978
БЛАГОДАРНОСТИ
Исследования по вопросам обработки изображений начались
в Южнокалифорнийском университете (КЖУ) в 1962 г. с очень
скромных по своим масштабам работ. Однако с ростом интереса
к этой области во всем мире они приобрели широкий размах.
В 1971 г. д-р 3. Капрелян, декан Инженерно-технической школы
и вице-президент университета по вопросам научных исследова-
исследований и административного управления, объявил о создании при
университете Института обработки изображений. В настоящее
время этот институт — один из крупнеших в мире исследователь-
исследовательских центров по данному кругу проблем, оснащенный первоклас-
первоклассным оборудованием. Все эти обстоятельства имеют непосредст-
непосредственное отношение к появлению данной монографии. Я призна-
признателен д-ру Капреляну за его роль в организации поддержки
университетом исследований в области обработки изображений.
Хочется поблагодарить членов ученого совета института, ока-
оказавших мне неоценимую помощь при подготовке рукописи, а
именно Г. Эндрюса, Л. Дэвиссона, В. Фрэя, А. Хабиби,
Э. Холла, Р. Гершеля, А. Джейна, Р. Крюгера, Н. Нахи,
Р. Невейшиа, Г, Робинсон, А. Савчука, В. Томпсона и Л. Уэлча.
Я благодарен также моим студентам И. Абду, Б. Ашьяри, В. Чену,
Ф. Даваряну, М. Юнсу, К-Мэнсиллу, Н. Мацаренасу, Дж. Роузу,
К- Ридеру и Р. Уэллису за техническую помощь при подготовке
книги.
Монография написана на основе конспекта лекций по курсу
«Обработка изображений», читавшихся на факультете электро-
электротехники КЖУ- Я признателен многим студентам за их замечания,
сделанные по первым вариантам этого курса. Хочется отметить
также работу по улучшению конспекта, проделанную профес-
профессорами КЖУ Г. Эндрюсом, Э. Холлом, В. Фрэем и А. Хабиби,
которые использовали этот конспект в процессе преподавания
курса обработки изображений.
Подготовка любой книги чрезвычайно трудная задача. Мне
очень повезло, что рукопись перепечатали сотрудницы КЖУ
Флоренс Теббетс, Джойс Сеге и Мэрилин Чен. Р. Шмидт и его
коллеги из Института обработки изображений выполнили необ-
необходимые фотографические работы; что касается графических
10 Благодарности
материалов, то заслуга их подготовки принадлежит Д. Хаул-
энду из ЮКУ. Приведенные в книге примеры изображений, по-
полученных с помощью ЭВМ, — это результат большой работы
С. Джонсона и Э. Казаняна по составлению вычислительных
программ. Фотографическая регистрация ряда изображений по
цифровым данным, полученным на ЭВМ, выполнена д-ром
К. Ридером (Ford Aerospace and Communications Corp., Пало-Аль-
то, Калифорния). Всем этим лицам я выражаю свою искреннюю
благодарность.
Наконец, я очень признателен Агентству перспективных иссле-
исследовательских работ (ARPA) и Бюро методов обработки информа-
информации, которое входит в его состав, за финансовую помощь,
а также персоналу Лаборатории измерений ВВС (контракт
№F-08606-72-C-0008) и военно-воздушной базы Райт-Паттерсон
(контракт №F-33615-76-C-1203) за проведение контрольных из-
измерений.
У. К. П.
Часть
1
Непрерывные
изображения
В этой книге рассматриваются главным образом цифровые,
а не аналоговые методы обработки изображений. Однако в боль-
большинстве случаев цифровое изображение получают из естествен-
естественного непрерывного изображения. Исключением являются искус-
искусственные изображения, например созданные с помощью ЭВМ
испытательные таблицы или томограммы. Следовательно, важно
понимать, как происходит формирование изображения с помощью
различных преобразователей и оптических систем, включая зри-
зрительную систему человека. Другой существенный вопрос — све-
световые измерения для количественного описания изображений.
Полезно также изучить пространственные и временные свойства
непрерывного светового поля, которые обусловливают характер
взаимосвязей между элементами цифрового изображения. Эти
вопросы рассматриваются в гл. 1—3. Глава 1 посвящена ма-
математическому описанию непрерывных изображений, в гл. 2
описываются психофизические свойства зрения, а в гл. 3 приво-
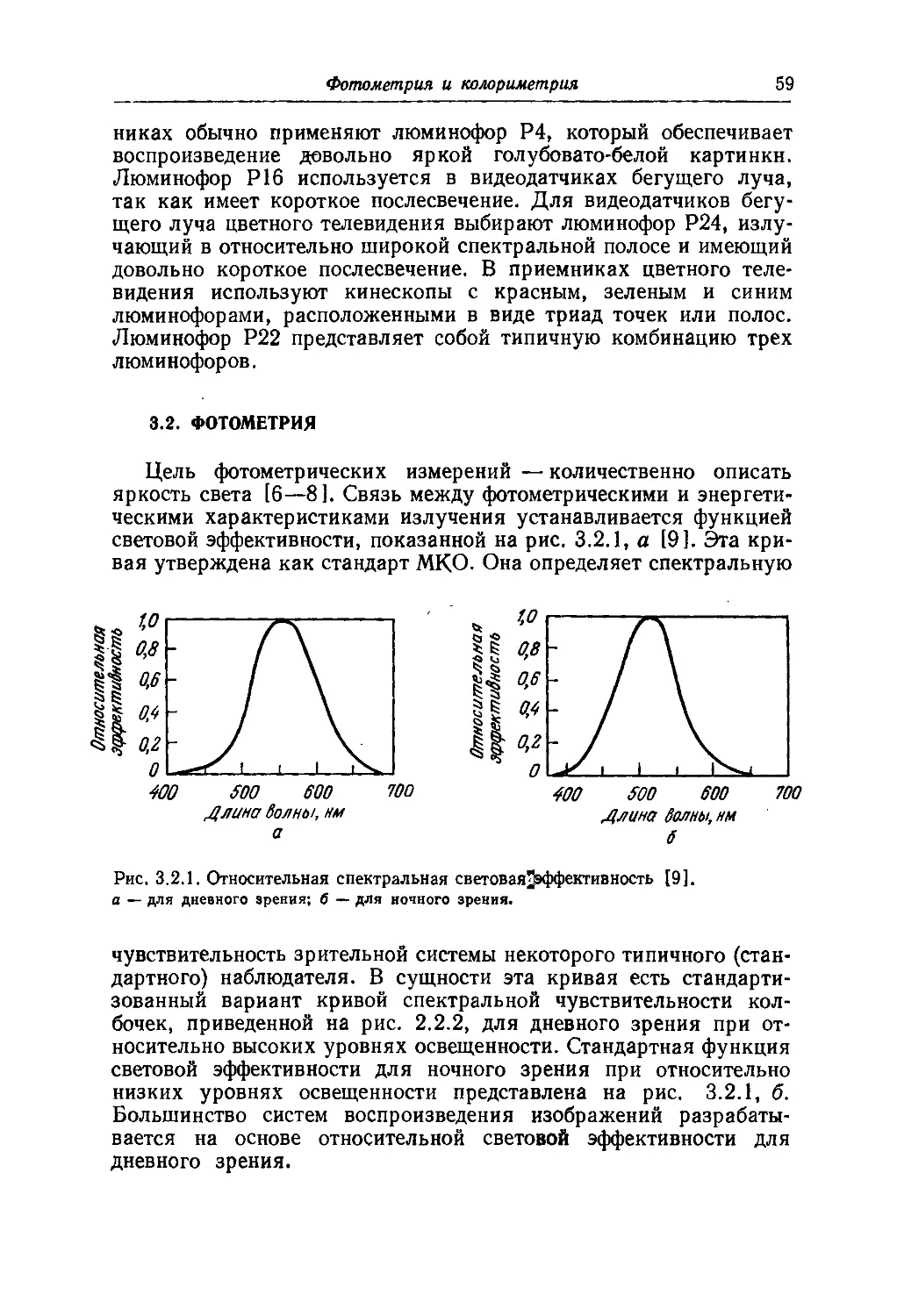
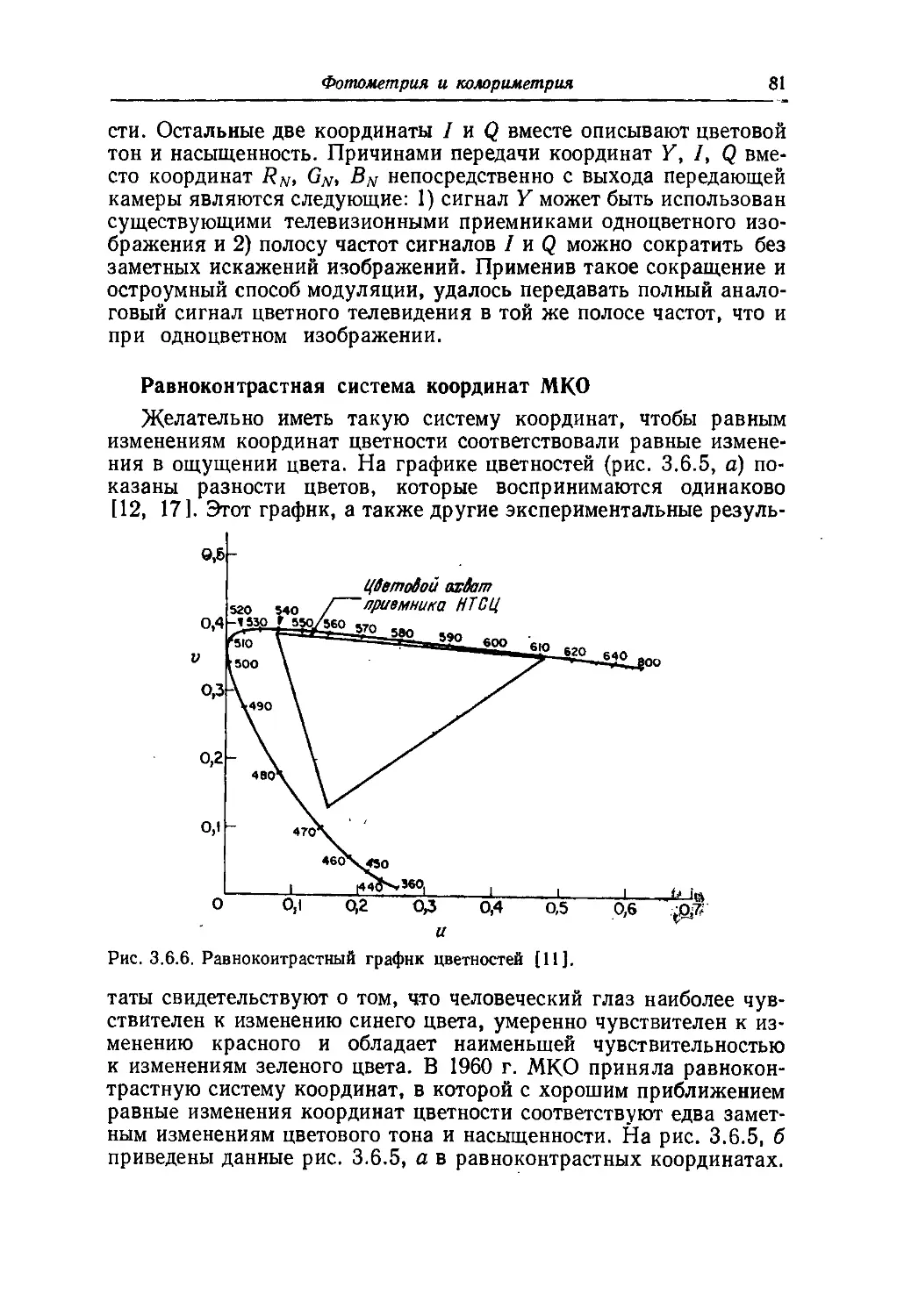
приводятся сведения по фотометрии и колориметрии.
Глава 1
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ
ИЗОБРАЖЕНИЙ
При разработке и анализе систем обработки изображений
удобно, а часто и необходимо иметь математическое описание под-
подлежащих обработке изображений. Существуют два основных
подхода к такому описанию: детерминированный и статистиче-
статистический. При детерминированном описании вводится математическая
функция, представляющая изображение, и рассматриваются
свойства изображения в каждой его точке. При статистическом
описании изображение определяется усредненными характеристи-
характеристиками. Следующие разделы посвящены как детерминированному,
так и статистическому описанию непрерывных изображений. Хотя
приведенный анализ относится к визуально воспринимаемым
изображениям, многие результаты могут быть распространены
на двумерные изменяющиеся во времени сигналы и поля общего
вида.
1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
Распределение энергии источника светового излучения по
пространственным координатам х, у, времени t и длинам волн "к
описывается функцией С (х, у, t, X). Энергия излучения пропор-
пропорциональна квадрату амплитуды электрического поля и поэтому
представляет собой действительную положительную величину.
В изображающих системах максимальная яркость изображения
ограничена из-за насыщения светочувствительной пленки или
перегревания люминофора кинескопа. Следовательно,
О < С (х, у, t, I) < A, A.1.1)
где А —максимальная яркость изображения. Размеры изображе-
изображения ограничены формирующей системой и средой, на которую
оно записывается. В целях упрощения будем считать, что все
изображения отличны от нуля только в прямоугольной области,
для которой
-Lx<x<Lx, A.1.2а)
—Ly<y<Ly. A.1.26;
Математическое описание непрерывных изображений 13
Изображение наблюдается в течение конечного промежутка вре-
времени, т. е.
—Г < * < Г. A.1.2b)
Таким образом, величина С (х, у, t, к) является ограниченной
функцией четырех ограниченных переменных. Будем считать
эту функцию непрерывной в области ее определения.
Ощущение светлоты, возникающее в зрительной системе
человека, обычно определяется мгновенной яркостью светового
поля, т. е. величиной
оо
Y (х, y,i)=\c {х, у, U Ц Vs(Цdk, A.1.3)
о
где Vs (к) —спектральная чувствительность человеческого зре-
зрения. Цветовые ощущения можно описать набором так называе-
называемых координат цвета, пропорциональных интенсивностям крас-
красного, зеленого и синего цвета, смесь которых дает заданный цвет.
Для произвольной красно-зелено-синей координатной системы
текущие значения координат цвета равны
00
R(х, y,t)=\c(х, у, t, к)Rs(к)dk, A.1 -4а)
о
оо
G (х, y,t)~\c (х, у, t, к) Gs (к) dk, A.1.46)
о
00
В(х, y,t)=\c(х, у, t, ЦBs(Цdk, A.1.4в)
о
где Rs (к), Gs (к), Bs (к) — удельные координаты для набора
основных цветов — красного, зеленого и синего, равные коорди-
координатам цвета монохроматического излучения единичной интенсив-
интенсивности с длиной волны к. В спектрозональных системах изображение
для 1-й спектральной зоны описывается выражением
со
Pi (*. y,t)=\c (х, у, t, I) St (к) dk, A.1.5)
о
где Si (X) — спектральная чувствительность 1-го датчика.
Для простоты будем во всех случаях описывать изображение,
сформированное некоторой физической системой, с помощью
функции F (х, у, t). Для одноцветной системы функция F (х, у, t)
представляет распределение яркости или какой-либо другой фи-
физической величины, связанной с яркостью. Для системы воспро-
воспроизведения цветных изображений F (х, у, t) есть одна из коор-
координат цвета. Функция F (х, у, f) используется также для описа-
14 Глгва 1
ния других полей, например меняющегося во времени простран-
пространственного распределения шума видеодатчика.
В соответствии с обычным определеним среднего значения
одномерного сигнала средняя по времени яркость изображения
в данной точке х, у определяется как
(F(х, у, t))T = Hm A/27) [ Fl(jc,>, 0 L{t)dt\, A.1.6)
где L (t) —временная весовая функция. Аналогично определя-
определяется пространственная средняя яркость в момент времени t:
<F(x, у, 0)s= Hm \{\IMxLy) \ \ F (x, y, t)dxdy • A.1.7)
Во многих системах воспроизведения изображений, например
в проекционных устройствах, изображение не изменяется во вре-
времени и переменная t может быть опущена. В системах другого
типа, например кинематографических, аргумент / меняется ди-
дискретно. В дальнейшем аргумент t функции, описывающей изоб-
изображения, будет обычно опускаться.
1.2. ДВУМЕРНЫЕ СИСТЕМЫ
В двумерной системе набор исходных двумерных функций
F\ (x, у), Fz(x, у), ..., FN (x, у) отображается в набор дву-
двумерных функций Gx (x, у), Gi{x, у), ..., GM (x, у), где х, у —
независимые непрерывные пространственные переменные, ар-
аргументы этих функций (оо < х, у < оо). Это отображение может
быть задано набором операторов От \ • } при т = 1, 2, ..., М,
которые связывают входные и выходные функции:
Gi {х, у) = Ох \F± (x, у) FN (x, у)),
A.2.1'
GM (х, у) = (Ум l^i {х, У) FN(x, y)\.
Число входных функций N может быть больше, меньше или рав-
равняться числу выходных. При N — М = 1
у)\. A.2.2)
В одномерных физических системах, в которых независимой пере-
переменной является время, выходной сигнал представляет собой
функцию прошлых и настоящих значений входного сигнала, но
не может быть функцией будущих значений. Такие системы,
называемые физически реализуемыми, удовлетворяют принципу
причинности. Двумерные системы в общем случае не обладают
Математическое описание непрерывных изображений 15
этим свойством: пространственные переменные х, у могут прини-
принимать отрицательные значения по отношению к некоторому началу
координат.
Чтобы продолжить обсуждение свойств двумерных систем,
необходимо познакомиться с некоторыми специальными видами
операторов.
1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ
Сингулярные операторы широко применяются при анализе
двумерных систем, особенно систем, в которых производится ди-
дискретизация непрерывных функций. Двумерная дельта-функция
Дирака есть сингулярный оператор, обладающий следующими
свойствами:
( оо, х = 0, г/==0,
' A.3.1а)
О в остальных случаях, ч '
О в остальных случаях, <L3'16>
8
Jjб(лг, y)dxdy=l при е>0, A.3.1в)
E, ri)б(дг — i, y-
Величина е здесь обозначает бесконечно малый предел интегри-
интегрирования.
Двумерная дельта-функция может быть представлена как
произведение двух одномерных дельта-функций ортогональных
координат х, у:
б (х, у) = 6 (х) 6 (у), A.3.2)
где одномерные дельта-функции удовлетворяют одномерным со-
соотношениям, аналогичным A.3.1). Дельта-функция может быть
также определена как предел некоторых функций [1, стр. 275],
например прямоугольной функции
б(х, y) = lim [a2rect{ca}rect{ay}], A.3.3а)
а-юо
круговой функции
= Нт [(a2/ji)cirk {a Уж* + у*)], A.3.36)
a->oo
гауссовой функции
§(х, у) = lim [a2exp {—а2я (л:2 + г/2)}], A.3.3в)
16 Глава 1
sinc-функции
6 (х, у) = lim [a2 sine {ал:} sine {он/}], A.3.Зг)
бесселевой функции
6 (х, у) = lim I—* , ¦=.—— , A.3.Зд)
где
) A-3.46)
sine {x\ = sin nx/nx. A .3.4b)
Другим полезным определением дельта-функции является сле-
следующее тождество [2, стр. 99]:
то
6 (х - I, у - ц) = A/4л*) j J exp \i [и (х - 5) +
—то
+ v(y-r\)]\dudv, A.3.5)
где i = У^Л.
1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
Двумерная система называется линейной, если для нее спра-
справедлив принцип суперпозиции. В частном случае отображения
функции в функцию для этого требуется, чтобы
О \aiFx (х, у) + a2f2 (х, у)} = ахО \FX (х, у)} + а,0 \F2 (x, у)), A.4.1)
где а]( а2 —некоторые постоянные (могут быть комплексными).
Определение свойства суперпозиции можно легко распространить
на отображение A.2.1) общего вида.
Используя свойство дельта-функции A.3.1г), функцию на
входе системы F (х, у) можно представить как взвешенную сум-
сумму дельта-функций:
F(x, y)= \\F(l, ц)Ь{х-1 y-ni)d?di\, A.4.2)
—оо
где F E, ц) — весовой множитель дельта-импульса, имеющего
координаты I, ц на плоскости (х, у) (рис. 1.4.1). Если функция
на выходе линейной системы
G(xty)~O{F{x,y)\, A.4.3)
Математическое описание непрерывных изображений
17
ТО
или
G(x, y)=
A.4.4a)
l 4H{f>(x-by-i\)\dldrl. A.4.46)
Для перехода от выражения A.4.4а) к A.4.46) был изменен по-
порядок выполнения операций линейного преобразования и интегри-
интегрирования. Линейный оператор действовал только на тот множитель
подынтегрального выражения A.4.4а), который зависит от про-
пространственных переменных х, у. Запишем второй множитель
подынтегрального выражения A.4.46) как
Н(х,у; I, ц) = О\Ь(х-1у-Щ. A.4.5)
Будем называть эту функцию импульсным откликом двумерной
системы. Импульсный отклик оптической системы часто назы-
Рис. 1.4.1. Представление функции, описывающей изображение, в виде супер-
суперпозиции дельта функций.
вается функцией рассеяния точки. Подстановка импульсного
откл"ика в соотношение A.4.46) дает интеграл суперпозиции
G(x, г/)=
, у;
A.4.6)
Линейная двумерная система называется пространственно-инва-
пространственно-инвариантной (изопланатической), если ее импульсный отклик зависит
только от разностей координат х — 5, у —tj. Для оптической си-
системы, показанной на рис. 1.4.2, это значит, что при перемещении
точечного источника в предметной плоскости изображение этого
18
Глава 1
источника в плоскости фокусировки будет также изменять по-
положение, но сохранять форму. Для пространственно-инвариант-
пространственно-инвариантной системы
Н{х,у\1,ц) = Н{х-1,у-т\) A.4.7)
и интеграл суперпозиции имеет особую форму, называемую
интегралом свертки:
G(x, y)= l\F{l ц)Н{х-1 у-У])йЫц. A.4.8а)
Операция свертки символически записывается как
G (х, у) = F (х, у) * И (х, у). A.4.86)
Интеграл свертки симметричен, т. е.
G(x, y)~ \\F(x-l, у-п)Н(Ь T|)d?Ai. A.4.9)
Процесс свертки иллюстрируется на рис. 1.4.3. На рис. 1.4.3, а
и 1.4.3,6 изображены функция F (х, у) на входе и импульсный
Входная
плоскость
Выходная
плоскость
Рис. 1.4.2. Изображение точечного источника света в оптической системе.
отклик. На рис. 1.4.3, в показан импульсный отклик при обра-
обращении координат, а на рис. 1.4.3, г —со сдвигом на величину
х, у. На рис. 1.4.3, д заштрихована область, в которой произве-
произведение F (|, r\) H (х — %, у — г)), входящее в подынтегральное
выражение A.4.8, а), не равно нулю. Интегрирование по этой
области дает величину G (х, у) для заданных значений коорди-
координат х, у. Таким образом, функция G (х, у) на выходе может быть
найдена сканированием входной функции скользящим «окном» —
обращенным импульсным откликом, и интегрированием по об-
области, в которой эти
Математическое описание непрерывных изображений
19
1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
Обнаружение и выделение контуров (границ) на изображении,
т. е. точек с резкими перепадами яркости, обычно осуществляются
дифференцированием функции F (х, у) по пространственным ко-
координатам и сравнением результата дифференцирования с по-
Рис. 1.4.3. Пример двумерной свертки.
рогом. Первые производные по пространственным координатам х
и у определяются как
dx = dF (x, у)/дх, A.5.1а)
dy = дР (х, у)/ду. A.5.16)
Производная по направлению г, составляющему угол Ф с гори-
горизонтальной осью, по определению [3, стр. 10] равна
V \F(x, y)\ = dF (х, y)Jdz = dx cos Ф + dy sin Ф. A.5.2)
Модуль градиента есть
A.5.3)
Вторые .производные по пространственным координатам х и у
по определению равны
dxx - d*F (x, уIдх\ A.5.4а)
A.5.46)
20 Глава 1
Сумма производных A.5.4) дает лапласиан
L \F (х, у)\ = dxx + dm = d*F(х, у)/дх* + d*F(x, у)/ду*. A.5.5)
Следует отметить, что лапласиан является скалярной величиной,
которая не зависит от направления на плоскости х, у, тогда как
градиент есть зависящая от направления векторная величина.
1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
В результате двумерного преобразования Фурье функции
F (х, у), описывающей изображение, получается спектр этого
изображения, который определяется как
оо
9- К, о>„) = \\ F (х, у) ехр {—i {щх + wyy)} dxdy, A.6.1)
— 00
где &х, &у—пространственные частоты, a i = V—1. Если
обозначить оператор преобразования Фурье через (УР\-\, то
можно записать
y)\. A.6.2)
В общем случае спектр 9" {(лх, &„) есть комплексная величина.
Его можно разложить на действительную и мнимую части:
ST К, u>y) = Л К, ю,) + iST К, ©,,) A.6.3а)
или представить с помощью амплитуды и фазы:
9" К, aty) = Ж {&х, ш,) ехр \if (©„ щ)\, A.6.36)
где
Ж К, ш,.) = \9Р К, а>„) + Я* К, (о,)]1/2, A.6.4а)
9 К Ю1/) == arctg \У К. <»у)/Я К, и)»I. A -6.46)
Достаточным условием существования фурье-спектра функции
F (х, у) является абсолютная интегрируемость этой функции,
т. е. условие
00
\\\F (x,y)\dxdy <оо. A.6.5)
—оо
Исходная функция F (х, у) может быть восстановлена обратным
преобразованием Фурье:
F(x, y) = (l/4n2) jJ#-K, ^)exp{t>^ + ©^)}dc0,dav A.6.6a)
Это соотношение в операторной форме можно записать как
F{x, у) = 0&\Г((ох, ®У)). A.6.66)
Математическое описание непрерывных изображений 21
Поскольку ядро двумерного преобразования Фурье разделимо,
это преобразование может быть выполнено в два этапа. Сначала
находится
» оо
^*»К, У) = j F(x, У) ехр {—/gvv} dx, A.6.7)
а затем
00
& К. «г,) = 1 #"У К- У) ехр {—Чу| dy. A.6.8)
— оо
Ниже приводятся несколько полезных свойств двумерного
преобразования Фурье. Их доказательства можно найти в книгах
[1, 21.
Функциональные свойства
. Если функция F (х, у) разделима по пространственным пере-
переменным, так что
F (х, у) = /, (дг) fy (у), A.6.9)
то
где fx ((лх) fL, (ыу) — одномерные фурье-спектры функций fx (x),
fu (у). Если &~ (ых, Ыу) есть фурье-спектр функции F (х, у),
то &"* (•—озх, —Ыу) является фурье-спектром функции F* (х, у).
(Звездочка обозначает комплексную сопряженность.) Если функ-
функция F (х, у) симметрична, т. е. F (х, у) = F (—х, —у), то
& ( ) & ( )
Линейность
Оператор преобразования Фурье линеен:
OSr[aFl{x, y) + bF2(x, у)} = а^-1(шж> %) + Ь<Г2(<ох, <оу), A.6.11)
где а, Ь — постоянные.
, Изменение масштаба
Изменение масштаба пространственных переменных приводит
к обратному изменению масштаба пространственных частот и
пропорциональному изменению значений спектра:
ar\F{ax, by)\ = (\/\ab\)&-((oja, cojb). A.6.12)
Следовательно, сжатие вдоль одной из осей плоскости (х, у)
приводит к растяжению вдоль соответствующей оси частотной
плоскости и наоборот. Происходит также пропорциональное из-
изменение значений спектра.
22 Рлава 1
Сдвиг
Сдвиг (изменение коордиант) на исходной плоскости приводит
к фазовым изменениям на частотной плоскости:
Ogr\F(x-a, у-Ь)\ = <Г(wx, wy)exp {—t(a>xa + wyb)}. A.6.13a)
Наоборот, сдвиг на частотной плоскости вызывает фазовые из-
изменения исходной функции:
}. A.6.136)
Свертка
Фурье-спектр функции, полученный в результате свертки двух
функций, равен произведению спектров исходных функций:
Су \F (х, у) * Н {х, у)\ = <Г (wx, wy) Ж (соЛ, ау). A.6.14)
Обратная теорема утверждает, что
Ogr\F(x, y)H(x, y)\ = (l/4n*)?-(wx, <*у)*Ж((ох, <оу). A.6.15)
Теорема Парсеваля
Два представления энергии изображения — через функцию
F (х, у) и фурье-спектр &~ (<лх, юу) —связаны следующим об-
образом:
\\ Jj wy. A.6.16)
Теорема о спектре автокорреляционной функции
Фурье-спектр двумерной автокорреляционной функции изоб-
изображения равен квадрату модуля фурье-спектра этого изображения:
= |#"К, <)|2. A.6.17)
Спектры пространственных производных
Фурье-спектры первых пространственных производных функ-
функции F (х, у) связаны с ее фурье-спектром следующими соотно-
соотношениями:
<Jp\dF(x, у)/дх\ = — i«>x&~(o>x, а>у), A.6.18а)
СУ \dF(x, уIду)\ = -"^Г(<о„ (*„)¦ A.6.186)
Следовательно, спектр лапласиана равен
(х,у)/дх2 + &F (х, у)/ду2} = — (а>1 + <4) &" (м*' ®v)- A-6.19)
Математическое описание непрерывных изображений 23'
1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ
ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Теорема о преобразовании Фурье свертки A.6.14) оказывается
очень полезным средством при анализе линейных систем. Рас-
Рассмотрим функцию F (х, у), описывающую изображение на входе
линейной системы с импульсным откликом Н (х, у). Изображение
на выходе описывается функцией G (х, у), получаемой в результате
свертки:
G(x, y)= \\F(a, Р)Я(х-а, y-P)dadp. A.7.1)
—оо
Выполнив преобразование Фурье обеих частей этого равенства и
поменяв порядок интегрирования в его правой части, получим
X ехр {—i (юхх + <йуу)\ dxdy \dad$. A.7.2)
Согласно теореме о сдвиге A.6.13), внутренний интеграл равен
произведению спектра функции Н (х, у) и экспоненциального
множителя фазового сдвига. Поэтому
оо
g? (со,, ю,) = J J F (а, Р) Ш К, wy) ехр \—i (ю/х + ю^)| da dp. A.7.3)
Выполнив преобразование Фурье, получим
9 К, ev) = 2ft {<лх, %) Т К, щ). A.7.4)
Наконец, обратное преобразование Фурье дает функцию, описы-
описывающую изображение на выходе:
оо
G (х, у) = A/4л2) J j 2ft К, <о„) & К, ©у) ехр \i {щх +
cfox(fay. A.7.5)
Выражения A.7.1) и A.7.5) представляют два альтернативных
способа определения выходного изображения линейной простран-
пространственно-инвариантной системы. Выбор того или иного подхода
зависит обычно от решаемой задачи.
1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
В разд. 1.4 были введены понятия линейности и суперпозиции.
Оппенгейм [4 ] ввел обобщенную суперпозицию с тем, чтобы рас-
распространить понятие линейности на более широкий класс систем.
24
Глава 1
Рассмотрим две функции, описывающие изображения, Fl (х, у)
и F2 (х, у), которые, взаимодействуя некоторым образом @), дают
функцию G (я, у):
G(x,y) = Fl(x,yHFt(x,y). A.8.1)
Пусть Са \ ¦ \ — оператор системы, преобразующей G (х, у), ко-
который обладает следующими свойствами:
Ов {FAx, У) О FAx, у)\ = OQ\FAx, У)\ О OQ \F2(x, y)\ A.8.2а)
0G \k :F(x, y)\=k: Oo \F(x, y)\, A.8.26)
где k — постоянная, а двоеточие обозначает обобщенное умно-
умножение на постоянную. В работе [4 ] показано, что если операция О
сводится к сложению векторов, а операция: — к умножению
вектора на скаляр, то оператор Cq \ • \ может быть представлен
в виде цепочки операторов, называемой гомоморфным фильтром
a
—0
*У)
Линейная
система
-г, ,
A i*J
, У)
LOG{»}
Линейная
система
ЕХР{.}
Рис. 1.8.1. Обобщенные линейные системы.
а — обобщенная система; б — представление обобщенной системы в виде гомоморфного
фильтра; в — мультипликативный гомоморфный фильтр.
(рис. 1.8.1). Первый оператор 0л{-} превращает операции
() и : в сложение векторов и умножение вектора на скаляр:
СА \FX (х, у) о F2 (х, у)} = 0А \Ft (х, у)\ + OA\F2 (х, у)\ 41.8.3а)
бА \k:F{x, y)\ = kOA {F(x, y)\. A.8.36)
Вторая ступень гомоморфного фильтра —обычная линейная си-
система. Третья ступень — оператор <УА1, который является обрат-
обратным относительно первого оператора, т. е.
O7?{0a\F{x, y)\\ = F(x, у). A.8.4)
Математическое описание непрерывных изображений 25
Рис. 1.8.1, в иллюстрирует частный случай гомоморфного
фильтра для мультипликативной системы [5], в которой функция
G (х, у) получается в результате перемножения функций Fx {х, у)
и F2 (x, у), т. е.
G (х, у) = Fx (х, у) о F, (х, у) = F, (к, у) F2 (x, у). A.8.5)
Прологарифмировав обе части равенства A.8.5), получим сумму
логарифмов функций Fx (x, у) и F% (x, у):
log{G(*t у)} = log {^ (jc, y)\+hg\F2(x, y)\. A.8.6)
Функция log G (л:, у) преобразуется некоторой линейной систе-
системой, а затем посредством экспоненциального преобразования воз-
возвращается в пространство исходных изображений. Операция
обобщенного умножения вектора на скаляр определяется как воз-
возведение в степень
G(x, y) = k:F(x, y) = [F(x, y)f. A.8.7)
Логарифмирование этого равенства дает
y)\. A.8.8)
Применение гомоморфной фильтрации при восстановлении изоб-
изображений рассмотрено в гл. 15.
1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ *
Часто бывает удобно рассматривать изображение как реали-
реализацию случайного процесса. Введем порождающую изображения
непрерывную случайную функцию F (х, у, t) трех переменных —
пространственных координат х, у и времени t.
Случайный процесс F (х, у, t) полностью описывается сов-
совместной плотностью вероятности
Р \Flt F2,..., F/, xlt уъ tlt хг, уг, U,..., xJt yJy tj\
для / значений функции F,- (xjt y;, tj) в точках отсчета xjt yh tr
Совместные плотности вероятности высокого порядка для изоб-
изображений обычно не известны, и их в общем случае трудно моде-
моделировать. Для плотности вероятности первого порядка р (F;
х, у, t) иногда удается подобрать удачную модель из физических
соображений или на основе измеренных гистограмм. Например,
плотность вероятности первого порядка случайного шума в элек-
*) Представленный в этом разделе материал предназначен читателю, зна-
знакомому с теорией вероятностей, случайными величинами и случайными процес-
процессами. Эти сведения можно найти в книгах [2, 6, 7]. Главная цель, которая пре-
преследовалась в этом разделе, — ввести соответствующие обозначения и рассмо-
рассмотреть вероятностные модели изображений.
26 Глава 1
тронных преобразователях изображений хорошо моделируется
гауссовой плотностью:
p\F;x, у, *} =
iр М A.9.1)
где параметры x\f (х, у, t) и op (x, у, t) есть среднее и диспер-
дисперсия шума. Гауссова плотность может также с приемлемой точ-
точностью служить моделью плотности вероятности коэффициентов
унитарных преобразований изображений. Плотность вероятности
яркости должна быть односторонней, так как яркость принимает
только положительные значения. В качестве моделей плотности
вероятности яркости применяются плотность распределения веро-
вероятностей Рэлея
(i.9.2a)
плотность логарифмически нормального распределения
P\F; х, у, t\ = [2nF\x, у, t)cF(x, у, t)]'1'2 x
ХеХР(
Щ(х, y,t)
и плотность экспоненциального распределения
p\F; х,у, t\ = aexp{-a\F(x, у, t)\\. A.9.2в)
Эти плотности определены при F >¦ 0, причем а — постоянная.
Двусторонняя экспоненциальная, или лапласова, плотность
p[F; х, у, /} = (a/2)exp{-a|F(x, у, t)\\, A.9.3)
где a — постоянная,гчасто используется как модель плотности ве-
вероятности разностей отсчетов функции, описывающей изобра-
изображение. Наконец, плотность равномерного распределения
p\F; х, у, /| = 1/2я, —n<F<n, A.9.4)
есть обычная модель для флуктуации фазы случайного процесса.
Для описания случайного процесса можно использовать также ус-
условные плотности вероятности. Условная плотность вероятности
значения функции F (х, у, t) в точке (хи уи tfx) при заданном зна-
значении этой функции в точке (х2, у2, Q определяется как
Р i^i; *i Уи к | F2; хъ уг, Ц =
_ Р {Fj, F2; Xj, yt, tt, дс2, уа, t2} ,. Q «
P {Fv x2, yv t2) • ^¦y-°>
Аналогично определяются условные плотности более высокого
порядка.
Математическое описание непрерывных изображений 27
Другой способ описания случайного процесса состоит в вычи-
вычислении средних по ансамблю. Первый момент, или среднее зна-
значение функции F (х, у, t), равен
%(х, y,t) = E \F (x, y,t)}= \F (x, у, t) p \F; x, y, I) dF. A.9.6)
—00
Второй момент, или автокорреляционная функция, определя-
определяется как
R (*i. Уи к> хъ Уг, h) =
= E\F(Xl, уъ yf*(x2l у2, 4)} =
ОО 00
= f f F (xlt yu k) F* (x2, y2, U) p \FU F2;
—-OO —00
*i> Vi, k, x2, y-i, t2\dF1dF2. A.9.7)
Автоковариационная функция изображения определяется как
K(xi> Уъ к> Ч, Уг, к) =
~E{[F(Xl, yu У-Т1,(Ж1, ух, у]х
х IF* (х3, у2, к) - т? (ха> уь h)]}. A.9.8а)
Автоковариационная и автокорреляционная функции связаны
соотношением
К (*i> Уи ti, x2, уъ h) = R (xlf у1У tt\ хг, г/2, ^г) —
— % fa, Уг, к) П*р (Хь Уг> 4). A.9.86)
Наконец, дисперсия процесса F (х, у, t) есть
о} (х, y,t) = K (x, у, t;j, y,"t). A.9.9)
Случайный процесс, порождающий изображения, называется
стационарным в строгом смысле, если его моменты не зависят от
переноса начала координат в пространстве или времени. Процесс
называется стационарным в широком смысле, если он имеет по-
постоянную среднюю яркость, а его автокорреляционная функция
зависит от разностей координат хх—хъ уг—уг, tx—12, но не от
самих координат. Для стационарного процесса F (х, у, t)
E\F{x,y,t)\=»4\F A.9.10a)
и
R (хи Уъ к> хй, у2, k) = R (хг — х2; ух —уг; tx — t2). A.9.106)
Выражение для автокорреляционной функции можно записать
в виде
R (т„ ту, т,) - Е [F (х + т», у + та, t + xt) F* (х, у, t)\. A.9.11)
Так как
К (-Ъ, -*» ~Ь) = R* (тЛ тв, т<), A.9.12)
28 Глава 1
для действительной функции F автокорреляционная функция
является действительной и четной. Энергетический спектр стаци-
стационарного изображения по определению есть результат трехмерного
преобразования Фурье его автокорреляционной функции:
+ <oyTl, + <otTt]\dTxdTudTt. A.9.13)
Во многих изображающих системах пространственные и вре-
временные процессы формирования изображений разделяются. В этом
случае стационарную автокорреляционную функцию можно за-
записать как
Ж*,, г у, Т/) = Лад(т„ ty)Rt(tt). A.9.14)
Часто для упрощения вычислений пространственную автокорре-
автокорреляционную функцию представляют в виде произведения автокор-
автокорреляционных функций для каждой пространственной переменной:
Rxy(**,*v) = RA*x)Ry(b)- A.9.15)
В изображениях объектов, созданных человеком, часто встреча-
встречаются горизонтальные и вертикальные структуры, поэтому аппрок-
аппроксимация автокорреляционной функции произведением A.9.15)
оказывается вполне приемлемой. В изображениях естественных
сцен обычно нет преобладающих направлений корреляции. Про-
Пространственная автокорреляционная функция таких изображений
близка к функции с вращательной симметрией и не является по-
поэтому разделимой.
Часто моделью изображения служат реализации двумерного
марковского процесса первого порядка. Автоковариационная
функция такого процесса имеет вид
Кх, у (тЛ ту) = К ехр {- Va2xx% + а\х1\, A.9.16)
где К, осх и ау — масштабные множители. Соответствующий
энергетический спектр равен
Часто делается упрощающее предположение, что автоковариаци-
автоковариационная функция марковского процесса может быть представлена
в виде
т,|-а,|т„|}. A.9.18)
Энергетический спектр этого процесса есть
+ «?)(aJ + «$]. A.9.19)
Математическое описание непрерывных изображений 29
При детерминированном описании изображений были оп-
определены средние по пространству и времени. При статистическом
описании также определяется среднее по ансамблю. Возникает
вопрос: как связаны друг с другом пространственно-временные
средние и средние по ансамблю? Ответ состоит в том, что для не-
некоторых случайных процессов, называемых эргодическими, про-
пространственно-временные средние и средние по ансамблю равны.
Очень трудно доказать эргодичность случайного процесса в общем
случае. Обычно достаточно определить эргодичность второго
порядка, при которой моменты первого и второго порядка, полу-
полученные пространственно-временным усреднением, равны соответ-
соответствующим моментам при усреднении по ансамблю.
1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ
В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ
Часто известны плотность вероятности или моменты случайного
поля, представляющего изображение, на входе некоторой системы
и требуется определить соответствующие характеристики для изо-
изображения на выходе этой системы. Если передаточная функция
системы представлена в виде алгебраического выражения, то
можно найти плотность вероятности на выходе посредством пре-
преобразования плотности вероятности на входе. Пусть, например,
функции, описывающие изображения на входе и выходе системы,
связаны следующим образом:
y,t)}, A.10.1)
где Ор {•} — монотонный оператор, действующий на функцию
Р (*> У, /)• Тогда плотность вероятности на выходе есть
n\G- х и t\ р {F (*' у> i)] A10 2)
Преобразование вида A.10.2) можно распространить на плотно-
плотности вероятности высокого порядка, однако часто полученные соот-
соотношения оказываются слишком громоздкими.
Мометны случайного поля на выходе системы могут быть полу-
получены непосредственно, если известна его плотность вероятности,
или в некоторых случаях косвенным путем, исходя из свойств
оператора системы. Если, например, этот оператор является ли-
линейным, то среднее значение поля G (х, у, t) есть
E\G(x, у, t)\ = E{0L{F(x, у, t)\\ = 0L\E{F(x, у, t)}\. A.10.3)
Можно показать, что если оператор системы линеен, а случайное
поле на входе системы стационарно в строгом смысле, то случай-
случайное поле на выходе также стационарно в строгом смысле. Если же
поле на входе стационарно в широком смысле, то в том же смысле
стационарно поле на выходе.
30 Глава 1
Рассмотрим линейную пространственно-инвариантную си-
систему, изображение на выходе которой представляется интегралом
свертки:
О(х,у, 0=Ш^(*-«> У-Р, t-y)H(a,$,.y)dadpdy, A.10.4)
—00
где Я (х, у, t) — импульсный отклик системы. Среднее значение
функции G (х, у, t) есть
E{G(x,y,t)\ =
-a, 0-р, *-7)}Я(а, р\ y)dad$dy. A.10.5)
Если случайное поле на входе стационарно, то среднее значение
г\р постоянно и может быть вынесено из под интеграла. Тогда
E{G(x,y,t)\ =
оо
= тцг J J J Я (а, р, Y) dad$dy = т^ @, 0, 0), A.10.6)
где 5# @, 0, 0) есть частотная характеристика линейной системы
в начале координат пространственно-временной частотной об-
области. Таким же способом легко показать, что автокорреляцион-
автокорреляционные функции входного и выходного полей связаны соотношением
Ra(*x, V т,) = ЯИтЛ т*. tt)*H{xx, xy, xt)*H*(—rx, —xy, xt).
A.10.7)
Выполнив преобразование Фурье обеих частей равенства A.10.7)
и используя теорему о преобразовании Фурье свертки, получим
соотношение между энергетическими спектрами входного и вы-
выходного полей
З^о К, «о», Щ) =
у, щ), A.10.8а)
2. A.10.86)
Этот результат будет полезен при анализе действия,шумов в изоб-
изображающих системах.
ЛИТЕРАТУРА
1. Goodman J. W., Introduction to Fourier Optics, McGraw-Hill, New York,
1968. [Имеется перевод: Гудмен Дж., Введение в фурье-оптику. — М.: Мир,
2. Papoulis A., Systems and Transforms with Applications in Optics, McGraw-
Hill, New York, 1968. [Имеется перевод: Папулис А., Теория систем и пре-
преобразований в оптике.—М.: Мир, 1971.]
Математическое описание непрерывны* изображений 31
Prewitt J. M. S., Object Enhancement and Extraction, in: Picture Processing
and Psychopictorics, Lipkin B. S., Rosenfeld A., Eds., Academic Press, New
York, 1970.
Oppenheim A. V., Generalized Superposition, Information and Control, 11,
528—536 (November, 1967).
Oppenheim A. V., Schafer R. W., Stockham T. G., Jr., Nonlinear Filtering
of Multiplied and Convolved Signals, Proc. IEEE, 56, 8, 1264—1291 (August
1968). [Имеется перевод: Оппенхейм, Щефер, Стокхэм, Нелинейная филь-
фильтрация сигналов, представленных в виде произведения и свертки. — ТИИЭР,
1968, т. 56, №8.]
Papoulis A., Probability, Random Variables, and Stochastic Processes, McGraw-
Hill, New York, 1965.
Thomas J. В., An Introduction to Applied Probability Theory and Random
Processes, Wiley, New York, 1971.
Глава 2
ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ
На выходе изображающих систем обычно создается фотоснимок
или изображение на экране, которые рассматриваются человеком.
Поэтому очевидно, что для эффективной разработки таких систем
очень полезно понимать механизм человеческого зрения. Зная
этот механизм, можно строить функциональные модели зритель-
зрительной системы. Такие модели очень важны при разработке систем
обработки изображений и создании критериев верности воспро-
воспроизведения и дешифрируемости изображения.
2.1. ВОСПРИЯТИЕ СВЕТА
Согласно словарю Вебстера [1], свет есть «лучистая энергия,
которая, действуя на органы зрения, дает им возможность вы-
выполнять зрительные функции». Физические свойства света изу-
изучены довольно хорошо, но механизм взаимодействия света с ор-
органами зрения еще не вполне понятен. Как известно, свет есть
форма электромагнитного излучения, лежащего в относительно
узкой области спектра в диапазоне длин волн от 350 до 780 нм.
Характеристикой источника света является интенсивность излу-
излучения заданной длины волны. В зрительную систему человека
попадает свет либо от самосветящегося источника, либо отражен-
отраженный от некоторого предмета, либо прошедший через него. Пусть
Е (К) есть спектральная плотность излучения первичного источ-
источника света, a t (к) и г (Я,) — коэффициент пропускания и коэффи-
коэффициент отражения соответственно. Тогда для предмета, пропуска-
пропускающего свет, спектральная плотность излучения наблюдаемого
света будет
С (Я) = t (К) Е (Я), B.1.1)
а для предмета, отражающего свет,
С (%) = г (%) Е (Я). B.1.2)
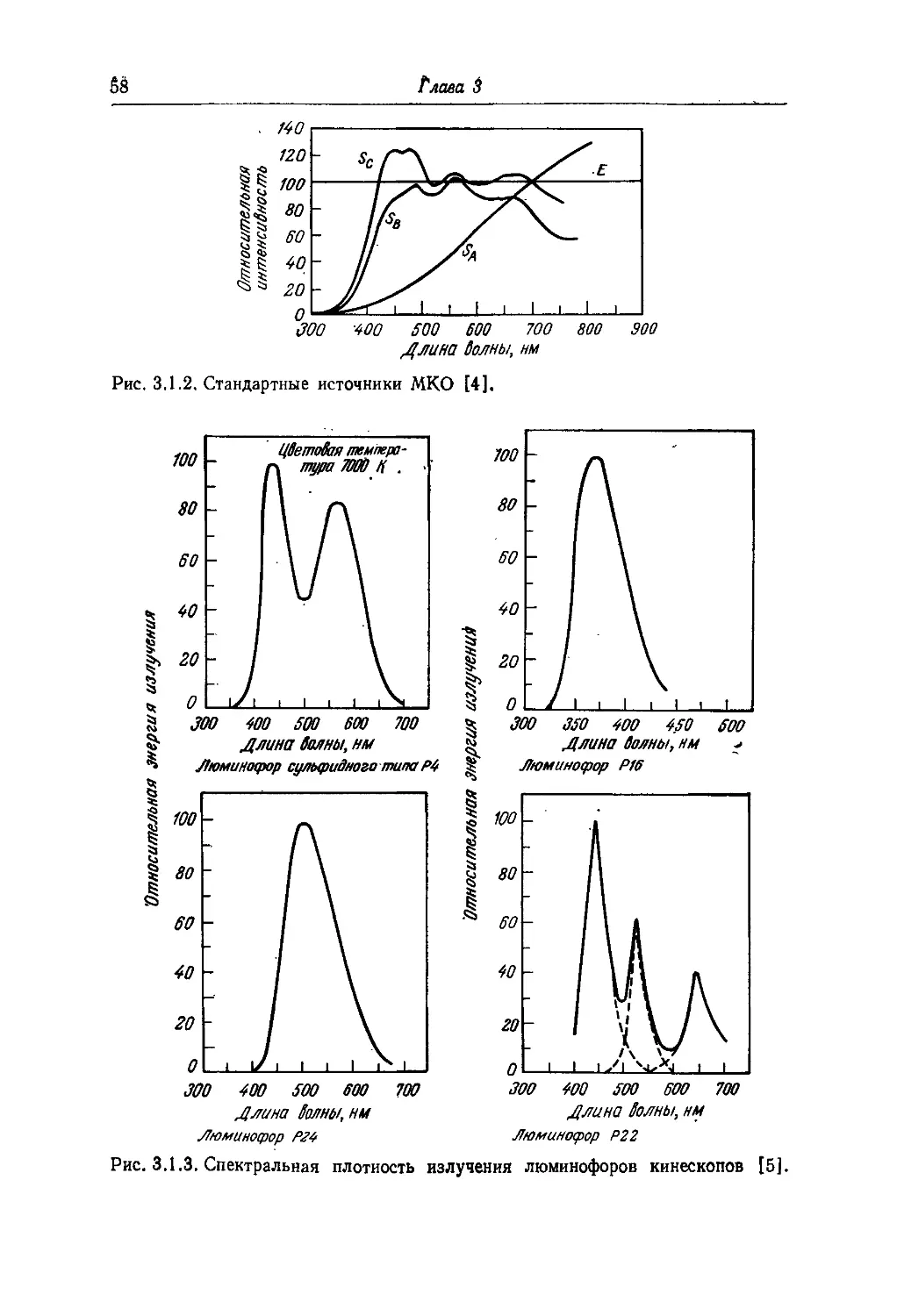
излНа Рис';^')^"реАставлены гРаФики спектральной плотности
в изюбра^. нейс*ЧШ^* обь'чных источников света, применяемых
^й11* С*е1^^ с°лнечного, вольфрамовой лампы на-
его й,Чода( ртутной дуговой лампы и
Психофизические свойства зрения
33
102 W3 ю4 105
Длина, баяны, нм
а
400 800 120 /600 2000
Длина Полны, нм
5
S20 S60 BOO 640
Длина fa/rm/, нм
В
600 800
длина Шны, нм
г
J20 S60 600 S40
Длина волны, нм
Й
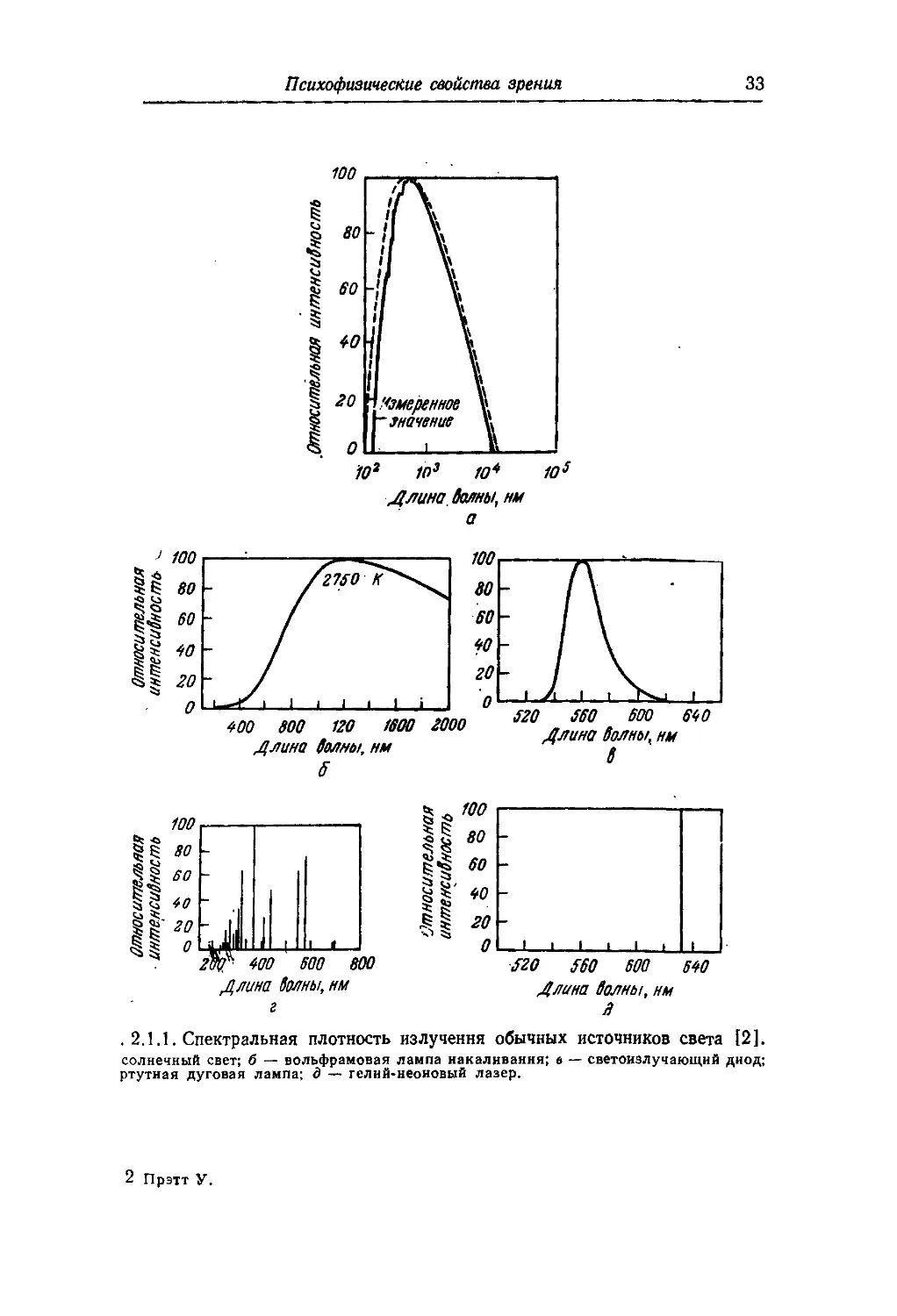
. 2.1.1. Спектральная плотность излучения обычных источников света [2].
солнечный свет; б — вольфрамовая лампа накаливания; 6 — светоизлучающий диод;
ртутная дуговая лампа; д — гелий-неоновый лазер.
2 Прэтт У.
34 Глава 2
гелий-неонового лазера. Свет от этих источников воспринима-
воспринимается зрителями по-разному. Солнечный свет кажется очень ярким
и желтовато-белым, а свет лампы накаливания —менее ярким
и довольно желтым. Светоизлучающий диод дает тусклый зеле-
зеленый свет, а ртутная лампа —очень яркий, голубовато-белый.
Наконец, лазер создает чрезвычайно яркий световой пучок чи-
чистого красного цвета. Эти наблюдения порождают много вопро-
вопросов. Например, полностью ли описывает спектральная плотность
излучения особенности восприятия этого излучения? Как будет
видно, получен только частичный ответ на этот вопрос.
Л Желтый
Красный
4ЛА
Голубой
Синий
Рис. 2.1.2. Преломление света в призме.
Существуют три основные характеристики ощущения света —
светлота, цветовой тон и насыщенность. Эти характеристики
рассматриваются ниже.
Если имеются два источника света с одинаковой формой спек-
спектральной плотности излучения, то источник с большей интенсив-
интенсивностью излучения воспринимается как более яркий. Известно,
однако, много примеров, когда предмет с одинаковой интенсивно-
интенсивностью излучения всех точек не воспринимается как имеющий рав-
равномерную светлоту. Следовательно, интенсивность света не яв-
является адекватной количественной мерой светлоты.
Признак, которым отличается, например, красный свет от зе-
зеленого, называется цветовым тоном. С помощью призмы и щели,
показанных на рис. 2.1.2, можно получать почти менохромати-
ческий свет различного цвета. Ясно, однако, что длина волны не
является адекватной мерой цвета, так как в природе встречаются
такие цвета, которые не наблюдаются в радуге, создаваемой приз-
призмой. Отсутствует, например, пурпурный цвет, который может быть
получен смешением в равных количествах узкополосных крас-
красного и синего света. Если два источника света с одинаковыми спек-
спектральными плотностями наблюдать в одинаковых условиях, их
цветовой тон будет одинаковым. Однако можно взять два таких
источника света с разными спектральными плотностями, которые
будут восприниматься как имеющие одинаковый цветовой тон
(такие два излучения называются метамерической парой.)
Психофизические свойства зрения
35
Третья характеристика ощущения света — его насыщенность.
Этот признак позволяет отличать спектральный цвет от пастель-
пастельного блеклого цвета такого же цветового тона. По существу насы-
насыщенность описывает «белизну» цвета. Можно измерять насыщен-
насыщенность в процентах, сравнивая данный свет со спектральным цветом
белый
Насыщенность.
Зеленый
красный
Черный
Рис. 2.1.3. Субъективные характеристики цвета.
на графике цветностей, изображенном на рис. 3.4.3. Однако обыч-
обычно насыщенность не используют как количественную характери-
характеристику.
Для классификации цветов удобно рассматривать их как точки
некоторого цветового пространства (рис. 2.1.3). Но для того чтобы
можно было делать количественные выводы, расстояние между
двумя точками в цветовом пространстве должно соответствовать
субъективно воспринимаемой разнице между нредставляемыми
цветами, где бы ни находилась эта пара цветов. Такие цветовые
пространства будут рассматриваться далее.
2.2. ГЛАЗ
Наиболее естественным подходом к разработке модели зри-
зрительной системы человека было бы, видимо, проведение физиоло-
физиологического анализа глаза, нервных путей от глаза к мозгу и тех
отделов мозга, которые связаны со зрительным восприятием.
К сожалению, мы не в состоянии решить эту задачу из-за того,
2*
36 Глава 2
что зрительная система состоит из огромного числа очень малень-
маленьких элементов. Однако в результате физиологических исследова-
исследований глаза уже получено много данных, полезных для создания
модели зрительной системы [4—7].
На рис. 2.2.1 показан поперечный разрез человеческого глаз-
глазного яблока. Передняя прозрачная наружная оболочка глаза на-
называется роговицей. Остальная часть наружной оболочки —
склера — состоит из плотных волокон. Следующий слой — со-
сосудистая оболочка, содержащая капилляры, которые снабжают
Височная сторона
Склера
Радужная
оболочка
Носо/ая сторона
Рис. 2.2.1. Поперечный разрез глаза.
глаз кровью. Внутри сосудистой оболочки находится сетчатка
с рецепторами двух типов —палочками и колбочками. Соединен-
Соединенные с сетчаткой нервные волокна выходят из глазного яблока
в виде пучка —зрительного нерва. Свет, попавший в глаз через
роговицу, фокусируется на поверхности сетчатки хрусталиком,
форма которого под действием специальной мышцы меняется для
обеспечения хорошей фокусировки предметов, (находящихся на
различном расстоянии от глаза. Радужная оболочка действует
как диафрагма, изменяя количество света, проходящее в глаз.
Палочки —это длинные тонкие рецепторы, а колбочки —
более короткие и толстые. Эти рецепторы действуют различным
образом. Палочки более чувствительны к свету, чем колбочки.
При малой освещенности палочки обеспечивают реакцию зри-
зрительной системы (ночное зрение). Колбочки функционируют при
большой освещенности, их реакция представляет дневное зрение.
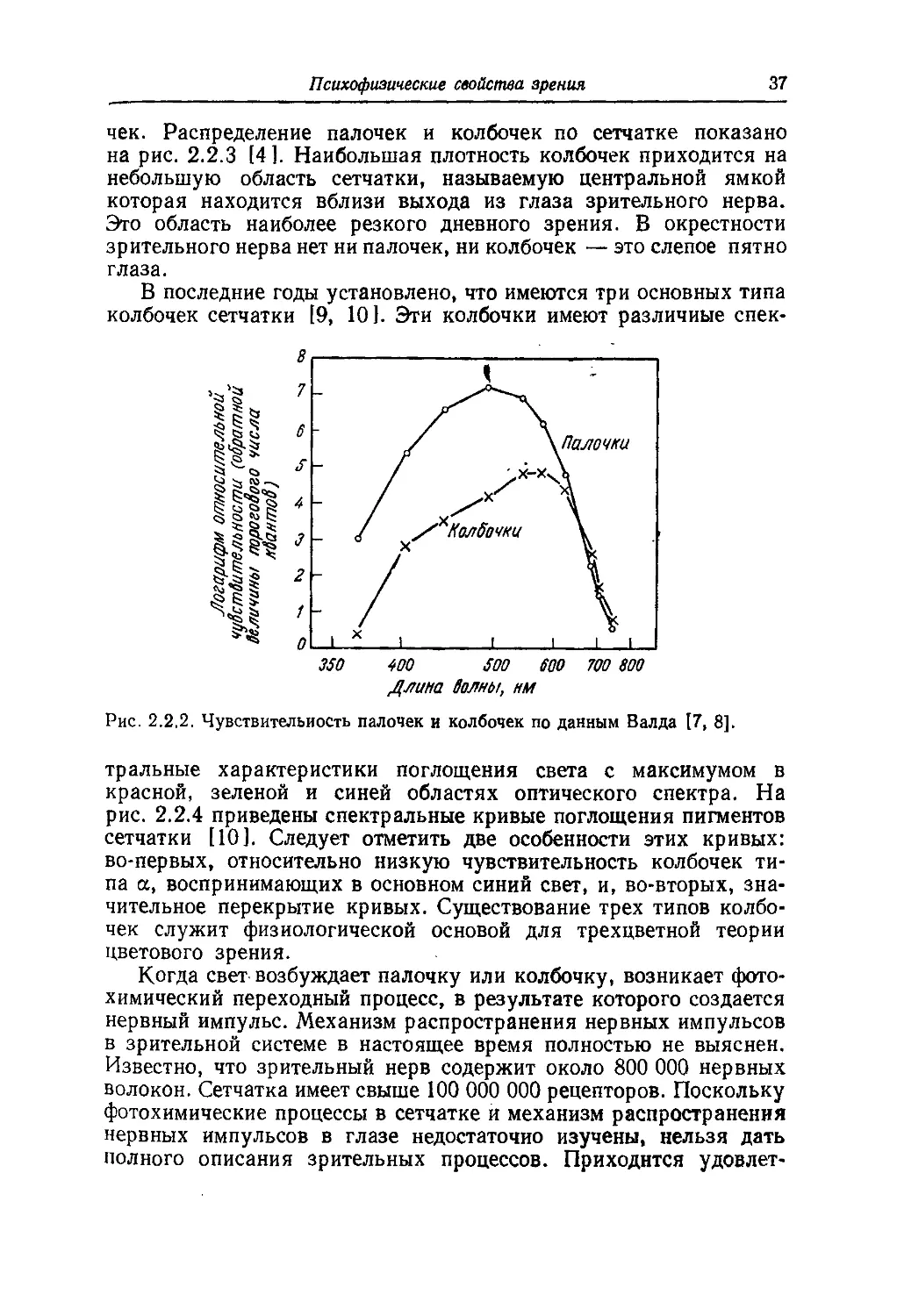
На рис. 2.2.2 приведены относительные чувствительности палочек
и колбочек в зависимости от длины волны воспринимаемого света
[7, 8]. Глаз содержит около 6,5 млн. колбочек и 100 млн. пало-
Психофизические свойства зрения
37
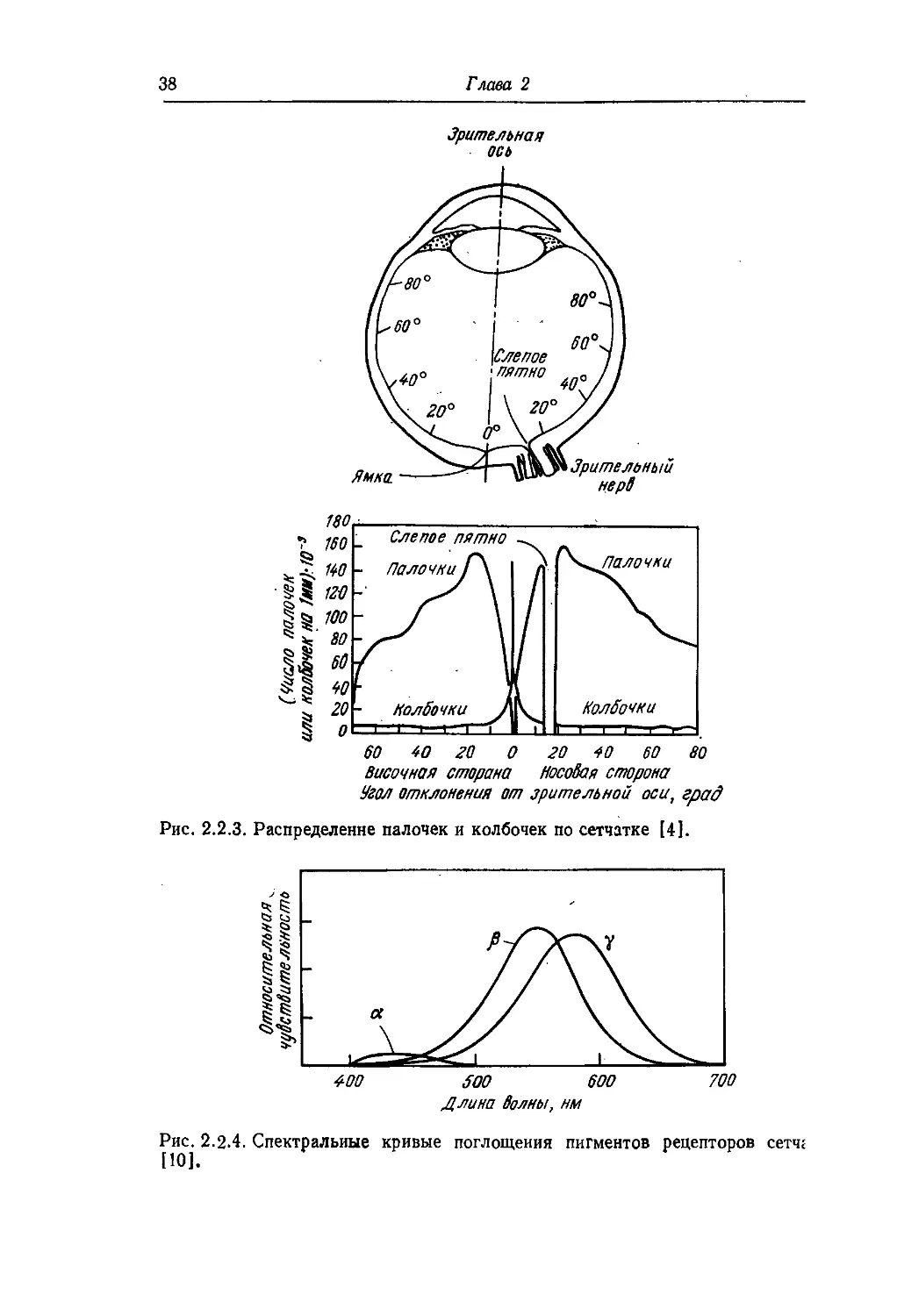
чек. Распределение палочек и колбочек по сетчатке показано
на рис. 2.2.3 [41. Наибольшая плотность колбочек приходится на
небольшую область сетчатки, называемую центральной ямкой
которая находится вблизи выхода из глаза зрительного нерва.
Это область наиболее резкого дневного зрения. В окрестности
зрительного нерва нет ни палочек, ни колбочек — это слепое пятно
глаза.
В последние годы установлено, что имеются три основных типа
колбочек сетчатки [9, 101. Эти колбочки имеют различные спек-
8
I
Hi
11
7 -
S -
4
3
г
t
о
_
-
-
1
/
X
/
1
КолВочки
i
\
\
\Палочш
\
\
i i i
350 400 S00 600
Длина волны, мм
700 800
Рис. 2.2.2. Чувствительность палочек и колбочек по данным Валда [7, 8].
тральные характеристики поглощения света с максимумом в
красной, зеленой и синей областях оптического спектра. На
рис. 2.2.4 приведены спектральные кривые поглощения пигментов
сетчатки [10]. Следует отметить две особенности этих кривых:
во-первых, относительно низкую чувствительность колбочек ти-
типа а, воспринимающих в основном синий свет, и, во-вторых, зна-
значительное перекрытие кривых. Существование трех типов колбо-
колбочек служит физиологической основой для трехцветной теории
цветового зрения.
Когда свет возбуждает палочку или колбочку, возникает фото-
фотохимический переходный процесс, в результате которого создается
нервный импульс. Механизм распространения нервных импульсов
в зрительной системе в настоящее время полностью не выяснен.
Известно, что зрительный нерв содержит около 800 000 нервных
волокон. Сетчатка имеет свыше 100 000 000 рецепторов. Поскольку
фотохимические процессы в сетчатке и механизм распространения
нервных импульсов в глазе недостаточно изучены, нельзя дать
полного описания зрительных процессов. Приходится удовлет-
38
Глава 2
Зрительная
ось
60 40 гО О 20 40 60 80
Височная сторона Носовая сторона
Угол отклонения от зрительной оси, град
Рис. 2.2.3. Распределение палочек и колбочек по сетчатке [4].
400
S00 600
Длина волны, нм
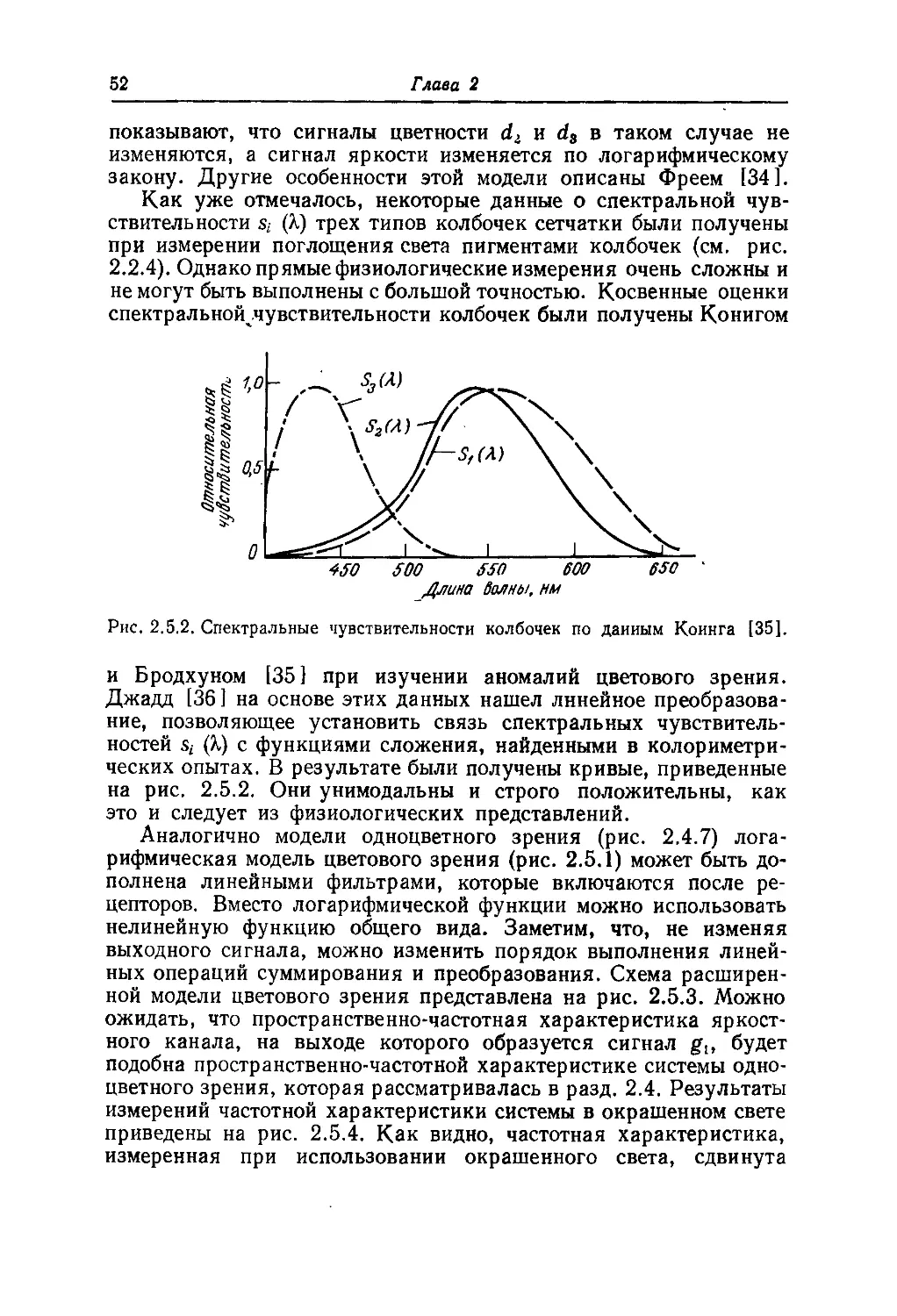
Рис. 2.2.4. Спектральные кривые поглощения пигментов рецепторов сетч;
[Ю].
Психофизические свойства зрения
39
вориться разработкой моделей, которые описывают и, будем на-
надеяться, предскажут реакцию зрительной системы человека на те
или иные изображения. В следующем разделе описываются неко-
некоторые явления, которые должны учитываться при моделировании
зрительной системы.
2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ
Описанные ниже зрительные явления взаимосвязаны, одни —
в меньшей степени, другие — в большей. Однако для упрощения
изложения, а также потому, что некоторые детали явлений не
ясны, эти явления рассматриваются вне связи друг с другом.
Контрастная чувствительность
Известно, что реакция глаза на изменение освещения является
нелинейной. Пусть пятно света, имеющее интенсивность I + А/,
окружено фоном интенсивности I (рис. 2.3.1, а). Нужно найти
Ингпенсибность I
Интенсивность /рона
Интенсивность 1
Рис. 2.3.1. Измерения контрастной чувствительности.
а — без фона; б — с фоном.
зависимость от / минимального приращения А/, которое замеча-
замечается наблюдателем. Установлено [11], что в широком диапазоне
интенсивностей отношение А7/7, называемое отношением Вебера,
имеет почти одинаковую величину — около 0,02. Этот результат
40 Глава 2
не имеет места для очень малых или очень больших интенсивно-
интенсивностей, как видно из рис. 2.3.1, а [12]. Более того, контрастная
чувствительность зависит от интенсивности окружающего фона.
Рассмотрим два пятна света с интенсивностями I и / + А/
(рис. 2.3.1, б), окруженные фоном интенсивности /0. Графики
зависимости отношения А/// от I для разных интенсивностей фона
/0 приведены на рис. 2.3.1, б (справа). Оказалось, что диапазон
интенсивностей, лри котором отношение А/// остается постоян-
постоянным, значительно уже, чем на рис. 2.3.1, а. Огибающая точек
минимума кривых рис. 2.3.1, б совпадает с кривой рис. 2.3.1, а.
Однако диапазон интенсивностей / для почти постоянного отно-
отношения А/// при фиксированной интенсивности фона /„ сравним
с динамическим диапазоном большинства электронных изобра-
изображающих систем.
Поскольку дифференциал логарифма интенсивности равен
d {log (I)\ = dill, B.3.1)
то одинаковые изменения логарифма интенсивности света можно
связать с одинаковыми едва заметными изменениями интенсив-
интенсивности в диапазоне, в котором отношение А/// остается постоян-
постоянным. По этой причине во многих системах обработки изображений
вычислительные операции проводятся с использованием лога-
логарифма интенсивности, а не интенсивности.
Полосы Маха
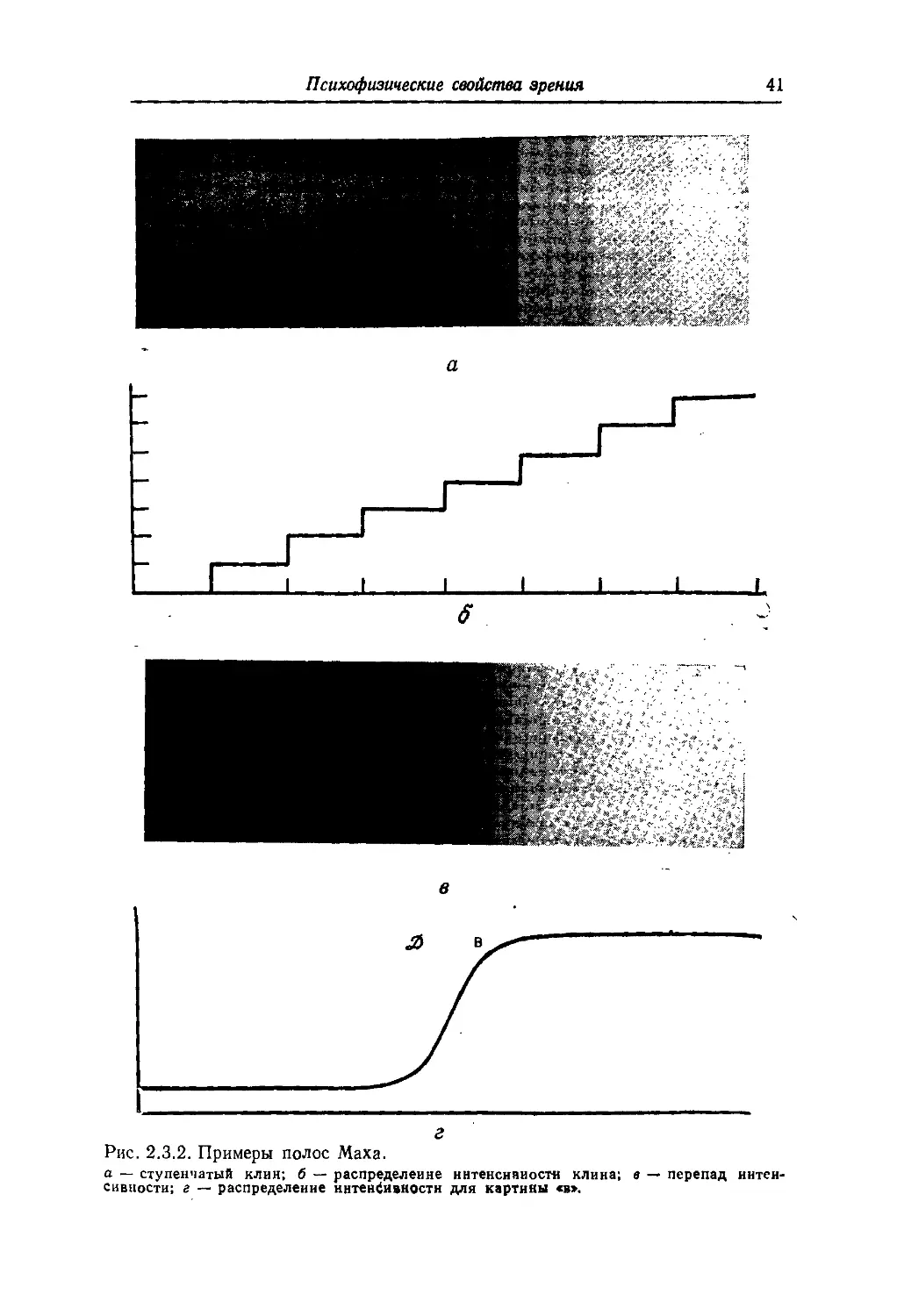
Рассмотрим ступенчатый оптический клин (набор полосок
различной светлоты), показанный на рис. 2.3.2, а. Интенсив-
Интенсивность света, отраженного от каждой полоски, одинакова по ее
ширине и отличается на постоянную величину от интенсивности
света, отраженного от соседних полосок. Однако правый край
каждой полоски кажется темнее левого. Это явление называется
эффектом полос Маха [13 ]. На рис. 2.3.2, в представлено изображе-
изображение с распределением интенсивности, которое показано на
рис. 2.3.2, г. На этой фотографии видны два столбика — яркий
(В) и темный (?>). Ни один из них нельзя предсказать исходя из
распределения интенсивности. Полосы Маха, т. е. кажущиеся
преувеличения изменений светлоты, можно объяснить исходя
из пространственно-частотной характеристики глаза. Как мы
увидим скоро, глаз обладает меньшей чувствительностью в об-
области низких и высоких пространственных частот по сравнению
с чувствительностью на средних частотах. Отсюда можно сделать
вывод, что при создании систем обработки изображений можно
в некоторой степени пожертвовать верностью воспроизведения
контуров, так как глаз не очень чувствителен к высокочастотным
перепадам светлоты.
Психофизические свойства зрения
41
Рис. 2.3.2. Примеры полос Маха.
а — ступенчатый клин; б — распределение интенсивности клина; в — перепад интен-
интенсивности; г — распределение интенсивности для картины ев».
42 Глава 2
Одновременный контраст
Явление одновременного контраста [7] иллюстрируется фото-
фотографией, приведенной на рис. 2.3.3. В действительности все
маленькие квадраты имеют одинаковую яркость, но из-за различ-
Рис. 2.3.3. Пример одновременного контраста.
ной яркости фона кажется, что их яркость разная. Цветовой фон
пятна света зависит также от цвета окружения. Белое пятно на
черном квадрате кажется желтоватым, если вся фигура окружена
синим фоном.
Цветовая адаптация
Воспринимаемый цветовой фон зависит от адаптации зрителя
[14]. Американский флаг, например, не сразу будет восприни-
восприниматься как красно-бело-синий, если человек перед этим смотрел
на интенсивный красный свет. Воспринимаемые цвета флага
будут смещены в сторону голубого цвета, который является до-
дополнительным к красному.
Цветовая слепота
Приблизительно 8% всех мужчин и 1 % женщин в той нли иной
форме страдают цветовой слепотой [15, стр. 405]. Существуют
разные степени цветовой слепоты. Некоторые люди, так назы-
называемые монохроматы, имеют только палочки или палочки и кол-
колбочки одного типа и поэтому им свойственно одноцветное зрение.
Другие люди — дихроматы — имеют колбочки двух типов. И мо-
монохроматы, и дихроматы могут различать цвета в той степени,
в которой они научились связывать различные цвета с разными
предметами. Например, они могут знать, что темные розы —
красные, а светлые —желтые. Но если покрасить красную розу
в желтый цвет, сохранив величину коэффициента отражения,
монохромат может назвать ее красной. Дихроматы также не-
неспособны точно определять цветовой тон.
Психофизические свойства зрения 43
Субъективные цвета [16]
В 1826 г. французский монах Бенидикт Прево заметил, что если
периодически освещать белый лист бумаги, помещая его в узкий
луч света в затемненной комнате, то на этом листе можно наблю-
наблюдать цветные полоски. Это было первое зарегистрированное
наблюдение субъективных цветов. Фехиер в 1838 г. наблюдал
субъективные цвета, появляющиеся на вращающемся диске,
Рис. 2.3.4. Диск Бенхэма.
выкрашенном наполовину в черный, наполовину в белый цвет.
В 1894 г. Бенхэм изобрел волчок, на верхней поверхности которого
был узор, показанный на рис. 2.3.4. Когда волчок вращается про-
против часовой стрелки, внешнее кольцо кажется красным, среднее —
зеленым, а внутреннее — синим. Вращение в противоположную
сторону приводит к тому, что цвета внешнего и внутреннего
колец меняются местами. Эти и связанные с ними явления частично
объясняются характером временной реакции зрительной системы
человека на вспышки света.
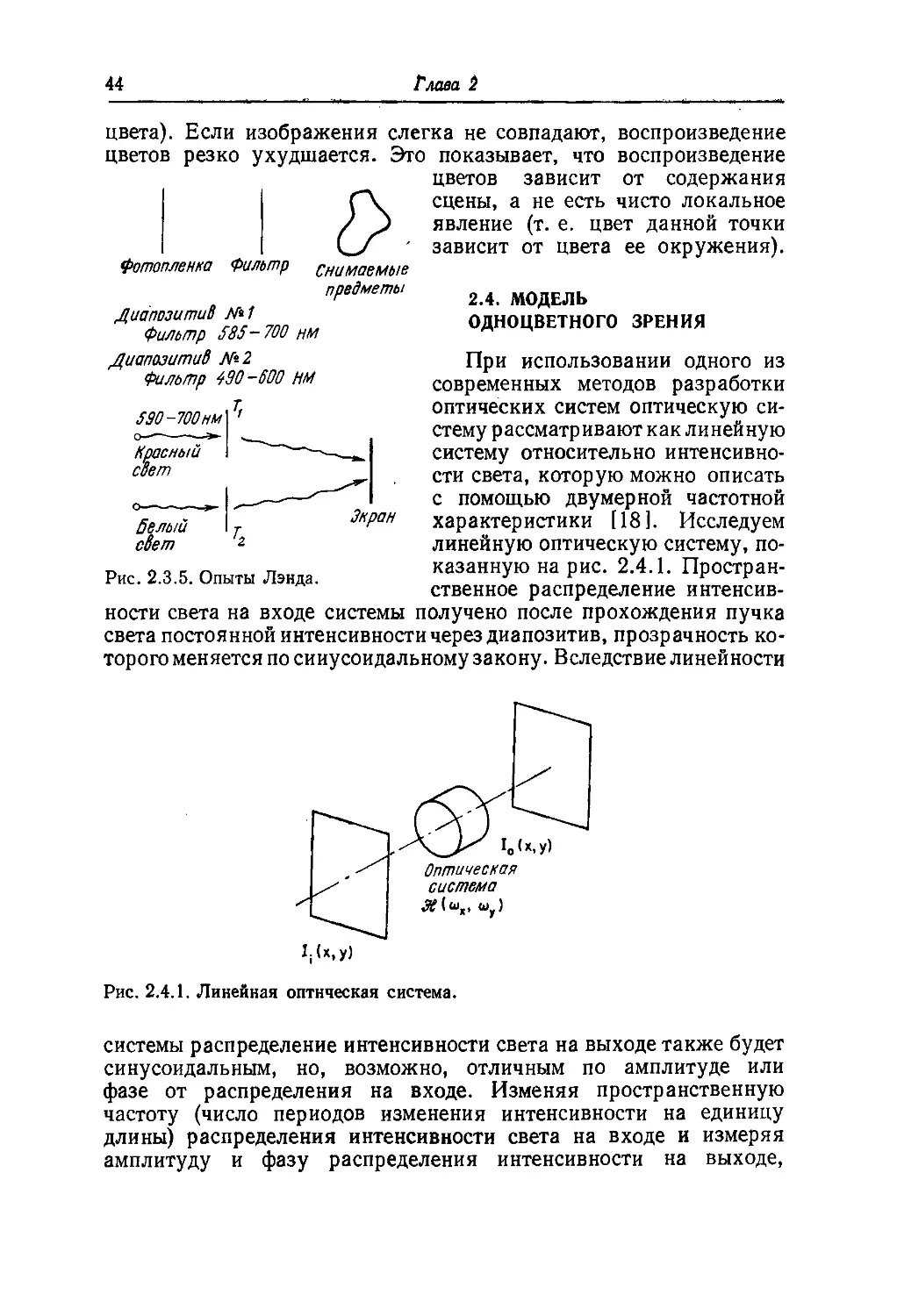
Опыты Лэнда
В начале 50-х годов Лэнд [17] провел интересные опыты,
показывающие возможность воспроизведения цвета с помощью
двух основных цветов. Один из этих опытов иллюстрируется на
рис. 2.3.5. Некоторая сцена фотографируется дважды: за филь-
фильтрами с полосами пропускания ~600—700 и —500—600 нм.
Изготавливаются два одноцветных диапозитива Тг и 7%. Затем
эти диапозитивы проектируются на один экран. Первый диапо-
диапозитив освещается красным светом (длина волны 600—700 нм),
а второй — белым. Наблюдается интересный эффект: когда оба
изображения совмещены, исходная сцена воспроизводится почти
в естественных цветах (плохо воспроизводятся только пурпурные
44
tjiaea
цвета). Если изображения слегка не совпадают, воспроизведение
цветов резко ухудшается. Это показывает, что воспроизведение
цветов зависит от содержания
сцены, а не есть чисто локальное
явление (т. е. цвет данной точки
зависит от цвета ее окружения).
Фотопленка Фильтр
Диапозитиб М*1
Фильтр S85-700 нм
Диапшти8 N'-2
фильтр 490-500 НМ
Снимаемые
предметы
2.4. МОДЕЛЬ
ОДНОЦВЕТНОГО ЗРЕНИЯ
S90-700 нм
При использовании одного из
современных методов разработки
оптических систем оптическую си-
систему рассматривают как линейную
систему относительно интенсивно-
интенсивности света, которую можно описать
с помощью двумерной частотной
характеристики [18]. Исследуем
линейную оптическую систему, по-
показанную на рис. 2.4.1. Простран-
Пространственное распределение интенсив-
интенсивности света на входе системы получено после прохождения пучка
света постоянной интенсивности через диапозитив, прозрачность ко-
которого меняется по сииусоидальному закону. Вследствие линейности
белый
свет
Рис. 2.3.5. Опыты Лэнда.
Экран
1.Сх,у)
Оптическая
система
Рис. 2.4.1. Линейная оптическая система.
системы распределение интенсивности света на выходе также будет
синусоидальным, но, возможно, отличным по амплитуде или
фазе от распределения на входе. Изменяя пространственную
частоту (число периодов изменения интенсивности на единицу
длины) распределения интенсивности света на входе и измеряя
амплитуду и фазу распределения интенсивности на выходе,
Психофизические свойства зрения 45
можно в принципе получить частотную характеристику оптиче-
оптической системы.
Пусть Ш (со*, со,,) — оптическая частотная характеристика
двумерной линейной системы, а со* = 2п1Тх, со, = 2п/Ту —
угловые пространственные частоты (Тх, Ту — периоды изменения
интенсивности вдоль координатных осей х и у). Пусть далее
/,- (х, у) обозначает распределение интенсивности света на входе
в предметной плоскости, а /„ (х, у) — распределение интенсив-
интенсивности света на выходе (в плоскости изображения). Тогда простран-
пространственно-частотные спектры распределений интенсивностей на
входе и выходе по определению будут равны
ЗГ, К, ©„)<=_[] /, (х, у) ехр \-1 К* + со,*,)} dx dy B.4.1)
оо
&0 К, ay) = J J Io (х, у) ехр{ —i (<лхх + *>уу)\ dx dy. B.4.2)
—со
Эти спектры связаны следующим соотношением:
&0 К, coj,) = Ж К, со^) ЗГ; К, ©„). B.4.3)
Распределение интенсивности света на выходе может быть полу-
получено обратным преобразованием фурье-спектра B.4.2):
оо
А> (х, у) = A /4я2) j j &0 К, coy) ехр {i (со^ + ЩУ) \ <К da>y. B.4.4)
Во многих случаях при разработке оптических систем интере-
интересуются только отношением амплитуд интенсивностей на входе
и выходе. Это отношение
I ЗГо К, со,) |/1 &, К, со,) | = | Ж К, со,) | B.4.5)
называется частотно-контрастной характеристикой (ЧКХ) опти-
оптической системы.
Много работ было посвящено вопросу использования понятия
линейной системы для описания свойств зрительной системы че-
человека [19—25]. Типичный эксперимент для проверки справедли-
справедливости линейной модели зрительной системы заключается в сле-
следующем. Наблюдателю показывают две решетки с синусоидаль-
синусоидальным изменением коэффициента пропускания. Одна из них —
опорная, с постоянным контрастом Т) и заданной пространствен-
пространственной частотой, вторая — испытательная, с переменным контрастом
и частотой, отличающейся от частоты опорной решетки. Кон-
1} Контрастом пространственно-периодического распределения интенсивно-
интенсивности называется отношение максимальной интенсивности к минимальной.
46
Глава 2
s
н
*,!\контраст
Л
Пространстбенная частота
а
В
8-1
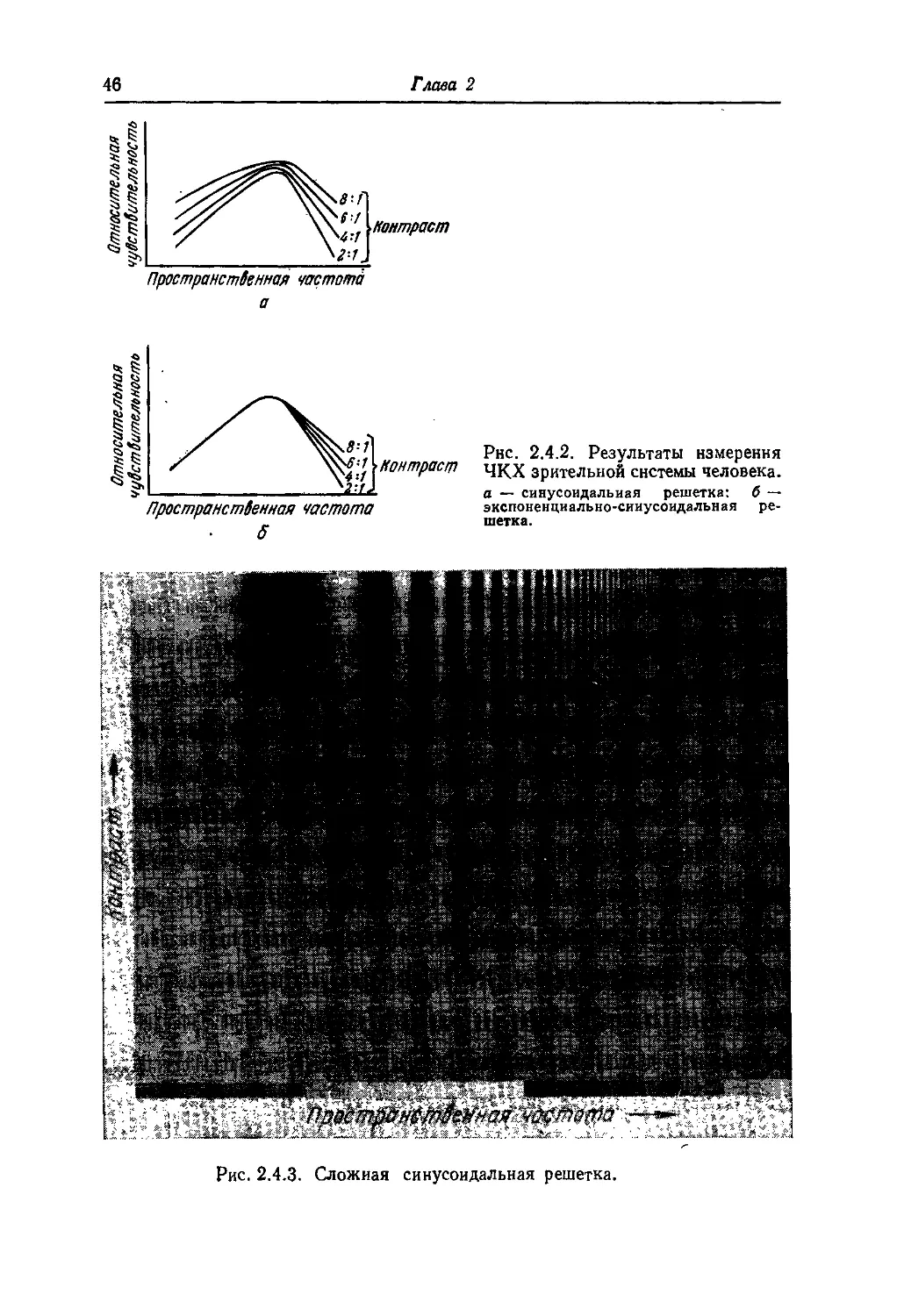
, ., Рнс. 2.4.2. Результаты измерения
&7 Г Контраст ЧКХ зрительной системы человека.
Z'ti. а — синусоидальная оешетка: б —
ПространстЦенная частота
6
а — синусоидальная решетка:
экспоненциально-синусоидальная
шетка.
ре-
Рис. 2.4.3. Сложная синусоидальная решетка.
Психофизические свойства зрения 47
траст испытательной решетки изменяется до тех пор, пока яркость
светлых и темных штрихов обеих решеток будет казаться одина-
одинаковой. Применяя набор испытательных решеток с разными про-
пространственными частотами, можно построить график ЧКХ зри-
зрительной системы человека. На рис. 2.4.2, а приведены графики
ЧКХ для разных контрастов входного сигнала. Представление
о форме ЧКХ можно также получить, рассматривая сложную
синусоидальную решетку, показанную на рис. 2.4.3. В этой ре-
решетке пространственная частота возрастает по одной координате,
а контраст — по другой. Огибающая различимых штрихов в об-
общем близка по форме к кривым рис. 2.4.2, а [24].
На рис. 2.4.2, а показано, что форма ЧКХ зависит от кон-
контраста распределения интенсивности на входе. Кроме того, она
меняется при вращении испытательной решетки вокруг оптиче-
оптической оси глаза. Таким образом, зрительная система человека
нелинейна и анизотропна (не обладает инвариантностью относи-
относительно поворота).
Было сделано предположение, что нелинейная реакция глаза
на изменения интенсивности имеет логарифмический характер.
Нелинейное преобразование осуществляется на первом этапе
обработки визуальной информации в зрительной системе. Преоб-
Jfoeapuqy-
мичесний
преобра -
в
рр
зовотем
Линейный1
фильтр
Выходной
сигнал
Рецептор
Рис. 2.4.4. Логарифмическая модель одноцветного зрения.
разованию подвергаются сигналы рецепторов (палочек и колбо-
колбочек) до того, как они вступают во взаимодействие друг с другом.
На рис. 2.4.4 приведена простейшая логарифмическая модель
глаза для одноцветного зрения. Если реакция глаза на величину
входной интенсивности действительно имеет логарифмический
характер, то, применив экспоненциальное преобразование ин-
интенсивности синусоидальной решетки, можно «линеаризовать»
зрительную систему. ЧКХ, полученная в результате измерения
с использованием экспоненциально-синусоидальной решетки
(рис. 2.4.2, б), хорошо аппроксимируется одной кривой на низких
и средних пространственных частотах. На рис. 2.4.5 приведены
результаты измерения ЧКХ, полученные Дэвидсоном [26] для
экспоненциально-синусоидального испытательного сигнала. Высо-
Высокочастотная часть этой кривой получена экстраполированием
входного сигнала среднего контраста.
Логарифмически-линейная модель глаза (рис. 2.4.3) позволяет
удовлетворительно предсказать реакцию зрительной системы
48
Глава 2
в широком диапазоне интенсивностей. Однако на высоких про-
пространственных частотах и очень низких или очень высоких интен-
сивностях наблюдаемая реакция отличается от предсказанной
на основе этой модели. Для того чтобы получить более точную
модель, необходимо детальнее рассмотреть физические процессы
в зрительной системе.
Нелинейная реакция палочек и колбочек на изменения интен-
интенсивности все еще служит предметом активных исследований. Были
высказаны гипотезы о том, что механизм этой нелинейности объяс-
ч!
И
10,0
6,0
4,0
2,0
'.о
0,6
0,4
111ll
ll I
0,18 0,60 1,8 6,0 18
Пространственная чостота,
число nepuodo&jzpqd
SO
Рис. 2.4.5. Результаты измерений ЧКХ зрительной системы человека с помощью
экспоненциально-синусоидальных решеток [26].
няется химической активностью, электрическими эффектами и
нервной обратной связью. Основная логарифмическая модель
предполагает, что
1о (х, у) = Ki log IK, + KsIi (x, у)], B.4.6)
где /Ci, К% и Кз — постоянные, а 1{ (х, у) и /0 (х, у) — входной
и выходной сигналы. В другой модели [7, стр. 253 ] предполагается
следующая зависимость выходного сигнала от входного:
/о (х, У) = [KJ, (х, у)]/[К2 + h (х, У)], B.4.7)
где Къ Кг — постоянные. Манное и Сакрисон [27 ] изучали раз-
различные нелинейности, используемые в аналитических мерах
верности воспроизведения изображения. Они установили, что
степенная нелинейная зависимость, когда
1о(х, У) = Ut (x, y)Y, B.4.8)
где s — постоянная, обеспечивает хорошее согласие между вы-
вычисленной верностью и субъективной оценкой качества изобра-
изображения. (Подробно результаты этой работы рассматриваются
в гл. 7.) Подбором постоянных, входящих в выражения B.4.6) —
Психофизические свойства зрения
49
B.4.8), соответствующие кривые могут быть достаточно хорошо
сближены в диапазоне средних интенсивностей.
Пространственно-частотные характеристики глаза объясняются
частично оптическими и частично нервными механизмами. Как
оптический инструмент глаз имеет ограниченную разрешающую
способность из-за конечных размеров апертуры линзы, опти-
оптических аберраций и конечных размеров палочек и колбочек.
Эти эффекты могут быть представлены в модели фильтром нижних
Логарифмические
преобразователи
Рецепторы ЯегпЛые
ттти и колбочки, ^жители
Рнс. 2.4.6. Схема латерального торможения.
0 !
Номер
сигнала
рецептора
пространственных частот, включенным между рецептором и нели-
нелинейным элементом. Наиболее существенный вклад в частотную
характеристику глаза вносит механизм латерального торможения
128]. Схема этого механизма приведена на рис. 2.4.6. Нервный
сигнал есть взвешенная сумма сигналов от многих соседних ре-
рецепторов. Некоторые рецепторы вносят тормозящий (т. е. отрица-
отрицательный) вклад в эту сумму. Весовые множители представляют
собой по существу импульсный отклик части зрительной системы,
находящейся после сетчатки. Двумерное преобразование Фурье
этого импульсного отклика дает соответствующую частотную
характеристику.
Восприятие светового импульса, попавшего в глаз, происходит
с задержкой. После окончания действия импульса ощущение
50
Глава 2
света затягивается на короткое время. Эти явления, возникающие
из-за ненулевой длительности временной реакции зрительной
системы, можно моделировать линейным временным фильтром.
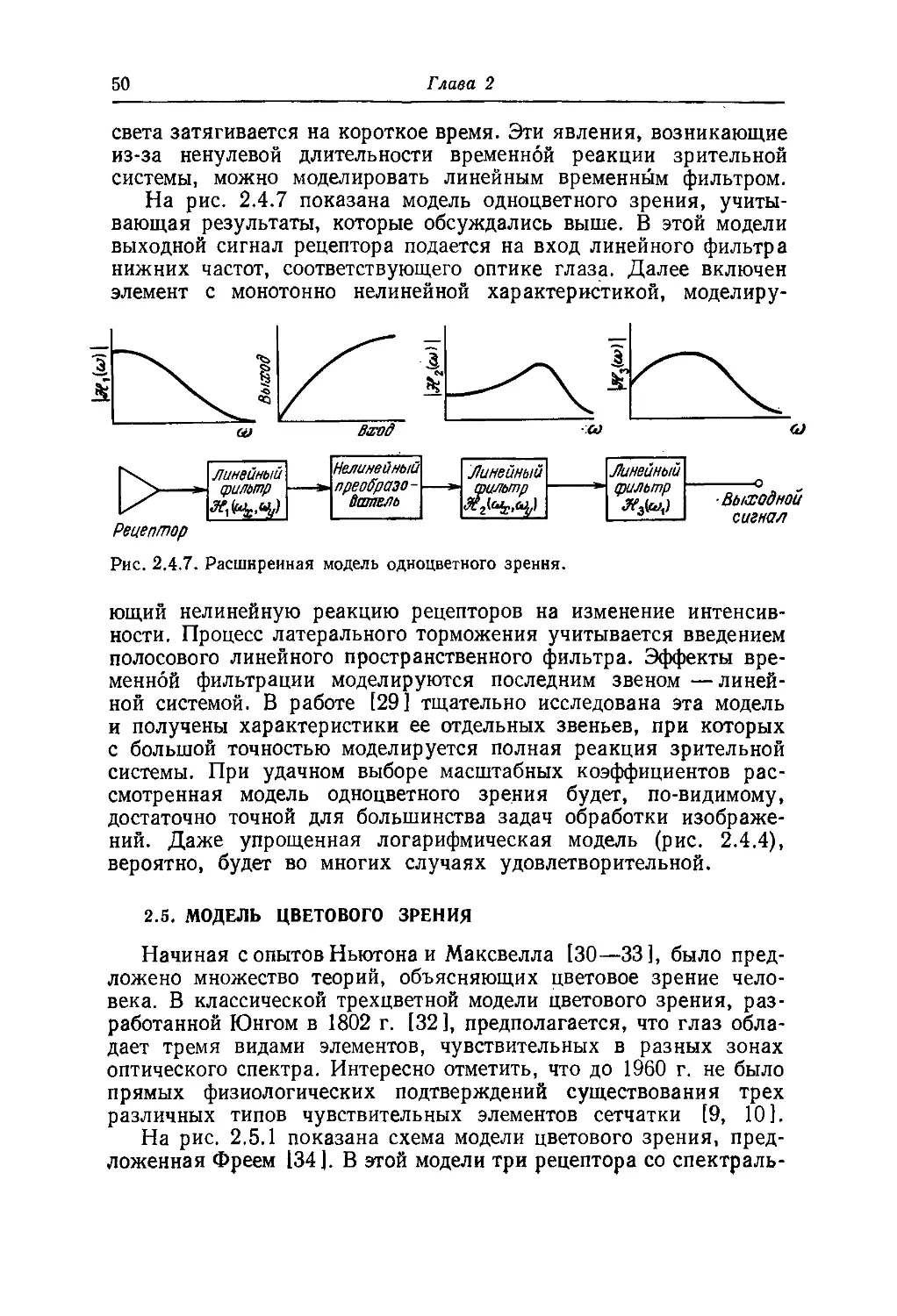
На рис. 2.4.7 показана модель одноцветного зрения, учиты-
учитывающая результаты, которые обсуждались выше. В этой модели
выходной сигнал рецептора подается на вход линейного фильтра
нижних частот, соответствующего оптике глаза. Далее включен
элемент с монотонно нелинейной характеристикой, моделиру-
Вход
м
Рецептор
Линейный
филыпр
Нелинейный
npeoffpaao-
Йсопвль
Линейный
тильтр
Линейный
фильтр
¦Выходной
сигнал
Рис. 2.4.7. Расширенная модель одноцветного зрения.
ющий нелинейную реакцию рецепторов на изменение интенсив-
интенсивности. Процесс латерального торможения учитывается введением
полосового линейного пространственного фильтра. Эффекты вре-
временной фильтрации моделируются последним звеном — линей-
линейной системой. В работе [29] тщательно исследована эта модель
и получены характеристики ее отдельных звеньев, при которых
с большой точностью моделируется полная реакция зрительной
системы. При удачном выборе масштабных коэффициентов рас-
рассмотренная модель одноцветного зрения будет, по-видимому,
достаточно точной для большинства задач обработки изображе-
изображений. Даже упрощенная логарифмическая модель (рис. 2.4.4),
вероятно, будет во многих случаях удовлетворительной.
2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
Начиная с опытов Ньютона и Максвелла [30—33], было пред-
предложено множество теорий, объясняющих цветовое зрение чело-
человека. В классической трехцветной модели цветового зрения, раз-
разработанной Юнгом в 1802 г. [32 ], предполагается, что глаз обла-
обладает тремя видами элементов, чувствительных в разных зонах
оптического спектра. Интересно отметить, что до 1960 г. не было
прямых физиологических подтверждений существования трех
различных типов чувствительных элементов сетчатки [9, 10].
На рис. 2.5.1 показана схема модели цветового зрения, пред-
предложенная Фреем 134]. В этой модели три рецептора со спектраль-
Психофизические свойства зрения
51
ными чувствительностями sx (Ц, s2 (К) и s3 (К), соответствующими
трем пигментам колбочек сетчатки, создают сигналы
е, = J С
К B.5.1а)
К B.5.16)
К B.5.1в)
где С (к) — спектральная плотность энергии источника падающего
света. Три сигнала еи eit e3 подвергаются затем логарифмическому
преобразованию и объединяются так, чтобы получились сигналы
di = log еъ B.5.2а)
d% = log e% — log ег — log (e^), B.5.26)
d3 = log e3 — log в! = log (е3/ег). B.5.2в)
Эти сигналы проходят через линейные фильтры с частотными ха-
характеристиками Жх (со*, со^), Ж% (cox, coj) и Ж3 (а>х, cofr); получае-
получаемые на выходе сигналы glt g2, g3 определяют восприятие цветов
в мозге.
Колбочко,
поглощающая
зеленый сбет
LOG
Колбочка,
поглощающая ,
желто-зеленый
едет
tOG
Шбочка,
поглощающая
синий свет
Выходной
' сигнал
Рнс. 2.5.1. Модель цветового зрения.
В модели рис. 2.5.1 сигналы d2 и d3 характеризуют цветность,
а сигнал d^ пропорционален яркости. Оказалось, что эта модель
позволяет очень точно предсказать многие явления цветового зре-
зрения и хорошо согласуется с основными законами колориметрии.
Известно, например, что если спектральную плотность энергии
источника света умножить на постоянную (одинаковую для всех
длин волн), то цветовой тон и насыщенность, описываемые коор-
координатами цветности, останутся неизменными в широком диапазоне
изменения интенсивности света. Выражения B.5.1) и B.5.2)
52
Глава 2
показывают, что сигналы цветности d2 и ds в таком случае не
изменяются, а сигнал яркости изменяется по логарифмическому
закону. Другие особенности этой модели описаны Фреем [34].
Как уже отмечалось, некоторые данные о спектральной чув-
чувствительности si (Я) трех типов колбочек сетчатки были получены
при измерении поглощения света пигментами колбочек (см. рис.
2.2.4). Однако прямые физиологические измерения очень сложны и
не могут быть выполнены с большой точностью. Косвенные оценки
спектральной .чувствительности колбочек были получены Конигом
и
1,0
0,5
0
/'
/
/
f-
V /
\ saM -У/
\ h
\ //
\ \
s,w \ \
\ \
\\
,\\
i i »^]^
450 500 5S0 600
Длина бмны, нм
650
Рис. 2.5.2. Спектральные чувствительности колбочек по даииым Коинга [35].
и Бродхуном [35] при изучении аномалий цветового зрения.
Джадд [36 ] на основе этих данных нашел линейное преобразова-
преобразование, позволяющее установить связь спектральных чувствитель-
ностей st (к) с функциями сложения, найденными в колориметри-
колориметрических опытах. В результате были получены кривые, приведенные
на рис. 2.5.2. Они унимодальны и строго положительны, как
это и следует из физиологических представлений.
Аналогично модели одноцветного зрения (рис. 2.4.7) лога-
логарифмическая модель цветового зрения (рис. 2.5.1) может быть до-
дополнена линейными фильтрами, которые включаются после ре-
рецепторов. Вместо логарифмической функции можно использовать
нелинейную функцию общего вида. Заметим, что, не изменяя
выходного сигнала, можно изменить порядок выполнения линей-
линейных операций суммирования и преобразования. Схема расширен-
расширенной модели цветового зрения представлена на рис. 2.5.3. Можно
ожидать, что пространственно-частотная характеристика яркост-
ного канала, на выходе которого образуется сигнал glt будет
подобна пространственно-частотной характеристике системы одно-
одноцветного зрения, которая рассматривалась в разд. 2.4. Результаты
измерений частотной характеристики системы в окрашенном свете
приведены на рис. 2.5.4. Как видно, частотная характеристика,
измеренная при использовании окрашенного света, сдвинута
Психофизические свойства зрении
53
к низким пространственным частотам по сравнению с частотной
характеристикой, измеренной с белым светом [37]. Латеральное
торможение должно приводить к изгибу частотной характеристики
Колбочка,
чувствительна
к зеленом и cSt
Линейный
фильтр
Нелинейный
пре образа -
датель
Мнеиныи
фильтр
<ая
<ету
Линейный
фильтр
колбочка, чувстви-
чувствительная к желто-зеле-
желто-зеленому свету
Нелинейный
преобразо -
датель
гч. Линейный
>—*¦ срильтр
Нелинейный^
поеобразо-
датель
Колбочка,
чувстдительная
к синему cffemy
Рис. 2.5.3. Расширенная модель цветового зрения.
9,
выдодныв
сигналы
на низких частотах. Этот изгиб получается, вероятно, на более
низких частотах, чем те, которые входили в исследуемый диапазон.
Воспринимаемый цвет — понятие относительное. Ощущение,
вызываемое светом с данным спектральным распределением энер-
энергии, зависит от окружающего фона и адаптации зрителя. Человек
1,0
«I
I I I I I I ||
0,1 0,3 1 3 Ю J0
, Пространственная: частота, число периодов/град
Рис. 2.5.4. Пространственио-частотиые характеристики зрительной системы че-
человека [26, 37].
А — для скрашенного света; Б — для белого света.
может очень хорошо адаптироваться к освещению сцены, исполь-
используя опорный белый свет или общий цветовой баланс. Это свойство
называется цветовой адаптацией.
В простейшей модели цветовой адаптации, предложенной фон
Крисом [38; 15, стр. 435], в схему зрительной системы (рис. 2.5.3)
54 Глава 2
между колбочками и первым линейным фильтром включается
блок автоматической регулировки усиления. Коэффициент уси-
усиления
[l[l B.5.3)
для i=l, 2, 3 устанавливается так, чтобы усиленный сигнал
колбочки равнялся единице при рассматривании опорного белого
света со спектральной плотностью W (к). Модель фон Криса
привлекает разумностью и простотой. Однако эксперименты по-
показали [15, стр. 438], что эта модель не полностью описывает
эффект цветовой адаптации. Уоллис [39] высказал предположение
о том, что цветовая адаптация может быть частично объяснена
действием механизма торможения, в результате которого ослаб-
ослабляются медленно изменяющиеся компоненты яркостного поля.
Этот механизм может моделироваться фильтрами с характеристи-
характеристиками Жи (ах, <йу) (рис. 2.5.3). Несомненно, оба механизма —
регулировки усиления и торможения —обеспечивают цветовую
адаптацию. Требуются дальнейший анализ и эксперименты, чтобы
правильно объяснить это явление и построить его модель.
ЛИТЕРАТУРА
1. Webster's New Collegiate Dictionary, G. and C. Merriam Co., The Riverside
Press, 1960.
2. Malitson H. H., The Solar Energy Spectrum, Sky and Telescope, 29, 4, 162—
165 (March 1965).
3. Munsell Book of Color, Munsell Color Co., 2441 North Calvert St., Baltimore,
Maryland.
4. Pirenne M. H., Vision and the Eye, 2nd ed., Associated Book Publishers,
London, 1967.
5. Polyak S. L., The Retina, University of Chicago Press, Chicago, 1941.
6. Davson L. H., The Physiology of the Eye, McGraw-Hill (Blakiston), New
York, 1949.
7. Cornsweet T. N., Visual Perception, Academic press, New York, 1970.
8. Wald G., Human Vision and the Spectrum, Science, 101, 2635, 653—658 (June
1945).
9. Brown P. K., Wald G., Visual Pigment in Single Rods and Cones of the Hu-
Human Retina, Science, 144, 3614, 45—52 (April 1964).
10. Wald G., The Receptors for Human Color Vision, Science, 145, 3636, 1007—
1017 (September 1964).
11. Hecht S., The Visual Discrimination of Intensity and the Weber-Fechner Law,
J. Gen, Physiol., 7, 241 A924).
12. Stevens S. S., Handbook of Experimental Psychology, Wiley, New York,
1951.
13. Ratliff F., Mach Bands: Quantitative Studies on Neural Networks in the Re-
Retina, Holden-Day, San Francisco, 1965.
14. Brindley G. S., Afterimages, Scientific American, 209, 4, 84—93 (October
1963).
15. Wyszecki G., Stiles W. S., Color Science, Wiley, New York, 1967.
16. Cohen J., Gordan D., The Prevost-Fechner-Benham Subjective Colors, Psy-
chophys. Bull., 46, 2, 97—136 (March 1949).
Психофизические свойства зрения 55
17. Land E. H., Experiments in Color Vision, Scientific American, 200, 5, 84—99
(May 1959).
18. Goodman J. W., Introduction to Fourier Optics, McGraw-Hill, New York,
1968. [Имеется перевод: Гудмен Дж., Введение в фурье-оптику. — М.:
Мир, 1970.]
19. Campbell F. W., The Human Eye as an Optical Filter, Proc. IEEE, 56, 6,
1009—1014 (June 1968).
20. Bryngdahl O., Characteristics of the Visual System: Psychophysical Measu-
Measurement of the Response to Spatial Sine-Wave Stimuli in the Mesopic Region,
J. Opt. Soc. Am., 54, 9, 1152—1160 (September 1964).
21. Lowry E. M., Depalma J. J., Sine Wave Response of the Visual System,
I. The Mach Phenomenom, J. Opt. Soc. Am., 51, 7, 740—746 (July 1961).
22. Lowry E. M., Depalma J. J., Sine Wave Response of the Visual System,
II. Sine Wave and Square Wave Contrast Sensitivity, J. Opt. Soc. Am., 52,
3, 328—335 (March 1962).
23. Sachs M. В., Nachmias J., Robson J. G., Spatial Frequency Channels in
Human Vision, /. Opt. Soc. Am., 61, 9, 1176—1186 (September 1971).
24. Stockham T. G., Jr., Image Processing in the Context of a Visual Model, Proc.
IEEE, 60, 7, 828—842 (July 1972). [Имеется перевод: Стокхэм, Обработка
изображений в контексте модели зрения. — ТИИЭР, 1972, т. 60, № 7.]
25. Pearson D. E., A Realistic Model for Visual Communication Systems, Proc.
IEEE, 55, 3, 380—389 (March 1967). [Имеется перевод: Пирсон, Реалисти-
Реалистическая модель системы передачи изображений. — ТИИЭР, 1967, т. 55, № 3.]
26. Davidson М. L., Perturbation Approach to Spatial Brightness Interaction
in Human Vision, J. Opt. Soc. Am., 58, 9, 1300—1308 (September 1968).
27. Mannos J. L., Sakrison D. J., The Effects of a Visual Fidelity Criterion on
the Encoding of Images, IEEE Trans. Inf. Theory, IT-20, 4, 525—536 (July
1974).
28. Ratliff F., Hartline H. K., Miller W. H., Spatial and Temporal Aspects
of Retinal Inhibitory Interaction, J. Opt. Soc. Am., 53, 1, 110—120 (January
1963).
29. Hall С F., Hall E. L., A Nonlinear Model for the Spatial Characteristics
of the Human Visual System, IEEE Trans. Syst., Man Cybern., SMC-7, 3,
161—170 (March 1977).
30. McCann J. J., Human 'Color Perception, in: Color Theory and
Imaging Systems, Enyard R. A., Ed., Society of Photographic Scientists and
Engineers, Washington D. C, 1973, pp. 1—23.
31. Newton I., Optiks, 4th ed., 1730; Dover Publications, New York, 1952. [Имеется
перевод: Ньютон И., Оптика. — М.: Наука, 1954.]
32. Young Т., Philosophical Transactions, 92, 1802, 12—48.
33. Maxwell J. С, Scientific Papers of James Clerk Maxwell, Neven W. D., Ed.,
Dover Publications, New York, 1965.
34. Frei W., A New Model of Color Vision and Some Practical Limitations, Uni-
University of Southern California, Image Processing Institute, USCEE Report
530, March 1974, pp. 128—143.
35. Konig A., Brodhun E., Experimentelle Untersuchungen uber die Psycho-
physische Fundamental in Bezug auf den Gesichtssinn, Zweite Mittlg. S. B.
Preuss Akademic der Wissenschaften, 1889, 641.
36. Judd D. В., Standard Response Functions for Protanopic and Deuteranopic
Vision, J. Opt. Soc. Am., 35, 3, 199—221 (March 1945).
37. Van der Horst С J. C, de Weert С M., Bouman M. A., Transfer of Spa-
Spatial Chromaticity — Contrast at Threshold in the Human Eye, J. Opt. Soc.
Am., 57, No. 10, 1260—1266 (October 1967).
38. von Kries J., Die Gesichtsempfindungen, Nagel's Handbuch d. Physiology
d. Menchen, Vol. 3, 1904, p. 211.
39. Wallis R. H., Film Recording of Digital Color Images, University of Southern
California Image Processing Institute Report No. 570, June 1975.
Глава 3
ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ
В гл. 2 зрение человека рассматривалось в качественном
аспекте и была сделана попытка построить модели одноцветного
и цветового зрения. Этим моделям можно придать количественный
характер, если ввести меры величин, определяющих восприятие
света человеком. Меры яркости изучаются в фотометрии, а цвета —
в колориметрии. В данной главе рассматриваются вопросы, отно-
относящиеся к обеим этим дисциплинам, а также источники света
3.1. ИСТОЧНИКИ СВЕТА
Источник лучистой энергии описывается спектральной плот-
плотностью С (К) — скоростью испускания энергии в единичном ин-
интервале длин волн. Полная мощность излучения источника опре-
определяется интегралом спектральной плотности — лучистым по-
потоком
оо
\k. C.1.1)
Эта величина обычно измеряется в, ваттах.
Тело, имеющее более высокую температуру, чем окружающая
среда, излучает электромагнитную энергию. Чем выше темпера-
температура, тем сильнее излучение. Идеальный тепловой излучатель
называется абсолютно черным телом. Лучистый поток абсолютно
черного тела при любом значении длины волны достигает макси-
максимума, возможного для заданной температуры. Спектральная
плотность излучения определяется законом Планка [1 ]
<312)
где К—длина волны излучения, Т—температура тела, Съ
С2 —постоянные. На рис. 3.1.1, а показаны графики спектраль-
спектральной плотности для разных значений температуры. В видимой
области электромагнитного спектра спектральная плотность из-
Фотометрия и колориметрия
57
лучения абсолютно черного тела может быть аппроксимирована
законом Вина [1 ]:
График функции Вина для видимой области спектра приведен на
рис. 3.1.1, б.
Главнейшим источником света является, конечно, солнце.
На рис. 2.1.1, а приведен график измеренного спектрального рас-
4 S 6
Дли но Волны,
а
78
400 SO0 600 700
д луна Волны, нм
б
Рис. 3.1.1 Излучение абсолютно черного тела [1].
а — закон Планка; б — закон Вина.
пределения энергии солнечного света [2]. Пунктирная линия на
этом рисунке, аппроксимирующая результаты измерений, пред-
представляет собой график спектральной плотности излучения абсо-
абсолютно черного тела при Т = 6000 К- Лампы накаливания также
часто приближенно рассматривают как абсолютно черное тело при
Т = 1500—3500 К [3].
Международная комиссия по освещению (МКО) утвердила
несколько стандартных источников света, спектральные плотности
излучения которых графически представлены на рис. 3.1.2 [4].
Источник Sa есть лампа накаливания с вольфрамовой нитью.
Источник Sb дает свет, близкий к прямому солнечному свету
в диапазоне 400—700 нм. Свет источника Sc близок к свету при
облачном небе. Источник Е с равномерной спектральной плот-
плотностью излучения часто применяется при колориметрических
расчетах.
В системах обработки изображений в качестве источников
света часто используются люминофоры кинескопов. На рис. 3.1.3
представлены спектральные плотности излучения нескольких
обычных люминофоров [5]. В одноцветных телевизионных прием-
13
о
ш
О
1
I
Относительная энергия излучения
w soo
%
I'll
- " ~
_
—_
1 ' 1
ъ
со
•о
я
о
1
я
i
00-
Относительная
интенсивность
Относительная энергия излучений
Со
Фотометрия и колориметрия
59
никах обычно применяют люминофор Р4, который обеспечивает
воспроизведение довольно яркой голубовато-белой картинки.
Люминофор Р16 используется в видеодатчиках бегущего луча,
так как имеет короткое послесвечение. Для видеодатчиков бегу-
бегущего луча цветного телевидения выбирают люминофор Р24, излу-
излучающий в относительно широкой спектральной полосе и имеющий
довольно короткое послесвечение. В приемниках цветного теле-
телевидения используют кинескопы с красным, зеленым и синим
люминофорами, расположенными в виде триад точек или полос.
Люминофор Р22 представляет собой типичную комбинацию трех
люминофоров.
3.2. ФОТОМЕТРИЯ
Цель фотометрических измерений — количественно описать
яркость света [6—8]. Связь между фотометрическими и энергети-
энергетическими характеристиками излучения устанавливается функцией
световой эффективности, показанной на рис. 3.2.1, а [9]. Эта кри-
кривая утверждена как стандарт МКО. Она определяет спектральную
I
ll
to
0,8
0,6
0,4
0,2
0
-
-
- j
j/
400
/
/
/
i I
soo
Длина
\
\
\
v
1 i4»^
600 70
долны, им
6
SOO 600
Длина волны, нм
а
Рис. 3.2.1. Относительная спектральная световаяЗэффективность [9].
а — для дневного зрения; б — для ночного зрения.
чувствительность зрительной системы некоторого типичного (стан-
(стандартного) наблюдателя. В сущности эта кривая есть стандарти-
стандартизованный вариант кривой спектральной чувствительности кол-
колбочек, приведенной на рис. 2.2.2, для дневного зрения при от-
относительно высоких уровнях освещенности. Стандартная функция
световой эффективности для ночного зрения при относительно
низких уровнях освещенности представлена на рис. 3.2.1, б.
Большинство систем воспроизведения изображений разрабаты-
разрабатывается на основе относительной световой эффективности для
дневного зрения.
60
Глава 3
Субъективное ощущение яркости, вызываемое источником света
со спектральной плотностью излучения С (к), определяется его
световым потоком, который выражается как
C.2.1)
где V (к) — относительная световая эффективность, a Km — по-
постоянная. Если световой поток измерять в люменах, то Кт —
= 685 лм/Вт. Источник монохроматического света мощностью
Точечный
источник
Точечный
источник
Рис. 3.2.2. К определению фотометрических величин.
а — излучение точечного источника; б — излучение элементарной площадки; к — осве-
освещенность, создаваемая точечным источником; г — освещенность, создаваемая протяжен-
протяженным источником.
1 Вт, длина волны которого соответствует максимуму кривой
относительной световой эффективности (т. е. при X = 555 нм),
дает световой поток 685 лм.
Другой важной характеристикой источника света является
пространственное распределение его излучения. Рассмотрим то-
точечный источник, испускающий световой поток во всех направле-
направлениях (рис. 3.2.2, а). Отношение бесконечно малого светового по-
Фотометрия и колориметрия 61
тока dF, излучаемого в бесконечно малый телесный угол do»,
к величине этого угла называется силой света
/ = dF/da. C.2.2)
Эта величина измеряется в канделах. Протяженный источник
характеризуется яркостью (рис. 3.2.2, б), равной по определению
В = dl (Q)/(da cos 9), C.2.3)
где dl (9) — бесконечно малая сила света, излучаемого с бес-
бесконечно малой площадки da в направлении, составляющем угол 9
с нормалью к поверхности. Единицей яркости является кандела
на 1 м2, или нит.
Протяженный источник света является диффузным, если спра-
справедлив закон Ламберта
dl (9) = dIN cos 9, C.2.4)
где dlN — бесконечно малая сила света, излучаемого перпен-
перпендикулярно поверхности. Для такого источника яркость
В = d!Nlda C.2.5)
не зависит от направления наблюдения. В изображающих системах
освещенное матовое стекло часто используется как приближение
к идеальному диффузному источнику света.
Яркость источника излучения есть мера светового потока,
излучаемого с единицы площади его поверхности в заданном на-
направлении в единичный телесный угол. Величина светового по-
потока, падающего на наблюдаемую поверхность, определяется ее
освещенностью. Пусть точечный источник испускает световой по-
поток dF в телесный угол da» под углом ср с нормалью к наблюдаемой
поверхности (рис. 3.2.2, в). Угол day охватывает площадку dA
на этой поверхности. Освещенность по определению равна
Е = dFldA. C.2.6)
Из соотношения C.2.2) и рис. 3.2.2 следует, что
dF = / (9) da = / (9) [(dA cos cp)/#2 ], C.2.7)
где R — расстояние от источника до поверхности. Следовательно,
при освещении точечным источником освещенность определяется
соотношением
Е = [/(9) cos ср]/#2, C.2.8)
которое выражает закон обратных квадратов для излучения.
Чтобы определить освещенность, создаваемую протяженным источ-
источником, его нужно представить в виде совокупности точечных
источников, а затем сложить освещенности, получаемые от этих
точечных источников. Обращаясь к рис. 3.2.2, г и выражению
C.2.8), получим, что бесконечно малая освещенность площадки dA
62
Глава 3
наблюдаемой поверхности, создаваемой площадкой da излучающей
поверхности, есть
dE = [dl (9) cos ср]/Я2. C.2.9)
Из выражений C.2.3) и C.2.9) получаем
dE = {В da cos 9 cos
C.2.10)
Для вычисления освещенности Е нужно интегрировать выражение
C.2.10) по поверхности освещающего предмета.
На основе приведенных выше теоретических положений можно
получить два важных фотометрических результата для оптиче-
Обобщенная
система
формирования
изображения
с/А
В
Изо5раокент%
Диаметр
D
с/А
Яркость В
Плоскость источника
Плоскость
изображения
Рис. 3.2.3. Связь яркости источника с яркостью и освещенностью изображения.
а — яркость источника и изображения: б — яркость источника и освещенность изобра-
изображения.
ской системы. Рассмотрим обобщенную изображающую систему,
показанную на рис. 3.2.3, а. Бесконечно малая площадка da
поверхности диффузного предмета с яркостью В отображается
в бесконечно малую площадку dA наблюдаемой поверхности, ко-
которая приобретает яркость В. Можно показать [8, стр. 189],
что Ъ = В, если коэффициенты отражения обеих поверхностей
Фотоме/прия и колориметрия 63
одинаковы. Таким образом, изображающая система не изменяет
яркость, если не принимать во внимание потерь из-за поглощения
и рассеяния света. На рис. 3.2.3, б показано, как происходит
отображение протяженного диффузного источника с яркостью В
на наблюдаемую поверхность посредством простой тонкой линзы.
Бесконечно малая освещенность на бесконечно малой площадке dA
[8, стр. 190] равна
6Е - (BnD2/4xl) cos4 9, C.2.11)
где D — диаметр линзы, 9 — угол пересечения главных лучей,
проходящих через центр линзы, и х2 —расстояние от центра
линзы до точки наблюдения. Таким образом, освещенность точек
плоскости наблюдения при удалении от оптической оси падает
как четвертая степень угла между данными направлением и
оптической осью. Заметим, что cos* 30° = 0,56. Дополнительные
потери освещенности вызываются поглощением и рассеянием
света в оптической системе. Кроме того, могут иметь место потери
из-за виньетирования, когда полностью теряются косые лучи,
составляющие большой угол с оптической осью.
В дальнейшем при рассмотрении систем обработки изображе-
изображений, для того чтобы не входить в излишние детали, будут по воз-
возможности исключаться вопросы, связанные с фотометрией. Кроме
того, как это обычно делается в литературе по обработке изображе-
изображений, термин «яркость» будет использоваться для обозначения све-
светового потока, силы света и собственно яркости.
3.3. УРАВНИВАНИЕ ЦВЕТОВ [10—14]
В основе трехцветной теории цветного зрения лежит возмож-
возможность представления произвольного цвета сложением в нужной
пропорции трех основных цветов. При аддитивном цветовоспроиз-
цветовоспроизведении, например в цветном телевидении, имеются три источника
света — красного, зеленого и синего, которые проектируются
на один участок поверхности, где и воспроизводится заданный
цвет. При субтрактивном цветовоспроизведении, на котором осно-
основаны цветная фотография и полиграфия, белый свет приобретает
нужный цвет, проходя последовательно через голубой, пурпур-
пурпурный и желтый фильтры.
3.3.1. АДДИТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
Опыты с аддитивным уравниванием цветов проводятся по схеме,
показанной на рис. 3.3.1. На поверхность идеального диффуз-
диффузного отражателя проектируется пятно света [С] (рис. 3.3.1, а)
с произвольной спектральной плотностью, приведенной на
рис. 3.3.2, а. На ту же поверхность проектируются пятно опор-
Глава 3
ного белого цвета [IF] со спектральной плотностью, показанной
на рис. 3.3.2, б, а также перекрывающиеся пятна [PJ, [Р.г], [Р3]
трех основных цветов со спектральными плотностями, представ-
Рис. 3.3.1. Уравнивание цветов.
а — три основных цвета; б — два основных цвета; « — один основной цвет.
ленными на рис. 3.3.2, в, г, д. Сначала интенсивности трех основных
цветов устанавливаются так, чтобы общая часть пятен имела
такие же светлоту, цветовой тон и насыщенность, как и опорный
белый цвет [W]. Интенсивности Ах (W), Аг {W), A3 (W) измеряют
в каких-либо физических единицах, например в ваттах. Они
являются величинами, уравнивающими опорный белый цвет.
Затем интенсивности основных цветов устанавливают так, чтобы
добиться уравнивания заданного цвета [С]. Если уравнивание
Фотометрия и колориметрия
65
достигается, записывают интенсивности Ах (С), At (С), Л3 (С)
и вычисляют нормированные величины
Т: (С) = Ас {C)/Ai (W), 1=1,2,3, C.3.1)
которые называются координатами цвета.
Если данный цвет уравнять не удается, от схемы рис. 3.3.1, а
переходят к схеме рис. 3.3.1, б. Один из основных цветов, на-
например [Ря], накладывается на пятно данного цвета, и интенсив-
интенсивности трех основных цветов подбирают до тех пор, пока не будет
woo
Р,(Х)
Р,(Х)
Р3(Х)
400
Рис. 3.3.2. Спектральная плотность энергии излучения.
а — произвольный цвет; б — опорный белый цвет; в — красный основной цвет; г — зе-
зеленый основной цвет; д — синий основной цвет.
достигнуто уравнивание общей части пятен [Рг] и [Рг] и общей
части пятен [Р3] и [С]. Если такое уравнивание получено, то
координаты цвета равны
7\ (С) = Аг (О/Л, (W), Т, (О = Аг (С)/А, (W),
Т3 (С) = -А, {С)!A, (W). C.3.2)
3 Прэтт У.
66 Глава 3
В этом случае координата Т3 (С) отрицательная. Если при такой
схеме добиться уравнивания не удается, нужно пробовать уравни-
уравнивать сочетание [РЛ ] и [Р3] с сочетанием [Р^] и [С]. Если уравни-
уравнивание будет достигнуто, координату Т2 (С) нужно взять со знаком
минус. Если и эта конфигурация окажется несостоятельной, нужно
попробовать уравнять [Р8]и [Р3]с [Р, ] и [С].Правильное уравни-
уравнивание в этом случае означает, что величина Ti (С) отрицательная.
Наконец, в тех редких случаях, когда не удается добиться
уравнивания ни по схеме рис. 3.3.1, а, ни по схеме рис. 3.3.1, б,
нужно два основных цвета наложить на данный цвет [С] и про-
пробовать уравнивать цвет общей частоты этих трех пятен с остав-
оставшимся основным цветом. Если уравнивание достигается для
схемы рис. 3.3.1, в, то две координаты цвета принимают отрица-
отрицательные значения:
Тг (С) = А, (Q/Аг (W), Т% (С) = -Аг (QM, (W),
Т3 (О = -A, (С)/А3 (W). C.3.3)
Если уравнивание по этой схеме не достигается, одна из двух
оставшихся комбинаций приведет к успеху.
Описанный выше процесс реализует прямой метод количествен-
количественного описания цветов. Он имеет два недостатка: является довольно
громоздким и получаемые результаты зависят от индивидуаль-
индивидуальных свойств единственного наблюдателя. В разд. 3.4 подробно
рассматривается стандартизованный метод количественного из-
измерения цветов.
3.3.2. СУБТРАКТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ
Схема опытов по субтрактивному уравниванию цветов приве-
приведена на рис. 3.3.3. Свет со спектральной плотностью Е (%) после-
последовательно проходит через три фильтра — голубой, пурпурный
и желтый. Спектральная кривая поглощения каждого красителя
зависит от его концентрации. Нужно заметить, что кривые погло-
поглощения используемых на практике красителей при изменении
их концентрации меняются нелинейным образом.
На первом этапе процесса субтрактивного уравнивания кон-
концентрации красителей трех фильтров изменяются до тех пор, пока
не будет достигнуто субъективное уравнивание опорного белого
цвета [W]. Эти концентрации являются уравнивающими величи-
величинами A-l (W), A2 (W), A3 (W). Затем концентрации изменяются
так, чтобы обеспечить уравнивание желаемого цвета [С]. Найден-
Найденные концентрации — уравнивающие величины Аг {С), Л2 (О.
А3 (С) — используются при вычислении координат Т1, (С), Т2 (С),
Т3 (С) согласно соотношению C.3.1). Очевидно, что между адди-
аддитивным и субтрактивным уравниванием цветов принципиальной
разницы нет. В субтрактивной системе желтый краситель дей-
Фотометрия и колориметрия
67
ствует как переменный поглотитель синего света, т. е. управляет
его интенсивностью. Таким же образом пурпурный фильтр управ-
управляет зеленым, а голубой — красным светом. Эти фильтры яв-
являются широкополосными и пропускают много света. Поэтому
их удобнее использовать в субтрактивных системах, чем узко-
белыц
свет
Сдетофильтры
Желтый Пурпурный Голубой
Окрашенный
едет
SO0 BOO 700 400 500 600 700 400 SOO BOO 700
Желтый краситель Пурпурный краситель Голубой красите/76
Рис. 3.3.3. Субтрактивиое уравнивание цветов.
полосные красный, зеленый и синий фильтры. Обычные красители
не обладают широким диапазоном изменения плотности. Чтобы
повысить контраст воспроизводимого изображения, в полигра-
полиграфии часто вводят четвертый фильтрующий слой —нейтрально-
серый. Субтрактивное воспроизведение цветов с реальными кра-
красителями, обладающими перекрывающимися кривыми поглоще-
поглощения, рассматривается в гл. 16.
3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ
Опыты по уравниванию цветов (как аддитивному, так и суб-
трактивному) проведены с большой точностью многими исследо-
исследователями. Установлено, что полного уравнивания иногда не
удается достигнуть при очень слабом'или очень сильном освеще-
освещении. Результаты уравнивания в некоторой степени зависят от
цветового окружения. Тем не менее оказалось, что простые пра-
правила уравнивания цветов остаются справедливыми в широком
диапазоне условий эксперимента.
Грассман [15] ввел восемь аксиом, определяющих трехцветное
уравнивание цветов, которые являются основой колориметрии:
1. Любой цвет может быть уравнен смесью не более чем трех
цветов.
2. Уравнивание, достигнутое при данной интенсивности света,
сохраняется в широком диапазоне интенсивностей.
3*
68 Глав! 3
3. Смесь цветов не может быть разделена человеческим глазом
на отдельные компоненты.
4. Яркость смеси цветов равна сумме яркостей ее компонент.
5. Закон сложения. Если цвет [М] эквивалентен цвету [N],
а цвет IP] —цвету [Q], то смесь цветов [М ] и [Р] эквивалентна
смеси IN] и [Q]*):
[М]А[Щ, [Р]&№=>[М]?[Р]^№А№. C.3.4)
6. Закон вычитания. Если смесь цветов [М\ и [Р] эквива-
эквивалентна смеси [N] a [Q] и если цвет [Р] эквивалентен цвету [Q],
то цвет [М ] эквивалентен цвету [N]:
[М]&[Р]А №Ш1 [P]&IQ]=>№A№. C.3.5)
7. Закон транзитивности. Если цвет [М ] эквивалентен цвету
IN], а цвет [N] —цвету [Р], то [М ] эквивалентен [Р]:
[M]&[N], [N] А[Р]=>[М]& [Р]. C.3.6)
8. Уравнивание цветов. Справедливо одно из трех соотношений:
а) С единиц цвета [С] уравнивают смесь М единиц [М],
N единиц [N] и Р единиц [Р]:
С А[С]Д М A[M]^N &[N] ДРА[Я]; C.3.7)
б) смесь С единиц [С ] и М единиц [М ] уравнивает смесь iV еди-
единиц [N] и Р единиц IP]:
СД[С]ДЛ* A[M)&NA[N] Д/>Д[/>]; C.3.8)
в) смесь С единиц [С], М единиц [М] и N единиц [ЛЧ урав-
уравнивает Р единиц цвета [Р]:
CA[C]?MA[M]&NA[N]&,'PA [P]. C.3.9
3.4. КОЛОРИМЕТРИЯ
Колориметрия —это наука об измерении цветов. Для измере-
измерения цветов используются различные системы координат.
Из восьмой аксиомы Грассмана следует, что цвет [С] может
быть уравнен смесью трех основных цветов [Рг], [Рг] и [Ра], т. е.
[С] А А, (С) A [PJ Д А, (С) А [Р2] Д Л (С) А [Р3], C.4.1)
где Л] (С), Л2 (С), Л3 (С) —уравнивающие величины цвета [С].
Так как интенсивности некогерентных источников света склады-
складываются линейно, то спектральная плотность смеси равна сумме
спектральных плотностей ее компонент. Согласно соотношению
C.4.1), спектральная плотность С (К) может быть заменена экви-
*) Вводятся следующие символы: А — уравнивание (эквивалентность),
А — аддитивная смесь, А — единица смеси.
Фотометрия и колориметрия 69
валентной спектральной плотностью смеси основных цветов, т. е.
С (Ц Д 4 (С) Р1 {%) + Л2 (С) Р2 (%) + А3 (С) Ра (I) =
= 2^ (С) Я, (А,), C.4.2)
где Ру (h)—спектральная плотность основного цвета [Р,].
Соотношение C.4.2) имеет простой смысл: спектральные плот-
плотности, связанные оператором эквивалентности 4 » вызывают оди-
одинаковое цветовое ощущение. В колориметрии используются коор-
координаты цвета, равные по определению
Г/(С) = Л;(С)/Л,(П C.4.3)
где Aj (W)—уравнивающая величина опорного белого цвета.
Подставив выражение C.4.3) в C.4.2), получим
С (Л.) Д'^Т, (С) Л, (У)/>,(*.). C.4.4)
Из четвертой аксиомы Грассмана следует, что яркость цвета
L (С) равна сумме яркостей его основных компонент. Следова-
Следовательно,
з
L (С) = | С (К) V {%) dX = ^ J А, (С) Р, (К) V (%) dk, C.4.5а)
з
L (О = S 1 Т' <С) А! (^) Р! М V M dK> <3-4-56)
где V (Я,) — относительная световая эффективность. Соотношения
C.4.4) и C.4.5) являются количественной основой колориметрии.
3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ
Прежде чем продолжить изучение процесса уравнивания цве-
цветов, полезно проверить, согласуются ли результаты эксперимен-
экспериментов и аксиомы уравнивания цветов с моделью цветового зрения,
рассмотренной в разд. 2.5. В этой модели реакции рецепторов трех
типов со спектральными чувствительностями st (К), s2 (%), Sg (X)
представлялись следующими величинами:
ех (С) = J С (%) sx {%) d%, C.4.6a)
C.4.66)
= \C(l)s3(%)d%. C.4.6b)
Если наблюдатель видит эквивалентную смесь первичных цветов,
а не исходный цвет [С], то замена спектральной плотности С (Я,)
70
Глава 3
эквивалентной спектральной плотностью, определяемой соотно-
соотношением C.4.4), не должна приводить к изменению сигналов
колбочек et (С). Следовательно,
з
Ч (С) = 2 Т, (С) A, {W) J P, {I) s, (к) dK C.4.7а)
(С) = 2 Ti
А!
Pi
з
е* (Q = 2 71/ (9
/=i
Определив коэффициенты
C-4.7В)
C.4.8)
можно переписать соотношения C.4.7) более компактно в матрич-
матричной форме
К21
«12
«22
«13
^23
«32 3
"Л
о
о
О
О
или еще короче как
е(С) = КАТ(С).
C.4.9)
C.4.10)
Векторы и матрицы, входящие в это соотношение, определены
выражениями C.4.7)—C.4.9). Следует отметить, что для заданного
набора основных цветов и опорного белого цвета элементы ма-
матриц К и А оказываются постоянными величинами. Поэтому
если известны сигналы колбочек et (С) для данного цвета [С],
то при условии, что существует матрица (КА), соответствующие
координаты цвета Т,- (С) могут быть вычислены по формуле
Т(С) = (КА)е(С). C.4.11)
Таким образом, при подходящем выборе величин Tt (С) любой
цвет [С] может быть заменен эквивалентной смесью основных
цветов; при этом сигналы колбочек останутся неизменными.
К сожалению, эти сигналы трудно измерить, поэтому соотношение
C.4.11) нельзя применить для непосредственного вычисления
координат цвета. Но это и не было целью приведенного вывода.
Наоборот, соотношение C.4.11) выведено для того, чтобы пока-
показать согласованность результатов экспериментов по уравнива-
уравниванию цветов с моделью цветового зрения.
Фотометрия и колориметрия
71
3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА
Координаты цвета произвольного излучения для заданного
набора основных цветов можно вычислить косвенным путем, если
для этого набора известны функции сложения, т. е. координаты
цвета спектральных (узкополосных) излучений единичной энер-
энергии. Типичные функции сложения показаны на рис. 3.4.1. Функ-
Функции сложения, определяющие колориметрическую систему, обо-
обозначаются как Тл (К), Ts2 (i), Ts3 (k), где X — длина волны спек-
спектрального цвета.
Синий
Зеленый л Красный
400 600
Длина Волны, нм:
Рис. 3.4.1. Функции сложения для типичных основных цветов — красного,
зеленого и синего.
Монохроматический свет [С$] с длиной волны ty и единичной
энергией имеет спектральную плотность б (Я, —1|з). При этом
справедливо следующее соотношение:
= S A, (W)Pj(l)Tsi^)si(X)dk.
C.4.12)
Рассмотрим теперь произвольный цвет [С] со спектральной
плотностью С (X). С (ф) единиц этого света при длине волны- 1|з
имеют координаты цвета Tsl (ф), 7\2 МО, Ts3 (ф). Следовательно,
C-4-
72
Глава 3
Интегрируя обе части этого равенства по г|> и используя основное
свойство дельта-функции, получаем
= J J С М 6 (А, -
C.4.14)
Сравнение этого равенства с соотношением C.4.7) показывает,
что координата цвета [С] есть
(i|>)di|>. C.4 15)
Как видно из рис. 3.4.1, координаты некоторых спектральных
цветов могут иметь отрицательные значения. С другой стороны,
координата цвета пропорциональна интенсивности основного
цвета, которая не может быть отрицательной. Отрицательные зна-
значения координат интерпретируются следующим образом: основной
цвет, соответствующий отрицательному значению координаты,
должен быть прибавлен к исходному цвету, после чего достигается
Желтый
Голубой
Цдетовой
Вектор
Треугольник
Максбелла
Красный
/синий
Рис. 3.4.2. Цветовое пространство для типичных основных цветов.
уравнивание смесью двух оставшихся основных цветов. В этом
смысле любой цвет может быть уравнен смесью любых основных
цветов. Однако цвета с отрицательными координатами не могут
быть воспроизведены с помощью реального устройства с задан-
заданными основными цветами (например, в приемнике цветного теле-
телевидения). К счастью, можно выбрать основные цвета так, чтобы
большинство обычных естественных цветов были воспроизводи-
воспроизводимыми.
Координаты цвета Тъ Т?, Т3 можно рассматривать как коор-
координаты точек в некотором трехмерном пространстве (рис. 3.4.2).
Данный цвет можно представить также как вектор. На рис. 3.4.2
показан треугольник, называемый треугольником Максвелла.
Расстояния от вершин этого треугольника до точки пересечения
Фотометрия и колориметрия
73
цветового вектора с плоскостью треугольника характеризуют
цветовой тон и насыщенность цветов.
Часто при описании цвета его яркость не представляет инте-
интереса. В таких случаях цветовой тон и насыщенность цвета [С]
-г,о
N 700 им
-1,0-
Рис. 3.4.3. График цветностей для типичных основных цветов.
можно выразить через координаты цветности, являющиеся нор-
нормированными координатами цвета:
tj. = 7УG\ + 7г + Т3), C.4.16а)
t% = 7У(Г, + Т, + Т3), C.4.166)
U = TJ(TX + Тг + Т,). C.4.16b)
Очевидно, что t3 = 1 —12 —tt и, следовательно, для описания
цветности необходимы только две координаты. На рис. 3.4.3
показан график цветностей для набора типичных основных цве-
цветов. С помощью реальных источников света можно физически
воспроизводить только те цвета, которые находятся внутри
треугольника, определенного тремя основными цветами.
3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ
Координаты цвета определяют данный цвет по отношению
к опорному белому цвету. Часто, однако, необходимо знать не
относительные, а абсолютные интенсивности основных цветов,
воспроизводящих данный цвет. Эти данные можно получить,
вычисляя его яркость.
Из выражений C.4.5) следует, что яркость L (С) цвета [С]
равна сумме яркостей его основных компонент:
L (С) =
t=i
Л7>
74 Глава 3
Интегралы
L(P{)= \Al{W)Pi(X)V(X)dX C.4.18)
называются яркостными коэффициентами основных цветов. Эти
коэффициенты представляют собой яркости основных цветов,
уравнивающих опорный белый цвет. Следовательно, яркость
цвета С можно записать как
L (С) = 7\ (С) L (Р.) + 7а (С) L (Р2) + Т3 (С) L (Ps). C.4.19)
Координата цветности цвета [С] определяется как
jiC). C.4.20)
Перемножив соответственно левые и правые части выражений
C.4.19) и C.4.20), после некоторых преобразований получим
Тг(С)= U1(C)L(C)V[t1(C)L(P1) +
+ t2 (С) L (Р2) + t3 (С) L (Р3) ] C.4.21а)
и аналогично
Т2(С)= [ti(C)L(C)]/lt,(C)L(P1) +
+ U (О L (Р2) + 4 (Q L (Рз) ], C.4.216)
7^з (Q = U3 (С) L (C)]/l*i (Q L (Р,) +
+ 4 (С) L (Р2) + t3 (С) L (Р3) ]. C.4.21b)
Таким образом, координаты цвета можно выразить через яркость
и координаты цветности.
З.б. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА
Из выражений C.4.7) следует, что набор основных цветов
можно выбрать многими способами. Если координаты цвета из-
известны для одного набора основных цветов, то простым преобра-
преобразованием координат можно найти координаты цвета для другого
набора [16]. Пусть [Pj], [P2], [Р3] есть исходный набор основ-
основных цветов со спектральными плотностями Рх (к), Р2 (X), Р3 (X).
Интенсивности, уравнивающие опорный белый цвет [W], обозна-
обозначим через Аг (W), Л2 (W) и А3 {W). Рассмотрим теперь другой
набор основных цветов [^1, [Р2], [Р3], имеющих спектральные
плотности Рх (X), Р2 (X), Р3 (к). Опорный белый цвет [W], который
может отличаться от исходного опорного белого цвета [W],
уравнивается при интенсивностях At (W), Аг (W), A3 (W) новых
Фотометрия и колориметрия
75
цветов. Произвольный цвет [С] имеет координаты Тх (С), Т2 (С),
Т3 (С) для исходного набора основных цветов и 7\ (С), Т2 (С),
Т3 (С) для нового набора. Из формулы C.4.10) можно получить
матричное соотношение
е(С) = KA(W)T(C) = KA(W')t(C). C.5.1)
Установим теперь единицы измерения новых координат цвета.
Взяв вместо цвета [С] новый опорный белый цвет [W], получим
е (W) = К A (W) T W = К A {W) f (W), C.5.2)
где Т1! {W) = Г, (#) = f3(W) = 1. Затем подставив в соотно-
соотношение C.5.1) новые основные цвета JPj ], fP2], [P3], будем иметь
е (Рх) = КА (Г) Т (PJ = К А (Г) Т (?!>, C.5.3а)
е (Р2) = КА (Г) Т (?,) = К X (f) f (Л), C.5.36)
е (Р8) = КА (Г) Т (Р3) = К А (Г)Т (?,), C.5.3в)
где „ _ „
0
0
О
о
о
Совместное решение системы матричных уравнений C.5.1),
C.5.2) и C.5.3) дает требуемое соотношение между координатами
цвета для исходного и нового наборов основных цветов:
Шс) =
Т,(С)
Т2(С)
Гз(С)
Г1(Л)
Г2(Р,)'
Гз(А)
Г,(Р,)
Г2(Р,)
7(РЛ
Ti(P2)
Т2(Р2)
Т3(Р2)
Г,(С)
Г2(С)
Тз(С)
г,(Л)
г2(Л)
Гз(Л)
Г,(Рз)
Г2(Р3)
7з(гз)
* цгз)
Г2(Р3)
Гз(Рз)
Г, (С)
Т2(С)
Тг(С)
/
/
1
1
1
Tt(W)
T2(W)
T3(W)
Тг(Рг)
T2(Pi)
т3(А)
г,(А)
Т* (Р \
Т (Р ~\
Tt(P2)
Т2(Р2)
T.(VV)
r2(VV)
T3(VV)
Г,(Я2)
Г2(Р2)
Т-\(Р2)
Ti(P3)
Т2(РЪ)
Гз(Рз)
Г,(Л)
Г2(Р3)
Гз(Рз)
T,(W)
T2(W)
T}(W)
C.5.4J
76
Глава 3
Можно переписать соотношение C.5.4), используя координаты
цветности ti (Pi), U (P2), U (Р3) новых основных цветов в коор-
координатной системе исходных основных цветов. В этом случае
г (С)
«11
m21
_«и
«и
m22
«м
/3
m3S
Г,
.Та
(С)
(Q
(С)
C.5.5)
где
тч = Д,7/Дь
А, = 7\ (#) Дц + Г2 (W) А12 + Г, (Г) А13,
А2 = Т, (W) Ли + Г2 (t) Ляя + Г, (Г) Д
Л, = Гх (t) Л31 + Т2 (W) Лз2 + Тз (t)
/ (p\f (P\ f lp\f tp\
2„
12
>) к (Л) -
i) к
3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА
Было показано, что цвет [С] может быть описан координатами
цвета Г3 (С), Т2 (С), Т3 (С) для данного набора основных цветов.
С другой стороны, цвет можно определить координатами цветности
h (С), t± (С) и яркостью L (С). Можно также описать цвет, исполь-
используя какую-либо линейную или нелинейную обратимую функцию
координат цвета или координат цветности и яркости. Из выраже-
выражения C.5.5) видно, что линейное преобразование координат цвета
есть просто переход к новому набору основных цветов. В прило-
приложении 2 приведены формулы преобразования координат цвета и
цветности для различных систем координат.
Для количественного описания цветов предложено много раз-
разных систем координат. Ниже рассматриваются те из них, которые
представляют исторический и теоретический интерес.
Фотометрия и колориметрия
77
- /
/
400
-
C\500
N. у
Длина
Д^(Х
(X) / \
л\
/ 600
Волны, нм
)
700
Система координат спектральных основных цветов МКО
В 1931 г. МКО разработала стандартный набор монохромати-
монохроматических основных цветов: красный с длиной волны 700 нм, зеле-
зеленый — 546,1 нм и синий —435,8 нм [4 J. Единицы измерения коор-
координат цвета выбраны так, чтобы координаты Rc, Gc, Bc белого
света с равномерной спектральной плотностью в видимой части
спектра были одинаковыми. Набор основных цветов определяется
0,4
I о,з
0,2-
0,1 -
-0,11-
Рис. 3.6.1. Функции сложения системы координат спектральных основных цве-
цветов МКО (красный — 700 нм, зеленый — 546,1 им, синий — 435,8 нм) [11].
кривыми сложения для спектральных цветов, приведенными на
рис. 3.6.1. Эти кривые получены в экспериментах по уравниванию
цветов с большим числом наблюдателей. По результатам экспери-
экспериментов был определен так называемый стандартный наблюдатель
МКО. Данные для поля зрения 2° были опубликованы в 1931 г.
Затем были получены результаты для поля размером 10°. В теле-
телевидении и фототелеграфии лучше использовать данные для поля
2°. На рис. 3.6.2 представлен график цветностей в системе коорди-
координат спектральных основных цветов МКО, а также цвета люмино-
люминофоров телевизионного приемника принятой в США системы цвет-
цветного телевидения НТСЦ. Треугольник, определяемый цветами лю-
люминофоров, охватывает цветности всех воспроизводимых цветов.
Система координат приемника НТСЦ
В телевизионных приемниках США используются кинескопы
с тремя люминофорами —красным, зеленым и синим [14]. Си-
Система координат приемника НТСЦ, определяемая цветами люми-
люминофоров, может быть связана с системой координат спектральных
основных цветов МКО простым линейным преобразованием. На
рис. 3.6.3 приведен график цветностей в системе координат прием-
приемника НТСЦ. В этой системе единицы измерения координат цвета
нормированы так, что значения координат, при которых уравни-
78
Глава 3
Основной цвет у
9с
500
Цветовой охват
/^-приемника НТСЦ
W
V0
Основной цвет г
Основной цвет х
-2,0 -1,5 -1,0 ~0,5 ЗВО О
-0,5 -
Рис. 3.6.2. График цветностей в системе координат спектральных основиы
цветов МКО [11].
.570
„S80
Ш I
5IQ»
5001
\
49С
1,5
5?0
^S53C
1,0
\
\ 0,5
48о\
i i \
-i;o -as
470Х
46С
0,5
540 .
\
-
0
360
-
Цветовой охват
' приемника НТСЦ
30
^560
Л.580
N. 6Ю
0,5 1,04.
\800
1
1,5
Рис. 3.6.3. График цветностей в системе координат приемника НТСЦ.
Фотометрия и колориметрия
79
вается опорный белый цвет, одинаковы. Люминофоры приемника
НТСЦ не являются источниками монохроматического света, по-
поэтому определяемый ими цветовой охват (совокупность воспроиз-
воспроизводимых цветов) уже, чем при использовании спектральных основ-
основных цветов МКО.
Система координат XYZ МКО
Система координат спектральных основных цветов МКО имеет
один недостаток для колориметрических расчетов: координаты
цвета иногда оказываются отрицательными. Столкнувшись с этой
трудностью, МКО разработала систему координат с искусствен-
искусственными основными цветами, в которой координаты цвета спектраль-
спектральных цветов являются положительными [4]. Искусственные основ-
цветовойотдат
приемника НТСЦ
УООНМ
0,1 0,2 0,3 Ofl 0,5 0,6 0,7 0,8 ".9 V>
х
Рис. 3.6.4. График цветностей в системе координат XYZ МОК [4].
ные цвета показаны на рис. 3.6.2. Они выбираются так, чтобы коор-
координата Y была эквивалентна яркости L (С) цвета С. На рис. 3.6.4
представлен график цветностей в системе XYZ МКО при опорном
белом свете с равномерной спектральной плотностью.
Система координат передаваемых сигналов НТСЦ
В системе цветного телевидения НТСЦ, разработанной в США,
передаются три координаты цвета Y, I, Q [14]. Координата Y
совпадает с координатой Y системы XYZ; она соответствует ярко-
80
Глава 3
520 °JU S40 m
V/0
\soo
0,3
0,2
0,1
480*
S70 580
590
600
о_о о—о о—о
a°
B20J30 S50HM
0,4
0,5
О, В
Рис. 3.6.5. Сравнение едва заметных цветовых разностей в системах координат
XYZ и UVW. Величины разиостей увеличеиы в 10 раз [12].
а — цветовые разности на графике цветиостей [х, у); б — цветовые разности на графике
цветностей (и, о).
Фотометрия и колориметрия
81
сти. Остальные две координаты / и Q вместе описывают цветовой
тон и насыщенность. Причинами передачи координат Y, I, Q вме-
вместо координат RN, GN, BN непосредственно с выхода передающей
камеры являются следующие: 1) сигнал Y может быть использован
существующими телевизионными приемниками одноцветного изо-
изображения и 2) полосу частот сигналов / и Q можно сократить без
заметных искажений изображений. Применив такое сокращение и
остроумный способ модуляции, удалось передавать полный анало-
аналоговый сигнал цветного телевидения в той же полосе частот, что и
при одноцветном изображении.
Равноконтрастная система координат МКО
Желательно иметь такую систему координат, чтобы равным
изменениям координат цветности соответствовали равные измене-
изменения в ощущении цвета. На графике цветностей (рис. 3.6.5, а) по-
показаны разности цветов, которые воспринимаются одинаково
[12, 17]. Этот график, а также другие экспериментальные резуль-
е,б-
ЦОетобой охдат
'приемника НТСЦ
ОД 0,4
и
Рис. 3.6.6. Равнокоитрастный график цветностей [11].
таты свидетельствуют о том, что человеческий глаз наиболее чув-
чувствителен к изменению синего цвета, умеренно чувствителен к из-
изменению красного и обладает наименьшей чувствительностью
к изменениям зеленого цвета. В 1960 г. МКО приняла равнокон-
трастную систему координат, в которой с хорошим приближением
равные изменения координат цветности соответствуют едва замет-
заметным изменениям цветового тона и насыщенности. На рис. 3.6.5, б
приведены данные рис. 3.6.5, а в равноконтрастных координатах.
82 Глава 3
Переход от координат X, Y, Z к равноконтрастным координатам
осуществляется линейным преобразованием. Координаты цветно-
цветности в обеих системах связаны следующими соотношениями [18]:
и = 4х/(—2х + 12у + 3), C.6.1а)
v = 6г//(—2х + \2у + 3). C.6.16)
График цветностей в равноконтрастной системе координат приве-
приведен на рис. 3.6.6.
Система координат U*V*W*
Система координат U*V*W* есть развитие системы координат
UVW с целью получения цветового пространства, в котором еди-
единичные изменения цветности и яркости воспринимаются одина-
одинаково. Координаты U*, V*, W* по определению [19] равны
U* = 13Й7* («— «„), C.6.2а)
у* = 13JF* (v —.»„), C.6.26)
W* = 25 (ЮОУI'3 — 17, C.6.2b)
причем единицы измерения яркости У выбраны так, что яркость
меняется от 0 до 1, а н0 и v0 —координаты цветности опорного
белого цвета.
Система координат S8W*
Координаты 5, в, W* есть просто полярные координаты для
системы U*V*W*. По определению они равны [11]
S = [({/•)¦ + (У*)*]1/2 = 1W* [{и - иоу + (v - vo)*]1/2, C.6.3a)
в = arctg [V*/U*] = arctg [(v - vo)/(u - u0)]. C.6.36)
Координата S определяет насыщенность цвета, а 0 — цветовой
тон.
Система координат Lab
Система координат Lab, будучи еще достаточно простой для
колориметрических расчетов, обеспечивает относительно точное
представление цветов в соответствии с системой цветов Мюн-
селла [20]. Координаты цвета в этой системе равны
L = 25 A00У/У0I/3 - 16, C.6.4а)
а = 500 t(X/X0I/3 - {Y/Yof'3], C.6.46)
Ь = 200 [(Y/Yof3 - (Z/ZoI/3 ], C.6.4b)
где Хо, Yo, Zo — координаты опорного белого цвета в системе
XYZ. Координата L определяет яркость цвета, а — соотношение
Фотометрия и колориметрия
83
красногб и "зеленого цвеп^рГ^—соотношение синего и желтого,
Многие колориметры, выпускаемые, промышленностью, дают
значения этих координат...
Система координат Карунена—Лоэва
Систему координат спектральных основных цветов, системы
XYZ, UVW и другие можно рассматривать как результат линей-
линейного преобразования системы координат приемника НТСЦ. Коор-
Координаты цвета RN, GN, BN приемника НТСЦ оказываются сильно
коррелированными друг с другом [21 ]. При разработке эффектив-
эффективных методов квантования и кодирования цветных изображений
удобно иметь дело с некоррелированными компонентами. Если
известна ковариационная матрица величин RN, GN, BN, то можно
построить систему ортогональных некоррелированных координат,
используя преобразование Карунена—Лоэва. Матрица преобразо-
преобразования М. = [niij ] состоит из собственных векторов ковариацион-
ковариационной матрицы и определяется следующим соотношением:
m,
п
тгз
mu m32
п
«12
«ir,
13
m
ll
m
12
тгз
C.6.5)
, «3
Л, 0 0"
0 Aa 0
0 О Л3
где Л1( Л.2, Л3 — собственные значения ковариационной матрицы
и
un = E\(RN-RN)% C.6.6a)
u2,~E{(GN-GNf\, C.6.66)
«а, = Е {{BN - Ъы)% (З.б.бв)
~GN)), (З.б.бг)
-BN)\, (З.б.бд)
-BN)\. (З.б.бе)
Система координат колбочек сетчатки
Как отмечалось в гл. 2, при рассмотрении моделей цветового
зрения человека. были проведены косвенные измерения спек-
спектральных чувствительностей st (i), s2 (A.), s3 (А.) колбочек трех типов.
4Ъ?
щ
&, --1
>f:..«ft ¦¦# 'Sl«*if*"'ltf
I '*
Рис. 3.6.7. Компоненты цветного изображения.
а — система координат приемника НТСЦ; б — система координат колбочек; в — система координат Карунена—Лоэва:
¦'1
Рис. 3.6.7. (продолжение)
г — система координат передаваемых сигналов НТСЦ; д — равноконтрастная система координат: е — система координат Lab.
88
Глава 3
Оказалось, что спектральные чувствительности связаны линейно
с функциями сложения, полученными по данным колориметриче-
колориметрических экспериментов. Следовательно, сигналы колбочек Tlt T2, Ta
можно рассматривать как координаты цвета. Эти координаты
связаны с координатами X, Y, Z следующим линейным преобразо-
преобразованием [22]:
ту
О
1,0
о
-0,46 1,359 0,101
0 0 1,0
'X'
Y
Z
C.6.7)
На рис. 3.6.7 приведены компоненты цветного изображения для
нескольких координатных систем. Следует отметить, что красная,
зеленая и синяя компоненты сильно коррелированы. В некоторых
координатных системах одна из компонент содержит большую
часть энергии изображения, а остальные кажутся менее деталь-
детальными.
3.7. ЦВЕТОВОЕ ТЕЛО
Как было показано в предыдущем разделе, существует много
систем координат, которые можно использовать для описания
цветов. К сожалению, нет способа определить, какая из этих си-
систем является оптимальной для большинства приложений. Для
выбора наилучшей системы следует сформулировать предъявляе-
предъявляемые к ней требования, а затем проверять, в какой степени им удов-
удовлетворяют те или иные системы. При количественном сравнении
координатных систем следует учитывать ограничения, накладывае-
накладываемые на способы представления цветов, и методы обнаружения
различий между цветами.
Для любой системы' воспроизведения естественных цветов су-
существуют два физических ограничения. Во-первых, интенсивность
света, излучаемого любыми источниками, может быть только поло-
положительной. Следовательно, если некоторый цвет имеет отрицатель-
отрицательные координаты, он не может быть воспроизведен в виде чисто
аддитивной смеси основных цветов. Второе ограничение связано
с диапазоном изменения яркости света, прошедшего через предмет
или отраженного от него.
3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА
Рассмотрим датчик сигналов цветного изображения, на выходе
которого получаются координаты RN (С), GN (С), BN (С) в системе
основных цветов [RN], [GN], [BN] телевизионного приемника
НТСЦ. Этот приемник может воспроизвести любой цвет, имеющий
Фотометрия и колориметрия
89
неотрицательные координаты. Такие цвета лежат внутри куба
цветового охвата, показанного на рис. 3.7.1, а. Вершины куба
соответствуют главным цветам приемника НТСЦ — красному,
зеленому, синему, голубому, пурпурному, желтому, черному и
/ Зеленый
щЖелтый
Голубой
Зеленый-
Голубой
Рис. 3.7.1. Цветовой охват приемника НТСЦ.
а — система координат R^, в^, В^; б — система координат X YZ; в — система координат
UVW; г — система координат Карунена—Лоэва.
белому. Посредством линейного преобразования перейдем к дру-
другой системе координат цвета Тл (С), Г2 (С), Т3 (С):
'Тг(СУ
Tt(C)
TS(C)
ти т12 т13'
tn2L m22 Шгз
m
32
-R»(CY
GN(C)
BN(C)
C.7.1)
В табл. 3.7.1 приведены координаты цвета и координаты цветности
главных цветов приемника НТСЦ для нескольких координатных
систем. Цветовой охват, который обеспечивается люминофорами
приемника НТСЦ, показан на рис. 3.7.1 в различных системах
90 Глава 3
Таблица 3.7.1
Координаты цвета и координаты цветности главных цветов
приемника НТСЦ для нескольких координатных систем
Rs
GN
BN
Гы
fo/
Ьы
X
Y
Z
X
У
z
Rc
Gc
Bc
rc
ge
be
и
V
w
и
V
w
Y
I
0
u*
V*
w*
s
в
w*
L
b
Красный
1,000
0,000
0,000
1,000
0,000
0,000
0,607
0,299
0,000
0,670
0,330
0,000
0,207
0,020
0,000
0,912
0,089
0,000
0,405
0,299
0,145
0,477
0,352
0,171
0,299
0,596
0,212
Зеленый
0,000
1,000
0,000
0,000
1,000
0,000
0.174
0,587
0,066
0,210
0,710
0,080
-0,026
0,133
0,010
-0,219
1,130
0,089
0,116
0,587
0,827
0,076
0,384
0.540
0,587
-0,273
-0,522
217,358-130,319
35,461 79,703
60,594 80,160
220,232
0,162
60,594
152,760
2,609
80,160
61,594 81,160
91,577-137,815
133,738 91,038
Синий
0,000
0,000
1,000
0,000
0,000
1,000
0,201
0,114
• 1,117
0,140
0,080
0,780
т0,026
0,028
0,200
-0,132
0,139
0,993
0,134
0,114
0,629
0,153
0,130
0,717
0,114
-0.322
0,315
Голубой
0,000
1,000
1,000
0,000
0,500
0,500
0,375
0,701
1,183
0,166
0,310
0,524
-0,052
0,161
0,210
-0,164
0,506
0,658
0,250
0,701
1,456
0,104
0,291
0,605
0,701
-0,595
-0,207
-24,558-108,566
-90.508 -17,913
39,265 86,081
93,781
4,445
39,265
40,265
52,227
-99,233
110,034
3,304
86,081
87,081
-81,411
-22,335
Пурпурный Желтый Белый
1,000
0,000
1,000
0,500
0,000
0,500
0,808
0,413
1,117
0,346
0,177
0,477
0,180
0,048
0,199
0,421
0,113
0,466
0,539
0,413
0,774
0,312
0,239
0,449.
0,41-3
0,272
0,526
100,385
-61,336
69,415
117,640
5,733
69,415
70,415
96,177
-47,269
1,000
1,000
0,000
0,500
0,500
0,000
0,781
0,886
0,066
0,451
0,511
0,038
0,181
0,153
0,010
0,525
0,446
0,029
0,521
0,886
0,972
0,219
0,373
0,408
0,886
0,322
-0,312
22,144
80,125
94,431
83,128
1,280
94,451
95,451
-16,977
115,670
1,000
1,000
1,000
0,333
0,333
0,333
0,982
1,000
. 1,183
0,310
0,316
0,374
0,154
0,181
0,210
0,283
0,333
0,384
0,655
1,000
1,601
0,201
0,307
0,492
1,000
0,000
0,000
0,000
0,000
99,040
0,000
0,000
99,040
100,040
0,000
0,000
Черный
0,000
0,000
0,000
0,333
0,333
0,333
0,000
0,000
0,000
0,310
0,316
0,374
0.0Q0
0.OQP
.0,00^)
0,283
0,333
0,384
0,000
0,000
0,000
0,201
0,307
0,492
0,000
•0,000
0,000
0,000
0,000
-17,000
0,000
0,000
-17,000
-16,000
0,000
0,000
Фотометрия и колориметрия
91
координат. Отметим, что в координатной системе Карунена —
Лоэва (рис. 3.7.1, г) цветовой охват представляется кубом, повер-
повернутым относительно осей координат.
Данный цвет может быть описан значениями цветности
tt (С) - Тх (С)/ [Г, (С) + Та (С) + Т8 (С) ], C.7.2а)
к (С) » Га (С)/[7\ (С) + 7\ (С) + Г» (С) ] C.7.26)
и яркости
Y (С) = L (С) = thxRN (С) + n22 GN (С) + ni3BN (С), C.7.2в)
где координаты цвета Tt (С) задаются соотношением C.7.1), а по-
постоянные tiij определены в приложении 2. Преобразование C.7.2)
Синий
Пурпурный
Кроеный
Ян
Рис. 3.7.2. Цветовой охват приемника НТСЦ в координатах цветности и яркости
(W. SN, Y).
координат цвета в координаты цветности является нелинейным.
На рис. 3.7.2 показан цветовой охват приемника НТСЦ в коорди-
координатах rN, gN, Y.
3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ
Большинство естественных изображений создается светом, от-
отраженным от непрозрачных предметов или прошедшим через про-
прозрачные среды. Диапазон изменения яркости такого несамосветя-
несамосветящегося предмета ограничен и зависит от его цвета. Мак-Адам
[23, 24 ] доказал, что цветовое тело максимального объема реали-
реализуется в том случае, когда предметы имеют коэффициенты отраже-
отражения или пропускания, представленные на рис. 3.7.3. Такие пред-
предметы физически не существуют; следовательно, цветовое тело реаль-
реальных предметов имеет меньший объем. Поясним это, ограничившись
для простоты только случаем предметов, отражающих свет. Эти же
рассуждения останутся справедливыми и в случае прозрачных
предметов.
92
Глава 3
Рассмотрим цвет [С], заданный координатами цвета
Х=\го(к)Е(к) Xs(к) dk, C.7.За)
Y = j г0 (к) Е (к) Y, (к) dk, C.7.36)
Z^ \ro(k)E(k)Zs(k)dk, C.7.3b)
где r0 (к) — спектральный коэффициент отражения, Е (к) — спек-
спектральная плотность излучения^ света, падающего на предмет,
1,0
§ 0,5-
1
5
400 1,500 ХгВОО 700
Длина болны, нм
а) Тип I
I
0,5-
0-
400 500 Л, 600 Лг 700
Длина. Волны, нм
$) Тип Д
Рис. 3.7.3. Оптимальные спектральные коэффициенты отражении или пропуска-
пропускания несамосветящихся предметов.
•^s (к), Ys (к), Zs (к) —функции сложения. Визуальная эффектив-
эффективность р определяется как отношение яркости предмета с коэффи-
коэффициентом отражения г0 (к) к яркости предмета с единичным коэффи-
коэффициентом отражения, т. е.
Р = j г0 (к)Е(к)Ys(к) dk\\E(к) Ys(к) dk. C.7.4)
Если предмет имеет коэффициент отражения такого типа, как по-
показано на рис. 3.7.3, а, его яркость равна
Xj 00
Y = J Е (%) Ys (\pk) dyk = р j E (%) Ys ($к) d\pk. C.7.5)
л, о
Предположим, что известна спектральная плотность Е (к) энер-
энергии падающего света. Тогда можно вычислить яркость предмета,
если известно значение визуальной эффективности р. Для задан-
Фотометрия и колориметрия
93
ного минимального значения длины волны Хх максимальное значе-
значение Х.2 можно найти численным методом из уравнения
л,
[
= У + [ Е Ш Ys (%
о
C.7.6)
Используя найденное значение Х2, можно вычислить координаты
цвета X, Z:
C.7.7)
C.7.8)
¦4
Z=}E(h)Zs(%k)dXk.
Координаты цветности х я у могут быть найдены по координатам
цвета. Если эту процедуру повторить для всевозможных значений
Рис. 3.7.4. Цветовое тело предметов в координатах цветности н яркости (X,
Y, Z) [23].
Xt при заданных значениях визуальной эффективности C, то можно
получить поверхность, ограничивающую тело возможных цветов
предметов, в координатах цвета или координатах цветности и яр-
яркости. На рис. 3.7.4 показана такая поверхность в координатах
цветности и яркости при освещении предметов источником белого
света. Отметим, что максимум яркости соответствует белой по-
поверхности.
94 Глава 3
ЛИТЕРАТУРА
1. Merrit Т. P., Hall F. F., Jr., Blackbody Radiation, Prot: IRE, 47, 9, 1435—
1442 (September 1959).
2. Malitson H. H., The Solar Energy Spectrum, Sky and Telescope, 29, 4, 162—
165 (March 1965).
3. Larabee R. D., Spectral Emissivity of Tungsten, J. Opt. Soc. Am., 49, 6,
619—625 (June 1959).
4. The Science of Color, Crowell, New York, 1953.
5. Fink D. G., Ed., Television Engineering Handbook, McGraw-Hill, New York,
1957.
6. Walsh J. W. Т., Photometry, Constable, London, 1953.
7. Morgan J., Introduction to Geometrical and Physical Optics, McGraw-Hill,
New York, 1953.
8. Born M., Wolf E., Principles of Optics, Pergamon, New York, 1970. [Имеется
перевод: Борн М., Вольф Э., Основы оптики. — М.: Наука, 1973.]
9. Weaver К. S., The Visibility of Radiation at Low Intensities, J. Opt. Soc.
Am., 27, 1, 39—43 (January 1937).
10. Wyszecki G., Stiles W. S., Color Science, Wiley, New York, 1957.
11. Hunt R. W. G., The Reproduction of Color, Wiley, New York, 1957.
12. Wright W. D., The Measurement of Color, Adam Hilger, London, 1944,
pp. 204—205.
13. Enyord R. A., Ed., Color: Theory and Imaging Systems, Society of Photo-
Photographic Scientists and Engineers, Washington D. C, 1973.
14. Bingley F. J., Color Vision and Colorimetry, Television Engineering Hand-
Handbook, Fink D. G., Ed., McGraw-Hill, New York, 1957.
15. Grassman H., On the Theory of Compound Colours, Phil. Mag., Ser. 4,7, 254—
264 (April 1854).
16. Wintringham W. Т., Color Television and Colorimetry, Proc. IRE, 39, 10,
1135—1172 (October 1951).
17. MacAdam D. L., Visual Sensitivities to Small Color Differences in Daylight,
J. Opt. Soc. Am., 32, 5, 247—274 (May 1942).
18. MacAdam D. L., Projective Transformations of ICI Color Specifications,
J. Opt. Soc. Am., 27, 8, 294—299 (August 1937).
19. Wyszecki G., Proposal for a New Color-Difference Formula, J. Opt. Soc. Am.,
53, 11, 1318—1319 (November 1963).
20. С I. E. Colorimetry Committee Proposal for Study of Color Spaces, Tech.
Note, J. Opt. Soc. Am., 64, 6, 896—897 (June 1974).
21. Pratt W. K., Spatial Transform Coding of Color Images, IEEE Trans. Com-
mun. Tech., COM-19, 12, 980—992 (December 1971).
22. Judd D. В., Standard Response Functions for Protanopic and Deuteranopic
Vision, J. Opt. Soc. Am., 35, 3, 199—221 (March 1945).
23. MacAdam D. L., The Theory of the Maximum Visual Efficiency of Colored
Materials, J. Opt. Soc. Am., 25, 8, 249—252 (August 1935).
24. MacAdam D. L., Maximum Visual Efficiency of Colored Materials, J. Opt.
Soc. Am., 25, 11, 361—367 (November 1935).
Часть 2
Представление изображений
в цифровой форме
При цифровой обработке изображений производится преобра-
преобразование непрерывного (аналогового) изображения в эквивалент-
эквивалентный цифровой массив. В этой части книги рассматриваются опе-
операции дискретизации и квантования изображения, с помощью
которых осуществляется такое преобразование. Описана также
обратная операция, позволяющая из цифрового массива получить
непрерывное изображение. Разработаны методы векторного пред-
представления изображений для детерминированных и случайных
цифровых массивов. В заключение рассмотрен вопрос о качестве
дискретизованных изображений, связанный с введением критериев
верности их воспроизведения и дещифрируемости.
Глава 4
ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ
НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
В системы цифровой обработки изображений обычно поступают
массивы чисел, полученные путем дискретизации реального изоб-
изображения по пространственным переменным. После обработки об-
образуются новые числовые массивы, используемые для восстанов-
восстановления непрерывного изображения, которое и рассматривает чело-
человек. Отсчеты изображения получаются в результате измерения не-
некоторых физических характеристик реального изображения, как,
например, яркости или оптической плотности. Любое измеритель-
измерительное устройство работает с какой-то погрешностью. Чтобы оценить
достоверность измеренных значений и создать методы компенса-
компенсации ошибок, важно иметь математическую модель ошибок измере-
измерения. Кроме того, часто не удается непосредственно измерить ха-
характеристики исходного изображения и вместо них измеряются не-
некоторые величины, относящиеся к другому изображению, которое
является функцией исходного. Для определения характеристик
исходного изображения эту функцию приходится «обращать».
Подобные операции обращения описаны в разделе, посвященном
вопросам исправления (реставрации) изображений. В данной
главе рассмотрены процессы дискретизации и восстановления
непрерывных изображений применительно к идеальным и реаль-
реальным системам.
4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ
И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ
При разработке и анализе систем дискретизации и восстанов-
восстановления непрерывных изображений обрабатываемые изображения
обычно принято рассматривать как детерминированные поля.
Однако в некоторых случаях удобнее предполагать, что входной
сигнал системы обработки изображений (особенно шумового про-
происхождения) является реализацией двумерного случайного
процесса. Ниже при анализе методов дискретизации и вос-
восстановления непрерывных изображений используются оба этих
подхода.
Дискретизация и восстановление непрерывных изображений 97
4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ
ИЗОБРАЖЕНИЙ
Пусть функция Ft (x, у) описывает исходное непрерывное изо-
изображение бесконечных размеров, представляя распределение
яркости, оптической плотности или какого-либо другого пара-
параметра реального изображения. В идеальной системе дискретизации
изображений пространственные отсчеты исходного изображения
I I I' I
V
Рис. 4.1.1. Набор дельта-функций, осуществляющих дискретизацию изобра-
изображений.]
получаются фактически путем перемножения этой функции с про-
странственно-дискретизирующей функцией
S (*,*)= 2 Ъ Ь(х-\хАх,у~иАу\ D.1.1)
/1==—00 /t==—00
состоящей из бесконечного числа дельта-функций, заданных
в узлах решетки с шагом (Аде, Ау), как показано на рис. 4.1.1.
Тогда дискретизованное изображение описывается соотношением
FP(x, y)~Fl{x
00 00
= S S FiUibx, J2Ay)b(x-hAx, y-hty), D.1.2)
в котором учитывается, что функцию F{ (x, у) можно внести под
знак суммирования и задать ее значения только в точках отсчета
(/i Ax, jt Ay). Для анализа процесса дискретизации удобно ис-
использовать спектр 9ГР((йх, (Оу), получаемый в результате непре-
непрерывного двумерного преобразования Фурье дискретизованного
изображения
оо
&-р (со,, coj,) = j j FP (x, у) ехр {—i (axx + ay/)} dx dy. D.1.3)
—OO
4 Прэтг У.
98 Глава 4
Согласно теореме о спектре свертки, спектр дискретизованного
изображения можно представить в виде свертки спектра исходного
изображения @~i((i>x, ц>у) и спектра дискретизирующей функции
9> (сол, со,,), т. е.
&-р К, ю,) = A/4я2) Г, К, ыу) * SP К, Ыу). D.1.4)
Двумерное преобразование Фурье дискретизирующей функции
дает в результате бесконечный набор дельта-функций в плоскости
пространственных частот с шагом axs = 2я/Д* и сом = 2п/Ау
14, стр. 22], т. е.
00 00
9> (со*, ц)у) = Dя2/Лх At/) II S б (со, — Дсо^,
/,=—оо /2=—оо
°>* —/>w)- D.1.5)
Будем предполагать, что спектр исходного изображения ограни-
ограничен по ширине так, что &"t (со,, со^) = 0 при ] со, | > (ахс и
| (йу | > со^,. Вычисляя свертку согласно равенству D.1.4), найдем
— а, со^ - Р) х
х Yi S 6(а~ />«. Р — jWy^dadp. D.1.6)
/,=-00 /,=-0О
Меняя порядок операций суммирования и интегрирования и учи-
учитывая основное свойство дельта-функции, получаем выражение
для спектра дискретизованного изображения
ОО 00
&~р(о)х, ъ)у)= A/АхАу) Yi I! ^"/К — />«, (Ну — /асо4-,)-
/,=—во /j=—оо
D.1.7)
Как показано на рис. 4.1.2, спектр дискретизованного изображе-
изображения получается путем бесконечного повторения спектра исход-
исходного изображения со сдвигом на величины, кратные Bл/Д*,
2я/Дг/). Следует отметить, что если Ах и Ау выбраны слишком боль-
большими по сравнению с шириной спектра #"/(<»*, а>у), то соседние
спектры будут перекрываться друг с другом.
Из отсчетов функции FP (x, у) можно получить непрерывное
изображение путем линейной пространственной интерполяции или
с помощью линейной пространственной фильтрации дискретизо-
дискретизованного изображения. Пусть R (х, у) есть импульсный отклик
интерполирующего фильтра, а М (соЛ, со^) —его частотная харак-
характеристика. Восстановленное изображение получается как свертка
последовательности отсчетов с импульсным откликом восстанавли-
Дискретизация и восстановление непрерывных изображений 99
вающего фильтра. Таким образсм, восстановленное непрерывное
изображение описывается соотношением
Подставляя FP (x, у) из равенства D.1.2) и вычисляя свертку,
получаем
00 ОО
Fr (х, У) = . Е Е Fj (/j A*, /, Ay) R(x- Д Ах, у - /, Ау).
/,=- ОО /j=—ОО
D.1.9)
Отсюда видно, что импульсный отклик R (х, у) выполняет роль
двумерной функции, интерполирующей отсчеты на всю плоскость.
Пространственно-частотный спектр изображения, восстановлен-
восстановленного согласно равенству D.1.8), есть произведение частотной ха-
Рис. 4.1.2. Типичный спектр дискретизовэнного изображения.
а — исходное изображение; б — дискретизованное изображение.
рактеристики восстанавливающего фильтра со спектром дискрети-
зованного изображения, т. е.
Pr К. ®у) = &р Ы «у) Л К, <а„). D.1.10)
С учетом равенства D.1.7) получаем
К. «>») = A /Д*
„ (Оу) Е Е *"/ К - />«>
/,=—оо /,=-оо
«» — /«»*»)¦¦ D.1.11)
Из этого выражения видно, что если спектры не перекрываются,
а множитель 5? (со*, со,,) подавляет все сдвинутые спектры при Д,
4*
100 Глава 4
/2 Ф 0, то спектр восстановленного непрерывного изображения
будет совпадать со спектром исходного изображения и поэтому.
изображения также будут одинаковыми. Для изображений с огра-
ограниченной шириной спектра первое условие выполняется, если
интервал дискретизации выбран так, что прямоугольная область,
ограниченная верхними граничными частотами спектра изобра-
изображения (сйхс, cow), лежит внутри прямоугольной области, опреде-
определяемой половинами частот дискретизации (ю^/2, <ow/2). Следова-
Следовательно, должны выполняться неравенства
Щс < "W2, а»,* < о>и/2, D.1 Л2а)
или
Ах =5 п/ахс, Ayszn/(uyi. D.1.126)
Это означает, что шаг дискретизации не должен превышать поло-
половины периода пространственной гармоники, соответствующей
самым мелким деталям изображения. Это условие эквивалентно
v теореме о дискретизации одномерных сигналов, в которой сформу-
сформулировано требование, что частота дискретизации должна хотя бы
вдвое превышать наивысшую частоту спектра сигнала. Если соот-
соотношения D.1.12) выполняются со знаками равенства, то изобра-
' жение дискретизуется с найквистовской х> частотой; если Ах и Аг/
меньше или больше, чем требуется по критерию Найквиста, то
говорят, что изображение дискретизуется с избыточной или недо-
недостаточной частотой.
-~ В тех случаях, когда пространственная частота дискретизации
изображения достаточна для^устранения наложения спектров
в дискретизованном изображении, исходное изображение можно
абсолютно точно восстановить путем пространственной фильтра-
фильтрации отсчетов с помощью соответствующего фильтра. Так, напри-
например, фильтр, частотная характеристика которого приведена на
рис. 4.1.3 н описывается выражениями
Я(<йх, (о&) = /С при \<йх\<а>а. и 1«>*1<ю*ь D.1.13а)
01 (<ах, фу) — 0 в остальных случаях, D.1.136)
где К — масштабная постоянная, удовлетворяет условию точного
восстановления, если axL > со^ и ayL > <abc. Функция рассеяния
точки (или импульсный отклик) данного восстанавливающего
фильтра имеет вид
Я {х, У) = (K®xiPyL/n2) isin KL*)/(co*Lx)] Isln Ki0)/(ffl,,i0)]. D.1.14)
При использовании этого фильтра изображение восстанавливается
с помощью бесконечной суммы функций вида sin с (х). Другим
2) В отечественной литературе это положение известно как теорема Котель-
ннкова. — Прим. перев.
Дискретизация и восстановление непрерывных изображений
101
фильтром, пригодным для восстановления изображений, является
«круговой» фильтр с частотной характеристикой (рис. 4, 1, 3, б)
Я((йх, со^) = /С при ]/"со^ + со^ <со0, D.1.15а)
в остальных случаях, D.1.156)
Рис. 4.1.3. Фильтры для восстановления дискретнзованных изображений.
а — прямоугольный; б — круговой.
если со§ < ale + <йуС. Импульсный отклик такого фильтра имеет
вид
R{x, 0) = 2яйо(/1КК*2 + уШ*2 + ^)> D.1.16)
где Ji (x) — бесселева функция первого порядка. Существует
много восстанавливающих фильтров (или соответствующих интер-
102 Глава 4
поляционных функций), которые можно использовать для восста-
восстановления изображений. Однако на практике в цифровой системе
воспроизведения изображений часто бывает сложно реализовать
оптимальный восстанавливающий фильтр. Одна из практических
трудностей состоит в том, что обычные интерполяционные функции
[например, заданные равенствами D.1.14) и D.1.16)] принимают
не только положительные, но и отрицательные значения, хотя
функции, описывающие восстановленные изображения, строго
положительны. Такие интерполяционные функции нельзя сформи-
сформировать оптическими средствами и, следовательно, не удается вос-
восстановить изображения путем последовательного их взвешивания
и сложения. Ричарде [6J нашел семейство интерполяционных
функций, которые можно применить для последовательной опти-
оптической интерполяции, поскольку их большие значения положи-
положительны.
4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8]
Выше при анализе вопросов о дискретизации и восстановление
изображений предполагалось, что функция Fj (x, у), описываю-
описывающая исходное изображение, является детерминированной. Было
показано, что если это изображение имеет спектр ограниченной
ширины, то совокупность отсчетов изображения, взятых с найкви-
стовской частотой в дискретных точках, достаточна, чтобы с по-
помощью интерполяции восстановить из отсчетов точную копию
исходного изображения. Подобный вывод справедлив и в случае
дискретизации случайных двумерных полей. Пусть Fj (х, у) обо-
обозначает непрерывный двумерный стационарный случайный про-
процесс с известными средним значением т^ и автокорреляционной
функцией
Rfj (хх, ту) = Е {Fj (хи уО F) (х2, у2)},- D.1.17)
где хх = хх — х2 и ху = ух — уг. С помощью набора дельта-функций
произведем дискретизацию этого процесса. В результате получим
FP{x, y)^F,(x, y)S(x, r/) =
= F,{x,y) Ц L Ь(х-иАх, y-jzAy). D.1.18)
Автокорреляционная функция дискретизованного процесса имеет
вид
Rfp (Хи х2; ух, у2) = Е {FP(xu yx)F*P (x2, y2)} =
- Е \F,{xh yi)F'r(x2, y2)) S(xh ^)S(x2, y2). D.1.19)
Первый сомножитель правой части этого равенства является
автокорреляционной функцией стационарного исходного изобра-
Дискретизация и восстановление непрерывных изображений 103
жения. Следует учесть, что стоящее в правой части равенства
D.1.19) произведение двух дискретизирующих дельта-функций
есть дельта-функция вида
S (*!, t/0 S (x2, t/2) = S (*! — х2, t/. — уГ) =
= S(t,, xy). D.1.20)
Следовательно, дискретизованное случайное поле, представляю-
представляющее изображение, также стационарно и имеет автокорреляцион-
автокорреляционную функцию
Rpp{rx, ry)^=RFl(rx, ry)S(xx, ту). D.1.21)
С помощью двумерного преобразования Фурье автокорреляцион-
автокорреляционной функции D.1.21) найдем энергетический спектр дискретизо-
ванного случайного поля. Согласно теореме о спектре произведе-
произведения,
WFp К, иу) = A/4я2) WF, К, со,) * 9> (со,, соД D.1.22)
где Wfj (со*. ®у) и Wfp (со*, Ыу) обозначают соответственно спек-
спектральные плотности исходного и дискретизованного изображений,
а 91 (соЛ, (Оу) — результат преобразования Фурье дискретизиру-
дискретизирующих дельта-функций. Далее, повторяя шаги, сделанные при вы-
выводе соотношения D.1.7), получим, что энергетический спектр
дискретизованного изображения можно записать в следующем
виде:
D.1.23)
К, 0),) = DЛ2/Л* Ау) ? ? ^F; К - /
/»=— °° /2=—»
Таким образом, энергетический спектр дискретизованного изоб-
изображения образуется повторением энергетического спектра непре-
непрерывного исходного изображения в пространственно-частотной
области через интервалы, кратные пространственной частоте
дискретизации Bя/Длс, 2л/Ау). Если ширина энергетического спек-
спектра непрерывного изображения ограничена так, что Wf, (&х<
ы>у) = 0 при | со* | > cow и | (лу | > (оус, где <оте и а^ — граничные
частоты, то в сумме D.1.23) отдельные спектры не будут наклады-
накладываться в том случае, когда интервалы дискретизации удовлетво-
удовлетворяют условиям Ах < л/сотс и Ау < п/(лус. Непрерывное случай-
случайное изображение FB (x, у) можно восстановить из отсчетов исход-
исходного случайного изображения с помощью интерполяции по фор-
формуле
оо оо
Fn (*> у) = !¦ !¦ F10iд^. У» Ду) Я (* - А Д^, «/ - ь Д^),
/,=— оо /2=-оо
D.1.24)
104
Глава 4
где R (х, у) —детерминированная интерполяционная функция.
Можно добиться, чтобы восстановленное поле и исходное изобра-
изображение были эквивалентны в среднеквадратическом смысле
[5, стр. 284], т. е.
E\\F1{x,y)-F]i{x, у)И = 0.
D.1.25)
Для этого достаточно, чтобы удовлетворялся критерий Найквиста
и в качестве интерполяционной функции была выбрана достаточно
А
<У-
ЛЛЛЛЛ
«¦V
Рис. 4.1.4. Спектры дискретизоваиного изображения, содержащего сигнал и
помеху.
а — сигнал; б — помеха; в — дискретизоваиный сигнал; г — дискретизоваиная помеха.
«хорошая» функция, как, например, бесселева или функция sine (x),
определяемые формулами D.1.16) и D.1.14).
Приведенные результаты можно непосредственно применить
к практической задаче о дискретизации суммы детерминирован-
детерминированного изображения и аддитивного шума, моделью которого служит
случайное поле. На рис. 4.1.4 показан пример энергетического
спектра дискретизованного зашумленного изображения. Этот
пример указывает на возможность возникновения серьезной труд-
трудности. Спектр шума может оказаться шире спектра полезного изо-
изображения, и если шум будет дискретизироваться с недостаточ-
недостаточной частотой, то в полосу пропускания • восстанавливающего
фильтра будут попадать «хвосты» шумового спектра. Это приведет
к увеличению искажений, вызванных шумом. Для устранения
этой трудности перед дискретизацией следует, конечно, профиль-
профильтровать зашумленное изображение с тем, чтобы сузить спектр
шума.
Дискретизация и восстановление непрерывных изображений
105
4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ
В реальной системе дискретизации изображений дискретизи-
рующая решетка имеет конечные размеры, ширина дискретизиру-
ющих импульсов заметно отличается от нуля, а отсчеты изображе-
изображения могут быть взяты с недостаточной частотой. Рассмотрим по-
последствия такой неидеальной дискретизации.
Основой для анализа будет служить типичная система ска-
сканирования изображений, показанная на рис. 4.2.1. Исходное изоб-
изображение, представленное в виде диапозитива, сканируется скачко-
скачкообразно перемещающимся тонким световым лучом. Свет, про-
прошедший через диапозитив, собирается конденсор ной линзой и на-
направляется на светочувствительную поверхность фотодетектора.
Электрический сигнал с выхода фотодетектора интегрируется за
период времени, в течение которого световой луч освещает данный
элемент изображения. В ходе анализа будем предполагать, что
в процессе дискретизации дополнительных шумов в сигнал не
Луч сдета
Диапозитиб
Конденсор
Рис. 4.2.1. Типичная система сканирования изображений.
вносится. Поэтому результаты предыдущего раздела, относящиеся
к дискретизации зашумленных изображений, нетрудно объединить
с выводами данного раздела. Следует также отметить, что ниже-
нижеприведенный анализ легко распространяется на широкий класс
реальных систем дискретизации изображений.
4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА
С учетом вышеупомянутых предположений дискретизованное
изображение можно описать функцией
FP {х, у) = F, {х, у) S (х, у),
D.2.1)
106 Глава 4
где дискретизирующая функция
S (х, 0)=1 1 Р (х - Д Д*. г/ - /, Ау) D.2-2)
/i— «^1 /2——^2
состоит из B/! + 1) B/г + 1) одинаковых импульсов Р (х, у),
образующих решетку с шагом (А*, Ау). Для упрощения обозначе-
обозначений пределы суммирования выбраны симметричными. Будем
считать, что дискретизирующие импульсы нормированы так, что
оо
\\Р(х, y)dxdy=\. D.2.3)
— 00
При анализе можно полагать, что дискретизирующая функция
была получена пропусканием конечного набора дельта-функций
DT(x, у) через линейный фильтр с импульсным откликом Р (х, у).
Таким образом,
5 (х, у) = DT (х, у) * Р (х, у), D.2.4)
где
DT(x, г/)= t t 8(x-hAx, y-j2Ay). D.2.5)
Подставив выражение D.2.2) в D.2.1), получим формулу для диск-
ретизованного изображения
Fp(x,y)= t ? F,(x, y)P(x-j1Ax, y-UAy). D.2.6)
Спектр этой функции имеет вид
3~Р К, соу) = A/4я2) Ti (со,, соу) * \ФТ (со,, со,) У (со,, со,)], D.2.7)
где & (со,, coy) — результат преобразования Фурье функции
Р (х, у). Преобразование Фурье конечной решетки дискретизи-
рующих импульсов описывается следующим соотношением [5,
стр. 105]:
sin \e
L
sin \e>x (j1+-r) Ал] sin
L \/ J
На рис. 4.2.2 приведен график функции 2bT (cov, coy). С увеличе-
увеличением /t и ].г правая часть формулы D.2.8) в пределе превращается
в набор дельта-функций.
В системе восстановления изображений непрерывное изобра-
изображение получается путем интерполяции отсчетов. Идеальные ин-
интерполяционные функции, такие, как sine (л;) и бесселевы [фор-
[формулы D.1.14) и D.1.16)], обычно определены на бесконечной пло-
плоскости. Если же дискретизирующая решетка имеет конечные
Дискретизация и восстановление непрерывных изображений
107
размеры, то на границах отсекаются «хвосты» интерполяционных
функций и вблизи краев восстановленного изображения появ-
появляются ошибки [9, 10]. Однако такие ошибки обычно становятся
пренебрежимо малыми при удалении от границ на 8—10 шагов
дискретизации.
Числовые значения отсчетов изображения получаются путем
пространственного интегрирования Fs (х, у) по некоторой конеч-
конечной площадке —элементу изображения. В сканирующей системе
DT (х, 0)
Рис. 4.2.2. Усеченная дискретизирующая последовательность и ее спектр.
(рис. 4.2.1) интегрирование фактически проводится на светочувст-
светочувствительной поверхности фотодетектора. Значение отсчета, соответ-
соответствующего (/j, /2)-му элементу, можно найти по формуле
= j j F1(x,y)P{x-j1Ax,y-j,Ay)dxdy, D.2.9)
ьЛх— Ах j2\y—Ay
где Ах и А„ обозначают наибольшие размеры этого элемента. Здесь
предполагается, что за время интегрирования в системе берется
лишь один отсчет. В противном случае приходится решать сложную
проблему перекрестных искажений. В рассматриваемой системе
дискретизации размеры элемента могут оказаться больше, чем
расстояние между отсчетами. Поэтому в модели допускается, что
последовательные (во времени) отсчеты соответствуют частично
перекрывающимся элементам изображения.
Простой заменой переменных равенство D.2.9) можно преобра-
преобразовать к виду
АХ Ау
Fs (/, Ах, /, Ау) = j j F, (jt Ax - a, /2 Ay - p) P (—a, —p) da dp.
D.2.10)
108 Глава 4
Поскольку предполагается, что за время интегрирования берется
только один отсчет, пределы в интеграле D.2.10) можно расширить
до бесконечности. В такой форме выражение D.2.10) можно рас-
рассматривать как результат свертки исходного изображения Ft (x, у)
с импульсным откликом Р (—х, —у) и последующей дискретиза-
дискретизации этой свертки в конечной области с помощью дельта-функции.
Тогда, пренебрегая эффектами, связанными с конечными разме-
размерами дискретизирующей решетки дельта-функций, получим
Fs (h Ах, /а Ay) = [F, {х, у)*Р {—х, —у)] 8 (х- /г Ах, у - /2 Ау).
D.2.11)
В большинстве систем дискретизации дискретизирующий импульс
симметричен, поэтому Р (—х, —у) = Р (х, у).
Несложное по форме соотношение D.2.11) полезно при оценке
эффектов, возникающих при дискретизации с использованием им-
импульсов конечной ширины. Если спектр изображения ограничен
по ширине, а Ах и Ау удовлетворяют критерию Найквиста, то
конечная ширина импульса приводит к тем же результатам, как
если бы исходное изображение перед идеальной дискретизацией
подверглось линейному искажению (смазыванию). В части 4
будут рассмотрены методы компенсации подобных искажений.
Однако конечность размеров дискретизирующего импульса не
всегда является недостатком. Рассмотрим случай, когда спектр
исходного изображения очень широкий, и поэтому оно дискрети-
зируется с недостаточной частотой. Импульс с конечными разме-
размерами фактически осуществляет низкочастотную фильтрацию исход-
исходного изображения, что приводит к сужению спектра и, следова-
следовательно, уменьшает ошибки, вызванные наложением спектров.
4.2.2. ЭФФЕКТЫ, СВЯЗАННЫЕ С НАЛОЖЕНИЕМ СПЕКТРОВ
Для безошибочного восстановления непрерывного изображе-
изображения необходимо ограничить ширину спектра исходного изображе-
изображения, взять отсчеты по пространственным переменным с частотой не
ниже найквистовской и интерполировать отсчеты изображения.
Вопрос об интерполяции рассмотрен в следующем разделе, а здесь
дан анализ эффектов, возникающих при дискретизации с недоста-
недостаточной частотой.
Если при такой дискретизации имеет место наложение спектров,
как отмечено штриховкой на рис. 4.2.3, то в восстановленное изоб-
изображение будут внесены ложные пространственные гармоники
[11, 12]. На рис. 4.2.4 показано, как выглядят на реальном изоб-
изображении ошибки, вызванные наложением спектров. Недостаточ-
Недостаточная частота дискретизации приводит к появлению в восстановлен-
восстановленном изображении ложных низкочастотных гармоник. В оптике
это явление называют муаровыми узорами или муар-эффектом.
Дискретизация и восстановление непрерывных изображений
109
Согласно равенству D.1.7), спектр дискретизованного изобра-
изображения можно представить в виде
ГР(и>„ со^О/ДяЛг/Н^со,, (¦>„) +fr-QК, (¦>„)], D.2.12)
где &~[ (ы>х, (иу) описывает спектр исходного изображения, диск-
дискретизованного с периодом (Ах, Ау). Слагаемое
/,=_00 /2=—00
/•+0
D.2.13)
описывает те компоненты спектра дискретизованного изображения,
которые получаются при повторении исходного спектра с перио-
Рис. 4.2.3. Спектры двумерной функции, дискретизованной с недостаточной
частотой.
дами a>xs = 2я/Дл" и юда = 2л/Ау. При отсутствии наложения
спектров оптимальную интерполяцию отсчетов изображения
можно получить, пропуская дискретизованное изображение через
идеальный фильтр нижних частот с частотной характеристикой
_ | К при | ах | < co,s/2 и | соу | < (dw/2, D.2.14а)
\ х, У'\ов остальных случаях, D.2.146)
где К — нормирующая постоянная. Если этот же метод применить
для восстановления изображения, дискретизованного с недоста-
4,2.4, Пример искажений, вызванных наложением спектров.
скодкое изображение; б — днскретвзованное изображение-
Дискретизация и восстановление непрерывных изображений
111
точной частотой, то получится изображение, описываемое функцией
Fr (*. У) = F, (х, у) + А (х, у), D.2.15)
где слагаемое
«W2
А(х, г/) = A/4я2) J J ^К, со,,) х
V2 /2
X ехр {/ [ыхх + (оуу]\
D.2.16)
соответствует тем деталям восстановленного изображения, кото-
которые появились вследствие наложения. Все коэффициенты, изме-
Предварительный
срильтр
Восстанадлидающш
фильтр
Рис. 4.2.5. К анализу ошибок, вызванных наложением спектров.
няющие амплитуду, входят в К. Ложную компоненту D.2.16)
можно существенно ослабить, если для интерполяции применить
фильтр, частотная характеристика которого согласована со спек-
спектром исходного изображения. Этот метод описан в гл. 15. Ниже
будет рассмотрен другой подход, при котором для уменьшения
наложения спектров изображение перед дискретизацией подвер-
подвергают низкочастотной фильтрации.
На рис. 4.2.5 представлена модель, служащая для количест-
количественного анализа эффектов, связанных с наложением спектров.
В ней предполагается, что исходное изображение F1 {x, у) яв-
является реализацией двумерного случайного процесса с известной
спектральной плотностью &"t (co^, coj. Исходное изображение про-
пропускают через предварительный линейный пространственный
фильтр с частотной характеристикой Э6 (со,., со#). Будем полагать,
что этот фильтр обеспечивает плавное ослабление высших простран-
пространственных гармоник (т. е. это не идеальный фильтр нижних частот
с резкой отсечкой). Затем отфильтрованное изображение дискрети-
зируется с шагом (Л*, Дг/) с помощью идеального пространствен-
пространственного дискретизатора. Далее отсчеты интерполируются в восста-
восстанавливающем фильтре и получается копия исходного изображения.
Согласно равенству A.10.8), спектральная плотность изображения
на выходе предварительного фильтра равна
*У0 К. <*у) = \ЯК, со„)|?Ж9г1 К, со,), D.2.17)
112 Глава 4
а спектр дискретизованного изображения
OS OS
,—оо D.2.18)
Желательно разделить эффекты, вызванные дискретизацией
с недостаточной частотой, и последствия неточного восстановления.
Поэтому здесь будем полагать, что в качестве восстанавливающего
фильтра взят оптимальный фильтр с частотной характеристикой
D.2.14). Мощность компоненты сигнала при Д = /а = 0, проходя-
проходящей через такой фильтр, при этом равна
"W2 "W2
ER = j J JTri К, соу) | Ж К, <о„)|* d(ox d«v D.2.19)
В идеальном случае частотная характеристика предварительного
фильтра должна совпадать с частотной характеристикой D.2.14)
восстанавливающего фильтра. При этом мощность дискретизован-
дискретизованного сигнала оказывается наибольшей и равна
«W2 «W2
?«м= J J *V/K, «v)cK<4- D.2.20)
Уменьшение резкости изображения, связанное с введением пред-
предварительного фильтра, можно выразить отношением
&л = {ЕцМ — Е%)/ЕцМ. D.2.21)
Ошибку, вызванную наложением спектров, обычно определяют
через энергию паразитных гармоник, принадлежащих смещенным
спектрам, попадающим в полосу пропускания восстанавливаю-
восстанавливающего фильтра. Предположим для упрощения, что частота дискре-
дискретизации довольно высока и вклад спектров, смещенных на
(±/1ил/2, ±h<uy,l2), пренебрежимо мал при /х > 2 и /2 >¦ 2.
Полная энергия ошибки, вызванной наложением спектров (см.
заштрихованные участки на рис. 4.2.3), равна
Ел = Ео - Ею D.2.22)
где
00 ОО
?„= J J *V,K, ю,)|#((ода <»у)\*d<asdxaa D.2.23)
ОО —ОО
есть энергия сигнала на выходе предварительного фильтра. Тогда
ошибку из-за наложения спектров можно определить как [11]
sp р 1р (АО 94Л
Дискретизация и восстановление непрерывных изображений 113
Эту ошибку можно уменьшить путем ослабления высших
пространственных гармоник Fj (x, у) в предварительном фильтре.
Однако любое ослабление гармоник, попадающих в полосу про-
пропускания восстанавливающего фильтра, приводит к ухудшению
резкости изображения. Таким образом, приходится идти на ком-
компромисс между резкостью дискретизованного изображения и ошиб-
ошибкой, вызванной наложением спектров.
Рассмотрим теперь соотношение между величиной этой ошибки
и степенью снижения резкости применительно к нескольким типам
предварительных фильтров. Вероятно, простейшим способом
пространственной фильтрации изображения, полученного в неко-
некогерентном свете, является пропускание изображения через линзу
с ограниченной апертурой. Пространственную фильтрацию также
можно осуществить, дефокусируя оптическую систему. На
рис. 13.2.2 показана зависимость частотной характеристики круг-
круглой линзы от степени ее дефокусировки. Даже при использовании
точно сфокусированной линзы, не имеющей аберраций, получается
некоторое смазывание изображения из-за дифракции на конечной
апертуре. Частотная характеристика безаберрационной круглой
линзы диаметром d, вносящей только дифракционные искажения,
равна [13, стр. 83]
Ж (со) == B/я) [arccos (со/ыо) — (со/соо) V1 — («ДооJ], 0 < | ш | < ш0,
D.2.25а)
D.2.256)
где ш0 = ndIR, a R — расстояние от линзы до фокальной пло-
плоскости. В предыдущем разделе было отмечено, что неидеальная
дискретизация, когда ширина дискретизирующего импульса ко-
конечна, эквивалентна идеальной дискретизации того же изображе-
изображения, но пропущенного через пространственный фильтр, импульс-
импульсный отклик которого (после изменения направления обеих коор-
координатных осей) совпадает с формой дискретизирующего импульса.
Таким образом, дискретизирующий импульс может производить
предварительную фильтрацию."
В некогерентной оптической системе сканирующего микроден-
микроденситометра дискретизирующий импульс имеет прямоугольную
форму:
1/Г2, |дг, у\<Т/2,
о, и;!>гд D-2-26»
Частотная характеристика в этом случае равна
sin
114
Глава 4
В электронно-лучевых трубках образуется световое пятно с дву-
двумерным гауссовым распределением яркости
D.2.28)
где аш характеризует ширину луча. Частотная характеристика ска-
сканирующей системы с гауссовым пятном имеет вид
D.2.29)
= ехр {-
На рис. 4.2.6 приведены графики зависимости потери резкости
и величины ошибки, вызванной наложением спектров, от <л0 для
безаберрационной линзы, а также для квадратного и гауссова пя-
пятен. Ширина квадратного пятна выбрана равной Т = 2п/ш0,
100
I SO
I 60
I
I 40
го
ZS
20
§ IS
I 10
I
Квадратное
пятно
Квадратное
пятно
it
{[гауссоВо
пятно
Линза
Рис. 4.2.6. Ошибка, вызванная наложением спектров, и потеря резкости для раз-
различных предварительных фильтров при т = 1.
так что первый нуль функции sine (x) совпадает с частотой отсечки
частотной характеристики линзы. Рассеяние гауссова пятна вы-
выбрано равным aw = 21 щ. В данном примере спектр исходного изо-
изображения моделировался функцией
Г Г, К. «*») = А1[\+ («>/<»/"]• D-2.30)
где А — амплитудный множитель, т — целочисленный параметр,
определяющий скорость, с которой амплитуда спектра умень-
уменьшается с ростом частоты, а сос — пространственная частота, на
Дискретизация и восстановление непрерывных изображений 115
которой амплитуда спектра уменьшается в два раза. Кривые, при-
приведенные на рис. 4.2.6, показывают, что предварительная фильтра-
фильтрация, осуществляемая при гауссовой и квадратной формах скани-
сканирующего пятна, дает примерно одинаковые результаты, а безабер-
безаберрационная линза с конечной апертурой при той же величине
ошибки, вызванной наложением спектров, дает несколько большую
потерю резкости. При использовании дефокусированной линзы
получаются самые плохие результаты.
4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ
В разд. 4.1 были сформулированы условия, необходимые для
точного восстановления изображения. Из исходного изображения
нужно взять отсчеты с частотой, вдвое превышающей наивысшую
пространственную частоту его спектра. Кроме того, восстанавли-
восстанавливающий фильтр (или эквивалентный интерполятор) должен быть
рассчитан так, чтобы пропускал без искажений основной спектр
при Д = 0, /а = 0 и полностью подавлял все побочные спектры
ПРИ /it h ?= 0- Ниже приведены некоторые соображения о том,
к каким результатам может привести применение неидеальных
восстанавливающих фильтров.
В большинстве систем цифровой обработки изображений элек-
электрические сигналы, представляющие собой отсчеты изображения,
поступают с выхода вычислительной машины последовательно,
согласно обычной схеме развертки. Эти «электрические отсчеты»
следует подать на устройство воспроизведения (синтеза) непрерыв-
непрерывных изображений, например на электронно-лучевую трубку (ЭЛТ)
или фоторегистратор. Ниже рассмотрены три способа выполнения
такой операции.
4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
На рис. 4.3.1 изображена схема некогерентной оптической си-
системы восстановления изображений. Маленькое световое пятно
сканками перемещается по экрану ЭЛТ, образуя растр; яркость
каждой точки модулируется пропорционально значениям отсчетов
изображения. С помощью проекционной системы, содержащей
некогерентный пространственный фильтр с желательными свой-
свойствами, картинку с экрана ЭЛТ можно затем отобразить на боль-
большой экран для просмотра или на фотопленку для записи. Как
правило, оптимальный фильтр, равномерно пропускающий спектр
изображения и имеющий резкую отсечку за пределами спектра,
физически реализовать не удается.
Для восстановления одноцветных изображений можно приме-
применить когерентную оптическую систему, схема которой приведена
на рис. 4.3.2. В этой системе сначала фотографируют картинку
116
Глава 4
с экрана ЭЛТ и изготавливают диапозитив, который освещают
коллимированным лазерным лучом. Свет, прошедший через диапо-
диапозитив, попадает на линзу, которая в своей задней фокальной пло-
плоскости создает световое поле с распределением интенсивности,
пропорциональным двумерному спектру Фурье пространствен-
Оптичеснии
фильтр
Фото-
Фотопленка
Рис. 4.3.1. Некогереитная оптическая система восстановления изображений.
ного распределения коэффициента пропускания диапозитива.
Можно рассчитать оптический фильтр, который желаемым обра-
образом изменял бы распределение амплитуды и фазы светового поля
в плоскости фильтрации, т. е. мог бы играть роль восстанавливаю-
восстанавливающего фильтра. Вторая линза также выполняет преобразование
Фурье и восстанавливает изображение на поверхности фотопленки.
Диапозитив Линза
Когерентный
оптический
срилыпр
Линза Фотопленка
Лазерное
излучение
Рис. 4.3.2. Когерентная оптическая система восстановления изображений.
Главным достоинством устройства, построенного на основе коге-
когерентной оптической системы, является сравнительная простота
изготовления восстанавливающего фильтра. Оптимальный фильтр
является просто диафрагмой, пропускающей только дифракцион-
дифракционную картинку нулевого порядка.
В системах восстановления изображений широко используются
электронно-оптические устройства. Так, например, можно весьма
просто осуществить интерполяцию путем электрической дефоку-
Дискретизация и восстановление непрерывных изображений
117
сировки луча на экране ЭЛТ. Недостатки такого метода состоят
в том, что трудно поддерживать на всем экране заданную форму
светового пятна, а интерполяция, как правило, оказывается суб-
субоптимальной. В сканирующих фоторегистраторах обычно восста-
восстанавливают непрерывное изображение, проектируя прямоугольное
световое пятно на фотопленку. В большинстве случаев размер
светового пятна выбирают равным шагу дискретизации с тем, чтобы
целиком заполнить все поле изображения. Такая интерполяция
Истинный
отсчет
/—Дополншпель -
/ ные отсчеты
Истинный
отсчет
—Дополнитель -
ные отсчеты
1
¦
К— — И
1
1. 1
1
1
1--- + --J
1
1
.--4--н
j
¦ 4- н
!
Рис. 4.3.3. Восстановление изображений методом подразвертки.
а — квадратное пятно: б — круглое пятно
выполняется просто, но она не является оптимальной. Если в вос-
восстанавливающем., устройстве удается сформировать очень малень-
маленькое световое пятно, то с помощью дополнительной подразвертки
можно с некоторой погрешностью синтезировать любую желаемую
интерполяционную функцию (рис. 4.3.3). Существуют три метода
получения значений промежуточных элементов изображения для
восстановления с подразверткой: подгонка пространственной функ-
функции, свертка и фильтрация в частотной области. В гл. 11 и 15 по-
подробно рассмотрено практическое применение этих методов.
4.3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
На рис. 4.3.4 приведены примеры одномерных интерполяцион-
интерполяционных функций. Как уже отмечалось, функция sine (x) обеспечивает
точное восстановление, но, как правило, ее трудно сформировать
в реальной системе воспроизведения изображений. Простейшей
интерполяционной функцией является прямоугольная функция,
с помощью которой осуществляется интерполяция отсчетов много-
многочленом нулевого порядка. Треугольная функция обеспечивает
линейную интерполяцию первого порядка. Подобную функцию
можно рассматривать как свертку двух прямоугольных функций.
Свертка треугольной функции с прямоугольной дает колоколооб-
118
Глава 4
разную интерполяционную функцию, изображенную на рис. 4.3.4,
г. Повторением этого процесса можно быстро прийти к гауссовой
интерполяционной функции, приведенной на рис. 4.3.4, е. Много-
Многочлены второго и более высокого порядка также пригодны для ин-
интерполяции отсчетов. Особенно удобным для интерполяции изоб-
изображений является кубический В-сплайн, поскольку в результате
Рис. 4.3.4. Одномерные интерполяционные функции.
а — sine (дг); б — прямоугольная: в — треугольная (свертка двух прямоугольных функ-
функций); г — колоколообразная (свертка трех прямоугольных функций); д — кубический
В-сплайн (свертка четырех прямоугольных функций); е. — гауссова
интерполяции получается функция, непрерывная и гладкая в уз-
узлах интерполяции. Кубический Б-сплайн определяется [14] соот-
соотношением
R (х) = (хK+ - 4 (дг - Дл:? + 6 (д: ~ 2 ЛхK+ - 4 (х - 3 Дд:K+,
где
zm,
О,
2>0,
г < 0.
D.3.1)
D.3.2а)
D.3.26)
Эту функцию, отличную от нуля только на четырех интервалах
дискретизации, можно получить, выполнив свертку четырех пря-
прямоугольных функций. Рис. 4.3.5 иллюстрирует процесс одиомер-
Дискретизация и восстановление непрерывных изображений
119
ной интерполяции с использованием функций sine (х), а также
прямоугольных и треугольных функций.
В табл. 4.3.1 даны определения нескольких двумерных разде-
разделимых интерполяционных функций, для которых R (х, у) =
~ R (x) R (у). Следует отметить, что операция двумерной линей-
линейной интерполяции (или интерполяция многочленами первого по-
порядка), аналогичная операции одномерной линейной интерполяции
Восстановленный
сигнал
1
1
1
1
I
1
6
Рис. 4.3.5. Одномерная интерполяция.
а — функция sine (*); б — прямоугольные функции (интерполяция нулевого порядка);
в — треугольные функции (интерполяция первого порядка).
(рис. 4.3.5, в), отличается от интерполяции с помощью двумерных
треугольных функций, представленных в табл. 4.3.1. Эту операцию
следует выполнять кусочно-линейным способом, как показано на
рис. 4.3.6, а. В области / отсчеты линейно интерполируются пло-
плоскостью, заданной точками А, В и С, тогда как в области // они
линейно интерполируются плоскостью, заданной точками В, С и D.
Непрерывный билинейный способ интерполяции, иллюстрируе-
иллюстрируемый на рис. 4.3.6, б, сводится к последовательной линейной ин-
интерполяции между парами точек, расположенных на прямых, па-
параллельных осям координат. В результате образуется некоторая
поверхность, проходящая через точки А, В, ChD (см. рис. 4.3.6, б).
Как правило, эта поверхность оказывается непдоской,
120
Глава 4
Таблица 4.3.1
Двумерные
Функция
Прямоугольная
Треугольная
Колоколообразная
Кубический
В-сплайн
Гауссова
разделимые интерполяционные функции
Определение
4 siaBnxjTx) sin BnyjTy)
К 'У) ТХТУ Bпх1Тх) Bпу1Ти) '
Тх = 2n/mxs, Ту = 2nle>yS
\0 в противном случае
\ 0 в противном случае
sin (&xTx/2) sin (<%7y2)
#i (*- У) = ^?о (х, у) * Ro {x, у)
Ri (х, у) — Ro (x, у) * Rt (x, у)
Я1 К-«if)*!(«*•"»)
*•(«*• «») = *t («*•»»)
i? (x, у) = [2Я01,]-1 expf %"^У 1,
I 2 J
Рис. 4.3.6. Двумерная линейная интерполяция.
в — кусочно-линейная интерполяция; б — билинейная интерполяция-
Дискретизация и восстановление непрерывных изображений 121
4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ
ФИЛЬТРОВ
Проанализируем теперь работу реальных систем восстановле-
восстановления непрерывных изображений. Будем предполагать, что входной
сигнал такой системы состоит из отсчетов некоторого исходного
изображения, полученных на найквистовской частоте с помощью
конечного набора дельта-функций. Согласно равенству D.1.9),
восстановленное изображение описывается функцией
Fr (х, У) = IS L Fj (j1 Ах, jt Ay) R(x — jx Ax, у - y2 Ay),
U=—'» /s=—Л
D.3.3)
где R (x, у) — двумерная интерполяционная функция. В идеаль-
идеальном случае восстановленное изображение должно быть точной
копией исходного, т. е.
00 00
Fr (х, у) = ? S р! (Д Дат, /2 Ау) #7 (х - h Ах, у — /s Ay),
J =—00 J gssi—00
D.3.4)
где R{ (x, у) обозначает оптимальную интерполяционную функ-
функцию, например заданную формулой D.1.14) или D.1.16). В этом
случае ошибка восстановления для произвольной точки изобра-
изображения равна
&d (х, У) = Jj ш . _2J F, (/, Ах, j, Ay) [R (x - jx Ах, у - \г Ау) -
'-Rilx-UAx.y-UAy)]. D.3.5)
Величина ошибки восстановления зависит от двух факторов:
а) в реальной системе интерполяционная функция R (х, у) мо-
может отличаться от идеальной интерполяционной функции
Ri С*! У)> б) восстановленное изображение имеет конечные раз-
размеры и поэтому интерполяционные функции отсекаются на его
границах. В большинстве систем, оперирующих с дискретизован-
ными изображениями, ошибками восстановления вблизи границ
обычно пренебрегают, так как они становятся весьма малыми при
удалении от границ изображения на несколько шагов дискретиза-
дискретизации. Неидеальность интерполяционных функций в принципе
приводит к ухудшению резкости изображения, а также к появле-
появлению паразитных высокочастотных составляющих.
Влияние неидеальности восстанавливающего фильтра удобно
исследовать, рассматривая структуру спектра восстановленного
изображения, определяемого соотношением D.1.11):
/2=—оо
<»ir — h«>ys)- D.3.6)
il22
Глава 4
В идеальном случае множитель 91 (со*, со,,) должен выделять со-
составляющие спектра нулевого порядка при \х = 0, /2 = 0, а все
остальные составляющие должны подавляться. В неидеальном
фильтре могут ослабляться составляющие спектра нулевого
порядка, что приводит к ухудшению резкости, и, кроме того, гар-
гармоники спектров более высокого порядка могут подавляться не
полностью, что искажает восстановленное изображение. На
Рис. 4.3.7. Энергетические спектры при идеальном н неидеальном восстановле-
восстановлении.
а — спектр дискретизоваяиого изображения: б — частотная характеристика идеального
восстанавливающего фильтра; в — спектр изображения после идеального восстановле-
восстановления; г — частотная характеристика восстанавливающего фильтра с интерполяцией нуле-
нулевого порядка; д — спектр изображения, восстановленного с интерполяцией нулевого
порядка.
рис. 4.3.7 приведен пример, показывающий характер искажений
спектра изображения при использовании неидеального восстанав-
восстанавливающего фильтра. Типичное сечение спектра дискретизованного
изображения представлено на рис. 4.3.7, а. При использовании
идеального восстанавливающего фильтра, когда интерполяцион-
интерполяционные функции имеют вид sine (л:), составляющие спектра нулевого
порядка выделяются, а все составляющие побочных спектров
полностью подавляются (рис. 4.3.7, в). На рис. 4.3.7, г показана
частотная характеристика восстанавливающего фильтра, осно-
основанного на интерполяционной функции нулевого порядка, когда
значения восстановленных элементов в окрестности точки отсчета
устанавливаются равными значению в точке отсчета. В результате
Дискретизация и восстановление непрерывных изображений 123
получается спектр (рис. 4.3.7, д), искаженный за счет ослабления
некоторых составляющих спектра нулевого порядка и появления
ложных высокочастотных составляющих.
Повторяя шаги, сделанные при выводе равенства D.2.21),
получим, что потери резкости, вызванные неидеальностью вос-
восстанавливающей функции R (х, у), количественно можно выра-
выразить с помощью отношения
D.3.7)
где интеграл
«W2 V/2
Ен- J J *VyK, ю„)|ЯК, ее,)!»*»,*», D.3.8)
представляет собой энергию тех составляющих неидеально вос-
восстановленного изображения, которые лежат в найквистовском диа-
диапазоне, а интеграл
j J K, *v)d<ox<4 D.3.9)
описывает энергию таких составляющих идеально восстановлен-
восстановленного изображения.
Ошибку восстановления, связанную с внесением ложных
высокочастотных составляющих спектра, можно определить от-
отношением
#н = ?н/?г, D.3.10)
где
00 SO
Ет = J j УГрР К, <о„) | Я! К, со,)|2 do* dco, D.3.11)
—00 —00
есть полная энергия восстановленного изображения, а
EH = ET-ER D.3.12)
представляет собой энергию всех спектральных составляющих
восстановленного изображения, лежащих вне найквистовского
диапазона.
В табл. 4.3.2 приведены значения ошибки восстановления 8Н
и коэффициента потери резкости &R, полученные при восстанов-
восстановлении с использованием некоторых двумерных разделимых интер-
интерполяционных функций.
124
Глава 4
Таблица 4.3.2
Ошибка восстановления и коэффициент потери резкости
для различных разделимых двумерных
интерполяционных функций
Функция
sine (х)
Прямоугольная
Треугольная
Колоколообр азная
Кубический В-сплайн
Гауссова, ош = ЗГ/8
Гауссова, ош = Г/2
Гауссова, ош= 5Т/8
Коэффициент
потери резкости
SR, %
0,0
26,9
44,0
55,4
63,2
38,6
54,6
66,7
Ошибка восста-
восстановления &fj, %
0,0
15,7
3,7
! М
0,3
10,3
2,0
0,3
Здесь предполагалось, что спектральная плотность исходного
изображения описывается формулами
К/2)а,
(©) = 0, О2 > (со4/2)а.
D.3.13)
Кроме того, предполагалось, что вклад, вносимый в ошибку
восстановления побочных спектров при /1( /8 > 2, пренебрежимо
мал. Из таблицы видно, что при восстановлении с использованием
прямоугольных интерполяционных функций (функций нулевого
порядка) коэффициент потери резкости и ошибка восстановления
получаются довольно большими. Применяя интерполяционные
функции более высокого порядка, ошибку восстановления можно
значительно уменьшить, но за счет дальнейшего ухудшения коэф-
коэффициента потери резкости.
ЛИТЕРАТУРА
1. Whittaker E. Т., On the Functions which are Represented by the Expansions
of the Interpolation Theory, Pfoc. Roy Soc. Edinburgh, Section A, 35, 181—
194 A915).
2. Shannon С E., Communication in the Presence of Noise, Proc. IRE, 37, 1,
. 10—21 (January 1949). [Имеется перевод: Шеннон К., Работы по теории
информации и кибернетике. — М.: ИЛ, 1963, с. 433—461.]
3. Landau H. J., Sampling, Data Transmission, and the Nyquist Rate, Proc.
IEEE, 55, 10, 1701—1706 (October 1967). [Имеется перевод: Ландау, Метод
выборок, передача информации н частота Найквиста. — ТИИЭР, 1967,
т; 55, № lOJ
4. Goodman J. W., Introduction to Fourier Optics, McGraw-Hill, New York,
' 1968. [Имеется перевод: Тудмен Дж., Введение в фурье-оптику. —¦ М.: Мир,
1970.] ¦•-..--
Дискретизация и восстановление непрерывных изображений 125
5. Papoulis A., Systems and Transforms with Applications in Optics, McGraw-
Hill, New York, 1966. [Имеется перевод: Папулис А., Теория систем н пре-
преобразований в оптике. —М.: Мир, 1971.]
6. Richards P. J., Sampling Positive Functions, Proc. IEEE (Letters), 54, 1,
81—82 (January 1966). [Имеется перевод: Ричарде, Дискретное представле-
представление положительных функций. — ТИИЭР, 1966, т. 54, № 1.]
7. Lloyd S. P., A Sampling Theorem for Stationary (Wide Sense) Stochastic
Processes, Trans. Am. Math. Soc, 92, 1, 1—12 (July 1959).
8. Shapiro H. S., Silverman R. A., Alias-Free Sampling of Random Noise,
J. SIAM, 8, 2, 225—248 (June 1960).
9. Brown J. L., Jr., Bounds for Truncation Error in Sampling Expansions of
Band-Limited Signals, IEEE Trans. Inf. Theory, 1T-15, 4, 440—444 (July
1969).
10. Helms H. D., Thomas J. В., Truncation Error of Sampling Theory Expan-
Expansions, Proc. IRE, 50, 2, 179—184 (February 1962).
11. Downing J. J., Data Sampling and Pulse Amplitude Modulation, in: Aeros-
Aerospace Telemetry, Stiltz H. L., Ed., Prentice-Hall, Englewood Cliffs, N. J.,
1961.
12. Childers D. G., Study and Experimental Investigation on Sampling Rate
and Aliasing in Time Division Telemetry Systems, IRE Trans. Space Electro-
Electronics and Telemetry, SET-8, 267—283 (December 1962).
13. O'Neill E. L., Introduction to Statistical Optics, Addison-Wesley, Reading,
Mass., 1963. [Имеется перевод: О'Нейл Э., Введение в статистическую оп-
оптику. — М.: Мир, 1966.]
14. Greville Т. N. Е., Introduction to Spline Functions, in: Theory and Appli-
Applications of Spline Functions (Greville T. N. E., Ed.), Academic Press, New
York, 1969.
Глава 5
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ
ИЗОБРАЖЕНИЙ
В гл. 2 были рассмотрены вопросы, связанные с математиче-
математическим описанием непрерывных изображений. В настоящей главе
даны способы формального представления дискретных изоб-
изображений с использованием как детерминированных, так и стати-
статистических моделей.
5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ
В данном разделе коротко рассмотрены встречающиеся в тексте
математические действия, выполняемые с векторами и матрицами.
Строгий вывод и доказательства теорем и положений, приведен-
приведенных ниже, можно найти в литературе A—5].
Вектор
Вектор-столбец f размера Nxl представляет собой совокуп-
совокупность элементов f (я), где п — 1, 2, ..., N, расположенных
в виде вертикального столбца
f ==
7(D
/B)
f(N)
E.1.1)
Вектор-строка h размера 1 X N представляет собой упорядоченную
совокупность элементов h (я), где я = 1, 2, ... N, расположен-
расположенных в виде горизонтальной строки
h = [h(\), hB), .... h(j), ..., h (N)l E.1.2)
В книге полужирными строчными буквами будут, как правило,
обозначаться вектор-столбцы. Вектор-строка будет обозначаться
как транспонированный вектор-столбец:
= [/A), /B),
f(N)l
E.1.3)
Математическое описание дискретных изображений
127
Матрица
Матрица F размера MXN представляет собой совокупность
элементов F (т, я), где т = 1, 2, ..., М и п = 1, 2, ..., N,
расположенных в виде строк и столбцов двумерной таблицы
E.1.4)
1) F{\, 2) ... УA, N)
FB, I) FB, 2) ... FB, N)
_F(M,
, 2) ... F(M,
Символ О обозначает нулевую матрицу, все элементы которой
равны нулю. Диагональная матрица — это квадратная матрица
(когда М = N), все элементы которой, не лежащие на главной
диагонали, равны нулю, т. е. F (т, п) — 0, если т Ф п. Еди-
Единичная матрица, обозначаемая символом I, есть диагональная
матрица, все диагональные элементы которой равны единице.
Индекс при символе единичной матрицы указывает ее размеры;
\N обозначает единичную матрицу размера NXN. Матрица F
может быть разделена на блоки (подматрицы) Fpq:
F =
Fi.i
FA1
Fl,2
Fp>2
Fl, Q
Fp,q
E.1.5)
Сложение матриц
Сумма двух матриц С = А + В определена только в том
случае, когда обе матрицы имеют одинаковые размеры. Матрица
С — сумма матриц А и В, имеет размеры MX.N, а ее элементы
С (т, п) = А (т, п) + В (т, п). ¦
Умножение матриц
Произведение двух матриц С = АВ определено только тогда,
когда число столбцов матрицы А равно числу строк матрицы В.
При умножении матрицы А размера МХР на матрицу В раз-
мера PXN получается матрица С размера MXN, элементы ко-
которой определяются равенством
С(т, я)=
р)В(р, п).
E.1.6)
При умножении матрицы А на скаляр k получается матрица С:
= k\, элементы которой С (т, п) = kA (m, п).
128 Глава 5
Обращение матриц
Если А — квадратная матрица, то матрица, обратная отно-
относительно нее и обозначаемая как А, обладает следующими
свойствами: АА = I и А~*А = I. Если матрица А существует,
то матрица А называется неособенной (невырожденной). В про-
противном случае она называется особенной (вырожденной). Если
у некоторой матрицы есть обратная, то эта обратная матрица
единственна. Матрица, обратная относительной обратной, сов-
совпадает с исходной матрицей, т. е.
[АГ1 = А. E.1.7)
Если матрицы А и В неособенные, то
[АВ] = В^АЧ E.1.8)
Если матрица А неособенная, а скаляр k Ф О, то
E.1.9)
Обращение особенных квадратных матриц и неквадратных мат-
матриц будет рассмотрено в гл. 8. Матрицу, обратную относительно
блочной квадратной матрицы
р _
можно представить в виде
i'Fnl
Fu|F12"|
F21 i F22 J
E.1.10)
—F22 F21 [Fu — F12F22 F2U
E-iE [г с c-ic i—i
— ГЦ Г12 1Г22 ~~ Г21ГЦ 1*12]
[F22-F21FnFu]
-Id 1-1
E.1.11)
при условии, что матрицы Fn и F22 не являются особенными.
Транспонирование матриц
При транспонировании матрицы А размера MXN образу-
образуется матрица размера NXM, которую обозначают через А7".
Строки матрицы А7" совпадают со столбцами, а столбцы — со стро-
строками матрицы А. Для любой матрицы А
[АГ]Г = А. E.1.12)
Если А = А7", то матрицу А называют симметричной. Для лю-
любых матриц А и В
[АВ]Г - BW. E.1.13)
Математическое описание дискретных изображений 129
Если матрица А неособенная, то матрица А7" также неособенная и
[АТГХ = [А-Т. E.1.14)
Прямое произведение матриц
Левое прямое произведение матрицы А размера PXQ на мат-
матрицу В размера MXN представляет собой матрицу размера РМХ
XQN:
В(\, 1)А|ВA,2)А
5B, 1)А |ВB, 2)А
C=A®B=
_B(M, 1)A|B(M, 2)A] ... \B{M,N)A_
... \B(l, N)A
... |ВB, N)А
E.1.15)
Аналогично можно определить правое прямое произведение.
В этой книге будет использоваться только левое прямое произве-
произведение. Прямые произведения В ® А и A (g) В могут разли-
различаться между собой. Ниже указаны свойства операций умноже-
умножения, сложения, транспонирования и обращения прямого произ-
произведения матриц:
E.1.16)
E.1.17)
E.1.18)
[А ® B]-i = A ® В. E.1.19)
След матрицы
След квадратной матрицы F размера NXN равен сумме ее
диагональных элементов и обозначается как
N
tr[F] = Sf(n, n). E.1.20)
л=«1
Если А и В — квадратные матрицы, то
tr[AB] = tr[BA]. E.1.21)
След прямого произведения двух матриц равен
tr(A(g)B) = tr(A)tr(B). E.1.22)
Норма вектора
Евклидовой нормой вектора f размера NXJ называется ска-
скаляр, определяемый как
IN = frf. E-1.23)
5 Прэтт У.
130 Глава 5
Норма матрицы
iMoft матр
шй след>
= tr[FrF]. E.1.24)
Евклидовой нормой матрицы F размера MXN называется
скаляр, определяемый следующим образом:
Ранг матрицы
Матрица А размера NXN имеет ранг R, если наибольший
из всех ее квадратных неособенных блоков имеет размер RXR.
Понятие о ранге используется при обращении матриц. Если мат-
матрицы А и В неособенные, а С — произвольная матрица, то
Ранг [С] = Ранг [АС] = Ранг [СВ] = Ранг [АСВ]. E.1.25)
Ранг произведения матриц А и В удовлетворяет неравенствам
Ранг [АВ] < Ранг [А], E.1.26а)
Ранг [АВ] < Ранг [В]. E.1.266)
Ранг суммы матриц А и В удовлетворяет неравенству
Ранг [А + В] < Ранг [А] + Ранг [В]. E.1.27)
Скалярное произведение векторов
Скалярным произведением векторов f и g размера NX1 яв-
является скаляр
fc = grf=fg, E.1.28)
или
N
k= I- g (n)f(n). E.1.29)
л=1
Матричное произведение векторов
g размера М X1 на i
E.1.30)
Матричным произведением вектора g размера М X1 на вектор f
размера WX1 является матрица
где А (т, п) = g (m) f (n).
Квадратичная форма
Квадратичной формой вектора f размера Nxl является ска-
скаляр
k=f\t, E.1.31)
где А — матрица размера NXN. Часто матрицу А берут симмет-
симметричной.
Математическое описание дискретных изображений
131
Векторная производная
Производная от скалярного произведения агх по х есть
д[агх]/дх = а, E.1.32)
а производная от скалярного произведения хга по вектору х
равна
д[хга]/дх = а. E.1.33)
Производная от квадратичной формы хгАх по х естьг)
E.1.34)
5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ
Известно, что любую матрицу F размера MXN, имеющую
ранг R, можно представить в виде взвешенной суммы матриц
единичного ранга размера М X N. Такое представление называ-
называется сингулярным разложением [6—8]. В последующих разделах
будет рассмотрено применение этого метода для обработки изоб-
изображений.
При сингулярном разложении используют унитарную матрицу
U размера MXN и унитарную матрицу V размера NXN, такие,
что
UrFV = Л
1/2
где матрица
E.2.1)
N-R
Л1/2 =
(.5.2.2)
M-R
имеет размеры М X N, а ее диагональные элементы" М2 (j) назы-
называются сингулярными значениями матрицы F. Поскольку матри-
матрицы U и V унитарны, то UU7" = 1М и VVr = lN. Поэтому
М
F = UAVV.
E.2.3)
Столбцы унитарной матрицы U являются собственными век-
векторами й,п симметричной матрицы FF7", т. е.
UT[FFT]U =
О
о
"о
») Формула E.1.34) справедлива в случае симметричной матрицы
А. — Прим. ред.
5*
132 Глава. 5
где К (у) — ненулевые собственные значения матрицы FFr.
Аналогично строки матрицы V являются собственными векторами
\п симметричной матрицы FrF, т. е.
VT[FTF]V = ¦•'.. ! О \R t E.2.5)
__AJR)| j _.
"о Г" о ~Jfjv-if
где К (у) — соответствующие ненулевые собственные значения
матрицы FrF. Нетрудно проверить, что равенство E.2.3) согла-
согласуется с E.2.4) и E.2.5).
Разложение матрицы F, задаваемое соотношением E.2.3),
можно представить в виде ряда
F= ?u1/2(y)u;v/. E.2.6)
Матричные произведения собственных векторов UjVT. образуют
набор матриц единичного ранга, каждая из которых умножа-
умножается на весовой множитель, являющийся соответствующим син-
сингулярным значением матрицы F. Согласованность разложения
E.2.6) с вышеприведенными соотношениями можно показать,
подставив его в равенство E.2.1). В результате получается
R
1=1 ! '
Заметим, что произведение иги7 дает вектор-столбец, /-й элемент
которого равен единице, а все остальные — нули. Вектор-строка,
получающаяся в результате вычисления произведения V/V,
имеет аналогичный вид. Поэтому в правой части равенства
E.2.7) образуется диагональная матрица, элементы которой равны
сингулярным значениям матрицы F.
Матричное разложение E.2.3) и эквивалентное представление
в виде ряда E.2.6) можно найти для любой матрицы. Поэтому та-
такое разложение можно непосредственно применить для обработки
дискретных изображений, представленных в виде матриц. Кроме
того, этими формулами можно воспользоваться для разложения
матриц линейных преобразований изображений. Применение ме-
метода сингулярного разложения для исправления и кодирования
изображений рассмотрено в последующих главах книги.
5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
В гл. 1 яркость, координата цвета или какой-то другой под-
подходящий параметр, описывающий изображение, представлялись
непрерывной функцией F (х, у, t). С помощью методов дискрети-
Математическое описание дискретных изображений
133
зации изображений, рассмотренных в гл. 4, непрерывное' изоб-
изображение, зафиксированное в некоторый момент времени, можно
представить в виде массива отсчетов F (j\, /2) в некоторой прямо-
прямоугольной области —/, === /,- =s Jt. Часто этот массив полезно
рассматривать как матрицу с NtxN2 элементами:
E.3.1)
где 1 < щ s? Nh а индексы отсчетов перенумерованы так, как
это принято в теории матриц.
Для облегчения анализа удобно перейти от матричного пред-
представления изображения к векторному, собирая элементы столб-
столбцов (или строк) матрицы F в один длинный вектор [9]. Фор-
Формально эту операцию можно представить с помощью вспомога-
вспомогательного вектора \п размера N^Xl и матрицы Nre размера
NtNz X Nu определяемых следующим образом:
О
•
О
1
О
1
П— 1
п
n+V
О
1
п— 1
п
л+1
E.3.2)
О N2 О N2
В этом случае матрица F будет представлена в векторной форме
с помощью операции упорядочения
f = t NnFvn. E.3.3)
n=l
Вектор vn выделяет /г-й столбец матрицы F, а матрица Nre помещает
этот столбец на место, отведенное для /г-ro отрезка вектора f.
Таким образом, вектор f содержит все элементы матрицы F,
последовательно считанные по столбцам. Обратная операция
преобразования вектора f в матрицу F описывается соотношением
n—=i
E.3.4)
С помощью формул E.3.3) и E.3.4) легко установить связь между
матричным и векторным представлениями двумерного массива.
Достоинствами представления изображения в векторной форме
являются большая компактность обозначений и возможность
непосредственного использования методов, разработанных для
обработки одномерных сигналов. Следует отметить, что выражения
E.3.3) и E.3.4) не только описывают лексикографическую связь
134 Глава 5
между матрицей и вектором, но и определяют некоторые опера-
операторы, которыми можно пользоваться при математическом анализе.
В последующих разделах приводятся многочисленные примеры
применения этих операторов упорядочения.
5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ
ИЗОБРАЖЕНИЙ [5, 10]
Статистические методы описания непрерывных изображений,
приведенные в гл. 1, можно непосредственно применить и для
описания дискретных изображений. В данном разделе получены
выражения для моментов дискретных изображений. Модели
совместных ^плотностей вероятностей приведены в следующем
разделе. ""
Среднее значение матрицы, описывающей дискретное изобра-
изображение, представляет собой матрицу
(rt1, nz)\]. E.4.1)
Если эта матрица разверткой по столбцам преобразована в век-
вектор, то среднее значение этого вектора есть
Ч/ = Ят- T'N^IFlv,, E.4.2)
Корреляция двух элементов изображения с координатами (пъ th)
и (п3, п4) определяется как
R К п2; «з, «4) = Е \F (пъ п2) F* К /г4)}. E.4.3)
Ковариация двух элементов изображения есть
К(пи n2; n3, nt) = Е {[F(nlt п2) — Е {F(nv n2)\] x
X [F*(n,, я4) - Е \F*(n3, я4)}]}. E.4.4)
И наконец, дисперсия элемента изображения равна
ora (tit, п2) = К («1, п2; «1, «г)- E.4.5)
Если матрица изображения преобразована в вектор f, то кор-
корреляционную матрицу этого вектора можно выразить через кор-
корреляции элементов матрицы F:
Rf = Е {ffr} =Е \\ I NmFvJ [ I v?F'rNrJ), (БЛба)
ИЛИ
R/= I I.N^"{FvnvjF*r}N;. E.4.66)
Математическое описание дискретных изображений
135
Выражение
F (Fv \TF*T\ — R {*, A 7\
представляет собой корреляционную матрицу m-ro и n-ro столб-
столбцов матрицы F и имеет размеры N^XN^ Следовательно, R;
можно представить в виде блочной матрицы
R1.1
R2. i
Rl, 2
R2,2
E.4.8)
Ковариационную матрицу вектора f можно получить на основе
его корреляционной матрицы и вектора средних значений с по-
помощью соотношения
К/ = R/ - y\mf. E.4.9)
Матрица дисперсий VF массива чисел F {пъ /г2) по определению
является матрицей, элементы которой равны дисперсиям соот-
соответствующих элементов массива. Элементы матрицы VF можно
непосредственно выделить из блоков матрицы Ц{:
VF(«i, «2) = Кп,п2 К «J. E.4.10)
Если дискретное изображение представляется массивом, ста-
стационарным в широком смысле, то его корреляционную функцию
можно записать в виде
R («ь Щ\ п3, n4) = R («х — п3, п2 — n4) = R (/, k), E.4.11)
где / = «1 — п3 и k = /г2 — /г4- Соответственно блоки ковариа-
ковариационной матрицы E.4.9) будут связаны соотношениями
Кт>л = К*, т>п, E.4.12а)
Кт,п=К1, т<п, E.4.126)
где k = | т — п | + 1. Таким образом, для стационарного в ши-
широком смысле массива
кх к2
К 2 Kl
к2
2—1 Кл/2—2
Ki
E.4.13)
Матрица E.4.13) является блочно-тёплицевой [11]. Наконец,
если корреляционную функцию изображения можно записать
в виде произведения корреляционных функций строк и столб-
столбцов, то ковариационную матрицу вектора f, представляющего
136
Глава 5
изображение, можно записать в виде прямого произведения ко-
ковариационных матриц для строк и столбцов:
К/ = Кс ® Кл =
1, 1)Кс К*A, 2)КС ... КлA, N2)KC
КяB, 1)КС КяB, 2)КС ... Кя B, tfa) Кс .Кл.л^
, E.4.14)
„ 2) Кс ¦ • •
где Кс — ковариационная матрица столбцов матрицы F, име-
имеющая размеры Л^ХЛ^, а Кл — ковариационная матрица строк
матрицы F с размерами N^XN^1).
Рассмотрим случай, когда ковариационная матрица строк мат-
матрицы F имеет следующий вид:
1
1
E.4.15)
где а2 — дисперсия элементов изображения. Эта ковариацион-
ковариационная матрица — аналог непрерывной автоковариационной функ-
функции вида ехр {—а\х\\ — описывает марковский процесс. На
рис. 5.4.1 приведены полученные Дэвиссоном [12] значения коэф-
коэффициентов корреляции элементов строки типичного изображения.
Экспериментальные точки хорошо аппроксимируются ковариаци-
ковариационной функцией марковского процесса с параметром р = 0,953.
Аналогично значения коэффициентов корреляции в направлении,
перпендикулярном к строкам, хорошо согласуются с марковской
ковариационной функцией при р = 0,965. Если ковариационная
функция может быть представлена в виде E.4.14), то коэффици-
коэффициенты корреляции по диагонали должны быть равны произведению
соответствующих коэффициентов корреляции вдоль строк изоб-
изображения и в направлении, перпендикулярном к ним. В данном
примере оказалось, что такая аппроксимация является достаточно
точной в области от нуля до пяти шагов дискретизации.
По аналогии с непрерывным энергетическим спектром A.8.11)
можно определить дискретную спектральную плотность дискрет-
дискретного стационарного двумерного случайного поля, представляющего
изображение, как результат двумерного дискретного преобра-
Х) Выражение E.4.14) должно иметь следующий вид:
A/о«) Kf = [A/о«) Кс] ® [A/а2) К;?],
где а2 — дисперсия элементов изображения. — Прим. ред.
Математическое описание дискретных изображений
137
зования Фурье х) автокорреляционной функции этого поля. Тогда
в силу равенства E.4.11) будем иметь
/,=о *=о
E.4.16)
@,953)"
@,965)П(Ц953)П=@,92)П
О 2 4 6 8 10 12
Расстояние между элементами ¦
14
Рис. 5.4.1. Пример корреляционных зависимостей между соседними элементами
изображения.
На рис. 5.4.2 приведены энергетические спектры марковских
процессов.
*¦) Свойства двумерных дискретных преобразований Фурье рассматриваются
в гл. 10.
138 Глава 5
5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ
ИЗОБРАЖЕНИЙ
Дискретное изображение, представленное массивом F (пъ tiz),
можно полностью описать с помощью совместной плотности ве-
Рис. 5.4.2. Энергетические спектры марковских процессов, моделирующих изоб-
изображения (N = 256, по вертикальной осн логарифмический масштаб).
а — разделимый спектр; б — спектр с круговой симметрией.
роятности его элементов. При задании F (пи л2) в матричной
форме эта плотность записывается как
p(f)=p{F(l, I), FB, 1), .... F(Nlt Nt)\, E.5.1a)
Математическое описание дискретных изображений 139
а в векторной форме — как
p(f) = p{/(l), /B), ..., f(Q)\, E.5.16)
где Q = Ni-N2 определяет порядок совместной плотности. Если
все элементы изображения статистически независимы, то совмест-
совместная плотность вероятности равна произведению одномерных
безусловных плотностей
P(t) = p{f(l)\p{fB)\ ••• P\f(Q)\- E-5.2)
Наиболее распространенным видом совместной плотности ве-
вероятности является гауссова плотность
р (f) = BяГд/21 К/ Г1/2 ехр {- -g" С - Ч,)Г КГ1 (f - Щ)},
E.5.3)
где Kf — ковариационная матрица вектора f, r\f — среднее зна-
значение f, а символом | К; | обозначен определитель матрицы К/.
Гауссова плотность^является полезной моделью совместной плот-
плотности вероятности коэффициентов, полученных в результате
унитарных преобразований изображений. Однако гауссова плот-
плотность не подходит для описания яркости элементов изображения,
поскольку яркость может быть только положительной, а гаус-
гауссовы случайные величины принимают как положительные, так и
отрицательные значения.
В литературе редко встречаются выражения для совместных
плотностей, не являющихся гауссовыми. Хунс [13] разработал
методику формирования подобных плотностей высокого порядка
на основе заданной безусловной плотности первого порядка и
заданной ковариационной матрицы элементов ансамбля. Для
плотности с нулевым средним эта процедура сводится к линейному
преобразованию набора независимых случайных величин g,
совместную плотность вероятности которых
Р(Ф = Р lg(l)\p lgB)\-'-p lg(Q)\ E.5.4)
можно записать в виде произведения заданных плотностей пер-
первого порядка. Тогда искомая совместная плотность вероятности
имеет вид
Pf(f) = |A|MAf)> E-5.5)
где
А = ЕА~1/2ЕГ, E.5.6)
а | А1 обозначает определитель матрицы А. Столбцы матрицы Е
являются собственными векторами заданной ковариационной
матрицы К/, а матрица А — диагональная и состоит из собствен-
собственных значений этой матрицы, причем выполняется соотношение
ErKfE = A. E.5.7)
•pte.y)
pte. Ц)
Рис. 5.5.1. Двумерные плотности вероятности пары коррелированных случайных величин (р = 0,8).
а — плотность распределения вероятностей Лапласа; б — плотность распределения вероятностей Рэлея.
Математическое описание дискретных изображений 141
На рис. 5.5.1 приведены двумерные плотности вероятности пары
коррелированных случайных величин, безусловные распределения
которых являются распределениями Рэлея или Лапласа. Много-
Многомерная модель с распределением Рэлея полезна при рассмотрении
совместной плотности вероятности яркостей элементов изобра-
изображения, а модель с распределением Лапласа применяется для
статистического описания последовательности разностных сиг-
сигналов, образующихся в системах кодирования изображений мето-
методом предсказания.
В следующей главе рассматривается методика квантования,
т. е. представления отсчетов с помощью дискретного набора
чисел, называемых уровнями квантования. Пусть г,- (q) обозна-
обозначает /,-й уровень квантования для элемента изображения, кото-
который занимает q-e место в векторе изображения f. Тогда вероят-
вероятность получения одного из возможных значений вектора f мо-
можно выразить через совместное распределение вероятностей
значений отсчетов следующим образом:
г,-2B), ..., /(Q) = r/Q(Q)}, E.5.8)
где 0 ==? jq ==g J — 1. Обычно для всех компонент вектора выби-
выбирают одинаковый набор уровней квантования и совместное рас-
распределение вероятностей принимает вид
rtq). E.5.9)
Распределения вероятностей значений отсчетов можно оценить,
измеряя соответствующие частоты. Так, одномерное распределение
q-й компоненты вектора
г,\ E.5.10)
можно оценить путем анализа большого набора изображений,
относящихся к одному и тому же классу, таких, например, как
флюорограммы, аэрофотоснимки полей и т. д. Оценкой одномер-
одномерного распределения вероятностей служит распределение отно-
относительных частот
НЕ (Г, q) = [Np(j)]/Np, E.5.11)
где Np — полное число исследованных снимков, a Np (j) — число
снимков, для которых / (q) = rjt j = 0, 1, ..., /— 1. Если ис-
источник изображений является стационарным, то одномерные
распределения E.5.10) будут одинаковы для всех компонент век-
вектора, т. е. не будут зависеть от q. Кроме того, если источник изоб-
изображений является эргодическим, то усреднение по ансамблю
(измерения при использовании набора снимков) можно заменить
усреднением по пространственным координатам. Если предполо-
142
Глава 5
жение об эргодичности справедливо, то одномерное распределе-
распределение можно оценить по частотам
E.5.12)
где Ns (/) — число элементов исследуемого изображения, для
которых / (q) = rjt причем 1 sg q s? Q, a 0 ^ / ==g J — 1.
На рис. 5.5.2 приведены одномерные гистограммы красной,
зеленой и синей координат цвета цветного изображения «Порт-
«Портрет». В большинстве естественных изображений темных элементов
О 5 • 10 15 20 25 30 35 40 45 50 55 60
10 15 20 25 30 35 40 45 50 55 60
10 20 30 40
У родни квантования
50
60
Рис. 5.5.2. Типичные гистограммы красной, зеленой и синей координат цвета
цветного изображении.
гораздо больше, чем светлых, и частоты с ростом яркости убывают
примерно по экспоненте.
Оценку двумерного распределения вероятностей для эргодиче-
ского источника изображений можно найти с помощью распреде-
распределения частот второго порядка, которые получают, подсчитывая
случаи совместного появления определенных пар значений эле-
Математическое описание дискретных изображений
143
ментов, разделенных заданным расстоянием. Допустим, что
F (mlt т2) и F (т3у /п4) есть два элемента изображения, разде-
разделенные отрезком длиной г, который наклонен к горизонтальной
(п3,п4)
(П|,П2)
Рис. 5.5.3. Взаимное расположенне пары элементов изображения.
оси под углом 9 (рис. 5.5.3). Поскольку элементы образуют пря-
прямоугольную решетку, параметры г, 9 могут принимать только
некоторые дискретные значения. Относительная частота второго
порядка есть
Hs(h, U: г, 9) = lNs{]lt h)]/QT, E.5.13)
Рнс. 5.5.4. Гистограммы второго порядка для изображения «Портрет».
где Ns (jb j2) — число пар элементов изображения, для которых
F (тъ т2) = rjt и F (т3, /п4) = г1г. Знаменатель дроби E.5.13) QT
представляет собой полное число пар элементов, которые разде-
разделены отрезками с одинаковыми параметрами (г, 9). Из-за краевых
эффектов QT < Q.
Гистограммы второго порядка для изображения «Портрет»
представлены на рис.5.5.4. Элементы изображения с увеличением
расстояния между ними становятся менее коррелированными, и
частоты распределяются по плоскости более равномерно.
144 Глава 5
ЛИТЕРАТУРА
1. Ayres F., Jr., Schaura's Outline of Theory and Problems of Matrices, McGraw-
Hill, New York, 1962.
2. Bellman R. E., Introduction to Matrix Analysis, McGraw-Hill, New York,
1970. [Имеется перевод: Беллман Р., Введение в теорию матриц.—М.:
Наука, 1969.]
3. Campbell H. G., An Introduction to Matrices, Vectors, and Linear Program-
Programming, Appleton, New York, 1965.
4. Cullen C. G., Matrices and Linear Transformations, Addison-Wesley, Rea-
Reading, Mass., 1966.
5. Graybill F. A., Introduction to Matrices with Applications in Statistics, Wads-
worth, Belmont, Calif., 1969.
6. Rau C. R., Mitra S. K.. Generalized Inverse of Matrices and its Applica-
Applications, Wiley, New York, 1971.
7. Golub G. H., Reinsch C, Singular Value Decomposition and Least Squares
Solutions, Numer. Math., 14, 403—420 A970).
8. Andrews H. C, Patterson C. L., Outer Product Expansions and their Uses
in Digital Image Processing, Am. Math. Monthly, 1, 82, 1—13 (January 1975).
9. Pratt W. K., Vector Formulation of Two Dimensional Signal Processing Ope-
Operations, /. Comput. Graphics Image Proc, 4, No. 1, 1—24 (March 1975) (Aca-
(Academic Press, New York).
10. Papoulis A., Probability, Random Variables, and Stochastic Processes,
McGraw-Hill, New York, 1965.
11. Grenander U., Szego G., Toeplitz Forms and Their Applications, University
of California Press, Berkeley, 1958. [Имеется перевод: Гренаидер У., Сегё Г.,
Тёплицевы формы и их приложения. — М.: ИЛ, 1961.]
12. Davisson L. D. (частное сообщение).
13. Huhns M. N.. Optimum Restoration of Quantized Correlated Signals, Uni-
University of Southern California, Image Processing Institute, Report USCIPI
600, August 1975.
Глава 6
КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
Любая аналоговая величина, подлежащая обработке в ЦВМ
или цифровой системе, должна быть представлена в виде целого
числа, пропорционального значению этой величины. Процесс
преобразования отсчетов, имеющих непрерывное множество зна-
значений, в отсчеты с дискретными значениями называется квантова-
квантованием. В следующих двух разделах дан математический анализ
процесса квантования, который справедлив не только для изоб-
изображений, но и вообще для широкого класса сигналов, с которыми
приходится сталкиваться в системах обработки изображений.
Затем рассматривается обработка квантованных отсчетов. В двух
последних разделах описаны субъективные эффекты, возникающие
при квантовании одноцветных и цветных изображений.
6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН
Рис. 6.1.1 иллюстрирует типичный пример квантования ска-
скалярного сигнала. В процессе квантования значение отсчета ана-
аналогового сигнала сравнивается с набором пороговых уровней.
Если отсчет попадает в интервал между двумя соседними по-
пороговыми уровнями, то ему приписывается значение фиксирован-
фиксированного уровня квантования, соответствующего данному интервалу.
В цифровой системе каждому квантованному отсчету ставится
в соответствие двоичная кодовая комбинация. В этом примере
применен равномерный код, имеющий постоянную длину кодовых
комбинаций.
Приступая к количественному анализу квантования скалярных
величин, допустим, что f и f обозначают соответственно значения
отсчета действительного скалярного сигнала до и после кванто-
квантования. Предполагается, что /—случайная величина с плотно-
плотностью вероятности р (/). Кроме того, предполагается, что / не вы-
выходит за пределы некоторого интервала:
aL<f<.aUt F.1.1)
где аи и aL — верхняя и нижняя границы интервала.
146
Глава 6
При решении задачи о квантовании необходимо выбрать такой
набор пороговых уровней ds и уровней квантования rjf что если
d,<f<dhl, F.1.2)
то исходный отсчет заменяется на число, равное уровню кванто-
квантования г.-. На рис. 6.1.2, а приведен пример размещения пороговых
уровней и уровней квантования на отрезке числовой оси, содер-
64-
63-
62-
I I I I I I
У родни нбантобания —,
i i i i ю
33-
32-
31 -
30-
юоооо
О I I I I I
О I I I 10
Исходный
отсчет
3-
2-
I -
О-
0000 10
000001
000000
Пороговые
уродни
КодоНые
комбинации
КВаитобанный
отсчет
Рис. 6.1.1. Пример квантования сигнала.
жащем J пороговых уровней. Другой распространенной формой
представления характеристики квантователя является ступенчатая
кривая (рис. 6.1.2, б).
Уровни квантования и пороговые уровни выбирают так, чтобы
уменьшить до минимума некоторую заданную величину, характе-
характеризующую ошибку квантования, т. е. степень различия между f
и f. В качестве меры ошибки квантования обычно выбирают
среднеквадратическую ошибку. Если J — число уровней кванто-
квантования, то среднеквадратическая ошибка квантования равна
аи ¦'-! ai+i
a^ /=0 di
F.1.3)
Если число J велико, то плотность вероятности значений кванту-
квантуемого сигнала на каждом из интервалов (d/, d/+1) можно считать
постоянной и равной р (rj). Следовательно,
¦1-Х dj+l
J f F.1.4)
J (f-
/=0
ai
Квантование изображений
147
или после вычисления интегралов
—i
з ^=0 / i+i I I 1
Оптимальное положение уровня квантования rs в интервале
(dj, dj+1) можно найти, решая задачу о минимуме ошибки &
как функции г,-. Приравнивая нулю производную
d&ldrj = O, F.1.6)
получаем
г, = (d/+1 + dj)/2. F.1.7)
Таким образом, при сделанных допущениях оптимальным поло-
положением уровня квантования является середина интервала между
Пороговые уровни
10 dj d2 a
аз dj-i dj dj>i
О-' О
O-i au
Уровни кйантобания
Выкидной
сигнал
Уробни
кдантобания
Пороговые
уровни
Вводной
сигнал
Рис. 6.1.2. Пороговые уровни и уровни квантования.
соседними пороговыми уровнями. Подставив соответствующие
величины в выражение для ошибки квантования, получим
ff-l/^fW/Hd/rt-d/]». F.1.8)
Оптимальное положение пороговых уровней можно определить,
находя минимум ошибки 8 методом множителей Лагранжа.
С помощью этого метода Пантер и Дайт [1] показали, что поло-
148 Глава 6
жения пороговых уровней довольно точно определяются по
формуле
d. = __^ +aL, F.1.9a)
где
g/=/K/-M+ab F196)
а / = 0, 1, ..., /. Еслл плотность вероятности значений отсче-
отсчетов равномерна, то пороговые уровни будут расставлены равно-
равномерно. При неравномерных плотностях пороговые уровни чаще
в тех участках, где плотность вероятности велика, и реже там,
где она мала. Для большинства видов плотности вероятности,
используемых обычно при описании изображений, интегралы
F.1.9) взять не удается и положение пороговых уровней прихо-
приходится находить с помощью численного интегрирования.
Если число уровней квантования невелико, то приближение,
с помощью которого получено равенство F.1.4), становится неоп-
неоправданным и следует использовать точное выражение для ошибки
F.1.3). Дифференцируя его по переменным ds и ri и приравнивая
производные нулю, получаем
dg/dd, = (d, - г,)* р (d,) - (d, - rM)« p (d,) = 0, F.1.10a)
d»/dr, = 2 J {f-r,)p{f)df = Q. F.1.106)
"/
После преобразований приходим к системе уравнений
ri = 2d!-ri_1, F.1.11a)
//= j fpifldfl j p(f)df. F.1.116)
Решая эти уравнения рекуррентным способом, можно для задан-
заданной плотности вероятности р (f) найти оптимальные значения по-
пороговых уровней и уровней квантования. Макс [2] решил такую
задачу для гауссовой плотности и составил таблицы оптимального
размещения пороговых уровней в зависимости от числа уровней
квантования. В табл. 6.1.1 указано расположение уровней кван-
квантования и пороговых уровней в квантователе Макса для плот-
Квантование изображений
149
Расположение
РаВномерное
Число
разрядов "i
1
2
г
3
4
-1,0000
0.0000
1,0000
-1,0000
-0,5000
-0,0000
0,5000
1,0000
-1,0000
-0,7500
-0,5000
-0,2500
0,0000
0,2500.
0,5000
0,7500
1,0000
-1,0000
-0,8750
-0,7500
-0,6250
-0,5000
-0,3750
-0,2500
-0,1250
0,0000
0,1250
0,2500
0,3750
0,5000
0,6250
• 0,7500
0,8750
1,0000
г,-
-0,5000
0,5000
-0,7500
-0,2500
0,2500
0,7500
-0,8750
-0,6250
-0,3750
-0,1250
0,1250
0,3750
0,6250
0,8750
-0,9375
-0,8125
-0,6875
-0,5625
-0,4375
-0,3125
-0,1875
-0,0625
0,0625
0,1875
0,3125
0,4375
0,5625
0,6875
0,8125
0,9375
уровней
Таблица 6.1.1
квантования и пороговых уровней
в_квантователе
Гаусса
d,
—ОО
0,0000'
00
—оо
-0,9816
0,0000
0,9816
00
—оо
-1,7479
-1,0500
-0,5005
0,0000
0,5005
1,0500
1,7479.
00
-00
-2,4008
-1,8435
-1,4371
-1,0993
-0,7995
-0,5224
-0,2582
0,0000
0,2582
0,5224
0,7995
1,0993
1,4371
1,8435
2,4008
оо
л
-0,7979
0,7979
-1,5104
-0,4528
0,4528
1,5104
-2,1519
-1,3439
-0,7560
-0,2451
0,2451
0,7560
1,3439
2,1519
-2,7326
-2,0690
-1,6180
-1,2562
-0,9423
-0,6568
-0,3880
-0,1284
0,1284
0,3880
0,6568
0,9423
1,2562
1,6180
2,0690
2,7326
! Макса
Лапласа
d,
-оо
0,0000
ОО
—оо
-1,1269
0,0000
1,1269
00
-оо
-2,3796
-1,2527
-0,5332
0,0000
0,5332
1,2527
2,3796
оо
-оо
-3,7240
-2,5971
-1,8776
-1,3444
-0,9198
-0,5667
-0,2664
0,0000
0,2644
0,5667
0,9198
1,3444
1,8776
2,5971
3,7240
оо
г*
-0,7071
0,7071
-1,8340
-0,4198
0,4198
1,8340
-3,0867
-1,6725
-0,8330
-0,2334
0,2334
0,8330
1,6725
3,0867
-4,4311
-3,0169
-2,1773
-1,5778
-1,1110
-0,7287
-0,4048
-0,1240
0,1240
0,4048
0,7287
1,1110
1,5778
2,1773
3,0169
4,4311
Рэлея
d,
0,0000
2,0985
ОО
0,0000
1,2545
2,1667
3,2465
ОО
0,0000
0,7619'
1,2594
1,7327
2,2182
2,7476
3,3707
4,2124
оо
0,0000
0,4606
0,7509
1,0130
1,2624
1,5064
1,7499
1,9970
2,2517
2,5182
2,8021
3,1110
3,4566
3,8588
4,3579
5,0649
оо
1
1,2657
2,9313
0,8079
1,7010
2,6325
3,8604
0,5016
1,0222
1,4966
1,9688
2,4675
3,0277
3,7137
4,7111
0,3057
0,6156
0,8863
1,1397
1,3850
1,6277
1,8721
2,1220
2,3814
2,6550
2,9492
3,2729
3,6403
4,0772
4,6385
5,4913
150
Глава 6
ностей распределений вероятностей Гаусса, Лапласа, Рэлея и
равномерного.
Нетрудно показать, что если пороговые уровни и уровни
квантования выбраны согласно равенству F.1.11), то среднеквад-
ратическая ошибка квантования уменьшается до величины
-s
J
V 'г 1
J fp\f\df-r) J p\f\df\, F.1.12a)
или в более короткой форме
j—i
/=0
F.1.126)
Для частного случая плотности равномерного распределения
вероятностей минимальная среднеквадратическая ошибка равна
#мин = 1/A2/2). F.1.13)
Для большинства других видов плотности вероятности ошибку
квантования приходится определять с помощью расчетов.
Неравномерное квантование можно све:ти к равномерному
с помощью нглингйного "преобразования, как показано на
Нелинейное
преобразование
Ч
Равномерный
кван-тоВате/гь
л
Обратное
преобразование
Рис. 6.1.3. Квантователь со сжатием.
рис. 6.1.3. Отсчет подвергается нелинейному преобразованию, за-
затем равномерно квантуется и подвергается обратному нелинейному
преобразованию [3]. Ё системах квантования с преобразованием
стремятся сделать плотность вероятности преобразованных отсче-
отсчетов на входе квантователя равномерной. Преобразованный от-
отсчет .(рис. 6.1.3) есть
g=T[f\, F.1.14)
причем нелинейное преобразование Т (•) выбрано таким, что
плотность вероятности g оказывается равномерной, т. е.
P\g\=l F.1.15)
в интервале — 1/i<g< V2. Если / — случайная величина с нуле-
нулевым средним, то искомая характеристика нелинейного элемента
имеет вид [4J
\\z\dz-ik. F.1.16)
Квантование изображений
151
Квантование с преобразованием
Таблица 6.1.2
Плотность вероятности
Гауссова р (J) —
— Bяа2)~1/2 X
X ехр— {/2/2а2}
Рэлея р (f) =
= (//а2) ехр { - /*/2а2}
Лапласа р (/) =
= (а/2)ехр{-а|/|},
Прямое преобразование
g —
_ехр- {—а/}), />0
-Va(i-
-ехр-{а/}), /<0
Обратное преобразование
?=[К2а«х
X In(l/(V2 — g))V/2
f =
-A/а) X
X In(l —2^),^>0
A/а) х
Xln(l+2g), ^<0
Таким образом, она совпадает с функцией распределения вероят-
вероятностей величины f. В табл. 6.1.2 приведены характеристики пря-
прямого и обратного нелинейных преобразований для плотностей
распределений вероятностей Гаусса, Релея, Лапласа.
6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН
Обычно квантование совокупности отсчетов выполняется пос-
последовательно. Каждый отсчет рассматривается как скалярная ве-
величина и квантуется независимо от остальных отсчетов с помощью
методов, описанных в предыдущем разделе. Однако часто удается
уменьшить ошибку квантования, если все отсчеты квантовать
совместно.
Рассмотрим сигнал f, представляющий собой вектор размера
NX 1. Будем полагать, что этот вектор является реализацией слу-
случайного вектора с Af-мерной плотностью вероятности
pQ) = Plh,h М- F-2.1)
При квантовании вектора f JV-мерное векторное пространство
разделяют на J ячеек квантования Dn каждой из которых соот-
соответствует один из J квантованных векторов. Векторный сигнал f
заменяется на квантованный вектор r/t если f попадает в ячейку Dr
На рис. 6.2.1 приведены примеры векторного квантования в одно-,
двух- и трехмерном пространствах. В подобной общей постановке
задачи о векторном квантовании векторный сигнал f преобразу-
преобразуется в вектор г,-, но компоненты Ректора f при этом не обяза-
152
Глава 6
тельно будут квантоваться по отдельности по набору дискретных
пороговых уровней.
Среднеквадратическую ошибку векторного квантования можно
представить в виде суммы
*=2 jtr к* - «¦/) (f - г/)г i p (f)df ¦ F-2-2)
Оптимальное положение квантованных векторов гу при фик-
фиксированных границах ячеек квантования Dj можно найти, при-
равнивая нулю частные производные
, ! / ! ошибки квантования по векторам г,.
" J. I*' 1 В результате получается система ин-
у ^'' тегральных уравнений
7)p(f)df. F.2.3)
= J(f-r
ft.
После преобразований находим
rl^\tp{t)dtj\p{t)dt. F.2.4)
Равенство F.2.4) определяет услов-
условное математическое ожидание векто-
вектора f, когда он попадает в ячейку Dt:
Т: = Е{{ |f ?Dt\. F.2.5)
В этом случае минимальная средне-
квадратическая ошибка квантования
равна
Рис. 6.2.1. Ячейки квантования
в векторном пространстве.
а — одномерное пространство; б —
двумерное пространство; о — трех-
трехмерное пространство.
/=о
F.2.6)
где R^ — корреляционная матрица
вектора f. Заметим, что при N == 1
формула F.2.4) сводится к F.1.11), а
выражение для ошибки квантования
F.2.6) переходит в формулу F.1.12).
Оптимальные положения квантованных векторов г;- при фик-
фиксированных ячейках квантования Dj невозможно определить,
не зная совместной плотности вероятности р (f). Однако часто
такая информация отсутствует. Еще одна существенная трудность
связана с фактическим вычислением интегралов в формуле
F.2.4). Поэтому часто приходится упрощать процедуру вектор-
векторного квантования. Так, можно квантовать все компоненты век-
Квантование изображений 153
тора f по отдельности, но задавать квантованные векторы г, с по-
помощью ячеек квантования Dy. Тогда в трехмерном пространстве
ячейки Dj превращаются в прямоугольные параллелепипеды.
Если при этом компоненты вектора f некоррелированы, то век-
векторное квантование сводится к последовательному квантованию
скалярных величин. Однако если отсчеты коррелированы, то
задача определения оптимального вектора г;, как правило, не
поддается решению без введения дополнительных упрощающих
предположений. Кэри [4] получил решения применительно
к совместным гауссовым плотностям, когда ячейки квантования D/
достаточно малы. Хунс [5] исследовал рекуррентный метод реше-
решения такой задачи, когда каждая компонента вектора определя-
определяется с помощью последовательных приближений на основе осталь-
остальных квантованных компонент вектора. Этот метод позволяет найти
решение задачи для множества различных плотностей вероятности:
в части 6 он рассмотрен как средство уменьшения ошибок кванто-
квантования в системах, использующих ИКМ и кодирование с преобра-
преобразованием.
Попытаемся теперь найти такой набор ячеек квантования Dn
при котором минимизируется среднеквадрэтическая ошибка кван-
квантования. Брюс [6] разработал метод решения этой задачи, осно-
основанный на динамическом программировании. Однако в общем
случае оптимальные формы ячеек квантования сложны и опреде-
определить их весьма трудно. Поэтому в большинстве методов векторного
квантования используется субоптимальный подход, когда для
каждой компоненты вектора задается фиксированное число
уровней квантования J (i), где i — 1, 2, ..., N, w. все компоненты
квантуются независимо. Задача оптимизации сводится в этом
случае к выбору величин J (i), произведение которых
N
nj(i) = J F.2.7)
есть фиксированное число уровней квантования для данного век-
вектора. Ошибка квантования t-ro отсчета равна
j (o-i
* @ = Е \? (i)} - Ъ г) (О Р [d, @ <: / @ < di+1 @). F.2.8)
В системах с цифровым кодированием число уровней квантования
обычно выбирают равным двоичному числу
У@ = 2*(|), F.2.9)
где Ь @ — целое число кодовых разрядов (бит) для t-й компо-
компоненты вектора. Общее количество кодовых разрядов должно быть
154 Глава 6
постоянно и равно
N
B=%b(i). F.2.10)
Такой способ квантования называется блочным.
Несколько специалистов [7—9] разработали алгоритмы рас-
распределения числа разрядов Ь (i) при фиксированном В, позво-
позволяющие минимизировать среднеквадратическую ошибку кванто-
квантования. При использовании алгоритма, предложенного Реди и
Уинцем [9] и применяемого для квантования независимых гаус-
гауссовых величин по методу Макса, следует выполнить следующие
операции:
1. Вычислить распределение числа разрядов по формуле
Ь @ = {BIN) + 2 lg [о" @1 - B/ЛО I- lg [а2 (/)], F.2.11)
/=i
где а2 (t) — дисперсия 1-го отсчета.
2. Округлить каждое из чисел Ь (i) до ближайшего целого.
3. Изменять полученное распределение, пока не будет выпол-
выполнено условие F.2.10)
Вывод соотношения F.2.11) основан на экспоненциальной ап-
аппроксимации зависимости F.1.12), связывающей ошибку кванто-
квантования t-ro отсчета и заданное ему число разрядов b (i). Если Ь (i)
невелико, то эта аппроксимация оказывается довольно грубой.
Более надежные результаты можно получить, пользуясь разра-
разработанным Прэттом [10] методом минимальной ошибки. Здесь
разряды последовательно отводятся отсчетам, которые имеют
наибольшую дифференциальную ошибку F.2.8). При квантовании
величин с нулевым средним алгоритм состоит из следующих
шагов:
Шаг 1. Определение начальных условий:
В — общее число разрядов в кодовой комбинации
блока,
N —длина блока,
а2 (п) — дисперсия компоненты,
Р {/ (п) \ — плотность вероятности компоненты,
Bs — индекс разряда (сначала равен нулю).
Шаг 2. Вычислить и запомнить коэффициенты дифференци-
дифференциальной ошибки
D[b(n)] = F[2J(n)]-F[J(n)],
где / (п) = 2* <"), а сумма
F[J(n)}= S raf[J{n))P{d,[J(n)]<i
<f{n)lo(n)<d,+l[J(n)]\
Квантование изображений 155
определяет коэффициент ошибки для случайных величин с еди-
единичной дисперсией, причем знаком тильды (~) отмечены уровни
квантования и пороговые уровни, относящиеся к таким величи-
величинам.
Шаг 3. Отвести один разряд той компоненте, для которой
произведение а2 (п) D [Ъ (п) ] имеет наибольшую величину; уве-
увеличить на единицу Ъ (п) и Bs.
Шаг 4. Если Bs = В, закончить процедуру; в противном
случае повторить шаг 3.
Коэффициенты дифференциальной ошибки D (•), необходи-
необходимые для данного алгоритма, можно вычислить заранее и хранить
в виде таблицы из N чисел. В этом случае алгоритм сводится к В
последовательным операциям распределения разрядов. Достоин-
Достоинства алгоритма состоят в том, что здесь не требуется громоздких
вычислений, а также отсутствуют ошибки аппроксимации и
округления, характерные для алгоритма с вычислением лога-
логарифмов дисперсий. Кроме того, метод минимальной ошибки опи-
опирается на модель плотности вероятности и поэтому его можно
эффективно применять для распределения разрядов при неодина-
неодинаковых плотностях вероятностей отсчетов.
6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН
Числа, описывающие изображения (например, представляющие
яркость или координаты цвета), обычно вводятся в цифровую
вычислительную машину в виде целочисленных кодовых комби-
комбинаций, соответствующих уровням квантования отсчетов. Так,
яркость одноцветного изображения обычно измеряют с помощью
линейной целочисленной шкалы, ограниченной числами 0 (уро-
(уровень черного) и 255 (уровень белого). Эти целочисленные кодовые
комбинации, однако, не следует рассматривать как арифметические
величины. Перед обработкой в машине кодовые комбинации сле-
следует преобразовать в действительные десятичные числа, соот-
соответствующие уровня квантования. Если этого не сделать, то мо-
можно получить совершенно неверные результаты. Так, если ко-
кодовые комбинации — номера уровней — изменяются вдоль шкалы
яркостей немонотонно, то их вообще нельзя использовать для
обработки. Рассмотрим теперь, что произойдет, если эти комбина-
комбинации изменяются монотонно и обрабатываются в ЦВМ без преоб-
преобразования в десятичные числа —значения уровней квантования.
Существуют две основные формы представления чисел в циф-
цифровых вычислительных машинах: как целое число и как действи-
действительное число. Целые числа изменяются от 0 до некоторого макси-
максимального значения. Так, в 16-разрядной мини-ЭВМ наибольшее
положительное целое число равно 32 768 B15). Если результат
арифметической операции определен как целое число, а в резуль-
156
Глава 6
тате получается дробное число, то дробная часть просто отбрасы-
отбрасывается. Отношение 8/3, например, будет представлено как целое
число 2 без десятичной точки и знаков после нее. Если обрабаты-
обрабатываемые величины определены как действительные числа, то
дробная часть итога операции будет сохраняться и содержать
Нелинейное
преобразование
Квантование
¦ и
кодирование
J
Восстановление
действительного
числа
rj
Нелинейное
преобразование
Целое
число
Действитель -
мое число
Действитель-
Действительное число
Кдантобание
и
иодирование
Преобразование
ubjwzo числа
в действительное
Нелинейное
преобразование
Целое
число
Действитель-
Действительное число
Действитель-
Действительное число
Рис. 6.3.1. Методы преобразования квантованных сигналов.
а — поэлементное преобразование непрерывных сигналов; б — преобразование кванто*
ванных сигналов, представленных действительными чнслаин: в — преобразование кван-
квантованных сигналов при замене кодовых комбинаций действительными чнсламн.
столько знаков, сколько позволяет получить разрядность машины.
Отношение действительных чисел 8./3. будет иметь вид 2.66...66.
На рис. 6.3.1 для сравнения представлены три способа обра-
обработки сигналов. На рис. 6.3.1, а непрерывная скалярная вели-
величина /, изменяющаяся в интервале aL ss / s? av, подвергается
преобразованию Ор \-\, в результате которого получается не-
непрерывная величина
g = Op{f\. F.3.1)
На рис. 6.3.1, б показана схема обработки, в которой скалярная
величина / перед обработкой подвергается равномерному кванто-
квантованию и кодированию. Целочисленные значения кодовых комби-
комбинаций определяются по формуле
F.3.2)
где символ [ • ]N обозначает округление аргумента до ближай-
ближайшего целого числа. Код /,. определенный как целое число, пре-
Квантование изображений 157
образуется в действительное число rt согласно соотношению
Г] = [(rj-i - ro)/(/ - 1)] / + го, F.3.3а)
или, что то же самое,
г = [(аи - aL)/J] I + [fa - aL);2J] + aL. F.3.36)
Далее с квантованным отсчетом Г/ выполняется необходимая опе-
операция и получается квантованный выходной сигнал
g1 = ap\rj\, F.3.4)
отличающийся от непрерывного выходного сигнала g, фигуриру-
фигурирующего в равенстве F.3.1), только из-за ошибки квантования ис-
исходной величины.
К сожалению, часто обработку квантованных сигналов произ-
производят неправильно—по схеме, приведенной на рис. 6.3.1, в.
Кодовая комбинация /, рассматриваемая как целое число, преоб-
преобразуется в действительное число ujy принимающее значения 0.,
1., 2., ..., (/ —1). . После этого по формуле
vJ = Op{ui\ F.3.5)
вычисляются значения выходного сигнала vjt определяемые как
действительные числа. В общем случае vf имеет и целую, и дроб-
дробную части. Если, например ы;- = 17., то после преобразования,
состоящего в извлечении квадратного корня с точностью до пя-
пятого знака, получается выходной сигнал v, = 4.12311. Ясно,
конечно, что ошибки квантования входного отсчета и,- проявятся
и в выходном отсчете v-r Однако существуют более серьезные
трудности, если считать, что vs может служить сравнительно
хорошей аппроксимацией непрерывного выходного сигнала g.
Предположим, что число уровней квантования достаточно велико
и поэтому
и,^(J—l)[(/ -aL)i(au -aL)\. F.3.6)
Тогда выходной сигнал будет равен
Vj f^Op \kj-\- k2], F.3.7)
где постоянные
ki = (J — 1)<(#и —¦ ^l)> F.3.8a)
kt = — [(¦/ — 1) а^]'(Я{/ — %). F.3.86)
Если преобразование <УР {¦ \ линейно, то
Vjtvkjpplft + kt F.3.9)
и
g^gj^ (vt- - k2)/kL. F.3.10)
Таким образом, выходной сигнал рассматриваемой системы
(рис. 6.3.1, б) будет хорошей аппроксимацией непрерывного
158 Глава 6
выходного сигнала системы с аналоговой обработкой (рис. 6.3:1, а),
если преобразование, выполняемое в системе, является линейным.
С другой стороны, если это преобразование нелинейно, то аппрок-
аппроксимация одного сигнала другим обычно оказывается очень пло-
плохой. Так, например, обычно логарифм квантованной переменной rt
существенно отличается от логарифма действительного числа и,-,
сформированного из кодовой комбинации, которая задает номер
уровня квантования для г-г
6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ
В системах передачи одноцветных изображений с применением
импульсно-кодовой модуляции (ИКМ) каждый отсчет квантуется
(обычно на основе линейной шкалы), и ему ставится в соответ-
соответствие двоичная кодовая комбинация. Как правило, применяют
равномерный код, и поэтому число уровней квантования свет-
светлоты выбирают из условия
L=2>, F.4.1)
где Ь — число двоичных разрядов (бит), отведенных для коди-
кодирования отсчетов.
В системах с ИКМ можно сократить цифровой поток простым
уменьшением числа разрядов в кодовых комбинациях. Если
имеется аналитическая мера качества изображений, передаваемых
с помощью такой системы, то величина Ь будет равна наимень-
наименьшему числу разрядов, при котором качество изображения еще
является удовлетворительным. При субъективной оценке каче-
качества величину Ь понижают до тех пор, пока эффекты, вызванные
квантованием, не выйдут за пределы допустимого. Глаз способен
определить от 10 до 15 градаций абсолютного значения светлоты,
однако он имеет гораздо большую чувствительность к различию
светлоты соседних элементов изображения. При уменьшении числа
уровней квантования прежде всего бросается в глаза эффект
появления контуров в тех областях, где светлота исходного
изображения изменяется плавно. Появление контуров вызвано
скачкообразным изменением светлоты квантованного изображе-
изображения при переходе от одного уровня квантования к другому. Наи-
Наименьшее число разрядов ИКМ, позволяющее предотвратить появ-
появление контуров в областях с плавным изменением светлоты,
зависит от ряда факторов, в том числе от линейности характе-
характеристик дисплея и свойств шума до и после преобразования изоб-
изображения в видеосигнал.
Предположим, что отсчеты на выходе датчика видеосигнала
пропорциональны яркостям элементов изображения. Возникают
вопросы: следует ли квантовать непосредственно сигнал яркости
изображения или же некоторую функцию от него и какой должна
Квантование изображений 159
быть характеристика квантователя — линейной или нелиней-
нелинейной? Последний вопрос скорее относится к практической реали-
реализации системы. Любую нелинейную характеристику квантователя
можно получить, осуществляя нелинейное преобразование кван-
квантуемого сигнала, равномерное квантование и обратное нелинейное
преобразование квантованного сигнала, как показано на схеме
рис. 6.1.3. В связи с этим здесь будет рассматриваться только
равномерное квантование отсчетов, которые предварительно могут
быть подвергнуты нелинейному преобразованию.
Известно большое число экспериментальных работ по опре-
определению количества (и расположения) уровней квантования,
необходимого для сведения к минимуму эффекта ложных конту-
контуров [11—14]. Гудолл [11] одним из первых проводил опыты
с цифровым телевидением и пришел к выводу, что для получения
хорошего качества необходимо квантовать яркостное изображе-
изображение на 64 уровня F разрядов), а при 32 уровнях E разрядах)
ложные контуры не слишком заметны. Аналогичные результаты
получили и другие исследователи. В большинстве работ в той
или иной мере затрагиваются вопросы о линейности характери-
характеристик системы воспроизведения изображений и ее калибровке.
Сигналы телевизионной камеры и видеомонитора, как правило,
нелинейно связаны с интенсивностью света. Фотоматериалы, при-
применяемые для регистрации изображений, также имеют суще-
существенно нелинейные характеристики. Отметим, наконец, что
любые шумы, создаваемые камерой или монитором, скрадывают
ложные контуры.
На рис. 6.4.1 и 6.4.2 представлены фотографии, квантованные
с разным числом уровней. На рис. 6.4.1 приведены изображения,
полученные равномерным квантованием яркости при числе уров-
уровней от 2 до 64 Aч- 6 двоичных разрядов). В темных частях изобра-
изображения заметны ложные контуры, когда число разрядов не пре-
превышает пяти. На рис. 6.4.2 показаны результаты машинного
моделирования процесса равномерного квантования оптической
плотности изображения. В этом эксперименте величины F (/, k) —
квантованные на 256 уровней (8 разрядов) отсчеты яркости,
значения которых лежат в диапазоне от 0 до 1, —были подверг-
подвергнуты логарифмическому преобразованию:
G (/, k) = {In [I + F (/, k)\ /In 2. F.4.2)
Величина G (/, k) была равномерно квантована на разное число
уровней. Функции G (/, к), описывающие изображение с кванто-
квантованной плотностью, были затем преобразованы в функции
F (/, k) = exp {G (/, к) In 2} - 1, F.4.3)
которые описывают изображения с квантованной яркостью.
Сравнение рис. 6.4.1 и 6.4.2 показывает, что при равномерном
160
Глава б
Рис. 6.4.1. Пример равномерного квантования яркости изображения.
Квантование изображений
161
Z разрядаj
'ис. 6.4.2. Пример равномерного квантования оптической плотности изобра-
изображения.
6 Прэтт У.
162
Глава 6
плотностном квантовании (рис. 6.4.2) эффект появления ложных
контуров выражен не столь заметно, как при равномерном ярко-
стном квантовании (рис. 6.4.1).
В гл. 19 рассматриваются методы цифрового кодирования
изображений, предназначенные для подавления ложных конту-
контуров, появляющихся при недостаточном числе уровней кванто-
квантования.
6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ
Цветное изображение можно описать с помощью красной,
зеленой и синей координат цвета или произвольной (линейной или
нелинейной) обратимой функции от этих величин. Если красная,
зеленая и синяя координаты цвета квантуются по отдельности,
то число и расположение уровней квантования выбираются по
тем же общим правилам, что и при квантовании одноцветных
изображений. Глаз реагирует на интенсивность света нелинейно,
и поэтому субъективно качество квантованного цветного изобра-
изображения оценивается выше, если перед квантованием подвергнуть
координаты цвета нелинейному преобразованию, сжимающему
их динамический диапазон. Известно, что глаз наиболее чувстви-
Источник
цветных
изображений
6
в
Преобразова-
Преобразователь
координат
цвета
т!1)
Х01,
Квантова-
Квантователь
?0) ^
Обратный
преобразова-
преобразователь
координат
цвета
в
в
цветной
дисплей
Рис. 6.5.1. Квантование цветных изображений.
телен к изменениям яркости в синей области спектра, умеренно
чувствителен к таким изменениям в зеленой области и наименее
чувствителен в красной области. Учитывая это, можно получить
более эффективное распределение уровней квантования, чем рав-
равномерное.
На рис. 6.5.1 представлена обобщенная блок-схема системы
квантования цветных изображений. Три координаты цвета RN,
GN, BN, описывающие исходное изображение, преобразуются
в три компоненты вектора х A), х B), х C), которые и поступают
в квантователь. Затем квантованные компоненты х A), х B)
и х C) преобразуются обратно в исходную координатную систему;
в результате получается три координаты RN, GN, BN. Кванто-
Квантователь (рис. 6.5.2) по существу разделяет на ячейки квантования
цветовое пространство, имеющее координаты х A), х B) их C),
и ставит в соответствие всем цветовым сигналам, попадающим
в ячейку, одно и то же значение. Для большей эффективности
следовало бы квантовать три цветовые компоненты х A), х B)
Квантование изображений
163
и х C) совместно. Однако по техническим причинам часто при-
приходится квантовать цветовые компоненты независимо. В этом
случае цветовое тело заключается в прямоугольный параллеле-
параллелепипед, который делится на прямоугольные ячейки квантования.
Если координаты цвета преобразуются в какую-то другую
координатную систему, то сразу же возникают трудности. Рассмо-
Рассмотрим, например, квантование координат цвета в системе UVW.
На рис. 6.5.2 показано тело воспроизводимых цветов для системы
/ Зеленый Желтый
Галу5ой
белый
/Красный
Голубой
Синий
'Пурпурный
Желтый
Красный
Черный у
Пурпурный
"Синий
UVW
Рис. 6.5.2. Тело воспроизводимых цветов в системах координат R^GNB^ и UVW.
Rf/jNBN, представленное в форме куба, а также дан вид этого
куба после преобразования его в координатную систему UVW.
Можно заметить, что куб RNGNBN превращается в параллеле-
параллелепипед. Если координаты U, V, W квантуются независимо друг
от друга, а диапазон квантования каждой из них охватывает
весь интервал от минимального до максимального значения, то
много ячеек квантования попадает в области невоспроизводимых
цветов и поэтому оказываются бесполезными. Было бы жела-
желательно размещать все ячейки квантования внутри параллелепи-
параллелепипеда воспроизводимых цветов, но, как правило, такую операцию
сложно осуществить на практике.
Предположим для упрощения анализа, что каждая компонента
квантуется равномерно на 2*(l) уровней, причем b (i) обозначает
число разрядов, отведенных для квантования компоненты х (i).
Общее число таких разрядов фиксировано и равно
^Б = Ь A) + Ь B) + ЬC). F.5.1)
Допустим, что аи (i) обозначает верхнюю, a aL (i) — нижнюю
границу диапазона значений компоненты х (i). Тогда размеры
ячеек квантования равны
?@ = [%@-М0]/2*(°. F.5.2)
164
Глава 6
Все цвета, цветовая компонента которых х (i) попадает в одну
и ту же ячейку, в ходе квантования будут заменяться одним
цветом с квантованным значением х (i) этой компоненты. Ошибка
квантования по каждой компоненте равна
е @ = | х @ - х @1 = [аи@ - aL (i)]/2b U)+1. F.5.3)
0,40
0,30
0,20
Зеленый
г y~~
Голу Sou %
L \
( Синий
Желтый
~3—
? белый
>
1 1
~~ 3=
* Пурпурный
i
Красный
^-
I
0,40
0,30
0,20
0,10
о,ю
Зеленый
0,20 0,30 0,40 0,50
и
а
Желтый
Голубой
Красный
О 0,10 0,20 0,30 0,40 0,^0
и
б
Рис. 6.5.3. Смещение цветов при равномерном квантовании изображения «Порт-
«Портрет» [15].
а — смещение цветов при квантовании в системе координат R^N^N' " — смещение цве-
цветов при квантовании р системе координат Yuv.
О 4 разряда на каждую из трех координат;
Л 5, 4, 3 разряда на соответствующие координаты.
Тогда координата квантованного цвета
x(i) = x(i) *e(t), F.5.4)
причем aL (i) «s x (i) =c av (i). Следует заметить, что значения
х (i) всегда будут находиться внутри наименьшего куба, окружа-
окружающего цветовое тело, для данной цветовой координатной системы.
Квантование изображений 165
На рис. 6.5.3 показаны смещения различных цветов при кванто-
квантовании в системах координат RNGNBN и Yuv [15].
Джейн и Прэтт [15] рассмотрели вопрос об оптимальном
распределении пороговых уровней при квантовании цветных
изображений, позволяющем уменьшить до возможного предела
цветовое расстояние между исходным цветом и его квантованным
значением. Было установлено, что квантование в координатной
системе RNGNBN дает лучшие результаты, чем в других распро-
распространенных цветовых координатных системах. Это объясняется
тем, что в системе RNGNBN эффективно используются все ячейки
квантования, а в других системах многие ячейки оказываются
незанятыми. Последнее, по-видимому, существеннее, чем метриче-
метрическая неоднородность цветового пространства RNGNBN.
ЛИТЕРАТУРА
1. Panter P. F., Dite W., Quantization Distortion in Pulse Code Modulation
with Non-uniform Spacing of Levels, Proc. IRE, 39, 1, 44—48 (January 1951).
2. Max J., Quantizing for Minimum Distortion, IRE Trans. Inf. Theory, IT-6,
1, 7—12 (March 1960).
3. Algazi V. R., Useful Approximations to Optimum Quantization, IEEE Trans.
Commun. Tech., COM-14, 3, 297—301 (June 1966).
4. Curry R., Estimation and Control with Quantized Measurements, MIT Press,
Cambridge, Mass., 1970.
5. Huhns M., Optimum Quantization Restoration, University of Southern Cali-
California, Image Processing Institute Report 600, September 1975.
6. Bruce J. D., Optimum Quantization, MIT Research Laboratory of Electro-
Electronics, Technical Report 429, March 1965.
7. Huang J. J. Y., Schutheiss P. M., Block Quantization of Correlated Gaus-
Gaussian Random Variables, IEEE Trans. Commun. Syst., CS-11, 3, 289—296 (Sep-
(September 1963).
8. Ready P. J., Wintz P. A., Multispectral Data Compression Through Trans-
Transform Coding and Block Quantization, Purdue University, Laboratory for Ap-
Applications of Remote Sensing, Information Note 050572, May 1972.
9. Wintz P. A., Kurtenbach A. J., Waveform Error Control in PCM Telemetry,
IEEE Trans. Inf. Theory, IT-14, 5, 650—661 (September 1968).
10. Pratt W. K-. Block Quantization Bit Assignment (частное сообщение).
11. Goodall W. M., Television by Pulse Code Modulation, Bell Syst. Tech. J.
(January 1951).
12. Cabrey R. L., Video Transmission over Telephone Cable Pairs by Pulse Code
Modulation, Proc. IRE, 48, 9, 1546—1551 (September 1960).
13. Harper L. H., PCM Picture Transmission, IEEE Spectrum, 3, 6, 146 (June
1966).
14. Scoville F. .W, Huang T. S., The Subjective Effect of Spatial and Bright-
Brightness Quantization in PCM Picture Transmission, NEREM Record, 1965,
pp. 234—235.
15. Jain A. K-, Pratt W. K-, Color Image Quantization, National Telecommu-
Telecommunications Conference 1972 Record, IEEE Publication No. 72 CHO 6Q1-5-NTC,
Houston, Texas, December 1972.
Глава 7
МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ
ИЗОБРАЖЕНИЙ
При кодировании изображений для хранения или передачи
с помощью минимально возможного количества цифр требуется
сохранить качество воспроизводимого изображения в допустимых
пределах. Для повышения визуального качества изображения
разрабатываются системы улучшения изображений. Системы ис-
исправления изображений предназначаются для компенсации иска-
искажений и создания изображений, приближающихся к тем, которые
были бы получены с помощью идеальной системы, не вносящей
искажений. Во всех трех задачах общим является вопрос о ка-
качестве изображения — о том, чтобы в процессе обработки изобра-
изображений поддерживать, повышать или восстанавливать его.
Качество изображения можно оценивать двояко: либо опре-
определяя верность воспроизведения, либо оценивая дешифрируемость
изображения. Верность воспроизведения характеризует степень
отклонения обработанного изображения от некоторого эталон-
эталонного, а дешифрируемость указывает, в какой степени человек или
машина может извлечь из изображения полезную информацию.
Чаще всего верность воспроизведения связана с небольшими раз-
различиями между обработанным и эталонным изображениями.
О дешифрируемости же, напротив, говорят, как правило, в связи
с большими различиями между этими изображениями. •>
Очевидно, что количественные меры верности и дешифрируе-
дешифрируемости изображения очень нужны для проектирования и оценки
систем воспроизведения изображений. Эти меры во многом по-
помогут избавиться от трудоемкой и подчас неточной современной
методики оценки изображений посредством субъективной экспер-
экспертизы. Кроме того, на основе количественных мер можно развивать
методы оптимизации систем обработки изображений.
В разработке количественных критериев верности и дешифри-
дешифрируемости изображений достигнуты значительные успехи. Однако
введенные критерии не являются достаточно совершенными:
очень часто можно привести примеры изображений, качество
которых формально оценивается как высокое, а субъективно —
как низкое и наоборот. Создание более совершенных критериев
оценки качества изображений связано, несомненно, с более глу-
глубоким изучением свойств зрительной системы человека.
Меры качества дискретизоеанных изображений 167
7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
В настоящее время наиболее распространенным и самым на-
надежным способом определения качества изображений является
субъективная экспертиза [1—7]. В некоторых случаях в качестве
экспертов привлекают наблюдателей-неспециалистов. Их оценки
определяют качество изображения именно так, как его воспри-
воспринимает «средний» наблюдатель. Кроме того, проводятся опыты со
специалистами, имеющими опыт обработки изображений, от кото-
которых следует ожидать более обоснованных оценок качества. Предпо-
Предполагается, что опытные наблюдатели замечают небольшие погреш-
погрешности изображения, которые неспециалист может проглядеть.
Существуют два вида экспертных оценок: абсолютные и сравни-
сравнительные. В первом случае наблюдатель должен оценить качество
изображения по какой-то заранее определенной шкале. При
некоторых методиках процесс оценивания облегчается тем, что
наблюдателю предоставляется также набор эталонных изобра-
изображений. Существуют и другие методики, когда наблюдатель вы-
вынужден принимать решение только на основании своего собствен-
собственного опыта. При сравнительных оценках наблюдатель должен
ранжировать набор конкретных изображений, т. е. расставить их
в ряд по убыванию качества.
Распространенным видом шкалы оценок является шкала
«общего качества», когда изображениям приписываются баллы,
которые соответствуют градациям от «неудовлетворительно» до
«отлично», приведенным в табл. 7.1.1 [1]. На практике каждое
изображение поступает к наблюдателю, и он выставляет балл той
категории, которая, по его мнению, в наибольшей степени соот-
соответствует качеству изображения. Вариантом данной шкалы яв-
является шкала «места в группе», или относительная шкала
(табл. 7.1.2), когда наблюдатель оценивает качество изображения,
сравнивая его со всеми другими изображениями, входящими
в рассматриваемую группу [2]. Еще одной распространенной
шкалой оценок является шкала погрешностей, согласно которой
наблюдатель должен оценить в баллах степень искажений, изме-
изменяющихся от «незаметных» до «крайне нежелательных». Эта
шкала, составленная Мерцем, Фаулером и Кристофером [3 ],
приведена в табл. 7.1.3. Несколько других шкал оценки качества
описаны в работе Пирсона [1].
Результаты экспертных оценок обычно выражают с помощью
среднего балла, определяемого как
Znft, G.1.1)
где nk — число изображений, отнесенных к k-й категории, &Ck —
соответствующий ей балл. Считается, что для получения надеж-
168 Глава 7
ной оценки качества изображения необходимо опросить не менее
двадцати наблюдателей. Одной из трудностей, связанных с балль-
балльными оценками, является возможная нелинейность шкалы. На
рис. 7.1.1 для сравнения помещены шкала абсолютного (общего)
качества (табл. 7.1.1), шкала погрешностей (табл. 7.1.3) и еще
Таблица 7.1.1
Шкала общего качества (абсолютная шкала)
5. Отлично
4. Хорошо
3. Посредственно
2. Плохо
1. Неудовлетворительно
Таблица 7.1.2
Шкала места в группе (относительная шкала)
7. Лучшее в группе
6. Заметно лучше среднего для данной группы
5. Несколько лучше среднего для данной группы
4. Среднее по группе
3. Несколько хуже среднего для данной группы
2. Существенно хуже среднего для данной группы
I. Самое плохое в группе
Таблица 7.1.3
Шкала погрешностей
1. Незаметные
2. Еле заметные
3. Вполне заметные, но слабо ухудшающие изображение
4. Ухудшающие изображение, но допустимые
5. Несколько нежелательные
6. Определенно нежелательные
7. Крайне нежелательные
одна шкала погрешностей, состоящая из трех градаций. Сравне-
Сравнение шкал выполнено на основе субъективных оценок [1].
Следует подчеркнуть, что на результаты субъективных эксперт-
экспертных оценок влияют характер рассматриваемых изображений и
окружающая обстановка (условия эксперимента). Если наблю-
наблюдатель видел подобные изображения, то он склонен более строго
оценивать погрешности, поскольку имеет сложившееся представ-
представление о структуре изображения. С другой стороны, в незнакомом
изображении искажения могут оставаться незамеченными, пока
наблюдателю не будет на них указано. Ясно, что условия экспе-
эксперимента должны в максимально возможной степени соответство-
соответствовать условиям наблюдения в реальной обстановке. Кроме того,
Меры качества дискретизованных изображений
169
следует с осторожностью пользоваться экспертными оценками,
если изменились условия наблюдения. Так, качество изображения
на экране обычного телевизионного монитора может быть расце-
0,0
0,1-
0,2-
0,3-
0,4-
0,5-
0,6-
0,7-
0,8-
0,9-
1,0-
т Отлично
. Не дидно никаких^ Незаметно
погрешностей
¦ Еле дидно
Хорошо
Посредственно
Плохо
Неудодлет-
Ьрительно
Определенно
дидно
- Еле заметно
Заметно, но слабо
ухудшает снимок
Ухудшает снимок, но
допустимо
Несколько нежела-
нежелательно
Определенно
нежелательно
- ¦ Крайне нежелательно _
Рис. 7.1.1. Сравнение шкал качества и погрешностей, применяемых для субъек-
субъективной оценки изображений.
нено как «хорошее», с «еле заметными» искажениями. Однако если
то же самое изображение будет представлено в виде фотографии,
снятой с помощью высококачественной аппаратуры, то все по-
погрешности, ранее скрытые нелинейностями телевизионного ус-
устройства, неожиданно могут стать очень заметными.
170 Глава 7
7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ
И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ
Телевизионные системы обычно проверяют и испытывают
с помощью эталонных изображений, которые либо генерируются
электронными устройствами, либо получаются обычным путем,
когда перед камерой помещают испытательные таблицы. Этот
Амплитуда
1,0
Рис. 7.2.1. Пример оценки искажений сигнала с помощью фактора К [8].
метод удобен благодаря его простоте, но связь результатов таких
испытаний с результатами субъективной экспертизы, как пра-
правило, оказывается весьма сложной.
В аналоговых телевизионных системах искажение сигнала в ка-
канале связи часто оценивают сравнением переданного и приня-
принятого сигналов. Рис. 7.2.1 поясняет полуколичественную мето-
методику такого сравнения [8]. Испытательный сигнал (рис. 7.2.1, а)
называют синус-квадратным импульсом. Принятый сигнал
(рис. 7.2.1, б) заключают в рамку допусков, размеры которой
определяются параметром /С, и находят наименьшее значение
параметра. Это значение выражает степень искажений.
С помощью испытательных электрических сигналов можно
проверить наличие геометрических искажений, линейность пере-
передачи яркости и разрешающую способность телевизионного мони-
монитора. На рис. 7.2.2, а и 7.2.2, б помещены фотографии сформиро-
сформированных электронными средствами испытательных изображений,
Меры качества дискретизованных изображений
171
применяемых для оценки геометрических искажений. Эти же
изображения позволяют обнаружить несведение лучей в цветном
телевизоре. Фотография шкалы градаций яркости, также сформи-
сформированной электронными средствами, приведена на уэис. 7.2.2, в.
Линейность передачи яркостей можно оценить сравнением ампли-
амплитуды сигнала с интенсивностью светового излучения от соответ-
Рис. 7.2.2. Фотографии испыта-
испытательных таблиц, сформирован-
сформированных на экране ЭЛТ.
а — точечная решетка; б — сетка:
в — яркостный клин.
ствующих вертикальных полос на экране. Для проверки цветных
телевизоров разработана таблица, состоящая из вертикальных
полос белого, желтого, голубого, зеленого, пурпурного, крас-
красного и синего цветов [9—11].
Разрешающую способность можно определить, измеряя рас-
распределение интенсивности излучения в направлении, перпенди-
перпендикулярном границам полос.
Применение испытательных сигналов и таблиц позволяет изме-
измерить некоторые физические характеристики изображающих си-
систем. Учитывая это, трудно переоценить полезность подобных
методов для калибровки и настройки таких систем. Однако ре-
результаты испытаний по сигналам и таблицам не могут служить
достаточно общими показателями качества изображения.
172 Глава 7
7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА
Первый шаг в создании критерия верности воспроизведения
изображения — это введение метрики для количественного изме-
измерения воспринимаемых различий в яркости, цветовом тоне и
насыщенности точечного источника света. Существуют два вида
мер различий характеристик света: глобальные и локальные.
Глобальные меры пригодны для описания свойств любых источ-
источников света независимо от конкретных особенностей восприятия
этого света. Локальные меры характеризуют только небольшие
изменения параметров, описывающих световые ощущения.
7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА
Рассмотрим источник белого света [Z,x], имеющий яркость Y
и расположенный в непосредственной близости от второго источ-
источника белого света [L2], имеющего такой же спектр излучения
и яркость Y + АУ. Измерения контрастной чувствительности,
описанные в разд. 2.3, показали, что отношение Вебера AYIY,
т. е. отношение едва заметной (пороговой) разницы яркостей к аб-
абсолютному значению яркости Y, в довольно широком диапазоне
значений Y почти постоянно и равно 1-—2 %. На этом основании
можно утверждать, что приращение светлоты второго источника
по отношению к первому должно определяться логарифмическим
выражением
I \ ] Y)\ogb(Y), G.3.1)
а не разностью яркостей AY. Поскольку дифференциал лога-
логарифма яркости равен
d[Ь& (Y)] = lim [log* (Y + AY) - log*(Y)] = log6 (e) (dY/Y), G.3.2)
ДУ-+О
то приращение логарифма яркости равно отношению Вебера.
Манное и Сакрисон [2] изучали возможность измерения верности
воспроизведения одноцветных изображений с помощью соотно-
соотношения B.4.8). В этом случае мерой приращения светлоты стано-
становится величина
A\Llt U} = {Y + AY)V-(Y)\ G.3.3)
где v—постоянная. В работе Корнсвита [12] было сделано
предположение о том, что отклик фоторецепторов сетчатки глаза
описывается нелинейным законом B.4.7). Тогда соответствующая
мера приращения светлоты
A {Lj, L2\ = [/С, (Y + AY)VlKt + (У + AF)] —
— KiYUKt+Y), G.3.4)
где Ki и Kz — постоянные.
Меры качества дискретизованных изображений
173
Меры G.3.1), G.3.3) и G.3.4) относятся к локальным мерам
изменения светлоты. Часто используются и глобальные меры,
которые служат для сравнения яркостей сильно различающихся
источников света. Такие меры были получены на основе эмпириче-
эмпирических моделей, построенных на экспериментальном материале.
На рис. 7.3.1 приведены графики зависимости светлоты Л от
Рис. 7.3.1. Шкалы светлоты.
25 SO
Яркость У, %
75
яркости источника белого света. Прист, Гибсои и Макниколс
[13] предложили простое соотношение
Л=(ГI/2, G.3.5)
где яркость измеряется в процентах @ ^ Y ^ 100), а светлота
изменяется от 0 до 10. Лэдд и Пинни [14] использовали шкалу
с кубическим корнем
Л = 2,468 (КI/3 - 1,636, G.3.6)
где яркость также измеряется в процентах. В дополнение к этим
зависимостям Фосс [15] ввел логарифмическую шкалу:
Л = 5 )g Y + 0,25. G.3.7)
Различие между тремя кривыми, приведенными на рис. 7.3.1,
обусловлено главным образом различием уровней фонового осве-
освещения, применявшегося в соответствующих экспериментах [16,
стр. 453]. Джадд [17] ввел шкалу светлоты, где учитывается
уровень фонового освещения YB. В этом случае светлота опре-
определяется выражением
Л = [0,1 Г (YB + 100) ]/(YB + Y). G.3.8)
Интересно отметить, что эмпирическая шкала Джадда по своей
форме аналогична соотношению B.4.7), описывающему нелиней-
нелинейную модель отклика фоторецепторов сетчатки.
174 Глава 1
7.3.2. МЕТРИКИ ЦВЕТА
Для определения цветовых различий можно ввести детермини-
детерминированную меру, если рассматривать цветовое пространство,
определяемое тремя координатами цвета, как евклидово простран-
пространство. Тогда цвет [С^], заданный значениями трех координат 7\,
Тг и Т3, будет отделен от цвета [Са] с координатами цвета 7\ +
+ Д7\, Тг + АТ2 и Ts + AT3 расстоянием A \Clt Сг], опреде-
определяемым соотношением
A2 \Clt С2] = (Д7\J + (АГ2J + (АГ3J. G.3.9)
Если данная мера различия цветов согласуется с субъективными
представлениями, то при всех значениях координат цвета одина-
одинаковые приращения А \Си Cz\ должны соответствовать одинако-
одинаковым едва заметным (пороговым) различиям цветов. Другими
словами, уравнение А2 {Сг, Сг\ = 1 должно описывать сферу
радиуса в одну пороговую единицу различия цветов с центром
в точке (Ть Тг, Т3). Исключением являются только те точки, ко-
которые соответствуют чистым основным цветам — красному, зеле-
зеленому и синему. Эксперименты показали, что человеческое зрение
наиболее чувствительно к единичным изменениям синей коорди-
координаты цвета, а наименее чувствительно —к зеленой [18].
Чтобы достигнуть лучшего соответствия меры G.3.9) резуль-
результатам субъективных испытаний, можно положить, что цветовое
пространство является римановым. По определению расстояние
в римановом цветовом пространстве выражается как
_|1^(,)(/) G.3.10)
где коэффициенты gtj являются функциями 7\, Т2, Т3. Прирав-
Приравняв выражение G.3.10) единице, получим уравнение эллипсоида
с центром в точке G\, Тг, Т3). Установлено, что цвета, едва за-
заметно отличающиеся от данного цвета, можно довольно точно
описать эллипсоидами в пространстве основных цветов.
Выражение G.3.10) применяется в колориметрии в качестве
меры различия цветов, если расстояние между ними не превышает
нескольких пороговых единиц. Если же цвета различаются силь-
сильнее, то следует суммировать элементарные приращения вдоль
кратчайшего пути, соединяющего соответствующие точки цвето-
цветового пространства. Тогда глобальная мера различия цветов будет
задана соотношением
d\Cv QHEM^, C2\.. G.3.11)
вдоль кратчайшего пути
Меры качества дискретизованных изображений 175
В евклидовом пространстве таким кратчайшим путем является
прямая линия. В римановом пространстве кратчайший путь,
называемый геодезической линией, в общем случае проходит вдоль
некоторой кривой. Мут и Перселс [19], а также Джейн [20]
составили программы для вычисления расстояний между цветами,
основанные на построении геодезических линий в пространстве
цветов. На основе этих программ удалось создать весьма точную
метрику цветового пространства, но для проведения вычислений
требуется много времени.
Пользоваться римановой метрикой G.3.10) сравнительно
сложно, поэтому естественно возникает вопрос, существует ли
такое отображение трехмерного пространства с координатами 7\,
Т2, Т3 на евклидово трехмерное пространство с координатами 7\,
Тг, Т3, при котором метрика различия цветов сохраняется неизмен-
неизменной. В этом новом пространстве приращения координат цвета
должны удовлетворять соотношению
А2 \С1г Сг\ = (ATt)« + (Af,J + (AfзJ, G.3.12)
так, чтобы поверхность едва различимых цветов представляла
собой сферу с центром в точке G\, Т~, Т\). Было показано [16,
стр. 513], что в общем случае не существует линейного преобра-
преобразования, в точности обладающего требуемыми свойствами. Однако
было найдено несколько линейных преобразований со свойствами,
близкими к заданным. Международная комиссия по освещению
(МКО) приняла систему координат UVW, основанную на работах
Джадда [21] и Мак-Адама [22]. В этой системе расстояния между
цветами на пороге различения оказываются почти одинаковыми.
На рис. 7.3.2, а приведены результаты измерений едва заметных
отличий цветов, выполненных Мак-Адамом [23]. Множества
едва отличимых цветов аппроксимированы эллипсами и пред-
представлены на графике цветностей в координатах х, у. Если эти же
данные представить на графике цветностей с координатами и, v
(рис. 7.3.2, б), то эллипсы становятся более близкими по разме-
размерам и заметно округляются. Фарнсуорт [24] нашел нелинейное
преобразование, в результате которого эллипсы Мак-Адама
(в пределах точности измерений Мак-Адама) превращаются
в окружности (рис. 7.3.3). К сожалению, это преобразование
выражается в виде сложной функции координат цветности х и у
и требует выполнения громоздких вычислений.
В системе координат UVW расстояние между цветами рав-
равняется
А2 \СЪ Сг\ = kt. (AUJ + A, (AVT + fc3 (АJ, G.3.13)
где kt — постоянные.
Человеческий глаз более чувствителен к изменению оттенков
темных цветов. Стремясь использовать это обстоятельство, МКО
176
Глава 7
0,6
Рис. 7.3.2. Эллипсы Мак-Адама для пороговых различий цветов в системах коор-
координат XYZ и UVW [23]. Размеры эллипсов увеличены в 10 раз.
а — график цветностей в координатах**, у; б — график цветностей в координатах и, V.
Меры качества дискретизованных изображений
177
временно ввела в качестве стандартов системы координат Lab
и U*V*W*, в которых изменения цветности и светлоты должны
быть заметны в равной степени [25]. В этих системах различие
цветов определяется величинами
Л2 \Си С2\ = h (ALJ + k2 (ДаJ + k3 (Ab)\ G.3.14a)
А2 \Clt Сг\ = h (AU*J + k2 (AV*J + h {AW*f. G.3.146)
Одним из недостатков меры различия цветов в системе U*V*W*
является неразличимость разницы в цветовом тоне и насыщен-
насыщенности цвета. Считается, что различия в цветовом тоне гораздо
более заметны, чем различия в насыщенности цвета. Поэтому
была введена система координат SQW, в которой S пропорцио-
5Я) 530 5ЗД 550
k-_ s,™ **Ss
MO %
^- ******
Рис. 7.3.3. Нелинейное преобразование эллипсов Мак-Адама на графике цвет-
ностей в системе координат XYZ [24].
нально насыщенности, а 0—цветовому тону [26, стр. 152].
Различие цветов в этой системе измеряется величиной
A2 \Clt Сг\ = ki. (ASJ + k2 (A6J + ks (AW*J- G.3.15)
Если цвет имеет очень слабую насыщенность, т. е. близок к серому,
то изменения цветовою тона не имеют особого значения. На этом
основании была введена еще одна мера различия цветов [26,
стр. 152]:
А2 \С1г С2\ = Ь (ASJ + k% [(Si + S8)/21« (A8J +
+ ka{AW*J. G.3.16)
178 Глава 7
Все приведенные выше формулы являются результатами попыток
создать субъективно-однородную меру цветовых различий. Экспе-
Экспериментов, которые позволили бы определить ценность каждой
из них, проведено мало, так что вопрос о выборе подходящей
меры все еще остается открытым.
7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ
ИЗОБРАЖЕНИЙ
Построению и развитию системы количественных мер верности
воспроизведения одноцветных изображений уделялось большое
внимание [27—32]. Разумные меры верности должны хорошо
согласовываться с результатами субъективных оценок для ши-
широкого класса изображений, не требуя при этом чересчур сложных
вычислений. Кроме того, желательно, чтобы эти меры имели
простую аналитическую форму и их можно было бы применять
в качестве критериев оптимальности при оптимизации или выборе
параметров систем обработки изображений.
Количественные меры верности воспроизведения одноцветных
изображений можно разделить на две группы: одиночные и пар-
парные. Одиночная мера представляет собой число, сопоставляемое
любому изображению на основе анализа его структуры. Парная
мера является числовым результатом взаимного сравнения двух
изображений.
Измерения верности в цифровой системе обработки изображе-
изображений можно провести, используя либо непрерывное изображение,
сформированное из массива отсчетов, либо сам этот массив. Обычно
предпочитают второй способ, так как он проще с практической
точки зрения. Однако, для того чтобы измерения на массиве
отсчетов согласовывались с результатами субъективных оценок,
воспроизводящее устройство не должно создавать больших или
по крайней мере непредсказуемых искажений изображения.
Ниже сначала будут введены меры верности изображений, полу-
получаемые на основе непрерывных двумерных функций, а затем пред-
представлены их дискретные варианты и описано соотношение между
ними.
Рассмотрим непрерывную функцию F (х, у), описывающую
изображение, которая определена в прямоугольной области —Lxss.
^i^ Lx, —L,j ^ у sg; Ly. Предположим, что эта функция
получена путем двумерной интерполяции массива отсчетов изоб-
изображения F (/, k) [при —J s=: / s^ J и —К «s k ==? К1 согласно
соотношению
F(x, </)== !¦ I F(i, k)R(x-jAx, y-kAy), G.4.1)
где R (x, у) — непрерывная интерполяционная функция, а А*
и Аг/ — шаги дискретизации.
Меры качества дискретизованных изображений 1?9
Одиночную оценку верности в общем виде можно представить
соотношением
Q= j j O\F(x, y)\dxdy, G.4.2)
где О \-\ —некоторый (возможно, нелинейный) оператор. Кри-
Критерии верности часто формулируют с использованием преобра-
преобразований Фурье. В таком случае обобщенная форма одиночной
меры верности имеет вид
оо оо
Q= j J О \@~(а>х, (o^dtojcdaij,, G.4.3)
—оо —оо
где & ((ох, со,,) — непрерывный двумерный спектр Фурье изоб-
изображения F (х, у). Одна из наиболее простых мер подобного рода —
предложенное Штрелем [33, стр. 461 ] отношение
00 ОО
I 1
f
dtox doty
. G.4.4)
где ^"/(co^, о)у) —спектр исходного изображения. Первоначально
это отношение использовалось для оценки качества элементов
оптических систем. Спектральные составляющие оптического
изображения в некоторой реальной оптической системе обычно
уменьшаются по величине и, возможно, изменяются по фазе по
сравнению с теми же составляющими в идеальной (безаберрацион-
(безаберрационной) оптической системе, свойства которой ограничиваются только
дифракционными явлениями. Составляющие с высокими про-
пространственными частотами, как правило, ослабляются в наиболь-
наибольшей степени. С учетом определения преобразования Фурье A.6.6а)
отношение Штреля G.4.4) сводится к F (О, 0)/F. (О, 0), т. е.
к отношению центральных отсчетов реального и идеального изоб-
изображений. Таким образом, отношение Штреля по существу является
простой мерой уменьшения контраста реального изображения по
сравнению с идеальным. Отношение Штреля в некоторой степени
соответствует субъективным представлениям о качестве изобра-
изображения, однако эксперименты показывают, что это соответствие
не всегда полное. В частности, известны примеры изображений,
которые обладали достаточно высокой дешифрируемостью, не-
несмотря на то что отношение Штреля для них было небольшим
[34].
180 Глава 7
Другим классическим примером одиночной меры верности
изображения служит величина эквивалентного прямоугольника
пропускания, равная по определению [35]
оо
G.4.5)
—оо —оо
При возведении в квадрат возрастает вес составляющих изобра-
изображения с низкими пространственными частотами, поскольку они,
как правило, имеют большую величину. Однако и эта мера также
не очень хорошо согласуется с результатами субъективных испы-
испытаний.
Попытки создания парных мер качества изображения имели
несколько больший успех. Рассмотрим пару изображений, со-
состоящую из некоторого эталонного (или идеального) изображе-
изображения F (х, у) и его искаженного варианта F (х, у). Одной из мер
«близости» двух изображений является их взаимная корреляция,
равная по определению
/F(x,y)F(x,y)dxdy. G.4.6)
~Lx ~Ly
Обычно взаимную корреляцию нормируют относительно энергии
эталонного изображения так, чтобы ее максимальное значение
равнялось единице. Нормированная взаимно-корреляционная
мера — коэффициент корреляции — имеет вид
j F(x,y)F(x*y)dxdy
\
G-4.7)
[F(x,y)Fdxdy
Согласно теореме Парсеваля A.6.16), значения коэффициента
корреляции можно вычислить по спектрам на основе соотноше-
соотношения
оо
I
jj | У (ах, <ov) |2 dax duty
ыу) dax da>y
G.4.8)
При восприятии изображений важную роль играют контуры
предметов. Поэтому Эндрюс [36] предложил пользоваться коэф-
Меры качества дискретиэованных изображений 181
фициентом корреляции лапласианов изображений, определяе-
определяемым как
оо
J J
К
Ж = ^=_ G.4.9)
Напомним, что в силу соотношения A.6.19) умножение спектра
?" (со*, o)j,) на квадрат частоты эквивалентно применению опера-
оператора Лапласа, что приводит к обострению контуров изображения,
описываемого функцией F (х, у). Эксперименты, выполненные
Эндрюсом на изображениях, которые были преобразованы с по-
помощью фильтров низких и высоких пространственных частот,
показывают, что обычный коэффициент корреляции остается до-
довольно большим даже в том случае, когда очень сильно подав-
подавлены высоко- и среднечастотные компоненты изображения и
субъективно оно воспринимается как низкокачественное, а коэф-
коэффициент корреляции лапласианов быстро уменьшается при су-
сужении полосы низкочастотного фильтра. Можно, однако, полу-
получить низкокачественные изображения с большими искажениями
в области низких пространственных частот, для которых коэф-
коэффициент корреляции лапласианов оказывается сравнительно
большим.
Еще одним парным критерием верности изображений является
нормированная абсолютная ошибка ¦— разность функций, описы-
описывающих эталонное и искаженное изображения:
J \
L h
\O{F{x.y))-O{F(x,y))\dxdy
G.4.10)
\O{F(x,y)}\dxdy
При обработке изображений в качестве меры ошибки чаще всего
применяется нормированная среднеквадратическая ошибка, рав-
равная
J fl0(F(x,y))-0{P(x,y))pdxdy
Ш^ LX "*¦* Ч G.4.11)
J ] [0{F(x,y)}l*dxdy
182 Глава t
На практике обычно предпочитают пользоваться среднеква-
дратической, а не абсолютной ошибкой, поскольку первая удоб-
удобнее для анализа, чем вторая. Именно поэтому проводились уси-
усиленные поиски таких преобразований, при которых средне-
квадратическая ошибка преобразованной функции была бы хо-
хорошо согласована с субъективными оценками. В основном, ко-
конечно, рассматривались пространственные линейные и поэлемент-
поэлементные нелинейные преобразования. Довольно много внимания уде-
уделялось степенным, а также логарифмическим преобразованиям.
Исследовались операторы линейных пространственных преобра-
преобразований, такие, как оператор градиента, оператор Лапласа и опе-
оператор свертки. Кроме того, рассматривались комбинации выше-
вышеупомянутых поэлементных и пространственных преобразований.
Выражение для ошибки можно также представить с помощью
спектральных характеристик. В этом случае нормированная
среднеквадратическая ошибка определяется соотношением
¦ (<лх, со,,)} — О [У (co.v, <Лу]
G.4.12)
Интересный частный случай линейного преобразования —это
частотное взвешивание, когда
О {Т К, со,)} = W К, о>у) Т (со,, о,), G.4.13)
где Ж (оо*, ау) — весовая функция. Выражение для частотно-
взвешенной среднеквадрэтической ошибки получается в виде
оо
J J | Г
J J
(<ох, щ) - Т К, в>у) |2 da>x da>y
G.4.14)
„ со^) |2 d<ox
Следует отметить, что формула G.4.14) совершенно эквивалентна
выражению G.4.11) для среднеквадратической ошибки, если опе-
оператор О \ •) соответствует свертке, осуществляемой линейным
фильтром с частотной характеристикой
5»К, «о„) = |У((о„ соу)|2. G.4.15)
Уайлдер [37] провел глубокое исследование свойств абсо-
абсолютной и среднеквадратической ошибок в дискретной форме
применительно к степенному, логарифмическому и градиентному
преобразованиям, а также к преобразованию Лапласа. Искажен-
Искаженные образцы изображений получались моделированием процесса
Меры качества дискретизованных изображений 183
кодирования исходного изображения с помощью различных
алгоритмов. Было выяснено, что поэлементные преобразования
в сочетании с критериями абсолютной и среднеквадратической
ошибок не позволяют получить критерия верности, согласующегося
с субъективными оценками. Меры ошибки, основанные на преоб-
преобразовании Лапласа и градиентном преобразовании, имеют наиболь-
наибольшую корреляцию с субъективными оценками, но коэффициент
корреляции не превышает 0,8, т. е. и эти критерии недостаточно
надежны.
Большинство попыток найти приемлемые критерии верности
изображения относится к частным случаям. Предлагается не-
некий критерий, основанный на каких-то физиологических пред-
предпосылках, а чаще просто удобный для анализа и вычислений,
а затем оцениваются его свойства. Другой подход к проблеме со-
состоит в копировании процесса выработки оценки человеком, т. е.
свойства изображения должны измеряться в той метрике, которая
присуща человеческому мозгу. При таком подходе оцениваемое
изображение сначала проходит предварительную обработку и
только потом оценивается его верность. При этом аппроксими-
аппроксимируются, насколько это возможно, процессы, фактически проис-
происходящие в начальных звеньях зрительной системы человека.
В гл. 2 была описана модель входного каскада зрительной системы
человека, состоящая из трех звеньев. Двумерная линейная система
с импульсным откликом #0 (*i У) представляет оптические эле-
элементы глаза. Звено, выполняющее поэлементное нелинейное
преобразование ON {•}, моделирует отклик фоторецепторов. Вто-
Вторая двумерная система с импульсным откликом HL (x, у) описы-
описывает процесс латерального торможения. Преобразование, выпол-
выполняемое всей моделирующей системой, описывается выражением
O\F{x, y)\ = HL(x, у)* <yN{H0(x, y)*F{x, y)\. G.4.16)
Манное и Сакрисон [2] провели обширные измерения для раз-
разработки надежного среднеквадратического критерия верности
одноцветных изображений, опирающегося на модель зрительной
системы человека. Эффекты в оптической системе глаза, приводя-
приводящие к ухудшению его разрешающей способности, при этом не
учитывались, и соотношение G.4.16) приводилось к более про-
простому виду:
a\F(x, y)\ = HL(x, y)*aN\F(x, y)\. G.4.17)
В этих экспериментах исходное распределение интенсивности,
описывающее исходное изображение, подвергалось поэлемент-
поэлементному нелинейному преобразованию по степенному или логариф-
логарифмическому закону, а затем —пространственной фильтрации с ча-
частотной характеристикой
И = [с + («о/ю/11 ехр {— (со/со/2}, G.4.18)
184
Глава 7
где с, klt k2 и (оо — постоянные. Далее в полученное изображение
вносились искажения, эквивалентные возникающим в процессе
оптимального кодирования с заданным средним числом двоичных
разрядов на элемент изображения. Затем искаженное изображе-
изображение подвергалось обратной пространственной фильтрации с ча-
частотной характеристикой 2вТ} (со) и обратному поэлементному
нелинейному преобразованию. В результате получалось искажен-
Угловая частота
а
Входной сигнал
8
Рис. 7.4.1. Характеристики $Bj_ (w) и О^ {•}, обеспечивающие наилучшее субъ-
субъективное качество изображений при моделировании процесса кодирования [2].
а — частотная характеристика; б — характеристика поэлементного нелинейного пре-
преобразования.
ное изображение в виде распределения интенсивности. Все эти
операции выполнялись над дискретным изображением. Подобная
процедура повторялась для различных изображений при разных
значениях среднего числа двоичных разрядов и других пара-
параметров. Качество полученных изображений оценивалось субъек-
субъективно по семибалльной шкале места в группе (табл. 7.1.2) и ран-
ранжированием. Оказалось, что при одинаковом среднем числе двоич-
двоичных разрядов на элемент наивысшие оценки и места в группе
получили те изображения, которые подвергались действию филь-
фильтра с частотной характеристикой, приведенной на рис. 7.4.1.
Кроме того, нелинейное преобразование по степенному закону
с показателем V3 дало гораздо лучшие результаты, чем логариф-
Меры качества дискретизобанных изображений 185
мическое преобразование. Исследования Манноса и Сакрисона
показали также, что предварительная обработка согласно равен-
равенству G.4.17), выполненная перед кодированием изображения,
создает более благоприятные условия для кодирования. Резуль-
Результаты этих исследований удостоверяют еще и полезность приме-
применения среднеквадратического критерия верности с метрикой
«геодезического пространства», характерного для человеческого
зрения. Для количественного изучения этого критерия верности
необходимы дальнейшие исследования.
В системах цифровой обработки изображений для определения
верности воспроизведения обычно гораздо удобнее использовать
дискретные отсчеты, а не аналоговые изображения. Поэтому
важно найти критерии верности на основе дискретных отсчетов,
которые хорошо согласуются с результатами субъективных оценок
непрерывных изображений.
Непосредственный способ получения таких критериев вер-
верности состоит в простой «дискретизации» соответствующих ана-
аналоговых критериев. Так, например, нормированную среднеквадра-
тическую ошибку (НСКО), описывающую различие между отсче-
отсчетами / (/, k) непрерывного эталонного изображения F (х, у) и
отсчетами F (/, k) непрерывного искаженного изображения F (х,
у), можно представить как
«•= I У [O\F(j, k)\-O{F-{j, k)\]*\l- I [0{F(j, k)}?.
G.4.19)
Можно показать, что эта мера совпадает с соответствующей
«непрерывной» мерой, описываемой соотношением G.4.11), если
при дискретизации обоих изображений удовлетворяется крите-
критерий Найквиста. К сожалению, в реальных системах обработки
изображений отсчеты, на основе которых создается воспроизво-
воспроизводимое непрерывное изображение, не являются его найквистов-
скими отсчетами, так как воспроизводящее устройство вносит
свои искажения и в нем трудно осуществить оптимальную двумер-
двумерную интерполяцию. Тем не менее необходимость часто вынуждает
пользоваться характеристиками, подобными G.4.19), даже в тех
случаях, когда они неточны.
В табл. 7.4.1 указаны некоторые наиболее распространенные
критерии верности, основанные на оценках нормированных
среднеквадрэтических ошибок (НСКО) для дискретных изобра-
изображений. Еще одним широко применяемым критерием верности яв-
является так называемая пиковая среднеквадратическая ошибка
(ПСКО), определяемая соотношением
ПСКО = (\/JK) S I [G (/, k) - G У, k)flA\ G.4.20)
/i fci
186 Глава f
где G (/, k) — преобразованное изображение, соответствующее
определению, приведенному в табл. 7.4.1, а число А равно макси-
максимальному значению G (/, k). Среднеквадратические ошибки часто
Таблица 7.4.1
Критерии верности, основанные на оценках
нормированных среднеквадратических ошибок,
для дискретных одноцветных изображений
Без преобразования
.' К J К
НСКО=? ? [F (/, A)-F (/,«)]«/Г- !¦ [F (/,*)]¦
7=1 fe=l /=i fe=l
С поэлементным преобразованием
нско = ? ? № </. *) - о (/. *)]s/? Г-1° (/• fe))s
/=i fe=i /=i ft=i
Степенной закон
где
G (/, А)
где
нско =
= F(/+I,
НСКО =
G(/,
G
>=2
*Н
Логарифмический
(/, fe) = fej log4 [?2 -f
С преобразованием
/С-1
23 [C,(j,k)—G(i,,
k=i
-F(/-I, A) + F(/,
С использованием
? [G (/, k) — G (/, ^
= [F(*. *)•#(*,»):
закон
- *з^ (/'. '
Лапласа
J-\
7=2
/C-1
U [G (/, fe)]2,
ft=2
A+l) + F(/, ft-I)-4F(/,A)
свертки
г
!)г//§ *
/C
I [0 (/.*)]«.
измеряют в децибелах и рассматривают как отношение сигнал/шум
(С/Ш):
(С/Ш)н = —10 lg (НСКО) G.4.21а)
или
(С/Ш)п = —10 lg (ПСКО). G.4.216)
Имея дело с операторами пространственных преобразований,
такими, как оператор Лапласа или оператор свертки (табл. 7.4.1),
Меры качества дискретизованных изображений 187
не следует забывать, что массивы отсчетов изображений имеют
конечные размеры. Поэтому пределы суммирования [в выра-
выражениях, подобных G.4.19) или G.4.20)] необходимо ограничи-
ограничивать центральными областями массивов G (/, k) и G (/, k) с тем,
чтобы избежать краевых эффектов, которые появляются при
аппроксимации непрерывных интегралов свертки дискретными
суммами. Более подробно эти вопросы рассматриваются в гл. 11.
7.5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ
ИЗОБРАЖЕНИЙ
Разработка количественных критериев верности воспроизве-
воспроизведения цветных изображений является гораздо более трудной за-
задачей, чем создание таких критериев для одноцветных изображе-
изображений. Это обусловлено не только увеличением числа величин,
описывающих изображение, но и необходимостью учета большего
числа психологических факторов, связанных с восприятием цве-
цветов. Критерий верности воспроизведения цветных изображений
должен согласовываться с мерой различия цветов и такими яв-
явлениями, как цветные полосы Маха и цветовая адаптация.
В разд. 7.3.2 было получено выражение для меры различия
цветов
Д* \CV С2\ = ? Б §ц А7-, AT,, G.5.1)
где АТ( обозначает разность координат цвета, a glf — весовые
коэффициенты, зависящие от координат цвета. Исходя из этой
формулы, примем за критерий верности воспроизведения цветных
изображений нормированную среднеквадратическую ошибку. По
определению эта мера равна
оо 3 3
J J S Sgti [Tt {Xi у) ~~ ^{х> у)] [Ti{х> у) ~ ^{х> у)] dxdy
il /1
^аз
If S Y>
l /1
If
_ОО J=l /=1
G.5.2)
где Т{ (х, у) и Ti (x, у) — цветовые компоненты эталонного и
искаженного изображений соответственно. Среднеквадратическую
ошибку довольно трудно вычислять по этой формуле, так как
в нее входят перекрестные члены — произведения различных
координат цвета. Кроме того, весовые коэффициенты gtj не по-
постоянны, а зависят от координат цвета. Как было отмечено при
188 Глава 7
рассмотрении вопроса о метрике цвета, не существует такого ли-
линейного преобразования, при котором перекрестные члены исче-
исчезали бы полностью. С помощью нелинейных преобразований
координат, описанных в гл. 3, осуществляется переход к цвето-
цветовому пространству U*V*W* или Lab, временно принятым МКО
в качестве стандартных пространств с равномерным распределе-
распределением яркости и цветности. В пространстве U*V*W*, например,
выражение для среднеквадратической ошибки имеет вид
ОО
J J (&i [U* (x, у) - U* (х, y)f + h2 [V* (x, у) - V* (x, у)? +
—OO
<g + &з W* (xt y) — W* (xt y)]2) dx dy rj g 2)
oo
j j {hi. [U* (x, y)\* + h2 [V* (x, y)\* + h3 [W* (x, </)]a) dx dy
—oo
При другом подходе к выбору среднеквадратической меры
верности воспроизведения цветного изображения используются
некоррелированные между собой координаты цвета, полученные
в результате преобразования первичных координат. Такую де-
корреляцию можно провести с помощью разложения Карунена —
Лоэва, описанного в гл. 3. Исчезновение перекрестных членов
в полученной таким образом мере интуитивно обосновывается тем,
что координаты цвета являются статистически некоррелирован-
некоррелированными. Преобразование Карунена—Лоэва определяется кова-
ковариационной матрицей координат цвета Т( (х, у) исходного изобра-
изображения, которую необходимо либо измерить (оценить), либо полу-
получить из модели данного класса цветных изображений. Система
координат YIQ оказалась довольно близкой к системе Кару-
Карунена—Лоэва [38]. По этой причине среднеквадратическую ошибку,
вычисленную для координат Y, I, Q, часто применяют как меру
верности воспроизведения цветных изображений. К сожалению,
пока нет достаточных данных, чтобы судить о согласованности
мер, рассмотренных в этом разделе, с результатами субъективных
оценок.
Третий способ определения верности воспроизведения цветных
изображений состоит в вычислении среднеквадратической ошибки
в цветовом геодезическом пространстве, согласующемся с некото-
некоторой моделью цветового зрения человека. Для подобной модели,
приведенной на рис. 2.5.3, среднеквадратическая ошибка имеет
вид
оо 3 I оо 3
* = 11 S Mi (х, у) - g, (х, у)? dx dy J J 2 UT, (x, У)? dx dy,
—00 t=l I -oo 1=1
Меры качества дискретизованных изображений 189
где gi (х, у) — сигналы, получаемые из сигналов колбочек ес (х,
у) с помощью следующих преобразований:
gt(х, у) = Ht(х, у) * logfa (х, у)], G.5.5а)
& (*, У) = Я2 {х, у) * log [-Jg-|-] , G.5.56)
§3 (х, У) = Н3 (х, у) * log [-jg$-] ¦ G.5.5в)
Переменные et (x, у) в свою очередь связаны с координатами цвета
Т( (х, у) некоторым линейным преобразованием
е = МТ, G.5.6)
где М—матрица преобразования размера 3x3. Как и в пре-
предыдущих случаях, экспериментальная проверка пригодности
геодезической меры ошибки почти не проводилась.
Приведенные выше меры верности воспроизведения непрерыв-
непрерывных цветных изображений можно приспособить и для оценки
дискретных цветных изображений, пользуясь методикой, приме-
примененной для дискретизации мер верности воспроизведения одно-
одноцветных изображений.
7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ
Очевидно, что одни изображения являются более содержатель-
содержательными, чем другие, т. е. имеют больше деталей или при анализе
из них удается извлечь больше данных. Детали, данные и другие
подобные понятия являются качественными и довольно расплыв-
расплывчатыми. Поэтому часто бывает необходимо ввести количественные
характеристики изображения, позволяющие оценивать предельные
свойства алгоритмов кодирования, исправления и анализа изоб-
изображений. Один из подходов к количественному описанию изобра-
изображений состоит в применении теории информации [39—42].
Согласно методике, описанной в разд. 5.3, допустим, что
матрица F размера NxN, составленная из квантованных отсчетов
изображения, будет заменена вектор-столбцом f размера QXl
(где Q = N2), полученным путем развертки матрицы F по столб-
столбцам. В принципе такие векторы можно рассматривать как изобра-
изображения на выходе некоторого источника, который может генери-
генерировать любой из возможных векторов. В одном из крайних слу-
случаев получается темное изображение с минимальной яркостью
всех элементов, а в противоположном случае—изображение
с максимальной яркостью. Между этими крайними случаями за-
заключено множество различных изображений. Если яркость каж-
каждого из NxN элементов изображения квантуется на / уровней,
то данный источник может создать Т = JQ различных изобра-
190 Глава 7
жений. Многие из них имеют хаотическую структуру и похожи
на реализации двумерного случайного шума. Лишь очень неболь-
небольшое число из Т возможных изображений будут такими, какие
дал бы реальный датчик при наблюдении за окружающим миром.
В принципе можно считать, что имеется априорное распределе-
распределение Р (ft) (где t = 1, 2, ..., Т) вероятности появления каждого
из возможных состояний вектора f. Измерить или промоделиро-
промоделировать это распределение очень непросто, но сама идея в конце
концов приводит к полезным результатам,
В 1948 г. Шеннон [39] опубликовал свою знаменитую книгу
«Математическая теория связи» в которой был дан способ коли-
количественного описания свойств источников данных и систем пере-
передачи информации. В основе шенноновской теории информации
лежит понятие об энтропии. При векторном описании изображения
среднее количество информации в изображении равно энтропии
источника:
!. G-6.1)
В данном определении энтропии применяются логарифмы с осно-
основанием два и энтропия измеряется в двоичных единицах. Энтропию
источника полезно знать при кодировании изображений, поскольку
согласно теореме о кодировании при отсутствии помех [39 ],
теоретически можно закодировать без искажений изображения,
создаваемые источником с энтропией Н (f), затратив на кодирова-
кодирование Н (f) + е двоичных единиц, где 8 — бесконечно малая поло-
положительная величина. И наоборот, в принципе невозможно зако-
закодировать изображения без искажений, если число двоичных
единиц меньше чем Н (f).
Вероятность появления ^-го вектора, описывающего изобра-
изображение, можно выразить через совместное распределение вероят-
вероятностей уровней яркости элементов изображения
^(Ъ) = Рг{/A) = гдA), /B) = r/2B), ...J(Q) = r/Q(Q)b G.6.2)
где rjq (q) —значение /-го уровня квантования для q-ro элемента х>.
Эту вероятность можно выразить также в виде произведения
условных вероятностей:
Я(г) = Рг{/A) = ГдA)}Рг |/B) = г/3B)|/A)}Рг |/C) =
= ОзCI/B), /A)} --.Рг{/(?) =
= rjg(q)\f(q-\), f(q-2) /B), /A)} • •• Pr{/(Q) =
= rIQ(Q)\f(Q-\), /(Q-2), ...,/B), /A)}. G.6.3)
1J Предполагается, что источник изображений ие обладает памятью в том
смысле, что распределение вероятностей для данного изображения ие зависит
от того, какие изображения были созданы источником ранее.
Меры качества дискретизованных изображений 191
Логарифмируя обе части равенства G.6.3) по основанию два и
учитывая определение энтропии G.6.1), получаем
-?: P(it) log [Pr{/ (q) = rig(q)\f(q-\), . . ., f (\)\) . . . .
G.6.4)
В равенстве G.6.4) q-e слагаемое, обозначенное через Н [f (q) \
\f (q — 1), ..., /A)], можно рассматривать как выражение для
средней информации, содержащейся в q-n компоненте вектор-изоб-
вектор-изображения f, при условии, что точно известны яркости предше-
предшествующих q — 1 компонент. Таким образом,
l G.6.5)
Это выражение, описывающее энтропию источника изображений,
является общим и не зависит от того, в каком порядке берутся
элементы изображения. Рассмотрим теперь вид формулы G.6.5)
для двух случаев: 1) изображение развертывается по столбцам
и 2) когда все элементы изображения поступают одновременно.
Можно показать, что при развертке изображения по столбцам
H[f(q)\f(q-\), ...f(q-j)]>H[f(q)\f(q-\), ...,f(q-k)],
G.6.6)
где / > k. Это означает, что информация, содержащаяся в q-n
точке, с увеличением числа полностью известных предшеству-
предшествующих элементов изображения в среднем только уменьшается.
Равенство обеих частей соотношения G.6.6) достигается только
тогда, когда яркости всех элементов распределены независимо 1К
Если количество известных предшествующих элементов неогра-
неограниченно увеличивается, то правая часть неравенства G.6.6) стре-
стремится к некоторому ненулевому предельному значению, обозна-
обозначаемому как Н [/ (q) | оо].
Если пренебречь малосущественными для достаточно крупных
изображений краевыми эффектами, то энтропию изображения
можно приближенно выразить в виде
c). G.6.7)
Х) Равенство в соотношении G.6.6) имеет место в том случае, если последо-
последовательность элементов, полученная в результате развертки, является марковской
последовательностью не более чем й-го порядка. При этом нет необходимости
неограниченно увеличивать число предшествующих элементов для получения
величины Н [/ (q) |оо]. — Прим. ред.
192
Глава 7
Таким образом, можно считать, что энтропия всего изображения
равна предельному значению условной энтропии одного элемента
изображения, умноженному на полное число элементов.
В системах с разверткой изображения предельная условная
энтропия определяется на основе конечной последовательности
предыдущих элементов. Так, если этих элементов было k, то
Я [ / (?) | оо ] «* Я If (q)\f(q — \), ..., f (q — k)]. G.6.8)
В явной форме
H[f(q)\f(q-\), ...,f(q-k)] =
>-jfc)]i°g{ рГЛУ-'dV" /(g~*"-
j-i
/o=0
f{q-k)\
G.6.9)
где совместное распределение вероятностей
= rik(q-k)\ G.6.10)
(r/(? —уровни квантования яркости). Для вычисления условной
энтропии G.6.9) необходимо либо ввести модель совместного
распределения вероятностей, либо измерить соответствующие
распределения частот для изображения или некоторого класса
изображений.
Таблица 7.6.1
Оценки энтропии изображения, полученные Шрайбером
Порядок
Первый
Второй
Третий
Функциональное выражение энтропии
HVD)\f(q-l)\
Я [/(9I/(<?-!). /W-2)]
Энтропия,
бит/элемент
4,4
1,9
1,5
Шрайбер [43 ] оценил энтропию первого, второго и третьего
порядка для нескольких изображений, квантованных на 64
уровня, измеряя распределения относительных частот того же
порядка. Полученные распределения были подставлены в фор-
формулу G.6.10) вместо соответствующих распределений вероятно-
вероятностей. При таком способе измерений предполагается, что источник
изображений является стационарным и эргодическим, т. е. усред-
усреднение по ансамблю изображений можно заменить усреднением
по отдельному изображению. Результаты измерений, проведенных
Шрайбером для конкретного изображения, приведены в табл. 7.6.1.
Для кодирования этого^изображения с помощью обычной ИКМ
Меры качества дискретизованных изображений 193
требуются шестиразрядные кодовые слова, т. е. затрачивается
6 бит/элемент. Теоретически для его кодирования достаточно
4,4 бит/элемент при условии, что все элементы кодируются по
отдельности. Если же использовать значение предыдущего эле-
элемента, то теоретический предел уменьшится до 1,9 бит/элемент.
Иначе говоря, предыдущий элемент дает 2,5 бита информации
об элементе / (q). Учет еще одного предшествующего элемента
дает всего 0,4 бита дополнительной информации. Таким образом,
оказалось, что в данном изображении большая часть дополни-
дополнительно извлекаемой информации содержится в небольшом числе
предыдущих элементов.
Выше был описан метод оценки энтроп-ии изображения, раз-
развернутого по столбцам, при котором предельная условная энтро-
энтропия Н [f(q) | оо] аппроксимируется условной энтропией, вычис-
вычисленной с учетом нескольких предыдущих элементов в том же
столбце. Такой метод можно применить для оценки энтропии
изображения, когда все его элементы поступают одновременно.
Допустим, что q = (Q + 1)/2 обозначает номер центрального
элемента вектора f с нечетным числом элементов. Тогда совмест-
совместное распределение вероятностей можно представить в виде
/>(f) = /> [f(\)]P f/(Q) 1/A)] Я lfB)\f(Q), f A)] ...
-P l Ш I f (Q). f (Q -1), .... / (я + О, / (я - О, ...
...,f B),f(\)l G.6.11)
Повторяя рассуждения, которые привели к соотношению G.6.7),
энтропию источника изображений можно выразить приближен-
приближенным равенством
Я (f) ~ QH [f (q) j / (Q), f (Q - 1), ..., f (q + 1), / (q - 1), ...,
/B),/(l)]. G.6.12)
Полученное «двустороннее» выражение для условной энтропии
можно в свою очередь аппроксимировать, учитывая только бли-
ближайшие элементы столбца:
Н (f) & QH \f (q) \f(q + k), ..., f (q + 1), f (q - 1), ...,
f(q-k)l G.6.13)
Развивая эту идею, можно включить в выражение для оценки
энтропии все элементы вектора, которые имеют достаточно силь-
сильные статистические связи с f (q). Во многих случаях такие эле-
элементы оказываются геометрически ближайшими к исследуемому.
Поэтому можно принять следующую оценку энтропии:
H(t)~QH\f(q)\f(q-\), f (q + 1), f (q - N),
f(q+N)], G.6.14)
7 Прэтт У.
194
Глава 7
где N —длина столбца, а энтропия элемента f (q) определяется
значениями ближайших четырех элементов, находящихся сверху,
снизу, справа и слева от него 1(.
Прейс [44 ] вычислял энтропию двухградационных факсимиль-
факсимильных документов, используя несколько предшествующих элемен-
элементов развертки. К сожалению, из-за чрезмерного объема необхо-
необходимых вычислений трудно оценить энтропию многоградационных
изображений даже с использованием упрощенной формулы
G.6.14). Для вычислений по этой формуле необходимо получить
распределение частот пятого порядка, причем число возможных
значений каждого аргумента равно числу уровней квантования
яркости. Приходится делать печальный вывод, что вычисление
энтропии в принципе позволяет оценивать «содержательность»
изображения, однако для многоградационных изображений такие
вычисления практически невыполнимы 2>.
7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ
ИЗОБРАЖЕНИЙ
Скорость создания информации некоторым источником опре-
определяет минимальную величину пропускной способности канала,
которая необходима для передачи сообщения с заданным допусти-
допустимым уровнем искажений в принятом сообщении относительно пере-
переданного [45, 46]. Был предпринят ряд попыток [2, 47—50] при-
Источник
информации
f*
Нодер
Канал
Декодер
Получатель
информации
Рис. 7.7.1. Блок-схема системы передачи информации.
способить теорию информации к задачам передачи изображений
с тем, чтобы определить предельные возможности систем кодиро-
кодирования изображений. В данном разделе приведены основные поло-
положения этой теории, сформулированные применительно к изобра-
изображениям на основе обзорной статьи Дэвиссона [50].
На рис. 7.7.1 приведена упрощенная блок-схема системы пере-
передачи изображений. Источник создает последовательность из Q
элементов изображения, каждый из которых квантуется на /
уровней. Эта последовательность образует вектор f размера QXl.
В кодере каждому из Т = JQ возможных сочетаний яркостей f,-,
где i — 1, 2, ..., Т, ставится в соответствие кодовая комбинация.
11 Вывод выражения для энтропии изображения, когда все его элементы
поступают одновременно, не вполне корректен. Оценка G.6.14) дает заниженное
значение энтропии. — Прим. ред.
2) Можно получить оценки энтропии изображения,, нсп ользуя его вероят-
вероятностные модели. — Прим. ред.
Меры качества дискретизованных изображений 195
После декодирования восстанавливается сочетание яркостей f*.
Характеристики системы передачи изображений можно описать
•¦ч •¦ч
с помощью условной вероятности Р [fk | f/ ] вектора fk на выходе
при условии, что кодированию подвергался вектор f,-. Если кодер
и декодер работают без ошибок, то входной и выходной векторы
изображения (при отсутствии ошибок в канале) будут одинаковыми.
Условная вероятность Р [f^lfj описывает работу системы пере-
передачи изображений при наличии искажений. На основании этой
условной вероятности и распределения априорных вероятностей
находим безусловное распределение вероятностей восстановлен-
восстановленных векторов
P(h)=YP(h\h)P(h). G.7.1)
Требования к пропускной способности канала определяются ко-
количеством взаимной информации, по определению равной
Iq (f, f) = Y I P (h) P (h I f,) log [P (f* | fdlP (?)]. G.7.2)
i—i k=\
При безошибочном кодировании это выражение упрощается:
Iq (I ?) = -!¦/> (f,) log [P (f {)] = H (f), G.7.3)
1=1
т. е. количество взаимной информации оказывается равным энтро-
энтропии источника. Если в процессе кодирования вносятся искаже-
искажения, то восстановленная последовательность ft содержит непол-
неполную информацию о состоянии /,• и требования к пропускной способ-
способности канала будут уменьшены.
Допустим, что функция D (f, f) представляет собой некоторую
меру искажений воспроизведенного изображения. Тогда для век-
вектора из Q элементов средняя величина искажений в расчете на один
элемент будет определяться равенством
Т Т
{)|=-il l-D(luU)P(h)P(U\h). G.7.4)
Определим для этого вектора скорость создания информации
в расчете на один элемент как
[L] G.7.5)
при. D <Dx x>. В принципе RQ (DJ и есть минимальная пропуск-
пропускная способность канала, необходимая для передачи информации,
1) Символ inf [¦ ] обозначает инфинум аргумента.
7*
196 Глава 7
создаваемой источником, когда искажения в среднем не должны
превышать некоторой максимальной величины D^. Скорость
создания информации источником R @%) можно найти, увеличи-
увеличивая длину вектора до бесконечности:
p (,)] G.7.6)
Q-Э-ао
Как правило, отыскать минимум количества взаимной инфор-
информации при условии, что средняя величина искажений не должна
превышать заданного предела D4, сложно как аналитическими, так
и численными методами. Получено несколько решений для кана-
каналов связи, используемых на практике. Одно из них относится
к источнику с гауссовым распределением вероятностей при оценке
искажений среднеквадратической мерой. Такое решение нельзя
непосредственно применить к задаче о кодировании яркостей эле-
элементов, поскольку яркость — неотрицательная величина. Кроме
того, среднеквадратическая мера искажений может оказаться не-
неподходящей. Однако решение, полученное для гауссова источника
и среднеквадратической меры искажений, позволяет указать пре-
предельные возможности системы кодирования для любых источников
с заданными вторыми моментами. Кроме того, это решение непо-
непосредственно переносится на задачу о кодировании с преобразова-
преобразованием. Поэтому ниже будут рассмотрены свойства скорости созда-
создания информации для случая гауссова источника и среднеквадрати-
среднеквадратической меры искажений.
Рассмотрим вектор f, образованный Q независимыми гауссо-
гауссовыми случайными величинами с нулевыми средними и известной
дисперсией а2. Среднеквадратическая ошибка определяется фор-
формулой
D (f, f) - 4- ? ? \lf(q) - f (</)]*}. G.7.7)
Было найдено [45], что скорость создания информации
G.7.8а)
D/ni D тл j
R @J - #с (А*) = ( о при a» < D,. G.7.86)
Таким образом, скорость создания информации равна половине
логарифма отношения мощности сигнала к мощности искажений,
если это отношение превышает единицу, и нулю в противном слу-
случае. Если элементы последовательности, создаваемой гауссовым
источником, коррелированы и ковариационная матрица К/ из-
известна, то скорость создания информации равна [50]
Ъ(Л.) " Т § "Г »°
Меры качества дискретиэованных изображений
197
где % (q) — q-e собственное значение матрицы К/, a D^ выбрано
так, что
с
* = ~о *- min^(?)> D**l- G.7.Ю)
При обработке изображений представляет интерес частный случай
двумерного разделимого марковского источника, когда все эле-
элементы имеют одинаковые дисперсии, равные а2, а коэффициенты
/о
Нормированная среднеквадратическая ошибка s/бг
У00
Рис. 7.7.2. Зависимость скорости создания информации от величины искажений
при одно- и двумерном кодировании изображений — реализаций марковского
поля.
корреляции вдоль строк и столбцов равны соответственно ря и рс.
Если предположить, что степень искажений невелика, то скорость
создания информации для однородного случая равна [501
а в двумерном случае
Я(Л.)=4-!
-]¦
G.7.-11)
G.7.12)
На рис. 7.7.2 приведены графики зависимости скорости создания
информации от величины искажений при различных значениях
коэффициентов корреляции. В гл. 24 проведено сравнение харак-
характеристик некоторых систем кодирования изображений с предель-
предельными характеристиками.
198 Глава 7
7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ
Определение количественной меры дешифрируемости изобра-
изображения, т. е. степени его пригодности для анализа наблюдателем,
является гораздо более сложной задачей, чем измерение верности
воспроизведения изображений. Факторы, влияющие на дешифри-
руемость, глубоко связаны со свойствами человеческого зрения.
Способность человека-наблюдателя извлекать из изображений ин^
формацию зависит, очевидно, от физических свойств зрительной
системы, которые определяются, в частности, оптическими свой-
свойствами глаза, нелинейной реакцией фоторецепторов на яркость и
наличием латерального торможения. Однако алгоритмы обработки
данных, поступающих от глаза в мозг, играют важную и, по-види-
по-видимому, решающую роль в процессе извлечения человеком визуаль-
визуальной информации из изображения. Поскольку механизмы зри-
зрительного восприятия пока изучены слабо, то в настоящее время
попытки создать критерий дешифрируемости изображений, осно-
основанный на модели зрительной системы человека, представляются
безнадежными. Следует скорее остановиться на каких-то частных
критериях, которые достаточно хорошо согласовывались бы с ре-
результатами субъективных оценок.
В большинстве экспериментов по экспертной оценке дешифри-
дешифрируемости изображений используются простые штриховые фигуры,
как, например, оптометрические таблицы, составленные из подоб-
подобранных случайным образом букв разного размера. На рис. 7.8.1
представлены четыре контрольные таблицы, применявшиеся
в экспериментах по распознаванию объектов 151]. Таблицы Лан-
дольта [52, 53 ] составлены из строк буквы С, которая может на-
находиться в любом из четырех (или восьми) возможных положений,
причем размеры букв от строки к строке уменьшаются. Цифровая
таблица составлена из «криволинейных» цифр 3, 5, 6, 8 и 9, ориен-
ориентированных случайным образом. В таблице из звездочек в каждом
символе отсутствует какой-то один из шести лучей. Наблюдатель
должен распознать символы во всех таблицах; результаты экспе-
эксперимента выражаются в виде зависимости^вероятности правильного
ответа от размера символа. Подобные эксперименты на дискретизо-
ванных вариантах четырех таблиц, показанных на рис. 7.8.1, про-
проводил Бернард [51 ]. Результаты приведены на рис. 7.8.2. В этих
экспериментах были дискретизованы изображения на диапозити-
диапозитивах, затем к отсчетам прибавляли гауссов шум и результаты запи-
записывались на фотопленке в виде диапозитива. Как и ожидалось,
с уменьшением размеров символов вероятность распознавания мо-
монотонно убывает. Бернард заметил также, что в экспериментах
с цифрами наблюдается больший разброс, чем в опытах со звездоч-
звездочками или с таблицами Ландольта. Кроме того, оказалось, что ве-
вероятность правильного различения цифр зависит от их ориентации.
Меры качества дискретиэованных изображений 199
Так, при распознавании повернутой цифры «3» ошибки делали
чаще, чем при распознавании такой же цифры, стоящей в нормаль-
нормальном положении. Можно предполагать, что в экспериментах со
С О О О С О О С -*» * "• Ь * о. J $и
С О С О О О О О™ о 6 ы »? <» «Ъ«о
осээосэоос %%з»$#ъъ%*
ОООСОООООС 6SP#">P«S<P%
СЭООСЭОООО *8#«43»'ttb«*
ОООСОООООО 9 Л «С *t S S J<^
СОООССОООССС |1)»»*'Л9Д%<Л
оооооосоооосоо » и 5 п j п ч 9« «
COOOOCCCOOOCOOOO J4»»efllMM«<«»
О9ОО0О9СОООО9ОЭС **"»«*JJ«»*n#*».4J »
пээиеаспспэоспэоос ии.итм »mui»h
Ji f
6
oocooooooo ^ •»- * •»- •»- ~ I * *
oooooooooc ******** *
ooocooocoooo ****** + + *¦+*
СОООООЭЭЭОО.С ***•********• +
OOOOOOOOOOCO »*4»***it**t
oooooooftoooooc #*****«¦¦****¦
ССОСЭОООСОООСЭОО »««« »*•»»*••¦»¦?*•¦?
эосоооссоооососооо «¦»¦»»»»«¦¦*¦*¦*•¦*
ООООЭОЭЭООЭООЭОСОООО
Рис. 7.8.1. Испытательные таблицы для экспериментов по распознаванию симво-
символов [51].
а — кольца Ландольта с четырьмя позициями; б — кольца Ландольта с восемью пози-
позициями; в — цифры; г — звездочки.
звездочками и таблицами Ландольда такой зависимости не наблю-
наблюдалось потому, что у этих символов нет «стандартной» ориентации.
Бернард [51 ] для предсказания результатов эксперимента по раз-
различению человеком символов в таблицах Ландольта применял
200
Глава 7
I
1,0
0,8
0,6
Q4
02
0
д наблюдателей
0,6
0,4
0,2
О
0,6
I
0,2
/7
г з ь 5
f/размер символа
редняя для трех
наблюдателей
Z 3 4 5
1/размер символа
Средняя для четырех
наблюдателей
4 наблюдателя
Теоретическая
кривая
' 2 д 4 S
f/размер символа
S наблюдателей
г j *
f/размер символа
Рис. 7.8.2. Результаты экспери-
экспериментов по распознаванию сим-
символов [51].
а — таблица цифр: б — таблица с
кольцами Ландольта (четыре пози-
позиции); в — таблица с кольцами Лан-
Ландольта (восемь позиций); г — таб-
таблица заездочек.
теорию согласованной фильтрации х>. Вероятность правильного
распознавания М ортогональных сигналов (М ориентации сим-
символа) в присутствии аддитивного гауссова шума аппроксимиро-
аппроксимировалась [54 ] выражением
Р =
со
J ехр (-г2) [72 + V,erf
G.8.1)
г> Анализ свойств двумерных согласованных фильтров представлен в гл. 19.
Меры качества дискретизованных изображений 201
где S/N — отношение мощностей сигнала и шума. Как показано
на рис. 7.8.2, б, в, теоретические и экспериментальные результаты
согласуются довольно хорошо.
Был проведен ряд опытов по оценке разборчивости цифро-
буквенных символов, переданных с помощью фототелеграфных
аппаратов. Арпс и др. [55] обнаружили, что для достижения
97,5 %-ной вероятности правильного распознавания необходимо,
чтобы разрешение при дискретизации символа было порядка одной
десятой наибольшего размера символа. Эрдман и Нил [56 ] изучали,
как изменяется разборчивость слов в зависимости от разборчиво-
разборчивости букв, связности текста и других семантических факторов.
Проводились также исследования с целью определения «ра-
«рабочих характеристик» человека при визуальном анализе много-
многоградационных изображений [57]. Однако исследования в этом
направлении все еще находятся на начальной стадии своего раз-
развития.
ЛИТЕРАТУРА
1. Pearson D. E., Methods for Scaling Television Picture Quality, in: Picture
Bandwidth Compression, Huang T. S., Tretiak O. J., Eds., Gordon and
Breach, New York, 1972.
2. Mannos J. L., Sakrison D. J.( The Effects of a Visual Fidelity Criterion on
the Encoding of Images, IEEE Trans. Inf. Theory, IT-20, 4, 525—536 (July
1974).
3. Mertz P., Fowler A. D., Christoper H. N., Quality Rating of Television
Images, Proc. IRE, 38, 11, 1269—1283 (November 1950).
4. Fredenhall Q. L., Behrend W. L., Picture Quality-Procedures for Evalu-
Evaluating Subjective Effects of Interference, Proc. IRE, 48, 6, 1030—1034 (June
1960).
5. Dean С. Е., Measurements of the Subjective Effects of Interference in Tele-
Television Reception, Proc. IRE, 48, 6, 1035—1050 (June I960).
6. Prosser R. D., Allnatt J. W., Lewis N. W., Quality Grading of Impaired
Television Pictures, Proc. IEE, 111, 3, 491—502 (March 1964).
7. Weaver L. E., The Quality Rating of Color Television Pictures, J. Soc. Mo-
Motion Picture Television Engineers, 77, 6, 610—612 (June 1968).
8. Lewis N. W., Waveform Responses of Television Links, Proc. IEE, 101, part
III, 258—270 A954).
9. Fisher J. F., Generation of NTSC Color Signals, Proc. IRE, 41, 3, 338—343
(March 1953).
10. Luther A. C, Methods of Verifying Adherence to the NTSC Color Signal Spe-
Specifications, Proc. IRE, 42, 1, 235—240 (January 1954).
11. Fink D. G., Ed., Television Engineering Handbook, McGraw-Hill, New York,
1957.
12. Cornsweet T. N.. Visual Perception, Academis Press, New York, 1970.
13. Priest I. G., Gibson K. S., McNicholas H. J., An Examination of the Mun-
sell Color System, I. Spectral and Total Reflection and the Muncell S;ale of
Value, U. S. National Bureau of Standards, Technical Paper 167, 1920.
14. Ladd J. H., Pinney J. E., Empirical Relationships with the Munsell Value
Scale, Proc. IRE (Correspondence), 43, 9, 1137 A955).
15. Foss С E., Nickerson D., Granville W. C, Analysis of the Ostwald Color
System, J. Opt. Soc. Am., 34, 7, 361—381 (July 1944).
16. Wyszecki G. W., Stiles W. S., Color Science, Wiley, New York, 1967.
202 Глава 7
17. Judd D. В., Hue, Saturation, and Lightness of Surface Colors with Chroma-
Chromatic Illumination, J. Opt. Soc. Am., 30, 1, 2—32 (January 1940).
18. Wright W. D., The Sensitivity of the Eye to Small Colour Differences, Proc.
Phys. Soc. (London), 53, 93 A941).
19. Muth E. J., Persels C. G., Computation of Geodesies in Color 3-Space by
Dynamic Programming, Proceedings 4th Hawaii Conference on System Sci-
Sciences, January 1971, pp. 155—157.
20. Jain A. K., Color Distance and Geodesies in Color 3 Space,/. Opt. Soc. Am.,
62, 11, 1287—1290 (November 1972).
21. Judd D. В., A Maxwell Triangle Yielding Uniform Chromaticity Scales,
J. Opt. Soc. Am., 25, 1, 24—35 (January 1935).
22. MacAdam D. L., Projective Transformations of ICI Color Specifications,
J. Opt. Soc. Am., 27, 9, 294—299 (August 1937).
23. MacAdam D. L., Visual Sensitivities to Color Differences in Daylight, J. Opt.
Soc. Am., 32, 5, 247—274 (May 1942).
24. Farnsworth D., A Temporal Factor in Colour Discrimination, Visual Pro-
Problems in Colour, II. National Phys. Lab. Symposium, No. 8, London, Her
Majesty's Stationary Office, 1958, p. 429.
25. Wyszecki G., Proposal for a New Color-Difference Formula, /. Opt. Soc.
Am., 53, 11, 1318—1319 (November 1963).
26. Hunt R. W. G., The Reproduction of Colour, Wiley, New York, 1967.
27. Barnard T. W., A Literature Survey on Image Quality Evaluation, The Per-
kin Elmer Corporation, Engineering Report ER-177, June 1971.
28. Frieden B. R., Image Evaluation by Use of the Sampling Theorem, /. Opt.
Soc. Am., 56, 10, 1355—1362 (October 1966).
29. Linfoot E. H., Quality Evaluations of Optical Systems, Optica Ada, 5, 1—2,
1 — 14 (March — June 1958).
30. O'Neill E. L., Introduction to Statistical Optics, Addison-Wesley, Reading,
Mass., 1963. [Имеется перевод: О'Нейл Э., Введение в статистическую оп-
оптику. — М.: Мир, 1966.1
31. Harris J. L., Sr., Image Evaluation and Restoration, J. Opt. Soc. Am., 56,
5, 569—574 (May 1966).
32. Harris J. L., Sr., Resolving Power and Decision Theory, J. Opt. Soc. Am.,
54, 5, 606—611 (May 1964).
33. Born M., Wolf E., Principles of Optics, 4th ed., Pergamon, New York, 1970.
[Имеется перевод: Борн M., Вольф Э., Основы оптики. —М.: Наука, 1973.]
34. Воусе В., A Summary Measure of Image Quality, Proceedings of a Sympo-
Symposium on Current Mathematical Problems in Image Science, Naval Postgra-
Postgraduate School, Monterey, California, November 1976.
35. Schade O. H., Modern Image Evaluation and Television, Appl. Opt., 3, 1,
17—23 (January 1964).
36. Andrews H. C, Computer Techniques in Image Processing, Academic Press,
New York, 1970. [Имеется перевод: Эндрюс Г., Применение вычислительных
машин для обработки изображений. — М.: Энергия, 1977.]
37. Wilder W. С, Subjectively Relevant Error Criteria for Pictorial Data Pro-
Processing, Purdue University, School of Electrical Engineering, Report TR-EE
72-34, December 1972.
38. Pratt W. K., Spatial Transform Coding of Color Images, IEEE Trans. Com-
mun. Tech., COM-19, 6, 980—992 (December 1971).
39. Shannon С. Е., The Mathematical Theory of Communication, University of
Illinois Press, Urbana, Illinois, 1949. (Orig. Pub., Bell Syst. Tech. J.. 1948.)
[Имеется перевод: Шеннон К., Работы по теории информации и киберне-
кибернетике. — М.: ИЛ, 1963, с. 243—332.1
40. Abramson N., Information Theory and Coding, McGraw-Hill, New York,
1963.
41. Ash R. В., Information Theory and Reliable Communication, Wiley, New
York, 1968.
Меры качества дискретизованных изображений 203
42. Gallagher R. G., Information Theory, Wiley-Interscience, New York, 1965.
[Имеется перевод: Галлагер Р., Теория информации и надежная связь. —
М.: Советское радио, 1974.]
43. Schreiber W. F., The Measurement of Third Order Probability Distributions
of Television Signals, IRE Trans. Inf. Theory, IT-2, 3, 94—105 (September
1956).
44. Preuss D., Comparison of Two-Dimensional Facsimile Coding Schemes, Inter-
International Communications Conference, 1975 Conference Record, Vol. 1, June
1975, pp. 7.12—7.16.
45. Berger Т., Rate Distortion Theory: A Mathematical Basis for Data Compres-
Compression, Prentice-Hall, Englewood Cliffs, N. J., 1971.
46. Andrews H. C, Bibliography on Rate Distortion Theory, IEEE Trans. Inf.
Theory (Correspondence), IT-17, 198—199 (March 1971).
47. Hayes J. F., Habibi A., Wintz P. A., Rate Distortion Function for a Gaus-
Gaussian Source Model of Images, IEEE Trans. Inf. Theory (Correspondence), IT-16,
507—508 (July 1970).
48. Sakrison D. J., Algazi V. R., Comparison of Line-by-Line and Two-Dimen-
Two-Dimensional Encoding of Random Images, IEEE Trans. Inf. Theory, IT-17, 386—
398 (July 1971).
49. Tasto M., Wintz, P. A., A Bound on the Rate-Distortion Function and Appli-
Application of Images, IEEE Trans. Inf. Theory, IT-18, 150—159 (January 1972).
50. Davisson L. D., Rate Distortion Theory and Applications, Proc. IEEE, 60,
7, 800—808 (July 1971). 1Имеется перевод: Дэвиссон. Скорость создания
сообщений. Теория и применение. — ТИИЭР, 1972, т. 60, № 7.]
51. Barnard T. W., An Image Evaluation Method, A Symposium on Sampled
Images, Perkin-Elmer Corporation, Norwalk, Connecticut, 1971.
52. Landolt E., Tableau d'Optotypes pour la Determination de l'Acuite Visuel,
Society Francois d'Ophthol, 1889, p. 157.
53. Cowan A., Test Cards for Determination of Visual Acuity, Arch. Ophthol, 57,
283—295 A928).
54. Schwartz M., Bennett W. R., Stein S., Communication Systems and Techni-
Techniques, McGraw-Hill, New York, 1966, p. 85.
55. Arps R. B. et al., Character Legibility Versus Resolution in Image Processing
of Printed Matter, IEEE Trans. Man-Machine Systems, MMS-10, 3, 66—71
(September 1969).
56. Erdmann R. L., Neal A. S., Word Legibility as a Function of Letter Legi-
Legibility with Word Size, Word Familiarity, and Resolution as Parameters, /.
Appl. Psych., 52, 5, 403—409 A968).
57. Snyder H. L., Image Quality and Observer Performance, in: Perception of
Displayed Information, Biberman L. M., Ed., Plenum Press, New York, 1973.
Часть
Дискретная линейная
двумерная обработка
В третьей части книги с единых позиций анализируются диск-
дискретные линейные операции, выполняемые при двумерной обра-
обработке. Даны определения обобщенных линейных операторов и опе-
операторов псевдообращения. Введено несколько видов дискретных
двумерных операторов суперпозиции и свертки и установлены
соотношения между ними. Представлены двумерные преобразо-
преобразования, такие, как преобразования Фурье, Адамара, Карунена —
Лоэва, и описаны быстрые алгоритмы вычисления. Рассмотрен
вопрос о применении двумерных преобразований как эффектив-
эффективного средства выполнения свертки. В заключение описаны рекур-
рекуррентные методы линейной обработки изображений.
Глава 8
ЛИНЕЙНЫЕ ОПЕРАТОРЫ
Многие операции, выполняемые при обработке изображений,
по своей природе являются линейными. В число таких операций
входят суперпозиция, свертка, унитарные преобразования и диск-
дискретная линейная фильтрация.
8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР
Рассмотрим массив F (щ, п2) из NtxN2 элементов, представ-
представляющий исходное (входное) изображение. При воздействии на
него обобщенным линейным оператором получается массив из
МгхМ2 элементов, описывающий преобразованное (выходное)
изображение
Л\ N
A 2 (u 1( п,; тъ тг), (8.1.1)
где ядро оператора О (пъ п2; тг, т2) представляет собой набор
весовых множителей, зависящих в общем случае от координат
элементов как входного, так и выходного изображений.
При анализе линейных операций по обработке изображений
удобно пользоваться векторными представлениями, описанными
в гл. 5 [1 ]. Поэтому будем полагать, что входной массив F (л1(
п2) представлен или в виде матрицы F, или в виде вектора f, полу-
полученного разверткой матрицы F по столбцам. Аналогичным обра-
образом допустим, что выходной массив Р {тъ m2) может быть пред-
представлен либо матрицей Р, либо в виде ее развертки по столбцам,
т. е. вектором р. Для упрощения обозначений ниже будет принято,
что матрицы, представляющие входное и выходное изображения,
квадратные с размерами Nx =* Nt =* N и Мг = Мг = М соот-
соответственно. Допустим теперь, что символ Т обозначает матрицу
размера M2xN2, с помощью которой вектор исходного изображе-
изображения f размера N2X\ линейно преобразуется в вектор
p = Tf (8.1.2)
выходного изображения размера М2х\. Матрицу Т можно разде-
разделить на блоки — матрицы Ттп размера MxN (число которых так-
206
Глава 8
же равно MxN) —и представить ее в следующем виде: ¦
ц Т,
Т •—
* 12
Г
»2i
(8.1.3)
В согласии с соотношением E.3.3) вектор выходного изображения
р можно выразить через матрицу входного изображения F:
=Г. TNnFvn.
п=\
(8.1.4)
Кроме того, с помощью равенства E.3.4) матрицу Р выходного
изображения можно выразить через вектор р того же изображения:
м
Р= Y Мттритт. (8.1.5)
Из этих формул получим выражение, связывающее между собой
входную и выходную матрицы:
М N
р--= L I- (л?та„) f (vni&). (8.1.6)
m=l л=1
Заметим, что операторы Мт и Nrt просто выделяют из матрицы Т
блок Ттп. Следовательно,
Р= I IVW). (8.1.7)
т=\ п=Л
Пусть линейное преобразование является разделимым, т. е.
матрицу Т можно представить в виде прямого произведения
Т = ТС®ТЙ, (8.1.8)
где Т6. и Тн — операторы преобразования столбцов и строк ма-
матрицы изображения F. В этом случае
Т«„-Тя(т, п)Тс. (8.1.9)
Следовательно,
I Тя(т,
l
(8.1.10)
Таким образом, матрицу выходного изображения Р можно полу-
получить путем последовательной обработки матрицы F по строкам
и столбцам.
При обработке изображений во многих случаях оказывается,
что оператор линейного преобразования Т имеет специфическую
структуру, позволяющую упростить вычислительные операции.
Ниже перечислены важные частные случаи, проиллюстрированные
Линейные операторы
207
на рис. 8.1.1, когда размеры входного и выходного изображений
выбраны одинаковыми, т. е. М = N.
а) При обработке матрицы F только по столбцам
T = diag[Ta, TC2) .... Та,), (8.1.11)
где ТС]- — матрица преобразования для /-го столбца.
• • • г
¦•. •
•
•
•
•
•
*
¦
•
•
. \
ГГГ.-.1
t.L'_U
1
•
•
•
•
*
•
•
•
• • • «у* • • •
7
'.
1 •
• 1 •
М. _ _ i
* 1 *
'¦• '•
. 1 .
. I •
_ _ i) ±
Г." -7
* ' 1 *
•
--•*-.-- -x
• • • •
• • • •
« • • •
• * • «J
• • • •
• • • «
•
•
\
"Г
•
•
•
•
•
L 1
• • • •
• • • •
• « • •
i—
•
•
i—*j
• • • •
• • • •
• • • •
•
•
•
•
i
•"•" .Л
• • • •
• • • t
ff
m
•
•
•
•
• • • •
• • • •
• • • •
•
•
•
•
Г
'.
• t • •
• • ¦ •'
• • • •
•
•
•
•
•
•
±
•
•
•
L_ 1
t • • «
• • • •
• • • •
• • • •
X
X
Рис. 8.1.1. Структура матриц линейного оператора.
а — общий случай; б — обработка только по столбцам; я — обработка только по стро-
строкам: г — обработка только по строкам и столбцам.
б) При одинаковой обработке каждого столбца матрицы F
Т = diag [То Тс> .... Тс] = Тс ® 1л,. (8.1.12)
в) При обработке матрицы F только по строкам
Tm4 = diag[TB1(m, n), ..., TnN(m, n)], (8.1.13)
где Тлу — матрица преобразования для j-Pi строки.
г) При одинаковой обработке каждой строки матрицы F
Т„!;, = diag[TR(m, n), TR(m, n), ..., TR{m, л)]. (8.1.14а)
Т = 1л,®Тл. (8.1.146)
д) При одинаковой обработке столбцов и одинаковой обработке
строк матрицы F "^
Т = Тс®1^ + 1л,®Тд. (8.1.15)
208 Глава 8
Число арифметических операций, выполняемых в каждом из этих
случаев, указано в табл. 8.1.1.
Из соотношения (8.1.10) видно, что если двумерное линейное
преобразование имеет разделимую матрицу, то его можно выпол-
выполнить путем последовательной одномерной обработки строк и столб-
столбцов массива отсчетов. Как следует из табл. 8.1.1, для таких преоб-
преобразований удается существенно сократить число необходимых
вычислительных операций: в общем случае при вычислении по
Таблица 8.1.1
Число арифметических операций при линейном преобразовании
Случай
Число умножений
и сложений
Общий
Обработка" по столбцам
Обработка по строкам
Обработка по строкам и столбцам
Обработка при разделимой матрице
N3
2N3 — N2
формуле (8.1.2) требуется МгЫг операций, но если можно восполь-
воспользоваться формулой (8.1.10), достаточно MN2 + М2М операций.
Более того, в этом случае матрицу F можно хранить в запоминаю-
запоминающем устройстве (ЗУ) с последовательным доступом, например на
диске или на барабане, и считывать строка за строкой, т. е. отпа-
отпадает необходимость хранения матрицы F в более дорогостоящем
ЗУ с произвольным доступом. Необходимо, однако, транспони-
транспонировать результаты преобразований по столбцам с тем, чтобы вы-
выполнить построчные преобразования. В работах [2, 3] описаны
алгоритмы транспонирования матриц, записанных в ЗУ с последо-
последовательным доступом.
8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ
ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ
Если массив отсчетов входного изображения является реализа-
реализацией случайного процесса с известными первым и вторым момен-
моментами, то для заданного линейного преобразования можно найти
первый и второй моменты также и для массива отсчетов выход-
выходного изображения. Среднее значение выходного массива равно
Е\Р(ти щ)\^Е\ } !¦ F(nlt nt)O (нх, п.г; ть щ)\.
(8.2.1а)
Линейные операторы 209
Однако оператор усреднения линеен, и поэтому
л/, Nt
E\P{mlt mz)} = Ц S ?{^(«1, щ)\0{пг, п„; тъ тг).
(8.2.16)
Корреляционная функция массива отсчетов выходного изображе-
изображения имеет вид
RP(my, тг; т3, m4) = ?'{P(m1, тг)Р*(т3, m4)| =
= ? Ц I! F(ni, n2)O(nlt n,\ nil, Щ) 2- 1; F*{n*, >h)x
U.n,=l n2=l " «3=1 n4=l
xO*K, л4; ms, m») }. (8.2.2a)
После перемножения рядов и вычисления среднего получается
выражение
RP(mv m,; m3, m4) —
Л/, Л, Л/, N,
S L S L
1 3 4
хО*(ил, п4; /я„ т4), (8.2.26)
где ^/г («b «z; «з. "J — корреляционная функция массива от-
отсчетов исходного изображения. Аналогично определяется и кова-
ковариационная функция обработанного изображения
/Ср(/и1( пи; тЙ, т4) =
Л', Мг N, N,
Y Ъ !' 1' KF{nlt 1ц; п3, п4H(пи п2; mu m2) x
1 1 1
(п3, п4; т„ т4). (8.2.3)
Если массивы отсчетов входного и выходного изображений пред-
представлены в векторной форме, то выражения для их моментов
можно записать более компактно. Среднее значение выходного
вектора р
Чр = Е |р| = Е |Tf 1 = Т? {f \ = Tr,f, (8.2.4)
а его корреляционная матрица
Rp = Е {$)**] = Е {Tff*ГГГ! = Т^Т*71. (8.2.5)
Ковариационная матрица вектора р
КР = ТК/ГГ. (8.2.6)
I [рименение этих теоретических положений к операторам суперпо-
суперпозиции и унитарного преобразования описано в последующих
главах.
210 Глава 8
8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ
При линейной обработке сигналов часто встречается задача
«обращения» преобразования вида
p = Tf (8.3.1)
с тем, чтобы выразить точное значение входного вектора f размера
Qx 1 или некоторую его оценку f через выходной вектор р размера
Pxl. Если Т —квадратная матрица, то очевидно, что
?=(ТГ1р, (8.3.2)
если обратная матрица существует. Если матрица Т не квадрат-
квадратная, то для отыскания решения можно воспользоваться псевдооб-
псевдообратной матрицей Т+ размера QxP. В этом случае
? = Т+р. (8.3.3)
Если решение существует и единственно, то «правильным» опера-
оператором псевдообращения будет тот, который обеспечивает точную
оценку, т. е. f = f. Это означает, что вектор f можно определить
по наблюдаемому вектору р без ошибок. Если решение существует,
но оно не единственно, то с помощью псевдообратного оператора
можно выбрать решение с минимальной нормой. Если, наконец,
точных решений не существует, то с помощью оператора псевдо-
псевдообращения можно найти наилучшее приближенное решение.
Более подробно этот вопрос рассмотрен в последующих разделах.
Разъяснения и доказательства многих из нижеприведенных поло-
положений содержатся в монографиях [4—6].
Первым из операторов псевдообращения будет рассмотрен опе-
оператор с обобщенной обратной матрицей Т", для которой выпол-
выполняются следующие соотношения:
(8.3.4а)
(8.3.46)
(8.3.4b)
(8.3.4г)
Обобщенная обратная матрица является единственной и при неко-
некоторых условиях ее можно записать в явном виде. Если Р > Q,
то систему уравнений (8.3.1) называют переопределенной, т.е.
число компонент наблюдаемого вектора р превышает число под-
подлежащих оценке компонент вектора f. Если при этом ранг матрицы
Т равен Q, то обобщенная обратная матрица
Г = (ТГТ)-1ТГ. (8.3.5)
Линейные операторы 211
В противоположном случае, когда Р < Q, систему (8.3.1) называют
недоопределенной. Если при этом ранг матрицы Т равен Р, то
обобщенная обратная матрица имеет вид
Т = Тг (Пт)-\ (8.3.6)
Нетрудно показать, что матрицы, определенные соотношениями
(8.3.5) и (8.3.6), удовлетворяют условиям (8.3.4). Если матрица
Т может быть представлена в виде прямого произведения (8.1.8),
то обобщенная обратная матрица имеет вид
Т~ = ТЕ <g> Jr , (8.3.7)
где T# и Тс — обобщенные обратные матрицы для линейных
операторов обработки строк и столбцов. В этом случае сокра-
сокращается объем вычислений, необходимых для обращения.
Еще один тип оператора псевдообращения имеет матрицу Ts,
называемую матрицей обращения методом наименьших квадратов,
которая определяется следующими соотношениями:
TTST = Т, (8.3.8а)
TTs = (TTs)r- (8.3.86)
И наконец, условно обратная матрица Т# определяется формулой
ТТ*Т = Т. (8.3.9)
Анализ определений всех трех видов оператора псевдообращения
показывает, что обобщенный обратный оператор является опера-
оператором обращения методом наименьших квадратов, а последний —
оператором условного обращения. Для любого линейного опера-
оператора с матрицей Т всегда существуют матрица обращения методом
наименьших квадратов и условно обратная матрица, но они могут
быть не единственными. Кроме того, для этих матриц обычно не
удается найти явное выражение в конечной форме.
Ниже приведены некоторые полезные соотношения для ма-
матрицы Т", которая является обобщенной обратной матрицей отно-
относительно матрицы Т размера PxQ.
Обобщенное обращение транспонированной матрицы
[ТТ«[Т-]Г- (8.3.10)
Обобщенное обращение обобщенной обратной матрицы
[ТТ = Т. (8.3.11)
Сохранение ранга
Ранг [Г] = Ранг [Т]. (8.3.12)
Обобщенное обращение произведения матриц
[ТГТГ = (Т)"(ТГ)"". (8.3.13)
= В-А", (8.3.14)
212 Глава 8
где А и В —матрицы ранга R, имеющие размеры PxR и RxP
соответственно.
Обобщенное обращение произведения ортогональных матриц
[АТВГ -* ВГГ-АГ, (8.3.15)
где А и В —ортогональные матрицы размера РхР и QxQ соот-
соответственно.
8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Систему линейных уравнений
p = Tf, (8.4.1)
где Т —матрица размера PxQ, можно рассматривать как систему
из Р уравнений с Q неизвестными. Возможны три случая:
*—,
1. Система уравнений имеет единственное решение Гдля кото-
которого Tf = р.
2. Системе уравнений удовлетворяют несколько решений.
3. Система уравнений не имеет точного решения.
Если система уравнений имеет хотя бы одно решение, то ее назы-
называют совместной, а в противном случае — несовместной. Системы
уравнений, не имеющие решений, часто получаются при исследо-
исследовании физических систем, когда вектор р описывает последователь-
последовательность измерений наблюдаемых величин, которые по предположе-
предположению являются следствием воздействия некоторой недоступной для
прямого наблюдения движущей силы, представленной вектором f.
Матрица Т получается посредством математического моделирова-
моделирования характеристик реальной системы, для которой вектор р яв-
является выходным сигналом. При исправлении (реставрации) изоб-
изображений вектор f обычно представляет исходное изображение,
вектор р — смазанное изображение, а матрица Т описывает диск-
дискретную математическую модель процесса, приводящего к смазы-
смазыванию изображения. Поскольку матрица Т и вектор р обычно
определяются с некоторой погрешностью, может оказаться, что
этот вектор не соответствует ни одному из возможных векторов
воздействия f.
Рассмотрим теперь вопрос о существовании решений системы
уравнений р = Tf. Из структуры системы уравнений видно, что
решение будет существовать тогда и только тогда, когда вектор р
может быть получен линейной комбинацией столбцов матрицы Т.
В этом случае говорят, что вектор р лежит в пространстве столб-
столбцов матрицы Т. Более строгой формулировкой условия существо-
существования решения является следующая [4]: система уравнений р =
= Tf имеет решение тогда и только тогда, когда для матрицы Т
существует условно обратная матрица Т#, удовлетворяющая
уравнению ТТ*р = р.
ЛипеСные операторы 213
Значит, для существования решения необходимо, чтобы при ото-
отображении из пространства наблюдаемых изображений в простран-
пространство исходных изображений (с помощью условно обратной ма-
матрицы Т#) и обратно (с помощью матрицы Т) снова получался
вектор наблюдаемых величин р. Если система уравнений является
недоопределенной (Р < Q), то решение существует тогда, когда
ранг матрицы Т равен Р, т. е. полному числу строк. Во всех
остальных случаях, в том числе и для переопределенной системы
уравнений, существование решения необходимо проверять.
8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ
УРАВНЕНИЙ
Установив существование решения системы уравнений
p = Tf, (8.5.1)
следует определить характер решения: является ли оно единст-
единственным или же решений несколько, а также какой вид имеет ре-
решение? Ответ на последний вопрос содержится в следующей фун-
фундаментальной теореме 14]:
Если решение системы уравнений р = Tf существует, то в об-
общем случае оно имеет вид
?=T*p4-(I-T*T)v, ' (8.5.2)
где Т# —матрица, условно обратная относительно матрицы Т,
a v — произвольный вектор размера QX 1.
Для доказательства умножим обе части соотношения (8.5.2)
на матрицу Т:
T?=TT*p4-T(I-T*T)v. (8.5.3)
Однако по условию существования решения ТТ#р = р. Кроме
того, согласно определению условно обратной матрицы, Т(I —
— Т*Т) = 0. Следовательно, Т f = р и вектор f является решением.
Поскольку Tf = p, то, умножив обе части этого равенства на
матрицу Т*, получим
Т*т?=Т*р, (8.5.4а)
или
Т*р-Т*Т?=0. (8.5.46)
ух
Прибавив к обеим частям вектор f, получим
f = Т*р _ Т*Т? + f = Т*р + (I - Т#Т)?. (8.5.5)
•^
Этот результат совпадает с соотношением (8.5.2), если вектор f,
стоящий в правой части формулы (8.5.5), заменить на произволь-
произвольный вектор v.
214 Глава 8
Поскольку обобщенная обратная матрица Т" и матрица Ts
обращения методом наименьших квадратов являются условно
обратными, то общее решение системы (8.5.1) также можно пред-
представить в виде
?=Tsp4-(l-TsT)v, (8.5.6а)
f=T-p + (l-T-T)v. (8.5.66)
Решение очевидно, будет единственным, если Т#Т = I.O^Bo всех
подобных случаях Т"Т = I. Исследовав ранг матрицы Т~Т,
можно доказать, что [4 ] если решение системы уравнений р == Tf
существует, что оно единственно тогда и только тогда, когда ранг
матрицы Т размера PxQ равен Q.
Отсюда следует, что если решение недоопределенной системы
уравнений существует, то оно не единственно. С другой стороны,
переопределенная система уравнений может иметь только одно
решение.
Пусть для системы уравнений (8.5.1) может быть получено
точное решение. Рассмотрим оценку
T+Tf, (8.5.7)
где Т+ обозначает одну из матриц, псевдообратных относительно
Т, которая не обязательно будет совпадать с этим решением,
поскольку произведение матриц Т+Т может не равняться единич-
единичной матрице. Величину ошибки, т. е. отклонение оценки ? от истин-
истинного значения f, обычно выражают через квадрат разности векто-
векторов f и f в виде произведения
&Е = $-ЪТ(*-Ь (8.5.8а)
или как
#? = tr{(f-?)(f-f)T}. (8.5.86)
Подставив выражение (8.5.7) в (8.5.8а), получим
9В = ? [I - (ГТ)Г] [I - (ГТ)] f. (8.5.9)
Значение матрицы Т+, при котором ошибка (8.5.8) оказывается
минимальной, можно найти, приравняв нулю производную от
ошибки ёЕ по вектору f. Согласно соотношению E.1.34),
д8Е1д\ =. О => 2 [I - (T+T)r] [I - (T+T)] f. (8.5.10)
Равенство (8.5.10) удовлетворяется, если матрица Т+ = Т, т. е.
является обобщенной обратной матрицей относительно Т. При
этом ошибка оценивания уменьшается до минимума, равного
arA.=.-fT[I-(T-T)]f, (8.5.11а)
Линейные операторы 215
или
^H = tr(ff[I-(T-T)j). (8.5.116)
Как и ожидалось, ошибка становится равной нулю, когда Т"Т =
== I. Это произойдет, например, если обобщенная обратная ма-
матрица Т~ имеет ранг Q и определяется соотношением (8.3.5).
8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ
ЛИНЕЙНЫХ УРАВНЕНИЙ
Несовместность системы уравнений р = Tf означает, что ни
для одной из возможных оценок f система не будет переходить
в тождество при подстановке f вместо f. В таких случаях систему
уравнений можно преобразовать к виду
p = Tf + e(f), (8.6.1)
где е (f) —вектор ошибки, зависящий от f. Найдем теперь такое
значение оценки f, при котором оказывается минимальной вели-
величина ошибки, выражаемая двумя эквивалентными соотношениями:
&м = [е (?)f [е (?)] = [р - Tff [р - Tf], (8.6.2а)
S'м = tr |[e (?)] [е (f)f} = tr ([p - Tf] [p - Tff}. (8.6.26)
Пусть символ Т+ обозначает псевдообратную матрицу, с помощью
которой получается оценка
?=Т+р. (8.6.3)
Прибавив и отняв произведение ТТ+р внутри обеих скобок соот-
соотношения (8.6.2а), получим
&м - [(I - ТТ+) р + Т (Гр - f)f [(I - TV) р + Т (Т+р - ?)].
(8.6.4)
После перемножения имеем
&м = [(I - ТГ) р]г [(I - ТТ+) р] + [Т (Т+р - f)f [T (Т+р - ?)] +
+ [(I - ГГ) р]г [Т(Т+р -?)] + [Т (Т+р - i)f [(I - ТГ)р]. (8.6.5)
Два перекрестных члена будут равны нулю, если ТТ+Т = Т
и (ТТ+) = (ТТ+)Г. Однако при выполнении этих условий матрица
Т+ является матрицей обращения методом наименьших квадратов,
т. е. Т+ = Ts. Тогда ошибка будет равна сумме двух положитель-
положительных слагаемых:
[Т(Т5р-?)Пт(Т5р-?)]. (8.6.6)
216 Глава 8
Второй член равенства (8.6.6) превращается в нуль, так как f =
= Tsp. Следовательно, ошибка уменьшается до величины
, (8.6.7а)
или, что то же самое,
#M = tr[ppr0-TTs)l. (8.6.76)
Как и ожидалось, ошибка равна нулю, если TTS = I.
Решение, полученное псевдообращением по методу наименьших
квадратов, может быть не единственным. Если при псевдообраще-
псевдообращении ввести дополнительные условия Т+ТТ+ = Т и Т+Т = (Т+Т)г,
при которых матрица Т+ является обобщенной обратной (т. е.
Т+ = Т"), то можно показать, что оценка, полученная с помощью
этой матрицы (f = T~g), является решением с минимальной нор-
нормой в том смысле, что
f г? < ТГТ, (8.6.8)
где f —¦ произвольная оценка, найденная методом наименьших
квадратов. Если обобщенная обратная матрица Т~ имеет ранг Q
и удовлетворяет определению (8.3.5), то произведение ТТ" не
обязательно равно единичной матрице, а ошибку можно найти из
соотношений (8.6.7). Если же матрица Т" имеет ранг Р, т. е. соот-
соответствует определению (8.3.6), то ТТ~ = I и ошибка равна нулю.
В последующих главах будет показано, как данные теорети-
теоретические положения применяются для исправления, анализа и ко-
кодирования изображений.
ЛИТЕРАТУРА
1. Pratt W. K-, Vector Formulation of Two Dimensional Signal Processing Ope-
Operations, J. Computer Graphics and Image Processing, 4, 1, 1—24 (March 1975),
Academic Press, New York.
2. Eklundh J. O., A Fast Computer Method for Matrix Transposing, IEEE Trans.
Computers, C-21, 7, 801—803 (July 1972).
3. Twogood R. E., Ekstrom M. P., An Extension of Eklundh's Matrix Trans-
Transposition Algorithm and Its Applications in Digital Image Processing, IEEE
Trans. Computers, C-25, 9, 950—952 (September 1976).
4. Graybill F. A., Introduction to Matrices with Applications in Statistics, Wads-
worth, Belmont, Cal., 1969.
5. Rao C. R., Mitra S. K-, Generalized Inverse of Matrices and Its Applications,
Wiley, New York, 1971.
6. Albert A., Regression and the Moore — Penrосе Pseudoinverse, Academic
Press, New York, 1972. [Имеется перевод: Алберт А., Регрессия, псевдо-
псевдоинверсия н рекуррентное оценивание.—М.: Наука, 1977.]
Глава 9
ОПЕРАТОР СУПЕРПОЗИЦИИ
Двумерный дискретный оператор суперпозиции определяется,
во-первых, как оператор дискретной линейной фильтрации, при-
применяемый к конечному массиву отсчетов, и, во-вторых, как дискре-
тизованный оператор аналоговой фильтрации. Обычно эти два
определения не эквивалентны. Ниже будут применяться оба опре-
определения. Кроме того, будет введен дискретный оператор суперпо-
суперпозиции с циклически (периодически) продолженной областью дей-
действия и описаны соотношения между тремя операторами.
9.1. ОПЕРАТОР СУПЕРПОЗИЦИИ КОНЕЧНЫХ МАССИВОВ
Рассмотрим сначала дискретный оператор суперпозиции конеч-
конечного массива отсчетов х) F (пи п2) (где п1г п2 = 1, 2, ..., N) с ко-
конечным массивом Н Aи /2; тъ т2) (где 1Ъ 12 = 1, 2, ..., L),
играющим роль импульсного отклика. В общем случае импульсный
отклик может изменяться в зависимости от координат (тъ т2)
отсчета в выходном массиве Q. Операция суперпозиции в ограни-
ограниченной области определяется соотношением
Q (mlt m2) = Г D F (nx, n,J H (m1 — nx -f 1,
n,=l n2=l -
' Щ — n2-h 1; mv m2), (9.1.1)
где mlt m2 = 1, 2, ..., M, а массивы Н и F имеют нулевые значе-
значения вне областей изменения соответствующих индексов. Анали-
Анализируя предельные значения индексов отсчетов импульсного от-
отклика, можно убедиться, что М = N + L — 1 и, следовательно,
выходной массив Q имеет большие размеры, чем исходный
(рис. 9.1.1).
Если массивы F и Q представлены соответственно в виде век-
вектора f размера N2x 1 и вектора q размера Мгх 1, то преобразова-
преобразование (9.1.1) можно записать как [1]
q = Df, (9.1.2)
Для простоты обозначений принято, что все массивы отсчетов квадратные.
218
Глава 9
где D —матрица размера M2xN2, содержащая отсчеты импульс-
импульсного отклика. Матрицу D оператора суперпозиции удобно раз-
Рис. 9.1.1. Суперпозиция конечных массивов отсчетов импульсного отклика
и исходного изображения.
А — массив из N X N отсчетов изображения; Б — повернутый на 180° массив из L X L
отсчетов импульсного отклика.
делить на блоки Dm>n размера MxN. Проанализировав пределы
суммирования в выражении (9.1.1), можно показать, что
¦>. 0 0
D
(9.1.
Произвольный ненулевой элемент матрицы D имеет вид
Dm,, пг {mlt п1) = Н(т1 — п1-}-1, т.г — п2 -)- 1; mlt m2),
(9.1.4)
где 1 ==? щ ^ N, а щ ^ т,- «; щ + L — 1. Отсюда следует, что
матрица D имеет регулярную структуру и заполнена довольно
редко, причем ненулевые блоки, группирующиеся в виде полосы
в средней части матрицы D, содержат зоны нулевых элементов.
Если форма импульсного отклика инвариантна относительно
сдвига (т. е. одинакова для всех точек выходного массива), то
структура матрицы D не зависит в явной форме от координат
(mi, т.,) выходного отсчета. Тогда
Dm2>n, = Dm!+i, „1+1. (9.1.5)
Оператор суперпозиции
219
Таким образом, все столбцы матрицы D образуются сдвигом пер-
первого столбца. В этом случае оператор суперпозиции называется
оператором свертки конечных массивов. На рис. 9.1.2,а приве-
приведены полученные на ЦВМ распечатки матриц, фигурирующих
в операции свертки конечных массивов, для случая, когда входной
массив имеет размеры 2x2 (N = 2), выходной массив 4x4 (М = 4),
а массив отсчетов импульсного отклика 3X3 (L — 3). Пары целых
12 13
22 23
32 33.
r\
и —
11
21
31
0
12
22
32
0
13
23
33
0
0
0
0
. о
0
11
21
31
0
12
22
32
0
13
23
33
0
0
0
0
i
i
i
i
i
i
i
i
1
i
i
i
i
i
i
i
1
1
1
I
1
I
i
t
i
i
i
i
i
i
i
0
0
0
0
11
21
31
0
12
22
32
0
13
23
33
0
0
0
0
0
0
11
21
31
0
12
22
32
0
13
23
33
Рис. 9.1.2. Примеры матриц операторов свертки конечных массивов.
а — общий случай, М
М = 16, N = 8, L = !
4, N = 2. L = 3; б — импульсный отклик гауссовой формы.
чисел (i, j) *) в матрице D обозначают (t, /)-й элемент матрицы
Н (t, /). Структура матрицы D лучше видна на примере матрицы
большего размера, показанной на рис. 9.1.2, б. В рассматриваемой
матрице М = 16, N — 8, L — 9, а импульсный отклик симметри-
симметричен и имеет гауссову форму. Заметим, что в данном примере раз-
размеры матрицы D равны 256x64.
Пользуясь методикой, примененной при выводе соотношения
(8.1.7), оператор суперпозиции можно представить в матричной
форме
Q= 2 Г Dm,nFvnuL (9.1.6)
m=l n=l
г) В этих парах отброшены запятые и пара индексов запнсывается как дву-
двузначное число. — Прим. перев.
220
Глава 9
Если импульсный отклик является инвариантным относительно
сдвига и разделимым, т. е.
H = hch?, (9.1.7)
где hc и Ья — вектор-столбцы, описывающие соответственно
характер изменения импульсного отклика по столбцам и строкам,
то
D = DC®DR. (9.1.8)
Матрицы DH и Dc имеют размеры MxN и структуру вида
M2) Ml>
ЛяC) Ля B)
^ir(L)
С S.I. 9)
Операция двумерной свертки в этом случае сводится к последова-
последовательному вычислению одномерных сверток по строкам и столбцам.
Таким образом,
? (9.1.10)
Для получения конечной свертки или суперпозиции в общем слу-
случае необходимо выполнить N2L2 арифметических операций, причем
в это число не входят умножения на нулевые элементы матрицы D.
Если же оператор является разделимым, т. е. удовлетворяет ра-
равенству (9.1.10), то достаточно выполнить NL (М + N) операций.
9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ
При цифровой обработке изображений во многих случаях
требуется перевести в дискретную форму интегральный оператор
суперпозиции, связывающий непрерывные изображения на входе
и выходе линейной системы. Такие явления, как смазывание изоб-
изображения, вызванное несовершенством оптической системы, апер-
турные искажения или искажения при наблюдении через турбу-
турбулентную атмосферу, можно описать с помощью следующего ин-
интегрального уравнения:
G(x,
, у; a,
(9.2.1а)
Оператор суперпозиции 221
где F (х, у) и G (х, у) описывают соответственно входное и выход-
выходное изображения, а ядро 7 (х, у; а, Р) представляет импульсный
отклик линейной системы 1). Импульсный отклик может быть
функцией четырех переменных — координат точек входной и вы-
выходной плоскостей. Если линейная система является пространст-
пространственно-инвариантной, то изображение на ее выходе можно описать
с помощью интеграла свертки
G(x, y)= Jj?(a, PO(x-«, y-P)dadp. (9.2.16)
—00
При дискретной обработке выходное изображение будет представ-
представлено отсчетами. Поэтому интеграл суперпозиции или сверт-
свертки следует преобразовать так, чтобы явно выразить связь отсчетов
выходного изображения со значениями функции, описывающей
входное изображение. Вопрос о дискретном представлении ин-
интегральных преобразований важен, поскольку получающиеся при
этом ошибки могут привести к большим ошибкам в обработанном
изображении или даже к потере устойчивости процесса цифровой
обработки. Кроме того, от выбора алгоритма дискретного пред-
представления, как правило, сильно зависит сложность самой обра-
обработки.
На первом этапе процесса дискретизации интеграла суперпо-
суперпозиции выходное изображение дискретизуется с помощью решетки
из B/ + 1) х B/ + 1) дельта-импульсов Дирака, разделенных
интервалом AS. В результате образуется массив отсчетов 2)
G (A AS, /2 AS) = G(x, у) Ь(х — 1г AS, у —и AS), (9.2.2)
где —J sr: /, s^ J ¦ Дельта-функцию можно ввести в подынтеграль-
подынтегральное выражение интеграла (9.2.1а); в результате получается соот-
соотношение
00
5 (j\ AS, U AS) = j J F (a, p) 7(]\ AS, /2 AS; a, p) da dp. (9.2.3)
— 00
Следует отметить, что дискретизация выходного изображения осу-
осуществляется по координатам плоскости наблюдаемого изображе-
изображения (х, у) и не затрагивает текущие переменные (а, {$), по кото-
которым проводится интегрирование.
*) В пределах данной главы знак ~ над символом функции указывает, что
соответствующие пространственные аргументы принимают значения обоих зна-
знаков, т. е. в интервалы их изменения входят отрезки как положительной, так и
отрицательной полуосей.
а) Для упрощения обозначений принято, что шаги дискретизации по гори-
горизонтали и вертикали одинаковы. Эффекты, связанные с конечными размерами
дискретизирующих импульсов, учесть нетрудно. Для этого импульсный отклик
следует заменить сверткой J (х, у; а, Р)*Р (—х, —у), где функция Р (х, у) опи-
описывает форму дискретизующего импульса.
222 Глава 9
На следующем этапе импульсный отклик следует ограничить
по длительности. Для этого положим
J (х, у; а, р) = 0 (9.2.4)
при 1 д: — а | > 7 и | г/ — р | > Т. Тогда
Ь AS+T j, AS+T
G & AS, /, AS) = j J F(a, pJ/tfiAS, /,AS; a, p)dadp.
/, AS-Г i, AS-Г
(9.2.5)
Следует отметить, что усечение импульсного отклика эквивалентно
умножению его на весовую функцию («окно») V (х, у), равную еди-
единице внутри квадрата | х\ < Т, | у \ < Т и нулю за его пределами.
Согласно теореме о спектре свертки, спектр получаемого после
усечения изображения равен свертке спектров изображения
G(x, у) и весовой функции (окна) V(x, у), причем спектр по-
последней есть двумерная sine-функция. Такое искажение спек-
спектра G (х, у) приводит к появлению паразитных компонент с
высокими пространственными частотами, группирующихся вблизи
частот, кратных 2я/7 (явление Гиббса). Искажения, вносимые
при усечении, можно уменьшить, используя более, совер-
совершенные весовые функции, такие, как окна Бартлетта, Блэк-
мана, Хемминга или Ханна1) [3], которые позволяют сгладить
нежелательные эффекты, связанные с наличием разрывов прямо-
прямоугольного окна. Выбор подходящего окна имеет большое значе-
значение, поскольку некорректность интегрального преобразования
(9.2.1а) может привести к резкому усилению искажений, вызван-
вызванных усечением импульсного отклика в процессе восстановления
изображения.
Следующий этап процесса дискретизации состоит в том, что
непрерывное исходное изображение F (а, Р) представляется набо-
набором значений описывающей его функции в узлах прямоугольной
сетки с шагом А/ и размерами BК + 1) х B/С +1). Эта опера-
операция является не взятием реальных отсчетов, а всего лишь матема-
математическим преобразованием, в результате которого получается мас-
массив
F {kx A/, kbM) = F (а, р) 6 (а — ^ А/, р —
- kz A/), (9.2.6)
где Кц s? k *s Km, причем Кц и Кш обозначают минимальное
и максимальное значения индекса ?;.
J) Иногда весовую функцию Ханиа. (U.von Harm) ошибочно называют «окном
Хеннинга». Хеннииг (harming) — операция умножения на эту весовую функ-
функцию. — Прим. перев.
Оператор суперпозиции 223
Если конечной целью является оценка непрерывного исходного
изображения путем обработки реальных отсчетов наблюдаемого
физического поля, то шаг А/ должен быть взят достаточно малым,
чтобы для исходного изображения удовлетворялся критерий
Найквиста. Это значит, что если исходное изображение имеет
спектр конечной ширины, то расстояние между узлами следует
положить равным соответствующему найквистовскому интервалу.
В идеальном случае это обеспечивает возможность точного вос-
восстановления изображения F (х, у) посредством интерполяции
оцененных значений F (kt A/, k2 A/).
Воспользовавшись формулами для приближенного вычисления
интегралов, в равенстве (9.2.5) интеграл можно аппроксимировать
суммой [2]. В этом случае реальные отсчеты изображения можно
описать выражением
G (Д AS, /2 AS) = ? X F fa А/, К A f) & fa, ft.) J (h AS,
/2AS; ^M, A, A/), (9.2.7)
где W (ki, k2) — весовые коэффициенты в конкретной приближен-
приближенной формуле, примененной для вычислений. Обычно пользуются
формулой прямоугольников, для которой все весовые коэффици-
циенты равны единице. В любом случае удобно объединить весо-
весовые коэффициенты и отсчеты импульсного отклика, так что
tff/iAS, /2AS; ^A/, КЫ) =
= Wfa, k2)J(]\AS, /,AS; k,M), *,A/)- (9-2.8)
Тогда
G (j, AS, j2 AS) = T' T, F (kt А/, К А/) Н (/\ AS,
/2AS; ^АЛ A, A/). (9.2.9)
Следует отметить, что функция Н не подвергалась дискретизации
по двум первым переменным. В формулах просто фигурируют ее
значения в соответствующих точках. Пределы суммирования
в равенстве (9.2,9) равны
где символ [• V обозначает округление до ближайшего целого
числа.
На рис. 9.2.1 приведен пример того, как реальные отсчеты
G (jx AS, /2 AS) выходного изображения сопоставляются с узловыми
224
Глава 9
F(a,O)
-5-4-3-2-1 0,1 2 3 4 5
/ с*
Рис. 9.2.1. Соотношение между отсчетами реального изображения и значениями
исходного изображения в узловых точках при численном представлении интег-
интеграла суперпозиции.
/Г
\!
!
( !
)!
/ 1
\ ¦
¦—¦
У
—-—__^
—.
^-—--_
—-
t
i )
! \
i /
1
к
Рнс. 9.2.2. Соотношение между областями расположения реальных отсчетов
и узловых точек при численном представлении интеграла суперпозиции.
А — исходное изображение; Б — область расположения отсчетов наблюдаемого изобра-
изображения; В — область расположения узловых точек.
Оператор суперпозиции 225
точками F (kt A/, fe2 Ы) исходного изображения. В данном при-
примере интервал между узлами выбран вдвое больше расстояния
между реальными отсчетами. Значения импульсного отклика,
использованные при вычислении суммы (9.2.9), показаны на этом
рисунке точками.
В связи с дискретным представлением (9.2.9) линейного ин-
интегрального преобразования следует сделать важное замечание:
независимо от соотношения между числом узловых точек и числом
реальных отсчетов площадь исходного изображения F (х, у), на
которой расположены узловые точки, влияющие на значения
реальных отсчетов, всегда оказывается больше площади дискрети-
зованного выходного изображения G (jt AS, /2 AS). Как показано
на рис. 9.2.2, размеры обоих изображений с точностью до одного
интервала дискретизации связаны соотношением
/ AS + Т = К А/. (9.2.11)
Итак, построена дискретная конечная модель линейного ин-
интегрального преобразования, которая связывает отсчеты выход-
выходного изображения G (j\ AS, /2 AS) со значениями элементов исход-
исходного изображения ~F (fej A/, fe2 А/) посредством математической
операции дискретного линейного преобразования. Такая операция
является аппроксимацией непрерывного преобразования, по-
поскольку импульсный отклик / (х, у; а, р) подвергался усечению,
а интеграл вычислялся по приближенным квадратурным форму-
формулам. Ясно, что, расширяя область определения импульсного от-
отклика, ошибку усечения можно сделать сколь угодно малой, хотя
это и связано с увеличением объема вычислений. Ошибки за счет
приближенного вычисления интегралов можно уменьшить, при-
применяя более точные квадратурные формулы, но также ценой услож-
усложнения вычислений. Следует, однако, отметить, что дискретный
вариант линейного интегрального преобразования является точ-
точной аппроксимацией последнего, если все функции пространствен-
пространственных переменных, входящие в формулу (9.2.1), имеют спектры
ограниченной ширины, а интервалы при дискретизации выходно-
выходного изображения и численном представлении исходного изобра-
изображения выбраны в соответствии с критерием Найквиста [4]. Воп-
Вопрос о точности и устойчивости дискретного представления рас-
рассмотрен в гл. 14.
Часто оказывается, что пользоваться соотношением (9.2.9)
удобнее, если оно представлено в векторной форме. С этой це-
целью нумерацию элементов массивов G и F следует изменить так,
чтобы образовались соответственно массивы размерами МхМ и
NN с положительными индексами. Допустим, что
F (щ. Д/, п2 Д/) = F {kx A/, k2 А/), (9.2.12а)
8 Прэтт У.
226
Глава 9
где щ = ki + К + 1, а
G (/«! AS, m, AS) = G (Д AS, /2 AS),
(9.2.126)
где m/ = // + / + 1. Кроме того, определим импульсный отклик
так, что
Я (mi AS, m2 AS; nt A/, n2 A/) =
= Я (Д AS, /2 AS; ^ A/, &2 A/). (9.2.12b)
На рис. 9.2.3 показаны геометрические соотношения между этими
функциями.
1 <
мг
б)
L,
1 < /,< Ц
6) Н(/г/г)
о) Fj(nvn2) 1<n2<N2
Рис. 9.2.3. Массивы отсчетов изображения и импульсного отклика.
Дискретное преобразование (9.2.9) применительно к сдвинутым
массивам имеет следующий вид:
F{ntM, na А/) Я (mj AS,
/n2AS; пг А/, п2А/), (9.2.13)
AS . 2
+
8, /n2AS)=
"i
где 1 sg т; «s Л1, а
Воспользовавшись методикой, описанной в гл. 5, можно сформиро-
сформировать векторы g и f, являющиеся разверткой матриц G и F по столб-
столбцам. Эти векторы связаны соотношением [1 ]
g=Bf, (9.2.14)
Оператор суперпозиции
227
где В — матрица размера М2 X N2, имеющая следующую струк-
структуру:
в =
в,.,
(Г-
Bi.t
о
(Г-В,
'M.N-L+1
Bm,N _
C,2.15)
Элементы матрицы В определяются равенством
Д»„ „2 К, nj = Н {щ AS, т2 AS; щ. AI, п2 А/) (9.2.16)
при 1 ==? т.-, ss М, mi ==s n,- ==s /n,- + Ь — 1, где L — [27/А/ ]N + 1
есть нечетное целое число, ближайшее к размерам импульсного
отклика, выраженным числом шагов дискретизации А/. В даль-
дальнейшем для простоты матрицу В будем называть матрицей сма-
смазывания. Если импульсный отклик инвариантен относительно
смещения, т. е.
Н (i\ AS, /2 AS; k, A/, k2 M) =
= Я (Д AS — kt A//2 AS — ife2 A/), (9.2.17)
то операция дискретной суперпозиции (9.2.13) превращается
в дискретную свертку:
, /n2AS)=
V2?/
"l=NlL "i
, n2AF)H(m1AS-
). (9.2.18)
Интересен частный случай, когда AS/A/ = k, где k — целое число.
При этом
m,/4-L— I m2k+L—I
Gf/njAS, m2AS)= Г j FfaM, n2 Al) H [m^k AI -
]. (9.2.19)
Теперь элементы матрицы смазывания равны
Bmi. п, К, nx) = Н \rnji А/ - щ. А/ + (L - 1) А/,
tn2k АГ - п2 AI-\-(L — 1)А/], (9.2.20)
где 1 ==s /п, г=: М и /n,- =s; n, «s /п, + ? — 1. Далее, если AS = A/,
то элементы матрицы смазывания принимают вид
Дя,./1, ("»i. «i) = Я («1 — «1 + ?, m2-n3 + L). (9.2.21)
Кроме того,
В
т,, я,
(9.2.22)
8*
228
Глава 9
Следовательно, все строки матрицы В получаются сдвигом первой
строки. Тогда оператор В является дискретизованным оператором
свертки, а представление суммы (9.2.19) упрощается:
G (т1г щ) =
—l m,+L—l
F (nlt n2)
— Лл +1,, щ — о, + L).
(9.2.23)
На рис. 9.2.4, а приведена распечатка матриц дискретизован-
ного оператора свертки, когда входной массив состоит из 4X4 от-
отсчетов (N=4), импульсный отклик представлен 3x3 отсчетами
(L=3), а выходной массив содержит 2x2 отсчета* (М = 2). На
рис. 9.2.4, б показан вид матрицы В для случая более высоких
размерностей, когда М =•= 8, N = 16, L = 9, а импульсный отклик
имеет гауссову форму.
в=
а
3
0
0
. 0
23
33
0
0
13
23
0
0
0
13
0
0
32
о
33
0
22
32
23
33
12
22
13
23
о; 31
12 ! 0
0|32
13 { 0
21
31
22
32
11
21
12
22
0
11
0
12
0
о
31
0
0
0
21
31
0
0
11
21
0"
0
0
11.
Рис. 9.2.4. Примеры матриц дискретизованиых операторов свертки.
а — общий случай, М = 2, N = 4, L = 3: б — импульсный отклик гауссовой формы,
М = 8, N = 16, L = 9.
Допустим, что импульсный отклик является пространственно-
инвариантным и разделимым, т. е.
В = Вс ® ВЯ)
(9.2.24)
где матрицы Вя и Вс размера MX.N имеют следующую струк-
структуру:
'hR(L) ML-D •'•
• М2)
о
L о
Mi)J
(9.2.25)
Оператор суперпозиции 229
В этом случае вычисление двумерной свертки сводится к последов
вательному выполнению сверток по строкам и столбцам матрицы
исходного изображения. Таким образом,
G = BcFBj. (9.2.26)
Для выполнения операции суперпозиции или вычисления свертки
в векторной форме нужно провести M2La арифметических опера-
операций, причем в это число не входят умножения на нулевые элементы
матрицы В. Если же оператор свертки разделим, то для вычисле-
вычислений в матричной форме достаточно ML (M + N) арифметических
операций.
Предположим, что при одном и том же импульсном отклике
размера LxL к массиву отсчетов изображения размера NXN
с целью моделирования процесса непрерывной суперпозиции
применены оператор суперпозиции конечных массивов и дискрети-
зованный оператор суперпозиции. Тогда массив, обработанный
первым оператором, совпадает с массивом, полученным в резуль-
результате действия второго оператора, который окружен полосой из
L — 1 лишних элементов 1), и наоборот, если размеры обработан-
обработанных массивов будут одинаковыми, то L — 1 пограничных элеме-
тов массива, полученного с помощью оператора конечной супер-
суперпозиции, окажутся искаженными. Таким образом, следует с осто-
осторожностью применять оператор суперпозиции конечных массивов
для моделирования непрерывных процессов.
9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ
При использовании оператора циклической суперпозиции
массивы отсчетов входного и выходного изображений, а также
импульсного отклика должны быть периодическими по простран-
пространственным переменным с одинаковым периодом. Для единства из-
изложения примем, как и прежде, что все эти массивы имеют конечные
размеры. Допустим также, что массив исходных отсчетов F (пъ па)
размером NXN помещен в левый верхний угол массива, содержа-
содержащего /х/ нулей (/ > N), т. е. образуется расширенный массив
^лК. п2) = Р(пъ пг) ПРИ 1<П/<Л^, (9.3.1а)
Ре К, п2) = 0 при N + 1 <s tit < J. (9.3.16)
Аналогично формируется расширенный массив отсчетов импульс-
импульсного отклика:
НЕ {1Ъ /2; тх, т2) = Н AЪ /2; щ, щ) при 1 < /, < L,
(9.3.2а)
НЕ{1Ъ /2; ть /п2) = 0 при L+l <li<J. (9.3.26)
х) Исключением является случай, когда вдоль границы входного массива
лежит полоса из (I — 1)/2 нулевых элементов. Реальным примером этого может
служить смазаииый снимок Луны на фойе ночного неба.
230
Глава 9
Далее образуем периодически продолженные массивы FE (пъ п2)
и НЕ AЪ 1г; тъ т2), повторяя (размножая) расширенные мас-
массивы с периодом в / отсчетов. Циклическая свертка этих массивов
по определению равна
j j
KE{mlt Щ) = Е Е FP(nlt nJHpini! — «!+ 1,
т2 — п2 +1; Щ, т2). (9.3.3)
Бросается в глаза сходство данного выражения с равенством
(9.1.1), описывающим суперпозицию конечных массивов. В самом
деле, если / выбрано так, что J = N + L — 1, то FE (тъ т2) =
= F (тъ т2) при 1 ==с mt ^ M. Следует также отметить сходство
циклической суперпозиции с суперпозицией дискретизованных
массивов. Эти соотношения становятся более ясными, когда ис-
используется векторное представление циклической суперпозиции.
Допустим, что массивы FE и К.е представлены соответственно
(Р X 1)-компонентными векторами iE и кЕ. Тогда для операции
циклической суперпозиции можно записать соотношение
k? = Cf?, (9.3.4)
где С — матрица элементов массива НЕ размера Р X Р. Оператор
циклической суперпозиции удобно выразить в виде блочной ма-
матрицы с блоками Cmin размера JxJ:
с =
C2.i
^ о
С2>
Cj.,2
Clj-L+2
(9.3.5)
^ о
где
Cm,, n, C"i. nl) = HB(k1, k2; mlt щ), (9.3.6)
причем 1 ==s Щ =s: / и 1 ss Щ === J, a kt = (mt — щ + l)modj и
#л (Of 0) = 0. Следует отметить, что каждая строка и каждый
столбец блочной матрицы С содержат L ненулевых блоков. Если
массив отсчетов импульсного отклика является пространственно-
инвариантным, то
Ст„ „, = Cmi+1. „2+i (9.3.7)
и любую строку (или столбец) можно получить путем циклической
перестановки блоков первой строки (или первого столбца). На
рис. 9.3.1, а приведен пример оператора циклической свертки
Оператор суперпозиции
231
[и 12 m
21 22 23
31 32 33 J
II
21
31
0
12
22
32
0
13
23
33
0
0
0
0
0
0
II
21
31
0
12
22
32
0
13
23
33
0
0
0
0
31
0
II
21
32
0
12
22
33
0
13
23
0
0
0
0
21
31
0
II
22
32
0
12
23
33
0
13
0
0
0
0
0
0
0
0
II
21
31
0
12
22
32
0
13
23
33
0
0
0
0
0
0
II
21
31
0
12
22
32
0
13
23
33
0
0
0
0
31
0
II
21
32
0
12
22
33
0
13
23
1
0 113
О1 23
о [зз
0 , 0
- - X
211 0
311 0
0 1 0
II ' 0
~ 1—
22 | II
32 | 21
1
0 , 31
12 | 0
23 ' 12
33 B2
1
0 1 32
13 | 0
i
0
13
23
33
0
0
0
0
0
II
21
31
0
12
22
32
33
0
13
23
0
0
0
0
31
0
11
21
32
0
12
22
23
33
0
13
0
0
0
0
21
31
0
11
22
32
0
12
i
12
|22
'32
1
.1
1
1
1
0
13
23
33
0
1
1
1
j_
1
0
0
0
0
11
¦21
1
1
i
31
0
0
22
32
0
13
гз
зз
0
0
0
0
0
11
21
31
32
0
12
22
33
0
13
23
0
0
0
0
31
0
II
21
22
32
0
12
23
33
0
13
0
0
0
0
21
31
0
II
Рис. 9.3.1. Примеры матриц оператора циклической свертки.
а — общий случай, J = 4, L = 3: б — импульсный отклик гауссовой формы, У = 1В.
L =и 9.
232
Глава 9
когда входной и выходной массивы имеют размеры 16x16 (J = 4),
а размер массива отсчетов импульсного отклика равен 3x3
(L = 3). На рис. 9.3.1, б показана структура матрицы того же
оператора при J = 16 и L = 9, когда импульсный отклик имеет
гауссову форму.
Если же импульсный отклик является пространственно-инва-
пространственно-инвариантным и разделимым, то
С = Сс ® СЛ, (9.3.8)
где Сл и Сс — матрицы вида
МО
M2)
0 S^«(L)
о 6ч
М2)'
МЗ)
о
(9.3.Э)
размер которых равен Ух У. При этом двумерная циклическая
свертка вычисляется в соответствии с соотношением
^ (9.3.10)
9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ: ОПЕРАТОРАМИ ,;
Из матрицы оператора циклической суперпозиции С можно
получить матрицы оператора суперпозиции конечных массивов D
и дискретизованного оператора суперпозиции В. Для этого сле-
следует ввести выделяющие матрицы
L-1
lfc! 0 }\К,
К J-K-L+1
(9.4.1а)
= [ 0 i 1К 1 0 '1}А, (9.4.16)
где 1К — единичная матрица размера К х К. Приведем соотно-
соотношения, связывающие эти матрицы с матрицами, полученными из
них обобщенным обращением и транспонированием:
(9.4.2а)
(9.4.26)
(9.4.2b)
(9.4.2r)
Оператор суперпозиции
233
Анализируя структуру различных линейных операторов, можно
показать, что
D = [SlSM) <g> SlSM)] С [Slf > ® Slf >]г, М > W, (9.4.3а)
Таким образом, матрица D образуется посредством выделения
первых М строк и N столбцов блока Ст> „ матрицы С. При этом
во всех других блоках также выделяются первые М строк и N
столбцов. Аналогично из матрицы С можно образовать матрицу В.
Элементы матрицы С, из которых формируются матрицы D и В,
на рис. 9.3.1, а заключены в рамки.
Из определения (9.3.1) расширенного массива отсчетов исход-
исходного изображения следует, что вектор отсчетов конечного исход-
исходного изображения f образуется из вектора расширенного изобра-
изображения fE при помощи операции выделения:
(9.4.4а)
F. (9.4.46)
Можно также показать, что выходной вектор оператора суперпо-
суперпозиции конечных массивов можно получить из выходного вектора
J-M
м
J-M
L-1 М . J-M-L+t %
J-M-L*1
JtNZM+L-1
¦ ¦¦ 5
Рис. 9.4.1. Расположение матриц Q и G в матрице Кя-
а — оператор суперпозиции конечных массивов; б — дискретизопаиный оператор супер-
суперпозиции.
оператора циклической суперпозиции с помощью операции выде-
выделения:
q = [SlS^* <S> SiS^*]^. (9.4.5a)
Между векторами существует и обратное соотношение
(9.4.56)
234 Глава 9
Для дискретизованного оператора суперпозиции
(9.4.6)
однако обратный переход от g к кЕ выполнить не удается в силу
недоопределенности дискретизованного оператора суперпозиции.
Преобразуя q и кЕ в матричную форму, из соотношения (9.4.5а)
можно получить равенство
Q = S ЪМЪ [SlljM) ® SlH NnK?vX- (9-4.7)
Поскольку оператор выделения обладает свойством разделимости,
формула (9.4.7) упрощается к виду
Q=[SlHK?[Slwf. (9.4.8)
Аналогично из равенства (9.4.6), относящегося к дискретизован-
ному оператору суперпозиции, можно получить соотношение
G=[S2w]K?[S2^)]r. (9.4.9)
На рис. 9.4.1 показано расположение элементов матрицы Кя,
из которых формируются матрицы для оператора суперпозиции
конечных массивов Q и для дискретизованного оператора суперпо-
суперпозиции G.
Итак, для обоих операторов выходные векторы можно полу-
получить из результата циклической суперпозиции с помощью опера-
операции выделения части элементов. Как показано в гл. 11, этот факт
позволяет упростить вычисления.
ЛИТЕРАТУРА
1. Pratt W. К., Vector Formulation of Two Dimensional Signal Processing Ope-
Operations, J. Computer Graphics and Image Processing, 4, 1, 1—24 (March 1975),
Academic Press, New York.
2. McCalla T. R., Introduction to Numerical Methods and FORTRAN Program-
ming, Wiley, New York, 1967.
3. Oppenheim A. V., Schaefer R. W., Digital Signal Processing, Prentice-Hall,
Englewood Cliffs, N. J., 1975. [Имеется перевод: Оппенгейм А. В., Ша-
Шафер Р. В., Цифровая обработка сигналов. — М.: Связь, 1979.]
4. Papoulis A., Systems and Transforms with Applications in Optics, McGraw-
Hill, New York, 1968. [Имеется перевод: Папулис А., Теория систем и пре-
преобразований в оптике. —М.: Мир, 1971.]
Глава 10
ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ
Существуют три основные области применения двумерных
унитарных преобразований для обработки изображений. Во-пер-
вых, преобразования используются для выделения характерных
признаков изображения. Так, например, постоянная составляю-
составляющая спектра Фурье пропорциональна средней яркости изобра-
изображения, а высокочастотные составляющие характеризуют величину
и ориентацию его контуров. Другой областью применения пре-
преобразований является кодирование изображений, когда ширина
спектра уменьшается за счет отбрасывания или грубого кванто-
квантования малых по величине коэффициентов преобразования. Третья
область приложений — это сокращение размерности при выпол-
выполнении вычислений. Иначе говоря, в процессе обработки (например,
фильтрации) малые коэффициенты преобразования можно отбро-
отбросить без заметного ухудшения качества обработки. В последую-
последующих главах эти применения будут описаны более детально. В этой
главе рассмотрены свойства преобразований, наиболее часто
встречающихся при обработке изображений.
ЮЛ. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
Унитарные преобразования являются частным случаем ли-
линейных преобразований, когда линейный оператор [см. (8.1.1)]
точно обратим, а его ядро удовлетворяет условиям ортогональ-
ортогональности [1, 2]. В результате прямого унитарного преобразования
матрицы изображения F (пъ п2) размера Ni X N2 образуется
матрица преобразованного изображения того же размера, эле-
элементы которой по определению равны
&~(тъ т2) = Y) Г р(Пь п2)А(п1г п2; тъ тг), A0.1.1)
где A (tti, 1ц; ти т2) — ядро прямого преобразования. Исходное
изображение можно получить с помощью обратного преобразо-
преобразования, описываемого соотношением
^(«i. 4) = Ъ 2j &(Щ, Щ)В{пь п2; щ, т.2), A0.1.2)
mi=l /п2=1
236 Глава 10
где В (пъ пг; тъ тй) — ядро обратного преобразования. Преоб-
Преобразование является унитарным, если выполняются следующие
условия ортогональности:
? ? А(пи п2; щ, т.г)А*{}ъ /2; m-jmj) = 6(пх — ]ъ пъ — ]2),
A0.1.3а)
*(]\, /.; "ь яц) = в (% — jlt л« —/»),
/л, т2
A0.1.36)
A0.1.3b)
Ij L ("i> ; ^i, Щ)В*{пъ п2; Аь ^2) = б(т1 —Аь т2 — k2).
(ЮЛ.Зг)
Преобразование называют разделимым, если оба его ядра
можно представить в следующей форме:
А (п1г tu; т1г т%) = Ас(пъ тх) AR (я2, щ), A0.1.4а)
В (nv п2; тъ тг) = Вс (nlt щ) BR (n2, щ), A0.1.46)
где через Ас (или BL) и AR (или BR) обозначены соответственно
одномерные операторы преобразования столбцов и строк. Резуль-
Результат воздействия оператора разделимого двумерного унитарного
преобразования можно находить в два этапа. Сначала выпол-
выполняется одномерное преобразование по всем столбцам матрицы
изображения, причем образуется матрица с элементами
P(mlt na)= ? F{nu n2)Ac(nu щ). A0.1.5)
Затем выполняется второе одномерное преобразование по всем
строкам полученной матрицы, в результате которого образуется
массив чисел вида
д-{т1Ущ)^ Б Р(Щ, п2)Ац(щ, яц). A0.1.6)
Унитарные преобразования удобно записывать с помощью век-
векторных обозначений [3]. Допустим, что F и f — матричное и век-
векторное представления массива отсчетов исходного изображения,
а &~ и f — матричное и векторное представления преобразован-
преобразованного изображения. Тогда двумерное унитарное преобразование
в векторной форме выражается соотношением
/ = Af, A0.1.7)
Двумерные унитарные преобразования 237
где А — матрица прямого преобразования. Обратное преобразо-
преобразование записывается как
/ = Bf, A0.1.8)
где В — матрица обратного преобразования. Очевидно, что
В — А. A0.1.9)
Для унитарных преобразований обратная матрица удовлетворяет
соотношению
А-' = А*Г. A0.1.10)
В этом случае матрицу А называют унитарной. Действительная
унитарная матрица называется ортогональной матрицей, и для
нее справедливо соотношение
A'^A7". A0.1.11)
Если ядра преобразования разделимы, так что
А = АС®АН, A0.1.12)
где Ад и Ас — унитарные матрицы преобразования по строкам
и столбцам, то матрицу преобразованного изображения можно
получить из матрицы исходного изображения с помощью ра-
равенства
#- = AcFA?. A0.1.13а)
Обратное преобразование определяется соотношением
где Вс = Ас1 и Вл = Aij1.
V Разделимые унитарные преобразования можно также пред-
представлять в виде взвешенной суммы матричных произведений
вектор-столбцов, сформированных из элементов матриц. Пусть
ас (ла) и ад (л2) обозначают пгй и п2-й столбцы матриц Ас и Ад.
Нетрудно показать, что
Nl N,
#"=!] U F(nu nJMnJaJK). A0.1.14a)
«1 = 1 «2 = 1
Аналогично
f= Б L ^
где bc (Щ) и bfl (m2) — тгй и т2-й столбы матриц Вс и В« соот-
соответственно. Матричные произведения векторов, входящие в суммы
A0.1.14), образуют последовательности матриц, называемых ба-
238 Глава 10
зисными матрицами, на основе которых и производится разложе*
ние матрицы F исходного изображения или преобразованного
изображения ЗГ.
Возможны различные интерпретации унитарных преобразо-
преобразований. Преобразование изображения можно рассматривать как
разложение исходного изображения в обобщенный двумерный
спектр [4]. Каждая спектральная составляющая характеризует
вклад соответствующей спектральной (базисной) функции в энер-
энергию исходного изображения. При такой трактовке понятие ча-
частоты можно обобщить так, чтобы оно было применимо не только
к синусам и косинусам, но и к другим функциям, на которых осно-
основываются преобразования. Подобный обобщенный спектральный
анализ полезен для изучения тех конкретных разложений, кото-
которые в наибольшей мере подходят для данного класса изображений.
Наглядное представление о преобразованиях изображений можно
получить и по-другому, рассматривая преобразование как пово-
поворот многомерной системы координат. Одним из главных свойств
унитарного преобразования является сохранение метрики. На-
Например, евклидово расстояние между двумя изображениями
равно евклидову расстоянию между их образами. Третья возмож-
возможность интерпретации преобразований заключается в том, что
равенство A0.1.2) можно рассматривать как способ составления
изображения из набора двумерных функций В (пь п2; тъ т2),
каждая из которых соответствует определенной точке (/nlt /щ)
плоскости обобщенных частот. В подобной интерпретации ядро
В (пь и2; тъ /га2) называют двумерной базисной функцией, а ко-
коэффициент ?Г (ть т2) указывает «вес» этой базисной функции,
необходимый для получения рассматриваемого изображения.
Для упрощения анализа свойств двумерных унитарных пре-
преобразований ниже в этой главе будет принято, что все массивы
являются квадратными и имеют размер N х N. Кроме того,
будут изменены обозначения и нумерация всех индексов в выра-
выражениях вида A0.1.1) и A0.1.2). Таким образом, массив отсчетов
исходного изображения будет обозначен через F (/, k), где /, k =
= 0, 1, ..., N — 1, а массив коэффициентов преобразования —
через ?Г {u,'v), где и, v = 0, I, ..., N — 1. С учетом этого прямое
унитарное преобразование записывается в следующем виде:
и, «) = Б Б F(l, k)A(J, k; и, v), A0.1.15a)
а обратное преобразование — как
F(j, k) = Б Б Г (и, v)B(j, k; и, v). A0.1.156)
Двумерные унитарные преобразования 239
10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
Дискретное двумерное преобразование Фурье матрицы отсчетов
изображения определяется [5—10] в виде ряда
ЛГ-1 JV-1
и, o) = 4"S 2 F(j'
/0 *
S 2
A0.2.1а)
где i = У—1, а дискретное обратное преобразование имеет вид
Л'-l N-X
F(l, *) = "г2 2 ^~{и' »)«р{-^-(«/ + »*)}• (Ю.2.16)
По аналогии с терминологией непрерывного преобразования
Фурье переменные и, v называют пространственными частотами.
Следует отметить, что не все исследователи пользуются опреде-
определением A0.2.1); одни предпочитают помещать все масштабные
постоянные в выражение для обратного преобразования, а другие
изменяют знаки в ядрах на противоположные.
Поскольку ядра преобразования симметричны и разделимы,
двумерное преобразование можно выполнить в виде последова-
последовательных одномерных преобразований по строкам и столбцам
матрицы изображения. Базисными функциями преобразования
являются экспоненты с комплексными показателями, которые
можно разложить на синусную и косинусную составляющие.
Таким образом,
A {I, k; и, v) = exp{—
= cos i~- (uj + vk)\ - isin i~- (uj + «fe)J, A0.2.2a)
В (j, k; u, v) = exp {ijL (uj + и/г)} =
= cos {-^- {uj + «ft)} + isin {-|L (uj + vk)\ ¦ A0.2.26)
На рис. 10.2.1 приведены графики синусных и косинусных со-
составляющих одномерных базисных функций преобразования Фурье
для Af = 16. Видно, что для низких частот эти функции являются
грубыми аппроксимациями непрерывных синусоид. С повышением
частоты сходство базисных функций с синусоидами теряется.
Для наивысшей частоты базисная функция представляет собой
меандр. Можно заметить также избыточность наборов синусных
и косинусных составляющих.
240
Глава 10
Спектр изображения имеет много интересных структурных
особенностей. Спектральная составляющая в начале координат
частотной плоскости
f N
, 0)-тг
if
/=о
j, k)
A0.2.3)
равна увеличенному в N раз среднему (по исходной плоскости)
значению яркости изображения. Подставив^в равенство A0.2.1а)
Номер базисной
функции,
О :
Номер базисной
(рункцш/
OL--
п
п
L»_ U U U
I I I I I I I I I I I I II I I I
О 4 8 12 16
а
• I I I I I I I I I I I I I I I II
О 4 8 12 16
Рис. 10.2.1. Базисные функции преобразования Фурье.
а — синусная (нечетная) составляющая; б — косинусная (четная) составляющая.
и = и +
и и = о + и#, где тип — постоянные, получим
дг_1 ЛГ-1
{
/=0
хехр{—2ш(т/ + п/е)}. A0.2.4)
При любых целочисленных значениях тип второй экспонен-
экспоненциальный множитель равенства A0.2.4) превращается в единицу.
Таким образом, при т, п = 0, ±1, ±2, ...
Т (и + mN, v + пЛО = ^ (и, и), A0.2.5
Двумерные унитарные преобразования
241
что свидетельствует о периодичности частотной плоскости.
Рис. 10.2.2, а иллюстрирует этот результат.
Двумерный спектр Фурье изображения является по существу
представлением двумерного поля в виде ряда Фурье. Для того
чтобы такое представление было справедливым, исходное изоб-
изображение также должно обладать периодической структурой, т. е.
(как показано на рис. 10.2.2, б) иметь рисунок, повторяющийся
по вертикали и горизонтали. Таким образом, правый край изобра-
Рис. 10.2.2. Периодическое продолжение изображения и спектра Фурье.
а — спектр; б — исходное изображение.
жения примыкает к левому, а верхний край — к нижнему-
Из-за разрывов значений яркости в этих местах в спектре изоб-
изображения возникают дополнительные составляющие, лежащие на
координатных осях частотной плоскости. Эти составляющие не
связаны со значениями яркости внутренних точек изображения,
но они необходимы для воспроизведения его резких границ.
Если массив отсчетов изображения описывает поле яркости,
то числа F (/, k) будут действительными и положительными.
Однако спектр Фурье этого изображения в общем случае имеет
комплексные значения. Поскольку спектр содержит 2Иг ком-
компонент, представляющих действительную и мнимую части или
фазу и модуль спектральных составляющих для каждой частоты,
может показаться, что преобразование Фурье увеличивает раз-
размерность изображения. Это, однако, не так, поскольку ^{и, v)
обладает симметрией относительно комплексного сопряжения.
Если в равенстве A0.2.4) положить тип равными целым числам,
то после комплексного сопряжения получится равенство
/.О А=0
A0.2.6
С помощью подстановки u — —и и v = —и можно показать, что
{и, и) = ?-*(—u + mN, —v + nN) A0.2.7)
f (/, k) ехр Ш- (uj + vk)\.
242
Глава 10
при т, п = 0, ±1, ±2, .... Из-за наличия комплексно-сопряжен-
комплексно-сопряженной симметрии почти половина спектральных составляющих
оказывается избыточной, т. е. их можно сформировать из осталь-
остальных составляющих. На рис. 10.2.3 области расположения избы-
избыточных составляющих спектра на частотной плоскости заштрихо-
заштрихованы. Избыточными составляющими можно, конечно, считать гар-
гармоники, попадающие не в нижнюю, а в правую полуплоскость.
о i
128
255
128
255
•///////////////77
Рис. 10.2.3. Частотная плоскость.
На рис. 10.2.4 приведены фотографии исходного изображения
и различных вариантов его фурье-спектр а. Поскольку динами-
динамический диапазон составляющих спектра гораздо шире, чем линей-
линейный участок интервала экспозиций фотопленки, то спектры необ-
необходимо подвергнуть сжатию. Сжатие динамического диапазона
можно осуществить путем ограничения больших спектральных
составляющих или логарифмическим преобразованием всех со-
составляющих спектра согласно соотношению
(и, v) = log [а + Ъ | Т (и, i-)|], A0.2.8)
где а и b — масштабные постоянные. На рис. 10.2.4, б приведены
(в логарифмическом масштабе са= 1 и 6 = 1) модули гармоник
спектра, вычисленных в соответствии с равенством A0.2.1а).
На рис. 10.2.4, в показан тот же спектр, в котором наибольшие
гармоники, составляющие 25 % всех компонент спектра, были
ограничены по величине. При математическом анализе непре-
непрерывных сигналов начало координат частотной плоскости обычно
Двумерные унитарные преобразования
243
помещают в ее геометрическом центре. Аналогично в дифракцион-
дифракционной картине, полученной с помощью когерентной оптической
системы для диапозитива с коэффициентом пропускания F (х, у),
Рис. 10.2.4. Преобразование Фурье изображения «Портрет».
а — исходное изображение; б — модули гармоник спектра (в логарифмическом масш-
масштабе, бея перестановки гармоник); в — спектр с ограниченными наибольшими гармони-
гармониками (без нх перестановки); г — спектр с ограниченными наибольшими гармониками
(посЛе их перестановки).
гармоника с нулевой частотой оказывается в центре. Двумерный
дискретный фурье-спектр, найденный с помощью вычислительной
машины, путем простой перестановки коэффициентов можно из-
изменить так, чтобы начало координат также оказалось в центре
массива. Тот же результат можно получить по-другому, если от-
отсчеты изображения предварительно умножить на коэффициенты
вида (—l)'+ft. Тогда квадранты спектра, рассчитанного согласно
формуле A0.2.1а), в процессе вычисления автоматически меняются
244
Глава 10
местами. Данное утверждение можно доказать с помощью соот-
соотношения A0.2.4), положив в нем т = п = г1г. Тогда в силу
тождества
(-l)i+k A0.2.9)
выражение A0.2.4) можно записать в следующем виде:
S 2 {^ } (Ю.2.10)
;=0 А=0
На рис. 10.2.4, г представлен спектр с переставленными гармо-
гармониками.
Прямое и обратное преобразования Фурье A0.2.1) можно пред-
представить в векторной фэрме
f = Af, A0.2.11а)
f = A*7f, A0.2.116)
где f и f — векторы, полученные соответственно путем развертки
по столбцам матриц F и ЗГ. Поскольку матрицу преобразования А
можно записать в виде прямого произведения
А = А6.®АД, A0.2.12)
где
Ая — \г -
С - ,/-Т7-
V"n~
Hffi^ *HP^ Hto^
урЛ урЧ Ж4
Ж"'1
Ж°
«(
, A0.2.13)
Ж—ехр\—2т/Щ, то матрицы изображения и спектра связаны
соотношениями
0? = АсРАд A0.2.14а)
и
F = Ac^A^. A0.2.146)
Понятно, что свойства преобразования Фурье, установленные для
рядов A0.2.1), сохраняются и при его матричной записи.
Хотя преобразование Фурье имеет много полезных для ана-
анализа свойств, у него есть и два существенных недостатка: во-
первых, все вычисления приходится производить не с действи-
действительными, а с комплексными числами и, во-вторых, ряды схо-
сходятся медленно. Последнее замечание, весьма существенное для
Двумерные унитарные преобразования
245
задач кодирования изображений, можно пояснить, переписав
определение A0.2.16) в следующей форме:
F(j, k)=
t
lim
r-s-{JV+l)/2
и, v?S(UT, VT)
A0.2.15)
где 5 (UT, VT) — низкочастотная область частотной плоскости,
которая на рис. 10.2.5 заштрихована. Если верхние границы UT
и VT зафиксированы, а размер изображения N сравнительно не-
невелик, то заключенная в квадратные скобки величина может
сильно отличаться от F (/, k), пока UT и VT не станут достаточно
N-1-VT
N-1
"N-1-UT
/ / / / / / / /
у/у//.',
^/У/У/'/у
N-1
Рис. 10.2.5. Низкочастотная область частотной плоскости.
большими. В дальнейшем вопрос о сходимости преобразований
будет проанализирован с количественных позиций. Качественно же
можно указать, что плохая сходимость преобразования Фурье
обусловлена скачками изображения, возникающими на линиях
перехода от левого края изображения к правому и от верхнего
к нижнему. Эти разрывы приводят к появлению в спектре больших
составляющих с высокими пространственными частотами.
10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ
Известно, что ряд Фурье для любой непрерывной действи-
действительной и симметричной (четной) функции содержит только дей-
действительные коэффициенты, соответствующие косинусным членам
246
Глава 10
ряда. В соответствующей интерпретации этот результат можно
распространить и на дискретное преобразование Фурье изобра-
изображений. Существуют [11] два способа получения симметричных
изображений (рис. 10.3.1). Согласно первому из них, к изображе-
изображению вплотную пристраивают его зеркальные отражения. По вто-
X
X
(j.k)
X
X
1
I F(j,M.
1
1
A
I
1
1
1
1
а 6
Рис. 10.3.1. Построение симметричного изображения, предназначенного для ко-
косинусного преобразования.
а — отражение относительно края: б — отражение относительно крайних элементов.
рому методу оригинал и отражения пристраивают, налагая край-
крайние элементы. Таким образом, из первоначального массива,
содержащего NXN элементов, в первом случае (называемом чет-
четным косинусным преобразованием) получается массив из 2NX2N
элементов, а во втором случае (называемом нечетным косинус-
косинусным преобразованием) — массив из BN — 1) X BN — 1) эле-
элементов.
Четное симметричное косинусное преобразование
Допустим, что симметричный массив образован путем зер-
зеркального отражения исходного массива относительно его краев
согласно соотношению
F(j, k) при j> 0, k^O,
f(-l-j, Л)при /<0, *>0,
(ЮЗЛ)
F(—\-j, —\~k) при /<0,
Построенный таким образом массив Fs (/, k) симметричен отно-
относительно точки j — —V2, k = —V2. Вычислив преобразование
Фурье для случая, когда начало координат находится в центре
симметрии, получим
N—l N—1
-N k=
A0.3.2)
Двумерные унитарные преобразования
247
где и, v = —N, ..., —1, О, 1, ..., N — 1. Поскольку массив
Fs (/", k) симметричен и состоит из действительных чисел, соотно-
соотношение A0.3.2) можно свести к виду
<ys (и, v) =
т
A0.3.3)
Номер
базисной
функции
¦ I I I I I I I I I I I I I I I I I
О 4 8 12 16
Рис. 10.3.2. Базисные функции косинусного преобразования.
С другой стороны, спектральные составляющие вида A0.3.3)
можно найти, вычисляя преобразование Фурье массива F (/, k)
по 2N точкам:
V V
k
k=Q
. (Ю.3.4)
Прямое четное косинусное преобразование по определению
[12] равно сумме A0.3.3), умноженной на нормирующий мно-
248
Глава 10
житель, т. е.
N—1 N-\
Г {и, v)~ ^-C
x cos [iLu (/+ 1)] cos [-5-0
/=0
j, k) x
y)]' A0-3-5a)
Phc. 10.3.3. Косинусное преобразование изображения «Портрет».
а — исходное изображение: б — косинусный спектр в логарифмическом масштабе по оси
амплитуд; в — спектр с ограниченными наибольшими гармониками.
а обратное преобразование определяется соотношением
N—1 N—\
С (и) С (и)*" (и, о) х
ы=0 о=о
x<
(ю.3.56)
Двумерные унитарные преобразования 249
где С @) = B)-1/., а С (w) = 1 при w = 1, 2, .... N — 1. Ока-
Оказалось, что базисные функции четного косинусного преобразова-
преобразования принадлежат к классу дискретных полиномов Чебышева [12].
На рис. 10.3.2 приведены графики базисных функций чет-
четного симметричного косинусного преобразования при N — 16.
Образцы спектра, получаемого при четном симметричном коси-
косинусном преобразовании, приведены на рис. 10.3.3. Начало коор-
координат расположено в верхнем левом углу каждого снимка, что
согласуется с принятым в теории матриц порядком. Следует от-
отметить, что здесь, как и в случае преобразования Фурье, основ-
основная часть энергии изображения концентрируется в области низ-
низких пространственных частот.
Нечетное симметричное косинусное преобразование
При нечетном косинусном преобразовании строение симмет-
симметричного массива определяется следующим образом:
F{j, k) при }, k^O,
F(-i.k) при /<0,*>0.
F(j, -k) при />0, k<0, {Ш-6Л)
F(—/» —Щ при /, &<0.
Вычисление двумерного преобразования Фурье от такого мас-
массива дает
JV-1 N— 1
а- I \ ! V V z? /• «Л
ir lit ТП = 7 у /• м р| у
'» ' ' 2W—-1 Zj Zj s^' ;
j=-N+l k=-N+l
A0.3.7)
где и, v — —N + 1, ..., —1, 0, 1, ..., W — 1. Поскольку преоб-
преобразование Фурье обладает свойством симметрии относительно
комплексного сопряжения, то для реальных изображений
Tt(и, v) = &1 (—и, —V). A0.3.8)
Следовательно, &"s (и, v) достаточно вычислять только при неотри-
неотрицательных значениях индексов («, v). Кроме того, поскольку
функция Fs (/, k) принимает действительные значения и симме-
симметрична, то #%(«, v) также имеет действительные значения. Таким
образом, соотношение A0.3.2) можно представить в следующем
виде:
JV-l JV-1
**. («. v) = 2ЛСТ 2 2 Р U> k) cos [ж=Т ju] cos [ 2ЛСТ
/=0 ft=0
A0.3.9)
250
Глава 10
где массив F (/", k) получается из матрицы изображения F (/, k)
взвешиванием ее элементов в соответствии с формулой
, k) при / = 0, k = 0,
) при / = 0, k^O,
V2F(j,k) при />0, 6 = 0,
при
A0.3.10)
Нечетное косинусное преобразование есть просто нормированный
вариант равенства A0.3.9), причем нормирование проведено так,
чтобы базисные функции стали ортонормальными. Таким обра-
образом, нечетное косинусное преобразование определяется соотно-
соотношениями
N-\ N-l
4 ? = °. у = °. (Ю.З.Па)
2
1=0
cos
=0
при и, v^O.
Такое же преобразование
JV-l N-1
A0.3.116)
A0.3.12а)
0
и=0 0=0
cos
S
u=0 0=0
при /,
A0.3.126)
дает матрицу взвешенных отсчетов F (/, ft). Тогда исходный мас-
массив можно восстановить с помощью формулы
4F(/, ft) при /=«0, ft —0,
2F (/, ft) при / = 0, ft ^ 0,
„ ' v * *- , (ю.3.13)
2F(j, ft) при ' • ~ ' -
F(/, ft) при
Базисные функции нечетного косинусного преобразования яв-
являются разделимыми, так что двумерное нечетное косинусное
преобразование можно выполнить с помощью последовательных
одномерных преобразований. Кроме того, нечетное косинусное
Двумерные унитарные преобразования
251
преобразование можно найти с помощью алгоритма преобразо-
преобразования Фурье при нечетном числе элементов, поскольку
f |Ч\*)ехр{-^(/« + Ц}.
A0.3.14)
10.4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ
Быстрое синусное преобразование, предложенное Джейном [ 13 ]
в качестве аппроксимации преобразования Карунена—Лоэва
для марковского процесса, в одномерном случае определяется
с помощью базисных функций вида
<«>¦*¦
где и, j = 0, I, 2, ..., N — 1. Рассмотрим матрицу, содержащую
ненулевые элементы только на главной диагонали и двух приле-
прилегающих к ней поддиагоналях (так называемую трехдиагональную
матрицу):
1 —а 0 ... 0
1
—а
0
0
1 —а
1
A0.4.2)
где а = р /A + р2), причем 0 г=: р ^ 1 — коэффициент корре-
корреляции соседних элементов марковского процесса. Можно пока-
показать [14], что с помощью унитарной матрицы А, в качестве эле-
элементов которой взяты базисные функции A0.4.1), матрицу Q
можно привести к диагональному виду х) в том смысле, что
= D) A0.4.3)
где D — диагональная матрица, составленная из элементов
м 1-Р* .
_ 2р cos [йя
A0.4.4)
при k = 1,2, ..., N.
х) Джейн [15] показал, что косинусное и синусное преобразования обла-
обладают общим свойством — с нх помощью удается приводить к диагональному
виду трехдиагональные матрицы.
252
Глава 10
Двумерное синусное преобразование определяется соотно-
соотношением
/=0 4=0
X
(Ш.4.5)
а обратное преобразование имеет тот же вид. Синусное преобра-
преобразование можно вычислить с помощью алгоритма преобразования
Номер базисной
функции
4=^
г^
L ¦
t
¦»:tf4flj HJ1
Рис. 10.4.1. Базисные функции синусного преобразования при N = 15.
Фурье. Допустим, что массив F (т, п) размером BN + 2) X
X BN + 2) образуется в соответствии с равенствами
?(/л+ 1, n-f l) — F(m, п) при 0 <т <: N — 1, 0
?(т, п) = 0 в других случаях
N — 1,
A0.4.6а)
A0.4.66)
Двумерные унитарные преобразования
253
Тогда, выделяя мнимую часть коэффициентов Фурье массива
F (т, п), можно найти синусное преобразование в виде
2ЛГ+1 2ЛГ+1
у
2ЛГ+1
2
Рис. 10.4,2. Синусное преобразование изображения «Портрет».
а — исходное изображение; б — синусный спектр в логарифмическом масштабе по осн
амплитуд: в — спектр с ограниченными наибольшими гармониками.
Графики базисных функций синусного преобразования при
N = 15 представлены на рис. 10.4.1, а на рис. 10.4.2 приведены
фотографии, полученные синусным преобразованием изображе-
изображения.
254
Глава 10
10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА
Преобразование Адамара [16, 17] основано на квадратной
матрице Адамара [18], элементы которой равны плюс или минус
единице, а строки и столбцы образуют ортогональные векторы.
Нормированная матрица Адамара N-vo порядка удовлетворяет
соотношению
HwHJv = Iat. A0.5.1)
Среди ортонормальных матриц Адамара наименьшей является
матрица второго порядка
Известно, что если матрица Адамара порядка N (где N> 2)
существует, то ./V делится на 4 без остатка [19]. Пока не удалось
определить, существуют ди матрицы Адамара для произволь-
произвольных N, удовлетворяющих этому условию, однако почти для всех
1 -1
1 1
1 -Ч
1 1
1 -1
z. _ _ __j
-1 -1
-1- 1
Число ,
изменении
знака
0
3
1
2
Н8 = —
1
1
1
1
1
1
1
1
1
-1
1
-1
1
-1
1
— 1
1
1
-1
-1
1
1
-1
-1
I
-1
-1
1
1
-1
-1
1
1
1
1
1
-1
__1
— 1
-1
1
-1
1
-1
-1
1
-1
1
1
1
1
-1
-1
-1
1
1
1
-1
-1
1
-1
1
1
__1
Число „
изменении
знака
0
7
.3
4
1
6
2
5
Рис. 10.5.1. Неупорядоченные матрицы Адамара четвертого и восьмого порядка.
допустимых N, доходящих до 200, найдены правила построения
соответствующих матриц. Наиболее просто удается построить
такие матрицы при N ~ 2п, где п — целое. Если HN — матрица
Адамара Л^-го порядка, то матрица
Haw —ТТя"
. . 1
FHjv J
A0.5.3)
Двумерные унитарные преобразования
255
также является матрицей Адамара, но порядка 2N. На рис. 10.5.1
приведены матрицы Адамара четвертого и восьмого порядка,
построенные с помощью соотношения A0.5.3).
Номер
базисной
функции
9
10
12
13
14
15
"LTLTLTLr
ишлллг
итлллпя.
"ШЛЛЛПЛГ
"[ЛЛЛПЛШЪ
'О1 И I4I I I 1.1 I I l,j I I I,,
Рис, 10.5.2. Базисные функции преобразования Адамара при N = 16.
Хармут [20] предложил частотную интерпретацию матриц
Адамара, имеющих блочную структуру A0.5.3). Число измене-
изменений знака вдоль каждой строки матрицы Адамара, деленное на
два, называется секвентой строки. Можно построить матрицу
Адамара порядка N = 2", в которой число изменений знака
в строках принимает значения от 0 до N — 1. Унитарные матрицы
с такими характеристиками называются матрицами с секвентным
свойством.
Строки матрицы Адамара, описываемой соотношением A0.5.3),
можно рассматривать как последовательность отсчетов прямо-
прямоугольных периодических колебаний (сигналов), период которых
кратен UN. Подобные непрерывные функции, называемые функ-
256
Глава 10
циями Уолша *) [21], связаны с импульсными функциями Раде-
махера [22]. Следовательно, матрица Адамара описывает преоб-
преобразование, связанное с разложением функций по семейству прямо-
-:¦>:
Л1.1.
¦ ¦ ¦¦ i ¦ i II i in
Рис. 10.5.3. Базисные изображения преобразования Адамара при N — 8.
Черный цвет соответствует значению +1, белый —значению —1.
ха-
хаугольных базисных функций, а не по синусам и косинусам,
рактерным для преобразования Фурье.
Для симметричных матриц Адамара порядка N = 2" дву-
двумерное преобразование Адамара можно представить в виде ряда
N-l N-1
(Ю.5.4)
/=0 4=0
г) Преобразование Адамара, определяемое с помощью матриц вида A0.5.3),
известно также под названием преобразования Уолша. Следует, однако, отметить,
что существуют матрицы Адамара (например, матрица 12-го порядка), строки
которых не состоят из отсчетов функций Уолша.
Двумерные унитарные преобразования
257
где
и, о)=
1=0
A0-5-5)
Переменные ы>, у,-, /(- и &,- равны цифрам в двоичном представлении
чисел и, v, j и k соответственно. Так, например, если и = 13,
то м3 = 1, ы2 = 1, Мх = 0 и и0 = 1. Если матрица Адамара упо-
упорядочена, т. е. строки ее переставлены в порядке возрастания
Рнс. 10.5.4. Преобразование Адамара изображения «Портрет».
а — исходиое изображение: б — спектр Адамара в логарифмическом масштабе по оси
амплитуд: в — спектр с ограниченными наибольшими гармониками
секвенты, то существует другая форма записи преобразования
Адамара. В этом случае
N-l JV-1
k)(—If lh *>UlV)t A0.5.6)
V29 Прэтт У.
258
Глава 10
где
причем
л-1
k, и, v)=
A0.5.7)
g-0 (и) = н„_1(
g-j (И) = «„_! + М„_2,
u) = м„_2 + м„_3,
A0.5.8)
«о-
Графики базисных функций преобразования Адамара с упоря-
упорядоченной матрицей для N — 16 представлены на рис. 10.5.2.
Базисные изображения, образованные с помощью матричного
произведения базисных векторов преобразования Адамара раз-
размера 8X1, приведены на рис. 10.5.3. На рис. 10.5.4 дан пример
преобразования Адамара (для упорядоченной матрицы Адамара).
10.6. ПРЕОБРАЗОВАНИЕ ХААРА
Преобразование Хаара [1, 23] основывается на ортогональной
матрице Хаара. Ниже приведены примеры ортонормальных
матриц Хаара четвертого и восьмого порядка:
1
/8
~ 1
1
V
0
2
0
0
0
н —
1
1
- 1
1
V2
0
1
1
2 К2 — V2
0
2
0
0
0
0
0
2
0
0
1
1
-J/2
0
1
1
-J/2
0
0
2
0
0
1
— 1
0
V2
1
1
0
J/2
0
0
2
0
1 '
— 1
0
— V2_
1
— 1
0
V2 -
0
0
— 2
0
1
-1
0
V2
0
0
0
2
A0.
1
— 1
0
-V2
0
0
0
—2
Матрицы Хаара более высокого порядка строятся по тем же пра-
правилам, что и матрицы A0.6.1) и A0.6.2). На рис. 10.6.1 приве-
Двумерные унитарные преобразования 259
дены графики базисных функций преобразования Хаара при
N = 16. Базисные изображения того же преобразования для
матрицы отсчетов, содержащей 8X8 элементов, представлены
на рис. 10.6.2.
Преобразование Хаара можно рассматривать как процесс
дискретизации исходного сигнала, при котором с переходом к сле-
следующей строке вдвое уменьшается шаг дискретизации.
Номер
базисной
функции
о ¦ =»
I 11 11 1111 11 11 I I I I
О 4 8 12 16
Рнс. 10.6.1. Базисные функции преобразования Хаара при N = 16.
В задачах обработки изображений хааровский спектр описы-
описывает распределение энергии компонент, соответствующих разно-
разностям яркостей соседних элементов, разностям средних значений
яркостей соседних пар элементов и вообще разностям средних
значений яркостей соседних групп из 2т элементов.
На рис. 10.6.3 приведен пример преобразования Хаара для
конкретного изображения. На снимке с логарифмическим масшта-
масштабом отчетливо заметна концентрация энергии, особенно в обла-
областях с высокими секвентами. Отметим, что в спектре Хаара наб-
наблюдается концентрация энергии также в областях с низкими сек-
секвентами.
i/a9*
260 Глава 10
10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ
В работах [24—26] предложено ортогональное преобразова-
преобразование, названное наклонным (slant transform). Это преобразование
обладает следующими особенностями: 1) среди базисных векторов
Рис. 10.6.2. Базисные изображения преобразования Хаара при N=8.
Черный цвет соответствует значению +1, белый — значению —1, штриховка — 0.
имеется вектор с одинаковыми компонентами (постоянный базис-
базисный вектор); 2) наклонный базисный вектор монотонно убывает
от максимального до минимального значения скачками постоянной
величины; 3) матрица преобразования обладает секвентным свой-
свойством; 4) существует быстрый алгоритм преобразования; 5) обеспе-
обеспечивается высокая степень концентрации энергии изображения.
При длине вектора N = 2 наклонное преобразование совпадает
Двумерные унитарные преобразования
261
с преобразованием Адамара второго порядка. Таким образом,
. A0.7.1)
Рис. 10.6.3. Преобразование Хаара изображения «Портрет».
а — исходное изображение; б — спектр Хаара в логарифмическом масштабе по оси ам-
амплитуд; в — спектр с ограниченными наибольшими гармониками.
Матрица наклонного преобразования четвертого порядка форми-
формируется по следующему правилу:
A0.7.2a)
9 Прэтт У.
1
а4
0
0
fr4
1
fl4
1
-at
0
64
0
h
]
fl4
262
Глава 10
ИЛИ
S'=7T
a4 —
1 1 1
я4 — bt —а4 4" bt —я4 — i
— 1 —1 1
—а4 — fr4 at -f- 64 —a4 -f- i
, A0.7.26)
где a4 и 64 — действительные коэффициенты, которые следует
выбирать так, чтобы матрица S4 была ортогональной, а величина
скачков при изменении второго наклонного базисного вектора —
постоянной. Из условия постоянства величины скачка можно
найти, что a4 = 2bt. Из условия ортогональности S4Sf = I
следует, что 64 = 1/1/5. Таким образом, матрица наклонного
преобразования четвертого порядка имеет вид v
111
3/J/5 1///5 — l/J/5
1—1—1
_ l/J/5 — 3///5 З/У'5
1
—3///5
1
A0.7.3)
Нетрудно проверить, что матрица S4 является ортонормальной.
Кроме того, она обладает секвентным свойством: число изменений
знака возрастает с увеличением номера строки от 0 до 3.
Матрица наклонного преобразования при N = 8 имеет вид
1
«8
0
0
0
-bs
-0
- 0
0
h
0
0
1
as
0
0
0
0
1
0
0
0
1
0
0
0
0
1
0
.0
0
1
1
~as
0
0
0
bs
0
0
0
bs
0
0
-1
as
0
0-
0
0
1
0
0
,0
.-1
0
0"
0
0
1
0
0
0
-1.
s4
0
*
0
UOJA)
Как и при построении матрицы S4, коэффициенты а8 и Ь8 подби-
подбираются так, чтобы наклонный базисный вектор убывал равно-
равномерными скачками, все строки матрицы являлись ортонормаль-
ными векторами, а сама матрица обладала секвентным свойством.
Обобщая соотношение A0.7.4), можно получить рекуррентную
формулу, связывающую матрицы наклонного преобразования
Двумерные унитарные преобразования
263
N-vo и (Л/У2)-го порядка:
'?
1 0
as bN
0
0 1
-bs aN
0
о
I(N/2)-2
•
I(N/2)-2
—as us i
0 | I(N/2>-2
~0 -1|
bN aN\ 0
0 ,~I(N/2)-2
Sn/2
0
0
г
A0.7.5)
где lK — единичная матрица /(-го порядка. Постоянные aN
и bN можно найти из рекуррентных соотношений [26]
оа = 1, A0.7.6а)
Ьы = [ 1 + 4 (а*/2J]-1/2, A0.7.66)
A0.7.6b)
Номер
базисной
Функции
¦ о
v^y^r
6
7 "~П
Ь
tP-
[>Чг
¦¦о- nJlTLTUkP
14
15
Рис. 10.7.1. Базисные функции наклон-
наклонного преобразования при Л^ = 16.
9*
12 , 6
264
Глава 10
или по формулам
3N* у/2
)
4Дп _
N* — 1 \i/2
)
A0.7.7a)
A0.7.76)
Рис. 10.7.2. Наклонное преобразование изображения «Портрет»,
а — исходное изображение: б — результат преобразования в логарифмическом масштабе-
по оси амплитуд; в — результат преобразования с ограниченными наибольшими гармо-
гармониками.
На рис. 10.7.1 приведены графики базисных функций наклон-
наклонного преобразования для N = 16. Пример спектра, получаемого
при таком преобразовании, показан на рис. 10.7.2.
Двумерные унитарные преобразования 265
10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА—ЛОЭВА
Метод преобразования непрерывных сигналов в набор некор-
некоррелированных коэффициентов разработан Каруненом [27] и
Лоэвом [28]. Как указывается в статье [30], Хотеллинг [29]
первым предложил метод преобразования дискретных сигналов
в набор некоррелированных коэффициентов. Однако в большин-
большинстве работ по цифровой обработке сигналов и дискретное, и непре-
непрерывное преобразования называют преобразованием Карунена—
Лоэва или разложением по собственным векторам.
В общем случае преобразование Карунена—Лоэва описыт
вается соотношением
N-XN-1
ЗГ(и, v) = ? 2 F(j, k)A(j, к; и, v), A0.8.1)
/=0 4=0
ядро A (j, k; и, v) которого удовлетворяет уравнению
К {и, v)A(j, k; и, у) =
JV-1 ЛГ—1
= 2 Е 'KAL А; /'- k')A(j', k'; и, v), A0.8.2)
/'=0 ft'=0
где Kf (/. k; f, k') — ковариационная функция дискретизован-
ного изображения, а 'к (и, v) при фиксированных и и v постоянна.
Функции A (j, k; и, v) являются собственными функциями кова-
ковариационной функции, а X (и, v) — ее собственные значения.
Как правило, выразить собственные функции в явной форме не
удается.
Если ковариационную функцию можно разделить, т. е.
KAi, k; /', k>) = Kc(i, ГЖЛК П (Ю.8.3)
то ядро разложения Карунена—Лоэва также разделимо и
A (j, k; и, v) = Ас (j, и) AR (k, v). A0.8.4)
Строки и столбцы матриц, описывающих эти ядра, удовлетворяют
следующим уравнениям:
KR (v) AR (k, v) = 2 Kr (k, k') AR (k', -v), A0.8.5)
ft'=0
M«) Ac (/, u) = 2 KcU, П Ac(j\ u). A0.8.6)
/'=0
В частном случае, когда ковариационная матрица описывает
разделимый марковский процесс первого порядка, собственные
функции удается записать в явной форме. Для одномерного мар-
марковского процесса с коэффициентом корреляции р собственные
функции и собственные значения имеют вид [3]
10 Прэтт У.
266
Глава 10
1-р»
— 2pcos[a>(«)]
A0.8.8)
где 0 :?. /, и sz N — 1, a w (и) — корни трансцендентного урав-
уравнения
te INw) - (l-p')»»nC>)
ё *• ' ~ cos (ю) — 2р + р» cos (w)
A0.8.9)
Собственные векторы можно также найти из рекуррентных фор-
формул [32]
^, и)-рАA, и)], A0.8.10а)
ГГ
A(N -1, и) = -^[-
— 1, A0.8.106)
2, u) + A(N—l, u)}, A0.8.10b)
положив в качестве начального условия Л @, и) = 1 и затем
пронормировав полученные собственные векторы.
Если исходное и преобразованное изображения представить
в векторной форме, то пара преобразований Карунена—Лоэва
будет иметь вид
/=Af . A0.8.11)
и
f=AV. A0.8.12)
Матрица преобразования А удовлетворяет уравнению
A0.8.13)
где К/ — ковариационная матрица вектора f; А — матрица,
строки которой являются собственными векторами матрицы К^;
Л — диагональная матрица вида
Л =
Mi) о . . .
0 ХB) . . .
\
0
о
\
\
0 0 ... K(N2)
Если матрица К/ разделима, то-
А = Ас0Ая,
[A0.8.14)
A0.8.15)
Двумерные унитарные преобразования
267
причем матрицы Ас и Ая удовлетворяют следующим условиям:
АЯКЯ = ЛЛАЯ, A0.8.16а)
АСКС = АСАС, A0.8.166)
а К (k) = XR (i) Kc (/) при i, j = 1, 2, ..., N_ [33].
¦Номер
базисной
функции-
О =
д
4! ' ' 'а1 ^ У
is
Рнс. 10.8.1» Базисные функции преобразования Карунена — Лоэва при W = 16.
На рис. 10.8.1 приведены графики базисных функций преоб-
преобразования Карунена—Лоэва одномерного марковского процесса,
для которого коэффициенты корреляции соседних элементов
р = 0,9.
10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ
Сингулярное преобразование [34] является двумерным уни-
унитарным преобразованием, основанным на сингулярном разложе-
Ю*
г
Рис. 10.9.1. Сингулярное преобразование изображения «Портрет». Все пред-
представленные массивы из 256 X 256 элементов получены из массивов размера
64 X 64 элемента посредством билинейной интерполяцнн.
а — исходное изображение, матрица F; б — результат сингулярного преобразования,
матрица f; в — матрица FF^; г —матрица F^F; д — матрица, состоящая из модулей эле-
элементов матрицы U; е — матрица, состоящая из модулей элементов матрицы V.
Двумерные унитарные преобразования
269
нии матриц (см. гл. 5). Прямое сингулярное преобразование по
определению равно
#- = AcFA?, A0.9.1)
а обратное преобразование
? = А?9-Ац. A0.9.2)
Матрица преобразования строк Ан обеспечивает выполнение
операции диагонализации
Ak[F7F]A?=A, A0.9.3)
где А — диагональная матрица, элементы X («) которой являются
собственными значениями матрицы FrF. Аналогично
Ac[FFr]A? = A. (Ю.9.4)
Подставив выражение A0.9.2) в равенства A0.9.3) и A0.9.4),
получим
#- = А1/2, A0.9.5)
где элементами диагональной матрицы А1/2 являются числа А,1/2 (и),
называемые сингулярными значениями матрицы F и равные квад-
квадратному корню из соответствующих собственных значений %(и).
fS dZ 48 64-
Номер сингулярного значения <
Рис. 10.9.2. Сингулярные значения изображения «Портрет».
Матрицу изображения можно записать в очень компактной
форме с помощью матричного произведения векторов, получае-
получаемых при сингулярном разложении. Согласно равенству A0.1.146),
=S ЗГ(и,и)Ъс(и)ЪТн(и),
и=1
A0.9.6)
где Ьс (и) и Ья (и) представляют собой векторы, состоящие
элементов м-х столбцов матриц в? и В^.
из
Рис. 10.9.3. Базисные изображения для изображения «Портрет».
Рисунки а, Ь, в, е, д, е соответствуют Ьс{1) 6^A), &cH)f>j?D),
? ^ ^
, ЬсA6)
Двумерные унитарные преобразования 27».
Пользуясь сингулярным преобразованием, матрицу изобра-
изображения F, содержащую NxN элементов, можно полностью опи-
описать N величинами, представляющими, собой N коэффициен-
коэффициентов &" (и, м). Однако следует отметить, что конкретные .значения:
элементов матриц преобразований по строкам и столбцам в этом;
случае зависят от элементов изображения.
На рис. 10.9.1 приведен пример сингулярного преобразова-
преобразования изображения. Здесь же показаны произведения FFr и FrF,
а также соответствующие матрицы преобразований по строкам (U)>
и по столбцам (V). Сингулярные значения рассматриваемого изо-
изображения представлены на рис. 10.9.2. На рис. 10.9.3 показана
несколько матричных произведений Ъс (и) Ъ% (и).
10.10. \ЛГОРИТМЫ ВЫЧИСЛЕНИЙ
В общем случае, чтобы выполнить унитарное преобразование
матрицы изображения, содержащей NxN элементов, и получить-
матрицу из NxN спектральных коэффициентов, необходимо про-
произвести примерно N* арифметических операций (умножений и
сложений). Если размеры матрицы изображения велики, то число^
операций становится чрезмерно большим. К счастью, для многих
унитарных преобразований существуют эффективные алгоритмы
вычислений, позволяющие ускорить выполнение преобразования.
Основной идеей этих быстрых вычислительных алгоритмов-
является разделение всей задачи на ряд этапов, причем резуль-
результаты, полученные на предыдущих этапах, многократно исполь-
используются на последующих этапах. В качестве примера рассмотрим1
процесс вычисления коэффициентов преобразования Адамара
с неупорядоченной матрицей для последовательности из четырех
элементов / (/)• При прямом способе вычисления находятся четыре-
величииы по формулам
/ @) = /(О) + / A) + / B) + f C), A0.10.1а>
/0) = /@)-/(!) + /B)-/C), A0.10.1б>
/ B) = / @) + / A) - / B) - / C), A0.10.1b).
/ C) = / @) - f A) - / B) + / C). A0.10.1г>
Для этого необходимо выполнить IN (N — 1I= 12 ариф-
арифметических операций (сложений и вычитаний). Однако коэффи-
коэффициенты преобразования Адамара можно найти по-другому, разбив^
процесс вычисления на следующие этапы:
Первый этап
а @) = / @) + / B), A0.10.2а>
а A) = / @) - / B), A0.10.2б>
о B) = / A) + / C), A0.10.2в>
а C) = / A) - / C). A0.10.2г>
:272
Глава JO
Второй этап
/ @) = а @) + а B),
f A) = а @) _ а B),
/ B) = л A) + а C),
/ C) = а A) - а C).
A0.10.3а)
A0.10.36)
A0.10.3b)
(ЮЛО.Зг)
-При этом для определения элементов матрицы Н4 требуется только
[jV log2 jV I = 8 операций, т.е. экономится четыре операции.
«10) о
до)
/C)
Рис. 10.10.1. Граф вычисления коэффициентов преобразовании Адамара для
четыредэлемеитиой последовательности. (Сплошные линии обозначают операции
¦ сложении, пунктирные — вычитания.)
Ход вышеуказанных вычислений мо.жно описать с помощью
графа (рис. 10.10.1). Общее число операций равно половине числа
ребер, соединяющих вершины графа. Другой способ представле-
представления того же процесса заключается в факторизации матрицы, когда
матрицу преобразования Адамара Н4 записывают в виде произ-
произведения двух разреженных матриц. Так, например,
Н4 =
1
0
1
0
1
0
—1
0
0
1
0
1
0
1
0
1
1
0
1
0
1
0
—1
0
0
1
0
1
0
1
0
—1
A0.10.4)
"Число операций равно половине числа ненулевых элементов в обеих
матрицах-сомножителях.
Принципы, описанные выше на примере преобразования Ада-
Адамара, можно применить для быстрого вычисления многих других
преобразований. Разработаны быстрые алгоритмы для преобра-
преобразований Фурье [35], четного косинусного [12], синусного [13],
Адамара [17], Хаара [1] и наклонного [26]. В общем случае
для преобразования Карунена—Лоэва быстрого алгоритма не
найдено, однако известны приближенные алгоритмы преобразо-
преобразования Карунена—Лоэва для марковских процессов.
Двумерные унитарные преобразования
Для большинства одномерных унитарных преобразований поря-
порядок требуемого числа арифметических операций равен N log2 N.
Исключением является преобразование Хаара, которое имеет
разреженную матрицу и поэтому может быть вычислено с помощью-
примерно 2N операций. Для унитарных преобразований пока не-
неизвестен общий метод построения эффективных вычислительных
алгоритмов [36]. В каждом случае приходится отыскивать эффек-
эффективную процедуру вычислений или способ представления матрицы,
в виде произведения разреженных матриц.
Унитарные преобразования, основанные на базисных векторах:
синусоидального характера (преобразования Фурье, косинусное,,
синусное), можно выполнить косвенным путем, пользуясь алгорит-
алгоритмом так называемого 2-преобразоваиия с ЛЧМ-фильтрацией. Преоб-
cos<ir|2/N)
cosdrj^N)
sin(irj2/N)
cosdri^N)
sindrj^N)
Рис. 10.10.2. Блок-схема алгоритма преобразования Фурье с использованием
метода г-преобразоваиия.
разование Фурье одномерной последовательности / (/) опреде-
определяется соотношением
W-1
/=o
Произведя замену переменных
2/а = р + ы2 — (и — jf,
274 Глава 10
можно получить выражение
A0.10.7)
Формула A0.10.7) описывает совокупность следующих операций:
1. Поэлементное умножение последовательности f (/) на мно-
множители с квадратично изменяющейся фазой ехр {—inj4N\.
2. Свертка результатов предыдущей операции с ядром
ехр \inj4N].
3. Поэлементное умножение полученной последовательности
на множители с квадратичной фазой ехр {inu2/N\.
На рис. 10.10.2 приведена структурная схема алгоритма вы-
вычисления коэффициентов преобразования Фурье с использованием
метода 2-преобразования с ЛЧМ-фильтрацией. Если обработка
производится в универсальной ЦВМ, то, как правило, применять
этот алгоритм не следует, поскольку для вычисления свертки тре-
требуется большее число операций, чем для прямого выполнения
преобразования методом БПФ. Однако с помощью аналоговых
трансверсальных фильтров очень легко осуществить г-преобразо-
г-преобразование с ЛЧМ-фильтрацией, что дает возможность вычисления
коэффициентов преобразования Фурье, а также косинусного и
синусного преобразований поточным способом.
10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ
ИЗОБРАЖЕНИЙ
Для создания эффективных методов квантования и кодирова-
кодирования преобразованных изображений необходимо знать статисти-
статистические свойства последних. В данном разделе определены первые
и вторые моменты спектральных коэффициентов. Следующий
раздел посвящен созданию статистической модели плотности
вероятности этих коэффициентов.
Если предположить, что массив элементов изображения
F (/, k) является реализацией двумерного случайного процесса
с известными математическим ожиданием и ковариационной функ-
функцией, то его спектр (результат унитарного преобразования)
N—lN—1
г(м)=ЕЕ^A,^(й;м) (Ю.П.1)
/=0 4=0
также будет реализацией случайного процесса. Согласно равен-
равенству (.8.2.16), математическое ожидание ЗГ (и, v)
Е \<Г (и, »)}=ES E \F (/, k)} A (j, k; ut v), A0.11.2)
Двумерные унитарные преобразования 275
где Е {F (/, k)\ — математическое ожидание F (/, к). С помощью
равенства (8.2.3) можно получить выражение для ковариационной
функции спектра ЗГ (и, v)
К&- к, vi, и„ »2)=SSSS^ (и, /2; К К)А (U. ki> «i. vi) x
*хЛ*(/2, к; «,, it,), (ю.п.з)
где через Kf (А. /г! ^i. k9) обозначена ковариационная функция
F (j, k). И наконец, дисперсия 9е" (и, v) равна
а^(и, о) = Кг{и, v; и, v). A0.11.4)
При векторном представлении унитарного преобразования век-
вектор, образованный разверткой по столбцам матрицы коэффициен-
коэффициентов преобразования, определяется соотношением
^-Af. A0.11.5)
Математическое ожидание этого вектора
а ковариационная матрица
К^-АК,А*Г. A0.11.7)
Матрица дисперсий коэффициентов преобразования V^- обра-
образуется из диагональных элементов ковариационной мат-
матрицы A0.11.7).
Рассмотрим теперь, как вычисляются первый и второй моменты
матрицы коэффициентов преобразования применительно к кон-
конкретным унитарным преобразованиям. Очевидно, что в общем слу-
случае все моменты можно получить в виде ряда или вектора, произ-
производя вычисления по вышеприведенным формулам. Однако для
проектирования и анализа систем желательно иметь аналитиче-
аналитические выражения моментных функций.
Сначала рассмотрим случай преобразования Карунена—Лоэва.
В общем виде ковариационная функция коэффициентов этого пре-
преобразования описывается равенством A0.11.3), которое можно
приставить в следующем виде:
Кг («1» vi> и2> »2> = '
= S S A*(j2, k2; «2, v2) S S KF(li, U К, 'kJA(h, ki, uu vt).
It k, it ft.
A0.11.8)
Однако формула A0.8.2) подсказывает, что вторая двойная сумма
совпадает с определением ядра преобразования Карунена—
Лоэва. Таким образом,
i, u2, :-2)= S S А*A*, К> «2. f2L«i, Щ)А(и, Ъ; ult vy),
i» k,
A0.11.9)
276 Глава 10
где К (и, v) — собственные значения ковариационной матрицы
изображения. Поскольку преобразование Карунена—Лоэва орто-
ортогонально, т. е.
Кдг (Ы1; Vi, Ut, V2) = К (и1г Oj б (иг - Ы2, 1>! - О,), A0.11.10)
то коэффициенты этого преобразования некоррелированы между
собой, а их дисперсии равны соответствующим собственным зна-
значениям:
а^г {и, v) = Я, (и, у). A0.11.11)
Преобразование Карунена—Лоэва является единственным уни-
унитарным преобразованием, в котором достигается полная декор-
реляция произвольного изображения. В других преобразованиях
между коэффициентами преобразования остается некоторая оста-
остаточная корреляция. Кроме того, преобразование Карунена—
Лоэва обеспечивает наибольшую среди всех унитарных преобра-
преобразований степень концентрации энергии спектра изображения.
Предположим, что коэффициенты произвольного преобразования
расположены в порядке убывания их дисперсий, т. е. о2 A) >
> о2 B) > ... > о2 (N2), и также расположены собственные зна-
значения корреляционной матрицы, т.е. X (I) > А, B) > ... >
> К (N2). Можно показать, что для любого верхнего предела
суммирования W < N2 выполняется неравенство
w w
Y Я(да)> Г о1 И. A0.11.12)
Чтобы найти аналитические выражения для моментов других
преобразований, необходимо задать статистические свойства эле-
элементов изображения. Если изображение стационарно в широком
смысле, то его математическое ожидание постоянно, и поэтому
е \р (и, v)\ = е \дг) ? 2 л (У, *; UfV). (io.11.13)
/ *
Но поскольку базисные функции являются ортогональными, то
результат суммирования отличен от нуля только для нулевой
базисной функции упорядоченного преобразования. Следова-
Следовательно,
Е{&-@, 0)\ = E{F) ? ? A(j, k; 0, 0) при и, v = 0, A0.11.14а)
/ k
v)\ = 0 при и, �. A0.11.146)
В тех преобразованиях, где в число базисных функций входит
постоянная функция, двойная сумма A0.11.14а) равна N.
Если изображение стационарно в широком смысле, соответ-
соответствующая ковариационная функция имеет вид Kf (ji — /21 ^i—k2).
Однако матрица коэффициентов преобразования будет стационар-
Двумерные унитарные преобразования 277
ной в широком смысле только тогда, когда ядро преобразования
обладает свойством пространственной инвариантности. Нагляд-
Наглядным подтверждением этого является преобразование Фурье.
Большинство обычно используемых преобразований изобра-
изображений являются разделимыми в пространственной области. Если,
кроме того, разделима по пространственным переменным и кова-
ковариационная функция изображения, то
Л>(«1. Ъ; th,-v3)=*Krc{uu u2)KgrR(vu v2), A0.11.15)
где
1, «2)= ? ? Kfc(H, 'h)Ac(ib иг)АЪ(к, u2), A0.11.16а)
/» /*,
Г2)= Е 2 **Л(*1, *а)Л«(*ь »1)Дй(*а, »»). (Ю.11.166)
Пр» этом дисперсия спектра (преобразованного изображения)
также разделима, т. е. ее можно представить в виде произведения
одномерных функций, описывающих изменение дисперсии вдоль
строк и столбцов:
(и, v) = a^R(u) oVc(i')- A0.11.17)
Одномерная дисперсия Фурье-спектра для стационарного в ши-
широком смысле изображения имеет вид
} A0.11.18)
где w — и или w = v, a zl — ji или zt = kt. Это выражение можно
переписать в следующем виде:
A0.11.19)
Вторую сумму можно рассматривать как одномерное дискретное
преобразование Фурье ковариационной функции, сдвинутой на z2
отсчетов. Согласно теореме о преобразовании Фурье смещенной
функции,
^ И = 4 2 ехр [^L wz2} ехр {- ^- wz2\ 8Z (w) = $z (w),
A0.11.20)
где (SZ (w) и Kfz (w) — пара одномерных дискретных преобразо-
Рис. ЮЛ i.L Ковариационные матрицы унитарных преобразований при N -
= 16, р ~ 0,9-
й — юждествевное преобразование; б — преобразование Фурье; в — косинусное; г
синусное; д — Адамаря; е — Хаярз; ж — иакло«яое; з — Карунена — Лоэва.
Двумерные унитарные преобразования
279
ваний Фурье. Из соотношения E.4.16) видно, что *&z (w) является
дискретным вариантом энергетического спектра Wfz (®) строки
(или столбца) изображения, уменьшенным на величину, равную
средней мощности изображения. Для процесса с нулевым мате-
математическим ожиданием
ofrz(w) = W*Fz(w). A0.11.21)
Рассмотренные ранее преобразования Адамара, Хаара и другие
не обладают свойством, которое для преобразования Фурье дается
теоремой о спектре сдвинутой функции. По этой причине для
этих преобразований не удалось получить в конечной форме
выражение для дисперсии или ковариационной функции.
Наклонное
Адамора
Хаара
Фурье
Карунена-Лозва (р = 0,95,,
косинусное и синусное
i ш I ¦ i . » ¦¦'¦ _ ¦
2 4 е 8 W 12
Номер базисной (рункции и
П
Рис. 10.11.2. Дисперсии коэффициентов унитарных преобразований при N =
= 16, р = 0,9.
На рис. 10.11.1 представлены ковариационные функции коэф-
коэффициентов некоторых унитарных преобразований отрезка дискрет-
дискретного одномерного марковского процесса, состоящего из 16 эле-
элементов, причем коэффициент корреляции между соседними эле-
элементами р = 0,9. Графики дисперсии коэффициентов преобразо-
преобразований приведены на рис. 10.11.2.
280 Глава JO
10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ
ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ
Было бы полезно знать плотность вероятности элементов пре-
преобразованного изображения для произвольного преобразования.
К сожалению, найти эту плотность нелегко, так как обычно мы
не имеем полного описания плотности вероятности исходного
изображения,. Кроме того, сами преобразования, как правило,
являются сложными математическими операциями. Однако рас-
рассмотренные выше преобразования, применяемые для обработки
изображений, сводятся к вычислению взвешенных сумм всех эле-
элементов исходного изображения. Поэтому, пользуясь центральной
предельной теоремой теории вероятностей, можно прийти к вы-
выводу о том, что плотность вероятности элементов преобразован-
преобразованного изображения близка к гауссовой с теми моментами, которые
были найдены в предыдущем разделе.
Коэффициенты преобразования Фурье являются комплекс-
комплексными числами, и их можно задавать с помощью действительной и
мнимой частей или же модулем и аргументом. В обоих случаях
каждому коэффициенту соответствуют два числа, которые необхо-
необходимо подвергнуть квантованию. Можно считать, что действитель-
действительная 3Гц (и, v) и мнимая &г1 (и, v) части коэффициента Фурье имеют
одинаковые гауссовы распределения, дисперсия которых <т2^-(и, v)
пропорциональна энергетическому спектру исходного изобра-
изображения. Таким образом,
(u, t>)]~1/2exp
,{и, v)) = [2no2<r(u, р)Г1/2ехр|-2^ц"Ч. A0.12.16)
Если действительная и мнимая составляющие имеют гауссово
распределение, то модуль коэффициента Фурье &~м{и, v) распре-
распределен по закону Рэлея. Таким образом,
J^J A0.12.2)
о&- (и, v) { 2о&- (и, v)
при &~м (и, v) > 0, а фаза ЯГр (и, v) имеет равномерное распре-
распределение
р[ЗГР(и, v)\= 1/2я, A0.12.3)
где —л < &~Р (и, v) < п.
Можно считать, что действительные коэффициенты других
преобразований имеют гауссовы распределения вида
(u, о)Г1/2ехр(- *7(»>РМ. (Ю.12.4)
{ ы&~ (и. ») J
Двумерные унитарные преобразования 281
Плотность распределения вероятностей Рэлея A0.12.2) часто
применяют в качестве модели плотности вероятности постоянной
составляющей #"@, 0) яркостных изображений, поскольку для
таких изображений коэффициент ^@, 0) всегда строго положи-
положителен. Рассмотренные модели плотностей вероятности широко
применяются при разработке методов кодирования с преобразо-
преобразованием изображений.
ЛИТЕРАТУРА
1. Andrews H. С, Computer Techniques in Image Processing, Academic Press,
New York, 1970.
2. Andrews H. C, Two Dimensional Transforms, in: Topics in Applied Physics:
Picture Processings and Digital Filtering, Vol. 6, Huang Т., Ed., Springer-
Verlag, New York, 1975.
3. Bellman R., Introduction to Matrix Analysis, McGraw-Hill, New York, 1960.
4. Andrews H. C, Caspari K., A Generalized Technique for Spectral Analysis,
IEEE Trans. Computers, C-19, 1, 16—25 (January 1970).
5. Cooley J. W., Tukey J. W., An Algorithm for the Machine Calculation of
Complex Fourier Series, Math. Comput., 19, 90, 297—301 (April 1965).
6. IEEE Trans. Audio and Electroacoustics, Special Issue on Fast Fourier Trans-
Transforms, AU-15, 2 (June 1967).
7. Cochran W. T. et al., What is the Fast Fourier Transform? Proc. IEEE, 55,
10, 1664—1674 A967). [Имеется перевод: Кокрен и др., Что такое «Быстрое
преобразование Фурье»? — ТИИЭР, 1967, т. 55, № 10.]
8. IEEE Trans. Audio and Electroacoustics, Special Issue on Fast Fourier Trans-
Transforms, AU-17, 2 (June 1969).
9. Cooley J. W., Lewis P. A., Welch P. D., Historical Notes on the Fast Fou-
Fourier Transform, Proc. IEEE, 55, 10, 1675—1677 (October 1967). [Имеется
перевод: Кули, Льюис, Уэлч, Исторические замечания относительно бы-
быстрого преобразования Фурье. — ТИИЭР, 1967, т. 55, № 10.]
10. Brigham Е. О., Morrow R. E,, The Fast Fourier Transform, IEEE Spectrum,
4, 12, 63—70 (December 1967).
11. Means R. W., Whitehouse H. J., Speiser J. M., Television Encoding Using
a Hybrid Discrete Cosine Transform and a Differential Pulse Code Modulator
in Real Time, Proceedings of the National Telecommunications Conference,
San Diego, California, December 1974, pp. 61—66.
12. Ahmed N., Natarajan Т., Rao K- R., On Image Processing and a Discrete
Cosine Transform, IEEE Trans. Computers, C-23, 1, 90—93 (January 1974).
13. Jain A. K-, A Fast Karhunen-Loeve Transform for Finite Discrete Images,
Proceedings of the National Electronics Conference, Chicago, Illinois, October
1974, pp. 323—328.
14. Jain A. K-, Angel E., Image Restoration, Modelling, and Reduction of Di-
Dimensionality, IEEE Trans. Computers, C-23, 5, 470—476 (May 1974).
15. Jain А. К. (частное сообщение).
16. Whelchel J. E., Jr., Guinn D. F., The Fast Fourier-Hadamard Transform
and Its use in Signal Representation and Classification, EASCON 1968 Con-
Convention Record, 1968, pp. 561—573.
17. Pratt W. K., Andrews H. C, Kane J., Hadamard Transform Image Coding,
Proc. IEEE, 57, 1, 58—68 (January 1969). [Имеется перевод: Прайт, Кайи,
Эндрюс, Кодирование изображений с использованием преобразования Ада-
мара. - ТИИЭР, 1969, т. 57, № 1.]
18. Hadamard J., Resolution d'une Question Relative aux Determinants, Bull.
Sci. Math. Ser. 2, 17, Part I, 240—246 A893).
10 Прэтт У.
282 Глава id
19. Ryser H. J., Combinational Mathematics, Wiley, New York, 1963. [Имеется
перевод: Райзер Г. Дж., Комбинаторная математика.—М.: Мир, 1966.]
20. Harmuth H. F., Transmission of Information by Orthogonal Functions, Sprin-
Springer-Verlag, New York, 1969. [Имеется перевод: Хармут X. Ф., Передача
информации ортогональными функциями. — М.: Связь, 1975.]
21. |Walsh J. L., A Closed Set of Orthogonal Functions, Am. J. Math., 45, 5—24
П923).
22. Rademacher H., Einige Satze von Allgemeinen Orthogonal-Funktionen, Math.
Annalen, 87, 112—138 A922).
23. Haar A., Zur Theorie der Orthogonalen Funktionen-System, Inaugural Dis-
Dissertation, Math. Annalen, 5, 17—31 A955).
24. Enomoto H., Shibata K-, Orthogonal Transform Coding System for Televi-
Television Signals, IEEE Trans. Electromagnetic Compatibility, EMC-13, 3, 11—17
(August 1971).
25. Pratt W. K-, Welch L. R., Chen W. H., Slant Transform for Image Coding,
Proceedings Symposium an Applications of Walsh Functions, March 1972.
26. Pratt W. K-, Chen W. H., Welch L. R., Slant Transform Image Coding,
IEEE Trans. Commun., COM-22, 8, 1075—1093 (August 1974).
27. Karhunen H., 1947, English translation by Selin I., On Linear Methods in
Probability Theory, The Rand Corporation, Doc. T-131, August 1960.
28. Loeve M., Fonctions Aleatories de Seconde Ordre, Hermann, Paris, 1948.
29. Hotelling H., Analysis of a Complex of Statistical Variables into Principal
Components, /. Educ. Psych., 24, 417—441, 498—520 A933).
30. Wintz P. A., Transform Picture Coding, Proc. IEEE, 60, 7, 809—820 (July
1972). [Имеется перевод: Уинтц, Кодирование изображения посредством пре-
преобразований. — ТИИЭР, 1972, т. 60, № 7.]
31. Ray W. D., Driver R. M., Further Decomposition of the Karhunen-Loeve
Series Representation of a Stationary Random Process, IEEE Trans. Inf. The-
Theory, IT-16, 6, 663—668 (November 1970).
32. Pratt W. K-. Generalized Wiener Filtering Computation Techniques, IEEE
Trans. Computers, C-21, 7, 636—641 (July 1972).
33. Friedman В., Eigenvalues of Composite Matrices, Proc. Cambridge Phil. Soc.,
57, Part 1, 37—49 A961).
34. Andrews H. C, Patterson С L., Outer Product Expansions and Their Uses
in Digital Image Processing, Am. Math. Monthly, 1, 82, 1—13 (January 1975).
35. Brigham E. O., The Fast Fourier Transform, Prentice-Hall, Englewood Cliffs,
N. J., 1974.
36. Gentleman W. M., Matrix Multiplication and Fast Fourier Transformations,
Bell. Syst. Tech. J., 47, 1099—1103 (July — August 1968).
Глава 11
ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ
Большинство алгоритмов обработки дискретных изображений
являются линейными: элементы обработанного изображения об-
образуются в виде линейной комбинации элементов исходного изоб-
изображения. Широкое применение линейных операций объясняется
тем, что выполнить их легче, чем нелинейные. Однако при обра-
обработке массивов большого размера часто не удается выполнить
даже линейные операции, если отсутствуют эффективные алго-
алгоритмы вычисления. В данной главе рассмотрены косвенные методы
вычислений, опирающиеся на унитарные преобразования и позво-
позволяющие проводить обработку более эффективно, чем при исполь-
использовании традиционных методов. Здесь также описаны методы
рекурсивной двумерной фильтрации.
11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ
Двумерные линейные преобразования можно определить в виде
ряда как
JV, N,
? ? л2; щ, щ). A1.1.1)
Это соотношение в векторной форме имеет вид
p = Tf. A1.1.2)
Ниже будет показано, что подобные линейные преобразования
часто можно выполнить более эффективно, если вместо непосред-
непосредственных вычислений по формулам A1.1.1) или A1.1.2) восполь-
воспользоваться косвенными методами с применением двумерных уни-
унитарных преобразований.
На рис. 11.1.1 приведена структурная схема косвенного ме-
метода вычислений, называемого обобщенной линейной фильтрацией
[1 ]. Массив F (tii, я2)> описывающий исходное изображение,
подвергается здесь двумерному унитарному преобразованию,
в результате которого получается массив коэффициентов преоб-
преобразования #"(«!, и2). Затем составляется линейная комбинация
этих коэффициентов, описываемая в общем случае формулой
N, N,
^ («i, и2) Т («!, и,; щ, и>г), A1.1.3)
i
Ui=l U,=l
10*
284
Гдава II
где ST («!, и2\ wly w2) — ядро линейного фильтрующего преобра-
преобразования. В заключение проводится обратное унитарное преобра-
преобразование, чтобы получить обработанное изображение Р (тъ т2).
Линейное
преобразода-
ние
K, пг).
Прямое
унитарное
преобраэода-
ние
Линейная
дкштрация fiM^
Обратное
унитарное
преобразо-
преобразование
P(m,,m2)
Рис. 11.1.1. Структура алгоритмов непосредственной обработки (а) и обобщен-
обобщенной линейной фильтрации (б).
Такой метод вычисления будет эффективнее, чем непосредственное
вычисление по формуле A1.1.1), если существуют быстрые алго-
алгоритмы унитарного преобразования, а ядро ST (uit м2; wlt w2) со-
содержит большое количество нулевых элементов.
Г
а
Рис. 11.1.2. Структура алгоритмов непосредственной обработки (а) н обобщен-
обобщенной линейной фильтрации (б) при векторном представлении изображений.
Процесс обобщенной линейной фильтрации можно также пред-
представить в векторной форме (рис. 11.1.2). Для упрощения обозна-
обозначений положим, что Ni = Ni ~ N, a Mi — М2 = М. Тогда
обобщенную линейную фильтрацию можно описать соотношениями
/ = (A*.)f, A1.1.4а)
/ A1.1.46)
. A1.1.4b)
Двумерные методы линейной^об работки 285
где Ajv« — матрица унитарного преобразования размера N2 X N2,
ir—матрица оператора линейной фильтрации размера M2XN2,
a AM2 — матрица обратного унитарного преобразования размера
М2ХМ2. Как следует из соотношений A1.1.4), векторы исходного
и обработанного изображений связаны между собой равенством
p = (AA,Jri?T(Aiv3)f. (П.1.5)
Приравнивая соотношения A1.1.2) и A1.1.5), найдем связь между
матрицами ST и Т:
Т - (Ад,.) ?Г (Ад,.), A1.1.6а)
?Г = (Ам.) Т (Адр.). A1.1.66)
При непосредственной обработке для выполнения вычислений по
формуле A1.1.2) необходимо провести kd (M2N2) арифметических
действий, где kd @ sg kd ^ 1) характеризует степень заполнения
матрицы Т ненулевыми элементами. При обобщенной линейной
фильтрации общее число арифметических действий равно:
Прямое преобразование: N* — при непосредственном вычисле-
вычислении;
2N2 log2 N — при использовании бы-
быстрого преобразования.
Линейная фильтрация: kaM2N2 умножений.
Обратное преобразование: М* — при непосредственном вычис-
вычислении;
2М2 log2M — при использовании бы-
быстрого преобразования.
Здесь к„(О^.к„'^ 1) — коэффициент заполнения матрицы ?7*
ненулевыми элементами. Если ka = 1 и производитсянепосред-
ственное вычисление унитарного преобразования7"то~~очевидно,
что обобщенная линейная фильтрация оказывается не столь
эффективной, как непосредственная обработка. Однако, если
применяются быстрые алгоритмы, подобные быстрому преобра-
преобразованию Фурье (БПФ), обобщенная линейная фильтрация будет
эффективнее, чем непосредственная обработка, если коэффициент
заполнения матрицы ZT удовлетворяет неравенству
kg<kd~ B/Мг) log.W - B/Л/2) log2M. A1.1.7)
Во многих случаях матрица ZT бывает разрежена и неравенство
A1.1.7) выполняется. Вообще говоря, унитарные преобразова-
преобразования часто приводят к декорреляции элементов матрицы Т л мат-
матрица гГ оказывается разреженной. Кроме того, матрицу ?Г часто
удается разредить без внесения больших погрешностей, если за-
заменить нулями ее малые по величине элементы [1 ].
В последующих разделах рассмотрена структура линейных
операторов суперпозиции, свертки и псевдообращения, для того
чтобы определить возможность применения метода обобщенной
линейной фильтрации для осуществления этих операций.
286 Глаза И
11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ
Операцию суперпозиции, описанную в гл. 9, часто удается
выполнить более эффективно, если вместо непосредственной об-
обработки проводить обработку с использованием преобразования.
На рис. 11.2.1, а, б приведены схемы непосредственного выполнения
конечной суперпозиции и дискретизованной суперпозиции. На
рис. 11.2.1, г, д представлены схемы осуществления операции
суперпозиции, когда вектор f подвергается унитарному преоб-
преобразованию, результат которого умножается на матрицу 3) (для
оператора суперпозиции конечных массивов) или матрицу $й
(для дискретизованного оператора суперпозиции). Обратное пре-
преобразование дает обработанный вектор. Согласно рис. 11.2.1, о, г,
в случае применения оператора суперпозиции конечных массивов
исходный и обработанный векторы связаны следующими соот-
соотношениями:
q = Df A1.2.1а)
)f. A1.2.16)
Поэтому матрицу 2Ь можно представить в виде произведения
^-(AM.)D(AA,,)-1. A1.2.2а)
Аналогично
-\ A1.2.26)
Чтобы непосредственно выполнить суперпозицию конечных мас-
массивов, требуется примерно N*L2 операций (здесь L — порядок
матрицы импульсного отклика). В этом случае коэффициент
заполнения матрицы D равен
kD=*(L/Nf. A1.2.3а)
Для суперпозиции дискретизованных массивов требуется около
M2L2 операций, а коэффициент заполнения матрицы В равен
kn = (LlM)\ A1.2.36)
На рис. 11.2.1, е приведена блок-схема циклической суперпози-
суперпозиции с преобразованием. В этом случае входным вектором к? слу-
служит так называемый расширенный входной вектор, получаемый
размещением матрицы исходного изображения F (nlt n2) в левом
углу квадратной нулевой матрицы J-ro порядка и разверткой
полученной матрицы по столбцам. Повторяя вышеприведенные
рассуждения, можно показать, что
кя = Cfв = (А,,)"* ^ (Aj,) f? A1.2.4а)
и, следовательно,
b-\ A1.2.46)
О' • ¦»
С
В
fS2^®S2^U
Рис. 11.2.1. Различные виды суперпозиции.
а — конечная суперпозиция; б — дискретизованная интегральная суперпозиция;
циклическая суперпозиция; е — конечная суперпозиция с преобразованием; д — ДН1
тизоваииая интегральная суперпозиция с преобразованием; е — циклическая с;
позиция с преобразованием.
288 - Глава 11
Как было отмечено в гл. 9, для суперпозиции конечных или ди-
скретизованных массивов эквивалентный выходной вектор можно
сформировать из кЕ, выбирая определенные компоненты послед-
последнего. Для суперпозиции конечных массивов
B, A1.2.5а)
а для суперпозиции дискретизованных массивов
q = [S2SM) ® S2(,A1)] kE. A1.2.56)
При суперпозиции конечных массивов матрица обработанного
изображения связана с расширенной матрицей изображения Ке
следующим образом:
Q = [SlV11»] Kb [Siy*»]1". A1.2.6a)
При суперпозиции дискретизованных массивов матрица обрабо-
обработанного изображения равна
A1.2.66)
Число арифметических операций, необходимых для вычисления
вектора кЕ путем обработки с преобразованием, можно найти
из приведенных выше формул, если положить М. = N = J:
Прямое преобразование: 3J*.
Быстрое преобразование: J2 + 4/2 log2 J.
Если матрица & разрежена, то многие из Р умножений, нуж-
нужных для операции фильтрации, выполняться не будут.
Из вышеизложенного нетрудно сделать вывод, что для эффек-
эффективного проведения суперпозиции следует подобрать преобразо-
преобразование, отвечающее двум требованиям: во-первых, для него дол-
должен существовать быстрый алгоритм, а, во-вторых, матрица
фильтрации преобразованных массивов должна быть разрежен-
разреженной. В качестве примера рассмотрим свертку конечных массивов,
получаемую с помощью преобразования Фурье [2, 3]. В соответ-
соответствии с рис. 11.2.1 положим
А^ = АХ®АХ, A1.2.7)
где
при х, у = 1, 2, ..., К- Кроме того, примем, что вектор ЬяК) раз-
размера К2 X 1 представляет расширенную матрицу пространствен-
пространственно-инвариантного импульсного отклика, описываемого форму-
формулами (9.3.2) при J — К. Преобразование Фурье от ЬвК) обозна-
обозначим через
#> f \ A1.2.8)
Двумерные методы линейной обработки 289
Полученные отсчеты преобразования расставим на главной диа-
диагонали матрицы размера /С2 X /С2
A1.2.9)
С помощью весьма громоздких выкладок можно показать, что
в спектральном пространстве матрицы оператора свертки конеч-
конечных массивов и дискретизованного оператора свертки можно
представить в следующем виде [4 ]:
# = З^М [Ро ® Ра] A1.2.10)
при N = М — L + 1 и
Я = Рв ® РвЯГМ A1.2.11)
при N = М + L — 1, где
PD(u.v)=-L- )~Zul '-!-!»> (П.2.12а)
A1.2.126)
(
Таким^образом, оба оператора свертки в спектральном простран-
пространстве содержат матрицу скалярных весовых множителей Ж(К)
и интерполяционную матрицу [Р ® Р], которая позволяет свя-
связать входной вектор размера N2 с выходным вектором размера М2.
Как правило, интерполяционная матрица Р ® Р содержит много
нулевых элементов, и поэтому свертка с использованием преоб-
преобразования выполняется весьма эффективно.
Рассмотрим теперь циклическую свертку, выполняемую с пе-
переходом в спектральное пространство. С помощью рассуждений,
"аналогичных вышеприведенным, было показано [4], что оператор
, фильтрации в этом случае сводится к скалярному оператору
:¦ # = .Ш>. A1.2.13)
Таким образом, как видно из равенств A1.2.12) и A1.2.13),
при свертке в пространстве спектров Фурье матрицу фильтра
удается выразить в компактной замкнутой форме. Для других
унитарных преобразований подобных выражений не найдено.
Эффективность .вычисления свертки с применением преобразо-
преобразования Фурье определяется тем, что оператор свертки С имеет
циклическую матрицу, а соответствующая матрица фильтра 42 явля-
является диагональной. Как можно увидеть из соотношений A1.1.6),
базисные векторы преобразования Фурье фактически являются
собственными векторами матрицы С [5]. Это не так для операции
суперпозиции общего вида, а также для операции свертки с приме-
применением других унитарных преобразований. Однако во многих слу-
290
Глава И
чаях матрицы фильтра й>, да и<? содержат сравнительно мало нену-
ненулевых элементов и обработка с преобразованием позволяет умень-
уменьшить объем вычислений.
Рис. 11.2.2. Матрицы операторов свертки одномерных сигналов с использова-
использованием преобразований Фурье и Адамара.
в — конечная свертка; б — дискретизованиая свертка', 8 — циклическая свертка*
На рис. 11.2.2 показан вид матриц спектров для грех типов
оператора свертки одномерного входного вектора с гауссовым
импульсным откликом с использованием преобразований Фурье
и Адамара [61. Как и ожидалось, матрицы коэффициентов преоб-
Двумерные методы линейной обработки
291
¦
Рис. 11.2.3. Матрицы операторов свертки двумерных сигналов с использованием
преобразования Фурье.
Конечная свертка: й — непосредственно выполняемая; б — с преобразованием,
Днскретизованная интегральная свертка: « — непосредственно выполняемая; г — с пре»
образованием.
Циклическая свертка: 9 — непосредственно выполняемая; е — с преобразованием.
292 Глава 11
разования оказались значительно более разреженными, чем
исходные матрицы. Кроме того, легко заметить, что для цикли-
циклической свертки с преобразованием Фурье матрица фильтра яв-
является диагональной. На рис. 11.2.3 показана структура матриц
трех операторов свертки двумерных сигналов [4].
П.З. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ
Как уже отмечалось, для оператора свертки конечных мас-
массивов или дискретизованного оператора свертки эквивалентный
выходной вектор можно найти, выбирая определенные элементы
расширенного выходного вектора циклической свертки кЕ или
соответствующей ему матрицы Кя- Это положение в сочетании
с равенством A1.2.13) приводит к весьма эффективной процедуре
вычисления свертки, состоящей из следующих этапов:
1. Записать матрицу импульсного отклика в левом верхнем
углу нулевой матрицы /-го порядка, причем J > М для случая
свертки конечных массивов и J >¦ N для дискретизованной сверт-
свертки. Выполнить двумерное преобразование Фурье расширенной
матрицы импульсного отклика
^ = А,Н?АУ. A1.3.1)
2. Записать матрицу исходного изображения в верхнем левом
углу нулевой матрицы J-ro порядка и выполнить двумерное
преобразование Фурье расширенной матрицы исходного изоб-
изображения
^? = A,F?Ay. A1.3.2)
3. Выполнить скалярное умножение
ЖЕ (т, п) = J3HE (т, п) ТЕ{т,п), A1.3.3)
где irs^m^Jnl^n^J.
4. Произвести обратное преобразование Фурье
Кя = (АУГ1ЛГ?(Ау)-1. A1.3.4)
5. После выбора нужных элементов сформировать искомую
выходную матрицу
Q,= [S1(A))]Ke[S1(M)]7' A1.3.5а)
или
G=[S2(M)]K?[S2(M)]7'. A1.3.56)
Важно, чтобы порядок J расширенных матриц ЖЕ и @~Е удовлетво-
удовлетворял соответствующим неравенствам. При J = N на левом и верхнем
краях выходной матрицы будут находиться полосы ошибочных
элементов, имеющие ширину в L — 1 отсчет (рис. 11.3.1, а, б). Они
образуются в результате так называемой циклической ошибки,
Двумерные методы линейной обработки
293
связанной с неправильным применением метода БПФ для вычисле-
вычисления свертки. Кроме того, при выполнении свертки конечных мас-
массивов (D-свертка) будут потеряны элементы выходного массива,
расположенные полосами в правой и нижней его частях. Если поло-
положить / = М, то при D-свертке выходная матрица будет полностью
заполнена правильными отсчетами. Чтобы вычислить Б-свертку
Ошибочные
отсчеты
J
Ошибочные
отсчеты
1-1
Верные
отсчеты
Рис. 11.3.1. Циклические ошибки. (Нижняя и правая стороны матрицы F от-
отсечены.)
а — фильтрация типа В; J = N, М = N — L + 1.
б — фильтрация типа D; J — N, М — N + L — 1.
в — фильтрация типа В; J — М, М — N — L + 1.
г — фильтрация типа D; J — М, М = N -\- L — 1.
при J = М, необходимо отсечь правый и нижний края исходной
матрицы. Однако в результате получится, что элементы выходного
массива, расположенные сверху и по левому краю, будут оши-
ошибочными.
При обработке сигналов во многих случаях оказывается, что
на различные входные массивы воздействуют операторы с одним
и тем же импульсным откликом и, следовательно, первый этап
алгоритма (вычисление 9@Е) достаточно выполнить только один
раз. При использовании алгоритма БПФ для случаев прямого и
обратного преобразований требуется выполнить примерно по
2J2 log2 J арифметических операций. Скалярное умножение про-
проводится за Р операций, т. е. всего требуется Р A + 4 log2 /)
операций. Если входная матрица содержит NxN элементов,
выходная MXiM, а матрица импульсного отклика LXL элемен-
294
Глава 1J
тов, то для вычисления конечной свертки требуется N*L2 опера-
операций, а для дискретизованной свертки M2L* операций. Если раз-
размер L матрицы импульсного отклика достаточно велик по сравне-
сравнению с размером N исходной матрицы, то свертка с преобразова-
преобразованием оказывается эффективнее прямой свертки, причем число
операций,* может уменьшиться раз в десять или более. На
рис. 11.3.2 приведен график зависимости L от N для случ?.",
В*
О 200 400 600 _ 800 1000
Размер исходной мотриць! М
Рис. 11.3.2. Сравнение эффективности двух методов получения конечной свертки:
прямого и с преобразованием Фурье.
когда оба метода вычисления свертки конечных массивов (прямой
и с преобразованием Фурье) имеют одинаковую эффективность.
Зубчатость графика объясняется тем, что с ростом N параметр /
изменяется скачкообразно, принимая значения 64, 128, 256 и т. д.
Для вычисления свертки с преобразованием Фурье требуется
меньшее число операций, чем в случае ее прямого вычисления,
если длина импульсного отклика достаточно велика. Однако если
обрабатываемое изображение также имеет большие размеры, то
относительная эффективность метода с использованием преобра-
преобразования Фурье понижается. Кроме того, при вычислении преоб-
преобразования Фурье больших матриц возникают трудности, связан-
связанные с обеспечением точности расчетов. Обе проблемы удается
разрешить, прибегая к блочной фильтрации изображения, когда
большую матрицу подразделяют иа ряд перекрывающихся бло-
блоков, обрабатываемых поочередно [2, 7—9].
На рис. 11.3.3, с показано, как из левого верхнего угла боль-
большой матрицы извлекается блок, содержащий NBxNB элемен-
элементов. После свертки его с импульсным откликом, состоящим из
LXL элементов, получается блок размера Мв ХМВ элементов,
который помещают в левый верхний угол выходной матрицы
Двумерные методы линейной обработки
295
(рис. 11.3.3, а). Далее из обрабатываемой матрицы извлекают
следующий блок размера NB x NB элементов и из него получают
второй блок обработанного изображения размера Мв х Мв,
примыкающий к первому. Как показано на рис. 11.3.3, б, второй
блок исходного изображения должен перекрываться с первым
блоком в полосе шириной L — 1 элемент. Тогда обработанные
блоки будут стыковаться без зазора. Этот процесс продолжается
Исходное
изображение
4
Лро<рш?ьтро-
бонное
-i1 изобрдженш
Рис. 11.3.3. Размещение блоков при блочной фильтрации изображения.
а — первый блок; б — вторые блоки в строке и столбце блоков.
до тех пор, пока не будут обработаны все блоки, прилегающие
к верхней строке матрицы. Если в этой строке блоков последний
блок окажется неполным, в него следует добавить нулевые эле-
элементы. Далее извлекают блок, находящийся в начале второй
строки и перекрывающийся с блоками первой строки в полосе
шириной L — 1 элемент. Процесс продолжается до тех пор, пока
не будут определены все элементы обработанного изображения.
Для получения свертки с помощью преобразования Фурье
требуется
0F = JV2 + 2fP\ogt N A1.3.6)
операций. При блочной обработке, когда размер блоков равен
NBxNB, необходимо
Ов = Я2 [N% + 2N% log2 NB] A1.3.7)
операций, где число блоков R — округленное в большую сторону
значение дроби Nl[NB + L — 1 ]. Хант [9] определил, как оп-
оптимальный размер блока зависит от величины матриц исходного
изображения и импульсного отклика.
296 Глава 11
11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Алгоритм свертки с применением БПФ, рассмотренный в пре-
предыдущем разделе, часто используют при машинном моделировании
линейных аналоговых фильтров. В данном разделе проанализи-
проанализированы ошибки, присущие такому методу моделирования, и опи-
описаны способы определения дискретной частотной характеристики
по заданной непрерывной частотной характеристике. В целях
упрощения изложения здесь описываются только одномерные
сигналы.
Рассмотрим длинный одномерный непрерывный сигнал /с (х),
спектр которого /с (со) равен нулю, если | со | больше частоты
среза со0. Нужно найти свертку сигнала с непрерывным импульс-
импульсным откликом hc (х), частотная характеристика которого 4С (со)
также ограничена частотой соо. Как упоминалось в гл. 1, свертку
можно выполнить либо в пространственной области в соответ-
соответствии с соотношением
00
?с(*)= J fc (<*) hc (х-a) da, A1.4.1а)
—00
либо в частотной области
00
gc(x) = A/2я) J /с((й)Лс(со) ехр {ио*} Жо. A1.4.16)
— 00
В гл. 9 описана методика дискретизации интеграла свертки
A1.4.1). Непрерывный импульсный отклик hc (x) необходимо
подвергнуть усечению, умножив его на весовую функцию у (х).
В результате получается взвешенный импульсный отклик
bc(x) = hc(x)y(x), A1.4.2)
где у (х) = 0 при | х\ > Т. Весовая функция уменьшает эффекты,
связанные с усечением. Интеграл свертки аппроксимируется
выражением.
gc(x)= j fc(a)bc(x-a)da. A1.4.3)
х-Т
Затем в 2J + 1 точке берут отсчеты выходного сигнала с интер-
интервалом А = я/со0, а непрерывный интеграл заменяют суммой с тем
же шагом А. В результате получается дискретное представление
S fc(kA)bc[(j-k)A], A1.4.4)
где К — целое число, ближайшее к значению дроби Т/А.
Для вычисления суммы A1.4.4) с помощью дискретного преоб-
преобразования Фурье можно следующим образом применить алго-
алгоритм, описанный в разд. 11.3. На первом этапе в качестве первых
Двумерные методы линейной обработки 297
L == 2Л" + 1 элементов /-элементной последовательности берутся
отсчеты взвешенного импульсного отклика, а в качестве после-
последующих J — L элементов — нули. Таким образом,
Ьэ(/) = Ьс(-К),...,Ьс{0),...,Ьс(К)к 0,. . ., 0, A1.4.5)
L элементов
где 0 =^ г sg Р — 1 • Элементы последовательности bD (<?) можно
получить из непрерывного импульсного отклика hc (х) и весовой
функции у (х), дискретизируя произведение этих функций, т. е.
+ KA-tA). (П.4.6)
На следующем этапе вычисляется дискретное преобразование
Фурье Ьо {() в Р точках
р-\
Ы«) -Yj^bD{i)^p{~^iu\, A1.4.7)
1=0
где 0 =^ и sg P — 1. После подстановки выражения для bD (/)
в формулу A1.4.7) и преобразований получается, что дискретная
частотная характеристика фильтра связана с аналоговой частот-
частотной характеристикой Лс (со) и спектром Фурье у (со) весовой функ-
функции соотношением
^ (")!i= 1STl^-exPH5t(iTLL)"}^(-T!L и). (П.4.8а)
*д(Р-и) = *Ь(и), A1.4.86)
где и = 0, 1, ..., Я/2, а ?с (со) = ^с (со) * у (со).
Равенства A1.4.8) задают искомую связь между дискретной
и непрерывной частотными характеристиками. Если непрерыв-
непрерывная частотная характеристика Лс (<*>) и спектр Фурье у. (со) весо-
весовой функции известны и заданы в аналитическом виде, то в прин-
принципе отсчеты дискретной частотной характеристики можно полу-
получить, выполниз аналитическим путем свертку A1.4.86) и находя
числовые значения полученной при этом функции в точках
Bлн/ЯА) для каждого значения параметра и. На практике часто
не удается вычислить свертку аналитически, особенно для дву-
двумерных сигналов, и оказывается проще выполнить обратное пре-
преобразование Фурье частотной характеристики Лс (со) для полу-
получения аналитического выражения импульсного отклика и затем
взять отсчеты bD (<?) в соответствии с формулой A1.4.6). Можно
использовать и другой подход: согласно равенству A1.4.8), взять
отсчеты дискретного обратного преобразования Фурье ^СBл«/ЯА),
умножить расширенную последовательность отсчетов импульс-
импульсного отклика на весовую функцию, а затем, выполнив дискрет-
дискретное преобразование Фурье, получить &р (и).
298
Глава 11
Умножение на весовую функцию, которое можно выполнить
согласно равенству A1.4.6) или неявно в спектральной области
с помощью соотношения A1.4.8), совершенно необходимо, если
нужно подавить описанные в гл. 9 циклические ошибки. При филь-
фильтрации изображений обычно делается типичная ошибка, когда
в качестве дискретного импульсного отклика берется последо-
последовательность отсчетов непрерывного импульсного отклика. Тогда
в общем случае все J элементов соответствующего расширенного
дискретного импульсного отклика будут ненулевыми, т. е. длина L
дискретного импульсного отклика, «погружаемого» в расширен-
расширенный вектор A1.4.5), неявно будет принята равной J. Поэтому
все профильтрованные отсчеты будут искажены из-за цикличе-
циклической ошибки.
Известно [10—12] несколько видов весовых функций, при-
пригодных для использования при дискретной линейной фильтрации.
Некоторые из них, чаще всего встречающиеся на практике, при-
приведены в табл. 11.4.1, а их графики — на рис. 11.4.1. На
рис. 11.4.2 представлены соответствующие спектры, состоящие
из главного лепестка и набора боковых лепестков, амплитуды
которых обычно уменьшаются с ростом частоты. Анализ выражения
Таблица 11.4.1
Весовые функции
Функция
Определение
Прямоугольная
Бартлетта (тре-
(треугольная)
Ханна
Хемминга
Блэкмана
Кайзера
w (я) =
ш(я) = 1, 0<я< L — 1
2я L — 1
1-1 ' 0</г< 2 :
2 —
2я
L — \
L — 1 ' 2
— cos
и) (я) = 0,54 — 0,46 cos ( ™ Л , 0<я<1 —
w (n) = 0,42 - 0,5 cos (~2^r) + 0,08 cos
0«n< L — 1
/„ {wa[({L - l)/2)»-[n-((L -
/o {cM(L -
0<n^L —1,
I a {•} — модифицированная функция Бесселя нулевого
порядка первого рода
Двумерные методы линейной обработки
299
A1.4.8) показывает, каким образом форма весовой функции и
ее спектра влияет на выходной сигнал. Форма главного лепестка
спектра весовой функции определяет искажение спектра сигнала
в диапазоне от 0 до со0. Боковые лепестки вызывают наложение
спектров, поскольку взвешенный импульсный отклик &с (ш)
имеет спектр неограниченной ширины. Плавные весовые функции
Прямоугольная
Л -
N-1 п
Рнс. 11.4.1. Одномерные весовые функции [10].
имеют слабые боковые лепестки, что уменьшает ошибки наложения
спектров, однако главный лепесток в этих случаях оказывается
более широким, что приводит к сглаживанию спектра сигнала.
При проектировании фильтров приходится находить компромисс
между этими двумя видами ошибок. Обе ошибки можно умень-
уменьшить, увеличивая длину взвешенного импульсного отклика,
однако при этом либо сокращается длина обработанного сигнала,
либо увеличивается объем вычислений.
11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ
Обработку с использованием преобразований можно с успехом
применить для получения обобщенных обратных матриц. Как
видно из соотношения A1.1.66), матрица ^"линейного оператора
в спектральном пространстве связана с произвольной матрицей Т
размера M2XN2 следующим образом:
а/ — \г\цх) I \J\fo\) , ^ 1 1.0. 1)
В тех же обозначениях обобщенная обратная матрица &" опре-
определяется как
ёГ" = (АЛ2) Т (Ам2)"х. A1.5.2)
Относительный уровень, дБ
Относи тельный уровень, дБ
i
от
?
Двумерные методы линейной обработки
301
-го-
-60
-80
-100
щ
I
I
о
-го
-40
-60
-80
-loo
Рис. 11.4.2. Спектры одномерных весовых функций [10].
а — прямоугольной; б — треугольной (Бартлетта); о — Ханна; а — Хемминга; д —
Блакмана.
где Т~ — матрица размера N2XM2. Соотношения A1.5.1) и A1.5.2)
являются самосогласованными, поскольку известно, что для
произвольной матрицы Z и унитарных матриц Р и R выполняется
равенство (PZR)" = R*rZ"P*r [13, стр. 100].
Если ранг матрицы Т равен ./V2, то, согласно формуле (8.3.5),
ТГ A1.5.3)
и нетрудно показать, что
&-' = (tr^try1 ZT*7. A1.5.4)
В противоположном случае, когда ранг матрицы Т равен М2,
из формулы (8.3.6) следует, что
Г = Т(ТТГ)-1 A1.5.5).
и обобщенная обратная матрица преобразования в спектральном
пространстве удовлетворяет соотношению
gr- = gr*T (zrtT*7)-1. A1.5.6)
Укажем для примера, что обобщенные обратные матрицы отно-
относительно матриц максимального ранга, соответствующих опера-
302
Глава it
торам суперпозиции Ф, $ и f, определяются равенствами
, A1.5.7а)
, A1.5.76)
9- = V\] A1.5.7b)
На рис. 11.5.1 представлены распечатки обобщенных обратных
матриц для операторов свертки одномерных сигналов с исполь-
Рис. 11.5.1. Обобщенные обратные матрицы операторов свертки одномерных
сигналов с использованием преобразований Фурье и Адамара.
о — конечная свертка; б — днскретиэованная интегральная свертка в — циклическая
свертка.
Двумерные методы линейной обработки 303
ш
зованием преобразований Фурье и Адамара. Хорошо заметно,
что эти матрицы более разрежены, чем исходные матрицы.
Более того, обобщенная обратная матрица оператора циклической
свертки с преобразованием Фурье является диагональной, по-
поскольку, как следует из равенства A1.2.13), матрица V — диаго-
диагональная.
11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ
В предыдущих разделах данной глары обработка с преобра-
преобразованием рассматривалась как косвенный метод выполнения дву-
двумерной линейной обработки. Было показано, что для обработки
с преобразованием часто требуется гораздо меньше арифметиче-
арифметических операций, чемТпри использовании стандартных методов.
В данном разделе будет рассмотрен другой способ линейной об-
обработки, называемый рекурсивной фильтрацией [14—16]. Иногда
рекурсивная фильтрация оказывается даже более эффективной,
чем обработка с преобразованием. Кроме того, в этом случае для
хранения данных требуется ЗУ меньшей емкости, чем при обра-
обработке с преобразованием.
^Рекурсивная фильтрация основывается на рекуррентном соот-
соотношении между входными и выходными переменными системы.
Для одномерных сигналов подобное рекуррентное соотношение
имеет следующий вид [14]:
г К
-l+l)-Y b{k)r{m- k+ 1), A1.6.1)
A2
где / (n), n = 1,2, ..., N — отсчеты входной последовательности,
г (т), т = 1, 2, ..., М — отсчеты выходной последовательности,
a b (k) и а (/) — весовые множители. Ключевой момент здесь в том,
что т-й элемент выходной последовательности зависит не только
от последнего п J — 1 предпоследних элементов входной после-
последовательности, но и от К — 1 предыдущих элементов выходной
последовательности.
Большинство методов синтеза и анализа рекурсивных филь-
фильтров основано на применении Z-преобразования. По определению
[17, 18] Z-преобразование N- элементной последовательности f (п)
дает образ
Лг)=? /(n)zi-«. A1.6.2)
Нетрудно показать, что Z-преобразование выражения A1.6.1)
дает образ
304 Глава 11
где а (г), 4 (г) и / (г) — образы соответствующих последователь-
последовательностей .
Двумерная рекурсивная фильтрация основана на следующем
рекуррентном соотношении между входным и выходным масси-
массивами [19, 20]:
R (Щ, Щ) -- Г I- А (/1; /2) F К - /х + 1, т2 - j, + 1) -
/•=1 Ь=1
-? I B(ki,k2)R(m1-k1+lm2-k2+l), A1.6.4)
?,=2 А2=2
где F (nx, n2) — входной массив из NiXN2 элементов, R (ть
пг2) — выходной массив из М^ХМ^ элементов, а В (klt Л2) и
А (Д> /г) — весовые множители. Предполагается, что процесс
рекурсивной фильтрации начинается с левого верхнего угла
входного массива. С помощью двумерного Z-преобразования из
равенства A1.6.4) получается
где s4- {гъ г2), Jf (г],, г2) и ^" (ги z2) — двумерные образы соответствую-
соответствующих массивов. Так, например,
•*(zi, г2)= !¦ Г Л(пь n2)z?-ni)z(tni). (П.6.6)
При синтезе рекурсивных фильтров требуется выбрать такие мас-
массивы весовых множителей А и В, чтобы выходной массив R (тът^)
оказался эквивалентным массиву, получаемому в результате
свертки функции F (пъ п2), описывающей исходное изображение,
с заданным импульсным откликом Н (tlt S2). Как правило, точ-
точного совпадения массивов добиться не удается и при синтезе
фильтров приходится пользоваться приближенными методами [21,
22]. При этом возникает вопрос об устойчивости рассчитанного
рекурсивного фильтра. Если фильтр неустойчив, то ошибки ок-
округления или шум, присутствующий во входном массиве, могут
в ходе обработки не ослабляться, а увеличиваться до очень боль-
большого уровня. Рекурсивный фильтр устойчив [20], если коэф-
коэффициенты К (/ь /а) разложения частотной характеристики фильтра
в ряд по степеням переменных гх и г2
00 00
-щ-j-——г- = л (zu z2) = 2
1 2 /.=1 /,=1
являются абсолютно суммируемыми, т. е. удовлетворяют условию
? ? 1*(/ь /2)|<оо. (и.6.8)
/.=1 h~\
Двумерные методы линейной обработки 305
Разработано несколько методов проверки рекурсивных фильтров
на устойчивость [23—25]. При обработке изображения согласно
равенству A1.6.4) требуется выполнить
NR = (JtJ» + KiKJ N,N2 A1.6.9)
арифметических операций. Здесь У,- и /С,- — размеры массивов
весовых множителей для входного и выходного изображений,
a N[ — размеры входного изображения. Если изображения и
массивы весовых множителей — квадратные (т. е. Jx == /2 —
= J, Ki — К% = К и Nt = ЛГ2 = N), то при рекурсивной филь-
фильтрации нужно выполнить
NR= (P + К2) N2 A1.6.10)
операций. Для сравнения укажем, что для получения конечной
свертки (см. разд. 9.3) требуется
NC=L*N2 A1.6.11)
операций, где L — размер импульсного отклика. Как показано
в разд. 11.2, для получения свертки с применением быстрого
преобразования Фурье необходимо примерно
A^ = Wa(l+41og2A0 A1.6.12)
операций. Степень относительной эффективности трех типов об-
обработки зависит от размеров массива импульсного отклика [27].
Если эти размеры невелики, то для прямого метода получения
свертки и рекурсивной фильтрации требуется почти одинаковое
число арифметических операций. В этом случае сравнить эффек-
эффективность обоих методов с эффективностью получения свертки
с использованием БПФ можно с помощью графика на рис. 11.3.2.
При больших размерах массива импульсного отклика быстрый
метод получения свертки оказался гораздо эффективнее прямого
метода. Сравнивая число операций в равенствах A1.6.10) и
A1.6.12), можно показать, что при больших размерах импульс-
импульсного отклика рекурсивная фильтрация оказывается эффективнее
быстрого метода получения свертки, если площади массивов коэф-
коэффициентов рекурсивного фильтра удовлетворяют неравенству
P + F^clogzN, A1.6.13)
где с — постоянная, принимающая значения от 1 до 20, причем
ее величина зависит от вида использованного алгоритма БПФ и
от того, насколько вычисления с комплексными числами проис-
происходят медленнее, чем с действительными.
306 Глава И
ЛИТЕРАТУРА
1. Pratt W. К., Generalized Wiener Filtering Computation Techniques, IEEE
Trans. Computers, C-21, 7, 636—641 (July 1972).
2. Stockham T. G., Jr., High Speed Convolution and Correlation, Proceedings
Spring Joint Computer Conference, 1966, pp. 229—233.
3. Gentleman W. M., Sande G., Fast Fourier Transforms — for Fun and Pro-
Profit, Proceedings Fall Joint Computer Conference, 1966, pp. 563—578.
4. Pratt W. K-, Vector Formulation of Two-Dimensional Signal Processing Ope-
Operations, J. Computer Graphics and Image Processing (March 1975) (Academic
Press, New York).
5. Hunt B. R., A Matrix Theory Proof of the Discrete Convolution Theorem,
IEEE Trans. Audio and Electroacoustics, AU-19, 4, 285—288 (December 1973).
6. Pratt W. K-. Transform Domain Signal Processing Techniques, Proceedings
National Electronics Conference, Chicago, Illinois, 1974.
7. Helms H. D., Fast Fourier Transform Method of Computing Difference Equ-
Equations and Simulating Filters, IEEE Trans. Audio and Electroacoustics, AU-15,
2, 85—90 (June 1967).
8. Ekstrqm M. P., Algazi V. R., Optimum Design of Two-Dimensional Non-
recursive Digital Filters, Proceedings 4th Asilomar Conference on Circuits and
Systems, Pacific Grove, California, November 1970.
9. Hunt B. R., Computational Considerations in Digital Image Enhancement,
Proceedings Conference on Two-Dimensional Signal Processing, University
of Missouri, Columbia, Missouri, October 1971.
10. Oppenheim A. V., Schafer R. W., Digital Signal Processing, Prentice-Hall,
Englewood Cliffs, N. J., 1975. [Имеется перевод: Оппенгейм А. В., Ша-
Шафер Р. В., Цифровая обработка сигналов. — М.: Связь, 1979.]
11. Blackman R. В., Tukey J. W., The Measurement of Power Spectra, Dover,
New York, 1958.
12. Kaiser J. F., Digital Filters, Chapter 7 in Systems Analysis by Digital Com-
Computer, Kuo F. F., Kaiser J. F., Eds., Wiley, New York, 1966. [Имеется
перевод: Кайзер Дж., Цифровые фильтры. Приложение к книге:JCcwm Б.,
Рэйдер Ч., Цифровая обработка сигналов.—М.: Советское радио, 1973.]
13. Graybill F. A., Introduction to Matrices with Applications in Statistics, Wads-
worth Publishing, Belmont, Calif., 1969.
14. Childers D. G., Durling A., Digital Filtering and Signal Processing, West
Publishing, St. Paul, Minn., 1975.
15. Oppenheim A. V., Schafer R. W., Digital Signal Processing, Prentice-Hall,
Englewood Cliffs, N. J., 1975.
16. Rabiner L. R., Gold В., Theory and Application of Digital Signal Processing,
Prentice-Hall, Englewood Cliffs, N. J., 1975. [Имеется перевод: Рабинер Л.,
Гоулд Б., Теория и применение цифровой обработки сигналов. — М.: Мир,
1978. J
17. Ragazzini J. R., Franklin G. F., Sampled Data Control Systems, McGraw-
Hill, New York, 1958.
18. Jury E. I., Theory and Applications of the Z-Transform Method, Wiley,
New York, 1964.
19. Shanks J. L., Two-Dimensional Recursive Filters, SWIEECO Record, Vol. 21,
19E1, 1969.
20. Farmer С. Н., Gooden D. S., Rotation and Stability of a Recursive Digital
Filter, Proceedings Two-Dimensional Signal Processing Conference, University
of Missouri, Columbia, Missouri, October 1971.
21. Hu J. V., Rabiner L. R., Design Techniques for Two-Dimensional Digital
Filters, IEEE Trans. Audio and Electroacoustics, AU-20, 4, 249—257 (October
1972).
22. Dudgeon D. E., Two-Dimensional Recursive Filter Design Using Differen-
Differential Correction, IEEE Trans. Acoustics, Speech, and Signal Processing,
ASSP-23, 3, 264—267 (June 1975).
Двумерные методы линейной обработки 307
23. Shanks J. L., Treitel S., Justice J. H., Stability and Synthesis of Two-
Dimensional Recursive Filters, IEEE Trans. Audio and Electroacoustics, AU-20,
2, 115—128 (June 1972).
24. Huang T. S., Stability of Two-Dimensional Recursive Filters, IEEE Trans.
Audio and Electroacoustics, AU-20, 2, 158—163 (June 1972).
25. Anderson B. D., Jury E. I., Stability Test for Two-Dimensional Recursive
Filters, IEEE Trans. Audio and Etectroacoustics, AU-21, 4, 366—372 (August
1973).
26. Pistor P., Stability Criterion for Recursive Filters, IBM J. Res. DeveL, 18,
1, 59—71 (January 1974).
27. Hall E. L., A Comparison of Computations for Spatial Frequency Filtering,
Proc. IEEE, 60, 7, 887—891 (July 1972). [Имеется перевод: Холл. Срав-
Сравнение трех методов цифровой пространственной фильтрации. — ТИИЭР,
1972, т. 60, № 7.]
ОГЛАВЛЕНИЕ
Предисловие к переводу 5
Предисловие 7
Благодарности 9
ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ
Глава 1. Математическое описание непрерывных изображений 12
1.1. Представление непрерывных изображений 12
1.2. Двумерные системы 14
1.3. Сингулярные операторы 15
1.4. Линейные операторы 16
1.5. Дифференциальные операторы 19
1.6. Двумерное преобразование Фурье 20
1.7. Анализ линейных систем с помощью преобразования Фурье ... 23
1.8. Обобщенные линейные системы 23
1.9. Вероятностное описание непрерывных изображений 25
1.10. Преобразование случайных изображений в изображающей системе 29
Литература 30
Глава 2. Психофизические свойства зрения 32
2.1. Восприятие света 32
2.2. Глаз 35
2.3. Зрительные явления 39
2.4. Модель одноцветного зрения 44
2.5. Модель цветового зрения 50
Литература 54
Глава 3. Фотометрия и колориметрия 56
3.1. Источники света 56
3.2. Фотометрия 59
3.3. Уравнивание цветов [10—14] 63
3.4. Колориметрия 68
3.5. Преобразование координат цвета 74
3.6. Системы координат цвета 76
3.7. Цветовое тело 88
Литература 94
ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ
Глава 4. Дискретизация и восстановление непрерывных изображений . . 96
4.1. Процессы идеальной дискретизации и восстановления непрерыв-
непрерывных изображений 96
4.2. Реальные системы дискретизации изображений 105
4.3. Реальные системы восстановления изображений 115
Литература , 124
Оглавление 309
Глава 5. Математическое описание дискретных изображений 126
5.1. Действия с векторами и матрицами 126
5.2. Сингулярное разложение матрицы 131
5.3. Векторное представление изображений 132
5.4. Статистическое описание дискретных изображений [5, 10] .... 134
5.5. Модели плотностей вероятности дискретных изображении .... 138
Литература 144
Глава 6. Квантование изображений 145
6.1. Квантование скалярных величин ,'.... 145
6.2. Квантование векторных величин 151
6.3. Обработка квантованных величин 155
6.4. Квантование одноцветных изображений 158
6.5. Квантование цветных изображений 162
Литература 165
Глава 7. Меры качества дискретизованных изображений 166
7.1. Субъективные оценки качества изображений 167
7.2. Оценка качества по контрольным сигналам и испытательным та-
таблицам 170
7.3. Метрики светлоты и цвета 172
7.4. Верность воспроизведения одноцветных изображений 178
7.5. Верность воспроизведения цветных изображений 187
7.6. Энтропия изображений 189
7.7. Скорость создания информации источником изображений . . . 194
7.8. Дешифрируемость изображений 198
Литература 201
ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА
Глава 8. Линейные операторы 205
8.1. Обобщенный линейный оператор 205
8.2. Статистическое описание изображений при линейном преобразо-
преобразовании 208
8.3. Операторы псевдообращения 210
8.4. Решение систем линейных уравнений 212
8.5. Решение совместных систем линейных уравнений 213
8.6. Приближенные решения несовместных систем линейных урав-
уравнений 215
Литература 216
( Глава 9. Оператор суперпозиции 217
i 9.1. Оператор суперпозиции конечных массивов 217
1 9.2. Дискретизованный оператор суперпозиции 220
\ 9.3. Оператор циклической суперпозиции 229
9.4. Соотношение между линейными операторами 232
: Литература 234
Глава 10. Двумерные унитарные преобразования 235
10.1. Операторы унитарных преобразований 235
10.2. Преобразование Фурье 239
10.3. Косинусные преобразования 245
10.4. Синусное преобразование 251
310 Оглавление
10.5. Преобразование Адамара : 254
10.6. Преобразование Хаара 258
10.7. Наклонное преобразование 260
10.8. Преобразование Карунена — Лоэва 265
10.9. Сингулярное преобразование 267
10.10. Алгоритмы вычислений 271
10.11. Статистический анализ преобразованных изображений .... 274
10.12. Модели плотности вероятности преобразованных изображений 280
Литература 281
Глава П. Двумерные методы линейной обработки 283
11.1. Обработка с использованием преобразования 283
11.2. Суперпозиция с преобразованием 286
11.3. Свертка с использованием БПФ 292
11.4. Фильтры на основе преобразования Фурье 296
11.5. Псевдообращение с преобразованием 299
11.6. Рекурсивная фильтрация 303
Литература 306
Уильям Прэтт
ЦИФРОВАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Старший научный редактор Л. П. Якименко
Младший научный редактор Е. П. Орлова
Художник В. И. Харламов
Художественный редактор Л. Е. Безручеиков
Технический редактор Н.^Д. Толстякова
Корректор Е. Г. Лнтвак
ИБ № 2371
Сдаио в набор 25.03.81.
Подписано к печати 29.10.81.
Формат 60x90Vi«.
Бумага типографская № 2.
Гарнитура литературная. Печать высокая.
Объем 9,75 бум. л. Усл. печ. л. 19,50.
Усл. кр.-отт. 19,50.
Уч.-изд. л. 16,61. Изд. № 20/0958.
Тираж 10 000 экз. Заказ № 596. Цена 1 р. 50 к.
ИЗДАТЕЛЬСТВО «МИР»
129820, Москва, И-110, ГСП,
1-й Рижский пер., 2.
Леиниградская типография № 6 ордена Трудо-
Трудового Красного Зиамени Ленинградского объеди-
объединения «Техническая книга» им. Евгении Соко-
Соколовой Союзполиграфпрома при Государственном
комитете СССР по делам издательств, полиграфии
и книжной торговли
193144, Ленинград, ул. Монсеенко, 10