Cubic Forms
Algebra, Geometry, Arithmetic
YU.I.MANIN
Mathematical Institute V.A. Stek/ov
Academy of Sciences of the U.S.S. R.
Moscow
Translated from Russian
by
M. Hazewinkel
Second Edition
.*:'!■
Щ
1986
NORTH-HOLLAND
AMSTERDAM • NEW YORK • OXFORD

© ELSEVIER SCIENCE PUBLISHERS B.V.. 1986
All rights reserved. No part of this publication may be reproduced, stored in a retrieval
system, or transmitted, in any form or by any means, electronic, mechanical,
photocopying, recording or otherwise, without the prior permission of the copyright
owner.
First edition 1974
Second edition 1986
ISBN: 0444 558136
Published by:
ELSEVIER SCIENCE PUBLISHERS B.V.
P.O. Box 1991
1000 BZ Amsterdam
The Netherlands
Sole distributors for the U.S.A. and Canada:
ELSEVIER SCIENCE PUBLISHING COMPANY. INC.
52, Vanderbitt Avenue
New York, NY 10017
U.S.A.
Library of Congress Cataloging-in-Publication Data
Manin. IU. I.
Cubic forms.
(North-Holland mathematical library ; v. 4)
Translation of: Kubichcskie formy.
Bibliography: p.
Includes index.
1. Surfaces, Cubic. I. Title. II. Series.
QA573.M2513 1986 516.3'6 83-20463
ISBN 0-444-55813 6 (Paperback)
Printed in the Netherlands

PREFACE TO THE SECOND EDITION
In the ten years since this book was published in English, there has been important
progress in a number of topics related to its subject. Were this book io be written anew,
its title could be Algebraic Varieties close to the Rational Ones. Algebra, Geometry,
Arithmetic. In fact, this class of varieties has crystallized as a natural domain for the
methods developed and expounded in Cubic Forms.
In this edition the original text is left intact, except for a few corrections, but an
Appendix is added together with a list of references to original papers, mainly of the last
decade.
This Appendix sketches some of the most essential new results, constructions and
ideas, including the solutions of the Liiroth and Zariski problems, the theory of the
descent and obstructions to the Hasse principle on rational varieties, and recent
applications of K-theory to arithmetic. Proofs are omitted since their complete
presentation would demand a new book. Meanwhile, this modest report will hopefully
be of use.
1 am deeply indebted to V. E. Voskresenski and M. A. Tsfasman for their help in
preparing this second edition.
Moscow, 1984. Yu. I. Manin

CONTENTS
PREFACE TO THE SECOND EDITION v
CONTENTS vii
INSTRUCTIONS TO THE READER x
INTRODUCTION ... 1
CHAPTER I. CH-QUASIGROUPS AND MOUFANG LOOPS 6
1. A survey of definitions and results 6
2. Symmetric Abelian quasigroups 11
3. CH-quasigroups 15
4. Commutative Moufang loops 21
5. The connection between CH-quasigroups and Moufang loops ... 25
6. Morphisms of CH-quasigroups and Moufang loops 28
7. The first structure theorem 30
8. The second structure theorem 33
9. Finite Fischer groups 34
10. Unsolved problems and bibliographical remarks 39
CHAPTER II. CLASSES OF POINTS ON CUBIC HYPERSURFACES 42
11. Admissible equivalence relations: a survey 42
12. Unirationality 46
13. Universal equivalence 54
14. R-equivalence: the basic properties 61
15. R-equivalence and quadratic extensions 65
16. Universal equivalence over local fields. Examples 69
17. Bibliographical remarks 76
CHAPTER III. TWO-DIMENSIONAL BIRATIONAL GEOMETRY 77
18. The main results 77
19. Monoidal transformations 82
20. Monoidal transformations and divisors 90
21. The main theorems on birational maps 100
22. Bibliographical remarks 110
vii

viii CONTENTS
CHAPTER IV. THE TWENTY-SEVEN LINES 112
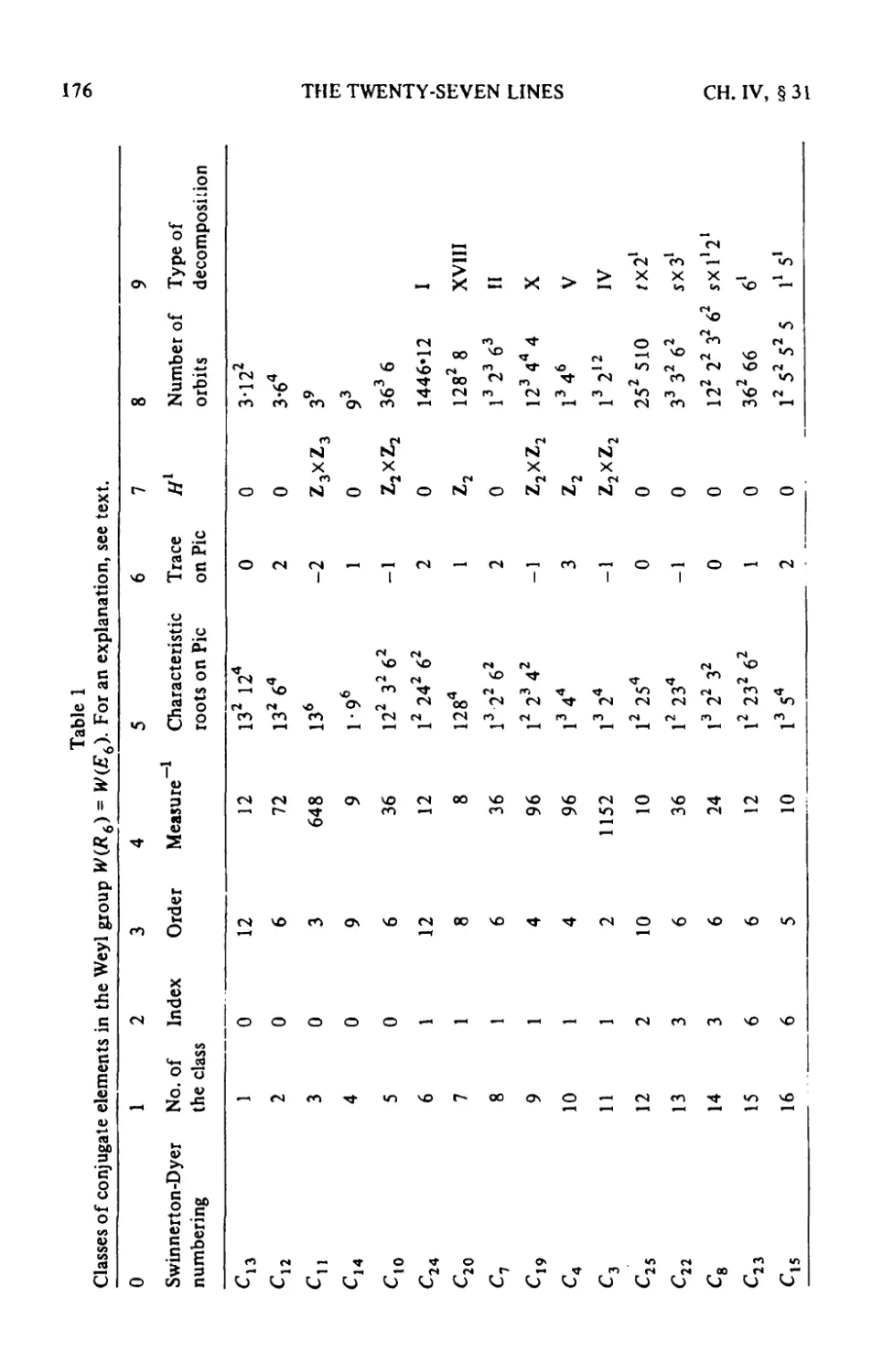
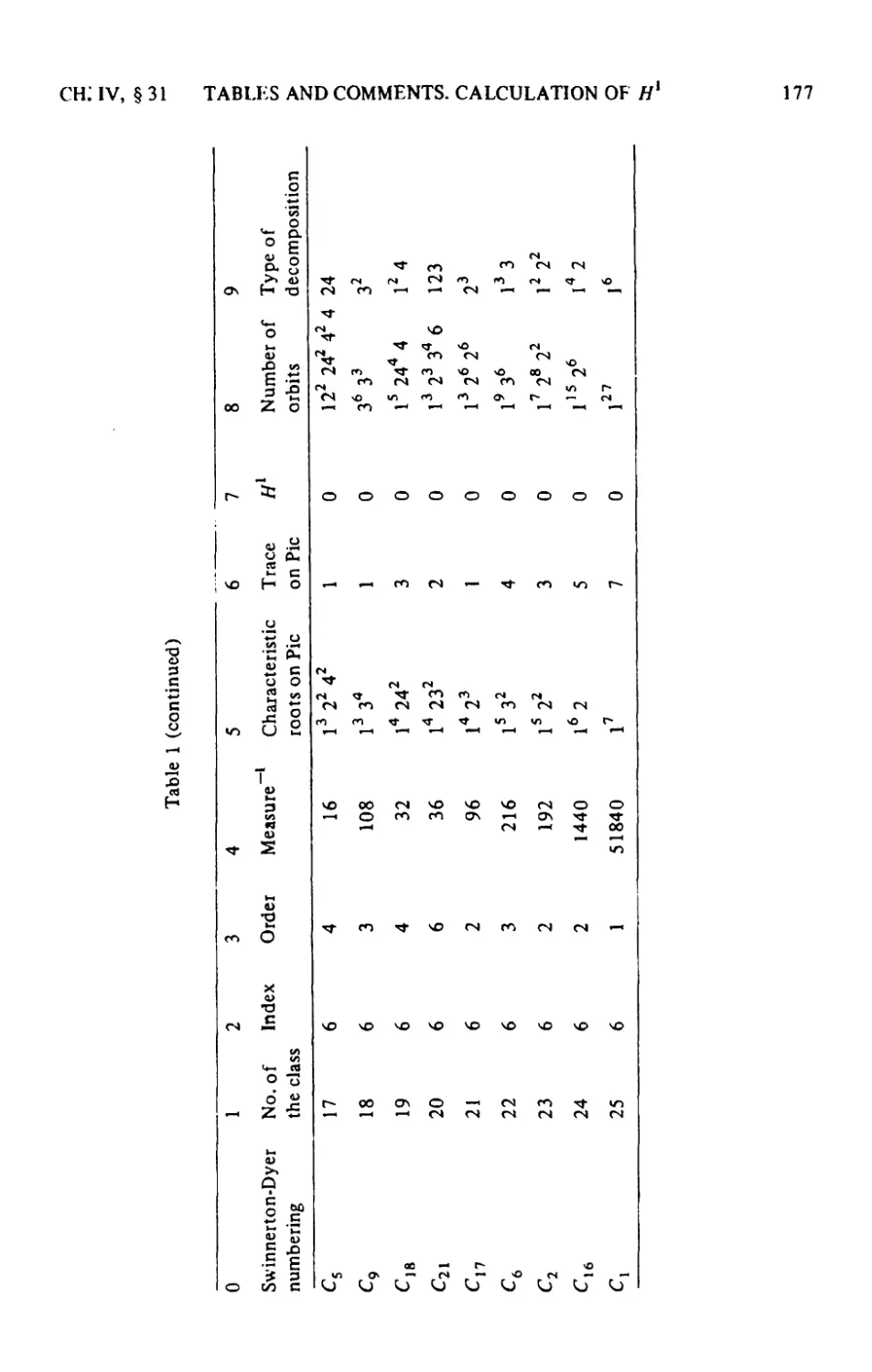
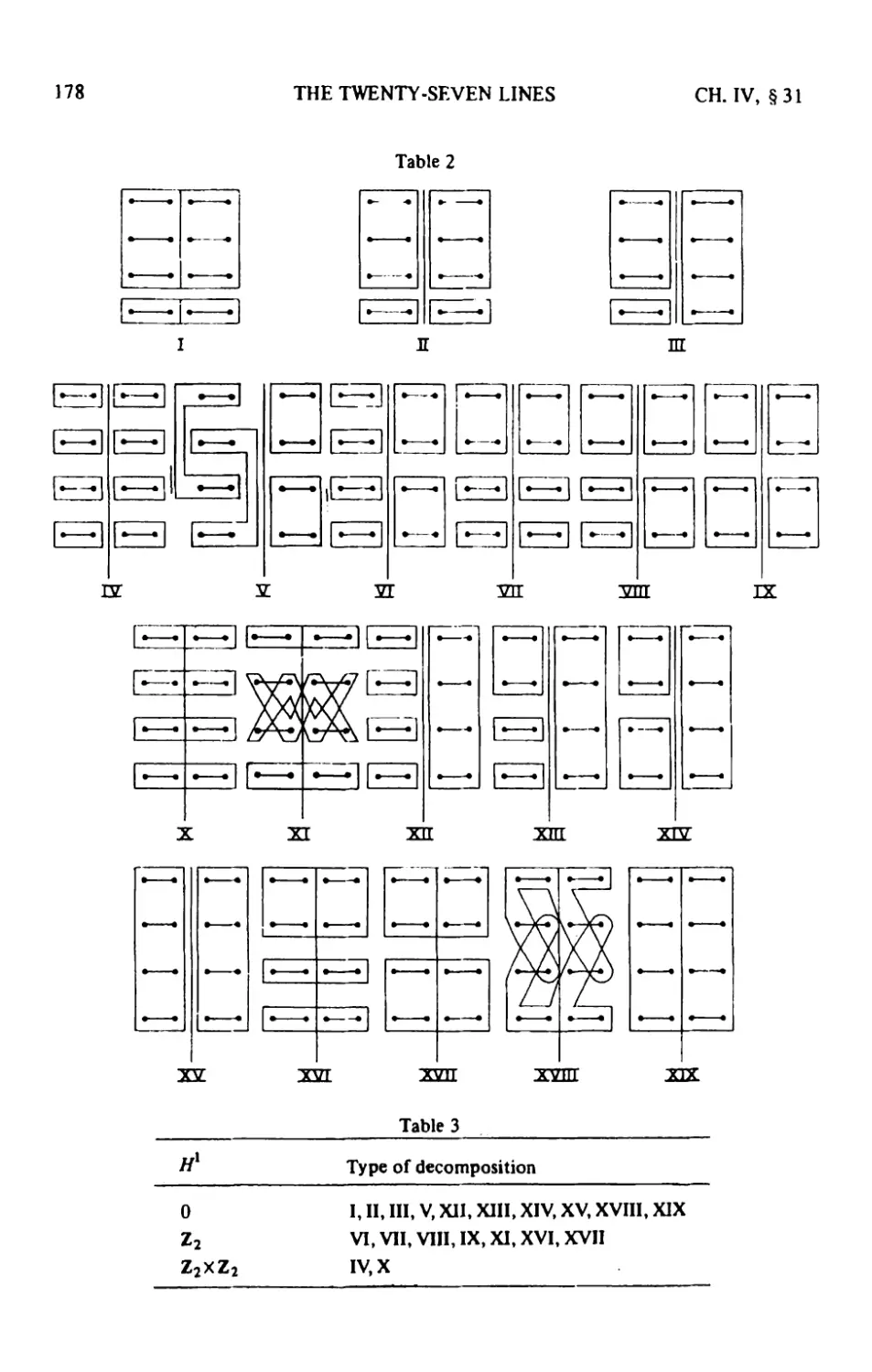
23. A survey of the results W2
24. Del Pez'zo surfaces 117
25. The Picard group and root systems 126
26. Exceptional curves and Weyl groups 134
27. The zeta function 143
28. Minimality and classes of conjugate elements in Weyl groups • • .151
29. A cohomological invariant and the degree of unirationality. . • .154
30. Rational points 162
31. Tables and comments. Calculation of//1. The theorem of Artin
and Tate 174
32. Bibliographical remarks 182
CHAPTER V. MINIMAL CUBIC SURFACES 184
33. A survey of the results 184
34. The fundamental birational invariant 189
35. A bubble space 195
36. Calculations on cubic surfaces 200
37. Birational non-triviality 202
38. Birational classification 204
39. Relations between the generators 206
40. Bibliographical remarks 219
CHAPTER VI. THE BRAUER-GROTHENDIECK GROUP 220
41. A survey of the results. Obstructions to the Hasse principle. . . . 220
42. The construction of Azumaya algebras 229
43. Brauer equivalence 234
44. The finiteness theorem 237
45. Calculations for Brauer equivalence. Examples 243
46. A negative result 264
47. Counter-examples to the Hasse principle 276
48. Bibliographical remarks 283
APPENDIX. ALGEBRAIC VARIETIES CLOSE TO THE RATIONAL ONES.
ALGEBRA, GEOMETRY, ARITHMETIC
Introduction 284
1. Galois cohomology, Picard groups and birational geometry .... 285
2. The Hasse principle and descent on rational varieties 288
3. Geometry of rational surfaces. Complements 294

CONTENTS ix
4. The Liiroth problem and the Zariski problem in dimension 5= 3 -302
5. Rational points and equivalence relations 306
6. Cubic surfaces and commutative Moufang loops (CML) 309
References (for the Appendix) 313
REFERENCES 318
AUTHOR INDEX 323
LIST OF SYMBOLS 324
SUBJECT INDEX 325

INSTRUCTIONS TO THE READER
1. The first sections of all chapters can be read consecutively,
independently of the remaining text. These sections contain a survey of the main concepts
and results of the book, as well as some motivation and examples.
2. Interdependence table of the chapters:
I
VI
(Dashed arrows indicate a weak dependence.)
3. Some standard notation:
Z - the integers,
Q - the rational numbers,
R - the real numbers,
С - the complex numbers,
Qp - the field of p-adic numbers,
Zn — the cyclic group of order n,
4. The list of references, the author index, a list of the most frequently
occurring symbols, and the subject index can be found at the end of the book.

INTRODUCTION
0.1. Every mathematician who is not indifferent to number theory has
felt the charm of Fermat's theorem on the sum of two squares of natural
numbers. A psychologist of the Jungian school would probably think that
such diophantine problems are archetypal to a high degree.
The basic idea for the book presented here arose from an attempt to find
out what happens in the case of sums of three rational cubes. Needless to say,
the result is not nearly so simple, fundamental and complete as the classical
pattern. The author has generalized the problem along all the lines which
occurred to him, and has used all technical resources known to him. He obtained
as a result the multitude of non-associative composition laws, monoidal
transformations and Galois cohomologies which make up this book.
0.2. The problem of the sum of three cubes has a respectable history. The
basic result by the classical mathematicians is the following (see Dickson [1]):
Theorem. Every rational number is a sum of three rational cubes.
First proof (Ryley (1825); Richmond (1930)):
/ *3-36 \3 /-Д3 + 35д+36\3 { I 3V + 3sfl \3
' 3V+34a+~36 / + W+~34<i+ 36 / + W + 34*+ 36/
This proof is simple, but not too illuminating. It would be nice to know what
lies behind this identity.
Second proof: After having added an extra coordinate Tq, we can write the
equation in homogeneous form:

2
INTRODUCTION
This is the equation of a smooth cubic sin face V in a three-dimensional
projective space. There are 'trivial'1 rational points on this surface, e.g. (0, 0, 1,-1).
Unfortunately these lie in the plane at infinity and do not give a solution to
our original problem. However, rational points on a cubic surface can be
multiplied, that is, we can construct new ones, starling from known points.
The first idea. Let x £ V be some rational point. Construct the tangent plane
to V at x and let us denote by C(x) its intersection with V.
'Generally speaking', C(x) is an irreducible cubic curve in this plane with x
as a double point. Through л* we draw all the lines in rational directions which
arc tangent to V. Each of these lines must intersect the cubic curve C(x) in three
points (counting multiplicities), but the intersection at x has multiplicity two,
which leaves only one point. The coordinates of this point are necessarily
rational. In fact, the coordinates of the intersection points in terms of the
parameters of the equations of the line are the roots of a cubic equation with
rational coefficients. This equation has a double rational root, corresponding
to x\ therefore the third root is also rational. After this one can apply the
same procedure to the rational points of the curve C(x) and so on.
Unfortunately, for x = (0, 0, 1, -T) the curve C(x) consists of three lines
which are conjugate over Q, and there are no rational points on it except for x.
The second idea. In this case we draw a line in an arbitrary rational direction.
We only take care that the two other points of intersection of this line with V,
say у and p, do not coincide and that the curves C(y) and C(y) are 'good' as
described above.
Then the previous argument on cubic polynomials shows that y9y are defined
and conjugate over some quadratic extension К of the field of rational
numbers Q. (It can happen'by accident thaty, у even have rational coordinates,
but then the problem is solved.)
As above, we construct lmany' points on C(y) with coordinates in A'. Take
one of those points, say z, construct its conjugate z, and draw the line through
z and z. Because z and z are conjugate, we can assume that the coefficients
of the parameter equation of this line are rational. The third (besides z and z )
of its intersection points with K, which we denote by z о z, then also has
rational coordinates (by the same argument on cubic polynomials).
Of course, if we start with z =>\ we simply return to>> о у = х, but it is not
difficult to show that other pointsz &C(y) give many new rational points
including points which do not lie in the plane at infinity.

INTRODUCTION
3
0.3. Although the second proof is considerably longer than the first, it
contains, in embryo form, interesting possibilities for establishing approaches
towards getting a review of all solutions of the equation, instead of giving only
an existence proof.
Multiplying points by means of C(x) gives an infinite family of solutions
of our diophantine equation. These solutions depend on as many independent
parameters as desired (the directions of the lines which occur in the construction).
Can all solutions be covered by a finite number of such families? How many
parameters are sufficient for this?
The composition law* и у is not defined everywhere (e.g., what is* <> x?);
all the same it permits us to obtain new solutions from old ones. Is it possible,
by combining this composition with the construction of points on C(x), to
obtain all solutions out of a finite number of them?
0.4. A positive answer to the latter question is known; not for cubic surfaces,
but only for cubic curves (without singular points), say aT^ + T\ + T\ = 0.
This is the famous Mordell-Weil theorem on elliptic curves. The algebra,
geometry and arithmetic of cubic curves (one could add analysis, e.g. theta functions)
constitute a vast and actively developing field; see the survey ot Cassels [3]
in the list of references.
The natural more-dimensional generalizations of elliptic curves, however,
arc the Abelian varieties (and homogeneous spaces over them) and in general
not the cubic (hyper)surfaces. Nevertheless, it turns out that over non-closed
fields (in particular over number fields), there is a whole series of results from
the theory of elliptic curves which admit non-trivial analogues in the theory of
cubic surfaces. (Sometimes the statement of the theorem carries over almost
verbatim, although the mechanics of the proofs in dimension 2 have nothing
in common with the one-dimensional case; see Section 33.)
Three fundamental parallels follow.
0.5. (a) The composition law xy = и о (х о у) (и fixed) on an elliptic curve
turns its set of points into an Abelian group. (As above, the point x *y is
defined by the property that л, у, х <^у are on one line.) On a cubic surface one
can divide the set of points into classes such that these classes can be composed
in a unique way by means of lines through representatives. After this the
composition law XY = U о (X о Y) turns the set of classes E into an 'almost' Abelian
group of exponent six. 'Almost' because this composition can apparently be

4
INTRODUCTION
non-associative. A slightly weaker associativity condition than the usual one,
which can be successfully proved, defines on E the structure of a 'commutative
Moufang loop'. This structure is studied in Chapter I of this book, and the
composition of classes of points in Chapter II.
(b)i The translations by means of a rational point generate almost all of
the group of birational maps of an elliptic curve into itself (more precisely,
they generate a subgroup of finite index). In the two-dimensional case, the
translation by x defines analogously a birational map tx: и »-► x о v of a surface
into itself. These maps (and similar ones connected with quadratic extensions
of the base field) also generate a subgroup of finite index in the group of all
birational maps of V into itself; in any case, if V is minimal. The proof (with
substantial specifications) is contained in Chapter V.
(c) An algorithm for settling the question of whether there are rational
points on a given plane elliptic curve has up till now not been found. The
first necessary condition is that there exist points 'everywhere locally'. This
being fulfilled, there is the second necessary condition that the so-called
Cassels -Tate form becomes zero. In Chapter VI it will be shown that the
second condition admits a quite general formulation, which is in particular
applicable to cubic surfaces. There we also obtain (rather restricted) results on
the quv ..tiv. is formulated in section 0.3. They give lower estimates for the
necessary number of parameters and for the number of generators of the set of
points.
These three subjects also represent, respectively, algebra, geometry and
arithmetic. Analysis and topology could essentially complete the picture.
For instance, starting with dimension 3, the 'intermediate Jacobians' of
A. Weil appear. In a less traditional direction we can expect that the group
generated by the maps tx has interesting ergodic properties. All this is not
touched upon in this book.
0.6. A part of the results expounded here has been taken from the journal
literature, old and new (including papers of the author). Another part is
published here for the first time, for example the discussion on universal
equivalence in Chapter II and almost all calculations of Chapter VI.
Mainly classical material is contained in Chapter IV, where the geometry
of the famous configuration uf the 27 lines and its generalisations and
applications are studied. Chapter III presents the necessary preparatory information
on birational maps.
The required algebraic—geometric background of the reader increases mono-

INTRODUCTION
5
tonically with the numbers of the chapters. In Chapter I, in general no algebraic
geometry is required. To understand Chapter 11, it suffices if the reader is
familiar with the lectures of SafareviC [2] (by no means to its fullest extent).
Chapters III-V require the mastery of approximately half of Mumford's book
[2], if the reader is willing to take a series of theorems on trust. Finally in
Chapter VI already the ghosts of Stale cohomology faintly stir. To understand
it, it is also necessary to have some acquaintance with class field theory
(structure of the Brauer group for local and global fields).
I.R. SafareviC taught me the algebraic—geometric approach to number
theory. Around ten years ago he drew my attention to cubic surfaces. He
conjectured, in particular, that some non-associative structure must play a
role in the description of the set of rational points. When these structures
started to appear, I was assisted in dealing with them by B.B. Venkov, A.I.
Kostrikin and V.A. Belousov. The talks with V.A. Iskovskih on the Brauer
group have been very useful to me. Some of the results of Chapter II are due
to A. Bel'skii; he has also been of considerable assistance in preparing the
manuscript for printing. The identification of the root systems Лг in
Chapter IV has been done by means of a method communicated to me by P. Deligne
in a private letter. To all these persons I am deeply indebted.
The papers of Grothendieck [2], Segre [3] and Chatelet [1] have most of
all influenced the formation of the new ideas of this treatise.
Moscow, 1969-1970
Yu. 1. Manin

CHAPTER 1
CH-QUASIGROUPS AND MOUFANG LOOPS
First Scene:
An open place. Thunder and lightning.
Enter three witches.
Shakespeare. Macbeth, Act I
1. A survey of definitions and results
In this chapter we introduce and study some algebraic structures which
emerge in the theory of cubic hypersurfaces. The first section contains a
survey of those results which have immediate applications in that theory. I
strongly recommend to restrict oneself at first to this survey and to go on
directly to the second chapter, returning to the first when necessary. Here
we give the exact definitions, state the theorems and give some motivation;
the proofs are contained in the next sections.
Definition 1.1. A set E with a binary composition law EX E^E: (x, y)
\->x у is called a symmetric quasigroup if it satisfies one of the following
equivalent conditions:
(i) The three-place relation L (x. y, z): .v о у = z is invariant under all
permutations ofx, y, z.
(ii) The following identities hold for all x, у t E:
x у = v * x . (1.1)
*•■(* >y)=y. 0-2)
The equivalence can be verified immediately.
The following geometric example may serve as background and motivation
6

СИ. 1. §1
DEFINITIONS AND RESULTS
7
for this definition: let E be the set of non-singular points of an irreducible
cubic curve V, embedded in a projective plane over a field k\ and let the
relation L(x,y, z) be 'the cycle x+y + z is the intersection of К with some line*
(counting multiplicities). Here condition (i) is geometrically obvious but
condition (ii) is easier to work with algebraically.
In this example the quasigroup E satisfies the following additional
property: let и 6 E be some fixed element; we introduce on E the new composition
law xy = и .* (x y). Then E becomes an Abelian group with и as unit element.
As the structure of Abelian groups is well known, one usually prefers to work
with this (new) composition law.
An axiomatization of this situation leads to the following:
Definition 1.2. A symmetric quasigroup E is called Abelian if it satisfies
one of the following equivalent conditions:
(i) There exists an Abelian group structure on E with composition law
(л\ y)*+xy,and there is an element с E£such that x о у =cx~ly [ for all
x,yE E.
(ii) For any element и 6= E the composition law xy = и о (х о у) turns E into
an Abelian group.
The equivalence of conditions (i) and (ii) will be verified in the next section.
Let us now consider an irreducible cubic hypersurface V of dimension > 2
embedded in some projective space; let E be the set of non-singular points. The
three-place relation L(x, y, z) on V is defined as before in the case of a cubic
curve. It is symmetric. However, in general, it does not come from a binary
composition law on V. This has to do with two geometric circumstances:
(a) When dim V = ], the point x ■ x is defined as 'the third intersection
point with V of the tangent line to V at x\ But, when dim V > 1, there are
many tangent lines at x: they fill up a whole tangent hyperplane.
(b) When dim V> 1, there can be lines completely lying in V. Vox two
points on such a line it is impossible to find a third such that the set of these
three forms the whole intersection cycle with some line.
In the next chapter we shall avoid these difficulties by considering instead
of E 2. quotient set of E such that the induced relation of'collinearity* comes
from a symmetric quasigroup composition law. We cannot guarantee that this
quasigroup will be Abelian, as in the one-dimensional case. However, any three
points of V are contained in the intersection of V with a plane. This intersec-

8 CH-QUAS1GR0UPS AND MOUFANG LOOPS CI I. I, 8 I
tion is a cubic curve. Hence, as the lines through these points and the points
derived from them all stay in this plane, we obtain the result that any set of
three elements of the quasigroup generates an Abelian quasigroup.
This justifies the following definition:
Definition 1.3. A CH-quasigroup (CH stands for Cubic Hypersurface) is
a symmetric quasigroup in which any three elements generate an Abelian sub-
quasigroup.
We shalJ now state the main known results on the structure of CH-quasi-
groups.
Let E be a CH-quasigroup. By analogy with the Abelian case we
introduce on E a new composition law xy =uo(x oy)y where и is some fixed
element. It is a remarkable fact that the structure thus obtained has been
introduced before in non-associative algebra theory, and has been thoroughly
studied by Bruck [2].
Definition 1.4. A set E with composition law (x,y)^xy is called a
commutative Moufang loop (henceforth abbreviated CML) if it satisfies the following
axioms:
(i) Commutativity: xy - yx for all x, у е Е.
(ii) Unit element: их = x for all x G E.
(iii) Inverses: there exists a map E ->E: x*-+x~l such that x~l(xy) =y
for all x, у Е E.
(iv) Weak associativity:
for three factors: x{xy) =x~y\
for four factors: (xy) (xz) = *2(yz),
x(y(xz)) =(x2y)z .
Theorem 1.5. If E is a CH-quasigroup, then the composition law
xy -u^ (x uy) turns E into a CML.
The axioms for a CML, as introduced in Definition 1.4, are not
independent. For example, it is possible to deduce (1.3), (1.4) and (1.5) from either
(1.4) or (1.5) alone. We have included these identities because they immedi-
(1.3)
(1.4)
(1.5)

CH. I, §1
DEFINITIONS AND RESULTS
9
ately show how close CML s are to Abelian groups; in particular, any Abelian
group is a CML. The structure theory for CML s, due to Bruck, specifies and
pinpoints this closeness. Before we formulate its basic results, we introduce
some auxiliary definitions concerning CMLs.
Morphisms of CML s are defined in the obvious way.
Let E f+ E} be a CML morphism. Its image f(E) is a Moufang subloop in
Zj'j. The kernel of/is defined as the inverse image of the unit element in h\.
A sequence of CML's and CML-rnorphisms,
/ К
1 -* E2 ~> E —> Ex -> 1 ,
where g is a surjective morphism, and/identifies ZT2 with the kernel of#, is
called an extension of E\ by E2\ frequently we shall denote this extension by
the CML E. The kernel of g defines completely the equivalence relation
induced by the map#, exactly as in the theory of groups. The equivalence
classes are the cosets of E with respect to f(E2). We write E^ = E/f(E2).
A subloop of the CMLE which is the kernel of some morphism is called
a normal subloop of E.
Definition 1.6. Let E be any CML. Then the set
Z(E) = {xEE\ x(yz) - (xy)z, Vv, :6£)
is called the associative centre of E.
Lemma 1.7. Eor any CML E, the associative centre Z(E) of E is an
associative subloop (and hence it is simply an Abelian group) in E; Z(E) is also a
normal subloop in E.
We can now state the main structure theorems.
Theorem 1.8. Let E be any CML. Then the quotient loop of E by its centre,
E/Z(E), is a CML of exponent 3; that is, in E/Z(E) the identity x3 = 1 is
satisfied.
Theorem 1.9. Let E be a finite CML of exponent 3. Then its centre is non-
trivial.

10 CH-OUASIGROUPS AND MOUFANG LOOPS CH. I, § 1
From this it follows in particular that any finite CML of exponent 3 is
obtained by successive extensions by Abelian groups of exponent 3; and its order
is hence of the form 3*.
Theorem 1.10. A ny CML of exponent 3 with a finite number of generators
is finite.
Thus any CML with a finite number of generators can be obtained by
successive extensions by an Abelian group and a chain of finite Abelian groups of
exponent 3: the non-associativity is caused by the non-triviality of these
extensions and V4s in' the 3-component. A non-associative CML has order at least
81 (Hall [2]; in that paper a different notation is used).
1.11. Theorems 1.9 and 1.10 are rather deep. There are two methods of
proving them that I know of.
The original method of Bruck [2] is based on a very complicated and in-
geneous inductive process and uses some hundreds of non-associative identities.
Here a different approach is offered, which is based on the fact that the
connection between CH-quasigroups and Moufang loops can be reversed. The results
on the classification of CML s of exponent 3 will then follow from the
classification of distributive symmetric quasigroups; that is, quasigroups which
satisfy
*, (y< z) = (xoy)o(x. z).
This was observed by Belousov [ 1 ].
Theorem 1.9 can then be obtained as a corollary of a purely group
theoretical theorem due to Fischer [1]. The proof of this theorem, although it uses
considerably less calculations than the proof of Bruck, is far from simple and
uses such deep results of the theory of finite groups as the Brauer-Suzuki and
Thompson-Feit theorems! Moreover, this proof neither yields Theorem 1.10,
which therefore is not proved here, nor does it give an explicit estimate of the
length of a composition series with Abelian quotients for a CML in terms of
the number of its generators. Bruck's method does furnish such an estimate,
though it is unknown how accurate it is.
I would like to bring this beautiful and subtle structure theory to the
attention of the algebraists. There is a scries of perplexing unsolved problems and
the proofs clearly can do with some improvements.

CH. I, § 2 SYMMETRIC ABELIAN QUASIGROUPS 11
Whether there are really non-associative CML's in the algebraic—geometric
theory of the next chapters I have been unable to clear up. This seems very
likely, but it is not impossible that only Abelian groups occur. In that case
the main algebraic constructions of this chapter of course turn out to be
superfluous for the sequel.
2. Symmetric Abelian qoasigroups
In this section we make use of Definitions 1.1 and 1.2 (i). Our main result
will consist of the statement and proof of some criteria for the commutativity
of a symmetric quasigroup E. First we introduce some notation which will be
constantly employed in the sequel.
Let E be a symmetric quasigroup. For an arbitrary element x E E, the
symbol tx : E -* E will denote the 'reflection7 tx(y) = x о у. It follows
from formulae (!.]) and (1.2) that t\ = 1 and that tx(y) = ry(x). We denote
by T{E) the group of permutations of the set E generated by all the tx, x GE,
and by T®(E) we denote its subgroup consisting of the products of an even
number of reflections tx.
Theorem 2.1. Let E be a symmetric quasigroup. The following properties
are equivalent:
(i) E is an Abelian symmetric quasigroup.
(ii) The group T°(E) is Abelian.
(iii) Vx, y.zSE, (txty tz)2 = 1.
(iv) For any element и E E, the composition law xy =uo (x о v) turns E
into an Abelian group.
(v) The same as (iv)for some fixed element и Е E.
Under these conditions E is a principal homogeneous space over T®(E).
Proof. We shall verify the following implications:
(i)«=(v)
/\ \

12
CH-QUAS1GR0UPS AND MOUFANG LOOPS CH. 1, $ 2
(i) =*(ii). Let x о у = cx~{y~x in terms of the composition law of an Abelhm
group structure on E. Then
txty(z) = cx~[(cy~lz-[yl = (x'ly)z .
Thus pairwise products of reflections are group translations and therefore they
commute. From this it follows that Г°(£) is commutative.
(ii) => (iii). Because the group Г°(/Г) is Abelian, pairwise products of
reflections commute, so that
(Hi) => (i).We first of all remark that for all x,y,z€- E we have
where w -у о (х о z). In fact, for an arbitrary и G E,
(the second equality follows from (iii): (/Y /yz/)2 = 1 =* txtytu = tutytx).
The commutativity of £ now results from the following lemma.
Lemma 2.1.1. Let и ЕЕ be a fixed element of the symmetric quasigroup
E with property (iii) of Theorem 2.1. Then the map E -► T®(E) :x>+x-tu tx
is a one-to-one correspondence, T®(E) is an Abelian group, and for all x,yEE,
x~c~y = TToU x _1 у ~l . (1.7)
Proof. It is clear that the map x *-* x is an embedding. By applying
formula (1.6) repeatedly to an arbitrary element of 7*°(2Г), it may be represented
as a product of just two reflections. Further, again by formula (1.6),
where v = x о (и о у). Therefore x ь* х is an epimorphism.

CM. I, § 2 SYMMETRIC ABELIAN QUASIGROUPS 13
The commutativity of T°(E) follows from Theorem 2.l(iii):
t t t -1 t t ** t t t t - t t t t ^ r v = v jc
'xluly LyluLx lulxlu'y lulyluLx ЛУ У*'
Finally, formula (1.7) is derived from formula (1.6) in the following way:
Here formula (1.6) is applied twice to the product of three reflections in
parentheses. This concludes the proof of the lemma.
(iii) =* (iv). We introduce in E the composition law xy = uo(xoy) and we
check the Abelian group axioms. The commutativity and the existence of an
inverse and of a unit element follow from the symmetry of the quasigroup E:
uy-uo(uoy)=y f
Xy = Uo(xoy) =Uo(y ox) -yX ,
X~{ =(llou)oX ,
XX~l = U о (х о (х о (и о и))) = U .
The associativity follows from the commutativity of T®(E):
(xy)z =uo(zo (xy)) = tu tz tu tx(y),
x(yz) = Uo (X o(yz)) = tu txtu tz{y) .
(iv) =>(v). Obvious.
(v) =>(i). We suppose that uo(x oy)= xy is the composition law of an
Abelian group. The commutativity of E will follow when we have proved
the formula
xoy = (u i> u)x~*y~]
And in fact this is equivalent to the identity
{xy)(xoy)-UoU ,
but
(xy) (X о v) = U о [(и о (х о у)) о(х<>у)] = U о U .

И CH-QUASIGROUPS AND MOUFANG LOOPS CH. I, § 2
Finally, the last statement of the theorem follows from the observation
made in the course of the proof of (i) =* (ii).
This proves the theorem.
As an application of the theorem, we give a simple geometric proof of
the commutativity of the quasigroup of points of a plane cubic curve. With
the usual definition, operating directly with the composition law и о (x oy)t
the associativity is extremely difficult to see.
Somewhat unexpectedly, it turns out that the equality (txtytz)2 = 1 has
a straightforward geometric interpretation.
Example 2.2. Let A: be a field, Kan absolutely irreducible cubic curve in
the projective plane over k. We denote by E the set of its non-singular k-
points. It is made into a symmetric quasigroup as described in Section 1. Take
three pointsx,y, г and an arbitrary point и on E (see Fig. I.l). The
equality (txt tz)2u = и means that by 'reflecting' и successively through x, y, z
and then again through x, y, z, we will arrive again at u. We shall show this.
We number the lines by means of which the successive reflections are
carried out starting with the line (uz). We denote by V\ the union of the odd
numbered lines (they are drawn boldly in Fig. I.l). This is a reducible cubic
curve. It intersects V in nine points, which are marked in the figure.
Fig. I.I.

CK. I, §3
CH-QUASIGROUPS
15
The curve K2 is the union of the three straight lines with even numbers;
obviously it passes through eight o( these points, but possibly not through u.
To prove that V2 also passes through u, we note that the projective space
of cubic forms of three variables is nine-dimensional. Consequently, the sub-
space ot those that become zeio in eight points of the plane is, 'generally
speaking', one-dimensional. Therefore the equation of the curve V-y is a linear
combination of the equations of the curves К and Г,, that is to say, V-,
passes through all the points of the intersection of V and Vx.
Ibis 'quasi-classical* argument has ьоте flaws. One of these is hidden
in the expression 'generally speaking'; this is partially dealt with by a theorem
in Walker's book 11 ]. The others are connected with the consideration of the
various cases of'not lying in general position' of л. у, z, и. Therefore it is
probably better, ultimately, to consider Fig. 1.1 as a geometiic illustration of the
theorem rather than to base the proof on it, although it shows the nature of
the relation (tx ty tz)2 - 1 very clearly.
We conclude this section with a corollary.
Corollary 2.3. Every subquasigroup and quotient quasigroup of an Abelian
quasigroup is again Abelian.
Proof. The symmetry is obvious and the commutativity follows from
properly (iii) of Theorem 2.1.
3. CH-quasigroups
We denote by CK the class of symmetric quasigroups in which any к
elements generate an Abelian subquasigroup. Evidently CK is contained in
CK + 1. For к > 4, CK coincides with the class of Abelian quasigroups. Indeed,
{txtytz )2u = u for all x, y, z, и £ t\ where E 6 CK. because for к > 4, x. y, zf и
belong to an Abelian subquasigroup of £". Therefore {txtyt:)2 - 1 within it
arid property 2.1 (iiij gives the desired result.
The class C3 is called the class of CH-quasigroups (ct\ Definition 1.3). The
remaining part of this chapter is dedicated to the structure theory of C3. It
certainly contains non-Abelian quasigroups: the smallest order of such a
quasigroup is 81 (see Example 3.4). Possibly the structure of 'he quasigroups
belonging to Cj and C2 also deserves a study.
Our first result on the structure of CH-quasigroups is analogous to part of
Theorem 2.1.

16 CH-QUASIGROUPS AND MOUFANG LOOPS CH. I, § 3
Theorem 3.1. Let E be a symmetric quasigroup. Then the following
properties are equivalent:
(i) E is a CH-quasigroup.
(\i)Vxfy£Et txtytxoy =ty(>y.
(hi) Let и G E be a fixed element. Then the map E -» T°(E): x*-»x=tutx
is an embedding and it has the following properties:
x~^y =й"ойхА y~x [xty] , (1.8)
where [x,y] = xуx _1 v ""]. Moreover,
vToV. belongs to the centre ofT(E) , (1.9)
[x,у ] commutes with x,у , (1.10)
1*.Л3 = 1 . (1.11)
Compare condition (iii) with Lemma 2.1.1. The group T°(E) can be non-
Abelian, but the properties (1.9), (1.10), (1.11) show that it is not too far from
being Abelian.
Proof, (i) => (ii). The equality txtvtXGy(z) = tyoy(z) can be checked within
the subquasigroup generated by x, v, z. But this one is Abelian because E is a
CH-quasigroup: formula (1.6) then gives the desired result.
(ii) => (iii). Here, and also further on, we shall use the notation /3(x) =дг .-> x.
We start by proving some identities.
Lemma 3.1.1. In any symmetric quasigroup E where the identity
*x ly rxoy ~ *в(у) holds* the following equalities are valid for all x, y, z G E:
(Xoy)oZ=Xo{yo(P(x)oz)), (1.13)
fxfy = lyop(x) Гх = Гу!хор(уу (,Л4^
Proof. Because of the symmetry of the composition law, we have
*хоУ*х{у = r0W Therefore ^ov = г&х)*у*х = *0(у)'х*у (the latter quality
holds because x о у = у ox). Formula (1.12) follows from this.

СИ. 1, §3
CH-OUASICROUPS
17
Furthermore,
> 'ж W2) = Vv)<2> =" 'xoy & = '* '> W)(Z) '
which is equivalent to formula (1.13).
Finally,
*x ^W=(.V^)ox^o(zo(«^) о x)) = />( Гл om>;)(z) .
The second equality of formula (1.14) is obtained by taking the inverses of
both parts of the first equality and interchanging x and y. This concludes the
proof of the lemma.
It is convenient for the statements of the following lemmas to call elements
a, b E T°(E) related if there exist elements jc, y, z € E such that a = tx ty and
b = txtz. Evidently this is a symmetric relation.
Lemma 3.1.2. IfE satisfies condition (ii) of Theorem 3.1 and if a, b £: T®(E)
are related, then я-1, b are also related.
Proof. Suppose a = txty, b = txtz; because of formula (1.14),
a =ty*x = txryop{x) '
which proves the lemma.
Formulae (1.10) and (1.11) now follow from the next lemma:
Lemma 3.1.3. Under the same conditions as before, let a, b £ T®(E) be
related elements. Then [a, Z?]3 = 1 and \a, b) commutes with a and b.
Proof. According to Lemma 3.1 2, a and b l are also related. Therefore we
can assume that a- txty, b = tztx. Using formula (1.12), we find
b4a4 = t 2 / 2 t 2 t 2 = (Paf .
02(z) p\x) 02(л') V\y)

18 CH-QUASIGROUPS AND MOUFANG LOOPS CH. I, § 3
After multiplying the first equality on the left by a and on the right by h, and
the second equality on the left by Z>~] and on the right by a _1, we obtain:
a3b3 =b3a3 =(ab)3 = (ba)3 .
From this it follows that
(ba)a3b3 ^ba(ba)3 = (ba)2(ba)2 = a2b2a2b2 = a2(ab)2b2 = a3bob2 ,
or, after multiplying this chain of equalities by b~3a~* on the right,
ba3 = д3/?; i.e., [b, a3] = 1. Because of symmetry, [a, b3] = 1.
Because the pair a~], b is also related, we have a~2b2 = ba~^ ba~[.
Multiplying this equality on the left by a3 and on the right by a, and using [tf3,£]= 1,
we obtain ab2a - ba2b, that is, [ab, ba] = 1.
Set c- [a,b] -aba' *b~[. Then [c,ab] = [c,ba] = 1; moreover, c3 = I,
because (ab)3 = (cba)3 = c3(ba)3 = (ba)3.
Finally, we show that [c, b\ = [c, a] = 1. Indeed, a2b2 = (ba)2 = (c~*ab)2 =
= c(ab)2 -abcab. Multiply this equality by а~л on the left and by Ъ~] on the
right to obtain ab = bca\ but ab = cba\ therefore [c, b] = \y and by symmetry
[ct a] = 1. This proves the lemma.
Corollary 3.1.4. The map (t\ d) *-> [c, d] on the subgroup of T®{E)
generated by a pair of related elements is a skewsymmetric bilinear form, that is,
[c,d\ - \d,c]"[ and [cxc2td] = [clfd] [c2,d].
This is a general group theoretic fact which follows from the centrality of
the commutator subgroup.
3.1.5. To prove formula (1.9), it suffices to check that tu t^ commutes
with all elements of the form txtin because these generate the group T\E).
We set a = tu tp(u)t b = tx tu. Then b2 = tpM tpM, from which ab2 = tu tp(x)
and further,
a(ab2)~l = tu tmt0{x)tu = tu(tx tu)2 tu = (tu tx)2
Consequently, [a, b2 ] = I, and as the commutator is bilinear and [a, b3] = 1,
it follows from this that [a, b] = 1.

СИ. I § 3
СИ-QUASIGROUPS
19
3.1.6. Finally, we derive the identity (1.8). Combining everything which has
been proved, we have:
= ,mW)/(3(m)W)/>'/",m^
= Т(й)х ~2y "] x l =j3(w) x~] yr l [x, y].
(in) => (i). Let E be a symmetric quasigroup which satisfies condition (hi)
of the theorem. Let и, х, у ЕЕ be any three elements. We denote by £0 the
subquasigroup generated by x, у, и, and we shall show that it is Abelian. The
image of £'n under the map z^+z = tutz clearly is contained in the subgroup
G С T°(E) generated by the elements /J(w), x, у ; this follows from the fact
that according to formula (1.8) the composition law о can be expressed in
terms of groups.
The commutator subgroup of the group G is in its centre and has exponent 3
We introduce on G the new composition law
а т b = ab [a, b\ .
We show that G with this composition law is an Abelian group G+. Indeed
a + b = ab [a, b] = ba [bta] = b + a .
Further,
(a + b)+c =ab[a,b] c[ab[a,h],c] =abc[a,b] [a,c] [btc] ,
a + (b + c) = abc[b,c\\aM'\b,c]\ =abc[a,b][a,c][b,c] .
(We constantly use Corollary 3.1.4.) The unit element and inverses in G
and G+ coincide.
From formula (1.8) it now follows that for all x]t x2 &Eq,
Ху~ох0 = ййм! - x. ~x2 .
Thus Eq can be embedded in an Abelian quasigroup constructed from the
group G+ and that means that Eq is Abelian. This concludes the proof of the
theorem.
Using this result we shall now describe one method of constructing CH-
quasigroups from groups which are given by generators and relations of a

20 CH-QUASIGROUPS AND MOUFANG LOOPS CH. I, § 3
special form. The structure of these groups has been studied by Fischer [1];
his results will be set forth in detail in Section 9. Here we only show that one
can construct non-Abelian CH-quasigroups by means of the Fischer groups.
Definition 3.2. A Fischer group is a pair (G, E) consisting of a group G and
a system of generators E С G satisfying the following conditions:
(i) VxEE, jc2 = 1.
(ii) Vx,у ЕЕ, (ху)3 = 1 andxyx EE.
From this definition one easily obtains some ele.nentary properties of
Fischer groups:
3.2.1. The set E constitutes a full class of conjugate elements ofG.
In fact, let jc, у EE\ the relation (xy)3 = 1 implies thatj> = (xy)x(xy)1.
We set F = x U xE\ this is clearly a system of generators in G, and for all
g E F we havegxg-1 ЕЕ. Therefore all conjugates of x are contained in E.
3.2.2. The commutator subgroup G' of the group G is generated by
products of pairs of elements of if; moreover G/G' = Z>> or {I}.
In fact, Vx,у ЕЕ, ху EG' becausex and>> are conjugate. On the other
hand,.* together with the products of pairs of elements of E generates G, and
*2 = i.
3.2.3. The pair (G//V, EN/N) is a Fischer group for every normal subgroup
/VCG.
Theorem 3.3. Let (G, E) be any Fischer group. We introduce a composition
law on E by setting
X о у =XVX .
Then E becomes a CH-quasigroupt and the map E -+ T(E): x •-> tx can be
extended to an epimorphism of groups with as kernel the centre of the group G.
Proof. The symmetry of E follows from the fact that
x cy = xyx = уху = у >x ,
x о (х ■? у) = л: (хух)х = у .

CH. I, §4
COMMUTATIVE MOUFANG LOOPS
21
The CH property is verified by means of property (iii) of Theorem 3.1:
lx ly lxoy (z) = x(y(yxy(z)yxy)y)x = yzy .
The last assertion of the theorem follows from the fact that tx acts on E as
conjugation by means of x
Tliis proves the theorem.
Remark. The identity relation |3(x) = x holds in E under the conditions of
Theorem 3.3.
3.4. Examples of non-Abelian CH-quasigroups. We fix an integer r > 4, and
construct a finite non-Abelian CH-quasigroup withr generators. Let B(3,r-\)
denote the Burnside group of exponent 3, generated by ax,..., аг_л with the
identity relation x3 = 1. Take the semi-direct product G of the groups Z2 = {1,jcq }
and В = B(3,r-1) with В as normal subgroup on which x0 acts according to
xoaixo=airl-
We set Eq = (xq, x^a^ . . ., x§ar _j). The product of a pair of elements of
Eq belongs to В and its third power is therefore equal to 1. Consequently Zf0
belongs to one class of conjugate involutions E\ one easily convinces oneself that
(G, E) is a Fischer group and that G' = B. It follows from Theorem 3.3 that Е
with the composition law x о у = xyx is a CH-quasigroup, while T®(E)= B/Z(G),
where Z(G) is the centre of G. But В is nilpotent of class 3 for r > 4 (a
theorem of Levi and Van der Waerden, cf. Hall [ 1 ]). The group T®(E) is therefore
non-Abelian, and consequently the CH-quasigroup £ is non-Abelian (Theorem
2.1).
4. Commutative Мои fang loops
We use the definition of a CML as stated in Definition 1.4. Before we start
with the proof of the main result of this section, Moufang's theorem, we state
some elementary properties of a CML E.
The unit element и G E and the map x ►-* jc"1 are uniquely defined: if
uxx = x = u2x, then because of property (iii) of Definition 1.4,
иj =(и1х)хл =(и2х)х~] -u2 ;

22 CH-QUASIGROUPS AND MOUFANG LOOPS CH. I, § 4
if x_,.v =м = yxy then х-1 -у. From this it follows immediately that
(.v-1)"-1 =x and (xy)~[ =х~лу~]. In fact,*""1 Осу) =у ^jc-1 = (xy)~{y ->
=>x~ly~l = (xy)t.
Finally, we deduce the identities (1.3) and (1.5) from (1.4). Substituting
z = и in eq. (1.4), we obtain eq. (1.3). Replacing^ by^"1 in eq. (1.4), we obtain
x2(y~ xz) = (y~ {x) (xz). Multiplying both parts by y2 and bringing a factory
in each of the four factors on the left and on the right according to formula
(1.4), we find (x2y)z = x{y(xz))y which is eq. (1.5).
Theorem 4.1 (Moufang's theorem). Let x, y, z be three elements in a CML
E for which the relation (xy)z = x(yz) holds. Then the subloop generated by
them is associative and hence is an Abelian group.
Corollary 4.1.1. Every two elements in a CML Egenerate an Abelian
subgroup; in particular, words in which only two variables occur may be handled
as if they belonged to an Abelian group, and one may disregard the distribution
of the parentheses.
In fact,(xy)u =x(yu)9 where и is the unit element, and x,y are arbitrary
elements.
The proof of Theorem 4.1 rests on two lemmas:
Lemma 4.1.2. Let E be a CML, x,y ^E two elements. Then the map
axy : E-*E defined by the formula
\y(z) = (xy)-Hx(yz))
is an automorphism of E.
Proof. It is clear that ax y is 1-1 and onto and that it takes the unit element
into itself. We must only verify that for all v, wGE,
It follows from formulae (1.4) and (1.3) that y(y(vw)) = (yv) ( уw).
Multiplying both parts by x2 and bringing a factor x in each of the factors on the left

CH. I, §4
COMMUTATIVE MOUFANG LOOPS
23
and on the right according to formula (1.4), we find
(xy)(x(y(uw))) = (x(yv))(x(yw)) ,
from which
x(y(vw)) = (xy)-*([x(yv)][x(yw)}).
Multiplying both parts by (xy)~l and on the right bringing a factor (xy)"* in
each of the factors in square brackets according to formula (1.4), we find,
finally,
\yipw)-axy(v)axy(w).
This proves the lemma.
We define the associator of three elements in E by
(x,y,z)=[{xy)z\[x{yz)\-x .
Lemma 4.1.3. Let the elements x, y, z €E satisfy the relation (x, y, z) = 1.
Then this relations remains valid
(i) under replacing any of the elements x, y, z by its inverse;
(ii) under all permutations ofx, y, z.
We say that elements x,y, z with this property behave associatively. Let
xt y> zf и be elements such that every three of them behave associatively. Then:
(hi) (x, y, zv) = 1.
Proof, (i). By definition,
(x,y,z)=\ о (xy)z=x(yz) <>aXpy(z) = z.
Because a is an automorphism, we have aY v(z~l) = z_1, and that means
(x,y, z-l) = 1. By symmetry, x can be replaced by x~l. The middle term needs
a bit more work,
(x,y, z) = 1 о у = z"1 (x~l (z(xy))) = z"1 {x-2 [x(z(xy))]}
= 2-1{х~г[(хгг)у\}*а .t(y) = y.

24 CI I-QUASIGROUPS AND MOUFANG LOOPS CH. I, § 4
Therefore the same argument as before shows that (x, y~x ,z) = 1. This proves
the first part of the lemma.
(ii). We note that x and z obviously can be permuted; the invariance with
respect to a cyclic permutation is verified as follows:
x-{(yz) = x-2[x(yz)] =х~2[(ху)г\ = y(xAz)=>(y,z,x~x) = 1
=*b\z,x)= 1 .
Finally,
ax y(z) = z and ax v(v) = v => ax y(zu) = zv^ (x, >\ zu) = I .
This proves the lemma.
4.1.4. Proof of Theorem 4.1. Consider a maximal subset F С E, containing
x, y, z, such that every three elements of F behave associatively. Such a subset
exists by Zorn's lemma. According to Lemma 4.1.3, F is closed under
multiplication and taking inverses and it is therefore an Abelian group. The
elements x, y, z generate a subgroup of it. This proves the theorem.
4.2. From Lemma 4.1.3 and Moufang's Theorem 4.1, the first part of
Lemma 1.7 follows: the associative centre of a CML is an Abelian subgroup.
The second part results from the following characterization of normal subloops.
Definition 4.2.1. A normal subloop H С E in the CML category is a subloop
which satisfies one of the following equivalent conditions:
(\) Я is the kernel of some morphism/: E -+ F oi CMLs.
(u)x(yH) = (xy)H for all jc, у ЕЕ.
Proof of the equivalence (outline), (i) => (ii). Let H be the kernel of/; then
f(y-\x-\(xy)H)))=f{y)-\f(x)-\f(x)f{y)))= \ ,
from which j>-1(.x~l((.xv)//))) С Я. The opposite inclusion is proved similarly;
one can also use the fact that ax y is an automorphism of E.
(ii) => (i). A subset <,(E of the form xH, where x € E, is called a coset with

CH. I, § 5 CONNECTION BETWEEN CH-QUASIGROUPS AND CMLs 25
respect to H. It is easy to sec that the cosets form a partition of £ into disjoint
subsets. On the set of cosets E/H one can define a CML composition law which is
induced by the multiplication in E, so that the canonical map E -> E/H is a
morphism with kernel H. The details are standard and are left to the reader as
an exercise.
4.2.2. It is clear from Lemma 4.2.1 that the normal subloops of a CML E
can be characterized as those subloops which are invariant with respect to the
automorphisms ax y for all x,yC E. By analogy with group theory, these
automorphisms are called interior automorphisms. They generate a group of
automorphisms of E; the elements of this group are also called interior
automorphisms.
5. The connection between CH-quasigroups and Moufang loops
In this section we shall prove the following two theorems:
Theorem 5.1. Let E be a CH-quasigroup and и G E an arbitrary element.
Then the composition law xy = и о (x^y) turns E into a CML with unit
element w. One obtains isomorphic CMLs for different choices ofu.
Theorem 5.2. Let E be a CML and с G Z(E)an arbitrary element of its
centre. Then the composition law x о у = ex ~^y _1 turns E into a
CH-quasigroup.
We note that here, in contrast with 5.1, one can obtain non-isomorphic
CH-quasigroups for different choices of с The precise description of those с
for which they turn out to be isomorphic will be given in Section 6.
5.1.1. Proof of Theorem 5.1. The formulae xy = yx and их = х are obvious.
The inverse element is found from the equationхх"-1 = и:
uc(xox'l) = u=>x"] =P(u)ox.
The identity x~*(xy) = у is verified as follows:

26 CH-QUASIGROUPS AND MOUFANG LOOPS CH. I, § 5
x~l (xy) = ио ((/3(w) ox) о (и о (x о у)))
= Хи hiu)oX (" ° (* °У)) = *х lu (" ° (* °У»=У >
in virtue of formula (1.14) .
Finally, we shall check formula (1.4). We note that in any CH-quasigroup
the identity t^)tzoxtz{y) ~ tx{y) holds, which can be rewritten as
(zox)o(zoy) = $(z)o(xoy). (1.15)
Taking into account formula (1.12) we find
(xy)(xz) = Wo((Mo(jC oy))o(U о (XOZ))) = /„^^^oz)
^Uo(p{u)o(P(x)o(yoz))) = Uo((uo^x))o(uo(yoz)))^X2(yz).
It remains to be shown that one obtains isomorphic CML s for different
choices of и G E. We set
xy =uo (x oy), x*y = vo(xoy)i
and we define a map/: E -+E by f(x) = w o(v ox). It is clear that/is bijective
and that/(w) = u. It is therefore sufficient to verify that/(xy) = /(x) * f(y).
In fact,
f(xy)-tutvtu(xoy)i
/М*/(^)=^(/(дг)о/Ы) = у/,(1/)^)(хо^)
This proves the theorem.
We shall now list three useful supplements to it.
5.1.2. Under the conditions of Theorem 5A,the operation xoy can be
represented in terms ofxy and the element ${u)asxoy = $(u)x~xy~x.
In fact,
P(u)(xy)-1 =Uo(p(u)o(P(u)o(Xy))) = Uo(xy)=Xoy.

CH. I, § 5 CONNECTION BETWEEN CH-QU/\SIGROUPS AND CMLs 27
5Л .3. The element P(u)is in the centre of the CML with composition law
и о (x о у).
In fact,
0(и) (ху) = и о (0(м) о (w о (х о у))) = tu /э(||) ги ty (х),
(М«)х)^ = 11о((ио(|»(||)оДг))о^) = Ги^ГиГЛм)(х).
It now remains to apply the result 3.1.5, according to which tut^u^ is in the
centre of the group T°(E).
(These observations show that the constructions of Theorems 5.1 and 5.2
are inverse to one another.)
5.1.4. The identity relation ($(x) = x in a quasigroup E is equivalent to the
relations jc3 = и and |3(u) = и in the corresponding CML.
Indeed, for all*,
0(x)=x ^fi(u)x~2 = x =*x3 =0(ы)=>*3 = /3(w) = u3 =i/.
Conversely, if x3 - и for all x and p(u) = и we have, in virtue of 5.1.2,
p(x) = 0(u)x-2=x-2=x.
5.2.1. Proof of Theorem 5.2. It is clear that x^y-y о х. Further,
хо(хо);) = а"1(а"У1)"1 -у,
as in an Abelian group, because ст х, у behave associatively.
It remains to check that the identity of Theorem 3.1 (ii) holds. We have
tyoy{z) = c((cy-2ylz-l)=y2z~l ,
again as in an Abelian group. But with the left part one must be a little careful
because it depends on four elements:
Xoy- CX~ly~* ,

28 CH-QUASIGROUPS AND MOUFANG LOOPS CH. I, § 6
txoy{z) = c((c-lxy)2-1) = (xy)2-1,
according to eq. (1.5). Finally,
txtytxoy(z) = cx-](c~{x(y2z-l))=y2z-1 .
This proves the theorem.
6. Morphisms of CH-quasigroups and Moufang loops
We describe the functorial properties of the constructions if the preceding
section. First of all it is clear that any morphism/: E -> F of CH-quasigroups
induces a morphism of the corresponding CMLs with unit elements u£.E,
v G F if and only if f(u) = f{v).
The inverse question is more difficult and more interesting. Let E, F be two
CMLs, and let cGZ(E), d € Z(F). Construct the two CH-quasigroups Ec and
Fd with the composition laws cx~^y~^ and du~*v~l, respectively. We shaJl
designate the unit elements of E and F by the symbol 1.
Theorem 6.1. Let f: E'c -* Fd be a morphism of CH-quasigroups. Then
d=f(c)f(\)2,andthemapg=f(\)Af:E~>FisaCML morphism. Here
g(c) = df(l)~\
Conversely, let there be given a CML morphism g : E -> F and an element
b E.F such that g(c) = db*. Then the map f- b~] g : Ec -* Ed is a morphism
of CH-quasigroups.
Before proving Theorem 6.1, we state two important corollaries:
Corollary 6.1.1. Let E be some CML, and let c, d E Z(E). The quasigroups
Ec, Ed are isomorphic if and only if there exist an automorphism g : E -+ E
and an element bEE such that g(c) = db*.
Example 6.1.2. Let E be an Abelian group of exponent 3. Its automorphism
group is transitive on the set of non-zero elements. Therefore from E one can

СИ. 1, § 6 MORPHISMS OF CH-QUA£lGROU?S A.ND CMU 29
obtain exactly two non-isomorphic CH-quasigroupsEc: one fore = 1 and the
other for с Ф \.
Corollary 6.1.3. The category of CH-quasigroups with the identity relation
&(x)=x and a distinguished element is equivalent to the category of CML s
of exponent 3.
The functor which establishes this equivalence transforms a quasigroup£*
with distinguished element и into the CML with the same underlying set E
and the composition law xy = и о (х о у). This CML has exponent 3 according
to 5.1.2 and 5.1.4, and the composition law x о у can be reconstructed asx"^y~K
Theorem 6.1 then shows that the morphisms of quasigroups which preserve
the distinguished elements are exactly the morphisms of the corresponding
CMLs.
6.1.4. Proof of Theorem 6.1. Let/: Ec -+Ed be a quasigroup morphism.
Then
f(cx-ly~l) = df(xr*f(yr* , (1.16)
from which we obtain/(c) = df(\)~2 by taking* =y = 1. Substitutingx = 1
and x = c, respectively, in eq. (1.16), we find
f(cx-l) = df(\)-lf(xrxt
f(y'1) =df(c)-lf(yr{=f(\)2f(y)~l ,
from which
Дх)-1 =d~*f(\)f{cx-x), (1.17)
/ОО-1-/OrVCr'). 0-18)
Substituting eqs. (1.17) and (1.18) in the right-hand side of eq. (1.16), we find
ficx-ly-1) = (ДОЛ0Г1)) (/(I)"2 Д^"1))).

30 CH-QUASIGROUPS AND MOUFANG LOOPS CH. I, § 6
Replacing cx~[ by* and j>-1 Ъуу, we obtain
/(^) = (/(0/W)(/(ir2/W).
Using the associativity formula (1.5) in which Jcl-*/(l)-*, у y+f(y) and
z^/O )/(*)> we obtain finally
from which, using eq. (1.4),
gipcy) =/(i)-1 /toy) =/(i)~2 (Л*)/О0)=*(*) *O0 -
This proves the first part of the theorem.
Conversely, let a CML morphism g : E -> F be given and let g(c) = dZ?3.
We set /= b~lg, it is clear that/(I) = b_1. We must verify the identity
f(cx-ly-l) = df(xrlf(y)-1 .
We have
/(cx-V1) = ft-!*(«-V_1) = 4_1(№3)(*(*)_I гЫ-1)) •
Since d is in the centre of F, we obtain from this
f{cx-xy-x) = d{b\g{x)-xg(yyx)).
On the other hand,
df{x)-lf{yTl =d{bg(x)-l)(bg(y)-l)=d(b4g(xrlg(yTl)>
again because of formula (1.4). This concludes the proof.
7. The first structure theorem
Definition 7.1. Let E be a symmetric quasigroup. Then E is called a
distributive quasigroup if it satisfies one of the following equivalent conditions:

CH. I, §7
THE FIRST STRUCTURE THEOREM
31
(i) T(E) is a group of automorphisms of E.
(ii) x о (у о z) = (x о у) о (х о z) for all х, у, z ЕЕ (distributivity).
(iii) if is a CH-quasigroup with the identity relation j3(x) =x.
Proof of the equivalence, (i) о (ii). Conditions (i) and (ii) are equivalent
because the group T(E) is generated by the reflections tx.
(ii) =* (iii). Substituting z =x in relation (ii) and multiplying both parts by
x oyy we obtain /3(x) = jc. Consequently,
0(*)o (yoz) = (Xo^)o(xoz) = ^)^(2) = txoytx{2)*txoytxty = ГЛх) .
Theorem 3.1 (ii) then shows that E is a CH-quasigroup.
(iii) -* (ii). This follows from formula (1.15).
7.2. Now let E be any CH-quasigroup, и ЕЕ a fixed element. As in Section
3, we consider the embedding E -> Г°(£): x^>jc =tutx. In addition, let
g : Г°(£) -> G be some group homomorphism. We denote by E' the image of
£ in G under the composed map x*-+g(x).
There is a unique quasigroup structure on E' such that E -*£' is a morphism
(of quasigroups). In fact, the composition law on £' С G can be expressed in
group theoretical terms by Theorem 3.1 (iii), and all relations then transform
into group theoretical relations. The homomorphism g obviously preserves
these relations.
We apply these considerations to the natural homomorphism
g : T°(E) -+ T0(E)/Zy where Z is the centre of the group Т°(Ю-
Theorem 7.3. As in 7.2, let us denote by E' the image of the composed map
E-+T°(E)S> T°(E)/Z. Then the following assertions hold:
(i) The equivalence relation on E induced by this map and the quotient
quasigroup E', the image ofE, do not depend on the choice ofu.
(ii) The quasigroup E' is distributive.
(iii) All fibres of the morphism E ~+E' are Abelian quasigroups.
Proof, (i).
Situtx)-g{tuty)otutx^tuty{mouZ)otxtyEZ,
and this condition clearly does not depend on the choice of w.

32 CH-QUASIGROUPS AND MOUFANG LOOPS С11. I. \ /
(ii). It is clear that E' is a CH-quasigroup; in virtue of Definition 7.1, il now
suffices to verify that £(0(*)) = g(x) for all л* <EE. And in fact, according lо
Theorem 3.1 (iii),
jffx) = /Г{м) х~2=Х~2 (mod Z)=x (mod Z) ,
because |3(w) EZ according to formula (1.9); and by formula (1.11) and
Corollary 3.1.4,x3 GZ.
(iii). lfg(x)=g(y), then
g(^) = Mg(x))=g(J(x)) = g(x).
Therefore the fibres of the map *->£(*) are closed with respect to composition.
They are Abelian because if x, у belong to one and the same fibre F С E,
then txtv belongs to the centre of the group T®(E), so that the group T®(F)
is Abelian.
This proves the theorem.
We shall now show that the interpretation of Theorem 7.3 in terms of
CMLs leads immediately to a proof of Theorem 1.8.
Theorem 7.4. Let E be a СИ-quasigroup, uGE a fixed element, and let
f:E-*E'bethe quasigroup morphism constructed in Theorem 7.3. We
introduce on Ea CML structure with multiplication xy =uo (x oy) and on E'
a CML structure with multiplication x'y' =/(w) о (x' oy'). Then f is a CML
morphism with identifies E' with the quotient loop of E by its centre.
Moreover, E* has exponent 3.
Proof. It is clear from the definition that for allx, у EE,vtehavex(y)=xy.
Therefore the group T°(E) coincides with the permutation group of Я which
is generated by the multiplication by all possible elements of /Tin the sense
of the CML composition law. In particular, the image of x coincides with the
image of и in£' if and only if x belongs to the centre of T®{E), that is,
for all;', zGE,
ЧУ (z)) =У(х (z))<*x(yz) = (xz)y.
By definition, this means that the kernel of/coincides with the associative
centre of E.

CH. I, § 8 THE SECOND STRUCTURE THEOREM 33
The last assertion of the theorem follows from the distributivity and
Remark 5.1.4.
8. The second structure theorem
In this section we shall show that the study of distributive quasigroups,
and therefore of CML s of exponent 3, to a large extent results in a purely
group theoretical problem. More precisely, the construction of CH-quasigroups
by means of Fischer groups (Definition 3.2) permits us to obtain all possible
distributive quasigroups.
Theorem 8.1. Let E be a distributive quasigroup. We embed E in T(E) by
identifying the element x e E with tx e T(E). Then the pair (T(E), E) is a
Fischer group, and the composition law onEis given, as in Theorem 3.3, by
the formula
x о у ~ x у х ~ уху'
Proof. Formula (1.14) gives (taking into account the identity /3(jc) =jc):
This proves what we wanted.
Remark 8.2.1. Using 3.2.2, we obtain from this that for a distributive
quasigroup E the group T°(E) is the commutative subgroup of T(E). The centre of
T(E) is trivial because of Theorem 3.3.
Remark 8.2.2. Let / be some set. We construct the free distributive
quasigroup generated by /. To this end we set G(I) = F(I)/N, where F(I) is the
free group generated by /, and N is the normal subgroup generated by the
words*2 and (sjxsjf1 ^.У^1)3 for allx,y 6/ and s^ s2 ^F{/). Let
E(I) С G(I) be the full class of conjugate elements which contains the image of
/. It is clear that (G(/), £(/)) is a Fischer group, so that there is a natural
distributive quasigroup structure on E{I). E(I) is free in the following sense: for

34 CH-QUASIGROUPS AND MOUFANG LOOPS CH. I, § 9
every distributive quasigroup£ and set of elements {*,}, / E/, there exists a
morphism E(I) -► £ which sends the image of / E / into xz- E £ The proof is
left to the reader as an easy exercise.
I do not know whether a free Fischer group G{I) with a finite number of
generators is finite. From Theorem 3.3, Bruck's Theorem 1.10 and Remark
5.1.4, it follows that in any case the quotient group of G(J) by its centre is
finite. A direct proof of this fact would in turn subsume Theorem 1.10. This
is an interesting group theoretical problem of the Burnside type.
9. Finite Fischer groups
The basic aims of this section are the proofs of Theorems 9.1 and 9.2,
which are due to Fischer. By combining them with earlier established results
we immediately obtain Theorem 1.9 on the structure of CML s of exponent 3.
Theorem 9.1. Let (G, E) be a finite Fischer group. Then the following three
assertions are equivalent:
(i) The commutator subgroup G' is nilpotent.
(ii) G' is a 3-group, and G/G' = Z2.
(iii) E consists of 3* elements.
9.1.1. Proof. (ii)=>(i). Obvious.
(ii) =* (iii). The group G acts transitively on E by conjugation; the centralizer
ZG(x)={y£G\xy=yx}
is the isotropy subgroup of an arbitrary element jc E E and it contains the
element x of order two. The order of G is equal to 2 ■ 3m; consequently the order
of ZG(x) is equal to 2 • 3', from which IEI = (G : ZG(x)) = 3m~l. (From now
on we shall denote by \M\ the order of the set M.)
(i) => (ii). Because the group G' is nilpotent, its only Sylow 3-group G3
is a direct summand. Because (G : G') = 2 or 1, G3 is the only Sylow 3-group
in G and is therefore a normal subgroup. But for all x, у Е Е we have
(xyj* = 1 =>xy EG3. Therefore the group G/G3 is generated by one involution,
which is obviously non-trivial because 2 divides IGI and 2 does not divide IG3 I.

CH. I, § 9 FINITE FISHER GROUPS 35
(iii) => (ii). This part of the proof lies deeper. We need two lemmas:
Lemma 9.1.2. Let N CG be a subgroup, N ПЕФфу and let NC\E be the
subgroup generated by NC\E. Then we have for every element xENnE,
N = {NnE}ZN(x).
Proof. N acts on E by conjugation. The orbit of jc EjVn£under this is equal
to jV ПЕ. Indeed, it is contained in N П E\ on the other hand,
yGNHE=>y = (xoy)ox = (xoy)x(xoy) ,
and x о у Е N П E together with x, y. Therefore (N : ZN(x)) = \N П E I. Since
the pair ({NC\E},NC\E)\% also a Fischer group, applying the same
considerations to it, we obtain
({NnE}:Z{mE](x))=\{NnE}nE\=\NnE\.
On the other hand, by an elementary theorem.(Hall [1], 1.5.5) we find that
the indices of the pairs of groups marked by (1) and (2) in the diagram
N
{NnE}ZN(x)
/ \j>
NHE ZN(x)
(2)| /
are related by the inequality (1) > (2). It follows immediately from this that
(N :{NП E}ZN(x)) = \y which proves the lemma.
Lemma 9.13,Let x € E and IE I > 1. There exists a Sylow 3-subgroup
HCG such that xHx = Я
Proof. Let у Е Е, у Фх, and let [x,y] С G be the subgroup generated by
л: and >>. Obviously {x,y}' = Z3. We denote by H the maximal 3-subgroup in
G with the properties
{x,y}'cH, xHx = H.

36 CH-QUASIGROUPS AND MOUFANG LOOPS CH. I, § 9
We show that Я is a Sylow subgroup in G. Otherwise it is contained in a larger
3-group, where its normalizer will be larger than itself. It therefore suffices to
check that a Sylow 3-subgroup F containing Я of the normalizer
N = {nEG\nHn = H) coincides withЯ. For this in turn it suffices to check
that F = HZp{x). In fact, xHZF(x)x = HZF{x)\ therefore ii follows from the
maximality of Я that HZF(x) = Я
The inclusion HZF(x) С F is obvious.
To prove the opposite inclusion, we first calculate {£ HN}'. We have
yeEnNoyeE.xyeH. (1.19)
Indeed,
ySEHN =>yHy = Я =>хуНух = H=>H {ху\ is a 3-grcup;
moreover, xH{xy}x =Н{ху}. From the maximality of Я i' then follows
that xy EH. Conversely, if xy EH and у ЕЕ, xhen yxHxy = H=>y EN.
The group {E CiN}' is generated by pairwise products of elements of
E П N\ it then follows from (1.19) that it is generated by some pairwise
products of elements of Я. In particular, {E П TV}' С Я, so that {E П /V}'
is a Sylow 3-group in {E П N}. But \E C\N] is a normal subgroup in ;V and
according to Lemma 9.1.2, TV = {ECiN}ZN(x). Therefore there exists in TV a
Sylow 3-subgroup F generated by{E CiN}' and the centralizer ZF(x). For this
we have F ={E ON}' ZF{x) CHZF(x). This concludes the proof of the lemma.
9.1.4. Proof of the implication (iii) => (ii). We return to Theorem 9.1.
Let x ЕЕ, and let Я С G be the Sylow 3-subgroup whose existence was proved
in Lemma 9.1.3. Considering the action by conjugation of G on Ц we find as usual
\E\ = (G : ZG(x)). Since l£*l = 3* by hypothesis, we have
(G : ZG(x))= (H : Z„(x)) = (//{*}: ZH {x} (x)).
On the other hand,
lEl = (H{x):Zff{x]{x))=\EnH{x}\.
Therefore E С H{x] =>G = И{х], which proves what we want.

CH. I, §9
FINITE FISHER GROUPS
37
Theorem 9.2. Let (G, E) be a finite Fischer group. Then the equivalent
assertions (i)-(iii) of Theorem 9.1 hold.
9.2.1. Proof. We proceed by induction on the order of G. We shall suppose
that the theorem is proved for Fischer groups of order < | G\. We distinguish two
cases, depending on whether there exists in G a minimal normal subgroup N
different from G'.
Case 1. There exists a minimal normal subgroup N С G different from G'.
Step 1. The group G is solvable. Indeed, choose x E E. Then N{x}^ G.
Otherwise,G = NUNx=>ECNx (because E П N = 0)=* G' С N. Therefore
{N{x]OE} is a proper subgroup in G, so that {N{x} Г)Е}' is nilpotent by the
induction hypothesis, and so {Лфс}П£} is solvable. It is clear that {N{x}CiE}nN
is a normal subgroup in N..
If there exists anxGf for which the intersection {N{x} nE}DN is non-
trivial, then TV has a non-trivial radical (that is a maximal solvable normal
subgroup). Because the radical of TV is a characteristic subgroup, it is a normal
subgroup in G. From the minimality of TV it follows that the radical coincides
with TV, that is, that N is solvable. By the induction hypothesis, G/N is solvable,
and hence G is solvable.
If Wx ЕЕ, {N{x}C\E}ПN ={1}, then V* ЕЕ, NxHE = (x). (In fact,
if у ENxDE, then j>jc E{N{x) П E] ON.) This means that there is a natural
isomorphism E ^NE/N, from which N С Z(G), because the action by
conjugation of N on E is then trivial. It follows from this that G is solvable because
G/N is solvable by the induction hypothesis.
Step 2. The group G' is nilpotent. Since G is solvable, there exists a normal
subgroup N CG such that N^Z where q is a power of some prime number
p. We note that if p Ф 3, then N С Z(G). In fact, if N <f Z(C), then there
are*, j> ЕЕ such that* Фу andxEyv>;but thenxv EN, so that I7VI = 0
(mod 3). We distinguish three possibilities.
(a)p Ф 2 or 3. Then N С Z(G) and N С G', because (\N 1,1 G/G' I) = 1. The
group (G/N)I(G'/N) s G/G' is Abelian, so that G'/N D {G/N)'. The group
(G/N)' is nilpotent by induction hypothesis. If G = G', then G/N= (G/N)' =
= G'/N so that G' is nilpotent. If G Ф G\ then (G/N)/(G'/N) ss Z2 and again
(G/N)' = G'/N. so that G' is nilpotent.
(b) p = 2. We have again jV С Z(G). If N С G', the same argument as in (a)
gives what we want. The case N £G' is impossible since then G = N X G' =>
=> G' = G" and (G/N)' = G' is a 3-group by induction hypothesis; but then
£ = (/v)MO-

38 CH-QUASIGROUPS AND MOUFANG LOOPS CH. 1, § 9
(c)p = 3. (G/N)' is a 3-group by induction hypothesis, so that G' is a 3-
group.
Case 2.G' is a minimal normal subgroup ofG. Following Fischer, we
deduce from this a contradiction, provided that G' ф Z3.
Lemma 9.2.2. Let E be a distributive quasigroup, and let x ^ xz be an
automorphism of order two (an involution) ofE. We set Ez = [x E E\x2 = x) and
for an arbitrary element x E E2 we set Ez x = [ у E EI у о у2 - x). The
following assertions hold'.
(i) Ev EZXCE are non-empty subquasigroups.
(u)EZXinE2X2 =<t)forxx ^x2,andE={Jxe£2Ezx.
(iii) The Ez x are isomorphic for different x. In particular, \ EI = \EZ I IE2 x I.
Proof. (\).y oyz E Ez for ally ЕЕ; х EEZX because of the distributivity.
Ez and Ez x are therefore non-empty. If x, у EEzt then x oy EEZ because z is
an automorphism. LeXy^, y2 EEZ x;then^j = xoyz[ andj>2 =x°Уг> ^rom
which y] oy2 =xo (y2^ о ^|)and (,Vj ^2)° (-^1 °У2У ~ x> so tnat
yloy2eEZtX.
(ii). Obvious.
(iii). Let jcj, x2 EEZ andjc3 =x^ ox2 EEZ. Then the тйру^+х^оу^х^ухз
establishes an isomorphism between Ez x and Ezx .In fact,
У\°У\ = x\ **хз°(У] °у])=х2 ^(^з0^)0^0^)2 =xi'
*3 ° (Ух сУ2) = (*3 °^!) ° (*3 °У2^ •
9.2.3. Conclusion of the proof of Theorem 9.2. Let (G, E) be a finite Fischer
group in which G' is a minimal normal subgroup and let z E G be any element
of order 2. It acts on E by conjugation.
We first show that there exists az with \EZ I > 1. In fact, suppose that this
is not the case. If \EZ I = 1, E2 = (y), then x о xz = j>, that is, x1 = уху for
all* ЕЕ, so that zy EZ(G) because G ={£}. This does not contradict the
minimality of G' only \iz~y ЕЕ. ThusE is the only class of conjugates
under the involution. For G Ф G', we have E П G' = 0, so that G' has odd

СИ. I, § 10 UNSOLVED PROBLEMS AND BIBLIOGRAPHICAL REMARKS 39
order and thus is solvable by the Feit- Thomson theorem. This is a
contradiction provided that G' ф. Zy For G = G', the group G must be simple. But any
two different elements x, у Е.Е belong to different Sylow 2-subgroups of 6'
because (xy)^ = 1. Therefore a Sylow 2-subgroup contains a unique element
of order two and that means that it is either cyclic or it is the generalized
quaternion group (Hall [1]). This contradicts the fact that the group is simple
(theorem of Burnside, Hall [1], and the theorem of Brauer and Suzuki [)]).
Thus, let z G G be an involution with \EZ I > 1. Then also Ez Ф E} because
otherwise z €Z(G), and the only possible case Z{G) = G' cannot occur in a
Fischer group. Thus E2X*E for all x 6 E2 (Lemma 9.2.2 (ii)). The groups
{Ez} and {Ez д} are Fischer groups of order < | G |; moreover, it is clear that
{Ez} П £ = Ez and {Ez x) П £ = Ez x. From the induction hypothesis, Lemma
9.2.2 and Theorem 9.i, it then follows that l£2l=3*, l£ I = 3b, so that
l£ I = 3a+b in virtue of Lemma 9.2.2 (iii). Theorem 9.1 then shows that G'
is a 3-group, which again is only possible for G' = Zy
This concludes the proof of Theorem 9.2.
9.3. Proof of Theorem 1.9. Let £ be a finite CML of exponent 3. The
composition law* о у = x~^y-l defines a distributive quasigroup structure on it,
for which the group Г°(£) coincides with the 'group of multiplications'
(translations) of the CML £. According to Fischer's theorem, T°(£) = T(E)'
is a 3-group and so it has a non-trivial centre. Theorem 7.4 then shows that
the centre of the CML £ is non-trivial.
10. Unsolved problems and bibliographical remarks
Symmetric quasigroups were introduced by Bruck [1] and CH-quasi-
groups were introduced by the author (Manin [6]); the investigation of their
structure theory was started in the same papers. Later, Venkov and Belousov
(see his paper [1]) indicated to the author the connection between CH-quasi-
groups and CMLs. The general case was analyzed in Manin [9]. Hall [2] has
obtained results similar to those expounded in Section 8; however, he used a
different notation. The proofs in Section 9 are taken from Fischer [1]. In the
latter paper, a more general case is dealt with; namely, the case where the
relation between the involutions has the form (xy)P = 1, with p prime.

40 CH-QUASIGROUPS AND MOUFANG LOOPS CH. I, § 10
An essentially different method (and the first) to study the structure of
CML s can be found in Chapter VII of Bruck [2]. In that book, the following
interesting unsolved problem is raised:
Let £ be a CML.
Definition 10.1. (i) Let EQ=E\ £/41 is generated by associators of the
form (xit y, z), where xt 6 Eh y,zEE. The series E0 D Ex D E2 Э . .. is
called the lower central series of the CML£.
(ii) E has nilpotency class ^ / if Et = (1).
Problem 10.2. What is the nilpotency class k(n) of the free CML with n
generators. What is its 3-order /(/?)?
Obviously, /(1) = 3, /(2) = 9, and Hall [2] proved that /(3) = 81.
Theorem 10.2.1 (Bruck [2], Chapter VII). 1 + [\n\ <k(n)<n-\ for all
n>3.
Obviously, k(\) = fc(2) = 1 (Moufang's Theorem 4.1). The first unknown
case is: k(5) = 3 or 4? This is a very curious question in itself, but also in view
of the following theorem of Bruck [3]:
ffk(5) = 3, then k(n) = 1 + [\n] for alln>3.
The upper estimate for k(n) is obtained by Bruck by a complicated induction
on л, and the lower one by means of the following interesting example of a
CML.
Example 10.3. Let L be a linear space over the field of three elements,
and let A*L= Ф^=о Л* ^ (its exterior algebra). Further we set E = L X A*L
and define on E the composition law
(a,x) (b,y) = (a+b,x + y + (x-y)ab) .
This turns E into a CML. (Why? Does there exist a more transparent
explanation than a formal verification of the axioms?)
The lower central series looks like E{ = (0,®^=7l-AxZ,), i>\. The proof
is by induction on i, making use of the identity
((j, jc), №, v), (c,z)) = (0,xbc +yca + zab).
In particular, if dim L = n> 3, and (jr.) is a basis of L, then the subloop£
generated by the generators (*,-, 1), / = 1, ... ,n> has nilpotency class \\n\ +1

СИ. I, §!0 UNSOLVED PROBLEMS AND BIBLIOGRAPHICAL REMARKS 41
10.4. Let 7'u(£)be the group.of multiplications of a free CML£"with n
generators (T°(E) is generated by the maps/T --> E: у *+ху). Then its nilpo-
tency class is equal to
t(n) = 2k{n)- 1 .
Using this» one can translate Problem 10.2 into the language of Fischer groups.
This problem for n = 5 should lend itself to analysis on an electronic
computer.

CHAPTER II
CLASSES OF POINTS ON CUBIC HYPERSURFACES
11. Admissible equivalence relations: a survey
Throughout this chapter, we fix some infinite field k. Unless it is stated
otherwise, ail algebraic varieties and schemes will be understood to be defined
over k\ and points will be geometric points with values in a subfield of some
fixed algebraic closure of A:.
The main objects of study in this chapter are cubic hypersurfaces defined
over k. By definition, such a hypersurface Fis given by a form of the third
degree: F(T0,..., Tn) = 0, where (T0,..., Tn) is a homogeneous coordinate
system in some projective space over k. Unless it is stated otherwise, the form
F will be assumed to be irreducible over the algebraic closure of/c; that is
to say, the scheme V is geometrically irreducible and reduced. (It is obvious,
however, that we shall also have to consider reducible hypersurfaces, e.g.,
intersections of К with a tangent plane.)
Let Vr(k) be the set of non-singular /c-points of the cubic hypersurface
V С P,;. (We recall that a point x = (f0,..., tn) is non-singular on V if in the
affine coordinate system with origin at* the equation of Fhas a non-vanishing
linear part; by putting this linear part equal to zero, one obtains the equation of
the tangent hyperplane to V at the point x.)
Definition 11.1. Three pointsx, y, z E V:(k), not necessarily different, are
said to be collinear if one of the following conditions is fulfilled:
(i) x +>• +z is the intersection cycle of V with some line in P", defined
over к (that is, each of the points x, y, z turns up equally often as the
intersection multiplicity of that line at this point).
(ii) x, y, z lie on some line defined over к which is completely contained in
V.
It is clear that the three-place relation L(x, y, z): \x, y, z are collinear' on
VT(k) possesses the following two properties:
42

СИ. И, § 11 ADMISSIBLE EQUIVALENCE RELATIONS: A SURVEY 43
11.1.1. The relation is symmetric, that is, invariant under all permutations
oix, y, z.
11.1.2. For any two pointsx, у € VT(k) there exists a point z £ VT(k) such
that x, y, z are collinear.
If, as in the one-dimensional case, the point z of Property 11.1.2 were
uniquely defined, then the three-place relation L(x, y, z) would give rise to a
symmetric quasigroup structure on V{(k) (see Definition 1.1). For the reasons
given in Section 1, this is in general not true. This circumstance suggests the
following definition.
Let, quite generally, P be some $eiyL CPX PX P a three-place relation
which satisfies Properties 11.1.1 and 11.1.2 (with P instead of VT (k)). Any
equivalence relation R CPX P defines a quotient three-place relation L/R on
the quotient set P/R. This quotient relation also satisfies Properties 11.1.2
and 11.1.2.
Definition 11.2. An equivalence relation R is admissible (with respect toL)
if L/R induces a symmetric quasigroup composition law on P/R (in the sense
of Definition 1.1).
It is clear that the set of admissible equivalence relations is non-empty (e.g.,
R = P X P is admissible).
The following simple result is independent of any additional assumptions
onPorZ..
Proposition 11.3. Under the conditions given above on P (and L) there
exists a unique finest admissible (with respect to L) equivalence relation. We
shall call this the universal equivalence relation.
Proof. Let {/?/}ze/ be some set of equivalence relations on P. We then define
a new equivalence relation R by
x ~ у (mod R)e*ViEI, x ~~y (mod R.).
We shall show that R is admissible if all /?,- are. This will prove the proposition
because we can take for/ the non-empty set of all admissible equivalence
relations. In fact, let X, Y, Z be equivalence classes mod R such that for some

44 CLASSES OF POINTS ON CUBIC HYPERSURFACES CH. II, § 11
x GXy у G Y, z EZ we have (x, y,z)ELAl is clear that X = nyY/f Y = П y/f
Z = flZy, where Xit Yh Z{ are the respective equivalence classes mod R{ of
xy y, z. Now letx'EAT, У G Y and (У, y',z')EL. We then have
(х',У, z')ez,=»v/, z'ezz.,
since all Д,- are admissible. Consequently, z ECljZ; = Z. The classes X, Y
therefore uniquely define the class Z in the three-place relation L/R, which is
what we wanted to prove.
Remark 11.4. Let R{f R2be admissible equivalence relations, and let
Ej ~P/Rj (i = 1, 2). If fij is finer than /?2> then the natural map E\ -» E2 is
obviously a morphism of symmetric quasigroups (with composition laws
induced by L/Rit i = 1, 2). The result of Proposition 11.3 therefore admits a
dual: there exists a 'largest' quotient quasigroup of P\ all others are quotients
of this one.
11.5. The main aim of this chapter is to introduce and study various
admissible (with respect to collinearity) equivalence relations on the set VT(k). We
shall systematically consider the following admissible relations:
(i) The universal relation (see Sections 13 and 16).
(ii) R-equivalence. Roughly speaking, two points x, у 6 Vz(k) are R-equiv-
alent if they can be connected by a chain of rational curves which lie
completely in F(see Sections 14 and 15).
In Chapter VI we shall introduce and study in detail:
(iii) Brauer equivalence. To define this, one considers 'Azumaya-Grothen-
dieck' algebras over V. Informally speaking, these are sheaves of simple algebras
over V. Each point x E VT(k) then defines a simple algebra A (x), the stalk of
A at x. Two points*, у G VT(k) are called Brauer equivalent if for all A the
elements of the Brauer group of к defined by A(x) and A (y) are equal. Brauer
equivalence is coarser than R-equivalence; its advantage is that by definition
it can be effectively calculated.
Given some mild restrictions on V, which we do not formulate here, one
gets the following facts:
Let S С VT(k) X VT(k) be some admissible equivalence relation, E- VT(k)/S
the corresponding symmetric quasigroup.

СН. II, § 11 ADMISSIBLE EQUIVALENCE RELATIONS: A SURVEY
45
Theorem W.6. E isa QW-quasigroup (cf Definition 1.3).
Now choose some class U G E and construct on E the commutative Moufang
loop with unit element U (see Definition 1.4). Let the dimension of Fbe
greater than one.
Theorem 11.7. The CML E = Vr(k)/S with composition law XY = U о (X о Y)
satisfies the identity X^ = \.In particular, the CML has a finite number of
generators if and only if it is finite, and then the number of elements is of the
form 2*3*.
In the case that the base field к is local or global one has some finiteness
theorems. Here is the local result:
Theorem 11.8. Let [k : Qp ] < «>. Then the points of V( (k) = V(k) are
partitioned into a finite number of classes under universal equivalence.
The global theorem will be proved in Chapter VI, but only for the coarsest
equivalence (i.e., Brauer equivalence).
We give some examples which show that admissible equivalence relations
can quite well be non-trivial.
Example 11.9. Let к = R and V a cubic surface over R such that V(R)
consists of two connected components Xq, Xy and such that Xq is convex. Then
this partitioning into components is admissible and the CML (Xq, X^) with
zero element Xq is isomorphic to Z2.
Using this, one can for any n ^ 1 construct an algebraic number field ky a
surface V over k, and an admissible equivalence relation S on Vx(k), such that
Zj С VT(K)/S. In particular we see that the set E can be arbitrarily large over
number fields. For more details see Example 16.2.
Example 11.10. Let к = Q2(0), #3= 1 (this is a non-ramified quadratic
extension of the 2-adic numbers). Let the surface УЫ given by the equation
Г0 + T\ + T2 + в Tl = ° •
Two points x, у G V(k) will be called equivalent if they coincide after
reduction mod 2. In Example 16.3 it is proved that this is an admissible equivalence
relation and that the corresponding CML is isomorphic lo Z3 X Z3.

46 CLASSES OF POINTS ON CUBIC HYPERSURFACES CH. II, § 12
Further examples are contained in Chapter VI.
We now list the main unsolved questions.
Problem 11.11. Can the CMLs E - VT(k)/S be non-associative (for some
k, V, 5)?
Problem 11.12. Is there a global finiteness theorem for universal equivalence
and R-equivalence?
Problem 11.13. Is it possible to parametrize an R-equivalence class by a
finite number of parameters; let us say over a field k, [k : Q] < °°?
These and related problems will also be discussed in Chapter VI, in
particular after we have studied the Chatelet example in which all main ideas can
be checked in detail.
Amongst the algebraic-geometric circumstances which influence the struc*
ture of VT(k) and its quotients £, the most important is, no doubt, the unira-
tionality of a cubic variety V. The next section is devoted to an elementary
study of this property.
12. Unira tionality
We recall the general definitions as regards rational maps of algebraic
varieties over a field k.
Let V, W be two varieties. We consider the set of pairs (U, <Д where L/C V
is a dense open subset of V, and <p\ V -* W is some morphism. Two such pairs
(Ux,\px) and (L/2, ^2) are equivalent if ^ \ихпи2 = "Pi ^U]nu2 • (Tne
symmetry of this relation is obvious, and the transitivity follows from the fact
that W is separable.)
Definition 12.1. An equivalence class/of pairs (Ut ip) is called a rational
map of the variety V into the variety W.
Among all morphisms \p : U -> W belonging to a given class there clearly
exists one with a largest domain of definition, the union of all U of the given
class. This open subset of V is called the domain of definition of/

СН. II, §12
UNIRATIONALITY
47
Let/: V^-W be a rational map, represented by the morphism \p : U-* W.
This map is called dominating if the image y(U) is dense in W. It is clear that
this property does not depend on the choice of the representing morphism.
Lemma 12.2. There exists a natural one-one correspondence between
dominating rational maps f:V->W and field inclusions f* : к (W) -+ к ( V) of
the rational functions on V, W (these are the local rings in the general points).
Proof. If/is dominating, then there exist open affine sets V{ С V, JVj С W
and a morphism у : V\-*VJ\ representing/such that y(Vy)CW\. The
general points of V and W lie in Vx and JVj, respectively, and as \p(V{) is dense
in IVj, the general point of JVj must belong to if(V^). Consequently, \p induces
an inclusion k(W) -*• k(V)\ it is obvious that this inclusion is independent of
the choice of \p.
Conversely, let there be given an inclusion k(W) -» k(V). We choose rings
of finite type А С k(W), В С k(V) such that ACB, and such that the quotient
field of A (resp.i?) coincides with k(W) (resp. k(V)). Each element of a fixed
finite system of generators of A is, as a function on W, defined on some dense
open subset of W. Therefore W and Spec (A) have a dense open affine subset
in common. By localizing A if necessary, we can assume that W^ = Spec (A)C W-,
analogously we can arrange things such that F, = Spec (В) С V. Then the
inclusion ACB defines a morphism V± -* W±. It is not difficult to check that
different choices of A and В yield equivalent morphisms.
The constructions of rational maps and field inclusions that we have just
described are inverse to one another; this proves the lemma.
Let/: V-* Wbe a dominating rational map. The number [k(V):f*(k(W))]
is called the degree of/
Suppose we have two rational maps V 4 W Д. Z. Then the composition of
/ and g can be defined in the obvious way if/is represented by a morphism
<p : U-*W such that y(U) has a non-empty intersection with the domain of
definition of g. In particular, the composition is defined if/is dominating.
Definition 12.3. The rational map/: V•+ W is called birational if the
following equivalent conditions are fulfilled:
(i)/is dominating, and there exists a representing morphism y?: U-+W
such that v? induces an isomorphism of schemes U^<p(U) С W.

48 CLASSES OF POINTS ON CUBIC HYPERSURFACES CH. II, § 12
(ii)/is dominating, and the field inclusion/*: k(W) -* k(V) is an
isomorphism.
We leave it to the reader to verify that conditions (i) and (ii) are equivalent,
using the proof of Lemma 12.2 as a model.
We note that the birational maps/: V -* V form a group which is canoni-
cally isomorphic to the group of isomorphisms of the field k(V) over к. А
birational morphism is any morphism which is birational as a (rational) map.
Definition 12.4. An «-dimensional variety V over the Field к is birationally
trivial if one of the following two equivalent conditions is satisfied:
(i) There exists a birational map ?n -* V defined over k.
(ii) The field of rational functions on V is a purely transcendental
extension of the field k.
From the diophantine point of view, this property says that 'almost all'
points of V which are rational over к are described in a one-one way by n
independent parameters with values in k. Two examples follow:
Example 12.5. Let К be a cubic hypersurface in P1 given by an absolutely
irreducible cubic form. Let * E V be a singular point which is rational over k.
We call it conical if any line in ?n which passes through* is either completely
contained in V or intersects V only at *. A two-dimensional cone with its
vertex at x and as a base a non-singular cubic curve is, of course, birationally
non-trivial, and the point x on it is conical.
We show that V is birationally trivial if the point x is not conical. Let Pw~l
be any hyperplane which does not pass through* (see Fig. 11.1). The function
/: ?n~] -> Vwhich maps a sufficiently general pointy 6P"-1 onto the point
(different from x) of intersection of the line through *, у with V is birational.
Indeed, let us write the equation of V in some affine coordinate system in
?n with* as the origin and P^_1 as the hyperplane at infinity:
q(Tv...,Tn) + c(Tr...,Tn) = 0.
Here (jTj, . . . , Tn) is at the same time a homogeneous coordinate system on
P""1; q is a quadratic form and с a cubic form. We have that q Ф 0 because jc
is non-conical; the linear part vanishes because* is a singular point.

СН. И, §12
UNIRATIONALITY
49
i
рЛ-1
Fig. II. 1.
We denote by UC Рл_1 the complement in the hyperplane of q = 0, c = 0;
and we find that for a point v = (t],..., tn) E U the line through x, v
intersects Fat the point
ДУ) = (Х/р...Д/„)*х = (0,0,...,0),
g(fp ■■■,*„>
cCp..-л)'
Therefore/induces an isomorphism/: £/~ K\ ({c = 0}U (^ = 0}).The
latter complement is open and dense in V, because V is irreducible.
Example 12.6. Let V С P3 be a cubic surface on which there are two non-
intersecting lines defined over k. Let </?, \p : P1 -* F be the embeddings of
these two lines in V. Construct the map </к ф : Р1 X P1 -+ K, which maps a
point (.x, v) E P1 X P1 onto the third point of the intersection of V with the
line passing througli v?(.y) and \p(y). This map is defined on a non-empty open
subset ofP1 X Pl; otherwise V would contain a plane (consisting of the lines
through one of the points y(x) and intersecting ^(P1))- Moreover, this map is
one-one on a dense subset of V, because one can pass through any point of P3

50
CLASSES OF POINTS ON CUBIC HYPERSURFACES CH. II, § 12
outside ^(P1) and \p(Pl) exactly one line which intersects both ^(Pl) and
ф(?]). By translating these geometric considerations into algebraic language one
easily convinces oneself that the map \p ф is birational.
A concrete example is the surface *q + x^ + x\ + x\ = 0 over a field which
contains a primitive cubic root of unity Q. This surface contains for example
the non-intersecting lines Xq + Jtj =jc2 + *з = 0 and xQ + jc3 = jcj + 0*2 = ®-
12.7. The interest of the following theory is connected with the fact that
cubic hypersurfaces are, generally speaking, not birationally trivial, even if
they have 'many' rational points. We restrict ourselves to non-singular varieties.
For these the following two facts are well known:
(i) dim V -2. If the field к is algebraically closed, then V \$ birationally
trivial, because it is then always possible to find a pair of non-intersecting
lines on V. Over non-closed fields there exist many birationally non-trivial
cubic surfaces. The problem of their birational classification and of the
structure of the group of birational maps has been thoroughly studied, although it
is not finished yet. The known results will be presented in Chapters IV and V.
An example of a non-trivial surface is
jfg + jrJ+*! + <wrj=0, a<£(k*)3 .
(ii) dim K> 3. The question of birational triviality is an unsolved classical
problem already in the case к = С and dim V = 3.1 Over non-closed fields one
can construct birationally non-trivial V\ however, no general results on the
classification are known to the author.
It is, however, extremely important for the following that most cubic
hypersurfaces have the following property, which is weaker than birational
triviality:
Definition 12.8. An ^-dimensional variety V over a field к is called unira-
tional if one of the two following equivalent conditions is satisfied:
(i) There exists a rational map of finite degree Pn -► V defined over k.
(ii) There exists a rational map Pm -* V defined over к which is
dominating (that is, it induces an inclusion of function fields k(V) -> k(?m)).
1 Clemens and Griffiths have recently shown that smooth three-dimensional cubic
hypersurfaces over С are birationally non-trivial.

СИ. II. § 12
UNIRATIONALITY
51
Proof of the equivalence, (i) =* (ii) is clear.
Conversely, let there be given a map/: ?m -> К with property (ii). There
exists a dense open set U С ?т such that /is defined at each point of U and
such that the dimension of the fibre is constant and equal to m - n on U.
Take a rational point x £ U and construct through it a linear subvariety
pw q pm which is defined over к and which is transversal to the fibre /~l (/(*))•
The restriction of/to ?n is an epimorphism in the general point and has
therefore finite degree. This concludes the proof.
If the variety V is unirational, then the set of its /c-rational points is dense
in the Zariski topology. Of course, the converse is not true, even for
non-singular cubic curves.
The main result of this section, however, establishes this property for a
large class of cubic hypersurfaces of dimension > 2. We need the following
definition.
Definition 12.9. Let КС Р" be a cubic hypersurface. A geometric point x
of V is called a point of general type if the following conditions are satisfied:
(i) jc is a non-singular point of V.
(ii) The intersection C(x) of the tangent hyperplane at x with V is
geometrically irreducible and reduced.
(iii) The singular point x G C(x) is not conical on C(x).
Example 12.10. If dim К =2, then a non-singular point x is not of general
type only if C(x) is geometrically reducible. One of the components is then
a line and passes through x.
A schematic picture of all possible shapes of C(x) is shown in Fig. 11.2.
Here x is of general type in the cases (a), (a^) and (b). In case (е),* is a conical
point on C(x). In case (a) there are two tangent lines to C(x) at x, defined
cK
(a) (a,) (b) (c) (d) (e)
Fig. II. 2.

52
CLASSES OF POINTS ON CUBIC HYPFRSURFACES CH. II, § 12
over the base field, in case (b) they are defined over some quadratic extension
and in case (a^) the two tangent lines coincide. Pictures (d) and (e) do not reflect
the action of the Galois group on the geometric components; it may be non-
trivial.
Theorem 12.11. Let V С ?п be a cubic hypersurface of dimension > 2
which contains a k-point x of general type. Then V is unirational and we have
in particular that the set V(k) is dense in the Zariski topology.
Proof. First we remark that the points of general type form an open set
on К In fact, each of the conditions (i), (ii) and (iiij is open: (ii) because it is
equivalent to the requirement that the tangent hyperplane at x does not
contain any linear subvariety P" 2 С V\ and (iii) because the condition 'conical*
can obviously be expressed by means of the matrix of values of the second
derivatives of the equation of V.
It now follows from the conditions of the theorem that the set of points
of general type on Fis dense. The variety C(x) is birationally trivial in virtue
of Example 12.5: the ^-points of general type on V, which lie in C(jc), form
a dense open subset U С C(x) and for each /c-point у G U we can form the
birationally trivial variety C(y) on V. Thus we obtain a system of birationally
trivial varieties C(y) on V, parametrized by the points of the birationally
trivial variety U. We need to show that this system forms a birationally trivial
variety and that its natural map into ^is epimorphic in the general point.
Leaving the details to the reader, we give a sketch of one of the possible trivi-
alization constructions of this 4birational fibre space' Uyeu C(y) -* (J (see
C(y)
fy(v)
Hn-1nD°-2(y)
C(x)
Fig. II. 3.

СН. II, §12
UNIRATIONALITY
53
Fig. II.3). Choose a hyperplane Un ] С ?п which is not tangent to Fat x.
Let D" ^(x) be the tangent hyperplane atx, and let H"~2 СЯИ be a
hyperplane in H"~l such that H" 2 Ф \\n l П Dw Цл'). Finally choose a point
z E Hn~ 1 \ H"~ 2. The hyperplane H""'2 is birationally mapped on the fibre
C(y) for almost all v in the following way. We project a point v E Нл"2 from
z onto the hyperplane D"~ l(y) П H""1 (inside H"_1). After that, draw the
line joining the point thus obtained toy (within D"~l(y))\ intersect this line
with V, and let Л,(и) denote the intersection point different from>\ The map
UXHn-2-+V:{y,v)t+fv(v)
is rational. It is epimorphic in the general point because otherwise its image
would be contained in C(x). But then we would have C(y) = C(x) for all v,
which is impossible because every pointy is singular in C(y), but (for a dense
set) non-singular in C(x). This proves the theorem.
Remark 12.12. A two-dimensional cone has no points of general type.
I do not know a complete description of hypersurfaces with such a
property. One can show that there are always geometrical points of general type on
a non-singular hypersurface, so that a non-singular hypersurface of dimension
> 2 over an algebraically closed field is always unirational.
To conclude this section we state the following simple result.
Proposition 12.13. Let x £ V be a non-singular k-point of the cubic
hypersurface V, and C(x) the intersection with V of the tangent hyperplane at x.
There exists a unique birational map over k, tx : V -► V, defined outside C(x)y
such that the points (x, y, tx(y)) lie on one line for у E C(x).
[We shall study the precise structure of tx later (see Section 21.2).]
Proof. Choose a homogeneous coordinate system (Г0, . . . , Tn) in which
x = (1, 0,. . . , 0) and Tx = 0 is the equation of the tangent hyperplane to V
at jc. The equation of V in affine coordinates will then be
-r + q\—...,rl + c\— y) = 0,
Jo vo V wo 'o7

54 CLASSES 0Г POINTS ON CUBIC HYPERSURFACES CH. II, § 13
and in homogeneous coordinates,
Г1Г02 + Г0^(Г1,...,Г/7) + с(71,...,^) = 0. (Н.1)
The line through the points (1, 0,..., 0), (/j,. . ., tn) e V has the
parameter representation Tq = X + дг0, 7j- = nti% i > 1. Substituting this in formula
(И.1) we find
\»{\tx + /i(2r0f, +^J,...,//7)) = 0.
On D+(Tj) we can take
X = 2y, +</(/,,...,/„),
from which
and therefore
'(i.c....©^ r«>=<ro'i+i('i. • • ■. '„)»-'?. - 'i'2 -v«>-
This is a morphism on D+(T^).
13. Universal equivalence
Let К be a fixed cubic hy persurface over k, Vt(k) the set of its non-singular
/c-points, and L С Vr(k) X V(k) X VT(k) the collinearity relation defined in
Definition 11.1. We start here the study of equivalence relations on VT(k)
which are admissible with respect to L in the sense of Definition 11.2.
We shall say that the pointsx, у € VT(k) are in general position if x Фу
and the line through x and у is not contained in V and is not tangent to V.
In this case, there exists a unique point z € VT(k) such that (x, y, z) are col-

СН. II, § 13
UNIVERSAL EQUIVALENCE
55
linear, and z = tx(y) = ty(x). From now on we shall write z =x су =у о х in
this case. This notation is justified by the following: if A', Y, Z are the classes
of xf y, z with respect to some admissible equivalence relation, then Z = X о Y
in the sense of the composition law induced by L.
Theorem 13.1. Let V be a cubic hypersurface of dimension > 2 having a
k-point of general type, let S be some admissible equivalence relation on Vx(k)
and E - VT(k)/S the corresponding symmetric quasigroup. Then the following
statements hold:
(i) Every equivalence class is dense in the Zariski topology. If к is
algebraically closed, then all points of VT(k) are equivalent to one another.
(ii) E is a CH-quasigroup.
(iii) Let B(V) be the group ofbirational maps of V generated by the maps
tx for all x G VT(k). Then there exists an epimorphism of groups
B(V) + T(E):tx»tX9
where X is the equivalence class ofx.
(We recall that tx : E -» E is the map tx(Y) = XoY.)
Proof, (i). We start with the following important remark:
Let x G VT(k) be any point, C(x) the intersection of V with the tangent
hyperplane at x. Then all the к -points lying on C(x), except possibly xy
belong to the same equivalence class. In fact, [{ у G C(x),у Фх, the line
containing x, у is rational over к and it is either tangent to V at the point x or it
is completely contained in V. The points (x, xy y) are therefore collineav and
that means that у Е X X, where X is the equivalence class ofx.
Applying these considerations to the points of general type^ E C(x) \ {*},
where x is some fixed point of general type, we get that all points of the
set UL(C(>')^ (y))(k)&xe in one and the same class (XoX)o(XoX). The
proof of Theorem 12.11 shows that this set is dense in the Zariski topology. At
least one 5-equivalence class Y is therefore dense.
Let X be any other equivalence class. We shall show that it is also dense.
Choose a point ;сп G X\ since it is non-singular, the points tXQ(y) are defined
for a dense subset of points у € У, they belong to the same equivalence class
X о Y and form a dense set. Now let y$ G Y be a point such that y§ and *0

56
CLASSES OF POINTS ON CUBIC HYPERSURFACFS CM. II, § 13
are in general position. Then again there exists a dense set of points of the
form ty tx (y) belonging to the same equivalence class, viz. the class X%
because it contains tyQtXQ(y0) = x0.
Finally, let к be algebraically closed. Then for each point x 6 VT(k) there
exists a line which either has a threefold intersection with V at x or is in V,
so that for any equivalence class X and x 6 X о X we have xEXoX=>X = XoX,
and all points of C(x) are equivalent. Therefore all points of Vy^Qx) ^Cv) W
are equivalent. But this set is obviously thick, that is, it contains all &-points of
some open Zariski dense set. The arguments of the preceding paragraph then
show that any equivalence class is thick and, as a consequence, all classes coincide.
(ii). To verify that E is a CH-quasigroup (Definition 1.3), one must establish
that any three classes X, Y, Z SE generate an Abelian subquasigroup. Since all
classes are dense, one can find points л: <~X,y€Y,z£Z such that the plane
through x, y, z intersects V in an absolutely irreducible cubic curve (Bertini's
theorem) on which x, y, z are non-singular points. The collinearity relation
induces the structure of an Abelian symmetric quasigroup on the /c-points of this
plane section of V (Example 2.2). The subquasigroup of E generated by X, Y, Z
is a quotient of this Abelian quasigroup and therefore is also Abelian (Corollary
2.3). Hence E is a CH-quasigroup.
(iii). To construct a homomorphism B(V) -> T(E), we first define an action
ofB(V)or\E. Let s= tXl... tx €5(Ю, YEE. Since У is dence, there exists
a pointy € К such that for all /, 1 </<«, the points xi and tXf+l ... *хп(у)
are in general position. We then define
s(Y) = ciass rY ... tY ( v).
To show that this is well defined we must verify that the definition does not
depend on the choice of y, or on the factorization s = tx ... tx , and that
s{(s2(Y)) = (sxs2)(Y).
The independence of the choice of у is verified by induction on /. The class
of tx (y) does not depend on the choice of у because the points (xn, y, tx (y))
are collinear and the classes of xn and у are fixed. The step from / + 1 to /
goes similarly. The independence of the factorization of s can be shown as
follows: we can choose a pointy E Y in the class Y such that for two given
factorizations s = /v ...tY = t. ...t7 we have that for all /= 1,..., n and
J- 1,.... m the points jc.-, tY ...tY (y) and z.-, Л,. ...t7 (y) are in general
'' л/+1 лп i ^y+i ^m
position. It is then obvious that tx ... tx (y) = tz ...tz (y) = s(y). Because
the class of the first and the second point does not depend on the choice ofy,

СН. П, §13
UNIVERSAL EQUIVALENCE
57
we obtain that the class s(Y) is well defined. A completely similar argument
shows that sx (s2(Y)) = (sxs2)(Y).
Thereby we have defined a left action of the group B(V) on E for which
tx (for all x G VT(k)) acts as t%, where X is the class of*. This defines the
desired epimorphism#(K) -* T(E) and completes the proof.
Theorem 13.2. Let the conditions of Theorem 13.1 be satisfied and
introduce on E a CML structure by means of the composition law XY=Uo (Xo Y),
where UGE is some fixed class. Then the relation X^ = 1 holds in E.
Proof. We show that the identity &(X) = P2(X) is true in E, where
P(X) = X о X. In fact, let X € E be any class, x € X a point of general type.
We choose on C(x) two ^-pointsу and z in general position. Then we clearly
have у о z E C(x), у о z Ф x. On the other hand, by the remark in the first
paragraph of the proof of Theorem 13.1 ,y, z, у о z E X о X. This proves our
identity. (The preceding arguments are due to A. Bel'skii; in [9], I have
proved this result in a more complicated manner and only for R-equivalence.)
Let us now put this identity in terms of the CML multiplication. In virtue of
5.1.2, we have X» Y = /3(1)X~lY~\ hence /3(X) = №)X~2 and 02(*) =
= ^(1)-1ЛГ4. Consequently,*6 = Д(1)2. This is true for all X, in particular for
X = 1 = U, therefore X6 = 1. This proves the theorem.
Corollary 13.3. E is the direct product of an Abelian group of exponent 2
and a CML of exponent 3.
In fact, it follows from Moufang's theorem (Theorem 4.1) that the map
x^xn is a CML morphism for every integer n. In particular, let Elt E^ С Е be the
subloops consisting of squares and cubes of elements of E, respectively. Then the
mapiT -+E2 X E3 : x *-* (x2, л*3) is a CML morphism. Its kernel is trivial, and
(u, v) *-► vu _1 is the inverse map. Finally,^ is a CML of exponent 3,and E3 is
an Abelian group of exponent 2. (We can of course prove a general theorem
on the decomposition of a torsion CML intop-primary components; (отрФЗ
these components are Abelian groups by Theorem 1.8.)
Corollary 13.4. If E has a finite number of generators, then it is finite and
consists of 2a3h elements.
Below, it will be proved that this result can be applied to complete locally cor
pact fields.

58 CLASSES OF POINTS ON CUBICHYPERSURFACES СИ. II, § 1 3
Sometimes one can show that the 2 or 3 component is absent. First of all,
by refining the considerations used for Theorem 13.1 (i) we obtain the
following useful result.
Proposition 13.5. We assume that any quadratic form in > r variables has
a non-trivial root in the field k, and that the conditions of Theorem 13.1 are
satisfied. Then the CH-quasigroup E is distributive if the dimension of V is
larger than or equal to r. In other words, the identity X-X о X holds in E for
all X and the identity X3 - 1 is satisfied in the CML with composition law
XY = U о (X о Y). In particular, a quasigroup E with this property and which
has a finite number of generators is finite, and its number of elements is of
the form 3K.
Proof. Let V С ?n+l, x E Vx(k) an arbitrary point. Choose in ?n+l a
coordinate system (TQ,... , Гл+1) such that jc = (1, 0,... , 0) and such that Tx = 0
is the equation of the tangent hyperplane at x. The equation of C(x) will
then have the form (in the hyperplane T\ = 0 with affine coordinates
Тт/То,...,Тяц/Т0):
(T2 Tn+l\ + (T2 Тпн\ п
where q is some quadratic and с some cubic form. If n>r9 then the equation
q = 0 has a non-trivial solution in k. This solution defines a line in C(x) which
is defined over к and either has a threefold intersection with V at x (when
с Ф 0), or lies completely in V (when с = 0). In both cases we obtain X о X = X,
where X is the equivalence class of x.
The remaining statements about the structure of £ follow from the results
of Chapter I; see in particular 5.1.4, and Theorems 1.9 and 1.10.
13.6. This result can be applied to a rather large class of fields; for example:
(i) If к С Fp (the closure of the prime field of p elements), then r = 3.
(ii) If к is a non-Archimedean local field, then r = 5.
(iii) If к is a purely imaginary extension of the rational numbers, then r = 5.
(iv) If A: is a CJ-field, then r = 24 1;
(v) If к has no non-trivial quadratic extensions, then r = 2.

СН. II, § 13
UNIVERSAL EQUIVALENCE
59
In addition we remark that the simplest example of a geometric CH-quasi-
group with the relation X о X = X is formed by the inflection points of a
complex non-singular cubic curve. There are nine such points, and the
corresponding CML is isomorphic to Z3 X Z3. The construction of Example 16.3
is based on this idea.
Bel'skii has shown that the 3-component is absent if К contains a line:
Proposition 13.7. We assume that the conditions of Theorem 13.1 hold and
that there is a k-line DC V of which not all points are singular on V, Then, if
we designate by U the class of points ofD{k) П VT(k), we have XoX= U for
allX ЕЕ. In particular, the CML E with unit element Uis an Abelian group
of exponent 2.
Proof. Let x € X be a point of general type, x $ Д Construct a plane P2
through x and £>. We can assume that the intersection Р2ПК decomposes
into D and a geometrically irreducible conic Q. Construct in P2 the tangent
P1 to Q at the point jc; let the intersection of P1 with D be y. It is clear that
у is non-singular on V\ moreover, 2x +>> is the intersection cycle of К with P1.
Therefore X о X = U, as we desired to prove.
Example 13.8.1. dim V= 2. There are 27 lines on V ® к (see Chapter IV),
but it can happen that none of them is defined over k.
Example 13.8.2. dim V = 3. For each sufficiently general point on V <8> к,
there are six lines passing through it; in terms of the notation of the proof of
Proposition 13.5, their union is given by the system
<i %)-4--£)-°- -•
If V is smooth, then the set of all lines on V ® к is parametrized by an
extremely interesting surface. Its Albanese variety is 5-dimensional; cf. Bombieri
and Swinnerton-Dyer [1 ]. I do not know whether the set of fc-lines on V can
be empty or infinite, for instance for a number field or a local field. This is
an interesting diophantine problem.
Example 13.8.3. dim V = n > 4. If the field к is such that any system of
equations of the form (II.2) is solvable, then E is trivial: there is no 2-com-

60 CLASSES OF POINTS ON CUBIC HYPF RSURFACKS CH. II, § 13
ponent according to Proposition 13.5, and no 3-component according to
Proposition 13.7. This argument can be applied to Crfields (dim V> 2l + 3'),
and probably also to local fields and purely imaginary global fields for dim V
sufficiently high.
13.9. To conclude this section, we point out an algebraic-geometric
description of universal equivalence on Vt(k) (cf. Proposition 11.3). This description
can be useful for a study of E with the methods of Chapter V.
Let B$(V) denote the normal subgroup oi'B(V) generated by elements of
the form txtyt2tx,tv>tz», where (x,y, z) and (x\y\z) run through all
possible triples of collinear points of Kr(/c). Define x ~у (mod U) if txty SBQ(V).
It is clear that U is an equivalence relation on Vt(k).
Theorem 13.10. Under the conditions of Theorem 13.1 ,U ».v the universal
admissible equivalence relation.
Proof. First of all, we show that U is admissible. Let (x, y, z) be collinear;
one must verify that the (/-class of z is defined by the (/-classes of x and v.
It suffices to verify that if л*' ~ x (mod U) and if (*', y, z ) are collinear,
then z ~z(mod (J). In fact,*' ~x(mod U) if and only if rxtx, €B0(V).
Moreover, tx ty tz tx.ty tz. EBq(V) by definition. Because Bq(V) is a normal
subgroup o(B(V), it follows that tztz, eB0(V), that is,z' ~z(mod U).
Now let S be any admissible equivalence relation. We shall show that
jc ~y (mod U) implies Jt ~ у (mod 5). Let E = V{k)jS and let у : B(V) -+ T(E)
be the homomorphism constructed in Theorem 13.1. Using the fact that E is
a CH-quasigroup and taking into account Theorem 3.1 (ii), for any collinear
triple of points (x, y. z) and (x',y, z ) we obtain
Here X, Y, ... are the classes of jc, y,... mod S. As a consequence, Bq(V) С
С Ker \p. Therefore, we have
л; ~.у (mod li)<*txty e В Q(V)**yp(t xt\.) = t xt Y = 1 <=> tx = ty *>X = Y .
Tliis concludes the proof.

СН. II, § 14 R-EQUIVALENCE: THE BASIC PROPERTIES
61
Corollary 13.11. Under the conditions of Theorem \3A,letE= Vt(k)[U
be the universal CH-quasigroup of classes of points on V. Then there is a
canonical isomorphism T(E) ^ B(V)/B0(V).
We remark that the group B(V)/Bq(V) can also be defined for hypersur-
faces over finite base fields. I do not know whether this group is necessarily
trivial in this case, at least when the number of elements of the field is
sufficiently large.
14. R-equivalence: the basic properties
Following Chevalley, we call a variety which is; irreducible over к special if
each of its points possesses an affine neighbourhood which is isomorphic to an
open subset of some affine space Spec к [7\,..., Tn ]. We shall say that a rational
map of varieties /: U -» V covers a point x E V(k) if there exists a point
и € U(k) such that /is defined at и and f(u) = x.
Definition 14.1. R-equivalence on V(k)is the weakest equivalence relation for
which any two points covered by one and the same rational map of a special
variety U into V are in the same equivalence class.
An amusing example is the following: Let Vbe an irreducible cubic curve
with a double point x. if the two tangent lines to V at x are both defined
over the base field, then all points of V{k) are R-equivalent. Otherwise, V(k)
splits into two classes, namely, {x}and the class of all other points. It is this
very phenomenon, however elementary, which is responsible for the existence
of a 2-component in our CML s (cf. Proposition 13.5).
Lemma 14.2. Two points xf у G V(k)are R-equivalent if and only if there
exists a finite sequence of points x = Xj, x2, • . ., xr = v, and morphisms
ft: P1 -* V, i = 1, . . ., r- 1, such that ft covers xt> x7+1.
Proof. It is clear that the condition is sufficient. To prove that it is also
necessary, we remark that it follows from the definition of R-equivalence that
there exist points л: = x\t х'2,.. . , xr =y, morphisms of special varieties
f'i : Uf -* V and points un, un G Ut{k) such that f^un ) = x\, //(u;-2) = *J+1.

62 CLASSES OF POINTS ON CUBIC HYPERSURFACES CH. II, § 14
If we could join the points mz1 and ui2 in £/z by a rational curve on which uzl
and ui2 are non-singular, then everything would have been proved. But also
sufficient is a weaker fact, which can be verified easily: Ид and ui2 can be
joined by two rational curves which intersect in an intermediate point v. In
fact, choose open neighbourhoods of the points u^ and ui2 which are
isomorphic to open subsets of an affine space, take a fc-point v in their intersection
and join lift to и by a line within the first neighbourhood and ui2 to v by a line
within the second neighbourhood (the 'lines' can of course be incomplete).
This proves the lemma.
Just as Definition 14.1, this lemma can of course be applied to any variety V.
We now return to cubic hypersurfaces.
Theorem 14.3. Let V be a unirational cubic hypersurface over k. Then R-
equivalence is admissible on Vf(k).
First we verify a necessary condition for admissibility (cf. the proof of
Theorem 13.1(i)).
Lemma 14.3.1. Under the conditions of Theorem 14.3, let x E Vr(k) be
any non-singular point, C{x) the intersection of V with the tangent hyperplane
at x. Then all k-points on C(x), except possibly x, are ^equivalent.
Proof. We distinguish several cases depending on the character of the
degeneracy of C(x):
(i) C(x) is geometrically irreducible.
(a)x is a conical point on C(x). In this case (Example 12.5), any line
joining* with the pointy Фх,у € C(x)(k), is completely contained in C(x).
Therefore у ~х (mod R), that is, all points of C(x)(k) are R-equivalent.
(b)x is not a conical point on C(x). The construction of Example 12.5
yields a rational map of a special variety into C(x) which covers all points of
C(x) except possibly x and points у Ф x for which the line joining у to x
is completely contained in V. Further, in the notation of Example 12.5, such
points correspond to a solution of the system q = с = 0 in k. The fc-points on q =0
are dense because к is an infinite field, and in particular there are solutions
of the equations q = 0, с Ф 0 because C(x) is geometrically irreducible. This
shows that the point x is also covered by the map of Example 12.5 and

СИ. II, § 14 R-EQUIVALENCE: THE BASIC PROPERTIES
63
that it is therefore R-equivalent with those points of C(x) for which the
line joining them to x does not lie completely in V. As a consequence, all
points on C(x) are R-equivalent also in this case.
(ii) C{x) is geometrically reducible. Then x lies on the intersection of two
or three irreducible components of C(x) <8> fc.
(a) C(x) ® 1c splits into a linear space and an irreducible quadric. Then the
splitting already occurs over k, and both sets of non-singular points of both
varieties are special. It is easy to see that the singular points on the quadric
are also R-equivalent.
(b) C(x) ® к splits into linear spaces. If this splitting arises from one over
the base field, everything is clear. Otherwise, the Galois group permutes the
components, and the к -points lie on the intersection of all conjugate
components, which is linear. This concludes the proof.
In addition to this we need two technical results:
Lemma 14.3.2. Let W be a normal curve, f: W-+ V some morphism,
x e V(k) andf(W) £ C(x). Then the morphism txf:W^Vis defined as the
composition of the morphism W 4 V and the birational map V Л V. If
f(w) G C(x) for some point w E W(k), then also (tx f) (w) G C(x).
Proof. The significance of the lemma lies in the fact that we cannot
calculate (fx/)(w) as /x(/(w)) since/(w) does not belong, generally speaking, to the
domain of definition of tx. However, the proof is truly easy. \f(txf)(w) =
= уф C(x), then (tx(txf))(w) = tx(y) £ C(x), because V \ C(x) belongs to
the domain of definition of tx and is invariant with respect to tx (Proposition
12.13). But tx(tx f) = /, which contradicts the condition f(w) e C(x).
Lemma 14.3.3. Let fi: Vi: -► V (i = 1, 2) be rational maps of special varieties
into the unirational cubic hypersurface V and suppose that ft covers the
points xf, у € V(k). Then there exist rational maps f\ :U\-*V such that U- is
a special variety and
(i) f\ covers the points xf, y(i= \y2);
(ii) the set of points of V(k) covered by both f[ and f'2 is dense.
Proof. The lemma states that if jcj ~y ~x2 (mod/?) and if each pair (xlfy),
(y, x2) is covered by one and the same map, then by changing the maps, jy can
vary over a dense set.

64
CLASSES OF POINTS ON CUBIC HYPERSURFACES CH. II, § 14
For the proof we consider some rational map g : Pr -► Fwith a dense image.
We can find a point a E VT(k) with the following properties:
(\)g coversд;
(2) a is in general position with respect to Xj, x2, y.
Let xi = fi(ui),y=fi(u'i)ya = g(b). Wc take V\ = J7,X Pr,
The rational map tafi is defined here in virtue of condition (2), and the
composition (tafj)^g is defined because the image of# is dense. Moreover,
f.(unb) = tjjiu^ogib) = (aoxi)oa=xi,
Finally, the domain of definition of the restriction of//to u\ X Pr is
nonempty and this restriction coincides with the rational map
t g\?r^V,
the image of which is dense. The points covered by this map are covered at the
same time by/j and fj, which proves the lemma.
14.3.4. Proof of Theorem 14.3. Let (x,y,z) and (x\ y. z') be collinear triples
of points of Vx(k) and let x ~ .x:'(mod R). If suffices to verify that then
z ^z'(mod R). According to Lemma 14.2, one can restrict oneself to the
case where there exists a morphism/: P1 -» Vcoveringx and*'.
If.v is in general position with respect to x and x\ then it is clear that the
morphism ty f: l)l -► V covers z and z\ so that this case is trivial. If у is in
general position neither with x nor with x\ then according to Lemmas 14.2
and 14.3.3, one can join x to x' by a chain of rational curves for which
the intermediate intersection points are in general position with respect to>>.
It is therefore sufficient to treat the case where у is in general position with
x\ but not with x In this connection one can even assume that x G C(y)\
otherwise, tv would be defined in x and the same considerations as above
would give the desired result.
Lei J\u)=xJXu')=x'. Then (r/)(w') = />.(/("'))= ty(x) = z\ since;- and

CU. П, § 15 R-EQUIVALENCE AND QUADRATIC EXTENSIONS
65
x are in general position. On the other hand,z' ~ (tvf)(u) (mod R). The point
z"=(fv/)(u)Hes on C(y) according to Lemma 14.3.2. The point z also lies on
C(y') because x G C(y) and (*, v, z) are collinear. From Lemma 14.3.1, one
immediately obtains that the points z and z" (and therefore z and z') are R-
equivalcnt in all cases, except maybe in the case that z-y, z" Фу and no lines
exist which are defined over к and either are tangent to V threefold at>' or
contain у and are completely in V. However, this is impossible. In fact, if
these conditions are fulfilled, then x Фу (because (x, у, у) are collinear) and
the line which passes through x, у does not lie in V and is tangent to V
twofold at>\ It follows from this that j> is the only specialisation of (A,/)(w>)
(where w is the general point of W) extending the specialisation w-*u.
Therefore z" =y, contradicting the assumption.
Remark 14.4. R-equivalcnce is, in contrast with universal equivalence, bira-
tionally invariant in the following sense: Let Vlt V2 be unirational cubic hyper-
surfaces and/: Vy -> K2 some birational map. Then/induces a set isomorpnism
Vl^(k)/R ~ V2j(k)IR (in general, the composition laws do not coincide!).
This follows easily from the fact that the R-equivalence classes are dense; we
leave the details to the reader.
In Chapter V it will be proven that for an important class of cubic surfaces
also the quasigroup V(k)jR is birationally invariant and so is even VT(k)/U
(where U is universal equivalence). This is a very subtle fact.
Remark 14.5. The only class of varieties for which the calculation of R-
equivalence succeeds completely in explicit form are the Chatelet surfaces.
This example is analysed in Chapter VI because for the proof one must also
use Brauer equivalence.
15. R-equivalence and quadratic extensions
In this section we study the behaviour of E = VT(k)/R under a quadratic
extension of the base field. Let К D к be an extension of A:. Then clearly
there exists a morphism of CH-quasigroups / = ij.jK : Ek = VT(k)/R -> EK =
= VI(K)/R which maps the class of a point x G VT(k) onto its class in VT(K).
We denote by XK the image of X G Ek in EK. It will be shown that when
К D к is a separable quadratic extension, there exists a 'norm' map in the
opposite direction (not necessarily a morphism):

66 CLASSES OF POINTS ON CUBIC HYPERSURFACES CH. II, § 15
Proposition 15.1. // [K: k] = 2 and К is separable over k, then there exists
a map of sets N = NK/k :EK-+Ek such that N о i(X) = P(X)for all XeEk.
(Recall that P(X) = XoX.)
Corollary 15ЛЛ. Let the conditions of Proposition 15.1 be satisfied and let
XtYe Ek. Then i(X) = i(Y) =» 0(X) = P(Y). In other words, the kernel of the
CML morphism i consists only of elements of order two.
In fact,i(X) = i(Y) =*Noi(X)=Noi(Y). in terms ofCML's: р(\)Х~2 =
= Q(\)Y~2 z+X2 - У2. One can obtain from this another proof of the identity
Xе = 1 in the CML Я = Г(А:)/Я (cf. Theorem 13.2):
Lemma 15.1.2. For all XeEk we have 0(ЛГ) = P2(X).
Proof. We show that there exists for each X EEk г separable quadratic
extension KDk such that i(X) = 0(/(Jf)) = *(P(X)). The result will then follow
from Corollary 15.1.1.
Indeed, let x G V(k) be some point, and X its R-class. We have already noted
that (C(jc)\ {x}) (к) С @(Х). Moreover, it can be seen from the proof of Lemma
14.3.1 that the point x does not belong to this class only if C(x) is
geometrically irreducible and if the quadratic tangent cone to C(x) at jc has no A>points
except x But then it surely acquires points in some quadratic extension of k,
which is separable, at least if к is perfect or if char (к) Ф 2. This proves what
we wanted.
15.1.3. Proof of Proposition 15.1. We construct the map NK/k in the
following way: for every class X E EK choose a point jc G X such that x, its
conjugate over k, is in general position with respect tox. Thenx ox G V(k). We
put NKik{X) =x ox (mod R) EEk.
We have to prove three statements: (1) it is always possible to choose an
x with the indicated property; (2) the class of x о х does not depend on the
choice of x\ (3) if X = i(Y), YEEk, ther\NK/k(X) = 0(У). In the proof
of the second and third statement we essentially use the fact that we work
with R-equivalence. I do not know whether the analogous facts hold for
universal equivalence, and I see no reason why they should.

СН. И, § 15 R-EQUIVALENCE AND OUADRATIC EXTENSIONS 67
(i) The choice ofx. We denote by RK/k the functor "restriction to the
base field1'' of Weil [2]. We recall that it associates with any quasiprojective
variety W defined over К a variety Rxfc(W) defined over к with the following
property:
Let X be an arbitrary variety over k\ then there are defined isomorphisms
which are canonical and functorial in X:
Hom^(X ®kK, W) 3 Horn^JT, RK/k (W)) .
If we apply this in particular to X = Spec (fc), we find that the K-points of the
variety Ware in one-one correspondence with the /c-points of RK^(W). Now
let W= V ® k K, where V is defined over k. Taking X = R&/k(W)t we obtain
HomK(RK/k(W) ®kK, V ®kK) = Homk(RK/k(W),RK/k(W)) .
Every automorphism of the extension K/k acts on the set on the left by means
of the second factors of RK/k(W) ®k К and V ®kK and that means that it
also acts on the set on the right. In particular, let K/k be normal and let
G = Gal (K/k). Then there is defined amapG-> Homk{RK/k(W)iRK/k(W))y
s^s(id), where id is the identity map of RK/k(W). One easily sees that this
map defines an action of G on К-к/к^)гог which the induced action on the k-
points of the variety R^/k{W) coincides with the action of G on the A'-points
of W= V®kK.
We now apply these general observations to the case where К is a cubic hyper-
surface over/c, К Эк is a quadratic Galois extension, and V = Rf^fk{V®kK).
Identifying V(K) with V(k), we first of all obtain that the set
{(x, x)\ (x, jc)E V(k)X V(k)} is closed (it is the graph of the conjugation mor-
phism). Moreover, the set of pairs (x, y) E V(k) X V(k) such that the
corresponding points in V(k) are not in general position is also closed. It follows-
from this that the set S of pointsx G V(K) = V(k) for which (x, x) are not
in general position on Vis closed in V(k). It remains to be shown that S does,
not coincide with all of V(k). Then, as V is unirational,5 cannot completely
contain any R-equivalence class ovei К because these classes are dense in V
and hence also in V.
To find points outside S, we intersect V with a sufficiently general 3-di-
mensional projective space, defined over ky and which passes through some
non-singular &-point of V. This intersection is then an irreducible cubic fc-sur-

68 CLASSES OF POINTS ON CUBIC HYPERSURFACES CH. II, § 15
face F on which the point x is non-singular and of general type. Consequently,
all points in some neighbourhood of x are of general type. Therefore, there
is only a finite number of lines on F (their union consists of the points not
of general type). Further, the set F(A) \ F(k) is dense in F (tor instance
because the set CF(x)(K) \ CF(x)(k) is dense in CF(x) for any point x E F(k)
which is of general type on F). One can therefore find a point x E F(A)\ F(k)
which does not lie on one of the lines on F. Then x Ф x, and the line joining
x and x intersects F(and V) in exactly one more point, which is defined over
k, and therefore different from x and x. It follows that x and x are in general
position, so that x ^ 5.
00^K/k is welldefined- Let XE Kr(A )/#. We choose two pointsx,yEX
such that (x, x) and (v, y) are in general position; we shall show that
x о x ~ у -о у (mod R) over k.
According to Lemma 14.2, there exists a sequence of poii.ts^-E V(k)y
x = Xq, jCj, . . . ,*r+i -y such that xv x/41 are covered by a A-rnorphisrn
fr?\®K^v®K, #о) = хг #~) = *,-+1.
In virtue of Lemma 14.3.3, the points jc^ . . . , xr can be varied over an
everywhere dense set. Therefore, according to the results of (i), we can assume that
Xj, x~j are in general position for all/ = 1, ..., r. We let the non-trivial
automorphism of the field K/k act on ?lk ® К and V ® К by means of the second
factor. This defines the morphisms/,. We set
6i Ji Ji к *
and by definition we have for all t 6 P1 (/c),
ф)=ф) о /;.(о.
In particular,^.(0) =xtox(, ^(°°) = jc/+1 с х/+1. It follows from this that the
pointsx оx =x0ox0 and>'oy = xr+1 • хж are R-equivalent over A:.
(iii) 77?e identity NKjk о /^ = j3. Let x EXE VT(k)/R. Again applying Lemma
14.3.3 and the results of (i), we can find a point v Ei(X) and a A-morphism
/: ?\ ® A' -* K® A such that>>,jp are in general position and such that
/(0) = x, /(«>) = y. The morphism g=fof:P^-+V defined as above covers
£(0) andj> о у. It is therefore sufficient to verify that £(0) Ep(X).

СН. II, § 16 UNIVERSAL EQUIVALENCE OVER LOCAL FIELDS
69
Let t E ?J. (k(t)) be a generic geometric point in the sense of A. Weil. In
the space in which V is embedded, the line L{ over k(t) is defined as the line
through the points/(/) and /(f). Its specialisation Z,0 for t = 0 is uniquely
defined (consider the morphism of P1 into the Grassmann variety of lines, which
maps t onto the line Lt). Moreover, LQ is tangent to К at the point x because the
two intersection points/(/) and/(/) coincide at x for t = 0. Because #(0)Е10,
it follows that £(0) E C(x). But according to Lemma 14.3.1, (C(x)\ {*})(*) С
С Р(Х); if #(0) = x, then the line LQ either has a threefold tangent point at jc,
or it is completely contained in V, and again a: E ($(X).
This concludes the proof of Proposition 15.1.
Developing the ideas of this proof a bit further, one can establish in some
other cases that the 3-component of the CML V(k)/R is trivial.
Proposition 15.2. Suppose that there exists a finite extension К D к of к
and a rational map f: P£ -» V ® К of finite degree, defined over K, with the
following properties:
(i) К D к is a tower of separable quadratic extensions.
(ii)fis a composite of separable rational maps of degree 2.
Then the CML E = V(k)/R is an Abelian group of exponent 2.
Proof. Let к denote the maximal separable 2-extensjon of the field k. Let
E = V(k)/R, E- V(k)/R and / = ikj%: E -*E the canonical map.
First of all we have that the kernel of/ consists of elements of order 2 in
virtue of Corollary 15.1.1.
We now show that Eis trivial, so that E = Ker iKfe . Indeed, by
assumption there exists over к a rational map/: Pr -* V ® к which decomposes as a
composition of rational maps of degree 2, Let U С Р/! be a non-empty open
set in the domain of definition of / on which/ is unramified. Then, by the
definition of the field k, f maps U(k) on all of W(fc), where W = f(U). As a
consequence, one of the R-equivalence classes is thick in the Zariski topology of
Kr(/c), and, as all classes are dense, they all coincide with VT(k).
16. Universal equivalence over local fields. Examples
In this section a local field will be a field of one of the following types:

70 CLASSES OF POINTS ON CUBIC HYPERSURFACES СП. II, § 16
(i\ The field of real numbers R.
(ii). A finite extension of the field of p-adic numbers Qp.
Let к be a local field. It carries a topology and is complete and locally
compact. In particular, the set of rational points V(k) of any algebraic variety V
over к is provided with a topology which is induced by the topology on k. We
shall call it the k-topology.
Theorem 16.1. Let V be a cubic hypersurface of dimension > 2 which has
k-points of general type. Then for any admissible equivalence relation on
VT(k) each equivalence class is open and closed in the k-topology.
Proof. It is sufficient to prove that each class is open since it is the
complement of the union of all other classes and hence is closed.
We show first that there exists a set U which is open in the fc-topology and
which is completely contained in one equivalence class. The proofs of Theorems
12.11 and 13.1 show that there exists a rational dominating map/: ?n -> V
such that all points in the image f(?n(k)) are equivalent; in the notation of
Theorem 12.11, the birational fibre space \JyGUC(y) is birationally equivalent
to ?n.
We can assume that n = dim V, by restricting/to a projective subspace of
dimension equal to dim f passing through a point in the domain of definition
of/. As/is of finite degree and separable, there exists a pointy G?n(k) such
that /is defined and unramified in y. But then /defines an analytic
isomorphism of some neighbourhood of у (in the £-topology) with some
neighbourhood U of the point x =/( v). This neighbourhood U lies completely in
one class.
We now show that for any other point у 6 V(k) there is a whole
neighbourhood lying in the class of y. (See Fig. II.4.) The set U is dense in the
Zariski topology. Therefore there exists a non-empty subset if С (/which is open
in the ^-topology such that у is in general position with respect to all points
x E U\ Choose*; then the same considerations show that there exists a neigh-

СН. И, § 16 UNIVERSAL EQUIVALENCE OVER LOCAL FIELDS
71
bourhood U" of the point x oy E ty(U') which is open in the fc-topology such
that all its points are in general position with respect to x. Moreover, they all
belong to one and the same class by definition. It follows that the set tx(U")
is an open neighbourhood of the pointy which belongs to the class of y. This
proves the theorem.
Corollary 16.1.1.Lev [k: Qp] <°°andlet V be a cubic hypersurface without
singular points. Then the set of classes of points on VT (k) with respect to any
admissible equivalence relation is finite and consists of 2a3b elements.
Proof. The set of ^-points Vr(k) = V(k) is compact in the /c-topology (as a
closed subset in ?n(k)) because by assumption there are no singular points.
Using Theorem 16.1, the finiteness follows from this. Corollary 13.4 yields the
second assertion.
Remark 16.1.2. One can extend the results of Theorem 16.1 and Corollary
16.1.1 to fields of formal power series with a finite residue field. To do this,
we need a more careful analysis of the construction of the rational map
/: Pw -> V to establish its separability. This can in any case easily be done for
characteristic Ф1, 3.
Corollary 16.1.3. Let к = R. Then universal equivalence and R-equivalence
coincide on V(R) and each class is a connected component of V(R). The
number of connected components of V(R) is equal to 1 or2\ the CML E= V(R)/R
is isomorphic to {1} or Z2, respectively.
Proof. It follows immediately from Theorem 16.1 that each class of an
admissible equivalence relation is a union of connected components. On the
other hand, an arbitrary rational dominating map/: ?n -*• V completely covers
exactly one connected component of F(R), and the points of different
components are cleaily not R-equivalent. The first assertion follows from this.
Further, if there existed three different connected components of K(R),
then by choosing a points on them and passing a plane through these points,
we would obtain a plane cubic curve with > 3 connected components, which
contradicts Harnack's theorem.
Example 16.2. Using the results on the calculation of V(R)/R just described,
we shall now show that the number of classes cf VT(k) can be arbitrarily large

72 CLASSES OF POINTS ON CUBIC HYPF.RSURFACES CH. II, § 16
for a fixed cubic surface while к varies over different algebraic number
fields (of growing degree over Q). Let V be such that V( R) = X0 U X{ (a
splitting into two connected components). We shall make use of the fact that the
inclusion VT(k) -> VT(K) sends R-equivalent points into R-equivalent points
for each inclusion of fields к С К.
We now fix some integer n > 0 and suppose that we have constructed an
algebraic number field k, n embeddings s{: к -> R and n points xi E VT(k)
satisfying
*,.(*.) e*0 с rr(R),
}(*,)£*, С KT(R),
for all /, / = 1, . .. , /7. The points jcj, . .. , xn G Vr(k) are then pairwise not
R-equivalent to each other because xit X: belong to different connected
components of V(R) under the embeddings S;: VT(k) -+ VT(R).
We now give an explicit construction of the example.
(i) Construction of V. Let V be given in affine coordinates by the equation
TJ + f\ = T2 (7*2 - 1). This surface is obtained by revolving the curve
f\ = T2(T\ - 1) round the T2 axis. (See Fig. II.5.) Let Xx be the convex
(compact) connected component of VT(R). The composition law on E= (Xq, X^) is
given by the formulae X\ о X^ = Xq, X\ ° X0 = X\, Xq о Xq= Xq.
(ii) Construction of'k, s(andxt. Let p]f. . . , pn be different primes. For
each /= 1,.... я, choose rational numbers t7j, ri2 ^ Q such that
t.- = t/j+t,-2Vp,>i.
-1<^ = t|-1-^Vp/<0;
Xl
((ТТЛ
АккУ
Ti
0 ,(^
Fig. II. 5.

СИ. 11, § 16 UNIVERSAL EQUIVALENCE OVER LOCAL FIELDS 73
it is trivial that this can be done. Farther we set
k = Q(l=v...A,rev...,en),
where
Finally, let the embedding s, : к -> R be defined by the formulae
*,•(£,•)=Vp/, y^';
(arbitrarily extended over 0). Then the points xi 6 K(fc) with coordinates
Г,=0, Т2=в,. 73=r,, +T/2f,.
possess the property
*,.(*.) e*0, s/(xi)exl for /*/.
This concludes the construction of the example.
We remark that the equivalence relation Tor all /,5z(x) "^ дЯ/О')' is admissible.
The CML constructed from this is Abelian with at least 2n elements. Later
we shall show that the construction of this example can be generalized to
arbitrary fields if we use Brauer equivalence.
Example 16.3. We now mention an example of an admissible equivalence
relation which yields the CML Z3 X Z3. We set к = Q2(0), 03= 1 (an unrami-
fied quadratic extension of the 2-adic numbers) and consider the surface V
over к defined by
7^ + Т\ + T\ + 0 T] = 0 .
There exists a map 'reduction modulo 21:
Р*(*Ир*0(*о>.
(И.З)

74
CLASSES OF POINTS ON CUBIC HYPERSURFACES CH. II, § 16
where P| = Proj k[TQ) T{, T2, Г3], A:Q = F4, the residue field of the ring of
integers of/:, and Pj* = Proj k0 [f0, f j, f2, f3]. This map carries a point with
homogeneous coordinates (/0,. .., /3), where the /;- E к are integers and
relatively prime, into the point with coordinates (r^, .. . ,73), rj- = ^(mod 2). This
is clearly well defined. Restricting this to V(k), we obtain a map
P(*)->K(*0), *^Jc , (H.4)
where V is given by the equation
fl + f I + f| + 0 f\ = 0 , 0=0 (mod 2) € F4 .
One easily verifies that this surface is non-singular.
We shall prove that the equivalence relation on V(k),
x ~y <=*jc = y ,
is admissible, and that the corresponding CML is isomorphic to Z3 X Z3. For
this, it suffices to verify the following two assertions:
16.3.1. The collinearity relation induces on K(fc0) a composition law of an
Abelian symmetric quasigroup, and T^(V{k^)) = Z3 X Z3.
16.3.2. If the points x, y, z E V(k) are collinear, then the points
x,y,z E V(k0) are also collinear.
Proof of 16.3.1. For all elements /6F4,we have r3 =0 or 1. Therefore
0EF4 cannot be represented as a sum of three cubes; it follows that all points
of V(kQ) lie on the plane section 7\ = 0. This is the non-singular cubic curve
Tq + T j1 + T2 - 0; all its points over F4 can be easily enumerated, they are
its nine inflection points. Choosing one of these as the origin, we obtain that
K(fc0) consists of the complete set of points of order 3 on a plane elliptic
curve. The desired assertion follows from this.
Proof of 16.3.2. We first of all observe that there are no lines on V defined
over к and also no lines on V defined over /c0. In fact, all of the 27 lines on the
surface 2?=n ai T? - 0 can be obtained as follows: dividing the four terms of the
left-hand side into two pairs and factorizing each sum, e.g., ax Т\ ^а^Т\ into
the product ГГ* (aj T{ +д|0,7,2), we represent the equation in the form

СН. II, § 16 UNIVERSAL EQUIVALENCE OVER LOCAL FIELDS 75
LlL2L3 + L\V2L\ = 0. The equationsZ,7 = L'f = 0 give 9 lines on V, resulting
from the given division into pairs, and there are in all 3 ways in which to
divide them. It follows from this that in our case all lines are defined over k(d*)
(respectively fcn(0*), but not over the base field. Consequently, the points
xt y, i E V(k) are collinear if and only if there exists a line / С Р| such that
/П K = x+.y+z.
The desired result will be found if we can show that for each line / С Р^
it is possible to define its reduction mod 2, i.e. a line T С P| such that the
following condition is satisfied:
lC)V = x+y+z=*TnV=x+y+z. (II.5)
Of course, there exists a general definition of the reduction of a closed sub-
scheme of a projective space, defined over a discretely valued field. We make
do with some special cases of this, treating Vt x, T separately.
(i) The construction of I. We consider the set M of all linear forms in
Tq, Ту, Т2, Г3 with coefficients in the ring A of integers in the field k, which
are zero on /. Because A is a principal ideal ring and M has no torsion, M is
free of rank 2 = <ЫткМ ®А к (because M ®A к is the linear space of forms which
are zero on /). Let us denote by M the space of forms of M, reduced mod 2 (we
reduce the coefficients and replace 7} with 7}). We shall show that the system
of equations M = 0 gives a line T in P| . First of all, dim^ M = 2. In fact, let
mx, т2£МЪе a free Л-basis forM If fhy +6^ = 0 for some e = e(mod2)EfcQ,
then {{my + em2) ^M, contradicting the choice of m{, m2 and the
maximally of M. Therefore, Г is a line since it is the intersection of two different
planes rhy = 0, m2 = 0.
(ii) Verification of property (11.5). Let M be the Л-module of linear forms
corresponding to a line / for which /П К = jc + j> + z. We consider the ideal
/ = (Mt T* + 7j* + T\ + в T%) in the ring of forms with integer coefficients and
we set В = A [T0, Tx, T2, Тъ\ //.
First of all, Proj В 5§A к is the scheme intersection V П /, / Cf. Vy so that
the Hilbert polynomial of В ®д к is equal to 3. Moreover, this is also
true for В ®A &0, because this is the scheme intersection Fn/and7<£ V.
Consequently, for / > /Q, Bf is a free Л-module of rank 3 (B = ®~0 Bt, graded
by the degrees of the forms), because 2-torsion in Bt would give superfluous
generators in /?, &Ak0 as compared to В <8>A к. It follows from this that
Proj В C?^ is a closed subscheme which is Hat over Spec (A ), its fibre over
the general point Spec (k) -> Spec (A) is equal to V П / and the fibre over the
closed point Spec(&0) -> Spec (A) is equal to V П T. Thus the underlying space

76 CLASSES ОГ POINTS ON CUBIC HYPILRSURFACES CH. II, § 17
of V П T coincides with the specialization of the underlying space of V П £
From this we obtain immediately that VnT=x+y+ztfxJ=y (or, which
is the same, if the points x, y, z are all different). Ifx -y, then alsox^z",
and the intersection V ОТ as a cycle consists of the point x with multiplicity
3 = dinijto/?/®^0,/>i0.
This concludes the construction of the example.
1 do not know whether the given partition is universal and in which relation
it is to the partition into R-equivalence classes.
17. Bibliographical remarks
This chapter is completely based on the papers Manin [6] and [9]. However,
the definition of admissible equivalence has been changed and universal
equivalence has been studied here for the first time. Also, the examples of Section
16 have not been published previously.

CHAPTER HI
TWO-DIMENSIONAL BIRATIONAL GEOMETRY
18. The main results
This chapter has an auxiliary character; we have collected in it some
information on the structure of rational and birational maps of surfaces; the
proofs have sometimes been omitted or are incomplete. This information will
be intensively used in Chapters IV and V which contain a 'subtle' theory of
cubic surfaces which does not carry over to higher dimensional cases. In the
first section of the present chapter we give a summary of the definitions we
work with and of the results, and some informal comments on them. The
logical presentation in the survey is different from that of the main part of the
chapter.
Let к be some algebraically closed field. We consider only smooth
projective surfaces over k. We denote by Pic V the Picard group of the surface V.
Lemma 18.1.1. Let f: V' -> V be a birational morphism of surfaces and let
/*: Pic K-> Pic V\ Then Pic V'lf*(P\c V) is a free Abelian group with a
finite number of generators.
Definition 18.1.2. The rank of this group is called the index of the mor-
phism/and it is denoted by /(/).
The map/* : Pic V-+ Pic V' has a trivial kernel, so that the index measures
how much the Picard group grows. It is the simplest numerical invariant of the
morphism /. One easily verifies that i(fo g) = /(/) + /(^).
Lemma 18.1.3. The following statements hold for the index i(f) of the
morphism f: V'-> V:
(i) ///(/) = 0, then fis an isomorphism.
(ii) ///(/) = n > I, then f can be represented as a composition
11

78
TWO-DIMENSIONAL B1RATIONAL GEOMETRY CH. Ill, § 18
where fj is a birational morphism of index one.
It is clear from this that morphisms of index 1 play a fundamental role.
Their geometric structure is described by the following result.
Theorem 18.2. Let /: V' -> V be a birational morphism of surfaces and let
(i) There exists a closed point xEV such that the restriction
f: V' \ f~x (x) -> V ^ x is an isomorphism. The point x is called the centre
off Thenf~* (x) ~ D is a curve isomorphic to P1 with self-intersection
number-].
(ii) Let f': V' -*V, f" : V" -> V be two birational morphisms with centre x,
Kf) ='(/') = 1 • Then there exists a unique isomorphism g : V' -» V" such
that f= fog.
(iii) Let fx : V' -+ VXJ2 : V -» V2 be two birational morphisms, i(fx) =
= '(/2) = 1 • Let xt E Vi be the centre off{ and suppose that /f1 (xj) =f2l(x2) ~
= D С V\ Then there exists a unique isomorphism g : V^ -+ V2 such that
g°f\ =/2-
In the situation as described in the theorem, the morphism of index one
/: V' -> V is called a monoidal transformation with centre x. The statements
(ii) and (iii) are uniqueness theorems: /is completely determined (up to
isomorphism) either by V and the centre x E V, or by V' and the inverse image
of the centre D =/~1 (x) С V'. Therefore the morphism/is also called
'blowing up the point x4 (from the point of view V) or 'collapsing the curve
D' (from the point of view V').
Theorem 18.3 (Existence theorem), (i) For every' closed point x E V there
exists a monoidal transformation with centre x.
(ii) For each curve D С V' such that D = P1 and (Д D) = -1, there exists
a monoidal transformation /: V' -> V with the point f(D) as its centre.
A curve satisfying (ii) is called exceptional.
In fact the theory starts with an explicit construction of a monoidal trans-

CH. HI, §18
THE MAIN RESULTS
79
formation with the point x as its centre. Thereafter the inverse image/_1(x)
is described. The role of these maps in the general picture becomes only
gradually clear; the formulations cited above are a survey of the results.
Since we are interested in birational maps (e.g. tx) and not only in morphisms,
we must clear up the place of the latter in the general picture. This is done by
the following theorem:
Theorem 18.4. For every rational map of surfaces y: V-*W, there exists
a birational morphism f\ V' -► V and a morphism g: V' -* W such that
This is the simplest form of the theorem on the resolution of singularities
of a rational map; for a more detailed discussion see the first part of Section 19.
Combining Theorems 18.4 and 18.3 gives:
Corollary 18.5. Every birational map can be split up into a product of
monoidal transformations and their inverses.
During the proof of these results, in the main text of the chapter we discuss
another three important themes:
(i) The actions of a monoidal transformation/: V -*» V ox\ Pic К and
Pic V' on curves of the surfaces V' and V and on their canonical classes (see
the resume in Section 34).
(ii) Galois descent: the transition from the algebraic closure of the base
field к to the base field itself.
(iii) Minimal models.
We shall say a bit more about the latter concept. Let К D к be an extension
of transcendence degree 2. A model of the field К (over k) is any pair
consisting of a (projective smooth) surface V over к and a fixed ^-isomorphism
у : k(V) -+K, where k(V) is the local ring in the general point of K, that is,
the field of rational functions on V. Two models (J^, v>i X ( ^2» ^2) аге са^ес^
equivalent if there exists a (necessarily unique) isomorphism/: V\ -> V2 such
that «pj of* = ^2- An equivalent definition is: to a model corresponds a set of
local rings in К corresponding to the points of V. Two models are equivalent
if and only if these sets coincide.
Definition 18.6. (i) A surface К is called minimal if every birational
morphism/: V ^ V' is necessarily an isomorphism.

80
TWO-DIMENSIONAI BIRATIONAL GEOMETRY CH. Ill, § 18
(ii) A model (V, ф) of the field A' is called minimal if the surface V is
minimal.
An important fact is that there exists for every surface V' a birational mor-
phism into some minimal surface. The group of automorphisms of the field
К over к has a completely different structure depending on whether there is
or is not a unique minimal model of this field. We investigate first the case
when к is algebraically closed.
18.7.1. The minimal model V is unique. Then it follows easily from the
definition that the group of automorphisms of the field A is isomorphic to the
group of ordinary automorphisms of the surface V% so that birational objects
reduce to biregular ones. Moreover, for surfaces 4of general type', on which
the sheaf ft., is ample, the automorphisms of V induce linear automorphisms
of the space //°(K, £l*y). If и is such that £lnv is very ample, then this yields
a faithful linear representation of the group of automorphisms of V and it is
easy to show that its image is finite.
18.7.2. Tlie minimal model V is not unique. It is known (cf. the book
"Algebraic Surfaces") that this is only possible in the case that A' has a model of
the form P1 X X, where X is a curve; in other words, A - k(t, u, i>), where
f(u, v) = 0 is the equation of the curve X for some polynomial/over k. If
genus (X) > 1, then all automorphisms of A" send the subfield К$=к(и, и)
into itself. On the other hand, A = A^q(/) and the automorphisms of A/Aq
are well known: they are the linear fractional transformations / -+(at+b)/(ct+d),
where a, by c, d EK{). Therefore there is an exact sequence
1 ~> PL(2, A0) -> Aut (K/k) -» Aut X -> 1 .
The kernel PL(2,Kq) here is infinite dimensional as a group over k\ the
functions a, b, с d can have arbitrarily high degree.
Finally, if genus (X) = 0, that is, A is the field of rational functions in two
variables, A = /c(/q, /j), the situation becomes even more complicated. One
can conclude from Noether's theorem that Aut (K/k) is generated by an
infinite dimensional subgroup PL(2, k(t0)) and the group of linear maps
0q, rl)>^(a0r0^ali] +a2, Vo + Vl + b2 ).

CH. Ill, §18
THE MAIN RESULTS
81
18.7.3. The geometric picture. Most of the results formulated in Sections
18.7.1 and 18.7.2 are obtained by means of a subtle analysis of the geometry
of exceptional curves. To illustrate the main ideas, we consider two extreme
cases:
(i). Let Vbe a surface on which there are no rational curves (including
singular ones). Then V is the unique minimal model of its function field. An
example is a surface V which is a product of curves of genus > 1. In fact, let
W be another minimal model. There exists a canonical birational map
</>: V-+W. Let /: V -* V,g: V' -► W be a resolution of its singularities, as in
Theorem 18.4. In virtue of Theorem 18.3,/can be factorised as a product.
of a finite number of monoidal transformations, each of which 4glues in' a
rational curve P1 in the place of a single point. As there are no rational curves on V,
the glued in curves on V' exhaust all rational curves.
The morphism^ collapses some sequence of curves P1. It is evident from
what has been said that all these must be contained among those produced
by/ But then some combinatorial analysis shows that all rational curves on V
must collapse, and the image of g is isomorphic to V,
(ii). Let V = ?{ X Pl,and let V' -> К be a monoidal transformation with
its centre at the point (jc, y) G V. Here there are many rational curves on V9
and two of these immediately become exceptional on V\ namely, the inverse
images of the fibres x X P1 and P1 X y. [This can be checked as follows: After
a monoidal transformation/: V' -* V with its centre at the point xGFof
multiplicity e on the curve D С V, we have
(rl(D),f-\D)) = (D,D)-e2.
Therefore, if there passes through x a curve P1 of self-intersection number zero,
then it becomes exceptional after blowing up x] In particular, by collapsing
/_1 (лХР1) and /-1 (P1 X y) we obtain a morphism V' -* P2. The surfaces
P1 X P1 and P2 are non-isomorphic minimal rational surfaces.
Besides these, there is a countable series of non-trivial fibre spaces ^-^P1
with base P1 and fibre Pl. The index n refers to the fibre space which has a
section with self-intersection number -n. This is the only curve on Vn
with a negative self-intersection number. Every minimal rational surface
over an algebraically closed field к is isomorphic to either P2 or Vn, where
n = 0 (then V = P1 X P1), or n > 2 (V{ is not minimal). The proofs of
these results can be found in the treatise of Nagata [1], in the book
"Algebraic Surfaces", Ch.V, and in the paper of Hartshorne [1].

82 TWO-DIMENSIONAL B1RATIONAL GEOMETRY CH. HI, § 19
However, the field К = k(t0, t{) has considerably more minimal models.
In fact, let (V, </?), where у : k(V) -> K, be one such model. Then for every
automorphism К %K we get another model (V, \p о {p)y so that the infinite
dimensional group Aut(K/k) acts on the left on the set of models. The
subgroup which leaves (V, ф) invariant is isomorphic to Aut^ V and it is not
difficult to see that it is finite dimensional. Finally, the classes of minimal
surfaces are exactly the orbits under the action of Aut (K/k) on the set of
minimal models of К
18.7.4. The case of a non-closed field k. Let K/k be the field of rational
functions in two variables over k. What can be said about the minimal models and
automorphisms ofK/kl The situation here is considerably more complicated
and interesting. In Chapters IV and V we shall study the case where К is the
field of rational functions on a cubic surface. Chapter IV investigates in detail
the non-minimal surfaces and Chapter V the minimal ones. Here a whole
spectrum of possibilities is realized:
(i) The field К can have a unique minimal model. (This is the case if the
cubic surface V is minimal and V(k) is empty.)
(ii) The minimal model can be not unique, although Aut (K/k) acts
transitively on the set of minimal models. (V minimal and V(k) contains points
which do not lie on an exceptional curve of V.)
(iii) The minimal model is not unique and Aut (K/k) does not act
transitively. (V non-minimal, for example V is birationally trivial.)
For more details see Section 33 in Chapter V.
19. Monoklal transformations
19.1. Let V, W be algebraic varieties over a field к and let/: K-* W be some
rational map. Our immediate aim is to study the singularities, the points wrier*»
the map/is 4not defined' and, in particular, to learn how to 'resolve* them
(in the case that dim V = 2).
A resolution (of singularities) of a map f in the widest sense of the word
shall be every commutative diagram of the form

CH. Ill, § 19 MONOIDAL TRANSFORMATIONS 83
V
'I \
v f , w
where g and h are morphisms and in addition g is birationaL
Adopting this definition, it is not difficult to indicate one general method of
resolution. Indeed, let /be represented by a morphism \p : U -> W, where U С V
is a dense open subset, and let Г^ С U X IV be the graph of \p. We consider the
embedding Г^ С U X W С Г X W and denote by K' = ry the cforore of Г^, in
V X IV. It is easy to see that V' does not depend on the choice of U\ it is
natural to call it the graph of the rational map f The projection morphisms of
V X W on V and:W induce morphisms#: V' ~+V and Л : F' -> W\ it is clear
that {V\ g, h) constitutes a resolution of singularities of the map/. This
method of resolution has two basic defects:
(i) Even if V and W are non-singular, V' can have singularities.
(ii) The structure of the birational morphism g is not explicit.
Therefore our theory of resolution will be developed by taking some other
ideas into consideration. However, resolution by means of the graph gives us
the basic construction of an important special class of birational morphisms #:
the monoidal transformations with a point as centre.
We start with the following classical example.
Example 19.2 (4linear projection*). Let An+l = Spec к [T0)..'., Tn] be an
affme space, ?n = Proj к [ Tq> .. ., T'n ] the projective space of lines in An+l
passing through the origin О = (0,... , 0). The usual 'projection of an affine
space onto the hyperplane at infinity'
*:A"+1M0}— P", *(V--'*)s(V-":r*)' <IIL1)
represents a rational map/: Aw+1 -+Pn. We shall now resolve the singularity
of this map by means of the graph.
First of all we recall that if у: Speol -► Spec/? is a morphism of affine
varieties, then its graph
Г С Spec>4 X SpecB = Spec(yl ® kB)

84 TWO-DIMENSIONAL BIRATIONAL GEOMETRY CH. Ill, § 19
is defined by the ideal (1 <g> b - y* (b) ® 1) С A ® B, where ^* : В -» A is the
homomorphism of function rings and b runs through all possible elements
of Я
Now let
n
p*= и d^t\) , o+(r;) = sPec*[^/7;,..., t^/t;] ,
1=0
и
А"+1=и/)ф, Z)(7\) =Specfc[r0>...,7;, l/7;.l.
/=0
Then the graph of \p restricted to£>(7)) X D+(T-) is given by the equation
т Г
Ti ri
in Spec k[TQ,... , Tn, 1/7}; Г^/Г/,. . ., 7^/7;']. (We have deleted the tensor
product sign for brevity.) It follows from this that in the product
An+lX?n=Pro\klTQ,...,Tn,T^...4rn]
(the ring is graded by total degree in the variables Tq, .. . , T'n), the graph Гу
of the rational projection is defined by the ideal with the system of
generators (TjTJ - TjT'i), i,j=\,...,n. In fact, this ideal defines a closed
irreducible subvariety, coinciding with Г at all points where the latter graph is
defined.
The geometric fibre of the graph Г over any point except the origin
consists of one point, and over О the fibre is isomorphic to P". Eq. (III. 1) gives
the geometrical reason for this: if the point (r0, ...,/„) approaches the
origin, while remaining on one and the same line through the origin (or, more
generally, on a curve with tangent), then the point ip(t0, . . . , tn) approaches
the point of the 'glued in' fibre corresponding to the direction of this line.
In other words, to resolve the singularity offwe replace the point where f is
not defined by the whole projective space of tangent directions at that point.
It is not difficult to verify that Гу is a non-singular variety.
The significance of this example for the general theory is illustrated by the
following circumstance.
Let I7 be an affine variety,л* G V a Appoint on it, and V^*An+^ a closed em-

CH. Ill, § 19 MONOIDAL TRANSFORMATIONS 85
bedding such that x is mapped onto the origin. Then the composed rational
map 'linear projection of V from the point x\ V^ An+l -> Pw, is defined. We
can again try to resolve the singularities of this map with the graph method,
and then we obtain a diagram (V't g, h). It turns out that this diagram does
not depend on the choice of the embedding Vе-* Ал+1 (up to a uniquely
defined isomorphism) but is defined by the point x G V alone. The morphism
g: V ^ V which we obtain by means of this construction is called the
monoidal transformation of V with centre at the point x.
To prove the invariance, we first give a new construction of monoidal
transformations, which will be invariant by definition, in a significantly more
general context. Thereafter we show that this coincides in our particular case with
the graph of a linear projection.
Lemma and Definition 19.3. (i) The local version: Let Abe a ring. IС А
an ideal, and
Я= ©7*s ®K>QaJ*laKei*}CA[T]
a graded ring (the variable T defines the grading). Then the embedding A<~+R
defines a morphism
K'=Projtf ^ Г = Spec Л,
which is called the monoidal transformation of the scheme V with its centre
in the closed subscheme Spec (A/I).
(ii) The global version: Let V be a scheme, J С Oy a sheaf of ideals and
R = ФГ=л IK a sheaf of graded Oy-algebras on V. Then there exists a uniquely
defined morphism
g: F' = ProjR^F
which locally on V gives the morphism constructed under (\\ // is called the
monoidal transformation of V with centre in the closed subscheme W defined
by the sheaf of ideals I.
Let V be a variety over a field k. Then V' is also a variety and g is a biratio-
nal morphism which induces an isomorphism V' \ g~^(W)fX V^ W.
Let Wbea k-point of V (with its structure as a closed subscheme), V an
affine variety. Then V' (together with g) is isomorphic to the graph of the
linear projection of V from the point x.

86 TWO-DIMENSIONAL BIRATIONAL GEOMETRY CH. Ill, § 19
Proof. To carry out the global construction of monoidal transformations,
one must verify, in terms of (i), that for any multiplicative system SCA and
any ideal /$= 1m (As ®д1) С As there is a natural isomorphism
oo oo
0 /*alm((© Г )®аАЛ.
к=0 ^к=0 ' I
This guarantees the possibility of gluing together the affine pieces. The
details are left to the reader.
If the ring A has no divisors of zero, then the same is true for R. \fA is
Noetherian and / = (fx,... , /„), then R = ©~=0 IK TK is generated by the
elements/j T,... , fnT over A. In particular, V = Proj/? is a variety if
V = Spec (A ) is a variety.
Every point x £ V \ W has an affine open neighbourhood U = Spec A on
which I \v- 0V. The restriction#|£-1 (CO '■ S~l(U)~* U to this
neighbourhood is isomorphic to the canonical isomorphism Proj A [ T] 2J Spec Л. The
monoidal transformation is therefore an isomorphism outside W.
Finally, we prove the last assertion; it is local on V. Let V = Spec Л; choose
an embedding Vе* Spec Jc[Tq, . .. , Tn] for which x goes over in the origin.
This is equivalent to choosing a system of generators (/0,... , fn) in the
A>algebra A such that (f0,. .., fn) = 1С A is the ideal of the point x Arguing
as in Example 19.2, we find that the graph of the linear projection of V for
this inclusion is embedded as a closed subscheme in
ftqj^[r0,....rll]/(....//7;.-//7;.,...).
There exists a natural homogeneous epimorphism of A -algebras
oo
A[T0 f„l/(... JfTf -ffr ...) -* Ф /к Г : class of Tt - f.T.
к=0
To conclude the proof of the lemma one must only verify that this induces an
isomorphism of Proj (®^=0 IK TK) with the graph.
In fact, this epimorphism of rings induces a closed embedding of V into
the graph of the linear projection of which the image is everywhere dense.
Consequently, the image of V' must be defined by a nilpotent sheaf of ideals, which
can only be the zero sheaf because the graph is a variety. This proves the lemma

СИ. III, § 19 MONOIDAL TRANSFORMATIONS 87
We shall now study the local structure of a monoidal transformation of a
variety V with its centre at a non-singular closed point. The geometric meaning
of the theorem following below is that, as in the case of the linear projection
in P", at the place of x a projective space (of tangent directions at x) is glued
in, and its embedding in V has the standard conormal sheaf.
Theorem 19.4. Let V be an n-dimensional variety defined over a field k,
x E V a regular closed point with residue field k(x), and f \ V' -+ V a monoidal
transformation with centre x. Then the following statements hold'.
(i) W' = f"l(x) = V' X vk(x) is isomorphic to ?n~] as a k(x)-scheme and
it is locally defined by a single equation in V{i.e., W' is a Cartier divisor).
(\\)Let 7'С 0у be the scheafofideals defined by W' in V\ Then the
conormal sheaf Г/1'21ц/';i' invertible and isomorphic to the standard sheaf
(iii) All points of W' are regular on V'\ in particular, if V is regular, then
V' is also regular.
(iv) // V is a projective variety, then V' is also projective.
Proof. All assertions except the last one can be verified by replacing V by
a sufficiently small affine neighbourhood of x.
(i). Since the local ring 0X of the point x is regular, we can choose n
elements fj,. . . , tn ^mx which generate the maximal ideal mx С 0Х.
Thereafter we extend all ti to a section of the sheaf Oy in some affine
neighbourhood of л: and we shrink this neighbourhood until (t{ tn) exactly
generate in it the sheaf of ideals of the point x. Thus we get the following
situation: V = SpecM, / = (t],. .. , tn) С A is the ideal of the point jc,
dim^ V = n.
We have
K' = Proj( e A,
and
W' = V'®Ak(x)~ Proj( Ф (/* ®^//)Wroj( 0 /K//K+l) .
4=0 ' 4=0 /
[To prove the last isomorphism, we take the tensor product over A of the exact
sequence 0->/-> A -> A /I -+ 0 with /K; this gives/ ®AI« -*/* -► IK ®AAII-+0y

88
TWO-DIMENSIONAL BIRATIONAL GEOMETRY CH. Ill, § 19
from which IK/IK+l = IK(g)AA/[.] Therefore, to prove the isomorphism
W' s pj^ it is sufficient to verify that 0"=O/K//K+1 = 5fcu)(///2) (the
symmetric algebra). [Indeed, it follows from the fact that x is regular that
dim^^///2) = n, because I/I2 is the Zariski tangent space.)
There exists a natural epimorphism of rings
oo
^W7/7^"* Ф/К//К+1 , (Ш.2)
к=0
which for elements a^,. . . ,aKEl and a. = a; (mod /2) is defined by the
formula
^(flj... дк) =fl1...flK(mod/K+1).
One immediately verifies that у is well defined. Further, both rings have a
natural grading, so that to prove that \p is an isomorphism it is sufficient to verify
that the homogeneous components of the same degree are of equal dimension:
«"»«*) w2)- ("+;_')=d"W7/*+i.
The last equality follows from the fact that the completion 0X of 0X is
isomorphic to the ring of formal power series in л,.. . , //7, because 0X is
regular, and /k//k+1 = mj/wj+1. Hence W = Pj^. Further,
K'=Proj( 0/*7*) = UD^T).
Here
^,T) = SPec(®o/^)(/ir) .Spec^,....£]
(the adjunction of tJtj to A takes place within the fraction field of the ring A).
The ideal defining W' within D+(rzT) is generated by the elements f-/1,
7=1,...,/?, that is, by the elements tJX and ///1, tJtif j Ф i. But the
elements tJti are regular in D+(/;T), therefore rf-/l = 0 gives the local equation
of W' within V'. This proves assertion (i).
(ii). We have already established that W' is locally given by one equation,

CH. Ill, § 19 MONOIDAL TRANSFORMATIONS 89
which is not a zero divisor. From this it follows aJready that the sheaf I'/I 'w
is locally free. Identifying W' with Pjjrl by means of the isomorphism (III.2),
we obtain that I'/I'2 is glued together from the structure sheafs on
W П D+(tjT)^ Proj k[tx/th . . . , rw/rz] by means of the transition
functions /,-//.-, but this cocycle describes the sheaf 0(1), as is well known.
(iii). To prove the regularity, it suffices to check this separately on the
open sets £>+(/,-Г) = Spec Л [^/г/,..., *ИД/]. An arbitrary point of W' lies in
the closed subset Spec (A [tl/tft..., tn/t(] /(/,-/!)) = A*j£\ (a part of the
projective space P£r\ on which one coordinate function is not zero). Since Р^Г
is regular and f,-/l is not a zero divisor in A [t{lth .,., /„//,-], the desired result
follows from this.
(iv). We restrict ourselves to the case that k(x) = ky that is, the point x has
degree 1. Let VC?N be some projective embedding. In Section 19.3, we
established that V is isomorphic to the graph of the linear projection of К into
?N~l from the pointx Therefore V'CVX ?*~l C?NX ?N~{, and the
last product, as is well known, is projective. This proves the theorem.
Remark 19.5. It is clear from 19.3 that monoidal transformations are
compatible with the extension of the base field in the following sense of
the word. Let V be a variety over k, W С К a closed subscheme over k, and
/: V' -> V the monoidal transformation with centre W. Then for every
extension of the field of constants К D к the morphism f<g)K: V' ®k-* К ® К
is the monoidal transformation of V ® К with centre W ® K.
In particular, let W = x be a closed point and let the extension k(x) be
separable. UK is a Galois extension containing k(x)y then W ® К С V ® К is the
disjoint union of [k(x): k] closed points (as a subscheme), and the monoidal
transformation with centre W ® К is a succession of monoidal
transformations with these points as centres, composed in any order. (We suggest that
the reader specifies this statement.)
Conversely, let К Э к be a separable closure of the field k, and let there be
given on V ®k К a closed subscheme W' which is a disjoint union of a finite
number of closed points which are conjugate over к (in the sense of the
action of the Galois group on V* ® k К through the second factor). Then
W = W®k K, where W С V is a closed point, and the monoidal
transformation with centre W' is obtained by extending the field of constants to К out
of the monoidal transformation with centre W.
These considerations permit us in particular to pass from the case of a per-

90
TWO-DIMKNSIONAL BIRATIONAL GEOMETRY CM. Ill, § 20
feet field к to the case of an algebraically closed field, which gives the
possibility of an account in terms of geometric points.
20. Monoidal transformations and divisors
In this section we shall study the effect of monoidal transformations on
divisors and invertible sheaves over an algebraic surface V defined over a field k.
We recall only the basic facts from divisor theory; for details we refer to
Mumford's book [2], lectures 9, JO and 12.
20.1. Effective divisors. An effective (Cartier) divisor on V is a closed sub-
scheme D for which the defining sheaf of ideals is locally smooth. (Since V is
a variety, in particular an integral scheme, this requirement is equivalent to
the invertibility of the sheaf of ideals.) Then the support SuppZ) is a
(generally speaking irreducible) curve or empty. Divisors can be added by
multiplying their ideals.
Suppose that we have two divisors Dy, D2CF such that the intersection of
their supports is zero-dimensional. Then the intersection /)j C\D2 as a scheme
(it is defined by the sheaf of ideals 7 j + 12* where IK defines DK) is affine
and zero-dimensional over k: Z)j OZ)2 = Spec A, where A is a
finite-dimensional ^-algebra. The number
(D]tD2) = dimkA
is called the intersection number of the divisors D\ and D2. The intersection
number is invariant with respect to extensions of the field of constants К D k\
(Dl®K,D2®K) = d\mK(A ®kA) = dim^/4 =(DVD2).
Because A = Ф^еБресЛ^л (waere Ax is the local ring of Spec A in the point
x ESpec Л), we have
(/>,,/),) = E *™kAx = S (P{fD2)x.
jteSupp Dxr\D2 *eSupp DlnD2
The ring,4л. can be calculated in the following manner: Let ty (resp. t2) be the

CH. Ill, § 20 MON01DAL TRANSFORMATIONS AND DIVISORS
91
local equation of the divisor Dl (resp.£>2) al tne point x, that is,7lJC = Qxtx,
72rx=0xf2.Then
Ax = 0xi(tvt2).
The dimension of this /c-algebra is the local intersection number of Dj and £>2.
It is equal to zero if one of the elements tlt t2 is invertible in 0X, i.e., if the
divisor /)j or D2 does not pass through x. It is equal to one if к (x) - к and
(fj, t2) = mx (the maximal ideal in О*), i.e., if/{(mod m£) and f2 (mod /w£)
are linearly independent over k(x). This means that D^ and D2 intersect each
other transversally at the point xt i.e., they have different tangents in x. In
general,
(DvD2)x = lk(X):k]dimk(x)0xl(rvt2).
The first factor here reflects the circumstance that the point x decomposes
into [k(x): k] geometric points over the closure of the field к (if k{x)jk is
separable); the second factor describes the intersection number of the divisors
Dy andD2 in these geometric points.
20.2. Let/: V' -* V be any morphism of surfaces,!) С К a Carrier divisor.
l(f(V') <£ Supp D, then the inverse image f*(D) is defined. It is a Cartier
divisor on V'\tf D is defined by the sheaf of ideals I C 0V, then/*(£>) is
defined by the sheaf of ideals/*(1) С Оу. We shall now investigate this inverse
image operation in the case where/is a monoidal transformation at a closed
point. The result can be more conveniently formulated if we make use of the
definition of a Weil divisor. An effective Weil divisor on К is a linear
combination of irreducible curves (that is, of one-dimensional closed subsets) on V
with non-negative integer coefficients (as an element of the free Abelian group
generated by all such curves).
If V is a non-singular surface, then the semigroups of Cartier and Weil
divisors are isomorphic. In fact, in this case any irreducible curve on V is locally
given by one equation (as a reduced subscheme) which permits us to construct
a Cartier divisor from a Weil divisor. The construction of the inverse map
rests mainly on the fact that the local rings of V are regular, and that therefore
the factorization of polynomials in them is unique (cf. Mumford [2], lecture 9).
Locally, therefore, every Cartier divisor can be uniquely represented in the
form of a linear combination of Weil divisors given by prime elements.

92
TWO-DIMENSIONAL BIRATIONAL GEOMETRY СИ. Ill, § 20
Definition 20.3. Let К be a non-singular surface over к, x G V a closed
point, D С V an effective divisor, and V' -* К the monoidal transformation
with centre x On V there exists a unique (Weil) divisor Ea^D,- = f~^(D) (the
/)7 are irreducible curves) such that:
(i) 2я,-/(/),) = D;
(ii) the coefficient of/_1(x) in/-1(/)) is equal to zero.
The divisor/-^(D) is called the proper inverse image of D.
In other words, the map/"1 is a homomorphism of semigroups which on
the generators is defined in such a way that for every irreducible curve D С V
the curve /"*(/)) is the closure of the inverse image of D \y^ix\ in V ^f~l(x).
It is clear that we have f~l(D) =f*(D) for every divisor О С V for which
x $. SuppD. However, if x GSuppD, thcn/*(D) =/-1(D) + some multiple
of/_1(jc). The divisor/-1 (*) is a projective line on V'\ we siull presently
describe the difference f*(D)-fl(D) and the behaviour of/_1(/)) in the
neighbourhood of/~*(jc). To be able to see things better geometrically, we restrict
ourselves to the case of an algebraically closed field k. The reader can without
difficulty supply the changes necessary in the general case, but for our
objectives this result will be sufficient in view of the compatibility of the basic
constructions with extensions of the field of constants.
Let t G 0X be a local equation of D in a neighbourhood of jc. Wc designate
by e = e(x, D) the number such that
temex^mex+i.
The number e is the multiplicity of the point x on D.
Further let J = t (mod w£+1) G mex/m€x+l s Se{mxlm2x) {d. the proof of
Theorem 19.4 (i)). In other words, T is some form of degree e in two variables
(a basis of mx\m\ over /c), the leading form* of the local equation of the
divisor/). We have therefore (using that к is closed)
7-lV,'' -
/ = )
where the 7£. G mxjm\ are different elements of the Zariski tangent space,
ei >0 and S[=1 ei - e. Geometrically this means that the divisor/) in a neigh-

СИ. III, § 20 MONOIDAL TRANSFORMATIONS AND DIVISORS 93
bourhood of x 4up to a higher order of smallncss' behaves itself as the union
of an enfold curve /j = 0, an e2-fold curve l2 - 0, and so on. Moreover, x
is a simple (of multiplicity one) point on each of the curves /,• = 0 (the
equations of these curves are only defined mod m^). We shall therefore describe
this situation by saying that the divisor/) hasr different tangents at x (with
multiplicities elt. . . , er, respectively).
Proposition 20.4. Let xG V be a regular closed point on a surface defined
over an algebraically closed field k, let f: V' -> V be a monoidal transformation
with centre xy D С V an effective Car tier divisor and x E Supp D, W =
= /-1 (x) = P£, the inverse image of the point xt is a Cartier divisor on V\
The following statements hold:
(i) /*(/)) = f~l (D) + e W\ where e is the multiplicity ofx on D.
(ii) Let D have r different tangents at x of multiplicities e j,... , er. Then
the intersection f~*(D) П W' consists ofr closed points x\,. . . , x'r which
naturally reflect the tangents ofD at x, and
xi
(Informally speaking, the monoidal transformation 'splits up' the branches
of D passing through x in different directions.)
Proof. Since/induces an isomorphism V' ч W' 2; F\{x], and as W' is
irreducible, it is clear that/*(D) -f~x(D) is some multiple of W\ We need
only show that this multiplicity is equal to e. Replacing V by a sufficiently
small affine neighbourhood of x, and W' by its inverse image, we can assume
that the following conditions are fulfilled:
(a) V = Spec A \ the ideal of the point x in A is generated by two elements
tlt t2 ЕЛ
(b) The divisor D on V is given by one equation t = 0, t G A; moreover,
te(tvt2y^{tltt2y+K
Then V = Spec (A [f j/fj])u Spec(,4 [t2/tx ]) and W' is given on these
two open sets by the equations t2 = 0 and tx = 0, respectively. It follows
immediately from condition (b) that
teA[t}/t2] t\y teA[t2/tx] t\.

94
TWO-DIMENSIONAL BIRATIONAL GEOMETRY CH. Ill, § 20
Since tj\ = 0 is the equation of /*(/)) within V', it follows from this that W turns
up in /*(£>) with multiplicity at least e. If this multiplicity were greater, then we
would have t E A [/ //21 /^+1. We shall show that it would follow from this
that/ 6 (/j, r2)f+1, which contradicts our assumptions. In fact, Л [fj/^] =
= ^[7,]/(r2r-f1),henceyl[/1//2]/(/1/l,r2/l)^^ir],whereA: = it(i)and
Tis the class of Г]Д2 modulo the ideal (^/1, b/1). If/^+1 divides /, then
tlte2£(txl\,t2l\)CA\t^t2],
but denoting by T =f(t^f T2) = /(mod m£+I) the leading form of t as a
polynomial in lv T2 (7, = ^(mod wx)), we have
/(Г, l) = (f/^(mod(yi,/2/l))
in Л [/1//2]/(/,/l, r2/l). The desired result follows because T Ф 0.
We shall now calculate the intersection/-1 (D) П W\ let us say within
Spec /4[/i//2]. The divisor f~*(D) is given by the equation ///2 = 0 and the
divisor W by the equation /2/l = 0; therefore
rl(D)nW' = SptcA[tl/t2]Kt1l\j/te2)
= Spec.4[/1/r2]/(rl/l,r2/l,rAp .
Taking first the quotient by (fj/1, /2/l) and then by i/te2 mod (/j/1, f2/l), we
obtain, in the previous notation,
f~\D) П W = Spec k[T] If(T,\) .
The various zeros of the polynomial/(T, 1) give the various points of the
intersection, and the multiplicity of each of them coincides with the multiplicity
of the corresponding zero. This completes the proof of the proposition.
20.5. The semigroup of effective divisors on V is included in the group
Div V, the elements of which are called divisors. Let/: V' -* Vbe some bira-
tional morphism defined over k. Then the map/* can be extended to a group
homomorphism /*: Div V -+ Div V'. and its image has a canonically defined
complementary direct summand in Div V'. Indeed, we define a homomorphism

СИ. Ill, § 20 MONOIDAL TRANSFORMATIONS AND DIVISORS 95
/+:Div K'->Div V,
in the following way: Let DC V' be an irreducible curve; then )\{D) is either
the curve/(D) (the set-theoretical image) or zero iff(D) is a closed point. It
is obvious that Д о /* is the identity map, so that
Div K'=/*(Div К) ©КегД .
In the case where/is a monoidal transformation with its centre at a closed
point, Ker Д =ZW\ where W' is the inverse image of that point. In the
general case, Ker/+ is generated by the collapsed curves (with respect to/). The
maps/*(resp. Д) transform Div into a contravariant (resp. covariant) functor
on the category of surfaces with birational morphisms.
20.6. The Picardgroup. Let D be a divisor on V, U С V an open set, / a
local equation for D on U. Those open sets on which D\y is given by one
equation constitute a basis for the open sets, and the presheaf
UH>rl\\U, 0V)
which is naturally defined over this basis is a sheaf. It extends uniquely to an
invertible sheaf on V% which is denoted by 0 y(D). The map D *-* class of
0 y(D) defines an epimorphism of groups Div V -* Pic V\ the kernel of this
map consists of the 'principal' divisors which can be given by one equation
globally.
Suppose that D is an effective divisor. Then 0 y(-D) is a coherent sheaf
of ideals on K, and there is a canonical exact sequence
0^0V(-D)^0V-+0D-+0,
where Op is the structure sheaf of D as a closed subscheme of V. In the case
where К is a projective smooth surface, this gives the possibility to point out
an important cohomologicat description of the intersection number.
Let L be an invertible sheaf on V\ we set
X(L) = &\mkH°(V, L) - d\mkHl(V,L) + <ЬткН2(У,Ь).
Then we have the following:

96
TWO-DIMENSIONAL BIRATIONAL GEOMETRY CH. Ill, § 20
Proposition 20.7. Let D]fD2C V be two effective divisors on a smooth
projective surface V and let their intersection be ^-dimensional. Then their
intersection number is equal to
(Dv Z>2) = X(0y) - xWyi-D^)- xiOyl-D^ + xiOyi-D^D2)) .
For a proof see Mumford [2], lecture 12. It is based on the fact that
(DVD2) = dimH°(V, 0D] ® 0z>2) = x(0Z)i® 0Dj),
and on the existence of the locally free resolvent for 0d( which was described
above.
The role of this result is that it permits us to give a canonical definition of
the intersection number as a scalar product on the whole Picard group y and
also on all divisors, even if their intersection is not 0-dimensional.
Lemma and Definition 20.8. Let Lj, L2 be two invertible sheaves over a
smooth projective surface V. We set
{LyL2) = x(0v)-x(Lil)-x(L-{)+x(Lil®L-1).
This 'intersection number is a bilinear symmetric scalar product, Pic VX Pic K-*Z,
which coincides with the geometric intersection number of divisors in those
cases where the latter is defined:
(0y(D])i0y(D2)) = (DvD2)i
and it can serve as a definition of(D^, D2) in the general case.
As regards the proof, we again refer the reader to the lectures of Mumford.
Now let /: Y' -► V be a monoidal transtormation with its cenire at the
closed point x, and let W' be the inverse image of this point.
Lemma 20.9. f induces an embedding of Picard groups f* : Pic К-►Pic V
(corresponding to the homomorphism f* of the divisor groups) which preserves
the intersection numbers:

CH. Ill, § 20 MONOIDAL TRANSFORMATIONS AND DIVISORS
97
(rLvrL2) = (LvL2)>
for all Lx, L2 ^Pic V. Moreover,
(W, W')=-d, d = [k(x):k] , (f*L, И/') = 0,
for all L G Pic V (we write W' instead ofOy,(W')).
Proof. The sheaf f*(L) is invertible on V for every invertible sheaf L on V\
in particular, if L - 0y (£>), where D is an effective divisor, it immediately
follows from the definitions that/*( 0V(D)) is canonically isomorphic to
0y(f*(D)). Therefore the maps/4 on the groups Div and Pic correspond.
The following general observations are useful for the calculation of (W, W').
Let L be an invertible sheaf and/) a curve on V\ Then
(/,, 0V. (D)) = deg(X^) = X(0D) - X(L~] \D)
(see Mumford [2],lecture 12). We now take D = W and /, = 0V.(W). It
follows from Theorem 19.4 that the curve W' is isomorphic to PL . , so that
x(Ow') = d. (Note that x is calculated by taking dimensions over k, and not
over k(x)\) Moreover, the sheaf of ideals I' defining W' С V' is 0y{-W)\
therefore, L~x \w> = V\w' = I 'Д'2 - 0pi (1) (Theorem 19.4 (ii)).
Consequently,
X(L-I\w.) = x(0pl (\))-dinhHu(?l 0(\))-^тН\?1к(хГ0(\))
vk(x)
from which, finally,
(0V'(W'),0v,{W')) = -d.
Now let DC V be an effective divisor and e the multiplicity of the point
x on IX According to Proposition 20.4,
f*(D)=f-l(D) + eW ,
and
(r\D)yW') = ed.

98 TWO-DIMENSIONAL BIRATIONAL GEOMETRY CH. Ill, § 20
[This has only been proved for d = 1; the general case immediately follows
from this by extending the field of constants if /c(jc)//c is separable; or it can
be verified by changing slightly the arguments of Proposition 20.4.] We find
from this
(/*(£>), W) = (Г1 (£>), W) + e(W\ W) = ed - ed = 0 .
Because the classes of the sheaves f*(D) generate /*(Pic K), we find that this
group is orthogonal to W'. Finally, let D]f D^ be effective divisors on V such
that their intersection is 0-dimensional and does not contain x. Then
iPvD2) = (r\Dx\rx(D2)),
because Dj П£>2 is contained in the open set K\ \x) and the restriction of
/to this set is an isomorphism. Further
(г1Ф1),/-1Ф2))=(ГФ,)-^^:г(^2)-е2н'')
= (f*(D1),f*(D2)),
because at least one of the two multiplicities e{, e2 of the point xonDj, D2
is equal to zero, and W' is orthogonal to/*(Pic V). But the sheaves
0y(D)y where D does not pass through x, generate Pic V. (The orthogonality
of/*(Pic V) and W' also follows immediately from this remark.) This
concludes the proof of the lemma.
Corollary 20.9.1. Under the conditions of Lemma 20.9, we have
Pic (/'=/* (Pic V)®Zw ,
where w is the class of 0y(W)and the subgroups f* (Pic V) and Zw
determine one another uniquely as orthogonal complements with respect to the
intersection number.
Proof. As was remarked in 20.5,
DivK'=/*(Div K) ®ZW' .

CM. Ill, § 20 MONOIDAL TRANSFORMATIONS AND DIVISORS
99
The kernel of the canonical homomorphism Div F'~> Pic V' is completely
contained in/* (Div V), because if/*(D) + aW is a principal divisor, then
0 = (f*(D) + aW,W')=-a.
Consequently, Pic V' = /*(Pic V) © Zw. The second assertion also follows
immediately from the lemma.
The last result of this section describes the behaviour of the canonical
class со ^G Pic V under monoidal transformations.
Proposition 20.10. Under the conditions of Lemma 20.9, we have
where w is the class of the sheaf Qv,(№) in Pic V.
Proof. It will be convenient to use the following constructive definition
of the class со. Let £1G П2 (k(v)/k) be some exterior form of degree 2 in the
field of rational functions on V, For every closed point л: G V, we define the
divisor К of the form CI in a neighbourhood of л: by the following condition:
if £2 = tdz^ Л dz2, where z j, z2 G mx are local parameters, then Ms a local
equation of К atx That this is well defined follows without difficulty from
the invertibility of the Jacobian under a change of the system of local
parameters. Under these conditions we have
cov= class 0V(K) .
Therefore
/*(coK)= class Oy.tf*(АО).
On the other hand,u>v>= class 0V,(K'), where A"' is the divisor of the form
/*(£2), the canonical image of CI in the field k(v) of rational functions over P'
which is identified with k(u) by means of/ The form О can be chosen such
that A' is not contained in the support of K. Then it is clear from the
definition that/*(/Q = f~l(K) and that K' - f*(K) is some multiple of №. To
calculate this multiplicity, it suffices to consider the situation locally in a
neighbourhood of a closed point jy G W'.

100
TWO-DIMENSIONAL BIRATIONAL GEOMETRY CH. Ill, § 21
Letzlt z2 be local parameters inx, £2 = tdz} л dz2, t invertible at д:. It is
clear from the proofs of Theorem 19.4 and Proposition 20.4 that (z]/z2, z2)
forms a local system of parameters in a neighbourhood of a typical closed
point on W'm Therefore we have
r(n) = tz2d(zx/z2)Adz29
and because / is invertible at x, tz2 is a local equation of W' on V' together
with z2. This proves the proposition.
21. The main theorems on birational maps
In this section wc shall formulate, guided by the ideas and results introduced
above, the main technical statements, which afterwards shall be used in the
birational theory of cubic surfaces.
Theorem 21.1 (Resolution of singularities of a map). Let V be a smooth
projective surface over a field kt W a projective variety and f: V -* W some
birational map. Then there exists a resolution off,
V
'w
(cf Section 19.1 )f in which g decomposes as an iteration ofmonoidal
transformations with their centres at closed points which lie over points where f
is not defined.
Proof (outline). First of all, any rational map/: V^ W of projective
varieties is defined in all normal points of codimension 1. For the proof of
the general case one first reduces to the case W = P1; we omit this reduction.
If W = P1, then/is represented by a rational function у on V\ at any normal
point x of codimension 1 on V, the function \p is either defined or it has a pole,
because 0x is a discretely valued ring, and poles correspond to the point at
infinity on P1. Therefore, points where/is not defined (in which the function

CH. Ill, § 21 THE MAIN THEOREMS ON BIRATIONAL MAPS
101
leads to 0/0) do not exist. In particular, if К is a smooth projective curve, then
every rational map of it is a morphism. If V is a surface, then the points where
/is not defined are isolated. To resolve/, it suffices to consider them
separately; moreover, we can again assume that W = Pl, so that we need to resolve
the points where a rational function is not defined; to do that, it suffices to
work locally. In order to illustrate the principles of the proof, we consider
some of the simplest cases:
Let у be a rational function on V and л: е'К a point where </? is not defined.
For simplicity, we shall assume that к is algebraically closed (or k(x) - k).
Further, let the divisor of <p in a neighbourhood of x be equal to Z)q —Д^,
where Dq and Ож are effective divisors which do not have a common
component. The character of the singularity of x is determined by the complexity of
the behaviour of Dq, D^ at the point x. Let us consider the behaviour of \p
and its divisor under a monoidal transformation /: V* -* К with centre jc
under various partial assumptions with respect toD0 and D^.
Case 1. The multiplicity ofx on Z)0, Dw is equal to 1, and Dq, D^ are not
tangent to each other at x. Then the divisor of \p on V' is equal to
in a neighbourhood of W' =f 1(jc); апё/~1(/>0),/~1(/>00) no longer
intersect in a neighbourhood of W' (cf. Proposition 20.4). In this simplest case,
therefore, the point of non-definition is removed by one monoidal
transformation.
Case 2. The multiplicity ofx on D0 and DTO is equal to 1, but DQ and D^
are tangent to each other. In this case, after a monoidal transformation with
centre*, the curves/-1(Do) and/-1 (A») will intersect each other in a
neighbourhood of W' at precisely one point, as before, but their order of tangency
does not increase, and after a finite number of repeated monoidal
transformations it diminishes.
Case 3. D0 has one tangent of multiplicity e$ at x and D^ has one tangent
of multiplicity e^ at x, and these tangents do not coincide. After a monoidal
transformation, the divisor of <p will have the form
rl(DQ)-f-l{DJ+{eQ-ejW
locally in a neighbourhood of W'.Toi e0 = e^, the point of non-definition
vanishes; for e0 > еж it emerges at a point of the intersection of /""^(A»)

102
TWO-DIMENSIONAL BIRATIONAL GEOMETRY CM. Ill, § 21
with W', and for eQ < еж at a point of the intersection of /~l(£>0) with W\
but the multiplicity of one of the components of W will be less than the
maximal multiplicity at x.
These examples give a sufficiently clear picture of the character of the
'simplification1 of points of non-definition and of the invariants which must
be watched. For more details we refer the reader to the lectures of Safarevic
[2] (surfaces over an algebraically closed field) or |l] (smooth 2-dimensional
schemes).
Example 21.2. The structure of the map tx. Let VC P3 be a smooth
cubic surface, x £ V(k) a &-point of general type. The map tx: V-*• К was
described algebraically in Proposition 12.13. In particular, it induces an
automorphism on the complement of C(x), the intersection of the tangent plane at x
with V. The geometric map tx looks as follows:
Let V' 4- К be the monoidal transformation with centre x. Then there
exists on V' an automorphism of order 2, t'x : V' -> V\ such that tx of = fo t'x.
Moreover/induces an isomorphism
кЧ(Н/'и/-1(ОД));Гчф),
and on this open set t'x acts precisely as tx on V^C(x). In addition, tx
interchanges W' and/-1(C(jc)). These two curves intersect at two different
geometric points (as shown in Fig. III.l) if C(x) has distinct tangents at*. If* is
\ /
\ /
V
\.
IV-
\
J
Cix)
Fig. III. 1.

CH. HI, § 21 THE MAIN THEOREMS ON BIRATIONAL MAPS
103
a cusp for C(jc), then W' and f~^(C(x)) are tangent to each other at exactly
one point.
A different method of looking at the map tx, which is often useful, is the
following: Let P2 С Р3 be a plane which does not pass through jc. The
projection from* of P3 on P2 is a rational map which is resolved by the monoidal
transformation U' ?> P3 with centre jc; it defines a commutative diagram
The composed map V' -* P2 is a morphism of degree 2, and tx is the
automorphism: interchange the sheets of this two-sheeted projection'. As an exercise,
we suggest that the reader should translate these assertions into algebraic
language and verify them.
Control questions'. How can one resolve the singularities of the map tx in
the case when x is not a point of general type on the surface? Can the map
tx be a morphism? {Answer: Yes, if C(x) consists of three lines intersecting
at the point jc.)
Example 21.3. Stereographicprojection. Let КС P3 be a smooth quadric.
It is well known that it is isomorphic to P1 X P1 (we here take the base field
to be algebraically closed). The intersection C(x) of the surface К with its
tangent hyperplane at an arbitrary point jc E К consists of two lines intersecting
each other at this point; these are the fibres with respect to the two projections
of V on P1. Let P2 С P3 be a plane which does not pass through jc. We
consider the rational map
r : K->P2 ,
which is a morphism outside C(x) and which is defined by: the points jc, у Е V
and r{x) E P2 are on one line. Its resolution looks like
V
+ P2

104 TWO-DIMENSIONAL BIRATIONAL GEOMETRY CH. Ill, § 21
where/is the monoidal transformation with centre*, andg is the monoidal
transformation with as its centre the two points of the intersection of P2 with
the components of C(x). In other words,/blows up*, and# collapses the
/-1 inverse image of C(x). This can be easily proved by a local analysis. We
remark that the components o( C(x) are isomorphic to P1; their
self-intersection numbers on ^are zero; after being lifted to V\ they become - 1, which
easily follows from Lemma 20.9.
Theorem 21.4 (Structure theorem for birational morphisms). Let /: V -> IV
be a birational morphism of smooth projective surfaces over a field k. Then
f is an iteration of monoidal transformations with their centres in closed
points. In other words, there exists a sequence of surfaces and morphisms
f f f
v -V v .L v i!L v -w
such that fi : J^ -* Vi is a monoidal transformation with its centre at a closed
point xtE V(and such that f = fr ofr^ о .. . o/1#
We omit the proof (cf. Safarevif [1] and [2]). However, its main feature
is needed for further applications, and therefore we formulate it separately.
Lemma 21.4.1. Let /: V-> W be as in Theorem 21.4 and let the rational map
/-1 be not defined at the closed point x E W. Then f decomposes into a
product V ~+ W' -v W, where h is the monoidal transformation with centre x,
and f' is some morphism.
Informally speaking, a 'not being defined' of the type of a 'monoidal
transformation' is the most economical kind of'not being defined' of a
rational map.
From Theorem 21 A, we immediately obtain the following useful
corollary:
Corollary 21.4.2. Let /: V -+W be a birational map of smooth projective
surfaces. Then in every resolution
-/,V

CH. HI, §21 THF MAIN THEOREMS ON BIRATIONAL MAPS 105
of [the morphisms g and h are iterations of monoidal transformations with
their centres at closed points, provided V' is smooth.
Examples 21.2 and 21.3 and the answers to die control questions can
serve as illustrations of this general principle.
Theorem 19.4 describes the structure of exceptional divisors, the inverse
images of a point jc under monoidal transformations with centre *. One of the
useful results is a partial converse to this theorem:
Theorem 21.5 (Collapsing theorem)./,?/ V be a smooth projective surface
over a field к and let W' С V' he an irreducible effective divisor on V\ which
as a scheme is isomorphic to ?%, where K/k is some finite extension. In
addition, let one of the two following equivalent conditions be satisfied:
(i) 7'/7 '~\W' is isomorphic to 0(1) on PlK (here T С Qw> is the sheaf of
ideals defining W').
(\\)(W\ W') = -[K:k].
llien there exists a birational morphism f: V' -> V which is a monoidal
transformation with as centre the regular closed point x =f(W')E V\ moreover, it
induces an isomorphism К ^ k(x). The morphism f which collapses W' is
uniquely defined up to isomorphism. The surface V is projective.
Proof (outline). We restrict ourselves to showing how to construct the
morphism/which collapses W'. For the verification of its nice properties, see the
lectures of Safarevic [1 ] or, for surfaces over an algebraically closed field, the
treatise of M. Artin [1].
Let d = [K : k]. Let L be a very ample sheaf on V' such that the following
conditions are satisfied:
Hl(V\L) = 0 ,
(/„ Qv,(W')) = ad, aeZ .
(As L one can take, for example, a sufficiently high power of an arbitrary
initial very ample sheaf.) We consider the standard exact sequence
0+ 0v,(-aW)-* 0v.-> QaW,^>Q ,

106
TWO-DIMENSIONAL BIRATIONAL GEOMETRY CM. Ill, § 21
and take its tensor product with the invertible sheaf L ®Qy. Qy^aW). The
exactness is maintained under this, and the third term remains as before.
Indeed, the sheaf L ® q ,0y(aW'), restricted to aW\ has degree
(I, Qv,(aW)) + (aW\ aW') = a2d -a2d = 0.
This restriction is therefore isomorphic to O^t because the invertible sheaves
on P1 are defined up to isomorphism by their degree (this same argument shows
the equivalence of conditions (i) and (ii) of the theorem). Therefore we obtain
an exact sequence of sheaves
0->L->L ®Qv,Qv,(aW')^0QW,^b,
which gives an exact sequence of groups of sections:
Let s0eH°(V\ L ®0r 0 y(aW')) be the inverse image of 1 eHQ(V,QaW>),
and let sly... , sn 6 /(# °( V\ L)) be a basis of this space. The &-morphism
/': V->?% defined by the sheaf L ®Qy 0 y(aW') and its set of sections
(Sty..., sn) is birational because it is an isomorphism with f(V) outside W''.
Moreover, for every jc € W' we have s0(x) Ф 0, s^(x) = ... = sn(x) = 0, so that
the whole divisor W' is collapsed into the point (1, 0, ... , 0) E P£.
This construction has the following geometric meaning. Let V' С ?™
from the very beginning, and let L' = 0(1) be the induced sheaf on V'. Replace
L' by L = L'e such that the conditions mentioned in the beginning of the proof
are satisfied. Then the zeros of the sections of the sheaf L on V' are geometric
sections of V' with hypersurfaces of degree e. The zeros of the sections of the
sheaf I ®Qy 0y(aW') form a linear system in which there is a linear
subsystem of codimension one consisting of hypersurface sections of degree
e plus aW'. All these sections are zero on aW and there is only one more
independent section Sq, which is constant on aW and which guarantees that there
is no 'not being defined1 in the points of W'.
21.6. The curves W' on V' which satisfy the conditions of Theorem 21.5 are
called exceptional curves. (In an older terminology, 'irreducible exceptional
curves of the first kind', in contrast with reducible curves which can be col-

CH. Ill, § 21 THE MAIN THEOREMS ON BIRATIONAL MAPS
107
lapsed by a birational morphism on the one hand, and on the other hand,
curves 'of the second kind' which can be collapsed under some birational map
with points on this curve where the map is not defined).
Combining Theorems 21.4 and 21.5 yields the following important concept:
Definition 21.7. Let К be a smooth projective surface over a field k. Then
Vis called minimal if one of the following two equivalent conditions is
fulfilled:
(i) Any birational &-morphism /: V-* V\ where V' is a smooth projective
surface over k, is an isomorphism (i.e., it is impossible to shrink V).
(ii) There are no exceptional curves on V.
We immediately remark that minimality can be destroyed by an extension
of the field of constants. This circumstance will repeatedly arise further on
because it is characteristic for surfaces which are birationally equivalent to
P2 over the closure of the base field. In order to follow this phenomenon, we
shall use the following criterion for minimality:
Theorem 21.8 (Minimality theorem). Let V be a smooth projective surface
over a perfect field kt and let G = Gal (k/k) (the Galois group of the algebraic
closure of the field k). We define the natural action ofG on the group
Div (V ® H) (by the action on the field of constants к and the trivial action
on V). The surface Vis minimal if and only if for every exceptional curve D
on V ®lc there exists an element sEG such that s(D) Ф D and the
intersection D П s(D) is non-empty.
Proof. In fact, suppose first that V is not minimal. Then there exists an
exceptional curve D on К It is easy to see that D® к on V® к splits as a
disjoint union of a finite number of exceptional curves which are conjugate
to each other. This follows from the fact that D is the inverse image of some
closed point x with respect to some monoidal transformation/: V-* V\ and
then/® к : V® к -► V1 ® к will be a monoidal transformation with as
its centre the subscheme x® к which splits up as a union of degx= \k(x)\ k]
conjugate closed points:
d d
x®k = U x.9 D®k=\J (f®k)~l(x.).
1=1 1=1
None of the components of the curve D®J<: satisfies the condition of the
theorem.

108
TWO-DIMENSIONAL BIRATIONAL GEOMETRY Of. Ill, $21
Conversely, let /)j be an exceptional curve on К® к such that all its
conjugates D| D4 are pairwise disjoint. We shall first of all show that D' -
- 2^=1 Z). comes from some divisor D on V: D' = D ® к . This is a particular
case of a useful general lemma on 'Galois descent*.
Lemma 21.8.1. Let V be an irreducible variety over a field kt К Э к а
Galois extension with group G. The natural map Div V -+ Div (V ® K):
Dt+D ® К identifies Div V with the subgroup of G-invariant divisors
(Div(K® K)f.
Proof. First of all, the map/) •->/) ® К is injective and its image belongs to
(Div(F ® K))G. Conversely, we shall show that any element Z)'e(Div(F®K))(
comes from a divisor on V. If suffices to consider the case when /У=2т../).,
where the D{ are effective and irreducible divisors over К which are conjugate
to one another (over k) and pairwise different. Indeed, such divisors constitute
a free system of generators for the group (Div(7 ® K))G.
As every divisor on V ® К is defined over some finite extension of the
field k, we can assume that K/k is finite. Let [K : k] = nd. We show first that
the divisor nD' comes from V. In fact, let jc € V be an arbitrary point, U3x
an affine neighbourhood such that the divisoiDj is given by one local
equation tx in U <8)K. Then t = Hje(75(/>1) is a local equation in 17® К for the
divisor nD'. However, t E Г (U ® A', Qv ф К )G= Г(И, Оу), and therefore
nD' = D ® A', where D is given over U by the equation t. (It is clear that when
multiplying t\ by an invertible element t is also multiplied by an invertible
element, so that the local equations for D are compatible.) Now we must show
that if an effective divisor/) G Div V can be divided by an integer m in
Div(K ® A'), then this can be done already in Div К It suffices to verify that if
D is irreducible, effective and not divisible by any integer > 1 in Div V, then
it is also not divisible in Div(F ® A'). We consider D as a closed subscheme
in V. Then the fact that it is not divisible in Div V implies that there are no
nilpotents in the structure sheaf Op. But because the extension К Э к is
separable, there are also no nilpotents in the sheaf Of) g> % = Qd ® ^. This
concludes the proof of the lemma.
21.8.2. We return to Theorem 21.8. We recall that an exceptional curve
D{ on V ® к is under consideration and that D2, •. • , Dd are the other
conjugates of/). Let tf^D. =D ® k,DG Div V. We shall show that D is an
exceptional curve on V. Wc exploit the criteria of Theorem 21.5. Clearly,

CH. Ill, § 21 THE MAIN THEOREMS ON BIRATIONAL MAPS
109
(D,D)= -d .
It is therefore sufficient to verify lhat (as a scheme over k)D is isomorphic to
PJ^, where К is the minimal field over which the curve Dx is defined (in other
words, К = kH, where H = {s e G I s(Dx) = Dx}).
We introduce а К -scheme structure on D as follows. The group G acts on
the structure sheaf 0p^ (as quotient sheaf of 0y^) and 0£>g>£ = ©Ф).®£>
where 0]o.®k is concentrated on the component Dt ® ~k С D ® k. The sheaf
coincides with the image of the homomorphism
(0Dl®b)H^(®0D.®-kf
f *►(...,v:...)
if G = иД, sz#, D, = s^. On the other hand, there is a natural sheaf of K-
algebra structures on (0# $$ к)** because kli = K. We now show that
the K-schemes D and Pj^ are isomorphic. They become isomorphic over
к because D ® k, as shown above, coincides with (Dj ® к)и ® £ ^ Pi
since Dj is an exceptional curve. Therefore £> is a form of the projective line.
It is known that a non-trivial form of the line over К has no /C-points; on the
other hand, there is an element of degree 1 in Pic D (induced by the conormal
sheaf to D), and its non-zero section becomes zero in a rational /C-point on D.
Consequently, D = PJ^, which concludes the proof of the minimality theorem.
Example 21.9. Minimal cubic surfaces. Let К be a smooth cubic surface
over a field к in P3. First of all we shall show that the exceptional curves D on
V ® к = Fare precisely the lines lying on V ® k. In fact,/) ^ pi, and there-
г k
fore
2pa(D)- 2 = (%, 0y (D)) + (0y(D\ Qy(D)) = -2 .
BecauseD is exceptional, (О^ф), 0y(D)) = - 1. It follows from this that
(О"1, 0 (/>))=! .

110
TWO-DIMENSIONAL BIRATIONAL GEOMETRY CH. Ill, § 22
But Q?} - ' *(0рз(1)), where /: V -► P3 is the usual embedding (cf. Safarevic'
[2], Chapter III, § 5). ThusD as a curve in P| has degree 1, and hence is a
line. By repeating these arguments in inverse order we obtain that the
self-intersection number of every line Don V © к is - 1, so that it is
exceptional in virtue of the criteria of Theorem 21.5.
A classical result is that there are precisely 27 lines on V ® ~ky so that
V ® к can never be a minimal surface. In Chapter IV we shall prove this and
study in detail the symmetry properties of this configuration of lines.
Meanwhile we restrict ourselves to the verification of the fact that the surface of
Example 16.3, for which all lines can be explicitly written out, is minimal.
Nothing prevents us to study a somewhat more general case. Let A: be a
field of characteristic Ф 3 containing a primitive cubic root of unity 0, and
let a £ (Л*)3. Let V be given by the equation
7^ + 7'3 + Г3 + я7;3 = 0.
Every line on V © к is described by one of the pairs of equations
7; + 0'"7: =0,
7} +0ля*Г3 = О,
where (/, 7, /) run through (0, 1, 2) such that / </, 0 < m,n < 2 and a1 is any
fixed root in к. The Galois group G only acts non-trivially on the coefficient д"3
in these equations and sends a* into Ba~y or 02а~ъ. Therefore the collection of
all lines splits up into 9 triples of conjugate lines. The lines of every triple
intersect at one point and they lie in one plane defined over k. It follows from
Theorem 21.8 that V is minimal.
Exercise 21.10 (Segre [2]). Show that the surface V given by 2?_0а-Т? = 0
is not minimal if and only if а^а.-а^а^ €.(k*) for some permutation of
(/, 7, /, h) of the indices (0, 1, 2, 3). If this condition is fulfilled, then onV <% к
there is a triple of conjugate lines which are pairwise disjoint.
22. Bibliographical remarks
The whole theory of this chapter orginated in the classical Italian school.

СИ. Ill, § 22 BIBLIOGRAPHICAL REMARKS 11 1
Contemporary accounts can be found in Zariski [1]. in the lectures of
Safarevic' [1] (the theorem on resolutions is also proved in the lectures [2]),
in the treatise of Lipman [ 1 ], and in the book 'Algebraic Surfaces'. This book
also contains a description of all minimal rational surfaces over closed fields;
for more expositions see the treatises of Nagata [1], Hartshorne [1] and also
Manin [3], where the classification of minimal surfaces with a group of
operators is obtained.

CHAPTER IV
THE TWENTY-SEVEN LINES
23. A survey of the results
Whole books have been devoted to the configuration of the 27 lines on
a smooth cubic surface (Henderson [1 ]; Segre [2]). Their elegant symmetry
both enthrals and at the same time irritates; what use is it to know, for
instance, the number of coplanar triples of such lines (forty five) or the
number of double Schlaffli sixfolds (thirty six)? The answer to this rhetorical
question is one of the two recurring themes of this chapter. In just a few
words: the classes of the lines on V ® к generate the group N(V) =
= Pic (V ® к ) and the action of the Galois group G1 = Gal (k/k) on N(V)
preserves symmetry and it implicitly contains an extremely large amount of
information on the arithmetic and geometry of V.
Here is a short list of valuable results.
Theorem 23.1. Let к he a finite field of q elements, F G G the Frobenius
automorphism z »-> z4, and let F* : N(V) -» N(V) be its action on the
Picard group. Let N denote the number of к-points of the surface V. Then
N = q2 + qTi F*+ I .
This theorem is due to Weil [3]. It is true for any smooth projective
surface over к which becomes birationally trivial over k.
Now let к be a global field, that is, [k : Q] <°°. Let \ denote the
character of the representation of G on N(V), and let L(s, x, k) be the Artin
function of the field к corresponding to the character x (cf. Serre [5]).
Theorem 23.2. Jlie Hasse-Weil zeta function of the surface V coincides
(up to a finite number of Elder factors) with the product
i(s,k)l;(s-2,k)L(s-\,x*k)-
112

СН. IV, §23
A SURVEY OF THE RESULTS
113
This result is also due to Weil.
Up till now we have had no means of determining whether a surface V
is birationally non-trivial over fc, whether it can be trivialised over к or
whether V(k) is non-empty. The (7-module N(V) itself is, generally speaking,
not a birational invariant (cf., however, Theorem 33.2 of Chapter V), but
on the other hand its first cohomology group is invariant.
Theorem 23.3. (i) The group H{ (G, N(V)) is a birational invariant of
the surface V\ ifV = ?2, then Hl(Gf N(V)) = 0.
(ii) Suppose that the surface V is unirationaL Then the degree of every
map P2 -> V over к is divisible by the exponent of the group //](G, N(V)).
Example 23.4. ft is impossible to describe all rational solutions of the
equation Tq + Г3 + T\ - 2 by means of rational functions in two
independent parameters. Let, in general, the field к contain a primitive cubic root
of unity, let a E k* and let Va be given by the equation
Г03 + Г3 + Г23 + а Г33 = 0 .
If a e (k*)3, then VQ is birationally trivial. But if a 3 (/с* )3, then
^(G^(Kfl))sZ3XZ3 .
(cf. Table 1 in § 31, or the direct calculation in Chapter VI).
Theorem 23.3 shows that the degree of unirationality of V is not less
than three. In Chapter VI we shall see that in this case no finite number
of two-parameter families of points can exhaust all points (over a number
field). Even more, except for the trivial case a G b(k*)-*, the surfaces VQ and
Vb cannot be birationally equivalent over k. This will follow in full gener-.
ality from the results of Chapter V. The cohomological invariant permits
us only to establish that VQ and Vb are not birationally equivalent over к
if the fields k(a'3) and k{&) do not coincide, that is, if a $ b±l (A:*)3. In
fact, in that case
Z3 X Z3 - H*{G2\(klk(£)\N(Va ® к(bh))
ф Hl(Gz\(k/k(b>)\ N(Vb ® k(bh)) = {0} .

114
THE TWFNTY-SF.VF.N LINES
CM. IV, §23
Informally speaking, this means that the problems of representing different
numbers as a sum of three cubes are independent.
23.5. The group H] (G\ ;V( K)), which here emerges ad hoc, acquires an
interesting interpretation in Chapter VI in lerms o[ Azumaya-Grothendieck
'sheaves of simple algebras'. Using this, we then shall be able to construct other
useful things, including the following:
(i) A new admissible equivalence relation on V(k), eminently calculable,
with an Abclian CML.
(ii) An obstruction to the Hassc principle which explains all
counterexamples known in the literature.
Returning to the survey proper we conclude our list with the following
criterion for minimality (Segre [1 ]).
Theorem 23.6. A smooth cubie surface V over к is minimal if and only if
N(V)C' - Zcjj/, where ojy is the class of the sheaf of differentials £ly.
All this sufficiently justifies our interest in the action of G on N(V). This
action preserves со у G N(V) and the intersection number; this permits a long
digression from algebraic geometry for the sake of the combinatorics of root
systems and their Weyl groups. This is the second theme pervading the present
chapter.
Definition 23.7. Letr> 1 be an integer. We consider a composed object
{Nr ojn ( , )}, where
(i) Nr = Zr+1 = 0{Ln Z/,-; (/,-) a chosen basis.
(ii)a}=(-3. 1,..., \)£Nr.
(iii) ( . ) is a bilinear form Nr X /Vr -> Z given by the formulae
('o-V*1* (/,./,) = -! if'•>!. (/,.,/,) = (> if»*/.
We define the subsets Rr, /,. CA'r by the conditions
(iv)/?r={/GiVrl(/. ык.) = 0, (/./) = -2}.
(v)/, = {/€,V,l(/. wr) = (/./) = -l}.
The main justification for these constructions is the following.

СН. IV, §23
A SURVEY OF THE RESULTS
115
Theorem 23.8. Let V be a smooth cubic surface over a perfect field k.
(i) The triple {N(V)} coy, intersection number] is isomorphic to the
object fyV6, co6, ( , )} described in Definition 23.7.
(ii) The Galois group G acts on N(V) and preserves i*>v and the
intersection number.
(iii) The set of classes of lines on V (&k goes over into Ir under the
isomorphism (i).
Remark 23.8.1. It is useful to consider all values of/*, and not only r = 6, for
two reasons: Firstly, because induction on r is often convenient in the proofs.
Secondly, and most important, the algebraic-geometric objects, the Del Pezzo
surfaces, can be connected with all values 0 < r < 8 and not only with r = 6.
The Del Pezzo surfaces with r < 5 are obtained as images of non-minimal
cubic surfaces under birational morphisms. The surfaces with r-1 and r = 8
are even more interesting, but shall not be investigated in detail here. All
these points have been omitted in the survey, so as not to drown the main
themes, but they occupy a large place in the main text of this chapter.
Remark 23.8.2. In the formulation of Theorem 23.8, nothing has been
said about the role of the set/?r It permits us to identify the symmetry group
of the lines with the Weyl group of type Ee.
Theorem 23.9. Let 3 < r < 8.
(i) The scalar product (with opposite sign) on R ® z Nr = Rr+1 induces
on the orthogonal complement ofoor the structure of a Euclidean space. The
set Rr is a root system in it of type A j X A 2, A4, Ds, Ee, E-j, ZT8, respectively
(the sum of the indices is equal to r).
(ii) The following groups coincide'.
(a) the group of automorphisms of the lattice Nr preserving cor and the
scalar product',
(b) the group of permutations of the vectors from Ir preserving their
pairwise scalar products',
(c) the Weyl group W(Rr) of the system Rr generated by the reflections
with respect to the roots.
Remark 23.10. Starting with r = 9, the system Rr beomes infinite. In

Мб
THE TWENTY-SEVEN LINES
CH. IV, §23
Chapter V, a basic role is played by some variant of the object {/V^, co^, ( ,)}
which, however, is best investigated by not losing sight of its
algebraic—geometric origin.
23.11. In principle, Theorems 23.8 and 23.9 permit us to give all information
on the action of G = Gal (k/k) on N( V) a tabular character. More precisely, the
representation of G in N(V) is described by a pair consisting of the invariant
subfield of the kernel of this representation (a finite extension of k) and the
image of G in the group Aut N(V)\ this image 'is' a class of conjugate subgroups
in W(E^). Its invariants constitute the formal part of the picture. Therefore a
good table must contain a list of the classes of conjugate subgroups // in W(Rr)
and for every class the values of at least the following invariants:
(a) Z/1 (//, Nr) (Theorem 23.3);
(b) the character of the representation Nr (Theorems 23.1 and 23.2);
(c) the multiplicity of the identity representation (Theorem 23.6);
(d) the decomposition of lr into Я-orbits (this is especially useful for the
calculations of Chapter VI).
Some information of this type for the values r = 6 and r - 5 can be found in
the last section of this chapter. For r = 7 and 8, it would be reasonable to
attempt a computer calculation.
23.12. The realisations of the systems £6, Ej, E% described in this chapter
in the form of Rr are different from the standard ones (cf. for example Serre
[4] or Bourbaki [1]) and in a number of respects they are more convenient.
One of the advantages is that in the space Rr+1, which has only one dimension
more than the rank of the system, together with Rr there is also room for the
system of'exceptional vectors' Ir. This can facilitate, for instance, the
combinatorial part of the theory of exceptional simple groups over a non-closed
field.
23.13. Realization problems. We have in mind the following group of
problems: Let к be a perfect field, and let V run through the smooth cubic curfaces
over k.
(i) Which subgroups of ЩЕ^) are realised as an image of the Galois group
by its representation on Pic ( V® k) for some VI
(ii) Which extensions of the field к correspond with kernels of such
representations?

СМ. IV, § 24
DFL PFZZO SURFACES
117
Of course, the answer must depend heavily on k. The derived groupW(Eb)
is simple, and the whole of it obviously cannot be realized over a local base field
which has only solvable extensions. On the other hand, according to Todd [1]
and Segre [1], W(E6) can be realized over some function field. The proof rests on
Lefshetz' theory: for K, one takes a general fibre of the bundle of sections
of a 3-dimensionaI cubic hypersurface. The local monodromy map for a
suitable choice of V generates all of W(E^). The more interesting case of a
number field is completely unknown. The search for a reasonable approach
to problem (ii) may involve a pattern for a non-commutative class field theory.
Here, it appears that topological-analytical considerations and something like
Hecke operators do not suffice. The lines on a 3-dimensional cubic, connected
with Abelian varieties, appear to be still more promising.
The final problem is:
(iii) To what extent does the G-module N(V) determine the surface VI
It is probable that this problem only becomes reasonable for minimal cubic
surfaces. An analogy with Tate's theorem for Abelian varieties permits us to hope
for an interesting answer.
24. Del Pezzo surfaces
In this section we suppose the base field к to be algebraically closed. We
shall introduce and study a certain class of surfaces: they are smooth and
projective surfaces over к and are singled out by simple invariant properties. From
the point of view of birational geometry, one naturally considers the surfaces
of this class simultaneously. We start with cubic surfaces.
Theorem 24.1. Let V be a smooth cubic surface over a field k. Tfien:
(i) V is birationally trivial
(ii) The anticanonical sheaf Q~y is ample. More precisely, il'y s()K(l)
under the usual projective embedding.
Proof. In virtue of Theorem 12.11, V is unirational. It follows that К is
birationally trivial over closed fields, for instance, by means of the rationality
criterion (see "Algebraic Surfaces", Chapter III, or Serre [1]).
Another, more elementary argument uses the fact that there exists a
line/) on V (Safarevic, lectures [2], p. 59). Taking the bundle of planes

118
THE TWENTY-SEVEN LINES
CH. IV, § 24
through this line, we obtain a bundle of conies on V complementary to D.
Writing down the equations of V and D explicitly, one can convince oneself
that precisely five of these conies in turn decompose into a pair of lines.
Choose one of these and repeat the process. This furnishes a line (the twelfth)
D' on V which crosses the first one. The rational map D X D' -> V:
(x,y)*-»x о у establishes the birational equivalence of V with P1 X P1 as in
Example 12.6.
Finally, the second assertion is well known in a wider context, namely for
hypersurfaces (and complete intersections) of arbitrary dimension. It follows,
for instance, from the addition formula, if one takes into account that £2рз =
= 0рз(-4) and 0?з(У)~ Орз(З). This proves the theorem.
Definition 24.2. A smooth birationally trivial surface V on which the sheaf
Г2^ is ample is called a Del Pezzo surface.
We recall that the property of being ample by definition means that there
exists an integer n > 1 and a closed embedding i : V*-* P^ such that Q.~^n =
— '*(0p/vO))- If one can taker* = 1, then the sheaf Sl'y is very ample. The
number d - (cjj/, coy) is called the degree of the Del Pezzo surface V, It
coincides with the projective degree of the image i(V) if co^1 = /*(0(1)).
Theorem 24.3. Let V be a Del Pezzo surface of degree d. Then
(i) 1 <d<9.
(ii) Every irreducible curve with a negative self-intersection number on V
is exceptional
(iii) // V has no exceptional curves, then either d = 9 and V is isomorphic
to P2, or d = 8 and V is isomorphic to?* X P1.
Proof. Assertion (i) is immediately implied by the following lemma if we
take into account that (ily, Slv)> 1 because Slv[ is ample, and that
rk Pic V > 1.
Lemma 24.3.1. For every (smooth projective) surface V which is
birationally trivial, the group Pic V is free with a finite number of generators and
rkPic V + (Q.y,£lv)= 10.

СИ. IV, § 24
DEL PEZZO SURFACES
119
Proof. Let V' -> К be a monoidal transformation with a closed point as
centre. It follows directly from the results of Section 20 (particularly from
Corollary 20.9.1 and Proposition 20.10) that the lemma is true for V if and
only if it is true for V\ The resolution Theorems 21.1 and 21.4 then show
that it suffices to verify the lemma for a single arbitrary surface, for instance
for P2. In this case, the lemma holds because ftp2 = 0?г(-3) and Pic P2 ~ Z.
This proves the lemma.
24.3.2. Proof of Theorem 24.3 (continued), (ii) Let D С V be an
irreducible curve and (Д D) < 0. Because £1^} is ample, (£), £l~}) > 0 (this is the
degree of the curve D, which divides n, if Sly" induces a projective embedding
of V and D). On the other hand,
2pa(D)-l = (ptD)~{D,£l-vX).
But pa(D) >Q,asD is irreducible. The only possibility is therefore the case
determined by the equalities
(D,D) = ~\ , p,(Z)) = 0.
The latter condition is only possible when D = P1. The curve D is therefore
exceptional (cf. Theorem 21.5 and Section 21.6).
(iii). If there are no exceptional curves on V, then V is minimal and by (ii)
it has no curves with a negative self-intersection number. But except for P2
and P1 X P1, there do not exist minimal rational surfaces with this property
(Section 18.7.3). On the other hand, they are both obviously Del Pezzo
surfaces. This proves the theorem.
By Theorem 24.1, a cubic surface is a Del Pezzo surface of degree 3. The
reason for considering all Del Pezzo surfaces is that this class is closed under
ordinary birational morphisms (cf. Corollary 24.5.2). The following theorem
gives the main geometric information on these surfaces.
Theorem 24.4. Let V he a Del Pezzo surface of degree d.
(i) // d = 9, then V is isomorphic to P2.
(ii) If d =8, then V is isomorfihic to either P1 X P1 or to an image of?2
under a monoidal transformation with its centre at one point.
(iii) // 7 > d > 1, then V is isomorphic to an image of?2 under a monoidal

120
THE TWENTY-SEVEN LINES
CH. IV, § 24
transformation with as centre the union of9-d closed points, no three of
which lie on one line and no six of which lie on one conic.
Conversely, any surface described under (i), (ii), (iii) for d>3 is a Del
Pezzo surface of the corresponding degree.
Remark 24.4.1. For 7 > d > 5, all Del Pezzo surfaces of the same degree
are isomorphic. In fact, the projective automorphisms of P2 act transitively
on systems of <4 points in general position.
Remark 24.4.2. The last assertion of Theorem 24.4 should remain true also
for d - 1,2 if the requirement on the 'general position' of the blown up points
is strengthened (see Theorem 26.2 for this approach).
24.4.3. Proof of Theorem 24.4. The minimal V have already been described
in Theorem 24.3 (iii). Let V be non-minimal. Then there exists a birational mor-
phism/: V-> W, where W is a minimal rational surface. W cannot be a non-
trivial ruled surface; otherwise there would be an irreducible curve/} on W
with self-intersection number -2; then (/^1(/)),/_1(D)) < -2, which
contradicts Theorem 24.3 (ii). Therefore either W = P2 or W = P1 X P1. In the
second case, let x £ W be a point where /_1 is not defined. According to
Lemma 21.4.1, the morphism/can be split up into morphisms V £ W'-> W,
where W' -> W is a monoidal transformation with centre x. But for W' in turn
there exists a morphism h : W' -> P2 collapsing the inverse images of the two
fibres of the projections of W on P1 which pass through x (cf. e.g. Example
21.3). The composed morphism V Л W Л Р2 gives also in this case a
birational morphism of V to P2.
We shall, as before, denote this morphism by/. Since under each monoidal
transformation with a closed point as centre, the rank of the Picard group goes
up by one, and the rank of this group for V is 10 -d (Lemma 24.3.1), /splits
up as a product of r = 9 - d of such transformations. In other words, the
index of/is equal tor in the terminology of Definition 18.1.2.
Let*j,. . . , xs EP2 be all closed points in which/-1 is not defined. Then
s = r necessarily. Otherwise, s < r, and then one of the monoidal transformations
of the decomposition of /would have its centre on the inverse image of some
point Xj, under the blowing up of this point. After that transformation, the
proper inverse image of/) (Definition 20.3) would have an intersection number
- 2, and on V this number could only diminish still more. This contradicts
Theorem 24.3 (ii).

СН. IV, § 24
DEL PEZZO SURFACES
121
Suppose that three of the points jcj, . .. , xr G P2 are on one line D. Then
(f l(D),f~*(D)) < -2 because the self-intersection number becomes 2
already after only blowing up those three points. Analogously, a conic on
which there are six of the points jcj, . .. , xr is converted into a curve with
self-intersection number < -2. All this is impossible according to Theorem
24.3(h).
Finally, we prove the last assertion. It follows from the much stronger fact:
Theorem 24.5. // the surface V is obtained from the plane P2 by means of
a monoidal transformation with as centre r < 6 closed points no three of which
are on one line and no six on one conic, then the sheaf со у is very ample and
its sections yield a closed embedding of V in a projective space of dimension
dim//°(K fl"1) - 1 = (£2K,ilv) = 9-r.
The set of exceptional curves is identified under this embedding with the set
of lines in the containing space which lie on V. The image of V has degree
9-r.
Proof. We divide the argument into a series of steps. Let jtlf. .. , xr E P2
be the points mentioned in the theorem.
First of all, we put/, = {s e H° (P2, Q~l)\ фгу) = 0 for all /}. Because £l~] =
=0р2(3),1 can be identified in any projective coordinate system with the
space of cubic forms which are zero in x^,. . . , xr. In particular, dim/. >\Q-r.
We now define a rational map
/;P2_pdimL-i =pr0j ф skl ^
which lets a point x G ?2(k) correspond with the point with homogeneous
coordinates (s^x), . . . ,sdimL(x)), if (s,-) is a basis for L (because the st
are sections of an invertible sheaf, their 'values' at a point x are defined up to
a common constant factor which can be fixed by choosing an isomorphism
of the fibres ft"1^ 0X).
(ar) The map f is defined everywhere outside Ц=] *,-; moreover, ify± ^y^
thenf(y{)*f{y2).

122
THF. TWENTY-SEVEN LINES
CH. IV, § 24
We use induction on r.
The first assertion of (a,.) follows from (ar 1). Indeed, let у Фх{. but/not
defined in y. This means that all cubic curves passing through xx ,xr auto-
matically also pass througli v. Denote by L' the space of cubic forms which are
zero in .Vj xr_y In virtue of (ar_j). there exists an s£// such that х(хг)Ф0.
It follows from our assumptions that the ratio s(xr): s(y) as a point in P1
remains constant. (In fact, if .Vj(jfr) ■ 5](у)Ф s2(xr) : s2{y), then there would be
some linear combination of st and .v2 which is zero in xr but not in v, that is,
/would be defined in v.) But then the map/' corresponding tox]t ... , .v j
would not distinguish xr and y, which contradicts (ar_)).
To prove the second assertion of (ar), we choose first of all two points i'j
and.v-) outside U/Lj xh and we suppose that /(Vj) ~f(y2). It suffices to lead
this assumption 10 a contradiction in the case where r is equal lo its maximal
possible value, six. In fact, if r < 6, we add toxj, . ... ,xr the missing number
of points 'in sufficiently general position'; the contradiction obtained for the
new system is one for the old system too. Thus, let r - 6. We denote by D the
line through j>],.у <>; let D also contain 2 - к points of (xp .. . , x6), where
к = 0. 1, 2. On D, we choose к additional different points.^/ different from
■*!,.... *6>>V1'2 •
The space of cubic forms is ten-dimensional. Therefore dim L > 4. Let
// = {s CL\s(y^) = s{ yV) = 0;. If s is zero in one of the points У], у2, then it
is also zero in the other, because /(у,) - f(y2) (cf. the arguments used above).
Consequently, dim L' > 3. Let L" = [seL'\ s(y2+i) = 0, / > 0} (L" = L'
if к = 0). Then dim //' > 3 - к > I. On the other hand, for ОФьЕ //', the
cubic curve s = 0 intersects the line D at the pointsy^, y2 and also at two
other points: those 2-к which are contained among the Uj,... ,x6), and the
к additional points>'2+/. Therefore/) is a component of the curve s = 0. Let
Q be the complementary component, a conic. For к = 2. it must pass through
all points .Vj,.... x6, which is a contradiction. For к = 1, it passes through
five of these points, missing, generally speaking, the one which lies on D. But
then dim L" ^ 2, and the conies constructed in this manner form a bundle
and one of its elements also contains the missing point, which is again a
contradiction. Finally, for к = 0 the conic Q passes only througli four points of
Xj,. . . , x6. but dim //' ^ 3 and we can again construct a conic passing through
the two additional points. This concludes the proof of (a,.).
(br). dim Л = 10- r.
This can be immediately obtained by induction from (a,). In fact, we
need to prove that adding a point xr to the pointsx^ xr--\ diminishes

СН. IV, §24
DEL PEZZO SURFACES
123
the dimension of L (it follows that it then diminishes by one). If this were
not so, then the map/' corresponding to*j,... , xr_\ would not be defined
in xr. This proves our assertion.
Now denote by V Д.Р2 the monoidal transformation with centre U/LjX,
and let /: V_+ P2 _>.P9~r be the composed rational map. The aim of the
following is to show that / is the morphism of a closed embedding. This will be
achieved by a local analysis of/ and g, but first we check that this implies the
main assertion of the theorem on the ampleness of £l~y^ and the dimension of
the space of sections of this sheaf.
Indeed, first of all we have g*(Sl~l) = П"1 ® 0(1^0.), where D. is the
inverse image of xi on K(cf. Proposition 20.10). Further, £* defines an
embedding of L in the space of those sections of #°(И, ЩХ ® 0(2f= { Dj)) of
which the zeros are contained in 2f=1 Dj. But the space of sections of 0(£f=1 Dj)
is one-dimensional. Dividing by a generator of it, we can identify/, with a sub-
space in #°(K, £1^}). Indeed, no other sections except those which come
from /. are contained in H°(V, Sly1): the projection into P2 of the zero divisor
of such a section must coincide with the zero divisor of some section of L
because (£>,, П^1) = 1, and this means that (s = 0) intersects all the Dj.
Consequently, dim №(Vt Щх) = dim L = 10 - r.
Finally, if we assume that it is known that / is a closed embedding, we
obtain immediately from its definition that Sly ^ /*(0 9_r (1)). Indeed, the
linear systems of the zeros of the sections of both sheaves coincide on V.
We now pass to the proof that / is a closed embedding. We shall employ the
following criterion. Suppose that it is already known that the map / is a
morphism at a point x 6 V. Then it is a closed embedding locally in a
neighbourhood of x if/ induces a local isomorphism of V and i(V) in neighbourhoods
of* and /(jc), respectively (because /(K)is closed in virtue of the fact that V
is projective). In turn, to verify this property, it suffices to know that the
differential dx: Tx-+ Тцх) has no kernel, where Tx is the tangent space at the
point jc, that is, the space of linear forms on mxjmx (where mx С 0X is the
maximal ideal). In fact, it follows from this that the dual map w^/mjLv -^rr^/rn^ is
epimorphic, so that, by Nakayama's lemma, /'* : 0цХ) -> 0X is epimorphic.
It is therefore an isomorphism because i(V) is two-dimensional.
We first apply this criterion to those points^ £ V in which g is a local
isomorphism. By (ar), / is a morphism in all such points. For convenience we can
assume that/ 6 P2 \ Ц=1*/ and consider/instead of/.

124
THE TWENTY-SFVF.N LINKS
CU. IV, §24
(c).Kerdv/=0.
Indeed, suppose that this is not true. As above, we can assume that r - b.
Then, using the notationsof the beginning of the proof of (tfr), the zero divisors
of all sections 56L wliich pass through.!' either have at least a double point
at у or they all have a common tangent. In both cases, there exists a line
i^CP2 for which the local intersection number with every curve (s = 0),
5 G L, is not less than two. Let D also contain 2 -к points of <x{y. , . , a6),
к = 0,1, 2, On/) choose к additional separate points (yt) different from
*!,..., *(,, y. After this, the proof of (a6) can be carried over verbatim to
this case. (An intuitive explanation is that the points Vj and j'2 from (a6) have
'fused' my, and D is the limit position of the line through y^ and>'2.)
(d). 'I he rational map i is a morphism in all points of V which He over
somexK>K = 1,. .. , 6.
If/ is not a morphism in some such pointy £ V9 then the proper inverse
image on V of the zero divisors of the sections jf:I must all pass through
this point. Let g(y) coincide with, let us say, x j; then all curves .v = 0 must
have a common tangent at Aj, the direction of which corresponds with y. We
show that this cannot be the case. To this end, we consider a reducible cubic
curve consisting of a conic Q which passes through A[, a2, x$, xa, and a line
D passing through x^y x^. In addition we can choose the conic Q such that its
tangent at jcj is any prescribed line. Indeed, take a system of coordinates in
P2 such \h2LXxl9x2,x3,X4 become (1,0,0),(0, 1,0), (0,0, 1),(1, 1, 1). The
equation of Q then has the form a 1\ T2 + b Г0 T2 + c T$ Л = ^» anc^ tuc ^ne
cTy + bT2 = 0 is its tangent atxj. (If с = 0 or b = 0, then Q decomposes, but
this does not interfere with the argument.)
(e). Ker d / = 0 in any point у G V.
Again let g(y) =л*1. We denote by /У the line on P2 through At in the
direction corresponding to y. Suppose that we have found two curves (s = 0),
s <E L, non-singular in Aj, which are tangent to D' at x^ and such that their
order of tangency to each other is one. Then their proper inverse images on V
go through>> in different directions. It follows easily from this that the kernel
of di at the point у is trivial. We now show how to find such curves.
Except for л:A, there is onD' at most one more point of (Aj,. . . , a6). Let
x2y *з, -v4, a5 be not on D'. We now apply the construction of (d) twice to
get conies wliich are tangent to D' at .Vj thiough [x^, x2, A3, a 4 ) and through
(a,, a2, a3, a5). These two conies, together with complementary lines, are
the curves we are looking for. l-ach of them is irreducible because the tangent
D' contains no points o( the quadruple other than a j ; ihey do not coincide

СН. IV, § 24
DEL PEZZO SURFACES
125
unless the conic through x±, x2, Xy *4, x5 happens to have D' as tangent line
at x j. In that case take the conic through x[t x2, Xy x4, x5 and the conic througii
x\> хъ ХУ z (wnere z is апУ sufficiently general point) with tangent D' at jcj.
In both cases the order of tangency at Xj of the curves is not larger than one
because otherwise their intersection number at this point would be > 3, and
they already have two other points of intersection: x2 and *3.
Finally, let D С V be an exceptional curve. Because (Д D) - (Д SIt}) =
= 2pa(D)-2 = -2 and (Д £>) = -1, we have (Д Sly1) = 1. This means that
the degree of D in the anticanonical embedding of К is equal to one, that is,
D is a line. This argument can clearly be reversed. This concludes the proof
of Theorem 24.5.
Remark 24.5.1. Theorem 24.5 ceases to be true for r - 7,8. The critical
part is of course the end of the proof of (ar): the dimension of the space L"
does not suffice. Indeed, for r = 7, the map defined by the sections of Sly- has
degree 2: any cubic curve which passes through Xj,... , Xj and the point у ^
necessarily also passes through some point y2. For r = 8, for the same reason,
the one-dimensional space of sections of Sl~y has a base point; its resolution
constitutes a bundle of curves of genus 1, parametrized by the projective line.
Corollary 24.5.2. Let V' ^ V be any birational morphism.
(i) // V is a Del Pezzo surface, then V is also a Del Pezzo surface.
(ii) // V is a Del Pezzo surface, rk Pic V < 7, and all curves on V' with a
negative self intersection number are exceptional, then V' is also a Del Pezzo
surface.
Remark 24.5.3. The restriction on the rank in (ii) should not be there, but
I do not know how to get rid of it.
Proof, (i). We use the following theorem of Moisezon and Nakai (cf.
Cartier [1]): the sheaf Sl~^ is ample if and only if we have (QV(D), Sly1) > 0
for all irreducible curves D. [It is clear that this condition is necessary. The
sufficiency is a much deeper fact, but geometrically it is plausible, for
instance, because the restriction of SI у to any curve, being a sheaf of positive
degree, is obviously ample.]
Now let D' С V\ D =/(/)') С V. Proceeding by induction on the index of
f we can reduce to the case where/is a monoidal transformation with a point
л- e Fas centre. Let e be the multiplicity of* on D. Then D' = f*(D) -eW\

126
THE TWENTY-SFVFN L1NF.S
CH. IV, §25
where W' is the inverse image of x. Moreover, (D\ Пг') > 0 because £2~y\ is
ample. But
(Д Я",1) = (ГФХГЩ1) = №'+ *W\ П"1,) = (D\ П"1,) + e > 0
(taking into account that (/*(£>), 0{W)) = 0). Therefore, Sl~y is an ample
sheaf and К is a Del Pezzo surface.
(ii). Now let К be a Del Pezzo surface. As in (i), we can assume that/is a
monoidai transformation with as centre a point л* G V. If V - P2, then the
assertion immediately follows from Theorem 24.5; for V ~ P1 X P1 it also follows
from Theorem 24.5, using the vstereographic projection' as in the proof of
Theorem 24.4. If V is not minimal, let V -+ P2 be its morphism, which exists
according to the proof of Theorem 24.4. At the point x € V, g is a local
isomorphism; otherwise jc would lie on one of the curves collapsed under g and
then the proper inverse image of this curve on V' would have self-intersection
number — 2, which contradicts the hypothesis. Therefore the composition
V' -i V Д P2 is a monoidal transformation with as centre a finite number of
points - the union of the centre ol g and /. g(x). All the points thus chosen
are in 'general position' as described in Theorem 24.4 (liij: in the opposite case
there would be on V' a curve with self-intersection number < -2. The last
statement of Theorem 24.4 then shows that V' is a Del Pezzo surface.
This result is useful for proofs 'by induction on the degree', as we shall see
in the following section.
25. The Picard group and root systems
This and the following sections are devoted to the proof of the results
described in Definition 23.7 and Theorems 23.8 and 23.9.
Proposition 25.1. Let V be a Del Pezzo surface of degree d which is not
isomorphic to?] X P1; we put r = 9 - d. There exists in the Picard group
Pic V a free basis (IqJ\ lr) such that
(Dco^-S/o + S^/,.
(ii) Co- 7o> = l " Vh '/) = -lfori>\,(md(li, lj) = Qfori*j.
Corollary 25.1.1. The object {Pic V, coy, intersection number} is, up to
isomorphism, only dependent on r and coincides with the object {Nr, со r,( , )}
described in Definition 23.7.

СМ. IV, § 25 THE PICARD GROUP AND ROOT SYSTEMS
127
25.1.2. Proof of Proposition 25.1. Let/: V -► P2 be the monoidal
transformation with a centre of r points (Theorem 24.4 (in)). Let /Q be the class of
/*(C)p2(l)), and let /• (i> l)be the classes of the sheaves 0v(Dt) where the
Di are the inverse images of the blown up points. They constitute a basis for
Pic V according to Corollary 20.9.1. The formula for ojv follows from
Proposition 20.10 if one takes into account that Пр2 ^ 0p2(-3). The
self-intersection numbers are calculated by means of Lemma 20.9. These establish
assertions 23.8 (i) and (ii).
We shall now occupy ourselves with the system R We keep all the
notations of Section 23.
Proposition 25.2. The orthogonal complement cj^ to cor in R ® Nr
equipped with the scalar product ofNr (with opposite sign), is a Euclidean
vector space of dimension r for r < 8. The vectors from Rr in it form a system
of roots of rank r.
Proof, (i). Obviously, the space R ® Nr is generated by the vectors
cor, /j,... , lr. Moreover,
(r \ r
w,feco +£ft7.) = (9--r)e- E *..
/=1 ' i=l
Therefore,
/ r \ r
(cj 0gj + Zy6./.)=0«(9-r)fl = S br
\ /=l ' /=l
The length of such a vector (with opposite sign) is equal to
(9-г).'-2«Йь,-Б**=-Л(1Ч)2-£ bl
/=1 /=1 X ' /=1
so that the intersection number on corl is negative definite.
(ii). We now check that the set Rr of vectors from Nr of length 2 and
orthogonal to (jjr forms a system of roots. According to the definition (cf. Serre
[4], Ch. 5.2), we must establish the following facts:
(iia) Rr is finite, generates oolr and does not contain zero. It is clear that
Nr П a;^ is a lattice in gj^\ it can therefore contain only a finite number of

128
THE TWENTY-SEVEN LINES
СИ. IV, § 25
vectors of a given fixed length. Finally, the r vectors l{ - /2,. . . , /j - lr,
/q - /j - /2 - /3 are linearly independent and have length 2.
(iib) For every element I E Rr, the reflection of the space а£,
5/(x) = jc + (x,/)/,
sends Rr into itself (Our formula for ^ is obtained from the usual one after
a change of sign of the scalar product if one takes account of (/,/) = - 2.) This
is obvious because the symmetry ^ preserves length and orthogonality to cjr,
and it sends Nr into itself.
(iic) 2(Lm)/(l,l)e.ZforalII, m ERr. This is obvious.
This proves the proposition.
To identify the root systems Rr which we have constructed, we establish
one of its invariance properties. In keeping with the notations of Bourbaki [1],
we consider the group Q(Rr) С <л1г generated by Rr and we set
P(Rr) = {ieojxr\(l,m)eZ for all meQ(Rr)}
(the dual lattice). Clearly, Q(Rr)CP(Rr) and therefore the quotient group
P(Rr)/Q(Rr) is finite. Its order is called the 'index of connectedness' of the
system Rr.
Proposition 25.3. For all r, 3 < r < 8, we have
P(Rr)IQ(Rr) = Z9_r.
Proof. It is easy to check that the vectors l{ -/2,.. . , l{ ~ lr Iq - /j l^'h
o{Rr generate NrC\ulr ; therefore they form a basis of the lattice Q(Rt.).
We now consider the homomorphism
for which
x(al0 + lb ty^bjCmodZ).

СН. IV, § 25 THE PICARD GROUP AND ROOT SYSTEMS 129
Writing out the condition that the scalar product of the elements я/0+2'=1 btlt
with /j - lf and /Q- /j - /2 - /3 must be an integer, we obtain b1 -6,-EZ and
a _ b}-b2 - b3 GZ;moreover,Зд - £'=12>, = О(orthogonality to cor). It
follows from this in the first place that Ker x = Q(Rr) = Nr ^ ^. And in the
second place,
a -- 3^ G Z ,
3a- rb^ G Z .
These conditions are equivalent to what we want: (9-r)btGZ. From this one
infers that x induces an isomorphism
A*r)/G(/g-^z/z,
which is what we desired to prove.
As was remarked by P. Deligne, the properties thus established for the
system Rr suffice to identify it uniquely as one of the classical root systems:
Theorem 25.4. Let Rrfor 3 < r < 8 be a root system of rank r with the
following properties'.
(i) The lengths of the roots are the same.
(ii)P(Rr)/Q(Rr)~Z9_r.
Then Rr is isomorphic to one of the following systems, which are ordered
according to increasing rank:
AlXAvA4,D5,E(>,EvEs.
Proof. We turn to the tables in the book of Bourbaki [1], pp. 250-275.
The systems of type Bif C), F4 and G2 do not satisfy condition (i). Of the
remaining systems, only E% has its index of connectedness equal to 1, therefore
R% = ZTg. The index of connectedness of a direct sum of root systems is equal
to the product of the indices of the summands. Therefore for 9 — r = 2, 3, 5
(primes) the systems/?,, do not decompose into a direct sum. For these values
of the rank and the index, the tables directly give R7 =£7, /?6 = E^, Л4 =Л4.

130
THE TWENTY-SEVEN LINES
CH. IV, § 25
For r = 5, the system D5 is the only indecomposable one of index 4. UR5
were decomposable, then its two summands would have to be simple, of
index 2 and their ranks must sum to 5. But Dj has index 4 and A[ has index /+ 1,
so that it is impossible to get R5 as a combination of these. One proceeds
analogously to identify R^ with Ax X A2. This proves the theorem.
We can now apply Theorem 25.4 in two directions: to obtain necessary
information on the groups Pic V, 'anticipating results' by looking in the
Bourbaki book, or to prove properties of Rr, using our new geometric
realization. We shall do both.
25.5.1. Diophantine equations for Rr Let
1 = 1
The condition / ERr means that the coefficients a, bi € Z satisfy the system
of equations
r
3a - T, bi = 0 ,
/=1
(IV. 1)
/=1
This interpretation is convenient in order to see that the Rr can be embedded
in each other as lattices,
r
R=R*n © R/..
r 8 /=o '
In particular, all calculations can be carried out in Л8, and for the remaining
Rr one simply 'omits the unnessary'. (The system R^= /T6, which corresponds
to a cubic surface, in this context does not particularly stand out in any respect.)
25.5.2. Hie number of roots and an explicit description of them. It is easy
to check that the following table lists all integer solutions of the system (IV. 1)
with the properties 0 <д < 3, 6j >b2> . . > b%.

СН. IV, § 25 THE P1CARD GROUP AND ROOT SYSTEMS
131
a
0
1
2
3
*l
1
1
1
2
b2
0
1
1
1
ьг
0
1
1
1
b4
0
0
1
1
*5
0
0
1
1
b6
0
0
1
1
h
0
0
0
1
bS
-1
0
0
1
(IV .2)
Proposition 25.5.3. All roots ofR% can be obtained from the roots (1V.2)
by reversing signs and permuting the bt in all possible ways.
Proof. First method. We consider an arbitrary solution (a, b\,.. . , Z>g) of
the system (IV. 1). Permuting the bj and changing signs if necessary, we can
assume that a > 0 and bY > . . . > b8. Then it follows from the first equation
of (IV.l) that a = \^%lbi <b} + b2 + Ъъ. Let / = (1,1,1,1,0,0,0,0,0). The
reflection with respect to / sends (af bx, , . ., b%) into (a+c, b^ +c, b2 + c, 2>3 +c,
64,... , /?g), where с = a - by - b2 - £3 < 0, and hence it diminishes д.
Therefore all roots can obviously be obtained from the table by applying to it not
only permutations of the bi and changes of sign, but also the reflection st. But
this reflection does not permit us to obtain a solution with \a\ > 3 because
\2a- bfj - b( - bj\< 3 for all the tabulated solutions and their opposites. This
proves the statement.
Second method. We denote by R9 the set of solutions of the system
(IV.l) with r = 9. We shall presently see that it is infinite and is not a root
system; Л8 is obtained from this set by omitting all solutions for which Ьд Ф 0.
The introduction of the auxiliary unknown Z?9 is convenient because the
equations (IV.l) with r = 9 are equivalent to the equations
9
3a - S b. = 0 ,
9 ' (IV.3)
E(^-3^.)2 = 18.
1=1

132
THE TWENTY-SEVEN LINES
CH. IV, § 25
In total there exist three essentially different representations of 18 in the
form of a sum of 9 squares of numbers which are in the same residue class
mod 3:
18 = 32 + 32 + 02 + ... + 02 = (±2)2 + (±2)2 + (±2)2 + (+1)2+ ... + (+1)2 .
Therefore, up to the enumeration of the fy, all solutions of (IV.3) are
contained in the following series:
(3b; b + 1, b - 1, bt... , b) , (3b±2;btbfbfb±\>...9b±\). (IV .4)
(b € Z; in the second series we must either take all lower or all upper signs.)
One easily sees that all solutions of (IV.4) for which one of the b( is equal to
zero can be obtained from the table by a permutation of the bt and a change
of sign.
The system Ry will be useful in the following section for the description of
exceptional curves.
Corollary 25.5.4. The number of elements ofRr is given by the following
table:
8
240
7
126
6
72
5
40
4
20
3
8
Proof. A direct calculation using Proposition 25.5.3.
25.5.5. Simple roots. The following proposition describes a system of simple
roots, or a basis in the terminology of Serre [4].
Proposition 25.5.6. (i) In terms of Table (IV.2), the following roots
constitute a basis Sg C/?8:
(0-1,1,0,..., 0),(0,0-1,1,0,...,0), (0,0,0,-1,1,0,0,0),... Д0,..., 0,-1,1]
(1,1,1,1,0,0,0,0)
(They are arranged as in the traditional Coxeter-Dynkin diagram (see 25.5.7).)
(ii) The intersection Sr=S$n (ф/[ R/ ) is a basis for Rr for allr^3.

СН. IV, § 25 THE PICARD GROUP AND ROOT SYSTEMS 133
Proof. We shall construct a basis for /?8, as described in Chapter 5, § 8 of
Serre [4]. We consider the linear form
8
feftp...,^)^^ Tj ibr
/=l
It takes on a positive value exactly for those roots which are obtained by
permutations of the bt of the first and third rows of Table (IV.2) and by those
permutations of the bt of the first row for which -1 occurs earlier than 1.
The indecomposable ones of these positive roots are precisely those listed in
the statement of the proposition. The second assertion is immediately obtained
from this.
25.5.7. We enumerate the roots described in Proposition 25.5.6:
rl r2 r3 r5 r6 rl r8
We denote by si the reflection with respect to r,-. Because sr(x) = x + (x, r) r,
we have the following explicit formulae:
s\ (a> b\> ьг>--> b^ = (a> bV b\> bV • • • > bS^ » * * *
*4(я, bv bv . .. , bs) = (a + cf b{ + c\ b2\c, b3 +c, b4,... , Z>g) ,
с -a- b. — by -Z?3 .
(s2 interchanges b3 and £4, s^ interchanges b4 and fr5, etc.)
25.5.8. The Weyl group W(Rr) is the group of permutations of the roots of
Rr generated by the reflections slt... , sr restricted to Фу=0 R/.
All relations between the generators s7 are consequences of the following:
(s;.s.)2= 1 if г., г- are not joined in the Dynkin diagram ,
(s.s.) = 1 if rif r. are joined
(cf. Bourbaki [1]).

134
THE TWENTY-SEVEN LINES
CH. IV, §26
26. Exceptional curves and Weyl group?
We keep the assumptions and notation of the previous section; in particular,
К is a Del Pezzo surface of degree d> and r = 9 -d.
Let DC V be an exceptional curve. Then the class / of the sheaf Oy(D) in
Pic V satisfies the condition
(/.«,,)=(/,/)=-1.
We shall call aU such classes exceptional
The isomorphism described in Proposition 25.1 of {Pic V, My, ( , )} with
{Nr cof, ( , )} identifies the set of exceptional classes in Pic К with the subset
lr С Nr described in Definition 23.7.
Let
r
/=1
The condition / GNr means that
r
3a - £ bt = 1 ,
(IV.6)r
*2-£/>,2=-i.
The problem of describing Ir for r < 8 is solved by means of two simple
arguments. Firstly,/,. = /8 П (©^jR/j-Xso that it suffices to calculate/8. Secondly,
the introduction in (IV.6)8 of an auxiliary unknown' bg - 1 immediately
reduces the question to the solution of the system
9
Ъа- £ Z>, = 0,
/=1
9
a2-Ttb}=-2, b9=\
/=1
(IV.7)
These solutions without the restriction b9 = 1 are described in (IV.4). A simple
computation yields the following result:

СП. IV, § 26 EXCEPTIONAL CURVES AND WEYL GROUPS
135
Proposition 26.1. All solutions of the system (\W.6\ are obtained by all
possible permutations of the b{ of the rows of the following table:
a
0
1
2
3
4
5
6
*l
-1
1
1
2
2
2
3
b2
0
1
1
1
2
2
2
*3
0
0
1
1
2
2
2
*4
0
0
1
1
1
2
2
*5
0
0
1
I
1
2
2
*6
0
0
0
I
1
2
2
*7
0
0
0
i
1
1
2
*8
0
0
0
0
1
1
2
(IV.8)
We can now derive the main theorem on exceptional curves on Del Pezzo
surfaces.
Theorem 26.2. Let V be a Del Pezzo surface of degree I <d < 7, and let
f: V -+P2 be its representation in the form of a monoidal transformation of
the plane with as centre the union of r - 9 -dpoints x^ ... , xr Then the
following assertions hold:
(i) The map D ь> (class of 0V(D)) G Pic V establishes a one-one onto
correspondence between exceptional curves on Vand exceptional classes in
the Picard group. These classes generate the Picard group.
(ii) The image f(D) in P2 of an arbitrary exceptional curve D С V is of
one of the following types:
(a) one of the points xt\
(b) a line passing through two of the points x^
(c) a conic passing through five of the points xf,
(d) a cubic passing through seven of the points jc7 such that one of them is
a double point;
(e) a quart ic passing through eight of the points xi such that three of them
are double points;

136
THE TWENTY-SEVEN LINES
CH. IV, § 26
(f) a quintic passing through eight of the points xi such that six of them
are double points.
(g) a sextic passing through eight of the points xi such that seven of them
are double points and one is a triple point.
{Of course, only for r = 8 the whole list must be used\for r-1 only (a) - (d);
forr = 6,5 omy (a) -(c); for r= 4,3 u,»y (a)-(b).
(iii) The number of exceptional curves on V is given by the following table;
8
240
7
56
6
27
5
16
4
10
3
6
Proof, (i). Let L be an exceptional sheaf on V, that is,
(L,L)-(£,nK) = -l.
Apply the Riemann-Roch theorem to it, take into account that pa{V)- 0,
discard Я1 and replace Я2 by its dual group. We then find:
dimH0{VJL)>{(LiL)-{(nv,L)^\-dimH0{V,nv®L-1)
= l-dim^°(K7nF®L-1).
But
{£l-\nv®L-l) = -d-\<Q.
Because the sheaf £lyl is ample, this means that £2 v ® L~l has no non-zero
sections. Thus dim H°(V, L)> 1.
Let s be a non-zero section of L, and D the divisor of its zeros, and let
D - "ZajDj, ai > 0, be its decomposition into irreducible components. Now
l=(nyl,D) = Eai(ny\Di)1
and from the ampleness of П^1 it follows that (SlZ1, D.) > 0. D can therefore
have only one irreducible component which is of multiplicity one. From the
condition on L it follows that pa(D) = 0, (D, D) = -1; therefore D is an
exceptional curve and L = 0y{D).
Two different exceptional curves belong to different exceptional classes:

СН. IV, § 26 EXCEPTIONAL CURVES AND WEYL GROUPS
137
0v(Dl)=0v(D2)=*(DvDl) = (DvD2),
but the first number is equal to -1 and the second is > 0 if Dx Ф02.
The last assertion of (i) is obtained immediately by induction on r, starting
with r = 3. For r= 2 (in the notation of Proposition 25.1) Pic К is generated
by the classes /0 - /j -/2 J\>h^ anc* a^ these are exceptional.
(ii). We keep the notation of Proposition 25.1. Suppose that/(£>) is not a
point. If the class / of Oy(D) is of the form al^-L^b^, then b.= (Д Л),so
that the point xi becomes a /^-multiple point onf(D) under the collapsing of
a curve of the class /;- into the point xf. Because D = /"* (/(#)), we have
r
class/*(/P)) = / + E ЬД = а10У
from which we get for the degree of f(D) the expression
(/(/)), 0p2(l)) = (/*(f(D)l/0) = fl.
It is now evident that the list (ii)(a)-(g) is a direct translation of Table (IV.8)
in geometric language. Finally, Table (IV.9) is obtained from (IV.8) by a
straightforward calculation.
Remark 26.3. We shall say provisionally that the points x j,..., xr G P2
are in general position if their blowing up leads to a Del Pezzo surface. As was
proved in Theorem 24.5, r < 6 points are in general position if and only if no
three of them are on one line, and no six of them are on one conic.
Theorem 26.2 permits us to extend this list of necessary conditions for
'general position' until r = 8: the curves described in conditions (ii)(b)— (g)
must have exactly the described set of multiplicities in the points Xj (in the
'non-general case* these multiplicities may jump). I do not know whether this
list of conditions is sufficient.
Ал analysis similar to the one carried out in Theorem 24.5 can become
more complicated here because 0,7/ can cease to be very ample, and for a
projective embedding of К by means of ЩР one must consider curves of
sixth and higher order.
Remark 26.4. The blowing up of r > 9 points on P2 can already lead to
surfaces К with infinitely many exceptional curves. For the exceptional

138
THE TWENTY-SEVEN LINES
CH. IV, §26
classes in Pic Kit is not difficult to verify this, by examining the system of
equations (IV.6). It is possible to show that on some surface Kail classes are
represented by curves, by means of the following geometric arguments (of I.R.
Safarevic):
We choose eight points on P2, leading to a Del Pezzo surface V of degree 8.
On it (ft^1, ft^1) = 1, and the zeros of the sections of ft^ form a bundle of
elliptic curves with one base point. Carrying out one more monoidal
transformation with as centre this base point, we obtain a Neron model for the general
curve of this bundle. Its sections, and only these, are exceptional curves,
and the composition law of the general fibre induces on them the structure
of a free Abelian group of rank 8. This situation is studied in more detail
in Manin [2].
In the following chapter, the case r = «> emerges in a somewhat different
context. It appears that the process of blowing up 'all points of the plane', 'all
points of the surface obtained', and so on, admits a reasonable and important
algebraic interpretation, and it leads, for example, to a description of the
group of birational maps of a surface onto itself.
Returning to the main theme, we shall now study the group of
automorphisms. We shall not recall the statement of Theorem 23.9 (i), which has
already been proved.
26.5. Proof of Theorem 23.9 (ii). We shall provisionally denote the groups
described in conditions (ii)(a) — (c) of the theorem by W^f H^, W3,
respectively.
There is an obvious embedding W$ С W± and a homomorphism W^ -> W2
which maps each automorphism of {/Vr,cor,(,)} onto the corresponding
induced permutation of Ir. We shall show that both these maps are
isomorphisms.
The kernel of W^ -+ JV2 is trivial because Ir generates Nr (Theorem 26.2 (i)).
On the other hand, let Z/r be the free Abelian group generated by Ir, let
ZIr -*yVr be the natural epimorphism, and let Kr be its kernel. We have
Kr= {Z.^lvee/,, Ъ.а.{ер е) = 0}, *.€/,.
This follows from the fact that on a rational surface linear equivalence of
divisors is the same as numerical equivalence. Of course this can also be
directly checked from the definition of Ir.

СН. IV, § 26 EXCEPTIONAL CURVES AND WEYL GROUPS
139
Further,
со = a Lj e (mod К ),
ee/r
where-a,:1 = 120,28,9,4,2, 1 for r = 8, 7, 6, 5, 4, 3, respectively. In fact, it
is clear from table (IV.8) that for r = 8, the map e н> -u>r -e, and for r = 7 the
map ей- -2cor-~e sends /r into itself (without fixed points). For r < 6, the
coefficient ar can be directly calculated without difficulty.
This description of Kr and cor shows that any permutation of the vectors
ez G Ir which preserves their pairwise intersection numbers induces an
automorphism TLlrjKr ^Nr. This automorphism preserves intersection numbers
and cor, so that Wx -* W2 is an isomorphism.
It remains to show that W{ contains no elements other than those of
И/3 = W(Rr). For r = 7,8, the full group of orthogonal maps of co^ which send
Rr into itself (4he extended Weyl group' W*(Rr)) coincides with W(Rr) (see
Serre [4]). However, for 3 < r < 6 the index of W(Rr) in W*(Rr) is equal to
2 because changing the signs of the roots,/^ -/, is not generated by the
reflections S/. We show that it does not induce an admissible automorphism of
Nr. Otherwise this automorphism would be the reflection with respect to the
vector сол in the space R ® Nr which sends the integral lattice Nr into itself.
Because the intersection number is a unimodular form, this is only possible
for (cor, cor) = ± 1, ± 2, that is, precisely for r = 7,8. Theorem 23.9 is now
completely proved.
26.6. We write down the orders of the group W(Rr) from the tables in
Bourbaki [1] (forr = 2 it can be directly calculated):
г 8 7 6 5 ~4 3 2~
\W(Rr)\ 21435527 210345-7 27345 273-5 233-5 223 2
A first result on transitivity is the following:
Corollary 26.7. (i) Under the natural inclusion Ir_x = /rO ©JTqZ/,- С In
the group W(Rr_x) is identified with the isotropy subgroup of the vector
lr e lr in W{Rr).
(ii) W(Rr) acts transitively on lr.

140
THE TWENTY-SEVEN LINES
СП. IV, § 26
Proof, (i). It is obvious that all reflections Sj, I E //._1, leave lr fixed.
Therefore W(Rr_y) is contained in the isotropy subgroup. Conversely, any element
of the isotropy subgroup induces an automorphism of(yVr_j, cor_j( , )} as a
sub-object of{Nr,u)r( , )}and therefore belongs to W(Rr__i') according to
Theorem 23.9.
(ii). The order of the W(Rr) orbit of the vector / is equal to the index
(W(Rr): W(Rr_\)) because of part (i). Comparing these indices, calculated
from the table in Section 26.6, with table (IV.9) of the orders of the Ir, we
immediately obtain the desired result.
More generally, every ordered subset (m^ . . . , nij) С Jr such that (mK, mj)
= 0 for к jfc/ will be called an exceptional subset of length i. It is clear that
such a set generates a Euclidean subspace of dimension i in R © Nr. As the
intersection number is indefinite on R <8> Nn i < r. As before we assume that
3<r<8.
Corollary 26.8 (i) The group W(Rr) acts transitively on the collection of
exceptional subsets of length i ifi Фг—\. If this condition is fulfilled, every
exceptional subset is contained in one of length r.
(ii) The group W(Rr) has two orbits in the collection of exceptional
subsets of length r-1: one of these consists of all maximal sets of this length and
the other of all non-maximal ones.
Proof. We use induction on /. As in Corollary 26.7, Ir^= Ir П ©^oZ/KC7r'
and W(Rr_j) is included in W(Rr) as the isotropy subgroup of the set
Cr-/fl Q-
Corollary 26.7 clearly leads to a proof of transitivity up to length r-2. The
step from r-2 to r— 1 is not possible on account of the fact that W(Rr) does
not act transitively on /2, and has two orbits: see the graph of Г2 in Section
26.9. One orbit consists of two non-intersecting classes, the other of one class.
This suffices for assertion (ii).
The following is an algebraic-geometric explanation of the meaning of a
maximal exceptional set of length r— 1: collapsing the corresponding curves
on a Del Pezzo surface of degree 9-r, we obtain the quadric P1 X P1 and not
the plane P2.
These corollaries are usually used as follows. Suppose we want to find out

СН. IV, § 26 EXCEPTIONAL CURVES AND WEYL GROUPS
141
how to construct the set of lines on a cubic surface V which intersect some
pair of crossing lines. We can take any pair, e.g. 1^ and /2, and read off
everything needed from Table (1V.8). In Section 30 we shall develop a whole series of
such arguments. There we shall also implicitly use some other assertions on
transitivity, for example, on pairs of intersecting lines, etc. We leave it to the reader
to formulate and prove such results.
26.9. Graphs of exceptional curves. We attach to the set Ir a graph Tr the
vertices of which are in one-one correspondence with the vectors of Ir, and the
number of simplices joining / with /' is equal to the scalar product (/, /').
It is sometimes useful to examine the following pictures for small r:
Here the vertices are labelled by the images of the exceptional curves on the
corresponding Del Pezzo surface under the map V -* P2: the Xj are the blown
up points, the /« the lines passing through xit xy.
Unfortunately, it is already impossible to depict Г4 in such a way that its
various symmetries become evident. It is even more difficult to draw Г5:
4 4
3 3
2 2
1 T
•
8
7
6
5
•
8
7
6
5
Here the simplices which join the vertices of the column on the left with the
vertices of the column on the right are not shown. They are reconstructed thus:

142
THE TWENTY-SEVEN LINES
CH. IV, § 26
The vertices of each column are connected with precisely one vertex of each
pair in the other column in the following way. The left (right) vertex of each
pair is joined with the left (right) vertex of the pair in the same row of the
other column and with the right (left) vertex of the other pairs. For example,
1 is joined with 5, 6, 7, 8 (in addition to 1).
After some trouble, the reader can check that precisely the same incidence
relations of exceptional curves on the image of a monoidal transformation of
P2 with centre x j,... , x5 are enumerated as follows:
1234567 8 T2345S78
/Q1 x2 *3 , *4 Xj /Q2 /Q3 /^ x0 ln /13 /]4 q /34 /24 /23
(q is the conic passing throughxx,... ,x5.)
The graph Г6 of the 27 lines (for us the most interesting graph) is
already very complicated, and I cannot draw it. Still more complicated are
Г7 (56 vertices) and Fg (240 vertices), where, in addition, vertices occur which
are joined twice (in Г7) or thrice (in Г8) by simplices. However, the involution
/ »-> -2cor - / of the graph Г7 permits us to reduce it to a graph of almost the
same order as Г6: r7/Z2 consists of 28 vertices, and the simplices reflect the
incidence relations of the 28 double tangents to a smooth quadric on P2.
A simple explanation of this is the following: Project a cubic surface
V С P3 onto some plane P2 С P3 from a point x G V that does not lie on P2
or on one of the lines of V. Resolving the unique singularity of this map by
blowing up the point jc, we obtain a morphism V' -► V -+ P2 of Del Pezzo
surfaces of degree 2 on P2. The degree of this morphism is equal to 2, its
branching curve, the projection on P2 of the 'apparent contour' of V from x,
is a quartic. The exceptional curves of V' are pairwise glued together and they
are projected onto a double tangent to this quartic: 27 of them are essentially
the images of pairs (a line on Vy a conic on V passing through jc and the line)
and the last one is the image of C(x). For some more detailed calculations see
the proof of Theorem 29.4.
Here is a reformulation in terms of the graphs Гг of some of the results
proved:
Let v G Гг+1 be any vertex of the graph. Then the subgraph of the vertices
which are not joined to u, together with the simplices joining them, is
isomorphic to Гг.

СН. IV, § 27
THE ZETA FUNCTION
143
The group W(Rr) is isomorphic with the full group of automorphisms of
the graph Гг. (The action of an automorphism on different simplices joining
one and the same pair of vertices is not taken into account; such simplices
only occur for r = 7,8.)
The group Nr is isomorphic to a quotient group of the zero-dimensional
chains of the graph Vr:
Nr^c\rf)l{^Vi^raivi\^K>I,ai(^vK) = 0},
where (vj, vK) is the number of simplices joining uz- to vK.
27. The zeta function
Let к be a finite field of q elements and let V be a smooth projective
surface over k. We denote by F the canonical generator of the Galois group G -
- Gal (k/k) : F(z) = z*l for all z 6 k. This is the Frobenius automorphism; it
acts on 7V( V) = Pic (V (g> к). We denote by TV the number of ^-points of the
surface V.
Theorem 27.1 (A. Weil). If the surface V® £ is Irrationally trivial, then
N = q2 + q1iF*+\ ,
where Tr F* denotes the trace of F in the representation of Gal (k/k ) on N( V).
Corollary 27.1.1. (i) W = 1 (mod q). In particular, the set V(k) is
nonempty.
(ii) \N- (q2 + \)\<rq, where r = rk N(V).
Corollary 27.1.2. Let Na be the number of geometric points of V over the
field ofqa elements, a = 1,2,... . Then
ZF(/) = exP(E Nat°/a)= [(\ -1) (I-q21) det (I-qF*t))'1 ,
where the characteristic polynomial det (l—qF*t) refers to the representation
ofFonN(V).

144
THE TWENTY-SEVEN LINES
CH. IV, § 27
Proof. Applying Theorem 27.1 to the surface V ®kka (wnere [ka :k]=a)
over the finite field ka, we obtain:
Na=q2a + qaTrF*a+\ .
Let/lf... ,/л EC be the characteristic roots of the representation of F* on
С® N(V). As the groupN(V) is finitely generated, all its elements are defined
over some finite field kb. Then Fb acts on N(V) as the identity, so that all the
ft are roots of unity. Assertion (ii) of Corollary 27.1.1 follows from this.
Further Tr F*a= Ц=х%. Therefore
oo oo f oo oo
£ Nf\a = E q2atala + T,T,<ff°tala+Tj ta\a
a=\ a=\ i=\ a=\ a=\
= -iog [о-^оо-оП (i-^.ol,
L 1=1 J
which proves what we want.
27.1.3. Proof of Theorem 27.1. We start with a survey of some necessary
algebraic—geometric results.
21Л A. Intersection number. Let К be a smooth «-dimensional projective
variety over some field k. The free Abelian group generated by the
irreducible subvarieties of V of codimension к is denoted by CK( V). Its elements
are called cycles o/(pure) codimension к.
The subvarieties ZA, Z2 of codimensions к, п-к, respectively, are said to
be in general position if their intersection is zero-dimensional and in the
local ring 0X of each point jc EZj C\Z2 there exists a system of generators
of the maximal ideal (flf... , fK ; gx, ... , gn_K) such that the first к
elements give a local equation for Zj, and the remaining ones give one for Z2.
Geometrically this means that the intersection is transversal. The sum
{Z^Z^)- 2xgZi nZ2 W*) : ^)is tnen caNed tne intersection number of Z{, Z2.
The cycles Z{ € C*(K), Z2 G Cn~ K(V) are in general position if each
component of Zy is in general position with respect to each component of Z2.
For such cycles the intersection number is extended by bilinearity.
The first step of the Weil theory consists in interpreting TV as an intersection
number. Let k be a finite field of q elements.

СН. IV, §27
THE ZETA FUNCTION
145
We denote by Д С VX V the diagonal, and by A(1) С VX V the graph of
the 'geometric' Frobenius morphism Ф : V-> V, which on an affine subscheme
Spec (A) is induced by the endomorphism A -+A, x ^+xQ (note that it preserves
the /c-algebra structure of A).
Lemma 27.1.5. The cycles А, Д^Е Cn(VX V) are in general position and
the number N ofk-points of the variety V is equal to
# = (Д,Д(1)).
Proof. It is clear from the definition of Ф that
АПА(1)={(х,х)ЕКХ У\Ф(х)=х}^У(к)
(as a set theoretic intersection). Let x be a closed point on V of the first degree,
0X its local ring on V, and t\,... , tn the generators of the maximal ideal of
0X. We denote by pt: VX V-* Vthe Ith projection, and let tP = p*(tk)9
i= 1,2. Then t\{ \ ... , t^\ tf)... , f^2) are generators of the maximal ideal
lu(x,x) ш tne rin8 ^(jc,jc) on ^* ^ ^ne ^oca^ equation for Д has the form
('Г "il2)' • •.: ' /(л } -'^2)) and A(1) is defined by the equations {t\^ - t^\
• • • ,№я~ *rP)^ is c^ear tnat tnese equations are independent modm? ,,
which proves the desired result because
(Д,Д(1))= £ (£(x):A:) = /V.
27.1.6. The lemma just proved naturally leads to the idea of establishing
an analogue of the Lefshetz formula for the number of fixed points (here of
the endomorphism Ф) and to apply it to the calculations of N The
corresponding formalism, however, is essentially linked with the possibility of
replacing Д and Д^) with cycles of the form E/Z^-X Z2/, where ZKi С C*(V),
without changing their intersection number. In topology this can be done by
passing to cohomology classes and using the Runneth formula H*(VX V)~
=H*(V) ® H*(V). A. Grothendieck has proved that there exists a
construction of cohomology groups with the necessary functorial properties also in
algebraic geometry over an arbitrary (in particular a finite) field.

146
THE TWENTY-SEVEN LINES
CH. IV, §27
In our particular case, however, we can get by without this profound theory
of Grothendieck, roughly speaking, because on rational surfaces and their
products kall cohomology classes arc algebraic'.
Before stating this result precisely, we shall first explain how algebraic
cycles are replaced by classes. A cycle Z £ CK(V) is called (numerically)
equivalent to zero if (Z, Z) = 0 for all Z' £ Cn~K(V) in general position with
respect to Z.
Lemma 27.1.7. The cycles equivalent to zero form a subgroup Z§(V) С
CZK(K).
For every two cycles Z± £ZK(V)y Z2 £Zn~K( V), there exists a cycle
Zq £Zq(K) such that Z^+ Z§ and Z2 are in general position. The intersection
number (Zj + Zq, Z2) does not depend on the choice ofZ§.
Corollary 27.1.8. We set A*(V) = ZK(V)IZ«(V). Then the intersection
number induces an everywhere defined non-degenerate pairing
AK(V)XA"-K(V)-+Z.
We omit the proof of Lemma 27.1.7.
Lemma 27.1.9. Let V be a birationally trivial surface over an algebraically
closed field k. Then
A°(V)~A2(V) = Z, Al(V)=?icV.
Proof. The map D н> class (Oy(D)) preserves intersection numbers of
divisors which are in general position. On the other hand, under our conditions
the group Pic V is free with a finite number of generators and the intersection
number is non-degenerate on it. The desired result follows easily from this.
Lemma 27.1.10. Let V]t V2 be two birationally trivial surfaces over an
algebraically closed field. Then the Kunneth formula holds:
A"(V}XV2)= Ф ЛЧИ,)®Л'(И2), 0<л<4.
i+j=n

СН. IV, §27
THE ZETA FUNCTION
147
Here, zj ®z2 denotes the class represented by the subvariety Zj X Z2 if
the classeszx ЕА1(УХ), z2 €А*(У2) are represented by me subvarieties
Z, С Vx andZ2 CK2.
I do not know a simple proof of this result. It can be deduced without
trouble from a general formula of A. Grothendieck which permits the
calculation of the Chow ring of a monoidal transformation of a given variety.
In fact, Kj X K2 can be obtained from P2 X P2 by a chain of monoidal
transformations 'along the fibres'. The result follows from this by induction
on rk Pic Vx + rk Pic K2.
Another variant consists in using an algebraic 'cellular decomposition' of
Kj X K2 and 'excision axioms' for the Chow ring,4*(Y), as in the expose of
Grothendieck [1]. For a more detailed study, see Manin [1].
Using Lemmas 27.1.9 and 27.1.10, we now calculate the classes of A, A^)
and their intersection number.
Lemma 27.1.11. Let (z,-) be an orthogonal basis in the space С ® Pic V,
V= V® k, Le.f (zjf Zj) = 6/y- (Kroneckersymbol). Then
r
class Д= \v®ev+ E z;. <g) z,-+ *V ® 1 G С ® A2(VX V) ,
where \yf ev are the canonical generators of the groups A®(V) and A2 (V):
the classes of V and of a point, respectively.
Proof. Let Z^ Z2 EA*(V) be cycles in general position. It is not
complicated to check, as in Lemma 27 J .5, that then the cycles A and Zj X Z2 are
in general position in VX К and that (A, Zj X Z2) = (Z1? Z2). In fact, that
А П (Zj X Z2) coincides with Zj П Z2 is obvious, and passing to the local
ring at the point x 6 А П Zj X Z2 linearizes the problem. Consequently,
(class A, 1 у ® ev) = (class A, ey ® 1 v) = 1 ,
(class A,z. ® zf) = (z.f z.) = 5- .
But the element written down in the statement of the lemma has the same
intersection numbers with the basis {\v ® ev, ey ® \v, z{ ® z.) of the group
С ®A2(V). The desired result now follows frr>m the fact that the intersection
number is non-degenerate and that A2(V X V) has finite rank.

148
THE TWENTY-SEVEN LINES
CM. IV, §27
27.1.12. We now compare the two Frobenius automorphisms: the 'algebraic'
one F. V -> V and the 'geometric' one Ф : V -» V. Let U = Spec (А) С V be an
open affine subset, and \ei 0 = U ® к С V. Then these morphisms act as
follows on the functions £ aigi € Тс ®kA, а{ Ek, gjEA :
Ф-^*,<)=£^.
Therefore their product is the 'complete' Frobenius morphism which acts on
Oy as 'raising to the power q\
We now remark that for any morphism of/c-varieties \p : V] -> V2 of the
same dimension, one can define two maps
4>*:AK(V2)-*A*(yj,
^:A*{Vx)-*AK{y2)
with the usual functorial properties. Both these maps are even defined on
cycles. In particular, for a subvariety Z С Vy we have </?#(Z) = d\p{Z), where
<p(Z) is the set-theoretical image, and d is the degree of the map Z -* </>(Z)
(zero if dim i/?(Z) < dim Z). Finally, if all elements are defined, the following
'projection formula' holds for intersection numbers:
(^Z,,Z2) = (Z1,^(Z2)),
which holds without restrictions for the cycle classes.
We apply this formalism to the morphism idr X Ф : К X V -> V X V. By
definition, ДО) = (idK X Ф)„ Д. Therefore
/V = (Д, Д°>) = (Д, (id v X Ф)+ Д) = ((id v X Ф)* Д, Д) .
We transfer this identity to classes of cycles. Note that (idr X Ф)*^, X Z2)
= Z, ® Ф*^). Further, it follows from the discussion on the action of F
and Ф that F* Ф* : Pic K-*Pic V coincides with multiplication by q, so that
Ф*(г) = 4(F*)"J (z) for all z G Pic К Moreover, Ф*( 1 r) - 1 Vt Ф*(еу) = q2ey
(q* is the degree of the morphism Ф). Combining all this, we find:

СН. IV, § 27
THE ZETA FUNCTION
149
N = q2 + qT< (z^^Y1^)* \ = q2 + qlx F* + \ ,
because Tr(F*)_1 = Tr F*: the representation has been obtained by an
extension of constants from a real one (even an integer one). This proves Theorem
27.1.
27.2. We now deduce from Theorem 27.1 the corresponding global results.
Let [k : Q] < °° and let V be a smooth projective surface over к which is bira-
tionally trivial over k. We denote by К D к a finite normal extension such that
all generators of the group N(V) = Pic (V ® k) are already defined over K.
Let x be the character of the representation of the group Gal (K/k) on N(V).
Theorem 27.3. The Hasse- Weil zeta function of the surface V coincides up
to a finite number of Euler factors with the product
S(s,k)S(s-2,k)L(s-\9x,K/k),
where L is the Artin function corresponding to the character x«
Proof. Everything reduces to a careful comparison of the definitions,
(i) Artin's L-function. Let А С к be the ring of integers, let pvCA run
through the prime ideals of A, and let qv be the order of the field A/pv. The
function L = UVLV is the product of the local factors. They are easily described
for those u, corresponding to the ideals pv9 which are unramified in K. Let В be
the integral closure of A in К and let Pv С В be any of the prime ideals lying
over pv. The automorphism z^+z v of the extension B/Pv over A/pv is
induced by some element Fv G Gal (K/k) = G, which is defined up to conjugacy.
We fix some finite-dimensional linear representation g^g* , G -> AutM,
overC. The value of det (\—F* t) does not depend on the arbitrariness of the
choice of Fv. Let x be the character of the representation. Then, by definition,
Lv(s, x, K/k) = det (1 - F'q-'Y1 ■ (IV.10)
The finite number of factors which correspond to the ramified and the
Archimedean v are more difficult to define; here there is no necessity to go into
the details. Instead of К we can take k, inserting the obvious modifications.
(ii) The Hasse- Weil function. There exists a model of the surface V *over
A\ that is, an A -scheme Vq of finite type, projective over Spec A, such that the
general fibre V0 <8> ^ Spec к is isomorphic to V. For almost all pv С A, 'the

150
THE TWFNTY-SFVEN LINES
CH. IV, §27
reduction' VQ v = K0 & л A/pv is a smooth surface over A/pv = k(v) which is
birationally trivial over A/pv = fc(u). Even more, for different choices of
models V'^, Vq their reductions are isomorphic for almost all u; we shall simply
denote them by Vv. The local factors of the Hasse-Weil /eta function are by
definition equal to
^(O^-O"1*1-^"1)-1 d«u-4]u"sO nv.n)
(сГ Corollary 27.1.2). Here F*is the representation of the local Frobenius
automorphism on N(VV).
Comparing formulae (IV. 10) and (IV. 11) shows that to identify the local
factors it is sufficient to construct a commutative diagram
ч>
Pic (V ® k) =f Pic ( Vv ® "Щ)
Pic (И® ft) ~ Pic (К ®Щ),
in which the map ip is an isomorphism for almost all v.
We choose a finite number of divisors Dt С V® к such that they are pair-
wise in general position, and such that the classes of the 0(!>,•) generate
Pic (К® £). As they are given by a finite number of equations over a finite
open covering of K, it is not difficult to check that for almost all v one can
define their reductions: the divisors D{ v С Vv, while the intersection numbers
(Djf D:) coincide with (D( t„ D v). Mapping the class of Op (£>,-) into the class
0y (Dj y), we obtain a homomorphism \pv. This is clearly an inclusion. A
comparison of the actions of G on V <g) к and of/7* on V ® k(v) shows that the
diagram (IV. 12) is commutative because these actions are already defined on
divisors.
It remains to show that the ypv are isomorphisms. First of all the ranks of
the groups Pic (V <2> Ik) and Pic (Vv ® ^c(v)) coincide: for instance, because
the first one is equal to 10- (ftp, ftp), and ftp reduces to CI у for almost
all v. This is already sufficient for comparing (IV. 10) and (IV.11) because
it follows from this that С ® <pv are isomorphisms. The triviality of the co-
kernel of ^, however, also follows easily from the fact that the 'intersection
number' form has determinant ± 1 already on the image of \pv. This proves the
theorem.

СН. IV, § 28 MINIMALITY AND WEYL GROUPS 151
28. Minimality and classes of conjugate elements in Weyl groups
Let К be a smooth projective surface over a field k. Obviously rk Pic V> 1;
the class of 0y{\) for any projective embedding has infinite order. If rk Pic V =
= 1, then the surface V is minimal: nothing on it can be collapsed. B. Segre
discovered that for cubic surfaces the opposite result is also true:
Theorem 28.1. Let V be a cubic surface over a perfect field к, and let
G = Gal (к/к). The following assertions are equivalent:
(ii) V is minimal.
Proof. It is clear that (ii) follows from (i). To prove the opposite
implication, we suppose that N(V)G Ф Zcov. Because (u>y, cjv) = 3, coy is not
divisible in N(V)\ consequently, there exists an element n€.N(V) which is
linearly independent of u>y.
Let / GiV(K) run through all exceptional classes. Then the intersection
number (n, I) takes at least two different values: otherwise from the equality
(n + (n, 1) u>y, I) - 0 for all / it would follow that n = - (n, 1){jOV, contrary to
our assumption.
Wcset
a = min (n, I), b = max (n, I),
/ /
Da= £ /, Db= Б /.
(/!,/)=* {П,1) = Ь
Each of the classes Da, Db is represented by a unique positive divisor on V
the components of which are lines L with (n,l)- a or b (because the divisors
are G-invariant; cf. Lemma 21.8.1). For brevity's sake we shall denote these
divisors also by Da> Db and we shall show that one of them can be collapsed
over к.
Suppose this is not so. Then there exist two different exceptional classes
la, l'Q (components of Da) such that (la, l'a) = 1 (Theorem 21.8; the intersection
number of exceptional curves on К cannot be greater than one). Analogously,
we can find componentslb and l'b of Db with (lb, /J,) = 1. We set

152
THE TWENTY-SEVEN LINES
CH. IV, §28
One immediately verifies that these are exceptional classes (their geometric
interpretation: /0 is the class of the third component of the intersection of V
with the plane passing through the lines which represent la and l'a).
From this we obtain
(i,-toK) = (nf/fl + /4/0) = 2fl+(/if/0)<2flr + bf
(Wf-w|r) = (WfZb + /; + /1) = 2b + (^/1)>2u + flf
which contradicts the inequality a < b. The theorem is proved.
Remark 28.1.1. This result is not true for minimal Del Pezzo surfaces of
degree d = 1,2,4: the rank of the group N( V)G can also be two.
28.2. We now use some arguments, connected with minimality, to introduce
a convenient principle for the classification of conjugate elements in the Weyl
group W(Rr). Tables for the classes for r = 6,7 can be found in the works of
Swinnerton-Dyer [2] and Frame [1]. Cartier [1] contains tables for all Weyl
groups. As always, when there is question of a finite number of data, the
methods of organizing them into a table are in principle indistinguishable from each
other. The principle proposed here firstly gives the possibility to use
induction on r and secondly is convenient for the calculation of the
algebraic-geometric invariants described in Section 23.11. A table for W(i?6) will be given
in Section 31; it would be worthwhile to compile the analogous tables for
W(/?7)and W(RS).
We now turn to the precise definition. We shall consider the system
Rr С Rr+1 = R ® Nr as given by its geometric realization, as described
in Sections 25 and 26;let7r CRr+1 be the set of exceptional vectors. We
consider some element s G W(Rr). A set (m^,..., mK) € Ir is called s-exceptional
if:
(i) (гпц mK) is s-invariant;
(ii) (mjf mj) = 0 for / Ф j.
(compare the definition preceding Corollary 26.8). The index i(s) is the
maximal order of an s-exceptional set.
Suppose that s is an element of the group Gal (k/k) acting on Pic (V <8> k).
Let К D к be the field of invariants of the cyclic subgroup (sn). Then i(s) is
the maximal number of geometric components of a divisor on V ® К which

СН. IV, § 28 MINIMALITY AND WKYL GROUPS 153
can be collapsed over k. In particular, if i(s) = 0, the surface V ® К is minimal.
For i(s) > 0 the corresponding divisor can be collapsed by a morphism
V-+ V\ and Pic V® к is obtained from Pic V' ® к in the well-known
manner.
These considerations are given concrete form in the following theorem:
Theorem 28.3. Let r>3t and let /0, /j,... , lr be the standard basis for the
space Rr+1. Choose a number 0 < / < r and let Sj denote the group of
permutations of the vectors (/r_,+1,... , lr)- Let W(Rr__i) be embedded in W(Rr),
as described in Corollary 26.7, as the isotropy subgroup o/(/r_r+1,..., lr).
(i) For every pair s G W(#r_z), t G Sif there exists a unique element in
W(Rr) which acts as s on /Q,... , lr_if and as t on /r_/+1,... , lr
(ii) The set of elements of the type described forms a representation of
all classes of conjugate elements of index > i in W(Rr), provided that i^r-\.
Proof, (i) (a) Existence. W(Rr_j) С W(Rr) coincides for all / with the
isotropy subgroup of the set (lr_j+\,.. . , lr)\ on the other hand, Sj is included
in W(Rr) as the subgroup of all permutations of this set which act trivially on
'о» • • • > /,-/(Proved as in Section 26.5). The product st, s G W(Rr_t\ teSh
under such an inclusion therefore possesses the desired property.
(b) Uniqueness. An element of W(Rr) acting trivially on /ft,. . . , /r_;,
'/•_/+p . •. , /r is the indentity on Rr+1.
(ii). Let s G W(Rr) be an element of index /, and let (mlf.. . , mfi С Ir be
a maximal ^-exceptional set. According to Corollary 26.8, for / Ф r-1 it is
possible to extend it to an exceptional set of length r (not necessarily s-in-
variant). Sending this maximal set by means of u> G W(Rr) into the part
(/j,... , lr) of the standard basis of Nr such that (wj,... , m^ go into
(fr-i+v • • - ' '/•)» respectively, we obtain that the element wsw~* maps the
set (/r_/+i,... , lr) into itself. Therefore it has the form described in (i).
The theorem is proved.
28.4. Theorem 28.3 permits us to give the following recipe to describe the
classes of conjugate elements in W(Rr):
(i). Write down the classes of elements of index 0 in W{Rr_i) for all / < r.

154
THE TWENTY-SEVEN LINES
CH. IV, § 29
(ii). Draw up the list of pairs (class of elements of index 0 in W(Rr_j)]
class of permutations on / letters).
(iii). Write down the classes of elements of index r-1 in W(Rr).
(iv). Make explicit which elements of (ii), (iii) are conjugate with one
another in W(Rr).
The result of this work for W{R^) is contained in Section 31. For r = 7
or 8, one essentially only needs to write down the classes of index 0; the
information on W(R^) can according to Theorem 28.3 easily be recast as
information on the classes in W(R-j) and W{R%) of index > 1 and > 2,
respectively.
We formulate as a theorem some properties of the classes in W(R^) which
I detected by looking closely at the table.
Theorem 28.5. (i) The index of an element s С W(Re) can only take the
values 0, 1,2,3,6.
(ii) The elements s, t E W(Re) are conjugate if and only if their sets of
characteristic roots in the space С ® N^ coincide.
Proof. See Table 1 in Section 31. The first result could also be established
by direct arguments, which are left to the reader as an exercise. I do not know
how to prove the second fact without sorting out all classes: it is possible
that it is also true for r = 7,8 or even for all Weyl groups. For instance, for
a symmetric group it is obvious since the set of characteristic roots can be
directly reconstructed from the set of the lengths of the cycles which occur in
the decomposition of the permutations of a class.
29. A cohomological invariant and the degree of unirationality
Let V be a smooth projective surface over a field к, G = Gal {к/к). In this
section we shall show that the group Hl{G, N(V)) is a useful birationai invariant
of К and shall in particular verify Theorem 23.3. An interesting interpretation
of this group and its further applications will be given in Chapter VI.

СН. IV, § 29 A COHOMOLOGICAL INVARIANT 155
Theorem 29.1. Letf: V1 -> V be a birational morphism of smooth
projective surfaces over k. Then the map of G-modules f* : N( V) -* N( V') induces
an isomorphism of Galois cohomology groups
f:Hl(G, N(V'))ZHl(G,N(V)).
Corollary 29.1.1. The maps V^H^ (G, N(V)) extend to a (contravariant)
functor on the category of smooth projective k-sur faces with k-birational maps
as morphisms. This functor takes every birational map into an isomorphism
of the groups Я1.
[To define ip* : H1 -> Hl for a birational map <p: V' -* V one must
consider some resolution of it,
and set y* = £*o(/z*)-1, using the fact that h* is an isomorphism. The
independence of the choice of the resolution is checked by standard diagram
chasing.]
Theorem 29.1 is a rather essential weakening of the following observation.
Let H С G be some open subgroup of finite index. The //-module Z (with
trivial action) then induces a G-module Z [G] ® ^щ Z of rank [G: H] on a
basis of which the group G acts by permutations, as on G/H. A direct sum of
a finite number of such G-modules shall be called trivial.
Lemma 29.1.2. Under the conditions of Theorem 29.1 there exists a trivial
G-module M such that
N{V') = N(V)®M.
Proof./* embedsN(V') in N(V) as a direct summand; its complement
M = Ker Д is generated by the classes of N(V) which are collapsed (under/)
and which are independent over Z; there are a finite number of them, and they
are permuted by the action of G on them. This proves the lemma.

156
THE TWENTY-SEVEN LINES
CH. IV, § 29
29.1.3. Proof of Theorem 29Л. According to Shapiro's lemma on the coho-
mology of induced modules
H\G, Z[G] ®Z[H] Z) &e H\H, Z) = Horn (Я, Z) = 0 .
Therefore Hl(G, M) - 0 for every trivial G-module Mt so that Theorem 29.1
follows from Lemma 29.1.2.
Corollary 29.1.4. If the surface Vis birationally trivial, then Hl{H, iV(K))=
= 0 for all closed subgroups H <ZG.
(In fact>//1(^,iV(P2)) =Я!(Я, Z) = 0.)
Using the tables of Section 31 and this criterion, it is easy to construct
birationally non-trivial Del Pezzo surfaces, in particular cubi: surfaces. We
now show that Я1 can also give more precise information on the birational
properties of V.
Theorem 29.2. Let Vbea smooth projective surface and let there exist a
rational map of finite degree ^ : P2 -> V. Then the degree of\p is divisible by
the least common multiple d of the exponents of the groups Я1 (//, N( V)) for
all possible closed subgroups HCG.
Proof. We remark first of all that the surface F(g) к is birationally trivial
over к, so that N(V) is a free group with a finite number of generators which
are all defined over a finite normal extension К Эк. Therefore all the groups
Я1 (Я, N(V)) are finite. Further, let G0 be the subgroup corresponding to K.
Then it suffices to take for Я a subgroup of the form Gq С Я С G and then
H\H,N(V))~HHH/GQ,N{V)).
(The standard 'restriction-inflation' sequence; see 'Algebraic Numbers', Ch.lV.)
The calculation of d is therefore a completely finite problem, and d is finite.
We now proceed to the proof. Let
•/\
P2 *• V

СН. IV, § 29 A C0H0M0L0G1CAL INVARIANT 157
be a resolution of singularities of the map </?, where g is a birational morphism
and Л is a morphism of degree deg \p. This diagram defines two homomorphisms
of G-modules:
h* : N(V) -> N(V),
and it is clear from the definitions that h^h* is multiplication by deg h =
= deg v? in the groupN(V). But Я1 (G, N(V')) = 0 (Corollary 29.1.4).
Therefore h^h* induces the zero homomorphism of the group H*(G, N(V)), so that
deg </? annihilates this group. Consequently, deg у is divisible by the exponent
of Hl(G, N(V)). Applying this result to the map
V®K:?2®K^V®K, K = kH
for an arbitrary closed subgroup Я С G, we obtain the desired result.
The proof of Theorem 29.2 shows that the following invariant of the
system Rr is important. Let Nr be the lattice generated by the vectors
^0' h> - • •»*r in tn^ standard realization of Rr (cf. Section 25). This group is a
W(/?r)-module. Let dT denote the least common multiple of the exponents of
the groups Я1 (G, Nr) for all possible subgroups G С W(Rr).
Theorem 29.3. The numbers dr are given by the following table:
r
dr
<4
1
5
2
6
6
7
2" в
8
2bySd
where a, b,c>\yd>0.
(The author has been too lazy to calculate the constants a, b, c, d\)
Proof (outline). Let p be a prime number. To see the contribution of p to
dn it suffices to restrict oneself to the calculation ofHl(H, Nr) for p-sub-
groups И С W(Rr).
Some details of the calculations for r < 4 are contained in the following
section. The results of the calculations for r = 5 are given in Table 3 in Section
31; in particular, Я1 = 0 for 3-subgroups and 5-subgroups.

158
THE TWENTY-SEVEN LINES
CH. IV, § 29
When passing from W(R5) to ИУ?6), the Sylow 5-subgroups and 2-sub-
groups do not increase (see the table in Section 26.6). Therefore d = 2-3K.
The table shows that к > 1. A more detailed computation, which is omitted
here,givesK = 1. When passing from W(tf6) to W(#7), the 3-subgroups and
5-subgroups remain as before. The 2-subgroup increases, which can lead to an
increase in the power of 2 in d1. (I do not know whether this happens).
Moreover, there appears a 7-subgroup G1 (see the table in Section 26.6).
However, it yields no contribution to d7 for the following reason. It is
cyclic of order 7 and therefore conjugate with the group of cyclic
permutations of /j,. . . , /7. The algebraic-geometric model of the situation shows
immediately that the G7-module /Vg is isomorphic to Z/0 ®Z[(z7], so that
tfl(G7,tf8) = 0.
Finally, the assertion concerning W(R%) follows from what has been shown.
(The 7-subgroup again does not increase.)
Theorem 29.4. Let V be a Del Pezzo surface of degree 9-r over a field k
and for r > 5 suppose that there is a point in V(k) which is not on any
exceptional curve. Then there exists a rational map <p : P2 -* V of degree 5r which
is given by the following table:
*r
<4
24
(IV. 14)
(For the calculation of deg \p the case of small characteristic of the field к
has been omitted; in particular, for r = 6 the characteristic is taken to be
different from 2.)
Remark 29.4.1. Comparing this with Theorem 29.2 and 29.3 shows that
for r < 6 the maps ^ described above possess 'generally speaking7 the lowest
possible degree. The stipulation relates to the circumstance that we have not
shown here that it is possible to realize all subgroups of W(Rr) as an image of
the Galois group in Aut N(V). Besides, examples which realize the largest
possible exponent o(Hl(G, N(V)) can be constructed without difficulty by means
of Table 1 in Section 31, at least for r < 6. See also the discussion in Section
23.13.

СН. IV, § 29
A COHOMOLOGICAL INVARIANT
159
Remark 29.4.2. The requirement that there exists a £-point outside the
exceptional curves for r = 5,6 will be removed in the next section.
Remark 29.4.3. I do not know whether there exists a unirational Del
Pezzo surface V of degree 1 for which the set V(k) is everywhere dense. Of
course, such a V must be minimal.
29.4.4. Proof of Theorem 29.4. We shall treat the cases for different r
consecutively.
(i) r - 0. According to Theorem 24.3, V® к is isomorphic to P|. Such
surfaces are called Severi—Brauer surfaces; it is well known that the existence
of an isomorphism V= P2 is equivalent to: V(k) is non-empty (see, for
example, Roquette [1]).
(ii) r = 1. According to Theorem 24.3, V® к is isomorphic either to a
2 11
monoidal transformation of P, with a closed point as centre, or to P- X Pr.
In the first case there exists a unique exceptional curve on V which can be
collapsed over k. This gives a fc-morphism V -* V\ where V' is a Severi—Brauer
surface; it is trivial if V(k) is non-empty, but this is always the case because
there is a £-point on the exceptional curve. In the second case, after a
monoidal transformation V' -> К with as centre а к -point of the surface V there
appear on V'® к three exceptional curves with the configuration •—•—* .
The union of the two 'extreme' curves can be collapsed over /c, which yields
a morphism V' -> V" onto a Severi- Brauer surface, which is trivial, as above.
(iii) r = 2. The same argument as in case (ii). We remark that the
exceptional curve 'in the middle* is isomorphic to P1: it is a form of P1 over к on
which there is an invertible sheaf of degree 1. Therefore for r - 2 the set
V(k) is always non-empty.
(iv) r = 3. If V is not minimal, everything goes as in one of the cases
already treated. Let Vbe minimal. Considering the graph Г3 in section 26.9,
one easily convinces oneself that all exceptional classes are conjugate over k\
therefore there is no /c-point on the exceptional curves.
Take a fc-point x E V(k) and perform the monoidal transformation
V' -> V with centre x It is evident from Corollary 24.5.2 that V' is a Del Pezzo
surface of degree 5. An argument as in Theorem 26.1 or a look at the graph
Г4 shows that the curve Д the inverse image of x, intersects the exceptional
curves/)^ D2, £>з on V'® fc in precisely three points. These curves do not
intersect each other pairwise and the image of each of them on V® к
intersects the pair of opposite sides of the exceptional hexagon Г3. Therefore the

160
THE TWENTY-SEVEN LINES
CH. IV, § 29
divisor Dy + Z>2 + />з is G-invanant and can be collapsed over k. This yields a
Л-morphism V' -> V'\ where V" is a Del Pezzo surface of degree 8, which
reduces everything to the case r = 1, which has already been analyzed.
(v) r = 4. If there is a £-point on К lying on the intersection of two
exceptional curves/)j, D2 on V® k, then DltD2 form a G-invariant pair. The set
of exceptional curves which do not intersect Dx от D2 on V® к is also G-in-
variant. A look at the vertices of Г4 in Section 26.9 shows that this set
consists of pairs of non-intersecting curves. Collapsing them over к reduces the
matter to the case r = 3, which has already been treated.
Suppose now that x £ V(k) does not lie on any exceptional curve. Take the
monoidal transformation V' -► К with centre л:; let D be the inverse image of x.
On V ® k, the curve D intersects five pairwise non-intersecting exceptional
curvesDlf... , D5.(For instance, if under the collapsing V'<8) к -»P|
D transforms to x0> and jc j,..., jc4 are the remaining centre points, then
Dx,... , Z)5 reduce to the four lines through xQ, jcz- and the conic through
*0> x\> • • • » x4-) Collapsing the (/-invariant divisor D± + .. . + Z>5 over к
reduces everything to the case r = 0.
(vi) г = 5. Let jc в V(k) be a point not lying on any exceptional curve. Then
the monoidal transformation V' -+ V yields a Del Pezzo surface of degree 3,
that is, a cubic surface on which the line Д the inverse image of x, is defined
over К The planes passing through D cut out a bundle of conies on V
complementary to D. These conies are the fibres of a A:-morphism V' -^P1 (the base
of the bundle). The curve D is a section of multiplicity 2 of this bundle. The
surface V' X , D is birationally trivial because there is a bundle of curves of
genus 0 on them, with one of the components of D X , D as a section. The
projection V' X , D -> V' is a morphism of degree 2.
(vii) r = 6 or 7.
(a) The construction of <P- Let x 6 V(k) be a point outside the exceptional
curves. Then there is a unique curve Dx of genus 0 over к passing through x
such that its inverse image under the monoidal transformation V' -> V with
centre x belongs to the class - 2ojv> - I for г = 7 or the class — ojy - I for
r = 6, where / is the class of the inverse image of x. (For r = 6, this is the
intersection of V with the tangent plane at the point jc).
Let у be the general point of the curve Dx\ we consider it as a closed point
of the first degree on the surface V®k k(y) over the field k(y), and we denote
by D the curve on this surface constructed from>> just asD^ fromx Finally,
let z be the general point of the curve D ; we can consider it as a geometric

СН. IV, § 29
A COHOMOLOGICAL INVARIANT
161
point of the surface Fover a pure extension of к of transcendence degree 2.
Its locus is the general point of V. This yields the map </?.
(b) Calculation of the degree ofV for r = 6. The degree of ^ is the number
of inverse images of a general point. Choose in the containing space P3 Э V a
coordinate system such that the point (1,0,0,0) is on V but not on one of the
lines of V. Denote by В the geometric locus of the tangent points with V of
the lines that pass through x and are tangent to V, generally speaking, outside
jc. (Classically В is called the apparent contour of the surface V from the point
x.) We shall show that the degree of \p coincides with the degree of B. Indeed,
V contains the section Dx of the tangent hyperplane at some point x by means
of which у is constructed. We construct tangent planes through the points of
Dx. The number of these planes which pass through (1,0,0,0) is also the
number of inverse images of (1,0,0,0) under the map </?.
We now show that the degree of В is equal to six. The equation of К has
the form
Г02/(Г) + 70^(Г) + с(Г) = 0,
where /, qy с are respectively linear, quadratic and cubic forms in T = (T^ T2, T3).
Any line through (1, 0,0,0) is uniquely determined by the coordinates of its
intersection point (ri,r2>Г3) witrl tne Plane Tq = 0. Let Tq = /0, 7} = r,-f j, / = 1,
2,3, be the parameter equation of this line. To find its points of intersection
with V outside (1,0,0, 0), we get the equation
t\ /(r) + tQ txq(T) + t\c{r) = 0 , г = (rx, r2, т3 ) .
The tangency condition means that
q2(T)-4l(r)c(r) = 0. (IV.15)
[The simultaneous equalities с = q = / = 0 are not possible; otherwise there
would be a whole line on V passing through (1,0,0, 0).] We shall assume that
the characteristic of A: is different from 2. Then the coordinates of the tangent
point look like
Т0 = Ф) , -7\= -^Я(г) , i= 1,2,3 . (IV.16)
The formulae (IV.16) define a morphism of the plane curve (IV.15) into
the space P3; В is the image of this morphism. Those points of the plane Гп= 0

162
THE TWENTY-SEVEN LINES
CH. IV, § 30
for which c(r) = q{r) = 0 remain fixed under this map, and those for which
l(t) = <?(r) = 0 are mapped onto (1,0,0,0). Therefore the degree of B, being equal
to the number of its points of intersection with a general hyperplane Z^o^T} = 0,
coincides with the number of solutions of the system consisting of eq. (IV. 15),
the equation
3
%Ф)- 4?(r)E V/ = 0, (IV.17)
/=1
and the inequalities q(r) Ф 0, с(т) Ф 0. This number of solutions is clearly
equal to six.
(c) Calculation of the degree of \p for r = 7. This is done analogously. We
refer the reader interested in the details to the note of Sermenev [I].
30. Rational points
We start with a useful addition to Theorem 29.4.
Theorem 30.1. Let V be a Del Pezzo surface of degree 3 or Л over a perfect
field k. If the set V(k) is non-empty, then it contains a point which does not
lie on an exceptional curve, provided one of the following conditions is
fulfilled:
(i) The field к is infinite.
(ii) The field к is finite and has > 22 elements in the case of degree 4 and
> 34 elements in the case of degree 3.
Remark 30.1.1. The lower bounds for the order of the field are probably
not the best possible. Yet some bound is necessary, as is shown by the following
examples:
(i). Let к be the field of two elements; there are in ?2(k) four points in
general position: (1,0,0), (0,1,0), (0,0,1), (1,1, 1). The remaining three points
are on lines through pairs of these points. Carrying out a monoidal
transformation with the four indicated points as centre, we obtain a Del Pezzo surface of
degree 4 for which all points are on exceptional curves. This surface is, of course,
not minimal and birationally trivial.

СН. IV, § 30
RATIONAL POINTS
163
Here is a more interesting example:
(ii). Let к be the field of four elements, 0 G к, в Ф 0,1. The surface V is
given by the equation
tI + t\ + t\ + в т\ = о.
All its fc-points are on the lines Г?+ TJ = 0, TK - Г3 = 0, where (/, /, к) is a
permutation of (0,1,2). Moreover, V is minimal (cf. Example 21.9) and bira-
tionally non-trivial, for instance because
Я1 (Gal(*/*), Pic (V® *)) ^ Z3 X Z3 .
It is unirational over &? The construction of Theorem 29.4 does not apply here,
and I do not know the answer.
30.1.2. Proof of Theorem 30.1. First let the field k be finite with q
elements. Then the number of /[-points on V is not less than q2 - aq + 1, where
a = 6 or 7 for degree 4 or 3, respectively (Corollary 27.1.1). On the other hand,
there are not more than \6(q + 1) and 27 (g +1) points, respectively, on the
exceptional curves. Comparing these estimates yields the desired result.
From now on we can therefore assume that the field k is infinite. We ana*
lyze the two cases each in turn.
Degree 4. If jc € V(k) lies on precisely one exceptional curve, then this curve
is defined over k. We collapse it and apply Theorem 29.4. Because a point of
V(k) cannot lie on the intersection of more than two exceptional curves, it
remains to analyze this case. Let x GD± П/^, ^jC V® k. The divisor
Z>! +/)2 is G-invariant. On the other hand, it is e3sy to see that there exists
exactly one more pair of exceptional curves D3, Z)4 on V® k such that
(D3, D4) = (D3, !>!) = (D4, D2) = 1. It is therefore also G-invariant; it satisfies
the relation 0V(DX + D2 + D3 + D4) s Пу1.
Let D be a divisor on V such that D ® ~k = D3 + D4. We have
(ДД) = 0, Pa(D) = 0, (Пк,Д) = -2;
moreover, dim H°(V, 0 V(-D) <8> Sly) = 0 because Z) is effective. The Rie-
mann—Roch theorem then gives
dim H°(V, 0V(D)) > ^(Д D) - |(ПК, Я) + 1 = 2 .

164
THE TWENTY-SEVEN LINES
CH. IV, § 30
Therefore the linear system of zeros of the sheaf QV(D) covers all of the
surface К Let Z)' be an element of this system which contains the point x.
Because (П^1, D') = 2, this is a curve of the second degree in the space which
contains V. There is a simple к -point x on it (for instance, because (£>j, D') =
= (Z)j, D) - 1). Consequently the set/)'(£) is dense in D', which proves what
we wanted.
Degree 3. If x E V(k) lies on precisely one line, then it is defined over k„
by collapsing it, we reduce the problem to the preceding case. If jc lies on
precisely two curves, then the complement in the plane section through them is
a line defined over k; collapsing it, we again obtain the desired result.
It remains to analyze the case where x lies on the intersection of three
lines on V ® k. (These points are called Eckhardt points: all/c-points of the
example 30.1.1 (ii) are of this type.)
Because the field к is infinite, in the containing space P3 "J V there exists
a line L through x which is defined over к and which intersects V at two
different geometric points >>, у which do not lie on the lines of V ® k. If these
points belong to V(k)9 everything is proved.
In the opposite case, they belong to V(K), where K/k is a separable
quadratic extension, and are conjugate over k. The surface V ®k К is unira-
tional over К in virtue of Theorem 29.4, so that the set V(K) is dense.
For every point z E V(K) we denote by z its conjugate point over k. We shall
show that it is possible to find points z, z in general position and such that
z oz Фх. (We cannot use the proof of 15.2: there we also supposed that
V(k) was dense.) Then, because j> о у =х, the closure of the set of points of
the form z о z" is at least one-dimensional, because it is irreducible; on the other
hand, this set is contained in V(k). This proves the desired result.
For the construction of z we denote by C(y) and C(y) the intersections of
V®kk with the tangent planes at the points>>, J\ respectively. Further, we pass
through the line L ®kK a plane P over К (in P^,) such that P Ф P and
PnC(^) = zU^,z^^. Then obviously P C\C(y) = z Uy and P ПР =
= L ®/cK. Therefore the line through the points z,I G V(K) does not
intersect L ®k K, so that z о z Ф x. This concludes the proof.
30.2. We now pass to the problem of the existence of /c-points.
Let [k : Q] <°°, i.e., A: is a number field. A necessary condition for V(k)
to be non-empty is that all the V(kv) are non-empty, where the kv are the
completions of A: for all possible valuations v. If this condition is also sufficient

СН. IV, § 30
RATIONAL POINTS
165
for all varieties of some class C, then we say that the Hasse principle holds
for C.
In Chapter VI it will be proved that the Hasse principle clearly does not
hold for the class of minimal cubic surfaces. For non-minimal surfaces,
however, we can say something positive.
Let К be a Del Pezzo surface over the field k. By analogy with the
definition in Section 28.2, the index of the surface V is the maximal number of
exceptional curves on V ® к forming a G-invariant divisor which can be
collapsed over k.
Theorem 30.3. Let V be a cubic surface.
(i) // the index of V is equal to 1, 2, 4 or 5, then the set V(k) is
nonempty and in the case where the index > 2, V is birationally trivial.
(ii) For the class of cubic surfaces of index 3 or 6 over a number field kf
the Hasse principle holds. The existence of k-points on such a surface is
equivalent to its birational triviality.
Proof. If the index of V is equal to 1, then there is a line on V together
with its fc-points. If the index is equal to 2, then the only case which is not
completely trivial is when the collapsible lines D +Z) are defined and conjugate
over a quadratic extension K/k of the base field. But let x €-. D (k)> then
x£D(K) and x о x G V(k). Theorem 29.4 then shows that V is
birationally trivial because after collapsing D + Dwe obtain a Del Pezzo surface of
degree 5 with a point.
In the case of index 4, let Е^Я,- be the collapsible four lines. Table (IV.8)
shows that there are precisely two lines which intersect all the Df. They do not
intersect each other and form a G-invariant set; we can therefore apply the
same arguments as for index 2.
Finally, let the index be 5, and let 2/^/),- be the collapsible divisor. If as
the result of collapsing a form P1 X P1 is obtained, then Table (IV.8) shows
that there is a unique line intersecting all the Dt, so that V(k) is nonempty;
on the other hand, after collapsing 2/LjD,- we can again apply Theorem
29.4. In the opposite case, there is precisely one line which does not intersect
all Dj, and everything is obvious.
We now pass to assertion (ii). By collapsing an exceptional six lines on V
(in the case of index 6) we obtain some fc-form of the projective plane, that
is, a Severi-Brauer surface. It is known that the Hasse principle holds for these
surfaces. [Using this argument it is not difficult also to construct a surface of

166
THE TWENTY-SEVEN LINES
CH. IV, § 30
index 6 without fc-points: one must take a non-trivial Severi-Brauer surface
and perform a monoidal transformation with as centre the union of 2 closed
points of degree 3. It is known that, let us say, over a number field, such
surfaces and such points on them exist.]
It remains for us to deal with the case of index 3. Collapsing the exceptional
triple of lines over k> we obtain a Del Pezzo surface of degree 6. Therefore it
suffices to prove that the Hasse principle holds for such surfaces. We shall
establish more precise results:
Theorem 30.3.1./,£/ V be a Del Pezzo surface of degree в over a perfect field
k. Let D С V be the divisor such that D® к is the sum of all the exceptional
curves on V ® 1c. Then the open subset V \ D is isomorphic with a principal
homogeneous space over some two-dimensional k-torus.
Theorem 30.3.2 (Ono and Voskresenskii). The Hasse principle holds for the
class of principal homogeneous spaces over two-dimensional k-tori if к is a
number field.
30.3.3. Survey of the theory of tori. Let G = Gal(fc/fc), and let S be a left
C-module which is free over Z and of finite rank «.Its group ring over к is
isomorphic to к [S] =k [Tv Tf\ .. . , Tn, T~l ]. The group G acts from the
left on к [S] - at the same time on the coefficients and the monoidals of
S. Let A(S) = к [S]Cr be the subring of G-invariant elements. It is a A>algebra
of finite type, so that T = Spec A(S) is an affine variety over к. Т is called a
torus, and S its group of characters. The following list of properties of T
justifies in particular its definition. The proofs can be found in the papers of
Ono [I], [2].
(i). The canonical map к ®^Л(5) -» к [S] is an isomorphism. In particular,
T®k = Speck[S] aGj- ,
where Gm г = Spec k[T, Г-1 ] is the multiplicative group scheme.
On T there is a unique group scheme structure such that T ® к =
= Spec fc [S] is an isomorphism of groups.
(ii). T(k) = Horn (5, P) as a G-module. Here, the action of G on T(k) is
defined such that
f(sx) = s(f(x)) for all f€A(S\x£T(k),seG ,

СИ. IV, § 30
RATIONAL POINTS
167
and the action of G on Horn (St k*) is given by the usual formula
f(sx) = s((s_1/}(*)) for all feS.xe T(k).
(iii). Letz ={xs) GZl(Gf T(k)) be some continuous cocycle. For an
arbitrary point x E T(k) we denote by m* : к [S] -* к [S] the homomorphism
corresponding to translation by x:
mx:T®k-*T®k,. mx(y) = xy.
The cocycle z permits us to define a new action of G on the ring к [S] by
means of the formula
*/ = w!(s/), sGG, f£k[S].
s
Since sm* = m^s, it follows from the 'cocycle' condition s(xt)x~fX5 = 1 that
this is well defined. The action on к clearly does not change; moreover,
sf=[(sf)(x5)]sf if fes.
(iv). Now let B(S) be the subring of invariants in к [S] with respect to the
new action of G. We set Tz = Spec B(S). The scheme Tz is a principal
homogeneous space over T, that is, there exists an exterior composition law
ГХ Tz -+TZ
with the usual properties.
(v). The principal homogeneous spaces T \ T 2 are isomorphic if and
only if Zj, z2 belong to the same cohomology class in H^(G, S). In particular,
the following conditions are equivalent:
(a) z is homologous to zero.
(b) Tz = T.
(c) Tz(k) is non-empty.
This is the usual context in which homogeneous spaces turn up in number
theory: the diophantine property (c) turns out to be equivalent to the coho-
mological condition (a); cf. Cassels [3], where an analogous formalism is
described for elliptic curves.

168
THE TWENTY-SEVEN LINES
CH. IV. § 30
30.3.4. A general construction. Let V be some variety over the field kt and let
{DJC V® к be a finite set of (irreducible and reduced) divisors. We denote
by S the group of principal divisors of which all components belong to D{ ,
and let R be the group of rational functions on V ® к with divisors from S.
We consider the usual exact sequence
0 -> A* -/?-£-► 1 . (IV.18)
It permits us to define a morphism of the complement to 1Щ into the
torus Spec к [S] in the following way. Because S is free of finite rank, there
exists a section v : £->/?. On the other hand, R С Г(Р \ UZ),, Oy), where
V= V® &. Therefore the choice of </? defines a homomorphism of к -algebras,
~k[S]->r(U,0D\ (IV.19)
where U = V \ U£>z, i.e., a morphism of fc-schemes
0 -» Spec * [S] . (IV.20)
We now suppose that the divisor £,■£,• is G-invariant. Then (IV.18) is a
sequence of G-modules, and SD, =Z) ® k, where D С F is some divisor, so
that £?=-- U®ky where l/ = K^D.
We want to construct a morphism analogous to (IV. 20) over k. This can be
done directly if (IV.18) also splits as a sequence of G-modules; then choosing
a G-section ip, we obtain a G homomorphism of algebras (IV.19) which
induces a homomorphism of the rings of invariants
k[S]G - Г((/, 0Df = r(U, Oy) , (IV.21)
and finally a morphism
U-+Speck[S]G = Г. (IV.22)
However, in general, the G-section \p need not exist. The obstructions have
a cohomological character: Consider the exact sequence of G-modules
obtained from (IV. 18),
1 -> Homz (£**)-> Homz (5, Л) -> Homz(S, S) + 1 .

СМ. IV, § 30
RATIONAL POINTS
169
(Take into account that (IV. 18) splits over Z.) The exact cohomology sequence
gives a boundary homomorphism
5 : HomG(S, S) = //°(G, Homz(S, S))-»Hl(G, Homz(S, **)) .
The image 6(id) of the identity map S -+ S is an obstruction to the splitting ot
(IV.18).We now remark that according to 30.3.3(ii),Homz(5, **)=7,(Л) (as
G'-modules), where T = Spec к [s)G. Therefore the obstruction written down
defines at the same time some principal homogeneous space Tz over Г (see
30.3.3 (iv), (v)). It appears that in the general case one only needs to replace
Г by it in the diagram (IV. 22).
Proposition 30.3.5. With the notation of the previous paragraph, there exists
a cocycle z in the class 5 (id) E Я1 (G, T(k)) such that it is possible to
construct a k-morphism
U^T2 (IV.23)
such that over к it is isomorphic to diagram (IV.20).
Proof. We proceed by an explicit calculation. To find a cocycle in the class
6 (id) we need first to construct some inverse image of id in Horn (S, R). This
is also a section y? : S-+R. After this, the formulae
МЯ = *И/)) [ФПГ1, /es, sec, (iv.24)
yield a cocycle
{zs)eZl{G,Hom{S,k*)),
the class of which also belongs to б (id). Since the map S -* k* : g и- zs (s~lg)
(for a fixed s EG) is a homomorphism, there exists also a uniquely defined
point xs E T(k) such that
zs(f) = (sf)(xs), feS, s€G. (IV.25)
From formula (IV.24) one easily deduces the explicit form of the condition
that {zs} be a cocycle:

170
THE TWENTY-SEVEN LINES
CH. IV, § 30
ФДЛ)^(г/)2л(Л-1 = 1.
Substituting formula (IV.25) in this we obtain that for all/ES,
<*r/)[svv*-l] = i,
that is, {xs}EZl(G, T(k)). The class of {xs} coincides with 5(id) under the
identification of Horn (S,k *) with T(k).
On the other hand, comparing formulae (IV.24) and (IV.25) gives for
fes,
s(v(f)) = (sf)(xs)[*(sf)}. (IV.26)
This equality can be interpreted as follows. We introduce on k[S] a new action
of the group G : /ь* sf, by the formula sf=m* (sf\ as in 30.3.3(iii). Then <p
extends to a G-homomorphism of A:-algebras
Ш->Ш0о). (IV.27)
Passing to the spectra of the subrings of invariant elements, we finally obtain
the desired morphism.
which concludes the proof.
' 30.3.6. Proof of Theorem 303 J. We apply the construction of 30.3.4 and 30.3.5
to the case where F is a Del Pezzo surface of degree 6 and {/),-} С V®k the
set of all exceptional curves on it. We shall show that in this case the map (IV.22)
is an isomorphism. For this it suffices to verify that it becomes an isomorphism
after replacing к by k. But over Tc all Del Pezzo surfaces of degree 6 are
isomorphic. Therefore we can carry out all calculations for one suitable model.
For this, we choose the surface Kq С P1 X P1 X P1 given by the equation
^O^O ^0 - ^ ^i 7^;' = 0 ,' (IV.28)
where (T0, Т{), (Tq, T[), (Tq, T"x) are homogeneous coordinates for the
first, second and third factor, respectively. To identify V, it suffices to observe

СН. IV, § 30
RATIONAL POINTS
171
that the projection p12 : V-* P1 X P1 presents К as a monoidal transformation
with as centre the pair of points ((0,1), (1,0)) and ((1,0),(0,1)).
Using the notation of Section 30.3.4, the group R is generated by k* and the
functions Tq/T^ , Tq/T[, Tq/T'y, restricted to V. The group S is free of rank
two (in virtue of relation (IV.28)), so that the torus Spec Jc [S] is
two-dimensional. One immediately verifies that the canonical map
U=V^D-* Spec * 1Г0/Г,, TJT0, Ц/Т[, Т[/Т^
is an isomorphism. This proves the theorem.
30.3.7. Proof of Theorem 30.3.2. Let Г be a torus over a number field к and
let K/k be a finite normal extension over which it splits, that is, T becomes
isomorphic to G^ K over K.
The deviation from the Hasse principle in the class of principal
homogeneous spaces over T is measured by the group
Ker [tf'(G, T(K)) - UvHl(Gv, T(KV))] ,
where v runs through all possible valuations of k, and Gv С G = Gal (K/k) is
the decomposition group of some extension of v on K. In fact, the non-zero
elements of this kernel correspond to those spaces which have a point
everywhere locally, but not globally. One can restrict oneself to the field К instead
of к because for a trivial torus the group Я1 is also trivial. The order of this
kernel will be denoted by i(T).
The Hasse principle holds if and отНу if i(T) = 1. Ono [2] proves that this
equality is satisfied in the following two cases:
(i) Suppose the torus Tsplits over a cyclic extension of the field k\ then
|(Г)= 1. This is Proposition 4.5.1 of Ono [2].
(ii) Let H2(G, f) - 0, where T is the group of characters ofT\ then
i(T) = 1. In fact, let T(AK) be the group of adeles of the torus 7\ and С =
= T(AK)/T(K). The exact sequence
H°(G, C)-+Hl(G, T(K)) ^Hl(G, T(AK))
shows that Ker \p - 0 \{H°(G, C) = 0. By Nakayama's duality theorem (see
Ono [2], Section 2.2)), 7/°(G\ C) = H2(G, f). Therefore Ker <^ 0 in our

172
THE TWENTY-SEVEN LINES
CH. IV, § 30
case. But Ker $ coincides with the kernel of Я1 (G, T(K))-* WVHX (Gv, T(KV)).
These two criteria can be combined by means of the following functorial
properties of the number /(Г):
(hi) i(T{ X T2) = i(Tx) • i(T2Yi(RK/k(T)) = i(Rtyk(T)) = i(T).
Here RK/k denotes the Weil restriction functor (to the base field) and R^jk(T)
is the kernel of the norm map. Using these criteria, Voskresenskii establishes
that i(T) = 1 for all two-dimensional tori Г by simply sorting out all cases.
We describe this in a few words.
We can assume that the representation G -> Aut (T) = GL(2, Z) is faithful.
Its image is a finite subgroup in GL(2,Z), which is defined up to conjugacy.
There are in all fifteen classes of such subgroups: all of them are mentioned
in the paper of Voskresenskii [1]. The intersection of any such subgroup with
SL(2, Z) is cyclic: every finite subgroup of SL(2, Z) is isomorphic with (1),
Z2, Z3, Z4 or Z6. Because criterion (i) immediately gives what we want for
cyclic groups, we need only consider those cases where the image of G is not
completely contained in SL(2, Z).
There are eight such classes. Criteria (iii) and (i) give the desired result for
all except two of them. There remain the cases G = ^(#3), the most
interesting case for us, because only this one (except G ^ Z6) can furnish a
minimal Del Pezzo surface. Therefore we shall analyze this one in more detail
(these are the groups 9a, b in the list of Voskresenskii).
(a) G is generated by (} "*), (° J) in GL(2, Z), f = Z X Z, in the natural
representation. Let G2 and G3 be the respective Sylow subgroups of exponent
2 and 3 of the group G. To show that #2(G, T ) = 0, it suffices to check this
for G2, G3. But G3 = Z3 and G2 = Z2 X Z2, and a direct, simple
calculation gives the desired result.
(b) G is generated by (| -1), (Д -1) in GL(2, Z), f = Z X Z. Here the
analysis is similar.
This concludes the proof.
As a corollary we indicate a class of minimal cubic surfaces for which the
Hasse principle is still correct:
Theorem 30.3.8. The Hasse principle holds for those minimal cubic
surfaces over a number field к which become non-minimal under some quadratic
extension.

СН. IV, § 30
RATIONAL POINTS
173
Proof. Let V be such a surface, and let H С G = Gal (k/k) be the subgroup
of index 2 corresponding to a field К over which V becomes non-minimal. We
write G = Я U sH. Let D G Div (V ® fc) be a sum of exceptional curves which
are conjugate over К such that this sum can be collapsed over K. Then the
divisor D + sD is G-in variant. Because К is minimal, we have according to
Theorem 28.1,
0K(D + jD)afl7, 7>1 .
On the other hand, letD consist of jc components each of which intersects n
components of sD. We have first of all:
(D + sD,Q-[) = 3y = 2x .
Consequently, jc = 0 (mod 3); but x < 6 and therefore x = 3 or x = 6. Further,
(D + sД D + sD) = 3>;2 = (2я - 2) x .
Therefore there are two possible cases:
(i) x = 3,j/ = 2, и = 3. The graph of the orbit D + sZ) is
(ii) Jc = 6,7 = 4,n = 5. The graph of the orbit D + sD is
Here every vertex is joined with five of the vertices of the other row— with all
except the opposite one. In the picture we have shown only five of these sinv
plexes. This configuration is classically called a 'conjugate Schlaffli sixfold'.
Case (i) is realized by means of a cyclic subgroup in W(R^): its generator
belongs to class 5 in Table 1 of Section 31. For case (ii), the cyclic subgroups
are not sufficient; we leave it to the reader as an exercise to check that it can
be realised.

174
THE TWENTY-SEVEN LINES
CH. IV, §31
We now suppose that the set V(kv) is non-empty for all v. Then also V(KV)
is non-empty for all v. Because the index of V® K, as shown, is equal to 3 or
6, it follows from Theorem 30.3 (ii) that the set V(K) is non-empty. Let
x € V{K), and let x be the conjugate point of x over k. Then x о х G V(k).
This proves the theorem.
Problem 30.4. Is it true that every cubic surface over Q has points over
some Abelian extension of Q? This is the simplest partial case of the Artin
hypothesis, to the effect that the maximal Abelian extension of Q is a
Cj-field (see Greenberg [1]).
31. Tables and comments. Calculation of //*. The theorem of Artin and Tate
In this section (pp. 176 — 178) there are three tables. Below is explained
their structure, possible use and method of calculation. Cf. also the
comments in Section 23.11. After describing the tables we mention one general
lemma on the calculation of Hl(G, N(V)) and the theorem of Artin and
Tate which connects the order of Я1 with other invariants of the
representation.
31.1. Table 1. This is a table of the classes of conjugate elements in the
Weyl group W(R£ = W(E^). It is obtained by slightly revising the tables of
Swinnerton-Dyer [2]. Needless to say that all responsibility for mistakes is
the author's.
(1). The first column of the table gives the number of the class. It does not
coincide with the Swinnerton-Dyer number, the designation of which (of
type Cj) is shown in the zeroth column.
(2). The second column gives the value of the index. For the definition,
see Section 28.2. We recall that the index is calculated in terms of the action
of W(E^) on the set of exceptional classes /6. If the corresponding element
of the group is realized as an automorphism of a cyclic extension K/k and acts
on N(V) = Pic (V ® K) for a cubic surface V, then the index is the maximal
number of lines on V which can be simultaneously collapsed over k. In
particular, the first five classes correspond to fc-minimal models, and the following
six to surfaces on which only one line can be collapsed, etc.
(3). The third column gives the order of an element in the class.

СН. IV, § 31 TABLES AND COMMENTS. CALCULATION OF H1 175
(4). The fourth column (measure-1) gives the quotient of the order of the
group and the number of elements of the class. The name is connected with
the Cebotarev—Artin density law; see Serre [7].
Suppose that К is a cubic surface over a number field к and that the image
of G = Gal (k/k) coincides with the whole group ЩЕ^). Then the measure
of the class of conjugate elements is equal to the DirichJet density of those
prime ideals of the field к for which the corresponding Frobenius
automorphism falls into that class (see Section 27).
(5). The symbol ambncP ... in the fifth column means that in the
canonical representation of W(R^) on W6 an element from the class under
consideration has as eigenvalues m primitive 0th roots of unity,/? primitive b^ roots of
unity, etc. For surfaces over a finite field of q elements, this column permits
us to calculate the zeta function if the class of the Frobenius automorphism
is known.
(6). The trace, which is mentioned in the sixth column, gives directly the
number of points; see Theorem 27.1 and its collaries.
(7). The seventh column contains the values of//1 {G, 7V6), where G is the
cyclic subgroup in W(R$) generated by some element of the class. Its algebraic-
geometric meaning has in part already been described. Some information on
the method of calculating it is given below.
Finally, the eighth and ninth columns yield information on the action of the
cyclic subgroup G on /6.
(8). In the eighth column, the symbol ambn ... means that there are m
orbits of order a, n orbits of order b, etc. . A notation of the type 63 6 means
that of four orbits of six lines, three have one type of connectivity and one
another. The type of connectivity is given by the matrix of the pairwise
intersection numbers and it is not explicitly given. It can be derived from the
second table of Swmnerton-Dyer [2], where all orbits are listed.
(9) The roman numerals in the ninth column for the classes 6-11 refer to
Table 2. There the numbers of the decompositions into orbits (with respect to
G) of the graph Г5 are shown; this graph consists of the vertices in Г6 which
are not joined to some G-invariant vertex.
For classes 15 —25 we show the type of the permutation which is induced
on the s-exceptional subset of length 6 in /6. Similar information is given for
the classes 12— 14; see the explanations in Sections 28.2 — 28.4.

Table 1
Classes of conjugate elements in the Weyl group W(R6) = W(E6). For an explanation, see text.
0
Swinnerton-Dyer
numbering
<^
Cn
<?u
Cl4
C,o
^24
cJ0
C-,
C„
C4
c3
Сгь
С 22
C6
C73
cls
1
No.
of
the class
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
Index
0
0
0
0
0
6
6
3
Order
12
6
3
9
6
12
8
6
4
4
2
10
6
6
6
5
4
Measure-1
12
72
648
9
36
12
8
36
96
96
1152
10
36
24
12
10
5
Characteristic
roots on Pic
~ТзМ?
1326a
136
1-96
1223262
I2 242 62
1284
132262
I2 23 42
1344
1324
12254
12234
I3 22 32
I2 232 62
1354
6
Trace
on Pic
0
2
-2
1
-1
2
1
2
-1
3
-1
0
-1
0
1
2
7
Я1
0
0
Z3><Z3
0
Z2XZ2
0
z2
0
z2xz2
z2
z2xz2
0
0
0
0
0
8
Number of
orbits
3-122
3-64
39
93
3636
1446*12
1282 8
132363
123444
1346
13212
252510
33 32 62
122 22 32 62
36266
I2 52 52 5
9
Type of
decomposition
I
XVIII
II
X
V
IV
ГХ21
5X31
sXl'21
6l
1!5!
tTJ
2:
H
ел
<
2:
Z
m
ел
О

Table 1 (continued)
0 12 3 4 5 6 7
Swinnerton-Dyer
numbering
c5
c.
^]8
Сгх
C,7
^6
c2
C,6
Ci
No.
of
the class
17
18
19
20
21
22
23
24
25
Index
6
6
6
6
6
6
6
6
6
Order
4
3
4
6
2
3
2
2
1
Measure l
16
108
32
36
96
216
192
1440
51840
Characteristic
roots on Pic
l3 22 42
1334
14242
14232
1423
Is 32
Is 22
162
Г
Trace
on Pic
1
1
3
2
1
4
3
5
7
Я1
0
0
0
0
0
0
0
0
0
8
Number of
orbits
122 242424
3633
l5 244 4
l3 23 34 6
l3 26 26
1936
l7 28 22
,is26
l27
9
Type of
decomposition
24
32
124
123
23
133
1222
142
I6
<
>
>
z
a
о
о
in
z
H
ел
О
>
К
a
r
>
H
о
z
о

178
THE TWENTY-SEVEN LINES
CH. IV, §31
Table 2
• • • ■•
• • » ■
I
*~ ■* III *■ —*
* • * •
• •• • •
EE3EEJ
F^ll—-
Ш
E3I
EEJ
E3
,E3
Q
* *
EB
• 9
—~*
• • •
•—-• > ■
rz
21
ШГ
УГГГ
Ш
ТГГУ
• • ♦ -•
• • • *
• • • •
Ш 4 > •
ХУ_
ТУГ XVII
Table 3
2ШГГ
xnr
//'
Type of decomposition
0
Z2XZ2
I, II, III, V, XII, XIII, XIV, XV, XVIII, XIX
VI, VII, VIII, IX, XI, XVI, XVII
IV, X

СН. IV, § 31 TABLES AND COMMENTS. CALCULATION OF Я1 179
31.2. Tables 2 and 3. Let Я С W(R5) be a subgroup such that under its action
on /5 no orbit is an exceptional set. When interpreted algebraic-geometrically,
these subgroups correspond to minimal Del Pezzo surfaces of degree 4.
И is some subgroup of the group of automorphisms of the graph Г5
described in Section 26.9, and it therefore decomposes the set of its vertices into
orbits. Table 2 contains all possible decompositions of this kind (to the cyclic
subgroups correspond only those five of them that are shown in column
nine of Table 1). In Table 3 the values of the groups H*(H, 7V5) are given for
each of these decompositions. The circumstance that Я1 depends only on the
decomposition and not on the group H itself is not entirely obvious. This will
follow from Proposition 31.3 below, which also gives a convenient direct
method of calculating Я1.
Tables 2 and 3 are taken from Manin [4], which contains a detailed proof
of the completeness of the list of decompositions. Originally, these data were
calculated in order to obtain an, albeit partial, birational classification of cubic
surfaces with one rational line.
The fact is that cubic surfaces of index > 2 with a non-empty set of points
are birationally trivial (Theorem 30.3), and for surfaces of index 0, the
birational classification coincides with the projective one (see Chapter V). Neither
the one nor the other is true for surfaces of index 1. For this transitional case
there are no decisive results, and H] is the only accessible birational invariant.
Proposition 31.3. Let V be a smooth projective surface over a field k, and
let {D};} С V ® к be a finite G-invariant set of irreducible curves the classes
of which generate N(V). Let S be the group of divisors generated by {/),},
let SqCS be the subgroup of principal divisors, and let H С G be a normal
subgroup of finite index which acts trivially on allDj. Finally we set
N = ( E s)eZ[G/H] .
4eG/tf '
Then
H^G,N(V)~(NSnS0)/NSQ.
(The isomorphism is not canonical.)
Proof. First of all, Hl(G, N(V)) a Hl(G/H, N(V)) (inflation). The exact
sequence of G/H modules

180
THE TWENTY-SEVEN LINES
CHMV, §31
gives
0 -+H-\G/H, ?\c(V®K))^ H°(G/H, S0) -> H°(G/H, S) ,
from which
H~l (G/H, Pic (V ® /C)) s« Ker (^/7V5Q -> SG/NS) = (NS П S0)/MS0 .
It now remains for us to observe that the canonical pairing
Pic (V ® К) X Pic (V ® /Q -> Z
(the intersection number) induces a pairing of cohomology groups
№ (G/H, Pic (К ® К)) X H~P(G/Hf Pic ( К ® £)) -> //°(С/Я, Z) ,
which is an exact duality. The proof of this is a slight generalization of the
argument of Theorem 6.6, Chapter XII, in the book of Cartan- Eilenberg.
As Pic(F ® K) is a free group of finite rank, the intersection number
permits us to identify Pic(K® K) and Horn (Pic (F® K), Z), which gives an
exact sequence of G/H modules,
0 -+ Pic(V ® K) -> Horn (Pic(V ® /Q, Q) -> Horn (Pic(K ® *). Q/Z) -* 0 .
Its boundary isomorphism
5 : //P(G/#, Horn (Pic(F ® AT>, Q/Z)) 5 /^+1 (G/H, Pic (К ® А))
can be combined with the Cartan-Eilenberg isomorphism, from which
Horn (H~P(G/H, Pic(F® *)), 0/Z) =* HP(G/H, ?ic(V®K)).
We omit the easy verification that this pairing is the same one as ihe one
defined earlier. This proves the proposition.
31.4. Application to the calculation oftf *. Let К be a Del Pezzo surface
of degree d < 7. For {£>,-} we take the set of all exceptional curves on V ® k.
We identify this set with the vertices of the graph Trj = 9 -d. Then S is

СН. IV, § 31 TABLES AND COMMENTS. CALCULATION OF Иl 181
transformed into the group of zero-dimensional chains of this graph, and 50
into the subgroup of chains Ед,/, for which ХдД/,-, /.•) = 0 for all /.- E (vertices
of Гг). Further, let (ZK) С S be the set of those chains which are sums of the
vertices of some Я-orbit, where H is the image of the Galois group in Aut Гг
We denote by zK the number of vertices in ZKi and by h the order of H. Then:
(i) The group TVS' is generated by the chains (h/zK) ZK = norm of a vertex
ofZ„.
(ii) The group NSq consists of the chains
UaK(h/zK)ZK\Wj^aK(h/zK)(ZKfZ^O}.
Here everything, except the number Л, depends only on the decomposition of
Гг into orbits. But this factor also ceases to play a role after passing to the
quotient group (NS П S^)/NS0: by the linearity for all h = 0 (mod zK), we
obtain one and the same value, and in practice it is convenient to choose
l.c.m. (zK) instead of h in (i) and (ii).
In this way Table 3 has been calculated for r = 5.
We cite, finally, a theorem of M. Artin and J. Tate.
Theorem 31.5. Let V be a smooth projective surface over a finite field k,
and let V® к be birationally trivial We denote by h1 the order of the group
Hl (G, N(V))y where G = Gal (k/k), and by (f) the set of characteristic roots
different from unity of the (algebraic) Frobenius automorphism acting on
N(V). Finally, let A be the determinant of the form 'intersection number' on
N(V)G. Then
П(1-П = Л1А-
Г
We omit the proof. This is a particular case of a considerably more general
fact which is established in Tate1s paper [1] not only for birationally trivial
surfaces. (In the paper this equality is only proved up to a factor which is a
power of the characteristic of the base field; but here this restriction can be
removed.) See also Milne [1].
The reader himself can verify as an easy exercise the next proposition.
Proposition 31.6. Let V\ V satisfy the conditions of Theorem 3L5, and

182
THE TWENTY-SEVEN LINES
CH. IV, § 32
let there exist some birational morphism V' -► V. Then Theorem 31.5 holds
for V' if and only if it holds for V.
This reduces the problem to minimal surfaces V. Applying this result to
Del Pezzo surfaces, and translating it in terms of our model with Weyl groups,
we obtain:
Conjecture 31.7. Let 3 < r < 8 and let И С W(Rr) be some cyclic subgroup
of the Weyl group of the root system Rr. We denote by hl the order of the group
#*(//, Nr), by (f) the set of characteristic roots different from unity of a
generator of the group H acting on Nr, and by Л the determinant of the met-
ric on N^. Then
r\0-$) = h]b.
I do not know a direct algebraic proof of this result; of course, it is easily
checked for W(E^) by means of the tables.
Problem 31.8. Does 31.7 generalize to the remaining Weyl groups?
32. Bibliographical remarks
Zeta functions of rational surfaces were computed by Weil [2]. He also
gave an outline of the applications of cohomology theory and the Lefshetz
formulae (the Weil conjectures). The detailed formalism is developed in the
recent paper by Kleiman [1].
The group of automorphisms of the set of twenty-seven lines has been
studied by Jordan [1 J; see also the bibliographies in Henderson [] ], Segre [1]
and Swinnerton-Dyer [2]. The treatment given here is based on Manin [3],
with imprcvements by P. Deligne. It is interesting to note that the simple roots
in the system Rr get an algebraic—geometrical meaning if Nr is realized as
the group N(V) for some 'degenerate' Del Pezzo surface V. A map on it by
means of Щ? collapses some configurations of curves with self-intersection
number —2 into 'rational' singular points. The classes of these curves precisely
constitute a system of simple roots; see Lipman [1 ]. The proof of Theorem

СМ. IV, § 32
BIBLIOGRAPHICAL REMARKS
t?>3
24.5 has been taken from SafareviS [1 ]. The cohomological invariant was
introduced in Manin [4]; its connection with degrees of unirationality is
explained in Manin [3].
The twenty-seven lines were discovered in 1849 by Salmon and Cayley. A
detailed bibliography of the study of them in the first 50 years is contained
in Henderson [1] and in the survey of Meyer [1]. We cite some fragments of
Henderson's historical summary:
"Indeed Sylvester once remarked, in his characteristical florid style:
'Surely with as good reason as had Archimedes to have the cylinder, cone and
sphere engraved on his tombstone might our distinguished countrymen W.ve
testamentary directions for the cubic eikosiheptagram to be engraved on theirs."
"If Cayley and Salmon had wished to follow Sylvester's advice and to insert
a clause in their wills, directing that an eikosiheptagram be engraved upon
their monuments, they would have had no certainty of the correct fulfilment
of their directions until the year 1869, when Christian Wiener made a model
of a cubic surface showing twenty-seven real lines lying upon it. This
achievement of Wiener, Sylvester once remarked, is one of the discoveries 'which
must for ever make 1869 stand out in the Annals of Science'."
"Klein exhibited a complete set of models of cubic surface.s at the World's
Exposition in Chicago in 1894, including Clebsch's symmetrical model of the
diagonal surface and Klein's model of the cubic surface having four real
conical points. Models of the typical cases of all the principal forms of cubic
surfaces have been constructed by Rodenberg for Brill's collection; and these
plaster models may now be purchased."
Henderson's book appeared in 1911. Sylvester's eloquence and the plaster
models disappeared together with the Victorian era ... .

CHAPTER V
MINIMAL CUBIC SURFACES
33. A survey of the result*
In this chapter, the base field к is perfect. We shall investigate the category
of minimal smooth cubic surfaces over к and birational maps, and prove the
following basic facts about them.
Theorem 33.1. Every niuimal cubic surface over к is birationally
non-trivial
Theorem 33.2. Two mvvmal cubic surfaces Vx, V2 over к are birationally
equivalent if and only if they are (projectively) isomorphic.
Hence it follows that all linear constructions with minimal surfaces have a
birationally invariant meaning. In particular the following corollary holds.
Corollary 33.3. // Kj, V*, are birationally equivalent, then the commutative
Moufang loops У^{к)1и, V2(k)/Uare isomorphic (U is the universal
equivalence relation; see Section 11).
We note that Theorem 33.2 is certainly not true for non-minimal cubic
surfaces. In particular, it does not say anything for algebraically closed fields.
Example 33.4. Let Vg be given as in Example 23.4 by the equation
т1+т\ + т} + аТ1 = Ъ.
If a = be*, then VQ and Vb are isomorphic: simply substitute Г3 = сТъ in the
equation of Va.
Exercise 33.5. If J ^ b(k*)*, then VQ and Vb are not isomorphic and
therefore not birationally equivalent.
184

CH.V, §33
A SURVEY OF THE RESULTS
185
Hint. (i). As in Example 23.4, it suffices to show that VQ and V x are not
isomorphic.
(ii). Every projective isomorphism of VQ and Vb must induce an
isomorphism of the sets of the 27 lines.
33.6. To describe the birational automorphisms of V, we need an additional
construction.
In this chapter we shall call a point jc E V(fe) good if it does not lie on the
union of the lines of V ® k. An unordered pair of points x, у E V(k) is called
good \{хФу and the line containing these points is not tangent to V® к and
does not intersect the union of the lines on V ® к in P^ . The point x о у =
= ^(.v) = tv(x) is then also good, as are all pairs from (д:, у, х о у).
The following identity holds:
'xW,='/*"/*• (V1>
In fact, x, x о yf у and a general point v E V lie in one plane; the intersection
with this plane is a cubic curve, and on this curve (tx txoy ty)2v = v (see
Theorem 2.1 (iii)).
Now suppose that the points x, у form a good pair and that they are defined
and conjugate over a quadratic extension К D k. The birational automorphism
tx txo tv is then also defined over Ky and, as an automorphism of the function
field on V ® K, it commutes with the conjugation o£K/k, acting trivially on V.
Galois theory then immediately implies that there exists a birational
automorphism sx v of the surface Fover к such that
s ® K = t t t . (V.2)
x,y x gxoy у v 7
We are now in a position to state theorems on the structure of the birational
automorphisms.
Theorem 33.7. Let W be the group of projective k-automorphisms of a
minimal cubic surface V, and let В be the group of birational maps generated
by the maps tx for all good points x E V(k) and the maps sx y for all good
pairs x, у Е V(k) which are defined and conjugate over a quadratic extension
of the field k. Then the full group Bir V of birational maps V-* V over к is
generated by the subgroups W and B.

186
MINIMAL CUBIC SURFACES
CH. V, § 33
Thus we have described the generators of the group Bir V. We note that W
is finite: its representation on the graph of the lines of V ® к is faithful
because the kernel of the representation acts trivially on the lines and hence its
elements arise from the automorphisms of the projective plane wiiich leave six
points fixed. Except for the identity, there are no such automorphisms.
On the contrary, the group В is very big, provided that V(k) is non-empty.
Meanwhile it is clear that it has many generators: the set {tx} indexed by the
points of V(k) (outside the lines), and the set^ } indexed by the pairs (a
point x с у of V(k)\ a line in P3 which is rational over к and which intersects
V in good points that are not defined over k). Thus the set of generators is
something like V(k) X ?2(k).
It turns out that there are not that many relations between them.
Theorem 33.8. All relations between the generators of the group BW are
consequences of the following ones:
(V.3)
In particular, BW is a semidirect product {with В as the normal subgroup).
We deduce two corollaries.
Corollary 33.8.1. Let Vbea minimal cubic surface over a field к with a
sufficiently large number of elements (infinitely many, for example). Then the
following assertions are equivalent:
(i) The set V(k) is non-empty.
(ii) The group Bir V ofbirational k-maps V -> V contains not only
projective maps.
(iii) The group Bir V is infinite.
Proof. (i)=* (ii). It follows from Theorem 30.1 that there is a good point
x G V(k)\ the map tx is then not projective.
(ii) =* (i). It is clear from Theorem 33.7 that if the birational maps of V are
not exhausted by the projective ones, then there exist maps of the form tx or
s z, with respectively jc G V(k) oryOzG V(k).

СН. V, § 33
A SURVEY OF THE RESULTS
187
(i) => (iii). According to Theorems 29.4 and 30.1, the set V(k) is big (it is
dense if к is infinite). Therefore there exists a gojd pair of points x.y G V(k).
One can then conclude from the relations (V -t Lhat the map txt in the
group BW has infinite order. It is even simpler to prove this by means of some
intermediate results (see Example 39.8.4 below).
(iii) => (ii). This has already been proved.
33.8.2. The second corollary permits us to say something about the
structure of the group В when comparing it to the orthogonal groups of rank three.
We shall assume that the characteristic of к is not equal to two. Let L be
some л-dimensional linear space over k, let/: L --> к be a non-degenerate
quadratic form on L, and let b : L X L -> к be the corresponding bilinear form
Let On{f) be the group of orthogonal automorphisms with respect to/
over k. A reflection тх € On(f),
T (y)=y frfr-JP.Y
is associated with every vectorx EL for which/(x) Ф 0 (see E. Artin [1]).
These reflections satisfy the relations
if x, y, z are linearly dependent. It is trivial to verify this. [As a matter of fact,
the rx generate On(f), and a complete system of relations looks like т\ = 1,
тх ту rz-ru, where и can be explicitly expressed in terms of xt y, z. This is
proved in Becken [1], but we shall not need it.}
Corollary 33.8.3. Let V С Р3 be a minimal cubic surface over the field k.
Let us choose:
(i) an arbitrary plane P2 С P3 over к;
(ii) an arbitrary point jc0 E Р3(Л) which is noi in V U P2;
(iii) an arbitrary non-degenerate quadratic form f on the linear space
L = P3 \ P2 which is zero at x0, and for which there are no isotropic
points on V(Le.. f(x) Ф 0 for all x G V(k)except the points at infinity
on(Vn?2)(k)).

188 MINIMAL CUBIC SURFACES CH. V, § 33
Then the map
t и-т
extends to a homomorphism of the subgroup B$ С В, generated by the tx
for all good points x G V(k), into the group O^f).
Proof. One only needs to compare the relations (V.3) and (V.4) and to
observe that the vectors in L corresponding to the points*, xoy and у on V(k)
are linearly dependent.
We note that this proof has a purely algebraic character and essentially uses
the fact that the system of relations (V.3) is complete. The geometric meaning
of the homomorphism described above is quite vague: the groups Bq and O^(f)
have an entirely different nature, and the possibility of largely varying/looks
strange.
Another astonishing property of the group of birational automorphisms of
К is that В is a normal subgroup in it. I do not know any natural
representation of this group with kernel B.
One would like to use Theorem 33.8 to obtain further information on the
group BW. For instance, 1 do not know the answer to the following problem.
Problem 33.8.4. Does В contain elements of finite order other than tx, syz
and their conjugates?
Maybe the homomorphisms of Corollary 33.8.3 are useful here.
For a better understanding of the structure of B, one may consider the
subgroups generated by those tx for which x belongs to some hyperplane section.
A pilot problem: H is some Abelian group (cyclic in the simplest case). Examine
the group B(H) generated by the generators tQ (for all a E H) with the
relations t\ = (ta tb t_a_b)2 = 1.
33.9. Remarks on the method of the proof In Chapter IV we used the
representation of Gal (к/к) on the object {N(V), cjv, intersection number}.
The group of birational maps of V does not, generally speaking, act biregu-
larly on any model of the function field on V: to resolve the singularities of
each given map, we must blow up some points of V, depending on this map.
A reckless solution is to blow up all points of all models; it turns out that this
can be carried out reasonably well, and one obtains an algebraic object which

СН. V, § 34 THE FUNDAMENTAL BIRAT10NAL INVARIANT 189
here will be called 'the fundamental birational invariant' and will be described
in the next section. It looks like {\imN(V), limoop,', lim (intersection
number), ...} over all birational morphisms V -* V. This monster has been tamed
by Max Noether and the classical Italian mathematicians; the contemporary
authors have only braided ribbons into its tail (cf. Deligne f Ц).
33.10. Comparison with other dimensions. If one replaces the words
'minimal cubic surface1 in Theorems 33.1, 33.2 and 33.7 by the words 'smooth
plane cubic curve having a &-point\ then the assertions remain true, although
the mechanism of the proof in the one-dimensional case is quite different.
However, the group of automorphisms of a cubic curve V with an empty set
of points V(k) cannot be exhausted by the projective automorphisms, because
Vq(!c) acts on V, where V^ is the Jacobian of V (see Cassels [1]). Apparently
this fact has no analogues in the two-dimensional case, but even the existing
parallelism is astonishing. On the other hand, for three-dimensional cubic hyper-
surfaces (let us say over C) the truth of the analogues of Theorems 33.1 and
33.2 would mean a solution to an old problem.
These problems have been neglected because they turned out to be very
difficult. Fano has spended some decades on experimenting and on carrying over
the methods of two-dimensional birational geometry to the
three-dimensional case. His series of papers [1] —[4] and others (see also the bibliography
in Roth [1]) contains a mass of interesting calculations but no coherent proofs
which can stand up to criticism.
Maybe the technique developed in this chapter can be carried over to higher
dimensions. The formal constructions, with the replacement of N(V) by the
Chow ring, may lead us far enough; all the material of Section 34 has
a reasonable generalization. Here the Todd genus and the calculations of the
Chow ring of a monoidal transformation by Grothendieck are used. The
difficulties start in Section 35, especially towards the end.
34. The fundamental birational invariant
In Chapter IV an important role was played by the triple{N(V), <jjyy
intersection number on N(V)}9 which can be constructed for every surface V.
In particular, the action of the Galois group and the group of automorphisms
of К on this triple yields essential invariants of the surface.

190
MINIMAL CUBIC SURFACES
CH. V, § 34
In this section we shall construct an 'infinite' analogue of this object which
is suitable for studying the birational maps of V.
We first collect the necessary facts from Chapter III. Recall that Pic V is at
the same time a covariant and a contravariant functor on the category of
surfaces with birational morphisms/: V -» V. The corresponding maps of the
Picard groups are denoted by Д and /*. The composition law in Pic V is
written additively. We denote the class of the canonical sheaf by со v E Pic V.
Lemma 34.1. Let f: V' -> V be a birational morphism.
(i) /* : Pic V -+ Pic V' is a monomorphism which preserves the intersection
number.
00/*/* = id>Pic v' = Im/* © Kei7* -
(iii) (f*(t)J) = (l',f*(l))fora!ltePic V\ lePic V. In particular, Im/*
and КегД are orthogonal with respect to the intersection number.
(iv)/#(wr) = wr
This result is easily obtained by induction on the index of/ (the number of
monoidal transformations into which/decomposes) from the following more
exact lemma which only deals with monoidal transformations.
Lemma 34.2. Let f: V' ~+ V be a monoidal transformation with a closed
point xEVas centre. We set d = (k(x): k) and D = f"l(x). Let IG Pic V' be
the class of the sheaf Qy(D). Then:
(i)Ker/, = Z/.
(ii)(/, /) = -</.
(iii)cor=/*(coK) + /.
In the following we shall most of all work with the group Pic(^® k),
which will be denoted by N(V). Lemmas 34.1 and 34.2 can be applied to this
group, making the obvious changes. It carries the following family of
structures.
34.3. (i). The Galois group G = Gal (k/k) acts linearly on N{V) through the
second factor of 1^® it.
(ii). The intersection number defines a G-invariant bilinear form
N(V)XN(V)-»Z.
(iii). There is a distinguished G-invariant semigroupN+(V) = {l£N(V)\ I is the

СИ. V, § 34 THE FUNDAMENTAL BIRATIONAL INVARIANT
191
class of a sheaf L such that dim//°(K® £, I)>0}(In other words,N+
consists of the classes of effective divisors.)
(iv). The dual cone N+{ V) = \ieN(V)\ (/. /') > 0 for all l'EN+(V)}. (It
does not necessarily coincide with 7V+: the exceptional classes, for instance,
belong to N+ but not to N+.)
(v). A distinguished element со у GN(V).
Now let /: V' -+ V be some fc-morphism. We shall for brevity write /*
instead of (/® к )* and so on. Then:
(vi)./*(^(K))CA^+(K'), f^N+(V'))CN+(V). (This is obvious from the
explicit construction of the action of/+ and/* on divisors: their effectivity
is preserved.)
(viO./JA^K)) CN+(V'). (This follows from Lemma 34.1 (iii) and the
preceding remarks).
34.4. We shall now prepare the necessary data for passing to the limit. Let
К Э к be some field and let g( V ® K) be the category of which the objects
are birational /C-morphisms V' -> V ® К (where V' is a complete smooth
A-surface). The morphisms in this category are the commutative triangles
„.—„.
V®K
For any two objects of B(^® K) the set of morphisms is either empty or it
consists of precisely one element. Therefore we shall often identify isomorphic
objects.
The set of objects of B(^® A") is naturally ordered by the relation: f>g
([dominates g) if Horn (/, g) is non-empty. The theorem on resolution of
singularities (Theorem 18.4) shows that this set is directed: for every two objects
gj. g2 there exists a third object/such that f> g{, f>g2. In fact, let
gx : V{ -> K® K, g2 : V2 -* V®K, and let //,-: K3 -> V( (i = 1,2) be the
resolution of singularities of the mapg-Jl r S\- Ihen f = g\ о hx = g2 с h2 dominates
g\ and#2-
Lemma 34.5. Replacing the base field к by К transforms B(V) into a
cofinal subset ofB(V® K) if the extension К D к is algebraic.
An informal explanation: Suppose we have, say, a projective system of
groups, indexed by the ordered set of birational nv-^hisms V' -* К® К.

192
MINIMAL CUBIC SURFACES
CH.V, § 34
Then we can take the limit, while restricting ourselves to those morphisms
which are defined over k.
Proof of Lemma 34.5. We must check that for every /C-morphism
/: V' -> V ® К there exists a £-morphism g: V" -► V such that g <8>K
dominates/. The idea of the proof is the following: Include the points of
indeterminacy of (/® fc)-1 on К® к in a G-invariant finite set, after having added
all conjugates, and blow up this larger set; this can be done over k.
To carry out this idea, however, it is necessary to take care separately of
the case when there are among the points of indeterminacy of/~l 'infinitely
close points* in the Italian terminology. In other words, in the decomposition
f = fn-.f\ into monoidal transformations, the centre of/, can lie on a curve
which collapses when, let us say,/^ is applied.
Therefore wc first define a canonical decomposition of the morphism
f:Vl-*V®K.l*txlC V <g> К be the smallest subscheme of V ® К
outside which/is an isomorphism. It is closed and zero-dimensional. Let/| : Kj -*
V® К be the monoidal transformation with centre jcj (the identity map
ifjCj is empty). The proof of the theorem on resolutions shows that
/dominates /j. If/~/i, then/j is called the canonical decomposition of/. In the
opposite case, the same construction, applied to Kj, gives the subscheme
x2 С Vx and its blowing up /2 : V2 ~* V\, whereby /dominates f2f\.
Continuing in this way, we obtain a canonical decomposition of/:
v'=vr - vr _!-►...-> vx -+ v®k.
The number r is called the length of the decomposition^^ set r = 0 if/is an
isomorphism. It is clear that the length does not exceed the index of/, but it
certainly can be strictly smaller: the length is one if there are no 'infinitely
close* points of indeterminacy.
We shall now establish the existence of a morphism £ (first paragraph of the
proof) by induction on the length r. If/is an isomorphism, i.e. the decompo-
id
sition length is zero, then for g we can take V -* V.
Suppose that everything has been proved for morphisms of decomposition
length r-T. We set f~ffr, where the length of/' is equal to /*—1,/': Vr^\^
V ® K. Without loss of generality we can assume that A' is a Galois extension
of the field к with group G.

СН. V> § 34 THE FUNDAMENTAL BIRATIONAL INVARIANT
193
Let g : U-> К be a &-morphism such that g ® К dominates/'. Consider
the commutative diagram
HerejJ. is the blowing up of a closed reducible subscheme x С Кг-1. This sub-
scheme x can be written as a union x' U x", where x" consists of all points in
which h is a local isomorphism. Let и € U ® К be the reducible subscheme
which is the union of all points conjugate over к with points of h~^(x") with
respect to the action of С There exists a subscheme и G U such that и ® K=u\
Let g": V" ^ U be the monoidal transformation with centre u. We put
g ~ gg": V" "* К The morphism g <8> К dominates /because h о (g" ® /Q is
not a local morphism at any of the points of x and thus it dominates the
monoidal transformation/,, with centre*. This proves what we want.
Definition 34.6. Z' (V) = lim N{V') and Z.(F)= lim N(V'). The limits are
taken with respect to the maps/* in the first case, and with respect to the/*
in the second case; V' runs over all possible birational &-morphisms
/: V' -> К or /c-morphisms V' -* K® A:: this is the same according to
Lemma 34.5.
Z'(V) plays the role of Ticard group of the field of rational functions on
V\ The group Za(V) will not play any role in the following: it has been
introduced for symmetry and some intermediate explanations.
All the structures described in Section 34.3 can be carried over to this
infinite level (and they shall be used in the following).
34.7. (i). G acts onZ\V). (Here it is important that we can take the limit
using the ^morphism/: V -» V, and then/* : Pic(K'<g> k)->P\c(V<g> k)
is a G-homomorphism. This also gives the action of G on the limit.)
(ii). The intersection number furnishes a G-invariant bilinear from
Z" (V) X Z' (V) -*Z (because/* preserves intersection numbers according to
Lemma 34.1 (i)).
(iii). Z;(K)= lim N+(V'). (Use property 34.3 (vi).)

194
MINIMAL CUBIC SURFACES
СИ. V, § 34
(iv).Z+'(*0 is not introduced by passing to the limit, but by duality:
Z+*(K)= {z eZ'(V)\(z,z')>0 for all z'eZ'+(V)}.
(v). £2 :Z'(V) -> Z is defined as the homomorphism wnich on the image
ofN(V) inZ"(^) coincides with the intersection number with coy:
n(z) = (/,wK)
if IEN(V) represents z. The result does not depend on the choice of/by
Lemma 34.1 (iii), (iv).
Thus, there is no 'canonical class' in Z' (V): it belongs to the dual group.
The reason for this is shown by Lemma 34.2: the limit of the canonical classes
would have to coincide with the sum of tov and all exceptional classes in
lirn N(V).
More formally, Lemma 34.1 (iv) shows that there exists a limit
£2 = lim и*,. €Z (V\ and, using 34.1 (iii), by means of the intersection num-
ber we can define a pairing
Z'(V)XZ.(V)-*Z
such that H(z ) = (z, £2) for all z GZ '(V). The details are left to the reader as
an exercise.
Theorem 34.8 (Theorem on the fundamental invariant). The composite
object Z(V) consisting of the groups Z' (K), Z. (V) and the structures described
in 34.7 (i) - (v) is a k-birational invariant of the surface V.
More exactly, the map V^Z(V) can be extended to a covariant functor
on the category of smooth projective k-surfaces and their birational maps. For
each birational map f: V' -+ V, the corresponding morphism Z(V') -+Z(V)
is an isomorphism.
In particular, the group of birational maps of V into itself is represented in
Z' (V) and preserves all the structures described.
Proof. Let /: V' -+ V be a birational map. To define the isomorphism
Z(V')-*Z(V) (which in the future we shall also denote by/for the sake of
brevity), we note that there are cofinal subsets in 8(V') and B(K) which
are identified by means of/ Namely, let g : Vм -► V\ h : V" -* V be any
resolution of the map /. Then B(K") is embedded in B(K') by means of g and
in B(V) by means of h. The images of these inclusions are cofinal.

СН. V, § 35
A BUBBLE SPACE
195
The independence of this construction from the choice of the resolution
and the functoriality in/are verified immediately and completely standard.
This proves the theorem.
In the following section we shall introduce a certain space which permits
us to indicate a convenient 'geometric' system of generators for the group
Z' (K) and to describe the structures introduced above in terms of it.
35. A bubble space
Definition 35.1. E(V) = (U V')/R, where V' £ V runs through all objects
of the category 8(F), and R is the following equivalence relation:
The points x' E V' and x" £ V" are equivalent if the canonical birational
map V' -* V" is an isomorphism of some neighbourhood of x with some
neighbourhood of x".
35.2. Comments, In order to imagine better what the space E(V) looks
like, we shall consider how to glue together with respect to R two surfaces
/: V' -* V connected by a monoidal transformation with as centre a point
x € V. R identifies V \ x with V' \ Z), where D =/"1(JC)- The closure of
this open set contains the disjoint union D U{*}. This is a typical case of a
non-separated scheme. If к = С, then/} (С) = P!(C) is the Riemann sphere;
thus ((KU V')/R) (C) as a topological space is obtained from the
four-dimensional space K(C) by attaching a two-dimensional 'bubble' Z)(C), blown up
from the point x (see Fig. V.l). Passing to E (V) means that we blow up
bubbles from all points of V, and then from all points of these bubbles, etc.
Fig.V. l.

196
MINIMAL CUBIC SURFACES
CH. V, § 35
35.3. All canonical maps iy,: V' -» E(V) are open embeddings. We call the
spaces iy(V) the leaves of E (V). Every leaf is dense in E (V). For brevity's
sake we shall say that a point x GE(V) lies on the surface V\ where
(V' -* V) E B(V), if * lies on the corresponding leaf.
There is a natural ordering on the set of points of E(V): We write *' <x"
and we say *' lies overx" if there exist surfaces V\ V" such that *' lies on V\
x" lies on V", and the canonical map V' -> V" is defined at the point *' and
sends it to*". In other words,*' <*" if*'lies on the bubble blown up out
of the point *", and < is the weakest ordering with this property. (To show
that these definitions are equivalent, one must refer to the proof of the
resolution theorem, as in Lemma 345.) The point x' lies over a surface V" if there
exists a point x" on the surface V" for which *' <x".
The geometric points of the space E(V) and the ordering relation on them
are defined analogously.
Definition 35.4. The symbol Z°(K) denotes the free Abelian group
generated by the geometric points of E{V) with values in the field k.
In other words, the elements of Z°(K) are the zero-dimensional cycles the
components of which are not only points of the surface Fbut also points
lying 'over' this surface.
35.5. We equip Z°(K) with the structure of a G-module by using the
natural action of the Galois group G on E(V) (k). We further define a scalar
product
Z°(V)XZ°(V)^Z
by setting (x, *) = -1 and (*, y) = 0 if* Фу, for all *, у G E(V)(k).
We now consider the orthogonal direct productN{V) XZ°(K) and define
a homomorphism
N(V)XZ°(V)-+Z'(V)
as follows. On the first factor it is the canonical map of an element of the
inductive system of groups \N(V')} in its limit.
Now let * GE(V)(k), and let * lie on the surface V\ (V -+V)G B(V).

СН. V, § 35
A BUBBLE SPACE
197
We blow up the closed point corresponding to jc on V'® k. LetD be its
inverse image on the resulting surface V". The composite morphism
V"-+ V® к -* V®k is in 8(F <£>£), and QV„(D) defines an element of
the group W(T"), which is canonically imbedded in Z'(V). We let the image
of the class of Oy(D) under this embedding correspond to the point x.
Briefly: each point x G E(V)(k) is put into correspondence with the class of
its blown up bubble; this map is extended to Z°(F) by linearity. It is easy to
see that the map is well defined.
The main justification for introducing the space E(V) is the following:
Proposition 35.6. The homomorphism just constructed,
N(V)XZ°(V)-+Z'(V),
is an isomorphism ofG~modules with scalar product.
The proof is obtained by the completely formal passing to the limit from
Lemmas 34.1 and 34.2. Roughly speaking, 'on a finite level' of one monoidal
transformation /: V' -* V with as centre the point x (over k), we write
Pic V' = Pic V Ф Zx ,
where (x, Pic V) = 0 by 34.1 (iii),Pic V denotes/* (Pic K)andx stands for
the class of Qv>{J-l(x)).
35.7. In future we shall identify Z\V) with N(V) X Z°(V) as
described in 35.5. The following intuitive interpretation suits this formalism.
Let IGN+(V). Then / is uniquely determined by the complete linear
systems of the zeros of the sections of the corresponding invertible sheaf.
Now let x € V(k) be some point. We consider the element 1-xS
N(V)XZ°(V) = Z'(V). Let/: V'-+Vbe the blowing up of x. Then 1-х
represents some element /' inTV(K'). We suppose that /' EN+(V') as well and
construct the linear system of the sections of the corresponding sheaf on V' and
its image under/in K. Then this will consist of precisely those sections of the
sheaf of / which pass through the point x.
Similarly, the element / - 2^-jc,- corresponds to those curves of the linear
system of / which pass through the point xx with multiplicity >aiy through
the point x2 with multiplicity >a2i etc. (cf. Lemma 35.10 below).

198
MINIMAL CUBIC SURFACES
CM. V, § 35
Needless to say that the inconvenience of this interpretation is connected
with the existence of Virtual linear systems with prescribed base points',
which are not linear systems at all. The groupN(V) X Z°(K) provides also a
convenient framework for such objects. The interpretation connected with
effectiveness is reflected in the structures of Z+' and Z+ .
Finally, we have started with the introduction ofZ' (V)because the
definition of this group is more invariant and more convenient for the verification
of functorial properties. On the other hand, the group N(V) X Z°(K) is well
suited for concrete calculations, as we shall see below.
Finally, we shall establish some auxiliary facts on the extra structures in
Z-(V).
Lemma 35.8. Let L be an invertible sheaf on V ® к which is isomorphic to
/*(0pr(l)), where f: V®k^?r is some morphism. Then the class l of this
sheaf inZ'(V) belongs toZ*'(V).
Proof. Obvious.
Lemma 35.9. The restriction to Z°(F) of the homomorphism
ft : N(V) X Z°(V) -> Z (see Section 34.7 (v)) is defined by the formulae
a(x) = -\foraUxEE(V)(k).
Proof. In fact, for every exceptional class / £ Pic (V' ® k) we have
(wK,,/)=-l.
Lemma 35.10. Let DC V® fc be some effective divisor, letxlf.. .xnED
be closed points, and let ni be the multiplicity ofXj on D. We denote by
lGN(V)the class of the sheaf 0V(D) and identify the points x{ with the
corresponding points of E (V)(k). Then
n
|-Б«лбг;(и)..
Proof. Let/: V -> V® к be the monoidal transformation with as centre
the union of the points xy. According to Proposition 20.4, the class /- EjLjrt/*/
represents in the group Pic V' the class of 0К<(/_1(Я))>where f~l(D) is the

СН. V, § 35
A BUBBLE SPACE
199
proper inverse image of D (Definition 20.3). As/_1(D) is effective, everything
is clear.
Corollary 35.1 \.Letx',x"eE(V)(k).Ifx,<x",thenx"-x,eZ'+(V).
Proof. Let x' lie on a surface V\ and x" on V'\ If the birational map
V' -> V" is locally the blowing up of x\ then the element x" ~x' represents
the element/-*' (in the group N(V)X ZQ(V') = Z'(V') = Z\V)\ where
/ is the class of 0y(D) and D is the inverse image of x" on V\ In this case,
the assertion follows from Lemma 35.10 because x lies onD.
In the general case, there exists a sequence of points x" = Xj > . . . >хп-х
such that (xt> x/+1) satisfy the preceding condition. Therefore xrxi+l E Z+(Ю>
and hencex" — x E Z\{V) because Z\ is a semigroup.
Corollary 35.12. Let I - S^x,- EZ+'(V), where IE N(V) and xt E E{V)(k).
Then:
(i)lEN + (V).
(ii) nf > 0.
(iii) л,- >Hj ifXj >Xj.
Proof. The element / - ^nixi represents some class /' EN(V') on a surface
V' L V. It is obvious from the definition that even /' EN+(V'). But then
l =/*('') €N+(V) because of 34.3 (vi).
Further, Xj EZl(V) (obviously) and xz- -x.- EZ+(V) if xt >x, (Corollary
35.11). Therefore
п^(1-ХП{х.,х.)>09
which concludes the proof.
Lemma 35.13. Let f: V' -* V be some birational map. We suppose that
there exists an element /' EN(V) С Z'(V')such that I = f(l')E_N(V) С
CZ'(V) and I is the class of some ample invertible sheaf on V. Then fis a
morphism (and hence /' =/*(/)).

200
MINIMAL CUBIC SURFACES
CH. V, § 36
Proof. Represent/as a composed map V'—> V^ -+ V, where g and h are
birational morphisms. We want to prove that h о g~l is a morphism, i.e., that
h collapses all curves which g~* blows up.
An easy induction on the index of g permits us to restrict ourselves to the
case where g is a monoidal transformation with a closed point x' E V' as
centre. Let /t EW^) be the class of the inverse image g_1(jc). Applying
Lemma 34.1 (ii), (iii), we find
0 = (^(О,/,) = (лЧ0,/1) = (/.л»(/1))-
It follows from this that h collapses the curve g~l(x): in tne opposite case the
class of /^(/j) EN(V) would represent an effective divisor, and the
intersection number of the ample class / with any non-zero effective divisor is positive.
This proves the lemma.
36. Calculations on cubic surfaces
We now apply the developed techniques to cubic surfaces. We start with
the calculation of the actions of the birational maps tx and sx • V-> V on
the group Z' (V) (see Theorem 34.8).
Lemma 36.1. Let V be a cubic surface over an algebraically closed field k,
let x ^ (resp. x^fx2)bea good point (resp. a good pair of points) on V (see
33.6). Then for any element
к
z=acjy^bixieN(V)XZ°(V)=Z\V)>
i=l
wherex. € E(K)(k) and х.Фх. for i Ф j, we have
к
tx(z) = (2a-bl)wv + (3a-2bl)xl+I}b.tx(x.), (V.5)
i=2
sx x (z) = (Sa-2bl -2b2)ojy + (ба-ЗЬ^ - 2b2)x}
к
+ (6a-2b,-3fc2)x2 +'Dbisx,{xi). (V.6)
/'=3

СН. V, § 36 CALCULATIONS ON CUBIC SURFACES 201
Proof. We start with the explanation of the symbols tx (xt) and sx x (xz).
Let V -► V be the blowing up of the point xx. Then E(V^){k) = Е(У)(к)^{хх}.
But tx is a (biregular) automorphism on V'\ see Example 21.2. Therefore
tx can be naturally extended to an automorphism of the space E(V) (к).
We denote the image ofxz- under this action by tx (xf) forxz- Фхх.
Similarly, we can check that sx x = ix tx ox tx acts biregularly on the
surface V" obtained from К by blowing up the points xx, x2 (but not xxcx2\).
This action can thereupon be extended to E(V")(k) = E(V)(k) \ {jcj, x2],
which permits us to define the points sx x (xz) for \Ф 1,2.
We now prove formula (V.5).
First step. Let/: V -» Vbe the blowing up ofJCj. We identify by means
of this moiphismZ'(V)=N(V) X Z°(V) withZ'(K') = N(V') X Z9(V) so
that E(V')(k) = E(V)(k) \ {xx} as above. Denoting by lx EN(V) the class
of the inverse image of xx, we then have
b)v = b)v,-l, xx=l, х1=х1ЦФ\),
so that
К
z=ao)v, + (b-a)l + Tj b.x.. (V-7)
;=2
Second step. For brevity let us denote by tx the automorphism of V
induced by tx on V. We calculate its action on the (for us interesting) elements
of Z'{V'). There is nothing to say about the action onxz; moreover, tx (cov,)-
~tOy,.
We now show that tx (/) = -coy,-L Indeed, let D С К be the intersection
of К with the tangent plane inx Thenx has multiplicity two on D, so that
class f*(D) = class f~l(D) + 21.
But
class/*(£>) = -f*(uv) = -cjv, + I,
so that
chssrl(D) + I= -ojv, , / = classf'l{x).

202
MINIMAL CUBIC SURFACES
CH. V, § 37
On the other hand, the geometric analysis (see Example 21.2) shows that the
curves f~*(D) 2Li\df~l(x) are interchanged under the action of tx . This
proves what we want.
Third step. Substituting tx (/) = -oov,-l in (V.3), we obtain
к
tx (z) = (2*-*)wr + (n-ft)/+£ty* (*.).
/=2
Finally, under the opposite identification of N(V') X Z°(K') with
N(V) X Z°(K), the class cov> goes to coK + x{, the class / to xh and ^ (*,-)
remains the same. This proves (V.5).
Formula (V.6) is obtained by a mechanical threefold application of formula
(V.5), if one takes into account that s„ v = f v tY nv fv . We omit this calcu-
v ' \**2 1 л1ил2 х2
lation; note, however, that precisely here the hypothesis is used that we
have 2l good pair (xx,x2) and not just two separate good points x^t x2.
36.2. Comments. From formula (V.5) it follows that
гх1(~ы|/) = -2сок~3;с1 •
According to Section 35.7, such an equality means that the linear system of
hyperplane sections of К goes into a linear system of intersections of V with
quadrics which have at least a threefold point inx1. If one prefers, the content
of the lemma is exhausted by this.
This classical terminology is completely adequate as long as points lying
over V do not turn up. Within the frame of our formulation, such geometric
difficulties are easily localized and separated from the purely algebraic theory
of the representation of birational maps in Z' (V).
37. Birational non-triviality
It is time to start gathering the fruits.
We start with the proof of Theorem 33.1, which is obtained as a corollary
of a much stronger result. To be able to formulate this exactly, we call a k-
surface Va surface with a rational bundle structure if it admits a /:-morphism
f:V->B such that the base and the general fibre have genus zero (the fibre is
supposed to be irreducible and reduced).

СН. V, § 37
BIRATIONAL NON-TRIVIALITY
203
Among these surfaces is for instance P1 X P1, so that the birationally trivial
surfaces belong to this class. It is a very large class; for instance, if к is a finite
field, then it contains representatives of all except a finite number of the
classes of surfaces birationally trivial over к modulo birational equivalence
over k. This is proved in Manin [4].
Theorem 37.1. A minimal cubic surface V over a perfect field к cannot be
birationally equivalent with any surface with a rational bundle structure.
Proof. Let Vbe birationally equivalent with such a surface. Then the image
i in Z' (K) of the class of some fibre of the bundle has the following
properties:
zGZ+(F)G, (z,z)=0, fl(z) = -2. (V.8)
In fact, all this is true in the Picard group of a surface with bundle structure
and it is preserved in Z* (V) according to Theorem 34.8. We shall show that
there are no such elements.
According to the minimality criterion 28.1, N(V)G - Zcjv. Therefore z
must have the form
К
z = -jcok- L/bixi .
/=1
Corollary 35.12 then shows that a > 0 and bi > 0 for all /.
Choose a z with the lowest possible value of a. By Proposition 35.6 and
Lemma 35.9, the last equalities of (V.8) can be written in the form
(V.9)
К
3 a - T/ b{ = 2 .
i=l
We can assume that b{ > b2 ^ . . • ^ bK > 0 (it is clear that not all bi can be
zero). According to Corollary 35.12 (iii), in any case one of the points of
maximal multiplicity Ьл must lie on the surface V and not over it. Let this point

204
MINIMAL CUBIC SURFACES
CH. V, § 38
bexj E V(k). We show that it is a good point. Otherwise it lies on some line
belonging to an exceptional class IEN(V). According to Lemma 35.10,
/ - x j 6 Z+ (V), from which
0<(l-xvz) = a-b} .
This, however, contradicts eqs. (V.9) because
Зд2 = Е h] < bx E bt < МЕа, + 2) =3abx ,
/=1 /-1 \/=1 /
which implies a < bx. Because Jtj is a good point, we can apply the
automorphism tx to V ® k and calculate its action or\Z'(V)by means of Lemma
36.1. Then
к
t (z) = -(2a~bl)cov-(3a-2bl)x1 -T*b.tx (x.) .
/=2
Moreover, by Theorem 34.8 the element tx (z) also satisfies conditions (V.8)
(just as z). But the coefficient of - cj K of it is equal to 2a - by < ay and this
contradicts the choice of z. This proves the theorem.
38. Birational classification
In this section Theorems 33.2 and 33:7 will be proved. They are both
contained in the following result:
Theorem 38.1. Let V, V' be cubic surfaces over some perfect field k, let
V be minimal and let f: V' -> V be some birational k-map. Tlien there exists a
birational k-map g: V-* V with the following properties'.
(i) g can be represented as a product of maps tx and sy z for good points
x 6 V(k\ respectively good pairs of points у, z G V(k) defined and conjugate
over a quadratic extension of the field k.
(ii) The composed map V—* V% V is an isomorphism.
Corollary 38.1.1. Under the conditions of Theorem 38.1, V' is also minimal.

СН. V, § 38
BIRATIONAL CLASSIFICATION
205
38.2. The derivation of Theorems 33.2 and 33.7. For Theorem 33.2 it
suffices to make sure that every isomorphism h : V' -*• V is projective; but
h*(£lyl) - Sly], and Sly1 is precisely the sheaf 0y(\) under the standard
embedding.
Theorem 33.7 is obtained by applying Theorem 38.1 to the case V' = V
and /an arbitrary birational map of V into itself.
38.3. Proof of Theorem 38.1. We set z =/(-coF0 eZ* (K). This element
possesses the following properties:
zeZ*\V)G ; (z,z) = ft(z) = 3.
Setting z = - jco у - I*=1 Z? .Jtj, as in Section 37, we find a > 0, b{ > 0 for all /
(we again use the minimality of V in the form of the equality N(V)G = Zaiy).
Further,
3a2-Efc?=3-
i=l
(V-10)
3j- Eby=3;
i=l
therefore a > 0. We suppose that not all the bi are equal to zero and set
bx >62>...>fcK>0.Wehave
К I К ч
3j2=Sb/2 + 3<b1( £^. + 31=3^ ;
/=1 ^ i=l '
consequently a < bx. (The equality sign is possible here only if b{ = 1, but
then a = 1, which contradicts (V.10).) It follows from this that there can be
no more than two points with the coefficient b\\ otherwise 3a - 2f=jfy <
<3a-3bx <0.
We now consider two cases separately; and these exhaust all possibilities.
Case 1. On the surface Flies exactly one point oixx,..., xK with
coefficient bx. Let this point be xv Exactly the same arguments as in Section 37
then show that Xj is good. Moreover, the element z is G-invariant, therefore
xx € V(k). Applying Lemma 36.1, we find from this,

206
MINIMAL CUBIC SURFACES
CH: V, § 39
к
tXi(z)= -{2a- b{)toy - (3a-2bl)x{ - Ety^x.) ,
so that the coefficient of -co у has diminished.
Case 2. On the surface V lie exactly two points of xx,. . . , xK with
coefficient bj. Let these bexj, x2. The pair (*i,*2) is G-invariant because z is G-
invariant. Consequently, either both points are defined over k, or they are
defined and conjugate over a quadratic extension ofk. In the first case it suffices
to apply tx to diminish the coefficient of a. In the second case we can make
use of sx x (see Lemma 36.1), but we must first show that (jcj, x2) is a
good pair.
Because both of the points xv x2 (having maximal multiplicity) are good,
difficulties can only arise if the line through x±, x2 is tangent to V at precisely
one of these points; but this is not possible because such a line is G-invariant.
The other bad case is when the point Xy о х2 lies on one of the lines. We
show that this is not possible. In fact, according to Lemma 36.1, the
coefficient of -coу in the decomposition of the element tx (z) is equal to 2a - b2,
and the coefficient for x± о x2 is equal to by But 2a-b<> -2a-by <&j;
therefore x^ о х2 is a point whose multiplicity in tx (z) is greater than that of
— go j/. The same arguments as in Section 37 applied to tx (z) instead of z
show that xx о x2 is a good point.
Conclusion of the proof. Repeating the above constructions, we construct
a map g : V ->• V by composing the maps tx and sx y such that the composed
map£o/: V' -> K-> К has the property go /(-co v.) - -atoy. Applying
Lemma 35.13, we immediately obtain that g о f is a morphism. But it can
collapse nothing because rkN(V') = rk N(V) = 7. Therefore g о /is an
isomorphism. This concludes the proof.
39. Relations between the generators
In this section, Theorem 33.8 will be proved, as a corollary of some more
general results.
Excepting the last two subsections, the base field k is supposed to be
algebraically closed in this section; Fis an arbitrary smooth cubic surface over k.

СН. V, § 39 RELATIONS BETWEEN THE GENERATORS 207
Definition 39.1. A birational map/: V ~+ К over к is called good if under
its action onZ*(T) the subgroup Zcjj/ + Z°(F) is mapped into itself.
Motivation: If/comes from a birational map of a minimal surface over some
subfield of A:, then /is good; this follows from Theorem 33.7 and Lemma 36.1.
We denote by В the group of good birational maps of V. The coefficients
of its representation in ZcoK +Z°(F) will be our main tool in the study of this
group. We therefore give the following formal definition.
Definition 39.2. The functions a, bx'.B -> Z(where x E E(V)(k)) are given
by the formula
/(«^«(/)ик + ^№. (v.ii)
For convenience of reference, we restate in this slightly more precise
context a series of results which have already been proved.
Lemma 39.3. For every element feB we have
*(/)>!, bx(f)>09 bx(f)>by(f)
ifx>y .
This follows from Corollary 35.1 2.
Lemma 39.4. Let x be a good point of V(k), and let (x, y) be a good pair.
Then tx eg, sxyeB, mid for all f SB, we have
a{txf)=2a(f)~bx(f)9
bx(txf) = 3a(f)- 2bx(/), (V.12)
bxoyHxn = byU) ify*x.
and
a(sXiyf) = 5a(f)-2bx(f)-2by(f), (V.Ba)
bx(-sx,y^ = 6aW - 3M/) - 2Ьу(П > (V-l3b>

208
MINIMAL CUBIC SURFACES
CH.V, §39
by(sXtyf) = 6a(f)-2bx(f)-lby(f), (V.13c)
KM*xyfi=biW ifz*x>y- <v-13d)
This is an obvious reformulation of Lemma 36.1.
Lemma 39.5. LetfeB.
(i)Ifa(f)> 1, then there exists a good point x E E ( V) (k) lying on V
such that bx(f) > a(f). No more than two points of E ( V) (k) satisfy this
inequality.
(ii) Let x, у € E (V) (k) be two good points lying on V such that bx(f) >
> by(f) > a(f). If at least one of these inequalities is strict, then they form a
good pair.
(iii)L£f*£ E (V) (k) be a good point lying on V. Then bx(f) =^flf(/); in
particular, in the conditions of (ii) one of the inequalities is certainly strict.
Proof, (i). We have
(/(w^)./(wv)) = (^K,coK) = 3 ,
^(/(^k))= ^(wk) = (wk»wk) = 3 »
from which
з*(Я2-Е^(/)2 = з,
(V.14)
X
After this, the argument goes on as in the beginning of the proof of Theorem
38.1.
(ii). Let (x,y) € E(V)(k) be two good points lying on К and such that
bx(f) > b (/) > a(f)y where at least one of the two inequalities is strict. To
prove that (x,y) is a good pair, we must check that the line through x,y is
not tangent to V in x,у and that x о у does not lie on the lines of V.
Suppose that this line is tangent to V at x (the case of у goes completely
analogously). The tangent plane to V at x intersects V in a curve which passes
through у and which has a double point at л\ This curve belongs to the class

СН. V, § 39 RELATIONS BETWEEN THE GENERATORS 209
of -co y. According to Lemma 35.10, — со у ~ 2x - у GZ\(V). Because
f(o>y) GZ*\V), we obtain from this
(-coK- 2x yJ(cov)) = 3a(f)- 2bx(f) by{f) > 0 ,
but this contradicts the condition imposed on x,y.
We now show that jc о у is a good point. In fact, by Lemma 39.4
a(tyf) = 2a(f) - by(f) < bx(f) = byox(ty f).
Vixoy lies on a line of class/, then/- x oyGZ'+(V) by Lemma 35.10. On
the other hand, tyf{- u>v) €2+'(K). Therefore
0 < (/ ■■ xoy, y(-w„)) = a(tyf) -byox(tyf) .
The contradiction thus obtained proves what we want.
(iii). Suppose that there exists a good birational map/GZ? and a good
point x E V(k) such that bx(f) -a(f). We choose an/with a smallest possible
a(f). It is clear that a(f) > 1; otherwise equation (V.14) could not be valid.
Let у G V(k) be a good point such that by(f) >a(f): it exists in virtue of
assertion (i). According to property (ii), (x,y) forms a good pair. From
Lemma 39.4, eq. (V.13), it follows that
a{S;tyf)=3a(f)-2by(f),
bx(\yf)=Mf)-2by(f).
But this contradicts the choice of/because sx yfis a good map and
3a(f) - lb ,(/) < a(f). This concludes the proof.
Lemma 39,6. a(f)= 1 if and only if f is a projective automorphism of V.
Proof. From (V.14) it is clear that all bx(f) = 0 ifa(f)= 1. Applying
Lemma 35.13 to the map/: V-+ V we obtain that/is a morphism. We have
already verified that in this case/is a projective isomorphism.
The last result parallels Theorem 33.7.

210
MINIMAL CUBIC SURFACES
CH. V, § 39
Theorem 39.7. The group В of good birational maps of V is generated by
the group W of projective automorphisms and the maps tx for all good points
Proof. Suppose that this is not the case. We consider an /EZ? with smallest
possible fl(/), which is not contained in the subgroup generated by W and the
tx. It is clear from Lemma 39.6 that a(f) > 1. According to Lemma 39.5 (i),
there exists a good pointy E V(k) for which by(f)>a(f). Then tyfEB and,
by Lemma 39.4,
a(tyf) = 2a(f)-by(f)<a(f).
This contradicts the choice of/because tyf does not belong to the group
generated by W and the tx if/does not. This proves the theorem.
We shall now occupy ourselves with the relations. The basic result of this
section is:
Theorem 39.8. The following relations between the generators w E Wand
tx of the group В generate a full system of relations:
x xoy ly ~ у xoy lx '
wtxw'1 =W>. <^15>
In particular, В is a semidirect product of W and the normal subgroup В
generated by all the tx.
39.8.1. Start of the proof That the first and the third of the relations (V.15)
hold has been proved earlier. The second easily follows from the fact that the
action of w is linear; therefore it can be extended to the whole space P3 and it
sends the lines by means of which tx is defined into lines. In particular, good
points and good pairs remain good.
We now occupy ourselves with the completeness of the system (V.15).
We denote by D the free product of the groups Z2 generated by the symbols
Tx and Sx v, one for each good point x E V(k) and one for each unordered

СН. V, § 39 RELATIONS BETWEEN THE GENERATORS
211
good pair of points x, у G V{k), with the relations Tx - s\ v = 1. Construct
the semidirect product DW with the normal subgroup/) on which W acts
according to the rule
wTxw'~l = Tw(x) . wSxtyw~X =Sw(x)M.v) •
There exists an epimorphismZW-*/? which is the identity on W and which
sends Tx into tx and Sx y into sx y = txtxoyty (by definition!).
To prove the theorem it suffices to verify that the kernel of the homomor-
phism DW-+B (as a normal subgroup) is generated by the elements
$x у Tx 7^L,V Ty. First we describe how to associate to each element of В some
uniquely determined inverse image of it in DW.
Each element unequal to the identity of DW can be uniquely written as
R\R2. * . Rn, where RfJ is one of the symbols w G W\{l}, Tx, Sxv, and Rt
for/< «-I is one of the symbols Tx, Sxv. Moreover, R^R^ for all /.
We shall say that this word starts with R j; the number n is called its length.
The identity is represented by the empty word of length zero. We shall identify
the elements of DW with such words.
We define canonical words by induction on the length. The definition uses
in an essential way the representation of\D!V on Z'(V) induced by the homo-
morphism/)W -> B.
Definition 39.8.2. (i) The empty word and all words of length one are
canonical.
(ii) The word TXF is canonical if and only if the word F is canonical and
satisfies the conditions
bx(txf)>a(txf),
bvOxf) < bx(txf) for all у lying on V,
where/is the image ofFinB.
(iii) The word Sx VF is canonical i( and only if F is canonical and satisfies
the conditions
М\,я=у*х,,/)>«<^,/).
The continuation of the proof of Theorem 39.8 has been split into several
lemmas.

212
MINIMAL CUBIC SURFACES
CH. V, § 39
Lemma 39.8.3. For every element g€B there exists a unique canonical
representative G in DW.
Proof. The existence of G is established by induction on the number a(g).
If a(g) - 1 > then g E W according to Lemma 39.6, so that the element G is
canonical. Let a(g) > ] and suppose that it has already been proved that there
exists a canonical representative for every fEB with a{f) <a(g). Find a
good point* G V(k) such that bx{g)> a(g) (Lemma 39.5 (i)). If in addition,
bx(g) > b (g) for every other point у on V, we set /= txg. Then a(f) =
= 2a(g)-~ bx(g) < a(g). Let F be a canonical representative of/. Then TXF
is a canonical representative of g by Definition 39.8.2.
If there exist precisely two points x,y on V such that bx(g) = by(g)> a(g),
they form a good pair by Lemma 39,5 (ii). We then set f=sx g. Applying
(V.13), we find a(f)<a(g). Denote by F a canonical representative of/;
then SxyF is a canonical representative of g.
Finally, the uniqueness of the canonical representatives follows from the
fact that the element it starts with is uniquely defined according to Lemma
39.5.
Example 39.8.4. If x, у €i V{k) form a good pair, then (TyTx)n is a
canonical representative of (tytx)n for a\\n> 1. In particular, the element tytx
has infinite order.
Proof. We set fn = (t tx)n. We first of all check that bz(fn) = b2(txfn) = 0
if z Ф x, yy x о у. This is true for n = 0, and it is easily established by induction
on n for the remaining n by means of Lemma 36.1.
The proof that (TyTx)n is canonical also goes by induction.
Induction hypothesis for n:
bx(fm)>bxoy(fm)<a(fm)<by(fm),
2а^т)>ЬхЮ^ЬуЮ f0ral! * <"><»•
(For n = 1 we have a(fx) = 4, bx(fx) = 0, by(f{) = 6, bxoy(f{) = 3, according
to Lemma 36.1, so that all inequalities are true.)
Corollary form the words (TyTx)m and TX(T Tx)m are canonical for
all 1 < m < n.

СН. V, § 39 RELATIONS BETWEEN THE GENERATORS
213
In fact, it is clear from the definition and the induction hypothesis that the
canonical representative of (tytx)m starts with Ty. Further, since
bx(txfm) = Mfm)-2bx(fm),
ЬХоу«хГт>ЬуЮ>
we have
bXOy«xfm)> >>y(txfm)<a{txfm)<bx(txfm) ,
so that the canonical representative of tx{tytx)m starts with Tx. Clearly, our
assertion follows from this.
The step from n /ои + l.We have, using Lemma 36.1 twice:
°(fn + l) = *°(fn)-2bx(Q-bXoy(fn)>
*,</„♦!)-У/я).
^(/и+1) = 6в(/и)-3*х(/и)-2^(/я),
W/« + l)s3e(/n)-2M/n)-
All inequalities of the induction hypothesis for и+1 can now be checked
mechanically. We leave the details to the reader.
Lemma 39.8.5. LetfEB and let x,y be points on V such that bx{f) >
> by(f) > <*(f)- Then the canonical representative of f has the form Tx Tx oy G,
where G is a canonical word.
Proof. It is clear from the definition and Lemma 39.5(i) that the canonical
representative of/starts with Tx. Therefore it suffices to verify that the
canonical representative of txf starts with Tx
It follows from Lemma 39.5 that the pair (x,y) is good; therefore x о у is
a good point. Moreover,

214
MINIMAL CUBIC SURFACES
CH. V, § 39
bXoy(bxn = by(f)>2a(f)--bx(f) = a(txf).
We check that bz(txf)<bxc.v{txf) for all гФх v. Uz=x, then
»A/) = Mf) - 2bx(f) < by(f) = bxiy(txf) .
And ifz Фху thenz = xou (и Фу,х\ and then the inequality we need,
hXcU('xf) = bu(f)<byU),
follows from Lemma 39.5. This concludes the proof.
We now prove the fundamental lemma from which Theorem 39.8 can be
deduced in a few words.
Lemma 39.8.6. The canonical representative of a product of elements of
В can be obtained from the product of the corresponding canonical
representatives by applying the relations (V. 15) (more precisely, their analogues in
the group D W) and the relation Sx y = Tx Txo y Ty.
Proof. It suffices to consider the product of two elements. Induction with
respect to the length of the canonical representative of the first of them
immediately reduces the matter to the case where it is equal to w, Tx or Sx .,.
Let Fbe some word in DW. We denote byFw (w E W) the word which is
obtained from F by conjugation:
Tx " TMx)> Sx.y " SMx)M>y Wl " WWl W~] ■
Obviously wF = Fww. Because the action of W on V is linear, F is canonical
if and only if Fw is canonical. This proves the lemma in the case where the
first factor is w.
If the first factor is equal to Sx y, applying the relation Sx v = Tv Tx, y Tx
we reduce the matter to the case of a first factor Tx. Only this case presents
difficulties.
Let F be a canonical representative of the second factor and let/be its
image in/?. We must examine the canonical representative of the element
txf and compare it with TXF.

СН. V, § 39 RELATIONS BETWEEN THE GENERATORS
215
The case a(f) = 1 is trivial. Suppose that a(f) > 1 and that the assertion
of the lemma for t g has already been proved for all g with a(g) < a(f) and
for all points;^ € V(k). The word TXF itself is canonical if the following
conditions are fulfilled:
Ъх(?хП > W*/} f°r a" X "У 1у1П8 °П V '
(Herex о у = tx(y) by definition.) Non-trivial possibilities arise only if these
conditions are not fulfilled. This can only happen in one of the following two
cases:
(i) bx(txf) < a{txf). The equality bx{txf) = a(txf) is impossible by Lemma
39.5(iii).
(ii) bx(txf) > a(txf); there is a point x о у on V such that bx(txf) <
<bxoy(txf).
We study these two cases separately.
Case (i). We have
bx{tj) - 3a(f) - 2bx(f)<a(txf) = 2a(f) - bx(f),
from which bx(f) > a(f). It is evident from the definition that the canonical
representative F of the element/either starts with Tx or with Sx y for some
point >'. If F = TxGy then G is a canonical representative for txf, which is
obtained from the product TX(TXF) by means of the relation 7^ = 1.
We now suppose that F = SxyG. We show that in this case the canonical
representative of txfis equal to Txoy TyG. This word is obtained from the
product TxSxyG by applying the relation Sx v = Tx Txoy Ty.
By definition, Sx VG is canonical if and only if the inequality bx(f) =
- by(f)> a(f) holds. Consequently, the pair (xty) is good and the point
x. -y is good. Therefore,
bxcy(txf) = by(f) >a{f) > 2a(f) - bx(f) = а(^/) > bx(rj).
Moreover, bXOz(txf) < bXQy(txf) for all z Фх, у by Lemma 39.5, which
shows that bz(f)<by(f) for such z. It follows from this that the canonical
representative of txf starts with Txcv.
It remains to show that the canonical representative of txoy tx /starts with
Ty. One needs to check that

216 MINIMAL CUBIC SURFACES CH. V, § 39
(V.16)
b/'xoy (*/) > bz^xoy <xf)> for a11 P°ints гфУ lying on V.
The first inequality of (V.16) follows from the relations
Wxoy '*/> = bxo{xoy)«xoytxf) = bx(txf) = Mf) - bx{f) ,
"('xoy '*/) = 2a{txf) - bxoy(txf) = 4a(f) - 2b//) - by(f) ,
because b (f) > a(f). The second inequality of (V.16) must be verified
separately for z = xoy and for all the remaining points z Фx,y, x oy, each of
which can be represented in the form z = txoy tx(u).
Uz =xoy, we have
Ьхоу('Хоу'хО = Mtxf) - 2bxoy(txf) - 6a(f) - 3bx(f) - 2by(f)
<by(txoytxf) = 3a(f)-2bx(f),
because bx{f) = by{f)>a(f).
U z = t tx(u), иФх.у, x о у, then
M'xo, *ХП - *„ (/) < W) - *,( Л = by('xoy txf) ,
because in the opposite case we would have
bx(f) + by(f) + bz(f)>3a(f).
which contradicts eqs. (V.14).
Case (ii). First of all, in this case
bx(f)<a(f),
by{f) = bxoy(txf) > bx(txf) = 3a{f) - 2bx(f) > a(txf) > a(f) .
Consequently, the pair (у, х o/) is good and the pointy is good. We show that
*,(/) < by(f) if г Фу. Indeed, if bz(f) > by(f), then z Ф x and

СН. V, § 39 RELATIONS BETWEEN THE GENERATORS 217
from which
W*/)+ bxoy('xf)+ bx(txn>Mtxf),
which contradicts (V.14). It follows from this that the canonical
representative of/starts with T It remains to check that the canonical representative
of Гу/starts with Txoy. For this one needs to establish two inequalities:
W/) >*('/),
(V.17)
bxoy(tyf) > bz(tyf) for all points z Ф х о у.
We have
w/>=**</> • a v}=Mf) - Vя •
and
ьх(П > НП - kby{f) >Mf)- by{f),
from which the first inequality of (V.17) follows. The second inequality will
be verified separately for z = y and for all other points z Фу, х oyy each of
which can be represented in the form z = ty(u). If z =y, we have
W/} = W > by°yf) = Mf) - 2by(f)'
because
bx(f) + 2by(f) > 2bx(f) + by(f) > 3a(f).
If z -у о u, then from the inequality
W'/)>W'/)
it would follow that bx(f) < bu(f), and therefore
мл+у/)+*«(/) > *x(/)+<3°(/) - 2M/»+*„(/) > w) •
which contradicts (V.14). Thus in case (ii) the canonical representative of/
has the form F = Ty TxoyG, where G is a canonical word.

218
MINIMAL CUBIC SURFACES
CH. V, § 39
If bXQy(txf) = bx(txf), then the canorical representative of f^/starts with
SXXOy^nd hence it is equal toSx xoy G, i.e., it can be obtained from
the product Tx Ty TXCVG by means of a standard relation. Finally, suppose
that bxo (txf) > bx(txf). Then according to Lemma 39.8.5 the canonical
representative of tx /has the form Txo TyG\ where G' is the canonical
representative of txg(g is the image of G). But the word TxayTyTxG is obtained
from the product TX(T TxoyG) by applying the standard relations Tx T Tx =
= Sx xoy Sx xoy = 1 > anc* tbe word G' is obtained from the word TXG by
means of the relations specified in the lemma in virtue of the induction
hypothesis because a(g) < a(f). (This is the only place where induction is used.)
This completes the proof of the lemma.
39.8.7. End of the proof of Theorem 39.8. Let the element F £DW belong
to the kernel of the homomorphism DW -> Б. By Lemma 39.8.6 this means
that by applying to F the relations in the group DW and the relation
Sxy = Tx Txoy Ty we can obtain the empty word. This completes the proof.
39.,9. Application to minimal surfaces. Starting at this point, к denotes a
perfect field, V is a minimal cubic surface over к, and G = Gal (к/к). We
denote by H some group of projective ^-automorphisms of V. We set Gj = G X #.
This group acts in the obvious way on N(V) and on Z'(V). The following
result contains Theorem 33.7 as the particular case where H= {]}.
Theorem 39.10. We suppose thatN(V)Gl = Zco^. Then the group ofk-bira-
tional maps of V which commute with the action ofG^ is generated by the
following maps:
(i) 1Ъе centralizer of И in Aut^ (V) С W.
(ii) The maps tx for H-invariant good points of V(k).
(iii) rThe maps s for G {-invariant good pairs x, у G V(k).
The relations between these generators are those described above.
Proof, Extending the action of G^ to E (V)(k) in the obvious way we
obtain for all g^G^:
gtxg = *gix)' gsx,y8 = sg(x\g(y) ■
We apply these relations to a canonical representative of a /omap which com-

СИ. V, § 40
BIBLIOGRAPHICAL REMARKS
219
mutes with G|. It remains canonical. Using its uniqueness, we obtain that all
components of length 1 which go into this representative must be Gj-invariant.
From this the assertion on the generators follows. A full system of relations
is obtained precisely as in the preceding theorem.
40. Bibliographical remarks
This chapter is completely based on material from Manin [3] and [8].
Theorem 33.1 was first proved by Segre [3]; an analysis of its proof, which
has been reproduced in other terms in Section 37, also led to a series of further
specifications. The arguments of Segre in turn go back to Max Noether, who
was the first to describe the generators of the group Bir P2 over an algebraically
closed field. Note that the relations between the generators in the theorem
were unknown to Noether.
As the group Bir Fis so closely connected with the fc-points of a minimal
cubic surface V, one may hope that this very group reflects the essential
arithmetical properties of К over local or global fields.
One should probably start with a study of the various topologies on Bir V
which are induced by the local topologies of the field. Does there exist a unique
invariant measure?
The group of projective automorphisms W is trivial for almost all surfaces
V (i.e. on a Zariski open subset of the space of coefficients). Some account
of the 'exceptional' V for which W is not trivial can be found in Segre [ 1 ].

CHAPTER VI
THE BRAUER-GROTHENDIECK GROUP
41. A survey of the results. Obstructions to the Hasse principle
41.1. We first recall the basic information on the Brauer group of an
arbitrary field к (see Bourbaki [2]; Serre [3, 6]; Cebotarev [1]).
A finite-dimensional A>algebra A is called a simple central algebra over к if
there exists an n > 1 such that A ®k к =Мп(к) where к is the algebraic
closure of A: and where Mn denotes the algebra of (n, n) matrices.
The tensor product induces on the set (of classes up to isomorphism) of
central simple algebras over к the structure of a commutative semigroup.
The following equivalence relation turns it into & group: An algebra A is
equivalent to В if there exist numbers m, n such that А ®кМп{к) is
isomorphic to В ®кМт(к). AM the matrix algebras over к are equivalent to one
another and they form the zero class. The class of the algebra A °, the opposite
algebra to A (that is, the algebra with the same elements and the same addition,
but with the multiplication performed in the inverse order) is the inverse to
the class of A. In fact, the canonical map A ®k A0 -> End^ ) (the endomor-
phisms of the linear space A) which associates multiplication by x on the left
and by у on the riglit to the element x ® у Е A ®k A0 is an isomorphism: its
kernel is trivial because A <8>k A0 is simple, and the dimension of A ®k A0
is the same as the dimension of End^ A, i.e., (dimkA)2.
The group of classes of central simple algebras over к up to equivalence is
called the Brauer group of the field к and it is denoted Brfc. It admits the
following cohomological description.
Let К Э к be some extension of the field k. It is called a splitting field of the
fc-algebra>! if Л ®kK ~Mn(K). Equivalent algebras have the same splitting
fields. Let Br (A:, K) be the subset of the Brauer group consisting of the classes
of algebras with splitting field K. It turns out to be a subgroup.
Suppose now that К Э к is a Galois extension with Galois group G. Then
one can establish the following fundamental isomorphism:
220

CH.VI, §41
A SURVEY OF THE RESULTS
221
Br (k,K) = H2(GtK*).
It admits various descriptions. We here indicate one of them which is needed
for the following: the so-called 'crossed product' construction. It consists of
an explicit construction of a central simple algebra over к given a 'factor system',
that is, a cocyc\e{aStt}GZ2(Gf K*). This algebra Л is constructed as follows:
A = Ф Kes ;
eSet=\test> Vs./€=G,
esa =s(a)es, \/seGfaeK.
Its dimension over к is clearly equal to [K : k\2. We omit the verification of
all the properties needed for the construction; we only remark that the
associativity of A is equivalent to the fact that the cochain of'structure constants'
{as t) is in fact a cocycle.
We now introduce the basis for the subsequent algebraic—geometric variant
of the Brauer group.
41.2. Let V be an algebraic variety defined over a field k, let К Э к be a
Galois extension with group G. Further, let и € Vhe the general point, let
k(v)(resp. K(v)) be the field of rational functions on F(resp. onK® K).
Each element of K(v) can be made to correspond to its divisor on V® K, an
element of the group of (Cartier) divisors Div (V ® K). The group G acts
accordingly on K(v) and Div (V ® K), which permits us to define a natural ho-
momorphism of cohomology groups /^(G, K(v)*) -> ffi(Gf D\\(V ® K)).
Definition 41.3. Br (V, K) = Ker [#2(G, K(v)*) ->/^(G, Div(K ® K))].
41.4. Because the divisor of a function measures its 'singularities', we can
intuitively represent the elements of Br (V, K) as those classes of algebras over
K(v) which split over K(v) and have no singularities on V. To give a precise formi
lation of this we need the following concept:
Definition 41.5. An Azumaya algebra over an arbitrary scheme V is a
locally free sheaf of O^-algebras/* Qn Fsuch that the following condition is
fulfilled:

222 THE BRAUER-GROTHFNDIECK GROUP CH. VI, § 41
The geometric fibre/4 (x) =AX ® Q k(x) = ^xlmx^x is a centra^ simple
algebra over the field k(x) for every point x G V.
Informally speaking, an Azumaya algebra is a continuous system of central
simple algebras, 'parametrized* by the scheme V.
Definition 41.6. Let Л,/? be two Azumaya algebras over a scheme V. They
are called equivalent it' there exist two locally free sheaves of (^-modules £
and F such that the Oj/-algebras A ®QV End£ and В ®QV End F are
isomorphic.
Thus the 4riviar algebras End$ E play the same role as the matrix
algebras over a field. The inconvenience of restricting oneself in the definition of
equivalence to matrix algebras over Qv becomes clear if one wants to retain
the triviality of the algebra A ® Qy Л0. In fact, the same arguments as those
over a field show that there exists an isomorphism of the algebra A ® Qv A®
with the algebra of endomorphisms of the 0 ^-module A, which in general can
be only locally trivial over v.
Grothendieck [2] has shown that the classes of Azumaya algebras over a
scheme form a group (relative to the tensor product) which admits a coho-
mological interpretation in terms of the etale cohomology of schemes. For
our purposes only the part of this group introduced in Definition 41.3 is
important. It has been constructed such that in the following investigations we
can avoid all except the more modest tools of etale cohomology theory: all
we need is concentrated in one lemma which the reader can take for granted.
Theorem 41.7. Let V be a smooth variety over a field k. Under the
conditions of41.2 and 41.3, there exists for every element a £ Br( V, K) an
Azumaya algebra A on V such that a = class A(v) over k(v) (v is the general
point of V). Moreover, any two algebras with this property are equivalent.
Corollary 41.8. Under the conditions of Theorem 41.7 every k-point
x S V(k) defines a specialisation homomorphism
Вт(У,К)-*Ът(к,К): а~а(х).
It associates to the class of an Azumaya algebra A the class of its fibre A(x).

CH.VI, §41
A SURVEY OF THE RESULTS
223
We have now concluded the preparations and can state the main results of
this chapter.
Definition 41.9. Under the conditions of Theorem 41.7, hi В С Br (V,K)
be a subgroup. The points x, у € V(k) are called B-equivalent if for all At В
wehavetf(x) = a(j>)-
Theorem 41.10. The B-equivalence relation is admissible for every smooth
cubic surface V over a field к and every group В С Br (Vf K) (see Definition
11.2).
Theorem 41.11. Under the same conditions we have:
(i) The CML E - V(k)/B is an A belian group of exponent a divisor of six.
(ii) // [k'. Q] < °°, the group E is finite.
Incidentally, it will be established that the quotient group Вг(КД)/Вг(£, к)
is an old friend of ours: it is isomorphic to the group Я1 (Gal (k/k), N(V)) of
Chapter IV.
This permits an effective calculation of ^-equivalence: all of Section 45 is
devoted to an analysis of examples. We here adduce the answer to the three
cubes problem:
Example 41.12. Let к contain a primitive cubic root of unity в, let a $(k*)3
and let V be given by the equation
70+Г13 + 72+*71 = 0-
We set
f J°+l)Tl { УГ2
1 T +T ' 2 T +T '
Finally, let К = k(a*). The points x, у E V(k) are Br (K, /Q-equivalent if and
only if
fi(x)lfi(y)eNK/k(K*), /=i,2.
Arithmetical considerations then permit us to give an upper estimate of how

224 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 41
large the 3-group E = V(k)/B is, in particular, its number of generators for
a global field k. For example, if к = Q(0), a E Z and d is the number of
different prime divisors of 3<z, then the number of generators of E is not larger than
2d-2. All this reminds one very much of the weak Mordell-Weil theorem
and first descent for elliptic curves, and this is no accident.
41.13. The second example of Section 45 are the Chatelet surfaces. For these,
in particular, it is proved that R-equivalence coincides with Brauer equivalence.
Chatelet has proved that in his examples each R-equivalencc class is
parametrized by four independent parameters; consequently there is a clear
redundancy from the dimensional point of view. It turns out, however, that over
number fields two-parameter coverings obviously cannot be sufficient. Section
46 is devoted to a proof of this; it stands somewhat apart.
41.14. Finally, the last section of this chapter is devoted to violations of
the Hasse principle for cubic surfaces. In Chapter IV this principle has been
proved for some special classes of surfaces, including all minimal ones. Here
counter-examples will be indicated. They are taken from the literature
(Swinnerton-Dyer [1]; Mordell [1 ]; Cassels and Guy [1]). Our contribution
consists in observing that the Brauer group gives a quite general
obstruction to the Hasse principle, and the calculations, which looked
accidental, do fit into a general theory. The idea of the construction of
this obstruction is so simple that we expound it here. We first recall some
definitions.
41.15. Let M be some class of algebraic varieties defined over a field k,
[k : Q] < °°. It is customary to say that the Hasse principle holds for the
class M if the following assertion is true:
Let VEM and V(kv) be non-empty for all places v of the field k. Then
V(k) is non-empty.
41.16. We start with the description of the language which is convenient
to employ when introducing and classifying obstructions to the Hasse principle.
Let Ov С ки be the ring of integers (which coincides with kv if и is
Archimedean), and let S be a finite set of places of the field k\ let As ={xEk\ xGOv
for all v $ S).
Each algebraic variety V has a model V defined over As for some S: in other

CH.VI, §41
Л SURVEY OF THE RESULTS
225
words, V is a scheme of finite type over Spec As and its general fibre over
Spec (k) is isomorphic to V. We choose such a model V' and for a finite set
S' D S of places of the field we set
V(As,) = {(xv)env v{kv)\ vvfS',xvGV\ov)}c\\v v(kv).
Here we identify V'(Ov) with a subset of V(kv). The product of the
/^-topologies on V(kv) induces a locally compact topology on V(AS,). The union
V(A)= U V(AS.)
S'dS
with the inductive limit topology does not depend on the choice of the model
V' and it is called the space of adeles of the variety V. It is non-empty if all
V(kv) are non-empty, which we shall presuppose in the following.
The canonical inclusions k^kv define an inclusion V(k) -> Uv V(kv), and
the image of this belongs to the space of adeles, as is not difficult to check;
it is called the set of principal adeles.
In itself the condition that the vector {xj G V(kv) belong to V(k) is
obtained by axiomizing the first conspicuous property of any fc-point: the
denominators of its coordinates are bounded.
The majority of the classical proofs that the set V(k) is empty use the
existence of some additional necessary conditions on an adele {xv} to be principal.
The author knows of three groups of conditions, using respectively the
product formula, the non-triviality of the class group of the field к and the
composition laws. The first two groups are on the whole well known from the practice
of proving that concrete diophantine problems cannot be solved, and I give
a systematic formulation only to show that a series of particular arguments
are of identical nature. The third group, however, was explicitly introduced
and subsequently studied only in the theory of Abelian varieties, where it led
to the scalar product of Cassels-Tate on the Safarevic' -Tate group. The
possibility of a general formulation (and new non-trivial applications) of this group
of conditions appears to be new.
Each 'condition' С which we shall consider formally means the specifying
of a subset V(A )c of the space of adeles which contains all the principal
adeles. The simultaneous fulfilment of a family of conditions Ci corresponds to
the intersection C\V(A)C., etc. To prove that V(k) is empty it suffices to
establish that a V(A)C is empty.

226 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 41
The first group of conditions in their simplest formulation is as follows.
Let/er(K, 0^); we set
v(A)f = {(xv)ev(A)\nv\f(xv)r^\}.
(The notation I £v will be explained in Section 46.5.)
41.17. The Artin-Whaples condition: V(k) CT\{V(A)f\fe Г(У, Oy))-
In practice this condition is sometimes applied to rational functions/on V,
but instead of V one then in fact considers only the complement to the
support of the divisor of/
The second group of conditions does not use the Archimedean component.
Let pv be a prime divisor corresponding to a non-Archimedean place v. Using
the previous notations we set
V(A)j = {(xv) GV(A)\ the divisor Пу p»</<*u» \s principal} .
41.18. The Kummer condition: V(k) dt\{V (Aff\fGY{V, 0*,)}.This
can be summarized and generalized as follows: Let с = Ucv: Ik -+ C* be an
arbitrary quasicharacter of thegroupof ideles(thatis,Gm04)) of the field к which is
trivial on the principal ideles (see "Algebraic Numbers4''). This means that the
product formula \\vcv(x) = 1 holds for all x € k*. We set
V(Aff = {(xv)GV(A)\nvc{f(Xv))= 1}.
Both of the conditions 41.17 and 41.18 are special cases of the following:
41.19. V(k)cncnfV(A)cff where/G T(V, 0*v\ and с runs through any
set of quasicharacters. It appears that this is a rather impractical recipe.
We now turn to the Brauer group. We recall that for every place и of the
field к there is defined the canonical embedding, the Mocal invariant',
invu:Br*w->Q/z,
which possesses the following property ('sum formula'):

CH.VI, §41 A SURVEY OF THE RESULTS 227
Z/invu(j) = 0 for all aGJZrk.
v
(For a more precise statement see Section 44.) The symbol invu here must be
understood to act on the image of a after the canonical base change homomor-
phism Br к -> Br kv. It must already be evident to the reader how to use this
formula for the construction of new obstructions.
Let В С Вг V be any subgroup of the Brauer-Grothendieck group. For
every element a SB, we set
V(A)a={(xv)GV(A)\ Suinvu(a(xu)) = 0}.
41.20. We have V(k) Cflje^ V(A)a. An important distinction from 41.18
and 41.19 is that the variety V can be complete. It is convenient to
reformulate this condition, so as to show firstly its connection with Brauer equivalence
and secondly its connection with the Cassels-Tate form for elliptic curves.
Definition 41.21. Two adeles (xv), (yv) E V(A) are calledB-equivalent if
(V aeB)(W) mvv(a(xv)) = invw(*(yj)
(cf. Definition 41.9).
Now let E = V(A)/B be the quotient set of the space of adeles modulo
inequivalence. Then every class X E E defines a character of the group B:
ix:B^ Q/Z, ix{a) = S inv^(a(xv)) .
Condition 41.20 is equivalent with the following.
41.22. V(k)C\Jix=0XCV(A).
In the examples of Swinnerton-Dyer and Mordell of Section 47, we take
В = Вг (К, к) for some field К and show that ix Ф 0 for all classes X.
The example of Cassels and Guy fits in by using a combination of the
Kummer condition 41.18 and 41.22.
41.23. To conclude, we show how our construction is connected with the
Cassels-Tate form. The reader can skip this explanation without endangering
his understanding of the following.

228 THE BRAUER-GROTHENDIECK GROUP CH.Vl, § 41
Let V be a curve of genus 1 over a field ky for example a plane cubic one; let
Vq be its Jacobian. We fix on V a structure of a principal homogeneous space
over KQ; then V defines a cohomology class ЛЕЯ1 (G, У$(к))у witn G =
= Gal(£/fc). Suppose that all the sets V(kv) are non-empty. Then h is
everywhere locally trivial, that is, it belongs to the Safarevifc- Tate group
Ul(V0)CHl(G,VQ(k)).
We now discuss the choice of a subgroup В С Br К, by means of which an
obstruction to V{k) being non-empty will be constructed. The most
economical choice is obtained when E consists of one class, i.e., if for all a G В and all
places v, the local invariant invv (a(xv)) does not depend on the choice of xv.
In this case the unique obstruction is the fact that the character
i'-B-+QIZy i(a)= £ inv^C*,)) >
is non-zero. Therefore we choose for В the subgroup of those elements
a G Вг(КД) which are 'everywhere locally constant', i.e.,
(Vu) a ® kv e image Br kv С Br (V ® к J .
This is immediately connected with ILL. In fact, there exists an exact sequence
Brk^Bi(V,k) X Hl(G, Pic K®£)-*0,
and an epimorphism
ф :Hl(G, V0(k))^Hl(G,?\c V®k)4
which is obtained from the exact sequence of G-modules
0 -+ Pic0 V ® к = V0 (к) - Pic К ® *-£?► Z - 0 .
For every elementя € £ we have <^(д) в ф(ILL(Fq)). The Cassels-Tate form
ILL X ILL -^ Q/Z will be denoted by <,). It emerges in our context as follows
(h is the class of V, and a£B):
Theorem 41/24. (h, i//-1 о у{а)) = i(a).
It is proved by a straightforward comparing of definitions.
From our point of view, the double role of LLL С Я1 is clearly visible:
as the group which classifies the forms of Kn, and as a part of the Brauer group
of the curve V.

СН. VI, § 42 THE CONSTRUCTION OF AZUMAYA ALGEBRAS 229
42. The construction of Azumaya algebras
The main aim of this section is the proof of Theorem 41.7 and some of its
consequences. We shall need:
Lemma 42.1. Under the conditions of Theorem A\.l,let A be an A zumaya
algebra on V such that its class A (v) in Br к (v) is zero. Then A is trivial
The proof is contained in Grothendieck [2], II, Corollary 1.10. It makes
essential use of the techniques of etale cohomology and of the smoothness
of К
42.2. Proof of Theorem 41.7. (i) Construction of an Azumaya algebra. Let
a G Br (VtK) be an element represented by the cocycle {ast}, ^r GAT(u)*; we
denote by (a^t) G D'\v(V ® K) the divisor of the function a^(. Then the co-
cycle {(fl4/)]GZ2(G, Div(K<g> K)) is a coboundary, i.e., there are divisors
DsGDiv(V®K)y seG,
such that
(\t) = sVt)-Da+Ds; s.tGG.
A Zariski open set U С V is called small if all the divisorsDs\y, sGG, are
principal on U. Because it suffices to prove the theorem under the assumption
that [K : k] < «>, we can assume that the group G is finite. Then the small
open sets form a basis for the Zariski topology on V, and every sheaf on V is
uniquely determined by its sections over these small open sets. We use this to
give an Azumaya algebra Л explicitly.
Let bs E K(v) be a local equation of D5 in the small neighbourhood U. We
set
T{U.A)= © Ш0у9К)Ь;1е CA(p),
s&G
where A(u) = (BseQ K(v)es is the crossed product over k(v) corresponding to
the cocycle {a^}. The definition of T(UtA) does not depend on the choice of
bs, because

230 THE BRAUER-GROTHEND1ECK GROUP CH.VI, §42
The restriction homomorphisms are defined in the obvious manner (they act
'identically' on the symbols e$) and it is clear that U V* r(U,A) is a locally
free sheaf on the small sets. Finally, the multiplication in,4(u) induces a
multiplication in the sheaf because, setting e's = bsAes, we have
e e = a e #,
S t S,t St '
and {\t)\y = 0 by definition, so that a's( E T(U, 0*yQK).
The fibre of A in the general point is clearly isomorphic to A(v) as a k(v)-
algebra. It therefore only remains for us to show that the fibre A(x) is a simple
central algebra over k(x) in any other point x E V. In fact, let x E U, where
U is a small neighbourhood; then, using the preceding notation, we have
A(x)= © {K®kk(x))e's, e's = e's(x),
seG
and the composition law is given by the cocycle {a'^t(x)} €Z2(G, К ® k(x)*)
(note that Г(£/, 0V ®K) = К ® Г((/, 0V) and that in particular
f(x)EK <8>k k(x) for every function fG r(Uf0V(S>K). This is not quite the
usual crossed product, because К ®л k(x) is not necessarily a field, but only
a sum of fields. However, one easily checks whether it is simple and central
over k(x) by a straightforward calculation exactly as in the case of products
over a field (Cebotarev [ 1 ], page 67).
(ii) Azumaya algebras which are equivalent in the general point are
equivalent. In fact, let A, В be Azumaya algebras over V such that A(v) and B(v)
are equivalent over k(v). Then (A ® B°)(v) is a matrix algebra. Therefore,
according to Lemma 42.1, A ® B° = End /Г, where E is some locally free
sheaf on V. Taking the tensor product with В of this isomorphism, we find
finally
A®(B<8>B0)=B®EndE,
which proves what we want, because the algebra В ® Z?° is trivial.
From the proof of the theorem we draw the following fundamental
corollary:

СН. VI, § 42 THE CONSTRUCTION OF AZUMAYA ALGEBRAS 231
Corollary 42.3. Let f: W -> V be some k-morphism of smooth varieties. For
every element a G Br (K, K) we denote by A some Azumaya algebra on V such
that the class ofA(v) is equal to a. Then f*(A)is an Azumaya algebra on W,
and the class off*(A)(w) (w is the general point of W) belongs to Bt(W, K).
This class only depends on a;denoting it byf*(a), we obtain a map
f* : BT(V,K)-+Er(W,K),
which turns Br (•, K) into a contravariant functor.
Proof. First of а!1,/*(Л) is clearly a locally free sheaf of algebras of finite
rank. Further, tor every scheme point w€W there is a canonical isomorphism
of algebras
f4A)(w) = k(w)0k{f{w))A(f(w))
so that/*(,4)(>v) is simple and central over k(w). Consequently f*(A) is an
Azumaya algebra on W.
Further, the algebra A &A" becomes trivial at the general point of V®K\
therefore, according to Lemma 42.1, A ® К = End E, where E is some locally
free sheaf on V ® K. It follows from this that f*(A) ® К s End (/ ® K)*E
on W ® K, so that the class of f*(A) in the general point w € IV belongs to
H2(G, K(w)*). An analogous argument shows that the class of f*(A) does not
depend on the choice of A. It remains to show that it is killed by the homo-
morphism K(w)* -> Div (W ® K). This is a quite general fact, which in the
Grothendieck theory simply follows from the circumstance that the cohomo-
logy class which interests us is represented by some Azumaya algebra on W.
In our special situation this can be established by the following
considerations. Let{^/}GZ2(G,^(u)*)be some cocycle in the class a. If all functions
a^t are regular in the image of the general point w E W(for instance, if / is
a surjective morphism), then the rational functions f*{as f) EK(w) are defined,
and they form a cocycle{f*(as ()}GZ2(G, K(w)*)\ and the class of this co-
cycle coincides with/*(fl) in virtue of the preceding considerations. Passing
to the divisors we can write the condition for triviality in the form
as above. Clearly, if f(w) is not contained in the union of the supports of the
divisors sDt (s, t в G), then

232 THE BRAUER-GR0THEND1ECK GROUP CH. VI, § 42
(/>,,,)> = *(/'W -f4D„) +/*(/),),
so that the image off*(a) in the divisor cohomology is zero.
The case where/(w) is in the support of a divisor (j^r) or s(Dt) is dealt
with by passing to a cohomologous cocycle. The details are left to the reader.
42.4. Specialisation. Let /: Spec к -> V be a A:-point x of the variety V.
Then for an element a E Br(F, £) it is convenient to denote f*(a) G Br(fc, /f)
by д(х) and to call a(x) a specialisation of the class a.
Theorem 42.5. Let f\W-+Vbea birational morphism of smooth surfaces
over k. Then the map
/*:Br(K,A0^Br(W,/O
is an isomorphism.
Proof. Every birational morphism of surfaces is a composition of monoidal
transformations with their centres at (scheme) points of V. In virtue of the
functoriality, it suffices to deal with the case of one monoidal transformation.
In this case, as is well known,
Div (W® K) =/*(Div(K® AT)) © E, Ker/* = 0 ,
where E is the group generated by the divisors which/® К collapses into a
point. A glance at the commutative diagram
H2 (G, JC(w)*)—4 H2 (G. /*(Div(V ® К))) Ф H2(G, E)
w v
H2(G,K(v)*) ► Я2(С, Div(K®JC))
proves what we want, because ф is an isomorphism with the first direct factor,
and the component of <p in H2(G, E) is equal to zero.
Corollary 42.6. Br (V, K) is a contravariant functor on the category of
smooth projective surfaces over к with the rational maps as morphisms. Jn
particular, the group of birational maps of a surface V into itself acts on
Bt(V,K).

СИ. VI, § 42 THE CONSTRUCTION OF AZUMAYA ALGEBRAS
233
Proof. Let ^ : W-+ V be some rational map. Its singularities can be resolved.
That is, we can construct a commutative diagram
w-*-*v
in which g is a morphism, and/is a birational morphism. We now define the
map y* : Br(V,K)-+ Br(W, K) as the composition
Bv(V,K) A* Bt(W',K) ^ Br(W,K).
The independence from the choice of /follows from the fact that any two
resolutions can be embedded in a commutative diagram
in which ti and ti' are birational morphisms (for this one needs to take for
(W"\ ti, ti') a resolution of the birational map С/')"1 о /" : W" -* W). After
this, some trivial diagram chasing, using Theorem 42.5 shows that \p* is well
defined. Analogously, one establishes the formula (у о ф)* = ф* о vp* in those
cases when the composition i£° ф is defined. This proves the corollary.
42.7. We now remark that there is a canonical homomorphism of groups
Br (k, K) -* Br (V, K) corresponding to the structure morphism V -► Spec k.
The image of Br (к, К) consists of the classes of 'constant' Azumaya algebras.
This map can have a (non-trivial) kernel.
For example, the algebra of the real quaternions decomposes over the
function field on the conic V : 7^ + T* + r| = 0. Therefore it follows from Lemma
42.1 that the homomorphism Br(R,C)-> Br (V, C) is zero.
However, if there is а к -point x on V, then the specialisation map
Br(K.tf)-» Br(*.*), a»a(x)

234 THE BRAUER-CROTHENDIECK GROUP CH. VI, § 43
shows that Br {к, К) is a direct summand of Br (V, K)y and in particular that
no non-trivial constant algebra becomes trivial over V.
In the following important case, the group Br (V, K) is exhausted by its
constant elements.
Theorem 42.8. Let V be a smooth projective surface or curve which is bi-
rationally equivalent to P2 or P1 over k. Then Br (V, K) = Br (к, К),
Proof. One can assume that V is isomorphic to P2 or P1. Denoting by Div0
the group of principal divisors, we have in this case
Div (V <g> K) = Div° {V®K)®Z.
(The projection on Z is 4he degree of the divisors'.) The exact sequence of
G-modules
1 -+ K* -+ K(v)* ^Di\° (V <8>K)-+ 1
shows that the image of Br (к, К) in H2(G, K(v)*) coincides with the kernel
of the homomorphism H2(G, K(v)*)-*H2(Gt Div0 (V® K)), but this kernel
is equal to Br (V, K) by the arguments indicated above. This proves what we
want.
43. Brauer equivalence
In this section we fix some subgroup В С Br (V, К). Recall Definition 41.9:
The points x, у E V(k) are called B-equivalent \ia{x) = a(y) for all a G B. One
can obviously assume that В contains all constant classes. The following result
implies Theorems 41.10 and 41.11 (i).
Theorem 43.1. Under the conditions stated above, let V be a smooth cubic
surface over k. The following assertions hold:
(i) B-equivalence on V(k) is admissible and is stronger than ^-equivalence.
(ii) The CH-quasigroup E = V(k)/B is Abelian and there is a canonical
embedding.
T°(E)^ Horn (Д/Br (к, К), Br (к, К)) .

CH.VI?§43
BRAUER EQUIVALENCE
235
Proof, (i). First of all, for all morphisms/: P1 -► V over k, and all elements
a E Br(V, K) and points xGP1 (k) we have a(f(x)) = f*(a)(x), and this class
does not depend on x, because the class f*(a) is constant according to
Theorem 42.8. Consequently, Я-equivalence is stronger than R-equivalence;
in particular, the classes of /^-equivalent points are dense.
Now let the points (x, y, z) and (*', y, z ) be collinear on V, and x ~~ x
(mod B)\ we shall show that z~z (mod B). We consider the diagram obtained by
resolving the singularities of the birational map t :
where/, g are birational fc-morphisms.
If у is in general position with respect to x and with respect to x\ then there
exist points w, w' G W(k) such that f(w) = jc, /(w') = x\ g(w) = z, g(w') = z'.
Then for any element a € Br (V, K) we have
^ Or*)"1/*(«)(*) = UT1/>)(*'),
that is, Sy(a)(x) = t*(a)(x'\ or a(z) =a(z').
Uу is not in general position with respect to x\ and the line through x\
y, z' is not completely contained in V, then a point u>' with all the necessary
properties can still be found.
Finally, if the points x', y, z' are on a line in V, then they are R-equivalent,
and hence /^-equivalent. A simple geometrical analysis then shows that
there exists a point w' G W(k) such that /(w') = g(w') =y = x' (mod B) =
= z (mod B\ and the previous arguments give the desired result.
This shows that ^-equivalence is admissible.
To prove the second part of the theorem we need two lemmas, which are
also of independent interest.
Lemma 43.1.1. For every smooth surface V with a dense set ofk-points
there is an isomorphism

236 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 43
Br(V, /O/Br (A:, A:) X Я1 (G, Pic (V ® K)) ,
which is functorial with respect to birational morphisms.
Proof. The exact sequence of G-modules
1 -► K(v)*/K* -> Div (V®K)-+ Pic {V ® K) -> 1
gives an isomorphism
tf^G, Pic(K® *)) 3 Ker [Я2(С, tf(u)*/K*) -> H2(G, Div(K® /Q)] .
On the other hand, the exact sequence
shows that
H2(G, K(v)*IK*) = H2(G,K(v)*)lH2{G, K*) ,
if one takes into account that the homomorphism tf3(G, K*) -* Я3^, #(u)*)
has a section 'specialisation at a point1 and therefore has a trivial kernel. This
proves what we want.
The functoriality can be established without difficulty.
Lemma 43.1.2. Let V be a smooth cubic surfacet and let x E V(k) be a good
point. Under the natural action on Br(F, К)/Вт(к, К) the homomorphism t*
is inversion.
Proof. Let W -* V be a monoidal transformation with centre x. It induces
a G-isomorphism Pic W ® К ^ Pic V ® К 0 Z and, according to Theorem
29.1, an isomorphism
Я1 (G, Pic (V ® AT)) з Я1 (G, Pic (W ® K)).
The group Pic (W ® £) is generated by the canonical class со and the divisors
which over к consist of exceptional curves of the first kind. The automorphism
tx becomes biregular on W; we denote it by the same symbol. For every class /
of an exceptional curve of the first kind on W ® Л we have
#o+/=-w.

СН. VI, § 43
BRAUER EQUIVALENCE
237
Indeed for curves coming from V this is clear from the following geometrical
considerations: the class f *(/) + / is represented by the intersection of V with
the plane passing through a curve of class / and the point x, and — со is
precisely the class of the hyperplane sections. In addition to these /, there are on
W two more exceptional curves - the inverse image of x and the inverse image
of C(x), which are interchanged by tx\ their sum is obviously also equal to -co
(cf. the proof of Lemma 36.1, second step). Thus t* acts on Pic (W ® A")/Zco
as changing signs. On the other hand, the exact sequence
0 -+ Zco -* Pic (W (8 K) -> Pic (W <g> £)/Zco -► 0
yields an embedding
0 -» Hl (G, Pic (W <g> К)) -> Hl (G, Pic (W ® /Q/Zco),
which shows that on Hl (G, Pic (W ® /Q) the map t* is also the changing of
signs. This proves the lemma.
43.1.3. End of the proof of Theorem 43.1. We set E = V(k)/B and define
a map
i : Г°(/Г) -+ Horn (B/Br (*. /Г), Br (*, К))
as follows: Let s E Г°(£). Since В is an admissible equivalence relation» by
Theorem 13.1 (iii) there exists in the group B(V) of birational maps of V
generated by the maps tx for all x E V(k) an element T which passes into s under the
natural homomorphism B(V) -* Г(£): fx *-* tx% x E Я. Further, let
h E В/Вт (к, K)\ we denote by ti E В some representative of this residue class
and set
/(!)(*) = Г*(А')-Л'.
First of all, this map is well defined. In fact, since s (and hence also J) is a
product of an even number of maps tx, T acts trivially on B/Bi(k, /0 by Lemma
43.1.2, so that T*(h') - Ы E Br(£, A"). This element does not depend on the
choice of h' in the class h because s* also acts trivially on the subgroup of
constant classes. Finally, let 7 be another lifting of s in B(v) and let x E V(k)
be a point in which J and ? are biregular. Then

238 THE BRAUER-GROTHFNDIECK GROUP CM. VI, § 44
S *(A') - A' = (ST *(A') - A')(*) = *'(*(*)) - Л'(*) ,
in virtue of the functoriality of s *, and, similarly,
But, by definition, ti is a function on classes of points modulo /^-equivalence,
and J and T induce the same permutation of these classes. Therefore i(s) (A)
does not depend on the choice of J either.
It is obvious that i(s)(h) is additive in A.
The map i is a homomorphism, because (using the obvious notations)
i(st)(h) = 7*s*(A')-A'
= 7*(s*(A')-A/) + 7*(A')-A/
= /(5)(A) + /(r)A
(taking into account that t* acts trivially on Br (к, К) С В).
Finally, the kernel of i is trivial. In fact, as above, let s be biregular in the
point jc G V(k)\ then
j*(A') - A' = 0 « (s\h') - h')(x) = 0
*h'(fx) = h'(x).
If s G Ker /, then the last equality must hold for all A' G В and for the
representatives x of all equivalence classes. This means that s acts trivially on E. This
proves the theorem.
44. The finiteness theorem
Our first result is elementary.
Theorem 44.1. Let V be a smooth projective surface and let V"(g) к be bh
rationally trivial. Then the group Br (V, К)/Вт (к, К) is finite for any Galois
extension К Э k.
Moreover, if ?ic(V<8> K) = Pic(F® k\ then
Br(F, AT)/Br (*, A') s Вг(К *)/Br (*, *) .

CH.VI, §44
THE FINITENESS THEOREM
239
Proof. We start with the second assertion. First of all it follows easily from
the classical exact sequence of Brauer groups of fields
0 - Br (*(«;), K(v)) -> Br (Jfc(u) Л (и)) -> Br (К (и), k(v)) ,
that there exists a canonical embedding Br (V, K)/Br(k, K)^> Br (V,~k)/Br (k,~k).
On the cohomology groups it is induced by the inflation, which commutes
with the isomorphism of Lemma 43.1.1.
We now consider the exact sequence
i inf , _
0 -► Я1 (Gal К/к, Pic V®K)-+ Я1 (Gal к/к, Pic V ® A:)
res _ __
—>Hx(G*\k/Ky Pic V®k).
From the hypothesis with respect to the field К it follows that the group
Gal(£//0 acts trivially on Pic V ® к = Pic V ®K.\i follows from the
rationality of V that Pic V® к is free. Therefore the last /У1 is trivial, which gives
the desired isomorphism.
As the field К one can take a finite extension of к because Pic V ® к has
finite rank, and each of its generators is 'defined' over a finite extension.
Therefore the group #l (Gal (k/k), Pic V ® k) is finite and hence this is also true
for every algebraic extension K.
Remark 44.1.1. It is not difficult to show by means of a slightly more
precise argument that Br (V, ^)/Вг (Л, К) - Br (Vt /c)/Br (к, к) \iV ®kK is bira-
tionally equivalent to P£.
Corollary 44.1.2. Suppose that in the group Br к there are only finitely
many elements of order dividing 6. Then the set E = V(k)\B is finite for every
smooth cubic surface V.
If in Br к there are no non-trivial elements of order dividing 6, then all
points of V(k) are B-equivalent.
The proof is obvious if one uses Theorem 43.1 and takes into account that
the relation X^ = 1 holds in T°(E), according to Tlieorem 13.2. Instead of this,
one can also refer to Theorem 29.3, which shows that the exponent of the
group Вг(Т, К)/Вт(к, К) divides 6.
This corollary is inapplicable in the most interesting case, namely, when к
is a number field. All the same, the finiteness theorem is also true in this case;

240 THE BRAUER-GROTHENDIECK GROUP СП. VI, § 44
its proof, which is in itself not complicated, rests, however, on deep number
theoretical results:
Theorem 44.2. Let [k : Q] < °°. Then the set V(k)/B is finite for any
smooth cubic surface Vover k.
Proof. To start, we state some well known facts on the structure of the
Brauer group of a field k.
Let p be a place of the field k, i.e., either a prime ideal in the ring of
integers of the field k, or an embedding k^ R, or a pair of conjugate complex
embeddings k^Q (Archimedean places). We denote by к the completion of
к in the topology corresponding to p.
Further, let К 3 к be some Galois extension with group G, and q some
place of the field K\ we shall write q \p if q induces p on k. As is well known,
kp ®k К?* П ,p Kq; the group G which acts through the factor К on the left-
hand side, permutes q transitively and the isotropy subgroup Gq of the place
q (the decomposition group) is isomorphic to the Galois group of the
extension/^/^.
We now give a list of the properties of the Brauer group which we need:
(i). If kp = C, then Ъткр = 0. If kp = R, then Bikp =\Ъ\Ъ\ the unique
non-trivial element is the class of the quaternion algebra.
(ii). Letp be non-Archimedean; then Br/c^ is canonicaliy isomorphic to
Q/Z and Br (к К ) coincides with the subgroup (1ДО Z/Z, where n =
= [K : kp]. In case the extension Kq/kp is unramified, this isomorphism is
obtained as follows. Denote by v : K* -> Z the valuation homomorphism and
construct the composed map
Mkp.Kq)XH2(Gq.K*)xH2(Gq,Z)6x Hl(Gq> Q/Z) l± Z/Z.
P
Here a is induced by means of vq, and 5 is the coboundary operator, which
corresponds to the exact sequence of trivial (7-modules 0 -* Z -> Q -* Q/Z -> 0,
and 7 is the map which to each element x £ Hl(Gq> Q/^) = ^om №q, Q/Z)
associates the number x(^) £ iMnp) Z/Z, where Fis the Frobenius
automorphism, a canonical generator of the group Gq (see Serre [6]).
(iii). There exists an exact sequence of the form

CH.VI, §44
THE FINITENESS THEOREM
241
0 ->Br*-i> 0 ВгЛ Л Q/Z-0.
Here the homomorphism i is the sum of the homomorphisms induced by the
embeddings k-+kp for all possible places P of the field kt and /, under the
canonical identification inv : Bikp -> Q/Z described above, is the sum of the
'local invariants'.
This exact sequence contains in compact form the following assertions:
(a) Each element of Br к is completely determined by its local invariants.
(b) Each element of Br к has a finite number of non-zero local invariants.
(c) For each system of local invariants (...,/..), L G Q/Z (or yZ/Z,
{0}, if kp = R, C) there exists a realization as an element of Br A; if and only if
/;; Ф 0 for only a finite number of places p and E / = 0.
We now state our basic lemma:
Lemma 44.2.1. Let К D к be a finite Galois extension, and a G Br {V. K)
some element. There exist a non-empty open set V С V and a finite set S of
places of к such that for all x G U(k) and p $ S the local p-invariant ofa(x)
is equal to zero.
44.2.2. Deduction of Theorem 44.2 from Lemma 44.2.1. It is clear from
Theorem 44.1 that it suffices to prove Theorem 44.2 for В = Br(F, K), where
К is a finite Galois extension К D к with group G. The group Br (K K)IBr(k,K)
is finite; let ^j,. . . ,anE Bi(V, K) be representatives of its generators
modulo 'constant' classes. Then there exist a U and an S which fulfil the
assertions of Lemma 44.2.1 for all the a^ an at the same time. From the
considerations in 43.1.3 it follows easily that for every element s G T®(E) the image
of the homomorphism
i(s) : Br(V,K)/Bi(k,K)^Bik
consists of the classes which have trivial invariants outside S.
In fact, suppose s~GB(V) is induced by sG T®(E)\ because U\s dense, one can
choose an x G U(k) such that J is defined in x and J(x) G U(k). Then i(s)
sends the classy into
J *(*.) -a^s >.) (x) a fix) = a.(sx) - a.(x) ,
so that the invariants of the image are trivial outside S.

242 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 44
Moreover, as remarked above, 6/(5) = 0. Consequently, Theorem 43.1 and
the result 44.2 (iii) establish an embedding
T°(E)<+Нот (Вг(К К)1Вт(к. K\ ®peS \Ъ\Т),
and both groups under the Horn sign are finite. This proves Theorem 44.2.
44.2.3. Proof of Lemma 44.2.1. Let{^,}GZ2(G, K(v)*) be a cocycle in the
class of a. We can find divisors Ds G Div(K ® K),sG G, such that
(\t)^(Dt)-Dst+Ds.
Denote by U the complement of the union of the supports of the divisors
s(Dt) in V ® K, s, tGG. Then for every point x G U(k) the cocycle {aSJ(x)}E
EZ2(G, K*) represents the class of the element a(x) G Br(/t, A"), and we must
investigate its local invariants.
First of all, include in S all the Archimedean places of к and all places in
which K/k is ramified. Then, according to 44.2 (ii), the local invariant of the
class a(x) in a place p GS is represented by the class of the cocycle
(uA'w)}ez2((vz)>
where q is any extension q \p of the place p on K.
We must now use the central result of A. Weil's theory of distributions
which we shall describe in a moment. The result cited below is obtained
immediately from Theorem 10 of Weil [1], with the obvious changes in notation.
Proposition 44.2.4. Let F be a group of divisors on V ® К whose supports-
are contained in the complement of a non-empty open set UС V ® К. Then
there exists a family of homomorphisms
indexed by the points x G U(k) and the non-Archimedean places q of the field
K, with the following properties:
(i) // (f)^Fisa principal divisor, then for all except a finite number of
places q of the field (the exceptions depend on f) and for all points x G U(k)
we have

СН. VI, § 45 CALCULATIONS FOR BRAUER EQUIVALENCE
243
V((/)) = V/W)*
(ii) For alls EG = Gal K/k and D E F,
We apply this result to the divisors (as t) which occur in the cocycle
[as t}EZ* (G, K(v)*). Because there are a finite number of them, we can
enlarge the set S of places q (while it remains finite) such that the assertion
44.2.4 (i) is true for all (as t). As a result we obtain that for <7 $ S and xEU(k),
uAr<*>>=VW - \* (°«)+ \JDs> ■
Restricting ourselves to the case s, t EGq and using 44.2.4 (ii), we obtain
Therefore for x E U(k) and q $ S the local invariant of the class a(x) is
represented by the cocycle
< V<^> - v<V+ V<°,»ez2«v z) •
which clearly is the coboundary of the cochain
{Aqx{Ds)}ec\c,q,Z).
This concludes the proof of the lemma and of the finiteness theorem.
Corollary 44.2.5. Under the conditions of Theorem 44.2, B-equivalence is
trivial on V(kp) for almost all places p of the field k.
1 do not know whether the analogous result holds for universal equivalence
or R-equivalence.
45. Calculations for Brauer equivalence. Examples
In this section, summarizing the preceding discussion, we shall describe an
effective algorithm to determine whether two given points xyy E V(k) are

244 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 45
/^-equivalent. Afterwards we shall apply this algorithm to concrete examples.
We start with calculating the Brauer group. We keep the notation of the
previous section.
Proposition 45.1. Let F be a G-invariant group of divisors on V (&K, the
classes of which generate Pic (V ® K). Then
Ът(КК)/Вт(к,К) s Ker [H2(G,L/K*) -+H2(G,F)),
where L с K(v) is the group of rational functions on V ® К of which the
divisors belong to F.
Proof. The commutative diagram of (7-modules
1 »L/K* >F *Pic V ® К >1
f f R
1 >K(v)*/K* >Div V ® К >Pic V ® К A
yields the commutative diagram
О-^ЯЧС, Pic V®K) >H2(G,L/K*) >H2(G,F)
0 -*Hl(G. Pic V ® K)—+H2(G,K(v)*IK*)^H2(G, DWV®K)
An appeal to Lemma 43.1 Л proves what we want.
45.2. We can now proceed with an informal description of the algorithm
for the calculation of Brauer equivalence.
(i). Choose a finite Galois extension K/k and a finitely generated group
of divisors F, generating Pic V ® Ky with a finite number of generators.
The typical situation is: For F, take the group generated by all the 27 lines
on K® k and for G a finite normal extension of k over which all these lines
are defined. Sometimes one can do with only part of these lines and a
correspondingly smaller field K.
(ii). Calculate a finite number of cocycles
{*j})ez2{G.L/K*)

СН. VI, § 45 CALCULATIONS FOR BRAUER EQUIVALENCE
245
of which the classes generate
Ker [H2(G, L/K*)-+H2(G, F)] .
Because G is finite, and F and L/K* are finitely generated groups, this step
can be carried out effectively. In practice it is usually convenient first to
calculate the cocycles which represent a system of generators of the group
H\G, Pic V ® K) = Hl(Gt F/F0) ,
where Fq С F is the subgroup of principal divisors, and to map them
afterwards into ffl(Gf L/K*) by means of the coboundary operator as in
Proposition 45.1.
(iii). Construct functions{asj}GL such that a$ = aft (mod AT*)(the S$
have been described in the previous step). It is not necessary for this to care
about whether the {ast} generate cocycles of C2(G,L*).
(iv). The final result: Suppose that the points x, у G V(k) do not belong to
a support of the divisors of the group F. Then x ~ у (mod B) if and only if all
of the following cocycles represent zero:
K?w
l«goo
€Z2(G,/T), i=l,...,r.
In turn, to check whether a given algebraic number theoretical cocycle is
trivial reduces to a finite number of local calculations.
(v). An important particular case: G is a cyclic group. The calculations are
simplified in this case thanks to the existence of an isomorphism (which
depends on the choice of a generator of G)
H2(G, K(v)*/K*)^H°(G, K(v)*/K*) ~ k(v)*/k*N(K(v)*) ,
where TV denotes the norm of K(v) into k(v). In this case each cocycle {a^\} can
be replaced by a single element 5(/) G k(v)*/k*N(K(v)*), and for that purpose
one can take a representative of this element,
6(/)Gfc(u)*.
Two points x, у G V(k) which do not belong to a support of the divisors (b^)
will be equivalent if and only if

246 THF. BRAUER-GROTHENDIECK GROUP CH.VI, §45
b(i\x)
b{i\y)
^ел^(Г), /-i,
Example 45.3. Let char кФЗ,аек*^ (Л*)3, and 03 = 1, where 0 €k is
a primitive root; iet К = к(а>), G = Gal K/k. We consider the surface
V: т1*Т\ + т\+аТ\ = Ъ,
and rational functions on it,
(these notations will be kept up to and including 45.7.5).
We shall prove the following result:
Proposition 45.4. The points x, у G V{k) at which 7$ + т\ Ф 0 and
Т0+Т2Ф0 are B-equivalent if and only if
fi(x)lfi(y)ENK/k{K*).
Proof. According to the recipe given in the beginning of this section, denote
by FE Div V ® К the group of divisors generated by the lines on V ® K, and
by F0 С Fthe subgroup of principal divisors. A choice of a generator in
G = Z3 yields the commutative diagram
H2(G.FQ) - H2(G,F)
H°(G,FQ) - H°(G,F)
II II
F$INFQ у FG/NF
where N = %sGGs. This diagram permits us to identify the group
Bt(V, K)lBi{k, К) ч
the kernel of the upper arrow, with the group

СИ. VI, § 45 CALCULATIONS FOR BRAUER EQUIVALENCE
247
F0CiNF/NFQt
the kernel of the lower arrow.
We now need to analyse in thorough detail the groups Fq, F and the action
of G on them; we start therefore by introducing some convenient notations.
Let к - 0,1 or 2, let (/, /) = (0, 1, 2)^-(к), /</', and let m, n run independently
through a full system of equivalence classes mod 3. The 27 lines on V ® A' have
the form
L(m,n):
(T{ +0wr. =0,
к З
(я3 El К is fixed once and for all). Further we put
Мк(т) = N(LK(m, #i)): 7} + 0mTf = 0 .
The nine divisorsMK(m) turn out to be free generators of the group NF.
Because they are plane sections, they are pairwise equivalent (linearly), so that
the group Fq П NF is generated by the pairwise differences of these divisors.
Further, the divisors
(/j)=M2(l)-M2(0),
if2) = Mx{<S)-M2(0)
belong to Fq О NF, and for the proof of Proposition 45.4 one needs to verify
that their classes constitute an (independent) system of generators for the
group F0 HNF/NF0.
Firstly, by means of considerations on invariants, we make sure that there
are precisely two generators. The following result can be derived from Table 1
in Section 31 or calculated by means of Propositions 31.3 and 3 1.5. For
completeness' sake we give another variant of the proof, taken from Safarevic's
lectures [1].
Lemma 45.4.1. H] (G, Pic (V <g> A")) = Z3 X Z3.
Proof. We recall the definition and fundamental properties of the 'Herbrand

248 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 45
quotient'. Let G be a finite cyclic group, A a G-module such that the orders
h\A) of the groups Н1{СА) (Tate cohomology) are finite.
The known periodicity Я7"1"2 = IP naturally suggests the introduction of
the following variant of the Euler characteristic
h(A) = h<>(A)lhl(A).
h(A) is called the Herbrand quotient of the G-module A, and it has the
following properties:
(i). Let 0 -> A -* В -> С -* 0 be an exact sequence of G-modules and
suppose that two of the three numbers h(A), h(B), h(C) are defined. Then the
third is also defined and
h(fi) = h(A)-h(Q.
(ii). Let A j, A 2 be G-modules which are free and of finite rank over Z. If
the G-modules R ®z,4j andR®z^2 are isomorphic, then h(A^) =h(A2)
(sec the book "Algebraic Numbers", Ch. IV, § 8).
We apply these properties to the calculation of Я1 (G, Pic V ® K). Because
V is minimal, (Pic (V ® K))G = Zcj^; but cjv is the class of a hyperplane
section; in particular, it contains the norm divisors MK (m). Therefore
H°(G, Pic V ® AT) = (Pic V ® Kf/N (Pic V ® K) = 0 ,
and
hl(?icV®K) = h(?ic V®K)~l .
Because the exponent of Я1 divides 3 (the exponent of G), it suffices to prove
that/21 =9,i.e.fc = £.
The space R ® z Pic V ® К is seven-dimensional; the group G acts on it, and
the identity representation turns up with multiplicity one in this representation.
Therefore, setting / = Z [G] /Z, we have
R ®zPicK®K = R ®(R®Z/)3
(as G-modules), because R ®z /is the unique irreducible representation of G
over R different from the identity. Using properties (i), (ii) of the Herbrand
quotient, we therefore find

СН. VI, § 45 CALCULATIONS FOR BRAUER EQUIVALENCE
249
h(I) = h{Z[G])/h(Z) = h(Zy* ,
Л(Ис V® K) = h(Z)h(I)3=h(Z)-2 .
But H°(G, Z) = Z3 and tf1 (G, Z) = 0, which concludes the proof.
We now return to the analysis of the configuration of the lines.
Lemma 45.4.2. Let V be a smooth cubic surface over a field К over uhich
all its lines are defined. Then the group of principal divisors, consisting of lines,
is generated by the pairwise differences of those plane sections which decompose
into three lines.
Proof. We choose six non-intersecting lines on V and collapse them by means
of a morphism/: V-+ P2. We introduce the following notation for the lines on V
(see Theorem 26.2): pj ,...,p6 arc those lines such that thef(pj) = pt;are points
on P2;/,y (/,/ ~ 1,. .., 6; /Ф}) are those lines such that the/(//,•) = '//.• are lines
on P2 passing through the points/?., Pj\Qj{i = 1,..., 6) are those Hnes for
which the /fa/) = qi are conies which do not pass through the point p..
With this notation, after some practice, we can easily see which lines
intersect. For instance, /12 does not intersect /13 because f 12 and /13 intersect on
P2 at the point /?j, which gels blown up and 'throws apart' these lines.
Similarly, /j3 does not intersect g4, but does intersect q^ and q^ (only one of the
intersection points of /13 and q^ on the plane is thrown apart). The plane
sections on V arc exactly the triples of pairwise non-intersecting lines, e.g., qi +/?• +
+ Ijj (iФ j) and //• + L + /r5, where (ijpqrs) is a permutation of (1 2 3 4 5 6).
Further, Fq represents the inverse image under/of the group of principal
divisors on P2 with components Т.. and qK. This group is clearly generated by
divisors of the form
Tij Trs> 5/ Я? *"l - /_23 " '45 •
Taking into account that /*(//.•) = ^- + Pt + P.-, /*fa/) = q{ + ^,>/Р/» we ^d *or
Fq the system of generators
'ij-b+Pl+Pj-Pr-Ps-
4t - Я; - Pt + Pf = (q, + Pj +lv)- (<7;- + Pt + 1ц) ,

250 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 45
«1 ~;23 "Z45 +^6 = ^1 +Рв +/1б)-(/16 + /23 +/45>'
The divisors of the last two types have already been represented in the form of
a difference of plane sections. As regards the first type we remark that firstly,
for / = r,
'if - hs+ Pj ~Ps = <■«,■+ hi+ P/) - to/+ h,+ p,) ,
and secondly, for (if) П (rs) = 0,
Tij-Trs = «i,~TiJ + (lis-Trs^
which reduces the matter to the previous case and concludes the proof.
From this lemma we deduce:
Corollary 45.4.3. Under the conditions tf/45.3,45.4, the group NF0 is
generated by the pairwise differences of divisors of the form
ЗМк(т)9 к,т = 0,1,2,
2
£ Мк(т), к =0,1,2.
m=0
2
ЕлГк(ш'), w' = 0,1,2.
Proof. We check that the divisors described are norms of all the plane
sections contained in F.
First of all, a straightforward calculation shows that each line LK(m, n)
intersects precisely nine lines
LK(m, ri\ LK(m'> n\ Li(mi> n\)> Lj(m2> пт) >
where n Фп,т'Ф т, and the indexes mlt n^, m2, n2 satisfy the following
conditions:
mx + nx =m + л (mod 3) if к </,

CH.VI, § 45 CALCULATIONS FOR BRAUER EQUIVALENCE
251
n.-m^=m+n (mod 3) ifK>/,
m2-n2=m-n (mod3) if / < к ,
m2*n2~n~m (m°d3) if/>K .
These nine lines in turn split up into five connected pairs, which together with
LK(m, n) constitute all triples of coplanar lines containing LK(m, n).
The first of the divisors described in Corollary 45.4.3 is the norm of the
triple T,^QLK(m, n)\ the second the norm of the triple ^»=o^K(m'» n) and,
finally, the last three are the norms of the remaining three triples, which the
reader can check himself with little trouble.
Corollary 45.4.4. We define the homomorphism
X:FQnNF->Z3XZ3,
by setting
*&атМк(тЪ = & Какт <mod 3>> 2 такт <mod 3» •
Then Кег х = NFo, an^ became
x((/,)) = (o,i), x((/2)) = (-i.o),
the classes {fx)(mod NF0) and (f2)(mod NF0)generate F0 П NF/NF0.
Proof. It is immediately clear from the formulae of Corollary 45.4.3 that
NF0 С Ker x. On the other hand,(/j)and (/2)generate in FQ DNF/Ker \a
subgroup of order 9, therefore Fq П TVF/Ker x, as a factor group of
F0 HNF/NFq = Z3 X Z3, must coincide with it. This concludes the proof of
Proposition 45.4.
We now apply it to number fields.
The local case. Let [k : Qp] < <», 7 : k* -> Z a valuation (equal to one on a
generator of the maximal ideal), and let А С k be the ring of integers, m its
maximal ideal and U = A *— m the group of units.

252 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 45
Proposition 45.5. If a is an integer and 3a G U, then for all points x G V(k)
in which 7* + т\ Ф 0, T\ + т\ Ф 0, we have
fl(x)GNK/k(K*), f2{x)GNK/k(K*y
In particular, all points of V(k) are Br V-equivalent.
Proof. Letx = (70, rj, t2, ^з)> where the t{GA are integral and relatively prime.
From the fact that 3a G U it follows that the extension К = к(а"ъ) is unramified
Therefore
^AA'(**) = {rE**,uW = 0(mod3)}.
We now examine the functions/t and/2 separately, distinguishing in turn the
possible cases.
Study offy(x).
0) u('o +'i) = u('o +Otl).Thtnv(fx(x)) = 0*>fx(x)GNK/k(K*).
(ii) r = v(t0 +t^)Фv(t0 +6tl) = s. Then y(r0) = u(r1)> and therefore
u(r0 + 02/j) = min (r, s). Because
2
II(r0 + 0/r1)+7V(r2 + a>r3) = 0,
/Ю
we obtain r + s + min (r, s) = 0 (mod 3), so that
Sfwc/y o//2(x).
(i) и (f3) = 0. Then u(/?+ r?) = 0 for all / */, /, / 6 (0, 1, 2) (from which
follows u(/2(jc)) = 0 =>f2(x)GNK/k(K*)). In fact, in the opposite case we
would have for к Ф i, к Ф j, к G (0, 1, 2),
а = (-^кГъ1)ъ (mod m)
( tn С A is the maximal ideal). Because 3a G Uy it would follow from this that
a G (/c*)3, in contradiction with the assumptions.
(ii) v(t^)>0, v(t0txt2)>0. Because r0, tx, t2, /3 are relatively prime,
for precisely one index / в (0, 1, 2) we have u(ry) > 0. If v(tx) > 0, then
u(fj + r2) = v(t0 + r,) = 0 => v(f2(x)) = 0. If u(/0)> 0, then v(tx) = v(t2) = 0,

СИ. VI, § 45 CALCULATIONS FOR BRAUER EQUIVALENCE 253
v(tQ + rt) = 0 and one must separately consider the case v(t^ + t2) > 0 only.
But then
v(tx +6t2) = v(tx + 02f2) = O
(we here use the invertibility of 1 - 0, a divisor of 3, in A), so that
v{tl +t2) = v(t] +t32) = v(t32 +<7/^) = 0(mod3)
and
v(f2(x)) = o(mod3).
The possibility v(t2)> 0 is dealt with in entirely the same way.
(iii) v (r3) > 0, v(t0tx t2) = 0. Then v(tj + ф = 0 for aU 1 =£/, f, / e (0,1,2)
(otherwise v(tK)> 0), so that v(f2(x)) = 0.
This concludes the proof.
A particular case, к = Q2(0), a = в. All the conditions of Proposition 45.5
are fulfilled, so that Br K-equivalence is trivial. On the other hand, it was
demonstrated in 16.3 that reduction mod 2 defines a non-trivial admissible
equivalence relation on the surface V.
Consequently, in this example Brauer equivalence is strictly coarser than
universal equivalence.
The global case. Now let [k : Q] < °°, let a G к be an integral algebraic
number, let p run through the non-Archimedean places (i.e. the prime ideals)
of the field k, and let EQ = K(/c)/Br V.
Proposition 45.6. Under the conditions described, the construction of
Theorem 43.1 yields an embedding
i : T*(Ea)^ Hom(Z3 X Z3, ©;p|3fl ±Z/Z) ,
where the prime on the direct summation sign means that we consider the
subgroup of those vectors whose components add up to zero.
In particular, let rk EQ denote the number of generators of the Abelian
group TQ(Ea) (or ofEQ with composition law U ° (X о Y), and let d be the
number of different prime ideals dividing 3a. Then rk Ea<2d- 2.

254 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 45
Proof. Using the notation of 45.3 take as h j, h\ € Br (V, K) the classes
of the algebras over V corresponding to the functions f\tfj' In Proposition
45.5 it was proved that if рХЪа and a $(k*)^y then the local p-invariants of
the classes of h\(x), h'2(x) G Br(kp) remain invariant under changes of x in
V(kp). This is also true for a E (kp)3 because the surface Vk ® k kp is bira-
tionally trivial in that case. The Archimedean places do not contribute to
Br к because 0 £ к and hence the field к is purely imaginary.
An explicit treatment of the construction of the embedding /given in 43.1.3
now immediately shows what we want.
45.7. We now state some unsolved questions.
45.7.1. Let cj, c2 € k* and [k : Q] < °°. Do there exist points x e V(k)
for which /}(x) € C/WW (K *), / = 1,2? It can be assumed that the necessary
local conditions are fulfilled.
45.7.2. To what extent can Br ^-equivalence be different from R-equivalence
and U-equivalence in this example?
45.7.3. Is there a bound for rk (Ea) as a runs through all possible numbers
of the global field kl 'ibis, clearly, is analogous to a well-known unsolved
problem in the theory of elliptic curves. For a discussion for the curve 7q + T* +
+ fl7,|=0,sccCasscJs [2].
45.7.4. Finally, it would be interesting to examine the case when в $ к
(for example, к = Q). Adjoining в gives a quadratic extension k(0), and on
V(k(6))9 Br F-equivalence is defined. It induces some admissible equivalence
relation B' on V(k); moreover, it is probably possible to define a norm map
Nk(0)lk:V(k^lhrV^V^lB'
(see the construction in Section 15 concerning R-equivalence.)
45.7.5. Do there exist connections between гк(#д) and the zeta function
of the surface VI

СИ. VI, § 45 CALCULATIONS FOR BRAUER EQUIVALENCE
255
We now pass on to the analysis of another example.
Example 45.8. We consider the surface studied by Chatelet [1 J, [2]. Let
char (к) Ф 2,aGfc*N (A:*)2, let ^t, a2, a^G/che three different elements,
and let К = k(\/a). The surface V is given by the equation
3
V: Т0(Т*~аТ1)=\\(Тг-а.Т0).
/=1
On V we consider the rational functions
= 73"gl70 3 -Д2Г0
Jl~T3-«3To' /2_73-"3V
This notation will be retained until the end of this section; let В = Br(K K).
Proposition 45.9. Two points x, у £ V(k) in which Г3 я,Т0 ФО.Т^Ф О,
/ = 1, 2, 3, are B-equivalent if and only if
fi(x)lfi(y)eNK/k(K*)i /=1,2.
Proof. Before starting the calculations, we point out one difficulty:
the surface V has two singular points (which are conjugate over k) on
the hypersurface at infinity Tq = 0: Tx ± Г2\/д"= 0. Therefore, under Brauer
equivalence on V we must understand the equivalence relation induced by
inequivalence on some non-singular model of V: this does not depend on the
choice of the resolution of singularities according to Theorem 42.5.
45.9.1. The construction of a non-singuiar model. In the direct product
P1 X P1 X P1 with threefold homogeneous coordinates (XQt Xx, YQt Yx, ZQ,
Zj) we define a surface WQ by the equation over k:
WQ: Z{(Z0 -«,Z1)Jfiri =X0Y0(Z0-a2Zl)(Z0 - ^Z,).
An easy local computation shows that Wq is smooth for а^а2а^ Ф 0: this can
be assumed without loss of generality because a non-singular linear
transformation of (Tq, Г3) permits us to obtain this.
There exists a birational morphism over K,

256
THE BRAUER-GROTIIENDIECK GROUP CH. VI, § 45
which on the generators of the field of rational functions К(v) is given by the
formulae
4—т^-)Лт;-а^
,ПА (zo \Yi
The surface W0 has a form W over к and a birational map \p : W -* V over
к such that ^0 = \p ® K. To describe W, we denote by t : ^q ->• Wq the
automorphism of order 2 induced by the permutation of the first two components
ofP1 XP1 XP1:
/*(*.)= K;, /*(Уу) = ^ f(Zt) = Z.9 i=lf2.
Further, let Z2 act on the fc-scheme WQ (£)k К as {id, r} on the first factor and
as G = Gal (Ay/:) on the second factor, and let Z2 act on V ®k К as the identity
on the first factor and as G on the second. The map ^0 is then compatible
with these actions, and that permits us to descend it to a map
yp : W = (WQ ®k K)IZ2 -> (V ®k K)IZ2 = V.
The surface W, being a form of Wq, is smooth. It is also the model of V on
which we shall carry out the calculations. We identify W ®к К and W0 ®A, K,
and also the divisor groups of these surfaces.
45.9.2. The geometry of W. To analyze the structure of the surface W and to
choose a group of divisors F С Div(Ii' ®к К) such that their classes generate
Pic (W®k K\ we consider two projections of W С P1 XP1 X P1: p, andp13.
(i) The projection ръ : W -> P1 on the axis (Zn, Z{). The fibres of this
morphism over the points (1,0), (jj, 1), (a2> 1), (а3,1) consist of two lines
which intersect each other transversely. Over any other point the geometric
fibre is isomorphic to P1.

СМ. VI, § 45 CALCULATIONS FOR BRAUER EQUIVALENCE
257
This morphism has two sections: the curves/)1: Xq = Y^ = 0, and
D2: X\ = Yq = 0. The configuration consisting of the two sections and the
components of the special fibres is indicated in Fig. VI. 1. The fibres have been
numbered in the order in which they were enumerated in the previous
paragraph. The pairwise intersection numbers of these curves, equal to 0 or 1, are
easily discovered from Fig. VI. 1. The self-intersection numbers turn out to
be as follows: (DJ. ,Df)= -1, (Df, D1) = -2. In particular, the D{are excep-
tional curves. The first equality follows from the fact that the fibres £>. + Dt
are pairwise equivalent to one another and do not intersect; consequently,
(£>', D) + Df) = (D\, D)) + 1 = (£>,', Dj + Df) = 0 , / Ф i.
The second equality is deduced from the equivalence of the divisors
(XQ=0)=D] +DlQ+D\ ,
from which
(Dl,D]) + 2 = (D\Dl + D]q +D\) = (D],D2 +D\ + /)*) = 0.
Finally, the generating element of the group G- Gal K/k interchanges the places
of Dx and D2 and the components of the fibres, sending each fibre into itself.
D20 D\ D% D\
\
\
\ /
/
-J—
/
Fig. VI. 1.

258 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 45
To calculate Я1 (G, Pic W ®k /C), it is necessary to know that DJ and Dj
generate the whole Picard group. To prove this we consider one other projection:
(ii) The projection p13 : W-+ P1 X P1. This morphism has the following
properties, the verification of which we leave to the reader as an easy exercise:
(a) p13 is a birational morphism which collapses the exceptional curves
Dl0>D\> D2> D\ int0 the P°ints (°> *> Ь °)> (°» ]> Jl> 0 0. °. J2> 0,(U 0, a3i\)y
respectively.
(b) The monoidal transformation of Pl X P1 with as centre the union of
the four points listed above is isomorphic to p13.
We now observe that the curves С =p13(Z)z) are fibres with respect to the
two projections of P1 X P1, so that their classes generate Pic ((P1 X Pl) ® k).
It follows from this that Pic W ® к is generated by the classes of
p*n(Cx) = Dx+Dl+D\,
dI,d\,d\,d\.
In particular, let F be the group of divisors on W ® К - Wq ® К generated
by all the Dj, DJ. Then the canonical map F-* Pic (W ® K) is surjective.
Moreover, property (a) shows that the surfaces W, WQ, К become birationally
trivial over K.
45.9.3. The calculation o/Br(W, K)IBr(k, K). Let FQ С Foe the subgroup
of principal divisors. Because G = Z2 is cyclic, we obtain as in Proposition 45.4,
Br (W, K)/Bi {k, K) £■ F0 П NF/NFQ , N = 1+ s, G = {1, s].
Let D E Fbe any divisor; because Fgenerates the Picard group, and because
numerical equivalence coincides with linear equivalence or. rational surfaces,
we have
DeFQ<*(D,DJ) = (D,DJ) = 0 for all /=1,2, / = 0,1,2,3.
Therefore, using the table of intersection numbers, we obtain without
difficulty that

СН. VI, § 45 CALCULATIONS FOR BRAUER EQUIVALENCE
259
^0 =
1 /=o /=o
tjd. = 2d\
«=0
On the other hand, NDi = Dl +D2 and7V£>/ = D\ + D2r Consequently,
NF,
0
3 3 \
iTtd^D)* D}) + 2dTj D]\
{ i=0 i=0 )
F0HNF =
He.(Pl + D*)
3
i=0
I 3
w=o
We define the map
X:F0rW-Z2XZ2
by the formula
x(E *•(#/ + 0?)) = (^ - e3 (mod 2), e2 - еъ (mod 2)).
\=0 I
One can easily convince oneself that x induces an isomoфhism
F0r\NF/NFo^Z2XZ2 .
In particular, this group is generated by the divisors of the functions
^<>-2»-^^)-^^2)-(D»+Df),
which also concludes the proof of Proposition 45.9.
In contrast with Example 45.3, we can make the following essential
supplement:

260 THE BRAUER-GROTHFNDIECK GROUP CH. VI, § 45
Proposition 45.10. On a Chatelet surface Vy Brauer equivalence coincides
with R-equivalence. More precisely, for every B-equivalence class X С V(k)
there exist a four-dimensional special manifold W and a k-morphism \p: W-*V
such that <p(W{k)) is a thick subset of X {that is, on a dense open subset
UCVwe have UDX=Un *(W(k))).
Informally speaking, the points of one B- (or R-) equivalence class on V are
parametrized by four independent parameters.
Proof. It is sufficient to establish this assertion for one equivalence class;
we take the class X0 for which/).(x) 6NKjk(K*)y i = 1,2, for all * eX0. To
construct W, we use the construction of 15.1.3. That is, we set V-Rj^^V® K)
Since the surface V ® К is birationally equivalent to P^, the four-dimensional
/r-manifold V is birationally equivalent to P^. Further, we identify V(k) with
V(K). There exists a birational map over k,V % V, such that for every point
x G V(k) = V(K) of which the conjugate (over к) х is in general position with
respect to x, we have
ф(х) = хох EV(k)C V(K)
(see the construction of the norm map in 15.1.3).
Let WC К be the dense special subset on which ф is defined, and let
ip : W -> V be the restriction of ф to W. Because ^-equivalence is stronger than
R-equivalence, Proposition 45.10 immediately follows from the lemma:
Lemma 45.10.1. *p(W(k)) is a thick subset of the class X0.
Proof. Following Chatelet, we shall establish this by a direct calculation.
Let x G X0 С V(k) and suppose that in the point x the sections Г0, Г3 - а{Г§
do not become zero. We shall prove that then there exists a point v in V(K) ~
- V{k) such that у о у = x. It is clear that the lemma follows from this because
y(W(k)) is completely contained in one ^-equivalence class.
We set /;- =7}/Г0, i- 1? 2,3. The argument consists of three steps:
(i) jcGI0« /3(*) - д. ENK/k(K*) for all /' = 1,2,3. In fact, because
fj(x)ENK/k(K*), by definition there exists an element c£k* such that
t3(x) - a{ €cNK/k(K*); moreover,
3
П (t3(x) - a.) = /1 (x)2 - at2(x)2 e NK/k(K*) ,
/=1

СН. VI, § 45 CALCULATIONS FOR BRAUER EQUIVALENCE
261
so that c3 GNK/k(K*) => с GNK/k(K*). The opposite implication is obvious.
(ii) There exists a point >>' G V(k) such that У and У are in general position
and such that the ^-coordinates of у о у' and x are the same:
t3(x)=t3(y'of).
We shall indicate the coordinates of such a pointy explicitly. We set
r3(x)-j|. = ii?-flu?=7vr(w/), w. = u.+y/av.eKt i= 1,2,3 .
Further, let
A = и>, - u>3 , •> /i = w. - w~ •
We construct a pointy with coordinates t\(y'), t2(y\ t^(y') which we find
from the equations
t^y^+y/at^y') =\w2w2,
t^y^-y/atjiy1) =/iw3w3 ,
>3(У) =*i +^.
It is easy to check that У G V(k). It is more difficult to verify that
t$(y' ° У) ~ *з(*)- Chatelet arrives at this after having calculated all the
formulas for the coordinates of the pointy oy' explicitly. I cannot suggest
anything better and therefore omit these rather cumbersome direct
calculations.
(iii) Conclusion of the proof. We consider now the affine curve Г defined
over kx by the equation r^ - ar2 - 1. This is a group with unit element (1,0);
it is the multiplicative group under the classical composition law of a Pell form.
It acts к -linearly on the surface V> preserving the projection of V onto the
f3-axis. Under this action, a pair of points x G V{k\ z G Г (A:) corresponds to
a point zx G V(k) of which the coordinates can be found from the formulae
t3(?x) = t3(x),
tx(zx) + \fct2(zx) = (t{(x) + \fct2(x)) (rx(z) + y/ar2(z)) .
The action of Г(&) on the set of Ac-points of each irreducible fibre of the f3-

262 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 45
projection is transitive. In fact, the ratio of two numbers of К with the same
norm in к has the norm of a unit (we restrict our considerations to an affine
part of V). Therefore there exists a point z € Г(£) such that z(y' о у') = x
On the other hand, from the /c-linearity of the action of z it is obvious that
z(y'oy')=;(zy')c(zy').
Consequently, the point zy' -y fulfils the conditions of the lemma. This
concludes the proof of Proposition 45.10.
Corollary 45.10.2. The CML E = V(k)jR isan Abelian group of exponent 2.
It is finite if к is an algebraic number field.
We shall now study the number field case a bit more in detail.
The local case. Let [k : Qp] < °° and и : к* -+ Z a valuation. Let А С к be
the ring of integers, and U = A* the group of units.
Proposition 45.11. If a, af are integers and 2a П^Дя,- - aj) £ Ut then for
all points x e V(k)for which Т0Ф0 and T3 - afT0 Ф 0, we have
f^)eNK/k(K*)9 1=1,2.
In particular, all these points are B- and ^.-equivalent.
Proof. Let jc = (fn, fj, t2, t3), where the /,- GA are relatively prime. The
extension К = k(\Ja) is unramified because 2a E U, so that
MK/k(K*) = {tek*\ i)(/) = 0(mod2)}.
The functions/j and/2 are transformed into one another if one renumbers
the at\ therefore it suffices to deal with/j(x). We consider two cases separately:
(i) v(t3 -axt0)= v(t3 -a3t0). Iben v(fx(x)) = 0*+fx(x)GNK/k(K*).
(ii) r = v(t3- a{t0) Ф v(t3-a3t0) = s. In this case
u('0) = u(r3> = u(r3 " Vo) = min (r' 5> •

СН. VI, § 45 CALCULATIONS FOR BRAUER EQUIVALENCE
263
Take into account that /n(f j -atj)- П/=1 (f3 - att^) and compare the
valuation of both parts. We obtain
min (r, s) + 2q = r + s + min (r, s).
Consequently, r = s (mod 2), so that v(fx (x)) = 0 (mod 2).
This proves the proposition.
We remark that if к = R, we have E = {1} or Z2, depending on whether
V(R) is connected or not, according to Corollary 16.1.3.
The global case. Now let [к : Q] < °°, let a, ai G к be integer algebraic
numbers, let p run through all possible (Archimedean and non-Archimedean)
places of the field к, and let E = V(k)/B = V(k)/R.
Proposition 45.12. Under the conditions described, the construction of
Theorem 43.1 yields an embedding
i : T°(E)^ Hom(Z2 X Z2> e^Z/Z) ,
where S consists of the real Archimedean places for which V(kp) is not
connected, i.e., p(a) > 0, p(af) E R, and the primes dividing 2a П (at - aj). In
particular, let ikE be the number of generators ofT®(E), let d be the number
of different prime divisors of 2a П (я, - aj), and let n\ be the number of real
places p: к -*Rfor which p(a) > 0. Then
ikE<2(d + n\)-2.
Proof. One repeats the arguments of 45.6 with the obvious modifications.
We note that in the construction of Example 16.2 we made use of
precisely the 'Archimedean part' of this result as we did not yet have available
the general theory.
Concerning the Chatelet surfaces one can also pose questions analogous to
those of 45.7.1,45.7.3 and 45.7.5. In particular, let cx, c2, c3 Ek* be
elements such that their product cxc2c^ ^NKik(K*). There exists a point
xE V(k)inthe class for which fj(x)£ сiNKjk(K*),i = 1, 2, if and only if the
system of equations (see 45 J 0.1 (i))

264
THE BRAUER-GROTHENDIECK GROUP CH. VI, § 46
is solvable in k. Eliminating /3 from this, we obtain the four-dimensional
intersection of two quadrics in P6:
(2:
icx(u\ -aiv\)-c2(ul-a2vl) = (a2-al)w2 ,
Conversely, starting with A>points on Qt one can construct points on V in the
corresponding R-equivalence class (this is clearly not a 1-1 connection, in
particular with respect to the choice of the sign of /j, t2).
If Q(kp) is non-empty for all places of the field k, does i; follow that Q(k)
is non-empty? This is a typical problem arising in connection 'vith Tirst
descent'.
46. A negative result
In the last example of the previous section, for Chatelet surfaces V over
number fields k, we obtained a rather complete qualitative description of the
structure of the set of rational points of V(k). Let us recall it once more in
outline:
2n
(i) V(k) decomposes into a disjoint finite union U,=i ДГ,- of classes with
respect to R- (or Br V-) equivalence.
(ii) These classes form an Abelian group E of exponent 2 with respect to
the composition law U о (X о У).
(iii) Each class (more precisely, a thick subset of it) is covered by a
morphism of a four-dimensional special variety.
Apparently it was precisely the unusual character of this description in
conjunction with the many calculations in Chatelet's work which caused the
fact that his construction did not attract attention for a long time. Chatelet
himself gave the decomposition E in terms of the functions/lf f2 by analogy
with the elementary proof of the weak Mordell-Weil theorem, and he verified
all properties of the composition law and of the classes by means of explicit
formulae.
From the point of view of our general theory, all characteristic features of

СН. VI, §46
A NEGATIVE RESULT
265
Chatelet's construction get an invariant explanation. In particular, E is a group
of exponent two, because V becomes birationally trivial over a quadratic
extension of the field & (Proposition 15.2). Moreover, this group is a birational invariant
of V over к and it does not depend on the choice of the model and formulae.
It can have arbitrarily large order (Example 16.2) but is finite over number
fields: this is always true for Br F-equivalence.
The only embarrassment may be raised by (iii): Why does one need to use
four parameters to describe the rational points of a /wodimensional manifold?
The main aim of this section is to show that over number fields two
parameters in any case do not suffice, so that Chatelet's result, even though it yields
some perfection at this point, is not improved in principle.
More precisely, we shall prove the following theorem:
Theorem 46.1. Let [k : Q] < °°, and let V be a cubic surface of general
type over к with a finite number of (geometric) singular points and a dense
set ofk-points V(k), while ^(РДС)) = {1}. Moreover, let there be given a finite
family of geometrically irreducible k-surfaces Vi (i = 1,. .. , n) and k-mor-
phisms ft -Vf^-V of degree > 1. Tlien the set
n
/=i
ofk-points of V which are not covered by this family is dense in the Zariski
topology.
The condition 7Tj (K(C)) = {1} is automatically fulfilled if V is smooth, and,
probably, in the general case.
In order to apply this result to the Chatelet surfaces, we choose for the V{
birationally trivial surfaces. Then the degree of any morphism/,: V{ -* К which
is surjective in the general point is greater than one, because the surface V is
birationally non-trivial: one has Br(^, A)/Br(fc, K)~Z2^ Z2. Because in
addition the number of R-equivalence classes is finite, it would follow from
the possibility of covering one class by a finite number of two-parameter
families of points that the whole surface could thus be covered, which contradicts
the theorem.
For general cubic surfaces, this result leads to the following alternative:
Corollary 46.2. Under the conditions of Jlieorem 46.1, // V is birationally
non-trivial over k, then at least one of the following two assertions is true:

266 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 46
(i) The set E = V{k)/R is infinite.
(ii) No class XE.E can be covered by a finite number ofmorphisms of
rational surfaces.
It is not impossible that both possibilities can be realized simultaneously.
Problem 46.3. Can every R-equivalence class be covered by a finite number
of morphisms of special varieties (of arbitrary dimension)?
46.4. Before turning to the proof of Theorem 46.1, we want to say a few
words as to its nature.
(i). We explicitly construct 'many' points on V(k) which are not
covered by a given family of morphisms. This construction is based on a method
of multiplying points on V(k) which has not been used up to now. Namely,
we consider a sheaf of hyperplane sections of which three base points are in
V(k). If it is sufficiently general, almost all sections are elliptic curves. On
most of them the group of ^-points has infinite order: the triple of base points
already generates an infinite subgroup. The union of these sets of rational points
(for all sections), generated by the three base points, already shows that a
covering by a finite number ofmorphisms is not possible.
(ii). To prove the latter assertion, we have to use in an essential way that
the base field к is global; the theorem is not true if к = R or Qp because of
obvious topological reasons (see the proof of Theorem 16.1). We reduce the
problem to an analogous question for curves of genus 0 or 1 and use all
the known qualitative results on rational points on curves. These results show,
roughly speaking, that the density of rational points on curves falls sharply
as the genus increases (Lemma 46.13). Therefore, if we have a morphism of
curves/: Y -► X, while the genus of X is 0 or 1 and the genus of Y is greater
than the genus of X, then the set/(y(*)) is so much smaller than X(k) that
even a finite number ofmorphisms cannot manage to cover it.
This concludes our informal remarks and we proceed to the techniques
needed for the proof.
46.5. Sun>ey of height theory. The height concept is the main tool in the
'counting' of /c-points on projective surfaces. It permits us to give a precise
meaning to the expressions 'many' and 'few1 points and it will be essentially

CH.VI,§46
A NEGATIVE RESULT
267
used in the following. We shall omit most of the proofs, referring the reader
to Lang [1] or to Manin [2].
Let у be a place of the field k. It uniquely determines a norm
which satisfies the following conditions:
(i) \x\v = I x' I, where x is the image of x under the embedding in R or C,
if у is an Archimedean place.
(ii) \p\v =p~1) if v is a non-Archimedean place corresponding to a divisor
of the prime number pGZ.
Further, let kv be the completion of к in the topology induced by i>, and
^t nv = [kv : QJ.
46.6. Definition and Lemma. For every system (xq, . . . , xn) G kn + l of
elements of the field k, not all of which are equal to zero, the number
h(xQy ...,xn) = |Щ| £ nv max(log \x.\J
(by definition, log 0 = -<») is well defined and has the following properties:
(i) /z(Xx0,..., Xxn) = h(x0,..., xn)for all X E k*. Therefore h can be
considered as a function on the k-points Рл (к) of projective space, once a
coordinate system has been chosen. This function is called the height.
(\i) h(x)>0 for all xG?n(k).
(iii) h(x) does not depend on the choice of the field to which the
projective coordinates ofx belong.
Example 46.7. Let к = Q, xt e Z, and g.c.d. (x0,..., xn) = 1. Then I xt\v < 1
for every non-Archimedean place v and there exists an index i such that
I Xj\v~ 1, so that max,- (log I X(\v) = 0. Consequently, in this case,
h(x0>... , xn) = max log Ы .
i
In particular, the number of points in P"(Q) for which the height is bounded
by some constant, is finite. Mere generally:

268 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 46
Lemma 46.8. Let О 0, d > 0, and d^Z\let?n be a projective space with
a fixed coordinate system. Then the set
{jcGPw(Q)IA(jc)<C, [k(x):Q]<d]
is finite.
The main inconvenience of this definition of height is the necessity of a
choice of a projective coordinate system. It turns out, however, that the height
only weakly depends on this choice. More precisely, let/j,/^ be two real-valued
functions on some set. We shall call them equivalent and write /j ~/2 ^
1Д -/21 is bounded.
Lemma 46.9. Let h\, h2 be two heights on ?n(Q)7 defined in two different
coordinate systems. Then hx ~ h2.
Henceforth, heights will be considered only up to equivalence; therefore
we shall be able to calculate them in any coordinate system. The reader can
convince himself that the truth of any assertion made does not depend on a
substitution of an equivalent height for the height considered.
We can now formulate the main general theorem on heights.
Theorem 46.10 (A. Weil). With each pair(V, L) consisting of a projective
variety V over a field к and an invertible sheaf L on it, there corresponds a
height function hL : V(k) -► R. This correspondence satisfies the following
properties, which determine each height uniquely up to equivalence:
(i) hL <ql ~~ hL +hL .
(u) // К = P", L = b(l), then h q{{) is the height defined in 46.6.
(iii) For every k-morphism vp : V -> W and L G Pic W we have h * щ ~~ hL о \р.
(iv) hL does not change under an extension of the base field.
We shall call the functions hL Weil heights. On Abelian varieties they have
an important additional property: they are quadratic with respect to the group
law.
Theorem 46.11 (J. Tate and A. Neron). Let V be an Abelian variety over к
and L an invertible sheaf on V. There exist uniquely determined functions
bL : V(k)X V(k) -> R and lL : V(k) -► R with the following properties:

СН. VI, §46
A NEGATIVE RESULT
269
(i) bLisa bilinear map, and lL is a homomorphism.
(ii) The Weil height hLis equivalent to the Tate-Neron height hL which is
defined by the formula
hL(x) = ±bL(x,x)+lL(x).
(iii) If the sheaf L is very ample, then the quadratic form bL(x, x) on V(k)
is positive definite modulo torsion. Moreover, lL=0 ifi*L = L, where i(x) =
= -xy i: V -* V {symmetric sheaves).
(iv) // L is in the connected component Pic0 V, then bL = 0.
For an elementary exposition in the case of elliptic curves see Cassels [3].
From this result and the functoriality of the Weil height we can derive
some properties of heights on curves which we shall need:
Lemma 46.12. Let V be a smooth projective curve over k, let L^ L2 be
two ample sheaves on Vf and let deg L7- > 0 be their degrees. Then the Weil
heights (1 /deg Lx)hL and (1 /deg L2) nt2 are asymptotically equivalent on
V{k)\thatis,
\hL (x) degLj
\hj (x) degL-
Proof, (i). If the genus of К is equal to zero and У(к)Ф 0,then V is isomorphic
to P1, and Li s 0pi 0У*'. The result therefore follows from Theorem 46.10(i).
(ii). Now let the genus of V be greater than zero, Jy the Jacobian variety of
the curve Vr and \pv : V->JV the canonical embedding(it is determined up to a
translation; as before, we assume that V(k) is non-empty).
Replacing L{ by L^8^/, ii=j, we can assume that degZ^ = degL2. LetAfj
be a sheaf on J у such that $y{M j ) ~ L j, and Mj ® Л/2! a sheaf on J у
which is in Pic°7^ and which induces L] ® Z,2 * on V. This sheaf exists
because deg Lx = degL2=>L1® L21 e Pic0 (K).
It follows from Theorem 46.11 that the quadratic parts of the heights hM
and hM coincide, and that these quadratic parts are non-degenerate (modulo
torsion;. Therefore the difference in the linear parts cannot affect the
asymptotic equivalence of these heights. Because hii ~hj\4i о <pv (Theorems 46.10
and 46.11), the lemma follows.
0 forhL{x)

270 THE BRAUER-GROTMENDIECK CROUP CH. VI, § 46
Lemma 46.13. Let V be a smooth projective curve of genus g such that
V(k) is non-empty, let L be an invertible sheaf on V of degree d>0.We
denote by NL (//) the number of points x <E V{k)for which hL(x) < H. Then
the following estimates hold for H -> °°:
(i)* = 0: NL(H) = c] ехр(2Яс/-1)(1+о(Г));
(ii) g = 1 . NL{H) = c2(H/dy/2(\ + o(l)), where r is the rank of the group
{m)g>]:NL(H)<c3\ogH.
Here the constants с j, c2, c$ depend on Vand к but not on L.
Proof (outline), (i). Suppose that к = Q and g = 0. Then V ^ P1. Example
46.7 shows that
hL(XwXx)~d max (log lxQl,log l^j I) ,
where xn, Xj £ Z are relatively prime. Therefore NL(H) coincides
asymptotically with half the number of primitive points in the integral lattice in the
square (I x0 I, \xx l)< exp(//d-1). It is well known that this number is
asymptotically equal to (12/тг2) ехр (2Hd~]).
Schanuel [1 ] deals with the case of an arbitrary field к (and ?n instead of
p>).
(ii). Now let g - 1. Instead of hL we can consider hL. According to
Theorem 46.11, the quadratic part of hL has ihe form db0, where b0 : V(k) -+ R is
positive definite and does not depend on L. The natural map V(k) -* V(k) ®z R
has as its kernel a (finite) torsion group and the image is a lattice in the
/'-dimensional Euclidean space V(k) ® z R. The metric on it is defined by the form b0.
Therefore the region hL(x)<:H in this space is a sphere of radius
(Hd~{ - #q)2, the centre of which andtf^ depend on the linear part of hL.
The number of points of the lattice in this sphere is proportional to its volume,
which establishes the desired asymptotic behaviour.
These arguments are due to Neron.
(iii). Finally, let g > 1. The estimate for NL(H) in this case was obtained
by Mumford [1]. According to the Mordell conjecture, one must have/v^(H)
< constant, but for our purposes the logarithm also suffices.
For Mum ford's proof one again considers a map of V(k) into a Euclidean
space Jy(k) ® R. The metric in the latter is induced by the quadratic part Z?0

CH.Vl,§46
A NEGATIVE RESULT
271
with respect to the standard ample sheaf 0(0) on Jv. The map
V(k) -> Jy(k) ® R is induced by \pv\ its image is contained in a sublattice in
the image of Jy(k), and the inverse image of each point contains no more
elements than the order of the torsion of Jy(k).
Mumford's basic result, which is obtained by means of a careful comparison
of the heights on a curve and its Jacobian using their functorial properties,
can be stated as follows (in a somewhat weakened form):
There exist two constants e > 0,r\ > 0 such that for any two vectors
x ^y€Jv(k) satisfying I (|| x || /|| у ||) - 11 < e, the angle between x and у
is greater than i?r provided that these points belong to the image of V(k).
In other words, vectors of almost the same length in V(k) cannot have
almost the same direction. On the other hand, the collection of vectors in a
Euclidean space of given dimension r such that the angle between any two of
them is greater than 77 has no more elements than some constant N, which
depends only on r and r\.
Consider now a set (at most countable) of points in Jy(k) ® R which
come from K, and arrange them in a sequence according to increasing length
jCj, дс2, . . . , xn . . . .It follows from what has been said that 11 xn+N 11 >
> (1 + e) \\xfl II for all n. Thus the lengths II jc„ II do not grow slower than in
geometric progression. This immediately establishes the estimate (iii). The length
/>п(х, x) and the height hL(x) differ by a factor d +o(l) and this can be taken
account of once and for all by enlarging the constant c3. This proves the lemma.
Lemma 46.13 permits us to establish a one-dimensional variant of the
main Theorem 46.1, to which we shall afterwards reduce this theorem.
In order to give an exact formulation we introduce the following definitions.
Let Vht a curve over к and let the set V(k) be infinite. We shall say that
almost all points of V(k) have some property P if
№L(H)
where Л^(Я) denotes the number of points which satisfy property P and the
condition hL(x)<H. Here L is some invertible sheaf of degree > \.h
immediately follows from Lemma 46.12 that this definition does not depend on the
choice of L.
We can now formulate:

272 THE BRAUER -GROTHENDIECK GROUP CH. VI, § 46
Corollary 46.14. Let f: V' -► V be a morphism of projective curves over k.
Suppose that the following conditions are satisfied:
(i) The curve V is geometrically irreducible and smooth, its genus is 0 or 1,
and the set V(k) is infinite.
(ii) For each irreducible component V-of V' the induced morphism
ft: Vx; -> V has degree > 1 and the genus of V\ is greater than one if
the genus of V is equal to one.
Then almost all points of V{k) do not belong to the set f(V'(kj).
Proof. It is obvious from the definition that if for every z'= 1,..., я,
almost all points of V(k) have property />,-, then almost all points have all
properties ?j simultaneously. It therefore suffices to consider the irreducible
components of V' separately, i.e., we can assume that V' is irreducible over k.
If, moreover, V'®k is reducible, then the ^-points of V cm only be at the
intersection of at least two conjugate geometric components; therefore there
are only a finite number of them, and the assertion is obvious.
Now let V' be geometrically irreducible, e > 1 the degree of the morphism
/. Then we have for every point jc € V'(k) that
hf4L)(x)~hL(f(x)) , deg/*(Z,) = edegL .
Therefore the number Nj(H) of points of L-heighth < H which belong to
f(V\k)) satisfies the estimate
А^(Я)<^(/)(Я)(1+о(1)).
Under the conditions of the lemma, this establishes the following inequalities,
where d= degL:
(i) Genus V is equal to zero:
^(Я) = с1(ехр2Я^-1)(1+о(1)),
!c'{exp 2H(de)~l if genus V = 0 ,
c'2Hr/2 ifgenusK/= 1 ,
c\ log Я if genus V'> 1 .

CH.VI, §46
A NEGATIVE RESULT
27 3
(ii) Genus V is equal to one:
NL(H) = c'2(HcTV^U+oO)), r>0,
because genus V' is by hypothesis greater than one.
This proves the corollary.
Finally we shall use the estimates of 46.13 to study the specialisation of
the group of sections of a bundle of elliptic curves.
Let В = P1 over k, V a smooth projective surface over k, p : V -> В a k-
morphism of which the general fibre is geometrically irreducible and has
genus 1. Suppose further that the geometric fibres of V do not contain
exceptional curves and that the A:-section a-q : В -> К of the morphism p is fixed.
Then on an open set K0 С V, the complement of the finite set of points
in which p is not smooth, there exists the structure of an Abelian scheme
over/?. In particular, the sections V(B) of the morphism p form an Abelian
group with a finite number of generators and with as zero s0(B) = S0.
On the other hand, for each point x GB(k), except a finite number, the
fibre Vx is a one-dimensional Abelian variety, and the intersection with Vx
induces a natural homomorphism
px:V(B)-*Vx(k).
The following lemma, in a slightly less precise form, was first proved by
A. Neron.
Lemma 46.15. The kernel of the homomorphism px is trivial for almost
allx<EB(k).
Proof. Let q > 1 denote an integer such that the order of the torsion group
in V(B) is relatively prime to q. The fibrewise multiplication by q is a
^-morphism q : Vq -> VQ (outside the points where p is not smooth).
Let Sq С Vq С V be the zero section. The inverse image q*(Sft) С VQ is
closed in К and contains 50 as an irreducible component of multiplicity one.
Let <7*(S0) denote its complement. Further, let Slt...,SNCV represent the
non-zero classes of V(B)/qV(B), and let

274 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 46
N
B^q^)^q%)
1=1
(the addition is in the divisor group on V). All the curves q*(Si) С К are closed
in К and defined over k. We denote by/: В' -+ В the restriction ofp to 5', and
check that the conditions of Corollary 46.14 are fulfilled for this morphism.
The genus of В is equal to zero and the set B(k) is infinite. Moreover, none
of the irreducible components of the curve B' is a section. This is obvious for
the components of the curves q*(S(), i>\, because 5,- Ф. q V(B), and for the
components of g*(Sn) because the torsion of V(B) is relatively prime to q.
Consequently, according to 46.14, almost all points o(B(k) do not belong
to/(£'(*)).
It therefore suffices to prove that if Ker \px : V(B) -> Vx(k)] Ф 0, then
there exists a pointy eB'(k) such that x =f(y). Utpx(S) = 0. If S fi qV(B\
then for some / > 1 and S' £ V(B) we have
S = St+qS', P^S^qp^S')
(the addition is in the groups V(B) and Vx(k)). Therefore, on the curve q*(St)
there is a fc-point over*: the intersection of S' with Vx.
We now consider the case S GqV(B). Let S = qaS' and S' not divisible by q
in V(B). Then either px(S') = 0, and the matter reduces to the previously
considered case, or рх(Б')Ф 0. In this case there exists an integer 1 < b < a
such that px(qbS') = 0, px(qb ~К?)Ф0. Set S" =qb~{S'. We have
qpx(S") = 0, Px(S")*0.
This means that on the curve q*(S$) there is a £-point over x, the
intersection of S" with an x-fibre, which does not belong to Sq. This concludes the
proof.
46.16. Proof of Theorem 46.1. We return, finally, to a cubic surface
V С P3 and a family of morphisms/j : Vt -> V. Let D{ С V be the branching
curve of^-; it is non-empty because deg^ > 1 and ^(КДС)) = {1}.
In the space P3, dual to P3, we consider the set of those points for which
the corresponding planes contain no components of the curves Diy no lines on
V, and no singular points on V. These points form a dense set. Because V{k)
is also dense in V, the set of lines in P3 which intersect V in three different
non-singular points of V(k) that do not belong to U"=1£>, or the lines of V,

СН. VI, §46
A NEGATIVE RESULT
275
is dense in the corresponding Grassmanian. Each of these lines determines a
bundle of planes in P3 passing through it, that is, a line in P3. Consequently,
in P3 there exists a fc-bundle of planes such that a general member of it has a
non-empty intersection with any component of the curves Diy but does not
contain singular points of V\ moreover, no plane of this bundle contains lines
on V, and the three base points of the sheaf of sections belong to
K(A:)\(U;=1/)z.Ulines).
Perform a monoidal transformation with as centre the union of these three
points and resolve the singularities of V; let V' be the resulting surface.
Replace the morphisms/J- : V,- -* V by morphisms// : V\ -> V\ where f\ is some
resolution of the composed rational map V( % V *- V\ As the assertion of
the theorem is of birational nature, it suffices to prove that the set
V\k) \U?=1 ftV\{k)) is dense in V{k).
We consider the morphism p : V -> В of the surface V into the base of the
bundle of plane sections. Again because of the birational nature of the
problem we can assume that this morphism satisfies the conditions described
preceding Lemma 46.15.
As the zero section in V'{B), we take the inverse image of one of the base
points of the bundle of sections of V, say x. Then the section, the inverse
image of another base pointy, has infinite order in the group V (B). In fact,
let 2 € V(k) be a point on one of the smooth irreducible sections of the
bundle. The result of the composition of z and у with the zero x on this section is
written as txtv(z) in our standard notation. Consequently, translating with
the inverse image of у in the group of sections V'(B) induces a birational map
of V which corresponds to txty on V. But in 39.8.3 it has been proved that
txty has infinite order, in any case when V is non-singular. The same method
can be used to prove this result also for singular surfaces V\ we omit the
details.
It follows in particular from this that the group V'(B) is infinite, and in
virtue of Lemma 46.15 that the group Vx'(k) is infinite for almost all x SB(k).
We denote by Bi the normalisation of the curve В in the field of rational
functions on V\ and consider the commutative diagram
, f'i
Vl >V
, P
Bt '-—+B
8i

276 ТНГ BRAUF.R-GROTHENDIKCK GROUP СИ. VI, § 47
We distinguish two cases.
(i) deg gj > 1. Then according to Corollary 46.14 almost all points of
B(k) do not belong to #,■(£,■ (£)). This means that on almost all fibres V'x
there are in general no points from the setf]'(VJ(k)), although there are
infinitely many /c-points on each of these fibres.
(ii) deg gj = 1. Then according to Bertini's theorem all except a finite
number of the fibres {V-)x x 6 B(k), are geometrically irreducible smooth curves.
Moreover, the genus of these fibres is greater than I, because all the Vx have
a zero-dimensional non-empty intersection with the branching curves/),' of
the morphisms//on V'. Applying Corollary 46.14 to the morphisms
(Vj)x -> V'Xi we obtain that on those fibres V'x for which V'x(k) is infinite, almost
all points on V'x(k) are not in the image of (V-)x(k).
Combining these results we obtain that in all cases almost all ^-points of
almost all fibres of the morphism p over x G B(k) do not belong to
U/Lj f{(VJ(k)). In particular, they certainly form a dense set on V'. This proves
the theorem»
Problem 46.17. Let h be the height on a cubic surface ГСР^3 induced by
its ample embedding. What is the asymptotic behaviour of the number
N(H)={xG_V(k)\ h(x)<H}?
How essentially does it depend on the minimality of VI
At first one would have to study this problem for surfaces over Q which
are obtained by a monoidal transformation with as centre six Q-points and
for 2jl0 7* = o.
47. Counter-examples to the Hasse principle
This section contains explicit calculations to illustrate the principles
described in 41.14 -41.22 of this chapter.
We start with an example of Mordell [ 1 J.
47.1. The surface V is given over Q by the equation
7"3(д1Г0+^7'з)(|12Г0+^27з)=П(Г0 + 0(/)Г1 +(0(/))27'2).

СН. VI, § 47 COUNTER-EXAMPLES TO THE HASSE PRINCIPLE
277
Here af, dj are integers, К = Q(0('*) is an Abelian cubic extension which is
ramified in one place p = 7 or 13. For each value of p there are defined two
series of congruences forfl,, d{: one of them ensures that K(Q ) is non-empty
for each q, the other ensures that the local components of the Brauer group
fit. (It is obvious that K(R) is non-empty, and the contribution of the real
places to the collection of local invariants is zero, because Br(K, К) consists of
elements of order 3.)
These series of congruences (see (A), (B), (C), (D) below) have infinitely
many solutions. Mordell constructs an additional sequence of examples,
corresponding to a field К which is ramified in p = 3; we omit it because it
necessitates some more minute calculations. The essential picture is
completely the same. Moreover, we restrict ourselves to an indication of the part of the
congruences which are sufficient to demonstrate the principle; the other
sufficient conditions can be found in Mordell's paper.
Let us now describe all data successively.
47.2. The field К and 0. Let f be a primitive root of unity of degree p.
К is uniquely determined as the cubic subfield of Q(f7) or Q(f 13). One of the
values of в is given respectively by the formulae
ff + Г1 +1, forp = 7,
f + f5 +f8+f12-4, forp=13 .
The number of classes of К is equal to 1; the ring of integers coincides with
Z[0]. The discriminant of в is equal top2.
In the field К the number p ramifies as p = p 3; the prime numbers q for
which
/±l(mod7) forp = 7,
И
l± l,±5(modl3) forp=13 ,
decompose completely. The remaining 4 stay prime.
47.3. The Brauer group of V. We restrict ourselves to a consideration of
two elements of Br (V, K). The divisors of the rational functions on V

278 THF BRAUER-GROTHliNDIECK GROUP CH. VI, § 47
belong to Л^д (Div V ® A'). As in the examples already analyzed, they
determine the elements of the Brauer group of V, which we shall also denote by/)-,
abusing brevity.
The local invariants inv (fj(x)) for x $ Supp (/)•) are represented by the
classes/)(л:) (mod ^Kj/q (&%))> where q divides q in K. One can restrict
oneself to points x ф Ц Supp (/)) because inv (/)(*)) is locally constant in the
*7-adic topology of V(QQ).
We shall now show how to ensure that the local invariants fit together.
This is an idea of Swinnerton-Dyer [ 1 ].
Proposition 47.4. Suppose that the sets V(QQ)for all primes q are
nonempty and that the following conditions are satisfied:
(A) 0 p fl| = a2(mod p),0£d\ = d2 — 1 (modp\ p = 1 or 13.
(B) g.c.d. (d\% d2) consists of primes which completely decompose in K.
Then for all q Ф p, x G V(Qp), the local invariants inv (fj(x))f / = \,2.are
zero. For q-p there does not exist a point x E V(Q J) for which
simultaneously
invp(/l(x)) = invp(/2(x)) = 0.
Therefore the set V(Q) is empty.
Proof. Let л: = (/0, /j, t2, f3) E Q be a point outside U Supp(/)■), with
coordinates which are relatively prime. We consider three cases separately.
(i) q completely decomposes in K. Then K- = Q and inv (/)•(*)) - 0.
(ii) q remains prime in K. Then N(K± ) ={x E Q* I vq(x) = 0 (mod 3)}.
If the equality
V'3<Vo + V3><Vo +^2/3^ = 0
holds, then it follows already from this that )\ (x) and f2(x) aic norms.
Suppose that this equality does not hold; then u- (/0 + r^B + t2$2)> 0 and hence
vq (t() > 0 for / = 0, 1, 2. Considering again the left-hand part of the
equation of V, we obtain vq(d\d2t\) = ^- ^гогп tne fact that /n, f,, t2, /3 are

СН. VI, § 47 COUNTER-EXAMPLES TO THE HASSE PRINCIPLE 279
relatively prime it follows that this is only possible if, say, v (dY) > 0. Besides,
in virtue of (B), vq(d2) = ^('3) = 0. Hence
V'3(Vo +<V3)(Vo +</2'з)) = VVu + V3) = 0(mod3)f
so that again/i(jc),/2(x) are norms.
(iii). q = p (i.e., 7 or 13). Then p = p 3 and и-- (0) = 1.
We show first of all that
VMVo+£/1'з)Ц'о+<V3)) = 0 •
In the opposite case, v- (/0 + txd + t262) > 0, from which и (/0) > 0 and
that means vp(dxd2i\)>0. By (A), vp(d{d2) = 0, so that up(/3) > 0, from
which ир(П(г0 + tx0 + t2d2))> 3. Consequently, 1^(/0 + f j0 + f202)> 3 and
t> (/j) > 0, vp(t2) > 0, which contradicts the fact that f0, f,, r2 are relatively
prime. Thus up(/,(x)) = vp(f2(x)) = 0. Moreover,/,(x)-/2(x) = dj - rf2 = 1
(mod p) by condition (A).
From this it follows already that/j(x) and/2(x) cannot simultaneously be
norms in K- because the norm of a unit has the form ± 1 (mod 7) (for p - 7)
and ± I, ± 5 (mod 13) (for p = 13).
This concludes the proof.
Lemma 47.5 (Lemma on local solvability),
(i) q = p. The set V(Qp) is non-empty if
ax=a2=dx-\ (mod7)}
d2=2(mod7)J
jj = a2 = 1 (mod 13)\
dx =A (mod 13)
d2 = 5(mod!3)
forp^l ,
for p ~ 13 .
(C)
(ii) q = 2or3. The set V(Qq) is non-empty if
<ij = 0 (mod q), д. cL £ 0 (mod 4) .
(iii) q > 3,q Ф p. rThe set ^(Q^) is always non-empty.
(D)

280 THE BRAUER-GROTHENDIECK GROUP CH. VI, § 47
Proof. In each case we give a non-singular Z/(q) point on the reduction of
the surface K(mod q). Well-known elementary arguments then permit us to
show that it lifts to a</-adic point. (The lifting must be done by steps from
mod qn to mod qn+l; to find the correction for each step, one obtains a non-
homogeneous linear equation; as the coefficients of this equation serve the
partial derivatives of the left-hand part F of the equation of V in the lifted
point (mod q\ Because this point is simple, not all of these coefficients are
zero.)
(i) q = p. Because vAO) > 0, the reduced equation of V has the form
^ = ^<?lfO+JIf3X?2fO+'?2f3)-fO=0-
Л verification using conditions (C) shows that x = (1, 0, 0, -1) lies on V
(mod q). It is non-singular because (dF/bT3)(x) Ф 0.
(ii) q = 2, 3. Conditions (D) show that the point jc = (0,0, 0, 1) lies on
V (mod q\ It is non-singular because (bF/bf0) (x) Ф 0.
(iii) q > Ъ,цФр. If q decomposes completely in K, then the right-hand
'norm type' part of the equation of V decomposes in Q into three linear
factors. Therefore on V there arc nine lines which are rational over (L. If q
remains prime in K, however, then У (mod q) has a non-trivial Z/(<7)-point x
by the classical theorem of Chevalley. If it is singular and double, then a line
through it in any Z/((/)-rational direction intersects V (mod q) in a non-singular
Z/(g)-point. Finally, a simple calculation, which we omit, shows that triple
points on К (mod q) do not exist.
47.6. To conclude, we describe the example of Cassels and Guy 11 ].
The surface V is giv°n by the equation over Q,
V: 57^ + 127^+97^ 107^ = 0.
That all the HQ^) are non-empty is verified without trouble. In fact, if ^7 > 5
is prime, then the surface К (mod q) is non-singular and it is well known that
it has Z/(</)-points, because the number of such points = 1 (mod q). On V
(mod 2) there is a simple point (1,0, 1,0), on V (mod 5) there is a simple point
(0, 2, 1, 0). Finally there exists a 3-adic solution with T0 = T{ = 1, T2 = 0.

CH. VI, § 47 COUNTER-EXAMPLES TO THE HASSE PRINCIPLE 281
Let f be a primitive cubic root of unity. Because к = Q(f) is a quadratic
extension of 0, V(Q) is empty if and only if V{k) is empty. We shall consider
к as the base field because the auxiliary fields kx = fc(^30) and k2 =k($90)
are normal over k. Cassels and Guy work with Q instead of A:, but all the for
us necessary number-theoretical information from their paper is easily carried
over to our base field.
The Galois group G = Gal (K/k) is generated by the automorphisms of
order three, s and t: s($30) = f ^30; r(^90) = ?^90; s acts trivially on къ
and t on fcj. The obstruction which Cassels and Guy construct lies in the
group of divisor classes of K. It is supplied by the function (cf. Section 41.18)
Г0+7\(^90)2/15
т2 + г3(>^зо)/з
The investigations fall into two parts: a local and a global part.
The local investigation. Let x = (x ) be some Q-adele of the surface V. We
shall say that the function/is defined in x if, firstly* ^ Supp(/), and,
secondly, Vq (f(xq)) = 0 for all q except for a finite number, where q is any
divisor of q in K.
Lemma 47.7. Let x be a Q-adele of the surface V in which fis defined.
Then the K-divisor
has the form
-T2c~lJ+Wz
(/(*)) = 3'5-V
-(1+5+S2)

282 THE BRAUER-GR0THEND1ECK GROUP CH. VI, § 47
where с is some K~divisor, and 3 and 5 are K-divisors defined by the equations
33 =(3),53=(5).
This is a straightforward reformulation of Lemma 1 of the paper of Cassels
and Guy. A proof (which there is also omitted as a matter of fact) is obtained
by an immediate calculation of exponents if one rewrites the original equation
of К in the form
5CT0 + 7^90)2/15)1 + r+'2 = - 9(72 + r3(#30)/3)1+s+s?
The global investigation.
Lemma 47.8. (i) 3 is a principal divisor and 5 is a non-principal divisor of
the field K.
(ii) Tlie class of the divisor с belongs to the subgroup of the class group which
is generated by the class of 5.
Cassels and Guy prove that the group of classes of the field
#0 = QC^O, >}^90) С К is isomorphic to Z3 and that it is generated by the
class of 5. The class of (/(*)) belongs to this subgroup, however, because/
even belongs to K0(v) and not only to K(v). Since К is a quadratic extension
of A'q, 5 cannot become a principal divisor in K: the class of 5 has exponent 3.
Corollary 47.9. V has no Q-points.
Proof. As a matter of fact, V does not even have Q-adeles a* in which/is
defined and the divisor (/(л*)) is principal in K. In fact, Lemmas47.7 and 47.8
together show that the class of the divisor (/(.*)) coincides with the class of
5 _1, because s and /, acting trivially on the class of 5. also act trivially on
the class of c, so that c1+r + r2 /c1+5+s is a principal divisor.
47.10. Discussion. Tlie author would like to connect this very choice of
the function/, of which the divisor of the values is investigated, with the
Brauer group of the surface V. This can be done with some stretching.
We extend the base field к to k' = k(\/36) and construct the fields k\ = k'k(,
K' = k'K. We write the equation for V (&k k' in the form

СН. VI, §48
BIBLIOGRAPHICAL REMARKS
283
15Г03 + (>?/5б Тх )3 + (ЗГ2)3 + ЗОГ3 = 0 ,
and we consider the two rational functions
Г0+'Л(^90)2/15
/rV" e*;(u),
#36Г,+ЗГ2
/2 = ^~ €*i(i,).
V36rt + 3r2
Then, on the one hand,/ = /^/2; on the other hand, as in Example 45.3:
Therefore/j and /2 define elements of the Brauer group of V (although over
different fields k\ and k'ly respectively). Thus Lemma 47.7 can be interpreted
as information on the connection between the local invariants of these two
elements on Q-adeles of the surface V.
It can be cleaily seen that the proof of Cassels and Guy is much too short
for the Procrustean bed of our general theory: the field k' is only needed for
the stretching of the limbs ....
48. Bibliographical remarks
The Brauer-Grothendieck group for schemes was introduced and
investigated by Grothendieck [2]. Its connection with the Safarevic-Tategroup(ina
different context) was explained in the same paper of Tate where the theorem
mentioned in Section 31 was proved. Brauer equivalence was defined in Manin
[9] ; the contents of Section 46 have been taken from Manin [5]. The
calculations in Section 45 and the construction of the general obstruction to
the Hasse principle are here published for the first time. A detailed survey of
analogous problems in the theory of elliptic curves has been written by
Cassels [3|; there one also finds an extensive list of references.

APPENDIX
ALGEBRAIC VARIETIES CLOSE TO THE RATIONAL ONES.
ALGEBRA, GEOMETRY, ARITHMETIC
Introduction
Let X be an absolutely irreducible algebraic variety over a perfect field k,
dim X = n. Recall three rationality properties of X.
(a) X is called ^-rational, or /c-birationally trivial, if a birational map Pnk -> X exists.
(b) X is said to be stably k-rational, if a birational map P™+n -> P™ x X exists for
some m ^ 0.
(c) X is called Л-unirational, if a rational map of finite degree P£-> A" exists.
When the mention of the ground field к is omitted, it is understood that the
corresponding property is valid over k.
One easily sees that (a) => (b) Ф (c). (To prove the last implication, choose in P™+"
an n-dimensional /c-rational subvariety У such that the composition У -> P™+n -> P™ х
A'-» A" is generically surjective. If /r is infinite one can find a linear subspace У with this
property.)
The somewhat loosely defined class of 'varieties, close to the rational ones' includes
fc-unirational varieties but is not exhausted by them. For example, let X-+ У be a
surjective rational map such that the base У and the generic fibre A^ are close to
rational. Then A" itself is close to rational. Fano's varieties (see Section 4 below) also
belong to this class.
Smooth cubic hypersurfaces, moduli spaces of curves of genus =^13, linear algebraic
groups and their homogeneous spaces are rational or unirational.
The classical problem of existence of unirational, but irrational varieties was solved in
1971, and a strengthening of this result, the existence of stably rational but irrational
varieties was proved only in 1983. A brief exposition of this remarkable achievement
is given in Section 4.
The irrationality proofs are partly based on the principles which were studied in
"Cubic Forms". Section 1 of this Appendix is devoted to the further connections
between the Galois cohomology of the Picard group (or the dual torus) and the
birational properties of the varieties, exploited in the simplest situations in Chapters IV
284

APPENDIX
285
and VI. Section 2 introduces the technique of descent due to Colliot-Thelene and Sansuc
which is the far-going generalization of the methods of Chapter VI, in particular of the
Chatelet surfaces theory. In Section 3 some new results on the geometry of rational
surfaces are expounded. This may be considered as a natural continuation of Chapter V.
Finally, Sections 5 and 6 are devoted to the questions about R-equivalence and
rational equivalence in connection with constructions of Chapter I. In particular, new
information about the structure of abstract CML's is discussed.
Unfortunately many interesting results not directly related to "Cubic Forms" had to
be passed over in silence. We refer the reader in particular to the recent survey articles
by V.P. Platonov [81], and V.P. Platonov and A.S. ftapincuk [82] for information on the
arithmetic of linear algebraic groups.
1. Galois cohomology, Picard groups and birational geometry
1. Permutation modules. Let G be a profinite group. A continuous G-module P with
discrete topology is called a permutation module if it admits a Z-free base on which G
acts by permutations (in IV.29 such modules are called trivial). Two G-modules Л/, N
are called similar \f M(B P~ M (BQ for approp» iaCe permutation modules P, Q.
Denote by [M] the similarity class of M. Since H\G, P) = 0 if P is a permutation
module, Hl(G, M) depends only on [M].
V.E. Voskresenskii [101], using Hironaka's resolution, has proved the following
generalization of Lemma IV.29.1.2. Let к be a field of characteristic zero, G = Gal к Ik,
X an absolutely irreducible variety over ky X - X ® k. There is an evident action of G
on Pic X.
2. Theorem. IfX, Y are projective smooth k-vaneties, then their birational equivalence
implies [?'\cX\ = [?icY\.
3. Corollary, (a) For any field extension KDk,Hl(K, Pic X) is a k-birational
invariant of a smooth projective variety X.
(b) IfX is k-birationally trivial, then H l(K, Pic X) = 0 for all KDk.
4. Semigroup of similarity classes. If a smooth projective variety X is rational (i.e., X
is birational to PI), the G-module Pic A^ is Z-free of finite rank.
The following group-theoretic definitions fit well with this situation. It is tacitly
assumed that all G-modules in these definitions are Z-free of finite rank.
Denote by Sc the semigroup of similarity classes of such G-modulcs with respect to
direct sum.

286
APPENDIX
If G is finite, H'(G,M) denotes the Tate cohomology, defined for all / E Z and
which satisfies the duality law tf'(G, М)* = Н'(С, Л/и), where Л* =Hom(^,Q/Z),
Л/п = Hom(M, Z). The group H~\G, M) can be defined also for profinite G as
lim H~\GIH, Mh)i where H С G runs over all open subgroups.
A G-module M is called flabby, if Я " l(G\ M) = 0 for all open subgroups G' С G.
The significance of this notion is explained by the following result due to Voskresenskii
[105]. Let ГЬе a /c-tonis, Xits smooth projective compactification, D the group of
divisors of A'supported at infinity X^T. Denote by Г the character module of T. Then
(a) Pic X is a flabby Gal klk-module.
(b) The module Trias a resolution
0-+f->D->P\cX->Q,
where D is a permutation module and Pic Xis flabby.
Axiomatizing this remark, call any exact sequence 0->M->P-»F-»0fl flabby
resolution of M, if P is permutation and Fflabby. Denote by FG С SG the subsemigroup
of similarity classes of flabby modules and set F°G = {[M{)]\ M flabby}. Finally, call a
G-module M invertible, if it is a direct summand of a permutation module. Let Uc =
FG П F°G be the subgroup of classes of invertible modules.
5. Proposition ([26]). (a) Each G-module M admits a flabby resolution
0->Af-^F^F->0.
(b) The class [F] depends only on [M]. Let
p{M) = p([M}) = [F], <т(М) = сг([М]) = р(М У.
(c) The map p (resp. o) induces a surjection SG -> FG (resp. SG -> F°G). The restriction
ofp (resp. o) to FG (resp. FG) induces mutually inverse isomorphisms FG -> FG
(resp. Fq-+Fg). The restriction ofp and a to UG induces -id.
(d) p(M) = p(N), iff there exist two exact sequencesQ-* M-* E-* ?-> 0,
0->N->£->/?-*0 where Py R are permutation modules.
The structure of the semigroup SG and its filtration was studied in the papers [43],
[70], [16]. We mention the following facts. If G is finite, then FG is a group (coinciding
with UG), iff G is metacyclic. For finite G, UG is an abelian group of finite type which
may be infinite.
Applications to birational classification. For a smooth variety X over к denote by
I(X) the group ДО*) Ik*. Let Kfk be a Galois extension with group G, XK = Xk® X.
The varieties Xy Y are said to be stably birationally equivalent over /c, if there exists
a birational map X x Pak-* Y x pbk for a certain a, b.

APPENDIX
287
6. Theorem. For X as above, let V С X be a dense Zariski open subset with Pic Uk = 0.
Then:
(a) The invariant p(X) = p(I(UK)) E FG depends only on the stable birational
equivalene class ofX over k. It vanishes for birationally trivial X.
(b)IfXisa k-torus split over K, then
p(T) = p(t) = [Pic XK)9
where Xisa smooth compactification of T.
(c) Let Z{Klk) be the semigroup of classes ofk-tori, split over K, with respect to stable
k-birational equivalence. Then p induces an isomorphism Z(K/k) ^ FG.
Part (c) was proved by V.E. Voskresenskii [103]. Parts (a) and (b), slightly
generalizing Voskresenskii's results, were obtained by Colliot-Thelene and Sansuc [26].
7. Invariant field of a cyclic group. Let/? be a prime, К = Q(x{,. .., xp ),and let С be
the group of cyclic permutations of (jc, ,..., jcp ). Swan [91] has found a necessary
condition for KG to be a pure extension of Q. Using the technique described above,
Voskresenskii [102] proved that it is also sufficient:
8. Theorem. KG is a pure extension ofQ iffeither p or-pis a norm of a number lying
i«Q(e2¥i,p).
9. Linear groups. Let Я be a connected linear algebraic group over a number field k.
Weak approximation is valid for Я, if the image of H(k) in the adele group H(Ak) is
dense. The obstruction group is denoted by
A(H) = H(Ak)IH(h).
Similarly, the obstructions to the Hasse principle for the class of principle
homogeneous //-spaces (or H-torsors) lie in the Safarevic-Tate set
Ш (Я) = Kerf Hl(k, //)-> U H\kv, H)]
L v J
If Я is semisimple and simply connected, A(H) = 0. If moreover Я has no £8 factor,
Ш(Я) = 0.
Set
В^Я - {b e Br H\ b splits over к), Вг.Я - В^Я/Вг к.

288
APPENDIX
10. Theorem. Let Hbea connected linear algebraic group without E8 factors, V its
smoth compactification over ky S the torus dual to Pic V. Then:
(a) А (Я), Ш (Я) are finite abelian groups, depending only on the stable k-birational
equivalence class ofH.
(b) There is an exact sequence
0-> Л(Я)-> Н\к, Pic V)*-> Ш (//)-> 0 •
Moreover,
//'(*, Pic К)* = ВгаК.
When His a torus, this was proved by Voskresenskii [105]. He also investigated the
general situation [101]. The given statement was proved by Sansuc [84] who used the
technique of pairing with the Brauer group developed in Chapter VI of this book.
2. The Hasse principle and descent on rational varieties
1. The Hasse principle. The theory of the Brauer obstruction to the Hasse principle
introduced in Chapter VI of this book was considerably extended and supplemented by
a general descent technique in the papers by Colliot-Thelene and Sansuc. This section
is devoted to their results. Our exposition is based particularly on the papers [27] and
[83], [24], [25], [21]. Cf. also [29], where interesting conditional results are deduced
from one of Schinzel's conjectures.
We recall, that for a class Tof algebraic varieties over an algebraic number field
к the Hasse principle holds, if for any X 6 T with all X(kv) non-empty X(k) itself is
nonempty. The classical Minkowski-Hasse theorem states that for the class of
projective quadrics the Hasse principle holds. Another such class consists of the
Severi-Brauer varieties, i.e., /c-forms of projective spaces. On the other hand, for cubic
curves (and abelian varieties of arbitrary dimension), cubic surfaces and conic bundles
over P\ the Hasse principle fails. A general method which sometimes allows to prove
that X(k) = 0 although X(kv) Ф 0 for all v consists in checking that the Brauer
obstruction is non-zero. This means that for all adelic points (xv) E X{Ak) there exists
an element A G Br X such that Lv invv A(xv) Ф 0 (see Chapter VI for details).
A quite general theorem proved by Birch [9] with the help of the circle method
means, roughly speaking, that complete intersections of large dimension verify the
strong Hasse principle. By definition, this means that if V°(kv) Ф 0 for all v, where V° is

APPENDIX
289
the set of smooth points of V, then V(k) Ф 0 for any projective model V of V. Here is the
exact statement of Birch's theorem.
2. Theorem. For the class Y(n ,h,d) of varieties in PnQ~l defined by h equations of
degree d and verifying the condition
n-\-d\mVsing>h(h + \)(d-\)2d\ l/.ng=V-V\ dim0=-l,
the strong Hasse principle holds.
It follows in particular that in the class of smooth complete intersections the Hasse
principle holds (a) for quadrics of dimension ^3 (n ^ 5); (b) for intersections of two
quadrics of dimension ^10 (n ^ 13); (c) for cubic hypersurfaces of dimension ^15
(Л*17).
As Sansuc [83] puts it, for each of these three classes one can define two numbersw(),
л, such that for n < n0 counterexamples to the Hasse principle are known, for n ^ nQ the
Brauer obstruction vanishes, and for n ^ n{, v Ф °° one has V(QV) ^ 0 so that the local
obstruction vanishes iff V(R) Ф 0. Namely, л0 = 0, л, = 5 for quadrics; n0 = 6, л, = 9 for
intersections of two quadrics; n{) = 5, nl = 10 for cubic hypersurfaces. Therefore one can
conjecture that for n < n{) the Brauer obstruction is the only obstruction for Hasse
principle and for n ^ л0 the Hasse principle holds. A remarkable recent theorem by
Heath-Brown [50] proves this for cubic hypersurfaces and n ^ nx = 10. Below we shall
describe certain new results for intersections of two quadrics.
3. Descent. Suppose that for a variety X a family of dominant morphisms 7Г,: Yt -» X
is given with the property X(k) = U . тгДУХЛ)). To prove that X(k) = 0 it suffices then
to demonstrate that for each Yt there exists a v such that Y,(&v) = 0 (and hence
Y,(k) = 0). On the other hand, if X(k) is nonvoid and the У, are in a sense simpler than
X, say, ^-rational, we get a passable description of Л^лг). This is the general idea of
descent which goes back to Fermat, Mordell, Selmer (for elliptic curves) and which
works well also for Chatelet surfaces (see Chapter VI, Section 45).
Colliot-Thelene and Sansuc developed a systematic procedure to generate the
'descent families' (Y;, тг,) starting from X. Under some natural conditions the following
can be proved:
(a) The obstruction to the existence of a £-point on X corresponding to (У,., тг,)
vanishes or not simultaneously with the Brauer obstruction.
(b) Brauer's obstruction for Yi vanishes: there is no 'second descent'.
One may hope that for a certain class of varieties X the members of the descent

290
APPENDIX
family Yt verify the Hasse principle. Results of this kind are proved in [21], [32].
We shall now describe the Colliot-Thelene and Sansuc method, following [27].
4. Torsors. Let S be a fc-torus X a k-scheme. A torsor (or, more precisely, an S-torsor
over X) is a ^-scheme / together with a morphism p,: J-+X and an action of S on 7
along the fibers of pr This action should make 7 a principal fibre space in the etale
topology of X.
Up to isomorphism a torsor7 is defined by its class [7] E Hl(X, S) (etale cohomol-
ogy). In particular, for X = Spec к we have f/'(Spec /c, S) = H\k, S(k)) (Galois
cohomology).
For each a E H\ky S) we shall denote by the same letter its inverse image in
H\X, S). On the other hand, given a point jcG X(k), a class [7] E Hl(X, S) can be
specialized to give [7J E H\k, S). The following simple fact is easy to verify:
[7J = 0 О xePj(J(k)).
Let us now choose a torsor 7 and denote by 0y: X(k)-* H\k, S) the mapx >-> [7J.
For each a E Hl(ky S) construct a torsorpa :Ja->X\r\ the class [7] - a E tf ^ 5). In
view of the above observation,
*(*)- LI a (•/.<*))= LI />„«,(*))•
attmej aeH4k,S),Ja(k)*«
Thus a choice of a fc-torus 5 and of a torsor 7 furnishes a descent family as defined in
Section 2.3. The following proposition shows that this family is finite in cases interesting
for arithmetic. Denote by ZQ(X) the group of 0-dimensional k-cydes on A'and extend в.
to a homomorphism 0,: Z0(X)~* H\k, S) by setting 0;(x) = covesk{x)lk([Jx]) for any
closed point x E X.
5. Proposition, (a) For proper X, cycles rationally equivalent to zero cycles lie in
Kerdj.
(b) //, in addition, к is either local or finitely generated over the prime subfield, then
the image ofdjinHl(k4S) is finite.
6. Universal torsors. For proper, smooth, rational X there is a canonical choice of 5.
Namely, set S0 = Pic X.
Moreover, among the 50-torsors over X there are distinguished ones called universal
by Colliot-Thelene and Sansuc. To define them, consider the map
^:Я1(^,50)^НотОа1(50,РюХ),

APPENDIX
291
such that the homomorphism *([/]) maPs a character Л : S0 ® к -> Gm ® к onto the
Gm-torsor Л*[У ® ас] which we identify with an element of Pic X.
7. Definition and Lemma, (a) An S0-torsorJis called universal, ifxilA)= idPlc *•
(b) The equivalence relation defined by 0, on Xfor a universal torsor J is stronger then
for any other torsor.
8. Existence and uniqueness of universal torsors. Suppose that X(k) Ф 0. Then the
extension of G-modules (G = Gal к Ik)
l-*k*~>k(X)*-+k(X)*lk*^l
is trivial. Following [25], we shall call the class of this extension the elementary
obstruction (to the existence of a k-po\nt). Its vanishing is related to the existence of
universal torsors.
9. Proposition (a) Let Xbea proper smooth rational variety, A universal torsor for X
exists iff the elementary obstruction for X vanishes. For a number field k, an equivalent
condition is the vanishing of the Brauer obstruction corresponding to the group
В = Ker[res: Br X^> U Br Xv /Br *„ ].
V
(b) The set of universal torsors is either empty or a principal homogeneous space over
//'(Mo).
10. Theorem. Let Xbea smooth proper rational variety admitting an universal torsor
J. Then for any smooth к-compactification У we have:
(a) Г is rational.
(b) Pic Iе is a permutation G-module.
11. A local description of universal torsors. For X as in Sections 2.9 and 2.10, the
Zariski open subsets U С A" with Pic ^7 = 0 form a base of topology. Choose such a U
and set F = X ^ U. Consider a torus Г dual to k[U]* Ik* and denote by M the
G-module of divisors X supported by F. The exact sequence of character modules
0-> ic[U]* Ik * -> M-> Pic X-> 0 induces the exact sequence of k-ton
1 -> S0-> M -> Г-> 1. Thus M becomes a 50-torsor over T. Set G = Gal klk.
Choose a G-spIitting k[U\* Z-k[U]* Ik* = t If U(k) * 0, one can put a,(cl /) =
flf(x) for x E U(k). Using this splitting we can define a G-homomorphism k[t]—»k[U]
and hence a £-morphism (pa\U-+T.

292
APPENDIX
The 50-torsor defined earlier induces then an S0-torsor over U. One can prove that it
is a restriction on (/of a unique (up to isomorphism) universal torsor/aon X, and that
all universal torsors are obtained in this way.
12. Theorem. Let Xbea smooth proper rational variety over a number field к
admitting a universal torsor У, and let X(kv) = 0/or all v. Then
(a) The obstruction for the existence of a k-point on X corresponding to the descent
family of universal torsors {pa : Ja-+ X\aE H]{k,S0)Ja (к) Ф 0} coincides with the
Brauer obstruction for X (i. e., they vanish simultaneously).
(b) The Brauer obstruction for JI vanishes.
The second assertion follows from Theorem 10.
As was remarked in Section 2.3, if X(k) Ф 0 and the varieties JQ with Ja (к) Ф 0 are
/:-rational, this theorem gives a description of X(k). Unfortunately, Ja may not be
k-rational even for a 3-dimensional intersection of two quadrics. E.g., let X be given in
Pr by the equationsx2 + y2 + z2 - uv = x2 + ly1 + t2-(u~ v){u - 2v) = 0. Then X(R)
consists of two connected components. Hence the same is true for/f(R) where J is an
universal torsor so that У is not R-rational.
13. Application to tori. Let now Г be a k-torus, X its smooth fc-compactification.
Since Pic f = 0, the local description of universal torsors over X given in Section 2.11 is
applicable to this case, with T= U. The /c-torus M, dual to the divisor group of X
supported in X > Г is k-rational, since it has a permutation character module. From the
exact sequence 1 -* Su-+ Л/-> Г-> 1 we derive the exact sequence
Af(*)-> 7W-* Hl{k, S0)-> 1- Splitting f-> k[T]*lk* with the help of identity 1 €
T(k) and applying the explicit construction we get the following results.
14. Theorem, (a) The decomposition T(k) = Un p0 (Ja (k)) described in Theorem 2.2
coincides with R-equivalence.
(b) The map д : T{k)-+ H\k, S0) induces an isomorphism T(k)/R2^, Hl(k, 50).
Both groups are finite if к is finitely generated over the prime subfield. In characteristic 0
wehaveT(k)IR~X(k)/R.
15. Applications to the generalized Chatelet surfaces. Consider an affine surface
y2 - az2 = п;м Р>( A), where a G k* ^ (it*)2, and the Pt(A) G A:[A] are irreducible
pairwise coprime polynomials. The descent method applied to a smooth compactific-
ation X of this surface leads to the descent family consisting of the following subvarieties
mAk :
V(cx,.. . , cr): 0 Ф /> (A) = ф] ~ av2)< i = 1,.. . , r ,

APPENDIX
293
where с, 6 /с*. In particular, if r - 2 and P,, P2 are quadratic polynomials, these descent
varieties are intersections of two quadrics in A5.
16. Proposition. Let Tbea certain class of generalized Chdtelet surf aces X, Wthe
corresponding class of descent varieties V(cl4.. ., cr). If the strong Hasse principle holds
for W, then the Brauer obstruction is the single obstruction to the Hasse principle in V.
17. The Hasse principle for the intersection of the two quadrics. In [32] the following
results are established. Let V be an intersection of two quadrics in P£, n ^ 4, over a
number field k. Assume that V is absolutely irreducible and non-conical. Assume
furthermore that in the k-pencil of quadratic forms containing V there are no k-rational
pairs of forms of rank 4.
18. Theorem. The strong Hasse principle holds in the class of intersections of two
quadrics with the described properties verifying one of the following additional
conditions:
(a) V contains a k-rational pair of lines.
(b) V contains a k-rational pair of singular points.
(c) V contains a smooth k-rational quadric surface.
From this theorem and Proposition 2.16 the following facts can be derived.
19. Theorem. In the class of smooth projective models of surfaces y2 - az2 = P( A),
deg P = 3 or 4, P without multiple roots, the following is true:
(a) the Brauer obstruction to the Hasse principle is the unique one.
(b) IfX(k) is non-void, then the Brauer obstruction to the weak approximation is the
unique obstruction, and X(k) IR — A\(X) {set ofQ-cycle classes of degree 1).
In particular, if deg P = 3 and P is irreducible, then Х{к)Ф§ and weak approximation
holds for X. If deg P = 4 and P is irreducible, then the Hasse principle holds for X and,
for X(k) Ф 0, weak approximation holds also.
In these cases the universal torsors J with J(k) Ф 0 turn out to be A>rational.
20. Example. Let к = Q, a = -1, P( A) = -A4 + n where n = 24' Mw > 0, m = 1(2),
0 ^ i"^ 3. Checking the local solvability conditions for x2 + y1 + A4 = n, (x, у, А) Е Q
and applying Theorem 2.18, we get that there are no solutions exactly in the following
cases:
(a)i = 0,ms7(8),
(b)i = 2,m«3(4).

294
APPENDIX
21. Example. The equation*2 + 3у2 = (л - A2)(A2 - n + 1), where л 7*0, lis an
integer, is solvable in Q, iff n > 1, and n * 32°" '(3/) + 2), д, b 6 Z, a ^ 0.
3. Geometry of rational surfaces. Complements
1. Del Pezzo surfaces and conic bundles. Let A' be a smooth projective surface over a
field k. We recall (cf. Section 24, Ch. IV), that X is called a Del Pezzo surface, if the
anticanonical bundle ft^1 is ample, i.e. X = Proj Г(®~ =0 ft^"). Then d = (Пд, • Q,x) =
dim ЦП;1) - 1 is called the degree of X. We have 1 ^ d ^ 9 and if d = 9 then X = P2
(and X is called a Severi-Brauer surface).
Zis called a conic bundle if there is a surjective morphism/ : X-* C, where С is a
smooth curve of genus zero and the generic fiber of/is also smooth of genus zero.
In papers by the author and V. A. Iskovskih the Enriques classification theorem for
rational surfaces was modernized and made more precise. In [59] it was finally proved in
the following form which describes the minimal models of all /:-birational classes.
2. Theorem. Every minimal smooth projective surface over к is isomorphic to a surface
of one of the following two families:
(a) Del Pezzo surfaces with Pic X ^ Z.
(b) Conic bundles with ?\сХ^Ъ®Ъ.
Moreover, surfaces of the first family are necessarily minimal. Surfaces of the second
family are not minimal in the following case:
(b1)(n^-n^) = 3,5,6or(njr-n^) = 8,Jf-F1.
Some conic bundles are also Del Pezzo surfaces. Namely, this happend in the
following cases:
(b2) (Пд • Ux) = 1,2 or 4 and X has two different representations as conic bundle.
(b3) (Cix • ilx) = 8 andX is not isomorphic to FNfor N^2.
Finally у there are no minimal rational surfaces with (Q,x • ilx) = 7.
Now, let G be a group. A G-variety is a variety with an action of G on it. A
G-morphism between G-varieties is a morphism commuting with the action of G. The
notions of G-minimal models, G-conic bundles etc. are self-evident.
In a paper of the author in 1967 it was shown, that if G is finite abelian, the analogue
of Theorem 3.2 is true for rational G-surfaces. In [59] the condition of abelianness was
removed, and the following result was established.

APPENDIX
295
3. Theorem. Let G be a finite group, X a minimal rational G-surface. Denote by P(X)
the subgroup of the Picard group generated by the classes ofG-invariant divisors. Then
either P(X) = Z or Z Ф Z and X is correspondingly either a G-Del Pezzo surface, or a
G-conic bundle.
This result reduces the classical problem of the classification of finite subgroups of the
Cremona group (up to conjugacy) to the problem of the classification of biregular
automorphisms of a well defined class of surfaces.
If G is infinite X may contain no G-invariant ample linear system. Here is a classical
example of such a situation.
Consider a pencil of cubic curves on P2 with nine base points and smooth generic
curve. Denote by X the result of blowing up the base points. The projection X~-+ Pl
onto the base of the pencil has nine distinguished sections, images of the base points.
Taking one for origin and defining on the generic fiber of X the structure of elliptic
curve, we get the group Z8 of translations acting upon X. No ample linear system is
stable with respect to this group. Xcan be thought of as a 'degenerate Del Pezzo surface
of degree zero', cf. Section 3.6 below.
In [48] M. Gizatullin proved that under some conditions on the action of G this
example is typical and classified elliptic bundles with non-discrete automorphism group.
We shall describe his results.
4. The surfaces Wt. In this and the next section к is algebraically closed of
characteristic ^5.
Consider on ?\ pencils of cubic curves containing the following pairs of curves:
Ai(y): {*г(*2 ~*o)(*2 ~ y^o) = 0, jc0x^ = 0}, -y a parameter ^0, 1 ;
A2: {*o*? + *2 = Mo = 0} ;
A3:{*o*; + *2 = 0,4x2=0};
A4:{*0x2 + r2 = 0,Agr,=0}.
Denote by W^y), W2, W3, W4 the result of blowing up the base subscheme of the
corresponding pencil. The surfaces W, are pairwise поп-isomorphic except that
Wl(p)^W](y)for I(P)= l(y),\vhcie l(p) = (p2 - p ^ \)Y\P ~ ^f Over the
base these pencils have two degenerate fibers each.
The group Gm acts on Wt in the following way:

296
APPENDIX
i=l: (x0:xl:x2)»(x0:txl:x2)\
/2*2: (x0:xx : x2)^(xQ: t3x{ : t2x2).
Roughly speaking, Wt exhaust all surfaces having a non-ample G-invariant linear
system and automorphisms which arc not translations along fibers. More precisely, the
following statement is proved in [48].
5. Theorem. Let Xbea rational G-minimal surface without an ample G-invariant
linear system. Assume however, that for each element gEG' there exists a non-principal
divisor Dg with (D 2) ^ 0 and such that Dg is linearly equivalent tog(Dg). Then
(a) ([\хПх) = 0,тк?кХ=\0.
(b) For some m, £l®m defines an elliptic bundle p : X-+ P1 without exceptional curves
in the fibers.
(c) If X is not isomorphic to one of the Wn then Aut X contains an abelian subgroup of
finite index inducing translations of the generic fiber of p.
Some interesting arithmetic results on a class of cubic surfaces, generalizing the
so-called Markoff surfaces were proved by El Huti [41]. He proves essentially that the
automorphism group acts on integer points with a finite number of orbits.
We now turn to generalized and degenerate Del Pezzo surfaces. Their geometry was
investigated by Timms [96] and Du Val [40] after Schlaffli and Cayley. For modern
versions, see M. Demazure [39], J. Bruce and C.T.C. Wall [14], J.-I. Merindol [74], H.
Pinkham [80], E. Looienga [73], Y. Naruki, T. Urabe [79]. The paper [37] by D. Coray
and M. Tsfasman is devoted to the arithmetic of degenerate Del Pezzo surfaces.
6. Definition, (a) A generalized Del Pezzo surface is a proper smooth rational surface
A'such that (l~l is almost ample i.e. the map X-> X' = Proj(®*=0 Г(И/))is birational.
(b) A generalized Del Pezzo surface is called degenerate if ^V is not smooth.
The structure of the nondegenerate Del Pezzo surfaces is described in detail in
Chapter IV. We recall one of the main results. Over к each nondegenerate Del Pezzo
surface X of degree 9 is isomorphic to P2, and if it is of degree 8 it is isomorphic to
P1 x Pl or F,. For 2 ^ d < 9 there exists a morphism/ : X-* P2 blowing down r = 9 - d
mutually non-intersecting exceptional curves. Their images can be any system of
г = 9 - d points in general position. The latter condition means that no three points lie
on line, no six lie on a conic, and, for г = 8, no cubic curve goes through all points having
one of them as double point. (In Chapter IV the necessity of this condition was proved

APPENDIX
297
for all r and sufficiency for r ^ 3. The proof of sufficiency for г = 1,2 can be found in
Dcmazure [39] and Iskovskih [59]).
Degenerate Del Pezzo surfaces can be characterized in the same way. However,
among the points to be blown up, infinitely near ones may exist. Assuming the ground
field to be algebraicly closed, we give the appropriate definition.
Let X = Xr -* Xr _ x -» ► Xx -* Xq = P2 be a sequence of monoidal
transformations with centers x• G Xt_,, 1 ^ r ^ 8.
7. Definition. The points (*,) are in almost general position if any of the following
equivalent conditions holds.
(a) No two points xt lie on an exceptional curve ttj l (Xj ); no four points lie on a line in
P2; no seven points lie on a conic in P2.
(b) AH points jc, lie on a smooth cubic curve in P2.
(Recall that a point x over a surface X is said to lie on a curve С С X, if it lies on the
proper inverse image of C.)
8. Theorem. Let Xbea generalized Del Pezzo surface of degree d. Then \^d^9 and
X is either isomorphic to P2, or to F2, or else toP'xP1, or finally to a blow up of 9 - d
points in almost general position over P2. Any such system of points leads to a generalized
Del Pezzo surface.
9. The Picard group and root systems. The analysis of the structure of Pic A", endowed
with intersection index and canonical class, made in Chapter IV for Del Pezzo surfaces,
is literally the same for generalized Del Pezzo surfaces. The essential difference between
the degenerate and nondegenerate case lies in the position of the cone of effective
elements in Pic X. The surface A'is a smooth model of the anticanonical surface X' and
the inverse images of singular points can be characterized by their classes in Pic X which
are very special effective elements of this group.
Let us give some more details. Denote by /0 E Pic X the class of a line on P2, by
/,,..., /r the classes of the inverse images of the blown up points. Set ш = -3/0 +
10. Proposition. Set
/?-{/6PicAr|/2 = -2,(/,^0) = 0},
Re{f(X) = {I ER\ I is effective);

298
APPENDIX
ВД = адиКс(Д);
Rt(X) = {IE RcU(X)\ I is irreducible} .
//3^r^8, then R(X) is a closed and symmetric part of the root system R, Rt(X) is its
base. The intersection graph ofR^X) coincides with the (dual) intersection graph of the
desingularization of the anticanonical model X'.
We recall that a subset P С R of a root system R is called closed, if a, /3 G P,
а + реЯфа + ДеР, and symmetric, if P = - P.
Now the problem of the combinatorial description of singularities of degenerate Del
Pezzo surfaces can be solved in two steps. First, one describes closed symmetric subsets
of root systems R. Second, one clarifies which of them have a geometric realization. The
first problem can be attacked by means of the following general result.
11. Proposition. Let Rbea reduced indecomposable root system, (a, ,... ,ar)its
base y a- n]a] H + nrar its maximal root. Then every maximal closed symmetric part
of R is a transform by an element of the Weylgroup of one of the following sets Я,, S,:
(a) Letl^i^r and nt = \. Then the base ofR, is {д.| /V i) and Л, consists of all
positive linear combinations of these roots in R.
(b) Letl^i^r and nt prime. Then the base ofS( is {- я, a}\ /V i) and S, consists of
all positive linear combinations E;r=1 m-ai in R with m, = 0(л,).
Using this description recursively, one can list also all non-maximal parts. The
resulting combinatorial object can be given by a table.
12. Theorem. Let 3 ^ r ^ 8. Then for any closed symmetric part PCRr there exists a
degenerate Del Pezzo surface of degree d = 9 - r realizing P, with the following
exceptions:
г = 7,? = (Л1)7;г = 8,Р = (Л1)8,(Л1)70г(Л1)4®О4.
As a matter of fact, appropriate realizations can be found in a family of degenerate
Del Pezzo surfaces whose base points lie on a fixed elliptic curve. For further details one
may consult the articles quoted in Section 3.5.
Assume now that a degenerate Del Pezzo surface X is defined over a non-closed field
k. In view of Theorem 3.2, it is still birationally equivalent to either a nondegenerate
Del Pezzo surface, or to a conic bundle. Now, the arithmetic of these standard models is
known to a certain degree. Hence one approach to studying X is to understand the

APPENDIX
299
geometry of the corresponding transform depending on the Galois action on Pic X and
singularities of X'. This program has been realized by D. Coray and M. Tsfasman [37].
13. Biratlonal automorphisms of rational surfaces. Certain sets of generators of Bir ?2k
were determined in the last century both for closed and non-closed k. In the second case
the description is fairly complex. In Chapter V of this book a modern version of the
method of 'virtual linear systems with prescribed singularities, is developed and applied
to minimal cubic surfaces X, giving a complete presentation of Bir X (in an earlier paper
by the author similar results were obtained also for minimal Del Pezzo surfaces of
degree 1 and 2).
V. A. Iskovskih ([63J, [64]) extended these results to Del Pezzo surfaces of lower
degree. Below we shall describe a part of his results.
14. Cremona group. Let к be algebraically closed. We shall realize the two-
dimensional Cremona group as the group of birational automorphisms of the quadric
F0 = P' xp\
Set A = PGL(2, k) x PGL(2, k) and denote by т : P1 x P1 -> P1 x P1 the involution
interchanging the factors. Then Aut FQ is A x {1, т}.
Let 7г: P1 x P1 -»P1 be the first projection. Denote by В С Bir F0 the subgroup of
birational maps, compatible with тт. В is a semidirect product PGL(2, k(t)) x
PGL(2, k). Choose a point x E P1 x P1. It defines a birational map ex: F0-+ F0 which
blows up x and blows down the fiber through x. To normalize all constructions, we shall
fix bihomogeneous coordinates (Mo^J^Vq,!;,) on F0, and pointsx0 = (0,1) x
(0,l),yo = (1.0)x(l,0)andset
е'оУо=еУое*а '• ("°' "J X fa» Ul)~fao, «l) X M. Ml»o) ,
t0:(«o.«i)x(^Wi)h(vp4))x("i.«o)-
Then the following result is true.
15. Theorem, (a) Bir F0 is generated by rand B.
(b) All relations between rand В are generated by
and the relations between т and A.
On the other hand, Gizatullin [49] described all relations between the classical

300
APPENDIX
generators of the Cremona group, i.e., the projective and quadratic transformations of
P2
We turn now to the case of non-closed k.
16. Theorem. Let Xbea minimal conic bundle with (Cix • ilx) ^ 0. Then Bir X
preserves the structure bundle and is a semidirect product Bir Xv* G, where G is a finite
group of automorphisms of the base and Bir Xv is the automorphism group of the generic
fiber.
This theorem is proved in [53]. In [59], [63], [64] Del Pezzo surfaces of degree d = 1,
2,3,4 with Pic X = Z 0 Z are studied. For d = 1,2 a full presentation of Bir X is given;
for d = 3,4 only generators are known. For example, if d = 1,2, Bir X is generated by a
subgroup preserving one of two conic bundles and by a classical involution (Bertini and
Geiser) interchanging the two existing bundles. For details see the original papers.
17. Structure of some groups related to cubic surfaces. In [67], [68] D. Kanevsky
investigated certain abstract groups defined by a presentation of the same type as Bir X
for a minimal cubic surface X. We shall describe below some of his results.
We shall call an abstract cubic a set S with a ternary relation L С S x S x 5, satisfying
the following axioms.
(a) L is invariant with respect to permutations of factors.
(b) If (x, y, z), (jr, y, z') E L and x Ф y, then z = z'.
The reflection group Gs of an abstract cubic S is generated by symbols tx,xES subject
to the following relations:
t] = \ forа11л:е5 ;
(txt,t:)2=\ forall(jr,y,2)e/,.
The following result is proved in [67].
18. Theorem. Let S be given effectively and LCS x S * S be decidable. Then:
(a) The word problem in Gs is decidable.
(b) The conjugacy problem in G$ is decidable.
(c) Any element of finite order in Gs is conjugate to either tx or to txtytJor appropriate
jc, y, z E 5. (Here of course the decidability ofL can be dropped).
The proof is based on a direct description of Gs as a limit of amalgamated sums.
In [68] it is established that S can be reconstructed from Gs if L contains no triples

APPENDIX
301
(jc, x, z). Moreover, under some additional assumptions it is proved that Aut Gs is
generated by Gs and permutations of S preserving L.
19. Unirationality and stable rationality. Let X be an absolutely irreducible algebraic
variety over k.
The so-called Zariski problem is the question whether a stably k-rational X is
necessarily /c-rational. Recently a negative answer to this question was given [6]: (a) in
the class of rational surfaces over a nonclosed field k\ (b) in the class of three-
dimensional varieties over С In this section we shall state some results of [6] for
surfaces. They refer to conic bundles. (Some unirationality constructions for Del Pezzo
surfaces can be found in Chapter IV, Section 29.)
20. Theorem. Let к be afield of characteristic Ф2, P E k[x] and irreducible separable
polynomial of degree 3 with discriminant aEk*^(k*)2. Then the surface X given by the
affine equation
y2 - az2 = P(x)
satisfies the following property: ?\ x Xis birational to ?5k.
The proof heavily uses the torsor technique. Using P and the Weil descent functor
from the field К = k[x] IP, the authors construct a ^-rational three-dimensional torus 5
and S-torsor J-» X with the following properties:
(a) J-> Xadmits a section. Therefore J is birational to X x S and X x P^.
(b) /can be realized as a Zariski-open subset of an intersection of two quadrics which
is birationally trivial.
This establishes that X is stably rational. On the other hand, V. A. Iskovskih has
proved in several papers the following theorem on the birational non-triviality of conic
bundles.
21. Theorem. Л k-minimal conic bundle with s ^ 4 degenerate geometric fibers is
birationally non-trivial over k.
In [53] this is proved fori 2* 8, in [54] for 5 = 5,6,7 and in [56] for s = 4.
It is not difficult to construct a minimal model for X from Theorem 3.20 and to
establish that 5 = 4. Moreover, the Gal £/fc-module Pic X turns out to be stably
permutational, i.e., similar to the zero module. Thus, we have:

302
APPENDIX
22. Corollary. There exists a stably k-rational, but not k-rational surface, with stably
permutational module Pic X.
4. The Luroth problem and the Zariski problem in dimension ^3
1. Luroth problem. In 1876 Luroth proved that every unirational curve is rational. In
1894 Castelnuovo proved that every unirational surface over the complex field is
rational. (For non-closed base field this is not true even for surfaces with fc-points, as the
example of minimal cubic surfaces shows.) The question whether all unirational
varieties of dimension ^3 over С are rational is called the Luroth problem. The question
whether all stably rational varieties are rational, as we mentioned already, is called the
Zariski problem. Until recently the answer to it was unknown even over non-closed
fields.
It was long conjectured that in dimention d ^ 3 the Luroth conjecture has a negative
solution, even for cubic threefolds. A very important contribution to this problem is due
to G. Fano ([45], [46], [47]) who has been studying for four decades the birational
geometry of three-dimensional hypersurfaccs and complete intersections of small
degree, later called after him the Fano varieties. Unfortunately, it was during these four
decades that the technique of Italian algebraic geometry ceased to suffice for adequate
treatment of the geometric problems accessible to the marvellous geometric intuition of
the founders.
The new algebraic geometry was built by the successive efforts of O. Zariski, A.
Weil, J.-P. Serre and A. Grothendieck. Only after the complete reconstruction of
foundations was accomplished and the new cohomological methods were developed, the
neoclassical period began, when old problems could be attacked with new weapons.
At the beginning of the sixties the Luroth problem was considered unsolved, contrary
to some claims in classical papers. A principle obstacle was the absence of an effective
invariant distinguishing unirational varieties from rational ones.
At the Tata Institute Algebraic Geometry Colloquium 1967, the author made a
report on the current status of the unirationality problem, where three approaches to the
proof of irrationality were discussed.
(a) The Fano method. It consists in studying of the group Bir X, or, more generally,
of the set of birational maps X-+ X' with the technique of virtual linear systems. If this
set is 'small', e.g., in the simplest case finite-dimensional, then Xis not rational.
(b) The method of intermediate motives. Let A" be a three-dimensional variety, h3(X)
its middle Grothendieck's motive. In a paper, published in 1968, the author noted that
blowing up a point on ЛГdoes not change h\X) and blowing up a smooth curve adds

APPENDIX
303
hx(Y) ® L" \ where L is the so called Tate motive. Hence in the group of classes of
3-motives modulo formal sums E aih\Yi) ® L lies a birational invariant of X.
(c) The Brauer group method. Let X be a smooth proper unirational variety over C.
Grothendieck noted that Br A' is a birational invariant of X isomorphic to НЪ{Х, Z)lors
(torsion subgroup). Hence A'cannot be rational unless H\X, Z)lors = 0.
(Unfortunately, for classical examples, e.g. cubic hypersurface, 3-torsion vanishes.)
In 1971-72 three independent papers appeared using all these three methods to
obtain various examples of unirational but irrational varieties. V. A. Iskovskih and Yu.I.
Manin [65] applied the Fano method to quartic threefolds A" in P4 and showed that Bir X
is finite (B. Segre earlier proved that some smooth quartics are in fact unirational). C.
Clemens and Ph. Griffiths [17], considering intermediate Jacobians instead of motives,
proved that the intermediate Jacobian of the rational threefold must be either a
Jacobian or a product of Jacobians, and that for a cubic threefold this property does not
hold. (It was long known that smooth cubic threefolds are unirational; in fact, they were
classical candidates for the role of counterexamples to the Luroth problem.) M. Artin
and D. Mumford [2] constructed unirational conic bundles A" over a two-dimensional
base space for which Z2 С H\X, Z). Since H\X, Z) = H\X x p", Z), their examples
are not even stably rational.
Finally, in 1984 A. Beauville, J.-L. Colliot-Thelene, J.-J. Sansuc and H.P.F.
Swinnerton-Dyer [6] solved negatively the Zariski problem, constructing non-rational,
although stably rational three-dimensional varieties over С. То prove stable rationality
they utilize the torsor technique, essentially for surfaces over a rational function field.
To prove non-rationality they, use the Clemens-Griffiths method.
Below we shall describe very briefly some recent results of three-dimensional
birational geometry. For further details the reader may consult reports by V. A.
Iskovskih [60], [61], A. Turin [98], [99], A. Beauville [5], S. Mukai and H. Umemura
[77].
We start with describing two classes of varieties, close to the rational ones, which
were most intensively studied. They are Fano's varieties (analogous to the Del Pezzo
surfaces) and birational bundles with rational base and rational generic fiber (analogous
to conic bundles).
2. The Fano varieties of the first kind. A smooth projective threefold X whose
anticanonical bundle £l~x = {ilx)~l is ample and generates in Pic X a subgroup of finite
index r, is called a Fano variety of the first kind and index r.
A thorough study of the anticanonical system on X made after Fano by V. A,
Iskovskih (cf. also [1]) led to a detailed classification scheme for the Fano varieties. We
reproduce it below, using the following notation: d = r~\tox{ • fix{ ■ 0.x{), r = index,

304
APPENDIX
g = genus of (йх • [lxl), й1,2 = the Hodge number, dimension of the intermediate
Jacobian. In Beauville's notation [5], the manifolds of index 2 and degree d form a class
A d, and those of index 1 and degree d form Bd. Here is a list of all Fano varieties of the
first kind.
(a) Index 4. P3, d = 1, g = 33; rational.
(b) Index 3. Quadric Q С P4, d = 2, g = 28, h1'2 = 0; rational.
(c) Index 2. Herein d^ 5.
Л1: sextic hypersurfaces in the quasihomogeneous projective space P(l, 1,1,2,3); it
can also be realized as a double covering of a Veronese cone; g = 5, й1,2 = 21. A
'general' manifold is irrational (proof by the intermediate Jacobian method, A.
Beauville (4]). Unirationality is unknown.
A2\ double covering of P3 ramified at a quartic, g = 9, A1,2 = 10; unirational;
'generally' rational (A. Beauville [4]); the Clemens-Griffiths method).
A3: cubic in P4; g = 13, A1,2 = 5; unirational; non-rational (C. Clemens, Ph. Griffiths
[5D-
Л4: complete intersection of two quadrics in P5; g = 17, й1'2 = 2; rational.
A5: linear section of the Grassmanian G(2; 5) in Plucker's embedding; g = 21,
A1,2 = 0, rational.
(d) Index 1.
B2\ double covering of P3 ramified at a sextic surface; g = 2, й1,2 = 52; non-rational
(proved in [61] by Fano's method); unirationality unknown.
B4: quartic in P4; g = 3, й' '2 = 30; irrational (proved in [65] by Fano's method). Some
smooth quartics are unirational; for a general quartic unirationality is unknown.
B'4: double covering of a quadric in P4, ramified at a surface of degree 8 (intersection
with a quartic);g = 3, A1,2 = 30; unirational; irrational (proved in [61] by Fano's
method).
fi6: complete intersection of a quadric and a cubic in P5; g = 4, й1,2 = 20; unirational;
irrational (proved in [61] by Fano's method).
Я8: complete intersection of three quadrics in P6; g = 5, й1 '2 = 14; unirational;
irrational (Beauville [4], the Clemens-Griffiths method).
Bw: intersection of a quadric with G(2; 5); g = 6, A1,2 = 10, unirational; 'generally'
irrational (A. Beauville [4], the Clemens-Griffiths method).
Bn: a subvariety of P8 (we omit a description which is rather cumbersome); g = 7,
A1,2 = 5; rational.
Bu: a linear section of the Grassmanian G(2, 6) in P14; g = 8, A1,2 = 5; unirational;
non-rational (in fact, it is birationally equivalent to a smoth cubic in P4, c.f. [61]).
Bd (d = 16,18,22): certain subvarieties in Pd/2+2; A12 = 11 - d/2, g = (d + 2) /2; all
rational, with the possible exception of some varieties B22. On B22 see also [77].

APPENDIX
305
Finally, we should note that for many Fano varieties A" V. A. Iskovskih described
geometric generators of Bir X. In some cases relations are also known.
3. Birational bundles. Let/ : X-> S be a morphism of a threefold to a rational
surface. If a generic fiber Xv is also a rational curve, then birationality properties of X
depend first of all on the existence of rational section of/ If it exists, A" is rational.
Otherwise it is a conic bundle, and birationality properties of A'are to a great degree
determined by the properties of the discriminant curve CCS of/ One can choose a
model X in such a way that over a smooth point of С the fiber of/is a union of two smoth
rational curves, transversally intersecting at a common point. One can also arrrange that
С has only nodes, over which/has double P1 as fibers. Below we shall assume that a
conic bundle X is chosen in this way.
There is also the second natural class of birational bundles which are fibered by
rational surfaces over a rational curve/: X-+ C. Here the generic fiber Xv has either a
model of Del Pezzo type over C^ = C(/), or a model which is a conic bundle over C4. In
the latter case X itself evidently has also a conic bundle model.
The varieties of this class are in general not well understood. One may conjecture
that a conic bundle with a curve of a sufficiently large degree (over a given 5) is not
unirational, but this remains unproved.
The following is known, however:
4. Theorem, (а) Л conic bundle over P with a discriminant curve of degree 5*6 is not
rational, since its intermediate Jacobian is not a product ofJacobians of curves (see [5]).
(b) Letf : X—>Sbe such a conic bundle with a discriminant curve C,thatH°(S,
(Cl5)A®05(C)) ^ 0. Then any birational automorphism ofX preserves /, and X is
irrational (see V. Sarkisov [86]).
5. Stably rational irrational varieties. Let us consider now surfaces, as described in
Theorem 3.20, over a field к = C(/):
y2-a(t)z2 = P(x,t),
where a(t) E C[t] is a polynomial without multiple roots which coincides with the
x-discriminant of an irreducible cubic polynomial in x, P(x, t) E C[x, t). Denote by Я а
model of С(дг, у, z, r). This variety is stably rational in view of Theorem 3.20. On the
other hand, one can find a conic bundle model of X and calculate its intermediate
Jacobian in terms of its discriminant curve. This gives the following result.

306
APPENDIX
6. Theorem. IfP(x, t) = 0isa curve of genus >2 whose projection onto the t-axis has
no points with ramification index 3, then the intermediate J acobian ofX is not a product
ofJacobians of curves. Hence X is irrational.
7. Open questions. Although the last decade has seen considerable progress in our
understanding of the geometry of threefolds close to the rational ones, it is clear that
only fragments of a complex picture emerged as yet. The following questions arise
naturally:
(a) What can be said about the classification of Fano varieties of dimension sM? Is
their anticanonical degree bounded (by a function of dimension)?
(b) Find efficient criteria of irrationality in dimension ^4. Is a cubic fourfold
rational?
(c) The same as (b) for unirationality.
(d) Can a smooth rational variety be a flat deformation of an irrational one?
5. Rational points and equivalence relations
1. Bloch's exact sequence. Let A'be a rational proper smooth geometrically
irreducible variety over a perfect field k, G = Gal k/k. Let A0(X) be the zero-cycle class
group of degree zero modulo rational equivalence. Denote by S the k-torus dual to
Pic X. If A" admits a universal torsor /, the map 0, described in Section 2.4 induces a
homomorphism which does not depend on /,
4>:A0(X)-+Hl(X,S)
(see Proposition 2.5). In fact, one can easily define Фdirectly without using/, cf. [28].
As in Proposition 2.5, Im <£is finite, if A: is absolutely finitely generated. S. Bloch in
[13], using algebraic ^-theory, has included (for dim X = 2) Ф into an exact sequence
giving important additional information.
SctF=k{X)J=k(X).
2. Theorem ([13]). //dim X = 2, there is an exact sequence
S(k)-> tf l(G, K2F/K2k)-+A0(X)-?>H\k, S)-* H2(G,K2FIK2k).
Colliot-Thelene in [19], using recent deep results by Merkuriev and Suslin [75],
proved the following facts (statement (b) was known earlier).

APPENDIX
307
3. Theorem. Let X be a rational surface.
(a) If к is a number field (or is finitely generated over Q and there is a k-cycle of degree
1 onX), then A Q(X) is finite. The same is true for a local field k\ if furthermore X has a
nondegenerate reduction, thenA0(X) = 0.
(b) //char к * 2 and cd к = 1, then A 0(X) = 0.
(c) If X is a conic bundle, char к Ф 2 and either X admits a 0-cycle of degree \,orkis
local or global, then Кег ф = 0.
Knowing qualitative properties of A 0(X) one naturally tries to calculate it by local
means. As an example we shall again consider the Chatelet surfaces
y2-dz2 = (x-el)(x-e2)(x-e3), dEk*^(k*)2, e^e^oii^j .
4. Theorem. IfX is a Chatelet surface, the following assertions hold:
(*)A0(X) = X{k)IR.
(b) Every element of AQ (X) is defined by local invariants: there is an exact sequence
Q^A0(X)^\lA0(Xv)->H\kJy
V
andH\k, S) - (Z/2Z)2.
Cf. also Theorem 2.19 where a different class of conic bundles is treated.
The following explicit calculations can be found in [28]. We shall denote by Xrs the
Chatelet surface with parameters (d,ex, e2, еъ) = (-1,0, r, s) over Q. Then we have the
following cycle groups:
(r,s)
A„W
(1,5)
гаг
0.3)
(Z/2Z)2
(3.7)
(гиг)'
(3.9)
(Z/2Z)3
(7.19)
(гигу
(1.17)
Z/2Z
No surface in this table satisfies the weak approximation principle.
5. Tsfasman's surfaces (cf. [37], [85]). There exist rational surfaces for which the
group
UlA0(X) = Ker(A0(X)-+U A0(X¥))

308
APPENDIX
does not vanish. Denote by Yah a smooth projective model of the surface
v2 - abz2 = (x2 - a)(x2 - b).
Let it be a number field, К = k(Va, V/>), G = Gal K/k, [K:k] = 4.
In this case Ш AQ(X) = Z/2Z iff there is no valuation v such that Gv = G\ otherwise
U1A0(X) = 0.
For example, if/с = g, we get a nonvanishing Ш i40for(a, b) = (p, q), where /?,
q = 1 mod 4 are primes such that (p/q) = "(plq)A(qlp)A = 1, e.g. (5,29), (13,17), (5,
41) Л13,29).
Tsfasman's examples, e.g. У13,7 have also the following interesting properties:
(a)BrY/BrQ#0.
(b) The Brauer equivalence on У is trivial.
(c) The /^-equivalence on У is non-trivial.
We now turn to the R-equivalence on intersections of quadrics. The following result
is stated in [32].
6. Theorem. Let X С ?"kbe a smoth intersection of two quadrics over a number field к,
n $* 7, X(k) Ф 0. Then the following assertions hold:
(а)ад/Я = П^ктг0(ВД).
(b) For archimedean v, X(kv)/R = 7r0(X(kv ))\for non-archimedean v, X(kv) /R = 0.
In a series of papers, D. Coray and coauthors have investigated the following
question. Following Colliot-Thelene and Coray [20], we shall say, that a variety X over к
satisfies condition (h), if there exists a finite set of extension fields К J к with relatively
prime degrees such that all X(K,) Ф 0. Obviously, (A) holds for*, itX(k) Ф 0. What can
be said about the opposite assertion?
7. Theorem, (a) From (h) it follows that X(k) Ф 0, ifXis a nondegenerate Del Pezzo
surface of degree ^4. This is true also for a smooth cubic X, if к is a local field.
(b) Assume that Xisa smooth cubic surface satisfying condition (h). Then there exists
an extension field Klk with [K:k] = 1,4or \0such thatX(K) Ф 0.
(c) Let Xbea rational conic bundle, r = 8 - (йх йх). JfXsatisfies (h) and
X(k) = 0, then X(K) Ф 0 for a certain К of odd degree [К: к] ^ s = max( 1, [r/2]), and
also X(L) Ф 0 for a certain quadratic extension field L.
In particular, for r ^ 5 from (h) it follows that X(k) Ф 0.
However, for r - 6 there exist conic bundles over Q^, for which X(Qp) = 0 but
X(K) Ф 0 for appropriate extensions of degrees 2 and 3.

APPENDIX
309
For proofs see D. Coray [34], D. Coray [35] and J.-L. Colliot-Thelene, and D. Coray
[20].
6. Cubic surfaces and commutative Moufang loops (CML)
1. Notation. Let A' be a smooth cubic surface over a field K. We shall consider three
admissible equivalence relations on X(K): U (universal), R and Br (Brauer equivalence
related to the full group Br X). Recall that for any admissible equivalence relation S
there is on X(K)/S a structure of CML of period 6 (depending on a choice of identity
class). We shall denote by 52,53 such equivalence relations that S = S2C\S3 and
X(K) ISm is of period m.
In this section we shall describe certain results on the structure of X(K) IS obtained
since the first publication of this book, and also results on the structure of abstract
CML's with finite number of generators, answering some questions raised in Chapter I.
We first note that the principal qualitative question on the structure of CML's of
cubic hypersurfaces remains unsolved: do there exist non-associative CML's of this
type? A key particular case of this situation is the following one. Let A" be a generic
cubic surface over the field Q(aijk), where the aijk are independent coefficients of an
equation of X and let jc, be four independent generic points of X. What CLM is
generated by *, over Q(aijk)?
We turn now to finite fields. Almost exhaustive information in this case is supplied by
the following result of Swinnerton-Dyer [95], which in a less precise form was
independently established by D. Kanevsky [66].
2. Theorem. Let Xbea smooth cubic surface over a finite field к with q elements. Then
X(K)IU = 0, except for certain cases when X contains no k-lines and all points ofX(k)
are Eckardtpoints. In the latter case we have either q = 2, card X(k) = 3, or q = 4,
card *(*) = 9.
The last case is realized for the surface jc3 + y* + г3 + St3 = 0, в2 + $ + 1 = 0,
considered in this book (Example 16.2). Swinnerton-Dyer proves that X(k) /R = 0 for
this surface, so that universal equivalence is strictly stronger than the R-equivalence.
Let now К be a local number field, к its residue field. Assume that X is defined by an
equation F with integer coefficients such that the reduction F defines a smooth /c-surface
X. Denote by H = \ dct(d2F/dx,dXj) the Hessian of X. It has integer coefficients and
has a reduction H.

310
APPENDIX
3. Theorem ([95]). Let X be a smooth cubic surface over a local number field К with a
smooth reduction. Then X(K)IV = 0 except for, possibly, the following cases:
(a) char к = 3 and either Й = 0,ог the surface // = 0 touches X at all k-points ofX.
(b)ch<iTk = 2andH = 0.
(c) char к = 2 and any rational point ofX is an Eckardt point.
4. Corollary. Let Xbea smooth cubic surface over a number field K. Then for all t>,
except for a finite number, X(KV) IV = 0.
The map X(K)-* Uv X(KV) IV induces on X(K) an admissible equivalence relation,
approximating V. To calculate it, we lack the understanding of the structure of
X(KV ) / £/ for exceptional cases in Theorem 6.3 and for degenerate reductions. In order
to go from к to K, the following result of Kanevsky [69] can be used.
5. Theorem. Let Xbea smooth cubic surface over a local number field К with possibly
nonsmooth reduction X. Assume that X(K) contains a point of general type and let
x E X(k) be a point in general position with certain pointy E X(k) (this means that the
line containing x and у does not touch X).
//char к Ф 2,3, then all points {x E X(K)\ x reduces tox) belong to the same
V-equivalence class, //char к = 2 (resp. 3), these points belong to the same class modulo
(73 (resp. V2) equivalence.
Finally, let LI К be a Galois extension with group G. An equivalence relation 5 on
X(L) is called G-invariant if the action of G preserves equivalence classes.
6. Theorem ([69]). If К is infinite and there is a point of general type in X(L), then V
and R are G-invariant. The same holds for Br, ifX is smooth and char К = 0.
We shall now turn to the structure theory of abstract CML's.
7. Nilpotence class. Question 10.3 on the nilpotence class k(n) of a free CML with n
generators was solved independently by L. Beneteau [7] and J.D.H. Smith [89]. They
proved that Bruck's upper bound is in fact achieved:
8. Theorem. k(n) = n-lforalln^ 2.
9. Beneteau's construction. The Beneteau proof is based on the following
construction, which generalizes an idea of Bruck (Example 10.5).

APPENDIX
311
Consider an associative ring R and a subset SCR with the following property: for
every triple x, v, z € S we have
x2 = xy + yx = Ъхуг = 0.
Denote by G the additive subgroup of /?, generated by all products of an odd number of
elements of S. Define on the set £ = G x G a multiplication law
(*i.хг)(У\* Уг) = (*i + У. + ^ifo " Уг)^ + Уг + ^2(^1 ~*.)) -
Then £ is a CML.
Beneteau applies this construction to the ring R = ® k=[j\kL where L is an
infinite-dimensional linear space over F3. Take a base of L for 5; then G =
. In the CML E= G* G consider a subloop Tn generated by the
following elements:
where lx,..., ln is a base of L.
Beneteau proved that the nilpotence class of Tn is n - 1 for all л ^ 2. In view of the
Bruck theorem, this proves Theorem 6.9.
10.3-order of a free CML. The second part of Question 10.3 on the 3-order l(n) of a
free CML E{n) with n generators is unsolved yet, but in a beautiful paper [90] J.D.H.
Smith formulated a conjecture on the value of l(n) and made some progress in proving
it. Let E(n) = £0 Э Е, Э • • • Э £„_, = {1) be the lower central series. Set 8(n) =
dimF ©/e," Ef-/E/+I.
11. Smith's conjecture. Set
0(z)=S &{n)zn/n\
n = 3
Then
Г ( l-2/2\ L z
+ res'-0 7T7 exP \z 7T7jsh 7 •

312
APPENDIX
Here70(2) = E^0(-l)'t(z/2)27(/c!)2is Bessel'sfunction. Setting S^=0 /Зкд:7(/с!)2 =
(JQ(2Vx)) l and a, = 0, aK = pK for к ^ 2, we can represent this conjecture in an
equivalent form:
in-l/2) „-2k-I , г / + - 1 \1
8(я)= X S „/, , 1Ч„—' ^—777 a«+( L «^3.
.=i ,=o р!(2к + 1)!(л-г2Ы)!г V p /J
Here are the first few values of this function:
6(3) = 1, 6(4) = 8, 5(5) = 44, 6(6) = 214, 5(7) = 1000, 5(8) = 4592.
In effect, Smith proves the following group-theoretic fact. Let G be a finite group,
containing a product of two symmetric groups Skx Sk. Denote by 5; (resp. ту) for
1 «s j < k the permutation of/cth and (k + l)th object in the first (resp. second) group
Sk. Set R = K[G] where К is a field. Then for k > 1 we have
codim, 2 (1 + a})(\ + т;)Я = |C| res, Vo(2Vz) V(* + ,) = |G|& .
A conjectural part of Smith's results relates this group-theoretical theorem to the
problem of computing 8(n). To make this reduction, Е(/Е{ f! is considered as a
module over a group permuting the free base of E(n). A conjecture on the structure of
this module is made which would follow from the 'triple argument conjecture' [89].

REFERENCES (FOR THE APPENDIX)
A.B. Altman and S.L. Kleiman, Foundations of Fano schemes, Compos. Math. 34(1) (1977)
3-47.
M. Artin and D. Mumford, Some elementary examples of unirational varieties which are not
rational, Proc. Lond. Math. Soc. 25 (1972) 75-95.
M.I. Basmakov and A.L. Cistov, On rationality of a certain class of tori, Trudy Steklov Inst.
48 (1978) 27-29 (in Russian).
A. Beauville, Varictes de Prym et jacobiennes intermediates, Ann. ENS 10 (1977) 309-391.
A. Beauville, Varietes rationnelles et unirationneles, Lect. Notes Math. 997 (Springer,
Berlin, 1983) 16-33.
A. Beauville, J.-L. Colliot-Thelene, J.-J. Sansuc and P. Swinncrton-Dyer, Varictes stable-
ment rationnelles non rationnelles, Ann. of Math. 121 (1985) 283-318.
L. Beneteau, Problemes de majorations dans les quasigroups distributifs et les groupes de
Fischer, Actes du Coll. Alg. Appl. et Comb., Grenoble (1978).
L. Beneteau, Free commutative Moufang loops and anticommutative graded rings, J.
Algebra (1979).
B.J. Birch, Forms in many variables, Proc. Royal Soc. London Ser. A 265 (1961) 245-263.
B.J. Birch and H.P.F. Swinnerton-Dyer, The Hasse problem for rational surfaces, J. Reine
Angew. Math. 274 (1975) 164-174.
S. Bloch, Lectures on Algebraic Cycles, Duke University Math. Series 4 (1980).
S. Bloch, Torsion algebraic cycles, Kz, and the Brauer group of function fields, in: Groupe de
Brauer, Lecture Notes in Math. 844 (Springer, Berlin, 1981) 75-102.
S. Bloch, On the Chow groups of certain rational surfaces, Ann. Sci. Ec. Norm. Sup. Scr. 4 14
(1981)41-59.
J.W. Bruce and C.T.C. Wall, On the classification of cubic surfaces, J. Lond. Math. Soc. (2)
19(1979)245-256.
A.L. Cistov, On the birational equivalence of tori with cyclic splitting field, Zapiski Nauc.
Sem. LOMI64(1976) 153-158 (in Russian).
A.L. Cistov, On the number of generators of the semigroup of classes of algebraic tori
modulo stable equivalence, Dokl. Akad. Nauk SSSR 242(5) (1978) 1027-1029 (in Russian).
С Clemens and Ph. Griffiths, The intermediate Jacobian of the cubic threefold, Ann. of
Math. 95 (1972) 281-356.
J.-L. Colliot-Thelene, Surfaces de Del Pezzo de degre 6, C.R. Acad. Sci. Paris 275 A (1972)
109-111.
J.L. Colliot-Thelene, Hilbcrt's theorem 90 for K2, with application to the Chow groups of
rational surfaces, Invent. Math. 71 (1983) 1-20.
J.-L. Colliot-Thelene and D. Coray, L'equivalence rationnelle sur les points fermes des
surfaces rationnelles fibrces en coniques, Compositio Math. 39 (1979) 301-332.
J.-L. Colliot-Thelene, D. Coray and J.-J. Sansuc, Descente et principe de Hasse pour
certaines varietes rationnelles, J. Reine Angew. Math. 320 (1980) 150-191.
J.L. Colliot-Thelene and W. Raskind, K2-cohomology and the second Chow group, Math.
Ann. 270 (1985) 283-318.
313

314 REFERENCES FOR THE APPENDIX
J.-L. Colliot-Thelene and J.-J. Sansuc, Torseurs sous des groupes de type multiplicatif, C.R.
Acad. Sci. Paris 282A (1976) 1113-1116.
J.-L. Colliot-Thelene and J.-J. Sansuc, Varietes de premiere descente attachees aux varietes
rationnellcs, C.R. Acad. Sci. Paris284A (1977) 967-970.
J.-L. Colliot-Thelene and J.-J. Sansuc, La descente sur une variete rationnalle definie surun
corps de nombres, C.R. Acad. Sci. Paris 284A (1977) 1215-1218.
J.-L. Colliot-Thelene and J.-J. Sansuc, La Л-equivalence sur les tores, Ann. Sci. Ec. Norm.
Sup. Ser. 4 10(1977)175-229.
J.-L. Colliot-Thelene and J.-J. Sansuc, La descente sur les varietes rationnelles, in: Journee
de Geometric Algebrique d'Angers, 1979 (Sijthoff-Noordhoff, Alphen aan den Rijn, 1980)
223-237.
J.-L. Colliot-Thclene and J.-J. Sansuc, On the Chow groups of certain rational surfaces: a
sequel to a paper of S. Bloch, Duke Math. J. 48 (1981) 421-447.
J.-L. Colliot-Thelene and J.-J. Sansuc, Sur le principe de Hasse et I'approximation faible, et
sur une hypothese de Schinzcl, Acta Arithm. 41 (1981) 33-53.
J.-L. Colliot-Thelene, J.-J. Sansuc and Ch. Soule, Ouelques theoremes de finitude en theorie
des cycles algebriques, C.R. Acad. Sci. Paris 294 (1982) 749-752.
J.-L. Colliot-Thclene, J.-J. Sansuc and Ch. Soule, Torsion dans lc groupe de Chow de
codimension deux, Duke Math. J. 50 (1983) 763-801.
J.-L. Colliot-Thclene, J.-J. Sansuc and P. Swinnerton-Dyer, Intersections de deux quadriques
et surfaces de Chatelct, C.R. Acad. Sci. Paris 298 (1984) 377-380.
K.R. Coombes and D.J. Muder, Zero-cycles on Del Pezzo surfaces over local fields, Preprint,
1983.
D. Coray, Arithmetic on singular cubic surfaces, Compos. Math. 33 (1976) 55-67.
D. Coray, Points algebriques sur les surfaces de Del Pezzo, C.R. Acad. Sci. Paris284 (1977)
1531-1534.
D. Coray, The Hasse principle for pairs of quadratic forms, in: Journee Arithm. (Cambridge
Univ. Press, 1982) 238-245.
D. Coray and M. Tsfasman, Arithmetic on singular Del Pezzo surfaces, Preprint, 1984.
M. Demazure, Sous-groups algebriques de rang maximum du group dc Cremona, Ann. Sci.
ENS. Ser. 4 3(1970) 507-588.
M. Demazure, Surfaces de Del Pezzo II, III, IV, V., Lecture Notes in Math. 777 (Springer,
Berlin, 1980)23-69.
P. Du Val, On isolated singularities which do not affect the conditions of adjunction I, II, III,
Proc. Cambridge Phil. Soc. (30) 1934,453-465,483-491.
El Huti, Cubic surfaces of Markov type, Mat. Sbornik 93(3) (1974) 331-346 (in Russian).
S. EndoandT. Miyata, Invariants of finite abelian groups, J. Math. Soc. Japan 25 (1973)
7-26.
S. Endo and T. Miyata, Quasi-permutation modules over finite groups I, II, J. Math. Soc.
Japan 25 (1973) 397-421; 26 (1974) 698-713.
S. Endo andT. Miyata, On a classification of the function fields of algebraic tori, Nagoya
Math, J. 56 (1975) 85-104.
G. Fano, Sopra alcune varieta algcbriche a tre dimensioni aventi tutti i generi nulli, Atti Ace.
Torino 43 (1908) 973-977.
G. Fano, Osservazioni sopra alcune varieta non razionali aventi tutti i generi nulli, Atti Ace.
Torino 50 (1915) 1067-1072.
G. Fano, Nuove ricerche sulle varieta algebriche a tre dimensioni a curve-serioni canoniche,
Comm. Pont. Acad. Sci. (1947) 635-720.
M.H. Gizatullin, Rational G-surfaces. Izv. AN SSSR, Ser. Mat. 41(1) (1980) 110-144 (in
Russian).

REFERENCES FOR THE APPENDIX
315
[49] M.H. Gizatullin, Defining relations for the plane Cremona group, Izv. AN SSSR, Ser. Mat.
46(5) (1982) 909-970.
[50] D.R. Heath-Brown, Cubic forms in ten variables, Proc. London Math. Soc. 47(2) (1983)
225-257.
[51] J.W.P. Hirschfeld, Del Pezzo surfaces over finite fields, Tensor 37 (1982) 79-84.
[52] W. Hurlimann, Brauer group and diophantinc geometry: a cohomological approach, Lect.
Notes Math. 917 (Springer, Berlin, 1981).
[53] V. A. Iskovskih, Rational surfaces with pencil of rational curves, Mat. Sb. 74(4) (1967)
608-638 (in Russian).
[54] V. A. Iskovskih, Rational surfaces with pencil of rational curves and positive square of
canonical class, Mat. Sb. 83(1) (1970) 90-119 (in Russian).
[55] V. A. Iskovskih, A counter-example for the Hasse principle for a system of two quadratic
forms in five variables, Mat. Zametki 10 (1971) 253-257 (in Russian).
[56] V. A. Iskovskih, Birational properties of surfaces of degree four in P4, Mat. Sb. 88(1) (1972)
31-37 (in Russian).
[57] V.A. Iskovskih, Three-dimensional Fano varieties. I, Izv. AN SSSR, Ser. Mat. 41(3) (1977)
516-562 (in Russian).
[58] V.A. Iskovskih, Three-dimensional Fano varieties. II, Izv. AN SSSR, Ser. Mat. 42(3) (1978)
504-549 (in Russian).
[59] V.A. Iskovskih, Minimal models of rational surfaces over arbitrary fields, Izv. AN SSSR, Ser.
Mat. 43 (1979) 19-43 (in Russian).
[60] V.A. Iskovskih, Anticanonical models of three-dimensional algebraic varieties, in: Sovremen-
nyc Problemy Matematiki 12 (VINIT1, Moscow, 1979) 59-157 (in Russian).
[61] V.A. Iskovskih, Birational automorphisms of three-dimensional algebraic varieties, in:
Sovremennye Problemy Matematiki 12 (VINITI, Moscow, 1979) 159-236 (in Russian).
[62] V.A. Iskovskih, Birational automorphisms of three-dimensional algebraic varieties close to
rational ones, in: Algebra, Vol. 1, Moscow University (1980) 40-49 (in Russian).
[63] V.A. Iskovskih, Generators and relations in the two-dimensional Cremona group, Vestnik
MGU, Ser. 1 5 (1983) 43-48 (in Russian).
[64] V A. Iskovskih, Generators and relations in the groups of birational automorphisms of two
classes of rational surfaces, Trudy Steklov Inst. 165 (1984) 67-78 (in Russian).
[65] V.A. Iskovskih and Yu.I. Manin, Three-dimensional quartics and counter-examples to the
Luroth problem, Mat. Sb. 86 (1971) 140-166 (in Russian).
[66] D.S. Kanevski, Classes of points on cubic hypersurfaces, defined over finite fields, Mat.
Zametki 20(1) (1976) 121-131 (in Russian).
[67] D.S. Kanevski, Structure of groups, related to cubic surfaces, Mat. Sb. 103(2) (1977) 292-308
(in Russian).
[68] D. Kanevsky, On cubic planes and groups connected with cubic surfaces, J. Algebra 80(2)
(1983)559-565.
[69] D. Kanevsky, Some remarks on Brauer equivalence for cubic surfaces, Preprint, Max Planck
Inst, fur Math., Bonn, 1983.
[70] B.E. Kunyavski, On tori with biquadratic splitting fields, Izv. AN SSSR, Ser. Mat. 42(3)
(1978) 537-542 (in Russian).
[71] B.E. Kunyavski and M.A. Tsfasman, Zero-cycles on rational surfaces and Neron-Severi tori,
Izv. AN SSSR, Ser. Mat. 48 (1984) 631-654 (in Russian).
[72] H.W. Lenstra, Rational functions invariant under a finite abelian group. Invent. Math. 25
(1974)299-325.
[73] E. Looijenga, On the scmiuniversal deformation of a simple elliptic hypersurface singularity.
II, Topology 17(1978)23-40.

316 REFERENCES FOR THE APPENDIX
J.-Y. Merindol, Les singularites simples clliptiques, leurs deformations, les surfaces de Del
Pezzo et les transformations quadratiques, Ann. Sci. ENS 15 (1982) 17-44.
A.S. Merkufev and A.A. Suslin, K-cohomology of Severi-Brauer varieties and norm
residue homomorphism, Izv. AN SSSR, Ser. Mat. 46(5) (1982) 1011-1046 (in Russian).
S. Mori, Threefolds whose canonical bundles are not numerically effective, Ann. of Math.
116(1982)133-176.
Sh. Mukai and H. Umemura, Minimal rational threefolds, in: Algebraic Geometry, Lecture
Notes in Math. 1016 (Springer, Berlin, 1983) 490-517.
J.P. Murre, Reduction of the proof of the nonrationality of a nonsingular cubic threefold to a
result of Mumford. Compos. Math. 27 (1973) 63-82.
1. Namki and T. Urabe, On singularities on degenerate Del Pezzo surfaces of degree 1,2,
Preprint, 1981.
H. Pinkham, Simple elliptic singularities, Del Pezzo surfaces and Cremona transformations,
Proc. Symp. Pure Math. 30 (1977) 65-84.
V.P. Platonov and A.S. Rapinchuk, Algebraic groups, in: Algebra. Topology. Geometry,
Vol. 21 (VINITI, Moscow, 1983) 80-134 (in Russian).
V.P. Platonov, Arithmetic theory of algebraic groups, Usp. Mat. Nauk 37(3) (1982) 3-54 (in
Russian).
J.J. Sansuc, Descente et principe de Hasse pour certaines varietes rationnelles, Sem.
Delange-Pisot-Poiton (1980-81) 254-271.
J.-J. Sansuc, Groupe de Brauer et arithmetique de groupes algebriques lineaires, J. Reine
Angew. Math. 327 (1981) 12-80.
J.-J. Sansuc, A propos d'une conjecture arithmetique sur le groupe de Chow d'unc surface
rationnelle, in: Seminaire deTheorie desNombresde Bordeaux, Vol. 33 (1981-1982).
V. Sarkisov, Birational automorphisms of conic bundles, Izv. AN SSSR 17 (1981) 177-202 (in
Russian).
W. Sokurov, Existence of a line on the Fano varieties, Izv. AN SSSR, Ser. Mat. 43(4) (1979)
922-964 (in Russian).
V.V. Sokurov, Smoothness of a generic anticanonical divisor or the Fano varieties, Izv. AN
SSSR, Ser. Mat. 43 (1979) 430-441 (in Russian).
J.D.H. Smith, On the nilpotence class of commutative Moufang loops, Math. Proc.
Cambridge Phil. Soc. 84 (1978) 387-404.
J.D.H. Smith, Commutative Moufang loops and Bessel functions, Invent. Math. 67 (1982)
173-187.
R.G. Swan, Invariant rational functions and a problem of Steenrod, Invent. Math. 7(1969)
148-158.
H.P.F. Swinnerton-Dyer, Two special cubic surfaces, Mathematika 9 (1962) 54-56.
H.P.F. SwinneTton-Dyer, Rational points on Del Pezzo surfaces of degree 5, in: Proc. 5th
Nordic Summer School in Math. Oslo (1970) 287-290.
H.P.F. Swinnerton-Dyer, The birationality of cubic surfaces over a given field, Michigan
Math. J. 17(1970)289-295.
H.P.F. Swinnerton-Dyer, Universal equivalence for cubic surfaces over finite and local fields,
Symp. Math., Bologna 24 (1981) 111-143.
G. Timms, The nodal cubic surfaces and the surfaces from which they are derived by
projection, Proc. Royal Soc. London A 119 (1928) 213-248.
M.A. Tsfasman, Arithmetic of conic bundles, Usp. Mat. Nauk 37(2) (1982) 239-240 (in
Russian).
A.N. Turin, Five lectures of three-dimensional varieties, Usp. Mat. Nauk 27(5) (1972) 3-50
(in Russian).

REFERENCES FOR THE APPENDIX
317
[99] A.N. Turin, Intermediate Jacobian of three-dimensional varieties, in: Sovremennye Prob-
lemy Matematiki, Vol. 12 (VINITI, Moscow, 1979) 5-57.
[100] V.E. Voskresenski, On the birational equivalence of linear algebraic groups, Doklady AN
SSSR 188(5) (1969) 978-981 (in Russian).
[101] V.E. Voskresenski, Birational properties of linear algebraic groups, Izv. AN SSSR, Ser. Mat.
34(1) (1970) (in Russian).
[102] V.E. Voskresenski, Rationality of certain algebraic tori, Izv. AN SSSR, Ser. Mat. 35(5)
(1971) (in Russian).
[103] V.E. Voskresenski, Stable equivalence of algeraic tori, Izv. AN SSSR, Ser. Mat. 38 (1974)
3-10 (in Russian).
[104] V.E. Voskresenski, On birational invariants of algebraic tori, Usp. Mat. Nauk 30(2) (1975)
207-208 (in Russian).
[105] V.E. Voskresenski, Algebraic Tori (Moscow, Nauka, 1977) (in Russian).
[106] V.E. Voskresenski, Problems of rationality of linear algebraic groups, Usp. Mat. Nauk 32(2)
(1977) 241 (in Russian).
[107] V.E. Voskresenski, On the reduced Whitehead group of a simple algebra, Usp. Mat. Nauk
32(6) (1977) 247-248 (in Russian).
[108] V.E. Voskresenski, On the R-equivalence of semisimple groups. Zapiski Nauc. Sem. LOMI
86 (1979) 49-65 (in Russian).
[109] V.E. Voskresenski, Projective invariant Demezure's models, Izv. AN SSSR, Ser. Mat. 46(2)
(1982) 195-210(in Russian).
[110] V.E. Voskresenski and A. A. Kliachko, Toric Fano varieties and root systems, Izv. AN SSSR
48(2) (1984) 237-263 (in Russian).

REFERENCES
Algebraic Number Theory, eds. J.W.S. Cassels and A. Frohlich (Academic Press,
New York, 1967).
Algebraic Surfaces, Tr. Mat. Inst. Steklov 75 (1965) (English Transl.: Proc. Steklov
Inst. Math. 75, Am. Math. Soc, Providence, R.I., i968).
E. ARTIN
[1] Geometric algebra (Interscience, New York, 1957).
M. ARTIN
[1] Some numerical criteria for contractibility of curves on algebraic surfaces, Am. J.
Math. 84(1962)485-496.
S. BECKEN
[1] Spiegelungsrelationen in orthogonalen Gruppen, J. Reine Angew. Math. 210 (1962)
205^215.
V.D. BELOUSOV
[1] On the structure of distributive quasigroups, Mat. Sborn. 50(3) (1960) 266-298
(in Russian).
E. BOMBIERI and H.P.F. SWINNERTON-DYER
[1] On the local zeta function of a cubic threefold, Ann. Scuola Norm. Sup. Pisa (3)21
(1967)1-29.
N. BOURBAKI
[1] Groupeset algebresde Lie (Hermann, Paris, 1968) chs. 4-6.
[2] Algebre (Hermann, Paris, 1958, 1959) chs. 1 -9.
R. BRAUER and M. SUZUKI
[ 1 ] On finite groups whose 2-Sylow group is a quaternion group, Proc. Natl. Acad, Sci.
USA 45 (1959) 1757-1759.
R.H. BRUCK
[1) Some results in the theory of quasigroups, Trans. Am. Math. Soc. 55 (1944) 19-52.
[2] A survey of binary systems (Springer, Berlin, 1958).
[3] An open question concerning Moufang loops, Arch. Math. (Basel) 10 (1959) 419-421.
H, CARTAN and S. EILENBERG
[l!] Homological algebra (Princeton Univ. Press, Princeton, N.J., 1956).
P. CARTIER
[1] Diviseurs amples, Sem. Bourbaki (1966) expose 301.
J.W.S. CASSELS
[ 1 ] Arithmetic on curves of genus 1. IV. Proof of the Hauptvermutung, J. Reine Angew.
Math. 211(1962)95-112.
[2] Arithmetic on curves of genus 1. VI. The Tate-Safarevi£ group can be arbitrarily large,
J. Reine Angew. Math. 214/215 (1964) 65-70.
[3) Diophantine equations with special reference to elliptic curves, J. London Math. Soc.
41 (1966) 193-291. (Corrigenda: ibid. 42 (1967) 183.)
318

REFERENCES
319
J.W.S. CASSELS and M J.T. GUY
[ 1) On the Hasse principle for cubic surfaces, Matematika 13(1966) 111 -120.
N.T. CEBOTAREV
[1 ] Introduction to the theory of algebras (Ogiz, Moscow, 1949) (in Russian).
F. CHATELET
[I ] Points rationnels sur certaines courbes et surfaces cubiques, Enseignement Math. 5
(1959)153-170.
[2] Points rationnels sur certaines surfaces cubiques, Colloq. CNRS Clermont-Ferrand,
1964 (Paris, 1966)67-75.
С CHEVALLEY
[1] Sem. C. Chevalley, Anneaux de Chow et applications (Secretar. Math., Paris, 1958).
P. DELIGNE
[ 1 ] Intersections sur les surfaces regulieres, SGA 7 (Inst. Hautes Etudes Sci., 1969) expose'
10.
A. DICKSON
[1 ] History of the theory of numbers, Vol. 2. Diophantine analysis (Washington, 1920).
G. FANO
[1J Su alcune varieta algebraiche a tre dimensioni aventi curve-sezioni canoniche, Scritti
Mat. offerti a L. Bersolari (Pavia, 1936) 329-349.
[2J Sulle varieta algebraiche a tre dimensioni a curve-sezioni canoniche, Mem. Accad.
Italia 8(1937) 23-64.
[3 j Su alcune varieta algebraiche a tre dimensioni razionali, e aventi curve-sezioni
canoniche, Comment. Math. Helv. 14 (1941) 202-211.
[41 Nuove ricerche sulle varieta algebraiche a tre dimensioni a curve-sezioni canoniche,
Comment. Pont. Acad. Sci. 11 (1947) 635-720.
B. FISCHER
[1] Distributive Quasigruppen endlicher Ordnung, Math. Z. 83 (1964) 267 -303.
J.S. FRAME
[ 1 ] The classes and representations of the groups of 27 lines and 28 bitangents, Ann.
Mat. Рига Appl. (4) 32 (1951) 83 -119.
F. GHERALDELLI
[1] Un osservazione sulla varieta cubica di P3, Rend. Sem. Mat. Fis. Milano 37 (1967)
157-160.
M. GREENBERG
[ 1 ] Lectures on forms in many variables (Benjamin, New York, 1970).
A. GROTHENDIECK
[ 1 ] Sur quelques proprietes fondamentales en theorie des intersections, Sem. С
Chevalley, Anneaux de Chow et applications (Secretar. Math., Paris, 1958).
[2] Le groupe de Brauer, I, II, III, in: Dix exposes sur la cohomologie des schemas
(North-Holland, Amsterdam, 1968) 46-66, 67-87, 88-188.
A. GROTHENDIECK and J. DIEUDONNE
[1] Elements degeometrie algebrique, Publ. Math. l.H.E.S. 4, 8,.. . (I960,...).
M.HALL
[1] Theory of groups (MacMillan, New York, 1959).
[2] Automorphisms of Steiner triple systems, Proc. Symp. Pure Math., Vol. 6 (Am.
Math. Soc, Providence, R.I., 1962) 47-66.

320
REFERENCES
R. HARTSHORNE
[ 1 ] Curves with high self-intersection on algebraic surfaces, Publ. Math. I.H.E.S.
36(1969) 111-125.
A. HENDERSON
(1) The twenty-seven lines upon the cubic surface (Cambridge Univ. Press, Cambridge,
1911).
С JORDAN
[1 ] Traite des substitutions et des equations algebriques (Gauthier-Villars, Paris, 1957).
S. KLEIMAN
[1J Algebraic cycles and the Weil conjectures, in: Dix exposes sur la cohomologie des
schemas (North-Holland, Amsterdam, 1968) 359-386.
S. LANG
[1] Diophantine geometry (Interscience, New York, 1962).
J. LIPMAN
[ 1 ] Rational singularities with applications to algebraic surfaces and unique factorization,
Publ. Math. I.H.E.S. 36 (1969) 195-279.
Yu. I. MANIN
[ 1 ] On the arithmetic of rational surfaces, Dokl. Akad. Nauk SSSR 152 (1963) 46 -49
(in Russian).
[2] The Tate height of points on an Abelian variety, its variants and applications, Izv.
Akad. Nauk SSSR Ser. Mat. 28 (1964) 1363-1390 (in Russian).
[3] Rational surfaces over perfect fields, Publ. Math. I.H.E.S. 30 (1966) 55 - 113 (in
Russian).
14) Rational surfaces over perfect fields, Mat. Sb. 72 (114) (1967) 161 -192 (in Russian).
[5] Two theorems on rational surfaces, in: Proc. Symp. Int. Geometria Algebraica
(Rome, 1967)198-207.
[6] Cubic hypersurfaces I. Quasigioups of classes of points, Izv. Akad. Nauk SSSR Ser.
Mat. 32 (1968) 1223-1244 (in Russian).
[7] Correspondences, motives and monoidal transformations, Mat. Sb. 77 (1968)
475-507 (in Russian).
[8] Hypersurfaces cubiques II. Automorphismes birationnels en dimension deux, Invent.
Math. 6 (1969) 334-352.
[9] Cubic hypersurfaces III. Moufang loops and Brauer equivalence, Mat. Sb. 79 (121)
(1969) 155 -170 (in Russian).
W.F. MEYER
11 ] Flachen dritter Ordnung, Encyclopadie Math. Wiss. Bd. Ill, 2 h.l 1, IIIc 10a (Berlin,
1928).
L.J. MORDELL
[1] On the conjecture for the rational points on a cubic surface, J. London Math. Soc.
40(1965)149-158.
[2] Diophantine equations (Academic Press, New York, 1969).
D. MUMFORD
[i] A remark on MordeiTs conjecture, Am. J. Math. 87(1965) 1007-1016.
[2] Lectures on curves on an algebraic surface (Princeton Univ. Press, Princeton, N.J.,
1966).
M. NAGATA
[1] On rational surfaces, I, H, Mem. Coll. Sci. Univ. Kyoto, Ser. A, Math. 32 (1960)
351 -370; ibid. 33 (1960/61) 271 ^293.

REFERENCES 321
T.ONO
[1] Arithmetic of algebraic tori, Ann. Math. 74(1961) 101-139.
[2\ On the Tamagawa number of algebraic tori» Ann. Math. 78 (1963) 47-73.
P. ROQUETTE
[1] On the Galois cohomology of the projective linear group and its applications to the
construction of generic splitting fields of algebras, Ann. Math. 150 (1963)411 -439.
L. ROTH
[1J Algebraic threefolds (with special regards to problems of rationality) (Springer, Berlin,
1955).
I.R. SAFAREVIC
[1J Lectures on minimal models and birational transformations of two-dimensional
schemes (Tata Inst. Fund. Res., Bombay, 1966).
[2] Fundamentals of algebraic geometry, Usp. Mat. Nauk 24 (1969) 3-184 (in Russian).
S. SCHANUEL
[1] Heights in number fields, Bull. Am. Math. Soc. 70 (1964).
B. SEGRE
(1] The non-singular cubic surfaces (Clarendon, Oxford, 1942).
[2) A parametric solution of the indeterminate cubic equation z2 = f(xf y), J. London
Math. Soc. 18 (1943) 226-233.
[3] The rational solutions of homogeneous cubic equations in four variables, Math.
Notae Univ. Rosario anno II, fasc. 1-2 (1951) 1-68.
[4] Arithmetical questions on algebraic varieties (London, 1951).
E. SELMER
[1J Sufficient congruences for the existence of rational points on certain cubic surfaces,
Math. Scand. 1(1953) 113-119.
AM. SERMENEV
[1] On some unirational surfaces, Mat. Zametki 5 (1969) 155 -159 (in Russian).
[2] On motives of cubic hypersurfaces, lzv. Akad. Nauk SSSR Ser. Mat. 34 (1970)
515-522 (in Russian).
J.P. SERRE
[1] Critere de rationalite pour les surfaces algebriques, Sem. Bourbaki (1957).
[2] Morphismes universels et differentielles de troisieme espece, Sem. C. Chevalley,
Anneaux de Chow et applications (Secretar. Math., Paris, 1958).
[3] Cohomologie Galoisienne (Springer, Berlin, 1964).
[4] Lie algebras and Lie groups (Benjamin, New York, 1965).
[5] Zeta functions and L-functions, in: Arithmetical algebraic geometry (Harper and
Row, London, 1965) 82-92.
[6] Local class field theory, in: J.W.S. Cassels and A. Frohlich, eds., Algebraic number
theory (Academic Press, New York, 1967).
[7] Abelian /-adic representations and elliptic curves (Benjamin, New York, 1968).
SNYDER
[ 1J The problem of the cubic variety in P3, Bull. Am. Math. Soc. 35 (1929) 607-642.
H J\F. SWINNERTON-DYER
[1J Two special cubic surfaces, Matematika 9 (1962) 54-56.
[2] The zeta function of a cubic surface over a finite field, Proc. Cambridge Phil. Soc.
63(1967)55-71.
J.TATE
[ 11 On the conjectures of Birch and Swinncrton-Dyer and a geometric analogue, in:
Dix exposes sur la cohomologie des schemas (North-Holland, Amsterdam, 1968)
189-214.

322
REFERENCES
J.A. TODD
[1 ] On the topology of certain threefold loci, Proc. Edinburg Math. Soc. Ser. 2, 4 (1935)
175-184.
A. TURIN
[1] On non-singular Fano cubic surfaces in P3, Izv. Akad. Nauk SSSR Ser. Mat. 34 (1970)
1200-1208 (in Russian).
V. VOSKRESENSKlI
[1] On two-dimensional algebraic tori, Izv. Akad. Nauk SSSR Ser. Mat. 29 (1965)
230-244 (in Russian).
R. WALKER
[1] Algebraic curves (Dover Publ., New York, 1962).
A. WEIL
[1) Arithmetic on algebraic varieties, Ann. Math. 53 (1951) 412-444.
[2] Adeles and algebraic groups, Matematika 8 (1964) 3-74 (a translation into Russian
of mimeogranhed notes).
[3] Abstract versus classical algebraic geometry, Proc. Int. Congr. of Mathematicians,
Amsterdam, Vol. 3 (1964) 550-558.
O. ZARISKI
[1] Introduction to the problem of minimal models in the theory of algebraic surfaces
(Tokyo, 1958).

AUTHOR INDEX
Artin, E., 181,187
Artin, M., 105
Becken, S„ 187
Belousov, V.D., 10,39
Bombieri, E., 59
Bourbaki, N.. 116,128,129,133, 139,
220
Biauer, R., 39
Bruck, R.H., 8,10,39,40
Car tan, H., 180
Cartier, P., 125,152
Cassels, J.W.S., 3, 167, 189, 224, 254,
269, 280, 283
Cebotarev, N.T., 220, 230
Chatelet, F., 5, 255
Deiigne, P., 189
Dickson, A., 1
Dieudonne, J., see A. Giothendieck
Eilenberg, S., see H. Cartan
Fano, G., 189
Fischer, В., 10,19,39
Frame, J.S., 152
Greenberg, M., 174
Giothendieck, A., 5, 147, 222, 229,
283
Guy, M.J.T., see J.W.S. Cassels
Hall, M., 10,21,35,39,40
Hartshorne, R., 81, 111
Henderson, A., 112,182,183
Jordan, С, 182
Kleiman, S., 182
Lang, S., 267
Lip man, J., Ill, 182
Manin, Yu.L, 39,57,76,111,138,
147,179,182,183,203,219,267,
283
Meyer, W.F., 183
Mordell, L.J., 224,276
Mumford, D., 5,90,91,96,97,270
Nagata,M., Ill
Ono,T., 166,171
Roquette, P., 159
Roth, L., 189
Safaievi6,1.R., 5, 102, 104, 105, 110,
111,117,183,247
Schanuel, S., 270
Segre, В., 5,110,112,114,117,182,
219
Sermenev, A.M., 162
Serre,J.P., 112,116,117,127,132,
133,139,175,220,240
Suzuki, M., see R. Brauer
Swinnerton-Dyer, H.P.F., 152,174,
175,182,224,278
Swinnerton-Dyer, H.P.F., see E.
Bombieri
Tate, J., 181
Todd, J.A., 117
Voskresenskii, V., 172, 166
Walker, R., 15
Weil, A., 112,182,242
Zariski, O., Ill
323

LIST OF SYMBOLS
P(x)
C(x)
ГФ)
rHo)
*r
N(V)
"r
R(-equivalence)
4ik
*,
sx,y
tx (reflection in a symmetric quasigroup)
tx (birational map)
ПЕ)
T°(E)
x о у (composition
x о у (composition
in a symmetric quasigroup)
of points)
Xo Y (composition of classes of points)
-p. 16
-p. 51
-p. 91
-p. 92
-p. 114
-p. 112
-p. 114
-p. 61
-p. 67
-p. 114
-p. 185
-p. 11
-pp. 14,53
-p. И
-p. 11
-p. 6
-p. 55
- pp. 45, 55
324

SUBJECT INDEX
Abelian (symmetric) quasigroup 7, 1 Iff
Admissible equivalence relation 43ff
Associative centre 9
Associator 23
Azumaya algebra 221, 229ff
^-equivalence 223, 227, 234ff
Biiational map 47, lOOff
Birational triviality 48
Blowing up of a point 78
Brauer equivalence 44, 220ff, 234ff
Brauer-Grothendieck group 220ff
Brauer group 220ff
Bubble space 195ff
Cartier divisor 90
Cassels-Tate form 227ff
Centre of a CML 9
CH-quasigroup 8, 15ff
Chatelet surface 255
CML 8, 21ff
Collapsing of a curve 78
Collinearity 6,7,42
Commutative Moufang loop 8, 21ff
Conical singular point 48
Del Pezzo surface 117ff
Distributive (symmetric) quasigroup 10,
30
Divisor 94
Dominating map 47
Effective (Cartier) divisor 90
Effective (Weil) divisor 91
Exceptional class 134
Exceptional curve 78,106
Exceptional subset 140
Fischer group 20,34ff
Fisher's theorems 34, 37
Fundamental birational invariant 189ff
General position, points in 54
General type, point of 51
Good point (pair of points) 185
Hasse principle 165, 166, 171, 172, 224,
276ff
Height 267ff
Index of a morphism 77
Index of a surface 165
Intersection number 90, 96
Л-topology 70
Minimal model 80
Minimal surface 79, 107, 184ff, 218
Model of a field 79
Monoidal transformation 78, 82ff, 85
Мои fang's theorem 22
Multiplicity of a point on a divisor 92
Picard group 77,95,126
Point in genera) position 54
Point of general type 51
Point over a surface 196
Principal homogeneous space 167
Proper inverse image of a divisor 92
Rational map 46
Reflection 133,187
R-equivalence 44, 61 ff
Resolution of singularities of a map 82ff,
lOOff
SafareviS-Tate group 228
Schlaffli sixfold 173
325

326
SUBJECT INDEX
s-exceptional set 152
Severi-Brauer surface 159,169
Special variety 61
Symmetric quasigroup 6
Torus 166
Universal equivalence relation 43, 44,
54ff, 69ff
Weil divisor 91
Weil height 268
Wey! group 133ff, 151 ff
Unirationality 46ff, 50, 154ff
Zeta function 143