М. С. МАЦКИН, Р. Ю. МАЦКИНА
Функции и пределы.
Производная
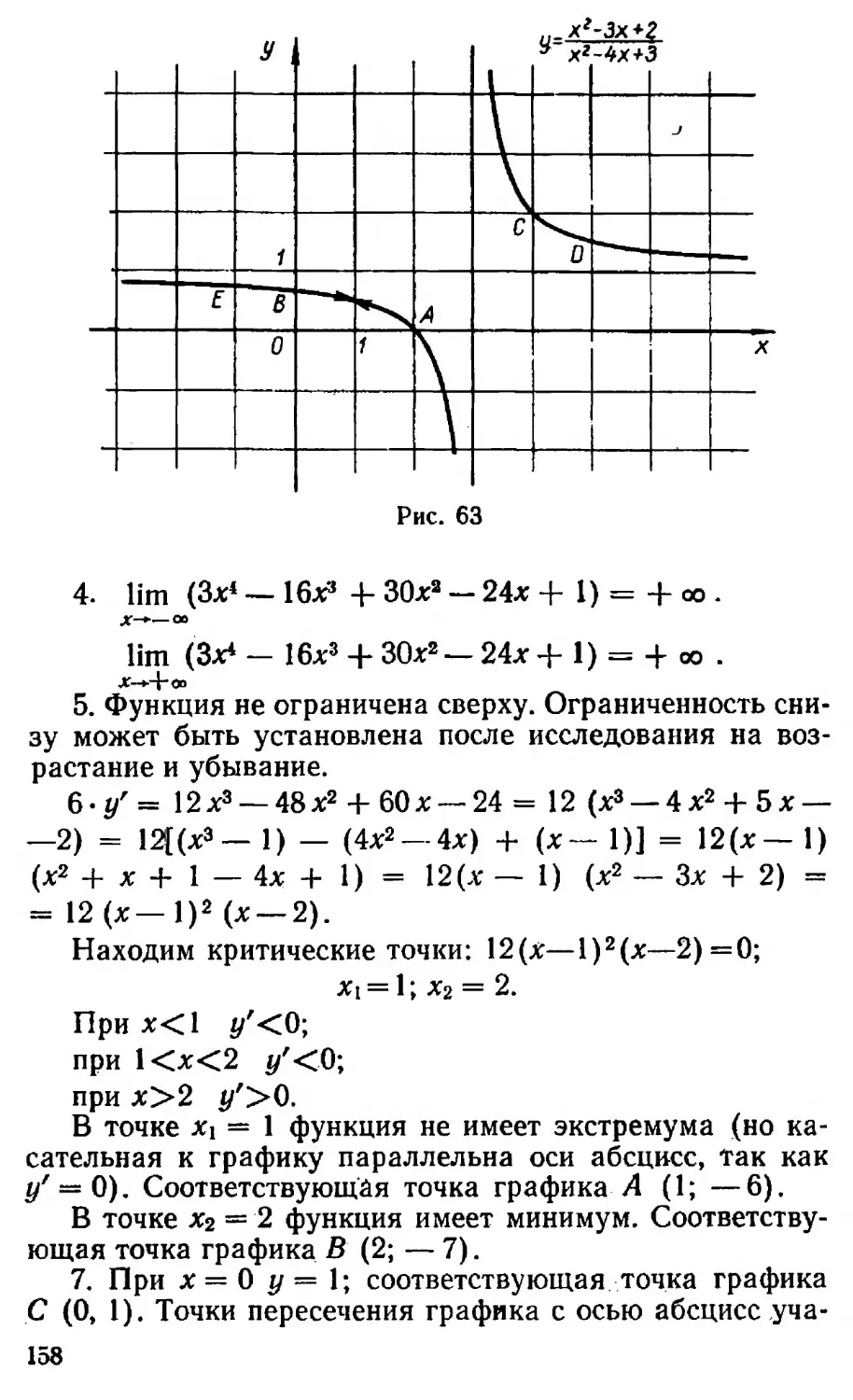
ПОСОБИЕ ДЛЯ УЧИТЕЛЕЙ
ИЗДАТЕЛЬСТВО «ПРОСВЕЩЕНИЕ»
Москва 1968
Мацкин М. С. и Мацкина Р. Ю.
М 36 Функции и пределы. Производная. Пособие для учителей. М,, «Просвещение», 1968 г.
182 с. с илл.
В предлагаемом пособии рассматривается один из возможных вариантов изложения программного материала: функции, пределы и производные.
Большое внимание уделено разбору примеров на исследование функций как элементарными средствами, так и с помощью производной.
517.2(07)
2-2-2
158-68
ВВЕДЕНИЕ
Бурное развитие современного производства, все большее внедрение в него различных средств автоматизации, механизация производственных процессов предъявляют все более высокие требования к подготовке подрастающего поколения. Особенно большое значение приобретает в настоящее время математическая подготовка школьников.
В связи с возрастающим проникновением математических методов в самые разнообразные отрасли науки и техники очень остро стоит задача повышения уровня математического развития и расширения математического кругозора учащихся, готовящихся стать квалифицированными рабочими или продолжать, свое образование в высших учебных заведениях.
Совершенно очевидной становится необходимость введения в школьное преподавание элементов высшей математики, в частности аналитической геометрии и математического анализа, без которых невозможно серьезное изучение техники, причем это важно особенно для тех, кто сразу после школы пойдет на производство.
Как известно, темы «Функции и пределы», «Производная и ее применение» были включены в школьную программу и изучались в средней школе в 1965/66 учебном году.
Мы имели возможность осуществить преподавание этих тем в Волгоградской школе № 8 ежегодно, начиная с 1963/64 учебного года. Преподавание велось и ведется учителями школы № 8 по нашим методическим разработкам, под нашим наблюдением и при нашем непосредственном участии. Следует отметить особенно большую работу учителей математики Е. Г. Ряховской и В. П. Яро*
шика, которые первыми провели в школе изучение указанных тем в 1963/64 учебном году.
В настоящем пособии описывается предлагаемый нами вариант изложения в средней школе вопросов, связанных с понятиями функции, предела функции и ее производной, который мы разработали с учетом опыта преподавания в Волгоградской школе № 8.
Непосредственное наблюдение на уроках преподавания указанных тем, а также результаты контрольных работ и зачетов, в проведении которых мы принимали участие, убедили нас в том, что предлагаемое изложение вполне доступно учащимся, вызывает у них живой интерес и успешно воспринимается ими. Это мнение разделя-. ют и учителя, проводившие преподавание.
Мы имели возможность проследить изучение тем «Функции и пределы», «Производная и ее применение к исследованию функций» уже начиная с 1963/64 учебного года, так как в связи с введением специальности монтажники электро- и радиоаппаратуры в этой школе был выделен один лишний час в неделю на преподавание математики, благодаря чему и появилась возможность несколько расширить программу по математике.
Мы убедились в том, что на изучение всех вопросов, включенных в тему «Производная и ее применение», выделенных 38 часов вполне достаточно. В школе № 8 изучали все эти вопросы, а также некоторый дополнительный материал (например,- производную частного, производную сложной функции). В то же время на изучение темы «Функция и пределы» желательно было бы выделить хотя бы 20 часов вместо 16, предусмотренных программой.
Надо сказать, что понятие предела функции вызывает наибольшие затруднения и усваивается не сразу. Однако в результате кропотливой работы над этим понятием учащиеся делают большой шаг в своем математическом развитии.
При изучении темы «Функции и пределы» мы знакомили учащихся, в небольшой мере, с понятием непрерывности. На наш взгляд, для изучения непрерывности следовало бы добавить дополнительно еще 3—4 часа.
Примеры и задачи, рассмотренные в данной работе, в основном взяты из сборника задач по алгебре П. А. Ларичева и сборника задач по математическому анализу Н. А. Давыдова, П. П. Коровкина и В, Н. Никольского.
Раздел I. ФУНКЦИИ И ПРЕДЕЛЫ
Как известно, с идеей функциональной зависимости учащиеся знакомятся на самых ранних этапах школьного обучения математике. Решение текстовых задач, построение графиков, вычисление значений алгебраических выражений и т. п. подготавливают школьников к восприятию понятия функции, которое в явном виде вводится в 8-м классе в теме «Функции и графики».
Введение специальной темы, посвященной функциям, обусловливается новым подходом к изучению функциональных зависимостей. Если до этого во всех вопросах, связанных с рассмотрением зависимостей между величинами, во главу угла ставился вопрос о вычислении конкретных значений величин, то здесь на передний план выдвигается задача изучения свойств самих функциональных зависимостей. Именно поэтому становится естественным введение функциональной терминологии.
Очень важно, чтобы задача изучения свойств функциональных зависимостей была достаточно мотивирована для учащихся. Ученики должны понимать, что введение математических понятий вызывается в конечном итоге потребностями практики и что, для того чтобы математика могла помочь в изучении различных процессов и явлений природы, нужно уметь выразить математически зависимости между величинами, участвующими в протекании этих процессов. Именно понятие функции отражает эту зависимость и изучение свойств функций помогает изучению закономерностей окружающего мира.
Достаточное число примеров из техники и других разделов естествознания, приводимых как в теме «Функции и графики», так и в дальнейшем при изучении конкретных функций, закрепляет в сознании учащихся важность
изучения функций как мощного инструмента в познании реальной действительности.
Тема «Функция и пределы» поднимает изучение функций на новую ступень. Здесь ставится задача отыскания общих методов исследования функций, и, кроме того, понятие функции используется для введения новых понятий, помогающих описывать явления природы, науки и техники.
Глава 1. ПОВТОРЕНИЕ И УГЛУБЛЕНИЕ ОСНОВНЫХ СВЕДЕНИЙ О ФУНКЦИИ
И СВОЙСТВАХ ФУНКЦИЙ
Повторение организуется таким образом, чтобы не просто воспроизвести в памяти учащихся необходимые определения и некоторые примеры, их иллюстрирующие, но и углубить, и в какой-то мере пополнить запас представлений, накопленных учениками к началу изучения темы.
Повторение рассчитано примерно на четыре урока. Оно завершается решением ряда задач на исследование функций элементарными средствами с использованием знакомой учащимся схемы исследования. При повторении большое внимание уделяется употреблению символа f (х) и построению графиков функций.
§ 1. ПОВТОРЕНИЕ ПОНЯТИЯ ФУНКЦИИ. ГРАФИК ФУНКЦИИ.
1 ОБОЗНАЧЕНИЕ ФУНКЦИИ В ОБЩЕМ ВИДЕ
Первый урок темы «Функции и пределы» посвящается повторению основных определений, связанных с понятием функции, и введению символа f(x). Рекомендуется на предыдущем уроке, давая задание, повторить определение функции, способы задания функции и определение графика функции и напомнить ученикам о значении изучения функций для познания закономерностей окружающего мира и решения важнейших задач науки и техники.
Урок начинается с повторения определения функции, известного ученикам из курса восьмилетней школы.
В итоге повторения даются следующие определения.
Областью изменения данной переменной величины называется множество всех тех числовых значений, которые может принимать данная переменная величина в условиях рассматриваемого вопроса, 6
Если две величины связаны между собой таким образом, что каждому значению одной величины из области ее изменения соответствует вполне определенное значение другой величины, то говорят, что между этими величина-ми_существует функциональная зависимость; первую величину называют аргументом (или независимой переменной величиной), а вторую — функцией от этого аргумента.
Мы считаем понятие области изменения переменной величины полезным само по себе и рекомендуем знакомить с ним учащихся еще в 8-м классе при изучении темы ^Функции и графики». (Кстати, в этом случае отпадает необходимость в специальном определении области изменения функции как множества всех тех значений, которые принимает сама функция.)
Внимание учащихся обращается на то, что функция водностью характеризуется областью изменения ее аргумента и тем законом соответствия, который каждому значению аргумента из области ее изменения ставит в соответствие вполне определенное значение функции.
V Область изменения аргумента называется областью Определения функции.
В зависимости от того, каким способом задается закон Соответствия между значениями аргумента и значениями функции, различают способы задания функции. Учащиеся: вспоминают известные им следующие способы задания функции:
1.	Задание функции с помощью одной или нескольких формул.
2.	Табличный способ задания функции.
3.	Графический способ задания функции.
4.	Задание функции путем словесного описания закона соответствия.
Приводятся примеры функциональных зависимостей, Заданных различными способами, встречающихся в математике и в смежных дисциплинах.
Укажем некоторые из них:
1.	Площадь круга /С есть функция его радиуса /?. Она может быть задана формулой	где R — аргумент,
а К — функция. Область определения — множество всех положительных чисел.
Аналогично, объем куба V есть функция длины его ребра.
В случае свободного падения тела пройденный путь S является функцией времени t. Если время отсчитывается от начала движения и отсутствует сопротивление воздуха, то эта функция может быть выражена формулой
S = Пусть Т — время от начала движения до падения на землю. Тогда область определения состоит из неотрицательных чисел, меньших числа Т, и самого числа Т. Коротко, область определения есть промежуток [0; 7] или
2.	В естественных науках и в технике зависимость между величинами часто устанавливается экспериментально или путем наблюдений. Полученные из опыта данные оформляются в виде таблицы, в которой для ряда значений одной величины указаны соответствующие значения второй величины. Такие таблицы, имеющиеся в технических справочниках, представляют собой пример табличного задания функциональных зависимостей. Областью определения функции служит множество, состоящее из конечного числа записанных в таблице значений аргумента.
Например, имеется такая таблица зависимости температуры кипения воды Г от давления р.
3.	Самопишущие при-х<0 боры, применяемые в раз-личных исследованиях и на производстве, вычерчивают кривую, которая графически задает соответствующую функцию.
Например, термографы и барографы записывают зависимость темпе-♦ ратуры и давления от вре-х мени.
4.	Примером функции, заданной словесно, может служить функция у = ~Е(х), где Е(х) —целая часть числа х, т. е. наибольшее целое число, не превосходящее х.
Разумеется, можно подобрать и много других примеров. Приводятся примеры функций, заданных несколькими формулами с иллюстрацией на графике.
Например:
1) Г х, если х < О, х2, если х > О (рис. 1);
2)	| 2х, если х < 1,
У ~ V х > 1 (рис. 2).
Следует подчеркнуть учащимся, что одна и та же функция может быть задана различными способами.
Ученики вспоминают, что область определения функции также может быть задана различным путем. Она может определяться конкретным физическим смыслом рассмат
риваемых величин и условиями, в которых они рассматриваются.
Область определения функции также может быть непосредственно указана. (Например, у=х2 при х> 0.)
Наконец, и это наиболее важный для исследования функций случай, если функция задана с помощью формулы, причем неизвестно, какие именно конкретные величины участвуют в функциональной зависимости, и нет никаких дополнительных указаний относительно области определения функции, областью определения функции считается множество всех тех значений аргумента, для которых соответствующая формула имеет смысл.
Например, для функции у=\гх—1 область определен ния состоит из значений х, удовлетворяющих неравенству х>1, т. е. представляет собой промежуток [1,+ оо).
ГТ	1
Для функции У= у область определения состоит из значений х, больших, чем — 3, т. е. представляет собой промежуток ( — 3, + со).
Вторая половина урока отводится введению символа f(x) и проведению ряда упражнений, связанных с его употреблением. Необходимость введения символа /(х) можно мотивировать примерно' следующим образом. В предыдущих классах учащиеся изучили целый ряд функций: линейную, квадратную, степенную, показательную, логарифмическую, тригонометрические. При изучении свойств этих функций каждый раз приходилось пользоваться различными приемами исследования. Возникает задача нахождения общих приемов исследования функций. В связи с этим удобно ввести специальное обозначение для произвольной функции, подобно тому как при переходе от арифметики к алгебре мы ввели в употребление буквы, понимая под буквой любое число. Для того чтобы записать в общем виде, что величина у является функцией величины х, не указывая, каков именно закон соответствия, связывающий эти величины, употребляют обозначение #=/(х), где х обозначает величину, являющуюся аргументом, у — величину, являющуюся функцией, а буква f обозначает в общем виде закон соответствия, связывающий эти величины. Если нужно рассмотреть две различные функции (без указания какие именно), то можно употреблять различные буквы для обозначения закона соответствия, например, писать у~ =f(x), £/=ср(х). Можно предложить, например,такие упражнения:
1.	Дана функция f (х) = 2х3 — Зх + 4.
Найти f (- 2), /(0), / (1), f (а).
2.	Дана функция ф (х) — 2 sin х + cos 2х.
Найти ф (0), Ф Ф(1), Ф(а).
3.	Дана функция <р (х) = х2. Что собой представляют функции у (х 4-1), <р (х 4- а), <р ( <р (х)4-1, у Л 1
+	Л-?(х),	k• <р [т(х — а)] 4- Ь,
<f(mx + n), <р(|х|), |<р(х)|, |<р(И)1?
Примеры обычно заготавливаются на переносной доске. Учащиеся решают их самостоятельно, а затем решение проверяется.
Аналогичные примеры, связанные с использованием символа f(x), задаются и на дом.
понятии графика функций на первом уроке нет времени подробно останавливаться. Здесь ученики только вспоминают и уточняют его определение. Графиком функции у = j(x) называется геометрическое место точек плоскости, у которых абсцисса является значением аргумента х., а ордината — соответствующим значением функции f(x). Мы считаем необходимым каждый раз давать учащимся задание по построению графиков функций, чтобы накопить достаточный материал для дальнейшего ^ведения новых понятий.
Отметим, что на первых уроках каждый раз дается материал для повторения к следующему уроку. Ко второму уроку учащиеся повторяют возрастание и убывание функций, а также вспоминают свойства всех известных им основных элементарных функций.
§ 2. МОНОТОННЫЕ ФУНКЦИИ. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ НА ДАННОМ ПРОМЕЖУТКЕ. ПОНЯТИЕ
О МАКСИМУМЕ И МИНИМУМЕ ФУНКЦИИ
При повторении свойств возрастания и убывания функций учащиеся формулируют определения этих свойств с помощью символа f(x). Это, с одной стороны, способствует закреплению в сознании учащихся как самих этих свойств, так и применения символа f(x). С другой Стороны, определения, использующие символ f(x), более удобны при исследовании функций. С помощью учителя учащиеся формулируют следующие определения возрастающей функции и функции, возрастающей на данном промежутке.
Функция у = f(x) называется возрастающей, если для любых двух значений xt и х2 из области ее определений из неравенства х2 > следует неравенство
Функция y~f(x) называется возрастающей на данном промежутке, принадлежащем области определения функции, если для любых двух значений xY и xt из этого промежутка из неравенства х2> л;1следует неравенство
>f(x1).
Такой промежуток называется промежутком возра-стания функции.
Аналогично определяются убывающая функция; функция, убывающая на данном промежутке, и проме-
жуток убывания функции. Учащиеся приводят примеры возрастающих и убывающих функций, а также /промежутков возрастания и убывания функций с иллюстрацией на графиках.	/
Надо сказать, что почти все графики тех функций, которые учащиеся строят в классе или дома, имеются в школе на таблицах, часть которых изготавливается с помощью самих учащихся. Поэтому все знакомые ученикам графики в любой момент могут быть использованы в классе. Понятия возрастания и убывания иллюстрируются на таких хорошо знакомых учащимся функциях, как квадратная, показательная, логарифмическая, тригонометрические и т. п., а также на графиках функций, рассмотренных на предыдущем уроке и построенных дома.
В связи с рассмотрением промежутков возрастания и убывания функций вводится понятие максимума и минимума.
Мы не пользовались терминами «локальный максимум (минимум)» и «абсолютный максимум (минимум)».
Термин «абсолютный максимум (минимум)» отнюдь не лучше хорошо известного и понятного ученикам термина «наибольшее (наименьшее) значение функции». Если же не пользоваться термином «абсолютный», то отпадает и необходимость в термине «локальный». Уже при самом введении понятия максимума (минимума) учащиеся не отождествляют его с понятием наибольшего (наименьшего) значения; они отчетливо представляют себе, что максимум (минимум) —это наибольшее (наименьшее) значение функции на некотором интервале, откуда вовсе не следует, что оно должно быть наибольшим (наименьшим) и вообще.
Понятие максимума и минимума функции может быть введено в связи с рассмотрением промежутков монотон.-ности функции (т. е. промежутков возрастания и убывания функции). После ряда упражнений, в которых требуется указать промежутки монотонности функций, внимание учащихся обращается на те значения аргумента, которые отделяют промежутки возрастания (убывания) от соседних промежутков убывания (возрастания) функции. Например, для функции у = —х2+1 таким значением аргумента Является число 0 (на интервале (— оо, 0) эта функция возрастает, а на интервале (0,+ оо) —
убывает), для функции у— sinx— значения аргумента вида +&л (где k — любое целое число) и т. п.
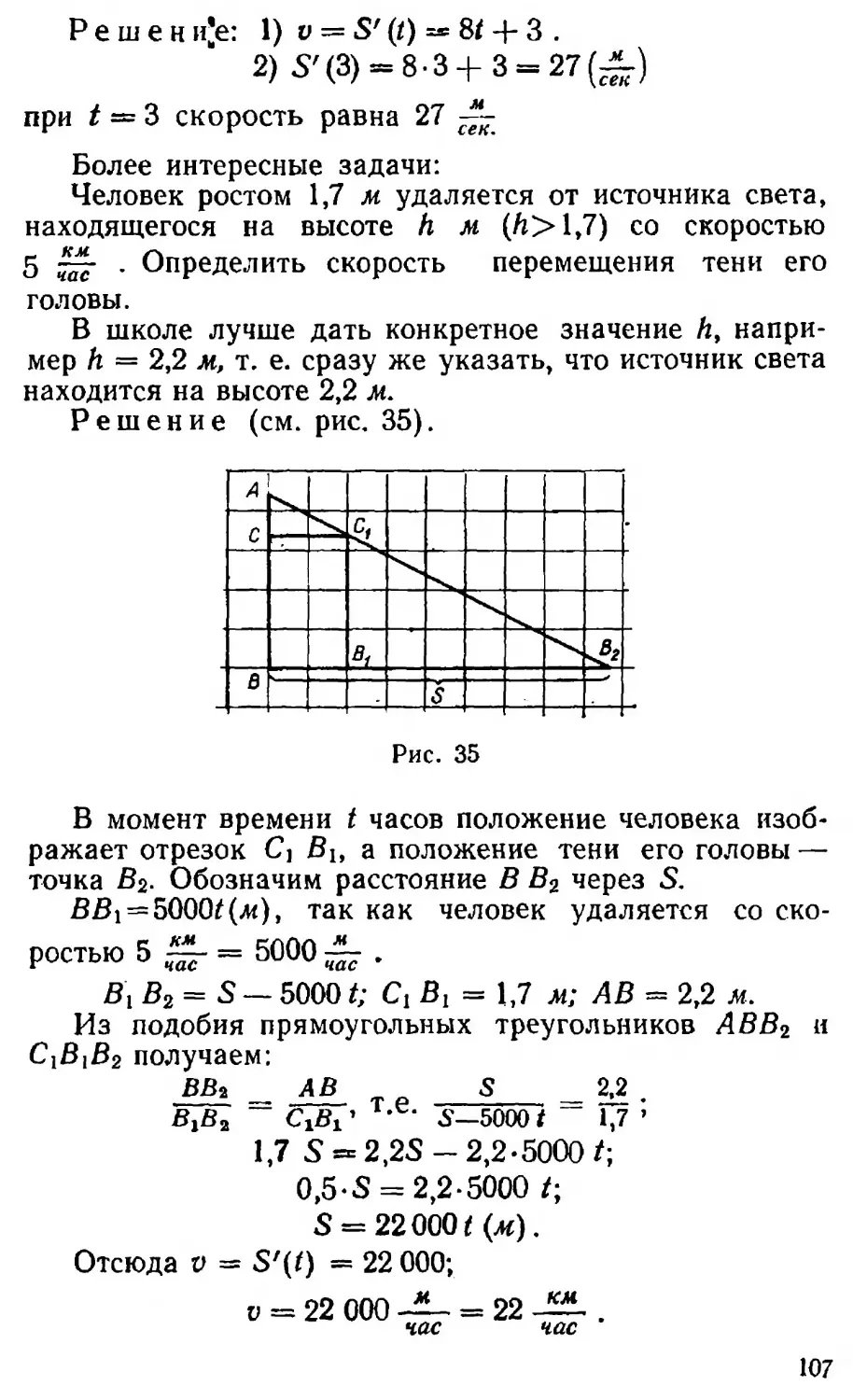
Рассматривается задача. На рисунке 3 изображен
1)	Найти по графику промежутки возрастания и промежутки убывания функции.
2)	При каких значениях х функция y=f(x) положительна; отрицательна; равна нулю?
3)	Найти, при каких значениях х функция y=f(x) имеет наибольшее (наименьшее) значение и какое именно.
Решая задачу, учащиеся выделяют значения аргумента х=—4; х=0; х=1; х=3, которые отделяют промежутки возрастания от соседних промежутков убывания. Очевидно, что при исследовании незнакомой функции и при построении ее графика очень важно уметь находить точки (значения аргумента), отделяющие промежутки возрастания от промежутков убывания. Учащиеся замечают, что все такие точки обладают следующей характерной особенностью, для каждой из них существует такой интервал, содержащий эту точку внутри себя, что значение функции в этой точке больше (меньше), чем значения функции во всех остальных точках этого интервала.
Точки, удовлетворяющие указанным условиям, получили специальное название точек максимума (минимума) функции.
Таким образом, вводятся следующие определения.
Функция у —f(x) имеет максимум в точке а?, если существует интервал, содержащий точку а, для всех точек которого, отличных от точки а, выполняется неравенство f(x) </(«)*.	/
Точка а при этом называется точкой максимума функции.	'1
Функция у =Дх) имеет минимум в точке aL если существует интервал, содержащий точку а, для ^сех точек которого, отличных от точки а, выполняется неравенство
Точка а при этом называется точкой минимума функции.	>
Минимум и максимум функции имеют общее название экстремум (соответственно точка экстремума функции).
Очевидно, что точки, лежащие на стыке промежутков убывания и возрастания функции, находятся среди точек экстремума. Следует, однако, заметить, что не всякая точка экстремума обязательно отделяет промежуток возрастания от промежутка убывания.
Рассмотрим, например, функцию
(1x1 +	х sin -4- при х¥=0,
2	X
О при х = 0.
(См. рис. 4.)
Очевидно, что точка 0 является точкой минимума. В этой точке значение функции равно 0, а все остальные значения на интервале (—оо^оо) положительны. В то же время ни на каком интервале, концом которого служит точка нуль, функция не является монотонной.
Если учитель пожелает привести этот пример учащимся, то график этой функции должен быть заготовлен в виде таблицы заранее. (Разумеется, кроме графика, ученикам даются соответствующие пояснения).
Мы избрали в качестве определения максимума (минимума) определение, которое обычно дается для так называемого собственного максимума (минимума), так как
* Мы не оговариваем здесь специально, что точка а и точки интервала, о которых идет речь, принадлежат области определения -функции, считая, что в противном случае неравенство /(х)</(а) не имеет смысла.
мы счйтаем, что для -средней школы лучше ограничиться этим наиболее характерным случаем. Вопрос о проме-жуткахутостоянства функции можно рассмотреть в дальнейшем Специально, когда эти промежутки встретятся в конкретных примерах.
Рис. 4
§ 3. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ. ФУНКЦИИ, ОГРАНИЧЕННЫЕ СВЕРХУ, И ФУНКЦИИ, ОГРАНИЧЕННЫЕ
СНИЗУ. ОГРАНИЧЕННЫЕ ФУНКЦИИ. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
Понятия четных, нечетных, ограниченных, периодических функций знакомы учащимся из предыдущего, и они обычно хорошо формулируют соответствующие определения и приводят примеры, если предварительно задать им повторить указанный материал. Затем учащиеся самостоятельно дают формулировки этих определений с использованием символа f(x).
Функция #=/(*) называется четной, если для любого принадлежащего области определения функции, —х также принадлежит ее области определения, и выполняется соотношение f (—х) =f (х).
Функция y=f(x) называется нечетной, если для любого х, принадлежащего ее области определения, —х также принадлежит ее области определения, и выполняется соотношение f(—х) =—f(x).
Функция y~f(x) называется периодической, е^ли существует такое положительное число /, называемое периодом функции, что для любого х, принадлежащего области определения функции, х-\-1 также принадлежит ее области определения и выполняется соотношение f(x+Z)=f(x). Обычно указывают наименьший период для данной функции.	!
Функция y=f(x) называется ограниченней сверху, если существует такое число М, что для любрго х, принадлежащего области определения функции, выполняется неравенство f{x)^.M.
Аналогично определяется ограниченная снизу функция. Функция, ограниченная и сверху и снизу, называется ограниченной.
Обращаем внимание учеников на то, как отражаются свойства функций на графиках этих функций. Например, графики четных функций симметричны относительно оси ординат, так как каждой точке графика с координатами (х, У), где f(x) =у, соответствует точка с координатами (—х,у), также принадлежащая графику, ибо —х также принадлежит области определения функции и f (—х) = =f(x)=l/.
График нечетной функции симметричен относительно начала координат. Пояснение аналогично предыдущему.
График периодической функции, очевидно, можно разбить на части, каждая из которых соответствует промежутку оси абсцисс с длиной, равной периоду функции I, причем каждая из этих частей может быть получена соответствующим параллельным переносом одной из них вдоль оси абсцисс.
График функции, ограниченной сверху, расположен весь ниже некоторой прямой, параллельной оси абсцисс; график функции, ограниченной снизу, расположен весь выше некоторой прямой, параллельной оси абсцисс; график ограниченной функции лежит весь между двумя прямыми, параллельными оси абсцисс.
Эта связь между свойствами функции и свойствами ее графика каждый раз поясняется и иллюстрируется на графиках конкретных функций.
Например, могут быть использованы графики таких хорошо знакомых учащимся функций, как у=х2, y=cosx (четные функции); у=х3, y=sinx (нечетные функции); y=sinx, y=cosx, t/=tgx, y==ctgx (периодические функции); 1—х2 (функция, ограниченная сверху); у — х2
(Функи ниченн
(функция, ограниченная снизу); t/=sinx, y = c,osx (ограниченные функции).
В с^язи с иллюстрацией свойств функций на графиках хорошей напомнить учащимся о значении графика функции. \
Кроме иллюстрации свойств функции, график может также служить для приближенного вычисления значений функции^ для графического решения уравнений.
В некоторых случаях приближенное построение графика функции по точкам, аккуратно выполненное, помогает обнаружить некоторые свойства этой функции, которые затем должны быть доказаны.
Обычно, чтобы построить график функции, вначале изучают ее свойства и затем строят график, учитывая эти свойства. Необходимо напомнить, что исследование свойств функции при построении ее графика целесообразно проводить по определенной схеме. Записываем один из возможных вариантов такой схемы, указывая при этом, что порядок следования пунктов этой схемы в зависимости от конкретных условий может быть изменен.
Схема исследования функции
1.	Область определения функции.
2.	Исследование на ограниченность сверху и снизу (если возможно, указать область изменения функции).
3.	Исследование на четность и нечетность.
4.	Исследование на периодичность.
5.	Исследование на возрастание и убывание; указание точек максимума и минимума ( если они существуют) и промежутков возрастания и убывания функции.
6.	Построение графика функции. (В процессе построения графика находят некоторые дополнительные его точки, уточняющие график. Полезно найти точки пересечения графика с осями координат.)
Надо обратить внимание на то, что не всегда удается полностью провести исследования по всем пунктам. В этом случае строят график, ограничиваясь теми сведениями, которые удалось получить. Иногда построенный таким образом приближенный график подсказывает наличие у функции тех или иных свойств, хотя он, конечно, не может служить доказательством этих свойств. Полезно сообщить ученикам, что в дальнейшем
2 Заказ 314
17
они познакомятся с новыми понятиями (предел функции, производная) и связанными с ними более сильными методами исследования функций.	/
Рассматриваются примеры исследования функций и построения их графиков. Например, решается задача.
Исследовать функцию #=х4—4х2+5 и построить ее график.	J
Исследование проводим по схеме.	
1.	Область определения (—+ «>)
2.	Функция ограничена снизу и не ограничена сверху.	ii
Чтобы убедиться в этом, преобразуем формулу, задающую функцию, у=х4—4х2+5—(х4—4х2+4) + 1; У= = (х2—2)2+1.
Очевидно, у>1 и легко показать, что при достаточно большом значении х у может быть сколько угодно большим (т. е, больше любого наперед заданного числа). Наименьшее значение, равное 1, функция принимает при х2 = 2, т. е. при Х1 = )/Ти Хг=— V 2.
3.	Функция четная, так как f (—х) = (—х)4—4(—х)2+ +5=х4—4х2+5=/(х). График ее симметричен относительно оси ординат.
4.	Легко видеть, что функция не является периодической.
Действительно, допустим, что данная функция периодическая и положительное число / является ее периодом. Тогда должно иметь место тождество (x+Z)4— —4(х+/)2+5=х4—4х2Ч-5 или (x-FZ)4—4(x-f-Z)2=x4—4х2
Полагая в этом тождестве х=0 и х=1, делаем вывод, что число I должно одновременно удовлетворять равенствам: /4—4/2==0 и (1-|-О-4—4 (1+Z)2=— 3. Так как Z>0, то из первого равенства получаем, что 1=2, Подставляя полученное значение во второе равенство, имеем З4—4*32=s—3, что неверно. Таким образом, наше предположение о периодичности данной функции привело к противоречию.
5.	Так как функция четная, то при исследовании на возрастание и убывание достаточно рассмотреть поведение ее при х>0. Мы уже знаем, что в точке Х1=]/г*2 функция принимает наименьшее значение. Поэтому рассмотрим отдельно поведение функции на интервале (О, V 2) и отдельно на интервале (1^2^+ оо),
Возьмем два произвольных значения Х| на (O.pf2) такие, что Xi<x2, т. е. 0<Х1<х2<уЛ2,
\	у®	г2	О*
I	1	Л2
И Х2 тогда
х2—2< х* — 2 <0; 1	а	’
2-xJ>2-x2’>0;
(2 - х‘)2 > (2 - xfr > 0:
(х* - 2)2 > (х2 - 2)2 > 0; X	А
(Л2_2)2+1>(х2-2)2-|-1. Ж	А
Итак, на (0,]/ 2) из неравенства xi<x2 следует неравенство f(xi)>f(x2), т. е. на этом интервале функция убывает.
Возьмем теперь произвольные значения хх. и х2 на интервале ()/2, + оо) такие, что хх<х2. Тогда
х >> х "> 1/2-
Лг л1 г *•,
х2 х2
х4 х1
2;
X2 - 2 > X* - 2 > 0;
2	1	’
(х“—2)2 > (х*—2)2; А	X
(<-2)’ 4- 1 > (х2 — 2)2-Ь 1. А	X
Мы видим, что на интервале (У^2, + со) функция возрастает. Легко сообразить, что так как функция четная, то на интервале (— У~2, 0), симметричном интервалу (0, 1^2), она возрастает, а на интервале (•— оо,—]/2), симметричном интервалу (У2\ + со), она убывает. В точках— 1/2 иУ'2 функция принимает наименьшее значение. В этих точках она, очевидно, имеет минимум. Точка 0 лежит на стыке двух интервалов (— }/2, 0) и (0, ]/2), на первом из которых функция возрастает, а на втором убывает.
Таким образом, в точке 0 функция имеет максимум. (Легко проверить, что значение в точке 0 будет
наибольшим среди значений х на интервале (—]/%, у 2). (При х = 0 у = 5,_а при х О, удовлетворяющем неравенству — |/ 2 < х < У*2>	0 < х2 < 2, / откуда
0<2 — х2 < 2, (2 —х2)2<4, (х2 —2)2 1.1 <j5, т. е. У<5).
6.	Строим график функции.
Так как функция четная, достаточно построить вначале график для х > 0. Строим характерные точки графика: А(0; 5), В(\Г2\ 1). От А к В кривая все время идет вниз, а правее точки В все время поднимается вверх.
Общий характер графика ясен. Однако чтобы построить его более точно, рекомендуется найти несколько дополнительных точек.
X	1	2	3
У	2	5	50
Построив правую часть графика, строим затем симметрично его левую часть (см. рис. 5).
На уроке и дома ученики проводят исследование еще нескольких функций с построением их графиков. Разумеется, в классе рассматриваются более сложные примеры с целью иллюстрации различных приемов исследования; на дом задаются примеры более простые.
Рассмотрим еще
один пример исследования функции, проводимого в классе. Исследуем функцию
1 ч
1.	Область определения функции ( — со, -f- со).
2.	Функция не ограничена ни сверху, ни снизу. Действительно, для выполнения неравенства
_ х > м,
О
(где М — любое наперед заданное число), или, что то же самое, неравенства х (-у х2—1 )>Л4, достаточно подо
брать такое значение х, которое, с одной стороны, больше I и, с другой стороны, удовлетворяет неравенству
О
Не нарушая общности, можно считать Л4>0, тогда очевидно, у>М при любом значении х, большем, чем УЗ(Л4 + 1).
Таким образом, функция не ограничена сверху.
Аналогично можно показать, что функция не ограничена снизу.
3.	Функция нечетная, так как область определения ее ('—оо, +оо) и выполняется условие
; ( _ х) =	- X)3 - ( - X) = -	=
4.	Функция непериодическая.
Здесь можно опустить доказательство, указав, что оно проводится таким же образом, как и в предыдущем
случае.
5.	Для исследования функции на возрастание и убывание выбираем два произвольных значения аргумента *1 и х2» удовлетворяющие неравенству х2>хь и сравниваем соответствующие значения функции
*/i = -у -к* — и у2 = -у- х* — х2,
х2 ~ *2 -	*1
0.
Очевидно, что при (xj < 1 и [х2| < 1
и, значит, у2 < ух. Легко видеть, что при xt — 1 и | ха | < 1, а также при | | < 1 и х2 = 1 имеет I место это же неравенство у2<У1- Таким образом, jia сегменте [ — 1, 1J функция убывает. Если xt > 1 и! xt > xt (или х2 < — 1 и х± < х»), то очевидно, 4- х’4—я- x.xt 4-
+ -д- х* — 1 > 0 н~ у2> уОтсюда получаем, что
на промежутках ( — со, — 1] и [ + 1, + °°) функция возрастает. Так как на промежутке (— со, — ]] функция возрастает, а на сегменте [ — 1, 1] — убывает, то значение ее в точке — 1 больше всех других значений на интервале (—со, 1), т. е. при х = — 1 функ-
ция имеет максимум.
Аналогично рассуждая, приходим к выводу, что при х= 1 функция имеет минимум.
			У ।			ж*3-л	6. Так как функция нечетная, то строим график функции вначале для положительных
							значении х. Строим прежде все-
							го точку графика А 1,—, соответству-
							V _	*5 / ющую минимуму функ-~	ТТ1Ш	nWllUC TTQAM
						т	ЦИИ. О di VIVI 0014*1X^/171 VIVI координаты нескольких
			и	J	Л А		х в частности точек пере-paupuuo rnpffiuwa Г ЛГЯ-
							ми координат. Получа- PM THUKU 1/	10	0^ •
							СМ lU4IX.rl ху	t в (Уъ, 0); с (2, 4-);
				-			D (3,6). Построив правую часть графика,
		1	Рис	6			строим затем левую его часть, симметричную с правой отно-
сительно начала координат (см. рис. 6).
Рассмотрев несколько примеров, обращаем внима-
ние на то, что при отыскании промежутков возрастания
и убывания функций каждый раз приходится применять специальные приему, что значительно затрудняет и$-следование.
Глава 2. ОБРАТНЫЕ ФУНКЦИИ
Как известно, школьники часто недостаточно хорошо усваивают важное понятие обратной функции. Изучению обратных функций в нашем изложении уделяется довольно много внимания.
Доказываются некоторые теоремы об обратных функциях, которые дают возможность легко и быстро исследовать свойства функций, обратных по отношению к известным функциям. Эги теоремы не вызывают никаких особых затруднений у учащихся. Опираясь на эти теоремы, проводятся, в частности, исследования свойств обратных тригонометрических функций.
На изучение обратных функций в школе по предлагаемому здесь плану достаточно четырех уроков.
§ 1. ПОНЯТИЕ ОБРАТНОЙ функции, график обратной функции
Понятие обратной функции в какой-то' мере известно учащимся, так как они знакомились с ним, например, при изучении логарифмической функции. На первом уроке, посвященном обратным функциям, после краткого повторения основных понятий, связанных с функциями (область определения функции, область изменения функции, график функции и т. п.), учащиеся вспоминают, что им было известно об обратных функциях, а затем после рассмотрения некоторых примеров взаимно обратных функций уточняется понятие обратной функции и дается следующее определение.
Пусть функция у =/(х) имеет область определения X и область изменения К Если каждому значению у из множества Y соответствует единственное значение х из множества X такое, что f(x) = у, то тем самым определена некоторая функция х = <р (у) с областью определения Y. Эта функция называется обратной по отношению к функции у =	.
Очевидно, что X является областью изменения фун-ции *=<p(f/) и что функция y=f(x) является обратной
по отношению к функции х=<р(у). Обычно такие функции у —f(x) и	называются взаимно обратными.
Примеры у=—2х и х=------у являются взаимно
обратными, как и функции у х3 и х ~Д/~У\ У = 2х и * = log2 у.
Очевидно, что графиком каждой пары из взаимно обратных функций служит одна и та же линия, только для функций вида х = ф(г/) значение аргумента служит ординатой, а соответствующее значение функции — абсциссой точки графика. Удобнее аргумент обратной функции обозначить снова через х, а функцию через у (сохранив ту же область определения ее и тот же закон соответствия).
В этом случае для функции у = —2х обратной функ-
цией будет функция у =---х; для у = х3 обратной
будет функция у = ух\ для функции же у = 2х обратной будет функция у = log2x. При этом графики прямой и обратной функции уже не совпадают. Значение аргумента, которое служило ординатой точки графика, будет служить ее абсциссой, а соответствующее значение функции, служившее ранее абсциссой точки, будет служить ее ординатой.
Таким образом, каж-
Рис. 7
дая точка графика функции с координатами (а, Ь) после переименования переменных перейдет в точку графика функции у = ф(х) с координатами (6, а) (см. рис. 7). Легко видеть, что точки с координатами (а, Ь) и (ft, а) располагаются симметрично относительно биссектрисы 1-го и 3-го координатных углов.
Действительно из равенства прямоугольных
треугольников	и ON2M2 следует 0М\ = 0М2 и
ЛМ{0М{= ZM2ON2. а тогда	£М20К и, значит,
ОК является биссектрисой в равнобедренном треугольнике ОМ\М2.
Из свойства биссектрисы равнобедренного треугольника следует, что 0К1_М\М2 и М\К=м2К, т. е. точки и М2 расположены симметрично относительно биссектрисы ОК.
Итак, графики функций у=[(х) и y = q(x) расположены симметрично относительно биссектрисы 1-го и 3-го координатных углов.
Так как график функции y=f(x) совпадает с графиком обратной ей функции х=ф(у), то графики функций y=f(x) и у = ф(х) расположены симметрично относительно биссектрисы 1-го и 3-го координатных углов.
Внимание учащихся обращается на то, что при доказательстве была выбрана точка Mi (а, Ь), расположенная в первой четверти и не на биссектрисе координатных
углов. Предлагается продумать ход доказательства при других возможных расположениях точки М{. В классе рассматриваются 1—2 таких случая, когда точка Afi расположена во второй, третьей или четвертой четверти или лежит на биссектрисе 1-го и 3-го координатных углов. Иллюстрируются заранее заготовленные графики взаимно обратных функций (см. рис. 8, 9, 10).
Построение графика обратной функции по известному графику данной функции обычно не вызывает затруднений, и здесь не требуется много упражнений.
§ 2. СВОЙСТВА ОБРАТНЫХ ФУНКЦИЙ
Сравнивая свойства взаимно обратных функций, изображенных на чертежах-таблицах, имеющихся в классе (например, рис. 8, 9, 10), учащиеся замечают, что если данная функция возрастает (убывает), то и обратная ей функция возрастает (убывает), а функция, обратная по отношению к данной нечетной функции, также является нечетной. Оказывается это не случайно. Докажем соответствующие теоремы.
Теорема I. Если данная функция возрастает, то и обратная ей функция возрастает.
Пусть у — f(x) и у = ф(х) — взаимно обратные функции, причем функция у = f (х) возрастает. Чтобы удобнее было воспользоваться определением обратной функции, рассмотрим функцию x = <p(r/), полученную из у = ф(х) заменой х на у и имеющую те же свойства, что y = q>(x) (свойства функции не зависят от того, какими буквами обозначены аргумент и функция).
Возьмем два произвольных значения у\ и у2 из области определения функции *=<₽(#) такие, что Уъ>У\- По определению обратной функции Xi=<p(i/i) есть такое значение аргумента функции y = t(x), при котором f(xi)=gi. Аналогично, если х2=ф(г/2), это значит, что f(x2)=y2- Нам нужно доказать, что ф(у2)>ф(У1)> т. е. что х2 > хь Проведем доказательство от противного. Допустим, что соотношение x2>xi, не имеет места, тогда либо Xi = х2, либо Xi > х2. В первом случае f(xi) = f{x2), т. е. У[ = у2, что противоречит выбору значений £/1 и у2. Во втором случае из возрастания данной функции y=f(x) следует, что f(xi)>f(x2), что также противоречит выбору значений у\ и у2.
Итак, предположение, что неравенство х2 > Х\ не выполняется, приводит к противоречию. Мы доказали, что х2 > хь Таким образом, функция х = ф(у), а значит, и функция у = ф(х) возрастают.
Аналогично доказывается, что если данная функция убывает, то и обратная ей функция убывает. Это доказательство проводят ученики самостоятельно в классе.
Теорема 2. Если данная функция нечетна, то обратная ей функция также нечетна.
Пусть дана нечетная функция y**f(x), для которой существует обратная функция.
Рассмотрим обратную функцию в форме х — ц)(у). Нам нужно доказать, что для любого у0, принадлежащего области определения обратной функции, — у^ также принадлежит ее области определения и <р(—уо) = = — фй/о)* Обозначим ф(*/о)=*о, тогда f(x0)=yQ. Так как функция у = f(x) нечетна, то —х0 входит в ее область определения X и /(—х0) =—f(x0), т. е. /(—х0) =—ifo. Последнее равенство означает, что —г/о входит в область определения Y обратной функции и ф(— Z/o) = —хо = —ф(Уо). Итак, ф(—Уо) ==— (Уо), т. е. обратная функция является нечетной.
Очевидно, что если данная функция не является нечетной, то и обратная не может быть нечетной (так как функции взаимно обратны).
Обращаем внимание на то, что, как это следует из определения, не для каждой функции существует обратная функция. Если каждое свое значение функция принимает только при одном значении аргумента, как это имеет место, например, для возрастающих или убывающих функций, то обратная функция существует. В противном случае обратная функция не может существовать, так как само определение функции требует, чтобы каждому значению аргумента соответствовало одно вполне определенное значение функции.
В частности, для четной функции, например, # = х2 обратная функция не существует, так как одно и то же значение функции соответствует двум различным значениям аргумента. По этой же причине обратная функция сама не может быть четной (так как прямая функция служит обратной функцией по отношению к ней).
Точно так же для периодической функции (например, y = sinx) не существует обратной функции и сама функция, обратная по отношению к некоторой функции, не может быть периодической.
Чтобы получить функции, обратные для функций, заданных формулами у=х2, y = sinx, y=cosx и т. п„ в качестве исходной функции берут функцию, заданную соответствующей формулой, но с областью определения не обычной, а специально подобранной так, чтобы обратная функция существовала. Для этого достаточно, как уже говорилось, чтобы в выбранной области определения исходная функция была возрастающей или убывающей, так как в этом случае каждое значение у 28
из ее области изменения У она принимает только один раз.
Например, функция у —х2, определенная на множестве X, представляющем собой промежуток [0, 4- со ), монотонно возрастает. Для нее существует обратная функция # = ]/х (знак радикала означает арифметическое значение корня). Легко получить свойства функции # = зная свойства прямой функции У = х\ определенной на промежутке [0, + оо).
1.	Область определения — промежуток [0, 4- со) (совпадает с областью изменения прямой функции).
2.	Область изменения — промежуток [0, 4-со) (совпадает с областью определения прямой функции).
3.	Функция не является ни четной, ни нечетной (так как прямая функция не является нечетной, а четной обратная функция вообще не может быть).
4.	Функция не является периодической (так как обратная функция не может быть периодической).
5.	Функция возрастает (так как прямая функция возрастает) .
6.	Для построения графика используется свойство графика обратной функции (график прямой функции правая ветвь параболы у=х2, см. рис. 11).
Аналогично рассматриваются свойства функции
У =1о£зх на основании свойств функции у=Зх и свойст-
ва функции у= logj*
2
на основании свойств функции
Следует отметить, что независимо от использования чертежей-таблиц при изучении обратных функций, как и в других случаях, ученикам обычно каждый раз предлагают построить дома те графики, которые предпола
гается рассматривать на следующем уроке.
Чтобы учащиеся лучше уяснили себе значение выбора области определения для существования обратной функции, полезно решить несколько упражнений, связанных с этим вопросом.
Например: 1) Существует ли функция, обратная функции у =	— х1 ?
Обратная функция не существует, так как данная функция четная.
2)	Существует ли~ функция, обратная функции y=sinx, определенной на сегменте , 4^] ?
Обратная функция существует, так как данная функция монотонно убывает.
3)	Существует ли функция, обратная функции определенной на множестве, состоящем из двух интервалов ^0, и	?
Обратная функция существует, так как различным
значениям аргумента данной функции соответствуют и различные значения функции. Это следует из того, что на каждом из интервалов [0,-£-) и я) данная функция возрастает, а для значений аргумента, принад-
лежащих различным интервалам, значения данной функции имеют разные знаки.
4)	Существует ли функция, обратная функции t/=sinx, определенной на полусегменте [0, л)?
Обратная функция здесь не существует, так как различным значениям аргумента могут соответствовать и одинаковые значения данной функции.
Действительно, если выбрать Х| такое, что 0<*1< то и Xi и л—Х| принадлежат полусегменту [О, л) и при этом sinxi=sin (л—Xi).
§ 3. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Как уже отмечалась выше, изучение свойств обратных функций позволяет легко и быстро рассмотреть основные свойства обратных тригонометрических функций на основании известных свойств тригонометрических функций.
Обратимся к функции у = sin х. Выберем такой промежуток, принадлежащий области ее определения, на котором эта функция монотонна (т. е. либо возрастает, либо убывает). Обычно выбирают про-
межуток £--F >	’ на КОТОРОМ Функция f/ = slnx
возрастает (его называют главным промежутком монотонности функции # = sinx). Тогда для функции
у — sin х, определенной только на промежутке [---, -^-1 существует обратная функция. Эту функ-
цию обозначают через t/ = arcsinx (с этим обозначением учащиеся уже встречались).
Рассмотрим свойства функции у *= arc sin х:
1.	Область определения [—1, 1] (совпадает с областью изменения прямой функции).
2.	Область изменения
ластью определения прямой функции).
к
(совпадает с об-
3.	Функция является нечетной (так как прямая функция нечетна).
4.	Функция не является периодической (так как обратная функция вообще не может быть периодической).
5.	Функция является возрастающей (так как прямая функция возрастающая).
6.	Строим график функции, используя свойства графика обратной функции (см. рис, 12). Иллюстрируем свойства функции на графике.
Функция y=arc cosx определяется как функция, обратная по отношению к функции у=cosx, заданной на промежутке [0, л]
Свойства функции y=arc cosx:
1.	Область определения [—1,1].
2.	Область изменения [0, л].
3.	Функция не является ни четной, ни нечетной.
4.	Функция не является периодической.
5.	Функция является убывающей.
6.	Строим график, используя свойства графика обратной функции (см. рис. 13).
Функция у — arctg'x определяется как функция, обратная по отношению к функции У = tgx, заданной
на промежутке
Свойства функции aretgx:
1. Область определения (— сэ, <к>
2. Область изменения
3.	Функция нечетная.
4.	Функция не является периодической.
5.	Функция является возрастающей.
6.	Строим график, используя свойства графика обратной функции (см. рис. 14).
									У ।								•		
			1				1 I					У-			r, /1				
							1 I								1 1 1				
		1 1 1	-												 1""! f r i				
		t J ,													1 t				
		/				~г f								i			y*ar		
		1 '							0										
	/ i										2L Z		/ /				f	у	
					г								* / t				t		
				- z									f				I		
				/													1 i f		
				I								i i				। i			
				1/	•							f 1				I i			
Рис. 14
Функция у — arcctgx определяется как функция обратная по отношению к функции y = ctgx, заданной на промежутке (0, л).
Свойства функции y = arcctgx:
1.	Область определения (—<*>, +°°)«
2.	Область изменения (0,л).
3.	Функция не является ни четной, ни нечетной.
4.	Функция непериодическая.
5.	Функция убывающая.
6.	Строим график, используя свойства графика обратной функции (см. рис. 15).
Все графики строятся с использованием заранее заготовленных графиков соответствующих прямых функций.
3 Заказ 314
33
Учащимся сообщают, что функции y = arcsinx, у= — arccosx, y = arctgx, arcctgx называются обратными тригонометрическими функциями.
Глава 3. ПРЕДЕЛ ФУНКЦИИ
Понятие предела функции — одно из существенно новых понятий, введенных в школьный курс математики. Это понятие ранее никогда не входило в программу по математике советской массовой средней школы, и естественно, что при изучении его учитель встречается с рядом серьезных трудностей как в отношении отбора материала, так и методики его изложения.
Разрабатывая пути ознакомления школьников с понятием предела функции, следует прежде всего уяснить себе, какие цели преследует введение этого понятия в школе и какие задачи могут и должны быть решены в процессе его изучения.
Известно, что понятие предела функции служит основой для последующего введения понятия производной. Однако ознакомление школьников с пределом функции имеет и самостоятельное значение, так как дает им воз
можность глубже овладеть идеей предельного перехода, играющей столь большую роль в различных областях математики.
Мы считаем, что при изучении понятия предела функции учащиеся должны получить отчетливое представление о сущности этого понятия и в то же время научиться четко и сознательно давать соответствующие определения и опираться на них при проведении рас-суждений в необходимых случаях.
Здесь следует использовать возможность показать переход от смутных представлений к четким математическим определениям. Чтобы проиллюстрировать важность введения таких определений, необходимо хотя бы на отдельных примерах дать образцы рассуждений, проводимых на основе этих определений.
Разумеется, школьное преподавание темы «Пределы и функции» не должно дублировать вузовское изложение этих вопросов в курсах математического анализа, однако это не означает, что изложение должно быть чрезмерно упрощенным и что следует всячески избегать всего, что как-то напоминает изложение материала в высшей школе. Главное — обеспечить научность и в то же время доступность изложения и добиться того, чтобы изучаемый материал с интересом воспринимался. В школьном курсе достаточно ограничиться определением предела функции по Коши, вполне доступным для учащихся и в то же время достаточно ясно отражающим суть дела.
Разъясняя определение Коши, можно решать конкретные примеры, поясняющие смысл произвольного е и соответствующего ему б, и использовать геометрические иллюстрации, помогающие составить наглядное представление о понятии предела функции.
Ввиду ограниченности времени подробную теорию пределов в средней школе развивать, по-видимому, невозможно, но хотя бы несколько доказательств, связанных с использованием определения предела функции, на наш взгляд, обязательно нужно провести.
Необходимо при изучении предела в какой-то мере познакомить с понятием непрерывности, хотя ныне действующая программа этого не предусматривает*.
* Проект новой программы предусматривает ознакомление учащихся с понятием непрерывности функции. «Математика в школе», 1967, № 1. стр. 22.
Мы пришли к убеждению, что целесообразно начать знакомство с пределом функции с изучения предела функции при х-+ оо (читается: при х, стремящемся к плюс бесконечности). Это значительно облегчает школьникам усвоение этого трудного понятия, так как позволяет связать изучение предела функции с ранее известным им понятием предела числовой последовательности.
После введения определения предела функции при х-> + со , рассматривая и строя графики функций, учащиеся неизбежно приходят к мысли, нельзя ли ввести понятие предела функции и при х-> —оо. Определение предела функции при х -> — со учащиеся обычно дают почти самостоятельно по аналогии с пределом функции при х -> + оо .
Усвоение учащимися понятий предела функции при х -> со и при х -> — со значительно облегчает введение определения предела функции при х -* а (читается: при xt стремящемся к а). На изучение предела функции отводится примерно 10 уроков.
§ 1. ПРЕДЕЛ ФУНКЦИИ / (х) ПРИ х -> + оо И х^ — оо
Для лучшего усвоения понятия предела функции в свое время должно быть уделено достаточное внимание изучению предела числовой последовательности. Учащиеся должны иметь отчетливое представление о сущности понятия предела числовой последовательности и хорошо понимать определение предела числовой последовательности *, что достигается решением достаточного числа задач, в которых нужно найти номер N, начиная с которого выполняется требуемое неравенство, сначала для конкретных значений е, а затем и для произвольного е, а также решением задач, в которых требуется доказать, что данное число является пределом данной числовой последовательности. Если обна
* Имеется в виду определение: «Число а называется пределом числовой последовательности а2, ...» %, • . • , если для любого наперед заданного положительного числа е можно указать такой номер N члена последовательности, что при n>N для членов последовательности выполняется соотношение \ап —д|<е>. В этом определении вместо «при	часто говорят «при	однако,
как легко видеть, это несущественно, так как легко убедиться в том, что оба эти определения равносильны.
руживается, что учащиеся недостаточно владеют понятием предела числовой последовательности, то необходимо выделить на повторение этого понятия специальный урок. Во всяком случае предполагается, что к уроку, посвященному первому знакомству' с пределом функции, учащиеся вспомнили понятие предела числовой последовательности и хорошо владеют его определением.
При введении на уроке понятия предела функции _ f (х) при X ->4-оо используется изучение функций и построение их графиков, которыми занимались на предыдущих уроках. В качестве домашнего задания к данному уроку (кроме повторения предела числовой последовательности) учащимся предлагается построить какой-либо график функции, на котором можно было бы проиллюстрировать понятие предела функции при х -> 4~ со . Например, можно задать построить график х® 4” 2
функции у	. Кроме того, на уроке привлека-
ются заранее заготовленные чертежи-плакаты графиков функций, уже знакомых учащимся.
Подойти к введению понятия предела функции при 4- °0 можно, например, следующим образом.
Во время краткого фронтального опроса в начале урока один из учащихся вычерчивает заданный график j^2 I 2
функции у = -^2	- на классной доске. (Желательно
иметь в каждом классе разграфленную в клетку доску или часть доски.) Затем перечисляются свойства рассматриваемой функции и уточняется ее график (см. рис. 16), после чего учитель приступает к объяснению нового материала.
Рис. 16
~F- 2
Глядя на график функции У = - х2 р-, учащиеся видят, что с возрастанием положительных значений х значения функции все меньше отличаются от 1. Если записать эту же функцию в форме у= 1 + JTZpf » то Уче’ ники легко догадываются, что при дальнейшем неограниченном возрастании аргумента х значения функции неограниченно приближаются к 1. Они ясно представляют себе, как должен выглядеть график функции при дальнейшем его продолжении. Точно так же, глядя на знакомый график функции У— ——2 (представленный в классе на чертеже-плакате, рис. 17), учащиеся считают очевидным, что при неограниченном возрастании значений аргумента х значения функции неограниченно приближаются к числу —2.
У
Рис. 17
Термин .«неограниченно приближаются» или другой сходный термин употребляют для выражения своих наглядных представлений, не вдаваясь в его точный смысл.
Учитель ставит перед учащимися задачу установить, какой точный смысл мы придаем словам: «Значения 38
функции неограниченно приближаются к данному числу при неограниченном возрастании значений аргумента х» (или «значения функции становятся сколь угодно близкими к данному числу при достаточно больших значениях х», или другим сходным выражениям), и указывает, что обычно в математике в том же самом смысле употребляется выражение: «Данное число является пределом функции /(х) при х -|~ со ».
Возникает задача уточнить выражение: «Данное число является пределом функции f(x) при х -> + со » — и, таким образом, дать определение предела функции при х -> Ц- со .
Здесь уместно использовать определение предела числовой последовательности, в котором в точных математических терминах описывается факт неограниченного приближения членов последовательности к некоторому числу при неограниченном возрастании их номеров.
Внимание учащихся обращается на то, что задание числовой последовательности означает в то же время задание некоторой функции.
Действительно, каждому значению п (номера члена) соответствует вполне определенное значение члена последовательности. Таким образом, общий член последовательности ап представляет собой функцию f(n), областью определения которой служит множество натуральных чисел, или, как говорят, функцию натурального аргумента ап
Неограниченное приближение членов последовательности а„ к ее пределу при неограниченном возрастании их номеров означает неограниченное приближение к этому числу значений f(n) при неограниченном возрастании значений ее аргумента. Поэтому число а можно назвать пределом функции f(n) при неограниченном возрастании значений ее аргумента п, или, как это принято обозначать, при п -> + со .
Таким образом, определение предела числовой последовательности приводит к следующему определению предела функции натурального аргумента (не для запоминания) Число а называется пределом функции при л -► + оо , если для любого наперед заданного положительного числа е можно указать такое значение аргумента N, что для всех значений аргумента n>N выполняется неравенство |’f(n)—а|<е.
Легко сообразить, что то обстоятельство, что аргумент функции f(n) принимает только натуральные значения, не является здесь существенным.
В таких же терминах можно выразить факт неограниченного приближения к некоторому числу b значений функции y—f(x) при неограниченном возрастании значений ее аргумента х, т. е. при х + оо *.
Таким образом, приходим к следующему определению: число b называется пределом функции у =/(лг) при х + оо , если для любого наперед заданного положительного числа в можно указать такое значение аргумента ш, что для всех х>тп выполняется неравенство \/(х)-Ь\<г . Обозначение: Ь = lim/(x).
Выбор т по заданному е иллюстрируется на графи-ке функции у —	, начерченном на доске и в
тетрадях учащихся (см. рис. 18).
Рис. 18
Учитель разъясняет, показывая это на чертеже, что для заданного положительного числа е можно подобрать не одно, а бесчисленное множество различных значений т, удовлетворяющих требованиям определения. Так, для числа ej мы подобрали число пц. Для числа Е2 число уже не подходит, мы выбрали для него число /Из. В то же время число т2 могло быть выбрано для числа 8[. Очевидно, что если для некоторого е подобрано
* Число, являющееся пределом функции, удобнее обозначить буквой 6, ибо так будет обозначен и предел функции при х -> а.
соответствующее число т такое, что для всех х>т выполняется неравенство |7(х)—<е» то для любого числа tn', большего чем т, тем более можно утверждать, что для всех х>т' выполняется последнее неравенство. Для того чтобы убедиться в том, что число b является пределом функции f (х) при х -> + оо , нужно проверить, что для любого положительного числа е можно
найти по крайней мере одно такое число т, что для всех значений аргумента х больших, чем т, выполняется неравенство |f(x)—6|<е.
Учитель показывает, как это делается, на примере j^2 —I— 2 рассматриваемой функции у— ~ла .
Вначале полезно взять конкретные значения е. Например, ставится задача: для числа б —0,01 найти такое число tn, чтобы для всех значений аргумента х, больших этого числа т, выполнялось неравенство
хН2
Чтобы найти число т, выясняется вначале, для каких вообще значений х справедливо это неравенство, т. е.,
другими словами, решается неравенство.
Преобразовывая неравенство, получают тгх! *
•Л I 1
1
Так как при всех значениях х выражение ~	।
ложительно, то знак абсолютной величины можно стать. Получается неравенство
0,01
100
по-опу-, от-
100 и х2>99. Отсюда ясно, что данное не-
равенство справедливо для всех х>/99 и для всех х<— /99.	_
Обозначив /99 через tn, учащиеся получают, что для всех х > т выполняется неравенство  „ , , — 1 <0,01. Итак, при е =0,01 в качестве т можно взять число ]/99.
Разумеется, что любое число, большее, чем 99, также можно было выбрать в качестве числа tn.
Если в качестве е взять число 0,001, то легко видеть, что ]/99 уже не сможет играть роль числа т. Действительно, при х — 10 > ]/99
х2+_2 — J — —— —!— •> 0 001 + 1	1	& + 1	101 >	•
мо-
за-со-
Однако, проведя аналогичные рассуждения, мы жем выбрать для « — 0,001 число т = У 999 .
Чтобы убедиться в том, что для любого наперед данного положительного числа е можно подобрать ответствующее значение т такое, что для всех значений х>т будет выполняться неравенство уу следует провести рассуждения в общем виде.
Рассуждения проводятся совершенно так же, как в случае конкретного е.
Пусть е — произвольное наперед заданное положительное число.
£
Решается неравенство
е;
2 >
Е

Е
неравенство справедливо вообще для х и в качестве т можно брать любое
Если е > 1, то всех значений число.
Если же е 1, то неравенство выполняется для всех значений х
и для всех значений
то окажется, что для'
е.
= 1. Опи-
F £
х < —1/	. 1. В этом случае, если обозначить
через т число у -j-
всех значений аргумента х>/и выполняется неравенство
Итак, каким бы ни было наперед заданное положительное число е, всегда возможно подобрать требуемое число т, а это и означает, что lim
раясь на введенное определение предела функции Дх) при х-*4-оо, можно теперь доказать и ранее подмеченный из наглядных соображений факт, что функция У =-j;—2 при х-> 4-оо имеет своим пределом число —2.
Пусть е — произвольное наперед заданное положительное число. Чтобы найти соответствующее чис-42
ло т, достаточно решить неравенство
е.
------2
е,
переписать в виде —|
Отсюда получается реше-
ИЛИ
Это неравенство можно е, или |х|
£
1 ние: х> —, или х<----------
£ ’ £
Ясно, что при /п = —для всех х>/п выполняется неравенство —------2 — (—2) <е.
Таким образом, lim ( —--------2 = —2.
Jf-^4-00 \ х	/
Примеры на доказательство того, что данное число является пределом данной функции при х->4-оо, даются только для иллюстрации смысла определения предела функции и использования определения при доказательствах. Не следует ни в коем случае идти по пути заучивания рассуждений; здесь самое главное добиться того, чтобы учащиеся понимали рассуждения учителя.
Можно рассмотреть еще несколько подобных до-казательств, например, для функции у = —, у = —-— .
А	«А
Полезно предложить учащимся продумать доказательство дома, а затем разобрать его в классе. Например, предложить для функции у — ---------— построить
график (см. рис. 19), догадаться, какое число является пределом функции при х -+ + оо , и доказать, что это число действительно является пределом.
Следует обратить внимание учащихся на то, что не всякая функция имеет предел при х 00 (так же как не всякая последовательность имеет предел). Например, хорошо известные ученикам функции у=х\ у=х3, y—sinx, у— cosx не имеют предела при х-> +со. Отсутствие предела не доказывается, но его легко пояснить на графиках этих функций, изображенных на чертежах-плакатах. В первых двух случаях значения функции неограниченно возрастают при неограниченном возрастании значений аргумента; в последних двух случаях значения функции при х—>-+оо не приближаются неограниченно ни к какому числу, так как имеются сколь
угодно большие значения аргумента х, при которых значения этих функций равны 1 и в то же время для сколь угодно больших значений аргумента значения этих функций могут быть равны —1.
Предел функции при х -> — оо рассматривается менее подробно. Используя ранее рассмотренные графики функций у =	, у = —-----2, у = и т. п.» обра-
щаем внимание на то, что представляет интерес не только изучить поведение функции при значениях х, неограниченно возрастающих, но и при значениях х, неограниченно убывающих, т. е. при х -> — оо. Нередко ученики сами приходят к этой мысли.
Естественно, по аналогии с понятием предела функции при х-> + 00 ввести понятие предела функции при X -> — со .
Это определение будет отличаться от определения предела функции при х + со только тем, что в этом случае значения функции как угодно мало отличаются от своего предела не для всех значений аргумента, больших некоторого числа, а для всех значений аргумента, меньших некоторого числа.
х2 Ч- 2
Например, учитывая четность функции у —	'-у ,
из наглядных соображений можно сделать вывод, что при х -> — со пределом функции у = — является
число 1. И действительно, вспоминаем, что, выбрав прр-
извольное положительное число е, мы получили, что неравенство i>l/A
е выполняется как для всех
— 1 , так и для всех х
довательно, обозначив через т число — у —----1 ,
мы получаем, что для любого положительного числа е можно выбрать такое число т, что при всех
х < т выполняется неравенство
б .
Повторив определение предела функции при х-> + оо, учащиеся почти самостоятельно формулируют следующее определение: число Ь называется пределом функции y=f(x) при х —>— со, если для любого наперед заданного положительного числа е можно указать такое число что для всех значений аргумента выполняется неравенство \f(x) — &]< е.
Обозначение: b = lim/(x).
X-*--09
Чтобы у учащихся не создалось ложного впечатления, что предел функции при х — со всегда совпадает с пределом функции при х -> + со, можно привести им примеры функций, для которых это не имеет места, с иллюстрацией их графиков на чертежах-плакатах. Например, 11m 1	* = 1, a lim ii_LLL = — 1 (см.рис.20);
lim 2х не существует, а Иш 2х = 0 (см. рис. 21); Х-+4"00	Х~* — оо
(1 Хх'	/ 1
-к-) = О, а Пт|-к-| не существует (см. рис. 22).
/	JC-+ — °о \ ~ /
Доказательство вышеуказанных соотношений обычно на уроке не удается провести, это рекомендуется сделать для интересующихся учащихся во внеурочное время.
Все ранее рассмотренные графики функций могут создать у учащихся впечатление, что значения функции всегда приближаются к пределу при х + оо или х ->— оо монотонно. Хорошим примером, опровергающим это мнение, может служить рассмотрение ,	sin X
функции у = ------ .
Так как эта функция понадобится и при дальнейшем изложении, то желательно изучить ее свойства и построить ее график.
из
двух интервалов (—оо, 0) и (0, -f- со). Эта функция четная, она обращается в нуль при всех значениях
Аргумента х вида k^, где k—целое число; на интер-алах (0,«); (— л, 0) и на всех интервалах вида 2А«, (2А 4-1)«) при k натуральных и интервалах вида (|2Л— 1)к, 2Лл) при k целых отрицательных значения функции положительны, а на всех интервалах вида ((2Л— 1)тс, 2Лп) при k натуральных и (2Ая,(2Л 4- 1)я) при k целых отрицательных значения функции отрицательны.
Опуская отыскание промежутков монотонности функции, так как в данном случае это было бы слишком громоздко, учащиеся строят график функции (см. рис. 23) по точкам, учитывая уже известные свойства. Желательно, чтобы у учителя имелись заранее вычисленные значения этой функции для ряда значений аргумента.
Рис. 23
Возникает затруднение в построении графика вблизи оси ординат. Оставляя пока график в этой части незаконченным, обращаем внимание на поведение функции при х -> + оо и при х — оо . Сосредо1очйваем внимание на том, что при неограниченном возрастаний значе-
ннй х график неограниченно приближается к оси абсцисс, проходя то выше, то ниже оси. Такая же картина на-,	sin х !
блюдается при х — со , так как функция у = —-—?
> + оо И при Докажем, на-
четная. Представляется очевидным, что число 0 является пределом функции y=f(x) при .
х -> — оо . Это нетрудно и доказать.
пример, что lira--— 0.
Пусть е — произвольное наперед заданное положительное число. Нам нужно выбрать такое число /п, чтобы для всех х>т выполнялось неравенство sin X
е или, что то же самое
е .
мечаем, что
подобрать такое /и, чтобы при х неравенство
х
и, следовательно, достаточно выполнялось е. Последнее неравенство справед
ливо при значениях х > — и при значениях х< — — .
Обозначив через т число — , получаем, что для всех х> т выполняется неравенство pi I sin х	n .
неравенство |------0 < е.
е, а значит, и
§ 2. ПРЕДЕЛ ФУНКЦИИ f(x) ПРИ х-+а (а —ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО)
На том же уроке, где рассматривается функция у = -у- , учащиеся подводятся к мысли о необходимости введения понятия предела функции при условии, что значения аргумента неограниченно приближаются к некоторому действительному числу. Перед нами стоит задача, как закончить построение графика функции у = вблизи оси ординат. Для этого нужно выяснить поведение функции, когда значения аргумента приближаются к числу 0. Вычисленные при х = тг , 2 о
Т’ Т’ П значения функции подсказывают, что при при-
ближении аргумента к нулю значения функции приближаются к 1. Чтобы убедиться в том, что при неограниченном приближении значений аргумента к числу 0 значения функции действительно неограниченно приближаются к числу 1, следует прежде всего уточнить смысл выражения: «При неограниченном приближении значений аргумента к данному числу значения функции неограниченно приближаются к некоторому числу», выразить этот факт в точных математических терминах, т. е. дать определение предела функции при х а (а — действительное число), или, как еще говорят, предела функции в точке а. Окончание построения графика функции sin х
у = х • откладывается до того времени, когда соответствующее определение будет введено и будет доказано, что при пределом функции у = —является число 1.
Прежде чем вводить определение предела функции при х -> а, полезно рассмотреть графики достаточно знакомых функций. Можно взять, например, такую как у=2х. Эта функция определена при всех значениях аргумента х. В частности, при х=1 значение ее равно 2. Рассмотрим значения аргумента, отличные от числа 1, но все меньше отличающиеся от него, и составим таблицу соответствующих значений функции.
X	0	2	0,5	1,5	0,75	1,25	0,9	1,1	0,99	1,01
У	0	4	1	3	1,5	2,5	1,8	1 2,2	1,98	2,02
Таблица показывает, что, выбирая значения аргумента, все более близкие к числу 1, мы получаем значения функции, все более близкие к числу 2. График подсказывает, что при неограниченном приближении значений аргумента к числу 1 значения функции неограниченно приближаются к числу 2.
Выясним, например, для каких значений аргумента значения функции будут отличаться от числа 2 меньше, чем на 0,01, т. е. будет выполняться неравенство 12л: — 21 < 0,01. Легко видеть, что данное неравенство может быть представлено в виде 2|х— 11< 0,01, что равносильно неравенству |х—1|< 0,005.
4 Заказ 314
49
Таким образом, для всех значений аргумента, дл* которых выполняется неравенство |х—1| <0,005 будет выполняться и неравенство |2х— 2|<0,01.
Легко сообразить, что если мы возьмем какое
угодно положительное число е, то для выполнялось неравенство |2х— 21 < е,
того чтобы достаточно.
€
неравенство [х—1[
чтобы выполнялось
Рис. 24
Можно проиллюстриро вать на чертеже геометрический смысл обоих неравенств (см. рис. 24). Для любого значения аргумента, попавшего внутрь интервала (Е	1	Е \
1—~2~ > 1 + _2_1на оси абсцисс, т. е. достаточно близкого к 1, соответствующее значение функции попадет в интервал (2— е, 2-}-е) на оси ординат, т. е. будет отличаться от числа 2 меньше, чем на е. (Необходимо напомнить, что неравенство |х— а|<е равносильно системе неравенств
а — е < х < а + е.)
похожую на ту, которую видели
Мы имеем картину, похожую на ту, которую видели при рассмотрении предела функции при х -> + со (или при х-> — оо ). Напрашивается мысль, что в данном случае число 2 может быть названо пределом функции при х -> 1 и что определение предела функции при х а может быть сформулировано аналогично тому как это делалось для предела функции при х ->- + со (или х -> — оо ). Здесь следует обратить внимание на то, что в нашем случае значение функции при х= 1 нас не интересовало, мы рассматривали значения аргумента, все более близкие к 1, но все же отличающиеся от 1.
Можно рассмотреть также функцию у = —~тт—~ » которая не определена при х—\, а при всех остальных 50
значениях х принимает .те же значения, что и рассмотренная функция у**=2х (см. рис. 25).
Естественно считать, что и функция у -------—
не определенная при х=1, имеет своим пределом при х-*- 1 число 2.
Наконец,
можно показать пример функции
которая при х=1 принимает значение 1, но пределом которой при х-+ 1, как это видно из графика (см. рис. 26), естественно считать число 2.
Таким образом, при определении предела функции при х -> а необходимо делать соответствующую оговорку.
После рассмотрения примеров должно накопиться достаточно представлений для сознательного восприятия определения предела функции при х -> а.
Определение. Число b называется пределом функции /(х) при х-+ а, если для любого наперед заданного положительного числа е можно указать такое положительное число 6, что для всех значений х отличных от а и удовлетворяющих неравенству |х—а| <б, выполняется неравенство |/(х) — &|<е.
Обозначение: & = lim f (x). (Разумеется, что не? х~^а
равенство \f(x) — &|<£ может выполняться и при х = а и при каких-либо значениях х, не удовлетворяющих неравенству |х — &|<В. Важно только, чтобы для х, отличных от а и удовлетворяющих неравенству |х—п|<8, неравенство |/(х) — &|<е обязательно выполнялось, а для других значений х оно может либо выполняться, либо нет.)
Возвращаясь к примеру функции у = 2х, проверим, исходя из введенного определения, что lim2x—2.
х-»1
Действительно, мы уже убедились в том, что, каково бы ни было положительное число е, для всех х, удовлетворяющих неравенству |х — 11	•, выпол-
няется неравенство |2х— 2| < е. Здесь является тем числом 8, о котором говорится в определении, и, таким образом, число 2 удовлетворяет определению предела для данной функции у = 2х при х-> I.
Следует показать примеры функций, не имеющих пределов в некоторых точках. Здесь уместно воспользоваться заранее заготовленными чертежами-плакатами (см. рис. 27, 28, 29).
Чтобы учащиеся лучше усвоили определение предела функции и научились проводить рассуждения, опи-
рающиеся на это определение, рекомендуется провести такие рассуждения еще в нескольких простых случаях, например доказать справедливость следующих утверждений:
1. lim-^^.-=2.	2. lim 5х~— =0,5.
л->1	**	1	л*->0,4 z
3. 11m (Зх — 5) = 4.
л->3
Полезно рассмотреть в качестве примеров дока; зательства утверждений lim sinx = 0 и lim cos х = 1, х -> 0	.v -> О
к которым учащиеся легко приходят из наглядных соображений. И сами эти утверждения и некоторые промежуточные выводы, полученные в процессе их доказательства, оказываются полезными при дальнейшем изложении.
При доказательстве того, что limsinA: = 0 нам х -> О нужно показать, что для любого наперед заданного положительного числа е можно подобрать такое положительное число 8, чтобы для всех х, отличных от 0 и удовлетворяющих неравенству |х| <8, выполнялось неравенство |sinx[<e.
Оказывается, для отыскания 8 по заданному е можно будет воспользоваться тем, что при всех х=/=0 | sin х | < | х |. Поэтому предварительно доказывается последнее неравенство.
Лемма 1. Если х#=0, то |sinx | < |х|*.
Рассмотрим вначале значения х, удовлетворяющие неравенству 0 < х <-s- • Построим угол в х радиан, который в данном случае является острым (см. рис. 30). Проведем дугу АВ окружности радиуса 1 с центром в верши-
не О данного угла. Легко видеть, что площадь треугольника АОВ меньше площади сектора АОВ.
Имеем: S&AOB<Z $ сект АОВ , HO S&AOB ~~7Г' ОА’ОВ X Ал
X sin х = -5- sin х (так как ОА — ОВ = \). В то же „„„ с	11 ОАг 1
время 5 сект аов =  -2~ х =-%-х. Таким образом, -g- sin х< -у- х или sin х <х. На интервале ^0,	х>0
и sin х > 0 и, следовательно, для рассматриваемых значений х выполняется неравенство |slnx| <|х|. Рассмотрим теперь значения х, удовлетворяющие
* Учащимся, разумеется, известно, что sin0 = 0 и. значит, '| sin 0| = 0.
Рис. 30
неравенству----
л<0. В этом случае, очевидно,
> 0 или 0 < — х < ~ и, значит, | sin (—л)| < <| — х |. Но | sin ( — х) | = | — sin х | — | sin х |, | — х = |х |, и таким образом, и в этом случае справедливо неравенство | sin х | < | х |. Для х, удовлетворяющих неравенству | х | > т. е. для х <----и для х >	,
выполнение неравенства | sin х | < | х | очевидно, так
как |sinx| < 1 <	. Итак, для всех значений
х 4= 01 sin х | < |л |.
Доказываем теперь, что lim sinx = 0.
л'->0
Пусть е — произвольное положительное число. Так как | sin х | < | х | при х =# 0, то, выбрав в качестве 8 само число е, получаем, что для всех х, отличных от 0 и удовлетворяющих неравенству |л|<8, обязательно выполняется неравенство I sin х | < е (| sin х| < |л | < 8 = е) .
Чтобы доказать, что limcosx=l, следует убе-л >0
диться в том, что для любого наперед заданного положительного числа г можно подобрать такое положительное число 8, что для всех значений х, отличных от 0 и удовлетворяющих неравенству |л|<8, выполняется неравенство | cos х— 11 < е. Здесь для выбора 8 полезным оказывается неравенство |cos х—1 |<|х|, справедливое также для всех х =£ 0. Поэтому преж
де всего доказываем это неравенство.
Лемма 2. Если, лг=/=О, то |cosx—11< |лг|.
Пусть х =^= 0. Преобразуем выражение | cos х—1|. I sin -к-| . Так как -=г|. Кроме того,
| cos х — 11 = 2 sin2 *2" = 21 sin --^-=#0, то по лемме 1 Isin -4-si n 4-1 < 1. Отсюда 2 sin -4-1
Теперь легко доказать, что lim cos х = 1. Дейст-
вительно, для произвольного наперед заданного положительного числа е достаточно выбрать в качестве 8 само это число е, и тогда для всех х, отличных
от 0 и удовлетворяющих неравенству выполняться неравенство cos х — 11
- 1 |<| Х| < 8 = е).
| х |< 8 , будет < е ([ cos X —
§ 3. ПРЕДЕЛ ОТНОШЕНИЯ СИНУСА К АРГУМЕНТУ, КОГДА АРГУМЕНТ СТРЕМИТСЯ К НУЛЮ
После введения определения предела функции и рассмотрения ряда примеров на приложение этого определения можно вернуться к поставленной ранее задаче исследования поведения функции у = —-— при значениях аргумента, близких к 0. Уже было высказано предположение, что если значения х неограниченно приближаются к 0, то соответствующие значения этой функции неограниченно приближаются к числу 1, однако эта догадка не была достаточно мотивирована.
Докажем теперь, что действительно Hm sinx — 1.
л-0 х
Здесь для произвольного наперед заданного положительного числа е требуется подобрать такое положительное число 8, чтобы для всех значений х, отличных от 0 и удовлетворяющих неравенству ] х | < 8, выполнялось неравенство тельно докажем две леммы.
Лемма 3. Если х у= 0 и [ х | < -£- , то | л] < | tg х |.
sin X
е. Предвари-
Рис. 31
Рассматриваем сначала значениях, удовлетворяющие неравенству 0 < х Строим угол в х радиан, который в данном случае является острым (см. рис. 31). Проводим дугу АВ окружности единичного радиуса с
центром в вершине О данного угла. В точке А восставим перпендикуляр к радиусу ОА до пересечения в точке С с продолжением радиуса ОВ. Легко видеть, что площадь сектора АОВ меньше площади треугольника ОАС.
Имеем. 5сект АО в *5 д а ос • Но *^сект а о в —g Зд аос = -к-ОА-АС = -С ОА-ОА-tgx = -i- tgx (так как ОА = 1). Получаем -|- х <	tg х, откуда х < tg х\ так
как х>0 и tgx>0, то |х| < |tgx|.
Пусть теперь х удовлетворяет неравенству —<х<0, тогда, очевидно, 0< — х<-£- , значит, I —*|<|tg(—л)|, откуда |х|< |tgx|.
Итак, для всех х О таких, что |х| <-у, выполняется неравенство | х| < |tgx|.
Лемма 4. Если х =# 0 и | х | <-£-, то| - — - — 11<|х|.
По условию х =/= 0 и |х|<С-к-, тогда по леммам Ги 3. имеем, ?что для рассматриваемых значений х выполняется, неравенство
| sinх] < |х| < |tgx| .
Так как | sin XgJ 0, то отсюда получаем
I X 1	. Itgx I
I sin X I | sin X I ’
1
sin x
1
I COS X I
Следовательно, 1> l>|cosx| . При рассматриваемых значениях xf—<x<0 или 0<x< yj cos x>0 и Sll^_ - > 0, поэтому в последнем неравенстве знак абсолютной величины можно опустить.
Имеем:	lj>—-—>cosx.
Преобразуем далее полученные неравенства:
„ sin х . .	,
0 > —---------1 > cos х — 1 ;
„	- sin х - 1
0 < I---------— <1 — cos х.
sin x
” Очевидно, здесь 1 —
и 1—cosx = |l— cos х |. Таким образом, 1	<
< 11—cosx| или, что то же самое, — 1 <[cosx—1|. Но по лемме 2 при х ¥= 0 | cos х — 1 | < | х | и, значит, в данном случае —- 1 < | х |.
Докажем теперь, что	1.
х->0 х
Пусть е — произвольное наперед заданное положительное число.
Если	то, выбрав в качестве ^6 само число
е, получаем, что для всех значений х, отличных от О и удовлетворяющих неравенству | х | < 8 ^8
I sin х л
вы-
полняется неравенство
е л
g — е
то достаточно выбрать в каче
стве 6 число -?г
получаем
sin х
е .
Таким образом, для любого наперед заданного положительного числа е можно выбрать такое положительное число 8, что для всех значений х, отличных от 0 и удовлетворяющих неравенству |х|<8, будет выполняться неравенство-------1 < е, т. е.
I JC	J
,.	sin X	1
hm--------- I.
х->0 х
Завершив доказательство, можно возвратиться к графику функции у = —— . Учитель показывает гото-вый график на чертеже-плакате, а учащиеся заканчивают построение графика в своих тетрадях (см. рис. 32).
Рекомендуется обратить внимание на то, что проводя рассуждения, аналогичные предыдущим, можно доказать, что для любого действительного числа k, отличного от нуля, lim sl"fex — 1. Нетрудно пока-х->0
зать, как это делается, на уроке или во внеурочное время для интересующихся учащихся.
Рис. 32
Действительно, при доказательстве лемм ничего не изменяется оттого, что вместо числа х рассматривается число kx.
Таким образом, можно считать доказанным, что при kx =# 0 и [	выполняется неравенство
sinkx i
Теперь покажем, как по произвольно заданному положительному числу е можно подобрать такое положительное число В, чтобы для всех значений х, отличных от 0 и удовлетворяющих неравенству е .
Чтобы при х 0 можно было воспользоваться неравенством
8, выполнялось неравенство I
sin kx
sin kx kx
достаточно, чтобы
2-, т. е. 1Л'1<^тср- Если же неравенство |Лх| справедливо, то для выполнения
sin kx kx требуемого неравенства достаточно, чтобы имело место |Axj < е, т. е.
чив через 8 меньшее из двух чисел
получаем, что при х=£0 и |х| < 811
Следовательно, обозна-
е И
мы
и вто же
E
время | х |
sin kx 4 kx
выполняется как неравенство
|kx|, так и неравенство ]Лх|<е, т. е.
имеет место неравенство.
sin kx
kx
Утверждение litnsl” —= 1 доказываем аналогично то-х ->0 “х
му, как это было сделано для утверждения lim sin-— = 1, а не пользуемся заменой kx — у, так х->0 х
как возможность замены переменных пришлось бы как то обосновать. Нельзя считать само собой разумеющейся возможность замены переменных в предельном переходе, так как этот вопрос не так прост, как может показаться на первый взгляд.
Рассмотрим такой пример:
/(*) = {
х при х =# 0,
1 при х = 0.
Очевидно, что limf(x) = 0.
С другой стороны, легко убедиться в том,что для функции £=<р (х) = x-sin —- Пт<р(х)=0.
х х ->о
Считая само собой разумеющейся возможность замены переменной, получаем lim / (<? (х)) — lim / (/)=0.
х О	t -> 0
В то же время нетрудно убедиться, что при сколь угодно малых по абсолютной величине значениях х вида , где k—целое число отличное от нуля, f I? (~т))= /(0) = 1, и, значит, число 0 не может быть пределом функции /(?(*)) при х-^0.
Мы не видим особой необходимости в использовании замены переменной при вычислении пределов функции в школьном курсе и поэтому не считаем нужным рассматривать условия, при которых такая замена возможна.
§ 4. ТЕОРЕМЫ О ПРЕДЕЛАХ
После того как познакомились с рядом примеров пределов функций при х -> а, ставится задача отыскания способов, облегчающих нахождение предела функции при х -> а. До сих пор при нахождении предела функции поступали следующим образом: каким-либо путем догадывались, какое число является, по-видимому, пределом функции в данной точке, и затем проверяли свою догадку, опираясь на определение предела функции в точке. Ясно, что в более сложных случаях догадаться, какое число является возможным пределом функции в данной точке, может оказаться затруднительным, да и проведение рассуждений, опирающихся на определение предела функции, может вызвать очень серьезные трудности.
Поэтому очень полезными могут оказаться теоремы, выражающие предел некоторой функции при х -> а через известные пределы других функций (также при х -> а).
Сообщаем, что для предела функции в точке (так же как, впрочем, и для предела функции при х -+ + со и при х -+ — оо ) имеют место теоремы, аналогичные тем теоремам о пределах, с которыми познакомились при изучении предела числовой последовательности.
Вспоминаем известные теоремы о пределе числовой последовательности, после чего формулируем основные теоремы о пределах функций.
Теорема 1. Если lim f (х) = b и Мт (х) = с, то х—а	х->а
Нт [/(дг) -|- <? (дс)] = b + с. (Сокращенная формули-х-*а
ровка: Предел суммы равен сумме пределов.)
Теорема 2. Если lim/(x) = b и к — некоторое х^а
действительное число, то lim \kf (дг)] = kb. (Сокра-х->а
щепная формулировка: постоянный множитель можно выносить за знак предела.)
Как следствие из теорем 1 и 2 немедленно получаем, что если lim f(x) = b и lim<p(x) = c, то х^а	х-*а
Ит[/(х)— ?(х)] = &— с . Действительно, lim[/(x) — х-*а	х^а
— <p(x)]=lim {/(х)4-[ — ?(х)]} = )lm/(x) + lim [( — !)• х~>а	х-^а
•<р(х)]=6 + (— 1)-с — Ь — с,
Теорема 3. Если lim/(x)=& и 11m <р (х) = с, то х^а	х-*а
Нш [/(•*)•? (х)] * Ъс. (Сокращенная формулировка:
предел произведения равен произведению пределов.)
Теорема 4. Если Пт/(х) = Ь и Нт <р (л)=с, причем х-*-а	х—а
с 0, то Нт	• (Сокращенная формулировка:
предел частного равен частному от деления пределов при условии, что предел делителя не равен нулю.) Рекомендуется обратить внимание учащихся на соотношение lim с — с (предел постоянной равен этой х -> а
постоянной), где с некоторое действительное число (lime понимается как предел при х^-а функции х^а
f (х) = с, т. е. функции, все значения которой равны с.)
Справедливость соотношения lim с —с обычно не х -г- а
вызывает сомнений у учащихся, однако интересно показать им, как оно может быть доказано на основании определения.
Пусть е — любое положительное число. Очевидно, что при /(х) = с неравенство |/(х)— с|<» справедливо при любом х. Следовательно, выбрав в качестве 8 любое положительное число, мы получаем, что, в частности, и при х^= а, удовлетворяющем неравенству |х— а К 8, справедливо неравенство |/(х) — —с | <Л.
Программа не требует доказательства теорем о пределах; однако мы считаем весьма полезным провести доказательства теорем 1 и 2.
Теорема 1 может быть доказана следующим образом. Известно, что lim f (х) = b и lim<p(x) = c. Тре-х^-а	х-+а
буется доказать, что lim {/(х) + <? (х)| = b + с.
х->а
По определению предела функции в точке нам надо доказать, что для любого наперед заданного положительного числа е можно указать такое положительное число 8, что для всех значений аргумента х, отличных от а и удовлетворяющих неравенству |х— а К8, будет выполняться неравенство | [/(*) + + ?(*)]— (& + <0|<8.
Для произвольного положительного числа е рассмотрим неравенство | [f (х) 4- ср (х)] — (Ь 4- с) | < е .
Преобразовывая левую часть неравенства, полу-чаем: | (х) + ср(х)] (Ь 4- с) | = | [/(х) —4 + [?(*) — d К !/(•*)—frl + l'pto-d.
(Учащиеся знают, что абсолютная величина суммы двух слагаемых не больше суммы абсолютных величин этих слагаемых.) Итак, чтобы выполнялось неравенство | [f(x) -|- <р(х)] — (Ь с)| < е , достаточно выполнения неравенства |/(х) — 6| + | <р (х) — с|< е . В левой части последнего неравенства стоит сумма двух слагаемых, и чтобы она была меньше е, достаточно, чтобы каждое из этих слагаемых было меньше -у- .
Так как d = lim/(x), то для положительного чис-ла-^-можно указать такое положительное число 8П что для всех х, отличных от а и удовлетворяющих неравенству ]х — а|<8ь выполняется неравенство
Так как с = lim<p(x), то для того же положитель-х-+а
£
ного числа -g- можно указать такое положительное число 82> что Для всех х, отличных от а и удовлетворяющих неравенству |х — а|<82, выполняется неравенство | <р (х) — С | <	.
Выберем меньшее из двух чисел 8Х и 82 и обозначим его через 8. Тогда для всех х, отличных от а и удовлетворяющих неравенству | х — а | < 8, будет иметь место [х —a|<8j и, значит, |Z(х) —	,
л?
в то же время 1х — а| < 82 и, значит, I <р (х) — с| <-4- •
Таким образом, для всех х, отличных от а и удовлетворяющих неравенству |х — а| < 8, выполняется неравенство |/(х)— b 4-|<р(х) — с|<е. Итак, мы доказали, что lim [/(х) + (х)J =Ь 4- с.
х-*а
Легко доказывается и теорема 2. Пусть k — некоторое действительное число.
Рассмотрим сначала случай, когда k #= 0. По определению предела функции при х -> а достаточно доказать, что для любого наперед заданного положительного числа е можно указать такое положительное число 8, что для всех значений х, отличных от а и удовлетворяющих неравенству |х —а|<8, будет выполняться неравенство |А/(х)—	Выберем
произвольное положительное число е и рассмотрим неравенство | kf (х) — kb | < е.
Преобразуя левую часть последнего неравенства, получаем | kf (х) — kb | = | k |  | f (х) — b |. Следовательно, чтобы выполнялось неравенство kf(x) — kb\<e, достаточно выполнения неравенства |k • |/(х)— Ь\<е. Так как по условию & = lim/(x), то для положитель-е	х-*а
кого числа -до 0) можно указать такое положительное число 8, что для всех х, отличных от а и удовлетворяющих неравенству |х —о|<8, выполняется и неравенство |/(х) — &|<-Дт-. Преобразуя последнее неравенство, имеем |£| -|/(х)— д|<е.
Таким образом, для всех х, отличных от а и удовлетворяющих неравенству |х — п| <8, выполняется неравенство |А| • |/(х) —&|<е или | kf(x) — kb | < е. Итак, при k =7^=0 доказано, что lim [kf(x)] = kb.
х^а
Если k — 0, то доказываемая теорема сводится к очевидному равенству lim [0./(х)] = 0. х-»- а
Проводить доказательства теорем 3 и 4 мы не рекомендуем, так как для этого пришлось бы привлечь дополнительный материал или проводить доказательство громоздким путем, что заняло бы много времени. Возможно было бы полезно в порядке упражнения провести доказательство следующей теоремы.
Если lim/(x) = 0, а функция <р(х) ограничена (т. е. х->а
существует такое положительное число М, что при всех значениях х из области определения функции ?(х)|<Л1), то lim [/(х)-<р(х)] = 0. После всего х-+а
рассмотренного ранее доказательство этой теоремы учащиеся могут провести почти самостоятельно примерно следующим образом.
Пусть е — произвольное положительное число. Рассматривается неравенство |/(х) • <р (х) | <е . Но I f (х) • <р (х) | < |/ (х) | -М. Следовательно, достаточно, чтобы выполнялось неравенство |/(х)|- Ж < е или равносильное ему неравенство | / (х) |	. Так как
lim/(x) = 0, то для наперед заданного положительно-х-+а
го числа можно подобрать такое положительное число 8, что при х=/=а и |х —а|<8 справедливо неравенство |/ (х) | < --^-или |/(х)|»Л1<е. Тогда при л^а и | х—а | < 8 имее т место ^неравенство | f (х) • <р (х) |< е.
Чтобы не увеличивать числа рассматриваемых теорем, мы не считали нужным формулировать в виде специальной теоремы утверждение, что любая функция не может иметь в одной и той же точке более одного предела. Это утверждение представляется учащимся очевидным, его можно проиллюстрировать на графиках функций. Следует сообщить, что единственность предела функции в данной точке может быть доказана на основании определения предела функции.
Вместе с тем для решения примеров на вычисление пределов функции важно обратить внимание на то, что значение предела функции при х -> а не изменится, если изменить значение функции при х=а, доопределить функцию для х=а, если она ранее не была определена при х=а, или исключить х=а из области определения функции. Это следует из того, что в определении предела функции выполнение неравенства | f (х)— 6|<е требуется только для значений х, отличных от а (и удовлетворяющих неравенству |х —а|<8). Поэтому при отыскании предела функции формулу, задающую функцию, можно тождественно преобразовывать, считая х п.
Решать много примеров на непосредственное применение теорем о пределах не представляет интереса. Учащиеся вскоре замечают, что дело сводится к подстановке в формулу, задающую функции, соответствующего значения аргумента. Необходимо указать, что это обстоятельству не случайно и что оно связано с так называемой непрерывностью функций, о которой вскоре будет идти речь.
Некоторое оживление вызывает решение примеров, в которых, прежде чем применить теоремы о пределах, приходится производить тождественные преобразования формулы, задающей функцию, или, как говорят, примеров «на раскрытие неопределенностей». Особенно увлекаться этими примерами не следует, так как они мало служат главной задаче, пояснения сущности понятия предела функции, однако некоторое число таких примеров необходимо решить, чтобы научить сознательно применять теоремы о пределах. Разумеется, если позволяет время, можно использовать решение их как упражнения, связанные с тождественными преобразованиями.
Приведем решение нескольких примеров.
j^3 _L Зх
1. Найти lim R а . В нашем случае непс-х -* о *
средственно использовать теорему о пределе частного нельзя, так как предел делителя равен нулю. Функция не определена при х—0.
Считая х ф 0, делим числитель и знаменатель на х.
_L 3
Получаем новую функцию t , значения которой во всех точках (кроме х = 0) совпадают со значениями данной функции. Так как при определении предела функции при х 0 ее значение в точке 0 не учитывается, то
lim
— lim
2. lim
= Нт
= lim
Рассуждения такие же, как и в предыдущем примере.
lim
lim
COS X
sinx
= lim------
lim —— r 0 cos x
lim cos x
л t. sin 5x
4. hm ——
x 0
= lim
x -> 0
sin 5x
= 5- lim ^=54 = 5. a > 0 OX
§ 5. ПОНЯТИЕ Q НЕПРЕРЫВНОСТИ ФУНКЦИИ
Ныне действующая программа по математике для 'средней школы не предусматривает ознакомления с понятием непрерывности.
Однако введение в курс математики средней школы шонятия предела функции позволяет без особых затруднений хотя бы в общих чертах познакомить с этим важнейшим математическим понятием.
При вычислении пределов функций с йспользовани-»ем теорем о пределах обращаем внимание на то, что в ;ряде случаев предел функции f(x) при х -> а совпадает (СО значением функции в той же точке.
Ясно, что для решения задачи вычисления пределов функций было бы очень полезно знать, в каких случаях мы можем считать, что пределом функции служит значение ее в соответствующей точке. Уже при решении примеров на вычисление пределов было указано, что «совпадайие искомого предела функции при х->а со :значеййем функции при х—а связано с понятием не-»прШйявности функции.
'Что же такое непрерывность?
Прежде чем давать определение непрерывности, обращаем внимание на ряд знакомых графиков функций, используя ранее заготовленные чертежи-плакаты.
Отметим, что все рассматриваемые графики не представляют собой одну сплошную линию, а распадаются на отдельные ветви. Возникает вопрос: с чем связана эта особенность данных графиков?
Рассмотрим подробнее каждый из представленных графиков. График функции у= ——2 состоит из двух частей (ветвей), одна из которых содержит точки с положительными абсциссами, а другая — точки с отрицательными абсциссами (см. рис. 17).
Можно сказать в этом случае, что график распался, «претерпел разрыва, при переходе аргумента через значение х — 0.
В то же время функция у =-^- — 2 не определена в точке 0 и не имеет предела при х -> 0. Аналогичное положение мы наблюдаем при рассмотрении графика функции у= 1 ”--*--(см. рис, 20), а также графиков
функций у— (см- Рис- и (х— I)*- (см- Рис- 28)
при переходе аргумента соответственно через значения х=2 и х=1. В обоих случаях функции не определены и не имеют пределов в соответствующих точках.
„ .	,	[ хя при х < 2, .	опч
График функции у= { г	(см. рис. 29)
( х при х > 2
также распадается на две ветви при переходе аргумента через значение х = 2. Однако в этом случае при х = 2 функция определена и разрыв графика, по-видимому, связан с тем, что не существует предела функции при х -> 2.
Аналогичный пример дает график функции при х ф О,
у = I х	(см. рис. 33).
О при х = О
У=
IXf
7 при х*0
О при х-0
Рис. 33
Рассмотрение графиков у= г~ (см- Рис- 25) и у= —si” < - (см. рис. 32) показывает, что график может претерпевать- разрыв при переходе аргумента через значение х- а и в том случае, когда существует предел рассматриваемой функции при х а, но функция не определена при х — а. Наконец, как показывает пример
функции у=
~ 1 к ’(см. рис. 26), график может
1 при X = 1
претерпевать разрыв при переходе аргумента через значение х = а и в том случае, когда функция определена при х=а и существует предел функции при ха, если значение функции не совпадает с этим пределом.
В рассматриваемых случаях график функции претерпевал разрыв при переходе аргумента через определенное значение. Из наблюдений заключают, что при переходе аргумента через другие значения график не претерпевает разрыва. При этом нетрудно показать, опираясь на теоремы о пределах, что для любых значений аргумента, кроме выделенных в каждом случае, значение предела функции совпадает со значением самой функции в соответствующей точке. Естественно указанное свойство, связанное с отсутствием разрыва графика, назвать непрерывностью функции в соответствующей
точке.
Таким образом, может быть введено следующее оп
ределение.
Функция y~f(x) называется непрерывной в точке а, если она определена при х — а и f(a)=\imf (х).
х^а
Вспоминая, что lira sin х=0 и sin 0=0, мы можем ска-х-*а
зать теперь, что функция у = sinx непрерывна в точке 0. Это можно проиллюстрировать и на графике функции у = sin х. Глядя на график, можно заключить, что, по-видимому, функция у = sinx непрерывна и при зна
чениях х, отличных от нуля.
Нетрудно доказать, что это действительно так. Нам нужно показать, что lim sin х = sin а, где а — лю-х^а
бое действительное число. Выберем произвольное no-
ложительное sinx — sinn]
sin х—sin a | = [2 cos — Итак, ]sinx — sinn|< честве В само число е
число е и рассмотрим неравенство С е. Нетрудно видеть, что при х а
4- а . х — al о - х—а ।	.
t-sin—1<2-1. — =|х-а|.
|х — п| и, значит, выбрав в ка-, мы получаем, что при хфа и удовлетворяющих неравенству |х — п| < В выполняется и неравенство |sinx—sin а
sin а I <
е.
Может возникнуть вопрос, нужно ли было проводить доказательство, раз и так ясно, что график функции у == sin х представляет собой сплошную линию (т. е. не претерпевает разрывов ни в каких точках). Здесь мож
но пояснить, что раньше при построении графика мы соединяли найденные точки графика сплошной линией, не задумываясь над тем, почему мы имеем право это делать. Именно понятие непрерывности даег возможность обосновать правильность построения графика таким путем.
Кроме соотношения limsinx = 0, ранее было до-казано и соотношение lim cosx=il, т. е непрерыв-ПОсть функции #=cosx в точке х = 0 (cos 0= 1). Непрерывность функции y = cosx в любой точке может быть доказана учащимися в порядке упражнения.
Заметим, что функция, непрерывная в каждой точке ее области определения, называется непрерывной функцией и что все известные нам основные элементарные функции (степенная функция, показательная функция, логарифмическая функция, тригонометрические и обратные тригонометрические функции) являются непрерывными функциями. Поэтому при вычислении пределов этих функций в тех точках, где они определены, мы можем заменить предел функции ее значением в соответствующей точке.
Для того чтобы вычислять пределы функций, которые могут быть построены из основных элементарных функций с помощью четырех арифметических, действий, пользуются теоремами о пределах.
Пользуясь теоремами о пределах, легко показать, что сумма, разность и произведение функций, непрерывных в точке а, есть функции, также непрерывные в точке а, и что частное от деления непрерывных в точке а функций есть функция, непрерывная в точке а, при условии, что значение делителя в точке а отлично от нуля.
При наличии времени было бы очень желательно познакомить школьников с некоторыми свойствами непрерывных функций.
Мы имеем в виду следующие теоремы.
Теорема 1. (О непрерывной функции, принимающей на концах сегмента значения разных знаков.) Если функция f(x) непрерывна на некотором сегменте [#♦ ft] и принимает на концах его значения разных знаков (т. е. f (a)nf(b)—числа разных знаков), то внутри сегмента
найдется по крайней мере одна такая точка ct в которой значение функции — 0 (т. е./(с)=0).
Теорема 2. (О промежуточном значении непрерывной функции.)
Если функция f(x) непрерывна на сегменте [а, &J и у0— какое-либо число, заключенное между f(a) и f(b) (т. е. /(а)<Уо</(&) ИЛИ	то внутри
сегмента [а, й] найдется по крайней мере одна такая точка с, что f(c)=y0.
Теорема 3. (Об ограниченности непрерывной функции.) Если функция f(x), определенная на сегменте [а, &], непрерывна, то она ограничена.
Теорема 4. (О наибольшем и наименьшем значении непрерывной функции.) Если функция f(x)9 определенная на сегменте [а9&], непрерывна, то среди значений ее обязательно имеются наибольшее и наименьшее.
Эти теоремы приходится сообщать без доказательства, так как в нашем распоряжении нет нужных средств для проведения таких доказательств. (Только 2-я теорема легко может быть доказана на основании первой.)
Мы знакомили учащихся с этими теоремами, правда несколько позднее, широко используя наглядные иллюстрации и пояснения.
Доказательства указанных выше теорем при наличии интереса у учеников могут быть проведены на внеклассных занятиях. При этом предварительно следует познакомить с принципом стягивающихся сегментов, с теоремой Больцано — Вейерштрасса о выборе сходящейся подпоследовательности, с понятиями верхней и нижней грани ограниченного множества, существование которых легко доказывается на основании принципа стягивающихся сегментов, а также доказать, что если lim f(x) = b9 то из условия lim хп == а, где хп — зна-х-+а	л—f-°o
чения аргумента, отличные от а, следует, что lim/(*„) = &.
Раздел II. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Понятие производной — одно из важнейших математических понятий, используемых в физике и в технике, и необходимость ознакомления с ним учащихся не вызывает сомнений. Помимо прекрасной иллюстрации практического применения математики, оно дает богатейшую возможность показать, как возникшее в связи с потребностями практики математическое понятие начинает играть важную роль в развитии математической теории и затем оказывается приложимым к решению задач, на первый взгляд далеких от тех, которые первоначально привели к возникновению этого понятия.
Изучение темы «Производная и ее применение» в средней школе очень тесно связано с изучением темы «Функции и пределы». Понятие скорости прямолинейного движения и задача вычисления этой скорости, используемая как пример задачи, приводящей к понятию производной, вначале рассматриваются как иллюстрация практического использования понятия предела функции. Само определение производной основано на понятии предела функции.
Исследование функций с использованием производной проводится по той же схеме, что и в теме «Функции и пределы».
Метод отыскания точек максимума и минимума функции и ее промежутков монотонности с помощью производной, значительно облегчающий исследование функций, легко усваивается. Успешное решение задач на исследование функций и построение их графиков при изучении темы «Производная и ее применение» обеспечивается достаточным опытом решения таких задач в теме «Функции и пределы».
При изучении темы «Производная и ее применение к исследованию функций» серьезное внимание уделяется различным случаям приложения понятия производной.
Кроме применения производной к вычислению скорости и ускорения прямолинейного движения рассматриваются и другие примеры использования понятия производной для определения и вычисления скорости протекания тех или иных процессов из различных областей науки и техники (скорость растворения вещества, протекания химической реакции, изменения температуры, изменения силы тока и т. п.).
Наряду с исследованием функций с помощью производных при построении их графиков решаются задачи с практическим содержанием, в которых максимум или минимум функции, обнаруженные с помощью производной, используются для нахождения наибольшего или наименьшего значения функции. Эти задачи вызывают большой интерес. Формула бинома Ньютона дается как еще один пример использования понятия производной в развитии математической теории. Учащиеся знакомятся с практическим применением этой формулы, решая задачи на приближенное вычисление натуральных степеней некоторых чисел.
Как уже говорилось выше, понятие производной вводится в связи с рассмотрением скорости (точнее, мгновенной скорости) неравномерного прямолинейного движения. Исходя из нашего опыта, мы считаем более целесообразным несколько отложить рассмотрение геометрического истолкования производной, так как понятие касательной как предельного положения секущей также является новым для учащихся.
Рассмотрение геометрического смысла производной проходит успешнее после того, как учащиеся несколько освоятся с самим понятием производной. В то же время геометрическое истолкование производной, как углового коэффициента касательной к графику функции в соответствующей точке, не так уж важно при выводе формул для вычисления производных, но играет очень большую роль при ознакомлении с методами исследования функций с помощью производной.
В соответствии со всем этим в предлагаемом изложении изучение темы «Производная и ее применение к исследованию функций» разбивается на два этапа. Пер-
вый из них посвящается введению понятия производной, способам ее вычисления и ее приложениям к решению различных задач, связанных с вычислением скорости изменения функции по отношению к изменению аргумента. Здесь рассматриваются следующие вопросы.
Скорость равномерного прямолинейного движения и понятие о мгновенной скорости неравномерного движения. Приращение аргумента и приращение функции. Определение производной. Примеры непосредственного вычисления производной на основании ее определения. Вынесение постоянного множителя за знак производной. Производная суммы функций. Примеры приложения производной в физике, химии и т. п. Теорема о приращении функции, имеющей производную. Непрерывность функции, имеющей производную. Производная степенной функции. Производная обратной функции. Производная частного двух функций. Производные функций у = sin х, у — cos х, у = tg х, у — ctgx. Понятие сложной ' функции. Производная сложной функции. Ускорение. Понятие о второй производной.
Задачи на применение производной решаются, разумеется, на протяжении всего изучения указанных выше вопросов.
Второй этап изучения темы «Производная и ее применение к исследованию функций», в основном посвященный различным случаям приложения понятия производной, содержит следующие вопросы:
Геометрический смысл производной. Касательная. Признаки возрастания и убывания функций. Нахождение максимума и минимума с помощью производной. Построение графиков функций с использованием производной. Графическое решение уравнений. Формула бинома Ньютона и ее применение к приближенным вычислениям.
При изучении признаков возрастания и убывания функции в большой мере используется геометрическая иллюстрация. В частности, достаточные признаки возрастания и убывания функций формулируются без доказательства на основе рассмотрения ряда примеров с привлечением графиков функций. К геометрическим иллюстрациям обращаются и во время вывода необходимого признака существования экстремума функции в данной точке и достаточных признаков существования 74
максимума и минимума, которые даются с доказательством.
Как это видно из вышесказанного, производная и ее [Применение даются в предлагаемом изложении нескользко шире, чем это предусматривалось программой средней школы, примерно в том же объеме, как это предусматривает проект новой программы. Мы убеждены, что это вполне посильно для учеников массовой школы. Более того, мы считали бы целесообразным еще несколько расширить объем материала, изучаемого школьниками, включив дополнительно теорему Ролля, теорему Лагранжа, доказательство с помощью теоремы Лагранжа достаточных признаков постоянства, возрастания и убывания функции, формулы для производной показательной и логарифмической функций, хотя бы без доказательства. Все это отняло бы не очень много лишнего времени и труда и в то же время сделало бы изложение более полным, более целостным и более интересным.
Глава 4. ПОНЯТИЕ ПРОИЗВОДНОЙ. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ.
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К РЕШЕНИЮ ФИЗИЧЕСКИХ И ДРУГИХ ЗАДАЧ
Выражение скорости прямолинейного движения как производной пути по времени сразу же выдвигает проблему вычисления производных известных функций. В связи с этим и доказываются теоремы о производной суммы, разности, произведения, частного, обратной функции и выводятся формулы для вычисления производных степенной функции и тригонометрических функций, а также вводится понятие сложной функции и доказывается теорема, дающая способ вычисления ее производной.
Как уже говорилось, задачи на применение производной решаются на протяжении всего изучения в школе рассматриваемого раздела. Понятие производной и основные способы ее вычисления можно рассмотреть в школе за 16—17 уроков.
§ 1. СКОРОСТЬ ПРЯМОЛИНЕЙНОГО движений. ПОНЯТИЕ ПРОИЗВОДНОЙ
Уже указывалось, что понятие скорости неравномерного движения дается прежде всего как одна из иллюстраций применения понятия предела функции.
Определению скорости неравномерного движения и введению понятия производной отводится один урок, полностью посвященный изложению нового материала.
Напомнив, что понятие предела функции было введено в связи с задачей изучения свойств функций и построения их графиков, переходят к одному из важнейших применений понятия предела функции в физике, а именно к использованию этого понятия для уточнения определения скорости прямолинейного движения.
В курсе физики понятие скорости было введено прежде всего для случая простейшего прямолинейного движения, для так называемого равномерного прямолинейного движения.
В этом случае в равные промежутки времени тело проходит одинаковые расстояния, и отношение пройденного пути ко времени, за которое этот путь пройден, не зависит от выбора отрезка времени. Это постоянное отношение пройденного пути к затраченному времени и называется скоростью данного равномерного прямолинейного движения.
Но, очевидно, не всякое прямолинейное движение является равномерным. В курсе физики ознакомились и с другими видами прямолинейного движения, например равноускоренным движением, частным случаем которого является свободное падение. Очевидно, что при неравномерном движении нельзя определить скорость движения как отношение пути ко времени, так как это отношение различно для различных промежутков времени.
Для характеристики движения за некоторый промежуток времени используется понятие средней скорости движения за данный промежуток времени. Средней скоростью за данный промежуток времени называется отношение пути, пройденного за этот промежуток времени, к величине этого промежутка.
Очевидно, что средняя скорость не дает полного представления о характере движения, так как в различ-76
ные периоды в течение данного промежутка тело могло двигаться то быстрее, то медленнее.
\ Возникает необходимость уточнить понятие скорости для неравномерного прямолинейного движения.
\ В физике, как известно, вводится понятие мгновенной скорости тела при неравномерном движении, как такой скорости, с которой двигалось бы тело, если бы начиная с данного момента времени его движение стало равномерным. Это определение в курсе физики иллюстрируется на опыте. Там же указывается, что средняя скорость за промежуток времени, начинающийся с данного момента, тем ближе к мгновенной скорости в данный момент времени, чем меньше рассматриваемый промежуток времени.
Однако приведенное определение мгновений скорости не указывает, как вычислить эту скорость в каждый момент времени при неравномерном движении даже и в том случае, если для каждого момента времени известен путь, пройденный от начала движения.
Понятие предела функции и позволяет ввести такое определение мгновенной скорости неравномерного движения, которое, с одной стороны, согласуется с понятием мгновенной скорости, указанным выше (как это подтверждено многолетней практикой), и, с другой стороны, позволяет вычислить скорость в любой момент времени, если известен закон движения, т. е. известна функция, которая каждому моменту времени t ставит в соответствие путь, пройденный телом от начала движения до данного момента.
Чтобы ввести определение мгновенной скорости (или скорости в данный момент времени /о), обозначим величину промежутка времени, начинающегося с данного момента to через Д/.
Как уже говорилось выше, из физики известно, что средняя скорость за промежуток времени Д/ тем ближе к мгновенной скорости в момент /0» чем меньше промежуток Д/. Поэтому естественно ввести следующее определение. Мгновенной скоростью прямолинейного движения тела в данный момент времени /0 называется предел, к которому стремится средняя скорость за промежуток времени А/, начинающийся с данного момента, при условии, что Д/ стремится к нулю; zr0 = lim яср.
Д/->0
Если известна зависимость vCJ, от Д4 то это определение позволяет вычислить Проиллюстрируем этб определение на примере такого хорошо знакомого дви/ жения, как свободное падение.
Как известно, путь, пройденный свободно падающи^г телом от начала падения, вычисляется по формуле crf2	»
о = —, где t — время, прошедшее от начала падения.
Скорость в каждый момент времени вычисляется по формуле v — gt.
Рассмотрим момент времени после пяти секунд от начала падения; tQ = 5 сек. Соответствующая мгновенная скорость v0= см/сек. Будем вычислять среднюю скорость за различные промежутки времени А/, начинающиеся с данного момента.
Для удобства введем следующие обозначения. Путь, пройденный за время А/, обозначим через AS, а /0+А/— через t. Очевидно, что AS можно найти как разность между путем S, пройденным за время /, и путем So, пройденным за время tQ. По формуле получаем:
2
S = см, So = —g— CM ~ 12,5g см,
AS =	_ 12,5g) cm.
Составим следующую таблицу (желательно заготовить ее заранее).
/0 = 5 сек, So — 12,5# см.
Д/ (в сек)	t (в сек)	S (в см)	AS (в cm)	Уср==^-(вслМек)
3	8	32 g	19,5 g	6,5 g
2	7	24,5 g	12g	6g
1	6	18g	5,5 g	5,5 g
0,5	5,5	15,125 g	2,625 g	5,25 g
0,1	5,1	13,005g	0,505 g	5,05 g
Мы видим, что значения оср в данной таблице дей-вительно тем меньше отличаются от = 5g , м меньше выбран промежуток времени ДА
Найдем limtu:
ДГ -ь о
g(4+AQ2
_ AS _ S —So _	2	2	_
~ M ~
g( 4 +	+ A*2 — to) gM (24 + AZ)
=	2Д?	2ДТ ~
= -f- (2/0 + AO;
v0 = limt>cp = lim -f- (2/0 + AZ) — -f- lim(2/0 + A/) —
Ы -Q Д/ч-O z	Z Д/ 0
2 ‘2^0 — g'o
Мы получили значение мгновенной скорости, совпадающее с ранее известным значением.
Пользуясь указанным выше определением мгновенной скорости, мы можем вычислить мгновенную скорость для любого прямолинейного движения, для которого известна функция S = 7(0» выражающая зависимость пути S от времени t:
Vo = lim ц.р = lim где AS = S — So = f(t) - f(tQ) =
А/ - 0 Д/ - 0
=f(to + до - fGo).
Д/ обычно называют приращением времени, AS — соответствующим приращением пути.
При вычислении мгновенной скорости мы рассматриваем уср как функцию, аргументом которой служит ДА и ищем предел этой функции при Д/->0. Таким образом, для данной функции S ==/(/) мы получаем новую функцию гср = (функцию аргумента А/) и ищем предел этой функции при Д/ 0.
Перед нами возникает задача найти наиболее рациональные способы вычисления указанного предела для различного вида зависимостей пути от времени.
Мы будем решать эту задачу в общем виде.
Пусть дана произвольная функция у = f(x). а х04-некоторое значение этой функции. Разность между любым значением аргумента х и данным значением х0 назовем приращением аргумента и обозначим через Цх:
х — х0 = А*; х, = х0 + А*-
Назовем приращением функции, соответствующим данному приращению Ах, разность /(х0 + Дх) —f(x0). Обозначим это приращение функции через Ду:
А«/ = f(*o + Ах) —f(x0).
Очевидно, что Ду является функцией Дх, т. е. каждому значению Ах соответствует вполне определенное значение Ау. В рассмотренном выше примере роль Дх выполняло АЛ а роль Ду играло ДХ. Нас интересует, следовательно, 11m—. Этот предел получил особое на-звание производной функции f(x) в точке Хо и обозначается через /' (х0).
Определение. Производной функции f(x) в точке лг0 называется предел отношения приращения функции к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю.
Г (х0) = 11m
АХ 0
Согласно этому определению скорость прямолинейного движения в момент времени t0 есть производная пути по времени, т. е. VQ=f'(to).
После введения понятия производной рассматриваются несколько примеров вычисления производных.
1. Пусть y = f(x) — х2. Найдем производную в точке х0:
Ду =• / (*о 4* Д*)	/(хо) = (-«о + М2,— X2Q= 2х0Дх + Дх2*;
Ду-------2х0Дх + Дх».. = 2
Дх	Дх	и - ’
f'(*o) = lim -g- = lim (2х0 + Дх) = 2х0.
Ах ► О *±х Дх -> О
Так как точка х0 выбиралась произвольно, то эти же рассуждения точно так же проводятся для любой точки х и мы можем записать f'(x)=2x, где х —произ-
* Дх* означает (Дх)2, Дх8 означает (Дх)8 и т. п.
вольное значение аргумента данной функции// = f(x) — 4 х2.
\ 2. Пусть у= f(x) = х3. Найдем производную в точке хй:
ку = (х0 + Дх)8 —Хд = Зх* Дх + Зх0Дх2 + Дх3’>
f' (х0) = lim = lim (Зх2 + Зх0 Д х -|- Д х2) = Зх2 .
Ал-0 0	0
Снова можно записать f'(x) = Зх2.
Для сокращения записи можно сразу в рассуждениях вместо х0 писать х.
3.	У = f (х) = х. Найдем f' (х): Д = (х -|- Д х) — х = Д х ;
f'(x) = lim 4т = lim 1 - 1 .
Дл -► 0 u л	Дх -> о
4.	У = /(х) = с (с — постоянная величина). Найдем Г(х):
Ьу = f (х -|- Д х) — f (х) = с — с = 0;
Лу. =	= о-
Д х Д х ’
f (х) = 11m 4т 11т 0 = 0 •
Длг -> 0 х Д.г О
В классе и дома ученики рассматривают еще несколько случаев вычисления производной непосредственно на основе ее определения. Например:
1.	у = /(х) — 2х.	Найти f'(x).
2.	у — f (x) ~ —х2 + 3.	Найти Г(х).
3.	у = ?(х) =х2 + 3.	Найти f' (х).
После выполнения ряда упражнений на вычисление производных учитель выписывает на классной доске следующие ранее полученные результаты:
у = /(х)=с;	ГМ=0;
У = 1(х)=х-,	f(x) = l;
y = f(x)=x2\	f(x)=2x;
У = f (x) = x3\	f'(x) = 3xJ
Обращаем внимание на то, что здесь были найдены не только конкретные значения производных в дан-
в Заказ ЗЦ
81
ной точке х0, но и получены общие формулы, позволяющие вычислить значение производной в любой точке области определения данных функций.	/
Для удобства в формулах, где нет указания на конкретную точку, вместо /' (х) можно писать у'.	!
Полученные формулы могут быть переписаны таЮ
У =	G	/=0;
у =	х;	у'=\\
у =	х2;	г/7—2х;
у =	х3;	у' = 3х2.
Эти формулы понадобятся в дальнейшем, и потому их надо записать и запомнить.
§ 2. ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ПРОИЗВОДНЫЕ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Решение примеров на вычисление производной на основании ее определения в конечном итоге приводит к мысли о желательности нахождения каких-то более рациональных приемов вычисления производных.
С подобной задачей учащиеся уже сталкивались при вычислении пределов числовых последовательностей и пределов функций. Первостепенное значение при вычислении пределов имеют теоремы о пределах, позволяющие, зная пределы некоторых функций, находить пределы других более сложных функций, полученных из них с помощью сложения, вычитания, умножения и деления. Возникает естественная проблема получить аналогичные теоремы и для прозводных. Некоторые догадки о возможности существования таких теорем возникают уже в процессе решения примеров, подобных рассмотренным выше.
Например, для функции у = х2 + х получают производную у'=2х+1, равную сумме производных функций у = х2 и у = х; для функции у = х3 + х2 получают производную у'=3х2+2х, равную сумме производных функций у = х3 и у = х2; для функции у = 3 х2 получается производная у'=6х, равная произведению постоянного множителя 3 на производную функции у = х2 и т. п.
Замечаем, что возможность вынесения постоянного множителя за знак предела и теорема о пределе суммы функций как будто переносятся и на производные. Ставится задача сформулировать и доказать соответствующие теоремы для производных.
Теорема 1. Если у = / (х) =£‘<р'(х), где с — некоторое число, а функция и= <р(х) в точке х0 имеет производи ную ?'(х0), то f'(x0) = с-у' (х0).
^Короче: постоянный множитель можно выносить за знак производной.
Доказательство:
= Пт
дх о
/(хр + Дх) —f(x0) Д х
Г (*о) = Ит
Дх -► О
= Ит
Д.г О
Ф(Х(,+Ах)—<у(х0) Дх
с- Пт
Дх О
= с-<?' (*<>)•
После доказательства примеров.
теоремы решается несколько
#'=5-2х=10х;
/=_3-3х2 = —9х2;
Теорема 2. Если у = f (х) = ср (х) + ф (х), причем функции и = <? (х) и v = ф (х) в точке х0 имеют производные соответственно равные ср' (х0)
и у (х0), то
Короче: производная суммы функций производных этих функций.
Доказательство:
= Нт Az = 11ш /(*.+**)•
равна сумме
lim
= lim
Дх -* о
Av
Легко доказать соответствующую теорему для случая любого числа слагаемых. Здесь можно применить метод математической индукции. (Желающим можно предложить провести это доказательство самостоя* тельно.)
Теорема 2-а. Если у = f (х) = (х) + <?2 (•*) + .. .4-+ <?„ (х), причем функции иг = (х), и2 = <?2 (х).
~ lim
к и , Av
Д и о А х
ип = <с„ (л:) в точке Jt0 имеют производные, соответственно равные (х0),	(х„)(х0), то /'(*о)/=
= ?' (*о) + ?' (*о) +	(*о) .	!
Краткая формулировка1 та же, что и в предыдущей теореме: производная суммы функций равна сумме производных этих функций.
При п=2 утверждение теоремы 2-а сводится к утверждению теоремы 2 и, следовательно, справедливо.
Допустим, что теорема верна для k слагаемых, и докажем, что в таком случае она верна и для (k + 1) слагаемых.
Пусть t/=f(x)=<p1(x) + ®2(x) + ... + т*(•«)+?* +1(*) и функции = <pj (х), и2 = <р2 (х), ... , «* = <?* (х), «4 + 1 ~ <р* +1 (х) в точке х0 имеют производные <р' (х0), ?' (*о), • • • >	(*о) >	+ 1 (*о) • Рассмотрим функцию
v = ф (х) = <р1 (х) -|-	(х)	... +	(х). Тогда согласно
индуктивному предположению ф' (х0) = <р' (х0)	<р(х0)+
+ •• + ?* (х9). С другой стороны, у = f (х) = ф*(х) + + ?*+1W и по теореме 2 f (х0) = ф'(х0) + ©*+, (х0).
Итак, f (х0) =	(х0) 4- <р' (х0) + ... + ?' (х0) +
+ сР*-|-1 (хо) •
Таким образом, утверждение теоремы справедливо при п == 2, и из справедливости его при п — k вытекает справедливость его при п = k + 1.
Согласно принципу математической индукции это означает, что теорема верна при любом п >2, т. е. для суммы любого числа слагаемых. Доказанные теоремы и выписанные выше формулы позволяют находить производную любого многочлена степени не выше третьей. В классе и дома учащиеся решают соответствующие примеры и задачи на применение производной, в которых рассматриваемые величины представляют собой функции, заданные с помощью многочленов не выше третьей степени.
Следует обратить внимание на то, что для нахождения искомого значения производной при некотором значении аргумента удобно получить сначала общую формулу, а затем подставить данное значение аргумента.
• . 11
Например: у = f(x) = —х3 +-=- х 4- -5-. Найти зна-Z	о
чение производной в точке х = — 2,5:
^ = rw = -3x3+4;
г ( - 2,5) = - 3( — 2,5)2 + 4 = - 18,25.
Чтобы иметь возможность вычислять производные многочленов любой степени, надо научиться находить производные функций у = хп при любом натуральном и.
Можно было бы получить соответствующую формулу, пользуясь определением производной (применяя, например, известную формулу деления разности п-х степеней на разность первых степеней тех же чисел), но проще воспользоваться теоремой о производной произведения функций.
Переходим к рассмотрению задачи нахождения производной произведения двух функций.
Попытаемся распространить на производные известную теорему о пределе произведения функций.
Простой пример показывает, что для производных аналогичная теорема неверна. Например: х3 = х2 • х. В то же время для i/==x3, у' = 3х2, для и—х2, и'= = 2х и для и=х, v'=l, Зх2=^2х-1, т. е. уже в данном случае производная произведения функций не совпадает с произведением производных этих функций.
Здесь уместно обратить внимание учащихся на то, что аналогия — очень хороший способ, чтобы натолкнуть на мысль о наличии свойства или соотношения, но она всегда нуждается в проверке.
Прежде чем вывести формулу для вычисления производной произведения функций, необходимо установить одно очень важное свойство функций, имеющих производные.
Лемма. (О приращении функции, имеющей производную.) Если функция y=f(x) имеет в точке х0 производную	то lim А у = 0 (где Д у — приращение
Дх-*-0
функции f(x), соответствующее приращению аргумента Ах в точке х0/
Доказательство:	j
»
ИтДу = limf-4^7 • Д-И = Нт-гг ИтДх = /'(хо)-О = О
Дх-*о Дх-*о\ ах /	Дх-^0	Ал->0
Доказанная лемма позволяет установить связь между понятием производной и понятием непрерывности функции.
Утверждение НтДу==0 в соответствии с опрсдс-ДХ-0
лением предела функции в точке означает, что для любого наперед заданного положительного числа в можно указать такое положительное число б, что при Дх^= О, удовлетворяющем неравенству | Дх—0| < В, выполняется неравенство | Ду —0| < е . (Очевидно, что при Дх = 0 Ду также равно нулю, т. е. неравенство | Д у — 01 < е выполняется и при Дх = 0.)
Учитывая, что Дх = х — х0, а Ду =/(х)—f(x0), можно утверждать, что условие limДу = 0 означает,
Дх-»-0
что для любого наперед заданного положительного числа 8 можно указать такое положительное число б, что из неравенства | х — х01 < 6 следует всегда неравен-ство |/(х) —f(x0)| <е, т. е. ЧТО lim/(x) = f(x0), х-+х0
Таким образом, условие lim А у = 0, по сути дела, Дх-*0
выражает непрерывность функции в точке Хо (иногда это условие берется в качестве определения непрерывности функции в точке х0).
Итак, согласно доказанной лемме, если функция fix) имеет в данной точке хй производную, то она непрерывна в этой точке.
Доказав лемму, переходим к производной произведения функций.
Теорема 3. Если у = fix) ~ у(х) • ф (х), причем функции и — (х) и v = ф (х) в точке х0 имеют производные, соответственно равные <р'(х0) и Ф'(хо)> то f (**о) = ? (-^о) ’ Ф (-^о) 4" ? (*0)  Ф (-^о)-
Другими словами: производная произведения двух функций равна производной первой функции, умноженной на значение второй функции, плюс значение первой функции, умноженное на производную второй функции.
Выразим Ду через Ди и Дц.
Для краткости вместо <р(х0), Ф(х0) и f(x0) будем писать соответственно «0, и0 и у0. Получаем:
Лх<>) ~ ?(Хо) 4* (х0) ~	/(х# 4“ &х) = f	&У=Уо~{~&Уt
<р (х0 4- Дх) = <р (х0) + Ди = «0 4- Ди;
| (х0 + Дх) = ф(х0) + До = р0 + Ду.
Отсюда by = f (х0 4- Дх) — f (х0) =
— (йо + ^и) • (уо+Д'1') ~ uovo = Auvo 3" uo^v + д« • Ду;
Ду Ди . До , Ди *
д7=д7-^ + “о--д7+ дГ-Ди’ откУда
lim = lim -4^- • у0 +мо lim ~л~' (так как lim Ду=0)-
Дх-0 А*	дх—о Д* 0	0	ДХ-0
Итак, f\x0) = ®' (х0) • <|> (х0) 4- ? (х0)<|/ (х0).
Для удобства запоминания можно пользоваться формулой у' — u'v 4- иг/ •
Примеры.
1.	у — х'. Найти у'.
1-й способ. Представим у = х2х2, тогда у' = 2х-х2 4- х2-2х = 4х8.
2-й способ. Представим у = х-х3, тогда у' = 1 • х3 4- х • Зх2 = 4х3.
2.	у = х®. Найти у'.
Представим у = х4-х, тогда у' = 4х3-х 4- -к4 -1 — 5х4.
Или иначе: y = xs-x2; у' — Зх2• х24-х3• 2х — 5х4,
3.	у = (х4 4- П (л® 4- Зх2 4- 2х);
у' = 4х3 (х® 4- Зх2 4- 2х) 4* (х4 4-1) (5х4 4~ 6х 4- 2) =
= 4х8 4* 12х® 4- Зх4 4- 5х8 4- 6х® -|- 2Х4 4- 5х4 4- 6х 4- 2 =
= 9х8 4- 18х® 4- 15х4 4- 6х 4- 2.
Применяя доказанную теорему о производной произведения, легко установить формулу для производной функции у = х " (и — натуральное число). Предварительно заготавливаются на доске или на чертежё-пла-
кате следующие ранее полученные формулы для вычисления производных:
1. у =
2.	у = х2;
3.	у = х3;
4.	у = х4;
5.	у = х5;
Замечаем закономерность в записанных формулах. Возникает предположение, что при любом натуральном показателе степени и формула для вычисления производной функции у — хп имеет такой же вид, т. е. у' = пхп~1. Как ее доказать? Очевидно, следует применить метод математической индукции.
I. Формула справедлива при п = 1.
Действительно, при п=1 имеем для у=х, у'=19 т. е. у'= Ьх°.
II. Допустим, что формула справедлива для некоторого натурального числа k, т. е. для у — xk, ,у' = kxk~} Докажем, что в таком случае формула будет справедлива и для числа k + 1, т. е. для у = х^1 у' = (k + 1)х* .
Для нахождения производной функции у = xfe+I воспользуемся формулой для производной произведения.
Имеем: у = xfe + i = xft-x,]
yf = kxk -1 x + V* 1 = kxk + xk = (k + 1) xk.
Итак, формула у' = пхп ~ 1 для функции у = хп справедлива при любом натуральном значении п.
Зная формулы для вычисления производной функции у = х п , мы, очевидно, можем вычислять производные любого многочлена, пользуясь теоремами 1 и 2.
Например: у ™ 5х10 — 12х7 + Зх2 — 2х + 1;
у'=5«Юх* — 12 • 7х6 + 3 2х — 2 • 1 = 50х9 — 84х6 + 6х—2.
Мы знаем , что функция у = у х является обратной для функции у=хп( в случае четного показателя степени разумеется, определенной на множестве неотрицательных чисел).
Возникает вопрос: нельзя ли воспользоваться этим обстоятельством, чтобы получить формулу для вычисле-88
НИЯ Производной функции у=р<ЛХ (или, что то же 1
самое, степенной функции у = х п )?
Другими словами, представляется целесообразным установить зависимость между производными взаимно обратных функций.
Прежде чем перейти к рассмотрению соответствующей теоремы, повторяем с учащимися определение обратной функции и при этом обращаем их внимание на то, что если функции у == f(x) и х = <р(у) взаимно обратны, то, как это следует из определения, при любом значении у f(<p(y))=y и при любом значении х = X.
Далее замечаем, что если приращению Ду аргумента у функции х = <р(у) соответствует приращение Дх самой функции, то, взяв это значение Дх в качестве приращения аргумента для функции у = f(x), мы получим, что соответствующее приращение этой функции равно ранее выбранному значению Ду. Это нетрудно и проверить.
Пусть Дх = ср (у -h Ду) — ср (у).
Тогда х + Дх = <р (у) + <р (у 4- Ду) — ср (у) = <р (у + Ду).
Отсюда /(х+Дх)—Дх)=/(ср (у-|-Ду))— У-=У+Ду—у =Ду.
Теорему о производной обратной функции мы формулируем следующим образом.
Теорема 4. Если функция х — ср(у) является обратной по отношению к функции у = f(x) и функция ==/(-*) имеет в точке xQ производную ff(x)^ 0, а данная функ4ия 6* = у(у) непрерывна в соответствующей точке у0 =/fx0), то существует производная функции X = ч(у) В точке у0 Причем <р'(Уо) =7^7 •
Чтобы убедиться в справедливости теоремы, необхо’» димо доказать, что
Имеем:
Дг/->0 f' lim = lim . д^->0
Приведенное преобразование допустимо, так как при Az/ ф 0 обязательно и Дх =# 0, что следует из самого определения функции, согласно которому одному и тому же значению х не могут соответствовать два различных значения у.
Благодаря сделанному выше замечанию, в выражении справа Ах можно считать приращением аргумента функции f(x), а самой функции.
Так как <?(у)
Это приводит
lim
Ay — соответствующим
непрерывна в точке #0,
К МЫСЛИ, ЧТО
&У _ Лу
приращением
то lim Дх=0.
А//-* О
(Сообщаем учащимся, что можно строго доказать, что если существует ду
0), a lim Дх = 0,
то
но мы этого ложение.)
Так как
1101 Й = l,m Й = •
Дх—>0 йх
не делаем, чтобы не загромождать из*
lim 4^
о/»
то lim т~ Ду-о^ Дх Итак,
а по условию f'(x0) у-- О,
1
, (по теореме о пределе частного).
Дх
Кратко утверждение тебремы можно записать в форме
Покажем, как можно доказать оставшееся недоказанным утверждение: если существует
1,01 Х7=П*о), а Нт Дх = 0, то lim = f’fxj.
Пусть е — произвольное' наперед заданное положительное число. Так как lim ^~—f (х0), то по задан-Дх—>0 а х
ному е можно указать такое положительное число 8, что при значениях Дх =# 0, удовлетворяющих неравенству |дх[<8, выполняется неравенство Ig-j-— -7'(*о)| <г-
С другой стороны, так как lim Дх = О, то по вы-Аг/ —>0
бранному 8 можно указать такое положительное число 8Ь что при всех значениях Ду=#0, удовлетворяющих неравенству |Ду|<_8и выполняется неравенство | Дх | < 8. Ввиду того что при Ду =# О имеет место Дх=#0, можно заключить, что при всех значениях Ду=#О, удовлетворяющих неравенству |Ду| < 8и вы* полняется неравенство
е,
Таким образом, по любому е>0 можно найти такое положительное число 8П что из неравенств &у =£ 0 и | Ду |<SX следует неравенство —/'(х0) а это и означает, что lim Лу -0
О/*
Применим полученную теорему к функции у =х п , обратной по отношению к функции у = хп с соответствующей областью определения. Для удобства обозначим переменные данной функции, т. е. рассмотрим 1
фукцию х = у п .
Согласно доказанной теореме при у #= 0 и, значит, Х^О имеем:	,
Возвращаясь к прежним переменным, получаем, что
-L 1	Д-[
при у—х п у = — * х п , т. е. правило дифференцирования здесь такое же, как и для степенной функции с натуральным показателем степени. (Исключение составляет точка нуль, но этот вопрос мы подробно не рассматриваем.)
1
Функции у = хп н у = х п представляют собой частные случаи степенной функции у = х«. где а — любое действительное число. Без доказательства следует сообщить учащимся, что при х¥= 0, выведенная формула справедлива для любой степенной функции, т. е. для функции у = ха , у1 — а-ха~1 (а — любое действительное число.)
Позднее школьники будут иметь возможность, используя формулы производной частного и производной сложной функции, в порядке упражнений проверить справедливость формулы при любом рациональном показателе степени.
Примеры.
1	2	^-1	2	-~
1.	у=х3; у'= -у х з ^-f-x	3‘
2.	& = х~°'12;	= —0,12х "0,12-1 - — 0,12х
3.	у= J- . х
Переписываем в виде у=х-1. Тогда у'=—1л-2=——г
4- У =	У=х~3 У' = —3-х-4 = —.
A*
1	__1_
8. у = У7+-^+0,1х“>-, у = х2 +* *+0,1X1";
__1	__3_	1	1
4
2
3__’
V t
AL 1
10.S=]/F(2/2 +77+ 1/3"); S =2t 2• + t 6 + ]/3/2;
He обязательно подробно записывать все выкладки. Желательно, чтобы то, что они могут, учащиеся делали в уме.
После решения ряда примеров и задач переходим к теореме о производной частного двух функций.
Теорема 5. Если у =/(лг)= причем функции а—$(х) и	в точке xQ имеют производные, соответственно равные и ¥(хъ) и	0, то
<Р'(*оН (Хо) ~ 9	ппггими ГЛМЯМ1Г
/ (-*о/ — ---------(<Цхо)]2----— ’ ДРУГИМИ словами,
производная частного двух функций в точке, где значение делителя не равно нулю, равна дроби, у которой в знаменателе стоит квадрат значения делителя, а в числителе— разность между производной делимого, умноженной на значение делителя, и значением делимого, умноженным на производную делителя.
Для доказательства, как и в случае теоремы 3, выразим Ау через Aiz и Ди.
Пользуясь, как и раньше обозначениями у0, uG, vQ вместо /(хв), <р(х0), ф(к0) и тем, что /(х0 + Дх) = у0 + + *У, <Р (*о + Дх) = «0 + Д«, ф (х0 + Дх) = v0 4- Ди, имеем:
Да Ду
д __ uQ + Да_____и0  	— Ду-а0 . Ау   &x‘Vq~u°' &х
vo + Ду Vo ~~ (уо + Ду)-уо ’ Дх (у0 + Ду)-у0»
(так
как lim Ди =0). Дх-^о
Итак,
t,( г x _ ?' M • Ж) - ? W  Ж) I \xw ~	[ф (Xo)]S
или для удобства запоминания, у' =
Примеры.
и'у — иу' ^2
2хаЧ-х + 1.	, _ (4х+ 1)(х2 -х+1) ~(2х2+х+ 1 )(2х-1)
х2 — ХЧ-1’	(х2 —х+1)2
4ха + х2 — 4ха — х + 4х -Р 1 — 4х3 — 2х2 — 2х J- 2ха + х4~ 1 (х2 — х 4-1)2
— Зх2 + 2х + 2 (х2 — X + I)2
1
Т
Доказанные ранее теоремы позволяют находить производные суммы, разности, произведения и частного двух функций, если известны производные каждой из этих функций (в случае частного в тех точках, где делитель отличен от нуля). Зная формулу для вычисления производной степенной функции, мы могли вычислять производные тех функций, которые получаются из степенных функций с помощью четырех арифметических действий, например производные многочленов и алгебраических дробей.
Однако для функций, которые не могут быть представлены таким образом, например для функции у = =sin х или y=cos х, для вычисления производных, мы не можем воспользоваться доказанными теоремами, и нам приходится обращаться непосредственно к определению производной.
1. Выведем формулу для производной функции у — = sinx. Возьмем произвольную точку х. Как обычно, обозначим приращение аргумента через Дх. Тогда соответствующее приращение функции
fay = sin(х+ Дх) — sin х — sinx-cos Дх + cosx-sin Дх--
— sinx= cosx-sin Дх-f- sinx(cos Дх— 1) =
= cosx sin Дх — 2sin x-sin2-^— .
sin*
= cosx-81"- —— 2sin x • —-r— e
Дх	Дх	Дх
yf = lim
Дх>0
by
bx
= cos л- Hm
Дх->-0
sjnAx Дх
sin
---^-sinx- lim
2
• lim Дх = cosx,
так ка^ lim —Ч-д*- =1 и НтДх = 0.
Итак, имеем: для функции y=sin х производная у'=cosx. Вывод формулы для производной функции у = sin х можно провести короче, например, так:
by = sin (х Дх) — sin х = 2 sin • cos (х 4- -4^1 ; А	\	~ f
bx
sln~ Л , Дх\ . Дх ,СОЦХ+ 2 ) ’
.	2 sin —
Ду _ ________
Дх Дх
Um ^-'=lim
Дх-0 ах
Дх sln-g-
• lim cos Дх->0
cosx.
Однако в таком случае пришлось бы ссылаться на возможность предельного перехода под знаком непрерывной функции (см. сноску на стр. 118).
2. Аналогично выводится формула для производной функции у = cos х. Возьмем произвольную точку х.
Имеем:
Ду = cos(x + Ах)— cosx = cosx-cosAx—Jsinx-sinAx— — cosx = —sinx-sin Ax^-|-[cosx-(cosAx— 1) =
= — sinx-sinAx — 2 cosx-sin1 2 -g-;
by
Дх
= —sinx-
sinAx
Дх
— 2 cosx-
Дх
— sinx-
sinAx Дх
1
----2" COS X
Дх\а sin-х- \ -Д— Ax;
Дх J ’
> V /
f 1, &У	•	1' sin Д*
У = Нш = — sinx- lim —г— Дх-4-О йЛ	Дх->0 a
так как
—^-cosx-
•ИтДх = — sin x;
Дх->0
sin(& • Дх) fc-Дх
lim
Дх->0
limAx •= 0.
Дх-*0
= 1 и
Итак, имеем: для функции г/=cosx производная у'=—sin х.
Формулы для вычисления производных функций $r=tgx и i/=ctgx выводят самостоятельно, пользуясь теоремой о производной частного двух функций. Рекомендуется запомнить выведенные формулы.
Появляется возможность решать более разнообразные примеры и задачи, в частности, содержащие тригонометрические функции.
Например:
1.	у = tgx. Найти у'.
У	у' - cosx cosx-sinx (-.sinx) * (заП0МнИть).
& COSX ’ 57	cos^x	COS2X '	7
2.	у = х• sinx — хя• cosx. Найти у'.
у’ — 1 - sinx 4- х-cosx — [2x-cosx 4- x2( — sinx)] — sinx 4-+ x • cosx — 2x • cosx 4- x2sinx = sinx — xcosx 4- x2sinx.
3.	s = .	. Найти s'.
1 4- sin/
— sin /•(I + sin t) — cosf»cos/ — sin/— 1  	1
(1 4- sin/)2	(1	s!n/)«	1 + sin/
4. У =
X’Sin x
> + tgx •
Найти у'.
(sin X 4- x-cos x)(l -j- tgx) — x-slnx- CQS»X (1 + tgx)«
1Ё
x cos2x 4- x cos3x 4- sin2x*cos x 4- x sinx cos2x—xsinx (cos x 4- sin x)2
Еще более расширяет возможности подбора интересных примеров и задач рассмотрение производной сложной функции. Учащиеся уже умеют, зная производные некоторых функций, находить производные более сложных функций, построенных из них с помощью четырех арифметических операций. Однако во многих случаях более сложные функции строятся из известных функций не только с помощью арифметических операций.
Рассмотрим, например, функцию у =prsinx=(sinx)2 . Для вычисления значения этой функции при некотором значении аргумента х0 мы прежде всего вычисляем значение функции sin х при х = х0, а затем полученное зна-1 чение sin х0 возводим в степень с показателем •
Таким образом, для вычисления значения данной функции нам приходится вычислять значения известных нам функций sinx и степенной функции с показателем степени -g- • Рассматриваемая функция построена, следовательно, из известных функций, но не с помощью арифметических операций.
Введем для удобства вспомогательную переменную /, обозначив / — sinx.	i
Тогда данная функция у = (sin х) 2 может быть представлена с помощью двух функций следующим образом:
1
t = sinx, у = t2.
Действительно, чтобы найти yQ = (sinx0) 2 , доста-
1
точно сначала найти /0 = sin х0, а затем у = /0 2 . Функция, которая допускает подобное представление, называется сложной функцией.
Дадим определение в общем виде. Пусть данная функция y=*f(x) может быть представлена в виде (х) — ф(ф(х), т. е. при введении вспомогательной переменной t ее можно представить с помощью двух функций:

Тогда данная функция y=f(х) =<р(ф(х)) называется сложной функцией.
Функция t = ф(х) называется внутренней функцией, функция у = <р(/) называется внешней функцией, а переменная t — промежуточным параметром.
В рассмотренном выше примере сложной функции 1
у = (sin х) 2 функция t = sin х является внутренней функцией, а функция у = t 2 — внешней.
Приведем еще один пример: y = tg(x2+l). Эту функцию можно рассматривать как сложную, введя промежуточный параметр (который можно обозначить любой буквой, например буквой z), следующим образом: z=x2+l, y = tgz.
Понятие сложной функции играет важную роль при вычислении производных, а именно имеет место следующая теорема о вычислении производной сложной функции.
Теорема 6. Производная сложной функции у = —Дл:)— ф(ф(•*)) в точке Хо равна произведению производной внутренней функции t— ф(л) в точке х0 на производную внешней функции <р(£) в соответствующей точке to = ф(Хо) при условии, что ф'(хо) и <₽' (^о) СУ" ществуют.
Л(*о) = Ф'(*о) • <?'(4) = ffohW-
Прежде чем доказывать эту теорему, обращаем внимание учащихся на следующее обстоятельство.
Пусть Дх — приращение аргумента внутренней функции ф(х), которое, очевидно, можно рассматривать и как приращение аргумента сложной функции ф(ф (хо)). Приращению аргумента Дх соответствует приращение внутренней функции А/ = !р(хо + Ах) ~ Ф(хо) и приращение сложной функции Ду == ср(ф(х0 + Ах)) — ?(Ф(х0)).
Имея в виду, что Ф(х0) = /0 и <Цх0 + Ах) = <|>(х0) + +	+ ДЛ получаем Ду = &(t0 + А/) — <р(/0).
Таким образом, приращение сложной функции Ду может рассматриваться и как приращение внешней функции <р(0, соответствующее приращению Д£ ее аргумента Л
Перейдем к доказательству теоремы.
гм
= lim Um
Дх-Оах Дх->0
Д< _ Д//1 . Дх Af J
™ lim
Дх->0
Д£
Дх
lim Ау ' Дх-*0 д<
=<|/(*0)-lim -Ъ.
Дх-0 щ
Так как по условию ф'(х0) существует, то функция t = ф(х) непрерывна в точке Хо и, значит, lim Д/ — 0.
Дх-*0
Вследствие этого напрашивается вывод, что lim тт- = Дх->0йГ
= lim ^гг = который может быть строго дока-де-0 "
зан. (В связи с доказательством теоремы об обратных функциях мы уже показывали, как могло бы быть доказано имеющееся там аналогичное утверждение см. стр. 91).
Итак, Г(Хо) =ф'(хо)’ф'(/о). Производную f'(x) функции y=f(x) будем обозначать через ух в отличие от производной <р'(/) функции y=<f(t), которую мы обозначим через у' /. Тогда выведенную формулу можно записать так: Ух = t’x-y't, или, что в некоторых случаях более удобно для приложений, у'х = y't-t’x.
Примеры.
1.	у — sin Зх. На йти у'.
i ~ Зх; у — sin t\
y'=y't‘t ';/' =3; У{ ~ cos t = cos Зх;
y' = 3 cos 3x,
2.	у = cos 4x. Найти у'.
Обозначаем t — 4x, у = cos/.
Используя формулу y'x = y't-i’x , сразу получаем:
у' — у'г— 4- (— sin /) = — 4 sin 4х.
•А	“	6
3.	= cosx3. Найти у'.
t = хч; у — cos /;
у' = Зх2-(— sin /) = — 3x2sin х3.
у = j^sin х. Найти у'.
t = sin х;
f	1	cos X
у' = cos X- —= .. 	.
2/1 2/sinx
5. у =]/3x2 + 2х 4- 1. Найти у'.
• __ 1
t = Зха 4- 2х 4-1; у =у t = f 3 ;
у' = (6х + 2).4-	= -4 —------------•
Зу(З-Г3 + 2х + 1)а
6.	у = jesin(jca + 1). Найти у’.
Применяем правило для нахождения производной произведения функций. Для вычисления производной функции о = sin (х2 + 1) используем правило для вычисления производной сложной функции.
Найдем v':
t = х2 -|- 1; v = sin t\ v'= 2xcos/ = 2x>cos(xs4- 1).
Находим у':
у' = l-sin(x24-1) 4-x-2x-cos(x® 4-1) =
= sinfx8 4-1)4- 2x®-cos(x* 4- 1).
7.	i/ = cos(3xs—l)4-sin4. Найти у'.
t = Зх2 — 1; у = cos 14- sin 4;
y’ = 6x( — sin / 4* 0) == — 6xsin(3x® — 1).
§ 3. ФИЗИЧЕСКИЕ И ДРУГИЕ ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ ПОНЯТИЯ ПРОИЗВОДНОЙ, ускорение.
понятие второй производной
Как уже отмечалось выше, на протяжении всего изучения способов вычисления производной учащиеся систематически решают примеры на нахождение производных, чтобы приобрести необходимые умения. Одновременно учатся применять вновь введенное математическое понятие к решению конкретных практических задач. Почти на каждом уроке решаются и задаются на дом одна-две такие задачи.
При решении задач с практическим содержанием не только применяют правила вычисления производных для нахождения значений величин, определяемых с помощью понятия производной, но и учатся самостоятельно давать новые определения, используя понятие предела функции и производной, по аналогии с тем, как это было сделано для мгновенной скорости прямолинейного движения.
Приступая к решению задач, отмечаем, что понятие производной имеет большое практическое приложение. В частности, производная применяется не только для вычисления скорости прямолинейного движения, но и для вычисления скорости протекания различных процессов физического, химического и другого характера.
Например, если при нагревании тела температура его изменяется с течением времени равномерно, т. е. в равные промежутки времени на одну и ту же величину, то скоростью изменения температуры называется отношение изменения температуры ко времени, за которое это изменение произошло.
Если же изменение температуры происходит неравномерно, то можно ввести понятие скорости изменения температуры в данный момент времени, подобно тому как было введено понятие мгновенной скорости (скорость в данный момент времени) неравномерного прямолинейного движения.
Можно показать, что скорость изменения температуры в данный момент времени есть производная функции, выражающей зависимость температуры от времени (так же как это было сделано для мгновенной скорости прямолинейного движения).
Решается, например, задача:
При нагревании тела температура его Т изменяется в зависимости от времени нагревания t по закону Т = 0,4 /2, где Т — температура в градусах С, t — время в секундах.
1. Найти среднюю скорость изменения температуры тела за промежуток времени от 6 = 4 сек до = 6 сек.
2. Найти скорость изменения температуры тела в момент t = 4 (т. е. в конце 4-й секунды от начала нагревания).
ДТ
Решение. 1) ц.р — Д/ = 6 сек — 4 сек = 2 сек-, ДТ = 0,4-62 — 0,4 • 42 — 0,4 (36—16) = 8 (градусов С);
- 4-=“ О •
2) .<4) = итЛ = ИтД_Г<4);
T = 0,4-f8;	0,81.
При t = 4 Г(4) = 3,2 1	7 к сек}
О т в е т. v (4) = 3,2
' 7	* сек
Затем ставится задача дать определение скорости изменения температуры с помощью понятия производной.
Средняя скорость изменения температуры тела за данный промежуток времени определяется как отноше-
ЬТ	А/
ние , где Дг — величина данного промежутка времени, а ДТ — соответствующее ему изменение температуры.
Как и в рассмотренной выше конкретной задаче, скорость изменения температуры тела в данный момент времени /0 определяется как предел средней скорости изменения температуры тела за промежуток времени Ы, начинающийся с момента времени /о, при условии, что Д/ стремится к нулю, т. е. v(Q = lim t/CD = lim дт-.
Д^О д^0аг
Если температура тела задана как функция времени Т то, очевидно, Д/ есть приращение аргумента этой функции, а Д7 — соответствующее приращение дт кции и, значит , lim -тт- = д<+0 {
Итак, v(t0) —	, т. е. скорость изменения темпе-
ратуры в данный момент времени есть производная температуры по времени, вычисленная для соответствующего момента.
Приведем еще несколько примеров решения задач с практическим содержанием.
Задача. Опытным путем установлено, что количество Р граммов вещества, уже растворившегося в воде за t секунд, есть некоторая функция переменного t, т. е. P=f(O-
1) Найти среднюю скорость (уср) растворения данного вещества в воде за промежуток времени от Л до t2.
2) Найти скорость v растворения в воде данного вещества в любой момент времени t.
Решение. 1) vcp есть отношение количества растворенного за данный промежуток времени вещества к
величине данного промежутка времени. Величина рассматриваемого промежутка времени Д/=/2—Количество растворенного за это время вещества равно:
др = /(4) - /(/,).
Отсюда оср = ‘s—‘1
2) Скорость и растворения в воде данного вещества в момент времени t, очевидно, равна lim tu.
Д/м-0
Отсюда v =•= lim vco — lim -гт- = lim 	~
д/-*0	Д/^-0 Д^О 1
Задача. При некоторой химической реакции за t секунд образуется Q граммов вещества.
1) Как найти среднюю скорость (оср) данной химической реакции за промежуток времени от t\ до считая Q — f(t)?
2) Как найти скорость (о) химической реакции в любой момент времени f?
Решение. 1. гср- -|г =	.
2.	lim vco = lim	= lim —	= НО•
Задача. Опытным путем установлено, что количество жидкости Q граммов, вытекающее через отверстие в сосуде за t секунд, определяется формулой Q = = 12014-?-------J-13.
1) Найти расход жидкости в момент времени t — —10 сек.	'
2) Через сколько секунд расход жидкости прекратится и какое количество жидкости выльется за это время из сосуда?
Примечание. Расходом жидкости называется количест-во жидкости, вытекающее в единицу времени (если бы вытекание проходило равномерно).
Редпение. Очевидно, что средний расход жидкости есть отношение количества жидкости, вытекшей за данный промежуток времени, к величине этого промежутка времени.
_ _	до _
Мы можем записать гср = -др. Расход жидкости г в данный момент времени t можно определить, как предел среднего расхода жидкости за промежуток времени Д/, начинающийся с этого момента, при условии, что Ы -+0.
г - lim гср = lim = Q'.
Д<->0	Д/-+0 “
Отсюда: 1) r(10) = Q'(10).
Так как Q = 120/-Н2 —-|-/3, то Q'= 120 + 2/-/2. г ( Ю) = Q' (10) = 120 + 2 • 10 — 10» = 40 (—) .
I сек ]
2) Найдем, через сколько секунд расход жидкости прекратится, т. е. при каком значении t выполняется условие r=0; r—Q'(t).
120 Ц-2 / —/2 = Q; /2 — 2/ — 120 = 0;
t == 1 ± V1 + 120; t = 12 (сек).
Отрицательный корень, очевидно, не имеет смысла. Получаем /=12 сек, т. е. через 12 сек расход жидкости прекратится. Чтобы определить, какое количество жидкости вытечет за это время из сосуда, надо найти значение Q при данном значении t = 12 сек.
Получаем <2(12) = 120-12 -Ь 12»---i- • 123 =
= 1440 + 144 — 576 = 1008 (г).
Ответ. Количество вытекшей жидкости равно 1008 г.
Желательно показать учащимся, что понятие производной может быть использовано в физике и других отраслях знания не только для определения скорости изменения величин с течением времени. Можно рассмотреть, например, понятие линейной плотности неоднородного стержня. Стержнем, как известно, называется тело, площадь поперечного сечения которого мала по сравнению с его длиной. Для однородного стержня вводится понятие линейной плотности как отношения массы стержня к его длине. Если стержень неоднородный, то можно рассматривать среднюю плотность его на различных его участках. Средней линейной плотностью данного участка стержня называется отношение массы данного участка стержня к длине этого участка.
Линейной плотностью стержня в данной его точке называется предел средней линейной плотности участка стержня, примыкающего к этой точке, при условии, что длина участка стремится к нулю.
Если через х обозначить длину участка стержня от начала его А до некоторой его точки В, то масса участка АВ, очевидно, представляет собой функцию аргумента х m=f(x) (см. рис. 34).
Длину участка, - II --------------1 примыкающего к
•------------точке В, можно счи-
тать приращением рис. 34	Дх аргумента х, а
массу этого участка — соответствующим приращением Ат функции m=f(x).
В таком случае линейная плотность стержня в точке В р(В) = lim , т. е. представляет собой произ-
водную функции т = Дх) в рассматриваемой точке х.
Разумеется, на уроках решаются и задачи, в которых используются уже введенные с помощью понятия производной определения.
Так, например, после определения скорости изменения тока как производной от функции, выражающей зависимость величины тока от времени, может быть решена задача:
Ток I ампер изменяется в зависимости от времени по закону 7=0,2 /2, где t — число секунд. Найти скорость изменения тока в конце четвертой секунды.
Решение, с/(4) = /'(4);	/ — 0,2/2;	/'(/) = 0,4/.
/'(4) = 0,4-4 = 1,6(^4; о(4) = 1,6^.
Решаются задачи на вычисление скорости прямолинейного движения.
Задача. Точка движется так, что путь S в метрах, пройденный ею за промежуток времени t в секундах,' выражается формулой:
S = 4/24-3£.
1) Найти скорость точки в любой момент времени.
2) Вычислить скорость точки в момент £ —3.
Решен и’е:
1) v = S'(t) = 8t + 3 .
2) S'(3) = 8-3+3 = 27(^)
при / = 3 скорость равна 27 —
Более интересные задачи:
Человек ростом 1,7 м удаляется от источника света, находящегося на высоте h м	со скоростью
5	• Определить скорость перемещения тени его
головы.
В школе лучше дать конкретное значение й, например h = 2,2 м, т. е. сразу же указать, что источник света находится на высоте 2,2 м.
Решение (см. рис. 35).
Рис. 35
В момент времени t часов положение человека изображает отрезок С] Вь а положение тени его головы — точка В2. Обозначим расстояние В В2 через S.
ВВ1 = 5000£(л<), так как человек удаляется со ско-ростью 5 ~ = 5000	.
В\ В2 = S — 50001; Ci Вг = 1,7 м; АВ = 2,2 м.
Из подобия прямоугольных треугольников АВВ2 и С1В1В2 получаем:
ВВ2 _ АВ	S 2,2 .
BiB2 ~ CiBt' Т‘е- 5—5000/ — 1,7 ’
1,7 S = 2,2S — 2,2-5000/;
0,5-3 = 2,2-5000 /;
3 = 22000/ (м).
Отсюда v = S'(t) — 22 000;
о = 22 000 — = 22 — . час час
После того как учащиеся познакомятся с понятием сложной функции, могут быть решены более трудные задачи.
Задача. Лестница длиной 5 м, прислоненная к вертикальной стене, падает, скользя одним концом о стену, а другим о пол. С какой скоростью опускается верхний конец лестницы в момент, когда нижний конец, ото
двигающийся от стены с постоянной скоростью 3
отстоит от нее на расстояние 4 м?
Решение. Чтобы найти скорость, с которой движется верхний конец лестницы, найдем закон движения,
т. е. функцию, выражающую зависимость расстояния S, пройденного верхним концом, от времени t (см. рис. 36).
Расстояние, пройденное верхним концом лестницы, отсчитывается от начального положения (на рисунке точка А), т. е. положения, которое занимал верхний конец, когда лестница стояла вертикально. Положение верхнего времени t обозначено на чер-
Рис. 36
конца в момент
теже буквой А г, положение нижнего конца в этот же момент времени — буквой Найдем зависимость расстояние S=AAj от времени /.
По условию АВ = АХВ{ — 5 м (длина лестницы). А{В=АВ—АА1=(5—5)(ж); ВВ1=ЗЦм) (так как нижний конец лестницы движется равномерно со ско-р°стью 3 -2L-).
Из прямоугольного треугольника 41ВВ] (/Л1ВВ1 = =90°) по теореме Пифагора имеем: Л]В2=.-41В12—BBj2,
т. е.
(5 — S)2 = 5\— (3/)а; 5 — S = У 25 - 9/2.
Здесь берется арифметический корень, так как рас-стояние Л]В = 5 — S не отрицательно. Отсюда S = 5 — —/25—9£2. Таким образом, мы нашли закон движения. Чтобы найти скорость в любой момент времени t, достаточно вычислить производную от полученной функции v — S'(t) ==	18*	_	9/	/ ж \
V ~	“ 2 /25 —9<» ” /25 — 9<« \сек ) ’
По условию нам надо найти скорость верхнего конца лестницы в тот момент времени, когда нижний конец находится на расстоянии 4 м от стены (т. е. когда ВВ^ = = 4 м). Так как нижний конец движется равномерно со скоростью 3	, то это произойдет в момент —
= (сек).
Соответствующая скорость о( получается из ранее найденной формулы для v.
4
— с' ZJL) —	‘ 3 = 4^—
1	\ 3 /	У 25—16	4	‘
Понятие ускорения определяется так же, как определялся с помощью производной ряд других физических величин.
Учащиеся знают, что при равноускоренном движении ускорением называется отношение приращения скорости ко времени, за которое это приращение произошло. Понятие ускорения можно ввести и для движения, которое не является равноускоренным, подобно тому как было введено понятие скорости для неравномерного движения. Очевидно, в этом случае придется говорить о среднем ускорении и об ускорении в данный момент времени.
Если за данный промежуток времени Д/ скорость v изменилась на некоторую величину До (положительную или отрицательную) или, как говорят, получила приращение До, то средним ускорением за данный промежуток времени Д£ называется отношение приращения скорости До ко времени Д/, за которое это приращение произошло:
_____До а<;р_•
Ускорением в данный момент времени to называется предел среднего ускорения за промежуток времени Д/, начинающийся с данного момента, при условии, что промежуток времени Д< стремится к нулю:
а =» lim ас0 = lim -¥т .
дг—»0	Д/-0 **
Если v есть некоторая функция аргумента t, v — <р(/), то по определению производной lim пгт = ?'(/0).
Итак, ускорение в данный момент времени есть производная скорости по времени, соответствующая данному моменту.
После введения понятия ускорения решаются две-три задачи перед введением понятия второй производной.
Задача. Скорость точки, движущейся прямолинейно, определяется формулой v = 3t 4- 2t2, где t — время в секундах, v — скорость в сантиметрах в секунду. Какое ускорение будет иметь точка в момент времени t = 4 сек?
Находим ускорение точки в любой момент времени/: a=v'(t) =3+4/,
Находим теперь ускорение точки в данный момент времени / = 4 сек:
а(4) = о'(4) = 3 + 4-4= 19PV) .
х 7 х 7	1	I сек* I
Задача. Уравнение движения точки:
s = 4-— + ^®+^ +1, О	Лл
где S — путь в метрах, /—время в секундах. Найти скорость и ускорение точки в момент времени / = 3 сек.
1) Находим скорость точки в любой момент времени /:
S'(t) = t* — t + 1.
Отсюда находим скорость точки в данный момент времени / = 3 сек:
р(3)==$'(3) = 9-3+1==7^.
2) Находим ускорение точки в любой момент времени t. Так как v — t2—f+1, то a=v'(t) =2t—1.
Отсюда находим ускорение точки в данный момент времени t — 3 сек:
а(3) = + (3) = 2-3- 1 =5/^-1.
х 7 х 7	I сек* I
Понятие о второй производной. Внимание учащихся обращается на то, что при решении последней задачи ио
нам пришлось вначале найти производную от данной функции S= t3-------g- /2 + / + 1, v = S '(t)=t2—t + 1,
а затем искать производную от полученной функции v, значение которой при каждом значении t представляет собой производную от данной функции S. Эта функция о = £'(£) носит название производной функции от данной функции £(/), а производная от производной функции, т. е. о'(О, называется второй производной от данной функции и обозначается через
Введем определение второй производной в общем случае.
Пусть дана функция y = f(x). Рассмотрим функцию у'=Г(х), значение которой при каждом значении х представляет собой производную от данной функции у = f(x).
Эта функция у'=1'(х) называется производной функцией от данной функции y=f(x).
Производная от производной функции f(x) называется второй производной от данной функции f{x) и обозначается через /" (л:). (Производную f(x) в отличие от второй производной обычно называют первой производной.)
Так как функция, выражающая зависимость скорости от времени, является производной функцией от функции, выражающей зависимость пути от времени, а ускорение есть производная скорости по времени, то, очевидно, что ускорение есть вторая производная пути по времени; $"(/).
Решается несколько задач, связанных с этим определением.
Задача. Поезд выходит со станции и через t часов находится на расстоянии 5 = /3+2/2 + 3/ километров от станции отправления. Найти величину его ускорения в конце t часов и в конце второго часа.
Решение. 1) а = S" (/);
S'(t) = 3t2 + 4/4-3;
S"(0 = 6/ + 4 .
Ускорение в конце t часов равно (6 t + 4)^^- ♦
2) а(2) = S"(2) = 6-2 + 4 = 16	.
Наряду с понятием скорости и ускорения при неравномерном движении можно рассмотреть угловую ско
рость и ускорение при неравномерном вращательном движении. Очевидно, что угловая скорость вращения в данный момент времени есть производная угла поворота по времени, а угловое ускорение в данный момент времени — производная угловой скорости по времени.
Задача. Вращающееся маховое колесо, задерживаемое тормозом, за t сек поворачивается на угол —rfi, где р, q, г—положительные постоянные. Определить угловую скорость и ускорение вращения. Через сколько времени колесо остановится?
Решение. Угловая скорость — <р' (/) == q — 2rt.
Угловое ускорение аугл = а/ «= /'(0 = —2 г.
Колесо остановится, когда ю = ср' (t) «= 0 .
Получаем уравнение q — 2 rf = 0.
Колесо остановится при t = (сек).
Как уже говорилось выше, задачи на применение производной решаются на протяжении всего изложения материала и наряду с ними решается достаточное число примеров, закрепляющих умение школьников вычислять производные.
В конце первого этапа изучения темы «Производная и ее применение к исследованию функций» дается контрольная работа, содержащая одну задачу на применение производной и несколько примеров на ее вычисление.
Глава 5. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ПРОИЗВОДНОЙ. ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНОЙ. РЕШЕНИЕ ЗАДАЧ, СВЯЗАННЫХ С НАХОЖДЕНИЕМ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИЙ.
ФОРМУЛА БИНОМА НЬЮТОНА
Как показывает опыт, знакомить с геометрическим смыслом производной лучше после того, как усвоено это понятие, тем более что здесь дается новое определение касательной, ранее неизвестное. Проделав достаточную работу по закреплению в сознании учащихся понятия производной и способов ее вычисления, можно переходить к вопросу о геометрическом истолковании произ-П2
водной в связи с задачей применения производной к исследованию функций.
Определение касательной к кривой в данной ее точке как предельного положения секущей не дается заранее, а вводится в связи с задачей геометрического истолкования производной. На ряде примеров учащиеся убеждаются, что это определение в общем соответствует их интуитивному представлению о прямой, касающейся данной линии (и известному им определению касательной к окружности), хотя и вносит в него нечто новое.
Геометрическая иллюстрация широко используется в дальнейшем при изучении методов исследования функций с помощью производной. В частности, при рассмотрении необходимых признаков возрастания и убывания функций геометрическая иллюстрация играет первенствующую роль, так как эти признаки не доказываются. Правда, мы считаем целесообразным познакомить школьников с теоремой Лагранжа и с ее помощью провести соответствующее доказательство. (Во всяком случае, для интересующихся учеников это можно сделать во внеурочное время.) Разумеется, геометрические иллюстрации играют важную роль и там, где доказательство соответствующих теорем проводится, например, при выводе необходимого условия существования экстремума и достаточных условий существования максимума и минимума.
В связи с рассмотрением нового, более рационального метода исследования функций решается довольно много задач на исследование функций и построение их графиков, а также задач с практическим содержанием, связанных с вычислением наибольшего и наименьшего значения функций. Построение графиков используется, в частности, для графического решения уравнений.
Изучение вопросов, рассматриваемых в данной главе, занимает в школе 20—21 урок.
§ 1. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Уже при введении понятия производной учащимся сообщается, что производная не только может быть использована при решении практических задач, но также помогает при изучении свойств функций. После того как заканчивается рассмотрение цикла вопросов, связанных
8 Заказ 314	ПЗ
с вычислением производных, напоминаем учащимся о задаче получения новых методов исследования функций с помощью производной.
Учащиеся уже знают, что для наглядного представления свойств функций большое значение имеет геометрическое изображение функции — график функции. Они вспоминают, что все рассматривавшиеся свойства функций получили какое-то отражение на графиках этих функций, что знание графика функции помогает лучше представить себе ее свойства. Поэтому, для того чтобы найти методы исследования свойств функций с помощью производной, следует прежде всего выяснить, какую геометрическую величину, связанную с графиком функции, выражает производная этой функции в рассматриваемой точке, т. е., другими словами, дать геометрическое истолкование производной.
Чтобы дать геометрическое истолкование производной или, как говорят, найти геометрический смысл производной, естественно обратиться к определению производной функции у ~f(x) в данной точке х0. Вспоминаем, что по определению производная функции y=f(x) в точке Xq есть предел отношения приращения функции Ду к соответствующему приращению аргумента Дх, при Дх, стремящемся к пулю, т. е. f'(x0)=lim .
Дх-0
Таким образом, следует прежде всего хорошо представлять себе изображение на графике приращения аргумента в данной точке и соответствующего ему приращения функции.
Привлекаются примеры простейших функций, рассматривавшихся при введении понятия производной.
1) у — х (см. рис. 37, а и б).
График функции у = /(х) =х представляет собой, как известно, прямую, проходящую через начало координат и образующую с положительным направлением оси абсцисс угол, равный-^- (считая от оси абсцисс до этой прямой в положительном направлении, т. е. против часовой стрелки).
Нетрудно заметить, что в случае, изображенном на рисунке 37,а, приращение аргумента Дх и соответствующее ему приращение функции Ду изображаются соответственно отрезками и NM. В случае, изображенном на рисунке 37,6, Дх и Ду отрицательны. Лег-114
ко видеть, что здесь длина отрезка MN равна — Ах = =|Ах|, длина отрезка MW0 равна —&у = [Д#|.В первом
Aw Л7И , к
случае	= tg -4-
= 1; во втором случае
Ду_[Af/| _ МИо Длг“"|Дх| ~ MN
= tg — == 1. Это соответствует тому, что,
как это было показано при вычислении производной, в
данном случае Ду = Дх,
2) у=х2 (см. рис. 38, а — е). Чертежи заготавливаются заранее в виде чертежей-плакатов или на переносных досках. Пояснение аналогично предыдущему случаю.
После рассмотрения конкретных примеров переходим к геометрическому изображению приращенйй Дх и Ду в общем случае для функции у ~ f(x) в некоторой точке х0.
Для простоты ограничимся рассмотрением случая, когда функция y=f(x) возрастает и Дх>0, тогда и Ду>0 (см. рис. 39).
Легко видеть, что AqA=MqN=&x-, B0B=NM = Ay. (MqAoIOX- MAJ-OX- M0N\\OX).
Чтобы получить геометрическое истолкование отношения проводим прямую ММ0, до ее пересечения с осью ОХ в точке К. Прямая ММ0, пересекающая кривую в данной точке А! о и некоторой соседней точке М, называется секущей.
Рис.
Угол, образованный секущей с положительным направлением оси абсцисс (отсчитываемый от оси абсцисс в направлении против часовой стрелки), т. е: ZAKM, обозначим через <р *.
Очевидно, что NM0M = АКМ. = <?. В таком случае из /\M0MN получаем:^- =
Нас интересует lim . Так как мы рассматрива-Дх-»0 х
ем случай, когда существует f'(x0), то lim Ьу = О.
Дх~*0
Следовательно, lim М0М = lim Y&х2 -|- by2 = 0, т. е. Дл-^0	Дх-+0
при Дл~> 0 точка М неограниченно приближается к точке Л10.
Когда точка М, двигаясь по кривой, приближается к точке. Aloi секущая MGM поворачивается около точки Мь Если при неограниченном приближении точки М к точке Мо прямая М0М стремится занять некоторое предельное положение ЛГоЛ то прямая MqT называется касательной к данной кривой в точке Л1о.
Определение. Прямая 7И0Т называется касательной к кривой в ее точке Ло, если она представляет собой предельное положение секущей 7ИО7И при условии, что
* Легко видеть, что в рассматриваемом случае угол у острый.
Точка М, двигаясь по кривой, неограниченно приближается к точке М0.
Чтобы убедиться в том, что некоторая прямая MqT является касательной к данной кривой в ее точке Л1о, достаточно показать, что острый угол между прямой MqT и секущей 7ИоЛ1 стремится к нулю при условии, что точка М, двигаясь по кривой, неограниченно приближается к точке Afo.
Используя определение касательной, можно показать, что если функция у = f(x) имеет производную в точке %о, то график функции имеет касательную в соответствующей точке Мо (х0; Ихо))-
Для этого достаточно доказать, что при Дх О (т. е. при Af->AJ0) величина угла ф, образованного секущей М0М с положительным направлением ОХ, стремится к определенному пределу а.
Так как tg ср —	, а ср острый, то <р — arctg^- .
Следовательно, lim ср = lim arctg £7- = arctg /'(x0) (так Дх->0	Ax->0
как lim = f'(x0), а внешняя функция arctg t яв-Дх>0
ляется непрерывной функцией своего аргумента/*).
Обозначим lim ср через а, т. е. lim ср = а;
Дх^О	Дх-0
arctg Л (х0) = а;
tg а =7' (*0).
Если провести прямую М0Т под углом а к положительному направлению оси абсцисс, то эта прямая и будет касательной к графику функции в точке Л1о,
Чтобы убедиться в этом, достаточно показать, что острый угол 0, образованный секущей MqM и прямой М0Г, стремится к нулю при М Af0 (в данном случае при Дх-> 0). Действительно, из чертежа легко усмотреть, что 0 = а — ф (см. рис. 39). Следовательно,
* Функция arc tg представляет собой сложную функцию
аргумента Дх, для которой внутренней функцией является . Можно совершенно строго доказать, что если внутренняя функция в некоторой точке а имеет предел, равный Ь, а внешняя функция в точке b непрерывна, то существует предел сложной функции в точке а, равный значению внешней функции в точке Ь.
lim 0= lim (a —<p)=0, так как lim <j>=a. Таким Дх^О Дх-*О	Дх^О
образом, прямая М0Т действительно является касательной. В то же время для угла а, который образует касательная MQT с положительным направлением оси абсцисс, было получено соотношение tga=f'(x0).
Таким образом, мы приходим к следующему геометрическому истолкованию производной f'(xQ).
Производная данной функции y=f(x)v точке представляет собой тангенс угла, который образует с положительным направлением оси абсцисс касательная к графику функции в точке Л10(лг0,
В своем изложении мы несколько отошли от традиционного пути рассмотрения вопроса о геометрическом смысле производной. Дело в том, что обычно постановка задачи о проведении касательной является одним из подходов к введению понятия производной. При этом, естественно, остается в стороне вопрос о том, что существование производной обеспечивает и существование касательной в соответствующей точке графика, и поэтому всегда возможно геометрическое истолкование производной как тангенса угла наклона ,этой касательной к положительному направлению оси абсцисс. Так как, переходя к геометрическому смыслу уже известной учащимся производной, мы ставили проблему выяснить, какую геометрическую величину выражает понятие производной, нам естественно нельзя было обойти вопрос о существовании касательной.
Для тех, кому предложенное нами рассмотрение вопроса о геометрическом смысле производной кажется слишком непривычным, мы предлагаем следующий, второй вариант изложения.
Прежде всего дается определение касательной, как предельного положения секущей, такое же, как дано на странице 117. Без доказательства учащимся сообщают, что если функция у — f(x) имеет производную в точке х0, то график этой функции имеет касательную в соответствующей точке М0(хо, f(xo)). Ставится задача найти угловой коэффициент касательной к графику функции y=f(x) в точке Af0* (см. рис. 39).
Из определения касательной следует, что если точка М, двигаясь по кривой, неограниченно приближается к точке Л1о, то угол 0 между секущей MqM и касательной
* Подразумевается, чго функция f(x) непрерывна в точке х0«
MqT неограниченно убывает. Это можно записать в форме Пт0=О, так как liniAfoA4==O (т. е. при Дх-* О точка М Дх-*0	Дх О
неограниченно приближается к точке Л40), что доказывается так же, как это было сделано на странице 117.
Из рисунка видно, что 0 = а—ф. Таким образом, lim (а—ф) =0, откуда следует, что Птф = а. Из последнего Дх — о	Дх -* о
соотношения можно сделать вывод, что Нп^ф=^а, так
Дх 0
как тангенс есть функция непрерывная в его области определения (см. сноску на стр. 118). Так как 1£ф=-£“, то отсюда получаем, что lim-4^ =tga, т. е. что tga=f(x0).
Дх-о х
На ряде примеров учащиеся получают возможность сравнить вновь введенное определение касательной с имеющимися у них представлениями. Они строят касательные к различным линиям, вычисляя угловой коэффициент касательной с помощью производной.
Так как учащиеся знают формулу для вычисления производной сложной функции, то возможно поставить задачу проведения касательной к окружности.
Задача. Провести касательную к полуокружности у=У 1—х2 в точке 7И0 (0,1). (Учащиеся знают уравнение окружности. В крайнем случае, пользуясь формулой для вычисления расстояния между двумя точками, можно показать, что любая точка графика функции у=]/ 1—х2 отстоит на расстоянии 1 от начала координат, т. е. что график есть часть окружности (смотрите рисунок 40, а, б).)
Вычисляем угловой коэффициент касательной в точке Mq (0,1):
у' = —,!=•( — 2х) =------~	,
2/1—х2	7	У 1—X*
4/'(0)=0, значит, tga=f/'(0)=0, т. е. угол наклона касательной к оси абсцисс равен 0 (или л). Касательная параллельна оси абсцисс, т. е. перпендикулярна радиусу ОМо, что согласуется с определением касательной к окружности, известным из школьного курса геометрии.
Интересно построить касательные к рассматриваемой полуокружности и в других точках, например в точках рп( 1 р^З \	/ -‘У 3 . 1 \ ,	лс\ \
и (—2— ’ ~2/ (см. Рис- 40» а) > вычис-
лив углы, которые они образуют с положительным
Легко показать, что касательная к окружности (в смысле нового определения) в любой ее точке 7И0 перпендикулярна к радиусу OMq (т. е. совпадает с касательной в смысле ранее известного определения).
Для простоты рассмотрим ту же полуокружность */=]/!—х2 и точку Л1о (*о, Уо) будем считать расположенной в первой четверти (см. рис. 40,6):
ОК = *0;	- so,	----
MqT — касательная к окружности в точке Л1о.
1
КМ0 = tg7 =	-
tg « = У'(Х0) = — -7=^=; р = л —a;
И-*0
tg? = - tg a	.-; lg? = ^Y = ctgi=tg^-J--Ty
Очевидно, что 0<р<л и 0<-п—у<л, (так как у—ост-рый угол), откуда следует, что ₽=-£—Y или Р+у=т- Та-ким образом, ZOM0T = n—(P+y) — -^- •
Итак, новое определение не противоречит ранее изве-стному определению касательной к окружности.
Последующие примеры показывают, что определение касательной к окружности как прямой, имеющей с окружностью одну общую точку, известное из школьного курса геометрии, не может быть перенесено на другие линии даже с точки зрения наглядных представлений. Самый простой пример — касательная к параболе г/—х2 в точке О (0, 0) (см, рис. 38). у, = 2х; у'(0) =0, т. е. tg а= =0; а=0 (или л). Касательная в точке О (0, 0) совпадает с осью абсцисс, что согласуется с интуитивным представлением о касательной. В то же время ось OY также имеет единственную общую точку с параболой, хотя явно касательной не является.
Для графика функцииy=sin х (синусоиды),касательной в точке	1) , очевидно, является прямая у=1
\ I
^'=cos х; = cos-^-=0^. В то же время эта прямая у=1 имеет бесконечно много общих точек с синусоидой j/=sin х (см. рис. 41).
Для лучшего ознакомления с новым определением касательной полезно решить следующую задачу.
Рис. 41
Найти угол касательной к кубической параболе у=х3
в точках: Xi = 0; х%=
Построить график функции и
соответствующие касательные (см. рис. 42).
Решение, tg а — yf = Зх2. tg 04 = у'(0) = 0 ; аА — 0;
tg =ИЦМ = 3>
Обращаем внимание учащихся на то, что первая касательная разбивает график на две части (одна часть лежит ниже, а другая — выше касательной г/=0).
Вторая касательная имеет с кривой две общие точки. Таким образом, то определение касательной к окружности, которое встречалось в школьном курсе геометрии (касательной к окружности называется прямая, имеющая с окружностью одну общую точку), годится только для окружности. Общее же определение касательной, которое было дано на предыдущем уроке, применимо к любой кривой и, в частности, к окружности.
Приведем еще несколько примеров решений задач, связанных с понятием касательной.
Рис.- 42
Задача. В какой точке касательная к параболе У=—х2 + 2х—3 наклонена к оси абсцисс под углом 0°; под углом 45°? (Построить график функции и касательные; см. рис. 43.)
Решение, tga=t/'=—2х+2.
1)	ai=Q; tgai=O; —2x-h2=0; Xi = l.
2)	«2=45°; tg <22= 1;—2x+2= 1; x2~-±-.
Задача. При каких значениях аргумента х касательные к кривым
y=f(x) =х3—X—1 и y=<f (x) = 3х2—4х+1, проведенные в соответствующих точках, параллельны.
Решение. Параллельность касательных означает, что они наклонены к оси абсцисс под одним и тем же углом, следовательно, при соответствующих значениях х обе функ
ции имеют равные производные.
Производная первой функции f'(x) = 3x2—1.
Производная второй функции «рдх)—6х—4.
Получаем уравнение: Зх2—1=6х—4;
Зх2—6х+3=0;
х2—2х+1=0;
Х! = Х2=1.
3	а да ч а. Под каким углом ось абсцисс на интервале/---
тангенсоида пересекает ; -£-) (Углом, под кото-
Рис. 44
рым кривая пересекает прямую, называется угол, который с этой прямой образует касательная к кривой в точке пересечения кривой и прямой. Например, на рисунке 44 кривая K.L образует с прямой АВ угол 0).
Решение. В данном случае нам надо определить угол наклона касательной к тангенсоиде в точке X6="0, где она пересекает ось абсцисс на интервале
(—5-; 4г) • Имеем У = tgx; tga=/=—;
\ -ь z у	о	cos2 а
tg ®о = cosW" ~ 1’ ao = 45°. (Иллюстрируем на таблице
с графиком функции y=tgx.)
Задача. Показать, что касательная в любой точке кривой у = 2х5+х3-Ь2х—5 наклонена к сен абсцисс пой острым углом.
Решение. tga=^'=’.10x4-(-3x2+2>0 при любом значении х. Это и означает, что a — острый угол.
§ 2. ИССЛЕДОВАНИЕ ФУНКЦИЙ НА ВОЗРАСТАНИЕ
И УБЫВАНИЕ И НАХОЖДЕНИЕ ТОЧЕК МАКСИМУМА И ТОЧЕК МИНИМУМА ФУНКЦИЙ С пбмбщью ПРОИЗВОДНОЙ
Приступая к изучению методов исследования функций на возрастание и убывание с помощью производной, очень удобно использовать график функции i/=sinx, заранее заготовленный на классной доске (или на переносной доске). Упражняясь в построении касательных, наносим на график касательные к синусоиде в точках
х —------£- (см. рис. 45).	V
Обращаем внимание На то, что в точках графика, абсциссы которых расположены на промежутках возрастания функции, касательная образует с положительным направлением оси абсцисс острый угол (производная в соответствующей точке, равная тангенсу этого угла, положительна); в точках графика,;абсциссы которых расположены на промежутках убываний функции, касательная образует с положительным направлением оси абсцисс ту* пой угол (соответствующая производная отрицательна); в точках, абсциссы которых разделяют промежутки убывания и возрастания (т. е. где функция имеет минимум или максимум) касательные параллельны оси абсцисс (производная равна 0).
Из наглядных соображений видно, что для данного графика функции указанная закономерность имеет место не только в выделенных выше точках, но и в других. В связи с этим возникает предположение о существовании зависимости между знаком производной и возрастанием или убыванием функции. Представляется вероятным, что если функция на промежутке возрастает, то производная в точках этого промежутка положительна, если функция убывает, то производная отрицательна, а там, где функция имеет минимум или максимум, производная равна 0. Также представляется правдоподобной справедливость обратных предложений: если во всех точках данного промежутка производная положительна, то функция на данном промежутке возрастает и т. п.
Более детальное рассмотрение вопроса показывает, что связь между знаком производной и возрастанием и убыванием функции, а также между обращением производной в нуль и наличием максимума или минимума действительно существует, однако не все, что представляется вероятным на первый взгляд, оказывается действительно справедливым.
Рассмотрим прежде всего возрастание и убывание функций. Покажем, что если функция возрастает на некотором промежутке, то из этого еще не следует, что во всех точках этого промежутка производная обязательно положительна. Убедиться в этом можно на примере хорошо знакомой функции */=х3. Эта функция всюду воз-126
растает. В то же время у'=3х2 и у =0, т. е. в точке 0 производная не является положительной. (Правда, во всех остальных точках производная положительна.)
Возникает вопрос: может ли у возрастающей функции производная в какой-либо точке быть отрицательной? Оказывается, имеет место следующая теорема.
Теорема. (Необходимое условие возрастания функции на данном промежутке.) Если функция y—f(x) на данном промежутке возрастает и имеет производную/'(>9, то в любой точкелго, принадлежащей этому промежутку, /W>0.
По определению /'(х0) = lim	. Так как
Дх-0 х
нас интересует предел функции при Дх -> 0, то можно ограничиться рассмотрением только таких значений Дх (достаточно малых по абсолютной величине), при которых х0+Дх принадлежит данному промежутку возрастания функции.
Тогда при Дх > 0 имеем х0 + Дх > х0 и f(x0 4- дх) > /(х0), т. е. 1 + ™ ~/(хо) >0, а при Дх<0 имеем х0-)-Дх<х0 и /(*04-Дх)</(х0), т. е. опять
1 (-*» + М — f (*о)	о
Дх
D	ж	/(хо+Дх)— f(Xo)
Все рассматриваемые значения функции -——-—-положительны. Можно доказать, что если все значения функции на некотором промежутке, содержащем данную точку а, положительны, то и предел ее в точке а не может быть отрицательным числом, откуда и следует, что f'(x9) = lim /(-To + .M-ZCxo)
Дх-0 ах
* Докажем, что если на некотором промежутке, содержащем точку а, ф (х) > 0 и 11m ф (х) существует, то lim ф (х) > 0. Обозначим х-+а	х-*а
11m ф (х) = k. Допустим, что k < 0. Возьмем е = — k > 0. По опре-х—а
делению предела функции для этого е существует такое число Ь, что для всех х а, удовлетворяющих неравенству |х — а|<&, выполняется неравенство ф (х) — k | < е. С другой стороны, при любом значении х |ф (х) — k = | ф(х)-|-(—k) |=| ф(х) + е |—ф(х)-Н > е, так как ф(х) > 0 и е >0. Итак, с одной стороны, для всех значений х из данного промежутка |ф(х) — Л| > е, а с другой стороны, для некоторых значений х из этого же промежутка |(<р(х)=«» — Л|< е, т. е. мы получаем противоречие.
Аналогично доказывается теорема, выражающая необходимое условие убывания функции на данном промежутке.
Если функция y=f(x) на данном промежутке убывает и имеет производную, то в любой точке х, принадлежащей этому промежутку, f'(x) 0.
Из наглядных соображений мы ранее пришли к выводу, что если во всех точках промежутка производная положительна, то функция на этом промежутке возрастает, а если во всех точках промежутка производная отрицательна, то функция убывает. К сожалению, приходится ограничиваться на уроке только формулировкой этих теорем, так как не рассмотрен ряд вопросов, необходимых для доказательства.
Теорема. (Достаточный признак возрастания функции на промежутке.) Если функция y=f(x) непрерывна на некотором промежутке и имеет положительную производную во всех точках, лежащих внутри этого промежутка, то на этом промежутке функция возрастает.
Аналогичную теорему, выражающую достаточный признак убывания функции на промежутке, формулируют сами учащиеся.
В качестве упражнений могут быть решены задачи.
Задача. В каких промежутках возрастают и в каких убывают следующие функции:
I)	у=х3— 12х24-48х—13;
2)	у=х3—х2—8x4-2;
3)	у=х3~Зх24-5;
4)	у=2х3~9х24-12х—3?
Задача. В каких промежутках возрастают и в каких убывают следующие функции:
1) t/=sinx, если х изменяется от 0 до 2л;
2) y=sin2x?
Приведем решение некоторых из них.
1. Исследуем функцию у=2х3—9х24-12х—3. /=6х2—18x4-12.
Решаем вопрос о знаке полученного квадратного трехчлена, для чего прежде всего находим его корни:
6х2—18x4-12=0;
х2—Зх4-2=0; Xi = 1; Ха=2.
На интервалах (—со ; 1) и (2; 4- со ) производная #'=6х2—18x4-12 положительна, а на интервале (1, 2) —
этрицательна. Функция у=2х3—9х2+12х—3 возрастает да промежутках (—т; 1] и [2; + ео) и убывает на промежутке [1; 2]. (Здесь концы промежутка могут быть в чего включены, так как рассматриваемая функция непрерывна.)
2. Исследуем функцию у — sin2x. у' = 2sinx»cosx = == sin 2х. > sin 2х > О при 2А^ < 2х < 2Ак + к или fen < х < kn где k — любое целое число.
sin 2х < 0 при 2Ак -f- тс < 2х < 2йтс 2тс или бтс -р < х < fat + к, где k — любое целое число.
Таким образом, функция y = sin2x возрастает на промежутках вида [£тс;	и убывает на про-
л»
межутках вида [Атс-|--^- ; + к], где k — любое целое число. (Концы промежутков включены в эти промежутки ввиду непрерывности функции f/=sinax.)
При решении упражнений еще раз убеждаемся в том, что при отыскании промежутков возрастания и убывания функции очень важно уметь находить точки максимума и минимума этой функции. Ставится задача получения признаков существования максимума и минимума,
Прежде всего на графиках функций f/—sin х, #=cos х, у~х2 еще раз иллюстрируется обнаруженный ранее из наглядных соображений факт, что для точек минимума и максимума касательная в соответствующих точках графика параллельна оси абсцисс, т. е. производная в точках минимума и максимума равна нулю. Для этих трех функций производная обращается в нуль только там, где эти функции имеют минимум или максимум. Однако пример функции у—х3 показывает, что производная может обращаться в нуль' и там, где функция не имеет ни максимума, ни минимума.
Таким образом, обращение производной в нуль в данной точке не является достаточным условием для существования в этой точке минимума или максимума. Можно показать, что это условие является необходимым, т. е. что в тех точках, где производная существует, но не равна нулю, функция не может иметь ни максимума, ни минимума.
9 Заказ 314	129
Теорема. Если в некоторой точкех0 функция y—f(x) имеет производнуюи fr(x$) =# 0, то в этой точке нет ни максимума, ни минимума.
Доказательство:
Пусть для определенности /'(л0) >
/'(х0)= lim 4- А*) — f (*о) Дх -* (J	Дх
Используем определение предела функции для функции
<р (Лх) = Нхо+Ах)^Нхо)
при Дх -> 0. (Вспоминаем определение предела функции в точке.) Выберем теперь в качестве 8 положительное число f(xo). Для этого числа е выберем такое 6>0, что при Дх =# 0 и | Дх | < 8 выполняется неравенство
f(x0 + Дх) — f(x0)	t,tv ч ______/(хо+Дх)—f(x0)	.
--------д7------------Г W <6 или	-------с <s (так как мы выбирали е=/'(хв)).
>0. Рассмотрим теперь произ-о- Вы-
Последнее можно записать с помощью двух не-f (хо + Дх) — f (х0)	.
равенств:	— е < —*----------------е < е,
откуда 0<- —	— - ^У^<2г. Итак, для всех Дх, удов-
летворяющих неравенствам Дх=#0 и | Дх|< 8, имеет мастп	f(xe + bx)—f(xe)
М v L1 U	.
Дх
вольный интервал (хх; х2), содержащий точку х,
берем положительное число Дх, меньшее, чем 8, так, чтобы х0 4- Дх принадлежало интервалу (хх; х2). Тогда, так как	>0 и Дх > 0, то
f (х0 + Дх) — Дх0) > 0 и, значит, / (х0 + дх) >/(х0).
Таким образом, на интервале (хх; х2) имеется точка х0 4- Дх, в которой /(х0 4- Д*) > f(xo), а так как интервал (хх; х2) выбирался произвольно, то это значит, что в точке х0 функция не может иметь максимум. (Напоминаем определение максимума функции.)
Возьмем теперь отрицательное число Дх так, чтобы | Дх [ < 8 и х0 4- дх также принадлежало интервалу (хх; х2). (Здесь Ха + д* < х0).
Так как	>0 и Дх < 0, имеем
/ (*о 4- Д*) — f (*0) < °> откуда f (х0 + Дх) < f (х0).
Получаем, что в точке х0 нет минимума (так как в любом интервале, содержащем эту точку, имеются точки, в которых значение функции меньше, чем f(x0)).
Итак, в точке х0 функция = не имеет ни максимума, ни минимума. Аналогично можно провести доказательство для случая, когда f'(x0) < 0.
Замечание. Функция может иметь максимум или минимум и в тех точках, где производная не существует.
Например, функция у =}/х2 имеет минимум в точке 0, так как при любом	>0, а при х»0
з _____
Vx2=O. В то же время #'(0)~linv	—— = lim	.
Дх-*0 Л •	Дх->0Д х
Но при Лх->0 э неограниченно возрастает по аб-у Дх
солютной величине, т. е. функция — не имеет у4 Дх
предела при Дх->0 и, значит, в данном случае у'(Р)
не существует (см. рис. 46.)
Итак, для того чтобы в данной точке существовал минимум или максимум функции, необходимо, чтобы в этой точке либо производная была равна нулю, либо не существовало производной.
Пусть теперь для функции y=f(x) в некоторой точке Хо производная f'(x0) равна нулю или не существует. Та-9*	131
1£ую точку в дальнейшем будем называть критической. В критической точке х0 функция может иметь минимум
или максимум, но может, как мы видели на примере функции у~х2, и не иметь ни того, ни другого. Возникает вопрос: как можно судить о том, имеется ли в действи-тельности в точке Хо максимум или минимум?
Ограничимся рассмотрением случая, когда существует интервал (хк х2), содержащий точку х0, на котором функ-
ция непрерывна и имеет производную во всех точках, кроме, быть может, точки Хо.
Рассмотрим следующие 4 случая:
1) На интервале (Xi; Хо) производная f'(x) положительна, а на интервале (хо; х2)— отрицательная (см. рис. 47).
Тогда на промежутке (хг, Хо] функция возрастает, а на промежутке [х0; х2) — убывает (по достаточным
признакам возрастания и убывания функции). Легко видеть, что в этом случае в точке х0 функция имеет максимум, так как значение функции в точке Хо больше, чем в любой другой точке интервала (xi; х2).
2)	На интервале (х^ Хо) и производная f'(x) отрицательна, а на интервале (хо; х2) — положительна. Тогда на промежутке (хй Хо] функция убывает, а на промежутке [х0; х2) функция возрастает. В точке х0 функция имеет минимум (см. рис. 48).
3)	Во всех точках интервала (х2; х2), кроме точки хо, производная положительна. Тогда функция возрастает на обоих промежутках (хк хо] и [х0; х2) и, как легко видеть, возрастает на всем промежутке (х^ х2). В точке Хо нет ни минимума, ни максимума (см. рис. 49).
4)	Во всех точках интервала (хк х2), кроме точки Хо, производная отрицательна. Функция убывает на промежутке (хй х2). В точке Хо нет ни минимума, ни максимума (см. рис. 50).
Правило, позволяющее судить о наличии минимума или максимума в критических точках, коротко формули-
руют так: если при переходе через критическую точку х0 провзводкая/'С?) меняет знак с пд&са ид минус (случай 1), то в точке(х) функцияДх) имеет максимум. Если же/'(х) меняет знак с минуса на плюс (случай 2), то в
Рис. 48
Рис. 49
точкехофункция/(х) имеет минимум. Если при переходе через критическую точку Хо производная /'(лг) не меняет знак (случаи 3 и 4), функция не имеет в точке лг0 ни минимума, ни максимума.
В качестве иллюст-
бх—4 = 0; х=А; х0= -L
рации правила решается несколько задач. Например, задача: исследовать на максимум и минимум функцию:
у = 3 х2 — 4х + 6.
Решение. у'— =6х—4.
Производная существует всюду. Ищем точки, в которых она обращается в нуль.
— критическая точка.
на интервалах I •— со;
6х— 4 < 0; при х >
(2 х
2 \	/ 2	\	2
т) ’ vT ’ 00 ) • При *
6х—4 > 0. Производная меняет
знак с минуса на плюс. В точке х0 данная функция имеет минимум. (Этот же результат мы могли получить, исследуя квадратный трехчлен г/ = 3х2— 4х+6 обычными средствами.)
Задача. Исследовать на максимум и минимум функцию i/=x3+5x-|-2.
Решение. у'=Зх2+5. Производная всюду существует и нигде не обращается в нуль. Функция не имеет ни минимума, ни максимума (*/'>0, функция возрастающая).
Задача. Исследовать на максимум и минимум функцию У = 4“ х3----х2 — 2х + 6 .
и	£
Решение, у' = х2 — х — 2; х2 — х — 2 = 0; xi = = —1; х2=2.
Критические точки: Xi =—1; х2 = 2.
По свойствам квадратного трехчлена заключаем, что t/z>0 на интервалах (—оо ; —1) и (2; + оо), у'<0 на интервале(— 1; 2).
Отсюда следует, что при переходе через точку Xi = — 1 производная меняет знак с плюса на минус. В этой точке функция имеет максимум.
При переходе через точку х2=2 производная меняет знак с минуса на плюс. В точке х2 функция имеет минимум.
Как говорилось выше, достаточные признаки возрастания и убывания функции даются учащимся без доказательства. Однако мы считаем возможным провести эти доказательства с помощью теоремы Лагранжа (хотя бы во внеурочное время). Разумеется, предварительно следует познакомить с самой теоремой Лагранжа.
К формулировке теоремы Лагранжа можно подойти в связи с задачей отыскания достаточных признаков возрастания и убывания функции, исходя из наглядных соображений. Рассмотрим графики возрастающей и убывающей функций (см. рис. 51,а и б).
Из рисунка 51, а, где функция f(х) возрастает на промежутке [р; легко усмотреть, что производная функции f(x) в любой точке промежутка [р; q\ положительна (касательная в любой точке графика образует с осью абсцисс острый угол). Возникает вопрос, как установить связь между этим обстоятельством и возрастанием функции на промежутке [р; <?].
Вспоминаем определение возрастающей на промежутке функции. Функция называется возрастающей на данном промежутке, если для любых двух значений аргумента и Хг, лежащих на этом промежутке, из не-
Рис. 51
равенства x2>Xi следует неравенство /(x2)>f(xi). Другими словами, возрастание функции на промежутке [р; q] равносильно тому, что '	Л*1?- >о для любых
значений аргумента xj и х2, принадлежащих данному промежутку [р -, 4
Выясним геометрический смысл последнего неравенства, выбрав на рассматриваемом графике функции (см. рис. 51, а) две произвольные точки М (xi; f(xi)) и N (х2; f (х2)). Легко видеть, что	= tg <р, где
ср — угол, образованный хордой MN с положительным направлением оси абсцисс.
Так как	> 0 , то любая хорда графика
образует с осью абсцисс острый угол. Ранее уже было замечено, что и любая касательная, проведенная к графику данной функции, образует с осью абсцисс острый угол. По-видимому, существует какая-то связь между этими двумя обстоятельствами. На данном графике проведена касательная TQT, параллельная хорде MN.
Если бы оказалось возможным для любой хорды графика провести параллельную ей касательную в какой-либо точке этого графика, то это означало бы, что если производная f'(x) во всех точках интервала (р; q) положительна (откуда следует, что касательные во всех точках графика образуют с осью абсцисс острые углы), то и все хорды графика образуют с осью абсцисс острые углы, т. е. для любых Х\ и х2 из промежутка г 1	f (Х2) — f (Xi) _ л
[р; q] выполняется неравенство	>0 и, зна-
чит, функция/(х) возрастает.
Таким образом, существенно найти условия, при которых каждой хорде графика соответствует некоторая касательная к графику, параллельная этой хорде, или, другими словами, для любых точек Х\ й Хг данного про-
---------------------------	г/ /	f(x«)— f(xt) межутка существует точка х такая, что f (х) —	
(f'(x) —тангенс угла наклона касательной, а f(x»)—J(x«)	.
—---------тангенс угла наклона хорды).
Оказывается, что существование производной во всех точках интервала (р; q) и обеспечивает для непрерывной функции существование для каждой хорды ее графика касательной, параллельной этой хорде. Это следу
Рис. 52
ет из теоремы:
Теорема Лагранжа. Если функция f(x) непрерывна на сегменте [а; &] и имеет производную в каждой точке интервала (а; &), то существует такая точка с, принадлежащая интервалу (а, &), что f '(c) = £•
Геометрически это означает, что существует касательная к графику функции f(x), параллельная хорде лВ, где A (a;f(a)),B (t>; f(b)) (см. рис. 52).
Прежде чем дать доказательство теоремы Лагранжа, приходится рассматривать ее частный случай, когда f(a)=f(b), который получил название теоремы Ролля.
Теорема Ролля. Если функция f(x) непрерывна на сегменте [а; &] и имеет производную на интервале (а; &), причем f\a) — то существует такая точка с, при-
Рис. 53
надлежащая интервалу; (а; &), что /'(О = 0.
Геометрическая иллюстрация такая же, как в общем случае теоремы Лагранжа, существует касательная к графику функции, параллельная хорде АВ, или, так как в этом случае хорда АВ параллельна оси абсцисс, существует касательная к графику функции, параллельная оси абсцисс (см. рис. 53, а и Ь).
Доказательство теоремы Ролля опирается на сформулированные выше (без д ок аз а те л ьс т -ва) свойства непрерывных функций.
Доказательство теоремы Ролля
Так как функция f(x) непрерывна на сегменте [а, Ь], то она принимает на этом сегменте как наибольшее, так и наименьшее значение.
Если функция f (х) на сегменте [а, 6] постоянна, то все ее значения, включая наибольшее и наименьшее, совпадают с	В этом случае f'(x)=O для
любого значения х, принадлежащего промежутку [а, &]. (Так как производная постоянной равна 0.)
Если функция f(x) не постоянна на сегменте (а, &], то !(а) =/’(&) не может одновременно быть и наибольшим и наименьшим значением функции и, значит, по
крайней мере одно из указанных значений функция при нимает в некоторой точке с, лежащей внутри сегмента [а, 6] (т. е. на интервале (а, Ь)).
В этом случае в точке с функция, очевидно, имеет максимум или минимум и /'(с)~0 согласно необходимому условию существования экстремума.
(Если теорема Ролля рассматривается до изучения необходимого условия существования экстремума, то утверждение /'(с)=0 в точке с интервала (а, Ь), где функция принимает наибольшее (наименьшее) значение, доказывается совершенно так же, как это было сделано выше при выводе необходимого условия существования экстремума.)
Доказательство теоремы Лагранжа
По условию функция y — f(x) непрерывна на сегменте [а, и имеет производную на интервале (а, 6); требуется доказать, что существует на интервале {а, Ь}
такое значение с, что f' (с) =
b — а
Рассмотрим вспомогательную функцию
?(*) = f(x) —-(х-а).
Очевидно, что ф(х) непрерывна на сегменте [а, Ь] и имеет на интервале (а, Ь) производную
?' (*) = Г(х) - !-^Е~ 
(По свойствам непрерывных функций и теоремам о производных.)	,
?(fl) = /(«) - (<*—«) =/(«};
? (Ь) = /(&)-	==	
Таким образом, <р(«) = ф(&), и функция ф(х) удовлетворяет всем условиям теоремы Ролля.
Следовательно, существует такая точка г, принадлежащая интервалу {а, Ь), что ф'(с)=0. Отсюда
Г (С) _ L -L Н = о
' ' '	b - - а
»-™ Г М -
Используя теорему Лагранжа, доказываем достаточное условие возрастания функции на промежутке <а, Ь> (т. е. на интервале (а, Ь), или на сегменте [а, 6], или на полуинтервале (а, Ь], или на полусегменте [я, Ь).
Теорема. Если функция y f(x) непрерывна на промежутке <а, Ь> и имеет во всех точках интервала (а, Ь) положительную производную, то эта функция возрастает на промежутке <а, Ь>.
Рассмотрим произвольные значения аргумента и х2, принадлежащие промежутку <atb> и удовлетворяющие условию X] < х2. Тогда, очевидно, сегмент [хь хъ] содержится в промежутке <а,Ь>. Функция у = — f(x) непрерывна на сегменте [Х],х2] и имеет производную во всяком случае на интервале (хьх2). В таком случае согласно теореме Лагранжа существует такая точка с, принадлежащая интервалу (хьх2), что
Но по условию f'(x) положительна во всех точках интервала (а, Ь) и, значит, f'(c)>0 или^^—> 0, и так как х2 - х, > 0 , то / (х2) - f (xt) > 0, т. е. f (х2) > /(xj.
Так как точки Xi и х2 на промежутке <а, Ь> выбирались произвольно, то это и означает, что функция у = f (х) возрастает на промежутке <£,&>.
Аналогично формулируется и доказывается достаточное условие убывания функции на промежутке.
С помощью теоремы Лагранжа может быть доказано и следующее условие постоянства функции.
Теорема. Если функция f{x) непрерывна на промежутке <а, Ь> и имеет во всех точках интервала (а, Ь) производную, равную нулю, то эта функция постоянна на промежутке <а, &>.
Рассмотрим произвольные значения аргумента х1 в х2, принадлежащие промежутку <я, Ь>. Пусть для определенности х1 < х2. Тогда сегмент [хь х2] содержится в промежутке <а,Ь>, а значит, функция f(x) непрерывна на сегменте [хь х2] и имеет производную f'(x) во всяком случае в каждой точке интервала (хьх2).
По теореме Лагранжа существует такая точка г, принадлежащая интервалу (хъ х2) (и, значит, интерва-
лу (а, &)), что Г(с)=	Так как f'(x) — О
во всех точках интервала (а, Ь), то f'(c) = 0 или — * ~~/	— 0, т. е. /(xj =/(х2). Итак, в любых двух
Х2 — Xi
точках промежутка < а, b > значения функции у — f(x) совпадают, а это и означает, что функция y~f(x) постоянна на промежутке < а, b > .
§ 3. ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНОЙ И ПОСТРОЕНИЕ ИХ ГРАФИКОВ. ГРАФИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЙ
В связи с изучением условий возрастания и убывания функций и признаков существования максимума и минимума учащиеся строят ряд графиков функций с небольшим исследованием этих функций.
Рассмотрим задачи.
Задача. Построить график функции
^=~4--¥г+2*-4->
определив предварительно промежутки возрастания и убывания; точки максимума и минимума; точки пересечения кривой с осями координат; несколько других точек кривой, уточняющих ее форму.
1)	Легко видеть, что область определения данной функции есть множество всех действительных чисел, т. е. интервал (— оо , 4- оо ).
2)	Чтобы обнаружить точки максимума и минимума функции и промежутки ее возрастания и убывания, находим производную данной функции:
= Н2 = -4<*~3). О	о
Ищемдсритические точки. Так как производная су-ЩССТОуётво всех точках области определения, то доста-2
точно решить- уравнение---%- х + 2 = 0 .
Получаем х = 3. Итак, имеется одна критическая точка х0 — 3.
Исследуем знак производной на промежутках 2
( — оо, 3) и (3, + оо). При х < 3-о-*.> — 2, откуда
/ —-----х 4-2 > 0. При х > 3------^-х <—2, откуда
у = _ 2 х + 2<0.
О
На интервале (— со, 3) функция возрастает, а на интервале (3, + оо ) —убывает. В точке х0 = 3 функция имеет максимум. Соответствующая точка графика
3)	Точки пересечения с осью абсцисс находим из со-ошения-----~ х2 + 2х-----1- = 0; х2 — 6х -|- 5 ---= 0;
Получаем точки В (1; 0) и С(5; 0).
Точку пересечения с осью ординат получаем, пола-гая х = 0. Тогда у = —Получаем точку D\ 0,
4)	Изображаем в прямоугольной системе координат
3
все полученные выше точки графика. Затем находим дополнительные точки:	Е( — 1: — 4):
3 Г
В заключение строим график функции (см. рис. 51).
Легко заметить, что данная кривая
есть парабола с вершиной в точке A и ее можно было построить и без использования производной.
Задача. То же условие, что и в предыдущей задаче, для функции у = х3 4 — 4 х2.
1. Область определения функции (— оо, 4*°° )•
2. Ищем промежутки возрастания и убывания и точки максимума и минимума: у'-4ха—8%; 4х3—8х = 0; 4х(х2—2)=0.	_	_
Критические точки: хк = 0; х2 = — ]/ 2 ; х3 — J 2 •
Исследуем знак производной на промежутках
У Т); (- [' 2"; 0); (0; У~2); (У 2; -Ь со).
На(— оо;—J/^ЗГ) у' = 4х(х2—2)<0 функция убывает.
На (—]/2 ; 0) у' = 4х(х2—2)>0функция возрастает.
На (0; У 2 ) у' = 4х(х2- 2)<0 функция убывает.
На (У 2 ; оо) у' — 4л (х2 —2) > 0 функция возрастает. Точки минимума х2 — —} 2 ; х3 = 1/Л2 . Соот
ветствующие точки графика А (—]/ 2 ; — 4);В (|/ 2, — 4)
Точка максимума xt = 0. Соответствующая точка графика О (0; 0)
3. Точки пересечения с осями: при у = 0 х4— 4х2 = 0; Х2(Х2 —4)=0; Х4-0; Х5 = -2; XG = 2.
Соответствующие точки графика О (0; 0); С (—2; 0);
0(2; 0).
При х = 0 у~0.
Строим все полученные точки.
Находим дополнительные точки графика £(1,-3);	F(—1; —3);
к (	I	•	.
Л \ 2	16 J ’
, (____1_.__15)
L \	2 ’	16 )
и строим график (см. рис. 55).
Построение упрощается, если заметить, что функция четная.
После того как усвоено исследование функции на возрастание и убывание, специальное время отводится исследованию функций и построению их
Рис. 55
графиков с применением понятия предела функции и производной. Схема исследования функции пополняется вычислением пределов функции на концах промежутков, из которых состоит область определения функции, в связи с чем находятся горизонтальные и вертикальные асимптоты графика функции, если они существуют *.
Нам представляется полезным в связи с построением графиков функций в процессе решения задач познакомить с бесконечными пределами и односторонними пределами. (Мы не считали целесообразным делать это раньше в теме «Функции и пределы», чтобы не перегружать обилием новых понятий.)
Дадим дополненную схему исследования функции.
1.	Область определения функции.
2.	Четность и нечетность.
3.	Периодичность.
4.	Пределы функции на концах промежутков, из которых состоит область определения функции. Горизонтальные и вертикальные асимптоты.
5.	Ограниченность сверху и снизу.
6.	Точки максимума и минимума и промежутки возрастания и убывания функции.
7.	Точки пересечения графика функции с осями координат.
Построение графика функции (с вычислением, в случае необходимости, координат еще нескольких его точек, кроме полученных ранее).
Иногда исследование удается провести не по всем пунктам, входящим в схему. Об этом следует предупредить, хотя и подбираются в основном такие примеры, где исследование может быть проведено полностью. Во всяком случае применение производной делает возможным во всех рассматриваемых примерах провести исследование на возрастание и убывание функций.
При построении графиков функций рекомендуется пользоваться миллиметровой бумагой.
Каждый этап исследования может потребовать немало рассуждений и выкладок. Поэтому целесообразно окончательные результаты исследования выписать на классной доске и в тетрадях в виде краткой схемы.
* Учащимся известно понятие асимптоты, как прямой, к которой как угодно близко приближается точка графика функции при удалении ее в бесконечность.
Иногда такую схему можно рекомендовать записать на миллиметровой бумаге рядом с графиком.
Разумеется, исследование функций с использованием понятий предела функции и производной проводится не только на специально отведенных этому нескольких уроков. Оно продолжается на протяжении всего дальнейшего изучения темы «Производная и ее применение к исследованию функций».
Первый пример исследования по дополненной схеме, занимающий обычно весь урок, рассматривается учителем, который по ходу дела дает нужные пояснения и вводит новые понятия, о которых говорилось выше.
Для исследования может быть выбрана функция
г/ \ х2 — 4
y =	хг_2х_3--
1. Очевидно, функция определена при всех значениях х, при которых знаменатель не обращается в нуль. Решаем уравнение:
х2 —2х —3 = 0;
X, = — 1; х2 = 3.
Отсюда область определения: (—со; (3, 4- оо).
9 ft ________(^х)2—4____ х2 4
*•'»' л) (—x)s>—2(—х)-3	Х2+2х—3V
-1); (—1; 3);
К	(—х)2-2 (—х)+3	х2—2х—3 ~	'
Функция не является ни четной, ни нечетной.
3. Докажем, что функция не является периодической. Допустим, что функция имеет период I. Тогда
(х + /)2 — 4	__ х2 — 4
(х + /)2 — 2(х + /) —3 ~ X* — 2х —3
верно-при любом значении х, в частности при х = 0, т. е. должно быть справедливо равенство
/2 _ 4	4
/2—2/—3 ~ Т’
Находим значение I:
3Z2—12 = 4Z2—8Z—12; Z2—8Z=0; и так как Z^O, то Z=8.
Следовательно, должно иметь место тождество: (х + 8)2 —4	Л-2-4	.
(х+8)2—2 (х-|-8)—3~ = х2-2х-3 = Б частности, при х = 1
должно иметь место равенство: (14-8)2—4	1—4 ж 77	3
(14-8)2—2(14-8)—3 ~ 1—2—3 ИЛИ 60 — 4 ’
что заведомо неверно.
Полученное противоречие показывает, что данная функция не имеет периода. (В дальнейшем доказатель-ство отсутствия периодичности проводить не обязательно. Достаточно указать, что это можно сделать точно так же, как в рассматриваемом примере.)
4. Находим:
lim
Х->— «
= lim
Х~>-—ОО
х2—4
х2—2х—3
Прямая у = 1 является горизонтальной асимптотой, к которой неограниченно приближается график функ-
ции при х -э—• °0;
.. . х3—4 -
lim -т—к—о =-„ х2—2х—3
lim
X > -| оо
При х—>4-°° график функции неограниченно приближается к той же асимптоте у — 1.
Далее следует найти предел функции при х = — 1. Точка х = — 1 является правым концом интервала (— оо ; _ 1) и левым концом интервала (— 1; 3). Желательно отдельно рассмотреть предел функции при х -> — 1 для значений аргумента, лежащих на интервале (— °0; —1), т. е. слева от точки —1, и отдельно для значений аргумента, лежащих на интервале (—1; 3), т. е. справа от точки —1. Первый из этих пределов мы называем пределом слева и будем обозначать через lim /(х)	, второй назовем пределом справа и
х->—1—0
будем обозначать через lim f (х).
1-|-0
Вообще, число Ь называется пределом слева функции f (х) при х, стремящемся к a (b = lim f (х)), если 0
для любого наперед заданного положительного числа е можно указать такое положительное число б, что для всех значений х, удовлетворяющих неравенству а — б < <х<а, выполняется неравенство |f(x)—6|<е. (Легко
видеть, что неравенство а — 6 < х < а равносильно системе неравенств < 8 и х< а.)
Аналогично определяется предел справа. Может случиться, что существует только один из этих пределов или существуют оба, но они различны. В этих случаях обычный предел lim f(x) не существует. Если су-х -> а
ществует limf(x) то, он, очевидно, является одновре-х а
менно пределом справа и пределом слева. С другой стороны, можно показать, что если в некоторой точке предел функции слева совпадает с пределом функции справа, то их общее значение является пределом функции в данной точке.
Итак, найдем Ит *2~4 • .
так как . lim (х2— 4) = —3, I—О
11m (х8 — 2х — 3) =0, 1—0
..	X2—4
то lim -т——х не существует.
Легко видеть, что при х — 1 — 0 абсолютная величина дроби неограниченно возрастает, причем числитель при х, достаточно близких к —1, отрицателен, а знаменатель при всех х <—1 положителен (квадратный трехчлен х2 — 2х — 3 положителен для значений х. меньших меньшего корня —1 и больших большего корня 3).
Следовательно, при х, стремящемся к —1 слева, дробь \g_2x— з~ неогРаниченно возрастает по абсолютной величине, оставаясь отрицательной для х, достаточно близких к —1. Этот факт мы условимся коротко за* f. ха — 4 писывать так: lim ——о--------б = — 00 •
х— t-о л2 — 2* — 3
Учащимся сообщается (не для обязательного запоминания) следующее определение.
Функция f(x) неограниченно возрастает по абсолютной величине при ж->а, если для любого наперед заданного положительного числа р можно указать такое положительное число 6, что для всех х #= а и удовлетворяющих неравенству |лг—al <8 выполняется неравенство 1Я*) I > р-146
Аналогично определяется неограниченное возрастание функции по абсолютной величине при х -> + 00 , х % х-+а — 0, х^а + 0.
Считается очевидным, что рациональная дробь неограниченно возрастает по абсолютной величине при х -+а (соответственно при х-^а—0; х -> а-|-0;х -> --р °°; х-> — оо), если при х->а (х->а —0; х-> а-|-0; х^-—	со),
предел ее знаменателя равен нулю, а предел числителя существует и отличен от нуля. Учащимся по
ясняют, что соответствующее доказательство могло бы быть проведено.
ция /(х) неограниченно возрастает по абсолютной величине, оставаясь положительной для значений, достаточно близких к а, то мы будем это записывать так:
Аналогично lim f (*) = х~+а lim f(x) = — оо).
оо
(lim f(x) = — оо .
Так KaKjta_o^2-_3 является вертикальной lim
оо
1 •	х2 — 4
°0: lim ——х—
то прямая х = —1 асимптотой. Очевидно, (График приближается к этой асимптоте и справа).
Аналогично находим .. *8 —  11т х* - 2х х-*з-о х—*х
Прямая х = 3 — вертикальная асимптота.
5. Функция не ограничена ни сверху, ни снизу, так как х^Гх4_з=-°°; -хг--~Гх-з = + °°-д /  2х(№ — 2х — 3)—(х2 — 4) (2х — 2)  
°* У “	(Х* —2х—3)2	~
_ •— 2х* + 2х — 8 __	2 х* — х + 4 ~	(х2-~2х —3)2	“ (ха —2х —3)2 *
при всех значениях х, значит, fz(x)<0 при всех значениях х, входящих в область определения функции. Таким образом, данная функция не имеет точек минимума и максимума и убывает па каждом из промежутков
10*
147
Следует заметить, что исследование на возрастание и убывание, проводится отдельно на каждом из промежутков, из которых состоит область определения функции.
7. Находим точки пересечения графика функции с осями координат. Чтобы найти точку пересечения графика функции с осью ординат, полагаем х = 0. Полу-чаем:	Искомая точка А (q. Чтобы найти
точки пересечения графика функции с осью абсцисс, полагаем у = 0. Получаем:
Т5А~—V = 0; Xs-4 = 0; х1>2 = ± 2.
л2*—2х—3	’	7
Искомые точки: В (—2; 0) и С (2; 0). Полезно проверить, пересекается ли график с асимптотой у === 1. При у = 1 получаем:
«1; х2 — 4 = х2 —2х —3; 2х-1=0;х-|.
Искомая точка D (-=- ; 1 ) .
Дополнительные точки графика находим в процессе построения графика по мере надобности. Строим график функции (см. рис. 56). Начинаем построение с проведения асимптот. Затем строим точки пересечения гра-
фика с осями координат. Далее на каждом из промежутков находим две-три дополнительные точки и строим соответствующую ветвь графика функции.
На промежутке (—<х>;— 1) строим, например, допол-
Л	Л	3
нительные точки с абсциссами х = —4 и х =---х- .
п v л _	16 — 4	4
При х —	4 у— 16_|_8_3 — 7 .
При х =------ у = — ~.
Искомые точки: Е( — 4;-у-};
Строим соответствующую ветвь графика, учитывая, что lim f(x) = 1, lim f(x) — — co .
—oo	X->—1—0
На промежутке (— 1; 3) строим дополнительные точ-л	1	5
ки с абсциссами х —---и х =	.
Ла	Лл
При х =----1- у = 2±~.
При х = у = — 1~.
При х = 1 у = А .
Искомые точки: К I-----; 2 -х-| ; Q I 1;-т-| ;
\ “ /  \ * 1
Строим соответствующую ветвь графика функции, учитывая, что lim f (х) = 4- оо и lim f (х) = — оо .
х->—1+о	х-З-о
На промежутке (3, + оо) строим дополнительные точки, например, с абсциссами х=3-|-;х=4;х=6. Получаем:
Прих=3-^-	=
При х =4	у = 2-|- .
При. х = 6	у = 1 4т- .
Искомые точки: Ml 3 -х- ;
\ xi
Строим соответствующую ветвь графика, учитывая, что lim f (х) = + оо и lim f(x) = 1.
В дальнейшем учащиеся дома и в классе самостоятельно проводят исследование функций и построение их графиков сначала для сравнительно простых, а затем и для более интересных случаев.
Самый простой случай, когда встречаются введенные в предыдущем примере новые понятия — хорошо знако-
А 1
мая функция у = — .
Учащиеся легко проводят ее исследование по рассмат* риваемой схеме.
1.	Область определения (— оо ; 0); (0 ; + со).
2.	Функция нечетная.
3.	Функция не является периодической.
4.	lim — — 0; lim — = 0.
Л—со X	’х-Н-оо х
у = 0 — горизонтальная асимптота.
1-1	П 1 I
lim — = —оо; lim — = + оо .
О Х	х->0-|-0 х
х ~ О — вертикальная асимптота.
5.	Функция не ограничена.
6.	у' =----. Производная существует при всех зна-
чениях х, отличных от нуля (т. е. всюду в области определения данной функции), у' < 0 при всех значениях х и точек экстремума нет. Однако из неравенства у' < 0 еще нельзя сделать вывод об убывании функции, так как соответствующее условие формулируется для функции, непрерывной на промежутке, а область определения данной функции не является промежутком.
На каждом из интервалов (—’оо ; 0) и (0; + оо ) функция непрерывна и, следовательно, из того, что у' < 0, сле-дует, что функция у = — убывает на каждом из этих
X
промежутков в отдельности.
7.	График функции у = — хорошо знаком учащимся.
X
Все рассмотренные свойства могут быть проиллюстриро< ваны на нем (см. рис. 57).
Вполне самостоятельно учащиеся могут провести и 1
исследование функции	при котором также
встречаются вновь введенные понятия пределов слева и справа и бесконечных пределов.
1. Область определения функции (—оо;
2. Функция четная.
3. Функция не является периодической.
4. lim т- 1 „ = 0; lim . 1 -- = 0. v‘2	4 * * * * 9	I _
у = 0 — горизонтальная асимптота.
П	1	1.	1
lim i-----z = — оо ; lim -------= 4
x—i-o 1 — x	x^-i-i-o 1 — xa
x = — 1 — вертикальная асимптота.
lim
lim -----
1—х2
х = 1 — вертикальная асимптота.
5. Функция неограниченная.
л f	1 о..	2х
У (Д2__ 1)2^ ’ ' =	1)Г •
Ищем критические точки.
Так как производная существует во всех точках области определения функции (т. е. при х — 1; х =# 1), то достаточно решить уравнение
откуда х0 = 0 — единственная критическая точка.
При х < 0 у' < 0, при х > 0 у' > 0, следовательно, в точке х0 = О функция имеет минимум. Соответствующая точка графика А (0; 1).
Функция непрерывна на каждом из интервалов (— оо ; -1); (-1; 1); (1; +оо).
Учитывая знак производной, получаем, что на интервале (—оо; —1) функция убывает, на полуинтервале (—1; 0] — убывает, на полусегменте [0; 1)—возрастает и на интервале (1; + оо) —возрастает.
7. Очевидно, что график функции не пересекает ось абсцисс. Точка пересечения с осью ординат Л (0; 1) уже была получена ранее. При построении графика учитываются все обнаруженные свойства функции (четность, пределы на концах промежутков и т. п.).
Дополнительно находим точки: В
С(2;---1); D(3;
Одновременно с этими точками наносим на график и симметричные им точки (см. рис. 58).
_L 2
Интересно исследование функции jT у =	,
график которой уже строился при введении предела функции при + оо (см. рис. 16).
1.	Область определения (— со ; + оо ).
2.	Функция четная.
3.	Функция не является периодической.
л 1, х* + 2	.	,. Xs + 2	1
4.	11m . т-J - 1; lim = 1.
r , X* + 1	х« + 1
л—►—00	Л—>1^00	'
у = 1 — горизонтальная асимптота.
х2 4- 2
5.	Т । > 1 — функция ограничена снизу.
х2 4- 2
~ 1 "I--ГЗП	—функция ограничена сверху.
Функция ограниченная. Ее график лежит в полосе между прямыми у — 1 и у = 2.
Рис. 58
/*	, _ 2х (хг + 1) — 2х (хг + 2)	2х
”• У ~~	(х2 + 1)2	—	(х2 + 1)2 •
Так как производная существует при всех значениях х, то критические точки находятся как корни уравнения
_____—___— О (х2 + 1)«	’
Единственная критическая точка х0 = 0.
При х < 0 if > 0; при х > 0 д' < 0.
В точке х0 = 0 функция имеет максимум. Соответствующая точка графика А (0; 2).
7. Строим график функции (см. рис. 16).
Рассмотрим еще несколько примеров исследования функций, с которыми учащиеся справляются самостоятельно или с небольшой помощью. (В большинстве случаев мы приводим только окончательные результаты исследования, записанные в виде схемы.)
у — f (х) = 2х2— х4 — 1.
1.	Область определения (—оо; + оо).
2.	Функция четная.
3.	Функция не является периодической.
4.	lim /(*) = — оо; lim /(*) = —оо - Вертикальных
X—►—со	X—*4“ 00
и горизонтальных асимптот нет.
5.	Функция не ограничена снизу, у^0—функция ограничена сверху. (у^0,таккаку = 2х2—х4—1 = — (х2—I)2.)
6,	Функция имеет максимум в точках х = — 1 и х =1 и минимум в точке х = 0.
Соответствующие точки 1 графика: А (—1; 0); В (1; 0); ' С (0; -1).
На промежутках (—оо;—1) Т и (0; Г) функция возрастает; на промежутках (—1; 0) и (1; + оо ) —убывает.
7. Точки пересечения графика функции с осями координат: А (—1; 0); В (1; 0); С (0; —1). (В первых двух точках график касается оси абсцисс.) График функции смотрите на рисунке 59.
ж2*— 1
ж2 + 1
1.	Область определения функции (— оо ; + оо).
2.	Функция четная.
3.	Функция не является периодической.
л f. Ж2 — 1	1 п Ж2 — 1	1
4.	lim г = 1; 11m	= 1.
х-г— а>* '	'
у = 1 — горизонтальная асимптота.
5.	у <1; У >— 1 — функция ограниченная.
6.	В точке х = 0 функция имеет минимум. Соответствующая точка графика А (0; — 1).
На промежутке (—оо;0) функция убывает, на промежутке (0; + со ) функция возрастает.
7.	Точки пересечения с осями координат: В (— 1; 0);
С (1;0); А (0; — 1).
График функции смотрите на рисунке 60.
_ х2 4 х 4- 1 _
& х2 — х 4- 1
1.	Область определения функции (— оо; + оо).
Рис. - 60
2.	Функция не является ни четной, ни нечетной.
3.	Функция не является периодической.
lim у = 1;
lim у = 1.
—1] функция убывает; на
у = 1 — горизонтальная асимптота.
Вертикальных асимптот нет.
5.	У>0; у^З—функция ограниченная *.
6.	В точке х=—1 функция имеет минимумов точке х = 1 — максимум.
Соответствующие точки графика А (— h-у); В (1; 3).
На промежутке о°;
[—1; 1] — возрастает; на [1; + оо)—убывает.
7.	Точка пересечения с осью ординат С (0, I). Допол-нительные точки D \2, -^-1; Е | — 2,	.
График функции смотрите на рисунке 61.
х
I.	Область определения функции ( — о?; + оо).
2.	Функция нечетная.
* Доказательство неравенства у < 3 может оказаться затруднительным для учащихся. 4
3.	Функция не является периодической.
4.	Ит = 0; lim ~ 0:
Х-^— оо 1 ~ Л	Л->4- 00 1 А
у = 0 — горизонтальная асимптота.
5.	у >-------------------функция ограниченная.
л	&
Рис. 61
б-	У' ~ (I -Ь- х»)г ' ПРИ х = — 1 функция имеет минимум, при х — 1 — максимум. Соответствующие точки графика А (—1» —g-); В fl, -g-j . На промежутках (— оо, —1] и [1, 4- со ) функция убывает, на сегменте [—1, 1 ] —возрастает.
Рис. 62
7. Точка пересечения с осями координат О (0; 0). Других точек пересечения с осями координат нет.
График смотрите на рисунке 62.
__ л8 Зх 4- 2
& ~~ х2— 4v + Д ’
1.	Область определения функции (—оо; 1); (1; 3); (3; + со ).
2.	Функция не является ни четной, ни нечетной.
3.	Функция не является периодической.
4.
lim
JC-* — «О
х2 — Зх -F 2
х2 — 4х + 3
lim
х2 ~ Зх 4- 2
х2 — 4х 4- 3
у = 1 — горизонтальная асимптота.
х2 — 3x4-2	<.	(х—1)(х — 2) п	х—2	1
—;—л—г?- = пт т-------гл?--от = ит----у- =
№ — 4x4-3	X^!_o(x—1)(х —3)	!_0 х—3	2*
lim
х 2 — Зх 4- 2
х2 — Зх -I- 2
х2 — 4х + 3
Отсюда Ит
lim х->3+0
Пт
х^з-о
X2 — Зх 4- 2
х2 — 4х 4- 3
___ сю
х2 — Зх 4- 2
х2 — 4х 4- 3
х = 3 — вертикальная асимптота.
5. Функция не ограничена.
я ttf _ (2х — 3) (х2 — 4х 4- 3) — (2х — 4) (х2 — Зх 4- 2)
°* У	(х2 — 4х 4-З)2
_ — х2 4- 2х — 1 _ (х — I)2	_	1 (х2 — 4х — З)2 “ (х — 1)2 (х — З)2	(х — 3)2 '
у' < 0 при всех значениях х, входящих в область опреде-ления функции. Функция убывает на каждом из промежутков (— оо ; 1); (1; 3); (3; 4-<*> ).
7. у = 0 при х = 2. В точке А (2; 0) график функции пересекает ось абсцисс.
2	(	2 \
При х = 0 у . В точке В ^0; -yj график функции пересекает ось ординат. Находим еще точки графика:
С(4;2); D (б; А) ; £*(—
Так как lim у =-5- , то график можно проводить через х->1	2
xi 1 >
точку (I; а затем стрелками показать, что эта точка не принадлежит графику (см. рис. 63).
у = Зх4— 16Х3 + 30 х2 — 24x4- 1.
1.	Область определения (— 00; + °0)-
2.	Функция не является ни четной, ни нечетной.
3.	Функция не является периодической.
Рис. 63
4.	lim (Зх* — 16л3 -Ь ЗОх3 — 24х + 1) = + а>.
Х—— ОО
lim (Зх* - 16х® + ЗОх2 — 24х + 1) = + оо .
5.	Функция не ограничена сверху. Ограниченность снизу может быть установлена после исследования на возрастание и убывание.
6-/= 12х3 —48х2 + 60х —24= 12 (х3 —4х2 + 5х — —2) = 12((х3— 1) — (4х2 —4х) + (х — 1)] = 12(х — 1) (х2 + х + 1 — 4х + 1) = 12(х — 1) (х2 — Зх + 2) = = 12 (х— I)2 (х —2).
Находим критические точки: 12(х—1)2(х—2)=0;
xt = 1; х2 = 2.
Прих<1 /<0;
при 1<х<2 «/<0;
при х>2 у'>0.
В точке Xi = 1 функция не имеет экстремума (но касательная к графику параллельна оси абсцисс, так как у' = 0). Соответствующая точка графика Л (1; —6).
В точке х2 = 2 функция имеет минимум. Соответствующая точка графика В (2; — 7).
7. При х = 0 у= 1; соответствующая точка графика С (0, 1). Точки пересечения графика с осью абсцисс уча-
щиеся найти не могут» так как не умеют решить данное
уравнение четвертой степени.
Находим точки графика D (3; 10), Е (— 1; 74).
График смотрите на рисунке 64.
Уже при построении графиков функций, в частности при решении последнего примера, замечаем, что график функции позволяет судить о корнях уравнения, левой частью которого является соответствующая функция. В рассмотренном примере точки пересечения графика с осью абсцисс не были найдены, так как уравнение 3 х4—6 х3+30 х2—24 х +1 — 0 учащиеся решить не могут. После построения графика можно сделать заключение, что данное уравнение имеет два действительных корня, которые, по-видимому, приближенно равны 0,1 и 2,8.
' Таким образом, построение графика функции может быть использовано для приближенного отыскания корней соответствующего уравнения. На специально
выделенном уроке этот вопрос рассматривается под* робнее.
Решим, например, графически уравнение х3— Зх2 + + 1 = 0. Исследуем функцию у = х3— Зх2+1 и построим ее график.
1.	Область определения ( — оо ; г 00 ).
2.	Функция не является ни четной, ни нечетной.
3.	Функция не является периодической.
4.	lim (х3—Зх2 + 1) = —оо; lim (х3—Зха+1)=+оо.
X ОО	-*•-»+ «
5.	Функция не ограничена.
6.	у1 = Зх2 — 6х = 3х(х— 2). Решаем уравнение Зх(х— 2) = 0;xi = 0; Хг = 2.
При х<0 у'>0‘, при 0<х<2 у'<0-, при х>2 у'>0.
Рис. 65
Xj — 0 — точка максимума; соответствующая точка графика А (0; 1); х2 — 2 — точка минимума; соответствующая точка графика В (2; —3). На промежутке (— оо; 0] функция возрастает; на промежутке [0; 2] функция убывает; на промежутке [2; + оо) функция возрастает.
7.	А (0; 1)—точка пересечения графика с осью ординат.
Находим дополнительно точки графика:
С (-1; -3); D (1; -1); Е (3; 1); F (4; 17). График смотрите на рисунке 65.
Используя график функции у = х3—3 х2+1, находим приближенно значения корней уравнения х3—Зх2-Ы=0.
Xi « — 0,5; х2 0,6; х3 ~ 2,8.
Можно показать, как уточнить полученные приближенные значения корней. (Удобнее всего, на наш взгляд, использовать метод хорд.) Рассмотрим первый корень х, — 0,5.
При х=—0,5 f(—0,5) — 0,13.
Так как на промежутке (—оо, 0) функция возрастает, то истинное значение корня меньше, чем (— 0,5).
Найдем значение функции при х=—0,6; f (—0,6) —
—0,29. Таким образом, —0,6<Xi<—0,5. Приближенное значение с одним десятичным знаком получено нами по графику достаточно точно. Чтобы получить более точное значение корня хь часть графика, соответствующую интервалу (—0,6; —0,5), заменяем отрезком прямой, соединяющим точки графика (—0,6; —0,29) и (—0,5; 0,13), и вычерчиваем в увеличенном масштабе на миллиметровой бумаге (см. рис. 66,а). Точка пересечения этого отрезка с осью абсцисс определяет более точно значение корня хь Получаем х——0,54.
Чтобы проверить полученное значение корня, можно вычислить f (— 0,54) — —0,03 *. Мы видим, что значение при х — — 0,54 очень мало отличается от нуля. Истинное значение Х\ больше, чем —0,54. Находим f (—0,53) = 0,09. Мы видим, что — 0,54 < Xi < — 0,53.
Приближенное значение Xi = —0,54 с двумя знаками достаточно хорошее. Если нужно, дальнейшее уточнение приближенного значения корня можно производить аналогичным образом.
Уточним значения остальных корней: f (0,6) — 0,135. На промежутке (0; 2) функция убывает х2 > 0,6; f (0,7) « — 0,129; 0,6 < %2 < 0,7. Поступая аналогично предыдущему, получаем х—0,65 (см. рис. 66,6).
f (2,8) ~—0,57. На промежутке (2, 4- <х) функция возрастает; хз>2,8; f (2,9) ~0,16. Используя чертеж (66в), получаем 2,88.
* В дальнейшем для экономии времени такую проверку можно не проводить.
При графическом решении уравнения f (х) = 0 иногда бывает, удобно записать это уравнение в форме q(x) = = ф(х). Например, уравнениех5—2х2+-1 =0 можно напи* " 1
сать в форме х5=2х2—к, а затем в одной и той же сис-теме координат построить графики функций у — х5 и у — = 2х2---к- (см. рис. 67). Абсциссы точек пересечения
этих графиков представляют собой искомые корни уравнения х5 = 2 х2 —• Их находят приближенно по графику. Дальнейшее уточнение производят так же, как в пре-
На графическое решение уравнений проводится примерно следующая самостоятельная работа. Решить графически на миллиметровой бумаге уравнения:
1. х4 — 4х— 1 = 0.
2. х4 — 2х3 + 9х2— 12х + 3 = 0.
Первый пример решается первым способом, второй пример — вторым способом (см. рис. 68 и 69).
§4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ
После двух-трех уроков, специально посвященных исследованию функций и построению их графиков, можно перейти к решению задач, связанных с нахождением наибольшего и наименьшего значения функции. В дальнейшем такие задачи решаются параллельно с исследованием функций и построением их графиков.
Учащиеся хорошо себе представляют, что максимум функции и ее наибольшее значение — это различные noil*	163
нятия (соответственно минимум функции и ее наименьшее значение)*
Теперь следует обратить внимание на то очевидное обстоятельство, что если функция, определенная, например, на интервале (а; 6), имеет единственную точку максимума с и на всем промежутке (а; с] функция возрастает, а на промежутке [г; Ь) убывает, то ее значение в точке с является наибольшим ее значением. (Аналогичное обстоятельство имеет место для функции, определенной на сегменте [а; 6], полусегменте [а; 6] или полуинтервале (а; &].) Точно так же, если функция, определенная на промежутке <а; Ь>, имеет в точке с единственную точку минимума и на промежутках <а, с> и <с, 6> соответственно убывает и возрастает, то ее значение в точке с является ее наименьшим значением.
Указанные положения позволяют применять исследование функции на минимум и максимум для нахождения ее наибольшего или наименьшего значения, что может быть использовано при решении практических задач.
Приведем примеры решения таких задач в школе.
Задача. Имеется 480 м проволоки. Этой проволокой требуется огородить в три ряда прямоугольный участок земли так, чтобы площадь участка была наибольшей. Найти длину и ширину такого участка.
Чтобы решить задачу, площадь участка нужно представить как функцию одного аргумента, например как функцию длины участка. Обозначим длину участка через х. Выразим через х ширину участка у.
Так как периметр участка равен 480 лг.3= 160 м, то
160 — 2х ОЛ / \
у = _ = 80—х	в таком случае площадь участ-
ка S(x)=(80—х)*х (ж2). Область определения полученной функции S(x) представляет собой интервал (0; 80), так как х>0 и 80—х>0.
Находим наибольшее значение функции S (х):
S(x)=80x—х2; S'(x) =80—2х; 80—2х=0; х=40.
На интервале (0; 40) 5'(х)>0, значит, функция возрастает. На интервале (40; 80) S'(x) <0, и, значит, функция убывает. При х = 40 5(х) имеет максимум, значит, и наибольшее значение. Итак, прямоугольный участок будет иметь наибольшую площадь, если его длина х=40 м и ширина у = 80 м—40 л< = 40 м. (Участок в этом случае имеет форму квадрата.)
Рис. 70
Задача. Из прямоугольного листа жести 3X5 дм2 нужно изготовить коробку (без крышки), вырезая по углам равные квадраты и загибая края листа. Какова должна быть сторона вырезаемых квадратов, чтобы объем коробки был наибольшим?
Сторону вырезаемых квадратов обозначим через х (см. рис. 70). Тогда площадь основания полученной коробки равна (3—2х) (5—2х) дм2, а высота ее равна х дм, объем ti(x) полученной коробки равен (3—2х)X з X (5—2х) х дм3. Очевидно, х>0 и х<-^.
Область определения функции v(x)—интервал 10,
V (X) = 4Х3 — 16Ха 4- 15х;
v'(x) = 12ха- 32х 4- 15;
12ха — 32х+ 15 = 0;
_ 16 ± /256—180	8 ± КЙГ .
Х~ 12	=	6
х2 не принадлежит интервалу (0; у! .
/ з \ Производная обращается в нуль на интервале ^0; yj только в точке Xt =---10,6. При x=xl v(x)
принимает наибольшее значение. (При 0 < х < xt з
t/(x)>0; При X, < X <-jj-< х.2 V* (х) <0 по свойству квадратного трехчлена 12х2 — 32х+15.)
Итак, сторона вырезаемых квадратов равна х1^8~4— ^0,6 (дм).
Задача. Требуется изготовить сосуд без крышки в форме прямоугольного параллелепипеда с квадратным основанием емкостью 32 л. Каковы должны быть размеры сосуда, чтобы на его изготовление пошло возможно меньше материала?
Сторону основания обозначим через х, тогда высота .	32
сосуда л= — .
128
Площадь поверхности сосуда S(x) —х2+4/гх=х2+ — . Эта площадь должна быть наименьшей. Область определения функции S (х) — интервал (0; + оо ).
—=0;
Л	Л?	л
На (0; 4) S,(x)<0; на (4, + оо) S'(x)>0. Наименьшее значение S(x) принимает при х=4.
Ответ. Сторона основания сосуда должна быть равна 4 дм, высота 2 дм.
Задача. Требуется изготовить из жести закрытый сверху и снизу цилиндрический бак вместимостью в 60 л. При каких размерах бака на его изготовление пойдет возможно меньше материала?
Требуется, чтобы полная поверхность бака была наименьшей. Обозначим радиус бака через х и выразим полную поверхность бака через х. Высоту бака h нахо* 60
лх2
60	.
дим из равенства irx2ft = 6С (<?ле3); h =
Полная поверхность S (х) = 2кх2 2ях> = 2яха 4-120
-4---. Область определения функции S(x)— интервал
АГ
itx* — 30
о/ / \	а 120
S (х) = 4кх--- = 4-
\ /	Ж2
л лх3 — 30 п тех3 — 30 п
4 •—^ = 0;^~ = °;
Легко видеть, что
а на интервале
функция S(x) принимает наименьшее значение.
60 1/"5л \2
60»
900 л
При этом h —
Ответ. Радиус основания^ ~дм, высота 21/ -~дм.
Поверхность бака будет наименьшей, когда высота его равна диаметру основания.
Задача. Окно имеет форму прямоугольника, завершенного полукругом, периметр фигуры окна равен 6 м. Каковы должны быть размеры окна, чтобы оно пропускало максимум света? (См. рис. 71.)	.й
Требуется, чтобы площадь окна была наибольшей. Обозначим основание окна „ через х и выразим площадь окна через х. * Чтобы найти h, воспользуемся равенст- Рис. 71
вом' х 2ft 4- я 4=г =6; ft = 3-------£-------- .
Отсюда площадь окна 3(х) = йх 4-	-з- — Зх —б—
О	£
—	4- тг = Зх — —1~4 -х2. Чтобы нагйти область оп-
4 о	о
ределения функции 3(х), учитываем, что х>0 и А>0, т. е.	<3; х<
Область определения функции 3 (х) — интервал (°; 2т^):	3~	3~	х==
=	• Легко проверить, что при х = — j- функ-
ция имеет наибольшее значение. При этом й = 3 — 12____________я 12	6
2 (к 4-4)	4 (к 4-4) 3=тг4-4
гх	*	12
Основание окна должно быть равно—г-г	высо-
Л 4 „	6 z
та прямоугольной части окна равна	(высота
прямоугольной части окна в два раза меньше основания окна).
Задача. В треугольник с основанием а и высотой h вписан прямоугольник так, что одна сторона его лежит на основании треугольника, а две вершины — на боковых сторонах треугольника. Доказать, что наибольшая площадь прямоугольника равна -	- (см. рис. 72).
Основание прямоугольника обозначим через х, а его площадь через S(x). Найдем наибольшее значение S(x). Составим формулу, выражающую функцию S(x) через х, для чего выразим через х высоту прямоугольника у. Из подобия треугольников
АВС и AKL получаем = й , откуда у = —
следовательно, S (х) — ху —	= hx—— хг.
а	а
Область определения функции S{x) — интервал (0, а): S'(x) = h—	^х=0; х = -^-.
Легко проверить, что при х = S (х) принимает наибольшее значение.
Таким образом, наибольшее значение площади вписанного прямоугольника равно S (-?-) = ft- ----— X
а2   ah
Х"4	4~ '
Задача. Известно, что прочность балки с прямоугольным сечением прямо пропорциональна ширине и квадрату высоты сечения. Найти размеры сечения балки наибольшей прочности, которую можно выпилить из круглого бревна, имеющего наименьший диаметр в d сантиметров.
Обозначаем ширину сечения через х (см. рис. 73). Тогда высота сечения h ~ V cP — зР . Прочность балки Q выразим через х, учитывая, что она пропорциональна
AC=d
Рнс. 73
ширине и квадрату высоты. Коэффициент пропорциональности обозначим через k (см. рис. 73):
Q (х) = kxh2 = kx (d2 — х2) = kd2x —kxs.
Область определения функции Q(x)—интервал (О, d).
Q' (х) = kd2 — 3/гх2; kd? — ЗЛ*2 = 0; d2 = 3x8; x = ± -£=
На интервале (0, d) лежит только корень уравнения
-/з •
/з
d
при -4=. < х < d Q' (х) < 0;
Г 3
При х— —т=. функция Q(x) имеет наибольшее значение на интервале (0, d).
Ответ. Балка будет наиболее прочной, если шири-d	d]^2~
на ее равна , а высота равна ’= .
Задача. Внутренняя поверхность бака с квадратным основанием без крышки равна 108 дм2. Каковы должны быть размеры бака, чтобы его объем был наибольшим?
Сторону основания обозначаем через х. Высоту бака h находим из уравнения х2 + 4 hx = 108, откуда .	108 — х4
Л — —j. 4х
Объем бака v{x) = х2Л =
Область определения функции и(х) — интервал (0; 6 |3), так как х>0 и 108 — ж2> 0, т. е. х </108 - 6 /ЗТ
®'(х) = 4- <108 -"Г <108 ~	“0’
108 — Зх2 = 0; х = ± 6.
Области определения функции принадлежит только один корень рассматриваемого уравнения Xi=6. Легко видеть, что для интервала (0; 6) f'(х) >0, а для интерва-
= -^-(108x-x=<).
ла (6; б/З) f(x)<0. Прих=6 о(х) принимает наиболь-шее значение. При этом h= -	=3 (дм).
Искомые размеры бака: 6x6x3 (дл3).
Задача. Из листа жести шириной а требуется согнуть открытый желоб так, чтобы поперечный разрез его имел форму трапеции, у которой AB=BC=CD=^rd. Какое значение надо придать углу <р, чтобы вместимость желоба была наибольшей? (См. рис. 74).
Вместимость желоба будет наибольшей, когда площадь поперечного сечения его будет наибольшей. Находим площадь поперечного сечения как функцию угла ф=л—<р:
АВ = ВС = CD = а;
BK.LAD-, CL^_AD-
h = ВК = Д- a sin Ф.
О
LD — АК — cos ф;
О
2	11
AD = -уa cosф + -у а = -у а (1+2cosф).
п	С / t \	"Ь	It
Площадь поперечного сечения 5(ф)== g-------л =
— #(1 + 2созф) +	I	1
= —--------5----------. -5-flsinp=-5-aasin ф(1+со$ф)=
Z	О	У
= -у а! sin ф +	a2 sin 2 ф.
Область определения функции 5 (ф) — интервал I г\ .2	\	тс
10; так как при <р желоба не получится.
5'(ф) = -5- °2 cos ф + -^агсо$2ф =4-a® (cos ф + cos 2 ф) = w	v7	v
2 « ЗФ ф = -g-a2cos-~- cos ;
2 „	3 Ф ф п ЗФ Фл
а2 cos —cos — = 0; cos ——- cos -5- = 0.
У	it,	Il
Общее решение тригонометрического уравнения
Зф ф л	. 2тс£ тс	,
cos -у- cos -j- = 0 имеет вид: ф = —g- + -д-, где k — целое число. Легко видеть, что только при k = 0 мы получаем корень уравнения ф0 = -д-, принадлежащий области определения функции.
На интервале (0;	0 < ф < -у ; 0 <	;
cos-|~>0; 6<# <-5-; cos-^->0; £'(ф)>0.
На интервале	ПГ<''1,<”Тк’Нг<:'’2'<'1Г’
COS-^->0;	< -|-ф <я; cOS-^- СО; 3'(Ф)<0-
/ 2тс \
Функция 5(ф) принимает на интервале (0; -о-1 наибольшее значение при ф0 = ~.
О
Ответ. Вместимость желоба будет наибольшей, ,	тс 2
когда угол <р0 равен ir—ф0 — к	*•
§ 5. ВЫВОД ФОРМУЛЫ БИНОМА НЬЮТОНА
И ЕЕ ПРИМЕНЕНИЕ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
Как уже говорилось, вывод формулы бинома Ньютона рассматривается как пример применения понятия производной в алгебре.
Учащимся сообщается, что во многих вопросах математики бывает важно уметь представить выражение (п+х)л, где и — натуральное число в виде ^многочлена:
С первых шагов изучения алгебры они встречались с частными случаями соответствующей формулы при и=2 и п=3 и их применениями.
Соответствующая формула, позволяющая записать (л+х) " в виде многочлена, получила название формулы бинома Ньютона. При выводе формулы внимание учащихся обращается прежде всего на то, что (а+х)л, представляя собой произведение п двучленов (а + х), является многочленом степени п относительно х и содержит (п+1) членов.
В общем виде можно написать:
(а + х)л = с0 + CjX + с2х2 + с3х3 + .
+ Сп _ 1 X" -
(0)
+ w 
Полагая х=0, получаем с0=ап.
Чтобы найти коэффициенты cj, с2, сз, . . ., cn-i, сп, используем то обстоятельство, что в левой и правой частях записанного равенства стоят тождественно равные функции, и, следовательно, производные их тождественно равны. Беря производные от левой и правой частей, получаем тождество:
п (а + х)”-’ = 1 -с, -|- 2сгх + 3csx2 + . . . +
+ (л — 1) cn-1 хл-2 + пспхп~х.	(1)
Полагая здесь х=0, получаем С1=па"~1. Мы снова можем взять производные от обеих частей тождества (1) и получим тождество:
п(п—1)(а +х)"-2 = 2г2 + 3-2с3х + . . . + + (л — 1) (л — 2) cn-i хл~3 + n {п — 1) спхп~2. (2)
Полагая х = 0, имеем с2 = —ап~2. Далее:
п(п—1)(л— 2)(а + х)л—3 = 3-2-1 -с3 + • • • +
4- (ft—1) (л—2) (л—3) c„-i хл~4 + п (л— 1) (л—2) с„хл-3. (3)
Полагая х = 0, получаем с3=	— ап-з
Берем производные от обеих частей тождества (3): л (л •— 1) (л — 2) (л - 3) (л + х)«-4 = 4-3-2-1-с4 + + 5-4-3-2.с5х+. . .+(n—1) (л—2)(л—3)(л—4)ся_1хл-5+ + л (л — 1) (л — 2) (л — 3) сяхл—4.	(4)
л	n(n— 1)(л — 2) (и — 3)	„ 4
Отсюда при х~ 0 имеем	—----------Рп „ /-— ал-4.
Если мы повторим процесс перехода к производным k раз то слева, на месте (а4-х)лмы получим п(п—1) X X (п—2) - - •[«—(k—l)](a4-x)n~fe, так как каждый раз при переходе к производной показатель степени при (а 4-х) уменьшается на единицу, а в коэффициенте появляется новый множитель, равный прежнему показателю степени. В частности, при k=n слева получается выражение:
п(п—1) (п—2) .,. [п—(п—1)](й4-х)п~п =
= п(п—1) (п—2) . .. 2-1.
В правой части тождества при повторении процесса перехода к производным k раз все члены, содержавшие х в степени, меньшей, чем kt очевидно, обратятся в нуль. Член ckxk обратится в k(k—1) ... 2 • 1 • с а члены, содержавшие первоначально х в степени, большей, чем k, все еще будут содержать х в какой-то степени.
Таким образом, после fc-кратного перехода к производным получаем:
п(п— 1) (п — 2). . . \п — (k— !)](#+ х)л~А =
= k(k— 1) • . . . -2.b^ + (jfe+ 1)А(£- 1)* . . . -2cft+ix + + . . .	— !)• . . . -[п — (k —
1-г	л	п(п—!)••••	» ь
Полагая х=0, получаем ck = 3—ьз-З-——~а k-
Эта формула справедлива при k = 1, 2, 3, . .. , п.
D	п(п— 1)-...-2	п(п—1)-...-2-1
В частности, гл_1=-7-^-5—ггя; сп	?—п— •
(Разумеется, выражения для сп_\ и сп можно упростить, но мы пока этого не делаем, так как желаем получить общую формулу.) Подставляя полученные значения коэффициентов с0,	с2, • • • , сп в фор-
мулу (0), получаем формулу бинома Ньютона в следующем виде:
(а 4- х)п = ап 4- пап~1х + Лап~2х2 4-
+ -\.2(3~2)аЯ-3х3+- • .+я(И~У;2^[П7(Й~1)1ап-М+ .	. п(п— 1). . . . • 2.1	,,
+ . . . 4--у о-<------хп . Мы видим, что член,
содержащий хк, содержит множитель аа~к и коэффициент при ап~к хк в этом члене равен
п (п — О- • •• 4” — (* - 01
Обозначим этот коэффициент через Вк.
D п(п— !)•... -п[п — (k— 1)] ^к	1-2- . . . -А
Для большей общности коэффициент 1 при ап обозначим через Во. Коэффициенты Во, Bt, . . . , Вп в разложении бинома (а + х)" называются биномиальными коэффициентами. Для удобства записи вводится обозначение А! для произведения k чисел 1,2, . . . , k, т. е. 1*2... k = k\ (читается k - факториал). Иногда обозначают 1 = 11 Тогда Вк = в И (л — !)• .. ..[и — (А — 1)1 прИ £ =	, д. в частно-
К1
п п п	п(п—1) п	п(п—1)(л — 2)
сти, = — ; В2 = -	, ; В3 =	----- , ... ;
Мы замечаем, что Вп = Вй— 1; Вп -1 = В2. Докажем, что и вообще Вп_к =а Вк, т. е. что коэффициенты членов, одинаково отстоящих от концов разложения бинома Ньютона, равны. Для этого преобразуем выражение для Вк.
___ л(л—1)< ...-[л —(А—1)] *__А!
л(л—1)-
.... [л—(А—I)] -(л- А) [л—(А + 1)1 
А! (л — А) [л — (А + 1)]. ... • 2-1
•2-1 п!
~ k!(n—k)! ‘
Найдем теперь Вп_к, подставив в полученное выражение п — k вместо А.
п!
п!
(л — А)/ [л — (л — А)]/ (л — k}!k! ~ к
Учитывая это, формулу бинома Ньютона запишем в следующем виде:
(a + x)n = an 4- tian -1 x 4- —%,—an ~2 x2 4-
n(rt—l)(n —2)	_ 3
31
~n(n—- [n—(*—1)£ an-kxk^_ 4- naxn-i 4- xn . R:
Можно предложить провести вывод формулы бинома Ньютона методом математической индукции без применения производной хотя бы для случая а=1.
Примеры.
1.	Разложить по формуле бинома (х+а)9. Замечаем, что разложение Должно иметь 10 членов, значит, достаточно вычислить только первые 5 коэффициентов, остальные получим, исходя из того, что коэффициенты членов, одинаково отстоящих от концов разложения, равны.
(а 4- х)9 = а9 + 9а®х +
а4х® 4-
Э-8-7-6
1-2-3-4
а8х4
Э-8-7-6
1-2-3-4
а2х7 4- Эол® 4- х’ = а9 4- 9а8х 4“ 36а7 х2 +
4- 84а6х-’ 4- 126а5 х4 4- 126а4х5 4- 84а8х®+36а2х7+ 9ах®4- х9.
2.	(/Г- 1)в=. [/Г4-(-1)]МК5)6 + б(/5)5(-1)+
Ьг! ~ 0я + Ш ~ О’ +г|0/5)я(“1)4+ + б/5"(- I)5 4-( — !)« =
125 - 150 /5 + 375— 100 /5 + 75 — 6 /5'+ 1 = = 576 - 256 /5 .
3.	Найти сумму всех биномиальных коэффициентов. Полагаем в формуле бинома Ньютона а=1, х=1. Тогда
(1+ 1)" = 1 + -р- + я(л °
п(п — 1).
k!
+ . . . + п + 1.
Справа стоит как раз сумма биномиальных коэффициентов, которая, как мы видим, равна 2п.
После решения ряда примеров с числовыми и буквенными данными на применение формулы бинома Ньютона учащиеся знакомятся с приложением этой формулы к приближенным вычислениям.
Если в выражении (1+х)л х мало, то обычно члены разложения, содержащие степени числа х с показателем, большим 1, оказываются настолько малыми, что не влияют на приближенный результат вычисления. В зависимости от требуемой точности вычисления члены разложения (1+х)я по формуле бинома Ньютона отбрасывают, начиная с третьего или с четвертого члена. Получают приближенные формулы вида:

или (1 + х)« «
-I- пх ;
1 + ПХ --L
Выбор формулы зависит от конкретных условий. (Иногда для большей точности сохраняют большее число членов.)
Примеры.
1.	Вычислить (1,002)7 с точностью до 0,001 (1 + 0,002)’ = 1 + 7-0,002 +	(0,002)® + ... Мы видим,
что уже третий член (0,002)2 = 0,000084 не оказывает никакого влияния на тысячные доли результата, так как он меньше одной десятитысячной доли, а остальные члены значительно меньше этого члена.
Следовательно, (1 + 0,002)’^ 1 ф- 7-0,002 = 1,014.
2.	Вычислить (1,03 )5 с точностью до 0,01.
(1 + 0,ОЗ)5 = 1 + 5-0,03 +	(О,ОЗ)8 +	(О,ОЗ)3 +
+ 5-(0,03)4(О,ОЗ)5.
Третий член	(О,ОЗ)8 = 0,009. Он близок к 0,01,
поэтому его надо сохранить. Остальные члены уже не влияют на точность вычисления, например: ^(0,03)3 = 10 -0,000027 = 0,00027 < 0,001.
Получаем:
(1+0,03)5^ 1 + 5-0,03-]- 10-(0,03)8= 1 +0,15 + 0,009= = 1,159^1,16.
3.	Вычислить (0,98)4 с точностью до 0,01.
(0,98)4 = (1 — 0,02)4 = 1 — 4-0,02 + 6 -0,0004 - 4 (0,02 )3 + - F (0,02)4.
Очевидно, здесь достаточно сохранить два члена разложения. (0,98)4 « 1 — 4-0,02 = 0,92.
4.	Вычислить (1,0б)т с точностью до 0,01.
(1,06)7 = (1 + 0,Об)7 = 1 + 7-0,06 +	• (0,06)2 +
+ тй-(0,06)’ + ...
Находим приближенно третий член разложения: 21-0,0036^0,076. Так как вычисление производится до 0,01, то этот член отбрасывать нельзя.
Оцениваем четвертый член разложения:
35-0,000216^0,008.
Этот член также можно сохранить. Остальные члены, очевидно, не будут влиять на точность результата и поэтому должны быть отброшены:
(1,0б)7	1 + 0,42 + 0,076 + 0,008 = 1,504 « 1,50.
(Если бы мы отбросили четвертый член, то результат был бы: (1,06)7 ~ 1 + 0,42 + 0,076 = 1,496~ — 1,50. Мы видим, что четвертый член не оказал влияния на приближенный результат. В большинстве случаев достаточно ограничиться не более чем тремя членами.)
5.	Вычислить (0,997)® с точностью до 0,001.
(0,997)e = (1 - 0,003)« = ] — 6.0,003 +	 (0,003)® + ...
1
Уже третий член по абсолютной величине значительно меньше 0,001 (он меньше, чем 0,0002).
(0,997)6^ 1 -6-0,003 = 0,982.
На изучение в школе формулы бинома Ньютона и ее применений достаточно выделить 3—4 часа.
ЛИТЕРАТУРА
-1. П. С. Александров и А. Н. Колмогоров. Свойства неравенств и понятие о приближенных вычислениях. «Математика в школе», 1941, № 2 (или «Вопросы преподавания математики». Сборник статей, под ред. П. В. Стратилатова. Учпедгиз, 1961).
2.	В. Г. Ашкинузе и Н. Н. Шоластер. Алгебра и элементарные функции. «Просвещение», 1964.
3.	В. М. Б р а д и с, Н. С. Истомина, А. И. Марк у ш е в и ч, К. П. Сикорский. Алгебра, под ред. А. И. Маркушевича. Учпедгиз, 1960.
4.	И. М. Гельфанд, Е. Г. Г л а г о л е в а, Э. Э. Ш н о л ь. Функции и графики. «Наука», 1966.
5.	Б. В. Гнеденко. Роль математики в развитии техники и производства. «Математика в школе», 1962, № 1.
6.	В. Л. Гончаров. Элементарные функции действительного переменного. Пределы последовательностей и функций. Общее понятие функции. Энциклопедия элементарной математики, т. 3. Гостех-издат, 1952.
7.	Н. А. Д а в ы д о в, П. П. К о р о в к и н, В. Н. Н и к о л ь с к и й. Сборник задач по математическому анализу. Учпедгиз, 1953.
8.	Я; С. Дубнов. Содержание и методы преподавания элементов математического анализа и аналитической геометрии в средней школе. «Математическое просвещение», вып. 5, 1960 (или Я. С. Дубнов. Беседы о преподавании математики. Сборник. «Просвещение», 1965).	4
9.	А. Н. Колмогоров. Функции, графики, непрерывные функции. «Математика в школе», 1965, № 6.
10.	А. Н. К о л м о г о р о в. Об учебниках на 1966/67 учебный год. «Математика в школе», 1967, № 1.
11.	А. Н. Колмогоров. Новые программы и некоторые основные вопросы усовершенствования курса математики в средней школе, «Математика в школе», 1967, № 2.
12.	Е. С. К о ч е т к о в, Е. С. К о ч е т к о в а. Алгебра и элементарные функции, ч. 1 и 2. «Просвещение», 1966.
13.	С. Г. Крейн, В. Н. Ушакова. Математический анализ элементарных функций. Физматгиз, 1963.
14.	П. А. Л ар и ч ев. Сборник задач по алгебре, ч. П. Учпедгиз, 1963.
15.	А. И. Маркушевич. Понятие функции. «Математика в школе», 1947, № 4 (или «Вопросы преподавания математики». Сборник статей, под ред. П. В. Стратилатова, 1961).
16.	А. И. М а р к у ш е в и ч. Об очередных задачах преподавания математики в школе. «Математика в школе», 1962, № 2.
17.	А. И. М а р к у ш е в и ч. Действительные числа и основные принципы теории пределов, Изд-во АПН РСФСР, 1948.
18.	Ю. Н. М а к а р ы ч е в. Система изучения элементарных функций в старших классах средней школы. «Просвещение», 1964.
19.	И. П. Натансон. Производные, интегралы и ряды. Энциклопедия элементарной математики, т. 3. Гостехиздат, 1952.
20.	И. И. П р и в а л о в, С. А. Г а л ь п е р н. Основы анализа бесконечно малых. «Наука», 1966.
21.	«Проект программы средней школы по математике». «Математика в школе», 1967, № 1.
22.	И. X. С и в а ш и н с к и й. Элементарные функции и графики. «Наука», 1965.
23.	С. Б. Суворова. Об опыте раннего введения начал дифференциального исчисления в девятых классах. «Математика в школе», 1966, № 4.
24.	Г. М. Фихтенгольц. Основы математического анализа, т. I. Гостехиздат, 1955.
25.	А. Я. X и н ч и н. Основные понятия математики в средней школе. Учпедгиз, 1940 (или «Вопросы преподавания математики в средней школе». Сборник статей, под ред. П. В. Стратилатова. Учпедгиз, 1961).
26.	А. Я. X и н ч и н. Педагогические статьи. Изд-во АПН РСФСР, 1963.
27.	А. И. Худо б ин, Н. И. Худ об ин, М. Ф. Шуршало в. Сборник задач по алгебре и элементарным функциям. «Просвещение», 1966.
ОГЛАВЛЕНИЕ
Введение
Раздел I. ФУНКЦИИ И ПРЕДЕЛЫ
Глава 1. Повторение и углубление основных сведений о функции и свойствах функций	6
§ 1.	Повторение понятия функции. График функции. Обозначение функции в общем виде................................. 6
§ 2.	Монотонные функции. Возрастание и убывание функции на данном промежутке. Понятие о максимуме и минимуме функции..................................................11
§ 3.	Четные и нечетные функции. Функции, ограниченные сверху, и функции, ограниченные снизу. Ограниченные функции. Периодические функции. Схема	исследования функции	15
Глава 2. Обратные функции	23
§ 1.	Понятие обратной функции. График обратной функции 23
§ 2.	Свойства обратных функций ....	27
§ 3.	Обратные тригонометрические функции	31
Глава 3. Предел функции	34
§ 1.	Предел функции f (х) при х>+°° и оо..............	36
§ 2.	Предел функции f(x) при а (а — действительное число) 48
§ 3.	Предел отношения синуса к аргументу, когда аргумент стремится к нулю .	56
§ 4.	Теоремы о пределах ...	61
§ 5.	Понятие о непрерывности функции	67
Раздел II. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Глава 4. Понятие производной. Вычисление производной. Применение производной к решению физических и других задач : : ; . ;............................................75
§ 1.	Скорость прямолинейного движения. Понятие производной. 76
§ 2.	Теоремы о производных. Производные некоторых элементарных функций ...........................................82
§ 3.	Физические и другие примеры использования производной.
Ускорение. Понятие второй производной................101
Глава 5. Геометрический смысл производной. Исследование функций с помощью производной. Решение задач, связанных с нахождением наибольшего и наименьшего значения функций. Формула бинома Ньютона	. 112
§ 1.	Геометрический смысл производной....................113
§ 2.	Исследование функций на возрастание и убывание и нахождение точек максимума и минимума функций с помощью производной .......................................125
§ 3.	Исследование функций с помощью производной и построение их графиков. Графическое решение уравнений . . . 140
§ 4.	Задачи на нахождение наибольшего и наименьшего значения функций...........................................   163
§ 5.	Вывод формулы бинома Ньютона и ее применение к приближенным вычислениям	. 171
Литература
179
Матвеи Семенович Мацкин Роза Юдовна Мацкина
ФУНКЦИИ И ПРЕДЕЛЫ. ПРОИЗВОДНАЯ
Редактор И. С. Комиссарова Художник И. Е. Сайко Художественный редактор В. С. Эрденко Технический редактор Л. Я. Медведев Корректор М. В. Голубева.
Сдано в набор 9/1—1968 г.
84х1081/82 Типографская
Уч.-изд. л. 9,02
(Тем. пл. 1968 г. №
Подп. к печ. 31/V—1968 г. № 2. Печ. л. 9.66 (5,75) Тираж 40 тыс. экз.
158)	А03919
Издательство .Просвещение* Комитета по печати при Совете Министров РСФСР
Москва» 3-й проезд Марьиной рощи» 41
Типография № 2 Росглавполиграфпрома,
г. Рыбинск, ул. Чкалова, 8.
Заказ 314	Цена 24 коп.
Школьные учебники (((Р
SHEBA.SPB.&U/SHKOLA