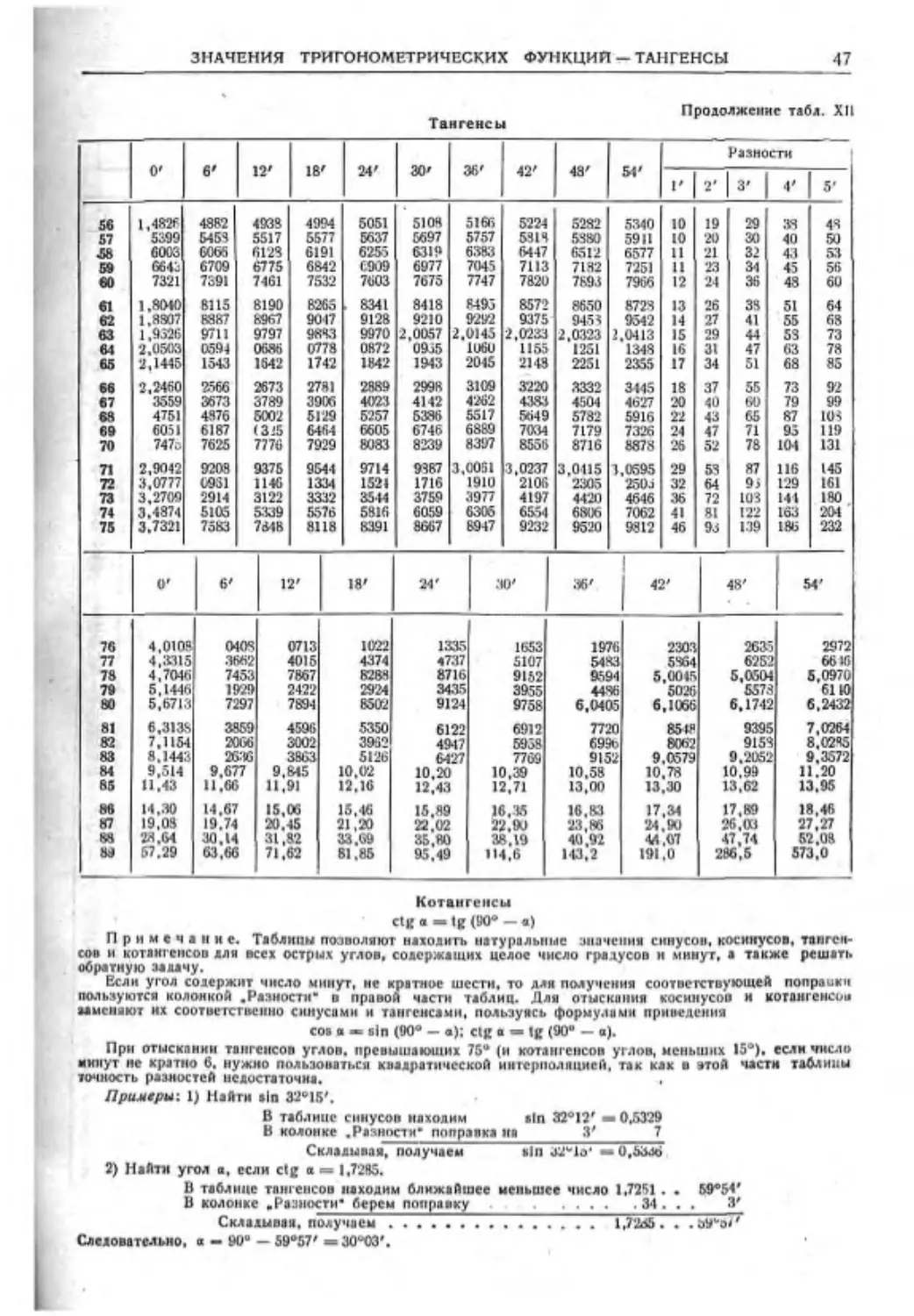
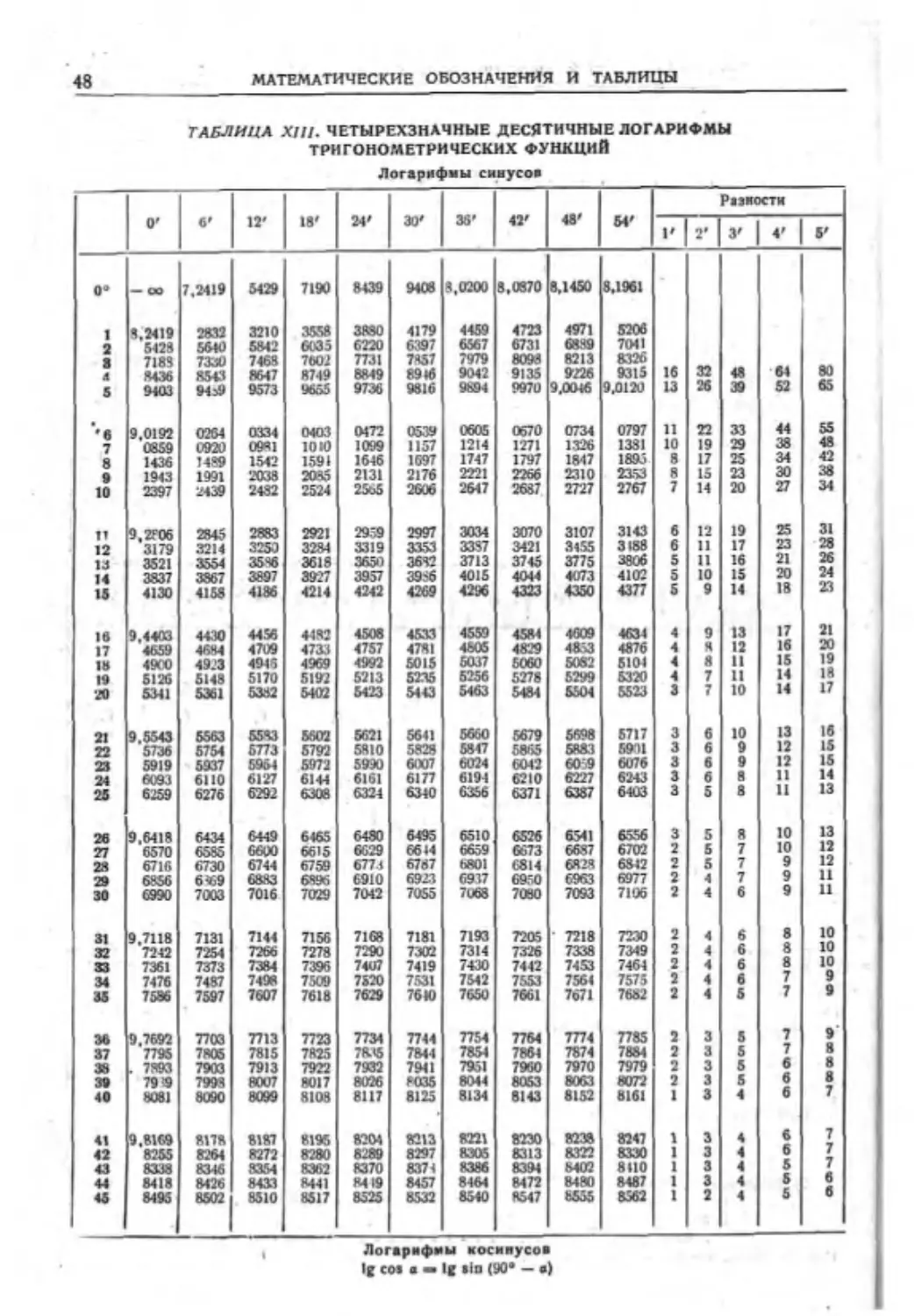
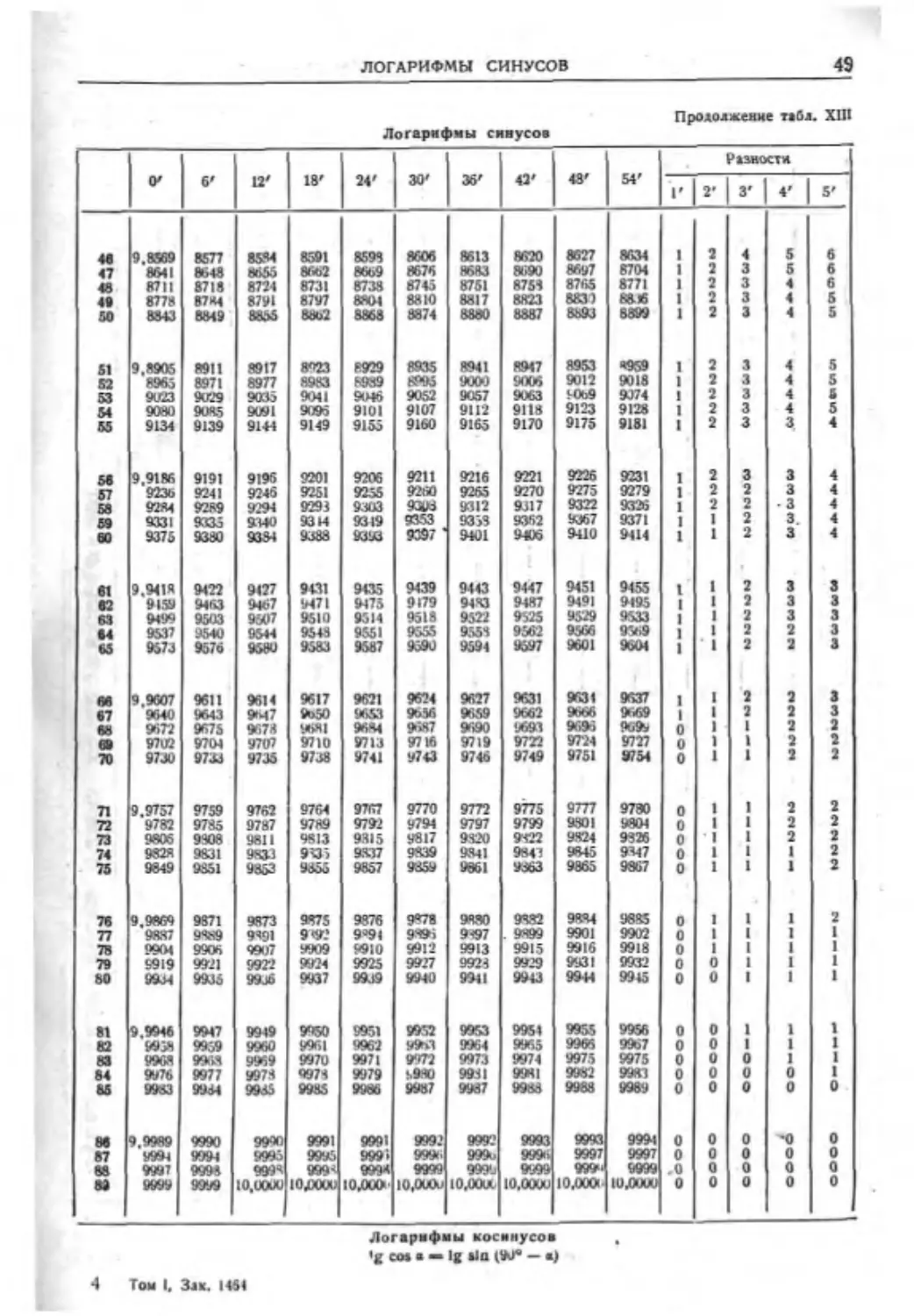
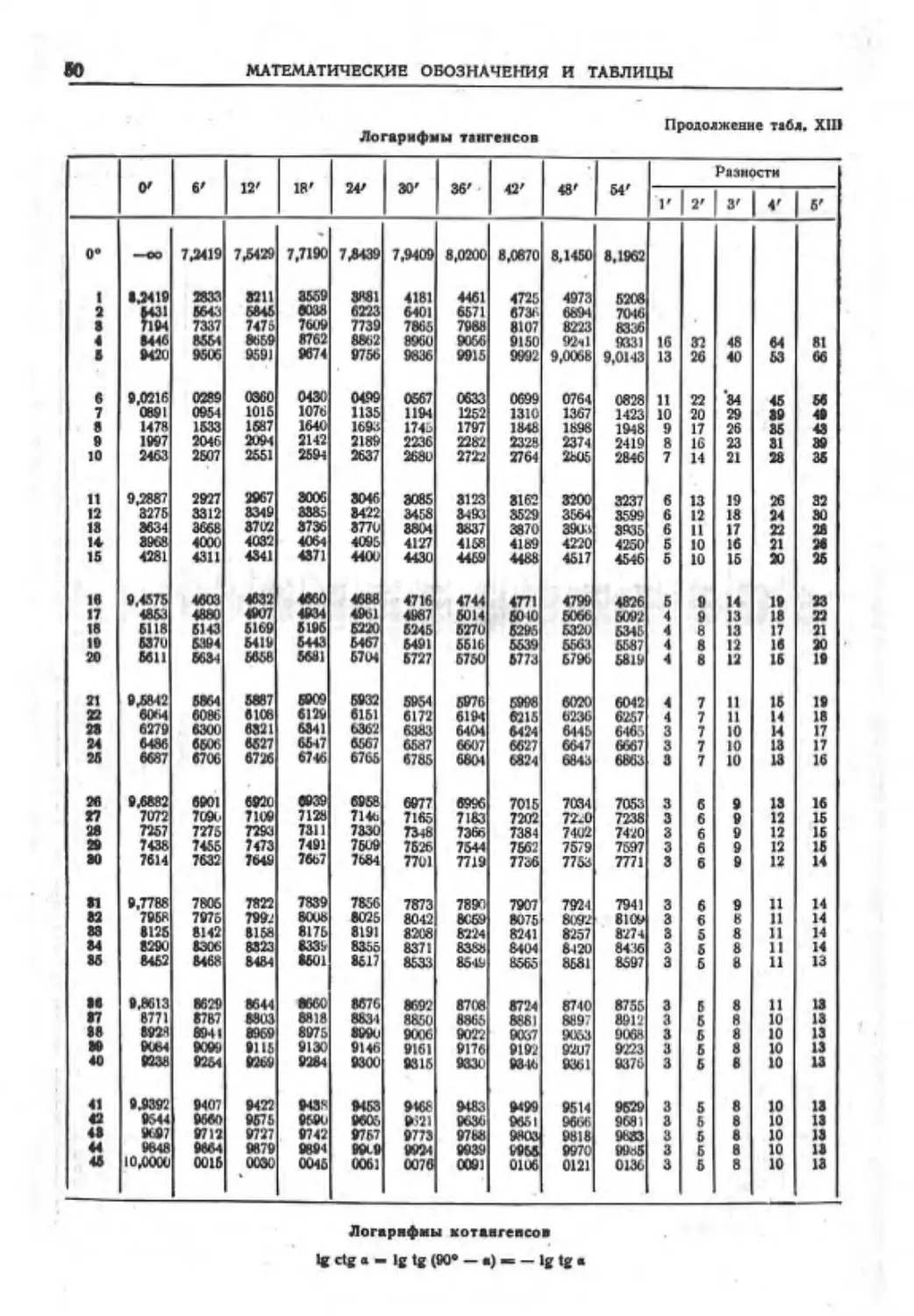
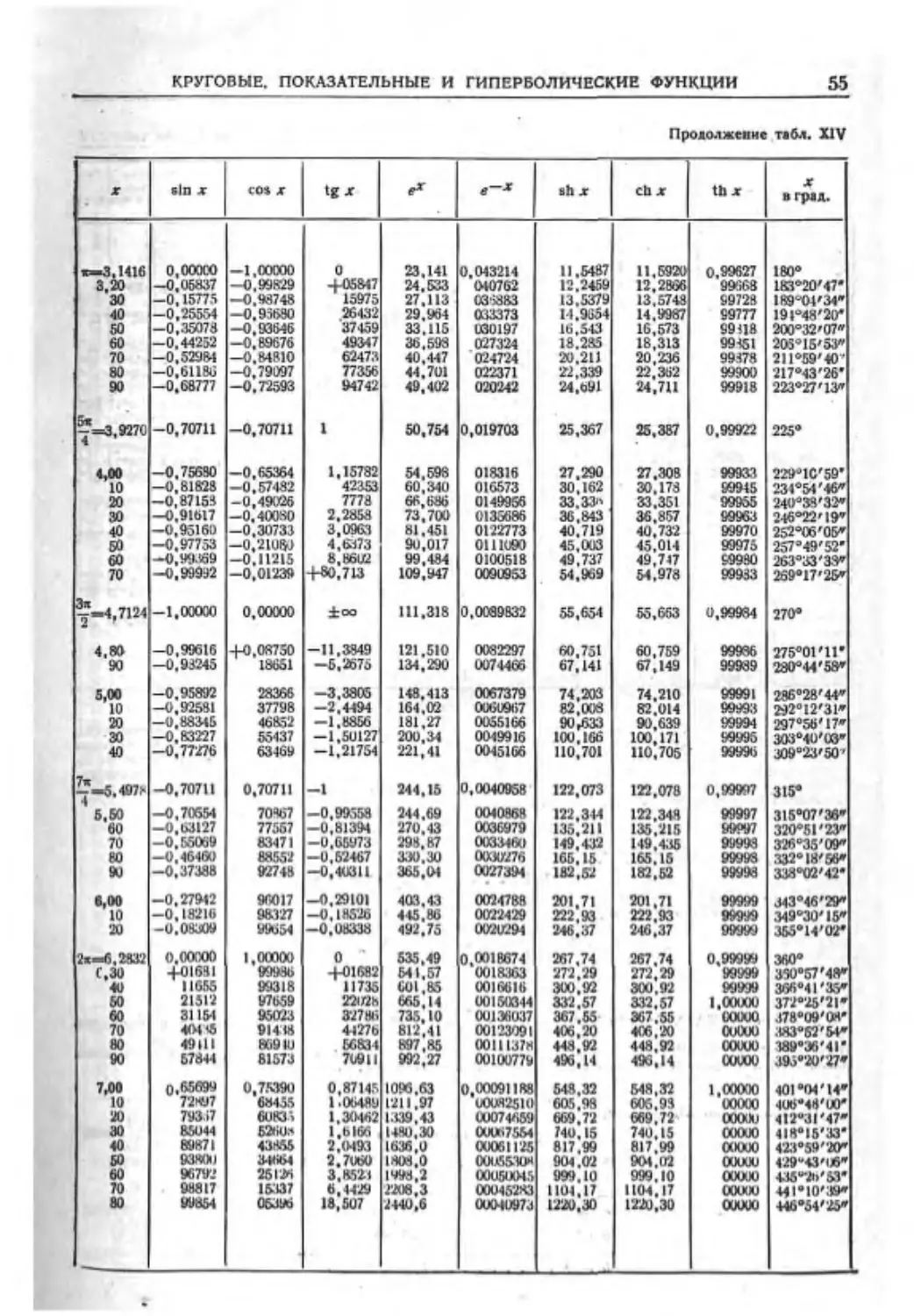
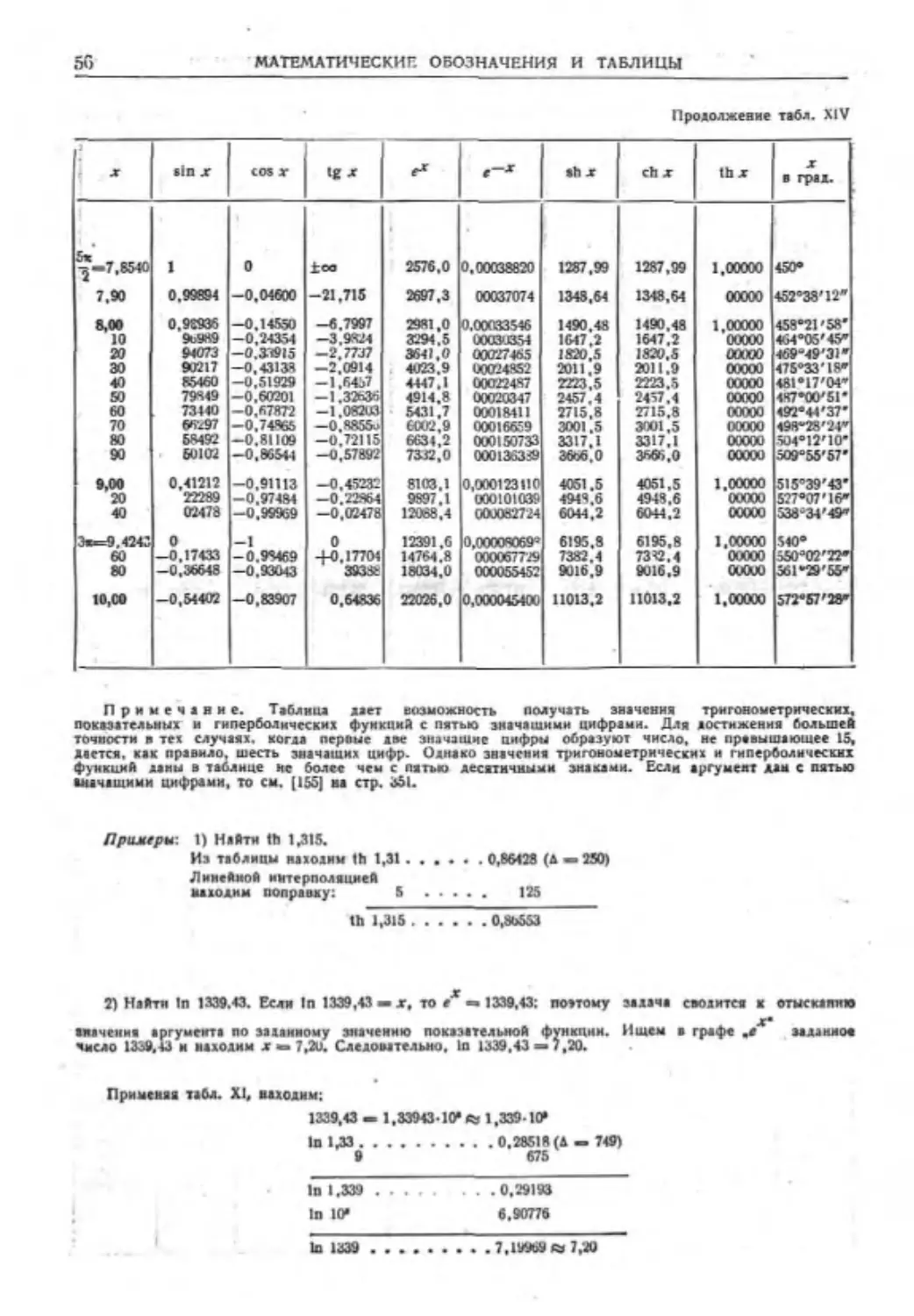
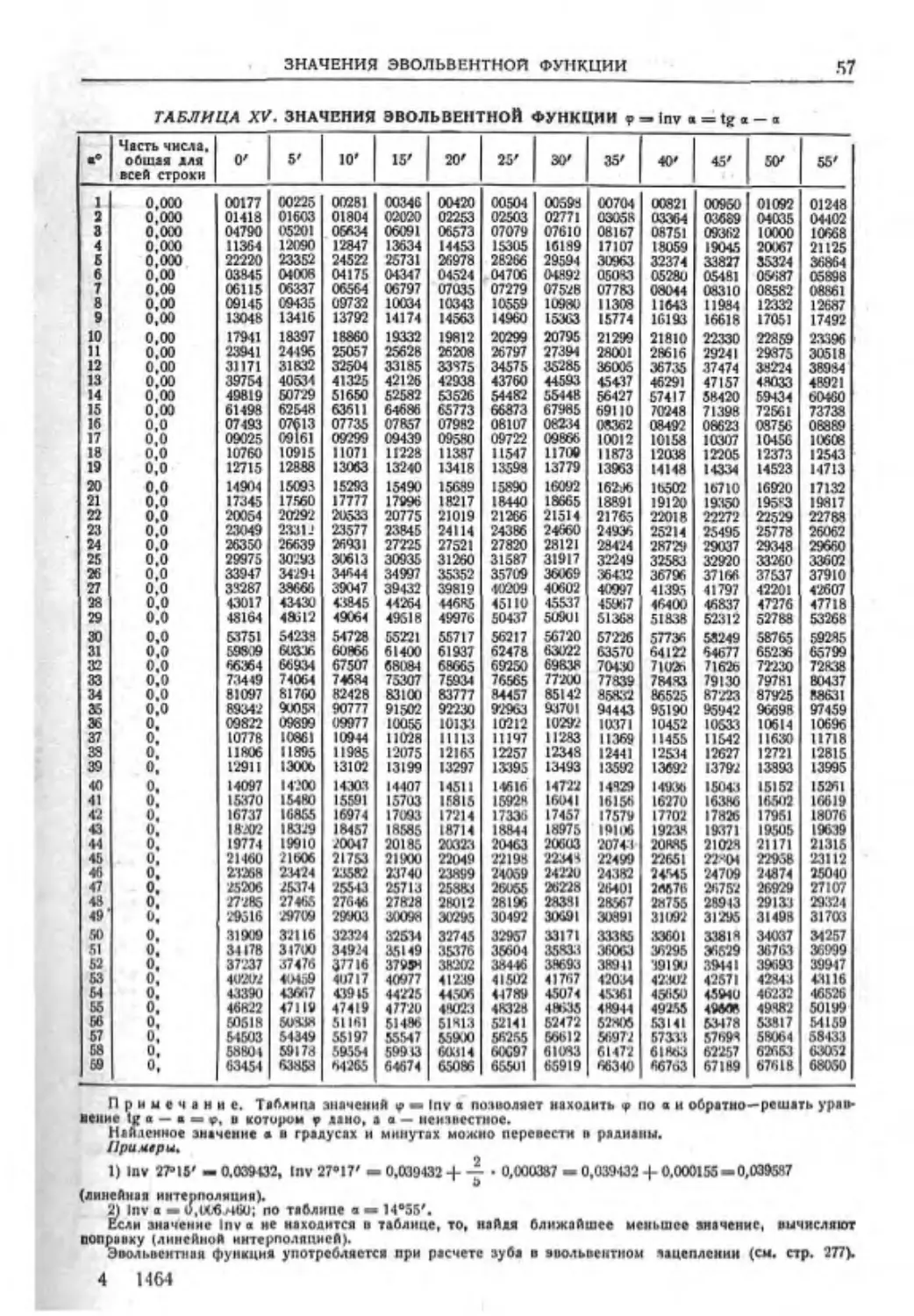
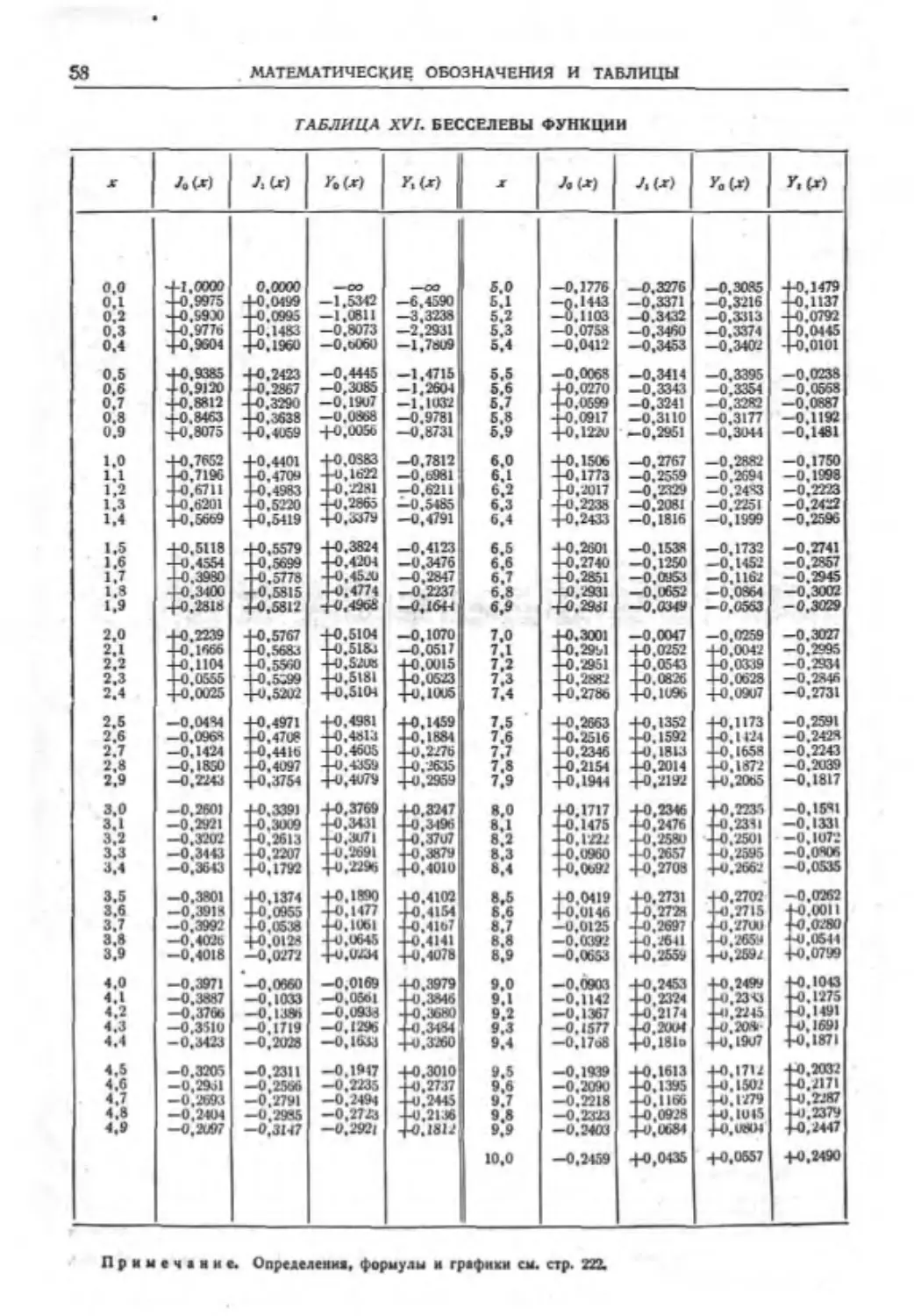
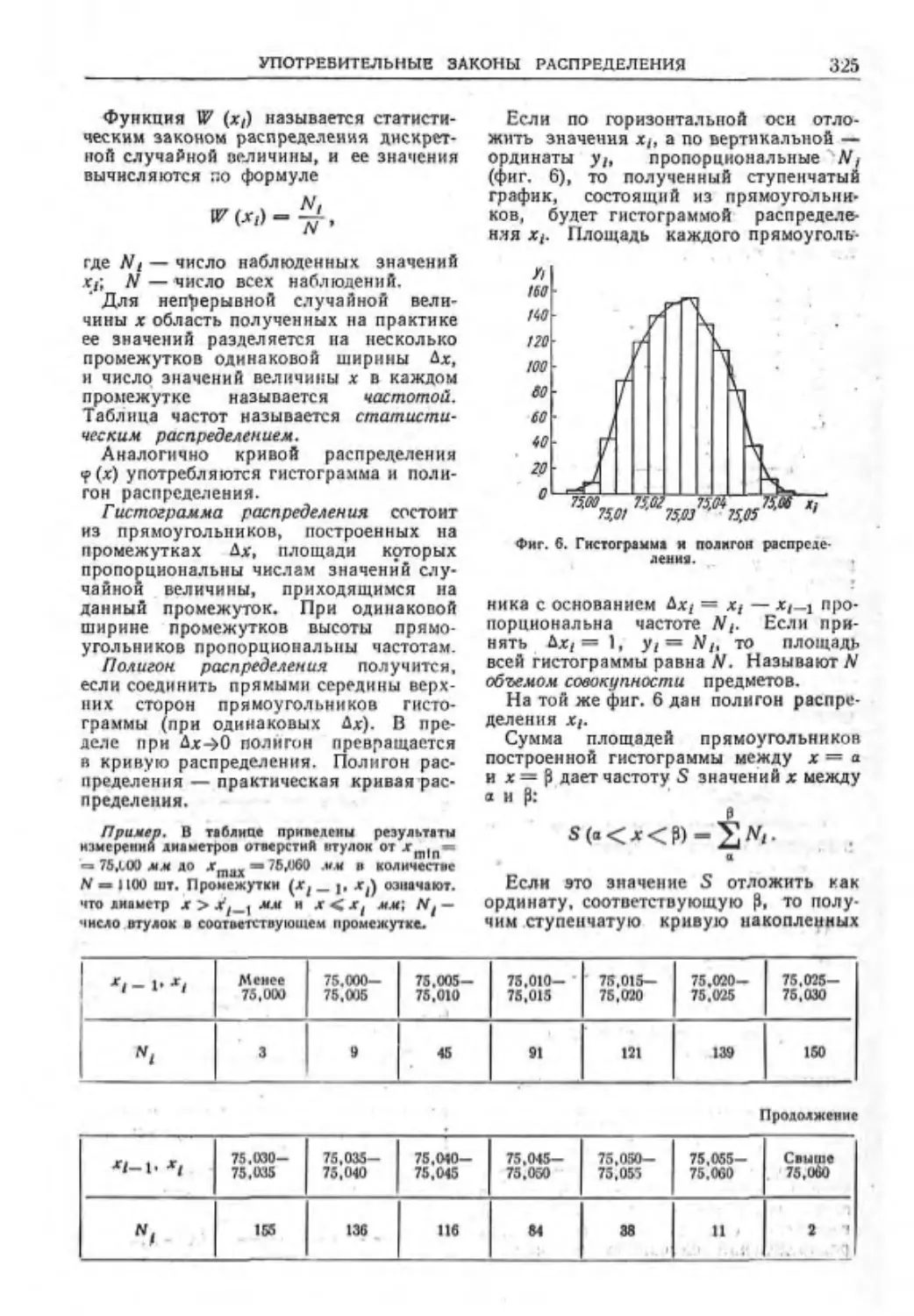
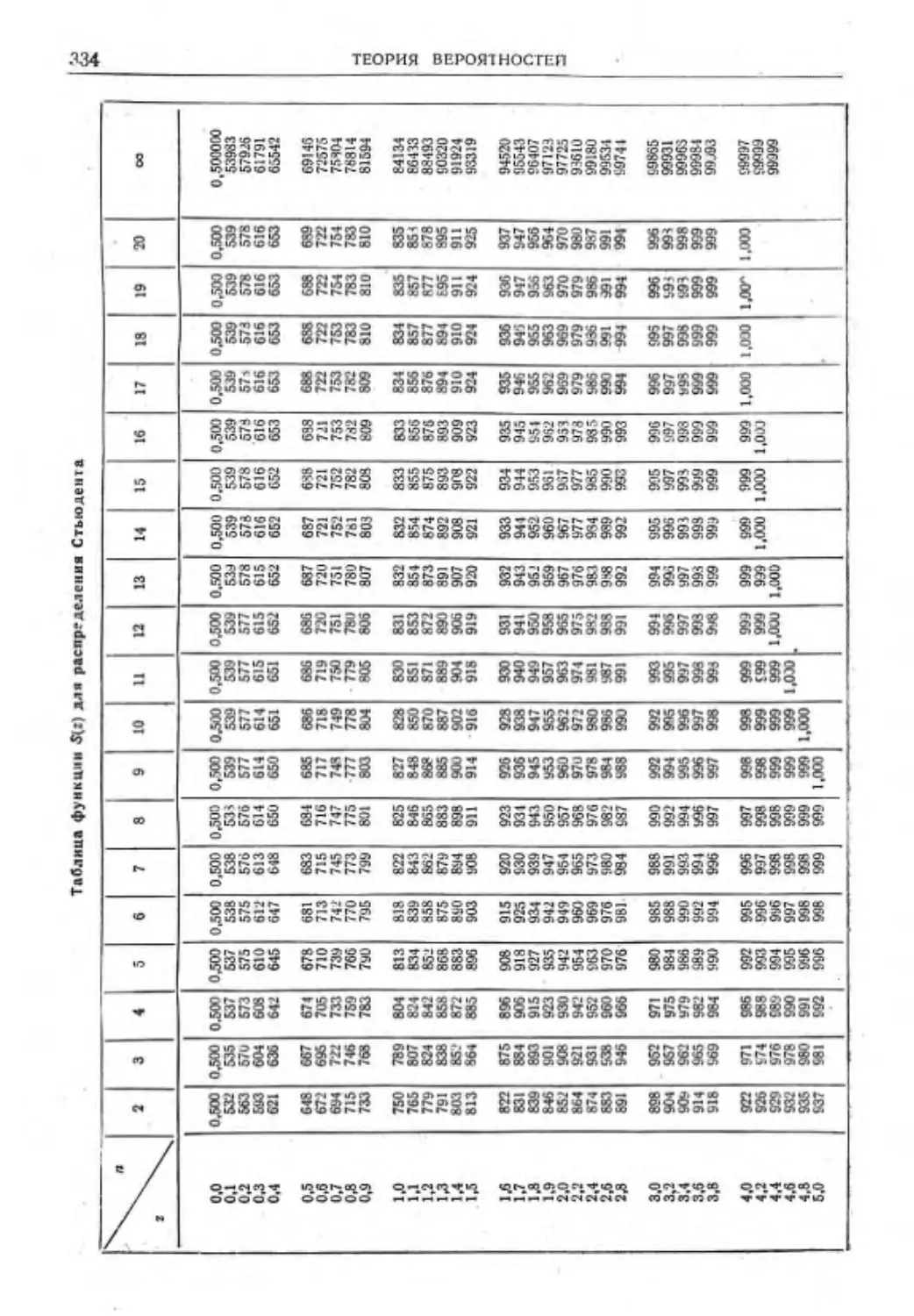
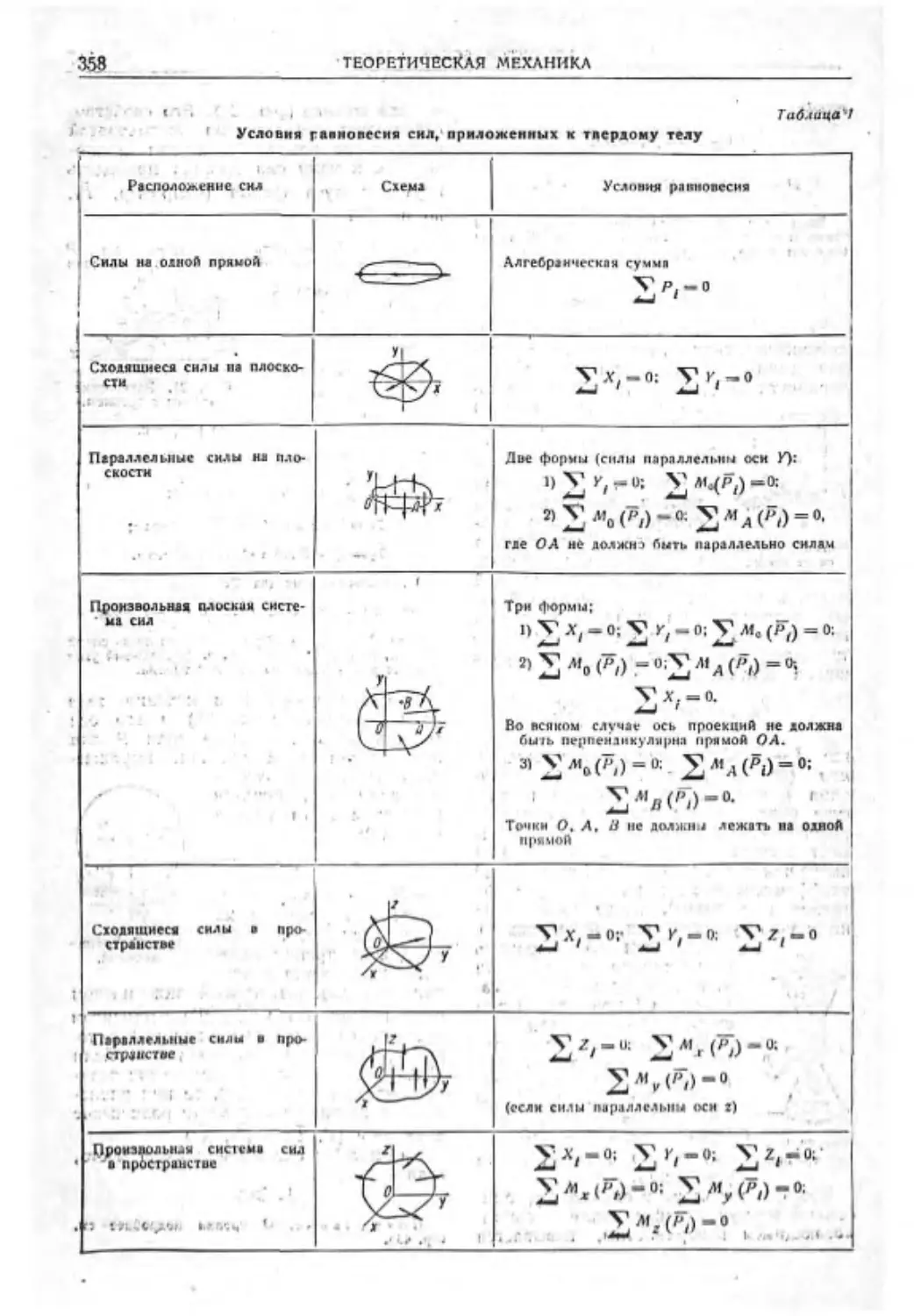
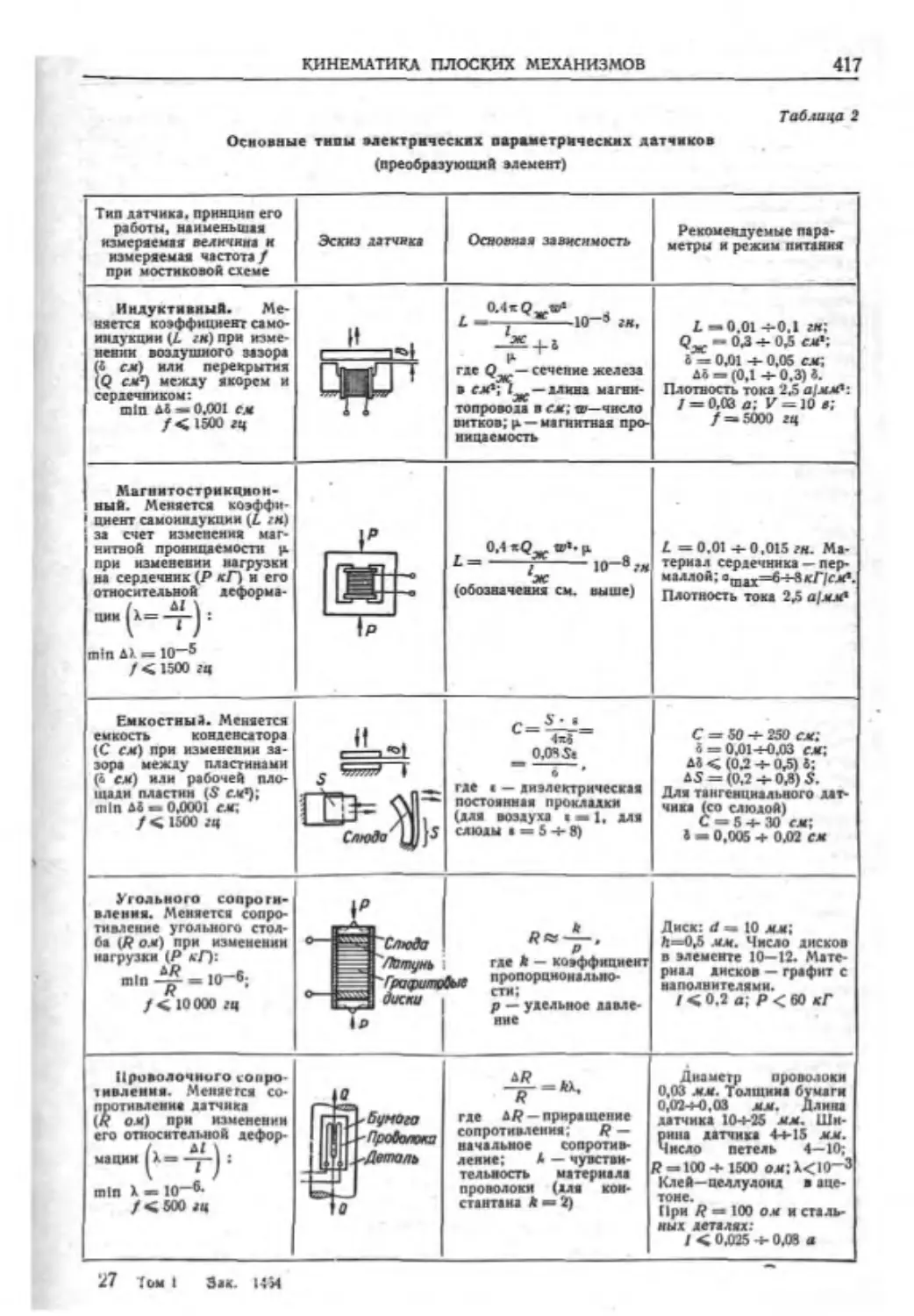
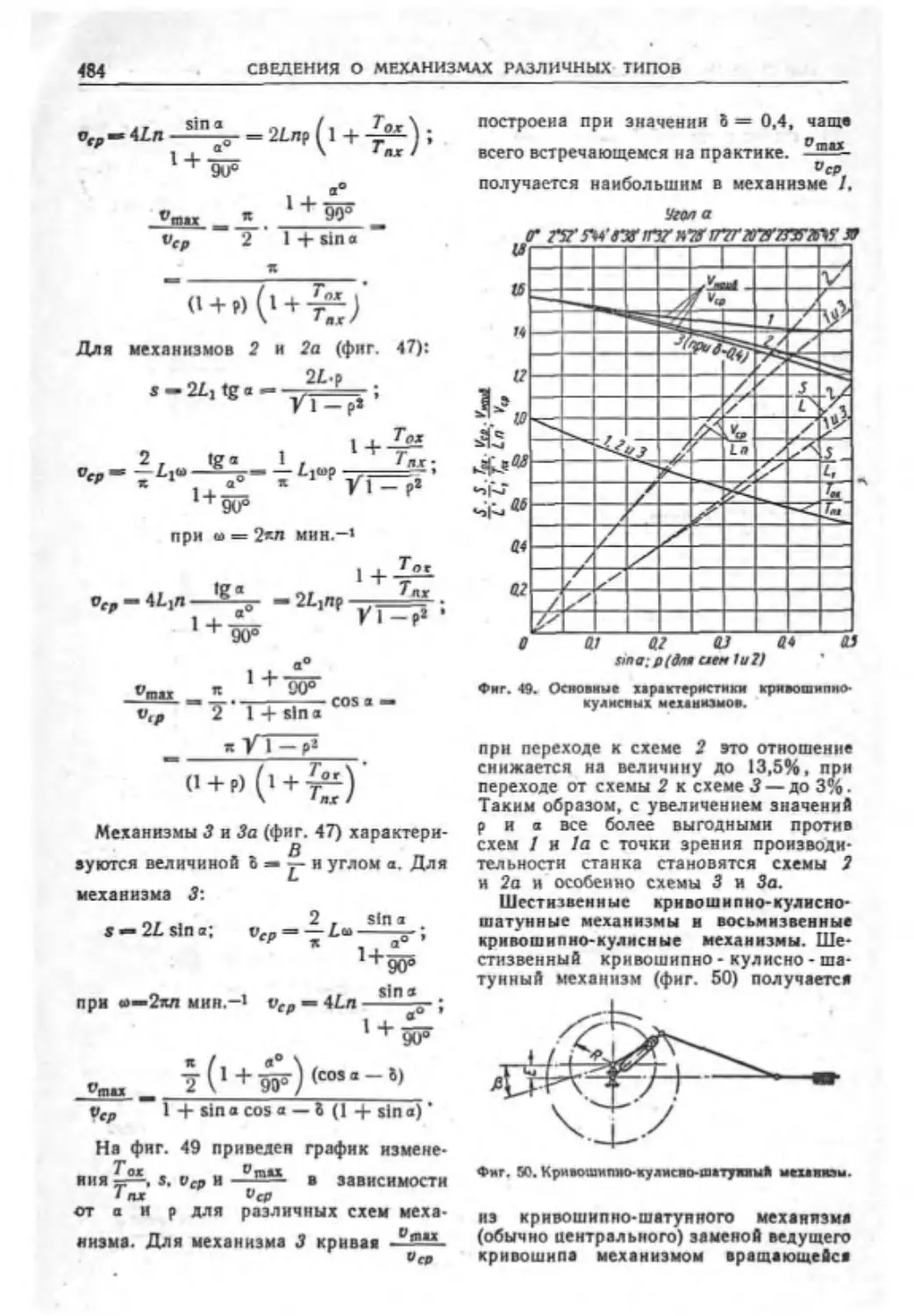
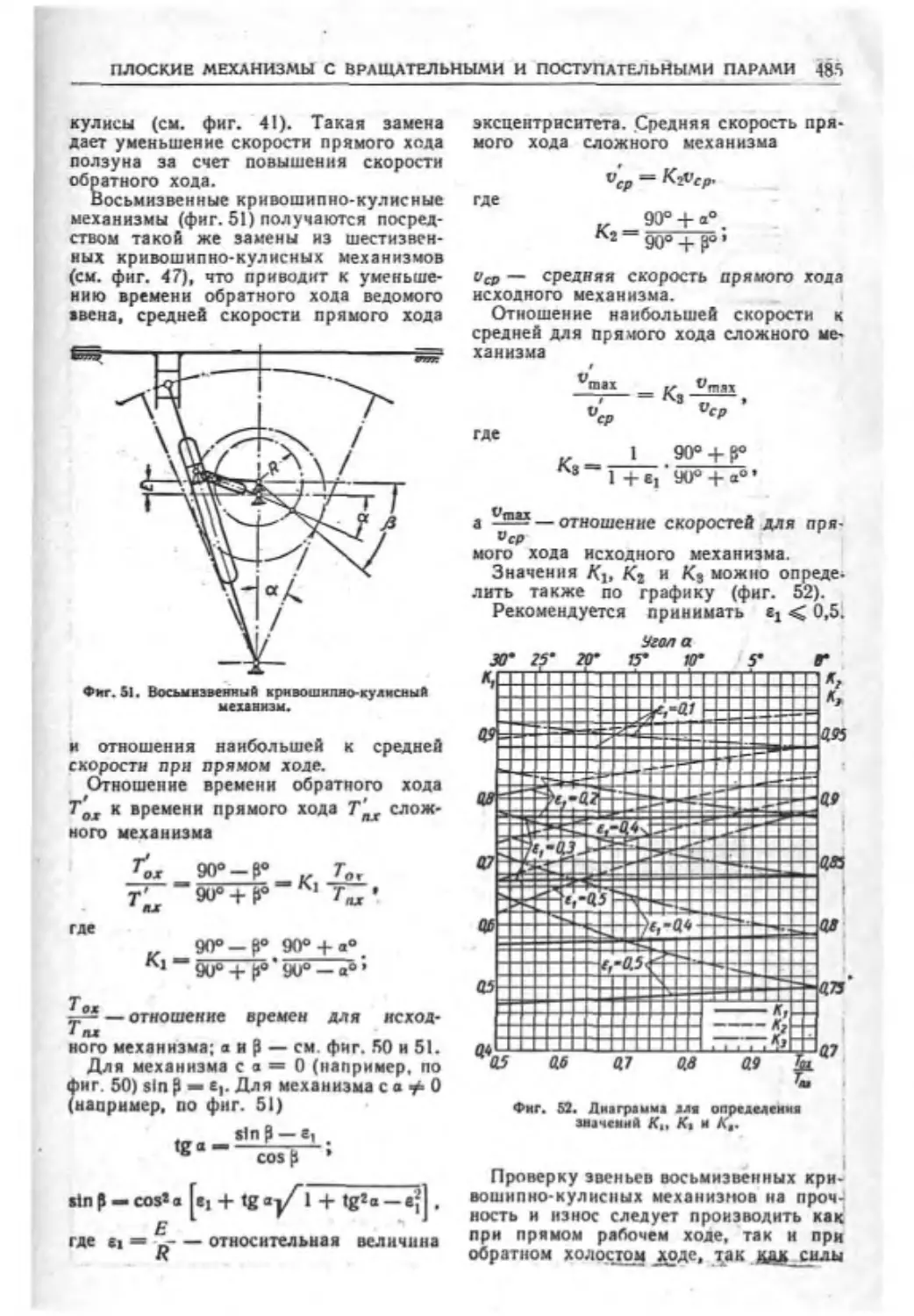
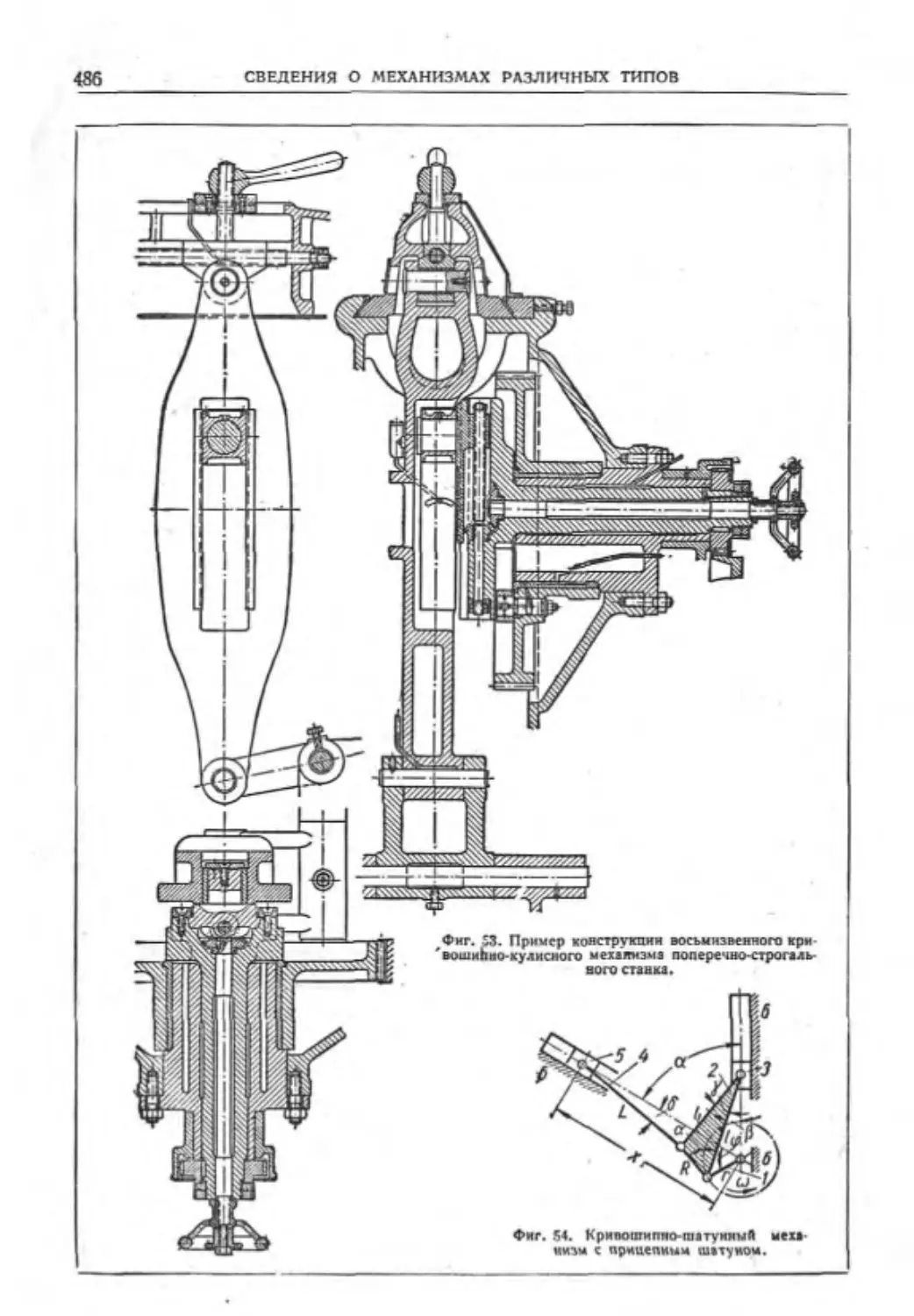
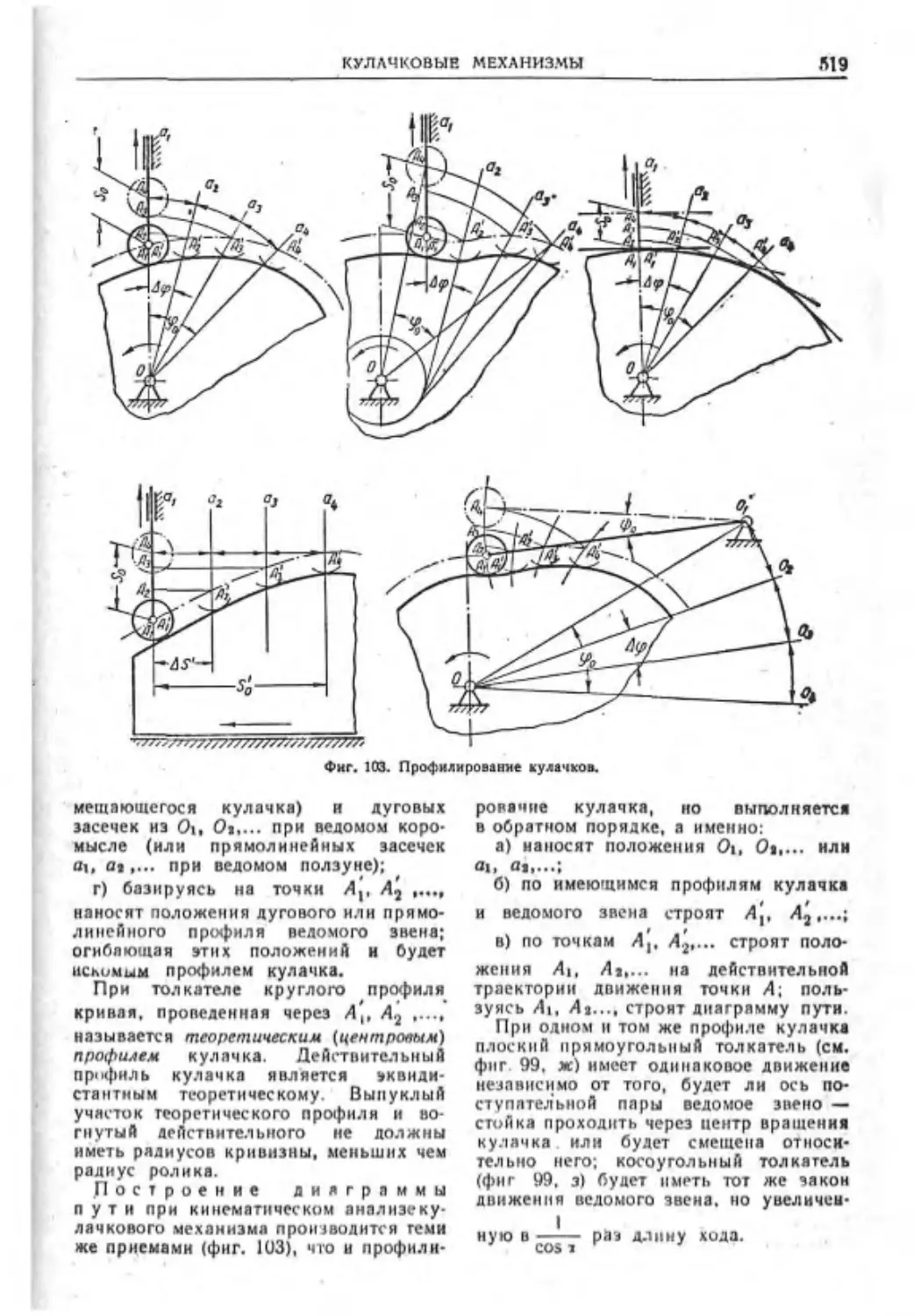
Текст
СПРАВОЧНИК
МАШИНОСТРОИТЕЛЯ
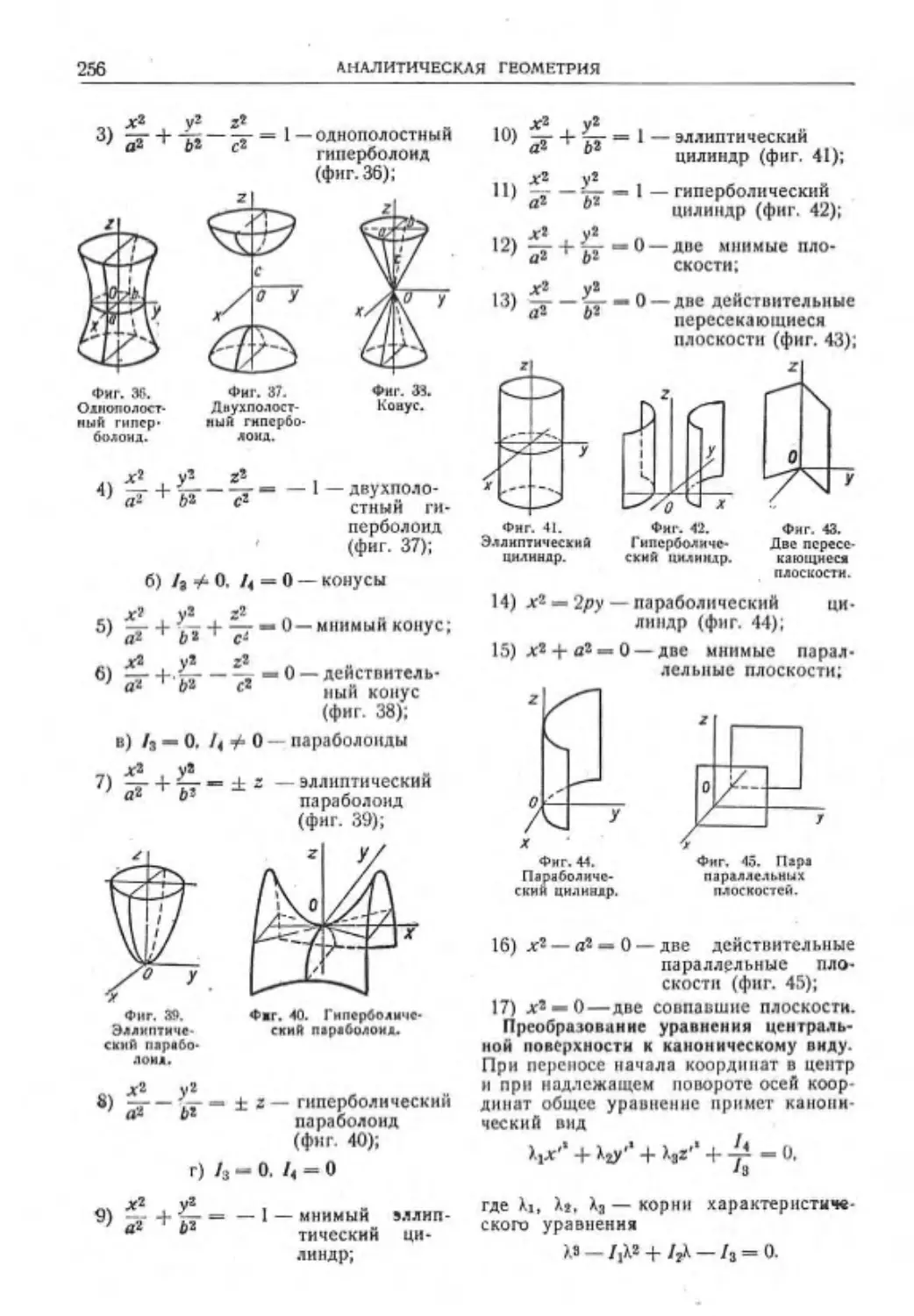
В ШЕСТИ ТОМАХ
УЗб^З
Том I
Главный редактор тома
д-р техн, наук проф. Н. С. АЧЕРКАН
Издание второе,
исправленное и дополненное
ГОСУДАРСТВЕННОЕ НАУЧНО-ТЕХНИЧЕСКОЕ ИЗДАТЕЛЬСТВО
машиностроительной литературы’
• Москва 19.56 X —.л
АВТОРЫ ТОМА
В. С. ЛЮКШИН, канд. физ.-мат. наук, Н. Я. НИБЕРГ, канд. техн, наук,
А. Н. ОБМОРШЕВ, д-р техн, наук, И. С. ПЛУЖНИКОВ, канд. физ.-мат. наук.
Редактор инж. М. Е. Маркус
Редактор графических работ инж. В. Г Карганов
Редакция справочной литературы
Зав. редакцией инж. М. Е. Маркус
Адрес редакции: Москва, ТретвяковскиВ пр., д. 1, Машгиз
СОДЕРЖАНИЕ
От издательства ................. . VD
МАТЕМАТИКА
Глава t. МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕ-
НИЯ И ТАБЛИЦЫ (пи фкз.-мат. наук
в. С. Люкшин кднл. фкз.-мат. наук
И. С. Плужников}.................. 1
Математические обозначения ....... I
Математические таблицы ......... 6
Глава П. ДЕЙСТВИЯ С ВЕЩЕСТВЕН-
НЫМИ И КОМПЛЕКСНЫМИ ЧИСЛАМИ
(кайл. фкз.-мат. наук И. С. Плуж-
ников} ...........................62
Вещественные числа ........... 62
О погрешностях и округлении приближен
иых чисел .......... .... 65
Оценка точности результатов вычнслеинй 66
Приближенные вычисления без точного
учета погрешностей .......... 67
Сокращенное умножение......... 67
Сокращенное деление ............69
Сокращенное извлечение квадратного
корм.......69
Вычисления е малыми числами и с числа-
ми. мало отличающимися от еаииинм . . 69
Непрерывные (цепные) дроби.......71
Действия со степенями.......... 74
Действия с корнями ... ........ 7S
Логарифмы........................76
Соединения...................... 79
Конечные ряды .................МО
Пропорции .а................... 82
Проценты ................ 84
Комплексные числа и действия с ннмч . . 84
Глава III. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
(каял, фнз.мат. наук И. С. Плужников} 47
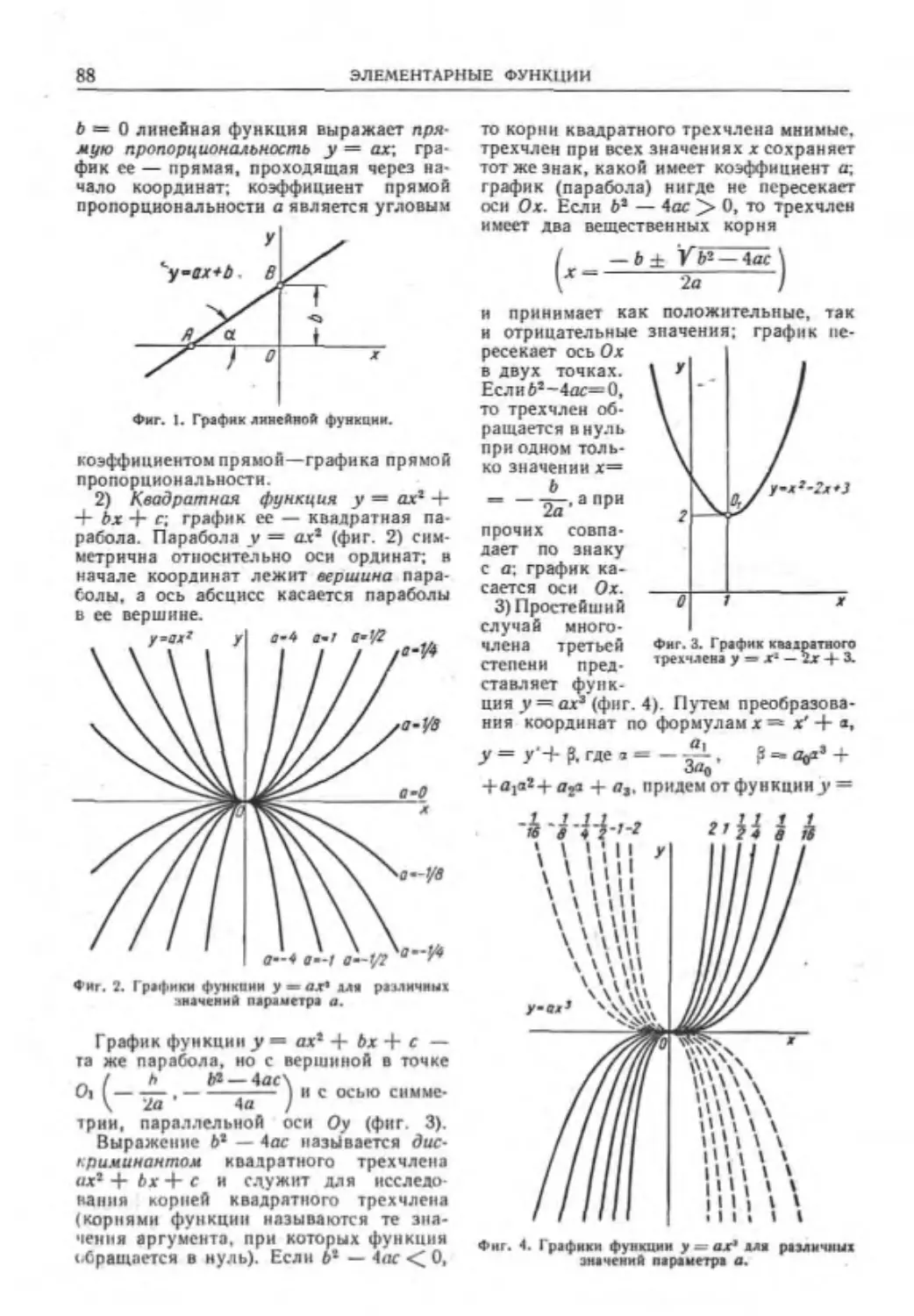
Понятие о Функции ............ 87
Целая рациональная функция ...... 87
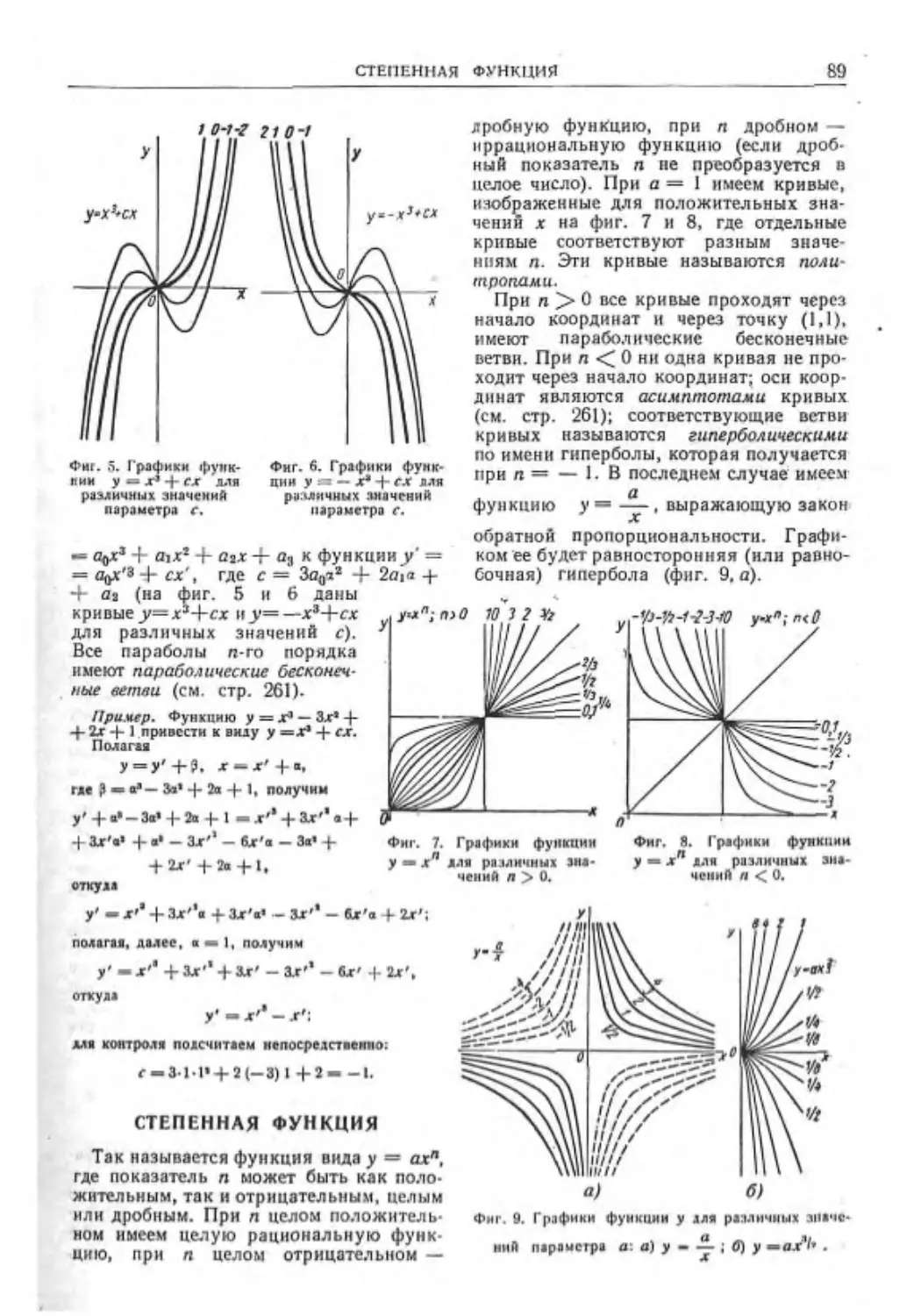
Степенная функция ............ 89
Рациональная функция......... 90
Функции алгебраические и Транснет»тент
иые................... 90
Обратные функции.................91
Показзтел»>иая и логарифмическая Функ
ши ........................... 91
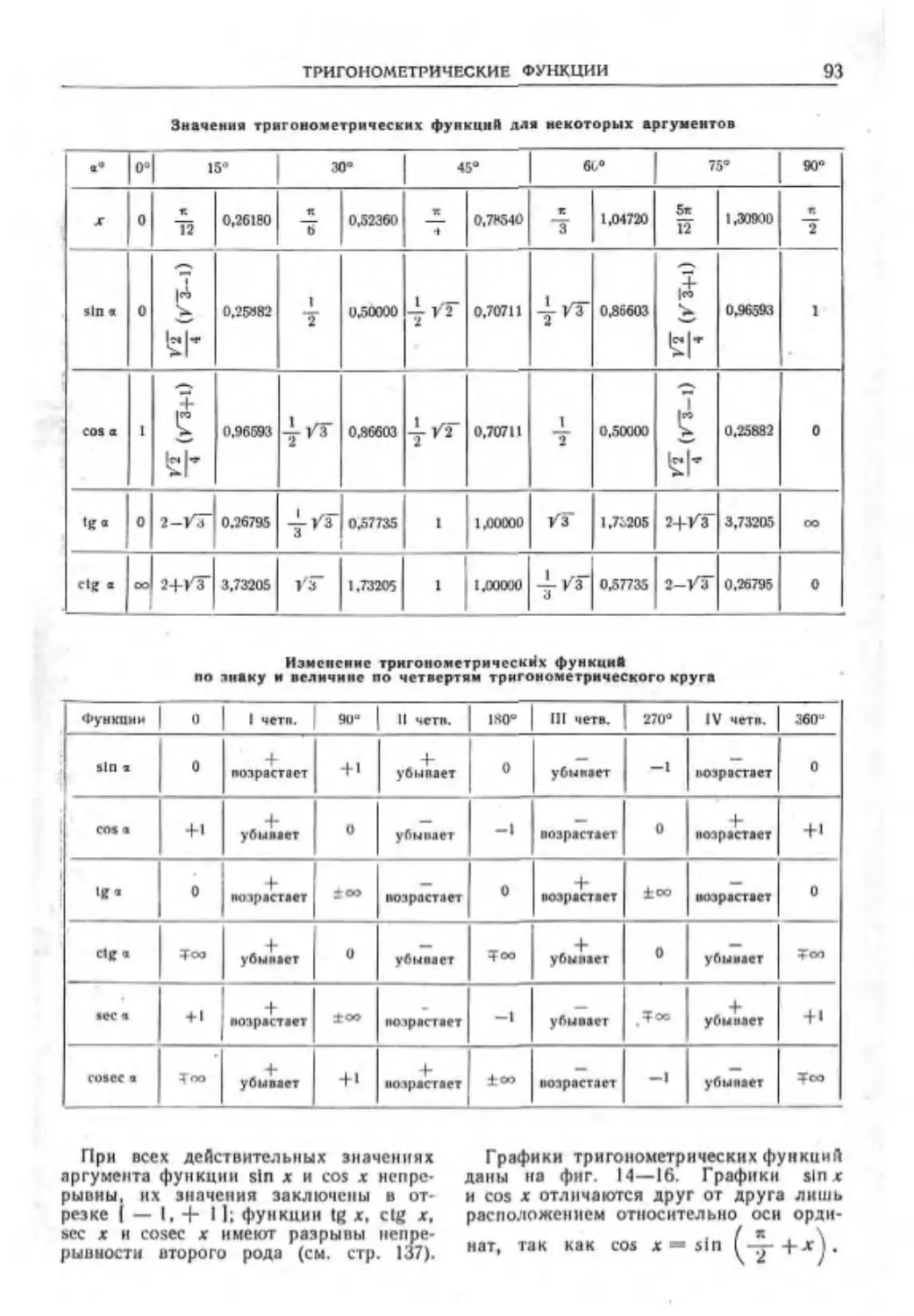
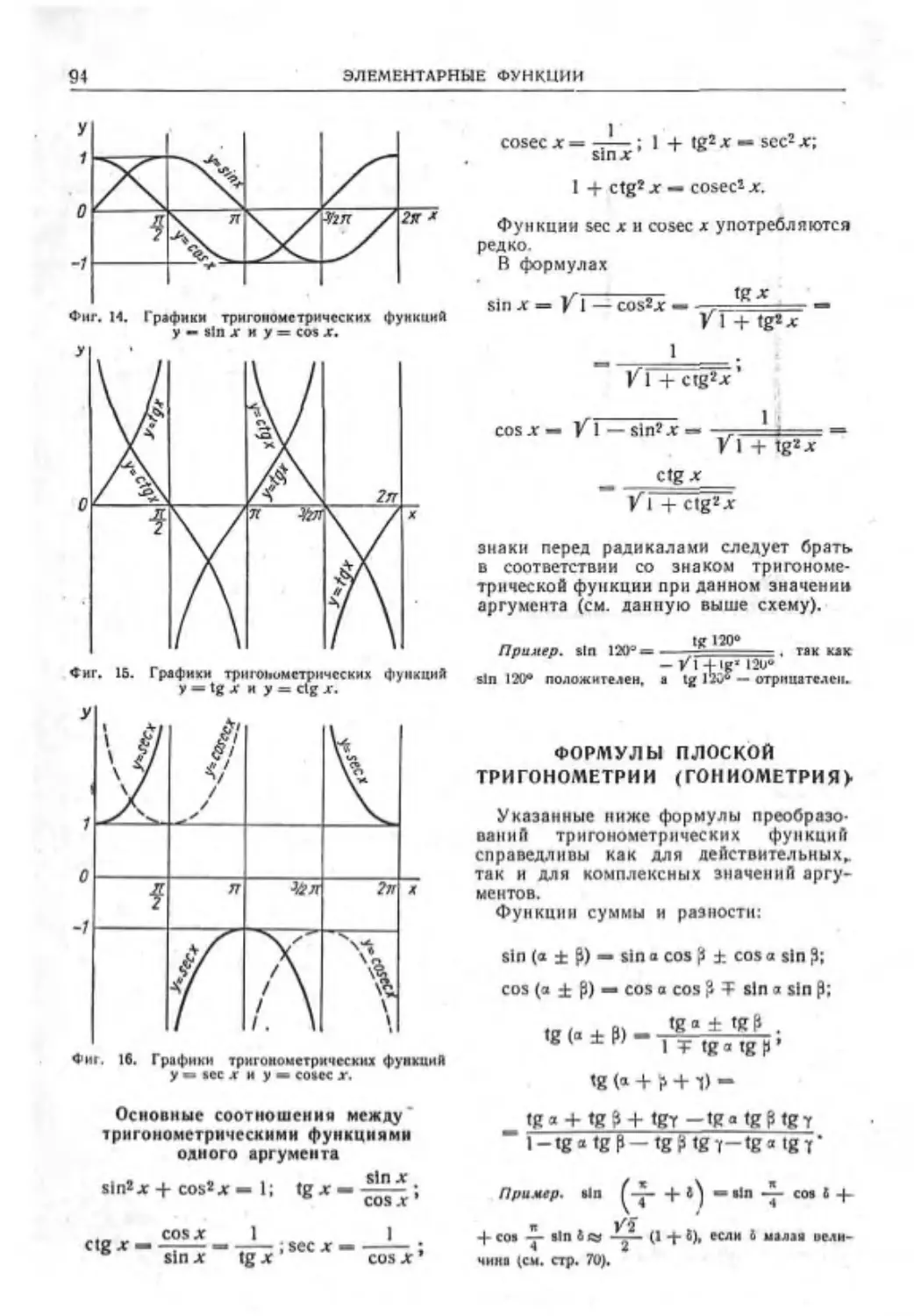
Тригонометрические функции ..... 91
формулы плоской тригонометрии (гонио
метрня) ........................ 94
Синусоидальные величины и их графики 97
Обратные тригонометрические функции 99
Гипсрболическне функции ........ 100
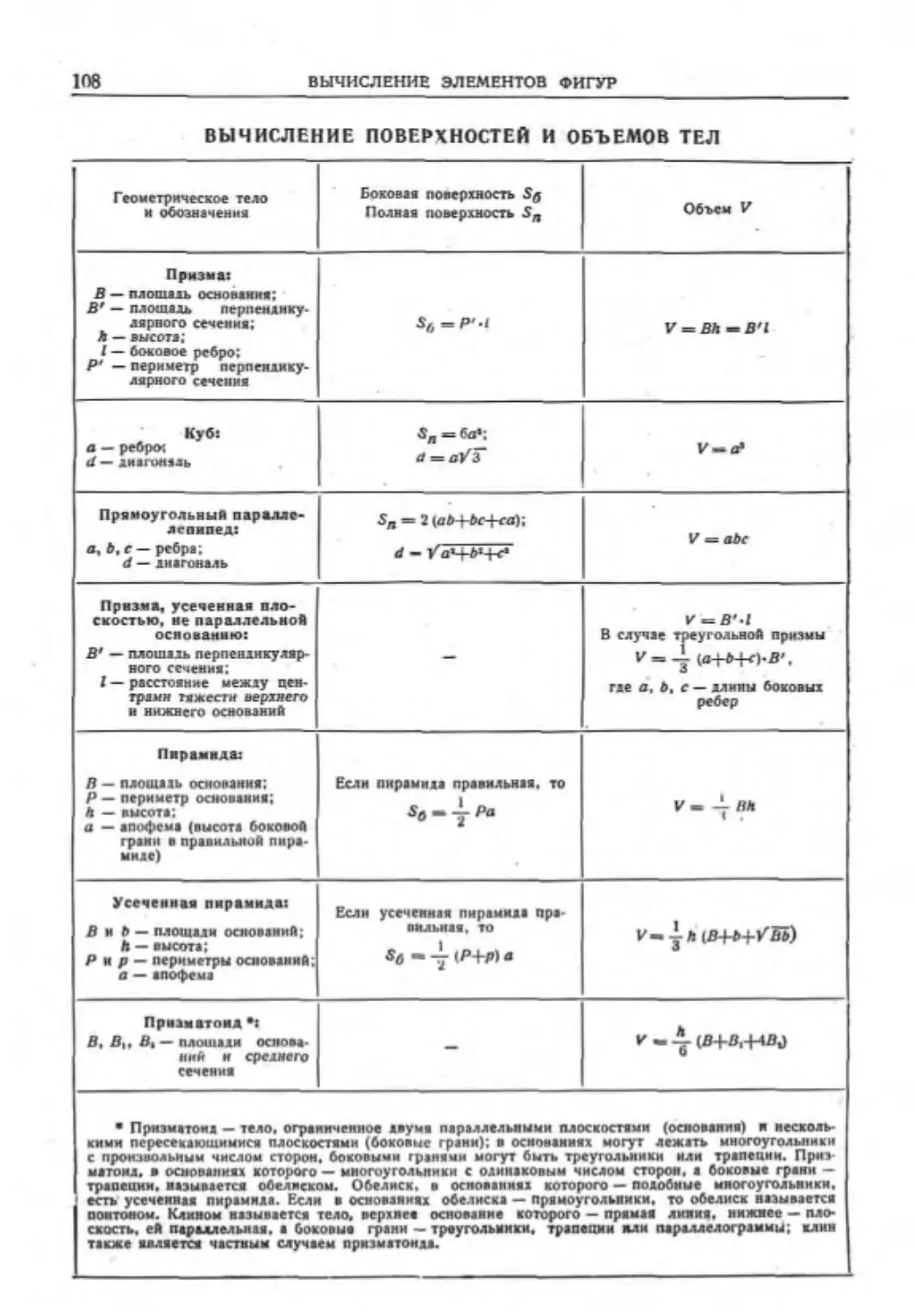
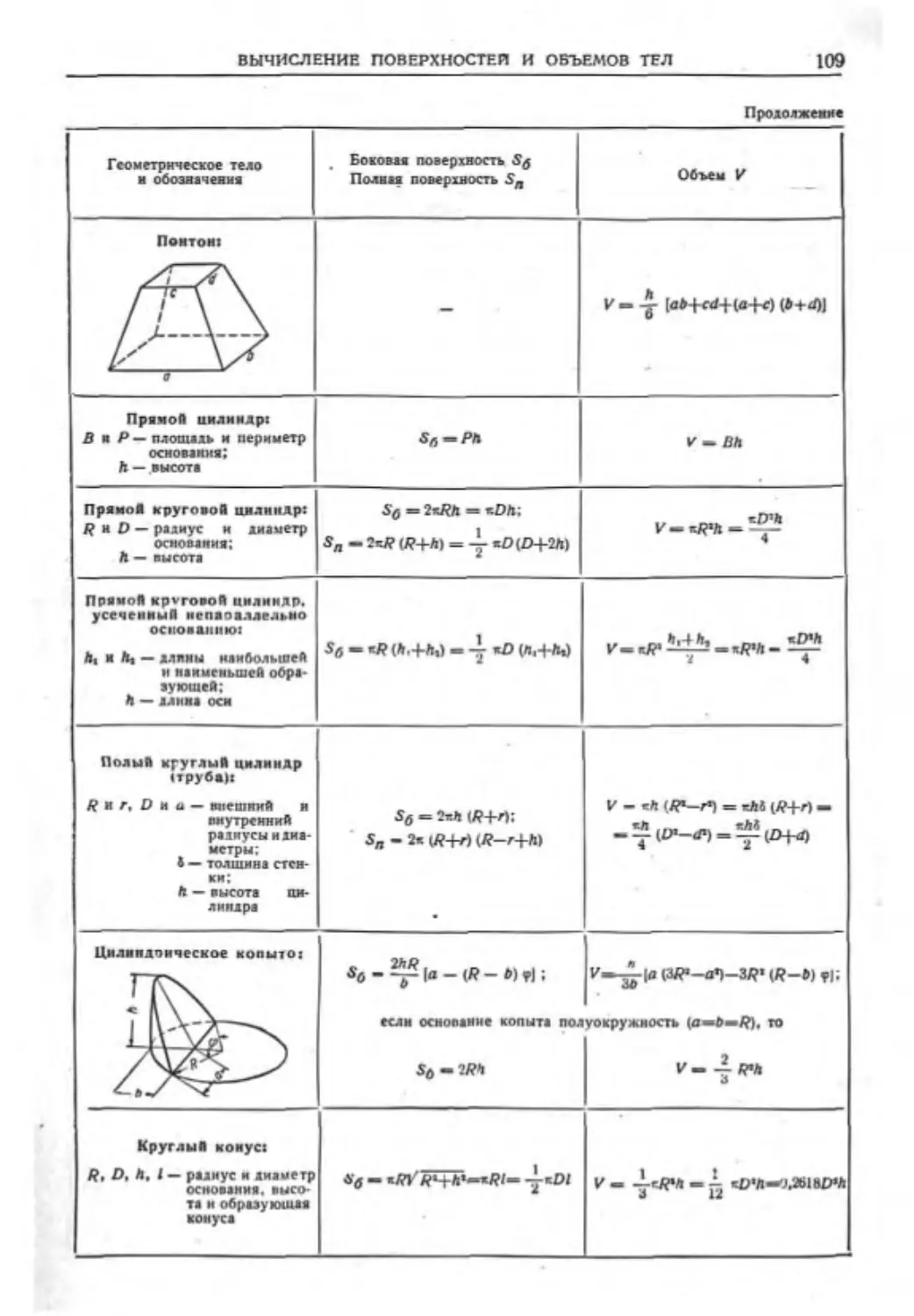
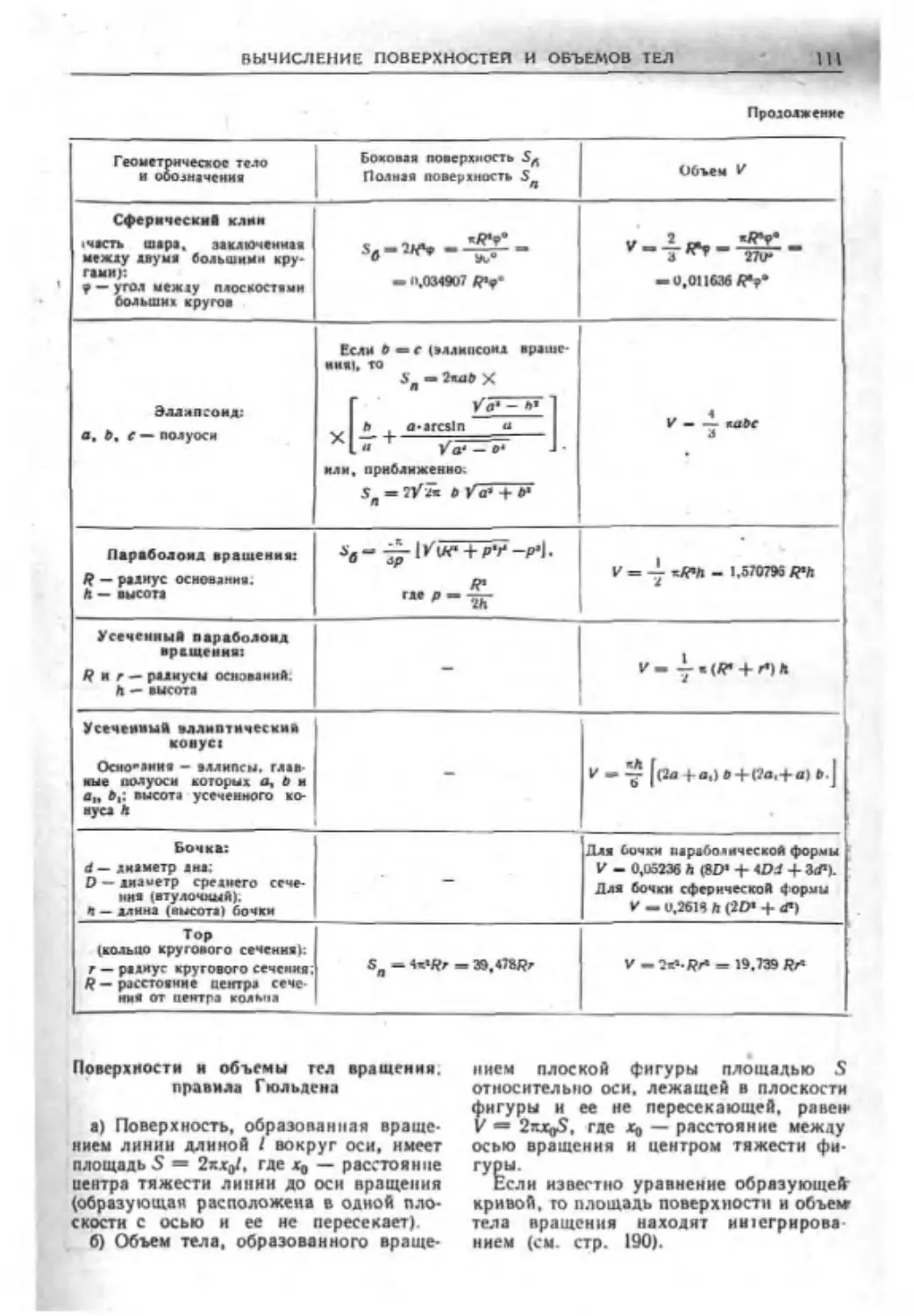
Глава IV. ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ
ФИГУР (кайл, фнз. мат. наук И. С. Плуж-
ников} ..........................102
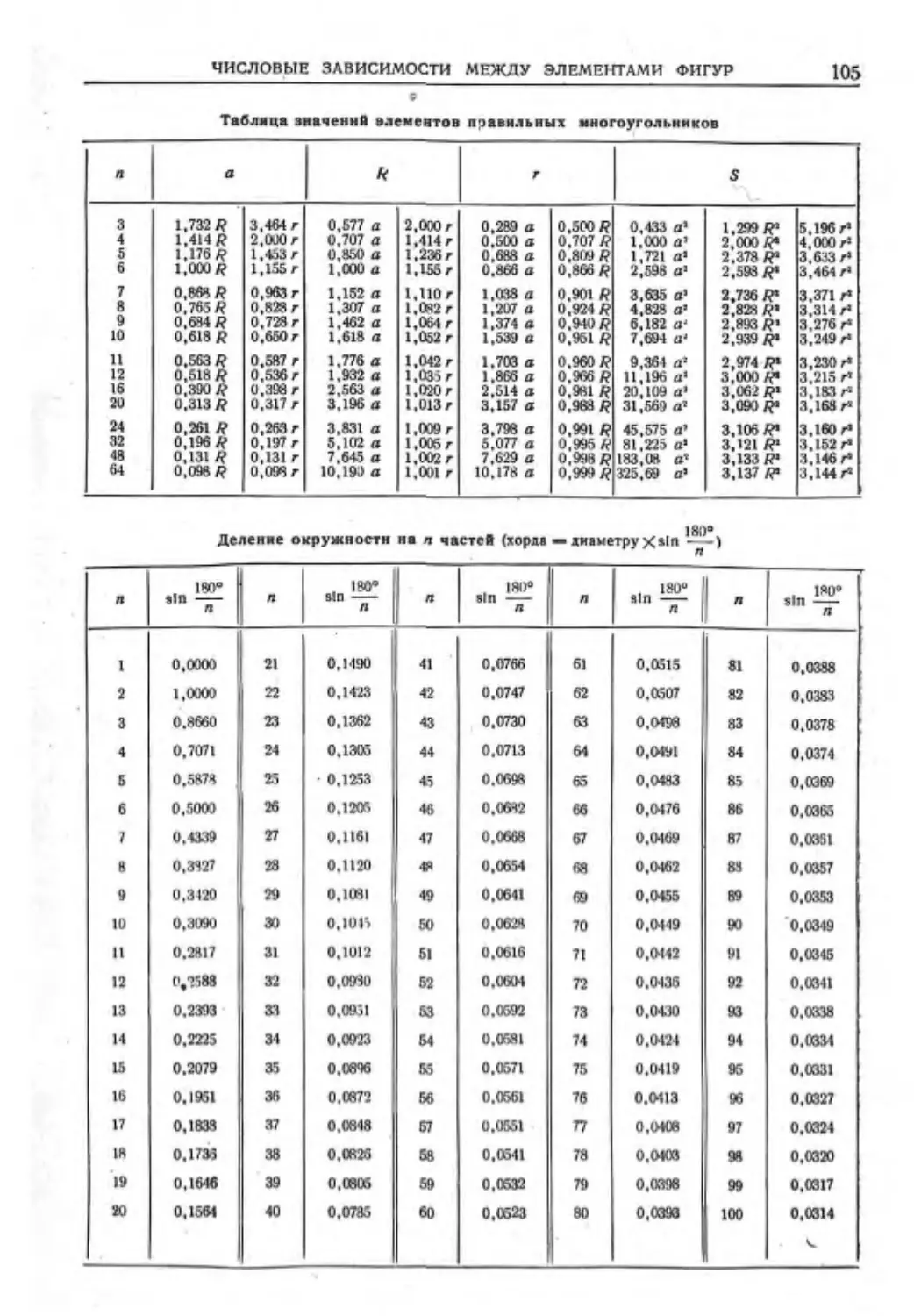
Числовые зависимости между моментами
фигур...........................102
Вычисление периметров н площадей пло-
ских фигур......................106
Вычисление поверхностей и объемов тел ИМ
Зависимости между тригонометрическими
функциями утлое треугольника . . 112
Основные случаи решения треугольников 112
Решение сферических треугольников ... 114
Глава V. РЕШЕНИЕ УРАВНЕНИЙ (кайл.
физ.-мат. наук И. С. Плужников}. ... 116
Определители н применение их к решению
линейных сметем ............ 115
Алгебраические уракнения ....... . па
Трансцендентные уравнении ...... |2(
Отделение корней ............ 123
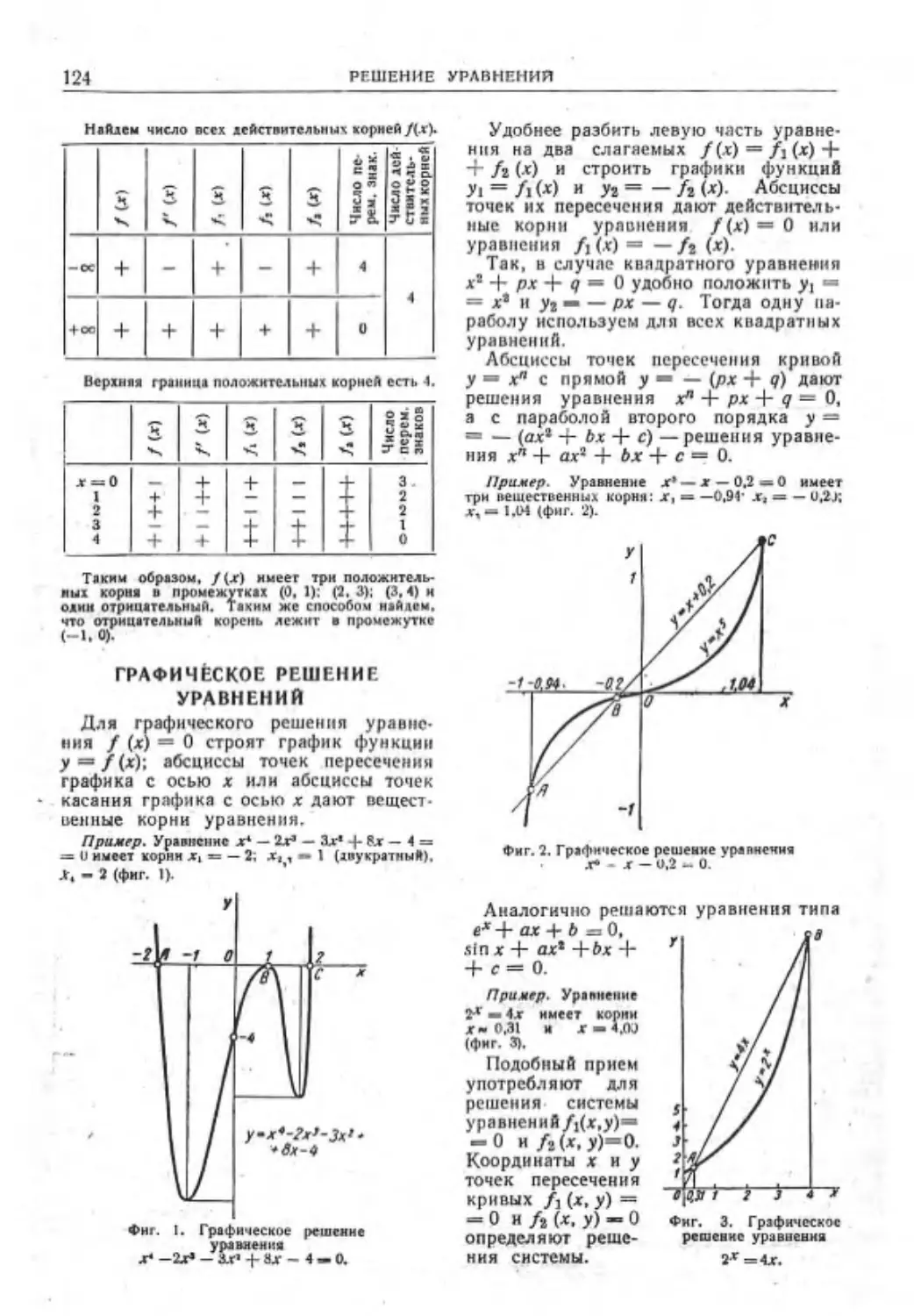
Графическое решение уравнений ..... 124
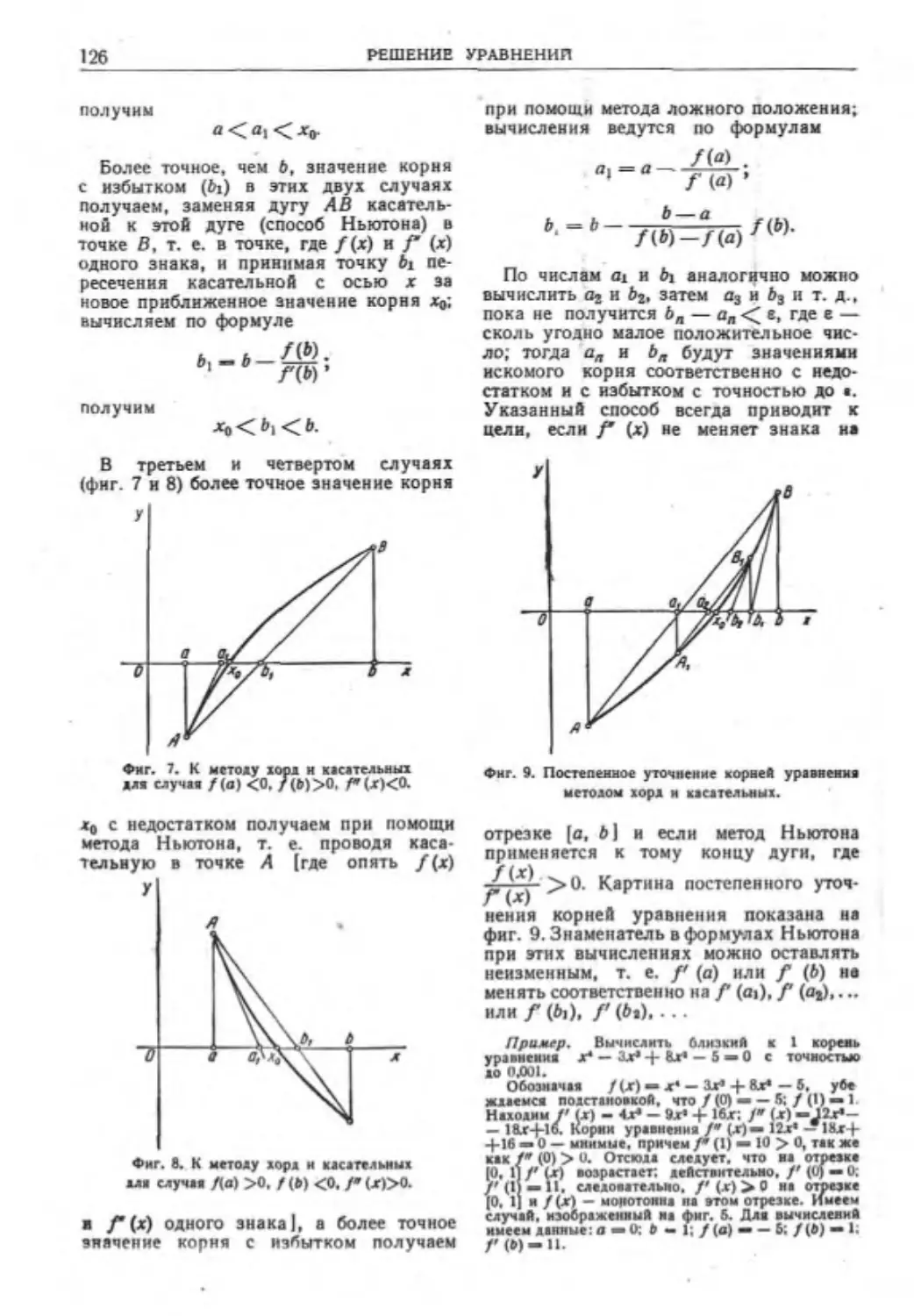
Численное решение уравнений .....125
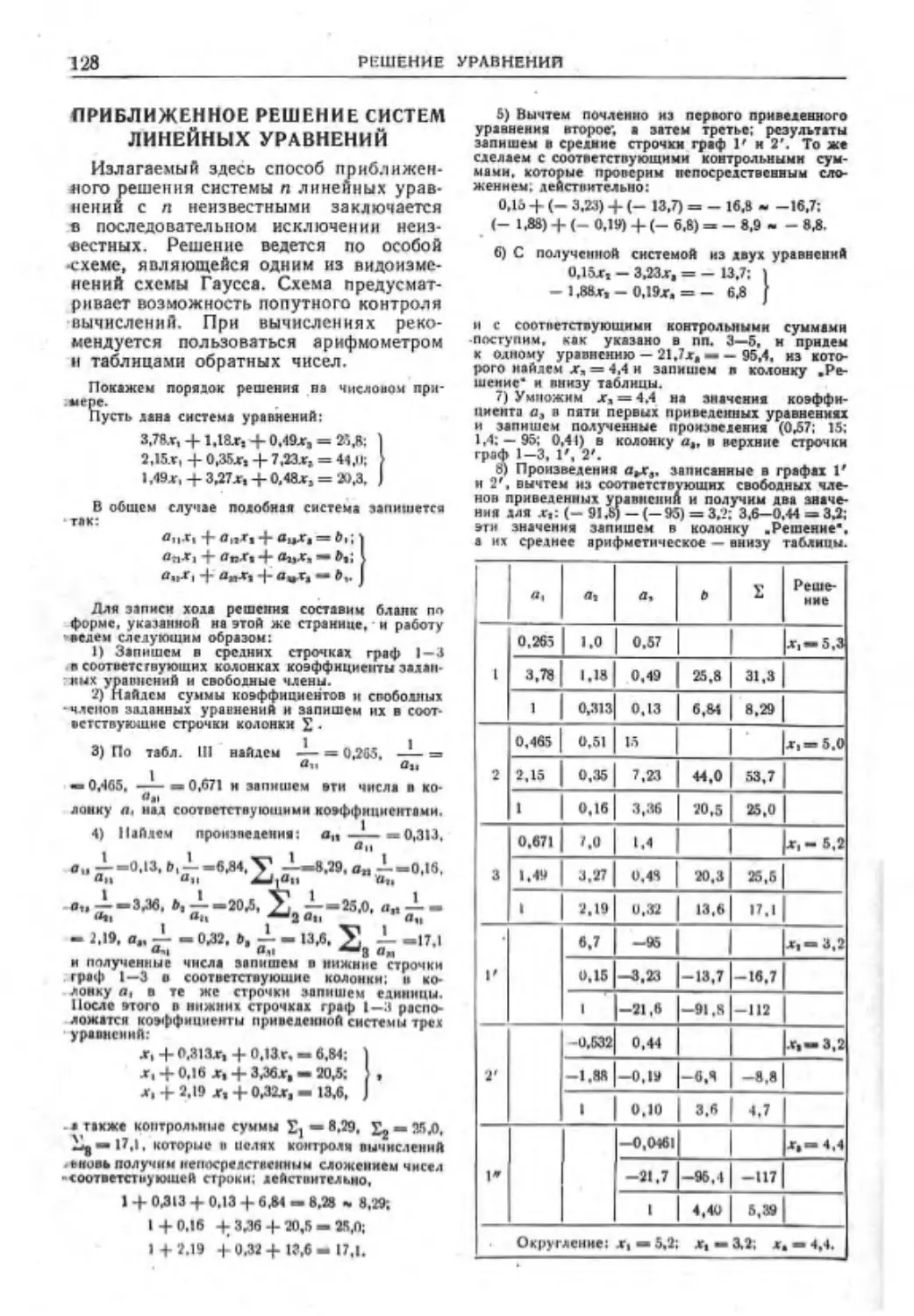
Приближенное решение систем линейных
уравнений ............... 128
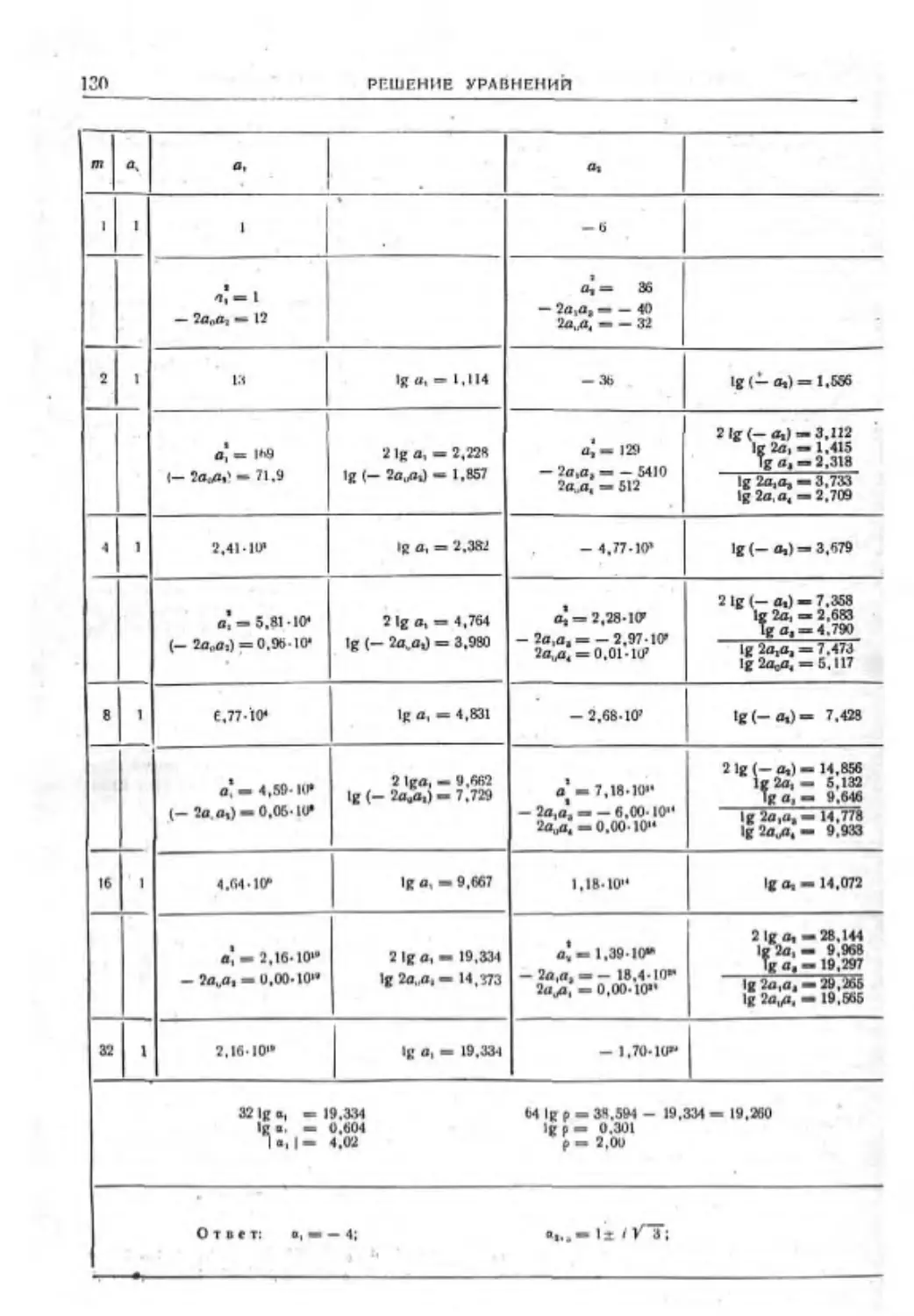
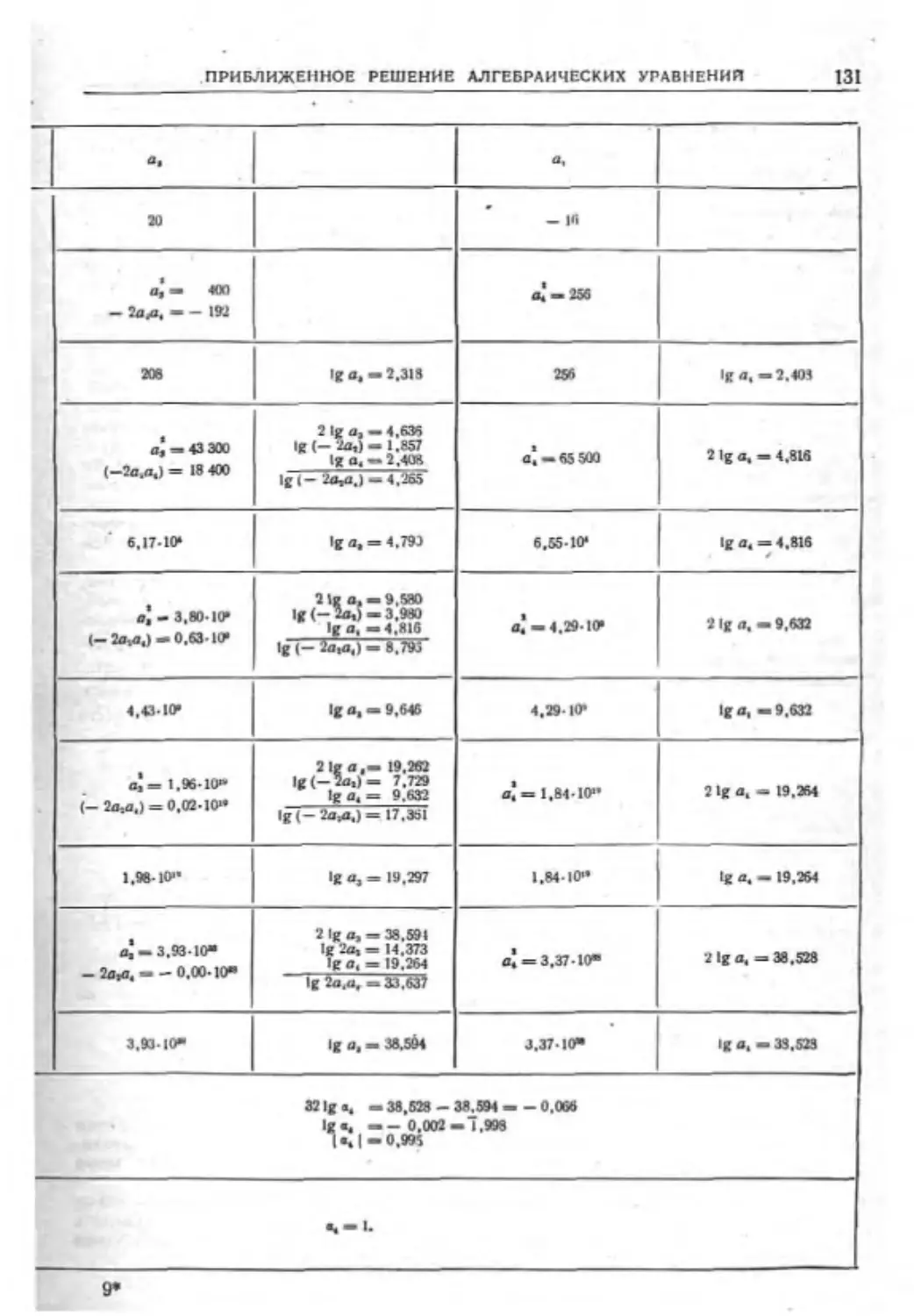
Приближенное решение алгебраических
уравнений по методу Н. И. Лобачевского 129
Глава VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИС-
ЛЕНИЕ (кайл.физ.-мат.наук И. С. Плуж-
ников} ................................|34
Осногиые понятия теории пределен» ... 134
Основные понятия дифференпияльного
исчисления ...................... 136
Формулы хиффереипнровлиия ...... 139
Основные теоремы ифференпиального
исчисление ...»................... 141
Раскрытие неопределенностей ...... (42
Графическое дифференцированно ..... 143
Функции многих переменных и их дифф»
ренпнроваяие ............ .-143
Дифференцирование неявных функций . 146
Определение вкстремдльных значении
функции ...........................»47
IV
СОДЕРЖАНИЕ
Числовые ряды и иссследовдннс их схо
димести .............................149
Фумкционвльяыс ряды; разложение функ-
ций и бесконечные ряды . • ...........151
Глава VU. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
(квнд. фих-мгт. мд ух И. С, Плужников) 154
Неопределенный интеграл и его свойства 154
Освой иые методы интегрирования ... 155
Иип-1 ри|х>|»аиие рациональных .функций 1.56
Инуцриро^ание иррациональных функций 160
Иитсгрнринанис элементарных трансцен-
дентных Функций.... ....... 161
Таблица неопределенных нитогралоп... 1(15
; Определенный интеграл и его свойства . . 172
Несобственные интегралы..............174
Интегралы Эйлера .....•.•*«•• 173
Таблица определенных нктсгралоп .... 173
п Приближенное вычисление определенных
интсгралор ...... ........ 182
Графическое интегрирование .••••_*. 153
Кратные интегралы . .,.»•••«• 184
Криволинейный интеграл .••••••.. 186
Интеграл пи роперхности .•••». ... 187
Придам, гни и интегрального исчисления
, , к геометрии и механике.........189
Интеграл Стильтьеса ... т ...... . 192
Глава VIII. ФУНКЦИИ КОМПЛЕКСНОГО
ПЕРЕМЕННОГО (КОМ. физ.-мат. наук
,И. С. Плужников)............ 194
4. • ‘
Основные понятия............ 194
. Элементарные функции комплексного пе-
ременней о. . ... 195
Днфферепинропанне функций комплекс*
• мою переменного ...................196
•Иите1рал по комплексному переменному 196
• • Ралложеннс аналитической функции и сте-
пенной ряд . ....... .... 197
Особые точки однозначной функции ... 199
‘Вычеты аналитической функции.....ЭЮ
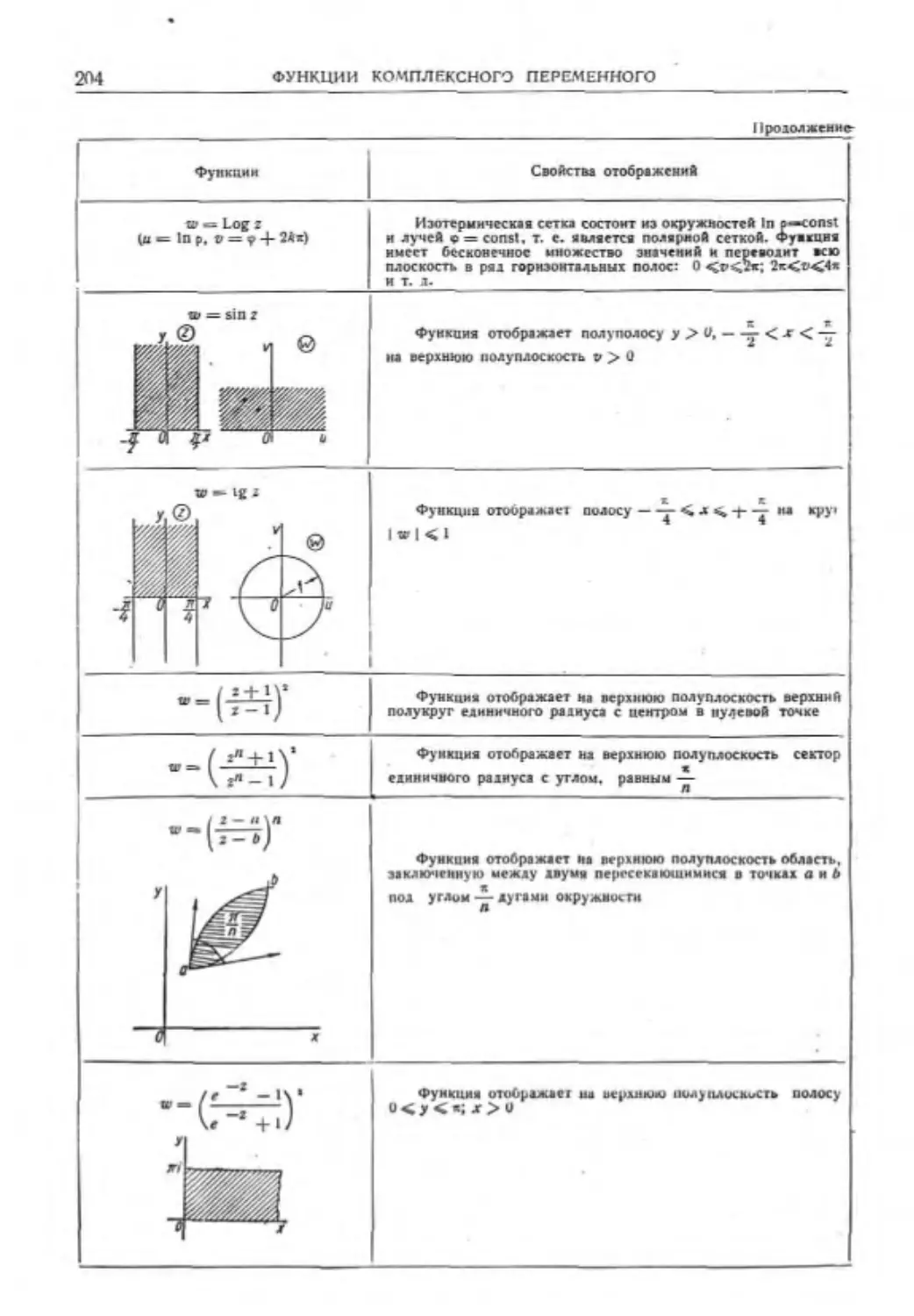
Конформные отображения .........201
Глава . IX. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВ-
НЕНИЯ (канд. физ.-мат. наук В. С. Люк-
шин] ............................ .206
Обыкновенные ура пиемия 1-го порядка . . 206
'Обыкновенные уравнения гысших поряд-
ке и и системы уравнений ........ 213
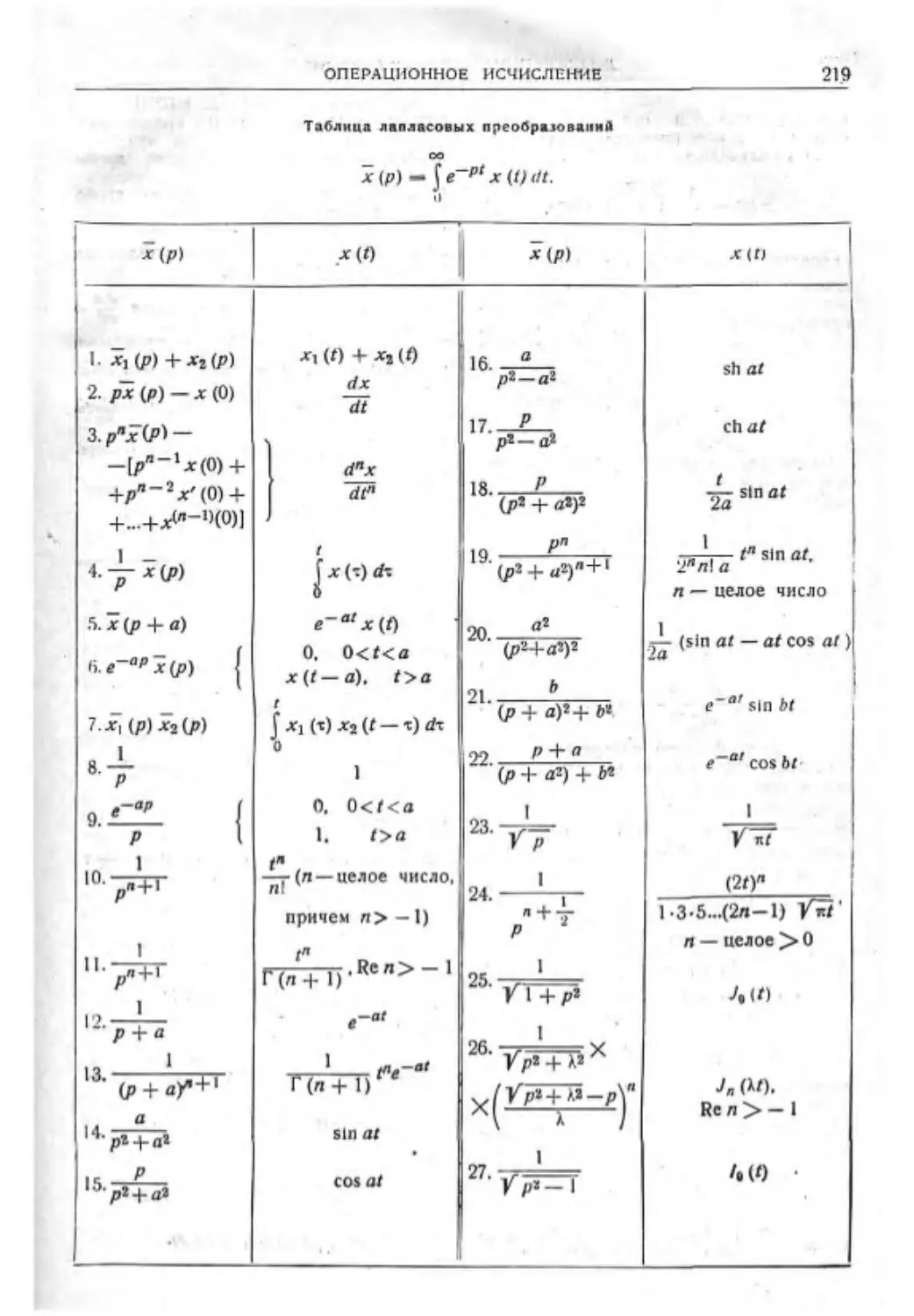
Операционное исчисление ••••••.. 213
1 Спи нальные Функции............. 221
Дифференциальные уравнения в частных
производных ............224
Глава Z . ВЕКТОРНОЕ и ТЕНЗОРНОЕ
ИСЧИСЛЕНИЕ (канд. фкз.-ыат. наук
Ь. С. 226
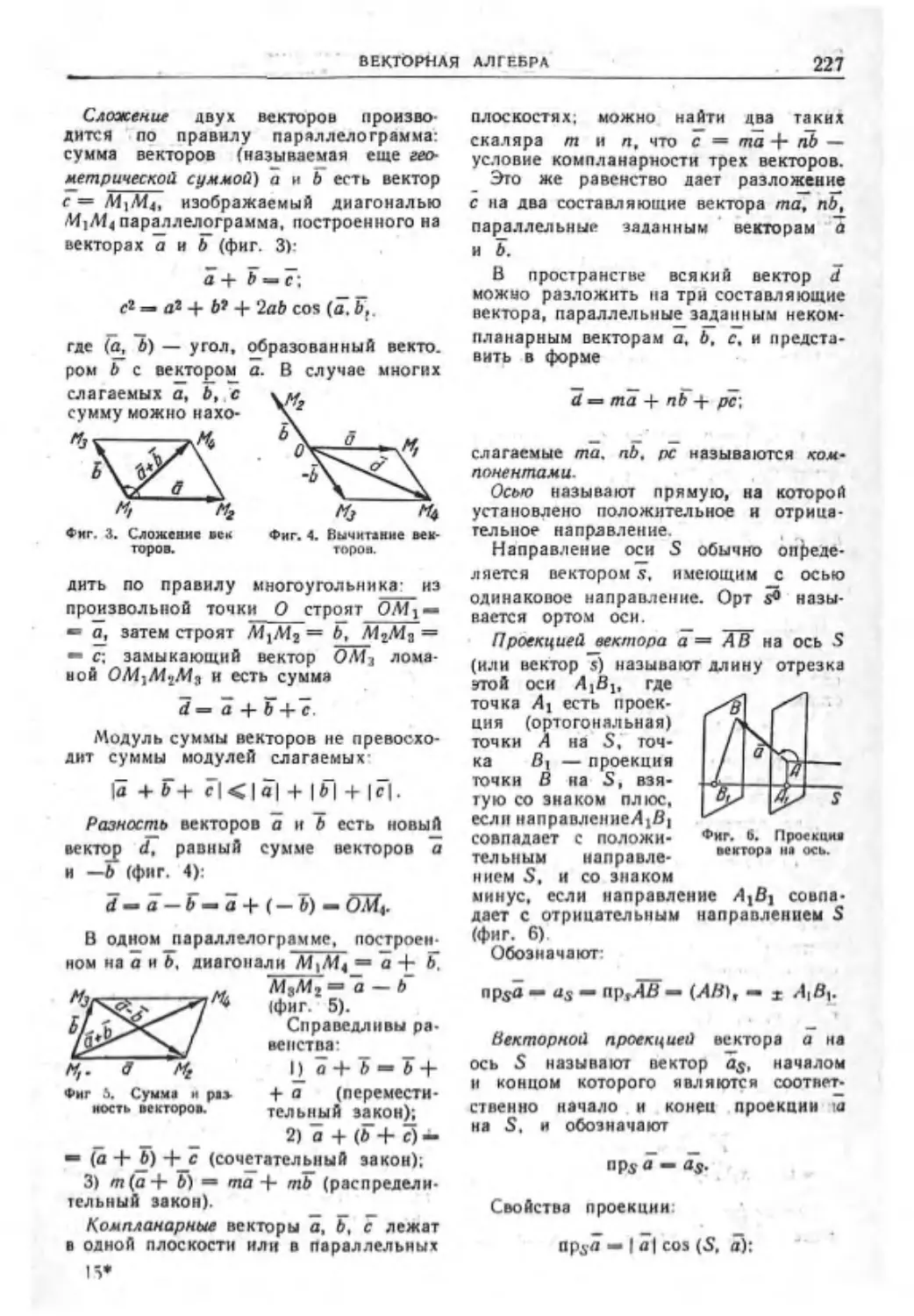
^-Векторная алгебра..................226
Векторный анализ ............ 230
Тензоры 234
Глава XI. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
(канд. фит,-мат. наук В. С. Люк шик) . . 238
Аналитическая геометрия на плоскости . 238
Аналитическая геометрия в пространстве 249
Глава XI/. ДИФФЕРЕНЦИАЛЬНАЯ ГЕО-
МЕТРИЯ (каид. фих-маг. наук В. С. Люк-
шик).............•..............2S8
Плоские кривые .................258
ПКоСтрацстггнны» кривыв . 282
.Теория поверхностей W3
Глава ХШ. РАЗНОСТНОЕ ИСЧИСЛЕНИЕ
И ИНТЕРПОЛИРОВАНИИ (каид. физ.-
Мат. наук В. С. Люкшин) ........ 301
Конечные рдтностн....301
Интерполирования........... ... 303
Глава ХЛ'. ПРИБЛИЖЕННОЕ АНАЛИТИ-
ЧЕСКОЕ ВЫРАЖЕНИЕ ФУНКЦИЙ
(мид. физ.-мат. наук В. С. Люкшин] . 305
Глава XV. НОМОГРАФИЯ (канд. фнз.-мат.
наук В. С. Люкшин]. . ....... 314
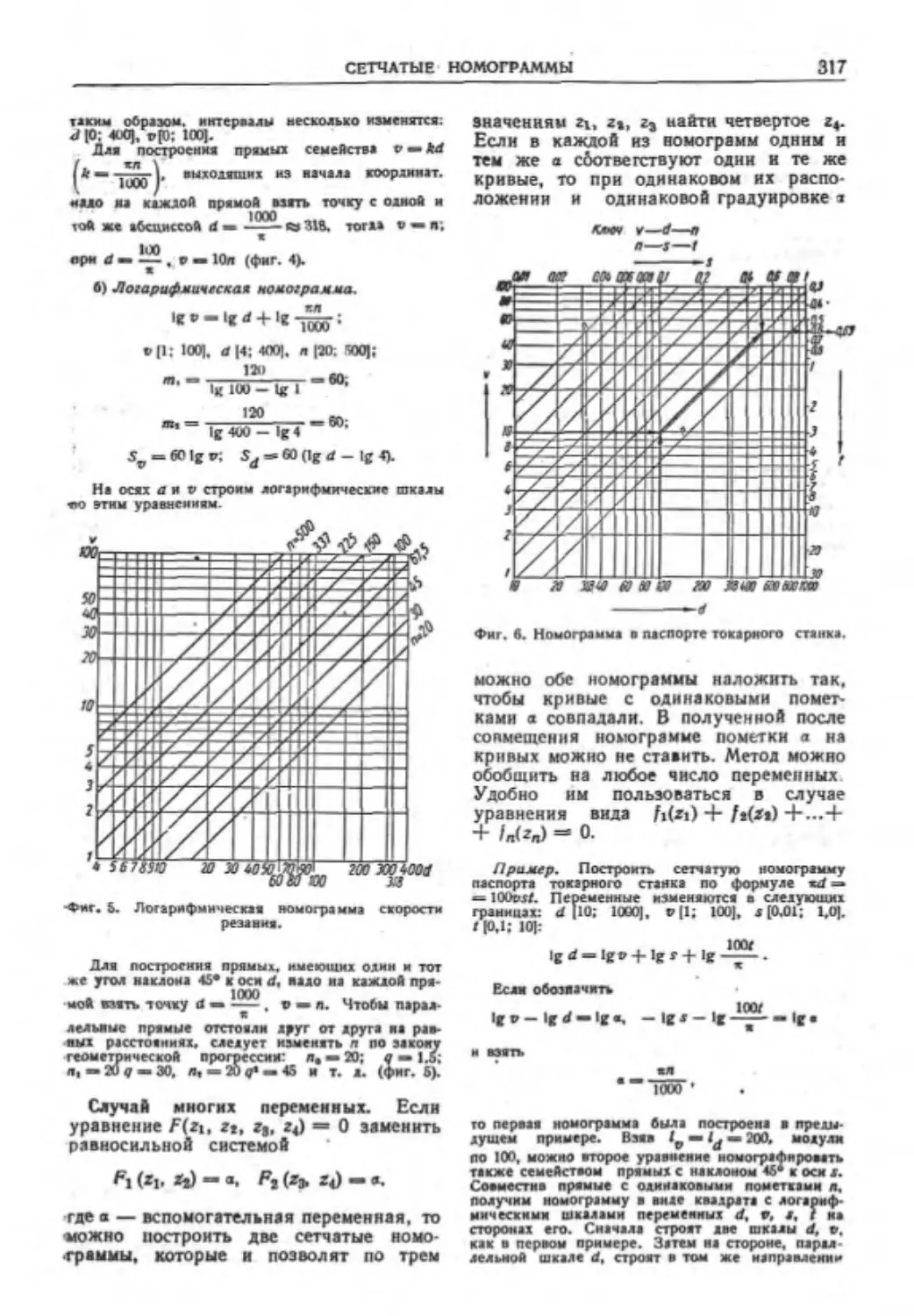
Сетчатые номограммы .......... 315
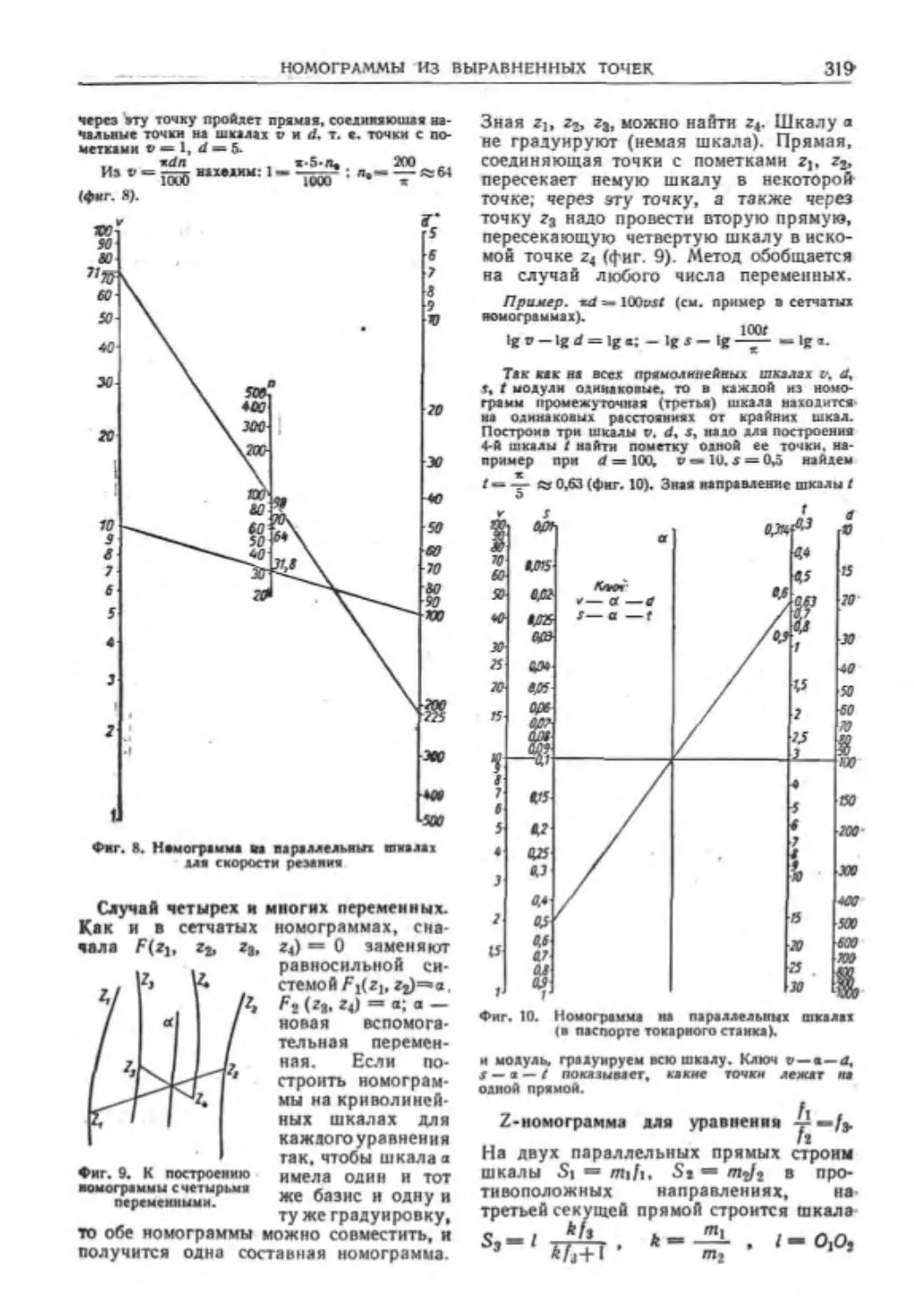
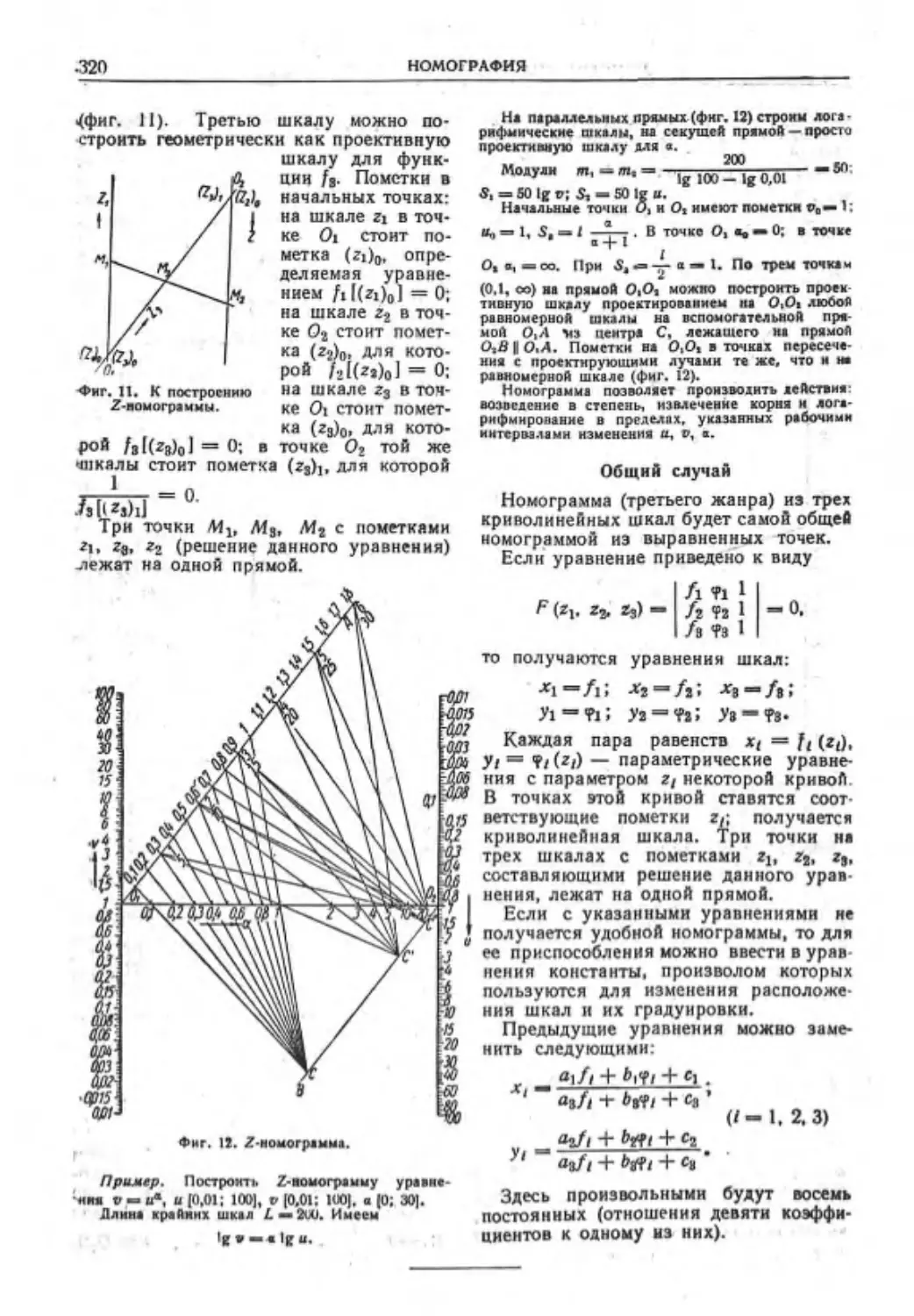
НоМ'Лраммы нт ьыр.тннсиных точек . 318
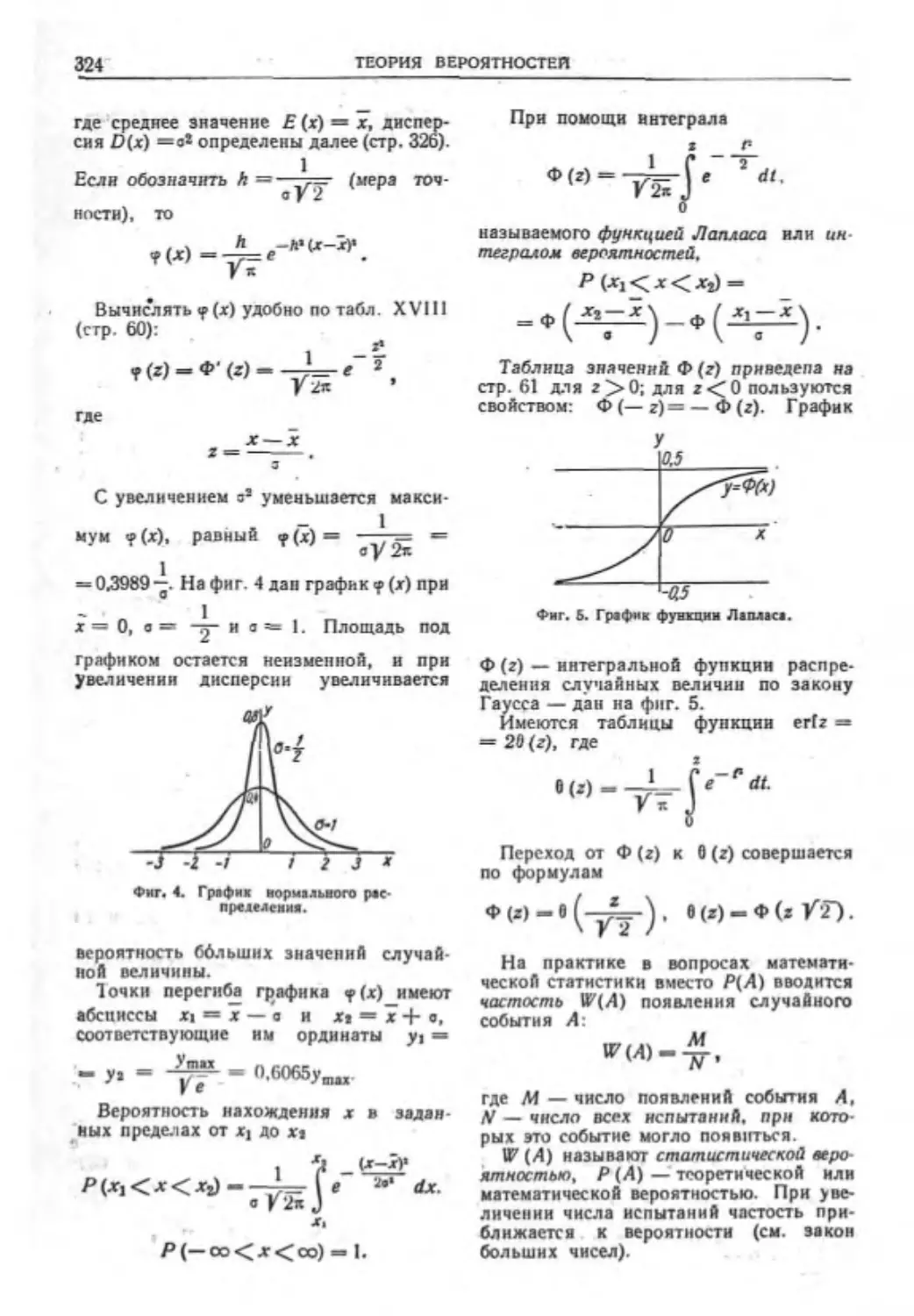
Глака XVI. ТЕОРИЯ ВЕРОЯТНОСТЕЙ С
ПРИЛОЖЕНИЯМИ К МАТЕМАТИЧЕ-
СКОЙ СТАТИСТИКЕ (канл. фна.-мат.
«>ук В. С. Люкшик\.................321
Основные noun ни н теоремы....... 321
Употребительные законы распределения 321
Вероятностные ................... 326
Закон большиз чисел и предельная тео-
рема .... . . . . . . 328
Теория ошибок н способ наименьших кпа-
дратов ... ь ................ . 330'
Способ наименьших квадратов.........332
Глава XVII. МАТЕМАТИЧЕСКИЕ ПРИ
БОРЫ (канл. фки.-иат. наук В. С. Jliun-
iuuhi ............................. . ЗЗв
Логарифмическая линейка............. . 336
Арифмометр ... ' ‘. 340
Планиметры и интеграторы...........342
Аттлтматическза вычислительная машина
с пропорциональным рычагом ... 343
Полуаптоматмческая вычислительная ма-
шина Точмаш, мотель КЕВ......... 347
Вычислительные машины ВК ...... . 348
ЛИТЕРАТУРА И ИСТОЧНИКИ К РАЗ-
ДЕЛУ .МАТЕМАТИКА-...................34»
МЕХАНИКА
Глава XVUI. ТЕОРЕТИЧЕСКАЯ МЕХА-
НИКА |л-р техн, наук А. Н. Обморшг.) 352
Статика .............................353
Геометрическая статика......352
Центр тяжести ............... . . 359
Графостатика .............. Зо4
Аналитическая статика ........ 308
СОДЕРЖАНИЕ
V
Кинематика. ........... 369
Кинематика точки . . .........369
Относительное движение точки ..... 374
Кинематика твердого тела.. . 375
Общий случай авижениа твердого тела . . 381
Сложение скоростей ори сложном движе-
нии твердого тела ............381
Динамика .................... 382
Механические единицы.......... 382
Динамика точки ............. 383
Динамика системы 388
. Моменты инерции ............ 392
Динамика твердого тела ......... 396
Динамика тела переменной массы .... 399
Удар.................... ...02
ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
Глава XIX. ОБЩАЯ ЧАСТЬ (пил. техн.
Маук Н. я. Нибгрг} ....... 407
Ст уктура и классификации механиз-
мов . ................... ... 407
Кинематика плоских механизмов ..... 413
Кинетостатика плоских механизмов ... 418
Д шамика механизмов и машин ...... 424
g g = з 62 £
Потерн механизмах и коэффициент по-
лезного дейстпив...........
Трение в механизмах ............
Износ деталей в мехаикзмлт .......
Основы теории точности механизмов ...
Проектирование плоских механизмов. . .
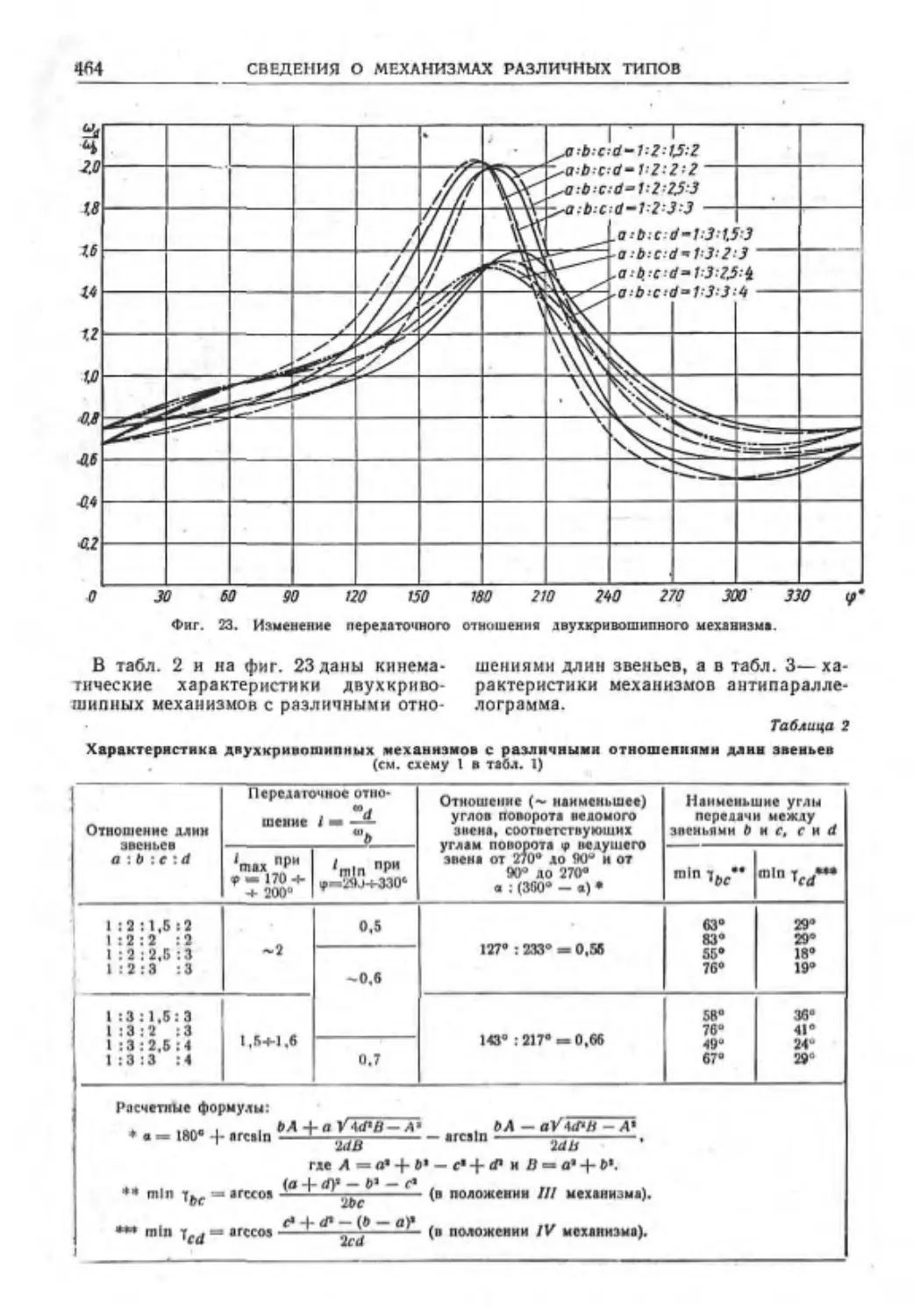
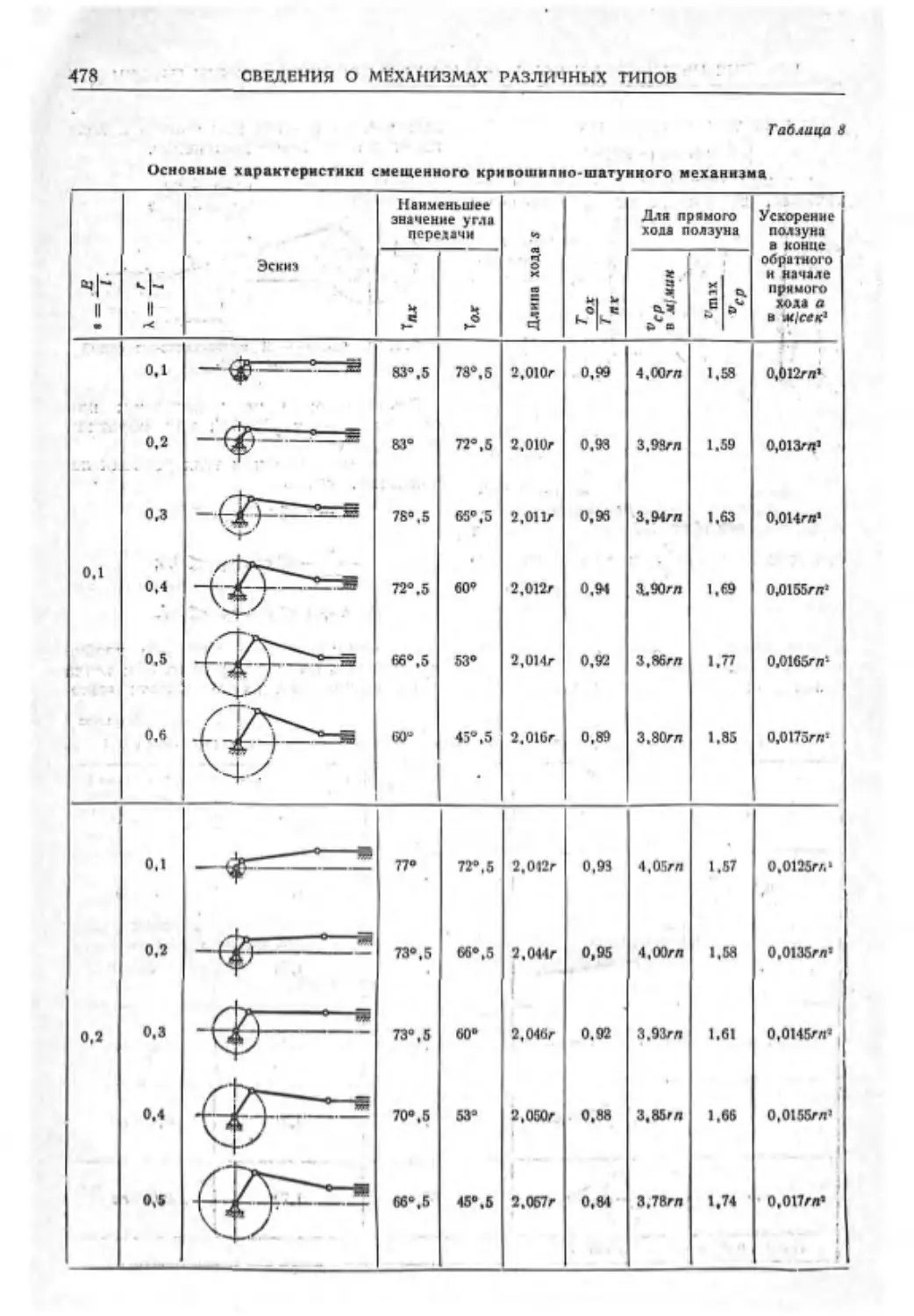
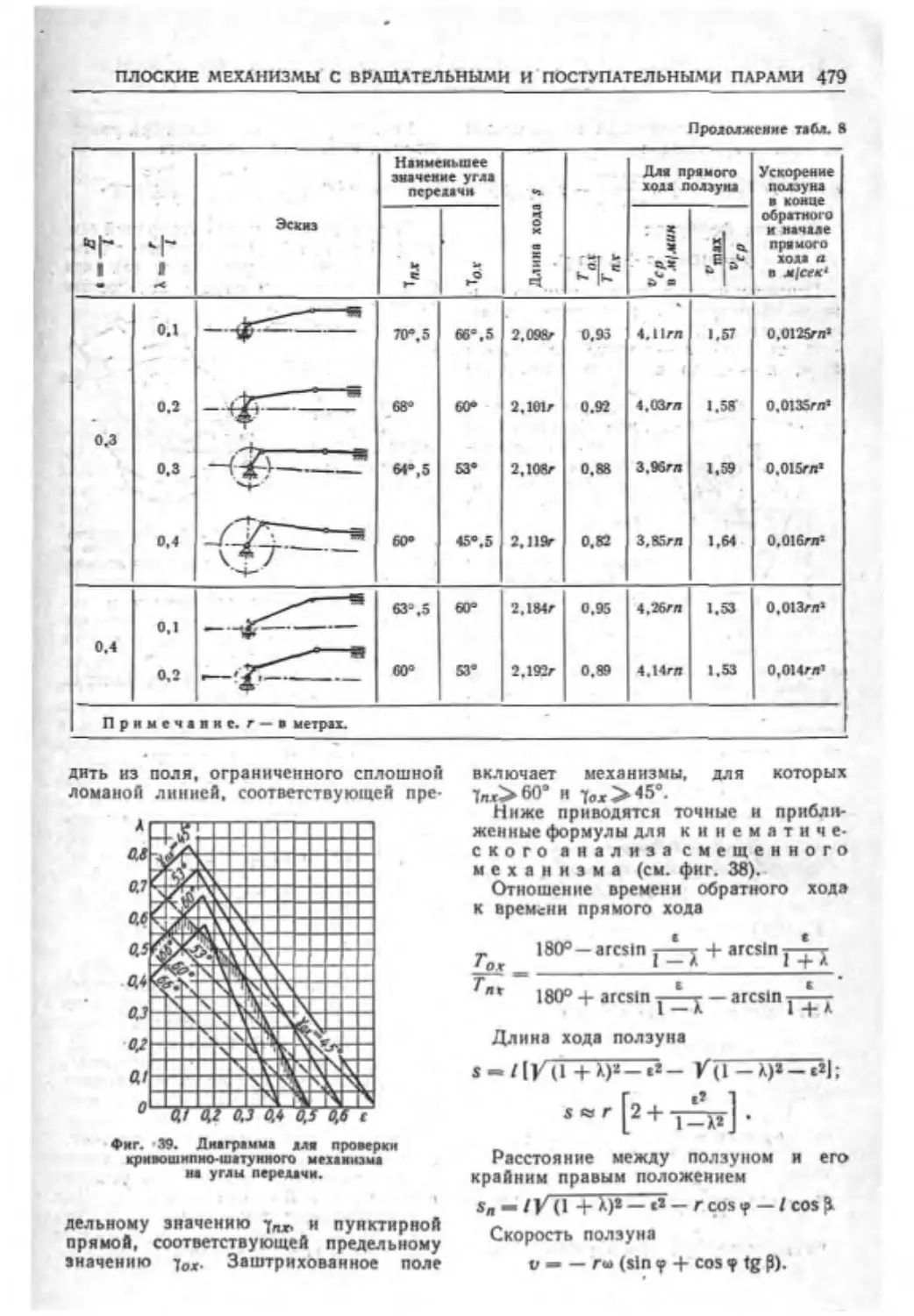
Слала XX. СВЕДЕНИЯ О МЕХАНИЗМАХ
РАЗЛИЧНЫХ ТИПОВ (канд. техн, наук
Н. Я- НиберЦ....................
Механизмы с одними поступательными па-
рами ..................
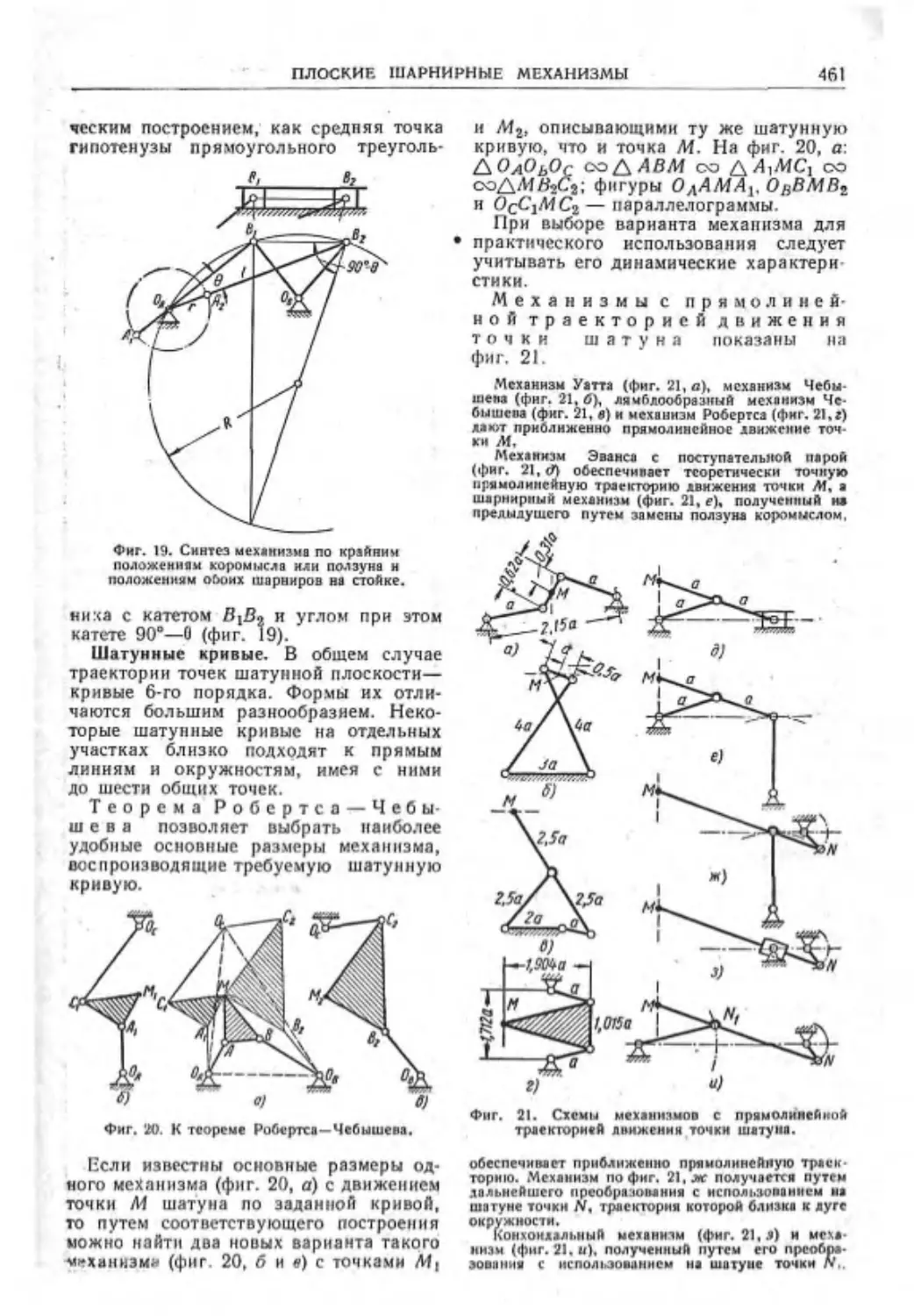
Плоские шарнирные механизмы..
Плоские механизмы с врашательныйи и
поступательными парами........
Винтовые механизмы с соосным располо-
жением кинематических пар •
Зубчатые механизмы ..*•••••*..
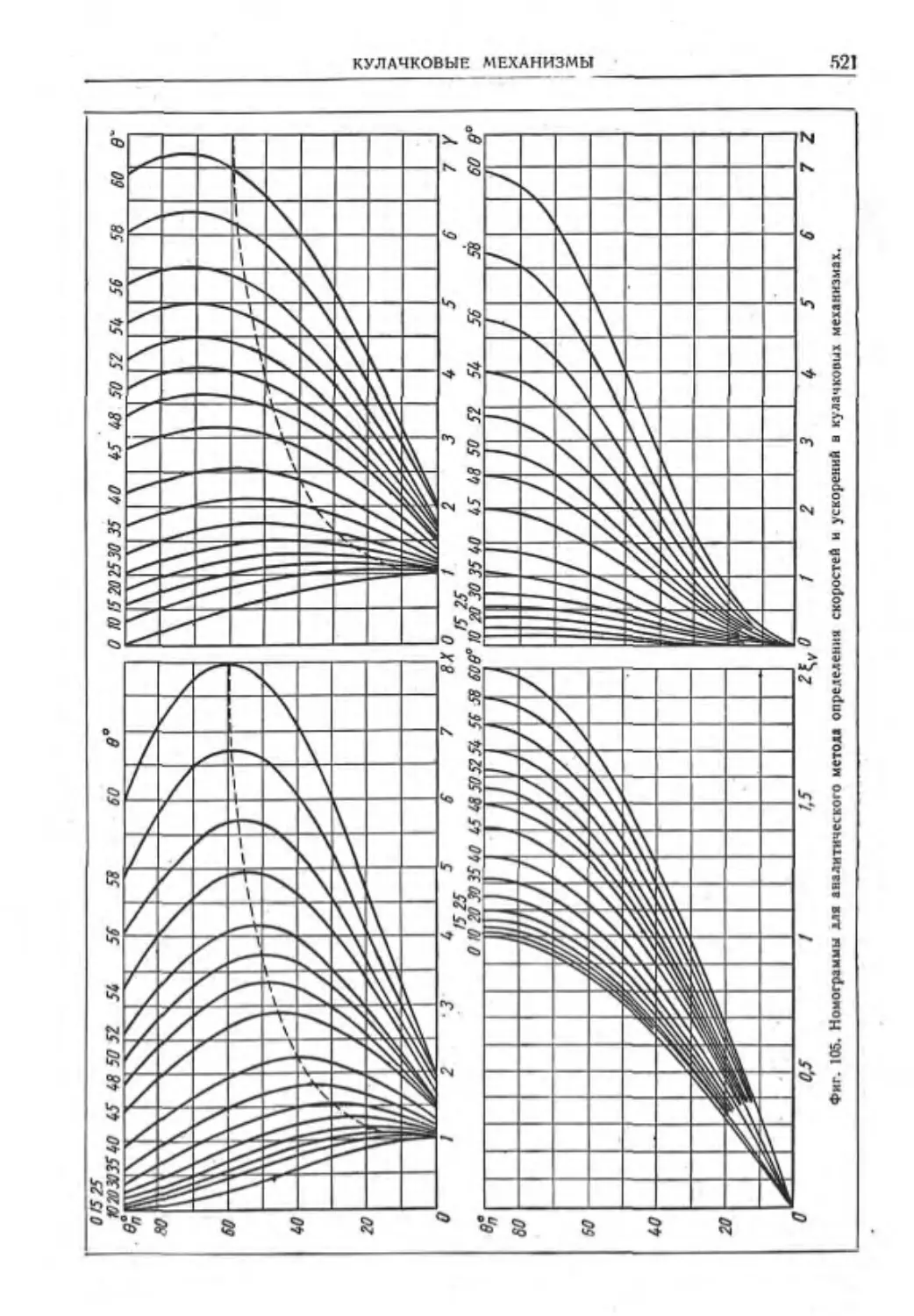
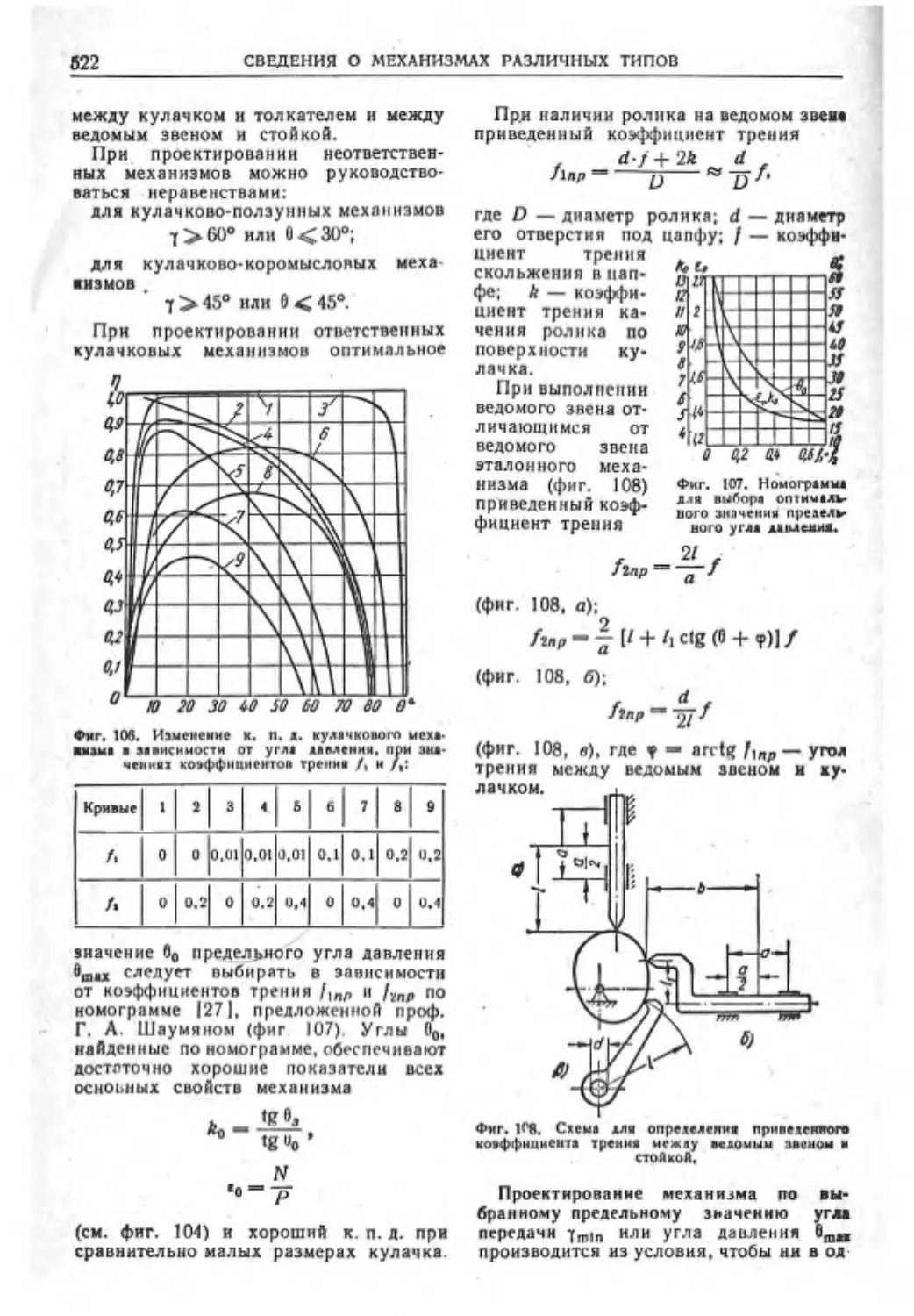
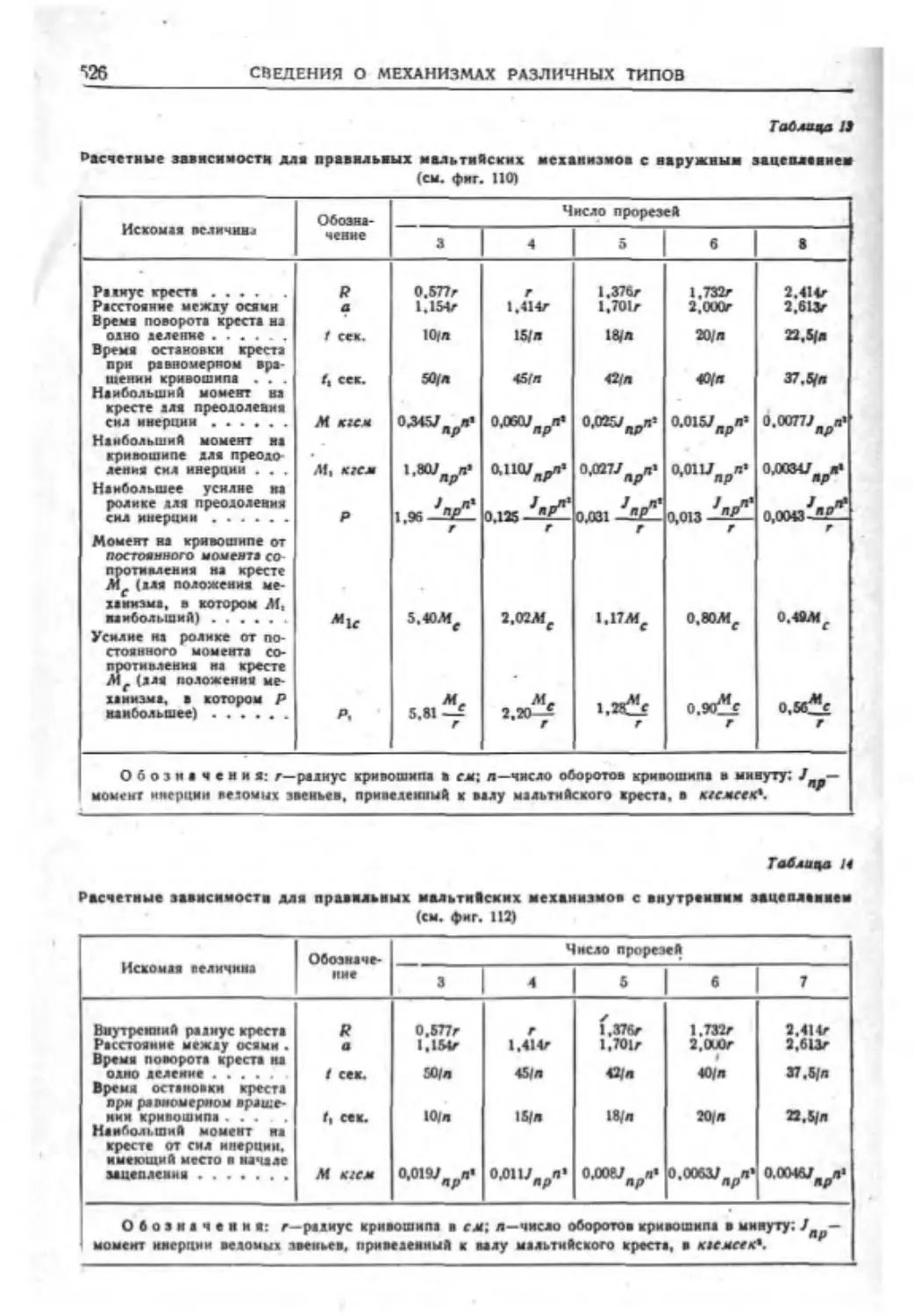
Кулачковые механизмы......••
Прочие механизмы ............
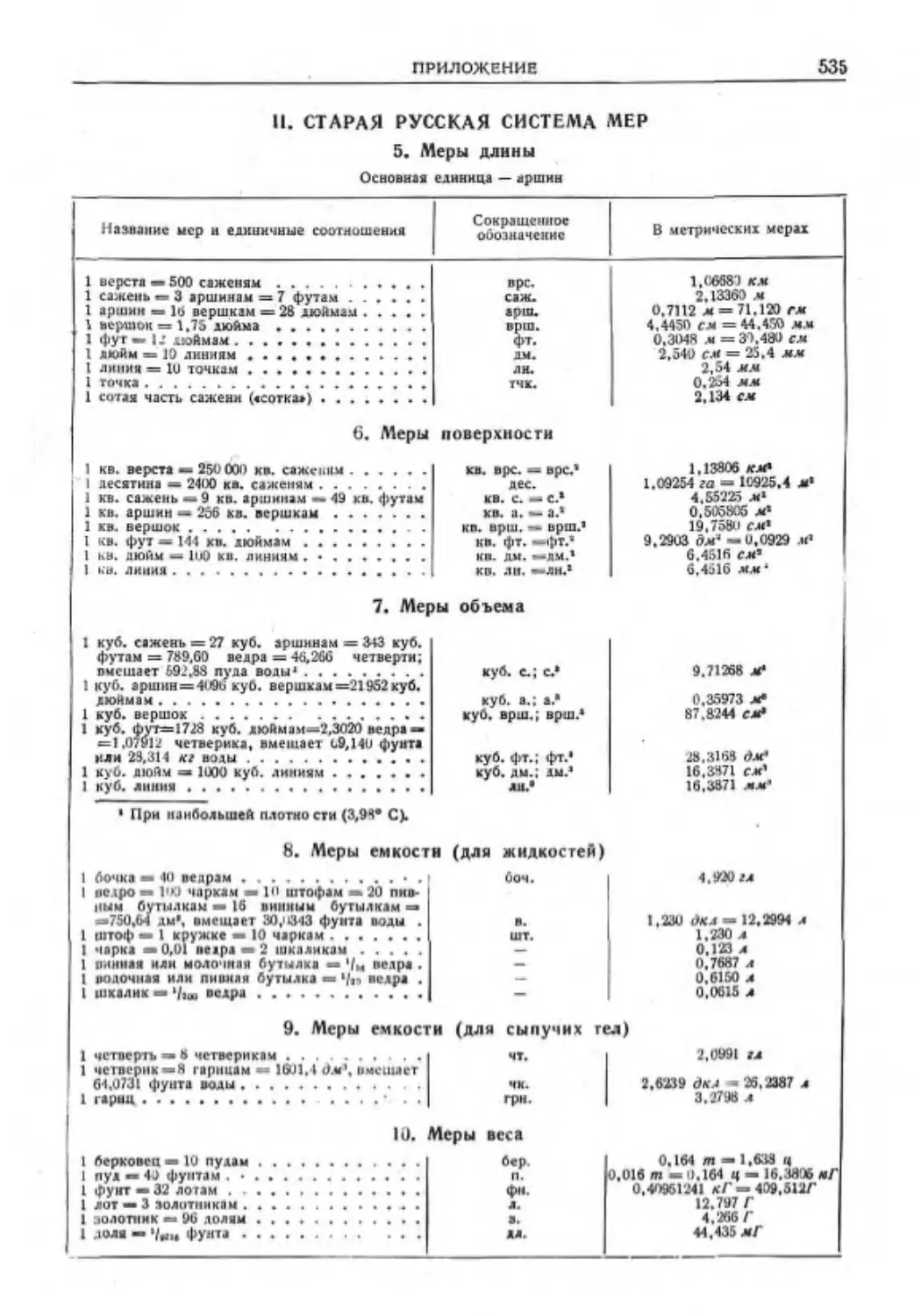
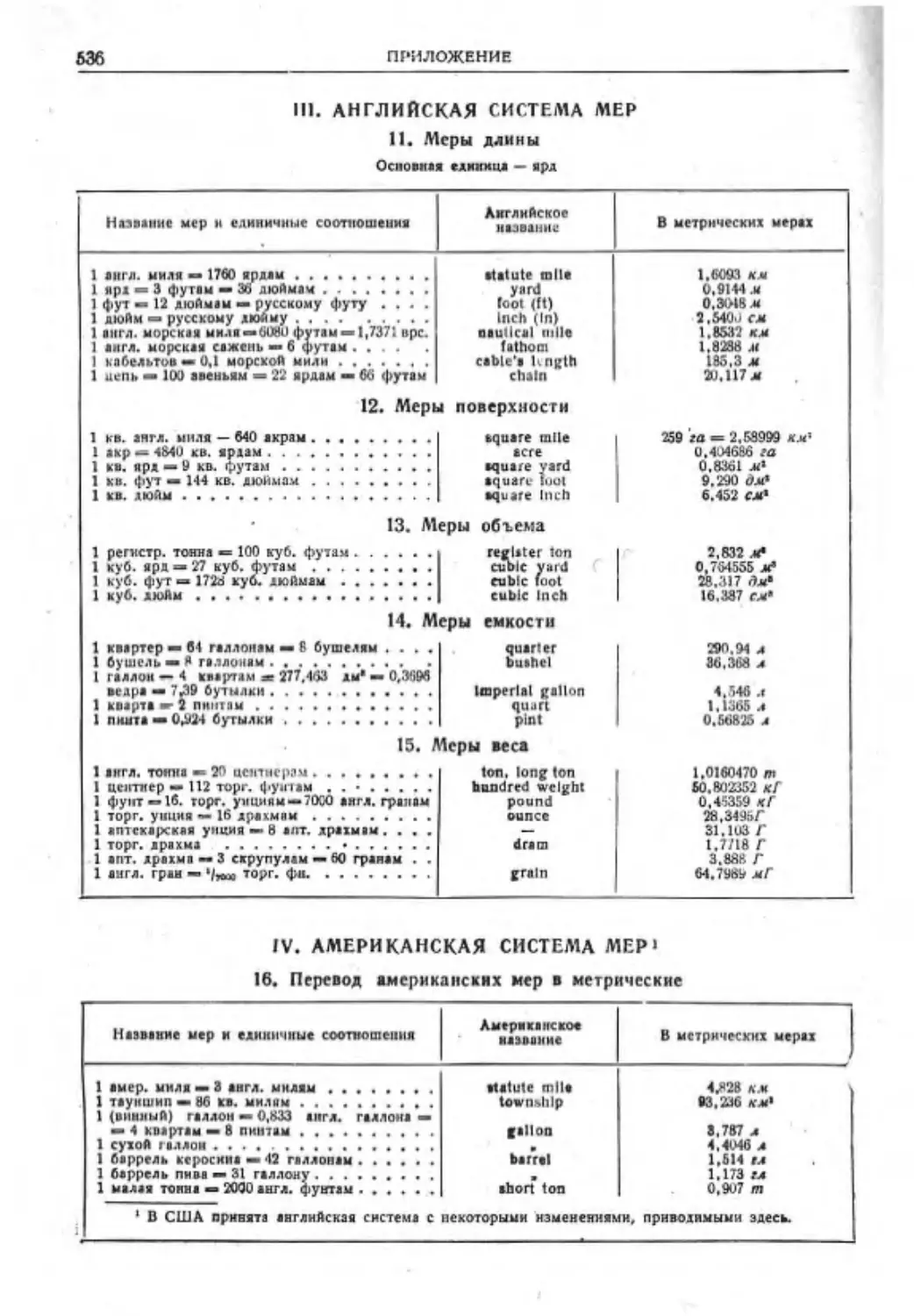
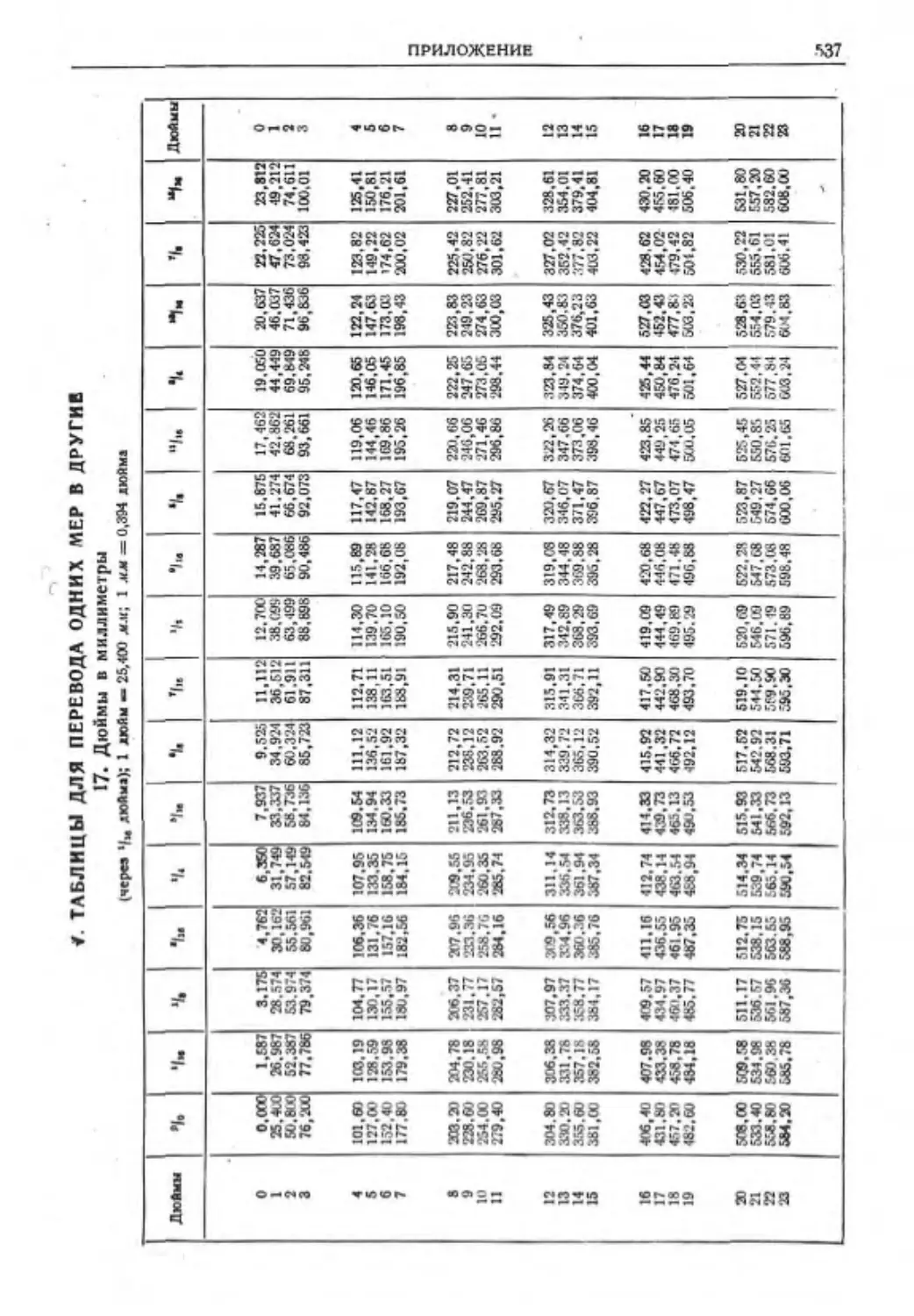
Прилажена,. ПЕРЫ И ЕДИНИЦЫ......
ПРЕДМЕТНЫЙ АЛФАВИТНЫЙ УКАЗА-
ТЕЛЬ (С. Л. XaCbMUMnuUJ ....... 548
ОТ ИЗДАТЕЛЬСТВА
При подготовке второго издания .Справочника машиностроителя*
были по возможности учтены замечания и предложения читателей по
первому изданию. Весь материал был внимательно проверен, ряд глав
подвергнут более или менее значительной переработке, некоторые главы
написаны заново, к другим сделаны существенные добавления.
Материалы, мало или редко используемые в практике работы машино-
строителя. конструктора и технолога, в новое издание справочника не
включены.
Устранены замеченные опечатки и ошибки в тексте и фигурах;
неясные или неудачно исполненные фигуры заменены новыми.
В соответствии с пожеланиями многих читателей новое издание
.Справочника машиностроителя* выходит в шести томах, что сделает
более удобным пользование справочником.
В первом томе даны сведения по математике, теоретической механике
и теории машин н механизмов.
Во второй том включены справочные данные по теплотехнике, химии,
оптике, акустике и гидравлике.
Третий том посвящен расчетам на прочность.
В четвертом томе даны сведения по расчету н конструированию
деталей машин.
Пятый том содержит сведения по технологии, необходимые конструк-
торам при проектировании деталей машин.
В шестой том включены данные по машиностроительным материалам.
По всем вопросам, которые возникнут у читателей при пользовании
.Справочником*, просим обращаться в Государственное научно-техни-
ческое издательство .Машгиз* по адресу. Москва. Третьяковский пр., д. 1.
МАТЕМАТИКА
ГЛАВА /
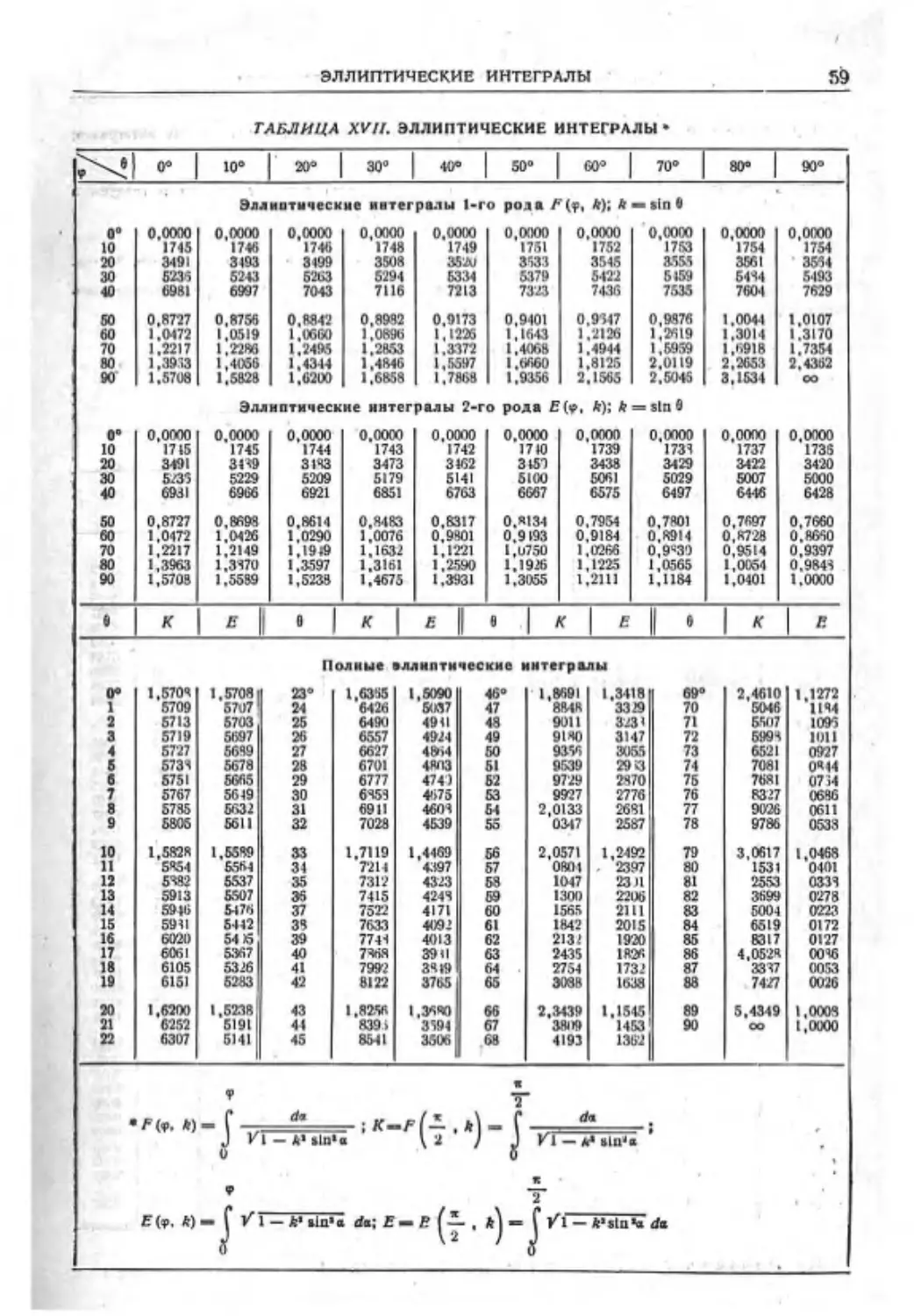
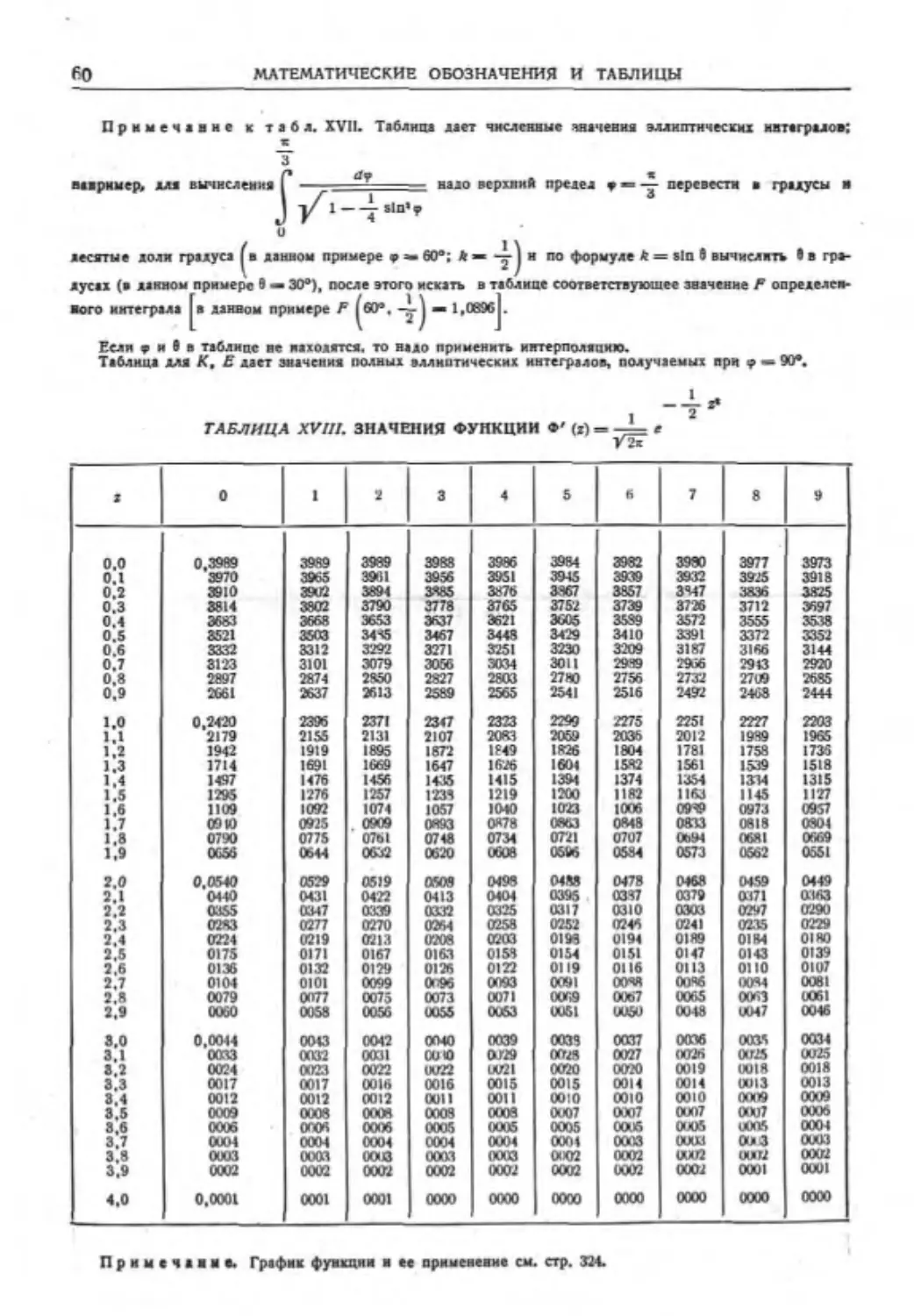
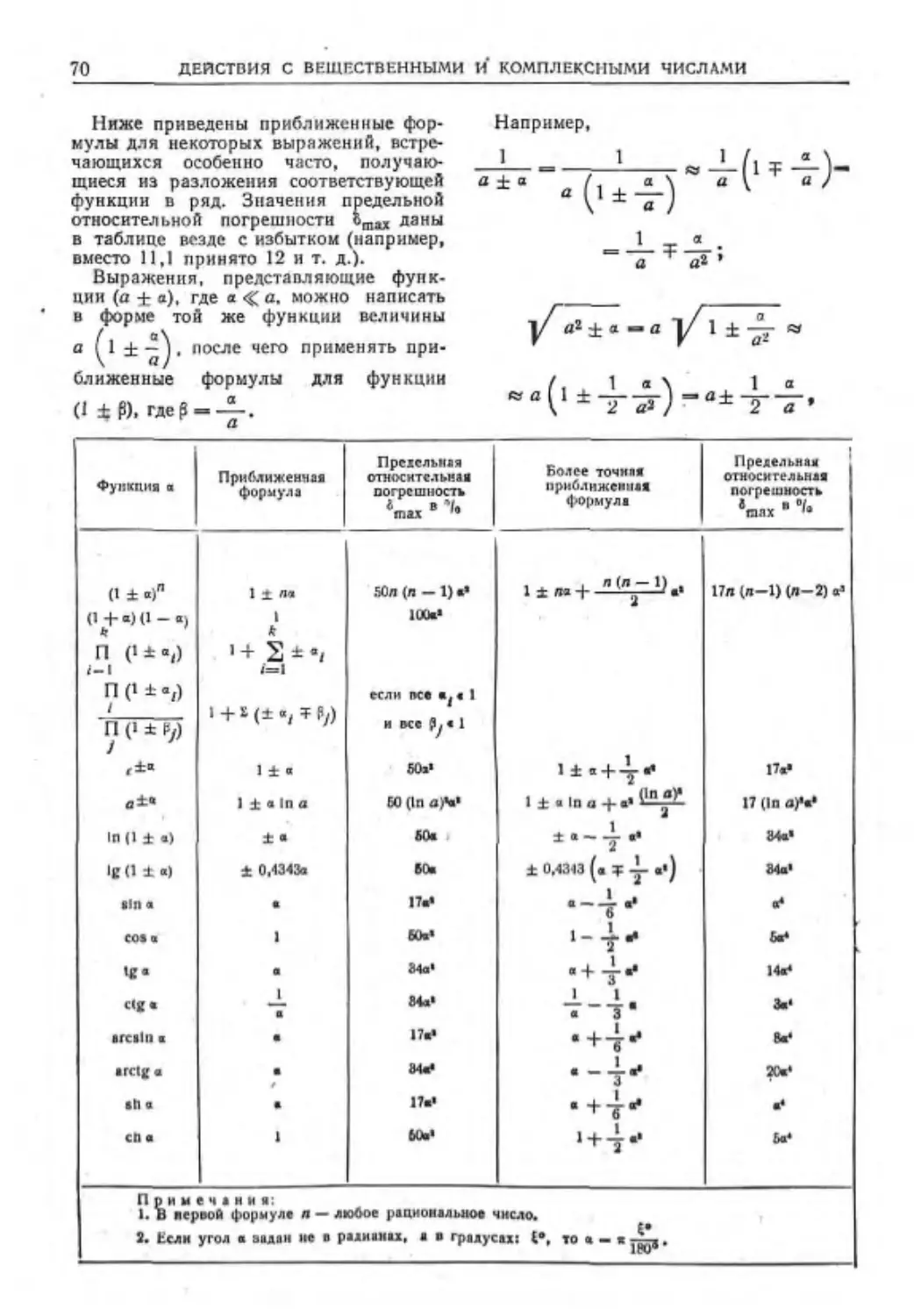
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
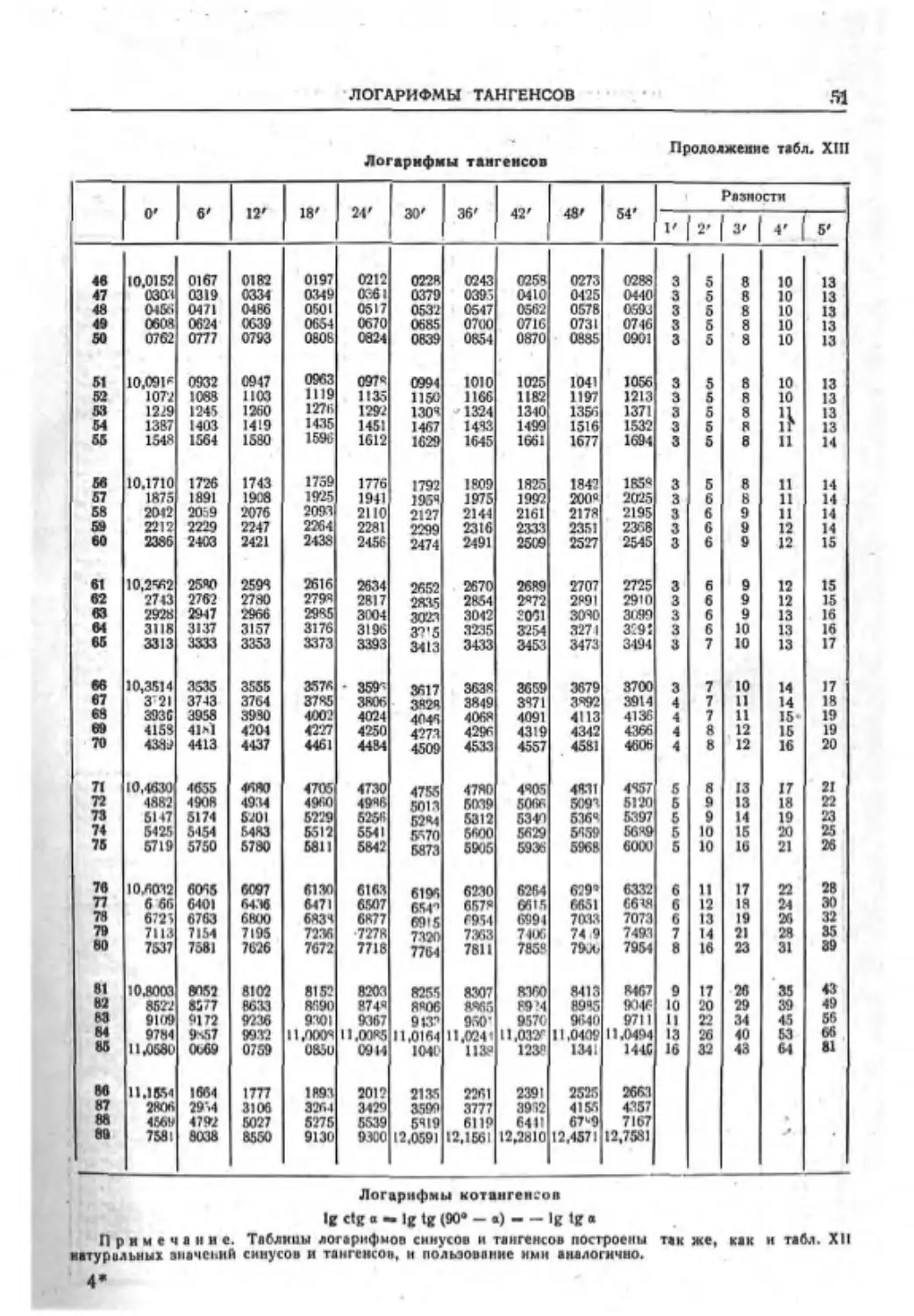
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ
Стандартные
Обозначение соотношений
= равно
s тождественно равно или тожде-
ственно
+ не равно
приближенно равно
< меньше
> больше
< меньше или равно
>больше или равно
< мало сравнительно с (значительно
меньше)
> велико сравнительно с (значительно
больше).
Алгебра
| а | абсолютная величина числа а
4- (плюс) сложение
— (минус) вычитание
• или X умножение. например а-Ь
или а X 6 или ab (знак умножения
часто опускается)
а
: или — деление, например а; b или у
о/0 процент
»/00 промилле (2°/00 — 0,002)
ат а в степени т
У квадратный корень
I квадратный корень из—I; i —
у' корень степени т при т 2
loge логарифм при основании Ь. Если
нет надобности указывать основа*
ние, то пишут log
ig логарифм при основании 10 (обык-
новенный или десятичный логарифм)
Ш логарифм при основании е»
— 2.71828 ... (натуральный лога-
рифм)
().[].{ ) скобки
л) факториал; л! — 1-2*3- • • • л.
1 Том I. 3« к.
Геометрия
х перпендикулярно
| параллельно
# равно и параллельно
~ подобно
АВ — отрезок прямой между точками
А и В. Это же обозначение упо-
требляется для отрезка, которому
приписывается направление от
точки А к точке В
АВ — тот же отрезок, если необходимо
отличить его от произведения АВ
Л треугольник: Д АВС
плоский угол
О или <-> дуга: о АВ, АВ
° градус 1 при обозначении вели-
' минута 1 чины плоского угла или
' секунда J дуги
Если обозначение и (градус). ' (ми-
нута) или * (секунда) относится к числу,
содержащему десятичную дробь, то оно
ставится над запятой. например.
б°5'.27; 8°4'2*,9.
При обозначении величины угла от-
влеченным числом подразумевается, что
вто число есть отношение данного угла
к радиану: радиан есть центральный
угол, длина дуги которого равна ра-
диусу; радиан — — 57“,29578 ...
к — отношение длины окружности к
диаметру.
Т ригонометрическне
и гиперболические функции
sin синус
cos косинус
tg тангенс
котангенс
вес секанс
созес косеканс
arcsln арксинус (у — arcstn х: у есть
дуга, синус которой равен х) (см.
стр. 99)
2
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ Н ТАБЛИЦЫ
arccos арккосинус
arctg арктангенс
arcctg арккотангенс
sh синус гиперболический
ch косинус гиперболический
ih тангенс гиперболический
cth котангенс гиперболический
Arsh ареа-синус гиперболический (см.
стр. 101)
Arch ареа-косннус гиперболический
Arth ареа-тангенс гиперболический
Arcth ареа-котаигенс гиперболический.
Для обозначения степени тригономе-
трической или гиперболической функции
показатель степени ставится при знаке
функции; например. sln2x (синус квадрат
икс) есть (sin х)г; th3 <? (тангенс гипер-
болический куб фи); arctg2х и т. д.
Математический анализ
а. Ь, с. . . . постоянные величины (при-
меняются преимущественно пер-
вые буквы латинского алфавита)
х. у, z, и. .. . переменные величины (при-
меняются преимущественно по-
следние буквы латинского алфа-
вита)
/( ). <р ( ). F ( ). Ф ( ). ... функции
одного или нескольких аргумен-
тов; например f(x), F (х. у, х)
const постоянное
со бесконечность
lim предел
-* стремится к . . . . например
I
х-ь a. lim (1 4- х) * — е
х-ьО
а приращение (греческая прописная
буква дельта)
Ь вариация (греческая строчная буква
дельта)
дифференциал
',v v обозначения
d
последователь-
ных производных от функции
одного переменного, например
f(x).y'.y,v./vU)
Если порядок производной обозна-
чается буквой или арабской цифрой, то
•та буква или цифра ставится в скобки;
например f®(x), /<о,(у)
первая производная функции одного
rfy df
переменного; например
dn
производная п-го порядка (л>1)
функции одного переменного; на-
№v
пример
<*7
dx*
fх' fXX' fxy
df^ df_
Ox ’ ду ’ дхг *
dxdy
V сумма; например
частные проча
полные функ-
ции / несколь-
ких перемен-
ных X, у, t . . .
по соответст-
вующий пере-
менным
V ик = U, 4- и, 4- . . . 4- ил
1=1
f интеграл
i
( определенный интеграл с нижним пре-
а
делом а и верхним пределом b
П произведение; например.
П«* = «!«?. ип.
J
Нестандартные
1 — V — 1 употребляется в злектро-
технике (чтобы не смешивать
с силой тока <)
R (х) или Rex действительная часть ком-
плексного числа х
1(х) пли hnz мнимая часть комплекс-
ного числа х
~х комплексное число, сопряженное с г,
например х — х 4- 1у, г — х — /у
|а] или Е (а) целая часть числа а; на-
пример
£(>0-3; Е (0.07)-(Ц-------------1
равномерно сходится, например
/(х)=£/(х)
ехрх — е*. например вместо в~‘рал
можно написать схр(—J Pdx)
sgn х обозначает функцию
{1, если х>0
0, если х — 0
— 1, если х<0
х-иа означает, что
О (? (х)) - /(х) при
-у-0 при х-> а
Шх)) —/(х) при
f (х)
fTx) 0ГРа,,мчеК0 ПРИ а
х-ь а означает, что
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ
3
яП произведение натуральных чисел, не
превосходящих п и одной с ним
четности; например
12!! = 2-4-6-8 -10-12
11U- 1-3*5-7-9-11
( я ) « С" — я(я—1),..(я —гя + 1)
число сочетаний из п элементов
по т
Arcsin. Arccos, Arctg. Arccig обозна-
чают многозначные обратные
тригонометрические функции (см.
стр. 99)
D знак производной; например Dy = у'
Dn знак производной я-го порядка
(п + 1); например D"y у1"*
*, . . . последовательные произ-
водные функции по переменному t;
например
и г. д.
d. <fl. dn дифференциал 1-го, 2-го. л-го
порядка
djf. dv и т. д. частный дифференциал;
например d^z
»
| знак двойной подстановки; например
а
Ь
| F(x)-F(b)-F(a)
а
С ( интеграл, распространенный на
площадь S, на объем V
f J двойной интеграл, распространенный
на область 5
J |J тройной интеграл, распространен-
ный па область V
JJ • • • j многократный интеграл
Г. f интеграл, взятый по кривой АВ.
по кривой L
ф интеграл, взятый по замкнутому кон-
I
ТУРУ L
>- следует за; например Ь>- л—элемент
Ь следует за элементом а
ч предшествует; например а -< б—эле-
мент а предшествует элементу b
£ принадлежит; например a G А —
элемент а принадлежит множеству А
о содержит; например D=> 8—область
D содержит область 8
с: влечет за собой; например А сВ—со
бытие А влечет за собой событие /<
Л совмещение событий; А п В чн
тается: А п В
U объединение событий; AUB чи
тается: А или В. *
Векторное исчисление
Векторы обозначаются латинскими
буквами жирного шрифта как пропне
нымн. так и строчными, а также латин
скнмн буквами нежирного шрифта с чер
точкой или со стрелкой над ними, напри
мер а. А. а. «- А. а. ы. а, А
АВ вектор. начало которого
в точке А. конец в точке В
до, а°, шо единичные векторы соот
ветственно того же напра
влення. что и векторы А
а. ш
i. J. k единичные векторы осей
прямоугольной системы
координат
«г- единичные векторы осей
любой прямолинейной си
стемы координат
п единичный вектор нормали
к поверхности или главной
нормали кривой
= | и]. | а | н я. | ш | = ш длина (абсо-
лютное значение) вектора
4 д 1 равенство, сложение (сумма).
д j вычитание (разность) векторов
mA. xi произведение скаляра на вектор
АВ скалярное произведение двух
векторов (точка между со
множителями не допу
скается)
А2 скалярное произведение век
тора на самого себя
А X В или [Ав] векторное произпе
дение двух векторов (точка между
сомножителями не допускается}
АВС=А |ВС] — векторно-скалярное про
изведенне
1|АВ] С] или (А X в) X С — двойное
векторное произведение.
Для обозначения порядка действий
применяются дугообразные скобки, на-
пример (А -р В) С — АС + ВС; (АВ) С,
К А - В) С|
4
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
Скалярный множитель при векторе
может быть отделен от него точкой,
например (АВ) С = АВ-С.
А/ составляющая (компонен-
та) вектора А по напра-
влению I
Ах. Лу, Аг составляющие вектора А
по осям х, у, z прямо-
угольной системы коор-
динат; А — Ах + Л у + Аг
Л], Аг, Л j составляющие вектора А
по осям X]. х2. х8 любой
системы координат: А =
•“ Л1 4- Л» 4- А%
Ai проекция (скаляр) век-
тора А по направлению I
Ах. Ау, Аг проекции вектора А по
осям х, у, 2 прямоуголь-
ной системы координат;
Axi — Ах и т. д.
В особых случаях проекции вектора
по осям координат могут обозначаться
тремя различными латинскими или гре-
ческими буквами нежирного шрифта.
Например, г = xi 4- yj 4- zk
V дифференциальный оператор
(d д д ) . . .
37’ 5Г’ •37р1,абла>
grad градиент скалярной фун-
кции (= v <f)
div Л расхождение (дивергенция)
вектора А (= vA)
rot Л вихрь (ротор) вектора А
(= [V Л] или v X Л)
а или V2 оператор Лапласа, дей-
ствующий на скалярное или
векторное поле
-j— я 1° v % производная скаляра по
данному направлению I
дА
производная вектора по данному
направлению /
Grad ч>, Div Л, Rot А поверхностные
(на поверхностях разрыва) гра-
диент, дивергенция, ротор.
Для ограничения действия оператора
V применяются дугообразные скобки.
Например, в выражении (\JA)B опе-
ратор V действует только на Л.
Теория ошибок (погрешностей)
измерения (сгандартные)
Общая часть
X истинное значение измеряемой ве-
личины
х, у, г, и. t, ... искомые значения
измеряемых величин
л число произведенных измерений
(где 2. 3............л) резуль-
таты отдельных измерений одной и
той же величины
pt (где I — 1. 2, 3. ... п) веса изме-
ренных значений величины
4i = —— (i — 1, 2, 3. . . . л) обратные
веса измеренных значений вели-
чины
L среднее арифметическое из равно-
точных измерений
Lo общая арифметическая середина
или среднее взвешенное из нерав-
ноточных измерений
1Л — 6 + 4 + • • • +
|я&] — a1bl ч- агЬг 4-
+ - - . + а„Ьл
(а&р] — 4-
+ а^грг+ ...+
+ «пЬпРп
I Р I “ Pi Рг
4- ...4-^
Р„
Л, ( = — X) (где I - 1. 2, 3.....л) —
случайная ошибка (погреш-
ность) измерения (случайное
отклонение от истинного зна-
чения)
О систематическая ошибка (по-
грешность) измерения
( — h — L) (где I — I. 2. 3. ... л) —
отклонение отдельного изме-
рения от среднего арифмети-
ческого
8 ( —. П А 11 j СрСдНЯЯ арифметическая
\ п /
ошибка ряда измерений
или в
средняя квадра-
т
тическая ошибка ряда изме-
рений
а111П предельная ошибка или наиболь-
шая возможная ошибка ряда
измерений
f ( — 0,6745м) вероятная ошибка рядя
измерений
(м \
— —7= I — средняя квадратн-
Ул/
ческая ошибка арифметиче-
ской середины (результатора)
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ
S
средняя квадратиче-
ская ошибка единицы веса
d случайная ошибка разности двойных
измерений.
Способ наименьших
квадратов
л,. bt. С/, dh ... коэффициенты при
неизвестных в уравнениях ошибок
или в условных уравнениях.
I свободный член в уравнениях оши-
бок и в условных уравнениях
U7 невязка в условных уравнениях
(1). (2). (3), (4), . . . поправки к изме-
ренным величинам (арабские
цифры в круглых скобках)
k коррелята
( — а, + b, + с, + ... + /|) суммы
коэффициентов н свободных чле-
нов уравнений ошибок.
Латинский алфавит
Греческий алфавит
Аа — а
ВЬ —бэ
Сс— цэ
Dd — дэ
Ее — е
Ff — эф
Gg — ге (же)
Hh — ха (аш)
II —и
JJ — йот (жи)
Кк — ка
L!— эль
Мгп — эм
Nn— эн
Оо — о
Рр — пэ
Qq—ку
Rr— эр
Ss — эс
Tt —тэ
Uu — у
Vv — вэ
Ww —дубль-ве
Хх — икс
Yy — игрек
Zz — зет
Аз — альфа
ВЗ — бэта
Гу — гамма
Д?> —дельта
Ег — эпсилон
ZC — дзэта
Нт) — эта
6М — тэта
it—йота
Кх — каппа
АХ — лямбда
Мр — ми
N-»— ни
— кси
Оо — омикрон
Пк — пи
В? — ро
Г<т — сигма
14 — тау
Го — ипсилон
Ф^> — фи
Ху—хи
4‘ф — пси
Q« — омс< а
в
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
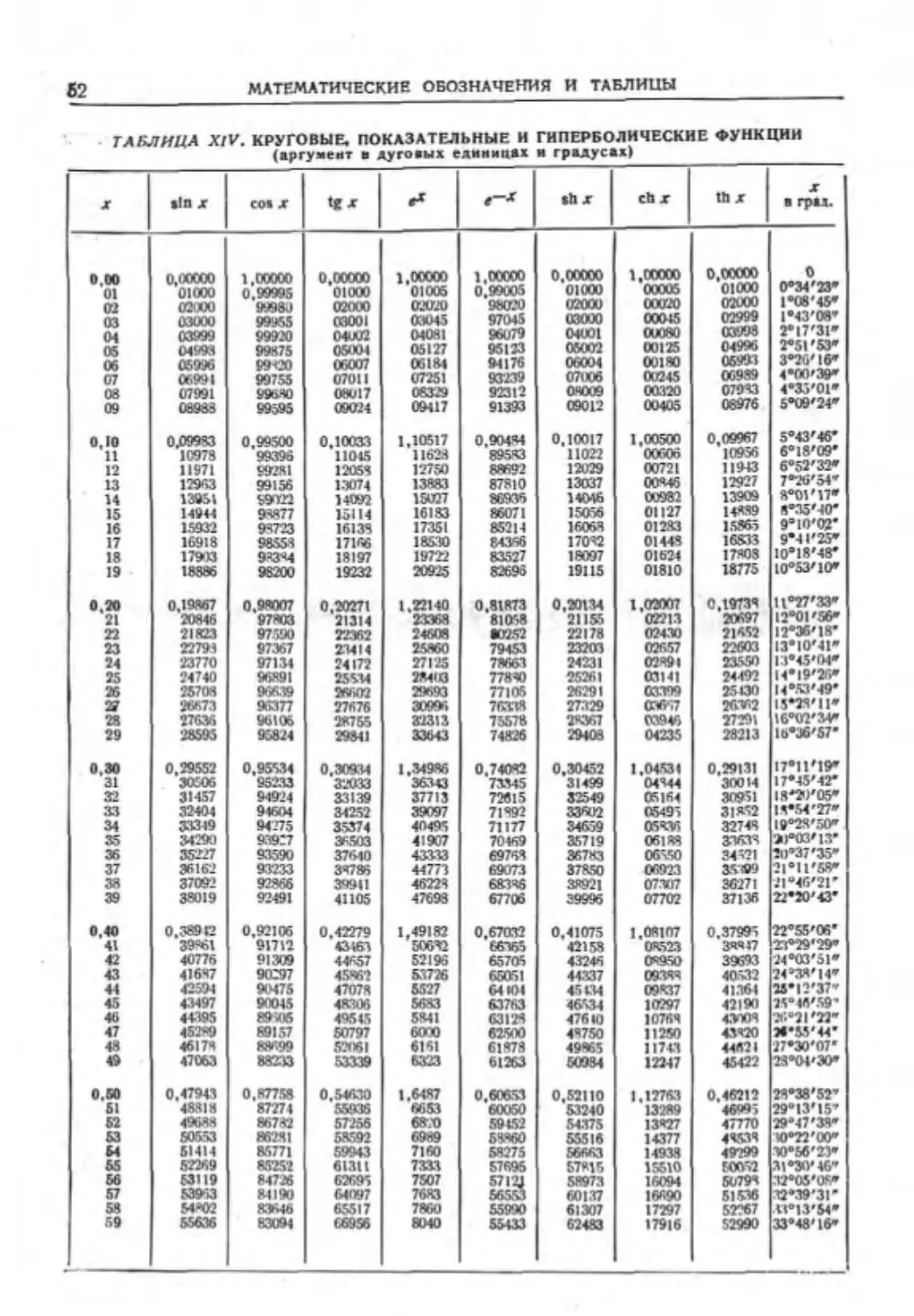
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
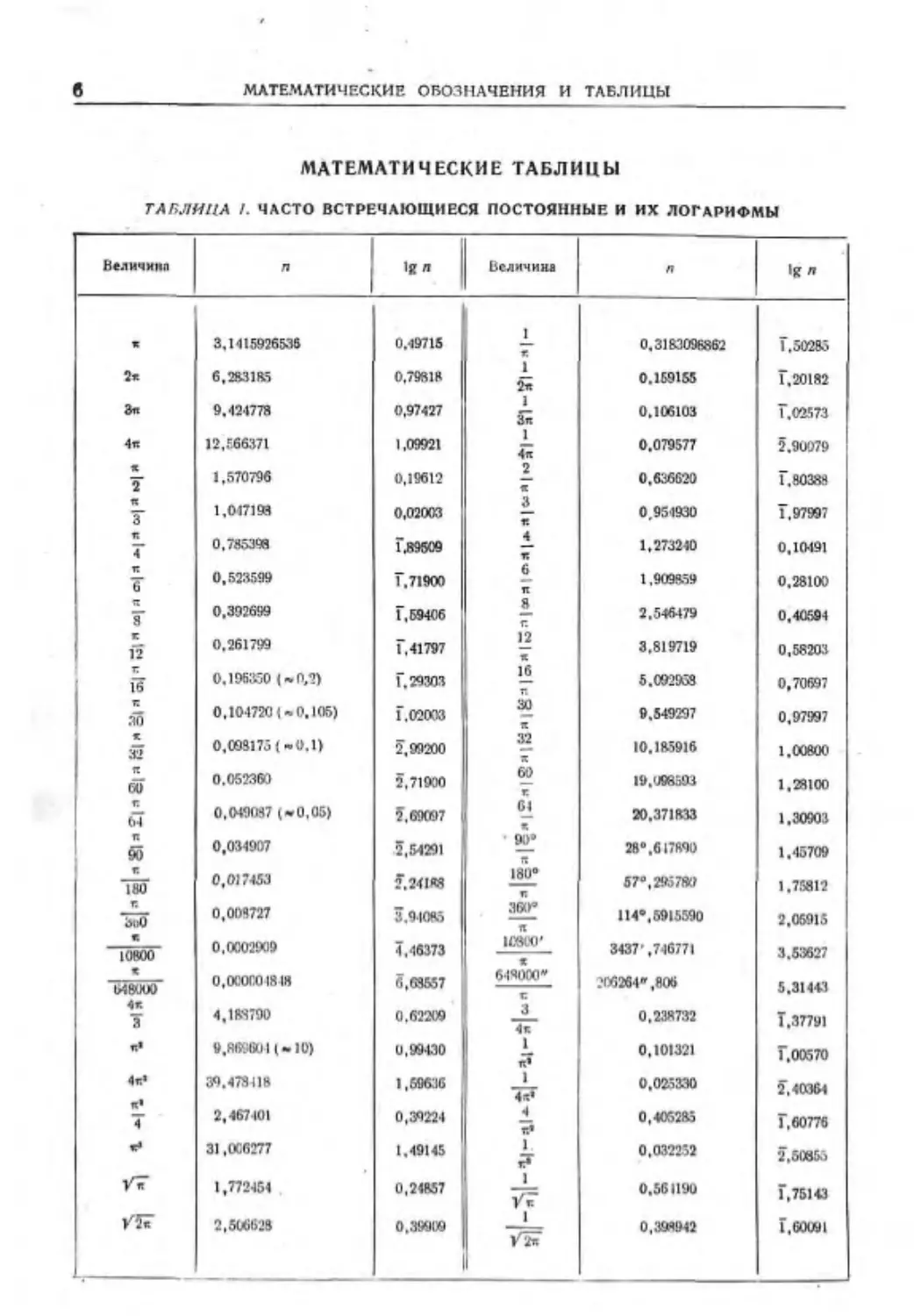
ТАБЛИЦА I. ЧАСТО ВСТРЕЧАЮЩИЕСЯ ПОСТОЯННЫЕ И ИХ ЛОГАРИФМЫ
Величина л Iff л Величина п >К "
К 3,1415926538 0.49715 £ г 0.3183098862 Г.50285
2» 6,283185 0,79818 1 Ъ* 0.159155 Г.20182
а» 9.424778 0,97427 1 & 0.106103 Г.02573
4я 12,566371 1,09921 1 4я 0.079577 2.90079
« т 1,570796 0,19612 2_ « 0,636620 Г.90388
я т 1,047198 0,02003 3 0,954930 Т.97997
к Г 0.785398 Г.В95М £ к 1,273240 0,10491
к (Г 0,523599 1,71900 6 я 1,909859 0,28100
я s' 0,392699 Г, 59406 £ 2,546479 0,40594
к 12 0.261799 Г, 41797 12 « 3,819719 0,58203
15 0.196350 (-0Л) Г. 29303 i_6 я 5.092968 0,70697
.40 0,104720 (-0,105) Г,02033 30 к 9,549297 0,97997
0,008175 (-0.1) 2,99200 .32 10.185916 1,00600
п 60 0.052360 2,71900 60 ш.иовзоз 1,28100
г. м 0,049097 (-0,05) ?, 69097 ? 20,371833 1,30903
п §0 0,034907 2,54291 28°.617880 1,45709
« Тео 0,017453 2.24188 180° 57°, 295760 1,75812
0,008727 3,94085 зесг я 114°,5915580 2,06915
« 0,0002909 0,000601848 4,46373 6,69557 icetti* 3437 ,746771 ? 171264".806 3.53627
иьи < ж 64*000*
мвооо с 5,31443
4* 3 4,188790 0,62209 3 0,238732 Т.37791
«• 9.869601 (-10) 0,99430 4 0,101321 Г,00670
4 т:’ «• 39,473418 1,59636 1 4«* 0,025330 2.40364
2,467401 0,39224 «• 0,40521» Г,60776
«• 31,006277 1,49145 1 0,032252 2,60в5.>
1,772454 0,24857 1 уг 0,561190 Г,75143
/5Т 2,506628 0,39909 __1_ 1 0,398942 1,60091
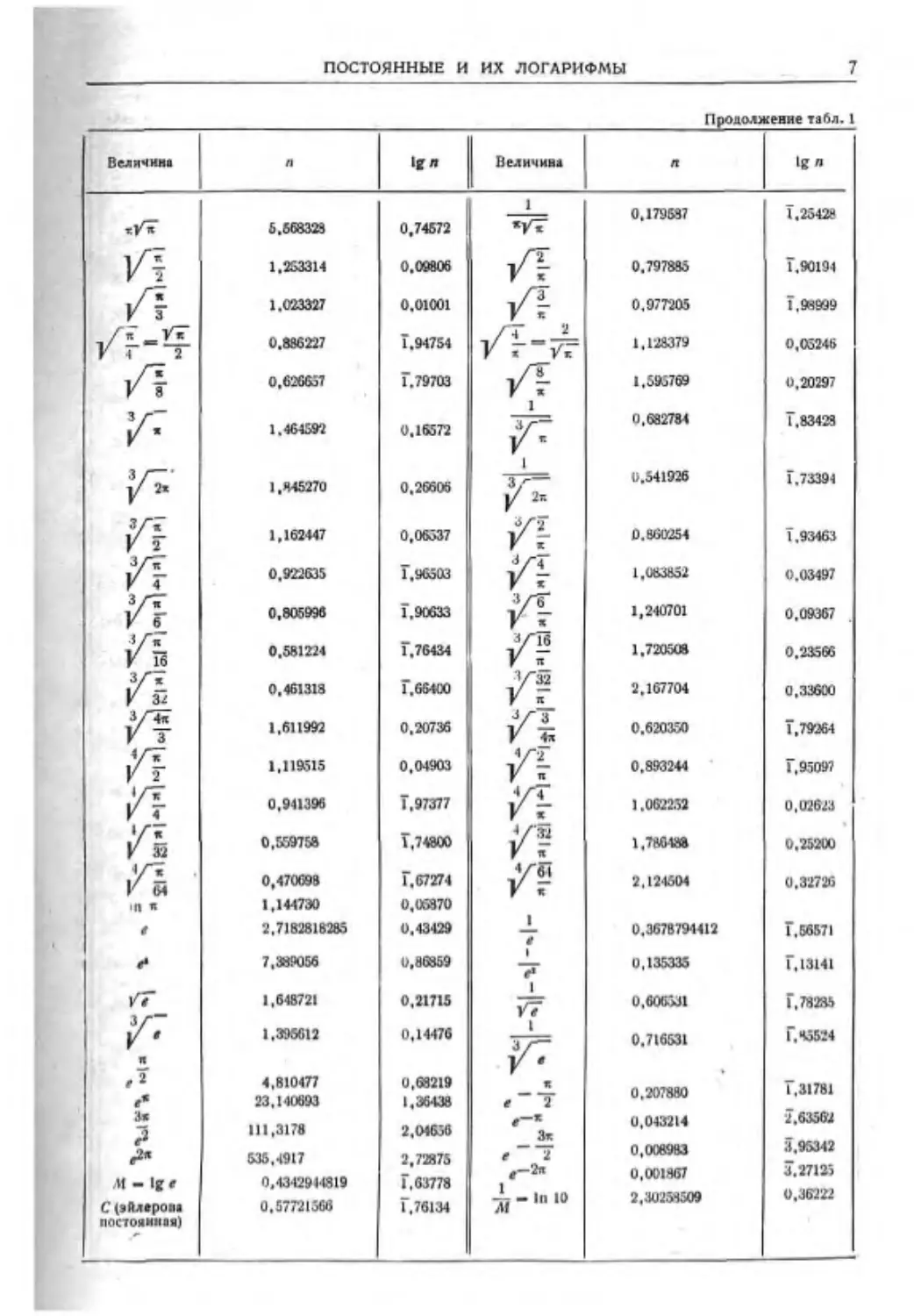
ПОСТОЯННЫЕ И ИХ ЛОГАРИФМЫ
7
Продолжение табл. 1
Величина Л 1g л Величина п 1g п
1 0,179587 1,25428
5.668323 0,74572 жу «
/т 1,253314 0,09806 /т 0,797885 Г.90194
\ з 1.023327 0.01001 у/Т 0,977205 1,98999
/£_ у«~ V 4 3 0.886227 1,94754 /Г -2. V а “Ук 1,128379 0,05246
0.626657 Г.79703 y/L 1,595769 0,20297
3/-” 1 3/— 0,682784 Г,83428
* 1.46459'2 0.16572
3 / 1/ 2» 1 0.541926
1,445270 0,26606 ЗГ— 1/ 2к 1.73391
3/Т 1,162447 0,06337 г 0.860254 1,93463
1 2
0,922635 1,96303 1,083852 0.03497
V 4
з/V V б 0,805996 Г.90633 F? 1,240701 0,09367
'г* V 16 0.581224 1,76434 VTe V я 1,720508 0.23566
з/7 V з2 0.461318 Г.654С0 )У- 2,167704 0,33600
У5 F 3 1,611992 0.20736 уТ 0.620350 Г.79364
/г F 2 1.119515 0,04903 0,893244 Г,95097
/I V 4 0,941396 Г,97377 </Т 1.062252 0,02623
•/« V за 0,569758 Г,74800 ^/•5 1,766-18» 0,25200
V 64 0,470698 Г.67274 2,124604 0,32726
Ifl я 1,144730 0,06870
г 2,7182818285 0,43429 1 г 0,3678794412 Г.56571
и 7,389056 0,86859 1 “г5" 0,135335 Г, 13141
/7" 1,648721 0,21715 1 vV 0,606331 Г, 78285
1,396612 0,14476 1 0.716531 Г. 85524
я
г» 4,810477 23,140693 0,68219 1,36438 « л“Т 0,207880 Г.31781
За 111,3178 0,043214 2.63562
э 2,04656 За
г* 636,4917 2,72875 f 2 0,008983 3,95342
г—2я 0,001867 3.27125
и - Ig t 0,4342944819 1,63778
С (s Плером постоянная) 0.57721366 Г,76134 „-.□10 2,30258509 0,36222
«
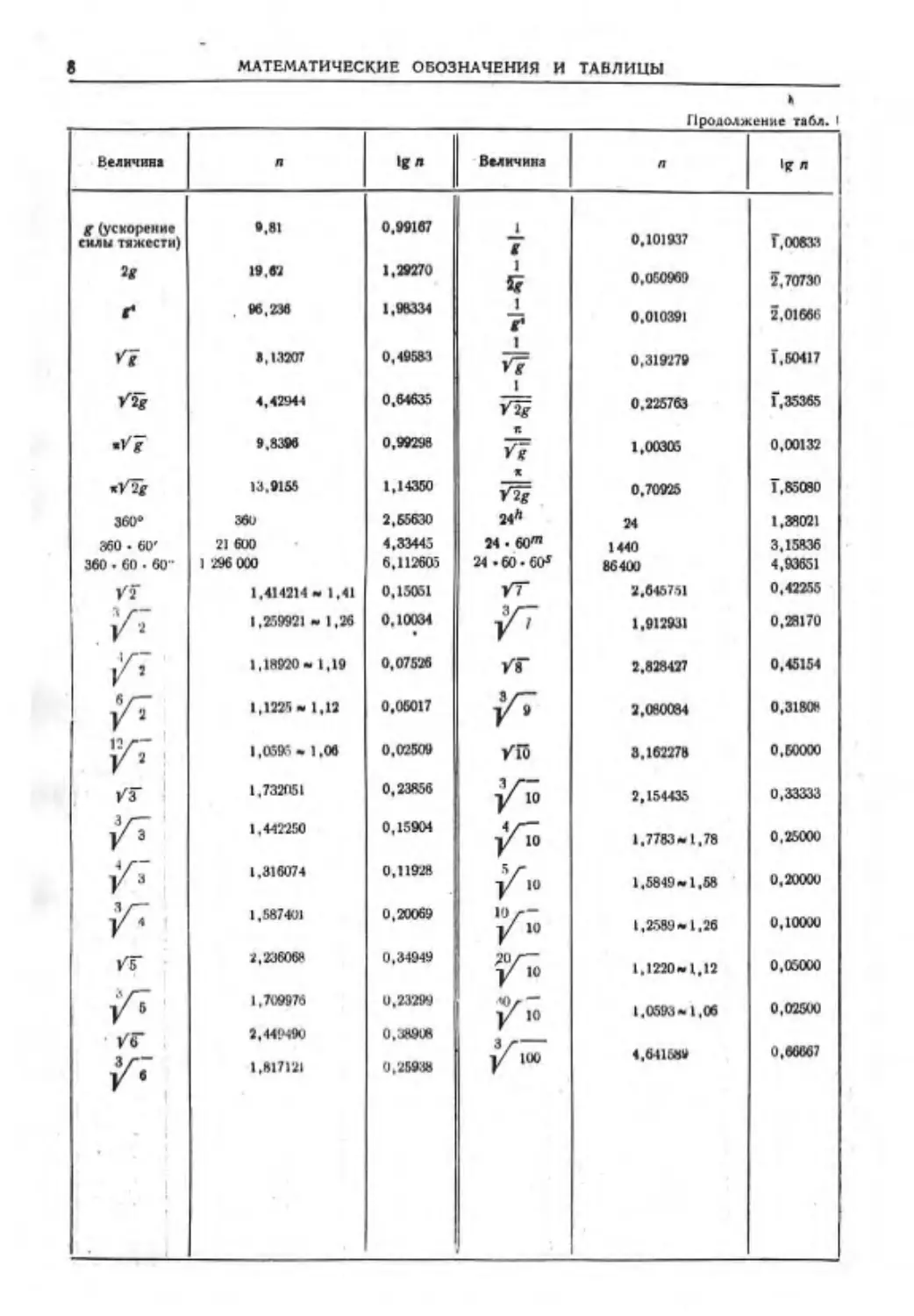
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
Продолжение табл. I
Величивд л If л Величина п •it л
g (ускорение e.el 0.99167 _1_
силы тижести) g 0,101937 Г,0063.1
19,62 1,29270 1 Sr 0,060969 5.70730
t 96,236 1,96334 i f 0,010391 2.01666
У1 1,1320? 0,40581 i »T 0.319279 f, 50417
Уй 4,42944 0,64635 1 Уй 0.225763 Г, 35365
г.
•Vg 9.8396 0,99298 Vg 1,00305 0,00132
ж
«/2Г 13,9166 1,14350 /5? 0.70925 Т, 85080
360“ 360 2,65630 24а 24 1.38021
360 • 60' 21 600 4,33445 24 • 60™ 1440 3,15836
360.60 60" 1 296 000 6,112605 24.60 - 6О1 864U0 4,93651
/г 1,414214 - 1,41 0,15061 УТ 2,645751 0,42255
|/ « 1,259921 - 1,26 0,10034 3/— г 1 1,912931 0,28170
1.IR920- 1,19 0,07526 УГ 2.828427 0,45154
6/— у 2 1,1225 » 1,12 0,05017 Я/— у9 2,080034 0,31808
п/— у 2 1,059ft- 1.06 0,02509 /15 8,162278 0,50000
/Г 1,733051 0,23866 1 /•— у 10 2,154435 0,33333
з/~ 1,442*250 0,15904 4/~
V 3 у 10 1.7783-1,78 0,25000
4/— 1.316074 0,11928 5/-
у IU 1,5849 — 1,58 0,20000
1.587401 0,20069 10/—
^ч/— у 10 1,2589-1.26 0,10010
/г 2.2Э606Н 0,34949 20Z~ у 10 1,1220-1,12 0,06000
j/T 1,709976 0,23299 «>/“ у 10 1.05173 - 1.06 0,02500
/г 2.44W9O 0.38908
1/ 100 4.641589 0,66667
V 6 1,817121 0.26938
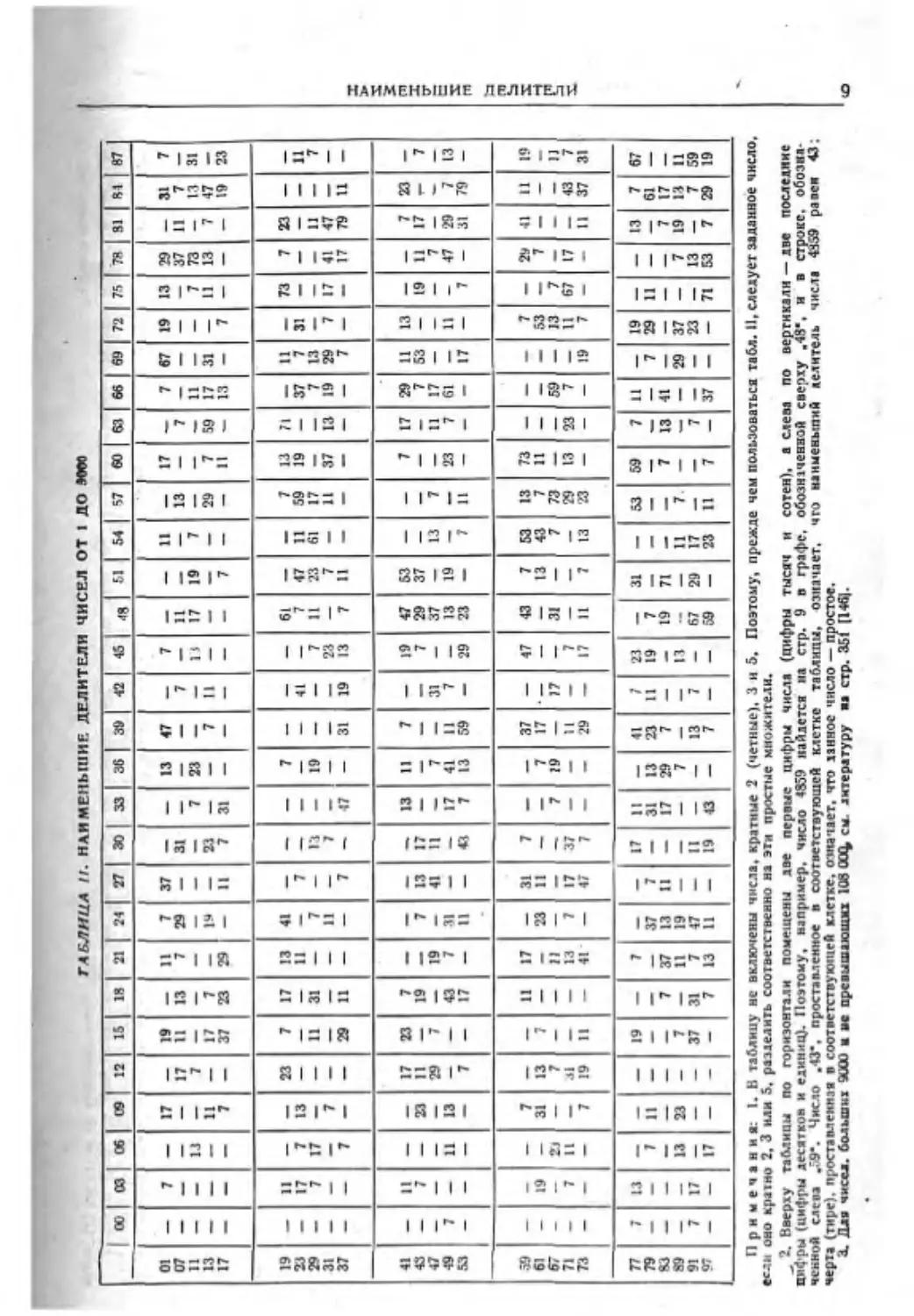
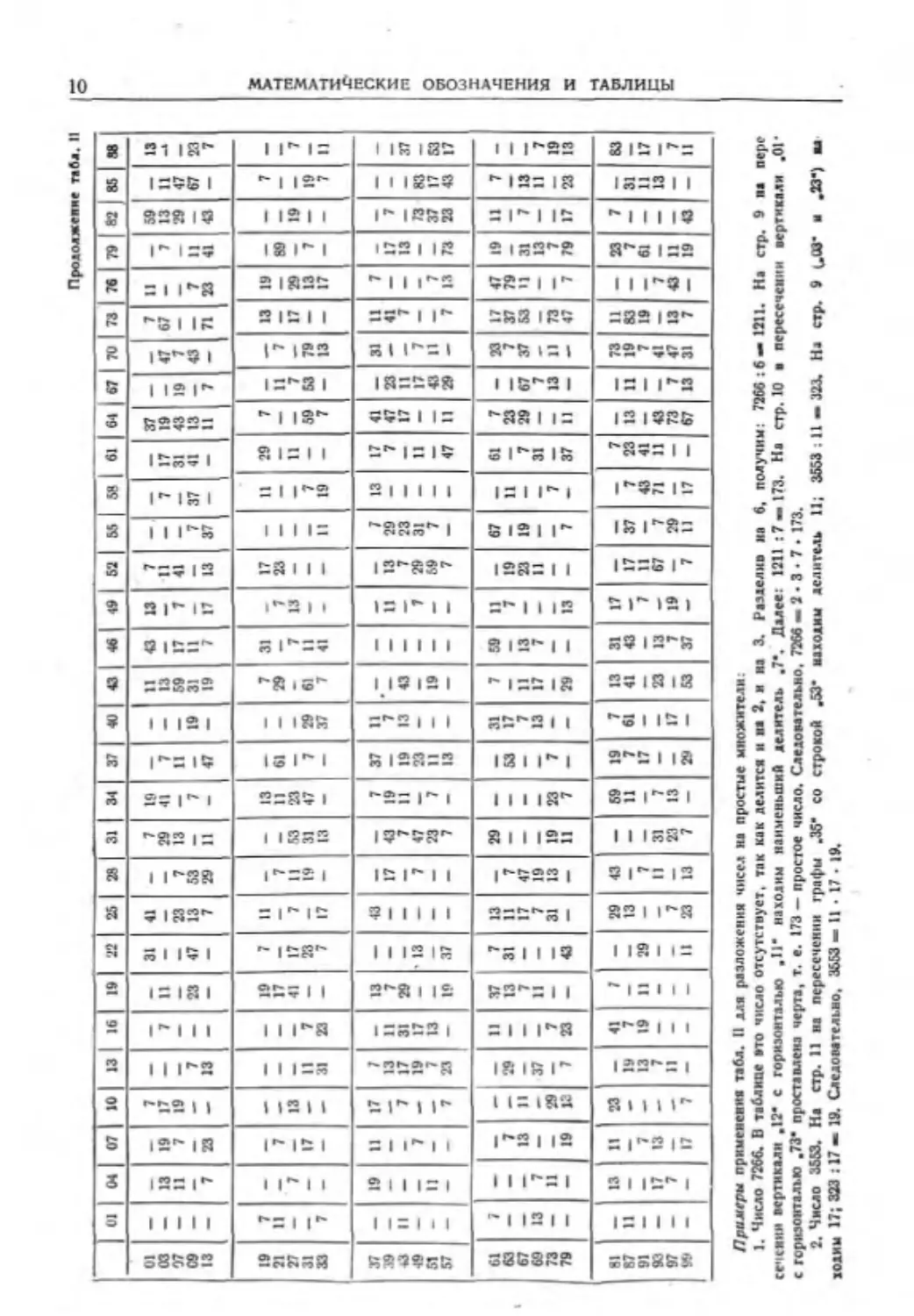
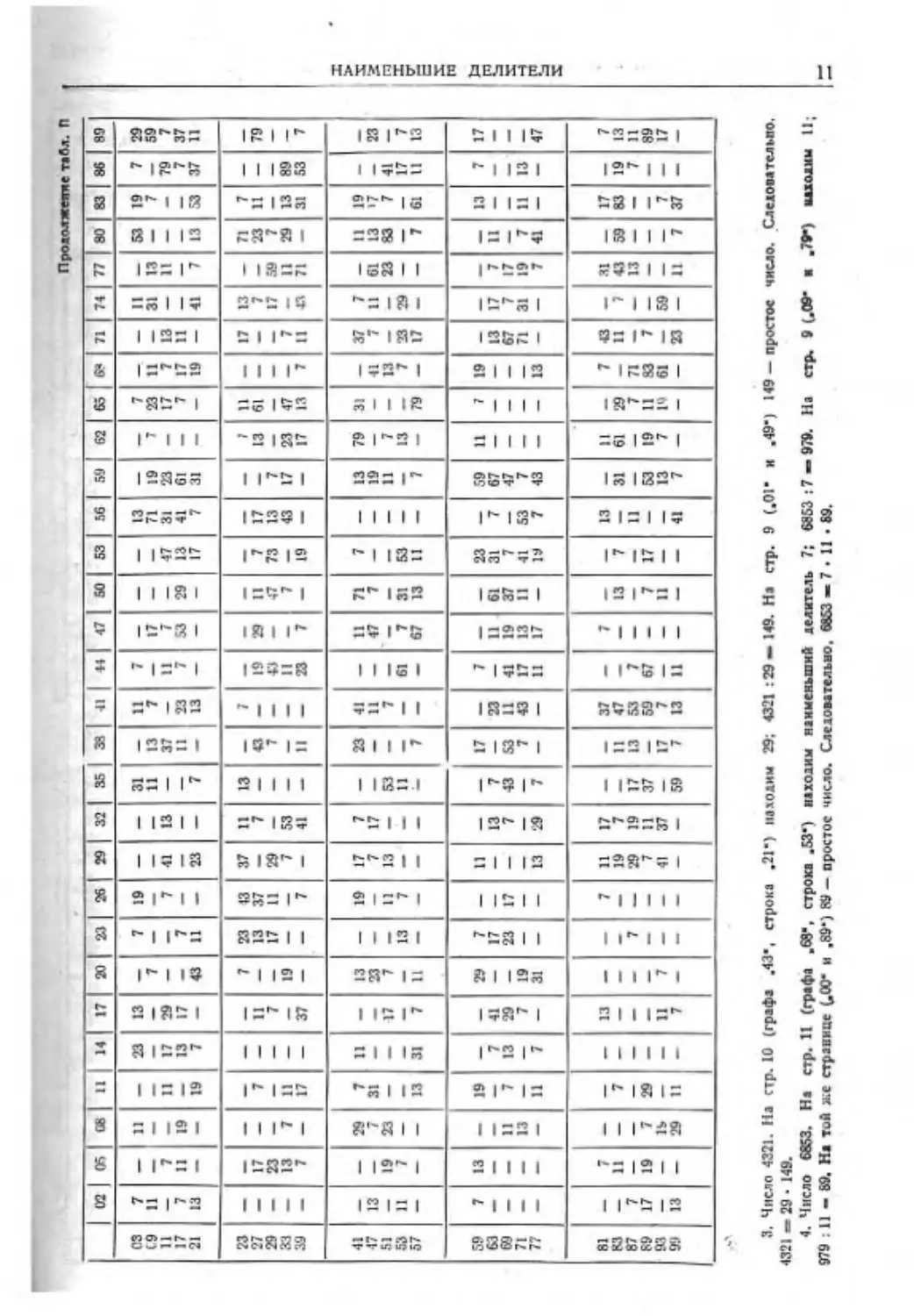
ТАЛЛИНА И. НАИМЕНЬШИЕ ДЕЛИТЕЛИ ЧИСЕЛ ОТ I ДО 8600
00 03 06 09 12 15 18 21 24 27 30 33 38 39 42 45 48 51 1 57 60 63 66 69 72 78 31 84 87
01 7 17 19 11 7 37 13 47 7 11 17 7 67 19 13 29 31 7
07 — — 17 11 13 7 29 31 __ 7 —- 11 __ 13 — 7 — — — 37 11 7 —
11 13 7 __ —— —— 7 23 —— __ 11 17 19 7 —— — — 11 —- — 7 73 — 13 31
13 11 17 7 __ 19 33 — 7 II —м 29 7 59 17 31 — 11 13 7 47 ж
17 — — — 7 — 37 23 29 — II 7 31 — — — — — 7 — — 11 *- 13 — — — — 19 23
19 11 23 7 17 13 41 7 61 7 13 71 11 73 7 23
23 — 17 7 13 11 — 7 — — — 41 7 47 11 59 19 — 37 7 31 — — — — 11
2» 7 17 —, —— 11 31 7 13 19 7 II 23 61 17 7 13 — 11 7
31 7 —— — И — 7 — — — 23 — 7 11 37 13 19 29 7 17 41 47 —
37 — — 7 — — 29 11 — — 7 — 47 — 31 19 13 7 11 — — — — — 7 — 17 79 11
41 11 17 23 7 13 11 7 19 47 53 7 17 29 11 13 7 23
43 7 23 11 19 —. 7 13 17 —— —— 7 29 37 — — — 7 53 — 19 11 17 7
47 — 29 7 19 — 41 11 —_ 7 __ 31 37 — 13 7 — 11 17 — — — 7 — »— —
49 7 11 13 — 43 7 31 ж 17 41 II 7 __ 13 19 — 23 7 61 11 — 47 29 7 13
53 — — — — 7 — 17 — II — 43 7 13 59 — 29 23 — 7 11 — — — 17 — 7 — 31 79 —
59 7 11 17 31 7 37 47 43 7 53 13 73 7 29 41 И 19
61 — 19 31 13 7 23 11 —— 7 17 • —— 13 43 7 11 —— .53 — 7 — — —
67 — 21 —— 7 11 — —« 7 19 17 —— 31 7 73 «ж — 59 13 7 — 11
71 — 7 11 —— 31 — 13 7 17 37 __ — и — 7 — — —. 29 13 23 7 11 67 17 — 43 7
73 — — — 7 19 11 — 41 — 47 7 — — 29 — 17 11 7 13 23 — — — 19 7 — — II 37 31
77 7 1.1 19 1 17 II 41 7 23 31 53 59 7 11 19 13 7 67
79 —_ ж 7 11 __ __ —_ 37 7 —— 31 13 23 11 19 7 — 7 29 11 — 61
S3 7 37 13 11 17 29 7 19 71 7 13 41 — 7 17
89 — 13 23 7 11 19 7 — __ 13 — 11 7 — 29 37 7 19 13 11
91 7 17 — —— — 37 31 7 47 II 13 7 67 29 17 __ — 7 23 — 13 — 7 59
97 — — 17 — — — 7 13 11 — 19 43 — 7 — — 59 — 23 11 7 — 37 — — 71 53 7 29 19
НАИМЕНЬШИЕ ДЕЛИТЕЛИ
При м еч ан ив: I. В таблицу не включены числа, кратные 2 (четные). 3 и 5. Поэтому, прежде чем пользоваться табл. II, следует заданное число,
•ели оно кратно 2. 3 нли 5, разделить соответственно на эти простые множители.
_ 2. Вверху таблицы по горизонтали помещены аве первые цифры числа (цифры тысяч и сотен), а слева по вертикали — две последние
цифры (цифры десятков и единиц). Поэтому, например, число 4359 найдется на стр. 9 в графе, обознтченной сверху .48". и в строке, обозна-
ченной слепа .59*. Число .43*. проста пл еиное в соответствующей клетке таблицы, означает, что наименьший делитель числа 4359 равен 43;
черта (тире), проставленная в соответствукичей клетке, означает, что данное число — простое.
X Для чисел, больших 9000 а ве превышающих 106 <ХХ^ см. литературу на стр. 351 [146].
иэ
Про лол же им г табл. II
01 (И 07 10 13 >6 >9 22 25 28 31 34 37 40 43 46 49 52 И 58 | 61 « 67 70 73 76 79 82 85 88
01 ». 7 31 41 7 19 11 43 13 7 __ 37 7 II 50 13
03 13 19 17 7 11 ж а— — 29 41 7 13 11 7 17 19 47 67 7 13 11 -8
07 11 7 19 ж ж ж ж 23 7 13 11 —- 59 17 7 41 — «» 31 43 19 7 — 29 47
С9 — — ж •» 7 ж 23 47 13 53 — 7 —- 19 31 II —— 7 37 41 13 43 7 И 67 23
13 7 23 13 — — 7 29 11 47 — 19 7 17 13 37 — — 11 7 71 23 41 43 7
19 7 19 7 11 13 7 31 17 11 29 7 13 19 7
21 II 7 ж — 17 7 — II 61 — 29 — 7 23 — И 7 89
27 — 7 • 13 ж 41 17 7 1) 53 23 — * 7 13 —- — 11 __ 7 17 29 19 — 7
31 — » 17 — II 7 — 23 — 19 31 47 7 29 61 II — 7 59 53 79 13 7 19
33 7 31 23 — 7 17 — 13 — — 37 7 41 — — II 19 — 7 13 — 17 — — 7 И
37 19 11 17 1 13 43 7 37 11 1 13 17 41 31 11 7
*9 —— «» »“ 13 11 7 ж 17 43 19 7 II 13 29 7 47 23 41 17 7
*3 II — — 7 17 31 29 —— 7 II 19 13 43 — 7 23 17 11 7 * 13 —. 37
49 — «к 7 19 17 — 13 7 47 ж 23 — »_ 7 29 31 — II —. 17 7 — 73 83
51 — 11 — 7 13 ж — —— 23 7 II • 19 — 59 7 — 43 11 7 37 17 S3
57 — — 7 23 — 19 37 — 7 — 13 — — — — 7 — — 47 11 29 7 13 73 23 43 17
61 1 * — 11 37 7 13 29 31 7 59 11 67 61 7 М 17 47 19 11 7
63 7 29 ж 13 31 11 7 ж 53 17 — 7 19 — 11 23 7 37 79
67 13 и V 7 •— 17 47 —— 7 11 13 —— 23 19 7 29 67 37 53 1 31 7 13
69 13 7 »- 37 II — 7 19 ж 13 17 7 II 31 7 13 II 7
73 11 — 29 — 7 — 31 13 19 23 7 А 7 —— __ 13 11 73 — 7 19
79 ““ 19 13 7 23 — 43 — 11 7 — — 29 — 13 — 7 37 11 47 7 79 17 23 13
81 — 13 II 23 __ 41 г 29 43 59 19 7 13 31 17 7 73 11 23 7 83
87 и — — * 19 7 13 >» 11 7 61 41 43 —- 17 37 7 23 13 11 19 83 7 31
91 — — 7 »• 13 19 II 29 * 7 — 17 в — 7 11 43 41 7 19 61 — 11 17
93 17 13 —- 7 ж — —• * II 31 7 — — 23 13 —. 67 7 71 11 43 — 41 7 — 13
97 7 «» »» II — * — 7 — 2'1 13 »* 17 7 19 —» 29 — 73 7 47 13 43 11 7
W - — 17 7 — 11 23 13 7 — 29 — 53 37 -» 7 и 17 — 67 13 31 7 19 43 — 11
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
Примеры применении табл. II лли разложения чисел на простые множители.
1. Число 7266. В таблице »то число отсутствует, так как делитсв и ва 2, и иа 3. Разделив ив 6, получим: 7266 : 6— 1211. На стр. 9 на перс
сечевик вертикали .12* с горизонталью .И* находим наименьший делитель .7*. Далее: 1211:7» 173. На стр. 10 в пересечении вертикали .01'
с горизонталью .73* проставлена черта, т. е. 173 — простое число. Следовательно, 7266 — 2 • 3 • 7 . 173.
2. Число 3663. На стр. II ва пересечении графы „38‘ со строкой ^3‘ находим делитель 11; 3563:11 — 323. На стр. 9 « .»") па
ходим 17; 823 :17 » 19. Следовательно, 3653 » 1| 17 19.
Проаолжеше табл. П
02 06 11 м 20 23 26 29 32 35 38 « « 50 S3 56 5У 62 65 6» 71 74 80 83 86 89
03 7 11 23 13 7 19 31 11 7 13 — 7 II 53 19 7 29
(9 11 7 и 13 7 17 — —- 71 19 7 23 и 31 13 —— 7 59
11 7 —— 11 17 29 7 41 13 37 — 11 7 47 31 23 17 7 13 II 79 7
17 7 11 19 13 17 7 —— — — 11 23 7 S3 29 13 41 61 __ 7 17 и — — — 7 37
21 13 — — 19 7 43 11 — 23 — 7 — 13 — — — 17 7 31 — — 19 — 41 7 13 S3 37 11
23 7 23 и 37 11 13 7 11 17 13 71 7
41 17 — 7 11 13 37 7 и — 19 29 11 7 17 13 61 — 7 23 И — 79
29 23 — — — 7 17 11 59 — 7 43 — 47 73 13 7 — 17 7 — — —
33 13 7 11 —— 19 —— — 7 53 II — 7 43 17 23 47 — 7 — 11 29 13 89 —
39 — 7 — 17 — 37 — — 7 — 41 — II — 23 7 — 19 — — 17 13 7 11 43 71 — 31 S3 7
41 29 7 11 13 19 17 7 23 41 11 71 7 13 79 31 37 7 11 19
47 13 — 7 31 23 — 7 17 — И 47 7 — —• 19 — — 41 7 11 61 13 >7 23
51 — 19 23 а— 17 7 11 13 53 7 — —— —— — 11 7 —— 13 _. «— 23 so 7 41 —
53 11 1 — —- 13 7 11 —- —— 61 7 31 53 — 13 — 7 23 29 — — — 17 7
57 — — — 13 31 7 11 — — — — — 7 — — 67 13 11 — 7 — 79 — 17 — — 7 61 II 13
59 7 13 19 29 7 11 17 7 23 59 11 7 19 13 7 17
63 — — 7 41 — 17 13 7 — 23 — 11 61 31 7 67 — — — 13 17 7 11 ж ж
69 ж 11 7 13 29 23 17 7 43 S3 11 41 19 37 7 47 — — 67 7 17 — — — __
71 А — 13 — 7 19 — 7 43 17 13 11 41 S3 7 — — 71 31 19 7 11 13
77 — — —* 11 7 — 31 — — 13 29 7 — — 11 17 — 19 7 43 — - 13 — — 7 41 — — 47
81 7 13 7 11 17 37 7 13 11 7 43 31 17 7
КЗ 11 — 7 — — — 19 7 11 47 13 7 — 31 61 29 «ж 11 7 43 59 83 19 13
87 7 7 29 19 17 13 S3 7 11 __ 7 71 13 — 7 11
89 17 19 7 29 — 7 11 37 — 59 67 7 17 53 19 11 83 7 89
93 — 1S «— —— 11 7 41 37 — 17 7 11 13 7 W 61 59 —— 7 17
99 13 — 29 11 — 7 — ~~ — — 59 7 13 11 — — — 41 7 — — 23 — 11 7 37 — —
НАИМЕНЬШИЕ ДЕЛИТЕЛИ
3. Число 4321. На стр. 10 (графа .43", строка .21") иахоаим 29; 4321 :29 — 149. На стр. 9 (.01" и .49") 149 — простое число. Слелооателыго.
4321 = 29 • 149.
4. Число 6853. На стр. И (графа .68*, строка .S3*) находим наименьший делитель 7; 6853 :7 — 979. На стр. 9 (.09* .79*) находим II;
979 ; 11 — 69. На той же странице (.00* и ,89*) R9 — простое число. Следовательно. 68S3 — 7 • 11 • 69.
12
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
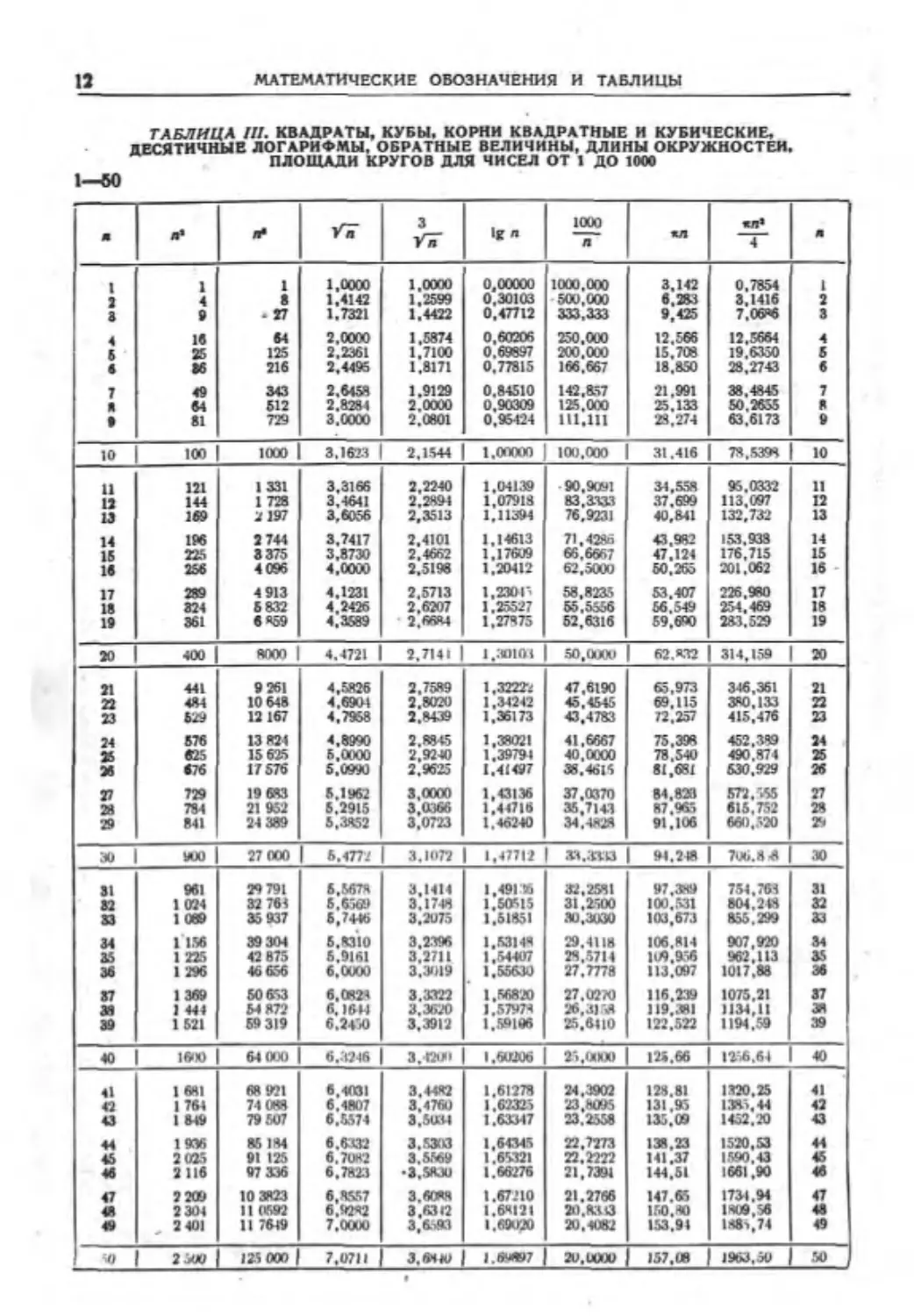
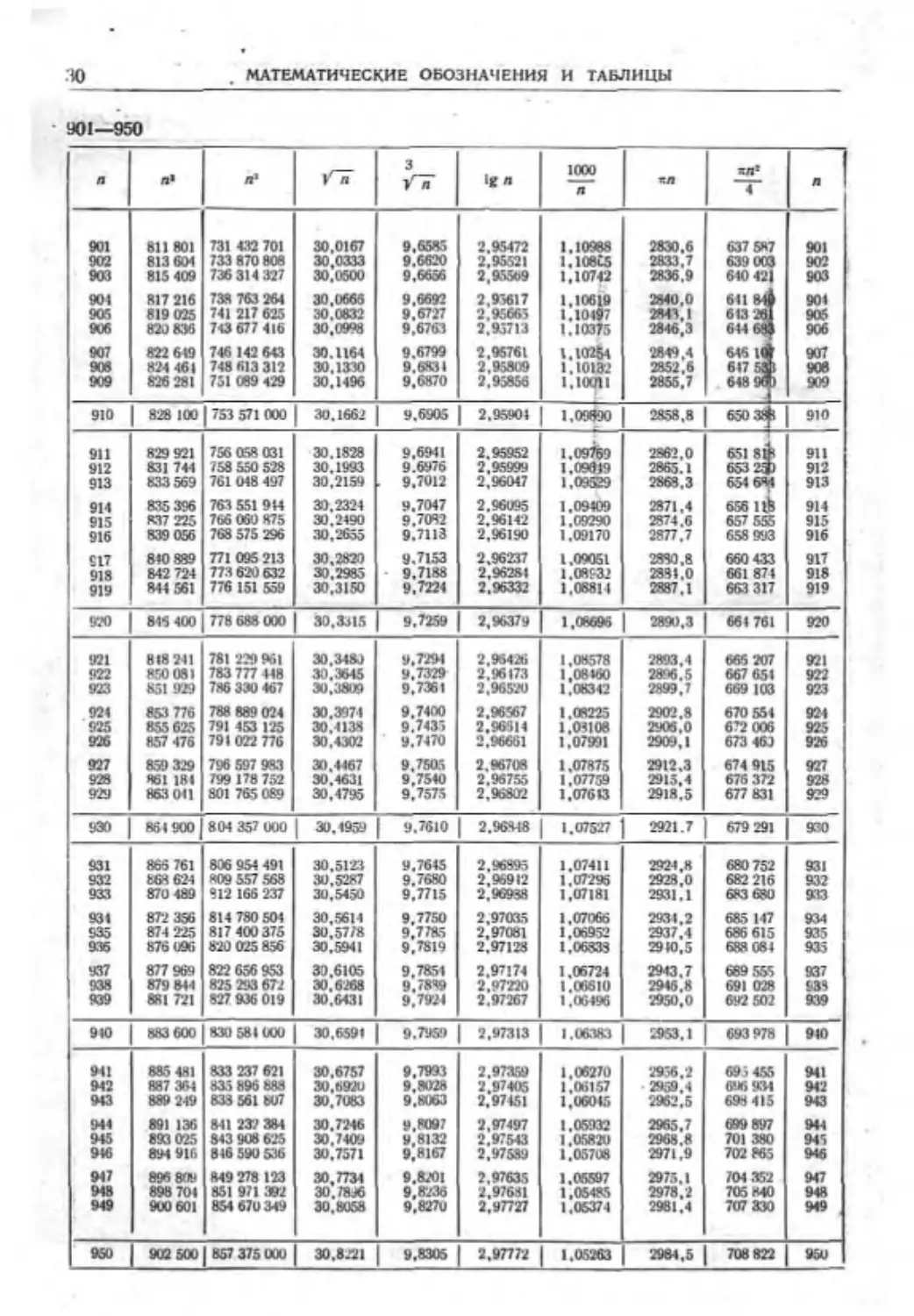
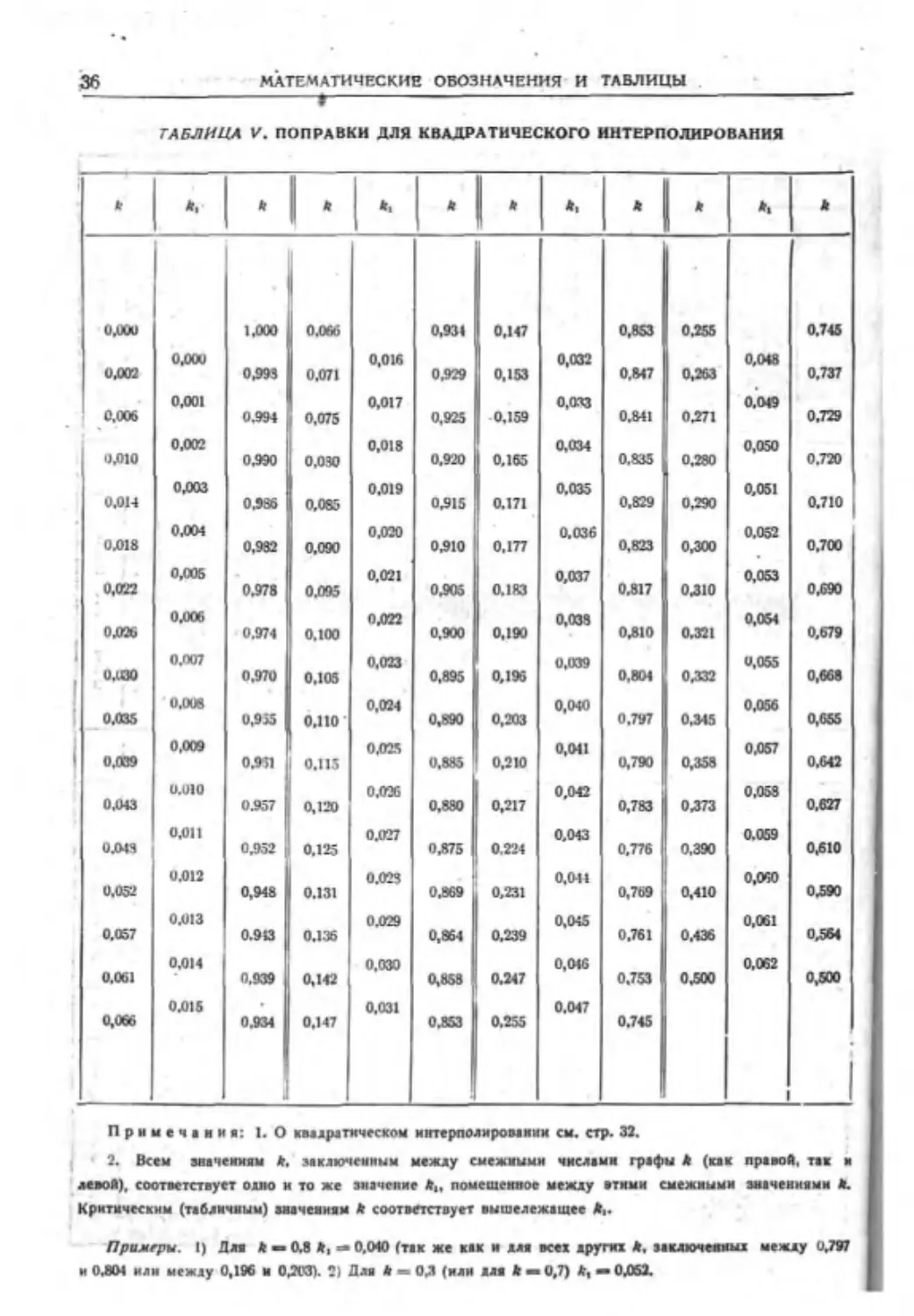
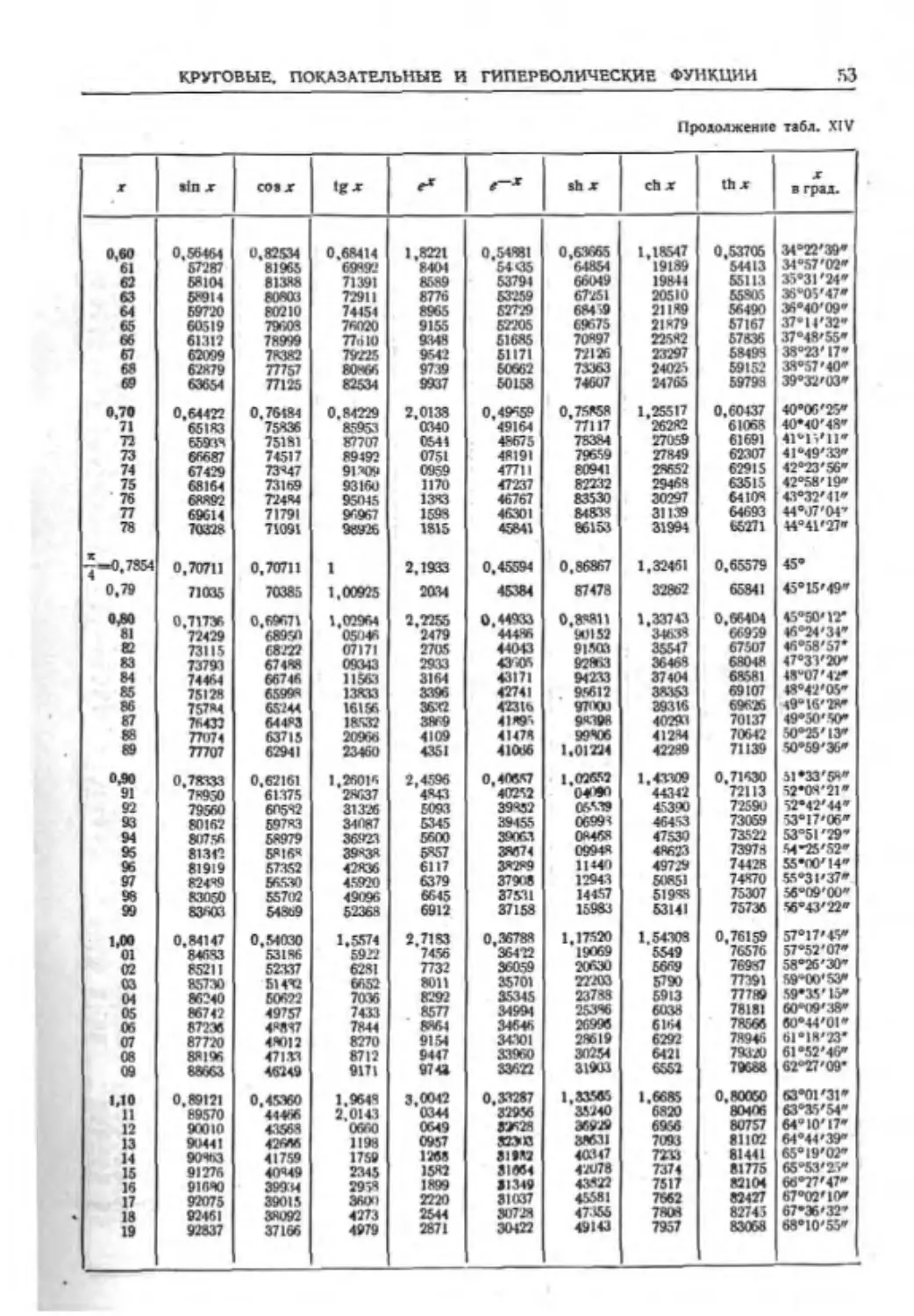
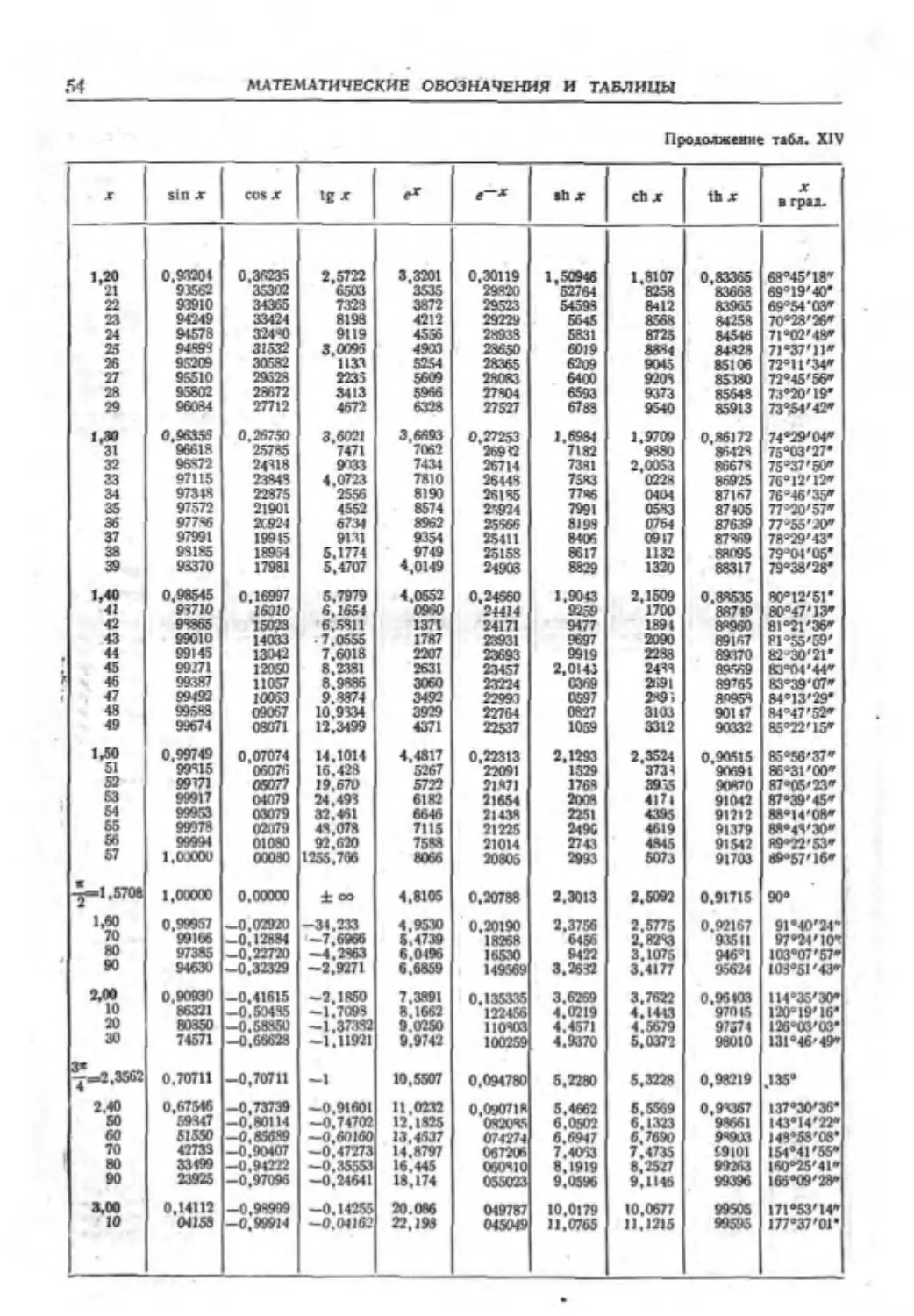
ТАБЛИЦА III. КВАДРАТЫ, КУБЫ. КОРНИ КВАДРАТНЫЕ И КУБИЧЕСКИЕ,
ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ, ОБРАТНЫЕ ВЕЛИЧИНЫ, ДЛИНЫ ОКРУЖНОСТЕЙ.
ПЛОЩАДИ КРУГОВ ДЛЯ ЧИСЕЛ ОТ 1 ДО 100*
1—60
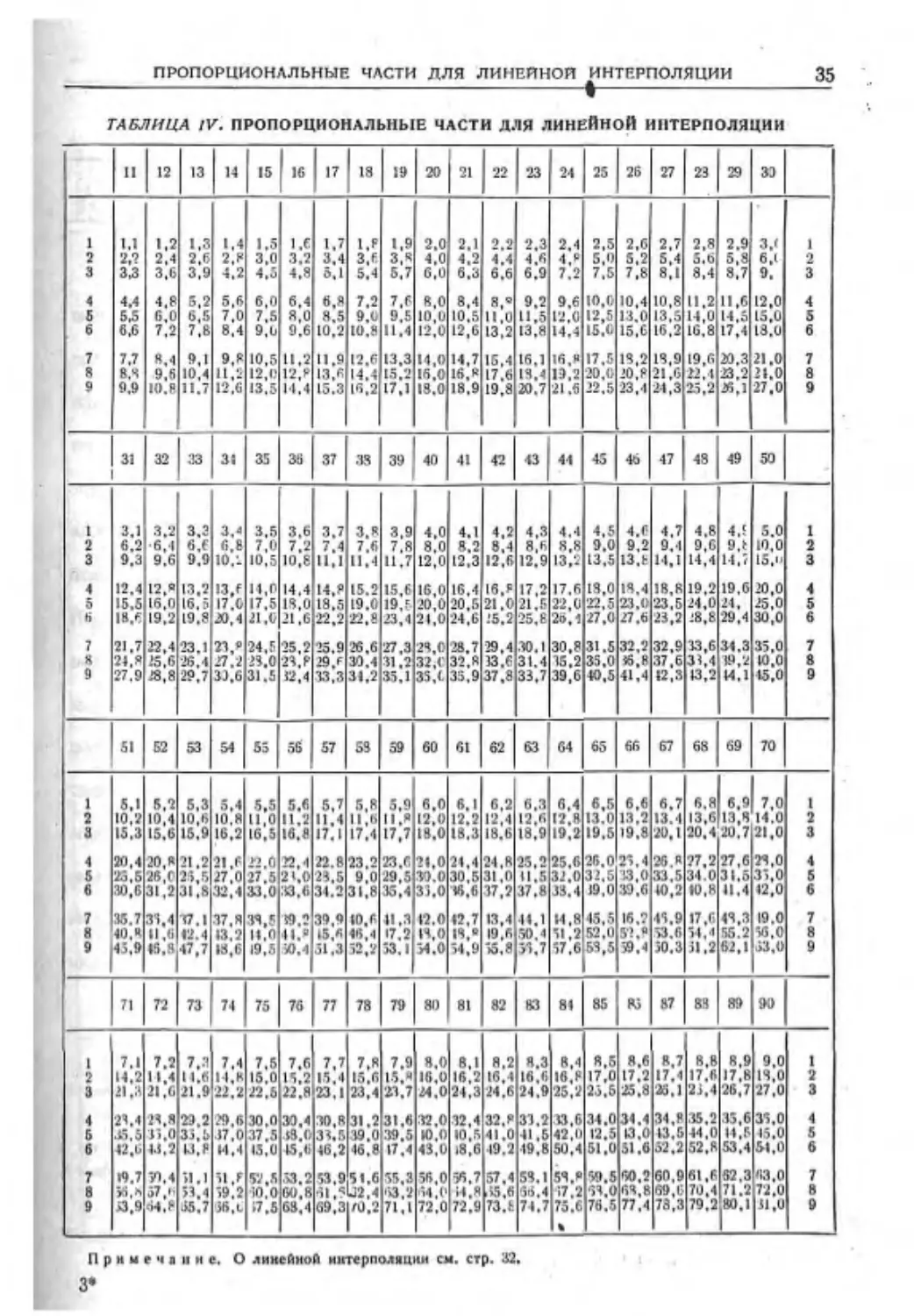
л Я* л* yf п 3 УГ 1g л 1000 п «Л «л» 4 л
1 1 1 1,0000 1,0000 0,00000 1000,000 3.142 0,7854 1
2 4 8 1.4142 1,2599 0,30103 500.000 6,283 3,1416 2
а 9 «27 1.7321 1.4422 0.47712 333,333 9,425 7,06*6 3
4 18 64 2.0000 1.5874 0,60206 250.000 12.566 12,5664 4
5 28 125 2.2361 1.7100 0.69В97 200,000 15.703 19.6350 5
< К 216 2,44% 1,8171 0.77815 166,667 18.850 28,2743 6
7 49 343 2.6458 1.9129 0.84510 142.857 21.991 38,4845 7
А 84 512 2.8281 2.0000 0,90309 125,000 25.133 50.2635 Я
• 81 729 3.0000 2.0801 0,96424 111.111 28,274 63.6173 9
10 100 1000 3.1633 2,1544 1.00000 100,000 31.416 78.5395 10
11 121 1 331 3,3166 2,2240 1.04139 90,9091 34.55Я 95,0332 11
и 144 1 728 3,44541 2.2894 1,07918 83,3333 37.699 113,097 12
13 169 2197 3.6056 2,3513 1,11394 76.9231 40,841 132,732 13
14 196 2 744 3,7417 2,4101 1,14613 71,4286 43,982 153.938 14
18 225 8375 3,8730 2.4662 1,17609 66.6667 47,124 176,715 15
16 256 4096 4,0000 2.5196 1,20412 62.5000 50,265 201,062 16
17 289 4 913 4,1231 2.5713 1,2301’ 58,82X5 53.407 226.980 17
18 824 8 832 4.2426 2.6207 1,25527 55.5556 56.349 254.469 18
19 381 6*59 4,3589 2.WM 1,27*75 52.6316 59.6W 283,529 19
20 400 8000 4.4721 2,7141 1.30104 50,0000 «2 АХ? 314,159 20
21 441 9 261 4,5826 2.7589 1,32222 47,6190 65,973 3-16.361 21
22 4*4 10 648 4.6904 2.8020 1.34242 45.4545 69,115 3*0.133 а
23 629 12167 4,7968 2.8439 1,36173 43,4783 72,257 415,476 а
24 576 13 824 4,8990 2.8845 1,38021 41,6667 75,398 452.3*9 24
28 825 15 625 6,0000 2,9240 1,39791 40.0000 78,540 490,874 25
26 676 17 576 5.0990 2.9625 1.41497 38.4615 81,681 530,929 26
27 729 19 683 6,1962 3.0000 1,43136 37.0370 84,820 572. .55 27
28 734 21 962 8.2915 3.0366 1.44716 35,7143 87.965 615,752 2*
29 841 24 389 8.3*52 3,07а 1.46240 34.4*28 91.106 660,520 29
30 JAJO 27 000 6.4772 3.1072 | 1,47712 X4.3XU 94.248 706.8 4 30
81 961 29 791 6.5678 3,1414 1,491 И 32,2581 97. 754,764 31
82 1 024 32 764 6,6-да 3.1748 1,5045 31,2500 100,531 804.248 32
33 1 (JH9 35 937 6,7446 3.2U75 1,51651 30,3030 100,673 855.299 33
34 1136 39 304 6.8310 3,2396 1,5314* 29,4116 106,*14 907,920 34
38 1 225 42 875 6.9161 3,2711 1,54407 28,5711 1О9.9Я6 962,113 35
38 1 296 46 656 6,0000 3.3019 1,55630 27,7778 113,097 1017.88 36
37 1 369 50653 6.0824 3.3322 1,56820 27.0270 116,23В 1075.21 37
1 444 54*72 6. 1614 3.3U0 1.5797* 26,3158 119,.4*1 1134,11 ЗЯ
39 1 521 59 319 6.24'4) 3.3912 1.58106 25,6410 122,522 1194,58 39
40 1600 64 000 6.3246 3.I2UO 1.Ш06 25,01100 125.66 1256.64 40
41 1 6*1 68 921 6,4001 3.44*2 1,61278 24,3902 128,81 1320,25 41
42 1 761 711X4 6.4807 3.4760 1.62323 23,8005 131,95 138». 44 42
43 1 649 79 507 6.6374 з,5аи 1.63347 а.2558 135,09 1432.20 43
44 1 9СУ» 88 1*4 6.6332 3.5Э13 1,64345 22,7273 138.23 1520,53 ♦4
45 2 025 91 125 6.70*2 3.556» 1.65.321 22.2222 141,37 1590,43 45
46 2116 97 336 6.7823 •3.5830 1.66276 21,7391 144,51 1661,90 46
47 2 209 10 3823 6,8557 ЗЛЯ* 1.67.40 21.2766 147.65 1734,94 47
4* 2 304 И (1592 6.92*2 3,63(2 1.6*121 20.83(3 150,80 1Кв,56 44
4» , 2 401 11 7649 7,0000 3.6A3 1.69020 20.4082 153,94 1*8(,74 49
80 гмо 125 000 | 7,0711 3.8*40 1.в***7 A'.LOM? 157,08 1963.30 50
КВАДРАТЫ, КУБЫ. КОРНИ. ЛОГАРИФМЫ. ОБРАТНЫЕ ВЕЛИЧИНЫ
13
51—100
Я л* л* У7 3 УТ 1g л 1000 п «Л Ж Л1 4 Л
61 2 601 132 651 7,1414 3,7084 1.70757 19,6078 160.22 2042,82 51
ч 2 704 140 608 7,2111 3,7325 1,716*90 19,2308 163,36 2123,72 52
S3 2809 148 877 7,2801 3,7563 1,72428 18,8679 166,50 2206,18 53
м 2 916 157 464 7,3485 8,7798 1,73239 18,5185 169,65 2290.22 54
ы 3 025 166 375 7,4162 3,8030 1,74036 18,1818 172,79 2375,83 55
и 3 136 175 616 7,4833 3,8259 1,74819 17,8571 175,93 2463,01 56
57 3 249 185 193 7.5498 3,8485 1,75587 17,5439 179,07 2551,76 57
М 3 364 195 112 7.6158 3,8709 1,7634.1 17,2414 182.21 2642,08 58
а 3 481 205 379 7.6811 3,8930 1,77055 16.9492 185.35 2733,97 59
50 3 600 216 000 7.7460 3,9149 1,77815 16,6667 188.50 2827,43 60
51 3 721 226 981 7.8102 3,9365 1.78533 16,3934 191,64 2922.47 61
62 3 844 238 зга 7,8740 3,9579 1,79'239 16,1290 194,78 3019,07 62
63 8 969 250 047 7,9373 3.9791 1,79904 15.8730 197,92 3117,25 63
64 ' 4 096 262 144 8,0000 4.0000 1,80618 15.6250 201,06 3216,99 64
66 4 225 274 625 8,0623 4,0207 1,81291 15,3846 204,20 3318,31 65
65 4 356 287 496 8,1240 4,0412 1.81954 15,1515 207.35 3421.19 66
67 4 489 300 763 8,1854 4,0615 1.82607 14,ММ 210,49 3525.65 67
88 4 624 314 432 8,2462 4.0817 1,83251 14,7069 213,63 3631.68 68
69 4 761 328 509 8,3066 4.1016 1,83885 14,4928 216, П 3739,28 69
70 4 900 343 000 8,3666 4.1213 1,84510 14.2857 219.91 3848,45 70
71 5 (Ml 357 911 8,4261 4,1408 1,85126 14,0845 223,06 3959,19 71
п 5 184 37.3 248 8,4853 4,1602 1,85733 13,8889 226,19 4071,50 72
73 5 329 389 017 8,5440 4,1793 1,86332 *13,6986 229,34 4185.39 73
74 5 476 405 224 8,6023 4,1983 1.86923 13,5135 232,48 4300,84 74
73 5 625 421 875 8,6603 4,2172 1,87506 13,3333 235.62 4417,86 75
76 5 776 438 976 8,7173 4,-2358 1,88081 13.1579 236,76 4536.46 76
п 5 929 456 533 8,7750 4,2543 1.8Я649 12,9870 241,90 4656,63 п
78 6 084 474 552 8,8318 4,2727 1,8921» 12,8205 245,04 477К..Ж 7В
79 6 241 МВ <А39 4.2908 I.R9763 248.19 4901,67 7»
80 6 400 512 (ИМ 8.9443 4,3089 1,90309 2,5000 251.33 5026,55 80
81 6 561 531 411 9.0000 4.3267 1,90849 12.3457 254.47 5153,00 81
82 6 724 551 368 9,0554 4,3445 1,91331 12,1961 257,61 5261,0В 62
83 6 889 571 787 9,1104 4,3621 1,91908 12,0482 260,75 5410,61 83
84 7 056 592 704 9,1652 4,3793 1,92428 11,9048 263,89 5541,77 84
86 7 225 614 125 9.2196 4,3963 1,92942 11.7647 367,04 5674,50 85
86 7 396 636 056 9,2736 4,4140 1,93450 11,6279 270,18 5808,80 86
87 7 569 658 503 9,3274 4.4310 1.93952 11,4943 273,32 5944,68 87
88 7 744 681 472 9.3ЯИ 4.4480 1,94448 11,3636 276,46 6082,12 88
89 7 921 704 969 9,4340 4,4647 1.94939 11,2360 279,60 6221,14 89
*? 8 100 729 000 9,4868 4.4814 1.95424 11,1111 282,74 6'161,73 90
91 8 281 753 571 9.5.194 4,4979 1.95904 10,9390 285,88 6503,89 91
92 8 464 778 688 9.5917 4,5144 1,96379 10,8696 289,03 6647,61 92
93 8 649 804 357 9,6437 4,5307 1,96848 10,7527 292,17 6792,91 93
94 8 836 830 584 9.6954 4,5468 1,97313 10,6383 295,31 69'19,78 94
96 9 025 857 375 9,7468 4,5629 1.97772 10,5263 298,45 7088,22 95
95 9 216, 884 736 9,7980 4,5789 1,93227 10,4167 301,39 7238,23 96
97 9 409 912 673 9,8489 4,5947 1,98677 10,3093 304,73 7389,81 97
98 9 604 941 192 9,8995 4,6104 1,99123 10,2041 307,88 7542,96 98
99 9 801 970 299 4,6261 1,99564 10,1010 311,02 7097,69 99
100 10 000 1000 000 1 10,0000 4,6416 2,00000 10,0000 | 314,16 7853,98 100
It
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
101-150
— я п* Л* КГ Л Гй IK " 10О> п кд ЖД1 гг
101 10 201 1 030 301 10,0499 4,6570 2,00432 9,90099 317.Х 8 011,85 101
ЮТ 10 404 1 061 'ЛЯ 10,0995 4,6723 2,00950 9.80:192 320,44 В 171.28 102
103 10 609 1 092 727 10,1489 4.6875 2,01284 9.70874 323.58 8 332.29 103
104 10 816 I 124 861 10,1990 4.7027 2.01703 9.61538 326,73 8 494.87 104
105 11 025 1 157 625 10,2470 4.7177 2.02119 9,52381 329,87 8 659.01 105
106 11 236 1 191 016 10,2956 4.7326 2,02531 9.43393 333,01 8 824.73 106
107 11 449 1 225 043 10.3441 4.7475 2.02938 9.34579 336.15 8 992.02 107
104 >1 664 1 259 712 10,3923 4.7622 2.03342 9.25926 339,29 9 160.84 108
109 11 881 1 295 029 10.4403 4.7769 2.03743 9,17431 342.43 9 331.32 109
110 12 100 1 331 000 10.4881 4.7914 2.04139 | 9,09091 345.58 9 503,32 НО
111 12 321 1 367 631 10,5357 4,8069 2,04532 9,00901 348.72 9 676,89 III
112 12 544 I 404 928 10.5830 4.8203 2,04922 8,92857 351.86 9 852,(3 11?
113 12 769 1 442 897 10$6301 4,8346 2.06308 8,84956 355.00 10 028,7 113
114 12 996 1 481 544 10.6771 4,8488 2.05690 8,77193 358,14 10207,0 114
115 13 225 1 520 875 10,7238 4.8629 2.06U70 8.69565 361.28 10 386,9 115
116 13 456 1 560 896 10,7703 4,8770 2.06446 8,62069 364,42 10 568.3 116
117 13 689 1 601 613 10,8167 4,8910 2.06819 8.54701 367,57 10 781,3 117
118 13924 1 843 032 10.8RS 4.9049 2,07183 8,47453 370,71 10 935.9 118
119 14 161 1 683 159 10,9087 4.9187 2.07555 8,40336 373,85 11 122.0 119
120 14 400 1 738 000 10,9545 4,9324 2.07918 8,33333 376,99 11 309.7 120
121 14 641 1 771 561 11,0000 4.Ш1 2,08279 8,26446 380,13 11 499,0 121
122 14 884 1 815 848 11,0451 4.9597 2,08636 8,19672 383,27 11 689,9 122
123 15 129 1 860 867 11,0906 4,9732 2.06991 8,13008 386,42 11 882,3 123
124 15 376 1906624 11,1355 4.9866 2.09342 8,06452 389,56 12 076,3 124
125 15 625 1 953 125 11,1803 5,0000 2.09691 8.00000 392.70 12 271,8 125
126 15 876 2 000 376 11,2250 6,0133 2,10037 7.93651 395.84 12 469,0 126
127 16 129 2 018 383 11,2694 5.0265 2.10880 7,87402 396,98 12 667,7 127
128 16 334 2 097 152 11.3137 5.0397 2.1072» 7,81250 402,12 12 868,0 128
129 16 641 2 146 689 11.3678 5.0524 2.11059 7,75194 405,27 13 069,8 129
130 16 900 2 197 000 11.4018 5,0653 2.11394 7,69231 408.41 13 273,2 130
131 17 161 2 248 091 11,4453 5,0788 2,11727 7.63359 411.55 13 478,2 131
132 17 424 2 299 968 11,4891 5.0816 2.12057 7.57576 414.69 13 684.8 132
133 17 689 2 352 637 11,5326 5,1045 2.123S5 7.51880 417.83 13 892.9 133
134 17 956 2 406 104 11,5758 5,1172 2,12710 7.4626Э 420,97 14 102,6 131
135 18 225 2 460 375 11,6190 5,1299 2,1303.3 7,40741 424.12 14 313.9 135
136 18 496 2 515 456 11,6619 5,1426 2,13351 7,35294 427.26 14 526,7 136
137 18 769 2 571 353 11,7047 5,1551 2.13672 7,29927 430,40 14 741,1 137
138 19 044 2 628 072 11,7473 5,1676 2.13983 7.24634 433.54 14957,1 138
139 19 321 2 685 619 11,7898 5,1801 2.14301 7,19424 436.68 15 174,7 139
140 19 600 2 744 000 11.8322 5,1923 2,14613 7,14286 439,82 15 393,8 140
141 19 881 2 803 221 11.8743 5,2048 2,14922 7.O922U 442.95 15 614,5 141
142 20 164 2 863 288 11.9164 5,2171 2,15229 7.04225 446.11 15 836,8 142
143 20 449 2 924 207 11.9583 5,2293 2.15534 6.99301 449,25 16 060.6 143
144 20 736 2 985 984 12,0000 5,2415 2.15836 6.94444 452,39 16 286,0 144
145 21 025 3 048 625 12.0416 5,2536 2.16137 6.89655 455,53 16 513,0 145
146 21 316 3 112 136 12.0630 5,2656 2.16435 6.84932 458,67 16 741,5 146
147 21 609 3 176 523 12,1244 5,2776 2.16732 6,80272 461,81 16 971,7 147
148 21 904 3 241 79.‘ 12.1655 5,2896 2,17026 6,75676 461.95 17 203,4 14-
149 22 201 3 307 949 12.2066 5,3015 2.17319 6.71141 463.10 17 436.6 149
160 22 500 3 375 000 | 12,2474 | 5,3131 2,17609 6.66667 471,24 17 671,5 130
КВАДРАТЫ. КУБЫ. КОРНИ ЛОГАРИФМЫ. ОБРАТНЫЕ ВЕЛИЧИНЫ
15
151—200
п л’ Л5 Vn 3 Уп 1Я п 10€К> п т.п кп* 4 п
151 22 801 3 442 951 12,2882 5,3251 2,17893 6,62252 474,38 17 907,9 151
152 23 104 3 511 яда 12.3288 5,3368 2.18184 6,57895 477.52 18145,8 152
153 23 409 3 581 577 12,3693 5,3485 2,18469 6,33596 480.66 18 385,4 153
154 23 716 3 652 264 12,4097 5,3601 2.18752 6,49351 483,81 18 626,5 154
155 24 025 3 723 875 12,4499 5,3717 2,19033 6,45161 486,95 18 869,2 155
156 24 336 3 796 416 12,4900 5,3832 2,19312 6,41026 490.09 19 113.4 156
157 24 649 3 8G9 893 12.5300 5,3947 2,19590 6,36943 493,28 19 359,3 157
153 24 961 3 944 312 12,5698 5,4061 2,19866 6,32911 496,37 19 606,7 158
159 23 281 4 019 679 12,6095 5,4175 2,20140 6,28831 499.51 19 855,7 159
160 25 600 4 096(100 12.6491 5.4288 2,20412 6.25000 502.65 20 106,2 160
161 25 921 4 173 281 12.6886 5,4401 2,206» 6,21118 505.80 20 358,3 161
162 26 244 4 251 52» 12,7279 5,4514 2,20952 6,17284 508,9-1 20 612,0 162
163 26 569 4 330 747 12,7671 5.4626 2,21219 6,13497 512,08 20 867,2 163
164 26 896 4 410 944 12,8062 5,4737 2,21484 6,09756 515,22 21 124,1 164
165 27 225 4 492 125 12,8452 5,4848 2,21748 6,06061 518,36 21 382.5 165
166 27 556 4 574 296 12,8841 5,4959 2,22011 6,02410 521,50 21 642,4 166
167 27 889 4 657 463 12,9228 5,5069 2,22272 5,9-88X12 524,65 21 9М,0 167
168 28 224 4 741 632 12,9615 5.5178 2,22531 5,95238 527,79 22 167.1 168
169 28 561 4 826 809 13,0000 5,5283 2,22789 5,91716 530,93 22 431.8 169
170 28 900 4 913 ООО 13,0394 5,5397 2.23045 5,88235 534,07 22 698.0 170
171 29 241 5 000 211 13,0767 5,5505 2.23300 5,84795 537,21 22 965,8 171
172 29 584 5 068 448 13,1149 5,5613 2,2355.3 5,81395 540,35 23 233,2 172
173 29 929 6 177 717 13,1529 5,5721 2,23806 5,78035 543,50 23 506,2 173
174 30 276 5 268 024 13,1909 5.5823 2,24055 5.74713 546,64 23 778,7 174
175 30 625 5 359 375 13,2288 5.5034 2,24304 5,71429 519,78 24 052,8 175
176 30 976 5 451 776 13,2665 5,6041 2.24551 5,68182 552,92 24 328,5 176
177 81 329 5 645 233 13,30-11 5,6147 2,24797 5,6497'2 556.66 24 605,7 177
173 31 684 Б 639 752 13,3417 5,6252 2.25М2 5,61793 559,20 24 881,6 178
179 32 Ml 5 735 339 13,3791 5.6357 2,25285 5,58659 562.35 25 164.9 179
180 32 400 5 832 000 13,4164 5,6462 2,25527 | 5,55556 565,49 25 446,9 180
181 32 761 5 929 741 13,4536 5,6567 2,25768 5,52486 668,6.1 25 730,4 181
182 33 124 6 029 568 13,4907 5,6671 2.261X17 5,49451 571.77 26 015,5 182
183 33 489 6 128 487 13,5277 5,6774 2,26245 5,46448 574.91 26 302*2 18.3
184 33 856 6 229 504 13,5647 5,6877 2.26482 5,43478 578.06 26 590,4 184
18.5 34 225 6 331 625 13,6015 5,6980 2,26717 5,40541 581,19 26 880,3 185
186 34 596 6 434 856 13,6382 5,7083 2,26951 5.37634 584,3-1 27 171,6 186
187 34 969 6 539 203 13,6748 5,7185 2,27184 5,34759 587,48 27 464.6 187
IBM 35 244 6 614 672 13,7113 5,7287 2,27416 6,31915 590.62 27 759,1 184
189 36 721 6 751 269 13.7477 > 5.7388 2,27646 5,29101 593,76 28 065,2 189
190 36 too 6 859 000 13,7840 5,7489 2,27675 5,26316 596,90 28 352,9 190
191 36 481 6 967 871 13,8203 5.7590 2,28103 5,23560 600,04 28 652.1 191
192 36 864 7 077 388 13,8561 5.7690 2,28330 5,20833 603,19 28 952,9 192
193 37 249 7 189 057 13,8924 5,7790 2,28556 5,18135 606,33 29 255,3 . 193
194 37 63о 7 301 384 13,9284 5,7890 2,28780 5,15464 609,47 29 559,2 194
195 38 025 7 414 875 13,9642 6,7989 2.29003 5,12821 612,61 29 864,8 195
196 38 416 7 529 536 14,0000 5,8068 2,29226 5,10201 615,75 30 171.9 193
197 38 809 7 645 373 14,0357 5.8186 2,29447 5,07614 618,89 30 480.5 197
198 39 204 7 762 392 14.0712 5.8285 2,29667 5,06051 622,14 30 790,7 194
199 39 601 7 880 699 14,1067 5,8383 2,29895 5,02513 625,18 31 102.6 199
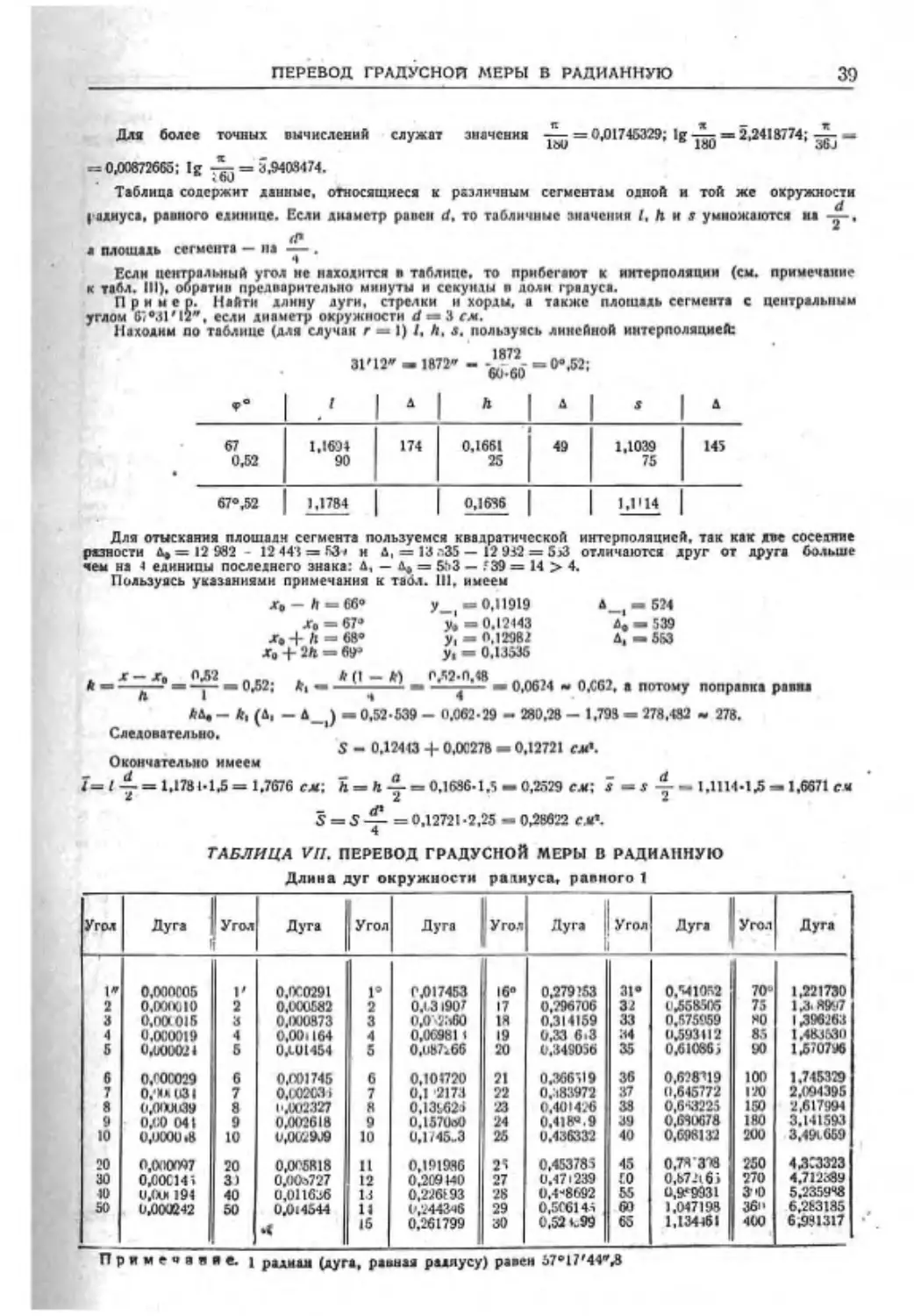
200 | 40 01» 8 000 000 14,1421 5.8480 | 2,341103 | 5,00003 | 628,32 | 31 415,9 | 200
16
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
201-250
п Я' ¥ п 3 ¥^п 1g п 1000 я жл «Л1 4 Л
201 40 401 8 120 601 14,1774 5,8578 2,30320 4,97512 631,46 31 730,9 201
202 40 804 В 242 408 14,2127 5,8675 2,30535 4,95050 634,60 32 047,4 202
203 41 209 8 365 427 14,2478 5,8771 2,30750 4,92611 637,74 32 365,5 203
204 41 616 8 489 6Ы 14,2829 5,8868 2,30963 4,90196 640,88 32 685,1 204
205 42 025 8 615 125 14,3178 5,8964 2,31175 4,87805 644,03 33 006,4 206
206 42 436 8 741 816 14,3527 5,9059 2,31387 4,85437 647,17 33 329,2 206
207 42 849 8 869 743 14,3875 5,9155 2,31597 4,83092 650,31 33 653,5 207
20В 43 261 8 998 912 14,4222 5,9250 2,31806 4,80769 653,45 33 979,5 208
209 43 681 9 129 329 14,4568 5,9345 2,32015 4.78469 656,59 34 307,0 20»
210 44 100 9 261 000 14,4914 5.9439 2,32222 4,76190 659,73 34 636,1 210
211 44 521 9 393 931 14,5258 5,9533 2.32428 4,73934 662,88 34 966,7 211
212 44 9+4 9 528 128 14,5602 5,9627 2,32634 4,71698 666,02 35 298,9 212
213 45 369 9 663 597 14.5945 5,9721 2.32838 4,69484 669,16 35 632,7 213
214 45 796 9 800 344 14,6087 5,9814 2,33041 4,67290 672,30 35 968,1 214
215 46 225 9 9.38 375 14,6629 5,9907 2,33244 4,65116 675,44 36 306,0 215
216 46 656 10 077 696 14,6968 6,0000 2,33445 4,62963 678,58 36 643,5 216
217 47 089 10 218 313 14,7309 6,0092 2.33646 4,60829 681,73 36 963,6 217
216 47 524 10 360 232 14,7648 6,0185 2,33846 4,58716 684,87 37 325,3 218
219 47 961 10 503 459 14,7946 6,0277 2,34044 4.56621 688,01 37 668,5 219
220 48 400 10 648 000 14.8324 6.0363 2,34242 4.54545 691,15 38 013,3 220
221 48 841 10 793 861 14,8661 6,0450 2,34439 4,52489 694,29 38 359,6 231
222 49 284 10 941 048 14,8997 6,0550 2.34633 4,50450 697,43 33 707,6 222
223 49 729 11 069 567 14,9332 6.0641 2,34830 4,18-130 700,58 39 057,1 223
224 50 176 11 239 424 14,9666 6,0732 2,35025 4,46429 703,72 39 406,1 224
225 50 625 11 390 625 15,(ХИМ 6.0822 2,35218 4,44444 706,86 39 760,8 225
226 51076 11 543176 15,0333 6,0912 2,35411 4,42478 710,00 40115,0 226
227 51 529 11 697 083 15,066.5 6,1002 2,35603 4.40529 713,14 40 470.8 227
228 51 984 11 862 352 15,0997 6,1091 2,35793 4,38596 716,28 40 828,1 228
Z29 52 441 12 008 989 15,1327 6.1180 2,35984 4,35681 719,42 41 187,1 229
230 52 900 12 167 000 15,1658 6,1269 2,3617.1 4,34783 722,57 41 547,6 230
231 53 361 12 326 391 15,1987 6,1358 2,36361 4,32900 725,71 41 909,6 231
232 53 824 12 487 168 15,2315 6,1416 2,36549 4,31034 728,85 42 273,3 232
233 5-1289 12 649 337 15,2643 6,1534 2,36736 4,29185 731,99 42 638,5 233
234 54 756 12 812 904 15,2971 6,1622 2,36922 4,27350 735,13 43 005.3 234
235 55 225 12 977 875 15,3297 6,1710 2,37107 4,25532 738,27 +3 373,6 21*5
236 55 695 13 1+4 256 15.3623 6,1797 2,37291 4.23729 741,42 43 743.5 236
237 56 169 13 312 053 15,3918 6,1885 2.37475 4,21941 744,56 44 115,0 237
238 56 644 13 481 272 15,4272 6,1972 2,37658 4,20168 747,70 44 488.1 238
239 57 121 13 651 919 15,4596 6.2058 2,37840 4,18410 750,84 44 862.7 239
240 87 6U0 13 824 000 15.4919 6.2146 2,38021 4,16667 753.90 •15 238,9 240
241 58 081 13 997 521 15,5242 6,2231 2,38202 4,14938 757.12 45 616,7 241
242 58 564 14 172 488 1.5,5563 6.2317 2,38382 4,13223 760,27 43 996.1 242
243 59 049 14 348 907 15,5885 6.2-403 2,38561 4,11523 763,41 46 377,0 243
244 59 536 14 576 784 15,6205 6.2488 2,38739 4.O9R3G 766,55 46 759,5 244
245 60 025 14 706 125 . 15,6525 6,2573 2,38917 4,0816.3 769,69 47 143,5 245
246 60 516 14 886 936 15,6844 6.2658 2,39094 4,06504 772,83 47 529,2 246
247 61 009 15 069 223 15,7162 6,2743 2,39270 4,04858 775,97 47 916,4 247
244 61 504 15 252 992 15.7480 6,2823 2,39445 4,03226 779,11 48 305.1 248
249 62 001 15 433 249 15,7797 6,2912 2,39620 4,01606 782,26 48 695,5 249
250 62 500 15 625 000 15,8114 6,2996 2,39794 4,00000 785,40 49 087,4 250
КВАДРАТЫ. КУБЫ. КОРНИ, ЛОГАРИФМЫ. ОБРАТНЫЕ ВЕЛИЧИНЫ
17
251 —30)
л л» а* V п 3 У п Iff л 1000 л «Л ХЛ* 4 Л
251 252 253 254 255 256 257 258 25» 63 001 63 504 64 00» 64 516 66 025 65 536 66 049 66 564 67 081 15 813 251 16 003 008 16 194 277 16 387 064 16 581 375 16 777 216 16 974 593 17 173 512 17 373 979 15,8430 15,8745 15,9060 15,9374 15,9687 16,0000 16.0312 16,0624 16,0935 6,3080 6,3164 6,3247 6,3330 6,3413 6,3496 6,3579 6,3661 6.3743 2,39967 2,40140 2,40312 2,40483 2,40654 2.40824 2,40993 2.41162 2,41330 3,98406 З.МЗЯ 3.96257 3,93701 3,92157 3,90625 3,89106 3,87597 3,86100 788,54 791,68 794.82 797,96 801,11 804,25 807,39 810,53 813,67 49 480,9 49 875.9 50 272,6 60 670,7 51 070.5 51 471.9 51 874.8 52 279,2 52 685,3 251 252 253 254 255 256 257 258 259
260 67 600 17 576 000 16,1245 6,3825 2,41497 3,84615 816,81 53 092,9 260
261 262 263 264 266 266 267 268 269 68 121 68 644 69 169 69 696 70 225 70 756 71 289 71 824 72 361 17 779 581 17 984 728 18 191 447 18 399 744 18 609 625 18 821 096 19 034 163 19 248 832 19 465 109 16,1555 16,1864 16,2173 - 16,2481 16,2788 16,3095 16,8401 16,3707 16,4012 6,3907 6,8881 6,4070 6,4151 6,4232 6,4312 6,4393 6,4473 6,4553 2.41664 2,41830 2,41995 2,42160 2.42325 2,42488 2,42651 2,42813 2,42975 3,83142 3,81679 3,80228 3,78788 3,77358 3,75940 3.74532 3.73134 3,71747 819,96 823.19 826,24 829.38 832,52 835,66 838,81 841,96 845.09 53 502,1 53 912,9 54 325,2 54 739,1 55 154,6 55 571А 55 990.2 56 410,4 56 83222 261 262 263 264 265 266 267 268 269
270 72 900 19 683 000 16,4317 6,4633 2,43136 3,70370 848,23 57 265.5 270
271 272 273 274 275 276 277 278 279 73 441 73 984 74 52» 75 076 75 625 76176 76 729 77 284 77 841 19 902 511 20 123 648 20 346 417 20 570 824 20 796 875 21 024 576 21 253 933 21 484 952 21 717 639 16,4621 16,4924 16,5227 16,5529 16,5831 16,6132 16,6433 16,6733 16,7033 6.4713 6,4792 6,4872 6,4951 6,5030 6,5108 6,5187 6,5265 6,5343 2,43297 2,43457 2,43616 2,43776 2,43933 2,44001 2,44248 2,44404 2 44560 3,68004 3,67647 3,66300 3.64964 3.63636 3,62319 3.61011 3,59712 3.58423 851.37 854,51 857.65 860,80 863,94 867,08 870.22 873,36 876,50 57 680.4 58 106,9 58 534.9 58 964.6 59 395,7 59 828,5 60 262,8 60 693,7 61 136.2 271 272 273 274 275 276 277 278 279
280 78 400 21 952 000 16,7332 6.5421 2,44716 3,57143 879,65 61 575.2 280
281 282 283 284 285 286 287 288 289 78 961 79 524 80 089 80 656 81 225 81 796 82 369 82 944 83 521 22 188 041 22 425 768 22 665 187 22 906 304 23 149125 23 393 656 23 639 90В 23 887 872 24 137 569 16,7631 16,7929 16,8226 16.8523 16,8819 16,9115 16,9411 16,9706 17,0000 6,5499 6,5577 6,5654 6.5731 6,5306 6,5885 6.5962 6.6039 6,6115 2,44871 2,45025 2,45179 2,45332 2,45484 2,45637 2.45788 2.1Г.9Н» 2.46000 3,55872 3,54610 3,53357 3,52113 3,50877 3,49650 3.48432 3,47222 3,46021 882,79 885,93 889,07 892,21 895,35 893,50 901,64 901,78 907,92 62 0153 62 458,0 62 901.8 63 347.1 63 794,0 64 242,4 64 692,5 65 144.1 65 597.2 281 282 283 284 285 286 287 288 289
290 84 100 24 389 000 17,0294 6.6191 2,462-10 3,44828 911.06 66 052.0 290
291 292 293 294 296 296 297 296 299 84 681 85 261 85 84» 86 436 87 025 87 616 88 209 88 804 89 401 24 6-12 171 24 897 088 25 153 757 25 412 184 25 672 375 25 934 336 26 199 073 26 463 592 26 730 899 17,'.158? 17,0880 17,1172 17,1464 17,1756 17,2047 17,2337 17,2627 17,2916 6,6267 6.6343 6,641» 6.6494 6,6569 6,6644 6.6719 6,6794 6,6869 2.46389 2,46538 2,46687 2.46835 2,46982 2.47129 2,47276 2,47422 2,47567 3,43643 3,42466 3,41297 3,40136 3,38983 3,37838 3,36700 3,35570 3,34448 914,20 917,35 920,49 923,63 926,77 929,91 933,05 936,19 939.34 66 508,3 66 966,2 67 4253 67 886,7 68 349,3 68 813,4 69 279,2 69 746,5 70 215,4 291 292 293 294 296 296 297 298 299
300 90 000 27 000 000 17,3205 6,6913 2,47712 3,33333 942.48 70 6853 300
2 ТМГЕЯ^- 1464
18
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
301-350
я я» в* / п 3 } п Ign 10» л КП* 4 Я
301 90 601 27 270 9П1 17.3494 6,7018 2.47857 3.32226 945.62 71 1573 301
302 91 204 27 543 603 17.3781 6.7Г.92 2.45001 3.31125 948.76 71 631Л 302
303 91 809 27 818 127 17,4069 6.7166 2.48144 3,30033 951,90 72 105,6 303
301 92 416 28 094 461 17.4356 6.7240 2.48287 3,28М7 955,04 72 583,4 304
3® 93 025 28 372 6® 17.4642 6.7313 2.4*130 3.27869 9j8,I9 73 061,7 3®
306 93 635 28 652 616 17.4929 6,7387 2,48572 3,26797 961.33 73 541,5 303
307 94 249 28 934 443 17,5214 6.7460 2,48714 3,25733 964.47 74 023,0 307
308 94 861 29 218 112 17,5494 6,7533 2,48855 3,24675 967.61 74 566.0 3»
309 95 481 29 503 629 17,5784 6,7606 2,48996 3.23625 970,75 74 993,6 309
310 96 100 29 791 000 17,6068 6.7679 2.49135 3.2/581 973,89 75 476,8 310
311 96 721 30 080 231 17,6352 6.7752 2,49276 3.21543 977.04 75 954,5 311
312 97 344 30 371 328 17,6635 6.7824 2.49115 3.20513 980.18 76 453.8 312
313 97 969 30 664 297 17,6818 6,7897 2,49554 3,19189 983.32 76 944,7 313
314 98 596 30 959 144 17.7200 6,7969 2,49693 3,1’471 986,45 П 437,1 314
315 99 225 31 255 875 17,7482 6.SH1 2,49831 .3,17460 77 931.1 315
316 99 856 31 554 496 17,7764 6,8113 2,49969 3,16153 992.74 78 426.7 316
317 100 489 31 855 013 17.8045 6,8185 2.50106 3.15157 995.88 78 923,9 317
318 101 124 32 157 432 17.8326 6.8256 2.50243 3.14465 999.03 79 422,6 314
319 101 761 32 461 759 17.8606 6,8328 2,50379 3.13480 1002,2 79 922,9 319
320 102 400 32 768 000 17,8885 6,8399 2,60515 3.12500 1003,3 80 421Л ЗД1
321 103 041 33 076 161 17.9165 6,8470 2,!4K51 3,11526 1008.5 80 928,2 321
321 103 684 33 386 248 17.9141 6.8541 2.50786 3,10559 1011.6 81 433.2 322
323 104 329 33 698 267 17,9722 6,8612 2,50920 3,09593 1014.7 81 939,8 3/3
324 104 976 34 012 224 18.0000 6,8683 2.51055 3,08612 1017.9 82 448,0 321
325 105 625 34 328 125 18,0278 6,8753 2,51183 3.07092 1021.0 82 957,7 325
326 106 276 34 645 976 18.0655 6,8824 2,51322 3.06748 1024,2 83 469.0 326
327 106 929 34 965 783 18.0831 б.яки 2,51455 3.05810 1027.3 83 981,8 327
328 107 584 35 287 552 18,1108 6.8964 2.51587 3.04*78 1030,4 84 496.3 328
329 10S 241 35 611 289 18,1384 6.9031 2,51720 3,03951 1033,6 85 012Д 329
330 108 900 35 907 000 18,1659 6,9104 2,5185) з.азазэ 1035,7 85 5299 330
331 109 561 36 264 691 18.1931 6,9174 2.51983 3,02115 1039,9 86 049,0 331
332 110 224 36 594 368 18,2209 6.9244 2.52114 3.01205 1043,0 86 569,7 332
333 НО 884 36 926 037 18.2483 6.9313 2.52241 з.иизоо 1046,2 87 092,0 333
334 111556 37 259 704 18.2757 6.93*2 2.52375 2.99401 1049.3 87 615,9 331
333 112 225 37 595 375 15.зато 6.9451 2,52504 2,98.507 1062,4 88 1413 335
336 112 896 37 933 056 18,3303 6,9521 2,52631 2,97619 1055,6 88 668,3 336
337 113 569 38 272 753 18,3576 6.9589 2.52763 2.96736 1058,7 89 196,9 337
3-18 111244 38 614 472 18.3818 6,9658 2,52892 2.95858 1061,9 89 727,0 335
339 114 921 38 958 219 18,4120 6,9727 2,53020 2.94985 1015.0 90 258.7
340 115 600 39 304 000 18.4391 6.9795 2.53148 2,94118 1068.1 90 7923 340
341 116 281 39 651 821 18.4662 6.9864 2,53275 2,93255 1071,3 91 326,9 341
342 116 964 40 001 688 18,4932 6.9932 2.53403 2.92308 10/4,4 91 863,3 342
343 117 649 40 353 607 18,6203 7.0000 2.53529 2,91545 1077,6 92 4013 . 343
344 118 336 40 70? 584 18.5472 7,0068 2.53656 2,90898 1080.7 92 940,9 344
345 119 025 41 063 625 18.5742 7.0136 2.53782 2,89855 1043.8 93 4*2.0 345
346 119 716 41 421 736 18.6011 7.0203 2,53903 2.89017 1067,0 94 024,7 346
347 120 409 41 781 923 18,6279 7.0271 2.5 КПЗ 2.88184 1090,1 94 569,0 347
348 121 104 42 144 192 18,6548 7,0338 2,54158 2.H73S6 1093,3 96 114.9 348
349 121 801 42 508 549 18.6815 7.0406 2,54283 2,86533 1096,4 95 6623 349
350 122 600 42 875 000 | 18.7083 | 7.0473 | 2,54407 2,85714 1099.6 | 9*2113 зм
КВАДРАТЫ. КУБЫ. КОРНИ. ЛОГАРИФМЫ. ОБРАТНЫЕ ВЕЛИЧИНЫ
19
351 —400
п п1 Я* 3 тПГ !g л I Я ял жл’ 4 п
3SI 123 201 43 243 551 18.7350 7,0640 2,54631 2.МЭО0 1102.7 95 761,8 351
.152 123 901 43 614 208 18.7617 7.0607 2,54654 2.84U9I 1105.8 97 314.0 352
353 124 609 43 986 977 18,7883 7.0674 2,54777 2,83286 1109.0 97 867.7 353
354 125 316 44 361 864 18,8149 7.0740 2.54900 2,82486 1112.1 98 423.0 354
355 126 025 44 738 875 18.8414 7.0807 2.55023 2,81690 1115.3 98 979.8 355
356 126 736 45 118 016 18,8680 7.0873 2,55145 2,80899 118.4 90 538,2 356
357 127 449 45 499 293 18.8944 7.0940 2.55267 2.80112 till.5 103 0» 357
351 12Я 164 45 882 712 18,9209 7,1006 2,55388 2,79330 1124,7 100 660 зм
359 128 881 46 268 279 18,9473 7,1072 2,55509 2,78562 1127,8 101 223 359
Збо 129 600 46 656 000 18.9737 7.1133 2.65630 2,77778 1131.0 101 7ЧЧ 360
361 130 321 47 045 881 19,0000 7,1» 2,55751 2.77008 1134.1 102 351 .161
362 131 041 47 437 928 19,0263 7,1269 2,55871 2,76243 1137.3 102 922 .162
363 131 769 47 832 147 19,05'26 7.1335 2,55991 2,75482 1140.4 103 491 363
164 132 496 48 228 544 19,0788 7,1400 2,56110 2,74725 1143.5 104 062 364
.165 1X1225 48 627 125 19,1050 7,1466 2,56229 2.73873 1146.7 104 635 365
366 133 956 49 027 896 19.1311 7.1531 2,56348 2,73224 1149.8 105'200 385
367 134 689 49 «0 863 19.1572 7.1596 2,56467 2.72430 1153,0 105 785 367
368 135 424 49 836 032 19.1833 7.1661 2.6КК 2,71730 1156,1 106 162 361
369 136 161 50 243 409 19,2004 7,1726 2,56703 2.71003 1159.2 106 941 369
370 1:16 900 50 653 000 19,2.64 7.1791 2.56820 2.70270 1162,4 107 521 370
371 137 641 51 064 811 19.2614 7.1855 2,56937 2,89542 1165.5 109 103 371
372 138 384 51 478 848 19,287.3 7,1920 2,570*54 2,64817 1168,7 106 687 372
373 139 129 51 896 117 19.3132 7.1984 2.57171 2.69007 1171.8 109 272 373
374 139 876 52 313 624 19.3391 7.2048 2,57287 2,67330 1175.0 100 858 374
375 140 625 52 7.44 375 19.3649 7,2112 2,57403 2.66667 1178.1 110 447 375
376 141 376 53 157 376 19,3907 7.2177 2.S7519 2.65957 1181,2 111 006 376
377 142 129 53 582 633 19,4165 7,2240 2,57634 2.65252 1184,4 111 628 377
378 142 884 54 010 152 19.442-1 7,2304 2,57749 2.64550 1187.5 112 221 378
379 143 641 54 439 939 19.4679 7.23% 2,57861 2,63852 1190.7 112 815 379
380 144 400 54 872 000 19.4936 7,2432 2,57978 2,63158 1193.8 113 411 380
381 145 161 55 306 341 19.5192 7,2496 2,58092 2,62467 1196,9 114 009 381
382 145 924 55 742 968 19.5448 7,2558 2,58206 2,61780 1200,1 114 608 382
383 146 689 56 181 887 19.5704 7,2622 2,58320 2,61097 1203,2 115 209 383
3°4 147 456 56 623 104 19,5959 7,24555 2.58433 2,60417 1206,4 115 812 381
385 148 225 57 066 625 19.6214 7,2748 2.58546 2,59740 1209,5 116416 385 <
386 148 996 57 512 456 19,64% 7,2811 2,58659 2,59067 1212,7 117 021 386
387 149 769 57 960 603 19.6723 7,2874 2.58771 2.58398 1215.8 117 628 387
383 150 544 58 411 072 19,6977 7.29П6 2.58881 2,57732 1218,9 118 2.37 зад
389 151 321 58 8413 8<?< 19,7231 7.299!* 2,58995 2,57069 1222.1 118 847 W9
Ж 1*4 100 59 319000 19,7484 7.3061 2.59106 2,.56410 1225.2 119 459 390
391 152 881 59 776 471 19,7737 7.3124 2,59218 2,55754 1228.4 120 072 301
Ж 153 661 60 236 288 19,7990 7.3186 2,59329 2.55102 1231,5 120 687 392
S3 154 449 60 698 457 19,8242 7,3248 2.59439 2,54453 1234.6 121 301 393
391 155 236 61 162 984 19.8494 7.3310 2.59550 2,53807 1237,8 121 9Z2 391
39.5 156 025 61 629 Р5 19.8746 7.3372 2.59660 2,53165 1240,9 122 542 3!<5
396 156 816 62 099 136 19,8997 7.3434 2,59770 2,52525 1244,1 123 163 396
397 157 609 62 570 773 19.9249 7,3496 2,59879 2,51889 1247.2 123 786 397
"98 158 4(Н 63 044 792 19,9499 7ЛБ5А 2.5935» 2,51456 1250,4 124 410 3(48
399 159 201 63 521 199 19.9750 7.3619 2,60097 2.50627 1253,5 125 096 :В9
<00 160 000 64 000 000 20.0000 7.3631 2.6U206 2,50000 1256.6 125 664 400
20
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
401—450
- п 1 Л* Л* V' п • 3 Ул |£ л 1000 л хД УЛ* 4 Л
401 160 801 64 481 201 20,0250 7,3742 2,60314 2,49377 1259,8 126 293 401
402 161 604 61 964 808 20,0499 7,3803 2,60423 2.48756 1262,9 126 923 402
403 162 409 65 450 827 20.0749 7,3864 2,60531 2,48139 1266.1 127 556 403
404 163 216 65 939 264 20,0998 7,3925 2,60638 2,47525 1269,2 128 190 404
405 164 025 66 430 125 20,1246 7.3996 2.60746 2.46914 1272,3 128 825 406
406 164 836 66 923 416 20,1494 7,4047 2.60853 2,46306 1275,5 129 462 406
407 165 649 67 419 143 20.1742 7,4108 2,60959 2,45700 1278,6 130 100 407
403 166 461 67 917 312 20,1990 7.4169 2,61066 2,45098 1281,8 130 741 408
409 4 167 281 68 417 929 20.2237 7,4229 2,61172 2.44499 1284,9 131 382 409
410 168 100 68 921 000 20.2485 7,4290 2,61278 2.43902 1288,1 132 ОН 410
411 168 921 69 426 531 20.2731 7,4350 2,61384 2.43309 1291,2 132 670 411
412 169 744 69 934 528 20,2978 7,4410 2.61490 2,42718 1294.3 133 317 412
413 170 669 70 444 997 20,3224 7,4470 2,61595 2.42131 1297,5 133 965 413
414 171 396 70 957 944 20,3470 7,4530 2,61700 2,41546 1300,6 134 614 414
415 172 225 71 473 375 20,3715 7,4590 2,61806 2,40964 1303,8 135 265 415
416 173 066 71 991 296 20.3961 7,4650 2,61909 2,40385 1306,9 135 918 416
. 417 173 889 72 511 713 20,4206 7,4710 2,62014 2,39806 1310.0 136 572 417
418 174 724 73 034 632 20,4450 7,4770 2,62118 2,3923-1 1313.2 137 228 418
419 175 561 73 560 059 20,4695 7.4829 2,62221 2,38663 1316,3 137 885 419
420 176 400 74 088 000 20,4939 7,4889 2,62325 2,38095 1319,5 138 544 420
421 177 241 74 618 461 20.5183 7,4948 2,62428 2.37530 1322.6 139 206 421
422 178 084 75 151 448 20.5426 7,5007 2,62531 2,36967 1325.8 139 867 422
423 178 929 75 686 967 20.5670 7.5067 2,62634 2.36407 1328.9 140 531 423
424 179 776 76 225 024 20,5913 7,5126 2.62737 2.35849 1332.0 141 196 424
425 180 625 76 765 625 20,6155 7,5185 2,62839 2,35294 1335,2 141 863 425
426 181 476 77 308 776 20,6398 7,5244 2,62941 2,34742 1338.3 142 531 426
427 182 329 77 854 483 20,6640 7,5302 2,63043 2,34192 1341,5 143 201 427
4’78 183 1М 78 407 752 20,6882 7.5361 2,63144 2,33645 1344,6 143 812 428
429 184 041 78 953 589 20,7123 7,5420 2,63246 2,33100 1347,7 144 545 429
430 184 900 79 507 000 20.7364 7.5478 2,63347 2.32558 1350.9 145 220 430
431 185 761 80 062 991 20,7605 7,5537 2,63448 2,32019 1354,0 145 896 431
432 186 624 80 621 568 20.7846 7.5596 2,63548 2,31481 1357.2 146 574 432
433 187 489 81 182 737 20,8087 7,5654 2,63649 2,30947 1360,3 147 254 433
434 188 356 81 746 504 20,832) 7,5712 2,63749 2,30415 1363,5 147 934 434
435 189 225 82 312 875 20,8567 7,5770 2,63849 2.29885 1366,6 148 617 436
436 190 096 82 881 856 20,8806 7,5828 2,63949 2,29358 1369,7 149 301 436
437 190 569 83 453 453 20.9045 7,5886 2,64048 2,28833 1372,9 149 987 437
438 191 844 84 027 672 20.9284 7.5944 2,64147 2,28311 1376,0 150 674 438
439 192 721 8-4 604 519 20.9523 7,6001 2,64246 2,27790 1379,2 151 363 439
440 193 600 85 184 000 20,9762 7,6059 2,64345 2.27273 1382,3 152 063 440
441 194 481 85 766 121 21,0000 76,117 2,64444 2,26757 1385,4 152 745 441
442 195 364 86 350 888 21.0238 76,174 2,64.542 2.26244 1388,6 153 439 442
443 196 249 86 938 307 21,0476 7,6232 2,64640 2,25734 1391,7 154 134 443
444 197 136 87 528 384 21.0713 7,6289 2,64738 2,25225 1394,9 154 830 444
445 198 025 88 121 125 21.0950 7,6346 2,64836 2,24719 1398.0 155 528 445
446 198 916 88 716 536 21,1187 7,6403 2,64933 2,24215 1401.2 156 228 446
447 199 809 89 314 623 21,1424 7,6460 2,65031 2,23714 1404,3 156 930 447
443 200 704 89 915 392 21,1660 7,6517 2,65128 2,23214 1407,4 157 633 448
449 201 601 90 518 849 21,1896 7,6574 2,65225 2,22717 1410,6 158 337 449
450 202 500 91 128 000 21,2132 7,6631 2,65321 2,22222 1413.7 159 043 450
КВАДРАТЫ, КУВЫ, КОРНИ, ЛОГАРИФМЫ. ОБРАТНЫЕ ВЕЛИЧИНЫ
24
451 —500
IB Д’ Я* п 3 V п 1g л 1000 л «Л ад’ т п
451 203 401 91 733 851 21,2368 7,6688 2.65418 2,21729 1416,9 I 159 751 451
4К2 204 304 92 345 403 21,2603 7,6744 2,65514 2.21239 1420,0 160 460 462
453 206 209 92 969 677 21,2838 7,6801 2.65610 2.20751 1423,1 161 171 453
454 206 116 93 576 664 21,3073 7,6857 2,65706 2,20264 1426,3 161 883 454
455 207 025 94 196 375 21,3307 7,6914 2,65801 2,19780 1429,4 162 597 455
456 207 936 94 818 816 21.3542 7,6970 2.65896 2,19298 1432,6 163 313 456
457 203 819 95 443 993 21,3776 7,7026 2.65992 2,18818 1435,7 164 030 457
458 209 764 96 071 912 21,4009 7,7082 2,66087 2,18341 1434,8 164 748 458
459 210 681 96 702 579 21,4243 7.7138 2,66181 2.17865 1442.0 165 468 459
460 211 600 97 336 000 21,4476 7,7194 2,66276 2,17391 1445.1 166 190 460
461 212 521 97 972 181 21,4709 7,7250 2,66370 2,16920 1448,3 166 914 461
462 213 444 98 611 128 21.4942 7,7306 2,66464 2,16450 1451,4 167 639 462
463 214 369 99 252 847 21,5174 7,7362 2,66558 2,15933 1454,6 168 365 463
461 215 296 99 897 344 21,5407 7,7418 2,66652 2,15517 1457,7 169 093 464
465 216 225 100 544 625 21,5639 7,7473 2,66745 2.15054 1460,8 169 823 465
466 217 156 101 194 696 21,5870 7,7529 2,66839 2,14592 1464.0 170 55-1 466
467 218 089 101 847 563 21.6102 7,7584 2,66932 2,14133 1467,1 171 287 467
463 219 024 102 503 232 21,6333 7,7639 2,67025 2,1.3675 1470.3 172 021 468
469 219 961 103 161 709 21.6564 7.7695 2,67117 2,13220 1473,4 172 757 469
470 220 900 103 823 000 21,6795 7,7750 2,67210 2,12766 1476,5 173 494 470
471 221 841 104 487 111 21,7025 7,7805 2.67.302 2.12314 1479,7 174 234 471
47-1 222 78-1 105 154 048 21,7256 7,7860 2,67.394 ’ 2,11864 1482,8 174 974 472
473 223 729 105 823 817 21,7486 7,7915 2,67486 2.11416 1485,0 175 716 473
474 224 676 106 496 424 21,7715 7.7970 2,67578 2,10970 1489,1 176 460 474
475 225 625 107 1 71 875 21,7915 7.8025 2,67669 2,10526 1492,3 177 205 475
476 226 576 107 850 176 21,8174 7,8079 2,67761 2,10084 1495,4 177 952 476
477 227 529 108 531 333 21.8403 7.8134 2,67852 2,09644 1498,5 178 701 477
478 228 484 109 215 352 21,8632 7,8188 2,67943 2.09206 1501,7 179 451 478
479 229 441 109 902 239 21,8861 7.8213 2,68084 2.0В76Я 1504.8 180 200 479
480 230 400 ПО 592 000 21,9069 7,8297 2,68124 2,08333 1503,0 180 956 480
481 231 36) 111 284 641 21,9317 7,8352 2,68215 2,07900 15И.1 181 711 481
482 232 324 111 980 168 21,9645 7,8406 2.68305 2,07469 1514,2 182 467 482
483 233 289 112 678 597 21,9773 7,8460 2,68385 2.О7ОЗЭ 1517,4 183 225 483
484 234 256 113 379 904 22,0000 7,8514 2,68485 2,06612 1520,5 183 984 484
485 235 225 114 084 125 22,0227 7.8568 2,68574 2,06186 1523,7 184 745 485
486 236 196 114 791 256 22,0454 7.8622 2.68664 2,05761 1526,8 18W506 486
487 237 169 115 501 303 22.0681 7,8676 2,68753 2,05339 1530,0 186 272 487
488 238 144 116 214 272 22,0907 7,8730, 2,68842 2,04918 1533,1 1Я7 038 484
489 239 121 116 930 169 22,1133 7.8784 2,68931 2,04499 1536,2 187 806 489
490 240 100 117 649 000 22,1359 7,8837 2,69020 2,04062 1539,4 188 574 490
491 241 081 118 370 771 22,1585 7.8891 2,69108 2,03666 1542,5 189 345 491
492 242 064 119 095 488 22,1811 7,8944 2,69197 2,03252 1545,7 190 117 492
493 243 049 119 823 157 22,2036 7,8998 2,69285 2,02840 1548,8 190 890 493
494 244 036 120 553 784 22,2261 7.9051 2.69373 2,02429 1551.9 191 665 491
495 245 025 121 287 375 22.2486 7,9105 2,69461 2,02020 1555,1 192 442 495
496 246 016 122 023 936 22.2711 7.9158 2,69648 2,01613 1558,2 193 221 496
497 247 009 122 763 473 22,2935 7,9211 2,69636 2,01207 1561.4 194 000 497
498 248 004 123 505 99-2 22,3159 7,9264 2,69723 2,00803 1564,5 194 782 498
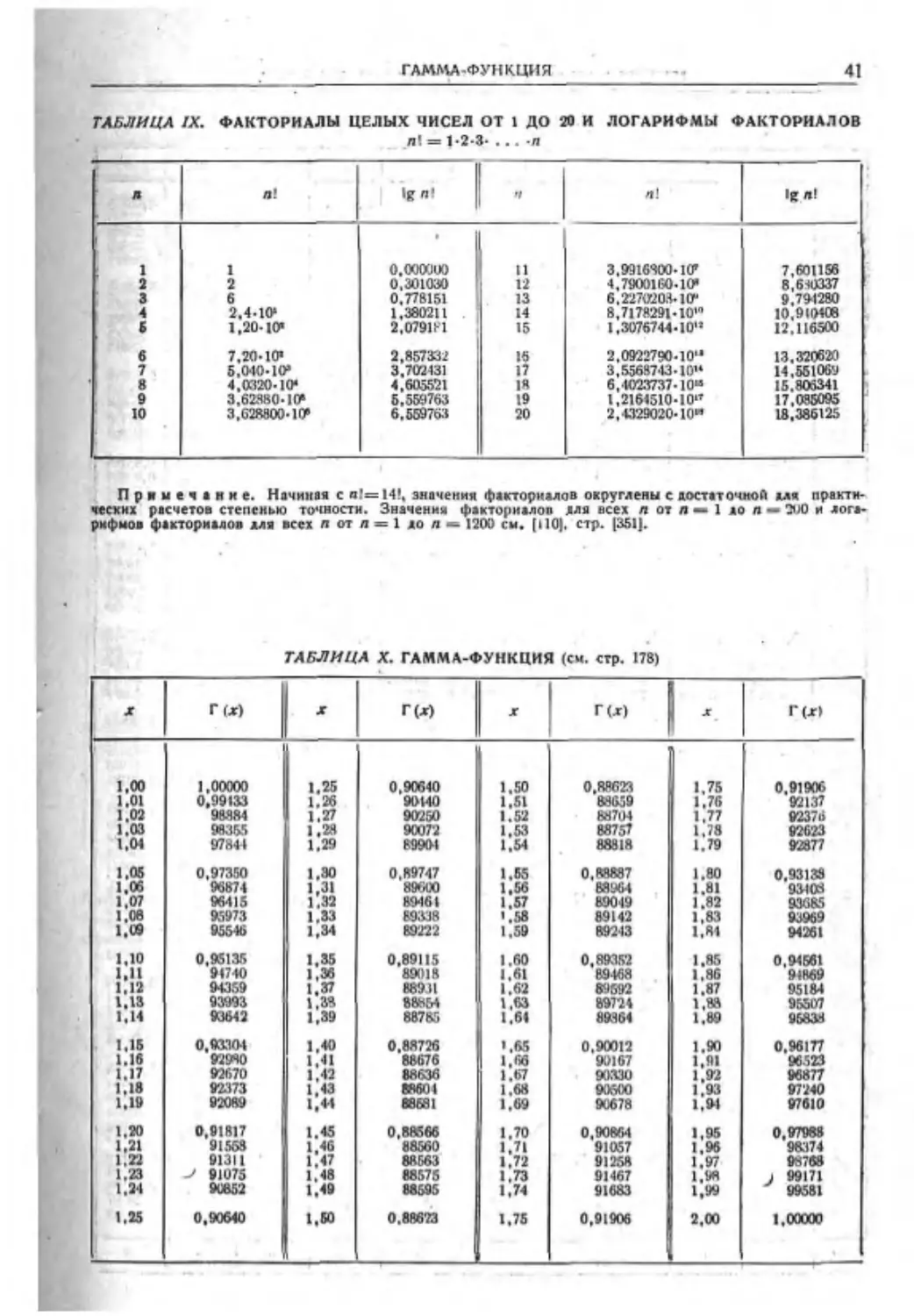
499 249 001 124 251 499 22,3383 7.9317 2,69810 2.00401 1567,7 195 565 499
500 250 000 125 000 000 22.3607 7,9370 2,69897 2,00000 1570,8 196 350' МО
22
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
501 —550
Л л» п* / Л 3 V н~ 1g Л 1000 Л Т.л «п* 4 Л
501 251 001 125 751 501 22,3830 7,9423 2.69984 1.99601 1573,9 197 136 501
502 252 004 126 506 ООН 22,4051 7.9-176 2.70070 1.99203 1577,1 197 923 502
503 253 00» 127 263 527 22,4277 7,9628 2,70157 1,98807 1580.2 193 713 501
504 25-1016 128 024 06-1 22,4499 7,9581 2.70243 1.98413 1583.4 199 504 504
505 255 025 128 787 625 22,4722 7,963*1 2,70329 1,98020 1586.5 200 296 605
506 256 036 129 554 216 22,49-14 7,9686 2,70415 1,97628 1589.6 201 090 505
507 257 049 130 323 843 22,5167 7,9739 2,70501 1.97239 1592.8 201 886 507
509 258 064 131 <195 512 22,5389 7,9791 2,70586 1.96659 1595.9 202 683 508
509 259 081 131 т 229 22,6610 7.9843 7,7'4*72 1.96464 1599,1 203 482 509
510 260 100 132 6S1 ООО | 22,5832 7,9896 | 2,70757 1,96078 1602,2 204 282 510
511 261 121 133 432 831 22,6053 7.9948 2,70842 1.93695 1605.4 205 ОМ 511
512 262 144 134 217 728 22,6274 8.0000 2,70927 1,95312 1608,5 205 887 512
513 263 169 135 005 697 22,6495 8,0052 2.71012 1.94932 1611,6 206 692 513
514 264 196 135 795 744 22,6716 8,0104 2,71096 1.94551 1614.3 207 499 514
515 265 225 136 590 875 22,6936 8,0156 2.71181 1,94175 1617.9 208 307 515
516 266 256 137 388 096 22,7156 8,0208 2,71265 1,93793 1621.1 209117 516
517 267 28» 138 188 413 22,7376 8.0260 2.71349 1.93424 1624,2 209 923 517
518 268 324 138 991 832 22,7595 8,0311 2.71433 1.93060 1627,3 210 741 518
519 269 361 139 798 359 22,7816 8,0363 2,71517 1,92378 1630,5 211 556 519 *
520 270 400 140 608 000 22,8035 8,0415 2,71600 1,92306 1633.6 212 372 520
521 271 441 141 420 761 22.825*1 8,0466 2,71684 1.91939 1636,8 213 189 521
522 272 481 142 236 648 22,8473 8,0517 2,71767 1,91571 1639.» 214 004 522
523 273 529 143 065 667 22,8692 8,0569 2,71850 1,91205 1643,1 214 829 523
524 274 576 143 877 824 22,8910 8,0620 2,719143 1,908*10 1646,2 215 651 524
525 275 625 144 703 125 22,9129 8.0671 2,72016 1,90176 1649.3 216 475 525
526 276 676 145 531 576 22,9347 8.0723 2.72099 1,90114 165'2.5 217 301 526
527 277 729 146 363 183 22,9565 8,0774 2,72181 1.89753 1655,6 218 124 527
525 274 784 147 197 952 22,9783 8,0825 2.72263 1,89391 1659.8 218 956 528
529 279 841 148 03.5 889 23,0000 8,0876 2,72345 1,89036 1661,9 219 787 529
330 2S0 900 148 877 000 23,0217 8,0927 2,72428 1.8867» 1665,0 220 618 530
531 281 961 149 721 2»! 23,0434 8,0978 2,72509 1,83324 1669,2 221 *152 531
532 2S3 021 150 568 768 23,0651 8.1028 2,72591 1,87970 1671,3 222 237 532
533 284 (Ю9 151 419 437 23,0868 8.1079 2,72673 1,87617 1674,5 223 123 533
534 2.85 156 152 273 304 23,1084 8,1130 2,72754 1,87266 1677,6 223 931 534
535 286 225 1.53 130 375 23,1301 23,1517 8,1180 2,72835 1,86916 1690,8 224 801 535
535 287 296 153 999 656 8,1231 2,72916 1,86567 1683,9 225 М2 536
537 268 369 154 854 153 23.1733 8.1281 2,72997 1.86220 1697,0 226 484 537
538 289 444 155 720 872 23,1948 8.13И 2,73078 1,85874 1690,2 227 ,329 538
53» 290 521 156 590 81» 23,2164 8.1382 2,73159 1.85529 1693,3 228 175 539
540 291 600 157 464 18X1 23,2379 8,1433 2.73239 1.85185 1696,5 229 022 5-Ю
541 292 681 158 340 421 23,2594 8,1483 2,73320 1,81843 1699,6 229 871 5-И
542 291 764 159 220088 23,280» 8,1533 2.73100 1.34502 1702.7 230 722 542
543 294 849 160 103 007 23,3024 8,1583 2,73180 1,94162 1705,» 231 574 543
544 295 936 160 989 НИ 23,3238 8.1633 2,73560 1.83324 1709.0 232 428 544
545 297 025 161 878 625 23.3452 8,1693 2,73610 1,83186 1712,2 233 283 515
546 298 116 162 771 336 23,3666 8.1733 2.73719 1,83150 1715,3 234 140 546
547 29» 269 163 667 323 23,3880 8,1783 2.73799 1.82915 1718,5 234 99Н 547
548 300 304 164 566 592 23,4094 8.1К13 2.73878 1.82482 1721.6 235 858 548
М9 301 401 165 469 149 23.4307 8.1882 2,73957 1.82149 1724,7 236 720 549
550 302 500 166 375 00Э 23,4521 8.1932 2,74036 1.81818 1727,9 237 583 550
КВАДРАТЫ. КУБЫ. КОРНИ. ЛОГАРИФМЫ. ОБРАТНЫЕ ВЕЛИЧИНЫ
23
55J - 600
а л* п* Ул 3 V п 1g л 1000 л «л1 4 Я
551 303 601 167 284 151 23,4734 8,1962 2,74115 1,81488 1731,0 238 448 551
552 304 704 168 196 608 23,4947 8,2031 2,74194 1,81159 173-1,2 239 314 552
553 305 809 169 112 377 23,5160 8,2081 2.74273 1,80832 1737.3 240 182 553
554 306 916 170 031 464 23,5372 8,2130 2,74351 1,80505 1740,4 241 051 554
555 303 025 170 953 875 23,5584 8,2180 2,74429 1.80180 1743,6 241 922 555
556 309 13G 171 879 616 23,5797 8,2229 2.74507 1,79356 1746.7 242 795 556
557 310 249 172 808 693 23,6008 8,2278 2.74586 1.79533 1749,9 243 669 557
558 311 364 173 741 112 23,6220 8.2327 2.74663 1,79211 1753,0 244 545 558
559 312 481 174 676 879 23,6432 8,2377 2,74741 1.78891 1756,2 245 422 559
560 313 600 175616 000 23,6643 8,2426 2,74819 1,78571 1759,3 246 301 660
561 314 721 176 558 481 23,6854 8,2475 2,74395 1,7825-3 1762,4 247 181 561
562 315 844 177 504 328 23,7065 8,2524 2,74974 1,77935 1765,6 248 063 562
563 316 959 178 453 547 23,7276 8,2573 2,75051 1.77620 1768,7 248 947 563
564 318 096 179 496 144 23,7487 8,2621 2,75128 1,77305 1771,9 249 832 554
565 319 225 180 362 125 23,7697 8,2670 2,75205 1,76991 1775,0 250 719 555
566 320 356 181 321 496 23,7908 8,2719 2,75282 1,76678 1778,1 251 607 566
567 321 489 182 284 263 23,8118 8,2768 2,75358 1.76367 1781,3 252 497 567
568 322 624 183 250 432 23,8328 8,2816 2,75435 1,76056 1784,4 253 388 568
569 323 761 184 220 009 23,8537 8,2865 2,75511 1.75747 1787,6 254 281 569
570 3*4 900 185 193 000 23,8747 8.2913 2.75587 1.75439 1790,7 255 176 570
571 326 041 186 169 411 23.8956 8,2962 2,75664 1,75131 1793,8 256 072 571
572 327 184 187 149 248 23,9165 8,3010 2,75740 1,74825 1797,0 256 970 572
573 328 329 188 132 517 23,9374 8.3059 2,75815 1,74520 1800,1 257 869 573
574 329 476 189 119 224 23,9583 8.3107 2.75891 1,74216 1803,3 258 770 574
575 330 625 193 109 375 23.9792 8,3155 2,75967 1.73913 1806,4 259 672 575
576 331 776 191 102 976 24,0000 8.3203 2.76042 1.73611 1809,6 260 576 575
677 332 929 192 100 033 24,0208 8,3251 2.76118 1,73310 1812,7 261 482 577
57В 33-4 084 193 100 552 24.0416 8.3300 2,76193 1.73010 1815,8 262 ЗН9 578
579 335 241 194 104 539 24,0624 8.3348 2,76'268 1,72712 1819,0 263 298 579
580 336 400 195 112 000 24,0832 8,3393 2,76343 1,72414 1822,1 264 208 580
681 337 561 19S 122 941 24,1039 8,3443 2,76418 1,72117 1825,3 265 120 581
682 334 724 197 137 368 24,1217 8,3191 2.76492 1,71821 1828,4 266 033 582
683 339 889 193 155 287 24,1454 8,3539 2,76567 1,71527 1831,6 266 948 583
584 341 056 199 176 704 24,1661 8,3587 2.76641 1,71233 1834,7 267 865 58-1
5Я5 342 226 200 201 625 24.1868 8,3631 2.76716 1.70910 1837,8 268 783 585
586 343 396 201 230 056 24.2074 8,3682 2,76790 1.70548 1841.0 269 703 586
587 344 569 202 262 0И 24,2281 8.3730 2,76864 1.70358 1844,1 270 624 587
588 345 744 203 297 472 24,2487 8,3777 2.76933 1.70068 1847.3 271 547 588
589 346 921 204 316 469 24,2693 8,3825 2.77012 1.69779 1850.4 272 471 589
590 848 100 205 379 000 24,2899 8,3972 2,77085 1.69492 1853,5 из W 590
591 349 281 206 425 071 24,3105 8,3919 2.77159 1.69205 1856,7 274 325 591
592 350 464 207 474 688 21,3311 8,3917 2,77232 1.68919 1859,8 275 254 592
593 351 649 208 527 857 24,3516 8,4014 2,77305 1,68634 1863,0 276 181 593
SSM 352 836 209 584 584 24,3721 а, 4061 2,77379 1,68310 1866,1 277 117 591
595 354 025 210 644 875 24,3926 8,4108 2,77452 1,68067 1869,2 278 051 595
596 355 216 211 708 736 24,4131 8,4155 2,77525 1,67785 1872,4 278 986 596
597 356 409 212 776 173 24,4336 8,4202 2.77597 1,6750-1 1875,5 279 923 597
598 357 604 213 847 192 24.4540 8,4249 2,77670 1.67224 1878,7 280 862 598
599 358 801 214 921 799 24.47-15 8,4296 2.77743 1.66945 1881,8 281 802 599
600 360 000 216 000 000 24,4919 8.4313 2,77815 1,66667 1885.0 | 232 743 | 600
24
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
601—650
Л л* л4 Уп , 3 If Л 1000 Г л *л жЛ* 4 Л
601 861 201 217 081 801 24,5153 8,4390 2;77887 1,66389 1888,Г 283 687 601
602 362 404 218 167 208 24,5357 8,4437 2,77960 1,66113 1891,2 284 631 602
603 363 609 219 256 227 24,5661 8.4484 2.78032 1,65837 1894.4 286 578 603
604 364 816 220 348 864 24,5764 8,4530' 2.78104 1.65563 1897.5 286 526 604
605 366 025 221 445 125 24,5967 8,4577 2.78176 1,65289 1900,7 287 475 605
606 367 236 222 545 016 24.6171 8,4623 2.78247 1,65017 1903,8 288 426 606
607 366 449 223 648 543 24,6374 8,4670' 2.78319 1,64745 1906.9 289 379 807
606 369 664 224 755 712 24,6577 8.4716 2.78390 1.64474 1910.1 290 333 608
600 ПО ОМ 225 866 529 24.6779 8,4763 2.78462 1,64204 1913.2 291 289 609
610 372 100 226 981 000 24.6982 8,4809 2,78533 1.63934 1916,4 292 247 610
611 373 321 228 099 131 24.7184 8.4856 2.78604 1,63666 1919,5 293 206 611
612 374 544 229 220 928 24,7396 8,4902 2.78675 1,63399 1922.7 294 166 612
613 375 769 230 346 397 24,7588 8.4943 2.78746 1,63132 1925,8 295 128 613
614 376 996 231 475 544 24,7790 8,4994 2,78817 1,62866 1928,9 296 092 614
615 378 225 232 608 375 24.7992 8,5040 2,78888 1,62602 1932.1 297 057 615
616 379 456 233 744 896 24,8193 8,5086 2,78958 1,62338 1935.2 29В 024 616
617 380 689 234 885 ИЗ 24,8395 8,5132 2.79029 1.62075 1938,4 298 992 617
618 381 924 236 029 032 24,8595 8,5178 2.79099 1,61812 1941.5 299 962 618
619 383 161 237 176 659 24,8797 8.5224 2.79169 1,61551 1944.6 300 931 619
630 384 400 238 328000 24,8993 8.5270 2.79239 1,61290 ‘ 1947,8 301907 620
621 385 641 239 483 061 24,9199 8,5316 2,79309 1,61031 1950,9 302 882 621
622 386 884 240 641 848 24,9399 8.5362 2.79379 1.60772 1954,1 303 858 622
623 388 129 241 804 367 24,9600 8.5408 2.79449 1,60514 1957,2 304 836 623
624 389 376 242 970 624 24.9800 8.5453 2.79518 1,60256 1960.4 306 815 624
625 390 625 244 140 625 25,0000 8.5499 2,79588 1.60000 1963,6 306 796 625
636 391 676 245 314 376 25,0200 8.5544 2,79657 1,59744 1966.6 307 779 626
627 393 129 246 491 883 25,0400 8,5590 2,79727 1,59490 1969,8 308 763 627
628 394 384 247 673 152 25,0599 8,5635 2,79796 1,59236 1972.9 309 748 62»
629 395 641 248 858 189 25,0799 8,5681 2,79865 1.58983 1976.1 310 736 629
630 396 900 250 047 000 25.0998 8.5726 2.7993-1 1.58730 1979,2 311725 630
631 398 161 251 239 591 25,1197 8.5772 2,80003 1,58479 1982,3 312 715 631
63-2 399 424 252 435 968 25,1396 8,5817 2.80072 1,58228 1985,5 313 707 632
633 400 689 253 636 137 25,1595 8,5862 2,80140 1,57978 1938,6 314 700 633
634 401 966 254 840 104 25,1794 8,5907 2; 80009 1,57729 1991,8 315 696 634
635 403 225 256 047 875 25,1992 8,5952 2,80277 1,57480 1994,9 316 692 63.5
636 404 496 257 259 456 25,2190 8.5997 2.80346 1,57233 1998,1 317 690 636
637 406 769 258 474 853 25,2389 8.6043 2,80(14 1,56966 2001,2 318 690 637
633 407 044 259 694 07 2 25,2587 в.вдая 2,80482 1,56740 2004.3 319 692 634
639 408 321 260 917 119 25.2784 8.6132 2.80550 1.66495 2007,5 320 695 639
640 409 600 262 144 000 25,2962 8,6177 ' 2.80618 1,56250 2010,6 321 699 | 640
641 410 881 263 374 721 25.3180 8.6222 2.80686 1,66006 2013,8 322 705 641
642 412 164 264 609 28» 25.3377 8.6267 2,80754 1.55763 2016,9 323 713 642
643 413 449 265 847 707 25.3574 8,6312 2,80821 1,55521 2020,0 324 722 643
644 1 414 736 267 089 984 25,3772 8.6357 2,80889 1,55280 2023,2 325 733 644
645 416 025 268 336 125 25.3969 8,6401 2.80956 1,55039 2026,3 326 745 645
646 417 316 269 586 136 25,4165 8.6446 2,81023 1,54799 2029,5 327 759 646
647 418 609 270 840 023 25,4362 8,6490 2,81090 1.54560 2032,6 328 775 647
М8 419 901 272 097 792 25,4558 8.6535 2,81458 1.54321 2035.8 329 792 648
649 421 201 273 359 449 25,4755 8,6579 2,81224 1,54083 2038,9 330 810 649
1 <22 500 274 625 000 25,4961 8,6624 2,81291 1.53846 | 9042,0 331 831 660
КВАДРАТЫ. КУБЫ. КОРНИ, ЛОГАРИФМЫ. ОБРАТНЫЕ ВЕЛИЧИНЫ
25
631—700
п . lit. л* /л 3 /т 1g Л 1(ХЮ п КП “Г- 4 Л
661 423 801 275 89-1 451 25,5147 8,6668 2,81358 1,53610 2045,2 332 853 651
652 425 104 277 167 808 25.5343 8,6713 2,81425 1,53374 2048.3 333 876 652
653 426 409 278 445 077 25.5539 8,6757 2,81491 1.53139 2051,5 334 901 653
654 427 716 279 726 264 25,5734 8,6801 2,81558 1,52905 2054,6 335 927 654
655 429 025 281 011 375 25.5930 8,6845 2,81624 1,52672 2057,7 336 955 655
656 4-30 336 282 300 416 25,6125 8,6890 2.81690 1.52439 2060,9 337 965 666
657 431 649 283 593 383 25,6320 8,6934 2,81757 1,52207 2064,0 339 016 657
6М 432 964 284 890 312 25.6515 8,6978 2,81823 1,51976 2067.2 340 049 658
659 434 281 286191 179 25,6710 8,7022 2,81889 1,51745 2070.3 341 084 659
660 435 600 287 496 000 25.6906 8,7066 2,81954 1,51515 2073,5 342 1.19 660
661 436 921 288 ЙМ 781 25,7099 8,7110 2,82020 1,51286 2076,6 343 157 661
662 438 244 290 117 528 25,7294 8,7154 2,82066 1,51067 2079,7 344 196 662
663 439 569 291 434 247 25,7488 8,7198 2,82151 1,50830 2082,9 345 237 663
664 440 896 292 7.54 944 25,7682 8.7241 2,82217 1,50602 2096,0 346 279 661
66.5 442 225 291 079 625 25,7876 8.7285 2,82282 1,50376 2089,2 347 323 665
666 443 556 296 408 296 25,8070 8,7.329 2.82347 1,50160 2092.3 348 368 666
667 444 889 296 740 933 25,8263 8,7373 2,82413 1,49925 2095,4 349 415 667
668 446 224 298 077 632 25,8457 8,7416 2,82478 1,49701 2098.6 350 461 668
669 447 561 299 418 309 25.8650 8,7460 2.82543 1,49477 2101,7 351 514 669
670 448 900 300 763 000 25,8844 8.7.503 2.82607 1,49254 2104,9 352 565 670
671 450 241 302 111 711 25,9037 8,7547 2,82672 1,49031 210S.0 353 618 671
672 451 584 303 464 448 25,9230 8,7590 2,82737 1.48810 2111.2 354 673 672
673 452 929 304 821 217 25.9422 8,7634 2,82802 1,49598 2114,3 355 730 673
674 454 276 306 182 024 25,9615 8,7677 2,82866 1,49368 2117.4 366 788 674
67b 455 625 307 546 875 25.9808 8,7721 2,829й> 1,49148 2120,6 357 847 675
676 456 976 308 915 776 26.0000 8,7764 2,82995 1,47929 2123,7 358 908 676
677 458 329 310 288 733 26,0192 8,7807 2,83059 1,47710 2126,9 359 971 677
678 459 684 311 665 752 26,0384 8,7850 2,83123 1,47493 2130,0 361 035 678
679 461 041 313 046 839 26,0676 8,7883 2,83187 1,47275 2133,1 362 101 679
680 462 400 314 432 000 98.QNB 8.7937 2,83251 1,47059 2136.3 363 168 680
681 463 761 315 821 241 26,0960 8,7980 2,83315 1,46843 2139,4 364 237 681
682 463 124 317 214 568 26,1151 8,8021 2,83378 1,46629 2142,6 365 308 682
683 466 489 318 611 987 26,1343 8,8066 2,83442 1,46413 2145,7 366 380 683
684 467 856 320 013 6OI 26,1534 8,8109 2,83506 1,46199 2118,8 367 453 684
6В5 469 225 321 419 125 26,1725 8,8152 2,83569 1,45985 2152,0 368 528 685
№6 470 596 322 828 856 26,1916 8,8194 2,83632 1,45773 2155,1 369 605 686
687 471 969 324 242 703 26.2107 8,8237 2,83696 1,45560 2158,3 370 684 687
6KS 473 344 325 660 672 26.2298 8.8280 2,83759 1,45349 2161,4 371 764 688
689 474 721 327 082 769 26.2488 8,8323 2,83822 1,45138 2164,6 372 815 689
690 476 100 328 509 000 26.2679 | 8,8366 2,81885 1,44928 | 2167,7 373 928 690
681 477 48) 329 939 371 26,2869 8,8408 2,83948 1,44718 2170,8 375 013 691
478 864 331 373 888 26,3059 8,3451 8,8493 2,84011 1,44509 2174,0 376 099 692
693 480 249 332 812 557 26,3249 2,84073 1,44300 2177,1 377 187 093
6SH 481 636 334 255 384 26,3439 8,8536 2,84136 1,44092 2180,3 378 276 «И
6% 483 025 335 702 375 26,3629 8,8576 2,84198 1,43885 2183,4 379 367 695
а«5 484 416 337 153 536 26,3818 8,8621 2.84261 1.43678 2186,5 380 459 696
697 485 809 338 608 873 26,4008 8,8661 2,843'23 1,43172 2189,7 381 553 697
698 487 204 340 068 392 26.4197 8,8706 2,84396 1,43266 2192,8 382 649 698
699 483 601 341 532 099 26,4386 8,8748 2,84448 1,43062 2196,0 383 746 1 699
700 «0000 343 000 000 26,4575 8,8790 2,84510 1,42857 2199,1 384 845 700
26
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
701—750
Л Л1 Л* /7 3 Ул 1g л 1000 л г.л ял» 4 Л
701 491 401 3-44 472 101 26,4764 8,8833 2.84572 1.42653 2202,3 385 945 701
702 492 804 315 918 408 26,4953 8.8875 2,8841 1,42450 2205,4 387 047 702
703 494 209 347 428 927 26.5141 8,8917 2.84695 1,42248 2208.5 388 151 703
7<М 495 616 348 913 664 •26,5330 8,8959 2,84757 1,42045 2211,7 389 256 704
70S 497 025 350 102 625 26,5518 8,9001 2,84819 1.41741 2214,8 393 363 705
706 498 436 351 896 816 26.5707 8,9043 2,84880 1,41643 2218,0 391 471 706
707 499 849 353 3№1 243 25,5995 8,9085 2,84912 1,41443 2221,1 392 580 707
708 501 264 354 894 912 26.6083 8,9127 2,8601И 1,41243 2224,2 393 692 708
709 502 681 356 400 829 26,6271 8,9169 2,85065 1.41044 2227,4 394 805 709
710 504 100 357 911 000 26,6458 8.9211 2,851’26 1,40845 2230,5 395 919 710
711 506 521 359 425 431 26,6646 8.9253 2.85187 1,40647 2233,7 397 035 711
712 505 944 360 944 128 26,6333 8,9295 2.85248 1,40449 2236,8 398 153 712
713 ми Э69 362 467 097 26,7021 8.9337 2,85309 1,40252 2240,0 399 272 713
714 509 796 363 994 344 26,7208 8.9378 2.85370 1,40056 2243,1 400 393 714
715 511 225 365 525 875 26.7395 8.9420 2.85431 1..39860 2246,2 401 515 715
716 512 656 367 061 696 26,7582 8.9.162 2.85491 1,39365 2249,4 402 639 716
717 514 089 369 601 813 26.7769 8,9503 2.85552 1,39470 2252,5 403 765 717
718 515 524 370 146 232 26,7955 8,9545 2,85612 1,39276 2255,7 404 892 718
719 516 951 371 694 959 26,8142 8,9587 2,85673 1,39382 2258.8 406 020 719
| 720 518 400 373 248 000 26,8329 8,9628 2.85733 1,38889 2261,9 407 150 720
721 519 841 374 805 361 26,8514 8,9670 2.85794 1,38696 2265,1 408 282 721
722 521 284 376 367 <И8 26,8701 8,9711 2.85854 1,38504 2268,2 409 415 722
723 522 729 377 931 067 26,8897 8,9752 2,85914 1,38313 2271,4 410 550 723
724 524 176 379 500 424 26,9072 8,9794 2,85974 1,38122 2274,5 411 687 724
725 525 625 381 078 125 26,9258 8.9835 2,нби:и 1,37931 2277,7 412 825 725
726 527 076 382 657 176 26.9414 8,9876 2.86094 1,37741 2280,8 413 965 726
727 529 529 384 240 583 26,9629 8,9918 2,86153 1,37552 , 2283,9 415 106 727
728 529 984 385 828 352 26,9915 8,9959 2,86213 1,37.163 2287,1 416 241 723
729 531 441 387 420 489 27.0000 9.0000 2,86273 1.37174 2293,2 417 393 729
730 532 900 369 017 000 27,0185 9,0041 2.86332 1,36986 2293,4 418 539 730
731 534 361 390 617 891 27,0370 9.0082 2,86392 1,36799 2296,5 419 686 731
732 535 824 392 223 161 27,0555 9,0123 2,86451 1,36612 2299,6 420 835 732
733 537 289 393 832 837 27,0740 9,0164 2,86510 1,36426 2302,8 421 986 733
734 538 756 395 446 904 27,0924 9,0203 2,86570 1,36240 2305,9 423 138 734
735 540 225 397 065 375 27,1109 9,0246 2,86529 1,36064 2309.1 424 293 735
736 541 696 393 688 256 27,1293 9,0287 2,86638 1,35870 2312,2 425 447 736
737 543 169 400 315 553 27,1477 9.0324 2,86747 1,35685 2315,4 426 604 737
738 541 644 401 947 272 27,1662 9.0369 2,86106 1 ,35101 2318,5 427 762 738
, 739 546 121 403 593 419 27,1846 9,0410 2,86361 1,35318 2321,6 428 922 739
740 547 600 405 221 000 27,2029 9.0450 2,86923 1,35135 2324,8 430 08-1 740
741 549 061 406 869 021 27.2213 9,0491 2.86932 1,31933 2327,9 431 247 741
742 550 564 408 518 418 27,2397 9,0632 2,870-Ю 1,34771 2331,1 432 412 742
743 552 049 410 172 407 27,2590 9.0572 2,87099 1,.34593 2331,2 433 578 743
744 553 536 411 831784 27,2761 9,0613 2,87157 1,34409 2337,3 434 746 744
745 555 02!> 413 493 625 27,2917 9,0654 2,87216 1,34228 2340,5 435 917 745
746 656 516 415 160 936 27,3130 9,0694 2,87274 1,34041 2343,6 437 087 716
747 558 009 416 832 723 27,3313 9,0735 2,87332 1,33869 2346,8 438 259 747
748 559 .504 418.509 992 27.3496 9.0775 2,87390 1,33693 2319,9 439 -133 748
749 561 001 420 189 749 27,3679 9,0816 2,87441 1,33511 2353,1 440 609 749
750 562 500 421 875 000 27,3361 9.0856 2,87506 1,33333 2356,2 441 786 750
КВАДРАТЫ, КУБЫ. КОРНИ. ЛОГАРИФМЫ. ОБРАТНЫЕ ВЕЛИЧИНЫ 27
751—800
Л Л* л* Т л 3 /7Г 1g п 1000 п Т.П 4
751 564 001 423 564 751 27.4044 9,0896 2,8756» 1,33156 2359,3 442 965 751
752 565 564 425 259 008 27,4226 9,0937 2,87622 1,32979 2362,5 444 146 752
753 567 009 426 957 777 27.4408 9,0977 2,87679 1,32802 2365,6 445 328 753
754 563 516 428 661 064 27,4591 9,1017 2,87737 1,32626 2364.В 446 511 754
755 570 025 430 368 875 27,4773 9,1057 2,87795 1,32450 2371,9 447 697 755
756 571 536 432 081 216 27,4955 9,1098 2,87852 1,32275 2375,0 448 883 756
757 573 019 433 79Я 093 27,5136 9,1138 2,87910 1,32100 2378,2 450 072 757
758 574 564 435 519 512 27,5318 9.1178 2,87967 1,31926 2381,3 451 262 753
759 576 081 437 245 479 27,5500 9.1218 2,88024 1,31752 2384,5 452 453 759
760 577 6.10 438 976 ООО 27,5681 9,1258 2.88031 1.31579 2387,6 453 646 760
761 579 121 440 711 081 27,5862 9.1298 2,83138 1,31406 2390.8 454 841 761
762 580 644 442 450 728 27,6013 9,1338 2,88195 1.3123» 2393,9 456 037 762
763 582 169 444 194 947 27,6225 9,1373 2,88252 1.31062 2397.0 457 234 763
764 583 696 445 943 744 27,6105 9,1418 2,88309 1.30890 2400,2 458 434 764
765 585 225 447 697 125 27,6586 9,1458 2,88365 1,30719 2403,3 459 635 765
766 586 756 449 455 U96 27,6767 9,149В 2,88423 1,30548 2406,6 460 837 766
767 588 289 451 217 663 27.6948 9.1537 2,88480 1,30378 2409.6 462 031 767
768 589 824 452 984 832 27.7128 9,157? 2,88536 1,30208 2412,7 463 247 768
769 591 361 454 756 609 27,7306 9,1617 2,88593 1,30039 2415,9 464 454 769
770 592 900 456 533 000 27,7489 9,1657 2,88619 1,29870 2419.11 465 663 770
771 .594 441 458 314 011 27,7669 9.1696 2,88705 1.29702 2422,2 466 873 771
772 595 904 160 04.9 648 27,7849 9,1736 2,88762 1.29534 2425.3 468 085 772
773 597 529 461 889 917 27,8029 9.1775 2.88818 1.29366 2428,5 469 298 773
774 599 076 463 684 824 27,8209 9.1815 2,88874 1,29199 2431,6 470 513 774
775 600 625 465 484 375 27,8388 9,1855 2.КВДЗО 1,29032 2434,7 471 730 775
776 602 176 467 268 576 27,8568 9,189» 2,88986 1,28866 2437,9 472 918 776
777 603 729 469 097 433 27,8747 9,1933 2,89012 1,28700 24(1.0 474 168 ТП
778 605 284 470 9104152 27.8927 9,1973 2,89098 1,28535 244», 2 475 389 ТП
779 606 841 472 729 139 27,9106 9,2012 2,89151 1,28370 2447,3 476 612 779
780 603 400 474 552 000 •n.vas 9.2052 2,89209 1,28205 2150,4 477 836 780
781 609 961 476 379 541 27,9461 9,2001 2,89265 1,280»! 2453,6 479 062 781
782 611 524 478 211 768 27,9643 9.2130 2,89121 1.27877 2166.7 480 290 782
783 613 089 480 048 687 27,9821 9,2170 2,89.176 1,27714 2459.9 481 519 783
784 614 656 481 890 304 28.0000 9,2209 2,89432 1,27551 246.3,0 482 750 784
785 616 225 483 736 625 28,0179 9,2248 2,89487 1,2738:1 2466,2 483 982 785
786 617 796 485 587 656 28.0357 9,2287 2,89542 1,27226 2469,3 485 216 796
787 619 369 487 443 403 28.0535 9,2326 2,89597 1,27065 2472,4 486 451 787
788 620 941 489 300 872 28,0713 9.2365 2.89653 1.'26901 2475.6 487 6ЧЯ 788
789 622 521 491 169 069 28,0891 9.2404 2,89703 1,26743 2478,7 488 927 789
790 621 100 493 039 000 28.1069 9.244.) 2,89763 1,26582 2481,9 490 167 790
791 625 681 491 913 671 28,1247 9,2482 2,89818 1,26422 2485.0 491 409 791
792 627 264 496 793 088 28,1425 9,2521 2,89873 1.26263 2188,1 492 652 792
793 628 849 498 677 257 28,1603 9,2560 2,89927 1,26103 2491,3 493 897 793
794 630 436 509 566 184 28.1780 9,2599 9,89982 1,25945 2494,4 495 143 794
795 632 025 502 459 875 28,1957 9,2638 2,90037 1,25786 2497,6 496 391 795
796 633 616 501 358 336 28,2135 9,2677 2,90091 1,25628 2500,7 497 611 796
797 635 209 506 261 573 28,2312 9,2716 2,90146 1,25471 2503,8 496 892 797
794 636 804 508 169 592 28,2489 9,2751 2,90200 1,25313 2507,0 500 1»5 796
799 638 401 510 092 399 28,2666 9,2793 2,90255 1,25156 2510,1 501 399 799
800 640 000 512 000 000 28,2843 9,2832 2,90309 1.254ЮО 2513.3 502 655 | 630
28 ' МАТЕМАТИЧЕСКИЕ‘ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
801—850
л Л* 1 3 V п 1g Л 1000 л пл ЯП» 4 Л
801 641 601 616 922 401 28,3019 9,2870 2,90363 1,24844 2516,4 503 912 801
802 643 204 515 849 608 28.8196 9,2909 2,90417 1,24688 2519,6 505 171 802
803 644 809 517 781 627 28,3373 9,2MB 2.9М72 1,24533 2522,7 506 432 803
804 646 416 519 718 464 28,3549 9,2986 2,90626 1,24378 2525,8 507 691 004
805 648 025 521 660 125 28,3725 9,3025 2,90680 1.24224 2529.0 506 958 80S
806 , 649 636 523 606 616 28.3901 9.3063 2,90634 1,24069 2532,1 510 223 806
807 651 249 525 557 943 28,4077 9,3102 2,90687 1,23916 2535,3 511 490 807
НОВ 662 864 527 514 112 29.4253 9,3140 2,90741 1,23762 2538,4 B137S8 80Н
НО9 654 481 529 475 129 28.4429 9,3179 2,90795 1,23609 2541,5 514 028 809
810 656 100 531 441 000 23,4605 9,3217 2,90849 1.23457 2544,7 515 300 810
811 657 721 533 411 731 28.4781 9.3255 2,90902 1,23305 2547,8 516 573 811
812 659 344 535 387 328 28,4956 9.32М 2.90956 1,23153 2S51.0 517 848 812
813 660 969 537 367 797 28.5132 9,3332 2.91009 1,23001 2554,1 519 124 813
814 662 596 539 353 144 28.5307 9,3370 2.91062 1,22850 2557,3 520 402 814
815 664 225 541 343 375 28,5482 9,3408 2,91116 1,22599 2560,4 521 681 815
81 Г> 655 856 543 338 490 28,5657 9.3447 2,91169 1,22549 2563,5 522 962 816
817 667 489 545 338 513 28,5832 9,3485 2,91222 1,22399 2566,7 524 245 817
814 669 124 547 313 432 28,6007 9,3523 2.91275 1.22249 2569.8 525 529 818
819 670 761 549 353 259 28,8182 9,3561 2,91328 1,22100 2573,0 526 814 819
820 «72 400 551 368 000 ' 28,6356 9,3599 2.91381 1.21951 2576.1 528 102 820
821 674 041 553 387 661 28,6531 9,3637 2,91434 1,21803 2579,2 529 391 821
822 675 684 555 412 248 28,6705 9,3675 2,91487 1,21655 2582,4 530 681 822
823 677 329 537 441 767 28,6880 9,3713 2,91540 1,21507 2585.5 531 973 823
824 678 976 559 476 224 28,7054 9,3751 2.91593 1,21359 2588.7 533 267 824
825 680 625 561 515 625 28,7228 9.3789 2.91645 1,21212 2591,8 534 562 825
826 682 276 563 559 976 28,7402 9,3827 2,91698 1,21065 2595,0 535 858 826
827 683 929 565 609 283 28,7576 9,3865 2,91751 1,20919 .2598,1 537 157 827
828 685 584 567 663 552 28.7750 9.3902 2,91803 1,20773 2601,2 538 456 823
829 687 241 569 722 789 28,7924 9,3940 2,91855 1,20627 2604.4 539 758 829
830 688 900 571 787 000 28,8097 9.3978 2.91906 1,20482 2607.5 541 061 830
831 690 561 573 856 191 28,8271 9,4016 2.91960 1,20337 2610,7 542 365 831
832 692 224 575 930 368 28,8444 9,4053 2.92012 1.20192 2613,8 543 671 832
833 693 889 578 009 537 28,8617 9.4091 2,92065 1,20048 2616,9 544 979 833
834 695 556 580 093 704 28.8791 9,4129 2,92117 1,1990-1 2620,1 546 288 834
835 697 225 582 182 875 28,8964 9.4166 2,92169 1,19760 2623,2 547 599 835
836 698 896 584 277 056 28.9137 9,420-1 2,92221 1,19617 2626,4 548 912 836
837 700 569 586 376 253 2В,9310 9,4241 2,92273 1,19474 2629,5 560 226 837
838 702 244 588 480 472 29,9482 9,4279 2,92324 1,19332 26742.7 551 641 83В
839 703 921 590 589 719 28,9655 9,4316 2,92376 1,19190 2635,8 552 858 839
840 706 600 592 704 000 28,9828 9,4354 2,92428 1,19048 2638,9 554 177 840
841 707 281 591 823 321 29.0000 9,4391 2,92480 1,18906 2642.1 555 497 841
842 708 964 596 947 688 29.0172 9,4-129 2,92531 1,18765 2645,2 556 819 842
843 710 649 599 077 107 29.0345 9,4466 2,92583 1.18624 2648.4 558 142 843
8-14 712 336 601 211 584 29,0617 9,4503 2,92634 1.18483 2651,5 559 467 844
845 714 025 603 351 125 29.0689 9,4541 2,92686 1,18343 2654.6 560 794 845
846 715 716 605 495 736 29.0861 9,4578 2,92737 1.18203 2657,8 562 122 846
847 717 409 607 645 423 29.1033 9,4615 2,92788 1,18064 2660,9 563 452 847
848 719 104 609 800 192 29.1204 9,4652 2,92840 1,17925 2664,1 564 783 848
849 720 801 611 960 049 29,1376 9,4690 2,92891 1.17786 2667,2 566 116 849
850 722 500 614 125 000 29,1348 9,4727 2,92942 1.17647 2670,4 567 450 850
КВАДРАТЫ. КУБЫ. КОРНИ. ЛОГАРИФМЫ. ОБРАТНЫЕ ВЕЛИЧИНЫ
29
851—900
Л л* л* V л 3 /Г 1g л 1000 п ПЛ г.л’ *т л
851 724 201 616 295 061 29,1719 9,4764 2,92993 1,17509 2673,5 568 786 851
852 725 904 618 470 208 29.1890 9.4801 2,93044 1,17371 2676,6 570 124 852
853 727 609 630 650 477 29,2062 9.4838 2,93095 1,17233 2679,8 571 463 853
854 729 316 622 835 861 29,2233 9.4875 2,93146 1,17096 2682,9 572 803 854
855 731 025 625 026 375 29,2404 9,4912 2,93197 1,16959 2635.1 574 146 655
856 732 736 627 222 016 29,2575 9,4949 2,93247 1,16822 2689,2 575 490 856
857 731 449 629 422 793 29,2746 9.4986 2,93293 1,16686 2692,3 576 835 857
858 736 161 631 628 712 29,2916 9.5023 2,93349 1,16550 2695,5 578 182 858
85» 737 881 633 839 779 29,3087 9,5060 2,93399 1,16114 2698.6 579 530 859
860 739 600 636 056 000 29,3258 9,5097 2,93450 1,16279 2701,8 1 580 880 860
861 741 321 638 277 381 29.3-128 9,5134 2,93500 1,16144 2704,9 582 232 861
862 743 044 610 503 928 29.3598 9,5171 2,93551 1,16009 2708,1 583 585 862
863 744 768 642 735 647 29,3769 9,5207 2,93601 1,15875 2711,2 5819-Ю 663
864 746 496 64 1 972 544 29,3939 9,5244 2.93651 1,15741 2714,3 686 297 864
866 748 225 64? 214 625 29,4109 9,5281 2,93702 1,15607 2717,5 587 655 865
863 749 956 649 461 896 29.4279 9,5317 2,93752 1,15473 2720,6 589 014 866
867 751 689 651 714 363 29,4449 9,5354 2,93802 1,15340 2?23,8 590 375 867
868 753 424 653 972 032 29,4618 9,5391 2,93852 1,15207 2725,9 591 738 868
86» 755 161 656 234 909 29,4788 9,5427 2.93902 1,15075 2730,0 593 102 869
870 756 900 658 503 000 29,4958 9,5461 2,93952 1,14943 2733,2 594 468 870
871 758 641 660 776 311 29,5127 9.5501 2,94002 1,14811 2736,3 595 835 871
872 760 384 663 054 848 29,5295 9,553? 2.94052 1,14679 2739,5 597 204 872
873 762 129 665 338 617 29,5466 9,5574 2.94101 1,14548 2742,6 598575 873
874 763 876 667 627 624 29,5635 9,5610 2,94151 1,14416 2745,8 599 947 874
875 765 625 669 921 875 29,5804 9.5617 2.94201 1,14286 2748,9 601 320 875
876 767 376 672 221 376 29,5973 9,5683 2.94250 1,14155 2752,0 602 696 876
877 769 129 674 526 133 29,6142 9,5719 2.94300 1,14025 2755,2 604 073 877
87Я 770 884 676 836 152 29.6311 9,5756 2,9-1349 1,13895 2758.3 6U5 451 878
879 772 611 679 151 439 29.6479 9.5792 2.91399 1,13766 2761,5 606 831 879
880 774 400 631 472 000 29,6648 9,5828 2,94448 1,13636 2764,6 608 212 880
881 776 161 683 797 841 29 6816 9,5865 2.94498 1,13507 2767,7 609 596 881
И2 777 921 686 128 968 29,6985 9,5901 2.94547 1,13379 2770,9 610 980 882
883 779 689 688 465 387 29,7153 9,5937 2,94596 1,13250 2774,0 612 366 883
884 781 456 690 807 104 29,7321 9,5973 2,91645 1,13122 2777,2 613 754 884
№ 7 КЗ 225 баз 154 125 29,7489 9.6010 2,94694 1,12991 то,а 615 143 885
886 781996 695 506 456 29,7658 9,6046 2,91743 1,12867 2783,5 616 531 886
887 786 769 697 861 103 29,7825 9,6032 2,94792 1,12740 2786,6 617 927 887
888 788 544 700 227 072 29.7993 9,6118 2,94841 1,12613 2789,7 619 321 888
889 790 321 702 505 369 29,8161 9,6154 2,94890 1,12486 2792,9 620 717 889
890 792 100 70-1969 000 29,8329 9,6190 2,94939 1,12360 2796,0 622 114 890
891 793 881 707 347 971 29.8496 9,6226 2,94988 1,12233 2799.2 623 513 891
892 795 66-1 '709 732 288 29,8664 9,6262 2,95036 1 ,’12108 2902.8 624 913 892
893 797 449 712 121 957 29.8831 9,6298 2,95085 1,11982 2805,4 626 315 893
894 799 236 714 516 98-1 29.8998 9,6334 2.95134 1.11SS7 2806,6 627 718 894
895 801 025 716 917 375 29,9166 9.6370 •2,95182 1.11732 2811,7 629 124 895
896 802 816 719 323 136 29,9333 9,6406 2,95231 1,11607 2814,9 630 530 896
897 804 609 721 734 273 29,9500 9,6442 2,95279 1,11483 2818,0 631 938 897
898 806 40-1 724 150 792 29,9666 9,6177 2,95328 1,11359 2821,2 633 348 898
890 808 201 726 572 699 29,9833 9.6613 2.95376 1,11235 2824.3 ШIW
900 | 810 000 729 000 000 30,0000 9,6549 | 2,95424 1,11111 2827,4 636 173 | 900
ю
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
901—950
л л1 п> 3 VЛ *< " 1000 fl пя ял* 4 “Л
901 811 801 731 432 701 30,0167 9.6585 2.95472 1.10988 2830.6 637 587 901
902 813 604 733 870 808 30.0333 9.6620 2.95521 1.106CS 2833,7 639 003 902
903 815 409 736 314 327 30,0500 9.6656 2,96569 1,10742 2836,9 640 42| 90.3
901 817 216 738 763 264 30.0666 9,6692 2.95617 1,10619 2840,0 641 еф 904
905 819 025 741 217 625 30,0832 9.6727 2.915665 1,10197 2843,1 613 261 905
906 820 836 743 677 416 30,0998 9,6763 2.95713 1,10375 2846,3 614 69» 906
907 822 619 746 142 643 30.1164 9,6799 2,95761 1,10254 2849,4 646 (Л 907
906 824 461 748 613 312 30,1330 9.6831 2,95»» 1,10182 2852,6 617 5® 908
909 826 281 751 (Я9 429 30.1496 9.6870 2.95856 i.ioqti 2855.7 648 9Я> 909
910 828 100 753 571 000 | 30.1662 9.6905 2,95904 1,09890 2858,8 650 910
911 829 921 756 058 031 30.1828 9.6941 2.95952 1.09769 2862,0 651 8» 911
912 831 741 /58 550 528 30.1993 9.6976 2.95999 1.09619 2865.1 653 2® 912
913 833 569 761 048 497 30,2159 9.7012 2.96047 1.09529 286S.3 654 684 913
914 835 396 763 551 944 30.2324 9.7047 2.96095 1,09409 2871,4 656 life 914
915 837 225 766 069 875 30,2490 9.70*2 2.96142 1,09290 2874.6 657 555 915
916 839 056 768 575 296 30,2655 9.7113 2,96190 1.09170 2877,7 658 993 916
£17 840 889 771 095 213 30,2820 9.7153 2,96237 1.09051 2880.8 660 433 917
918 842 724 773 620 632 30,2985 9.7188 2.96281 1.08132 2381.0 661 871 918
919 844 561 776 151 559 30,3150 9,7224 2.96332 1.06811 2387,1 663 317 919
920 846 400 778 688 000 30,3315 9.7259 2,96379 1,08696 2890,3 664 761 920
921 818 241 781 229 961 30,3483 9,7294 2,96426 1,08578 2893,4 665 207 921
922 850 081 783 777 118 30,3645 9.7329 2.96173 1,08160 28%. 5 667 651 922
923 851 9J9 786 330 467 30.3809 9,7361 2,96520 1,06342 2899,7 669 103 923
921 853 776 788 889 024 30.3974 9.7400 2,96567 1,08225 2902.8 670 554 921
925 855 625 791 453 125 30,113* 9.7435 2,96114 1,0*108 2905.0 6*2 006 925
926 857 476 791 022 776 30.4302 9.7470 2,96661 1.07991 2909,1 673 461 926
927 859 329 796 597 983 30,4467 9.7505 2.96708 1,07875 2912.3 674 915 927
928 Н61 1HI /99 178 752 30,4631 9,7540 2.96755 1,07759 2915,4 675 372 928
929 863 011 801 765 089 30,4795 9,7575 2.96802 1,07613 2918.5 677 831 929
930 №1900 804 357 000 | 30,1959 9.7610 2.96*48 1,07527 2921.7 679 291 930
931 865 761 806 954 491 30.5123 9.7645 2.96*95 1,07411 2924,8 680 752 931
932 888 624 *09 557 568 30.5287 9.7680 2,9691'2 1.07296 2928,0 682 216 932
933 870 489 812 166 237 30,5450 9.7715 2.96938 1,07181 2931.1 683 680 933
931 872 336 814 780 504 30,5614 9.7750 2,97035 1,07066 2931.2 685 147 934
935 874 225 817 400 375 30,5778 9,7785 2,97081 1,06952 2937,4 686 615 935
936 876 096 820 025 856 30.5941 9,7814 2.97128 1,06838 2910,5 688 081 935
937 877 969 822 656 953 30,6105 9.7851 2,97’74 1,06724 2943,7 689.555 937
938 879 814 825 293 672 30.6268 9.78*9 2.97220 1.06610 2946.8 691 028 93*
939 881 721 827 936 019 30.6431 9.7924 2.97267 1.06196 2950,0 692 502 939
910 883 600 830 581000 30.6591 9.7959 2,97313 1.06383 2953.1 693 978 940
941 88.5 481 833 237 621 30,6757 9,7993 2.97359 1.06270 2956,2 69,455 941
942 887 364 83> 896 888 30,6920 9.8028 2,97406 1.06157 2459,4 1W6 434 942
943 889 249 833 561 807 3O.7U83 9.8063 2,97451 1,06045 2962,5 698 415 943
944 891 136 841 232 384 30.7246 9.8097 2.97497 1,05932 2965,7 699 897 944
945 893 025 843 908 625 30.7409 9,8132 2.97543 1,05820 2968,8 701 380 945
916 894 916 816 590 536 30.7571 9.8167 2.97589 1.05708 2971,9 702 865 946
947 896 809 849 278 123 30,7734 9,8201 2.97635 1,06597 2975.1 /04 352 947
948 898 701 851 971 392 30.7896 9,8236 2,976*1 1,05485 2978,2 705 840 948
949 900 601 854 670 349 30,8058 9.8270 2,97727 1.06374 2981,4 707 330 949
9150 902 500 857 375000 30.8221 9.8305 2,97772 1.05263 2964,5 70S 822 950
КВАДРАТЫ, КУБЫ, КОРНИ, ЛОГАРИФМЫ. ОБРАТНЫЕ ВЕЛИЧИНЫ
31
951—1000
п Л> 3 /л 1g п 1000 п «Л Лж5 4 Л
951 904 401 860 085 351 30,8383 9,8339 2,9781» 1.05152 2987.7 710 315 951
962 905 304 862 801 408 30,8.54-5 9,8374 2.97864 1,05042 2990,8 711 809 952
953 903 209 865 523 177 30,8707 9,8403 2,97909 1,04932 2993.9 713 306 953
954 910 116 868 250 664 30.8869 9,8443 2,97955 1,04822 2997.1 714 803 954
955 912 025 870 933 875 30,9031 9,8477 2,98000 1,04712 3003.’ 716 303 955
966 913 986 873 722 816 30.9192 9,8511 2.98046 1,04603 3003.4 717 804 956
957 915 849 876 467 493 30,^354 9,8546 2.9Н091 1,04494 3006,5 719 306 957
958 917. 764 879 217 912 30,9516 9,8530 2,9’137 1,0434 3009.6 720 810 958
959 919-681 881 974 079 30,9677 9,8614 2,93182 1,04273 3012.8 722 316 959
960 921600 884 736 000 30,6339 9,8648 | 2.93227 1,04167 | 3015,9 | 723 823 | 960
961 92$ 521 887 503 651 ЗЬ.ОООО 9.8683 2,93272 1,04058 3019,1 725 332 961
962 925 444 890 277 128 31.0161 9.8717 2,98318 1.03950 3022,2 726 812 962
963 92? 369 893 056 347 31,0322 9.8751 2,91363 1,03842 3025,4 .728 351 963
964 929296 695 841 344 31,0483 9.8785 2,98408 1,00731 3028,5 729 867 961
955 931 225 898 632 125 31.0644 9.8819 2,98453 1,03627 3031,6 731 382 955
956 933 156 901 428 696 31,0805 9.8851 2,98493 1,03520 3034,8 732 899 966
967 935 089 904 231 063 31.0066 9.8888 2,98543 1,03113 31X17,9 734 417 967
963 937 024 907 039 232 31,1127 9,8922 2.985-8» 1,03306 3041,1 7359.17 968
969 938 961 909 853 209 31,1288 9,8996 2,98632 1,03199 3044.2 737 458 969
970 910 930 912 673 003 31,1448 . 9,8990 2,98677 i.osose 3047.3 738 981 970
971 942 841 915 498 611 31,1609 9,932-1 2,98722 1,02987 3050,5 7-10 506 971
972 944 784 918 330 018 31,1769 9,9058 2,98767 1.02881 3053,6 742 032 972
973 945 729 921 167 317 31,1929 9,9092 2,98311 1.02775 3056.8 743 559 973
974 943 676 924 010 424 31,209.1 9,9126 2,93856 1,03660 3059,9 745 088 974
975 П50 625 926 859 375 31,2250 9.9163 2,98900 1,02564 3063,1 746 619 975
976 952 576 929 714 176 31,2410 9,9194 2,93945 1,02159 3066,2 748151 976
977 954 529 932 574 833 31,2570 9,9227 2,98989 1,02354 30641.3 749 685 977
97Я 956 481 93.5 44 1 352 31.2730 9,9261 2,99034 1,02249 3072.5 751 221 978
979 958 441 9.38 313 739 Э1.2Я9:> 9,929.5 2,99078 1,02145 3075,5 752 758 979
980 960 400 911 192 000 31.3050 9,9329 2,99123 1,02041 3078,8 754 296 ИЮ
9S1 962 361 944 076 141 31.3209 9,9363 2,99167 1,01937 3081,9 755 837 <1В1
982 964 324 946 966 168 31.3369 9,9391 2.99211 1.01 ваз 3085.0 757 378 982
983 966 289 949 862 087 31,3528 9,9430 2,99255 1,01729 3088.2 758 922 983
984 968 256 952 763 904 31,3688 9.9464 2.99300 1,01626 3091.3 760 -166 984
985 970 225 955 671 625 31.38-17 9,9497 2,99344 1,01523 3094.-5 762 013 945
996 972 195 958 585 2.56 31,40011 9,9531 2,99388 1,01420 3097,6 763 561 <iv,i WVJ
987 974 169 961 501 803 31,4166 9,9565 2,99432 1,01317 3100.8 765 111 •37
9ЧЧ 976 141 964 430 272 31.4325 9.9598 2,99176 1,01215 3103,9 766 652 9хч
989 978 121 967 361 669 31,4481 9.9632 2,99520 1,01112 3107,0 768 214 981*
990 980100 970 299 000 31,4643 9,9666 2,99561 1.01010 3110,2 769 769 1 990
991 982 08*1 973 242 271 31.4802 9,9699 2,99607 1,00908 3113,3 771 3!В 991
992 984 054 976 191 488 31,4960 9,9733 2,99651 1,00806 3116,5 772 882 992
993 986 049 979 146 657 31,5119 9,9766 2,99693 1.1X1705 3119,6 774 441 993
994 988 036 982 107 784 31,5278 9,9800 2,99739 1,0060-1 3122,7 776 0V2 994
995 990 025 £8.5 074 875 31,5436 9,98'13 2,99782 1,00503 3125,9 777 564 9J5
996 992 016 988 047 936 31,5505 9,9866 2,99826 1,00402 3129,0 779 128 996
997 994 009 991 026 973 31,5753 9,9900 2.99S70 1,00301 3132,2 780 693 997
996 996 001 994 ОН 992 31,5911 9,9903 •2,99913 1.00200 3134.3 782 260 998
999 998 001 997 002 999 31,6070 9,9967 2,99957 1,00100 3138.5 783 828 999
ИХ» 1000 000 1000 000 004) 31,6228 10.0000 3,00000 1,00000 3141,6 785 390 1000
32
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
Примечание. Табл. Ill позволяет для целых л от 1 до 1003 находить квадраты, кубы, квад-
ратные и кубические корни, десятичные логарифмы, обратные величины, длину окружности и пло-
щадь круга диаметром л.
Если данное число х, над которым требуется произвести одну нз указанных операций, находится
в первой или последней графе, то ответ получается непосредственно в соответствующей графе.
Если же I < х < 1О::о и х не равеи целому л, то л<х<л + 1, и тогда необходимо прибегнуть
к интерполяции (см. интерполяционные формулы, стр. 3(B). Обычно употребляется линейная интерпо-
ляция.
Если х, = х0 -f- Л (в табл. Ill h равно единице) — два значения аргумента, которым соответ-
ствуют значения функции у„ — / (х0), у, —/(х,) = у, 4- Ду» (Ду0 — разность первого порядка), то при
линейной интерполяции принимают
/(х)-у»+
JC “ Jfa X “ Хл
Интерполяционную поправку " Ду» — Аду», где А =--—-, можио вычислять по табл. IV
А А
(стр. 35), даюшей произведения Ду» (от П до 90) ва 0,1, 0,2,... 0,9.
Погрешность линейной интерполяции не превышает единицы разряда последней значащей цифры,
если только разности второго порядка Д'у» — Ду, — Ду» меньше по абсолютному значению 5 единиц
последнего знака. В противном случае следует взять следующий член интерполяционной формулы.
В табл. 111 везде можио брать линейную интерполяцию, кроме вычисления / (х) =- д', где следует
-пользоваться квадратической интерполяцией по формуле
,, . . ' . *(*-1) ( А’У-1 + А’Уа \
/ (х) - у» + АДу» + —S——--------4--------J
/ W - У. 4- АДу, - А, (Ду, - Ay_j),
где А, = * ~ ; ДУ—j — у» — у_р таким образом, для нахождения /(х) для значения X, лежащего
между х» и х„ следует использовать предшествующее значение аргумента х—] — х, — Л и соответ-
ствующее в таблице значение у..
Величина А, находится из табл. V на стр. 36. ____ _ ___
Возведение в квадрат для л < х < п 4- 1.
Примеры: 1) у = (506,8)'; х» — л — 506;
у. — 506'= 256 036;
у, - SOT' = 257 049; А*“ ” 1013'
у, - 508* = 258 064. Ау‘ “ 1015’
Разность Ду» и интерполяционную поправку обычно выражают в единицах разряда последней зна-
чащей цифры табличного значения функции, не выписывая нулей и запятой впереди. Д'у» — 1015 —
— 1013 — 2 < 5; применяется линейная интерполяция: Ду» = 10-1004- 13; 0,8-10-100— 800; из табл. IVt
•0^-13-10,4; поправка Ад у, - 800 4-10,4 — 810,4; у = 506> -f- 810,4 = 256 846,4 или у— 256 846 с точ-
ностью до 1.
2) у — 0,0456'; по таблице 456* — 207 936; у должен содержать 8 десятичных аиаков, следовательно,
у - 0,00207936.
Возведение в куб для п < х < п 4- 1.
Пример, у — 23,01'. Так хак в таблице аргумент л — трехзпачиое число, то можио искать 200,4*,
•а затем, уменьшив результат в 10* раз, найдем отпет:
y_j — 199» — 7 880 599;
АУ_1—1 19 40!;
у» — 200> = 8 С00 000; 1 Д'у_1 — 1200,
Ду» —120 601: ..
у, в. 201*-8 120 601; 4 1218О7. А'Л- 1206.
у, — 202* — 8 242 408;
Чтобы применить квадратическую интерполяцию, находим:
Ду„ — 12-10 ООО + 60-10 + 1; 0,4-12-10 ООО — 48 ООО;
0,4'60 10 — 240 ; 0,4-1—0,4; АДУо — 48 000 + 240 + 0,4 — 48 240,4;
А — 0,4; А, — 0,060 (по табл. V);
200,4' - 200*4- 48 240,4 - 0,06 (121 807 - 119 401) — 200* ф- 48 240,4 - 144,36 — 8 048 096,04,
что отличается от точного результата (200,4)* — 8048096,061 на 0,024, т. а. ошибка меньше 0,1.
Ответ: у « 8048,0960 со всеми верными значащими цифрами.
Извлечение квадратного корня.
Примеры: 1) /672 = 25,9235;
2) /67,2 находится с применением лилейной интерполяции:
у, —/67 — 8,1854;
бое;
у, - К 68 - 8,2462;
Ду, - 6OI;
у, - /69 - 8,3066.
КВАДРАТЫ, КУБЫ. КОРНИ. ЛОГАРИФМЫ. ОБРАТНЫЕ ВЕЛИЧИНЫ
33
Поправка: 0,2-608 — 120 +1,6 - 121,6;
= 8,1854-|- 0,01216 = 8,19766 ~ 8,1976.
3) /о,0?32 = V 732 - 27,0655 = 0,270555 со всеми верными знаками.
4) /0,00732 = V73,2 и следует вычислить /73,2 с линейной интерполяцией, во можно исполь-
зовать графу л как квадратный корень из чисел, находящихся в графе л*.
Из таблицы находим
/731025 = 855 | --- /732> ОО
. ,_____ У / 73,2— 8,55;
/732736 — 856 )
/0,0иТ32 - 0,0855.
Применение обратной линейной интерполяции
на таблицы выписать первые четыре знака:
у0 - 7310;
у, = 7327
и мы находим
.310 ..... 865
10 . ... 6
7320......8556
/732000.
/0,00732.
уточнит результат. В данном примере достаточно
Ду« = 17;
(по табл. Ill)
855,6;
• 0,06556.
Поправка 6 по табл. IV находится так: в колонке под разностью 17 ищем число, ближайшее к
числу К), и в первой (последней) колонке находим соответствующее ей число 6.
Извлечение кубического корня.
Примеры:
I) /646 = 8,6401;
3________ . 3 ,
2)/0,000731 —-JJj/W* —^-9,0082 = 0.090082;
3
3)/64,5 находится применением линейной интерполяции:
3
у,-/Я-4.0000:
Ду. - 207;
3
у, - /65 - 4,0207; 4*У» “ ~
Ду,-206;
3 ’ • '
у, —/66 - 4,0412. ,
Поправка: ДДу, —0,5-207 — 103.5;
3________________________________________
. /6/3 » 4,0104.
Как и в предыдущем случае, можио использовать графу л как кубически* корень из чисел, нахо-
дящихся в графе л*:
3 /--- 1 3 /-----
у 64,5 — -jj- я/ 64vOO; ищем ближайшие к 64 500 числа, кубические корки из которых отличаются
3_____________________________ 3____________ 3 _
на 1; находим по таблице /MOW —40, /68 9^1 —41, таким образом, /64,5 •> 4,0,
Но можио подкоренное число увеличить в 100* раз:
3 /" 1 3 / । з / 1
У «-s-iay в4’5100,-ЁйУ64И)01100
и ло таблице находим:
3 ? • 3
/64481201 - 401; /64964806 - 402; / 64,5 - 4,01.
1
Том I. Зак 1464
34
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
(разность a Vo = 4S)
(по табл. IV)
64&Г
Применение обратной линейной интерполяции лает
у0 — 6441.....................................401
. ... 04
40104
3 _
V 64Л = 4,ОКИ.
Нахождение логарифма (десятичного) трехзначного числа производится непосредственно по та-
блице, а зля числа с тремя значащими цифрами нз таблицы берется мантисса, характеристика же
устаиав.1ипастся по правилам алгебры. Например
lg 0.0731 = 7.86392.
Дли числа с четырьмя и более значащими цифрами мантиссу следует искать с применением линей-
ной интерполяции (как обычно и пятизначных логарифмических таблицах), если л > 100, а если
п < 1<<0, — искать мантиссу в 10 раз большего числа.
Примеры-. 1) 1g 731.0 находится с применением линейной интерполяции:
у. - 1g 731 = 2,86392;
Ay. = 0,00369;
у, - |g 732 = 2,86151.
Поправка ААу. = 0,5-0,00059 = 0,00030;
lg 731Л — 2,86392 4- 0,00030 = 2,86122.
2) lg 73,15 искать пс в графе, где п - 73 и п ф-1 = 74, а в графе, где п = 731, л -f- 1 = 732; ман-
тисса логарифма числа 731,0 равна 86 422, следовательно, 1g 73,15 = 1^16122.
Нахождение обратных .величин лается графой . Для чисел с тремя значащими цифрами
обратная величина находится из таблицы; следует только привести даунос число умножением или
делением на степень десяти (Шк) к целому трехзначному числу и полученный по таблице результат
соответственным образом исправить. Для четырехзначных чисел применяется линейная интерполяция
(поправку вычитать, а не прибавлд '
Примеры: 1)Х —0,341. Найти
находим
2)
3)
4)
34,1
1 » 1(100
— —-------—-----ж 2.9325а.
X 0.Л1 .41
">*™ 6W=jSr",°- ЯГ = >0-2^-293255.
ЯГ “-ЙО -^ = ^•2.^-^93265.
ю 1 loco
34,15 - 341,5 ” 1<А» * 3«1и>"
Применяем линейную интерполяцию:
у. = ^? = 2.93255;
Ду. ж - 0,00857;
ООО „
** “ 312 “ ->92383;
Л — 0,5; поправка 0,5-0,00857 - 0,00428;
Ж 2,93251 - 0,00428 = 2,92827;
^-0.0297827.
Нахождение длины окружности н площади круга для диаметра <1. равного целому числу л
от 1 до ЮиО, производится непосредственно по таблице. В случае d < I или d > 1000. но с тремя
значащими цифрами следует находить длину окружности (площадь круга) для диаметра, в 10* раз
большего или меньшего, чем заданный, и помнить, что при увеличении (уменьшении) диаметра в 10* рад
длина окружности увеличивается (уменьшается) п 10* раз, а площадь круга увеличивается (умень-
шается) в 102* раз.
При чер. d - 34,1; KW — 341; длина окружности равна — 107,13, а площадь
91326,9
1(Ю — 913..69.
Если d имеет значащих цифр больше трех, то следует применить интерполяцию.
Эта же таблица позволяет находить диаметр окружности и круга по заданной длине
или плошали кругл.
Пример. Найти диаметр окружности, длина которой 144,3 см. По таблице находим
— ««46; d — «• 46. Но так как в графе ял можно искать 10-114.3,, то получим —«ж 459;
3*45.1 1443 . 1НЛ „„
-----ж 4W; поэтому------ •> 459, а следовательно, d ж---- > 45,9.
круга равна
окружности
141,37
* » ы>.
ПРОПОРЦИОНАЛЬНЫЕ ЧАСТИ ДЛЯ ЛИНЕЙНОЙ ИНТЕРПОЛЯЦИИ
35
ТАБЛИЦА IV. ПРОПОРЦИОНАЛЬНЫЕ ЧАСТИ ДЛЯ ЛИНЕЙНОЙ ИНТЕРПОЛЯЦИИ
II 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 23 29 33
1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.6 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2,6 2.7 2.8 2.9 3.1 1
2 2,? 2,4 2.6 2.8 3,0 .3.2 3.4 3/ 3,8 4.0 4.2 4.4 4.6 4,® 5,0 5.2 5,4 5.6 5,8 6.1 2
3 3.3 3.6 3.9 4.2 4.5 4.8 O.I 5.4 5.7 6,0 6.3 6.6 6.9 7.2 7.5 7.8 8,1 8.4 8,7 9. 3
4 4.4 4,8 5.2 5,6 6,0 6.4 в.Я 7.2 7.6 8.0 8.4 я,« 9.2 9.6 10,1. 10,4 10,8 11.2 11,6 12,0 4
5 5,5 6.0 6,5 7,0 7.5 8.0 8.5 9.0 9.5 10,0 10.5 11.и 11.5 12,(1 12,5 14.0 13.5 14.0 14.5 15.0 5
6 в .6 7.2 7.6 8.4 9.6 9.6 10,2 10,8 11.4 12,0 12,6 13,2 13.8 14.4 15.6 15.1 16.2 16.8 17,4 18,0 6
7 7.7 8.4 9,1 9,8 10.5 П.2 11.9 12.6 13.3 11,0 14,7 15.4 16.1 16.“ 17.5 18.2 18.9 19.6 20.3 21.0 7
R 8,8 9,6 Ш.4 11,2 12,г 12/ 1.3/ 14,4 15/2 15.0 16.“ 17.6 18.4 19,2 20, Я 21.6 22.1 23.2 21.0 8
9 9.9 10.Р П.7 12.6 13.5 14.4 15.3 16.2 17.1 18.0 18.9 19.8 20.7 21.6 22.5 23.4 24.3 25.2 26,1 27.0 9
31 32 33 31 35 36 37 .38 39 40 41 42 43 44 45 46 47 48 49 50
1 3.1 3.2 3.3 3/ 3.5 3.6 3.7 •3.8 3.9 4.0 4.1 4.2 4,3 4.4 4.5 4.6 4,7 4.8 4.! 5.0 1
2 6.2 6,4 6/ 6.8 7,0 7.2 7.4 7.6 7.8 8.0 8.2 8,4 я.к 8,Я 9.0 9.2 9.4 9.6 9/ 10,0 2
3 9.3 9.6 9.9 10.1 10.5 10,8 11.1 11.4 11.7 12,0 12,3 12,6 12.9 13.'. 13.5 13.8 14,1 14,4 14,7 15,> 3
4 12.4 12.= 13,2 13/ И.о 14.4 14,8 15.2 15,6 16,0 16,4 16,8 17.2 17.6 18,(1 18,4 18,8 19.2 19,6 20,0 4
5 15,5 Ih.fl 16.5 17,С 17.5 18,0 18.5 19.0 19,' 20,0 20,5 21.0 21.Г- 22,(1 22.5 23.0 2'1,5 24,0 21. 25.0 5
6 18/ 19.2 19.8 20,4 21.(, 21,6 2'2,2 22,8 23,1 21,0 24.1: 15.2 25.8 2о,1 27.0 27.6 2.8,2 28/. 29,4 30,0 6
? 21.7 22,4 23.1 23,® 24,5 25,2 15.9 26.6 27.3 2“/ 28.7 29,4 30.1 30, я 31.5 32,2 32,9 13/ 31.3 35.0 7
к 21, я .’5.6 26.4 27.2 23.0 2V 29,f 33.4 31.2 323 32,8 13.6 31.4 15,2 35.0 45,8 37,6 31,4 19,'2 10.0 8
9 27.9 *8.8 29,7 3J.6 31.5 12.4 13,3 31.2 35.1 35,1 35.9 37.8 33,7 39,6 40.5 41.4 12,3 Й.2 И,1 15.0 9
51 52 53 54 55 56 57 S3 59 60 61 62 63 64 65 66 67 68 69 70
1 5.1 5.2 5,3 5,4 5,5 5.6 5,7 5,8 .5,9 6.0 6.1 6,2 6,3 6,4 6,5 6.6 6.7 6.8 6,9 1,.. 1
2 10.2 10,4 10,6 10.Я п.0 11.2 II 4 II,» II." 1’2.0 12.2 12,4 12.6 12.8 11,0 13.2 13.1 13,6 13,4 14,0 2
3 15.3 15.6 15.9 16.2 16,5 16,8 17.1 17.4 17,7 18.0 18.3 18.6 18.9 19,2 19,5 19.8 20.1 20,4 20.7 21,0 3
4 211,4 20,“ 21.2 >1.1- ►2.0 22,4 22.8 23,2 23.0 1.0 21.4 24/ 25,2 25.6 26,0 23.4 •26 “ 27.2 27.6 28,0 4
5 2.1,5 26,1 21/, 27.0 27.5 2 40 >8,5 9.0 29,5 зз.о ,111,3 31.0 11.5 32.0 32.5 «.о 33.5 34.0 31,5 35.0 5
« 411, Б 31.2 31.8 .32,1 3.1,0 33.11 31.2 31,8 33.4 31.0 Vi.11 37,2 37.8 18.4 19.0 39.6 40,2 10,8 11.4 12,0 6
7 з 1.4 37.1 37.8 38,5 В.! 39,0 10/ 41.3 12.0 12,7 13,4 II.1 14,8 4.5,5 16.2 4'1.9 17.11 <8,3 19.0 7
Я 41>. “ II,в 42.4 13,2 и,о 41.» >5,« 46,4 17.2 И.О 18/ 19.6 30.4 >1,2 52,11 5>.“ >3.6 51,4 55.2 56.0 8
45,9 45.8 47,7 18,6 19,5 Ю.4 51.3 72.'.- 53.1 и.о >4,9 55,8 53.7 57.6 58,5 Я.4 10.3 >1,2 62,1 >3.0 9
71 72 73 74 75 76 77 78 79 80 81 82 83 81 85 № 87 88 89 90
1 7.1 7.2 7.3 7.4 7.5 7.6 7.7 7.8 7.9 8,0 8,1 8.2 8.3 8.4 8,5 8.6 8.7 8,8 8,9 9.0 1
2 Н.2 11.4 11.6 14,6 15,0 15.2 15.4 15.6 15. - 1(1,0 16.2 16.1 111,6 16/ 17.0 17.2 17.1 17,6 17,8 18,0 2
3 -'1.3 21.6 21.9 22.2 22.fi 22.8 23.1 2.1.4 23.7 24.0 24.3 24.6 24.9 23.1 25,5 25.8 23.1 23.4 26,7 27,0 3
4 24.4 21,8 2J.2 .*9.6 30.0 3'3.4 30.6 31.2 31.6 12.0 32.4 32.8 33,2 43/ ИЗ 34.4 34," 15.2 ь,6 3'1,0 4
Б .45.5 11.(1 31,6 17.0 37.5 45.1 .14.5 19.0 39.5 ю.о 10,5 41.0 41.5 42,1 12.5 й.о 13,5 44,0 11,5 15.0 5
6 12,ь 13.2 13.8 14,4 15.0 15.11 16,2 46.8 17.4 43.0 .8,6 19.2 19,8 50,4 51.0 31.6 ,>2.2 52.8 53.4 51,0 6
7 19.7 71.4 51.1 и/ 52.5 53.2 53,9 51.6 55,3 56,0 56.7 57.4 58.1 58.» 59.5 60.2 6П, 9 61.8 S2.3 63.0 7
8 >i,h 57,- И. 4 -.9,2 10.0 60.6 61.5 52,4 '>3,2 54.1 14.8 “5.6 1».4 17.2 >4.0 68,8 69,1 70.4 71.2 72.1 8
9 □ .9 64/ 35.7 >6,1 17.5 68.4 09,3 /0.2 71,1 72.0 72.9 73/ 71.7 75.1 76.5 77.4 78,3 79,2 80.1 41.0 9
*
Примечание. О линейной интерполяции см. стр. 32.
3*
36
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
------9-------------------------------
ТАБЛИЦА V. ПОПРАВКИ ДЛЯ КВАДРАТИЧЕСКОГО ИНТЕРПОЛИРОВАНИЯ
* А. А 1. А, А I- А. А А А
U.UUU 1.000 0.066 0,931 0,147 0,853 0.255 0,748
0.002 о дои 0Д93 0,071 0,016 0.929 0,153 0,032 0.847 0,263 0,048 0,737
0.006 0,001 0.994 0.075 0,017 0,925 I 0,159 0,033 0.841 0.271 0.049 0,729
ОЛЮ 0,002 0,990 0.030 0,018 0.920 0.165 0.034 0.835 0,280 0,050 0.720
0,014 0Д03 0,986 0,065 0,019 0,915 0.171 0.035 0,829 0,290 0,051 0,710
0Л18 0Л04 0.982 0.090 0,020 0,910 ОЛП 0.036 0,823 0,300 0.052 0,700
0,022 0,005 0.978 0.095 0,021 0.905 0.183 0,037 0.817 ОДЮ 0,063 0,690
0Д26 о.ооб 0.974 0.100 ОД22 0.900 0,190 0,038 0Д10 0.321 0.064 0,679
0,1X10 0.007 0.970 0,105 0,023 0,895 0,196 0.039 0,804 0,332 0.055 0,668
0.035 0.008 0,935 0,110 0,024 0,890 0,203 0,040 0,797 0.345 0,056 0,655
0.039 0,009 ОДП 0,115 одез 0,885 0,2Ю 0,041 0,790 0,358 0Д67 0,642
0.043 0.010 0.957 0,120 0,036 0,880 0,217 0.042 0,783 0,373 0,053 0,627
0Л49 ОДП 0.952 0,125 0Д27 0,875 | 0.224 0.043 0,776 0,390 0.059 ОЛЮ
0.052 0.012 0,948 0.131 0.023 0,869 0.231 0,041 0,769 0,410 0.060 0.590
0.057 0Д13 0.913 0.136 0.029 0,864 0,239 0,045 0,761 0.436 0,061 0,564
0.061 0Д14 0.939 । 0,142 0.030 0,858 0.247 0,046 0.753 0.500 0,062 0,500
0,066 0Д15 0.934 0,147 0,031 0.8S3 0.255 0.047 0.745 1
Примечав» а: 1. О квадратическом ишерполироваиии см. стр. 32.
2. Всем значением А. заключенным между смежными числами графы А (как правой, так и
лево*), соответствует одно и то же значение А„ помешенное между атими смежными эшчеамами А.
Критическим (табличным) значениям k соответствует вышележащее А,.
Примеры. I) Дм А — 0.8 А, » 0.040 (так же как и дм всех других А. заключенных между ОДЯ
и 0.804 или между 0,196 и 0,2031. 5) Дли А = 03 (или ала А — 0,7) А, — 0,062.
ЭЛЕМЕНТЫ КРУГА
ТАБЛИЦА VI. ЭЛЕМЕНТЫ КРУГА: ДЛИНА ДУГИ, СТРЕЛКА. ДЛИНА ХОРДЫ
И ПЛОЩАДЬ СЕГМЕНТА КРУГА ДЛЯ РАДИУСА г - - 1
Централь- ны! угол Дамка жути 1 Стрелка Л Данна хорды 3 Площадь сегмс ri а 1 Централь- кий угол f* Длина дуги 1 Стрелка Л Длина хорды з л ! с i Г
1 0,0175 0.0000 0.0175 0,00000 51 0.8901 0.0974 0.8610 0,05649
2 0,0349 0,0002 0.0349 0,00000 52 0,9076 0.1012 0,8767 0,05978
3 0,0524 0,0003 0,0524 0,00001 53 0.9250 0,1051 0,6924 0.06319
4 0.0698 0,0006 0,0696 0,00003 54 0.9425 0,1093 0,9010 0.06673
5 0.0873 0,0010 0.0872 0,00005 55 0.958» 0,1133 0,9235 0.07(39
6 0,1047 0.0014 0,1047 0,00010 56 0.9774 0.1171 0.93 9 0,07417
7 0.1222 0,0019 0,1221 0,00015 57 0,9948 0,1212 0,91543 0,07808
8 0,1395 0.0024 0.1383 0.00023 58 1.0121 0.1254 0.9695 0.08212
9 0,1571 0.0031 0.1569 0,00032 59 1,0297 0,1295 0.98Я 0,05629
10 0.1745 0.0038 0,1743 0,00044 60 1,0472 0.1310 1,0000 0.С9059
11 0,1920 0,0046 0,1917 0.000* 61 1.0647 0.1384 1.0151 0,09502
12 0,2094 0,0055 0.2091 •0.00076 62 1,0821 0,1428 1.03Л 0,09956
13 0.2269 0,0064 0.2264 0.00097 63 1,0696 0.1474 1.0450 0,10428
14 0.2443 0,0075 0,2437 0,00121 64 1,1170 0,1520 1.0694 0,10911
15 0,2618 0.0086 0,2611 0.00149 65 1.1315 0,1566 1.0716 0,11408
16 0,2793 0.0097 0.2783 0.00181 66 1,1519 0,1613 1.0893 0,11919
17 0.2967 0.0110 0.2956 0.00017 67 1.1994 0.1661 1,1039 0.12443
18 0.3142 0,0123 0.3129 0.00257 68 1.1 №>8 0.1710 1.1184 0,12982
19 0,3316 0,0137 0.3301 0.00302 69 1.2U43 0.1759 1,1328 0.1353.5
20 0,3491 0.0152 0,3473 0.00352 70 1.2217 0.1804 1,1472 0.14102
| 21 0.3665 0,0167 0.3645 0.00«Н 71 1.2392 0.1859 1,1614 0,14683
22 0.3840 0,0184 0.3816 0.00468 72 1.2566 0.1910 1,1756 0,15279
23 0.4014 0.0201 0.3367 0.00535 73 1.2741 0.1961 1,1896 0,15889
24 0.4189 0.0219 0.4158 0,00607 it 1,2915 0,2014 1.2036 0.16514
25 0,4363 0,0237 0.43?) 0.00686 75 1.3U9O и. л»; t.2175 0,17151
26 0,4538 0.0256 0,4499 0,00771 76 1,3265 0,2120 1,2313 0.17808
27 0,4712 0,0276 0.4669 0,00862 77 1,3439 0,2174 1.24.50 0,18477
28 0.48*7 0.0297 0.4838 0.00961 78 1,3611 0,2229 1.25В 0.19160
29 0,5061 0.0319 0.5003 0,01067 79 1.3788 0,2234 1.2722 0.19859
30 0.5236 0,0341 0,5176 0.01180 Л) 1.3963 0,2340 1.2856 0,20673
31 0.5411 0,0364 0.5345 0,01301 81 1.4137 0.2396 1.2989 0.21301
32 0.-5585 0.03 87 0.5513 0.01429 82 1,4312 0.2Q 1,3121 0,22045
33 0.5760 0.0412 0.5680 0.01566 83 1.4486 0.2510 1.3252 0.22804
34 0.5934 0,0437 0,5847 0 01711 84 1,4661 0.2569 1.3383 0.23578
3S 0.6109 0,0463 0,6011 0.01864 85 1,4835 0.2627 1.3512 0,24367
35 0.6283 0,0489 0.6180 0.02027 86 1,5010 0.2686 1,3540 0,25171
37 0,6458 0.0517 0,6346 0.02198 87 1,5184 0.2746 1.3767 0.25090
38 0,66.12 0.0545 0.6511 0.02378 88 1,5358 0,2807 1,3893 0.26825
39 0,6807 0,0574 0.6676 0.02568 89 1,5533 0,2867 1,4018 0.27675
40 0,6981 0,0603 0.6840 0.02757 90 1.570» 0,2929 1,4142 0,28510
41 0.7156 0,0633 0.7004 0.02976 91 1,5882 0.2991 1,4265 0.29420
42 0,7130 0,0664 0.7167. 0,01195 92 1,6057 0.3U63 1,4387 0.30316
43 0,7505 0,0695 0.733О 0.03125 93 1,6232 0.3116 1,4507 0,31226
44 0.7679 0,0728 0,7492 <7.03664 94 1.6406 0,3180 1,4627 0.32152
45 0.7854 0,0761 0.7654 0,03915 95 1,6580 0,3244 1,4746 0,33093
46 0.8029 0,0793 0,7815 0,04176 96 1,6755 0,3309 1.4863 0.34060
47 0,8203 0.0829 0.7975 0,04448 97 1,6930 0,3374 1.4979 0.35021
48 0,8378 0,0865 0,8135 0,04731 98 1.7104 0,3439 1,5094 0,36608
49 0.8552 0.0900 0,8294 0.05025 99 1.7279 0,3.06 1,5208 0,37009
60 0.8727 0,0837 0.8462 0,05331 100 1.7453 0,3572 1,5321 0.38028
.38
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
Продолжение табл. VI
Централь- ный угол а3 Длина дуги 1 Стрелка Л Длина хорды 3 . Площадь сегмента 9 Централь- ный угол »* Длина дуги 1 Стрелка Л Данина хорды 3 ' 5 3 о С сегмента $
101 1,7628 0,3639 1,5432 0.WO5S 141 2,4609 0,6662 1,8853 0,91580
102 1,7802 0,3707 1.5543 0,40101 142 2.4734 0,6711 1,89)0 0,931.35
103 1,7977 0,3775 1,5652 0,41166 143 2,4958 0,6827 1,8966 0,94700
104 1.8151 0,3843 1.5760 0.42242 144 2,5133 0.6910 1,9021 0,96274
105 1,8326 0,3912 1.5867 0,43333 145 2,5307 0,6993 1,9074 0,97858
106 1,вЗС0 0.3982 1,5973 0,44439 146 2,5482 0,7076 1,9125 0.99449
107 1.8675 0,4062 1.6077 0,45560 147 2,5656 0,7160 1.9176 1.010513
108 1,8850 0,4122 1,6180 0,46695 148 2.5831 0,7244 1.9225 1,02653
109 1,9024 0,4193 1,6282 0,47844 149 2.6005 0,7323 1,9273 1,04275
ПО 1,9199 0,4264 1,6383 0,4901В 150 2.6180 0.7412 1,9319 1,05901
111 1,9373 0,4336 1,6183 0,50187 151 2,6354 0,7496 1,9363 1.07532
112 1,1518 0;4403 1.6581 0.5137» 152 2.6529 0,7581 . 1,9406 1,09171
113 1.9722 0,4481 1,6678 0,52586 153 2,6704 0,7666 1,9447 1,10818
114 1,9897 0,4531 1,6773 0,53907 154 2.6878 0,7750 1,9487 1,12472
115 2,0371 0.4627 1.6468 0.55011 155 2.7053 0,7836 1,9526 1,14132
116 2,0246 0,4701 1.6961 0.56’89 156 2,7227 - 0,7921 1,9563 1,15799
117 2,0420 0,4775 1,7053 0,57551 157 2.7402 0.8006 1,9598 1,17472
its 2,0195 0.4Я50 1,7143 0,58827 158 2.7576 0,8092 1,9633 1.19151
119 2,076!» 0,4925 1,7233 0,60116 159 2.7751 0,8173 1,9665 1,20835
120 2,0944 0.5 00 1.7321 0.61418 160 2,7925 0,8261 1,9696 1.22525
121 2,1118 0,5076 1.7407 0,62731 161 2,8100 0,8350 1,9726 1,24221
122 2, Г.93 0.5152 1,7492 0,61063 162 2,8271 0,8436 1,9754 1,25921
123 2,1463 0,5228 1.7576 0.65404 161 2.8449 0,8522 1,9780 1,27626
124 2,1612 0,5305 1,769» 0.66759 161 2.8623 0,8603 1,9805 1,29.335
125 2,147 0.5383 1,7740 0.6*125 165 2.8791 0,869.5 1,9829 1,31019
126 2,1991 0,5160 1,7820 0.69505 166 2.8972 0,8781 1,9851 1,32766
127 2,2166 0,5538 1,7899 0.70497 167 2,9147 0,8868 1,9871 1 ,34487
128 2.2340 0,5616 1,7976 0.7210] 168 2,932? 0,8955 1,9890 1,36212
129 2,2515 0,5695 1,8052 0,73716 169 2,9196 0,90-12 1,9908 1,37940
110 2,2689 О.Г774 1,8126 0.75144 170 2.9671 0,9128 1,9924 1.39671
131 2.2861 0,5853 1,8199 0,76584 171 2,9845 0,9215 1,9338 1,41-104
132 2,3(38 0,51'33 1,8271 0.78034 172 3,0020 0,9302 1,1961 1,9963 1,43140
133 2,3213 0,6013 1,8341 0.79497 173 3,0194 0,9390 1,44878
134 2,3387 0,6093 1,8410 0,80970 174 3,0369 0,9477 1,9973 1,46617
135 2, 562 0,6173 1,8478 0.82454 175 3,0543 0 9.561 1,9081 1,483.59
136 2.3736 0,6251 1,85-14 0,83919 176 3,0718 0,9651 1.9968 1,50101
137 2,зап 0,6335 1,8608 0,85165 177 3,0892 0,9738 1.9993 1.51845
138 2,40'6 0,646 1,8672 0,86971 178 3.1067 0,9825 1.9997 1.53589
139 2,4260 0,6194 1,8733 0.88497 179 3,1241 0,9913 1,9999 1.55334
10 2.4435 Г,6.тЯ) 1,8791 0.1 (ИХ И 180 3.1416 1,0000 2,6000 1,57060
Примечание. Если <1 — 2г — диаметр окружности, то при принятых и таблице ободиаченпах:
1) длина дуги I — «4 - 0,0087274-? я» у/**+ Л*;
5) стрелка Л - — (l- coi-|) »d sin* у — — lg -J-;
3) длина хорды д — 4 sin ;
4) площадь сегмента S '£ ( if* — aln ?) i
5) площадь сектора раина = 0,002182н'-?.
ПЕРЕВОД ГРАДУСНОЙ МЕРЫ В РАДИАННУЮ
Для более точных вычислений служат значения = 0,01745329; 1g= 2,2418774;«
Idu lw jbJ
= 0.00672665; Ig -4- = 3,9408474.
, би
Таблица содержит данные, относящиеся к различным сегментам одной и той же окружности
радиуса, равного единице. Если диаметр рами d. то табличные значения I, h и s умножаются на -у.
а плошать сегмента — на — .
Если центральный угол не находится в таблице, то прибегают к интерполяции (см. примечание
к табл. Ill), обратив предварительно минуты и секунды и доли градуса.
Пример. Найти длину дуги, стрелки и хорды, а также плошадь сегмента с центральным
углом 67*31'12", если диаметр окружности d = 3 сж.
Находим по таблице (для случаи г = 1) /, А, л. пользуясь линейной интерполяцией:
1R72
31'12» - 1872» - -'°'- = О» ,52;
-UU
ф® 1 4 * 4 3 &
67 0,52 1,1694 90 174 0.1661 2S 49 1,1039 75 145
67»,52 1,1784 0,1686 1.1'М
Для отыскания плошали сегмента пользуемся квадратической интерполяцией, так как две соседние
разности а» = 12 982 - 12 441 = 53< и а, = 13 .'.35 — 12 942 = 5зЗ отличаются друг от друга больше
чем на 4 единицы последнего знака: Д, — а, = 553 — 739 = 14 > 4.
Пользуясь указаниями примечания к таил. 111. имеем
ж, - А = 66»
х, - 67»
X, + Л = 68»
х„ + 2А = «»’
У_,
У»
>i
У1
= 0,11919
= 0.12143
= 0,12982
= 0,13536
— 524
Д. = 539
б, =5»
. х-х, OJW . *(!-*) ОЛ2.П.4Я
* = —у = —— = 0,52; А. = ——-----------=---------— = 0,0624 ~ 0.062, а потому поправка равна
ла. - *,(4, - Д_ ) =0,52-539 — 0.062-29 - 260.28- 1.795 - 278,482 ~ 278.
Следовательно.
$ - 0.12443 + 0,00278 - 0,12721 см*.
Окончательно имеем
1=/-у —1,1781.1.5=1,7676 см; Л = А у = 0,1686-1.5 — 0,2529 см; t — Г -у - 1,1114.1 JS —1,6671 си
5 = 3у = 0,12721-2,25 — 0,28622 сМ1.
ТАБЛИЦА VH. ПЕРЕВОД ГРАДУСНОЙ МЕРЫ В РАДИАННУЮ
Длина дуг окружности радиуса, рапного 1
Угол Дуга Угол Дута Угол Дуга Угол Дуга 1 Угол Дуга Угол Дуга
1» 0,1X10005 1' 0,000291 1» 0X117453 16е 0,279’53 31» 0.541052 70» 1,221730
2 0,000610 2 0,100562 2 0.131907 17 0,296706 32 1,558506 75 1ДЯ997
3 O.nOOlS 3 0,000873 3 0,0 Z.60 18 0,314159 33 0,575959 но 1,396263
4 0,000019 4 0,00.164 4 0.06981 1 19 0,33 6.3 34 11,593412 8.5 1,4835311
Б оиюоол Б 0.101454 5 0,087,66 20 6,349056 35 0,610665 МО 1,5'0796
6 0,700029 6 0,001745 6 0,101720 21 0,366519 Зв 0,628719 100 1,7453»
7 О.» »(в 1 7 0,1,020.31 7 0,1 2173 22 0,183972 37 0.645772 ГД) 2.094395
8 0,(8520.39 8 1 .,002327 я 0,131.621 23 0,40142-6 39 0,613221 150 2,617994
9 0,'Я 041 9 0,(872618 9 0,1570о0 24 0.418“.9 39 0,680678 180 3.141593
10 0,0000.8 10 (.',002929 10 U,1745.3 25 U.436332 40 0.698132 200 3.491669
20 0.000097 20 0,005818 11 0,191986 25 0,453785 45 0,78 398 250 4 „323323
30 0Ж141 3) О.(КХ->727 12 о^евно 27 0.47,239 .’0 0,87216» 270 4.712389
11) 0,001194 40 0,011636 13 0,226193 28 0,4-8(92 55 Оде М81 З-'О 5.235988
50 0ДХК42 50 0X2(4344 11 (Д443»6 29 0,506141 6П 1,047198 36" 6,283185
4 15 0,261799 30 0,52 о 99 65 1,134461 400 6391317
Примечание, i радиан (луга, равная радиусу) равен 57»17'44"3
40
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
Примеры:
1) Выразить в радианах 52’37'23». Вычис-
ления располагаем так:
50“ - 0,872665
2“ —0.081907
30' — OfiMlll
’ V — 0/102036
20» - 0.000097
3» = ОДООП15
52*37'23» - 0,918447 - 0.91845 ра-
мака (сложение удобно выполнять нв счетах).
2) Выразить в градусной мере 5,645 рази-
ана. Вычисления располагаем так:
5,645 радиана
5,2359 48 =300“
0,404012
0,401426 — 23*
0,<Л 0556
0/06818 — 20'
6,001768
О/Ю1745 - 6'
03)00023 ______________5’
5,645 радиана — 323 26'5»
/ п\ т п — т /я
ТАБЛИЦА VIII. БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ 1-С С -
< \т/ п п \п — т
Примечания: 1. Лав больших значений п биномиальные коэффициенты вычисляются по
обшей формуле для С„* (см. стр. 79), причем следует пользоваться тем, что С„ т = с” , т. е.
л
при четных значениях п нужно вычислять коэффициенты лишь до т -- — , а при нечетных л — до
ж_±±1.
2
2, При вычислении удобно пользоваться зависимостью । ‘
Пример. Биномиальные коэффициенты для л — 15с
ат. ь Ряд биномиальных коэффициентов для данного случае 1; 15; 105; 456:1365 ; 3003:5006. 6435; 6433:
6006; 3003; 1365; 455; 105; 15; 1.
а. Значения биномиальных коэффициентов для всех л от л —0 до л — 100 см. [110J, стр. 361.
ГАММА-ФУНКЦИЯ
41
ТАБЛИЦА IX. ФАКТОРИАЛЫ ЦЕЛЫХ ЧИСЕЛ ОТ 1 ДО 20 И ЛОГАРИФМЫ ФАКТОРИАЛОВ
л! = 1*2-3- ... -л
— л л! 1g п'- Л1 1g «1
1 1 0.000000 3,9916300* 1СР 7,601156
2 2 0,301030 12 4,7900160*10* 8,640337
3 6 0,778151 13 6.2270203*10' 9,791280
4 2,4-10* 1,380211 14 8,7178291*10"’ I0.91O4C8
Б 1,20*10* 2.0791П 15 1,3076744*10” 12.116500
6 7.20-10" 2,857332 16 2,0922790-10” 13.320620
7 5.0*10* 10* 3.702131 17 3,5568743*10” 14,551069
8 4,0320-10* 4.605521 18 6,4023737*10” 15.806341
9 3,62380* 10" 5.555(763 19 1,2161510*10” 17.085096
10 3,628800*10* 6.559763 20 2,1329020* 10й 18,386125
f
Примечание. Начиная с «1= 141. значения факториалов округлены с «остаточной для практи-
ческих расчетов степенью точности. Значения факториалов для всех л от л - 1 ю л - 200 и лога-
рифмов факториалов для всех л от л = 1 до л = 1200 см. (НО), стр. (351).
ТАБЛИЦА X. ГАММА-ФУНКЦИЯ (см. стр. 178)
X гм 1 г (л) X Г (л) Грг)
1,00 1,00000 1.25 0,90640 1,50 0.88623 1,75 0,91906
1.01 0,99133 1.26 90140 1,51 84659 1,76 92137
1,02 98884 1.27 90250 1.52 887U1 1.77 92376
1,03 98355 1.28 90072 1,53 88757 1.78 92623
1.04 97844 1.29 89901 1.54 88418 1.79 92877
1,05 0,97350 1,30 0,89747 1,55 0,88837 1.80 0,93138
1.06 96874 1,31 89600 1.56 88964 1.81 93103
1,07 96*115 1,32 89461 1,57 89049 1.Я2 93685
1,08 95973 1,33 18338 (.58 89142 1,83 93969
1.09 95546 1,34 89222 1,59 89243 1,84 94261
1.Ю 0,95135 1,35 0,89115 1.60 0.89352 1,85 0,94561
1.11 917Ю 1,36 89018 1,61 89468 1,86 91Н69
1.12 94359 1.37 88931 1,62 89892 1,87 95184
1.13 93993 1,38 88ЧМ 1,63 89724 1,88 95507
1.14 93642 1.39 88785 1.М 89364 1.89 95834
1.1Б 0,9030*1 1,40 0,88726 • ,65 0,90012 1,90 0,96177
1.16 92980 1,41 88(176 1,66 90167 1,111 96523
1.17 926711 1.42 88036 I 1.67 90330 1.92 96877
1,18 92373 1,43 88601 1,68 90500 1,93 97240
1,19 92089 1,44 88681 1,69 90678 1,91 97610
1,20 0,91817 1.45 0,88566 1.70 0,90864 1,95 0,97988
1.21 91558 1,46 885(50 1.71 91057 1.96 98374
1.22 91311 1.47 88563 1.72 9)258 1.97 98768
1.23 > 91075 1.48 88575 1,73 91467 1.98 J 99171
1,24 90852 1.49 88695 1,74 91683 1,99 99581
1.25 0,90640 1.50 0.88823 1,78 0,91906 2,00 1,00000
12
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
ТАБЛИЦА XI. НАТУРАЛЬНЫЕ ЛОГАРИФМЫ ЧИСЕЛ
0 « 2 3 5 6 7 8 9
1.0 0.00000 0,00995 0,01980 0,02956 0.03922 0,04'79 0,05827 0.06711 0,0'696 0,08618
1'1 09531 10431 11333 12222 131U3 13976 14812 15700 16551 17395
1.2 18232 19062 19 «5 20701 21511 22314 23111 23912 •24616 25164
1.3 2623'1 27003 27763 28518 29267 30010 3::?48 .114 <1 32203 32910
1.4 33-47 31359 35066 35767 36164 37156 37844 38526 39201 39678
1.6 0,40547 0,41211 0,41871 0,42527 0,43173 0.43825 0,44459 0,45108 0,45742 0.46373
1.6 47000 47623 48243 48858 49170 50078 60682 51282 51’79 52173
1,7 53063 53319 51232 54812 55389 55932 66531 57098 57651 Е8Э2
Л 58779 59-133 59884 60432 60977 61519 62053 62591 631'27 63356
1.0 64185 64710 65233 65752 63 269 66783 67294 67803 68310 68813
2,0 0.69315 0,69813 0,70310 0.70904 0.71295 0,71784 0,72271 0,72755 0,73237 0,73716
2«1 74194 74669 75142 75612 76081 765-17 77011 77-73 77932 78-90
2.2 788-16 79299 79751 80200 НО64Ч 81093 81536 81978 82418 82855
2,3 83291 83725 84157 84587 IViOJb 85442 83866 86289 86710 87129
2.4 87547 87933 88377 88739 R92Q0 8951-9 90016 90422 90326 912'28
2,5 0,91629 0,92028 0.92Г26 0,92822 0,90216 0.93609 0.91001 0.95391 0,94779 0,95166
2,0 95551 95935 0,95317 0,94694 0,97078 0.97156 0.97КП 0.9R20S 0.96582 0,9 3954
2,7 0,99325 0,99695 1,00063 1.00433 1,00796 1,01160 1,01523 1.01885 1.02245 1,02601
2.8 1,02962 1,03318 03674 04023 04310 04732 05062 05431 16779 06126
2,0 06471 06815 07158 07500 07641 08181 03519 06856 09192 1.932/
3,0 1,09861 1,10194 1.10526 1.10858 1,11186 1,11514 1,11841 1.12168 ‘1.12493 1,12817
3.1 13140 13152 13783 14103 14422 14740 15057 1537. 1.5614 16002
3,2 16315 16627 16933 17248 17557 17965 18173 18479 18734 19339
3,3 19392 19695 19996 20297 20597 20196 2119! 21191 21784 22083
3,4 22373 22671 22964 23256 23547 23337 24127 24115 24703 24990
3,5 1,25276 1.25562 1,25846 1,26130 1,26413 1,26695 1,26976 1,27257 1.27536 1,27815
3,6 28093 2R37I 28647 28923 29191 29473 29746 30019 30291 30563
3,7 31»;3 31103 31372 31641 319-19 32176 32442 32701 32972 33287
3,8 3351Ю 33763 34025 34216 31547 34’07 350И7 3’325 35584 35811
3,9 36093 33354 35609 35864 37118 37372 37624 37877 33123 31379
4,0 1,33629 1,38879 1,39128 1,39377 1.39124 1.39372 1,40118 1,40361 1,40610 1,40454
4,1 41099 41312 41585 41828 42070 42311 42552 42792 43031 43270
4.2 43508 43746 43934 44220 44-156 41692 41927 45161 45395 45629
4,3 45852 46091 46326 46557 46787 47>Л8 47247 47176 47705 4,933
4,4 43160 48337 48614 49340 49365 49290 49515 49739 49962 50185
4,5 1,60403 1,50630 I.8MM 1,51072 1,51293 1,51513 1,51732 1,51951 1,52170 1,52398
4,6 52606 52323 53039 53256 53471 5:1617 53102 54116 54230 54543
4,7 54756 54969 56181 55.193 55604 65814 56,25 56231 56441 56653
4,8 56862 57070 57277 574’5 57691 57.91 58104 583 9 58515 88718
4,9 58924 59127 59331 59534 59737 59939 60141 60312 бОа-43 60744
5,0 1.60914 1.61144 1,61343 1,61542 1,61741 1.61939 1,62137 1,62334 1.62531 1,62728
5,1 62924 63120 63315 63511 63705 6391X1 64 '»4 61187 64431 • ||'|| .1
5,2 64866 65058 65230 65141 65632 658'23 61X113 66203 66.191 06582
S3 66771 66959 67147 67335 67523 67710 6789>i 04083 И169 63455
5.4 68640 68825 69010 69191 69378 69562 69745 69928 70111 70293
5.5 1.70475 1,70656 |,70°38 1,71019 1,71199 1,71380 1,71560 1.71740 1,71919 1,72093
5.6 7'2277 72455 72633 7241 72918 73166 73142 73519 73595 7М71
5,7 74947 74222 74-97 74572 74746 74920 75094 75267 75140 75613
5,8 75746 75958 76130 76302 76473 7-611 76115 76085 77156 7)326
5,9 77495 77665 77834 781872 78171 78339 78507 78675 78842 79Л19
6,0 1,79176 1.7942 1,79109 1,79275 1,79140 1,80005 1,80171 1,81X336 1.80500 1,80.165
6,1 80429 80993 611.56 81319 81412 81645 81808 81970 82132 82291
6,2 82155 82616 82777 82918 8'1098 83 .'58 81’418 83578 83737 83196
6,3 84055 84214 84372 84530 84 188 84 45 85033 851 ;о 85317 й!>ч?з
6,4 85630 85786 85942 86097 86253 86108 86565 86718 86872 87026
6,5 1,87180 1,87331 1,87487 1.87641 1,87791 1,87917 1.88099 1,88251 1,88403 1,88555
«,6 83707 88858 89JI0 89160 89311 89162 89212 897-2 899Г2 люб!
6.7 90211 90360 9и6С9 90358 9>1МХ> 91.931 91102 91'250 91398 91.ИЗ
6,8 91692 91839 919 6 Я.'132 92279 92425 92571 92716 92882 93J07
6.9 93152 93297 93442 93586 93733 93874 91018 9-1162 91305 941м8
0 1 1 2 з ч 1 s « 1 » « 9
НАТУРАЛЬНЫЕ ЛОГАРИФМЫ
43
Продолжение табл. XI
N 0 I Г 2 3 « 5 6 » »
7Л 7,1 7.2 7Л 7,4 1,91391 96 X» 97408 l,MW 2.00148 1,94731 96150 97.547 1.9-921 2,60283 1.94876 96291 97685 1.99061 2.00418 1,95019 96131 97824 1,99198 2,00653 1.96161 96571 97962 1.99334 2.00687 1.95303 96711 98100 1.9947J 2.00621 1.95445 УЖ51 98238 1.99606 2,00956 1.95586 96991 98176 1,99742 2.01069 1.95727 97130 98513 1,99677 2,01223 1,95869 97269 1,98650 2.00013 2,01357
7.5 7Л 7,7 73 7.» 2.01490 02815 04122 084)2 06686 2/1624 62946 04252 05540 66813 2.01787 03078 04381 08668 06939 2.01890 13209 04511 05 96 07065 2,02022 13310 0 610 059’4 07191 2,02155 03171 04769 06 «51 07317 2.02287 03 Ю1 04894 06179 07413 2.02419 03732 (5027 0636 07568 2.00551 0386? (4155 («40 07691 2.02683 03992 05284 06560 07619
8,0 8.1 8Л 8.3 8.4 2.07914 09186 10113 11626 12823 2.08069 09310 10535 11746 12942 2.08194 09433 10657 11 И! 13061 2,0*318 L9556 10779 11986 13180 2,08443 09679 10900 12106 13293 2.08567 49602 11021 1ЯИ 13417 2,08691 (.9921 1442 12316 13535 2,06815 10047 11263 12465 13653 2.08939 10169 11384 125*5 13771 2.09Г63 10291 11505 12704 13389
8Л 8.8 8.7 M 83 2,14007 15176 16332 17475 186® 2.14124 15292 16447 17589 18717 2.14242 1.5409 16)62 17702 18830 2,14359 15524 16677 17*16 18942 2.14476 1564U 16791 17929 19051 2.14593 15756 16905 18042 19165 2,14710 15871 17620 18155 19277 2.14827 15987 17134 18267 19389 2.14913 16102 17241 18380 1S500 2.15060 16217 17361 1*493 19611
9Л 9,1 »л 9.3 8,4 2.19722 20827 21920 mu 24071 2.19834 20937 22-/29 23109 241)7 2.19944 21017 22138 23.45 24281 2,20055 21153 22246 23324 24590 2,20166 21265 22351 23431 2.493 2.20276 2137$ 22462 23331 2ЛЮ1 2,20387 21 «5 22570 2364’, 24707 2.20 «97 21594 22678 23751 24813 2.20607 21703 22786 23858 24918 2.30717 21812 22*91 23965 23024
9.3 9.9 8.7 83 M 2.25129 26176 27213 28238 29253 2.26234 26280 27316 28340 29354 2,27339 26381 27419 28442 29455 2.25444 26488 27621 28.544 29556 2.25549 26592 27624 28646 29657 2.25«54 26695 27727 28717 29757 2.25759 26799 27829 M я 29858 2.X5*63 26903 2 932 28950 29958 2,259*8 27,06 28КИ 29031 30068 2.26072 27109 281.86 29152 30158
N 0 2 3 < 1 » в 7 « •
/ In 10' = 2.ЭО2585О9 tn 1№ - 4.60517 In 10* = 6.9,-776 In 10* = 9.21034 In 10» = 11.51293 In 10» = 13,81551 In 1(7 = 16,11810 In 17 = 18.42061 In 1C8 - 20.72327 In 10*“ - 23.00585 In 10*‘ -25.3M44 In 10" —27,63102
Примечание- Таблица содержит пггидиачные натуральные логарифмы чисел от 1 до 9.99.
Поэтому дли нахождение натурального логарифма числа N оно должно быть представлено в виде
N = W-10* ш, глс 1 < N' < 10; тогда In N — In N' ± In 10я*; In N' находиты непосредственно мд
таблицы, а значение In In*" указано внизу нее дав всех т < IX
Примеры. In 728,4 “ 7
728.4 - 7.281 IIP: In 728,4 — la 7.234 + tn 1№.
Из таблицы
In7.28... 1.98513(A— 137)
.4 84.8
In 7.284 — 1.98<68
In l< • = 4.6П517
In <28.4 — Ь.эЭмбЗ
In 0.00242 - ?
0,00243 - 2,42-ю—s; In 0.00242 — In 2.42 — Io I03
- In 10» - - 6.9O77S
In 2.42 - I ,88377
Ш 0,00242 — —
44
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
ТАБЛИЦА XII. ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Синусы
0 6' 12' 13' 24' 30' 36' 42' 48' 54' Разности
1' I2' 3’ 4' 1 5'
0° 0,0000 0017 0035 0052 0070 0087 0105 0122 0140 0157 3 6 9 12 15
1 0175 0192 0209 0227 02-44 0262 0279 0297 0314 0332 3 6 9 12 15
2 0349 0356 азм 0401 0419 0436 0154 0171 0488 (В06 3 6 9 13 15
3 0523 0541 0551 0576 0593 0610 0628 0645 0663 0680 3 6 9 12 15
4 0093 0715 0732 0750 0767 0785 0802 0819 0837 0851 3 6 9 12 14
5 0872 0889 0906 0924 0941 0958 0976 0993 1011 1028 3 6 9 12 14
в 0,1045 1063 1090 1097 1115 1132 1149 1167 1184 1201 3 6 9 12 14
7 1219 1235 1253 1271 1288 1305 1323 1340 1357 1374 3 6 9 12 14
8 1392 14.9 1426 1444 1461 147К 1495 1513 1530 1547 3 6 9 12 14
9 1554 1532 1599 1516 1633 1650 1668 1685 1702 1719 3 6 9 12 14
10 1736 1754 1771 1788 1806 1822 1840 1857 1874 1891 3 6 9 11 14
’11 0,1905 1925 1942 1959 1977 1994 2011 2028 2045 2062 3 6 9 11 14
12 2079 2096 2113 2130 2147 2164 2181 2198 2215 2233 3 6 9 11 14
13 2250 2267 2284 2300 2317 2331 2351 23 S8 2385 2402 3 6 Я 11 14
14 2419 2-136 2153 2470 2487 2504 2521 2.533 2554 2571 3 6 Я 11 14
15 2583 2605 2622 2639 2656 2672 2699 2706 2723 2740 3 6 8 11 14
16 0,2756 2773 2790 2807 2823 2840 2857 2874 2890 2907 3 6 8 11 14
17 2924 2940 2957 2974 2993 3007 3024 ЗОЮ 3057 3074 3 6 8 11 14
18 3090 3107 3123 3140 3156 3173 3190 3206 3223 32*19 3 6 8 11 н
19 3256 3272 3299 3305 3322 3338 3355 3371 3387 3401 3 5 8 11 14
20 3420 3-137 3453 3469 3436 3502 3518 3535 3551 3567 3 5 8 11 W
21 0,358-1 3600 3616 3633 3649 .366-5 3681 3697 3714 3730 3 5 Я 11 14
22 3746 3762 3778 3795 3811 3*27 3843 3859 3875 3891 3 5 я 11 14
23 3907 3923 3939 3955 3971 3987 4003 4019 4035 4051 3 5 8 11 14
24 4067 4033 4099 4115 4131 4147 4163 4179 4195 4210 3 5 8 11 13
25 4226 4242 4258 4274 4289 4305 4321 4337 4352 4368 3 5 Я 11 13
2В 0,4384 4399 4415 4411 4440 4462 4478 4490 4509 4524 3 Б 8 10 13
27 45-Ю 4555 4571 4586 4002 4617 4633 4648 4664 4679 3 5 8 10 13
2Я 4695 4710 4726 4741 4756 4772 4787 4802 4’18 4813 3 5 8 10 13
29 4848 4863 4879 4691 49:» 4921 4939 4955 4970 4985 3 5 8 10 13
30 5000 5015 5030 5045 5060 5075 5090 5105 5120 5135 3 Б 8 10 13
31 0,5150 5165 5180 5195 5210 5225 5240 5255 5270 5284 2 5 7 10 12
32 529!> 5314 5329 5344 5.353 537.1 5388 5402 5117 5432 2 5 7 10 12
33 5446 5461 5176 5-190 5.W5 5519 5534 5548 556.3 5577 2 5 7 10 12
34 559.' 5606 5621 56:15 ИБО 5664 5678 5693 5707 5721 2 5 7 10 12
35 5736 5750 5764 5779 5793 5807 5821 5835 5850 5864 2 6 7 9 12
.13 0,5878 5892 5906 5920 5934 5048 5952 5976 5990 6001 2 Б 7 9 12
37 6018 6032 6046 6060 6074 6088 6101 6115 6129 6143 2 Б 7 9 12
38 6157 6170 6184 6193 6211 6225 6239 6252 6266 6280 2 5 7 9 11
38 629(1 63'17 6320 6131 6347 6361 6371 бЗЯ* 6401 6411 2 4 7 9 11
40 6428 6441 6455 6468 6481 6191 6508 6521 6531 6547 2 4 7 У 11
41 0.6561 6571 6587 6600 6613 6626 66.39 6652 6665 6678 2 4 7 9 1!
42 6691 6704 6717 6730 6743 6756 6769 678*2 6794 6807 2 4 6 9 11
43 6Я2О 68.33 6845 6958 6871 6884 6896 60.9 6921 6934 2 4 6 8 11
44 69-17 6959 6972 1-984 6997 7009 7022 7034 704-1 7U59 2 4 6 8 10
45 7071 7083 7096 7106 7120 7133 7145 7157 7169 7181 2 4 6 8 10
Косинусы
col •• aln (90е — а)
ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИИ - СИНУСЫ
45
Продолжение т«6л. XII
Синусы
Разности
V 6' 12' 18' 24' 30* ЗУ 42* 48* 54' V V 3' «' 1 8'
44“ J 48 « 50 St 52 S3 54 55 Зв СТ 58 59 «0 61 62 63 64 63 66 67 68 68 70 71 72 73 74 75 76 71 78 7» 80 81 82 83 М 85 яв 87 88 0.7193 7314 7431 7547 7660 0,7771 7 <80 79» 8093 8192 0.СТ90 8387 8480 8572 8660 0.8746 8829 8910 8938 9J63 0,9135 9206 9272 9336 9097 0.9455 9511 9563 9613 9659 0.9703 9744 9781 9816 9848 0.9477 9903 ЙЙ £916 9962 0.9976 99* 9993 7206 7325 7443 7659 7672 7782 7591 7997 8100 8202 8300 8396 8197 8SSI 8669 8755 8818 8918 8996 9070 9143 №12 9278 9342 9403 9461 9516 9568 9617 9664 9707 9748 9735 9820 9851 9880 9905 9928 9947 9963 9977 W7 9995 9999 7218 7337 7455 7570 7683 7793 7902 8007 8111 ЮН 8310 8406 8499 8590 8678 8763 8846 8926 9003 9078 9150 №19 9285 9348 9409 9466 9521 9573 9622 9668 9711 9751 9789 9023 9654 9882 9907 9930 9949 9965 9978 од 4$ ИМ 9999 7230 7349 7466 7581 7694 7804 7912 8018 8121 8221 8320 8415 8308 8599 8686 8771 8454 8914 9011 9085 9157 9225 9291 9354 9415 9472 9527 9578 9627 9673 9715 9755 9792 9826 9657 9WS 9910 9932 9951 9966 9979 9989 9999 7242 7361 7478 7193 7705 7815 7923 8328 8131 8231 8329 8425 8517 «607 «695 8-780 8862 8942 9018 9092 9164 9232 9198 9361 9421 9478 9532 9583 9632 9377 9720 97'9 9793 9 <29 9360 9888 9912 9934 9952 9968 9980 9990 9996 9999 7254 7373 7490 764М 7716 7826 7934 8039 8141 8241 8339 8434 8526 8616 8704 8788 8870 8919 9026 9100 9171 9239 9304 9367 9426 9483 9537 9538 9636 9681 9724 9763 9799 9833 9363 9890 9914 9936 9954 9969 9981 9950 9997 1.0000 7266 73“ 5 7501 7615 7727 7837 7944 3019 8151 8251 .8348 8443 8536 8625 8712 8795 8878 8967 9033 9107 9178 9245 9311 9373 9432 94® 9542 9593 9641 9686 9728 9767 903 9436 9866 9893 9917 9938 9956 9971 99® 9991 9997 1.0000 7278 7396 7513 7627 7738 7848 7955 8059 8161 8261 8358 8453 8545 8634 8721 8ЭД5 8886 8935 9041 9114 9184 9257 9317 9379 9433 9494 9548 9698 9646 9690 9732 9770 9806 9839 9869 9895 9919 МВ 9957 9972 9983 95*92 9997 1,0000 7290 7408 7524 7638 7749 7859 79*16 «070 8171 8271 8368 8462 8554 8643 8729 8813 8м»| 8973 9048 9121 9191 9259 9333 9385 9444 9500 9653 9603 9650 9694 9736 9774 9810 9842 9871 9898 9921 9942 9959 9973 9984 9993 9998 1,0000 7302 7420 7536 7*49 7760 7869 7976 КЮ 8181 8281 8377 8471 8.563 8652 8738 WT21 8902 8980 9056 9128 9198 9265 9330 1191 9449 9505 9558 9608 9655 9699 9740 9778 9813 9845 9874 9900 9923 9943 99*Ю 9974 9985 9993 9994 1.0000 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 4 4 4 4 4 4 4 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 ' 2 2 2 2 2 1 I 1 1 1 1 1 1 1 1 0 0 0 0 0 6 6 6 6 6 5 5 5 5 5 5 5 5 4 4 4 4 4 4 4 3 3 3 3 3 3 3 2 2 2 2 2 2 2 1 1 1 1 1 1 1 0 0 0 8 8 8 8 7 7 7 7 7 7 6 в 6 6 6 в 5 5 5 б S 4 4 4 4 4 3 3 3 3 3 3 2 2 2 2 2 1 1 1 1 I 0 0 10 10 10 9 9 9 9 9 8 8 8 8 8 7 7 7 7 6 6 6 6 8 5 5 5 5 4 4 4 4 3 3 3 3 2 2 2 2 2 1 1 1 0 0
Косинусы
со»« «. Мп (90* — в)
46
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
Продолжение табл. XII
Тангенсы
0' 6' 12' 18' 24' 30' 36' 42' 48' 84' Разности
*'1 2' 3' 4' | 5'
0’ 5.«ХЮ 0017 0035 0052 0070 0087 0105 0122 0140 0157 3 6 9 12 15
1 0175 0192 0209 0227 0244 0262 0279 0297 0314 0332 3 6 9 12 15
2 0149 0367 0344 04й 0419 0437 0451 0472 0489 0507 3 6 9 12 15
3 0524 0512 0559 0577 0591 0612 0629 0647 0664 0662 3 6 9 12 15
4 0699 0717 0734 0752 0769 0787 0805 0822 0810 0’57 3 6 9 12 15
5 0375 0892 0910 092* 0945 0953 0951 0598 1016 1033 3 6 9 12 15
6 1,1051 1069 1086 1104 1122 1139 1157 1175 1192 1210 3 6 9 12 15
7 1224 12-16 1263 12S1 1299 1317 1334 1352 1370 13’8 3 6 9 12 15
8 1405 1423 1411 1459 1477 1495 1512 1530 154'8 1566 3 6 9 12 15
а . 15 4 1.02 1620 1631 1655 1673 1691 1709 1727 1745 3 6 9 12 15
10 1763 1781 1799 1817 1835 1653 1871 1890 1908 1926 3 6 9 12 15
11 0,1944 1962 1980 199- 2016 2035 2053 2071 2089 2107 3 6 9 12 15
12 2126 2144 2162 2180 2199 2*217 2235 2251 2272 2290 3 6 9 12 15
13 2309 2327 2345 2361 2382 2401 2419 243’ 2456 2475 3 ti 9 12 15
14 2494 2512 2530 2549 ЖИЯ 2545 2605 2623 2642 2661 3 6 9 12 16
16 2679 2698 2717 2736 2754 2773 2792 2811 изо 2349 3 б 9 13 16
10 3,2867 2886 2905 2924 2943 2972 2981 3000 3019 3038 3 fi 9 13 16
17 3057 3076 3095 3115 3134 3153 3172 3191 3211 3230 3 6 10 13 16
18 3249 3269 3288 ЗТО7 3327 3316 3365 3385 3404 3424 3 6 10 13 16
19 3443 3463 3182 3502 3522 3511 3561 3581 3503 3620 3 7 10 13 16
20 3040 3659 3679 3699 3719 3739 3750 3779 3799 3819 3 7 10 13 17
21 0,3539 .3859 3879 3899 3919 3939 3959 38П 4000 4020 3 7 10 13 17
22 4040 4061 40*1 4101 4122 4142 4163 41 ИЗ 4204 4224 3 7 10 14 17
23 4215 4265 42-6 47107 4327 434’ 4359 4390 4411 4131 3 7 10 14 17
24 4452 4473 4494 4515 4536 45.57 4578 4599 4621 4642 4 7 11 14 18
25 4663 4684 4706 4727 4748 4770 4791 4813 4334 4855 4 7 11 14 18
26 0.4*77 4’99 4921 4942 4964 4986 5004 5029 5051 5073 4 7 11 15 18
27 5015 5117 5139 5161 51Н 5205 5224 5250 5272 5295 4 7 II 15 18
28 5317 5340 5362 53’4 5107 5430 5452 5475 5198 5520 4 6 11 15 19
2» 5543 55% 55 9 5612 5635 565s 5681 Б7О4 5727 57.50 4 Я 12 15 19
30 5774 5797 5820 5344 5867 5’90 5914 5938 5961 5955 4 8 12 16 20
31 1,15009 6012 6056 6080 6104 «12« 6152 6176 6200 6224 4 Я 12 16 20
32 6249 6273 6297 6322 6345 1э371 6395 6420 6445 64«9 4 8 12 16 20
33 6494 651» 6514 6569 «591 6619 6644 «669 «694 6720 4 8 13 17 21
34 6745 «771 6796 «822 6Ч47 6S73 6В99 «924 6950 6976 4 9 13 17 21
35 7002 7028 7054 7030 7107 7133 7159 7186 7212 7239 4 9 13 18 22
36 1.7265 7292 7319 7346 7373 7400 7427 7454 7481 7508 в 9 14 18 23
37 7531 7553 7590 7618 764. 7673 7701 772» 7757 пм 5 9 14 18 23
3J> 7813 7841 7469 7-9' 7926 7951 7983 8012 8010 8069 5 9 14 19 24
3» 4091 8127 8156 8IK5 8214 8243 827.1 8302 8332 8361 5 10 15 20 24
40 6391 8421 8451 8481 8511 8541 8571 8601 8832 8662 В 10 15 20 25
41 J.9093 8724 8754 8785 8816 8847 8878 8910 8911 8972 5 10 16 21 26
42 9004 «136 9067 К® 91.31 9163 9195 9228 9260 9294 5 II 16 21 27
43 9325 9354 9391 9411 9457 #523 9556 9690 9523 « 11 17 22 28
44 9657 9.91 9725 9759 9793 #.427 9’Ы 9 96 9930 №5 6 II 17 23 29
46 1 ,<КИХ) 0035 0070 0105 0141 0176 0212 0247 02.-й 0319 6 12 IS 24 30
46 0055 0392 042’ 0461 0501 0538 0575 0612 0649 0686 6 12 18 25 31
47 0724 0761 0799 0КЧ7 0-75 0913 0051 0991) 102’ 1067 6 13 19 25 32
48 1106 1145 1144 12-24 1263 1303 1343 13’3 1423 1403 7 13 20 27 33
49 1501 1544 1585 1626 1667 170> 1750 1792 1833 1875 7 14 21 2’ 31
50 1918 I960 2002 2045 20.88 2131 2174 2218 2201 2305 7 14 22 29 36
61 1.2349 2393 2437 2482 2527 2572 2617 2662 2708 2753 8 15 23 30 38
52 2799 2846 2М72 293’ 29'5 3032 3079 3127 3175 3222 н 16 21 31 39
53 327п 3319 3367 3416 3465 3514 3584 3613 36.53 3713 в 16 25 33 41
34 3764 3814 3465 3916 39 Н 4019 4071 4124 4176 422» 9 17 да 34 43
55 4281 4335 4388 4442 4496 455.1 4605 4659 4715 4770 9 18 27 36 45
Котангенсы
Ct£ « - tg <9J’ - .)
ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ — ТАНГЕНСЫ
47
Продолжение табл. XII
Тангенсы
0' 6' 12' IB' 24' 30' 36' 42' 48' 54' Рааностн
•' 2' 3' «'
56 1,4826 4882 4938 4994 5051 5108 5166 5224 5282 5340 10 19 29 :н 43
57 5399 5458 5517 5577 5637 6697 5757 5818 5380 5911 10 20 30 40 50
58 6003 6005 6128 6191 6255 6319 6383 6447 6312 6577 11 21 32 4.1 53
59 664с 6709 6775 6842 С909 6977 7(45 7113 7132 725! II 23 34 45 56
60 7321 7391 7461 7532 7603 7675 7747 7820 789.1 7966 12 24 36 48 60
61 1,8040 8115 8190 8265 8341 8418 8493 8572 8650 8723 13 26 38 51 64
62 1.8S07 8887 8967 9017 9128 9210 9292 9375 9453 9542 14 27 41 55 68
63 1,9326 9711 9797 9КЧ.З 9970 2,0057 2.0145 2,0233 2.0323 ’.0413 15 29 44 53 73
64 2,0503 0694 0686 0778 0872 09x5 1060 1155 1231 1348 16 31 47 63 78
65 2,1445 1543 1642 1742 1842 1943 2045 2148 2231 2355 17 34 51 68 85
66 2.2460 2.566 2673 2781 2889 2998 3109 3220 3332 3445 18 37 55 73 92
67 3559 3673 3789 3906 4023 4142 4262 4504 4627 20 40 60 79 99
68 4751 4876 5002 5129 5257 5386 5517 5649 5782 5916 22 43 65 87 105
69 «Oil 6187 (315 6454 6605 6746 6889 7034 7179 7326 24 47 71 93 119
70 747с. 7625 7776 7929 8083 8239 8397 8556 8716 8878 26 52 78 10-1 131
71 2,9042 9209 9375 9544 9714 9387 3,0051 3,0237 3.0415 3,0695 29 53 87 116 145
72 3,0777 0931 1146 133-1 1521 1716 1911) 2106 2305 2503 32 64 9> 129 161
73 3,2700 2914 3122 3332 35-И 3759 .3977 4197 4420 4646 .36 72 103 141 180
74 3,4874 5106 5339 5576 5816 60.59 6306 6554 6306 7062 41 81 122 163 20-1
75 3.7321 75КЗ 7648 8118 8391 8667 6947 9232 9520 9812 46 93 139 186 232
0' 6' 12' 18' 24' .30' 36' 48' 54'
76 4,0108 0408 0713 1022 1335 1653 1976 2303 2635 2972
77 4,3.31.5 3662 4015 4374 47.37 5107 5483 5864 6252 6616
78 4,70k, 7453 7867 8288 8716 91.52 9594 5,0045 5,0504 5,0970
79 5,1446 1929 2422 2924 34.35 3955 4486 5026 5578 «ПО
80 5,671.1 7297 7894 8502 9124 9758 6.0405 6,1666 6,1742 6,2432
81 6,3138 3859 4596 5350 6122 6912 7720 8548 9395 7,0264
82 7,115-1 2066 3002 3962 49.17 5938 6996 8062 9158 8,0285
83 8.1443 2636 3863 5126 6427 7769 9152 9,0579 9,2052 9,3572
84 9,514 9,677 9,645 10.02 10,20 10,39 10,58 10,78 10.99 11.20
85 11,43 11.66 11,91 12.16 12,43 12,71 13.00 13.30 13,62 13,95
86 14,30 14,67 15,06 15.-16 15,89 16,35 16,83 17,34 17,89 18,46
87 19,08 19,74 20.45 21,20 22.02 22.90 23,85 24.90 26,03 27,27
м 28.64 30,14 31,82 33.69 35.80 38,19 40.92 46.07 47,74 52.08
57,29 63,66 71,62 81,85 95,49 114,6 143,2 191,0 286,5 573,0
Котангенсы
etg в »tg (00* — «)
Примечание. Таблицы позволяют находить натуральные значения синусов, косинусов, танген-
сов и котангенсов лля всех острых углов, содержащих целое число градусов н минут, а также решать
обратную задачу.
Если угол содержит число минут, не кратное шести, то для получения соответствующей попраикч
пользуются колонкой .Разности" а правой части таблиц. Для отыскания косинусов и котангенсов
заменяют нх соответственно синусами и тангенсами, пользуясь формулами приведения
со» в — sin (90* — «); etg в = lg (90° — в).
При отыскании тангенсов углов, превышающих 76“ (и котангенсов углов, меньших 15“). если «тело
минут не кратно 6. нужно пользоваться квадратической интерполяцией, так как в »той части таблицы
точность разностей недостаточна.
Примгры-. 1) Найти sin 32*15'.
В таблице синусов находим sin 32*12' 0,5329
В колонке .Разности" поправка на______3*______7
Складывав, получаем sin З2“1а‘ 0,5&Ш
2) Найти угол в, если etg в = 1.7285.
В таблице тангенсов находим ближайшее меньшее число 1,7251 . . 59*54'
В колонке .Разности" берем поправку_______ .... . 34 . . . 3'
Складывая, получаем........................... 1J285. . . а9"о)'
Следовательно, в - 90“ — 59*57' = 30“03'.
48
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
ТАБЛИЦА XIII. ЧЕТЫРЕХЗНАЧНЫЕ ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Логарифмы синусов
0' 6’
0* — со 7,2419
1 4.2419 2832
2 5424 5640
8 7183 7330
4 8436 KS43
5 94U3 94 э9
9.0192 0264
7 0859 0920
8 1436 14*9
9 1943 1991
10 2397 -'439
п 9,2106 2845
12 3179 3214
и 3521 3554
14 3837 3367
15 4130 4158
16 9.4403 4430
17 465» 4684
49С0 49.3
fitsst sasss esaas sasaa ass
5126 5148
5341 5361
9.5543
5736
5919
6093
6259
9,6418 6570 6716 6856 6990 6434 6585 6730 б%9 7003
9,7118 7131
7242 7254
7361 7373
7476 7487
7586 7597
9,7692 7703
7795 7806
. 7893 7903
79® 7998
8061 8090
9,8169 8П8
8255 8264
8338 8346
8418 8426
8495 8502
5563
5754
5937
5110
6276
12' 18' 24' 30' 36' 42' 48' 54' Ревности
1' 2’ 3' |
542» 7190 8439 9408 4,0200 8,0870 8.1450 8,1961
3210 3558 3880 4179 4459 4723 4971 5206
5842 6035 6220 6397 6567 6731 68*9 7041
7468 7602 7731 7457 7979 «093 8213 8326
8647 874» 8819 89*6 9042 9135 9Л6 9315 16 32 48 64 80
9573 9655 9736 9816 9094 9970 9,0046 9,0120 13 26 » 52 65
0334 0403 (М72 0539 0605 0670 0734 0797 11 22 33 44 55
0981 ЮМ) 1099 1157 1214 1271 1326 1331 10 19 29 38 48
1М2 1591 1646 1697 1747 1797 1847 1895 8 17 25 34 42
2038 2085 2131 2176 2221 2266 2310 23М 8 15 23 30 38
2432 2524 25о5 2606 2647 2687 2727 2767 7 14 20 27 34
2883 2921 2959 2997 3034 3070 3107 3143 6 12 19 25 31
3253 3284 3319 3353 3387 3421 3455 3188 6 11 17 23 28
3586 3618 3650 3682 3713 3745 3775 3806 5 11 16 21 25
3897 3927 3957 39-6 4015 4044 4073 4102 5 10 15 20 24
4186 4214 4242 4269 4296 4323 4350 4377 5 9 14 18 23
4456 4482 4508 4533 4559 458* 4609 4631 4 9 13 17 21
4709 4733 4757 4781 4805 4829 48.13 4876 4 ч 12 16 20
49*1 4969 4992 5015 5037 5060 5062 5101 4 8 11 15 19
5170 5192 5213 5235 5256 5276 5299 5320 4 7 И 14 Г8
53.42 5402 5423 5443 5463 5484 5504 5523 3 7 10 14 17
5583 5602 5621 5641 5660 5679 5698 5717 3 6 10 13 16
5773 5792 5810 5828 5847 5865 5«81 5911 3 6 9 12 Г5
5954 5972 5930 6007 6024 6042 60 9 6076 3 6 9 12 15
6127 6144 6161 6177 6191 6210 6227 6243 3 6 8 11 14
6292 6308 5324 6340 6356 6371 6387 64U3 3 5 8 и 13
6449 6465 6480 6495 6510 6526 6 >41 6556 3 5 8 10 13
ббоо 6615 66'29 66*4 6659 6673 6687 6702 2 5 7 10 12
6744 6759 6771 6787 ЬЙ01 6814 6Я2Ч 6412 2 5 7 9 12
68.43 6896 6910 692Л 6917 6950 6963 6977 2 4 7 9 11
7016 7029 7042 7055 7068 7080 7093 7106 2 4 6 9 11
7144 7156 7168 7181 7193 7205 7218 72.30 2 4 6 8 10
7266 7278 7290 7302 7314 7326 7338 7349 2 4 6 8 10
7384 7396 7407 7419 7430 7442 7453 7464 2 4 6 8 10
7498 750» 7520 7531 7542 7553 7564 7575 2 4 6 7 9
7607 7618 762» 76Ю 7650 7661 7671 7682 2 4 5 7 9
7713 7723 7734 7744 7754 7764 7774 7785 2 3 8 7 9
7815 7825 78. <5 7844 7854 7864 7874 7«84 2 3 5 7 8
7913 7922 7932 7941 7951 7960 7970 7979 2 3 5 6 8
8007 8017 8026 ><115 8044 8U53 8063 8072 2 3 5 6 8
8099 8108 8117 8125 8134 8143 8152 8161 1 3 4 6 7
8187 8196 8204 8213 8221 8230 8238 8247 1 3 4 6 7
8272 8280 8289 8297 8306 8313 М22 8330 1 3 4 6
«54 8362 8370 8371 8386 8394 «402 8110 1 3 4 5
8431 8441 8419 8457 8464 8472 8480 8487 1 3 4 5 5
8510 8517 8525 8532 8340 8547 8555 8362 1 2 4 5 б
Логарифмы косинусов
If сов а — lg aio (90* — в)
ЛОГАРИФМЫ СИНУСОВ
49
Продолжение пйя. XIII
Логарифмы синусов
О' 6' 12' 18' 24' 30' 36' 42- 48' 64’ Разности
2' 3' 1 «' 1 S'
4в 9,8369 8577 8584 8591 8593 8606 №13 №20 8627 №34 1 2 4 s 6
47 8641 а.+в 8655 8662 8669 8676 8683 8690 №97 6704 I 2 3 5 6
48 8711 8718 8721 8731 8738 8745 8751 8754 8765 8771 1 2 3 4 в
40 8778 87*4 8791 8797 8810 8817 8823 883) 8816 1 2 3 4 5
50 КПЗ 8849 8805 8862 8868 8874 8880 8887 8593 8899 1 2 3 4 5
51 9.8905, 8911 8917 8923 6929 РВД.5 *941 8947 4953 »959 1 2 3 4 5
52 8965 8971 8977 8983 5989 *43 900) 9012 9018 1 2 3 4 5
53 9163 9029 9033 9041 9046 9052 9057 9063 S0b9 9374 1 2 3 4 6
54 9080 9045 9091 9095 9101 9107 9112 9118 9123 9128 1 2 3 4 5
55 9134 9139 9144 9149 9155 9160 9165 9170 9175 9181 1 2 3 3 4
5в 9,9186 9191 9196 9201 9206 9211 9216 9221 9226 9231 1 2 3 a 4
57 9236 9241 9240 9251 9235 9260 9255 9270 9275 9279 1 2 2 3 4
58 9284 9289 9294 9291 9-303 91)3 9312 9117 9322 93® 1 2 2 • 3 4
59 9331 9335 9140 93 И 9319 <П53 9338 9352 9U67 9371 1 1 2 3. 4
во 9375 93® 9354 93SS 9393 9397 9401 9406 9410 9114 I 1 2 3 4
в1 9.941" 9422 9427 9431 9435 9439 9443 9447 9451 9455 1 1 2 3 3
62 91» 9463 94417 9471 9175 9179 94 S3 9487 9491 9195 1 I 2 3 3
вз 94IN 9503 9507 95IU 9514 9518 9522 9525 9529 4533 1 1 2 3 3
•4 9537 9540 9544 9548 9551 9555 9558 9362 9566 99,9 1 1 2 2 3
«3 «73 9576 9580 9583 9587 9390 9594 9397 9601 9604 1 1 2 | 3
9.9607 9611 9614 9817 9621 9624 9627 9631 9631 9637 1 1 2 2 3
•7 9640 9643 9М7 4»>5О 9»ЛЗ 9" тЛ 9*Л9 9662 9666 9Л9 1 1 2 2 3
№ 9672 9675 9678 96*4 9W7 5*,90 9691 969> «699 0 1 l 2 2
в» 9702 9704 9707 9710 9713 9716 9719 9722 9724 9727 0 1 I 2 2
то 9730 9733 9736 9738 9741 9743 9746 9749 9751 9754 0 I I 2 2
71 9.9757 9759 9762 9764 9767 9770 9772 9775 9777 9780 0 1 1 2 2
72 9782 9785 9787 9789 9792 9794 9797 9799 9301 9804 0 1 1 2 2
73 9805 9808 9811 4S13 9415 9817 9S2O 9822 9424 9826 0 1 1 2 2
74 9828 9831 9831 953, 9837 9439 9841 9*4! 9*45 9847 0 1 1 1 2
75 9849 9851 9853 9855 9857 9359 9861 9363 9865 9867 0 1 I 1 2
76 9.9869 9871 9873 987$ 9876 9*78 9ЧЯ0 9482 9884 9885 0 1 I 1 2
П 9ЯЧ7 9889 9*91 9<У.’ 9*91 98»' 9*97 . 98!» 9901 9902 0 1 1 1 1
7В 9904 9906 4907 4909 9910 9912 9913 9915 9916 9918 0 1 1 I 1
79 9919 99'1 9922 9924 9923 99’7 9924 9929 9931 9932 0 0 1 1 1
60 9944 9933 99® 9937 99.19 9941) 9911 9943 9944 9945 0 0 1 1 1
81 9.9646 9947 9949 9950 9951 9952 9953 9951 995$ 9956 0 0 1 1 1
82 99» 9939 9960 9961 9962 9964 9965 9966 9967 0 0 1 I 1
63 9968 9968 9969 9970 9971 тад 9973 9974 9975 9975 0 0 0 1 1
84 9976 9977 9978 9974 9979 s9*0 9941 99*1 994’ 9981 0 0 0 0 1
Ш 99.53 9934 9935 9985 9960 9987 9987 9988 9988 9969 0 0 0 • 0
80 9.9989 9990 99*1 9991 9991 9992 999'.’ 9993 9993 9991 0 0 0 "O 0
87 9994 9994 9995 9995 999» (лис 999о UtXb. 9997 9997 0 0 0 0 0
88 9997 9994 999* 999' 9«94 9990 Z»r 9l<99 999» 9999 .0 0 0 0 0
В) 9999 -У-Г-Пт ю.ооои ЮА*» 10 АО I0.0UX. ioax* 10,0000 10.0001 10АЮ0 0 0 0 0 0
Логарифмы косинусов
*g cos в — lg ala 1*1* — в)
4 Том I, Зан. 1464
80
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
Продолжение табл. ХШ
Логарифмы тангенсов
Разности
0' 6' 12' 18' 24' 30' 36' 42' 48' 54'
1' 2' 6'
0* —«о 73419 7,5429 7,7190 7,8439 7,9409 8,0200 8,0670 8,1450 8,1962
1 4.2419 2833 8211 3559 ЗМ1 4181 4461 4725 4973 52<:в
2 543’. 664.1 6845 8038 6223 6401 6571 8731 6894 7046
з 7104 7337 747» 76U9 7739 7865 7968 8107 8223 8336
4 8446 ММ 8659 8762 8Ж>2 8960 9066 9150 92ч 1 9331 16 3? 48 64 81
• >420 9506 9591 9674 9756 9836. 9915 9992 9,0068 9,0143 13 26 40 53 66
6 9,0216 0289 0360 0430 0499 0567 0633 0699 0764 0828 и 22 34 45 56
7 0891 0954 1016 1076 1135 1194 1252 1310 1367 1423 10 20 29 39 49
8 1478 1633 1587 1640 169.1 174» 1797 1845 1898 1948 9 17 26 35 43
» 1997 2045 21Л4 2142 2189 2236 2282 2328 2374 2419 8 16 23 31 89
10 2463 2607 2551 259ч 2637 2680 2722 2764 2805 2846 7 14 21 28 35
11 9,2887 2927 2967 эом 3045 3085 3123 8162 32О> 3237 в 13 19 26 32
12 3275 3312 8349 8885 8422 3458 84И 3529 3564 3599 6 12 18 24 80
18 8634 3665 8702 8736 8770 3801 8837 3870 390.1 3935 6 11 17 22 28
14 8968 4000 4032 4064 4095 4127 4158 4189 4220 4250 5 10 16 21 34
15 4281 4311 4341 4871 4401' 4430 4469 4488 4517 4546 5 10 15 20 25
16 9.4575 4603 4632 4860 4688 4716 4744 4771 4799 4826 5 9 14 19 23
17 485.1 4880 49U7 4934 49Ы 4987 6014 6010 6066 6092 4 9 13 18 22
18 5118 5143 6169 8196 5220 6245 6770 6295 5320 534Ь 4 8 13 17 21
10 5370 5394 5419 5443 5467 6491 6516 5539 6563 Б5в7 4 8 12 16 20
20 МП 6634 6658 5681 5704 5727 6750 8773 6796 6819 4 8 13 15 19
21 9,5842 5864 5887 6909 5932 5954 6976 6998 6020 6042 4 7 11 15 19
22 60M 6080 вкж 6129 6151 6172 6194 8215 6236 6257 4 7 11 14 18
28 6279 6300 6321 6841 6362 6383 6404 6424 6445 «46. 3 7 10 14 17
24 64Ж; 660». 6527 6647 5567 6587 6607 6627 6647 6*345? 3 7 10 13 17
25 6687 6706 6726 6746 6765 6785 66М 6824 6843 6883 3 7 10 U 16
26 9.6882 6901 6920 6939 69М 6977 6996 7015 7034 7053 3 в 9 13 16
n 7072 71® 711» 7128 7140 7165 7183 7202 72.0 7238 3 6 9 12 15
28 7257 7275 779.1 7311 7330 7348 7366 7384 7402 7420 3 6 9 12 15
a 7438 7455 7473 7491 7509 7526 7544 7662 7579 7597 3 6 9 12 15
Ю 76)4 7632 7649 7667 7584 7701 7719 7736 7753 7771 3 6 9 12 14
(1 9,7788 7806 7822 7839 7856 7873 7891 7907 7921 794) 3 6 9 11 14
82 7958 7975 799: 8008 8025 8042 8СБУ 8075 8092 8109 3 б 8 11 14
88 8125 8142 8158 8175 8191 8208 8224 8241 8257 8274 3 5 8 11 14
84 8290 8306 8323 8335 8355 8371 8388 8404 8120 8416 3 5 8 11 14
85 6452 5468 8484 8601 8617 8533 8541. 8565 8681 8597 3 5 8 11 13
И 93613 8629 8644 660 8676 8692 8708 8724 8740 8755 3 5 8 И 13
37 8771 8767 8803 8818 88.14 8850 8Ж>.‘, 8861 8897 8912 3 Б 8 10 13
88 8924 ЮН йога OIK1.’ 8975 39®. 9006 9022’ 9007 9053 9058 3 Б 8 10 13
W SUM 90Ю 9115 9130 9146 916) 9176 9192 9207 3 5 8 10 13
40 «238 9254 9269 «284 9300 9315 9330 «ЗЮ №61 9376 3 5 8 10 13
41 93392 9407 9422 9435 9455 9W8 9483 К 99 9514 9620 3 5 8 10 13
42 9544 9660 9575 9МИ. 9605 №21 94134, 9661 66*341 9681 3 5 8 10 13
4» 9U7 9712 9727 9742 9767 9773 9758 9803 9818 9ЫИ 3 5 8 10 13
44 9М8 9М4 9679 9694 9®9 9924 9934 4955 9970 W-.5 3 Б 8 10 13
46 ю.оооо 0016 осво 0045 0061 0076 0091 отв 0121 0136 3 5 8 10 13
Логарифмы котангенсов
ctg а - 1g tg (SO* — a) — — 1g tg a
ЛОГАРИФМЫ ТАНГЕНСОВ
51
Логарифмы тангенсов
Продолжение табл. ХШ
0’ 6' 12' 18' 24' 30' 36' 42' 48' 54' Разности
2- 3' * 5'
46 10,015? 0167 0182 0197 0212 0228 0243 0258 0273 0288 3 5 8 10 13
47 0301 0319 0334 0349 оаб1 0379 039", 0410 0425 0440 3 5 8 10 13
48 0466 0471 0466 0501 0517 0532 0547 0562 0578 0593 3 5 8 10 13
49 0608 0624 0639 0654 0670 0685 0700 0716 0731 0716 3 5 8 10 13
50 0762 0777 0793 0808 0824 0839 0854 0870 0835 0901 3 5 8 10 13
51 10.09И 0932 0917 0963 0974 0994 1010 1025 1041 1056 3 5 8 10 13
52 1072 1089 1100 1119 1135 1150 1166 1182 1197 1213 3 5 R 10 13
53 12'9 1245 1260 1276 1292 ISO’ 1324 1340 1356 1371 3 5 8 11 13
54 1387 1403 1419 1435 1451 1467 1483 1499 1516 1532 3 5 в 1Г 13
55 1548 1564 1580 1596 1612 1629 1645 1661 1677 1694 3 5 8 11 14
56 10.1710 1726 1743 1739 1776 | ?Г| 1 1809 1825 1843 185« 3 5 8 и 14
57 1R7S 1891 1908 1925 1941 1958 1975 1992 200“ 2025 3 6 8 11 14
58 2012 20 9 2076 2093 2110 2127 2144 2161 2178 2195 3 6 9 II 14
59 2212 2229 2247 2264 2281 2299 2316 2333 2351 2368 3 6 9 12 14
60 2386 2403 2421 2438 2456 2474 2491 25С9 2527 2345 3 6 » 12 15
61 10,2582 2580 2598 2616 26.34 2652 2670 2689 2707 2725 3 6 9 12 15
62 2713 2762 2780 2798 2817 2Я3.5 2854 2872 2891 2910 3 6 9 12 15
63 2928 2947 2966 2985 ЗС04 3021 3042 2061 3080 31.90 3 6 9 13 16
64 311В 3137 3157 3176 3196 <Р’5 3235 3254 3271 3'9! 3 6 10 13 16
65 3313 3333 3353 3373 3393 3413 3433 3453 3473 3494 3 7 10 13 17
К 10,3514 3535 3555 3676 - 359- 3617 3638 3659 3679 3700 3 7 10 14 17
67 3 21 3743 3764 3785 3806 382» 3849 3871 3492 3914 4 7 11 14 18
68 3936 3958 3980 400.’ 4024 4W 4068 4091 4113 4136 4 7 и 15- 19
W 4158 41Ы 4204 <227 4250 4273 4296 4319 4342 4366 4 8 12 15 19
70 4339 4413 4437 4461 4484 4509 4533 4557 4581 4606 4 8 12 16 20
71 10,4630 4655 4680 4705 4730 47М 47ЯО 4805 4831 4857 5 Я 13 17 2!
72 4882 4906 4934 494Л 4986 5013 5039 5066 509? 5120 Б 9 13 18 22
75 5147 5174 5201 5229 52.56 52М 5312 S344 536“ 5397 5 9 14 19 23
74 5425 5454 5483 5.512 5541 5S70 5600 5629 5559 5649 5 10 15 20 25
75 571» 5750 5780 5811 5842 5873 5905 5936 5968 «ООО 5 10 16 21 26
76 10.5072 6055 И97 «130 6163 61 % 6230 6264 629’ 6332 6 11 17 22 28
п 6 56 6401 64W 6471 6507 бМ'1 657» 6615 66.51 «688 6 12 18 24 30
78 672 > 6763 бию 6834 6877 6915 6954 6991 7033 7073 5 13 19 26 32
79 711.1 7154 7195 7236 7278 7320 7363 7406 74 9 7491 7 14 21 28 35
60 7537 7581 7626 7672 7718 тгы 7811 7859 7М6 7954 8 16 23 31 39
61 10.ЮТО 8052 8102 8152 8203 8255 8307 8160 8413 8467 9 17 26 35 43
82 85?.' 8577 663.3 8590 874’ Я"О6 89’4 «985 9М6 10 20 29 39 49
КЗ 91<>» '•172 92.16 9301 9367 913? 9.50" 9576 9640 9711 II 22 34 45 56
84 9784 9x57 9932 11,0008 11.0785 11,0164 11,024- 11,033" 11,0«lt' 11.0494 13 26 40 53 66
86 11.0581 0069 0759 0850 0914 1041 1138 123" 1341 144С 16 32 43 61 81
86 11.1554 1664 1777 1893 201? 2135 2261 2381 2525 2661
87 2806 29.4 3106 3264 3424 3599 3777 3912 4135 4’57
88 4669 4792 5027 6275 5539 5819 6119 64И 67“9 7167
80 7581 8038 8550 9130 9300 12,0591 12,1561 12,2810 12,4571 12,7581
Логарифмы котангенсов
1g «<К « — lg 1g (90* — •) — — lg tg в
Примечание. Таблицы логарифмов синусов и тангенсов построены так же, как и таб.1. XII
натуральных аиачеьнй синусов и тангенсов, н пользование ими аналогично.
4*
62
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
ТАБЛИЦА XIV. КРУГОВЫЕ. ПОКАЗАТЕЛЬНЫЕ И ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
(аргумент в луговых единицах н градусах)____________ ________
X tin X СО1 X tx н t~* •h x ch x th X X В rpll.
1 0.00 0,00000 1,00000 0,00000 1,00000 1,00000 0.00000 1,00000 0,00000 в
01 01000 0.99995 0101» 01006 0,99005 01000 OOOUS 01000 0’34’23*
02 021 ХЮ 9ОД) 02000 02020 98020 02000 00020 02000 1"'4'4 S’
03 (КИЛО 99А5 03001 03045 97045 озооо 000*5 02999 i*43'oe»
04 03МЮ 99920 04UU2 04081 96079 04001 ouoso 03098 2*17'31'
05 (ИМИ 99Н75 0500* 05127 95123 06X472 00125 04996 2*51 '53*
06 06996 99*00 06007 06184 94176 06004 00180 06991 3’26'16»
07 06991 99755 07011 07’251 93239 07006 0*7245 06999 4*00'39*
08 07991 9960 O8UI7 06329 92312 04009 00.320 07983 4*33'01*
09 06968 99595 09024 09417 91393 08012 00403 06976 5*09'24'
0,10 0,09983 0,99500 0,10033 1.10517 0,9044 0,10017 1,00500 0,099*57 5*43'46*
11 10978 99396 11045 1162,8 89583 11032 00606 10956 6’18'09’
12 11971 «Г2Л1 12053 12750 88692 12029 00721 11943 6’52'32*
13 12963 99156 1.3074 13883 87810 13037 00Мб 12927 7*26'54’
14 1305* 994’2 14WQ 15027 86935 140*6 00982 13909 8’01'17'
15 14944 98877 15114 16183 86071 15056 01127 14*89 8’35'40*
16 15932 98723 16138 17351 85214 16068 012,83 15965 9’10'02'
17 16918 98558 17156 18530 84366 17082 01448 16S33 9’41'25»
18 17903 9-3-4 18197 19722 83527 18097 01624 17*03 KPitMS*
19 18386 98200 19232 20925 82696 19115 01810 18775 10’53'10»
0,20 0,19867 0,98007 0,20771 1,22140 0,81873 0.20134 1,02007 0,19738 11’27'33*
21 20346 97803 21314 23368 81058 21155 02213 20697 12’01'56*
22 21823 97590 2236? •24606 •0252 22178 02430 21*52 12’36'18'
23 22791 97367 23414 25860 79453 232(13 02657 22603 13*10'41*
24 23770 97134 24172 27125 78663 24231 02*91 23550 13’45'IH*
25 24740 96891 25834 2*4'13 77840 25261 011*1 24*92 14*19'26*
26 2S708 966.® 2® «2 29693 77105 26’291 03399 2.5430 14*5.3'49*
2? 26673 96377 27676 30996 7(5338 27329 (X*®17 26362 15*28'11'
28 27636 96106 28755 32313 7557» '2*367 03946 27291 16’02'34*
29 28593 95824 29841 33643 74826 29408 04235 28213 10*36'57*
0.30 0,29552 0.95534 0,309’34 1,34986 0,74082 0,30452 1.0453* 0,29131 17*11'19*
31 ЗССОб 952,33 32033 36343 73345 .31499 04844 этом 17*45'42*
32 31457 94924 33139 37713 72615 32549 05164 30951 18'2(1'05'
33 32401 9*604 34252 39097 71892 3360’2 05495 31*52 18*54'27*
34 33349 94275 35374 40495 71177 34659 osw 32748 19*28'50*
35 34290 93927 36503 41907 70469 35719 06188 33638 Ji’oa'is*
36 35227 93590 37640 43333 69768 36783 06550 34*21 20’37'3.5-
37 36162 93233 38786 44773 69073 37850 06923 35309 21’11'5**
38 37092 92.866 39911 46228 68385 38921 07307 36271 .'1’46'21*
39 38019 92491 41105 47698 67706 39996 07702 37136 22*20'43*
0,40 0,38912 0,92106 0,42279 1,49182 0,67032 0,41075 1,0*8107 0.37995 22’55'06’
41 39 ЧЙ 91712 43*63 500*2 66365 42158 08523 3*47 23’29'29’
42 40776 91309 44R57 52196 65705 43246 08950 39693 24*03'51'
43 41687 90297 45862 53726 65051 44337 09388 40532 24’3*'14»
44 42594 91.475 47078 5527 64 МН 45134 09837 41.16* 28*12'37’
45 43497 90045 4*306 5683 63763 46534 10297 42190 IV 16'59 •
46 44395 И> «Об 49515 5841 63128 476*0 10768 4.3HN '№21'22»
47 452«9 99157 50797 «юо 625.Ю 48750 11250 43’20 38*55'44*
48 46178 88699 52061 6161 61878 49865 11743 44621 27*30'07*
49 47063 882:13 53.339 6323 61263 5OO»4 12247 45422 24*04'30»
0,50 0,47943 0,87758 0,54630 1.6487 0,60653 0,52110 1,12763 0,46212 28*38'52’
51 48818 87274 55936 6653 60050 53240 13269 дА(Ю; 29’13'15’
52 49588 86742 57255 681) 59452 54375 13«?7 47770 29'47'38»
53 50553 86281 58592 58960 55516 14377 48538 «’22'00*
54 51414 85771 59943 7160 58275 56663 14938 49290 30*56'23*
55 5'2269 85252 61311 7333 57695 57*15 15510 W.2 31*30'46»
56 63П9 84726 62695 7507 57I2J 58973 16094 50798 12’05'08'
57 53953 84190 64W7 7683 56553 60137 16W 51536 32*39'31 *
58 54*02 8»«46 65517 7860 55990 61307 17297 52767 *1’13'54*
59 55636 83094 €6956 8040 554.33 62483 17916 52990 33’48'16»
КРУГОВЫЕ, ПОКАЗАТЕЛЬНЫЕ И ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
S3
Продолжение табл. XIV
X »1п X COST •е* и th х ch X Du В rpiJL
0,60 0,56464 0.82534 0.68414 1.8221 0,54881 0,63665 1.18547 0,53706 34*22'39*
«1 67287 81965 69**'.' мм 54 <15 вам 19139 54413 34 “57’02’
62 №104 81388 71391 8589 53791 6601» 19841 5511.3 35’31'24’
63 58914 80*01 72911 8776 53259 67251 20510 SSW* 36“05'47’
м 69720 80210 74454 8965 527-29 684® 211*9 56490 36*40'09*
65 60519 7Ю0Ч 76020 9155 52205 69675 21879 57167 37*11'32’
66 61312 7Я9Ч9 77.110 аич 51685 70897 22582 57436 37’48'55’
67 62009 78182 7W2S 9М> 51171 72126 23297 58498 38-23' 17*
68 62879 77757 80466 9719 50662 73363 24025 59152 38’57'40*
63654 77125 82534 9937 50158 74607 24765 59793 39’32'03’
0,70 0,64422 0,76484 0.84229 2,0138 0.49659 0,75858 1,25517 0,60437 40’06'25*
71 65183 75836 &5953 0340 49164 77117 26282 61668 40*40'48’
Т2 Ь59Г’ 75181 87707 0541 48675 73384 27059 61691 41’15’11*
73 66687 74517 89492 0751 48191 7965» 27849 62307 41’49'33’
74 67429 73М7 91X19 0959 47711 80941 28652 62915 42’23'56*
75 68164 7311® 93160 1170 47237 82232 29468 63515 42’58' 19*
76 68892 72484 96045 1383 46767 83530 30297 64108 43*32'11"
77 69614 71791 *>967 1598 46301 84838 31139 64693 44*Я'ОГ
78 70328 71091 98926 1815 45841 86153 31994 66271 44-41'27’
0,77)711 0,70711 1 2,1933 0.45594 0,86867 1,32451 0,65579 45*
0.7» 71005 70385 1,00925 2034 45384 S7478 3’2862 65841 45’15'49’
030 0,71736 0.6*171 1.W29M 2.2255 0.44933 0,88811 1,33743 0,66404 45-90' 1Г
81 72429 689® 05О46 2479 444*. 90152 34»>3’ 66979 46*24'34"
К 73115 68222 07171 2705 44043 91503 ММ7 67507 46-58'57*
83 73791 67488 09343 2933 43’4)5 92863 36468 68048 47’33'20-
84 74464 66746 11563 3164 43171 94233 37404 68581 18-07'42*
85 7512Я 6599ч 13833 3396 42741 95612 ЗЯ'151 69107 48’42'05’
86 757*4 65244 16156 363? 4231b 97X11 39316 696-26 49“ 16'28*
87 7МП 644«3 18532 3869 41*9 953* 402*1 70137 49*50'50"
88 771174 63715 20966 4109 41474 99806 412М 70642 50*25'13*
89 77707 62941 23460 4351 41066 1.01224 42289 7113» 50-59'36*
0,90 0.78333 0.62161 1.26014 2,4.596 0.40687 1.02657 1,43309 0.71430 51*33'58'
91 789.50 61375 28637 4843 40252 041*' 44342 72113 52*08'21'
92 79560 60582 31326 5093 39452 0653» 45390 7'259" 52*42'44’
S3 90162 59783 34'187 5345 39455 06991 46453 73069 53’17'06’
94 80756 5*979 36921 5600 390ГЛ 0М6Я 47530 73522 53-51'29’
95 81ЗП 5Я1«Ч 39*3* 5457 ЗЯА74 0994« 48623 73978 54-25'52*
96 81919 57352 47KJ6 6117 38289 11*4*1 49729 74428 55*00'14’
97 R244Q 56530 45920 6379 37918 12943 50651 74870 55-31'37'
98 R3050 557(12 49096 6645 37531 14457 51988 75307 56*09'00*
99 83603 54369 52368 6912 37158 15983 53141 75736 56’43'22*
1.00 0.84147 0,54030 1,5574 2.7183 0,36788 1.17520 1,54303 0.76159 57*17'45*
01 ивв 531*6 5922 7456 36412 19069 5549 76576 57’52'07*
02 85211 52337 6281 7732 36059 20630 5&® 76987 58’26'30’
03 857» 51482 6652 8011 35701 7.-203 5790 77391 59-00'53*
(И 86240 50672 70.36 8292 15345 23783 5913 77789 59*35'13*
05 86742 49Ш 7433 8577 349W 25'186 6038 78181 бочч'.й’
06 87236 4-887 7844 №64 34646 26996 61**4 78566 80*44'01’
07 87720 4*012 8270 9154 34.301 2861» 6292 78946 61*18'23*
OR 8Я1Ч6 471X1 8712 9447 33960 30254 6421 79320 61*52'46*
09 88663 46249 9171 9743 33622 31*4 6553 79668 62-27'09*
1,10 0,89121 0.45М0 1.9648 3.0О42 0,33287 1.33565 1,6685 0,80050 63*01'31’
11 *•9570 44*/- 2.0143 0344 32956 35240 6.820 80406 63*35'54*
12 90010 4.Ч56Я 0660 0649 FJ524 3W29 6956 80757 64’10'17*
13 90441 42МА 1198 0957 ЯЭП 38611 7093 81102 64“44'39"
14 |МН 41759 1759 ГЛ8 IIH3 40347 7233 81441 65’19'02*
15 91276 40449 2345 1587 31*4 4Л178 7374 81775 65*53'2**
И 916*0 399М 29>* 1.899 31349 4382? 7517 82104 68*27'47*
17 92075 39015 360" 2220 31037 45581 7662 82427 67*02'10*
18 92461 3*092 4273 2544 30728 47155 7*04 82745 67-36'32’
1» 92837 37166 4979 2871 30422 49143 7957 83068 68*10'55*
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
Продолжение тебе. XIV
X sin х СО» X •* н е~* sb х ch х th х в rpai.
«« 22 23 24 25 26 27 28 29 1,30 31 32 33 34 35 36 37 за 39 1.40 41 42 43 44 45 46 47 48 49 1,50 51 52 53 54 65 66 57 -у-1,5708 1,«0 70 80 90 2,00 10 И 30 ^=2,3562 2.40 50 60 ТО 80 90 3,00 10 0.93201 93562 93910 вм 94573 94498 95209 95510 95802 96034 0.96356 96618 96872 97115 97318 97572 977ЭД 97991 ВПК 93370 0.98545 93710 9ЯЯ65 99010 99145 99271 99387 99492 99588 99674 0.99749 99815 99171 99917 99953 99078 тггя 1.00000 1,00000 0.99957 99166 97385 94630 0.90930 86321 80350 74571 0,70711 0,67546 5947 51550 42733 33499 23925 0,14112 04159 0.36235 35302 34365 33424 324*0 31532 30582 29628 28672 27712 0.26750 25785 24118 23848 22875 21901 2Г921 19945 18954 17981 0,16997 16010 15023 14033 13042 12050 11057 100*3 09067 09071 0.07074 06076 05077 04079 03079 02079 01080 00030 0.00000 -0,02920 -0.12884 -0.22720 -0.32329 -0.41615 —0.50485 —0,58850 -0.66628 -0,70711 -0,73739 -0,80114 —0,85689 —0.90407 -0,94222 -0,97096 -0,98999 —0,99914 2.5722 6503 7328 8198 9119 3,0095 1133 2233 3413 4672 3.6021 7471 9033 4.0723 2556 4552 6734 9П1 5,1774 5.4707 5,7979 6.1654 6,5811 7.0555 7.6018 8,2381 8.9886 9.8874 10,9334 12,3499 14.1014 16.428 19.670 24,493 32,461 48.078 92.620 1255.766 ± «ю -34.233 -7.6966 —4.2363 -2,9271 —2.1850 -1.7093 -1,37382 -1,11921 —1 -0.91601 -0.74702 -0.60160 —0.47273 -0.35553 -0.24641 -0,14255 -0,04162 3,3201 3535 3872 4212 4556 4900 5254 5609 5966 6328 3,6693 7062 7434 7810 8190 8574 8962 9354 9749 4,0149 4,0552 0950 137! 1787 2207 2631 3060 3492 3929 4371 4,4817 5267 5722 6182 6646 7115 7588 8066 4.8106 4.9530 5,4739 6,0496 6,6859 7,3891 8,1662 9,0260 9,9742 10,5507 11.0232 12,1825 13,4637 14.8797 16,445 18,174 20.086 22,198 0.30119 29820 29623 2922» 28933 28650 28365 280R3 27804 27527 0.27253 26912 26714 1ШВ 26135 25924 25666 25411 23158 24903 0,24660 24414 24171 23931 23693 23457 23224 22991 22764 22537 0,22313 22091 21*71 21654 21438 21225 21014 20805 0,20788 0,20190 18268 16530 149569 0,135335 122456 110*03 100259 0.094780 0.090718 082085 074274 067206 060810 055023 049787 045049 1,50946 52764 54598 5645 5831 6019 6209 64.30 6593 6783 1.6964 7182 7381 7583 7786 7991 8198 8406 8617 8829 1,9043 925S 9477 9697 9919 2,0143 0369 0597 0827 1059 2.1293 1529 1768 2008 2251 2496 2743 2993 2.3013 2,3756 6456 9422 3,2632 3,6269 4,0219 4,4571 4,9370 5,2280 5,4662 6,0502 6.6947 7.4063 8,1919 9,0596 10,0179 11.0765 1,8107 8258 8412 8568 8725 8884 9045 9208 9373 9540 1.9709 98») 2,0053 02-28 0404 0583 0764 0917 1132 1320 2,1509 1700 1891 2090 22*8 241* Э191 2X9. 3103 3312 2.3524 3731 3935 417| 4395 4619 4845 6073 2,5092 2.5775 2,82*3 3.1075 3,4177 3,7622 4,1443 4,5679 5,0072 5,3228 6,5569 6,1323 6,7690 7.4735 8,2527 9,1146 10,0677 11,1215 0,83365 83663 83965 84*58 845-46 84828 85106 85180 85648 85913 0,86172 86-12* 86678 86925 87167 87405 87639 П9М 8ЯЛ95 88317 0,88535 88719 88960 89167 89370 89569 89’65 8«95* 90117 90332 0.90515 90691 90X10 91042 91212 91379 91542 91703 0,91715 0.92167 93SII 946*1 95624 0.96 ЮЗ 97015 97*71 90010 0,98219 0,9*367 9*661 9*903 €9101 99263 99396 99506 99595 68’45'18* 69*19'40' 69’54’03» 70*28'26* 71*02'48» 71*37'11» 72*11'34» 72’45'56» 73*20'19* 73’34'42» 74’29*04* 75’03'27’ 75*37'50» 76’12'12» 76’46'35» 77*20'57» 77*55'20» 78*29'43’ 79*01'05’ 79’38'28* 80*12'51* 80’47'13» 81*21'36» 81*55'59' 82’30'21* 80*01’44» 83*39'07* 84’13'29’ 84’47'52» 85’22'15» 85’56'37* 86*31'00» 87*06'23* 87’39'45* 88*14'08* 88’48'30' 89*22’53» «*57'16» 90’ 91’40'24’ 97*24’10* 103’07'57* 104*51'43» 114’35'30* 120*19'16’ 126*00'03* 131’46-49* .135’ 137*30'36* 143’14'22» 148’58'06* 154’41'55* 160’25'41» 166’09'28» 171*53'14» 177’37'01’
88S SStktf BE i ;8 -is* у 1 88388 > S Tf 888с СП ** 1 £ II w 1 8 88 C 38888858 -Z 88588888- 5 § a И
НЯ 0,65099 72KU7 793-17 K5O44 89871 ПРИ 1П6» 9И<» ине 5ISI5 59911 , I89IO+ —0,27942 -0.18216 -0.0930» 0.00000 -0.63127 -0.55069 -0.46400 -0.37388 2 I H 22222 22 1 Й1Й И 1 ШШ s^sags ct. Si Qi 51 СЛ K>(CW О ii । 1111111 се о ooooooo ii I !ййй 0,00000 -0.05837 а »<
w9o itrti W1I95 кки-с |?1Й ГИ18 01658 мне РЧ 0,70711 70867 77567 83471 88552 92748 96017 98327 99654 1.00000 t С 8883В S aassg sS § «С -J К? 00 о» ►-© с i-J ; & 1 1 1 1 1 1 1 эоорссо c 35*§'||'SS s ;88SgB2 c ШШХ 1ййй 11 II cos х
QBO-. Ctf КЗ Bt*sg '‘feSrl Wt 9919*1 Wl <whoi s'HZS'O 4-011582 11736 221 72h 32766 44276 66834 76911 Ш. • ill Ш1 £$3S2S 1 1 о ** g Н2Т5Т- 25105*1- 9989*1- 4611*5- 9оее*с- 495*9- H 8 i ± eoe^ com sse'gka Eq?Sj SS 1 1,15782 42353 £3 Е8У«а' Ssaas ^3 М4С «СП t h
= S sss “«“=>’=8532 gg§sg 888 Ш§£ t 5=834 388 £8368 S ^§328 £5 = 8$?3а882 8 ±ks8£ g§ g меМКй'й £ 8£8888У£8
rzfiowx) EWSHWO S'MOSnOO «neswino 0,00091138 00082510 00074659 0UU.7554 00061125 88888888 85 ifliflii Ii 9821500 HFZ500 9Z2OC0O 09ИИЮ 6269600 II 991SHX) 9166КЮ wtssoo flKrtWl 0149956 0136686 0122773 0111000 0100518 0000053 0,0039832 0082297 0074466 0067379 022371 020242 0,019703 018316 016573 (В >883 033373 030197 027324 IW1TO4 0.043214 040762 <* I
sVssteas's 1Ш№ Z888588 Г4 LX LV.'Wt. 06'552 IZ‘105 135,211 149.432 166.15 182.62 122,073 122.344 5S83S 38 8 £8888883 8 £й Й1*§§ bs 2 ¥Й§8¥Й M W я* h
11.5487 12.2459 13.5379 14.9654 16,543 18.285 XI 911
sbo'sssssa ZS885S8S Wjb salsa S sssss зз a £ssa888a в BSfiBg 3 83SSS Sg 8 sVsaggqg 8 ScnS o= S-Зле to<o ы a.oa 3 £8 Й1 Г. И
11,6920 12,2866 13,5748 14.9987 16,573 18,313 >П 7ЧЛ
iiiiiiiii fifiini in ini e c © on 4Q С0ф <C tA«0 <040 *-C (flip (Л И tfi Й ITHfi CO rK 4^ »n ёВ flB ди to to it* io Й ! i 1!!!! ii 1 ! И оос: о teuste«> “ Ф '£> Ю Ю ДОМ 0 И
цшш.-. ggassha st л Ш№ Ift Sf=g2 а а g§ § Is O • С о о о о c o о о S J388«g £2 3S 3 ^8 Й i ч5 S l3 jc 2 о 8S=g8£8B8 aassaa^g’ в гряд.
КРУГОВЫЕ. ПОКАЗАТЕЛЬНЫЕ И ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
5G
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
Продолжение табл. XIV
J X sin x COS г ш * И f—X th л в грех.
y-7.8540 1 0 too 4 2576,0 0.00038820 1287,99 1287.99 1,00000 450»
7.90 0,99894 -0.04600 -21,715 2697,3 00037074 1348,64 1348,64 ооосю 452”38'12"
5,00 0,90936 -0.14550 -6.7997 2981,0 0.00033546 1490,48 1490.48 1,00000 458-21'58'
10 9вМК9 —0.243М —3.9824 3294.5 U003J34 1647,2 1647.2 ооооо 464-05'45»
20 94073 —0.3x915 -2,7737 3641.0 00027465 1820,5 1.820.5 «ДОО 469'49 '31*
30 90217 —0,43138 -2.0914 4U23.9 WOJ4852 2011,9 2011,9 ооооо 475-33'18»
40 R5460 -0.51929 — 1.6457 4447.1 00022487 2223,5 2223.5 ооооо 481-17'04’
S3 79649 -0.60201 -1.32636 4914.8 00020347 2457.4 2457.4 ооооо 447-00'51'
60 73440 —0,67872 — 1.0821x3 5431,7 00018411 2715,8 2715.8 гюлоо 492*41'37’
70 66297 -0,74865 —0.8855.* 6002,9 000166'9 3001.5 3001,5 (XXJOO 498*28'24*
80 58492 -0,81109 -0,72115 663 4,2 000150733 3317,1 3317,1 ооооо 504-12'10-
90 60102 -0.86544 -0,57882 7332,0 0001363® Збоб.О 3666.0 ооооо 509-55'57’
9,00 0,41212 -0.91113 —0,45231 8103.1 0,000123110 4061.5 4051.5 1.ооооо 515"39'43'
20 22289 -0,97484 -0.22864 9897.1 00010103?) 4948.6 4948,6 ооооо 527’07'16»
40 02478 -0,99969 -0,02478 12068,4 000082724 6044,2 6044,2 ооооо >38 34'49»
Эк=9.4243 0 -1 0 12391.6 0,00008069' 6195,8 6195,8 1,00000 540*
60 —0,17433 -0.98469 +0.17704 14764.8 000067729 7382.4 7382.4 оиооо >50-02'22»
80 -0,36648 —0.93043 3938: 18034.0 000055452 9016.9 9016,9 ООООО 561*29'55*
10,00 -0,54402 —0.83907 0,64836 22026,0 0,000045400 11013,2 11013.2 1,00000 572*57'28»
Примечание. Таблица лает возможность подучать значения тригонометрических,
показательных и гиперболически! функций с пятью значащими цифрами. Для аостижения большей
точности п тек случаях, когда первые аве значащие цифры образуют число, не превышающее 15,
лается, как правило, шесть значащих цифр. Оаиако значения тригонометрических и гиперболических
функций даны в таблице ие более чем с пятью десятичными знаками. Если аргумент дам с пятью
ааичашими цифрами, то см. (155] на стр. 351.
Прихгры I) Найти th 1,315.
Из таблицы находим th 1,31...... 0,86428 (А — 250)
Линейной интерполяцией
шкодим поправку: 5 ..... 125
th 1.315 ..... 0,80553
2) Найти In 1339.*3. Если In 1339,43 — X, то еХ — 1339,43: позтому задача сводится к отысканию
лг*
течения аргумента по заданному значению показательной функции. Ищем в графе .« заданное
число 1339,43 и находим х^Т^и. Следовательно. 1п 1339,43 » 7,20.
Применяя табл. XI. находим:
1339,43 — 1,33943-10* to 1,339-19
In 1,33.................0.28518 (А — 749)
9 675
In 1.339 ........... Г. .0,29193
In 10* 6.90776
In 1339 ................ 7,19969 «7,20
ЗНАЧЕНИЯ ЭВОЛЬВЕНТНОЙ ФУНКЦИИ
57
ТАБЛИЦА XV. ЗНАЧЕНИЯ ЭВОЛЬВЕНТНОЙ ФУНКЦИИ р =. Inv а = tg « - а
•° Часть числа, общая для всей строки 0' 5' 10’ 15' 20' 25' 30' 35' 40' 45' W 56'
I 0,000 00177 00225 00281 00346 00420 00504 00598 00704 О0Я21 00960 01092 01248
2 0,000 01418 01603 01804 02020 02253 02503 02771 0ЖХ5К 0X364 03689 04035 04-102
3 0,000 04790 05201 066.34 06091 06573 07079 07610 08167 08751 09362 10000 10668
4 0,000 11364 12090 12347 13634 14453 15305 16189 17107 18059 19045 20067 21125
Б 0,000 22220 23352 24522 25731 26978 28266 29594 30963 32374 33827 35324 36864
6 0,00 03845 04175 043+7 04524 04706 04892 05083 05280 05481 05687 05898
7 0,00 06115 06337 06564 06797 07X35 07279 07528 07783 08044 08310 0X582 08861
8 о.оо 09145 09-135 09732 11(034 103+3 10559 1О9Я0 11308 11643 11984 12332 12687
9 0,00 13048 13416 13792 14174 14563 14960 15363 15774 16193 1661R 17051 17492
10 0,00 17941 18397 18860 19332 19812 20299 20795 21299 21810 22330 22859 23396
11 0,00 '23941 24196 25057 25628 26208 26797 27394 28001 28616 29241 29875 30518
12 13 0,00 0,00 31171 39754 31832 40534 32504 41325 33185 42126 33875 +2938 34575 43760 35285 4+593 36006 +5+3? 36735 4629) 37474 47157 Х8224 48033 38984 48921
14 0,00 49819 50729 51650 525-82 53526 54482 55448 56427 57417 58420 59434 60460
15 0,00 61499 62548 63611 64686 65773 66873 67985 69110 70248 71398 72561 73733
16 0,0 07493 07613 09161 07735 07857 07982 08107 08214 08362 08492 08623 08756 08889
17 0,0 09025 09299 09439 0958О 09722 09866 10012 10158 10307 10456 106®
18 о.о 10760 10915 11071 11228 11X47 11547 11709 11873 12038 12205 12373 12543
19 0,0 12715 12888 13063 13240 13418 13598 13779 13963 14148 14334 14523 14713
20 о.о 14904 15093 15293 15490 15689 15890 16092 162J6 16502 16710 16920 17132
21 0.0 17345 17560 17777 17996 18217 18440 18665 18891 19120 19350 195’3 19317
22 0,0 20054 20292 20.533 20775 21019 21266 21514 21755 22018 22272 22529 22788
23 0.0 23049 2X11J 23577 23845 24114 24386 24660 24936 25214 25495 25778 26062
24 0.0 26350 26639 26931 27225 27521 27820 28121 28424 28729 29037 29348 29660
25 0,0 29975 30293 30613 30935 31260 31587 31917 32249 32583 32920 33260 33602
26 0,0 33947 34294 34644 34997 35352 35709 36069 36+32 36796 37166 37537 37910
27 0.0 38287 39666 39047 39432 39819 40209 40602 40997 41395 41797 42201 42607
28 0.0 4'1017 43430 41845 44264 <4685 45110 45537 45X17 46400 46X17 47276 47718
29 о.о 48164 48512 49664 49518 49976 50437 50901 51368 5183Я 52312 52788 53268
30 0,0 53751 54239 54728 55221 55717 56217 567'20 57226 57736 58249 58765 59235
31 0,0 598.» 60X16 6ОЯ65 61400 61937 62478 63022 63570 64122 64677 65236 6.5799
32 0,0 66364 66934 67507 68084 68665 69250 69X18 70430 71026 7162b 72230 72838
33 0.0 73449 74064 746.84 75307 75934 76565 77200 77839 78483 79130 79781 80437
34 0.0 81097 81760 .82428 8310О 83777 84457 8514'2 85832 86525 87223 87925 83631
33 0.0 89342 90058 90777 91.502 92230 9-2963 93701 94443 95190 95942 96698 97459
36 0. 09822 O9S99 09977 10055 101 зл 10212 1029'2 10371 10452 10533 10614 10696
37 0. 10778 10861 10944 11028 1111.3 11147 11283 11369 11455 11542 11630 11718
33 0. 11806 11895 11985 12075 12165 12257 12348 12441 12534 12627 12721 12815
39 0. 12911 13006 13102 13199 13297 1X195 13493 13592 13692 13792 13893 13995
40 0. 14097 14.*00 14303 14407 14511 1-1616 14722 14829 I4V-W) 18043 15152 15261
41 0. 15370 15480 15581 15703 15815 15928 16041 16156 16270 16386 1X5(2 16619
42 0, 16737 16X15 16974 17093 17214 17336 17457 17579 17702 17826 17951 18076
43 0. 18302 18329 18457 18585 18714 18844 18975 191П6 192X8 19371 19505 19639
44 0. 19774 19910 20017 20185 2X123 20463 2X103 •207+1 20845 21028 21171 21315
45 0. 21460 21606 21753 21900 22049 22198 22348 22499 22651 22-04 22958 23112
46 0, 21268 21424 23582 23740 23899 24X59 24Z2O 24.382 2+545 2471» 24874 25040
47 0. 25206 25374 255+3 25713 25881 26065 26228 26401 26676 2*175’2 26929 27107
48 0. 27285 27465 276-16 27828 28012 28196 2ЯЗЧ1 28567 28755 28913 291X1 29324
49 о, 29316 .>9709 299U3 30098 30295 30492 3OG9I 30891 31092 31295 31498 317X1
50 0. 31909 32116 32324 32534 327+5 32957 33171 333 ft5 33601 33818 34X17 34257
51 0. 31178 3(700 34924 351<9 35376 35604 358X1 .36063 36295 36529 36763 36999
52 0. 37237 37476 J77I6 37VK 38202 38446 38693 38911 39190 39141 39693 39917
53 о. ХМ. >8 4(1717 40977 41239 41502 41767 42034 42302 42571 4284.1 +1116
54 0. 43390 43667 43915 44225 +4.506 44789 45074 +5161 45650 +51HU 46232 46526
85 0. 46822 47119 47419 47720 48023 48328 48635 4W44 442.55 49882 501)»
56 0, 60518 5ОЧ.И 51161 51+86 51813 52141 52472 52.405 53141 ХМ 78 53817 54159
57 0, 54503 54349 55197 55547 559X1 56255 56612 56972 573X1 57698 58064 58-133
58 0, ЬЧНО| 59178 59554 59913 60314 Ы«97 61043 6147'2 61863 62257 62653 03052
69 0, 63454 63858 64265 64674 65086 65501 65919 66340 66763 67189 67618 68050
Примечание. Таблица значений подноляет находить ч> по а и обратно—решать урав-
нение tg а — а = р, а котором у дано. а а — иеизпеспюе.
Найденное значение а в градусах и минутах можно перевести и радианы.
При три,
1) Inv 27’15' - 0.039432, Inv 27’17' — 0.И9432 4- — • 0,000387 — 0,039-132 0.000156 -0,039587
9
(линейная интерполяция).
2) Inv а — 0.1Х.6М60; ПО табднпе а — 14’55'.
Если значение Inv а не находится п таблице, то, найдя ближайшее меньшее аилчеинс, вычисляют
поправку (линейной интерполяцией).
Эвольиснтная функция употребляется при расчете зуба в аяольпеигиом зацеплении (см. стр. 277).
4 1464
S3
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
ТАБЛИЦА XV/. БЕССЕЛЕВЫ ФУНКЦИИ
X л<+) л Ст) П(ж) Л (-Г) Х.СГ) У. IV)
0.0 +1.00» 0.0000 5.0 —0,1776 —0,3276 -0,30.45 +0.1479
0.1 --0,9975 +0.0499 —1,5342 -6.4590 5.1 -0-1443 —0,3371 -0,3216 -41.1137
0.2 - -0,9930 - -0.0995 —1,0811 —3,3238 5,2 —0,1103 —Ю.3432 —0.3313 - -0,0792
0.3 - -0.9776 --0,1483 —0.8073 —2.2931 5.3 -0.0758 —0.3460 -О;3374 •-0.0445
0.4 Ц-0,9604 4-0.1960 -0.U060 —1,7809 5,4 —0,0412 —0,3453 -0,3402 4-0.0101
0.5 4-0,9385 -f-0,2423 -0.4445 -1,4715 5.5 —0.0068 —0.3414 —0,3395 —0.0238
0.5 0,9120 4-0.2867 -0,3085 —1,2604 5.6 4-0,0270 —0.3343 —0,3354 —0.0668
0.7 +0.8812 --0.3290 —0.191)7 -1,1032 5.7 --O.O599 —0,3241 -4+3282 —0.0887
0.8 +0.8*53 - -0,3638 —0.0868 -0.9781 5.8 +0.0917 -0.3110 -0,3177 -0.1192
0.9 --0.8075 - -0.4059 +0.0056 —0,8731 5.9 --0.I22U —0,2951 —0.3*344 —0.1481
1.0 +0,7652 +0.4401 +0,0583 -0,7812 6.0 +0.1506 —0.2767 —0,288*2 -0.1750
1.1 --0.7196 • -0.4709 -0,1622 —0,6981 6.1 --0.1773 -0.2559 -0,2694 -0.1998
1.2 --0,6711 41.4983 - 41.2281 -0.6211 6.2 - 41.2017 —0.2329 -0.2483 —0,22*23
1.3 - -0.6201 --0.5220 • 4)Л86а —0,5485 6.3 --O.2238 -0.2081 -0,2251 —0,2422
1.4 4о.5669 +0,5419 441.3379 —0,4791 6,4 441.2433 -0,1816 —0,1999 -0.2596
1.5 +0,5118 -4-0.5579 1-0,3824 -0,4123 6,5 +0,2601 -0,1538 -0,1732 -0.2741
1.6 -41.4554 --0,5699 • 41.4204 -0.3476 6.6 --0.2740 —0,1250 -0,1452 -0,2857
1.7 --0,3980 --U.5778 • 41,4520 —0,2847 6.7 - -0.2851 —0,0953 -0,1162 -0.29+5
1.8 --0.3100 • -0,5815 •41,4774 -0.2237 6.8 - 41.2931 -0,0652 —0,0864 -0,3002
1.9 --0.2818 - -0,5812 -41.4965 —0,1644 6,9 --0,2981 —О.АЯУ —0.0563 - <1,3029
2.0 +0.2239 4-0,5767 +0,5104 -0.1070 7.0 4-0.3001 —0,(ХМ7 —0.0259 -0.3027
2.1 -1-0.1666 -41.5683 - 41.5183 —0,0511 7.1 - 41,2991 +0,0252 +0,004*2 -0,2995
2.2 +0.И04 -41.5560 - -0,5208 +0,0015 7.2 --0.2951 -41,0543 --0.0339 -0.2931
2.3 --0.0555 --0.K3I9 -41,5181 4о,05'23 7.3 - -0, 2882 -41.0826 -41.0628 -0.2.846
2 4 - -0 0025 - -o.w? - -0,5101 4*0 1005 7.4 . -0 27Ье --0 Иво --0 U9U7 —0.2731
2.5 -0.0484 +0.4971 +0,4981 +0,1459 7.5 +0,2663 +0,1352 +0,1173 -0,2591
2.6 -0.0964 41.4708 --0,4813 • -0.1*441 7.6 --0.2516 - -0.1592 -0.1124 —0.2+28
2.7 -0,1424 •41,4416 --0,4605 - 41,2276 7.7 -41.2346 -0,1813 -0.16-58 -0.2243
2.8 —0.1850 --O.4U97 - 41,4359 - -0.2635 7.8 - -0.2154 - -0.2014 - -0.1872 -O,2iJ39
2,9 —0'224.1 4-0 3754 4-0.4079 441.2959 7.9 4-0.1944 442,219*2 441,2065 -0,1817
3.0 -0.2601 +0,3391 +0,3769 +0,3247 8.0 +0.1717 +0,2346 +0,2235 —0.15Я1
3.1 -0.2921 • 41.3009 --0,3431 41,3496 8.1 41.1475 • 41.2476 41,2341 -0.1331
3.2 —0.3202 41,2613 -41,3071 • 41.3707 8.2 -0.1222 - 42,2580 41,2501 -0,1072
з.з -0.34 43 -41,2207 -0.2691 41,3879 8.3 -41.0960 - 41,26.57 -0,2595 -0,0806
3.4 -0,3643 441.1792 4-0.2296 4-0.4010 8.4 4-0,0692 40,2708 4+1.2662 -0,0535
3.5 -О.ЗЯ01 +0.1374 +0.1*90 +0.4102 8.5 +0,0419 +0.2731 +0.270*.’ -0,0262
3.6 -0.3918 4-0,0955 -41.1477 •41,4154 8.6 4-0,0146 --0,27» 41,2715 +0.0011
3.7 —0.3992 4-0,0538 • -0,1061 41.4167 8.7 -0,0125 41,2697 - 41.2700 Н.0280
3.8 —0.4О2ь +0.0128 - 41.064.5 -41.4141 8.8 -0.0392 41.2641 -0.2ИМ +0.0641
3.9 -0,4018 —0,0272 -|-и.или 4о.4078 8.9 -0.0653 4-0.2559 4-0,259.* 4-0.0799
4.0 -0.3971 -0,0660 —0,0169 +0,3979 9.0 -0.0903 +0,2453 +0,249? +0.1043
4.1 -0.3887 -0,1033 -41,0561 --О.ЗМЪ 9.1 -0.1142 - -0,2324 • 41.23-4 -0.1275
4.2 -0.3766 -0,1386 -0.0931 -41,3680 9.2 -0.1367 - 41,2174 41,2245 41,1491
4.3 —0,3*510 -0.1719 -0,1296 - 41.3484 9.3 -0.1577 • 41.201М -0.20* 41.1691
4.4 — 0.3423 —0,2028 —0,1633 40,3260 9.4 -0.17о8 4-0,181о 4-0,1907 441.1871
4.5 -0,3205 —0.2311 —0,1917 4-0,3010 8.5 —0,1439 4-0.1613 +0.1712 +0,203.’
4.6 -0,2931 -0,2566 -0.2235 +0,2737 9.6 -0,2090 - -0,1395 -U.I5O2 -0,2171
4.7 -0.269.1 —0,2791 -0.2494 - 41,2445 9.7 -0.2218 - -0.1166 41.1279 -0,2287
4.8 -0,2404 —0,2935 -0,2723 4J.2IJ6 9.8 —0.2323 - -0,0928 41,1015 41,2379
4.9 -0.2097 -0,3147 —0.2921 40.1812 9.9 -0.2400 Jo, 0684 141.2447
10,0 -0.2459 +0,0435 +0.0657 +41.2490
Пр м • ч I на. Определенна. формулы и графика см. стр. 222.
ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
59
ТАБЛИЦА XVII. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ»
XI 0» | 10» 20» 30» W° 50» 60» 70» 80" 90»
0“ 0.0000 Элл 0,0000 иотическ 0,0000 не иитег 0,0000 ралы t-г 0,0000 о рода А 0,0000 (7. А); А 0,0000 — sin < 0,0000 0,0000 0,0000
10 1745 1746 1746 1748 1749 1751 1752 1753 1754 1754
20 3491 3193 3199 3508 3520 3533 3545 3555 3561 3314
30 5236 5243 5263 5294 5334 5379 5422 5159 5484 5493
40 6981 6997 7043 7116 7213 73'23 7436 7,535 7604 7629
50 0,8727 0,8756 0,8842 0,8992 0.9173 0,9401 0,9'547 0,9876 1,0044 1,0107
60 1.1M72 1,0519 1.0660 1.0896 1,1226 1,1643 1.2126 1,2619 1,3014 1.3170
70 1,2217 1,2286 1,2496 1,2853 1.3372 1.4068 1.4944 1.5959 1,1.918 1.7354
80 1,39.13 1,4066 1.4344 1.4846 1,5697 1.6660 1,8125 2.0119 2,2653 2.4362
90 1,5708 1,5828 1,6200 1,6858 1,7868 1,9356 2,1565 2,5045 3,1534 СО
Эллиптические интегралы 2-го рода Е(р, А); к = sin 9
10 20 30 40 50 60 70 80 90 О.ООПО 1715 3491 5/33 6931 0,8727 1.0472 1,2217 1,3963 1,5708 0,0000 1745 34 <9 5229 6966 0,8698 1,0426 1,2149 1.3870 1.5589 0,0000 1744 3183 5209 6921 0,8614 1,0290 1,1949 1,3597 1,5238 0,0000 1743 3473 5179 6851 0,8483 1,0076 1,1632 1,3161 1,4675 0,0000 1742 3462 5141 6763 0,8317 0,9801 1,1221 1,2590 1,3931 0.0000 17Ю 3453 5100 6667 0.8134 0.9193 1.0750 1,1926 1,3055 0,0000 1739 3438 5061 6575 0,7954 0,9184 1,0266 1,1225 о.опоо 1738 3429 5029 6497 0,7801 0.МИ4 0,9“3'1 1,0565 1,1184 0.0000 1737 3422 5007 6446 0,7697 0,8728 0,9514 1,0054 1,0401 0,0000 1736 3420 5000 6428 0,7660 0.8660 0,9397 0,9848 1,0000
1. 2111
« К 1 > • 1 К £ 1 8 | Г £ » 1 * В
Полные еллнптнческие
интегралы
0» 1 1,5708 5709 1,5708 5707 23» 24 1,6355 6426 1,5090 5037 46» 47 1,8691 8848 1,3418 3329 69» 70 2,4610 5046 1,1272 1184
2 6713 5703 25 6490 4911 48 9011 3231 71 5507 1095
3 57)9 5697 26 6557 4924 49 9140 3147 72 599ч 1011
4 5727 мм 27 6627 4864 50 93W 3055 73 6521 0927
5 5738 5678 28 6701 4803 51 9539 2913 74 7081 0« 44
в 5751 5665 29 6777 474) 52 97'29 2870 75 7681 0714
Т 5767 5649 30 6859 4675 53 9927 2776 76 8327 0686
8 5785 5632 31 6911 4603 54 2,0133 2681 77 9026 0611
9 5805 5611 32 7028 4539 55 0317 2587 78 9786 0533
10 1,5828 1,5589 33 1,7119 1,4469 56 2,0571 1,2492 79 3,0617 1,0463
11 S454 6564 34 7214 4397 57 0801 2397 80 1531 0401
12 5382 5537 35 731'2 4323 53 1047 23>1 81 25S3 0338
13 5913 5507 36 7415 4248 69 1300 2206 82 3699 0'278
14 5946 5476 37 7522 4171 60 1565 2111 83 5004 0223
15 5911 5442 39 7633 4092 61 1842 2015 84 6519 0172
16 6020 54 S 39 7744 4013 62 2132 1920 85 8317 0127
17 6061 5367 40 7868 394 63 2435 1826 86 4,05'28 0086
18 6105 5326 41 7992 3419 64 2754 1732 87 3337 0053
10 6151 5283 42 8122 3785 65 3088 1638 88 7427 0026
20 1,6200 1,5238 43 1.8256 1,3680 66 2,3439 1.1545 89 5,4349 1,0008
21 22 6252 6307 5191 5141 44 45 8391 8541 3594 3506 67 68 3809 4193 1453 1362 90 оо 1,0000
f z- - ! K~F
J /I - A* Sin*a
V
di______
Kl — *• slu'a
£(ф. А)
к' sln*a da; Е — В
/1 — A*sln4 da
fio
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И ТАБЛИЦЫ
Примечание к табл. XVII. Таблица лает численные значения эллиптических интегралов:
х
т
ванример, для вычисления I ----- а? — нале верхний предел • — -7 перевести в градусы
и
десятые доли градуса (в данном примере * * 60е; * — -у) и по формуле Л = sin 6 вычислить I в гра-
дусах (в данном примере 9 а» 30е), после этого искать в таблице соответствующее значение Р определе*-
него интеграла ^в данном примере F ^60*. -у) — 1,0В9б|.
Если е и ) в таблице не назовется, то надо применить интерполяцию.
Таблица для К. Е дает значения полных эллиптических интегралов, получаемых при е — 90е.
•' (х)
ТАБЛИЦА XVIII. ЗНАЧЕНИЯ ФУНКЦИИ
1 0 1 3 3 4 5 6 7 8 9
0.0 0.3989 3989 3989 3988 3986 3984 39-92 39190 3977 3973
0.1 3970 3965 3961 3956 3951 3945 39-19 3932 3925 3918
0.2 3910 39U2 3894 3885 3876 3867 3857 347 3836 3825
0.3 3814 3802 3790 3778 3765 3752 3739 3726 3712 3697
0.4 3683 3668 3653 3637 3621 3605 3589 3572 3555 3538
0.S 3521 3503 3445 3467 3448 3429 3410 3391 3372 3352
0.6 3332 3312 3292 3271 3251 3230 3209 3187 3166 3144
0.7 8123 3101 3079 3056 3034 ЗОН 2949 '29и6 2913 2920
0.8 2897 2874 2850 2827 2803 2780 2756 2732 2709 26-85
0.9 2661 2637 2613 2589 2565 2541 2516 2492 2463 2444
1.0 0,2420 2396 2371 2347 2323 2299 2275 2251 2227 2203
1.1 2179 2155 2131 2107 2063 2059 2035 2012 1989 1965
1.2 1942 1919 1895 1872 1849 1826 1804 1781 1758 1735
1.3 1714 1691 1669 1647 1626 1604 1582 1561 1539 1518
1.4 1497 1476 1456 1435 1415 1394 1374 1354 1314 1315
1.5 1295 1276 1257 1238 1219 1290 1182 1163 1145 1127
1.6 1109 1092 1074 1057 1040 10-23 1006 0989 0973 095?
1.7 09 И 09’5 0909 0Я93 0878 086.1 0848 0833 0818 «804
1.8 0790 0775 0761 0748 0734 0721 0707 0694 0681 0669
1.9 0656 0644 0632 0620 0608 0596 0584 0573 0562 0551
2.0 0.0540 0529 0519 0508 0499 <мм 0478 1468 0459 0449
2.1 0440 0431 0422 0413 0404 0395 0387 037» 0371 0163
2.2 0.155 0347 0339 0332 0325 031? 0310 озоз 0297 0290
2.3 0243 0277 0270 02М 0258 0252 <7246 0-241 02.35 0229
2.4 0224 0219 0213 0208 0203 0199 0194 0189 0184 0180
2.5 0175 0171 0167 0163 0159 0154 0151 0147 0143 0139
2.6 0136 0132 0129 0126 0122 0119 0116 0113 ОНО 0107
2.7 0104 0101 0099 01-96 0093 0091 0088 а 186 0084 0081
2,8 0079 0077 0075 0073 0071 0069 0067 0065 0063 0061
2.9 0О60 0058 0056 0055 0U53 0051 UU5D 0048 UO47 0046
8.0 0,0044 0043 0042 0040 0039 0039 0037 О4П6 0035 0034
3.1 0033 003-2 0031 СОЮ 0729 04128 0027 1W26 (ХГ25 0025
3.2 0024 0023 0022 О4В2 UU2I 0020 0020 0019 0018 0018
8.3 0017 0017 0016 0016 0015 0015 0014 0014 0013 0013
3.4 0012 0012 0012 ООН ООП ООЮ ООЮ оою 0X19 ах»
3.5 0009 0008 00» 0008 оооа 0U07 0007 «XI? 0017 алл
3.6 0006 <ИО4 0006 0005 0005 0005 0005 0005 14X15 0004
3.7 0004 0004 0ОО4 0004 0004 ООО! 0003 UJU3 ОоЗ 0UU3
3.8 0003 0003 ООО 0001 (Ш 0002 0002 0002 ши 0ОГ2
3.9 0002 0002 0002 000-2 0002 0002 0002 ООО! oom oool
4.0 0.0001 0001 0001 0000 0000 оооо 0000 оооо оооо оооо
Примечание. График функции и ее применение см. стр. 324.
ФУНКЦИИ ВЕРОЯТНОСТЕЙ
61
ТАБЛИЦА XIX. ЗНАЧЕНИЯ ФУНКЦИИ Ф (z)
1 •(») 2 •(») 1 •(») • Ф(2) ♦(») Ф(е)
0,00 0,0000
0,01 0,0040 0,46 0,1772 0,91 0.3186 1,36 0,4131 1,81 0.4649 2,52 0.4941
0,02 0.0080 0,47 0,1808 0,92 0.3212 1,37 0,4147 1,82 0.4656 2.54 0.4945
0,03 0,0120 0.48 0,1844 0,9.3 0,3'238 1,:и 0,4162 1.83 0.466» 2.55 0.4948.
0,04 0,0160 0.49 0,1879 0,94 0.3264 1,39 0.4177 1,84 0.4671 2,53 0.4951
0,05 0.0199 0.50 0,1915 0,95 0,3289 1,40 0,4192 1,85 0,4678 2.60 0,4953
0,06 0.0239 0,51 0.1950 0,96 0,3315 1.41 0,4207 1,86 0,4686 2,62 0,49.56
0,07 0.0279 0,52 0,198.5 0,97 0,3340 1.42 0,4222 1.87 0,4693 2.64 0,4959
0.1В 0,0319 0,53 0.2019 0,98 0,3365 1.43 0,4236 1.88 0,4699 2,66 0,4951
0,09 0,0359 0,54 0,20.54 0,99 0,3389 1.44 0,4251 1.89 0,4706 2,68 0,4963
0,10 0,0393 0.55 0,2088 1,00 0,3413 1,45 0,4265 1.90 0,4713 2,70 0,4955
0,11 0,0438 0,56 0,2123 1,01 0,3438 1.46 0,4279 1,91 0.4719 2,72 0,4967
0,12 0,0478 0,57 0,2157 1,02 0.3461 1.47 0,4292 1.92 0.4726 2.74 0,4969
0,13 0,0517 0,58 0,2190 1,03 0.348.5 1,48 0,4306 1 1.93 0.4732 2.76 0,4971
0,14 0,0557 0.59 0.2224 1,04 0.3506 1,49 0,4319 1.91 0,473я 2.78 0,4973
0,15 0,0586 0.60 0,2257 1.06 0.3531 1,50 0,4332 1,95 0,4744 2,80 0.1974
0,16 0,0635 0,61 0,2291 1,06 0,3554 1,51 0.4345 1,95 0.4750 2,82 0,4976
0.17 0,0675 0.62 0,2324 1.07 0.3577 1,52 0.4357 1.97 0,4756 2.84 0,4977
0.1» 0.0714 0.63 0,2357 1,08 0,3599 1,53 0.4370 1,98 0,4761 2,86 0,4979
0.19 0.0753 0.64 0,2389 1.09 0.3621 1,54 0.4382 1.99 0.4767 2.88 0,4980
0,20 0.0793 0,65 0,2422 1.Ю 0,3643 1,55 0,4394 2,00 0,4772 2,90 0,4981
0,21 0,0832 0.66 0,2454 1.11 0,3665 1,56 0,4406 2,02 0.4783 2.92 0,4982
0.22 0.0871 0.67 0,2486 1.12 0,3686 1.57 0,441» 2.04 0.4793 2,91 0,4984
0.23 0,0910 0.68 0,2517 1,13 0,3708 1,58 0,44'29 2.05 0.481X1 2,96 0.4985
0.24 0.0948 0,69 0,2549 1.14 0,3729 1,59 0,4441 2,08 0.4812 2,98 0,1946
0,25 0.09В7 0,70 0,2590 1,15 0,3749 1.60 0,4452 2,10 0,4821 3,00 0,49865
0,25 0,1026 0,71 0,2611 1,16 0.3770 1,61 0.4463 2,12 0,4830 8,20 0,49931
0,27 0,1064 0,72 0,2642 1,17 0.3790 1,62 0.4474 2.14 0,4Ж« 3.40 п.вм
0.2Я 0.1103 0,73 0.2673 1,18 0,3810 1.63 0,4484 2,16 0,4816 3.60 0,499841
0,29 0,1141 0.74 0,2703 1,19 0,3830 1,64 0,4495 2,18 0,4854 3.80 0,499928
0,30 0,1179 0.75 0,2734 1.20 0,3849 1,65 0.4506 2,20 0,4861 4,00 0,499968
0,31 0,1217 0.76 0,2764 1.21 0,3869 1,66 0,4515 2,22 0.4868 4,50 0,499997
0.32 0.1255 0.77 0,2794 1.22 0,3888 1,67 0,4525 2,24 0.4875 5,00 0,4999997
0.33 0.1’293 0.78 0,2823 1.13 0,3907 1.68 0,4535 2,26 0,4881
0,34 0,1331 0,79 0,2852 1.24 0,3925 1,69 0,4515 2,28 0,4887
0,33 0,1368 0,80 0,2881 1.25 0,3944 1.70 0,4554 2.30 0,4893
0.36 0,1406 0.81 0,2910 1,26 0,3962 1.71 0,4564 2,32 0,4898
0,37 0.1443 0.В2 о,29:и» 1.27 0,3980 1,72 0.4573 2.34 0,49111
0.3« 0,1430 0,83 0,2967 1.28 0,3997 1,73 0,4582 2,36 0,4109
0.39 0,1517 0,84 0,2995 1,29 0,4015 1.74 0,4591 2,38 0.4VI3'
0.40 0,155-4 0,85 0,3023 1,30 0,4032 1,75 0,4599 2,40 0,49181
0.41 0,1591 0,86 0,3051 1,31 0.4049 1,76 0.4608 2,42 0,4922
0,4'2 0,1628 0,87 0,3076 1,32 0,4066 1,77 0,4616 2,44 0.4927
0.41 0,1664 0,88 0,3106 1,33 0,4082 1,75 0.4625 2,45 0.4931
0.44 0,1700 0.89 0,3133 1.34 0,4099 1,79 0,4633 2,4& 0,4934
0.45 0,1736 0,90 0,3159 1.35 0,4115 1,80 0.4641 2,50 0.4938
Примем II и е. График функции и ее применение см стр. 324.
ГЛАВА П
ДЕЙСТВИЯ С ВЕЩЕСТВЕННЫМИ
ВЕЩЕСТВЕННЫЕ ЧИСЛА
Понятие о числе является основным
понятием математики. В результате
счета предметов, составляющих неко-
торое множество, получаются нату-
ральные (целые положительные) числа 1,
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д.
Число, обозначающее одну или не-
сколько равных долей единицы, назы-
вается дробью.
Дробь можно рассматривать как от-
ношение двух целых чисел: */», */*, ’/«,
’/., »/., »/„, .
Дробь, знаменатель которой есть сте-
пень десяти, называется десятичной и
записывается без знаменателя (*/)0 = 0,3;
,ts/i« = >.25); остальные дроби назы-
ваются обыкновенными или простыми.
Числа появляются и в результате из-
мерения различных величин. Измерить
величину значит сравнить ее с неко-
торой определенной величиной того же
рода, принятой за единицу меры (мас-
штаб). Каждой конкретной величине
может быть сопоставлено измеряющее
ее число (значение величины), которое
существенно зависит от принятой при
измерении единицы.
Простейший пример величины — пря-
молинейный отрезок. Если измеряемая
величина соизмерима с единицей меры,
например, отрезок, принятый за едини-
цу, или какая-нибудь его часть уклады-
вается целое число раз в измеряемом
отрезке, то в результате измерения по-
лучается целое или дробное число.
Во многих вопросах приходится рас-
сматривать величины противоположных
значений (разных знаков, например,
тепло и холод; прибыль и убыток; иму-
щество и долг н т. п.), — тогда числу,
соответствующему измеряемой величи-
не, приписывают энак-h или —, и такое
3491371, w ри1.
И КОМПЛЕКСНЫМИ ЧИСЛАМИ •
число называют соответственно поло-
жительным (+ 2; + а/д) или отрица-
тельным (— 1,2; — 5/т).
Отрицательное число можно рассма-
тривать также как разность, когда
уменьшаемое меньше вычитаемого. Нуль
также можно рассматривать как раз-
ность, когда уменьшаемое равно вычи-
таемому (а —а = Ь — 6 = 0).
Все целые и дробные числа, как по-
ложительные, так и отрицательные, а
также число нуль образуют класс ра-
циональных чисел. Всякое рациональ-
ное число можно представить как отно-
шение двух целых чисел.
Всякая рациональная дробь может
быть представлена или в виде десятич-
ной дроби с определенным числом де-
сятичных знаков (конечной десятичной
дроби), или в виде бесконечной перио-
дической дроби.
Десятичная дробь называется беско-
нечной, если число ее десятичных зна-
ков бесконечно велико. Бесконечная
десятичная дробь называется периоди-
ческой, если в ее изображении повто-
ряется в одной и той же последова-
тельности некоторая группа десятичных
знаков, называемая периодом, напри-
мер 2,363636 .... 0,5232323 . . .; пе-
риодические дроби пишут сокращенно
так:
вместо 2,363636 . . . пишут 2,(36);
» 0,5232323 ...» 0,5 (23).
Периодическая дробь называется чи-
стой, если период в ней начинается тот-
час же после запятой, например 2,(36).
Периодическая дробь называется слу-
шанной, если между запятой и периодом
есть неповторяющиеся цифры, напри-
мер, 0,5 (23).
Если знаменатель обыкновенной дро-
би не содержит никаких иных множи-
телей, кроме 2 и 5, то такая дробь
обращается в конечную десятичную
дробь.
ВЕЩЕСТВЕННЫЕ ЧИСЛА
63
Если знаменатель обыкновенной несо-
кратимой дроби содержит множители,
отличающиеся от 2 и 5, то такая дробь
обращается в периодическую чистую,
если знаменатель совсем не содержит
множителей 2 и 5, или смешанную, если
знаменатель наряду с другими множи-
телями содержит и множители 2 или 5.
Бесконечные десятичные дроби могут
быть и непериодическими.
Если измеряемая величина несоизме-
рима с избранной единицей меры (на-
пример, диагональ квадрата несоизме-
рима с его стороной), то результат из-
мерения есть иррациональное число (на-
пример, V 2, к). Иррациональное число
не может быть представлено как отно-
шение двух целых чисел и может быть
изображено бесконечной непериодиче-
ской десятичной дробью, например.
У2 = 1,41421356 ....
к= 3,1415926535897932384626433832795...
На практике иррациональные числа
заменяют рациональными с требуемой
степенью точности; например полагают
т. = 3,14 (с точностью до 0,01).
Иррациональные числа могут быть
положительными или отрицатель-
ными.
Числа рациональные и иррациональ-
ные образуют класс вещественных (или
действительных) чисел.
Каждому прямолинейному отрезку
(каждой величине) соответствует (при
избранном масштабе) определенное ве-
щественное число, и обратно: каждому
вещественному числу при избранном
масштабе можно сопоставить отрезок
определенной длины и направления или
некоторую точку (конец отрезка) на
прямой, называемой в этом случае чи-
словой прямой, если все отрезки, соот-
ветствующие разным числам, отклады-
вать на прямой от общего начала.
Основные арифметические действия
Наименование действии Пример Первое число (35) называется Второе число (5) называется Наименование результата
Сложение Вычитание Умножение Деление 35 4- 5 - 40 35 — 5 — 30 35-5 — 175 35 :5 — 7 35 , или — = 7 О 1-е слагаемое Уменьшаемое Множимое (1-й сомножитель) Делимое 2-е слагаемое Вычитаемое Множитель (2-й сомножитель) Делитель Сумма Разность Произведение Частное (отношение)
Основные лакомы действии
Формула Нвимеионание закона
я-J-b — e-f-a ................................Переместительный для сложения
а-Э — Ь-а.................................... а а умножения
а + (в + е) вж (а 4" В) -|- е ...............Сочетательны* лля сложения
а-(Э-с) — (а-М-с.............................. > » умножения
(a -f- Ь)-с в а-с -f- Ь-с ................ Распределительный
Действия с положительными
(+ в) + ( + Ь) — + (а 4- Ь) — а 4- b
( +а)+ (-*)- +(а-й)- — (Ь~а)
( + а) — ( + *)-( + fl) + ( — b)
( + а)-(-&)-( + а)-|-( + б)
( + д)-( + Ь)- + ab
( + д)-(-й)---ab
( + в): (4- Ь) — + -у
( + д):(-6)----у
(в 4- Ь) (с + d) — ас 4- be + ad 4- bd
(а — b) (с + d) — ас — be + ad — bd
и отрицательными числами
(— я) 4- (— Ь) — — (а 4- Ь)
(—а) 4- ( 4- 6) - — (а—Ь) - 4- (Ь-а>
(-а) — (_*)«(_в)4-(4-*)
(-д)-(4-*)“(-в)4-(-Ь)
( —д)-( 4- b) — —ab
( — в)-( — *)— +ab
(-в):(4-й)-
(—«):( — *)- +-%-
(а 4- 5)-(с — d) ас + be — ad — bd
(а — b) (c — d) — ас — be — ad 4- bd
64
действия с вещественными и комплексными числами
Действия с нулем
а + 0 = а; а — 0=а; а-О-О-л-О,
— — 0, если а^О-, деление на нуль невозможно.
Действия с обыкновенными дробями
а ат
b Ь>т
Д1 . ‘h Д1 + «з
b ь “ ь
Д1 . Дт _ а1^г ~г Д?^1
b<yl btbtd
а а-т
b т“ b
а а: т
1> = Ь: т
Д1___Дт Д1 —
b b “ b
Д1 _ Ог ajbj — a^bi
btd btd “ W
a ma
m'~b~~ b
а1 . Д? — Дг«э
b% Ь\'Ь%
b c a-c
a: — — a-— = -r-
c b b
Д] e аг a\ b‘> Д| *bf
bi bj h Oj bi-аг
Изменение десятичной дроби от
перенесения запятой. От перенесения
запятой вправо (влево) на п знаков де-
сятичная дробь увеличивается (умень-
шается) в 10я раз, например 237,5 =
= 2,375 . 10*; 0,002375 = 2,375 ; 10* =
= 2,375 . Ю”* 3.
Обращение простой дроби в деся-
тичную. Для обращения простой дроби
в десятичную нужно числитель дроби
делить на знаменатель, обращая после-
довательно получаемые остатки в деся-
тые, сотые, тысячные, . . . доли.
Примеры:
I) Обратить дробь -у и десятичную.
Имеем:
23 I 8 23
~7U “ЗДЙ- • '«"’‘"«“•о, — - 2,875.
60
40 ,
2
2) Обратить дробь и десятичную.
Л
Имеем
’ ™«он«тельно, -1-0, (6).
•Л»
20
1
3) Обратить дробь -1 и десятичную.
Имеем
-^о^зЗЗ... ; «е*о«теяьво, у - 0,8(3).
20
а»
2
Обращение периодической дроби
в простую. Чтобы обратить чистую
периодическую дробь в обыкновенную,
берут ее период числителем, а в зна-
менателе пишут цифру 9 столько раз,
сколько цифр в периоде.
Примеры: 0,(7) - -1 ; 2,(05) - 2 .
Чтобы обратить смешанную перио-
дическую дробь в обыкновенную, вычи-
тают из числа, стоящего до второго
периода, число, стоящее до первого
периода, и полученную разность берут
числителем, а в знаменателе пишут
цифру 9 столько раз, сколько цифр в
периоде, со столькими нулями на конце,
сколько цифр между запятой и первым
периодом.
,, 352 -Я зю
Примеры: 0,3 (52) - ——— - -дт-!
0,26 (4) -
2М - 26 _ ?Я8 114
9UU “ MU “ 45U
О ПОГРЕШНОСТЯХ И ОКРУГЛЕНИИ ПРИБЛИЖЕННЫХ ЧИСЕЛ
65
О ПОГРЕШНОСТЯХ И ОКРУГЛЕНИИ
ПРИБЛИЖЕННЫХ ЧИСЕЛ
В технических расчетах обычно
приходится иметь дело не с точными
данными, а лишь с приближенными.
Выполняя вычисления, всегда необхо-
димо помнить о той точности, которую
нужно или которую можно получить.
Недопустимо вести вычисления с боль-
шой точностью, если данные задачи не
допускают или не требуют этого (на-
пример, не следует пользоваться семи-
значными логарифмами при вычисле-
ниях с числами, имеющими пять верных
значащих цифр). Исходные числовые
данные многих технических расчетов,
являясь приближенными, содержат обыч-
но не более трех-четырех значащих
цифр, последняя из которых бывает, как
правило, верна лишь ориентировочно
(сомнительная цифра); поэтому в боль-
шинстве случаев достаточно произво-
дить вычисления с числами, содержа-
щими не более четырех значащих цифр.
Если в процессе вычислений появляются
числа с большим количеством значащих
цифр, то их следует округлять до нуж-
ного количества цифр.
Разность между точным числом х и
его приближенным значением а назы-
вается погрешностью данного прибли-
женного числа. Если |х — а|<Дв, то
величина До называется предельной
абсолютной погрешностью приближен-
на .
кого числа а; отношение — «• Ь- Ha-
il “
зывается предельной относительной по-
грешностью-, ее часто выражают в про-
центах, реже в премил лях (Ja% = 1005.,;
4e°/oo= 1000ie).
Пример. Д14 является приближенным мичп-
ннем числя к-3,14150205.... погрешности его раки*
0/ХЛ59265 ...: предельную абсолютную погреш-
ность можно считать рапной 0,0016, а предельную
. n.ooie
относительную погрешность — раиной ———
- U,00061 — 0,051%.
Если предельная абсолютная погреш-
ность величины а не превышает одной
единицы разряда последней цифры чи-
сла а, то говорят, что у числа а все
знаки верные. Иногда требуют, чтобы
погрешность не превышала половины
единицы разряда последней цифры при-
ближенного числа. Приближенные чи-
сла следует записывать, сохраняя толь-
ко верные знаки. Оценить погрешность
Ь Том 1. Зак, .404
приближенного числа можно, указав,
сколько верных значащих цифр оно со-
держит. При подсчете значащих цифр
не считаются нули с левой стороны,
если же нули помещаются в середине
или в конце числа (справа) и обозна-
чают отсутствие единиц соответствую-
щих разрядов, то они считаются знача-
щими цифрами. Нули справа в целом
числе иногда ие идут в счет значащих
цифр, если они поставлены взамен не-
известных цифр; в этом случае нули
лучше заменять соответствующей сте-
пенью 10.
Примеры. 1) Если предельная абсолютная по-
грешность числа 52 4U0 рении 1UJ, то »то число
должно быть записано в виде 521-10* или 5,24-10*.
2) 1 куб. фут = 0,0283 лс* — три перина знача-
щих цифры.
3) 1 дюйм = 2,5400 см — пять верных значащих
цифр.
Предельная относительная погреш-
ность числа, которое имеет абсолютную
погрешность не больше половины еди-
ницы в п-й цифре и начинается с циф-
ры г, определяется формулой
8-------1—г.
Соответствующая таблица ? °/0 имеет
вид:
Пример. Если число а — 47,542 получено и
результате действий над приближенными числами
н известно, что 6 - 0,1»/л то а имеет три мер-
ных знака (см. таблицу).
Если приближенное число содержит
лишние или неверные знаки, то его сле-
дует округлить. При округлении сохра-
няются только верные знаки, лишние
знаки отбрасываются, причем если пер-
вая отбрасываемая цифра больше 4,
то последняя сохраняемая цифра уве-
личивается на единицу. Если отбрасы-
ваемая часть состоит только из одной
цифры 5, то округляют обычно так,
чтобы последняя цифра оставалась
четной.
Примеры. 273,54 - 273,5; 273542.2735-10*;
1.0)03 - 1,000; 273,55 ~ 273,8; 0,27345 - 0,2731;
749,86 ~ 800,№.
66
ДЕЙСТВИЯ С ВЕЩЕСТВЕННЫМИ И КОМПЛЕКСНЫМИ ЧИСЛАМИ
ОЦЕНКА ТОЧНОСТИ
РЕЗУЛЬТАТОВ ВЫЧИСЛЕНИЙ
а) Предельная абсолютная погреш-
ность алгебраической суммы равна сум-
ме предельных абсолютных погрешно-
стей слагаемых.
б) Относительная погрешность суммы
заключена между наибольшей и наи-
меньшей из относительных погрешно-
стей слагаемых.
в) Относительная погрешность про-
изведения и частного равна сумме отно-
сительных погрешностей сомножителей
или соответственно делимого и делителя.
г) Относительная погрешность л-й
степени приближенного числа в п раз
больше относительной погрешности
основания (как для целых, так н для
дробных п).
Примечание. При подсчете погрешностей
следует иметь в виду указанное иышс соотношение
откуда
Примеры:
l,₽ “ D^~d
ДО , .
“ D Г и-а •
2)x = Vl-f-xy; -
' * 2 l+xy
“ 2 ’ 1 + xy
3) Нейти предельную абсолютную погрешность
значения плошали круга диаметром 22 мм, гели
погрешность ди и метра ис преаышает 0.U5 мм и
принято г. — 3,14.
„ nd*
И» формулы * — —— следует:
«$ -»ж+2^-0,0006+2 - - 0.005.
По табл. Ill находим 5 — 380,133 мм1, слело-
яателыю, &£ — 380,133-0,006 а> 2 мм1.
Отсюда следует заключить, что уже третья
цифра числа <S япляетгн сомнительной, и резуль-
тат следует представить и ииле
S — 390 жж* (± 2 лк').
Если требуется получить результат
с определенной точностью, то, выведя
указанным способом формулу для по-
грешности результата, определяют из
полученной формулы допустимые по-
грешности первоначальных данных.
Пример. р — d — d ’ ТР*®5Г,ГСЯ определить р
с точностью до I0». D приблизительно в 5 раз
больше d. С какой точностью должны быть взяты
D и dt
Допуская для D и d рапные предельные абсо-
лютные погрешности, получим (см. выше при-
мер 1)
АП 24П
D +^<0-01' ИЛИ 3^D<0’01-
т. е.
lD < < °'°"3 “ °-3*^
с*
Погрешность при вычислении зна-
чений какой-либо функции, аргументы
которой заданы приближенно, может
быть оценена с помощью дифференциала
этой функции. Погрешность функции
есть не что иное, как возможное при-
ращение функции, которое она получит,
если ее аргументам дать приращения,
равные их погрешностям. Так как
погрешности бывают обыкновенно доста-
точно малыми, то практически вполне
допустима замена приращений диффе-
ренциалами. Если известны только пре-
дельные абсолютные погрешности аргу-
ментов, то при вычислении дифферен-
циалов необходимо для всех производ-
ных брать их абсолютные значения.
Примеры:
1) у «= sin х: dy — cos х dx;
д
ду - | со» X |ДХ; ty - -> - I dir х |АХ;
213-/F+F;
3 ж* + у’
8 - *« -Х'лх+
I I х>4-у> •
3) и — е~ал со» Sy;
Дц — |a<r~ *-t cos ?y I Дж + | (J.«—“•* sin 0y | Ду.
При оценке точности результата
вычислений по предельным погрешно-
стям нужно иметь в виду, что факти-
чески погрешность результата обычно
значительно меньше вычисленной пре-
дельной. Ошибки отдельных этапов
вычислений, а также погрешности исход-
ных данных нередко оказываются раз-
ных знаков и отчасти компенсируют
друг друга. Поэтому при не слишком
сложных вычислениях результат берут
с одним лишним знаком по сравнению
с тем, что дается оценкой предельных
погрешностей. Разумеется, нельзя со-
хранять в результате больше знаков,
чем в любом из исходных данных.
Для функции, значение которой нахо-
дится при помощи таблиц, оценка
погрешности может быть произведена
крайне просто. Если аргумент задан
СОКРАЩЕННОЕ УМНОЖЕНИЕ
67
с погрешностью Дх, то для определе-
ния погрешности f (х) находят, поль-
зуясь линейной интерполяцией, при-
ращение функции, соответствующее ±4г-
Абсолютная величина этого приращения
и дает предельную абсолютную по-
грешность /(х).
Примеры:
1) Если диаметр круга D =5,9? ем имеет по-
грешность Др = О,ОШ с.и, то соответствующие
погрешности длины окружности и площади круга
равны соответственно icm. табл, Ш) 0.U16 см и
0,0. см'.
2) Если te « = 0,818 ± 0,002, то (см. табл. XII)
— 39-17' ± 0"4'.
ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
БЕЗ ТОЧНОГО УЧЕТА
ПОГРЕШНОСТЕЙ
При массовых вычислениях, когтя
не учитывают погрешности каждого
отдельного результата, пользуются
следующими правилами подсчета цифр.
1) При сложении и вычитании при-
ближенных чисел в результате следует
сохранять столько десятичных знаков,
сколько их в приближенном данном с
наименьшим числом десятичных знаков.
2) При умножении и делении в резуль-
тате следует сохранять столько зна-
чащих цифр, сколько их имеет прибли-
женное данное с наименьшим числом
значащих цифр.
Исключение (сохранить еще одну
цифру!) можно сделать в том случае,
если произведение начинается с еди-
ницы, а наименьшее точное число —
с какой-либо другой цифры.
3) При возведении в квадрат и куб
и результате следует сохранять столько
значащих цифр, сколько их имеет воз-
водимое в степень приближенное число
(последняя цифра квадрата н особенно
куба при этом менее надежна, чем послед-
няя цифра основания).
4) При извлечении квадратного и
кубического корня в результате сле-
дует брать столько значащих цифр,
сколько их имеет подкоренное число
(приближенное). Последняя цифра ква-
дратного и особенно кубического корня
при этом более надежна, чем последняя
цифра подкоренного.
5) При вычислении промежуточных
результатов следует брать одной циф-
рой более, чем рекомендуют преды-
дущие правила; в окончательном резуль-
тате эта .запасная цифра* отбрасывается.
5*
6) Если некоторые данные имеют
больше десятичных знаков (при сложе-
нии и вычитании) или больше значащих
цифр (при умножении, делении, воз-
ведении в степень, извлечении корня),
чем другие, то их предварительно сле-
дует округлить, сохраняя только одну
лишнюю цифру.
7) Если данные можно брать с произ-
вольной точностью, то для получения
результата с п цифрами данные сле-
дует брать с таким числом цифр, какое
дает п + I инфпу я результате.
8) При вычислении посредством
логарифмов одночленного выражения
следует подсчитать чисто значащих
цифр в приближенном данном, имею-
щем наименьшее число значащих цифр,
и взять таблицу логарифмов с числом
десятичных знаков на I большим. В окон-
чательном результате последняя зна-
чащая цифра отбрасывается.
При соблюдении этих правил можно
считать, что в среднем полученные
результаты будут иметь все знаки вер-
ными, хотя в отдельных случаях воз-
можна ошибка в несколько единиц
последнего знака.
Примеры:
1) Сумму чисел 83,27 ; 0.4377; 273,1; 1,102
следует искать так:
273,1
83,27
1,Ю
0,49
358,0
2) 1,2-37,82-27 380 ~ 1,2-37,8-27 400 — 1,2-10».
3) 17,63-0,88 ~ 0,88-17,6—15,5 (« не 15).
4) 43,2 : 0,63162 - 43,2 : 0,6345 — 68,1.
При вычислениях следует избегать
вычитания близких друг к другу чисел,
так как точность результата оказы-
вается в этом случае весьма малой по
сравнению с точностью исходных дан-
ных. Для этого расчетные формулы сле-
дует соответствующим образом изме-
нить.
Пример. Площадь сечения тонкостенной труб-
ки с внутренним диаметром D = 127,4 мм и тол-
щиной стенки 8 — 0,15 мм следует вычислять по
приближенной формуле
и-127,4-0,15,
а не как разность площадей кругов диаметра
127,4-f-2-0,15 “ 127,7 мм и диаметра 127.4 мм.
СОКРАЩЕННОЕ УМНОЖЕНИЕ
Для того чтобы получить произве-
дение двух чисел с k верными знача-
щими цифрами, следует:
а) сомножитель с ббльшим числом
значащих цифр округлить так, чтобы
6Я
ДЕЙСТВИЯ С REUIECTREHHHMH И КОМПЛЕКСНЫМИ ЧИСЛАМИ
в нем осталось лишь на одну цифру
больше, чем у второго сомножителя;
б) под множимым подписать пере-
вернутый (т. е. с цифрами, написан-
ными в обратном порядке) множитель
так, чтобы его последняя цифра нахо-
дилась под (А 4- 2)-й цифрой множи-
мого;
в) найти частные’ произведепия сле-
дующим образом: на последнюю цифру
множителя умножить часть множимого
от его первой цифры до той (включи-
тельно), которая находится над послед-
ней цифрой множителя; на предпослед-
нюю цифру множителя умножить часть
множимого от первой цифры до той
(включительно), которая находится нал
предпоследней цифрой множителя; на
третью от конца цифру множителя
умножить часть множимого от первой
цифры до той (включительно), которая
находится над третьей от конца цифрой
множителя, и т. д.; все полученные
таким способом частные произведения
написать в виде столбца так, чтобы
последние цифры их находились на одной
вертикали, и сложить; в полученном
результате будут верны по меньшей
мере первые k значащих цифр;
г) в тех случаях, когда произведе-
ние первых значащих цифр сомножи-
телей больше девяти (т. е. >10), послед-
нюю цифру перевернутого множителя
можно подписывать не под (k 2)-й,
а под (ft Ц- 1)-й цифрой множимого;
при этом вычислительная работа умень-
шается, в произведении получается по
меньшей мере- к верных цифр, но при-
ближение получается более грубым,
чем при соблюдении правила .6*;
д) при выполнении указанных выше
операций запятых в сомножителях не
ставить, а место запятой в произведе-
нии определять перемножением в уме
весьма грубо округленных сомножи-
телей.
Примеры;
I. Найти произпеденне х — Я2,49.3,7563 с
двумя верлыми значащими цифрами.
Здесь * — 2, *4-2 — 4. В качестве множителя
берем число 82,49; и перевернутом тис 9428;
следовательно, под множимым 37 563 нужно под-
писать множитель 9428 тдк. чтобы его последняя
цифре находилась под (*-(-2)-й— четвертой —
цифрой (цифрой 6) множимого.
87563
9-128
30048
7.50
14Я
27
3U9,73
Честные произведения получены
здесь следующим обрезом;
8-37о6 - 30048
2-375
750
148
4-37
9-3 — 27
Если взять в качестве множимого число 82, 49,
то перевернутый множитель будет 36 573, и вы-
числение примет следующий вид (всхобках справе
пояснен способ получения частных произьедеиий):
8249
36573
24747 (3-8249 — 24747)
5768 (7-824 — 57(H)
410 (5-82 — 410)
48 (6-8 — 48)
309,73
— получен тот же результат.
В данном случае произведение первых цифр
сомножителей 8-3 = 24 > 9. Следовательно, можно
воспользоваться правилом, приведенным в п .г*,
н так как * 1 = 3. то получится;
37563 8249
<428 или 36573
306,6 306,6
Точное значение: X = 82,49-3,7563 = 309,857187.
Следовательно, при пользовании правилом .6*
верными получились первые три знака, при вычи-
слении по правилу .г* верны первые два знака
произведения в соответствии с поставленным тре-
бованием.
2. Найти х = 0,478563k с четырьмя верными
значащими цифрами.
Значение числа к берем с семью значащими
цифрами, так как второй сомножитель имеет их
шесть, т. е. принимаем к = 3,141592: в перевер-
нутом пиле: 2 961413. Пользуясь правилами .г*
(так как 4-3 = 12 > 9) и .6’, получим соответ-
ственна-
478563 478563
2961413 2951413
143568 1435689
4785 47856
1912 19140
47 478
20 235
36
1>Й32 1.503434
Вычисленное по семизначным таблицам лога-
рифмов значение х — 1,60845. Таким образом, при
гокрашенном умножении по правилу ,г* резуль-
тат имеет четыре верные значащие цифры, как и
требовалось, при пользовании правилом .6* —
пип- верных цифр.
Из приведенных примеров видно, что
если один из сомножителе.’ имеет я
значащих цифр, то (А + 1)-я цифра
у другого сомножителя (см правило „а")
далеко не всегда нужна: в зависимости
от того, каким правилом („б* или .г*)
пользуются, множитель может иметь
такое же число цифр, как и множимое,
либо даже на единицу меньшее. Однако
чтобы не анализировать всякий раз необ-
ходимое число цифр, проще всего поль-
зоваться правилом ,а*: как видно из
примеров, избыточные цифры не ослож-
няю! вычислений.
ВЫЧИСЛЕНИЯ С МАЛЫМИ ЧИСЛАМИ
69
СОКРАЩЕННОЕ ДЕЛЕНИЕ
•Для того чтобы получить частное
двух чисел с k верными значащими
цифрами, следует:
а) то число, которое имеет больше
значащих цифр, чем другое, округлить
так, чтобы в нем осталось лишь на одну
цифру больше, чем у второго числа;
б) взять делитель с (k + 2) цифрами,
разделить на пего делимое обычным
способом и определить таким образом
первую цифру частного; первый частный
остаток разделить на делитель, взяв при
этом в последнем только (А + 1) цифр,
и получить таким образом вторую циф-
ру частного; второй частный остаток
разделить на делитель, взяв при этом
в последнем только k цифр, и получить
таким образом третью цифру частного,
и т. д. до тех пор, пока не будут най-
дены k значащих цифр частного;
в) при выполнении этих операций
запятых в делимом и делителе не ста-
вить, а место запятой в частном опре-
делять делением в уме обоих грубо
округленных чисел; удобно при этом
передвинуть в них запятые на одина-
ковое число знаков так, чтобы делитель
имел перед запятой только одну цифру.
Примеры-.
1. Найти частное jc = 412 175 :31 485 е четырьмя
верными значащими цифрами.
Здесь * 2 =- 6; поэтому припишем к дели-
телю о:
412175 1 314 850
(1-314 850) 3148501 1з.оа~
97325
(8-31 485) 944-5
2870
(0-3148); (9-314) 2826
44
Более точное значение: х — 13,0912. Следова-
тельно, четыре цифры верны.
2. Найти значение — С шестью еерными циф-
рами. Так кек здесь * + 2 — 8, то берем я' Дели-
теле восемь значащи! цифр. т. е. « —3,1416926:
ЮООООООО | 31415928
(3-31415926) 94247778 | 3183099
67522X1
(1-3141592) 3141592
5610630
(8-314159) 2513272
973-8
(3-31415) 94245
3113
(0-3141); (9-314) 2826
237
(9-31) 279
Получено 0,3183099. Точнее, —=0,31830989...
Такны образом, верны шесть значащих цифр.
СОКРАЩЕННОЕ ИЗВЛЕЧЕНИЕ
КВАДРАТНОГО КОРНЯ
Для того чтобы извлечь из числа
квадратный корень с А верными знача-
щими цифрами, следует извлечь обыч-
ным способом корень с числом значащих
пифр, бдльшим ; после этого осталь-
ные значащие цифры находятся деле-
нием половины остатка на найденное
приближенное значение корня.
Примеры-.
1) Найти/7263 с пятью верными значащими
цифрами.
а) /7275=85,2 6)^1:852= 1^--
64 ча
165 «63 = гтс = 0.23 [239(
5 825 |<2
1702 в) V72» — 85,223 [239(
~396
Более точное значение этого корня равно
85,223236: таким образом, в действительности
верны семь значащих цифр.
2)' Найти Кп с семью верными значащими
цифрами.
а)/3',14* 15'92 — 1,772 6)1^: 1772-^1
1 2010 1 443
27 214 1772 1453?
7 189 2380
347 "2513 2218
7 2429 1650
8542 «692 1329
2 7-184 32Ш
1G4-8
в) /я — 1,772483(7]. Более точное значение:
/7- 1.77245385.
Таким образом, при пользовании способом со-
кращенного извлечения квадратного корня полу-
чено в данном случае семь верных значащих цифр
с малой погрешностью в восьмой цифре.
ВЫЧИСЛЕНИЯ С МАЛЫМИ
ЧИСЛАМИ И С ЧИСЛАМИ, МАЛО
ОТЛИЧАЮЩИМИСЯ ОТ ЕДИНИЦЫ
В технических расчетах нередко при-
ходится производить вычисления, в кото-
рых фигурируют различные функции
малых величин а или I ± а, где а < I,
или а ± а, где а < а. В подобных слу-
чаях можно значительно упростить
и сократить вычислительную работу,
пользуясь первыми членами разложе-
ния таких функций в ряд Тэйлора (см.
стр. 152—153). Предельная относитель-
ная погрешность результата, вычислен-
ного таким способом, может быть опре-
делена, как указано иа етр. 65.
70
ДЕЙСТВИЯ С ВЕЩЕСТВЕННЫМИ И КОМПЛЕКСНЫМИ ЧИСЛАМИ
Ниже приведены приближенные фор- Например,
мулы для некоторых выражений, встре- чающихся особенно часто, получаю- 1 _ 1 4lZ ‘ L
щиеся из разложения соответствующей а функции в ряд. Значения предельной относительной погрешности бт1Х даны в таблице везде с избытком (например, вместо 11,1 принято 12 и т. л.). Выражения, представляющие функ- ции (a -t а), где < а. можно написать - .(1±з.) - «V “ =4*т^;
в форме той же функции величины а U ±-). после чего применять при- |/ аг ± а — а j/
ближенные формулы для функции «‘О* 2 в1)" 1 а
(i ±₽),где₽--^-. а± 2 а ’
Функция к Приближенная формула Предельная относительная погрешность ‘max в '!• Более точная приближенная формула Предельнам относительна! погрешность 'max «
(1 ± «)П 1 1М 50л (Л — 1) «• 1±да + Л<^.. 17л (л-1) (л-2) в*
(!+«)(!-в) 1 А 100а*
п 0±«() 1-1 П(>±«,) 1 + S ± •< 1=1 если гке 1
П (1 ± ₽/) 1 + £ (± Т Ру) и все 0у а 1
»*« 1 ± « 50а* 1 ± я + -у •* 17«*
0±« 1 ± a In а 50 (In а)*а* 1 ± tlna + t*il£y£ 17 (In о^о*
Ш (1 ± •) ± • 50я - ± •-у «• 84я*
ig (1 ± «) ± 0,4343а 60а ± 0,4343 (• ¥ -J- ••) 34а*
111 а • По* а*
сою 1 бОв* ‘-Т- 6а*
tg« а 34а* •+ т"1 14«*
c<g« 1 • 34а* 1 1 Т~Т* За*
rcaln • 1?я* •+4* (U*
arctg а • 34о* • -Т"* 20а*
th к • По* •+ти •*
cn « 1 Ы-* >+4“ 5а*
Примечания: 1. В иервой формуле я — любое рациональное число.
2. Если угол а задан не я радианах, а а градусах: (•, то а — я
НЕПРЕРЫВНЫЕ (ЦЕПНЫЕ) ДРОБИ
71
или отсюда также
аг ± акз
сП + а
а
Другой пример:
Каждая дробь, представленная в виде
отношения двух целых чисел или в виде
десятичной дроби, может быть обра-
щена в непрерывную следующим обра-
зом.
„ р -
Если а — ---несократимая дробь,
то после выделения из а его целой части
Е(а) = 01 получится
+-L,
ч ч ’
или отсюда также
]/es ±а * 4 (2а+•
Если угол а мал и о < <у. то можно
пользоваться приближенными форму*
лани ^для углов :
sin (<? ± о) « sin ч> ± в cos ч>:
cos (<Р ± а) га COS f Т а sin
tg(T±a)ra tg?±-^-.
где
или также
г<4‘
Так как ^->1, го. выделив целую
часть £ ( —) = о», получим
НЕПРЕРЫВНЫЕ (ЦЕПНЫЕ) ДРОБИ
Число вида
где все числа а, (/= 1.2, ... , л) —
целые положительные, называется
непрерывной или цепной дробью. Она
получается следующим образом: целое
положительное число at складывается
с дробью, у которой числитель — еди-
ница, а знаменатель — целое положи-
тельное число as, сложенное с дробью,
у которой числитель—единица, а знаме-
натель—целое положительное число д9,
сложенное с дробью. . . , и т. д.
Сокращенное обозначение непрерыв-
ной дроби:
а — (°1. °?. а»..вя).
Если а> = О, т. е. а — правильная
дробь, то обозначается
а - (0, о,, о,...оя).
то, продолжив ату операцию, всегда
дойдем до г„ — 0.
Десятичную дробь для обращения
в непрерывную следует предварительно
'превратить в обыкновенную несократи-
мую дробь.
72
действия с вещественными и комплексными числами
105
Пример. Превратить дробь —— в Непперы:
до
у их
105
38
2
-(2, 1. 3, 4, Т).
е.
Вычисление щ, а», а-,. . . . — непол-
ных частных непрерывной дроби — удоб-
нее производить способом последователь-
ного деления, причем писать каждое
частное над соответствующим делите-
лем.
Для взятой в качестве примера
дроби —- вычисление расположится еле-
О0
дующим образом:
2 1 3 4 2
105 38 29 9 2 1
76 23 27 2
29 9 2 1 0
Если задана непрерывная дробь — —
— (ai, aj, as.....а„), то т-Й подходя-
щей дробью называется обыкновенная
дробь
т" - («1. ..... ат).
где
т < п.
Например, лая непрерывной дроби -{я- — (2,1,
«ю
1, 4, 2) подходящие дроби
последняя подходящая дробь равна точному виа-
чеиию непрерывной дроби.
Р Р
Равенство —=— гарантирует правильность
Чп Ч
разложения обыкновенной или десятичной дроби
в непрерывную.
Правило вычисления подходящих
дробей
а) Первая и вторая подходящие дроби
вычисляются непосредственно (см. при-
веденный выше пример).
б) Все остальные подходящие дроби
— вычисляются по фор-
Чг Че Чп
муле
Л _ Л-i а> + Pl-2
4t 4i—iai + 4i—2 *
где 1=3, 4.......л, a pt, qh а, имеют
значения, указанные выше.
Пример.
- (2, 1, а. 4, 2);
р, 3-3 + 2 11 .
q, “ 1-3 4-1 ” 4 1
р, 11-4 4-3 47
«.”4-4 4-1 " ЛГ
р, 47-2 4- 11 106
«, “ 17-2-1-4 “Д'*
Вычисление удобно располагать так:
Неполные частные не- прерывной дроби . Числитель подходя- щей дроби . . Знаменатель подходя- щей дроби (21 2 1 (1) 3 1 3 11 4 4 47 17 4 1U5 34
Для каждого иачшия к
-±—L-,
•/4-1 •/ ’(*44-1
для нечетных виачемий I нта разность полежи-
те льна, для четных — отрацатедыи.
НЕПРЕРЫВНЫЕ ЩЕПНЫЕ) ДРОБИ
73
Так, для взятого примера
Каждая подходящая дробь—дробь несократимая.
Приближенные значения конечной
непрерывной дроби
а) Каждая из подходящих дробей
представляет приближенное значение
непрерывной дроби.
б) Точное значение — непрерывной
дроби лежит между каждыми двумя со-
седними подходящими дробями; оно
больше каждой подходящей дроби не-
четного порядка (первой, третьей, пя-
той, . . .) и меньше каждой подходящей
дроби четного порядка (второй, четвер-
той, шестой. . .), т. е.
Pi _^Р р‘+'
для всех i нечетных и
Pi_>£> Р/+1
Я1 Ч Я1+1
для всех / четных.
в) Точное значение непрерывной дро-
би ближе к последующей подходящей
дроби, чем к предыдущей, т. е.
Р р‘+' < P.—1L
Я Я1+1 Я 4t
для каждого значения I. Каждая под-
ходящая дробь ближе к точному значе-
нию непрерывной дроби, чем всякая
другая дробь с меньшим знаменателем.
г) Погрешность, получающаяся при
замене точного значения непрерывной
дроби подходящей дробью —, меньше
4i
каждого из следующих трех чисел:
1__. 1 _!_•
ЯА^1 ’ ’ я* ‘
Пример. Подобрать сменные шестерен для
нарезания резьбы с шагом а ~ 3,03 мм на токар-
но-винторезном станке с ходовым винтом шага $=»
= — (5 ниток на 1*). ,
О
Передаточное отношение сменных колес (а на-
правлении передачи от шпинделя к ходовому
, , s 3,13 3.03 303 п
винту) /=—= ^-г5-г = —=—. При
помощи табл. II находим, что числа ЗЭЗ н 503
Следовательно, пег = (0, 1, 1, 2, 10, 1, 8).
Находим все подходящие дроби:
(0) (1) 1 2 10 1 ч
0 1 1 3 31 34 303
1 1 2 5 52 57 из
Наилучшее приближение;
р. «
«. 57
31 2 17 20 85
ОНО удобно потому, что gy — -у • — — jjjj-
(для выполнения условия сцепляемости нужно
V ' ‘6Б’)' * * невор» сменных колес шестерки
с числами зубьев 20, 30, 85 н 05 (а также 4U и
60) имеются.
Погрешность передаточного отношения
* 1 1
* < бГыЙ 29 010 •
д относительная погрешность
4, %, - |!— : -100 -
” ^67-503 5UO) STJ01
Шаг резьбы, нарезанной при применении ука-
занных сменных шестерен с I •* уу , будет
X-I.s-Jt . “Д- — - 3,03017 мм,
s-i.s- ы ’-J—“М24 о.иоидг жж,
т. е. ошибка шага будет меньше 0.2 м/с, что
вполне допустимо.
74
ДЕЙСТВИЯ С ВЕЩЕСТВЕННЫМИ И КОМПЛЕКСНЫМИ ЧИСЛАМИ
ДЕЙСТВИЯ СО СТЕПЕНЯМИ
Если п — произвольное натуральное
(т. е. целое положительное) число, то
N = а-а-а- ... -а = а",
где а — основание степени; л — пока-
затель степени; N = ап — л-я степень
основания а. Действие называется: воз-
вышение числа а в л-го степень.
(+ а)гп = + агп; (+ а)2л+‘ =4- в'!"+,;
( — в)2" = + агп, ( — а)-'я+1= — а-п *’*.
Следовательно, ( — 1)” = 4- 1, если
л четное , и ( — 1)” = — I, если л нечет-
ное.
= 1, если а — конечная величина.
(ап)т ~ апт — (ая,)в;
(а 4- — а? + 2аЬ ч- Ь-;
(a — — 2ab + Ь*,
(а + 6)« - а* + Загь ч- 3abi + frJ;
(а — b)» — о2—ЗаЧ> + Заб2— Ь»;
(в ± Ь)< — а*±4а3Ь 4- 6а?йг ± 4аЬ3 4- Ь*,
в»-bl - (а 4- Ь) (а—Ь);
а3 + Ь» — (а 4- b) (аг — ab ч- 42);
а» — bi - (а — b) (ai+ab+ bl);
an — b" — (а— b)(an~x 4-ап-г-&+ап-’
Иногда для производства вычислений
могут быть полезны следующие фор-
мулы:
(а 4- Ь)г — (а — b)i 4- 4аЬ;
al 4- bl — (д — b)i 4- 2аЬ;
(а 4- Ь ч- с)2 » а.14- bi + с* 4" ~аЬ 4-
4- 2ас 4- 2Ьс,
(а — b 4- c)i = а2 4- Ы 4- cl — 2аЬ 4-
4- 2ас — 2Ьс;
(а — Ь — c)l- al + Ы + сг — 2аЬ —
— 2ас 4- 2Ьс;
а* 4- г>< - (ai + bi+ V2 ab) (а* 4-
4. ьг — /2 ab).
Бином Ньютона
(Д-М)”- S (2)
или
(a4-h)"= Vc*a"-*b*.
Здесь (2) = С* — число сочетаний
из л элементов по k элементов в соче-
тании.
Таблица значений всех от л= 1
до л — 12 дана на стр. 40.
Для больших значений л биномиаль-
ные коэффициенты вычисляются по фор-
муле сочетаний С" (см. стр. 79), при-
чем следует пользоваться тем, что
С, = С”-”. При вычислении ряда бино-
миальных коэффициентов удобно поль-
зоваться зависимостью
•Ы + ... 4- а" * 14--.-4-в *л_24-*п-1);
av> _ bV> _ (а + 6) ( а2л-1 _ а2п-2. ь + а3л-а. ьг _. ф + 1 )Я-1 а2П~» ,4*-1 +
д2лЧ-1 + 62лЧ-1 _ (Д 4- fr) (а!Л _ а2"-1.* ч- а2"-2-*2 —... Ч-
4-(—1)*-а2л-*.Ь*ч-,.. —в-Ь2"-’ Ч- Ь»).
действия с корнями
75
Биномиальные коэффициенты могут
быть найдены также при помощи тре-
угольника Ласкали:
_• -» *
I
1 6 15 20 15 6 I
1 7 21 35 35 21 7 I
Этот треугольник легко продолжить
вниз, так как каждое число любой стро-
ки есть сумма двух соседних чисел выше-
расположенной строки (например, 7 =
= 1+6, 21 = 6+15,35= 15 + 20 чт. д).
Имея треугольник Паскаля с. доса-
точным количеством строк, можно сра-
зу получить из него все биномиальные
коэффициенты для любого значения л,
для чего нужно в-ять л + 1-ю строку
этого треугольника (например, 8-я стро-
ка дает С7' = 1, С) = 7, С? = 21, С?-
= 35 и т. д.).
Бином Ньютона в развернутом виде;
• (а + Ь)п - а" + у а"-1 -Ь +
+ —П("~-- ая~2.Ы +
+ ?(Я~Г11У:~2)ал-3^ + -..+.
1 aZ*O
, л (л—I) (п —2)... (л — (А — П| ,
+ 1-2-3-...А Х
Хоп-*-.&» + ... + 1 abn-' + 1Л
Аналогично:
(а — Ь)п — ап —" ап~1-Ь +
+ —”.7 ° а"~*ьг ~ +(“ ’>* X
л(я — 1) (л — 2)., |л — (й — 1)|
* 1-2-3-.. А Х
Хая-*+*+ ... +( —1)"-‘.а+я“' +
+ ( - 1)"+".
При отрицательных и дробных (см.
стр. 152) значениях показателя л в пра-
вой части разложения получается бес-
конечный ряд.
ДЕЙСТВИЯ С КОРНЯМИ
Если хп = а, где л и а заданы, причем
Л _
л — натуральное число, то х = У а;
а — подкоренная величина (подкорен-
ное количество); л — показатель корня;
п
Va—корень л-й степени из а. Дей-
ствие называется извлечением корня
л
л-й степени из числа а; Уа имеет л
различных значений, причем если а —
положительное число, то один из кор-
ней положителен; он называется ариф-
метическим значением корня л-й сте-
пени из а.
•2п
Уа, где л — натуральное число,
а>0, имеет два вещественных значепия,
одинаковые по абсолютной величине, но
различного знака; остальные 2л — 2
корней — комплексные (см. стр. 86);
т
У^а, где п — натуральное число,
а < 0, не имеет вещественных значе-
ний; все 2л корней — комплексные;
2/l-f-l _
V а, где а — вещественное число
н л — натуральное, имеет лишь одно
вещественное значение, положительное
при а>0 и отрицательное при а<0;
остальные 2л корней — комплексные;
я / л \<п и ,
-а"’
76
ДЕЙСТВИЯ с вещественными и комплексными ЧИСЛАМИ
У а"*
У а 4- УТ = )^а4-6 + 2‘Уа&
Бином Ньютона;
1 __2 _ О
—-.(j-x) „,4.__»(_д) +
4- (_ х),+Ь2Н-»><-«> (_ ху +
-b-,~2U;.^4)(~s> <-x)‘+...-i+2x+
4- Зл» 4- 4л» 4- 5х* 4- ...
Это равенство справедливо, если — 1 < х < 1
(см. стр. 152).
Действия с корнями:
4 4 4
/Т /27 = /81 = ±з:
1Д 3__ 3 8_
/10 = /1о» = /1й) - 4,6416 (из графы /л
табл. III).
3
3/ _ _8 /^ = — 2________2_
1/ 125 "З = 4- 5 = 6
У /TS
(остальные два корня—комплексные).
У 4 /Г- 2/15 - |/ 4/Г- /60 ->
Уа— уЬ—Уа + Ь— 2Vab, (а>Ь)
__=Л . Л (У~а — Г»),
У а + Vb “ « — b
Л Л ( /а 4- Vb) .
Уа — Vb " a — b
/ГГуГ- j/a+y2at~b +
/а-ГТ-
. /а- Vcfl — b
" V 2
Примеры. Действия со степенями:
( 3 \~® /7 V 313 . _
2377* — (2380 - 3)’ ~ 239». 10» - «.2380 4- 9:
ИЗ графы л* табл. 1U: 238"»56 644; следов*,
тсльмо,
2377’ = 5 (64 4004- 9 — 14 280 - 5 650129-
86" - ЗБ" « (85 4* 35)*(85 - 35) - 120-50 - «ООО.
4 4
“ /45 - /Г.
Проверка:
/45-/5 -/з /Т4-/Г-аУз » б -/Г—
- У 4 /Г- 2 /15 .
ЛОГАРИФМЫ
Логарифмом числа N при основании
а называется показатель степени л, в
которую нужно возвысить основание а —
постоянное положительное число (обычно
о> I). чтобы получить число N. Сле-
довательно, зависимость ап = N можно
написать в виде
я — ,ойа Л^-
Символ log N обозначает: логарифм
числа N при произвольном основании.
Из определения логарифма имеем
oioiaN - V.
ЛОГАРИФМЫ
77
Основные свойства логарифмов:
log (u-v) = log и + log v;
log — — log u — log u;
log un — n log u;
" - I
log Ku — — log u.
Пример.
— m lojr t 4- в log и — p log p-— log 4
Справедливы также равенства
llm log N = — oo;
W-o
Um log W = + oo
N—co
(при основании логарифмов, большем
единицы);
log 1 — О; loga а — I;
loga N • log a — log» N • log b.
где logo н log b берутся при произволь-
ном, но одинаковом основании; в част-
ности, log» N = loge N log» а или в
мнемонической форме
. «, log N
loga N — г-5—
6,1 log а
(N — вверху, а — внизу в обеих частях
формулы; в правой части — логарифм
при произвольном основании);
loga ь log*а = 1 или 1о2а о — , * ...
logo о
логарифма следует:
Для вычислений в технических рас-
четах применяются часто логарифмы
с основанием а = 10 — десятичные
(обыкновенные) логарифмы. Вместо logmiV
установлено (ОСТ 573) обозначение IgV.
Из определения
1g 10я — л, т. е.
1g 10-1
Igloo = 2
lg 1000 — 3
Ig 1UOOJ — 4 I t, 1
1g 0,1 - _ 1
Ig 0.01 - — 2
tg 0,001 = — з
lg 0,0001 = — 4
Иногда удоб"ее пользоваться лога-
рифмами при основании е = 2,71828133
(см. стр. 135). Они называются нату-
ральными логарифмами. Вместо log, V
установлено (ОСТ 573) обозначение
In У.
Пользование натуральными логариф-
мами особенно удобно, когда в выраже-
ние вычисляемой величины входят чис-
ла вида е±ж, как это встречается, на-
пример, в расчетах колебаний при нали-
чии сил сопротивления, в расчетах
ременных передач, некоторых бессту-
пенчатых фрикционных вариаторов,
тормозов и пр.:
Ige-ln 10- 1,
т. е.
Ig е — , \л и In 10 = —•
6 In 10 Ig е ‘
Ig е — 0.43429448... — Л1 — модуль де-
сятичных логарифмов;
In 10 - 2.30258509... -.
Л1
ig N = lg е • In N — /И • in N
и
In N ~ ilg N-
Если IOn<N < 10"+* in—целое чис-
ло), то n < Ig N < n 4- I, t. e. lg N —
= n + положительная дробная часть.
Целое число п, которое может быть
положительным или отрицательным, на-
зывается характеристикой десятичного
логарифма, положительная дробная
часть — мантиссой.
Десятичные логарифмы чисел, отли-
чающихся друг от друга только поло-
жением запятой, имеют одну и ту же
мантиссу.
Для чисел, ббльших единицы, харак-
теристика десятичного логарифма на
единицу меньше числа цифр до запятой
(числа целых знаков). Для чисел, мень-
ших единицы, характеристика отрица-
тельна и по абсолютной величине на еди-
ницу больше числа нулей после запятой
(т. е. равна общему числу нулей); так
как мантисса всегда положительна, то
минус, который в этом случае отно-
сится только к характеристике, пишется
над последней. Например (см. столбец
Ig п в табл. III):
Ig 27600 — 4,44091
Ig 2760 — 3,44091
Ig 276 — 2,44091
lg 27,6 - 1.441»!
Ig 2,76 - 0,44091
Ig 0,276 — 1,44094
Ig 0.0276 — 2.44091
Ig 0.00276 = 3,44091
И T. Д.
7Я ДЕЙСТВИЯ С ВЕЩЕСТВЕННЫМИ И КОМПЛЕКСНЫМИ ЧИСЛАМИ
Логарифмы неполной фор-
мы — с отрицательной харак-
теристикой и положительной
мантиссой-записывают иногда,
прибавляя к характеристике
4* 10, т. е., например,
вместо 1,44091
пишут 9,44091 — 10
или просто 9,44091;
вместо 3,67564
пишут 7,67564 — 10
или просто 7,67564.
Так делают, например, в
таблицах для логарифмов
тригонометрических функций,
меньших единицы.
Отыскание логарифма задан-
ного числа (логарифмирование)
и числа по заданному лога-
рифму (антилогарнфмировапие
или потенцирование) выпол-
няется по таблицам.
Действия над логарифмами
производятся так же, как над
другими десятичными дробями.
Если характеристика лога-
рифма отрицательна, а ман-
тисса положительна (лога-
рифм в неполной форме), то
логарифм может быть обращен
в отрицательное число (лога-
рифм в полной форме) сле-
дующим образом:
а) абсолютное значение ха-
рактеристики уменьшается ня
единицу (т. е. характеристики
увеличивается на единицу);
б) мантисса вычитается из
единицы, для чего все цифры
ее, кроме последней значащей,
вычитаются из 9, а послед-
няя значащая цифра — из 10;
в) перед полученным числом
ставится знак минус, напри-
мер, 3,44091 = — 2,55909;
- 1,20800 = 4- 0,79200.
Этим превращением лога-
рифма в полную форму прихо-
дится пользоваться при умно-
жении, делении, возвышении в
степень, иногда и при вычи-
тании (см. ниже, пример 2).
Аналогичным способом про-
изводится переход от полной
формы логарифма к непол-
ной.
Примерке
1) 1g 0,04293 = 2^63276. Найти In 0,04293. In 0,04293 —
— -jj-lg 0,04293 — 2,3025851 • 2 63276. Так как 2,63276 —
«=-1,36724, то In 0.0-1293——2,3025851-1,36724. Дла получе-
ння этого проитьелепия с шестью периымх значащими цифрами
пользуемся правилами сокращенного умножения (стр. 68):
23025851
* 427631
230258л1
6907755
1381548
161175
4Ш
920
31 481883
Следовательно, In 0.04293—— 3,14813. Пользуясь табл. XI
натуральных логарифмов, получили бы (fl,04293 = 4,293-10 )t
_о
In 4,29 .. . 1,45629 (233); In 10 — - 4,60517 —
3 _____70 _ 5,39483;
1_, 45699
6,39483
In 0,04293 = -Е 85182 —
— — 3,14818: тот же результат.
/ 1.734.0,561,а -0,435°'18 tg 12»41' tg 12*41'
, 7(й п ,.Л34 ‘ СОВ25’15/”*л'СОВ 25“1л>
Вычисление произвести с помощью четырехзначных лота*
рифыов. Имесы:
lg X - -1- 1g у + 1g tg 12’41' - lg cos 25’15', ru
lg У-lg 1734 4-1,2 1g 0,56 4-
4-0,18 lg 0,435 - lg * - lg 2,708 - 0.34 lg 0,2451
lg 1,734 — 012390
lg 0,56—1^6978
0,18 lg 0,435 -T.9349
— lg к — Г.5028
- lg 2,708 - TjS673
- 0,34 Ig H.245 — 0,2077
lg у -T. 1-195
-j- lg у -T5748
Igtg 12’41' — T.3523
- lg cos 25’15' — U.Obn
lg X — 2>7U7
X — 0,09348 > 0,093
lg 1,73.........0,2330 [25]
4.............10
lg 1,734 - 0,2390
lg 0,56 — T.7482 — - 0,2518
2518
— 0JUJ21U
ж 1,6978
lg 0,435 - Ц6385 - - 0.3815
X 0,18
28920
3615
— 0,065070
- 1.9319
Igo - 0,49721 lg 2.703 - 0,432?
- lg 0,245 — - 1,3892 — 4-0,6108
X0.34
24432
18324
4- 0,207672 .
« 0.207T
lg cos 25’15' — + 1,9564- -0,043»
"2,9707
03 ...... 934 [5]
V _____________8
0,09348
СОЕДИНЕНИЯ
79
СОЕДИНЕНИЯ
1) Размещения (обозначение: Д) из
л элементов по т (т<^п): соединения,
различающиеся либо составом, т. е. са-
мими элементами, из которых образо-
ваны соединения, либо порядком эле-
ментов. Например, все возможные раз-
мещения из четырех элементов а, Ь, с, d
по два: ab, ас, ad, ba, be, bd, ca, cb, cd,
da, db, de.
Если в размещениях допускается
повторение одних и тех же элементов,
то число их больше. Для взятого при-
мера добавились бы еще четыре разме-
щения: аа, bb, сс, dd.
Число всех возможных размещений
из п элементов по mt
а) число размещений без повторений
в них элементов
А„ = л(л — 1)Х
где л! — символ факториала, т. е. п! —
- 1-2-3. . . . л;
б) число размещений с повторениями
элементов
9
Например: <4} = 4-3 — 12 нлн также
Л 41 1.2-3-4
Л4“ —-------Г7Г-
12;
2(no«m)
4
— О — 1в.
А
2) Перестановки (обозначение: Р)
из л элементов: частный случай разме-
щений, когда т “ п, т. е. когда в
каждое соединение входят все п элемен-
тов и поэтому соединения различаются
только порядком элементов.
Если в совокупности из л элементов
некоторые повторяются, например один
элемент повторяется р раз, другой — q
раз, третий — г раз и т. д. , то при
комбинировании их по л элементов
получаются перестановки с повторени-
ями.
Число всех возможных перестановок
из л элементов:
а) число перестановок без повторений
в них элементов:
1-2-3-... -л - л!
6) число перестановок с повторениями:
р
гп(р, q. г,...) plqlrl...
Например: Pg = 1-2-3-4-5-6-7-8 —
40 320 (см. стр. 41, табл. IX);
р ___________81____
^В(3.2.3) “3,2)31 °
1-2-3-4-5-6-7-8
-i-2-3.1-2-1-2-3-560-
3) Сочетания (обозначение: (?) из л
элементов по т: соединения, различаю-
щиеся только составом, т. е. самими
элементами, из которых образованы
соединения; порядок элементов в соеди-
нении не имеет значения. Так, например,
из четырех элементов a, b, с, d можно
получить только следующие сочетания
по два элемента: ab, ас, ad, be, bd, cd;
комбинации ba, ca, da, cb, db, de не
являются новыми сочетаниями, так как
отличаются от написанных только по-
рядком элементов (Ьа и ab, са и ас, cb
и Ьс и т. д.), но не самими элементами.
Если в сочетаниях каждый из л эле-
ментов может повторяться т раз, то
получаются сочетания с повторениями.
Число всех возможных сочетаний из
л элементов по т [обозначение: (?” или
/ п \1
также ( ) I:
а) число сочетаний без повторений »
них элементов
с'п-( п\ -
л \т/
л (л — 1) (л — 2)... |л — (л» — И |
l-2-З-..-я
или также в другой форме
л (л— 1)(л — 2)...3-2-1
1-2-3-...-in l-2-З... (л—
и!_______Рп
т\(п-т)\ “ Рт-Рл-т '
б) число сочетаний с повторениями:
сл сл 4-m-l ( т )
_ (л + т - 1)1 _
" ml (Л — 1)1 “ Рт Pa-t ’
«о
действия с вещественными и комплексными числами
Число всех возможных сочетаний
из п элементов без повторений
(?)+(?) + (;)+ + (.-.) +
+ O-2--I.
Основные свойства сочетаний:
этим
свойством
, — п
удобно пользоваться, когда т > —
оапример:
— 21 вместо более
длинного
7-«-5-4-3 Л
1-2-3-4-5 6Ш
=21.
ГЛ-2
б)( = этим свой-
’ \ т + 1 ] \т J т + 1
ством сочетаний удобно пользоваться
для вычисления биномиальных коэффи-
циентов;
...пример: (•)-(’) + (’)-(’) + (’)-
-ТЗ+1Т5-’,+»-ж
Если считать, что (Д)={’"Р««=»
то будет иметь место соотношение
где т и k — произвольные натураль-
ные числа, совершенно не зависящие
друг от друга.
КОНЕЧНЫЕ РЯДЫ
Прогрессии
1) Арифметическая прогрессия (или
также арифметический ряд 1-го по-
рядка): последовательность чисел —
членов прогрессии—в|, аг, о8......
ар ... > ап, в которой разность каждых
двух последовательных членов — по-
стоянная величина. Разностью ариф-
метической прогрессии d называется
разность между любым членом ее н
предшествующим. Следовательно,
аг = в| + Ct, а3 = + 2d....
af = в, 4 (j— I) d;
последний член арифметической про-
грессии
в|.-<’1 + (л— !)<*•
Сумма л членов арифметической про-
грессии
или также
о _ (2/7, + (Л —l)-rf|-W
•>«- 2
Любые три из пяти величин а, (или
вообще ау). d, п, ап н Sa вполне опреде-
ляют арифметическую прогрессию.
Пример. Задави: а, = 2S; d = 6; “ 735.
Слелоительво.
а, - а, - 3d = 25 — 3-6 - 7;
прогрессия 7; 13: 19; 2S; 31 и т. а.;
£±±«-^".,735 иди (< + Зл)л—735;
Зл>+ 4л-735-0;
отсюда
- 2 + V 4 + 3-735 -2 + 47
" а “ —а— “151
ая - ои - и, + (л - 1) d - 7 + 14-8 - 91.
Проверка:
_ - (?+ 91). 15
---— 49-15 = 735.
2) Геометрическая прогрессия (или
также геометрический ряд): последова-
тельность чисел—членов прогрессии-
at, а3, а8, . . . ,а„, в которой отношение
каждых двух последовательных чле-
нов — постоянная величина. Знамена-
телем геометрической прогрессии q назы-
вается отношение любого члена ее к пред-
шествующему. Следовательно, а. = atq\
а» = anj*; . . ; aj >= акИ-1; . . . послед-
ний член геометрической прогрессии
Яр-Щ qn~l.
Сумма п членов геометрической про-
грессии
с — дл? —г»1
q — 1 •
или также
<- «I — D
0-1 •
КОНЕЧНЫЕ РЯДЫ
81
Если прогрессия—убывающая (q <2 I),
то удобнее пользоваться формулой
«1 — аяЧ
---Г^Г’
или также
g,(l-g")
»-?
Любые три из пяти величин а* (или
вообще aft, q, п, а„ и 5Я вполне опре-
деляют геометрическую прогрессию-
Пример. Числа оборотов минуту шпинделей
металлорежущих станнин обычно образуют геоме-
трическую прогрессию. Если а, — наименьшее
число оборотов шпинделя в минуту, ап — наи-
большее, q — знаменатель раза чисел оборотов,
п — число ступеней скорости шпиндели, ап - а, —
- R — диапазон регулирования этих скоростей,
то
ajl= R-q"~l ,
“1
ОТКУДА
lg V lg q
Этими формулами пользуются в ьниематиче-
скиа расчетах коробок скоростей станков. Вы-
брано. например: R « 50. IM при атом
и
должно быть сше соблюдено условие q • К10,
где £ — целое число ид ряда 40, 20, 10 и 5, а л по
условиям конструкции должно иметь форму
п -1Е..3Е,, *М £ м Е, — также целые числа.
Получаем
lg/10
Принимая последовательно Е—40, 20, 10. 5. по-
лучаем я—69. 35, 18, 10. Удовлетворяет поставлен-
ным условиям лишь значение л = 18 — 2-3*. При
10
этом знаменатель рвал р= 110 г<* 1,26), и дей-
ствительный дилпачон регулирования оборотов
10 IT
К =• IIя - 1 = (Ий) . lg R = 17-0,1 = 1.7000.
и /с—50.12-очень близко к требуемому значению.
Числа оборотов шпинделя в минуту: а, = ПЛ;
Iff 10
о,- пл Но -ПЛ-1.26 —14.5; л, —ПЛ-(Ио)* -
10_
- ПЛ-1.58 - 18Д; а, - ПЛ-(Но)’ - 11,5-2 -23
Арифметические ряды порядка
выше 1-го
Ряд чисел Дау, образованный раз-
ностями последовательных членов за-
данного ряда а/, называется рядом раз-
ностей f-го порядка. Аналогично из
ряда членов Дау образуется ряд Д:ау раз-
ностей 2-го порядка, из ряда членов
Д’а/ — ряд Д’ау разностей 3-го порядка
и т. д. Если ряд Д*ау состоит из равных
чисел, то ряд а/ называется арифме-
тическим рядом й-го порядка. Следо-
вательно, иначе: арифметическим рядом
к го порядка называется такой ряд, у
которого разности I-го порядка обра-
зуют арифметический ряд (к — 1 )-го по-
рядка.
Примеры-.
I) а- 1 6 14 18 22 41 101 239 503
Ла- & 8 4 4 19 60 138 264
/‘а, 3 —4 0 15 41 78 126
Д*а. -7 4 15 26 37 48
Л'а. 11 II И 11 П
Следовательно, этот ряд—4-го порядка.
2) Рал квадратов натуральных чисел
а. I 4 9 16 25 86 49 64
ла. 3 5 7 9 II 13 15
2 2 2 2 2 2
есть арифметический ряд 2-га порядка.
3) Ряд четвертых степеней натуральных чисел
а, I 16 81 256 625 1296 2401 4096
ла. 15 65 175 369 671 1106 1695
ДЧх 50 ПО 194 302 434 590
А. 60 84 10В 132 156
Д*а^ 24 24 24 24
есть арифметический ряд 4-го порядка.
Арифметический ряд fe-ro порядка
однозначно определяется первыми чле-
нами самого ряда и всех рядов его раз-
ностей, т. е. величинами: ai, Aai,
Д’аь .... A*aj.
Сумма Sfl первых n членов арифме-
тического ряда fe-го порядка:
д.-( f)«, + (; )ы, +
Бесконечно убывающая геометриче-
ская прогрессия: прогрессия аь а^.
aiff*. . . , ayq". где q < I и л-»со.
Для такой прогрессии предел суммы п
членов Jim 5Я = , поскольку
л-со ' Я
lim qn = 0.
0-00
Пример. Вычислить сумку
5я-1, + 2’+Э’+4’-|-. .. + «*
Составляем ряд разностей:
a. 1 8 27 64 125 216 343 612 729
Ла. 7 19 37 61 91 127 169 217
Л'а. 12 18 24 30 36 42 48
А’ву 6 6 6 6 6 6
б Том I. Зак. 1461
82
ДЕЙСТВИЯ .С ВЕЩЕСТВЕННЫМИ И КОМПЛЕКСНЫМИ ЧИСЛАМИ
Получен арнфметическнй ряд 3-го порядка
«я - (?) » + (") ’+ (") « + (?) 6 = - + 7+ П-Ь
+ Л(*~П("!72)(Я~3) в-АИ+14(я_|) + 8(я_1)(я_2) + (Я_1Ня_2)(П_ЗН.
Чд - М + вя*-34я + 18 4-Я» - вя*-f-Пи-б) - А (я*-(-2л’f л)- £(Я« +2и + IJ-
_ и» (а 4- If _ [яй+пр
Например, сумма кубов первых «ватаги натуральных чисел
21СЯ-44 100.
Некоторые конечные числовые ряды
1) 1+2 + 3 + -.. + (л — 1) +л~ П(П+ 1} ;
2) Р + (р + 1) + (Р + 2) + ... + (q - 1) + q ^(Я+р)(Я^\-р>.
3) 1 + 3 + 5 + ... + (2л — 3) + (2л — 1) = л1;
4) 2 + 4 + 6 + ... +(2л — 2) + 2л = л (л + 1);
5) 1» + 2» + 32 + ... + (л - 1Р + о» - Я + ^(2л + ;
6) I* + 2* + 3* + ... + (л — 1)* + л3 — [-("2+ П]\
7) 1« + У + У + ... + (Я-1И + л2- "<"+П(2л+^)(Зл« + Зл-П .
8) 1» + 3» + 5» + ... + (2л -3)2 + (2л - 1)2 - я (2я + -^(2я ~ П =я<4я1~D ;
9) 1» + 3» + 5» +... + (2л - 3)» + (2л — 1)» - л»(2Л»— I);
10) 1.2« + 2-3» + 3-4« + ... + л (л + 1)2 = я<>?+ Шл+.ЗРл + б).
11) 1 + 2q + 3?2 4-... 4- л?»--1 - 1 ~ (я * nq"+— ;
12) Ь2 + ГЗ + 3+ + '" + (л — 1) л “ ~И~ ’
ПРОПОРЦИИ
Г. Я1
Если два отношения + и -= равны.
0| Dy
то, соединяя их знаком равенства, полу-
чим пропорцию (геометрическую)
bi bj'
Основное свойство пропорции: ajfty =
= ajbi — произведение средних членов
пропорции равно произведению ее край-
них членов. Следовательно, для опре-
деления любого члена пропорции необ-
ходимо и достаточно знать три осталь-
ных члена ее.
Из равенства = ag6| следует;
» г-г; 2)
3) 4)b«h,
' ft, at at'
ПРОПОРЦИИ
83
т. е. в пропорции можно менять местами:
а)‘ или средние члены, б) или крайние
члены, в) или одновременно те и
другие.
Из того же равенства следует:
5) 6)
Ц) ^2 Д1 И
О» fl, Di О]
т. е. в пропорции можно обменивать
местами предыдущие члены обоих отно-
шений (О| и аг) с последующими (Ь} и Ьг)
(ср. 5 с I, 6 с 2 и т. л.).
Из пропорции = v следует
&1 &2
также:
' га, + t-b, r-at + l-bt
]m Г«1 + g at P-b\ 4- g-b
rax -r Г‘Ьу 4- t-bi *
где p, q, rt t — произвольные множи-
тели — положительные или отрицатель-
ные, целые или дробные, действитель-
ные или комплексные. Из производных
пропорций (9) и (10) получается,
в частности:
11) «1 4- Ь, Д1 = аг ± Ьг аг
12) а, -<• Л. Д» 4 bt
bi Ьг
13) а\ i bi аг ± bi - — • “ Дя’
14) «1 ± ь. ь>.
аг ± Ьг ьг'
15) а, 4- Ь, аг ± Ьг
а, + Ь,
16) «1 ± д» Д| _г Ь, ± Ьг bi
17) Д1 ± Д» Ь, ± Ьг
д2 Ьг
18) Д1 ± Дя Ь, ±
Д| Т flj ' bi^b2
19) «1 ± аг bi ± bi £1. bi'
20) at А аг Ь, ± Ьг о»
6е
-. 09
Из пропорции — — —- следует
также:
откуда по указанным выше правилам
получаются различные производные про
порции, например:
а™ _ аТ Ь” — Ь*
о” ~ = ’’
Lffl I.WT
Д1 - 61 а> - Ь2 .
ь” ь” ’
/п т т гл
Уа, + У/ь Уа? + уг,
т гл ~~ т ~т
Уа,- Vb, Vat- Vbt
и т. д.
Из равенства нескольких отношений
Ц| о. ак
ь> ь
следует:
V < + < + • + < „}
Дя = . . - д*
Ьг Ьк ’
где п и к — любые натуральные числя.
В частности, справедливы равенства
Д1 4- о< 4~ Дя 4- 4- Пу _ д,
4- bi 4- bt 4" • • • 4- bK b,
b i ”' ьк ’
и если известны сумма У а/ = и
/ ।
числа Ь/, пропорциональные а/, то из
этой формулы можно определить все а/.
Прилир. Разделить МО и» части, пропорцио-
нальные 3, 5, 8, 9 и 10.
Пользуясь последней формулой, получаем:
о. ’*> N0 < о ч
~“ЯЗ+а+ЭТй’зГ Т-
Щ 4 1 « .л. а1 * .
_-т . о,_5.<-Л; — --j-;
а, -4.8 -32
и т. д.
84 , ДЕЙСТВИЯ С ВЕЩЕСТВЕННЫМИ И КОМПЛЕКСНЫМИ ЧИСЛАМИ
Если обя средних (или оба крайних)
а х
члена пропорции равны, т. е. — =у
/ х Ь \
( или, что то же, — — — ), то х =*
\ _ а х)'
= Va-b—среднее геометрическое чисел
а и Ь.
ПРОЦЕНТЫ
При начислении простых процентов
по процентной таксе р% начальная
сумма К обращается через t лет в
При начислении сложных процентов
один раз в год начальная сумма Л' через
t лет обращается при процентной таксе
Р% в
Kt = К (1 + цХ))/> "л“ Kt = K q‘.
если обозначить
’ + ТОО = 9’
КОМПЛЕКСНЫЕ ЧИСЛА
И ДЕЙСТВИЯ С НИМИ
Комплексное число — выражение ви-
да а -|- р/, где я и fl — вещественные
(действительные) числа: i — так назы-
ваемая .мнимая единица', определяемая
условием i* = — I.
Если и—любое целое число, то /*•= 4-1;
/1я+1 - I; /4"+2 - -1; /,я+3 - — Ве-
щественные числа я и 3 называются со-
ответственно вещественной (действитель-
ной) и мнимой частью комплексного
числа я= а4-^'; обозначения: я= R(a),
fl — /(а) или я ” Rea, fi *- Ima.
Если ji= 0, тоо“ а (действительные
числа — частный случай комплексных
чисел); если я = 0, то а = fii (чисто
мнимые числа).
Геометрически комплексное число а «=
= я 4- fi< изображается точкой с коор-
динатами х = я, у = fl ня так назы-
ваемой комплексной плоскости (точка
эта называется аффиксом комплексного
числа); действительные числа изобра-
жаются точками оси абсцисс (действи-
тельная ось), чисто мнимые — точками
оси ординат (мнимая ось). Так как
каждая точка плоскости вполне опреде-
ляется радиусом-вектором этой точки,
то каждому комплексному числу соот-
ветствует определенный вектор, лежа-
щий в комплексной плоскости и идущий
из полюса в точку, соответствующую
комплексному числу. Таким образом,
комплексные числа могут изображаться
как точками, так и векторами. Часто
говорят о точке а - я 4~ вместо того,
чтобы говорить о числе а — а 4- fU’.
Два комплексных числа считаются
равными, если равны отдельно их дей-
ствительные и их мнимые части, т. е.
Я| 4“ 8i/ — *2 Н- ЗзЛ если — яа и
Pi = рг; отсюда следует а 4- -К = О,
если я = 0 и ? = 0.
Равным комплексным числам соответ-
ствуют равные векторы, их изображаю-
щие. Понятия „больше* и .меньше* для
комплексных чисел не существуют.
Выражение комплексного числа а —
= я 4- 3( называется алгебраической
формой его записи.
Если вместо декартовых координат
точки, изображающей комплексное
число, ввести ее полярные координаты
(р. <р), то получим тригонометрическую
форму записи комплексного числа:
а = о (cos <р + i sin у);
р —длина радиуса-вектора соответ-
ствующей точки — называется модулем
комплексного числа; угол <р (в радиа-
нах) — аргументом комплексного числа.
Обозначения: р = | а |, <р = arg а.
Связь между р, <р и а, р — та же, что
и между декартовыми и полярными ко-
ординатами точки:
а «• р cos <р; Р “ ? sin ®;
Р - К»2 4- <t - arctg ;
а
при этом 0 < р < оо, — оо < <Р < 4-со;
для данного комплексного числа
аргумент <р имеет бесконечное множе-
ство значений, отличающихся друг от
друга на 2йгс (fe — целое). Главное зна-
чение аргумента заключено в проме-
жутке —< 4- ir. Число нуль имеет
модуль, равный нулю; arg 6 — вели-
чина неопределенная.
Норма комплексного числа А(«) "
= а* 4- 3* = Р*-
Показательная форма записи ком-
плексного числа: а = ре*\ где р — мо-
дуль, <р — аргумент; эта форма записи
основана на применении формулы Эй-
лера
е*1 — cos ? 4- i sin ?.
КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ С НИМИ
85
Пример. I 4- Уз"! (алгебраическая форма) =
= 2 (cos i (тригонометрическая
форма) — 2ел (показательная форма).
Если не ограничиваться главным значением
аргумента, то
1 + V31 =2 (cos (у + 2An j +
+ ' *|П (т + 2*’') = *
Два комплексных числа называются
взаимно сопряженными (обозначаются
а и а), если их действительные части
равны, а мнимые отличаются знаком.
Точки, изображающие на комплексной
плоскости сопряженные числа, распо-
ложены симметрично относительно дей-
ствительной оси. Модули сопряженных
чисел равны, аргументы отличаются
знаком:
а — а + $ = р (cos <? + I sin f) = ре’’1:
а — а — &< = р (cos ф — I sin ч») = pe_|f“.
Сложение и вычитание двух или не-
скольких комплексных чисел выпол-
няется по формуле
(“I + 010 + (“з + 0гО — (аз + 0зО + • • • =
=а (<Xi 4- а2 — о3 4- ...) +
+ (01 + 02 - 03 + --•)/-
Умножение двух комплексных чисел
выполняется по формуле
(“1 + 010 (3s + ЗгО “ (’)’• — 010г) +
+ (“101 + 01“г) !
Если числа даны в тригонометриче-
ской форме, то
|Р1 (cos ft + I sin 4>j) 1 IР> (cos <ft 4-
+ isinft)] - p)?:[COS (f| + ft) +
+ I sin (ft 4- <Pi)}.
t. e. модуль произведения равен про-
изведению модулей, аргумент произве-
дения равен сумме аргументов сомно-
жителей.
В частности, произведение двух со-
пряженных комплексных чисел даст
квадрат модуля (т. е. норму) каждого
из них:
аа - (я + 0/) (« - 00 -
— а2 4. р — дг (Я) _ л (д).
Деление двух комплексных чисел
определяется как действие, обратное
умножению.
В тригонометрической форме
[pi (cos ft 4- i sin ft)]: [p2 (cos ft 4-
4- i sin f-J| >=» |cos (<f>t — ?г) +
Pi
+ i sin (ft — ft)],
t. e. модуль частного равен частному
модулей делимого и делителя, аргумент
частного равен разности их аргументов.
При делении комплексных чисел в
алгебраической форме „уничтожают мни-
мость в знаменателе” (аналогично уни-
чтожению иррациональности в знаме-
нателе), для чего умножают числитель
и знаменатель на число, сопряженное
знаменателю, и получают в знамена-
теле вещественное число.
Вообще вычисления над комплексными
числами а + 01 можно производить так
же, как и над обыкновенными двучле-
нами, полагая Р = — ).
Примеры:
1) _!_ =______1^5_____=
« + Р1 («Г₽1)(а-М
. «~Я « 3 ,
- 4-₽» = «• 4-Р ««4-0>'-
«.+Ы (о, 4-М (я,-3,0
’ -+ы .*+?;
_ в|Я1 -|- I ,
+7ГГ‘-
(3 - 4/) (1 - 101 - Я) . (10 4- 71) I
•-------ГТЗ?------+ ------
-2(3 - 40(12.4- 50 , 7—104
-------гтя------+ “Г““
-2(50-330(1-30 7- ИН
(14-31) (1-ЗО 5
— 2(—43 — 2011) , 7—101
" W +—~ “
- 4-(50+ 1911) = 10 4-ЗЯ,21.
Возведение в п степень комплексного
числа в тригонометрической форме про-
изводится по формуле
[р (cos<p + I sin f)|" —
= ₽л (cos Л<р + i Sin Лф),
т. е. модуль возводится в л-ю степень,
а аргумент умножается на п. Эта фор-
мула применима при любом значении л:
целом, дробном, положительном, отри-
цательном (при дробном л необходимо
86
ДЕЙСТВИЯ С ВЕЩЕСТВЕННЫМИ И КОМПЛЕКСНЫМИ ЧИСЛАМИ
учитывать многозначность результата —
см. ниже).
В частности, при р = 1 получается
формула Муавра:
(cos? 4- i sin ?)" = cos л? 4- i sin л?.
Извлечение корня л-й степени про-
изводится по формуле
л _ Л
Уа = У f (cos ? + i sin ?) —
- y^cos*±-2*." +/s,n ,
k = 0. 1, 2..л — 1.
Л
В этой формуле V p — арифметиче-
ское значение корня л-й степени из
положительного числа р = Ка* 4-
?0— главное значение аргумента ком-
плексного числа; каждому из л раз-
личных значений числа k соответствует
одно из значений корня л-й степени
комплексного числа, который, следова-
тельно, имеет п различных значений.
Точки, изображающие на комплексной
п _
плоскости У а .являются вершинами
правильного л-угольника с центром в
полюсе, следовательно, лежат на окруж-
л
ности радиуса Ур и делят ее на п
равных частей.
Примеры.
з
,, ./т — 2*4 < . . 2*«
I) У1 —со« —— ;
0 0
* — 0,1, 2^три мычания: 1;
дна значения:
В частности.
Л
УТ = t*. * — 0. 1.2..., л—I,
где
2т. 2л
е = cos------h1 sin —;
л п ’
где I. У a )i --—одно из п значений корня
(безразлично, какое), а еА принимает
все значения корня л-й степени из еди-
ницы.
Всякое равенство между комплекс-
ными числами, обе части которого со-
ставлены только при помощи действий
сложения, вычитания, умножения н
деления, остается верным, если каждое
из комплексных чисел заменить сопря-
женным с ним числом.
ГЛАВА III
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ *
ПОНЯТИЕ О ФУНКЦИИ
Совокупность вещественных чисел х,
удовлетворяющих неравенствам а
называется отрезком (или сег-
ментом), а удовлетворяющих неравен-
ствам а < х < 6 — проме жутком (или
интервалом). Символ отрезка: [а, Ы;
символ промежутка: (а, Ь). Переменная у
называется функцией переменной * (ар-
гумента), определенной на отрезке [а, д]
или в промежутке (а, Ь), если каждому
значению * из указанного отрезка или
промежутка поставлено в соответствие
одно (если функция однозначная) или
несколько (если функция многозначная)
значений переменной у. Отрезок |а, 6)
или промежуток (а, Ь) — область опре-
деления (или область существования)
функции. Символ функциональной зави-
симости: у = f (х); вместо буквы f ста-
вят любую другую букву, например F,
Ф, ф и т. д.; пишут также у = у (х).
Значение функции f (х) при значении
аргумента х ™ а обозначают символом
/(а); например, если / (х) “ cos х, то
/(0)=cos0 = 1. Если переменная и
является функцией нескольких незави-
симых переменных х, у, г..I, то пи-
шут и = f (х, у, г,...,(). Численное зна-
чение, этой функции при х = в, у = Ь,
г = c,...,l “ k обозначают символом
/ (a, b, c,...,k); например, если /(г. у)=
- х* + у», то /(1,2) = )’ + 2* = 5.
Функция может быть задана форму-
лой, таблицей, графиком. Средн функ-
ций, заданных формулой, различают
функции, заданные явно, когда дано
выражение у через х [у= / (х)1; неявно,
когда хну связаны уравнением
IF (х, у) = 0] (например, х* + у* —
— в1 “ 0) и параметрически, когда со-
ответствующие друг другу значения х
и у выражены через некоторую третью
• Си. литературу па стр. 349 [5], (30), [35], (ЗГ|.
величину I, называемую параметром
(х=<р(0,_у=ф(<)1 (например, х=а cos t;
у = a sin t).
Функцию можно задать таблицей,
если указать два множества соответ-
ствующих друг другу числовых зна-
чений переменных х и у (см., например,
математические таблицы в главе Г).
Если функция задана формулой, то,
задавая аргументу х различные число-
вые значения (из области определения
функции), можно вычислить при помощи
формулы соответствующие значения
функции у; совокупность всех полу-
ченных пар значений х и у опять со-
ставит таблицу.
Пользуясь той или иной системой
координат (см. главу XI), можно изо-
бразить каждую пару соответствующих
друг другу числовых значений пере-
менных х и у, взятых из таблицы,
точкой плоскости; соединив полученные
точки плавной кривой линией, получим
график функции, заданной формулой
или таблицей. Иногда функцию непо-
средственно задают графиком без фор-
мулы и таблицы. Нередко графики
получаются автоматически при помощи
самопишущих приборов.
ЦЕЛАЯ РАЦИОНАЛЬНАЯ ФУНКЦИЯ
Явная функция, выражаемая много-
членом
у - оох" + apr"-1 + ... + an_tx + а„,
где а0, аи...,ап — какие угодно посто-
янные, а л — целое положительное по-
стоянное число, называется целой ра-
циональной функцией одного аргумента,
а ее график — параболой п-го порядка.
Частные случаи:
I) Линейная функция у = ах 4- Ь; гра-
фик ее — прямая линия АВ (фиг. 1);
а = 1g »—угловой коэффициент прямой,
b = ОВ — начальная ордината. При
88
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Ь = 0 линейная функция выражает пря-
мую пропорциональность у = аг, гра-
фик се — прямая, проходящая через на-
чало координат; коэффициент прямой
пропорциональности а является угловым
Фиг. I. График линейной функции.
коэффициентом прямой—графика прямой
пропорциональности.
2) Квадратная функция у = ах1 4-
-4- Ьх + с; график ее — квадратная па-
рабола. Парабола у = ах* (фиг. 2) сим-
метрична относительно оси ординат; н
начале координат лежит вершина пара-
болы, а ось абсцисс касается параболы
Фиг. 2. Графики функции у = ax' ала различных
значений параметра а.
График функции у “ ох1 4- Ьх + с —
та же парабола, но с вершиной в точке
/ Л tfl — 4ac\
0\ (-----,---------- | и с осью симме-
\ 2а 4а )
трин, параллельной оси Оу (фиг. 3).
Выражение Ь* — 4ас называется дис-
криминантом квадратного трехчлена
ах* + Ьх + с и служит для нсследо
нация корней квадратного трехчлена
(корнями функции называются те зна-
чения аргумента, при которых функция
обращается в нуль). Если Ь* — 4ас < О,
то корни квадратного трехчлена мнимые,
трехчлен при всех значениях х сохраняет
тот же знак, какой имеет коэффициент а;
график (парабола) нигде не пересекает
оси Ох. Если Ь* — 4ас > 0, то трехчлен
имеет два вещественных корня
— b ± VЬ- — -\ас
'2а
значения; график не-
Фнг. 3. График ккахратиохо
трехчлена у = ж* — 2х 4- X
и принимает как положительные, так
н отрицательные
ресекает ось Ох
в двух точках.
Если62~4ос= О,
то трехчлен об-
ращается в нуль
при одном толь-
ко значении х=
Ь
= - 2^,апрн
прочих совпа-
дает по знаку
с а; график ка-
сается оси Ох.
3) Простейший
случай много-
члена третьей
степени пред-
ставляет функ-
ция у = ах* (фиг. 4). Путем преобразова-
ния координат по формулам х =* д' + а,
У = У‘+ ₽. где а = - ? =. <vJ +
4-aja*+ aft + аг. придем от функции у =
Фиг. 4. Графики функции у — ох* али рамнчиых
значений параметра а.
СТЕПЕННАЯ ФУНКЦИЯ
89
дробную функцию, при л дробном —
иррациональную функцию (если дроб-
ный показатель л не преобразуется в
целое число). При а = 1 имеем кривые,
изображенные для положительных зна-
чений х на фиг. 7 и 8, где отдельные
кривые соответствуют разным значе-
ниям л. Эти кривые называются поли-
тропами.
При л > 0 все кривые проходят через
начало координат и через точку (1,1),
имеют параболические бесконечные
ветви. При л < 0 ни одна кривая не про-
ходит через начало координат; оси коор-
динат являются асимптотами кривых
(см. стр. 261); соответствующие ветви
кривых называются гиперболическими
по имени гиперболы, которая получается
при в = — 1. В последнем случае имеем
а
функцию у = —, выражающую закон
— Ojx3 4- a-ix* 4* ajx 4- 03 к функции у' =
= Oqx'3 4- ex', где с = Зо0т2 4- 2a'ia 4-
+ аа (на Лиг. 5 и 6 даны
кривые _у=х34*сх иу=—х*4-«
для различных значений с).
Все параболы л-го порядка
имеют параболические бесконеч-
ные ветви (см. стр. 261).
Пример. Функцию у = л» — Зх* 4-
4- 2х 4- 1 привести к виду у
Полагая
обратной пропорциональности. Графи-
ком ее будет равносторонняя (или равно*
Сочная) гипербола (фиг. 9. а).
где Э — а'— За1 -|- 2а 4- I, получим
у'+ а»-3«« + 2в + 1 --*'* + 3*'*
р*п;п>0 10 3 2 Ъ
Фиг. 7. Графики функции
у — х" лля различных зна-
чений л > 0.
0,1
гл
%
02
Фиг. 8. Графики функции
у — х” для различных зна-
чений л < 0.
4-Зж'а* 4- — Зх'1 — вх'а — За’ 4-
4- 2х' 4* 2а -|-1,
откуда
у' — х’’ 4- Зх/,к 4- Зх'к’ — ЗХ'* — бх'а 4- 2х';
полагая, далее, ami, получим
у' — ж'* 4-Зх'* 4- Зх' — Зх’* — вх' 4- 2л',
откуда
у' — ж'* - ж';
для контроля подсчитаем непосредственно:
с—3-1-1’4-2(-3) I 4-2- -I.
СТЕПЕННАЯ ФУНКЦИЯ
Так называется функция вида у = ахп,
где показатель л может быть как поло-
жительным, так и отрицательным, целым
или дробным. При л целом положитель-
ном имеем целую рациональную функ-
цию, при п целом отрицательном —
Фиг. 9. Графики функции у для различных значе-
ний параметра а: а) у - -2.; б) у —ax'l' .
90
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
3
2
График функции у = ах называется
полукубической параболой. На фиг. 9.6
изображены полукубические параболы,
соответствующие различным значениям
параметра а.
РАЦИОНАЛЬНАЯ ФУНКЦИЯ
Функция вида
а^г" + о.Xя-1 + .. • + оя-1Х + дп
У «’еХт4-а1хл,-1 + ...4-ая,_|ж4-ат
называется дробной рациональной функ-
цией, или просто рациональной функ-
цией. Простейший случай этой функции
представляет дробнолинейная функция
тх + п
У “ px + q •
а
которая приводится к виду у = — при
помощи преобразования координат х =
= х' + а, у = у' + ₽, где а =--,
т . , пр-та
? — — (Р * 0). причем а = . .
Графиком всякой дробнолннейной функ-
ции будет равнобочная гипербола, а
Фиг. 10. График дробнолинейной функции
полученное после преобразования урав-
а .
некие у = — будет ее уравнением от-
носительно асимптот, проходящих через
точку (я, fl) и параллельных старым
осям координат (фиг. 10).
+ В)
Пример. Привести функцию у » 2ж 4- 4
к простейшему виду.
Положим у = у* 4* 3» х = х* + •» где ® • —’А
F = 4- 3; получим
или
6 (х'~ 2) 4- 13
2 (X'-2) 4-4 '
откуда
Действительно, здесь
пр — mq 26 — 24 1
“ - р* ” 4 “ 2 •
ФУНКЦИИ АЛГЕБРАИЧЕСКИЕ
И ТРАНСЦЕНДЕНТНЫЕ
Все рассмотренные функции относятся
к числу явных алгебраически* (за ис-
ключением случая степенной функции,
когда п — иррациональное).
Явная функция от х называется алге-
браической, если над аргументом после-
довательно выполняются в конечном
числе только основные действия (сложе-
ние, вычитание, умножение, деление,
возвышение в целую положительную
степень и извлечение корня с целым
положительным показателем). Если в
формулу, которой задана явная алгебра-
ическая функция, не входят радикалы,
то явная алгебраическая функция на-
зывается рациональной, в противном
случае иррациональной. Например, яв-
ная алгебраическая функция у = V 1—х1
есть функция иррациональная.
Если х ну удовлетворяют уравнению
F (*> У) “ 0, гАе F — символ целой ра-
циональной функции от хи у, то одну
из переменных называют алгебраической
неявной функцией от другой. Считая v
за функцию, уравнению можно придать
вид
fo (*) У" + fi (х) ул~* + ...+
+ Тя_1 (х) У + <?„ (х) - О,
где <fo (*)• fi (*). fa (*) — иелые ра-
циональные функции от х.
Всякая неалгебраическая функция
(явная или неявная) называется транс-
цендентной; среди них выделяют еле-
нектарные трансцендентные функции,
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
91
к числу которых относятся степенная
трансцендентная функция (х1, где s —
иррациональное число, например, дг*^)»
а также показательные, логарифмиче-
ские, тригонометрические, гиперболи-
ческие функции. Все алгебраические
функции также относятся к числу
элементарных.
Любую функцию можно взять за ар-
гумент для другой и получить слож-
ную функцию у = F If (х)], например
у = tg У1 — х*. у = lg sin х. Такне
комбинации дают всевозможные элемен-
тарные функции.
ОБРАТНЫЕ ФУНКЦИИ
Функции /(х) и <<> (х) будут взаимно
обратными, если / I? (х)| = х и
¥[/(*)] = х- Например, функции хя и
1 1
х " взаимно обратные, так как (х ” )я=х
1
п
и (Xя) = х. Имея явную функцию у =
= /(х), можно получить обратную ей,
если принять у за аргумент, а х считать
функцией от у и решить относительно х
написанное уравнение.
Для получения графика функции ?(х),
обратной данной функции / (х), доста-
точно построить кривую, симметричную
графику функции f (х) относительно
биссектрисы первого координатного угла.
Если прямая, параллельная оси Ох,
пересекает график функции у = / (х)
больше чем в одной точке, то обратная
функция будет многозначной: прямая,
параллельная оси Оу, пересекает график
функции в нескольких точках. Напри-
мер, квадратной функции у = х* соот-
ветствует обратная двузначная функция
у “ ± VV. графиком которой будет
та же квадратная парабола, но симмет-
ричная относительно осн х.
ПОКАЗАТЕЛЬНАЯ
И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
Функция у “ а*, где а — постоянная-
называется показательной. При поло-
жительном а всегда у > 0 (фиг. 11).
Функция, обратная показательной, на-
зывается логарифмической: у = log„x
(фиг. 12). Наибольшее употребление
имеют показательная и логарифмическая
функции с натуральным основанием е-
(см. стр. 135).
Если у = е*. тоотсюда х = in .у (лога-
рифмическая функция с натуральным
основанием). Итак, функции е* и 1я х —
взаимно обратны.
Фиг. 11. Графики показательной функции у а*
для различных значений параметра а.
Фиг. 12. Графики логарифмической функции у«
“ 1оцах ала различных значений параметра а.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Тригонометрические, или круговые,
функции sin х, cosx, tg х, etgx, sec х и
cosec x являются простейшими периоди-
ческими трансцендентными функциями.
Функция у — / (х) называется периода-
92
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
ческой, если при некоторых значениях h
н при любых значениях аргумента х
имеет место равенство f (х + й) =
= /(*)•
Наименьшее из чисел й. обладающее
указанным свойством, называется пе-
риодом функции.
Для вещественных значений аргумента
тригонометрические функции определя-
ются геометрически при помощи круга
(тригонометрического круга) и построен-
ных в нем отрезков (тригонометриче-
ских линий) (фиг. 13).
Фиг. 13. Геометрическое истолкование
тригонометрических функций.
Зависимости между
тригонометрическими функциями
дополнительных углов
sin а = COS (90’ — а);
sin (45° 4- я) = cos (45° — я);
tg я = ctg (90* — а);
tg (45° + а) = etg (45° - я).
При я > 90° ^я > следует поль-
зоваться формулами приведения:
sin я — cos (я — 90°) = sin (180° —а) =
= — cos (270° — я) — — sin (360° — я).
cos я-—sin (я — 90°)= — cos (180° — а)—
-------sin (270° — я) - cos (360° — я);
tg я= — etg (а—90°) =• — tg (180° — я)=ж
= cig (270е —а) - — tg (360° — я);
Clga=—tg(a —90°)= — Ctg (180° — я) =
= tg (270° — а) - - cig (360° - а).
Пример. со» 210" = — sin (270" — 210"» —
= - sin 60" - - 0.Н6ЙШ.
При радиусе круга, ранном единице,
аргумент х представляет собой длину
дуги АС, а функции sinx, coax, tgx.
ctg x, sec x, cosec x соответственно
длины отрезков CD, OD, AE, BF, OE
и OF, взятые co знаком + или — в за-
висимости от направления этих отрез-
ков (см. таблицу на стр. 93),
Аргумент х равен удвоенной площади
сектора АОС (в круге единичного ра-
диуса).
Длина дуги АС является (при О А = I)
мерой в радианах центрального угла
АОС.
Один радиан равен приблизитель-
но 57’17'44*,8.
Радианное измерение дуг и углов
употребляется в анализе.
При решении геометрических задач
за аргумент тригонометрических функ-
ций чаще всего принимается величина
центрального угла АОС, выраженная
в градусах, минутах и секундах (Г =
= 60' 3600* <в 0,01745 радиана;
180’ = я радиан).
Перевод градусов в радианы и обратно
см. в табл. VII и XIV.
Функции sin х, cosx, sec х, cosec х —
периодические с периодом 2к; функции
lg *• ctg х — периодические с перио-
дом ж.
Для я > 360° (х > 2х) следует исполь-
зовать свойства периодичности триго-
нометрических функций; при любом
целом п
sin я — sin (я — 360“ л);
cos я — cos (я — 360е л);
tg я — tg (a — 180° л);
ctg я — ctg (я — 180° л).
Пример. sin 118S" - »1п (1185’-a-МО») Ш
- (In 1<й‘ - sin (180" - 105») = sin 75“ - 0,96553.
Функции cos хи secx— четные функ-
ции; sinx. tgx, cigх. cosecх—нечет-
ные, т. е.
cos (— х) — cos х; sec (— х) — sec х;
sin (— х) — — sin x; tg (— x) = — tg x;
ctg(—x)= — etgx;
cosec {— x) = — cosec x.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
93
Значения тригонометрических функций для некоторых аргументов
ао 0° и» 30° во» 75° 90“
X 0 12 0,26180 Я "в 0.52360 X 4 0,78540 к Т 1.04720 5к 12 1,30900 f
sin а 0 d 0.25882 1 т 0,50000 0.70711 т** 036603 (К з+О 0,96593 1
сов а 1 + £ 0.96593 0.86603 0,70711 1 2 0,50000 £ th 0,25882 0
tga 0 0.26795 Туг 0.57735 1 1.00000 Уз 1,75205 2+/Г 3.73205 оо
etg в оо 2+/3- 3.73205 1 г 1.73205 1.аюоо 4/з" 0,57735 2-VT 0.26795 0
Изменение тригонометрических функций
по знаку и величине по четвертям тригонометрического круга
Функции ° 1 четп. 90“ 11 четп. 180° III чете. 270° IV четп. 360“
sin a 0 + возрастает + 1 4- убывает 0 убывает —1 возрастает 0
сов а +1 + убывает 0 убывает -1 возрастает 0 •h возрастает +1
Igl 0 + HOlpBCTBCT возрастает 0 + возрастает ±оо возрастает 0
Cig я Топ ♦ уоыяает 0 убывает Too л + убывает 0 убывает Топ
вес « 4-1 + возрастает ±<» возрастает —1 убывает ф°о + убывает + 1
совес Too + убывает +1 1 подрастает ±оо возрастает —1 убывает Тео
При всех действительных значениях
аргумента функции sin * и cos * непре-
рывны, их значения заключены в от-
резке ( — I, + 11; функции tg х, etg х,
sec х и cosec х имеют разрывы непре-
рывности второго рода (см. стр. 137).
Графики тригонометрических функций
даны на фиг. 14—16. Графики sin х
и cos х отличаются друг от друга лишь
расположением относительно оси орди-
нат, так как cos х “ sin
94
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Фиг, 14. Графики тригонометрических функций
у — sin X и у = COS X.
Фиг. 16. Графики тригонометрических функций
у •» sec х и у — cosec х.
Основные соотношения между*
тригонометрическими функциями
одного аргумента
sin2x 4- cos2x — 1; tg х — .sln-x •
' b cos x’
ctgx —
cos X I I
—;— — -— ; sec x —-----:
sin x tg x cos x ’
cosec x = -Д—; 1 + tg2 x — sec2 x;
sin x
I + ctg2 x — cosec2 x.
Функции sec x и cosec x употребляются
редко.
В формулах
sin х = К1 — cos2x — - - X------—
/1 + tg»x
_______1
V1 4- Ctg2X ’
COS X — К1 — sin2 X «- r Li—= =
/1 + tg* ж
__Ctgx_
’ Kl +Clg2X
знаки перед радикалами следует брать,
в соответствии со знаком тригономе-
трической функции при данном значении
аргумента (см. данную выше схему).
Пример, sin 120s =-----* — — . так как
— /I -Нкж 120“
sin 120* положителен, a tg 12й® — отрицателен.
ФОРМУЛЫ плоской
ТРИГОНОМЕТРИИ (ГОНИОМЕТРИЯ)-
Указанные ниже формулы преобразо-
ваний тригонометрических функций
справедливы как для действительных,,
так и для комплексных значений аргу-
ментов.
Функции суммы и разности:
sin (я ± Р) — sin « cos р ± cos я sin Р;
cos (а ± р) cos a cos р Т sin я sin р;
±Р1 ] т tg я tg р *
’g (» + Р + 1) -
tg » 4- tg Р 4~ tgy -tga tgp tgT
“ I-tga tg₽— tg p tg f—tg a tg "
Пример, tin -f- 4^ — atn cos 4 4-
в . /2
4- cos — aln 4 ks —j— (1 -r 8), если 4 малли вели-
чина (см. стр. 70).
ФОРМУЛЫ ПЛОСКОЙ ТРИГОНОМЕТРИИ (ГОНИОМЕТРИЯ)
95
Функции кратного аргумента
sin 2а «• 2 sin а cos а;
COS 2л •= COS* а — sin* а —
= 1 — 2 sin* а •» 2 cos* а — 1;
sin За — 3 sin а — 4 sin3 а;
cos За — 4 COS3 а — 3 COS а.
Чтобы найти cos ла и sin ла при лю-
бом целом положительном л, поль-
зуются формулой
COS ла + Z sin Ла = (COS а -|- Z sin а)я.
Применив к правой части биномиаль-
ную формулу (см. стр. 74) и сравнивая
вещественные части между собой, а
мнимые между собой, получим общие
формулы для sin ла и cos ла.
Пример, со» 4а i sin 4а = (cos а 4- i sin «)• =
= cos* «4-41 cos’ а sin а — 6 cos’ * sin’ а —
— V сов а sin’ а 4- sin1 а,
откуда
со* 4а = cos’ а — 6cos’ « sin* а (-sin* а;
Sin 4а — 4 cos* а sin « — 4 cos а sin’ а —
— 4 cos а sin а (cos’ а — sin’ а>.
Степени sin х и cos х
I « о
sin2 лг = —-----— cos2x;
, ’ , 1 п
cos* х — — 4- -у cos 2х;
3 1
sin3 х =• — sin х---— sin 1г,
4 4
. 3 I
cos» x = — cos x 4- —r- cos 3x;
4 4
3 1 I
sin4 x = —------— cos 2x 4- -j- cos 4x;
О 2 О
cos4 x = -4* 4- -4- cos 2x 4- cos 4x;
0 4 О
5 5
sin5 x = — sin x----— sin 3x -f-
o lo
+ -Lsin5x;
Функции половины аргумента
a _ / 1 — cos з
Sinv ± V ~2— ;
a / I + COS a
CO’-T- * V —2—>
± |/ 1 -.co.sa =
8 2 1 V 14- COS a
Sin a I — COS а
1 4- cos a = Sin a
Все тригонометрические функции дан-
ного аргумента выражаются рациональ-
но через тангенс половины аргумента:
sin х —-----------.
1 + tg* ’
1 - tg» 4
COS X —--------------.
I + tg* 4 ’
•gx---------------- .
1 - tg’ —
. я , 5 *
COS5 X — — COS X + -nr COS 3x -r
о ID
+ -jbcosJU;
5 15
—COS2x +
3 . 1 -
4- -nr cos 4x —яд- cos 6x;
lb 32
, л L 1Я о
c°s«x-— + -^- cos 2x4-
+ 4cos 4x + icos6x:
. , I 1
sin* x cos x — —— cos x------г- cos 3x:
4 4
cos*x sin x — -4- sin x -f- -4~sln3x.
4 4
Пример.
co»’ x tin* ж • (-j- + — co» X
X(-L_±c0,2x)--L_-Lcol’2x.
- T - T (t + T co* - T - Г” u-
96
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Легко выразить через синусы и ко-
синусы кратных дуг любые степени, а
также произведения степеней синуса и
косинуса, если воспользоваться форму-
лами Эйлера:
соях =
откуда
= cos х 4- i sin х;
e~xl — cos х — / sinx.
Пример.
= U3*' - 3e^‘-e-^ (-
КГ’
+ 3<r/.,-2xi _(-3xi) _
- - jj- f*3" - Зе*‘ 4 3*~xt - a-4’’') =
1 _ e-3xl eici _ e-xi ,
** “ 4 2J ~ 3‘ 2< J “
•= — y- (sin 3x — 3 sin x) —
3 . I . «
= — sin x-------sin 3x.
4 4
Преобразование сумм
в произведения и произведений
в суммы
sin а 4- sin р — 2 sin^-i-5 cos a^~";
sin e — sin p — 2cos —y-** sin ~y~ »
cos a 4- cos 3
„ s + J a — 3
— 2 cos —-— cos —;
cos « — cos p — 2 sin —sin -'-1
tg a + tg p -
Sin (« 4- p) ,
cos a cos p ’
sin a sin p =
= -5- (cos (“ — ?) — cos (a 4- P)l;
cos a cos 3 »
- -7* lcos —W + cos (“ + ₽)i»
sin a cos p =
= 4" [sin (a — P) 4- sin (a 4- P)l-
Пример,
1 4 sin я 4- со» я 4- tg я = (1 4 cos я) 4-
4 <»ln я t tR о) — 2 cos’ у 4- tg я (1 4- cos a) =
= 2 co»’ I Ig s-2 cos’ у = 2 co»’у (t 4*g ») ’•
“ 2 co»’ у (tg 45» 4- tg я) =1 co»’ у X
МП (45° 4- ») 2V'2'co«’y ’Int^+a)
COS -SO’ CO» a cos »
Для преобразования суммы в произ-
ведение иногда приходится применять
метод введения вспомогательного угла.
Пусть А и В — какие угодно выра-
жения (не только тригонометрические).
полагая
Тогда А — В = А ^1 4- # ;
В
— — tg 4 (что возможно, так как тан-
генсом может быть всякое число), по-
лучим
Л 4- в —Л(1 4- tgf) - Л
sin (45° 4- ф).
cos 4ли cos ф *
для вычисления правой части равенства
найдем сначала при помощи таблиц
вспомогательный угол ф, пользуясь
В
соотношением tg (? — .
Тем же способом получим
tg a - tg p -
sin (a — p) .
COS a COS p *
Л-fi-
. sin (45° — у).
cos 45° cos f *
sin1 a — sin2 3 — cos2 P — cos^a —
— sin (a 4- p) sin (a — P);
COS2 a — sin2 P cos2 p — Sin2 a —
-» COS (я 4- p) cos (а — p);
^±e _,s («•+,».
Выражение A 4- В преобразуется
проще, если известно, что А и В —
СИНУСОИДАЛЬНЫЕ ВЕЛИЧИНЫ И ИХ ГРАФИКИ
97
_ о -
одного знака. Тогда полагаем —j- = tg-?
А
и получаем
А + В — А (1 -г tg2?) —
. , А
= A sec2 ? = —=—.
т COS2?
Если А и В положительны и А > В,
Л
то, полагая —т- -= sin2?, получим
/1
А — В = А(1 —sin2?) = A cos2?.
Если А < В (при А > О, В > 0), то
берем сначала А — В — — (В — А),
после чего В — А преобразуем, как
раньше.
Примеры:
I) a sin а £ в соз к •=. a ^sln а ± «и а) =
= a (siп а ± tg ф сов а) =
a fain я cos ф ± «к « sin a' a sin it ± gi
cos ₽ сое» f
л
при lg ф = — .
Г а* т сов t =
•» Т'(а 4- Ь |- -- 2а 6 И -у cos а| —
Ш<1 сов‘ —
Inb
— — сов*
(а 4- *)’
»(а 4- b) V1 — sin’ ф — |a -f- о, сив
причем
In Ф —
2 УТ*
а + t>
а
С0,Т“
СИНУСОИДАЛЬНЫЕ ВЕЛИЧИНЫ
И ИХ ГРАФИКИ
Из определения тригонометрических
функций при помощи тригонометри-
ческого круга единичного радиуса вы
текабт способ построения графиков.
Для построения графика функции
у = sin х (синусоида) необходимо по-
строить слева от оси Оу круг единич-
ного радиуса с центром на оси Ох
(фиг. 17); разделить окружность на
Произвольное чцсло равных частей, на-
пример, на 16; полученные на окруж-
ности точки перенумеровать в после-
довательном порядке, начиная с нуля,
идя по окружности в положительном на-
правлении (т.е. против часовой стрелки),
причем отметку 0 поставить на оси Ох;
1 Том 1. Зак. 1461
через точки деления на окружности
провести прямые, параллельные, оси Ох
(горизонтали), которые окажутся пере-
нумерованными (нулевая горизонталь
совпадает с осью Ох); отложить на оси
Ох длину окружности и также разделить
ее на такое же число равных частей
(в данном случае на 16); точки деления
перенумеровать, причем нулевая точка
совпадет с началом координат; через все
точки деления оси Ох провести верти-
кали, которые также окажутся пере-
нумерованными; точки пересечения го-
ризонталей и вертикалей с одинако-
Фиг. 17. Построение графиков функция у = sin х
и у — сое х.
выми номерами будут лежать на сину-
соиде; плавная ливня, соелиняющая чти
точки, образует график функции у =
— sin х.
График тригонометрической функции
у = COS X e sin + “2“ j можно полу-
чить, передвинув только что построен-
ный график на отрезок -у влево по оси
Ох или перенеся начало координат на
Такой же отрезок вира по.
Дли построения графиков функций
у — sin шл, у — соз шх
можно применить прежний метод, ну-
меруя, однако, точки на окружности
(и горизонтали) не подряд, я через
каждые « делений.
На фиг. 18 построены графики фун-
кций у “ sln2x, у- sin-^-.
98
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Так же можно построить и кривые
у = A sin «х, у — A cos «х, нужно толь-
ко вспомогательную окружность описать
радиусом А вместо единицы.
Кривая у = A sin (их 4- а) заключает,
как частный случай, все рассмотренные
кривые и может быть построена тем же
методом, если только вспомогательную
окружность построить радиусом А.
точки деления на окружности нумеро-
вать через каждые « делений и отметку О
на окружности поставить в конце дуги «.
Фиг. 19. Построение графика функции
у-2 со. (xr
На фиг. 19 дан график функции
у — 2 cos ^Зх — — 2 sin ^Зх 4 у
Синусоидальные величины встречаются
при изучении колебательных движений,
явлений переменного тока и т. п.
Пусть точка М движется по окруж-
ности радиуса А с постоянной угловой
скоростью о», причем при t " 0 точка М
находилась в точке Ма (конец дуги а)
(фиг. 20). Проекция точки М на ось Оу
Фи,. ;*и. Мемииш простого
гармонического комбанка.
(точка W) совершает колебательное дви-
жение по отрезку CD оси Оу, это дви-
жение называется простым гармони-
ческим колебанием и совершается по
закону у = A sin (ы1 4- а), где С озна-
чает время. В этой формуле А назы-
вается амплитудой колебания, « —
частотой (<> есть угловая скорость вра-
щения радиуса).
Период Т функции у соответствует
времени полного оборота радиуса во-
круг центра и определяется из соот-
ношения шТ =• 2ж, так что Т = и
ы
2х 2* Л
и — выражение — дает также дли-
ну волны синусоиды. Очень часто вместо
частоты •> вводят число периодов или
число оборотов в единицу времени;
это число п определяется по формуле
I •>
" “ Т “ *
откуда ш = 2кп.
Переменный угол «Z + ч называется
фазой синусоидальной величины, а —
начальной фазой; изменив начало от-
счета времени, всегда можно начальную
фазу привести к нулю; так как <»( 4 о —
= ш t 4- —— , то для этого достаточно
отсчитывать время от момента t =
Если даны две синусоидальные вели-
чины одинаковой частоты <»
у, = Aj sin и/, уг — Лг cos ut.
но с разностью фаз , то их сумма
также представляет синусоидальную ве-
личину той же частоты:
У — У1 + Л — Л sin («Г 4 а),
где
л-/а’ + <;
Сумма синусоидальных величин yi =
= Я1 sin (•>( 4- в»), у» = Al sin (u>t 4- а,)
есть синусоидальная величина
у — A sin («/ + а),
где ____________________________
3 - р/Л' 4- Aj + 2A|Aj cos (в|— а-J.
а угол а определяется равенствами
A| cos «1 4 A cos а.
------------ ,
, A, sin а, 4 А> sin
Sin □ — —=----;——----s.
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
99
Для фактического определения ве-
личин А и а удобнее использовать гео-
метрическое представление синусоидаль-
ных величин одинаковой частоты. Из
точки О плоскости
(фиг. 21) строим
два вектора: один —
длиной Ai (накло-
ненный к оси Ох
под углом <ц), дру-
гой — длиной Аг
(наклоненный к осн
Ох ПОД углом а*);
тогда длина векто-
ра, полученного
сложением двух
названных векто-
ров, даст ампли-
туду А искомой синусоидальной вели-
чины, а угол наклона этого вектора-
суммы к оси Ох даст начальную фазу
величины у.
ОБРАТНЫЕ
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Обратные тригонометрические (или
обратные круговые) функции — аркси-
нус, арккосинус, арктангенс и т. д. —
определяются следующим образом:
у — Arcsin х, если х — sin у;
у = Arccos х, если х — cos у;
у = Arctg х, если х -= tg у
и т. д.
Таким образом, арксинус от х есть
дуга, синус которой равен х (.аркус*
означает .дуга*).
и сопоставление его с графиком функции
у = eln X.
Функции Arcsin х и Arccos х имеют
вещественные значения, если—
<4-1; функции Arctg х и Arcctg х имеют
вещественные значения при любом ве-
щественном значении х. Обратные три-
гонометрические функции суть функ-
ции многозначные (фиг. 22—24).
Фиг. 23. График функции у —
Arceos х н сопоставление его
е графиком функции у — сот х.
Г ладными значениями функций Arcsin х
и Arctg х называются такие их зна-
чения, которые берутся на отрезке
2 ’
;они обозначаются arcsinx
arctg х.
Гладными значениями функций Arccos х
и Arcctg х называются такие их зна-
чения, которые берутся на отрезке
(О, я); они обозначаются arccosх
и arcctg х.
Связь между любыми значениями
обратных тригонометрических функций
Фиг. 24. График функции у — Arctg X и сопоста-
вление его с графикой функции у —tg х.
7
100
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
и их главными значениями выражается
формулами
Arcsin х — *п -г (— 1)" arcsln х;
Arccos х = 2*п ± arccos х;
Arctg х = arctg х + пл.
Arcctg х = arcctg х + ял.
Для вычисления главных значений
обратных тригонометрических функций
полезны формулы
arcsln (— х) — — arcsln х;
arccos (— х)«- я — arccos х;
arclg (— х) * — arctg х;
arcctg ( — х) — я — arcctg х;
arcsin х -|- arccos х = ;
arctg х + arcctg х = -у-.
При вычислениях с обратными триго-
нометрическими функциями нужно учи-
тывать их многозначность. Так, напри-
мер, нужно иметь в виду, что формулы
arcsin х — arccos Vl — хг;
arccos х — arcsin — x2;
arcctg x — arctg —
справедливы только для x > 0.
Точно так же формулы
arcsln и + arcsin v =
— arcsin (u Vl — «2 + v У1—u2);
arccos u + arccos v ~
» arccos (uv — VI — иг V1 — v!);
и 4- v
arclg и + arctg v — arctg j_ ц-
всегда справедливы, если и и о поло-
жительны, а сумма членов, стоящих
„ я
слева, не больше — ; в других случаях
они верны не всегда.
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
К элементарным трансцендентным
функциям относятся также гиперболи-
ческие функции sh х, ch х, th х, cth х
(последняя функция употребляется
редко).
Для вещественных значений аргу-
мента они могут быть определены гео-
метрически как длины некоторых от-
резков (фиг. 25), связанных с равно-
бочной гиперболой х'2—у'* = 1, при-
чем аргументом функции является удво-
Фиг. 25. Геометрическое истол-
кование гиперболических
функций.
енная площадь гиперболического сек-
тора ОАС. Для любых значений аргу-
мента (вещественных и комплексных)
гиперболические функции определяются
формулами
sh х
2
ch х
Отсюда имеем
ch г ) sh х - ch х — sh х —1~*•
Гиперболические функции связаны
следующими соотношениями:
ch*x — sh2x — 1;
1 sh х
th x = —г— — -г— ;
cth х ch х ’
sh (a ± P) — sh a ch p ± ch a sh p:
ch (a ± p) — ch a ch p ± sh a sh p;
sh 2a — 2 sh a ch •;
ch 2a — ch2 a -|- sh1 a — 2 sh? a + 1 >
— 2ch2a— 1;
, □, th a ± th P
th(a±P)"i±thathp>
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
1л1
cth (в ± ₽)
1 А с th а с th 3
= cth а £ Cth jJ
sh а ± sh р = 2 sh ~y~ ch ° ;
ch« + ch₽ = 2ch
eh ( — a) — — sh a; ch ( — a) = ch a;
th (— a) » — th a;
Cth ( — a) — — Cth a.
Графики гиперболических функций
даны на фиг. 26 и 27. Для всех веще-
ственных значений х
ch х > I; — 1 < th х < 4 1;
cth х < —1 при х<0 и cth х> + 1 при
х>0; shx изменяется от — со до 4-со.
Обратные гиперболические функции
Arsh и, Arch и, Arth и (ареа-синус, ареа-
косинус, ареа-тангенс гиперболический}
определяются соответственно решениями
уравнений и = sh х; и = ch х; и =
= th х. В области вещественных зна-
чений функция Arsh и однозначна и
может быть выражена через логариф-
мическую функцию посредством фор-
мулы
Arsh и = In (и 4- Уи1 4 1).
Функция Arch и имеет в той же
области два значения:
Arch и — ± 1п (и 4- Уat — 1) —
- Т In (и - Ум»—1) (и > I».
Функция Arth и имеет действител!г
ные значения только при | и | < I; он?
может быть представлена в виде
ГЛАВА IV
ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ ФИГУР •
ЧИСЛОВЫЕ ЗАВИСИМОСТИ
МЕЖДУ ЭЛЕМЕНТАМИ ФИГУР
Треугольники (фиг. I)
Обозначения', а. Ь, с — стороны; о, 3.
7— противолежащие углы; Ла. hb. ht —
высоты, опущенные соответственно на
стороны а. Ь. с; та. ть, те — медианы,
делящие пополам соответственно сто-
роны а. Ь, с; 1а, 1Ь- 1С — биссектрисы
углов а, 3. Т, R — радиус описанной
окружности; г — радиус вписанной
(теорема косинусов);
окружности; га— радиус вневписанной
окружности, касающейся стороны а и
продолжений сторон b и с; аналогично
а + Ь + с
гь и ге; р —---g-------полупериметр;
та + нт» + те
у ~ —=———£ полусумма ме-
диан', S — площадь; d — расстояние
между центрами описанной и вписанной
окружностей; d„, db. de — расстояния
между центрами описанной и внеьпи-
• См. литературу « стр. И» |5). |в|. |7j.
санных окружностей. Если треугольник
прямоугольный, то а и Ь — катеты, с —
гипотенуза, у — прямой угол.
Зависимости между элементами тре-
угольника:
» а+ 3 + 7- 180»;
2) —-— = —-— — с - — 2R
Sin a sin й sin 7
(теорема синусов);
3) а2 = Ь* + с* — 2bc cos а
(теорема тангенсов);
5) 2 ;
7) а + 6 — 4/? cos -1- cos ° ;
8) а — b — 4R sin — sin * ;
9) р 4R cos -у- cos ~ cos -i-;
в в V
10) p — a — 4R cos — sin — sin -i ;
11) p — b — 4R cos sin sin J-;
12) p — c — 4R cos -i- sin sin -y;
ЧИСЛОВЫЕ ЗАВИСИМОСТИ МЕЖДУ ЭЛЕМЕНТАМИ ФИГУР
103
,3>
abc abr
15
2 sin 7
____________________________ be
4 Vр(р — а) (р—Ь) (/>—с)
И) г= 1/ ~ а> ~ ~ с) _
' Р
abt 5 Л О . " I & • т
- йГр “ Т “ 4R Stn VSin —S,n —-
a . 8 7
-=₽tg —
25) ма - Ц- V2 (Г- + Л -at
= -j- V4- с- -г 2Ьс cos я ;
аналогичные формулы — для т6 и те;
20) Шд 4- т2ь 4- = 4"(в! + 62 + с*):
27) м* 4- mJ 4- т* — 4- Ь* + с«);
/>(/> — »)<?- <)
>5) r,
p-a
— ——— — p tg ;
p — a H 6 2
аналогичные формулы — для Гц и
16) ГдГ^е — p*r,
17)
"a
1 1
ht r *
±—L + JL
*<. Гц rt
аналогичные формулы—для hb и
19) 7"-у- + J—у*;
re Пц nt ла
аналогичные формулы—для гь и
20) га 4- Гц + Ге — г «4/?;
21) d1 — R* — 2Rr (формула Эйлера);
22) < - R» + 2Rr„
аналогичные формулы — для dt и dt;
23) Ло — 2R sin 3 tin т— b sln*T—csln3 =.
— — Ур(р—а) (р—Ь) (р—с) —
= — 2(р —л) га _
~ а и
18)
he.
аналогичные формулы — для cos 3 и cos т;
29) sin “ /ISHP^c).
2 г be
3
аналогичные формулы —для sin
II Sin-1-;
з
аналогичные формулы — для cos
н cos-1-;
3D tg -у
- М (р — с)
р(р—а)
В т
аналогичные формулы для tg и tg -у
Для поямо1/еольноео треугольника
а + р — 90*. at 4- Ь* — с* (теорема Пифа-
гора); а — с sin □ — с cos 3 “ b tg я —
— Ь ctg 3- аналогичные формулы для Ь:
_ 2(р — />) гь 2(p — e)'fr
а ~ а '
аналогичные формулы — для hb и Лг;
24) /в — У Ьср (р — а) —
и -г с
--jj— V ЬсЦЬ + ср-а*] -
о + с
2Ьсcos-л- ,
_______2 a sin р sin т
Ь + С (sin р + sin 7) sin -j-
•налогичные формулы—для 1ц и te;
Четырехугольника
)) Во всяком четырехугольнике се-
редины сторон служат вершинами па-
раллелограмма; отрезки, соединяющие
середины днух пар противоположных
сторон, и отрезок, соединяющий сере-
дины диагоналей, проходят через одну
точку и делятся в этой точке пополам
(фиг. 2); при этом Л в* + ВС* -h CD1 4-
+ DA* - AC* 4- BD* + 4£Л.
2) Сумма квадратов сторон паралле-
лограмма равна сумме квадратов его
диагоналей. '
104
ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ ФИГУР
3) В выпуклом четырехугольнике,
вписанном в круг, произведение диаго-
Фиг. 2. Спойспш четырехугольника.
налей равно сумме произведений про-
тивоположных сторон (теорема Пто-
ломея).
Правильные многоугольники
Обозначения: п — число сторон; а —
длина стороны; R— радиус описанного
круга; г— радиус вписанного круга;а —
центральный угол; р — внутренний угол
многоугольника; S — площадь много-
угольника; ап и Ь„ — длины сторон пра-
вильных л-угольников, из которых
один вписан в круг радиуса R. а другой
описан около него.
Зависимости между элементами пра-
вильного многоугольника:
.. 360’.
2) 180“ — а [сумма внутренних
углов во всяком многоугольнике равна
180“ (л - 2)1;
on .’8°’ о . >80°
3) а — 2R sin----— 2r tg ----—
п п
- 2 К «» - г» ;
5) г-
в , 180° „ 180°
ту Ctg----— R cos ------—
2 л л
Окружность
Обозначения: г — радиус; d — диаметр;
L — длина окружности; S — площадь
круга.
Числовые зависимости:
L L
2* °* 6,28318
0,56419 /5;
d = — ~ ттгт™ “ ’'12838
п 3,14159
Пример. Рвмелить на 33 части окружность
круга, диаметр которого 24 см. Для этого надо
откладывать по окружности циркулем отрезок,
равный 24-0,0У61 ей 2,2а см (см. таблицу на
стр. 105).
Проекции
Обозначения: а —длина проектируе-
мого отрезка; а^ — длина его проекции
на ось; а — угол между проектируемым
отрезком и осью; S —площадь проек-
тируемой плоской фигуры; Si — площадь
ее проекции на другую плоскость; у —
угол между плоскостями.
Формулы: ai => a cos a; S> e S cos <р.
Телесный угол представляет собой
часть пространства, заключенную внутри
одной полости конической или пирами-
дальной поверхности с замкнутой на-
правляющей. За меру а телесного угла
принимают отношение площади S, вы-
резаемой телесным углом на поверхно-
сти шара произвольного радиуса с
центром в вершине телесного угла, к
квадрату радиуса этого шара: а =
= . Телесный угол, образованный
тремя взаимно перпендикулярными пло-
скостями, равен . Единица меры
телесного угла (стереорадиан) есть тв-
лесный угол, для которого S “ R.
ЧИСЛОВЫЕ ЗАВИСИМОСТИ МЕЖДУ ЭЛЕМЕНТАМИ ФИГУР
105
Таблица значений элементов правильных многоугольников
п а к Г У
3 1.732 7? 3,464 г 0,577 а 2,000 г 0.289 а 0.500 7? 0,433 а' 1,299/?* 5,196 г'
4 1,414 R 2,0)0 г 0.707 а 1,414 г 0.500 а 0.707 7? 1,000 а' 2,000 У?» 4,000 г'
& 1,176 7? 1,4дЗг 0,850 а 1,236 г 0.688 а 0.809 7? 1,721 а' 2.378 7?» 3,633 г1
б 1,000 7? 1,155 г 1,000 а 1,155г 0.866 а 0.866/? 2,598 а1 2.598/?» 3,464 г1
7 0,86ч 7? 0,963 г 1,152 а 1,110г 1,038 а 0,901 R 3,635 а' 2,736 7?» 3.371г»
8 0,765 7? 0,828 г 1,307 а 1,042 г 1,207 а 0,9217? 4.828 а’ 2,828 7?» 3,314 г1
9 0,694 7? 0,723 г 1,462 а 1,064 г 1,374 а 0.940 7? 6,182 а‘ 2,893 7?' 3,276 г»
10 0.618 7? 0,660 г 1,618 а 1,052 г 1,539 а 0.951 7? 7,694 а* 2,939 7?» 3,249 г»
11 0,563 7? 0,587 г 1,776 а 1,042 г 1,703 а 0.960 7? 9,364 а' 2,974 /?• 3,230 г1
12 0,518 /? 0.536 г 1,932 а 1,035 г 1.866 а 0.956 7? 11,196 а' 3,000 А" 3,215 г’
16 0,390 7? 0.398 г 2,563 а 1,020 Г 2,514 а 0.981 7? 20,109 а' 3,062 /?' 3,183 г»
20 0.313 7? 0,317 г 3,196 а 1,013 г 3,157 а 0.988 7? 31,569 а' 3,090/?' 3,168 г»
24 0,261 R 0,263 г 3,831 а 1,009 г 3.798 а 0.991 7? 45,575 а’ 3,106 А" 3,160 г»
32 0,196 7? 0,197 г 5,102 а 1,005г 5,077 а 0,995 7? 81,225 о1 3,121 /?' 3,152 г»
48 0,131 7? 0,131 г 7.645 а 1,002 г 7,629 а 0,998 7? 183,08 а' 3,133 /? 3,146 г»
64 0,096 7? 0,098 г 10,193 а 1,001 г 10,178 а 0,999/? 325,69 а> 3,137 3,144 г»
деление окружности на п чаете! (хорда — диаметру % xln-)
Л
Л 180е aln Л Л . 180е з!п л Л sin— л 1 • вШ*^ Я 1 . , 1*0® sin л
1 0,0000 21 0,1190 41 0.0766 61 0.0515 81 0.0388
2 1,0000 22 0,1423 42 0,0747 62 0.0507 82 0.0383
3 0.8660 23 0.1362 43 0,0730 63 0.0496 83 0,0378
4 0,7071 24 0,1305 44 0.0713 64 0.0191 84 0,0374
5 0,5878 25 0.1253 45 0.0696 6S 0,0483 85 0.0069
6 0,5000 26 0.1206 46 0.0682 66 0.0176 86 0,0365
7 0.4339 27 0.1161 47 0.0668 67 0.0469 87 0,0351
8 0,3827 28 0.1120 4Я 0,0654 68 0.0462 89 0.0357
9 0.3420 29 0.1081 49 0.0641 69 0.0455 89 0,0353
10 0,3090 30 0,1015 м 0.0628 70 0,0149 90 0.0349
11 0.2817 31 0.1012 51 0.0616 71 0.0142 91 0.0345
12 0,2588 32 0.0980 52 0.0604 72 0,0436 М 0,0341
13 0,2393 33 0.0961 53 0,0692 73 0,0430 93 0,0338
14 0.2225 34 0,0923 54 0.0681 74 0.0424 94 0.0334
15 0.2079 35 0.0896 55 0.0671 75 0,0419 95 0,0331
16 0.1961 36 0,0872 56 0.0561 76 0.0113 96 0,0327
17 0.1833 37 0,0648 57 0.0551 77 0,0408 97 0,0324
18 0.17» 38 0,0626 58 0,0541 78 0.0400 98 0,0320
19 0,1646 39 0,0806 59 0,0632 79 0.0698 99 0,0317
20 0,1564 40 0,0785 60 0,0523 80 0,0390 100 0,0314
106
ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ ФИГУР
ВЫЧИСЛЕНИЕ ПЕРИМЕТРОВ
И ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР
Обозначения: S — площадь; L — пери-
метр (см. также стр. 102).
Треугольник:
S — -^-a/ia = J- ай sin т —
a* sin 0 sin т ora, , , о .
= ---;т—;---- = 2R* Sin В Sin е Sin 1 =
2 sin a
a be • a 8 т
- 4K-r’c,g-Tc,g — c,gV =
- P1 tg -y tg -%- tg -y - Pr =•
— (/> — a) ra = (p — b) rb = (p — e) rc =
- "aTt/e -
— / P(P~a)(p — b)(p~c) —
4 ,_________________________
— -у к ч «i — «г — mt>) (я—•
Если угол т прямой, то
5 - у- ab = a* tg 3 — 4- «* ctg * -
1 . »
=-J-c1 sin 2a.
Если треугольник задан координатами
его вершин (х«. у,). (*2, yj, (х» у,). то
5 “ “5" — -чя) + <х»у» — -чъ) +
I
I
I
*1
+ (-ЧУ< — *1Уч)1 - -у
У|
Я
У»
причем площадь получится положитель-
ной при положительном обходе вершин
треугольника, т. е. если при движении
по периметру от 1-й вершины ко 2-й и
от 2-й к 3-Й треугольник будет нахо-
диться с левой стороны.
Четырехугольник:
S — -у «v sin f — -у (А, + *g) v.
где и и о — длины диагоналей; у —
угол между ними; Л( и Л» — длины
перпендикуляров, опущенных из про-
тивоположных вершин на одну и ту же
Лиягональ длины р.
* Здесь — определитель 3-го порядка, см.
стр. 1Нь
Трапеция:
S — -у Л (а + b) = mb.
где а и 6 — длины параллельных сторон;
a + й
Л — высота; m =—--------средняя ли-
ния трапеции.
Параллелограмм:
5 = ab sin з = ah,
где a — угол между двумя непарал-
лельными сторонами а и й; Л — высота,
опущенная на сторону а.
Ромб (и дельтоид — четырехугольник,
симметричный относительно одной из
своих диагоналей):
S-^-\
где <fi и di — диагонали ромба (или
дельтоида).
Многоугольник:
S - -у |(х1у*— xjy() + (x,_y, — х,ух) +
+• .. + - XLV,)].
где (хт, у,). (х», у«),...,(хя, ув) — коор-
динаты вершин многоугольника. Поря-
док следования этих вершин соот-
ветствует положительному обходу пери-
метра многоугольника.
Правильный многоугольник:
, , 180“
па1 ctg -----
Л
I о, , 2fVT 180’
—- nRt sin-------— nrt tg------
2 ft • Л
где a — сторона; л — число сторон,
R и г — радиусы описанного и вписан-
ного кругов.
Круп
L - 2r.R - kD; S - r.Rt -
« _L „DI _ 4- LD - <1,78539616 D’.
4 4
где D — диаметр, R — радиус круга.
Круговое яольио:
S- k(R»-H)
— у- к (Dl — <Р) — 2«А
где R, D и г, d — соответственно ввеш-
ВЫЧИСЛЕНИЕ ПЕРИМЕТРОВ И ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР
107
ние и внутренние радиусы и диаметры
Л + г .
кольца; р — —---------средний радиус
кольца; 8 = R — г — ширина кольца.
Круговой сектор:
aR*-
a°T.Ri
360°
1
2
S~-~IR
= 0,0087266-7?г-а*.
где I — длина дуги
Кольцевой сектор:
сектора; а® и а —
центральный угол
соответственно в
градусном и в ра-
дианном измере-
нии.
Круговой сег-
мент (фиг. 3)
5 = 1 /?»(«-
— Sin а) —
R(l-b) + bh
“ 2
где а — центральный угол; ₽ и 6 —
средний радиус и ширина кольца.
Эллипс. Длина дуги между точками
В и М (фиг. 4)
ф
/ — a J У1 — «* sin2a rfa — аЕ (<р, е),
Va‘-b‘
где а «•------------эксцентриситет; а и
Ь — полуоси эллипса; <р — угол между
полуосью эллипса ОВ и радиусом-век-
тором ОМ'; <f «= arcsin — , где х — абс-
цисса точки М; Е (<р, е) — J У~1 — е* sin» а
о
di — эллиптический интеграл второго
рода (см. табл. XVII, стр. 59).
Полная длина эллипса
_/Ь3\2 е« /ЬЗ-Чуе* 1
\.2-4/ 3 5 “
“ at • причем функция f
дается таблнцей:
а 0.1 0,2 0.3 0,4 ОД
'(т) 4.0640 4.2020 4.3860 4,6026 4,8442
ь а 0.6 0,7 03 0.9 1.0
'(4) 5,1064 5,3824 5.6723 5,9723 6,2832
Площадь эллипса- S — каЬ.
Площадь эллиптического сектора
О/ЪМ: 5 — -^-S', где S' — площадь со-
и
от ветст в у юще го кругового сектора
ОА'М' (Af 'Af || ОА).
Параболический сег-
2
менг (фиг. 5):5 - — bh;
□
h
если -г- мало, то длина
дуги
I <5> Ь
5
Фиг. 5. П»р»бо-
шческий с«г-
м««т.
Площади фигур произвольного вида
и длины дуг находятся интегрирова-
нием — аналитически или при помощи
математических инструментов (см.
стр. 189 и 342).
108
ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ ФИГУР
ВЫЧИСЛЕНИЕ ПОВЕРХНОСТЕЙ И ОБЪЕМОВ ТЕЛ
Геометрическое тело и обозначения Боковая поверхность Sg Полная поверхность Sn Объем V
Призма: В — площадь основания; В' — площадь перпендику- лярного сечения; Л — высота; 1 — боковое ребро; Р' — периметр перпеидику- ляркого сечения Sg-P'-l V = Bh — B'l
Куб! а — ребро: d — диагональ * 09 " И й П ч? V-ef
Прямоугольный паралле- лепипед: а, Ь, г — ребра; d — диагональ $я = 2 (nP-f-Ac-f-ca); d - УоЧ-Р’-и* V-= abc
Призма, усеченная пло- скостью. не параллельной основанию: В' — площадь перпендикуляр- ного сечения; I — расстояние между пен- трамн тяжести верхнего н нижнего оснований — V -=B' l В случае треугольной призмы V- 4 (л+б+О-В'. гае а, Ь. с — длины боковых ребер
Пирамида: В — площадь основания; Р — периметр основания; Л — высота: а — апофема (высота боковой грани в правильной пира- миде) Если пирамида правильная, то «б-уА» у - 4
Усеченная пирамида: В и б — плошали оснований; * — высота; Р и р — периметры оснований; а — апофема Если усеченная пирамида пра- вильная, то «б «-7<А+Л« у-| л (B+6+/S5)
Призматоид •: в, В„ В, — плошали основа- ний и среднего сечения — у - 4
• Призматоид — тело, ограниченное двумя параллельными плоскостями (основания) и несколь- кими пересекающимися плоскостями (боковые грани); в основаниях могут лежать многоугольники с произвольным числом сторон, боковыми гранями могут быть треугольники или трапеции. Приз матоил, в основаниях которого — многоугольники с одинаковым числом сторон, а боковые грани — трапеции, называется обелиском. Обелиск, в основания: которого — подобные многоугольники, есть усеченная пирамида. Если в основаниях обелиска — прямоугольники, то обелиск называется понтоном. Клином называется тело, верхнее основание которого — прямая линия, нижнее — пло- скость. ей параллельная, а боковые грани — треугольники, трапеции вли параллелограммы; клин также является частным случаем призматоида.
ВЫЧИСЛЕНИЕ ПОВЕРХНОСТЕЙ И ОБЪЕМОВ ТЕЛ
109
Продолжеаяе
Геометрическое тело н обозначения Боковая поверхность Полная поверхность S„ Объем И
ПОНТОН! / Iе \ \ / 1 \ \ 1 в * — V--J- юн-с-Жв-Н) (*+<0)
Прямой ЦИЛИИДр: В и Р — площадь и периметр осиоииия; Л — высота 5б-Рй V - ВЛ
Прямой круговой цилиндр: R н D — радиус и диаметр основания; * — высота $0 = 2*Яй = <DA; S„ - 2кЯ (Я+й) = 2- кО(£Н-2й) V-eR>ft-^
Прямой круговой цилиндр, усеченный иепапаллельио основанию: Й< я Л, — длины наибольшей и наименьшей обра- зующей; Й — длина осн $6 - «Я (Й.-НМ - -у «О (Л,+ЙЦ и-кя>_<Я*Й-
Полы* круглы* цилиндр <труба>| R и г, D и u - mieuRw* н пиутренний ратиусы и диа- метры: & — толщина стен- ки; й — высота пи- линз ра 5в «= 2чй <Я+П; Sn - 2к (Я+d (Я-Н-й) V - ей (R'-r*l = кй« (R+H —
Цилиндрическое копыто: 2h/? Se-~|a-(R-»)p); если основание копыта по. S0-?R4 (ая’-ап-зя1 (₽-») м; уокружиость (О—Л—Я). то V- -1я«й а»
Круглый коиус: Ц, D, й, 1— радиус и диаметр основания. высо- та н образующая конуса Ив - кЯ1ЯНй*-«Я/- -укХИ V - 4-*J?** - A cD'A-A'AieDM Л 1л
по
ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ ФИГУР
Продолжение
Геометрическое тело и обозначения Боковая поверхность Полная поверхность 5Я Объем V
Усеченным конус: R, г, D, А — радиусы и ди»* метры нижнего и верхнего осно- ваний; + п/ - -j-<0 + <ni. - J- «А (D* + d> + DA
*. 1- высота и обра-
эующдя усечен- ного конуса
Тетраэдр (четырехгранник), одна из вершин которого на- ходите! в начале координат, а координаты остальных Ut. Л х.К Ut. У* X»), (-*•• Ух» х,) —
1'= — В лг»УЛ *хУЛ -ХхУА
Шар: R н D — радиус н диаметр шар. в . „ г- ЗУ ей 5 — 4« А" — «О" — — — — v - 4 •=4- ‘««я* -= 4- ’О*= 4 0 -ОЛ2Э6№ R . 0,62035 /F
Шароеоб сегмент: R — радиус шара: А — высота сегмеота; а — Vh (2₽ - Л) — радиус ос- иовамия сегмента Sfl - 2«J?A -.«(«•+• »); * 2А V-rt.(₽- ». I - 4 «А (3*4*)
Шаров о! слой: So — 2*RH. (а>0) У=± «Л> + -1яв.* + + Д <б’Л - 77- <** + >’•* + 3»*1.
/ Ъ 1 а!
\ 2Л ) * т ! 1 ж 3 то (*•--?)
Шаровой сектор: R — радиус шара; й — вы< от а соответствующе- го сегмента. а — VH (2/? - Л) - радиус ос- нования сегмента (У. е. радиус мругоаото ребра сектора! Se — *Н UH 1- в» V - у - 2,09МЯ'Л . - » 0,623«DM. О
* Здесь — определитель з-ео порядка; см. стр. 116.
ВЫЧИСЛЕНИЕ ПОВЕРХНОСТЕН И ОБЪЕМОВ ТЕЛ Щ
Продолжение
Геометрическое тело и обозначения Боковая поверхность 5Л Полная поверхность S. Объем У
Сферически! клин «честь шера. заключенная между двумя большими кру- гами): у —угол межау плоскостями больший кругов » -',036907 <?•»' V ™ — я*» — ’Я'?* 3 27V — о.о) 1вэб
Эллипсоид: а, Р. с — полуоси Если 0 — с (кллипсонл ераше- ине), то 5в - 2«д» X V - — tube 3
V д' - »• , 0 , п-агсМп а •
Ч<< 1 или, приближенно. $я = » /а» +
Параболоид арашеиия: Ц — радиус основаинн. к — высота --5- ги Р- — р ад V = -J. «ДНД - 1,570796
Усеченный параболоид крашения: R и г — радиусы освэмиий. h — высота у .(₽• + /•)»
Усеченные нддиптичесина конус: Осмо-инне - аллипсы. глее яые полуоси которых о, b я а„ высота усеченного ко- нуса а [(2л-р л.) » + (?<». + «) »•]
Бочка: d — диаметр дна; D — диаметр среднего сече- ние (втулочный). в — длина (высота) бочки - Для бочки иарабоаическоА формы V - 0,16236 Л »D' + <D4 + 3rf>). Для бочки сферической Формы V — 0,2616 h (2D» + </»)
Тор (колыю кругового сечения h г — радиус кругового сечения; R — расстояние венгр* сече имя от иеитпэ кольца s « = ЗЭ.дТВДг п V — = 19,739 Rr«
Поверхности и объемы тел вращения,
правила Гюльдена
а) Поверхность, образованная враще-
нием линии длиной I вокруг оси, имеет
площадь S = где Хо — расстояние
центра тяжести линии до осн вращения
(образующая расположена в одной пло-
скости с осью и ее не пересекает)
б) Объем тела, образованного враще-
нием плоской фигуры площадью S
относительно осн, лежащей в плоскости
фигуры и ее не пересекающей, равен-
V = 2nxoS, где *о — расстояние между
осью вращения и центром тяжести фи-
гуры.
Если известно уравнение образующей*
кривой, го площадь поверхности и объеы
тела вращения находят ии>егрирова-
нием (см. стр. 190).
112
ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ ФИГУР
ЗАВИСИМОСТИ МЕЖДУ тригонометрическими ФУНКЦИЯМИ
УГЛОВ треугольника
sin а 4- sin 3 4- sin 7 =
. а 8 т
— 4 cos cos - j- cos
sin« + sin? — sin?—
а 8
4 sin -y sin cos
sin2 а + sin’ 3 4- sin17 —
— 2 cos a cos 3 cos т 4- 2
cos’ a 4- cos2 3 4- cos2 7 =
— 1—2 cos a cos 3 cos 7
tg 0 4- tg p 4- tg 7 — tg a tg 3 tg 7
sin 2а 4- sin 23 4- sin 2j —
= 4 sin a sin? Sin7
cos 2а 4- cos 23 4- cos 27 =
— — 4 cos a cos 3 cos 7 — 1
ctg a cig 3 4- cig? Ctg 7 4- Ctg 7 Cig а — 1
COS а 4- COS ? 4- COS 7 =
— 4 sin -y sin —• sin -y 4- 1
COS а 4- COS 3 — COS 7 —
a fi 7
— 4 COS -y cos -y sin --1
sin2 а 4- sin5 ? — sin*7 — 2 sin a sin ? cos 7
cos2 а4” COS2 ?—COS2 7— 1 —2 sin a sin 3 cos 7
eg + ctg у 4- ctg -L -
а ж В 7
- Cig -у Ctg -j- Ctg -±-
sin 2а 4- sin 2? — sin 27 — 4 COS a cos ?sin 7
cos 2а 4- cos 23 — cos 27 —
— — 4 sin i sin ? cos 7 4-1
а 3 Вт
tg-ytg-y+tg-ytg-j- +
+ tg
основные случаи ргшения треугольников
Решение прямоугольных треугольников (обозиачеине см. иа стр. 102)
1 Зайко ж £ •И X Решение I 1 Решение
а. а ь с S £ = 90* —а b — a ctg « а С в — sin а Я* 5 = -rctg« а. 0 а 3 с 5 II Я п си „| Ч я -а. ч» II = М II И И II !I-U 1 1
о. « Э а с S h-U III 1 л. « М <0
... • 3 » 5 •in. — —: с
co.3--y; a — *4-/sj » — Ус* — o’ — У (с 4- a) ic — а)- — сCOla — С tin? S—-jy<c4-e)(c — »1—-5 ас tin?
г, • о b S а — с Ып > С сое а 1 S “ tin а соа а — - tin 2а
ОСНОВНЫЕ СЛУЧАИ РЕШЕНИЯ ТРЕУГОЛЬНИКОВ
113
Решение косоугольных треугольников
(обозначения см. на стр. 102)
Задано Найти Решение
• «к Т С « 3 S с = У о* + Ь' — 2яй сот 7 а sin Т , a aln т sin a — ; tg a — — 1— c b — a cos 7 amp, *21111 ;tgp = *«'"T r “r a — b cos t $ __ ab sin 7 При пользовании логарифмами удобнее формулы Найдя в — 3 и «+?. получим а и 0; a sin т затем с Bln в
О. ?. т. ИЛИ а, «, или а. а» I « IT. ₽) 6 с S « = 180’ — (? + 7): 7 — 180’ — (a h a sin 3 = a sin p slu a sin (3+7) c — a *ln 1 — ° T sin e sin (3 + 7) У a'sin psln 7 a' 2 sin s 2 ictg 3 + ctg + 3); 0 = 180'-(а+7) т>
а. Ь, с а 3 т 5 o, “I-1 »=1‘® “Iя I 1 n II + ’’X '’x i 'Ъ "O *B 1 TS 1 t 1 ъ | » ? В % S S is i; • ? 1 Ol 5 | 5 | € Г Г 1 1 al а a 7 I - 1 - 1 - 1 al » о / (Р - я) (я - б) (р - с) г V р о — а / (Р — а) (р — й) (р — с) г V Р =Р—Ь / (р - а> (р — ») (р - с) ш г V Р р —с гр
a. b, a «>>*) ? Т с $ Bln 3 - Ь *дЛ * (3 — острый угол. 3 < a) 7-180"-(a + ?) c — a cos 3 + b cos a — 2212-1 = ft cos a -f- ]/ a' — ft1 sin' a sin а r s = ',b *ln 1 — *** ,ln * 2 i
а. Ь, а (а <61 3 т « S Решение возможно лишь при условии, что а > b aln a 1) Если а “ b sin а. то 0 = 90" — решение единственное 2) Если а > b sin я, то получаются два решения соотоетспешю дау к ана- ченияы угла 3: 0, — arcsln -~дП— (острый угол); - b sin а , 3, — _ arcsin —-— (тупой угол); 7, с и S — как и предыдущем случае
Н Том 1 Зак. 1404
114
ВЫЧИСЛЕНИЕ ЭЛЕМЕНТОВ ФИГУР
РЕШЕНИЕ СФЕРИЧЕСКИХ
ТРЕУГОЛЬНИКОВ
Сферический треугольник образуется
па сфере дугами трех больших кругов.
Если радиус сферы равен единице, то
длины сторон сферического треуголь-
ника (а, Ь, с) являются мерами углов
между радиусами сферы, проведенными
к соответствующим вершинам сфериче-
ского треугольника. Углы при вершинах
сферического треугольника (я, р, -у)
являются мерами двугранных углов
между плоскостями больших кругов,
дуги которых образуют треугольник.
Сферический треугольник опреде-
ляется любыми тремя из шести основ-
ных элементов а, Ь, с, а, р, 7, так как
углы при вершинах треугольника не
связаны друг с другом какими-либо
соотношениями. Остальные три эле-
мента определяются из следующих трех
основных соотношений:
sin а _ sin b _ sine
sin я = sin р — sin 7
(теорема синусов);
cos а = cos bcos с 4- sin I sin c cos i
(теорема косинусов).
Углы я, р, 7 противолежат сторонам
а, Ь, с и не превосходят г..
Площадь сферического треуголь-
ника:
5 - «R2.
где R — радиус сферы; в — а + р + 7 —
— к — сферический избыток, определя-
емый по формулам
а , b
cig у etg у 4- cos 7
С,8Т---------------ан,----------1
где р — у (а 4- Ь + с).
Если угол 7 прямой, то основные фор-
мулы принимают вид:
sin а — sin с sin я; sin b — sin с sin р;
cos с — cos a cos b.
Из основных соотношений вытекают
формулы
cos а — — cos ₽ cos 7 4- sin р sin 7 cos a;
cos a sin b — sin a cos b cos 7 4- sin C cos я;
cig a sin b — sin 7 cig я 4- cos 7 cos b.
cos я sin p = sin 7 cos a — sin я cos p cos c;
etg я sin p = sin c etg a — cos c cos P;
a _ Г — cos я cos (a — a)
£ T" = V cos (a — p) cos (a — 7)
где 0 — у (a 4- p 4- 7);
a _ Г sin (p — b) sin (p — c)
g ~2~ ~ V sin p sin (p — a)
где p -If- (a + b + c).
Все формулы допускают циклическую
замену букв а, Ь, с, я, р, 7 соответ-
ственно буквами Ь, с, а, р, 7, я и с,
а, Ь, 7, а, р.
Все шесть элементов сферического
треугольника связаны соотношениями
7 , а 4- b , с a — р
sin -у- sin -у- = sin у cos —у ;
7 а 4- b с а 4- Р
sin cos —-— = cos у cos ;
7 . а — b , С . а — р
cos sin -у- = sin у sin -у-;
7 а — Ь с,я4-р
cos -i- cos —“ cos ~2~ sln —у ’
Отсюда следует:
2
a 4- b
tg —J---------tg
При решении прямоугольных сфери-
ческих треугольников употребляются
также формулы
cos я — cos a sin р; cos р — соз b sin a;
lg п = sin b tg я; tg b — tg c cos «;
COS C — Ctg a Cig p.
ГЛАВА V
РЕШЕНИЕ УРАВНЕНИЙ •
ОПРЕДЕЛИТЕЛИ
И ПРИМЕНЕНИЕ ИХ К РЕШЕНИЮ
ЛИНЕЙНЫХ СИСТЕМ
Группы из л элементов, отличающиеся
друг от друга только порядком элемен-
тов, называют перестановками.
Отмечая элементы индексами 1, 2,
3,.... л, рассмотрим перестановки ин-
дексов.
Перестановка 1 2 3 ... л называется
главной. Если больший индекс стоит
впереди меньшего, то первый индекс
образует со вторым инверсию, или
беспорядок. Инверсии подсчитывают так:
считают, сколько цифр стоит левее 1,
и записывают; затем вычеркивают 1 и
считают, сколько цифр стоит левее 2
(не считая зачеркнутой единицы), и т. д.
Пример. Число инверсий в перестановке
6 3 12 4 6 буает шесть.
Перестановка четная, если число ее
инверсий четное, и нечетная, если
число инверсий нечетное.
Пример. Перестановка 2 3 1 четна* (две
инверсии).
Главная перестановка всегда четная
(нуль инверсий).
Квадратной матрицей из л1 эле-
ментов называется таблица
«и аа • • • в1я
аП а13 а!л
L аи: *л1--- апя
Определителем п-го по-
рядка из л элементов мат-
рицы называется алгебраи-
ческая сумма л! членов, каж-
дый из которых есть про-
изведение л элементов, взя- При вер.
тых по одному и только
по одному из каждой стро-
* См. литературу на стр. 319—351
И. 10. R5). 111/1.
а*
ки и каждого столбца матрицы,
причем знак каждого члена будет + или
— в зависимости от того, будет ли в
этом члене четной или нечетной пере-
становка вторых индексов, когда эле-
менты в каждом члене расположены
в порядке возрастания первых индексов.
Знак каждого члена определяется
множителем (—1)*, где t — число инвер-
сий во вторых индексах члена. Опреде-
литель л-го порядка имеет одинаковое
л!
число -g- положительных и отрицатель-
ных членов. Обозначение определителя
л-го порядка:
*п в12-*-*1л
*Я ап... д^
=1*01(0-1.2.., л);
«л1 агЛ • --апп
л’ элементов определителя л-го порядка
образуют л горизонтальных рядов
(строки) и л вертикальных (столбцы)
Первый индекс в обозначении эле-
мента есть номер строки, второй — но-
мер столбца.
Минором Мцопределителя | Ду |, соот-
ветствующим элементу ац, называется
определитель, образованный из дан-
ного вычеркиванием i-Й строки и /-го
столбца.
Алгебраическим дополнением {адыонк-
той) Ац элемента Ду называется его
минор со знаком плюс или минус, со-
ответственно формуле
’ аа............................аю
- ...................................а и
в„... Я|Я
*••••• "Зл
'•I е«/ e^t
ЯЛ2°Л9 * ’ авл
116
РЕШЕНИЕ УРАВНЕНИЯ
Свойства определителей
1) Величина определителя не изме-
няется при замене строк столбцами.
2) Определитель меняет знак при
перестановке двух столбцов (или строк).
3) Определитель равен нулю, если
два его столбца (или две его строки)
состоят из соответственно равных или
пропорциональных элементов или если
все элементы какого-нибудь столбца
(или строки) — нули.
4) Множитель, общий всем элемен-
там какой-либо строки (или столбца),
можно выносить за знак определителя.
5) Определители можно складывать
по формуле
Вычисление определителей: 2-го по-
рядка по формуле
«и ап
ati ав
— «цДа— «ц«я;
3-го порядка — по правилу Саррюса
(снизу приписываются первые две
строки):
—«н«22«м+<3ааа?я18 +
+«31®и«м—«si«a«n—
—«п«зт«а—«а«12«ю-
«и «И • • • «1л
«а • • • «гл
9
«Ц all--.ain
«21 ая.. л»я
anl ап1 • • • апп
«11- -*l?n«'n
Л21 «я •«и
«ш а"1' • • а"п
где ап - «J। ± «« - «п ± “it........
6) Определители можно перемножать
«11 «12 • • «1л
«а
6ц ЬЛ...Ь1Я
6а Ьа. • - 6гя
ап1 ап2” апп
6л1 6nj... Ь„п
«« «я1 • • • «лл
«Л1 — «л| ± ая1
по формуле
®11 Сц...«1Л
СЯ СЦ...С2Л
СЛ1 сл2 • • • елл
Определители
л-го порядка сво-
дят к определите-
лям 3-го или 2-го
* порядка, приме-
няя свойство 8 не-
обходимое число
раз; предваритель-
но определи-
тель преобразуют,
пользуясь осталь-
ными свойствами,
преимущественно
свойством 7, чтобы
обратить в нуль
возможно большее
число элементов.
п
где Си •» ОцЬу + ОцЬу -f-... + atrfinj — S «i»^W-
А-1
Пример.
D-
12 3-4
10 12
7) Величина определителя не изме-
нится, если ко всем элементам какого-
нибудь столбца (или строки) прибавить
соответствующие элементы другого
столбца (строки), умноженные на одно
и то же число.
8) Определитель можно разложить по
элементам любой (/-й) строки и лю-
бого (/-го) столбца по формулам
D — ацАц 4- а^Ап +... + а,я 1(я;
D — а^Ау 4- a^Aij 4- ...4- anjAnj.
где Atj—алгебраические дополнения
соответствующих элементов.
3-1-1 0
12 0 5
Булем .аелать нули- в последней строже, оставлял
без изменения первый элемент: из элементов 2-го
столбца вычтем соответственные влемевты 1-го
столбца, умноженные на t. нз элементов 4-го
столбца вычтем элементы 1-го, умноженные иа 5:
полу-шы
D -
I 0 3-
1-2 1 —
3 —7 -1 -15
I О О
(свойство 7)
I I
1 1
I 5
(свойство 8)
(свойство 4)
1<Я
Применяя этот прием, можио свести
вычисление определителя любого по-
ОПРЕДЕЛИТЕЛИ
117
рядка к вычислению одного определи-
теля 3-го порядка, постепенно понижая
порядок определителя.
Система п линейных уравнений
с п неизвестными
«11*1 + «12*2 + • + «1лл'л —
аПх1 + «й>х2 + -.. + Ощхп = Ьг
«л 1*1 + «л2*2 + • + аппхп =
решается по формулам Крамера: Ж/ =
— (1= 1,2,...,п). где D —главный
определитель — составляется из коэффи-
циентов при неизвестных
D =
anait- • • «и
«К«И... 02л
«л'«л2 • • -«лл
все Dt — дополнительные определите-
ли — получаются из главного заменой
«-го столбца свободными членами урав-
нений
Dt = Mil • • • «1л 62«2! • •• «2л ;о2- «11^1 • • • «1я «Д*2 • «2л
^Л«Л2 • • «лл ал)&„... а„„
и т. д.
ПрнЛ 0 система имеет единственное
решение; при D — 0 и 0,^0 система
несовместна (т. е. не имеет решений);
при D *= 0 и D, — 0 система неопреде-
ленна (имеет бесчисленное множество
решений).
Пример. Решим систем/:
JT.-f-x,ж,-|-лг,-5;
лг, + 2х, - х, 4- 4ж. — - 2;
2ж, - Зж, - х, - Ьг, — - 2:
Ьг. 4-ж, 4-2г. 4-11 Ж, —0;
1111
12-1 4
° “ 2 -8 -1 -6 “ ~ ’
3 I 2 11
6 111
-2 2-1 4
-2 -3-1 -5
О 1 2 II
16 11
1-2-1 4
2 -2 -1 -5
3 0 2 II
1 1 5 1
1 2 -2 4
D, - 2 -3 -2 —5 - - 426
3 1 0 11
1 1 1 5
1 2 -1 -2
D. - 2 -3 -1 -2 — 142
3 1 2 0
Система т линейных уравнений
с п неизвестными (гп может быть равно
или не равно л):
«11*1 + «12*1 + • • • + «1л*л " &1I
«21*1 + а^г + • • • + атхп = Ь2;
ат;х\ + атЪхг + - • - + атпхп = Ьт.
Пусть А — матрица из коэффициентов
системы, а В — расширенная матрица
(получается из А присоединением столб-
ца свободных членов):
А-
В -
«и«12 ... а1я
«а«а-.-«2л .
«п«12 •• • «!«*!
«а«з: • • • агльз
«ml«m2 • •• атп^т
Определитель 1-го порядка из эле-
ментов, принадлежащих одновременно
каким-нибудь t строкам и t столбцам
матрицы, называется определителем
матрицы; каждый элемент матрицы на-
зывается определителем 1-ео порядка.
Матрица имеет ране г, если среди
определителей r-го порядка матрицы
есть хотя бы один, отличный от нуля,
а все определители более высокого по-
рядка равны нулю.
Пример. Для матрицы
1 2 3 4
1-245
1 10 1 2
118
РЕШЕНИЕ УРАВНЕНИИ
ранг г — 2, так как все определители 3-го порядка
матрицы — нули. но среди определителей 2-го по*
рядка есть не равные нулю:
lUI
Система т линейных уравнений с п
неизвестными совместна тогда и только
тогда, когда ранг матрицы А равен
рангу расширенной матрицы В. Если
г = п, то имеем л независимых урав-
нений с л неизвестными; отбросив за-
висимые уравнения, решаем систему по
формулам Крамера и получим единствен-
ное решение. Если г < л, то число не-
зависимых уравнений (г) будет меньше
числа неизвестных; перенеся л — г лиш-
них неизвестных (свободные неизвест-
ные) в правые части, решим систему
относительно остальных г неизвестных;
задавая свободным неизвестным про-
извольные значения, получим бесчислен-
ное множество решений.
Примеры-. 1. Систем»
ж, — ж, 4~ 2ж, • 1,
х, — 2ж, — ж, — 2;
Зж, — «г» + 5лг, = 8;
-2х, + 2х, 4- Зж, = - 4 ,
совместна, так как матрицы А и В имеют одина-
ковый ранг г — 3, и допускает единственное рсте-
ине. Отбрасывая четвертое уравнение, из первых
10 1 2
трех получим х, — -у ; ж, —-----— ; ж, — — у
2. Система
вое решение). Для того чтобы система
л однородных линейных уравнений с л
неизвестными имела ненулевые решения,
необходимо и достаточно, чтобы глав-
ный определитель системы был равен
нулю.
Для системы двух однородных урав-
нений с тремя неизвестными
Л;Х + biy 4- Cjz = 0; 1
4- b>y 4- c2z = 0, f
если ранг матрицы системы равен двум.
получаем
X у Z
I bi ci I = |q «11 “ I «1 »i I •
|c2«2l I «2^1
ИЛИ
—‘1й2к-‘12::к-‘12й1=
k — произвольный множитель пропор-
циональности, а все три определителя
2-го порядка получаются из матрицы
»«1 *1 «1 1|
последовательным вычер-
«2 с2 ||
киванием столбцов (для среднего неиз-
вестного столбцы полученного таким
образом определителя 2-го порядка ме-
няются местами).
ж, — х, 4-х,— ж,— I;
X, — ж, — ж, 4- ж, — 0;
л. - ж, - 2ж. 4- 2л, - - у
совмсстна, так как матрицы А и В имеют одина-
ковый ранг г “ 2, ио здесь г < л, поэтому си-
стема имеет бесчисленное множество решений;
первые два уравнения независимы (определитель
их коэффициентов при ж, и ж, в этих уравнеииях
не равен нулю); отбрасываем третье уравнение
и переносим свободные неизвестные ж, и ж, в пра-
вую часть, получаем л, — ж, — —-; ж, — ж, 4--J",
Однородная система уравнений
«11*1 + «12*2 +... + «1яхя - 0; '
«2|Х| 4- «22*2 + . . . + «2ЛХЛ “ 0;
emlxl + «юз-Ч + • • • + атнх„ - 0 ,
всегда совместна (х> л = ... ™ хя= О
есть одно из решений системы — нуле-
АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
Алгебраическое уравнение п-ft степени
Р (х) В «ох" 4- Д|ХЯ-1 4- Одх"-2 4-...
... + «я "О
имеет п корней, вещественных или ком-
плексных, различных или равных; ко-
рень уравнения Р(х)« 0 называется
корнем многочлена Р (х). Если а — ко-
рень Р(х), то />(х) делится на (х— а)
без остатка; в общем случае остаток
от деления Р (х) на (х — а) равен Р (а).
Если Р (х) делится на (х — а)*, но не
делится на (х — a)*+l, то а называется
й-кратным корнем уравнения Р (х) = 0;
в этом случае а является общим кор-
нем многочлена Р (х) и его производных
до (А — 1)-го порядка включительно,
т. е. Р (в) =• Р' (а) = Рг (а) — .. . —
= Р*-,(а) = 0, но р" (а) уЬ 0. Если Р (х)
имеет корни а, р, 7, ... соответственно
АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
119
кратностей Л, I, т.......то Р (х) =
- До (х — «)* (х — 0)' (х — т)" ... Ком-
плексные корни уравнения с веществен-
ными коэффициентами могут быть только
попарно сопряженными, т. е. если такое
уравнение имеет корень а = а + Ы, то
оно имеет также корень 0 — а — Ы и
притом той же кратности. Произведение
(х—а)(х — 0) в этом случае дает
(х — а) (х — 0) = х2 + рх + q,
где р — — (а 4- 0) — — 1а. q = a0 = аг 4-
+ b*. откуда Поэтому мно-
гочлен с вещественными коэффициентами
можно разложить в произведение ве-
щественных множителей первой и вто-
рой степени
Р(х) = д0(х-а1)*‘Х
X (х — «г)*1 ... (х» + PiX + q^ X
X + Р2х + q^1'.
где все числа ah pb q, будут веществен-
ными и —?/<0.
Уравнение нечетной степени с веще-
ственными коэффициентами имеет по
крайней мере один вещественный ко-
рень. Число вещественных корней, за-
ключенных между любыми числами а
и Ь, может быть точно определено при
помощи теоремы Штурма (см. стр. 123).
Коэффициенты алгебраического ура-
внения и его корни связаны соотноше-
ниями
Х1 + х,+ ... +х„-
“О
*\Хг + Х1Л| + ... + х}хп 4- х^х9 + ... +
+ ;
XjXjX, + Х!ХгХ4 4-... 4- Xn_3x„_ix„ +
+ *л-й*а-1*я “ . *»
x}xtxt...x„ -(— 1)"
Квадратное уравнение ах2 4- Ьх +
4-с — О:
— Ь ± / № — 4ас
Л'-2------------Й
_ — & А У' М -4- (а — с)2— (д 4- с)2
2а
Квадратное уравнение х! 4- рх 4- q =0;
Квадратное уравнение ах1 4- 20х 4-
4- с - 0 (20 = ьу.
- 0± Я2^"
*1,2-------3
Если коэффициенты вещественны и
6" < 4ас (или соответственно < 4ц,
0* < ас), то корни — сопряженные ком-
плексные числя.
Для квадратного уравнения
b
Xj + х2 = — — = - р,
X'Xl--L._q.
Кубическое уравнение дх9 4- 1>хг 4-
4-сх 4-^=0 приводится к виду у* 4-
4- ру 4- q — 0, если положить х — у —
о-(|)--3-(т)*>
Если дискриминант уравнения у* 4-
4- рх 4- q = 0 положителен, т. е. Д =
/?8
£-4- ip то 510 уравнение имеет
один вещественный и два комплексных
корня:
У! — и + и;
I VT
У2 “---2“ + 0 + < 2
у,-------(114-е)-/ y^-(u—v).
Алгебраические уравнения 2-й, 3-й
н 4-й степени можно решать по гото-
вым формулам.
0,86603
120
РЕШЕНИЕ УРАВНЕНИИ
где и и v — действительные значения
кубических корней:
/Г;
v= у/-у- •
лВ аг
Если Л + 4 < 0. то асе ТРИ
корня действительны и определяются
формулами:
Л =• -у /з КГЯ cos ?;
у2 - А Уз УГЯ cos (Т ч- 120°);
О
У» = 4- Уз Уй cos (<? - 120°)»
О
где
I -ЗУЗ<?
<р =-у arccos -2-|/>|ty
Примеры. 1, Решим уравнение х* — 6х |-
-|- 6 “» 0.
Здесь р - в: <7 - 6; 4 = 7 “ 1:
п=|Л+ /Л -|/-3+1 --|/Г:
v — --^-УГ-|/-3-1-- Э|/Г 1
3 _ з ______
у, - U 4- » - - У 2 - У 4 - 2.847;
у, - - 4- (* + t>)-H W - ») - ‘.*24 + О.2НЗД
1 VT"
У. “ - у (« + »)-1 у- <и - ») - 1-421 - 0.783У.
2. Решим уравнение л*12лг*-f-24лг — 51 — 0.
Полагаем
получим
Здесь
у» _ 24 у — 32 = 0.
«Ул у _ 8 УТ-32
2 I р !*/• “ 2-2?
УГ.
Эр - 45» ; р = 15* ;
у, - -J- V 3 У24 cos 15» = 4 У 2 cos 15“ - 5,4&
у, = 4 УТ cos 135’ =-4:
Va“ 4 УТ cos ( — 105») = 4 УТ сов 105“ =
= — 4 У 2 cos 75’ •> — 1,45.
Найдя одни корень уравнения, ’можно свести
решение уравнения 3-й степени к решению квад-
ратного уравнения. Например, в данном случае мм
нашли, что у. = — 4. Делим у" — 24у — 32 на
у -{• 4 и приходим к уравнению у' — 4> — 8 — 0;
решая его, получим у = 2 ± У44-8 — 2 ± 2 УТ.
что и ласт остальные два корпя.
Возвратное уравнение 3-й степени
яхя4- 6х2 + Ьх + а = 0 имеет корень
х = —1: два других корня являются
корнями квадратного уравнения ах1 4-
4- (Ь — а) х 4- а =* 0, которое получим,
деля левую часть кубического уравне-
ния на х + I.
Уравнение ас* 4- Ьх* — Ьх — а = 0
имеет корень х=4-1 и два корня,
являющиеся корнями уравнения ах2 4-
4- (Ъ 4- в) х 4- о = 0.
Уравнение 4-н степени ах*Ьх3+
сх* 4- dx 4- е — 0 подстановкой х = у —
---приводится к виду у<4-ру14-‘
4- qy 4- г = 0. Корпи этого уравнения
имеют вил
У1 - -j’ (^*У+
л=4“ (~ ~
у»--у-(—V z?4 /Jj—УК);
л - - /«14- vъ),
где ?|, г», ?я—корни уравнения 3-й
степени (резольвенты)
za 4- 2рг‘ 4- (р3 — 4г) г — q3 — 0.
Квадратные корни У*2»
выбираются с такими знаками, чтобы
удовлетворялось равенство
Уд? - VaJ------------q.
Пример. Решим уравнение X1 — Зх' 4- —
-2 — 0; здесь р — — 3: « »б: г « — 2. Кубиче-
ская резольвента будет
1»-61«4-171-Зв-0.
Заметим, что целые корни уравнения с целыми
ковффициентами и со старшим коэффициентом
единицей являются делителями свободного члена;
ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ
121
подвергая испытанию делители свободного члена,
находим, что уравнение имеет корень г, = 4. Дела
левую часть уравнения иа г — 4, придем к ква
дратному уравнению 1* — 2z 4- 9 — О. корни кото-
рого будут вторым и третьим корнями резоль-
венты : h — 1 -f-/ /в” , I, “ I — I /3 . Таким обра-
вом, У”г, = ± 2; У* — ± У 1 -f-У'— 8 ; УТ, —
— ± У 1— У— 8 . Если применим формулу
У7ГТГ--|/“±Х^±
то получим
VT, - ± (УГ + /); Ул — ± (УГ - /).
Так хак должно быть выполнено условие
УК- Vh УК — — Я — — 6, то можемположить
УК—-2; УК-УТ4-h УК —/2 — t
Окончательно имеем
*|-4-(УК4-УТ4-У’Ю--Ч-/Т;
X, - -1 (УК - УК - УК) - -1 - УТ;
Л, _ -1. (- УК 4- /К - УК) - 1 4-
х,--^-(-УТ, -Уй + /Ю -1 - •-
Биквадратное уравнение ах* 4- Ъх'- 4-
+ с а 0 имеет корня
х|>2 - ± V'i (-* + :
« ± j/-±- (-6- уИ-4ас).
Если b* — 4ас < 0, то все корни яв-
ляются комплексными числами с одним
и тем же модулем
возвратное уравнение 4-й степени
ах* + Ьх3 4- сх* 4- Ьх + а = 0 подста-
. J I
новкой х 4—— = у приводится к квад-
ратному уравнению
в(у» — 2)4-*У 4-е —0.
Уравнение степени выше 4-й в общем
случае нельзя решить алгебраически
(т. е. в радикалах), т. е. нельзя выразить
его корни через коэффициенты с помощью
конечного числа рациональных действий
и извлечения корней. Уравнения с чис-
ленными коэффициентами решаются либо
графически, либо при помощи различ-
ных приближенных методов (см. стр. 125).
Решение системы двух алгебраических
уравнений соответственно т-й и л-й
степени с двумя неизвестными сводится
к составлению уравнения (т-п)-й сте-
пени с одним неизвестным путем исклю-
чения из системы другого неизвестного;
после отыскания корней составленного
уравнения они подставляются в одно
из уравнений заданной системы для
определения другого неизвестного.
Два уравнения с двумя неизвестными
(алгебраические или трансцендентные)
’ (х. у) = 0 и f (х, у) = 0 будут неза-
висимы, если их якобиан (см. стр. 185)
df df
О (f, <f) dx dy
D (x, _y) “
dx ~Sy
не обращается в нуль тождественно.
ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ
Если Дх) —трансцендентная функция,
то уравнение f (х) = 0 называется транс-
цендентным. Оно может иметь бесконеч-
ное множество корней, из которых
часть (или все) могут быть комплекс-
ными. Некоторые трансцендентные урав-
нения не имеют решений (например,
уравнение е* = 0). Большинство транс-
цендентных уравнений решается только
приближенно н лишь некоторые сво-
дятся к алгебраическим.
Показательными называются урав-
нения, в которых неизвестное входит
в состав показателя степени. Пусть х
или Р (х) (многочлен) находится только
в показателях степени некоторых ос-
нований а, 6, с...; такое уравнение
сводится к алгебраическому в следую-
щих случаях:
1) если над степенями а₽* Ьр'
не производится сложения и вычитания;
в этом случае уравнение следует про-
логарифмировать при любом основании;
2) если а, Ь, с,.., — целые или дробные
степени числа k (а = k', Ь = Ь?, с —
= А7,...); в этом случае, полагая у —
= kx, решают алгебраическое уравне-
ние относительно у и определяют х из
таблиц: х — : в некоторых слу-
чаях показательные уравнения решаются
без таблиц.
122
РЕШЕНИЕ УРАВНЕНИИ
Примеры:
I) 3*=4ЛГ—2-2*; х log 3 — (ж — 2)-log 44-
+-4 log 2;
_______2 log 4_____
Ж = log 4 — log 3 4- log 2 ‘
Я jx—1 „gx—2 _ дХ—2. 2Г 2^* 2^* .
4 8 V ’ 2 Ы 16 •
полагая 2* — у, получим у* — 4y* — 32y — ft
откуда у, — '2*‘ —8: yt —2Ж* — —4; y, = 2*» = ft
-Ti—3: других действительны! решений не суще-
ствует.
3) V~2*- V 3х —38; 22 -32 — в»; б2 —
— в»; -у-2: х = 4.
8_)Зх-2
4) 72-Зх.5Зх-2 _ |.
Зх —2 = 0; х = |.
Логарифмическим называется уравне-
ние, содержащее неизвестное под зна-
ком логарифма. Пусть х или Р (х)
(многочлен) находятся только под зна-
ком логарифма; такое уравнение сво-
дится к алгебраическому в следующих
случаях:
1) если уравнение содержит логарифм
от одного и того же выражения; в этом
случае, принимая логарифм за новое
неизвестное, решают полученное алге-
браическое уравнение и потенцируют
его решение;
2) если уравнение будет вида
m log„ Pi(x)4- л log4 Pi (x) + ... = 0,
где Pi (x). ₽«(x),... — многочлены; в
этом случае уравнение приводится к
алгебраическому потенцированием.
Примеры:
I) х'Х * — lOOr; fig х)‘ — 2 4- lg x обозначим
lg x = у, получим у* = 2 4- у, откуда у, — 1g х, —
— 2; у, — 1g х, — — I; х, — 100. х, — ftl.
2) lg (Зх - 11) + 'It (х - 2J) - 3; lg ((Зх —11) X
X(x — 27)| - lg 1«U; (Зл - U)(x - 27) - 1000;
X,—37; x. — -
Тригонометрическим называется
уравнение, содержащее неизвестное под
знаком тригонометрической функции.
Применяя тригонометрические формулы,
стремятся прийти к алгебраическому
уравнению от какой-либо одной тригоно-
метрической функции, определив ко-
торую находят далее х, вообще го-
воря, из таблиц; при этом следует иметь
в виду многозначность решения.
Причеры:
1) ctg (270» — х) — 3 ctg х; tgx — -L-; tg х —
“ ± Уз"; х, — 60’ 4- 180>п; х, = — «0» 4-1»Гл.
т. е. вообще X — 180'л ± 60* (или «п ± -у j .
2) sin 5х — s(n 4х: sin Sx — sin 4x — ft
X Qr r r
2 Sin — COS — - 0 ; sin y- — 0 ; i — 180»л:
x = 360»n; cosy-0; ^-ЯГ4-180«л; X-
- 20° 4- 10»n.
3) sin* x — 2 sin x cos x = 3 cos* x; делим обе
части ns cos*x(* 0); tg’ x— 2tgx=>3; tg x -
= —1; х=1ЧС»л —45»; tgx = 3; x = НЮ*я 4-
4-71*33'54" (по таблицам).
4) a sin X -f- b cos x = c.
Первый способ. Уединив a sin X, воз-
водим обе части уравнения в квадрат и замечаем
sin* х через 1 — соя* х; средн найлеииыд значе-
ний х будут посторонние.
Второй способ. Заменяем aln х —
2t«T
1+ig* 4
i-ig* 4
•4-«<*-|-
t> ал учим
cos X =
уравнение, квадратное отноентельио tg —.
Третий способ (введение вспомогатель-
ного угла). Разделим обе части уравнения на b и,
полагая — = tg ». будем иметь tg 9 sin х 4-
О
4- cos х = —, sin ?slnx4-co$eco»x = -—cos * ;
D D
cos (x — el — — cos e | « найдем no таблицам из
условия Igo “4) ’
Гиперболические уравнения сводятся
к показательным.
I (н + »-*)
Пример. 3 ch х - ah х 4- В; ? ---- “
- 4.»; е* 4- ЯГ-* - » - ft обоава-
2
мая Xх — у, получим у + •— — 9«О; /• — •/+
+ J_ft x-mJLtl^..
Действительные корни некогорыж
трансцендентных уравнений:
1) tg х — г, *1 в 0; xj = 4,4934; хя =»
- 7.7253; ж, — 10,9041; х5 = 14,0662;
17,2208; при п>6хя«е^л -д)*.
2) * lg х = а.
Значение параметра л и,01 0.10 0,30 0.50 0.70 0.90
Наимень- ший корень 0.10 0.31 0.52 0.66 0,75 0,82
ОТДЕЛЕНИЕ КОРНЕЙ
123
Продолжение
Знаменка параметра а 1,00 1.50 2.00 3,00 4.00 5.00
Наимень- ший корень 0,86 0.99 1.08 1,19 1.26 1.31
Значение
параметра
а
10,0 30,0 100
Наимень-
ший корень
3) tg х = th х; х0 = 0; х\ — 3,927; хг =
= 7,069; х8- 10.210; х4 - 13,352; х8 =
— 16,493; при п > 5 х„ «э 16,493 + к X
Х(«-5).
4) tg х — — th х; х0 — 0; х, = 2,365;
х2 — 5,498; при п > 2 хя я» 5,498 + л X
Х(»-2).
ОТДЕЛЕНИЕ КОРНЕЙ
Модуль любого корня, действительно-
го или комплексного, многочлена /(ж) —
= Орх" 4* а^-1 4* ... + а„ меньше
числа 4* 1, где А — наибольший из
модулей коэффициентов вь аз,, а„.
Все действительные корни многочлена
f (ж) заключаются внутри промежутка
"(кг+1)........i^T + L
Отыскание промежутков, в каждом нз
которых лежит один и только один
действительный корень уравнения, на-
зывается отделением корней.
Метод Штурма отделения корней
применяется к многочленам с действи-
тельными коэффициентами, но имеющим
только простые корни; поэтому нужно
освободить многочлен / (ж) от кратных
корней. Для этого следует:
а) найти наибольший общий делитель
D (ж) многочлена / (ж) и его производ-
ной f (ж) (см. сноску на стр. 159);
б) разделить / (ж) на О (ж).
f(x)
Многочлен Q (ж) — -р имеет те же
корни, что и /(ж), но простые.
Пусть /(ж) — многочлен с действи-
тельными коэффициентами, не имеющий
кратных корней т е. взаимно простой
со своей производной f (ж) (их наи-
больший общий делитель — постоянное
число, отличное от нуля).
К функциям / (ж) и f (ж) присоединим
ряд новых функций /1(х), /8(х), .... со-
ставленных следующим образом: (ж)
есть остаток от деления /(ж) на f (ж),
взятый с обратным знаком; /2 (ж) — оста-
ток с обратным знаком от деления f (ж)
на f\ (ж), и т. д., пока не придем к по-
стоянному числу.
Составляется ряд функций Штурма.
/ (ж), f (х), /, (х), /, (ж). /в (х),...
При составлении функций Штурма
положительные постоянные множители
не играют роли; такие множители можно
вводить или отбрасывать для упрощения
вычислений. Обозначим через $ (а) число
перемен знаков в ряду функций Штур-
ма при ж = а; тогда имеем теорему
Штурма: S (а) — S (5) = й, где й —
число корней функции /(ж) в промежутке
(а, 4). причем а < Ь.
Теорема Штурма позволяет прежде
всего определить число всех действи-
тельных корней. Для значений х, до-
статочно больших по абсолютной вели-
чине, каждая нз функций Штурма имеет
знак своего старшего члена; поэтому
можно легко найти число перемен
знаков в ряду функций Штурма для
достаточно больших положительных и
отрицательных значений ж, т. е. 5 (4- со)
и S (—со). Тогда S (—со) —S (4- со)
дает число всех действительных корней
функции /(ж).
Допустим, что действительные корни
многочлена /(ж) содержатся в проме-
жутке (а, 4). Разбивая этот промежуток
на более мелкие промежутки, можно,
пользуясь теоремой Штурма, опреде-
лить число корней, содержащихся в
каждом из них. Если в некотором про-
межутке содержится более одного корня,
то его можно снова разбить на более
мелкие. Этот процесс продолжаем до
тех пор, пока каждый корень не ока-
жется заключенным в отдельный про-
межуток.
Пример, /(ж) - ж* - вж* + аж’ 4- 4л - 4.
Составляем функции Штурма:
-1 /' (ж) - 2х> - 9л* + 8ж + 3;
/, (ж) - иж* - звл 4-10:
/,(л)-7л- 16;
/.(л) = 4 t-
124
РЕШЕНИЕ УРАВНЕНИЯ
Таким образом, /(л) имеет три положитель-
ны! корна в промежутках (0,1): (2.3); (3,4) и
вами отрицательный. Таким же способом найдем,
что отрицательный корень лежит в промежутке
(-1.0)-
ГРАФИЧЁСКОЕ РЕШЕНИЕ
УРАВНЕНИЙ
Для графического решения уравне-
ния / (х) = 0 строят график функции
У = /(*); абсциссы точек пересечения
графика с осью х или абсциссы точек
касания графика с осью х дают вещест-
венные корни уравнения.
Пример. Уравнение х* — 2т3 — Зл4 -ф 8_т — 4 =
= и имеет корни х, = — 2; х,, — 1 (авукратный).
X. - 2 (фиг. 1).
Удобнее разбить левую часть уравне-
ния на два слагаемых /(x) = /j(x) +
+ fl (х) и строить графики функций
У1 = /1(х) и У2=—/2(х). Абсциссы
точек их пересечения дают действитель-
ные корни уравнения /(х) = 0 или
уравнения /,(х) = —/2 (х).
Так, в случае квадратного уравнения
Xs 4- рх + q = 0 удобно положить у| “
= х* и уг “ — рх — q. Тогда одну па-
раболу используем для всех квадратных
уравнений.
Абсциссы точек пересечения кривой
у = Xя с прямой у " — (рх + q) дают
решения уравнения Xя + рх + q = 0,
а с параболой второго порядка у =
= — (ах* + Ьх + с) —решения уравне-
ния хп + ах* + Ьх + с = 0.
Пример. Уравнение х* — х — 0.2=0 имеет
три вещественных корня: х, = —0,94- х. = — 0,2л
ж, = 1.04 (фиг. 2).
Фиг. 2. Графическое решение уравнения
х* х — 0.2 -0.
Фит. I. Графическое решение
уравнения
л4 —2ж> — Зх3 -ф 8х - 4 — 0.
Аналогично решаются уравнения типа
ех 4- ах 4- Ь =з 0,
sin х 4- ах1 4-&х 4-
+ с = 0.
Пример. Уравнение
2х > 4х имеет корни
X- 0,31 и х — 4.00
(фиг. 3).
Подобный прием
употребляют для
решения системы
уравнений А(х,у)=
-0 и/г(х,у)-0.
Координаты х и у
точек пересечения
кривых /, (х, у) =
= 0 и /» (х, у) — 0
определяют реше-
ния системы.
Фиг. 3. Графическое
решение уравнения
2х =4х.
ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
125
Првмр- Системе уравнений x' + y'^IS,
ху — И соответствуют окружность радиуса s
с центром в начале координат н равнобочная
гипербола, отнесенная к асимптотам. График пока-
зывает (фиг. 4), что все четыре решения системы
действительные: jr, = — 4; у, = — 3: хг = - 3;
у, = - 4; х, = + 3: у, = 4- 4; х4 = 4- 4: у( = 4- 3.
Для графического решения уравне-
ний применяются также номограммы
(см. главу .Номография*).
Графические методы применяются,
когда требуется найти только прибли-
женное решение или сделать предвари-
тельный расчет для более точного ре-
шения численными методами.
рень уравнения, а числа а я ft могут
быть приняты за его первое приближе-
ние: с недостатком (число а) и с избытком
(число ft).
Возможны следующие случаи:
1) /(*)<<); /(*)>0; /" (х) > 0 — на
отрезке [a, ft] (фиг. 5);
2)/(д)>0; /(ft)<0; /-(^ХО-на
отрезке |а, ft] (фиг. 6);
3)/(а)<0; /(ft)>0; fW<O-M
отрезке (a, ft] (фиг. 7);
4)/И>0; /(6)<0; /'(х)>О-на
отрезке [в, 6] (фиг. 8).
Точки А и В кривой соединим хордой
и точку пересечения ее с осью х примем
Фиг. S. К метолу хоря и касательных ала
случай / (а) < 0, / (») > 0, f° (х) > 0.
за новое приближенное значение корня
Хп, заменяя тем самым дугу АВ хордой
АВ (метод ложного положения).
ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
Метод хорд н касательных
Если действительные корни уравнения
отделены, tq задача вычисления корней
сводится к дальнейшему уменьшению
промежутков, в которых заключаются
корни. Существуют различные методы,
позволяющие ускорить этот процесс;
остановимся на комбинированном при-
менении двух методов: ложного поло-
жения (простого интерполирования) и
метода Ньютона.
Пусть графически или вычислением
обнаружено, что вещественный корень
уравнения / (х) = 0 лежит между чис-
лами а и ft |/(а) и / (ft) —разных знаков]
н при этом /' (*) и f* (х) нигде на от-
резке |а, ft) не обращаются в нуль, сле-
довательно, сохраняют свой знак на леем
отрезке. Тогда между а и ft лежит
только один вещественный простой ко-
Фиг. 6. К методу хорд и касательных л ла
случае /(а) > 0. /(б) < 0, f (л) < 0.
В первом и втором случаях точка
пересечения at (фиг. 5 и 6) дает более
точное, чем а, значение корня х0 с не-
достатком; вычисляем по формуле
ft— а .
7 (Я);
126
РЕШЕНИЕ УРАВНЕНИИ
получим
при помощи метода ложного положения;
вычисления ведутся по формулам
Более точное, чем Ь, значение корня
с избытком (61) в этих двух случаях
получаем, заменяя дугу АВ касатель-
ной к этой дуге (способ Ньютона) в
точке В, т. е. в точке, где /(х) и f (х)
одного знака, и принимая точку bi пе-
ресечения касательной с осью х за
новое приближенное значение корня х^;
вычисляем по формуле
b -Ь-Ш-
Г(Ь) ’
получим
«I = а
/(а) .
f (а) ‘
b— а
По числам ах и bi аналогично можно
вычислить аг н бу, затем а3 и Ь3 и т. д.,
пока не получится Ьп — ая < е, где е —
сколь угодно малое положительное чис-
ло; тогда а„ и Ь„ будут значениями
искомого корня соответственно с недо-
статком и с избытком с точностью до а.
Указанный способ всегда приводит к
цели, если f’ (х) не меняет знака на
В третьем и четвертом случаях
(фиг. 7 и 8) более точное значение корня
Фиг. 9. Постепенное уточнение корней уравнения
методом хорд и кдсдтельных.
с недостатком получаем при помощи
метода Ньютона, т. е. проводя каса-
тельную в точке А (где опять /(х)
Фиг. 8. К метолу хорд и касательных
*ла случае Да) >0. / (») <0. /• (ж)Х>.
/*(х) одного знака], а более точное
значение корня с избытком получаем
отрезке (о, 6) и если метод Ньютона
применяется к тому концу дуги, где
f (х)
>0. Картина постепенного уточ-
нения корней уравнения показана на
фиг. 9. Знаменатель в формулах Ньютона
при этих вычислениях можно оставлять
неизменным, т. е. f (в) или f (Ъ) не
менять соответственно на f (щ), f (а»),.
или Г (61), /'(61)....
Пример. Вычислить близкий к 1 корень
уравнений л4 — Зл* 4- 8л* — 5-0 с точностью
ао ОДП.
Обозначая / (х) — Л* — Зл* 4- 8л* — в, убе
жлаемса похстаноакой. что / (0) — — 5; / (I) — 1
Нахолии /' (ж) - 4л* - »х« 4- 16л; /» (л) -Д2л«-
— lBx-j-16. Корни уравнения J* (л) — 12л* — ULr-f-
4-16 — 0 — мнимые, причем f (I) •• 10 > О, так же
как /» (0) > О. Отсюаа слелует, что на отрезке
[О. 11 /' (л) возрастает; лействительно. /' (О) — 0;
/'(11 —11. слеловательно. /'(л) > 0 на отрезке
[0. 1) я / (л) — монотонна на атом отрезке. Имеем
случай, изображенный на фиг. 6. Для вычислений
имеем ленные: о — О; » - 1; / (а) — — 6; /(В) — 1;
/’(»)-И-
ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИИ
127
Производим вычисления
___-____-____ / (a) 9 — — 0,8333;
/О) 10
/'1»)= Н
-0.9090.
/(О,)--0.6986; /(»,) — 0.C3S8. /'(».)-10.1118.
Такны образом, искомый корень х0 лежит в пре-
делах 0.9049 < л. < 0,9.51. Г. е. с точностью до
ОД» х„ — 0.905.
Если х = х,,, у = у9 — приближенное
решение системы уравнений Д (х, у) =0,
/1 (*• у) = 0, то более точным решением
является
Г f ЗА f d_h
dy dy
.dx ’ dy ~t)y dx
У
У1 “ У» +
Г f dh f dfx
fx~dx~f'~3x
. dx dy dy dx.
Эти формулы могут последовательно
повторяться, как в способе Ньютона для
уравнения с одним неизвестным.
Метод итераций
Простейшим способом исправления
приближенного значения корня уравне-
ния х®, найденного с небольшой точ-
ностью, является метод итераций (тер-
мин .итерация* означает .повторение*).
Приведем данное уравнение к виду
х = ?(х), что легко сделать, переписав
уравнение f (х) “ 0 в такой форме:
х — х + / (х) и обозначив правую часть
•того уравнения через ? (х). Подставим
исходное значение корня в правую
честь уравнения х= ф(л) и получим
первое приближение корня at ™ <f (ад);
подставив at в правую часть уравнения,
получим второе приближение Oj=f(ai)
и т. д.
Если при надлежащем выборе функ-
ции <f>(x) последовательность чисел
о®. «1 = ФИ»), flj - Т (“1)... ая —
— ? («л_|). а„+1 = <? (ая) .. . стремится
к пределу a = lim ал, то этот предел
Л—оо
и является корнем данного уравнения.
Числа «о, о1( аг,..., а„,... будут прибли-
женными значениями для корня урав-
нения, причем эти приближенные зна-
чения должны стремиться к корню урав-
нения по мере возрастания номера при-
ближения п.
На практике ведут вычисления, т. е.
повторяют подстановки до тех пор, пока
два последовательных приближенных
значения не окажутся равными в пре-
делах тех десятичных знаков, с какими
ведется вычисление-
Итерации дают последовательные при-
ближения к искомому корню тогда
и только тогда, когда | у' (х) | < 1 в окре-
стности корня, в частности в точке х=а9-
Если |ф'(а0)|>1, то для применения
способа итераций уравнение х = ф (х)
заменяют уравнением х = ф to* r*e’
ф (х) — функции, обратная функции
Т to-
Погрешность каждого нового прибли-
жения будет равна погрешности пред-
шествующего приближения, умножен-
ной на правильную дробь | ф' (а,)
если процесс сходящийся.
Прихгр. Найти наименьший положительный*
корень уравнения х — tg х.
Построив графики функций у — х и у = tg с.
упихни, что наименьший положительный корень
уравнения близок к —. повтому полагаемо.— — —
= 4,7124 (см. табл. I). Так как (tg л)' — sec* х >1
то данное уравнение заменим уравнением х —
— arctg х. и вычисления ведем по схеме, поль-
зуясь таблицами Б. И. Сегала и К. А. Семснхяе»
(см. стр. 351 (1S5J):
п °яф-1 - %
0 4,71» 4,5033
1 4.5U33 4.4919
2 4,493“ 4.4934
3 4.4934 4.4934
Получим корень а — 4.4934 с точностью до
четвертого десятичного знака.
Метод итераций
систем уравнений,
уравнений типа
применим и для
в частности дл»
х - (х. у).
У - Ф (*. Л
128
РЕШЕНИЕ УРАВНЕНИИ
ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ
ЛИНЕЙНЫХ УРАВНЕНИЙ
Излагаемый здесь способ приближен-
ного решения системы п линейных урав-
нений с п неизвестными заключается
в последовательном исключении неиз-
вестных. Решение ведется по особой
схеме, являющейся одним из видоизме-
нений схемы Гаусса. Схема предусмат-
ривает возможность попутного контроля
вычислений. При вычислениях реко-
мендуется пользоваться арифмометром
и таблицами обратных чисел.
Покажем порядок решения ва числовом при-
мере.
Пусть лава система уравнений:
3.78л, + 1,18Ла +0,49л, = 23 Д 1
2,15л, + 0,35л, + 7,23л, = 44,и; >
1,49л, + 3,27л. + 0,48л, = »,3. J
В общем случае подобная система запишется
так:
о,,.!, -f- a„tt+ я„л, = #,; 1
ЛцЛ| + ОпХ, 4- ЯиЛ, = 0,; \
о.нТ, 4- а„л, 4- а„г, — )
Для записи хода решения составим бланк по
форме, указанной на этой же странице, и работу
ведем следующим образом:
1) Запишем в средних строчках граф 1—3
в соответс гвуюших колонках коэффициенты залай-
пых уравнений и свободные члены.
2) Найдем суммы коэффициентов и свободных
-членов заданных уравнений и запишем их в соот-
ветствующие строчки КОЛОНКИ S .
3) По табл. Ill найдем = 0,265. =
— 0,465, —— = 0.671 н запишем вти числа а ко-
ланку л. над соответствующими коэффициентами.
4) Найдем произведения: л„ —1— = 0,313,
0,1
а„ -!_=о,13,1>, — -634. V — =8.29. л„ —=0,16,
а>, e,i “if"
а„А_ЗДб, б ' «20Д Xj—ОД. а„ —-
- 2,19, а» — — 032. — 13Д У — «17.1
е-i “з а„
и полученные числя запишем н хижине строчки
граф 1—3 и соответствующие колонки, в ко-
лонку л, в те же строчки запишем единицы
После этого в ни жни, строчках граф 1—3 распо-
ложатся коэффициенты прицеленной системы трех
уравнений:
л, 4- 0.313л, 4- 0.13г. — 6,84; ]
л, 4- 0.16 л, 4- 3,36л, = 20,5; ,
Л. 4- 2.1» х» + 0.32л, - 13Д J
а также контрольные суммы = 8.29. Vj = 25/1,
Lj « 17,1, которых1 в целях контроля вычислений
вновь получим непосредственным сложением чисел
-соответствующей строки; действительно,
14- 0313 4- 0.13 4- 6,84 - 8,28 ч 8.29;
I 4- 0,16 4- 3,36 4- 20,5 = ОД
1 4-2.19 4-0.32 4- 13,6 =17,1.
5) Вычтем почленно из первого приведенного
уравнения второе, а затем третье; результаты
запишем в средние строчки граф 1' и 2'. То же
сделаем с соответствующими контрольными сум-
мами, которые проверим непосредственным сло-
жением. действительно:
0,15 4- (- 3.23) 4- (- 13,7) = - 16,8 - -16,7:
(- 1.88) 4- (- 0,19) 4- (- 6.8) = - 8,9 - - 8,8.
6) С полученной системой из двух уравнений
0,15л, - 3,23л, = - 13.7; |
-1,88л,-0,19л. = - 63 J
и с соответствующими контрольными суммами
поступим, как указано в пп. 3—5, и придем
к одному уравнению — 21,7л, = —95,4, из кото-
рого найдем л. = 4,4 и запишем в колонку .Ре-
шение* и внизу таблицы.
7) Умножим л, = 4.4 иа значения коэффи-
циента а, в пяти первых приведенных уравнениях
и запишем полученные произведения (0,57; 15;
1,4: —95; 0,41) в колонку а„ к верхние строчки
граф 1-3, 1'. 2'.
8) Произведения а^г,. записанные в графах 1'
и 2'. вычтем из соответствующих свободных чле-
нов приведенных уравнения и получим два значе-
ния для л,: (— 91,8) —(—95) =3.2; 3,6—0,44 = 3.2;
эти значения запишем в колонку .Решение*,
а их среднее арифметическое — внизу таблицы.
О| «1 а. 6 I Реше- ине
1 0,265 1.0 0.57 Л, = 5.3
3.78 1.16 0,49 25.8 31,3
• 0,313 0,13 6.М 8.29
2 0,465 0.51 15 ж|в 5,0
2.15 0.35 ’.23 44.0 53,7
• 0,16 3.36 20.5 25,0
3 0.671 1.0 1.4 л, - 5,2
1.49 3.27 0.48 20,3 25,6
• 2,19 0,32 13,6 17,1
1' 2' 6.7 -95 л, — 3,2
0.15 -3.23 -13,7 -16.7
1 -21,6 —91,8 -112
-0,532 0,44 л,-3,2
-1.ЯЯ -0,19 -6,8 -8.8
1 0,10 3.6 1 4.7
1» -0,0161 -Г.— 4.4
-21.7 -96.4 -117
1 4,40 5,38
Округление: л. « 5,2; л, => 3.2. в. = 4.4.
ПРИБЛИЖЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
129
9) Умножим х, = 34 их значений коэффициен-
тов в] в трех первых приведенных уравнениях и
запишем полученные произведения (Где 0,51; 7j0>
в колонку а, в верхние строчки граф 1—3.
|С) Произвехекия а^х, и арг„ записанные в гра-
фах 1—3. вычтем нз соответсгиуюшнх свободны!
членов приведенных уравнений и получим три
значения *ля X, : 6,84—1,0—0,57 — 53; 203-031 —
—15 —5Д 13,6—74—1,4 ~ 54; вти значения запи-
шем в колонку .Решение*, а их среднее арифме-
тическое — виизу таблицы.
II) Полстаиовхой в данную систему уравнений
убедимся, что числа 5,2; 34; 4.4 лают решение
системы с точностью до двух диаков.
ПРИБЛИЖЕННОЕ РЕШЕНИЕ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
ПО МЕТОДУ Н. И. ЛОБАЧЕВСКОГО *
Пусть уравнение арх" 4- ajx"-1 4-
+ Ojx"-2 4* • • 4- о„ — 0 имеет корни яд,
°г. яя-
Составление по данному такого урав-
нения Аогл 4- Aizn~1 + Ляг"-2^- .. .+
+ Ая = 0, корни которого будут
2 2 2 2
— а,, — oj, — 03,..., — ап , называется
квадрированием. Коэффициенты преоб-
разованного уравнения вычисляют по
формулам
Л - aj; At - aj — Ai-a] —
— 2a.a, 4- 2aoa«; A, - a] — 2a&< 4-
4- 2а,а4 - 2а„ал;...; A, - a2.
Выполняя квадрнрованне последова-
тельно k раз, приходят к уравнению,
корнями которого будут —а”, —а.”,
— а"....— а”, где т = 2 называется
степенью квадрировання.
Сущность метода Лобачевского состоит
в образовании по данному уравнению
путем ряда квадрированнв нового урав-
нения, корни которого были бы столь
высокими степенями корней данного
уравнения, чтобы по коэффициентам пре-
образованного уравнения можно было
вычислить с требуемой точностью корни
данного уравнения. Эго делается сле-
дующим образом.
Пусть все корни данного уравнения —
вещественные и различные:
«1> 11>“1>-->ад-1 >“«
Тогда при достаточно большом числе
квадрированнй будут справедливы с тре-
• Этот метод опублмкоми Н. И. Лоблчекким
я 1834 г.; см. литературу на стр. 351 |П7]. (151).
9 Том 1 Зак. 1461
буемой точностью следующие равенства:
_т А, . .ля А) . — А, . .
1 “ А. ’ 2 А, ’ ’ Ад.....
из которых и получаются абсолютные
значения вещественных корней. Знак
каждого корня определяют, подставляя
его со знаками плюс или минус в дан-
ное уравнение.
Всего квадрированнй нужно сделать
столько, чтобы в последнем преобразо-
ванном уравнении каждый коэффициент
стал равен (с требуемой точностью)
квадрату соответствующего коэффициен-
та предпоследнего уравнения; при вы-
числениях с помощью логарифмов ло-
гарифмы коэффициентов преобразован-
ного уравнения окажутся в 2 раза
больше логарифмов соответствующих
коэффициентов преобразуемого уравне-
ния. В этом случае говорят, что коэффи-
циенты при квадрированнй изменяются
правильно.
Число квадрированнй тем меньше,
чем больше отличается от единицы
отношение наиболее близких по абсо-
лютной величине корней и чем меньше
требуемая точность. При вычислениях
с пятью-шестью знаками достаточно
в большинстве случаев шести-семи квад-
рированнй.
Если некоторые коэффициенты данного
уравнения при последовательных квад-
рированиях не показывают тенденции
возводиться в квадрат (в подобном слу-
чае говорят, что эти коэффициенты изме-
няются неправильно), то данное урав-
нение имеет либо кратные, либо ком-
плексные корни, либо н те, и другие.
Если при квадрированиях какой-
либо коэффициент А, меняет свой знак
и расположен между правильно изменя-
ющимися коэффициентами А/-( и Ац_1э
то это является признаком наличия
в данном уравнении простой пары сопря-
женных комплексных корней р (cos ft
±1а1пф), модуль которых определяют
с заданной точностью по формуле
-"/F-
Если в том же уравнении имеются
пары смежных коэффициентов, например.
130
РЕШЕНИЕ УРАВНЕНИИ
т а. А» Оз
1 1 1 — 6
0? — 1 — 2а„а, — 12 1 к? 11 11’ 11 Й4 8i •
2 ! 13 1g а, - 1,114 - .3b lg (— a,) = 1.556
А* « |Ь9 <— 2а«л? — 71.9 21g а. - 2,228 1g (— 2а,дО — 1.857 «Ц— 129 — 2a,a, — - 5410 2a.a. - 512 21g (-a,) —3,112 lg 2a, — 1,415 Tg а, —2,318
lg 2a,a, — 3,733 lg 2a, a, —2,709
4 1 2.41-Ш1 lg а, = 2.382 - 4,77-10“ |g (— a,) — 3,679
а’ — 5.8110" (- 2а,fl,) = 0.96-10“ 2 1g а, = 4,764 lg (— To.aJ = 3,980 0^ = 2,28-10“ — 2a,a, = —2.97-10“ 2a, fl, = 0,01-10’ 2 lg (- a,) - 7,358 lg 2a, = 2,683 Tg a, = 4.790
lg 2a,a, = 7,473 lg = 5,117
8 1 £.77 10“ lg а, — 4,831 -2.68-10’ lg(-a,)= 7.428
а* — 4,59- IO* (— 2а. о,) — 0.06- 118 2 Iga, - 9.662 lg (- 2a,a,) — 7.729 a' — 7,18-10“' - 2a,a*. — - 6,00-10» 2a.,a, — 0.00-10» 21g (- a») — 14,856 lg 2a, - 5,132 Iga,- 9.646
lg 2a,a, — 14,778 Ig2a„a. - 9,933
16 1 4.64-108 1g a, - 9,667 1,18-10» lg a, -14,072
а' — 2,16-10» - 2а.,а, - 0,00-10» 2 Iga, - 19,334 lg 2a„a, — 14,373 a'- 1,39-10» - 20,0,-- 18,4-10* 2a jO, — 0,00-10“' 2 Iga,-28,144 lg 2a, — 9,968 Tg a, -19,297 lg 2a,a, — 29,265 lg 2a,fl. — 19,565
32 1 2.16-10'* lg a, — 19,334 — 1,70-10*
32 1g а, - 19.334 64 lg р — 38.594 - 19,334 — 19,260 1g в. — 0,604 1g р — 0.301 1 а, 1— 4.02 р - 2,00
От бет: а, — — 4; “i..“ 1± ‘ fVTl
ПРИБЛИЖЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЯ
131
а» <2.
10 -16
а,'— «оо — 2ах>, — — 192 aj —256
206 1g а, — 2,318 286 lg a, - 2,401
а?-43 300 (—2а,а.) = 18 «00 2 1g а, - 4.636 lg (- 2л,) -1.857 1g а,-2,408 1g (-2<ца.) - 4.2S5 a*-65 500 21g a, = 4,816
в.17-10* lg a, = 4,799 6,55-10* lg at» 4.816
а’ - 3,80-10* (— 2а,а,) — 0,63-10* 2 lg а, — 9.580 lg (-1а,) — 3,980 lg а, —4,816 tg (- 2а,а,) - 8.791 a," — 4,29-10* 2 lg a. - 9,632
«,43-Ю* lg а, - 9,646 4,29-10* Igo, —9,632
а! = 1.96-10» (-2а,а,) = 0,02-10» 2 1g а,- 19,262 tg (- 2а,) — 7,729 Igo, = 9,632 lg(— 2а,а.) = 17,351 a? = 1,84*10» 2 lg a. - 19.264
1.98-10» lg a, = 19.297 1,84-10» tg a, - 19.254
/ц-3.93-10- — 2^«а4 • — 0.00* 10- 2 Igo, = 38.591 lg 2а, = 14.373 lg a, = 19,264 lg 2а.а, — 33.637 aj =3.37-10» 2 1g a, =38.528
3.93-10» lg a, - 38,501 3.37-10» lg a. - 33.523
321g 11. -38,528 - ЗЯ,594 --0.066
1g «. — - 0,002 —1.998
К 1-0.995
— I.
9»
132
РЕШЕНИЕ УРАВНЕНИЯ
Л, и Лу_р изменяющихся правильно, то
уравнение, кроме указанных комплекс-
ных корней, имеет и простые веществен-
ные корни, абсолютные величины кото-
рых определяют по формуле
Допустим, что данное уравнение не
имеет кратных корней, что можно об-
наружить, не решая уравнения |см.
стр. 1181.
Определив все вещественные корни
данного уравнения и модули всех ком-
плексных корней, найдем их аргументы.
Если уравнение имеет одну пару
комплексных сопряженных корней с мо-
дулем р, то их аргумент ? находится
из равенства
,, Я1
хр COS <р = - -2 — а, - «, — ... —
где аь а*....ап—2 ~ все простые ве-
щественные корни.
Если уравнение имеет две пары ком
плексных сопряженных корней с моду-
лями pi и ps, то их аргументы и
находятся из системы уравнений
2pj cos if 1 + 2рг cos <р2 =
-cos ?1 + -cos Т2-
°1 “X •«*
Если уравнение имеет несколько пар
комплексных сопряженных простых кор-
ней, то, чтобы найти вещественную
часть р какой-нибудь пары р £ qi
с модулем р, делим левую часть данного
уравнения на трехчлен ха— 2рх + р1,
оставляя р неопределенным, пока не
получи»! остаток 1-й степени относитель-
но х: Р (р) х + Q (р). Затем находим
общий наибольший делитель многочле-
нов Р (р) и Q (р) и приравниваем его
нулю. Полученное уравнение и опре-
делит величину вещественной части р
корня, а мнимая часть находится по
формуле
Если при вычислении окажется, что
шесть или семь квадрирований не от-
деляют корней, а присутствие отрица-
тельных коэффициентов в преобразо-
ванных уравнениях укажет на суще-
ствование комплексных корней, то это
значит, что модули комплексных корней
весьма близки между собой. Тогда
вычисления следует начать вновь, пред-
варительно преобразовав уравнение вве-
дением новой неизвестной у — х — Ъ,
пГ~а'
где Ъ к; I/ —2 . В уравнении с неиз-
вестным у модули корней, соответствую-
щих прежним корням с равными моду-
лями, будут уже не равны между собой
Указанным выше способом найдем ком-
плексные корни преобразованного урав-
нения и понизим его степень (см. при-
мер 1); следовательно, в уравнении
могут остаться лишь близкие или рав-
ные между собой вещественные корни,
число и присутствие которых обнару-
жатся по изменения»! коэффициентов при
последовательных квадрированнях.
Если при квадрировании уравнения,
освобожденного от комплексных корней,
окажется, что между правильно изменяю-
щимися коэффициентами А/ и А^г по-
мещаются коэффициенты »<+1, А/+г,...,
Af+r_t, изменяющиеся при повторном
квадрировании так, что имеют место
равенства
lg^+1-21g^+1-lg([);
'g A’-h-i - 2 ‘g A-h-i - ’г (г 11).
то уравнение имеет вещественный ко-
рень кратности г, определяемый по
формуле
Если корни уравнения не равны
между собой, а лишь весьма близки,
то указанные равенства имеют место
лишь приближенно.
Чтобы убедиться, в точности ли корни
равны между собой, надо применить
указанный на стр. 118 прием отыскания
равных корней.
ПРИБЛИЖЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЯ
133
Пример I. Положим, нашли, что уравнение
X1 2л* 4- х 4- 2 — и имеет пару комплексны*
сопряженных корней с модулем р = I; тогда у левой
части уравнения имеется трехчленный делитель
вида г — 1рх 4- р*, т. е. х' — 2рх 4-1. Требуется
найти комплексные корни уравнения и освободить
его от комплексных корней.
Ищем р. Делим по правилу деления много,
членов иг" 4- 2jr* 4- -*4-2) 2рж4-1\ остакляч
р неопределенным. В частном получим х' 4-
4-2(Р 4- О X 4- up' 4- Ар — !>, В остатке (Яр1 4
4- 8р* — Ар — 1) х — .(р1 4- 4р — 3). Искомая вели-
чина р есть общий корень уравнений Нр" 4- Яр1 —
— 4р — I « О и 4р* 4- 4р — 3 — U. Ищем последо-
вательным делением общий наибольший делитель
иного'хлеипи: в р4 -f- Яр1 — Ар — I и Ар' 4- Ар — а.
находим 2р — I.
Полагая 2р — 1 — С, получаем искомое зна-
чение р — i , Следовательно, мнимая часть
комплексного корпя в — Кр* — р' — j/ I — -j- —
/А
— —. Уравнение имеет комплексные корпи
1 н
у ± । . Леля левую часть уравнения на трех-
член г* — х 4-1, освобождаем его от комплексных
корией и приходим к урапиеиию д’ 4- лж 4- I — О.
Пример 2. Решить по методу Лобачевского
урапнеиие
r" + x--«иг> +20*-15-а
Выполняем квадрнроеания, располагая выпи
слеииа но схеме на стр. 130—131 и пользуясь лога-
бифмамн, начиная со второго квалрнрования.
ычисления ведем с точностью до трех знаком.
После пятого кнадрнроваиия замечаем, что лога-
рифмы коэффициентов a,, a* at начали удваи-
ваться, т. е. сами коэффициенты возводятся в квад-
рат. а коэффициент а, изменяется неправильно и
меняет свои знак. Приходим к выводу, что урав-
нение имеет ааа вещественных корня в я я, и два
комплексных сопряженных "р .соа у ± I aln у).
Определим вещественные корни и модуль ком-
плексных корней по формулам .
„32 А, ,64 _ л> . «32 _ А<
I А?' ₽ А? 4 А.
(расчет см. к конце таАлмом).
Округляв результаты до двух злаков и опре-
деляя подстановкой в уравнение знаки веществен-
ных корней, получим at — — 4; р — 2; et 1.
Определяем аргумент комплексных корней по
формуле
а,
2р соз » — — — — 1, — а4,
4 сое ф — -• I f 4 — I,
откуй
I <
COI J-- ; » — —-.
4 о
Следовательно,
“2,3 “ ( cot V * ? ,1л т) “1 * 1 УТ'
Итак, данное уравнение имеет корня — 4,
1 ± 1 /з, I.
Пример 3. Пусть при последовательном ква-
дриролании оказалось, что коэффициенты А, и А,
изменяются правильно, а коэффициент А, после-
дукицего уравнения приближенно равен половине
квадрата соответствующего коэффициента преды-
дущего уравнения, т, е. 1ц А.^ — 2 lg А, —1g 2; за-
ключаем, что ураииенна имеет двукратный корень,
абсолютную величину которого определяем по
формуле
гае т — степень явадриронения.
ГЛАВА VI
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ*
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ
ПРЕДЕЛОВ
Предел функции. Пусть функция
у = f (х) определена на некотором от-
резке, за исключением, быть может,
некоторого числа а, принадлежащего
этому отрезку. Тбгда символ limy = b
х-ьа
(.предел у равен Ъ при х, стремящемся
к а‘) обозначает следующее: задав про-
извольно малое положительное число е,
можно указать такое положительное
число 8, что при любых значениях х,
взятых из области определения функции
н удовлетворяющих условиям | х — а | <8.
х =£ а, соответствующие значения функ-
ции у = / (х) будут удовлетворять не-
равенству |у> — 6| < е.
Коротко: lim у = Ь, если у сколь
Х—а
угодно близко к Ь при х, достаточно
близком к а.
Пример. Um | 2х -f- 3 | — 5, так как при любом а
иеравеиство | С2х 4- 3) — 5 | < « будет выполнено
при любом значении х, удоалетворяющем нера-
венству | X — 11 < — ; адесь » — —.
Равенство lim у =6 обозначает, что у
сколь угодно близко к Ь при доста-
точно больших положительных х. Анало-
гично определяется равенство limy ™ Ь.
Х-—<»
Символ llmy= -f со (или — со) обо-
х-а
вначает, что при х, достаточно близ-
• См. литературу ил стр. 343—350 [30J. |33|,
РЧ рбЬ |40J. ЭД"
ком к а, у как угодно велико по абсо-
лютной величине, оставаясь с некото-
рого значения положительным (или от-
рицательным).
Примеры.
.. 1
Um ~г —4-со;
л-0
3 3
lim V~i — 4- lim Vx — — оо.
ЛГ— 4-оо X——те
Предел числовой последовательности.
Бесконечное множество чисел, зануме-
рованных всеми натуральными числами
и расположенных в порядке возрастания
номеров, называется числовой последо-
вательностью ui, ид, и„, ип — об-
щий член числовой последовательно-
сти — функция целочисленного аргумен-
та-. и„ = f (п).
Пределом числовой последовательно-
сти называется предел общего члена
последовательности при п -> оо.
3 4
Примеры: 1) Последовательность 2, —, —,
- .5
5 л 4-1
— , ..., и„ «• —j—.... имеет пределом еди-
ницу. так как Um ил — I; деДстьительио,
2) Последовательность
п — 1
ия — —— , если п— нечетное,
вя “ -Jf • вслм п ~ четное,
предела не имеет: ип — I прн л нечетном и
и„ — 0 при п четном. В пом случае говорит, что
последовательность имеет два предельных зна-
чения: Ом I; ид них второе нашвается паи-
большим пределом.
Ограниченная величина. Функция
у “ f (х) называется ограниченной
4 1 б
Т • о • 7........
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ПРЕДЕЛОВ
135
сверху (или снизу) на множестве М,
если существует число С такое, что
/(*) < С [или / (х) > С| для всех х,
принадлежащих множеству М.
Бесконечно большая величина Функ*
иия у = f (х) называется бесконечно
большой при х — а, если 11m |у| = + со.
л+а
Бесконечно большая величина либо
стремится к -f-оо, либо стремится к —оо,
либо не стремится ни к какому пределу,
принимая значения то положительные,
то отрицательные, но по абсолютной
величине безгранично возрастающие.
Пример, у — (— Ijn. п при л -оз (л — целое)
ест» бескоие'шо большая, предела не имеет.
Бесконечно малая величина Функ-
ции у — f (х) называется бесконечно ма-
лой при х -> а, если 11m у — U
х— а
Примеры-. 1) сое л — бесконечно малая при
л - — , так как 11m cos я — U.
2 к
**2
2) — — бесконечно малая при х — ± оо, так
как lim -j- —О.
х - ± ОО
Величина, обратная бесконечно малой,
есть бесконечно большая.
я
Если Пт — = 0, то говорят, что 3 —
«-о ®
бесконечно малая более высокого по-
рядка, чем а. Если порядок бесконечно
малой а принят за единицу и Um— =
а-0 а"
= A 0, где А — постоянное число,
то 3 — бесконечно малая порядка п.
Две бесконечно малые а и р назы-
ваются равносильными (эквивалент-
я
ними), если 11m у = 1. Если В — а 4-
+ е, где а, ₽, а — бесконечно малые,
причем е — бесконечно малая высшего
порядка по сравнению с а, то а назы-
вается главной частью 3; тогда аир —
равносильные бесконечно малые.
Примеры.
. 2 till* Д-
1 — сок я J
I) lira - ----—11m --------г- —
... ... Цту
В1П*
I 2 1
* —- Um — — « — , следовательно,
... М ) .
1 — сок я есть бесконечно малая 2-го порядка отно-
сительно к.
2) Um 8ln г — I, следомтельно, х и sin X —
х-0 х
равносильные бесконечно малые при к-0.
Основные свойства бесконечно малых.
Пусть а, р, 7,...—бесконечно малые
при х -* а; тогда:
О »±3±Т±... — бесконечно малая,
если число слагаемых ограничено;
2)а-и — бесконечно малая, если и —
ограниченная при |х — а|<т;, где
т) — достаточно малое положительное
число;
3) -— бесконечно малая, если
и
Нт и =h 0.
х-а
Основные теоремы о пределах
1) lim А = А (Л — постоянное);
2) 11m [/ (х)4-<? (х) —ф (х)| = lim/(x) +
4- Um f (х) — Um ф (х);
х-а х-а
3) lim [/ (х) ? (х) ф (x)J - lim / (х) X
X Нт ? (х) Пт ф (х);
/ “ Пт/(х)
4) Пт —— — —з-г-, если
х-а ? (*) И® * (*)
11т ? (х) 0.
л-а
5) Если ? (х) < / (х) < ф (х) и
Нт о (х) — 11т ф (х) — А, то
х-а х-а
11т/(х) = А.
л—а
Признак существования предела после-
довательности Для того чтобы по-
следовательность чисел O1, о^..., ап---
имела предел, необходимо и достаточно,
чтобы при любом а > 0 можно было
указать такой член Од/ последователь-
ности, что любые ее два члена, стоящие
после a/у, будут отличаться друг от
друга на число, меньшее а, т. е.
| а/ — а,1 <« при /> N и />Л/.
Важнейшие пределы:
Нт ^1 + -hy ~е «2,71828...; число в
служит основанием системы натураль-
ных логарифмов;
11га (1 + 4 + -т + ••• + Т” 1пл) "
Л-*ОО \ X О П /
— С я» 0,57722...; число С — постоянная
Эйлера;
136
•ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
о Sin* 1 и .
Um--------- 1; Um -=— — 1;
ж—0 X ж—О х
Um а* — 1; Um — — 0;
ж-0 я—оо
Um (l-f- —V — 4х; Um ~ 1 « I;
Я—ОО \ п / ж-о х
Um я*~ 1 _ Ina; Um _f^_-0(e>0);
Х-*0 X X—со
Um - 0'(* > 0); Um M1 + *> - 1;
X-oo x* X-*0 x
Л __ 'у T
Um Vp = 1 (p > 0); Um у -t “ 0;
«-♦DO n-»DO '**
lim Vx — 1;
X-oo
Um —- — A; lim n*x" - 0,
x-0 X B-oo
если | x | < 1;
0, если 0 < a < 1;
И . «>1;
(П n \П
Va+ Vb j _
'2 /
Hm <*"~ П -1 > • • • t**-**1 ~ 1) _
**i (л-I) (jfl-1),..(л*-I)
Л (л — 1) ... (л — A -f-1) f n\
“ 1.2... А "Ча г
l» + 2* + ... +л* I
Um----------------------це-
n
лое положительное);
(A — целое положительное);
Um •
л-оо
1 2 + 3-...-2л
У nt + I
— — I;
hm fL+J + -+"-Z\_
«»«. \ n + 2 2/
Um 1* + 3» + У + ...-К?я-1)» 4.
Л — оо Ла d
Um Ь2+2-Ч-3-4+.--+л(л4-1) = 1 .
Я — ОО па 3 '
Если f (к) конечна для всякого ко-
нечного значения х. то
1) llmf/(x+l)-/(x)|-llm №1 ;
Ж—оо Л-оо(_ X I
2) 11m [ZX* + Ч] - Um f/(x)J ! '
Ж—оо I f (X) J ж-co1
Um -----—— = VTn.
я-co nn-e~n У n
(формула Стирлинга);
! [ 2-4-6..,2л p 1 r.
я-ое [1-3-5...(2л—1)J ’ 2л ” 2
(формула Валлиса).
ОСНОВНЫЕ понятия
ДИФФЕРЕНЦИАЛЬНОГО
ИСЧИСЛЕНИЯ
Функция у “ f (х) называется непре-
рывной при х = а (в точке а), если
lim /(*) = /(а), т. е. предел функции
ж-а
при * -► а существует и равен числен-
ному значению функции при х — а.
Если функция непрерывна, то беско-
нечно малому приращению аргумента
соответствует бесконечно малое прира-
щение функции, т. е. Ау -♦ 0 при -» 0,
где Дх = х — а и Ду w у — /(а) — при-
ращения соответственно аргумента и
функции.
Значение х — а, при котором у =•
— / (х) не является непрерывной, назы-
вается точкой разрыла.
В точке разрыва предел функции лиЛо
вовсе не существует, либо не совпадает
со значением функции в этой точке.
Если в точке разрыва х в а не суще-
ствует предела функции f (х), то могут
существовать так -называемые предель-
ные значения функции справа и слева,
ОСНОВНЫЕ ПОНЯТИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
В7
обозначаемые символами / (а + 0) и
f (а — 0), так что
/ (а + 0) = 11m/ (а 4- ft) = Htn / (х);
Л-0 х-а+-о
/(а -0) = 11m f(a- ft) - lim/(x);
a-о x-a-0
(ft > 0).
Если f (x) непрерывна в точке x — a,
то имеют место равенства
/(a-0)=/(a) -f(a + 0).
Функция, непрерывная в каждой точке
отрезка [а, 61, называется непрерывной
на отрезке [а, 6]. При этом в точке а
требуется лишь непрерывность справа,
т. е. соотношение / (а 4- 0) = / (о),
а в точке b — непрерывность слева,
т. е. соотношение f (а — 0) = J (а).
Если при х " а оба предельных зна-
чения функции / (х) (справа и слева)
существуют и конечны, но не равны
между собой, то говорят, что при х = а
функция имеет точку разрыва 1го рода.
Функция имеет при х = а точку раз-
рыва 2-го рода, если не существует по
крайней мере одного из предельных
значений функции — справа или слепа;
в частности, это имеет место, если
функция стремится к бесконечности
в окрестности точки а, т. е. если по
крайней мере одно из значений функции
/ (а 4- Л) или / (а — Л) стремится к бес-
конечности при Л -» 0 (Л > 0).
Примри-.
г 1, если х > 0>
П 0 •
| -» . X <0s
точке 0 функция ие непрерывна ин слева, ни
справа; разрыв 1-го рода (фиг. 1).
Фиг. L Разрыв первого Фиг. 2. Разрыв второго
рола. рода.
имеет в точке О разрыв 3-го рода бесконечный
скачок) (фиг. ТК
Функция у — / (х), непрерывная ив
отрезке 1а, 61, ограничена на этом от-
рет ке и имеет на нем наибольшее и наи-
меньшее значения. Непрерывная функ-
ция между любыми своими двумя зна-
чениями обязательно принимает все
промежуточные значения.
Функция у = / (х) называется неубы-
вающей на отрезке [а, 6], если пр»
а < х, < х2 < Ь всегда / (хО < f (х,);
если же при том же условии всегда
/(Xi)>/(X2). функция /(х) называется
невозрастающей на отрезке (а, 6).
Неубывающие и невозрастающне
функции вместе образуют класс моно-
тонных функций.
.Монотонная функция может иметь
точки разрыва только 1-го рода. Л\оно-
тонная ограниченная в промежутке (а, 6>
функция имеет в точке а правый,
в в точке b — левый предел; здесь под
буквами а и Ь можно подразумевать
либо действительное число, либо один
из символов со или — оо. В частности,
если возрастающая числовая последова-
тельность ограничена сверху, то она
сходится (т. е. имеет предел при п -+ оо).
Производная н дифференциал. Пучь
функция у = [ (х) непрерывна на неко
тором отрезке. Если аргументу х0 дать
приращение Дх0. т. е. от точки х0
перейти к точке Хо 4- Ахф то функция у
получит приращение Ду — f (х^ 4- Дх0) —
— /(хц). Отношение
/<хЛ + Дх0) — /(г,)
Дхв
дает среднее приращение функции, рас-
считанное на единицу приращения аргу-
мента. Предел этого отношения при
Дхо -* 0, если он существует, назы-
вается производным числом функции /(х)
в точке Xq. Если функция имеет произ-
водное число в каждой точке отрезка,
то говорят, что она имеет производную
функцию на этом отрезке.
Обозначения производной:
-Df(x)- lira llm
ax-»o Ax Ax
Функция, имеющая производную, на-
зывается дифференцируемой. Дифферен-
цируемая функция непрерывна, но обрат-
ное не всегда имеет место.
Если функция у“/(х) изображена
кривой в декартовых координатах, го
f (х) —• tg 1, где а — угол, который
касательная к кривой в данной точке
138
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
образует с положительным направлением
оси х.
Непрерывная функция / (х), не диф-
ференцируемая в некоторой точке
х = х0, может иногда иметь в этой точке
так называемые правую и левую про-
изводные, обозначаемые символами
/' (X# + 0) и f (х0 — 0) и определяемые
как пределы, к которым стремятся от-
ношения
/ (х0 4- Л) - f (v0) f(xn - Л) -/ (х„)
--------Л " =Л ’
если величина Л стремится к нулю,
оставаясь положительной. В этом слу-
чае график непрерывной функции имеет
так называемую угловую точку, абсцисса
которой равна х0 (фиг. 3).
Кривая называется кусочногладкой,
если она имеет конечное число угловых
точек; при этом угол наклона касатель
ной к кривой является непрерывной
функцией абсциссы переменной точки
кривой во всех промежутках, соответ-
ствующих участкам кривой между угло-
выми точками.
Второй производной функции назы-
вается производная от производной
/*(х), третьей производной—
производная от второй производной
т; \
— /• (л); вообще л-й производной
называется производная от (л — 1)-й
производной: —/<л) (х). Производ-
ные четвертого и более высокого поряд-
ков часто обозначаются римской цифрой
без скобок, например /v (х).
Дифференциалом функции называется
произведение производной на произ-
вольное приращение аргумента: dy —
=/' (х)Дх; дифференциал функции есть
главная часть приращения функции:
Ду - / (х 4 Дх) - / (х) = Г (х) Дх + е;
при стремлении Дх к нулю величина е
будет бесконечно малой более высокого
порядка по сравнению с Дх.
В частном случае для у = х имеем
дх “ Дх, поэтому dy — f (х) dx.
Производная 1-го порядка равна от-
dy
ношению дифференциалов:/' (х) = .
Геометрический смысл дифференциала
Фи1. 4. Геометрическое истолкоа»-
ыис дифференциал* функции.
Дифференциал л-го порядка опреде-
ляется как дифференциал от дифферен-
циала (л —1)-го порядка. Дифференциал
аргумента считается при этом постоян-
ным. Таким образом:
d’y м f (х) dx*.... dny — /*л) (х) dx".
Дифференциал л-го порядка dny яв-
ляется бесконечно малой л-го порядка
по сравнению с дифференциалом dx, если
последний стремится к нулю.
Пусть у / (и) и и » f (х). Функция
у = / |<р (х)| = у (х) называется в этом
случае сложной функцией переменной х.
Производные сложной функции:
_ Пт У(х-Ь Дх)-у(х) -
dx ax-o Дх
I?' (X)]1 + f (a) <f' (X);
g-/“(«) I?' (x)P +
4 3f (и) <f’ (x) f (x) ф /• (U) yw (x)
И T. Д,
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
139
Дифференциалы сложной функции.
Если у = /(и) и и = и (х), то
dy = f («) du;
d*y = f (и) <Pu + f (u) du2;
ДЯу = f (u) <Pu + 3f (u) <Pu du 4-
+ f” (u) du*
11 T. д.
Цепное правило дифференцирования
сложных функций. Если у—/(и),
у
“ = К (V). V — <9 (w). W = Ф (х), то =
-/*(«)£' (V)4>'(W) ф‘(х).
Дифференцирование функций, задан-
ных параметрически. Если х=?(0,
dx ср’ (Г) dx*
_ < (У) ф" «) - ф' (П Г (О
<р(0
Нередко дифференцирование по пара-
метру t обозначается точкой, поставлен-
ной над дифференцируемой функцией,
тогда
V- L v’ ху—ух
У i dx' v
dx d,y — d v tflx #
dx* *
здесь dx, dy, d*x, d*y — дифференциа-
лы l-го и 2-го порядков от л и у по
аргументу t.
Если у = f (х) и х = ?(у) являются
взаимно обратными функциями, то
’ °0 " 77х) ' ’ °’’ “ 1Г (х)р :
’ W I/* (JT)|«
31Г (х)|*
I/' (х)|» •
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
с' — 0 (с — постоянная);
х' -1;
(u + v — w)' — и' 4- o' — w‘ (u, V, w —
функции от х);
(си)' — си'\
(uv)' — и v + uv';
(uIu1...ue)'-u,u,.,.u„-|-
+ uiu'2...u„ + ... + u,ut...u'n =
/ ui “1 \
1*3*1 1 Л |
/ и \' vu' — uv' #
хТ”) “ о2 *
(Ж’
/ с\' со'.
\ V ) ~ V* ’
(Xя)' = «Xя-1;
(4)'-^
(VxY-----L=-
2Vx
(”/T)----^1=-;
П |/ х«-1
(е')' — в*-,
(я*)' = ах In а;
(>«*)•-1:
(sin х)’ — cos х;
(cos х)’ — — sin х;
(ctg х)' - - - - (1 + ctg2x);
sinx
(sec x) — —=— — tg x sec x;
cos* x b
.. cosx
(cosec x) — - --- — —ctg x cosec x;
(In sly r)' « ctg x;
(In cos x)‘ — — tg x;
‘«у) --ЙН7 -co$ecx5
но
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
,п (-г + — I = —'— = scc х;
[ \ 4 2 ) | си$л
(□resin xY = - . - 1 — ;
F I - x‘
(arccos jrj’ -------- 1 ;
V i - x<
. (aretgx)'- pJ-_;
farcctgx)'----ГТП?;
(arete XY= °
la,C,g а) а^х‘ *
( Arch —)------‘ ;
\ a / / x« — a‘
(Arth x)' - j _
(-1 <x<+ I);
(Arcth xY — t J
(#") «• _
(д*Х)1Л| — |n д)",Д*Х-
Лп r)'" _ (_ I)"-' ;
(arcsec xY —;
X Vx‘ - I
(arccosec х)' Л V с< - 1 ’ 1
in Ct 4- ± а* )1 —
I X» ± и*
[ 1 in'-"]’- 1 .
| 2л X + а J х* — а! ’
I 1 )пл + 1Г- J
| 2а л - х | Л» — X? ’
(sh xY — ch x\
(ch xY — sh x\
.(,hx) "‘chTT’
(cth xY —----4—
(sinx)f" - sin (* + * y);
(cos x)'"' — cos (x + n ;
(sin Ax)'n — kn sin (fcx + n у) ;
(со» Ax)1" — A" cos ^Ax + I
- m (m — 1) (m -2)...X
X ... (m — n + I) x" " (при целом /ян
n>m производная л-го порядка равна 0);
(jk)'Л - (—D"m(m + 1)(л» + 2)...Х
(Arsh x)'
X (« к"-»—4
(Arch x)'
(^/7уя)-(_1)я-' 4, </п-1)(2/п-1)_Х
X ... |(л — 1) т — 1) ~ 1 _ ;
,/ „/ЯЛ—4
ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
141
(ио)(л' — и'"1- v + ли1"'” •«' +
П ~ 1* и1"-21 -v* + ... + uv'a (фор-
Формула Коши:
/(ft)-/(fl) Г (с)
Ф (ft) — ф (а) “ ф' (с) ’
мула Лейбница);
(«”)' = vuv~l -и' + uv in u-v‘ (и и v —
две функции одного аргумента).
d (и -|- v — w) = du + dv — dw,
d(uv) — vdu 4- udv;
При меры. I) (29*n'-r)' = 2stn‘ x In 2 (Bin' xY «»
- < sl“! * • In 2-2 sin x cos x - 2”n' л In 2 sin 2л;
2) у “ ж**пж ; логарифмируем; tn y—sinjr In x'.
у r
дифференцируем полученное равенство: ——
, , sin x ,
— cos ж In ж 4-, отсюда у' » у (cos x In x -f-
+ “ •*sl“ x ( cos ж In ж 4- J j; этот
прием известен как метол логарифмического
дифференцирования;
3) х « a cos f. у» о aln г; — — a aln ti
' dt
dv d>x <Лу
— — a cos Г. — — a cos Г; - — — a sin t;
al df df
dv a cox I <py
dx “ — a sin t “ C £ dx'™
ж I — о sin О I — a sin Л — a cos << — о cos 2)
t —a aln /)’
I
“ a sin11 '
ОСНОВНЫЕ ТЕОРЕМЫ
ДИФФЕРЕНЦИАЛЬНОГО
ИСЧИСЛЕНИЯ
Теорема Ролля. Пусть функция /(х),
непрерывная на отрезке (а, 6], имеет
в каждой внутренней точке этого от-
резка конечную производную f (х), а на
концах отрезка принимает равные зна-
чения / (а) = f (ft). Тогда между а и &
найдется такое число с, что f (с) — 0.
Геометрически теорема Ролля озна-
чает, что на графике функции у = /(х),
удовлетворяющей указанным условиям,
существует точка с абсциссой х = с,
|в которой касательная к графику па-
раллельна оси Ох.
Формулы конечных приращений.
Формула Лагранжа:
(ft -a)f (с).
«где a<c<ft;
где a<c<ft.
Предполагается, что функции /(х) и
Ф(х) непрерывны на отрезке (а, 6],
имеют конечные первые производные в
каждой внутренней точке отрезка [a, ft]
и ф'(а) не обращается в нуль ни в
одной из точек внутри отрезка (а, 6).
Геометрически формулы конечных
приращений означают, что на кривой,
Фиг. 5. Геометрическое истолкование фор-
мул конечных приращений.
заданной уравнением у =/(х) или урав-
нениями у = f (0, х = ф (0, существует
точка с абсциссой х = с, в которой ка-
сательная к кривой параллельна хорде,
соединяющей точки с абсциссами х " а,
х = b (фиг. 5).
Формула Тэйлора:
/ (х) — / (в) 4-—у-~/* (а) 4-
+ т£^/Ж(а) + ,,,+
где Rn - (x-Z-g21/("> (а 4- 8 (х - а)|
(остаточный член в форме Лагранжа),
причем 0<8< 1;
/?л - (л (Т2\),
(остаточный член в форме Коши),
причем 0< 6 < I;
142
ДИФФЕРЕНЦИАЛЬНОЕ исчисление
я.-оЛлУ /-’(х-ог-'л
О
(интегральная форма остаточного члена).
Формула Маклорена:
/(*) =/(0) + xf (0) + (0) + ... +
Полагая * — t, Л =0.01. получим I Л < <
I я •
< — (0.01)".
Последнее яыряжемме становится меньше, чем
0,5*10 при п =4, поэтому берем четыре члена
разложения:
Ш 1J0I = in 1 + + « 0.0099504.
1 < •»
РАСКРЫТИЕ
НЕОПРЕДЕЛЕННОСТЕЙ
где Ra — /<я) (Ох) (остаточный член
в форме Лагранжа);
(остаточный член в форме Коши);
(интегральная форма остаточного члена).
Формулы Тэйлора и Маклорена по-
зволяют вычислять приближенно значе-
ния функции /(х); для этого сумми-
руют первые л слагаемых правой части
и отбрасывают остаточный член Rn,
точное значение которого неизвестно.
Величина оценивается путем замены
неизвестного значения f*n> [а + 0 (х—а)|
или значения подинтегральной функции
максимальным по модулю значением
этих функций, принимаемым ими в про-
межутке изменения аргумента.
Примгр. Вычислить In 1,01 с семью верными
легитимными жалами.
По формуле ТвАлора:
1п(х + а)-1пх + Л. _1+*(__•.) +
ПС
h
л (а — 1)1 J + а _ д"
Если /(а) = су (а) = 0 или / (х) и <р (х)
одновременно стремятся к бесконеч-
ности при х —• а, то
lim _
х —а f (X)
lim£W
х—а <? (X)
при условии существования предела в
правой части равенства (правило рас-
\ 0 оо \
к рыт и я неопределенностей — и — к
В случае, когда f (а) = <₽ (а) — 0 или
когда f (х) в f‘ (х) стремятся при
х -► а к бесконечности, то lim —
х-а?'(х)
f (х)
“ ',гп • ’ели он существует, и т д.
Правило применяется и тогда,
когда ищется предел отношения
/(х)
ПРИ стремлении аргумента х к
бесконечности, если функции / (ж), (х)
при этом одновременно стремятся к
бесконечности либо к нулю.
Применением этого правила могут
быть раскрыты неопределенности видов
со — оо ^предварительно преобразуем
так:
/(х)-ф(х)- [-J- - :/и)т(л))
и 0-оо ^предварительно преобразуем
Г(х)»(х)-/(х):^Ьу).
Там нал I измемется от 0 до Л, то П - / > 0,
П
а потому | | <
Неопределенности вида О’. 1°°. оо*
приводятся к предыдущему виду при
помощи логарифмирования: если ув
— / (*)’ то In у — ч> (х) In [/ (х)]. Если
будет найден предел логарифма рас-
сматриваемой величины, то последующее
потенцирование приведет к раскрытию
и этого рода неопределенностей.
ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ И ИХ ДИФФЕРЕНЦИРОВАНИЕ
143
Примеры-.
1) Иш
.. — sin х -
» Нт -------1-----------;— 0.
Х-.0 «О® X + сое X — X sin X
4) Пш х*; In (х*) = х In х: Um (х In х) —
х-0 х-0
(1 \
I =11т (-х)-О;
___!_ / х-0
х«/
Пт х* — = 1.
х-0
ГРАФИЧЕСКОЕ
ДИФФЕРЕНЦИРОВАНИЕ
Построение по графику функции у =
= /(х) графика ее производной у' =
™ Г W называется графическим диффе-
ренцированием и выполняется следую-
щим образом.
Пусть имеем график функции у «
™ f (х) (кривая MABCN на фиг. 6).
Фиг. 6. Графическое яифференииромиие.
Разобьем проекцию кривой на ось Ох
на столь малые отрезки, чтобы соот-
ветствующие части кривой по возмож-
ности мало отличались от прямолиней-
ных отрезков. Эти элементарные отрезки
оси Ох не должны быть обязательно
равными; их следует брать меньшими
в тех частях, где функция изменяется
быстрее. Проведем ординаты аА, ЬВ,...,
соответствующие серединам а, Ь... всех
элементарных отрезков. Затем, отметив
на горизонтальной осн полюс Р на рас-
стоянии ОР — 1, станем проводить через
него прямые, параллельные касательным
к заданной кривой в точках А, В,...
Наконец, через точки пересечения этих
новых прямых с осью Оу (а',
проведем прямые, параллельные оси Ох,
до пересечения с соответствующими ор-
динатами (или их продолжениями) в точ-
ках А', В',... Кривая, соединяющая эти
точки, и будет искомой.
ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
И ИХ ДИФФЕРЕНЦИРОВАНИЕ
Функция г™/(х, у) непрерывна в
точке (х0, уд), если
lira /(х. у) -/(х* Уо).
Ж
Функция от многих переменных при
фиксированных значениях всех незави-
симых переменных, кроме одной, может
рассматриваться как функция от этой
одной переменной.
Ее производная по этой переменной
называется частной производной функ-
ции от многих переменных.
Первые частные производные функции
г = f (х, у) обозначаются так:
дг д/ (х, у) д. .
^fx^.y)-Dxf(x.yY,
гх df(x,y) д
ду ду ду 7 у’
- fy (*. у) (х, у) -
- fy (•*,>)- Dyf (x,yY
При дифференцировании первых част-
ных производных получаются четыре
частные производные второго порядка:
Ill
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
= /Г2(*.У) - 0^/(х. у);
г)«г r«
Udy“fvAx- y)-fyx^y)
= /Ji(xy) = y);
d’z ,-r
Jyj ” fvv (X. У) = fyy (x. y) =
= /и (X. у) = D\vf (x. у).
Если смешанные производные/^ и /”х
непрерывны, то /'у — f”x.
При непрерывности частных произ-
водных п-го порядка значение смешан-
ных производных того же порядка за-
висит от числа дифференцирований по
каждой из независимых переменных,
«о не зависит от порядка дифференци-
рования.
Пример, z — х>; J^ — ужУ-•;
^-хУЮж; ££-у(у-1)жУ-’|
5^ — X* (In хр.
Для производных 1-го и 2-го порядка
от функции «=/(*, у) употребляются
часто обозначения Монжа:
дг дг . №
~~ дх 1 Ч “ ^у ’ r “ Ojfl ’
дЧ . . дЧ
S ” дхду * ” Jy*'
Функция г=/(х, у) называется диффе-
ренцируемой в точке (х0, уо), если ее
полное приращение Дг — f (х + Дх,
у + Ду) — /(х, у) может быть предста-
влено в форме Дг = ЛДх + Я Ду -f- ер,
где А, В — постоянные; Дх, Ду — про-
нзвольные приращения аргументов; р =
— У(Дх)к + (Ду)* и О при р -► 0.
Линейная часть приращения диффе-
ренцируемой функции, являющаяся глав-
ной его частью, обозначается посред-
ством dz и называется полным дифферен-
циалом функции/ (х, у). Таким образом,
Дг — dz -j- ер.
Если функция дифференцируема в
точке (х0, Уо), то постоянные А, В всегда
оказываются равными частным про-
dz dz
взводным -3—, -г- в этой точке; еле-
дх ду
довательно, dz — Дх -+ -4^- Ду.
дх ду 7
В соответствии с определением диффе-
ренциала
dx — Дх, dy — Ду.
поэтому
dz — dx + dy.
дх ду 7
„ дг, дг .
Выражения dx, dy называются
частными дифференциалами-, таким об-
разом, полный дифференциал функции
есть сумма ее частных дифференциалов
Пример, г — In Уж*4-у": -у,;
dt У . xiix + ydy
Оу Х' + У' х' + у’ •
Если г = / (х, у), причем х = <р (0.
. ... dz dz dx , dz dy
у_Н0>то—-_—+—^-(фор-
мула полной производной от сложной
функции). В частности, если г=/(х, у),
. , dz dz дг dy
а у — а (x), то -г— = -г—h -г-T—.
7 T' ' dx dx dy dx
Формулы, аналогичные приведенным
выше, имеют место для функций многих
переменных с любым числом незави-
симых переменных.
Полным дифференциалом 2-го порядка
функции f (х, у) называется полный
дифференциал от ее полного дифферен-
циала 1-го порядка. Так,
(Г-z - d (dz) — dxt +
. . dx dy 4- -т-т dyV
dxdy ' dyt 7
Полным дифференциалом п-го порядка
называется полный дифференциал от пол-
ного дифференциала (п—1)-го порядка.
При последовательном составлении
дифференциалов более высокого порядка
приращения dx, dy, dz независимых
переменных х, у, г считаются постоян-
ными.
Выражение дифференциала n-го по-
рядка для функции и = / (х, у, z) может
ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ И ИХ ДИФФЕРЕНЦИРОВАНИЕ
145
быть представлено символическим ра-
венством вида
означающим, что после формального
возведения в л-ю степень трехчлена,
стоящего в скобках (при этом символы
д, дх, ду, дг рассматриваются как не-
которые количества), следует затем
полученную таким способом дифферен-
циальную операцию применить к функ-
ции /.
Частные производные сложной функ-
ции. Если w — f (х, у, г), где х — л (а. о),
у = у (и, о), 2 = z (а, о), то
die dw дх dw ду , dw дг .
ди дх ‘ ди ду ди ' дг ди *
dw dw дх dw ду dw дг
”* дх * ~дй + ду до дг ’ до
Пример, tv = х* 4- у’ + я»; х = uv; у = euv :
• — »1п (uv); = 2xv +!yveuv 4- 2tV cos (uv):
— - 2xu + 2yueav 4- 2zu cos (uv).
Полный дифференциал сложной
функции. Если функции w =• f (и, о),
и — <f> (х, у, г), v = ф (х, у, г) диффереи-
. dw . , dw .
инруемы, то dw — dx + dy +
, dw . df . . df .
4- -j— dz — -f- du 4- do. где полные
дг du до
дифференциалы функций и и и
. ди . , ди ди .
du--57dx+dJ^ + -drdr'
. до .до .до .
do-.-^dx^-^dy + —dz.
Полные дифференциалы 2-го и более
высоких порядков сложной функции
w — f (и, о), где и = 4> (х, у, г),
v — ф (*> У> г)> определяются последо-
вательно как дифференциалы от диффе-
ренциалов; при этом полные дифферен-
циалы любого порядка функций и и о
рассматриваются как переменные, за-
висящие от х, у, г. Символическая фор-
мула для дифференциала любого порядка
(д д \ л.
-т— du 4- — dv ] /
ди до )
справедлива как в том случае, когда
и и о — независимые переменные, так
и в том случае, когда они — линейные
функции независимых переменных. Если
же du и do нельзя считать постоян-
ными, то символическая формула уже
не будет справедливой, и выражение
для дифференциала л-го порядка будет
более сложным.
Пример. Пусть w =• / (и, v), где и — у (х, у),
v -Их, у).
Тогда
4w = dи 4- dv;
ди dv
d'w=^-du'+2 ^4- dudv 4- dvs 4
ои' dudv dv'
4- V-<Pu 4- “ tdv.
• Ли ’ An
Формула конечных приращений для
функции нескольких переменных:
F(x 4- ft, у 4- k. 2 4-1) — F (x. у, г) —
= h-F'x (x -f- 6h.y 4- 0ft, z 4- «О 4-
4- ft Fy (x 4- Oft, у 4- Oft, 2 4- W) 4-
4- Z-E*(x 4- Oft, у 4- Oft, 2 4- 0Z);
(O<0< 1).
т. e. полное приращение функции при
переходе от точки М к точке М' равно
полному дифференциалу функции, вы-
численному в некоторой промежуточной
точке отрезка, соединяющего точки
М и М'.
Формула Тэйлора для функции двух
переменных:
F(x + h.y + k)-F(x,y) +
+ (A^+Aw)F(x,-y)+
+ 5f F<x’^ +
+ --- + (7Г=Л)|(Й^ +
где R„ — остаточный член;
R»“4r(A^+H?)"F(x+
f Oft. у 4- Oft); 0 < 0 < 1.
10 Том I Зак. 1464
146
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Другая форма:
ДР(х. у) — dF (х. у) 4-
+ -^Г^(х. у) + ...+
+ 5ГГТ)!‘'И-,1''<'-» +
+ ’ dwF (х + вл. у + 8Л).
Аналогичные формулы имеют место
для функций любого числа переменных.
ДИФФЕРЕНЦИРОВАНИЕ
НЕЯВНЫХ ФУНКЦИЙ
Если неявная функция у одного не-
зависимого переменного х задана урав-
F (х,у) -0.
яением
то
dF
dV(dr V-i^F dF aF i
tPy &*• \ dy ) ix ду ’ дх ду + dy*
Если / (x) то g - .
Если функция г (x, у) задана уравне-
нием
F (х. у, z) — 0.
то
dF dF
dz _ Ox . di ду
дх dF ’ "Эу" ” dF '
Si ~di
Пример. Урамеиие jd -f- y* -f- x* — A" опреде
лает г как неявную функции х и у. И маем
*____й«_2..
оу 2а а
Если несколько переменных связаны
уравнениями, число которых меньше
числа переменных, то, вообще говоря,
можно рассматривать любые т нз этих
переменных как неявные функции
остальных.
Пусть неявные функции у»,..., ут
переменных xi...... хп определяются
как решения системы уравнений
^i(*i...у>....у„) - 0;
Рг(*1...дг»; У1.>т)-о;
....>1.......ут)-°
Тогда производные определяются пу-
тем решения системы уравнений
ду i ox,dyt дх.
ЭЪ dym dF}
дУт дх, дх
dfn, ду, dfw dya + +
ду, ' dx\ оуг Эх, dym дх,
9?., относительно неизвестных
STI аналогичныесн-
dx| dxi
стемы уравнений составляются
для определения производных
по другим аргументам..
Пример. Система уравнений
2х4-3х-и —4: 1
XI + уи — i I
определяет переменные гни как функции пере
ценных хну. Найдем
дг дх ди ди
дх' Эу ‘ дх' Ту'
1-й способ. Дифференцируем оба ураак»
ими по Xt
1 + ай-37“<х ‘+'£ + >Е“°-
______________________________ да
Решав ати апа уравнение относительно -jj-
ди .
к g-j . кайдем:
дх _ 2у х , ди 2х — Яг
Тх “ Зу-|-х ’ Тх “ Зу 4-х ’
Подобным образом дифференцируем оба ура»
веяна по у, найдем:
дх______и ди _ _ За
Зу“ »у 4-х ’ ду“ Эу4-х‘
1-й способ. Дифференцированием находим
хна уравнения, саяэынаишие дифференциалы всея
четырех переменных: .
24Х -)- Здх — ди — 0;
х их 4- к дх 4- у du 4- u ду - 0.
ОПРЕДЕЛЕНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИИ ФУНКЦИИ
147
Решая аги уравиеиия относительно аг и Ла,
жжхолмм*.
_ &V + г) ах + иву ,
аг^ Зу+х
(2х — за) ах — Зилу
“ “ Зу + х
откуда
Л »у 4-в . дг а
Зх“ Зу + х ’ Зу“ Зу + х '
Ла 2х — Зд. ви _ Ли
Зх““3у+х' Зу ” Зу4-х"
ОПРЕДЕЛЕНИЕ ЭКСТРЕМАЛЬНЫХ
ЗНАЧЕНИЙ ФУНКЦИИ
Функция f(x) возрастает при неко-
тором значении х, если знак разности
(ж + А) — / (х) одинаков со знаком А.
Функция /(х) убывает при некотором
значении х, если знак разности /(х +
+ А) — / (х) противоположен знаку А.
Те промежутки, в котовых f (х) > О,
суть промежутки возрастания функции,
а те промежутки, в которых f (х) < О,
суть промежутки убывания функции.
Говорят, что функция /(х) имеет
максимум в точке х “ хе, если ее зна-
чение /(хе) в этой точке больше всех
ее значений в ближайших точках, т. е.
если
/(хо + А)-/(хо)<0
при всяких А, как положительных, так
и отрицательных, достаточно малых по
абсолютному значению.
Если же выполнено условие
/(х® + А) —/(Хф) >0
при всяких А, достаточно малых по
абсолютному значению, то функция /(х)
имеет минимум в точке х = хф.
Максимум и минимум функции назы-
вают одним словом акстремум (что
значит .крайняя величина*).
Для нахождения тех значений х, при
которых /(х) имеет экстремум, следует:
1) найти f (х);
2) определить те значения х ™ дф.
при которых f (х) обращается в нуль
или не существует;
3) исследовать изменение знака f (х)
при переходе через эти (критические)
значения Хф если знак /' (х) меняется
в точке Хд с минуса на плюс, то имеем
в точке х0 минимум; если знак f (х) ме-
няется в этой точке с плюса на минус,
то имеем максимум.
10» •
Можно также применять следующие
достаточные условия экстремума функ-
ции :f (х9)=ГUo)---------/""’’(ле) - 0.
но /*"* (хф) =# 0, причем л — четно. Если
при этом /<я)(Xq)<0. то функция /(х)
имеет при х = хв максимум; если
/я) (хо) >°, то функция /(х) имеет
при х = х« минимум. Если же при вы-
полнении УСЛОВИЙ f (хф) ” f (Хф) —
(хе) - Ц /Л)(х,)^0
л — нечетно, то при х •*> х» нет экстре-
мума, а имеется точка перегиба (см.
стр. 264).
а
Пример. f (х) = V (1 — х»у; /' (XI —
<г
3 V 1-х’
При х ™ О производная обращается куль, к
при переходе через точку х —• 0 знак произвол-
вой меняется с плюса на минус, следовательно,
функция при х — и имеет максимум. При х =± I
производная имеет разрыв, и при переходе через
точки х = ± 1 знак производной меняется с ми-
нуса на плюс, следовательно, в точках х — ± 1
функция имеет два минимума.
Совокупность значений x1=X|,xt —
= Ху....х„ — х°„. при которых диффе-
ренцируемая функция многих перемен-
ных /(Xi, хя,. ...Хф) может иметь
экстремум (однако не обязательно его
имеет), должна быть решением системы
уравнений
df
dxi
= 0.
*-о.
выражающей необходимое условие су-
ществования экстремума.
Для отыскания тех значений хну,
при которых /(х, у) действительно
имеет экстремум, следует:
I) решить систему уравнений
£-о.
дх ду
2) полученные решения (х>, уд под-
<Я/ d»/ Э»/
ставить ’ W
вить дискриминант
<Pf W
дх» дхду
4 “ d»/ Э»/ 5
дудх ду»
Y48
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
если Д > 0, то f(x, _у) имеет максимум
дг/ дЧ
П₽Н ~dxt<'Q и М,|НИЫ>'М "Ри
если Д < 0, то f(x, у) не имеет экстре-
мума при' исследуемых значениях аргу-
ментов. Если же Д = 0, то имеет место
сомнительный случай; тогда нужно
исследовать функцию f (х, у) при зна-
чениях аргументов, близких к (х(, _у/),
непосредственно убеждаясь, имеет ли
здесь место максимум или минимум, или
ни то, ни другое.
Пример. Точки возможных экстремумов
функции
I - 4- ху« 4- 4- у*
находится путем решения системы уравнений:
dz
— _бж« +уч-iox-а
^-?Х,4-2у-в.
Система имеет четыре решения: 1) х=О,
у — V; 2) х---|-; у-О; 3) х - - I: у - 2;
4) х = — 1: у - - 2.
Так как - 12х + 10, = 2х 4- 2,
ox* df*
2у, то величина Д и двух первых точках
положительна (экстремум), а в третьей и четвер-
той — отрицательна (экстремума нет). В первой
точке > 0, и функция имеет минимум, а ио
второй точке -г-;< 0, и функция имеет максимум.
Для нахождения наибольшего значе-
ния функции, заданной в некоторой об-
ласти, надо найти ее максимумы внутри
области и сравнить их со значениями
на контуре. Наибольшее из всех этих
значений и будет наибольшим значе-
нием функции в данной области. Ана-
логично находится и наименьшее зна-
чение функции в данной области.
Пример. Ня плоскости дан треугольник ОЛЬ
(фиг. 7), обрэзоваипый осями координат и прямой
х 4- у — 1 « 0. Найти такую точку треугольника,
для которой сумма квадратов ее расстояний до
вершин треугольника Пыла бы наименьшей. Вер-
шины Д и В имеют координаты (1,0) и (0,1). Сумма
квадратов расстояний переменной точки (д', у) до
вершин треугольника будет г — 2x* 4-2у* 4-
+ (х-НЧ- (У - 1)*-
Приравнивая нулю частные производные 1-го
порядка, получим л—у •»-у; этим значениям
соответствует минимум д »*/,. Исследуем теперь
виачеиня д на контуре треугольника. Для иссле-
дования г на стороне ОД надо в выражении для а
положить у — О:
г - 2х« +(д - I*» + 1.
причем х может меняться на отрезке (0.1). Убе-
ждаемся. что z на стороне ОД принимает наимень-
шее значение я = */, в точке С, для которой
X = */». Точно так же н
на стороне О В наимень-
шее значение г будет
равно •/, и достигается
в точке D. для которой
у - */,. Для исследова-
ния значений г на сто-
роне АВ надо в выра-
жении Z положить у —
“ 1 — х (согласно урав-
нению прямой):
Z - Зх*+- 3 (X- 1)*.
Фиг. 7. К примеру на-
хождения наибольшего
значения функции в не-
которой области.
причем х может ме-
няться на отрезке [0.1].
В этом случае наимень-
шее значение д будет
Z = 4i и достигается
в точке Е, для которой х — у = “)». Сравнивав
возможные наименьшие значения функции Ч„ »/,.
*),. видим, что наименьшее значение Д —•), до-
стигается в точке F(-=-, — ].
Если разыскивается экстремум функ-
ции нескольких переменных, которые
не являются независимыми, но связаны
между собой одним или несколькими
уравнениями (число уравнений меньше
числа переменных), то говорят об от-
носительном (или условном) экстре-
муме. При решении задачи пользуются
методом неопределенных множителей.
Пусть требуется найти экстремум
функции /(х, у, г) при добавочных
условиях: (х, у. г) — а, ф (х, у. г) = Ь.
где а и Ь — постоянные. Составим
функцию
Р (х. у. г) — f(x. у, х) 4- (х, у. г) 4-
4- рф (х. у, г).
где X и р — неопределенные множители.
Необходимые условия экстремума
функции / (х,у, г) выражаются системой
уравнений
, ь- dF n dF
^-а; ф-fe.^-O.
0.
^--0.
дх
Пусть совокупность чисел х0, v®, г0,
Xe, pg получена при решении указанной
системы. Если при любых приращениях
dx, dy, dz, удовлетворяющих равен-
ствам df = 0, <(ф = 0, знак полного
дифференциала 2-го порядка функции
F (х, у, г) сохраняется положительным,
то в точке (х0, уо, г0) функция имеет
минимум; если знак дифференциала 2-го
порядка сохраняется отрицательным, то
функция в этой точке имеет максимум.
ЧИСЛОВЫЕ РЯДЫ И ИССЛЕДОВАНИЕ ИХ СХОДИМОСТИ
149
Пр амер. Найти такие точки на окружности
X* + у* — 2а*, произведения координат которых
достигают максимума или минимума.
В этом случае г-^х^. F =• ху 4-1. (к* 4- у*),
и система уравнений “ У + 2*-г ” °> в
— X + 2Ау — 0, р х* + у* — 2а* имеет решения:
1) к — а; у — а: А — — А ;
2) к-ж у--а; X-As
»)-г--а: у-а; А-А;
Ох--а;у —-н;Х--А.
В первой к четвертой точках функции кости
гает условного максимума, так как
= “57; чх* 4-2 dx dy 4- — dy* =•
ox' Ох Оу dy*
— 2Xdx* 4- 2dx dy + 2Xdy*.
а из соотношения ? = x’ 4- у* = 2a' получаем
dy = 2x dX 4- 2y dy — 0. откуда о данных случаях
имеем dx = — dy; поэтому
(d»F) t--------4dx><0.
Во второй и третьей точках (d’F) , —
К"“
•г idx* > 0 (таи как соотношение dy — 2xdx4-
4- 2у dy - 0 хает dx — dy). следовательно, фуик
ния достигает условного минимума.
ЧИСЛОВЫЕ РЯДЫ И ИССЛЕДОВАНИЕ
ИХ СХОДИМОСТИ
оо
Выражение V и„ — а, 4- Uj 4- ... 4-
Я=1
+ составленное из членов чи-
словой последовательности, называется
сходящимся числовым рядом, если су-
ществует предел л-й частичной суммы
п
5Я = 2 “* — “1 + “2+ ••• + «я при
/?=1
безграничном увеличении числа л ее
членов. В противном случае ряд назы-
вается расходящимся. Предел части ч-
я
ной суммы S " lim V л* называется
Я-ОО
А— I
суммой ряда.
Необходимый я достаточный признак
сходимости Коши. Ряд сходится в том
и только в том случае, если при любом
наперед заданном а > 0 можно найти
такое число л, что при произвольном
целом т будет иметь место неравенство
|°л4-1 + ••• + "я+я |<»- EcAHjinJufllrU,
то ряд расходится.
Если ряд V |«„|, составленный из
Л=1
абсолютных значений членов данного
ОО
ряда V ип, сходится, то и данный ряд
Л»1
сходится и называется абсолютно ско-
дящимся рядом.
Абсолютно сходящиеся ряды можно
почленно перемножать как конечные
суммы (распределительный закон); члены
их можно произвольно переставлять
(переместительный закон) и группиро-
вать (сочетательный закон), не нарушая
этим сходимости ряда и не изменяя его
суммы. В частности, всеми этими свой-
ствами обладают сходящиеся ряды с
положительными членами.
Если некоторый знакопеременный ряд
сходится, но ряд, составленный из абсо-
лютных значений членов данного ряда,
расходится, то данный ряд называется
условно сходящимся. Изменение порядка
его членов может привести к измене-
нию суммы ряда и даже к превращению
его в расходящийся ряд.
Существуют достаточные признаки,
по которым можно обнаружить схо-
димость или расходимость данного ряда.
Теоремы сравнения. Сравниваются
оо оо
два ряда: У, |«я| и У |оя|. I) Если
Л=1 г. -1
для всех n>N (N — некоторое постоян-
ное) выполняется неравенство | иа | <
<|соя|.гдес — любое число, не за-
висящее от л, то из сходимости второго
ряда вытекает сходимость первого ряда,
а из расходимости первого ряда следует
расходимость второго ряда. 2) Если
существует конечный lim LAd а= К + О
я-со| vn |
(причем |оя|*А0). то оба ряда одно-
временно сходятся или одновременно
расходятся.
Ряды для сравнения:
СО
у aqn — сходится, если и
расходится, если
2 -j — сходится, если k > 1, и рас-
л=1
ходится, если k < 1.
При k = 1 получается гармонический
ряд:
I + ’/« + •/> + Че + ... (расходится).
150
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
и расходи-
Признак сходимости
мости Даламбера. Ряд V । Ц/| | схо-
дится, если lim 1——— < 1; ряд рас-
Л—ОО | и„ |
холится, если Нт । >» 1; в случае.
л-оо | ип I
I и при любом п
когда 11m
отношение
1 > 1, ряд расходится;
в остальных случаях, когда Нт
л-сх
= 1, требуется дополнительное иссле-
дование для того, чтобы судить о схо-
ди мости ряда.
Признак Коши. Если
оо
то ряд У I и„ I сходится; если
п=1
lltn у'Г“П>1,
Л —оо F
то ряд расходится; если
|lm
л-*оо
л ____
* у I “я1 > 1 ПРИ любом л.
то ряд расходится Во всех прочих
случаях, когда
Um }/ГйП - >.
л—оо
для суждения о сходимости ряда тре-
буется дополнительное исследование.
Интегральный признак- Пусть / (х) —
положительная, непрерывная и убы-
вающая функция для всех х, ббльших
некоторого значения х = а, и | и„ | —/(л).
ОО оо
Ряд 2 l“nl сходится, если j /(х) dx
n—I а
сходится, и расходится, если интеграл
расходится (см. стр. 175).
Признак В. П. Ермакова*. Пусть
/(х)— положительная, непрерывная и
* В. П. Ермаков— профессор Киевского
университета и член-корреспондент Академии
паук. Спой примак он опубликовал в .Матема-
тическом сборнике* в 187U г.
убывающая функция для всех х, ббль-
ших некоторого значения х = а, и
оо
I «Л I =/(«)• Ряд 2 I «Л| СХОДИТСЯ, если
Л=1
|,га —тг-т—<1. и расходится, если
л-оо J\X)
этот предел >1.
Признак Лейбница (для знакочере-
дующихся рядов). Ряд |«1| — |и2|-|-
+ | и8 ] — | и4 | + ... сходится, если:
1) I "Лк!. < 1 при любом п и
Л I "л I
2) lim и„ = 0. Сумма ряда S < и4.
Л-»оо
. + оя*-|-...:
Примеры.
1) a + + +
0, если | а | < t
оо, • I о | > 1
Следовательно, ряд сходится, и притом абсо-
лютно. для | а | < 1, расходится для \а | > 1.
При а — ± 1 рад расходится, так как | ип | не
стремится тогда к нулю.
VI
—т- . где Л—любое число больше пула
лЗ "
(при А < О ряд. очевидно, расходящийся^. Здесь
—т*
Пя Xя
По признаку Ермакова
оо, если * < 1
0, . * > I.
По интегральному признаку
Отсюда есно. что
( оо, если А < I;
Следовательно, ряд будет сходащимса. если
А > 1, и расходящимся, если А < 1.
о° |
«2 (-1)»-1* v-i-/,+•/.-•!. + •.*
л—1
Так как I > *h > Ч. и 11ш и —
" л-оо "
— Ilm — — 0, то ры сходится, но сходится
л-оо "
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
151
услопно, так как рад I Ъ -f- -(- */« + • • • рас-
ходится.
Если. принять сумму данного ряда равной
I — ‘Ь 4- Ч- — . .. + ( — 1)« — 1 • — , то отбро-
Л
венный остаточный член выражается бесконечным
радом Rn = ( - 1)« [ J_- .
причем j R | < .—1—. Итак, в этом случае по-
" Л -г I
грешность не превышает
ФУНКЦИОНАЛЬНЫЕ РЯДЫ;
РАЗЛОЖЕНИЕ ФУНКЦИЙ
В БЕСКОНЕЧНЫЕ РЯДЫ
Если задана бесконечная последо-
вательность функций fi (х), /а (х),...,
/,,(х),.... обладающая тем свойством,
что при любом фиксированном значении
аргумента х = х< на некотором отрезке
[a. b I числовой ряд fa (хЦ 4- Л (xi) 4-
4- . . 4- fn (*»> 4- .. • сходится, то выра-
жение fi (х)+/а (х)4- . . +/я (х) + . ..
называется сходящимся на отрезке (а. 6)
л
функциональным рядом, a lim V, /*(х)=
«-’“5=1
“ f (х) — его суммой.
ОО
Функциональный ряд У, falx) назы-
вается равномерно сходящимся иа от-
резке |а, ft], если при любом задан-
ном i>0 можно указать такое целое
число N, не зависящее оз х, что при
n> N неравенство | Rn (х) | = | /„ (х) +
4- fb+i (х) 4- ... | < • будет иметь место
для любого значения х на отрезке [a. ft].
Сумма равномерно сходящегося на
отрезке |а, ft 1 функционального ряда,
члены которого /Цх), /,(х),... являются
непрерывными функциями, предста-
вляет непрерывную функцию /(х)~
ОО
= У, /«(*) "а том же отрезке.
л—1
Если ряд /|(x)f/!(x)+ ... сходится
ОО
равномерно на отрезке [a. ft] и £Л(х)=
Л=1
*= fix'). то j f(x)dx = У J /л(х) dx
а л—1 а
(т.е. ряд можно почленно интегрировать).
Если ряд /( (х) 4- fa (х) 4- ... схо-
дится равномерно на отрезке [a, ft], то
Л=1
(т. е. ряд можно почленно дифференци-
ровать).
Степенным рядом называется ряд
вида
Оо + П1 (х — «) 4" а» (х — а)’ + ... 4-
4- ап (х — а)п 4- .,.,
где ао, ад, аз, .... а„ и а — постоян-
ные; в частности, может быть а = 0.
Степенной ряд сходится абсолютно
для всех значений х, удовлетворяющих
неравенству | х — а | < р, где р — радиус
сходимости степенного ряда, который
определяется по формулам
2_= 11m ' в"4-1 । -
р «-со I ап |
На границах промежутка сходимости
(а —р, а 4- р) ряд может сходиться или
расходиться. Всякий степенной ряд с
радиусом сходимости р>0 есть равно-
мерно сходящийся на любом отрезке,
принадлежащем промежутку его схо-
димости.
Пример. Ряж I4.i4.2l + ... f — 4--’.
имеет — — Um Я — 1, т. е. р — 1, н рях
? Л-ОС «
сходится абсолютяо для —1 <х<4-1; при
х — — 1 ряж сходится условно, а при х — I ряд
расходится.
Если при безграничном увеличении
числа членов формулы Тэйлора иля
формулы Маклорена остаточный член
R„ стремится к нулю в некотором про-
межутке (а, 0), то степенной ряд
/<«>+>’<*>+(а)+
сходится к функции /(х) в этом про-
межутке-
1*2
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Разложения некоторых функций в сте-
пенные ряды:
1) (1 4- хУ - 1 + ух + х» +
я(я-1)(а_2)
т 1-2-3 х--г ... т
, а (а-!)...(«-л 4-1) „
* 1-2-3...п ’
Разложение имеет место для |х|< I;
ряд, стоящий в правой части равенства,
называется биномиальным; поведение
его на концах х = ± 1 промежутка его
сходимости определяют по таблице
X = 1 а>0 Абсолютно сходится
- 1<« <0 Сходится условно
«<- > Расходится
в> 0 Абсолютно сходится
.<0 Расходится
2) -j—J—- — 1 — х 4-хг — х® + х4 —.1 <х< 4-1);
1 “г л
3) T^j-- 1 +-J4- -з- + -^ + -..(х>1 И х< —I);
4) К 1 т X — (1 4- х) J - I 4-4-X— ~ х® + J А х» ,? ЛДг X* 4-
= I 4- -у х — 2- х» + -^ х» — х< 4- — (— К X < 4-1);
2 о ID 12о
5) ]/Т+"х М1+х)~-1+у.х-^х,4-^*-^х‘ + — хв-
—1 <х< 4- 1);
то 1 . * ЬЗ - 1-3-5 . , 1-3-5-7 . 1 ,
6) 7Щ-1-2-е+Т4ж,-ТГьл* + !ОТ8^“---"1“'2'х +
4- х> х® + -j^g- х* — I <х < 4- I).
7) ' -|_^+^«ж.+ ^ж._ «ул.*...<-1<л<+1М
У 1 4-Х
»> ^<ТТ77- , * £ л * **....
где р>0 и 9>0(— 1 <х< 4- I);
9) **-1 +т + у7 + т£з+’*4
Ю) в-х-1_^ + _^_т^_+„,
11) ! 4--^х4-^~^х®4-д^ух’4-...(с>0);
12) in(1 4- х) — х—4- -j-f + ••• (— 1 <х< 4- 1);
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
153
13) In (1-х)- _(х+^- + ^-(—1 < х < + 1);
HHn-Lii - 2(ж+ 4 + 4 + 4 +...)(-1 О < + 1);
И) 1»г±1_2(±+11- + _^.+ 7Lr + .„)u<_| „ Ж> + »;
|6> ‘ - 2 {ттт + т(ттт)’+ т(ттт)’+ -} <’ > и:
17) Inx-(x-l)-l(x-l)*+-j(x-l)»-...(0<x<2);
19) >„ (. + л) _ и а + 2 + | + + -}
(л>0; Х> —в);
, х Xs . х6 У
20) sinx- , --^273+ i.2.3-4-5 1 2-3-4-5-6-7 +",;
21) созх- 1 — y-j + Ь2.3.4 - 1.2.3.4.5-6 + "• ’
22) tg x — x 4- у х» + yr х» + -gjjr x*+ •«*+••• (lx I <-j) ’•
23) ctgx-l-lx-A-xe-^-xS-^ x»-...(|x|<«. кроме мо-
чения x = 0);
... . , 1 x9 , ЬЗ x6 ЬЗ-5 х^ . . ...
24) arcsinx-x++ + 2.4.б'"7~ +
25) arctgx-x-^- + y--y-+...(|x|<l);
26, !Ьх-^ц^_ж+14г+г54Г5+..!
Я)Л„«ц^_,+^+п^+....
26) + +
. . 1 Xе ЬЗ х5 ЬЗ-5 х» ,
29) Arshx-x—г— .-.-у-—?.-7-+...(|х|<1);
30) Arthx-x +-у + -у- + Т‘ + ,”(,х|<1)-
ГЛАВА VII
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ*
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
И ЕГО СВОЙСТВА
Если F' (х) = /(х), то функция F (х)
называется первообразной или прими-
тивной для функции /(х). Всякая не-
прерывная функция /(х) имеет беско-
нечное множество первообразных, отли-
чающихся друг от друга постоянным
слагаемым. Выражение F (х) + С, из
которого можно получить любую перво-
образную для /(х). придавая постоян-
ному С определенные значения, назы-
вается неопределенным интегралом от
/(х) и обозначается символом у/(x)dx.
т. е. j / (х) dx = F (х) + С, где F (х) —
некоторая первообразная от / (х);
С — произвольная постоянная, f (х)—
подинтегральная функция-, f(x)dx—
подинтегральное выра жение-, f — знак
интеграла.
Основные свойства неопределенного
интеграла:
dy/(x)dx —/(x)dx;
|J/(x) dx]' — f{xY,
J dF (x) - F (x) + C
j A/(x) dx — A j /(x) dx. если A - по-
стоянная;
У [/(x) + f (x)-ф(х)| dx-
— J f (x) dx + J f (x) dx — f ф (x) dx.
Таблица осаоааых аат«гр«ло* (постоаняи интегрированна С мм* опушена
и пожразуыемется)
<*-»
f dx ...
I — = ln|x|
f e* dx - e*
у-^-й
У sin x dx — — cos x
У sh x dx — ch x
У cos x dx — sin x
j ch x dx — sh x
У lg X dx — — In COS X
У Ih x dx — In ch x
У etg x dx = In sin x
У cth x dx — In sh x
f dx
dx
ch»7
— etg x
— cth x
vatc,gv
------arcctg —
a a
Сш литературу "• стр. M9-3S0 (ЗЦ. РЧ. psj, (36|, (87|.
ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
155
= In (х + /х* + а»)
(для Iх|<|а|)
С dX 1 . ... Ж
I я—zr “ — Ar,h — “
J а*—х* а а
1 1па + х
(для |х|<|в|)
(для |х|>|а |)
( ** - Arch 4--
J /х* —а* в
= In (х + Ух*— а*)
(для Iх|>|аI)
ОСНОВНЫЕ МЕТОДЫ
ИНТЕГРИРОВАНИЯ
Метод непосредственного иитегриро-
. вання состоит в непосредственном
применении таблицы интегралов, для
чего в случае необходимости полннте-
гральное выражение предварительно
подвергают некоторым преобразованиям.
При этом руководствуются следующим.
I) Если возможно, представляют под-
интегральную функцию как сумму не-
скольких функций, от которых инте-
гралы уже известны.
2) Если известен j f{x)dx = F (х), то
р(ах) dx — --L F (ах);
j"/(x + 6) dx -= F (х + *);
J f(ax + b)dx — F (ax + ft).
3) Если подннтегральное выраже-
ние — дробь, числитель которой есть
дифференциал знаменателя, то интеграл
равен логарифму знаменателя:
4) Если подинтегральная функция
есть произведение двух функций, из
которых одна может быть представлена
как степень функции, производной от
которой является другая, то применяют
формулу
f (/(*))"•/' (ж) dx - •
J « т •
В случае необходимости вводят так
называемый поправочный коэффициент,
пользуясь правом выносить (или вво-
дить) постоянный множитель за знак
интеграла.
Примеры.
р dx = Г (sin1 X -I- cos’ x) dx _
J »tn’ х cos* х ” J sin’ x сое’ x
j) j АН-Здх--Lr^+’+C.
’> j^Tl-T,B|^ + 4 5, + c
1
_ 2. <’ + +c-/TTF+c.
T
Метод подстановки состоит в том.
что введением новой переменной инте-
грирования стремятся заменить данный
интеграл таким, метод интегрирования
156
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
которого уже известей; этот метод осно-
вывается на формуле
f/(x)dx- МтСОН'ЮЛ.
где х = <р [/].
Примеры.
—±ЕЕ+с.
2жАг-л|-
1 Г (z - 1) dz 1 Г dz _
= 2 J Z’ “ 2 J 1
-4,^-4“-+4+с-
-т|"» + « + 17ГТч + с;
Метод интегрирования по частям
состоит в применении формулы J udv —
= uv— j vdu.
Примеры.
1) / — J ж sin х dx; полагаем х — и; slnxdx—
— dv; тогда dx — du; j sin x dx — — cos x — tr.
применяя формулу, получаем / — — x cos x 4
4 J со» x dx — — x cos x aln x + C.
2) I “ f In x dx; полагаем a — In x: dv — dx;
dX r
тогда du — — , t>—x, поатому /—x la x— J dx—
— x In x — x + C.
Обратные тригонометрические функции иите-
грнруютс» так же.
3) / — J еах со» bx dx; полагаем и —еах; dv —
—со» bx dx; тогда da—аеах dx. V — ~у~ > сле"
, еах »ln bx ° С .
допательяо, Z —--------------— I еах sin bx dx;
и и J
полагая еще ра» и — r“l, dv — aln bx dx,
олучим / — —------*^n ------р со*бх—
— J cos bx dx
или
, e“ (.a cos bx + » »ln Bx) a* ,
'--------------bi--------------V
откуда
. e** (a cos Эх 4 * lln bx>
“ « + »•
ИНТЕГРИРОВАНИЕ
РАЦИОНАЛЬНЫХ ФУНКЦИЙ
Первообразная любой рациональной
функции является элементарной функ-
цией. Чтобы найти се, следует сделать
следующее.
1) Разделить числитель на знамена-
тель по правилу деления многочленов
(если степень числителя не ниже сте-
пени знаменателя) и представить рацио-
нальную функцию как сумму много-
члена и правильной алгебраической
дроби.
2) Найти все корни знаменателя пра-
вильной алгебраической дроби и раз-
ложить знаменатель на вещественные
линейные и квадратные множители
(см. стр. 119); каждому вещественному
корню кратности т в знаменателе будет
соответствовать линейный множитель
вида (х — а)т; каждой паре сопряжен-
ных комплексных корней кратности п
в знаменателе будет соответствовать
квадратный множитель вида (х1 + рх +
3) Представить правильную алгебраи-
ческую дробь в виде суммы так назы-
ваемых элементарных дробей первого
и второго типа, т. е. выражений вида
Ль и Мьх 4- А'»
(х —a)* (jfl + px + q)*’
где Лд, Мл, Nь — постоянные, пока еще
не известные. Дроби Первого типа по-
являются при наличии вещественных
корней у знаменателя, причем каждому
вещественному корню кратности т будет
в сумме элементарных дробей соответ-
ствовать сумма из т дробей
Л; , Лд Ат
х —а + (х — а)» • • • л" (Х __ ауп •
Дроби второго типа появляются при
наличии сопряженных комплексных
корней у знаменателя, причем каждой
паре сопряженных корней кратности п
будет соответствовать сумма из п дро-
бей
М\Х Л- N\ М*х -1- Nt .
х» + рх + q + (х« -|- рх 4 «)»
М„х + Ыя
(х« -4 рх + q)n ’
ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИИ
157
4) Найти числа Дд, Л1ц, Nk, для чего
можно применить метод неопределенных
коэффициентов, состоящий в следующем:
приводят все элементарные дроби к
общему знаменателю н приравнивают
числитель полученной дроби числителю
данной дроби, расположив оба числителя
по степеням х; сравнивая между собой
коэффициенты при одинаковых степе-
нях х и свободные члены, получают
систему уравнений с неизвестными
коэффициентами Д4, Мр, N*. которые
♦1 определяются. После этого заданная
правильная алгебраическая дробь ока-
жется разложенной на элементарные
дроби, и интегрирование правильной
дроби сведется к нахождению инте-
гралов
Г dx Г dx
J x~a ' J (x — a)m •
Г (Mx 4-N) <tc.
Jx*+px + q ’
(Mx + N)dx
(jfl+px + 9)" ’
где тип — натуральные числа.
5) Интегрирование многочленов и
дробей первого типа производится не-
посредственно:
dx ____________1________
(1 — т) (х — «)"“* +
(«¥-1)
6) I (Mx + N) dx
J jfl+px + q
N-*f\dx
x* + px + q
-у (2х + р) dx
х2 + px + q
—j In|x4-px4-?| +
C dx
чтобы взять интеграл I -=-----------—
J xl + Px + 4
преобразуем квадратный трехчлен, стоя-
щий в знаменателе, в двучлен: хг -|-
+ рх + q - (х + + (q — ;
так как корни знаменателя — комплекс-
ные, то q — > 0; поэтому
Г dx =
J х» + px + q ~
Первый интеграл подстановкой х* 4-
+ px + q — и преобразуется в таблич-
. М С du D .
ный: — I . Второй интеграл под-
становкой и=2х+р приводится к инте-
гралу вида
du If du
(u? + kt)a = ** J («* +
1 f u2du ...
J (из + *2)4 » (* “ 4<? P^
При помощи интегрирования по ча-
стям второй интеграл правой части
равенства приводится к первому, после
чего удается установить рекуррентное
соотношение
du _________________и__________ +
(«* + *2)" “ 2*»(П_ 1) (ui + ftX)"-1
2л —3 f du
2Л»(п —I) J (B»4-*2)«-> ’
позволяющее последовательно умень-
шать показатели степени и в конечном
итоге свести задачу к отысканию инте-
грала
Прашры.
. Г 2л*+л*-Зл« + гг-1 .
*> ' - J -
158
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Делим числитель на знаменатель
2л*+л"-ЗХ« + 2х-1 _
х*-Зх’4-Зх-1 т
, 23Х* - 36л +14
+ ж» - Зх» 4- Зх - 1 ’
Разлагаем знаменатель дроби на множители и
налагаем
23л1—36x4-14 А, А. _ А,
U-l/ “(X-1р‘*‘(Х-1Р + х —Г
Приводим правую часть к одному знаменателю
о сравниваем числители:
23х* -Э6х4-М-А,4-А,(Х-1)4-
4- А,(ж- 1Р- А»х«4-(А,- 2А.)х 4-
4-<А.-А, 4-АД
Сравниваем коэффициенты при одинаковы!
степенях х:
А, — 23; А. - 2А, — - 36: А, — А, 4- А, = 14;
отсюда
А, — 23; А, — 10; А, = I.
Имеем
/- J (2л1 4-4. 16)<ix4- f 4-
Г 104х Г_И4х __2 x*4--Lx«4-
+ J (х - 1/ J X - 1 4 л- -Г 2 л- -г
4-,&х “ “ 73ГГ 4-23 Ш 1 ж - 11 4-с-
Г X dx
4 J (л 4-1) (ж 4-2) (л-3) '
Помгмм
*_______________________ л
U4- 0U4-2) (л - а» = х4-1
откуда л — А (л + 2) (л—3) 4- В (л 4- П (л — 3) 4-
4- С (х 4- 1) (х 4- 2К Написаииое равенство спра-
ведливо при любом значении х. полагая х — — I,
получим — 1— — 4А; А — полагая л — — X
найдем В — — •/,; полагая х — 3, найдем С — "1—
Теперь найдем
/» 4 . Г i . Г 3 .
I —Г dx I----г dx ( dx
1 4 16 I JU
'“J At + J-7+3- + J7=T-
«4 tn|x4-l|— *>1x4-214-
4-2- ln|x —314-C.
” J xix"4-4)(2x*4-ix4-2)
Полагаем
?x« - 3x« 4- 18X14- 8 A
X (X* 4- 4) (2л1 4- lx 4- 2) “ x +
Bx4-C , О(4x4-3)4-g
' x’4-4 ' 2x,4-3x4- x ‘
Otck.ui
2x* — 3x* 4-16x> 4- 8 — A (x« 4- 41 (2r* 4-3x4-214-
4-Bx’(2xa4-3x4-2)4-Cx(2x>4-3x4-2)4-
4-Dx (4x 4-3) (X* 4-4) 4-Ex (x* 4-4).
Раскрывая сковки и группируя подобные (отно-
сительно ж) члены, получим
2х« —Зх«4-16х«4-8 —(2А 4-2В 4-4D) х‘4-
4-(ЗА 4- 3B4-2C4-3D4-E)x*4-(10A4-
4-2В4-ЗС4-16О)х«4-
4-(12А 4-2С 4- 12D 4-4Е) X 4-84.
Приравнивая друг к другу коэффициенты при
одинаковых степенях х и решая полученную
систему пяти уравнений, найдем: А «1; В —— 1;
С-0; D-4,;
Следовательно.
- 2- 1п(х« 4-4) -~1п|2х» 4-3x4-2]—
последний интеграл берется так:
Г dx (• Мх
J 2х«4-Зх4-2 “ J Шх* 4-24х 4-16 ”
С Мх 8 - <Х4-3
"j (4Х4-3)" 4-7 “ 4/Т Г^Т
+с-Л,га,Тт*+с-
• ‘~ Jи-ВВ-т»- <г'
Полагая
2х-х« А В
(Л - 1Г (л« 4- !)• ~ х - I + (X - IP +
, СХ4-Р . Ех + В
ж* 4- I IX"4- IP "
найдем методом неопределенных коэффициентов
A--4;B-4;C-J.;D-£;E-^I
F — — 1. Следовательно,
4- 4 Ш IX* 4-1)4- — »ГС1< х 4-
+ 4 J UH-1F
ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИИ
159
Далее.
ПоследккА интеграл берем оо частям. ооласвя
GrnF‘w“
1 _ Г X* dx х
•“ 2(х-4- 1) и JU’+IP" 2(x*4-li
+ J 2U* + D " ~ 3(X*4- I) + T ,ГС’г X + C
Итак.
которых по крайней мере на единицу
меньше степени соответствующего зна-
менателя. Чтобы определить их коэффи-
циенты, дифференцируем обе части по-
следнего равенства и получим
у(х) Р(х)м (Х)-ы(Х) Р'(Х)
/<Х) ” Р*(х)
«) (X)
Q(X) •
Приводя к общему знаменателю,
отбрасываем его; приравняв коэффи-
циенты при одинаковых степенях х, най-
дем коэффициенты многочленов и (х) и
«1 (х).
Полином Q (х) имеет только простые
корни (см. стр. 123). Поэтому
<»i (х) dx
Q(x)
+-L tn и* +1) + J-„clg x _ _L_ _
" ,rct« x - aWi + T ,rrte ' + c “
выражается при помощи логарифми-
ческих и обратных круговых функций.
_ “ (х>
в то время как дробь представляет
алгебраическую часть интеграла, пол-
ностью выделенную.
4- Д la (л« + i) - -j- arctg x + C.
Метод M. В. Остроградского. Если
днаменатель дроби не удается разложить
на множители, то можно определить
алгебраическую часть интеграла мето-
дом Остроградского. Этот метод выгодно
применять также, когда знаменатель
можно разложить на множители.
»(х)
Пусть у-------правильная несокра-
тимая дробь. D (х) — общий наиболь-
ший делитель знаменателя / (х) и его
производной /' (х), a Q (х) — частное
от деления /(х) на D(x)*. Тогда
Т(х) Br “(jr) ж Г»' <х>
/ (х) D (х) + J Q (х)
rf.r.
где ы (х) и «1 (х) — некоторые неизвест-
ные многочлены, степень каждого из
•D(x) нааодгг лгтодом лослеЛтаотельяодо
вямния. ш чего делят / (л) ил /' (х), затем
/' (х) — ва первый, остаток и т. д., пота деление
не будет выполнено бе, остатке. делитель • по-
следнем делении и будет общим иакблльшим де-
лителем DlxK
Примр. I - J ‘
/<х) - < f + х -НУ; /' (х) - 2 (л* + х + I) (Дг« +
-MX D(x> - хЧ-х-Ь I: Q(х)-х* + х + I.
По формуле Остроградского получим
Зх*-?хЧ-х + 1 л А.х' + Ва + С,
1ХЧ-Х4-1У д'4-х 4-1
Диффереипироваиие дает
Зх» — ?х* 4-х 4-1
итЧ-х-НГ
(Х«4-х4->) (2Льг4-аа - (ХИ4-П (Аы>*-НМ+С0
(ХЧ-Х4-1У
Освобождаясь or зиамевагела и приводя в»
лобные члены, получим:
!*• - JX* + х + I — Аи* + (Вя - А.) *• +
4-Ия + С, - 2В,) х* 4-(А, 4-А, 4-в. - ЗС,) ж* ч-
4-(2А, 4- С, 4- в,) х 4- В, - С. 4- С,.
Приравнивая ковффиииеиты при одинаковы»
степени х. получим систему шести уравнений,
откуда иайдсм А,—№ А, — 3: В,—2: В, — Л
С, - 2: С, - I.
160
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Следовательно,
3**4- I
ИНТЕГРИРОВАНИЕ
ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
Интегрирование иррациональных
функции приводит, вообще говоря, к
неэлементарным трансцендентным функ-
циям. Лишь в некоторых случаях ре-
зультат интегрирования удается выра-
зить в элементарных функциях.
л Г { ах-\-Ь\* / ах 4- Ь\9
cx+d
dx
(R — символ рациональной функции;
о, ₽,. . . — рациональные числа) приво-
дится к интегралу от рациональной
функции при помощи подстановки
ах -J- Ь ,
-----—т “ г", где п есть общее нанмень-
сх + d
шее кратное знаменателей дробей а, ?,...
Примеры.
Vajfl 4- Ьх 4- с — Vа (х — а) (х — р) —
-z(x —а).
Первая подстановка употребляется в
случае а>0, вторая— в случае с>0,
а третья — в случае, когда кории трех-
члена аир действительны.
Пример. I I ------—*** - .
_______________J * У4*т -|- 4* 4-3
гдем У 4*! 4- 4* 4- з = г — 2х, т. е. z
4- V <*’ 4- 4* 4- 3 . Возвышая первое равенство
J " и _
Пола
квадрат, находим
4(1+д)« *S
, _ £' + 2г 4- 3
<0 4-г)
тогда >'<*• 4- 4* 4-3
2dx
--Lin
Уз
3) Подстановки Эйлера всегда ре
шают задачу, однако применение их
приводит к громоздким вычислениям.
Поэтому отметим некоторые случаи,
когда интеграл рассматриваемого вида
можно взять без применения подстановок
dx
У ах2 4- Лх 4- с
сводится к одному из основных инте-
гралов (см. стр. 155) при помощи извест-
ного преобразования квадратного трех-
члена (выделение полного квадрата)
(см. стр. 157).
При игры,
dx
Эйлера. Так, например,
тельно.
2 arete
. Полагаем * . Х
ildi
**>(! 4-<‘)“
«тгй?-л-2,ге,в*+
. — 4z4z _
! dx => (| _ г»). •
; полагаем х» у*, от-
V 404-20* 4-1U0**
куда dx — 6y-<iy. Тогда / 6
Г Vndx
J У 60 - 8 U - Зох-
И. откуда х
Vi - Тх - 3*‘
dx
Умй - («* 4- 7)*
-L.rc.ln ^±14-С.
Ум»
Уго dx
2) J R |х. Vax* + bx + c] dx.
где R — символ рациональной функ-
ции, приводится к интегралу от рацио-
нальной функции при помощи одной
из подстановок Эйлера:
Vax2 + Ьх + с = х ± х Ya ;
V ах* 4- дх 4- с — хг ± Vс;
_У&Г ах __________________________.
J Узэ-|-(1и*4- 1у 1и
+ У'211 (&*• 4-* 4-2) | 4- С.
4) К рассмотренному интегралу сво-
С Мх 4- (V
днтся интеграл типа I _________dx.
Если числитель
ной подкоренного
представляют так:
+»>+"- м..
не равен произвол-
количества, то его
Л4*4-JV--^(2ax+
получая в скобках
ИНТЕГРИРОВАНИЕ ТРАНСЦЕНДЕНТНЫХ ФУНКЦИИ
161
производную от подкоренного коли-
чества. Затем представляют задан-
ный интеграл как сумму двух интегра-
лов. из которых первый берется непо-
средственно, а второй является интегра-
лом рассмотренного типа:
f Mx + N
J У дл* + frx + с
Г (2дх 4- b) dx
~ ‘Ь J Удл*+ Ьх 4-с
' 2а J J Yax-+ Ьх + с
= — • 1 ах2 + Ьх + С 4-
а
\ 2а ] J y^ajfl+bx-t-c
5) J Yx2± a2 dx н j Va2 — xt dx
можно найти так:
С ix2±a2dx - С aL dx -
J J Л' ± a'
f xIrfx аг f dx
J Y*2 ± a* ± ° J Yx*± a*‘
К первому интегралу применим фор-
мулу интегрирования по частям:
. х dx
и = х; dv = — ;
У х*± а2
du dx; v — Yx2 ± а2.
Следовательно,
J Yx* ± a-dx — -у- Yx2 ± а- ±
± -у- In I л+ Yх* ± а- | +С.
Аналогично берется ) р дг— х2 dx.
6) Интегралом от биномиального диф-
ференциала (или дифференциального би-
нома) называют ( Xя (а 4- bxrfdx, где
т, п,р — рациональные числа. П. Л. Че-
бышев доказал, что такие интегралы
выражаются в элементарных функциях
только в следующих трех случаях:
а) когда р — целое число; б) когда
«4-1 . m + 1 ,
—-------целое число; в) когда--------)-
л л
4- р — целое число.
II Том 1 Зак 1!в1
В первом случае, если р положитель-
но, раскрывают скобки по биномиаль-
ной формуле и интегрирование выпол-
няют непосредственно; если же р —
целое отрицательное число, то подста-
новкой г = ?, где р — общий знаме-
натель дробей т и п, освобождают под-
интегральную функцию от иррацио-
нальности.
Во втором случае полагают а 4- Ьхп=я
“ х*, где s — знаменатель дроби р =
г
= _
I
В третьем случае полагают а 4* />хЯв
=
ИНТЕГРИРОВАНИЕ
ЭЛЕМЕНТАРНЫХ
ТРАНСЦЕНДЕНТНЫХ ФУНКЦИИ
I) ft# (sin х> cos *)dx, где R — сим-
вол рациональной функции, подстанов-
кой u " tg -р приводится к интегралу
от рациональной функции перемен-
ной а.
162
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Если функция /? — нечетная относи-
тельно cos х, т. е. если R (sin х, —cos х)=
= — R (sin х, cos х). то быстрее к пели
приводит подстановка sin х ™ t.
Если R( — sin х, cos х) = — /?(sln х,
cos х), то пригодна подстановка cos х = t.
Если R ( — sin х, — cos х) ™ R (sin х,
cos х), то следует пользоваться подста-
новкой tg х — и.
При меры.
. , Г спа х dx _ , X
a) I — I ---------: положим tg •" о.
1 I + COS X I
тоги
' - Т I - в.
С°» *----------Г “ ТПЙ ; х“2 *ГС,Е
I + ««• ф Т
240 „ , Г 1 и' .
dx — ; слелпаательно, I — I ,----du.
I + o’ J 1 + и‘
г dx
б) / — I у ; положим 1g х “ о. откуда
1 аи
cos’ х = -г-—г : х ~ arctg о: dx = - ;
1 + «’ 14-о’
следовательно, / «= I (I 4- и’| du.
2) Если подинтегральная функция ра-
циональна относительно sin kx, cos lx,
Igpx, ctggx, где Л, I, p, q — целые
числа, то зга функция преобразуется
в рациональную относительно sin х,
cos х при помощи формул
sin тх — ( ™ ) cos",_’x sin х —
— ( т. cos’1-3 х sin3 х 4-
\ •> /
4- ( ™ cos'" 5 х sin5 х—...;
cos тх = cos'" х — ) cos'" 2xsin2x4-
4- ) cos'"—‘x sin1 x — ...
Если числа k, I, p н q — дробные,
то нужно привести их к общему знаме-
иателю к — —-, / — —, р — -CJ-. о —
л п ’ г п * 4
и заменить — через у, после чего
функции sin ky, cos ly, tg py, ctg qy
выразятся рационально через sin у, cosy.
Пример.
обозначим
у, тогда dx = 64y и I
aln у dv
aln
-3 f -p-
J »>ny
4- 12 cos у 4- C
-6
-9
cos’ у — 3cos у aln* у
2 sin у cos у y
— >ln’ у
sin у
>s 3y 4y
In 2y
“*LLtfy
aln у ’
In у dv
3) ( sin mx cos nx dx, J cos mx cos nx dx,
( sin tnx sin nxdx находят, пользуясь
известными формулами тригонометрии,
преобразующими произведение тригоно-
метрических функций в сумму (стр. 96).
Вообще интеграл jcos(ax4-*)cos(aiX4-
4- *i) . . cos (пл 4- М dx
путем последовательного применения
формулы cos и cos v = ;cos (м4-о)4-
4-cos(u — о)| приводится к интегралу
вида j S cos (Л/X 4- fl() dx.
4) J sinmx cos"x dx приводится к ин-
тегралу от рациональной функции под-
становкой t sin х(если п нечетно) или
/« cos х (если т нечетно): если же оба
числа тип положительные и четные,
то нужно подинтегральную функцию
выразить через тригонометрические
функции кратных дуг.
Примеры, al J aln* х dx — f aln’ х aln х dx
— f (I—cos’ x> sin x dx — | cos x—T; —sin x dx
_ at I _ _ ((I-П) dt—+C — - cos x
4-^+C.
-l±^dx--£-4-
— i sin’ 2x dx
!1L1£ + C.
32
I—cos 4x .
----T---<lx
5) j tg" x dx^ J tg" 2 x (sectr — I) rfx —
— j tg"“<rd tg x — j tg"~br dx —
и. ____£_ _ ( tg"-2 x dx; применяя этот
n — I J
прием, приведем интеграл при п четном
к j dx " х, а при л нечетном — к
j tg х dx — — 1 п | cos x |. Аналогично
находится j ctg"x dx.
ИНТЕГРИРОВАНИЕ ТРАНСЦЕНДЕНТНЫХ ФУНКЦИИ
163
Формулы приведения
Г т , я . COS1"-1 X sln"+1x , т — if m—2 , - ,
1 cos"1 x sin" x dx --------------------— I cos x sin" x dx—
J m + n m -f- n J
sin"-1 x cosm+Ix , n— 1 f _. . я_2 .
—-----------------------------I cos'"x sin" xdx;
m -f- n m + л J
f dx __ 1 _________________m -( n — 2 C________dx_______
J cos"xsinmx = n — Г stn1»-* x cos»"1 x + Л—I J sin^x cos"-2x
= _ 1 ________I________ m + n—2 C dx__________________,
m~ • sinro-lx cos"-1x m—1 J sinm-2xcos"x
fcosmx . cos"+1x m — n + 2 f cosmx .
J sin x (n— 1) sin" *x n—1 J sin" *x
cos^-'x m— 1 f cosm~2xrfr _
“ (m — n)sin"“‘x + « J sin"x
Последовательное применение этих формул, если тип — целые, приводит
заданный интеграл к одному из следующих:
г . . г . f sin xdx fens xdx f , .
dx; sin x dx; I cos x dx; I---------: I —;-------; I sinx cos x dx;
J J •> cos x ’ sin x • 1
dx
sin x cos x
dx
sin x
dx
cos x
7) je^PfsIn x, cosx) dx, где P (slnx,
cos x) — полином от sin x, cos x, выра-
жается при помощи элементарных функ-
ций. Произведения sin"1 xcos" х следует
представить в виде суммы синусов и коси-
нусов кратных дуг (см. стр. 96), после
чего задача сводится к отысканию инте-
гралов J?1* cos nxdx, Je®* sin nxdx, кото-
11*
рые берутся интегрированием по частям
(см. стр. 156. пример 3).
8) jxmeaxcos bx dx, J xm«<rslnfcx dx (I)
можно найти, дифференцируя по пара-
метру а левую и правую части равен-
ства. определяющего интеграл пред-
шествующего типа (дифференцирование
в левой части производится под знаком
интеграла).
164
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
9) Интегралы Г dnax I Р“ (л) P,v (х)
более общего вида \Р (х) cos ахdx = I Р(х) - ^4- — I 4-
от полиномов J L ' *
Р(х, е", sin bx, cosax[P'(x) Р" (х) Pv(x) 1 г
Ыпсх..... + ~ + —-J + С;
... cos gx. , sin дх Г i-Х ( у 1 Qi n ft r/7 V — — 1 РЧх) P~(x) Pv(x)
coslix,...) (Il) J a a* 1 aS
могут быть так- _ “LZf Р (х) -^1 + _
же выражены че- а L аг а*
рез элементарные
функции, так как
при помощи тригонометрических пре-
образований интеграл приводится к
сумме интегралов вида (I), умножен-
ных на некоторые постоянные коэффи-
циенты.
10) Интегралы от полиномов Р(х,
arcsin х) и Р (*, In х) при помощи под-
становок arcsin х = / и 1п х = t при-
водятся к интегралам от полиномов
вила (II).____________________
11) Пусть R (х, К ах1 4- Ьх -г с) — ра-
цнональная функция от х и Vах*-\-Ьх+с,
a v(x)—элементарная трансцендентная
функция; если функции R и <? такого
рода, что первообразная функции R и
производная функции ? (х) также яв-
ляются рациональными функциями от х
и У'ах* + Ьх + с, то интегрирование
функций вида R (х, Уах2 4- Ьх + с)<?(х)
можно, пользуясь формулой интегриро-
вания по частям, свести к задаче об
н нтегри рова и и и некоторой рациональ-
ной функции от х и Vах* 4- Ьх + с •
Трансцендентными функциями по-
добного рода являются, например.
13) Если рациональная функция R
представляется суммой полинома
х я -А
и элементарных дробей типа ——
Вх 4- С Л
(х~4- Ьх 4- <)" * ТО1 вообщс ГОВ°РЯ* ин*
теграл типа 12 не является элементар-
ной функцией. В том случае, когда
в выражение рациональной функции
входят только дроби первого типа,
можно, применяя нужное число раз
формулу, интегрирования по частям
и простейшую замену переменной,
представить рассматриваемый интеграл
через элементарные функции и следую-
щие интегралы, не представимые в эле-
ментарных функциях:
Каждый из этих интегралов опреде-
ляет новую трансцендентную функцию,
именно:
R(x. V I — х«) arcsin х;
R (х, Уах2 4- бх 4- с) arctg х;
R (х. Уах2 4- йх 4- с) In х.
12) Интеграл от функции вида
R(x) sin х, R(x) cos x, /?(х) e"4. где R(x)—
рациональная функция, не всегда выра-
жается через элементарные функции.
Возможность выразить интеграл через
элементарные функции представляется
в том случае, если R (х) — полином;
при этом многократно применяется
формула интегрирования по частям.
Если Р (х) — полином, то
интегральный синус
SI (х) — J- dt ( —со<х<оо);
интегральный косинус
О(х)-—(0<х<оо);
интегральный логарифм
X
“W-jw <»<'<»•
и
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Существуют таблицы значений этих
функций (см. литературу, стр. 351,
Ц'591).
14) К интегралам предыдущего типа
приводятся также интегралы вида
f R (In х) xmdx; j R (arcsln x) xmdx,
причем попрежиему буква R служит для
обозначения рациональной фУ,<ки>,и1
первый из интегралов приводится под-
становкой 1пх = I, второй — подстанов-
кой arcsin х = t и последующим при-
менением тригонометрической формулы
2 sin и cos v = sin (и + v) + sin (и — г)
или других аналогичных формул.
15) При интегрировании иррацио-
нальных функций, не содержащих
никаких других радикалов, кроме ра-
дикалов вида или У а2 — х2,
удобно пользоваться тригонометриче-
скими подстановками.
Если подинтегральная функция не
содержит никаких других радикалов,
кроме Vаг — х*. то берется подста-
новка х = a sin t или х = a cos_t____
Для интегралов, содержащих Ух’4-02.
берется подстановка х = a tg t или х •=
= a sh t. _____
Для интегралов, содержащих V xi—а1,
берется подстановка х = -------- или
cos2t
х = a ch t.
Примеры-.
a) f У а' — х‘ dx=* |х—л sin t; dx=a cos /rff !=
«= a’ J cos1 Г dt = tl 4- cos It) dt
= + c = £.rcsm£+±yft-r^4-C;
6) f-----------|х-щг:дх = Л->
Jlx'-j-ljVl-j-x’ I co»
= I — . — f cos t dt = sin t -|- C =
J sec» t cos' t J 1
в) / = JV(x« - IP dx-1 x—ch t; rfx=shY<rfl =.
---* j ch 2Г dt 4- -i- j dt —j" (ch It -f-Ddf —
_ ’ sh 2/ + -1- r ’ ,h 4/- 4- sh 2/4-^/-f-C;
4 4 04 ч n
так как sh At = 2 sh 2t ch 2/ = -I ch t sh t (ch’t 4-
-f sh’ Г) = 4x Ух’ - I (2x* - I), t = Arch x =
= In ix 4- Vx‘ - 1>, то I =4 (2x»-5x)X
_____ 3 , —
x VX’-1 4- -j- in (x-f- Vx‘ - 1) 4- C.
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
(постоянная интегрирования С везде опущена и подразумевается)
Интегралы от рациональных функций
1) у<« + М^_“±‘«’."+‘!
2) ) хт (а + bx)n dx берется почленно после разложения (а 4- йх)в по бино-
миальной формуле, если п — целое положительное.
3) Если же т < п или если п — число дробное или отрицательное, а т —
целое положительное, то применяется формула
j хт(а 4- bx)ndx — j xmzndx —
уй+г]’
где (z— а)т разлагается по биномиальной формуле: здесь г= а + Ьх.
4) Если т и п — целые положительные, то
f xmdx Г xmdx _ I Г (z — a}mdz I ml (— a)s гт~я~^'у
J (а 4- Ьх)" J z" 1>т^1 J ьт ' 1 ^(гн—s)!sl (m—n—a+l)
• J—О
166
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
за исключением случая, когда т — п — s + 1 = 0; в последнем случае соответ-
ствующий член в квадратных скобках заменяется выражением
т! (— а)",-"+1
(т — п 4- 1)1 (п — 1)!
г = а 4- Ьх.
6> ]’тттг-т'”|“ + 4л1-
7) С х dx 1___________~ 1_____________2._____
’ J (д + “ ьг (п - 2) (д + Ьх)я~2 + (п — 1) (в + Ьх)я~'
8) Jttr?-тг[в + *x-fllnIa + М].
9) с x*dx_____LГ + _ °г
J(a + bx)n [(л—З)(а4-дх)”-3 (я-2)(а4-Мя-2 (я-Щв-Ь^х)"-1
10) 2~“2в(в + М+в2|П|а + 6х|] ’
11) Если т и п — целые положительные, то
'т-|-л-2
— I у (т 4-я — 2)!гя|-д~|(- ЬУ
am+n-i Zj (m + я —a —2)ls!(m-s—Пл’”-1-1
за исключением случая, когда т — s— 1 = 0; в последнем случае член в ква-
дратных скобках заменяется выражением
(т -Ь я — 2) I _ . )Я1_1
(/я—1)Ця-1)|' 1
1Я f , “ , [Д±*«_atol«±*£| » 1.
’ J (а 4- bxy а* [ х | х | а 4- Ьх J
а
161 Js4W_7ij"rc,8/4x'
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
167
17) f —*hri = -4=- ln Ig—- -7= Arth (ab > 0).
ja—bx* 2yab \a — xYab -fab V a
|S>
,Q. f x*dx x a C dx , . ...
,9) ——rjro^’CM ф°Рмулу ,6)-
C jfidx xl a f dx 1 , x*
20) I — . — — ---—— In a 4- bx*\. 21)1 —-—, — x— In f—, . .
J a + bx* 2b 2b* J x (a + bjfl} 2a [a 4- fcxJ]
22) J ^(a + bxij “ “ 4 “ 4 J lC* Ф°РМУЛУ l61‘
231 f **________________!___b In xi
' J x«(a + bxZ) 2ajfi 2a* |a + *x»|’
24) У(~+Ъ)-»-2а(аХ4-»х2) + 4Ja4^1CM' Ф°рмулу 16b
25) f x d* =____________!_____
' J (a 4- bx2)* 2b (a 4- *x*) *
(• x*rfx x , 1 C dx , . ...
26) J (a+W ~ - 2b(a + bx*) + 2b J a^bjfl lCM‘ Ф°Р"УЛУ 16b
ЭТ) j (a 4- bJfl)* " Sb* (a 4- bx*) + 5Ji ln 1 a + ftx*l •
28) J x (a 4- bjfl)* " 2a (a 4- bx‘) + 2a* In | a + bx* I *
<v« f dx Г 1 , 3bx 1 1 3bx f dx , . 1C1
2») J *{а + Ь*р = - [ST + 25tJ a-T^ - 25Г Ja-+^ >C“- Ф°РМУЛУ l6b
30) j x* (a 4- Ьхф “ [ 2ax* + a* J a 4- bx* tfi | a 4- bx* |
31) f-----arctg -- + -- ; (ac -b*> 0).
J a -t- 2bx 4- ex* Yac — b* Vac — b*
32) Г------ *Х ,-----; (ac-&2-.0).
J a 4- 2bx + ex* b + ex
33) rtx _ 1
J a 4- 2bx 4- ex* 2 у bx _ ac
ex + b — У h* — ac
ex -t- b 4- Уb*—ac
(ac —h*<0).
C dx_________________ _________1___________________b + ex
J (a+2bx 4- cx*)P “ 2 (ac — b*) (p — 1) ' (a + ‘2bx 4- ex*)"-1
+ (2/> — 3) с Г , dx__________________
2 (ac — b2) (p — 1) J (a 4- 2bx 4- схг)р~1
168
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
J (а« + жГ -2(„ll)e4(ai-rх-Г~‘ +('2П 3) J (а^х^~‘ I *
С________dx______ I р(1 — s»*"+"-s»f£ /_ .г - л
J(x — a)m(x-b)'1 “ —J I® ’• V =л -« ;
Интегралы от иррациональных функций
37) fl/e + Z>xdx= -=-( У л -г Ох )». 38) f—— УТ^Тх.
J Г 3d J К«-</Х "
39) С “ ±jf_ dx - (ЗаЬ -2л> + fox) /и-г Ьх.
J Va + bx ЗЬ-
40) ( У а* — x*dx — ~ У а* - х- -г arcsin —.
J • “ а
41) Ух» ± a1 dx — -у У\х2 ± д» ±-у-1п'х+ Ух* ± л» |.
42) С(х» + arf1' dx =^~ (2хп- + 5л’) Y х* + а* 4- In | х + Ух2 + а: |.
J о Ь
43) I х- Ух- -г a- dx = (2хг + а1) /х2 + а» — In | х 4- \ х- -р а* |.
Jo о
44) f--—--------^4----..
J (х2 ч- л'2) Ь лгух2 4-«г
f dx 1.1 * I
45) |~ — In ------------- -----.
J x У ж» 4- л» a | a 4- x^ 4- «• I
46) C dx -r? + at .
Jx»Kx»4-e» " aiJC
47) f Vx*4- a‘‘ , 1 I «+ /x 4- <1*
J x»VJflTa^ “ + 2л» | x
48) J Уa'1 dx , _ У»1 + х2 . 4-1п|ж+/д» + х*|.
49) f---fX- - — — arccos —.
J x Vx*-a* “ x
50) f . Ух‘-а^
J Jfi Vx* — <fi “
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
169
ад. Г Yx^ — a^dx .г---— а
°2) I -------------- V jfi — я* —a arccos —.
53) f (в» — xn’h dx - (5аг — 2х?) Ya^-xt ± — а* arcsin —.
jo b а
м> j /у=тг_,|.|«+^-л1|.
56) С dx _ _ У '*ах - х-
J х yiax—jfl ах
57) Г__—______________Х~°
I (2ах — х*)’** at Y'2&x — х2 *
,и. Р xdx х
Об) I ------г— — -----, = . -— т
1 (2ах — х2) h a Y2ах — х2
59) С —=^Аг= — In | х + а + Y2ах + ifi |.
J |/ 2ах + х2
ад. С dx . х—а
60) I —• — arcsin---.
J /гах — Х‘ а
61) ( — ах =. — -J=r In 12сх + b + 2 Yc у'а т Ьх + схг|; (с>0).
J у а + Ьх -г ext у с
62) j Ytt + bx -t- ex2 ax — ‘-~^+ b Y a -t- bx + c.<t —
— — ~ьДС In 12cx + b + 2 Yc~ Va + bx + cx* |; (c>0).
ber*
C dx I . 2cx — b
63) | -------— —- arcsin - : (C>0).
J Ytt + bx — ext у c у bi + 4ac
64) j Ka + bx— схг dx = У a + bx — ext -f-
. Ы + 4дс 2ex — b
d-----г--arcsin —--=_; (c > 0).
oc*' Vb*+*ac
170
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
65) С X(ix _ У<> + Ьх + сх*----------b 1п । + +
J Уа + Ьх + сх» « 2е'’
4-2 /с Уа + Ьх + сх* |; (е > 0).
66) f |/ dx = К(а 4- х) (ft 4- х) + (д —ft) In I Va 4- х + Kft + x ].
€7) ( 1/ a~x dx - K(a — x) (ft 4- x) 4- {a 4- ft) arcsin 1/i-iA.
J F ft 4-x Г a-hb
68) [ j/^Zx~ dx = — K(a 4- x) (ft — x) — (a 4- ft) arcsin |/ * ~
-n. C a* n . 1 / *—a
69) I — 2 arcsin!/ т-—.
J /(x-a)(ft —x) V b-a
Интегралы от трансцендентных функций
70) xne*dx ~ е* [Xя — пх"-'-у-п(п — 1)х"~2 — ... 4-(— 1)"л!].
71) j In х dx — х In x — x. 72) J -1ПуГ-\. dx — — (In x)*+l .
та> jIE?'(Дт-Нйй)-
75) J sin2 x dx = x-sin 2x. 76) J cos2 x dx = x 4- sin 2x.
77) tg2xrfx — tgx —x. 78) J ctg!xrfx — — etg x — x.
’«fro-H’Tl- в’Ует-ь|«(т+т)|-
81>
83) I sinxcosxrfx — 4-sln’x или l-coa<x. 84) ( ———-— ln|tgx|.
‘ J 2 2 J sin x cos x io>
85) f ig" x dx » — С tg'1-2 x dx.
J 11 — I J
86) Jctg',xrfx— ~~ _ | Г — ^ctg"-2xdX.
o_ C . . j sin (m 4- л) x . sin (m — л) x , - , .
87) J sin mx sin nx dx------4- 2(т~ я) - 5 И* * «ли
от2 о. д2 _ см. формулу 75].
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
171
оо. f . sin (т 4- л) х , sin (т — п) х. , . , ,
88) I cosmxcosnxdx — ;—-—Ь-тгт-------t—I и2 л’; если
' J 2(л» + л) 2(т — п) 1
тг = л2 — см, формулу 76].
от f j cos (т + л) х cos (т — л) х , , , .
89) | sin тх cos пх dx ---5-)-------------5—'-----; т2 + л2;
J 2 (т + л) 2 (т — л) 1
если л»2 = л2 — см. формулу 83].
а + b cos х — уes _ агс 2 ( у а 4- b й 2 ) ’ >
91)
dx____________1
a 4- b cos x у fti_a2
In
yb-atg-^-+ Vb + a
Уь — а tg — — Vb 4- a
; (а<Ь).
92)
dx
----------------— — arctg
a -f-&sinx у а‘—Ь2
atg~-+b
г-; (a > &».
93)
dx
a 4- b sin x ~ у^2____a‘
In
e tg + ft — V b- — a2
atg-j-4* b+ Vbt-a*
94)
dx
----------------— — arc
a2cos2x 4- &2sin2x ab
95)
„r , . . e°e (a sin bx — ftcos 6.r)
eat sin bx dx —
а2 + b-
96)
ea r cos bx dx
еах (Л sin bx 4- a cos bx)
a* 4- b*
97)
eax sin" bx dx
ear gin'»-1 bx (a sin bx — nb cns bx)
a- 4- n-b*
2
1
л (л — 1) b'
а2 4- л2/»2
in 2bxdx.
98)
„ . . ea'cosn~* bx (a cos bx 4- nb sin bx) ,
cos" bx dx —-------------- „Д-------------------- 4-
a2 4- n-o*
Л (л — 1) Ь- Г ал а—2 l j
д* + л*2 J* cos bxdx-
172
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
99) С хт sin ах dx = —cosax + — 1 хт 1 cos ах dx.
J ° " J
100) j хт cos ах dx = sin ах-----J хм~1 sin ах dx.
101) j arcsin xdx — xarcsinx -г У 1—хг.
102) arccos x dx = x arccos x — У1 — x1-.
103) arctgxdx — xarctg x-----In (1 + x1).
104) j arcctg xdx — x arcctg x 4- -y- In (1 4- x2).
105) j Arsh xrfx =• x Arsh x— У 1 + x*. 106) j Arch xdx = x Arcli x — Vx2 — 1.
107) J Arth xdx = x Arlli x 4- In (1 — x2).
108) f Arcth xdx = xArclh x 4- In (x-— I).
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
И ЕГО СВОЙСТВА
Пусть отрезок (а, 6|, на котором
определена некоторая функция y = f (х),
разбит точками а = х0 < xi <х». . . <
< Xfl_j < хп Ь на частичные отрезки
так, что длина любого частичного от-
резка меньше определенного положи-
тельного числа Ъ, т. е. |х/ — xt_} |<8.
Обозначая через 5, некоторое произ-
вольное значение переменной х на частич-
ном отрезке [Х/_р х,|, составим сумму
л
•*r-i)> которая называется
интегральной суммой.
С уменьшением 8 число частичных
отрезков п увеличивается. Если суще-
ствует такое число А, что разность
между этим числом А и любой инте-
гральной суммой стремится, к нулю при
стремлении 8 к нулю, то -функция /(х)
называется интегрируемой, а предел А
называется определенным интегралом от
этой функции на отрезка [а. 6| и обо-
ъ
значается символом f/(x) dx. Числа а
.<
и Ь называются нижним и верхним
пределами интегририаиния.
Основные свойства определенного ин-
теграла
а е
I’ К/ (х) dx = К (х) dx (К — постоя н-
а а
ное);
а
J 1/1 (X) + Л (•»•) — /»(-*) ] -
а
b h b
- J /1 (X) dx 4- f /г (х) dx — J /а (*) dx-,
а и а
b а
\f(x)dx- -f/(x)rtr,
J/(x)rfx-0;
а
b С С
j / (х) dx 4- ( / (х) dx - J /(х) dx.
а о а
Определенный интеграл не зависит
от обозначения переменной интегриро-
вания, так что
» t> ь
j/(xjrfx-j’/U)<«-J/(y)dy и т. д.
а а а ,
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
173
Теорема о среднем значении интеграла.
Если f (х) и ? (ж) непрерывны и (г)
сохраняет постоянный знак па отрезке
[а, 6], то
ь ь
J/(*) f W dx - /U) J Ф W dx,
а а
где
a<l<b.
В частном случае, если ?(х) = I.
ь
j/(x)dx- (b
Теорему о среднем применяют при
оценке величины интеграла, не произ-
водя его вычисления. Различают оценку
сверху, т. е. разыскание числа, которое
больше заданного интеграла, и оценку
снизу.
Пример. Найти оценку сверху дли ните-
1
града f *tn-Xa- dx. По теореме о среднем имеем
J 1 +•**
1 1
Г sin х . . . Г dx
ТТ*”
= sin Е [arctj x]J sin Е.
Так хак на отрезке (0,1| функция sin ж воз-
растает, то sin Е < sin I, следовательно.
Производная определенного интеграла
с переменными пределами. Если / (х)
непрерывна, то
-£-1 -/(X);
ь
b
Связь определенного интеграла с не-
определенным (формула Ньютона —
Лейбница). Если F' (х) = /(х), то
»
j/(x)dx= F(b)—F(a). Таким образом,
а
вычисление определенного интеграла сво-
дится к отысканию для интегрируемой
функции первообразной, в которую
вместо аргумента подставляется сначала
верхний предел, а затем нижний и из
первого результата вычитается второй.
Записывается это так:
» ь
J7(x) dx - F (х) | - F (b) — F (a)
или
J/(x) dx - (F (x)]‘ - F (b) - F (a),
a
Пример:
Неопределенный интеграл можно представить
так:
j fix) dx = J /(/) dt - E(x) - Fla),
где а произвольно.
Формула замены переменной в опре-
деленном интеграле. Пусть требуется
ь
вычислить f/(x)dx, где /(х)—непре-
а
рывная на отрезке [а, 6] функция.
Пусть х = ф(/), причем: 1) ф (/) опре-
деленна и непрерывна на некотором
отрезке [«, ₽]; 2) *(а) = а, ф(?) = Ь;
3) на отрезке [а, существует непре-
рывная производная ’f'(f). Тогда спра-
ведлива формула
о »
J/ (x)rfx-f/ [ф(О]ф' (О dt.
а «
Пример.
Формула интегрирования по частям
для определенного интеграла
в »
J’ и dv — — j’ v du.
174
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Интегралы от четных н нечетных функ-
ций. Функция f(x) называется четной,
если/(—х)’=/(х)' Функция f(x) назы-
вается нечетной, если /(—х) — —f (х).
Примеры: )) Функции COS X. X*. х*4-Х* 4*
+ 1 — четные.
2) Функции aln х, tg х, х 4- х* — нечетные.
Если /(х)—четная функция, то
4 о а
J /(х)4х-2 \f(x}dx.
—а б
Если f (х) — нечетная функция, то
J /(x)rfx-O.
Дифференцирование
определенного интеграла
по параметру
Если функции /(*, «) н Д(х, в) непре-
рывны, то непрерывна н дифференциру-
ема функция
F (“)- J7(X, «)rfx.
а
причем
»
F‘ («) - (х- •)ах-
В общем случае, когда
F («) — J /(•*• ®)rfx-
Ti t«)
имеем
*>(«)
F' (“) “ j Л <*• “) 4-
•i <•>
+ i (•)» °] —/In («). “J -V'- .
Пример. ~ j tln dx — \ co» (xy) dx +
< к
2y 2y
aln y* , "“T / \ . 3»lny*
+ —v)v~-
Вычисление некоторых определен-
ных интегралов может быть произведено
при помощи дифференцирования опреде-
ленного интеграла по параметру.
Пример. Найдем
I
(* X*-1 - хв-1
—ЙГ7-----"•
v
если а > 0. Ь > 0. Имеем
1
Отсюта / — —- J ^ = — In а 4- С. nu С не
зависит от а. При а—Ь, I = 0, поэтому С —In о,
/= tn —.
а
Интегрирование
определенного интеграла
по параметру.
/(х, a) da > dx.
если /(х, а) ограничена во всей области
а <. х < Ь, а, < а < <4 и, за исклю-
чением. может быть, конечного числа
прямых * = const на— const, непре-
рывна в этой области.
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Если с возрастанием b до бесконеч-
»
ности интеграл I — j/(x) dx стремится
а
к определенному пределу, то этот инте-
грал называется сходящимся. Предел
этого интеграла, обозначаемый симво-
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
175»
оо
лом|/(х)</х, называется несобственным
а
интегралом функции /(х) на полубес-
конечном промежутке (а, оо). Таким
образом,
ОО О
(* f(x)dx — Нт | f(x) dx,
а о-*с*> а
Если же при Ь -> оо интеграл / не
стремится ни к какому пределу, то
этот интеграл называется расходящимся,
оо
и символ f (х) dx в этом случае смысла
а
не имеет.
Аналогично определяется значение
символов
ъ
J /(x)dx
и j /(x)rfx
Если /(х) обращается в бесконечность
при х —» Ь, то
»
j/(x)dx
а
В
определяют равенством j /(x)dx =
а
b—«
™ Hm I /(х) dx, (« > 0), если этот пре-
-о л
дел существует.
В этом случае интеграл называется
сходящимся, а предел интеграла назы-.
вается несобственным интегралом от
неограниченной функции f(x) на проме-
жутке (а, Ь}.
Если же этого предела не существует,
то интеграл называется расходящимся,
•
н тогда символ j/(x) dx теряет смысл.
а
Аналогично определяется несобствен-
ный интеграл в случае, когда точки
разрыва совпадает с нижним пределом.
Если точка разрыва х — с функции / (х)
лежит внутри промежутка (а, Ь), то
J/(x)dx — llmj /(x)dx-f-
» г
4-Hmj /(x)dx;
при этом положительные величины
и »3 стремятся к нулю независимо друг
от друга.
Интеграл от функции с бесконечным,
разрывом всегда может быть преобра-
зован в интеграл с бесконечным пре-
делом и обратно.
Примеры'.
-=llm { -1 W +3 ) =«.
•-0
4-00
f di
2) 1 -----(а > О) при а > I сходится »г
J **
а
имеет значение -------!-----, в при а < 1 рао-
(« -1) а»-1
ходится.
dj Полагая х — . получим
а 4- оо
Г dx с dy
J Vx J •
и I
Вопрос о сходимости или расходи-
мости интеграла с бесконечным преде-
лом, если подинтегральняя функция f(x)
сохраняет положительное значение,
легко решить, применяя слсдующие-
критерии сравнения.
I) Если при х > а имеет место нера-
венство /(х) < <р (х), то из сходимости
too 4-оо
j (х) dx следует сходимость f /(x)dx.
а а
' +«»
а из расходимости j /(x)dx следует
-f-oo а
расходимость j у (х) dx.
а
f (jc)
2) Если существует Ilm —• =
x-4«TW
— с (0 < с <4- с»), то оба интеграл»
( <r(x)dx и [ /(x)dx сходятся или
а а »
расходятся одновременно.
Предположим, что подинтегральнаж
функция f (х) меняет свой знак и про-
межутке интегрирования. Если сущест-
вует (т. е. сходится) интеграл |/(x)|dx,.
а
то существует и интеграл J / (х) dx„
а
176
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
который в этом случае называется
абсолютно сходящимся, а функция /(х)—
абсолютно интегрируемой на отрезке
[a,-f-co]. Если же интеграл ( /(x)dxcy-
а
шествует, а интеграл f |/(х) | dx несу-
а
шествует, то первый интеграл назы-
вается неабсолютно сходящимся.
Аналогично устанавливаются поня-
тия об абсолютно сходящихся и не-
абсолютно сходящихся несобственных
интегралах всех прочих видов.
Признаки Коши сходимости н рас-
ходимости несобственных интегралов,
у]
I) Если |/(х) | < где А и р—поло-
жительные постоянные и р> I. то не-
собственный интеграл ( f(x)dx абсо-
а
у}
лютно сходится. Если же |/(х)|>-^
и р< 1, то указанный несобственный
интеграл расходится.
Условие сходимости будет выполне-
но, если существует конечный предел
lim {/(х) х1’}, (р > !)• условие же рас-
ходимости имеет место, если суще-
ствует lim (/(х) х^}, (р < 1), отличный
x--fco
от нуля (конечный или бесконеч-
ный).
Иначе говоря, если при х -» оо функ-
ция /(х) является бесконечно малой
порядка р > 0 ^по сравнению с ,
-Н»
то интеграл | / (х) dx сходится или рас-
а
ходится в зависимости от того, будет
ли р > 1 или р < 1.
Указанные признаки применяются и
к несобственным интегралам f f (х) dx
и f/(x)rfx.
— ОО
2) Если /(х) при х = b обращается
в бесконечность, а при х, близких к Ь,
удовлетворяет условию | / (х) | <
. Л
гле Л и р — положитель-
("“Аг
ные постоянные и р < 1, то несобствен-
ь
ный интеграл J /(x)dx сходится абсо-
“ А
лютно. Если же I/(х) | >и
р > 1, то указанный несобственный
интеграл расходится.
Условие сходимости будет выполнено,
если существует конечный предел
lim (/(х) (& — хУ\ , (р < 1). условие
х-о
же расходимости имеет место, если
существует lim {/(х)(& —хУ\, (р >1),
х-ь
отличный от нуля (конечный или бес-
конечный).
Иначе говоря, если при х -> Ь функция
f (х) является бесконечно большой по-
рядка ,р>0 ( по сравнению с »
ь
то интеграл i f(x}dx сходится или рас-
а
ходится в зависимости от того, будет ли
р < 1 или р > 1.
Аналогично можно применить ука-
занные признаки к случаям, когда f (х)
обращается в бесконечность при х = в
или в некоторой точке х = с промежутка
интегрирования.
Примеры;
+~
С dx
1) I ----7=^ сходится, так как
J xs VI + х’
lim I------' X1 1 — 1. т. е. полннтеграль-
x--H»lx»Vl-j-x* J
ная функция представляет собой бесконечно малую
порядка 3 относительно бесконечно малой -у
+ “»
m I х ' dx
2) J расходится, так как
и
I +1
х —|-оо J ——j — 1, т. е. похинтетряльная
функция представляет собой бесконечно малого
порядка -i- относительно бесконечно малой —.
—-----, т. о подиитегральная функция продета-
•____
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
177
•лкет собой бесконечно большую поралкл -J- ог-
оеительпо бесконечно большей i _
Равномерно сходящиеся интегралы
Несобственный интеграл | f(x,a)dx
а
называется равномерно сходящимся
относительно а на отрезке (а0, ai],
если при любом заданном числе к > О,
сколь бы мало оно ни было, существует
такое число д, что при всяких значе-
ниях N > п
ннях
и прн любых значе-
взятых на отрезке |а0, сч ],
выполняется неравенство
< е, причем число п зависит только
от е и не зависит от а.
Признак Венерштрасса.
Интеграл j /(х, о) dx сходится абсо-
лютно и равномерно относительно а на
отрезке а(|, если можно указать
такое число N и такую функцию (х)
(.мажорирующую функцию*), что при
х > N и а0 < а < а1 выполняется не-
равенство | /(х. а) | < | у (х) | и схо-
дится интеграл j | <f> (х) | dx.
а
Пример. Если л > I, то f -ln Лх по-
J гя
»игся равномерно лля всех значений у. так как
Свойства равномерно схо-
дящихся интегралов
I) Если функция fix. а) непрерывна
прн х > а и при изменении а на отрезке
lij.a,] и если интеграл j'/(x, a) dx
а
равномерно сходится, то он есть непре-
рывная функция от а при
2) При выполнении условий свойства
i-го имеет место формула интегриро-
вания под знаком интеграла
•1 +" +2° *1
1 da ( f(x.a)dx — I dx j f(X. a) da.
к. и й к.
3) Если прн непрерывности /(х, а) и
df(x, а)
— —- несобственный интеграл схо-
Т V (*• ») м
дится. а интеграл I —* — dx схо-
а
дится равномерно, то имеет место фор-
мула дифференцирования под знаком
интеграла
J /(х> e) dx
f^dx.
J da
Главное значение несобственного
интеграла
Пусть функция /(х) имеет разрыв в
точке с, лежащей внутри промежутка
интегрирования. Тогда несобственный
интеграл определяется равенством
J/U ) dx =
причем предел должен существовать
при независимом предельном переходе
по <1 и по В некоторых случаях,
когда этот предел не существует, ока-
зывается полезным рассмотреть предел
того же выражения, если и и с* стре-
мятся к нулю, оставаясь равными.
Если этот предел существует, то его
называют главным значением несобствен-
ного интеграла и обозначают символом
V-p'.
о
V-p-j fWdx-
а
— lim | J f(x) dx + j’ •/ (x) dx
Аналогично определяется главное
значение интеграла с бесконечными
пределами интегрирования
+~ -И»
V р- | /(x)dx- lim | f(x)dx
-Joo a-+ooj0
1'2 Том I Зак. H«l
178
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Пример. Ишеграл J х — с < е < *“
а
'Ссобствеииый иг существует, так как пырежеиие
г—a, Ь
Г ах , Г ал . а - с .
I Г=7 + I — + '“V
я Л
«е имеет огрсдсдсипого предела, если с, и ct стре-
мятся оба к нулю независимо друг от друга. Но
। данное значение ггоги интеграла существует:
Р
Iax , Ь —с
---------1л .
л-с с-а
а
ИНТЕГРАЛЫ ЭЙЛЕРА
Интеграл Эйлера 1-го иода (бэта-
функция)
1
В(р. <?)- j -xf-'dx
и
имеет конечное значение при р>0.
<?>().
Интеграл Эйлера 2-го рода (гамма-
функция)
Г(р)- J х*-' г~*Чх
U
имеет конечное значение при р > 0.
Огненные свойства:
В (?. Я) — В «?. ру, В (р, I) — у;
в (р. Я) -
_____________1-2-3..,(ф- I)________
“ (р + я— I) (Р+• Я—2)...(р4 hp*
если 9 — целое и больше I;
В (р, «) Г (f )£(.<?)♦
41 Г \р + д) ’
Г (р) —
- Ilm _____________12 3.. .р, >
.-«Ь (р + 1)(р + 2)... (р+т)/’
где т — целое.
Г (р + 1)-р-Г(р).
Если известны значения Г (р) дл»
всех р, заключенных между любыми
двумя последовательными целыми чис-
лами. то последнее равенство лает воз-
можность выразить функцию I (р) для
любого значения р. Таблицы значений
Г обычно составляют для отрезка [I, 2|
(см табл. X, стр. 41). Если р содержится
между 0 и I, то
Г (р) Г (1 — р) = * ;
sin /тх
r(4)-/i
Если п — целое положительное то.
Г(л) = (л — 1)! = I -2-3 . . (л — 1).
ТАБЛИЦА ОПРЕДЕЛЕННЫХ
ИНТЕГРАЛОВ
(Буквы лит везде в таблице означают
целые положительные числа; р, ?, t —
рациональные числа)
1
I) j (I — хУ> x'-'dx -
и
I
— j(l —X),-pxP<tt —
и
= pit (1 —р) cosec рх;
(Р®< »>-
।
— — cosec .
Я Я
3) ( xPdx рп
J (1 -хИ1 " Bin рх
I
f ^РДх _ х
J (I _хИ’+1 ” Slnpx
(Р»<|)
dx — — X Ctg рх.
6)
ТАБЛИЦА ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
179
7)
dx — ж cosec дх.
8)
x^-'dx
(I -х)»(| 4-дх)
= (TT7Fcosec<?r-
Г x*-‘dx
J (1-х)»(х+д)
J
д'7-*11
“йТ^СОЗеС^
(1 — х") dx
(1 +x)',+l (1 — x)
I
17) f хеХЛх -.±-1.
I
18) J In (q 4- PX\ dx
о
4 •+ P- In (</ 4 p) — In 7 — I.
i
С я*
19) । In x In (1 — x) dx — 2---- .
и
20) j xrt-1 In (1 — xirf.r- — “V1
и
i
21) । In x In (I 4x) dx-^1— p — 2 In L
и
(I -X)»-1
п
» v
2Л'Н aL * •
I
II) f(l - Viy-'dx-------7-2r-n«
J ₽ (P -I- и
f_______dx_______
121 J (I — дх) fT~=~T "
u
* — 1 arcsin l/p
?Кр(1-д) r
I
13) | .-----d-X- - = — arc tjj p.
j /(I 4- д»х)(|^7) P
I
14) f ax
J V(i - pU)(1 -x) P I— p
15) [-------.
J (1 + x<) /I -x« «
I
16) j xe^dx - 1|(9-!)«*+ ||.
u
I
26) j in (I — / v) dx — — y.
u
180
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
35)
*; (p>0).
I
28) j arcsin px dx —
и
— arcsin P + ~ I' i — /Iя — .
i
29) | arccos px dx —
*» arccos p + —-----— /1 -P-’
P P
36)
37)
и
и
nl
(p>0. и>0).
30)
Jarctgpxrtr—arctgp—In (1+p1),
и
38)
u
2
(p>0).
31)
£ arcctg px dx «
— arcctgp + ~ In (1 + pi)
2"p 2
39)
dx - I - In 2.
u
32)
f arcsin ( Vx ) dx
i
40)
j sin (qx + r}dx —
u
- ZTZTj w cos л + p sin r).
и
4
41)
33)
dx
r.
2pd
J e px cos (qx + r) dx =
u
= „t 1 (p COS r — <? sin r).
34)
42)
cos qx dx
и
m , ПХ
m sin —
m
(0<n<«).
2
_ r.
*; (P > 0).
43)
cos(a*)<L*=^
и
cos pr cos qr. (p > q).
44)
и
COS sx—------—
4 r* — Л*
— — cos2pr; (p ~ q\
+ у cos pr sin qr, (p < Я)-
ТАБЛИЦА ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
181
оо оо
С tg X . С Sln*X . л
*’ J х
и и
I COS р.Г — COS (?JC . X л
*7> ) --------— ах - у (Я — РУ (Р > 0. Я >
ОО
48) j In (1 + /fix*) d*~ = ~ In (1 + pq).
и
со
49) j In (pt + jfl) - 7 In (p + q).
u
50) fln(l— 2p cos x +/>*) Лс = | 0’
6 I 2xlnp; (pt > 1).
51) [?^rfXeL In(l+;>)
V lb **
U
2 2
52) j In sin x dx = J In cos x dx = — j = — у In 2.
и и и
ж ж
"Т 2
53) Jsin2 * * *"+'xrfx -j cos**' xdx - 3.-У;6-(^2; l}.
о и
54)
cosT”x dx
1-3-5...(2n—I)
2-4-6...2л
•i
55) f________dx__________
J (pt cost x + ql sin- x)n “*
и
Л
2{|2(л-*)-1|!!Р(»-1) - l|
, Я fr=l__________________________________________________________
2* (л - 1)1 ' д^»-'
* Символ *1! (оолуфикториал) обозначает проимеление всех нечетных чисел от I до 4, если а
счетное, или произведение всех четных чисел от X до А. если k четное.
1*2
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
2
56) f Ain^'ACOS^+'x^-l.—
J 2 (л + m + 1)
u
471 f cin1" xdx — <2Л ~ ” (2т ~ ’
57> j sin х cos xdx----------(2л+355)1,------7 •
и
Вычисление интегралов
при помоши рядов
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ
ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
ОС
Если /(х) = Vu„(x) и ряд равно-
ьх’рно сходится на отрезке la, b |. то
В оо Ь
j f(x)dx = У J «я(х)<(х.
а я-1 а
58) SI (X) - f 512/ dt = х - 1 - +
J I м «Э1
Формула трапеций. Промежуток ин-
тегрирования (а, Ь) делится на п рав-
ных частей точками х0 = а, хь х», . . . ,
хя = Ь;
+ У1 + п+-- + у<_1).
Здесь
Уо •= / (а). У| - / (Xi)........у« - f (М
59) CI (х) = - j dt = С + In х -
-гэг+Нт— <*>0)-
60) LI (х) — J - С + In I In х | +
1 (In х)’ | (In х)« ,
+ lnx+-r-5r- + 7.-3j-+...
(0<х<)).
В последних двух формулах С =
-= 0.57721566 — постоянная Эйлера (см.
стр. 135).
61) -р--у-4-
и
• Символ АН (полуфхггорихл) обозмачвет про*
из ведение всех мечетных чисел »«т 1 ло >, если А
мечетное, иди пронтнедемне все* черных чисел
мт 2 ди А, если А четкие.
Формула Симпсона. Промежуток ин-
тегрирования делится на 2л разных
частей точками Хд = a. х», х». ...
*za — b;
к
J/(x) rfxej |у0 +У!л +
4 4 СУ1 +У»+ ...4 У2я_|) 4
4- 2 (у, + у. 4 ..-Ч-У^-аМ.
Здесь
Уо - / - f (*1)....Уы - /(»)
Разность /?я между точным значе-
нием определенного интеграла и при-
ближенным его значением
- -Ь -Г (5) (Для формулы
трапеций);
Пя - - 785^/П(В) (дяя '1'ОРМУЛЫ
Симпсона).
Здесь 5 — некоторое значение пере-
менной интегрирования из промежутка
(а. Ъ).
ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ
183
Рормулы Чебышева
4
[/ (х) dx «а у I/ (0,2113/) + / (0,7887/));
О
* 4 I/(0.1464/)+/(0Л/) +
+ /(03536Л1;
<= У (0-1027/) + f (0.4062/) +
-I- ((0,59380 + f (QA413l)\-,
«ь У (0.0838/) + / (0231270 +
+ /(0,50 + /(0,68730 +
+ / (0,9162/)).
Формулы Гаусса
J / W dx s» / |0,5/ (0221130 +
4- 0,5/ (U.78870);
о / (022778/ (0.1127/) +
+ 0.4+44/ (0,52) +
-+ 022778/ (0,8873/) |;
о I |0.1739/(0.0691/) +
+ 0,3261/(03300/; +
+ 03261/(0.671)0/) +
+ 0.1739/(0.9306/));
ч» ) 10,118.5/(0,04690 +
+ 0.23ЧЗ/ (0.2308/) +•
4 0,2814/ (0,5/) +
•а 022393/ (0.7692/) ь
+ 0.1185/(0,9531/)).
Г^АФИЧРСКОЕ ИНТЕГРИРОВАНИЕ
Для получения графика первообразной
х
функции a=F(x)= | j (*) dx строится
график функции у = /(х) и построен-
ная кривая AAi (фИР. I) точками В,
В.....делится на части АВ, ВВ.....
криволинейная трапеция А А А ,А| де-
лится прямыми ВВ .fi.s’. . .. на по-
лосы АА' В'В, ВВ'ВуВу, . . . Каждую
полосу заменяем равновеликим прямо-
угольником, для чего на дугах АВ,
В В...выбираем (на глаэ)точкн С, С|.. ч
через которые проводим горизонталь-
ные прямые; точки C.Ci, . . . выби-
рают так, чтобы площади, ограниченные
кривой и этими горизонтальными пря-
мыми, были соответственно равны (на
чертеже эти площади заштрихованы).
На оси Ох влево от начала отклады-
вается отрезок OP = 1. и точка Р (по-
люс) соединяется с точками А*, В"...
которые являются проекциями точек А,
В, . . . на ось Оу.
Фиг. I. Графическое иитегрнрэпкиие.
На осн Оу берется произвольная
точка О‘. которая принимается за на-
чало ноной системы координат к'О'г
(см фиг. 1). Через точку Q пересече-
ния новой оси О'х' с вертикалью А'А
проводится прямая, параллельная лучу
РА*, до пересечения с вертикалью С'С
в ючке 5. Через точку S проводится
примам, параллельная лучу РВ’, до
пересечения с вертикалью CtCt в точке
R и т. л- Многоугольник с вершинами
Q. S, R. .. . образован кясягельны44
к интегральной кривой, точки пересе-
чения его сторон с вертикалями
В В, B'tBt,. . . являются точками каса-
ния, следовательно, принадлежат инте-
гральной кривой, которую можно вы-
чертить по лекалу. Ордината г по-
строенной кривой (в системе координат
х О г) дает значение интеграла г "
X
“ J / U) «и.
184
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
КРАТНЫЕ ИНТЕГРАЛЫ
Вычисление двойного интеграла
Пусть функция /(х, у) определена
п некоторой замкнутой области Р из-
менения независимых переменных.
С геометрической точки зрения области
Р соответствует на координатной пло-
скости ху некоторая плоская фигура,
ограниченная одной илн несколькими
кривыми. Разобьем эту область на
частичные области />>, р», . . . Пусть а,
обозначает площадь частичной области
Pj. a значение функции/(х, у),
которое она принимает в некоторой
точке М, частичной области с номером /.
Выражение V / (5/, rtl) а, называется
двумерпой интегральной суммой, если
наибольшая хорда любой из частичных
областей меньше некоторого числа 8
В зависимости от способа разбиения
основной области Р и от выбора точек
Mt внутри частичных областей р, инте-
гральная сумма может принимать бес-
численное множество значений. Если
существует такое число А, что разность
между этим числом А и любой инте-
гральной суммой стремится к нулю при
стремлении 8 к нулю, то функция/*.», у)
называется интегрируемой в области
Р, а предел А, обозначаемый символом
| j /(х, у) ds, называется двойным инте
Р
грамм от функции /(х, у), распростра-
ненным на область Р. Одним из воз-
можных разбиений области Р является
разбиение этой области прямыми, парал-
лельными координатным осям. В этом
случае для обозначения двойного инте-
грала служит символ /(х, у) dx dy.
С геометрической точки зрения двой-
ной интеграл можно истолковать как
объем некоторого цилиндрического тела,
ограниченного частью координатной
плоскости ху, цилиндрической поверх-
ностью с образующими, параллельными
осн Ох, построенной на контуре области
Р, и поверхностью, заданной уравне-
нием x — f(x,yY
Теорема о среднем. Если функции
/(х,у) и Т (*• У) непрерывны в области
Р и"функция <f (х, у) сохраняет посто-
янный знак, то всегда можно найти
внутри области Р точку с такими коор-
динатами т), что будет иметь место
равенство
JJ/ (х.у) Т (X.y)ds-J (S. ч) ? (х. у) ds.
Двойной интеграл, распространенный
на область Р, ограниченную прямыми
х = а, х = Ъ, у =* с, у = d, вычис-
ляется при помощи двукратного инте-
грирования
а та з
Jj/(x.y)rfx dy — J К f(x,y) dxj dy -
В случае произвольной области
f(x.y}dxdy — I f(x,y} rfy} dx.
a U.U' j
причем у = ?i (x), у = <pi (x) — уравне-
ния нижней (ANB) н верхней (AMB)
частей контура области Р (фиг. 2); а.
Фиг. 2. Случай произволь-
ной «ыпуклой области при
вычислении двойного инте-
грал»
Ь — абсциссы конное отрезка, яаляю-
щегося проекцией области Р на ось
абсцисс. При выполнении интегрирова-
ния по у (вычисление внутреннего ин-
теграла) величина х считается посто-
янной.
Пример. Интеграл I от функции / (х. у) -
sKjr’y. распространенный по области, ограничен-
ной биссектрисой координатного угла хОу и дуюй
окружности радиуса г с венгром ма оси Ох. ка-
сающейся в начале координат оси Оу (фиг. 3),
можно вычислить так:
КРАТНЫЕ ИНТЕГРАЛЫ
185
Если сначала интегрировать по переменной х,
то интеграл выражается так:
Фиг. 3. К примеру на
вычисление двойного
интеграла (область
интегрирования).
Пределы внутрен-
него интеграла в обоих
случаях определяются
из уравнений биссек-
трисы у=х и окружно-
сти х> -|- у* = 2гх; »ти
уравнения решаются в
первом варианте отно-
сительно у. а во вто-
ром — относительно х.
Формула замены переменных в
двойном интеграле. Уравнение х =
= /(u, v). j =f(u. v) устанавливают
соответствие между координатами (х. у)
точек некоторой области Р плоскости ху
и координатами (u, и) точек другой обла-
сти Р], расположенной на координат-
ной плоскости ио. Пусть функции
/(и, о) н <f (и, о) непрерывны вместе
с первыми частными производными вну-
три области Pi, и соответствие между
точками обеих областей взаимно одно-
значно, т. е. каждой точке («, о) обла-
сти Pi соответствует определенная точ-
ка (х, у) области Р, и обратно: каждой
точке (х, у) области Р соответствует
определенная точка (и, о) области Рг,
в этом случае область Р называется
взаимно однозначным образом области Pj.
Тогда определитель
df df
D(f,f) du оо
U(u.v) " ()y *
Ou dv
называемый якобианом, или функцио-
нальным определителем, сохраняет знак
в области Pi и
F(x.y) dxdy
" П FV(и- v)- f <“• v)l | |rfu dv.
поэтому
f^/(x.y)dxdy-
— I [f (р cos 0, р sin 0) pdpdO.
Р,
Тронной интеграл и его вычисление
Аналогично двойному интегралу опре-
деляется тройной интеграл как предел
трехмерной интегральной суммы:
.Of F У- г> djc dy dx —
— lim VF(«(1 Vj.
Вычисление тройного интеграла мо-
жет быть сведено к трехкратному вычис-
лению обыкновенных определенных
интегралов:
J| J F ^х' У' dy dz =
tX. VI 1
J | J F(x. y. z) dz) dx dy —
p 1ф. (Ж, у) J
b (X) Гф, (x, VI
j F (x. y, z) dz
a U, <x) k lx. v)
dv) dx.
Область G ограничена поверхностями
t = <|>i (x, >). z = фа (ж, у) н цилиндри-
ческой поверхностью Ф(х, у) =• 0, про-
ходящей через контур плоской области
Р плоскости ху, на которую проекти-
руется область G. При интегрировании
по переменной z переменные х и у счи-
таются постоянными. Определение пре-
делов интегрирования <р( (х), ft (х), а, Ь
выполняется так же, как при вычисле-
нии двойного интеграла по области.
Замена переменных в тройных
интегралах. При замене переменных
х = /(«, о, w), у=<р(и, и, ш), г =
= ф(«, о, w) имеет место формула
F (х. у, :) dx dy dz
В случае перехода от декартовых
координат к полярным
х-рсозв;у-рй1пв;£1±^_р,
JJJ F[f(u, v. w). <p (u. v. w),
ф (u, v, w)| I — T' I du dv dw,
‘ | U (u, v. w) I
186
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
причем область G — взаимно одно-
значный образ области Gt, и якобиан
D Ц. ?. 40
D (и. V, w)
а/ d/ df_
ди dv ow
dip Ар fAp
du ov dw
di|> dip d<p
du dv dw
ные дуги точками, абсциссы которых
будут х,. х,,.... х^^......... хя_|,
причем будем считать а = Xq, Ъ = хп
Внутри каждой частичной дуги, ограни-
ченной точками деления с абсциссами
•*/. возьмем произвольную точку
(5/( Td, С#) и составим сумму
п
’lb (х, — х^,).
Г"1
сохраняет знак в области Gi.
В частности, при переходе от декар-
товых координат к цилиндрическим (см.
стр. 2.51) элемент объема в декартовых
координатах dxdi/dz заменяется эле-
ментом объема в цилиндрических коор-
динатах pdprfddz, а при переходе к сфе-
рическим координатам (см. стр. 251) —
элементом объема в сферических коор-
динатах p*sin ’WprfOdip, так как в послед-
нем случае У ** — ptstn 6, где 8 —
D (р. «. <р)
угол между радиусом-вектором р и
осью х.
Пример. Интеграл
«реастаалеет тройкой интеграл от фуикпин
г ж* т- у' -г г‘. распространенный на ту часта
сферы х‘ 4- у1 + г' — /?*, для которой ж > и,
у>0. а>П.
Если внести вместо декартовых координат сфе-
рические. то
КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
Пусть в некоторой области простран-
ства задана непрерывная функция
Р (х, у. X) и кусочно-гладкая кривая L,
целиком лежащая в указанной области
и соединяющая точки А и В.
Обозначим через а и b абсциссы то-
чек А и В и разделим кривую на частим-
Если неограниченно увеличивать чис-
ло частичных дуг и одновременно
устремлять к нулю их максимальную
длину, то существует предел этой суммы,
называемый криволинейным интегра-
лом функции Р (х, у, z) по переменной х.
взятым вдоль дуги АВ кривой; этот
интеграл обозначается символом
f Р(х, у, х) dx.
АВ
Наиболее общий вид криволинейного
интеграла
j (Р dx + Q dy + R dz) —
- f P (x. y. x) dx + f Q (x. y, x) dy -p
AB AB
+J R (x. y, x) dz
представляет сумму криволинейных
интегралов от функций Р, Q, R соот
ветственно по переменным х, у, х.
При интегрировании вдоль замкну-
той кривой начальная и конечная точки
Лив совпадают, и криволинейный инте-
грал не зависит от выбора этой точки,
но зависит от направления обхода кри-
вой при движении от начальной точки
к конечной; при изменении направления
обхода знак интеграла меняется, абсо-
лютная же величина интеграла остается
неизменной.
Вычисление криволинейного интеграла
сводится к вычислению определенного
интеграла:
J Р(х,у, x)dx-
(О./1(0./а (О!/!
причем х = /> (О, У = /1 (Л, х = /|(/) —
уравнения кривей АВ; а и jj опреде-
ИНТЕГРАЛ ПО ПОВЕРХНОСТИ
187
л я юте я из уравнений а “ f\ (a), b “ f\ (?)
(а и b — абсциссы точек А и В).
Криволинейный интеграл часто при-
меняется при вычислении работы.
Пример. Силы поля обратно пропорциональны
расстоянию их точек приложения от оси О:, пер-
пендикулярны этой оси и направлены в сторону
оси О’.
Найти работу сил поля при движении точки
по окружности х — сох да, у = I. i=sln^ от
точки Af (1. I, 0) до точки N (0, 1, 1).
Согласно условию модуль лектора силы F —
«= -----, где й —кояффипнент пропорциональ-
У*' + У"
кисти.
Направляющие косинусы вектора силы равны
COJJ =
со» 7 — О;
проекции силы на координатные осн
Л —------if— F — — —» 0.
х х* + у» • у х< 4- у» • гг
Для определения работы заметим, что элемент
работы равен скалярному произведению вектора
силы на иектор элемента пути. Поэтому вся работа
выразится криволинейным интегралом по дуге MN
А ~Jn + V* + PtdI> -
- (
MN
. (* х ах + у а у
J Х- + ? -•
A1.V
Переходим к обыкновенному интегралу, пола-
гая х — соар; dx — — aln vat: у — I: rfy — 0;
при атом у изменяется от 0 (точка М) до ——
почка N); получим
и
т
, f - гоя у tin »ау
Л “ ~ * J ----(-HU.4--------
и
г
т
—-----у In |1 4- cot’ «) | —-i-ln2.
о
Интеграл и — Г (Р dx 4- Qdy) не за-
ла
iTiCHTor кривой АВ, соединяющей точки
А и В и заключенной в некоторой одно-
ввязнои (т. е. ограниченной одним кон-
туром) области D, если вл всей агой
области выполняются условия
В этом случае, если точка А (х0, уо)
фиксирована, интеграл является функ-
цией только координат х, у точки В,
т. е. и = Ф(х, у), причем эта функция
удовлетворяет уравнению в полных
дифференциалах
du = Р dx 4- Q dy.
Интеграл V — f (Pdx 4- Q dy 4- Rdz).
An
взятый вдоль пространственной кри-
вой АВ. соединяющей точки А и В и за-
ключенной в некоторой пространствен-
ной односвязной (т. е. ограниченной
одной поверхностью) области G, не
зависит от кривой АВ. если во всей
этой области выполняются условия
dP dQ dQ d/? . dP dP
ду Ох ' dz ду ' Ox dt *
Если в этом случае точка А фикси-
рована, то интеграл V является функ-
цией только координат х, у, z точки В,
т. е. V = ‘Г (х, у. z), причем
dV — Р dx 4- Q dy 4- R dz.
ИНТЕГРАЛ ПО ПОВЕРХНОСТИ
Пусть правильная поверхность 5
(см. гтр. 190) разбита на п частичных
поверхностей St, Sn, . . . , s„ и пусть
в|, ....... ся — площади частичных
поверхностей.
Дана непрерывная функция А'(Л1>
точек поверхности 5 •; F(Mt) — значение
функции в произвольной точке Mt чя
стичной поверхности s,. Предел суммы
V F(Mt) в| при безграничном умень
щеннн во всех измерениях каждой иэ
частичных поверхностей называется
поперхностным интегралом / типа и
обозначается символом
[f F (М) dz.
Если поверхность S задана параме
трическнми уравнениями
х = х (и, и), у = у (и, V), г — г («,</),
дР r)Q
•S7--57-
” Функцию трех не1«п"снмых переменим! мпмгно
рассмктрннать как функцию томе* прдетркистнк.
188
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
ТО
F(M) = Ф|х(и, о),
у (и. о), г(и, р)| = /(и. о).
я поверхностный интеграл сводится
к двойному:
f f F (М) da = I f Ф (x. у. г) da =
$ S
И
R
f (a. o)
К EG — F* du d p.
где
-(£)’Ч£)’Ч£)'=
«Ч^’Ч^УЧ^У’
_ дх дх , ду ду dz dz ,
ди dv ~ ди dv ди dv ’
[D(u.v)J
д ГР(х,х)|« [ D (у,z) ] *
[D(u.v)] + [ D (а, V)] ’
а область R есть отображение поверх-
ности 5 на плоскость uv.
Если поверхность задана уравне-
нием г " г(х, у), то
я
F (Л<) ~ Ф[ х. у, г(х, у)|
PMf) да -
Ф(х. у. »(х. у)| х
X /'Ч£УЧ£)'-"-
Область D есть проекция поверхно-
сти $ на плоскость ху.
tlpu*ep. KoopumiTU nenrps тяжести посьмла
части сферы X1 4- у’ + т‘ — /?•, вырезанной коор-
аинатиымн плоскостями х = 0, v «и. а =0 и
расположенной в первом октанте, вычисляются
так:
А* sin1 6 со» pd>
так как уравнения сферы в криволинейные коир-
липллах в (широта) н о (холгота) будут
г = R stn 3 соя о: у =. R sin 0 sin •;
г — R cos ».
а потому
<Ь - У ЕО- Р» <ЛЛа - R1 sin tdtdp.
Пусть в точках правильной поверх-
ности S задана некоторая функция
R(x, у, г}. Выберем на поверхности опре-
деленную сторону за внешнюю и ра-
зобьем поверхность^ на части я. ®я.- •
s„. В каждой части st выберем произ-
вольную точку Mi(xt, yt, г,), вычислим
в ней значение функции R (xh у,. zt) и
умножим это значение на проекцию 5,
части Si на плоскостьху. Прн этом числу 8,
приписываем знак плюс или минус в
зависимости оттого, образует ли пормаль
к поверхности в точке Mt, направлен-
ная но внешнюю сторону, острый или
тупой угол с осью Ог. Составим сумму а
л
таких произведений а= V Rtxh yt,
и перейдем к пределу, неограниченно
уменьшая во всех измерениях каждый
элемент sf. Этот предел называется по-
ьерхностным интегралом // типа от
R (х. V, г), распространенным на вы-
бранную сторону поверхности, и обо-
значается символом | [ R lx. у, z) dx dy.
Наиболее общим видом поверхностного
интеграла II типа служит интеграл
(Р (х. у. z)dydi + Q (х, у, г) dxdx +
+ R (х, у. z) dx dy}.
Связь поверхностных интегралов /
и // типа дастся формулой
Jj (Pdydz + Qdzdx + Rdxdy}^
= jf (P cos a 4- Qcos 3 + R cos f) da.
где a, ₽, у — углы нормали к поверх-
ности с осями координат.
Формула Остроградского (см. также
стр. 233)
(Р cos а 4- Q cos ? 4- R cos 7) da =
— 4-—Jrfxrfyrfz.
ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ
184
где 5 — поверхность, ограничиваю
щая область G; а, 3, -j — углы, соста-
вляемые внешней нормалью к поверх-
ности с осями Ох, Оу, Ог; функции
Р (х, у, г), Q (х. у, 2). R (х. у, г) непре-
рывны в области G вместе со своими
первыми производными.
Формула Стокса (см также стр 233):
#[(«->)**♦
о •
f dR dQ\ .
+ (*-—эг)*уЛ +
\ dz dx J J
= | (Pdx + Qdy + Rdz).
Здесь P (x, у, г), Q (x, у, г), R(x. у. г)
непрерывны вместе с первыми частными
производными в некоторой трехмерной
области, содержащей внутри себя пра-
вильную поверхность S; С — замкну-
тый контур поверхности S, интегриро-
вание вдоль которого ведется в поло-
жительном направлении. т. е. так, что-
бы обход контура представлялся наблю-
дателю, расположенному на выбранной
стороне поверхности S, совершающимся
против стрелки часов, если система
координат хуг — правзя.
Частным случаем формулы Стокса
для плоскости является формула
И (1» “ ** " ^(Pdx+Qdy),
где L — контур плоской области D,
интегрирование вдоль которого ведется
в положительном направлении, т. е.
так, чтобы область D при обходе кон-
тура L оставалась слева, если система ко-
ординат правая ;
рывны в области
Р' О'д~Г ' 7Г "'"Р*
dy dx
О и на ее границе.
ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО
ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ
И МЕХАНИКЕ
Вычисление площади плоской фигуры
(S). Если фигура ограничена кривой
у = /(х), осью х и ординатами х = а,
х = Ь, причем функция /(х) непре-
рывна, положительна и однозначна на
ь
отрезке 1а, б), то S = j/(x)dx.
а
Если график функции у = /(х), за-
данной на отрезке |а, 61. пересекает
в
ось Ох, то определенный HHTerpaaJ/(x)dx
а
будет представлять алгебраическую сум
му площадей, заключенных между гра
фнком, крайними ординатами х — а.
х = Ъ и осью Ох. Величины площадей
расположенных выше оси Ох. войдут в
эту сумму со знаком плюс, а величина
площадей, расположенных ниже оси Ох.
войдут со знаком минус.
Если кривая задана уравнениями в па-
раметрической форме х = ? (0> у — ф U)
так, что у (6) — а, у (/») = Ь, то пло-
щадь, ограниченная этой кривой, осью
х и ординатами х <« а, х Ь. будет
S - f 'У (/) у- (t) dt.
Если фигура ограничена кривой ? —
= /(«> (в полярных координатах р и 0>
и прямыми 0 = а, 9 = Ц, то
в
Площадь фигуры, ограниченной пло-
ской замкнутой кусочно-гладкой кри-
вой С, не имеющей двойных точек, удоб-
но вычислять при помощи криволи-
нейного интеграла по формулам
5 =. — fy dx — j.r dy — ^(xdy—ydx).
Криволинейные интегралы берутся
в положительном направлении, т. е.
так, чтобы при обходе контура С опре
деляемая площадь оставалась слева
(при правой системе координат).
Площадь плоской фигуры, ограни-
ченной замкнутым контуром, опреде-
ляют часто при помощи двойного инте-
грала S — I j dx dy (в декартовых коор
дниатах), где D — плоская область,
площадь которой определяется, или
S = jj fdfdU (в полярных координатах).
190
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Вычисление длины дуги (£.). Если
кривая задана уравнениями x = /i(t),
У = /г(О, г = /а (/). то
а
где а, Ь — значения параметра t на кон-
мах кривой.
Для плоской кривой х —sp (О. у = Ф (О
»
Если плоская кривая задана урав-
нением у = f (х). гае /(х) — однознач-
ная и непрерывная функция, то
в
L = S Г+1/' ix)\*dx.
а
Если плоская кривая задана уравне-
нием в полярных координатах
где /(6) — однозначная и непрерывная
функция, то
“ j р* -f- р - <Л,
ч
гдеО|. fit — полярные углы для концов
кривой
Вычисление площади поверхности
тела вращения:
в
S — 2я J/(x) К I + |/ (x)Fdx.
а
Здесь у = /(х) — уравнение образую-
щей, а, b — абсциссы ее концов; х —
ось вращения.
Вычисление площади кривой по-
верхности. Пусть поверхность S за-
дана параметрическими уравнениями
х = /(и, о), у «= у (и, о), г = ф (и. и).
где и, о — произвольные криволиней-
ные координаты точек на поверхности
(фиг. 4). Функции /. <р, ф —однознач-
ные, непрерывные и имеют непрерыв-
ные частные производные в некото-
рой области R плоскости ио. ограни-
ченной контуром L, причем ни в од-
ной точке области R якобианы
D(a. v)
D (х. z) D (у. г)
-тт----г. —- не обращаются одно-
D (и. v) О (u, V) *
временно в нуль. Поверхность S назы-
Фиг.4. Коорлннатные линии
на поверхности и элемент
плошали поверхности.
вается в этом случае правильной
Площадь поверхности
Здесь область R является отображе-
нием поверхности S на плоскость ио;
ЕС-/п.\°^У1\г +
(Р(х.х)р , [Р(у.х)Р
+ [p(u.v)J + I D (и. v)J *
Если поверхность задана уравнением
г = /(х, у), то
о
Здесь область D — проекция поверх
вости S иа плоскость ху.
Вычисление объема тела вращения:
о »
V - f F(x) dx - я JI/ (x)|»dx-
a a
Здесь F (x) — площадь поперечного
сечения тела, перпендикулярного к оси
вращения Ох; к — абсцисса сечения
а, b — абсциссы сечений на концах
у = /(х) — уравнение образующей.
Вычисление объема тел произьольно»
формы. Если тело ограничено поверх
ностью. которая пересекается лини-
ями, параллельными оси Ог. в двух
ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ
19»
очках, го объем V этого тела может
быть представлен в виде разности
v /1 (X У) d-rrfy — j j /г (X у) dx dy.
причем область интегрирования D
является проекцией тела на координат-
ную плоскость ху, а поверхности, огра-
ничивающие тело сверху и снизу, заданы
уравнениями
г = /1(ху). х —/г(х,у).
при
Объем тела определяется также
помощи тройного интеграла:
V= (jfdxdydz (в декартовых коор-
динатах);
fe цилиндрических
координатах);
У=У^У г’sin-prfr dO (в сфериче-
и*
ских координатах), где G — область,
занятая телом; г, р, U — цилиндри-
ческие координаты точки; г, ?. U —
сферические координаты, причем <р —
угол между радиусом-вектором г и осью
Ог.
Объем тела выражается также при
помощи поверхностных интегралов
И — j I х dy dz — I ( у dx dz —
{xdydz +
+ у dx dz + г ax dy)
причем интеграл распространен на
внешнюю сторону поверхности S. огра-
ничивающей тем.
Вычисление массы тела:
в (л. у. г) dx dy dz.
где ft (х, у, z) — переменная плотность,
заданная как функция координат точ-
ки; dm — элемент массы, G — область,
занятая телом.
Координаты центра тяжести:
Если плотность во всех точках тела
постоянна, то
и
где V — объем тела; dV — элемент
объем:.
Если ищется центр тяжести массы
плоской фигуры, то тронной интеграл
заменяется двойным. В случае одно-
родной поверхности (плотность всюду
одинакова) имеем для координат центра
тяжести площади плоской фнг/ры
для координат центра тяжести площади
поверхности
где интегралы берутся по поверхно
сти 5; da — злемент поверхности.
Момент инерции:
R*dm.
где dm — элемент массы; R — расстоя-
ние (переменное) элемента массы or
осн или от точки, относительно кото-
рых вычисляется момент;
dm — bdV.
х dm
где i — плотность, dV — элемент объема
Момент инерции плоской фигуры
J - jj R'dxdy;
D
в частности, Jt — 11 y‘dxdy, Jy —
192
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
x*dxdy—моменты инерции площади
относительно осей Ох и Оу; Jo =
F’+
+ уг) dx dy — момент инерции площади
относительно начала координат (поляр-
ный момент инерции).
ИНТЕГРАЛ СТНЛЬТЬЕСА
Пусть на отрезке (а, Ь | заданы две
функции /(л) н Ф (х), принимающие
в каждой точке этого отрезка конеч-
ные значения.
Разделим точками а x0<xi <х,<
<. . . <х„ « Ь отрезок |а. 6] на частич-
ные отрезки. Выбрав в каждом из ча-
стичных отрезков |x,_ltxj по точке
вычислим соответствующее значение
/ (•/)> умножим его на приращение функ-
ции Ф (*j) — Ф (xz_|) и составим сумму
/Л) |Ф(Х/)-Ф(Х(_,)|.
Если при стремлении всех разностей
к, — *1_1 к нулю сумма в имеет опре-
деленный конечный предел, не зави-
сящий ни от способа разбиения отрезка
(а, 6], ни от выбора точек с, в частич-
ных отрезках, то этот предел
называется интегралом Стилыпьеса
функции f(x) по функции Ф (х).
Интеграл Стилы ьеса обозначается
символом
о
(S)j/(JT)4/<J> (X).
а
гак что, по определению,
о
(S) j / (х) аФ (х) -
а
л
— lim 2£/(«()|Ф(х/)-Ф(х/_1)|.
«““'.-I
Функция у(х) называется интегрируе-
мой, функция Ф(<) — интегрирующей
Обычный определенный интеграл
можно рассматривать как частный слу-
чай интеграла Стнльтьеса, когда в ка-
честве интегрирующей функции Ф (х)
нзята незаписнмая переменная Ф (х) “ х.
Вычисление интеграла Стнльтьеса.
Если функция /(л) непрерывна на от-
резке [а, Л|, а функция Ф(х) имеет на
этом отрезке ограниченную интегри-
руемую производную Ф'(х), то
ь
(S) J fW йФ (х) =
а
Ь
— у f (X) Ф' (X) dx,
а
где в правой части — обычный опреде-
ленный интеграл.
Формула остается справедливой и
в том случае, когда на отрезке (a, b I
имеется конечное число точек, где про-
изводная Ф’ (х) не существует, но функ-
ция Ф(х) продолжает бытп непрерывной.
В общем случае, когда /(х) непре-
рывна на отрезке [а, 6], а функция
Ф(х) и Meet разрывы в точках а, бив
конечной! числе внутренних точек
с,, с,....сц, а между этими точками
имеет ограниченную интегрируемую
производную Ф' (х), интеграл Стиль-
тьеса вычисляется по формуле
» ь
(S) J’/(x) йФ (х) — ]’/(х) Ф' (х) rfx +
а а
+ / (д) [Ф (л + 0) — Ф (а)] +
*
+ V/(C<) |ф (с, + 0) - Ф (с, — 0)| +
<=i
+ /(6)|Ф (*)-♦(<»-0)1-
Эта формула верна и в случае, если
одна (или обе) из точек а или Ь есть
точка непрерывности, так как тогда
соответствующее слагаемое / (а)[Ф (а-|-
+ 0) — Ф (а)| или /(6) |Ф (б) — Ф (б—0)|
само собой исчезает.
Интеграл Стнльтьеса имеет приме-
нение как в различных областях мате-
матики (теория вероятностей, теория
Функций, функциональный анализ),
так и при решении технических задач.
Одно ! из важнейших проблем, решенных
интегралом Стнльтьеса, является про-
блема измерения моментов.
Поставим задачу измерить моменты
разных порядков относительно начала
координат некоторой массы М, распре-
деленной по прямой (осн абсцисс).
Если масса М вся сосредоточена в
одной точке х, то имеем:
момент статический h = |х|-Л4;
момент инерции /> = х’-Л! и т. д.
ИНТЕГРАЛ СТИЛЬТЬЕСА
193
Пусть масса Л1 распределена по всему
отрезку |а, i>] прямой. Разделим отре-
зок на частичные отрезки и в каждом
частичном отрезке Х/1 массу со-
средоточим в одной точке Е/. Если
обозначить через /(*) любую из функ-
ций |х|, |x*|, |х®|, . . .,|хя|, . . а через
Ф (х,) — массу на отрезке [a, xj, то
разность Ф (xj — Ф (xz_j) выражает
массу отрезка (x/_I, xj, а произведение
/(5/) 1Ф (xj — ФС*^)! выражает момент
того или иного порядка относительно
начала координат всей массы отрезка
1х<—11 х(1, которую мы сосредоточили
в точке Е/. Отсюда ясно, что
л
Ит £/(«/) |Ф (х/) -Ф (х,_,)] =
= (5) f/(X) (X)
а
даст момент того или иного порядка
относительно начала координат для
массы всего отрезка [а, 6]. При этом
масса может распределяться по отрезку
непрерывно, а также может быть со-
средоточена в отдельных точках, так
что функция в случае измерения момен-
тов хотя и может иметь конечное
число разрывов, но должна обладать
следующими свойствами:
а) Ф (х) — неубывающая функция от х;
б) Ф (х) — непрерывная справа функ-
ция от х.
Функции, обладающие этими двумя
свойствами, называются функциями рас-
пределения. Они заслуживают особого
внимания, так как наиболее часто встре-
чаются в приложениях интеграла Стиль-
тьеса.
Примеры-.
1) (S) J СО8’ х d (cos х)=»
о
= Jco*xd(co«x)=[^]'--4.
и
2
2) (S) J хМФ (х). где Ф (х) •» 0, если 0<х< 2:
2 2
Ф (2) - 5: (S) У хМФ (х)— j x’-Odx +
и и
-f- 2* [5 - 01 = 20.
3
3) ($) j х’</Ф (X),
если
(х° при 0 < х < 2;
х* при 2 < х < 3.
Точкой разом па будет точка х = 2. При «том
Ф (2 — 0) = 8; ф (2 — 0) — 16. В остальных точках
отрезка (0,3) функция Ф(х) имеет проиэнодную
Ф' (х), причем
I Зх* при 0 < х < 21
Ф'(Х> = I 4х» при 2 < х < 3.
Следовательно,
3 3
(S) j х"<М> (х) = j х"Ф' (х) <Гх + 2* (16 - 8)=-
2 3
- J л*ЗХМх 4- j x4x*dx + 2’ (16 - 8] -
2 3
- 3 \ хМх + 4 \ л*Дх 4-32 - 494 ~ .
13 Том I Зак. V1M
ГЛАВА VIII
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО •
ОСНОВНЫЕ ПОНЯТИЯ
Функция комплексного переменного
W = /(г). где 2 = х 4* «У. w = и 4- iv,
определена, если изаестны две веществен-
ные функции от двух вещественных
переменных: и = и(х, у), v = v (х, у).
Пример. Если w — г', то в -|- Iv = (х 4- /у)’ =
— х* — у' + Мху, т. е. и = х* — у’, t> = 2ху.
Функция w — f (?) дает точечное пре-
образование (или отображение} пло-
скости г на плоскость w: каждая точка
21 переходит в соответствующую точ-
ку Wi; кривая х = х (/), у = у(/) пере-
ходит в кривую и — u[x(t), у (01, о =
= о(х(0, j(Ol(Z — параметр); коорди-
натные линии у = с переходят в линии
и = и (х, с), v = и (х, с), где х — пара-
метр; координатные линии х = Ci пере-
ходят в линии и = и(щ,у), и = о(сь у),
где у — параметр.
Пример, w — 214-11, т. с. Г 4-/о —2 (х 4-
+ I (-Г - 1у} - (2-г + У) + I (х + 2у). откуп
и — 2х + у, v — х -|- 2у. Линии у — с переходи г
Фиг. 1. Отображение, осушестнлаемое функцией
комплексного переменного w — 21 4- It-
хинин в — 2х 4- с, о — х 4- 2с, т. с. о прямые
и . 3
® — — 4- -j- с. лннин х — с, переходят я прямые
® —2л—8с, (фиг. 1): яаштрнховлниая область
(квадрат) переходит я заштрихованную (ромб).
* См. литературу иа стр. 349: (43), [44]. (45].
ИЧ. (4?).
Если г = х 4* iy — комплексное пе-
ременное, а а = а 4- ib — такое посто-
янное число, что |г — я|-> 0, то говорят,
что комплексное переменное г стре-
мится к пределу а, и пишут: lim г =
= а. или г -* а.
Если г -+ 0, то г называется беско-
нечно малым комплексным числом. Гео-
метрически условие г + а равносильно
тому, что аффикс г беспредельно при-
ближается к аффиксу а.
Условие lim (х + /у) = а 4- ib равно-
сильно тому, что lim х = a, lim у = Ь.
Поэтому основные теоремы о пределах,
установленные для вещественных пере-
менных, остаются в силе и для комплекс-
ных переменных. Если | г | -> оо, то го-
ворят. что г -» со, или lim г = оо.
Непрерывность функции комплекс-
ного переменного определяется так же,
как и в случае функции вещественного
переменного. Непрерывность функции
w = f(z), если w =* и + iv, равно-
сильна непрерывности функций и(х, у)
и о (ж, у).
ОО
Ряд с комплексными членами У, а'л=
л—I
“ 1₽1 + к'а 4- ... 4- И1п 4- . . . , где
wn = и„ 4- называется сходящимся,
если s„ “ wi 4- tr*4--- + wn имеет пре-
дел s при п -> оо; s= lim s„ называется
Л •* оо
суммой ряда. Сходимость комплексного
ОО
ряда V w„ равносильна сходимости
л—I
оо оо
двух вещественных рядов и„ и “я!
Л=1 Л—)
если при этом сумма первого веществен-
ного ряда есть в, а второго Ь, то сумма
комплексного ряда s = e + ib.
Комплексный ряд называется абсо-
лютно сходящимся, если сходится ряд
модулей |wi| 4- |ша| +. • • + 1«’л1 +• • •
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
195
Если комплексный ряд сходится, то
его л-й остаток r„ = S — (w, + t»i +•
4- +wn) стремится к нулю при п -»оо,
т е. |гя|<б, как только индекс п сде-
лается больше некоторого числа <V, за-
висящего от выбранного произвольно
малого положительного числа » Ком-
плексный ряд функций от г называется
равномерно сходящимся в области G,
если для произвольно заданного поло-
жительного а можно выбрать такое зна-
чение индекса N. чтобы неравенство
|гя |< • было справедливо при любом
л>А/ и прн всяком произвольном г из
ОО
области G. Если члены ряда У:ся (г) —
Л—1
непрерывные функции от г в области G
и если ряд сходится равномерно в об-
ласти G, то сумма S ряда также непре-
рывная функция от г в области G.
ОО
Если все члены ряда У tr„ (г) в об-
№1
лястн G удовлетворяют условию
| w„ (г) | < а„. где о„ — постоянные по-
ложительные числа, причем числовой
оо
ряд Уо„ сходится, то данный комплекс-
ный ряд сходится равномерно и абсо-
лютно в области G.
Степенным называется ряд ee4-cra-f-
4-С|Д, + ...+ свгя4-.„, где коэффициенты
с0, Ci, сг..с„ ... — постоянные ком-
плексные числа, аг — независимое ком-
плексное переменное. Для всякого сте-
пенного ряда существует круг с центром
в нулевой точке (круг сходимости) и
с радиусом R (радиус сходимости),
внутри которого (т е. при |г| < R)сте-
пенной ряд абсолютно сходится, а вне
которого (т е. при | г | > R) ряд рас-
ходится В некоторых точках окруж-
ности круга сходимости (т. е. при
|г|= R) ряд может сходиться, в дру-
гих расходиться Всякий степенной
ряд равномерно сходится в круге) г | <г,
если r<R- Степенной ряд, для кото-
рого /?>0, изображает непрерывную
функцию внутри его круга сходимости
Степенной ряд можно, не меняя его
круга сходимости, дифференцировать и
интегрировать почленно сколько угодно
раз.
Радиус сходимости степенного ряда
СО
У, ctzl определяется по формуле Коши—
4-0
13*
Адамара
где
/- lim \ |с„ |.
Я*оо
т. е. t — наибольший предел последо-
вательности чисел |ся| (см. стр 134).
Пример. Для рям + +
с я — I, если л — anaipimic число, и с — О
• протипиом случае: послехомтельность | е, |,
п _____
предельные точки: 0 н 1: I — lim 1/ |с I -I
п—оо "
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Показательная функция —
—г* (cos у 4- i siny) удовлетворяет соот-
ношению е,,ег* = и имеет период
2п/; д2*** — + 1; г(2*+1)ж2 — 1. если
k — целое число.
Показательную функцию можно пред-
ставить степенным рядом
X Г* уЗ ГП
* “ 1 + Ii + 21 + 3! + - + “ЙГ +—•
сходящимся во всей плоскости.
Функция, обратная показательной, есть
логарифм-, при г = ге”
w = Log г = In г 4- i (? 4- 2Д-).
Это функция многозначная (k—лю-
бое целое число)
Главное значение логарифма, обозна-
чаемое через log г. подчинено условию
— к < /ж log z <. к.
Степенная функция w — z“ — е',1лг’
многозначна, если а не является це-
лым числом.
Тригонометрические функции:
tgz-
ctg г —
sin г е
cos г 1
cos г
sin г *
196
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Для них имеют место все обычные
тригонометрические соотношения, в
частности, первые две имеют период 2т.
и две вторые — период п.
Гиперболические функции:
е*-е~2
CllZ =
sh z =-----
Тригонометрические и гиперболиче-
ские функции связаны соотношениями
sin iz = i sh z; cos iz = ch z.
Любое соотношение между тригоно-
метрическими функциями sinz и cos z
переходит в соответствующее соотно-
шение между гиперболическими функ-
циями shz и chz, если в этом соотно-
шении заменить sinz через /shz, а
cos г — через ch z.
Обратные тригонометрические и ги-
перболические функции определяются
так же, как и для действительного пере-
менного. Напри.мер, w = arcsin z, если
z = sinw. Эти функции выражаются
через логарифмы
arcsin z = — / log (iz + V I — z2) ;
arccos z — / log (z -r i ]/1 — z2);
. 1 , 1 4- /z
arctg z = ^-log —;
Arsh z — log (z 4- Vz‘ -f- l) ;
Arch z — log (z + V z* — 1);
. 1 , 1 -*• z
Arth z — — log -г---.
2 s 1 — z
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Для того чтобы однозначная и непре-
рывная в окрестности точки г функция
w = f (г) имела производную
f(z)- llra /(Zj-y-/(a)
At-0 flZ
(где Az-»0 любым способом), необхо-
димо и достаточно, чтобы выполнялись
условия Даламбера - Эйлера
du dv ди _ dv
дх = ~3у ’ ~йу дх *
Функция w = /(г), дифференцируемая
в точке г. называется моногенной. Функ-
ция к» = /(г), моногенная в каждой
точке области G, называется аналити-
ческой (или регулярной) в области G,
и тогда о каждой точке области гово-
рят, что в ней данная функция анали-
тическая, и каждую точку называют
обыкновенной или правильной точкой
функции /(г). Всякая неправильная
точка функции /(г) называется се особой
точкой.
Пример. Функция и =3* (« = № — у1, о =>
= 2ху) — везде аналитическая: функция «• =
— 1г 4- iz (и = 2х у, V — X 4- 2у) — везде не-
аналитическая.
Правила дифференциального исчисле-
ния о производной суммы, произведе-
ния, частного, сложной и обратной функ-
ции остаются верными и для функций
комплексного переменного. Сумма, про-
изведение, частное регулярных в G
функций также регулярны в G (част-
ное — за исключением точки, где зна-
менатель обращается в нуль).
Для регулярной функции w = /(z)=
= Ч (*. У) + io (х. у)
,, . . ди , . dv dv .ди
Функция, аналитическая в области G,
имеет в ней производные всех по-
рядков.
Действительная и мнимая части ана-
литической функции /(г) удовлетво-
ряют уравнению Лапласа
. д*и , д'-и .
Ьи s , _ 4" -г-г “ О,
дх* оу2
т. е. и и v — гармонические функции
в области G.
ИНТЕГРАЛ ПО КОМПЛЕКСНОМУ
ПЕРЕМЕННОМУ
Интеграл от функции комплексного
переменного /(г) по дуге кривой С
определяется как предел суммы
л
[/(z)rfz- lim V /(^(z, — Zj-i),
С Л~оо)=ж1
где точки zi. zs, .... Zt_t, zt .... z„_l
разбивают дугу С от точки а = z0 до
точки Ь = гя на п частей, причем при
переходе к пределу наибольшее рас-
стояние между двумя соседними точ-
ками должно стремиться к нулю.
РАЗЛОЖЕНИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ В СТЕПЕННОЙ РЯД
197
Если уравнение линии С г = г (f)
(«< то
$f(z)dz z' (f)dt~
С
- " R(0 dt + i f I (t) dt.
где R (0 и /(Z)—действительная и
мнимая части выражения / |г (01 г' (О-
Таким образом, вычисление интеграла
по комплексному переменному приво-
дится к вычислению обычных опреде-
ленных интегралов.
+»
Пример. Вычислить I | х I Л: а) по отрезку
[ — 1, + 1] и 6) по верхней половине окружности
радиуса 1 с центром О:
t* 2 V
>)/=( | х I dz - Г 111 dz -+ Г Ixl Л=/»+/,:
-1 —i о
x-r. dz-dt. I,.. t(_f)di-.L-.I,-
—1
-Г‘Л-т:/-т+т-,: •
и
в) I — ^1 x I dz. где x — «**, I x I — 1. dz —
••i
0 I 0
- Ze<T df. I = J d* - | -i.
X X
Теорема Коши: если замкнутая кри-
вая С расположена вся внутри неко-
торой односвязной области, в кото-
рой функция /(г) является аналитиче-
ской, то
j/(z)rfz-O.
Значение функции, аналитической в
области, ограниченной контуром С,
определяется по ее значениям на кон-
туре по формуле Коши
/(«)
1 f/(О Л
2rjJ С — z ’
где г — любая точка области внутри
контура С, причем интегрирование со-
вершается по контуру С в положи-
тельном направлении.
Производные аналитической функции
даются интегралами
Z14
Пример. Вычислить, пользуясь интегральной
формулой Коши, интеграл / = J • гсл|’ (-
С
обозначает окружность | С — i ( — 1 единичною
радиуса с центром и точке I.
Преобразуем интеграл так:
Функция аналитическая всюду, кроче
точки С — — г, лежашей вне окружности IC—/I »I:
точка С = I лежит внутри окружности С (это
центр кругах Применяя формулу Коши к функции
,-J—Г при J = <. получим
Если С — произвольный замкнутый
контур, содержащий внутри себя точку а.
то
а)" dz-0(m-О, 1.2....);
3-->-
РАЗЛОЖЕНИЕ АНАЛИТИЧЕСКОЙ
ФУНКЦИИ В СТЕПЕННОЙ РЯД
Функция /(г), аналитическая в точ-
ке а, имеет в этой точке производные
всех порядков и в окрестности точки а
разлагается в ряд Тэйлора-.
J (z) -/(а) + ~^~Г (в) + •. - +
Окружность круга
имеет центр в точке
реэ ближайшую к
точку функции.
сходимости ряда
а и проходит че-
точке а особую
198
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Функцию /(г) называют голоморфной
в точке а, если она в некоторой окре-
стности этой точки разлагается в сте-
пенной ряд относительно г — а. Свой-
ство голоморфности функции комплекс-
ного переменного в точке а эквива-
лентно свойству ее аналитичности в той
же точке.
Нулем функции /(г), голоморфной
в области G. называют всякую точку г$
этой области, в которой имеет место
равенство f (гф = 0.
Говорят, что z0 есть нуль порядка т
для функции /(г), если разложение
функции в степенной ряд в окрестно-
сти точки г0 имеет вид
/(z) - Ст (Z - :„)т +
Функция /(г), аналитическая внут-
ри кольцевой области г < | г — а |</?
(где г > 0, R <оо), ограниченной двумя
концентрическими окружностями с ра-
диусами г и R и с центром в особой
точке а, разлагается в этом кольце
в ряд Лорана:
-иОО
/(*)- v c„(z — а)л =....+
Л=—СО
С_ з С_______2 ( £_|
+ (z — в)* + (z — a)*~^ z — а +
4 Со + С| (z — fl) + Cj (z — в)1 +
+ Cj(z —в)’+ ...;
коэффициенты определяются здесь по
формуле
1 Г /(OrfC
2с'У(С-в)"+1 ’
где Г — кривая, окружающая внутрен-
нюю окружность и расположенная внут-
ри кольца. Кольцо сходимости ряда
Лорана, в который разложена некото-
рая функция / (z), ограничено двумя
концентрическими окружностями, про-
ходящими через особые точки.
Ряд Тзйлора — частный случай ряда
Лорана Часть ряда Лорана, содержа-
щая положительные степени z — о, на-
зывается регулярной или правильной
частью ряда Лорана, а часть ряда,
содержащая отрицательные степени
г —а, называется главной частью.
Правильная часть ряда Лорана схо-
дится всюду в круге |z —flj<)?. Глав-
ная часть представляет степенной ряд
« « 1
относительно переменной Z- —------— .
следовательно, он сходится всюду вне
круга |г —о|>г. Ряд Лорана, кото-
рым представлена функция /(г), анали-
тическая в кольце г < | г — а|</?,
равномерно сходится в любой замкну
той области, принадлежащей этому
кольиу
Ряд Лорана можно почленно диффе-
ренцировать и интегрировать сколько
угодно раз без изменения области его
сходимости.
Иногда внутренний радиус сходимо-
сти ряда Лорана бывает равен нулю,
т. е. областью сходимости является
круг с выброшенной центральной точ-
кой.
Если в ряде Лорана имеется лишь ко-
нечное число членов с отрицательным i
степенями г — а, то внутренний радиус
сходимости ряда Лорана обязательно
равен нулю.
Найденное любым способом разложе-
ние аналитической функции в ряд по
положительным и отрицательным сте-
пеням z — а является лорановским
разложением этой функции.
Пример. Рассмотрим некоторые разложения
в pax Jaliiopa и рал Лорана функции
1= U — 1) (z — 2) = I — г ~ 2—л'
Особые точки этой функции а — I, г — J (по-
люса») *. В точках О и оо эта функция аналити-
ческая.
я) Внутри круга 111 < t / (I) регулярна и раз-
лагается а ряд Тэйлора:
6) Внутри круга 1t — t | < 1 функция f <1) ре-
гулярна. исключая центра —I. гае находи гея
полюс, а потому разлагается я ряд Лорана:
1 tX> “ Г^т ~ I — (я — I) ”
- --Ц - I - (я - 1) - U - 1У - ...
2 — 1
• Вблизи полюса аналитическая фуикимя стре-
мится к бесконечности.
ОСОБЫЕ точки однозначной функции
199
в) Вне Круг» I г | > 2 функция / U) регулярна
и разлагается и ряд:
г) В кольце между окружностями с центром О
и радиусами 1 н 2 (t < |al < 2)/(г) регулярна
и разлагается в ряд Лорана:
ОСОБЫЕ ТОЧКИ
ОДНОЗНАЧНОЙ ФУНКЦИИ
Если однозначная функция /(г)
является аналитической в окрестно-
сти точки а, за исключением самой
этой точки, то точка я называется изо-
лированной особой тонкой. В окрестно-
сти такой точки /(г) разлагается в ряд
Лорана, сходящийся в некотором
круге с центром я, исключая самую
точку а.
Различают три типа изолированных
особых точек в зависимости от пове-
дения функции /(г) в нх окрестности.
Точка а называется устранимой осо-
бой точкой, если существует конечный
Ига/(г).
>*а
Тонкая называется полюсом, если /(г)
является бесконечно большой при при-
ближении г к я, т. е. существует
lira/(г) — оо (это означает, что |/(г)|
z+e
неограниченно возрастает при г -> я).
Точка я называется существенно осо-
бой точкой, если Пт/(г) не суще-
t+a
ствует.
Для того чтобы а была устранимой
особой точкой функции / (г), необхо-
димо и достаточно, чтобы лорановское
разложение / (г) в окрестности точки а
не содержало главной части.
Устранимую особую точку можно
«устранить», полагая /(я) — lim/(a) =
г-а
= Со, после чего функция /(г)
аналитической и в точке я.
Для того чтобы точка я была
сом функции /(г), необходимо
статочно, чтобы главная часть
булет
полю-
н до-
лора-
новского разложения f[z) в окрестно-
сти я содержала лишь конечное число
членов. Наибольший отрицательный по-
казатель называется порядком полюса.
Полюс 1-го порядка называется про-
стым. Если п — порядок полюса, то
. о(Д)
в окрестности его /(г) д ,
где ф(г) — аналитическая функция, не
равная нулю в точке я. Если точка а
есть нуль порядка т для функции f(z)
(или полюс порядка т), то та же точка
1
для функции будет полюсом
порядка т (соответственно нулем поряд-
ка т при условии = 0). Видим,
J (г)
что нули и полюсы аналитических функ-
ций весьма просто связаны друг с дру-
гом.
Точка я тогда и только тогда является
существенно особой для функции/(г),
когда главная часть лорановского раз-
ложения /(г) в окрестности точки а
содержит бесконечно много членрв.
В любой окрестности существенно осо-
бой точки функция /(г) принимает все
значения, за исключением, быть может,
двух (причем сосчитается также зна-
чением функции).
Функция /(г) имеет точку а суще-
ственно особой точкой одновременно
. 1
с функцией ууту-
Итак, изолированная особая точка бу-
дет устранимой, полюсом или существен-
но особой точкой, смотря по тому,
будет ли в окрестности такой точки
данная функция ограниченной, беско-
нечно большой или неопределенной.
Примеры-. 1| Функция е г имеет при г —О
существенно особую точку. Разложение Лорена
к окрестности втой точки
200
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
. cos г ,
2) Функция etg г — $|п г имеет полюс 1-го по-
рядка при нуле функции sin г.
Разделив формально степенные ряды для cos z
и sin z. получим:
разложение справедливо я окрестности нулевой
точки.
ВЫЧЕТЫ АНАЛИТИЧЕСКОЙ
ФУНКЦИИ
Вычетом функции f (г) в изолирован-
ной особой точке а (обозначение: res /(я)|
называется число f(z)dz. где
т
7 — достаточно малая окружность
| г — о | = р. Величина вычета не зависит
от величины р для достаточно малых р.
Вычет функции /(г) в особой точке а
равен коэффициенту при минус первой
степени в лорановском рахчожении /(г)
в окрестности а.
В устранимой особой точке вычет
функции всегда равен нулю. Если а
есть полюс л-го порядка функции /(г),
то
res/(e)—
- 1 ,п|1т -«>" /
<Л— I)I a-u dz" '
Для полюсов I-го порядка имеем фор-
мулу
res/(e) — Hm |(2 — a) /(z)).
z-aa
Если в окрестности точки а функция
/(г) определена как частное двух ана-
литических в этой точке функций
причем <? (а)/-О, а ф(г) имеет в а нуль
1-го порядка (тогда /(z) имеет в а
полюс l-го порядка), то имеем формулу
res / (а) — *.
* «О
Попмгр Ндйти гычет функции —-— относ»-
СО» X
тельио простого полюса а — (2л -ф И-—
Имеем
™* (cos fl) “ С~ ’ 11114 *“
-----------!---- - I-
МП (2Л + IJ —
Теорема о вычетах
Интеграл аналитической функции по
замкнутому контуру, содержащему вну-
три конечное число изолированных осо-
бых точек, равен сумме вычетов отно-
сительно этих точек, умноженной на 2к/:
£/(*) Л - res /(«)•
Теорема о вычетах имеет важные при-
менения, в частности при вычислении
интегралов функций действительного пе-
ременного.
Сущность методов вычисления инте-
гралов, основанных на применении тео-
ремы о вычетах, состоит в следующем.
Пусть требуется вычислить интеграл от
действительной функции f(х) по ка-
кому-либо (конечному или бесконеч-
ному) отрезку (л. Z»] оси х. Допол-
ним отрезок некоторой кривой С, ко-
торая вместе с отрезком |«. 6] соста-
вит замкнутый контур С, ограничиваю-
щий некоторую область G, и возьмем
некоторую вспомогательную функцию
/ (г), аналитическую в области G, кроме
конечного числа особых точек, причем
такую, чтобы на отрезке |а. ft| значе-
ния вспомогательной функции были
равны значениям интегрируемой функ-
ции вещественного переменного. К вспо-
могательной функции применим теорему
о вычетах и получим
»
f/(z)dz = j / (x)dx + C/(z)dz=2=//?,
С а С*
где R — сумма вычетов f (z) в обла-
сти G.
Если интеграл по С удается вы-
числить или выразить через искомый
интеграл, то задача вычисления иско-
мого интеграла будет решена. В не-
которых случаях вспомогательную функ-
цию /(г) выбирают так, чтобы задан-
ная на |а. 6| функция была ее дей-
ствительной или мнимой частью; тогда
искомый интеграл находится соответ-
ственно отделением действительных или
мнимых частей. В случае бесконечных
отрезков (в, 6| обычно рассматривают
семейства неограниченно расширяю-
щихся контуров интегрирования, кото-
рые строят так, чтобы в результате
предельного перехода получить инте-
грал по (а. 6). В этом случае инте-
грал по С можно не вычислять, а лишь
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
201
найти его предел, причем часто оказы-
вается, что он равен нулю. Так, если
функция g (г), определенная в точках
некоторой полуокружности С радиуса R
(т. е. | г| == R), стремится к нулю рав-
номерна относительно arg г при R-»co,
то для любого положительного числа
X Ilm [ g (z) е*‘гй -= 0 (лемма Жор-
/?-оо С
дана).
Пример. Для вычисления интеграла Лапласа
оо
, fcns.rrfx
“J •*’• + «*
и
flz
выберем вспомогательную фуикпию /(я)=
и булям ее интегрировать по периметру С полу-
круга, составленному из отрезка оси .г (с концами
в точках — R и /?> и полуокружности С (с ра-
диусом R > а). Функция / (х) будет аналитической
во всей плоскости комплексного переменного за
исключением точки al, где она имеет простой
полюс (так как при z = al, j (д) = оо). По теореме
о вычетах имеем
+.* .
I e^dz _ Г elxdr . I e^dz
J г' -|- a' J дг* + а' + г‘ 4- а‘ “
С -R С
- hl res f (о/).
Так как /<г) представляет частное двух функ-
ций, то вычет определим по формуле
"•'—ш
и пахучим
"•/w—тзг~Ь-
Следовательно,
+ #
Г e,xdx Г e,2dz ве~п
J х‘ + и‘ ,) !• 4- а' “ а '
- R
Предположим, что R - оо.
Заметим, что I I» -|- а* | > | * | — | а» |, откуда
|да + <,.| < Пр —«•« «« точек к*
окружности I I | » R, ТО функция g (я) аа-!_
а* 4- а’
на С удовлетворяет неравенству |?(i)| < .
и д(т), при А' - оо, стремится к нулю независимо
от значений arg : (т. е. равномерно относи-
тельно arg Л). Следовательно, по теореме Жордана
f е'гаг н.
ilm I —-—- — о:
R,oo J * + *
поатому
Заменяя е*х — cos х -f-I sin х, получим
Отделяя в этом равенстве вещественные части,
получим
а так как подинтегральная функция — чеглаа, го
откуда окончательно
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
Преобразование плоскости, осуще-
ствляемое аналитической функцией w =
= /(г), обладает свойством, что в окре-
стности точки г, для которой
бесконечно малые векторы всех напра-
влений: 1) увеличиваются (или умень
шаются) по своей длине в одно и то
же число раз, равное | го' | (с точностью
до бесконечно-малых высшего порядка),
и 2) поворачиваются на один и тот же
угол, равный argw. Фигуры в беско-
нечно малой области преобразуются в
себе подобные, т. е. сохраняют форму,
поэтому преобразование называется
конформным-, оно является обобщением
преобразования подобия. Конформное
отображение сохраняет постоянными
углы между любыми двумя линиями
отображаемой фигуры; в частности,
координатные линии * « const, у “
= const преобразуются в два семейства
взаимно ортогональных кривых, и об-
ратно: для любого конформного ото-
бражения существует некоторая ортого-
нальная сетка кривых (изотермическая
сетка), которая преобразуется в декар-
тову прямоугольную сетку.
Пример. Преобразование w — 2s + iz не кон-
формно (см. фиг. 1К Преобразование w — s1 кон-
формно координатные линии переходят и дна
семейства софикусиых взаимно ортогональных
парабол (фиг 2); и точке i-п конформность
нарушается (w'—U). первый координатный ква-
дрант переходит в верхнюю полуплоскость.
202
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Важнейшие конформные отображена!
Функции
Линейная функция
« — аг + »
(в-РгТб
Свойства отображений
Преобразование может быть разложено ва три:
t — ef‘ i — поворот плоскости около нулево* лиши на
угол о:
г — р-г — подобное растяжение в р раз;
ш г + Ь — параллельный сдвиг на вектор Ь.
Фигуры плоскости г преобразуются в саба подобные,
причем поворачиваются и сдвигаются. Точки г, —‘
и г, — оо переходят сами в себя
Точка х с радиусом-вектором р и полярным утлом о
преобразуется в точку с радиусом-вектором — и углом —
Преобразование состоит из инверсии относительно едияич-
вого круга • и зеркального отражения относительно оси Ол.
Круги переходят в круги (считая прямую частным случаем
круга с радиусом оо). Точка 0 переходит в оо. точки 1 и —1
остаются неподвижными. Конформность нарушается при
1-0
ДроОво-лниейная функция дх -р » ” = сг + d Преобразование может быть рязложеаао на три: t “ сх + d (линейная Функция); з =-р- (инверсия); и ~ + (аа — bet s (линейная функция). Дробно-линейная функция переводит круг в круг (счи- тая прямую частным случаем круга); две точки, удоалетяо- реющие уравнению х ——г-г • ие сдвигаются. Вся пло- С2 + и скость отображается на самое себя. Отображение опреде- ляется тремя парами соответствующих точек Xi. Ха. х, и «, Wi. v, и может быть записано в виде г —г. х,— х, _ w —ш, ш. — «>» X — Ха X, — X, W — Wa W, — Ш>
1 - аг (а — комплексное число, сопряжен- ное числу д) себя, если 1 а | < 1; при | а | > 1 функция переводит вну- тренность круга I х 1 < 1 во внешнюю часть круга | в 1 < 1. Точка х — д переходит в точку ш~0. Направление т а точке а переходит в направление действительной оси
• Ингерсией относительно данного круга радиуса R называется преобразование точек пло-
скости, при котором точка Л, находящаяся на расстоянии d от центра круга, переходит в точку Л',
находящуюся на радиусе ОА или его продолжении, ио ид расстоянии d, — — (см. фигуру); при
«том преобразовании точки, лежащие же круга, переходят внутрь его и обратно.
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
203
Продолжение
Функции Свойства отображений
Функция отображает верхнюю полуплоскость иа единич- ный круг (| ® | < J). Точка z » а переходит в точку w = 0. Направление т в точке а переходит в направление действи- тельной осн
4- tf ш — f—г . где a. b. с, d — ее- cz 4-« щестаенные числа Функция отображает верхнюю полуплоскость иа верх- нюю (если ad — be > 0) или инжпюю (если ud — be < 0) полуплоскость
а
w = z
to — вешествениос)
Функция переводит угол с вершиной в начале и вели-
чиной л в угол величиной ал. В частности, угол в <|>увк
к
. а
цией w = z переводится в полуплоскость
Вся плоскость z переходит в двойную плоскость ш. Изо
термическая сетка плоскости г состоит нз двух семейств
гипербол и — х* — у1 и v » 2лу. Конформность нарушается
при г = 0. Точки 0 и 1 неподвижны
Функция двузначная; пси плоскость переходит: I) в верх-
нюю полуплоскость. 2) в нижнюю полуплоскость. Изотерми-
ческая сетка плоскости z состоит из двух семейств софо-
кусиых парабол с фокусом в начале и с осями, совпадаю-
щими с положительными и отрицательными направлениями
оси х (см. фиг. 2 иа стр. 2U5). Конформность нарушается
при г-0. Неподвижны точки 0 и 1
Показательная функция мет отображение полосы
а < у < 3, причем J р — к | < 2т., на угол а < р < р с вер-
шиной п начале. пол у пол оса а < у < р, л > п переходи г
в сектор в < р < 0. г < еа
20-1
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Функции Свойства отображений
w Log г (в = 1п р. о = у + 2 А к) Изотермическая сетка состоит на окружностей In a—const и лучей о = const, т. е. является полярной сеткой, функция имеет бесконечное множество значений и переводит всю плоскость в ряд горизонтальных полос: 0 <т>Ч2к; 2к<т/<4« и т. л.
= sin 2
Функция отображает полуполосу у > U,----j- < л < —
на верхнюю полуплоскость V > О
Функция отображает полосу-----— Ч л ч -Г *т м Ч"У’
функииа отображает на верхнюю полуплоскость верхний
полукруг единичного радиуса с центром в нулево* точке
Функция отображает на верхнюю полуплоскость сектор
ж
единичного радиуса с углом, равным —
Функииа отображает на верхнюю полуплоскость область,
заключенную между двум* пересекающимися в точка* а н Ь
пол углом — дугами окружности
Функция отобрали*! На ЬГрХНЮЮ ПОИ) плоскоеГЬ ПОЛОС)
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
205
Фиг. 2. Отображе-
ние, осушсспияе-
мое функцией ком-
плексного перемен-
ного w =. 2’.
отображение
Имея произвольную аналитическую
функцию, мы можем рассматривать раз-
личные конформные отображения, ею
ос уществл немые.
Таблицу важнейших
конформных отобра-
жений см. на стр.
202 -201.
Для практических
целей больший инте-
рес представляет зна-
чительно более труд-
ная обратная задача,
так называемая о с-
н о в н а я задача
теории кон-
формных ого-
бра жений: заданы
области G и G*; тре-
буется построить
функцию, осущест-
вляющую конформное
ч! области на другую.
Эту задачу можно решать, подбирая
надлежащие комбинации элементарных
функций
При конформных отображениях важ-
ную роль играет принцип соответствия
границ и принцип симметрии Римана-
Шварца: 1) если аналитическая функция
устанавливает взаимно однозначное соот-
ветствие на границах областей, то соот-
ветствие взаимно однозначно и внутри
области; 2) если границы областей D
и А содержат дуги круга сир которые
•соответствуют друг другу при конформ-
ном отображении, то отображение про-
должается в областях D 4- D' и А 4-
+ Д', где D', Д' — инверсии областей D,
А относительно дуг с, р, причем симме-
тричные точки относительно с области
и -f- D' переходят в симметричные отно-
сительно р точки области А 4- Д'.
В ряде вопросов играет важную роль
отображение, реализуемое функцией
Н. Е. Жуковского w =у 4- -у) .
Оно переводит внешность круга | г | > г
и одновременно внутренность круга
|а|<—(<>1) во внешность эллипса
а { . I X а { 1 X
с полуосями — i г + у } и I г —
В частности, внешность и внутренность
единичного круга переходят на пло-
скость с разрезом у = О, — а<х<4-а.
Отображение верхней полуплоскости
на внутренность ограниченного много-
угольника реализуется функцией Кри-
стоффеля-Шварца: если apt, ......аПп
(0<aK<2. А —1, 2.....л)—углы мно-
гоугольника при вершинах, a at, аг,....
а„ — точки вещественной оси, соответ-
ствующие вершинам многоугольника, то
отображение дается функцией
г
w = С J (z — аО®' ~ 1 (z — aj)** ~,... (г -
и
- ал)*"-1 dz 4- <Г,
где С и С — некоторые постоянные.
Та же формула может быть применена
к отображению круга на многоуголь-
ник; при этом ак будут точки окруж-
ности, соответствующие вершинам мно-
гоугольника.
ГЛАВА IX
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ »
Уравнение называется дифференциаль-
ным, если, кроме независимых пере-
менных и неизвестных функций этих
переменных, оно содержит произвол
ные неизвестных функций (или их диф
ференнналы).
Дифференциальное уравнение назы-
вается обыкновенным, если неизвестные
функции зависят от одной независимой
переменной
Уравнение в частных производных
содержит несколько независимых пе-
ременных, функции этих переменных
и частные производные этих функ-
ций.
Порядком дифференциального уравне-
ния называется наивысший порядок
производной неизвестной функции, вхо-
дящей в уравнение.
Решением дифференциального уравне-
ния называется система функций, под-
становка которых вместо неизвестных
обращает уравнение в тождество.
В случае обыкновенных дифференци-
альных уравнений решения могут быть
общие (содержащие столько произволь-
ных постоянных, каков порядок урав
нения, см. стр. 213), частные, полу-
чающиеся из общих при частных зна-
чениях произвольных постоянных, и
особые, которые вообще не содержатся
в общем решении, т. е. не получают-
ся из него при частных значениях
произвольных постоянных (см стр.
210).
Решение дифференциальных уравнений
в частных производных содержит про-
извольные функции.
Надлежащим выбором произвольных
функций получается частное реше-
ние. •
• Св. «итературу Im стр. 349: (Б»], [35], [25].
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ
1-го ПОРЯДКА**
Виды уравнений:
неявный вид
F (х. у. у') = 0.
где
у'-^;
у dx'
У'-/(х у).
явный вид
или
М (х, у) dx + N (х. у) dy — 0.
Общее решение у = ? (х, С) содержит
одно произвольное постоянное С.
Соотношение Ф (х, у. С) = 0 назы-
вается общим интегралом уравнения,
если у как неявная функция есть реше-
ние дифференциального уравнения. Част-
ный интеграл получается из общего при
частном значении С. Особый интеграл
не содержится в общем интеграле.
Если х, у — координаты точек пло-
скости, то кривая, соответствующая
решению С^, называется инте-
гральной кривой дифференциального
уравнения; общему решению у = у (х. С)
или общему интегралу Ф (х, у, С) «= О
соответствует семейство интегральных
кривых дифференциального уравнения.
Дифференциальное уравнение /™/(х, у),
связывающее координаты х. у точки
интегральной кривой и угловой коэффн
ииент у касательной к кривой в этой
точке, выражает свойство, общее всем
кривым семейства
При выполнении условий теоремы
о существовании и единственности ре-
шения (стр. 210) через заданную точку
(х0. Уо) проходит единственная инте-
гральная кривая
м См. литературу на стр. 349: (58), (54). (51J, ]49),
1ЭД-
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ 1-го ПОРЯДКА
207
Чтобы выделить частное решение,
надо задать С или задать значение _ув
искомой функции у, принимаемое при
х= х0.
Решить (проинтегрировать) дифферен-
циальное уравнение — значит, найти все
его решении.
В следующих случаях удается выра-
зить общий интеграл в конечном виде
или через неопределенные интегралы
(в квадратурах)
Уравнение с разделенными перемен-
ными имеет вид
М (х) N О) dx + Р (х) Q (у) dy - 0.
Общий интеграл его
С М « Хх 4- f $ № Вм Г
J + J -NMdy~C-
В некоторых случаях предваритель-
ной подстановкой уравнение сводится
к атому типу. Например, уравнение
dv
~ — f(ax+ by). где а. Ь — постоян-
ах
ные, заменой функции у новой неизвест-
ной функцией и = ах + by сводится
к виду
— bf (а) + а.
ах
Оанородные уравнения. Функция
F(x, у) называется однородной, если она
удовлетворяет условию F (lx. ty) =
= tmF (х. у); т — степень однородности.
Дифференциальное уравнение M(x,y)dx+
4- N (х, у) dy = 0 называется однород-
ным, если Л( и N—однородные функции
одной н той же степени однородности
Уравнение можно преобразовать к виду
.Ул
'Ф-
Замена и= приводит его к уравне-
нию с разделенными переменными.
Уравнение вила
rfy _ . / ах 4- by 4-е \
dx “ ' \ а,х + Л|у + е, / ’
где а. Ь, с, ai. bi, ci — постоянные,
приводится к однородному подстановкой
х — и 4 «. у • в + Р; постоянные «. В
находятся решением системы уравнений
аа + Pfi -ф С = О, О|Я 4 6|р1 + С| = 0
при условии abi — aib 4 0. Если же-
ab> — aib = 0, то дифференциальное-
уравнение преобразуется к виду ,^ =
= (ах 4 бу); подстановка о — ах 4 by
приводит уравнение к виду с разделен-
ными переменными.
Пример. Найти форму зеркала, которое ке
лучи, выходящие из точки О, отражало бы парал-
лслыю данному направлению. Ищем форму зер-
кала в виде поверхности вращения с осью Ох
(данное направление), точка О — начало коорди-
нат. Пусть сечение поверхности меридианной
плоскостью хОу есть у =/(х) — искомая кривая.
At U, у) - текущая точка. Дифференциальное
уравнение получится, если приравняем (фиг. 1>
Фиг. I. К определению формы зеркала.
тангенсы углов ВМТ и ОМ Г, (угол паления равен,
углу отражения) ОМ — падающий луч. МВ —
отраженный. MN — нормаль: tg ВМТ *
ах
^OMN = <. Z.BMN - Z MNO - Zfc
Z« = Zfc ON - ОМ- ¥х*4у*;
- PN
OMT, = — - tg OMT, = ctg • = ctg 3 = — :
отрезок PN - PO 4 ON = - X 4 Ух*4у». Диф-
ay — x 4 ¥ x*-t- v*
ференпиальнле уравнение -у— —---------——
илн^- = — — 4^(у) +I — однородное. За-
у tty Ва ,
мена « " — "X" У “ "X. — х 4 и при-
_____________________ чаи
водит уравнение к виду , —--------я»
¥l 4а* - (I + к1)
— — уравнение с разделенными переменными.
Но пройм решать уравнение искусственно:
у Ду 4 X dr — Ух* 4 у* Дх;
Х(Х*4У*> _ dx. d уха + у. _
2Уе* + у
откуда /х* 4 у* — X 4 С или у* — ЗСх 4 С* —
плраболн с фокусом п начале координат. Искомая
фирмл зеркала — параболоид иращемия.
208
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Линейное уравнение 1-го порядка
^4-Р(х)у = Q(x).
л dV
В случае Q (х) = 0 в уравнении +
-4- Р (х)у = 0 (однородное относительно
у и \ переменные разделяются, и его
общее решение имеет вид у = С<? (х),
<? (х) = е~ P|jr) dx Решение неоднород-
ного (исходного) уравнения ищем в форме
у = u<f (х) (метод вариации произволь-
ной постоянной). Общее решение имеет
«ид
у = е~ ipdx (С + j Qeipdx dx).
Уравнение Бернулли
у'+Р(х)у = Q(x)/1
сводится к линейному уравнению под-
становкой г = у-я+1.
Уравнение Риккати
У' — а (х)у2 + b (х) у + с (х)
вообще пе интегрируется в квадратурах,
но решение существует в силу теоремы
Коши (см. стр. 210). Если известно
одно частное решение у! (х), то подста-
новка у = У1 -|- г приводит к уравне-
нию Бернулли относительно г.
Уравнение в полных дифференциалах.
Уравнение
М (х, у) dx -f- N (х, у) dy — О,
дМ dN
Ъу“Ш
в котором
(условие
интегри-
руемости), называется уравнением в
полных дифференциалах. Левая часть
Mdx -|- Ndy есть полный дифференциал
некоторой функции и: du = Mdx-\-
+ A dy = О, и решение имеет вид
и — { М (х, у) dx +
+J [n (х.У) - & (х, у) dx
dy-C.
Если М dx+ N dy не является полным
дифференциалом некоторой функции, то
существует так называемый интегриру-
ющий множитель р (х, у), умножением
на который уравнение приводится к
виду в полных дифференциалах. Условие
d(uM) d(pN)
интегрируемости —' есть
уравнение в частных производных, слу-
жащее для определения р.
Пример. Линейное уравнение имеет интегри-
рующий множитель
Уравнения 1-го порядка, не разре-
шенные относительно производной.
В общем виде уравнение 1-го порядка
F (х, у, р) = 0, где р = , определяю-
щее р как неявную многозначную функ-
цию от х, у, разрешают относительно р:
Р~А (* >’). Р = А (*• >)• • •/»= /л(*. У)
(Ji — однозначные, непрерывные ветви
многозначной функции р). Если общие
интегралы этих уравнений Ф1(х,у. С)= О.
Ф» (х, у, С)=0.....Фп (х, у, О — 0, то
общий интеграл исходного уравнения
имеет вид
Ф! (х. у. С) Ф, (х. у. С).. Ф„ (х.у. 0=0.
* В некоторых случаях можно найти
общий интеграл без того, чтобы искать
явные функции р от х, у.
1. Если уравнение имеет вид Е(х, р)=0
и может быть решено относительно х.
то, дифференцируя х= f(p), получим
dx — f (р) dp\
так как dy — pdx. то
dy =pf(p)dp.
Общий интеграл дается параметриче-
ским представлением
x-f(p). У-C + jpf (р) dp.
Исключая параметр р, можно общий
интеграл получить в виде Ф(х,у,С)“О.
2. Аналогично рассматривается урав-
нение F (у, р) = 0. Если у = f(p), то
3. Если F (х, р) = 0 можно параметри-
зовать:
х — ц (Г), р — и((), и Р |и (/), и(01=0.
то
dy — р dx — v (0 и' (0 dt.
Получаем общее решение в параме-
трической форме:
х — и (f), у — | v (0 и' (0 dt + С.
4. Аналогично получается общее ре-
шение уравнения в случае, когда
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ 1-го ПОРЯДКА
209
F Р) = 0 можно параметризовать:
y=u(f), р = v(t), тогда
Пример, р* — у> (а — р) — о. Пусть у = рг;
М данного уравнения
at1 аР
Р !+«• ' 14-Г» •
Из соотношении dy — р dx получаем
dx =
£+_£ a(3P-f-P)„,
at‘ ' (1 + W
откуда
X- I rf/ = / + 2arctgZ -bC.
J 1 -г *
Решение:
л/®
jr-/+JiretBr + C; y-j-y^.
5. Если уравнение F . /Л = О
можно параметризовать в виде
2- » «(/). р _ v (0. F [« (/). v (/)] = 0.
то, дифференцируя соотношение у=хи (/)
по х, получим
dy , du dt
dx~u + x~didx'
откуда
, dt
v — и = хи —
dx
dx u‘
или — — v _ ~ dt — уравнение с раз-
деленными переменными. Общее реше-
ние:
Cu’dt
л —CeJe-«; у —хи (I).
6. Если уравнение F (х, у, р) — 0 со-
держит у или х в первой степени, на-
пример у = /(х, р), то dy = pdx,
df df dp
P dx^dpai- " если для последнего
уравнения найдем общее решение р “
= 4>(х, С), то общее решение исходного
уравнения
j-/(x, у(х. С)).
Уравнение Лагранжа y — x<f(p) 4-ф(р)
решается указанным приемом. После
дифференцирования по х получаем
Р-Т(Р)+ (Р) + Ф' (Р)1
Считая х искомой функцией, р —
аргументом, находим [ф (р) у-р]:
_ У (Р) х = Ср)
dp p-f(p) = р -<?(]>)
— линейное уравнение. Общий инте-
грал его вместе с исходным дифферен-
циальным уравнением дает параметри-
ческое представление общего интеграла
уравнения Лагранжа.
Если <р(р) — р = 0 имеет корнем
р = Со, то у = ч> (Си) х -г ф (Со) есть осо-
бое решение уравнения Лагранжа.
Уравнение Клеро у = px -f- ф (р)
тем же методом дифференцирования при-
водится к уравнению
Й (•>' + -И = °-
а) = 0, р =С. Общему интегралу
у = Сх + ф (С) соответствует семейство
прямых.
б) Ф' (р) — х = 0; исключая р из
ф' (р) 4- х = 0, у = px -г ф (р), получим
особый интеграл уравнения Клеро. Гео-
метрически особый интеграл означает
огибающую семейства прямых, предста-
вляющего общее решение (см. стр. 210).
Пример. Найти кривую, отрезок касательной
которой между осами координат равен а = const.
Если у « /(х) — искома! кривая в системе лОу,
то касательная У — у = у' (X — х) отсекает на
осях отрезки ОВ — у —
-ху „оа-2^1
(фиг. 2).
Получаем уравнение
Фиг. 2. Фиг. X Астроида.
(у - хрУ 4- У* - или у — хр ±
уравнение Клеро.
аС
. Осо-
Общее его решение у _ -(-С1
бый шгтеграл получим, исключая р из уравнений
х ±-------—— —0и у — хр ± ; пстамяя
d+p’ff />+Р‘
сюда х — Т ------г- . найдем у — * —-д-.
(I+/>’) '• , t И +₽•»*'<
Исключение р дает х'!> -f- у’^а — а% (астроида)
(фиг. 3).
14 Том I
Зак. 1МИ
210
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Теорема (Коши) существования и
единственности решения дифференци-
ального уравнения 1-го порядка у' =
—/(х, у): если /(х, у) есть однознач-
ная, непрерывная функция в некото-
рой области D изменения переменных х,
у и если для любых пар точек (х, у,),
(х, уг) в этой области /(х, у) удовлет-
воряет условию Липшица \f(x, yj)—
fix, Уз)1 < N lyi—ys|, где N—некоторая
постоянная, то существует единствен-
ное решение у = <#> (х) заданного ура-
внения, определенное и непрерывное
внутри D, принимающее при хв х0
значение у,,. причем точка (х0. Уо) при-
надлежит области D. Считая х0 посто-
янным, а у0 параметром, меняющимся
в некотором промежутке, получим за-
висящее от одного параметра у0 = С
семейство решений у = <р(х. С), т. е.
общее решение. Если существует не-
df
то суще-
прерывная
ствует %.
производная
Условие Липшица выполняется, если
/(х, у) имеет в области D ограниченную
частную производную
df п
. В этом слу-
чае постоянная W равна верхней гра-
df(x, у) , п
нице —— в области £>.
dy
Особые точки. Если условия преды-
дущей теоремы в точке (х0, у0) не выпол-
няются, то такую точку называют осо-
бой точкой уравнения! Если вблизи
точки (х0, уо) функция /(х, у) является
. 1
неограниченной, то -г;------г—ьОпри
(х, у)-♦ (Хо. Уо); примем
/ (•*«. Уо) ” °’
dx 1
тогда для уравнения -г- — -т-.-s уело-
rfy /(х.у)
вия предыдущей теоремы выпол-
нены.
Особая точка называется изолиро-
ванной, если условия теоремы выпол-
няются вблизи некоторой точки везде,
кроме самой точки. Примером такой
d\'
точки (х<, уе) будет случай =
Р (х. v)
“ (Г(х’ "у) ’ еСЛИ Р (Ч’ >oJ = °’ Q (Хв’ Ув)~
я О В частности, уравнение —
ах
“ I с д I * ° имсет в точке (0-0)
изолированную особую точку. Поведе-
ние интегральных кривых в ее окрестно-
сти зависит от корней квадратного
уравнения X* — (6 + c)k+ Ьс — ад = 0.
Точка может быть узлом (интегральные
кривые проходят через (0,0)], седлом (две
прямые проходят через (0,0) |, фокусом
[спиральные интегральные кривые при-
ближаются к (0,0) асимптотически),
центром [замкнутые кривые окружают
(0,0) f.
Особое решение. Особым решением
называют такое решение дифференциаль-
ного уравнения, которое во всех своих
точках не удовлетворяет свойству един-
ственности, т. е. в окрестности каждой
точки (х, у) особого решения сущест-
вуют по крайней мере две интеграль-
ные кривые, проходящие через эту
точку. В частности, если /(х, у) непре-
рывна во всей области D, то особые
решения могут проходить через те точки,
в которых не выполняется условие
Липшица. Последнее не выполняется
в тех точках, где — становится бес-
dy
конечной.
Такой простейший случай встречается,
когда f(x, у) — иррациональная функ-
ция от у в уравнении р = /(х, у).
Освободившись от иррациональности,
получим Fix,у, р) = 0 — алгебраическое
уравнение п-й степени относительно р.
Если составить
dF 1х, у, р>
dp
и исключить р из этих двух уравнений,
то получается Ф (х, у) = 0 — дискри-
минантная кривая (стр. 268). Если функ-
ция у=<р(х), определенная этим урав-
нением дискриминантной кривой,
является решением дифференциального
уравнения F (х, у, р) “ 0, то такое ре-
шение (вообще говоря) особое.
Если дискриминантная кривая яв-
ляется особым решением, то она — оги-
бающая обыкновенных интегральных
кривых.
Дискриминантная кривая может не
являться особым решением уравнения,
тогда она состоит из особых точек
обыкновенных интегральных кривых.
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ 1-го ПОРЯДКА
211
Если известен общий интеграл
Ф (*. У, С)=0 дифференциального урав-
нения, то огибающая этого семейства
интегральных кривых дает особое ре-
шение (см. стр. 268).
Поле направлений. В каждой точке
области D можно из уравнения у' “
“ /(х, У) получить направление каса-
тельной к интегральной кривой, про-
ходящей через эту точку. Совокупность
этих направлений образует поле напра-
влений. Поле направлений удобно пред-
ставить при помощи изоклин. Линия
/ (х, у) “ С называется изоклиной, каж-
дой точке такой линии соответствует
одно и то же направление с угловым
коэффициентом С. Проинтегрировать
уравнение значит построить кривую,
выходящую из данной точки (хв. ув),
которая, проходя через точку поля,
касалась бы в этой точке уже постро-
енной стрелки, указывающей напра-
вление поля.
Приближенные решения.
1. Способ Эйлера. Чтобы построить
интегральную кривую уравнения у*=
“ /(-*. У), проходящую через точку
Фиг. «. Пифическое интегрирование.
Л1в (х0, Уа>. наяо через эту точку про-
вести луч с угловым коэффициентом
Уо) я° пересечения его в точке
с прямой * = *1, параллельной Оу. Ор-
дината у) точки А41 определяется из
равенства у, — у. = /(х<>, у») (х, — х0).
На фиг. 4 = х> — Хо. NMy =
— У1— Уо- АМ<| I РАа. te ( 2. ОРАЛ) =
- /(Хе. Уо> - ; ОАо - fix* у.), если
0Р= I.
Из точки М|(*ь У1> проводят луч
Л1|Л1« с угловым коэффициентом Дхь у()
до пересечения с прямой х = х»; тогда
У« — У| “ /(xi, .yi) (xt — xi) и т. д. Если
надо определить у для заданного х, го
отрезок |х<н xl делят на п частей точ-
ками х», дд,.. последовательно
вычисляют ординаты yi, уд, , ya_t
14*
по предыдущим формулам, последнюю
ординату У находят по формуле
^-У»-1=/(хя-р Уп-1)(*-*.-1)и
полагают у as У
Пример. Найдем peoiemw уртонеииа у' — — ,
у дойдет иордюшее аачддьиому условию у (О) > 1.
Положим х, — ’х, — ... — <*4-1 — Х^—0,1;
х.-0;у>+1-/л-ау.
Вычисления рдеполлаем в форме следующей
таблицы:
Л V XV 2 АУ-^О.*
и 1 и 0
0.1 1 0.05 0,005
0,2 1,005 0,1005 0,0101
0.3 1,0151 0.1521 0,0152
0.4 1,0301 0,2001 0.0206
0.5 1,0500 0.2627 0,0263
0,6 1,0772 0.3232 0.0323
0.7 1.1086 0.33S3 0,0354
0,3 1.11ЯЗ 0.4593 0,0159
0.9 1.1942 0.5374 0.0537
2. Способ последовательных прибли-
жений. Уравнение у' = /(х, у) перепи-
X
сываетсч в виде у = у0 4- J / (х. у) dx.
Первое приближение:
х
У1 — Уо + ( / <*• Уг> Л*?
второе: у, — у0 + ( / (х. ур dx... п-ое
«в
г
приближение у„ — у0 + j f (х. у„_,) dx.
••
Последовательность уо, ут„ .. . у„. . .
сходится, lim уя (х) = у (х) — точное ре-
Ч—оо.
шенке уравнения. причем у(Хф) у^
3. Применение рядов. Можно искать
решение в виде ряда Тейлора
, ’ , (X —X0)f и ,
у — УЬ + (X - Хв) у0 + --у0 +
|Л ~ у" I I (•C-X0)" yW
з1 Уи +-+ Si у •
е • «•»
коэффициенты Уо, у№ Уо-.- находятся иэ
у' = / (х,у) последовательным дифферен-
цированием и вычислением производных
при х = дв, у = уо-
?р
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
4. Метод акад. С. А. Чаплыгина *.
Пусть в некоторой области D плоскости
dy
(х. у) дифференциальное уравнение —
=/(х, у) обладает единственным реше-
нием у (х), удовлетворяющим условию
У (<о) — Уе> т- е- интегральная кривая
у =» у (х) проходит через заданную
точку Л!0(х0,у0) области D (см. стр. 210,
теорема Коши).
Метод Чаплыгина для приближенного
dy .
интегрирования уравнения /(х,у)
состоит в том, чтобы в области D
найти такие проходящие через данную
точку Л1о две кривые у = и(х) и у= о(с).
из которых кривая у = и (х) лежит
ниже интегральной кривой у=у(х).
т. е. «(х)<у(х), а кривая у= о(х)
лежит выше интегральной кривой у =
= у(х), т. е. v (х) > у (х). и чтобы эти
кривые были близки друг к другу.
Кратко такую пару кривых будем обо-
значать [и(х), »(х)]. В точке 'А10
о (*о> = о (*о) ” У W = Уо-
Такая пара функций |и, о| удовле-
творяет неравенствам
g-/(x. В)«У, g-/(x, v)>tt
Для решения этих неравенств следует
выбрать две функции /1 (х, у) u /2(х, у),
между которыми заключена данная функ-
ция f (х, у), т. е.
/>(*. У)</(х. у)<Л(х.у),
причем эти функции должны быть та-
кими, чтобы легко интегрировались
уравнения
dv dv
- h (*• У) н - /?(*. У)- (D
Решения этих уравнений и(х) и и(х),
удовлетворяющие условиям и (х,,) “
= f(xe) = Ув. образуют требуемую
пару |и, о].
Чаплыгин предложил в качестве та-
ких дифференциальных уравнений (I)
использовать линейные дифференциаль-
ные уравнения. Это возможно, если
d»/
производная сохраняет знак в рас-
сматриваемой области D.
Первая пара (щ (х), и (х) | выбирается
произвольно. Тогда, если известна пара
|ця(х), х»я(х)], то следующая пара
[“„.р, с'я_|_|| получается как решение
двух линейных уравнений:
dy / (х, оя) — /(х. и„)
dx v„ - и„
(У - «„)+
+ /(-*• «»);
(] У 9
U- “ J (У — Ил) + / (*• ««)•
Решения и„+|. о„+1 должны удовле-
творять условиям: ия (х^> = т^^^Хц) —
= У в Пара оя+11 находится вну-
три пары [ця, v„] и сама содержит
внутри себя искомую интегральную
кривую у = у (х).
Получается последовательность пар
|ui,vi], lui, pi],...,[ид.проходящих
через точку Мй(х^ у0), содержащих каж-
дая все следующие за ней и как угодно
близко подходящие к искомой инте-
гральной кривой у = у(х).
Для оценки разности 8я(х) = о„(х) —
— и„ (х) мы обозначим через [xq,Xi] тот
отрезок, на котором производится
приближенное интегрирование данного
dv
уравнения = /(х, у)- Пусть длина
отрезка Xi — х0 = I >0. Обозначим че-
рез 1 и |х два положительных числа,
превышающих абсолютные значения
IУ) j и (<х. у) [ в рассматри-
ваемой области О:
14<*.У)|<*. |/уу(х. У)|<1*.
е-м
Обозначим . ^сли псРвая
пара |щ (х), с>1 (х)| удовлетворяет усло-
вию, чтобы на всем отрезке |xe. xj
выполнялось неравенство
(ж) - Vi (ж) — “I <ж) < С.
то все дальнейшие разности 6я(х) не-
обходимо удовлетворяют неравенству
справедливому для всех значений х на
отрезке lx#, xj.
5. Численное интегрирование* (ме-
тод Рунге-Кутта). Для нахождения
точек интегральной кривой, проходя-
щей через (х#, у»), берут Л = Лх — При-
Си. литературу nt стр. М9 |4Ц.
Си. литерптуру iu стр. 351 (124).
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
213
ращение аргумента — и составляют
величины kt, kt. kt по формулам
*i = / (х0, Уо) Л;
а» = / |^х0 + ^; Уо + "j ) Л;
А» — / » Уо + у) А;
^л — f (х0 4- Л); Уо + Аа) к-
Полагают Ду = (ki + 2Ат + 2AS4-
Ч-kt). Находят «!= х0 + Л. yi = Уо+ ЛУ-
Таким же образом вычисляют (ха, yj
и т. д. Зная хп, у„, находят
*i — /(*«>• Ул) А'. '
. , / Л , АА .
*з - / (-»я + у; Ул + -у)h’
А« = /(-*л + А; ул + л»)й;
Ду — — (А, + 2А2 + 2Ад -т А<);
хя+1 = х„ + Л; уп+1 - у„ + Ду.
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ
ВЫСШИХ ПОРЯДКОВ
И СИСТЕМЫ УРАВНЕНИЙ
Обыкновенное дифференциальное
уравнение л-го порядка имеет вил
F (х, у, у', у".у(»>)= 0. Функция
у™?(х, Ci,... ,СЯ), содержащая л про-
извольных постоянных и обращающая
уравнение в тождество, называется
общим решением уравнения. Соотно-
шение Ф (х, у, Ci, Ct.С„) = 0, опре-
деляющее общее решение как неявную
функцию независимой переменной, на-
зывается общим интегралом уравнении.
Произвольные постоянные Ci, Ct, ,Сп
должны входить в общее решение (или
в общий интеграл) так, чтобы надле-
жащим выбором для них частных зна-
чений можно было получить любое
частное решение, соответствующее лю-
бым начальным условиям: при х “ х0
искомая функция у н ее производные
У',. .. ,у(л-,) принимают заданные на-
чальные значения у0, у'о, . -, y<f Суще-
ствование и единственность решения
обеспечиваются теоремой Коши (см.
стр. 214).
Понижение порядка. Важным мето-
дом решения уравнения F (х, у, у',
у*, . , у<“') = 0 является замена пере-
менных, приводящая к уравнениям низ-
шего порядка.
1. Уравнение= /(»)• Последова-
тельным интегрированием получаем об-
щее решение
У * f - - J/(х) dx* + Сух"-1 +
-г Сухл "7 + •. • + Ся
или
X
Хо
2. Уравнение F (х, у**’, у(*+"...
у(»1) = о заменой к = —приводится
к уравнению F (х, и, и',... ,u^n~le>) = Q.
Используя решение последнего и =
, dky
= и (х), находим у из уравнения =
= и (х).
Пример, у* — ху’" 4-(у'*У “0. Зышу’а
» р прицедит к уравнению Клеро
Обшее решение
В-С.Х +С},
ОТКУДА
С,х* С,-**
У-^ + -Т-4-Сыг + Сг
3. Уравнение F (у. у’, у".Уя)) — 0
сводится к уравнению (л—1)-го порядка
dy (fly dp
после замены - р;
Пример, у»» —у’’ — 0; у'-р; у» —р^-;
VP -jj- -Р'-0, откуп р -0; y-j^ -P-U.
214
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Первое уравнение лает у = С„ а второе уравне-
ние дает у = причем при С, - О полу-
чается первое решение.
4. Уравнение F (х, у, у', у*,. .. ,у<л)) =
= 0 называется однородным порядка k
относительно у, у', у"...., у<л', если имеет
место тождество F (х, /у, ty', ty*,...) =
= t*F (х, у, у', у*,...). Заменой y^=e-2dx
порядок уравнения понижается на I.
Пример. Уравнение хуу" —2ху'*-|-уу ’-=0— одно-
родное 2-го порядка отиосителнип у, у', у". Замена
tldx , fldx „ fzdx
>«< , у'-и у» ™(x' + z4e
j
лает t' —- г1- уравнение Бернулли, обший
интеграл которого z = — (С, — hl ж)- *. Отсюда
1пу- J tdx - J —+1п С,; у =
С,
“ С, - In х •
Система п дифференциальных уравне-
ний 1-го порядка с неизвестными функ-
циями yj, уг,.. .,у„ в нормальной форме
’ ’ << .
rfVt . , ,
77 “Zi (х.уу.....уя)
= /я (Х.У1.... 0’л)
имеет единственную систему решений
у» = <?Дх) (I = 1.2,... ,л), определен-
ную и непрерывную п некотором про-
межутке |х — х0 | < й, принимающую
при х — х0 заданные начальные значе-
ния у/ (х0) = (/= I,... ,л). если функ-
ции ft (х, у>,... ,уя) непрерывны отно-
сительно х, у],. . ., уя и удовлетворяют
условию Липшица
l/i <х. У1 4- Дм..Уд + Дуд) —
-Л (x,y).....y„)|<K(|5yi|+
+ • • • + I Д?'л I )
для значений х, yt и у( + Д.Уо лежа-
щих в некоторой области вблизи их
начальных значений; К > 0 — некото-
рое постоянное (теорема Коши).
Уравнение у<п| =/(х, у, у', у*....
у(»—П) приводится к системе в нормаль-
ной форме из п уравнений I-го по-
рядка вида у' - у,. у, - у„.... у^_! -
-‘/{Х,У.у1.уг.....у„_{) с искомыми
функциями у, ylt Уз....,у„_1 и аргу-
ментом х.
Система дифференциальных уравнений
порядка выше первого аналогично при-
водится к нормальной форме введением
новых неизвестных функций.
Нормальная система уравнений экви-
валентна, вообще говоря, одному урав-
нению порядка л. Чтобы его получить,
надо 1-е уравнение дифференцировать
по х:
(Р\у _ ФЛ ЭД dyy , dZi dy„
dx* = дх дуу dx •••т dyn dx
или
(Руу dt. .dfy dfy
djfl“ дх ‘ ду/' + ‘“+ 1у/п
= (х. У1.....Уд)-
Полученное уравнение надо снова
дифференцировать по х:
dx* = дх+ ду/1 + •• + dvnfn
-Fs(x. У1....Уд)
и т. д.; последнее равенство получим
в виде
_ . .
jpr = ^я (х.Л. - - -.>„)-
Если теперь из системы
определить л — 1
dy,
через х, уь ,
величин у», у»,. .. .у,
^Л-1У1
.. .-----Н- и подста-
dx"-1
пить их в последнее
d"yt
уравнение -
=и Fя, то получим одно уравнение л-го
порядка:
d"v.
dx”
-• Ф
dn~\y,
dx”'
заменяющее систему. Если решение
этого уравнения у»,(х) дифференцировать
dv. d"~lvt
и вычислить -р-1.......гН“-то можно
dx dxn~'
получить уз, уз...уя как функции х,
удовлетворяющие системе.
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
215
Линейные дифференциальные
уравнения
Линейное относительно неизвестной
функции и ее производных дифференци-
альное уравнение имеет вид
+ /»я_>(х)У + Рп <х)у - /(х)
и называется неоднородным, если
/(х) 0. Функции ру(х) (j = 1,2.л),
f (х)— непрерывные. В случае /(х)=0
уравнение называется однородным или
без правой части. Если в однородном
уравнении ру-(х) те же самые, как и
в неоднородном, то однородное уравне-
ние называется соответствующим дан-
ному неоднородному уравнению.
Если ylf У?,-.., Уа— частные реше-
ния однородного уравнения, то у =
= Ciy। 4- .. •+ С*у* — также решение
того же уравнения, где Су — произ-
вольные постоянные. Система функций
У1 = Vi (х), . .., уя = уя (х) называется
линейно независимой, если их линейная
комбинация Cjyj -f- ... 4- Сяуя ни при
каких значениях Ct, Ct,..., Ся, кроме
Ci = Ct “ ... "• С„ = 0, не обращается
тождественно в нуль. Необходимым и
достаточным условием линейной неза-
висимости У1,...,уя является неравен-
ство
>1
1Г_ У............... Уп •
U7 называется определителем Вронского
для ylt уз,..., ул. Если функции уь у2,..
у„ суть линейно независимые частные
решения однородного уравнения, то их
называют фундаментальной системой
решений.
• Общее решение однородного уравне-
ния имеет вид у = С}уу + ... + Сяу„,
где У),--., Ул— фундаментальная си-
стема решений, Су — произвольные
постоянные. Последние можно опреде-
лить так, чтобы частное решение удо-
влетворяло начальным уелрвиям у=Ув,
У' “ Уо. • • • = Уо1-” ПРИ * и *о-
Если известен частный интеграл yf(x)
однородного уравнения, то подстанов-
кой г = — , а затем г' = и получим
линейное уравнение порядка п — I.
Общее решение неоднородного урав-
нения есть сумма какого-нибудь част-
ного решения неоднородного уравне-
ния и общего решения соответствую-
щего однородного уравнения.
Если известно общее решение Cjyj +
4-С2У3+ ... 4* Сяуя соответствующего
однородного уравнения, то решение не-
однородного уравнения можно найти ме-
тодом вариации произвольных по-
стоянных. Решение имеет вид у "•
— Ct (х) у: 4- Ct (х) yt + • - - 4-С„(х)уя,
где неизвестные функции Су (х) нахо-
дятся из системы линейных алгебраи-
ческих уравнений относительно произ
водных —:
dx
dC' ,
yi~dT +
dC.
=0;
dx
уГ2>^ + .„+ЛЛ-2)^.=0.
r> ^Cy . .
Решив систему и получив — Т;(х).
находим Су квадратурами: Су =
— fay (х) dx + Ay; А/ — постоянные ин
тегрирования.
Линейное однородное уравнение п-го
порядка с постоянными коэффициентами
у(я) + а1у<я-,,4- ... 4- в„_1У'4-Пл> = 0
имеет решением функцию где k —
корень характеристического уравнения
kn 4- Д1ЛЛ ' 4- ... 4- вя-1л 4" оп = 0
Если все корни kt, kt,..., kn различны,
то e*lX, е*,х.е*яХ образуют фундамен-
тальную систему решений и у = Cie*,x4-
4- ... 4- Сяе*яХ — общее решение задан-
ного (однородного) уравнения; С»......
С„ — произвольные постоянные.
Если корни k комплексные, то они
попарно сопряженные (при веществен-
ных а....... а„), например kr = e4_ |W,
to X _ 1 i-У
“ « — р/, тогда e ' . e заме-
няются действительными функциями
e^cosfx, elXsln8x, и получается новая
фундаментальная система.
216
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Гели k = имеет кратность т, то в
фундаментальную систему решений,
кроме е**, надо включить функции хе s .
х>Лг......
Если k = я 4- jtf — корень кратно-
сти гп (а — fW — корень той же крат-
ности, если ai,,. ая — вещественные),
то в фундаментальную систему реше-
нии входят функции
е™ cos fix; e*-r sin Зх;
xeajr cos fix; xe** sin px;
д.ст—1 e«x cos jjx, xm~l елх sin fix.
Неоднородное уравнение Ул) 4-
+ Oxy1"-1* 4- ... + апу •= f (х) решается
методом вариации произвольных по-
стоянных. Его частное решение _у(х)
можно найти по формуле
7(х)-j Y(x-t)f(f)dt,
и
где У (х) — решение соответствующего
однородного уравнения с условиями
Г(0) = 0; У'(0)
)ДЛ~2) (0) _ 0. у(и-1) (0) = |;
тогда общее решение имеет вид у=>•+ г,
причем г — общее решение соответ-
ствующего однородного уравнения.
Частное решение у неоднородного
уравнения находится методом неопреде-
ленных коэффициентов в случае, когда
/(х) — еах |Р (х) cos bx + Q (x) sin fcx],
где Р и Q — многочлены от х. Реше-
ние У подбирается а форме правой ча-
сто / (х):
у = е?х [Pj (х) cos Ьх 4- (?! (х) sin b.r|,
если а 4- Ы не является корнем ха-
рактеристического уравнения для соот-
|стствующего однородного уравнения,
и в форме
у xmc°‘ |Р] (х) cos bx 4- Q] (х) sin йх|,
если а 4- bt — корень кратности т ха-
рактеристического уравнения. Здесь Р\
и Qi — многочлены от х с неопреде-
ленными коэффициентами степени, со-
впадающей с наибольшей из степеней Р
и Q.
Если f (х) = б (х)_4- Jt (х),то частное
решение у = ух 4- >'?, где _У1 — реше-
ние уравнения у|л,4-... 4-алу =/j(x),
yt — решение уравнения _у1л)4~ . .. 4“
+ апУ “ ft (*)
Пример. у!У 4. у" » х 4- *Х sln х + х cos х.
Характеристическое уравнение я* -f- ** icij
имеет корни: А, — А, » 0; *„ •» <; А,« — I.
Фундаментальная система решений: е^х = 1.
хеОх — х, е*х, e~ix, причем е~1х заменя-
ются функциями cos х, sin х. Общее решение
соотвстствуюшсго однородного уравнения
С,4- CjX-f- С,coax 4- С, sin х.
Частное решение ншем в внае
У “ У. 4" У1 4-У»,
где у,—частное решение уравнения у^+у' — х;
у, — частное решение уравнения у1’ 4- У" “
= ех sin х; у, — частное решение уравнения у*У 4-
4- у* = X COS X.
Полагаем
у, = х« (Ах 4-S):
yi = ex (С cosx 4- р sin х):
у, - х |(,М,х 4- Л',) cos х 4- (Aisx 4- №) sin xj.
Иычнсляя y*. yiv, подставляя в соответствую-
щее неоднородное уравнение, приравнивая коэф-
фициент при одинаковых степенях х из обеих
частей равенства, получаем
СА = 1; В = 0; вС = -1; О = 2С=-4-:
ЛГ, = 0; 4V, = - 5; ЧА1- = - 1; N, = 0.
Общее решение неоднородного уравнения
шеег вид
у •• С, 4- Ci t 4* С, cos х 4- С, sin х 4-
4- -1- х*4 е* -g- cos х — -1- sin xj 4-
4- х j - -у- cos х-y х sin xj .
Уравнения, приводящиеся к уравне-
ниям с постоянными коэффициентами.
I, Уравнение Эйлера
(л* 4- &)л5 + ai(ax 4- b)n~l 4-
• . ctv
4- ... + o„_i (ax 4- b) -4- a„y - f(x)
заменой x новым аргументом t no
формуле ax 4- b ~ e1 приводится к
уравнению с постоянными коэффициен-
тами.
ОБЫКНОВЕННЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
217
2. Уравнение (1—х*) —
4- пгу = 0 заменой х = cos
d^y
дится к виду + пгу — 0.
ментальная система решений:
приво-
Фунда-
_У1 = cos (п arccos х); у2 = sin (п arccos х).
При целом п функция У] (х) является
многочленом степени п, так как cos л?
выражается в виде многочлена от cos <?;
У1
в этом случае —
называется
поли-
= Уд0*- Общее решение неоднородной си-
стемы
+ влУ| + - - - + в/лУл = Vt (х)
а = 1.2,.....п)
имеет вид
У1 - У1 + «г,
У» = Ув+ Zj,
номом Чебышева л-й степени (см. стр. 224).
Ул = Ул + z„.
Система линейных
дифференциальных уравнений
Решением линейной однородной си-
стемы уравнений
dy«
+ апУ1 + в«Уг + ... + а1пу„ — 0
(/=1, 2. .... ж)
называется совокупность функций
у-, (х), •••. уя (х), удовлетворяющих то-
ждественно системе уравнений. Здесь
а/Л — функции от х, непрерывные на
некотором отрезке S (xi х < xj).
л частных решений _у^, у^......у^1
(Л = 1,2, ..., л) образуют фундамен-
тальную систему решений, если опре-
делитель
УМ’ ....у<‘>
У^У?»
v<2)
/О
уГ’у^’
на отрезке S. Общее решение системы
уравнений имеет вид
У1 - Оу”’ + Qyf” + - - + Слу,1я);
Л - Cjyj” + СгуМ + ... + Сяу<я); (2)
Ул-С^'Ч С^ + .-.+ Слу*-».
где произвольные постоянные Ci,.... С„
можно определить так, что функции
У1...Ул бУЛУТ ПРИ X = Х0 (xt < х.<х,)
удовлетворять начальным условиям
У1 (х#) - У?. Уг (х0) - у!°>,.у„ (х0) =
где yi..... уп — некоторое частное ре-
шение неоднородной системы, a zj,. . . ,
г„ — общее решение соответствующей
однородной системы
— aazt + ... + а1пг„ = 0
0=1.....п).
Решение неоднородной системы мо-
жет быть найдено методом вариации
произвольных постоянных, если изве-
стна фундаментальная система решений
соответствующей однородной системы.
Считая в равенствах (2) С, неизвест-
ными функциями х, мы из уравнений
VU) dCx 4-
у‘ dx * У’ dx
А"> ‘Ч1- = У.;
1 dx *’
Л) dC± (2)dCj dC^ v
Уп dx t >n dx T ••• 4- Уп ax v"
найдем — v/(x); Ct — j <f/(x)rfx+
-|- Л, — постоянные (i = 1, ... n).
Линейная однородная система
с постоянными коэффициентами
+ Я11У1 + — + вглУл " °;
+ лаУ1 + • - • + в;лУл °!
d v л . , л
~ + «Л1У| + - . - + ДллУл - 0
14 1464
218
ДИФФЕРЕНЦИАЛЬНЫЕ УРАПНЕНИЯ
имеет частное решение вида
>1 ~ Я = • ••:>« =
где постоянная к удовлетворяет ура-
внению
А (к) =
а11 + к .«11....... «1л
«л «а + к.... а:„
«=0.
«л! «?.•••• апп + к
которое называется характеристиче-
ским. а постоянные , 7, удовле-
творяют линейной системе уравнений
(«и + к) 71 + Д1г7г + • • • + ai«7« = О-
«nil + (Ди + к) 7г + • • + ДглТл = 01
.................................(3)
«ЯП1 + «лЯг + • • • + («ям + к) 7, - 0.
Если все л корней к>....Ав характе-
ристического уравнения различны, то
ранг матрицы
|«п + к....д1а
............
«яЬ • •• • влл + к
для любого корня А, равен п — 1 /т. е.
но крайней мере один определитель
(п — 1)-го порядка матрицы М от-
личен от нуля). Из системы (3) при
k=kf определяются 71/*....7^, с точ-
ностью до произвольного множителя
пропорциональности Ср
где ........ — алгебраические до
полнеиия любой строки определителя
Д (к/), для которой они не все равны
нулю. Корню соответствует частное
решение системы (полагаем Ct = 1)
ytf>.........................
(0 _ МО/Н.
• п п
При (= 1,2,.... л получаем л раз-
личных частных решений, образующих
Фундаментальную систему решений.
Если корень А4 характеристического
уравнения имеет кратность mz, то ре-
шения системы дифференциальных
уравнений следует искать в виде
л = у> = Paix)Sr*i •••;
У я - Pi» (*) •
где Рп (ж), .... Р1я (х) — многочлены
степени, не большей чем —1. Для
нахождения общего решения надо со-
ставить для каждого корня kj выраже-
ния указанных видов с неопределен-
ными коэффициентами, подставить эти
выражения в данную систему дифферен-
циальных уравнений и решить относи-
тельно неопределенных коэффициентов
полученную линейную систему уравне-
ний. Число неизвестных коэффициентов,
остающихся произвольными, равно крат-
ности корня.
- Общее решение представится в виде
У/ - PyW**1* + pij(х)+ ••• +
+ ^/(x)e,?f •
где j — 1.2...л; mt + т.+... + /п,=л.
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ*
Функция х(р), определенная равен-
ством
х(р) e~ptx(t)dl.
и
называется лапласовым преобразованием
(L-иэображением) функции х ((). Пред-
полагается, что комплексная величина р
имеет положительную действительную
часть: Rep— а0>0. Функция х(р)
определена для всех р, для которых
1в-ч,х(Л dt существует.
Примеры:
и и
сооо преобрлэооеиие ж (Л " I.
00
2) I e~P,eat di — —— — лапласооо npeoo
J р — а
О
рмомняе X — е°' при условии Re р > Re а.
Ниже приведена таблица лапласовых
преобразований наиболее употребнтель-
• См. литературу мл пр. 350; |-73), f74)
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
219
Таблица лапласовых преобразований
x(pl- \e~ptx(t)dt.
Х(р) x(t) x.n 1
1. х, (р) + хг(р) 2. рх (р) — х (0) 3. рах(р) — _[р"~*ж(0)4 +рл“2х' (0)4 +„.+/"-‘)(0) 5. х (р + а) 6. е~ арх(р) 7. x; (р)хо(р) 9. * а” 1 xj (0 + *t <0 dx ~dt dnx dtn |х(т)Л e~at x{f) 0, 0<t<e x(t—a), t>a t J *1 (t) *1 (t-r)dx 0 ) 0, 0<t<a 1. t>a t" . —r(n — целое число, л! причем л> — 1) !7мПГ*ея> 1 е-о‘ . 1 tne~al 0+1) sin at • cos at 16. 35—1 pi —e2 17.—P pt — a2 18 £ (рг + a»)2 19 Pl ' (рг + «2)л+‘ 20. — (p^+a'-y 21. - (p + e)»+ b* 99 P + о ’ (p 4- at) + bt и 1 sh at ch at — sin at 2a — tn sin at, 2ял! a n — целое число (sin at — at cos at) e~ar sin bt e~a' cos bl 1
Р 10р"+« ,Ьр-И ‘-р + а 13‘ (р + д/,+ 1 14-р« + а» ,5р» + а» 23. r — V P 24. Ц— /+- 25‘ Vl+pi “7Йтэх v/Vp»+>.»-pV A / 27- V-—г Kp»-I /"ST (2t)" 13-5...(2n-l) n — целое > 0 J, it) j„ an. Re л > — I /.(O •
220
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
пых функций (см. стр. 219). Суще-
ствует обратное преобразование (фор-
мула Римана-Меллина)
«+«» _
eplx(p)dp, (4)
too
определяющее функцию х(0 по ее ла-
пласову преобразованию х(р) и спра-
ведливое при условиях: x(t) имеет не-
прерывную производную, |x(Z)K*erZ,
где k нс — положительные постоян-
ные. Интеграл берется по прямой,
параллельной мнимой оси в плоскости
комплексной переменной р и располо-
женной где угодно справа от всех особых
точек функции х (р).
Пусть дано линейное дифференциаль-
ное уравнение с постоянными коэффи-
циентами
решение х (Z) можно найти проще: раз-
(л)
лагаем "а простейшие дроби
(стр. 156), для каждой простейшей дроби
находим по таблице лапласовых преоб-
разований соответствующую функцию;
искомое решение равно сумме найденных
таким образом функций.
Пример. Найти решение уравнения — —
(Рх dx
_ — -f- 4 —----4х = cos 2t, удовлетворяющее
начальным условиям х0 и 0, X, =0, X, “ 1. Здесь
/(Z) = cos 2/;J(p)-
е pt cos 2tdt. Из таблицы
Р -г Я
Применение лапласона преобра-
зования к уравнению дает
<р’ - Р* + <Р - - 1 + •
Решение этого уравнения, удовлетво-
ряющее начальным условиям х = л0,
dx dn~
л ’ dt"~l
может быть найдено следующим обра-
зом. Над каждым членом данного урав-
нения совершаем лапласово преобразо-
вание и обозначаем Д(р) = рп 4- aip"~l4-
+ ... + an_fP + ая. Если принять во
внимание начальные условия, то полу-
чается уравнение
Д (р)х(р) - (рл-,х0 + ... +
+ Р*„-2 +*„_,) +
+ а1(рп~'-х, + ...+ рхп_3^ х„_2)+
+ вя-2(/«д + *1) +
+ ля_1Х0 + 7(р)-?(р),
называемое вспомогательным уравне-
нием для данного дифференциального
уравнения с данными начальными усло-
виями. Отсюда
Искомое решение находим по фор-
муле (4). Если ? (р)' — многочлен, то
Уравнение р3 — р'+ *р — 4 — 0 имеет кори»
р, — 1, p.j_ 3 = £ 2), слсдоиательнп.
- Р Р‘ ТР т
<Р‘ + *)(Р — 1)Х 1Р) = 1 + —,<1“ *= р<-р4
откуда
х(Р>-
р! 4- 4- 4
(Р-1) ЦЯ-НН’
Разлагаем правую часть на простейшие дробя
- , 4 . «л 4-е . 1Лр + ы
р-i + и>‘ + 4р + р»4-ч
и находим
- , в I 1 П . I <
х(р} ~ IT “ Т ф‘-М)* s (Р’-Hi-
ts /» 3 2
“ Л ц»+4 25 р» 4-4 '
Из таблицы находим
х W — / — -j- tin 2/ 4- ^-.^-(tln It —
— It cot 2Z)---cot 2t — ~ tin it
2d .XI
ИЛИ ’
X (0 - 4- e‘ - (tin 2/4-2 cot 2/)-
- ^(7 tin И-f-24 cot 2/).
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
221
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
Пусть _ylt уг — фундаментальная си-
стема решений линейного однородного
дифференциального уравнения
у* 4- ру (х) у' + pt (х) у - 0.
Если известно одно частное решение
У1(х), то второе частное решение
(5)
где С — произвольное постоянное.
Общее решение неоднородного уравне-
ния
У* + А (*) У' 4- Рг (*) У = / (•*)
имеет вид
dx —
y-yif_2^
J У1У2 — УгУ[
— У г f—, dx + Аууу + Av?.
ЛУ1У2 —УгУ|
где A|, At — произвольные постоянные;
>1. У? — фундаментальная система ре-
шений соответствующего однородного
уравнения.
Если в уравнении
Ро (-«)У* + pt (х) у' -f- рг (х) у = /(х)
функции р0(х), Pl(X), Рг(Х), /(*)_
многочлены или разлагаются в степен-
ные сходящиеся ряды из целых неотри-
цательных степеней х — х0, причем
Во(*о) у4 0, то решения уравнения тоже
выражаются сходящимися рядами по
степеням х — х0. Чтобы найти решение
вида
У — 4> 4- Ау (х — х0) 4- Аг (х — х0)« 4- ....
следует подставить этот ряд в урав-
нение и, приравняв коэффициенты при
одинаковых степенях х — х0, получить
уравнения для Ао, Аь Л8,...
Если Ро(*о) = 0, то в некоторых слу-
чаях тем же методом можно получить
решение в виде сходящегося ряда
у — А, (х — хв)г 4- (х — хв),+1 4-
+ А(*--г(/+г4-....
где г — вообще нецелое число.
В частности, уравнение
*гУ" 4- Рг (х) ху' 4- рг (х) у = 0
имеет при х = 0 особую точку. Если
Рг = я0+а*+ 02*’+—. Рг=*о+ &1*~г
4- btx1 — . . то решение можно
искать в виде
ОО
у-х'У АкХл
к-0
причем Ао =# 0. Для неопределенных
коэффициентов получаются уравнения
1Г (г — 1) 4- 4- Ьо] Ад = 0;
|(г 4- О г 4- ад (г 4- 1) 4- &0] А; 4-
4" О]ГД) 4- ij/lo = 0;
1(г 4- 2) (г 4- 1) 4- (г 4- 2) 4" ^ol Аг 4-
4" О) (г-f-1 )Д> + O’r.4o-|-fci/li4" Ь»Яо = О, (6)
Из уравнения г (г — 1)4- «о г + Ьв = 0.
называемого определяющие, находим
корни Г| и г2. Если разность Г|—г г не
оо
равна целому числу, тоУ1 = х'1
А—О
оо
у, = хл’У| А^х* определяют фунда
к-о
ментальную систему решений. Здесь Ал
и А* получаются нз системы линейных
уравнений (6), где г заменяется через
Гу для получения А* и через г» для по-
лучения А*; АутЫ), Ау ч*0—произ-
вольные постоянные. Ряды сходятся в
том же промежутке, где сходятся ряды
Рг М и рг (х).
Если Г| — rt есть целое положитель-
ное число или нуль, то, вообще говоря,
получается указанным способом одно
решение уу. Решение у2, независимое
линейно от А, отыскивается при помощи
формулы (5).
Фундаментальная система решений
имеет вид
ОО
у, и у, - Вуу In х 4- Z’ У в»х*
А=0
где в “ const, В* =• const.
Уравнение Бесселя, х’у* 4- *У +
4- (х’ — ч’) у = 0; ч — постоянное. Опре-
деляющее уравнение г (г — 1) + г — ч1
= г* — ч’ =- 0 имеет корни г = ± ч.
222
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Решением будет у — х" (Д04-Л1х4-
4- Aix*+ . . .),
где Ло — произвольное постоянное; 4j=0;
Лг 2 (2^4- 2) ’ А,“0:
л _ ________-4>_________
М 2-4 (2ч + 2) (2ч + 4)
Ль — 0 и т. д.
Бесселевы функции *. Решение урав-
нения Бесселя, принимающее при х —
= 0 конечное значение и при Ло —
=-------!-----, определяет бесселеяу
2T(v+ 1)
(или цилиндрическую') функцию ч-го по-
рядка 1-го рода
У’<Х) 2Т(»+1) [* 2(2v+2) +
+_________£*___________1 _
2-4-(2ч 4-2) (2ч 4-4)
у (-П* / х х >+2А
“ Г (ч 4-Л-г 1)1^ )
*=о ' 7
Здесь Г(г) — так называемая гямма-
функцня (см. стр. 178).
Бесселевы функции нулевого и пер-
вого порядка (1-го родя):
(iVU)’+ wGr)*“
Ряды равномерно сходятся при вся-
ком < (вещественном и комплексном).
Графики 20 и Ji изображены нафиг.5.
При ч = п 4- у (я — целое число) функ-
• См. литературу на стр. ЗА»: (3&|, |36(, (75), |66;.
ция Бесселя выражается через элемен-
тарные функции, например
J,(x) •=
При ч, не равном целому числу,
общее решение уравнения Бесселя имеет
вид
у = C]JV (X) 4- CjJ_, (х).
Если ч = п — целое число, го
/_в(х) = (—1)л/я(х). В этом случае
вторым решением уравнения Бесселя,
линейно не зависимым от функции Jп,
является функция Бесселя 2-го рода
Фиг. 5. Графики бесселевых функций А(х), Л (х).
порядка л (функция Вебера), определяе-
мая формулой
Yn(x)-^Jn (x)(ln^+c)-
1 V(" — * — 1)1 I x \-п+2»
«Zl Л! ' \ 2 )
*—о
J V <—D* ( х\"4-Д*
it All’ (л 4- A 4- I) \ 2 ) Л
*—о
где С—постоянная Эйлера (см. стр. 135).
*
и при к — О V — означает пустую сум-
му, т. е. нуль. В случае ч нецелого функ-
ция Бесселя 2-го рода определяем
формулой
Л (X) СОЗ чя — J-ч (X)
» 1 “ sin чя
Отсюда при ч -► л, л — целое число.
предельным переходом получается ) л1х).
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
223
Разложения Х0(х) и h (х) в ряды:
у r0W-(c+lni)j,M +
+Ф‘-^6У*
1 , 1 . 1
(3!)« Ш
у Г,(дг)-(с+1п-£) Jt (х) —
1 nV (—1)* ^лг>1+а*
х Zj k\(k + \)\\2) '
л=о
х [2(1+Т+-’ + т)+ ттт
У1 (X) Уо(х).
У, (х) вещественны. Функции У,(х) и
У,,, (х) не имеют общих нулей, кроме,
может быть, х = 0, но между двумя по-
следовательными нулями функции У, (х>
лежит один и только один нуль функ-
ции У, и функции У,, р Нули У,(х) —
простые, кроме х = 0.
Если п = 0, I, 2..., то | Jп (х) | < I.
HAW <1-
dx"
Бесселевы функции мнимого
мента определяются формулой
яргу
/,(х) = ( ’У,(*х) - r (v + |)
Щт4- I) 2! (у + 1)(у+ 2)
Графики Y0(x) и Fi (х) даны на фиг. б.
Зависимости между бесселевыми функ-
циями:
— У, (х) - Jw_1 (х) + У^., (х) *,
2 У, (х) — У._, (х) — У, н(х).
Такие же зависимости имеются для
У,(х).
'dx ' ’ dx ’ nx
При вещественном у функция Jм (х)
имеет бесчисленное множество веще-
Фиг 6. Графики бесселеаык функций
К. (х). >'. (хК
ственпых нулей [значений х. при кото-
рых У,(х) = 0] и конечное число чисто
мнимых нулей. Если J ,(х) = 0. то
J,(— х) = 0. При у > — I всё нули
и удовлетворяют уравнению
х2у* + ху' — (х* + у2) у — 0.
О свойствах ортогональности функций
Бесселя см. стр. 311.
Функции Лежандра [86], [35] опреде-
ляются как решения дифференциального
уравнения Лежандра
(I — х») у' — 2ху* + п (п + 1) у — О.
Для п целого (и п = 0) решениями
являются полиномы Лежандра л-й сте-
пени (шаровые функции)
Р tx\ (2п — 1) (2я — 3)... 3-1
Г л(Я-1)
х L 2(2л—I)
п<я — 1) (я —2) (л —3) п-4_ ]
2-4(2я-1)(2я —3) х
1 d"
РО(Х) - 1;
Pi (х) - х;
Рг (х) = 1 (Зх* - I);
GW =7 (5х3 — Зх);
224
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
^<(Х) = i(35x«-30x* + 3);
о
Р6 (•*) = 4- (63х» — 70x3 + 15х) ;
о
Р«(х) = —(231х« —315x4 + 105x2 — 5).
Рекуррентная формула:
(л + l)P„+i (х) -
— (2л + I) хРп (х) — пР„_у (х).
Ря(х) имеет п простых корней в про-
межутке (—1, 4- 1).
Свойство ортогональности:
Pn(x)Pm(x)dx
0, если т =£ п
2
2^+1 • еслп т-п'
На отрезке — 1 < с < I функции
i^wi. я» |р»<х)|’ i р"(х)1 нс
превосходят единицы. Рп (1) = 1.
Полиномы Чебышева [35], (67)
Тп (х) — ^д_1 cos (л arccos х) удовле-
творяют уравнению
(1 — х*) у' — ху' + л*у = 0;
Тп(х)- <4-|(х+ /х®-1)"4-
+ (х-У7г=1)"|. (л>1);
Т0(х) а 1; Ту — хГ0 — х; Г2 — xTj —
л-1-i ” х7„ 1 п_। (л > 2),
Г4(-х)-(-1)вГя(х);
-Ы
С Т"тт 4r _ ( 01 <”*»»)
J VI—х® I к:22я-,1 (л —/п).
Все корни Т„ (х) — простые, действи-
тельные и лежат на отрезке (— 1,1). Эти
полиномы наименее уклоняются от нуля
в промежутке (—1,4- I), Т. с. по срав-
нению с любым полиномом л-й степени
с вещественными коэффициентами и
коэффициентом 1 при хп полином Т„
таков, что max | Тя| в промежутке (—1,
4- 1) имеет наименьшее значение.
Фиг. 7 — 12. Графики полиномов Чебышева:
Г,. Г„ Г„ Г,. Т,. Г..
Графики Т1, Tt, Та. Ti, Т5, Тя даны на
фиг. 7 —12, причем масштаб на осн Оу
увеличен в 2Я~* раз.
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ В ЧАСТНЫХ
ПРОИЗВОДНЫХ «
Линейные уравнения 1-го порядка.
Решение однородного уравнения
дг
дх2
"л^Г”0-
где х>, . . . , хя— независимые пере-
менные, Xi........ Хп зависят от хь
X», . . , хя и имеют непрерывные про-
изводные, г — искомая функция, равно-
сильно решению системы обыкновенных
уравнений
rfxi dxt dxn
Ху ” Хг " хя •
Если <ft(xi,. . . хя)" C,(,t — 1,2.....
л — 1) — решение этой системы, то
г = Ф (<?ь ч>», . .<РЛ_|) — общее реше
ние уравнения в частных производных,
причем Ф— произвольная дифференци-
* См. литературу на стр. 3S0: [58|, (50), (59).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ
225
руемая функция своих п — I аргумен-
тов. В случае неоднородного уравнения
где R зависят от ж», . . . , х„, г,
общий интеграл г определяется из ра-
венства Ф fa, . . . , ?д) = 0, где Ф —
произвольная дифференцируемая функ-
ция, a <f>( (xi.хв, г) = Сt(i = 1.2...
..., я) — система интегралов системы
уравнений
dxx dx„ dz
х, ”••• ““XT” /? *
Линейное уравнение 2-го порядка.
Наиболее часто встречаются следующие
уравнения, называемые уравнениями
математической физики:
I) волновое уравнение
д'-u
• ^г-дгд“-
где Д — оператор Лапласа (см. стр. 234),
описывающее колебания некоторой
среды;
2) телеграфное уравнение
+ 2А4+С“
<Ри
"ох* ’
3) уравнение распространения тепла
%-™-
4) уравнения теории потенциала:
Ли " 0 — уравнение Лапласа; Ли =
= 4 т. р(х, у, г) — уравнение Пуассона.
Обычно ищут частное решение, удо-
влетворяющее начальным и граничным
условиям.
Пример. Решить волновое уравнение (коле-
бании закрепленной струны) = а' по не
О1* ох1
тоду Фурье с условиями а (дг. Г) | — /(х);
I ,_д - » (X), 0 < х < I (начальные
условия): z (О, f) = z (I, f) — О, I > 0 (граничные
условия). Ищем решение в виде произведения
функции от х на функцию от < : х = Х(х) Г(().
X* TN
Подставляя г в уравнение, получим —- = —jy_.
Левая часть не зависит от t, а правая не зависит
от х, поэтому равенство отношений возможно,
если каждое из них — постоянное: X* — XX, Г" —
•=<М, X—const. Из первого уравнения X —
= С, sh V X х + С, ch V X х. Условие г (О, 0 —
= О хает С, — 0. Условию z (I. /) — О можно удо-
влетворить только считая X отрицательным;
из условия 0_— С, »1> Ух (, или th /X (=0, (С,*0).
или »ln<Vx (—О (см. стр. 196). получаем
iV X I — ел. 1 —------(л — 1, 2, . . .): тогда
(sh х =sln I VTTx — sin —рх; следовательно.
„ „ , члх
X — С, sin—j— .
Второе уравнение лает решение
_ Па* . . к . па*
Тп = апст — ' + ЬЛ —
общее решение
ОО
V1 ( ПаЖ ж Я А. я П(ХК Л ПЖ
г , |лп cos —— I 4- Ьп sin —— t j sin -у- x
л—1
(с произвольными постоянными ап, бд, куда
включен С,). При t = 0 должны быть выполнены
начальные условия:
£ansln -у-х-Г(х);
Л = 1
V1 б ЯЯВ ля
7, —t-----Sin-J-X = • (х).
Л=|
Используя формулы разложения /(х) и у(х)
и рях Фурье, получим:
„ I
2 г , . . п«х .
- — v (JT) «In -J- dx,
я ла« J •
и искомая функция х « з (х. Г) опрехелена.
Теорема о существовании решений си-
стемы уравнений в частных производ-
ных принадлежит великой русской уче-
ной С. В. Ковалевской.
ГЛАВА X
ВЕКТОРНОЕ И ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ*
ВЕКТОРНАЯ АЛГЕБРА
В существующей литературе, посвя-
щенной векторному и тензорному исчис-
лению, имеет место большое разнообразие
в терминологии и в обозначениях одного
и того же понятия Ниже приняты
наиболее употребительные обозначения
и термины
Величины разделяются на скалярные
и векторные.
Скалярная величина (скаляр) при
избранной единице меры вполне харак-
теризуется одним числом, отрицатель-
ным или положительным, например,
масса, работа, температура, объем
Векторная величина (вектор) опре-
деляется числом, измеряющим ее в не-
которых единицах, и направлением в
пространстве, например, скорость, уско-
рение, сила
Изображают вектор (см. стр. 3)
направленным отрезком MiMj— а
(фиг. 1). Длина отрезка (в некотором
масштабе) есть число.
характеризующее век-
fy''' тор; оно называется, мо-
S дулем вектора, длиной.
численным значением
вектора и обозначается
. Га I = а — | Af]Afx | > 0.
*“ I. Вектор Направление вектора
отмечается на отрезке
стрелкой. Прямая, на которой лежит
вектор, называется носителем его, ли-
нией действия вектора
Векторы бывают: I) свободные, т. е.
не связанные с линией действия;
2) скользящие (переносятся вдоль
носителя) и 3) неподвижные, связан-
ные с точкой своего приложения.
Фиг. 2. Кодлинеармые
•скторы.
В дальнейшем рассматриваются сво-
бодные векторы
Вектор равен нулю, если его модуль
равен нулю
Равными векторами называются
векторы одинаковой длины и одинаково
направленные: а = b Вектор Ь = —а,
если длины равны, b = а. но направле-
ние а противопо-
ложно направле-
нию 3.
Векторы а и —а
называются про-
тивоположными
друг другу
Произведение ве-
ктора а на ска-
ляр т обозначает-
ся та или ат и
есть новый век-
тор, модуль которого равен произ-
ведению |а| на абсолютную величину
|/п | : | та\ = |/п| . |а|; направление та
совпадает с направлением а. если
m > 0, и противоположно а. если
т < 0 (на фиг. 2 |т| = 2).
Векторы а и та лежат на одном
носителе или на параллельных носите-
лях.
Коллинеарные векторы а и b лежат
на параллельных прямых (носителях).
Условие коллинеарности
Ь — та
Единичный вектор а0 вектора а (орт
направления- а) одинаково направлен
е вектором а и имеет модуль, равный
единице, |а°| = I; имеем
* Со. литературу U стр. ЗЬО: (89). [9||. |МЗ(.
а — аа°.
ВЕКТОРНАЯ АЛГЕБРА
227
Сложение двух векторов произво-
дится по правилу параллелограмма:
сумма векторов (называемая еще гео-
метрической суммой) а и b есть вектор
с=;М|Л<4, изображаемый диагональю
И|Л14 параллелограмма, построенного на
векторах а и Ь (фиг. 3):
а 4- ft —Г;
с2 = аг 4- ft? + 2ab cos (а. Ь,
где (а, Ь) — угол, образованный некто,
ром b с вектором а. В случае многих
слагаемых а, Ь, с \м
сумму можно нахо- X/2
""г 1
В, Мг Mj Ml
♦кг. 3. Сложение аек Фиг. 4. Вычитание век-
торов. торов.
лить по правилу многоугольника: из
произвольной точки О строят 0Л71 —
« а, затем строят ЛТрИг = Ь, МгМъ =
и с; замыкающий вектор ОЛ1, лома-
ной ОМуМ^Мц и есть сумма
d •= а 4- ft 4-7
Модуль суммы векторов не превосхо-
дит суммы модулей слагаемых
|а 4- ft 4- 7|<|в| 4- |ft| 4- |7|.
Разность векторов а и Ъ есть новый
вектор d, равный сумме векторов а
и —ft (фнг. 4):
d — a—F—а4-( — &) —
И,. d Мг
Фиг S. Сумма н рав
кость векторов.
В одном параллелограмме, построен-
ном на о и ft, диагонали М= а + 6,
=Ъ-Ь~
(фиг. 5).
Справедливы ра-
венства:
IJ о 4- Ь - b +
4- а (перемести-
тельный закон);
2) а 4- (ft + с) -
“ (а + Ь) +_с (сочетательный закон);
3) т(а+ ft) = та -f- mb (распредели-
тельный закон).
Компланарные векторы a, ft, с лежат
в одной плоскости или в параллельных
плоскостях; можно найти два таких
скаляра тип, что с = та -f- nb —
условие компланарности трех векторов.
Это же равенство дает разложение
с на два составляющие вектора та, nb,
параллельные заданным векторам а
и ft.
В пространстве всякий вектор d
можно разложить на три составляющие
вектора, параллельные заданным неком-
планарным векторам а, Ь, с, и предста-
вить в форме
а = та 4- nb 4- рс,
слагаемые та, nb, рс называются ком-
понентами.
Осью называют прямую, на которой
установлено положительное и отрица-
тельное направление.
Направление оси S обычно опреде-
ляется вектором я, имеющим с осью
одинаковое направление. Орт $° назы-
вается ортом осн.
Проекцией вектора а= АВ на ось S
(или вектор з) называют длину отрезка
этой оси AjBi, где
точка <4j есть проек-
ция (ортогональная)
точки А на S, точ-
ка 0| — проекция
точки В на S, взя-
тую со знаком плюс,
если направление<4|В|
совпадает с положи-
тельным направле-
нием S. и со знаком
минус, если направление совпа-
дает с отрицательным направлением S
(фиг. 6).
Обозначают:
Фнг. 6. Проекты
вектора на ось.
пр$<з — ид — пр,ЛВ в (АП), х <4|в|.
Векторной проекцией вектора а на
ось S называют вектор а$, началом
и концом которого являются соответ-
ственно начало и коней проекции ш
на S, и обозначают
пр$ а — as.
Свойства проекции:
орле — | л| cos (S, о);
228
ВЕКТОРНОЕ И ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ
прд (а + b + с) •= npsa 4- пр$6 -4- пр^с;
пр$ (та) — тпр^а — та^.
' Проекции вектора а на оси коорди-
нат х. у, г вычисляются по формулам:
ах — a cos (х, а);
а,— a cos (у. л); (1)
аг = a cos (х, а).
Вектор а можно представить в виде
а = axi + ayJ + aJi.
где i, j, k — единичные векторы (орты)
положительных направлений осей коор-
динат Ох, Оу, Ог. Эти проекции назы-
вают также координатами вектора и
обозначают а (ах, ау, а,} или а = (а,,
ау, в*}- Для модуля вектора а имеем
а = а* 4- а£ 4- аг-
Вектор о=0, когда а, = ау—ау= 0.
Равенство векторов а = Ь равно-
сильно трем алгебраическим равен-
ствам:
at = bx, ау — by, аг =• Ьг.
Направление вектора определяется
направляющими косинусами по фор-
мулам (1).
Для единичного вектора а® имеем
а® — Feos (х. а) + J cos (у. а) 4-
4- * cos (г. а).
Радиус-вектор точки М (ж, у, ?) есть
вектор г. соединяющий начало коорди-
нат с точкой М. Координаты г —
декартовы координаты конца вектора-
7 (х, у, г| или
г — Тх+Уу +Лж
Вектор, определяемый двумя точ-
ками Mylxt.yt, Х|) и Л1г(х;, у,, gt), равен
MiAty— Гу — г, —
- 4- (yt - У|) 7+ (Zy - Ж|)1
Скалярным произведением двух век-
торов а и Ь называется скалярная
величина, равная произведению их
модулей на косинус угла между ними;
она записывается в виде а Ь:
ab — ab cos (а. А).
Отсюда
- -г а b
cos (а . Ь) = —г-;
ао
ab= ап ра А — Апрйа .
Координатное выражение а о:
a b = ajfbjt + ayby 4- агЬх
Свойства
а Ь = Ь а; т(а Ь) = (та) Ъ = a (mb);
(а 4- А) с = ас 4- be.
Если векторы взаимно перпендику-
лярны, то а b = 0.
Если а = Ь, то обозначают произве-
дение аа = а’ и называют скалярным
квадратом вектора а; он равен квадрату
его модуля а* = а*.
Скалярные произведения координат-
ных ортов:
Л — I; 7*= 1; **= 1; 77=77=0;
7* = *7-о. *7—71 — о
Пример. Если * параллелепипеде известны три
ребра а, о, г и образованные ими попарно углы,
то (»иг. 7). введя векторы М^М, — о. М,Л1.— с,
М,М, — в. получим.-
ЛМГ, -3-
-3+ » + ?:
? . (о + • + ёу -
-3« 4-H + <i +
•+ 2а 6 + 2аё+ 2аё
Фиг. 7. Сложение тре>
пекоыпланариыа вех
торов.
или
<Л-о«4-а* + <, + 2оАа»(а. ») +
+ 2ве со» (Ь, ё) 2св сов (с. а)
формула для квадрата лиагопали. Она же лает
кватра: стороны чстыренуголытнка как простран
ствепного, так и плоского.
Векторным произведением двух век
торов и н b называется вектор с, модуль
которого
е — ab sin (а. Ь)
ВЕКТОРНАЯ АЛГЕБРА
229
равен площади параллелограмма, по-
строенного на векторах а и Ь (фиг. 8),
и который направлен по перпендикуляру
к плоскости, проходящей через и и 6
таким образом, что а,
с образуют правую
тройку, т. е., если
X. X. смотреть с конца век-
тора с, то поворот от
Фиг. 8. Векторное первого множителя а
произведение. к0 второчу * в парал.
лелограмме, ими об-
разованном, совершается против часо-
вой стрелки.
Обозначения:
г = а / 6 = [а Ь |.
Свойства:
ЬХа-------(аХЬ);
если а X b = О, то а и b коллинеарны
или один из перемножаемых векторов
равен нулю; если
а | Ь. то | а X & I = ab;
(та) X b — m(ax'b) = а X (mb);
(a +b) Х~с = а X с 4 ЬХ 7.
Проекции векторного произведения на
оси координат:
«л - (в X b)t — ауЬг — а^у,
су— (аХ — агЬл — ахЬг,
Сх — (а X Ь)у — axb v — йуЬх.
Выражение а х Ь через координаты
сомножителей:
а X Ь —
7 7 k
й f а у (1^
bx by bt
Векторные произведения координат-
ных орто»:
7x7-0; ГхГ—о; лхл-0;
7x7-й; 7хл-Г; лхГ-Л
7хТ- -k, kxT-------Т, Тхк--7.
Примеры'. I) Момент силы F с точкой при-
ложения А (ОА= г) относительно точки О ранен
5Г —г XF. отсюда, к частности, Мt—yFt—iF .
2) Если точка А совершает вращение вокруг
осн 0L с угловой скоростью <», тогда и данный
момент вектор скорости (фиг. S) о »<• Хл.
3) В пирамиде 41,41,41.41,, заданной своими
вершинами 41,(2, 3, 1); 41,(1.— 2,0); 41,(0. 2, 1);
41,(3, 1, 4), вычислить площадь д,4,41,41, и
двугранный угол при ребре 41,41,. Векторы:
41-41, { — 1.4. 1), 41,41, {1. 5. 1). AliAl?{2,3,4|.
Вычисляем вектор .V, J.6 41,-4,41,:
N, = 41,41. X 41,41. =
г 7 *
I 5 I
— 14 1
- Т - 2/ -)- 9Л.
ПлОШ1ДЬ
е.41.41,41,- -L | Я; | = -1 /1 + 4-Н1 - 4
Вычислим вектор
_ M_J_ д 41.41,41,;
тогда угол (,V„ N,) будет измерять двугранный
угол при ребре 41,41,:
М - 4ТА17 X 41Г4Г —
Г 7 *
_ 2 3 4 “
- I 4 I
= - 137-6/+ 115;
со. (.4.
- 13-1-6-(-2)П-В * *•
/1<»в + ?ъ + 121 Vai
«0.535.
Фиг. S. Вектор
скорости во вра-
щательном дв»
женим.
Сложные произведения векторов.
1) Смешанное или векторно-скалярное
произведение трех векторов а. Ь, с:
а Ц е — а (Ь Хе)
«л "у "л
b't by ь,
Сл Су сг
равно по абсолютному значению объему
параллелепипеда, построенного на а.
Ь. с, как на ребрах.
Свойства а /> с =_Ь с а — с а b —
— — c~b и = — Ь а с — — ас Ь. Если
~а b с — 0, то векторы компланарны
2) Двойное векторное или векторно-
векторное проиоведение трех векторов а.
*• F;_ ________________ __
яХ(7Хс) — b (а с) — ё (аё).
3) (в X b) (сХ d)- lic)Jbd)-{ad)_(bc}.
4) (в X_b) X(cXd) - J («ХЮ । ”
— а ( b (с X Ю) — b (a cd) — a(b cd).
5) 1(7 X 5) X«J Х_5 - (a7)_CbX Ю-
-(FJ) (аХд) - с (в ЬО) - (а ХЬ) (« 3).
230
ВЕКТОРНОЕ И ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ
Выражение через скалярные произве-
дения:
I) скалярного квадрата векторного
произведения
(а К? + (я X Ь? = а * Ь*;
2) квадрата смешанного произве-
дения
а а а Ь а с
—
la b с)1 •= ba 'b b t> г
с а с b с с
Основные векторные уравнения
Неизвестными являются вектор г и
скаляры х, у, г, а остальные величины
векторные и скалярные известны
Уравнение Решение
II в — В S — а
тг — а >«|В II |К
3)| f X ~г “ * | г/ — т ас ас
4) а X г - » • t - 5 Хе е — пронзаемьныа скаляр
5) аг « я» - т - . . ' — —я+сХл с — проинимьимЯ вектор
• «а. 1 1 1 !□;« ft ю «(» Xrl-f-fl(exe) + т(я К»)
а»?
7) aXr-4-mr — S г а(йа) 4-л><» + л> (»Х«)
«•(«• + т>)
В) ё—ха Г-Г*+ ж-ё. к- ?й. Т-^. abe abr aie
ВЕКТОРНЫЙ АНАЛИЗ
Если я изменяется по величине и по
направлению, являясь функцией ска-
ля риой величины I. то его обозначают
о(0 и называют аекторнай функцией
от I. Если начало всех векторов поме-
стить в одной точке О, то конец о
опишет кривую, называемую годовра-
фом вектора а(0-
Производная векторной функции а (О
rfo = 1||Д 4-АП-о llm ia
dt д/-»о А/ аг-о at
есть вектор, направленный по касатель-
ной к годографу вектора а (О Коор-
динаты а(0 (ах. ау. аг} суть скаляр
ные функции от Г. Координаты произ-
водной:
rfa f T day da‘ 1
dt I dt ’ dt * dt Г
Производная единичного переменного
вектора о0 есть вектор, перпендику-
лярный к дифференцируемому вектору:
. „о
dt -L
Правила дифференцирования вектор-
ных функций:
d . d<t - , da
dt dt dt dt
где <p и a — скалярные функции от
аргумента /;
л . т. da db
—— (а + Ь) — — + ——;
dt dt dt
d -j-. da r . - db
-jt (a b) “ 777 b + a
at at at
k j- da K .t . db
ZU (Л X й) - -57 Xi + «X -37 ;
dt dt dt
da 11 (s) | da dt
ds “ dt ds ‘
Скалярное поле
Скалярным полем называется часть
пространства, в каждой точке которого
определена функция и (функция поля),
зависящая только от координат «той
точки.
. в — а (х, у, д) или и — и (г).
Поля, которые не зависят от времени,
называются стационарными; поля
векторный анализ
231
называются переменными, если и =
= и (л, у, г, /) Скалярные функции,
далее рассматриваемые, непрерывны,
с непрерывными частными производ-
ными.
Поверхность, определяемая уравне-
нием и (х, у, г) = const, называется
поверхностью уровня.
Скорость изменения и (х, у, Z)в
точке М по направлению вектора Л1ЛГ
определяется производной по направле-
нию ММ':
du ,, Дм
—- — Ит --------;
ds |
Дм
lim ——
г—J -ts
где As = IMM'I- Предел не изменится,
если вместо отрезка ММ' взять любую
кривую 7 =7(0 |х(0. у(0. «(<)}. ка-
сающуюся в точке М прямой ММ".
Если длину дуги этой кривой обозна-
чить S, длину дуги от гочки М до сосед-
ней точки Л1| — через Дз, то производ-
ная сложной функции и = и (х (t), у (t),
г(0) по дуге s и есть производная по
направлению касательной ММ' (фиг. 10):
— 6,0 , du dv ди dz
ds дх ds ду ds дх ds '
Градиентом скалярной функции
и(х,у. г) называется вектор (направлен
оо нормали п к поверхности уровня)
ь‘и — ди
дх 1 + ~ду
ди г
Л-grad-;
du
ds
"Krad“ ds “
— grad, и — MMt (фиг. 10).
где т — —------единичный вектор каса-
aS
тельной к кривой ЛПИь
Полный дифференциал функции равен
скалярному произведению градиента на
радиус-вектор точки Mt du = grad и dr.
Производная поля и в точке М по
направлению п нлн grad и обозначается
du
—— и равна
dn
.df- |gradn|-
Нормаль к поверхности уровня ука
зывает направление , наибыстрейшего
изменения (ро-
ста — в сторону
grad и, паде-
ния — в про-
тивоположную
сторону) ска-
лярной функ-
ции и, а модуль
градиента — аб-
солютную вели-
чину скорости этого изменения.
Пример. Потенциал электростатического поля
с заряаом е в начале координат определяется фуни
иней и — у-, где « — coast; г= V х'-Ь у’-гТ*
расстояние от точки Л! яо начала координат. По
верхвисти уровня —с или -r*-f-y,-t-r' — | -у) -
— const — концентрические сферы.
du е Or ex ex
Ox ~ Ox “ <*'
du ey du n
о у ~ /• Ог~ t*
t. e. дгаД u направлен к центру сферы по ради
усу — это и есть направление наибольшей скоро
сти изменения данной функции.
Оператор набла V рассматривается
как символический вектор:
V-14- +7 — +к-^~
дх оу dz
Градиент и можно рассматривать как
произведение набла на скаляр:
g.adn-7^ + 7^+^-Ve-
Векторное поле
Векторное поле есть часть простран-
ства, в каждой точке которого опреде-
лен некоторый вектор а = я(х, у, г). ко-
ординаты его at, av, аг — функции
х, у, г: например, поле скоростей в дан
ный момент в движущемся теле, поле
градиентов данной скалярной функции.
Модуль а определяет интенсивность
поля.
Векторные поля, не зависящие от
времени, называются стационарными,
каковые далее и рассматриваются.
Векторными линиями (силовые ли-
нии) векторного поля называются кри-
вые, касательные к которым о каждой
232
ВЕКТОРНОЕ И ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ
точке совпадают с направлением век-
тора а= а (х. у. г) в той же точке.
Они определяются системой дифферен-
циальных уравнений
dx dy dz
d & У @2
Общий интеграл этой системы
Fi (х, у, г) = с,. F2(x, у, г) = сг дает
искомые векторные линии; постоянные
интеграции Ci и сг вычисляются зада-
нием одной точки.
Если а есть вектор скорости движу-
щейся частицы некоторой жидкости, то
векторные линии будут линиями тока
жидкости.
Элементарным потоком поля а че-
рез элемент площади Да* на поверх-
ности а называется
л*л*Да,
где а* — вектор а, взятый в точке
М (х*. у*, г*) иа Да*; л* — единичный
вектор нормали к поверхности в той
же точке.
Потоком поля а через поверхность а
называется
Нт У} а* л’*До* - П.
т-оо ,_i
который равен поверхностному инте-
гралу
П — jy a da — у f a „da —
• •
— (У (ar соз л + a, cos + аг cos у) da —
р
— JJ atdy dz + av dz dx + аг dx dy.
rmt Sa^r^da — вектор, направленный
no нормали л к о, | da | — da, й® (cos а.
cos 0, cos |.
Если г — /(ж, у) есть уравнение по-
верхности а,
dz dz
р “ дх ’ 4 ** ду ’
то
П - уу (— раг — qa, 4- a,) dx dy.
О
что является поверхностным интегралом
второго тип* (см- стр. 18в>.
Если поверхность а определена век-
торным уравнением г = г (и, о), то
n = yja(r“ Хг,,) dudv
О
В случае, если а — вектор скорости
точки жидкости, то поток определяет
количество жидкости, протекшей за
единицу времени через поверхность а.
Пример. Найти поток вектора й<=д_у/-|-
-f-zx / 4- tk через часть сферы х1 + у* + z" — 1,
находящуюся и первом октанте.
Вычисляем
П- УУ (Джу + i)dxdy.
Заменяем г = -f- V 1 — х* — _у*. проекция по-
верхности □ на хОу есть S — четверть круга: х* +
4 у‘ < I. х > 0, у>0; направляем нормаль ао
хне сферы, тогда
П = | у (2ху VI — х« — y')dx ay.
в
Первый интеграл
Второй интеграл вычисляем а полярных ыюр-
аннатах:
Расхождением (дивергенцией) век-
тора а в данной точке называется ска-
лярная величина div а, равная отнесен-
ному _к единице объема потоку век-
тора а через поверхность бесконечно-
малого объема, окружающего данную
точку:
div а — lim JJ a„ da —
•
даЛ да,, даг
“ дх + ду + az •
ИЛЛ
div а — V а
векторный анализ
233.
Теорема Остроградского. Поток векто
ра а через замкнутую поверхность а
равен интегралу от div а, взятому по
объему V.ограниченному поверхностью^:
Л ап da -
j | j div a dv.
где нормаль л,— внешняя.
Если рассматривать поле а как поле
скоростей стационарного течения жидко-
сти, то поток поля через замкнутую
поверхность о. ограничивающую неко-
торую область V, равен объемному
расходу жидкости из области V или
объемному расширению жидкости в
области V за единицу времени. Дивер-
генция поля скоростей жидкости есть
расход жидкости в данной точке, отне-
сенный к единице объема.
В случае любого поля а принимают,
что div а есть расход поля в данной
точке, отнесенный к единице объема.
Линейным интегралом вектора а
вдоль кривой L называется скаляр
I a dr — [ ат ds — ( | а | cos (х, а) ds =
ill
— f ах dx + dy + a, dz.
являющийся криволинейным интегра-
лом no L, причем г есть радиус-вектор
точки кривой L, т — орт касатель-
ной к L.
Циркуляция Г вектора а вдоль зам-
кнутого контура L есть линейный
интеграл по этому контуру при задан-
ном направлении обхода
Г
I
Линейный интеграл вектора а по L
представляет собой работу вектора а
при перемещении точки приложения а
вдоль L.
Вихрем (ротором) вектора а назы-
вается вектор rot a (curl а), координаты
ноторого определены формулами
rot, о —
da, да?
dy dz ’
rot,, a
dax da,
~oi dx •
_ da„ oax
rot, a = —t----5—.
dx dy
При помощи оператора набла ротор
выражается следующим образом:
rot а = V X а •=
I j k
д д д
Их dy дг
Q Л CL у LJg
Теорема Стокса. Циркуляция век-
тора а по замкнутому контуру L равна
потоку его вихря через любую поверх-
ность », ограниченную данным кон-
туром:
(£ a dr = г о!„ ado —
о
/дах даД
+ 1^--37ГО5^я) +
do.
где п — орт внешней нормали, ах, а у.
а, — непрерывныефункции с непрерыв-
ными частными производными 1-го по-
рядка.
Для плоского поля это равенство
имеет вид
ср Idav дах\
axdx + a,d, - Н J dx dy.
Пример. Если а сеть скорость жнлкостн,
го rot о"л»ет уапоемпую угловую скорость прл
шеи и а частив жнакого тел».
I
Потенциальное векторное поле а есть
поле градиентов некоторой скалярной
функции, т. е. существует функция и —
—и (х, у, г) такая, что а — grad и или
ди ди ди ~
а, — ——, в. —-я-- Функин»
* дх у ду ‘ dz '
и (х, у, г) называется потенциалом поля.
Чтобы поле а было потенциальным, необ-
ходимо и достаточно выполнение равен-
ства rot а = 0. Например, если жидкое
тело свободно от вихрей, rot и = 0, то
и = grad и. Циркуляция потенциаль-
231
ВЕКТОРНОЕ И ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ
«ого вектора по замкнутому контуру
равна нулю, если контур может стя
гиваться в точку поля, нс пересекая
границ поля. Линейный интеграл потен
циалыюго вектора не зависит от формы
липин, а только от ее концов
(*о- Уа- го > « М (х. у. г)
М_ _ А!
I а dr “ I grad и dr =
ж.
ж
— du - и (х. у. х) — u (x, уо. г,).
Для потенциального поля дивергенция
. d*u д^и <Ри .
dlvu-dlvgradu-^-E — + — -До.
где
(Г- гР
«Й + d7* + ЗУ» “ д “ v
называют оператором Лапласа.
Соленоидальное векторное поле а есть
такое поле, для которого div <7=0. Оно
обладает характерным свойством- поток
поля равен нулю через всякую замкну-
тую поверхность, которую можно стянуть
в точку, не пересекая границу поля
В таком поле векторные линии или за-
мкнутые, или уходят в бесконечность,
или начинаются и кончаются на границе
поля
Поле вихрей любого векторного
поля о есть поле соленоидальное, т. е.
div (rot я) — 0.
Если данное векторное поле 3 =
= rot а, то а называется векторным
потенциалом данного поля b
Точечным источником соленоидаль-
иого поля называется граничная точка
поля, изолированная от других граиич
них точек.
Поток поля через любую поверхность,
ограничивающую н'-точник, есть вели-
чина постоянная, называемая мощно-
стью или обильностью источника.
Источник соленоидального поля с
отрицательной мощностью называют
также стоком поля.
Если потенциальное поле o’f—grad и)
есть и соленоидальное, то div а =
•= div grad и = 0 или Ди ™ 0 (урав
пенне Лапласа)
Функция и, удовлетворяющая этому
уравнению, называется гармонической
Некоторые выражения при помощи
набла
div (rot о) = V (VX а) -0;
div (grad u) = 7 (Vu> = V2u — Ди;
rot (grad u) -= V X (V“) = 0
rot (rot a) — V X (V X «) -
= lWV-fVVH“
= grad (div a) — V2 °-
где V!“ — вектор, проекции которого —
Дах. Да^, До,
ТЕНЗОРЫ •
Если xt. х», х,—прямоугольные коор
дипаты точки Л1 относительно системы
координат Oxixix3. a Xj.. хг, Ху —
прямоугольные координаты той же
точки М в новой системе координат
0хгх,.х3,, то преобразование коорди
наг определяется формулами (стр 250)
х1- “ а/1х1 + “<!•*! + “гэхз =
з
— 2 “ I. 2,3).
Л=1
гле atk — cos (хг, х^). Штрих при
индексе указывает, что соответствую-
щая величина рассматривается отно-
сительно новой системы координат
Обратные формулы
я
X, - £ (/ — I, 2.3)
В дальнейшем рассматриваются так
называемые аффинные ортогональные
тензоры. называемые просто тензорами
Тензором Тео порядка (валентности,
ранга) называется всякая совокупность
зрех величин а., а3. преобразую
щихся в величины а(.. а2,, ал, при
переходе от одной системы координат
х* к другой системе х,,. по формулам
а
*/< 1-2.3) (2)
*—I
Всякий вектор в пространстве есть
тензор 1-го порядка, причем можно рас-
сматривать как один вектор, так и поле
векторов (компоненты суть функции
координат точки).
* См. литературу па стр. МО: (41). |V5|. |tU|. ДО.
ТЕНЗОРЫ
235
Тензором 2-го пормко называет:»
совокупность 3* = 9 величин а*, (его
компоненты) в данной координатной
системе, которые при переходе к новой
системе координат преобразуются в ве-
личины at,f. по формулам преобразо-
вания
з з
arf e S S ~ 1.2.3). (3)
Аналогично определяются тензоры
Это. 4-гои т. д. порядков н в простран-
стве любого числа измерений
Тензор 1-го порядка, или вектор
а [О]. а«, аз), иногда обозначают общим
компонентом а,.
Тензор 2-го порядка Т, определяемый
компонентами а*(. записывают в виде
матрицы
ап Д1Т в)я
av ап ап
“si азг азз
или обозначают общим компонентом а*(.
Аналогично обозначаются тензоры выс-
ших порядков.
. Примеры.
Цензор упругих иапражеяи*.
•«смотрим внутри упругого тел» некоторый
.^ъем и. ограниченный повермюстъю S. На каж-
дый влемеит aS »той поперт пости асйстиует сила
l’adS со стороны частно тела, лежащих вне V.
Сила рп. отнесеннае > единице плошали. зависит
от нормали л к рассматриваемому влемеиту и
называется напряжением на площадку *•$ с нор
малью п. Напряжение р вообще ве совпадает е
о "
отравлением я. Для каж.хпй иг осей координат
(дг.. X,. х.) мы можем определить соответствую-
щее напряжение как вектор: р. (р„. р„. р„).
Р. I/Ь.. Рп- Pul . Р. (р... Рп. Р&).
Совокупность втих тоет векторов (или матрица
вз влементов определяет тензор П, вазыеае-
мый тензором упругие напряжений в данной
точке.
Применение начала Даламбера дает равенство
р„ - р, со» (я. X.) + о. сов (я. ж,) + р, сов (я. Kjb
справедливое ДЛЯ всякого направления я . Отсюда
а.’» тред взаимно перпендикулярны» новы» напра-
влений <j«, Ху, ху получаем
.<
•/' “ 2 U - I. 1. 3).
*-1
Вели | р/-|», P/’j-. Р/'з» ) — координаты пек.
тоо« й/. по новым осям, то р/гу. — ЛРд^.Й/' "
3 9
“2\*"₽V"* И“ •зД-Ду»
поэтому
3 3
Ц'Г -2 2\*«/,р*,(‘./-=1.2.3)
t=l 6-1
На последние равенства можио смотреть как па
формулы преобразования р^ при перезоле от од
ной яоораинатиой системы к другой. Так как »ти
формулы совпадают с формулами (3). то веля
чины р4/ образуют тензор
2)Единичиый тенаор
Ч:::1
так как припав в одной системе координат
° и “ *• ° г* ”0 •'**> • "«во* другой си-
стеме будем иметь на основании формул (3):
3 3
ai'l' ” S ‘?Л “ “•’ г ~ 2 *<*’/* — о « ♦ д
3) Д н а я а. Если даны дм вектора а ( в,, а,
а, }. 9 { Pt. Й»), то можио составить ма-
трицу
{а,й, о,К, «,*. 1
aj> аф, aj>, >.
aj>, аф, e,9, I
которая определяет тензор, называемый бяаЛоО
и обозначаемый а *. Действительно, величины
рд1 — o^bi преобразуются по формулам (ЗУ тав
как в силу формул (2)
3 3
-г - 2 ••*“» »г - 2 «х*<
ж—। /—।
мы будем иметь
3 3
v»r-2 2 ••*•//’**)• 2. л
й=1 t—
т. е. если обозначить иуу то влемеиты
матрицы преобразуются по формулам (3).
Диада
{й,а, б,в. 9.0, т
b,a, D,a, t>,a, 1
РЛ М. '
отличив от диады а Ь. •-
Сумма (разность) двух тензоров
одного порядка а,у, Ъц есть новый тен
эор, определяемый равенством
еЧ “ аЧ + *4-
Тензор ац называется симметриче-
ским, если ац = ац, и кососимметри-
ческим, если а,/» —ajf.
Тензор 2-го порядка можно разложить
на сумму двух тензоров — симметриче-
ского и кососимметрического:
aU в <®|/ + а//) + j («у — Яд)‘.
236
ВЕКТОРНОЕ И ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ
здесь первая скобка есть симметриче-
ский тензор, а вторая скобка — косо-
симметрический тензор.
Симметрированием тензора по группе
нижних индексов называется сложение
этого тензора с теми, которые из него
получаются всевозможными переста-
новками индексов данной группы;
сумму обозначают
аи । i I *>= аш> + а*Л‘
где знаком |/| отделяют не участвующий
в симметрировании индекс.
Альтернирование тензора отличается
от предыдущей операции тем, что в соста-
вленной сумме исходный тензор и тен-
зоры, полученные из него четными пере-
становками индексов, берутся со знп
ком плюс, а остальные — с минусам.!,
и сумму обозначают
в[0*1 “ йб* ~ ачч + аич — апь +
+ — алп-
Симметричность тензора по I, ]
можно записать в виде а[(/| t “ 0, а
кососимметричность ацк по i. j — в виде
°W * = 0
Умножение тензоров производится
по следующему правилу: каждый ком-
понент первого тензора умножается на
каждый компонент второго тензора;
порядок получаемого тензора ранен
сумме порядков перемножаемых тен-
зоров.
Примеры.
1) Диад» есть произведение двум тензоров. ид
которых кажзий 1-го порядка.
2) Произведение тензора 2-го поряди» на
тендер l-го порядка !>* есть новый тендер 3-го
порядка — ауьь (4> Л * 1.1 Л « »• *
Свертыванием ортогональных аффин-
ных тензоров по двум каким-нибудь
индексам (индексы свертывания) назы-
вается следующая операция: из компо-
нентов тензора некоторого порядка,
например atlk, составляются суммы
вп* + «и* + «•«*-»» (*- 1.2.3).
н получается тензор с* порядка на 2
единицы меньше. Здесь индексами свер-
тывания являются i и /.
В случае тензора 2-го порядка ау
свертывание дает
яп + «н + оя
скалярную величину, называемую ин-
вариантом тензора.
Умножение и свертывание приводят
к новым тензорам, иногда называемым
внутренними произведениями. Напри-
мер. из тензора aybk можно получить
два внутренних произведения: ct =»
з
•= У и1кЬк (свертывание по у и й) и с , «
А=1
3
=• У, ак/Ьк (свертывание по < и k). из
которых каждый есть тензор 1-го
порядка, т. е. вектор. Вектор с {с», с». Cg|
(а также с') называется линейной век-
mop-функцией вектора b (bi, bt, ба);
компоненты с выражаются линейным
однородным образом через компо-
ненты Ь, причем коэффициентами явля-
ются компоненты тензора а1к Если
этот тензор обозначить через Т, то
рассматриваемое произведение можно
условно записать в виде
7 = ть.
На тензор Т, называемый аффинором
можно смотреть как на оператор, пре-
образующий вектор b в вектор с.
Тензорный признак системы вели-
чин Если для любого вектора bt
•
величины У aj/6/суть компоненты неко-
. ‘“1
торого вектора, то ау образуют тензор.
В общем случае вместо bt берется
тензор любого порядка н производится
свертывание.
Примеры:
I) Пусть упругое тело подвергается действию
сил, вы luitiiiouinx его смещение н деформацию.
Пусть Д1 - какая-либо точка. М, — близкая точка.
» действукхине силы за малый промежуток вре-
мени приведут точки М и Л1, в точки М' и Alj.
Основное положение теория упругости заключается
а том, что вектор Л1'Л1| подучается и» сектор»
ЛГИ, воздействием тензора Т
Л1’л<; - г (ЛЁй,>.
так как аналитически компоненты ( К, Г,.
Г, ) выражаются через компоненты МЛ1, | Л» Аь.
X, ) по формулам
3
’'l-S 31.
А—I
В силу предыдущего признака система вели-
чин ообразует тензор, обозначенный через Г.
ТЕНЗОРЫ
237
2) Пусть твердое тело вращается около непо-
движной точки 0;<й { ш„ «>,. т, ) — вектор угло-
вой скорости, ОМ = г ( X,. X,. х, ) — радиус-
вектор точки Л1 тела. Скорость этой точки М
v-^'X.r.
Главный момент количества движения L тела
относительно точки О равен
Z - f Г Х(«ХЙ dm
ат — элемент массы в точно Л1. Так как
' Х(“ X') — — ё(гй) -
— ш (xj 4- х2 4- х3) — г |х,». 4- хи», 4- хл»,|.
то координаты вектора £ {L,. L„ L, I определи-
«отся формулами:
£< = 4“ /»т®т 4-/.У"1-
£т — 4" 4" А*®».
£. = /„», +- 1„ш, 4- /«ш,.
еде Л< — J (-г2 + -,з) dm
И Т. Л.
In “ - J x.x»tfm
В силу иридии кт коэффициенты /^-образуют
тензор (обозначим его I), называемый отеклоро.н
моментов инерции; I — симметрический теиаор
Можно кратко записать:
Г-/1.
т. е. вектор момента количества лвижеиия является
линейной вектор-функцией вектора угло1*ой ско-
рости. /и» — внутреннее произведение тензора на
лектор.
Координатный метод в геометрии,
наряду с величинами существенно геоме-
трическими, дает и величины случай-
ные, связанные с выбором системы
координат. Тензорное исчисление раз-
вивает такие вычислительные приемы,
которые позволяют отличать геометри-
чески существенное от привнесенного
выбором координат. Такими приемами
являются операции сложения, умноже-
ния тензоров, операция свертывания
тензора; эти операции инвариантны по
отношению к преобразованию коор-
динат.
Если ввести более общие формулы
преобразования координат, то получим
более общие тензоры как системы вели-
чин, преобразующихся по некоторым
новым формулам.
л
ГЛАВА XI
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ*
Аналитическая геометрия изучает
свойства различных геометрических об-
разов (линий, поверхностей и др.) при
помощи метода координат Методом ко-
ординат называется способ определения
положения одного геометрического об-
раза относительно другого при помощи
чисел Исходя из условий задачи и ис-
пользуя введенные координаты, соста-
вляют уравнения. Решение геометриче-
ской задачи сводится к исследованию
и решению уравнений.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
НА ПЛОСКОСТИ
Прямоугольные (декартовы) коор-
динаты. На плоскости проводятся две
взаимно перпендикулярные прямые Ох и
Оу (фиг. i), на каждой из которых выбрано
положительное направление; они назы-
У
в “
д' д*
«иг. 1. Прям»
угольные коор-
динаты
отрезок т за
веются осями прямоуголь-
ной системы координат,
а точка О их пересече-
ния называется началом
координат. Положение
любой точки М плоско-
сти относительно осей
координат определяется
двумя отрезками: О А =
- ВМ я AM (AM | Оу).
Если выбрать некоторый
масштаб, го два отеле
чеиных числа хну
X- —
т
AM
т
называются координатами точки Л1.
Число х называется абсциссой точки М
* См. литературу и» стр. 3*.»: (18], (81. 161 |Э0|.
и берется со знаком плюс, если напра-
вление отрезка ОА совпадает с поло-
жительным направлением оси Ох, в про-
тивном случае — со знаком минус.
Число у называется ординатой точки М’
и берется со знаком плюс или минус
в зависимости от того, совпадает ли
направление AM с положительным
направлением Оу или нет.
В записи М (х, у) на первом месте
всегда стоит абсцисса точки.
Каждой точке плоскости соответ-
ствует единственная пара чисел (коор'
ди и ат) и обратно.
Расстояние между точ-
ками М^х,. уО и М^хг, у!)
<*- + У —-*1)’+ (Уз—У|)’
Расстояние г от точки Л1(х. у) до-
казала координат О (0. 0)
г = X» 4 у*.
Деление отрезка в дан-
ном отношении. Если Ah(X|, yi)-
и Mi(xi, у г) — начальная и конечная
точки отрезка MiMt, то координаты х
и у точки Л1, делящей отрезок в данном-
М,М
отношении Х = .определяются по
AiAi-t
формулам:
л, 4 Ххе у, -(- ху,
1 + X ’ ’ I + (
Если М является серединой отрезка.
ТО А — I И
Х| 4 л, у, 4- yt
2 ' 1 1
Отрицательным значениям А соот
встствует деление отрезка внешним-
образом
Косоугольные координаты. В косо-
угольной системе координат оси Ок
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
239
и Оу образуют угол ш уь На каждой
осн можно взять свой масштаб: mi=OEi
на оси Ох, т» = OEt на Оу (фиг. 2).
Положение всякой точки М плоскости
определяется координатами
ОД AM
тг
AM II Оу.
7П|
Такие координаты еще называются
х
аффинными. В случае <> = -у, но
/п> -У- ш* координаты хну также назы-
ваются аффинны-
ми Прямоуголь
ум ные координаты
представляют ча-
стный случай аф-
-X финны» при ту =
к
♦ит. 2. Косоугольные = т, ш .j •
коорлнвлты. в дальнейшем
рассматривается
прямоугольная система координат.
Преобразование координат. Если
даны на плоскости две системы коор-
динат хОу и х'О'у', то формулы пре-
образования координат позволяют по
координатам д', у' точки М вычислить
координаты х, у той же точки и обратно.
а) Формулы переноса на-
чал а. Если оси *;0 у соответственно
параллельны осям хОу, (а. Ь) — коор-
динаты 0‘ относительно хОу, то
х — х‘ + а; у — у' + Ь.
б) Формулы поворота
осей координат. Если обе си-
стемы имеют общее начало О, угол
(Ох, Ох‘) = а, то
х — х' cos я — / sin «;
у — х' sin « + у' cose,
где а > 0, если поворот совершается
против часовой стрелки.
в) Общее преобразова-
ние системыкоординат со-
стоит из поворота хОу на угол а =
" / (Ох, О'х) и переноса начала в
точку О'(а, Ь):
X •• х' COS а — у' sin а + а;
у — г' sin я + у' cos я -|- Ь.
Полярные координаты. Полупрямая,
выходящая из некоторой точки, назы-
вается лучом. Положение всякой
точки М можно определить относительно
луча х, выходящего из точки О (фиг. 3),
ОМ
двумя числами: г =-----. где т — мае-
т
штаб, ОМ = |ОМ | — длина вектора
ОЛ4, и величиной угла отсчитывае-
мого от луча х до направления век-
тора ОЛ4. Называют <р полярным углом,
г — радиисом-вектором точки М,
луч х — полярной осью, точку О —
полюсом, систему координат — поляр-
ной. Полярный угол считается поло-
жительным в направлении против часо-
вой стрелки и отрицательным в обрат-
ном направлении.
При указанном на фиг. 3 расположе
нии прямоугольной системы координат
и полярной оси переход от (г, <р) к (х, у}
одной и той же. точки Л4 совершается
по формулам:
х — г cos ч»;
г- V х» + у»;
у = г sin ?;
т= Arclg -£
Полюс имеет координаты г = 0, у —
произвольно. Чтобы получить все точки
Фмг. а. Полярные ко
орлннлты.
»(1П, 9>'Я)
Фиг. 4. Поляриие
коорлиняты
плоскости, достаточно брать г > 0 и-
угол ? изменять от 0 до 2л.
Для построения точки М(г, у), где
г < 0, следует провести луч ОМ под
углом f + к к полярной оси и на нем-
отложить |г| (фиг. 4).
Расстояние d между точками /И> (ri.fi)
и Л4*(Г1, f»)
<Р — Г? + — 2Г|Гг cos (^ — f|).
Геометрическое значение уравнения
Всякое уравнение F (х, у) " О, если
в нем рассматривать х, у как коорди-
наты в прямоугольной системе коорди-
нат, определит на плоскости совокуп-
ность точек М, координаты которых х, у
удовлетворяют данному уравнению. Та-
кую совокупность точек называют
линией, a F (х, у) = 0 — уравнением
этой линии (см. стр. 258).
Если F(x, у) — многочлен л-й степени
относительно х, у, то линия называется
алгебраической л-го порядка.
240
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
При повороте осей и переносе начала
координат степень уравнения алгебрам
ческой кривой сохраняется
В полярной системе координат ли-
ния будет определяться уравнением
/ (г, <?) = 0.
Переменные х, у (или г, <р), связан-
ные одним уравнением, называются те-
кущими координатами точек данной
линии. Если точка (xq, у0) лежит на
линии, то F (х0, j0) = 0, и обратно: если
некоторая пара чисел (хв, Уо) является
решением уравнения F (х, у) = 0, то
точка (xq, jo) лежит на линии, изобра-
жаемой этим уравнением
Пример. Совокупность точек, координаты кото-
рых удовлетворяют уравнению л* 4- у" = о', прел-
ставляет окружность с центром в начале координат
и радиусом а, так как левая часть уравнения есть
квадрат расстояния точки .М (х, у) от начала ко-
ординат. а правая часть — величина постоянная.
Уравнение геометрических мест.
Если данную линию можно рассматри-
вать как геометрическое место точек,
обладающих одним каким-либо общим
для всех этих точек геометрическим
свойством (геометрический закон обра-
зования линли), то, выбрав систему
координат, можно это свойство записать
в аналитической форме; получается за-
висимость между координатами произ-
вольной точки линии; эта зависимость
и есть уравнение геометрического места
точек
Примеры:
I) Составить уравнение окружности как гео
метрического мест» точек, удалейших от центра
С (л, й) иа постоянное расстояние г. Пусть х. у —
текущие координаты точки окружности относи-
тельно прямоугольной системы координат (фиг. 5).
Тогда СЛ( «• г или (х — а*) + (у — б>’ “ г* —
уравнение окружности.
2) Стержень АН длиной I скользит своими кои-
иами по сторонам прямого угла. Составить У pan
•иеиис траектории, описанной той точкой М
стержня, которая отстоит от одного конца А иа
расстоянии а. Если выбрать за оси координат сто-
роны данного прямого угла (фиг. 6), то ввиду
параллельности О А и РМ получаем-^- —
л УЙ — У* X* У*
- -------ндн — + - 1; геометри-
ческое место точек М есть эллипс. На этом осяо-
вано устройство эллипсографа — прибора для вы-
черчивания эллипса.
Прямая линия
Нормальное уравнение прямой Если
положение прямой относительно хОу
определить двумя параметрами: углом ф,
отсчитываемым от положительного на-
Фиг. 7. Параметры нормального
уравнения прямой.
правления оси х до направления пер-
пендикуляра, опущенного из начала
координат на прямую, и р — длиной
этого перпендикуляра (фиг 7). то урав-
нение
х cos ф + yslnit — р = 0,
(Р >0).
где х, у — текущие координаты точки
на прямой, называется нормальным
уравнением прямой
Общее уравнение прямой Всякое
уравнение первой степени
Ах + By + С — О
есть уравнение прямой; оно называется
общим уравнением прямой и приводится к
нормальному уравнению умножением на
нормирующий множитель ± y^_==,
в котором берется знак, противополож-
ный знаку С.
Пример. Уравнение 5х + 4у -(- 20 « 0 приво-
дится к нормальному виду умножением на
Параметры, определяюшие положение прямой:
соя ф — Д=. я!п Ф — — .
/41 VTT
Следует вычислить по tg ф — -4- угол первой
четверти Фо « arctg -у, тогда ф — к + Фо (фиг. 8).
Частные случаи: Ах + С 0 — урав-
нение прямой, параллельной Оу. By 4-
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
241
+ С = 0 — прямая || Ох; х = 0 — урав-
нение оси Оу; у = 0 — уравнение оси Ох;
Ах + By = 0 — уравнение прямой, про-
ходящей через начало координат.
Расстояние от точки до прямой.
Расстояние d от точки Мо (х0, у0) (фиг. 7)
до прямой равно левой части нормаль-
ного уравнения этой прямой х cos ф +
+ у sin ф — р = 0, в которую вместо
текущих координат подставлены коор-
динаты данной точки
d = х0 cos ф + у# sin ф —р
или
Если в результате вычисления <f>0,
то начало координат О и точка М9
лежат по разные стороны от прямой,
а если d < 0, то
Фиг. 8. К примеру при-
ведения уравнения пря-
мой к нормальному
пилу.
точки О и Мо ле-
жат по одну сто-
рону от прямой.
Припер. Расстояние
от точки .Mn (4.1) ао
прямой 5л ( 4/ т 30 =
= О (фиг. 8):
_ 5-4 4-4-1 4-20
-УГГ
44
КдГ
Точка М* отстоит от
прямой на расстоянии
44
| <1 | = . и лежит вместе с началом координат
по одну сторону от прямой.
Уравнение прямой с угловым коэффи-
циентом. Уравнение прямой (не парал-
лельной Оу) можно представить в виде
у — Их + Ь.
где х, у — текущие координаты; пара-
метры, определяющие положение пря-
мой: b—отрезок («0), отсекаемый прямой
на осн у (начальная ордината); k =
= tg а — угловой коэффициент, причем
угол а отсчитывается от положительного
направления оси х до прямой в напра-
влении против часовой стрелки (см.
фиг. 7).
Уравнение прямой, параллельной Оу
и отсекающей на Ох отрезок а,
х — а.
Уравнение прямой, проходящей через
данную точку (jq, ух).
16 Том I Зак. 1464.
называется уравнением пучка прямых
(k — переменный параметр, см. стр. 242).
Уравнение прямой, проходящей через
две данные точки (xt, _yi) и (xi, уг):
X —Ху У — У1
-Ч—*1 Ух—У1’
Параметрические уравнения прямой
проходящей через точку (xj, _yj):
X = Ху + It,
У “ У1 + mt,
постоянные /нт пропорциональны
cos я и sin в, где угол в образован пря-
мой с осью Ох : 1g а = —. Параметр /,
изменяемый от —оо до 4-оо, опреде-
ляет положение точки на прямой: при
( = 0 получается данная точка (xj, yt),
прн / > 0 получаются точки па прямой
по одну сторону от Му, а при /< 0 по-
лучаются точки по другую сторону
от Му.
Уравнение прямой в отрезках. Урав-
нение прямой, не проходящей через на-
чало координат, можно представить
в виде
где параметры а н Ь — отрезки (с учетом
знака), отсекаемые прямой соответствен-
но на осях Ох и Оу (см. фиг. 7).
Угол 0 между двумя прямыми у —
= kyx 4- 6i и у — ktx 4- by опредс
ляется по формуле
8 I + Mi
Фиг. 9. Угол межяу
прямыми.
Угол 0 отсчитывается от первой
прямой ко второй против часовой стрел-
ки; tg 6 > 0, тогда
О — 0| — острый угол
между прямыми;
tg в < 0, тогда 0 =
=91—тупой угол меж-
ду прямыми (фиг. 9),
91 = к — О».
Если прямые даны
уравнениями
АуХ + ВуУ -f- Су = 0
И
А>х + ВуУ 4- Cj — 0,
242
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
ти
tg в
Условие принадлежности трех точек
(хр у(). (хг. Уг). (xs. yt) одной прямой:
AjBj — АгВу
4]Дг + В\Вг
Условие параллельности прямые
A, Bi . .
л, “ в7 ил" ** “ **'
Х3 — X! Уя —У1
Хг У» У1 ’
У1 1
или АС» У» 1 -0.
АС» У» 1
Условие перпендикулярности прямых:
Д1Д1 + S|Sj — 0 или — — I.
Примеры:
1) В треугольнике МуМ.М,. заданном своими
вершинами Mi (1, — IX Al, (2, — 3), М, (4, 2), про-
вести через вершину А!, прямую, параллельную
стороне .М,М^ и составить уравнение икоты, опу-
шенной из точки М, па М,.Ма.
Уравнение М-.М,:
х — 2 у + 3
4 — 2 — 2 + 3
пли у + 3 = »/, (х — 2): ее угловой коэффициент
* — Ч,; уравнение искомой параллельной прямой
у +1 ~ •/. (л — 1) или 5х — 2у - 7 — 0; урав-
нение искомой высоты
y + l-(_«/J(x - 1) или 2х + 8/ + 3-а
2) Найти уравнения прямых, пересекающих
данную прямую у » 2г + 1 в точке М (1.3) пол
углом ( — 45е. Так как tg 45» — 1 и если обо
значить угловой коэффициент дайной прямой й„
причем й,=2, то угловой коэффициент А, искомых
прямых найлется яз равенств
. *>-2
1 “ , | - ИЛИ 1 “
Уравнение пучка прямых. Пучком
прямых называется совокупность пря-
мых, проходящих через данную точку
(см. стр. 241). Если последняя дана пе-
ресечением прямых Д|Х 4- Siy4- Ci —
= 0, Aix 4- Ssy 4- С»= 0, то уравне-
пие всякой прямой, проходящей через
эту точку, имеет вид
Д1Х + В\у + С] + X (А2х + ВгУ 4- Су)=0.
где А — переменный параметр.
Уравнение биссектрис углов, обра-
зованных двумя прямыми Ахх + Siy-f-
,4- С] = 0 и Л 2-Г 4“ В-1У + С* = 0:
Л]Х + Вуу + С, __ + Дух + Bjy + С2
Л? 4- Л? у/Д^ + ^
Уравнение прямой в полярных миор-
динатах
p-rcos (ф — 4»),
откуда получаются два значения 1) А, =- — 3,
соответствующая прямая- у — 3 — — 3(х — 1) или
у = — Зх + 6; 2) ki = ЧК прямая у — 3 - '1,(х — 1)
ИЛИ у = ‘/НГ+*/г
Координаты точки пересечения пря-
мых Лух + Btf + Ci = 0 и А>х + В*у +
+ Сг = 0:
X — • V — С1А — .
А1В2 — BjA2 ’ AyBi — B2Ai ’
(Afc - ВхАг + 0).
p Д| B\ . C|
Если , то прямые na-
Д1 Bi С»
раллельны; если -J- = -I = -Д, то пря-
Лг Bi Сг
мые совпадают.
Условие пересечения трех прямых
Aix + Bty 4- Ci = 0, Aix + S»y + C>
•= 0, A^x 4- Sjy 4- C| = 0 в одной точке:
где (г, ф) — текущие полярные коорди-
наты точки М на прямой; положение
Фиг. 10. Полярное
уравиеиие прямой.
прямой относительно полярной оси Ох
определяется перпендикуляром р и
углом 4* (фиг. 10).
Если прямая проходит через полюс,
то уравнение луча ОМ имеет вид
4»—Ф —(фиг. II), а для луча ОМ’
(продолжение ОМ) ф — ф“-у.
Hj Si
A2 B2
A> В2
Ci
C-
Cj
= 0.
Кривые 2-го порядка
Окружность. Уравнение вида
хг 4- У1 4- Ах + By + С — 0
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
243
определяет окружность с центром в
точке ( х0 = — А , у0--------и ра-
т /~?Р в*
диусом а = I/ —— -|— -----С . если
Г 4 4
А2 , В2 _
~ > С; уравнение может быть
приведено к виду
(х — х0)2 + (у — ув)« = а».
Параметрические уравнения окруж-
ности:
х = *0 + a cos t, у — уо + а sin t.
где переменный параметр t изменяется
от 0 до 2г. и геометрически означает
угол, отсчитываемый от положитель-
ного направления Ох к подвижному
Фиг. 12. К уравнению окруж-
пости в прямоугольных коор-
динатах.
Фиг. 1». К урав-
нению окружности
и полярных коор
динатах.
Параметрические уравнения окруж-
ности с центром в точке (0, 0)
х •- a cos /; у = a sin t.
В полярных координатах (г, <р) урав-
нение окружности с центром в точке
(г«. Vo) и радиусом а имеет вид
г* — 2rr0 cos (<р — fo) + r*Q — а2;
если центр лежит на полярной оси и
окружность проходит через полюс, то
уравнение имеет вид (фиг. 13)
г — 2а cos у;
уравнение окружности с центром в по-
люсе
г — а.
Эллипс. Эллипсом называется гео-
метрическое место точек М, для каждой
из которых сумма расстояний г, и гг
до двух данных точек Fx и (фоку-
сов) есть величина постоянная: г. 4-
+ г, = 2а.
При расположении осей Ох и Оу на
фиг. 14 каноническое уравнение эллипса
имеет вид
где х, у—текущие координаты (точки Л1);
2а = А В. 2b = CD—большая и малая осн
эллипса; Ь = у а2 — с2, с = F\Ft. экс-
центриситет эллипс^ е = -^-<1. Фо-
кальный параметр (половина длины
H-Zc---
---2а---
Фиг. 14. Эллипс н его элементы.
хорды, проведенной через фокус парал-
лельно малой оси) р = —.
а
Точки А, В, С, D — вершины эллипса,
точка О — центр эллипса.
Директрисы — прямые К\Е\ и KtEi,
параллельные малой оси и находящиеся
на расстоянии OKi = OKt =f — от нее.
е
Для каждой точки Af (х, у) эллипса
г’ г2 п
= е- Рациональные выра-
ЛтС| Л1С2
ження для радиусов-векторов п и г»
точки М:
г, = а 4- ех\ r2 = а — ех.
Диаметром эллипса называется гео-
метрическое место середин параллель-
ных хорд. Если Л| — угловой коэффи-
циент этих хорд, й2 — угловой коэффи-
циент диаметра, то kikt =--------;
а1
направления, определяемые ki и kt.
называются сопряженными. Если а
и {1,—острые углы сопряженных диа-
метров с большой осью (ki = tga, kt =
•" — *g 3) и длины их 2ai и 261, то а, +
4- б, = а’ + Ь2 и at6i sin (а 4- Э) = ab
(теоремы Аполлония) (фиг. 15). Взаимно
сопряженные и перпендикулярные дна-,
метры—главные диаметры эллипса,
они же—оси симметрии.
Уравнение касательной к эллипсу
в точке М (х, у)
2^4-22.1.
а» т Ьг
где X. У — текущие координаты точки
касательной. Нормаль и касательная
16*
244
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
(фиг. 16) в точке касания являются бис-
сектрисами соответственно внутреннего
(«у = fi) и внешнего (ф = ф1) углов
между г» н г».
Фиг. 15. Сопряженные
диаметры мл и пса.
Фиг. 16. Касательная
и нормаль эллипса.
и AiO каждый в отдельности делим на
одинаковое число равных частей, нуме-
руя точки, начиная от At. Лучи, иду-
щие из Di и Bi через точки деления
отрезков AiO и AiB с одинаковыми
номерами, пересекаются в точке М на
эллипсе.
Эллипс с полуосями а и Ь есть проек-
ция окружности, построенной на боль-
шой оси эллипса как на диаметре, если
плоскость окружности наклонена к пло-
скости эллипса под углом 0 = arccos —.
Гипербола. Г иперболоИ называется
геометрическое место точек М, для
Радиус кривизны в точке М (х, у)
R = а2Л2 (— + —) =(rir*) __ Р
\ a* b*) ab . sin8^'
В вершинах А и В (см. фиг. 14)
R = а — р\
в вершинах С и D
R^ai-.b.
Фиг. 19. Гипербола.
Фиг. 20. Директрисы
гиперболы.
Параметрические уравне-
ния эллипса:
х — a cos t; у •= b sin t,
где параметр t — угол хОА (фиг. 17),
соответствующий точке М на эллипсе.
Построение точек эл-
липса.
1. Через общий центр О двух окруж-
ностей радиусов а и о проводим пря-
мую под углом t к Ох, пересекающую
окружности в точках А и В (фиг. 17).
Фиг. 17. Эллипс как Фиг. 18. Построение
проекция окружности. точек аллипса.
Точка пересечения прямых AM Ц Оу и
ВМ || Ох лежит на эллипсе.
2. В прямоугольнике ABCD разме-
рами АВ = 2а, ВС — 2Ь через сере-
дины Al, Bi, Ci, Di сторон проводим
осн координат (фиг. 18), отрезки AiB
каждой из которых разность расстояний
Г\, Гг до двух данных точек Ft и Ft (фо-
кусов) есть величина постоянная; п —
— гг = 2а (правая ветвь); гг — п =
= 2а (левая ветвь).
Относительно системы координат хОу
(фиг. 19) каноническое уравнение гипер-
болы имеет вид
£*._
а* Ы
где х, у — координаты точки /И; b =
- с - -1- FiFp 2а - АВ -
отрезок осн х между вершинами гипер-
болы; ось симметрии Ох, которую ги-
пербола пересекает, называется дей-
ствительной осью гиперболы; вторая
ось симметрии Оу не пересекает гипер-
болу н называется ее мнимой осью;
а—действительная полуось; b—мни-
мая полуось.
Точка О — центр гиперболы, фокаль-
ный параметр (половина хорды, прохо-
дящей через фокус параллельно Оу)
р= — ; эксцентриситет е™ — > I.
Директрисы — прямые КгЕг и Ki£|,
параллельные мнимой осн и находя-
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
215
щиеся на расстояниях от нее OKt =
— OKi= ~ (фиг. 20). Для всякой
точки М (х. у) гиперболы
Радиус кривизны
Af£j MEt
Рациональные формулы для радиусов-
векторов точек правой ветви п = а -Ь
ex, ri = — а + ех и левой ветви г>=
= — а — ех, г» = а — ех.
Диаметром гиперболы называется гео-
метрическое место середин параллель-
ных хорд. Если Й1 — угловой коэффи-
циент этих хорд, ki — угловой коэффи-
циент диаметра, то kikt = ; напра-
вления, определяемые hi и >2, назы-
ваются сопряженными. Взаимно сопря-
женные и перпендикулярные диаме-
тры — главные диаметры, они же —
оси симметрии.
Асимптоты гиперболы — прямые,
определяемые уравнениями
Асимптоты гиперболы — самосопря-
женные диаметры.
Расстояние от точки гиперболы до
асимптоты неограниченно убывает при
удалении точки по кривой в бесконеч-
ность.
Если за оси координат принять асимп-
тоты, то уравнение гиперболы (в аффин-
ных координатах) имеет вид
ху-С.
Фиг. 2). Ккатеаьам нормаль гиперболы.
Касательная к гиперболе в точке
М (х, у) имеет уравнение
«» м
X, Y — текущие координаты.
Касательная и нормаль — биссектри»
сы соответственно внутреннего (ф=4'1)
н внешнего (f = ft) углов между л
и г» точки касания (фиг. 21).
(W р
ab sin* ф *
В вершинах R = Ь1 : а — р.
Отрезок касательной TTi между
асимптотами делится в точке касания
пополам: МТ = МТг (фиг. 22). Пло-
щадь {\TOTi между касательной и
Фаг. 22. Отрезки касательной между
асимптотами гиперболы.
асимптотами равна ab (для всякой
точки М). Если МР и MQ параллельны
асимптотам, то произведение отрезков
MPMQ = (а* + **) — -Lс*.
Построение точек гипер-
болы. имеющей данные асимптоты и
проходящей через
данную точку М:
через эту точку М
проводят всевоз-
можные прямые,
на которых от то-
чек пересечения с
асимптотой (лю-
бой) откладывают
отрезки AiAfi, рав-
ные МAt; геомет-
рическое место то-
чек М1 есть гипер-
бола (фиг. 23).
Сопряженн
х* V»
- МВ I и -X— — I
а» b* bt а*
Фиг. 23. Построение
точек гиперболы.
ые гиперболы
1 имеют
общие асимптоты. Действительная ось
каждой из них является мнимой осью
другой. Если обозначить через 2щ
и 26| длины двух сопряженных диа-
метров этих гипербол, то а, — =
= а1 — b*, ab = а>б| sin (а> — ai) (тео-
ремы Аполлония), где в| и а> — углы
диаметров с осью Ох.
246
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Площадь сектора (фиг. 24)
оли-1л»(| + х)-
— тг ab Arch —.
2 а
Равнобочна
(у которой а = Ь)
я гипербола
имеет уравнение
х*—у* ~ аг\ ее
асимптоты у= ±х
взаимно перпенди-
кулярны.
Уравнение рав-
нобочной гипербо-
лы относительно ее
асимптот, приня-
Фиг. 24. Гнперболиче- ТЫХ За ОСИ КООрДИ-
скиЙ сектор. I
нат: ху= —.
Параметрические урав-
нения: I) х = a ch t; у = b sh I
(правая ветвь); I изменяется от —оо
до 4-со; 2) х = a sec I; у = b tg при
к , , я
---< t < -у получается правая
ветвь, при — левая ветвь.
Парабола. Параболой называется
геометрическое место точек М, для
каждой из которых расстояние г до
данной точки F
Фиг. 2S. Парабола и ее
элементы.
(фокуса) равно
расстоянию d
до данной пря-
мой (директри-
сы А Е): r^d —
= ME (фиг. 25).
Относи-
тел ь н о хОу
на фнг. 25 ка-
ноническое ура-
внение парабо-
лы имеет вид
у» — 2рх.
где х, у — координаты точки М\ р —
фокальный параметр — расстояние от
фокуса до директрисы и в то же время
половина хорды, проходящей через
фокус перпендикулярно оси симметрии.
Вершина параболы удалена на рас-
стояние от фокуса и от директрисы.
Расстояние от всякой точки параболы
Л1(ж, у) до фокуса
Эксцентриситет параболы принимает-
ся равным единице, так как
Диаметр параболы (геометрическое
место середин параллельных хорд с угло-
вым коэффициентом k) параллелен оси
симметрии Ох; уравнение диаметра
у . Ось симметрии параболы —
главный диаметр (перпендикулярный
хордам, через середины которых он
проходит).
Касательная к параболе в точке
М(х, у) имеет уравнение
Уу-р(Л+х).
где X, Y — текущие координаты.
Касательная и нормаль являются бис-
сектрисами углов между г и диаметром,
проходящим через точку касания (?=4>i;
Ф=ф1). Если касательная в точке М
пересекает Ох в точке 7, Оу — в точке 2
и ОР = х, то ОТ = OP; TF = FM;
TQ = QA4; TFME — ромб (фиг. 25).
Построение параболы. 1)Да-
на вершина, ось симметрии и одна
точка М (фиг. 26). Разделив в прямо-
угольнике OQMP стороны OQ и QM
каждую в отдельности на п равных
частей (фиг. 26, п = 4), нумеруют
Фиг. 26. Построение Фиг. 27 Построение
параболы. параболы.
точки деления от О к Q и от 0 к М.
Точка пересечения любой прямой, про-
ходящей через О с соответствующей
прямой, параллельной осн симметрии,
лежит на параболе.
2) Дан параметр р, вершина О и ось
симметрии Ох (фиг. 27). От вершины О
в отрицательном направлении оси х от-
кладывают отрезок 2р = ОА и строят
окружность, проходящую через точку А,
с центром в любой точке оси Ох.
Точка Л4 пересечения QM || Ох и
PM II Оу лежит на параболе у2 = 2рх.
Радиус кривизны
з
(р + 2х)~' _ р _ №_
Ур sin* 4* р4 *
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
247
где W—длина нормали MG (фиг. 25).
В вершине О радиус кривизны R = р.
Параметрические урав-
нения параболы: х = ‘2р(г,
у = 2pt, где t изменяется от —со
до 4- оо.
Уравнение кривых 2-го порядка в по-
лярных координатах имеет вид
I — е cos ?
Для эллипса е<1, полюс в левом
фокусе; для гиперболы е>1, полюс
в правом фокусе; для параболы е = I,
полюс в фокусе.
Общая теория кривых 2-го порядка.
Общее уравнение второй степени
"цх2 4- 2д12ху 4- ОпУ2 4- 2л13х 4-
4- 2вау 4- ая = О
определяет линию, называемую линией
(кривой) 2-го порядка.
Если это уравнение не имеет веще-
ственных решений, то говорят, что оно
определяет мнимую линию.
Линия 2-го порядка определяется
вообще пятью точками, задание которых
позволяет определить отношение всех
коэффициентов alk к одному из них.
При преобразовании прямоугольной
системы координат хОу в прямоуголь-
ную х'О'у' уравнение той же линии
2-го порядка примет вид
апх'г 4- 2д'12х'у’ + а'22уЧ 4-
4- 2e[3x’4-2a^y'4- а'м - 0.
Функции коэффициентов уравнения, не
меняющие своих значений при указан-
ном преобразовании х, у, называются
инвариантами. Инварианты уравнения
кривой второго порядка относительно
преобразования координат (поворот
осей и перенос начала координат):
Л “ дп 4- «я — яц 4- «22;
Я11 я1! «11 «12
ап «а «21 «и
Я11 я13 «18 «11 «12 «13
/ г f
«?1 «22 «И «21 «а «23
«31 язг «аз «31 «32 «33
где в целях симметрии пишут ац = aJ3<
“л — «иь вза = аа-
Центром линии 2-го порядка назы-
вается точка, в которой делятся пополам
проходящие через нее хорды этой линии.
Координаты центра находятся из си-
стемы
аах 4- д12у 4- а13 = 0;
«их 4- «22У 4- "га — °-
При 1г = а1'Я12 =А 0 центр суще-
1яаяи1
ствует, при 1г — 0, т. е. при - — =
Я21
«]2 j «1*» «Ц
= —, центра нет, при —— =
«22
= — = — центров бесконечное мно-
«22 «23
жество (линия центров): линия 2-го
порядка состоит из двух параллельных
прямых.
Вид линии определяется знаками
инвариантов.
Центральные кривые получаются при
Гг * 0:
/, >0 /, + 0 Эллипс а) ДА < 0 — действительный 6) 1,1, > 0 — мнимый
/, = и Точка
/, < 0 1, + 0 Гипербола
/, - 0 Пара пересекающихся прямых
Нецентральные кривые получаются
при /г “ 0: парабола, если /а + 0, и
пара прямых, если /д — 0 (параллель-
ных при а23 — яцЯ,а> 0, совпавших
прн я,3 — aua„ = 0 и мнимых прн
в13 — «‘««38 <°)-
Примеры:
I) 4jr« — ixy 4-у» — 4х4-2у—3 — О.
/,-4-1 -(-2)»-0;
°ч — Я|> — д °1» — 2
слелояательно, линия распадается ил пару парал-
лельных прямых. Уравнение можно переписать
в виде
(2л — у)» — 2 (2л — у) — 3 = 0.
Ойо квадратное относительно 2х у — г, и его
левая часть раскладывается иа два множителя
г» - 2л - з - (X - 3) (Я 4-1) — a
Уравнение определяет пару прямых
2л - у — 3-0 И 2Х—y-j-i—O.
248
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Уравнения, определяющие центр.
4х _ 2у - 2 — О,
-2x4-.у 4-1=0
сводятся к одному уравнению 2х — у — 1 = 0 —
линии центров.
2) Jf — Аху 4- 2уг 4- 2х — 2у = 0.
Кривая— гипербола. Характеристическое урав-
нение
X* — 5Х — Эб = 0
линия центральная, гиперболического типа. Вы-
числяем
дает корни X, = 9, X* = — 4.
следовательно, линия представляет собой пару
пересекающихся прямых.
Координаты центра определяются из уре пиемий
ж-4> + , = °: +
откуда
х = 2, у = 2.
Из систем
X = 0; 2ji* - 2у — 0;
у = 0; x'-f-lx =0
Фиг. 28. Построение гиперболы.
находим координаты точек пересечения линии с
осями координат: (0.0), (0,1), ( —2.0). Так как пря-
мые проходят через центр, то уравнения, на ко-
торые распадается данное уравнение, имеют вид
Каяоинческое уравнение
у-х — 0; л-гу + 2-=а
Преобразование уравнения централь-
ных линий к» каноническому виду
И расположение кривых относительно
осей координат. Если дана линия 2-го
порядка общим уравнением, то, вычис-
лив /а, /3, составляют каноническое
уравнение линии
+ W1 + -г - о
•г
в некоторой системе х‘О'у'< причем Ап
>.» — корни характеристического урав-
нения
*«— /Л + /2-0;
оси О'х' и О'у' — главные диаметры.
Находят центр кривой О' и определяют
направление О'х' как одного из глав-
ных диаметров по угловому коэффициен-
ту k из формулы
k — fl|t _ ^1 ~ аи
ч — a-а ап *
где Ат — тот корень характеристиче-
ского уравнения, который в канониче-
ском уравнении есть коэффициент при
л'1.
Система уравнений
5x4-бу-11-0, Вх-6у=0
опреаеляст центр О'(1,1). ПрнХ, = 9 угловой
коэффициент
. __£>* 6 — —
X, - Ou 9 — 0 3
определяет направление О'х'. Расположение ги-
перболы см. иа фиг. 28.
Если взять X, - — 4, X, — 9, то уравнение
И-— — _ j ддет ту же гиперболу, но отно-
сительно другой системы координат, отличаю-
щейся от первой заменой О'х' иа О'у' и обратно.
Преобразование уравненяя параболы.
В случае параболы /2 “О, /8 уь 0.
Каноническое уравнение имеет вид
y'i — 2x' / — /в : - 0
в системе х'О'у'.
Уравнение главного диаметра (ось
О'х') имеет вид
an-*"bflit>' + eis + -^(вах+втдУ+а2з)“0-
Решая это уравнение совместно с урав-
нением параболы, определяют вершину
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
249
последней О'. Чтобы определить распо-
ложение ветвей (симметричных относи-
тельно главного диаметра), следует
найти еще одну точку параболы, на-
пример пересечение параболы с осью
Ох или Оу.
Припер. — -try + У1 — х — 2 — 0.
Z,=5; /,-0; /,= --L.
Линия — napafoAi, ее каноническое уравнение
Главный анаметр имеет уравнение
1 2
** - 2/- — - — (- 2х 4-у) =0
или
5(2х-у) = 1.
Реша» это уравнение совместно с уравнением
параболы (в котором всегда старшие члены дадут
полный квадрат суммы нлн
разности двух членов)
(Xr-yp-jr-H.
получаем координаты вер-
шимы:
_1«.
25
Построив главный диа-
метр. прохадншнй через
♦иг. 29. Построение вершину. можно далее
параболы. строить точки параболы по
ее каноническому урав-
нению. Легко найти пере-
сечение параболы е осью Оу:
г » 0, у» - 2 — ft
откуп
у, — V~2 , у. — — /Т (ем. фиг. 29).
Конические сечения. Кривые 2-го
порядка могут быть получены пересе-
чением прямого кругового конуса пло-
скостью.
Фиг. 30. Конические сечение.
Если секущая плоскость не проходит
через вершину конуса, то сечение будет
гиперболой, параболой или яллипсом
в зависимости от того, будет ли секу-
щая плоскость параллельна двум, одной
или ни одной образующей конуса. Если
секущая плоскость перпендикулярна
оси конуса, то получается окружность
Если плоскость проходит через вер-
шину конуса, то в сечении получается
пара пересекающихся прямых. Парил
лельные прямые в сечении получаются,
если конус вырождается в цилиндр
(фиг. 30, а—г).
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
В ПРОСТРАНСТВЕ
Метод координат. Положение точки М
в пространстве относительно той или
иной системы координат определяется
тремя числами — координатами.
Прямоугольная декартова система
координат состоит из трех пересекаю-
щихся в точке О взаимно перпендику-
лярных осей координат Ох, Оу, Ог, на
которых их орты <, j, k указывают
♦иг.З). Прямя систем»
координат.
Фнг. 32. Левая си-
стема координат.
положительные направления осей.
Длина этих единичных векторов т
взята за масштабную единицу. В зави-
симости от взаимного расположения
осей может быть правая система коор-
динат (фиг. 31) и левая система коор-
Ринат (фиг. 32). Система называется
правой, если вращение вокруг оси г
положительного направления осн* к по-
ложительному направлению оси у пред-
ставляется наблюдателю, совмещенному
с положительным направлением оси г,
происходящим в направлении против
часовой стрелки. В дальнейшем при-
нята правая система.
Оси координат попарно определяют
координатные плоскости. Если точку М
ортогонально спроектировать на оси
координат в точки Ai, Ае, А», то числа
(положительные или отрицательные)
х — (абсцисса), у = —- (ордн-
т т
ната), г — (аппликата) называют
250
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
прямоугольными (декартовыми) коор-
динатами точки М и записывают:
М(х, У, г).
Радиус-вектор точки М
ОМ = г = хГ-Ь у/ 4- zk.
Направляющими косинусами луча L
(направленной прямой, осн) называются
косинусы углов а = /_(х, L), 3 —
~ Z (У- £). 7 ~ / (г. L) между поло-
жительными направлениями осей коор-
динат и направлением луча L. Единич-
ный вектор е (орт) луча L имеет своими
координатами направляющие косинусы
е = 7 cos a +J cos g 4- k cos 7;
cos* a -j- cos* 3 + cos* 7—1.
Вместо cos a, cos 3, cos 7 мо жпо взять
пропорциональные им величины I, т, п,
определяемые условиями
/ _ т _ п
cos а — cos р — cos 7 ’
иногда I, т, п называют угловыми коэф-
фициентами прямой (луча) в простран-
стве. За величины (, т, п можно при-
нять разности одноименных координат
любых двух точек прямой.
О координатах вектора см. на стр. 228.
Деление отрезка, соединяющего точки
М j (Xi, у1, 2i) и M.(xt,yi, гг) в данном
. М,М
отношении А — .... : координаты точки
Л1ЛЬ
деления М(х, у, г) определяются фор-
мулами
х, 4- . У| 4- Ху, .
Х 1 4-Х ’ У 14-Х’
Z) +Xs,
r+V-
Середина отрезка определяется коор-
динатами
.. *1 + *«. .. >i 4- У, . _ z, 4-z,
— 2 >г“ 2 •
Расстояние между двумя точками At,
н Л1а равно
________d - AfjAf , -
- V(-*» — 4- (Уз - У1)‘ 4- (*з - «Г)’-
Преобразование прямоугольных коор-
динат. Перенос начала коор-
динат с сохранением направления
осей определяется формулами
х — х' 4- а; у — у' 4- b; z — z' 4- с,
где х, у, г — координаты точки М
в.старой системе Охуг; х‘, у', г' — коор-
динаты той же точки М в новой системе
O'x'y'z'; а, Ъ, с — координаты О' отно-
сительно старой системы.
Поворот осей (с сохранением
начала координат). Новые осн Ох'у'г'
образуют со старыми осями Охуг углы,
косинусы которых даны таблицей
где первый индекс относится к старым
осям, второй индекс — к новым осям,
например а28 = cos (у. г') и т. д. Фор-
мулы преобразования имеют вид
X = ацХ7 4- ацу' 4- аг>27;
у = адх7 4- “»У' + ’гзг';
Z = “six' 4- “32У' 4- “вд2';
х = ацХ 4- “гзУ 4- “siZJ
у'=ацХ 4-®аУ + ®з»2;
«' в “13* + а2зУ 4- a3sZ.
Девять косинусов а(А (/ = 1, 2, 3;
k = 1, 2, 3) связаны соотношениями
4-»2/»2ft 4- “зг’ад —
или
( 0, если i=£ k
I 1, если i= k
“n»M + + “га’ля ”
0, если i k
1, если I — k
Независимых углов — три. Примем
в качестве таковых углы Эйлера: <р,
ф, 0 (фиг. 33), где f — угол между Ох
и ОР — прямой
пересечения пло-
скостей ху и х'у';
ф— угол между
ОР и Ох'; 0 —
угол между Ог и
Ог', он же — дву-
гранный угол ме-
жду плоскостями
ху и х'у'; тогда
формулы преобра-
зования координат
х — х7 (cos f cos ф — sin sin ф cos 0) 4-
4- у' (— cos <? sin ф — sin ? cos ф cos 0) 4-
4- z' sin sin 0;
у — x7 (sin <f cos ф 4- cos sin ф cos 8) 4-
4- y' (— sin <f> sin ф 4-cos f cos Ф cos 9) —
— z' cos <? sin 0;
Z — x' sin ф81п 0 4- у' cos у sin J 4- z' cos 8.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
251
Цилиндрическая система координат
Если проекция точки М на хОу есть
точка Р (х. у) с полярными координа-
тами (г, ?), то положение точки М
вполне определяется тремя числами г,
Г, г, называемыми цилиндрическими
координатами (фиг. 34). Имеем
х = rcos <f>;
y = rsin<p; z = z;
r — Vx2+ y2; <p = arctg= arcsiny •
Чтобы получить все точки простран-
Фиг. 34. Цилиндри-
ческие и сфериче-
ские координаты.
ства, достаточно из-
менять г от О до
4- оо, ф от 0 до 2п,
z от — оо до — оо.
Сферическая система
координат
Если проекция точ-
ки М на хОу есть
Р (r< расстояние
ОМ = р, угол между
О г и лучом ОМ есть
в, то р, <?. О — сферические (полярные
в пространстве) координаты точки М
(фиг. 34). Имеем
х = р sin в cos <р; р = Ухг + yi + z2;
у
у = р sin0 sin?; <р = arctg ;
л Ух» 4- у:
z = р cos в; в = arctg----------—
Если изменять р от 0 до со, ? от О
до 2к (или от — и до 4- я). О от О док.
то получим все точки пространства,
Координатной поверхностью назы-
вается такая поверхность, в каждой
точке которой одна координата — посто-
янная; координатная линия — такая ли-
ния, в каждой точке которой две коор-
динаты постоянные.
В декартовой системе координат через
точку Af(x#, у0, г0) проходят три пло-
скости: х = х0, у = уо, г = г0 (коор-
динатные поверхности), параллельные
плоскостям координат и пересекаю-
щиеся по трем прямым, параллельным
осям координат.
В цилиндрической системе через точ-
ку М (г0, |рэ, г0) проходят координатные
поверхности:г=ги (цилиндр). (пло-
скость, проходящая через Ог), г = г0
(плоскость, перпендикулярная к Ог).
В сферической системе координат
через точку М (р01 >?0, проходят коор-
динатные поверхности: р = р0 (сфера),
F — -ри (плоскость), 9 — 0о (конус с
осью Ог).
Плоскость
Уравнением плоскости называется
соотношение между координатами (те-
кущими) всякой точки плоскости.
В дальнейшем г [х, у. z) обозначает
текущий радиус-вектор точки плоскости
или прямой; ro|xo, у0, z0), п. rt и т. д.—
радиусы-векторы заданных точек.
Общее уравнение плоскости. Всякое
уравнение первой степени Ах + Ву-|-
А- Сг + D = 0 определяет плоскость.
Здесь А, В, С — координаты вектора А/,
перпендикулярного к плоскости.
Векторное уравнение плоскости: •
7 N + О = 0.
Уравнение всякой плоскости есть
уравнение первой степени относительно
х, у, г.
Если А = 0 (или 0 = 0, или С = 0),
то плоскость параллельна оси Ох (со-
ответственно Оу, или Ог); если А =
— В = 0 (или А = С = 0, или В =
= С = О), то плоскость параллельна
плоскости хОу (соответственно хОг,
или уОг). Если D = 0, то плоскость
проходит через начало координат. Если
.4=0 = 0 (B = D = 0. или C=D = 0).
то плоскость проходит через Ох (соот-
ветствен по через Оу, или через О г}.
Если А = В — D = 0 (или А = С —
= 0 = 0, или В = С = D = 0), то
уравнение принимает вид г = 0
(у = 0, или х = 0), изображающее пло-
скость xOv (соответственно хОг, или
уОг).
Нормальное уравнение плоскости.
Положение всякой плоскости относи-
тельно Охуг можно задать параметрами:
единичным вектором п (cosa, cosp, cos 7),
направленным от начала координат
перпендикулярно плоскости, и длиной
перпендикуляра р, опущенного из на-
чала координат на плоскость.
Векторная форма нормального урав-
нения:
г п — р — 0,
скалярная форма:
х cos а 4- у cos j) 4- z cos 1 — p — 0.
Общее уравнение приводится к нор-
мальному умножением на нормирующий
множитель -----7- * , где знак
С*
берется противоположный знаку D.
252
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Расстояние а яг точки Af(Xo. Уо-
До) до плоскости х cos а + у COS Р +
4- z cos 7 — р = 0:
d — х0 cos а + Уо cos 3 + Zo cos 7 — р.
Если d > 0, то точка Мо и начало
координат лежат по разные стороны от
илоскости: если d < 0 — по одну сто-
рону от плоскости.
Уравнение плоскости, проходящей
через данную точку А40 (х^, у0, ze),
аерпендикулярно данному вектору
V(X, В, С):
А (х— хв) + В (у —уо) + С (х—ж9) — 0.
Векторная форма этого уравнения
(г - М V= 0.
Это же уравнение при любых А, В, С
есть уравнение связки плоскостей —
оовокупностн плоскостей, проходящих
через данную точку Мв.
Если точка /о!-*®- Уо< го1 Д®на пересе-
чением трех плоскостей г Nt 4- Dt = 0,
rNt+£h=0, г A/j-r- D3 = 0, то связка
плоскостей может быть записана урав-
нением
rAG + Di + KfrjTj + Dt) +
+ Р (r N» + Оа) = 0.
где X, р — переменные параметры.
Уравнение плоскости, проходяще* че
рез три точки Mi (Г)). М- (r}). М3(г3):
(7 — ~i) (ri — П) (— П) - 0.
где левая часть есть смешанное (век-
торно-скалярное) произведение, или
*-*! У~У1 »—»|
*1— Ух-У, Zx —Z,
JTJ —*1 У|~У1 2» —«1
-а
Если четыре точки лежат
в одной плоскости, то выпол-
няется условие
(*Ч — й) (г»— П)(<7— П) - 0.
Уравнение плоскости в отрезках:
Уравнение илоскости, проходящей:
а) через две точки Л1о (r^, Mt (г>)
параллельно прямой с направляющим
вектором S {/. т, л):
X— х0
X, —х0
I
У —Уо
У1 — Уо
т
-0
или
(~r — 7j) (rt — г0) S = 0,
б) через одну точку М^г^) и парал-
лельно двум_ прямым с направляющими
векторами St (/», mi, ni|, Sj (/», /пг, л»).
Р-^)^3»=0;
в) через линию пересечения двух пло-
скостей
Atx -г В^у 4- CfX т Dt “= 0
н
Агх + Вгу + C^z + D, — 0:
з4|Х + Biy + C,z + Dj +
+ А (4jX + В-у 4- С^г + Dt) — 0.
Последнее равенство есть уравнение
пучка плоскостей. Меняя X от —со
до -Ь со, получим все плоскости пучка.
Точка пересечения трех
плоскостей находится совместным
решением трех уравнений плоскостей
относительно х, у, г.
Пример. Найти проекпию прямой, и тайной
пересечением двух плоскостей 'Lx — у fl” ин
Ас — 7У+-111 — 8 — 0 на плоскость x-y'iy-j-г +•
4-1 = 0. Чтобы в пучке плоскостей 2x-y-t-i-f-
4-Л(4х - 7» + 111 -8) - 0 или U4-4X)x44-|-
— ?МУ + (• + 11А>* — а* —о найти Проектирую-
щую плоскость, слеаует записать условие перпсаа-
ликулкрмостн хвух плоскостей:
!-<2 4- «х» 4- 2-(-1 - А) 4-1.(1 4- IU) - о.
откуда X — — 1, искомая плоскость
X — Зу4-51 — 4 — О.
Лроекпиа эалаииой прямой па данную пло-
скость определится кек пересечение двух пло-
скостей:
ж-Эу4-й-4-0: ж4-2у + х + ‘-о-
Прямая и ее уравнения
Параметрические уравнения прямой.
Если_ прямая проходит через точку
МЛ(г^ и параллельна вектору S {(,т. л},
который называется направляющим век-
тором, то векторное уравнение прямой
имеет вид
1.
(г — r#) X 5 = 0;
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
253
параметрическое уравнение в векторной
фэр мо
7 = 70 + ts
•содержит переменный параметр t, опре-
деляющий положение точки на прямой.
В скалярной форме параметрические
уравнения имеют вил
х = 4 И; у = у0 + mf,
z «= z# 4 nt
Каждая пара уравнений есть параме-
трические уравнения проекции прямой
на соответствующую координатную пло-
скость. В дальнейшем 5 (Z. т, л),
-Si {/1.ЛП.Л1} и т. д. суть направляющие
векторы соответствующих прямых.
Канонические уравнения прямой:
Х — Хд _ У—Уд Z — Zg .
I т п ’
каждое уравнение
<^x0=yZLy ft или
I т т п ’
X — X(| z — Zq
ИЛИ —= —
решают систему относительно остав-
шихся неизвестных.
Канонические уравнения имеют вид
х — Хд у—уд г —Z()
НЖ W
Пересечение прямой с плоскостью.
Чтобы найти точку пересечения пря-
мой х = х0 4 It, у = у0 4 mt, г =
= г04л< с плоскостью Ах ф By 4
4 Сг + D = 0, надо в уравнения пря-
мой подставить
. _ _Ахд 4 Вуд -4- Cig 4- D
At 4 Вт 4 С п
Равенства
Ax’® 4 Вуд 4 Cig 4 0= 0,
At 4 Вт 4 Сп = О
являются условиями того, что прямая
лежит в плоскости.
Кратчайшее расстояние
между двумя скрещиваю-
X—X, у—V,
щ и м и с я прямыми —;—! — -—— —
h т1
= *—„ x—xt у —уг _ г —z..
«I 1г “* тг пг
есть уравнение пло-
скости, проектирующей
прямую на соответствую-
щую координатную пло-
скость.
Уравнения прямой,
проходящей через данную
перпендикулярно дайной
Ах 4 By 4 Сг 4 D = 0:
d _ /г т2 п2 I _ (— г J 5; Ог .
ЛТrwi I* , I л,/| I» , | />«, 13 I «1 X S, I
У +1/^1
точку Мо (7(0 Условие, при котором
плоскости Две прямые лежат в одной
плоскости:
Х — Хд у - Уо Z—Zg
А “ В ~~С~'
Уравнения прямой, проходящей через
две точки Af0 (Гд> и (Г;):
Х — Хд У — уо . Z — 20
--*0 “ У1 — Уо = -1~го'
Прямая как линия пересечения двух
плоскостей определяется совместным
рассмотрением уравнений этих пло-
скостей:
AiX 4 Bty 4 CyZ 4 Di = 0,
A2x 4 Bjy 4 CjZ 4 Dj — 0.
(/•» — Г|)$1$“0
или
X, -X!
А
1г
Уз —У|
^1
тг
«2—31
«1
Пг
-0.
Это же равенство есть и условие
пересечения двух прямых,
если только прямые не параллельны,
т. е. Si хЗ«4 0. Если две прямые
даны пересечением двух пар плоскостей,
то условие пересечения этих прямых
имеет вид
Чтобы привести эту форму к канони-
ческим уравнениям, следует найти одну
точку (х0, у0, г0) на прямой, для чего,
задав одну координату произвольно,
В.
Вг
i.
Сг &г
Са D3
Ct Dt
0.
Лз
254
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Расстояние от точки Мх (о)
-х — хп V—уя 2— z»
до прямо й—-— =--=---—:
г / т п
первое кз них есть условие перпендикулярности
искомой прямой со второй из данных прямых, а
второе — условие пересечения искомой прямой
с первой из хлнных прямых. Из двух однородных
. Iam^xsI
а •=-:-----
Уравнения общего пер-
пендикуляра двух скре-
щивающихся прямых полу-
чим, если составим сначала уравнение
плоскости Р, проходящей через одну
прямую параллельно другой прямой,
а затем составим уравнения двух пло-
скостей, перпендикулярных к Р и прохо-
дящих через каждую из заданных
прямых. Уравнения этих двух плоско-
стей н дадут искомый перпендикуляр.
Пример. Составить уравнения прямой, про-
ходящей через точку (1. 1, 1). пересекающей
X — I у 4-1 г
прямую —— = — — — и перпендикулярной
* I J
ДГ у Т
к прямой Уравнения искомой
прямой
г — 1 у —I _ в — 1
I т ~ п *
гае отношения I: т : л находятся из условий
I 4- 2m 4- 4л = 0;
514- 2m — 4л — 0;
уравнений с неизвестными I. т, л находим
I» — 16*. т — 24*. л - — 8*.
Уравнения искомой прямой
Х-1 У —1_т~1
4 “ —3 “ I '
Условия параллельности:
двух плоскостей
4-=^. = ^. пли ATiX^-O;
двух прямых
4=4-4.„ли SixS = 0:
♦2 «2
прямой н плоскости
А1 4- Вт 4- Сп = 0 или N S — 0.
Условия перпендикуляр-
ности:
двух плоскостей
4" В]Вч 4" — 0 или Л/j Лг^ в 0-
Угол между плоскостями и поямыми
Угол между Уравнение Формула
двумя плоскостями A,x+B,y+Ca+D,-0. А»я 4- Л»У 4- С.«4- О.—0- В векторной форме: rf7,4-D,-O; W,4-D.-0- го— ^Д.4-я.я,4-с.с. СОЯ» = — ; у/ (л;4-в;4-С?) (л,4-в,4-С.) TT,N, ЛОТ
авумв прямыми x — xt г — h 1, m, л, ’ l9 я* В векторной форме: (г—гЭх^—0; (7-/Ьх£—о сов^ Л/»-4“ / «4-:-н:)(^-:) ’ S, '“•“SA
примой и плоскостью •г-Л, у-у, х-з, 1 m ” л Ах By 4- Cl 4- D = 0 В векторной форме: rN + D-0. а(п. - |Д«+Д<"4-Сл| . / (ЛН-ДЧ-ОК/Ч-жЧ-лЧ •ln’--NS
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
255
двух прямых
/1^2 + т^т^ 4- Л]П2 ™ 0 или 5] » 0;
прямой и плоскости
илн ^хЗ = о.
I т п
Общая теория поверхностей 2-го порядка
Общее уравнение поверхности 2-го
порядка
“и*2 + аиу2 + a33z* 4- 2апху + 2eayz 4-
+2anzx + 2aux+2aity 4- ‘la^z + а44 — О.
Пример. Уравнение
г* + У’ 4- «* + 4- 2«иУ 4- 2л»г + “и - О
изображает сферу» так как после преобразования
к виду
(X 4- в..)* + 0 4- <’«)' + (г + “э.)' =
tit
“ Ок + яи 4- — °«
и обозначения — а„ = а, — а,, — Ь, — аи - с,
“к + в« + — в« “Г получим уравнение
(ж —в)1 4-(у -б)«4-(а-ер = ^,
которое имеет тот смысл, что расстояние от лю-
бой точки М (л, у, г) ло точки С (а. О. с) есть
величина постоянная г. Геометрическое место то-
чек Л1 есть действительная сфера при условии
“к + “м + “»• — аи > 0.
Инварианты поверхности 2-го порядка
(некоторые функции коэффициентов atk
предыдущего уравнения, которые не
меняют своего значения при переносе
начала и повороте осей координат):
Л “ “и + ап + “за!
/, = I “11 “12 I J. I “11 “S3 1,1 “11 “|я|;
I “si агз I ~ I “яз “за I I “ai “за Г
“11 Д12 Ящ
“11 “и “а »
“ai “зз “зз
/»-
где
“11 “12 “12 “14
“21 “22 “23 “24
“31 “32 “KI “34
“41 “4? “« “44
“1* “ “*/•
Вид поверхности зависит от знаков
инвариантов.
Центром поверхности 2-го порядка
называется точка, в которой делятся
пополам все проходящие через нее
хорды. Координаты центра находятся
нз системы уравнений
“и-* + “12У + “иг + “и = 0;
“я-X + “22.V + “2Я2 + “24 “
“3I-* + “«У + “S32 + “м “ 0.
Определитель этой системы равен Zs.
Определение вида поверхности 2-го порядка
1) /,+0 (центральные п о в е р х н ост и>
1,1, >0, Z, >0 1,1, <0 илн /,<0
/. <0 Эллипсоид Двухполостяый гиперболоид
Л > о Мнимый эллип- соид Однополосгный гиперболоид
— 0 Мнимы» конус Конус
2) /,-0 (нецентральные поверхнос ти>
/, < О I /, > 0 - эллиптический параболоид
1, > U | /,<0— гиперболический параболоид
/, = U I Цилиндры и пары плоскостей
В последнем случае система, опреде-
ляющая центр, сводится: а) или к двум
независимым уравнениям (имеется ли-
ния центров), поверхность будет или
цилиндрической с направляющей ли-
нией 2-го порядка, или парой пересекаю-
щихся плоскостей;б) или только к одному
уравнению (имеется плоскость центров),
поверхность состоит из двух параллель-
ных плоскостей.
При кер. 2лг> 4- у’ 4- 2д« - Чху - 2уг + 4л -
- 2у — 0.
0 1-20
I I -I —I
0-1 2 0
2-100
В сечения поверхности с плоскостью г “ 0 по-
лучается 2л’ 4- у' - 2ху 4- 4ж - 2у = 0. Этому
уравнению соответствует действительный эллипс:
следовательно, поверхность является эллиптиче-
ским цилиндром.
Канонические уравнения поверхностей
2-го порядка
а) /3 + 0. /4 О
X2 У2 Z2
«5-Н&+5-
— I — эллипсоид
(фиг. 35);
Фиг. 35. Эллипсоид.
к2 v2 z2
2) —= + 5-7 + — — —1— мнимый
“г “ с эллипсоид;
256
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
3) +
> at + bi с»
4)
*1 ,-vl_z’’
a t Ы с1
= 1 — ОДНОПОЛОСТЯМИ
гиперболоид
(фиг. 36);
Фиг. 36.
Охиополост-
ный гипер-
болоид.
Фиг. 33.
Конус.
— 1 — двухполо-
стный ги-
перболоид
(фиг. 37);
б) /, 4- 0. Ц = 0 — конусы
r'i у2 Z--
5) -z-4-vx-l—г — 0 — мнимый конус;
' аг b t ct
6)
jfi у» _ z}
а* 4 Ы ct
— О —действитель-
ный конус
(фиг. 38);
в) /3 — 0. /< + 0— параболоиды
7> £+£--*
— эллиптический
параболоид
(фиг. 39);
Фиг. 39.
Эллиптиче-
ский парабо-
лоид.
х2 V2
8) ~— <=- — ± z — гиперболический
ь параболоид
(фиг. 40);
г) /3 - 0. /4 = О
у2 V2
9) -у + гг = — 1 — мнимый эллип-
в ® тический ци-
линдр;
хг у2
10) — 4- <— = 1 — эллиптический
а ° цилиндр (фиг. 41);
х2 V1
11) -д- — ~ -= I — гиперболический
а ° цилиндр (фиг. 42);
X 2 у 2
12) -у + гг — 0 —дие мнимые пло-
я2 о1 гиоетн
X2 У2
13) — гг “ 0 — Две действительные
а~ ь~ пересекающиеся
плоскости (фиг. 43);
Фнг. 41. Фиг. 42. Фиг. 43.
Эллиптический Гиперболиче- Две Пересе-
цилиндр. ский цилиндр. кающиеся
плоскости.
14) х2 — 2ру — параболический ци-
линдр (фиг. 44);
15) х2 4-а2 = 0 — две мнимые парал-
лельные плоскости;
Фиг. 45. Пара
параллельных
плоскостей.
16) х2 — а2 = 0—две действительные
параллельные пло-
скости (фиг. 45);
17) х2 —0—две совпавшие плоскости.
Преобразование уравнения централь-
ной поверхности к каноническому виду.
При переносе начала координат в центр
и при надлежащем повороте осей коор-
динат общее уравнение примет канони-
ческий вид
).]Х' + Х^у' Xjz' 4—р “ 9-
'з
где Х1( X», Ха — корни характеристиче-
ского уравнения
X2 — /|Х2 4- /уХ — /3 = 0.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
257
Достаточно знать знаки инвариантов,
чтобы определить одну из шести цен-
тральных поверхностей.
Число положительных корней среди
М, X», Х8 равно числу перемен знаков
в ряде четырех чисел: I, — h, 1г. —13.
Пример, х' 4- у* + 5г* — битv 4- 2хх — 2уг —
— 4х 4- 8у — 12* -f-14 = 0.
В ряду чисел 1, —7, 0, 36 имеются две пере,
йены знаков, характеристическое уравнение К* —
— 7Х14-36 =0 имеет два положительных корня:
4=3, 4 — 6, А, = — 2, поверхность — двухпо-
лостпый гиперболоид; каноническое уравнение по-
верхности
Зх'* 4-бу'* — 2г'г 4-6=0.
Преобразование уравнения параболо-
ида к каноническому виду. В случае
13 — 0, 1 а 0 общее уравнение при-
водится к каноническому виду
М-*71 + ^2У” ± 2 У — Ц-izZ' = 0,
где знак перед радикалом выбирается
любой; Xj, Х2, ^з=0 — корни харак-
теристического уравнения
» — /,Х« -|- /jX = 0.
Примеры'.
1) 2х! 4-2у’+ зт» 4-4ху + 2хж 4-2у? - 4.
4- бу — 2г 4- а-d;
I, - 7. /, - 10, - 0, - 125.
Характеристическое урапнеине А* — 7Х» 4- ЮА=
— 0 имеет корни л, =5, X, = 2. А, = 0; канони-
ческое уравнение поверхности имеет вил Sx'1 4-
4-2у'‘ ±2д' “0 “ли 5х'*4-2у'’ —
= В У 2 г' — эллиптический параболоид.
2) г = тху;
/,-0; /,.о;
4 1о
Характеристическое уравнение имеет корни
A[(j = ± -у-, А, = и; каноническое уравнение
поверхности г' = (х'* — у’1) — гиперболи-
ческий параболоид.
То же получим, если вокруг оси г слелап
поворот осей хОу на угол « — 45° н перейти к
Vz Vz
новым осям х = — (х' — у'), У — -у(Х' 4- У').
г — г*.
Прямолинейной образующей поверх-
ности называется прямая, всеми своими
точками лежащая на этой поверхности.
Действительные прямолинейные обра-
зующие имеют однополостный гипербо-
лоид, гиперболический параболоид, ко-
нические и цилиндрические поверх-
ности.
х~
Однополостный гиперболоид 4-
у2 *2
+ -------з- — 1 имеет два семейства
()*
прямолинейных образующих:
Гиперболический параболоид г =
х2 V2 -
= —------т— имеет два семейства прямо*
дг 0^
линейных образующих:
2> “(т+т)-" ’(т-f)"”'-
Изменяя отношения параметров р : q,
и: и, получаем различные прямые в ка-
ждом семействе.
Задав точку (х0, уа, Zj) на поверх-
ности, можно найти отношения и : о,
p:q; из каждого семейства выделится
по одной образующей, проходящей через
данную точку.
17 Том I Зак. 1411.
ГЛАВА XII
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ •
ПЛОСКИЕ КРИВЫЕ
Линия (кривая) может быть задана;
1) явным уравнением, 2) неявным
уравнением, т. е. уравнением, опреде-
ляющим одну декартову координату
как неявную функцию другой, и
3) двумя уравнениями, определяющими
обе декартовы координаты точки как
функции некоторого вспомогательного
параметра.
I) П РОСТОЙ дугой линии
на плоскости называется геометриче-
ское место точек, координаты которых
удовлетворяют при надлежащем выборе
осей координат уравнению
>-/«. О)
где Дх) на отрезке а < х < 6 одно-
значна, непрерывна и имеет непрерыв-
ную производную.
2) Кривой, заданной не-
явным уравнением
F(x, у)-0, (2)
называется геометрическое место точек,
координаты которых удовлетворяют
уравнению (2) и в окрестности каждой
из этих точек из той области D пло-
скости ху, где F (х, у) определена,
геометрическое место точек образует
простую дугу. Зги точки называются
обыкновенными.
Такая кривая, называемая регуляр-
ным куском кривой в области D, суще-
ствует, если функция F(x, у), ее частные
производные первого порядка Fx, Fу
непрерывны и
Fj + F® у. 0. (3)
т. е. частные производные одновременно
в нуль не обращаются.
Точка, координаты которой удовле-
творяют уравнению (2), но не обыкно-
венная, называется особой.
• См. лип-рятуру mj стр. 349: (22). (9|. |21).
3) Линией в параметри-
ческом представлении на-
зывается геометрическое место точек,
координаты которых определяются урав-
нениями
х —х(0. у-у(0, (4)
если функции х(0, у (0 в (а, 61 одно-
значны, непрерывны, имеют непрерыв-
ные производные первого порядка и удо-
влетворяют условию регулярности
х’«(0 + у'«(/)у.О. (5)
Эти условия определяют регулярный
кусок кривой.
Точки кривой, в окрестности которой
линия представляет простую дугу, на-
зывается обыкновенной. в противном
случае — особой. В окрестности всякой
внутренней точки интервала регуляр-
ности линия представляет простую дугу.
Если функции х (0, у (0 — аналити-
ческие, могущие не удовлетворять усло-
вию регулярности (5), то линия (4).
состоит из регулярных кусков кри-
вой, разделенных точками, в которых
х' (0 = 0. у' (0 = 0. В окрестности
такой точки [нарушения условия (5)1
линия может представлять простую
дугу и может не являться простой дугой.
В последнем случае точка является
особой точкой кривой (4). О направле-
нии на кривой см. стр. 282.
Линия может задаваться уравнениями
в полярных координатах:
З)г-г(Г). ? = ?(0.
В каждом из трех способов задания воз-
можен переход от одного способа к дру-
гому способу задания кривой.
Параметр t может иногда иметь гео-
метрический или механический смысл.
Составляя таблицу значений функций
х(0, >(0 по формулам хя = х(1Й).
ПЛОСКИЕ КРИВЫЕ
259
Уп m yUn)> мы Можсм по точкам по-
строить кривую (фиг. 1) и нанести
пометки параметра / около этих точек
(шкала значений /)
Переход к параметрическому пред
ставлению (параметризация) возможен
многими способами: взять функцию
Фиг. I
х=х (t) произвольно,
у получить из уравне-
ния F [х(П, у] = О.
Параметризация
' = /(<?>
X —/(?)COS?;
>—/(?) sin?.
где параметр ? имеет геометрический
смысл—полярный угол точки на кривой.
Пример, Полярное уравнение спирали Архн-
мс18 r-ау заменяется в декартовых координатах
параметрическими уравнениями
х — дф cos ф; у ® оф sin ф.
Длина дуги. Если линия задана пара-
метрическими уравнениями (4). то длина
дуги от точки /Ио(/= (0) до точки
/Hi (t = /1) равна
дифференциал дуги ds находится из
формулы
ds2 = dx2 + dy2
Для кривой у = /(*)
s— j VI +'y'2dx.
Для кривой г = /(?)
2) Для цепной линии у — в -f- е а j ’
или у — a ch , длина дуги s т точки Л (0. а)
до текущей точки М (х. у) (фиг. 2) рамы
Свойство цепной линки: ( ~ (“7^ = I.
Касательная, нормаль н отрезки, свя-
занные с ними. Касательной в точке
Л! (х, у) па кривой называется предель-
ное положение секущей прямой ММу
(Л(1 — точка на кривой), когда М -> М.
В каждой внутренней точке М про-
стой дуги существует непрерывно вра-
щающаяся касательная при перемеще-
нии точки касания М по дуге.
Нормалью называется прямая, прохо-
дящая через М перпендикулярно каса-
тельной.
В обыкновенной точке (х. у) кривой уг-
ловой коэффициент касательной At=iga—
<fy Vе (/)
"'5х“лг(7) ЛЛ" уравнений (1) и (4)
и k — = — FX:F v для уравнения (2).
Если X, Y —текущие координаты точек
касательной или нормали, то уравне-
ния последних имеют вид, представлен-
ный в таблице:
«о
rfs* - r'fdt2 + dr2.
Прам»ры-.
1) Вычислить длину дуги одного нитка дркнме-
допой спирали г - ар от полюса ♦ «О и точки
»-!«
2к
— в: л — a J / I + p'dp —
U
-a VTT₽ + 410 <• + 'r'—|
a. a ln/l+4* + -j to (2n + /Ж?)1.
Формл уравнения кривой Уравнение касательной Уравнение нормали
(1) г-у- -/»(х)(Х-х| К-у- —гТЙ1Л-л’
(2) 4-/’>(Г-у)-н /ух-х)- -Рх1Г-У)-0
(4) Х-л_ Г-у х'(0 *“ и' (Л-х(х’<П+ -КК—у)у'(О—°
17'
260
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Здесь л =^Ы);
* дх ’ у ду ’
входящие производные ВЫЧИСЛЯЮТСЯ в
данной точке.
Для формы (6) уравнения кривой
угол р между радиусом-вектором г
точки М и касательной (фиг. 3) вычис-
ляется по формулам
Г Л<?) _ rdf
г' /'(?) dr ’
dr
cos p — -j—
ds
sin p =
rdf
ds
Угловой коэффициент касательной
fc=tga = tg(T + p)=Jy±^.
Пример. Из точки -f-.0 j «не кривой
= 11 прогсети к этой кривой касатель-
*ше. Из уравнения кривой находим производную:
4jr-f-6yy'=0;
*7
?ЛГ
В уравнение касательной Х-у» (X—X).
где (л, у) — неизвестная точка касания, подстав
паяем X = -у . Y — 0 и из полученного уравне-
ния Зу’ + 2х’---— = 0 совместно с aamiuu
уравнением находим х = 2, У = ± I. Касатель-
ные: Г± 1 - iy (Х-2).
Фиг. 3. Угол между Фиг. 4. Отрезки каса
касательной и радиу тельной и нормали,
сом-вс ктором.
Отрезок касательной Т от точки ка-
сания М до точки А пересечения ее
с осью х называется длиной касательной
(фиг. 4)
Отрезок нормали N от точки М до
точки В пересечения нормали с осью х
называется длиной нормали
N -МВ- — —
COS а
Подкасательная
S/ = прхТ = У Ctg а.
Поднормаль
Sn-npxN = ytg<x.
Для параметрически заданной линии
Г -Л КX't + у'». N-^т Yx'*+y-* •
S,-’4, S.-Л.
' у' ’ " *
где х', у' — производные от х(0. у (Г)
по Z и вычисляются для заданной точки М
при I = to-
При задании линии уравнением (1)
Т-^г Г1 + у'«; Д-З ‘ Л
У Х/У'
N = у У 1 + у'« ; -х'уУп*
- Л; sn = уу'. °\У / 7
Все отрезки рас- V»
сматриваются по фиг 5. По.,яриые
абсолютной вели- резки,
чине.
Если в точке М (г, ?) на кривой г =
= / (?) провести касательную и нормаль
до пересечения с прямой АВ, прохо-
дящей через полюс перпендикулярно
радиусу-вектору точки М, то (фиг. 5)
получаются так называемые полярные
отрезки касательной, нормали, подка-
сательной, поднормали, обозначаемые t,
П. «Г. «Л?
п- МВ--Р-------Кг«+Г'- ;
Sin р
St-OA = rtgp--^-;
а„ - OB - г cig р - г1.
Примеры'.
I) Для плрлболы у* — Чрх
Г - »'«<р + 2Х>; N - Уу + л> -
— Vpilx-i-py, St — 2л; Sn= р.
Во всякой точке плраболы у* = 2рх полнор-
мяль — величии* постоянная.
2) Для архимедовой спирали г — а?
аь УI + »; п = а V1 -у »•:
Во всякой точке архимедовой спирали поляр-
ная поднормаль есть величина постоянная.
ПЛОСКИЕ КРИВЫЕ
261
Углы касательной н нормали с осями
координат. Если положительное напра-
вление касательной (в сторону возра-
стания дуги s) образует с положитель-
ным направлением осн х угол а, то
dx , dv о
cos а = ; sin а = = cos 8,
ds ds
где p= ------а есть угол касательной
с осью у.
Положительное направление нормали
получается из положительного направле-
ния касательной поворотом последней на
угол — против движения часовой
стрелки. Угол а, положительного на-
правления нормали с осью х равен
“I = “ + -у;
cos ах
rfy . . dx
— . » Sjn 11 = -г-
as 1 ds
Асимптоты. Бесконечно удаленной
точкой на линии называется точка,
у которой одна или обе координаты
обращаются в бесконечность.
Асимптотой кривой в ее бесконечно
удаленной точке называется прямая,
расстояние до которой от точки на кри-
вой стремится к нулю, когда точка по
кривой удаляется в бесконечность.
Ветвь кривой, уходящая в беско-
нечность, но не имеющая асимптоты,
называется параболической ветвюо.
Если для кривой х = х(/), у = у(0
при I = t0, х (t0) » се, у (/0) = b + со,
тоу = Ь — асимптота, параллельная Ох;
если х (/ц) “ а + оо, у (/0) = со, то
х = а — асимптота, параллельная Ov.
Если х(1п) = оо, у (/0) — со, то асимп-
тотой (наклонной) в точке t = t0 на
кривой будет прямая
у — kx + b,
где
k - Um 2-LO. • b - 11m |y (/) — *x(/)|,
t-toX(l) t-h
если эти пределы существуют.
Для кривой у = Дх) асимптоты на-
ходятся так же, если положить х = /.
Если существуют пределы
(О
то у = kx + Ь, как предельное положе-
ние касательной в бесконечно удаленной
точке, есть асимптота.
В случае алгебраической кривой
F (х, у) = 0, где F (х, у) — многочлен
относительно х, у степени п, наклонная
асимптота у = kx -|- 11 находится по
правилу: в уравнение кривой вместо у
подставляют kx 4- Ь и в получен-
ном равенстве F (х, kx + b) = А^г” -+
+ A,x"~1 4- ... + Ал_,х + А, = 0 по
лагают Ао = 0, Ai = 0, откуда находят
действительные значения для k и Ь.
Асимптота, параллельная оси Оу, х=а,
найдется из уравнения F (я, у) = 0, в
котором коэффициент при старшей сте-
пени у приравнивается нулю н опреде-
ляется соответствующее значение я.
Для кривой г = /(?)?=?« опреде-
ляет асимптотическое направление, если
г = I (?с> = оо. Положение самой асимп-
тоты найдется, если еще знать расстоя-
ние р от полюса до этой асимптоты:
р = lim г sin (? — <fo).
Примеры:
1) Найти асимптоты алгебраической кривой
F(x. у) -з х' - ду 4- у - О; Р(х, Их 4- ft) = (I -
- Л) х' + (*-») X 4-Ь -0. Аа - 1 - к = 0; 4, =
с- к — Ь = О, откуда к = 1, 6 = 1; уравнение
асимптоты у = х -f I.
Для нахождения асимптоты х = в соегавляел
Ца, у) п (I -aty-f-a" =0.
В уравнении алгебраической кривой 2-го по-
рялкя отсутствует член у’. Приравняв нулю коэф-
фициент прн у, находим о = 1; кривая имеет
асимптоту X — 1. Нет асимптоты у =• Ь, парал-
лельной Ох, ибо при старшем члене х* коэффи-
циент ранен I.
2) На линии Xwj-^-р. у = беско-
нечно удаленные точки имеются при t, — I;
» — 1; t, — X со. Исслеломине концов ветвей дает
при 1=1 X — 4 оо, 1-тоо, *_||Шу=>
-ЙЛ7¥Т)-4’ 6-ilm'»-*x)-
- Л — t* 3
— Пт-----------—------- ; мы нашли наклонную
1-. । - (Г - О *
1 В
аси.мптогу у « — х---; при t» I + а х —
где Y — ордината точки асимптоты, у — орди-
ната точки липни (фиг. в); при t = — I,
I I
х =------j , у — ± оо, асимптота X =-— . при-
чем при / — —i 4-е, х > — , у-»4-оо(и<
< • - 0); 1 — - 1 - а. X < — — , у - — оо
(О < I - 0); при t - — оо, X - - оо, у - 1Г
оставаясь отрицательным; при t » -( оо, х -(- оо,
262
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
у - 0. оставаясь положительны»; получается одна
и та же асимптота у = 0 при Г — ± «а.
3) Гиперболическая спираль г = — имеет бес-
конечно удаленную точку в = 0, Ига г = со;
я-0
Фиг. 6 . Построение кривой.
асимптота параллельна полярной оси. Расстоя-
ние от полюса до асимптоты (фиг. 71
р = Ilm г sin р =
Фиг. 7. Гиперболическая
спираль.
Особые точки.
В особой
точке Af0(/0)
кривой (4)
(см. стр. 258)
одновременно обе производные: х’(/0)=
= 0, у'(/о)=О. Из этих уравнений
находится ta. Может случиться, что при
t = zo будет
с' - х' - х"' - .., - х0"-0 - 0;
х(м) ('о) + 0;
у' — у* — /" —... — — 0:
yw(f0) * 0.
Уравнение касательной в особой точке
х0 — х (/0). Уо — у «о): при п — т
Х — Ъ _ У —Уо .
г*")(/о) “ у<">(<0) ’
при п > т касательная параллельна Ох
у — Уо “ 0: при п < т касательная
параллельна Оу: х — ха = 0.
Обозначим наименьшее из чисел п,
т через k и составим выражение
S*+( - *<*у*-Н) _
где производные вычислены при t= 1л.
Пусть 5#+1 — “ $*+0—|=Ч
но 5А_|_р 0; тогда, если k — нечетное.
р — нечетное, то в точке Мй кривая
лежит по одну сторону касательной и по
разные стороны нормали; если k —
нечетное, р — четное, то Л1о — точка
перегиба: если k — четное, р — нечет
ное, то Мо — точка возврата 1-го рода
(фиг. 8); если k — четное, р — четное,
то /Мо — точка возврата 2-го рода
(фиг. 9).
Фиг. 8. Точка во»- Фиг. 9. Точка воз-
врата 1-го рода. ирата 2-го рода.
Только в двух последних случаях
окрестность точки Мл не является про-
стой дугой; точки возврата 1-го и 2-го
рода являются особыми точками кри-
вей (4)
Пример. Параметрические уравнения обыкно-
венной циклоиды -г — а (г — sin /); у —
— а (I — со» П: а — радиус образующего круга.
Из уравнений
X* «. а (I — соя Л — 0. у* = a sin t — О
находим общие корни
t — 2тж,
где т — любое целое число.
Вычисляем:
у—сом: »;-S4B,-«*os
число * — 2.
Вычисляем:
х'“ — а сов t: при t“ 2ms х " — а;
у'” — — о sin Г; при t у'" « 0:
составляем
= х"у"' _ у»х~ - о-о- аа - - о1 + О,
следовательно, р — 1. Точки при I — 2ms суть
точки возврата 1-го рода (фиг. 10).
Фиг. 10. Циклоида.
В особой точке кривой (2) одновре-
менно удовлетворяются три уравнения:
F(x. у) = 0; fx(x, _у) = 0; F^x. у) = 0.
ПЛОСКИЕ КРИВЫЕ
263
Если одна действительная пара реше-
ний этой системы (х0, у0) не обращает
в нуль хотя бы одну из частных пропз-
мр
водных 2-го порядка Fxx — — . Fxy=
<ГР d’F * .
= fad) * F” = df* •To TO4Ka Уо)
называется двойной (или двукратной).
Если для координат точки на кривой
нее частные производные до (п — 1)-го
порядка от функции F (х, у) равны нулю,
а производные л-го порядка не все ранны
нулю, то такая точка — п-кратная.
Уравнение совокупности касательных
и двойной точке (х0, у<|)
А(х — х0)« + 2В (х — ха) (у — ув) 4-
+ С(у-уо)2 = 0.
где А = Fxx (х„, у0). В = Fxv (х* yQ\
С— Fyv(x9, уо), представляет пару дей-
ствительных ’ разных, действительных
совпадающих или мнимых прямых в за-
висимости от того, будет ли дискрими-
нант Д — Вг — АС > 0, = 0 или < 0.
Угловой коэффициент этих касательных
определяется по следующей формуле:
о
Если Д>0, то точка (Xq, _Vq) назы-
вается /узловой с двумя касательными
(фиг. 11).
При Д < 0 точка называется изолиро-
ванной', вблизи этой точки нет других
Фиг. 12. Точка
самой ри косно
Кения.
Фиг. 13.
Точка само-
прик-снове-
инк.
I X
Фиг. II.Узлом»
точка.
точек кривой. При Д = 0 точка может
быть точкой возврата (фиг. 8 и 9),
точкой самоприкосновения (фиг. 12 и 13)
или обыкновенной точкой.
В трехкратной точке (хр, у») сово-
купность касательных к кривой опре-
деляется уравнением
(х Xp)*Fxt4r + 3 (х х0)*(у — y^Fxxy +
+ 3 (х — х0) (у - у0)3 Fхуу +
+ (У — yoJ’^yry - 0,
где частные производные от F (х, у)
вычислены при х = х0, у = у0.
Это уравнение дает или три действи-
тельные касательные (разные, совпа-
дающие), или одну действительную и
две мнимые касательные.
Если х0 = у0 = 0 является двойной
точкой алгебраической кривой, то урав-
нение не содержит свободного члена
и членов с первыми степенями х, у
и имеет вид
Ах- 4- 2Вху 4- Су* + £>х« +... = 0
Начало координат — двукратная точ-
ка; касательные в этой точке опреде-
ляются урявне.нисм
4х* 4- 2Вху 4- Суг = 0.
0
Примеры-.
I) Для уравнения уI * * * * * * 8 4-х*
Fx - 2х- Зх8; Fy - 2у; Fxx-2- fix:
Р =0: F =»2.
ху ' гуу
В особой точке х = у — 0 производные 2-го по-
рядка ранны: Л = 2. В = О, С = 1. Так как к —
— — 4, то начало координат является нзолироваи-
Фиг. 14. Изолнро- Фиг. IX. Узловая точка
ванная точка кри- лемнискаты 2а‘ (х8 — у8) —
вой у8 4-х’ — х* — — (Х‘ 4-/’г “ °-
>0.
ной (особой) точкой. Форма кривой (фиг. 14) опре-
делится исследованием явного уравнения у =»
- ± Ул* (х — I). Прн 0 < X < 1 соответствую-
щие у — мнимые.
2) Для лемнискаты Бернулли 2я8 (х8 — у8) —
— (х8 4- у8)* = ч начало координат является у в то-
вой точкой, так как Д > И. Совокупность каса-
тельных в агой точке определится из уравнения
Фнг. 16. Точка самоприкос-
новения кривой V8 — 6х8у 4-
4- fix' - X* - 0.
х8 — у* — 0: в начале координат — две действи-
тельные касательные у “ х. у = — х (фиг. 15).
Кривая симметрична относительно осей коор-
динат. Полярное уравнение етой кривой г* —
— 2а8 cos 2» показывает, что 0<r<a/fi
кривая замкнутая.
3) Для кривой у8 - 6х*у 4- 8х* - х* - 0 начато
координат — особая точка; Д — 0. Совокупность
264
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
касательных и «той точке: у> — 0, т. е. ше со-
ппалаюшие с осью Ох прямые. Исследование
явных уравнений
у =. х» (3 4-УI -f-х); у = х>(3- VT+*)
пока:'ымст, что обе веган лежит по ому сторону
касате-<ы<ой (так как при | х | < I, у > <>). Осо-
ба» точка — точка самоприкосновения (фиг. (б).
4) Для кривой ах (х* — у‘) — (х’ 4- у‘р = 0 на-
чало координат — трехкратная особая точка, так
как в уравнении отсутствуют члены ло 2-го по-
рядка включительно. Совокупность касательных
Фиг. (7. Трехкратная точ-
ка кривой ах (х‘ — у*)—
-и» -|- ^)« = 0.
в начале координат
определится уравне-
нием д’(д’— у»)®0.
Уравнение распадается
на три уравнения:
X » 0, у — дг, V — — Д'.
Кривая симметрична
(л нигнтелысо Ох. Урав-
нение кривой в поляр-
ных коорхиилгах г о
« а сох ф сох 2ф пока-
зывает. что кривая за-
мкнутая (фнг. 17).
Другие особые точки, кроме рассмо-
тренных, могут быть, если нарушается
непрерывность функций или производ-
ных функций, входящих в уравнение
кривой.
Если при движении по кривой у =
= / (х) функция после прохождения
через точку (х0, уа) перестает существо-
вать или становится мнимой, то эта
точка называется точкой прекращения
или точкой остановки-, например, кри-
вая у = х In х имеет в начале координат
точку прекращения (фиг. 18).
Фнг. 18. Точка Фиг. 19. Угловая
прекращения кри- точка кривой
пой у — х In х. у в 4-«'/Х).
Точка на непрерывной кривой, в кото-
рой направление касательной претер-
певает разрыв непрерывности, назы-
вается угловой.
Уравнение у —---------— содержит
1 + ех
1
функцию ех , которая имеет разрыв
при х ™ 0. Сама кривая непрерывна,
</у
но имеет разрыв непрерывности
при х “ 0 (фнг. 19).
Алгебраические кривые не имеют ни
угловых точек, ни точек прекращения.
Выпуклость, вогнутость, точки пере-
гиба. Пусть касательная в точке
М (х, у) кривой у = f(x) не параллельна
Оу; вблизи точки М кривая имеет
вогнутость в сторону 4- у, если точки
yi), достаточно близкие к точке. М
с обеих ее сторон, находятся по одну
сторону от касательной в точке М,
причем для одной и той же абсциссы х
ордината кривой больше ординаты
касательной. Вогнутость в сторону 4- у
характеризуется условием > О
(фиг. 20).
Аналогично определяется вогнутость
в сторону — у, характеризуемая уело-
вием < 0. Вогнутость в сторону
4-J при у > 0 есть
в то же время вы-
пуклость к оси Ох
(условие уу' > 0), а
вогнутость в сторо-
ну 4- у при у < 0
есть вогнутость к
оси Ох (условие
уу'<0). Точка на
кривой, в которой
Фиг. 20. Вогнутость
в сторону 4- У-
вогнутость в одну сторону меняется на
вогнутость в другую сторону, назы-
вается точкой перегиба. В этой точке
касательная пересекает кривую. Зна-
чение х точки перегиба кривой у =/(х)
находится из условия у = 0, если
у* 0. В общем случае в точке пере-
гиба
у* " в ... » у»2*» — 0; у(’*4-Ч у, о.
Если касательная параллельна Оу, то
точки перегиба находятся из уравне-
d*x „
ния —— = 0
dy1
Для кривой х —х(0, у —• у (0 значе-
ния I, соответствующие точкам пере-
гиба, находятся из условий х'у" —
—/ = °- Х'У" — х,ну' +
Для кривой /'(х, у) = 0 возможные
точки перегиба определяются условиями
F(x. у)—0; О
(F,P Fxx ~ 2PxF,Fxy 4- (fx)1?» - 0-
Примеры-.
1) Найти точки перегиба параболы 5-го порядка
У — х 4- л‘:
у - 14- 5х‘; у* - 20х»; у™ — flux’;
— lau; yV _ Jau>
ПЛОСКИЕ КРИВЫЕ
265
И» уравнения у" = 2UX1 — и находим х = О, и
так как все производные до 4-го порядка вклю-
чительно равны вулю при -г = О, во у * О, то
начало координат — точка перегиба.
В промежутке 0 < х < оо кривая обращена
вогнутостью в сторону -I- у. в промежутке — оо <
< X < 0 — в сторону — у.
2) Для нахождения точек перегиба кривой
(X* т У")’ — 2®’ (X2 3 4 s — У’) = Ь* — а' (овал Кассини)
вычисляем:
Fx = 4x(x«4-y’-e’):
/5>-<у (^4-у’4-о’);
•хх = 4(3х«4-у’-"’):
>j,»«xy;
Фиг. 21. Овал Кассини, р = 4 (Зу’ а1).
Условия (•) принимают вид:
(л14- У’Р - 2«’ (X* - У’) ~ »* 4- о* - °-
((х* 4- У’У - «‘I [<-*’ + У*)* - о’ (X* - У‘)1 4-
4- йп‘х*у’ = 0;
из этих уравнений находим
получаются четыре точки перегиба, дейсгштлъ*
иые при условиях
откуда
а /2 > Ь > а (фиг. 21).
Исследование и вычерчивание кривой
по уравнениям х = х(/), у = у (/) про-
изводятся по следующей схеме.
1. Находят дифференциальные эле-
менты: производные х , у', х“, у', х”, ум;
dy у' (Ру _ у“х' — х"у'
dx ““ х' * dx‘ “ х'»
2. Находят бесконечно удаленные
точки кривой, т. е. значения t, при
1л 1л
которых ——- = 0 или —= 0.
„ „ y(t)
3. Находят асимптоты.
4. Определяют экстремумы х и у.
5. Находят пересечение кривой с
осями координат.
6. Определяют t, при которых воз-
можно изменение знаков параметриче-
ских производных, т. е. такие значе-
ния t, при которых х'(0 = 0. У'(О — 0.
7. Строят шкалу переменной t и
таблицу изменения х, у по определен-
ной схеме (см. пример на стр. 265—266).
8. Находят особые точки.
9. Находят вершины кривой (см.
стр 268).
10. Находят точки перегиба.
II. Находят дополнительные точки,
например узловые, т. е. находят такие
(0, б. при которых х (1J = х (/1), у (/о) =
= У(Ь).
12. Построение схематического чер-
тежа надо начинать с вычерчивания
бесконечно удаленных ветвей, а затем
от точки при /= —оо пройти по всем
интервалам изменения t в соответствии
с таблицей и закончить точкой I = 4- оо.
На кривой стрелками указывают на-
правление обхода.
Пример. Исследовать форму кривой X ~
Р !
“ Г - I ’ У ~ Р — Г
Вычисляем
т а - 2).
(< — >)•
У'
С» —1 .
(/•-О'*
tfy Р I
ах"~ ~ /«_ 2)« + !)'•
Бескоисчио улалениые точки / =±1, Т=±оо
и асимптоты найдены выше (стр. 261). Для каждой
из функций х, у. х', у' находим те значения I,
при которых пи функции обращаются в и или
я оо:
х = 0 при г = 0;
у = О . Г = 0; / = ± оо,
х' = 0 . t — u, t — 2;
у' = О . I — ± оо;
х = ± оо при t = 1;
у — ± оо . /« х I;
х' = — оо . r= I;
у' = — оо , г = ± 1.
Имеется экстремум х при г-0 и при / = 2;
в этих точках касательные параллельны осн у и
кривая лелеет поторот. Составляется чертеж
(см. фнг. б); аля этого соелнняотся плавными ли-
ниями бесконечно ужаленные «етви и отдельные
точки с укатанном направленна движения по
кривой от t = — со.
266
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
IUiui переменкой t (ось Г).
Таблица изменения х и у
t Г У
7 о - « | 8 •• о — «4 Т 1 + 4- 4- В охр. от -со до —Ча • • — ‘Ii ДО 0 Убыв, от 0 до —оо . > 4-оо до 4 Возр. от 4 до 4-со Убыв, от U до —со • • Т00 *0 0 , 0 до —со 2 . - 4-оДО j . . -j до 0 Асимптота у — 0 прн t — ± оо Асимптота х — — ‘|t при Г = —1 1 3 Асимптота у - — х —- прн Г = 1
Точка самопересечения ветвей кривой в про-
межутках — оо < 4 < — 1 и 0 < Г, < 1 находится
из уравнений (см. и. 11 схемы исследования)
t I
Z. _ z, 6 _ А .
—1 <.-»'/_! /_1
I в
Если разделить второе равенство па первое,
то получается Г* — Г — Г, — t, или после сокра-
щения (I. * Q
«. + *. —-1.
Если первое уравнение преобразовать к виду
/АЛ-4)
то после сокращенна получается
1.Г. • /, 4- /. или Г.4 « — I.
Следовательно, /, и I, удовлетворяют кваарат
ому уравнению
«• + < — 1— 0.
Кории
, — 14-/!
4--------j--nt,- — --------
Соприкосновение кривых. Две кривые
у=Цх) и у=<?(х) имеют в общей
точке (Др, уо) соприкосновение л-го
порядка, если
/(•*в) - ? («•);
/’ (Jfo) - Г’ (-«о);
Если одна кривая дана уравнением
F (х,у) = 0, а другая — уравнениями
х = х (I), у = y(t), то условия сопри-
косновения л-го порядка в точке (/=/©)
имеют вид
<р (4) - 0; Ф' (4) = 0; Ф' (4) - 0.
Ф^/о) — о, ф(«4-1> (tj ф о,
где
Ф(0-Е|х(П. у(/)|-
Пример. Найти окружность, которая в точна
х« — — ок, у0 = 0 имела бы соприкосновение
л-го порядка с архимедовой спиралью г — оу.
Обшее уравнение окружности х* -f- у’ -f- 1Лх 4-
+ ЪВу 4- С — 0 содержит три параметра: А, В. С.
Составляем Ф =. Xs + у* -j- /Ах + 2Ву + С. где
надо заменить .г ж ay cos ». у = оу sin у (уравне-
ние спирали), причем я = «. Вычисляем
Ф' “ 2 \хх' 4- уу' 4- Ах' 4- By') = 0;
-2 |х*’ 4- у'*4-хх* 4- уу* + Ах* 4- Ву*|-0;
кроме того.
ф - х* 4. у«4- 2А х 4- 2Ву 4- С - О.
Вычисляем х. у. х’. у', х*. у* прн у — я, и
прелыхущне уравнения принимают вид
о*ч‘ — 2окА 4" С — 0;
с’я — а А — акВ “ 0;
о 4- А«-гв-а
откуда
оя п“<'4-«'1 .
искомое уравнение окружности
(2 4- я»)(X* 4- У*) 4- 2акх 4- 2а (I 4- «*) У — »*“0-
Соприкасающаяся окружность. Кри-
визна линии, радиус кривизны, центр
кривизны. Окружность (х — в)1 4- (у —
— />)*= R*. имеющая с кривой х=х(/),
у = у (/) соприкосновение в точке х, =
“ х (/(Р, уо = у(/о) 2-го порядка (или
ПЛОСКИЕ КРИВЫЕ
267
выше при некоторых значениях Zq), на-
зывается соприкасающейся окружностью
(круг кривизны). Ее центр (а, Ь), на-
зываемый еще центром кривизны, и
R — радиусом кривизны, находят по
формулам
Для центра (а, 6) кривизны
//у
а =х — Rsina =х----------;
da
. . dx
b — у + R cos а — у + —.
Центр кривизны лежит на нормали
кривой в сторону ее вогнутости. Если
Л>0, то центр кривизны лежит иа
положительной части нормали.
Кривизна в каждой точке прямой
линии постоянна и равна нулю.
Кривизна в каждой точке окружности
с радиусом R постоянна и равна по
абсолютной величине ——.
R
Для кривой у= /(х):
Примеры:
1) Для обыкновенной циклоиды (фиг. 22)
х = а (Г — sin О, у — а (1 — сва /)
R - (-- -+-/*) ’ .
У
Для кривой F(x. у) = 0:
радиус кривизны
R — — 4а | sin -i-1 .
Знак минус указывает, что центр кривизны
всегда находится на отрицательной части нормали.
Координаты (х„ у,) центра кривизны
х, = a (t -|- sin О. у, = — а (1 — cos f),
и так как у, = — у, at — х = х, — at, то центр
кривизны С и точка М кривой симметрично рас-
положены относительно точки Л на прямой МАС.
Фиг. 22. Длина нормали и радиус кривизны ци-
клоиды.
77 — FyFrt ~ 2FxFyFХу + /• уу.
Для кривой г = / (f):
о (rt + г'2)
R~ ^ + 2^ -
Величииа К " -рг называется кривиз
• V
ной кривой. Если а — угол касатель-
ной с осью Ох, Ла — угол между каса-
тельной в данной точке и касательной
в соседней точке, As — длина дуги кри-
вой между этими точками, то
4д-0 As ds
Радиус кривизны равен удвоенной длине нормали:
R • МС *2ЛМ
2) Ралнус кривизны логарифмической спирали
г — вкя*'Р:
г' ~ атет* “ те, г* — ат,ет'е » яг'г;
радиус кривизны
R-rVl-pm',
т. е. в каждой точке логарифмической спирали
радиус кривизны пропорционален радиусу-вектору
точки.
Для нахождения координат (х„ у,) центра кри-
визны составим параметрические уравнения лога-
рифмической спирали:
х — аете cos у; y»aem*stny;
х’ «1 ас'"? (т еоа у — sin у);
у' _о,тя ;т ,|0 * -|-cosp);
268
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
х* — аега^ (лг; cos в — 2т sin » — cos у);
у* — ает? (m* sin ? 4- 2т cos о — sin у К
х’*+ у'* («* 4- I) а*»21"? ;
х'у' - ух* - «п* 4- 1) а**2"»»:
X, — — ает* т sin у; у, - <ит? т cos у.
Дм каждой точки (х, у) логарифмической спи-
рали координаты (л,, у,) центра кривизны легко
построить по формулам
х, — — ту; у, — тх.
Для построении нормали в точке (л, у) спирали
пало соединить точки (л, у) и (л„ у,). Для по-
строения касательной к спирали надо к построен-
ной нормали провести перпендикуляр а точке
<Х. у).
Вершина кривой. Обыкновенная точ-
ка (не особая) кривой, для которой
радиус кривизны достигает максимума
или минимума, наибольшего или наи-
меньшего значения, называется верши-
ной кривой. Соответствующие значе-
dR
ния t находятся из условия — = О
и исследования R на наибольшее или
наименьшее значение.
В вершине порядок касания соприка-
сающейся окружности с кривой выше
двух.
Точка пересечения кривой с осью
симметрии (если точка обыкновенная) —
вершина кривой.
Пример. Для циклоиды /? = — 4а *1п ,
dR . t t п
— = — 2а сов —- ; при сое — = 0, т. е. при
/ = (2й 4* ) < (* — любое целое число). циклоида
имеет вершины (фиг. 2Z).
Натуральное уравнение кривой есть
соотношение вида F (R, s) — 0 или
R = f (s); оно определяет псе свойства
кривой, кроме ее положения на пло-
скости.
Натуральные уравнения некоторых
кривых:
а) окружности (стр. 242): R = а —
= const;
б) логарифмической спирали: R — ms;
в) эвольвенты окружности: R* = 2as,
где а — радиус окружности;
г) циклоиды: /?*4-д*= 16а’;
$з
д) цепной линии: R — a -f- — •
Семейство линий. Дискриминантная
кривая. Огибающая- Уравнение
F (х, у, с) = 0 определяет одиопара-
метрическое семейство линий; каждое
значение с выделяет из семейства инди-
видуальную кривую (фиг. 23). Система
уравнений
F (х, у. с) - 0. - - 0
при некотором с определяет так назы-
ваемую характеристическую точку на
выделенной кривой (с) из данного се-
мейства.
Характеристическая точка на кри-
вой (с) вообще является предельной
для точки пере-
сечения кривых (с)
и (с 4- Дс) при
Дс-ь 0.
Координаты ха-
рактеристической
точки зависят от фМг. 23. Огибающая,
с :*х=х(с), у=у(с).
При переменном с геометрическое место
характеристических точек определяет
дискриминантную кривую. Неявное урав-
нение дискриминантной кривой можно
получить, если исключить с из F — 0,
“ 0. Если точка |х (с),> (с)] является
обыкновенной точкой кривой семейства
(F, существует и -И*0). то дискрими-
нантная линия касается кривой се-
мейства в этой точке (фиг. 23). Если
точка (х (с), у (с)) является особой точ-
кой. то касание не всегда бывает
Дискриминантная кривая или ее
часть, касающаяся каждой своей точкой
соответствующей кривой семейства, на-
зывается огибающей семейства.
Примеры;
I) Семейство кривых (у 4-е)* — (х 4-е>* полу-
чилось параллельным переносом полукубической
параболы у* = л*. острие которой перемещается
по прямой у - X. Системе
F -О: /*г = 2(у 4-е)-»tx -t-ef-u
рмпзаается на лее системы-
F~0; Ж 4-е “°
и
Г-О; ж + е--у.
Дискриминанта* линия состоит из двух ветвей:
в) х - — с; у — — с или у - х;
4 8 4
ЫЖ---Г, у-^-еклиу-х--.
Кажи* точка перной ветви является осо'юй
(точка возврата l-то ролл) точкой кривой семей-
ПЛОСКИЕ КРИВЫЕ
269
ствв. Угловой коэффициент и точке (с. с) касатсль-
ной к первой ветви дискриминантной линии ра-
вен 1, а угловой коэффициент касательной в той
же точке на соответствующей кривой семейства
равен нулю. Прямая у = х не является огибаю-
щей. Вторая ветвь является огибающей. Дискри-
точку, координаты (х, у) характерней)
ческой точки находятся из системы
минантная кривая
состоит из огибаю-
щей к геометриче-
ского места особых
точек (фиг. 24).
X = X [t. с); у = у (/. с);
дх ду
()с дс
дх ду
dt dt
0.
Фиг. 24. Дискриминантная Фиг. 23. Огибаю-
линия семейства кривых шаясемсйствакри-
(У тсЕ = (л -|-ср. вых у* = ( х 4-е)’.
dt
Из последнего равенства
один параметр через другой: t = t (с).
Дискриминантная кривая определится
уравнениями
х - х (б(с). с); у-у(/(с). с).
Пример. Найти огибающую семейства окруж-
ностей
выражают
2) Семейство у! — (л 4-ср имеет огибающую
у=0—ось Ол, состоящую нз особых точек кри-
вых семейства (фиг. 25).
3) Уравнение (л — ср 4- У’ = I — с* определяет
семейство окружностей, диаметры которых
ЛЯд.Ол являются хордами окружности
(фиг. 26). Система F=0, F — — 2 (л - с) 4- йг= 0
определяет характеристические точки л — 2с.
у’= 1 — 2с1, откуда получаем огибающую
г’
2
+ У’ “ 1. т. е. эллипс с полуосями tG и 1; при с,
близких к единице, эллипс не будет касаться
соответствующих окружностей из данного семей-
ства (фиг. 26).
(Х-хУ4-(Х-уУ = о*
постоянного радиуса а, центр которых (л, у) дви-
жется по заданной линии л = л(с). у=у(с).
Огибающая называется эквидистантной кривой
(или параллельной) заданной линии.
Уравнение семейства окружностей
(X- ж ЮГ+ | Г-У (*)]• = «•
можно переписать в параметрической форме:
X=х (с) -|- а со» I;
у = у (с) 4-a sin/,
где X, У — текущие координаты точки на окруж-
ности. Уравнение
ОХ
Ос
ОХ
Of
ОУ
Ос
ОУ
Of
о
Фиг. 2й. Огибающая
семейства окружностей
(л — с)14- у> — I — с’.
откуда
tR t
принимает пил
х* см / + у' sin / - 0,
со» I =-----
•in г
искомая огибающая состоит из двух ветвей:
Фиг. 27. Дискриминант-
ная линия семейства
кривых у*—(х4- с)*—0.
X
У
4) Каждая кривая семейства F-y*-(л4-ср=0
имеет точку перегиба, лежащую на Ох. Прирав-
нивая F нулю, получим — 3 (л 4- <•)* = 0 или
л 4* с «• о.
Дискриминантная кривая у = 0 нс является
огибающей? она — геометрическое место точек
перегиба, в которых 6^,-0 (фиг. 27).
Для случая задания семейства кри-
вых параметрическими уравнениями
х = х (6 с), у = у (б, с), где с выделяет
из семейства определенную кривую,
a t выделяет на кривой определенную
Эволюта. Эволютой илн разверткой
данной кривой х = х (0,у = у (0 назы-
вается геометрическое место центров
ее кривизны (х,, yi). Параметрические
уравнения эволюты (см. стр. 267).
Уг = У +
х'-’+у'2
Х'у’-у'х' Х-
Нормаль в каждой точке М (фиг. 28)
данной кривой есть касательная MN
270
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
к эволюте в точке N (xi, yi) (центр кри-
визны):
=_____1_
dxj dy
dx
Эволюта кривой есть огибающая ее
нормалей. Приращение дуги а эво-
люты равно приращению радиуса кри-
визны R кривой:
'-'WjWI=|s2 — oj | = | Rz — #il
'I = IrfRI-
Вершинам данной
кривой соответствуют
на эволюте точки
возврата (фиг. 29).
Фиг. 29. Вер-
шима кривой.
Радиус кривизны р эволюты:
р
R^-
ds
где з — дуга данной кривой.
Примеры:
1) Эволютой циклоиды будет кривая
х, = а (/ 4- sin О: у, = — я (1 — cos 0-
Если ввести новый параметр и. топо-
лучим
X, » а (/, — sin 6) — як; у, • а (1 — cos Г,) — 2а.
Эволюта циклоиды есть такая же циклоида, по
смешенная по оси Оу впил на 2а (диаметр обра-
зующего круга) и оо оси Ох на ак (фиг. 30).
Фиг. 30. Эволюта циклоиды.
2) Эволюта логарифмической спирали r — aeп^',
изобразится уравнениями
х, — — яте”1* sin «; у, — amemf сов у.
Если ввести т, «ф + — и обозначить а, —
к
-<П-Т
•" ате ‘ , то предыдущие уравнения примут
вид:
х, — я1ея,Ч,| сое р(; у, — а,ет9< sin у,.
Эволюта логарифмической спирали — такая же
спираль г,~- а,ет^, полученная из первой вра-
щением вокруг полюса против часовой стрелки
на угол и изменением радиуса-вектора в т раз.
Эвольвента. Эвольвентой или развер-
тывающей данной линии NaNt назы-
вается кривая МаМа, эволюта которой
есть данная линия (см. фиг. 28). Если
xi = xi (о),_ут = yi (о) — уравнения дан-
ной линии N0Nt, где о — длина ее дуги,
то уравнения эвольвенты будут иметь
вид
* = Х|(я) — (о — Со) —;
У = У1(°)— (о — ®о)
где о0 — постоянная величина, длина
дуги эволюты, которая определяет по-
ложение точки Na. являющейся общей
для эволюты и эвольвенты. Меняя а0<
получаем бесчисленное множество
эвольвент с одной и той же эволютой.
Построение эвольвенты: на каждой
касательной к данной линии (в текущей
точке N) откладывается в отрицательном
направлении отрезок NМ = о NNa =
= о — а0. Конец (точка М) опишет
эвольвенту (или развертывающую) дан-
ной линии.
Эвольвенты ортогональны касатель-
ным эволюты. Расстояние между двумя
эвольвентами по нормалям к
стоянно, поэтому эвольвенты
той же эволюты обра-
зуют параллельные (эк-
видистантные) линии
Пример. Эвольвенте окруж-
ности х + у — я1. По окруж
пости от точки N„ (фиг. 31)
отложим лугу A'JV — at. He
касательной и точке N отло-
жим отрезок NM — at. При
качении касательной по окруж-
ности точка М опишет еноль
ним по-
одной и
Ai
Фиг. 31. К при-
меру об вволь-
пейте окруж-
ности.
центу окружности. Координаты
точки Л: х, •• a cos t; у, — я stn г; о — at; ах, —
— — я sin t dt; dy, ••я cos Г dt; de — a dt; при от-
счете «от точки N. о, — 0. Уравнении вволькенты
rfx,
do
|cos t +1 eln /|:
а
У-У> — |sln t — /сов If.
Эвольвенту окружности иногда мдаива ют раз-
верткой круге.
ПЛОСКИЕ КРИВЫЕ
271
Траектории Траекторией кривых не-
которого семейства называется линия,
пересекающая все кривые семейства
по некоторому закону.
Изогональной траекторией семейства
кривых F (х, у, с) = 0 называется
линия у = / (*), пересекающая кривые
семейства под постоянным углом 7.
Углом между линиями называется угол
между касательными к ним в их точке
пересечения. Если X. Y текущие коор-
динаты изогональной траектории, то
gT \dX dx } Д1 + dX dx )•
Изогональные траектории опреде-
ляются дифференциальным уравнением
Р.\
+ т-р;)
dY
dX
_ m - О,
I
+
где постоянная т = tg 7, в производных
Fx, F х заменены к, у на X, У и, нако-
нец, параметр с исключается при по-
мощи данного уравнения F (X, Y, с) «= 0.
Ортогональная траектория пересе-
к
кает кривые семейства под углом 7 = -у
Дифференциальное уравнение ортого-
нальных траекторий получится исклю-
чением параметра с из системы урав-
нений
dY Fr
F(X. У. с)=0; | =0.
dx r v
Эвольвента кривой есть ортогональная
траектория касательных к этой кривой
Пример. Линия, пересекающая ясе прямые
пучке, исколяшие из начала координат, у —ст-о,
пол углом г = сопм есть
логарифмическая спираль
(фиг. 32).
Дифференциальное урав-
нение принимает кил
(X- mY)dY- (л»Х +
•ф К)</Х —0.
Фиг. 32. Логариф-
мическая спираль.
Это олноролное урание-
ние 1-ю порядки решается
полстаиопкой К-кХ и
имеет общий интеграл
I - z
„ т' ,,С1« Т
• Се т х.
VX‘ 4- У*
В полярных координата!
г - Се* С,К Т-
Образование линий при движении
плоскости по плоскости (рулетты).
По неподвижной центроиде С (центре-
идей или полодией называется геоме-
трическое место мгновенных центров
вращения плоской фигуры, движущейся
в своей плоскости) х = х (t). у — у (О
в плоскости П катится без скольжения
подвижная центрои-
да С, данная уравне-
ниями* = *(/),
— >(0 относительно
системы координат
хОу в плоскости П,
жестко связанной с С
(фиг. 33), поэтому
<sAaA = о Л„Л; если
началу дуг Ао на С
соответствует I = 10,
на С соответствует /
а
началу дуг Да
то
/ Кх’* T7'dt- • + y4dt. (7)
*• £
Если (и, р) — координаты точки М
в плоскости П относительно хОу, то
для координат X, Y этой точки в пло-
скости П относительно хОу имеем фор-
мулы:
Х-гМ+^*-,
где
, _ <и —х(Й) dx+ (о —y(7))rfy
ds
(v — y(l})dx — (u — x(i))dy
Т] — -------_=-------;
из двух параметров Г и Г остается один
в силу зависимости ds = ds или (7).
Уравнения (8) определяют траекторию
точки М по плоскости П, называемую
рулеттой.
Если в плоскости П (вместо одной
точки /И) дана кривая L: и= и (т), о —
= и (т), то при движении П по П полу-
чается в плоскости П семейство кри-
вых параметрами являются t иг
или t и з.
272
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Примеры;_
1) Прямая С. принятая за ось Ох. катится по
окружности С: д’ 4- У1 = Я*-
Параметрические уравнения нейтрона:
С : х — R sin t; у R cos Г, dx — R cos t dt',
dv « — R sin t dt; s = Rt; ds = R dt;
C ; x = 7; у = 0; dx=> dt; dy = 0; 5 — ft
ds=~ dt.
Прямая С, называемая производящей, обкаты-
вает окружность С по часовой стрелке, параметр t.
определяющий положение С. отсчитывается от
оси Оу по часовой стрелке (фиг. 34). По формуле
Фиг. 34. Качение пря-
мой по окружности.
Rt = t н по форму-
лам (9) вычисляем
5 - и — Г» и — Rt;
1)-О.
Траектория точки
М(а, ») в плоскости П
определяется относи-
тельно хОу уравнени-
ями (8):
X = (R+p) sin /ф
4- (а — Rt) cos t;
У — (R4-v) cos t—
— (a — RO sin t;.
(K>)
полученная рулетта называется явольвентой ок-
ружности (обыкновенной, если 41 на прямой &,
укороченной прн v > О и удлиненной при v < 0).
Уравнения обыкновенной эвольвенты прн и — О,
и •= 0 (траектория точки О) имеют вид
X — R (sin t — t cos t);
У = R (cos 14-1 sin t).
Чтобы получить уравнения эвольвенты при ка-
чении (Г по С против часовой стрелки и с исход-
ной точкой А, на оси Ох, следует рассмотреть
траекторию точки М, (и — —R, a-о) и мм«-
иить-у — /«/’; получим
X = Rfcos f 4* f sin /');
К— R(sin f — V cos 1')-
При u=a (т).р=т>(т) получаем кривую Т в пло-
скости П; уравнения (10) определяю* семейство
этих кривых в плоскости П при движении П по П,
осуществляемом качением прямой С по окруж-
ности С.
2) Окружность радиуса г (центроида С) катится
без скольжения по прямой С. принятой за ось Ох
в плоскости //. При расположении осей н цен-
троид на фиг. 35 получаем:
для С:
х = ft у = 0; dx = dt; dy — О; s = t; ds = dt;
для C:
x “ r sin 7; у = л(1 — cos 7);
dJr = rcos7d7; dy = л sin 7d7;
a = л 7; ds=*rdi; rt ~ I.
Находим
£ = и cos 7-f- (p — r) sin 7;
t) = (p — r) cos 7— a sin 7-|-r.
Уравнения рулетты будут иметь вид:
Х-х 4- Е = г (7— sin ft 4- и cos 7-f- Р sin ft
У = ц = г (1 — cos t) -f- v cos t — и sin 7.
(11)
Рулетта (11) есть циклоидальная кривая; обык-
новенная циклоида для точки Л1 на С, укорочен-
ная циклоида для точки Л1 внутри круга С и удли-
ненная циклоида для точки Л1 вне С.
Уравнения траектории точки 5 («=• 0, р — 0):
Х = г (7— sin 7). У = г (1 — cos t).
В начальный момент системы хОу и хОу сов-
падают. Если и = и (т). v *»р (т) —- уравнения кри-
вой Д в плоскости П, то уравнения (II) опре-
деляют семейство Д при движении П по П. осу-
ществляемом качением крута С по прямой С.
3) Окружность радиуса 7 (центроида С) катится
без скольжения по окружности радиуса R (це»-
троида С) (фиг. 36).
Уравнении цен-
троиды С
х — R sin ft
у а» R COS ft
Уравнения цен-
троиды С
х — г sin 7;
у - г (I — cos 7).
Уравнения ру-
летты точки Л((и.»)
(эпициклоиды) име-
ют вид
X — (R 4- л) sin 14- (р - г) sin (» 4" 0 +
4- и cos (/ 4- 7);
У = (R 4- л) cos л 4- (р — л) сое (( 4" 0 —
— a sin (/ -|- 7),
где R! > л7. При качении окружности С по вну-
тренней стороне С (штрихпунктярная окружность
ПЛОСКИЕ КРИВЫЕ
273
н< фиг. 36) уравнения рулетты (гипоомклонш)
имеют аил
X = (/? — г) sin I + и со» (1 — 0+
+ (?+/) sm (/ — о;
Z- (R — г) cos I — и Sin (f — О +
+ (С + г) со» (/ — ъ.
гм Rt - ri.
Если а — и (т), v “ в (г) — уравнения кривой t
в плоскости П, то уравнении рулетт лллут урав-
нения семейства кривы» 1. при укамшаом дви-
жении П по П.
В вопросах плоского зацепления и
в теории инструмента кривая L и оги-
бающая семейства L называются взаим-
но сопряженными кривыми. Для полу-
чения огибающей надо к предыдущим
уравнениям семейства присоединить
уравнение
дХ дУ
dt dt
дХ дУ
~дГ~дГ
= 0.
чем устанавливается связь т и t (или т
и I) и на каждой кривой L выделяется
соответствующая характеристическая
точка.
Кривые, употребительные в технике.
1. Конхоиды. Конхоидой для ос-
новной (направляющей) кривой отно-
сительно некоторой точки О называется
4?________
X
Фиг. 37. К образсминню
конкомаы прямой.
геометрическое ме-
сто концов отрезка
постоянной дли-
ны Ь, откладывае-
мого от точек М
основной кривой
по лучам из точ-
ки О (фиг. 37).
Пусть точка О—
полюс, уравнение
направляющей кривой г = /(?), тогда
уравнения конхоид будут иметь вид
где г,?— полярные координаты Vohkh М;
р, f — полярные координаты точек Mi
илн Mi.
Свойства:
1) направляющая и ее конхоида имеют
одну и ту же поднормаль
" df df *
2) угол рц между касательной и ра-
диусом-вектором точки конхоиды на-
ходится по формуле
dr
tgu _ г .
tgf*i "г+Р
3) в приложениях к инструменталь-
ному производству угол а между пер-
пендикуляром к радиусу-вектору и каса-
тельной к кривой называется углом
. в _
задней заточки: а“ Для кон’
в
хонды соответственно «1 = у —
свойство второе можно переписать
tg »i г
виде 1 -= —.
tga р
Наиболее употребительные конхоиды:
а) Конхоида прямой (или Ннкомеда).
Уравнение направляющей (прямой OiAf)
Фиг. 38. Коихсиш пря-
мой с узлопоП точкой.
Фиг. 39. Конхоим
прямой с точкой
возврата.
г = —(фиг. 38). ее конхоида р «=
cos ?
— а— + Ь (Ъ > О). В декартовых ко-
сое f
ординатах получается кривая 4-го по-
рядка:
(х* + у2) (х — в)* — — 0.
Конхоида состоит из двух ветвей, ко-
торые асимптотически приближаются
к направляющей, и имеет в полюсе
особую точку: при Ь > в — узел (фиг. 38);
при Ь = а — точку возврата i-го рода
(фиг. 39); при Ь < а (штриховая линия
на фиг. 39) — изолированную точку.
Если начало координат перенести
в точку 0>, то уравнение конхоиды пря-
мой примет вид
x»y»-(x + a)«(ft»-x«)
или
У - ± У
18 Том I
Зм. 11Ы.
274
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
б) Конхоида окружности с полюсом
в одной из ее точек (улитка Паскаля).
Из уравнения окружности с радиусом а
(фиг. 40) г = 2а cos <f> получаем уравне-
ние конхоиды окружности относительно
точки О:
р — 2-1 cos <р ± b (Ь > 0).
В декартовых координатах получается
замкнутая кривая 4-го порядка
(хг + уг _ ах)2 = (xi -I- у»)
начале координат
с особой ТОЧКОЙ .8
Фиг. ТО. Конхоида
окружности (4а >
> Ь > 2а).
Фиг. 41. Конхо-
ида окружности
(Ь > 4а).
При 2а<б<4а полюс — изолиро-
ванная точка. Кривая имеет две точки
с касательными || Ох, четыре точки
с касательными || Оу, две точки пере-
гиба.
При Ь > 4а конхоида не имеет точек
перегиба (фиг. 41).
Фиг. 42. Конхоида Фиг. 43. Конхоида
окружности (кар- окружности
диоила, b - 2а). I» < 2а).
При b “ 2а получается кардиоида:
р = 2а (cos <р 4- 1). Полюс — точка воз-
врата 1-го рода (фиг. 42).
При Ь < 2а полюс — узел; кривая
имеет четыре касательные || Ох н че-
тыре касательные [| Оу (фиг. 43)
в) Конхоида логарифмической спирали
(см. стр. 276).
г) Конхоида спирали Архимеда (см.
стр. 275).
2. Спирали. 1) Спиралью Архи-
меда называется траектория точки, рав-
номерно движущейся по лучу ОА, кото-
рый в то же время равномерно вра-
щается вокруг неподвижной точки О
(фиг. 44).
Параметрические уравнения архиме-
довой спирал» для полчрных координат
г = vt; <р = wt.
где о — скорость равномерного движе-
лучу; ш — скорость равне-
ния точки по
мерного вращения
луча; t — время.
Уравнение в по-
лярных коорди-
натах
г = а?,
где
о
а = — = const.
ш
Фиг. 44. Построение
«рхимеловой спирали.
Параметрические уравнения в декар-
товых координатах
х = a<f cos <р; у —a^sin<f>.
Неявное уравнение в декартовых
координатах
V х‘ + уг —a-Arctg^; — 0.
Построение спирали по точкам: ок-
ружность радиуса 2аг. делят на п частей
(фиг. 44, п = 12), радиус (отрезок 2ат.)
также делят на п частей и на лучах из
полюса О откладывают соответствую-
щие отрезки (на луче номера А—отрезок,
. Л2ак\
равный • Конец отрезка лежит
на спирали.
Постоянный параметр а есть радиус-
вектор г той точки, для которой поляр-
ный угол f = 1 радиану (57е 17'44*,8);
ОА
2к ’
Свойства:
а) Спираль Архимеда — симметрич-
ная кривая
кулярной к
ной оси прямой, про-
ходящей через полюс
(на фиг. 45 симмет-
ричная часть вычер-
чена штриховой ли-
нией, соответствую-
щей ?<0). В полюсе
спираль касается по-
лярной оси.
б) При изменении <р
относительно перпенди-
поляр-
Фиг. 45. Архиме-
дом спираль.
арифметической
прогрессии с разностью Д? радиус-
в
ПЛОСКИЕ КРИВЫЕ
275
вектор г изменяется в арифметической
прогрессии с разностью Дг = яД<р
Кривая совершает бесчисленное мно-
жество оборотов
Фиг. 46. Поднор-
маль спирали Архи-
меда.
вокруг полюса
Шаг спирали —
расстояние по лу-
чу между соседни-
ми витками — равен
2ал = const.
в) Полярная под-
нормаль есть велн-
чина постоянная:
s„ = а. Построение
нормали и касатель-
ной в заданной точке
(г, ?) показано ня фиг. 46.
г) Дифференциал дуги
ds = в/1 + <?*d?.
Длина дуги, считая от полюса.
S — у V1 4- <?* + Arsti ?].
д) Радиус кривизны
/? = а
3
(1 + <р?)2
2 + т» *
е) Конхоидой спирали Архимеда г —
=* является также спираль Архимеда
р = a? + b с тем же параметром в, но
Ъ
повернутая на угол — радиана:
р — a<f -f- Ь — а
аО;
0_<р-А
т а
ж) Архимедовой спиралью г — а?
пользуются для деления любого угла <?о
на п частей, для чего отрезок г “ ар0
делят на п равных частей и из полюса,
как из центра, засекают дуги окруж-
ностей радиусами rt “ —, г» = -^2-
п п
и т. д.; на спирали получаются точки
с полярными углами: , ^2 и т. д. *
Применение архимедовой спирали
имеет место, например, в производстве
фасонных фрез с профилем по этой
спирали. Определение углов <п задней
заточки для конхоид архимедовой спи-
• Тем же спойсшпм обладает квадратриса
Дннострята:л
рали производится по формуле tg ij =
г .
-у tg3.
2) Логарифмической спиралью назы-
вается кривая, определяемая в поляр-
ных координатах уравнением
г = ает^-
Уравнение г = абт₽ также изобра-
жает логарифмическую спираль, так
как, положив m In mt, получаем
Параметрические уравнения:
х — ает* cos -f; у я= ает" sin ?.
Постоянный параметр а = г0 при ?=0.
Другой параметр т определяется зада-
нием q при ? = 1 (радиан):
т —- )п —.
а
Построение спирали по точкам про-
изводится при помощи таблиц патураль
ных логарифмов по формуле
In г — In а + mq>.
Свойства:
а) При изменении <? в арифмети-
ческой прогрессии с разностью Д? ра-
диус-вектор г изменяется в геометри-
ческой прогрессии со знаменателем
q = при <р-> со, г—»оо; при у-0,
г — а; при —оо, г-+0. Полюс есть
асимптотическая точка спирали: кри-
вая совершает бесчисленное множество
оборотов, неограниченно приближаясь
к полюсу.
б) Во всякой точке спирали etg р ™
= т = const.
Нормаль образует с радиусом-векто-
ром ОМ угол a = arctg т = const. Эго
свойство позволяет построить нормаль
(по тангенсу tga = гл) и касательную
в точке М.
В той же точке М (г, ?) поднормаль
sn = тг, что позволяет так же легко
построить нормаль и касательную к ло-
гарифмической спирали в точке Л1
(фиг. 47).
в) Уравнение г ••= ает*+р изображает
ту же логарифмическую спираль, но
повернутую наугол — радиана (фиг. 47).
т
Такую спираль называют подобной дан-
ной г = ае""*, так как при умножении
радиуса-вектора всякой точки на
18*
276
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
k = const получаем р = ое"’*- k “
- ae«’+ln * = ае”8, где 6 — <р - — .
т
Изменение параметра а приводит
к вращению одной и той же логариф-
Фиг. 47. Логарифмическая спираль.
мической спирали около ее асимптоти-
ческой точки.
г) Полярный отрезок нормали спи-
рали п = Г У 1 + т- — —-—.
г . COSO
д) Радиус кривизны R — = п
е) Центр кривизны — см. на стр. 267.
ж) Эволютой спирали является та же
спираль, но повернутая относительно
. 11п т я \
основной на угол ( —------— 1 .
з) Конхоидой спирали будет новая
кривая р = г + Ь, в точках которой
угол |Ai у*, const:
tg (Ч — (г + Ь): тг.
Угол а, нормали с радиусом-вектором
точки конхоиды находится по формуле
Фнг. 48. Коихонао
логарифмической
спирали.
tg «I - у tg «•
При <р-»соточка At]
конхоиды описывает
бесчисленное множе-
ство оборотов, р-»со.
При <р= 0 р = а-t- Ь.
При <р —► — оо р -> Ь,
т. е. окружность с
радиусом Ь является
асимптотической для
конхоиды логарифмической спирали
(фиг. 48).
Логарифмическая спираль приме-
няется при затыловании зуба фасонной
фрезы.
3) Гиперболической спиралью назы-
вается кривая, определяемая в поляр-
а
ных координатах уравнением г = ~
(см. стр 262). При <р -> со кривая
неограниченно приближается к полюсу.
При <р—»0 г —» оо; имеется асимптота
(см. фиг. 7).
Если образовать семейство концен-
трических окружностей с центром в по-
люсе и на каждой из них, начиная от
полярной оси, отложить дугу длины а,
то полученные на окружностях точки
лежат на гиперболической спирали.
Длина полярной подкасательной спи-
рали постоянная и равна а.
3 Эвольвента окружно-
сти. Уравнения (10) примера 1 (стр. 272)
при и = 0, о = р, R = а — радиус
основной окружности и при замене осей
хну между собой принимают вид
х = (а 4- р) cos t + at sin /;
у = (в + р) sin t — at cos t.
где t — угол хОВ. При р < 0 — эволь-
вента удлиненная (фиг. 49), при р > 0 —
эвольвента укороченная (фиг. 50), при
Фн|. 49. Уллииеккая
•аолыинта.
Фиг. SO. Укороченная
»волкпеита.
р " 0 — эвольвента обыкновенная
(фиг. 51).
Параметрические уравнении в поляр-
ных координатах:
1-й вид: •
, , . а + р „
г — (а + р) sec а, tg а — в,
где параметр а есть угол ВОМ и связан
с углом t формулами
(р а = ——— ; <s — t — а;
а + р ’ Т
2-й вид: ____________
г — У аП- + (а + р)*,
at
?./_arctg—.
Явное уравнение
? - ± (4 V(а + Р)‘ - arccos
ПЛОСКИЕ КРИВЫЕ
277
Фиг. 51. Обыкно-
венная эвольвента.
определяет ветвь, соответствующую
t > 0, если перед скобкой взять плюс,
и ветвь, симметричную относительно
Ох. если взять минус перед скобкой.
Частный случай удлиненной эволь-
венты: при р = — а удлиненная эволь-
вента обращается в
спираль Архимеда
г=а(<р-Ь-^У ось
симметрии Ох
Общее свойство
удлиненной, обыкно
венной и укорочен-
ной эвольвенты: если
построить окружность
радиуса а 4- о (р = 0)
с центром в полюсе,
из какой-нибудь точ-
ки М эвольвенты про
вести касательную к
этой окружности, че-
рез полученную точ-
через полюс О про-
ку касания Л
вести вспомогательную прямую АО,
провести в точке М нормаль к эволь-
венте до точки N пересечения нормали
с ОА, то np0AMN = р = const.
Для построения удлиненной и укоро-
ченной эвольвент следует построить
обыкновенную эвольвенту и от точек
последней по касательной к ней откла-
дывать отрезок р.
Уравнения и свойства обыкновенной
эвольвенты окружности-, а) кроме урав-
нений. полученных
р — 0, удобен вид
х — a sec a cos
где <f = tg а — а
вентной функцией. При
и
из предыдущих при
у — a sec a sin<р.
и называется вволн-
помощи таблицы
Фиг. 52. Построение эяольоеиты
окружности.
этой функции (стр. 57) можно вычис-
лять декартовы координаты точек эволь-
венты.
Геометрический способ построения
эвольвенты окружности основан на свой-
У
Т
Фиг. S3.
стне эвольвенты как развертывающей
кривой.
На фиг. 52 дуга АС окружности раз-
делена на п (п = 8) частей^ на ее каса-
тельной в точке С строится отрезок CD,
равный дуге АС, и делится на п частей.
В точках деления
окружности прово-
дят касательные,
на которых откла-
дываются отрезки
I1'=D1, 22'=D2,
33' = D3 и т. д.
Точки Г, 2',3'...—
точки эвольвенты.
б)Эволютой эволь-
венты является
окружность. Точка
является центром кривизны в соответ-
ствующей точке М эвольвенты (фиг. 53).
Отрезок МВ производящей прямой
есть радиус кривизны эвольвенты в
точке М:
В
на окружности
MB ~<jAB-at = Yr*—a* _ /?.
в) Изменение радиуса кривизны про-
порционально изменению центрального
угла Z:
Д/? = аМ-
г) Производящая прямая — нормаль
к эвольвенте в точке М. Касательная
к эвольвенте в точке М параллельна
радиусу ОВ окружности. Угол между г
и касательной р = а. Угол а назы-
вается в теории эвольвеитных зацепле-
ний углом давления:
д) Эвольвентная функция обозна-
чается ? Inv а “ tg а — а. При
помощи эвольвентной функции полу-
чается следующий параметрический вид
уравнений эвольвенты в полярных ко-
ординатах:
г —л sec a; <р —inva,
который применяется для построения
эвольвенты по точкам в полярных коор-
динатах.
Свойства эвольвентной функции;
Inv 0—0; inv y — оо;
Inv (— a) — — inv а.
278
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Функция имеет разрывы прн а = ± j,
Зя 5ж
±2-....
_ dinva . _
Производная —j— = tg2 в > О,
Л о
функция все врем» возрастает. График
функции в декартовых координатах
у — inv х дан на фиг. 54. Эвольвентной
функцией пользуются для вычисления
толщины зуба зубчатых колес:
Тг = 2гг + inv a, — inv о,] ,
где «1 и ч» — углы давления в точках
эвольвенты 41 и 4г; Т\— толщина зуба
на дуге окружности с радиусом г>; Тг —
толщина зуба на окружности с радиу-
сом г».
е) Эвольвента симметрична относи-
тельно Ох. В пересечении с осью Ох
находятся точка возврата 1-го родя при
» 0 и узловые точки прн ? = ± к.
Фиг. S6. Длит пор- Фиг. М. Экви-
шли шимьпепты хистаптиые вволь-
окружпосш. ввиты окружности.
j; 3«|; параметр а для зтих точек
определяется по таблице эвольвентной
функции из равенства
Inv в — kx,
после чего вычисляется г = в sec а.
ж) Шина нормали Alfli= N =
— a |tg/ — (| (фиг. 55).
з) Длина дуги от точки Я((ж 0) до
Q
текущей точки М(() s = -у или s =
Площадь сектора 0ММ> (фиг. 55)
между ОМ ~ г. 0Л»1 = Q и дугой
эвольвенты ЛМ11 равна
-^-(tg’a,—tg’a).
и) Из каждой точки Л| основной
окружности, как из начальной точки,
выходит эвольвента этой окружности,
эквидистантная эвольвенте из точки А.
Если угол AOAi = с, то уравнения
х — a |cos i + (Г — с) sin/].
у = a (sin t — (t — с) cos Т|
определят новую эвольвенту, получен-
ную из прежней поворотом вокруг точ-
ки О на угол с (фиг. 56).
4. Циклоидальные кри-
и ы е.
I) Циклоиды — рулетты, полученные
при качении окружности по прямой
(см. стр. 272).
Если положить и = 0 и обозначить
р = г — v — расстояние от некоторой
точки плоскости круга до его центра,
1 = у ~ угол поворота круга относи-
тельно прямой, соединяющей центр
круга с точкой касания Ох, то из урав-
нений (11) на стр. 272 получаются урав-
нения циклоиды
х = лр — р sin у;
у = г — pcosf.
которые определяют при р = G^M" <г
укороченную циклоиду (фиг. 57), при
Фиг. 57. Циклоиды: обышомниак. уалиигниаа
к у корсчета!.
р “ ОХМ “ г — обыкновенную цикло-
иду, при р " О^М' > г — удлиненную
циклоиду. Укороченная или удлиненная
эпициклоида или гипоциклоида назы-
вается также трохоидой.
ПЛОСКИЕ КРИВЫЕ
279
Явное уравнение н декартовых коор-
динатах первой половины парной арки
цнклонды имеет вид
х — г arccos ~~ — У Р2 — (г~ У)2!
для второй половины той жг арки
х — г ^2к — arccos +
+ V Р» — (г—У)г-
Свойства обыкновенной циклоиды.
а| Кривая имеет точки возврата 1-го
рода при ч> = 2Лп; k — целое число.
б) Построение: отрезок оси х, равный
тк, делят на п равных частей (на фиг. 58
Фиг. 58. Обыкпоиеннхя циклоида.
п = 8) и полуокружность также делят
на л частей. Точка циклоиды, например
Р.., получается от пересечения двух дуг
окружностей: одна
Фиг. SP. Касательная
и юрналь к циклоиде.
окружность радиу-
сом 03' имеет центр
в точке 3, другая —
с радиусом 33' —
имеет центр в точ-
ке О.
в) Касательная
и нормаль к ин
клонде в точке М
(фнг 59) пересе-
кают окружность
и концах диаме-
тра. проходящего
через точку А касания окружности
с осью Ох. Угол касательной с Ох
циклоиде парал-
угла <р (фиг. 59).
2r sin yrff.
О до
а в — — —— *
2 2 ‘
г) Касательная к
дельна биссектрисе
д> Дифференциал дуги ds
е) Длина дуги от точки f “
текущей точки l-й арки «“4г —сс
Длина дуги одной арки s= 8г.
ж) О длине нормали, радиусе кри-
визны, эволюте см. выше (стр. 267, 270).
Во всякой точке удлиненной и укоро-
ченной циклоид нормаль проходит
через точку касания катящейся окруж-
ности с прямой Ох.
Для построения этих циклоид надо
построить обыкновенную циклоиду и по
каждому радиусу окружности, направ-
ленному в точки обыкновенной цикло-
иды, отложить от центра отрезок р.
2) Эпициклоиды— рулетты, полученные
при качении окружности по окружности
(касание внешнее). Если в формулах
примера 3 (стр. 272) положить и = О,
и = г — р, где р — расстояние от цен-
тра О\ подвижного круга до его некото-
рой точки М, то при замене осей х на у
и у на х получим уравнения
х — (R + г) cos t — р cos (t 4-t).
у — (R + r) sin t — psin(t + t),
определяющие при p= O^M’ < г уко-
роченную эпициклоиду, при p ™ OjAf =
™ г — обыкновенную эпициклоиду.
Фиг. 60. Эпициклоиды: о6мкнп|>снкп1Г.
уллкненим, укороченная
при р " 0[М' > г — удлиненную эпи-
циклоиду (фиг. 60). В этих формулах
следует оставить (=^/ДОВ или ("
= £ВО\М иа основании зависимости
Rl = rt.
R
Если «обозначить — Xй
» (m — I) I,. то
x — rm cost — pcos mt,
у •— rm sin t — p sin mt.
Свойства:
а) Если m — рациональное число,
то эпициклоида будет алгебраической
кривой; в этом случае кривые полу-
чаются замкнутыми.
280
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
б) В случае R = г = р (т = 2) обы-
кновенная эпициклоида называется кар-
___ диоидой (фиг. 61).
/”у?\ При г — со эпицн-
rVT\fe> клоиды превращаются в
"I JmlAAJ-» эвольвенты неподвижной
\ окружности.
.S в) В каждой из эпи-
Фиг. 61. циклоид нормаль прохо-
Кардиоила. дит через точку каса-
ния кругов.
г) Обыкновенная эпициклоида (г — р)
имеет точки возврата 1-го рода при
2ft* п
t =----г, ft — целое число. Если про-
т—1
вести диаметр катящегося круга через
точку касания кругов, то касательная
и норМаль в данной точке эпицик-
лоиды проходят через концы этого диа-
метра.
д) Угловой коэффициент касательной
< я dy
к обыкновенной эпициклоиде -г =
dx
= tg W * У Касательная парал-
лельна биссектрисе угла/. Дифференциал
дуги
ds = 2(R + г) sin dt.
Радиус кривизны равен
Ar (R + г) sin у)
2г 4- К
е) Эволютой обыкновенной эпицикло-
иды является обыкновенная эпицикло-
ида, сжатая в постоянном отношении
l:fl 4- 2 по лучам, выходящим из
_ rit
точки О, и повернутая на угол-jj.
К
У этой эволюты радиус катящегося
rR
круга г, = -т,—, , радиус неподвиж-
/?г
ного круга эволюта по-
добна основной эпициклоиде.
ж) Для построения обыкновенной
эпициклоиды следует по неподвижной
окружности отложить лугу А0С =
= оД0В0 — половину длины подвиж-
ной окружности (фиг. 62), каждую дугу
разделить на п равных частей (на фиг 62
п = 4). Через точки I, 2, 3, 4 провести
из центра О лучи, а через точки Г, 2', <?',
4' провести концентрические окруж-
ности с центром О; эти окружности
пересекут диаметр 4BSn в точках /, //,
HI, IV, а лучи из центра О — соответ-
ственно в точках ai, аг, ав, Af<. От
последних точек по этим дугам концен-
трических окружностей надо отложить
II - аМ; 11 2’ = а?Л1г; HI 3' - а^А»
Точки Ло, Alj, Мг, М3, Af, — точки
эпициклоиды.
Построение удлиненной и укорочен-
ной эпициклоид производится при
помощи предварительно построенной
обыкновенной эпициклоиды; на прямой,
соединяющей центр Oi (фиг. 60) с точкой
обыкновенной эпициклоиды, отклады-
вают от центра О| отрезок р; конец
отрезка опишет удлиненную или укоро-
ченную эпициклоиду.
3) Гипоциклоиды — рулетты, получен-
ные при качении окружности по окруж-
ности (внутреннее касание, г < R).
Уравнения
х — (₽ — r)cos / 4- р cos Г ~Г-t\,
у-(Я —г) sin/—р sin г Г-/)
определяют укороченную (р < г), удли-
ненную (р — рх > г) и обыкновенную
(р = г) гипоциклоиды (фиг. 63).
р
Если отношение — рационально, то
гипоциклоиды — алгебраические кри-
р
вые, замкнутые; если — — 1 = т, го
х — rm cos t 4- р cos mt,
у — rm sin t — p sin mt.
ПЛОСКИЕ КРИВЫЕ
2ЯТ
При р = г = — (т = 3) гипоцикло-
4
ида называется астроидой (фиг. 64), и
уравнения принимают вид
х — R cos4;y=R sin81 или х '*+у l,=R ’*•
Касательная и нормаль обыкновенной
гипоциклоиды имеют свойства, одина-
ковые со свой-
ствами эпици-
клоиды.
Во всякой
точке каждого
типа гипоци-
клоиды нор-
маль проходит
через точку ка-
сания кругов.
Построение
Фиг. 63. Гипопиклоихи: ГИПОЦИКЛОИД
обыкновенна!, удлинении. аналогично ПО-
укорочешиа. строению ЭПИ-
ЦИКЛОИД.
При /•“ yR (m = 1) получается
эллипс:
х — (г -J- р) cos Г; у <= (г — p)s\nt\
прн г = р — X /? гипоциклоида обра-
щается в прямую — ось Ох.
При г. близком к R, удлиненные
гипоциклоиды могут иметь вид, пока-
занный на фиг. 65.
Фиг. 64. Астроии.
Фнг. 65. Удлинении
гипоциклоида.
R
НИИ 1
Эволютой обыкновенной гипоцикло-
иды является также обыкновенная гипо-
циклоида, только повернутая на угол
и растянутая в постоянном отноше-
^по всем лучам, выходя-
щим из начала координат. Радиус катя-
Rr
щегося круга rx = — радиус не-
подвижного круга Rx = ——д-. Радиус
<\
кривизны обыкновенной гипоциклоиды
равен
4r(R — г) sin (-j-y-)
2r — R ’
Фиг. 66. Обышовсннав
перициклом!!
Фиг. 67. Спрямление
окружности.
4) Перицик.юида описывается точкой
плоскости круга, катящегося без сколь-
жения по непо-
движной окружно-
сти, причем по-
следняя содержит-
ся внутри катяще-
гося круга.
Обыкновенная
перипиклоида опи-
сывается точкой
катящейся окруж-
ности (на фиг. 66
при г = 2R).
Удлиненная и укороченная перипи-
клонды описываются точками, лежа-
щими соответственно вне и внутри ка-
тящегося круга.
Перициклоида есть всегда некоторая
эпициклоида, причем неподвижный круг
имеет радиус Rx = R, а радиус подвиж-
ного круга и =* г — R.
Спрямление дуги окружности. Для
откладывания дуги окружности по дуге
другой окружности или по прямой имеет-
ся несколько спо-
собов.
1. Способ Че-
бышева. Дуга
окружности д =
= с централь-
ным углом а при-
ближенно равна
сумме боковых сто-
рон равнобедрен-
ного треугольника
АМС, построен-
ного на хорде АС
этой— дуги и
/4
у ее стрелки, т. е. ОМ =• Л
(фиг. 67):
имеющего высотой
s * 2ЛМ.
Точная величина ошибки
Дд — аг — 2АМ —
-Г [а-2 SID* Л + _ СОЗ .
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
282
Разложение в ряд дает
Величина относительной погрешно-
сти
Д« 1 / а \«
Лля
D
Фиг. 68. Спрямле-
ние окружности.
2. Способ Репкина,
спрямления дуги АВ окружности
/фиг. 68) с центральным углом а поло-
вину хорды АВ от-
кладывают на ее про-
должении АС=±АВ.
Радиусом СВ из точ-
ки С, как из центра,
засекают точку D на
касательной AD к
окружности: отрезок
AD Л1^АВ = s. Точ-
ная величина ошибки
о АВ — AD — Дд — аг—AD —
аг— г sin ^cos
1080
При а О (57*17'44*.8)
га* ,
900 ’
Дд н
"s"<' 900 ’
При углах, не больших ЗСГ, относи
тельная ошибка составляет около 0,006° u
измеряемой величины.
В обратной задаче — на окружность
наложить данный отрезок AD — надо
последний разделить на четыре равные
о
части (фиг. 68) и радиусом С\1) = -rAD
4
из точки С|, как из центра, засечь
окружность в точке в. Длина дуги
АВ сз AD. Точная величина ошибки
равна аг — AD (см. выше).
Для откладывания длины дуги одной
окружности по другой надо сначала
дугу спрямить, а затем полученный
отрезок построить на другой окруж-
ности.
3. Способ хорд состоит в том.
что дугу д заменяют ее хордой I. Точная
величина ошибки при такой замене
равна (фиг. 68).
Дд - s — / — 2г (j — sin .
Если д = , то Дд о 0,00002г, -у «
ж 0,0002 = 0,02%. Чтобы спрямить дугу
АВ, надо ее разделить на п равных
л 48 г
частей, причем длина дуги----- < .
п 10
„ АВ
Хорду дуги — откладывают по пря-
мой л раз, и полученный отрезок AD ж
«а о АВ с ошибкой в л раз большей.
АВ
чем при замене дуги -^-соответствую-
щей хордой.
ПРОСТРАНСТВЕННЫЕ КРИВЫЕ
Уравнения. Линия может быть задана:
1) уравнениями
У-/(х). т-у(х). (12)
определяющими на отрезке о < х < Д
простую дугу кривой, если в [а. Д|
функции / (х). у (х) непрерывны и
имеют непрерывные производные 1-го
порядка;
2) параметрическими уравнениями
х-х((). у-у(П. х-х(0 (13)
гли векторным уравнением
г-г (*) — 7д(/)+7у(О+*«(0. (14)
определяющими на отрезке
простую дугу кривой если—
х(0, у (0, г (0 непрерывны с непре-
рывными производными 1-го порядка,
которые не обращаются в нуль одно-
временно, т. е. модуль | ~| з* 0, н если
взаимно однозначно соответствуют точ-
ки дуги Л10Л1| значениям отрезка
Uo. М- (Определение регулярного ку
ска см. стр. 2.58.) При изменении t аг
t0 до tj, соответствующая точка М
пробегает простую дугу только один раз
в одном направлении, которое назы-
вается положительным направлением
кривой. Оно зависит от выбора пара-
метра t.
dr
В особой точке кривой — =0.
ПРОСТРАНСТВЕННЫЕ КРИВЫЕ
2ЯЗ
Из трех уравнений (13) каждая пара
определяет проекцию пространственной
кривой на соответствующую коорди-
натную плоскость;
3) уравнениями в неявной форме
F (*• У, г) •• 0. Ф (ж. у, z) — 0. (15)
определяющими геометрическое место
точек и такое, что в окрестности каж-
дой из этих точек имеется простая дуга
кривой.
Последняя существует, если в окре-
стности какой-нибудь точки (х0, у0, г0)
F и Ф непрерывны, обладают непрерыв-
ными частными производными l-го по-
рядка, н в этой точке ранг функциональ-
ной матрицы ?У равен 2.
Уравнения (15) можно параметри-
зовать, если задать одну координату
как произвольную функцию I.
Длина дуги. Простая дуга спрямля-
ема. и ее длина s от некоторой точки
до текущей точки М (/) нахо-
дится по формуле (см. стр. 190)
*0
ds — j/dx1 -)- dy‘ -f dz1-
Выразив t через s из уравнения
s= ф(0> можно получить новые пара-
метрические уравнения той же кривой
* — /| (s), у — ft (з), г — /я ($).
При таком задании положитель-
ному направлению на кривой соот-
ветствует го. в котором отсчитывается
длина з.
В дальнейшем производные по $ и по
t обозначены соответственно штрихом
и точкой:
4/ _ f. rfy Л df_ <Pf
ds • ds1 '..............dt “ '* dt1
Касательная. Касательной к про-
странственной кривой в точке М на
кривой называется предельное положе-
ние секущей через данную точку М и
точку кривой Л1| при ЛЬ-к/И.
Касательная в точке М (Г) на кривой
определяется направляющим вектором
а± - lim - lim Уд-МЛ-НП =
dt st-о St
— 7 — /ж (/) +7у (Г) + kz (О;
dr — idx + jdy -f kdz,
который называется касательным век-
тором, направленным в положитель-
ную сторону кривой.
Модуль касательного вектора
I г | — V хг + уг + гг; | rf г [ — ds.
Единичный вектор касательной (орт)
т — — 7' — /ж' + /у' + Л z'-
Направляющие косинусы касатель-
ной
X , у
COS а = ——- — Ж'; COS fi = j-f-г = у ;
COSy-^-Z',
где а, р, -j — углы г с осями коор-
динат.
При неявном задании кривой (15)
координаты касательного вектора
dx — XDji dy — KD4; dz — W8,
°-l5; ill-
где Л — произвольная функция x, у, г,
F г, Фх и т. д. — частные производные
функции (15)
Нормальная плоскость к кривой в
точке М есть плоскость, перпендику-
лярная к касательной в этой точке.
Все прямые, перпендикулярные к каса-
тельной и проходящие через точку М,
называются нормалями кривой и лежат
в нормальной плоскости.
2«4
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Главная нормаль и кривизна кривой.
Производная от орта касательной по
дуге
-=r* =7х +jy” + *z*
называется вектором главной нормали
(пли вектором кривизны) и определяет
прямую главную нормаль кривой, про-
ходящую через данную точку М. Глав-
ная нормаль лежит в нормальной пло-
скости (t’l т).
Орт главной нормали обозначается >:
d-.
ds
Kv,
где скаляр К = | называется кри-
визной кривой в точке М.
Кривизна в точке М
К = lim JL
Дз~0 АХ
где ? — угол смежности лнух касатель-
ных к кривой в точках М и Mi (угол
между касательными); 6s — длина
дуги кривой МЛ11
Кривизна характеризует отклонение
кривой от прямой.
Радиус кривизны:
I
₽"7Г*
Орт главной нормали:
> — р? — р (I-Xя +]у" + kt’Y
Спрямляющая плоскость кривой в
точке М—плоскость, перпендикулярная
к главной нормали.
Соприкасающаяся плоскость. Сопри-
касающейся плоскостью в точке М на
кривой называется предельное поло-
жение плоскости, проходящей через три
точки на кривой М, Мъ Мг, когда
УИ1 —» М, Л1г -* М.
Соприкасающаяся плоскость — пре-
дельная для плоскости, проходящей
через касательную в точке М и сосед-
нюю точку Afi при /Hi -е М. Сопри-
касающаяся плоскость проходит через
касательную и главную нормаль.
Бинормалью кривой в точке М назы-
вается прямая, перпендикулярная к
соприкасающейся плоскости в этой
точке.
Орт бинормали:
(16)
Сопровождающий трехгранник. Три
взаимно перпендикулярные прямые —
касательная, главная нормаль и бинор-
маль в точке М на кривой — назы-
ваются главными направлениями в этой
точке.
Три орта этих направлений v,
£ образуют правую тройку векторов
(как три координатных орта 7, J, k)
и связаны равенством (16).
Направляющие косинусы главных
направлений суть координаты ортов
Т, V, р.
Три плоскости, соответственно пер-
пендикулярные кт, у. р — нормаль-
ная,спрямляющая и соприкасающаяся,—
образуют в каждой точке кривой (не
особой) трехгранник (триэдр), называ-
емый сопровождающим, основным,
подвижным, естественным трехгран-
ником Френе. О его движении см.
стр. 292.
Кручение пространственной кривой.
Вектором кручения, имеющим напра-
вление главной нормали (в ту или
другую из ее сторон), называется вектор
Т = = — 77.
ds
Скаляр Т, являющийся относитель-
ным числом, называется кручением кри-
вой в точке М и по абсолютной вели-
чине есть
Пт
Д4-0 Дх | ds |
где ip — угол смежности двух бинормалей
(или двух соприкасающихся плоско-
стей) в точках Л1 и Л1| кривой; As =
-о А4Л1,.
Для плоской кривой Т = 9;
| сохраняет постоянное направление;
соприкасающаяся плоскость — пло-
скость самой крипой.
Если 7 уь 0, то чем больше абсолют-
ная величина кручения, тем быстрее
отклоняется кривая от соприкаса-
ющейся плоскости
Радиусом кручения называется вели-
чина
ПРОСТРАНСТВЕННЫЕ КРИВЫЕ
285
Таблица Л
Основные формулы уравнения, выраженные через производные но дуге s
Векторные формулы Координатные формулы
<Тд » I dr 1 ds — VAr'-J- dy" -t- dz*
1 T-Zr' +7y' +*»'
'-141 К-У х*’+У + У
- 1 К ' ds g*» +7<+ъ-)
5-<Х’ , I 77 * 1
_ - J_ /- </т О'-. \ ' ds = № Р as ’ ax’’ • I x’y'f Г-у, x-y’z-
Продолжение табл. А
Элементы трехгранника Векторные уравнения Координатные ураапеипя
Касательная ₽=7+иР Х~х _ Г-у _ Z-г х' ~ у’ ~ г'
Нормальная плоскость (*-7)й-0 х> (Х_х»+у'(К- p)4-z'(Z-i)=0
Главная нормаль IK II IK IK
Спрямляющая плоскость K«(X-x) + y«'(X-n+*'(Z-»)-0
Conpmtacaiouiiici пло скость (#-7)г'7»-о IX-jr r-y z-t x' f »' -0 1 *• v e
Бинормаль Р-7+kG'X^) 13|I 1 1 "-7 । ч 4 N мч 1 a - m
Здесь г, jr, у, Д — радиус-вектор и координаты точки А! на кривой; ₽, X, У, Z — текущий радиус-
вектор и текущие координаты праной или плоскости; и — скалярный параметр текущей точки.
285
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Винтона» линия. Обыкновенной или
цилиндрической винтовой линией назы-
вается траектория точки М, участвую-
щей одновременно в двух движениях:
во вращательном вокруг оси г и
в поступательном параллельно этой оси
с постоянными скоростями.
Обозначим расстояние от точки М
до Ог через «, угловую скорость — че-
рез ы, скорость в поступательном дви-
жении через »; для угла поворота ?
во вращательном движении точки М за
время t имеем ? = <в/; поступательное
Фиг. 69. Винтовая
линия.
Фиг. ТО. Правая
и левая винтовые
линии.
2
Если исключить ? “ из системы
г- + / “ V = 'S V.
то получаем винтовую линию как пере-
сечение двух поверхностей: х* у* =
= о2; у =х tg — — круглого цилиндра
и прямого геликоида (коноида). В даль-
нейшем положено ы = 1.
Параметрические уравнения
ж = a cos /, у = a sin t. г = ht
определяют правую винтовую линию
при h > 0 и левую винтовую линию
при й < 0. На фиг. 70 для правой
винтовой линии при I 5» 0 ветвь Л/И
лежит над ху, при t < 0 ветвь М;1/1—
под ху; для левой винтовой линии при
/>0 ветвь 4/И1 лежит под ху, при
t <0 ветвь МгА — над ху.
В дальнейшем вычисления сделаны
для правой винтовой линии, записан-
ной векторным уравнением
г — ia cost -|-У a sin t + kht.
перемещение за то же время г = vt
или г = й?, где h = Если к урав-
нениям ж — a cos ?, у = a sin ? тра-
ектории точки М во вращательном дви-
жении присоединить уравнение г Iry,
то получим параметрические уравнения
искомой траектории (фиг. 69).
Геометрический смысл h (приведенный
шаг, параметр винта) есть перемеще-
ние точки М параллельно Ог при
повороте на I радиан.
Полный шаг Н — 2кй есть переме-
щение || Ог при одном обороте во-
круг Ог.
Винтом называется совокупность
двух коллинеарных векторов ш и и
Вектор угловой скорости лежит на оси
винта Ог.
Проекция винтовой линии на хОу
есть окружность ж ™ a cos?, у = a sin ?,
называемая далее основной окружно-
стью; проекция на уОг: у = a sin ?,
г = Л? есть синусоида, так как нсклю-
чением ? получается у = a sin Про-
екция на хОг есть косинусоида.
dr — [/(— а sin/) +/а cos/4-Ай] dr;
ds — | dr | — yra*-|- li-dt',
x — dr: ds —
i (— a sin /) -4-/1 cos t -f- Ай
.- /(— a cos/)-)-/(— asin/)
U* - ****
V а* т
— I a cos/—/ a sin/
d''ds---------ai + he
. ia sin t — ja cos t
4(r->----------------------dt'
la sin t — ja cos /
d (И: ds -----------, -ЗГ---------------r- ,
‘-|£l
a . o?|- ft2 в
a2 4-ft2 ’ P “ a •
ПРОСТРАНСТВЕННЫЕ КРИВЫЕ
287
* = pr* = — i cos t — / sin t:
-- Ihsint— ihccst-{-ka.
= s X ----------r------------•
Va‘ + Л*
Уравнения элементов трехгранника
а точке M (t) кривой
касательной
X— a cos i __ Y — asint___Z — ht .
— a sin t — a cos t = Л *
нормальной плоскости
Ха sin t — Ya cos t — hZ 4- hit = 0;
главной нормали
X—acost____ К — a sin t _ Z — ht .
cost sint U *
спрямляющей плоскости
X cos t + Y sin t —a — 0;
соприкасающейся плоскости
Л sin r— Y cos Z — at — 0;
бинормали
A — a cos / Y—asint _ 7. — ht
h sin t — n cos t a
Свойства винтовой ли
нин. Длина дуги винтовой линии,
отсчитываемой от точки A (t = 0)
(фиг. 70)
S= Va^ + ht f.
для того же t дуга а окружности —
проекции винтовой линии на хОу:
а — at\ s пропорциональна а;
-vMtX-
Уравнения винтовой линии с пара-
метром s:
х — acos—r-S- , у — a sin—.
Ка»+Л* Val-tKt
hs
х = ---------
Уа» + Л*
Направляющие косинусы:
касательной
I — a sin / a cos t h )
Ув« + Л* ’ yd^+hi ’ V^hi] ’
главной нормали
( — cos t. —sin t, 0);
бинормали
(Л sin t — ft cos a
Va*+n‘ ' Va* + h* * Va'+h*
Касательная образует с осью винт»
постоянный угол т, для которого
Л
cos 7 — .------,
/п» + Л»
или иначе — винтовая линия пересекает
образующие цилиндра, на котором она
лежит, под постоянным углом 7.
Угол 90° — 7 = 0 между винтовой
линией и основной окружностью или
между касательными к ним, называ-
емый углом подъема винтовой линии,
определяется из формул
sin 0 = ~-т * —; cos 0 = — а ;
«в=4-
Отношение полного шага Н к длине
основной окружности есть tg 0:
Проекция главной нормали на хОу:
У = Xlgt.
Главная нормаль во всякой точке
М пересекает ось винта и перпенди-
кулярна ей. Главная нормаль совпа-
дает с нормалью к цилиндрической
поверхности. Винтовая линия — гео-
дезическая на цилиндре.
Бинормаль образует постоянный
угол Ф с осью винта, равный углу
подъема винтовой линии:
cos Ф = а ; tg Ф = —,
Уо« + Л* «
Всякая прямая. находящаяся на
кратчайшем расстоянии г от оси винта
и образующая с осью винта угол Ф,
определяемый равенством
. h
tg ф - 7.
называется лучом винта. Бинормали
всех винтовых линий данного винта
суть лучи винта; они образуют ком-
плекс (со3) лучей.
Во всякой точке винтовой лини»
кривизна и кручение постоянны. Пра-
?88
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
вая винтовая линия имеет положитель-
ное кручение, для левой винтовой линии
кручение отрицательное:
<у»_ А
Таблица В
Основные формулы я уравнения криво* (13). (14) с произвольным параметром t
Выражение кривизны и кручения
через угол в:
,z cos2 0 т cos20tg6 s)n20
<\ 43 ~~~— J * — . в
Векторные формулы Коорлиматиые формулы
dr — rdt 7—7jt + 7i+K
di — | dir | — ]/~^dt = | r | dt
5 — 1 r’ IX 4- /> + *2
5
* p r — 1 x-f- j у -f- a j
= dr:iii-~ —
s ii-JiJt+yy-t-II
77*
r yCr eX/“
x у г
IrxT l = K?
Уй?-(77У К A
t* 1И+?+?)'«
J ’-T 1г1**1+ 7|«'| + *bn.|]
I;x4 A I ly XI |x xl lx у 1 J
J- b'|»f.|+7
1 ' ll?x?l A 1 1* xl lx у| 1* »IJ
xy i
• • • • ,
1 • ««
(rx“)’ r-xr x у i X у X
И нагла лучше вычислять » оо схеме тайл. А, причем потребуется
dt
di
ПРОСТРАНСТВЕННЫЕ КРИВЫЕ
289
Продолжение табл. В
Элементы трехгранника Векторные уравнения Координатные уравнения
Касательная Нормальная плоскость «• — R-r + ur (R-r)r-n X-x Y-y Z-z x ♦ у i (X-_r) i 4-lr-y) y4-(Z-*)s-0
Главная нормаль Спрямляющим плоскость R — r + ur х(гХг) (₽-г)г (rXr)-O (X- X- l;i +( Г il z - Y- l.'i I* У + (>• -1? r Z i‘ii -я И- — i i 3 1 1 ; 11+
Сопри касающаяся пло- скость (~R-~r)r r-0 X-jT Y-y Z-z * у. i x v г = 0
Бинормаль R—r + u (rfr) X-x У i У Z i x : x к _ z - г 1Й1
Смысл г, х, у, г, R. X. Y, Z, и см. на сгр. 285. табл. А.
Общие винтовые линии
(линии откоса)—кривые, касательные к
которым образуют постоянный угол с
заданным направлением. Они лежат на
цилиндре с образующими, параллель-
ными данному направлению, и пере-
секают их под постоянным углом. Глав-
ная нормаль общей винтовой линии
совпадает с нормалью к цилиндриче-
ской поверхности.
Во всякой точке общей винтовой ли-
нии К'Т = const. Эволюты (простран-
ственные) всякой плоской кривой—общие
винтовые линии
Пример, инлиилро-коничсская ниитовая линия
х — aeml cot I,
у aemt sin/, г « beml
лежит ил конусе
4- у* - tg’ 3,
пересекает его образующие под постоянным углом
и проектируется на плоскость в логарифмическую
спираль
г = aemh а — b tg 9.
Найти же ее ллемеиты.
Состаиляем производные по t:
X « aeml (m cos / — aln I);
у = aemt (m sin 14- cos 0;
i = bmemt;
x *- aemt (m’ cos t — 2m sin t — cos 0;
у —• aemt (m1 sin t 4- 2m cos / — sin /);
'i x bm,eml.
x = aemt (ma cos t — 3m’ aln t — 3m cos 14- sin 0;
y — aeml (nt’ sin I 4- 3m’ cos t — 3m sin r — cos /);
j _ bm ’e"11;
i = .
где
t = /o' 4- m’ (o' 4- b»y,
a (m cos t — sin <) j-,
и»
19 Том I Зак. НМ
290
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Здесь проще сначала искать de:
- Гт в (— m sin Г — cos /) ,
* “ ----------------------------+
+ г (т со» / - Un 0] dt
и затем
df j- о (— m sin Г — cos t)
ds ” c'emt
7 “ l rncos t — а|п 0 .
I df | ° Vffl4- 1 . _ e'e"1' .
= I ал|= г<гт.‘ ' P a » i
* ~ У m- + 1
x l- Л™ sin t + со» o + J(m cos t — etn 0].
Иногда проще сначала искать г X г, что- впро-
чем. полезно сейчас сделать
, « imt
гХ' = «
I
а (от cos t — sin 0
а (тг cos t — 2т sin t — cos f>
и, вычитая из третьей строки вторую строку
с предварительным умножением ва т, получаем
7Хг = r^mt |— 7abm (т соа t — sin 0 —
— 7 at>m (m sin t4- cos 0 4- * o’ (m* 4- 0)1
IrX r I — uc I m‘ 4- 1 e2m/ — Kf;
— Tbmim cos f — sin 0
При вычислении определителя г г г следует
сделать такие же упрощения, как выше, и полу-
чается
гг~г^ а'Ьт (шЧ-1) еДя,/;
г _ р1 (Г г ~) _ “т __
“ c>tm‘ ’
Треть» координата т постоянная, поэтому дан-
ная крина» имеет постоянный угол | с Од, следо-
вательно, вта кривая- общая виитопая линия, она
пересекает псе образующие цилиндра, основанием
которого является логарифмическая спираль, а
образующие II Ог, под тем же постоянным углом |,
0m , » Vm' -К I
«I-—: ‘ст —’кЭ—
Кривая пересекает образующие конуса под
углом р. ял» которого
соа т
cos 0 *
Отношение
„ _ а Ут" 4- I
К : Г ---------------- tg т - const.
Основные формулы н уравнения
кривой, заданной неявными
уравнениями [15]
dx — XDJt dy = XD2, dz = XDt
(см. стр. 283);
ds - X |/ D? + + Dj = ХД;
dr = X (<D] 4- jDi + kD^)\
i = -^ = 4-I7D>+A + *D?l.
as A
J *
a (m sin t -|- cos 0 t>m
a (m* sin t 4- 2m cos t — sin 0 dm*
Далее бывает удобно, чтобы исполь-
зовать табл. Д, искать производные по
дуге и выражать их через дифферен-
циалы:
г' = т = dr: ds;
г’ — rfr: ds —
(Prds - dr<Ps .
ds»
Но бывает удобнее выразить искомые
величины только через дифференциалы
х, у, z и s:
iftx — \dD) 4- DjrfX; <Рх — d ((PxY,
(Ру •» >dDi 4- DttfX; (Ру — d ((Ру};
(Pz - XdD, 4- D„rfX; (Pz - d (d»z).
(Ps-ldA +AdK;
В дальнейшем обозначено:
Zdy dr IS Id.- dx U Ida dy h _
о у d"y d4 I " |d,j d'ar | • Id’s d>y |
— ds у (d'ar)» 4- (d'y)' 4- td‘j? - (dM»»;
K - -A = — i
ds* p
ПРОСТРАНСТВЕННЫЕ КРИВЫЕ
291
n — Р [Г((Рх ds — dx (Ps) +
4- j (tPy ds—dy (Ps) + A (d*z ds—dzdis}};
7 7 a
dx dy dz 1
d*x (Py <Pz
P*
— ds*
T
dx dy dz
<Px (Py (Pz
(Px (Py (Pz
Уравнения:
касательной и нормальной плоскости —
см. стр. 285, 283;
главной нормали
Х — х _ Y — y _ Z-z .
Ids dx I Ids dy I Ids dz I ’
I <Ps <Px I | (Ps (Py | I (Ps (Pz I
спрямляющей плоскости
*-Ч£Х1+"'-’’1ИХ1+
+<z-«|XXI-0;
соприкасающейся плоскости
Х — х Y — y Z — z
dx dy dz
(Px (Py (Pz
бинормали
X-x Y—y Z-z
Idy dz~T Idz dx I = Idx dy
I (Py (Pz I I (Pz (Px | | (Px (Py
flpuMtp. В течке (я, a, a YT) л икни
x* + У» + Д* - «o’.
x* 4 У» — '(OX — О
найти главные направления, кривизну н кручение.
Днффереинироваиие уравнения приводит к линей-
вой однородной относительно dx, ay, dz системе
уравнений:
х dx у оу 4- » dz — 0;
(Ж — а] ах + у оу — 0,
откуда
dx оу dz
W W l~’.l ’
или
ах — — Луг; dy — Ад (ж — я): яд — Рау,
ds “ Л К/д» 4-д" (х — я)» 4 а*у‘—
— Ла Г4и» - г»,
где коэффициент пропорциональности А — неиз-
вестная функция от х, у. г.
Если обозначить:
dx = Ля, dy = Л?, dz = *т, ds — AS,
где
а = — уд, 3 = г (х — я), т = оу. о =» я УЧа1 — х‘.
то:
(Рх — Л da 4 add; (Рх Л(Рл 4 2dzdP 4 шРЛ;
<ру = ляз + зол; (Ру = лач> 4 jo?oa ₽я«л-,
(Pz = Pdf 4- -[dp; (Pz = P(P( + 2ЯуЯЛ 4- усРА;
d>s = Pdi 4- Ш ;
или
(Ps - aP —~~.ax. 4- Я У4я» -ж» dp.
Via'-x*
Находим вектор
т f —~У* 1 (r ~ nl- У 1
la V"4a»- x'' a VPa' - x»' Yia*^~P J ‘
Уравнения касательной а данной точке
Х-я У-a Z-aYY
~7Т“ " “ 1
Вычисляем
1 “ | Я»у Я»Д I “ * ! Pd& + 8ЯЛ Pdy 4 ТЯЛ | =
”**!<« dt I-
Аналогично
л.-И1^|-Л»| J ’ I;
| (Pz (Рх I I dt da I
п =
rfy| = A'l 1 13 I
(Px (Py I I dz d) I
Далее находим:
d* — — у dz — z dy = — Л |ay* 4- P (x — a)|;
Яр — д dx 4- U — я) >‘г — Л | — уд» 4 (x — «> «У|;
dt — a ay = Аяд (x — a).
При x»»o, у — a, t — a Y? получаем:
e — - YY я»; 3 — 0; т — я»;
dz — — PcP; Я? — - Л2я’: Ят— 0;
t— P*2a'; m—— Л’я’; я — A»2 VT o'.
Уравнение бинормали
X-a У—a Z-aYT
I iVT
Вычисляем
I (Px (Ps I I AOa 4- <zdp Pdi 4 tdp I
'-|яхоз|-*| . * h
t da di I
— x Ox a t »«
Л — a —=^==. —-----, .
Y ia«— x* V *a‘— x‘
19*
292
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
При х
1,= - ; т. = - Ал2 V3 а>;
V 3
Ураннення манной нормали
Кривизна
Vt‘ 4 т1 -|- и» __ k'&yia _ VB
<Ь* <Аг‘3 /з з у-з д’
будет численно равняться времени).
Предыдущие формулы представляют
уравнения движения трехгранника.
Трехгранник движется с поступательной
скоростью t (скорость его вершины М)
и со скоростью вращения U
вектор скорости вращения трехгран-
ника
S’ = 4. Тг
определяет мгновенную ось вращения
и численно (по модулю) равен угловой
скорости вращения трехгранника (век-
тор Дарбу). Производные ортов t, у, ?
выражаются через Q:
Имеем далее
dx dy di
d'x <Py d":
tPx d*y (Ft
I « 3 1
= ** <«« «гз <h
i d’a <P? d*t
и инчиглчем
d*« — — |oy* 4- д’ (x — а)| dk — h [’ey dy 4-
4- 2z (x — e) dx + i'dx |;
”’₽ “ I— ys* 4- «У (x — e)l d* 4- A | — f’dy —
— 2yt dx J- a (x — e) dy 4- ay dx];
a’T = a: (x — a) di 4- la |(x — a) dx 4- г dx).
Расположение кривой вблизи данной
точки. Если данная точка М взята за
начало координат, направления осей
При X = a, у — я, г — а У2 получаем
— — a*dA 4- 2 V2 a'tfl,
a>3 — — 2a’d* - 3 VI я’*’;
<ПТ » —2я'А>.
|! точке At (a, a, a I'll А имеет мочение
- я' VI 0 o'
й “ *• — o’ — 2a’
0 - Ida' 3V5.
2VIa’-8V5a<- 2o‘
1 ручеине и данноА точке
Производные ортов главных напра-
'леннй (формулы Френе)
координат взяты по t, v, В в этой точке,
то координаты х, у, г близкой точки Mi
кривой имеют вид
X - As - 1 к» (As)» - 1 KK'(bs)<+ ..
О о
у-1к(Дд)»4- +
При перемещении точки М по кривой
можно считать движение сопровождав
ющего в точке Л1 трехгранника про-
исходящим с постоянной (по модулю)
скоростью, равной единице (путь s
4- (К' - К» - КГ») (As)4 4- -..;
г - -1кГ(Дд)»4-д(КТ +2К'Т)(Ав)<+..,
ТЕОРИЯ ПОВЕРХНОСТЕЙ
25)3
где As — длина дуги ММг.К, Т взяты
в точке М. Проекции пространственной
кривой на плоскости сопровождающего
трехгранника имеют вид, показанный
на фиг. 71, я — в для случая Т > О
и показанный на фиг. 72, а — в, для
Т <0.
Фнг. 72. Лем>е
кручение.
Если в данной точке Т > 0, то кри-
вая имеет форму правого винта, а если
Т<0 — форму левого винта (см. фиг. 70).
ТЕОРИЯ ПОВЕРХНОСТЕЙ
Уравнение поверхности. Поверхность
может быть задана:
1) явным уравнением
Г-/(Х, у) (17)
в той области изменения х, у, где / (х, у)
и ее частные производные 1-го порядка
It (*• У). 1у (*. — непрерывны; гео-
метрическое место точек, координаты
которых удовлетворяют уравнению
(17), называется простым куском поверх-
ности-,
2) неявным уравнением
Р(х. у, х)-О, (18)
определяющим геометрическое место
точек и такое, что в окрестности каж-
дой из этих точек имеется простой ку-
сок поверхности; каждая такая точка
называется обыкновенной точкой.
Это геометрическое место точек назы-
вается регулярным куском поверхности.
Последний существует, если функция
F (х, У. г) и ее частные производные
первого порядка Ft, F v, Ft в некоторой
области пространства непрерывны и
Fx, Fy, Ft одновременно в нуль не
обращаются.
В особой точке (х0, у0, z0) одновре-
менно удовлетворяются уравнения
Р (х0. Уо. «о) = 0. Ft - Р v - Рг = 0;
3) поверхностью в параметрическом
представлении, заданной тремя функ-
циями
х = х(и, v), у = у (и, о), х = г (и, и) (19)
или векторной функцией
г — 7 (и, V) = Их (и, о) +
+ /У (ц. V)+*Z (а. V), (20)
называется геометрическое место точек,
образуемых концом радиуса-вектора г,
когда параметры и, v пробегают область
своего изменения I) и когда в окрест-
ности каждой точки (и0, v9) области D
точки (*, у, г), определяемые формулой
(19) или (20), образуют простой кусок
поверхности. Точка (х0, у«, г0), соответ-
ствующая точке (п0. о0) из Ь, называется
обыкновенной точкой поверхности
Поверхность существует, если функ-
ции к (и, в), у (а, о), г (и, о) и их
частные производные первого порядка
в области D непрерывны и в каждой
области ранг функциональной матрицы
(х у“ 1“) <21>
_ дх(и, о)
равен двум. Здесь хи — —— и т. д.
Из трех уравнений (19) исключени-
ем и, v получается одно уравнение
F (х, у, z) = 0, определяющее регуляр-
ный кусок поверхности.
При и = а = const уравнение г —
= 7 (о, v) определяет линию на по-
верхности. При V = Cj = const Г — г(|». <j)
определяет другую линию на поверх-
ности.
Каждой паре значений (и, о) из
области D однозначно соответствует
точка (х, у, г) поверхности, и обратно.
Параметры и, о называются криволи-
нейными координатами точки на по-
верхности. Два семейства линий и = ci.
v — cs образуют сеть (правильную)
координатных линий.
Точка, в окрестности которой поверх-
’ ность не представляет простого куска
поверхности, называется особой точкой.
Необходимым условием, чтобы точка
294
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
поверхности (19) или (20) была особой,
является обращение в нуль трех опре-
делителей матрицы (21).
Пример. Уравнение прямого геликоида(аинго-
иая поверхность) у = х tg 1 можно параметризо-
вать, если положить
х = и cos v; у = и sin v; s = v.
При и» с, точка Л! (ж, у. г) этой поверхности
опишет винтовую линию на цилиндре с рааи-
усом к; при v = c, точка Л1 опишет прямую ВМ —
пересечение плоскости л = о с плоскостью
у = X tg v (фиг. 73).
Линию на поверхности
г = г (u, v) можно задать присоедине-
нием к уравнениям поверхности урав-
нения <? (и, о) = 0 или системы урав-
нений и = и (/), v = v (t), причем
функции непрерывны и имеют непре-
рывные производные 1-го порядка; в
этом случае уравнение линии имеет
вид
г - г (и (П, v (0).
Вектор касательной к этой линии
dr — ~radu 4- rvdv.
-dr - dr
ГДС
Линейный (элемент поверхности.
Дифференциал дуги линии м = и ((),
v = v (.Г) на поверхности г = г (и, и)
выражается формулой
ds2 — (dr)2 — (rudu + rvdv)2 —
- Edu2 4- 2Fdu dv 4- Gdv',
где du — u' (() dt; dv — v' (/) dt",
; - dxdx , dy dy dz dz
',r° ~ du dv + du ~dv + du dv
G — (rvP -
<>v / + \ dv / \ ~5v )
Если F = 0 в каждой точке M (и, v),
то координатные линии и = q и v = Cj
ортогональны.
Выражение Edu2 4- 2Fdudv 4- Gdv2
называется первой (основной) квадра-
тичной формой поверхности или линей-
ным элементом поверхности.
Пример. Для поверхности конуса .г
= —coifWv), у = —sin (VT v), 1» —~
/2 VI V2
имеем
= 4- ««(/b); - -k .in
dw у 2 du у 2
dz _ 1
du y'J '
4^- =— U »tn (V2v); —u COB (V2v);
A — l, G — u. F = 0; da* —dn’-f-uW.
Угол 0 между двумя кривыми (т. е.
между касательными к ним) на поверх-
ности г = г (и, v) и пересекающимися
в точке М вычисляется по формуле
drt> г
cos» — , . „ _ , —
I dr 1| Ьг |
Edu lu + F (du Ъу 4- bu dv) 4- Gdv *v
“ rfsSs ’
где d — знак дифференциала для 1-й ли-
нии; Ь — знак дифференциала для 2-й
линии.
О площади поверхности см. стр. 190
Касательная плоскость я нормаль к
поверхности. Через всякую обыкновен-
ную точку М поверхности проходит
бесчисленное множество регулярных
кривых, принадлежащих поверхности.
Касательные ко всем этим кривым в
точке М лежат в одной плоскости,
называемой касательной плоскостью к
поверхности в точке М. Прямая, про-
ходящая через М перпендикулярно
касательной плоскости, называется
нормалью к поверхности в точке М.
Касательная плоскость проходит через
векторы ги и rv, касательные к линиям
соответственно и= сги u = c, в точке М.
ТЕОРИЯ ПОВЕРХНОСТЕЙ
295
Вектор
нормали
N='i
орт нормали
// = |n|= Veg-
Di = ул4 — .W Dt - z„x„ - ZpX.;
Dj = xayv —xvya.
В случае задания поверхности урав-
нением (17) имеем
"{-£• -г- sr}-«-V*+W
р = гх, q = zy; вектор л, лежащий на
нормали, образует острый угол с осью Ог.
В случае задания поверхности урав-
нением (18) имеем
N-у/ Fj + Fj + F’.
Уравнения нормали
X — г ст о У — г sin в Z — /(г)
/' (г) cos р = /' (Г) sin » ” —1
Проекция нормали на плоскость хОу
K-Xtgp
проходят через начало коорхниат, следовательно,
сама нормаль пересекает Ог.
Кривизна поверхности. Кривизна К
линнии = и (О, о= о (0 на поверх-
ности г «= г (и, о) определяется из фор-
мулы
dr - du , - do
где х = „ = r- _ + _ _ единич-
ный вектор касательной к линии; v —
единичный вектор главной нормали той
же линии.
Ту же кривизну К имеет плоское сече-
ние поверхности соприкасающейся пло-
скостью линии.
Если С — плоское сечение поверх-
ности в точке М, С„—нормальное
сечение плоскостью, проходящей через
Уравнения касательно! ялоскоств а вормаля к поверхность
Задание поверхности (стр. 293> Касательная плоскость НО|>маль
(1Л (1!) (19) (20) Z-a»j*lX-jr)4-«r-y> (Х-ж)Л +(Г-4-(Z-r)A -0 J • D,(X— л) + О,(У - у)+D,(Z-a)-0 (ft_;)N-0 Ь Im Im *1111 $1 1 s 1 N IN |N e i ь?! I “j i
В таблице я. у. г, г — координаты и лк поверхности и через ё к С, К — радиус-вектор точки М поверхности; кривизна С, Ка — кривизна С„, то X, Y, Z, R — текущие координаты и радиус-вектор точки касательной пло- Х„—КсозО-» скости или нормали; все производные „ . , , , п,. вычисляются в точке М. Ddut + tD'dudv+D'difl E du--\- 2F du dv + G did • Пример. Показать, что нормаль в точке >, у, х) к поверхности ьрамеяия * — г cos у. - - - у ~ rain у, д— /(г) пересекает ось вращения: где 0 “ / (к, л), к — главная нормаль С я — сову, у — aln у: г —/'(г); <ФЯГ- 74>: знаменатель есть rfs»; чнсли_- г__ *. f ' . тель Ddu1 + 2D'dudv + D"dv* — — drdn м о e. jif - о. я называется второй квадратичной фор- D, - - rf (у)an t; D, — - rf (г) ain D,—г. мой поверхности; коэффициенты этой
296
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
формы определяются
г 7 г 1
п ' о»' “ Р
°-------Н-----Н
D’-
rw гигу
н
формулами
хии Уив гов .
хв У и гв I ’
xt> Уе zo I
1хаьУиь гиь .
хи У и «в ’
xv Уи *ь
2
н
хт Ут *vu
ха У и «нВ
xv Уь «в I
Я- VEG—Ft.
В случае задания поверхности урав-
нением (17) вторая квадратичная форма
имеет вид
г dx4- + 2s dx d y 4- 1 dy1
/1 +р» + ф»
где
t = zyr.
Q e Zyt Г Zjuc* $ —
P = «х.
Если R„ = -J-, R = — радиусы
Aa A
кривизны соответствующих сечений C„
и С (фиг. 74), то Racos 0 =/? (теорема
Меиье). R„ берется
со знаком плюс,
Фиг. 74. Нормальное
сечение поверхности.
если л направлен
в сторону вогну-
тости кривой С„,
и минус, если л
направлен в сто-
рону выпуклости.
Для каждого
нормального сече-
ния С„ его кри-
визна
Кв = К, cos1? 4-
4- K2sin»?
(формула Эйлера),
где ?— угол между плоскостями нор-
мальных сечений с кривизной Кп и /Ср
Величины Ri “ Rt — J------------глав-
ные радиусы кривизны, т. е. наибольшее
и наименьшее значения R„.
Средняя кривизна поверхности в точ-
ке (и, о)
.. 1 DG-IDF+D’E
М “ 2 (К> + ----T(EG — Ft) •
Полная (гауссова) кривизна поверхно-
сти, в точке (и, о)
у ху РУ-О'»
> t Л AjAl C(j — Ft ’
Главные радиусы кривизны суть кор-
ни квадратного уравнения
KRt — 2Af/?4- 1 =0.
Нормальные сечения поверхности,
имеющие кривизны Ki и Kt. называ-
ются главными нормальными сечениями
do
поверхности, и направление этих
сечений (взаимно перпендикулярных)
определяется из квадратного уравнения
+ (FD — ED) -0;
коэффициенты квадратичных форм £, F.
G, D, D' D' вычисляются в данной точке
(и, о) поверхности.
Классификация точек поверхности.
Если в точке М (и, с) поверхности вели-
чина DD'— D"1 >0, то точка назы-
вается эллиптической; Ri и Rt — одно-
го знака; вблизи точки М поверхность
расположена по одну сторону касатель-
ной. Если DD" — D'1 <0, то точка
называется гиперболической; Rt и /?2 —
разных знаков. Поверхность пересе-
кается касательной плоскостью в точке
М. и вблизи этой точки поверхность
имеет вид гиперболического параболо-
ида. Если DD’ — Dt = 0, то точка
называется параболической. R\ или Rt
равен оо.
Геодезической кривизной Kg в точке AI
линии Г на поверхности называется
кривизна в той же точке кривой Г’,
являющейся проекцией Г на касатель-
ную плоскость поверхности в точке М.
Кривизна К линии Г, Кг и нормальная
кривизна К„ кривой Г (кривизна нор-
мального сечения плоскостью, прохо-
дящей через т кривой Г и через п
к поверхности в
точке М) связа-
ны соотношениями
(фиг. 75)
Яг-Кз1п0;
К„ — К cos в;
кривизны
71 ра-
диус геодезической
I
Фиг. 75. Центр геодези-
ческой кривизны.
кривизны, Kg =
Ci — центр геодезической кри-
внзны.
Геодезической линией на поверхности
называется такая линия, в каждой
точке которой Kg = 0. Вдоль геодези-
ТЕОРИЯ ПОВЕРХНОСТЕЙ
297
ческой линии ее главная нормаль сов-
ладает с нормалью к поверхности.
Расстояние по геодезической линии
между двумя ее достаточно близкими
точками меньше расстояния между теми
же точками по всякой другой кривой,
проходящей через эти точки.
Если поверхность дана в форме (17),
то дифференциальное уравнение геоде-
зических линий имеет вид
(| +'’ + ’*) +
+ (2ра - qr.
Огибающая семейства поверхностей.
Уравнение А'(х, у, г, 7) = 0 определяет
однопарамстрическое семейство поверх-
ностей; I — параметр.
г с л с dF (х< У< г> 0 п
Если из F = 0 и Ft = ——-й------=0
' at
исключить t, то получится урав-
нение поверхности, называемой дискри-
минантной Для каждого значения t
два уравнения F = 0. Ft = 0 опреде-
ляют линию, называемую характери-
стикой той поверхности, которая выде-
ляется из семейства при этом значении t.
Дискриминантная поверхность есть
геометрическое место характеристик.
Огибающей семейства поверхностей
называется дискриминантная поверх-
ность или ее часть, касающаяся каждой
своей точкой некоторой поверхности
семейства. Огибающая касается поверх-
ности семейства вдоль характеристики.
На огибающей поверхности характе-
ристики образуют семейство линий.
Если это семейство линий имеет оги-
бающую, то последняя называется
ребром возврата семейства поверхно-
стей или огибающей; ребро возврата
определяется уравнениями
(,гр
F—0‘, Ft — 0; Fti-~-0.
Из трех уравнений можно получить
параметрические уравнения ребра воз-
врата
x-x(t), y-y(t).
В случае задания семейства поверх-
ностей параметрическими уравнениями
X = х(и, V, I). у = у (и, V, t), Z = Z (и, V, I)
огибающая находится присоединением
к этим трем еще одного уравнения:
*и Уи
Xv У®
У/
ги
«р
г(
= 0.
(22)
Развертывающейся поверхностью на-
зывается огибающая однопараметри-
ческого семейства плоскостей F = Лх -4-
+ fly 4- Сг + D = 0, где Л. fl. С. D —
функции t.
Характеристика плоскости нз данного
семейства есть прямая: Лх 4- Яу 4-
4- Сг 4- D = 0, А'х+ В‘у+ С‘г +
4- D' = 0, где А', В', С, D' — про-
изводные по /.
Развертывающаяся поверхность —
линейчатая поверхность (стр. 298).
Ребро возврата
опрсделяется урлв- 47
нениями
F - 0. к
Ft - 0. <^71
Fz, = 0.
— Фи:. 76. Ребро |юз-
Развертывающая* ярата.
ся поверхность со-
стоит из касательных ее ребра возврат»
(фиг. 76), являющихся характеристи-
ками. Каждая плоскость семейства —
соприкасающаяся плоскость ребра воз-
врата. Касательная плоскость к раз-
вертывающейся поверхности — одна и
та же вдоль характеристики и совпадает
с соответствующей соприкасающейся
плоскостью ребра возврата.
Развертывающаяся поверхность нало-
жима (без складок и разрывов) на пло-
скость. Во всякой точке развертываю-
щейся поверхности полная кривизна
К = 0.
Пример. Огибающая семейств» плоскостей
F я х sin t — у cos t г — nt = о, где t — вора-
метр, * ™ const, найдется исключением t из F — И,
F. — 0, Если положить г — А/ = и, то можно по-
лучить параметрические уравнения огибающей
х — Л cos t — и sin t;
у — A sin t 4* и cos I;
г - lit -f- n,
определяющие пнптооую поверхность.
Ребром полира га будет х — П со» Л у — П sin /,
1» nt — винтовая линия иа круглом цилиндре
С радиусом А.
Образование поверхностей линиями.
Если линии двупараметрического се-
мейства
Fj (х, у, z, а, 3) — 0, F2 (х, у, z, а,(1) = 0
2Т8
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
пересекают некоторую направляющую
4>! (ж. у. z) — 0, Фг (х, у. г) - О.
то исключением х, у, г из этих четырех
уравнений находят соотношени® между
параметрами: о (а, 5) = 0. Исключая
а, р из трех уравнений Ft = 0, Fг = 0,
V (’• ?) = 0. получают поверхность
F (х, у, г) = 0 как геометрическое
место кривых, выделенное из двупара-
метрического семейства линий.
а) Цилиндрическая по-
верхность есть геометрическое
место прямых, параллельных данному
вектору I и пересекающих данную
направляющую Ф1 =0, Фг — 0.
Прямые семейства
Ах + By + Cz = а, Л,х + Bjy + Ctz = ?
параллельны >,, если
i.ii I
I л, в,
i
с
Су
Если ? (а, р) = 0 — результат исклю-
чения х, у, г из четырех уравнений, то
ф (Ах 4- By 4- Cz, Ахх+Вуу 4- Суг) = О—
общий вид уравнения цилиндрической
поверхности.
6) Коническая поверх-
ность— геометрическое место прямых
х — х0 = “ (г — Zq), у — Уо = " (« —
— гв), проходящих через точку (х0.
Уо. ?о) н пересекающих направляющую
Ф1 = 0, Фо “ 0.
Уравнение конуса
г —А>/
где ? (“. ₽) = 0 — результат исклю-
чения х, у, г из четырех уравнений.
в) Поверхность враще-
ния образуется вращением данной
линии вокруг прямой (осн). Можно
х — а
поверхность вращения с осью—j— =
у — b г — с .
«= *---=------ образовать движе-
т п
нием круга (х — fl)* 4- (у — б)1 +
4- (г — с)* = /х + ту + пг = р,
плоскость которого перпендикулярна
оси вращения, центр лежит на оси, а
радиус изменяется так, чтобы окруж-
ность круга встречала данную линию
Ф> = 0, Ф1 “ 0. Если <f> (а, й = 0 —
результат исключения х, у, г из
четырех уравнений, то
V (/ (х — л)- + (у — б)2 4- (z — е)*.
1х 4- ту 4- ла) = 0
уравнение поверхности вращения.
г) Линейчатые поверхно-
сти образуются движением прямой
^образующей) с направляющим вектором
X (о) {/ (ti), m(v), л (о)} вдоль напра-
вляющей линии р =
-₽(»){х(р),у(р).г(п)}.
Уравнение линей-
чатой поверхности
г— р4- вХ,
где и (фиг. 77) —
параметр, определяю- Фиг. 77. Линейчл-
ЩИЙ текущую ТОЧ- ™ поверхность,
ку М на образующей;
г(Х, У, Z} — текущий радиус-вектор
точки М; «А = РМ
Уравнение касательной плоскости
(«-₽)Х(л+в^)“0>
где /? — радиус-вектор
ной плоскости.
Равенство
точки касатель-
dl
dm
dn
I
т
л
dx
dy
dz
rfp X ЛХ = 0 или
= 0
есть условие того, что линейчатая по-
верхность — развертывающаяся.
д) Винтовые поверхности
(геликоиды) образуются винтовым
Фиг. 7В. Профиль
гелниони.
приведенный шаг
движением дан-
ной кривой вокруг
оси. Если Ог — ось
винта (см. стр. 286),
/•=/ (х)—профиль
геликоида (сеченне
его плоскостью,
проходящей через
Ог), v — угол пло-
скости профиля с
хОг (фиг. 78), Л—
или параметр винта,
то
х — и cos V,
у — и sin V.
г — f («) + Av
параметрические уравнения гели-
коида; и — расстояние от точки про-
филя до осн Ог.
ТЕОРИЯ ПОВЕРХНОСТЕЙ
299
При винтовом движении прямой г =
= ± х ctg -j + Ь, пересекающей Ог
под углом 7, геликоид
х = и cos V,
у = и sin v,
hv ± и ctg 7 4- b
называется архимедовой винтовой по-
верхностью; в сечении г = const полу-
чается спираль Архимеда (фиг. 79).
Поверхность — нсразвертывающаяся.
В общем случае пусть Охуг — непо-
движная система координат. O'XYZ —
подвижная система, совершающая вин-
товое движение с параметром Л вокруг
Ох (фиг. 80). Координаты х, у, г точки
хИ (X,Y,Z), совершающей вместе с ПО-
Фиг. 79. Архимедова
винтовая поверхность.
Фиг. Я0. Криволиней-
ная образующая вин-
товой поверхности.
лвижной системой винтовое движение,
выражаются формулами
х—Лсозо — К sin о;
у — X sin v 4- У cos v;
г — Z 4- hv,
(23)
где. v — угол поворота О'Х YZ вокруг
Ог. Если X, Y, Z — постоянные, то
точка М опишет винтовую линию. Если
X, Y, Z — функции одного перемен-
ного параметра:
Х-Л(и). r-/t(«). Z-/s(«).
то мы имеем линию в системе O'XYZ
(образующую), которая опишет винто-
вую поверхность:
х — Д (“) cos v —fi (u) sin v;
у — /> («) sin v 4- fi (u) cos v,
*—/»(«) + Л»-
Если образующая дана уравнениями
и цилиндрических координатах р =/(0),
Z = F (0), то геликоид определится
уравнениями
* = /(#) cos (0 4- с);
у =/(0) sin (0 4- у);
z = F(b) + hv (фиг. 80).
Если образующей является прямая
/И0Л(, составляющая ^7 с осью Ог, ее
не пересекаю-
щая и находя-
щаяся от Ог
на кратчайшем
расстоянии а
(фиг. 81),
X— а
0
Фиг. 81. Линейчатая винто-
вая поверхность.
У
sin 7
cos 7
причем ось X направлена по кратчай-
шему расстоянию, то получается линей-
чатый геликоид:
x = ecosv— u sin о;
у = a sin v 4- “ cos v,
2 = Ли 4- и ctg 7,
где положено и = a tg 6 = I sin 7. Все
прямолинейные образующие геликоида
касаются основного (круглого) ци-
линдра радиуса а с осью Ог и в об-
щем случае пересекают винтовую
линию х = a cos о, у = a sin о, г =hv
на этом цилиндре, образованную точкой
Л10 (фиг. 82). Полученный геликоид,
Фиг. 82. Конво-
лютная вннговая
поверхность.
Фиг. 83. Эвольвент-
вав винтовав по-
верхность.
называемый конволютным — иеразвер-
тывающийся В пересечении с пло- •
скостью z=0 получается удлиненная
(прн Л tg 7 > а) или укороченная (прн
300
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
AtgT<a) эвольвента окружности с
радиусом h tg 7:
х = a cos v 4- vh tg 7 sin v,
у = a sin о — vh tg 7 cos v.
В частности, если образующая
является еще и касательной к винтовой
линии на основном цилиндре, то линей-
чатая винтовая поверхность будет раз-
вертывающейся, называемой авольвент-
ной, условием чего является равен-
ство Л = а etg 7 (фнг. 83).
Винтовая линия на основном цилин-
дре является ребром возврата эволь-
вентного геликоида; в пересечении с
плоскостью г = 0 получится эволь-
вента окружности с радиусом а.
Винтовая поверхность может полу-
читься и как огибающая семейства по-
верхностей, образованного винтовым
движением некоторой поверхности (пло-
скости. конуса и т. д.)
Если X, У, Z — функции двух пере-
менных параметров:
X-h (u.f);
Y~fi(u.t)-,
2 — t).
(24)
то имеем в системе O'XYZ поверхность.
При винтовом движении O'XYZ полу-
чится семейство поверхностей, опреде-
ляемое уравнениями (23), в которых
X, У, Z заменяются по формулам
(24).
Огибающая — винтовая поверхность
получится, если к уравнениям (23)
присоединить равенство (22).
ГЛАВА XIII
РАЗНОСТНОЕ ИСЧИСЛЕНИЕ И ИНТЕРПОЛИРОВАНИЕ*
КОНЕЧНЫЕ РАЗНОСТИ
Если имеется ряд значений функции
У = I (х): у0, уь у....... соответст-
вующих значениям аргумента х: х*
х»...,хп, то величины yt—у0,у; — у>...
у„—уя—1 называются разностями
1-го порядка. Обозначают Ду* = у*.,., —
— у*; разность т-го порядка есть раз-
ность 1-го порядка от разности (т—1)-го
порядка- Дту* — Am~1yft^| — Дя,~1уг*.
Удобно разности располагать в таблицу
(диагональная таблица разностей):
Употребляется также горизонталь-
ная таблица разностей:
^тУи ” д<п—1У* 1У*-1>
Д”у* = 1«.У*+Л ! ДтУ* “ Д"У*-т-
* См. литературу на стр. 351 (ПЭ]. |124|. ||12].
Если значения аргумента даны через
равные промежутки h = х* — ж*_: =
= const, то
Уо —/(*);
>1 — /<-« + л>-. ч у*—/ (х + **);
дУо - / U+А) —/(х); ..Ду* -
-/(х+ Л+ТЛ) -/(X + му,
Д1у0 — Ду, — Ду„ «= Д/(Х + А) — Д/ (X) —
= /(х + 2й)-2/(х + Л) +/(х);
Дяув-
-/(х + пЛ) - (")/(х + !ГПл» +
+ (")/ (х +Т^2Л) + ... + (-))«/ (X).
где обозначено
Значение уп >=/ (х + пй) выражается
через разности по формуле
>« = У» + (") дУо +
+ (2)Л1ув+—+ 4"y>
Конечные разности простейших
• функций
Степенная функция Xя н многочлены:
Дг" — (х + Л)я—Xя —
Разность первого порядка многочлена
у — Ojx" 4- fljx"-1 + ... 4- а„ есть много-
302
РАЗНОСТНОЕ ИСЧИСЛЕНИЕ И ИНТЕРПОЛИРОВАНИЕ
член степени л — I. Разность порядка
л есть постоянная ayil/i'1; разность
(л + 1)-го порядка от многочлена рав-
на нулю.
Показательная функция а*-
Ьл* - ax+h -ax = ax(ah — 1).
Тригонометрические функции:
Д sin х => 2 sin -j- ein (х + -у+ ;
Д cos х = 2 sin — cos ( x + + у ) »
Д" sin (ax -+•&) —
(n , ah\n . ( ... <2/1+
«=(2sin-y-J sin ^ax 4- b + n—-—J.
Факториальная * функция опреде-
ляется формулой
xW-
— х (х — Л) (х— 2Л).•. (х— п — 1й).
Для нее
Дх*я| — лйх (х — Л)... (х — л —2й) —
- пх|л-,|й;
Д*х|я| — п (п - 1)... (л - Д^П) X
X
ллх)л| .. п • Л".
Разложение по фактори-
альным функциям всякой
функции f (х), имеющей производные
до (л +1) порядка:
/(*) - л+ (х—Хо) +
+ГГЙ Хв)1” + (х ~ Хв)|Э| +
+ -+vr$- +
где
Уо —/(Jfo); (х —Хо)1*1 —
- (X — Хо) (X — Xi)... (X— Х*_!).
х*_, — Хд + (k — 1) h:
/Я'Н)(С)
(«4-1)!
Rn= (х-Х0) (х—X!) . . . (X—Хд)
-Го < С < Хд.
Если / (х) — многочлен степени л, то
Д'Ч-1 у,, = 0. и в его разложении по
факториальным функциям остаточный
член /?„ = 0.
Для /чх) = Xя. й — 1. .«о = 0. уо -= О'*
имеем
„ ДО" . Д2О" ,
х ’ 11 4* 2! х л ) "Ь
ДХ)"
-+• у х(х— 1) (х-2) +
_____
+ + -уу-Х(Х — 1)...(Х — Л— 1).
причем числа Д*0" даются следующей
таблицей:
Приложение к экстраполяции (про-
должение таблицы для следующих зна-
чений аргумента). Так как для поли-
нома I (т) л-й степени Д'7 = const,
то для вычисления Дя/ достаточно знать
л + 1 значение функции. Вычисляя по-
следовательно Д"-1 f, Ья~г1 и т. д., мож-
но экстраполировать таблицу значений
полинома в случае равноотстоящих зна-
чений аргумента.
Пример. Состакить таблицу аиачеииЛ функ-
ции у — л* — Аг» 4- Вх яла нелыт «качений х от 0
до 10.
Для четырех значений мепосредственно ммчис«
лясы
/(0)-0; /(1) — 5; /(2)-в; /(3>- 15
и по ятнм мгяченияы составляем разности.
JT У Ду Д<у Д»У
0 1 2 3 0 5 8 1S 3 3 7 • -2 4 1 <> 1
ИНТЕРПОЛИРОВАНИЕ
303-
Зная, что a’y0=fi= const = 4'у, = л,у1 и т. л.,
мы далее последовательно находим по формуле
4Я,-1У*4-1 — л"** + 4“-1>й:
A’ji = Дяу, Д*У » $+< го;
Л у, - Д’у, 4- Ду, - !0 4- 7 - 17:
/«) - у. « лу, + у, - 17 + 15 - 32.
Аналогично находятся / (5), j (в) ... выпол-
аеннеы только сложения.
ИНТЕРПОЛИРОВАНИЕ
Задачи интерполирования: I) опре-
деление значений функции, заданной
таблицей, для тех значений аргумента,
которые находятся между двумя сосед-
ними значениями, находящимися в таб-
лице; 2) построение такой функции,
которая для данных значений аргумента
принимала бы данные значения. Наи-
более употребительной интерполирую-
щей функцией является многочлен <р (х) —
= а0 + aix + . . . + а„хп (параболи-
ческая интерполяция), а для перио-
дических функций применяется триго-
нометрический полином (тригонометри-
ческая интерполяция) (стр. 306, 313).
Какова бы ни была заданная функция
/ (х) или ее л 4- I значений для узловых
точек х0, xj, х»..хп, всегда суще-
ствует единственный многочлен л-й
степени ? (х) такой, что (х*) = f (хц),
4=0. I......п.
Формулы Стирлинга и Бесселя удоб-
ны для интерполирования значений
Формула Стирлинга
/(х) « <р(х) —
, ду0 + Ду_,
= Уо + —|Т^—(х ~ Хо) +
Д2У—1
4 2! Л» ^Х ~ +
Д’У_| + Д,У-2
4 —тгтгт;—2 <х — х«>(х — Х,)х
О1 П9•А
Д<У-2
X (X - х_|) + (х - х0)« х
X (X — Х|) (X — х_!) + .. .
Интерполяционные формулы
для равноотстоящих узловых точек
Первая формула Ньютона дает раз-
ложение по факториальным функциям
через диагональные разности
J (х) » Т (х) — у0+ (х — х0) +
+ -^7 (х — х0) (х — х,) + ... +
+ -*»)—(*-x«-i).
где х* = х0 + kh\ употребляется для «,
близких к х0.
Вторая формула Ньютона выражаекя
через горизонтальные разности
/(X) <s ? (X) — Ул + (X — хя) +
+ -^7 (Х-Х„) (X- A„_t) -f-... +
+ (х—х„) <*—хл-1> •• • (х—х,>;
употребляется для х, близких к хч.
В схеме подчеркнуты сплошной чер-
той разности, взятые в формуле Стир-
линга.
Формула Бесселя
f (X) «з <f> (х) =
_ Уо + У1 , дУо / , _ Xi 4- х0 \
“ 2 4 ПЛ \ 2 М
ДТУ|> + дгУ-1
+ — >l„zv - - - х№ - х1)+
4 “ОТ <х “ х°)(х ~ +•
+ Д<У~4|^.2У~- (х - хо)(х - х>)Х
X (X —x_j) (х —Xi) +
Д5У_»
+ 5! ^-(Х — х0) (х — Х1)Х
Х(х — х_,)(х— хг) ^х—Х)
В схеме подчеркнуты пунктирной
линией разности, взятые в формуле
304
РАЗНОСТНОЕ ИСЧИСЛЕНИЕ И ИНТЕРПОЛИРОВАНИЕ
Бесселя. Формула особенно удобна для
интерполяции на середину при
•*1 + -*о
2 •
Интерполяционная формула Лагранжа
для неравноотстоящих узловых точек
/(X) « <р(х) -
= (х — X]) (х - Хг)... (X — хя)
(Х0 — X,) (Хо — Xj) ... (хо — Хя) Уо
(* — Хд) (X х;) . . (X — хя)
(Xj — Хо) (Xj — X,)... (Xj — хя) л
. (X — Х0) (X — X,) (X — Хд-1)
(дд—Ло) (Хя —Х])...(ХЛ Хд—j)
Пример. Построить ноликом у —/(Ж) по зна-
чениям г, у, прицеленным н таблице:
л 0 1 2 5
V 2 3 12 147
По формуле Лагранжа получим
_ (х - 1)(Л — 2)(л - 5)
’ (U — I) (U — 2) (О — о) "Г
ж(л — 2)(.r -S) л(л - 1)(X - 5)
+ 1(1-2)11-6) 2(2-1) (2-5)
+
х(х- 1)(л-2)
5 (5 — 1) (о — 2)
147 = X1 + х«-X 4- 2.
Остаточные члены интерполяционных
формул
Погрешность прн интерполировании
можно оценить, если вычислить остаточ-
ный член R * I (х) — <р (х).
I) Для формулы Лагранжа
R-
/я4'1)(6) у
(л + 1)1
X (х — х0) (х — Xj)... (х — хя).
где 6 — промежуточное значение между
наибольшим и наименьшим из чисел х0,
«1. •.*/!•
2) Такое же выражение имеет R и
для формул Ньютона, если аналити-
ческий вид / (х) известен. В противном
случае можно заменить
А*+ ' у0
Л"+'
в первой формуле Ньютона и
/<"+«)(6) « Д"+» ^
ДЛ+1
во второй формуле Ньютона.
3) Для формулы Стирлинга
/(2л-Ы)(М
•(2д + п , (х — -«-о) (х — Xj) X
X (х — X_j) ... (X — х„) (X — х_д).
Здесь можно заменить
2Л2я+*
4) Для формулы Бесселя
/^)
К~ (2л + 2,1 Х
X (X — Хв) (X — Xj) (X — x_j) ...
. . . (X — Х„) (X — х_д) (X — хя + j).
Здесь можно заменить
/(2П4-2)(5) *
Д2я+гу_д_, + А2л+ау_я
2л'2я+*
Численное дифференцирование
и интегрирование
Для приближенного (численного) диф-
ференцирования f (х) последняя заме-
няется одной из интерполяционных
формул <р (х):
по формуле Стирлинга
(*У\ =± [^4-^-1 _
\ rfx/x=x, ft 2
I ДЗУ—1 4- ।
6 2'
1 дау_, + д»у_, 1
-Г 30 .j -Г"-]»
по формуле Ньютона
(44 e Jr [Ду°_ -г
\ «X / XmJT0 "I ‘
+4- *8л-**+•••] •
Для приближенного (численного)
интегрирования I (х) следует эту функ-
цию заменить интерполяционным мно-
гочленом f (х) Интегрирование ? (х)
приводит к формулам трапеций. Симп-
сона и др. (см. стр. 182).
ГЛАВА XIV
ПРИБЛИЖЕННОЕ АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ
ФУНКЦИЙ*
Задача приближенного представления
функции 1(х), заданной аналитически
(формулой) или эмпирически (таблицей),
решается выбором аппроксимирующей
функции Sn (х) вида
5Я (х) = «оТо (х) 4- Crfi (х) +
+ • • • + с n't л (х).
Здесь ^х), ?i(x)... <?л(х) — неко-
торые заданные функции, а коэффициенты
со, Сг, . . , сл подбираются так, чтобы
выполнялись требования наилучшего
приближения на отрезке [а<х<й].
Близость функции /(ж) к S„(x) оцени-
вается различными способами; в зави-
симости от этого получается то или дру-
гое наилучшее приближение.
Наиболее употребительным является
такое приближение 5„(х), для которого
величина
»
С[/(х)~5п(х)рАх
имеет наименьшее значение. Величина »
называется средней квадратической по-
грешностью.
Употребляется еще наилучшее при-
ближение с оценкой по обобщенному
среднему квадратическому отклонению
с весом р (ж), т. е. такое приближение
Вп(х), для которого наименьшее значе-
ние имеет величина
р(х) (/(х)-5я(ж)]»Дг.
причем функция р(х) > 0 яа отрезке
(в, *1-
• См. авпрктуру п стр. МЭ PS], [вР]. (К].
2о Том I Зак. 1*и
Функции fa(x). ?i(x).-.. иа отрезке
а < х Ь называются ортогональными,
если
а
jfm (*)<Сп (x)dx = 0. т=рп.
а
где т, п = 0, 1, 2...
Обозначим
ь
kn- |[ТЯ (x)]«rfx;
и
тогда система функций
Фа (X) = уу <Гп (X)
называется ортогональной и нормиро-
ванной, так как обладает свойством
j (х) ф„ (х) Лх = {?
в
При оценке по среднему квадратиче-
скому отклонению коэффициенты наи-
лучшего приближения определяются по
формулам
Ь
с«-|/(ОФ«(П^ («-О. 1. 2.
Эти коэффициенты называются обоб-
щенными коэффициентами Фурье функ-
ции Дх) относительно системы Wx).
Рядг\, ф0\х) 4- о(х) 4- с«Фз (х) 4- -..
называется обобщенным рядом Фурье
функции /(ж).
Когда Дх) задана графически или
таблицей, то интегралы (для сп) вычис-
ляются по формулам численного инте-
грирования (см. стр. 182).
Система функций фо(х), ф1(х),.„ на-
зывается на отрезке а < х < b полной,
если для любой непрерывной функции
306
ПРИБЛИЖЕННОЕ АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ ФУНКЦИИ
Цх) на [а, 61 всегда можно подо-
брать п и коэффициенты с0, ft,..., сп
так, что среднее квадратическое откло-
нение Sn = С0ф0 (х) + (х) + ... +
+ с„фл(х) от Дх) становится меньше
любого сколь угодно малого положи-
тельного числа. Условие полноты си-
стемы ортогональных функций фо(х),
ф^х),... выражается равенством
i«=O а
В этом случае говорят, что s„(x)
сходится в среднем к функции Дх).
Среднее квадратическое отклонение
s„(x) от /(х) находится из равенства
(b-a) I’-firwF
а 1^-0
Примеры полных ортогональных систем функ-
ций: 1) Система функций
гиг „и „ гг
cos —j- , eos 2 -j— , cos 3 -j—....
me me * r
Sln-y-, Slu2-y-, sln3-=-,...
полна и ортогональна на отрезке 0 < х < 21.
Полнота этой системы впервые доказана А. М. Ля-
пуновым.
2) Система бесселевых функций
VxJ, («,х), («»г), Ух70 («^)....
полна н ортогональна иа отрезке (0, Z), если
«* (А = 1, 2, 3, . . . ) — корень уравнения
Л(«*0=° (см. бесселевы функции, стр. 222, 311).
Тригонометрический ряд Фурье
При разложении Дх) на отрезке
—I < х < I в основной тригонометри-
ческий ряд Фурье
-у + at cos ~ + at cos 2 + ...
-Mi sin ~ + ^sin2-y- + ...
коэффициенты вычисляются по форму-
лам Эйлера: *
°о "J
e*"‘Tj cos *
—I
/ (t) Sin k Tt- dt
(k = 1, 2. 3,...). В дальнейшем сумму
ряда Фурье для Дх) обозначим через
Ф(х).
При приближенной замене Дх) три-
гонометрической суммой (тригонометри-
ческим ПОЛИНОМОМ) 5П (X) = Од -f-
п
+ cos k-^- + fi* sin k средняя
iK
квадратическая ошибка t)2 I (/(/) —
—sn(f)|*d( будет наименьшей, если
a* = о*, fi* = 6* — коэффициенты Фурье
данной функции.
Для всякой ограниченной н кусочно-
непрерывной функции Дх) ее ряд
Фурье сходится в среднем к этой функ-
ции, т. е.
-Н
Hm J[/(0-s„(r)]W-0.
Л—ОО_|
Функция Дх) называется удовле-
творяющей в промежутке (а, 6) условиям
Дирихле, если в (а, 6) Дх) или непре-
рывна, или имеет конечное число разры-
вов 1-го рода (стр. 137), имеет конечное
число экстремумов; существуют конеч-
ные пределы /(а + 0) и ЦЬ — 0).
Иначе: Дх) — ограниченная, и отре-
зок (а, 6) можно разбить на конечное
число таких отрезков, внутри каждого
из которых /(х) — непрерывная и моно-
тонная.
Теорема Дирихле. Если Дх), заданная
в ( —/, /), удовлетворяет условиям
Дирихле, то ряд Фурье этой функции
сходится во всем промежутке (—I, 1)
и сумма этого ряда: 1) равна Дх) во
всякой точке непрерывности Цх);
2) равна у |Дх + 0) + Дх — 0)] в
точке разрыва непрерывности; 3) равна
| 1Д-/+ 0) + Д/ - 0)1 при х= -(
и х и + 1.
Сходимость ряда будет абсолютной
и равномерной на всяком отрезке, не
содержащем точки разрыва.
Если пользоваться рядом Фурье вне
(—I, I), то Дх) должна быть продол-
жена вне (—/, /) периодически с перио-
дом 21. Концы х = ± Z явятся для
продолженной таким образом функции
ПРИБЛИЖЕННОЕ АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ ФУНКЦИИ
307
точками разрыва, если /(—I + 0) =#
+ Ц1 - 0).
Ряд Фурье в комплексной Форме
имеет вид
fW - X W ‘ ’•
А»—оо
с*“ ‘Л J /(0* ‘ ‘ *
ik-0, ±1. ±2....).
3) Если /(—I + х) = —Цх), т. е.
отрицательная полуволна есть перевер-
нутая около Ох полуволна положитель-
ная (фиг. 3 и 4), то
Если Цх) принимает на (—I, + I)
только действительные значения, то
I 1 ,
у ао’’ СЛ"~ ~2~ ^а* ~ ,Ь^ '
"гл = “ 0;
i
«24^1 — у-J/(0 COS (2* +• \)~dt;
c-k — ("* + ibx)> A — 1. 2, ...
2 С Kt
*2*+>-----т J f (0 sln (2А + 1) Т dt’
Специальные случаи разложения
1) Если / (х) — четная функция, т. е.
К—х) = Цх). то
i
Ьх — 0. я*—у-J/(/) cos А-у 44;
и
Фмг. 4.
СК?
ф (х) — J} a2fr+, cos (2А + 1) ~ +
+ ^2*-г1 Sin (2Л + 0 "у.
(А — 0. 1, 2....).
4) Если /(х) четная и. кроме того.
/(— I + х) — — / (х), то Ьх — аи — 0;
4
2
*2*+1 “ -уУ 1 (П cos <2* + *> “У Л;
2) Если f (х) — нечетная функция,
т. е. 1(—х) — —Цх). то
Ф (х) — V а2Н_| cos (2ft + I) -у.
ал — 0; bx — -у j f (t) sin A dt;
u
co
Ф (X) — V bx sin А -у (фиг. 2X
*— 1
5) Если Цх) четная и /(x)—/(Z —х),
то ьь= a?*+i= 0;
1
в» - -у J/W cos2A-y dt
о
(А -0. I, 2....);
2О‘
зов
приближенное аналитическое выражение функций
*=i
6) Если / (х) нечетная н / (— I 4- х) =
= — f\x). 10 ац = bu - 0-,
I
2
^2*4-1 “ ”7"У s'n + 1) —р dr,
оо
Ф (X) — ^2*4-1 s'n (24 + П—у .
л— о
7) Если/(х) нечетная и f(l — х)—
= — / (*)• то ал ~ й2А+1 - 0;
I
4»--y J/(0«ln2*-y<ft;
о
ф (X) — V Ьы tin ‘2k -
л-1
Одну и ту же функцию f(x), задан
ную на 0 < х < /, можно разложить в
различные ряды Фурье, дающие в этом
промежутке /(ж):
а) Ф] (х) — -у 4- А] cos 4-
4- «»соз 2^ + ... 4- а„ cos л 4-
4-... 4- sin 4- Ьг sin 2 ~ 4-
у
4-... 4- fr* sin л 4-...;
периодом Ф,(ж) будет I. Коэффициенты
1
** “ "Т jcos *"т Л;
I
»»-4j/U)sin
и
в) ф»(х) - -у- 4- а, соз ~ 4-
4- ввсоз2у 4-... 4- a„cosn -у 4-...;
периодом Ф»(х) будет 21. Ф»(х) совпа-
дает с f(x) в 0 < х <1; в промежутке
—I < х < 0 ряд Ф»(х) дает симметрич
ное относительно Оу продолжение.
Коэффициенты находятся по формулам
специального случая 1.
в) Ф» (х» — b} sin 4- sin 2 4-...
...4- fe„sinA ~р + ...; период Ф»(х)ра-
вен 21. Ф3(х) дает на (—I, 0) продол-
жение, симметричное относительно на-
чала координат, и совпадает с Дх)
в промежутке 0 < х < /.
Коэффициенты находятся по формулам
специального случая 2
г) Ф4(х) = ^-4-а,со5 2-^4-
4-04 соз 4, период Ф4 (ж) ря-
вен I; коэффициенты находятся по фор-
мулам случая 5 и т. д.
Интеграл Фурье. Если /(ж) удовле-
творяет условиям Дирихле на любом
конечном отрезке н |Дх)| dx схо-
дится, то
/w=4-
/ (Г) cos a (t — х) dt
Это выражение для Дх) называется
интегралом Фурье функции Дх).
Если Дх) четная, то
соз их du
J / (/) cos at dt.
ч
Если Дх) нечетная, то
fix)
f(t) sin utdt
Примеры некоторых разложений в
ряд Фурье. Ниже даны разложения в
ряд Фурье некоторых простейших
функций, заданных на некотором от-
резке и продолженных вне этого отрезка
периодически. Изменением масштабов по
ПРИБЛИЖЕННОЕ АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ ФУНКЦИЙ
309
Ох и Оу, а также переносом коордн- Интегрированием рядов, а также
ватных осей • можно получить другие сложением и вычитанием получаются
разложения. новые разложения
- 1 ••
I. с1 + «г 1 2 (с» — <?i) [, « I I , i кл , I
1> 4-----J---- ^sln-r-f--5-sln3-r-+-.t.-1-Efqpjsin(2A+ 0 —+ ...J —
Фнг. 5.
Ci при —/<дг<0
ct прн 0<х</
при ж —0, ±1. ±21,...
310
ПРИБЛИЖЕННОЕ АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ ФУНКЦИЯ
8) “7Г [cos— +ycos3 — + mcos5—+•"] +
У
АА
21 31 х
Фнг. Н. (к ри.южению 10}.
Фиг. 13.
,л. 1 । 1 ЯХ 2 1 — | 2*Х .
,0) 7+ 2е05 — -vlrr^-l00’— +
1 4*х 1 бюг ,
+ 4-^П cos ~Г - 4^=1 003 - +
11)
2zslnxz [1 cosx , cos2x cos3x ,
[2х*“ г»-1 ^г»—2»"х» —3» +
*х I
COS-y пря-у<х<у
0 ПР" у<л</
0 при- 1<х<-
— COS XX при — К X < к
ПРИБЛИЖЕННОЕ АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ ФУНКЦИЯ
311
Разложение в ряды по бесселевым
функциям
Если at < as < ... < a„ < .... Корин
уравнения Jo (a^Z) = 0 175). 1151], k —
= 1,2, ..., то имеет место свойство
ортогональности с весом р(х) = х:
j xj» (алх) Jo (amx) dx => 0 (k + т);
и
если k = т, то
/
2 J xJ2(aftX) dx = ZVQ2 (a*Z) = ZV2(OfcZ).
и
Для функции Цх) сумма
л = ciJo (“!•*) + CtJo (“3х) +
дает наилучшее приближение с оценкой
по обобщенному среднему квадрати-
ческому отклонению с весом р = х,
причем коэффициент ск находится па
формуле
/
(«*0 ск = 2j xJ0 (a*x) f (х) dx.
достигается для коэффициентов
к J j/1 — х*
ИЛИ
2*-i V
сь -------- 1 / (cos 9) cos М rfO;
« J (Л-IA..J
Со = -i- J f (cos в) dB.
' Притер. Разложить | x | по полиномам Чебы-
ICM. f
— J* | cos 9 | cos Аб <И =*
—и
А 1
_ — J J со» 8 со» А4 Л —
«
~ т
Аналогичные разложения имеют
место по функциям Бесселя высших
порядков.
Ряд lim 5л(х) сходится в |0, Z] к Цх).
П-оо
имеющей непрерывную производную
с ограниченной вариацией.
Разложение в ряды по полиномам
Чебышева
Полиномы Чебышева (см. стр. 224)
удовлетворяют свойству ортогональ-
1
иости с весом р " . Наилучшее
У I — х>
приближение Цх) полиномами Чебы-
шева Тп(х) на отрезке (—1, I], т. е.
многочленом
я
s" “ f+Е е*г*
А=1
с оценкой по обобщенному среднему
квадратическому отклонению с весом
е.-р J |соа»|Л--р{
— Ж
*2л-Н “°
п—I “ т
Первые приближения:
|х|<м-2-4-лГ,4-«кГ,-да (-18x‘+3<ix--t-3).
312
ПРИБЛИЖЕННОЕ АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ ФУНКЦИИ
Двойные ряды
Функцию f(x, у) можно приближенно
представить двойной суммой
Smn (х.у) - V V Cwn (х)
а«=1 г=1
где <рДх) и ф/(у) — специальные функ-
ции, определяемые характером задачи.
Прн замене /(х, у) этой суммой $тп
коэффициенты с*/определяются из усло-
вия, чтобы интеграл
У) f (.*. У)Р dx dy
был наименьшим; вес р(х, • у) >• 0.
Примеры-. >
1) Разложение /(ху у) с периодом 2х как пох,
гак и по у п рад Фурье (область D — прямо-
угольник):
оо
/U, У)«= S («ы со» *л сое (у+
А, 1-0
sin hx со» Гу -f-Гу со» Ах к!п Гу +
4- dkl *1п Ах »1п Гу),
гае
{*/„ если А = Г =' 0;
*4, если А = 0, Г > 0 или А > О, Г -— О;
1, если А > 0, I > 0.
°АГ = г J J / (л. У) СОК Ах со» Гу Дх Ду;
— Ж — Ж а 1 *
J / (X. У) *1п Ах со» rydx <Jy;
— Ж — Ж
4-и +«гг
CW - -L J J / (X. у) со» Аж »1п Гу Дх Ду;
— Ж —ж
+«+•
"*/ “ ~Г ) j У (Л, у) »1п Аж »1п Гу dx dy.
— к —я
2) Если область р — круг радиуса а и р, • —
оларКМе координаты, то функцию / (г, ₽), обра-
шающуюс» к нуль на окружиосга, можно раз-
ложить и двойной ряд
оо 1
/(г.Т)- 2-,Г1"АГ,)<ЛАГс*",’+вАГ ,|в/«'
- J J/(г.(•*/)«>•;, «мд»,
**- • -*4, • *
1—0, 1, А- 1, 2, . .1
(Г, А — 1. 2. 3,...); а.. находятся из ураииеимя
2 f 'г <*Af)' * “^J2 (я^а) - eV?+1 («д/Ч.
Практический гармонический анализ *
Для большинства технических рас-
четов достаточно взять первые 10—12
гармоник периодической функции /(х):
fenx , . , ктл
"A cos — + Ь„ sin -у -
— 4» sin + п);
к = 0, 1,.,., 12. Здесь Д* — амплитуда,
<рА — начальная фаза k-Л гармоники;
они определяются по формулам: а* =
= X^slnfa, Ьц= A^cosfi, или 42 =
= °а+6A>tS’?* = ириче“ И8 Д«У«
значений <fb, отличающихся на к, выби-
рают то, прн котором знак simp* совпа-
дает со знаком ац и знак соз совпа-
дает со знаком
Последовательность амплитуд Ло>
41,.,. образует спектр периодической
функции (фиг. 15).
i3’
6,2 I I
I . .
* 5 6 7 69 К
Фиг. 15.
Для приближенного вычисления коэф-
фициентов ряда Фурье следует заменить
интегралы суммами по одной из формул
приближенного интегрирования, напри-
мер по формуле трапеций.
Обозначим период 21 = Т и возьмем
для периодической функции у /(х)
ее значения у0. _>>», уз,..., ya,-i (Ут^Уа)
для равноотстоящих значений аргумента
Т Т Т
°’ .................
• См. лмтерятуру ил стр. 3® (35], (112), [125].
ПРИБЛИЖЕННОЕ АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ ФУНКЦИЙ
31$
Тригонометрическая сумма
Разность
— «о+ fli cos — -j- аг cos 2 —у +
1 . 2кх . . . 2хх
4-... + ая cosn —sin т | ...+
<Ц“У1 — Уп и т. ju
Сумма
Разность
А'о 3] <$2 $3
$в Зь $4
Со С| С% Cj
д2
rfj d? de
d6 d<
eI ®2 ®8
*1 ®2
4- ь _. sin (n — 1) Дальнейшие вычисления производятся
я 1 Т ’ по следующей схеме:
_« { А» Ь. — а.
ода •t
ол -с. •• |
Сумм! ' II 1 и • 11 1 II
Сумма 1 + И 12a, ба. ба, 60, 60, —
Развость 1 - II 12a, ба, ба, Ьй. 60, 60. 60,
где
in—1
i S у*:
4=0
2л-1
1 V ь
e»’“ — L >*cosft v
A=U
2д —1
bm~"7T у*в|пЛ ^,«-1.2...л
*—о
(6„—0) является интерполирующим мно-
гочленом для периодической функции
(тригонометрическая интерполяция) и
дает наилучшее квадратическое прибли-
жение для Цх).
Для вычисления коэффициентов при-
меняются вычислительные схемы и
шаблоны |35|. |114|, 11171, а также
специальные приборы — гармониче-
ские анализаторы || 171.
Ниже приведена схема Рунге вычис
ления коэффициентов для 12 ординат.
Вычисляются суммы и разности ио
столбцам:
Уо У| Уг Ув Уа У» У»
Уп Ую Уо У» Ут
Сумма s0 s, s2 ss s, st st
s0 - Уо- «1 - У1 + Уп и т. д.
( I... . .1 . .
Здесь вместо с, д, а, & должны быть
помещены соответствующие суммы и-
разности, умноженные настоящие в той
же строке слева множители. В каждом
столбце сумма полученных таким обра-
зом величин обозначена I или II.
Гармонический синтез
Если дан ряд Фурье некоторой перио-
дической функции Цх), то можно вы-
ft ~
числить ее значения при х = та Т,
где Т — период /(х), k — 0, I, 2. 3,..,11,
при помощи той же схемы Рунге.
Предполагается, что в пределах допу-
стимой точности можно ограничиться
о ряде Фурье первыми шестью гармони-
*ами. Положим Sq= а^, а» = в»,...,
s# = og; di = bi, d« = tg... d6 — 68,
где ak, ft* — заданные коэффициенты
ряда. Затем производим вычисления
согласно схеме до получения величин
“0- “1. “3. °8- “4. а8- Р». ?»• i5». Р4
соответствующих величинам 12а^, (хц,
ба», 6a3, ba(, бсц, 12о8, 61>». 66>, 66а,
614, 60й, помещенным в двух послед-
них строках таблицы.
После этого находим-
Уо-0!»; Уо — “4-Р₽<; у» —°4 — fU;
У1 “ °» + hl У» — “8 + Рб’> Ув “ °8 — Psi
yt“ei + fe Уо —1 at‘ У»п —»»—№
Уа — ®з + ?в; у? — Уп — «8—₽*•
ГЛАВА XV
НОМОГРАФИЯ *
Номограммой называется графическое
изображение функциональной зависимо-
сти между несколькими переменными,
позволяющее находить приближенные
числовые значения одной из перемен-
ных по заданным значениям других.
Прямолинейной функциональной шка-
лой функции /(х) называется прямая
(носитель шкалы), на которой от неко-
торой точки (начальная точка шкалы)
откладываются отрезки 5 = т!(х} и в
конце каждого отрезка ставится по-
метка х, соответствующая значению
у = Цх); т — модуль шкалы — число
миллиметров в единице масштаба. В на-
чальной точке ставится пометка х®,
для которой /(Хф) “ 0. В одну сторону
шкалы откладываются S > 0. в другую
сторону S < 0. при х = Хф S = 0.
Уравнение функциональной шкалы
S « т/<х) позволяет построить шкалу.
На практике приходится строить функ-
циональные шкалы для некоторого ра-
бочего интервала |а С х < 6], поэтому
заменяют данное уравнение следующим:
3 = m[f<x) — f(a) |.
Назовем пометку х = а, для которой
3 = 0, начальной пометкой шкалы.
Модуль т выражается через L — длину
шкалы — по формуле
L
т ~ f(b)—f(a) ’
Для построения шкалы необходимо
по уравнению составить таблицу:
X а=х„ х, ...
0 s, ... L
где 3* = m|f(x*)— Ца)|, х* — те значе-
ния. которые чаще всего встречаются
при вычислениях.
* См. лкгериуру IU стр. 351 [130], (131), (137].
Равномерная шкала имеет уравнение
3-—(х—а);
о — а
одинаковым приращениям х соответ-
ствуют равные отрезки на шкале.
Логарифмическая шкала имеет урав-
нение S = т 1g х с начальной пометкой
х0 = 1. Построение S = znlgx можно
производить графически, проектируя
3 = 2501g х из одной точки плоскости
Фиг. 1. Логарифмический шабхоа.
на параллельные прямые. С полученного
логарифмического шаблона (фиг. I) можно
снимать 3 “ т 1g к для всякого т и
для всякого рабочего интервала.
Проективная шкала или спросто
проективная шкала» — шкала функции
у = , которая может быть по-
лучена проектированием равномерной
шкалы нз некоторого центра на вы-
бранную прямую (носитель шкалы)
(см. пример на стр. 320).
СЕТЧАТЫЕ НОМОГРАММЫ
315
Проективная шкала функции Цх)
есть шкала функции
а/(х) + »
У Cf (X) + 0 '
Криволинейной шкалой называется
линия (базис шкалы) с нанесенными
пометками г, построенная по параме-
трическим уравнениям
Sj = "»i/i («К “ тг/г (*).
причем Si строится по оси Ox, St —по
оси Оу, в прямоугольной или косо-
угольной системе координат
Функциональная сетка Если на осях
координат построить шкалы Si =
St = (фиг. 2), то точке А пло-
скости соответствуют координаты (х, у)
в- так называемой функциональной (не-
равномерной) сетке, образованной пря-
мыми, проведенными параллельно осям
координат через точки с пометками к на
олной оси и через точки с пометками у
на другой осн.
Проектируя А на оси координат, по-
лучим декартовы координаты той же
л S| Зд
точки 4: и — , v = —, если началь-
т т
ные точки шкал совпадают с началом
координат. Формулы перехода и
= — h(x), v — — ft(y) позволяют напи-
zn т
сеть уравнение кривой F h (ж),
= 0 в виде F(u, 0=0. В сетке
(х, у) получается иная кривая, нежели
в сетке (и, 0. Соответствующим выбором
функциональных шкал на осях кривую
можно выпрямить.
Наиболее употребительными номо-
граммами являются сетчатые номограм-
мы и номограммы из выравненных точек.
СЕТЧАТЫЕ НОМОГРАММЫ
Уравнение с тремя переменными
F(x, у, г) = 0 всегда можно номогра-
фировать, если считать две из пере-
Фиг. 3. Сетчатая номограмма.
мениых, например л, у, текущими де-
нартовыми координатами точки кривой,
а третью г — параметром семейства
кривых. Полученное семейство кривых
(не пересекающихся в рабочей части
области изменения переменных) и есть
сетчатая номограмма (из кривых линий)
или абак Декарта. Если задать х=х>,
у = yi, то соответствующее значение
г = ?| получим на фиг. 3 как пометку
той кривой, на которую попадает точка
(xi. Ух).
Если точка (х, у) не попадает на
готовую линию, то пометку г, соот-
ветствующую той линии семейства,
которая должна через эту точку (х, у)
пройти, надо оценить приближенно при
помощи двух рядом стоящих пометок
на двух проведенных кривых се-
мейства.
Прямолинейный декартов абак —
семейство из прямых линий. Общая
форма уравнения, допускающего пря-
молинейный абак в координатах ж, у,
имеет вид
/1 (ж) х + /,<г) v + /«(г) - 0.
Условие выпрямляемое™ абака Де-
карта. Семейство линий F (ж, у, г)—0
можно выпрямить, если это уравнение
может быть приведено к виду /!(x)<f(x)-|-
+ /г(г) ф (y)-f-/g(«) = 0. Если на осях
316
НОМОГРАФИЯ
координат построить функциональные
шкалы ф(х) и ф(у), то получим семей-
ство прямых
/1 (*)« + h (2) V + /«(«) = 0.
где и = <?(х), о = ф(у) — формулы, пре-
образующие декартову сетку в функ-
циональную.
Необходимое и достаточное условие
выпрямляемости семейства кривых
F(x, у, г) = 0 состоит в том. чтобы
dF dF
отношение-^ можно было пред-
ставить в форме произведения трех мно-
жителей, из которых каждый зависит
лишь от одного аргумента.
Если ~ — М (х) ЛЧу) Р (г), то
формулы преобразования декартовой
сетки в функциональную имеют вид
и - ^Al(x)rfx + Сь
Пример, .rx -f- ух1 2х»х — 2у — 1 — 0.
-»
т. с. уравнения выпрямляем. Находим
4-вж’)Дх-х4-2л>4-С,;
» = J ау = у 4- с,;
ураннение семейства прямых преобразованного
абака примет вид
(и - С,)х 4- (о - С,) (я* - 2) - 1 -0.
Общая форма сетчатых номограмм.
Одно уравнение F (и, v, w) " 0 эквива-
лентно системе
Л(«. х, у)-0, ft(v, х, у)-0.
fa (w. х, у) — 0.
Каждое из этих уравнений опреде-
ляет на плоскости х, у семейство кривых;
и, о. w —• пометки на кривых в соот-
ветствующих семействах. Совокупность
этих трех семейств лает сетчатую
номограмму самого общего типа. Задав
и, о, найдем w как пометку той кривой
семейства ш « const, которая проходит
через точку пересечения кривых с по-
метками и и V.
Если все три семейстиа — прямоли-
нейные, то F = 0 равносильно системе
(“) + У Ф1 (ц) + 1 — 0;
Л*» (V) 4- уф? (V) + I — 0;
+ УЫ») +1-Л
Три прямые пересекаются в одной
точке, если определитель системы равен
нулю. Так как и, о, и> связаны урав-
нением F (и, о, ш) = 0, то последнее
эквивалентно такому уравнению:
?1(“) Ф1(«) 1
фг(о) 1
Тз (w) фз (tp) I
-0.
Определитель в левой части равен-
ства называется определителем Marco.
Если уравнение F(u, о, w) = 0 приво-
дится к этому виду, то его можно изоб-
разить прямолинейной сетчатой номо-
граммой.
Практически удобно употреблять ло-
гарифмические сетки (на обеих осях
шкалы логарифмические) или полу-
логарифмические сетки (на одной оси
шкала равномерная, на другой — лога-
рифмическая). Уравнение вида ® =
— иЛи? приводится логарифмированием
к виду
lg w — a 1g и + ₽ lg V.
следовательно, при х = 1g и. у =* Igo
получим семейство прямых.
Пример. Построить сетчатую номограмму
«/л
формулы скорости резания о -• причем
ханы рабочие интервалы переменных, v |1; 1001,
а [4; 4С0|, п (20: 500]; ллины шкал 120.
I
На осях а и v строим равномерные шкалы по
уравнениям S. — 0,3d; S, — 1Л», т. а. модули
рамы; л», - «2? j *• ЧД “ Ml
СЕТЧАТЫЕ НОМОГРАММЫ
317
таким образом, интервалы несколько изменятся;
d]0; ОО), Р(О; 100].
Для построения прямых семейств» о — kd
(4 —выходящих из качала коорлииат.
мало иа каждой прямой взять точку с одной и
1000
го» же абсциссой d “-------яэ 316. тога» о — я;
«
100
арм d — — . v « 10я (фнг. 4).
6) Логарифмическая номограмма.
»[1; 100). d |4; 400|. я |20; W0);
1211
1Я| — я .ам а в
1g 100 — tg I
= 60 lg V, Sj =» SO (lg d — lg 4).
На осях ано строим логарифмические шкалы
no этим уравнениям.
Для построения прямых, имеющих один и тот
же угол наклона 45* к оси d, пало иа каждой пря-
__. 1000
мой «пять точку d «--, о — л. Чтобы парал-
лельные прямые отстояли друг от друга на рав-
ны» расстояниях, следует изменять л по закону
геометрической прогрессии: я. — 20; а — 1.5;
л, — 20 q — 30. я, — 20 qt — 45 и т. л. (фиг. 5).
Случай многих переменных. Если
уравнение F(xi, г», гг, г<) = 0 заменить
равносильной системой
Р\ (*». *»)-». Pt (г» г<) - «•
где а — вспомогательная переменная, то
можно построить две сетчатые номо-
граммы, которые и позволят по трем
значениям «д, г», г4 найти четвертое г4.
Если в каждой из номограмм одним и
тем же а сйотвегствуют одни и те же
кривые, то при одинаковом их распо-
ложении и одинаковой градуировке в
Фиг. а. Номограмма в паспорте токарного станка.
можно обе номограммы наложить так.
чтобы кривые с одинаковыми помет-
ками а совпадали. В полученной после
сопмещсння номограмме пометки а на
кривых можно не ставить. Метод можно
обобщить на любое число переменных
Удобно им пользоваться в случае
уравнения вида +/»<Л)+•••+
+ 1п(^ - о.
Промер. Построить сетчатую номограмму
паспорта токарного станка по формуле ad -*
«= ЮОолУ. Переменные изменяются в следующих
границах: d (10; КЮО]. о(1; 100], л [0.01; 1.0).
»КМ; 10):
100Г
lg d = Igo -]- lg г + lg —— .
Если обозлачнт»
100/
lg V - lg d — lg a, - |g л - lg - lg a
н взять
ВЯ
• “ алм .
1000 .
го первая номограмма выла построена в преды-
дущем примере. Взяв — 200. модуля
ПО 100, можно второе уравнение номографировать
также семеАством прямых с наклоном 46* к оси л.
Совместив прямые с одинаковыми пометками я.
получим номограмму в виде квадрата с логариф-
мическими шкалами переменных d, е. л. } иа
сторонах его. Сначала строят две шкалы d, о.
как в первом примере. Затем на стороне, парал-
лельно» шкале d, строят в том же направлении
318
НОМОГРАФИЯ
шкалу л. Прямые семейства пол 45’ проводят без
пометок. Чтобы построить шкалу Г, надо найти
пометку одной из ее точек, а яатем, зная мо-
дуль т = 100 и напраюение возраста ним г, до-
страивают всю логарифмическую шкалу t (фиг. в).
При d —100, v — 10, г — 0,5 получаем / =
= — сз 0,63. Ключ иа фиг. 6 показывает, при
помощи каких координат строят точки, лежащие
на прямой с одной и той же пометкой л.
НОМОГРАММЫ
ИЗ ВЫРАВНЕННЫХ ТОЧЕК
Номограмма из выравненных точек
состоит из трех шкал (прямолинейных
или криволинейных) с пометками пере-
менных соответственно a, it, г* Три
точки, пометки которых являются реше-
нием уравнения F(ii, гг, г3) = 0, лежат
на одной прямой.
Такие номограммы более удобны для
построения и пользования. Однако не
всякое уравнение представляется номо-
граммой из выравненных точек.
В дальнейшем fb <f,. <]ч и т. д. обо-
значают функции от одного перемен-
ного г(.
Номографическим порядком чиалне
ния F(zi, г5, г8) = 0 называется число
различных функций, зависящих каждая
от одной переменной, входящих в урав-
нение и соединенных действиями сло-
жения и умножения. Произведение друх
функций от одного аргумента считается
новой функцией.
Например, г£га + ?i = 0 —
уравнение 3-го порядка- полагая Zi=fb
2гд“ /в, -j г3 — ft, получим
ЛА + А/» + /1 “ О-
Уравнение г? + г8=0 —
5-го порядка.
Уравнение F(Zi, г», г8) = 0 номо
графируется. если оно не выше 6-го
порядка. Для построения номограммы
надо уравнение привести к канонической
форме.
Наиболее общая форма
уравнения (форма
номографируемого
Масео)
^(«i, *г. *ti) =
-0.
Канонические формы — частные слу
чаи формы Массо. Иногда можно урав-
нение r(ft, гг, zs) “ 0 привести к виду
ЛА + #ФВ + С^В — ft
где А, В, С — функции zi и Zj. Обо-
А В
значим = и, = о. Из ат их двух
равенств исключим гь потом г8. Если
после исключения получаются два ли-
нейных уравнения
“Л + «ft + to - О;
“А + «Тх + Фг = 0
и, кроме того,
«А + ^Рв + Фв •“ ft
то, приравняв нулю определитель згой
системы, мы получим F(zlt Zj. r8) = ft
в форме определителя, а поделив строки
на элементы одного из столбцов, при-
ведем определитель к форме Массо.
Жанром номограммы называется
число криволинейных шкал, составляю-
щих номограмму.
Номограммы нулевого жанра
Номограмма с тремя
шкалами для уравнения
На крайних пря-
мых строят функ-
циональные шкалы
по уравнениям Si =
= -$2 = на
промежуточной па-
раллельной прямой
строят ш кал у S8= mgfg.
т<тг
гле т* “ ~Z, 1 •
/Л| -f- Ш’2
Расстояния о и &
между Si, S8 и Sg, S2
связаны соотноше-
нием а : b = Щ| : mg
(фиг. 7)-
параллельными
/i + /г “ /а-
Фиг. 7. Схема рее
положения шкал
и номограмме для
уравнения Л +
Пример. р- Той) * интервалы
v [1; 100], а |5; £00], я |20; 500]. I* — I* - ДЮ;
1К о-*—.
я», — я>, » КО; т, — “ 50.
Уравнения .шкал: S, •> 100 lg о\ $ — 100-Х
X<lR <» - 'К 5>-
Фуикцни 1g о и 1g а входят в формулу с про-
тивоположными знаками, поэтому направленна
возрастании отредкоп S, и S, противоположны.
Шкала S.-SOpg-lIL.-lg-^.) направлена
и одну сторону со шкалой S,. Пометка л, к на-
чальной точке найдется на требования S,»U,'
НОМОГРАММЫ ИЗ ВЫРАВНЕННЫХ ТОЧЕК
31»
через тгу точку пройдет прямая, соединяющая на-
чальные точки на шкалах и и d. т. «. точки с по-
метками о •= 1, d = 5.
.. »dn _ . я-5-я. 200
и’’ = iotf 1 --ййГ : -Г « ы
Фмг. 8. Немогрямма в» «радлелъяъп ипли
скорости ремяик
Случай четырех и
Как и в сетчатых
чала F(zi, г* г».
♦иг. 9. К построению
иомогра мыы с четырем я
переменными.
то обе номограммы
многих переменных,
номограммах, сиа-
г4) = 0 заменяют
равносильной си-
стемой F^Zi, ?!)= а.
Ft (г». г«) = а; а —
новая вспомога-
тельная перемен-
ная. Если по-
строить номограм-
мы на криволиней-
ных шкалах для
каждого уравнения
гак. чтобы шкала а
имела один и тот
же базис и одну и
ту же градуировку,
можно совместить, и
получится одна составная номограмма.
Зная 2], zj, za, можно найти z4. Шкалу а
не градуируют (немая шкала). Прямая,
соединяющая точки с пометками zt, zj,
пересекает немую шкалу в некоторой
точке; через згу точку, а также через
точку za надо провести вторую прямую,
пересекающую четвертую шкалу в иско-
мой точке (фнг. 9). Метод обобщается
на случай любого числа переменных.
Пример, *4 — 10ОЮТ (см. пример в сетчатых
номограммах).
100Г
Igp — lgd = lg«; - lg s— lg—— —lg».
Тек пк на всех прямолинейных шкалах в. 4,
т, t модули одинаковые, то в каждой из номо-
грамм промежуточная (третья) шкала находится-
на одинаковых расстояниях от крайних шкал.
Построив три шкалы о. d, а, надо для построения
4-й шкалы t найти пометку одной ее точки, на-
пример при d = 100. о — 10. а = 0,5 найдем
t — — сз 0,63 (фиг. 10). Зная направление шкалы t
О
♦иг. 10. Номограмма на параллельных шкалах
(в паспорте токарного станка).
и модуль, градуируем всю шкалу. Ключ »— в— d,
1 — и — t покатывает, какие точки лежат иа
одной прямой.
Z-иомограмма для уравнения -1
На двух параллельных прямых строим
шкалы Si = mi/i, 3» “ т^г в про-
тивоположных направлениях, на
третьей секущей прямой строится шкала
R+T • '"°'0’
*/a+l
•320
НОМОГРАФИЯ
4фнг. 11). Третью шкалу можно по-
строить геометрически как проективную
шкалу для функ-
ции ft- Пометки в
начальных точках:
на шкале zi в точ-
ке 01 стоит по-
метка (Ti)0, опре-
деляемая уравне-
нием fi |(zj)0] = 0;
на шкале гг в точ-
ке О2 стоит помет-
ка (гг)0, для кото-
рой /21(г»)01 = 0;
на шкале г3 в точ-
ке 01 стоит помет-
ка (гз)о. Для кото-
точке О3 той же
шкалы стоит пометка (г3)ъ для которой
Л h z»)i J
Три точки Mi, М3 с пометками
Т|. г8, гг (решение данного уравнения)
лежат на одной прямой.
Фиг. 12. Z-номограмма.
Пример. Построит!. Z-еомограмму уравие-
ния ® —и (0,01; 100), р (0.01: НЮ). в (0; 30).
Длина крайних шкал I —201. Имеем
lg «-«1g и.
На пяралдельиых прямых (фнг. 12) строим лога-
рифмические шкалы, на секущей прямой— прости
проективную шкалу для а.
Модули i8 ,00^0.6—"80
S, = SO lg v; 5, — 50 Ig и.
Начальные точки О, и О, имеют пометки еп— 1;
к, = 1, S, “ I . В точке О, я. — 0: в точке
О, в, —оо. При 5, -= к — 1, По трем точкам
(0.1, оо) на прямой 0,0, можно построить проек-
тивную шкалу проектированием на 0,0, любой
равномерной шкалы на вспомогательной пря-
мой О,Л м» центр» С, лежащего на прямой
О,В | О.А. Пометки на 0,0, в точках пересече-
ния с проектирующими лучами те же, что я на
равномерной шкале (фиг. 12).
Номограмма позволяет производить действия
возведение в степень, извлечение корня и лога-
рифмирование в пределах, указанных рабочими
интервалами изменения о, о, к.
Общий случай
Номограмма (третьего жанра) из трех
криволинейных шкал будет самой общей
номограммой из выравненных точек.
Если уравнение приведено к виду
F (ж,. z» г,) -
Л Ti 1
А Тг 1
/а fa 1
-0.
то получаются уравнения шкал:
*1—/11 Xi“/1!
Л = ?15 Л —W y»-Ta.
Каждая пара равенств xt = ft (xtf,
У> = Т/(Д/) — параметрические уравне-
ния с параметром г, некоторой кривой
В точках этой кривой ставятся соот-
ветствующие пометки гк получается
криволинейная шкала. Три точки на
трех шкалах с пометками zlt z3, г,,
составляющими решение данного урав-
нения, лежат на одной прямой.
Если с указанными уравнениями не
получается удобной номограммы, то для
ее приспособления можно ввести в уряв
нения константы, произволом которых
пользуются для изменения расположе-
ния шкал и их градуировки.
Предыдущие уравнения можно заме-
нить следующими:
g|/i 4- b,<fi 4- С) .
' а»А +• М/ + й ’
(/ — 1. 2. 3)
аг/| -i- М + сг
1 atfi + М/ + й ’
Здесь произвольными будут восемь
постоянных (отношения девяти коэффи-
циентов к одному ыэ них).
ГЛАВА XVI
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
С ПРИЛОЖЕНИЯМИ К МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ*
ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ
В технике приходится иметь дело со
случайными событиями и связанными
С ними случайными величинами. Напри-
мер, получение размера детали в задан
ных границах—случайное событие;
отклонения размера сделанной детали
от номинала, ошибки измерения — слу-
чайные величины.
Под вероятностью события А пони-
мают отношение числа т случаев, бла-
гоприятствующих данному событию А,
к числу п всех случаев (ранноиозмож-
ных, единственнонозможных и несовме-
стимых, т. е. взаимно исключающих
друг друга) и обозначают
Невозможному событию (т = 0) соот-
ветствует вероятность 0, достоверному
(благоприятствуют все п возможных
случаев) — вероятность 1. Вероятность
случайного события заключена меж-
ду 0 и I.
Несовместимые случайные события,
сумма вероятностей которых равна 1,
образуют полную группу событий
Пример. П партии, содержа шей 100 деталей,
имеются Г> деталей с отклонением 0,05 от номи-
нала; 10 деталей с отклонением O.IU; ДО деталей
с отклонением 0,1$; :с> деталей с отклонением 0.211
и К деталей с отклонением 0,25. Если размер
«датой детали отличается от номинала не менее
0,15 н не более 0,20, то такая деталь может быть
употреблена при сборке без пригонки. Найти
вероятность события А. состоящего в том, что
если взять нз данной партии деталь наудачу, то
сборка будет произведена бе» пригонки. Случай-
ным событием является появление той или иной
детали при взятии ее из партии. Все события
ревновозможиы. едипственновозиожны и несов-
местимы. Число всея таких случаев равно |1Х>.
Число случаев, благоприятствующих сборке без
пригонки, равно 75 (40 деталей с отклонением и,15
* См. литературу иа стр. 350: (103|, (107]. ]110|,
|К«1. |10Г).
21 Том 1 Зак. 1 !С1
и 35 деталей с отклонением С.20). искомаа верой i
74 Я
поста Я (А) = — = — .
100 4
Если имеется бесконечное множество
равновозможных, единственновэзмож-
ных и несовместимых случаев и всей
совокупности их может быть дана коли-
чественная характеристика S в некото-
рых мерах длииы, плошали и т. п,
а части этой совокупности, благоприят-
ствующей наступлению рассматривае-
мого события А, может быть дана анало-
гичная характеристика в виде значе-
ния .4 в тех же мерах, то вероятность
появления события А определяется отно-
шением
о
Нримгр, При ныло л не и и и нското|н>й резня-
точной операции наносится разметочная ТОЧКА в
пределах круге диаметром 1 мм, причем положе-
ние точки в любом месте круге пре а пол а гнется
равно в па ножным. Найти вероятность события А.
состоящего в том, что точка окажется в пределах
операционного допуска ± 0,2 мм по одной коор-
динатной оси и ± ИЛ мм по другой оси. Центр
круга — в нпчале координат.
Количественной характеристикой бесконечного
множества всех вотможимж случаев является
площадь круге «0,78 mjP. Количествен-
ной характеристикой бесконечного множества слу-
чаев. благоприятствующих событию А, является
плошали прямоугольника з = и.4-0,6 = 0.24 мм‘.
Отсюда Р|А) — '-^~ - 031.
Теорема сложения. Вероятность Р
появления любого из нескольких несо-
вместимых событий, входящих в одну
полную группу, равна сумме вероятно-
стей этих событий.
Если п несовместимых событий Л(,
Ав....Ап образуют полную группу, т. е.
Р (А,) т Я (Аг)+ . +Р (А„) - I,
то вероятность того, что появится или
событие Ат, или Ад.......или А* (А<л),
равна Р (или Ат. или А», . .. или А*) —
= Р(А,} + Р(А#) Г . . .+ Р(А*).
322
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Пример. Пусть в примере с партией в 100
деталей (стр. 321) взятые наудачу детали с одним
из отклонений есть событие А где ( — номер
отклонения от 1 до 5* в указанном выше порядке.
По определению вероятности можно составить
таблицу распределения вероятностей этих собы-
тий:
а А. А. А, А. А.
р (Л) 5 10 40 35 10 5 V . 100 , i
IUU LL4J ИА) ИА» ИМ
Событие, состоящее в том, что взятая деталь
имеет отклонение от номинала не менее 0,15 и не-
более 0.2. имеет по теореме сложения вероят-
ность
41) Зп
Р (или А„ или AJ = — = 0,73.
I vU 1U J
Теорема умножения. При рассмотре-
нии нескольких случайных событий они
называются независимыми, если веро-
ятность любого из этих событий не за-
висит от наступления или непоступле-
ния других рассматриваемых событий.
Вероятность совместного появления
нескольких независимых событий равна
произведению вероятностей этих собы-
тий
Р(и Д. «4..., и Лд) =
-Р(Л1)Р(Л2)..../’(Л*).
Пример. В урне п шаров с двумя призма*
ками. Пусть вероятность вынуть шар с первым
признаком есть р, вероятность вынуть шар си вто-
рым пришв ком равна q = I — р. При визира ще*
ним шора обратно в урну вероятность вынуть
подряд 2 рам шар с первым при дни ком равна р\
вероятность вынуть подряд 2 раза шар со вторым
признаком ql, вероятность вынуть подряд в опре-
деленном порядке сначала шар с первым призна-
ком. зятем со вторым равна pq. такова же вероят-
ность вынуть шары с разными признаками, но
и другой последовательности. Вероятность вынуть
шары с разными признаками, мо безразлично, и
каком порядке, равна pq -f- qp —2pq,
Если события А н В зависимы, то
условной вероятностью события В назы-
вается вероятность, вычисляемая в пред-
положении, что произошло событие А,
и обозначается через Р(В)Л. Если обо-
значить Р (и Л, и В) — Р (4В), то
Р(АВ)-Р(А)Р(В)Л;
из этого равенства можно найти услов-
ную вероятность Р(В)А.
Случайные величины
Если дискретная случайная величина
может принимать любое значение от х<
ас хя, то совокупность (распределение]
вероятностей р всех возможных значе
ний является количественной характе-
ристикой дискретной случайной вели-
чины.
Распределение вероятностей задается
таблицей
X, X । ••••I xn
P(xp p(x.) P (X,) p{xn) Vp up = l I
Функция р (х/) называется законом
распределения дискретной случайной ве-
личины.
Если случайная величина является
непрерывной, принимающей всякое зна-
чение в некотором промежутке (области)
ее значений, то количественной характе-
ристикой такой случайной величины
является плотность вероятности или
дифференциальная функция распределе-
ния ?(х), т. е. предел отношения вероят-
ности того, что случайная величина X
окажется в промежутке (х, х + Ах),
к длине Дх при Дх -* 0:
Р (х < Х< X + Дх)
?(-»)
=» hm
JX-U
Дх
График функции <р(х) называется
кривой распределения случайной вели-
чины.
Вместо законов распределения р(х,)
и ч>(х) количественной характеристикой
может служить интегральная функция
распределения F(x) — вероятность того,
что случайная величина X имеет зна-
чение, меньшее данного значения х:
Л(х)-Р(Л<х).
Если х принимает значения от а до Ь,
го F(х) " 0 для х < a, F(x) = I для х > Ь
Для дискретных случайных величин
F(х) = Sp (xj, где х(<х; вероятность
I
тсго, что случайная величина х нахо-
дится в заданных пределах
**<* <Х/.
равна по теореме сложения
<
Р(х„ < X < X,) - V р (х,)
*>
УПОТРЕБИТЕЛЬНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
323
Для непрерывных случайных величин
Г dP
П*) = I ?(*) rfx. г (*) - ^7;
— оо
P(x'<x<x") = J ?>(x)dx-
X'
= F(x") — F(x').
УПОТРЕБИТЕЛЬНЫЕ ЗАКОНЫ
РАСПРЕДЕЛЕНИЯ
Часто встречаются следующие два
закона распределения дискретных слу-
чайных величин.
I. Биномиальный закон распреде-
ления встречается в задаче о вероят-
ности сложного события при повторных
испытаниях над простым событием
с постоянной вероятностью р в каждом
отдельном испытании.
Пусть X/ принимает значения х( =
= 0,1, 2, . . .,п: тогда при п испытаниях
вероятность появления события xt раз
равна
/> (*,)-С?'/'(1-/9 "-Х'-
П * -Г/ П—X.
- \(п х)1Р (1~^
Х| I (Л — X,) I
Примеры:
I) При р — Ч„ п — 5 закон распределения сим-
метричный (см. фиг. I):
р (0) — 1/32 га 0,<В р (3) — 10/32
р(1)»5/32 р (4)- 5/32
р (2) — 10/32 р (5) — 1/32
РС/>
Фиг. I. Симметри-
ческое распределе-
ние случайных ве-
личии о биноми-
альном законе.
РП.)
020
Фиг. 2. Симметрическое
распределение случайных
величии и биномиальном
законе.
2) р — 1/2, л — 20,
Р 10) - ЯПГ’. Р (D- 20 (1/2)»: Р (2) - (1/27»;
. . .. Р (Ю) - Сда (1/2)» га 0,176........ (20) -
-(1Я)“ (Фиг. 2).
21*
3) При р * 1/2 закон распределения несимме-
тричный.
Если р = 1/4. л = 5, то
А>.4
ОМ;
11________
° I 2 J « S X,
Фиг. 3. Несиммет-
рическое распреде-
ление и биноми-
альном :м»коие.
р (О) = (3/4)*-1 - 0.21,-
p (1) = (3|4)*.о/3 - >>.40;
р(2) = (3/4)*.-^-Ц - й.д6;
Р(4)= га 0,015;
р (5>= (1НУ =
- 7^- - 0.901 (фиг. 3).
4) При p = t/t, л = 20 несимметричность умень-
шается. При вычислениях следует полызоиагься
таблицами факториалов и степеней целых чисел.
При больших значениях Х| и п можно
использовать приближенную формулу
1 -- 1
где
ДГ / Л
z = —-------; а = пр; а = у npq,
о
q = 1 — р; Ф'(г) см. в табл. XVIII
(стр. 60).
2. Распределение по закону Пуассона
встречается в задаче о вероятности по-
вторного события, если р->0 при л-* со.
причем пр = а = const:
Нанвероятнейшее число */ = (Х/)т
появлений события при биномиальном
распределении находится из неравенства
np-q<(xl)m<np+p,
если np—q и пр + р — дроби, и из
равенств
(х/)т - ПР — Я! Мл-ц “ пр + р.
если эти числа целые; в этом случае
вероятности (х()т и (JQ)mti одинаковы.
Пример. При р — 1/2, q — 1/2. л — 5 имеем
пр - q = 5-(1/2) - (1/2) - 2: пп + р - 5-(1/2) +
+ (1/2) — 3, т. е. числа 2 и 3 иаивсрояшсйшие
числа появлений события. Их вероятности одина-
ковы (см. выше пример 1) и самые большие.
Для непрерывных случайных вели-
чин имеет наибольшее употребление
нормальный закон распределения слу-
чайных величин (закон Гаусса)
Т(*)
324
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
где среднее значение £ (х) = х, диспер-
сия О(х) =о» определены далее (стр. 326).
„ . 1
Если обозначить л =—(мера точ-
о У 2
ности), то
Л _ Л’(х—х»
?(Х) -y^g •
Вычислять <р (х) удобно по табл. XVI11
(стр. 60):
Г («)-♦'(«)-
где
С увеличением о2 уменьшается макси-
мум ?(*). равный <f(x)= * — =
О у 2.Т*
= 0,3989—. На фиг. 4 дан график f (я) при
1
х = 0, а — -у и « * 1. Площадь под
графиком остается неизменной, и при
увеличении дисперсии увеличивается
Фнг. 4. Графин иортльиосо рас-
пр«»лснм.
вероятность ббльшнх значений случай-
ной величины.
Точки перегиба графика <р(х) имеют
абсциссы Xi = х — о и х» = х 4- о,
соответствующие нм ординаты у> =
“ У> = yf-- 0.6065ум,
Вероятность нахождения х в задан
ных пределах от Xj до х«
1 tx-i)*
А>(Х1<ж<хх)--------!= а ₽ dx.
о У 2к J
Р (— СО < X < со) = I.
При помощи интеграла
z__________________г_
Ф<'>_-Йгр
называемого функцией Лапласа или ин-
тегралом вероятностей.
P(*l <X<Xi) =
Таблица значений Ф (г) приведена на
стр. 61 для г>0; для z<0 пользуются
свойством: Ф(—z)= —Ф(х). График
Фаг, 5. График фующиы Лапласа.
Ф (?) — интегральной функции распре-
деления случайных величин по закону
Гаусса — дан на фнг. 5.
Имеются таблицы функции erf г =
= 20 (г), где
Переход от Ф (z) к 0 (z) совершается
по формулам
Ф (ж) - в (-у=-) . О(х)-Ф(х УТ).
На практике в вопросах математи-
ческой статистики вместо Р(А) вводится
частость IF(4) появления случайного
события Л:
ИЧЛ)--$-.
где М — число появлений события Д,
V — число всех испытаний, при кото
рых это событие могло появиться.
U7 (4) называют статистической веро
ятностью, Р (Д) — теоретической или
математической вероятностью. При уве-
личении числа испытаний частость при-
ближается к вероятности (см. закон
больших чисел).
УПОТРЕБИТЕЛЬНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
325
Функция W' (xi) называется статисти-
ческим законом распределения дискрет-
ной случайной величины, и ее значения
вычисляются по формуле
где Nt — число наблюденных значений
xt; N —число всех наблюдений.
' Для непрерывной случайной вели-
чины х область полученных на практике
ее значений разделяется па несколько
промежутков одинаковой ширины Ьх,
и число значений величины х в каждом
промежутке называется частотой.
Таблица частот называется статисти-
ческим распределением.
Аналогично кривой распределения
? (х) употребляются гистограмма и поли-
гон распределения.
Гистограмма распределения состоит
из прямоугольников, построенных на
промежутках Дх, площади которых
пропорциональны числам значений слу-
чайной величины, приходящимся на
данный промежуток. При одинаковой
ширине промежутков высоты прямо-
угольников пропорциональны частотам.
Полигон распределения получится,
если соединить прямыми середины верх-
них сторон прямоугольников гисто-
граммы (при одинаковых Дх). В пре-
деле при Дх-)0 полигон превращается
в кривую распределения. Полигон рас-
пределения — практическая кривая рас-
пределения.
Пример. В тдблиае приведены результаты
измерения диаметров отверстий втулок от xm|n =
•= 75,100 мм до Х(пах » 75,060 мм о количестве
N “ 1100 шт. Промежутки (х( _ |, х() означают,
что диаметр х > мм и х<х( мм; Nt —
число втулок • соответствующем промежутке.
Если по горизонтальной оси отло-
жить значения X/, а по вертикальной —
ординаты у,, пропорциональные Nt
(фиг. 6), то полученный ступенчатый
график, состоящий из прямоугольни-
Фиг. 6. Гистограмма и полигон распреде-
лениа.
ника с основанием Дх/ = х/ — x/_j про-
порциональна частоте Nt. Если при-
нять Дх/= J, У/= Ni, то площадь
всей гистограммы равна N. Называют N
объемом совокупности предметов.
На той же фиг. 6 дан полигон распре-
деления X/.
Сумма площадей прямоугольников
построенной гистограммы между х = а
и х — р дает частоту S значений х между
аир:
0
S(«<*<P)-jXl.
в
Если это значение S отложить как
ординату, соответствующую р, то полу-
чим ступенчатую кривую накопленных
Х( _ „ Ж, Менее 75,00) 75.000- 75,005 75.005- 75,010 75,010— 75,015 75,015— 75,020 75.020- 75,025 75,025— 75,030
Nl 3 9 45 91 121 139 150
Продолжение
*1-1. *< 75.000- 75.035 75, ОМ- 75, 040 75,040— 75,045 75,045- 75.060 75,050— 75,055 75,055— 75,060 Свыше 75,000
Nf 155 136 116 84 38 11 2 1 2
326
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
частот, что соответствует интеграль-
ной кривой распределения (фиг. 7).
Огивой называется ломаная линия,
соединяющая точки, абсциссы которых
соответствуют границам частных интер-
валов Дх<, а ординаты суть суммы
частот, соответствующие всем интервалам
слева от взятой границы Дх/ (фиг. 7).
ЧОО
т-
900-
Р800-
t 700-
%600-
„500-
S W-
$300-
зм-
ию-
0^
75.01 75.03 15.05
Фиг. 7. Огив».
Широтой распределения называется
разность хт„ — Хщщ Для случайной
величины х.
В случае двухмерного распределения
непрерывных случайных величин (х, у)
указывается область значений х, у
и плотность вероятности <f (х, у).
Функция f(x, у) определяет поверх-
ность распределепия; объем, ограни-
ченный этой поверхностью и плоскостью
ху, должен быть равен 1:
j f ?(Jf, y)rfxrfy= 1.
-СО —00
Вероятность нахождения точки Л(х, у)
в заданной области R равна
P(AcR) - (“J<f (х. y)dxdy.
Точка плоскости с координатами
lg*
Ло - j J ?(•*, у) X dx dy;
— СО —оо
4-р°+?°
Уо-J J ?(*. У) У dx dy
-оо —оо
называется центром группирования.
ВЕРОЯТНОСТНЫЕ
ХАРАКТЕРИСТИКИ
Характеристики (некоторые пара-
метры) расположения и рассеивания
случайных величин позволяют численно
выразить существенные особенности
распределений случайных величин
Характеристикой расположения слу-
жит среднее значение Е (х) случайной
величины, которое определяет центр
распределения (группировки, рассеива-
ния) значений случайной величины, т. е.
такую точку, около которой группи-
руются значения случайной величины
Если случайная величина х прини-
мает значения xi, xj, . . . , хп с вероят-
ностями соответственно pi, р«..рп, то
п
Е (х) - 2 Р'х1-
1
Для непрерывных случайных величин
Е (х) -= j х<? (х) dx.
—ОО
Среднее значение Е (х) еще называют
математическим ожиданием случайной
величины. Оно обозначается М(х) =
= Е (х) = М. О. х =- х = а^_ Далее бу-
дем обозначать Е (х) = х.
Характеристикой рассеивания служит
дисперсия D(x) случайной величины
D (х) = V, (X/ — x^Pi - Е (х —х)>
/*|
и
D(x) = J (х — x)2f (x)dx.
—co
Дисперсия постоянной, т. е. неслу-
чайной, величины равна нулю.
Среднее квадратическое отклонение,
или стандарт, я связан с дисперсией
формулой as — D (х).
а
Отношение -=- называется козффици-
х
ентом изменчивости или вариации.
Практически удобно вычислять х
и а следующим образом: если х< встре-
чается Л/ раз, “ п, то среднее ариф-
метическое (средняя взвешенная)
- _ SnfX( _ а S ft (*| — а)
п “ п
где а — произвольное число и подби-
рается так, чтобы числа xt — а были
возможно меньше;
д, 'Sin/fxi-x')*
п
- Я< ~ а}г — (х — а)\
ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ
327
При «ер. Если величин! х = 2, 3, 4, Я, б по-
явилась соответственно nf — 3, 8, 1U, 7, 2 раза, то
гзя» о = 4. вычисляем:
х = < + ^ = <-°л = э.э;
а.= ^-(33-4)» = ^-С.Р-
— 1,167- 0,01 « 1,16.
Для характеристики средней части
всей области изменения х употребляются
мода и медиана.
Мода — наивероятнейшее значение
случайной величины х.
'Медиана (Me) — такое значение х,
что вероятность х <Z Me равна вероят-
ности х> Me.
Для непрерывной случайной вели-
чины
Me оо .
j ? (х) dx = г f (х) dx = —.
-оо Ale z
Средним арифметическим отклоне-
нием d случайной величины х называется
rf- Six,—x\pt
I
и
d — j’ |x — 7|f (x) dx.
-00 ,
Вероятным отклонением г случай-
ной величины х называется такое откло-
нение от медианы Me, что вероятность
отклонений, меньших его по абсолют-
ной величине, равна вероятности откло-
нений, больших его по абсолютной вели-
чине, т. е.
Лс+м- j
I <? (х) dx - -у.
Mi-r 2
Свойства а: I) дисперсия D и стан-
дарт а суть меры рассеяния, т. е. чем
больше дисперсия или стандарт вели-
чины х, тем более рассеяны около сред-
ней се значения, тем Солее она измен-
чива; с уменьшением D и а рассеяние
и изменчивость х уменьшаются;
2) стандарт имеет размерность вели-
чины х, для которой он вычислен;
3) средний квадрат отклонений х от
какой-нибудь величины, отличной от
средней, будет более D;
4) сложение средних и дисперсий:
если для нескольких совокупностей,
например трех, с объемами щ, л», п3 их
средние суть х(, х2, Xj и дисперсии
°1> а2> ал< то Длн общей совокупности
объемом л = Л1 + пг 4- Лз средняя
- _ л,!, 4- и?хг 4- Лдх»
л *
а дисперсия
п,о’ 4- лга| 4- лз«>з
°------------п--------+
Л1(х,—х)24-л2(х2-х)г 4- л3 (х,—х)»
п
Это свойство показывает изменение D
при соединении в одну совокупность
нескольких однородных статистических
совокупностей.
Для рассмотренных выше законов
распределения имеем:
1) для биномиального распределения
среднее значение х = E(xj) = пр-, дис-
персия £>(х.) = npq, стандарт в== Vnpq;
2) для распределения по закону Пуас-
сона х = a, D — а, а = У а; равен-
ство x — D характерно для закона
Пуассона;
3) для нормального распределения
1 _ . -
Ч> (х) ———= в '**' .среднее значение
о у 2п
£(х) = х, дисперсия D(x) = о*, среднее
квадратическое отклонение есть я.
Для этого распределения существуют
следующие зависимости между откло-
нениями о, d, г и мерой точности й;
0 •" Д1» I.253J яз 1.432г р/4
d - 1/ — о ft 0,798о г е Г_Я8 1,143г
Г — V А ft 0.6750 Vк p«/ft 0Л15г/
л = 1 0.707 I 1 0.М111 ₽ _ 0,477 = « —— S3 . « ——
Здесь р - 0, l7a9.ll ...
328
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Для отклонения За вероятность того,
что |х| <За, равна Р (|х| < За) = 0,9973,
т. е. за пределами ± За, Судет 0,27%
отклонений (при средней х = 0).
Пример. Если прн нормальном распределении
числовой характеристики х качества изделия пре-
дельные отклонения х от ее средней х принять
равными — 3» и -f-За, то количество брака, обусло-
«леиного тем, что х < х — За или х > Т-|-Зо.
составит Qt27°l9.
• Если в данной совокупности S, назы-
ваемой генеральной, содержится N пред-
метов, имеющих отметку х, и если эта
отметка принимает значения xi, х«. , ,,
х., частоты которых суть соответственно
Ni, Nt.. .., Ns (S.Vt = (V), то число N
называется объемом генеральной совокуп-
ности, а среднее значение х называется
генеральной средней-, а =
Если выбрать из S наудачу п пред-
метов (возвращая взятый предмет
обратно в S), то образуется повторная
случайная выборка-, xi, х», . . ., xs
с частотами щ, щ.........ns (tn, = я);
если же взятый предмет ье возвращается
в S, то образуется бесповторная слу-
чайная выборка. Средняя выборки назы-
вается выборочной средней: х= ^^о/х|.
При большом п и N п имеем а ю~х.
Распределение Стьюдента приме-
няется для оценки вероятности откло-
нения выборочной средней от генераль-
ной средней. Если случайная величина
,= *~а- , где х—выборочная средняя.
а — генеральная средняя,
а
а—
V п
п
xt — выборочные значения, то
любом значении н>2 величина t
при
имеет
дифференциальным законом распределе-
ния вероятностей выражение
. fl \ 2
где
Г
Г(х) — функция гамма (стр. 178, табл. X
на стр. 41). Функция s(/) представляет
плотность вероятностей в распределе-
нии Стьюдента.
Этим распределением пользуются для
п<20; если п >20, то распределение
Стьюдента можно заменить нормальным
(со средней 0 и дисперсией 1).
В табл, на стр. 334 даны значения S (г)
интегральной функции распределения
для закона Стьюдента
s
S(z)~$s (t) dt.
— ОО
Величина S (г) есть вероятность
неравенства —со</<г для данного л.
Вероятность неравенства —
Р( — х</<х) = ) s(t)dt-
—Я
z
- 2 f 5 (/) dt = 2S (z) — I.
Вероятность
P(|fl>«)-2[1 -5(x)J.
Пример. Найти вероятность значений t таких,
что 1t1 > 2Д для выборок объема л — 7. По
табл, ва стр. 334 дли г = 2,5 находим 5 (г) — ",9765,
следовательно,
Р (|Г| > 2,5) = 2 (1 - 0,9765) — 0.047.
Значит, вероятность значений Т, лежашнх
между — 2 j и 2,5, рдяна 1 — 0,047 — 0.953.
ЗАКОН БОЛЬШИХ ЧИСЕЛ
И ПРЕДЕЛЬНАЯ ТЕОРЕМА
Закон больших чисел устанавливает
близость между вероятностью случай-
ного события и частостью появления
его при большом числе испытаний. Наи-
более общая форма этого закона дана
П. Л. Чебышевым и А. А. Марковым.
Теорема Чебышева. Пусть xi, х», ...
.. ., хп — независимые случайные ве-
личины с математическими ожида-
ниями ai, аг, ... , ап и дисперсиями
а,, о|, . . . , aj. Обозначим через х сред-
нее арифметическое наблюденных зна-
чений величин хр
~ S xi
Х-----л ’
а через х0 — среднее арифметическое
математических ожиданий:
1
ЗАКОН БОЛЬШИХ ЧИСЕЛ И ПРЕДЕЛЬНАЯ ТЕОРЕМА
ЗЛ>
Если дисперсии ограничены
где L — постоянная, то вероятность Р
выполнения неравенства
|х —х0| < е
удовлетворяет условию
Таким образом, при неограниченном
увеличении п вероятность Р становится
сколь угодно близкой к достоверности,
как бы мало ни было положительное
число е.
Частным случаем теоремы Чебышева
является теорема Пуассона: если при л
независимых испытаниях вероятность
наступления события А при хи испы
тании равна рк и если т — общее
число появлений А при п испытаниях, то
Частным случаем теоремы Пуассона
является теорема Бернулли: если
о, = const = р, то
\ | п | / лс2
Теорема Чебышева имеет применение
в теории ошибок наблюдений. Пусть
измеряется некоторая неизвестная физи-
ческая постоянная а. Производим ряд
независимых друг от друга измерений.
Результат каждого из этих измерений
будет случайной величиной. Пусть *|,
ха......хп — эти случайные величины.
Допустим, как это делает теория ошибок
наблюдений, что средние значения этих
величии одинаковы и равны как раз
измеряемой постоянной а, т. е.
Е (X,) - ... — Е (х„) - а.
Это первое допущение означает, что
наши измерения свободны от система-
тических ошибок.
Допустим, далее, что дисперсии x)t
xi. • • > • хп равномерно ограничены,
т. е.
О(х1)<£,...,О(жя)<£.
где L — постоянная.
Это второе допущение означает, что
случайные рассеяния результатов наблю-
дений вокруг измеряемой величины
не могут безгранично возрастать.
Сделанные два допущения позволяют
применить к величинам xi, х»......хп
теорему Чебышева:
Jim Р (|П-1-.5* +••• + *« -«[<«) .1.
Это значит, что. увеличивая число
наблюдений, можно достичь практи-
ческой уверенности в том, что среднее
арифметическое из результатов наблю-
дений будет как угодно мало отличаться
от измеряемой постоянной.
Теорема Маркова. Пусть xi, х«,. . . .
х„ — независимые случайные величины
с математическими ожиданиями Oi.
at, ... , ап и дисперсиями af = 61.
«2=6»,..., а2п = Ьп, которые та-
ковы, что при п -> со
^1 + 6г + • • + 6Я
Л2
Обозначим через х среднее арифмети-
ческое наблюденных значений величин
х/, через х» — среднее арифметическое
математических ожиданий:
Д1 + ... + ап
--------л-----*
Тогда, какова бы ни была положи-
тельная постоянная в,
Р (I X - хп | < в) > I - .
Л-с-
Теорема Чебышева получается отсюда
как частный случай, когда все Ьк равно-
мерно ограничены.
При вычислении Р на основании пре-
дыдущих теорем получается недоста-
точно точный результат.
Более точное значение Р получается
при помощи следующей предельной
теоремы Л. М. Ляпунова.
Теорема Ляпунова. Пусть xi, х», . . .
хп — независимые случайные всличн' ы
с математическими ожиданиями <л,
at, . . . , а„ и с дисперсиями а*,
330
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Обозначим
V в? - В и d, - E\xt —а,^,
1=1
по которой находим г, г= , мо-
жем определить объем бесповторной
выборки.
где е — положительное постоянное.
Если
Пш 4+4 + -- +4 „о.
— •в1+т
Примеры-.
1) Из пяргии, содержащей 1000 метелей, сде-
лана выборка в IU0 шт., п которой оказалось
10 деталей бракованных. Найти вероятность, что
во всей партии брак нс превышает 15%. Здесь
N = 1000, я = 100, от = 10, — = , Р - неиз-
П 1U
вестно, но шах [-5L_, [ = g-j£| = °X».
то вероятность Р неравенства
л л
с увеличением п неограниченно прибли-
жается к значению интеграла
1 л* ——
е 2 dz.
Оценка частости. Если в генераль-
ной совокупности, состоящей из W пред-
метов (V — объем совокупности),
имеется М предметов с признаком 4, то
вероятность появления А при одном
М
испытании равна р = Пусть сде-
лана бесповторная выборка, объем кото-
рой п < N и признак А появился т раз;
тогда частость BZ(A) = -~яер. Для
оценки этого приближенного равенства
пользуются приближенной формулой
-Р
где
о
। - т)
л»
И,
а в называется точностью.
Если задана е, то находят Р
обратно, задав Р, можно найти в. Имеем
откуда
I
Зн?я объем генеральной совокупно-
сти N, точность « н вероятность 4>( г),
Вычисляем:
XIX,
стр. 61);
Ф (1.75) = 0,4599 (по табл.
Р = 0,92.
2) Если ЛГ = 1000, точность а — 0.05 и вероят-
ность Р = 0,95, следовательно, Ф | ) = 0,475, то
по табл. XIX (стр. 61) — = 1,96. откуда в = .
О 1
Находим
" ~ 4 0,061 | ~ ” б-бчоо = 277
1д«» ШиО
Это означает, что, взяв случайную выборку
п > 278, мы получим, что с вероятностью и,95
будет выполняться неравенство
-2- - 0,05 < р < + ода.
п п
ТЕОРИЯ ОШИБОК И СПОСОБ
НАИМЕНЬШИХ КВАДРАТОВ
Полученные из опыта (наблюдение,
измерение) величины содержат случай-
ные ошибки, которые не поддаются
точному учету и в каждом отдельном
измерении действуют различно. Учесть
такие ошибки можно только в среднем.
Если исследуемые величины опреде-
ляются непосредственно, то обработка
полученных результатов ведется стати-
стическими приемами. Если же вели-
чины определяются косвенным путем
(посредственные измерения), то при
наличии случайных ошибок и случай-
ных величин обработка результатов
производится по способу наименьших
квадратов.
ТЕОРИЯ ОШИБОК И СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ
331
Непосредственные измерения
Обозначим измеряемую постоянную
величину через а, полученные при изме-
рении значения — через xi, хт. . . х„
н предположим, что эти измерения —
равноточные или одинакового веса (т. е.
они произведены одним инструментом,
при одинаковых условиях, одним наблю-
дателем).
Искомая величина
п
Оценка этого приближенного равен-
ства состоит в том, что если X/ — слу-
чайные величины, подчиняющиеся нор-
мальному закону распределения веро-
ятностей
то требуется указать вероятность
Р (х — е < а < х + «).
Для любых п > 2 величина /=--
*
подчиняется закону распределения
Стьюдента, причем
_ , / 2^—х)»
х |/ л (л-1) *
Величины xt — х называются оста-
точными погрешностями (или кажу-
щимися ошибками).
Вероятность
Р(х — в<в<х-(-е) =
— 2 Г s
где в=гз-, т. е. с вероятностью а можно
утверждать. что_значение а заключено
между числами х — га- и х + га—.
В частности, с вероятностью 0,682
можио утверждать, что
а — х ± l.Hoj
л — х ± 1Х>6з-
а — х dt 1,04а -
ДЛЯ
л-5;
п- 10;
л - 15
Для л > 20 вероятность Р (| а — х | <
<е)=2Ф^ — У Поэтому с той же ве-
роятностью 0,682
а = х ± а- ;
с вероятностью 0,50 •
a-i±r-.
где г— — вероятная ошибка,
2
г- = 0.6745а- «з — а_.
X X 3 X
Вероятная ошибка г есть такая вели-
чина, что вероятность того, что ошибка
измерения окажется между г и — г,
1
есть — , и вероятность того, что
ошибка окажется вне этих пределов, есть
1
также ~2“, иначе
Р(|л — х | < г) — ОД
В случае неравноточных измерений
(с разными весами) вес измерения опре-
деляется по формуле
tt>i — а0. а,,
где з0 — число, совпадающее с одним
из чисел сЛ или произвольное (чтобы
w, были удобными для вычислений
числами), принимаемое как средняя
квадратическая ошибка измерений на
единицу веса.
Часто принимают и>/= л,, где л,—
число независимых и равноточных изме-
рений хд, хи, - • Лшл подчиненных
одному и тому же нормальному закону
в серии с номером I.
Наконец, иногда приближенно при-
писывают одним измерениям меньший
вес, другим — больший вес в зависи-
мости от качества инструментов н надеж-
ности работы лиц, производящих изме-
рения.
За приближенное значение величины
а можно принять так называемое сред-
нее взвешенное:
я я
«** — V
332
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Средняя квадратическая ошибка изме-
рения я0 находится по формуле
2 Wi(xt-xy
Средняя квадратическая ошибка
с редневзвешенного
/27,
2 (X/ — X)2
(«—1>2 w<
где £ берется от i *= 1 до п.
Результат измерения
а = х ± о-
или
а = х х г- .
Пример. Найти результат измерения по по-
лученным неравноточным отдельным измерениям:
Здесь л •= 5, II по предыдущим формулам пы-
чксляем:
». - 3,92;
3,92
/13
1.В;
/•_ =.0,674*. 1,23 - 0,83.
Результат: а —17.2 ± 1,2 (± средняя кеадраттН
ческая ошибка) или а ~ 17,2 ± U.8 (± яерокгная
ошибка).
Последний столбец я таблице дан для контроля:
сумма ранка нулю, если х вычислено без приблн-
жеимя, и не превышает 0,%.1У — 0,5, если х вы-
числено с точностью до 0,05.
Посредственные измерения
Если определяемая величина / яв-
ляется .известной функцией несколь-
ких непосредственно измеряемых неза-
висимых между собой величин, / =
= /(х, у, г), прячем ошибки измерения
х, у, г (с нормальным распределением)
достаточно малы, то можно приближенно
заменить f членами 0-то и 1-го порядка
ряда Тэйлора. Для значения искомой
постоянной X, принимаемой за истин-
ное, имеем приближенное равенство
Xnf'—f (х. у. х) ±
где значок 0 обозначает, что нужно
подставить х = х, у = у, z = гв произ-
водные; в—, , а— означают средние
квадратические ошибки.
СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ
Пусть искомые величины х, у, г
определяются системой уравнений:
/Дх. у, 2)-/, 0-1, 2.......л).
где реличины /, получаются измерением
и содержат погрешности. Число урав-
нений, называемых условными, больше
числа неизвестных; система, вообще
говоря, несовместна.' Если величины
х, у, г имеют нормальное распределение,
то считают наиболее вероятной ту сис-
тему значений неизвестных, для которых
сумма квадратов остаточных погреш-
ностей е, = ft—I, будет наименьшей.
Случай условных линейных уравнений
Если данная система состоят из линей-
ных условных уравнений
я,х + Ь,у + С/Х — //.
причем все // получены в результате
равноточных измерений, то подстановка
каких-либо х, у, г в это уравнение дает
вообще
Я/Х + + C/Z — // — 8/^0.
Для наиболее вероятных неизвестных
сумма
наименьшая. Из этого требования полу-
чается система линейных нормальных
уравнений для определения наиболее
вероятных неизвестных:
[ая] х + |аЬ]у + (ас] г “ lflZb
[Ьд]х+ |W|y + (dc| х - |W|; (•)
(са( x + У + l«l* - lc/l
СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ
ЙЗ
(см. |оа], |ай 1, . . в <Обозначениях>,
стр. 1). Для получения fc-го нормаль-
ного уравнения надо каждое условное
уравнение умножить на коэффициент при
/?-м неизвестном в этом условном урав-
нении н все уравнения сложить.
Чтобы проконтролировать вычисле-
ние коэффициентов нормальных уравне-
ний, следует вычислить суммы
S| — в/ 4- bt 4- С) 4- h,
и тогда должно иметь место для коэффи-
циентов первого нормального уравне-
ния тождество
[аа] + [лЛ] 4- |лс| 4 [а/] = (аз|.
Аналогичные тождества имеют место
для остальных уравнений.
Если систему (*) решать при помощи
определителей, то выражения
D D D
И’'=Лз
называются весами неизвестных, где
D — определитель системы (*), Ап, А^,
Ад» — алгебраические дополнения эле-
ментов главной диагонали определителя.
Если система (•) решается по способу
Гаусс» последовательным исключе
нием х, затем у и получается линейное
уравнение Аг = б, тогда А = »z;
остальные веса находятся аналогично,
т. е. опять из последнего уравнения,
если начать исключения с другой неиз-
вестной.
Подставив полученные значения неиз-
вестных в уравнение
atx + Ь>У + С/Х — /# = «/,
можно вычислить остаточные погреш-
ности е(. Средняя квадратическая
ошибка за на единицу веса вычисляется
по формуле
«о = 1«] = (« — *).
где s — число неизвестных (в данном
случае s = 3).
Средние квадратические ошибки опре-
деляемых величии находятся по фор-
мулам
' °о . °о
°Х“ ’
У wx V wr ) v>.
Искомые величины
X — х ± Y — У ± Ор ± аг.
где х, у. г — решения нормальных урав-
нений.
Если ошибки е( в величинах lj (оста-
точные погрешности) имеют разные
веса, то надо каждое нз первоначаль-
ных уравнений умножить на корень
квадратный из соответствующего веса,
а затем составлять нормальные уравне-
ния вида
х + |weft] у 4- [trac| г — |шп/|
и т. д.-, получаются взвешенные нор
мальные уравнения.
В случае нелинейных зависимостей
сначала находят каким-либо способом
приближенные значения неизвестных;
обозначают эти последние через хв, у0, г»,
затем разлагают каждое fj в ряд по сте-
пеням Е = х — Хд. т, = у — С =
= г — го- Ограничиваясь первыми сте-
пенями 6, т], С, получают линейные
условные уравнения
А/Е + В/Т] + Cf. — lt — ft (Xg. Уд Xg).
из которых определяют наиболее вероят-
ные значения поправок Е, т]. С-
Здесь
А . в d/<(Xg.y,.xj).
r dft (Хд. у». Хд)
С‘--------37-----
Пример. Рассмотрим маячу иадожлепия выпи
рической формулы по полученному нэ опита рллу
значений х и у. енамины, функциональной дави
симостью. Них последней задается или подби-
рается по виду графика.
Найти формулу вида y», + Jx при вадаяки:
X 03 1 13 2 23 3
У 0,31 0.Я2 1.29 1.83 2.S1 3.02
В задаче о нахождении эмпирической <|ор
мулы иеизпеетяими являются параметры аир;
я — 6. Условные уравнения имеют вне
a-f-030 — 0Д1;
• + 19-033;
а4-130-1.29;
• + 20- 135;
• 4-230 - 23U
«+ 30-3 ДИ.
Составляем нормальные уравнения:
6в 4-1030 - 93;
103« 4- 22.750 - 21.945.
Определитель системы
о- 1103 ejsl-2®-»: А,-22.75; А.-в.
Таблица функции $(:) для распределения Стьюдента
п 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 СО
0,0 ОЛОО 0,500 0.500 олоэ 0,500 0,500 олоэ 0,500 олоо олоо олоо олоо 0.500 0.500 ОЛОО олоо олоо ОЛОЭ ОЛОО 0.500000
0.1 532 535 537 537 538 538 534 539 539 539 539 53.4 539 519 539 539 539 539 539 53983
од 563 570 573 575 575 576 576 577 577 577 5771 578 578 578 573 57, 573 578 578 57926
0.3 593 604 608 610 612 613 614 614 614 615 615 615 616 616 616 616 616 616 616 61791
0.4 621 636 642 645 647 648 650 650 651 651 652 652 652 652 653 653 653 65.3 653 65542
0.5 G48 667 674 678 681 683 684 685 «46 686 686 687 687 648 638 688 685 688 689 69145
0,6 672 696 705 710 713 715 716 717 718 719 720 720 721 721 721 722 722 722 722 72575
0,7 694 722 733 739 742 745 747 748 749 750 751 751 752 752 753 753 753 754 754 75804
0,8 715 746 759 766 770 773 775 777 778 779 780 780 7»1 782 782 782 783 783 783 78814
0.9 733 768 783 790 7УБ 799 801 803 8^4 ЗД5 806 807 803 808 809 809 810 810 810 81594
1.0 750 789 804 813 818 822 825 827 828 830 831 832 832 833 ЮЗ 834 834 835 835 84134
1.1 765 807 824 834 839 843 846 848 «50 851 853 854 854 855 856 856 857 857 85) Е6433
1,2 779 824 84’ 852 858 862 865 868 870 871 872 873 874 875 875 876 877 877 878 88493
13 791 838 85.1 868 875 879 883 865 887 889 893 891 892 893 893 894 894 895 *95 90320
1.4 803 85.* 872 883 890 894 898 90U 902 904 906 907 908 903 909 910 910 911 911 91924
13 813 964 885 896 903 908 911 914 916 918 919 920 921 922 923 924 924 924 925 93319
13 822 875 896 908 915 920 923 926 928 930 931 932 933 934 935 935 936 936 937 94520
1.7 831 884 905 918 925 930 931 936 938 940 941 943 941 944 945 945 945 947 947 95543
13 839 893 915 927 914 939 943 945 947 949 950 952 952 953 951 935 955 9» 956 96407
1.9 846 901 923 935 942 947 950 953 955 957 958 959 961) 961 962 962 963 963 964 97123
2.0 852 W8 930 942 949 954 957 96J 962 963 965 967 967 967 953 969 969 970 970 97725
2.2 864 921 942 954 960 965 968 970 97’ 971 975 976 977 977 978 979 979 979 98*3 9361U
2.4 874 931 952 963 969 973 976 978 9<8О 981 982 951 954 965 985 986 936 9S6 987 99180
2,6 883 938 960 970 976 980 982 984 986 У87 938 968 989 990 990 990 991 991 991 99534
23 891 94» 966 976 98) 984 987 988 990 991 991 992 992 993 993 994 994 994 991 99741
3.0 898 952 971 980 985 988 990 992 992 993 994 994 995 995 996 996 995 996 996 99865
3.2 904 957 975 984 988 991 992 994 905 995 996 991 Ул) 997 997 997 997 99 < 991 99931
3.4 909 962 979 986 990 993 994 995 996 997 997 997 993 993 993 993 993 ‘.•93 998 99963
3.6 914 965 982 989 992 991 996 996 997 998 993 993 993 999 999 999 999 999 999 99984
3.8 918 969 964 990 994 996 997 997 998 993 908 999 999 999 999 999 999 999 999 99J93
4.0 922 971 986 992 995 996 997 998 998 999 999 999 999 999 999 1,000 1.030 1ДГ 1.003 99997
4.2 92» 974 989 993 996 937 998 998 999 599 9М 999 I.OJO 1.000 1.009 99999
4.4 929 976 £в\< 994 996 9S8 998 999 999 999 1Лои 1.000 99999
4.6 932 978 990 995 997 998 999 999 999 1,0»
4.8 935 980 991 996 996 ЮЧ 9*39 999 1,000
5.0 937 981 192 996 998 999 999 1 ЛОО
334 ТЕОРИЯ ВЕРОЯТНОСТЕЙ
СПОСОБ НАИМЕНЬШИХ КВАДРАТОВ
335
Решение нормальной системы
« = -0.285, 3 = 1.1.
Искомая зависимость булет
у = 1.1х-0Д85.
Веса искомых величия
26,25. 26.25
*' “ 2 А 75 ‘ ’
Вычисление остаточных погрешностей:
а, — — 0.285 + 03-1.1 - 031 - - 0/М5.
I, = - 6,281 + 1,1 - 032 - - 0.006;
«,«-0385 4- 1Д.1,1 - 1,29-0/175;
а, — - 0,285 4-2-1,1 - 135 - 0,065;
., - - 0,285 4- 2Д-1.1 - 2,51 - - 0/И5;
«. = - 0,285 4- 3-1,1 - 3.02 = - О/ХВ.
Наложим |и| — U314.
Вычнсленне средних квадратических ошибок:
на единицу веса
I /" 0ЛН-22.75 „
"ЗУ 26.25 -°-°66;
- 1 _ п га
2 У 26,25 М
Результат решения:
к - - 0.285 ± 0,056; р «= 1.1 ± 0/В.
ГЛАВА XV/1
МАТЕМАТИЧЕСКИЕ ПРИБОРЫ*
ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА
Счетная логарифмическая линейка
позволяет производить над заданными
числами действия умножения, деления,
возведения в степень, извлечения
корня, а также действия с тригонометри-
ческими функциями. Результат вычисле-
ния получается приближенный, с тремя
значащими цифрами.
На фиг, I представлена логарифми-
ческая линейка длиной 250 мм, которая
состоит из корпуса К, движка D
и бегунка В (с визирной линией посе-
редине). На корпусе нанесены следую-
щие шкалы.
I) Равномерная шкала А
с модулем 250; уравнение шкалы s =
= 250)' (см. «Номографиям, стр. 314),
причем у изменяется от 0 до I через
0,002, пометки I, 2, ... ,9 означают
что у “ 0,1; 0,2; . . . 0,9: в начале
шкалы у « 0, в конце шкалы у = I.
2) Логарифмическая шка-
ла L функции у = 1g х с моду-
лем 250; уравнение шкалы 5» = 250 1g х;
х изменяется от 1 до 10. От 1 до 2 деле-
ния даны через 0,01; от 2 до 4 — через
0,02; от 4 до 10 — через 0,05.
3) Логарифмическая шка-
ла Q с модулем, вдвое меньшим; ее
уравнение Si " 125 1g ж, х изменяется
от I до 100, причем шкала состоит нз
двух тождественно равных участков
с пометками ж от 1 до 10 и от 10 до 100
От 1 до 2 деления даны через 0,02; от 2
до 5 — через 0,05; от 5 до 10 — через 0.1,
Шкала Q называется шкалой квадра-
тов.
4) Логарифмическая ш к а-
„ с 250 .
л а С имеет уравнение = -у lg ж,
она состоит из трех тождественно равных
участков, поэтому ж изменяется от I до
* См. литературу на стр. 351: 1112), 1114), 1117),
4123), [144), )14й), |113»).
1000. Цена делений такая же, как на
шкале Q. Шкала С называется шкалой
кубов.
На лицевой стороне движка имеются
две шкалы: L' тождественна со шкалой L
и Q' тождественна со шкалой Q.
На обратной стороне нанесены логариф-
мические шкалы S, Т и (S и Т) тригоно-
метрических функций (см. ниже).
При помощи корпуса и визира можно
находить логарифм числа, число по ло-
гарифму, возводить в квадрат и в куб,
извлекать корень квадратный и кубичный.
Если установить визирную линию
на ж шкалы L, то мы прочитаем 1g ж на
шкале А в пересечении с ней визирной
линии. Прочитанное число является ман-
тиссой 1g ж, а характеристика 1g ж
устанавливается по взятому числу ж.
На фиг. 1 визирная линия отмечает на
шкале L число ж = 1432 (взято 143
н на глаз Vs самого мелкого деления,
получилось число 1432). Мантисса лога-
рифма этого числа равна 156, следова-
тельно, указанное положение визирной
линии дает 1g 1,432 = 0,156; 1g 14,32 —
- 1,156; lg 0,1432 =» 1,156 и т. д.
Чтобы найтиж по данному 1gж.
надо визирную линию установить на точ-
ку шкалы А, пометка которой равна ман-
тиссе данного логарифма. На шкале L
в пересечении с ней визирной линии
читаем ж; запятая ставится соответ-
ственно характеристике.
Для возвышения в квад-
рат ж устанавливают визирную линию
на х шкалы L и в пересечении ее со шка-
лой Q читают ж’. Если отсчет ж* полу-
чается в правой половине шкалы Q
(между 10 и 100), то число знаков ж*
налево от запятой равно удвоенному
числу знаков ж налево от запятой; если
же отсчет ж* получается на левой поло-
вине шкалы Q (между I и 10), то число
знаков ж’ налево от запятой равно удвоен-
ному числу знаков ж налево от запятой
ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА
337
22 том I Зак. 1484
без единицы. На фиг. 2: 7,88s = 62,1;
на фиг. 3: 1,628s = 2,65.
Правило определения числа знаков
верно и для возвышения в квадрат пра-
вильной дроби, если условиться «число
знаков» понимать как отрицательное
число, содержащее столько единиц,
сколько нулей содержится между запя-
той и ее первой значащей цифрой.
Пример. Дробь 0,00375 имеет (—2) знака; ее
квадрат прочитывается иа правой половине
шкалы Q и должен поэтому иметь 2-(— 2) — 4
знака, что дает (0,00375)* = 0,0000141.
Извлечение квадратного корня: V~x.
Данное число х разбивают, начиная от
запятой, па грани по две цифры в каж-
дой грани. Если в первой грани высших
единиц окажется одна цифра, то х нужно
брать в первой половине шкалы Q.
а если в этой грани будут две цифры
то х нужно брать во второй половине
шкалы Q. Результат извлечения квад-
ратного корня из х читают на шкале L.
Число знаков в этом результате равно
числу граней, на которые разбивается
целая часть х. Если х — правильная
десятичная дробь, то разбивают на грани,
начиная от запятой вправо. Число х
берут в первой или во второй половине
шкалы Q в зависимости от числа цифр
в значащей части первой значащей
грани. В результате нужно, кроме нуля
целых, взять до значащих цифр столько
нулей, сколько граней, состоящих исклю-
чительно из нулей, находится в данном
числе х.
Примеры: V4'S0 *21,2;
/6^3648 = УО.ОО'бГИО - 0,0305.
При возведении в куб
пользуются шкалой С: против пометки *
на шкале L читают х8 на шкале С. Пусть
целая часть х имеет п знаков. Если х>
получается в первой трети шкалы С,
т. е. в промежутке от 1 до 10, то резуль-
тат содержит Зп — 2 знака. Если х8
получается в средней трети шкалы (от
10 до 100), то результат содержит Зп — 1
знак. Если х8 заключается в последней
трети шкалы (от 100 до 1000), то число
знаков в результате равно Зп.
При извлечении кубического корня
нз данного числа нужно разбить послед-
нее, начиная от запятой, на грани по
три цифры в каждой грани. Если в пер-
вой грани слева оказывается одна цифра,
то число нужно брать в первой трети
шкалы С; если в первой грани две цифры,
то число надо брать во второй трети
шкалы С, и, наконец, если в первой
838
МАТЕМАТИЧЕСКИЕ ПРИВОРЫ
грани три цифры, то число берут в
последней трети шкалы С.
Число знаков в корне кубическом
равно числу граней.
В случае правильной десятичной
дроби следует разбить это число на
грани, начиная от запятой, и вопрос
о том, в какой из трех частей шкалы С
нужно брать данное число, решается
по числу цифр в значащей части первой
аначащей грани.
На фиг. 2 и 3 даны произведения
6,30 1,250 = 7,88 и 223-7,30 = 1628
(последний знак взят на глаз, как 0,8
деления).
Это правило справедливо и тогда,
когда один или оба сомножителя суть
правильные десятичные дроби, если
«число знаков> рассматривать как отри-
цательное число (см. возвышение в квад-
рат).
Фиг. 2. Положение движка .вправо* при умножении 6,30 • 1.250.
Фиг. 3. Положение движка .влево* при умножении 223.7,30.
Для умножения ху берут х на шкале L
и, продвигая движок направо,
устанавливают начало шкалы L' про-
тив х шкалы L. Против у, взятого на
шкале L', читают при помощи визирной
линии на шкале L число, равное произ-
ведению ху.
Если пометка у на £' выйдет за пре-
делы L, то передвигают движок влево,
устанавливают коней шкалы L' против х
на L, а затем опять против у читают
на шкале L число, которое равно •
Для умножения каких угодно чисел
надо округлять их так, чтобы они имели
не более трех верных значащих цифр.
Правило знаков. Если при
перемножении движок передвигается
направо, то число знаков в целой части
произведения равно сумме чисел зна-
ков сомножителей без единицы, если
же движок передвигается налево, то
число знаков произведения равно сумме
чисел знаков сомножителей (см. стр. 316).
Пример. Для проилведепич 0.0124-Я1,21, полу-
чаем (- 1)4-2» 1 эадк (движок влево). что
дает 1.007.
При перемножении нескольких чисел
промежуточные результаты не про-
читываются, а отмечаются визирной
линией, с которой совмещается началь-
ное или конечное деление движка при
следующем умножении. Нужно заме-
чать, в какую сторону передвигается
движок и сколько раз, чтобы подсчи-
тать число знаков произведения.
Пример. 2,7СОД1-Б,2В-О.ОЯ6. Стрелки аниду
укиивают. «право или
и ок. Число знаков:
Опит: 0,423.
„ X
Для деления —-
помощи визирной
шкалы L у шкалы
чают иа шкале L как пометку той ее
точки, которая приходится против
начала движка или конца движка, в запи-
лено перемещается лвн-
4-0—l-f-l4-(— 1) —0
устанавливают при
липин против х
L' и частное полу-
ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА
339
снмостн от того, пришлось ли передви-
нуть движок направо или налево для
этой установки.
Правило знаков. Если част-
ное читается против начала движка
(передвижение направо}, то число зна-
ков частного на единицу больше раз-
ности чисел знаков делимого и дели-
теля, если же частное читается против
конца движка (передвижение налево),
то число знаков частного равно раз-
ности чисел знаков делимого и делителя
Примеры.
I) 0,001464 : 0,0646; число лмков: — 2 — (— 1) —
— — 1. Ответ” (',0226.
2) 0.795 :2Д4; число зввков 0-14-1=0.
Ответ: 0.355.
В комбинированном умно-
а-Ь-с
женин и делении d е j удобно вести
вычисления по схеме a:d b:e-c:f.
_ 0.787-32Л-О/ОЧ
Пример. 633-5,76 1(3
— 0.787 : 633-32.5 : 6,76-0,024 :113.
Число shikob равно 0—14-1 4-2 — 1 — 14-
+ (- 1)-3+ 1 — -3. Ответ 0,000143.
Обратная сторона движка
служит для нахождения синуса
(шкала 5) и тангенса (шкала Г) по
углам и, обратно, углов по синусам и тан-
генсам. Шкала (S и Т) (посередине) слу-
жит как для синусов, так н для танген-
сов, для углов х от 34' до 5’44'.
Для вычисления тригонометрических
функций необходимо вытащить движок
и в перевернутом виде вдвинуть его
в паз корпуса линейки так, чтобы
шкала S оказалась на месте Q' и чтобы
начальное деление S совпало с началь-
ным делением Q.
Чтобы найти sinx, нужно взять х®
на S и прочесть на неподвижной шкале L
число, стоящее против х®. Эго число,
разделенное на 10, даст sinx.
Чтобы найти х no sin х, следует
10 sin х установить на шкале L и на
шкале S прочитать х®.
Примеры:
I) ж = 22“ не $; ил I читаем 3,75; слглаве-
твлвио, »1п 22* — 0,378.
2) Дли 11 п х — ОЛИЗ, берем 6.43 ил L. и «л 5
читаем X = 40“.
Эти же действия можно производить
без перевертывания движка.
В корпусе линейки с обоих концов
(иногда с одного) имеются вырезы. На
боках этих вырезов штрихами указаны
положения начала и конца шкалы L,
22*
Чтобы найти sinx, надо, не перевер-
тывая движка, выдвинуть его вправо
так, чтобы отсчет х ня S пришелся про-
тив штриха в вырезе. Против конца L
с лицевой стороны движка получится
отсчет 10sinx на шкале L'; sin х равен
результату деления этого отсчета на 10.
Для нахождения х no sinx передви-
гают движок направо так, чтобы отсчет
10 sin х шкалы L' пришелся против
конца L, тогда на обратной стороне
линейки читают угол к на $ против
черты в вырезе.
Для углов от 34' до 5°44’ (их синусы
изменяются от 0,01 до 0,1) используется
шкала (S и Г), но только при нахожде-
нии синуса по углу надо отсчеты на L
целтъ не на 10, а на 100; при на-
хождении угла по синусу (<0,1) надо
на L' устанавливать 100 sin х.
Нахождение tg х, или х по tg х. про
изводится так же, как и в случае sin х,
во с заменой шкалы S шкалой Т. При
втором способе двнжок надо выдвигать
не вправо, а влево и читать на шкале L'
против начала (а не конца) шка-
лы L.
Особые штрихи иа шкалах
отмечают некоторые употребительные
числа: на L, L', Q, Q' отмечается осо-
бым штрихом к; штрих С (на L' и на £)
отмечает число У4ж, употребительное
при вычислении площади S круга по
„ r.<P /d\t
диаметру его d;\ ; иногда
имеется штрих Ci = V 40:х, заменяю-
щий С.
При применении С или Ci результат
прочитывается на одной или другой
половине шкалы Q. Этим можно поль-
зоваться при производстве вычислений,
в которых участвует площадь S.
Штрихи р*. ?' на L и L’ служат для
перевода угла, заданного в градусах,
минутах и секундах, в дуговую меру
(в радианы) и обратно; ₽' соответствует
180-60-60
число----------= 206265 и р соот-
ветствует -—-—= 3437',75. Угол к*
в дуговой мере равен -р-, а угол х'
равен у.
Примеры:
1) Перевести угол 24'17» реликты. Соине-
шлем отсчеты 24 и р' швлл L и Д'; ил 1 против
«он ил £' читлеы Н9Я. Дли вл в число эилвов «л
340
МАТЕМАТИЧЕСКИЕ ПРИБОРЫ
24
иого — равно 2 — 4 = — 2, то получаем 24' =
— 0,00698 рпхиава. Так же совмещаем отсчеты 17
и р" шкал L н L' и против конца L' читаем
на L результат: 17* = 0,0000824. Окончательно,
округма, находим 24'17* =0,00706 радиана.
2. Перевести угол 1,75 ралканп в градусную
меру. Умножая на линейке числа 1,75 и р', нахо-
дим результат: 0020' = 11W-20',
АРИФМОМЕТР
Арифмометр (на фиг. 4 — русской
конструкции Однера) имеет в верхней
части (коробка) девять прорезов, в кото-
рых передвигаются рычажки. Сбоку
прорезов нанесены цифры; передвигая
вдоль каждого прореза рычажок, можно
•.поставить на рычагах* любое девяти-
значное число.
Внизу под рычагами находятся два
рядя окошечек (подвижная каретка):
одни, более крупные, числом 13 справа,
другие, меньшие, слева, числом 8.
Ряд окошечек справа образует резуль-
тирующий счетчик, а ряд слева — счет-
чик оборотов. Номер окошечка на счет-
чике указывает место единиц, какого-
либо разряда числа, стоящего на этом
счетчике.
Справа и слева каретки видны
барашки (ласточки), служащие для
сбрасывания цифр, появляющихся на
этих счетчиках. Повертывая барашки
до тех пор, пока они не щелкнут, мы
убираем все цифры на счетчиках, оста-
вляя нули.
На коробке машины справа от про-
резов имеются две стрелки, на концах
которых стоят плюс ( + ) и минус ( — ).
С правой стороны машины имеется
ручка, которую можно повертывать
в направлении плюс (по часовой стрелке)
и в направлении минус (против часовой
стрелки).
Пусть на результирующем счетчике
и на счетчике оборотов стоят нули.
Поставим на рычагах какое-нибудь
число, например 231705 896, и повер-
нем ручку в направлении плюс. После
одного оборота на результирующем счет-
чике появится то же число 231 705 896.
Сложение н вычитание. Чтобы сло-
жить несколько чисел, надо поставить
эти числа одно за другим на рычагах
и после каждой установки 1 раз повер-
нуть ручку в направлении плюс. На ре-
зультирующем счетчике появится сумма
всех чисел.
При вращении ручки в обратную сто-
рону на результирующем счетчике по-
явится разность между числом, стоявшим
в нем до начала поворота, и числом,
поставленным на рычагах.
Умножение. Каретка арифмометра
может передвигаться вдоль машины
вправо и влево, и под прорезом для
единиц можно поставить различные око1
шечки результирующего счетчика.
Когда каретка находится в крайнем
левом своем положении, то против еди-
ниц па рычагах находится место единиц
на результирующем счетчике; при одном
обороте к числу на этом счетчике при-
бавляется число, установленное на рыча
гах. Если каретку сдвинуть вправо на
одно место (на один разряд), чтобы
против единиц на рычагах оказалось
второе место (десятков) результнрую
щего счетчика, то при одном обороте
в направлении плюс к числу на резуль-
тирующем счетчике прибавляется число,
равное 10-кратному числу, поставлен
ному на рычагах. Передвигая каретку
на т разрядов вправо, мы будем при
одном обороте в направлении плюс
прибавлять число, в 10т раз большее
числа, поставленного на рычагах.
Число оборотов, сделанное ручкой,
появляется на счетчике оборотов. Если
производятся обороты в направлении
плюс и в направлении минус, то на
счетчике оборотов появляется алгебра-
ическая сумма числа оборотов, считая
число оборотов в направлении плюс
положительным, а в направлении ми-
нус — отрицательным. Отрицательное
число оборотов отмечается на счет-
чике оборотов красными цифрами.
Чтобы умножить установленное на
рычагах число, например, на 538, надо
передвинуть каретку так, чтобы против
находящейся над счетчиком оборотсв
стрелки приходилось третье справа
окошко этого счетчика (окошко, соот-
ветствующее номеру высшего разряда
множителя), и начинают вращать ручку
АРИФМОМЕТР
341
в направлении плюс. Сначала вращают
ручку 5 раз; передвигают каретку на
одно место влево и вращают ручку 3 раза,
наконец, после следующей передвижки
каретки влево вращают 8 раз На счет-
чике оборотов окажется множитель 538,
а иа результирующем счетчике — про-
изведение установленного на рычагах
числа на множитель 538. Для умень-
шения числа оборотов можно при вто-
ром положении каретки накрутить не 3
раза, а 4 раза, н затем, после передвижки
каретки влево на одно место, вращают
ручку в направлении минус 2 раза
(что соответствует вычитанию 2 раза).
При таком умножении иасчетчике обо
ротов появится число 542, где знак 2
означает красную цифру 2.
Для вычисления суммы произведений
вида ab + cd 4- ef + . надо поста-
вить а иа рычагах, накрутить в счетчике
оборотов Ь; на результирующем счет-
чике появится ab; сбрасывают Ь со
счетчика оборотов. Затем ставят d на
рычагах и, накрутив на счетчике оборо-
тов с, получают иа результирующем
счетчике сумму ab + cd и т д.
Деление. Делимое устанавливают на
результирующем счетчике так. чтобы
цифра высшего разряда находилась
в крайней левой части этого счетчика,
после чего со счетчика оборотов сбрасы-
вают все цифры. Затем устанавливают
на рычагах делитель, начиная с крайнего
левого разряда. Каретку ставят в такое
положение, чтобы из стоящего на резуль-
тирующем счетчике делимого можно
было вычесть делитель, причем так, что
если сдвинуть каретку вправо на одно
место, то вычитание стало бы
невозможным (фиг. 5). После
этого вращают ручку в на-
правлении минус до тех пор,
пока на результирующем
счетчике не останется число,
меньшее делителя. Тогда пе-
редвигают каретку на одно
место влево и снова вычн*
Фиг. 5. Подо- та ют, и т. д. За числами,
* ""корпута остающимися на результн-
рмфионетр! рующем счетчике, можно не
при лелеиии. следить, крутя просто до
тех пор, пока не раз-
дастся звонок. Тогда делают один обо-
рот назад (т. е. в направлении плюс),
затем передвигают каретку и продол-
жают вычитать. Частное появляется
на счетчике оборотов, изображенное
красными числами. Запятую в частном
ставят по смыслу (см. стр. 346). На ре-
НОЖНО
Мели*
зультнрующем счетчике будет оста-
ток.
Деление можно производить и другим
способом. Делитель устанавливают на
рычагах. Каретку передвигают так,
чтобы против цифры высшего разряда
делителя приходилось по крайней мере
предпоследнее с левой стороны око-
шечко результирующего счетчика. За-
тем вращают ручку в направлении плюс
и набирают на результирующем счет-
чике делимое. Как только набралось
на результирующем счетчике число, бли-
жайшее меньшее к делимому, надо ка-
ретку передвинуть на 1 разряд влево. За-
тем опять вращают ручку в направлении
плюс до получения на результирующем
счетчике ближайшего меньшего числа
к делимому и т. д. Частное появляется
на счетчике оборотов, запятая в частном
ставится по смыслу.
Извлечение квадратного корня. Если
известно приближенное значение квад-
ратного корня, то можно получить
более точное значение того же корня
следующим образом. Пусть Va = х-
Первое приближение xi искомого корня х
можно найти, например, при помощи
счетной линейки. Для второго прибли-
жения надо найти поправку Ci (поло-
жительную или отрицательную), чтобы
(Х| + Ь)’ = а. Пренебрегая полу-
чаем из этого уравнения вместо Ь
о-х?
поправку cj = —2^— и второе прибли-
жение х» = xi 4- Е; = •
Посредством арифмометра вычисляем
а а , _
—,------Их, и, наконец, х». Отиоситель-
Xt Xj
ная погрешность второго приближения
составляет всего лишь половину квад-
рата относительной погрешности пер-
вого приближения, и второе прибли-
жение имеет вдвое больше верных зна-
чащих цифр, чем первое. Далее можно
искать третье приближение х» =
ит *
Пример. Найта У'П1. Счетам линейка нет
первое приближение ж, *» 15,1. Деление — лает
15.03311. Второе приближение ж, — -i- (15.1-f-
4- 15.1ВЗИ) — 15.06655. Затем лепим ИТ иа 15Дв№Б,
получаем 1S.U664KK3 и налолим третье приближе-
ние ж( — 15,056519. п т. Л.
342
МАТЕМАТИЧЕСКИЕ ПРИБОРЫ
ПЛАНИМЕТРЫ И ИНТЕГРАТОРЫ
Планиметры и интеграторы служат
для вычисления площадей и определен-
ных интегралов.
Полярный планиметр. В полярном
планиметре (ведущей линией является
окружность) два стержня АВ и ОВ
(фиг. 6) находятся в точке В на одной
оси. В конце стержня ОВ имеется острый
штифт (полюс О), которым этот конец
укрепляется неподвижно к чертежу.
Фиг. 6. Планиметр.
В конце стержня АВ имеется острие А,
которым обводят по контуру обмеряемой
площади; на другом конце К того же
стержня насажено колесико с острым
ободом; плоскость этого колесика пер-
пендикулярна стержню АВ. К этому
колесику прикреплен второй обод с деле-
ниями, по которым отсчитываются угол
поворота колесика и число его полных
оборотов.
Чтобы изморить площадь Q (фиг. 7),
ограниченную контуром Г, укрепляют
Фиг. 7. Измерение пл опции планиметром.
полюс планиметра к чертежу, ставят
острие п любую точку на Г, производят
отсчет л0 положения колесика указа-
телем и затем обводят острием по кон-
туру Г; когда острие после полного
обхода Г снова придет в исходную
точку, те делают второй отсчет Пу поло-
жения колесика. Искомая площадь
Q = Л(Л| — nfl), где коэффициент про-
порциональности k = rt, г — радиус
колесика, I = АВ—длина стержня.
Если же полюс О помещается внутри Г,
то
Q — А] + * (nj — По),
где k и Ai — постоянные планиметра,
определяемые из размеров его частей.
Но эти постоянные можно определить
опытным путем. Взяв квадрат илнокруж-
ность определенной площади, делают
обвод контура, и если отсчеты до и после
обвода равны п9 и tti , то при положении
полюса вне контура
ЙЬ —- * •
Л1 —«о
Определив k, делают обвод контура
при внутреннем положении полюса.
Пусть соответственные отсчеты п0 и щ;
тогда ky — Q — k(n} — л0).
Обычно определение площади фигуры
планиметром производят при внешнем
относительно контура положении по-
люса. Если же размеры фигуры велики
и невозможно при внешнем положении
полюса сделать обвод контура, то фигуру
разбивают на несколько частей и опре-
деляют площадь каждой части в отдель-
ности.
Правила пользования
планиметром. 1. Перед упот-
реблением необходимо планиметр про-
верить. Ось колесика и стержни не
должны шататься в гнездах и должны
быть чистыми; вращение должно быть
свободным.
2. Очень важно, чтобы ось колесика
была параллельна вертикальной пло-
скости, проходящей через точку враще-
ния В и ось ведущего острия А.
3. Все определения площади должны
быть многократными; обвод контура
надо производить в двух направлениях:
по часовой стрелке и против нее; кроме
того, следует менять положение полюса.
4. Необходимо очень внимательно
относиться к тщательному обводу кон-
тура так, чтобы все его изгибы были
захвачены. Обвод должен производиться
со средней постоянной скоростью. При
случайном уклонении в какую-либо сто-
рону необходимо сделать примерно
такое же уклонение в противоположную
сторону.
5. Следует избегать шероховатых
поверхностей как бумаги, так и доски,
на которой лежит бумага; это спо-
собствует излишнему вращению коле-
сика. Надо избегать и тщательно шли-
фованной поверхности, так как умень-
шение трения способствует скольжению
колесика там, где должно быть его каче-
ние.
Дисковый планиметр содержит осо-
бый диск, по которому (а не по чертежу)
АВТОМАТИЧЕСКАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
343
и катится колесико К. Вращение диска
пропорционально повороту стержня ОВ,
благодаря чему увеличивается поворот
колесика в большее число раз, а
значит, увеличивается точность отсчета
угла Л1 — По; кроме того, показания
прибора точнее, так как устраняется
возможность скольжения колесика.
Относительная погрешность при
обмере площади величиной около 100 см*
обыкновенным планиметром не превосхо-
дит 0,5%, а дисковым планиметром 0,1%.
Интегратор в простейшем своем виде
отличается от планиметра только тем,
что точка В стержня АВ ведется не
по окружности, как у планиметра, а по
данной прямой х (фиг. 7), и можно
»
вычислять j ](х) dx. Площадь изме-
а
ряется той же формулой Q = k(n-i — па).
В интеграторе имеются два доба-
вочных колесика, пользуясь которыми,
можно найти: 1) статический момент
обводимой острием А площади Q отно-
сительно оси х и 2) момент инерции этой
площади относительно той же осн.
Линейка АВ (с колесиком К) соеди-
нена с двойным зубчатым сектором,
с которым соединены два зубчатых
колеса /Ин/ равных радиусов; послед-
ние снабжены каточками, по которым
делаются отсчеты.
Статический момент М площади Q
вычисляется по формуле
М - А (л, —Пр),
где л( и Лц — отсчеты по каточку
колеса М после и до обвода.
Момент инерции / площади Q вычис-
ляется по формуле ,
j - С(Л1 —Ло) + В(л' —Лц),
где ль л0 — отсчеты по колесику А;
л,, nJ — отсчеты по каточку колеса /.
Коэффициенты А, В, С находят из опыта
тем же способом, каким определяют
постоянные k и k\ для полярного
планиметра. Зная моменты инерции
двух разных фигур (круг, квадрат), обво-
дят их планиметром и получают два
уравнения для неизвестных В и С.
Интеграф позволяет найти определен-
ный интеграл с переменным верхним
пределом. Если функция Цх) дана гра-
Jhkom, то интеграф вычерчивает график
ункцни
X
F(A)-j/(x)dx
АВТОМАТИЧЕСКАЯ
ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
С ПРОПОРЦИОНАЛЬНЫМ РЫЧАГОМ
Автоматы этого типа производят дей-
ствия (сложение, вычитание, умножение
и деление) автоматически с помощью
электродвигателя, питаемого от освети-
тельной сети. Вычислитель устанавливает
исходные данные на клавиатуре и нажа-
тием кнопок и рычагов производит дей-
ствия. Клавиатура имеет 12 разрядов,
счетчик результатов имеет 12 разрядов и
Фиг. S. Автоматическая вичислительпаа машина.
счетчик оборотов—6 разрядов. В машине
имеется накапливающий счетчик (запо-
минающая шкала) и дополнительные
кнопки.
Средний ряд клавишей (фиг. 8), окра-
шенный в красный цвет, разделяет кла-
виатуру на левую половину /, имеющую
пять разрядов (или вертикальных рядов)
и правую половину 2 с семью разря-
дами, куда включается и красный ряд.
В каждом ряду имеется деоять кла-
вишей, служащих для установки цифры
одного разряда числа: самый правый
ряд для установки единиц, следующий
ряд влево для установки десятков и т. д.
Если клавиш неверно нажат, то при
нажатии другого клавиша в том же
ряду, первый автоматически освобо-
ждается. Чтобы гасить цифры в каком-
нибудь ряду, надо нажать одновременно
два клавиша.
Рычаг закрепления клавиатуры 3
при передвижении от себя (положе-
ние М) закрепляет установленные циф-
ровые клавиши; при передвижении
344
МАТЕМАТИЧЕСКИЕ ПРИБОРЫ
к себе (положение А) клавиатура авто-
матически гасится после каждого хода
машины, происходящего после нажатия
кнопки сложения 4 или кнопки вычи-
тания 5. При нажатии этих кнопок,
отмеченных на корпусе машины зна-
ками ( + ) и ( — ), число, установлен-
ное на клавиатуре, передается в счет-
чик результатов 10 с соответствующими
знаками, т. е. машина складывает или
вычитает.
Кнопки с правой стороны I, II, III
или соответственно 6, 7, 8 служат для
гашения: / — для счетчика оборотов,
/I — для счетчика результатов и III —
клавиатуры.
На каретке (подвижной части
машины) кроме счетчиков результатов 10
и оборотов 11 имеется шкала счетчиков
результатов и оборотов 12. Рычаг заслон-
ки счетчика результатов 9 передвигает
планку, в которой имеются окошки
для замены дополняющего числа до 10*
(в случае отрицательного результата)
самим числом; например, если в счет-
чике результатов появилось дополни-
тельное число 9999648, то надо пере-
двинуть рычаг 9 вправо, и в верхних
окошках того же счетчика результатов
читаем 0000352. Но в случае, когда
в последнем окошке виден нуль (окра-
шенный в красный цвет), то к прочитан-
ному числу надо прибавить 10, для
чего на клавиатуре устанавливается
единица в разряде десятков и передается
на счетчик нажатием на кнопку ( —).
Рычаг 13 служит для умножения чисел
с числом знаков больше шести. Пере-
движение рычага к себе как бы соеди-
няет обе половины клавиатуры в одно
целое и дает возможность установить
множимое вплоть до 12-значного.
Рычаг 14 служит для ограничения
количества знаков в частном при деле-
нии. Рычаг может быть установлен в
одно из трех положений,соответствующее
числу цифр, которые будут получаться
в частном при установке рычага.
Кнопка 15 служит для управления
счетчиком оборотов при сложении, вычи-
тании и умножении чисел. Если кнопка:
а) поднята вверх, то счетчик оборотов
работает в том же направлении, что
и счетчик результатов; б) закреплена
в среднем положении, то счетчик оборо-
тов совсем не работает; в) полностью
нажата, тогда счетчик оборотов рабо-
тает с обратным знаком относительно
работы счетчика результатов, т. е.
работает на вычитание от нажатия
кнопки (+ ) и па сложение от нажатия
кнопки ( —).
Кнопка деления 18 и кнопка умно-
жения 19 включают машину для авто-
матического деления и умножения.
При выполнении действия деления от
кнопки 18 положение кнопки /5 не
влияет на работу счетчика оборотов.
Рычаг 16 управления счетчиками
оборотов и результатов при умноже-
нии и делении служит для получения
суммы и разности произведений и част-
ных. Если рычаг установлен в положе-
ние « + », то оба счетчика работают
в направлении, соответствующем знаку
пусковых кнопок. Если рычаг уста-
новлен в положение «— >, то I) при
выполнении умножения от кнопки 19
оба счетчика работают со знаком минус
и может быть получена разность произ-
ведений и разность множителей; 2) при
выполнении деления от кнопки 18 счет-
чик оборотов работает с обратным зна-
ком и может быть получена разность
частных.
Положение рычага 16 не влияет иа
оба счетчика при выполнении действий
сложения и вычитания.
Рычаг 17 — прерыватель деления —
используется для прерывания автома-
тической работы при делении.
Исходным положением машины счи-
тается следующее: счетчики и клавиа-
тура погашены; рычаг 3 в положении «А»
(к себе); рычаг 9 в положении налево;
рычаг 14 в положении от себя; рычаг 16
в положении от себя.
Сложение и вычитание чисел, после
того как машина поставлена в исход-
ное положение, производятся так же,
как и на арифмометре: число устанавли-
вается на клавиатуре и переносится
в счетчик результатов при помощи нажа-
тия кнопок ( + ) или ( — ). Счетчик
результатов (результирующий счетчик
в арифмометре) и счетчик оборотов
имеют то же назначение.
Для того чтобы счетчик оборотов
отсчитывал количество вычитаемых
в том же направлении, что и при сло-
жении, перед производством вычитания
нажимают до отказа кнопку 15.
Если при сложении и вычитании не
требуется автоматически гасить уста-
новленные на клавиатуре числа, то
рычаг 3 ставится в положение «ЛЬ.
Для облегчения работы на клавиатуре
машины имеются специальные раздели-
тельные линейки, выступающие на
несколько миллиметров над клавиатурой
АВТОМАТИЧЕСКАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
MS
как по вертикали, разделяя разряды,
так и по горизонтали. При известном
опыте можно ощупью находить соот-
ветствующую область и в ней нужный
клавиш.
Умножение чисел, имеющих не более
шести знаков. Машина ставится в исход-
ное положение и рычаг 13 — в поло-
жение от себя.
Множимое устанавливается в правой
половине клавиатуры и так, чтобы низ-
ший разряд приходился в первом справа
ряду, а множитель — в левой половине
и низший разряд попадал бы на крас-
ный ряд. Нажимают кнопку (X), и ма-
шина сначала делает два подготовитель-
ных хода, после которых множитель пе-
реходит в мультипликатор (невидимый
снаружи умножающий механизм), мно-
жимое остается на месте, а каретка авто-
матически передвигается вправо на
число разрядов множителя без единицы.
Затем начинается процесс умножения,
продолжающийся до возвращения ка-
ретки в начальное положение и освобо-
ждения кнопки (X)-
Произведение получается на счет-
чике результатов, множитель — на счет-
чике оборотов, а множимое — на кла-
виатуре. Положение запятой в произ-
ведении находится обычным способом
(см. «Правило знаков» ниже).
Если на счетчиках уже находились
некоторые числа, то на счетчике резуль-
татов получается сумма произведений,
в на счетчике оборотов — сумма мно-
жителей. Чтобы получить разность
произведений, надо рычаг 16 установить
в положение < — », и тогда новое произ-
ведение вычитается из числа, имею-
щегося иа счетчике результатов.
Гашение счетчиков и клавиатуры
производится одновременным нажа-
тием на кнопки /, //, 111.
Умножение чисел, если один из сомно-
жителей имеет более шести знаков, но
само произведение содержит не более
12 знаков. Устанавливают рычаг 13
в положение «к себе».
Множитель с меньшим числом зна-
ков устанавливается в левой половине
клавиатуры так, чтобы низший разряд
множителя приходился в красном ряду.
При помощи нажатия кнопки (X) мно-
житель передается в мультипликатор
машины. Затем на клавиатуре уста-
навливают множитель, имеющий более
шести знаков, и так, чтобы его низший
разряд приходился на первый справа
разряд клавиатуры.
После этого переводят рычаг 13 в поло-
жение «от себя», что вызывает автомати-
ческий процесс умножения, который за-
канчивается возвращением каретки в
исходное положение, а кнопки (X) — в
нормальное положение.
На счетчике результатов получится
произведение, а на счетчике оборотов —
меньший множитель.
Деление. Машина устанавливается
в исходное положение, а рычаг 15
в среднее положение.
Делимое устанавливают в левой поло-
вине клавиатуры, начиная с крайнего
левого ряда ее; делитель устанавливают
в правой половине, начиная с красного
ряда; нажимают кнопку (:), машина
выполняет процесс деления и останавли-
вается. Запятая в частном устанавли-
вается по обычным правилам (см. ниже).
Гашение производится кнопками 1,
Н, III.
Если вычислитель забудет установить
делитель и нажмет кнопку (:) (деление
на нуль), то двигатель начинает работать
беспрерывно. Для выключения двигателя
надо рычаг 17 (прерыватель деления)-
отвести к себе, и двигатель остановится.
Чтобы возвратить каретку в на-
чальное положение, надо нажать кноп-
ку (X).
Рычагом 17 останавливают деление
и в том случае, когда при делении полу-
чилось достаточное число знаков.
Если при делении делимое имеет более
семи знаков, то, установив делимое
на клавиатуре в крайнем левом положе-
нии, нажатием на кнопку (+) пере-
дают его на счетчик результатов. Полу-
чившуюся на счетчике оборотов еди-
ницу гасят кнопкой II. Затем устанавли-
вают делитель так, чтобы его высший
разряд приходился в красном ряду
и нажимают кнопку (:). На счетчике
оборотов получается частное.
Правило знаков при.
умножении и делении. Обо-
значают через Na число цифр в целой
части числа а (а > I) или число нулей
после запятой до первой цифры, отлич-
ной от нуля, при а<1, причем
No > 0 при а > 1 и число Na берется
с минусом или равно нулю в случае
а< I.
Для произведения ab число
Nab “ Na + Nb.
если первая значащая цифра пронзве-
346
МАТЕМАТИЧЕСКИЕ ПРИБОРЫ
дения ab меньше первой значащей
цифры хотя бы одного нз сомножителей, и
Nab =* Na-\- Nb — 1.
если первая значащая цифра произве-
дения ab больше первой значащей
цифры хотя бы одного из сомножи-
телей.
Если первые цифры сомножителей
и произведения равны, то судят по
вторым цифрам и т. д.
Для частного а : Ь число
Natb-Na-Nb.
если первая значащая цифра делимого
меньше первой значащей цифры дели-
теля, и ,
Nafb “ Na—Nb + 1,
если первая значащая цифра делимого
больше первой значащей цифры дели-
теля.
Пример. 0.48 : 0,00192 “ 25U, т. е. в часпюы
4tyxer три знака до платой, так как
“alb - Na ~ Nb 4- ! - 0 - (- 2) + 1 - 3.
Комбинированные вычисления. Одно-
временное умножение двух множимых
на один общий множитель. Если со-
множители имеют небольшое число зна-
ков, то их устанавливают в правой
половине клавиатуры (с небольшим
интервалом между ними), а общий мно-
житель — в левой половине. Нажи-
мают кнопку (X) и на счетчике резуль-
татов получают оба произведения.
Если сомножители не устанавли-
ваются в правой половине, то исполь-
зуется рычаг 13.
Последний переводится в положе-
ние .к себе". Общий множитель устана-
вливается на левой половине, и нажатием
на кнопку (х) множитель переводится
в мультипликатор машины. Затем на
клавиатуре устанавливаются оба мно-
жителя с некоторым интервалом между
ними (чтобы произведения на счетчике
оборотов не слились). Рычаг 13 пере-
водится в положение .от себя*, и ма-
шина производит умножение. Оба про-
изведения, разделенные друг от друга
нулями, читаются на результирующем
счетчике.
Вычисление суммы произведений
<hb\ ± a»bi ±.... На машинах моделей
37 и 38 эта операция производится
при помощи рычага 16. Алгебраическая
сумма читается на счетчике резуль-
татов; если эта сумма отрицательна,
то появляется дополнение до 10*.
Само отрицательное число получится
после передвижения рычага 9 вправо
на <—».
в] ог
Вычисление суммы частных
Деление производят обычным способом,
но счетчик оборотов не гасят, а на нем
накапливают сумму частных, регули-
руя знаки частных рычагом 16.
В машинах этого типа имеется на
капливающий счетчик (иля запоминаю-
щая шкала), помещаемый над счетчиками
оборотов и результатов,!! дополнительные
кнопки М, 3 и SL, находящиеся на
правой стороне машины выше кнопок I,
II, III.
Накапливающий счетчик управляется
кнопками 3 и SL, а именно: нажатием
на 3 число, стоящее на счетчике резуль-
татов, передается на накапливающий
счетчик; кнопкой SL это число обратно
передается на счетчик результатов.
На счетчике результатов получают
отдельные произведения, а на накапли-
вающем счетчике — сумму этих произ-
ведений.
Кнопка М служит для многократного
умножения и возведения в степень.
При нажатии кнопки М число из левой
половины счетчика результатов пере-
дается в умножающий механизм (неви-
димый снаружи), и в специальном
окошке над левой стороной счетчика
результатов появляется буква М (меха-
низм занят).
Если требуется найти произведение
abc, то сначала устанавливают число а
в левой половине клавиатуры (как
множитель при умножении) и кнопкой
(+) передают его на счетчик резуль-
татов, а затем нажатием на кнопку М
передают его в умножающий меха-
низм.
Набирают число Ь на правой половине
клавиатуры. Нажимают кнопку (х)>
и в левой половине счетчика результа-
тов появляется произведение ab, а на
счетчике оборотов — число а.
Гасят клавиатуру и нажимают
кнопку М, после чего произведение ab
перейдет в умножающий механизм;
в правой половине клавиатуры устана-
вливают третье число с и умножают пв
предыдущему.
ПОЛУАВТОМАТИЧЕСКАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
347
ПОЛУАВТОМАТИЧЕСКАЯ
ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
ТОЧМАШ, МОДЕЛЬ КЕВ
Полуавтоматическая клавишная вы-
числительная машина Точмаш, модель
КЕВ (фиг. 9), имеет клавиатуру /
(установочный механизм) с восемью ря-
дами, что позволяет установить на ней
самое большое восьмизначное число.
Линейки-разделители 2 выполняют
функции запятых для клавиатуры.
Фмг. 9. Полуавтоматическая вычислительная
машина Точмаш, модель КЕВ.
Клавиши 3 служат для поразрядного
гашения клавиатуры.
Пусковые кнопки 4 со знаком <—»
н 5 со знаком <+> служат для вычитания
и сложения. Кнопки 6 со знаками ««-»
и «-»» служат для передвижения ка-
ретки влево и вправо.
Чтобы передвинуть каретку на один
разряд, надо сделать короткий удар
по кнопке, а для передвижения каретки
на несколько рядов надо держать кнопку
нажатой до соответствующего момента.
Кнопка гашения 7 гасит весь набор,
установленный на клавиатуре.
Кнопка закрепления набора 8 может
быть нажата и поднята. Если кнопка
нажата (устанавливается при сложении
и вычитании), то набор гасится автома-
тически после каждого хода машины.
Если же кнопка поднята (устанавли-
вается при умножении и делении), то
набор на клавиатуре закреплен, т. е.
не гасится после хода машины: набор
гасится при помощи кнопки гашения 7.
Рычаг 9 управляет счетчиком оборо-
тов. При положении «к себе» (или
положении «+») направление счет-
чика оборотов соответствует знаку
пусковой кнопки, суммирует положи-
тельные и вычитает отрицательные
обороты.
При положении «от себя» (нлн поло-
жении «—») счетчик оборотов работает
в обратном направлении, т. е. вычитает
при нажатии кнопки «+» и складывает
при нажатии кнопки «—».
Рычаги 10 служат для гашения счет-
чиков оборотов и результатов, для чего
их надо передвинуть вправо. Счетчик
оборотов 13 имеет шесть разрядов (око-
шек), шкала 11 счетчика оборотов
имеет нумерацию окошек и передвижные
запятые 14. Стрелки 12 являются
указателями положения каретки.
Счетчик результатов 17 имеет 12
разрядов (окошек), шкала 16 счетчика
результатов имеет нумерацию окошек
и передвижные запятые 14.
Вертушки 15 служат для установки
чисел на счетчике результатов без
использования клавиатуры. Шкала 18
для клавиатуры имеет нумерацию раз-
рядов. Контрольные окошки 19 пока-
зывают число, установленное на кла-
виатуре.
Исходное положение машины для
выполнения сложения и вычитания
следующее: клавиатура и счетчики пога-
шены, рычаг 9 в положении <+».
кнопка 8 нажата и закреплена, каретка
на 1-м разряде, т. е. неподвижная запя-
тая 12 указывает на I-й разряд по шкале
счетчиков оборотов и результатов.
Сложение и вычитание производятся
как на арифмометре или на автомате
модели 37.
Для умножения исходное положешк
машины следующее: счетчики и кла-
виатура погашены, каретка установлена
на 1-й разряд, кнопка закрепления
набора 8 поднята. Рычаг управление
счетчиком оборотов 9 установлен в по
ложение «к себе».
Устанавливают множимое на клавиа-
туре (в правой части ее) и умножение
производится последовательным сложе-
нием (как на арифмометре) с передви-
жением каретки из одного разряда
в другой для умножения на отдельные
разряды множителя.
В счетчике результатов появляется
произведение, в счетчике оборотов —
множитель.
При умножении на цифры больше «5»
можно применять сокращенные умно-
жения, как на арифмометре, но при •то»’
348
МАТЕМАТИЧЕСКИЕ ПРИБОРЫ
благодаря наличию передачи десятков
в счетчике оборотов последний пока-
зывает ответ прямыми цифрами (а не
красными, как на арифмометре).
Для деления исходное положение та-
кое же, как для умножения, но рычаг 9
находится в положении «—».
Передвигают каретку вправо до конца,
устанавливают делимое па клавиатуре
в левой ее части и нажатием на
кнопку «+» передают делимое в счетчик
результатов, затем гасят клавиатуру
и счетчик оборотов. Делитель уста-
навливается на клавиатуре также в
левой се части, как на арифмометре. Де-
ление производится последовательным
вычитанием. Нажимается кнопка «—» и
держится в таком положении, пока
машина автоматически не остановится
(пока не сработает автостоп); затем
передвигают каретку на один разряд
влево и опять нажимают на кнопку <—»
и т. д. При появлении девяток в высшем
разряде счетчика результатов машина
останавливается не сразу, а сначала
автоматически дает корректирующий ход.
Делимое можно устанавливать на счет-
чике результатов при помощи вертушек 15.
Частное читается на счетчике оборотов.
ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ ВК
Вычислительная клавишная машина
ВК бывает с ручным приводом (модель
ВК-1), полуавтоматическая с электро-
двигателем (модель ВК-2) и автомати-
ческая (ВК-3).
Машина модели ВК-1 (фиг. 10)
является усовершенствованным ариф-
мометром, в котором рычажки заменены
клавиатурой с десятью клавишами 1
для установки числа.
Справа находится клавиш 2 для
передвижения каретки в левое положе-
ние (используется при делении после
установки числа на клавиатуре).
Рычаг <? служит для гашения уста-
новленного числа. Рукояткой 4 произ-
Фиг. 10. Вычислите л ьнл я машин* ВК-1.
водят те же операции, что и в арифмо-
метре. Окошко красного сигнала 5
показывает направление работы счет-
чика оборотов. Рычаг б гасит счетчик
оборотов. Окошки счетчика оборотов 7
и счетчика результатов S имеют то же
назначение, что и на арифмометре.
Имеется контрольное окно 9. Рычаг 10
гасит счетчик результатов.
Слева от клавиатуры находятся две
кнопки ««-» и «-»», из которых первая
(11) служит для передвижения каретки
влево на один разряд, а вторая — для
передвижения вправо.
На машине модели ВК-3 можно авто-
матически применять сокращенный
прием умножения на цифры больше
<5», что невозможно в автоматах,
описанных выше, а при делении можно
автоматически применять рациональ-
ный прием деления, состоящий в попе-
ременном использовании кнопок сло-
жения и вычитания.
ЛИТЕРАТУРА И ИСТОЧНИКИ
Алгебра
1. К уро ш А. Г., Курс высшей алгебры,
Гостехиздат, М. — Л, 1933.
2. О к у н е в Л. Я., Высшая алгебра, Гостех-
«здат, М. - Л. 1949.
3. С у ш к е в и ч А. К., Основы высшей
алгебры, Гостехиздат, М. — Л. 1941.
4. Ш а п и р о Г. М., Высшая алгебра, Учпед-
гиз. 1937.
Элементарная геометрия
и тригонометрия
5. Перепелкина А. Н. и Новосе-
лове. И., Геометрия и тригонометрия для учи-
тельских институтов, Учпедгиз, М. — Л. 1947.
6. Перепелкин Д. И., Курс элементар-
ной геометрии, ч. 1 (геометрия на плоскости);
ч. II (геометрия в пространстве), Гостехиздат,
М. - Л. 1948 и 1949.
7. С т е п а и о в Н. Н., Сферическая триго-
нометрия, Гостехиздат, М. — Л. 1948.
Аналитическая и дифференциальная
геометрия
8. В ю in г е н с С. С„ Аналитическая геомет-
рия, ч. I н II, ОНТИ, М. - Л. 1939.
9. Б ю ш г е н с С. С., Дифференциальная гео-
метрии, Гостехиздат, М. — Л. 1910.
10. Выгодский М. Я., Дифференциальная
геометрия, Гостехиздат, М. — Л. 1949.
II. Делоне Б. Н. и Р а й к о в Д. А. Анали-
тическая геометрия. Гостехиздат, М. — Л., т. 1,
1948; т. II. 1949.
12. Е ф и м о в Н. В., Краткий курс аналитнче
ской геометрии, Гостехиздат. М. — Л. 19.51).
13. Каган В. Ф., Основы теории поверхно-
стей, Гостехиздат, М. — Л., ч. 1, 1917; ч. II, 1948.
14. Л о и ш и ц А. М.. Амалитнческая геомет-
рия, Учпедгиз, 65. 1948.
15. 61 и л и и с к и й В. И., Дифференциальная
геометрия, изд. Кубуч, Л. 19.31.
16. М у с х е л ii ш в и л и Н. И., Курс аиали-
тичесиой геометрии, Гостехиздат, М. - Л. 1917.
17. Норин А. П.. Дифференциальная гео-
метрия. Учпедгиз, М. 1918.
18. П р и в а л о в И. И., Аналитическая гео-
метрия. Гостехиздат, М. — Л. 1952.
19. Рашевский П. К., Курс дифференци-
альной геометрии, Гостехиздат, М — Л. 1950.
20. Ф и и и к о в С. П., Аналитическая геомет-
рия. Учпедгиз. М. 1932.
21. Ф и и и к о в С. П., Дифференциальная гео-
метрия, Учпедгиз, М. 1939.
22. Фиников С. П., Курс дифференциальной
геометрии. Гостехиздат, М. 1952.
23. Фиников С. П., Теория поверхностей
ОНТИ, М.-Л. 1934.
К РАЗДЕЛУ «МАТЕМАТИКАэ
Общие курсы анализа
24. Б е р м а и т А. Ф.. Курс математического
анализа для втузов, Гостехиздат, М. — Л., ч. I,
19S3; ч. II. 1953.
25. В а л л с-П у с с е н , Курс анализа беско-
нечно малых, т. I и II, Гостехиздат, М. — Л. 1933.
26. Власов А. К.. Курс высшей математики,
т. 1 и II, Гостехиздат, М. — Л. 19S2.
27. Гребенча М. К. и Новосе-
лове. И., Курс математического анализа, Учпед-
гиз. М.. т. I. 1963. т. II, 1953.
28. Г у р с а Э., Курс математического анализа,
т. I - 111, ГТТИ, 1933 - 1934.
29. К у р а и т Р„ Курс дифференциального и
интегрального исчисления, ч. 1 и II. ГНТИ.
М. - Л. 1931.
30. Л у з и в Н. Н., Дифференциальное исчи-
сление, .Советская наука", М. 1953.
31. Л у з и я Н. Н.. Интегральное исчисление,
.Советская наука". М. 1953.
32. Нем ы ц к и й В. В.. С л у д с к а я М. И..
Черкасов А. Н., Курс математического ана-
лиза, т. I и И. Гостехиздат, М. — Л. 1914.
33. П о с с с К. и П р и и а л о и И.. Курс диф-
ференциального исчисления, ОНТИ. М. — Л. 1939.
34. П о с с е К. и Привалов И.. Курс
интегрального исчисления, ОНТИ, М. — Л. 19'19.
35. С м и р н о в В. И.. Курс высшей математики.
Гостехиздат, М. — Л., т. I, 1953; т. И. 1953: т. Ill,
ч. 1-я, 1953; т. Ill, ч. 2-я, 1953 т. IV, 1953: т. V, 1947.
36. Ф и х т е и г о л ь ц Г. М„ Курс дифференци-
ального н интегрального исчисления, Гостехиздат.
М.-Л..Т. I, 1951; т. II. 1951: Т. 111. 1949.
37. Фихтенгольц Г. И.. Математика для
инженеров, ГТТИ, М. — Л., ч. 1,1934; ч. 11,‘вып. 1,
1932; ч. II. вып. 2. 1903.
38. Ф р а н к л н и Ф.. Математический анализ,
ч. I и II. Издательство иностранной литературы.
М. 1950.
39. X и н ч и и А. Я., Восемь лекций по мате-
матическому анализу, Гостехиздат, М. — Л. 1948.
40. X и н ч и н А. Я., Краткий курс математи-
ческого анализа, ГТТИ, М. 1953.
Функции комплексного переменного
41. Г у р а н т ц А., Теория аналитических и
эллиптических функций. ГТТИ. М. — Л. 1933.
42. Курант 1’., Геометрическая теория фуи»
ций комплексной переменной, ГТТИ. М.—Л. 1934.
43. Л а а р с и т ь е в М. А.. Конформные отоб-
ражения, Гостехиздат, М. — Л. 19-16.
44. Лаврентьев М. А. и 111 а 6 а т Б. В.,
Методы теории функций комплексного перемен-
ного. Гостехнздпт, М. — Л. 1951.
45. МаркушевичА. И., Теория аналити-
ческих функций. Гостехиздат. М. —Л. 1952.
46. Привалов И. И.. Введение в теорию
функций комплексного переменного. ГОНТИ,
М. - Л. 1948.
47. ФуксБ. А. нШабат Б. В., Функами ком-
плексного переменного. Гостехиздат. М. Л. 1949.
48. Я и ч с в с к и й С. А., Функции комплекс-
ного переменного, изд. Кубуч. Л. 1937.
350
ЛИТЕРАТУРА И ИСТОЧНИКИ К РАЗДЕЛУ «МАТЕМАТИКА»
Дифференциальные уравнения
49. А й н с Э. Л., Обыкновенные дифференци-
альные уравнения, ОНТИ Украины. Харьков 1939.
S0. Вебстер А. ► Сеге Г., Дифференци-
альные уравнения в частных произволных мате-
матической физики, ч. 1 и II, ГТТИ, М. — Л.
1933 — 1934.
51. ГребенчаМ. К., Обыкновенные диффе-
ренциальные уравнения, Учпедгиз, М. 1937.
52. К а и к е Э., Справочник по обыкновенным
дифференциальным уравнениям. Издательство ино-
странной литературы. 1951.
S3. К р ы л о в А. Н., О некоторых дифференци-
альных уравнениях математической физики, имею-
щих применение в технических вопросах, Гостех-
издат. М. —Л. I960.
54. Петровский И. Г., Лекции по теории
обыкновенных дифференциальных уравнений, Гос-
техизлат, М. — Л. 1952.
55. Петровский И. Г., Лекции об уравне-
ниях с частными производными, Гостехизлат,
М. — Л. 1953
56. П и а д ж и о. Интегрирование дифферен-
циальных уравнений, ГТТИ, М, —Л. 1933,
57. С т е к л о в В. А.. Основы теории интегри-
рования обыкновенных дифференциальных уравне-
ний. ГИЗ, М. - Л. 1927.
58. С т е п а н о в В. В., Kvpc дифференциаль-
ных уравнений, Гостехизлат, М. — Л. 1953.
59. С о 6 о л е в С. Л.. Уравнения математиче-
ской физики, Гостехизлат, М. — Л. 1947.
63. Тихонова. Н. и С а м а р с к и й А. А.,
Ураииеиия математической физики, Гостехизлат,
М. 1951.
Специальные вопросы анализа
61. А х и е з е р Н. И., Лекции по теории ап-
проксимации, Гостехизлат, М, —Л. 1947.
1938^' Б а Р и Н. К., Теория рядов, Учпедгиз, М.
63. Ватсон Г. Н., Теория бесселепых функ-
ций. Издательство иностранной литературы, ч. 1.
64. Г а р л и Г.. Иитсгрнрованне ыемептарных
функций, ОНТИ, М. - Л. 1935.
65. Г е р о и и м у с Я. Л.. О применении мето-
дой Чебышева к задаче уоапновешнваннп меха-
низмов, Гостехизлат, М. - Л. 194*.
66. Г л и в е и к о В. И., Интеграл Стильтьеса,
ОНТИ, М. - Л. 1936.
67. Гончарове. Л.. Теория интерполиро-
вания и приближения функций Гостехизлат.
М. - Л. 1914.
66. Г р е й Э. н М » т ь ю з Г. Б.. Функции Бес-
сели и их приложения к физике и механике. Изда-
тельство иностранной литературы, М. 1953.
69. Джексон Д. Д, Ряды Фурье и ортого-
нальные полиномы. Издательство иностранной
литературы, М. 1948.
70. Д и т к и и В. Л. н Кузнецов П. И..
Справочник по операционному исчислению. Гос-
техизлат, М, —Л. 11151.
71. 3 и г м у и д А.. Тригонометрические ряди.
ГОНТИ. М.-Л. 1939.
72. К а р м а н Т. и Б и о М., Математические
методы в инженерном деле. Гостехизлат, М. — Л.
1948.
73. К а р с л о у X. и Е г е р Д., Операционные
методы в прикладной математике. Издательство
иностранной литературы, М. 1949.
74. К о н т о ро в н ч П. Г., Операционное ис-
числение, Гостехизлат, М. — Л. 1949.
75. К у з ь м и и Р. О., Бесселевы функции,
ГТТИ, М. - Л. 1935.
76. Курант Р. и Гильберт Д.. Методы
математической физики, т. 1 и II, I остехиадат.
М. - Л. 1951.
77. Лаврентьев М. А. и Лю стер-
инк Л- А„ Курс вариационного исчисления
ОНГИ. М. - Л. 1938.
78. Л у р ь е А. И., Операционное исчисление,
Гостехизлат, М. — Л. 1950.
79. М и х л и н С. Г., Прямые методы в мате-
матической физике. Гостехизлат, М. — Л. 1950.
80. Натансон И. П.. Конструктивная тео-
рия функций, Гостехизлат, М. — Л. 1919.
81. П с т р о в с к и й И. Г.. Лекции по теории
интегральных уравнений, Гостехизлат. М. — Л.
1943.
82. П р и в а л о в И. И., Ряды Фурье, ОНТИ.
М. - Л. 1934.
83. Серебренников М. Г., Гармониче-
ский анализ, Гостехизлат. М. — Л. 1918.
84. С т е ф е н с о и И. Ф., Теория интерпо-
ляций. Гостехизлат. М. — Л. 1936.
85. Т и т ч м а р ш Е., Теория функций, Гостех-
излэт, М. — Л. 1951.
86. Уиттекер Е. Т. и Ватсон Г. Н., Курс
современного анализа, ч. 1 и II, Гостехизлат.
М. - Л. 19 И, 1934.
87. Фихтенгольц Г. М. и Натан-
сон И. П., Криволинейные и кратные интегралы.
ОНТИ. М. - Л. 1937.
88. Э л ь с г о л ь ц Л. Э„ Вариационное исчис-
ление. Гостехизлат. М. — Л. 1952.
Векторное и тензорное исчисление
89. Г о л ь д ф а й н И. А., Элементы вектор-
ного исчисления, Гостехизлат, М. — Л. 1918.
90. Д у 6 н о в Я. С., Основы векторного исчис-
ления. Гостехизлат. Мг — Л., ч. 1. 1950; ч. II. 1952.
91. К о ч и н Н. Е.. Векторное исчисление и на-
чата тензорного исчисления, ГОНТИ, М. — Л.
1951.
92. Рашевский П. К., Римаиова геометрия
н тензорный анализ, Гостехизлат. М. — Л. 1953,
93. фиников С. П.. Векторный анализ.
ГНТИ. М. - Л. 1931.
94. Широкой П. А.. Тензорное исчисление,
ч. I, Алгебра тензоров. ГТТИ, М. — Л. 1934.
95. Э й з е и х я р т Л. П., Рнманова геометрия.
Издательство иностранной литературы, М. 1»46.
Теория вероятностей
н математическая статистика
96. Арлей, НнльсиБух.Ранаер К..
Введение в теорию вероятностей и матемап-ческую
статистику. Издательство иностранной литературы.
1951.
97. Б е р и ш т е й и С. Н., Теория вероятностей,
Гостехизлат. М. — Л. 1916.
68. Боев Г. П., Теория вероятностей. Гостех-
издат, М. - Л. 1950.
W. Г л и а е и к о В. И.. Курс теории вероят-
ностей. ОНТИ. М. - Л. 1919.
10Э. Г и е д е и и о Б. В.. Курс теории вероятно-
стей, Гостехизлат. М. — Л. 1931.
1П1. Г н е д е к к о Б. В. и X ними и А. Я..
Элементарное кяслсиие в теорию вероятностей.
Гостехизлат, М. — Л. 1962.
102. Гончаров В. Л., Теория вероятностей.
Обороигиз. М. 1939.
10-1. Л а х т и и Л. К.. Курс теории вероятностей.
Госиздат. М. 1924.
104. Марко и А. А.. Исчисление вероятностей.
Госиздат, М. 1924.
105. М а р к о в А. А., Избранные труды. Теория
чисел. Теория вероятностей. Изд. АН СССР, 1931.
106 Р о м а н о в с к и й В. И.. Математическая
статистика, ОНТИ. М. - Л. 1918.
|07. Р о м а и о в с к и й В. И.. Элементарный
ку|>с математической статистики, Гостехизлат.
ЛИТЕРАТУРА И ИСТОЧНИКИ К РАЗДЕЛУ «МАТЕМАТИКА»
35»
108. Романовский В. И., Основные задачи
теории ошибок. Гостехиздат, М. — Л. 1947.
109. Ф е а а а р В.. Введение в теорию вероятно-
стей и ее приложения (Дискретное распределение).
Издательство иностранной литерагуры, 1952.
110. Ф р а й Т.. Теория вероятностей для инже-
неров. ГТТИ, М. - Л. 1904.
Ill. Чебышев П. Л., Теории вероятностей,
лекции 1879-1880 ГГ„ АН СССР М. — Л. 1936.
Приближенные вычисления
112. Б еэикович Я- Приближенные вычисле-
ния, Гостехиздат, М. —Л. 1949.
113. Г е л ь ф о н д А. О.. Исчисление конечных
разностей, Гостехиздат, М. — Л. 1962.
113а. Г и и о л м а и 8. А., Механизация учета
и вычислительных работ. Машгиз. М. 1950.
114. 3 а и л е и Г., Элементы прикладного ана-
лиза, ГТТИ. М. - Л. 1932.
115. Нильсон И. И.. Способ наименьших
квадратов, ГТТИ, М. — Л. 1932.
116. К а и т о р о в и ч Л. В. и К р ы л о в В. И.,
Приближенные методы высшего анализа, Гостех-
излат. 1952.
117. Крылов А. Н., Лекции о приближенных
вычислениях, Гостсхиздат, 1950.
118. Л а р ч е я к о Е. Г., Техника вычислений,
Геодезнзлат, М. 1952.
119. М а р к о в А. А., Исчисление конечных раз-
ностей, Матезнс, Одесса 1911.
(20. М и л и В. Э., Численный анализ. Издатель-
ство иностранной литературы, М. 1961.
121. О п п о к о в Г. В., Численное интегрирова-
ние дифференциальных уравнений, Гостехиздлт,
М. - Л. 1932.
122. II а нов Д. Ю.. Справочник по численному
решению дифференциальных уравнений в частных
производных, Гос1ехнздат, М. — Л. 1951.
123. П а и о в Д. Ю„ Счетная линейка. Гостех-
нзлат, М. — Л. 1953.
124. Скарборо Дж.. Численные методы ма-
тематического анализа, ГТТИ, М. — Л. 1934.
125. Уиттекер Э. и Робинсон Г., Мате-
матическая обрабожа результатов наблюдений,
ГТ1И. М. - Л. 1933.
126. Фадеева В. Н., -Вычислительиые методы
линейной алгебры, Гостехиздат, М. — Л. 1950.
127. Чаплыгин С. А., Новый метол прибли-
женного интегрирования дифференциальных урав-
нений, Гостехнэаат. I960.
12Я. Шилов П. И., Способ наименьших ква-
дратов. Геодезизлат. 1941.
Графические методы исчисления
129. Б л о к Л. С., Основные графические ме-
тоды обработки опытных данных, Машгиз. М. — Л.
1951.
130. Ге pee II нов И. М« Основы номогра-
фии. ГН1 И. М. 1932.
131. Глаголев Н. А., Теоретические основы
номографии, О ИЗИ, М. — Л. 1916.
132. Головнин Д. II.. Графическая матема-
тика. ГНТИ, М. - Л. 1931.
133. Графический справочник по математике.
Атлас кривых под пел. А. Ф. Берманта.
ч. I, ОНТИ, М.-Л. 1937.
134. Мелентьев П. В., Номография, ГНТИ,
М. 1933.
135. Невский Б. А., Методика построения
номограмм. ОНТИ. М. — Л. 1937.
136. Пентковский М. В., Номография,
Гостехиздат, М. — Л. 1919.
137. Справочник по номографии под рел.
Н. А, Глаголева, ОНТИ, М. - Л. 1937.
138. Швердт 1\ Номография на основе гео-
метрии отображения. ГНТИ Украины, Харьков
1935.
Таблицы и справочники
139. А и л р е е n II, П., Математические табли-
цы, Гоестатиэдат, М. 1952.
140. Бакингем Э., Руководство по проекти-
рованию зубчатых передач, ч. 1, Математические
таблицы, Машгиз, М. 1946.
141, Барлоу, Таблицы квадратов, кубов, ква-
дратных корней, кубических корней и обратных
величии всех целых чисел до 12 605, Издательство
иностранной литературы. М. 1950.
142. Бронштейн И. Н. и Семен-
ля е в К. А., Справочник по математике, для ин-
женеров и учащихся втуюв, ГТТИ, М. — Л. 1953.
143. Ватсон Г. Н.. Теория бесселевых функ-
ций, ч. II. Таблицы бесселевых функций. Издатель-
ство иностранной литературы, М. 1919.
144. В и л л е р с Ф. А., Математические инстру-
менты, Издательство иностранной литературы,
М. 1949.
145. Выгодский М. Я., Справочник по вле-
ментарной математике, Гостехиздат, М. — Л. 1952.
146. Граве А. А., Элементарный курс теории
чисел, Киев 1913 (п втом курсе лапа таблица на-
именьших делителей чисел до 108 000).
147. А ва йт Г. Б.. Таблицы интегралов и дру-
гие математические формулы, Издательство ино-
странной литературы, М. 1948.
148. Делоне Б. Н.. Краткий курс математи-
ческих машин, ч. I, Гостехиздат, 1952.
149. Л истеря их Л. А., А к у ш с к и й И. Я.
и Д и т к и в В. А., Таблицы бесселевых функ-
ций. вып. I, Гостехиздат, М. — Л. 1949.
150. М а й з е л ь В. М.. Справочное руководство-
по машиностроению. ГНТИ Украины. Харьков 1937.
151. .Машиностроение". Энциклопедический
справочник, т. 1, кн. 1, Машгиз, М. 1947.
152. Никитин А. А., Таблицы процентных от-
ношений. изд. ЦУНХУ Госплана СССР, М. 1940.
15 .1. О. Рурк, Таблицы умножения, Гостех-
издат. М. 1949.
154. Рыжик И. М. и Г р а л ш т е й н И. С..
Таблицы интегралов сумм, рядов и произведений,
Гостехиздат, М. — Л. 1951.
155. Сегал Б. И. и С е м е и а я е в К. А..
Пятизначные математические таблицы, изд. АН
СССР, М,-Л. 1950.
156. X р е и о в Л. С., Пятизначные таблицы три-
гонометрических функций, Гостехиздат, М. — Л.
1949.
157. X р е н о в Л. С., Семизначные таблицы
тригонометрических функций, Гостехиздат.
М. - Л. 1951.
158, Ш у м я г с к и й Б. М„ Таблицы для реше-
ния кубических уравнений, Гостехиздат, М. — Л.
1950.
169. Я н к е Е. и Э м д я Ф-. Таблицы функций
с формулами и кривыми, Гостехиздат, М.— Л.
МЕХАНИКА
ГЛАВА XVIII
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
СТА ТИКА
ГЕОМЕТРИЧЕСКАЯ СТАТИКА
Основные положения
Сила, приложенная к точке, изобра-
жается вектором, равным по величине
данной силе и направленным в сторону
ее действия.
Механической системой называется
совокупность материальных частиц,
в которой движение каждой частицы
зависит от положения и движения
остальных.
Механическая (или материальная) си-
стема называется неизменяемой (или
абсолютно твердым телом), если рас-
стояние между каждыми двумя ее точ-
ками постоянно; в противном случае
система называется изменяемой, или
деформируемой.
Твердым телом называется система,
в которой при исследовании или изу-
чении данного механического явления
можно пренебречь взаимными смеще-
ниями частиц. Силы взаимодействия
между частицами (или телами) данной
системы называются внутренними, тогда
как силы, действующие со стороны тел,
не принадлежащих к системе, назы-
ваются внешними. Системы сил, произ-
водящие на тело одно и то же действие,
называются эквивалентными. Сила, эк-
вивалентная системе сил, называется ее
равнодействующей. Силу, не нарушая
ее действия, можно в абсолютно твердом
теле переносить в любую точку, лежа-
щую на линии ее действия. Сила может
быть сосредоточенной (если она прило-
жена в одной точке) или распределенной
(по длине, поверхности или объему дан-
ного тела).
Связи. Условия, стесняющие свободу
движения механической системы, назы-
ваются связями. Сила, заменяющая
действие связи, называется реакцией
связи; реакции — силы пассивные; прочие
силы (обычно задаваемые) называются
активными. Связи реализуются в виде
каких-то тел (не входящих в изучае-
мую систему).
Основные типы связей:
1. Гладкая опорная по-
верхность; реакция направлена
по нормали к опорной поверхности
Фиг. 1. Типы связей.
(фиг. 1, а, б, в, г — схематическое изо-
бражение).
2. Опорная точка при опираю-
щейся гладкой поверхности (фиг. 1, <?);
реакция направлена по нормали к опи-
рающейся поверхности.
3. Скользящая муфта, а
также подшипник (фиг. 1, а); реакция
располагается в плоскости, нормальной
к направляющей оси.
4. Неподвижная точка,
например, шарнир, подпятник
(фиг. I, ж, з, и); реакция проходит
через эту точку, но ее направление
заранее не известно.
ГЕОМЕТРИЧЕСКАЯ СТАТИКА
353
5. Заделка (фиг. 1, к); помимо
неизвестной реактивной силы возни-
кает момент.
6. Жесткий стержень
(фиг. 1, л); реакция (усилие) направлена
вдоль стержня (растяжение или сжатие).
7. Гибкая нить (фнг. I, ж);
реакция (натяжение) направлена по
нити.
Сложение и разложение сил
Правило параллелограмма сил Равно-
действующая двух сил, приложенных
в одной точке, выражается диагональю
параллелограмма, построенного на этих
силах (фиг. 2):
/?=]//’? + (Л. Р,);
_____
sin (Pi,/?) sin(Pb/?) sin(P,.Pi)
(1)
Всякую силу можно разложить в пло-
Фнг. 2. Параллелограмм сид.
скости по двум произвольным направле-
ниям. Для это-
го следует по-
строить парал-
лелограмм» диа-
гональю кото-
рого является
эта сила, а сто-
роны имеют за-
данные напра-
вления. эти стороны — искомые соста-
вляющие, или компоненты силы.
Правило многоугольника сил. Равно-
действующая произвольного числа схо-
дящихся сил (или пучка сил) выра-
жается замыкающей стороной сило-
вого многоуголь-
ника (фнг. 3) Она
называется геомет-
рической суммой
составляющих сил
и не зависит от по-
рядка слагаемых*
(2)
Фиг. 3. Многоугольник
сил.
В случае равновесия системы сходя-
щихся сил силовой многоугольник сам
собой замыкается.
Если все силы действуют вдоль одной
и той же прямой, то геометрическое
сложение вырождается в алгебраиче-
ское.
23 Том I 3»*. 1454
Правило параллелепипеда сил. Равно-
действующая трех сходящихся сил,
не лежащих в одной плоскости, выра-
жается диагональю параллелепипеда,
построенного на
этих силах (фиг. 4),
Разложение силы
по трем направле-
ниям, не лежащим
в одной плоскости,
можно осущест-
вить либо при по-
мощи построения
параллелепипеда,
либо путем дву-
кратного разложе-
ния силы. В ПО-
Фиг. 4. Параллелепи-
пед сил.
следнем случае
проводим две плоскости через силу R
и одно направление, а затем через два
других направления, и находим линию
пересечения (23) этих двух плоскостей.
Разложение очевидно из чертежа.
Задачу разложения можно решить
в ортогональных проекциях |/, 321
(фиг. 5). Дана сила R и направления /,
Фиг. 6. Разложение силы и ортогональным
проекциях.
2, 3. Через конец /? проводим прямую,
параллельную направлению /, отмечаем
точки A (a', а*) н В (У, Ь*) на напра-
влениях 3 и 2, которые вместе с точ-
кой О (o', о") определяют плоскость 2, 3;
находим точку С (с‘, с") пересечения
упомянутой прямой с этой плоскостью.
Прямая ОС (о'с', о'с') соответствует
прямой (23) на фиг. 4.
Таким образом, приходим к двукрат-
ному разложению силы R — Р\ +
Р, + Р,. Для нахождения величин
354
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
сил надо найти их вертикальные соста-
вляющие (например. Р-,гУ. тогда
и т. д.
Можно также воспользоваться соста-
вляющими в горизонтальной плоскости,
перпендикулярными к оси проекции,
Т- е.
и т. д.
Разложение по осям координат.
В прямоугольной системе координат
(фиг. 6) имеет ме-
сто разложение
Р = Xi + Yj + Zk.
гдеХ, Y, Z—проек-
ции силы на осн,
а Л /, k — еди-
ничные векторы
Фиг. 6. Разложение силы (орты), оп редел я lo-
ne «ом коорливлт. щне направления
осей. Проекции вы-
числяются либо через углы а, fl. у
силы с осями координат, либо же через
два угла: угол 1 с одной из осей
и угол ? (азимут), определяющий по-
ложение плоскости, в которой действует
сила:
X — Pcos в = Р sin f COS Ip;
Y = P sin ? = P sin т sin
Z — Pcos 7.
(3)
Если сила лежит в плоскости хОу,
то Т р= 90°. Д = 90е
' X Р COS а.
Y — P sin a.
Кроме указанного расположения осей,
образующих правую систему, приме-
няется также расположение, получае-
мое перестановкой осей к и у, дающее
левую систему
Равновесие трех
непараллельных
сил в плоскости.
Для равновесия
трех сил необхо-
димо и достаточно,
чтобы их линии
действия пересека-
лись в одной точке,
а силы образовали
замкнутый силовой
стр.’353).
Фиг. 7. Графическое
определение опорных
реакций балки.
треугольник (см.
опо-
Пример. Балка АВ (фиг. 7) с шарнирной
гой А и гл аде ой опорой В шгружеш cocpexojo-
чегаюй силой Р. Линия действия реакции в В
известна; слеаовятельаю, реакция а А проходит
через точку О. Из силового треугольника (сы.
внизу фиг. 7) находим величины реакций.
Сложение двух параллельных сил.
Равнодействующая двух параллельных
сил (фиг. 8, а и б), направленных в одис
или в противоположные стороны (в по
следпем случае, если Pi == Pt), равна их
алгебраическдй сумме (/? = Pt ± Pt) и
делит прямую, соединяющую точки при-
ложения данных сил, внутренним или
внешним образом на части, обратно
а с .
Wl
\ О) С)
Фиг. 8. Два случая сложения
двух параллельных сил.
пропорциональные этим силам. В обоих
случаях имеют место соотношения
ЛС ВС_ АВ
Pt ° Pi ” R ‘
Пользуясь этими соотношениями,
можно денную силу R разлагать на две
параллельные Pi и /'я в различных
случаях (например, зная точки прило-
жения обеих сил).
В общем случае равнодействующая
произвольного числа параллельных сил
(если она существует) равна их алге-
браической сумме
R - 2 Pt- (4>
Моменты сил н пар
Момент силы относительно центра
Моментом силы Р относительно некото-
рого центра (или относительно точки)
О Называется произведение величины
силы Р на ее плечо h относительно
центра (т. е. кратчайшее расстояние от
центра точки О, называемой центром
момента, до линии действия силы). Чи-
сленно момент равен
МЛ(Р)-РН. (5)
Момент силы относительно центра
изображается вектором, перепендику-
лярным к плоскости, проходящей через
силу и центр момента так, чтобы нэ
его конца вращение силы вокруг центра
представлялось против часовой стрелки
ГЕОМЕТРИЧЕСКАЯ СТАТИКА
355
(это — в правой системе, в левой —
наоборот). Тогда момент может быть
представлен в ниде векторного произ-
ведения радиуса-вектора точки при-
ложения силы на силу (фиг. 9)
W₽)=7x/<
При рассмотрении плоских систем
сил все векторы-моменты параллельны;
тогда геометрические операции заме-
няются алгебраическими, причем момент
считается положительным при вращении
против часовой стрелки и наоборот.
%(Р)
♦иг. 9. Геометриче-
ское предстаьлеиие
момента силы относи-
тельно точки.
Фиг. 10. Алгебраи-
ческие значения мо-
ментов двух сил.
Пример. На фиг. 10 лены дне силы, для ко-
торых
М.(А) = + Р.Л.;
(А) - - РЛ?
Момент силы относительно оси.
Моментом силы Р относительно осп Д
называется алгебраическая величина,
равная проекции на эту ось момен-
та силы относительно какой-либо точ-
Фиг. 11. Момент силы отно-
сительно оси.
ки О оси (фиг.
II). Иначе го-
воря, это есть
момент проек-
ции Рц силы
на плоскость N,
перпендикуляр-
ную к оси, от-
носительно точ-
ки О пересече-
ния оси с пло-
скостью:
Л/Л (Р) - iM0(/J) cos <р =. AM/5*,). (б)
Если X, У, Z — проекции силы, а х,
у, г — координаты точки ее приложения,
то моменты силы относительно осей
координат соответственно равны
МХ(Р) -yZ-zV;
Му (Р) - zX—xZ;
Мг(Р) -хУ-уХ.
(7)
Момент силы относительно оси равен
нулю, если сила пересекает ось или па-
раллельна оси
Пример. Ня конец С рукоятки ворота
(фиг. 12) действует сила Р, образующая с
зонтом угол 0; угол между
вертикальной плоскостью,
проходящей через силу, к
плоскостью xAz (азимут)
ранен «. Длина рукоятки I,
расстояние между опо-
рами Л:
X = — Р cosa соя 0;
Х= Р sin « сое 0;
г = - р sin ?.
По формулам (7) нахо-
дим (х = 0, у = I, z = Л):
ЛИС
Гори-
Фит. 12. Вычвслв-
иие момеитоя силм
относительно осе*
координат.
М r = — Р U am 0 + Л sin « cos 0);
Л( v = — Ph cos я cos 0; Мг = Pl cos » cos p.
To же можно найти н проектированием силы
иа плоскости, перпендикулярные к соответствую-
щим осям.
Пара сил. Парой сил называется со-
вокупность двух численно равных па-
раллельных сил, направленных в раз-
ные стороны. Рас-
стояние Л между
линиями действия
сил пары назы-
вается ее плечом
(фиг. 13). Пару
Фит. 13. Геометриче-
ское представление мо-
мента пары.
нельзя заменить
(а следовательно,
и уравновесить)
одной силой. ,
Момент нары. Моментом пары иазы
вается произведение одной из сил пары
на ее плечо (фиг. 13):
т - Ph. (8)
к
я,
Фит. 1-1. Сложение пар
в пересекающихся пло-
скостях.
Момент пары изображается вектором,
перпендикулярным
пары и приложен-
ным в любой точ-
ке. Направление
этого вектора, а
также алгебраиче-
ское представление
момента пары для
случая плоской за-
дачи подчиняются
тем же правилам,
что и момент си-
лы. Пары с гсо-
равнымн моментами экви-
плоскости действия
метрически
валентны.
... Сложение
скольких пар получается, новая (резуль
пар. При сложении не-
23*
856
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
тирующая) пара, момент которой равен
геометрической (в плоскости — алге-
браической) сумме моментов пар состав-
ляющих (фиг. 14):
М - S т,. (9)
Равновесие пар имеет место тогда,
когда геометрическая (в плоскости —
Фнг. 1S. Определе-
ние опорных реак-
ций белки, находя-
щейся по* дсй-
ствием пары.
алгебраическая) сум-
ма нх моментов равна
нулю.
Пример. Но балку с
пролетом I действует попа
с моментом т («риг. 15).
Так кок пару можно урав-
новесить лишь порой с та-
ким же численно момеи-
том, то имеем
RA = RB =
т
I
Произвольная система сил
нарушая ее дей-
Фиг. 16. Привел с
мне одной силы к
клятому центру.
Параллельное перемещение силы.
Всякую силу Р, не
ствия, можно пере-
нести параллельно
самой себе в любую
точку О (фиг 16),
присоединив при этом
пару с моментом, рав-
ным моменту силы Р
относительно точки О:
— М0(Р).
Приведение систем)
ному центру. В результате указанной
операции, применяемой ко всем силам
системы, получается сило-
вой мотор (фнг. 17), т. е.
совокупность результирую-
щей силы — главного век-
тора "R и результирующей
пары с главным моментом
Lo, причем
7г- S?(;
Го-2-Мо(Л). (Ю)
е случаи приведения:
1) R = 0, Lo = 0 — равновесие;
2) R — 0, Lo + 0 — пара;
3) R ч4, 0, £п= 0 — равнодействующая;
4) R + 0, £0 0, ф — 90“ — переме-
ной центра О сводится к предыдущему;
5) /?=#=0, Lo=£O, «=0 или 180“ —
динама, силовой или динамический винт;
6) R=pO, £0т*0, — произвольный
угол; переменой центра О приводится
к предыдущему.
в
<p/i~o
о
Фиг. 17.
Силовой
мотор.
Если система приводится к равно-
действующей, то имеют место следую-
щие две теоремы:
1. Момент равнодействующей отно-
сительно какого-либо центра равен гео-
метрической (в плоскости — алге-
браической) сумме моментов всех соста-
вляющих относительно того же центра.
II. Момент равнодействующей отно-
сительно какой-либо осн равен алге-
браической сумме моментов всех со-
ставляющих относительно той же оси.
Условия равновесия сил, приложен-
ных к твердому телу, приведены в
табл. I (стр. 3.58).
Равновесие сочлененных систем.
Систему делят на части, прикладывая
н местах разделения попарно противо-
положные и равные силы. Если всего
л частей, то можно либо составлять
уравнения равновесия для всей системы
ил — 1 части, либо же только для л
частей.
Если число уравнений достаточно
для определения неизвестных сил, си-
стема называется статически опреде-
лимой, в противном случае — стати-
чески неопределимой.
Пример. Да» равны* бруска АС к СВ
(фнг. 18) с шарнирами в точках А, В, С загру-
жены а своих серединах вертикальными силами
Фиг. 18. Определение реакций в плоской сочле-
ненной системе.
(например, своими весами) Р, и Pi. Пусть АВ =»
- 41. Берем всю систему. Так как в шарнирах
направленна реакций заранее неизвестны, мы вво-
дим их составляющие — горизонтальную Н и вер-
тикальную V-.
^х^нЛ-нв^о-.
2*4“ V-A-J-M-0;
' - Ид-4 + Р,-» + ₽,-! =0,
отсюда
va - 4(3Pi+р,г- ив“4(/’,+зр,>-
Разделяем систему по шарниру С, отбрасываем
правую часть и ввозим силы Vq, Hq (левая
часть представлена отлелыю):
2-x = «a + «c=o:
2Г=ИЛ+ИС-Р, = О;
2*C=«A-2- VA-2 + ₽,!= °.
ГЕОМЕТРИЧЕСКАЯ СТАТИКА
357
4^u>u
PC--L(P1_P,);
нл--яс-«л=4<А + АК
Если бы мы составляли
также и для правой части,
бы силы — Vct — Hq,
уравнения равновесия
то и точке С ввели
Системы с трением
Трепне скольжения. Если силы, при-
ложенные к телу А, стремятся его сдви-
нуть (или же двигают) по опорной по-
верхности В (фиг. 19), то в месте со-
прикосновения помимо
нормальной составляю-
щей реакции Д' возни-
кает касательная соста-
вляющая, направленная
против движения дей-
ствительного или воз-
можного, обусловленная
шероховатостью соприка-
сающихся поверхностей
силой трения. Наиболь-
Фиг. 19. Трение
скольжения.
н называемая
шая величина силы сухого трения про-
порциональна нормальному давлению
трущихся поверхностей друг на друга
(закон Кулона):
Tmax=fN или T<fN. (11)
где f — коэффициент трения скольже-
ния (безразмерная величина). Вели-
чина f зависит от материала и каче-
ства обработки (а также и от темпе-
ратуры) трущихся поверхностей. В мо-
мент начала движения (Т = Гт„) /
имеет наибольшее значение (статический
коэффициент трения или коэффициент
трения при покое), после чего сразу
несколько уменьшается, изменяясь в
дальнейшем со скоростью
сравнительно мало. При
этом для большинства ма-
у--у териалов / при увеличении
\1 / скорости уменьшается.
„jjKL, Углом трения называется
угол междУ полной реак-
/)?У\ чией и нормальной реак-
/-ХУХ цией. При Т =Тт.* этот
угол называется предельным
Фиг. 20. Ко- целом трения (фиг. 19): обо-
нус трения. значая его через <р, имеем
f ” arctg /.
Конус с углом растворения 2f, опи-
санный вокруг общей нормали к сопри-
касающимся поверхностям, называется
конусом трения (фиг. 20). Его свойство:
для равновесия тела на шероховатой
поверхности равнодействующая прило-
женных к нему сил должна проходить
внутри конуса трения (например, А,
но не Pt).
прн наличии
Пример. Исследовать равновесие груза Р
(фиг. 21) на шероховатой
гири Q.
Если вес гири Q
мал. то
V X - Р«1п
- q _ Г, - 0;
Фиг. 21. Равновесие
если он велик, то системы с трением.
2 X — Р sin « - Q + Г, = 0.
В обоих случаях
Г, - Р sin < - Q <fN — fP cos
T, — Q - P sin « </N =fP eos a.
Получаем условия ДЛЯ Q:
P(sln .-/cos«)<(?< P(Sln « -f-/roa <0.
Если Q = 0 (груз P удерживается лишь силой
трения), то tg «</.»< <р. т. е. предельный угол
наклона равен предельному углу трения.
Фиг. 22. Трение
качения.
Трение качения. При качении тела
по поверхности (фиг. 22) к его оси
должна быть приложена сила Р для
преодоления сопротивления, выражае-
мого моментом сопро-
тивления при качении
(моментом пары трения
качения):
m — kN, (12)
где N — нормальное да-
вление (в случае фиг. 22
равно весу G); It — ко-
эффициент трения каче-
ния (выражается в еди-
ницах длины), называемый также плечом
пары трения. Пара (N't N‘) с моментом
т смещает нормальную реакцию N в сто-
рону движения на расстояние k. Если
Q есть касательная составляющая реак-
ции (вследствие вмятия), то прн равно-
мерном качении имеет место равновесие
двух пар: (Р, Q) И (G, N').
Качение без скольжения имеет место,
если
i lr>k.
Примечянне. О трении подробнее см.
стр. 43).
358
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
• t » * 4 • Таблицй'*!
Условия равновесия сил, приложенных к твердому телу
.. ' • 1. . • 1 Расположение сил Саем* Условия рлпнопесия
Силы ИЛ ОДНОЙ прямой I 1 ^7 - Алгебраическая сумма Lp'-°
Сходящиеся силы на плоско- сти .» • ч а * е 1 н с 1 х" СИ
Параллельные силы на пло- скости । • » < 4* * * Г "Tr-|-Jf7 Две формы (силы параллельны осн У): И V к, - о: V лцр,) =о: пе ОА не лолжн! йыть параллельно силам
•*? 1 Произвольная плоским систе- ма сил .4 А.. » 1 X’’ <• ,и Г 1 1 У , f Три формы; 1) у Xt - 0; у Yt _ о; у Л». (Р,) = 0: г>2Л,»<^) =0;2?,д('7/)=0’ V х; = о. Во всяком случае ось проекций не должна быть 11ерпенанкулирн.т прямой О А. з>уЛ1(>(Р() = о: V Л1Д (₽,) = <>; Тонки О, Л, в не должки лежать иа одной прямой
1 1 Сходящиеся силы а про- странстве г , иЛ А / ХУ * /’ * У X, - 0-,- у И, - 0; у Z, - 0 • * * • 3 /
Параллельные силы про- странстве • I ♦ I ” ? * i % » |Г Vz?-u; ум^.о. 2Л1т(/Т/>-° (если силы параллельны оси г)
произволыия СИС1СММ сил ’ я пространстве • . ?3 t>L >£>•>» !.-• Лц ’ Т « • АГ • •.? ‘ । ух,-о; у г,-о; yz,- o; ул>ж(р;)-о: Vm^^-O; : , . ....
ЦЕНТР ТЯЖЕСТИ
359
ЦЕНТР ТЯЖЕСТИ
Основные определенна
Центр параллельных сил. Центром
параллельных сил называется точка С,
через которую проходит равнодействую*
Фиг^ 23. Центр парал-
лельных сил.
тая системы па-
раллельных сил
(фнг. 23) незави-
симо от их напра-
вления
Координаты
центра параллель-
ных сил:
v/-1, ’ с ’
где к,, yt, г, — координаты точки при-
ложения СИЛЫ /?,.
Центр тяжести Центром тяжести г ма-
териальной системы (или тела) назы-
вается центр параллельных сил, прило-
женных ко всем частицам системы , и
пропорциональных весам этих частиц.
Эта точка, ня'зываемая также центром
масс, имеет координаты
.
- * м ' Ус .и ’
2Е
АГ
(И)
Центры тяжести однородных' тел-
Общие -принципы:
1) Если тело симметрично относи-
тельно некоторой точки, его центр тя-
жести совпадает с этой точкой.
2) Если тело симметрично относи-
тельной некоторой оси, его центр тя-
жести лежит на этой оси.
3) Если тело симметрично относи-
тельно некоторой плоскости, его центр
тяжести лежит в этой плоскости.
Центры тяжести одно-
родных линий:
_ S АЕ>х, . _ S Д^<У|.
е L ’ Уе“ L ’
где ЛЕ, — элементы длины линии; L **
= ^ЛЕ, — полная длина линии.
Центры тяжести одно-
родных поверхносг е‘й:
_ £ЛРрг, _ у АЛ,у, . ;
с = F ’ Уе~ Г ’
. х di
где АЛ, — элементы плогаяиг » поверх-
ности. Л — £АЛ, — полная площадь по-
верхности.
Центры тяжести однород»
ных объемов:
где mt — массы частиц с координатами
M ж 2уп, — масса всей си-
стемы (теля); ^m,x,. ^т,у„ —
статичен кие моиенты массы тела
относительно координатных плоскостей
руг. г0\. \')ч
В этих формулах под гп, можно ра-
вумедь (ак«е
массы конечных элемен-
тов теля', а под у,,
tt— координаты центров
тяжести утих элементов.
Если тело имеет поло-
сти, то- их можно счи-
тать дважды заполнен-
ными положительной и
.отрицательной* мае-
где ДУ, — элементы объема тела;
™ £ДУ, — полный объем тела.
Написанные СП" группы формул могут
(170
У -»
Г
быть
Фиг. М. Оппе- сами
(елеинг центра
тяжести «и. гуры //риито. При определении
с выреши. центра raweciK икка с лнре-
том (<|я<|. . можно счиигь
систему состояшей нт егЬосииогб тили (м тиуса If
с положительна!» массой Л( и пустоты ратиуса г
с ахлмтстаукшиси .осушительной* массой я.
истолкованы ааояко.
I) при реэбненин систем». на конечиде вл*
менты 4Д(1 оЛоаивчаюс сои rue ret ее мио
длину. плошаХь Лбъем алемента. » y(w —
коортмнлтм его ..(игра тйжес-га. .
Л при ппрслелеини' центра тажеттмХ непрй-
ровно распмхстейныт.масс ограниченные чжлл»-
тнческиыи крн ычи илн понераи<1сгнми могушим)!
быть нреаст «влеимымн м-ааме уважении, суммы
псречолаг а ииКчралн распространенные rt>
«лине. <ю»ер>искобъему:
7"1
При приМижериоч пире делении печтрл тиим»-
стм имеем MUHC4MMC суммы ИМ4КГМ МШ«Г
360
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
В случае плоских фигур имеем для
линий
е L ’ у' - L
и для площадей
хс “ р • Ус — —р — •
Центры тяжести од
здесь “ 5Ж — статический мо-
мент площади относительно оси г,
^^Ftxi= Sy — статический момент этой
площади относительно оси у.
Если центр тяжести лежит на какой-
либо оси, то соответствующий стати-
ческий момент обращается в нуль.
Формулы для координат центров тяже-
сти однородных фигур и тел приве-
дены в табл. 2.
Таблица 1
родных фигур и тел
Периметр треугольника. Центр тяжести находится и центре круга, вписанного в треуголь- ник А,В,С„ вершины которого находятся в серединах сторон данного треугольника; расстояние центра тяжести от стороны а у »+ 7е 2 а + Ь -|- с
S'* Sy* а pCJaj*! 7 ’4 Дуга окружности х -"г!*“±-5?.мвг •!"£, е 1 а г* ’ где 1 — длина дуги; а — угол в радианах; 2л при «“ = 90“ (полуокружность) xf = — 0,6366г 2Ь<2» . а" = 46» — 0,9003г , а° — 30“ X — — — 0,9549г
У| Дуге параболы 2 ^ = -3 *
с **• в Площадь треугольника. Центр тяжести находится в точке пересечения медиан, отсекая от каждой из них Ч, (считая от стороны); его расстояние от сто- роны ВС — а Вообще *t - 4 +*«+- 4 ^+*•+х,,: te—4 +*+*•>< где а сковках — координаты вершин А, В, С
»<уг. tjc в * с / '• • н8 а я в о в Площадь трапеции . Л о -f~ 2b . - Л 2д -f- б а з а в ' В 3 а У в Графическое построение: а) Откладывают СР — а. АЕ — Ь и проводят прямую ЕР, которая пересекает медиану MN в центре тяжести. б) Делят одну из боковых сторон на три равные части СЕ~ЕР~ — ЕВ, проводят DfaAP. Центр тяжести лежит на пересече- нии Ос || АВ и медианы MN- в) трапецию разбивают диагональю на ава треугольника, центры тяжести которых г, н с,; центр тяжести находится иа пересече- нии MN н с,с.
Площадь произвольного четырехугольника. Диагоналями АС и BD производится двоякое разбиение на тре- угольники с центрами тяжести г„ с„ с„ с,; центр тяжести всей фигуры находится на пересечении г,с, и с^с,
ЦЕНТР ТЯЖЕСТИ
361
Продолжение табл. 2
Площадь кругового сектор*
2г» 2 г sin« г sin •” г*3
^“-зГ-Т —-------------М-,ЭТ-Г~** v*
где I — длина дуги; F — площадь. « — угол в радидвдд.
При «* — 80° (полукруг) xt — ~ •= 0.4244г
. «• — 45° (км драит) . 2 »0,6002г
. «-«30» (секстант) xf — — г = 0,6366г
Площадь кругового сегмент*
V 2л* sin*• 4 г sin**
"‘г “ ЙЛ 3f ” 3 ' 2а — sin 2* '
где и — угол в радианах, Р — площади сегмент*
Площадь части кругового кольца
* >1п
3 Я4 - Г>
где а — угол в радианах
36.197
sin
Площадь кругового треугольника.
Круговой треугольник получается вычитанием квадранта из
квадрата
10 — Зя „
——Г = 0,2234г:
Ое — хе /Г— 03159г
Площадь аллиптического квадранта (четвертой части вллипса)
X, — ~ “ 0.4244а; у. - - 0.4244»
Площади, ограниченные параболой.
Параболический полусегмент О А В'
Параболический треуголвшк ОС в :
3
ЯС* “ 10
3
Бокова поверхность призмы (вообще наклонной).
Центр тяжести с боковой поверхности призмы (а также цилиндра)
с параллелыгымм основаниями лежит в центре тяжести пери-
метра среднего сечения
362
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Продолжение табл. 2
I г Боковая поверхность пирамиды и кЬиуса <<=4* с лежи? на прямой SO, где О — центр тяжести периметра осно- вания
'?<жиГ^ч>г 8^ Полна» поверхность треугольной пирамиды. Центр тяжести находится и центре шара, описанного а пирамиду A,H,CiD„ иершины которой совпадают с центрами чжести гра- ней; его расстояние от грани АВС hn ра + рв + рс с 4 pa + pb + pc + pd ’ где Гл, Fg. Fq, Fd — плошали граней, противолежащих верши- нам А, В, С. D
£ Боковая поверхность усеченной пирамиды Л <+** •» #* + Я • где Р и р — периметры нижнего и верхнего оснований: О и О, — их центры тяжести
/ л », -VA"*- •.!»‘ Боковая поверхность усеченного конуса h Н+ 2г т«= a R + r
Сферическая поверхность шарового пояса (в частности, сегмента) I » ' - П • ’е-Т» • - т
ftdl > . i’ Объем призмы (вообще наклонной). Цен гр тяжести с объема призмы (а также цилиндра) с парал- лельными основаниями лежит и центре тяжести плошлдн сред- него сечения • • . о '
D 5^» ' t Объем 1 ре)СОЛЬНОЙ пирамиды. Центр тяжести всякой треугольной пирамиды лежит в точке пере- сечения прямых, соедиикалиих какие-либо две ее иершины с Петрами тяжести противоположных iрайей, отсекая от каждой из них Ч, (считая от грани). - Если Л — высота пирамиды, то — л. Вообще 0 I 4 ! ... ! яг - - J (ж, + х, + X, + ж,); Ус — 4-1*» + У» V» + ЯЛ 1 1 1 ге - -у Ц» + > -f ». + *«). где в скобках — кооп я сил ты вершин |
‘ " ‘Л а J i > Объем наклонно усеченною прями, о круг лого цилиндра: г у€ 4л * с 1 ь/х хдась >' . i ’* * “ U (лшах ~ лш1п) |
центр тяжести
353
Продолжение табл. 2
ЛЭ - Л-
Н' - Л1
//
h ;
Объем обелиска
на прямой, соединяющей
центры тяжести
Ч!
1
Объем цилиндрической полой подкопы:
3 Р* _ 3
' ~ 16 " R> - г' ' ‘с S1
В случае сплошной подковы (г = 0. ft = О) ,
’'с=Лб*л ^=-а’
Объем пирамиды и конуса:
с лежит на прямой SO. где О — центр тяжести плпшади осноианни
Объем усеченной пирамиды
плошали соответственно нижнего и перхнего основа-
ний; О и О, — их центры тяжести
Объем усеченного конуса:
А» 4- Wr 4- лэ
ah -р ah, 4. я,» 4-Зо.в
Центр тяжести лежит
плошалей оснонаикй.
Л 0 4-е,
2 ‘ 2а 4- а,
Для клипа (»,
Объем uiapoaoi'o сектора:
4<2г-*>
для полушара (а* — 90»)
Объем шарового сегмента:
Объем параболоида вращении:
Объем вллнпсонлальиого октанта (восьмой част» вллнпсоида)
3 к. 3
364
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Теорема Паппа — Гульдена.
1. Площадь поверхности, полученной
вращением плоской линии около осн,
лежащей в ее плоскости, но ее не пере-
секающей, равна длине этой линии,
умноженной на длину окружности, опи-
сываемой ее центром тяжести:
F-Z.-2wf. (18)
2. Объем тела, полученного враще-
нием плоской фигуры около оси, лежа-
щей в ее плоскости, но ее не пересе-
кающей, равен площади этой фигуры,
умноженной на длину окружности, опи-
сываемой ее центром тяжести:
V = F-2r.re. (19)
Пример. Вращением окружности вокруг оси г
(фиг. 25). Вычислить его поверх-
основании указанных двух теорем
Фиг. 2Б. Центр тяже-
сти равнобокого
уголка.
получаете» тор
кость и объем.
На
Г — 2тг - 2п7? = 4r.'Rr:
к = «г«.2н/г = гп’Ят1.
Фиг. 25. Тор.
Пример. Равнобокий уголок (МЮ.ОСТ 10014-39,
фиг. 26) имеет размеры п мм: Ь = 100, d = 10.
R “ 12, г •и 4. Площади отдельных частей (о леи’):
ЛЕ, «24; ДЕ, — 12,5; ЛЕ, — 860; ЛЕ, =31;
ЛЕ, = 960; ЛЕ, = 24; ЛЕ, = 12.5.
Полная площадь Е= 1924 лиЕ. Части 1,3, 5,6-
нрямоугольники, 2 и 7 - квадранты. / - круго-
вой треугольник;
•г.-3; л, = 6 +1,7 =7,7; х, -5;
X, - 10+ 2.68 = 12.6»; х,-48; х,-98;
.Г,-96+ 1.7 -97,7;
54521
Е “ 1924 “ 38,3 у;
Определение координат центров тя-
жести при помощи интегрального ис-
числения см. стр. 191. Графический ме-
тод определения координат центров тя-
жести, см. стр. 365. Кроме того, суще-
ствует еще предложенный проф. А.А. По-
повым графо-аналитический метод, так
называемый метод ортогональных фоку-
сов, который использует специальные
шаблоны [25].
ГРАФОСТАТИ КА
Веревочный многоугольник
Сложение снл. Дана плоская система
сил Pi, Рг, Р3 (фиг. 27., в). Начиная из
произвольной точки А (фиг. 27, 6),
строят силовой многоугольник A BCD,
определяющий величину и направление
(но не линию действия) равнодействую-
щей, иначе говоря, главный вектор R.
Фиг. 27. Сложение сид с помощью иеревочвшо
многоугольника. Общий случай.
Если из произвольной точки О, назы-
ваемой полюсом, провести к вершинам
А, В, С, D лучи О А, ОВ, ОС, 0D, по-
лучается силовой план ОA BCD. Обо-
значая лучи через а, 12, 23, ш, прово-
дим (фиг. 27, а), начиная из произволь-
ной точки т, прямые, параллельные
соответствующим лучам: а — до пересе-
чения с линией действия Pi в некото-
рой точке а, 12 — до пересечения с ли-
нией действия Рг в точке Ъ и т. д По-
лучаемая фигура maben называется
веревочным многоугольником. Продол-
жая до взаимного пересечения его край-
ние стороны о и «>, получаем точку К,
лежащую на линии действия равнодей-
ствующей. Длины лучей представляют
величины составляющих данных сил
вдоль соответствующих сторон много-
угольника maben (т. е. натяжения
участков веревочного многоугольника).
Если полюс взять в другой точке О',
то стороны нового веревочного много-
угольника будут пересекаться с соответ-
ственными сторонами прежнего в точках
т, I, II, III на прямой, параллельной
ОО'.
Частные случаи. I) Силовой много-
угольник замкнут, а веревочный разом-
кнут (фиг. 28, а и б). Система приво-
дится к паре, составляющие силы
которой равны совпавшим лучам а и и,
а плечо Л.
ГРАФОСТАТИКА
365
2) Силовой н веревочный многоуголь-
ники сами собой замыкаются (фиг. 29, а
и б). Система сил находится в равно-
весия.
Фиг. Я. Случай пхры сил.
Применение веревочного многоуголь-
ника к определению опорных реакций
Так как реакции совместно с задавае-
мыми нагрузками дают равновесие, то
оба многоугольника замыкаются
Случай произвольно на-
правленных сил (фиг. 30, а и б)
При построении силового многоуголь-
ника (фиг. 30,6) заданные силы можно
Фиг. 30. Определение опорным реакций фермы,
ил холящейся поя действием произвольно и лира
•ленник сосре.ютоиениык сил.
обходить в любом порядке, но тот же
порядок соблюдать и при построении
веревочного многоугольника (фиг. 30, а).
Его первая сторона At должна быть
проведена через неподвижную опору,
в которой направление реакции заранее
неизвестно. Сторона ЗВ доводится до
пересечения с линией действия -реакции,
известной по направлению. Параллельно
замыкающей В А строится луч, приво-
дящий уже к определению обеих реак-
ций.
Случай параллельных
сил (фиг. 31, а н б). Поскольку в пред-
ставленном случае направления обеих
реакций очевидны, построение веревоч-
ного многоугольника можно начинать
с любой точки, лежащей на линии дей
ствия реакции. Этот многоугольник
а) 6)
Фиг. 31. Определение опорных релкций бллки,
нлхохншейен пох хействиеч сосредоточенных па-
раллельных сил.
является многоугольником моментов, так
как отрезки вертикальной прямой, про
ходящей через какую-либо точку С
балки (фиг. 31.а), заключенные между
двумя смежными сторонами веревочного
многоугольника (или их продолжения-
ми). будучи умножены на полюсное
расстояние Н силового плана (фнг.31,6)
дают моменты соответствующих сил от-
носительно точки С. Например, отрезок
между сторонами А1 и 12 определит мо-
мент силы Pt Отрезок ус между сто-
ронами, называемый ординатой вере-
вочного многоугольника, умноженный на
Н, дает сумму моментов сил, лежащих
слева от точки С относительно этой
точки, или изгибающий момент в се-
чении С:
Мс - усН. (20)
Применение веревочного миогоуголь-
иика к определению центра тяжести
плоской фигуры. Делят фигуру на части,
центр тяжести каждой из которых
известен (хотя бы приближенно). В этих
центрах тяжести строят систему парал-
лельных сил (фиг. 32, а и б), пропор-
циональных площадям частей.
При помощи веревочного многоуголь-
ника а — 12—23 — о» находят точку Si,
лежащую на линии действия равнодей-
ствующей. Далее поворачивают напра-
вления сил на 90“ и строят веревочный
многоугольник а' —1'2' —2'3' — <•', сто-
роны которого перпендикулярны сто-
366
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
вонам предыдущего; находят точку S».
Центр тяжести с лежит на пересечении
двух взаимно перпендикулярных пря-
мых, проходящих через Si и S».
Фнг. 32. Определение положения ucirrpa тяжести
плоской фигуры.
Веревочная кривая. Если дана рас-
пределенная по некоторому закону на-
грузка интенсивностью р (рассчитанной
на единицу длины), то заштрихованную
на чертеже (фиг. 33, а) грузовую пло-
щадь делят на несколько частей. Центры
Фиг. 33. Веревочная кривде для
распределенной нагрузки.
тяжести этих частей, которые, например,
можно приближенно принять за трапе-
ции, находят одним из изложенных
способов, и строят веревочный много-
угольник. При увеличении числа деле-
ний новые веревочные многоугольники
Стремятся к веревочной кривой, вписан-
ной во все эти многоугольники. Диффе-
ренциальное уравнение веревочной кри-
вой
В честности, если р« const, имеем
параболу
У ““ & + Ctx + Сг-
Уравновешивание данной силы тремя
силами, линии действия которых за-
даны. Пусть силу Р требуется урав-
новесить силами, действующими по пря-
мым 11, 32, ДО,-(фиг. 34, о). Находим
точку М пересечения силы с одной нэ
прямых и точку N пересечения двух,
других прямых. Затем (фиг. 34, б>
из произвольной точки О строим силу Р,
прямую ОК || MN, а далее силовой
Фиг. 34. Уравновешивание данной
силы тремя силами.
четырехугольник, построение которого
очевидно. Тем самым находим искомые
силы Si, Sj, Sg.
(
АНАЛИТИЧЕСКАЯ СТАТИКА
Работа. Мощность
Элементарная работа. Элементарной
работой силы Р на пути ds называется
произведение проекции силы на напра-
вление пути на величину пути (фиг. 35):
d'A = Pds cos -f — Pdtds. (22)
m dr
Фиг. 35. Элв-
ыеитарная ра-
бота силы.
Здесь знак ' поставлен вследствие
того, что элементарная
работа вообще не есть
дифференциал. В вектор-
ной форме работа выра-
жается скалярным про-
изведением силы на пе-
ремещение:
dM-P-dr.
где Idrl — ds. При ?<90° d'A>0; при
«Г > 90’ d’A < 0.
В аналитической форме
выражение работы
А - имеет вид
d'A - Xdx +
dZ —+ Ydy + Zdz. (23)
m ^9 Где X, У, Z —проек-
ции силы на оси ко-
Фиг. 36. Работа си- пппикят як v z —
ли при вращатель- ординат, а X, у, г
пом движении. координаты точки
приложения силы.
Работа при вращатель-
ном движении. Элементарная ра-
бота силы при вращении тела, на которое
сила действует (фиг. 36), равна пронз-
АНАЛИТИЧЕСКАЯ СТАТИКА
?67
ведению момента силы относительно оси
вращения на угол поворота:
d'A - Мл (Р) d?. (24)
Работа на конечном пути. При дви-
жении точки приложения силы по траек-
тории MN (фиг. 37) работа выражается
посредством криволинейного интеграла.
взятого на пути MN:
А - J Pvds - £ (Xdx-г Ydy + ldzh (25)
MN MN
где Pv — проекция силы P на скорость
(которая направлена по касательной).
Р(Ре>
Фиг. 37. Рлбот» силы Фиг. 38. Графическое
иа конечной пути. вычисление работы.
Если проекцию силы на касательную
(обозначим ее просто Р) выразить в
функции пути з и представить зависи-
мость графически (фиг. Зв), откладывая
по оси абсцисс в единице длины
единиц проходимого пути, а по оси
ординат в единице длины единиц
силы (масштабные множители), то ра-
бота на пути от я до м пропорциональна
заштрихованной площади:
А = p-pp-jP-
Пример. Пусть I»- « 0-5 Kl'lMM. и, “ 0,2 м)мм.
Р а НЮ млР; тотл» .. — 10 кГм.
Мощность- Мощностью N в момент
времени I называется предел отноше-
ния элементарной работы к соответ-
ствующему промежутку времени:
(»)
Если известна функциональная зави-
симость совершаемой работы от вре-
мени, то мощность является производ-
ной работы по времени. Мощность
может быть представлена так:
N — P„v к! м/сек — P„v л. с —
“ |ТЕ ,27’
Для случая вращательного движения
N = Л(д (/-*) ы кГmi сек —
"= Л4Д (Р) ы А. С. =
МЛ(Рьл M^iPin
“ ~7~Ле----------й7Г~ кат-™
где ы — угловая скорость в сек-*, п —
число оборотов в минуту.
Потенциальная энергия
Определения. Если работа силы, при-
ложенной к точке, не зависит от формы
траектории, то говорят, что сила имеет
потенциал. Работа, совершаемая силой
при перемещении точки приложения
из некоторого фиксированного нулевого
положения в заданное, называется сило
вой функцией силы U, являющейся
функцией координат точки. Работа,
совершаемая при перемещении из дан-
ного положении в нулевое, называется
потенциалом силы V, или потенциале
ной энергией точки П-
FI-V--U. (2Э)
Область действия сил, имеющих по-
тенциал, называется потенциальным
силовым полем. В таком поле элемен
тарная работа является полным диффе-
ренциалом силовой функции, а проекции
силы на осн координат — частными про-
изводными ее по соответствующим ко-
ординатам:
d'A — dU - — dll;
х-*± у™ {3а>
ax ’ dy ’ dz
Фиг. 39. Рлботв ев
лы тяжести
Все сказанное для точки обобщается
и на случай системы.
Сила тяжести. Если за нулевое по-
ложение принять произвольную гори-
зонтальную плоскость хОу (фиг. 39) и на-
править ось г вверх,
то
U — — mgz = — Ох;
П-Gz.
где т — масса тела;
G — его вес; г — ко-
ордината . центра тя-
жести.
Работа на пути MN
(< Л-0 (ht - Ад) (31
368
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Обобщенные координаты н силы.
Если положение системы можно пол-
ностью определить посредством неко-
торого числа k независимых величин
71, 7s,которыми, в частности,
могут быть декартовы координаты, то
эти величины называются обобщенными
координатами, k — числом степеней
свободы, а коэффициенты Qj, Qs,...,Qk
при дифференциалах координат в выра-
жении элементарной работы
д'А = Qidqi + Qtfiqv + • • + Qed<]i, (32)
называются обобщенными силами.
В потенциальном силовом поле
о _dU_________дП_
1 <*9i <*91
Q, = ^_ = _^L. (33)
<>9* <*9*
Пример, При вращении теля около нелодаиж
ной осн з> обобщенную координату принимают
угол поворота р. Так как d'А — Л1д dy, то обоб-
щенной силой является момент силы (или сумма
моментов) относительно оси, называемый при таю-
щим моментом.
Принцип возможных перемещений
Определения. Возможным, или вир-
туальным, перемещением системы (обоз-
начается символом 8) называется всякое
элементарное перемещение ее, допускае-
мое в данный момент связями. Переме-
щение, при котором система не покидает
связи, называется неосвобождающим, в
противном случае — освобождающим.
Связь, не допускающая освобождающих
перемещений, называется удерживающей,
неосвобождающей, или двусторонней;
если же связь допускает освобождающие
перемещения, она называется неудержи-
вающей, освобождающей, или односто-
ронней. Связь называется идеальной, если
сумма работ ее реакций на всяком воз-
можном перемещении равна нулю.
Принцип возможных перемещений.
Для того чтобы система, подчиненная
идеальным удерживающим связям, на-
ходилась в равновесии, необходимо и
достаточно, чтобы сумма элементарных
работ всех приложенных к ней сил на
всяком возможном перемещении рав-
нялась нулю:
2 Рр*1 cos (?!• - 0) (34)
или в аналитической форме
S (Xfix, + Yfiyt + Z^z) = 0. (35)
В обобщенных координатах
Ql-QI=.=Q* = o. (36)
В потенциальном силовом поле
d/7 d/7 дП - о
<*9i <*9з <*9*
Это — условия, необходимые (но еще
недостаточные) для экстремума функ-
ции П.
Пример. К рукоятке винтового пресса (фиг. 40)
приложена пара с моментом л; шаг винта Л. По-
ступательное перемещение винта 4д, угол пово-
рота ip; iz : Л «• : 2х. Если реакция сжимаемого
тела равна Р. то т4р —
— PSz — 0. или
("
Фиг. 40. Винтовой
пресс.
0;
здесь
<?
f* =0.
следовательно,
Л
Устойчивость равновесия. Равнове-
сие материальной системы называется
устойчивым, если при ее достаточно
малом отклонении из этого положения
она стремится в него возвратиться
(фиг. 41, а). Если же при отклонении
система стремится
VlZ удалиться от поло-
41 Л в) жения равновесия,
равновесие назы-
Фиг. 41. Различные слу- вается неустойчи-
чаи равиомсия. вым (фиг 41(у)
Если, наконец, си-
стема не проявляет тенденции ни к воз-
вращению в положение равновесия, ни
к удалению от него, равновесие назы-
вается безразличным (фиг. 41, а).
Теорема Лагранжа — Ди-
рихле. Если в данном положении
равновесия потенциальная энергия си-
стемы имеет минимум, равновесие устой-
чиво.
Теорема Ляпунова |17].
Равновесие системы неустойчиво, если:
I) отсутствие минимума потенциаль-
ной энергии узнается уже по членам
второго порядка (в ее разложении в ряд
Тейлора) без необходимости рассмотре-
ния членов высших порядков;
2) потенциальная энергия в рассма-
триваемом положении равновесия имеет
КИНЕМАТИКА ТОЧКИ
369
максимум, определяемый членами наи-
низшего (но не обязательно второго)
порядка в разложении потенциальной
энергии.
Если потенциальная энергия П есть
квадратичная форма относительно обоб-
щенных координат
I /
то необходимое и достаточное условие
устойчивости заключается в положи-
тельности всех главных миноров ма-
трицы:
Сц clg . . с)я
С21 е22 • • «гл
*Л1 СМ • • сяп
где dj = Cjt, т. е.
где нуликами отмечены значения част
ных производных потенциальной энер-
гии в положении равновесия. Суммиро
ванне производится по всем индексам
от 1 до k, если k — число степеней
свободы. При отсчете потенциальной
энергии от положения равновесия (что
наиболее часто встречается) член (П\>
исчезает.
Теоремы Лагранжа — Дирихле и Ля-
пунова относятся к силам, имеющим по-
тенциал. Для силы тяжести иллюстра-
цией может служить тяжелый шарик на
поверхности (фиг. 41). Вообще, если при
малом отклонении опертого твердого
тела от положения равновесия его центр
тяжести повышается, равновесие устой-
чиво, если понижается — неустойчиво,
наконец, если остается па прежнем
уровне — безразлично.
Пример. В некоторых замках нз системы с
одвой степенью свободы потенциальная энергия
имеет них
Сц>0,
Qieu
c2ica
>0, ...
С11 с12 • • е1л
«а css • • с2л
Сл1 cnZ ♦ • cnn
это есть так называемый критерий
Сильвестра.
Теорема Ляпунова предполагает воз-
можность разложения потенциальной
энергии системы в окрестности поло-
жения равновесия в ряд по степеням
обобщенных координат, отсчитываемых
от этого положения:
п-№+-я-2 2 М/+
тэг222(^).«а,+....
П = Cj -( <зд* + а,ф + a,fl*
гае а4. <ъ. а,... — постоянные.
Требуется сделать заключение об устойчивости.
Постоянная а, не имеет существенного значе-
ния. Если а, > 0, равновесие устойчивое (по тео-
реме Лагранжа — Дирихле); если а, < 0. равнове-
сие неустойчивое (по теореме Ляпунова»; если,
наконец, а, = 0, то аналогично рассматривают а,.
Вообще, если первый, не равный нулю, коэффи-
циент положителен, равновесне устойчиво, если
отрицателен. — неустойчиво.
Устойчивость на опрокидывание. Or-
ношение момента удерживающего (или
момента устойчиво-
сти) к моменту опро-
кидывающему назы-
вается коэффициен-
том устойчивости на
опрокидывание х.
Фиг. 42. Устойчи-
вость плотины.
Пример. Пусть плотина
(фиг. 42) подвергается аей-
стаию давления иолы Pt иа
высоте Я( и земли на высоте Л у, вес плотины О
действует на расстоянии б от ребра О.
Коэффициент устойчивости на опрокидывание
вокруг ребра
О»
КИНЕМА ТИКА
КИНЕМАТИКА ТОЧКИ
Прямолинейное движение точки
Закон движения. Положение точки М
на прямой (фнг. 43) определяется ее
расстоянием s = ОМ от некоторой фик-
сированной точки О — начала отсчета
24 Тоы I Зак. 1464
расстояний. Расстояние считается в одну
сторону положительным, в другую — от-
рицательным. Если точка, выйдя в не-
который начальный момент времени t^O
из начального положения Мо, переме
стнлась сначала в положение (Иц а за
тем в Мя, то расстояние MoMi назы
370
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
вается перемещением точки,
а арифметическая сумма
+ Л1)М> — ее путем.
Закон движения дается либо
уравнением
(37)
либо таблицей соответствую-
щих друг другу значений s и t,
либо графически.
~~0 Mi н "г м,
toL-l
Фиг. 43. Определение
положения точки в пря-
молинейном движении.
Скорость. Если sl = /(/1),
s? — / то средней скоростью
точки за промежуток времени
h — ti называется выражение
,, fr-i| _ As
tt — <i й1 •
Скоростью точки в момент
времени I называется
v=Jlm (38)
д/-п \ д/ / at '1О'
где точка над буквой обозна-
чает дифференцирование по
времени (см. стр. 3).
Размерность скорости: - л 111111
время'
Ускорение. Если скорости
У] и и» соответствуют момен-
там времени и £, то сред-
ним ускорением точки за про-
межуток времени 1г — I, назы-
вается выражение
ви _ у» — о» _ Av
h — h Ы ’
Таблица 3
Ускорением точки в момент времени t
называется
\ A< ) “ dt “ dt* “ S- (39)
n длина
Размерность ускорения .
Скорость v и ускорение а иногда на-
зываются соответственно истинной ско-
ростью и истинным ускорением
Если знаки s и s одинаковы, то ско-
рость но абсолютной величине возра-
стает, и движение называется ускоренным.
в противном случае — замедленным.
Основные задачи кинематики прямоли-
нейного движения приведены в табл. 3.
Пример. Движение носил в течение несколь-
ких секунд после его птлилв от станции выра-
жается уравнением
а — тР — я/*.
тле т и п — некоторые коэффициенты. Для опре-
деленности можно считать, что 3 выражается
в метрах, t — в секундах.
Предполагая, что после достижения скоростью
максимума движение поезда стали равномерным,
определить эту скорость установившегося движе-
ния. время /, ее достижения, а также наибольшее
ускорение в этот промежуток времени.
По формулам (38) и (39) находим
v •» * — ЗтР - &пР, а — а — бят/ - JOnP.
Цдя отыскиний максимума и полагаем
v — У — — 20л/» — 0,
откуда
_ ЛЗд> -91”1
1 “ У 1ол • "max "" 'Агя '
КИНЕМАТИКА ТОЧКИ
371
Аналогично находим а — а •= 6m — &>nt — О;
Графики движения
1. График расстояние — время
(s — Л (фиг. 44). По оси абсцисс от-
кладывают время t в масштабе р.у,
т. е. в единице длины (например, в I мм)
единиц времени
(сек.); аналогично
по оси ординат
в единице длины
(1 леи) отклады-
вают р, единиц
расстояния (м) от
откладывают р*
/ Ot, | t2 t, (pt)
Фиг. 44. Графин рас- на,'а-1а отсчета.
стояние — время. До точки С, где
касательная гори-
зонтальна, графики расстояния и пути
совпадают; после С графиком расстоя-
ния служит кривая CD, а графиком
пути — ее зеркальное отражение СЕ.
Секущая АВ определяет среднюю ско-
рость за время tj — ilt а касательная
в точке А — истинную скорость в мо-
мент
v* = tg р; у lg ».
2. График скорость — время (о — Л
(фиг. 45). По оси абсцисс откладывают
время t в масштабе р,, по оси орди-
нат —скорость о в масштабе р„, т. е. в
единице длины откладывают единиц
Фиг. 4Ь. График ско-
рость — время.
Фиг. 46. График
ускорение — время.
скорости например м/сек Аналогично
предыдущему
— ‘й»1-
Н/ Pt
Площадь F определяет с точностью
до масштабного множителя перемеще-
ние s — Sq:
s — Др = V-vV-t?-
3. График ускорение — время (а — Г)
(фиг. 46). По оси абсцисс отложено
время t в масштабе р,, по оси
ординат — ускорение а в масштабе
ра (т. е. в единице'длины отложено
ра единиц ускорения, например м/сек*).
Площадь Е) пропорциональна прира-
щению скорости v — v9.
V — Vq = PaP/Fp
4. Прямая задача кинематика
(фиг. 47k Дан график расстояние —
время Графическим дифференцирова-
Фиг, 47. Построение графика
скорость - нремя по графику
расстояние — время.
кием можно получить график ско-
рость — время. Для этого делим про-
межуток времени па интервалы (обычно
равные, но отмечаются также моменты,
соответствующие экстремуму кривой и
точкам перегиба). Проводим касатель-
ные к кривой ($ — t), затем из неко-
торой точки Р, лежащей на оси абсцисс
на расстоянии h от начала, проводим
параллельные нм лучи до встречи
с осью ординат. Из полученных точек
проводим прямые, параллельные оси
абсцисс, до пересечения с ординатами
соответствующих точек, Через получен-
ные точки строим плавную кривую —
график (о — t). Масштаб р„ = —.
Таким же образом по графику (о—О
строится график (а — t).
Фиг. 48. Построение грифит рис-
стояние время — по графику ско-
рость — время.
5. Обратная задача кинематики
(фиг 48) Дан график v — t. Графи-
ческим интегрированием можно полу-
24»
372
теоретическая механика
чить график s — I. Промежуток вре-
мени делим на интервалы, для каждого
из которых проводим среднюю орди-
нату кривой. Полученные точки проек-
тируем на ось ординат, проводим из Р
(на произвольном расстоянии Л от О)
лучи, параллельно которым, начиная
из О, строим ломаную, являющуюся
приближением кривой з — /. Масштаб
р5= Лррр/. Часть кривой, лежащая ниже
оси t, указывает на отрицательность s.
Таким же образом по графику а — t
строится график о — t.
5. Комбинированные
а) Даны графики
(фиг. 49). Очевидным
* М j
задачи.
5 — t H V — I
из чертежа по-
строением мож-
но получить
(Мд
о
о
t
(И
0
Фиг. 30. Построение гр»-
фи о время — расстояние
по графику скорость —
расстояние.
Фиг. 49. Построеня» графика
скорость — расстояние по гра-
фикам расстояние — время и
скорость — время.
р, и Н> еохра-
график о —з; масштабы
няются, р, ие фигурирует.
б) Дан график и — s (фиг. 50). Для
получения графика t — s делим s иа
интервалы и берем средине ординаты.
Из точки Р справа от О проводим лучи
в проекции точек деления, а затем,
начиная нз точки О, строим ломаную,
стороны которой перпендикулярны со-
ответствующим лучам. Эта ломаная есть
приближение кривой t — з. Масштаб
Из
я/ -лт:
Частные случаи
I. Равномерное движение (о = const):
s — s, + vt; а — 0. (46)
2. Равномерно-переменное движение
(а “ const):
аР
v — v0 4- at; s — s, 4- vot 4- -у. (47)
3. Свободное падение тел в безвоз-
душном пространстве у поверхности
з< мл и:
V-gt- T2gn, (48)
где Л — высота падения, g — ускорение
силы тяжести (табл. 4).
Таблица 4
Ускорение g для некоторых пунктов
4. Гармоническое колебательное
движение. Такое название носит
движение, происходящее по за-
кону синуса (или косинуса):
s — Л sin (kt 4- ?). (49)
где Л — амплитуда колебания;
k — круговая, угловая или цикли-
ческая частота колебания; угол
<f = fef-j-fi — фаза колебания;
р — начальная фаза колебания.
Наименьший промежуток време
ни Т, через который движение вос-
производится, называется перио
колебания, а число колебаний в
дом ___________
единицу времени—частотой колебания ч:
(50)
Скорость и ускорение:
v = Ak cos (kt 4- ?);
a - - AHsIn (kt 4- P) - - **»•
Криволинейное движение точки
Траектория. За-
кон движения.
Кривая С, которую
описывает точка М
при своем движе-
нии (фиг. 51), на-
зывается ее траек-
торией. На траек-
тории устанавли-
вается начало от-
счета О», расстоя-
ние от которого по
кривой в любой
Фиг. .1. Определение
положения точки я крн-
волнмеймом движеими.
момент времени определяется законом
движения по заданной траектории;
«-/(О-
КИНЕМАТИКА ТОЧКИ
373
Положение точки Л) определяется
также либо радиусом-вектором г отно-
сительно некоторой точки О, либо коор-
динатами х, у, г по отношению к системе
отсчета Охуг. Тогда закон движения
может быть задан тремя уравнениями:
*=Л(/); у=Л(О;
«-Л(0:
Вектор ускорения лежит в соприка-
сающейся плоскости к траектории в дан-
ной точке и направлен в сторону вогну-
тости. Его проекции на оси координат
<Рх
аг-
d2y
dt*
tflz --
°* ар °" 2
(56)
исключив из них время, получаем урав-
нения траектории.
Пример, х = If <0 а, у = mf(f)-j-b; г=-
= я/(Г)-|-е, г« /(О — произвольная функция
времени. Исключая время, имеем
х - а у - b 2-е
I т п *
Полное ускорение определяется моду-
лем и направляющими косинусами:
а — Иа, + ву + а*; (57)
т. е. траектория — прямая в пространстве, прмо-
сяшая через точку (а, Ь, с) и имеющая направляю-
щие косинусы, пропорциональные числам I. т, п
(стр. 250 и 253).
Скорость. Скорость точки М в дан-
ный момент времени t выражается в
векторной форме
— ь Or
cos (а, х) = ; cos (а, у) = —
. “ . Л»
cos (a, z) — — л
(58)
и в алгебраической
rfs
Hi
(52)
Вектор скорости направлен по каса-
тельной и траектории. Его проекции на
оси координат
Ускорение может быть разложено на
тангенциальное а‘ (по касательной) и
нормальное ап (по главной нормали)
ускорения (на фиг. 52 _я
а‘ и ап—тангенциальная I
и нормальная составляю- \ а
щие ускорения). Проек-
ции ускорения на каса-
тельную и главную нор- -t
маль °
оу-
rfy
dt
dvx tPs
“ dt ~ dt't
. v*
(59)
Величина скорости (модуль)
(53)
Фиг. 52. Pnmo-
женис ускоре-
ния на танген-
циальное и нор-
мальное.
« - I I - | | • (54)
Направление определяется косину-
сами
cos (и, л)
V, . Vy
— —; cos (о. у) — -д •
о ' V
где р — радиус кривизны траектории
Полное ускорение
а - /(а')Ч-(вл)». (60)
Его угол с нормалью
Н- arc'g-^r* (61)
cos (v, а) - .
(55)
Ускорение. Ускорение точки М в дан-
ный момент времени t выражается в
вектор ной форме:
Ускорение а образует острый угол
со скоростью V в ускоренном движении
и тупой — в замедленном: оно перпен-
дикулярно и в равномерном движении
или в моменты экстремума о,: ал исче-
зает в прямолинейном движении, в точке
перегиба траектории, в начальный и ко-
нечный моменты криволинейного дви-
жения. а также в моменты мгновенной
остановки точки.
374
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Здесь могут быть применены все
формулы и графики для прямолинейного
движения, где только вместо ускоре-
ния а следует брать а'.
Движение точки в плоскости, отне-
сенное к полярным координатам. Закон
движения точки (фиг. 53) определяет-
ся двумя уравне-
ниями:
f - /»(0. J
где угол назы-
ваемый полярным
углом, принято из-
мерять в радиа-
нах.
Средней угловой
скоростью радиу-
Фиг. 53. Исслеховоиие
движения точки в по-
лярных координатах.
са-вектора точки за промежуток вре
мен и — /j называется выражение
в ?2~У1 _
/2—z, Д/ •
Угловой скоростью (или также истин-
ной угловой скоростью) точки в момент /
называется
“—1,т (4?)=(бз)
. дг-о \ / at
Размерность угловой скорости: (вре-
мя)- 1.
Средним угловым ускорением радиуса-
вектора точки за промежуток времени
Z, — называется выражение
ы, — ш, Дш
h-h "лГ*
Угловым ускорением (или также истин-
ным угловым ускорением) точки в момент
t называется
в-Нт (64)
Д/-0 \ AZ j dt dt* J '
Размерность углового ускорения:
(время)-*.
Проекции скорости и ускорения точки
на направление радиуса-вектора назы-
ваются соответственно радиальными
скоростью vr и ускорением аг, а на
направление, перпендикулярное к ра-
диусу-вектору. — трансверсальными ско-
ростью и ускорением а?. Формулы
для вычисления скорости:
dr ,
* - V v’ + . (65)
Формулы для вычисления ускорения
о о dr
ar-—-r^-, ^-2^.4- ге;
а = Vа1г 4- а? .
(66)
Если через F обозначить площадь
(фиг. 54), описываемую радиусом векто-
ром точки, начиная от какого-либо
фиксированного положения ОМ о, то
выражение
dF
dt
(67)
называется секторной, или секториаль-
ной, скоростью точки в момент вре-
. - длина* _
менн t. Ее размерность: —^^ёмя- • <^ек"
торная скорость равна половине момента
скорости точки относительно непо-
движной точки:
« — vh — -i- mom0 (v), (68)
i A
Фнг. Круговое дви-
жение точки.
Фиг. М. Секторная
скорость точки.
В декартовых координатах
« —-у (•«> —yvx). (69)
Движение точки по окружности
(фиг. 55). В этом случае г = р = R =
= const; о, — u — Rw, а1 = а* = Re;
а" — — аг — Здесь радиальное
направление прямо противоположно
нормали, а трансверсальное совпадает с
касательной.
ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ
ТОЧКИ
Основные определения. Если точка М
(фиг. 56) движется по отношению к си-
стеме отсчета 2Ет,С, которая, в свою
очередь, движется по отношению к си-
стеме Охуг, принятой за неподвижную;
то движение точки Л! по отношению
к системе называется относитель-
КИНЕМАТИКА ТВЕРДОГО ТЕЛА
375
Фкг. 56. Относи-
тельное движение
точки.
ным, по отношению к системе Охуг —
абсолютным, а движение системы
по отношению к системе Охуг — пере-
носным или движением влечения
Скорость и ускорение точки М по
отношению к системе 26г£ называются
соответственно отно-
сительной скоростью
ц, и относительным
ускорением а0. а по
отношению к системе
Охуг — абсолютной
скоростью va и абсо-
лютным ускорением ал.
Скорость, а также
ускорение точки, не-
изменно связанной с системой я
совпадающей в данный моменте движу-
щейся точкой М, по отношению к си-
стеме Охуг называется переносной ско-
ростью оп. соответственно — переносным
ускорением а„.
Сложение скоростей. Абсолютная
скорость точки равна геометрической
сумме скоростей переносной и относи-
тельной:
v, = va + К (70)
Сложение ускорений. Абсолютное уско-
рение точки равно геометрической сум-
Вектор относительной скорости про-
ектируется на плоскость, перпендику-
лярную к оси переносного вращения,
полученная проекция поворачивается
на 90° в сторону вращения относитель-
ной траектории и умножается на удво-
енную угловую скорость.
Поворотное ускорение обращается
в нуль в случаях: 1) переносное дви-
жение поступательное (<>„ = 0); 2) мгно-
венная остановка точки в относитель-
ном движении (t»o= 0); 3) относи-
тельная скорость параллельна оси вра-
щения (0=0 илн к).
Пример. Стер-
жень ОВ (фиг. 58)
равномерно вра-
щается вокруг оси
0.4 с угловой ско-
ростью «'n=w. обра-
зуя с осью постоян-
ный угол а. По
стержню равномер-
но движется пол-
зушка М со ско-
ростью . On ре-
делнть абсолютные
скорость и ускоре-
ние ползушки Af,
принимаемой за точ-
ку. в функции рас-
стояния ОМ = л.
Переносная ско-
рость
® = шг sin «;
и
Фиг. 58. Определение ско-
рости и ускорения н слож-
ном движении.
»а — У««з> ДО а в* .
Переносное ускорение
ап — ш'з sin к.
Поворотное ускорение
ак — 2ми tin а.
Так как относительное ускорение aQ — 0, то
оа m ш tin я /ш’а* + 4и',
Фиг. 57. Построение поворотного ускорения.
ме трех ускорений: переносного, отно-
сительного и поворотного (или уско-
рения Кориолиса):
а» “ 4п + ао + лк- (71)
В общем случае переносное и отно-
сительное ускорения разлагаются на
тангенциальное и нормальное:
ап - а‘п + апп;
о» - «о + "о •
Поворотное ускорение
«к-2ыпХ «о
ИЛИ _л_
- 2*>воо sin (»„, vo). (72)
Поворотное ускорение определяется
по правилу Жуковского (фнг. 57).
КИНЕМАТИКА ТВЕРДОГО ТЕЛА
Сл
Поетупа-
лвижеиие
Фиг. 59.
тельное
твердого ’ила.
Поступательное движение
Определение. Траектории. Поступа-
тельным движением твердого тела назы
ваетоя такое его дви-
жение, при котором
всякая прямая, неиз-
менно связанная с те-
лом, перемещается па-
раллельно самой себе
(фиг. 59). При посту-
пательном движении
тела траектории всех
его точек предста-
вляют собой кон-
груентные кргвые
(Сд и Ср), т. е. кривые, совмещающиеся
при наложении.
376
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Скорости. Ускорения. При поступа-
тельном движении тела в любой момент
времени все его точки имеют геометри-
чески равные скорости (од= vg) и
геометрически равные ускорения
(вА = ав)-
Стедовательио, при поступательном
движении все точки тела движутся оди-
наковым образом.
неподвижную ось
Фиг. GO. Вращение
твердого тела во-
круг неподвижной
оси.
Вращение вокруг иеподвижиой оси
Заком движения. Угловая скорость.
Угловое ускорение. Если тело имеет
АВ (фиг. 60), то его
положение в произ-
вольный момент вре-
мени t определяется
двугранным углом ?
между начальным по-
ложением ЛЛ10Я не-
которой плоскости,
проходящей через ось
вращения, и ее поло-
жением АМВ в дан-
ный момент.
Закон в р а щ а-
тельногодвиже-
п и я твердого тела
вокруг неподвижной
оси (или просто: закон вращения) вы-
ражается уравнением
?=/(Ф (73)
Любая точка М описывает круговую
траекторию в плоскости пер-
пендикулярной к оси вращения; полу-
чается рассмотренный случай кругового
движения (см. стр. 374).
Угловая скорость опреде-
ляется равенством
" “ “ * (74>
и изображается вектором, приложен-
ным в любой точке оси и направленным
вдоль нее так, чтобы, смотря из его
конца в сторону начала, видеть враще
ние происходящим против часовой
стрелки.
Угловое ускорение опре-
деляется равенством
rf<u /Ар ••
<75)
Таблица 5
Основные задачи кинематики вращательного
движении
Дано Отыски- ваются । Расчетные формулы
1- 9 — 9 (0 Ш» S <?9 UI —— ' *. dt '•$ <га>
2. ш = » (0 Ф» t ?=»>+j •=4г <”>
3. ш •* оо(ф) Л • Фо
4. а - а (0 «а Ф t • «=<•» + [ tflt; t 9 — 9e + a>dt (81)
5. • - (9) «®, t Ш “ 1/ *• (82) Фо
6. • = • (“) г. t Q> /• цм/а» . 9-9.+ ша -к (83)
и изображается вектором, направлен-
ным вдоль ы в ту же сторону, если
вращение ускоренное (<р и '<? имеют
одинаковые знаки), и противополож-
но и», если вращение замедленное
(<р и имеют разные знаки); на фиг. 60
это условно показано обозначениями
*+
КИНЕМАТИКА ТВЕРДОГО ТЕЛА
377
Угловая скорость ш сек-1 связана
с числом оборотов в минуту п зависи-
мостью
у --?£-0.10472л; (76)
JU
обратно:
п - — _ 9.549Ш, (77)
It
Основные задачи кинематики враща-
тельного движения даны в табл. 5.
Между зависимостями, связываю-
щими и», е, /, и зависимостями, свя-
зывающими а, и, a, t для прямолиней-
ного движения, имеется полная анало-
гия, вследствие чего здесь могут быть
использованы приведенные выше гра-
фические построения.
Частные случаи
1) Равномерное'вращение
(w = const)
? — fo + «*. е — 0. (84)
2) Р а в н о м е р н о-п временное
вращение (с = const)
“"“о + £С9 =<?от“о1 + у. (to)
3) Гармоническое колеба-
ние
<Р = a sin (kt + ₽). (86)
где а — угловая амплитуда колебания;
остальные величины имеют те же на-
именования, что и в прямолинейном
колебании.
Скорости и ускорения точек вра-
щающегося тела. Здесь имеют место
Фиг. 61. Диаграмме Фиг. 62. Ди»,
скоростей. грамма ускоре-
ний.
те же формулы, что и для кругового
движения точки (см. фнг. 55), а именно:
s = fr, (87)
а1 — er; ап — к>2г; (89)
а — г К“4 + е2; tg и — -Ц-, (90)
UI*
где г — расстояние точки от осн вра-
щении: d — диаметр соответствующей
окружности.
Скорости и ускорения пропорцио-
нальны расстояниям точек от оси
вращения: отсюда следуют диаграммы
скоростей (фиг. 61) и ускорений (фиг. 62).
Винтовое движение
Определение и свойства. Движение
твердого тела, состоящее из враща-
тельного и поступательного, напра-
вленного вдоль осн
вращения, назы-
вается винтовым
(фиг. 63, а и б).
Различают движе-
ния правовинтовое
(фнг. 63. а) и лево-
винтовое (фиг. 63,6).
РасстояниеЛ, прой-
денное проекцией
какой-либо точки
тела на ось винта
при одном обороте,
называется шагом
Фиг. 63. Винтовое дви-
жение и двух вариан-
тах.
винта. Отношение
поступательной скорости и к угловой <о
называется параметром винта р:
_ v_____h
Р ~ ш ~ 2л
(91)
Подъем винтовой линии
(траектории произвольной точки М
на расстоянии г от оси винта) равен
<9»
Скорость точки М равна*
vM — V v2 + г2*»».
Ускорение при равномер-
ном винтовом движении
ам = гы*;
в общем случае определяется по правилу
сложения ускорений.
Плоско-параллельное движение
О п редс лен и я. Плоско параллельным
движением твердого тела называется
движение, при кото-
ром все точки тела
движутся в плоско-
стях. параллельных
некоторой неподвиж-
ной плоскости. Эго
движение определяет-
ся движением плоской
фигуры — проекции
Фиг. 64. Определе-
ние положения пло-
гела на плоскость, ской фигуры,
параллельно которой
происходит движение (фиг. 64). Поло-
жение фигуры определяется координа-
378
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
тами х0, уй произвольно выбранной точ-
ки — полюса — и углом поворота вокруг
полюса. Уравнения движения:
•v0 - Л (0; Л - /»(0; г=Л (О- (93)
Первые два определяют поступатель-
ную часть движения, зависящую от вы-
бора полюса, последнее — вращатель-
ную часть, от этого выбора не зависящую.
Так, угол поворота <р, угловая скорость
<•>=<!> н угловое ускорение с = <?
фигуры относительно любой точки —
одни и те же. Если координаты произ-
вольной точки М в подвижной системе Е,
5, а в неподвижной — х, у, то
•х - х0 + Е cos v — т] sin <?; j
У = уо + 6 sin <? + т( cos <р. /
Фиг. 6S. Ско-
во-
65):
(95)
(96)
Распределение скоростей. Скорость
я# любой точки фигуры равна геоме-
трической сумме скоро-
сти полюса vo и скоро-
сти вращения оЛ1О
круг полюса (фиг.
VM_= vq + Vaio!
и mo — “ • ОМ.
рость произ- Та точка Р фигуры,
доской скорость которой в лан-
гуры. ный момент равна нулю,
называется мгновенным
центром скоростей, а совпадающая с ней
точка неподвижной плоскости — мгно-
венным центром вращения. Во всякий
момент времени скорости точек фигуры
распределяются так, как если бы фи-
Фиг. 66. Определение положения мгно-
венного пснтря скоростей в двух слу-
чаях.
гура вращалась вокруг мгновенного
центра скоростей (фнг. 66, а и б):
од = м.РЛ, Ов = ы-РВ.
Для нахождения Р по од и <о находим
о )
АР=— и откладываем перпендику-
лярно од сообразно знаку ?. Для на-
хождения Р по скоростям двух точек сле-
дует восставить перпендикуляры к этим
скоростям, а в случаеихслияния провести
еще прямую через
концы скоростей. Точ-
ка Р может оказаться
в бес конечности. Тогда
имеет место движение,
Фиг. 67. Проекции
скоростей авух то-
чек отрезки и» его
направление.
при котором скорости
всех точек фигуры в
данный момент вре-
мени равны между со-
бой, т. е. скорости распределяются так,
как если бы фигура совершала посту-
пательное движение. Однако ускорения
различных точек фигуры вообще не
равны друг другу.
Проекции скоростей любых двух то-
чек фигуры на прямую, их соединяю-
„ щую (фнг. 67),
уъ—равны между со-
Уу} ‘ б°Й: °Л “ °в'
тыр"»«нноммехГ
ниэме (фиг. 68) с не-
Фиг. 68. Четырехэвенвый подвижным звеном
механизм. 0,0,
Од сое (а - 90е) — vB cos (? - 90°),
откуха
ш, a sin а = а>, b sin 0.
Геометрическое место мгновенных
центров вращения (ня неподвижной пло-
скости) (фиг. 69) называется неподвиж-
ной центроидой (или полоидой), a
геометрическое место
трое скоростей (на
движущейся фигу-
ре)—подвижной цент-
роидой (или полои-
дой). При движении
фигуры подвижная
центроида // катится
по неподвижной /,
имея точкой касания
мгновенных цен-
Фиг. 69. Центро-
иды.
(97)
мгновенный центрско-
ростей Р Скорость
любой точки фигуры
1>Л1 = ы - РМ. Скорость перемещения
мгновенного центра
Р-1»
I Pi i ps I ’
и —
где р< и рз — радиусы кривизны цен-
троид; плюс берется в случае, когда
центроиды обращены выпуклостями друг
КИНЕМАТИКА ТВЕРДОГО ТЕЛА
379
а# любой точки
Фиг. 70. Ускорение
произвольной точки
плоской фигуры.
к Другу, минус — в противоположном
случае.
_ Распределение ускорений. Ускорение
фигуры равно геоме-
трической сумме уско-
рения полюса ао и
ускорения амо во вра-
щательном движе-
нии вокруг полюса
(фиг. 70):
аМ “ ао + ^МО- <98)
Это ускорение раз-
лагается на танген-
циальную составляю-
щую а‘мо (вращатель-
ное ускорение) и нормальную составляю-
щую а^10 (центростремительное уско-
рение):
а‘мо = ^-ОМ‘, ]
(99)
eMO = I
Направление а‘мосогласно с направле-
нием Сумо, если f и <р одинаковых зна-
ков, и противоположно, если разных.
Ускорение амо определяется по вели-
чине и направлению формулами
Для нахождения Q по ускорению
аА
одной точки А находим AQ = z
У <!>' С2
е
и угол fi = arctg -^7, который отклады-
ваем от ад в сторону вращения, если
и ф одного знака, и в противополож-
ную— если разных знаков. Для нахо-
ждения Q по ускорениям двух точек сле-
дует построить от-
носительное уско-
рение аЛВ, найти
его угол (ж с отрез-
ком АВ и отло-
жить этот угол от
ал и ав.
Пример. Кривошип
ОМ = I (фиг. 7'2), вра-
щающийся с постоянной
угловой скоростью о»»,
приводит к движение
линейку Д2? эллипсогра-
фа, причем АМ = МВ = 1. Здесь мгновенный центр
скоростей Р находится на перпендикулярах АР н
ВР к скоростям Рд н Ьд: = <е4- ОМ = Ш х
X МР (гае ш — угловая скорость линейки). Тек
как МР = /, то ш — ш0 — const, следовательно.
а=0; тогда угол ц — О; мгновенный центр уско-
рений линейки находится в О;
2 2 2
аЛ(~“о'г; ад = “о-ОЛ; ад-^о-ОВ.
аМО ~ ОМ V
(100)
Точка Q фигуры, ускорение которой
в данный момент равно нулю, назы-
Фиг. 71. Определение положение
мгновенного центре ускорений.
вается мгновенным центром ускорений.
Во всякий момент времени ускорения
точек фигуры распределяются так, как
если бы она вращалась вокруг мгновен-
ного центра ускорений (фиг. 71). Тогда
аА “ СМ + **; Яд « QB -|- »*;
Движение тела около неподвижной
точки
Определение положения тела. В слу-
чае движения твердого тела около
неподвижной точки, называемого также
сферическим движением, положение
тела определяется углами Эйлера
(фнг. 73, а): углом прецессии ф, углом
Фиг. 73. Углы Эйлера в двух вариантах.
нутации в и углом собственного вра-
щения <р. Эти углы характеризуют
положение координатного трехгранника
Oxvz, связанного с телом, по отноше-
нию к неподвижному трехграннику ОЬ)С.
3«0
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Линия ON пересечения двух координат-
ных плоскостей, принятых за основные,
называется линией узлов.
Акад. А. Н. Крылов [15] указал па
ряд видоизменений выбора углов Эйлера,
удобных при изучении движения артил-
лерийского снаряда, корабля или само-
лета (см., например, фиг. 73, б).
Уравнения движения
® = Л (О;
♦ -/.(О;
(101)
Распределение скоростей. Во всякий
момент времени существует проходящая
через неподвижную точку прямая OQ
Фиг. 75. Скорост» про-
школьной точки тела.
Фиг. 74. Аксонам.
(фиг. 74), скорости всех точек которой
равны нулю. Это — мгновенная ось
вращения тела. Геометрическое место
мгновенных осей вращения в непо-
движном пространстве есть коническая
поверхность, называемая неподвижным
аксоидом (/), а в движущемся теле —
подвижным аксоидом (//). При движе-
нии тела аксоид II катится по аксонду /
(снаружи или внутри), имея общей обра-
зующей мгновенную ось.
Проекции угловой скорости ш на
оси х, у, г, связанные с телом, выра-
жаются через углы Эйлера (фиг. 73, а)
формулами (кинематические уравнения
Эйлера):
— Ф sin 0 sin + 6 cos г:
-j — ф sin 0 cos f — 6 sin f;
— Ф cos 8 + ф,
(102)
где точками обозначены производные
по времени. Скорость любой точки М
(фиг. 75) равна моменту вектора угло-
вой скорости относительно этой точки.
В векторной форме
vм - « X Г;
в координатной — через координаты
точки (формулы Эйлера):
vx-=M^-»xy; |
V, = ыгх — м>Лг; I (103)
—“И- )
Распределение ускорений. Угловое
_________________ бы
ускорение а = -гг представляет
собой скорость конца
нне произвольной
точки М (фиг. 76)
а — а" 4- а*> (104)
<г> = ы*МС есть
цент ростре ми-
тел ь ное ускоре-
ние, направленное
перпендикуляр-
но мгновенной оси;
ав = гЛ (где h —
перпендикуляр,
опущенный на а)
есть вращательное
ускорение, предста-
вляющее собой по
Фиг. 76. Ускорение про-
извольной точки тела.
величине и напра-
влению момент углового ускорения от-
носительно точки М.
Пример. Бегун ра ануса R раппомерпо катится
по перпеиаикулёриоА к'нему плоскости; скорость
центра рама vq (фиг. 77).
Фиг. 77. Кияематмческое исслкло-
каиие аенжепик бегуна.
Мгаокеимак ось ON\ угловая скорость
"С .
"“«со».* 2
”С *С >.
7г,г*'
VM “•’W cos я - 2Vf.
м 7*С
а R »С
°-И “ ’ аГп а “ R со* я ’
СЛОЖЕНИЕ СКОРОСТЕЙ ПРИ СЛОЖНОМ ДВИЖЕНИИ
381
(ам) +(°'m)
2
-|- 2а'на\( со» (к—2в)=
vc _____________
—-----У 6 — 4 cos 2я
Keota
ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ
ТВЕРДОГО ТЕЛА
Определение положения тела. Приме-
няются три системы координат (фиг. 78):
Фиг. 78. Определение поло-
жения твердого геля
в общем случае.
*0-/:(<);
’ю-Л (О;
Со-Л(О;
ctjC — неподви-
жная; 05'ч'С' —
имеющая на-
чало, связанное
с произвольной
точкой тела,
и перемещающая-
ся поступатель-
но; Охуг — свя-
занная с те-
лом. Получается
шесть уравне-
ний движения:
?—/<(0; |
Ф-Л«); («о*)
о-Л (О- I
Первые три уравнения определяют
поступательную часть движения, осталь-
ные — вращательную.
Скорости и ускорения точек нахо-
дятся, как для сложного движения.
СЛОЖЕНИЕ СКОРОСТЕЙ
ПРИ СЛОЖНОМ ДВИЖЕНИИ
ТВЕРДОГО ТЕЛА
Сложение поступательных движений.
Результирующая скорость V (фиг. 79)
равна геометрической сумме составляю-
щих скоростей:
(106)
Фнг. 79. Сложение Фиг. Яи. Сложение парал-
скоростей поступи- лсльных угловых скоро-
тельных движений. стей в двух случаях.
Сложение вращений вокруг параллель-
ных осей. При сложении двух вра-
щений вокруг параллельных осей
(фиг. 80, а и б) результирующая угло-
вая скорость S2 равна алгебраической
сумме составляющих угловых скоростей,
и мгновенная ось делит расстояние
между осями внутреннем или внешним
образом обратно пропорционально этим
скоростям:
2 “ ± “2>
АС СВ АВ
Wj Ш] U
(107)
В случае фиг. 80, б предполагается,
что <ui yfc их. Совокупность двух чис-
ленноравных, но противоположно напра-
вленных угловых скоростей называется
парой угловых скоростей (фиг. 81). Эта
пара в смысле рас-
пределения линейных
скоростей эквивалент-
на мгновенному по-
ступательному движе-
нию со скоростью Vj"—
поступательной ско-
ростью, равной мо-
Фиг. R1. Пара угль-
пых скоростей.
менту пары: одг =
= w • АВ. Обратно, всякую поступа-
тельную скорость можно представить
как пару угловых скоростей.
В случае произвольного числа вра-
щений вокруг параллельных осей их
угловые скорости складывают последо-
вательно.
Сложение вращений вокруг пересекаю-
щихся осей Результирующая мгновен-
ная угловая скорость Si (фиг. 82) равна
геометрической сумме составляющих
угловых скоростей:
Фиг. ЯЗ. Угловая
скорость кониче-
ских зубчатых ко-
лес.
2- (Ю8)
Фиг. 82. Много-
угольник угловых
скоростей.
Пример. По неподвижному коническому ауб-
мятому колесу А катится шестеренка В (фиг. 83).
Миюненная ось ОС. Переносная угловая ско-
рость «»п (угловая скорость оси шестеренки), от.
яосительная «о и абсолютная удоялетаоряют
соотношениям
"п
sin J
о = а .
sin « sin (я -НО ’
’п + “о + !“п“о с<>‘ (•
(109)
382
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Сложение вращений вокруг скрещи-
вающихся осей. Параллельным пере-
носом «>» в точку приложения
(фиг. 84) с присоединением пары, экви-
валентнрй поступательной скорости о,
задача сводится к сложению поступа-
тельного и вра-
Фиг. 84. Сложение
вращений вокруг
скрещивающихся
осей.
Фиг. в5. Мбтор
скоростей.
Сложение поступательного и враща-
тельного движений. В результате при-
ведения поступательных и угловых ско-
ростей в данный момент времени к дан-
ному центру О (фиг 85) получается
мотор скоростей, т. е. совокупность V
и Q.
Различные случаи приведения:
1) V — 0; 2=0 — покой или мгно-
венная остановка;
2) V <Л 0; О = 0 — мгновенное посту-
пательное движение (только по отноше-
нию к скорости);
3) И = 0; 2 «А 0 — вращение вокруг
мгновенной оси;
4) V чь 0; 2 * О. ч> = 90’ — мгно-
венное плоско-параллельное движение;
5) V ч^ 0; й 0; ? = 0 или 180° —
мгновенное винтовое движение (кине-
матический винт);
6) V 0; Й 0; — произвольный
угол — переменой центра приводится
к предыдущему.
Таким образом, наиболее общий слу-
чай движения твердого тела приводится
к кинематическому винту, подобно тому
как наиболее общий случай системы
сил приводится к динамическому винту.
Общая теория винтов разработана рус-
ским ученым, геометром и механиком
А. П. Котельниковым (12).
ДИНАМИКА
МЕХАНИЧЕСКИЕ ЕДИНИЦЫ
Измерение механических величин
В основе измерения всех механиче-
ских величья лежат три единицы, назы-
ваемые основными, через которые могут
быть выражены все прочие единицы,
называемые производными. По роду
и величине основных единиц различа-
ются следующие системы * (согласно
ГОСТ 7664-55):
Система МКС (метр — килограмм —
секунда)
Сиоема СГС (сантиметр — грамм —
секунда)
Система МКГСС (метр—килограмм-
сила — секунда)
В первых двух системах величинами,
соответствующими основным единицам,
являются:
Длина L, масса М, время Т.
В третьей системе величинами, соот-
ветствующими основным единицам,
являются:
Длина L, сила К. время Т.
• См. твкже .Справочник машиностроителя-,
т. 2. гл. XII, .Электротехника*, табл. I.
Каждая единица в любой системе
имеет свой размер, под которым разу-
меется формула, выражающая данную
единицу через основные единицы
(табл. 6).
Способ получения производной еди-
ницы [Q] из основных единиц для изме-
рения некоторой величины Q записы-
вается в виде формулы, называемой
формулой размерности. Формула раз-
мерности имеет вид:
а) в системе МКС и СГС
|(?]=Е*М’Г (П0>
б) в системе МКГСС
[Q]^LkK^T\ (Ill)
Показатели степени «, Р ... т называ-
ются размерностями измеряемой вели-
чины.
Какие бы величины ин входили в
уравнение, выражающее какой-либо
механический процесс, все члены этого
уравнения должны быть однородны от-
носительно каждой из трех основных
единиц.
ДИНАМИКА ТОЧКИ
383
Системы едмвмц
Таблица б
Наименование системы
Название ВСЛИЧННЬ Метр-кнлограмы-секувда Саитиметр-г^аум<скуяда Метр-килограмм-сида-секуила МКГСС
Еднииил н ее размер Размер- ность* величины Езннииа и ее размер Размер- ность величины Еаивина и ее размер
Длина . Масса . Время . Силл Скорость Ускорение Частота . Угловая скорость Угловое ускорение Работа и энергия Мощность Давление • Относ Метр (м) Килограмм (кг) Секунда (сек) Ньютон (л)=1 кг. м сек’ мсек мсек1 Гери (гя)-1 ‘сек рад сек рад сек* Джоуль (<br)=l н. м. ватт (лш)=1 дж-сек п/м‘ итсв к системам МКС L* М' Л DM' Т-* и Г-* £.* Т-* Т~‘ T-* T-* L'M'T-* и М‘ т -> М‘ Т~' и СГС. Сантиметр (см) Грамы (г) Секунда (сек) Дика К)аи)=1<. См сек', см’сек см сек’ Гери (гц)=1 ' сек рад сек радсек* эрг (»pe}-\ дин см грг сек денем' D L-че-г Г К1 и Т~' и т~* Г-‘ Г-* Т-* L1 Ю L' К1 Т~* L-* Ю Метр (ж) кГсекЧм или кГ. сск'.м Секунда (сек) Килограмм-сила (клс или кГ) м сек мсек'- Герц (еч)=1 ‘,’сек рад!сек радсек кГ. м или кГ. м кГ. м сек, или кГ м сек кГ,'м‘ или Kl'jM'
Внесистемные единицы и главнейшие
соотношения между единицами различ-
ных систем (на основании ГОСТ
7664-55).
М а с с а. 1 тонна (тн) — 10* кг = 10сг=
= 101,972 кГ-сеюм; 1 кГ-сек*1м =
=9,80665 «=9806,65 г.
Сила. 1 тонна—сила (тс) = 10»л/’=
= 9.86665- 10s н; 1 н = 0,101972 кГ.
Работа. I дж =10” эрг =
= 0,101972 кГ -м; 1 ватт час (вт. ч) =
=3.6-10» дж; 1 кГ. м = 9.80665 дж.
Мощность. 1 лошадиная си-
ла (л. с.)=75 кГ. м сек = 735.499 вт;
1 вт = 0,101972 кГ-мсек.
Д а в л е н и е. 1 миллиметр ртутного
столба (мм рт-ст) = 133,322 нм*;
1 миллиметр водяного стол-
ба (мм вод. ст.)=9,80665 м/ж»; 1 техни-
ческая атмосфера (ат или кГ/см*) =
= 9,80665-10* н,м*.
Примечем и*. При расчетах с точностью
е свыше 0.1* вместо чисел 0.101972 и 0,980665.
умноженных на степени 10. берут соответственно
0.102 и 0.98.
ДИНАМИКА ТОЧКИ
Основные законы
Закон инерции. При отсутствии
сил материальная точка находится
в покое или движется равномерно и
прямолинейно (1-0 закон Ньютона).
Системы отсчета, в которых этот закон
выполняется, называются инерциальны-
ми. С достаточной в большинстве слу-
чаев степенью точности такой системой
является система, связанная с Землей.
Закон об ускорении и силе. Основное
уравнение динамики. Ускорение мате-
риальной точки пропорционально при-
ложенной силе и направлено в сторону
силы (2-й закон Ньютона). Математи-
чески это выражается в форме основно-
го уравнения динамики
та-Р. (112)
где т — масса точки; а —ее ускоре-
ние; Р — приложенная сила (фиг. 86).
Если вес тела G. уско-
рение силы тяжести g. то
G
-------. (ИЗ)
g
Для средней широты
g=9,80665 м/сетд; округ- фиг- 86- Сила “
ляя, имеем g=9,8 м/сек*. У“ор*""«
— =0,102 сек*/м (см. стр. 372. в част-
ности. табл. 4).
Закон действия и противодействия.
Силы взаимодействия двух материаль-
ных точек всегда равны друг другу п»
величине и противоположны по напра-
влению (3-й закон Ньютона).
3R4
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Этот закон имеет место не только
при относительном покое частиц или
тел, но и при их движении.
Закон независимости действия сил.
Под действием нескольких сил мате-
риальная точка получает , ускорение,
равное геометрической сумме ускоре-
ний, получаемых при действии каждой
силы в отдельности.
Закон всемирного тяготения. Две
материальные точки притягиваются
друг к другу с силой, пропорциональ-
ной произведению их масс и обратно
пропорциональной квадрату расстоя-
ния между ними:
P~f
т,т^
(Н4)
где / — гравитационная постоянная.
В системе CGS
/ = 6,67-10-8 сж3-в-1-сек~г.
О' т ~рз
Фиг. 87. Прямолиней-
ное авижеине точки.
Прямолинейное движение точки
Дифференциальное уравнение прямо-
линейного движения точки. Если от-
нести точку с массой т, находящуюся
под действием силы Р, к координате s
(фиг. 87), дифференциальное уравнение
движения имеет
вид
(Ps
<115>
При задании за-
кона движения д —
— /(О (прямая или первая задача дина-
мики) сила находятсядвукратным диффе-
ренцированием. При задании силы Р =*
= Р (t, s, s) (обратная или вторая
задача динамики) закон движения на-
ходится интегрированием дифференци-
ального уравнения движения. Две по-
стоянные интеграции Ci н Cg опреде-
ляются из начальных условий: при
t = t9, s = зд, s = ve. Когда P за-
висит только от одной переменной (t,
s или s), задача решается так, как
указано выше в разделе «Основные за-
дачи кинематики точки» (случаи 4—6).
Пример. Из зенитного орудия выпушен сиарях
• вертикальном направлении с начальной скоро-
стью Vj (Ф<п . 88). Сила сопротивления воздуха
предполагаете* пропорциональной квадрату ско-
рости < /? — fro*; О = mg).
Уравнение авижепия тл — — лад — До*. Ввозим
*• — • Тогда д = — g(1 + *‘о'). При («О,
mg
кота), s — 0;
0
Г (время атлета) smaI = ti
Фиг. 88.
Вос-спящее
движение
сварила.
Н =
“Wln
о
arctg *о0
Здесь постоянные С, и С, не вводились, так
как интегралы взяты определенные.
Криволинейное движение точки
Дифференциальные уравнения криво-
линейного движения. В декарто-
вых координатах уравнения
движения свободной материальной точки
имеют вид
тх = X; ту = У; тг = 2.. (116)
где т — масса точки; х, у, г — ее коор-
динаты; X, У, Z — проекции действую-
щей силы, являющиеся вообще функ-
циями от t,x,y, г, х, у, г. Шесть постоян-
ных интеграции определяются по началь-
ным условиям: при t = t0 (обычно^ = 0)
х = х»; у = у* г = г»; * = У =
= Уо> г — *0-
В случае несвободной точки к X, У,
Z добавляются реакции связи N х,
Ny. Nr
В естественной форме (т. е.
в проекциях на касательную, главную
нормаль и бинормаль) уравнения дви-
жения свободной материальной точки
имеют вид
m^-"‘P»i 0~Pt.(117)
at р
где р — радиус кривизны траектории;
Pt, рь ~ проекции действующей
силы.
Если точка несвободна,то добавляются
реакции Nt (Nt = 0 при идеальной
связи), N„, Nt.
Пример. Днижеине тела (принимаемого за
точку), брошенного наклонно к горизонту и пу-
стоте (фиг. 89); начальна» скорость о*, угол бро-
сания а. Здесь Р — mg; X — 0; У — — mg; Z — 0.
mx —0; my — — mg; г не рассматриваем, так
как очевидно, что движение происходит в плоско-
сти хОу.
Первые интегралы
i-C,; у--д<4-С,
ДИНАМИКА ТОЧКИ
38-5
Вторые интегралы
* “ C.14- С,; у — —j дт* + С.г +• С,.
Начальные условна: Г — 0; х — у — О; X —
- «,яна; у = aln а;
С, — е0со»«; Ся = о0»1п«; С, —С,—о.
Фнг. 89. Движение тяжелой
точки, брошенной наклонно
к горизонту.
Уравнении движения:
. X — г>„1 сов а; у — sin «--------у- gf.
Траектория — парабола:
i •» * «------------------------Л
SvJ со»’«
Наибольшая высота польем»
о,
Л — »1П’ в.
Дальность no-itrr.i
Ра
I •=--- «Ш 2а.
g
Радиус кривизны траектории можно опреде-
лить из второго уравнения в естественной форме-
«А О’ О’
и — як те со» •; р —----------------------.
р gсов ф gv„со» в
гак как
о со» т " ту, со» в;
о -г/ ej — tVogt aln в + g'f ,
Математический маятник. Плоским
математическим маятником
круговым
Фиг. НО. Математи-
чески* маятник
называется матери-
альная точка, дви-
жущаяся по дуге ок-
ружности в верти-
кальной плоскости
под действием силы
тяжести (фнг. 90).
Уравнение движе-
ния
Ф — —*1пч>. (118)
где I — длина маятника; f — угол or-
клонен и я от вертикали.
25 Том I Зак. 1’61
Период колебания (полного)
[1 + (1Г slnTl +
(119)
где а — амплитуда колебания.
Функция Да), стоящая в скобках,
имеет значения, приведенные в табл. 7
|2|
Таблица ’
Функции угла а
а ГМ I- гм 1 • Г (к)
О" 1,00000 15" 1,00430 S0" 1,1800
2е 1.00005 30" 1,01741 120" 1,3753
5" 1,00048 45" 1,0400 150" 1,7800
10" i.ooim 60" 1,0732 180" ОО
Хорошее приближение дает формула
'-’•/уО+ТБ-). <1а“>
где угол а выражен в радианах,
малых
Для
(121)
углов
Г-2х
При а < 8° погрешность зтой фор-
мулы <0,1%, при а <22° погреш-
ность < 1%.
Движение точки переменной массы
Точка переменной массы. Точкой
переменной массы называется тело,
некоторая часть которого в процессе
решения данной задачи исключается нз
рассмотрения или, наоборот, к массе
которого присоединяются новые массы,
ранее не' включенные в рассмотрение;
при этом предполагается, что, во-первых,
можно пренебречь относительным пере-
мещением центра инерции по отношению
к телу вследствие изменения массы,
а во-вторых, можно пренебречь кине-
матическими элементами вращательного
движения по сравнению с кинемаги-
ческими элементами поступательного-
движении (|31, |10|, |16|).
386
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Предполагается также, что масса
может быть выражена в виде непре-
рывной функции от времени
т = т (/)-
Уравнение Мещерского,
или основное уравнение динамики точки
переменной массы,
та = Р + рреакп, (122)
где т — масса точки в данный момент
времени; а — ее ускорение (точнее—
ускорение центра инерции); Р — при-
ложенная сила; рргакт — реактивная
сила, равная
(123)
Здесь v — абсолютная скорость массы
точки т (/) в данный момент времени;
и — абсолютная скорость массы, при-
соединяющейся (dm > 0) или отделяю-
щейся (dm < 0).
В координатной форме
тх = X + -
= Х + т (и„ — х);
ту = У + уреакт =
- У+т(иу — у)-,
mz = Z+ zpeaKm =
— Z + т (аг— г).
(124)
Частные случаи
1. Абсолютная скорость присоеди-
няющейся или отделяющейся массы равна
нулю (и = 0):
d . — —
-^(ти)-Р. (125)
Эго есть 2-й закон Ньютона в его
первоначальной формулировке: произ-
водная по времени количества движе-
ния материальной точки геометрически
равна приложенной силе.
При постоянной массе получается
основное уравнение динамики (112).
2. Относительная скорость присо-
единяющейся или отделяющейся массы
павна нулю (и — о ™ 0):
do s-
п -<г-р-
(126)
где т — не постоянная. 8 зависящая
от времени величина.
Пример. Подъем ракеты в поле силы тяже-
сти. Предполагается: т = m^e~ai ; g = const.
= и - v = const; сопротивлением пренебрегаем:
Из уравнения (124), где
Z - - mg, zPeaKm — — mvh,
имеем
о,
или
« — —д + «Ро.
□ткул.
»— -i («* - Г) <* + V/.
Общие теоремы динамики точки
Количество движения. Импульс силы.
Теорема количеств движения. Количе-
ством движения материальной точки
называется вектор
К = mv (127)
с проекциями тох, тоу, тиг.
Импульсом силы за промежуток вре-
мени t называется вектор
t _
l=^Pdt (128)
t t t
с проекциями §Xdt, f/dt j Zdt.
ooo
Размерность / и К — одинаковая, рав-
ная в абсолютной системе единиц
L‘MlT~\ в технической /ОТ1.
Теорема количеств дви-
жения. Геометрическое приращение
количества движения материальной
точки за некоторый промежуток времени
равно импульсу силы за тот же проме-
жуток времени:
t _
mV/— mv0 — j Pdt.
где vt и o0 — скорости точки соответ-
ственно в конечный и в начальный мо-
менты времени. В проекциях на оси
t
mvlr — mvM — f Xdt — Ix;
t
mvty — mv0> — f Y dt — !y;
mvu — mv<u
Момент количества движения точки
Теорема моментов количеств движения
Момент количества движения мате-
риальной точки относительно центр»
ДИНАМИКА ТОЧКИ
387
и осн определяется совершенно так же,
как момент силы. Момент количества
движения точки относительно начала
координат есть векторное произведение
радиуса-вектора точки на ее количество
движения:
Go = г X то.
Моменты количества движения точки
относительно осей координат:
= m (yvz — xvv) — 2znaw;
Gy = m (xvjr — xvt) — 2mafr;
G2 — m (xvy — yvx) — 2лизх>,
(130)
где Syt, azt, aIV — секторные скорости
проекции точки на соответствующие
плоскости.
Теорема моментов коли-
чества движения. Производная
по времени от момента количества дви-
жения материальной точки относительно
некоторого неподвижного центра равна
моменту приложенной силы относи-
тельно этого центра:
-^=Л«в(Р).
В координатной форме.
dG. - dG9 —
(131)
Если момент силы относительно
какой-либо оси равен нулю, соответ-
ствующая секторная скорость по-
стоянна. Например, если Мж(Р)=0,
то Oyi => const.
Если М9 (Р) = 0 — сила центральная,
тогда имеет место теорема площадей:
прн действии центральной силы точка
описывает плоскую кривую с постоян-
ной секторной скоростью.
Кинетическая энергия. Теорема об
изменении кинетической энергии.
Кинетической анергией или живой си-
лой материальной точки называется
половина произведения массы точки на
квадрат ее скорости:
Т mifl
2
(132)
Теорема кинетической
энергии. Приращение кинетиче-
ской энергии материальной точки на
некотором перемещении (элементарном
25*
или конечном) равно работе приложен-
ных сил на этом перемещении:
где Л есть работа всех сил или работа
равнодействующей. Т имеет размерность
работы.
• Если силы имеют потенциал, то имеет
место закон сохранения
механической энергии:
Т+Л=Т0 + /70, (134)
где П — потенциальная энергия.
В случае несвободной точки, подчи-
ненной идеальным связям, не зависящим
от времени, формулировка теоремы
живых сил не изменяется. Если же связи
не идеальные или зависят от времени
(подвижная поверхность), к работе
активных сил добавляется работа реак-
ций связей.
Кинетостатика точки. Относительное
движение
Сила инерции. Силой инерции Ф
материальной точки называется сила,
равная произведению массы точки на
ее ускорение и направленная противо-
положно ускорению:
Ф = - та. (135)
/
Принцип Даламбсра. Если к мате-
риальной точке приложить силу инер-
ции то активная сила Р (точнее, равно
действующая всех активных сил), реак-
ция связи N и сила инерции Ф будут
в равновесии (фнг. 91):
Р + N + ф - 0. (136)
На фиг. 91 R " та — деятельная сила
(? — потерянная сила (уравновешн
Фиг. VI.
Принцип
Далаибера.
Фиг. Я. Ра»
аожеиие силы
инерции.
Разложение силы ^нерции. В общем
случае (фиг. 92) Ф разлагается на
тангенциальную или касательную силу
388
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
инерции Ф/ и нормальную или центро-
бежную силу инерции Ф„:
(137)
где р — радиус кривизны траектории-
В случае кругового движения (радиус
окружности г)
Ф( =- mt г, Фя — /пш2г. (138)
Пример. Ручка центробежного регулятор»
длиной I с грузом О на конце равномерно вра-
щается вокруг вертикали с угловой скоростью •>.
Пренебрегая несом
ручки, найти угол в и
Фиг 93. Отклонение
от вертикали ручки
центробежного регу-
лятора.
усилие N в ручке
(фиг. 93).
Здесь = 0;
Ф. = — sin *.
Л g
Для системы сходя-
шихся сил составляем
уравнения равновесия:
V х = — •*>/ sin Я — N aln « = 0;
2 К — N cos я - G = 0;
отсюда
В — arccba .
шЧ
Относительное движение точки
Система O'fr|C — инерциальная, Охуг—
неинерциальная, т. е. движущаяся по
Фиг. 94.
Динамик» относитель-
ного движения.
отношению к пер-
вой вообще нерав-
номерно и непря-
молинейно (фи г.94).
Чтобы составить
уравнения движе-
ния точки массы т
в этой подвижной
системе, следует к
заданным силам и
реакциям связи
прибавить силы
инерции перенос-
ную Фп_и корио-
лисову Фк:
та “ Р + N + Фп + Фк,
В координатной форме:
тх - Рж + Nx + Фпх 4- Фжх;
my-P,+ Ny+ Фву + Фм;
тх — Рг 4- Nt + Фш + Фй.
(139)
Теорема кинетической энергии сохра-
няется. но добавляется работа перенос-
ной силы инерции.
о
Фиг. 95. Аксе-
лерометр.
Пример. Акселерометр лля определения уско-
рения вагона о, представляет собой маятник дли-
ной I (фиг. 95).
Для составления уравнения
движения маятника добавляем
силу инерции Фп:
dv
т со» <р— о sin т.
но
Ф4 = та,; О = mg; о — 4;
следовательно,
ф _ сов р — y *|п »•
При относительном равновесии у = у». » — О
о» — У ‘В Оо-
ДИНАМИКА СИСТЕМЫ
Общие теоремы динамики системы
Количество движения. Теорема ко-
личеств движения. Количеством дви-
жения системы или, точнее, главным
вектором количеств движения системы
называется геометрическая сумма коли-
честв движения всех точек системы
К — S «W (140)
В проекциях:
К,-"% три.
Если М — полная масса системы,
ие— скорость центра масс (или центра
инерции), то
K-Mvc. (142)
Теорема количеств дви-
жения (в дифференциальной форме).
Производная по времени от главного
вектора количеств движения системы
равна главному вектору внешних сил:
(143)
где Ф„ = — та„; Фж — — так (ап—
переносное ускорение точки т, аж —
поворотное).
ДИНАМИКА СИСТЕМЫ
389
В координатной форме:
dKt
dt
= Rxi
dK,
dt
-R,;^- = Rt. (144)
В координатной форме дифференциаль-
ные уравнения движения центра масс
Мхс—Rx; Myc-=RX, Mzc=Rx. (149)
Теорема импульсов (тео-
рема количеств движения в конечной
форме). Геометрическое приращение
главного вектора количеств движения
системы за некоторый промежуток вре-
мени равно сумме импульсов всех
внешних сил за тот же промежуток:
К-Ко-2 Л- (1«)
Пример. Автомобиль
на расстояние I моль
формы весом О, со
скоростью и по отно-
шению к платформе
(фиг. 97). Пренебрегая
сопротивлениями.найти
перемещение s и ско-
рость v платформы,
если в начальный мо-
мент v “ 0.
Здесь Ех — Rj.—0.
а поетому Kj—K^—О,
т. е.
весом О, перемешается
желелиоаорожной плат-
♦нг. 97. Перемещение
автомобиля на плат
форме.
В координатной форме:
Кх — — 2
Kf—-- 2
Kz — Kjo = 2 hr
О,в
’ бг+о;-
(146)
В случае уравновешивания внешних
сил К = Ко = const.
Теорема количеств дви-
жения для жидкости (тео-
рема Эйлера). Главные векторы объем-
Из уравнения движения центра инерции
Мх — 7? находим:
♦иг. 96. Теоремх
Эйлера.
через выходное.
ных и поверх-
ностных сил н
векторы коли-
честв движе-
ния массы жид-
кости, проте-
кающей в еди-
ницу времени
(фиг. 96) через
многоугольник:
входное сечение
трубы н с об-
ратным знаком
образуют замкнутый
Кинетический момеит. Теорема мо
ментов количеств движения. Главным
моментом количеств движения системы
или кинетическим моментом системы
относительно некоторого центра (иапри-
мер, начала координат) называется
геометрическая сумма моментов коли-
честв движения всех точек системы
относительно этого центра:
Go = 2 тото (mtv,) = S X (150)
Mvt - Mvt + R°6 + Rno> = 0. (147)
где M = — , a Q — весовой расход
жидкости.
Теорема о движении цен-
тра масс (также центра инерции,
центра тяжести). Центр масс системы
движется, как материальная точка, в ко-
торой сосредоточена вся масса системы
и к которой приложены все внешние
силы, действующие на систему.
Если хс, ус, г с — координаты центра
масс. ае — его ускорение, М — масса
системы. R — главный вектор внешних
сил, то
. Мае - R. (148)
Проекции Go на оси координат, про-
ходящие через О, называются главными
моментами количеств движения си-
стемы (или кинетическими моментами)
относительно осей; они равны соот
ветвенным алгебраическим суммам ми
ментов относительно этих осей:
Ох — 2 тот.< (т^,) —
- S /И, (ури - ztvty);
Gy— 2 тот у (m/V/) —
- 2 (wu — х^ии);
G, — 2 mom, (m,vt)
- 'Si'ntfXiVty —
(151)
Кинетический момент системы отно-
сительно некоторого неподвижного
39Э
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
центра равен геометрической сумме мо-
мента количеств движения центра масс
системы, в котором сосредоточена вся
ее масса, относительно данного центра
и кинетического момента системы отно-
сительно центра масс в относительном
движении по отношению к осям, про-
ходящим через центр масс и движу-
щимся поступательно:
Go •» тота (Mvc) + Ge =
-KXMvc + O'c, (152)
где штрих означает, что надо брать
относительные скорости.
Теорема моментов коли-
честв движения или теорема
о кинетическом моменте.
Производная по времени от кинетиче-
ского момента системы относительно
некоторого центра (неподвижного или
же относительно центра масс) равна
главному моменту внешних сил относи-
тельно того же центра:
VJ?0(A,)- <153)
В координатной форме:
= д • _ / - dGf _ / (154)
dt Lx' dt У dt r ' '
Если Ln = 0, to (ja = const по вели-
чине и направлению. Gr, Gy. G, выра-
жаются через секторные скорости о<
отдельных точек:
Од " т1я1уг> О» ™ 2 У. mflirn
Gt - 2 V т,з1ху.
В случае обращения в нуль одного
нз главных
моментов сил, например
£х = 0, имеет место
интеграл площа-
дей
V т(з1уг “ const.
Фиг. 98. Пру-
жинный регула- *
тор.
Аналогичные выраже-
ния получаются в слу-
чаях —0 или L, — 0.
Пример, При изменении угловой скорости
и •_ ю » грузы пружинного регулятора (фиг. 98),
вышине иа рзсстоинин I от оси. перемешаются
на расстояние д. Массой псеа частей механизма,
кроме грузов, пренебрегаем. Определить ш.
Решение. i -1.-0; О, - Jmr -
Щ • • *У
“ conal; Ло, — (/ + др ш, отсюда
Р
-“(ТПл*
Кинетическая энергия системы.
Теорема кинетической энергии. Кине-
тической энергией или живой силой
системы называется сумма произведе-
ний масс всех ее точек на квадраты их
скоростей:
(155)
Кинетическая энергия системы равна
сумме кинетической энергии центра
масс системы, в котором сосредоточена
вся ее масса, и кинетической энергии
в относительном движении системы по
отношению к осям, проходящим .через
центр масс и движущимся поступательно:
Т
Moi
(156)
2
где штрих означает, что надо брать
относительные скорости.
Теорема кинетической
энергии для системы. При-
ращение кинетической энергии системы
на некотором перемещении (элементар-
ном или конечном) равно сумме работ
всех приложенных сил как внешних,
так н внутренних:
Т - Тй = + 2?"’уя* • (,57>
Если система неизменяемая, то
Роль наложенных связей та же, что
в случае точки. При движении в по-
тенциальном поле имеет место закон
сохранения механической энергии:
Т -f- П в /р 4- riff — const, (158)
Фиг. 99. Движение
вягииеток пи на-
клон и им плоско-
стям.
где П — потенциальная энергия си-
стемы. В этом случае система назы-
вается консервативной.
При игр. По наклонным плоскостям с углом а
движутся вагонетки яссом О, и О, {О, > О,).
Определить скорость него
меток, когда они нз со-
стояния покоя пройдут
путь « (фиг. 99). Трением
пренебречь.
Злесы Г, — 0; Г —
-.°, -t-g'-c.; П.-Л-
2g
— (Gj — Gj J aln a;
Г<О« ~ s 8
У
ДИНАМИКА СИСТЕМЫ
391
Общие принципы динамики системы
Принцип Даламбера. Если ко всем
точкам системы приложить силы инер-
ции. то активные силы, реакции связей
и силы инерции будут уранновеши
ваться.
Уравнения равновесия составляются
таким же образом, как в статике, н
носят название уравнений кинетоста-
тики (см. стр. 387)
Обшее уравнение кинетостатики.
Объединение принципа возможных пере-
мещений и принципа Даламбера гла-
сит: сумма элементарных работ всех
активных сил, приложенных к мате-
риальной системе, подчиненной идеаль-
ным неосвобождающим связям, и сил
инерции на всяком возможном переме-
щении равна нулю, т. е.
V{(^ —m/jrjLc, + (r/-m/y<)eyJ4-
+ -0, (159)
Фиг. 100. Центробеж-
ный регулятор.
где X,, Yt, Zt — проекции активных
сил; г,. у(. г, — координаты точек
их приложения
Пример. Центробежный регулятор состоит ил
хвух шаров весом О, « Ох = О. муфты весом О,
и четырех стержней,
весами которых можно
пренебречь |фи|. КО).
Размеры указаны. Оп-
ределить угол и. если
о, = const.
Если силы инерции
шаров обозначить че-
рез Ф • Ф, » Ф то об-
щее ypai исние «иието-
статмки примет вил
ОЛ». 4- 2О»у +
4-2ФЙЖ-О,
ГМ
у. — 2а сов ; у, — у( — v — ( со» о;
ж, — — ж, ии х — I »1п у;
тогда
— 2аО„ tin * — 2/0 tin в +•
f/у нФ ЯП у со»»)*.—О.
По коиструктиаатым сооЛражеииям » * 0. еле-
Уравнения Лагранжа 1-го рота.
В случае несвободной системы коорди-
наты ее точек должны удовлетворить
уравнениям связей
г/Ивл.*......** у»- г«> - °;
у-i. a,.... s.
(160)
Уравнения движения в форме Ла-
гранжа:
(161)
Из этих уравнений и уравнений свя-
зей определяются все Зп -Ь s неизвест-
ных: Зп координат и s множителей
связи kj.
Пример. Движение точки по гладкий иоосрк-
НОСТК
fix. у. 0.
Урашгепия Дагранжз принимают вид
Эти уравнения интегрируются совместно с
уравнением покерхпогти Н торне члены правых
частей являются проекциями нормальной реакции
поверхности, величина реакции
N - |А|
Ура имен и я Лагранжа 2-го рова. При
отнесении движения системы к обоб-
щенным коораниа1ям qlt qi, .... q* урав-
нении движения имеют вид:
(162)
/-1. 2....,*,
где Т — кинетическая энергия системы;
йь 9». • . 9» — обобщенные скорости;
Qi, Qi.....Q, — обобщенные силы.
В потенциальном поле
О _ - - —_______dfz
V/ “ дц, “ " иЧ,9
rae U — силовая функция; V — потен-
циал, П — потенциальная энергия.
392
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Фиг. 101. Двм-
Пример. Блок весом радиус» г с массой,
распределен»)* оо ободу (фиг. 101). приводится
во ирдшеиие канатом (весом пренебрегаем), несу-
щим грузы G, и G, (О, > <?,).
Определить угловое ускорение
барабана.
Здесь (угол поворота):
Г --jL (0, + О, + О,) гЧ*;
Л = ОЛ, + ОА
гае Н, — Л, -f- лр; Н, — ч, —гр
(Л,. Л, — начальные высоты
грузов над произвольной гори
эоиталыюй плоскостью):
под действием лт j
грузов. —г- — — (О« + Oi + 0,1 е*ч;
К
дП
= (0, -б,)г;
(Oat O.-bq.Ul.- + (01 _ ед r о *
g ft-о, К_
” 0.-1-О, +о. ’г •
Принцип Остро градского — Гамиль-
тона. Если сравнить действительное
движение консервативной системы
(«прямой путь») с любым кинематически
возможным, бесконечно близким к нему
(«окольный путь»), происходящим в
течение одного и того же промежутка
времени и между одними и теми же
положениями («конфигурациями»), то
вариация «действия» при переходе
с прямого пути к окольному равна
нулю:
6
В ((Г - /7) dt - 0. (163)
где интеграл представляет собой дей-
ствие^
Устойчивость движения. Если дви-
жение системы, определяемое реше-
нием дифференциальных уравнений прн
некоторых определенных начальных
условиях, принять за основное или
невозмущенное, например в обобщенных
координатах
?i-/i(fl: ...
<?<-/<«).
то движение, определяемое изменен-
ными начальными условиями (коорди-
натами и скоростями), называется воз-
мущенным, а величины изменений на-
чальных условий — возмущениями.
Пусть поведение системы в возму-
щенном движении по сравнению с ее
поведением в невоэмущенном движении
определяется совокупностью величин
МЛ. «г(0 5я(0. могущих быть
разностями координат (в основном и
возмущенном движении), скоростей или
их функциями.
Невозмущенное движение системы на
зывается устойчивым по Ляпунову, если
прн всяком наперед заданном положи-
тельном числе е можно указать такое
положительное число 6. зависящее от е,
что при начальном возмущении |s/0)| <
<3 в последующем возмущенном дви-
жении системы будут справедливы в лю-
бой момент времени неравенства
1*/(01 < *
Если, кроме того, все в, -»0 при
t -»оо. то невозмущенное движение
называется асимптотически устойчи-
вым по Ляпунову
В случае равновесия системы У) =
= Уу .ук = являются- также
частными решениями дифференциальных
уравнений движения, вследствие чего
совершенно так же определяется устой-
чивость равновесия по Ляпунову.
МОМЕНТЫ ИНЕРЦИИ
Основные определения
и соотношения
Моментом инерции J тела относи-
тельно точки, оси или плоскости назы-
вается сумма произведений элементов
массы тела на квадраты их расстояний
до точки, оси или плоскости.
J - f r*dm. (164)
Размерность момента
инерции: в абсолютной системе
L*Ml (е-см* или т-жЛ; в технической
системе LWT* (кГ-м сек*).
Если М — полная масса тела. G —его
вес, /4 — радиус инерции тела отно-
сительно осн Д, то момент инерции
относительно осн Д
-0,102G(’ кГ м-cetA (165)
Маховой момент тела относительно
оси есть произведение его веса на ква-
драт диаметра инерции (D 4 — 2/д):
К4 - GD} - 40/д - 39,2/д кГж». (166)
МОМЕНТЫ ИНЕРЦИИ
393
Теорема о параллельных
осях. Момент инерции тела относи-
тельно какой-либо оси равен сумме мо-
мента инерции относительно оси, парал-
лельной первой и проходящей через
его центр масс, и произведения массы
тела на квадрат расстояния между
осями:
J - Jt + Mh*.
(167)
Момент инерции тела относительно
оси А, проходящей через начало коор-
динат и образующей
углы а, р, f с осями
(фиг. 102), равен
1Л = УхСО$*а +
♦иг. 102. Onpeie-
леиме каправлениа
оси трема углами.
+ JyCOS* р 4- 1г C0S*7—
— 21 уг COS Р COS Т —
— 2J,X COS T COS a —
—2Jxy COSa COS P, (168)
где Jjp Jy Jt — моменты инерции отно-
сительно осей координат, а Уу1. 1гх,
1 ху ~ центробежные моменты инер-
ции, илн произведения инерции:
Л = J (У1 + г*) dm:
J г — J (z* + х*) dm:
У,-|(х» + у»)</щ;
Jyt - J У* dm:
Jxx = I tx dm:
Jxv-jxydm.
(169)
Фиг. юз. Поворот
координатного трех-
гранника вокруг
одной из осей ко-
ординат.
Если оси 5, v), С параллельны осям х.
у, г и проходят через центр тяжести
тела, то
Ууг^МусХс + (170)
и т. д.
Ось х называется
главной осью инерции.
если J уу — J гх = 0.
Если тело симмет-
рично относительно
оси, то »та ось глав-
ная. Если тело сим-
метрично относительно плоскости, то
всякая прямая, перпендикулярная к зтой
плоскости, есть главная ось.
Поворот осей координат
вокруг одной нзосей (фиг. 103)
В этом случае
4+4 “4 + 4г! 07П
Л, — Jxy COS 2» + -|- (Jx—Jy) Sin 2a. (172)
Моменты инерции относи-
тельно Н'ачала (•/„) и плоско-
стей координат (Ууог. JtOx. JxOyy.
Л = J (х* + у* + »*) rfm =
•" у Ux + Jу + Л)>
yyOj-jxMm;
JxOy -$***
Jx = JiOx + JxOy
И T. Д.
Для плоских фигур (2=0)
Jx-J0 -Л + ^r
Моменты инерции однородных тел
1) Объемное распределение масс плот-
ности р:
Л - Р-бЛ И; (173)
У 2^ — момент инерции объема.
2) Поверхностное распределение масс
плотности в:
4 - ’ZP; - j (174)
yjfl— момент инерции поверхности
(в частности, площади фигуры).
3) Линейное распределение масс плот-
ности К:
УД-КДЧ //’-.JrVL; (175)
У — момент инерпии длины.
Моменты инерции однородных тел
приведены в табл. 8.
394
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Таблица 3
Моменты инерции однородных тел
г Идеально тонкий стержень: . Afz* 1 .
0$ 7, = —- — — MP sin’ о. При а = 90’ . МР Jt Г
1 ’ Материальна» дуга окружности: 1 **r* i sln , Air* /. aln '« ?у- — (*+— J (• — угол в радианах) Полная окружность (а * ж) •
V / Л
Прямоугольный параллелепипед «кк г, у, г проходят через центр тяже сти и параллельны соответственно сторонам а, Ь. с):
Jx “ 77(®' + JV “ Ъ+
/\
Jt - 4 ю* + »•). При с -» <1 получаем прямоугольную пластинку. Куб со стороной а: J -J -У А “Л
Tj
у?
/X V
1 \у Четырехугольная пирамида с прямоугольным основанием, и — центр тяжепн; Jjt - -£ (« + ЗЛ9-. /у - + W. OU J ои м J* “ T7le'
ь—
• г о_ Прямой круглый цилиндр, О — иентр тяжести Л,-А,—£<*- + *•); При Л — 0 получаем диск.
.. S7 Для боковой поверхности цилиндра 77'*'* + *П:
1 J. Полый цилиндр, О — Hemp тяжести. «'х - >у - —- W +з/-+л,>; А --р'*• + »*). При h + 6 получаем »фугов»»е кольцо
Jj ( Я| '» Прямая приема или пил ни др, О — центр тяжести, ось а паралледьн- ребрам или образующим: 77 + w»): J4 -’^77 +WC): А “ ^3' гае у — плотность; F — плошаю, нормального сачения; 1^. 7 — мо меяты «версии плота ан г среднего сечеиия относительно осей а.у.д
МОМЕНТЫ ИНЕРЦИИ
395
Продолжение табл. 8
прямой Круглый конус, О — центр тяжести: /,-^-5Г*(^ + 4)5 Для боковой поверхности конуса А—Г*''
Z • к Прямой усеченный круглый конус: j - 3 <0 М к> - Л • Для боковой поверхности усеченного конуса J, “~у *(«• + *•)
/О, Прямая пирамида или конус. О, — центр тяжести основания, ось z перпендикулярна основанию; 'а - “Т^Г' где f — плотность: F — плошадь основа ина; J*,, — моменты инер- ции плошали основания относительно осей у', г
Шар: 2 —ЖА Для поверхности тара /.-4м’*
Полый шар:
Шаровой сектор: jt — 4^ (3^ - м—4" •* -с<>* •> р+“* •>• 2 В случае полушара • * 90*. Jt м» — Mf*
0 Шаровой сегааеп: , Mh - 1«г» + Зй«
'«"1м - аг-й '
396
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Продолжение табл, в
Эллипсоид:
/ж_ A(t. + C.): 7j(_ *.(4.+ вЧ;
(О* + »•)
Параболоид вращения
Кольцо прямоугольного сечения
+ 4-»’): G--£(«*+-5-»•+»’)
Кольцо круглого сечения (тор):
Кольцо эллиптического сечения:
Кольцо с сечением, симметричным относительно оси z', параллельной
оси вращения 2. Ось х — любая ось, перпендикулярная к оси z (вообще не
проходящая через центр тяжести сечения):
>г - р.2п/? (ЛЯ* 4- vj,); /х - ₽•«/? (Я/г« 3jf, 4- vx).
где Jx, J?, — моменты инерции площади F относительно осей х, а';
р — плотность
ДИНАМИКА ТВЕРДОГО ТЕЛА
Вращение тела вокруг неподвижной оси
В дальнейшем за ось вращения при-
нята ось z; вращающий момент (сумма
моментов всех сил относительно оси
вращения) обозначен через AG; осталь-
ные обозначения уже применялись.
Кинетический t момент относительно
оси вращения
ог - (176)
Кинетическая энергия
Г -1J^. (177)
Дифференциальное уравнение враще»
ния
j, “ М* (178)
что записывается еще так:
Jt — — Мг или Jtt — Mt.
Прямая задача [дано ? ™ /(/), тре-
буется определить AG] решается диффе-
ренцированием, обратная (отыскание ?
по Мг) — интегрированием дифферен-
циального уравнения. Мг вообще зави-
сит от t, <р, f- Если Al, зависит только
динамика твердого тела
397
01 одной из этих величин, задача ре-
шается так, как указано на стр. 376,
(Основные задачи кинематики враща-
тельного движения» (случаи 4—6).
Уравнение кинетической энергии
2
(179)
это уравнение дает непосредственно
интеграл, если Мг = Мг(у) или Мг—
— const.
Уравнение кинетического момента
г
— Згшй = j Mtdt. (180)
и
это уравнение дает непосредственно
интеграл, если Mz~ Мг(() или Мг =
= const
О мощности см. стр. 366, (Аналити-
ческая статика».
Физический маятник. Физическим
маятником называется твердое тело,
колеблющееся около не-
подвижной осн (обычно
горизонтальной) под дей-
ствием силы тяжести
(фиг. 104).
Точка пересечения оси
подвеса с плоскостью, ей
перпендикулярной и про-
ходящей через центр
фиг км Фиш- тяжести, называется точ-
;«екийм;.™«. подвеса.
Дифференциальное ура-
внение колебаний маятника
/и^Л ,
? --------J- Sin f,
Jo
(181)
где т — масса маятника; Л — расстоя-
ние его центра тяжести от точки под-
веса; Ja — момент инерции относи-
тельно оси подвеса.
Эго уравнение тождественно с урав-
нением колебаний математического
маятника, имеющего длину
(,82>
называемую приведенной длиной физиче-
ского маятника. Конец К отрезка /
(фиг. 104) называется центром качания
маятника. Если центр качания сделать
точкой подвеса, прежняя точка подвеса
станет центром качания, и период
колебаний маятника не изменится.
Приближенная формула для периода
колебаний
Л (183)
(см. стр. 385, (Математический маят-
ник»).
Опытное определение момента инер-
ции при помощи качаний. Известны
О. Л, Т; тогда
''-°* (S-у)- <184)
где Jс — момент инерции относительно
оси, проходящей через центр тяжести
и параллельной оси подвеса.
Давление вращающегося тела на
опоры. А, В —точки опоры (подшип-
ники или подпятники); О — произ-
вольная точка на оси вращения
(фиг. 105). Полные реакции опор ела
гаются из статических, определяемых
по правилам статики, и добавочных
динамических, перпендикулярных к оси,
вращающихся вокруг нее вместе с телом.
Фиг. 108. Реакции, обуслов-
ленные главным вектором (а)
и главным моментом (б) сил
ниерцин.
Фиг. 105. Да-
вление вращаю-
щегося тела на
опоры.
Последние, в свою очередь, распадаются
на реакции N\, N'v обусловленные
главным вектором М7 сил инерции, и
Wp Л^. обусловленные главным мо-
ментом сил инерции (фиг. 106, а
и б) ((16), (23]):
R7 — mre V м<4-(»;
М} - у4J}z + Ах/-* + •’' • (185>
где т — полная масса тела; ге—рас-
стояние центра тяжести от оси вра-
щения. В практических случаях одна
из осей х или г есть главная; тогда
один из центробежных моментов инер-
398
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
ции обращается в нуль, а другой вычис-
ляется с помощью формулы (172).
О наиболее общем случае см. 116],
123).
Тогда, если h = hi 4- ht,
(186)
Условия свободной оси
(добавочные давления отсутствуют): ось
вращения должна быть главной (7>г =
= Jzx = 0) и центральной (хс = уе =0)
осью инерции. В этом случае имеет
место динамическая уравновешенность;
если же выполняется только второе
условие (xf = уе = 0), уравновешен-
ность называется статической.
Плоско-параллельное движение
Пусть К — сечение тела неподвижной
плоскостью, проходящей через центр
тяжести с; R — главный вектор всех
сил; Мс — их главный момент отно-
сительно оси, проходящей через с,
перпендикулярной плоскости (фиг. 107);
Фиг. 107. Динлмикд Фнг. К». Динамика
плоско-паряллельииго движения около непо-
дикжения тела. авнжной точки
тельно этой осн. Дифференциальные
уравнения плоско-параллельного дви-
жения:
— Я о тус — Ry, Jcif— М,
Кинетическая энергия
г mv‘ .
2 + 2 ‘
(187)
(188)
Пример. Кинетическая анергия катящегося
однородного цилиндра весом О равна
2 2^2
г _ О °C 1 Ol* Ve 8
“г’~Г+Т’2г’»*”Т’ g •
Движение около неподвижной точки
Положение осей х, у, г, связанных
с телом, по отношению к неподвижным
осям 6, т„ С определяется углами Эйлера
р, ф, 0 (фиг. 108). За оси е, у, г прини-
маются главные оси инерции тела.
Скорость и конца кинетического
момента О'0 относительно неподвижной
точки О равна главному моменту Ма
всех приложенных сил (теорема Резаля).
Проекции Go на осн х. у, г (или
кинетические моменты относительно
осей):
Gx Jхшх' Оу У^У'
О? =
Кинетическая энергия
7’-4(-,x“x + V5+-/^)- (190)
Уравнения движения тела, отнесен-
ные к осям х, у, г (динамические урав-
нения Эйлера):
(189)
Jx + (Л — Jyl “у"д — Мх>
(гЭ у
•ly —I" (Лг — А) гад“х “ Му ;
А + (jj, — Jx) ШХШУ = Мг.
(191)
где Мх, Му, Мг — главные моменты
сил относительно осей х, у, г. Эти
уравнения интегрируются совместно
с кинематическими уравнениями Эйлера
(см. стр. 380).
Фиг. 109. Гироскоп.
Г нроскоп
Гироскопом (или жироскопом) назы-
вается симметричное абсолютно твердое
тело вращения, быстро вращающееся
вокруг своей оси ма-
териальной симме-
трии (фиг. 109).
Если угловая ско-
рость собственного
вращения ш( много
больше угловой ско-
рости 0>2 осн гироско-
па, то принимается,
что кинетический мо-
мент гироскопа Go,
называемый собственным моментом,
направлен вдоль o>t и равен
Оо - Л-|. (192)
где Jg — момент инерции относительно
оси симметрии.
ДИНАМИКА ТЕЛА ПЕРЕМЕННОЙ МАССЫ
399
Сумма моментов всех сил инерции
гироскопа относительно неподвижной
точки называется гироскопическим мо-
ментом; в векторной форме он прибли-
женно равен
Л1? = х “*•
я алгебраической
Mg = Уг<01«>2 sin fl. (193)
Действие гироскопического момента
на связи называется гироскопическим
эффектом.
Правило Жуковского —Грюэ.
При повороте оси быстро вращающегося
гироскопа возникает лара сил с момен-
том Mg, стремящаяся привести к совпа-
дению вектор угловой скорости «>]
собственного вращения с вектором ь>2
наложенного вращения
Гироскопический момент Mg равен
и противоположен моменту Ма актив-
ных сил и реакций.
Вращение оси гироскопа с угловой
скоростью «>2 при fl = const называется
регулярной прецессией. Момент внеш-
них сил, обеспечивающий регулярную
прецессию при любых Ш] и <*>2, равен
Л!о= +^£Z<5.^cosfl), (194)
где J г — момент инерции гироскопа от-
носительно оси, проходящей через не-
подвижную точку и перпендикулярную
к оси гироскопа г.
Эта точная формула совпадает с при-
ближенной при 0 = 90° и может быть
«вменена приближенной при о»! > <>».
Примеры'.
1. К оги ураоноигшениого гироскоп» с тремя
степенями свободы (Фиг. IЮ) я кдрд»-
поаом поялесе приложено сил» Р ио расстоянии Л
Фиг. ПО. Гироскоп с
тремя степенями сво-
боды.
Фиг. Hi. Гироскоп с
двумя степенями сво-
боды.
от О (например, добавочный грузик). По теореме
Резяля скорость кони»
и “ О„а>» “ •" М, — РА
Отсюда угловая скорость прецессии <о, -=--.
'г*'
2. Оси гироскопа с двумя степенями
свободы (фиг. 111) сообщено принужденное
вращение с угловой скоростью О А = ОН к.
Здесь М, есть момент реактивной пари ;R, R”).
приложенной к оси гироскоп», я Mg — момент
пары давлений (Р, Р"), приложенной к подшипни-
кам. стремящейся повернуть всю установку в со-
гласии с правилом Жуковского — Грю». Очевидно.
Р-Р
Общий случай движения твердого
тела
Составляются три уравнения движе-
ния центра инерции, три динамических
и три кинематических уравнения Эйлер»
для движения тела относительно посту-
пательно движущихся осей координат,
имеющих начало в центре инерции.
ДИНАМИКА ТЕЛА ПЕРЕМЕННОЙ
МАССЫ
Тело переменной массы. Телом пере-
менной массы называется тело, масс»
которого изменяется вследствие про-
цесса присоединения к нему или отде-
ления от него элементарных частиц, т. е.
частицы, изменяющие массу, не возни-
кают и не исчезают, а лишь вводятся
в рассмотрение или исключаются из
него (|3|, [101, (16|).
Теорема количеств движения. Про-
изводная по времени от главного век-
тора количеств движения тела перемен-
ной массы, вычисленная в предположе-
нии постоянства масс, равна сумме
главного вектора внешних сил и глав
ного вектора реактивных сил:
- R + (195)
at
где
d*K VI dv, dK \ldrn!-.
dt “ dt “ dt dt
Rp‘aKn _ («/ - V) )1 (196>
v, — абсолютная скорость точки массы
m,(t); и, — абсолютная скорость при-
соединяющейся (dm, > 0) или отде-
ляющейся (dm, < 0) массы.
4ГК)
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
В координатное форме:
dt
d*K,
~di~
- Ry + RpeOKm ;
(197)
нии постоянства масс, равна сумме
главного момента внешних сил и глав-
ного момента реактивных сил относи-
тельно того же центра-
-^5- = £в + . (200)
d*Kt
dt
R, + RPfaKm.
где
Теорема о движении центра инерции.
Точка тела переменной массы, совпа-
дающая в данный момент с его центром
инерции, имеет ускорение, какое имела
бы материальная точка, обладающая
массой тела в рассматриваемый момент,
под действием всех внешних и реактив-
ных сил:
М - R + RPea“m. (198)
— у тОтй _ v-)) „
= S Р/Х й, (й/—v()}; (201)
Здесь ас есть ускорение точки тела,
совпадающей с центром инерции, иначе
говоря, ускорение центра инерции тела
при постоянной его массе, равной массе
в данный момент (т. е. без учета пере-
мещения центра инерции внутри тела
вследствие изменения массы)
vt — абсолютная скорость точки массы
m,(0; “z — абсолютная скорость при
соединяющейся (dm, > 0) или отде-
ляющейся (dmi <Г 0) массы.
В координатной форме:
d*Gx
dt =
Lx + LPxeaKm ;
dt •
где vc есть скорость центра инерции
при постоянной массе, причем
М (О V* - К.
где К есть главный вектор количеств
движения тела в данный момент вре-
мени без учета присоединения или от-
деления частиц.
Уравнения движения центра инерции
• координатной форме:
У > , г реакт ,
—йГ = + у •
^~Lt + LPfalcm.
(202)
Пример. На барабан, имеющий горизонталь-
------------------- ------• ‘ - весом р на гаи
MaCJt -R„ + RP‘axm;
- Rv + ;
Ма„ - R, + Rp,a*'n .
(199)
где M = M(f).
Теорема моментов количеств движе-
ния. Производная по времени от кине-
тического момента системы относительно
«екоторого центра (неподвижного или
же относительно центра эафиксирован-
«ых масс), вычисленная в предположе-
кую ось, намотан трос алиной /
вицу длины. Радиус барабаиаг,
его момент инерции /„. Прене-
брегав сопротивлениями, опре-
делить скорость троса в тот
момент, когда он весь сойдет
с барабана (фиг. 112).
Пусть ось ж направлена по
оси барабана за чертеж, ось
у— горизонтально вправо, а ось
а — вертикально вниз. Разре-
зав трос о месте его схода е
барабана и вводя силу натяже-
ния N, рассматриваем отдельно
барабан с убывающей массой и
свешивающуюся часть троса е
возрастающей массой. Тогда
для барабана
d"O,
-^.Ljs + LP^m,
и
фиг. ИХ Дни
жение барабана
под влиянием
троса.
для Трос»
л* к.
Так как скорость сходящих е барабана элемен-
тов троса равна окружной скорости барабана, то
относительная скорость их равна нулю, а понтону
ДИНАМИКА ТЕЛА ПЕРЕМЕННОЙ МАССЫ
401
главный Moueirr реактивных сил масс, отделяю-
щихся от барабана, и главный вектор реактивных
сил масс, присоединяющихся к свешивающейся
части троса, равны нулю, т. е.
~ о.
Далее:
4Х ~ Nr; Rt = pi — N;
+ft'-*>'•]
*x = f
d’K о do,
— —i t. — ! -— —
dt g dt
Подставляя в исходные уравнения и принимая
во внимание, что — «г. имеем
f х i -px - W.
Исключаем TV:
(Z>K + />*'•) X — pgr'l-
Введем обозначение
IP,_____Ш-r-.
Jtg +pit*
Тогда
»• A’x.
Так как зякь
то. интегрируя, имеем
V* . А>Х< + с.
При f-0, х~1№ е—0, т. a. В МО-
мант схода х — Окончательно
е-*УР-в.
Теорема кинетической энергии. Диффе-
ренциал кинетической энергии тела
переменной массы равен сумме элемен-
тарных работ всех внешних, внутрен-
них и реактивных сил, приложенных
к данному телу, и кинетической энергии
присоединяющихся (dm, > 0) или отде-
ляющихся (dm! < 0) масс за соответ-
26 Том I Зак. )«и
ствующий элементарный промежуток
времени, обусловленный их переносным
движением:
-7-2^-
= 2 (<Г
+rf ,Ар,акт) + -2 V dmtv-, (203)
где штрихи показывают, что соответ-
ствующие элементарные величины вооб-
ще не являются дифференциалами, а
d' А/*™” (и!- о,) dr, =
= «i ((«<ж — vlx)djt! +
+ (uly — va) dy, + (au — vu) dz,) (204)
причем u( — абсолютная скорость при-
соединяющихся или отделяющихся ча-
стиц; vt —абсолютная скорость частиц,
остающихся связанными с телом.
Если ввести дифференциал кинетиче-
ской энергии в предположении неизме-
няемости массы за данный элементар-
ный промежуток времени, то
<ûà - S (<7Амеш + d’tW +
где
+ d'APeaKm), (2(b)
Уравнения движения твердо го телу
около неподвижной точки:
Jg + ~ ***** ”
- Af, + ;
Jу + (J л — J A “x“x =
- My + MP,ait,a;
d*i».
(206)
- Mt + AffaKm .
Эти уравнения относятся также к слу-
чаю движения свободного твердого Пй«
около центра инерции.
402
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Здесь х, у, г — главные оси инерции
в неподвижной точке (или в центре инер-
ции), вообще непрерывно меняющие свое
положение в теле вследствие присоеди-
нения или отделения масс. Производные
от шх, ыу, шг вычислены в предположе-
нии неизменного положения осей коор-
динат в теле соответственно распределе-
нию масс в данный момент времени;
Jх, Jу, Jz — мгновенные значения глав-
ных моментов инерции относительно
этих осей; Мх, Мг — главные мо-
менты приложенных к телу сил (вра-
щающие моменты); Мрракт-
мреакт — глаВцЫС моменты реактивных
сил.
УДАР
Основные положения. Ударом назы-
вается явление, происходящее в меха-
нической системе, характеризуемое рез-
ким изменением скоростей ее точек
за весьма малый промежуток времени
и обусловленное кратковременным дей-
ствием весьма больших сил. Этими си-
лами, называемыми мгновенными, могут
быть как силы активные, так и реакции
мгновенно налагаемых связей. В послед-
нем случае удар называется неупругим,
если наложенные связи сохраняются при
дальнейшем движении системы; удар на-
зывается упругим (вполне или не вполне),
если за мгновенным наложением связей
следует мгновенное снятие связей. Дей-
ствие мгновенной силы Р измеряется ее
импульсом:
1 - j Р dt (2Q1}
или в проекциях
JXrf/;
J Zdt,
о
(208)
где X, Y, 2 — проекции силы 7s на оси
координат; т — время удара. Импульс 7
называется ударным импульсом или
просто ударом. Импульсами конечных
сил (неударных) при ударе пренебре-
гают.
Улар точки о поверхность. Скорость
падения (до удара) и и скорость отраже-
ния и' (после удара) разлагаются на
нормальные и тангенциальные соста
вляющие:
vn = v cos a; vt = о sin «;
v'n = o'cosо, = о' sin р,
где аир — углы падения
(фиг. 113).
Для проекций скоро-
стей имеют место соот-
ношения (16]
и отражения
Фиг. ИЗ. Улар
точка о поверх-
ность.
(209)
где k — коэффициент
восстановления; X—ксаф-
фициент мгновенного трения. Эти физи-
ческие константы определяются экспе-
риментально для каждой пары соударя-
ющихся тел (здесь — частица и поверх-
ность). Предельные случаи:
k = О— тела абсолютно неупруги;
k — 1 » » упруги;
X — 0 > » гладки;
X — 1 » » шероховаты.
Вообще 0 < £ < 1, 0 < X < 1; при
этом по большей части полагают Х=0.
В общем случае
h
tg-ug?--^.
Пример. Шарик падает с высоты Ло ил гори
эонтальную плиту, от которой отражается, до
тигля высоты Л.
Здесь v* — t>t —0.
Коэффициент восстановления
Vn __ Гh
vn ” FA.’
Общие теоремы динамики системы
в применении к удару
Теорема количеств движения. Прира-
щение главного вектора количеств дви-
жения системы за время удара равно
сумме всех внешних ударных импуль-
сов:
ДКж- S/ul
дк, - 21„.
ДА - £ 7,
(210)
УДАР
403
Теорема о движении центра инерции.
Приращение количества движения
центра инерции в предположении, что
в нем сосредоточена вся масса системы,
за время удара равно сумме всех внеш-
них ударных импульсов:
- 2 hx.
M^Vff ~ 2/!*•
(211)
AMvc — 27/
Теорема моментов количеств движе-
ния Приращение кинетического мо-
мента системы относительно некоторой
неподвижной точки за время удара
равно сумме моментов всех внешних
ударных импульсов относительно этой
точки:
ДО,-
= ^,тотг (/,);
« 2 тот0 (!,} = 2 тот у (7/);
*0,-
— 2 *яо/я/ (7().
Принцип возможных перемещений для
удара. Этот принцип выражается урав-
нением Остроградского
Sl(7/jr~*’^V/jr) 4у/+
+ (Л< — U,| — 0 (213)
и может быть высказан так: потерян-
ные количества движения системы при
ударе уравновешиваются ударными им-
пульсами (на потерн указывают знаки
минус перед и т. д.).
Теорема о потере кинетической энер-
гии (теорема Карно — Остроградского).
При мгновенном наложении связей
потерянная кинетическая энергия си-
стемы равна кинетической энергии
потерянных скоростей:
+ Ь/ “ +(»/.“ <«)*] (214)
Удар двух тел
Определения Прямая, проходящая
через точку соприкосновения тел при
ударе, направленная параллельно отно-
сительной скорости их центров тяжести
в начале удара, называется линией
удара. Удар называется центральным,
если линия удара проходит через
центры тяжести тел, в противном слу-
чае — эксцентричным или внецентрен-
ным. Удар называется прямым, если
линия удара перпендикулярна элемен-
тарной площадке соприкасания тел при
ударе, в противном случае он назы-
вается косым.
Время удара -с делится на два периода
(t = ci + cj): 1-й период — от момента
соприкасания до момента наибольшего
сближения; 2-й период — от момента
наибольшего сближения до момента
разъединения.
Формулы для k и X принимают вид
k
V«1-Vn^Vn
—-----«1; l-X---«----—,(215)
vn.’ vra— ”n '
т. e. сюда входят относительные ско-
рости.
Прямой центральный удар. Пусть
mi и "и — массы тел; t>i и vj—
скорости до удара (берутся со знаком
плюс или минус в зависимости от их
направления вдоль линии удара); oj
и t>2 — скорости после • удара; о —
общая скорость тел в момент наиболь-
шего сближения. Тогда
mjvJ + mtv'2 — («| + mj) v —
— »»|Vi + mjcij; (216)
t’2 — oj = It (V| — Oj);
v «io, -f- ищ
/П| -Г «2
«I - v + k —T2 -;
JR] -f-
(217)
v't - v + A (v, — СЧ) .
• ni\ -j- tWj
Импульсы взаимодействия в 1-й и 2-й
периоды удара (считая о, > щ)
; (у, - У;) .
1 “ mt + т, ’
к _ т/Л^А (t>i - <ч)
«I 4- тг
(218)
404
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Полный импульс за все время удара
j _ (У| — о?) (1 4- Л) (219)
“ + л*»
Потерянная кинетическая энергия
(V! — о,)* 1 2 (1 — Л’)
------------2 («, + «,) ’ t220)
где Г* — кинетическая энергия поте-
рянных скоростей.
«!(»,-»',)’+л (о,-<4)’-
"»!*> (Р, — О0* (1 Ч- *)* (22П
2 («, + «,) * ' '
♦иг. 114.
Забивка
сваи.
Частные случаи:
1) Л-0; Го— 7 = Т*;
2) Л-l; Т9-Т = 0.
Пример. Баба копра несом G, кГ падает с вы-
соты h см ва сваю весом О, кГ и забивает сс
в грунт (фиг. 114). Найти среднее
сопротивление К грунта, если за
л уларов свая углубилась на г ем.
Улар можно считать неупругим
(*-0).
Здесь о, - F'577. th-O. М —
— Л 4 — — средняя высота пале-
ния бабы за л ударов.
я.»?
Г. —у1 -О.«;
"•"«’’1 o,(hH .
” 2 («а, -I- ла.) “ О. 4 О, ’
G?H
r-T.-tr.-D-g^.
По теореме кинетической энергии
-«>" «О?
К~ (О. 4 о,) 1 (* + г)"
Общий случай удара двух тел. Общие
уравнения удара. Ось X неподвижной
системы OX FZ направлена параллельно
нормали к общей элементарной пло-
щадке в точке соприкосновения тел при
ударе (нормали удара); С», С» — цен-
фиг. 115. Общий случай улара двух
тел.
тры масс 1-го и 2-го тел (фиг. 115);
к, у, г — главные оси инерции 1-го
тела; ?, -эд, С — главные оси инерции
2-го тела; mi, mi — массы тел; JljCt
J ’ J\v х — их моменты
инерции; обозначения линейных и угло-
вых скоростей — обычные, причем ско-
рости после удара отмечены штрихом
сверху. Скорости центров масс обозна-
чены просто о, и о,, а скорости точек А
и В соударения тел йд, vB. 12 кинема-
тических величин являются известными:
°ly uli> v2l« °2ip рх> “и,
“|у, “и- <“2tj- “» *2 — искомыми:
°lx> °ly vlz> °2i’ в2ч> °Х> “|х> “1у
“1т« “»• “2г “X-
Скорости точек А и В могут быть по
кинематическим формулам выражены
соответственно через от, •»>, о», ы* и
координаты точек А и В.
В общем случае должно быть всего
12 уравнений, семь из которых не зави-
сят от физической природы тел, именно
118].
Лд (“и - -и) - «1 { УА (4, - Vu) - Хд (о]у - Оу)] - 0;
Лу («]у - “1л) ~ *1 рА « - »и) - *А («И - Vu)] - 0;
Л,(в>;,-«и)-«1 [ХА Ну — М — >А«-®1г)] -°;
тг (<4с -"к) - «г,)] -°;
•'2ч(“2,-“2,)-т1 MVk -«») -^в(«Х -®х)] “°-
Jk (“« - -х) - mt - w2,) - ’le (их - V»E)] “ °:
(222)
УДАР
405
+ m2v2X = mlvlX + m2t,2X- (223)
Восьмое уравнение зависит от коэф-
фициента восстановления:
v'bx ~vAX = k («АХ - vbx>- (224)
В развернутой форме уравнение (224)
имеет вид
[»2Х + (ш^в — "с Чв) cos (Е. X) +
+ (“с?в — ^b)cos(t), *) +
+ (ШЁТ1В — “^в) cos (С. X)] —
~ Нх + ("/а — “ЁУл) cos (х. X) +
+ (“Иа — v'^a) cos (у. X) +
+ (“хУд — “Ил) cos <*• "
- * (frix + (“На — “хУа) cos (X, X) +
+ (“На — “На) cos (у, X) +
+ (“хУа — “На) cos (г. X)] — [«« +
+ ("‘J.B — “fie) cos (;, X) +
+ (“<58 — ш^в) cos (tj. X) +
+ (<*eiB — “т*в) cos (С. X) |}.
Остальные четыре уравнения зависят
от шероховатости тел.
Случай абсолютно гладких
тел (А = 0). Ударный импульс /,«»—72
перпендикулярен плоскости YOZ:
®1Г— V1Z—о|2 —0; |
, , } (22э)
°2У — v2Г " °’ V2Z — °2Z “ °- J
Случай абсолютно шерохо-
ватых тел ()»1). В месте сопри-
косновения тел скольжение отсутствует:
«ЛУ-»Вг; v'AZ-v'BZ. (226)
В развернутой форме:
Промежуточный случай
(0 < А < 1). Последние два уравне-
ния сохраняются; недостающие два
уравнения находятся путем исключения
нормального импульса I взаимодей-
ствия тел из системы:
«1 (v'ix — vix)-Л
«1 (®Jy— ®1У) — — Л cos у;
®i (vjz —v1Z) “ - Л sin?,
где /—коэффициент трения
тел в месте соударения;
? — угол между осью Y
и осью и, по которой
происходит скольжение
поверхности 1-го тела
по поверхности 2-го
(фиг. 116).
Уравнения для опреде-
ления О] у и viz:
скольжения
Фнг.116. Вззнм-
но€ проскаль-
зывание тел в
месте контакта
при уларе.
«; х - о, у - f (®;л - V, х) cos ?;
VIZ — ®1Z - f (v'\x — »ix) s,n f •
(229)
Зная Оуу и viz, можно из уравнений
(228) найти о'2У и o^z-
В частных случаях, с которыми
обычно приходится иметь дело, число
неизвестных бывает меньше 12, и тогда
достаточно использовать только часть
указанных уравнений, структура кото-
рых в этих практических случаях также
оказывается более простой.
v^r+(«/А —“ЁУл) cos (х. У) + («Ёхд-«>x)cos(y, У)+
+ (“хУА — “у^л) cos (*. и “ V2Y + (“лСВ — “сЧв) COS (Е. У) +
+ (“с»в—“ев) cos (Т(, У) 4- («Ёчв—“Ё^в) cos (С, У);
v'lZ + (“/А — “ЁУа) cos + (“i^A —“^а) COS (y,Z) +
+ (“хУЛ — “ЁЛа) COS (z. Z) — VjZ 4 («^в — “сЧв) cos (Е. Z) +
+ (“Ё^в — ы^в) cos (1). Z) + («(Х|в — “vfl)cos (С, Z).
Сюда добавляются еще два уравне-
ния:
mivlZ’^m*v2Z““'niVtZ'^ miv2Z •
(228)
Действие удара иа вращающееся
твердое тело
Для твердого тела, вращающегося
вокруг оси г и подвергающегося дей-
ствию ударов, имеет место уравнение
ЛЛш “ S momt (I/),
406
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
где Дш = <и' — ш есть изменение угло-
вой скорости за время т действия
импульсов /j, It,... Ниже приводятся
условия, при которых
ось вращения АВ
тела (фиг. 117) не ис-
пытывает действия
улара /, приложен-
ного в точке К тела
(ось г — ось враще-
ния, ось х проходит
через точку К):
1) удар 1 должен
быть направлен пер-
пендикулярно осн
вращения;
быть направлен пер-
пендикулярно плоскости, проходящей
через ось вращения и центр тяже-
сти с (следовательно, точки К и с
должны лежать в одной плоскости с
осью г);
3) ось вращения должна быть глав-
ной осью инерции в точке пересечения
ее с плоскостью хОу, проходящей через
= Jyt = 0):
4) точки с и К должны лежать по
одну сторону оси вращения, причем
должно иметь место равенство
(230)
Фиг. 118.
Маятнико-
вый копер.
где it — радиус инерции тела относи-
тельно оси z. Это — формула, опреде-
ляющая приведенную длину I физиче-
ского маятника. Точка К в этом случае
называется центром удара.
Если тело имеет плоскость матери-
альной симметрии, перпендикулярную
к оси вращения (напри-
мер, плоскость хОу), то
точки К и с лежат в этой
плоскости.
Пример. Маятниковый копер
Шарли для испытания материалов
ударом (фиг. 118) имеет пло-
скость симметрии (хОу). В таком
случае центр удара К и центр тя-
жести е лежат на осевой лилии
маятника (ось Ох); при атом
Легко видеть, что все четыре условия удовле-
творены, и ось вращения (От) не испытывает дей-
ствия удара.
ЛИТЕРАТУРА И ИСТОЧНИКИ
1. А и ано в Г. Д„ Метод ортогональных
проекций в задачах механики. Гостехизлат, 1948.
2. А с т а ф ь е а А. ф„ Инженерная справоч-
ная книга, т. 1. Машгиз, 1947.
3. Ь у т е и и и И. В., Л а з е е в С. И., По-
лов Е. П.. Курс теоретической механики, ч. I
и II, ЛКВВИА. IW8-1&0.
4. Волохов А. Н., Опытное определение
моментов инерции, .Труды НАГИ*, вып. 285, 1936.
А. Порой ков И. М., Курс теоретической
механики, Гостехизлат, 1940.
6. Добровольский В. В., Теория меха-
иизмог, Машгиз, 1951.
1. Жуковский Н. В., Полное собрание
сочинений, лекции, вып. 3-6, НКАП СССР ГИОП,
1939.
8. К и р п и ч е в В. Л„ Основания графической
статики, ГТТИ, 1933.
9. Космодемьянский А. А., Курс тео-
ретической механики, Учпедгиз, 1949.
IU. Космодемьянский А. А., Механика
тела переменной массы, изд. ВВИЛ им. Жуков-
ского, 1947.
II. Космодемьянский А. А„ Очерки
по истории теорсгнческой механики в России,
.Ученые записки МГУ, вып. 122, т. II, изл. МГУ,
1918.
12. К о х е л ь и и к о и Л. П.. Винтовое счисле-
ние и иске! рые его приложения к геометрии и
механике. .Ученые записки Казанского универси-
тета*, Казни, |Ь95.
13. Котельников А. П„ Точки Бурместра,
Их свойства и построение, .Математический сбор-
ник*. т. 34, иып. 3—4, 1927.
14. Котельников А. П„ Заметки по гра-
фической динамике. .Труды Московского механи-
ко-машиностроительного института ни. Баумана*,
вып. 29-30, I 37.
15. Крыло» А. Н. и К рут коп 10. А.,
Общая теория гироскопов к некоторых техниче-
ских их применений, АН СССР, 1942.
16. Л о й ц я и с к и й Л. Г. и Л у р ь е А. И..
Курс теоретической механики, ч. 1 и II, Гостех-
нзлат. 1948.
П. Л я п у и о в А. И.. Общая задача об устой-
чив ости движения, ОНТИ, 1935.
18. Энциклопедический справочник, .Машино-
строение*, т. 1. ки. 2. Машгиз, 1947.
19, Мещерский И. В., Курс теоретической
механики, ч. I и II. Гостехизлат, 1930.
20. Н е к р а с о в А. И., Курс теоретической
механики, Гостехизлат, я. I, 1950. я. II. 191x3.
21. Николаи Е. Л..Теоретическая механика,
я. I и II, Гостехшаат, 1950.
22. Обморшев А. Н., О видоизменении
способа Риттера расчета ферм, .Труды Москов-
ского механико-машиностроительного института
им. Баумана*, вып. 31. 1935.
23. о б ы о р ш е в А. Н., Вычисление опорных
реакций нраииюшегося твердого тела. .Труды
кафедры теоретической механики МВТУ им. Бау-
мана*-, изд. МИГУ, 1949.
24. О с т р о г р а л е к в й М. В., Собр. соч.,
АН СССР, 1946.
25. ПопояА. А., Новый метоа интегрирова-
ния с помощью ортогональных фокусов, Гостех-
нэлат. 1947.
26. С е л о я Л. И., Методы подобая и размер-
ности п механике, Гостехизлат, 1951.
27. С е и а Л. А., Единицы измерения физиче-
ских величии, Гостехизлат, 19W.
28. С м и р и о я Л. П., Кинематика механизмов
и машин. Госиздат, 1926.
2. . Справочник по технической механике под
рел. акад. А. Н. Линника. Гостехизлат, 1949.
30. С у с л о в Г. К., Аналитическая механика,
Гостехизлат, 1544.
31. Техническая аицнклопедия, ж >3, Гостах
издат, 1941.
32. Уманский А. А., Пространственные
системы, Стройиздат, 1948.
ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
ГЛАВА XIX
ОБЩАЯ ЧАСТЬ
СТРУКТУРА И КЛАССИФИКАЦИЯ
МЕХАНИЗМОВ
Основные понятия
Деталь — отдельная неделимая часть
машины, состоящая из монолитного ма-
териала или из нескольких кусков,
соединенных сваркой или другими по-
добными способами.
Звено — одна или несколько непо-
движно скрепленных деталей. Твердые
звенья принимаются за абсолютно жест-
кие по отношению к любым деформа-
циям, гибкие звенья — за абсолютно
жесткие по отношению к некоторым де-
формациям (нерастяжнмые нити и т. п.).
Кинематическая пара — подвижное
соединение двух твердых звеньев, на-
кладывающее ограничения на их отно-
сительное движение.
Элемент кинематической пары — по-
верхность или совокупность поверх-
ностей каждого эвена, входящих в
соприкосновение при образовании ки-
нематической пары. Таким образом, ки-
нематическая пара имеет два элемента.
Кинематическая цепь — ряд звеньев,
связанных между собой кинематическими
парами.
Механизм — кинематическая цепь с
одним неподвижно закрепленным звеном
(стойкой), в которой при заданном дви-
жении одного или нескольких звеньев
(ведущих) все остальные звенья (ведо-
мые) получают вполне определенные
движения. Ведущим звеном называется
звено, закон движения которого задан.
Не следует смешивать ведущее звено
с движущим, к которому приклады-
вается движущая механизм сила. На-
пример, у поршневых двигателя и ком-
прессора ведущими являются криво-
шипы, а их движущие звенья — разные:
у двигателя—поршень, у компрессора —
тот же кривошип.
Структура и классификация
кинематических пар
Степени свободы и условия связи.
Отдельно взятое звено (твердое тело)
имеет в пространстве шесть степеней
свободы. Если два звена связаны между
собой кинематической парой, то на дви-
жение одного из них относительно дру-
гого налагаются ограничения, выражаю-
щиеся условиями связи — зависимостями
между значениями координат относи-
тельного положения звеньев илн равен-
ством некоторых координат постоянным
величинам. Оставшееся в относительном
движении звеньев число степеней сво-
боды
W - 6 - S.
где 5 — число условий связи кинемати-
ческой пары, для которой оно является
основной структурной характеристикой.
По числу условий связи
кинематические пары разделяются на
пять классов (табл. I). При 5 = 6 кине-
матическая пара вырождается в непо
двнжное соединение |1].
По характеру соприко-
сновения элементов кинематиче-
ские пары разделяются на низшие,
высшие и смешанные. Низшие пары
имеют соприкосновение элементов по
поверхностям, высшие — по линиям
или в точках.
Низшие пары применяются в прак-
тике шести типов: шаровая и плоскост-
ная (111 класс), цилиндрическая
(IV класс), вращательная, поступатель-
ная и винтовая (V класс).
Во всех низших парах, кроме винто-
вой, условия связи исключают возмож-
ность определенного числа движений
относительно соответственно выбранных
осей прямоугольной системы координат,
в винтовой же паре четыре условия
связи исключают возможность четырех
из указанных движений, а пятое условие
408
ОБЩАЯ ЧАСТЬ
Таблица /
Классификация кинематических пар
Низшие пары и примеры высших пар (стрел-
ками показаны мозыожнис движения)
Шанхая Плкюатт
Класс I* *
Число условий
связи 1. Число
степеней сво-
боды 5
Класс II’
Число условий
связи 2. Число
степеней сво-
боды 4
Класс 111*
Число условий
связи 3. Число
степеней сво-
боды 3
Класс IV*
Чнслоуслоиий
связи 4. Число
степеней сво-
боды 2
Класс V*
Число условий
связи 5. Число
степеней сво-
боды I
*) Возможны только высшие пары с то-
чечным контактом.
•) Возможны только высшие пары.
’) Возможны как высшие, так и низшие
пары (показаны все типы низших пар).
устанавливает зависимость между остав-
шимися двумя движениями (hx и ух):
где hx—линейное перемещение звена
вдоль оси *; <рг— угловое перемещение
эвена вокруг осн х в радианах; t —
постоянный шаг резьбы, равный пере-
мещению звена вдоль оси х за один
оборот.
Элементы шаровой, плоскостной и
цилиндрической пары могут состоять
соответственно из концентрических ша-
ровых поверхностен, параллельных пло-
скостей, соосно расположенных круглых
цилиндрических поверхностей. В шаро-
вых и цилиндрических парах каждый
элемент обычно состоит из одной по-
верхности, в плоскостной паре — из
одной или двух поверхностей.
Элементы вращательной пары могут
состоять из любых поверхностей вра-
щения, но практическое применение
находят простые по форме и легко обра-
батываемые частные виды этих поверх-
ностей— плоскости, цилиндрические, ко-
нические и шаровые поверхности.
На расположение поверхностей в эле-
менте вращательной пары наклады-
ваются следующие условия: плоскости
должны быть перпендикулярны геоме-
трической оси элемента, оси цилиндри-
ческих и конических поверхностей
должны совпадать с осью элемента, а
центры шаровых поверхностей должны
лежать на этой оси.
Элементы поступательной пары обра-
зуются из любых цилиндрических по-
верхностей. Применение имеют про-
стейшие по форме частные виды этих
поверхностей — плоскости и круглые
цилиндрические поверхности, а также
некоторые частные виды некруглых ци-
линдрических поверхностей — эволь-
вентного профиля и др.
На расположение поверхностей в эле-
менте поступательной пары наклады-
вается следующее условие: образующие
всех цилиндрических поверхностей и
все плоскости должны быть параллельны
направлению относительного движения
звеньев, связываемых парой.
Элементы винтовых пар получаются
из соосно расположенных винтовых по-
верхностей одинакового шага и напра-
вления. Применение в элементах вин-
товой пары наряду с винтовыми поверх-
ностями также круглой цилиндриче-
ской поверхности облегчает получение
точного центрирования и направления
звеньев.
Высини пары возможны всех пяти
классов и неограниченного числа ти-
пов— со всевозможными сочетаниями
условий связи.
Особенно большое распространение
на практике получили высшие пары:
а) кулачкового типа, позволяющие осу-
СТРУКТУРА И КЛАССИФИКАЦИЯ МЕХАНИЗМОВ
409
ществлять движение ведомого эвена,
вообще говоря, по любому наперед за-
данному закону; б) зубчатые, обычно
используемые для передачи вращатель-
ного движения или преобразования вра-
щательного движения в прямолинейно-
поступательное с постоянными отно-
шениями скоростей.
Кинематические пары могут быть
геометрически .замкнутыми или геоме-
трически незамкнутыми. В первом слу-
чае постоянное соприкосновение эле-
ментов пары обеспечивается их формой
(все пары в табл. 1), во втором — ка-
кой-либо силой — веса, упругости пру-
жин, магнитного притяжения (силовое
замыкание) — или ограничениями, нала-
гаемыми на относительное движение
связываемых звеньев другими звеньями
механизма (замыкание через кинема-
тическую цепь).
Примеры выполнения кинематических
пар
Подвижные скользящие соединения
вала с сопряженными деталями вы-
полняются при помощи шпонок или
с применением некруглых профилей.
Шпонка прикрепляется винтами к
охватываемой или охватывающей де
тали или удерживается от осевого сме-
щения посредством выступов или хвоста
(фиг. I). Иногда шпонка выполняется
Фнг. 1. Примеры крепление скользящих
шпонок.
за одно целое с валом. При малых на-
грузках шпонка может быть заменена
штифтом или винтом с лысками на конце
Фиг. 2. Применение штифтов и пинтой
в полпн» ных соединениях.
(фиг. 2, а), при очень малых нагрузках—
штифтом или винтом без лысок
(фиг. 2, б).
Характерными примерами некруг-
лых прсфилей подвижных соединений
являются прямоугольный (прямобоч-
ный) шлицевый (фиг. 3, а), эвольвент-
ный шлицевый (фиг. 3, б), фасонный
(фнг. 3, а) и профиль в виде правильного
многоугольника (фиг. 3, г). Профили
по фиг. 3, а выполняются с числом
Фнг. 3. Примеры нскруглых профилей для
подвижных соединений.
шлицев (зубьев) от 3 до 20. Наиболь-
шее распространение имеет шестишлн-
цевый профиль. Для лучшего центри-
рования обычно предусматривается ка-
сание не только по боковым граням
шлицев, но и по наружному или вну-
треннему диаметру вала. Сопряженные
поверхности соединения по фиг. 3, в
легко обрабатываются на обеих дета-
лях шлифовальным кругом. Однако,
несмотря на простоту обработки, ука-
занное соединение не нашло широкого
применения вследствие некоторых экс-
плуатационных недостатков.
Направляющие для прямолинейного
движения ползунов и салазок особенно-
широко применяются
щнх станках, прес-
сах и других рабо-
чих машинах.
Направляющие в
форме ласточкина
хвоста (фиг. 4) об-
разуют геометриче-
ски замкнутою пару.
Их преимущества: ма-
лая высота, малое чи-
сло клиньев для под-
тягивания. Недоста-
ток — невыгодное вое-
принятие отрываю-
щих усилий. Направляющие по первому
варианту фиг. 4 хорошо удерживают
смазку и пригодны для Сбльшнх ско-
ростей, чем направляющие по двум
другим вариантам той же фигуры.
V-образные, прямоугольные и круг-
лые направляющие (фиг. 5), имеющие
на нижней детали углубления в виде
желобов, хорошо удерживают смазку,
но подвержены загрязнению.
Применяются для больших скоростей
при наличии хорошей защиты от
стружки.
в
Фнг. 4. Направлаю-
шке в форме ла-
сточкина хвоста.
410
ОБЩАЯ ЧАСТЬ
При широких столах применяется со-
четание из одной V-образной и двух
плоских направляющих. Круглые на-
правляющие позволяют удобно осуще-
ствить выгодную фрикционную пару:
закаленная сталь — чугун.
Направляющие, имеющие на нижней
детали выступы (фиг. 6) с горизонталь-
ными и особенно с вертикальными и
наклонными плоскостями, не препят-
ствуют свободному удалению стружки
Сочетание одной круглой направляю-
щей в виде стержня и одной плоской
обеспечивает возможность временного
использования пары в качестве враща-
тельной или цилиндрической.
Фиг. 5. Профили иа- Фиг. 6. Профили напра-
правляюшнх, хорошо влкюших, и» прспят
ухержимюших сыахку. ствуюшнх свободному
удалению стружки и
грнаи.
и грязи, но плохо удерживают смазку.
Поэтому эти направляющие приме-
няются при малых скоростях к таком
выполнении пары, при котором поверх-
ности скольжения на нижней детали
обнажаются во время работы.
Удерживание ползуна или стола от го-
ризонтальных смещений одной напра-
вляющей (принцип узкого направления)
дает более надежное направление и
почти не препятствует тепловым дефор-
мациям звеньев.
Для получения геометрически замкну-
тых пар у направляющих предусматри-
вают планки (фиг. 6).
Регулирование зазора в направляю-
щих осуществляется:
а) клиньями с продольным (фиг. 7, а)
или поперечным (фиг. 7, б) перемеще-
нием;
б) закладными поджимными планками
(фиг. 7, в);
в) накладными поджимными (фиг. 7,е)
или пригоняемыми (фиг. 7, д) планками.
Направляющие в виде двух, трех или
четырех круглых стержней применяются
при нагрузках, не вызывающих силь-
ного изгиба стержней.
Фиг. 7. Типы регулировочных клиньев
и планок.
Направляющие кругового движения
применяются для обеспечения жестко-
сти круглых горизонтальных столов,
главным образом в металлорежущих
станках. Такие направляющие обычно
выполняют в виде желобообразного углу-
бления на нижней детали, что обеспечи-
вает хорошее удерживание смазки. За-
щита направляющих кругового движе-
ния от загрязнения трудности не пред-
ставляет.
Для кругового движения применяют-
ся V-обраэная, коническая или плоская
направляющие в сочетании с центри-
рующим пальцем
или осью (фиг. 8).
а для столов боль-
шого диаметра (не-
сколько метров) —
большей частью
сочетание V-образ-
ной направляющей
с центрирующей
осью; для кольце-
вых столов обычно
сочетание V-образ-
ной и плоской на-
правляющей без
осн.
Наиболее простой в изготовлении
является плоская направляющая, не-
сколько сложнее — коническая, значи-
тельно сложнее — V-образная. Плоская
направляющая плохо воспринимает ра-
диальные нагрузки и применяется при
их небольшой величине; плоская и ко-
ническая допускают свободны* тепловы»
Фиг. 8. Профили на-
правляющих аля кру-
гового движения.
СТРУКТУРА И КЛАССИФИКАЦИЯ МЕХАНИЗМОВ
411
деформации стола; V-образная хорошо
воспринимает осевые и радиальные уси-
лия и отчасти опрокидывающие момен-
ты; применяется в ответственных слу-
чаях.
Направляющие скольжения сильно
нагруженных и тяжелых столов, вра-
щающихся под нагрузкой, частично
разгружаются от вертикальной силы
регулируемым по высоте подпятником
качения или посредством гидравличе-
ского поджима. Направляющие сколь-
жения делительных столов, поворачи-
вающихся без нагрузки, разгружаются
полностью на время поворота подни-
мающимся подпятником качения или
частично — гидравлическим поджимом.
Пара качательного движения часто
служит для передачи больших усилий
Фиг. 9. Пары качательного хяижеика
для передачи больших усилий одном
направлении.
Фиг. 10. Пары качательного движение
ала передачи больших усилий в одном
направлении.
а одном направлении н малых — в дру-
гом. Такие требования предъявляются.
например, к шарнирам рычажных н кри-
вошипно-шатунных механизмов прессов
и поршневых машин.
Конструкция пар должна обеспечить
достаточно большую площадь опорных
поверхностей и отсутствие или по край-
ней мере уменьшение изгибания оси
шарнира при передаче усилия в одном
направлении. Это обычно достигается
использованием для передачи усилия
внешней цилиндрической поверхности
одного звена (фнг. 9) или почти всей
длины оси шарнира (фиг. 10).
Шаровые пары, применяемые, напри-
мер, в соединении шатуна с ползуном
кривошипного пресса (фиг. 11, а), по-
фиг. 11. Примеры ясполяенив шаровых пар.
зволяют просто решать вопрос регули-
рования длины шатуна и дают возмож-
ность иметь меньшее, чем при враща-
тельной паре, число пассивных связей
в механизмах.
В малонагруженных парах при до-
статочно твердых поверхностях охваты-
ваемого элемента охватывающий эле-
мент может быть изготовлен с кониче-
скими поверхностями, на которых пояс-
ки шаровой поверхности образуются
в результате смятия (фиг. II, б). Геоме-
трическое замыкание неответственных
шаровых пар мо-
жет быть достиг-
нуто путем заваль-
цовкн (фиг. 11, в).
Отдельные ша-
ровые пары сколь-
жения (шарнир- Фиг. И. Шаровой шар-
НЫв ПОДШИПНИКИ, няриый пидшипник.
фиг. 12) представ-
ляют собой два кольца с особыми
выемками, позволяющими вводить их
одно в другое при нерабочем относи-
тельном положении.
412
ОБЩАЯ ЧАСТЬ
Кинематические пары (условные)
с промежуточными телами качения ха-
рактеризуются малыми потерями на
трение и малым износом. Между эле-
ментами пары закладываются шарики
или ролики.
Примерами вращательных и шаровых
пар являются радиальные и сфериче-
ские подшип-
ники качения.
Примеры посту-
пательных и
винтовых пар
представлены
на фиг. 13.
Элементы по-
сту п ател ьной
пары имеют
продольные ка-
навки для тел
качения или
выполняются в
форме напра-
вляющих (см.
Фиг. 13. Примеры пэр выше). Тела ка-
качения. чения движутся
свободно по ра-
бочим и возвратным канавкам, поме-
щаются в поступательно движущийся
сепаратор (при небольшом ходе) или
включаются в роликовую цепь типа
Галля (при большом ходе).
В винтовой паре возвратная канавка
выполняется в гайке.
При свободном движении тел качения
для уменьшения потерь на трение ре-
комендуется чередовать рабочие ша-
рики или ролики с промежуточными,
имеющими несколько меньший диаметр.
Кинематические пары (условные)
с промежуточными деформируемыми те-
лами характеризуются отсутствием отно-
сительных смещений звеньев за счет
зазоров.
Вращательная пара для малых угло-
вых смещений (фиг. 14, а) применяется
в измерительных приборах типа мини-
метров и др.
Особенности—отсутствие мертвого хо-
да, легкость поворота подвижного звена.
Поступательная пара для очень
малых относительных перемещений
звеньев (фиг. 14, б) применяется в при-
борах, например в индуктивном датчике.
Особенности — простота конструк-
ции, отсутствие мертвого хода и легкость
перемещения подвижного звена нз-эа
отсутствия сил трения.
Пара обкатывания (фнг. 14, в) ши-
роко применяется в приборах и
станках для получения точного качения
одного звена по другому без проскаль-
зывания и мертвого хода.
Фиг. И. Примеры пэр с упруго деформируемыми
деталями.
Структура механизмов
Структура механизма определяется
числом звеньев, числом и типами кине
магических пар, порядком соединения
звеньев между собой посредством пар,
общими условиями па взаимное распо-
ложение кинематических пар в меха-
низме.
Число степеней свободы IV' механизма
равно числу независимо изменяемых
координат положений ведущих звеньев
или, иначе, числу обобщенных коорди-
нат, определяющих положение всех
звеньев механизма. Структурный ана-
лиз и синтез ставят своей основной за-
дачей определение IV' механизма или
составление структурной схемы меха-
низма с заданным IV.
Структурная формула определяет W
в зависимости от числа подвижных
звеньев (п) и числа пар различных клас-
сов (pi, pt . . .).
Структурная схема определяет число
звеньев, порядок их соединения в ме-
ханизме и типы применяемых для
этого кинематических пар; размеры
звеньев в структурной схеме не учи-
тываются.
Кинематические пары в механизме
накладывают определенные условия
связи, стесняющие движения звеньев.
Каждая связь (точнее, условие связи)
может быть выражена одним уравне-
нием, которое устанавливает какую-
либо зависимость между координатами,
характеризующими положения звеньев.
КИНЕМАТИКА ПЛОСКИХ МЕХАНИЗМОВ
413
Если уравнение является следствием
уже имеющихся, то новая связь ника-
кого дополнительного условия на дви-
жение звеньев не накладывает, на число
степеней свободы механизма не влияет
и поэтому называется пассивной.
Классификация механизмов
Структурная классификация, осно-
ванная на учете общих условий связи,
разработана советскими учеными [10].
Общие условия связи исключают воз-
можность некоторых движений одина-
ково для всех звеньев механизма. Не-
которые из общих условий связи могут
быть пассивными.
Индивидуальными условиями связи на-
зываются такие, которые нс удовлетво-
ряют определению общих. Они также
могут быть активными и пассив-
ными.
Влияние индивидуальных условий
связи на W7 механизма учитывается
структурной формулой, определяющей
IF механизма как разность между чи-
слом степеней свободы, оставшимся
после наложения на звенья общих усло-
вий связи, и числом индивидуальных
условий связи.
Структурная формула для общего
случая пространственных механизмов;
IF - 6л — 5pt — 4р< — 3/>я — 2р^ — pf, (1)
для пространственных механизмов с по-
ступательным движением звеньев, для
общего случая плоских механизмов и
для сферических механизмов:
IF-Зл —2/>г—pj (2)
для плоских механизмов с поступа-
тельным движением звеньев и для вин-
товых механизмов с соосным располо-
жением пар:
W-,2n-Pl. (3)
В приведенных формулах: л — число
подвижных звеньев (стойка не учиты-
вается); pt, .... р8 — число кине-
матических пар, налагающих соответ-
ственно одно, два, . . пять индивиду-
альных условий связи (в формуле для
общего случая пространственных меха-
низмов индекс при р соответствует
классу кинематической пары).
Индивидуальные пассивные условия
связи разделяются на структурные,
пассивный характер которых опреде-
ляется структурными признаками ме-
ханизма, и размерные, которые могут
стать пассивными только при опреде-
ленных соотношениях между основными
размерами механизма. Структурные пас-
сивные связи учитываются дополни-
тельным членом структурной фор-
мулы.
Например, в формуле для плоских ме-
ханизмов с одними низшими парами
W — Зл — 2р2 + f,
где f — число структурных пассивных
связей или число в схеме замкнутых
контуров из звеньев, связанных одними
поступательными парами.
Размерные пассивные связи могут
быть обнаружены только по кинемати-
ческой схеме механизма, учитывающей
основные размеры звеньев.
Наибольшее распространение в со-
временном машиностроении имеют пло-
ские механизмы.
Пространственные механизмы приме-
няются главным образом в машинах со
сложным движением рабочих органов,
например в сельскохозяйственных ма-
шинах.
Основоположником теории про-
странственных механизмов является
Н. И. Мерцалов.
КИНЕМАТИКА ПЛОСКИХ
МЕХАНИЗМОВ
Кинематическая схема
Кинематическая схема механизма,
кроме структурных характеристик, учи-
тывает его основные размеры, т. е. раз-
меры звеньев, влияющие на кинематику
механизма (радиус кривошипа и длина
шатуна в центральном кривошипно-ша-
тунном механизме и т. п.).
В схемах, служащих для пояснения
устройства механизма или машины (ин-
струкции по эксплуатации, паспорта ма-
шин), не всегда соблюдается правиль-
ное соотношение между основными
размерами; в такие схемы обычно вклю-
чаются некоторые сведения по устрой
ству машины (типы подшипников, элек
тродвигатели и т. п.).
Условные обозначения для кинема
тических схем механизмов и машин пре
дусмотрены ГОСТ 3462-52.
414
ОБЩАЯ ЧАСТЬ
Задачи и методы
кинематического анализа механизмов
В задачу кинематического анализа
входит:
I) определение положений всех
звеньев механизма по заданным поло-
жениям ведущих звеньев;
2) определение линейных скоростей
и ускорений характерных точек меха-
низма, а также угловых скоростей и
ускорений звеньев.
Результаты кинематического анализа:
а) позволяют судить о степени соответ-
ствия кинематических свойств механиз-
ма требуемым; б) используются при
динамическом, анализе механизма.
Кинематическое исследование меха-
низма может быть произведено: а) ана-
литически; б) графически или графо-
аналитически по кинематической схеме;
в) экспериментально по имеющемуся
образцу или специально изготовленной
модели.
Аналитический способ, не требуя точ-
но вычерченной кинематической схемы,
может обеспечить любую наперед задан-
ную степень точности. Его удобно при-
менять для исследования движения ве-
домых звеньев в механизмах распро-
страненных схем, для которых имеются
готовые формулы. Для сложных меха-
низмов аналитический способ мало при-
годен
Графический способ дает меньшую
точность результата, но характери-
зуется наглядностью.
Планы скоростей и ускорений (см.
стр. 455) графически дают векторы ско-
ростей и ускорений характерных точек
всех звеньев в одном ИЛИ нескольких
положениях механизма.
Кинематические диаграммы s=h (/),
и а =/,(/) (см. стр. 515)
графически дают законы изменения
пройденного пути s, скорости и и уско-
рения а в движении одного эвена непре-
рывно за весь цикл работы механизма.
Кинематические диаграммы находят
применение главным образом для звень-
ев с вращательным или прямолинейно-
поступательным движением: а) при ана-
лизе и синтезе кулачковых механизмов,
б) реже при анализе механизмов с низ-
шими парами, например, механизма ка-
чающейся кулисы поперечно-строгаль-
ного станка.
Диаграммы могут быть построены на
основании аналитических расчетов или
по изображениям механизма в последо-
вательных положениях и по планам
скоростей и ускорений.
Более простым, но значительно менее
точным является построение по одной
имеющейся диаграмме двух других спо-
собами графического дифференцирова-
ния и интегрирования (см. стр. 516).
При анализе обычно легко получить
диаграмму s = ft (/) элементарными по-
строениями на чертеже механизма;
тогда две остальные диаграммы строятся
путем двукратного графического Диффе-
ренцирования. При синтезе кулачковых
механизмов часто задается закон изме-
нения ускорения а = /8 (/), двукрат-
ным графическим интегрированием ко-
торого получают диаграммы v =
= и з = (0- Последняя исполь-
зуется для профилирования кулачка.
Для кулачковых механизмов при-
меняется "также построение диаграммы
пути или ускорения на основании ана-
литических подсчетов с последующим
ее графическим интегрированием или
дифференцированием.
Более точные результаты получаются,
если вместо графического интегриро-
вания и дифференцирования пользо-
ваться способами численного интегриро-
вания и дифференцирования.
Экспериментальные методы
исследования
Исследование упрощенной модели ме-
ханизма обычно позволяет проверить
зависимость движения звеньев от основ-
ных размеров.
Исследование образца механизма по-
зволяет выявить фактические характе-
ристики движения звеньев при нор-
мальных или искусственно созданных
условиях работы механизма. При этом
учитываются факторы, влияние которых
трудно поддается предварительной ко-
личественной оценке (жесткость звеньев,
вибрация, влияние загрязнения, про-
скальзывание в парах трения, тепловые
деформации, характеристика привод-
ного двигателя и т. и.).
Цель исследования при нормальных
условиях работы — проверка точности
и устойчивости работы механизма в це-
лом, выявление отклонений от расчет-
ных данных и их причин. Цель исследо-
вания при искусственно созданных усло-
виях работы — выявление работоспо-
собности механизма на различных ре-
жимах, проверка отдельных частей ме-
КИНЕМАТИКА ПЛОСКИХ МЕХАНИЗМОВ
415
ханизма, изыскание способов улучше-
ния механизма.
Испыта1ельная аппаратура. Вслед-
ствие дифференциальной зависимости
между перемещением, скоростью и
ускорением каждая из указанных вели-
чин может измеряться непосредственно
или при помощи другой величины с по-
следующим автоматическим дифференци-
рованием илу интегрированием в соот-
ветствующей аппаратуре. При отсут-
ствии прибора для автоматического диф
ференцнровання и интегрирования по-
следующая обработка результатов
измерения производится графическими
или приближенными аналитическими
способами.
При измерении переменных величин
может потребоваться определение мгно-
венных или средних их значений, отне-
сенных к определенному промежутку
времени.
В случае измерения быстро изме-
няющихся величин их мгновенные зна-
чения могут быть уловлены только при
помощи регистрирующих устройств, за-
писывающих кривую изменения иссле-
дуемой величины в зависимости от дру-
гой— обычно от времени, или пути,
проходимого другим звеном.
Всякая установка для измерения ме-
ханических величин в общем случае
состоит из трех функционально различ-
ных устройств: приемного, передаточ
ного и отмечающего [30].
Приемное устройство
(I на фнг. 15) воспринимает измеряемую
величину — перемещение х (фнг. 15, а),
угловую скорость и (фиг. 15, б), уско-
рение а (фиг. 15, в) — чувствительным
органом и в случае надобности преоб-
разует ее в первичное перемещение х
(фиг. 15, б).
Передаточное устройство
(// на фиг. 15) передает первичное пе-
ремещение от приемного в отмечающее
устройство. При зтом первичное пере-
мещение х может: а) передаваться без
изменений; б) увеличиваться в механи-
ческих передачах, т. е. в каскаде уси-
ления Б (фиг. 15, а и б) до величины X;
в) преобразовываться в процессе пере-
дачи в удобное для передачи и реги-
страции перемещение жидкости, газа,
луча света или изменения электриче-
ского тока (гидравлические, пневмати-
ческие, оптические и электрические
передаточные устройства); г) преобра-
зовываться и усиливаться а процессе
передачи, например проходя через ка-
скад основного преобразования А, преоб
разующий первичное перемещение х
в электрический сигнал у, каскад уси-
ления Б, усиливающий сигнал у в си-
гнал Y, и каскад вспомогательного
преобразования В, преобразующий си-
гнал )' в удобный для регистрации
сигнал У1 (фиг. 15, в).
Фиг. 1S. Схемы установок для измерения механи-
ческих величии.
Отмечающее устройство
(/// на фиг. 15) регистрирует изме
ряемую величину, поступающую в виде
перемещений X, электрических сигна-
лов У и г. п., посредством указателя
и шкалы (устройства указывающего
типа — фиг. 15, а и б) или путем записи
ее в виде кривой (устройство записываю-
щего типа —фиг. 15, в).
Указанные устройства и их элементы
могут быть оформлены в виде одного
прибора (фиг. 15, а и б) или в виде
нескольких приборов и аппаратов
(фнг. 15, в)
Приемное устройство и преобразую-
щий элемент передаточного устройства,
выделенные из общей системы в виде
отдельного прибора, носят название
датчика (фнг. 15, в).
•116
ОБЩАЯ ЧАСТЬ
Большее распространение имеют ме-
ханические и электрические переда-
точные устройства, меньшее — опти-
ческие, пневматические и гидравличе-
ские.
Электрические датчики делятся на
три основные группы:
I) параметрические, в которых пер-
вичное перемещение преобразуется
в соответствующее изменение одного из
параметров электрического контура —
индуктивного сопротивления, емкости,
омического сопротивления;
2) генераторные, характеризую-
щиеся тем, что первичное перемеще-
ние вызывает в них появление электро-
движущей силы, величина которой со-
ответствует этому перемещению (пьезо-
электрические и фотоэлектрические эле-
менты) или его скорости (электродина-
мические постоянного и переменного
тока);
3) импульсные, в которых первичное
перемещение, например, вызывает попе-
ременное замыкание контактов, обеспе-
чивающее сначала зарядку, а затем
разрядку конденсатора; сила тока на
выходе изменяется в зависимости от
скорости разрядки, а следовательно, и
от скорости первичного перемещения.
В табл. 2 приведены основные типы
электрических параметрических дат-
чиков [30].
Включение датчиков обычно произ-
водится по схеме мостика Уитстона. Прн
использовании принципа частотной мо-
дуляции наименьшая величина, измеряе-
мая емкостным датчиком, уменьшается
до 2-10—6 сл, и диапазон измеряемых
частот расширяется до предела О—
20 000 гц. Такое же расширение диапа-
зона дает включение датчика проволоч-
ного сопротивления в потенциометри-
ческую схему.
Измерение перемещений. Измерение
полной длины перемещения произво-
дится теми же способами, что и линей-
ных размеров.
Измерение перемещений а промежу-
точных положениях движущегося звена
производится в функции времени или
перемещения другого подвижного звена.
Для записи больших пе-
ремещений во времени поступа-
тельно движущегося или поворачиваю-
щегося на неполный оборот звена при-
менима простейшая установка, которая
состоит из неподвижного отметчика вре-
мени, производящего запись на прикре-
пленной к подвижному звену ленте, или
из подвижного отметчика и неподвиж-
ной ленты. Недостаток — вынужден-
ный масштаб записи, ограничивающий
ее точность.
В качестве механического отметчика
времени может быть использован не
большой электродвигатель переменного
тока (лучше синхронный) с отмечаю-
щим усом на валу. Чтобы избежать уста-
лостного разрушения уса, последний
рекомендуется делать из материала орга-
нического происхождения — щетины,
стержня гусиного пера, дерева и т. п.
Ленга или линейка для механической
записи (желательно с миллиметровыми
делениями) на нужном участке покры-
вается слоем легко снимаемой краски
или копоти.
Для записи перемеще-
ний во времени посредством осцил-
лографа пользуются электриче-
скими датчиками. Для измерения угло-
вых перемещений вращающегося звена
обычно употребляют индуктивный дат-
чик, сердечник которого замыкается и
размыкается вырезами и выступами
стального диска, вращающегося вместе
с исследуемым эвеном. Роль диска может
выполнять также зубчатое колесо, а прн
использовании этого способа для пря-
молинейно-поступательного движения—
невращающнйся ходовой винт с под-
ходящей по размеру резьбой.
Колебания тока, вызванные измене-
нием индуктивного сопротивления дат-
чика, записываются осциллографом
одновременно с записью 50-периодного
тока для масштаба времени.
Кроме индуктивных датчиков, для
указанной цели могут быть использо-
ваны также датчики других типов, вклю-
чая электроконтактные, в виде коллек-
торного кольца и щетки по образцу
применяемых в электрических маши-
нах.
Применение двух датчиков — на ве-
дущем и ведомом валах — с одновремен-
ной записью их показаний позволяет:
а) весьма точно определять передаточ-
ное отношение передач (например, фрик-
ционных) прн различных нагрузках;
б) исследовать процессы неустановив-
шегося движения при включении муфт
и т. п.
Недостаток рассматриваемого спосо-
ба — невозможность иметь очень малый
шаг на диске датчика, что ограничи-
вает точность измерений. Положитель-
ная особенность — независимость ре-
зультатов от силы электрических сигна-
КИНЕМАТИКА ПЛОСКИХ МЕХАНИЗМОВ
417
Основные типы ыектркческах параметрических датчиков
(преобразующий злемеит)
Таблица 2
Тип датчика, принцип его работы, наименьшая измеряемая величина к измеряема» частота / при мостиковой схеме Эскиз датчика Основная зависимость Рекомендуемые пара- метры и режим питания
Индуктивный. Ме- няется коэффициент само- индукции (L тк)при юме- веихи воздушного зазора (4 см) или перекрытия (Q слг*) между якорем и сердечником: min Л4 — 0.001 см /<1500 гц И 0.4 к (? =.• L ————10-d гл. где Qx— сечение железе в гл1; —длина магни- топровода в ел; V—число витков; р — магнитная про- ницаемость L = 0.01-4-0.1 гм; <?ж — ОД =0,5 см"’ а = 0Л1 -г- 0.06 см; До— (0,1 ч-0.3) а. Плотность тока 2 j о/диг*: 7 = 0,03 а; И = 10 в; / = 5000 ац
Магнитострикцион- ный. Меняется коэффи ' циент самоиндукции (£ ги) за счет изменения маг- нитной проницаемости р при изменении нагрузки на сердечник (Р кГ) и его относительной деформа- цми^Х=-—-): min Л1 = IO-5 / < 1500 гц г ол«гж-.р L 1 - IO-8 гл Ж (обозначения см. выше) L =0.01 -е-0,013 гя. Ма- териал сердечника — пер- маллой; аши=6=8 кГ/сдИ. Плотность тока 2,5 а/.им'
Емкостный. Меняется емкость конденсатора (С см) при изменении за- зора между пластинами (i см) или рабочей пло- щади пластин (5 с. и*); mln Д4 — 0ДЮ01 ем; f < 1500 гц 5 JLat С=^= 4x4 _ °'IBSe гае г — аизлектрическаа постоянная прокладки (для воздуха а «1, ала слюды а — 5 -4- 8) С = SO-г-250 см: а = охнч-одз ем; ла < (од -<- од а; AS = (0,2 4-0,8)$. Для тангенциального дат- чика (со слюдой) С - 5 -ь- 30 см; а - 0.005 4- 0Л2 см
^Л|)}5
Угольного сопроти- вления. Меияется сопро- тивление угольного стол- ба (/? он) при изменении нагрузки (Р кГ); mln - 10-4; /С 10000 гц 1' iP "Слюда fcnjHb duciw где А — коэффициент ж., пропорционально- сти; р — удельное давле- ние Диск: d = 10 лиг; Л=0Л лиг. Число дисков в элементе 10—12. Мате- риал дисков - графит с иаполнителямн. 1 < 0.2 а; Р < 60 кГ
Проволочного сопро- тивления. Меняется со- противление датчика (Я ом) при изменении его относительной дефор- мации — -y-j : mln X — 10-4- /<«00 ац iff 2* *1 Я • где А/? - приращение сопротивления; R — начальное сопротив- ление; * — чувстви- тельность материала проволоки (для кон- стантана *“2) Два метр проволоки 0,03 мм. Толщина бумаги 0,02-г-0,03 мм. Длина датчика 10-4-25 лиг. Ши- рина датчика Фа-15 мм. Число петель 4—10; R —100 -4-1500 ом; Х<10~3 Клей—целлулоид в аце- тоне. При R = 100 ом и сталь- ных деталях. /< 0.025-4-0,09 а
ri щ.-/ fyHOia 'робота
27 Том I Зак. 1454
418
ОБЩАЯ ЧАСТЬ
лов, что повышает надежность изме-
рений.
Для записи средних и
малых перемещений во вре-
мени применяются: а) при длине хода
до 100 мм — емкостные датчики с изме-
нением активной ' площади пластин;
б) при длине хода до I мм — емкостные
датчики с изменением расстояния между
пластинами, индуктивные и другие типы
электрических датчиков; в) механиче-
ские самописцы; г) оптические записы-
вающие приборы. Точность измерений
малых перемещений может быть дове-
дена до 0,01—0,001 мм.
Для точного измерения
больших и средних переме-
щен и й во времени или в зависимости
ОТ перемещения другого звена поль-
зуются эталонным устройством, точно
воспроизводящим такое же движение
(обычно равномерное), какое должно
иметь исследуемое звено. При измере-
нии перемещений в зависимости от дви-
жения другого звена эталонное устрой-
ство приводится от последнего, при
записи перемещений во времени — от
синхронного электродвигателя (приме-
няется реже). Контролю подвергается
отклонение в положении исследуемого
звена относительно эталона; ввиду ма-
лых значений этих отклонений их можно
измерить весьма точно измерительными
йриборами типа индикатора-миниметра
или записать посредством установки
С электрическими датчиками.
Измерение скоростей. Для непосред-
ственного измерения скорости механи-
ческим путем используются: а) измене-
ние нормальных ускорений и сил инер-
ции при вращательном движении — цен-
тробежные тахометры; б) изменение
сопротивления среды — крыльчатые
тахометры, велосиметры для больших
скоростей. Для непосредственного изме-
рения скорости электрическим путем
используется зависимость от нее индук-
тируемой электродвижущей силы —
таходннамо.
Для определения среднего числа обо-
ротов в минуту за определенный про-
межуток времени используется счетчик
оборотов, соединенный в один прибор
с секундомером.
Измерение ускорений. Для непосред-
ственного измерения ускорений, как
прямолинейно-поступательных, так и
вращательных движений, используется
зависимость силы инерции или инерци-
онного момента от ускорений.
Некоторая масса может перемещаться
внутри корпуса прибора или датчика
за счет деформации пружины. Величина
деформаций пропорциональна силе инер-
ции, а следовательно, и ускорению дви-
жения корпуса прибора. Для получения
достаточной точности измерений необ-
ходимо иметь настолько малые смеще-
ния массы относительно корпуса, чтобы
они не давали существенной разницы
между абсолютными движениями кор-
пуса и массы.
Перемещение массы относительно кор-
пуса может фиксироваться при помощи
механического самописца или осцилло-
графа. В последнем случае применяются
емкостные, индуктивные н др. датчики.
Возможна такхсе постановка электри-
ческого датчика, реагирующего на уси-
лие. В этом случае пружина не требуется.
КИНЕТОСТАТИКА ПЛОСКИХ
МЕХАНИЗМОВ
В кинетостатике задача динамики об
определении сил, возникающих в меха-
низме при его заданном движении,
приводится на основе принципов Далам-
бера к статической задаче равновесия
под действием внешних сил, сил инерции
и реакций в кинематических парах.
Задачи кинетостатики:
1) определение давлений в кинема-
тических парах, сил, действующих на
звенья, и уравновешивающих сил по
заданному закону движения механизма
и внешним силам;
2) уравновешивание движущихся масс
в механизме.
Определение сил инерции звеньев
Для звена массы т, движуще-
гося поступательно с уско-
рением а, равнодействующая сил инер-
ции
Ри — — та
приложена к центру тяжести звена;
линия ее действия параллельна напра-
влению движения.
Для вращающихся звеньев,
имеющих плоскость симметрии, перпен-
дикулярную к осн вращения:
а) прн и = const и положении центра
тяжести на оси вращения (г^ = 0)
силы инерции элементарных масс
взаимно уравновешиваются;
б) прн <о = const и ra + 0 равввдай-
ствующая
Ра — mrsufl
КИНЕТОСТАТИКА ПЛОСКИХ МЕХАНИЗМОВ
419
приложена к центру тяжести и имеет
радиальное направление от оси (цен-
тробежная сила);
в) при w const и rs =0 силы инер-
ции приводятся к паре с моментом
M = -Jsz.
где Js = Jrfdm = mp- — момент инер-
ции звена относительно центра тяже-
сти; р — радиус инерции звена; s —
угловое ускорение;
г) при ы -A const и rs -А 0 силы инер-
ции приводятся к равнодействующей
Ра = — mrs V «4 4- в®,
приложенной к центру тяжести звена,
и к паре с моментом
Нормальная и тангенциальная соста-
вляющие Ра будут соответственно
Рпи - - mrsa\ Р'и- — mrf,
Ра и М могут быть также сведены
к одной равнодействующей Ра, прило-
женной в центре качания, который на-
ходится на радиальной прямой, прохо-
дящей через центр тяжести. Расстояние
от оси О вращения до центра К качания
Л
ОК-Г,+ —.
mrs
Для звеньев, сов ер шага-
щ и х сложное плоское дви-
жение, силы инерции приводятся
к равнодействующей
Ри - - rnas,
приложенной к центру тяжести, и к
паре с моментом
M--JSV
В приведенных формулах а?— уско-
рение центра тяжести звена, /д — мо-
мент инерции звена относительно оси,
проходящей через центр тяжести пер-
пендикулярно плоскости движения
Ри и М могут быть также сведены
к одной равнодействующей
Ри — — mas,
линия действия которой отстоит от
центра тяжести звена на расстоянии
в4
где ps — радиус инерции звена, соот-
ветствующий J$. Моменты инерции про
стейших геометрических тел даны
в табл., 8. гл. XVIII (стр. 394—396).
Для облегчения подсчетов моментов
инерции тел вращения удобно пользо-
ваться таблицей единичных моментов
инерции [181 для участков цилиндри-
ческой формы.
В табл. 3 приведены значения еди-
ничных моментов инерции, умноженные
на 10*, стальных цилиндрических тел
различных диаметров и длиной 1 мм.
Ступенчатые детали илн группы де-
талей разбиваются на цилиндрические
участки, моменты инерции которых
затем суммируются При подсчете
момента инерции пустотелых деталей
наличие полостей учитывается путем
вычитания моментов инерции цилиндри-
ческих участков, соответствующих раз-
мерам полостей.
Момент инерции каждого цилиндри-
ческого участка определяется умноже-
нием табличного значения J^-IO8 на
длину участка / в л.и и на К)-®.
При сложных подсчетах удобнее опе-
рировать значениями /,-Ю'1 вместо Je
и лишь при окончательном определе-
нии момента инерции детали получен-
ный результат умножить на 1Q—».
Момент инерции конического участка
может быть приближенно определен по
формуле
j- io-«y
где • 10® — сумма табличных зна-
чений единичных моментов по арифмети-
ческому ряду диаметров, начиная со зна-
чения, соответствующего наименьшему
диаметру конуса, и кончая значением,
соответствующим наибольшему диа-
метру; г — число членов суммы tJt-10®;
I — длина конического участка в мм.
Если отдельные детали изготовлены
из материала, удельный вес которого от-
личается от удельного веса стали (7,8),
то для них табличные значения Jt-16*
следует умножить на k " 0,3—дли
алюминия и его сплавов (уд. вес 2,7),
k = 0,92 — для чугуна (уд. вес 7,2)
и k = 1,12—для бронзы (уд. вес 8,7).
Примеры П Определить момент ниериии чу-
гунного диска диаметром 300 ям н толшиио®
20 ММ.
По табл. 3 находим
if. 10» — «3 200.
J - (*,•>»’) - в3 200-2и-0,92-10“J -
— l,lt> »t
420
ОБЩАЯ ЧАСТЬ
Габлица 3
Значения единичного момента инерции, умноженные на 10*
4-10. в Kl'cM ctK? юг а р 1 • и d в мм 7-10* в кГсм сек' ш /г-10> в кГсм сек' 3 а Ч 1 4 юг а г ‘J 3 во *• V1' в кГсм'ПК'
10,0 0,0780 L 0,395 20,0 1,25 25,0 3,05 37.5 15.4 60 48.8 75 W
10,2 0,0844 15,2 0,416 20,2 1,30 26,5 3.30 33.0 16,3 51 52,8 76 260
10,4 0.0S13 15,4 0,439 20,4 1.35 26.0 3,56 33,5 17.1 52 57,0 77 274
10,6 0,0984 15.6 0.461 20,6 1,40 26,5 З.К5 39.0 18,0 53 61,5 78 289
10,8 0,106 15,8 0,486 20,8 1,46 27,0 4,15 39.5 19.0 51 66,3 79 304
11,0 0.114 16,0 0,611 21,0 1,52 27,5 4.46 40,0 20,0 55 71.4 80 320
П.2 0,123 16.2 0,537 21,2 1,58 28,0 4,79 40,5 21.0 56 76,7 81 336
11.4 0,132 16.4 ’ 0,565 21.4 1,64 24.5 5,15 41.0 22.0 57 82,3 82 353
11.6 0,141 16,6 0.592 21,6 1,70 29,0 5,52 41,5 23.1 58 88,3 83 370
11,8 0,161 16,8 0,621 21,8 1,76 29.5 5.91 42,П 24.3 69 94.5 81 333
12.0 0,162 17.0 0,651 22,0 1,83 30,0 6,32 42.5 25,5 60 101 85 407
12,2 0,173 17.2 0.683 22,2 1.® 30.5 6,75 43.0 26,7 61 108 86 427
12.4 0.184 П.4 0.715 22,4 1,95 31.0 7,20 43,5 27,9 62 118 87 447
12.6 0,197 П.6 0,748 22,6 2,04 31,5 7,68 44,0 29,2 63 123 88 458
12,8 0,209 17,8 0,783 22,8 2,11 32.0 8,18 44.5 30.6 64 131 89 4®
13,0 0,223 18.0 0,819 23,0 2,18 32,5 8,70 45,0 32.0 65 139 90 512
13.2 0,237 18,2 0,856 23,2 2,26 33.0 9.25 45,5 33,4 66 148 91 535
13,4 0,251 18,4 0,891 23,4 2,34 33,5 9,82 31.9 67 157 92 559
13,6 0,267 18,6 0.934 23.6 -2,42 34,0 10.4 46,5 36.5 68 167 93 584
13,8 0,283 18,8 0.974 23,8 2,50 34.5 11.1 47,0 38.1 69 177 94 609
>4.0 0,300 19.0 1,02 24,0 2,59 35,0 11.7 47,5 39.7 70 187 96 635
14,2 0,317 19.2 1,06 24,2 2.68 35.5 12.4 48,0 41.4 71 196 96 662
>4,4 0,335 19.4 1.10 24,4 2.77 36.0 13,1 48.5 43,2 72 210 97 691
14,6 0,354 19,6 1,15 24,6 2,86 36.5 13,8 49.0 45,0 73 222 98 720
14,8 0.374 19,8 1,20 24,8 2,95 37.0 14.6 49.5 46,8 74 234 99 749
100 780
Примечание. Значения У(,10* для диаметров от I до 10 н от 100 до 1000 мм получаются
соответственно делением или умножением табличных значений <1 на 10 и табличных значений
3^10» ва 10*.
КИНЕТОСТАТИКА ПЛОСКИХ МЕХАНИЗМОВ
2) Определить момент ннерпни стальной коми
ческой детали с наименьшим диаметром 39,5 ЛЛ,
наибольшим 46 мм к длиной 100 мм.
По табл. 3 для d = 40; 42; 44 и 46 мм находим
значения Имея в виду, что z = 4, получим
7 « МГ* 2 V10* = 10~* -V *
X (20,0 н- 24,3 29,2 + 34,9) = 0,0027 к Гем сек!'.
При подсчете моментов инерции сложных де-
тален и групп леталеЛ расчетные данные целе-
сообразно заносить во вспомогательную табличку.
Для упрощения подсчета момента инерции по
чертежу общего вида измерения диаметра участ-
ков удобно производить угольником или линейкой,
имеющими шкалу единичных моментов инерции,
что делает излишним обращение к табл. 3.
Определение давлений
в кинематических парах
Определение давлений в кинематиче-
ских парах возможно для механизмов,
являющихся статически определимыми
относительно рассматриваемой си-
стемы сил. Для плоского механизма,
нагруженного силами, лежащими в его
плоскости, решение возможно при от-
сутствии индивидуальных пассивных
условий связи.
Решение, полученное по плоской ки-
нематической схеме, правильно для ме-
ханизма, все кинематические пары ко-
торого симметричны относительно его
главной плоскости. При больших от-
клонениях от указанного условия не-
обходимо учитывать смещения сил в
перпендикулярном к плоскости меха-
низма направлении и считаться с кон-
струкцией кинематических пар
Графо-аналитический способ решения
задачи по плоской кинематической
схеме предусматривает построение пла-
на сил (см. стр. 456).
Определение приведенных
и уравновешивающих сил
Приведенной называется сила, кото-
рая при малом возможном перемещении
механизма совершает работу, равную
сумме возможных работ всех действую-
щих на механизм сил. При рассмотре-
нии условий равновесия механизма все
действующие силы могут быть заменены
приведенной. Точку приложения приве-
денной силы обычно выбирают на ве-
дущем звене и называют точкой при-
ведения. Звено, на котором распола-
гается точка приведения, называется
звеном приведения.
Построение диаграмм приведенной
силы и ее момента в зависимости от
угла поворота звена приведения упро-
щает динамический анализ механизма
(см. стр. 426).
Уравновешивающей называется сила,
уравновешивающая действие прило-
женных к механизму сил. Она равна
по величине и противоположна по на-
правлению приведенной силе. Урав-
новешивающий момент равен момен-
ту приведенной силы и противополо-
жен ему по знаку.
Определение приведенных и уравно-
вешивающих сил и моментов может про-
изводиться по плану сил (см. стр. 456)
или при помощи теоремы Жуковского
о жестком рычаге.
Теорема Жуковского основана на
принципе возможных перемещений
Если рассматривать повернутый на 90’
план скоростей как жесткий рычаг
с осью вращения в полюсе, то из усло-
вий равновесия этого рычага под дей-
ствием сил, перенесенных с механизма
в соответственные точки повернутого
плана скоростей, можно определить ве-
личину уравновешивающей силы с вы-
бранными линией действия и точкой
приложения.
Уравновешивание вращающихся
масс
Инерционные силы неуравновешен-
ных вращающихся деталей дают допол-
нительную нагрузку на опоры, часто
являются источником вибрации и спо-
собствуют расшатыванию машины и
фундамента. Поэтому уравновешивание
быстро вращающихся масс в современ-
ных машинах является обязательным.
Неуравновешенность, получающаяся
за счет конструктивных особенностей
детали, может быть устранена добавле-
нием уравновешивающих масс (проти-
вовесов), величины и расположение
которых определяются расчетом или
графическим построением. При этом
уравновешенные части детали, симме-
тричные относительно осн вращения,
не учитываются.
Неуравновешенность, получающаяся
при изготовлении детали вследствие
неточностей в размерах, отклонений от
правильной формы и неоднородности
материала (пустоты в литье и т. п.),
может быть уменьшена до допустимых
пределов лишь путем статической или
динамической балансировки детали на
специальных установках.
Уравновешивание в одной плоскости,
перпендикулярной к оси вращения,
достаточно для узких деталей с при-
422
ОБЩАЯ ЧАСТЬ
близительно симметричным относи-
тельно этой плоскости распределением
массы.
При расчете обычно задается радиус
расположения г0 центра тяжести уравно-
вешивающей массы т0. Величина ее
определяется по формуле
г
П1л — ГП--,
/'О
где т и г — величина и радиус распо-
ложения центра тяжести уравиовеши-
ваемой массы.
Центры тяжести масс т и должны
лежать на противоположных концах
прямой, проходящей через ось вращения
и перпендикулярной к лей.
Для статической балан-
сировки деталь насаживается на
специальную оправку или сопряжен-
ный с ней вал и
уста на вл и вается
на легко вращаю-
щиеся ролики
(фиг. 16, а) или
выверенные по
точному уровню
горизонтальные
стержни (фиг. 16.6).
Снятием метал-
ла с утяжеленной
стороны детали
(обычно высверли-
ванием), реже —
добавлением с об-
легченной стороны
(обычно напаива-
нием) добиваются
безразличного рав-
новесия оправки
с деталью, что
служит признаком
статической урав-
новешенности последней. Для облегче-
ния процесса балансировки часто на-
клеивают на деталь грузик (из воска),
по весу которого определяют количе-
ство подлежащего снятию металла.
Иногда роликовую балансировочную
установку снабжают сверлильным при-
способлением, позволяющим удалять
излишний металл без снятия детали
С установки.
, Для балансировки сменных деталей !
(фиг. 17) (шлифовальные круги и т. п.)
предусматриваются переставные гру-
зики 2, заложенные в круговой паз
фланца.
Дисбаланс детали количественно оце-
нивается смещением г ее центра тяже-
сти от оси вращения.
Действие дисбаланса
при заданном числе п
об/мин удобно оценивать
отношением возникаю-
щей силы инерции Ри к
весу детали О:
Ра ш-r п*г
G g — 90 (ХЮ *
где г — в см.
Необходимость балан-
сировки в каждом кон-
кретном случае устанав-
ливается путем сравне-
ния наибольшего смеще-
ния, получаемого при
изготовлении детали, с
допустимым смещением
9000(1Ря
'•=—слпри^ при-
нятом отношении -g5-.
Фиг,!7. Устрой-
ство для креп-
ления шлифо-
вального круга
с у ра внове ши-
веющими грузк-
кдми.
Уравновешивание в двух плоскостях
требуется для деталей значительной
длины.
Графическое построение для опреде-
ления уравновешивающих масс пока-
зано на фиг. 18.
Силы инерции нескольких сосредо-
точенных масс (mt. т->, т3) (фнг. 18, а)
могут быть уравновешены двумя мас-
сами znj и /и,’, расположенными в двух
произвольно выбранных плоскостях ис-
правления S и S". Величины и угловые
положения уравновешивающих масс
находятся следующим образом.
В плоскости S' строим векторы /П|Г|.
/nsr8, пропорциональные центро-
бежным силам заданных масс. Замыкаю-
щая многоугольника нз этих векторов
дает вектор тг, пропорциональный
уравновешивающей силе (фиг. 18, б).
Далее, в плоскости S' строим век-
торы /П|Г| х Я. Щаг» X г». mare X гц,
пропорциональные моментам соответ-
ствующих центробежных сил. Замыкаю-
щая многоугольника из этих в< Кторов
дает вектор moro X г0, пропорциональ-
ный уравновешивающему моменту
(фиг. 18, в).
Как известно, момент изображается
вектором, перпендикулярным к плоско-
сти, содержащей вектор силы и центр
момента, и направленным так, что если
смотреть со стороны стрелки вектора,
КИНЕТОСТАТИКА ПЛОСКИХ МЕХАНИЗМОВ
423
момент будет казаться действующим
в направлении движения часовой
стрелки.
Делением модуля вектора ту0 х
на модуль вектора г9 найдем модуль
вектора т^го, пропорциональный ураз-
Фиг. 18. Графическое определение уравновешивающих масс.
в)
новешивающей силе в плоскости испра-
вления S*. а вторичным делением
на выбранное г$ определим величину
уравновешивающей массы ,
го
Угловое положение уравновешивающей
массы устанавливается в соответствии
с приведенным выше правилом век-
торного изображения моментов.
Уравновешивающая масса в плоско-
сти 5' определяется геометрическим сло-
жением т.г0 и тг и последующим де-
лением модуля этой суммы V тг на
выбранный радиус г'о (фиг. 18, а):
> 2
>п0- Г-.
го
Динамическая баланси-
ровка производится на специальных
машинах, позволяющих определять ве-
личину и угловое положение уравно-
вешивающих грузов в двух выбранных
плоскостях исправления, а на некото-
рых машинах также устранять дисбаланс
изделия, например путем высверлива-
ния лишнего материала специально пре-
дусмотренным для этой цели сверлиль-
ным шпинделем.
Во всех балансировочных машинах
используются колебания, передаваемые
на опоры быстро вращающегося несба-
лансированного изделия. По амплитуде
и фазе возникающих колебаний опре-
деляют соответственно величину и угло-
вое положение уравновешивающих гру-
зов. Необходимые измерения выпол-
няются механическими, оптическими
или, особенно часто, электрическими
способами. Различают балансировочные
машины с качающейся рамой и с по-
движными опорами.
В машине е качающейся рамой изделие уста-
навливается • опорах, помещенных на раме, кото-
pa а удерживается а среднем положении пружи-
нами. Сначала ось качания рамы устанавливают
в первой плоскости исправления. Тогда величина
направление дисбаланса во второй плоскости
исправление определятся амплитудой колебание
рамы и угловым положением изделия я момент
наибольшего отк аонеииа рамы от среднего поло-
жения. Посла «того ось качаниа рамы устанавли-
вают во второй плоскости исправления и таким же
образом определяют дисбаланс в первой плоскости.
В машине по фиг. 19 рама 3, нд которой уста-
навливается изделие /, укреплена на четырех
упругих стержнях 3, допускающих колебания а
горизонтальной плоскости. Для удобства измене-
ния оси качания рамы предусмотрены две пере-
ставные попеременно включаемые опоры 4. Изме-
рение искомых величин производится алеятриче-
скнм способом при помощи индуктивного датчика S
424
ОБЩАЯ ЧАСТЬ
генераторного типа. Датчик состоит из механи-
чески связанной с колеблющейся рамой катушки,
помещенной в поле сильного постоянного магнита.
Измеряя генерируемый в катушке ток соответ-
ственно тарированным прибором, опрехеляют не-
обходимую величину уравновешивающего груза
при заданном плече его расположения. Угловое
расположение уравновешивающего груза в ма-
шине по фиг. 19 определяется при помощи меха-
нического выпрямителя. Выпрямитель состоит из
синхронно вращающегося с изделием кулачка б и
поворотного кольца 7 с контактным устройством 8.
Через выпрямитель пропускается переменный ток
от того же датчика. Частота тока равна числу
оборотов изделия, фаза зависит от углового поло-
жения дисбаланса. Выпрямитель осуществляет
переключение направления тока на противополож-
ное в течение одного полупернола. При повороте
кольца показания контрольного миллиамперметра
постоянного тока будут изменяться от максимума,
когда переключения производятся и моменты пе-
рехода тока датчика через нуль (фиг. 19, б), ло
нуля при переключениях в моменты экстремаль-
вых значений тока (фиг. 19, в). Угол поворота
кольца, отсчитанный по соответствующей шкале,
при нулевом показании миллиамперметра опреде-
лит угловое положение уравновешивающего груза.
Фиг. 19. Схема балансировочной машины
с качающейся рамой.
I
Я машинах с подвижными опорами (фиг. 20)
изделие /, приводимое в движение ремнем 2,
имеет возможность горизонтального плоско-парал-
лельного движения и колеблется относительно вер-
тикальной геометрической оси, положение кото-
рой зависит от распределения дисбаланса и ха-
рактеристики опор 3. Обе опоры связаны с индук
тнвнымн датчиками в генераторного типа.
Эталонная деталь с дисбалансом только в пер-
вой плоскости исправления будет колебаться около
осн, положение которой не зависит от величины
дисбаланса. Лагчикн будут генерировать перемен-
ные токи pniuiux частот и со сдвигом фаз в 18(1“.
Выравнивая амплитуды напряжений при помощи
потенциометра 5, добиваются их взаимного гаше-
ния, что контролируется нулевым показанием мил-
ливольтметра. После замены эталонной летали
балансирувмым изделием показания милливольт-
метра будут зависеть только от величины дис-
баланса во второй плоскости исправления. Урав-
новешивающий груз на заданном плече опреде-
ляется по тарированному для данных изделий мил-
ливольтметру.
Угловое положение уравновешивающего груза
в машине по фиг. 2(1 определяется стробоскопиче-
ским методом. Бсвинерционная газосветная лампа в
включается в электрическую схему машины таким
обрааом, что за каждый оборот изделия она зажи-
гается (приблизительно на 10 7 сек.) при пере-
ходе напряжения датчика через куль. На враща-
ющемся изделии укрепляется шкала 7. на ста-
нине — указатель 8. Освещенное такой лампой
изделие кажется неподвижным. По делению шка-
лы. находящемуся против указателя. определяют
угловое положение уравновешивающего груза во
второй плоскости исправления.
Фиг. 20. Схема балансировочной машины
с подвижными опорами.
Дисбаланс в первой плоскости исправления
определяется аналогичным образом.
На крупных машинах для определения угло-
вого положения груза используется вспомогатель-
ный генератор. Генератор приводится во вращение
с тем же числом оборотов и минуту, что и изделие.
Переменный ток генератора имеет частоту, рав-
ную частоте тока датчика. Фаза тока генератора
может изменяться поворотом его статора. В ка-
честве контрольного прибора используется ватт-
метр, катушки которого питаются электроэнер-
гией от датчика и генератора. Показания ватт-
метра пропорциональны косинусу угла сдвига
фаз. Поэтому, изменяя фазу тока генера-
тора путем поворота статора, можно получить
нулевое показание прибора. Угол поворота ста-
тора, отсчитанный по шкале, определит углоное
положение уравновешивающего груэ.1-
Электрические схемы балансировоч-
ных машин обычно имеют ламповые
усилители, иногда частотные фильтры,
устраняющие влияние посторонних ви-
браций на показания приборов.
Современные машины для динами-
ческого балансирования определяют
смещения центра тяжести изделий
средних размеров относительно оси
вращения до 0,001 мм.
Замена динамической балансировки
статической для длинных деталей не
достигает цели и может даже увели-
чить динамическую несбалансирован-
ность.
ДИНАМИКА МЕХАНИЗМОВ
И МАШИН
Динамика машин решает на основа-
нии силового и энергетического ана-
лиза следующие основные задачи:
1) определение передаваемых машиной
ДИНАМИКА МЕХАНИЗМОВ И МАШИН
425
сил и работы; 2) определение движе-
ния машины под действием приложен-
ных сил; 3) регулирование хода ма-
шины.
Характерные периоды движения
машины
Уравнение движения машины, осно-
ванное на законе живых сил:
7g — 7j = A# — Апе — Ак i- Ая. (1)
где Ti — кинетическая энергия машины,
равная сумме живых сил всех ее звеньег,
для момента времени fj; Tg — то же
для последующего момента времени tt\
Лэ—работа движущих сил за проме-
жуток времени (/g— /]); Лп, — то же
сил полезного сопротивления; Ак— то
же сил вредного сопротивления (тре-
ния, сопротивления среды); А„—то же
сил веса звеньев.
Установившееся движение наблю-
дается при нормальных условиях ра-
боты машины и может продолжаться
неограниченное время.
Различают равновесное и неравно-
весное установившееся движение.
Равновесное движение характеризует-
ся постоянством скоростей (участок
Фиг. 21. Периоды движения машины.
кривой а на фнг. 21). Такое движение
могут иметь ротационные машины —
турбины, электродвигатели и т. п.
Для любого промежутка времени рав-
новесного движения
7»! -Лц —0.
где
Ли " Лд АЯс Авс i Ая.
Неравновесное движение характери-
зуется периодическим изменением ско-
рости движения (участок кривой б на
фиг. 21). Такое движение имеют, напри-
мер, поршневые машины.
Для любого промежутка времени
неравновесного движения
T^/Tg и Л12^0.
а для цикла
Ti — Tg и AIt — 0.
Циклом называется промежуток вре-
мени, через который повторяются ра-
27 1464
бочие процессы машины; в начале ка-
ждого цикла звенья машины занимают
одни и те же положения. Например,
в паровых поршневых машинах цикл
равен времени одного оборота криво-
шипа.
Неустановившееся движение продол-
жается ограниченное время.
Период разбега имеет место при пуске
машины или переходе ее на режим ра-
боты с большей скоростью.
Характерные неравенства Т\ < Тг
и Лц>0 всегда справедливы; а) в ма-
шинах с равновесным установившимся
движением для любого промежутка вое-
мени периода разбега(участок кривой в
на фиг. 21); б) в машинах с неравно-
весным движением для промежутка вре-
мени, за который машина совершает
движение, соответствующее циклу, —
чаще всего один оборот ведущего звена
(участок кривой г на фиг. 21).
Период выбега наблюдается прн оста-
новке машины или переходе се на ре-
жим работы с меньшей скоростью.
Характерные неравенства 7*] > Тг и
Л1г< 0 всегда справедливы: а) в маши-
нах с равновесным установившимся дви-
жением для любого промежутка времени
периода выбега (участок кривой д на
фиг. 21); б) в машинах с неравновесным
установившимся движением для проме-
жутка времени, за который машина
совершает движение, соответствующее
циклу, — по большей части один оборот
ведущего звена (участок кривой е на
фиг. 21).
Определение скоростей и ускорений
механизма
Задача исследования движения меха-
низма под действием приложенных сил
и моментов может быть сведена к ана-
логичной задаче для одного вращаю-
щегося звена, называемого звеном при-
ведения. Для этого необходимо: а) все
действующие в механизме внешние силы
и силы сопротивления заменить приве-
денной к указанному звену силой или
моментом приведенной силы (см.стр.421);
б) массы и моменты инерции всех
звеньев заменить приведенным к тому
же звену моментом инерции.
Иногда в качестве звена приведения
удобно принять звено с прямолинейно-
поступательным движением. В этих слу-
чаях требуется определить приведенную
силу и приведенную массу.
В машинах с неравновесным устано-
вившимся движением приведенный мо-
426
ОБЩАЯ ЧАСТЬ
мент действующих сил и приведенный
момент инерции изменяются в зависи-
мости от положения звена приведения.
Для определения скорости звена приве-
дения в заданных положениях, степени
неравномерности его движения, а
в случае надобности—средств умень-
шения этой неравномерности до допу-
стимых пределов, требуется найти зна-
чения приведенного момента инерции
и кинетической энергии механизма
в функции угла поворота звена при-
ведения.
Приведенный момент инерции ме-
ханизма выражается общей формулой
где J и <> — момент инерции относи-
тельно оси вращения и угловая скорость
звена приведения; Jot и и>0/ — моменты
инерции относительно оси вращения и
угловые скорости остальных вращаю-
щихся звеньев механизма; т, и vt —
массы и скорости поступательно
движущихся звеньев механизма; т$1, v$i,
J$i и u>si — массы, скорости центров
тяжести, моменты инерции относительно
осей, проходящих через центры тяжести,
и угловые скорости звеньев, совершаю-
щих сложное плоское движение.
Для простых зубчатых механизмов
имеем
Jnp“J + S • (3)
где — передаточные отношения между
рассматриваемыми звеньями и звеном
приведения.
Приведенная масса выражается общей
формулой
где тио — масса и скорость поступа-
тельно движущегося эвена приведения.
Определение Jл„ и m,t/, выполняется
аналитически по привело ням формулам
или чаще графо-аналитически с исполь-
зованием плана скоростей и указанных
выше формул. Для удобства графо-
аналитического решения в формулах (2)
и (4) величины угловых скоростей заме-
няются отношениями линейных скоро-
стей к соответствующим радиусам (дли-
нам звеньев); тогда отношения линейных
скоростей во всех слагаемых могут быть
заменены отношениями отрезков плана
скоростей с добавлением в формулы не-
которых размеров звеньев механизма.
Кинетическая энергия механизма
в ряде его последовательных положений
определяется методом графического ин-
тегрирования диаграммы приведенного
момента в функции угла поворота звена
приведения. Так как при интегрирова-
нии нас интересует лишь приращение
Фиг. 22. Построение днпгрвммы кинетической
•иергии.
площади, заключенной между осями
координат и кривой приведенного мо-
ы’нта, то задачу можно ре пить следую-
щим более наглядным построением
(фиг. 22, д). Строим раздельно кривую
М) — /({?) приведенного момента дви-
жущих сил с учетом сил тяжести
звеньев и кривую Ме — /. (?) приведен-
ных моментов сил полезных и вредных
сопротивлений,
Ординаты кривых, несмотря па раз-
, личные знаки моментов, откладываются
в одну сторону.
Интегрирование ведут по площади,
заключенной между построенными кри-
выми, причем участки площади, ограни-
ченные сверху кпчвой Л!j •« f\ (?) и
снизу кривой Л1,-"/г(?), означают
увеличение кинетической энергии ме-
ханизма и принимаются за положитель-
ные (заштрихованы на фиг 22, а вер-
тикально). Участки, ограниченные
сверху кривой Мс = /.(?), а снизу
кривой МЦ (?), принимаются за от-
рицательные (заштрихованы горизон-
тально).
Масштаб рг кинетической энергии на
диаграмме Т = f (?) (фиг. 22, б) пока-
ЛИНЛМИКЛ МЕХАНИЗМОВ И МАШИН
427
зывает, сколько кГм содержится в 1 мм
ординаты:
Р кГм!мм-
где (хд, — масштаб моментов в кГм!мм
на диаграмме М = /3 (</>); ц» — масштаб
угловых перемещений в радмм на той
же диаграмме; р — полюсное расстояние
в мм при графическом интегрировании
диаграммы Ма — Мс ft (f) (см. ниже
стр. 516) или переходный параметр в мм
при интегрировании путем измерения
площадей, что в данном случае удобнее.
Масштаб кинетической энергии меха-
низма, измеренной соответствующей пло-
щадью диаграммы М = /а (if), будет
Нт — кГлЧммХ
Интегрирование, произведенное от на-
чала движения механизма, позволяет
найти абсолютные величины его кине-
тической энергии; интегрирование, про-
изведенное на отдельном интервале дви-
жения (например, в цикле установив-
шегося движения), дает лишь прираще-
ния кинетической энергии.
Скорость звена приведения в зави-
симости от угла поворота определяется
при помощи вспомогательной диаграммы
в координатах
7„ри7'(фиг.23).
Кривая вспомо-
гательной диа-
граммы строит-
ся по точкам,
каждая из ко-
торых соответ-
ствует опреде-
ленному поло-
жению меха-
низма. По уг-
лам ф наклона
лучей, прове-
денных из на-
Фиг. 23. Вспомогательная
хк Iграмма ала определенна
угловой скорости звени
приведении.
чала координат
к соответствующим точкам кривой, на-
ходят угловые скорости « звена приве-
дения в различных положениях:
Угловое ускорение звена приведения
в зависимости от углового перемещения
строится следующим образом.
Графическим дифференцированием (см.
стр. 516) диаграммы •> = / (?) получают
du>
кривую = f (?). Перемножая орди-
du>
наты кривых <> = f (?) и — / (?) и
деля результат на некоторый постоян-
ный параметр pt в мм, находим орди-
наты искомой кривой е= /"(?).
Масштаб угловых ускорений на по-
строенной диаграмме
2
ц =— — рад-сек~~1мм,
* V^P\
где ц» и ц» — масштабы угловой ско-
рости в рад сек~1 /мм и углового переме-
щения в рад!мм на диаграмме <» = f (?);
Pi — полюсное расстояние в мм, приня-
тое при графическом дифференцировании.
Время в зависимости от углового пере-
мещения звена приведения определяется
графическим интегрированием кривой
— [0 (?), которая может быть по-'
строена по известным значениям о>.
После определения скорости и уско-
рения звена приведения можно произ-
вести кинематический анализ всего меха-
низма.
Регулирование скорости
установившегося неравновесного
движения (расчет маховых масс)
Средняя угловая скорость звена при-
ведения за время t
t
6
Коэффициент неравномерности 6 вра-
щения звена приведения за цикл
j _ “щах — “mln
"ср
Y tg ф-сек_|,
где м? и (ду — масштабы приведенного
момента инерции в кГмсек'/мм и кине-
тической энергии механизма в кГм/мм
на диаграмме Jn„ = F (Т).
, По найденным значениям ы можно по-
строить диаграмму
“-/(?)•
Средине допустимые значения >
для различных машин
Генераторы переменного тока . 1/200—1/300
Генераторы постоянного тока . 1/100—1/200
Двигатели внутреннего сгора-
ния и компрессоры . . . 1/110—1/ЦЮ
Судовые двигатели .... 1/20—1/100
Металлорежущие станки, ткац-
кие, полиграфические и муко-
мольные машины.................1/20—1,<80
Сельскохозяйственные машины . . 1/10—1/50
Насосы, иашииы ударного лей-
ст инк ...................... 1/5—1/30
423
ОБЩАЯ ЧАСТЬ
Определение 6 для спроектированной
машины производится по углам наклона
Фпих и Фпил лучей, касательных к за-
мкнутой кривой диаграммы Jna = F (Г)
(фиг. 23):
3 о Vtg Vшах VФшШ
Ktg
Фтах + V tg 4.га|п '
Если величина 8 выходит за допусти-
мые пределы, необходимо повысить
равномерность движения вращающегося
звена за счет увеличения его момента
инерции путем установки махового ко-
леса или замены имеющегося махового
колеса другим, обладающим большим
моментом инерции.
Определение момента инерции махо-
вого колеса по заданному коэффициенту
неравномерности может быть выполнено
различными способами. Ниже приведены
два из них.
Определение JM при помощи диа-
граммы Jnp = Fj (Л Т), Строят диа-
грамму Jnp = F\ (ДГ) для цикла (фиг.24).
Приращение кинетической энергии ДГ
отсчитывается от кинетической энергии
в исходном положении механизма, в ко-
тором ДГ принимают равным нулю. По
заданному 6 определяют
, . 1 Л 8 V 2
tg'i'min 2 |у \ 2/ Ш'р'
По подсчитанным углам <рга„ и фпцп
проводят два касательных луча к за
Фиг. 24. Диаграмм» ллк
определения требуемого
момент» инерции махового
колеса.
мкнутой кри-
вой диаграммы
(фиг. 24). Точ-
ка пересечения
лучей дает по-
ложение нача-
ла координатО'
диаграммы
Jnp + J м — •
- F (Т).
Расстоя ние
между точка-
ми О и О' по
вертикали рав-
но кинетиче-
ской энергии
(Го) механизма в исходном положении
(в масштабе ру кГм/мм), по горизон-
тали — искомому моменту инерции ма-
ховика (в масштабе р/ кГмсекУмм).
Если точка О' пересечения лучей
выходит за пределы чертежа, то JM
определяется через отрезок I мм. от-
секаемый указанными лучами иа оси
ординат диаграммы Jnp = Гу (ДГ). по
формуле
р_/
Ju — - „ кГмсек*.
8-“-„
ср
Определение JM по диаграмме ДМ =
= Л (?)*• По диаграммам Ма — ft (?) и
Mc^fiit) строим диаграмму прира-
щения момента Д/И — Mg — Мс= (?)
на протяжении цикла (фиг. 25).
Фиг. 25. Диаграмма для определения тре-
буемого момента инерции махоиого колеса
по способу И. И. Артоболевского.
Для нахождения значений ?, при ко-
торых угловая скорость звена приведе-
ния приобретает максимальное значение,
строим в том же масштабе, что и ДУИ.
вспомогательную кривую:
Г 2
+'•4 *)].
где во, — угловое ускорение вращаю-
щихся звеньев; а, — ускорение посту-
пательно движущихся звеньев; а$, и
tst _ тангенциальное ускорение центра
тяжести и угловое ускорение для
звеньев, совершающих сложное плоское
движение. Остальные обозначения те же,
что и в формуле (2) на стр. 426. Уско-
рения определяются при
“ “ “max “ “ср (' + "2^ “ const.
В пересечении кривых ДМ = ft (?) и
ДЛ4! — ft, (?) получаем точки Л. В, С и D.
соответствующие экстремальным значе-
ниям “.Точка с максимум максиморум “
• Способ разработан И. И. Артоболевским.
ПОТЕРИ В МЕХАНИЗМАХ И К. П Д.
429
соответствует действительной наиболь-
шей угловой скорости эвена приведения
'"тю “ + “5“); остальные экстре-
мумы имеют условный характер.
Точки, в которых ш имеют максимумы
(В и D на фиг. 25), выявляют из общего
числа полученных точек (А, В, С, D)
пересечения кривых путем определения
знака площади, заключенной между
осью абсцисс, кривой ДМ = (<р) и
двумя вертикалями, проведенными через
соседние исследуемые точки: если пло-
щадь — положительна, последующий
экстремум (максимум) больше преды-
дущего (минимума), и наоборот. Из
отобранных точек таким же способом
определяют точку, соответствующую
максимуму-максиморум и.
На фиг. 25 этой точкой и является
точка В.
Указанный способ определения точки
с максимумом-макснморум <» базируется
на практически приемлемом допущении,
что изменения относительно
малы и не влияют на распределение
максимумов и минимумов “ между
точками А, В, С и D
Для определения значения ?, при
котором угловая скорость звена прнве-
ления приобретает наименьшую
величину “т,п=Игр (1 —ш _ 1
строим вторую вспомогатель- К J
ную кривую ДЛ4- = fA (?) на
основании соотношения
Точки А| и С, пересечения кривых
ДМ ™ (?) и ДЛ42 = 4 (?) соответствуют
экстремальным значениям ы, среди кото-
рых минимум-миннморум равен наи-
меньшему значению угловой скорости
прн заданном коэффициенте неравномер-
ности: ®га)п = шСР (1 - -у ) . Точки А|
и Cj, соответствующие минимумам ш,
располагаются вблизи ранее полученных
точек Л и С условных минимумов; по-
этому для выявления точек А( и С|
можно ограничиться проведением не-
больших участков кривой ДМ2 — (?).
Определение точки С| с мииимумом-ми-
ниморум ш производится выявлением
знака площади, заключенной между кри-
вой ДМ, — Д (?), осью абсцисс и верти-
калями, проходящими через А> и Ci.
Момент инерции махового колеса (зве-
на приведения)
гЯ
2 J bMdf—Jnp.Bu>mtx+Jnp.Clb>mln
----------------------------
«2 -«2,
max mln
где j &Mdf пропорционален соответ-
”ci
ствующей площади на диаграмме ДЛ4=
= fa (?) в м.и?(на фиг. 25 заштрихована),
умноженной на масштабы и ?в
и — значения угла ? соответственно
при “max и <*П|П;Л1де и JnPjC\ — значе-
ния Jnp в положениях, соответствую-
ЩНХ “Шах и “mln-
Если приведенные моменты инерции
малы по сравнению с моментом инерции
махового колеса, то можно пользоваться
приближенной формулой
’в
f ДЛ4 df
yCT
. 'ашср
Угловая скорость в любом положении
г , 'В
Ju + Jno. В ? 2 (* .. .
где [ ДМ df подсчитывается по со-
9 К
ответствующей площади диаграммы
фиг. 25.
ПОТЕРИ В МЕХАНИЗМАХ
И КОЭФФИЦИЕНТ ПОЛЕЗНОГО
ДЕЙСТВИЯ
Основные понятия и определения
В процессе преобразования, передачи
и использования энергии для выполне-
ния определенной технологической за-
дачи в машине всегда имеет место потеря
части энергии, основная масса которой
обычно превращается в тепловую и рас-
сеивается.
Уменьшение потерь дает экономию
энергии и снижает нагрев частей ма-
шины, что благоприятно влияет на
их работоспособность и стойкость. Энер-
гия потерь, отводимая с продуктами
430
ОБЩАЯ ЧАСТЬ
выделения (отработанный пар и воздух,
отводимый поток жидкости), производит
меньший нагрев частей машины, чем
энергия, выделяемая внутри машины, и
может быть более удобно использована.
Чрезмерный нагрев деталей при не-
возможности дальнейшего уменьшения
потерь устраняется: а) увеличением по-
верхности охлаждения машины, напри
мер введением ребер; б) введением при-
нудительного потока охлаждающего
воздуха (например, в электрических ма-
шинах); в) введением естественной или
принудительной циркуляции охлаждаю-
щей жидкости, проходящей через соот-
ветствующее охлаждающее устройство
(например, в двигателях внутреннего
сгорания); г) применением охлаждаю-
щих устройств для масла в системе
циркуляционной смазки.
Немеханнческие потери являются спе-
цифичными для машин с различными
рабочими процессами. Потери энергии
от неполного расширения, перепада да-
вления и утечек газообразного илн
жидкого рабочего тела характерны для
пневматических и гидравлических ма-
шин.
Потери этого рода рассматриваться
здесь не будут.
Общими для всех видов машин и ме-
ханизмов являются механические потери
от сил вредных сопротивлений, а именно:
а) от сил трения, имеющих большое
значение как в тихоходных, так и
в быстроходных машинах; б) от сил со-
противления окружающей среды — со-
противление воздуха (существенно толь-
ко для очень быстроходных машин),
сопротивление смазывающей жидкости
(может быть сведено до незначительной
величины правильным выбором системы
смазки; так, например, поливка шестерен
струей масла в быстроходных машинах
сильно снижает потери по сравнению со
смазкой саморазбрызгиванием).
Абсолютная величина потерь равна
работе сил вредных сопротивлений за
рассматриваемый промежуток времени.
Коэффициент потерь <р характеризует
относительную величину потерь в меха-
низме.
Для установившегося равновесного
движения
А„
— const
б',)
Для установившегося неравновесного
движения вследствие периодического
аккумулирования кинетической энергии
отдельными звеньями пользоваться ве-
личинами мгновенных значений ? прак-
тически неудобно; в этих случаях поль-
зуются его средним значением, равным
коэффициенту потерь за один цикл:
В формулах Ак и Nge — работа в-
мощность (теряемая) сил вредных сопро-
тивлений за любой промежуток времени
равновесного движения или за время
цикла неравновесного установившегося
движения; Ал и N,,— работа и мощность
(подводимая) движущих сил за тот ж&
промежуток времени.
Коэффициент полезного действия Ч
характеризует относительное количество
энергии, используемой в машине по пря-
мому назначению:
. т) — 1 —
Для установившегося равновесного
движения
ЧА,
-const
A)
Для установившегося неравновесного-
движення средняя величина к. п. д.
равная к. п. д. за один цикл, будет
В двух последних формулах Ате и
Nnc— работа и мощность (полезная) сил
полезных сопротивлений за рассматри-
ваемый промежуток времени.
Общий к. п. д. нескольких последо-
вательно соединенных передач или ме-
ханизмов
’)- Wk-le
Общий к. п. д. нескольких парал-
лельно соединенных передач илн меха-
низмов
т|| + Ми?тд 4-N.xch +.. • + tyja’ln
1----------------ъ----------- “
__________N"
nrl , net , ‘^пгз , , ^псп
ra + V + “пГ + •" + "ЧТ
в формулах тр, тЛ, Т]ц.Чл —К. п. д.
отдельных передач или механизмов;
Л/<й, N ог, No».... — Мощности
ПОТЕРИ В МЕХАНИЗМАХ И К. П. Д
431
движущих сил в отдельных передачах
(разветвлениях); Ndl + N,n+ NM+ ... +
+ Non ~ Nd> Nnd, Nnc2, Nпсз t • • •
Nnen— мощности сил полезных сопро-
тивлений в отдельных передачах (раз-
ветвлениях); iVn€| + Л^г + ЛГпса +... +
“Ь Ne Nде-
Общий к. п. д. смешанного соединения
передач (механизмов) определяется пу-
тем совместного использования формул
для последовательного и параллельного
соединений.
Если для какой-либо машины отдель-
но известны к. п. д., связанные с раз-
личными источниками потерь, например,
электрический к. п. д. электродвига-
теля т;э, объемный к. п. д. насоса -q0,
механический к. п. д. от трения ц, то
общий к. п. д. машины определяется
как произведение этих к. п. д.
Механический к. п. д. одной и той
же машины зависит от режима ее ра-
боты — скорости и нагрузки. С возра-
станием полезной нагрузки от нуля (хо-
лостой ход) до наибольшей величины
к. п. д. сначала возрастает от нуля до
максимума (при оптимальной нагрузке),
а затем снижается; часто на исполь-
зуемом диапазоне нагрузок к. п. д. не
достигает максимума.
На фиг. 26 в качестве примера при-
ведена зависимость к. п. д. от нагрузки
для передней
бабки токарно-
го станка с ше-
степенной ко-
робкой передач
на 12—18 ско-
ростей и с диа-
пазоном регу-
лирования чи-
сел оборотов
шпинделя- по-
рядка 50.
Зависимость
к. п. д. от ско-
рости является
бодее сложной.
При очень боль-
ших скоростях
Фнг. 26. Примерна! зави-
симость к. п. Л. передней
бабки токарного стайка от
нагрузки.
шпинделя, по-
рядка 5000—10 000 об/мин, у некото-
рых станков среднего размера наблю-
далось снижение к. п. д. до 0,3—0,1.
Мощность холостого хода Nxx цели-
ком расходуется на работу сил вред-
ных сопротивлений. Мощность холо-
стого хода благодаря легкости ее изме-
рения часто служит сравнительным по-
казателем величины потерь, характе-
ризующим в меньшей степени качество
конструкции и в большей степени каче-
ство изготовления механизма (тща-
тельность обработки трущихся поверх-
ностей, наличие перекосов, перетяжка
подшипников и т. п.).
На фиг. 27 в качестве примера при-
ведена зависимость мощности холостого
Фиг. 27. Примерные записи мости мощности холо-
стого хода передней бабки токарно-винторезного
стнккд модели 1Дь2 от включенного числа оборо-
тов, температуры смазки и времени с момента
пуска.
I
хода N хх от включенной скорости —
числа п об/мин шпинделя, температуры
смазки ГС и времени Т с момента
пуска для передней бабки токарного
станка 1Д62 (ДИП-200) с 18-скоростноЙ
шестеренной коробкой передач на под-
шипниках качения и смазкой в мас-
ляной ванне.
Способы повышения к. п. д.
Схема механизма оказывает суще-
ственное влияние на его к. п. д. Ра-
циональная с точки зрения к. п. д.
схема должна обеспечивать: а) короткие
кинематические цепи с малым числом
кинематических пар — источников по-
терь на трение; б) полное отключение
кинематических цепей, не участвующих
в передаче мощности при данных вклю-
чениях, что важно для быстроходных
машин; в) отсутствие значительных
432
ОБЩАЯ ЧАСТЬ
блуждающих мощностей, когда скорости
и усилия в кинематических парах соот-
ветствуют большей мощности, чем пе-
редается механизмом (примерами таких
механизмов могут служить планетар-
ные редукторы): г) рациональный за-
кон изменения передаваемой мощности
по циклу механизма с неравновесным
установившимся движением (учиты-
вается влияние движущих сил на по-
терн в различных положениях меха-
низма); при этом необходимо иметь
в виду, что движущие силы могут не
только увеличивать, но и снижать по-
тери, если они приводят к уменьшению
инерционных давлений в кинематиче-
ских парах.
При проектировании механизмов пе-
речисленные требования не всегда могут
быть полностью удовлетворены.
В некоторых механизмах, передаю-
щих незначительные мощности, к. п. д.
имеет второстепенное значение.
Конструктивное выполнение меха-
низма также влияет на его к. п. д
С целью повышения к. п. д. следует:
а) не применять сильно увеличенные
против расчетных размеры звеньев,
особенно диаметры подшипников; б) без
необходимости не применять механиз-
мов с большим числом пассивных свя-
зей, требующих строгого соответствия
между размерами звеньев для хоро-
шей сборки механизма; рекомендуется,
например, применять самоустанавли-
вающиеся подшипники на сильно про-
гибающихся валах; в) использовать
вместо пар скользящего трения под-
шипники качения (для быстроходных
валов лучше шариковые или цилиндри-
ческие роликовые), а также поступа-
тельные и винтовые пары с трением
качения; г) обеспечить надежное вы-
ключение фрикционных муфт, особенно
многодисковых, на вертикальных валах
и в реверсивных механизмах (трение
дисков с большой относительной ско-
ростью приводит к заметным потерям);
д) применять для быстроходных машин
жидкую смазку вместо консистентной;
е) применять систему принудительной
смазкн от насоса (например, смазку пере-
дач шестеренных коробок и редукторов
производить поливкой вместо масляной
ванны).
Качество изготовления механизма
сильно влияет на его к. п. д
Тщательная обработка трущихся по-
верхностей снижает потерн на тре-
ние.
Неточности во взаимном расположе-
нии сопрягаемых поверхностей в дета-
лях механизма (отклонения от соосности
и параллельности осей цилиндрических
поверхностей и т. п.) могут привести
к неправильному распределению давле-
ния на поверхностях трения, к заеданию
и т. д. Все эти явления увеличивают
потери в механизме. Эксперименталь-
ное исследование влияния отклонений
подшипников от правильного положе-
ния для вала, приводимого во вращение
через муфту и передающего движение
через зубчатую передачу, показало сле-
дующее: а) неп а рал дельность валов
в плоскости их расположения мало
влияет на потери в зубчатой передаче,
непараллельность в перпендикулярной
плоскости дает заметное увеличение
потерь; б) даже весьма малая несоос-
ность подшипников скольжения при-
водит к значительному увеличению по-
терь на трение; в) шарикоподшипники
допускают бдльшие отклонения, чем
конические роликоподшипники.
На фиг. 28 показано влияние угло-
вого смещения а подшипника качения
и линейного его смещения 8 в плоскости,
перпендикулярной к плоскости распо-
ложения валов, на момент трения вала
с одной зубчатой передачей прн л ™
= 680 об/мин (фиг. 28, а) и при л =
— 1450 об/мин (фиг. 28, О): при точной
установке шарикоподшипников (кри-
вая /); при линейном смещении шарико-
подшипников на 8 = 0,3 мм, 8 = 0,6 мм
и 8 =* 1,2 мм (соответственно кри-
вые?, 3и 4); при угловом смещении шари-
коподшипников на а = 20' и а = 40'
(кривые 5 и б); при точной установке
конических роликоподшипников (кри-
вая 7); при угловом смещении роли-
коподшипников на а — 5' и а = 10'
(кривые 8 и 9).
Осевой натяг конических ролико-.н ша-
рикоподшипников оказывает заметное
влияние на величину момента трения;
для уменьшения потерь рекомендуется
регламентация предварительного иа-
тяга.
Неровности поверхностей трения и
небольшие отклонения от правильного
контакта последних между собой могут
быть частично исправлены обкаткой
машины после ее изготовления. При
этом поверхности несколько изнаши-
ваются н прирабатываются друг к другу,
создавая лучший контакт.
Обкатка новой машины или меха-
низма может проводиться на холостом
ТРЕНИЕ В МЕХАНИЗМАХ
433
Фнг. 23. Нлняяне перекосов и смешений полшип-
иккоо на момент трения пала с одной зубчатой
передачей (по данным ЭНИМСК
ходу или с неполной искусственно со-
зданной нагрузкой, с нормальной смаз-
кой или со смазкой, имеющей тонкую
абразивную примесь для ускорения про-
цесса приработки.
Кроме заводской обкатки, практи-
куется приработка машин на регламен-
тированном пониженном режиме работы
в начальный период их эксплуатации
28 Гон > Зак. 1461
(например, ограничение наибольшей
скорости автомашин на первой тысяче
километров пробега). Эта мера заметно
удлиняет срок службы машины.
ТРЕНИЕ В МЕХАНИЗМАХ
Виды трения
Трением называется сопротивление
относительному перемещению соприка-
сающихся тел, возникающее в месте их
контакта.
По характеру относительного дви-
жения трущихся тел различают:
I. Трение скольжения, которое может
возникнуть при соприкосновении тел
по поверхности, по линии или в точке.
Под линейчатым понимается касание
по малым площадям, протяженность
которых в одном направлении практи-
чески мала и зависит от смятия поверх-
ностей. Под точечным подразумевается
касание по еще меньшим площадям,
имеющим во всех направлениях малую
протяженность, зависящую от смятия
поверхностей.
2. Трение качения, возникающее при
перекатывании одного тела по другому.
Касание тел может быть линейчатым
(по прямой) или точечным. Мгновенная
ось вращения одного тела относитель-
но другого при чистом качении совпа-
дает с прямой касания или проходит
через все точки касания.
3. Трение верчения, которое может
появиться при точечном соприкоснове-
нии (обычно в одной точке). Относи-
тельное движение тел — вращение во-
круг оси, проходящей через точку ка-
сания по нормали к соприкасающимся
поверхностям.
На практике часто один вил трения
сопровождается другим.
По характеру смазки трущихся по-
верхностей различают:
чистое трение прн отсутствии на тру-
щихся поверхностях следов посторон-
них веществ (в механизмах не встре-
чается, может быть получено в вакууме);
сухое трение при отсутствии смазки
(в механизмах возможно при хорошей
изоляции трущихся поверхностей от
системы смазки);
полусухое трение, сочетание сухого
и граничного;
граничное трение при очень тонкой
масляной пленке (0,1 мк и менее),
прочно удерживающейся на трущих-
ся поверхностях (на этот вид треиия
434
ОБЩАЯ ЧАСТЬ
гидродинамическая теория смазки не
распространяется);
по луж ид каст ное трение — сочетание
жидкостного и граничного;
жидкостное трение, когда трущиеся
поверхности полностью разделены слоем
смазки. Попадание достаточного коли-
чества смазки в зазор между трущимися
поверхностями обеспечивается: а) само-
затягиванием при достаточной скорости
движения и при наличии соответствую-
щих поверхностей, образующих масля-
ный клин в сочетании с явлением ка-
пиллярности; б) подачей смазки в зазор
под давлением, что обеспечивает жидко-
стное трение при сколь угодно малой
скорости относительного движения по-
верхностей (применяется, например,
для смазки направляющих некоторых
станков).
Основные понятия и законы
трения
Вектор силы трения лежит в пло-
скости. касательной к трущимся поверх-
ностям, и направлен против скорости
относительного движения.
Сила трения покоя имеет место до
начала движения при действии сдви-
гающей силы. Величина неполной силы
трения покоя равна приложенной сдви-
гающей силе; величина полной силы
трения равна предельному значению
сдвигающей силы, при котором может
начаться относительное движение тел.
Сила трения движения возникает при
относительном движении тел. Ее вели-
чина не зависит от движущей силы,
превышение которой над силой трения
вызывает ускорение движения тела.
' Величины силы трения движения и
предельной силы трения покоя при
скольжении зависят от следующих фак-
торов: а) нормальной силы, б) удель-
ного давления на трущихся поверхно-
стях, в) скорости относительного дви-
жения, г) материалов трущихся тел,
д) гладкости трущихся поверхностей,
е) смазки и ж) загрязнения трущихся
поверхностей.
Величина силы трения качения, кроме
перечисленных факторов, зависит еще от
радиусов кривизны поверхностей в месте
их соприкосновения.
Ввиду недостаточного развития теории
трения наиболее надежным способом
определения сил трения является исполь-
зование экспериментальных данных,
полученных в условиях, близких кана-
лизируемому случаю.
При нежидкостном трении наиболь-
шее влияние на величину силы тре-
ния в среднем оказывает нормальная
сила.
Трение скольжения. Трение сколь-
жения за исключением жидкостного
характеризуется формулами (фиг. 29):
для силы трения движения
F =fN;
для предельной силы трения покоя
Фиг. 2». Конус тре-
пня.
где f — коэффициент трения движения;
/о — коэффициент тре-
ния покоя; N — нор-
мальная сила.
Формула F — С+
-|- fN дает лучшие
результаты для диа-
пазона малых давле-
ний, но пользование
ею затрудняется из-за
отсутствия достаточ-
но полных экспери-
ментальных данных
для С и f.
Коэффициенты трения дол-
жны учитывать влияние перечислен-
ных выше факторов на силу трения.
Для большинства случаев > f. Обыч-
ный характер изменения коэффициента
трения в зависимости от скорости сколь-
жения показан на фиг. 30, а (1 — при
Фиг. 30. Зпписиыость коэффициента треки* от
скорости скольжсни» и даклеии*.
малой нагрузке, 2 — при средней, 3 —
при большой) и от удельного давле-
ния — на фиг. 30, б. Значения коэффи-
циентов трения см. стр. 437.
Угол трения ф образуется
вектором полной реакции R поверх-
ности трения и нормалью: tg <р — f\
tg То - fa
Введение понятия угла трения часто
упрощает выводы и расчеты.
Конус трения имеет ось, нор-
мальную к поверхности трения, и угол
между образующей и осью, равный углу
ТРЕНИЕ В МЕХАНИЗМАХ
435
Таблица 4
Приведенные коэффициенты трения
для некоторых подвижных соединений
Посгупателыю перемещающийся или вращаю-
щийся стержень в двух коротких опорах или
в одной опоре с зазором
Л= о/
пр а
мтр “ Q'np ~
'пр а '
f — коэффициент
трения скольжения
Поступательно перемещающийся или вращаю-
щийся стержень а одной опоре без зазора
Ториевая опора (пята)
V'Образнаи напраил Пр( икмиая симметринного )фН.1й Р-Ч'пр / 1— 'пр aln •
Подкладные катки трения в Колеи с учетом тр (ли колеса, без учета юдши пинках 'пр D к— коаффиииент трения качения ения и подшипниках 4-/+2» fnp~ D
2S*
трения (фиг. 29). При движении изме-
нение направления относительной ско-
рости вызывает соответственное изме-
нение направления полной реакции R
с сохранением ее на поверхности конуса
с углом ф. При покое изменение вели-
чины и направления сдвигающей силы
дает такое изменение вектора полной
реакции R, при котором он остается
внутри конуса трения. Когда сила тре-
ния покоя достигнет предельного зна-
чения, полная реакция будет находить-
ся на боковой поверхности конуса с
углом ?0.
Смещение реакции у звеньев
с вращательным движением вызывается
возникающим моментом сил трения
(фиг. 31). Смещение b — f-r является
плечом пары сил N
и R„ = — (V, кото- I |
рая даст момент тре- Jm-— *- <
ния Мтр, действую- / ____
щий против движу- / \ \
щего момента. I Р'ГыУЛ }
Окружность Т I к> / /
трения описы- \ J
вается радиусом, рав- X.
ным смещению реак- —
ции Д. Во время дви- ф1(г. зь о
жения при любом на- иосп. трепня,
правлении реакции Rn
ее вектор должен касаться окружности
трения (фиг. 31). Окружность трения
используется при учете трения во вра-
щательных парах механизмов.
Приведенный коэффициент
трения fnp — понятие, используе-
мое для сложных сопряжений, имею-
щих обычно несколько мест трения и
особенности во взаимном расположе-
нии действующей силы и трущихся
поверхностей и т. п.
fna равно отношению приведенной
силы трения к перпендикулярной ей
компоненте действующей силы.
Значения приведенных коэффициентов
трення для некоторых случаев даны
в табл. 4.
Жидкостное трение характеризуется
формулой для силы внутреннего трения
с с
кГ,
где и — динамический коэффициент вяз-
кости в кГсек/мг; S — площадь тру-
щихся
диент
поверхностей в жг;
скорости в сек “ *•
гра-
436
ОБЩАЯ ЧАСТЬ
Характер изменения силы трения от
скорости при обильной смазке показан
па фиг. 32.
Формула для определения ц по из-
меренной величине относительной вяз-
кости Е в градусах Энглера
р=10-6-7 (о,737£-кГсек1лА,
где 7 — удельный вес жидкости в
о кГ/лА
Жидкостное трение обеспечивается,
если несущая способность масляного
слоя будет рав-
на нормальной
силе при задан-
ной скорости
относительного
движения и при
_ толщине масля-
ного слоя, пре-
f вы шлющей сум-
му высот
ровностей
поверхностях
трения. Прн не-
(с наибольшей
Полужидлостное
трепце
Жидкостное
трение
Фиг. 32. Изменение силы
1 рения и за fatten и ости от
с корсета скольжении при
обильная емвзке.
йе-
на
большой шероховатости
высотой неровностей до 0,1 толщины ма-
сляного слоя) получаем надежное жид-
костное трение с характером движе-
ния жидкости в зазоре, близким к ла-
минарному. В таких случаях резуль-
таты подсчетов F по приведенной формуле
получаются близкими к действитель-
ности. При более шероховатых поверх-
ностях трения и большой скорости от-
носительного движения поверхностей
движение жидкости в зазоре стано-
вится турбулентным, и потери на тре-
ние сильно возрастают. Получающийся
вследствие этого нагрев масла в зазоре
и снижение его вязкости создают опас-
ность разрыва масляного слоя и нару-
шения жидкостного характера трения.
Разновидностью жидкостного трения
является трение с газовой смазкой (воз-
душной, водородной). Особенности тео-
рии такого трения обусловливаются
сжимаемостью смазочного вещества.
Трение качения, возникающее при пе-
рекатывании круглого цилиндра по
плоскости, характеризуется формулами
(см. фиг. 33):
для силы трения
для момента трения
N,
где N — нормальная сила; г — радиус
цилиндра; k — коэффициент трения
качения, имеющий линейную размер-
ность, может быть представлен как ве-
личина смещения нормальной реакции
Rn = — N в сторону движения (фиг. 33).
Прн покое сила и момент трения
будут соответствен но равны
приложенной силе или приложенному
моменту. Предель-
ные значения:
силы трения по-
коя
Fe = Atf.
* момента трения
покоя
^отр = ^0*^ •
Фиг. 33. Трение пече-
ние.
где йд — коэффициент трения покоя для
случая качения.
Значения коэффициентов трения
и моментов трення
Значения приведенных коэффициентов
трения для некоторых часто встречаю-
щихся случаев даны в табл. 4.
Величины коэффициентов тре-
ння. найденные в лабораторных условиях
(табл. 5 и 6), могут быть использованы
лишь для ориентировочных расчетов
ввиду возможного несоответствия реаль-
ных условий работы трущейся пары
условиям проведения экспериментов
в лаборатории.
Более точными и надежными являются
величины коэффициентов трення для ти-
пичных случаев трущихся пар с учетом
условий их работы в механизме. Эти
данные устанавливаются на основании
длительного опыта эксплуатации соот-
ветствующих механизмов или специ-
ально проводимых испытаний.
Значения / и h для конкретных пе-
редач и соединений даны в соответствую-
щих разделах, посвященных расчету
деталей машин.
Моменты трення в подвижных со-
единениях машин,работающих насильно
меняющемся режиме (например, метал-
лорежущие станки общего назначения),
удобнее определять по формулам, от-
личным от
Мяр - Q/r.
ТРЕНИЕ В МЕХАНИЗМАХ
437
Таблица 5
Ориентировочные значения коэффициентов трения скольжения
Материалы трущихся тел Коэффициент трения /
покоя движения
Насухо Со смазкой Насухо Со смазкой
Металл по металлу Сталь — сталь Сталь — мягкая сталь Сталь — чугун Мягкая сталь — чугун Сталь - бронза Мягкая сталь — бронза ..... Чугун — чугун ... ....... Чугун — бронза Бронза — бронза 0,15 0.3 0,2 0,15 0.2 0,1-0,12 0,1-0,15 0.18 ОЛ 0.15 0.2 0,18 0.18 0.15 0.18 0.15 0.15-0,2 0.2 0,05-0,1 0,1 -0.2 0.05-0,15 0,06-0,15 0,1 -0,15 0,07-0,15 0,07-0.12 0.07 -0.15 0,07-0.1
Металл по дереву Мягкая сталь — вяз Чугун — дуб .......... Чугун — вяз. тополь 0.6 O.GS 0.6 0,12 0.4-0.6 0.25 0.3-0,5 0.4 0Л 0,1 0.2 0.1
Прочие пяры Дерево — дерево Кожа лицевой стороной — дуб . . Кожа бахтармой — дуб ...... Кожа — чугун Резина — чугун Пеньковый канат — луб ..... о.а-о,б 0.6 0.4 0,3—0,5 ол 0,1 0,15 0,2-0,5 0.3-0.5 0,3-0,4 0,6 0.8 0.5 0.07-0,15 0,15 0.5
Ранее приведенные диаграммы (см. фиг. 28) иллюстрируют характер изме- нения момента трения Мт1> в зависи- Таблица 6 Ориентировочны. значения коэффициентов трения качения для катка иа плоскости
мости от передаваемого через вал кру- тящего момента М„ при различных числах оборотов в минуту. Как видно, прпувелнченни Л1« отнуля величина Мтр увеличивается от некоторого начального значения. Такой характер зависимости от нагрузки значительно лучше выра- жается формулой типа л*тР-(Р+/’рЯ)4» где Р—сила трения, не зависящая от нагрузки; /'—коэффициент в слагаемом, Материалы трущихся тел Козффицгсиг трения k и с.л
Мяп Зака Т.П И . 1 Чугу Дер< Дер< сан сталь — мягкая сталь ленная сталь — алкал си- аль в в в о 0,005 0,001 0,006 0.03-0,04 0,05-0,08
и — чугун ыао — сталь ;ао — дерево ......
Таблица 7
Моменты трепня в подшипниках и зубчатых зацеплениях коробок передач,
определяемые по формуле вида Мтр =• (P-\-f рп)~^
Трущаяся пара Момент трения в кГмм Примечание
Я 5 Т а S 1 с к 1 Шариковые и цилин- дрические ролико- вые '^Ip-<o-M5rf+°-oo,₽n)4 Рп — нормальная сила в к Г', d - жнаметр вала а мм. Спра- ведливо при л «. 1000 об/мин и умеренной смазке разбрызги- ванием. При консистентной смазке и смазке в масляной ванне коэффициенты в первом слагаемом следует угпличить в 1Д> раза
Комические и сфери- ческие роликовые ^tp-(°-c25d+o’oo2₽n)4
438
ОБЩАЯ ЧАСТЬ
табл. 1
Трущаяся пара
Момент трения в кГмм
Примечание
При ~ > 150.
достаточном подво-
де смазки н неболь-
ших кромочных да-
влениях
Мтр
При < 1И.
или прн высоких
кромочных давле-
ниях
Мтп
тр
₽я — нормальная сила в кГ\
d. I — диаметр и длина под-
шипника в мм; А — диаме-
тральный зазор в л«ж;
— п — число обомни; р.— вязкость
масла в сантипуазах; р — срел-
р нее удельное давление в кГ/см*
Для одного кольиа
обыкновенного тина
при d — 20-1-80 мм
Л< =0,01
тр
d — диаметр вала в мм
При шлифованных
•jyhLBX
Прн нешлифованных
Зубьях
Мтр = ^+,0.08 2"
,Иетр= (10-“>С- fr/₽4?4- 0,10 Р„
Р, — окружное усилие в «Г;
dt. b — диаметр начальной ок-
ружности и ширина шестерни
о'лги; о — окружная скорость
в м/сек; р — вязкость масла
п сантипуазах; с - кож|к|>ициеит.
равный 3 — 6 при струйной
сназКе, 5—10 при смазке погру-
жением на высоту зуба и до-
ходящий до 60 прн погруже-
нии на бблыную глубину
П JL
Примечание. Формулы составлены по экспериментальным данным ЭНИМС [-’0| и др.
для подшипников и зубчатых передач средних pan,еров.
выражающем силу трения, зависящую
от нагрузки; Рп — сила, действующая
d
на трущуюся пару; — — г — плечо, на
котором приложена сила трення.
Формулы и значения необходимых
коэффициентов для определения М,пр
в кинематических парах зубчатых коро-
бок передач приведены в табл. 7.
ИЗНОС ДЕТАЛЕЙ В МЕХАНИЗМАХ
Виды износа
В практике встречается нормальный
и катастрофический износ. Первый мо-
жет быть заранее оценен и учтен при
планировании ремонтных работ, второй
выводит машину из строя внезапно.
Уменьшение величины нормального
износа и вероятности катастрофиче-
ского дает увеличение общего срока
службы машины, а также снижает стои-
мость и продолжительность ее ремонтов.
Износом называется постепенное
поверхностное разрушение материала,
сопровождающееся отделением от него
частиц, переносом частиц на сопряжен-
ное тело, а также изменением качества
поверхности — ее геометрии и свойств
поверхностных слоев материала.
Износ происходит вследствие меха-
нического, теплового, химического и
электрического воздействия на материал
соприкасающегося с ним трущегося
тела, воздействия свободных твердых
частиц другого материала или окру-
жающей среды.
Износ, так же как н трение, связан
со сложными, недостаточно изученными
явлениями в поверхностных слоях ма-
териала.
Истирание наблюдается при относи-
тельном движении прижатых друг к дру-
гу поверхностей. На истирание расхо-
дуется часть энергии трення.
Процесс истирания объясняется сле-
дующими явлениями: а) выступающие
неровности соприкасающихся деталей
при движении задевают друг за друга
н механически отрывают частицы ме-
талла с поверхностей; б) поверхности
приходят на отдельных участках в моле-
кулярное соприкосновение, как бы при-
ИЗНОС ДЕТАЛЕЙ В МЕХАНИЗМАХ
43Э
вариваясь друг к другу; при дальнейшем
относительном движении "происходит
разрушение мест приварки, сопрово-
ждающееся отрывом приставших частиц
с сопряженных поверхностей; в) аморф-
ные слои приработанных поверхностей
в отдельных точках сильно нагреваются
и размягчаются; при относительном
движении поверхностей размягченные
частицы переносятся со своих мест на
значительные расстояния, по пути за-
стывают и оказываются отделенными.
При истирании, невидимому, имеет
место сочетание перечисленных явлений.
Абразивный износ наблюдается при
попадании на трущиеся поверхности
мелких частиц высокой твердости (абра-
зива шлифовального круга, окалины,
песка и т. д.).
При жидкостном трении свободные
частицы, имеющие размеры меньше тол-
щины масляного слоя, оказывают
сравнительно слабое влияние на износ
поверхностей.
При нежндкостном трении, а также
когда размер частиц превышает толщи-
ну масляного слоя, наблюдается интен-
сивный износ поверхностен.Следы износа
имеют вид мелких продольных канавок.
Когда одна трущаяся поверхность
имеет малую твердость, абразивному
износу подвергается главным образом
другая поверхность; это объясняется
более прочным удерживанием частиц a6J
разива на менее твердой поверхности
за счет их вминания и, следовательно,
меньшим движением частиц абразива
относительно мягкой поверхности, чем
относительно твердой.
Задирание заключается в быстром
образовании продольных канавок зна-
чительной глубины (до 1 мм и больше).
Явление задирания для большинства
машин относится к категории катастро-
фического износа Процесс образования
задиров объясняется сцеплением тру-
щихся поверхностей в отдельных местах,
вырыванием значительного количества
металла с одной поверхности и появле-
нием нароста на другой. При дальней-
шем относительном движении поверх-
ности нарост вызывает появление за-
дира и дальнейшее прогрессивное
разрушение поверхности.
Ббльшая опасность задира получается
при поверхностях из одинаковых метал-
лов. Попадание абразивных частиц мо-
жет послужить самостоятельной при-
чиной задира (при достаточно крупных
частицах) или способствовать началу
описанного выше процесса вследствие
повышения удельного давления в точке,
расположенной впереди зерна абразива,
где происходит выпучивание металла.
Усталостное выкрашивание заклю-
чается в отслаивании частиц металла
с трущихся поверхностей в резуль-
тате усталости при периодически изме-
няющихся нагрузках. Явление уста-
лостного износа обычно наблюдается
в высших кинематических парах, глав-
ным образом при обильной смазке.
Последнее объясняется внедрением
жидкости в микрощели поверхности, что
способствует разрушению последней.
Постепенное смятие наблюдается при
недопустимо больших удельных давле-
ниях или при плохо обработанных, не
прошедших предварительной приработ-
ки. поверхностях.
Коррозионный износ является след-
ствием химического или электрического
воздействия среды; на интенсивность
коррозии оказывает большое влияние
нагрев поверхности детали, ускоряю-
щий процесс износа.
Факторы, влияющие на износ тру-
щихся поверхностей: а) материалы тру-
щихся поверхностей и их термообра-
ботка; б) качество поверхностей трения;
в) степень загрязнения мест трения;
г) характер и род смазки; д) величина
удельного давления; е) величина удель-
ной работы трения; ж) скорость.
Обычно износ металлов получается
гем меньше, чем выше их твердость.
Поэтому для повышения износостой-
кости рекомендуется применять терми-
ческую обработку стали и чугуна, на-
сыщение поверхностных слоев соответ-
ствующими веществами (цементация,
азотизация), а также поверхностные
покрытия износостойким материалом
(например, хромом).
При необходимости закалки отдель-
ных участков крупных стальных н чу-
гунных деталей производится поверх-
ностный нагрев нужных мест токами
высокой частоты или газовым пла-
менем.
Высота и характер неровностей на
трущихся поверхностях оказывают боль-
шое влияние на первоначальную ста-
дию износа и изменение размера де-
тали после приработки.
Характер неровностей оценивается
опорной кривой (фиг. 34, б), Дающей
возможность определять, какую часть
полной площади поверхности, профиль
которой показан на фиг. 34, а, соста-
440
ОБЩАЯ ЧАСТЬ
вляет опорная площадь в различных по
высоте сечениях. Очевидно, вначале
износ поверхности будет более интен-
сивным вследствие малой опорной пло-
щади. Высота неровностей характери-
зует зону интенсивного износа. ГОСТ
2789-51 дает классификацию чистоты
поверхностей по среднему квадрати-
ческому отклонению микронеровностей
И средней высоте микронеровностей.
Применение отделочных операций при
обработке поверхностей уменьшает вы-
соту неровностей и несколько улуч-
шает форму опорной кривой, обеспе-
Фнг. 34. Профиль поверхности и опорихя кривая.
чияая в верхних сечениях значительную
опорную площадь.
Улучшение поверхностей трения про-
исходит также в процессе первоначаль-
ной приработки, которая для устране-
ния опасности задиров часто произво-
дится на пониженных режимах работы
(см. стр. 433).
По материаламЭНИМСизиос стальных
закаленных направляющих (сталь 45.
Rc — 50) токарных станков в среднем
на 20% меньше, чем чугунных неза-
каленных; применение щитков для
защиты направляющих уменьшает
износ последних на 30—50%, примене-
ние принудительной смазки — на 15—
20% |19].
Условия работы изнашивающихся
деталей
Распределение износа между трущи-
мися поверхностями, а также по их
длине и ширине имеет большое значение
для работы механизма, долговечности
деталей н стоимости ремонта.
В каждой трущейся паре предпочти-
телен более сильный износ? простой и
легко заменяемой детали и менее силь-
ный — сложной и дорогой. При кон-
струировании машин это учитывается
соответствующим выбором материалов:
сложная деталь делается нз более твер-
дого металла и часто подвергается тер-
мической обработке н поверхностным
покрытиях»; простая деталь (например,
втулки, вкладыши и т. л.) выполняется
из более мягкого металла.
Распределение износа по поверхности
трения зависит от формы последней
и от условий работы пары.
Во вращательной паре
с одним неподвижным и одппм враща-
ющимся элементами имеют место три
следующих характерных случая распре-
деления износа:
1. Нагрузка постоянного направле-
ния — износ вращающегося элемента
будет равномерным по всей поверхности,
а неподвижного элемента — сосредото-
чен на одном участке поверхности. В
результате ось вращения сместится в
сторону местного износа; при этом
центрнчность вращения детали и ее
балансировка не нарушаются. Неподвиж-
ным может быть как охватывающий,
так и охватываемый элемент (фиг. 35, а).
2. Вектор нагружающей силы следует
за движением вращающегося элемента
(фиг. 35, 6) — износ неподвижного эле-
мента получается равномерным, изнов
вращающегося элемента — местным.
Ось вращения после износа поверхно
износ деталей в механизмах
441
стей соприкосновения не изменит своего
положения, но вращающаяся деталь
сместится относительно нее в сторону
местного износа, что может привести
к заметному увеличению дисбаланса.
3. Вектор нагружающей силы и по-
движный еле мент пары вращаются
с различными угловыми скоростями
(фиг. 35, в) — износ обеих трущихся
поверхностей получается равномерным.
К этому же случаю относится враще-
ние с различной скоростью двух эле-
ментов при постоянном направлении век-
тора нагружающей силы (фиг. 35, г).
В двух первых случаях линейный
суммарный износ может получиться
меньшим, если из более износостойкого
(твердого) материала будет изготовлена
деталь с местным характером износа.
Однако на практике обычно применяется
обратное соотношение твердостей мате-
риалов по следующим соображениям:
а) Сочетание слабого равномерного
износа Д> одной детали с более сильным
местным износом Д2 другой детали
(фиг. 36, а) не приводит к существен-
ному нарушению характера контакта
Фиг. 36. Характер контакта изношенных пар.
поверхностей. Незначительное по вели-
чине уменьшение радиуса кривизны
твердой равномерно изнашивающейся
детали компенсируется местным изно-
сом другой детали; при этом зона
контакта я (фиг. 36, а) практически не
уменьшается, и. удельное давление на
поверхностях не возрастает.
Если же соотношение твердостей
взять обратным рассмотренному, то
сильный равномерный износ А более
мягкой детали при слабом местном
износе Д2 твердой детали приведет к
значительному уменьшению зоны кон-
такта я (фиг. 36, б), увеличению удель-
ного давления и повышению интенсив-
ности износа.
б) Замена детали с местным износом
новой восстанавливает нарушенное
первоначальное'положение оси враще-
ния или центричность вращения. Равно-
мерное распределение износа в сочета-
нии с большей твердостью металл»
обеспечивает незначительный износ бо-
лее сложной и дорогой детали без
нарушения в ней центричности изнаши-
вающейся поверхности; местный харак-
тер износа в сочетании с мягким метал-
лом концентрирует износ на дешевой,
легко заменяемой детали (обычно—втул-
ка пли вкладыш), благодаря чему ремонт
машины упрощается.
Третий случай (фиг. 35, в и г) харак-
теризуется наименьшей величиной ли-
нейного суммарного износа поверхно-
стей. Смещения оси вращения вслед-
ствие износа здесь не произойдет, на-
рушение же центричности вращения
будет равно сумме радиальных взносов
обоих элементов Удельная работа тре-
ния, приходящаяся на единицу пло-
щади поверхности и равная произве-
дению силы трения на относительное
перемещение поверхностей, будет оди-
накова и равномерно распределена по
обеим поверхностям. Поэтому выбор
соотношения твердостей поверхностей
диктуется только желанием сконцен-
трировать износ на той или иной детали
по соображениям удобства ремонта.
Обычно в таких случаях обе поверхно-
сти стремятся выполнить с возможно
большей износостойкостью. Третий слу-
чай в чистом виде на практике встре-
чается редко. Примером использования
рассмотренного принципа может слу-
жить посадка неподвижного наружного
кольца шарикоподшипника в корпус
механизма с небольшим натягом; как
установлено практикой, кольцо при
работе постепенно поворачивается,
обеспечивая равномерный износ дорож-
ки, по которой катаются шарики.
В поступательной паре
всегда наблюдается тенденция к нерав-
номерному износу поверхностей в связи
с тем, что отдельные участки последних
периодически выходят из соприкосно-
вения.
Для количественной оценки ожида-
емой неравномерности износа можно
пользоваться диаграммами распреде-
ления удельной мощности сил трения
по поверхностям. Для построения этой
диаграммы требуется установить распре-
деление относительного скольжения по
поверхностям трения и закон изменения
удельного давления в зависимости от
перемещения деталей для различных
442
ОБЩАЯ ЧАСТЬ
точек поверхностей трения. Построе-
ние диаграмм относительного сколь-
жения для разных соотношений между
длиной хода и размерами поверхно-
стей трения показано в табл. 8.
Таблица Д
/яспрехеление относительного скольжении
по длине поступательно движущихся
деталей
г— длина хода верхней летали относи
тельио нижней: I — длина верхней летали;
L - длина нижней детали; — наибольшее
возможное или действительное относительное
скольжение
Наибольшая величина относитель-
аого скольжения
s-л
“°= “зо~ мсек'
где I — длина хода в м; п — число
двойных ходов в минуту.
В том случае, когда равнодействую-
щая Q сил, нагружающих верхнюю
деталь, находится на ее середине, для
двух первых случаев, указанных в
табл. 8, удельное давление между дета-
лями остается постоянным, и диаграмма
относительных перемещений будет одно-
временно диаграммой удельной мощно-
сти сил трення.
Величине м/сек на диаграмме
удельных скольжений будет соответ-
ствовать удельная мощность сил трения
*0 •“f Pvae М/секслА,
где / — коэффициент трения; р0—удель-
ное давление 'между поверхностями
в кГ.смА.
В трех последних случаях табл. 8
диаграммы удельной мощности требуют
кропотливых построений с учетом не-
равномерного распределения давления
ня поверхности трения при выходе верх-
ней детали за пределы нижней. Диа-
граммы распределения давлений и не-
обходимые формулы приведены в табл. 9.
Таблица 9
Удельное давление на соприкасающихся
поверхноС1их пои линейном законе
Крайняя точка нижней детали харак-
терна тем. что на нее наиболее длитель-
ное время действуют максимальные да-
вления. получающиеся в связи с выдви-
жением верхней детали за пределы
нижней.
График на фиг. 37 дает возможность
быстро определить мгновенное р и
среднее рср значения удельногэ давле-
ния в крайней точке нижней поверхно-
сти при перемещении верхней детали
из положения, в котором крайние точки
обеих деталей совпадают, в положение
наибольшего выдвижения верхней де-
тали.
Для крайней точки нижней поверх-
ности удельная мощность сил трення
у* -я/.^.р-и кГм/сек-слА.
где Рср — среднее удельное давление,
определяемое при помощи графика на
фиг. 37, в кГ/см'-, и — относительное
скольжение в М{сек. определяемое по со-
ИЗНОС ДЕТАЛЕЙ В МЕХАНИЗМАХ
+13
ответствующей диаграмме (табл. 8) или
по формуле
•1
“ = “° s ’
где /) — величина выдвижения детали.
Неравномерный износ поверхностей
со временем приводит к искажению их
формы и нарушению правильного кон-
такта. Чтобы ослабить это явление,
следует для детали, имеющей равномер-
ное или близкое к нему распределение
удельной мощности сил трения, выби-
рать менее твердый материал, чем для
Фиг. 37. График хля определения давлений в край-
ней точке ипжией поверхности скольжении.
сопряженной детали, работающей с
сильно изменяющейся по длине удель-
ной мощностью сил трения.
Постоянство режима ра-
боты пары облегчает борьбу с изно-
сом. Например, если вал работает с по-
стоянным числом оборотов в минуту,
имеется возможность выбрать для его
подшипников наивыгоднейшнй режим
жидкостного трения; если же число
оборотов в минуту меняется в преде-
лах I : 50 (металлорежущие станки),
становится невозможным обеспечить
жидкостное трение в подшипниках на
всем диапазоне скоростей вращения.
В этом случае выгодно применять под-
шипники качения.
Режим работы кинематических пар
нарушается при разбеге н пыбеге ма-
шины. Наблюдениями установлено, что
подшипники автомобильного двигателя
за периоды разбега и выбега изнаши-
ваются больше, чем за все время рабо-
ты при установившемся движении.
Сдной из действенных мер борьбы с по-
вишенным износом при разбеге машины
является обильная подача смазки насо-
сом или ручным лубрикатором перед
пуском машины.
Пути изучения износа
Явление износа связано со сложными
процессами в поверхностных слоях ма-
териала. Изучение явлений износа бази-
руется на экспериментальных работах.
Основные направления изучения про-
цесса и получения практических данных
по износу следующие:
1. Лабораторные испытания, прово-
димые на образцах установленной формы
и размеров. Эти работы дают материал
для теоретических выводов, а также
выявляют зависимость износа от от-
дельных факторов (материал, термообра-
ботка, состояние поверхности, смазка
и т. п.). Результаты исследований могут
найти ограниченное использование в
практике, главным образом —для срав-
нительных оценок различных трущихся
пар.
2. Лабораторные (стендовые) испы-
тания, проводимые на образцах, соот-
ветствующих встречающимся на прак-
тике парам (например, различным чер-
вячным, винтовым и другим передачам).
Условия проведения испытаний близки
к практическим условиям работы.
Строгий учет отдельных факторов, воз-
можный в лабораторной обстановке,
позволяет выявить влияние отдельных
причин на интенсивность износа иссле-
дуемых пар. Результаты такого иссле-
дования могут быть использованы при
конструировании машин, испытания
могут выявить новые, более целесо-
образные конструкции пар рассматри-
ваемого типа.
3. Наблюдения за износом деталей
в условиях производственной работы
машин. Преимуществом этого пути
изучения износа является полное соот-
ветствие его результатов практическим
. условиям работы машин. Недостатки:
трудность учета влияния отдельных
факторов, трудность надежного кон-
троля за условиями работы отдельных
пар, менее тщательные, чем в лабора-
торных условиях, замеры. Для устра-
нения случайных причин необходимо
большое количество наблюдений. По-
лученные результаты могут быть ис-
пользованы как лицами, занимающи-
мися эксплуатацией машин, так и кон-
структорами.
444
ОБЩАЯ ЧАСТЬ
Для изучения износа деталей машин
используются все три указанные на-
правления в работе.
ОСНОВЫ ТЕОРИИ ТОЧНОСТИ
МЕХАНИЗМОВ
Основные понятия
Факторы, влияющие на точность
работы нового механизма:
а) отклонения от заданного движе-
ния, зависящие от выбранной схемы
механизма, встречаются главным обра-
зом в механизмах с одними низшими
парами для приближенного осуществле-
ния движения;
б) технологически неизбежные откло-
нения в размерах и форме деталей —
имеют значение для большинства ма-
шин — регламентируются стандарти-
зованной системой допусков;
в) упругие деформации звеньев под
влиянием действующих сил — жест-
кость звеньев имеет существенное зна-
чение для большинства механизмов;
г) температурные деформации звеньев—
особенно сильно проявляются при не-
равномерном нагреве последних;
д) относительные смещения деталей
под действием сил за счет неплотно-
стей и деформаций контактных поверх-
ностей в неподвижных соединениях; со-
противляемость смещению носит на-
звание жесткости стыков; она имеет
большое значение для машин с высо-
кой общей жесткостью, например для
металлорежущих станков;
е) смещения звеньев за счет зазоров
и толщины слоев смазки в кинемати-
ческих парах; влияние зазоров особенно
сильно проявляется при нежидкостпом
трении в геометрически замкнутых па-
рах, которые находятся под действием
изменяющихся по направлению нагру-
зок; влияние толщины масляного слоя
сказывается при жидкостном и отчасти
при полужидкостном трении.
Для механизмов и машин важна не
только их первоначальная точность ра-
боты, но и способность сохранять эту
точность при длительной эксплуатации,
а также при длительном хранении ма-
шины.
Дополнительные факторы, влияющие
на точность работы механизма, нахо-
дившегося в эксплуатации:
а) износ трущихся поверхностей, осо-
бенно за счет истирания и смятия (см.
стр. 438);
б) остаточные деформации деталей,
особенно смятие в неподвижных соеди-
нениях плохо обработанных поверхно-
стей, испытывающих большие удельные
давления;
в) постепенные деформации деталей
(коробление) за счет остаточных напря-
жений, полученных при технологиче-
ских процессах, связанных с их нагре-
вом до высоких температур. Эти дефор-
мации особенно существенны для круп-
ных литых деталей (например, станин),
не прошедших естественного или искус-
ственного старения, и появляются хек
во время эксплуатации машин, так и
при длительном их хранении.
Влияние всех перечисленных факто-
ров на точность работы механизмов
еще не вполне изучено.
В задачу раздела теории точности
механизмов, изучающей теоретически
неизбежные для некоторых схем меха-
низмов отклонения получающегося дви-
исепия от заданного движения, входит
определение основных размеров меха-
низма (метрический синтез) из условия
получения наименьших отклонений на
интересующем нас участке движения.
В настоящее время объектами иссле-
дования являются плоские механизмы
с одними низшими парами. Эти меха-
низмы благодаря разнообразию движе-
ния шатуна дают возможность прибли-
женно воспроизводить практически
почти любое плоско-параллельное дви-
жение. Необходимые сведения по этому
вопросу имеются в специальной лите-
ратуре.
Основоположником указанного раз-
дела теории точности механизмов являет-
ся П. Л. Чебышев, разработавший
теорию яаилучшего приближения тра-
ектории точки шатуна к заданной
кривой.
Практически более важный раздел
теории точности механизмов посвящен
изучению нарушений заданного движе-
ния механизма вследствие ошибок в раз-
мерах и форме звеньев. Основоположни-
ками этого раздела теории точности
являются советские ученые Н. А. Калаш-
ников (15) и Н. Г. Бруевич |8|. Боль-
шинство ошибок имеет случайный ха-
рактер, вследствие чего и теория
точности механизмов носит теоретико-
вероятностный характер. В задачу этого
раздела входят определение ожидаемых
величин ошибок в размерах звеньев н
нахождение по ним интересующих нас
ошибок механизма.
ОСНОВЫ ТЕОРИИ ТОЧНОСТИ МЕХАНИЗМОВ
445
Основные определения
Идеальным механизмом принято на-
зывать механизм с абсолютно точными
размерами всех звеньев; действитель-
ным механизмом условно называют ме-
ханизм, имеющий ошибки в основных
размерах и форме звеньев (первичные
ошибки).
Первичные ошибки делятся на:
а) систематические — постоянные или
изменяющиеся по определенному закону;
б) случайные —величины которых нельзя
заранее предугадать; в) грубые — недо-
пустимо большие ошибки, подлежащие
устранению (обычно отклонения, выхо-
дящие за пределы допусков).
Распределение ошибок по указанным
группам зависит от того, анализируется
ли конкретный экземпляр механизма или
достаточно большая серия одинаковых
механизмов без учета индивидуальных
особенностей каждого экземпляра.
Часть первичных ошибок является
технологически неизбежной (например,
ошибки во взаимном расположении эле-
ментов кинематических пар в звене и
отдельных поверхностей в элементе ки-
нематической пары), часть представляет
собой отклонения, необходимые для обес-
печения надлежащих эксплуатационных
свойств механизма (например, зазоры,
заполненные смазкой, в быстроходных
вращательных парах).
Первичные ошибки могут быть ска-
лярными или векторными, плоскими и
пространственными. Плоская векторная
сшибка может быть заменена двумя
скалярными, пространственная — тремя
скалярными.
Ошибки механизма характеризуют от-
клонения движения ведомых и некото-
рых промежуточных звеньев от иде-
ально точного движения
Ошибкой положения механизма на-
зывается разница положений ведомых
звеньев действительного и идеального
механизмов при одинаковых положениях
ведущих звеньев.
Ошибкой перемещения механизма на-
зывается разница перемещений ведомых
звеньев действительного и идеального
механизмов при одинаковых перемеще-
ниях ведущих звеньев обоих меха-
низмов.
Ошибками положения и перемещения
ведомого звена механизма называются
разницы гоответственно положений и
перемещений ведомых звеньев действи-
тельного и идеального механизмов, по-
лученные не только вследствие первич-
ных ошибок механизма, но и от неточ-
ности положений ведущих звеньев.
Ошибками скоростей и ускорений
механизма называются разности между
скоростями и ускорениями ведомых
звеньев действительного и идеального
механизмов при одинаковых положениях
ведущих звеньев.
Динамическими ошибками механизма
называется разность сил реакций в дей-
ствителыюм.и идеальном механизмах при
одинаковых положениях ведущих звень-
ев. Эти ошибки получаются в виде от-
клонений сил реакций или реактивных
импульсов.
Нахождение ошибок положения
и перемещения механизма
по первичным ошибкам
Для встречающихся в практике малых
величин ошибок по сравнению с разме-
рами звеньев справедливы следующие
положения:
1. Влияние каждой первичной ошибки
на ошибку положения ведомого звене
не зависит от других первичных оши-
бок (принцип независимости действия
первичных ошибок).
2. Ошибка положения механизма, вы-
званная какой-либо одной первичной
ошибкой, равняется произведению по-
следней на передаточное отношение пре-
образованного механизма, равное отно-
шению скорости его ведомого звена
к скорости ведущего.
Преобразованный механизм строится
таким образом, чтобы он давал соответ
ствующее перемещение ведомого звена
при перемещениях, имитирующих изме
некие размеров звеньев действительного
механизма на величины первичных оши
бок (фиг 38).
Ошибка положения механизма, так
же как н ошибка положения ведомого
звена механизма, мзжет быть найдена
графическим, графо аналитическим или
аналитическим способом.
Графический способ состоит в выявле-
нии преобразованных механизмов — осо-
бого для каждой первичной ошибки или
общего для всех первичных ошибок —
и построении для них планов малых
перемещений с помощью обычных при-
емов построения планов скоростей Пол-
ная ошибка положения механизма опре-
деляется алгебраическим суммированием
ошибок положения, каждая из которых
получается от одной первичной ошибки,
или непосредственно построением плана
44Г>
ОБЩАЯ ЧАСТЬ
малых перемещений с учетом сразу
всех первичных ошибок.
В качестве примера на фиг. 38 и 39
показано определение ошибок положе-
ния ползуна 4 смещенного кривошипно-
шатунного механизма (фиг. 38, а) по за-
данному угловому положению ведущего
Фиг. 38. Схемы анализируемого кривошнпно-ша-
туммого механизма и преоОразоивнных механизме».
кривошипа 2 (угол а) и известным пер-
вичным ошибкам в основных размерах
звеньев механизма.
По схеме преобразованного механизма
(фиг. 38, б) путем построения плана
малых перемещений (фиг. 39, б) опре-
деляют ошибку Дх» положения ползуна,
получающуюся вследствие известной по
величине первичной ошибки в длине
шатуна 3. Далее по схеме на фиг. 38, в
и соответствующему плану на фиг 39, в
определяют ошибку &хг положения пол-
зуна, получающуюся вследствие пер-
вичной ошибки Д</1 в величине ра-
диуса кривошипа 2. И, наконец, по
схеме на фиг. 38, г' или 38, г’ и плану
на фиг. 39, г' или 39. г' определяют
ошибку Дх» положения ползуна, полу-
чающуюся от первичной ошибки Д<?1 в
величине смещения центра шарнира О
от прямолинейной траектории движения
точки В. Полная ошибка положения
ползуна Дх = Дх1 + Дх» -г- Лхз. где
ошибки, направленные вправо, счита-
ются положительными, направленные
влево — отрицательными.
Полная ошибка Дх положения ползуна
может быть также получена 'построе-
нием одного плана малых перемещений
(фнг. 39, д) для преобразованного меха-
низма, имеющего схему по фиг. 38, д'
или по фиг. 38, д'.
Во всех построенных планах малых
перемещений: 1-1 — параллельно АВ,
11-11 — перпендикулярно АВ, ! Il-
li 1 — параллельно направлению движе-
ния точки В, IV-IV — параллельно О А,
V-V — перпендикулярно направлению
движения точки в (см. фиг. 38 и 39).
Ввиду малых величин первичных оши-
бок план малых перемещений строится
в сильно увеличенном масштабе, что
благоприятно влияет на точность ре-
зультата.
Фнг. 39. Планы малых перемещений крипошнпио-
шатуииого механизма по фнг. 38.
формул на базе геометрических зависи-
мостей плана малых перемещений.
Аналитический способ целесообразен
для сравнительно простых часто повто-
ряющихся схем механизмов.
ПРОЕКТИРОВАНИЕ ПЛОСКИХ МЕХАНИЗМОВ
447
Ошибка перемещения механизма
равна разности ошибок положения ме-
ханизма в конечном и в начальном поло-
жениях последнего. Та кая же зависимость
существует между ошибками перемеще-
ния и положения ведомого звена меха-
низма.
Пользуясь указанным соотношением,
легко определить ошибки перемещения
по найденным ошибкам положения.
ПРОЕКТИРОВАНИЕ ПЛОСКИХ
МЕХАНИЗМОВ
Основные положения
Теория механизмов занимается неко-
торыми основными вопросами проекти-
рования машин и механизмов.
Качество выполнения основной задачи
и экономическая эффективность являют-
ся критериями целесообразности приме-
нения всякой машины.
Экономическая эффективность машины
определяется: 1) производительностью.
2) степенью автоматизации, 3) перво-
начальной стоимостью машины, 4) сро-
ком службы машины. 5) расходами по
эксплуатации.
Большое значение имеют также малая
металлоемкость и минимальное приме-
нение дефицитных материалов прн изго-
товлении и эксплуатации машины
На отдельных этапах проектирования
конструктор должен учитывать ряд кон-
кретных требований, количественная
оценка влияния которых на работу и
на экономическую эффективность ма
шины часто бывает весьма затруднитель-
ной; в качестве примеров подобных
требований можно привести такие, как
легкий доступ к отдельным узлам ма-
шины, легкий монтаж и демонтаж,
удобное расположение органов управле-
ния и т. п.
Прежде чем приступить к проекти-
рованию, выбирают принцип действия
машины, исходя из ее назначения и ос-
новных условий работы. Выбор прин-
ципа действия требует от конструкто-
ра большого опыта и знания характе-
ра рабочего процесса машины. Далее,
основное задание преобразовывают в ки-
нематическое и расчленяют его на кине-
матические задания для проектиро-
вания отдельных узлов (механизмов)
машины.
На этом подготовительная работа за-
канчивается, и можно приступить к про-
ектированию.
Процесс проектирования механизма
можно разбить на следующие этапы:
1) выбор типа механизма и составле-
ние структурной схемы; 2) составление
кинематической схемы; 3) конструктив-
ная разработка механизма.
Выбор типа механизма
и составление структурной схемы
Выбор типа механизма в каждом от-
дельном случае является весьма ответ-
ственным этапом проектирования, ока-
зывающим большое влияние на простоту
и эксплуатационные качества механизма.
Плоский механизм может быть приме-
нен тогда, когда кинематическое задание
предусматривает движение всех звеньев
в параллельных плоскостях. После того
как возможность применения плоского
механизма установлена, решается вопрос,
какой тип механизма возможно и целе-
сообразно использовать для выполнения
поставленной кинематической задачи
Кинематическая задача заключается
в воспроизведении заданных или обу-
словленных движений или, точнее, в пре-
образовании движения ведущего звена
в заданные или обусловленные движения
ведомых звеньев. Так как возможность
воспроизведения движений для каждого
механизма определяется характером при-
меняемых кинематических пар, то с этой
точки зрения плоские механизмы удобно
разбить ня три следующих типа: I) меха-
низмы с одними поступательными пара-
ми; 2) механизмы с одними вращатель-
ными или с вращательными и поступа-
тельными парами; 3) механизмы, имею-
щие высшие пары.
В механизме с одними поступатель-
ными нарами относительное движение
любых двух звеньев получается прямо-
линейно-поступательным и отношение
между скоростями звеньев постоянным.
Таким образом, механизмы первого типа
пригодны для преобразования прямоли-
нейно-поступательного движения веду-
щего звена в прямолинейно-поступатель-
ные движения ведомых звеньев с посто-
янным отношением скоростей и с соблю-
дением заданных направлений движения
звеньев.
В механизмах с одними вращатель-
ными или с вращательными н посту-
пательными парами для получения
сложного относительного движения двух
каких-либо звеньев приходится вводить
между ними промежуточные звенья. При
помощи рассматриваемых механизмов
448
ОБЩАЯ ЧАСТЬ
точно воспроизвести заданное относи-
тельное движение двух звеньев в общем
случае невозможно, и приходится удо-
влетворяться приближенным решением
задачи. Обычно на относительное дви-
жение интересующих нас звеньев накла-
дывается лишь некоторое конечное число
условий. Примером последних может слу-
жить требование, чтобы в своем движе-
нии звенья проходили через несколько
заданных относительных положений. Чем
точнее требуется воспроизвести задан-
ное движение звеньев или чем большее
число условий приходится налагать на
их движение, тем большее число звеньев
и пар должен иметь механизм, тем более
•сложным он получается. Поэтому до-
статочно точное решение сложных кине-
матических задач при помощи механиз-
мов второго типа может привести к ме-
ханизмам с довольно большим числом
звеньев.
В механизмах с высшими парами
сопряженные звенья могут совершать,
вообще говоря, любое наперед заданное
относительное движение, характер кото-
рого определяется соответствующим про-
филированием элементов пары. Эго цен-
ное свойство высшей пары позволяет по-
лучать механизмы, которые при малом
числе звеньев воспроизводят весьма
сложные движения.
Из приведенной характеристики меха-
низмов 1-го, 2-го и 3-го типов видно,
что все задачи о воспроизведении дви-
жений, решающиеся при помощи плоских
механизмов с одними низшими парами,
могут быть решены посредством меха-
низмов, имеющих высшие пары.
Замена механизма с одними поступа-
тельными парами механизмом 3-го типа
•никакого выигрыша в числе звеньев не
дает и может оказаться целесообраз-
ной в том случае, когда желательно
сократить число пассивных связей ме-
ханизма
При одинаковых возможностях приме-
нения механизмов 2-го и 3-го типов необ-
ходимо учитывать следующие преимуще-
ства механизмов с одними низшими пара-
ми: а) удобство регулирования относи-
тельного движения звеньев путем изме-
нения одного илн нескольких основных
размеров механизма; решение подобной
задачи в механизмах с высшими парами
встречает ббльшие конструктивные труд-
ности и поэтому редко осуществляется;
б) легкая компенсация износа в шар-
нирах и поступательных парах посред-
ством соответствующих регулировочных
устройств (например, клиньев в напра-
вляющих станка).
Отдать предпочтение тому нлн иному
варианту в сомнительных случаях можно
лишь в результате совместного рассмо-
трения кинематических схем или даже
конструктивных чертежей механизмов.
Обычно о сравнительной сложности
механизмов можно судить по их струк-
турным схемам.
Структурная схема должна обеспечить
принужденность движения механизма
и возможность спроектировать меха-
низм, звенья которого совершали бы
заданные или соответствующим образом
обусловленные движения.
Необходимыми условиями получения
механизма принужденного движения
являются: а) правильное соотношение
между числом звеньев и числом кинема-
тических пар различных типов, устана-
вливаемое соответствующими структур-
ными формулами; б) правильный порядок
соединения отдельных звеньев в меха-
низм посредством кинематических пар.
Второй вопрос структурного синтеза
заключается в выборе структурной
схемы, по которой можно было бы по-
строить механизм для выполнения того
или иного конкретного задания.
Составление кинематической схемы
Как было указано, кинематическая
схема в отличие от структурной имеет
основные размеры, определяющие кине-
матику механизма. Отыскание этих раз-
меров и является задачей так называе-
мого метрического синтеза механизмов.
Все существующие методы метрического
синтеза предполагают наличие структур-
ной схемы.
Исключение составляет эксперимен-
тальный метрический синтез, заключаю-
щийся в отыскании методом проб точек
плоской системы, траектории движения
которых относительно другой плоской
системы мало отличаются от окружно-
стей нлн шатунных кривых. В этом слу-
чае структура механизма зависит от си-
стем, при рассмотрении относительного
движения которых нам удалось найти
упомянутые точки, и от вида траекторий
этих точек (окружности или шатунные
кривые).
Метрический синтез механизмов про-
изводится по заданию, в которое вклю-
чаются не только чисто кинематические
условия, но также условия динамические
и даже конструктивные.
ПРОЕКТИРОВАНИЕ ПЛОСКИХ МЕХАНИЗМОВ
449
К динамическим условиям относят вы-
держивание в известных пределах угла
передачи или угла давления, сильно вли-
яющих на работоспособность механизма.
Углом давления в называется угол
между . вектором абсолютной скорости
той точки ведомого звена, к которой
приложена движущая сила, и вектором
движущей силы без учета его отклоне-
ния вследствие трения в кинематических
парах.
Углом передачи । называется разность
между прямым углом и углом давления.
Для различных типов механизмов
можно пользоваться не приведенными
здесь общими определениями 0 и -у, а бо-
лее удобными частными определениями;
некоторые из них указаны далее.
К конструктивным относятся условия,
налагаемые на расположение отдельных
шарниров, и предварительное задание
некоторых основных размеров звеньев.
Составление кинематических схем ме-
ханизмов 1-го типа сводится к опреде-
лению углов расположения поступатель-
ных пар и трудностей не представляет.
Метрический синтез механизмов 2-го
типа представляет большие математиче-
ские трудности. Аналитическое решение
практически применимо только в эле-
ментарно простых случаях, что заста-
вляет пользоваться графическими и
графо-аналитическими методами (см.
стр. 459). Практическое значение имеет
экспериментальный синтез плоских -ме-
ханизмов.
Метрический синтез механизмов 3-го
типа заключается в профилировании эле-
ментов высших пар н выгодно отли-
чается своей простотой от синтеза ме-
ханизмов 2-го типа. Последнее обстоя-
тельство часто является решающим при
выборе того или иного типа.механизма.
Нахождение конструктивных вариантов
(преобразование механизмов)
Для получения новых •кинематических
схем и вариантов конструктивных ком-
поновок механизмов с одной и той же
кинематической схемой используются
следующие практические приемы пре-
образования механизмов:
1. Превращение в стойку различных
змньев кинематической цепи дает но-
вые кинематические схемы механизмов.
Призер. Из кинематической цепи, состоящей
из звеньев I, 2, 3 и 1 и имеющей три вращатель-
ные и охну поступательную пару, можно получить
кривэшипио-шхтуииый (фиг. 40. а), крнпошипио-
'29 Том I Зак. 1461
кулисный с вращающейся кулисой (фиг. 40, б),
кривошип но- кулисный с качающейся кулисей
(фиг. 40. в) и коромыслово-ползунный (фиг. 40, г)
меуяниамы.
Фиг. 40. Преобразование механизма путем пре-
вращения н стойку различных его jueiibetu
2. Расширение цапф вращательных
кинематических пар до конечных зна-
чений радиуса дает различное оформле-
ние механизмов бед изменения кинемати-
Фиг. 41. Преобразование мехаиизмоп путем рас-
ширенна шпф и обращение кинематических пар.
ческой схемы; прн расширении до беско
нечно большого радиуса — превращение
вращательной пары в поступательную.
3. Обращение кинематических пар (ме-
няются местами охватывающий и охва-
тываемый элементы пары) дает новые
450
ОБЩАЯ ЧАСТЬ
оформления механизмов без изменения
кинематической схемы.
Пример. Используя способы расширения цапф,
обращения пар и ограничивая элементы пар от-
дельными участками, получаем различные вари-
анты кривошипно-шатунного механизма с неизмен-
ной кинематической схемой (фиг. 41, а—лс), а при
увеличении радиуса элемента охной пары ао бес-
конечности — кривошипно-кулисный механизм с
поступательно движущейся кулисой (фиг. 41, з).
На фиг. 41. а—исходный кривошипно-шатунный
механизм; б — механизм, полученный из исходного
путем расширения цапфы шарнира А; в — меха-
низм, полученный из исходного путем расширения
цапфы шарнира В (кривошип обратился в эксцен-
трик. шатуи получил кольцевую форму); г — гео-
метрически незамкнутый механизм, полученный
в результате совместного расширения цапф швр-
ниров В и С (кривошип обратился в эксцентрик,
шатун принял форму полумесяца); д — механизм,
полученный нз исходного путем расширенна одного
участка цапфы шарнира С (фигурный шатун поме-
шается п фнгурвзм вырезе ползуна); е — меха-
низм, полученным путем расширения цапфы шар-
нира С (шатун приобрел кольцевую форму, пол-
вуи — круглую внешнюю форму); ж — механизм,
полученный из предыдущего путем использования
отдельного участка кольцевого шатуна (шатуи при-
обрел форму дугового кулисного камня, ползун —
форму дуговой кулисы с прорезью); з — криво-
шипно-кулнеиый механизм, полученный из преды-
дущего посредством дальнейшего расширения
цапфы шарнира С до радиуса, равного бесконеч-
ности (шатун обратился в кулисный камень, пол-
зун — в поступательно движущуюся кулису).
В результате преобразований спосо-
бом расширения цапф внешние очерта-
ния звеньев часто меняются до неузна-
ваемости; например, стержень с двумя
шарнирам» на концах приобретает форму
кольца, эксцентрика, полумесяца, дуго-
вого кулисного камня и т. п.
Примечание. Список использованной
литературы см. па стр. 831—532.
ГЛАВА XX
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
МЕХАНИЗМЫ С ОДНИМИ
ПОСТУПАТЕЛЬНЫМИ ПАРАМИ
Общие сведения
Назначение. Плоские и пространствен-
ные механизмы с одними поступатель-
ными парами пригодны для преобразо-
вания прямолинейно-поступательного
движения ведущего звена в прямоли-
нейно-поступательнысдвижения ведомых
звеньев по заданным направлениям и
с постоянным отношением скоростей.
Эти механизмы применяются, например,
в вырезных и вытяжных штампах, в при-
способлениях к станкам, в сложном
инструменте и т. д.
Структура. Применение находят глав-
ным образом механизмы, все звенья ко-
торых связаны кинематическими парами
со стойкой.
Наибольшее распрострапепие имеют
механизмы с наименьшим числом звеньев,
преимущественно трехзвенные. Необхо-
димость введения промежуточного звена
между ведущим и ведомым звеньями вы-
зывается главным образом взаимным
pai п сложением последних, реже — жела-
нием улучшить динамическую характе-
ристику механизма (см. ниже).
Для удобства анализа многозвенные
механизмы могут быть соответствую-
щей разбивкой приведены к трехзвен-
ным.
Роль поступательных пар в механиз-
мах могут выполнять также подходящие
кинематические пары более низких клас-
сов, если замена пар не изменит числа
степеней свободы механизма и не нару-
шит общих условий связи, т. е. если
сокращение числа условий связи, нала-
гаемых парами, произойдет в результате
уменьшения числа пассивных связей
механизма.
Такая замена часто практикуется, так
как позволяет упростить форму элемен-
тов пар и сократить объем пригоночных
29*
работ или число размеров, которые не-
обходимо выдерживать по жестким до-
пускам.
В трехзвенном механизме допу-
скается замена цилиндрическими па-
рами (IV класс) одной, двух или трех
поступательных пар. Возможна замена
одной поступательной пары плоскостной
(III класс) или высшей парой I или
II класса. Можно заменить также одну
пару цилиндрической И одну пло-
скостной или высшей парой II класса,
две пары цилиндрическими и одну пло-
скостной.
Кинематика. Отношение между пере-
мещениями, скоростями и ускорениями
отдельных звеньев механизма постоянно.
План перемещений плоского механизма
является одновременно планом скоростей
и планом ускорений (при замедленных
движениях звеньев — повернутым на
180°). Построенный план сохраняется
для любого положения механизма, ме-
няется лишь его масштаб в зависимости
от величины перемещения, скорости и
ускорения ведущего звена.
Трехзвенный механизм
Свойства механизма. Свойства меха-
низма характеризуются:
а) передаточным отношением iv, рав-
ным отношению скорости ведомого звена
к скорости ведущего;
б) коэффициентом передачи силы if,
равным отношению усилия на ведомом
звене к усилию на ведущем;
в) к. п. д. механизма т) =
Для трехзвепного механизма (фиг. I)
. s|na< .
*" в| " sinaj ’
aln (я2 — Уп) — cos (а, — ?.ц) tg
sin (aj 4- <р12) + COS (a, -h y12) tg
4*2
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
И при ?U = ЭД ,
I sin(<n —эд —ЭД)
₽ ~ sin (в] + <?15 +• эд) ’
где эд. эд, — углы трения в кине
магических парах, соединяющих ссот
ветственно звенья / и 2, 1 и 3, 2 н<?.
Для трехзвенного механизма, передаю-
щего движение под углом 90° (фиг. 2),
tg«,;
i I ~tg(-»! +Ук)<гэд
p lg 1’1 + fix) + tg ЭД
и при эд = эд
‘р — ctg (“Г + эд т эд).
Влияние конструкции механизма на
трение в кинематических парах учиты-
. вается подстанов-
Фиг. 3. Трехзнечиый
меминам с консольный
неком ым зныоы.
кой в формулы ДЛЯ
определения ip уг-
лов трения, соот-
ветствующих при-
веденным коэффи-
циентам трения
(см. стр. 435).
В качестве приме-
ра на фиг. 3 по-
казан трехзвенный
механизм с кон-
сольным звеном 2;
приведенный коэф-
фициент трения
/» яр “ tg эд нр = ( 1 4- 3 —tg эд.
Передаточное отношение в механиз-
мах обычно меньше единицы: углы
между направлениями движений веду-
щего и ведомого звена большей частью
равны 90° или 180®. В последнем слу-
чае необходим механизм с промежуточ-
ным звеном, который разбивается на
два трехзвенных, каждый — для пере-
дачи под углом 90°.
На фиг. 4 приведен график изменения
гр, гр и Т; в зависимости от угла sj для
трехзвенного механизма, передающего
Фиг. Г. Перем-гочное отношение, коьффициеш пе-
релачм силы и к. я. д. трехзоекяого иежяниэыа
л зависимости от угла Клима.
движение под прямым углом. Углы тре-
ния 3° соответствуют работе в масляной
ванне хорошо изготовленного механизма,
углы трения 5е — обыкновенным усло-
виям работы хорошо изготовленного
механизма, углы трения 8’ — плохим
условиям работы грубо изготовленного
механизма.
Надежность работы. В трехзвенном
механизме кинематически может быть
осуществлено любое передаточное отно-
шение, если угол («]-)-«г) между напра
вленнямн движения звеньев не равен 0”
или 180®. Однако при некоторых значе-
ниях угла («1 4- «*). передаточного отно-
шения и углов трения в кинематических
парах к. п. д. механизма снижается до
нуля, и его работа становится невоз
можной из-за самоторможения при пере-
даче движения в прямом направлении —
от ведущего к ведомому звену.
В зоне, близкой к самоторможению,
работа механизма ненадежна ввиду не
устойчивости значений углов трения.
Ппов«вку надежности работы меха-
низма рекомендуется производить путем
ПЛОСКИЕ ШАРНИРНЫЕ МЕХАНИЗМЫ
453
определения его к. п. д. по приведенным
формулам с введением коэффициента на-
дежности, равного 2—3, на который
умножаются величины углов трения.
Меньшие значения коэффициента надеж-
ности берутся при больших углах тре-
ния, бдльшне — при малых.
Если подсчитанный таким образом
к. п. д. окажется меньше нуля, работа
механизма ненадежна, и необходимо ус-
ложнение его схемы введением проме-
жуточного звена.
На фиг. 4 надежной работе механизма
соответствуют участки кривых ip и т(,
показанные сплошными линиями. Коэф-
фициенты надежности здесь приняты
равными 3 при углах трения 3°, 2,5 —
при 5°, 2 — при 8°.
Примеры применения. На фнг. 5 по-
казан вырезной штамп с боковыми пу-
ансонами. Конструкция поступательных
пар, связывающих ведущее звено с го-
ризонтальными ползунами, позволяет
передавать движение последним только
на определенном участке перемещения
Фиг. 5. Штамп с боковыми пуансонами.
ведущего звена, удерживая их непо
двнжно на других участках перемеще-
ния. Наклонным ползунам-пуансо-
нам движение передается посредством
высших кинематических пар с точеч-
Фиг. 6. Каиново* маками» зажимного
пряспособаеима.
На фиг. 6 показан механизм зажим-
ного приспособления с гидравлическим
цилиндром; механизм имеет две цилин-
дрические и одну поступательную пару.
ПЛОСКИЕ ШАРНИРНЫЕ
МЕХАНИЗМЫ
Общие сведения
Назначение. Назначение плоских шар-
нирных механизмов различно в зависи-
мости от их схемы. На практике они
применяются довольно широко.
Структура и классификация Исчер-
пывающая классификация плоских шар-
нирных механизмов с одной степенью
Фиг. 7. Группы згепьев, не ихменякхпис числа
степеней свободы, н обраэооаиие нз них схемы
восьмизвсяного механизма.
свободы по структурному признаку и
метод образования структурных схем
таких механизмов предложены русским
ученым Л. В. Ассуром и в дальнейшем
разработаны советскими учеными.
Образование схем механизмов пронэ-'
водится путем последовательного при-
соединения к ведущему или исходному
кривошипу * (фиг. 7, «) кинематических
пеней или групп звеньев (фиг. 7,6—е). не
изменяющих числа степеней свободы
механизма, к которому они присоеди-
няются (фиг. 7, ж).
При анализе структуры механизма его
схема разбивается на ведущий кривошип
со стойкой и группы.
Класс механизма определяется наибо-
лее высоким классом группы нз числа
встречающихся в механизме. Порядок
механизма определяется наиболее высо-
ким порядком группы из числа встре-
чающихся в механизме групп наиболь-
шего класса.
Структурная формула группы:
W - Зл — 2р — О.
• Здесь под исходным кривошипом понимаете^
звено, с г ценное со стойкой прлщлте лигой парий.
Не «двисммо от того, совершает ли оно крапптель-
ное или хачателькив движение.
45»
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
Возможные числа звеньев (л) и шар-
ниров (р), удовлетворяющие структур-
ной формуле:
л-2; 4; 6; 8; 10;...
р-3; 6; 9: 12; 15;...
По классификации И. И. Артоболев-
ского группы звеньев делятся на классы
в зависимости от числа сторон имею-
щегося в группе действительного или
возможного замкнутого контура.
Кривошип, шарнирно связанный со
стойкой (фиг. 7, а), характеризуется от-
сутствием замкнутого контура или фор-
мально имеет контур с одной стороной.
Поэтому такая группа звеньев отно-
сится к I классу. Указанная группа обра-
зует самостоятельный механизм I класса;
в составе механизма более высокого
класса эта группа является ведущей
его частью.
Двухповодковая группа
(диада, фиг. 7, б) характеризуется нали-
чием эвена с двумя шарнирами, которое
формально может считаться составлен-
ным из двух шарнирно связанных по
обоим концам стержней, образующих
замкнутый контур с двумя сторонами.
Поэтому двухповодковая группа отно-
сятся ко II классу.
Трехповодковая группа
(фиг. 7, в) и более сложные группы
(фиг. 7, г), характеризуемые наличием
звена с тремя шарнирами, относятся к
111 классу, так как упомянутое звено
можно считать составленным путем шар-
нирного соединения трех стержней, об-
разующих замкнутый контур с тремя
сторонами.
Группы IV класса (фиг. 7, д
и е) и более высоких классов характе-
ризуются наличием замкнутого контура,
составленного из четырех и более шар-
нирно связанных звеньев.
Порядок группы любого класса опре-
деляется по числу шарниров, которыми
группа присоединяется к первоначаль-
ному механизму.
Таким образом, двухповодковая группа
(фиг. 7, б) является группой 2-го поряд-
ка, трехповодковая (фиг. 7, в) — груп-
пой 3-го порядка, четырех поводковая
(фиг. 7, е) — группой 4-го порядка. При-
веденные в качестве примера на фиг. 7, д
в е группы IV класса относятся соот-
ветственно ко 2-му и 3-му порядкам.
Механизм (фиг. 7, ж), структурная
схема которого образована последова-
тельным присоединением к кривошипу 1
двухповодковой группы 2—3 и трех по-
водковой группы 4—5—6—7, относится
к 111 классу, 3-му порядку в соответ-
ствии с классом и порядком наиболее
сложной группы звеньев (трехповод-
ковой), входящей в состав меха-
низма.
Практическое применение находят
почти исключительно механизмы I и II
классов, а также 111 класса 3-го порядка.
Более сложные механизмы вследствие
многозвенности имеют пониженную
жесткость и малую, быстро теряющуюся,
точность работы.
Рассмотренный метод может быть
использован также для образования пло-
ских шарнирных механизмов с несколь-
кими степенями свободы путем присо-
единения групп к нескольким ведущим
кривошипам.
В зависимости от положения меха-
низма в классификации к нему могут
быть применены те или иные методы
анализа н синтеза.
Пассивные связи. Механизм с одними
вращательными парами V класса имеет
общие пассивные связи в количестве,
равном утроенному числу иеповторяю-
щихся замкнутых контуров в схеме.
Наличие пассивных связей увеличивает
жесткость механизма, но усложняет его
изготовление. В случае надобности об-
щие пассивные связи могут быть устра-
нены илн число их уменьшено путем
замены некоторых вращательных пар
(V класс) подходящими кинематическими
парами II, III и IV классов, например,
парами с одним элементом, образован-
ным шаровой поверхностью, и одним —
цилиндрической поверхностью (см.
табл. 1 на стр. 408), шаровыми парами,
цилиндрическими парами.
Кинематика механизмов II класса
2-го порядка. Применяются графический
и графо-аналитический методы, а для
простейших механизмов — также анали-
тический метод. .
Построение положений
всех звеньев механизма при заданном
положении ведущего эвена расчленяется
иа построение положений двухповодко-
вых групп, выполняемое методом засе-
чек: из известных положений крайних
шарниров радиусами, равными длинам
звеньев, проводят дуги, пересеченна
которых дает положение среднего шар-
нира.
План скоростей (фиг. 8). Если
звено OtA считать ведущим, то при за-
ПЛОСКИЕ ШАРНИРНЫЕ МЕХАНИЗМЫ
455
данной его угловой скорости ш = const
получим для скорости точки А величину
од = ы/0,д, где/01д — длина эвена О»Л.
План скоростей для рассматриваемого
механизма строится по следующим век-
торным уравнениям, составленным на
основании разложения движений анали-
зируемых звеньев на переносные и от-
носительные:
Чв= £д + ГЯд
для двухповодковой группы, присоеди-
няемой к стойке;
VE = £с + £₽с
и
VE = Vp +
для двухповодковой группы, не связан-
ной со стойкой.
Здесь ид, ид — абсолютные скорости
точек А и В; Vba— скорость точки В
относительно точки А; одной чертой
снизу подчеркнуты векторы, известные
по направлению, двумя чертами — из-
вестные по величине и направлению.
Определение скорости точки С (фиг. 8, а)
звена по известным скоростям двух
других его точек Лив производится
построением на плане треугольника
относительных скоростей (&abc), ко-
торый подобен изображению звена
(Д АВС) и сходственно с ним распо-
ложен. Масштаб плана скоростей
м £ек~1/мм показывает, сколько м/сек
содержится в I мм чертежа.
Порядок построения плана скоростей
(фиг. 8, б): в выбранном масштабе
откладывают 0„а = 1>д; проводят Ov&£
L О В и ab 1 АВ. ас £ Ас и be £ ВС,
0,d £ OD и bd £ BD. de £ DE и се £
j_CE.
План ускорений. План уско-
рений (фиг. 8) строится после построения
плана скоростей иа основании следую-
щих векторных уравнений:
£я +£а “ £а + £ва +£/ы
для двухповодковой группы, присоеди-
ненной к стойке;
аЕ “ £с + £гс + дяг
и
аЕ + £еО_+ aED
для двухповодковой группы, не связан-
ной со стойкой.
Здесь ая, ад, а1д—соответственно
ускорение точки В и его нормальная
и тангенциальная составляющие; аЯд,
Одд> яЯд — ускорение точки В в ее
движении относительно точки Л него
нормальная и тангенциальная состав
ляющие; одной чертой снизу подчерк-
Фнг. 8. Пл«ны скоростей и ускорений
шесткзвсиного механизма.
„уты векторы, известные по направле-
нию, двумя чертами — известные по
величине и направлению.
Все нормальные составляющие уско-
рений определяются графически или
подсчитываются по известным скоростям
и размерам.
Определение ускорения третьей точ-
ки С (фиг. 8, а) звена по известным уско-
рениям двух других его точек Л и В
производится построением в плане уско-
рений треугольника относительных уско-
рений (Дайс), который подобен изо-
бражению звена (ДЛВС) и сходственно
с ним расположен. Масштаб плана
ускорений >>„м-сек~2/мм показывает,
сколько м/сек* содержится в I мм чер-
тежа.
Порядок построения плана ускорений
(фиг. 8, в):
в выбранном масштабе отклады-
вают Оаа " ад; проводят подсчитан-
ное вдд || АВ и адд £ АВ, подсчитан-
ное Од || 01В и ад£0 в; строят
Л abc со & АВС и Л Oabd со Д О» 3D;
проводят подсчитанное аяс || СЕ и
а^С _]_££, подсчитанное agD || DE и
«‘еоЛ-ОЕ. .
456
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
Кинематика механизма III класса
3-го порядка (фиг. 9). Определение по-
ложений, скоростей и ускорений вну-
тренних шарниров (£, F, G) трехповод-
ковой группы по положениям, скоростям
и ускорениям внешних шарниров (С, D
и 08) производится следующим обра-
зом.
Построение положения
трех поводковой группы выполняется ме-
тодом ложных положений. Из С, D и 0л
радиусами, равными длинам поводков,
проводят дуги. Произвольно выбирают
несколько положений шарнира Е на
первой дуге, засечками определяют со-
ответствующие положения шарнира F
Фиг. 9. Построение плана скоростей трехпооол-
ковоА группы метолом ложных положений.
на второй дуге и шарнира G — на пло-
скости чертежа. Полученные положения
шарнира G соединяют кривой, пересе-
чение которой с третьей дугой дает
действительное положение шарнира О.
При построении большого числа поло-
жений механизма удобнее пользоваться
шаблоном-калькой с нанесенными на нее
шарнирами Е, F и Q.
План скоростей трехповод-
ковой группы строится методом ложных
положений или методом особых точек
(см. (29]).
При некоторых схемах механизма
можно упростить построение плана ско-
ростей трех поводковой группы, если на-
чать его не с ведущего, а с какого-либо
другого звена, связанного со стойкой.
Так как скорость этого звена заранее
не известна, план строят в неопределен-
ном масштабе, который может быть под-
считан только после построения вектора
скорости ведущего звена.
Метод ложных положений основан на
разложении скоростей внутренних шар-
ниров (£, F, G) на переносные и отно-
сительные и использовании условия по-
добия F\efg со /\EFG (фиг. 9).
Построения, показанные на фиг. 9
штриховыми линиями, выполнены по
фиг. 8, б.
Порядок дальнейших построений: че-
рез с проводят e^0J_£C, через d —
fJ0±E)F, через О„ — gag^±P3G:
произвольно выбирают на точку ei
проводят ej/i_L££, hgiA-FO и
eigi±£G; через gi и точку пересече
ния и /о/о проводят прямую, пере
сечение которой с g0g0 дает точку g;
проводят ge±£G и gl A.FG.
План ускорений трехповод-
ковой группы строится также методом
ложных положений или методом осо-
бых точек.
Метод ложных положений основан на
тех же приемах, что и при построении
планов скоростей, но осложнен необхо-
димостью разложения ускорений ряда
точек на нормальные и тангенциальные
составляющие.
Кинетостатика. Задача сводится к оп-
ределению реакций в шарнирах, урав-
новешивающей силы и необходимого
движущего момента, прилагаемого к ве-
дущему звену. Известными являются
действующие на звенья внешние силы,
силы тяжести и силы инерции. Трение
в шарнирах не учитывается. Решение
задачи выполняется графо-аналитиче-
ским способом (построение плана сил).
Начав с наиболее удаленной от веду-
щего кривошипа группы звеньев, после-
довательно решают все группы до ве-
дущего кривошипа. Определив уравно-
вешивающую силу, действующую на ве-
дущий кривошип, находят реакцию его
опоры и необходимую величину движу-
щего (приводного) момента.
Группы звеньев и механизмы, имею-
щие только общие пассивные связи,
являются статически определимыми от-
носительно сил, лежащих в плоскости
механизма.
Построение плана сил для механизма
II класса 2-го порядка. На фиг. 10, а
показан шестизвенный механизм с дей-
ствующими на его звенья силами Pt,
P»i каждая из которых является
равнодействующей внешних сил Q, силы
инерции Ри и веса звена G. Например,
Pt “ Q& + Рцп+ 6'j.
Двухповодковая группа 4—5
отдельно показана на фиг. 10, б со всеми
действующими на ее звенья силами и
реакциями (кроме /?64 и /?«)
ПЛОСКИЕ ШАРНИРНЫЕ МЕХАНИЗМЫ
457
Реакции в крайних шарнирах С и D
разлагают на составляющие, действую-
щие вдоль звена «J, и R^- и действую-
Фиг. 10. Построение плени сил иля шестизисниого
механизма.
щие поперек звена — R^ и «у,, после
чего подсчитывают
R/___0 hi . nt п hft
а *35
Построением многоугольника сил
« "< + *24 + «4 + Ъ + *35 + Е» - 0
определяют реакции в шарнирах С и D
(на фиг. 10, д — сплошными линиями).
Проводя дополнительную диагональ в
соответствии с уравнением
«4 + §4 + «м + «м " 0.
находят реакцию в шарнире Е В урав-
нениях одной чертой подчеркнуты век-
торы. известные по направлению двумя—
известные по величине и направлению.
Двухповодковая группа 2—3
(отдельно показана на фиг. 10, в).
Подсчитывают
nt —
К*2 4 ’
nt ---- + Pr-Эм r
«03--------.
пристраивают к плапу сил многоуголь-
ник (иа фиг. 10, д — штриховыми линия-
ми) по уравнению
«12 + «12 + «2 + «42 + «и + «и +
+ «оз + «оз “
Реакцию в шарнире В находят построе-
нием по уравнению
«12 + «U + «2 + «42 + «32 “ 0.
Ведущий кривошип 0—1 от-
дельно показан на фиг. 10, г. Пристраи-
вают к плану сил треугольник (на
фиг. 10, д — штрихпунктирными линия-
ми) в соответствии с векторным уравне-
нием
«I + «а + «о! “ 0.
Уравновешивающий момент подсчиты-
вают по формуле
Mj = Pj/lj — «21^n-
Построение плана сил для механизма
III класса 3-го порядка. При решении
трехповодковой группы используется
метод особых точек (см. (291).
Чстырехзвенные шарнирные
механизмы
Четырехзвенные шарнирные механиз-
мы широко применяются для преобра-
зования равномерного вращательного-
движения в неравномерное вращатель-
ное, качательное илн в сложное плоское
движение. Онн используются как само-
стоятельные механизмы или как часть
более сложных механизмов.
Соотношение между дли-
нами звеньев определяет разно-
видности механизмов
По характеру движения в механизме
различают следующие типы звеньев
(фиг. II): стойка О — неподвижное
звено; кривошип 1 — звено, связанное
со стойкой и имеющее возможность
совершать вращательное движение на
полный оборот; шатун 2 — звено, несвя-
занное со стойкой, совершающее слож-
4 'Я
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
ное плоско-параллельное движение; ко-
ромысло или балансир — звено, связан-
ное со стойкой и имеющее возможность
качаться на угол, меньший 360s. Коро-
мысла разделяются на односторонние (J)
и двухсторонние (<?') в зависимости от
того, располагается ли угол качания
по одну или по обе стороны линии
стойки.
В зависимости от типа звеньев, свя-
занных со стойкой, различают двухкри-
вошипные, кривошипно-коромысловые и
двухкоромысловые механизмы.
Фаг. 11. Типы звеньев шарнирного механизма.
Обозначения длин звеньев: а — дли-
на наименьшего звена, d — наиболь-
шего, b и с — двух остальных.
Если а + d Ь + с, получаем меха-
низмы: двухкривошипный — при обраще-
нии в стойку d; кривошипно-коромыс-
ловый — при обращении в стойку звена,
прилегающего к а. которое будет кри-
вошипом; двухкоромысловый — при об-
ращении в стойку звена, противолежа-
щего а.
Если а + d > b + с. получаем двух-
коромысловые механизмы независимо от
того, какое звено обращено в стойку.
Частные случаи соотношений между
длинами звеньев см в табл. I.
В качестве двухкоромысловых часто
используются кривошипно-коромысло-
вые и двухкривошипные механизмы
с ограничением углов попорота их
звеньев, связанных со стойкой.
Мертвым положением называется
такое положение механизма, в котором
условиями связи допускается переме-
щение ведомого звена в' двух противо-
положных направлениях. Это имеет
место, когда ведомые кривошип или
коромысло располагаются на одной пря-
мой с шатуном, что встречается: а) в ме-
ханизмах с а + d i 6 + с при соответ-
ствующем выборе ведущего звена;
б) в механизмах с а + d = 6 + с неза-
висимо от выбора ведущего звена, так
как у таких механизмов имеется одно
положение, в котором все звенья распо-
лагаются на одной прямой, а в частном
случае, когда звенья попарно равны,
имеются даже два таких положения.
Получающаяся неопределенность дви-
жения при выходе из мертвого положе-
ния на практике недопустима и должна
быть устранена инерцией движущихся
звеньев или другими способами.
В мертвых положениях механизма
угол передачи (см. стр. 449) равен нулю,
и к. п. д. при подсчете получается
отрицательным.
Кинематика. Нахождение скоростей
может быть упрощено построением по-
вернутого плана скоростей на схеме
механизма: из О' проводится ив || О'А
(фиг. 12).
Отношение между угловыми скоро-
стями (фнг 12>-
Если О находится вне отрезка О'О* —
скорости одинаково направлены; если О
лежит на отрезке О'О*—скорости про-
тивоположно направлены.
Фиг. 12. Повернутый план скоростей чстырехзве»
кого механизма.
Формулы для аналитиче-
ского определения положе-
ний скоростей и ускорений.
Угловые координаты положений звеньев
(фиг. 12):
тз +Л рз
2т/
Т1 " ~ ’г'со»
ж» - Л + /?«
Тш-агссоз—------
где
. , . г sin?
г sin у г cos ? + L
т — —-----—------------
si" Tn.
Угловые скорости:
г sin (у — ?.>.
“isiniyi-yj’
Г Sin — f|)
"* “ “ К sin vfa - ?o
ПЛОСКИЕ ШАРНИРНЫЕ МЕХАНИЗМЫ
459
Угловые ускорения
— ГЫ» COS (<f — <ft) — re sin (? — <?s) — COS (?. — ??) + Rv}
/ sin (<?j — <fj
«I —
Гы* cos (? — f ]) + ГС sin (<р — ?1) + /<Л, — Ruj COS (<f-2 — чц)
К Sin (<f>2 — <?j)
0 пределен не основных размеров меха-
низмов (синтез) графическим способом
по заданным положениям шатунной
плоскости.
1. Заданы два положения Si и St
шатунной плоскости положениями ле-
жащих в ней шарниров А и В (фиг. 13).
Фиг. 13. Синтез механизма по двум заданным
положениям шатуна.
Требуется определить положения шар-
ниров Од и Од на стойке. Построение;
из середины отрезков Д(Да и BtBt вос-
станавливаем перпендикуляры, на кото-
рых должны лежать центры шарниров
Од и 0в.
Положения шарниров Од и Ов на
перпендикулярах определяются на осно-
вании каких-либо дополнительных усло-
вий. Например, можно обеспечить полу-
чение двух кривошипного или криво-
шипно-коромыслового механизма, необ-
ходимых углов а и 3 поворота звеньев
ОдД и ОдВ при переходе механизма
из l-го во 2-е положение (фиг. 13, а)
Если центр одного звена удалить в
бесконечность, то получаем коромыслово-
шатунный механизм (фиг. 13, б). Если
положения шарниров совпадают (на пе-
ресечении перпендикуляров), то четырех-
звениый механизм вырождается в двух-
звенный: шатунная плоскость соединяет-
ся шарниром О со стойкой (фиг. 13, в).
2. Заданы два положения Si и St
шатунной пло-
скости положе-
ниями закреп-
ленного на ней
отрезка MN и,
кроме того, по-
ложения шар-
ниров Од и Ов
на стойке. Требуется определить поло-
жения шарниров А и В на шарнирной
плоскости (фиг. 14).
Рассматриваемую задачу приводим
к предыдущей методом обращения дви-
жения: шатунную плоскость условно
закрепляем, а стойку рассматриваем как
шатунную плоскость. Для этого, не
меняя относительного положения Од,
Ов и MtNt, совмещаем отрезок M^N?
с MiNi. Новое положение шарниров 0А
и Ов получаем засечками из точек Afi
и Nr. Од —радиусами ОдЛ^ и 0АЫъ
Од — радиусами OgMt и 0gNt. Из сере-
дины отрезков ОдОд и 0^0в восстанав-
ливаем перпендикуляры, на которых
и должны располагаться шарниры А
и В в первом положении шатунной пло-
скости. Выбор точек А и В может быть
произведен с учетом дополнительных
условий (см. п. 1).
Фиг. 14. Синтез меха-
низма по двум поло-
жениям шатунной пло-
скости и положениям
обоих шарниров на
стойке.
Фиг. IS. Синтез меха-
низма по трем зала»
мыы положением ша-
туна.
3. Заданы три положения Si, St и
St шатунной плоскости и положения
на ней шарниров А и В. Требуется опре-
делить положения шарниров Од и Од
на стойке (фиг. 15).
Построение: из середин отрезков Д|Д>
и ДуДд восстанавливаем перпендику-
ляры, в точке пересечения которых рас-
полагается центр шярииря Од; из сере-
дин BiBt и восстанавливаем пер-
пендикуляры, в пересечении которых
располагается центр шарнира Од.
460 . СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
4. Заданы три положения Sj, Sj и St
шатунной плоскости положениями
скрепленного с ней отрезка MN и.
кроме того, положения шарниров Од
и Од на стойке (фиг. 16). Требуется
определить положения шарниров А и В
на шатунной плоскости.
Задачу приводим к предыдущей путем
обращения движения приемом, указан-
ным в п. 2.
ине шарнира В в плоскости второй»
звена.
Воспользуемся приемом обращения
движения, для чего, не изменяя относи-
тельного положения Аг и МтОд, совме-
щаем MjOg с М^Од и, не изменяя от-
носительного положения Л8 и М^Од,
совмещаем Мг0д с МхОд, вследствие
чего получаются новые положения шар-
нира А — At и А3.
Фиг. 16. Снятез механизма по
трем положениям шатунной
плоскости и положениям обоих
шарниров на стоАке.
Фиг. 17. Синтез механизма по
хвум соответствующим поло-
жениям звеньев, связанных со
стойкой. и положению второго
шарнира на одном из звеньев.
Фнг. 18. Синтез механизма по
трем соответствующим поло-
жениям звеньев, связанных со
стойкой, и положению второго
шарнира на одном из звеньев.
Шарнир А в первом положении ша-
тунной плоскости находится в пересе-
чении перпендикуляров, восстановлен-
ных из середин отрезков ОдОЛ н ОдОд!
шарнир В — в пересечении перпенди-
куляров, восстановленных из середин
отрезков ОВОВ и ОВОВ.
Определение недостающих основных
размеров механизмов по заданным соот-
ветствующим положениям звеньев, свя-
занных со стойкой.
5. Заданы два положения одного
звена и соответствующие им положе-
ния другого звена, а также положе-
ние шарнира А на звене ОдА. Требуется
определить положение шарнира В на
прямой, связанной со вторым звеном
(фнг. 17). Для решения пользуются ме-
тодом обращения движения, делая услов-
но звено ОдМ стойкой и ОдА — шату-
ном. Для этого, не меняя относительного
положения Л2 и ОдМв, совмещаем OgMs
с OgMi, после чего из середины отрезка
Л|Л2 восстанавливаем перпендикуляр,
в пересечении которого с прямой ОдМ^
находится искомое положение шарни-
ра Вх.
6. Задано три положения одного
звена и соответствующие им три по-
ложения другого звена, а также по-
ложение шарнира А на одном из ценнее
(фиг, 18). Требуется определить положе-
Из середин отрезков Л^2 и Л2Л3
восстанавливаем перпендикуляры, пере-
сечение которых дает положение шар-
нира В иа плоскости звена ОдВ в его
первом положении.
Определение основных размеров кри-
вошипно-коромыслового (а также кри-
вошипно-шатунного) механизма по край
ним положениям коромысла.
7. Заданы крайние положения коро-
мысла (или ползуна) и положения шар-
ниров- В — на коромысле, Од и Од — на
стойке (фиг 19).
Радиус кривошипа
ОлВ.-ОдВг
2 '
Длила шатуна
I - ОдВ, 4- г.
8. Заданы крайние положения коро-
мысла (или ползуна) и отношение вре-
мени обратного хода к времени пря-
мого хода
Искомое положение шарнира Од дол-
жно находиться на окружности радиуса
R - -Ml где о - 180° Центр
2 sin « « т I
окружности может быть найден графи-
ПЛОСКИЕ ШАРНИРНЫЕ МЕХАНИЗМЫ
461
ческнм построением, как средняя точка
гипотенузы прямоугольного треуголь-
Фиг. 19. Синтез механизма по крайним
положениям коромысла или ползуна и
положениям обоих шарниров на стойке.
низа с катетом BjJ3. и углом при этом
катете 90°—0 (фиг. 19).
Шатунные кривые. В общем случае
траектории точек шатунной плоскости—
кривые 6-го порядка. Формы их отли-
чаются большим разнообразием. Неко-
торые шатунные кривые на отдельных
участках близко подходят к прямым
линиям и окружностям, имея с ними
до шести общих точек.
Теорема Робертса — Чебы-
шев а позволяет выбрать наиболее
удобные основные размеры механизма,
воспроизводящие требуемую шатунную
кривую.
Фиг. 20. К теореме Робертса—Чебышева.
Если известны основные размеры од-
ного механизма (фиг. 20, а) с движением
точки М шатуна по заданной кривой,
то путем соответствующего построения
можно найти два новых варианта такого
механизм» (фиг. 20, б и «) с точками Л1,
и М2, описывающими ту же шатунную
кривую, что и точка М. На фиг. 20, а:
£\0а0ь0г со&АВМ оо /\AyMCy со
соД.И/йСз; фигуры ОдАМА^ ОцВМВ2
и OcCiMCt— параллелограммы
При выборе варианта механизма для
• практического использования следует
учитывать его динамические характери
стики.
Механизмы с прямолиней-
ной траекторией движения
точки шатуна показаны на
фиг. 21.
Механизм Уатта (фиг. 21, в), механизм Чебы-
шева (фиг. 21, б), лямблообразиый механизм Че-
бышева (фиг. 21, л) и механизм Робертса (фиг. 21.а)
дают^ приближенно прямолинейное движение том
Механизм Эванса с поступательной парой
(фиг. 21, <П обеспечивает теоретически точку»
прямолинейную траекторию движения точки М, а
шарнирный механизм (фиг. 21, е), полученный на
предыдущего путем замены ползуна коромыслом.
Фиг. 21. Схемы механизмов с прямолинейной
траекторией движения точки шатуне.
обеспечивает приближенно прямолинейную траек-
торию. Механизм пофиг. 21. ж получается путем
дальнейшего преобразования с использованием на
шатуне точки N, траектория которой близка к ауге
окружности.
Конхоидальный механизм (фиг. 21,3) и меха-
низм (фиг. 21. и), полученный путем его преобра-
зования с использованием на шатуне точки №..
462
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
Фиг. 22. Схема
подъемного крана.
на отдельном
имеющей траекторию движения, близкую к дуге
окружности, дают приближенно прямолинейное
движение точки М.
Механизмы с прямолинейным движе-
нием точки шатуна в настоящее время
используются, например, в самопишу-
щих приборах для •
воспроизведения дви-
жения записывающе-
го штифта, в подъем-
ных кранах для обес-
печения горизонталь-
ного перемещения
точки подвеса груза
(фиг. 22). Кроме то-
го, механизмы с дви-
жением точки шатуна
астке траектории по
прямой илн по окружности использу-
ются как составная часть многозвенных
механизмов с остановами (см, фиг. 26).
Сложное плоско-параллельное движе-
ние шатунов (плоских систем) исполь-
зуется для выполнения некоторых тех-
нологических операций (тестоме-
силки, сельскохозяйственные и другие
машины).
Типы механизмов. В табл. I приве-
дены типы четырехзвенных шарнирных
механизмов, получающиеся при различ-
ных соотношениях между длинами
звеньев, а также при предельных и
частных случаях этих соотношений.
Механизмы по схемам 2, 7 и особенно
5, 8 (табл. 1) требуют специальных мер,
обеспечивающих прохождение их через
мертвое положение, и поэтому мало
пригодны для практического исполь-
зования.
Таблица I
Типы четырехзвениых шарнирных механизмов
Двухкривошип и не
Общий случай бвухкравошапного лиха-
нилма
а 4- d <Н<; а — стойка при а< b<c<d или
a<c<b<d
Мертвых положе-
ний нет
Наименьший угол
передачи —между
доеньями cud
mlny^-
c*4-rfx-(»_op
rcco‘-2F5-------
X ерактернстю см. табл. 2 и фнг. 23
Продолжение табл, 1
Двухкривошипные
Предельный случай дву.хнривошипного меха-
низма
о -}-</“ б + с; а — стойка
при а < b < с < d или а < с < b < d
Не дает существенно новых возможностей по
сравнению с механизмами погхеме/, имея ухуд-
шенную динамическую характеристику вслед-
ствие наличия мертвого положения
Шарнирный параллелограмм (противоле-
жащие звенья попарно равны)
а = с; b — d
Схема 3
Прохождение через мертвые положения обес-
печивается за счет инерции звеньев или за
счет усложнения механизма (см. фиг. 24)
Шарнирный антипараллелограмм (проти-
волежащие звенья попарно равны)
а — с; b — d
Получается ид шарнирного параллелограмма
искусственным ренеренропанием ведомого зве-
на и мертвом положении (см. табл. 3 и
фиг. 27)
Примечание, а, Ь.с, «/—длины звеньев
в порядке их соединения.
ПЛОСКИЕ ШАРНИРНЫЕ МЕХАНИЗМЫ
463
Продолжение табл, I
Продолжение табл. 1
Двухкривошипиые
Кривошипно-коромысловые
Деулкрааошилямй желоиадл Галловея
(соседние вменяя попарно равны)
а — »; с а; а < г: а или » — стойке
Сит б
При большом велушем кривошипе малы* кри-
вошип в мертвых положениях может остано-
виться, тогда механизм обращается в двухзвеи-
ный: стойка — кривошип
Кривошипно-корОмыеловый меканием
Галловея (соседние меняя попарно равны)
а — »; а < г. с — Л с илн d — стойка
В мертвом положении ведомое коромысло
может остановиться, тогда механизм обра-
щается и дпухзпенимй стойка — кривошип
Кривошипно-коромысловые
Двухкоромысловые
С односторонним коромыслом
о -р </ < Й -р С. 0 или d — стойка
при а < b < с < d или а < с < о < d
Схема 6
Мертвых положений при ведущем кривошипе
нет, при ведущем коромысле — I и III
С двусторонним коромыслом
a+d-b+г, b или d —стойка при а<О<с<гГ
или в<с<0<</
Схема 7
За 1 оборота кривошипа коромысло делает
одно двойное качание. При искусственном
реверсчроваиии ведомого звена в мертвом по-
тожеиим механизм работает аналогично ме-
ханизму по схеме в
С двумя односторонними кора кыслами
Схема 9
Мертвые положения
при ведущем тиене Ь
IV mV
b*+e*-(a+d)’ pc±c‘-(d-aV.
•«•tccos— ---------—arccos —!— — - ё
2»c ibc
3=arccos ————---------arccot
ICu
Zed
С двумя двусторонними коромыслами:
А) а -р а > о -р с: стойка — любое звено
или a<e<b<d
, ____ (d — ер - в* - »>
- 1г«ов-----STZ------
р—2 атссоа
Мертвые положения
прн ветушем звене б:
А) / и V!
Б) И. V и VI
На схеме показав
более предпочтитель-
ный вариант А
Zau
Так как в механизмах по схемам 9 и 10 мерт-
вые положения совпадают с крайними поло-
жениями ведущего звена, получается трудно
устранимая неопределенность движения н пло-
хие динамические характеристики механизма.
Поэтому авухкоромысловые механизмы ис-
пользуют с углами качания меньше « и 9
464
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
В табл. 2 и на фиг. 23 даны кинема-
тические характеристики двухкриво-
шипных механизмов с различными отно-
шениями длин звеньев, а в табл. 3— ха-
рактеристики механизмов антипаралле-
лограмма.
Таблица 2
Характеристика двухкривпшнпных механизмов с различными отношениями длин звеньев
(см. схему 1 в табл. 1)
Отношение длим звеньев а : b : е : d Передаточное отно- шение 1 w —— Отношение наимсиьшее) углов попорота ведомого звена, соответствующих углам поворота <₽ ведущего звеиа от 270“ до 90“ и от 90“ до 270“ в : (300’ — •) • Наименьшие углы передачи между звеньями й и с, с и d
'max П₽и Р - 170 -ь + 200“ mln he” mln Tf(/—
I 1:2:1,5:2 1:2:2 :2 ~2 0,5 127’ : 233’ * 0,56 63’ 83“ 55“ 76’ 29“ 29“ 18“ 19“
1 :2 : 2.5 :3 1:2:3 :3 ~0.6
1 :3 :1.5 : 3 1:3:2 :3 1 :3:2.5:4 1:3:3 :4 1,54-1 ,в 143’ : 217“ = 0,66 58“ 76“ 40“ 67“ 36“ 41* 24“ 29“
0.7
Расчетные формулы:
* • “ 1Й0Ч- «realn —Т- -------------- - .ream--------—----------.
где Л = о* 4- »• — с* -J- <Л и В = а' 4- Ь*.
(о 4- rf)« - О’ - <* , ...
mln = Brecon----------!----—----------(в положении III механизма).
*•» mln = arccos f*- ! ----— (в положении IV механизма).
I
ПЛОСКИЕ ШАРНИРНЫЕ МЕХАНИЗМЫ
465
Таблица 3
Хараастериетаки шарнирных аигипараллелограммов с различными отношениями длин звеньев
(см. схему 4 в табл. I)
Отношение радиуса кривошип* к длине шатуна а : & Передаточное отношение / ® —— Отношение (наименьшее) углом по- вороте ведомого звена, соответствую- щих углам поворота « везущего звена от 270“ до 90“ и от 90" до 270“ а : (360“ - «), где а=2.ГС31П|^-1):(1’+1)|
'mln = при » = 140“ ‘|МХ= при ф = 0е
1 :3 0,50 2,00 106“ : 254“ = 0.42
1 :4 0,60 1.67 122“ -.238’ =0,51
. 1 :6 0,72 1.40 142“ : 218“ = 0.65
1 :8 0.78 1.29 152“ : 2О«“ — 0.73
• 1 :10 0.82 1.22 157“ :203“—0.77
Многозвенные шарнирные механизмы
с одной степенью свободы
Многозвенный шарнирный механизм
допускает:
а) передачу движения от одного ве-
дущего к нескольким ведомым звеньям,
связанным со стойкой;
б) получение таких преобразований
движения, которые невозможно выпол-
нить при помощи четырехзвенного ме-
ханизма, а также решение других задач,
не выполнимых посредством четырех-
звенного механизма
Большинство многозвенных меха-
низмов построено на базе четырехзвен-
иых.
Многозвенные механизмы шарнирного
параллелограмма. Применение двух ша-
тунов (фнг. 24. а и б) обеспечивает
принудительный переход механизма че-
рез мертвые положения, уменьшение
усилий в кинематических парах и новы
шеиие среднего к. п. д.
В механизмах с несколькими ведомыми
кривошипами (фиг. 24, в) мертвые поло
жения устраняются при условии, что
на шатуне центры шарниров 4, В и С
не будут лежать на одной прямой. Me
ханизмы такого типа применяются в при-
воде ведущих колес электровоза, в при-
воде шпинделей многошпиидельной
сверлильной головки и т. д.
Если в механизме применяются только
вращательные пары V класса (см. табл. I
на стр. 408), то добавление к четырех-
звенному механизму каждого дополни-
тельного шатуца или кривошипа увели-
30 Том I Зак. 1464
чивает число общих пассивных связей
на 3 и индивидуальных — на 1.
Фиг, 24. Устранение мертвых положений меха-
низма шарнирного параллелограмма.
Шестизвенные кривошипно-коромыс-
ловые механизмы (фиг. 25). Такой ме-
ханизм может сообщать коромыслу не-
сколько качательных движений за один
оборот кривошипа. Путем изменения
основных размеров механизма при
регулировании можно удобно изменять
характер качания ведомого коро-
мысла.
Два качательных движения коро-
мысла на одинаковые углы (фиг. 25, а)
и на разные углы с двумя совпадаю-
щими точками реверсирования (фиг.25,б)
466
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
можно получить посредством механизма,
схема которого составлена путем при-
соединения шатуна 4, связанного с ве-
домым коромыслом 5, к коромыслу 3
первоначального кривошипно-коромыс-
лового механизма О—1—2—3.
Фиг. 25. Механизмы с двумя качаниями коромысла
за одни оборот кривошипа.
Определение основных размеров ме-
ханизма по заданным положениям ревер-
сирования ведомого коромысла трудно-
сти не представляет.
Более сложное движение коромысла
с двумя и тремя качаниями за цикл мо-
жет быть получено посредством меха-
низма, схема которого составлена путем
присоединения шатуна, связанного с
ведомым коромыслом, к шатуну перво-
начального четырехзвенного меха-
низма. ..
Определение основных размеров та-
ких механизмов значительно сложнее.
Механизмы с остановами. В этих
механизмах при непрерывном движении
ведущего звена ведомое звено некото-
рое время остается неподвижным или
почти неподвижным.
Шестиэвенный шарнирный механизм,
работающий с остановами, строится на
базе четырехзвенного механизма, у ко-
торого точка М шатуна движется по
траектории, имеющей участок, близко
подходящий к дуге окружности с цен-
тром 0м и радиусом R. Точку М ша-
туна посредством промежуточного звена
длиной R связывают с точкой N ведо-
мого коромысла, траектория движения
которой проходит через центр 0,ц
(фиг. 26, а). Шестизвепиый механизм
может иметь один, два и более остановов
ведущего звена.
Указанный принцип синтеза механиз-
мов с остановами распространяется
также на механизмы, имеющие поступа-
тельные пары. При построении кулисных
механизмов с остановами используются
шатунные кривые с приближенно пря-
молинейными участками (фиг. 26, б).
Механизмы инверсоров. Инверсией на-
зывается такое соответствие между
двумя кривыми, когда остается по-
стоянным произве- «
дение расстояний
от центра инвер- <%.
сии О (фиг. 27) --------
до точек М к N |
пересечения крн-
вых с прямой, про- I/
ходящей через О. ” '^y^yh
Инверсия окруж- / 1
ности, проходящей ~~
через О, — пря- I
мая, нс проходя- ®
щей через О — ОК- Фиг. 27. Механизмы
ружность Другого инверсоров,
радиуса.
Шарнирные механизмы, осуществляю-
щие инверсию, используются для теоре-
тически точного воспроизведения пря-
мой линии или дуги окружности боль-
шого радиуса.
На фиг. 27, а показан инверсор,
основанный на схеме анти-
параллелограмма.
Инверсор Лнпкина (фиг. 27, 6)
основан на схеме шарнирного ромба или
ромбоида; механизм инверсора — восьми-
звенный. Вследствие большого числа
звеньев рассматриваемый механизм мо-
жет оказаться практически менее точ-
ным, чем четырехзвенные механизмы
с приближенно прямолинейным движе-
нием точки шатуна (см. фиг. 21).
Шарнирные механизмы
с двумя степенями свободы
Направляющие механизмы. В отли-
чие от передаточных и преобразующих
механизмов назначение направляющих
ПЛОСКИЕ ШАРНИРНЫЕ МЕХАНИЗМЫ
417
механизмов — налагать определенные
ограничения на движение какого-либо
звена или его части (точка, прямая
линия). Особенность направляющих ме-
ханизмов — отсутствие явно выражен-
ных ведущих и ведомых звеньев.
Механизм с одной степенью свободы
обычно используется для направления
движения точки по прямой (см. фиг. 21
и 27) или по дуге окружности большого
радиуса.
Механизмы с двумя степенями сво-
боды обычно используются для выпол-
нения следующих задач:
1. Трехзвенные — для сохранения
перпендикулярности оси элемента ци-
линдрической или вращательной пары
Фиг. 28. Трехзвенвые п|лравлаюшие ыехааизыы.
Фиг. 29. Семшмииые иапрамиишме
механизмы.
к плоскости механизма. Практически
применяются для обеспечения нужного
направления инструмента в радиально-
сверлильных станках с шарнирным ру-
кавом (фиг. 28, а), в копировальных
станках для огневой резки металлов
(фиг. 28, б) и т. п.
2. Семизвенные — для сохра-
нения поступательного характера дви-
жения определенного звена плоского
механизма. Практически применяются
в чертежных приборах для обеспече-
ния неизменного направления линеек
(фиг. 29, в), в трансляторах для воспро-
изведения без изменения масштаба одной
или нескольких новых кривых по имею-
щемуся образцу (фиг. 29. б), в копи-
ровальных станках с пантографом для
пространственного копирования (см.
фиг. 33) и т. п.
Механизм пантографа. Механизм слу-
жит для воспроизведения одной или не-
скольких кривых, подобных имеющемуся
образцу. Копирование производится без
изменения или чаще с изменением мас-
штаба, без поворота или иногда с пово-
ротом кривой на некоторый угол.
30е
Механизмы пантографа применяются
в специальных чертежных приборах,
в копировальных устройствах, например
для правки профильного шлифовального
круга, в копировальных станках — фре-
зерных, гравировальных и др. для кон-
турного и объемного копирования, в
оптических профильно-шлифовальных
станках и т. п.
Пантограф представляет собой одно-
кратно
изменяемую плоскую кинемати-
ческую цепь, имеющую три и более
рабочих точек, обладающих следующими
свойствами: при любом изменении формы
пантографа отношение расстояний между
точками сохраняется неизменным, точки
остаются на одной прямой или в вер-
шинах подобно-изменяемого треуголь-
ника.
Плоский механизм панто-
графа с двумя степенями свободы
получается после присоединения (по-
средством вращательной пары) указан-
ной кинематической цепи к стойке.
Если для присоединения к стойке
использовать одну из рабочих точек
пантографа, а другую вести по контуру
образца, то все остальные рабочие точки
опишут кривые, подобные и сходственно
расположенные относительно контура
образца. Все’ рабочие точки, располо-
женные на прямой по одну сторону не-
подвижного шарнира, движутся по кри-
вым с одинаковым угловым положением;
расположенные на той же прямой, но
по другую сторону неподвижного шар-
нира — по кривым, повернутым на 180*
относительно первых; расположен ньг?
468
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
в вершинах подобно-изменяемого тре-
угольника — по кривым, повернутым
относительно друг друга на угол при
вершине треугольника, совпадающей с
неподвижным шарниром. Подавляющее
большинство применяемых на практике
пантографов имеет схему шарнирного
параллелограмма: с тремя рабочими точ-
ками (фиг. 30, а) для копирования без
Фиг. 30. Схемы пантографов.
поворота кривой; с четырьмя рабочими
точками (фиг. 30, б) для копирования
с поворотом па 180“; с тремя (фиг. 30, в)
и четырьмя (фиг. ЗЮ, е) рабочими точ-
ками для копирования с поворотом кри-
вой на угол <f. Пантографы по другим
схемам для копирования без поворота
(фиг. 30, д) и с поворотом на 180°
(фиг. 30, е) имеют меньшую жесткость
и точность работы из-за большого числа
звеньев.
В основе параллелограммных панто-
графов лежат большей частью схемы
с расположением рабочих точек на
прямой.
Основные схемы кинематических испей таких
пантографов прицелены » табл. 4.
Наибольшее возможное число рабочих точек и
параллелограммном пантограф* ранио числу его
3ueni.cn. Каждая рабочая точка, совпадающая с
центром шарнира, уменьшает общее число рабо-
чих точек пантографа иа 1.
Применение пятитвеииого параллелограммпого
пантографа при исполыюиании нс всех рабочих
точек оправлывается повышением жесткости си-
стемы благодаря появлению дополнительных пас-
сивных связей.
Точность механизма пантографа
в каждом его положении характеризуется откло-
нениями Др и Дф полярных координат или откло-
нениями &х и А декартовых координат воспроиз-
водимой точки it теоретически правильных. На-
Таблица 0
Схемы кинематических цепей
параллелограммных пантографов
si Число рабочих точек (обозначены • )
н 3 4 5
ЧетырехзВенные гХ^Х^ —
Пятизвенные
Примечания:!. В схемах с четырьмя рабочими точками могут ныть МВММ0М1Ш только три рабочие точки, и схемах с пятью рабочими i tклми — только три или четыре точки. 2. Схемы 5, 12, 13. 17. IX. 19 лают помп женные жесткость и точность работы меха-
чало обеих систем координат берется и точке
соединения паитогра<|>а со стойкой. Ось Ох
декартовой системы проходит через теоретически
правильное положение поспронзиодимой точки.
Точность полученной кривой и
каждой точке характеризуется ее отклонением
Д от теоретически правильной кривой, измерен-
ным по нормали к последней:
6atV Др-HpV со»(«+М
или •
А «а У Д* -г Ду соя (я + Ц),
4р dx
где я = arctg ~ — arctg — угол подъема тео-
ретически правильной кривой в исследуемой точке;
ПЛОСКИЕ ШАРНИРНЫЕ МЕХАНИЗМЫ
469
Р^е ду
f- = arctg ~ = arctg — угод между радиусом-
лР Аж
вектором исследуемой точки и вектором откло-
нения.
Две кривые Др =/,(₽), Дф=/,(р) или Д^ —
= А СО» Ьу = А (О полностью определяют точ-
ность пантографа я могут быть найдены графи-
ческими, графо-аналитическнмн млн аналитиче-
скими способами по первичным ошибкам в основ-
ных размерах звеньев пантографа.
На фиг. 31 изображен пантограф наиболее рас-
пространенного типа с идеально точными разме-
рами звеньев / и с размерами, имеющими откло-
Фнг. 31. Определение ошибок пантографа.
пения 2. Точные формулы для определения ошибок
механизма по фиг. 31:
Д -ж -fL-л ±-ж
ж е *, с a da'
где
Ау-ус ~d+vd~
1
yrf“ye
7е AD'.b “АВ' е~ вс' d-CD, f- BE,
OF действительные размеры звеньев; с. н
*i — идеально точные (номнидльиые) размены
звеньев; xf — абсцисса ведущей рабочей тонки е.
Расчеты по приведенным формулам должны про-
изводиться весьма точно, желательно на арифмо-
метре, с учетом повторяющихся действий.
В копировальных станках обычно при-
меняют инструмент не с точечным, а с
линейным (лезвие резца) или объемным
(фреза, шлифовальный круг) режущим
элементом. В этом случае воспроизво-
димая поверхность получается как оги-
бающая последовательных положений
режущего инструмента. Для обеспече-
ния подобия воспроизводимой поверхно-
сти н поверхности образца необходимо,
чтобы режущий и ощупывающий эле-
менты были подобны по форме И соот-
ветствовали масштабу копирования по
своим размерам. Кроме того, если ре-
жущее лезвие неподвижно закреплен-
ного на пантографе резца не проекти-
руется на плоскость механизма в точку,
совпадающую с соответствующей рабо-
чей точкой пантографа, то во избежание
искажений нужно обеспечить одинако-
вые угловые положения режущего и
ощупывающего элементов путем закре-
пления их на противолежащих звеньях
параллелограммного пантографа.
Постоянные пантографы обычно имеют
масштаб уменьшения до 1 : 25, регули-
руемые — до 1 : 10. Пример выполнения
пантографа копировально^фрезерного
станка с уменьшением, регулируемым
в пределах 1 : 1,5 — 1:7, показан на
фиг. 32.
Пространственный меха-
низм пантографа с тремя сте
пенями свободы получается после при
соединения плоской кинематической
цепи пантографа к стойке посредством
кинематической пары или соединения
с промежуточным эвеном, допускающих
поворот не только вокруг оси, перпеп
дикулярной к плоскости пантографа,
но и вокруг осн, лежащей в этой пло-
скости. Тогда свободные рабочие точки
будут описывать подобные кривые в про-
странстве. Это дает возможность обра-
батывать сложные пространственные по-
верхности, геометрически подобные по
верхности образца.
Если ощупывающий штифт н инстру'
мент закрепить непосредственно на пан-
тографе, то угловые положения штифта
относительно образца и инструмента
относительно обрабатываемой поверхно
стн будут в процессе работы изменяться
470
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
что затруднит обработку. Чтобы устра-
нить указанный недостаток, применяют
систему нз пантографа и направляющего
механизма.
Пример копировального устройства,
построенного по такой схеме, показан
на фиг. 33. Пантограф t имеет возмож-
ность качаться вокруг горизонтальной
оси 2. Направляющее устройство со-
стоит из салазок 3, перемещающихся
Фиг. 33. Копировальное устройство ставка.
по вертикальным направляющим, и двух-
параллелограммного шарнирного меха-
низма 4, который обеспечивает посту-
пательное движение эвена, несущего
инструмент 5 и ощупывающий штифт 6
при копировании в масштабе 1 : 1 без
пантографа. При копировании с панто-
графом на месте штифта 6 может быть
закреплен еще один инструмент для одно-
временной обработки второй детали.
Двухзвенный направляющий механизм 7
обеспечивает поступательное перемеще-
ние оси ощупывающего штифта 8, ко
торый шарнирно связан с рабочей
точкой пантографа и перемещается по
образцу 10 вручную — посредством ру-
коятки 9.
Другая рабочая точка пантографа шар-
нирно связана с последним звеном двух
параллелограммного механизма через
продольные и поперечные салазки, позво-
ляющие переходить на любую степень
уменьшения (в пределах 1 4 1,5 — 1:7)
без перестановки обрабатываемой де
тади Л. :
ПЛОСКИЕ МЕХАНИЗМЫ
С ВРАЩАТЕЛЬНЫМИ
И ПОСТУПАТЕЛЬНЫМИ ПАРАМИ
Общие сведения
Назначение. Назначение плоских ме-
ханизмов с вращательными и поступа-
тельными парами различно при разных
схемах. Основное применение — для
преобразования вращательного движе-
ния в прямолинейное возвратно-посту-
пательное или наоборот.
Структура и классификация. Наличие
поступательных пар в плоском меха-
низме с одними низшими парами
(V класс) приводит к структурным осо-
бенностям, которые должны быть учтены
при определении числа степеней свобо-
ды механизма и при построении струк-
турных схем.
Структурная формула для механизмов
с вращательными и поступательными
парами (смешанных механизмов):
Г = Зл - 2Л + Т.
где UZ — число степеней свободы меха-
низма; п — число подвижных звеньев
в механизме (исключая стойку); рг —
число кинематических пар в механизме;
7 — число замкнутых контуров, имею-
щих одни поступательные пары.
Так как смешанные механизмы не
всегда удовлетворяют условию отсут-
ствия индивидуальных пассивных свя-
зей, пассивный характер которых опре-
деляется структурой механизмов, обра-
зование структурных схем методом
последовательного присоединения групп
звеньев (см. фиг. 7) на эти механизмы
распространяется с известными ограни-
чениями, а именно:
1. Замена в шарнирных группах
звеньев (см. фиг. 7) некоторых враща-
тельных пар поступательными не должна
приводить к образованию замкнутых
контуров, имеющих одни поступатель-
ные пары, а также сквозных контуров
с одними поступательными парами, про-
ходящих по цепи от одной внешней пары
до другой. Замена, проводимая с соблю-
дением указанного условия, позволяет
получить все возможные смешанные
группы звеньев, не влияющие на число
степеней свободы механизма, к которому
они присоединяются.
2. Образование смешанных механиз-
мов методом последовательного присо-
единения смешанных и шарнирных групп
звеньев к ведущему кривошипу или
ПЛОСКИЕ МЕХАНИЗМЫ С ВРАЩАТЕЛЬНЫМИ И ПОСТУПАТЕЛЬНЫМИ ПАРАМИ 471
ползуну (см. фиг. 7) дает возможность
получить все возможные структурные
схемы смешанных механизмов прину-
жденного движения без индивидуальных
пассивных связей.
3. Метод устранения бездействующих
шарниров в построенном по п. 2 меха-
низме дает возможность получить все
возможные структурные схемы плоских
смешанных механизмов принужденного
движения с индивидуальными пассив-
ными связями структурного происхо-
ждения. Указанный метод состоит
в объединении звеньев, связанных вра-
щательной парой, но не имеющих воз-
можности в механизме поворачиваться
относительно друг друга вследствие
наложенных поступательными парами
условий связи. В механизме с бездей-
ствующим шарниром (фиг. 34, а) устра-
нение последнего не приводит к измене-
нию кинематики механизма (фиг. 34, 6).
Фиг. 31. Устранение бездействуш-
шего шарнира.
Для смешанных механизмов поль-
зуются обычно также классификациями
Ассура или Артоболевского, которые,
однако, для этих механизмов не являются
столь строгими и исчерпывающими, как
для плоских шарнирных механизмов.
Индивидуальные пассивные связи,
пассивный характер которых опреде-
ляется соотношениями между основными
размерами механизма, при составлении
структурной схемы не могут быть учте-
ны; они выявляются при рассмотрении
кинематической схемы.
Пассивные связи Смешанный меха-
низм с парами V класса имеет: а) общие
пассивные связи в количестве, равном
утроенному числу неповторяющихся
замкнутых контуров в схеме; б) инди-
видуальные пассивные связи, зависящие
от структурных признаков механизма,
в количестве, равном числу замкнутых
контуров, образованных одними посту-
пательными парами.
Число общих пассивных связей может
быть уменьшено путем замены некоторых
пар V класса парами 1,11, 111 и IV классов,
йапример, парами с одним элементом
по шаровой поверхности и другим по
плоскости или цилиндрической поверх-
ности (см. табл. 1 на стр. 408), плоскост-
ными парами, цилиндрическими па-
рами и т. п.
Число индивидуальных пассивных
связей структурного происхождения мо-
жет быть уменьшено теми же средствами,
а также введением бездействующих шар-
ниров (мало рационально).
Кинематика смешанных механизмов
II класса 2-го порядка. Применяются
графические., графо-аналитические и
аналитические методы.
Построение положений
всех звеньев механизма при заданном
положении ведущего звена расчленяется
на последовательное построение положе-
ний двухповодковых групп по положе-
ниям центров крайних шарниров и осей
крайних поступательных пар. На фиг. 35
показаны эти построения для четырех
возможных типов смешанных двухповод-
ковых групп. Основные размеры звень-
ев— г, и, Л, Л1 и а — заданы.
В группе с одной крайней поступа-
тельной парой (фиг. 35, а) положение
среднего шарнира определяется как пе7
ресечение прямой, проведенной парал-
лельно заданной оси поступательной
пары, и дуги, описанной из заданного
центра крайнего шарнира; в группе
с одной средней поступательной парой
(фиг. 35, б) ось последней определяется
а) б)
Фаг. 35. Построение положений
двухпоиодковой группы.
как касательная к двум дугам, описан-
ным из заданных центров крайних шар-
ниров; в группе с двумя крайними по-
ступательными парами (фиг. 35, в) поло-
жение среднего шарнира определяется
как пересечение двух прямых, парал-
лельных заданным осям поступательных
пар; в группе со средней и крайней по-
ступательными парами (фиг. 35, г) ось
средней пары определяется как пря-
мая, составляющая требуемый угол а с
472
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
заданной осью крайней поступательной
пары и касающаяся дуги, описанной
из заданного центра шарнира.
Планы скоростей и уско-
рений строятся последовательно для
всех двухповодковых групп, начиная
с прилегающей к ведущему кривошипу.
При построении планов скоростей и
ускорений для каждой двухповодковой
группы известными являются скорости
и ускорения центров крайних шарниров
и всех точек звеньев, к которым иссле-
дуемая группа присоединяется крайними
поступательными парами. Требуется оп-
ределить скорости и ускорения точек
обоих звеньев, составляющих группу.
Для этого находят скорости и ускорения
двух точек каждого звена со сложным
плоским движением и одной точки звена
с вращательным или прямолинейно-по-
ступательным движением. Таким обра-
зом, для звена с крайним шарниром,
движение которого задано, требуется
определить скорость и ускорение еще
одной точки. Это же относится к звену,
присоединенному к стойке посредством
поступательной пары.
Зная скорости и ускорения двух точек
звена, можно легко определить скорость
и ускорение любой третьей его точки
путем построения треугольников отно-
сительных скоростей и ускорений.
В табл. 5 приведены векторные урав-
нения, при помощи которых строятся
планы скоростей и ускорений для раз-
личных типов двухповодковых групп
с поступательными парами. Уравнения
составлены на основании разложения
движений на переносные и относитель-
ные. Так как переносное движение часто
получается в виде вращательного, в
большинстве уравнений фигурирует ко-
риолисово ускорение. При наличии по-
строенного плана скоростей величины
кориолисовых а* и нормальных ап уско
рений подсчитываются или определяются
построениями, их направления из-
вестны; тангенциальные ускорения а'
известны только своими линиями дей
ствия, совпадающими с линиями дей-
ствия соответствующих скоростей.
Кинетостатика смешанных
механизмов отличается от кинетостатики
шарнирных (см. стр. 456) тем. что при
построении планов сил приходится опре
делять наряду с величинами и напра-
влениями реакций в шарнирах величины
и положения реакций известных на-
правлений в поступательных парах (по-
дробнее см. [3|).
Таблица 5
Векторные уравнения для построения планов
скоростей и ускорений двухповодковых
групп с поступательными парами
(смешанных)
С одной крайней поступательной парой
- , -Л . , -н , -I
аА +аВА “ аВ, + аВВ, + аЯД,
гле авв, “ ^вв, •
- - . -* . -t
аС “ “С, 4- “вв, 4- «ВВ,
——» : _ . „
- - , -л . -I
°ВА 4- пВА
—fl I . •“/
в# + " ДД; + aBBl + авв, •
—A j —t
”с ~ дд 4- авв, 4- два,
С одной средней поступательной парой
ёд 4- рд.л “ ^а + ёд,в;
»Д,
PB 4- Рд,а " ёд 4- ёД|Я.
ав,
ал +аВ>Л + аН,А +Д/?|/?+
г“ ав,в ~ °юв,в
aAi ~аА + aBlB^‘aBiB
ПЛОСКИЕ МЕХАНИЗМЫ С ВРАЩАТЕЛЬНЫМИ И ПОСТУПАТЕЛЬНЫМИ ПАРАМИ 47?
Продолжение табл. 5
С одной средней поступательной парой
аВ, аА,
-п , -I - -к , ~t
«В, т аВ, — а В + аН,В + аВ,В
V_A, = РА + рА,А •
РВ, = РАД, '
аВВ,
-п -f ~ -к -t
°А, + ° А, ” аА + аВВ> — аВВ,,
гг~ ’
гже аВВ, “ 2“РВВ,
С двумя крайними поступательными
пароли
VB-VB, + VAA,' РС—”С. + РАА.:
«А
где “ДА.-^АА,!
“AA’^AA.:
- , -к , -t
аВ“^ + “ДА, + °АА,:
- .
°C ~“С. + аАА, + °АА,
Продолжение табл. 5
С двумя крайними поступательными
парами
”а д;ал4-раа,;
РС = аС1 + *А \ •
аА ~aA, +aAAi+aAAt •
~-к , -t
аС " “С, + аАА, +°АА,
— *
«А_= °А + аАА, + °АА,;
- , -к , -t
а В “аВ, + аАА, + а ДА,
С крайней и средней поступательными
парами
VB “ рЯ,+ рЛ А, + РД,Д,!
рС-рС,+ рД,А, »
“Д>
ад + аА,Д 4-° Л,А ~ aA, + “AiA,-b“A,A>
гм “дм **л.д: “д.д, “ ’"'ЧА,;
аВ + aA,Af + аА,Л, ~
~ (аА,А 4-Да,д) !
“С ” “Cj+ ДД,А. + “А,А,
474
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
Продолжение табл. 5
С крайней и средней поступательными,
парами
1 _°±_
-* , -Г - . -Л , -I
аА, -Ь аЛ, " а А, + °Д,Д,+ аЛ,А, ’
° В -aBj + aA,At + a^A, ~
~ (ал, + ал,) •
- - -A -t
“С = ДС, +ДЛ,Л( + Д 1,Л,
Дд," ДД + «А,А
Примечания: 1. Л, В, С — точки.
изображенные на чертеже, принадлежат одному
звену или сразу двум (шарниры); Л,, Д., Д, и
Д, - точки, принадлежащие звеньям 1,3,3 и
4 и совпадающие и данном положении меха-
низма с точкой А; В„ В, и В, - то же, но с
точкой В; С„ С„ С, и С, — то же, ио с точ-
кой С.
2. Обозначения некто,юн с одиночным ин-
дексом относятся к абсолютным скоростями
ускорениям, с двойным индексом — к относи
тельным.
3, Векторы, подчеркнутые одной чертой,
известны только по направлению, подчеркну-
тые двумя чертами - известны по величине
и направлению.
4. Векторное уравнение графически может
быть решено (построено), если неизвестны два
вектора по величине или один — по величине
и направлению.
5. Построение планов производится в той
последовательности, в которой приведены век-
торные уравнения.
Четырехзвенные механизмы
с вращательными
и поступательными парами
Эти механизмы служат для преобразо-
вания равномерного вращательного дви-
жения в прямолинейное возвратно-по-
ступательное, в неравномерное враща-
тельное, в качательное или в сложное
плоское движение. Используются в ка-
честве самостоятельных механизмов или
как часть более сложных механизмов
Типы механизмов. Четырехзвенные
механизмы разделяются на типы в зави-
симости от числа поступательных пар,
их расположения и от соотношения
между некоторыми основными разме-
рами, влияющими на характер движения
звеньев (табл. 6). При числе поступа-
тельных пар более двух механизм вы-
рождается в плоский механизм с посту
нательным движением звеньев.
Механизм по схеме 2 (табл. 6) требует
специальных мер для прохождения через
среднее положение и поэтому мало при-
годен для практического использования.
Кривошипно-шатунные механизмы слу-
жат для преобразования вращатель-
ного движения в возвратное прямоли-
нейно-поступательное и наоборот.
Кривошипно-шатунные механизмы
имеют широкое распространение; они
применяются в поршневых двигателях,
насосах и компрессорах, в станках
с прямолинейным движением резания
и т. д.
С целью сокращения числа общих
пассивных условий связи для облегче-
ния сборки механизма некоторые из
кинематических nap V класса (см
табл. 1 на стр. 408) могут быть заменены
парами более низкого класса. Так, за-
мена одной пары на цилиндрическую
дает сокращение числа общих пассивных
условий связи до 2, поступательной и
одной вращательной пары на цилиндри-
ческие — до I, одной пары на шаровую-
до 1, одной пары на шаровую и одной
на цилиндрическую — до 0. В послед-
нем случае заменяемые пары не должны
Прилегать к одному звену.
Центральный кривошнпно-шатунный
механизм- (фиг. 36) характеризуется
отношением размеров Х = Это отно-
шение К должно быть таким, чтобы
угол передачи (см. стр. 449) в соеди|
(нении шатуна с ползуном не снижался
ниже определенного предела.
ПЛОСКИЕ МЕХАНИЗМЫ С ВРАЩАТЕЛЬНЫМИ И ПОСТУПАТЕЛЬНЫМИ ПАРАМИ 475
Таблица 6
Типы чегырехзвениых механизмов с враща-
тельными н поступательными парами
Продолжение табл. 6
С одной поступательной парой
С одной поступательной парой
Схема 6
В)
Длина хода ползуна
для механизма а
равна 2г, для меха-
низма 6 прнблнзн-
Кривошипно-ша -
тунный:
а — центральный
б — смешенный
тельно равна 2г. Имеет весьма широкое при-
менение
Схема 2
'jZ/t Кривошипно-ша-
тунный с увеличеи-
—ным ХОЛОМ ползуна
При равномерном крашенки кривошипа лает
движение ползуна по закону гармонических
колебаний с длиной хода 4г
Коромыслово-ша-
тунный
"Применяется для получения большого вы-
игрыша в силе н зажимных уетронствах.
прессах и т. п.
Схема 4
Кривошипно-ку-
лисный с качаю-
щейся кулисои
Ч Дает медленный ход
. при движении ку
I лисы в одну сторону
и быстрый — при
движении и другую
сторону. Применяется в металлорежущих
стайках и других машинах
Схема 5
Кривошипно-кулис-
ный с арашающей-
ся кулисой
Передаточное от-
ношение механизма
меияется в зависи-
мости от угла по-
вороте кривошипа:
среднее значение за оборот <rD — I. Имеет
широкое применение в сочетании с другими
* [ механизмами
Кривошнпно- ку-
лисный с равно-
мерно вращаю-
щейся кулисой
£ = г
Угловая скорость
кулисы во всех по-
ложениях мела-
сь,” сойду
ннзма равна
половине угловой скорости кривошипа.
Применяется редко
С дьумя поступательными парами
Кривошипно-
кулисный с по-
ступательно
движущейся
кулисой:
<х — прямой,
б — наклонной
Схема 7
Прн ранномерпом вращении кривошип дает
движение кулисы по закону гармонических
колебаний. Имсбт широкое применение прн
малых длинах хода. Применяется а счетных
приборах (синусный механизм)
Двух кулисный
Характери-
зуется равен-
ством угловых
скоростей всех
подвижных
звеньев.
Применяется в виде соединительных муфт,
допускающих смещение осей (крестовые
муфты, муфты Ольдгема)
Схема 10
Дяухползуниый
Траектория точки
А — окружность,
’ других точек ша-
туна — в.тлипс.
Применяется в эллипсографах, в прессах
для получения большого выигрыша в силе
и т. п.
476
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
Наименьшие одинаковые значения
угол передачи 7 приобретает I раз при
прямом и I раз при обратном ходе. Реко-
мендуется принимать 7 >60°. Тогда
X<cos 7<0,5. Чем меньше тем в луч-
ших условиях работает механизм и тем
выше его к. п. д.
При Х = 1 получается механизм с дли-
ной хода з = 4г и с движением ползуна
по закону гармонических колебаний.
Прн использовании кривошипа в каче-
стве ведущего звена механизм имеет
мертвые положения в средней точке хода,
т. е. при угле между кривошипом и ша-
туном, равном 0°. Для прохождения
Фнг. 35. Центральны* кривошипно-шатунный
механизм.
мертвых положений в рассматриваемом
механизме рекомендуется иметь спе-
циальные устройства, так как использо-
вание инерции звеньев не является здесь
достаточно надежным.'Механизм с).= 1
не имеет широкого применения.
При Х> I кривошипно-шатунный ме-
ханизм обращается в коромыслово-ша-
тунный, который на практике приме-
няется весьма редко.
Ниже приводятся точные и прибли-
женные формулы для кинемати-
ческого анализа механизма.
Приближенные формулы получены путем
разложения У1—X2sln»<? в ряд; они
дают достаточно точные результаты при
малых Х>
Отношение времени обратного хода
к времени прямого хода
Тог ।
Длина хода ползуна s = 2г.
Расстояние между ползуном и его
крайним правым положением (фиг. 36):
зя — г 11 — cos V + -I (I — cos 0) I ;
s„ « г f 1 — cos ? + ~ (I — cos 2<f)
Скорость ползуна
v — — гш (sin у + cos -f tg (s);
v a — гш (sin v + -y sin
2
v'p “ V r“:
при
itn .
30 CCK "‘
где n — число оборотов кривошипа в
rn
минуту, vcp = -j^-; прн ш = 2ют мин.-1,
vcp = ______
vmax «г Гш (1 + X2) V1 — X2.
Ускорение ползуна при равномерном
вращении кривошипа:
а - _ Гм1 (cos <f - sin ? tg 3 + A J;
a « — r<u* (cos <f> + X cos 2?);
amu « (1 + *)•
Ускорение ползуна при неравномер-
ном вращении кривошипа:
а «в — r«>2 (cos ? + X cos 2?) —
— re0 (sin f + y sin2f) ,
где eq— угловое ускорение кривошипа.
Координаты центра тяжести шатуна:
xs — г cos ч> + li cos Р;
сз г cos <р + /1 (1---j" sin2 ;
y^ — ZjAsin?.
Скорость центра тяжести шатуна:
vx — — г<*> ( sin ? + — cos <р tg p);
гш A. cos ; V “
Ускорение центра тяжести шатуна при
равномерном вращении кривошипа:
— гш2 у- sin <у.
Угловая скорость шатуна
“ cos р
Угловое ускорение шатуна
——
ПЛОСКИЕ МЕХАНИЗМЫ С ВРАЩАТЕЛЬНЫМИ И ПОСТУПАТЕЛЬНЫМИ ПАРАМИ 477
Во всех точных формулах
Р = arcsin (К sin <р).
заться наименьшим; при обратном ходе
имеется одно такое положение.
Значения основных показателей ме-
ханизма, зависящих
Фиг. 37. Планы скоро-
стсй и ускорений крн-
вошитю-щату иного
механизма.
от К, приведены
в табл. 7.
В таблице: г —
радиус кривоши-
па в ж, л — чис-
ло оборотов кри-
вошипа в минуту.
Построение пла-
нов скоростей и
ускорений (фиг. 37)
производится теми
же приемами, что
и для плоских
шарнирных меха-
низмов.
Смещенный кри-
Прямой гав
t Обратный хой
Фиг. 38. Смещенный кривошипно-шатунный
механизм.
вошипно-шатун-
ный механизм (фиг. 38) характеризуется
. г Е
отношениями *• — у н 6 = "р которые
должны быть такими, чтобы угол
Рекомендуемые углы передачи: при
прямом ходе уях > 60е; при обратном
ходе 7ог > 45°.
Для удовлетворения этих условий не-
обходимо, чтобы
Л — е COS "fajr 0,5:
передачи в соединении шатуна
с ползуном не снижался до слишком
малых значений. При прямом ходе ме-
ханизм проходит через два положения.
в которых угол передачи может ока-
. ।’С cos In л < 05;
I + е < cos 70Ж < 0,7.
Проверку основных размеров удобно
производить по графику (фиг. 39): точка
с координатами X и е не должна выхо-
Таблица 7
Основные характеристики центрального кривошипно-шатунного механизма
Х“”Т Эскиз Наименьшее значение угла передачи Т Отношение ско- ростей ползуна v max vrp Наибольшее уско- рение ползуна (в крайней привой точке) а к м/сяк’
0.1 — (И 84’ 1.69 0,012га’
ил —" 1 ж 78е.5 1,60 0,013га’
0.3 72» ,5 1.63 0,014га’
0.4 -g 66», 5 1.71 0,0155га’
0,5 ф 60’ 1,79 0,0166га’
Примечание. г — а метрах.
478
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
Гнблшщ в
Основные характеристики смещенного кривошипно-шатунного механизма
ч|~ II * II Эскиз 1 Наименьшее значение yt.ui передачи Длина хода s Тох Гяг Для прямого хода ползуна Ускорение ползуна в конце обратного и начале прямого хода а в иг/сек1
2 >— § >— ttmrlrr а dJa X i ь 1
0.1 83= .5 78»,5 2,010г 0,93 4.00m 0,012m1
•:i ; I. 58
; - 0.2 03 83° 78».5 72» ,5 65», 5 2,010г 2,011г 0.98 0.96 3.98m 3,94гп 1.59 1,63 0,013m1 0,014m1
0.1 03 _С < 72=. 5 60» 2,012г 0.94 3.90m 69 0Д155т*
У 1«
0,5 ZI Г" , • 66»,5 53» 2,014г 0.92 3,86m 1. 77 0,0165т1
0.6 Z-i 60" 45’ .5 2,016г 0,89 3.80m 1. 85 0,0175т1
0.1 77® 72»,S 2.012г 0,93 4,05m 1.57 0,0125т1
0.2 / У*1! 73»,5 66»,S 2.044г 0,95 4,00m 1.58 0,0135т1
0.2 0.3 73»,5 60» 2,046г 0,92 3.93m 0,0145т1
1.01 1.66
0.4 70»,5 S3» 2,060г 1 0,88 3,85m 0,0155т1 i
• f
<1 7*\—— 1
0.5 4—-А 66»,Б 45»,5 2,067г 0,84 3,78m 1.74 О.ОПгд’ !
у
— . •
ПЛОСКИЕ МЕХАНИЗМЫ С ВРАЩАТЕЛЬНЫМИ И ПОСТУПАТЕЛЬНЫМИ ПАРАМИ 479
Продолжение т»Ьл- В
1 « ч- 1 Эскиз Наименьшее значение угла передачи Длина хода f Гот Гпх Для прямого хода ползуна Ускорение ползуна в конце обратного и начале прямого холя а в jtlcttc*
5 »— и VCp и м/мин S о.
о.з 0.1 0.2 о.з 0.4 70е, 5 68“ 64°,5 60» 66°.S 60“ 63“ 45«,5 2.098г 2.101г 2,10Вт 2.119г 0.95 0.92 0,88 0.82 4. Игл J < 4.03m 3.96m 3,85гл 1.57 1.58 1.59 1.64 0.0125m" 0.0135m" 0.015m" 0.016гл"
Ч’
п
0.4 0.1 0.3 W i 1 63“ .5 60° 60° S3* 2.184т 2.192г 0.9S 0.89 4.26гл 4.14m 1.53 1.53 0.013m’ 0,014m’
Примечание, т — метрах.
дить из поля, ограниченного сплошной
ломаной линней, соответствующей пре-
дельному значению и пунктирной
прямой, соответствующей предельному
значению tox. Заштрихованное поле
включает механизмы, для которых
7лл>60’ и 7<,x>45°.
Ниже приводятся точные и прибли-
женные формулы для кинематиче-
ского анализа смещенного
механизма (см. фиг. 38).
Отношение времени обратного хода
к времени прямого хода
_ 180° — arcsin , * г + arcsin у
• ох _1 — ** ~г *
180° + arcsin . * а — arcsin j * -
I ““ A I *7“ A
Длина хода ползуна
« - /1У (1 +*)*-•*- F(l — Х)« —а«|;
**г[2+т^г]-
Расстояние между ползуном и его
крайним правым положением
sn — /У (1 + X)» — — г cos — / cos
Скорость ползуна
v — — гш (sin ? + соз ? tg ₽).
480
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
Ускорение ползуна при равномерном
вращении кривошипа
а . - гыЛ ( cos ? + К - sin ? tg ?j.
Во всех формулах
£ = arcsin (в + X sin у).
Фиг. 40. Кривпшнпио-
кулисный механизм
с качающейся кулисой.
Основные показатели смещенного кри-
вошипно-шатунного механизма приве-
дены в табл. 8.
В таблице г — радиус кривошипа
в ж; л — число оборотов кривошипа
в минуту.
Построение пла-
нов скоростей и
ускорений произ-
водится так же,
как для централь-
ного механизма
(см. фиг. 37).
Кривошипно-ку-
лисный механизм
с качающейся ку-
лисой (фиг. 40)
служит для преоб-
разования враща-
тельного движения
кривошипа в кача-
тельное движение
кулисы с плавно
изменяющимися угловой скоростью и
угловым ускорением на всем угле ка-
чания.
Отношение времени обратного (бы-
строго) хода к времени прямого хода
у. 90° — arcsin
90° 4- arcsin -д
Полный угол качания кулисы
2а — 2 arcsin
Угловое положение кулисы
. . г sin?
V — arclg-;------—.
А 4- г cos
Угловая скорость кулисы:
A cos -f- г
КЗ По - Т--1 •
Аг 4- 2Ar cos 4- •
“к max “ <> -. , при прямом ходе;
Л Т '
max <• -д----- при обратном ходе.
/» ~~ г
Угловое ускорение кулисы при равно-
мерном вращении кривошипа
_ , А (г — Л)2 sin ?
“ Г“ (Л* 4- 2Ar cos ? 4- Г*)’ *
При построении плана ускорений (см.
"табл. 5 на стр. 472) необходимо учиты-
вать кориолисово ускорение, так как
в рассматриваемом
движением являет-
ся вращение ку-
лисы.
Рекомендуется
принимать
Т<0’5:
тогда 2а < 60°.
Кривошнпно-ку-
лисный механизм
с вращающейся
кулисой (фиг. 41)
служит для пре-
образования рав-
номерного враща-
тельного движения
случае переносным
Фиг. 41. Крнвошнпио-
кулисный механизм с
вращающейся кулисой.
кривошипа в не-
равномерное вращательное движение
кулисы. Отношение времени поворота
кулисы от ф = 90° до ф = 270° и от
ф = 270° до ф = 90° при равномерно
вращающемся кривошипе
F
9СГ — arcsin —
Tj r
90° 4- arcsln —
Отношение углов поворота кулисы
за время поворота кривошипа от? = 90°
до ? = 270° и от ? = 270° до ? = 90°
Е
ъ 90° 4-arctg т
90° — arclg -у-
Положение, угловая скорость и угло-
вое ускорение кулисы определяются по
формулам для механизма с качающейся
кулисой (вместо А подставляется Е).
Кривые изменения передаточного отно-
шения в зависимости от угла поворота
ведущего звена для механизмов с раз-
личными соотношениями между основ-
ными размерами показаны на фиг. 42.
При построении плана ускорений необ-
ходимо учитывать кориолисово ускоре-
ние (см. табл. 5 на стр. 472).
Рекомендуется принимать
«1-
ПЛОСКИЕ МЕХАНИЗМЫ С ВРАЩАТЕЛЬНЫМИ И ПОСТУПАТЕЛЬНЫМИ ПАРАМИ 481
Механизм с прямо-
угольной к ул исо й (фнг. 44).
Длина хода кулисы s = 2г.
Координата положения кулисы
х = г(1 —соз ?)..
Скорость кулисы:
v = гы sin = м V'2rjc — х*,
2
Vraax = г“-
Ускорение кулисы:
Кривошипно-кулисный механизм с
равномерно вращающейся кулисой (см.
схему 6 в табл. 6) осуществляет пере-
дачу вращательного движения между
параллельными валами с постоянным
передаточным отношением. Этот меха-
низм получается из предыдущего
(фиг. 41), когда г.
Передаточное отношение
/-^=1.
ш 2
При «= 180° механизм имеет мертвое
положение: не может передавать крутя-
щего момента от кривошипа к кулисе
и допускает возможность независимого
движения кулисы.
Прохождение через мертвое положе-
ние может быть обеспечено инерцией
ведомого эвена илн применением сдвоен-
ного механизма с крестовой кулисой
(фиг. 43).
♦иг. 43. П«рм«ч«
С ПОСТО1ИКЫМ ntp.ia-
точимы отношением.
Фиг. 44. Крнвошипио-
кулисный механизм с
посту летел ьно-заижу-
шсйся прямоугольной
кулисой (ползуном).
Кривошипно-кулисные механизмы с
поступательно движущейся кулисой слу-
жат для преобразования вращательного
движения в прямолинейно-поступатель-
ное. При равномерном вращении кри-
вошипа движение кулисы происходит
по законам гармонических колебаний.
а — r«at cos f = (г — х) »*',
flmax — 0,0110 гл1 М/сек*.
Фиг. 45. Крноошипяо-
кулисмый механизм с
посту п 1 те л ьно-хвнжу-
щейся наклонной му
лисой (поииуаом).
где г — радиус кривошипа в ж; л —
число оборотов кривошипа в минуту.
Механизм с
наклонно й к у-
л и сой (фнг. 45)
применяется ред-
ко.
Для анализа ме-
ханизма можно
пользоваться фор-
мулами для меха-
низма с прямо-
угольной кулисой,
если вместо г под-
г
ставить ----и на-
cos а
чало отсчета угла у
сместить иа угол а.
Ползунно-кулисный механизм (см.
схему 8 в табл. 6) служит для преобра-
зования прямолинейного возвратно-по-
ступательного движения ползуна в кача-
тельное движение кулисы или наоборот
Координата положения ползуна х —
= A tg ф. Угол передачи •j = 90* — ф.
Рекомендуется 7 > 60*; тогда угол
качания кулисы 2а <60*, длина хода
ползуна s < 1,154.
Двухкулисный механизм (см. схему
9 в табл. 6) имеет одинаковые угловые
скорости вращения кулис, что исполь-
зуется в плавающих соединительных
муфтах (типа Олъдгема). При относитель-
ном смещении валов с соблюдением их
параллельности угловые скорости оста-
ются одинаковыми. Если поступательны»
пары заменить плоскостными, как
обычно и делается в плавающих муфтах,
то при относительном повороте осей
валов на небольшой угол муфта рябо
31 Тох I 3«. 1464
482
СВЕДЕНИЯ о МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
Фнг. 46. Дпухползунный
механизм.
тает как шарнирная за счет смещений
в плоскостных кинематических парах.
Звено, не связанное со стойкой (двой-
ной кулисный камень), движется таким
образом, что закрепленная неподвижно
на стойке точка описывает на нем эллипс.
Это свойство механизма может быть ис-
пользовано для обработки эллиптиче-
ских профилей. Изменяя расстояние
между центрами вращательных пар на
стойке, можно получать эллипсы с раз-
личными фокусными расстояниями; при
совпадении цен-
тров получает-
ся окружность.
Двухползун-
ный механизм
(см. схему 10
в табл. 6) при-
годен для пере-
дачи прямоли-
нейно- поступа-
тельного двнже-
иия под углом с передаточным отноше-
нием, изменяющимся от 0 до со. При I,
близком к нулю, получается значи-
тельное увеличение силы.
В передаче под углом 90е (фиг. 46)
{ _ V» _ X
V1 ~ - х’ *
Угол передачи в соединении шатуна
с ведомым ползуном изменяется от 0°
до 90° при уменьшении * от наибольшей
величины до нуля.
Рекомендуется 7 > 30°, тогда
х</соз30° - 0.86/;
у >/510 30° -0.5/.
С целью сокращения числа общих
пассивных условий связи вращательные
пары V класса могут быть заменены
цилиндрическими или шаровыми,
Траектория движения средней точки
шатуна—окружность, остальных точек—
аллнпсы. Это свойство двухползунного
механизма используется в эллипсогра-
фе — приборе для вычерчивания эллип-
сов.
Многозвенные механизмы
с вращательными и поступательными
парами
Механизмы с числом звеньев более
четырех применяются: а) для передачи
движения от нескольких ведущих или
к нескольким ведомым звеньям, связан-
ным со стойкой; б) для получения двн-
жения звеньев с такими кинематиче-
скими и динамическими характеристи-
ками, которых не дает четырехзвенный
механизм.
Шестизвениый кривошипно-кулисный
механизм с качающейся и поступа-
тельно-движущейся кулисой (схема 1
на фиг. 47), а также его модификации,
показанные на остальных схемах фиг. 47,
используются преимущественно в метал-
лорежущих станках для привода глав-
ного движения резания.
Назначение механизмов — преобразо-
вание вращательного движения в пря-
молинейное возвратно-поступательное
с плавным изменением скорости и уско-
рения ведомого звена на всей длине
хода и значительной разницей средних
скоростей при прямом и при обратном
ходе.
Механизмы 1, 1а и 2 (фиг. 47) отно-
сятся ко 11 классу, 2-му порядку,
а механизмы 2а, 3 и За—к III классу,
Фиг. 47. Типы шестишенных кри|юшипно-кулисиыа
механизмов дли лреобраховопнп врачительниго
движении в прямолинейное вотврагпо-лоступа-
тельное.
3-му порядку по классификации Арто-
болевского. Наличие трех поводковых
групп в механизмах по двум последним
схемам значительно осложняет их кине-
матический анализ по сравнению с меха-
низмами /, 1а, 2 н 2а.
Механизмы характеризуются:
а) длиной хода ведомого звена з мм\
б) средней скоростью ведомого звена
при прямом ходе vcp м/мин;
ПЛОСКИЕ МЕХАНИЗМЫ С ВРАЩАТЕЛЬНЫМИ И ПОСТУПАТЕЛЬНЫМИ ПАРАМИ 483
в) отношением ——-------наибольшей
°ср
скорости к средней скорости прямого
хода, влияющим на производительность
станка;
т
г) отношением — времени обрат-
‘ п*
ного хода к времени прямого хода ве-
домого звена, определяющим потерн вре-
мени на холостой ход.
Закон движения ведомого звена и
определяемые им отношения tl,naj‘- и
Г щ
зависят от схемы механизма и его
' пх
основных размеров. Уменьшение С’Д||Ц-
7 ох
и =—. выгодное с точки зрения произ-
• пл
водительности станка, ограничивается
допустимыми силами инерции.
У механизмов 1а и За законы движе-
ния ведомых ползунов незначительно
отличаются от законов движения ползу-
нов соответственно у механизмов по
схемам 1 и 3.
Механизмы 1, 1а, 2 и 2а характер!!-
. г
зуются величиной р = = sms, где
г — радиус ведущего кривошипа; А —
расстояние между осью вращения кри-
вошипа и осью качания кулисы; а — по-
ловина угла качания кулисы. Значение р
рекомендуется брать не более 0,5.
В механизме по схеме 1 (фиг. 47 и 48):
координата положения ползуна
. sin у
х — Lf - -- ;
У 1 -f- р» -|- 2р cos <f
скорость ползуна
р _ £шр (1 COSf+p(l + COS»?).
(I + р2 + 2р cosy/1’
ускорение ползуна
В механизмах по схемам 3 н За х, он
а обычно определяются графически.
График изменения скорости и уско-
рения ползуна в механизме по схеме 1
(см. фиг. 47) приведен на фнг. 48.
Фиг. 48. Изменение скорости и ускоре-
ния ползуне крипошипио-кулмемого
механизма.
Для всех шестизвенных кривошипно-
кулисных механизмов
70х 90° - а°
?лх
Для механизма / (фиг. 47):
s — 2£ sin а — 2/_р;
а - — Lafy ~ Р* + Р4) *|п ? 4- (2 — р 4- 2р* — Р8) 9 cos у 4- (4р 4- Зр1) sin у cos*у
(I 4- р* 4- 2р cos у)’1»
В механизмах 2 н 2а (фиг. 47)
, sin у
х — Ltf ------i---•
' r 1 4- р cos у ’
2 , Sin а
- «£“—=
’ + Уб5
лх
V - £.Шр — cos у 4-р (I—2 cos*у) .
г (14-рсоьур ’ ________
, г (4р —2ра) sin у cos у 4- (1 — 2р-) sin у 4- 15р* sin у cos?y 4- 8p>cos»y
®“ Ц“Р (I 4“ Р cos у)1
при а» м 2пл МИН.-1
31*
484
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
о„-4£л = 2£лр (1 + ;
9и°
а°
Vm„ П 14~9^
vCp “ 2 ’ 1 + sin а ’
Для механизмов 2 и 2а (фиг. 47):
л — 2л, tg» ;
2, fg« 1 , 1+-7^.
*"r90°
при ы = 2«л мин.—’
Механизмы 3 и За (фиг. 47) характери-
зуются величиной 8 — — и углом а. Для
механизма J:
п. , 2 , sin а
я — 2£sina; vf» = —£•>------я-i
l + g05
i л r «Ina
при •>—2хл мин,—1 veo — 4 Ln------т- ;
‘ + 5J3-
Одм ?(*
Vep “ 1 4- sin a COS a — В (1 4- Sin а) *
На фиг. 49 приведен график измене-
ния ». vep и ~^5Й- в зависимости
‘ пх t>CP
от а и р для различных схем меха-
низма. Для механизма 3 кривая
VCP
построена при значении 8 = 0,4, чаще
всего встречающемся на практике.
°ср.
получается наибольшим в механизме 1.
Фиг. 49. Основные характеристики кривошипно-
му лисиых механизмов.
при переходе к схеме 2 это отношение
снижается на величину до 13,5%, при
переходе от схемы 2 к схеме 3 — до 3%-
Таким образом, с увеличением значений
р и а все более выгодными против
схем 1 и 1а с точки зрения производи-
тельности станка становятся схемы 2
и 2a и особенно схемы 3 и За.
Шестнзаениыс крнвошипио-кулисно-
шатунные механизмы и восьмизвенные
крнвошнпно-кулисные механизмы. Ше-
стизвенный крнвошипно - кулисно - ша-
тунный механизм (фиг. 50) получается
Фиг, 50. Кривошнпио-мулмсяо-ивтужяы» меииюм.
из кривошипно-шатунного механизма
(обычно центрального) заменой ведущего
кривошипа механизмом вращающейся
ПЛОСКИЕ МЕХАНИЗМЫ С ВРАЩАТЕЛЬНЫМИ И ПОСТУПАТЕЛЬНЫМИ ПАРАМИ 485
кулисы (см. фиг. 41). Такая замена
дает уменьшение скорости прямого хода
ползуна за счет повышения скорости
обратного хода.
Восьмизвенные кривошипно-кулисные
механизмы (фиг. 51) получаются посред-
ством такой же замены нз шестизвен-
ных кривошипно-кулисных механизмов
(см. фиг. 47), что приводит к уменьше-
нию времени обратного хода ведомого
звена, средней скорости прямого хода
Фнг. S1. Восшнзмнный арнаошипво-кулисяыА
мехаакзм.
и отношения наибольшей к средней
скорости при прямом ходе.
Отношение времени обратного хода
Тох к времени прямого хода Т'^ слож-
ного механизма
К» 90°-3° „ Т„,
где
90е-?0 9О° + «»
K1"9U° + |JO’‘MIO — а®’
— отношение времен для ксход-
' nt
кого механизма; аир — см фиг. 50 н 51.
Для механизма с а = 0 (например, по
фнг. 50) sin р » «|. Для механизма с а у- 0
(например, по фнг. 51)
tg а
sin р — е,
cos р
sin Р — COS* a ^S| + tg 1 + tg*a— ,
Е
где st ------относительная величина
К
эксцентриситета. Средняя скорость пря-
мого хода сложного механизма
vcp = К^ср.
где
Кг =
90° + а°.
90° + р°’
Vcp — средняя скорость прямого хода
исходного механизма.
Отношение наибольшей скорости к
средней для прямого хода сложного ме-
ханизма
где
к 1 90° + р»
8 1 + в) ’ уц° + а° ’
V«Bsx
а -== — отношение скоростей для ПрЯ-
^СР
мого хода исходного механизма.
Значения К\, Кг и К, можно опреде-
лить также по графику (фиг. 52).
Рекомендуется принимать ву < 0,5.
Угол а
Фиг. 52. Диаграмма ала опрглелсима
значений К„ К, и К,.
Проверку звеньев восьмизвенных кри-
вошипно-кулисных механизмов на проч-
ность и износ следует производить как
при прямом рабочем ходе, так и при
обратном холостом ходе, так силы
486
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
ПЛОСКИЕ МЕХАНИЗМЫ С ВРАЩАТЕЛЬНЫМИ И ПОСТУПАТЕЛЬНЫМИ ПАРАМИ 487
инерции в этих механизмах могут дости-
гать значительных величин.
Пример конструкции восьмизвенного
кривошипно-кулисного механизма по-
перечно-строгального станка с регу-
лированием длины хода ведомого звена
приведен на фиг. 53.
Кривошипно-шатунный механизм с
прицепным шатуном применяется в
миогоцилнндровых поршневых маши-
нах (двигателях), в которых несколько
цилиндров, расположенных под углом,
работают на один кривошип коленча-
того вала. Кинематический анализ ос-
новной части механизма /—2—3—6
(фиг. 54) производится по соответствую-
щим формулам для центрального кри-
вошипно-шатунного механизма.
Положение И скорость ползупа 5
для механизма с углом расположения
цилиндров а, равным углу шатуна
прн шарнире кривошипа, подсчиты-
ваются по формулам:
х = г cos у + R cos p + L cos 8;
{г Г R sin (<f + o) cos (7 -(- a>
Sln * + ЦГ [----------- cosl" -------------
sin (y —7) cos (y — 7)
+ L cos 8
где
cos 8 - j/l — у sin* (y — 7).
Скорости и ускорения механизмов
с прицепными шатунами легко опре-
деляются также построением планов
скоростей и ускорений.
Кривошипно-рычажные механизмы
служат для преобразования вращатель-
ного движения в прямолинейно-поступа-
тельное. Применяются главным образом
в прессах небольшой мощности (фиг. 55).
Кривошипно-коленные механизмы
служат для преобразования вращатель-
ного движения в прямолинейно-посту-
пательное со значительным возрастанием
усилия на ползуне в конце его хода.
Применяются в различных зажимных
приспособлениях и в прессах средней
и большой мощности (фиг. 56).
Ползунно-коленные механизмы слу-
жат для преобразования прямолинейно-
Фиг. 56. Кривошипно-коленные механизмы.
поступательного движения ведущего
звена в прямолинейно-поступательное
Фиг. 57. Ползунно-коленные механизмы.
движение ведомого ползуна со значи-
тельным выигрышем усилия в конце
хода последнего. Применяются, напри-
мер, в пневматических (фиг. 57, а) и
488
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
гидравлических (фиг. 57, б) прессах,
а также в различных зажимных устрой-
ствах.
Рычажные механизмы с качающимся
цилиндром (кулисные) служат для
преобразования прямолинейно-поступа-
тельного перемещения поршня относи-
тельно качающегося цилиндра в прямо-
линейно поступательное движение ведо-
Фнг. 53. Пневматический пресс
с качающимся цилиндром.
*юго ползуна с выигрышем усилия. Та-
кне механизмы применяются, например,
а пневматических зажимных устрой-
ствах и в мелких пневматических прес-
сах (фнг. 58).
. ВИНТОВЫЕ МЕХАНИЗМЫ
С СООСНЫМ РАСПОЛОЖЕНИЕМ
КИНЕМАТИЧЕСКИХ ПАР
Общие сведения
Назначение. Винтовые механизмы
с соосным расположением кинемати-
ческих пар пригодны для преобразо-
вания с постоянным отношением ско-
ростей винтового, вращательного и пря-
молинейно-поступательного движений
в любых сочетаниях. Основное исполь-
зование — получение медленного пря-
молинейно-поступательного движения с
большим выигрышем силы (домкраты, за-
жимные устройства) или с точным отсче-
том пройденного пути (измерительные
приборы, станки). В винтовых механиз-
мах легко достигается самоторможение.
Структура. Звенья механизма могут
соединяться винтовыми, вращательными
и поступательными парами (V класса).
При составлении структурной схемы
необходимо следить за тем, чтобы в ме-
ханизме не образовалось групп звеньев
с независимой подвижностью. Незави-
симая подвижность одного звена полу-
чается при соединении его с соседними
звеньями двумя поступательными, двумя
вращательными или двумя винтовыми
парами одинакового шага. Независимая
подвижность группы из двух звеньев
имеет место, например, при соединении
их между собой поступательной и с со-
седними звеньями двумя вращательными
парами или между собой вращательной
и с соседними звеньями двумя посту-
пательными парами.
Число общих условий пас-
сивных связей в механизме
с одними парами V класса равно учетве-
ренному числу неповторяющнхея за-
мкнутых контуров в схем?. Уменьшение
числа пассивных условий связи может
быть достигнуто путем за юны некото-
рых пар V класса парами более низких
классов без нарушения подвижности
механизма. Вращательные пары могут
быть заменены шаровыми, плоскост-
ными (Ш класс) или высшими, поступа-
тельные — плоскостными или высшими,
винтовые — высшими (например, в виде
штифта, входящего в винтовую ка-
навку).
Кинематика. Винтовое движение со-
стоит из двух составляющих — враще-
ния и осевого перемещения. В винтовом
механизме с одной степенью свободы
отношение между осевыми и угловыми
перемещениями всех звеньев постоянно
и равно отношению между соответ-
ствующими скоростями и ускорениями.
В механизмах с несколькими степенями
свободы та же зависимость наблю-
дается при постоянном отношении между
сообщаемыми перемещениями, скоро-
стями и ускорениями ведущих звеньев.
Кинематический анализ и синтез выпол-
няются аналитически или графически.
Аналитический способ отличается про-
стотой и практически любой точностью
подсчетов, графический более нагля-
ден.
На фиг. 59 приведено построение пла-
на перемещений, скоростей и касатель-
ных ускорений винтового механизма.
Шаги правых резьб (sj, Sn) отклады-
ваются в положительном направлении
оси абсцисс: Н = 2кг, где г — радиус
цилиндрической поверхности, к которой
приводятся перемещения, скорости и
ускорения. Масштабы по оси абсцисс
ВИНТОВЫЕ МЕХАНИЗМЫ С СООСНЫМ РАСПОЛОЖЕНИЕМ ПАР
48»
и оси ординат выбираются произ-
вольно.
Осуществление винтового движения ве-
дущего звена не вызывает затруднений
при ручном приводе, но обычно требует
дополнительных устройств при механи-
ческом приводе. Из винтового движения
ПраВая резьВа
Фнг. 39. Построение планоа переме-
щений. скоростей н касательных уско-
рений для винтового механизма.
tpl'CJlVt)
S}l’l
fleBm резьба
ведомого звена часто используется
только одна его составляющая — осевое
перемещение.
Двухзвенные механизмы
Механизм имеет стойку и одно по-
движное звено. Использование отдель-
ных составляющих винтового движения
в качестве самостоятельных движений
позволяет двухзвенный механизм при-
менять для преобразования поступатель-
ного нлн вращательного движения в
винтовое (направляющий механизм), вра-
щательного — в поступательное.
Получение винтового движения часто
требуется для обработки соответствую-
щих поверхностей. Например, в зубодол-
бежных станках, работающих шестер-
ней-инструментом, при нарезании винто-
вых зубчатых колес применяются винто-
вые направляющие для долбяка, в при-
способлении для шлифования винтовых
шлицевых валиков применяется направ-
ляющая гайка и так называемый мастер,
винт.
В ряде механизмов в качестве веду-
щего движения, выполняемого от руки,
используется вращательное, а в каче-
стве ведомого — осевое прямолинейно-
поступательное перемещение одного и
того же подвижного эвена. Значитель-
ная разница между перемещениями по
оси и по окружности при малом шаге
винта дает возможность просто осуще-
ствить точный отсчет меняющейся в зна-
чительных пределах координаты осевого
положения подвижного звена; это ши-
роко используется в измерительных при-
борах с прямолинейной шкалой для от-
счета целых миллиметров н шкалой по
окружности для отсчета долей милли-
метра.
Например, винтовой механизм микро-
метра (фиг. 60) имеет микрометрический
винт I (с шагом 0,5 мм), на котором
закреплен барабан 2 с круговой шкалой
для отсчета сотых долей миллиметра
Фиг. 60. Микрометр.
ограничивающая кру-
прн вращении винт»
и трещотка 3,
тящий момент
пальцами руки; стебель 4 с продольной
шкалой для отсчета половин миллиметра
закреплен в скобе 5 и несет гайку 6 и
направляющую втулку со стопорным
устройством 7.
Трехзвенные механизмы
Трехзвенные винтовые механизмы
имеют большое распространение.
Многозвенные механизмы с одной
степенью свободы для удобства ана-
лиза, как правило, могут быть соответ-
ствующей разбивкой приведены к треху
звенным.
Рассматриваемые здесь механизмы слу-
жат для преобразования винтового дви-
жения в винтовое, винтового во враща-
тельное или наоборот, винтового в пря-
молинейно-поступательное или наоборот,
вращательного в прямолинейно-поступа-
тельное нлн наоборот.
490
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
Наиболее употребительные типы трех-
звенных механизмов с различным взаим-
ным расположением кинематических
пар приведены в табл. 9.
Другие виды механизмов по приведен-
ным в табл. 9 схемам могут быть полу-
чены путем обращения винтовых пар:
охватывающий и охватываемый элемен-
ты меняются местами.
Механизмы • по схеме 1 применяются
редко, по схеме 2 находят применение
при ведущем звене с вращательным
движением, по схеме 3 применяются
для получения очень малых поступа-
тельных перемещений за один оборот
ведущего звена.
Механизмы по схемам 4 и особенно 5
имеют наиболее широкое применение иа
практике.
Потерн на трение в поступательных
парах сильно зависят от их конструк-
тивного выполнения и расположения
действующих внешних сил, поэтому учет
этих потерь в общем виде затруднителен.
К- п. д. винтовой пары с одним не-
подвижным элементом
п *gg
tg (? + «) ’
где а — угол подъема резьбы по сред-
нему диаметру; — угол трения в резь-
бе, соответствующий приведенному коэф-
фициенту трения. К. п. д. механизма
по схеме 5 табл. 9 без учета потерь
в поступательной паре
ч-----------'^-г--------.
tg (? + «) + ~ tg ч>|
Таблица Я
Типы трехзвенпых винтовых механизмов с одной степенью свободы
Тип механизма Характер движения эвсиьсп Схема Кинематические зависимости
Со средней поступа- тельной парой Винтовое н винтовое Схема J, А «1 ° «i; V) + ts; е, = з,л,: —А Vi *1
С крайней вращатель- ной и средней по- ступательной па- рами Винтовое и вращательное г Схема л» — л»; Vi = 0; V, «в 5» Л»
С крайней поступа- тельной парой Винтовое и прямолинейно- поступи- t г Схема У, яа^-sa. £ п, — 0; v, * Vi — (л, - Л) л,
С крайней поступа- тельной и.средней праща тельной ла- рами тельное р Схема r.i »Д WBR о Л 1 1 1 5 о £
С одной крайней вра- щательной и другой поступательной па- рами Вращательное и прямоте нсйнп-ппсту- пательное г Схема 5 о о 5 1 1 J с о £
Примечаниям. Угловые перемещения р и скорости л считаются положительными, если при рассматривании мезаннзма слепа вращение происходит по часовой стрелке. Линейные перемещении и скорости v считаются положительными при движении вправо. Величина шага а оинтовой пары считается положительной при припой резьбе, отрицательной - при левой. 1. Приведенные кинема >ическне зависимости справедливы также ала перемещений за определен- ный отрезок времени и для ускорений.
ВИНТОВЫЕ МЕХАНИЗМЫ С СООСНЫМ РАСПОЛОЖЕНИЕМ ПАР
431
где г — средний радиус резьбы; и и
fi—радиус приложения силы трения и
угол трения в кольцевой опоре.
К- п. д. механизма по схеме 3 табл. 9
без учета потерь в поступательной паре
П tg ai — r2 tg аг
Г\ tg (fl + tg (fj-aj) ’
где ai, fi и rt — соответственно угол
подъема резьбы по среднему диаметру,
угол трения и средний радиус резьбы
для винтовой пары, прилегающей к
стойке; 32, fj и г2 — то же, но для
винтовой пары, соединяющей виптс пол-
зуном.
Ошибки положения механизма по
схеме 5 табл. 9, получающиеся вслед-
ствие деформации винта, зависят от ха-
рактера и расположения опор.
Для механизма, в котором осевое
усилие воспринимается опорой, рас-
положенной со стороны привода винта
(фиг. 61, а), ошибки положения от одного
Фиг. 61. Ошибки положения механизма
«следствие деформаций ходового винта.
растяжения винта и от растяжения
и скручивания изобразятся на графике
соответственно наклонными прямыми
/] и /. Для механизма, в котором осе-
вое усилие воспринимается опорой, рас-
положенной со стороны свободного
конца винта (фнг. 61,6). ошибки поло-
жения от одного сжатия винта и от
сжатия и скручивания изображаются на
графике прямыми 2t и 2.
Если растяжению или сжатию под-
вержен тот же участок винта длиной /1(
который испытывает деформацию скру-
чивания, то ошибка положения будет
р/
Д “ TF ° + *>•
где Р — осевое усилие, действующее на
винт; Е — модуль упругости материала
винта; F — площадь условного расчет-
ного сечения винта диаметром, равным
наружному диаметру винта за вычетом
удвоенной рабочей высоты профиля:
k — коэффициент.
Для механизма с нормальной трапе-
цондальной резьбой шага s и номиналь-
ного наружно-
го диаметра d0
значение коэф-
фициента k мо-
жет быть взято
по графику ня
фиг. 62; при
учете к.п.д. вин-
товой пары при- Фиг. 62. Лидгремма для
веденный угол определения котффици
трения принят сига *"
равным 5°.
Когда растяжению или сжатию под-
вержен один участок винта длиной /г,
а скручиванию другой — длиной /8, то
Дв_^(/2 + А/а)-
Винты обычно выполняются цельны-
ми, очень длинные — составными на
нескольких секций. Резьба применяется
чаще всего трапецеидального профиля,
реже—прямоугольного и треугольного.
Прямоугольная резьба обеспечивает
относительно высокий к. п. д. механизма
и малую ошибку положения, вызывае-
мую биением винта; однако такая резьба
сложна в изготовлении (невозможно
фрезерование) и быстро изнашивается.
Применяется иногда в домкратах и в
очень точных винтовых механизмах.
Треугольная резьба с малым шагом
и углом при вершине профиля 30® или
60“ применяется для точных ходовых
винтов делительных и контрольных
машин.
Гайки винтовых механизмов по схеме
5 выполняются закрытыми (фиг. 63, а
и в) или открытыми (фиг. 63, биг),
постоянными (фиг. 63, а и б) или отклю-
чаемыми (фнг. 63, в и г). Закрытые
гайки лучше направляют винт и дают
осевое усилие по центру винта; открытые
гайки позволяют применять промежу-
точные опоры для винта и часто упро-
щают сборку механизма. Осевой зазор
в резьбе при постоянных открытых и
отключаемых открытых и закрытых
гайках может быть устранен регули-
рованием их положения в поперечном
направлении. В постоянных закрытых
гайках возможность осевого смещения
вннта относительно гайки за счет зазора
в резьбе устраняется регулированием
или саморегулированием гаек. Такие
492
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
гайки выполняются двойными: одна часть
закрепляется на салазках, а другая
имеет возможность незначительно пере-
мещаться относительно первой. Такое
перемещение может быть осевым, угло-
вым нлн винтовым и осуществляется под-
тягиванием установочных винтов, гаек
Фиг. 63. Типы гаек ходовых ви|гтоп.
илн клиньев (регулирование) нлн под
действием пружины, гидроцилиндра, са
моэатягнвания (саморегулирование)
Винтовые механизмы с несколькими
степенями свободы
Четырехэвенные механизмы, образо-
ванные из простой замкнутой кинема-
тической цепи с винтовыми, вращатель-
ными и поступательными парами, имеют
две степени свободы, пятизвенные —
три, шестизвенные — четыре и т. д.
Практическое применение находят
механизмы с двумя и с тремя степенями
свободы; они используются, в част-
ности:
а) для перемещения салазок от двух
приводов, когда требуется независи-
мость действия последних с целью со-
хранения определенного положения ки-
нематической цепи одного привода при
пользовании другим приводом; напри
мер, поперечная подача круга в шлифо»
вальных станках — путем вращения
гайки от механизма подачи и быстрый
подвод и отвод круга — осевым переме-
щением гайки посредством гидравличе-
ского цилиндра (W = 2);
б) для компенсации ошибок ходовых
винтов измерительных машин и неко-
торых точных станков при помощи
Фиг. 64. Винтовые механизмы е компенсацией
ошибок по шагу ходового винта и его тепловых
деформаций.
соответствующим образом спрофилиро-
ванных коррекционных линеек.
В механизме по фиг. 64, а преду-
смотрена компенсация ошибок по шагу
ходового винта, осуществляемая при
перемещении салазок 1 путем поворота
гайки 3, от неподвижной лнненки 4, про-
филь которой соответствует ошибкам
шага ходового винта 2 по длине. В ме-
ханизме по фиг. 64, 6 предусмотрены
компенсирующие поворот и осевое пере-
мещение гайки 3 относительно корпуса
салазок 1. Поворот гайки 3 осуще-
ствляется от профильной линейки 4, a
компенсирующее осевое перемещение —
посредством втулки 5 с резьбой и наклон-
ной линейки 6 прямолинейного профиля
(компенсация тепловых деформаций).
Возможно весьма большое число схем,
винтовых механизмов cW' = 2hIF=3,
различающихся типами кинематических
пар и их взаимным расположением.
ЗУБЧАТЫЕ МЕХАНИЗМЫ
Общие сведения
Назначение. Зубчатые механизмы де-
лятся на плоские и пространственные.
Зубчатые механизмы применяются
преимущественно для передачи враща-
тельного движения с постоянным отно--
шением скоростей и для преобразования
вращательного движения в прямоли-
нейно-поступательное и наоборот.
ЗУБЧАТЫЕ МЕХАНИЗМЫ
493
Зубчатые зацепления
Движение зубчатых колес, передаю-
щих вращение между двумя параллель-
ными валами с постоянным передаточ-
ным отношением, можно представить
как качение без проскальзывания двух
цилиндрических поверхностей, называе-
мых начальными цилиндрами. Проекции
этих поверхностей на плоскость, перпен-
дикулярную к осям вращения колес, на-
зываются начальными окружностями;
точка касания их называется полюсом
зацепления траектория точки касания
двух профилей зубьев — линией зацеп-
ления. Линия зацепления проходит через
•полюс зацепления. Профили зубьев
должны удовлетворять следующему усло-
вию: общая нормаль к точке касания
профилей в любой момент зацепления
должна проходить через полюс зацепле-
ния, или, иначе, профили зубьев должны
быть взаимно огибаемыми в относи-
тельном движении зубчатых колес.
Профили, удовлетворяющие указан-
ному условию, называются сопряжен-
ными. Вообще говоря, почти для любого
заданного профиля можно найти сопря-
женный. Однако практическое приме-
нение имеют только некоторые техноло-
гически удобные сопряженные профили:
мольвенткый, циклоидальный и цевоч-
ный.
Эвольвентное зацепление. Боковые
стороны зубьев очерчиваются по эволь-
вентам окружности, описываемым точ-
ками производящей прямой прн ее
качении без скольжения по основной
окружности, концентричной начальной
окружности колеса (фиг. 65), причем
линия зацепления в этом случае полу-
чается прямой с рабочим участком МЫ;
угол между линией зацепления и пер-
пендикуляром к прямой, соединяющей
центры колес, называется углом заце-
пления, Для нормальных зацеплений
стандартная величина угла зацепления
по ГОСТ 3058-45 □ - 20’.
Шаг зацепления — расстояние между
двумя одноименными точками двух со-
седних зубьев, взятое по какой-либо
окружности зубчатого колеса.
Дуга зацепления — дуга окружности,
на которую поворачивается колесо од-
ной парой сцепляющихся зубьев.
Степень или коэффициент перекры-
тия — отношение дуги зацепления
к шагу зацепления.
Модуль зацепления — отношение шага
зацепления к числу к. Величины моду-
лей стандартизованы (ОСТ 1597): с 0,3
до 0,8 через 0,1 мм; с 1 до 4,5 через
0,25 мм; с 4,5 до 7 через 0,5 мм; с 7
до 16 через 1 .им; далее 18, 20, 22, 26,
28, 30, 33, 36, 39, 42. 45 мм и далее
через 5 мм.
Делительной окружностью назы-
вается окружность, диаметр которой
равняется произведению стандартной ве-
личины модуля на число зубьев ко-
леса.
Головка зуба — часть зуба, высту-
пающая за пределы начальной окруж-
ности. Высота головки he = kt-m; для
нормального зуба ke = 1, для укорочен-
ного kt = 0,8.
Ножка зуба — часть зуба, располо-
женная внутри начальной окружности.
Высота ножки hH = kH-m; для нормаль-
ного зуба kH = 1,25, для укороченного
*и = 1.
На фиг.65показано нормальное эволь-
вентное зацепление двух зубчатых колес,
одно нз которых имеет подрезание ножки
зуба 5 со снятием участка эвольвенты тп.
Начальные окружности 1 и /' касаются
друг друга в полюсе зацепления Р,
через который под углом зацепления а
проходит линия зацепления 4 с рабо-
чим участком МЫ. Производящая пря-
мая 3 в изображенном на фиг. 65 поло-
жении совпадает с линией зацепления
и касается обеих основных окружно-
стей 2 и 2'. Шаг по начальной окруж-
ности t = кт, шаг по основной окруж-
ности /0 = кт соз а.
Свойства эвольвентного зацепления:
1. Эвольвентные колеса не являются
парными — каждое колесо с зубьями
нормального профиля при одном н том
же модуле может сцепляться с колесом
того же модуля, имеющим любое число
зубьев (образуют серию определенного
модуля).
2. При изменении расстояния между
центрами колес правильность зацепле-
ния не нарушается, передаточное числ
сохраняется постоянным.
494
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
3. При бесконечно большом радиусе
основной окружности эвольвента обра-
щается в прямую, поэтому зуб рейки
получается с прямолинейным профилем.
Это позволяет пользоваться сравни-
тельно простым в изготовлении, точным
и легко контролируемым инструментом
прямолинейного профиля (гребенка, чер-
вячная фреза, шлифовальный круг)
при обработке эвольвентных зубьев ме-
тодом обкатки — копирования движе-
ний зубчато-реечной передачи (фиг. 66).
Фиг. 66. Корригирование эвольвентных
эубьеп смещением реАкн-ммструментэ.
Движение инструмента относительно за-
готовки можно представить себе разло-
женным на две составляющие: одну,
обеспечивающую движение режущих
лезвий по плоскостям, ограничивающим
объем воображаемой производящей
рейки (например, прямолинейное воз-
вратно-поступательное главное движе-
ние резания гребенки, имеющей про-
филь производящей рейки), и вторую,
обеспечивающую зацепление производя-
щей рейки с заготовкой (например, про-
катывание заготовки по <неподвижной>
производящей рейке в станках, рабо-
тающих гребенкой).
Начальная окружность заготовки в ее
зацеплении с производящей рейкой но-
сит название делительной окружности
колеса. В нормальных зацеплениях де-
лительные и начальные окружности ко-
лес совпадают; в корригированных заце-
плениях (см. ниже) эти окружности не
совпадают.
Изготовление и контроль реек-дета-
лей являются также достаточно про-
стыми.
4. При' нарезании зубьев методом
обкатки одним и тем же рейкой-инстру-
ментом или шестерней-инструментом
можно нарезать колеса одинаковых мо-
дулей с различными числами зубьев.
5. Легко выполняется корригирование
профиля зуба, предпринимаемое с целью
улучшения качества зацепления, в част-
ности, для устранения подрезания ножки
зуба в процессе обработки.
Подрезание ножки зуба заключается
в образовании на ножке выемок, сни-
мающих часть эвольвентного профиля и
ослабляющих зуб в опасном сечении
(см. фнг. 65). Срезание части эвольвенты
прн подрезании приводит к уменьшению
коэффициента перекрытия а, что небла-
гоприятно влияет на плавность работы,
прочность и износоустойчивость переда-
чи. Коэффициент е желательно иметь по
возможностибольшим(недопустнмов< I).
Величина е определяется аналитически
илн графически как отношение длины
рабочего участка линии зацепления
к шагу по основной окружности.
Опасность подрезания возникает прн
малом числе зубьев (см. т. 4 гл. VH)-
Для профилирования корригирован-
ных зубьев пригодна производящая
рейка нормального профиля. Корриги-
рование профиля достигается смеще-
нием инструмента в направлении от
центра (иногда к центру) заготовки.
На фнг. 66 показано положение 2 про-
изводящей рейки прн нарезании зуба 1
нормального эвольвентного зацепления
(с подрезанием ножки зуба) и сдвинутое
на величину х положение 4 той же про-
изводящей рейки при нарезании зуба 3
корригированного профиля. В обоих слу-
чаях делительная окружность 5 и дели-
тельная прямая б остаются неизмен-
ными.
Величины смещений прн обработке
обоих колес выбираются с таким расче-
том, чтобы, достигнув необходимого
корригирования профиля, не получить
в то же время слишком большого окруж-
ного зазора между зубьями сцепляю-
щихся колес.
Прн проверке корригированных зубьев
на отсутствие подрезания кг берется со-
ответствующим высоте головки зуба
рейки-инструмента, измеренной от дели-
тельной прямой до конца зуба (даст не-
сколько завышенное значение гт1п) илн
до начала закругления вершины зуба
(дает несколько уменьшенное значе-
ние Г„щ).
Циклоидальное зацепление (фиг. 67).
Головка зуба очерчивается по эпици-
клоиде 3 (нлн 3' для другого колеса),
иожка — по гипоциклоиде 4 (или 4'),
т. е. по кривым, которые описываются
точками производящих окружностей 2"
и 2 (или 2 и 2') при их качении без
скольжения соответственно по наруж-
ной или по внутренней стороне началь-
ЗУБЧАТЫЕ МЕХАНИЗМЫ
495.
ной окружности 1 (или /') колеса.
Линия зацепления MPN состоит из двух
дуг окружности. Колеса с зубьями цик-
Фнг. 67. Циклоидиль-
пое зацепление.
лоидальпого про-
филя — парные.
Каждое колесо мо-
жет правильно
сцепляться только
с тем зубчатым
колесом, на рабо-
ту с которым оно
рассчитано. Цик-
лоидальный про-
филь, приближен-
но очерченный ду-
гами окружностей,
имеет применение
в механизмах ча-
сов и других при-
боров.
Цевочное зацепление (фиг. 68). Если
профиль зуба одного колеса предста-
вляет собой точку 2, то профиль зуба
сопряженного с ним колеса очерчивается
эпициклоидой 2', получающейся при
качении начальной окружности 1 пер-
вого колеса по начальной окружности Г
второго. После за-
мены этих теоре-
тических профи-
лей практически
выполнимыми эк-
видистантными
профилями полу-
чаем на первом
колесе профиль
зуба в виде ок-
ружности 3 (сече-
Фиг. 6В. Цевочное
цепленне.
ние цевки — штифта или ролика) и на
втором колесе — с боковыми сторонами
по эквидистантным к эпициклоидам
кривым 3’. Профиль зуба второго ко-
леса обычно очерчивается приближенно
дугами окружностей.
Цевочное зацепление имеет ограни-
ченное применение. Оно используется
главным образом для передач с большой
редукцией в общем машиностроении и
в точной механике.
Типы зубчатых пар
Различают пары для передачи враща-
тельного движения (зубчатые передачи)
и пары для преобразования вращатель-
ного движения в прямолинейно-посту-
пательное или наоборот (реечные пере-
дачи).
Зубчатые передачи делятся на пере-
дачи между параллельными, пересекаю-
щимися и скрещивающимися валами.
Во всех
шение
случаях передаточное отно-
=
“I
«I
г?
где <>! и шг—угловые скорости; X) к
Xj—числа зубьев соответствующих колес.
В передачах между парал-
лельными валами зубчатые ко-
леса имеют цилиндрическую форму и
снабжаются прямыми, косыми, угло-
выми или шевронными зубьями.
Прямые зубья имеют направление no-
образующим цилиндра.
Передачи с прямозубыми эвольвент-
ными колесами получили наибольшее-
распространение в
практике.
Косые зубья —
наклонные на про-
изводящей или
рабочей рейке,
винтовые па коле-
се (фиг. 69) —
дают касание со-
пряженных зубьев
по линии.
Преимущество
передач косозубы-
ми колесами — по-
вышенная плав-
ность работы.
Недостаток—на-
личие осевых уси-
лий.
Фиг. 69. Передача ци-
линдрическими коле-
сами с косыми эубьими
Угловые или шевронные зубья состоят
из двух (или белее) участков косых зубь-
ев с противоположными углами наклон»
к образующей. Осевое усилие в пере-
даче отсутствует. Одно колесо обычно
делают самоустанавливающимся в осе-
вом направлении. Недостаток передач —
сложность обработки зубьев и невоз-
можность их шлифования производи-
тельными методами.
В передачах между пере-
секающимися палами зубча-
тые колеса обычно имеют коническую
форму. Работа передачи может быть
представлена как качение без проскаль-
зывания двух начальных конусов с вер-
шинами в общей точке. Колеса снаб-
жаются прямыми, косыми или криволи-
нейными зубьями.
Прямые зубья имеют направление по
образующей конуса, касание сопряжен-
ных зубьев — по прямой. Боковые сто-
роны зубьев ограничены некрутыми
коническими поверхностями. Теорети-
чески точный эвольвентный профиль
49Г>
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
может быть построен методами сфериче-
ской геометрии. Для графического по-
строения и исследования профилей поль-
зуются приближенным методом, заклю-
чающимся в замене сферической поверх-
ности двумя дополнительными конусами
с последующей разверткой их на пло-
Фиг. 70. Коническая и плосхо-цилии-
лрическая передачи между пересекаю-
щимися валами.
скость (фиг. 70, «). Дополнительные
конусы имеют углы при вершине
27[ - 180° - 2п и 27г = >80°- 2ц
(где 271 и 2-ja — углы при вершине на-
чальных конусов соответствующих ко-
лес) и касаются сферы по линиям ее
пересечения с начальными конусами,
что обеспечивает удовлетворительное
совпадение дополнительных конусов со
•сферой в зоне, прилегающей к линии
касания. Развертка дополнительных ко-
нусов позволяет рассматривать профили
зубьев конических колес как цилиндри-
ческих с диаметрами начальных окруж-
ностей
rf«,“dM,:cos7i “mzi:cos Т1
и «
— dH : cos 7j — mz2: cos yj,
где и dNi — диаметры начальных
окружностей конических колес (фиг.70.а).
У колес с углом при вершине началь-
ного конуса 180’ (плоское колесо) допол-
нительный конус обращается в цилиндр,
а профиль зубьев на развертке послед-
него соответствует прямолинейному про-
филю зубьев рейки.
Широкое практическое применение
имеют колеса с теоретически неточными
зубьями, спрофилированными плоским
производящим колесом (на фиг. 70, а по-
казано штрихпунктириыми линиями)
с прямолинейным профилем зубьев и
углом при вершине начального конуса,
равным или близким к 180’. Обработка
таких колес возможна инструментом
с прямолинейной режущей кром-
кой.
Косые и криволинейные зубья обеспе-
чивают большую плавность работы пе-
редачи. Название зуба соответствует его
форме на плоском производящем колесе.
Средние линии косых (тангенциальных)
зубьев касаются некоторой концентри-
ческой окружности на плоском колесе.
Из криволинейных зубьев технологиче-
ски наиболее удобным является круго-
вой, допускающий производительные
методы нарезания и шлифования зубьев.
Плоско-цилиндрическая передача
(фиг. 70, б) состоит из цилиндрического
колеса и сопряженного с ним плоского
колеса, зубья которого имеют сложную
форму и нарезаются тестер ней-долбя-
ком, соответствующим цилиндрическому
зубчатому колесу передачи. В плоско-
цилиндрической передаче касание зубьев
происходит по линии. Такая передача
применяется, например, в токарных
зажимных патронах.
Передачи между скрещи-
вающимися валами выполняются
винтовыми колесами, гипоидными коле-
сами, червячной па-
рой, глобоидной чер-
вячной парой.
Винтовые колеса
(фиг. 71) имеют ци-
линдрическую форму
и снабжены винто-
выми зубьями, геоме-
трическая характери-
стика которых та же,
что и косых (см. вы-
ше). Передача рабо-
тает с большим отно-
сительным скольже-
нием зубьев, имею-
щих точечное касание. Поэтому такие
колеса используются главным образом
для передачи малых усилий. Оси ко-
лес могут скрещиваться под любым
углом.
Гипоидные колеса представляют собой
конические вантовые колеса. Передачи
с типоидными колесами применяются
главным образом в автомобилях.
Фиг. 71. Пер«Д1ч>
винтовыми коле-
сами.
ЗУБЧАТЫЕ МЕХАНИЗМЫ
497
Червячная передача (фиг. 72, а) со-
стоит из цилиндрического винта (чер-
вяка) и сопряженного с ним зубчатого
(червячного) колеса. Ось червяка пер-
пендикулярна оси колеса. Профиль резь-
бы архимедова червяка соответствует
профилю стандартной рейки, шаг резьбы
где т — модуль, z4 — число заходов.
Зубья червячного колеса имеют слож-
ную форму — нарезаются червячной фре-
вой, получающей относительно заго-
товки такое же движение, какое должен
Фиг. 72. Черничные перехачи.
иметь червяк относительно червячного
колеса. В передаче касание зубьев про-
исходит полинни; скольжение трущихся
поверхностей — значительное- Передача
применяется для малых и средних
мощностей прн значительной редукции.
Глобоидная червячная передача
,'фнг. 72, б) имеет червяк, начальная по-
верхность которого выполнена по гло-
боиду. Благодаря большому числу нахо-
дящихся в соприкосновении зубьев и
хорошему их контакту такая передача
прн одинаковых габаритах может пере-
давать значительно большую мощность,
чем обыкновенная червячная передача.
Глобоидная червячная передача находит
применение главным образом в транс-
портных машинах.
Реечные передачи различных типов
получаются нз зубчатых при обращении
одного колеса в рейку (при увеличении
радиуса его начальной окружности до
бесконечности). Передача, в которой ось
шестерни перпендикулярна направле-
нию движения рейки, получается из
передачи между параллельными валами.
Выполняется с прямыми, косыми, иногда
с угловыми зубьями.
32 Той t Зак. 1464
" Передача с расположением оси ше-
стерни под острым углом к направле-
нию движения рейки получается из пе-
редачи винтовыми колесами. При малом
числе зубьев шестерни (I—6) обращается
в пару червяк — зубчатая рейка (фиг. 73).
Фиг. 73. Передача чер-
вяк—зубчата* рейка.
Фиг. 71. Передача
червяк -черничная
рейка.
Такие передачи отличаются повышенной
плавностью хода и могут обеспечить
малое перемещение рейки за один обо-
рот червяка.
Передачи с осью червяка, параллель-
ной к направлению движения рейки, по-
лучаются из червячной передачи. Пара
червяк — червячная рейка (фиг. 74)
является разновидностью винтовой —
с коротким винтом и длинной открытой
ганкой. Такие передачи, как и винтовые,
отличаются хорошей плавностью хода.
Недостаток передачи — трудность раз-
мещения на осн червяка приводной
шестерни достаточно большого диаметра,
так как над шестерней проходит чер-
вячная рейка; иногда (в металлорежу-
щих станках) отказываются от отдельной
Фиг. 75. Непосрехстзениый привод червяк»
в передаче по фиг. 74.
приводной шестерни и нарезают зубья
непосредственно ня червяке, что позво-
ляет несколько увеличить диаметр их
начальной окружности (фиг. 75).
Зубчатые механизмы
с неподвижными осями колес
Механизмы имеют одну степень сво-
боды. Делятся на непереключаемые (на-
пример, редукторы) и переключаемые
(например, коробки передач).
498
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
При анализе зубчатых механизмов
с неподвижными осями принято вклю-
чать в кинематическую цепь только по-
движные звенья (валы) без учета их
связи со стойкой.
Непереключаемые механизмы харак-
теризуются передачей движения всегда
через один и те же звенья.
Различают механизмы с простой от-
крытой, разветвленной и замкнутой
кинематическими цепями.
Механизмы спростой от-
крытой цепью передают движение
от ведущего к ведомому валу через не-
сколько последовательно соединенных
зубчатых передач. Общее передаточное
отношение механизма
I»ij-ij-ij...,
где /1, it, is... — передаточные отноше-
ния отдельных передач. Применяются
для уменьшения числа оборотов в ми-
нуту (редукторы), для передачи враще-
ния между далеко друг от друга и не-
удобно расположенными валами, а также
между валами, установленными на дви-
жущихся друг относительно друга
звеньях (в таких случаях используются
скользящие вдоль вала или уширенные
шестерни).
Механизмы сраэветвлен-
ной цепью передают движение от
ведущего к ведомому валу через не-
сколько параллельных ветвей кинема-
тической цепи. При симметричной кон-
струкции дают уравновешивание уси-
лий, действующих на центральные валы
в месте разветвления и соединения парал-
лельных ветвей.
Недостаток — необходимость прини-
мать меры для равномерного распреде-
ления передаваемой мощности между
отдельными ветвями (за счет точности
изготовления или применения промежу-
точных упругих элементов).
Применение — в компактных редук-
торах средней и большой мощности.
Механизмы с замкнутой
цепью (фиг. 76, а и б) позволяют
иметь большую циркулирующую мощ-
ность при малой мощности приводного
электродвигателя 1, равной потерям
в цепи. Обеспечивают привод вводного
и одновременное нагружение выводного
вала обкатываемой (испытуемой) пере-
дачи 2. Целесообразны для испытания
передач большой мощности со сравни-
тельно высоким к. п.д. Особенно удобны
для одновременной обкатки двух оди-
наковых передач (фиг. 76,6). На фиг. 76,в
для сравнения показана схема обык-
новенной испытательной установки
с приводным электродвигателем 1 боль-
шой мощности и тормозным устрой-
ством 3 в виде генератора
При обкатке передач с жесткой кине-
матической связью в цепи создается
*,-МЛп
М-ЮкИя!
натяг обычно за счет деформации упру-
гих звеньев (закручивания валов). При
обкатке передач,
работающих с
проскальзыванием,
регламентирован-
ная нагрузка мо-
жет быть создана
выбором такого
передаточного от-
ношения цепи, ко-
торое обеспечивает
определенную по-
стоянную величи-
ну проскальзыва-
ния обкатываемой
передачи; этот спо-
Фнг. 76. Схемы мспыте-
тельных установок с
замкнутой и открытой
кинематической цепью.
соб неприменим
при включении в
замкнутую цепь
двух передач, ра-
ботающих с * проскальзыванием.
Рассмотренная схема применяется
в испытательных установках—производ-
ственных и лабораторных — и для
выполнения некоторых технологических
процессов (обкатка зубчатых колес,
предварительная обкатка механизмов).
Переключаемые механизмы характе-
ризуются передачей движения через
различные звенья при разных включе-
ниях. Механизмы особенно часто исполь-
зуются для изменения скорости враще-
ния выводного вала (коробка передач)
или направления его вращения (ревер-
сивные механизмы). Переключения осу-
ществляются разобщением одних ветвей
кинематической цепи и замыканием
других ветвей.
Разобщение кинематических цепей
производится: I) размыканием зубчатых
зацеплений и 2) разобщением в месте
соединения зубчатых колес с валами
или валов между собой.
Размыкание зубчатых зацеплений осу-
ществляется:
а) поступательным перемещением зуб-
чатого колеса вдоль вала; применяется
для цилиндрических прямозубых колес,
иногда для конических колес;
б) винтовым перемещением зубчатого
колеса по валу с винтовыми шлицами;
шаг винтовой линии шлицев должен
ЗУБЧАТЫЕ МЕХАНИЗМЫ
499
быть равен шагу винтовой линии зубьев
колеса, что обеспечивает легкое пере
ключей не без относительного поворота
валов; применяется для цилиндрических
косозубых колес;
в) радиальным (поперечным) первые
щснием зубчатого цилиндрического ко-
леса обычно с прямыми зубьями.
Разобщение в месте соединения зуб
чатых колес с валами или валов между
собой осуществляется:
а) зубчатыми или кулачковыми муф-
тами;
б) фрикционными муфтами;
в) вытяжными шпонками.
Переключение путем размыкания за
цеплений способствует повышению к.п.д.
механизма и уменьшению его износа
за счет устранения работы передач
вхолостую.
Применение фрикционных муфт по-
зволяет производить переключения на
ходу без каких-либо мер предосторож-
ности, в то время как другие способы
переключения требуют предохранения
от поломок зубьев на шестернях и ку-
лачков ня муфтах, для чего приходится
производить переключения только прн
малых скоростях вращения, вводить син-
хронизаторы и т. п.
Зубчатые коробки передач
дают ступенчатое изменение скорости
ведомого вала. В приводе шпинделей
металлорежущих станков целесообразно
принимать ряд скоростей или передаточ-
ных отношений по геометрической
прогрессии:
«1. — «if- «а “ «I?2 - •.. "к — «i?*-1.
Такой ряд обеспечивает одинаковый
относительный перепад скоростей при
переходе от любой скорости к соседней
на всем диапазоне регулирования
Я1
Значения коэффициента (знаменателя)
геометрических рядов нормализованы:
? = 1,12; 1,26; 1,41; 1,58, 1,78; 2,00.
Геометрический ряд передаточных от-
ношений в коробках передач обычно
выдерживается приближенно. Иногда
требуется получение точных передаточ-
ных отношений по арифметическому
или другому ряду. Для этой цели при-
годны только некоторые схемы коробок
передач.
Коробки со сменными ше-
стернями являются .простейшими
типами коробок передач. Они выпол-
с2*
ня юте я с постоянными или с регули-
руемыми межосевымн расстояниями.
Двухваловая коробка с постоянным
межосевым расстоянием для получе-
ния К различных передаточных отно-
шений требует: а) 2К сменных шестерен
при одних замедляющих или одних уско-
ряющих передачах, б) К сменных ше-
стерен при симметричном диапазоне
регулирования (когда для получения
каждой ускоряющей передачи меняются
местами сменные шестерни соответ-
ствующей замедляющей передачи) и от-
сутствии передачи I : 1; в) К + 1 смен
ных шестерен прн симметричном диа-
пазоне регулирования и наличии пере-
дачи 1 : I
Часто число замедляющих передач
К3 превышает число ускоряющих Kv.
тогда для получения К = К3 4- Ку
различных передаточных отноше-
ний требуется 2К3 шестерен (пере-
дача I : 1 включается в число заме-
дляющих).
Практически приемлемый диапазон
регулирования днухваловой коробки до
ходит до 8—12.
Трехваловая коробка с постоянными
межосевыми расстояниями представляет
собой две последовательно включенные
двухваловые передачи Сменные ше-
стерни одной передачи могут быть
использованы также для второй. Диа-
пазон регулирования практически до-
ходит до 50—100
Коробки передач со сменными тестер
нями и регулируемыми межосевыми
расстояниями выполняются с так назы-
ваемой гитарой — поворотной деталью,
в пазах которой в нужном положении
закрепляются одна или две оси с на-
детыми на них втулками, несущими по
две сменные шестерни. Такая конструк-
ция позволяет использовать значительно
большее число различных комбинаций
шестерен и обычно применяется для
подбора точных передаточных отноше-
ний (например, в металлорежущих
станках).
Коробки передач со сколь-
зящими вдоль валов шестер-
ня м и выполняются с числом скоростей
до 36 и более. Диапазон регулирования
не ограничен.
Оценка степени сложности коробок
передач, выполненных по различным
схемам, но с одним и тем же числом
ступеней скорости, может быть произве-
дена путем сопоставления чисел валов
и шестерен.
яю
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
По принципу построения схем разли-
чают два следующих типа коробок пе-
редач:
1. Коробки с передачей движения через
одни и те же валы при включении
любой скорости. Такая схема может
быть условно разделена на ряд после-
довательно соединенных двухваловых
групп. Каждая группа характеризуется
числом передач д, и коэффициентом <р(
гео метр и чес ко го ряда их передаточных
отношений. Пронумеровав группы в по
рядке возрастания if,, получаем для
первой группы Ki и для второй—
А» и = Т*'» для третьей — К3 и if» =
К К
= <р и т. д. Общее число скоростей
коробки К = K^Kt диапазон регу-
„ К- I
пирования Д =
Варианты схем получаются различ
ним разложением К на множители и из-
менением последовательности располо-
жения найденных групп. Обычно группы
располагаются в порядке возрастания
у,. Наибольший приемлемый диапазон
регулирования между двумя валами
Д ' = 8 (при ускоряющей передаче 2 : 1
и замедляющей I : 4).
Различные передачи между двумя ва-
лами могут включаться посредством
одного нлн нескольких зубчатых блоков
Прн наличии нескольких блоков воз-
можность поломки зубьев вследствие
одновременного включения двух передач
(«замок») должна быть устранена кон-
струкцией механизма управления (бло-
кировка при нескольких рукоятках или
♦иг. П. Осевой размер простри исты. неоАхоаимого мя
переключении зубчатых блоков.
согласованное переключение нескольких на одной
•убчатых блоков одной рукояткой).
Двухвенцовые зубчатые блоки допу-
скают управление коробкой передач
с выборочным включением — возможен
непосредственный переход с любой ско-
рости на любую другую без промежу-
точных включений.
Трех- и четырехвенцовые блоки дают
определенную последовательность пере-
хода от одной скорости к другой. По-
следовательное включение скоростей при-
водит к ненужным промежуточным вклю-
чеиням — к потере времени иа пере-
ключения и повышенному износу торцов
зубьев ня шестернях.
Осевой размер пространства, необхо-
димого для переключения двухвенцо-
вого блока (фиг 77, а), обыкновенного
трехвенцового (фиг. 77, б) и трехвен-
цозого для переключения передач в по-
рядке увеличения пли уменьшения пе-
редаточных отношений (фиг 77, в), по-
лучается меньше при перемещении бло-
ков с близко расположенными венцами
(размер Вд и больше при перемещении
блоков с расставленными венцами (раз-
мер Bt), несмотря на одинаковую длину
S полного осевого перемещения зубча-
того блока в том и другом случаях.
2. Коробки, в которых при включе-
нии разных скоростей изменяются число
и последовательность валов, передаю-
щих движение.
При конструировании таких коробок
стремятся:
а) чтобы в передаче движения на
каждой скорости участвовало наимень-
шее число зубчатых зацеплений и валов:
б) чтобы зацепления и валы, не не-
редающие нагрузку, полностью отклю-
чались.
Это приводит к повышению к. п. д.
и уменьшению износа деталей.
Указанные факторы имеют
особое значение:
а) для быстроходных коро-
бок с большим диапазоном ре-
гулирования, когда большое
число передач требуется для
осуществления необходимой
редукции лишь при малых
скоростях выводного вяла,
а сокращение числа передач
при больших скоростях дает
существенное увеличение
к. п. д.;
б) для коробок, условия
эксплуатации которых преду-
сматривают длительную работу
или нескольких основных
скоростях и кратковременную работу
на других, меньших скоростях.
Примером такой коробки может слу-
жить типичная автомобильная коробка
передач (фнг. 78), у которой основная
ЗУБЧАТЫЕ МЕХАНИЗМЫ
501
скорость включается муфтой .напря-
мую*. Коробка передач с включением
.напрямую* должна иметь не менее трех
валов.
Коробки передач с вытяж-
ной шпонкой, накидной ше-
стерней и многократными
ступенями возврата приме-
няются главным образом в коробках
подач металлорежущих станков
Переключаемые передачи с вытяжной
шпонкой н. двумя валами (фиг. 79. а)
для получения К различных передаточ-
ных отношений требуют 2К шестерен.
Такие же передачи с тремя валами
и двумя вытяжными шпонками без по-
вторяющихся передаточных отношений
требуют меньшего числа шестерен, рав-
ного ЗУ~К. Перемещение шпонки вы-
ключает предыдущую пару шестерен
и подготовляет включение новой, ко-
торое осуществляется при вращении
ведущего вала зяскакнняннеч шпонки под
действием пружины в паз шестерни.
Переключаемые передачи с зубчатым
конусом и накидной шестерней (фиг. 79. б)
требуют K-f-2 шестерен для получения
Фиг. 79. Схемы переключаемых передач с вытяж-
ными 1ШЮИК1МИ, MBKMJUIMMH ШССТСрНКМИ И Ы1ЙОГО
KpaiMMMM степенями возврата.
502
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
К различных передаточных отношений.
Переключение передач производится
выборочно путем отвода накидной ше-
стерни в поперечном направлении, пе-
ремещения ее вместе с рычагом в осе-
вом направлении и ввода в зацепление
с новой шестерней зубчатого конуса
поперечным перемещением. Эти опера-
ции выполняются одной рукояткой, за-
крепленной на поворачивающемся и пе-
ремещающемся вдоль вала рычаге или
двумя органами управления, один нз
которых выполняет поворот, а другой —
осевое перемещение рычага (применяет-
ся в коробках закрытой конструкции).
Переключаемые передачи с многократ-
ными ступенями возврата (.меандр') и
скользящей по валу шестерней (фиг. 79.в)
требуют не менее 4К — 2 шестерен для
получения К различных передаточных
отношений.
Переключение передач происходит в
определенной последовательности. Пе-
редачи выполняются для большого у
(см. стр. 499), обычно равного 2.
Передачи с многократными ступе-
нями возврата и накидной шестерней
(фиг. 79, е) требуют не менее 2К шесте-
рен для получения К передаточных от-
ношений.
Во всех многоваловых коробках ско-
ростей число шестерен увеличивается
при наличии повторяющихся переда-
точных отношений и уменьшается при
использовании одних и тех же шесте-
рен для переключаемых передач между
разными валами.
Простые реверсивные меха-
низмы служат для изменения напра-
вления вращения ведомого вала прн не-
изменном направлении вращения веду-
щего. На практике применяются главным
образом механизмы с цилиндрическими
прямозубыми (фиг. 80, а — д) или кони-
ческими (фиг. 80, е—з) зубчатыми
колесами, с переключением посредством
перемещения шестерен вдоль вала (фнг
80, б, в, г, е) или при помощи муфт
(фнг. 80, д, ж, з).
Реверсивные механизмы с цилиндри-
ческими колесами должны иметь не
менее трех валов, а при одном включе-
нии «напрямую* — не менее четырех
валов; механизмы с коническими коле-
сами должны иметь соответственно не
менее двух или трех валов.
Помимо своего прямого назначения
рассматриваемые механизмы часто осу-
ществляют также изменение величины
передаточного отношения при ревер-
сировании (фиг. 80, в, г, д, з). характе-
ризуемое частным от деления переда-
точного отношения ia прямой передачи
на передаточное отношение обратной
передачи.
Фнг. 80. Типи зубчатых
реверсивных механизмов.
Реверсивные механизмы реже выпол-
няются в виде самостоятельных меха-
низмов, чаще встраиваются в коробки
передач (см. фиг. 78).
Зубчатые механизмы с подвижными
осями колес (дифференциальные
и планетарные)
Зубчатый механизм с подвижными
геометрическими осями колес по про-
стейшей схеме (фиг. 81) состоит нз
ЗУБЧАТЫЕ МЕХАНИЗМЫ
гл
степени свободы:
♦иг. Я|. Схема зиф-
фереишылыюго зуб-
ка того механизма.
следующих звеньев.поводка или водила 4.
планетных колес или сателлитов 2,
центральных или солнечных колес / и 3,
стойки 5. Поводком называется вращаю-
щееся звено, несущее оси сателлитов,
которые находятся в зацеплении с цен-
тральными колесами. Различают диффе-
ренциальные и планетарные зубчатые
механизмы.
Дифференциальным называется меха-
низм с несколькими степенями свободы.
Например, механизм пофиг. 81 имеет две
принудительное дви-
жение одного из
звеньев /, 3 и 4 по-
лучается прн опре-
деленном движении
двух других.
Планетарным на-
зычается механизм с
подвижными осями
колес и одной сте-
пенью свободы. Пта-
нетарный механизм
получается из дифференциального в ре-
аультате наложения дополнительных
условий связи — закреплением одного
из центральных колес или соединенней
передачами центральных колес и по-
водков (замкнутая планетарная пере-
дача). Например, механизм по фиг. 81
может быть обращен в планетарный
закреплением звена 1 или 3, а также
соединением передачей звеньев 1 и 3,
1 и 4 или 3 и 4.
Если закрепление звена производить
управляемым тормозом, то механизм
может заменить муфту включения. Если
в планетарный механизм включить пере-
дачу с бесступеичато изменяемым в не-
больших пределах передаточным отно-
шением, то можно получить планетар-
ный вариатор с кинематически неогра-
ниченным диапазоном регулирования.
Все механизмы удобно подразделить
для рассмотрения на неуправляемые и
управляемые.
Неуправляемые механизмы характе-
ризуются неизменными структурой и
кинематической характеристикой. К ним
относятся зубчатые дифференциалы н
планетарные редукторы.
Дифференциальные меха-
низмы практически используются
для следующих целей:
а) сложения нескольких движений
в одно — применяется в металлорежу-
щих станках для получения независимых
кинематических настроек иа различные
•лементы изделий (например, на число
зубьев и на угол наклона зубьев наре-
заемой косозубой шестерни), в универ-
сальных делительных устройствах для
облегчения настройки на заданное число
делений, в счетнэ-решающнх механиз-
мах для суммирования параметров;
б) разложения одного движения на
слагаемые — применяется в приводе ве-
дущих колес автомобиля для устранения
проскальзывания их относительно до-
роги вследствие различной длины пути,
проходимой правым и левым колесами
на поворотах* и неровностях дороги, а
также вследствие некоторой разницы
в диаметрах колес.
Для дифференциального механизма
с одним поводком соотношения между
угловыми скоростями звеньев выража-
ются формулой
или
где «и —угловая скорость первого цен-
трального колеса /; — угловая ско-
рость поводка; — угловая скорость
второго центрального колеса к; —
передаточное отношение между звень-
ями / и к при неподвижном поводке:
. zc
Угловые скорости следует подставлять
в формулы с учетом знака (направ-
ления вращения); ilx имеет знак плюс,
если направления вращения звеньев /
и к одинаковы при остановленном
поводке, знак минус — если направле-
ния их вращения различны. Формула
остается справедливой, если вместо «j
и •>* подставить угловые скорости лю-
бых промежуточных зубчатых колес,
взяв соответствующее illt.
Распространенные типы дифференци-
альных механизмов приведены в табл. 10.
Благодаря своей компактности наиболь-
шее применение имеет механизм по
схеме 3.
В обычных случаях применения диф-
ференциальных механизмов (см. выше)
их к. п. д. не имеет большого значения.
Простые планетарные ре-
дукторы делятся на две группы
в зависимости от знака передаточного
604
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
Таблица 10
Твои зубчатых дифференциальных
механизме*
отношения /| между центральными ко-
лесами при остановленном поводке.
Редукторы с отрицательным iilc (схе-
мы I и 2 табл. 11) пригодны для не-
большого снижения угловой скорости
(до 1 : 10), имеют высокий к. п. д.;
применяются в качестве многосателлит-
ных компактных редукторов средней и
большой мощности, например, в авиа-
ционных двигателях. При подборе чисел
зубьев шестерен учитывают возмож-
ность и удобство сборки; должны быть
соблюдены условия
пир
к
21 -I- Zg
-ь z-z4
z3K
-G;
в
желательно также выдержать
Здесь К — число сателлитов; Ci и С»—
целые числа; г1( гг, Zg, г4 — числа
зубьев шестерен в редукторе по схеме 1
табл. II.
Редукторы по схеме 2 (редукторы
Джемса) имеют большее распростране-
ние, чем по схеме I.
Редукторы с положительным 1[я
(схемы 3 и 4 табл. II) пригодны для
значительного уменьшения угловой ско-
рости (передаточное отношение до
1 : 10 000); вследствие низкого к. п. д.
применяются для передачи малых мощ-
ностей, например в приборах.
Кинематические возможности редукто-
ров по схеме 3 приведены в табл. 12.
Несколько ббльшую унификацию ше-
стерен в редукторах с некорригирован-
ными зубьями одного модуля можно по-
лучить при Zj = г8 и г2 — г4; тогда
(Zi + Z?) (Z| - z2)
и при нечетном числе (zi + г2), обозна-
чаемом далее через 2z^
, 2га 2
<ш,п= (Хв + 0Л)« C3z0+l ’
Zi — z0 — 0.5 и Zj = z0 + ОД
В редукторах с нскорригнрованнымн
зубьями разного модули при нечетных
числах
2zo и 2z„ = 2 — Zo (см. табл. 12):
. __________\ тг /________________
°"п “ 9 т, 1 ( тх .» ’
если
zj — ze — 0.5;
z2 — ze + 0.5; z3 — г0 + 0,5
mt
и
/Я1 ле
Z< - —L Zo - 0.5.
”•2
Подбор нужных 2z0 и 2^' производится
следующим образом: отношение модулей
записывается в виде простой дроби
с числителем Ci и знаменателем С» —
целыми числами, не содержащими общих
множителей; принимая различные зна-
чения множителя С, подбирают иужныа
значения 2z^ = С>С н 2zu = С2С:
2Zq С| С)С
2-и п:2 С2 С2(-
Простые пяанетариые реятжторм
Гоблнчн П
Назначение
характеристика
Схемы
Формулы перелаточных
отвошемиА
Формулы ала к. п. л. релуггора
с закрепленным веемом < *
Але небольшой релук-
пине высоким ж. л. л.
(не ниже ж. п. л.
обыкновенной зубча-
той передачи, как
правило, ч >
Обычно прнменаетса
несколько сателлитов
Закреплен поволок
сх. *>2в~г?
•• *»*•
Сх.2)^---Ь
•• •»
За креп лево мело 4
<x,)^“‘+ss
Сх. J) Л-1 + -Ь-
•я X»
Закреплено звено I
« + (т$
где Qa — петгобежяая сила сателлита;
О — окружное усилие и а оси сателлита.
Дла тнхоходлых редукторов
Але большой рехук-
цин эначеине к. л. л.
низкое (может ока
мтыга меньше *(•).
Обычно стаеитса охни
сателлит
Закреплен поволок
а.м
", Й.Ч
Закреплено звено 4
Закреплено звено I
Сх, 2) 4 е»
р ллв опор центральных колес и сателлитов
приматы олимлковы ми
ЗУБЧАТЫЕ МЕХАНИЗМЫ
* По способу проф. Л. Н. Решетова.
в к в •S + 'i
Примечаний: I. Величина смешение окружного усилив *иу ла/, точнее Д — — ш/ при а.ыц и Д — — mf------ при ч > или < ч
элесь m — ыолуль заоеплеииа f — ковффиииеит трение п зубьал: а, — коеффипиент перекрытие за полюсом запеплеииа; ч—то же. во перед полю-
сом; — а, + ч — полный козффиписит перекрытие.
X Ралиус крута трение р — fnp'w Tit 'пр ~ лРнм*еппый коэффициент трении; гц — радиус цапфы.
3. г„ г,. г, — радиусы начальных окружностей шестерен.
S06
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
Таблица 11
Передаточимн отношения простого планетарного редуктора с внешним зацеплением
при четном 2х.
• Передаточное отношение /_ Щ — 1 _ th п, хи.
Схема Исполнение Формула для наименьшего значения Нхниеньшаа неличиы прн Z.
30 <ю 100
1 Модули одинаковые т, м /л, X, + Z, = I, + 3. - 2г„ . _ 2 ш|п мч при z, - г, — х,; х, = хь - 1; Z. - /„ +1 1 15,5 1 30,5 1 юТЗ
Модули различные П»! > Д1в Zi 4" в *. + х.-2^Х. 7 их, " 2 — z0 должно быть це- лым четным числом j '.7 „6 8If - - - сч 1 )* 1 1 1
_гЛ*л’’ 2 а» при х. — х„ - Я>< , “ •• Э|Э Г * 1 >’ » 1 SI3 - а|?г <-^4. =- + । 1 ~ •ж 9U.42 при - 1.2 180,46 при ^i-1,2 m, 300.475 при ^1-1.2 '‘l
1 Модули одинаковые» зубы корригированные т, = т, х, + z« * г, -Ь х. 'mln при г, = х. = х»; х, •= х0 — 1; х» = хи + 1 1 Зид 1 3600 1 10UUO
Для получения четного 2г„ один или
оба множителя Cj и С должны быть
четными, для получения нечетного 2z0
оба множителя Ci и С — нечетные.
Те же правила относятся к 2г0.
В редукторах с корригированными
эубьямн для упрощения конструкции
иногда объединяют оба сателлита в одну
шестерню (принимают г2 = Zg). Тогда
«4 - «1 ± 1 И i - ±~-
*4
Кинематические возможности редукто-
ров с внутренним зацеплением по схеме 4
(табл. 11) удобно оценивать по формуле
t _ л, _ Azi--az4| __
Пп Z* — *1 (Azn — Az41)
______Azig-Azji_____
“ (z4 - (z4 - Az«J ’
где
Azu — Zj — «г -• z< — Zj;
Az4) — Z4 — Zj — Zg — Zj.
Закреплено колесо с числом зубьев г».
Для получения возможно малых I же-
лательно Az)t и Az4I иметь наимень-
шими. На выбор Дг4) никаких кон-
структивных ограничений не налагается,
оно может быть взято равным I. Вели-
чина Дг12 прн неисправленных эволь-
вентных зубьях не может быть взята
сколь угодно малой вследствие интер-
ференции зубьев, т. е. внедрения зубьев
одного колеса в зубья другого; в цевоч-
ных зацеплениях и корригированных
эвольвентных Дг|г может быть взято
сколь угодно малым.
Разработанный советскими учеными
способ корригирования внутреннего
эвольвентного зацепления для получе-
ния малой разницы в числах зубьев
сцепляющихся колес |25] позволил по-
лучить передачу с Azlg = 1, более про-
ЗУБЧАТЫЕ МЕХАНИЗМЫ
507
етую в изготовлении, чем цевочная пере-
дача.
Редукторы по схеме 4 (табл, II) при-
годны для значительного уменьшения
угловой скорости. Например, при zi =
— 60, г4 = 61, Дг41 = I и Дг1г = 6
(зубья некорригированные) получаем
i = I : Б50. а при &га= I (зубья кор-
ригированные) 1=1: 3600.
Частным ви-
дом планетар-
ного редуктора
с внутренним
зацеплением
является его ис-
полнение с од-
ной парой зуб-
чатых колес.
механизмах, в текстильных машинах
и т. п.
Если в схеме 4 табл. 11 с неподвиж-
ным солнечным колесом 4 принять Zi — zt
и заменить эту пару колес муфтой,
допускающей относительное круговое
поступательное движение связываемых
звеньев, то получится редуктор по рас-
пространенной схеме (фиг. 82, б). Муфта
имеет пальцы, входящие в отверстия
сопряженного звена, диаметр которых
превышает диаметр пальцев на двойную
величину эксцентриситета ведущего
поводка.
Передаточное отношение редуктора
/ _ ЛХ = — *' ~ g;
2g
Если бы в механизме по схеме 4
табл. 11 с неподвижным солнечным
колесом 4 принять гя = г4, чтб при
обыкновенном зацеплении практически
невыполнимо, то угловая скорость сател-
лита будет равна нулю, и колеса 3 и 4
можно заменить механизмом плавающей
муфты, связав нм звено 2 со стойкой
и обеспечив таким образом круговое
поступательное движение сателлита 2.
Полученный редуктор (фиг. 82, а) со-
стоит из центрального ведомого колеса /,
сателлита 2, ведущего эксиснтрика-по-
водка 3 и промежуточного звена 4 меха-
низма плавающей муфты, которое со-
вершает прямолинейное возвратно-по-
ступательное движение.
Передаточное отношение редуктора
/—Л — ~zi .
“л *1 *
например, при Zj = 60 и Zt = 54 полу-
чаем /=1:10, при Г| = 60 и Zj= 59
получаем / = I : 60. Редукторы по такой
схеме применяются в грузоподъемных
Замкнутые планетарные
редукторы получаются из диффе-
ренциального механизма обычно путем
соединения центральных колес постоян-
ной передачей. Редукторы дают возмож-
ность получать чрезвычайно сильное
уменьшение скорости, но при очень
низком к. п. д. Центральные колеса
получают вращения с близкими по вели-
чине угловыми скоростями, на поводок
дифференциала передается их разность.
Примерами таких редукторов слу-
жат:
а) редуктор с центральными колесами,
связанными шестеренной и двумя чер-
вячными передачами (фнг. 83, а), для
которого при zi = zs = 1
Мд _ — z'lZ'' 1 ,
2Z(242s 2-10» *
б) редуктор Гуляева (фиг. 83, б), для
которого
«“а _ 2гДя - x.zg 1 .
И] ^-^-5 ’
5СЯ
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
в) редуктор Гоммеля (фиг. 83, в), для
которого
ма __ — ZiZt2g^t 1
*“1 “2^8 (V8 + ~8*т) 10®
Сложные планетарные ре-
дукторы образуются посредством
объединения нескольких простых редук-
торов в один механизм. Цель — полу-
чение достаточно большой редукции
(до 1 : 300) при высоком к. п. д. Иногда
удается получить некоторое упрощение
механизма Путем использования зубча-
тых колес одной передачи в качестве
колес следующей.
♦иг. (И. Сложные пл«»етарные редукторы.
Примеры сложных планетарных ре-
дукторов. применяемых в электроталях.
приведены на фиг. 84.
Для редуктора по фиг. 84, а:
“1 ”
_________________г'г<г1_________
(Z|Zt+XJZ4+Z»Zt) Зио’
Для редуктора по фиг. 84,6:
*7 1
“I liVe + <-» + *!> -^|J ’
Управляемые механизмы служат:
а) для включения и переключения кине-
матических цепей — планетарные меха-
низмы включения; б) для изменения
знака передаточного отношения — ре-
версивные механизмы; в) для ступен-
чатого изменения величины передаточ-
ного отношения — планетарные коробки
передач; г) для бесступенчатого измене-
ния величины передаточного отношения
в больших пределах — планетарные ва
рнаторы.
Практически применяемые механизмы
часто выполняют не одну, а несколько
указанных функций.
Управление механизмами осуще-
ствляется: а) включением и выключе-
нием привода отдельных звеньев —
обычно индивидуальных электродвигате-
лей; б) торможением и освобождением
отдельных звеньев механизма; в) со-
единением и разъединением некото-
рых звеньев муфтами включения —
обычно фрикционными; г) изменением
передаточного отношения между неко-
торыми звеньями — обычно фрикци-
онными бесступенчатыми переда-
чами.
Планетарные механизмы
включения служат для соединения
и разобщения кинематической цепи по-
средством тормоза. Механизм получается
из дифференциала путем присоединения
двух звеньев к валам и одного — к тор-
мозу. При освобожденном тормозе ме-
ханизм имеет две степени свободы, и
передача движения от одного вала
к другому не происходит. При включен-
ном тормозе механизм имеет одну сте-
пень свободы — движение от одного вала
к другому передается. В этом случае
механизм работает как планетарный
(если тормоз действует на центральное
зубчатое колесо) или как передача
с неподвижными осями (если тормо-
зится поводок).
В зависимости от схемы механизма
и его кинематической характеристики:
а) передача вращения может происхо-
дить с изменением или без изменения
направления и величины угловой ско-
рости, б) тормозной момент может быть
меньше передаваемого, что облегчает
управление и сокращает размеры тор-
моза. Например, для часто применяемого
механизма по схеме 2 табл. 11 с воздей-
ствием тормоза на звено 1 тормозной
момент М\ < ЛЦ.
Применение планетарных механизмов
включения вместо простых фрикцион-
ных муфт может оказаться целесообраз-
ным там, где желательно одновременно
получить уменьшение (увеличение) угло-
вой скорости или изменение направле-
ния вращения, а также при наличии
особо высоких требований к надеж-
ности и легкости управления.
Дифференциальные меха-
низмы быстрых перемеще-
ний используются в рабочих машинах
(например, в станках) для выполнения
вспомогательных движений частей ма-
шины, имеющих сравнительно медлен-
ные рабочие движения — подачу, с по-
вышенной скоростью.
ЗУБЧАТЫЕ МЕХАНИЗМЫ
509
♦иг 85. Схемы лиф.
ференциальиых мех»,
иэмов быстрых пере-
мещений.
В механизме используется дифферен-
циал, одно из звеньев которого присо-
единяется к кинематической цепи пере-
мещения соответствующей части ма-
шины, другое приводится от цепи рабо-
чего движения, третье — от привода
быстрых перемещений.
Привод быстрых перемещений, как
правило, состоит из отдельного электро-
двигателя, соединенного с соответствую-
щим звеном диф-
ференциала: 1) по-
средством само-
тормозящейся чер-
вячной передачи—
фиг. 85, а; 2) непо-
средственно или
через несамотор-
мозящуюся пере-
дачу — фиг. 85,6.
В первом случае
быстрое вращение
вала 1 может быть
получено от элек-
тродвигателя 3 не-
зависимо от цепи
привода рабо-
чего движения
(фиг. 85, а). Во
втором случае в
цепь привода вво-
дится одно из следующих устройств:
а) муфта обгона, допускающая передачу
движения только от вала электродвига-
теля к дифференциалу; б) тормоз, автома-
тически включающийся при выключе-
нии тока электродвигателя; в) тормоз,
управляемый самостоятельно (фиг. 85,6).
Л1уфта обгона и тормоз, включаю-
щийся при выключении тока, дают
возможность включать быстрое пере-
мещение электродвигателем независимо
от цепи привода рабочих движений и
изменять направление быстрого переме-
щения за счет реверсирования электро-
двигателя. Тормоз, управляемый само-
стоятельно, кроме того, дает возмож-
ность разобщать цепь привода рабочих
движений: передача рабочего движения
от вала 2 к валу 1 прекращается при
выключении электродвигателя 3 и осво-
бождении тормоза 4 (фиг. 85, 6).
Удобство дифференциальных механиз-
мов быстрых перемещений заключается
в легкости и простоте управления.
Планетарные реверсивные
механизмы служат для изменения
направления вращения выводного вала
при постоянном направлении вращения
вводного. Реверсирование обычно со-
провождастся изменением передаточ-
ного отношения.
Переключения осуществляются фрик-
ционными муфтами и тормозами. Кон-
струкция тормоза может быть выполнена
проще, чем фрикционной муфты, так
как позволяет переключающие дви-
жения сосредоточить на иевращ-'ю-
щнхея деталях; подвод тока в электро-
магнитный тормоз не требует контакт-
ных колец.
Схемы с одним простым планетарным
механизмом не дают возможности обой-
тись без фрикционных муфт.
Пример конструкции механизма, вы-
полненного в виде реверсивного шкива,
управляемого муфтами с разжимными
кольцами, приведен на фнг. 86.
Реверсивные механизмы с переклю-
чением муфты и тормоза строятся на
базе различных дифференциалов. Пре-
имущественное применение имеет меха
Фиг. 86. Пример конструкции планетарного
реверси иного шкииа.
ниэм по схеме 2 табл. 11, у которого
тормоз действует па поводок, а фрик-
ционная муфта может соединять любые
два звена. При включении тормоза такой
механизм работает как простая передача
с неподвижными осями; момент тормо
жения
Мт - М, + Mt.
где М\ и Л)4 — крутящие моменты со-
ответственно на вводном и на вывод-
ном валах. При выключении тор-
моза и включении муфты получаем
вращение выходного вала в дру-
гую сторону, относительное движение
510
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
звеньев /, 4 и подводка отсутствует;
момент на муфте при ее установке
между поводком и ведущим звеном 7
Мм = М!-'+^-,
* гг ’
между поводком и ведомым звеном 4
г1
между звеньями 1 и 4
Мя = Ж,.
Прн выключении тормоза и муфты дви-
жение от вводного вала к выводному
не передается.
Реверсивные механизмы с переклю-
чением посредством двух тормозов, (без
муфт) наиболее удобны в управлении.
Однако это удобство достигается за счет
аначительного усложнения системы пе-
Фиг. 87. Пример конструкции планетарного рекер-
си иного механизма. ynpaiMueuoro посредстиом
хпух электромагнитных тормозов.
редающих зубчатых колес. Поэтому та-
кие механизмы применяются ня практике
редко. Пример конструктивного выпол-
нения механизма, управляемого двумя
электромагнитными тормозами, показан
на фиг. 87.
Планетарные коробки пе-
р е д а ч служат для ступенчатого изме-
нения передаточного отношения Пере-
ключения производятся тормозами и
фрикционными муфтами. Различают две-
основные схемы механизма.
I Схема пмстпго планетарного ме-
ханизма, имеющего более двух цен-
по-
оси
соответствующее
Фнг. 88. Схема четырех-
скоростной плаветарно»
коробки передач.
тральных колес
число сателли-
тов, закреп-
ленных на
движной
(фиг 88). Два
из центральных
звеньев (цен-
тральные коле-
са и поводок)
соединяются с
вводным и вы-
водным валами.
Торможением
каждого из ос-
тавшихся цен-
тральных звень-
ев устанавли-
вается соответствующее передаточное
отношение. Кроме того, добавлением
одной фрикционной муфты может
быть дополнительно получена передача
«напрямую*. Таким образом.общее число
ступеней будет равно числу централь-
ных колес, число переключающих тор-
мозов и муфт — числу передаточных
отношений. По такой схеме выполня-
ются коробки передач на малую мощ-
ность и небольшое число ступеней. На
фиг 88 приведен пример четырехско-
ростной коробки передач, различные пе-
редаточные отношения которой вклю-
чаются тормозами /, //, Р и муфтой III.
2. Схема с последовательным соеди-
нением простых планетарных механиз-
мов, каждый из которых дает два раз-
личных передаточных отношения путем
переключения фрикционной муфты и тор-
моза, приведена нафиг.89. Коробка пере-
ЗУБЧАТЫЕ МЕХАНИЗМЫ
.'11
дач, построенная по этой схеме, обеспе-
чивает большие кинематические возмож-
ности: общее число различных переда-
точных отношений коробки равно двум
в степени, равной числу последовательно
соединенных простых планетарных меха-
низмов. Например, коробка передач по
фиг. 89 дает реверсирование включением
муфты В или тормоза Н, а также восемь
различных передаточных отношений
включением тормозов и муфт 1—3—5,
1—3—6, 1—4—5, 1—4—6, 2—3—5,
2—3—6, 2—4—5 и 2—4—6.
Планетарные вариаторы
служат для изменения угловой скорости
(часто и направления вращения) вывод-
ного вала при постоянной угловой ско-
рости вводного вала.
Применение планетарной схемы дает
возможность кинематически неограни-
ченного расширения диапазона регули-
рования входящей в вариатор бессту-
пенчатой передачи.
Существенным недостатком планетар-
ных вариаторов является их низкий
к. п. д. при малых угловых скоростях
выводного вала.
Различают вариаторы по простой и
по замкнутой планетарной схеме (под-
робнее см. главу X «Фрикционные пе-
редачи и вариаторы» в т. 4).
ные цилиндры, что достигается соответ-
ствующим профилированием зубьев.
Передачи с циклически изменяющимся
межцентровым расстоянием дают воз
можность не только плавного изме-
нения величины передаточного отноше-
ния, но и его знака.
Практический интерес представляют
частные виды таких передач, входящие
в механизмы для преобразования враща-
тельного движения в прямолинейное
Фнг. 90. Типы лерехач яскруглыми
зубчатыми колесами.
Зубчатые пары с переменным
передаточным отношением
Передачи с циклически изменяющимся
передаточным отношением выполняются
ва редким исключением между парал-
лельными осями.
Различают передачи с постоянным и
с изменяющимся межцентровым расстоя-
нием.
Передачи с постоянным межцентро-
вым расстоянием бывают: 1) с некруг-
лыми колесами эллиптической или дру-
гой криволинейной формы; передаточ
ное отношение изменяется плавно; сред
яяя его величина за цикл должна выра-
жаться простой дробью 1:1, 1:2, 1:3;
примеры схем см. на фиг. 90, а—д;
передачи сложны в изготовлении и по-
этому имеют ограниченное применение
на практике; 2) с колесами, состоящими
из нескольких концентрических круго-
вых зубчатых секторов (фнг. 90, а), ха-
рактеризуются скачкообразным измене-
нием передаточного отношения; при-
годны только для малых скоростей;
3) с круглыми по форме зубчатыми ко-
лесами, имеющими некруглые началь-
возвратно-поступательное (фиг. 91, о
и б) или в качательное (фиг. 91, в иг)
с жесткой кинематической связью ме
жду ведущей шестерней I и ведомым
звеном 2. Шестерня 1 помещается на
ползуне 3 и приводится во вращение
через вертикальный шлицевый валик и
коническую зубчатую передачу или дру-
гим способом. Вспомогательный пол-
зун 3 получает движение от аамкнутой
канавки на звене 2, в которую входит
ролик, сидящий на конце вала ше-
стерни 1.
Зубчатый элемент звена 2 может быть
составлен из отдельных реек и зубча-
тых секторов, что облегчает его изго-
товление.
1. Механизмы посхемамаиб (фиг. 91)
прн равномерном вращении ведущей
шестерни обеспечивают: а) движение
ведомого ползуна в обоих направлениях
с постоянными и равными по величине
скоростями на среднем участке длины
хода; б) реверсирование ползуна на
сравнительно коротких участках пути
с изменением скорости по закону гармо-
нических колебаний.
512
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
Фнг. 91. Схемы зубчатых механйэмов для преобразования равномерного вращательного
движений в прямолинейное возвратно-поступательное или качагельное движение.
Время одного двойного хода ползуна
т-£(А,,)^
где ш, X, — угловая скорость и число зубьев
везушеА шестерня; х, — полное число зубьев на
везомом звене. Знак плюс относится к механизму
е наружным зацеплением (схема б), знак минус —
я механизму с внутренним зацеплением (схема а).
Для участка равномерного движения:
длина хода ведомого ползуча 2
л«= клад';
время движения
скорость ползуна
см.
г <н — модуль запеплеиия.
Для участка реверсирования (обозначения
иа фиг. 92):
длина участка ревер-
сирования ползуна 2
(см. фиг. 91)
реверсирояа-
длина хода ползуна J
а, — 2г;
время реверсирова-
ния
„ гкг
координата положе-
ния ползуна 2
участке
скорость ползуна 2
*в — *м.г СОЗ » — Аае, Ул» — Л* ;
ускорение ползуча 2
п, — — *‘ui!r aln г — —
для ползуна 3
у — —г cos у;
О, — k*>,r sin ? = А«о,л;
о, “ А*ш j г со» р = АЧ» J /А— ж*.
В приведенных формулах г = т ( г* ± г'
с—А •,/, где t — время, отсчитываемое с момента
начала реверсирования; А •» ——Знак паях
* ± 2^
берется при наружном зацеплении, знак минус —
при внутреннем. Положительными считаются ли-
нейные перемещения, скиросги и ускорения, напра-
вленные горизонтально вправо и вертикально
вверх, а угловые скорости — с направлением по
движению часовой стрелки.
2. Механизмы по схемам вне (фнг. 91)
дают постоянные, но не одинаковые при
прямом н при обратном ходе передаточные
отношения на среднем участке (а) угла
качания и реверсирование ведомого
звена на сравнительно небольших
участках угла качания с плавным изме-
нением скорости.
Зависимость между углом равномерного пово
рота ведомого звена, числами зубьев и радиусами
начальных окружностей секторов выражается фор-
мулами (см. фиг. 91, » и г)
• в . - 180* .
г2 —тх2 : '3 — ,, «»2 .
где Xj и г2 — число зубьев и радиус качельной
окружности малого центрального сектора; г? и
г2 — то же, ио большого центрального секторе.
9 9
»2 и г2 — то же. но смешенного реверсирующего
сектора с углом 1Ю*.
КУЛАЧКОВЫЕ МЕХАНИЗМЫ
513
Время охного двойного кхчания ведомого лоенд
определяется по приведеиио» выше формуле для
ремепн двойного хода мекднидмов по сяемям
о и б.
Для участил быстрого равномерного поворота:
время поворота
Г' - — • — ;
•. А
угловая скорость ведомого двеиа 2
Для участка медленного равномерного поворота:
В формулах верхние знаки относятся к меха-
низму по схеме а. а нижние — к механизму по
. схеме г; в подставляет-
' ся в радианах.
/ Для участка ревер-
сировання (обозначения
----г ем. на фиг. 93):
, ' I угол реверсирова-
/ / \ ння ведомого эвена
arcsin-g-;
длина хода ползуна J
S.-V;
время реверенром-
2«г .
координаты положе-
ний твепьев
пгоростн звеньев:
Р С 05 Я —
Фиг. 93. Работа меха-
низма по фиг. у|, я на
участке реверсирования.
г sin V
соя,
= ireslnj2^i;
Значения г, у и * — те же, что и для механи».
ыов по схемам а и б.
ускорения звеньев:
C"w*/?r sin е
Конструкция механизмов по схемам
б на может быть упрошена применением
цевочного зацепления. Тогда зубчатый
элемент поступательно-движущегося илн
качающегося эвена выполняется в виде
одного ряда цевок, а ведущая шестерня—
с соответствующим профилем зубьев
(см. фиг. 68).
Если требуется получить одинаковые
скорости равномерного движения прн
33 том । Зак. 1«и
качании в обе стороны, то механизм
строят на базе конического зацепления.
Такой механизм применяется, например,
в станке для нарезания угловых и ше-
вронных зубьев.
Зубчатые передачи с неполнозубыми
колесами
Такие передачи дают возможность по-
лучать периодическое вращение (фиг. 94,
а и б), а также канательное (фиг. 94. в)
Фиг. 91. Примеры зубчатых передач с неполно-
зубыми колесами.
и прямолинейное возвратно-поступатель-
ное (фнг 94, г) движение ведомого
знена 2 прн непрерывном вращении ве-
дущего эвена 1.
Зубчатые колеса во время работы
расцепляются и снова входят в зацепле-
ние. Чтобы не произошло поломки
зубьев, необходимо обеспечить опреде-
ленное относительное положение веду-
щего и ведомого звеньев в начале за-
цепления. В механизме по фиг. 94, а
предусмотрено запирающее устройство
в виде цилиндрической поверхности на
ведущем колесе / и дуговых лысок
на ведомом колесе 2. В механизме по
фиг. 94, б на ведущем звене / преду-
смотрен свободно поворачивающийся
сектор; после того как ведомое колесо 2
вступит в зацепление с подвижным сек-
тором, движение ведомому валу не будет
передаваться, пока ведущее звено не
повернется на угол а и не начнет толкать
сектор.
Рассматриваемые передачи работают
с толчками и не пригодны для больших
скоростей.
КУЛАЧКОВЫЕ МЕХАНИЗМЫ
Общие сведения
Назначение. Кулачковые механизмы
характеризуются наличием одной или
нескольких высших кинематических пар
кулачкового типа; остальные пары обыч-
но выполняются вращательными и посту-
SH
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
петельными, иногда в виде зубчатых
ваиспленнй и др.
Кулачковые механизмы дают возмож-
ность воспроизводить движение ведо-
мых звеньев, вообще говоря, по любым
веданным законам. Это свойство меха
инзмов, а также сравнительная простота
синтеза (профилирования кулачков) обес-
печили широкое их использование в
различных отраслях машиностроения.
Наибольшее распространение получили
Фиг. 95. Схемы гулачковнх механизмов ui по-
лучения аинжеииа точки ,М по малиной криво*
с веоДусловлеииой или обусломеииой скоростью.
плоские трехзвенные механизмы с одной
парой кулачкового типа, а из простран-
ственных кулачковых механизмов —
трехзвенные с барабанными или торце-
выми кулачками.
Структура. Необходимое а механизме
число пар кулачкового типа равно числу
функциональных зависимостей между
параметрами движения звеньев. Так,
если требуется воспроизвести движение
точки по определенной плоской кривой,
то задание в прямоугольной системе ко-
ординат выражается одной функциональ-
ной зависимостью у = f (*); для получе-
ния нужного движения достаточно иметь
механизм с одной высшей парой кулач-
кового типа (фиг. 95, а и б), обеспечи-
вающей движение точки М по заданной
кривой с необусловленной скоростью.
Если же требуется воспроизвести дви-
жение точки по определенной плоской
кривой с постоянной скоростью, то за-
дание выразится любыми двумя зависи-
мостями нз числа следующих:
у-/(х); x-/i(ft у-У» (Г).
где t — время. Для воспроизведения
такого движения требуется механизм
с двумя высшими парами кулачкового
типа (фиг. 95, в и а), обеспечивающий
движение точки М по заданной кривой
с постоянной скоростью.
Кинематическая пара ку-
лачкового типа имеет линейча-
тый или точечный контакт. Элемент
пары из ведомом звене обычно выпол
няется по технологически простой по-
верхности — круглой цилиндрической
или плоской, реже по шаровой или
бочкообразной. Элемент на ведущем
звене имеет более или менее сложную
форму поверхности, которая опреде
ляется заданным относительным движе-
нием связываемых звеньев. Такое звено
называется кулачком. В наиболее рас-
пространенной плоской паре кулачко-
вого типа (относительное движение
звеньев совершается в одной плоскости)
элемент кулачка имеет некруглую ци-
линдрическую поверхность. Сечение
кулачка указанной плоскостью назы-
вается его профилем.
При точечном контакте элементов ку-
лачковая пара налагает одно условие
связи; при контакте по прямой линии
плоского элемента с сопряженным цн
линдрическим — два условия связи; прн
контакте по прямой линии неплоских
элементов — три условия связи Однако
из этих условий связи для ограничения
свободы движения связываемых звеньев
в каждой паре может быть удобно ис-
пользовано лишь одно, а именно устра-
няющее относительное движение эле-
ментов по общей нормали к поверхно-
стям в точке нх контакта. Остальные
условия связи относятся к общим пас-
сивным, приводя к нарушению правиль-
ного контакта при недостаточно точном
соблюдении соответствия между основ-
ными размерами звеньев или при де-
формации последних (перекосы и т. п.).
Фиг. 96. Рэмюяихппсти книемэтичееккх вар
кулачкового типа.
Основные разновидности кинемати-
ческих пар кулачкового типа: с боч-
кообразным роликом или пальцем
(фнг. 96, а), с плоским элементом
(фиг. 96, б), с цилиндрическим роликом
или пальцем (фиг. 96, а). Сплошными
стрелками на фиг. 96 показаны движе-
ния, возможность которых устраняется
активными условиями связи; пунктир-
ными стрелками показаны движения.
КУЛАЧКОВЫЕ МЕХАНИЗМЫ
515
обычно не устраняемые парой, но при-
водящие к нарушению правильного кон-
такта элементов (в механизмах являются
пассивными условиями связи).
Применение бочкообразного ролика
устраняет пассивные связи в контуре,
замыкаемом парой кулачкового типа.
Кинематика. Кинематический
анализ ставит своей целью опреде-
ление положений, скоростей и ускоре-
ний ведомого эвена при работе имеюще-
гося или спроектированного кулачко-
в) построением диаграммы скорость—
время посредством планов скоростей
(без определения радиусов кривизны
профиля) и диаграммы ускорение—
время однократным графическим диффе-
ренцированием;
г) расчетным путем с использованием
или без использования номограмм; этот
способ рассмотрен далее;
Большинство указанных способов до-
статочно полно разработано только для
плоских кулачковых механизмов.
Фнг. 91. Различные типы анаграмм: ускорение - время, скорость — время
и пут» - время.
вого механизма. Решение начинается
с построения кинематической диаграм-
мы путь — время или, что то же,
путь — перемещение равномерно дви-
жущегося ведущего звена. Построение
производится рассмотренным далее гра-
фическим способом, а при заданном
уравнении кривой профиля кулачка
(например, при круглом эксцентрике)
может быть выполнено аналитически.
Выявление скоростей и ускорений
ведомого эвена в различных положе-
ниях механизма и построение диаграмм
скорость — время и ускорение — время
производятся следующими способами:
а) двукратным графическим дифферен-
цированием; недостаток — низкая точ-
ность результатов вследствие накопле-
ния ошибок при вычерчивании;
б) построением планов скоростей и
ускорений, для чего в каждом положе-
нии кулачковый механизм заменяется
кинематически эквивалентным меха-
низмом с шарнирами и поступатель-
ными парами; недостаток — необходи-
мость определять радиусы кривизны про-
филя, что обычно затруднительно;
33*
Кинематический синтез
заключается в правильном выборе диа-
граммы путь — время и в построении
по ней профиля кулачка.
Кулачок обычно имеет рабочие и
холостые участки. На рабочих участках
характер движения ведомого эвена опре-
деляется рабочим процессом в машине
(например, технология обработки ня
металлорежущих станках обычно тре-
бует постоянства скорости подачи). На
участках холостого хода выполняются
вспомогательные движения; здесь жела-
тельно произвести перемещение ведо-
мого звена за возможно более короткое
время при наименьшем перемещении
ведущего звена (кулачка); препятствием
к сокращению времени перемещения
являются динамические условия, кото-
рые могут привести к неспокойной ра
боте механизма.
Диаграмму путь — время для участка
холостого хода получают двукратным
графическим или аналитическим инте-
грированием принятой диаграммы уско-
рение — время. Употребительные виды
диаграмм показаны на фиг. 97. Во всех
516
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
случаях отсутствуют удары первого
рода — скачкообразное изменение ско-
рости, в результате которого ускорения
и силы инерции теоретически возра-
стают до бесконечности. Диаграммы а
и в приводят к удару второго рода —
скачкообразное изменение ускорения и
силы инерции на конечную величину
Диаграммы б и д дают скачкообразное
изменение производной от ускорения.
Наиболее плавную работу обеспечивает
диаграмма г.
Здесь, так же как и в дальнейшем изложении,
звенья механизма примяты за абсолютно жесткие.
В действительном механизме процесс передами
движения от кулачка к ведомому звену ослож-
няется упругой деформацией звеньев, ’гго приводит
к некоторому искажению кинематических диа-
грамм.
Максимальная величина ускорения
ат„— k —— (обозначения см. на
«ы*-* Т'-
1 о
фиг. 97). На фиг 97 диаграммы распо-
ложены в порядке возрастания k, т е.
возрастания величины, характеризую-
щей инерционное воздействие движу-
щихся звеньев на механизм. Для изго-
товления кулачков диаграммы вне
(тригонометрические) более удобны.
Графическое дифференцирование
и интегрирование
Применяются два способа г р а фи
ч е с к о г'о дифференцирова-
ния (фиг. 98).
1. Способ касательных:
на диаграмме з—t проводят касательные
1—1, 2—2,..., а иа диаграмме v—t—
параллельные им лучи 1—1, 2—2,...
(//> выбирается произвольно с учетом
желательного масштаба построений/;
из точек пересечения лучей с осью v
проводят горизонтали до пересечения
с разделяющими вертикалями /, 2,...;
через полученные точки проводят кри-
вую v—I. Построения, относящиеся
к рассмотренному способу, показаны
пунктирными линиями. Подобным же
образом строится диаграмма а—t по
полученной диаграмме о—I.
2. Способ хорд: на диаграмме
в—t вместо касательных проводят
хорды 0—1, 1—2..... в на диаграмме
v—t — параллельные им лучи 0—1,
1—2,..., из точек пересечения которых
с осью v приводят горизонтали; кривую
v—t ведут через середины отрезков
горизонталей между соответствующими
разделяющими вертикалями или, точ-
нее, таким образом, чтобы площади Ли1
и Fi2 и £*2 ... были на глаз равны
между собой. Построения, относящиеся
к этому способу, показаны сплошными
линиями.
Подобным же образом строится диа-
грамма а—t по полученной диаграм-
ме v—t.
Графическое интегриро-
вание производится в обратном по-
рядке: сначала по заданной диаграмме
а—t строят v—t, а затем по v—I
строят з—/. В обоих случаях построе-
ния выполняются одинаковыми прие-
мами.
Рассмотрим в качестве примера
построение диаграммы s—t по v—t
(фиг. 98). На диаграмме проводят раз-
деляющие линии /, 2.... а затем гори-
зонтали с таким расчетом, чтобы иа
глаз F„, = F'nv F,, = F"n далее
выбирают произвольно Hi с учетом
желательного масштаба построений и
проводят лучи 0—1, 1—2,,.., парал
лельно которым на диаграмме з—t
проводят отрезки прямых б—/, I—2... и
по полученным и пересечениях с разде-
ляющими прямыми точкам строят кри-
вую 3—I.
КУЛАЧКОВЫЕ МЕХАНИЗМЫ
517
Формулы для определения масштабов
диаграмм:
при графическом дифференцировании
и. = _!5£_. ц =-££-
Из
при графическом интегрировании
Ро — Р-айгНъ Из “ tW-^l —
где р/, p.s, Ро и ра — масштабы, равные
соответственно числу сек., м, м/сек и
м/сек*, содержащихся в 1 мм чертежа;
/А и Я» — полюсные расстояния в мм.
Плоские трехзвенные кулачковые
механизмы
Структура и классификация. Из ку-
лачковых механизмов наибольшее рас-
пространение получили плоские трсх-
звенные механизмы, имеющие одну пару
кулачкового типа и две низшие пары —
вращательную и поступательную или
обе вращательные. Ведущим звеном, как
правило, является кулачок, редко —
сопряженное с ним звено.
В механизмах с кулачковой парой по
фиг. 96, а пассивные условия связи от-
сутствуют, в механизмах с парой по
фиг. 96, б имеется одно и по фиг. 96, в —
два общих пассивных условия связи.
Для удобства анализа и синтеза из
многозвенных кулачковых механизмов
часто оказывается возможным выделить
плоские трехзвенные.
Трехзвенные кулачковые механизмы
(фиг. 99) разделяются:
1) по характеру движения ведущего
эвена — на механизмы с вращающимся
(а—и), качающимся или поступательно-
движущимся (л—т) кулачком;
2) по характеру движения ведомого
эвена — па кулачково-ползунные (с по-
ступательно движущимся ведомым зве-
ном — а, б, г, д, ж, з, л, м, о, п) и ку-
лачково-коромысловые (с качающимся
относительно неподвижной точки ведо-
мым звеном —остальные исполнения на
фнг. 99);
3) по выполнению элемента кулач-
ковой пары у ведущего звена — на меха-
низмы с открытым кулачком (все,
кроме г, д, е, о, п, р) и с пазовым кулач-
ком (геометрически замкнутые меха-
низмы — г, д, е, о, п, р);
4) по выполнению элемента кулачко-
вой пары у ведомого звена— на механизмы
с плоским толкателем (ж, з, и, к, с, т}
и с круглым толкателем (остальные
исполнения на фиг. 99). Толкатели
более сложного, а также заостренного
профиля применяются редко;
Фиг. 99. Различные типы трехзвенных кулачковых механизмов.
sis
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
5) по расположению элемента ку-
лачковой пары ведомого звена относи-
тельно осей вращения и направлений
поступательного движения как веду-
щего, так и ведомого звеньев — ня
центральные (а, г) и смещенные (б, д),
с прямоугольным (ж) и косоугольным (з)
толкателем, с центральным (и, с) и сме-
Фиг. 100. Примеры геоме-
трически замкнутых меха-
ниаыое с открытыми кулач-
ками.
Фиг. 1С1.Схемы ме-
ханизмов с много-
оборотными кулач-
ками.
шейным (к, т) коромыслом, с передачей
поступательного движения под прямым
(л, о) н косым (ж, л) углом.
В механизмах с плоским'толкателем
и с поступательным движением кулачка
и ведомого звена касание элементов
кулачковой пары происходит всегда
в одной точке профиля кулачка. Такой
кулачковый механизм вырождается в ме-
ханизм для передачи прямолинейно-
поступательного движения с постоянным
отношением скоростей, т. е. кинемати-
чески становится идентичным механизму
с одними низшими поступательными
парами.
При открытых кулачках геометриче-
ское замыкание может быть достигнуто
выполнением элемента кулачковой пары
ведомого эвена с двумя поверхностями
круглого (фиг. 100, а и б) или прямо-
линейного (фиг. 100. в н г) профиля.
В этих случаях пргфнль кулачка дол-
жен обеспечить постоянное касание
с ведомым звеном в двух точках.
Если цикл работы механизма должен
совершаться за два и более оборотов
кулачка, то паз последнего выполняется
с соответствующим числом оборотов
незамкнутым (фиг. 101, а) или замкну-
тым (фнг. 101, б). Первое исполнение
пригодно, если кулачок делает несколько
оборотов в одном, а затем в противо-
положном направлении. Второе испол-
нение требует специальных мер против
попадания ведомого ролика в другую
ветвь в месте пересечения пазов; наи-
более просто это достигается примене-
нием вместо круглого ролика башмака
продолговатой формы (фиг. 101, б).
Кинематика. Профилирование
кулачков по имеющейся диаграмме
пути выполняется графическим построе-
нием огибающей последовательных по-
ложений профиля ведомого звена (тол-
кателя) в его движении относительно
ведущего. Для этого используется метод
обращения движения
или поступательно
движущийся кулачок
условно останавли-
вают, а стойке сооб-
щают движение со
скоростью кулачка,
но в противополож-
ном направлении
(фиг. 102).
При практическом
применении указан-
ного метода ограничи-
ваются построением
необходимого мини-
мума линий (фиг.
разделяется на следующие этапы:
я) пользуясь имеющейся диаграммой
пути s = /«(?). s » /«(s'),. <|» = /»(?)
или 6 e /«(s') на дуговой или прямо-
линейной траектории движения харак-
терной точки А ведомого эвена, наносят
положения Л|, At...... которые эта
точка будет занимать через равные при-
ращения угла поворота А? или линей-
ного перемещения As' кулачка;
б) наносят положения О>, О«,.....
центра неподвижного шарнира ведомого
коромысла или положения о«, at,...
прямых, проходящих через А в напра-
влении поступательной пары ведомого
ползуна в обращенных положениях
механизма;
в) определяют положения Л[ , Ла-
точки А в обращенном движении как
пересечение дуговых засечек из центра О
вращающегося кулачка (или прямоли-
нейных засечек, параллельных напра-
влению движения поступательно пере-
Фиг. 102. О6р»Щ»-
ние движений
кулачкопом мехл-
ниме.
103). Построениа
КУЛАЧКОВЫЕ МЕХАНИЗМЫ
«19
Фнг. 103. Профилирование кулачков.
метающегося кулачка) и дуговых
засечек из Oi, Оз,... при ведомом коро-
мысле (или прямолинейных засечек
ai, at.... при ведомом ползуне);
г) базируясь на точки Л(| А2 ,...,
наносят положения дугового или прямо-
линейного профиля ведомого звена;
огибающая этих положений и будет
искомым профилем кулачка.
При толкателе круглого профиля
кривая, проведенная через At, А2 ,...,
называется теоретическим (центролым)
профилем кулачка. Действительный
профиль кулачка является эквиди-
стантным теоретическому. Выпуклый
участок теоретического профиля и во-
гнутый действительного не должны
иметь радиусов кривизны, меньших чем
радиус ролика.
Построение диаграммы
пути при кинематическом анализеку-
лачкового механизма производится геми
же приемами (фиг. 103), что и профили-
ровачие кулачка, но выполняется
в обратном порядке, а именно:
а) наносят положения Oi, Оз,... или
в», аз,...;
б) по имеющимся профилям кулачка
и ведомого звена строят 4J,
в) по точкам Л'2,... строят поло-
жения Л|, At,... на действительной
траектории движения точки А; поль-
зуясь 41, 4з..., строят диаграмму пути.
При одном и том же профиле кулачка
плоский прямоугольный толкатель (см.
фиг 99. ж) имеет одинаковое движение
независимо от того, будет ли ось по-
ступательной пары ведомое звено —
стойка проходить через центр вращения
кулачка илн будет смещена относи-
тельно него; косоугольный толкатель
(фнг 99, э) будет иметь тот же закон
движения ведомого эвена, но увеличен-
I
ную в раэ длину хода.
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
520
Аналитический способ
определения скоростей и
ускорений в кулачковом меха-
низме (22| основан на следующих
формулах:
скорость ведомого эвена
v -
ускорение ведомого звена
2/ X . Y , Z \
Чп«, . v анЧ»,-«I.
’ = COS 0 ’ COS®<J *
у _ 2 cos (8Л — 0) — cos 8 cos 8„
” cosiu *
где р, — о»/? — окружная скорость ку-
лачка в месте его касания с ведомым
эвеном: «— угловая скорость кулачка
(считается положительной при подъеме
ведомого эвена, отрицательной при опу-
скании); р — радиус кривизны профиля
в точке касания (положительный при
вогнутом профиле и отрицательный прн
выпуклом); R — радиус-вектор ку-
лачка, т. е. расстояние от центра его
вращения до точки касания; / — длина
ведомого коромысла от точки касания
до центра поворота (считается положи-
тельной. если при своем движении
радиус-вектор стремится удалиться от
коромысла, и отрица-
тельной — если стре-
мится приблизиться
к нему); 8„ — угол
подъема кривой ку-
лачка (считается
всегда положитель-
ным); в — угол да-
вления (считается
всегда положитель-
ным — см. далее);
6Л — 0 = 8 — угол
смещения между R
и направлением дви-
жения ведомого эве-
на эталонного меха-
низма (фиг. 104).
Для упрощения расчетов удобно
пользоваться номограммами (фиг. 1С5).
Во многих частных случаях кулачко-
центра качания
Р
Фиг. IM. Схема
•талонного меха-
низма.
вого механизма расчет сильно упро
щается.
Углы передачи и углы давления
Углом передачи у называется угол
между направлением движения ведомого
звена и направлением обшей касатель-
ной к профилям в точке их соприкосно-
вения; углом давления 6 — угол между
перпендикуляром к направлению дви-
жения ведомого звена и направлением
общей касательной (фиг. 104);
7 + в - 99°.
Величина угла передачи
или угла давления должна
одновременно возможно полнее удовлет-
ворять двум противоречивым требова-
ниям:
с точки зрения сокращения размеров
кулачкового механизма выгодно умень-
шать у или увеличивать 8;
с точки зрения надежности механизма
против заклинивания, т. е. самотор-
можения при передаче движения от
ведущего звена (кулачка) к ведомому,
выгодно увеличивать у или уменьшать 8.
Надежность работы механизма характе-
ризуется коэффициентом надежности
. Ctgy, -
* гдеь "’э-углы.
прн которых начинается заклинивание
механизма.
С точки зрения к. п. л. механизма
выгодно, чтобы предельные значения
у и 0 находились в некоторой средней
зоне, не подходя близко ни к О’, ии
к 90°.
На фиг. 106 (271 приведен график
изменения к. п. д. эталонного кулачко-
вого механизма (см. ф>-г. 104) в зави-
симости от угла давления 8, а также
коэффициентов трения между кулачком
и ведомым звеном (/») и между ведо-
мым звеном и его опорами (/»)-
К. п. д. центрального кулачково-
ползунного механизма
1 — ЛлдАп/» — (finp + flap) tg 8
71 I + fmp Ctg e
К. п. д. смещенного кулачково-пол-
зунного или кулачково-коромыслового
механизма
I —fxnpftpp— (finp+finp) tg t8,—8)
l+/)Vc‘g8<> ’
гае hnp н Imp — коэффициенты трення,
приведенные прн отклонении механизма
от эталонной схемы (см. фиг. 104).
КУЛАЧКОВЫЕ МЕХАНИЗМЫ
622
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
между кулачком и толкателем и между
ведомым эвеном и стойкой.
При проектировании неответствен-
ных механизмов можно руководство-
ваться неравенствами:
для кулачково-ползунных механизмов
7>60° илн 0<30°;
для кулачково-коромысловых меха
иизмов
7 >45° или 6 <45°.
При проектировании ответственных
кулачковых механизмов оптимальное
♦иг. 106. Изменение к. п. д. кулачкового меха-
ими а ад виси мости от угла давлении, при зна-
чении! ковффиииентоп трепне /, и
Кривые 1 2 3 4 S 6 7 а 9
А 0 0 ОДП 0.01 0,01 0.1 0.1 0.2 о.2
А 0 0.2 0 0.2 0.4 0 0.4 0 0.4
значение в0 предельного угла давления
вшжх следует выбирать в зависимости
от коэффициентов трения 1]пр и /упр по
номограмме |271, предложенной проф.
Г. А. Шаумяном (фиг 107) Углы 0о,
найденные по номограмме, обеспечивают
достаточно хорошие показатели всех
основных свойств механизма
N
«о = -р
(см. фиг. 104) и хороший к. п. д. при
сравнительно малых размерах кулачка.
При наличии ролика на ведомом звем
приведенный коэффициент трения
. d-f+2k d
—«o'
где D — диаметр ролика; d — диаметр
его отверстия под цапфу; / — коэффи-
циент трепня
скольжения в цап-
фе; k — коэффи-
циент трения ка-
чения ролика по
поверхности ку-
лачка.
При выполнении
ведомого звена от-
личающимся от
ведомого звена
эталонного меха-
низма (фиг. 108)
приведенный коэф-
фициент трения
Фиг. ЮТ. Номограмма
для выбора оптималь-
ного значения предель-
ного угла дамемиа.
flnp
(фиг. 108, а);
2
ftnp “ — (/ + li etg (в + <р)] /
(фиг. 108, б);
d
21
(фиг. 108, в), где v — агсЦ Ц„р— угол
трения между ведомым звеном и к у-
Фиг. 108. Схема для определения прнведеииогв
кояффициента трения между ведомым звеном и
СТОЙКОЯ.
Проектирование механизма по вы-
бранному предельному значению угла
передачи 7ГО|П или угла давления 6шИ
производится из условия, чтобы ни в од
524
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
б) от точек Л,, Л2, ... по горизон-
о
тали откладывают отрезки у = —,
СО
где v — линейная скорость ведомого
звена в данном положении, прини-
мается за положительную прн напра-
влении вверх и за отрицательную при
направлении вниз; <> — угловая ско-
рость кулачка считается положитель-
ной при вращении по часовой стрелке
н отрицательной при вращении против
часовой стрелки; положительные отрез-
ки откладываются вправо от точек Л,,
Л2, . . . , отрицательные — влево;
Фиг. 109.' Определение зоны воз-
можного расположения оси кулачка
по предельным значениям углов
заиления.
в) точки tij, В2 . . . и flj, В2 . . . со-
единяют плавной замкнутой кривой.
При вращении кулачка против движения
часовой стрелки участок кривой, про-
веденный сплошной линией, соответ-
ствует подъему ведомого звена, а про-
веденный пунктирной линией—опуска-
нию. При вращении кулачка по дви-
жению часовой стрелки подъему ведо-
мого эвена соответствует участок, про-
веденный пунктирной линией, опуска-
нию — сплошной линией;
г) проводят касательные тт и т'т'
к кривой под предельно допустимыми
углами давления 0тах и 0^а!( к верти-
кали.
Центр вращения кулачка может рас-
полагаться в любой точке заштрихован-
ной области (фиг. 109). Наиболее ком-
пактный механизм Получается при вы-
боре центра в точке Oi пересечения
касательных.
Для пазовых кулачков (см. фиг. 99,
г и 3) и открытых кулачков, работаю-
щих с вращением в обе стороны, бе-
рется 0п1ах — 0^и. Для открытых кулач-
ков с вращением в одну сторону утл
давления, соответствующий опусканию
ведомого звена под действием пружины,
может быть выбран большим: 0шмх<С
®тах‘
Если ведомое звено перемещается
проектируемым кулачком только в одну
сторону, а возвращается в исходное по-
ложение каким-либо другим устройством
при отсутствии соприкосновения ролика
с кулачком, то область возможных по-
ложений центра вращения кулачка огра-
ничивается только одной касательной.
Например, для механизма со скоростью
о, направленной вверх, и угловой ско-
ростью я» против движения часовой
стрелки эта область лежит по левую
сторону линии тт (фиг. 109).
Кулачково-коромысловые
механизмы.
1. В механизмах с поступательным
движением кулачка (см. фиг. 99, н н р)
в-вл — ф:
tg 0 = ^4-. —Ц tg ф.
к с/ соз ф т
Подбор основных размеров механиз-
ма при проектировании рекомендуется
производить путем пробных вычерчива-
ний с последующей проверкой по при-
веденным формулам.
2. В механизмах с вращающимся ку-
лачком (см. фиг. 99, в н е) положение
центра последнего определяется графи-
чески. От описанного выше построения
(фиг. 109) рассматриваемый случай от-
личается следующим: траектория центра
ролика вместо прямой является дугой
окружности: отрезки у откладываются
в радиальных направлениях; вместо
одной касательной тт приходится про-
водить пяд прямых /П|/П|, тгт2. . . через
точки В|, В2, . . . под углом 7m(n —
— 90° — к радиальному направле-
нию. Эти прямые образуют ломаную
линию (в пределе — кривую), которая
и ограничивает область допустимых
положений центра вращения кулачка
Таким же образом строится вторая
граничная линия вместо касатель-
ной т'т'.
ПРОЧИЕ МЕХАНИЗМЫ
525
ПРОЧИЕ МЕХАНИЗМЫ
Мальтийские механизмы
Механизмы служат для прерывистого
поворота ведомого звена (креста) при
постоянном вращении ведущего звена
(кривошипа). Наибольшее распростра-
нение получили так называемые пра-
вильные механизмы (фнг. НО), характе-
ризующиеся поворотом ведомого звена
на равные углы с постоянной продол-
жительностью поворотов и остановок.
Для безударной работы механизма тре-
буется, чтобы направление скорости
центра ролика
Фиг. ПО. Мальтий-
ский механизм для
пзкорота везомого
звена на равные
углы.
или пальца кривошипа
при входе в прорезь
креста и при выходе
из нее совпадало с
направлением оси
прорези. При соблю-
дении этого условия
отношение между вре-
менем поворота и
временем остановки
будет зависеть только
от числа прорезей
на кресте.
Если требуется со-
кратить время оста-
новок, применяют
кривошипы с двумя
и более роликами,
равномерно распо-
ложенными по окружности. Если тре-
буются различные продолжительности
Фиг. Ill. Мальтий-
ский механизм для
поворота ведомого
эое на на различ-
ные углы.
Фиг. 112. МальгиАскиА
механизм с пнутреи-
ним зацеплением.
остановок, ролики на кривошипе раз*
мещают неравномерно. При необходи-
мости получить неодинаковые углы по-
ворота креста ролики располагают на
разных расстояниях от оси вращения
кривошипа, а крест выполняют не-
правильной (несимметричной) формы
(фнг. 111). Наконец, если нужно зна-
чительно увеличить продолжительность
остановок, кривошип периодически оста-
навливается, когда крест находится в
положении покоя.
Мальтийские механизмы с внутренним
зацеплением (фиг. 112) отличаются от
механизмов с наружным зацеплением
(фиг. 110) большей плавностью пово-
рота. Это достигается за счет умень-
шения времени остановки и увеличения
Фиг. 113. Диаграммы изменения скорости и уско-
рения искомого эиспа и мальтийских механизмах
с наружным и с внутренним зацеплением.
времени поворота, а также лучшего
соответствия траектории движения ро-
лика движению прорези (вращение ве-
дущего и ведомого звеньев происходит
в одном направлении).
На фиг. 113 показаны диаграммы из-
менения угловой скорости ш и углового
ускорения е трехпазового креста с на-
ружным (фиг. 113, в) и с внутренним
(фиг. 113,6) зацеплением за время по-
ворота на одно деление в зависимости
от угла поворота кривошипа а.
Фиксация ведомого звена во время
его остановки осуществляется: а) по-
фиг. 114. Мальтийский ме-
ханизм с принудительной
фиксацией ведомого звена.
Фиг. 113. Мальтий-
ский механизм е
пружишюй фик-
сацией ведомого
ямка.
средством концентрически расположен-
ных цилиндрической поверхности на
S26
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
Таблица 13
рвсчетиые зависимости для правильных мальтийских мехаиизмоа с наружным зацеплением
(см. фиг. ПО)
Искомая величина Обозна- чение Число прорезей
« * 5 6 8
Ра «иус креста ₽ 0.577л г 1.376г 1.732г 2.414г
Расстояние межху осанн 1,154г 1.114г 1,701г 2,000г 2.613г
Время поворота креста иа одно деление 1 сек. 10ТЯ 15/л 18/п 20/л 22,5/л
Время остановки креста прн равномерном ара щенки кривошипа . . . /а сек. 50/л 45,'л <2<л 37.Цл
Наибольший момент на кресте для преодоления сил инерции М кгем °-^«z 0-0К/прп’ 0.015/__л» п1
Наибольший момент иа кривошипе для преодо ления сил инерции . . . Наибольшее усилие ка /И, кгем мм^е 0,110/яут’ 0Ж/я^« ОДЛ!/ л’ лр ОЯВМ^гР
ролике для преодоления Лол* •'ey” /--Л* J.„nl
сил инерции Момент на кривошипе от постоянного момента со противления на кресте (для положения ме хаммзма, в котором 3ft наибольший) р 1.96— г б.ЙОЖ, 0.125 яр 0 031 пр П 013 пр
*1С г 2,О2Ме г \Л7МС 0,80Mf 0.4ЙА«г
Усмане на ролике от по- стланного момента со- противление на кресте Mf (зле положения ме- ханизма. в котором Р наибольшее) р. м, 5.81 —£ м, 2.20-= 1.28^?£ O.«£c О.и^с
Г Г Г Г г
Обозначения: г—рахиус кривошипа а см; л—число оборотов кривошипа в минуту:
момент инерции везомих звеньев, припсхсиный к валу мальтийского креста, в к/смсск1.
Таблица Н
Расчетные зависамоств для правильных мальтийских механизмов с внутренним аацеплаиаам
(см. фиг. 112)
Искома* величина Обозначе- ние Число прорезей
s * 6 « 1
Виутрскний раанус креста л 0.577г г Г,376г 1,732г 2,414г
Расстояние межху осями . Время поворота креста на а 1.154г 1.41 V 1.701г 2.0U> t 2,613г
одно деление .... Время остановки креста при равномерном краше- 1 сек. 50/Л 45/л 42/л Ю/л 37.5(л
ими кривошипа . . . . Наибольший момент иа кресте от сил инерции, имеющий место в начале 7, сек. 10(л 15/л 18/л 20/л 22,5/л
зацеплекни ...... М кгем °-0,w»n"’ *• р 0Д1иярЯ« °ДЮ?Уярл« o.ooea^yp 00tM&/np"'
ОАоаначеииа: г—рахиус кривошипа в см; л—число оборотов кривошипа в минуту; 1 пр-
момеит инерции везомых звеньев, привезенный к валу мальтийского креста, в клсмсск*.
ПРОЧИЕ МЕХАНИЗМЫ
.527
кривошипе и соответствующих выемок
на кресте: б) посредством специальных
фиксаторов, например принудительно
действующих (фиг. 114) или пружинных
(фиг. 115).
Второй способ обеспечивает большую
точность и надежность фиксации, а по-
атому применяется преимущественно
в ответственных механизмах.
Зависимости для геометрического, ки-
нематического и динамического расчета
мальтийских механизмов приведены
в табл. 13 и 14.
Кроме рассмотренных основных типов
мальтийских механизмов, существует
значительное число различных вариан-
тов их исполнения. В частности, в при-
борах и тихоходных малонагруженных
машинах применяются механизмы, у ко-
торых условие безударности работы не
выполнено (фиг. 115).
Храповые механизмы
Механизмы допускают свободное от
аосительное движение звеньев в одном
направлении и препятствуют относи-
тельному движению в противоположном
направлении. Храповые механизмы ис-
пользуются: а) для преобразования
качательного или прямолинейного воз-
вратно-поступательного движения в пре-
рывистое вращательное или прямоли
нейно-поступательное, а прн многозвен-
ных механизмах — в непрерывное вра-
щательное с пульсирующей скоростью;
б) для устранения возможности переме-
щения какого-либо звена в одном на-
правлении — запирающие устройства
в подъемных механизмах и т. п.; в) для
обеспечения свободного проворачивания
связанных звеньев а одном направле-
нии — муфты обгона (муфты свобод
ного хода).
Различают зубчатые и фрикционные
храповые механизмы.
Зубчатые храповые механизмы со-
стоят из зубчатого храпового колеса
Фиг. Ив. Типы зубчатых храповых ыехаииаыоа
ли зубчатой рейки и коромысла или
ползуна с закрепленной на них собачкой.
Храповое колесо выполняется с на-
ружными, внутренними или торцевыми
зубьями (фиг. 116). Профиль зуба бе-
рется: несимметричным трапецеидаль-
ным (фиг. 117, а) или треугольным
(фиг. 117, б) при работе механизма
в одну сторону; симметричным трапе
цондальным (фиг. 117, в) для работы
механизма в обе стороны; эвольвент
ным (фиг. 117, г) при одновременном
использовании храпового колеса в ка
честве шестерни зубчатой передачи.
Фнг. 117. Храповые механизмы с собачками ра»
личного типа и зубьями различного профиля.
Собачки выполняются чаще поворот-
ными— прямыми (фиг. 117, а), обрат-
ными (фиг. 117, б) или перекидными
двусторонними (фнг. 117, а), реже с рас-
цеплением посредством поступатель-
ного перемещения (фиг. 117, г). В по-
следнем исполнении направление ра
боты механизма может быть изменено
на обратное поворотом собачки вокруг
собственной оси на 180°. Прижатие со-
бачек к храповому колесу выполняется
пружинами, иногда собственным весом
собачки. Для устранения возможности
отхода собачки под нагрузкой поло-
жение оси ее поворота выбирается так.
чтобы нормальное усилие на ее рабо
чую поверхность создавало крутящий
момент, при-
жимающий со-
бачку к коле-
су. Выполнение
этого условия
и желание ус-
транить ради-
альную нагруз-
ку на колесо
(важно для
Фиг. HR. Профиль «уб»
храпового KO.U-CB ллх боль
ШИХ И«1 рузок.
сильно нагру-
женных механизмов) приводит к необхо
димостн поднутрения зуба. На фиг. 118
показан профиль поднутренного зуба,
предназначенного для больших нагру
so к; размеры зуба даны в зависимости
от модуля т, соответствующего наруж-
ному диаметру колеса.
Если ось качания коромысла совпа-
дает с осью поворота храпового колеса
или направление движения ведущего
ползуна совпадает с направлением
528
СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
движения храповой рейки, то при рабо-
чем ходе собачка не имеет движения
относительно колеса или рейки, что
создает благоприятные условия работы
механизма. При невозможности выдер-
жать указанное соответствие, напри-
мер при поступательном движении од-
ного звена и вращательном — другого,
необходимо стремиться к возможно
меньшим отклонениям действительной
траектории движения центра поворота
собачки от наивыгоднейшей траектории
Отрицательное влияние поворота со-
бачки относительно зубьев можно отча-
сти уменьшить увеличением радиуса за-
кругления рабочего конца собачки и дна
нпадины между зубьями на колесе.
Регулирование мгла поворота храпо-
вого колеса за одно качание коромыс-
ла производится;
а) изменением
угла качания ко-
ромысла , б) пере-
становкой щитка
(фиг. 119).
Устранение шу-
ма от прыгания
собачки по зубьям
при обратном хо-
де обычно осуще-
ствляется: а) про-
Фиг. 120. Схемы меха
ни «МОП с опюдом со-
бпЧКИ ОТ xp.lfiotaoi‘0 ко
леса при обратном ходе.
Фнг. НУ. Хрипотой ме-
ханизм с регулиродеч
ным щитком.
буксовывающнм пружинным кольцом,
надетым с натягом на неподвижный
цилиндр (фиг. 120. а): б) ведущим
шатуном (фиг. 120, б).
Устанавливая К собачек с относи
тельным смещением каждой на шага,
можно уменьшить угол поворота хра-
пового колеса до оборота, где
г — число зубьев храповика.
Кроме рассмотренных зубчатых меха-
низмов обычного типа, встречаются спе-
циальные конструкции, как, например,
с цевочным храповым колесом и виль-
чатой собачкой, с собачкой в виде цн-
линдрического ролика; они приме-
няются в запирающем реечном меха-
низме домкрата (фнг. 121, а), в иефрик-
циоииом механизме муфты обгона
с выемками на обеих звеньях
(фиг. 121, б).
Фиг. 121. Хрпповыс механизмы с
собачкой и аиле цнлнваричсского
ролика.
Фрикционные храповые механизмы
применяются при больших скоростях
и необходимости обеспечить возмож-
ность сцепления связываемых звеньев
при их любом угловом относительном
положении.
Механизмы характеризуются выпол-
нен нем элемента одного из связываемых
звеньев по поверхности, геометрически
не препятствующей относительному дви-
жению последнего в обоих направле-
ниях. Возможность движения в одном
направлении устраняется силами тре-
ния на указанной (фрикционной) поверх-
ности, возникающими при заклинивании
промежуточных звеньев. Фрикционные
поверхности звеньев с вращательным
движением выполняются большей
частью цилиндрическими, причем фрик-
ционную поверхность предпочтительнее
делать с внутренней стороны, так как
это уменьшает габариты механизма и
облегчает обработку обычно более слож-
ной поверхности сопряженного звена.
Различают роликовые, кулачковые,
колодочные И пружинные фрикционные
храповые механизмы
Роликовые механизмы
(фиг 122, а и б) применяются главным
образом в муфтах обгона и в бессту-
пенчатых импульсных вариаторах. При
назначении размеров механизма необхо-
димо соблюдать неравенство
где а — см. фиг. 123; ?— меньший
из углов трения между роликом и со-
прикасающимися с ним поверхностями.
ПРОЧИЕ МЕХАНИЗМЫ
^29
Для случая по фиг. 123
Л — (7?— r0) cos а — r0; cos а = Г° .
К —
Обычно для муфт обгона принимают
a rs 7’.
Храповые механизмы
с кулачками или эксцен-
триками (фиг. 122, в и е) приме
8) е)
Фиг. 122. Типы фрикционных храповых
маханишов.
вяются, например, для зажима деталей
при их обработке на станках.
Фиг. 123. Основные
размеры роликового
храпового мехаикама.
При назначении размеров этих меха-
низмов необходимо соблюдать неравен-
ство (фиг. 124)
4/0
n/"mln ’
где <₽ — угол трения на фрикционной
поверхности; / — коэффициент трения
между кулачком и осью или гнездом;
Г1 — радиус оси или опорной поверх-
ности кулачка; гт)п — наименьшая ве-
личина радиуса-вектора кулачка.
Колодочные механизмы
(см. фиг. 122, д) имеют ограниченное
применение. Они отличаются от всех
остальных фрикционных храповых ме-
ханизмов тем, что имеют контакт рабо-
чих поверхностен по площади.
Пружинные фрикцион-
ные храповые механизмы
(фиг. 122, е) пригодны для легких усло-
вий работы; они применяются, напри-
мер, для закрепления валика рукоятки
патефона.
Основной деталью механизма является
витая пружина, прикрепленная своим
концом к одному звену и посажен-
ная с некоторым натягом на наруж-
ную поверхность другого эвена.
Блокирующие механизмы
Блокирующие механизмы служат для
предохранения машины от несовмести-
мых включений или самовключений
(например, от одновременного включе-
ния двух скоростей в коробке передач
автомобиля, одновременного включения
продольной и поперечной подач в обык-
новенном токарном станке), а также
от неправильной последовательности
включений (например, от включения
главного привода машины при невклю-
ченной системе смазки).
Блокирующие механизмы запираю-
щего действия широко используются в
устройствах управления (переключения).
При двух блокируемых звеньях и
малом расстоянии между ними проме-
жуточных звеньев обычно не требуется.
Каждое звено снабжается элементами
двух запирающих кинематических пар.
Когда оба звена находятся в блокируе-
мых (средних) положениях, элементы не
соприкасаются. При перемещении одно-
го из звеньев в соприкосновение входят
элементы пары, допускающей движение
этого звена и препятствующей движе-
нию другого. Выполнение механизмов
без промежуточных звеньев возможно
при любом взаимном расположении бло-
кируемых звеньев, кроме соосного для
поворотных и параллельного для посту-
пательно-перемещающихся. Классифи-
кация механизмов для блокирования
двух звеньев приведена в табл. 15
34 Том I Зак. 1464
530 СВЕДЕНИЯ О МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
Первые варианты схем 2 и 8 (табл. 15)
не обеспечивают двустороннюю фикса-
цию одного звена при всех положениях
другого. Различные варианты схемы 11
дают одностороннюю фиксацию обоих
звеньев, одностороннюю одного звена и
двустороннюю другого, двустороннюю
обоих звеньев.
Пример выполнения блокирующего
механизма в фартуке токарно-винторез-
ного станка показан на фиг. 125. Меха-
низм устраняет возможность одновре-
менного включения подач от ходового
валика и от ходового винта. Подача от
ходового валика включается рукояткой,
сидящей на валу 1 и связанной с бло-
кирующим упором 2, который препят-
ствует замыканию сходящихся полови-
нок гайки ходового винта при включен-
ной подаче и не позволяет включить
подачу при замкнутой гайке, когда бло
кирующие пазы 3 надвинуты на упор 2.
Таблица М
Блокирующие механизмы запирающего действия для двух звеньев
Примеры принципиальных схем
Примеры принципиальных схем
Беа промежуточных
звеньев (расстояние
между блокируемыми
звеньями небольшое)
С промежуточными
звеньями типа фикса-
торов (расстояние
между блокируемыми
звеньями большое)
Без промежуточных
звеньев (расстояние
между блокируемыми
авеиьямн небольшое)
С промежуточными
звеньями типа фикса-
торов (расстояние
между блокируемыми
звеньями большое)
Оба звена поворотные
Оси поворота звеньев совпадают
Схема 1
Одно звено поворотное. другое с прямоли-
нейно-поступательным движением
Оси поворотных и направления перемещений
поступательно движущихся звеньев параллельны
Оси попорота звеньев параллельны
Схема 2 Схеме 3
Схема б
Схема •
Осн поворотных и направления перемещений
поступательно движущихся звеньев перпенди-
кулярны
Оба звена с прямолинейно-поступательны м
движением
Направления перемещений поступательно движу-
щихся звеньев параллельны
Схема 10
Осн поворота звеньев скрещиваются
Направления перемещений поступательно дви-
жущихся звеньев перпендикулярны
Схема 12
Схема* Схема S
Схема П
ПРОЧИЕ МЕХАНИЗМЫ
531
При большом расстоянии между бло-
кируемыми звеньями механизмы вы-
Фиг. 125. Блокирующий механизм п фартуке
токарно-винторезного станка.
полняются с промежуточными звень-
ями. обычно в виде поступательно пере-
мещающихся стержней-фиксаторов или
поворотных рычагов-фиксаторов с конус-
ными или клиновыми концами, входя-
щими в соответствующие гнезда блоки-
руемых звеньев (табл. 15).
В табл. 16 приведены схемы механиз-
мов для блокирования трех звеньев.
Механизмы допускают перемещение
одного из звеньев лишь при определен
ных положениях двух других.
Пример конструктивного выпол-
нения механизма см. на фиг. 78,
стр. 501.
Блокирующие механизмы запирающего действия для трех звеньев
Таблица 16
Область возможною применения схемы
Пригодна для блокировании поступательио-
псрсмсшаюшихся звеньев в параллельных
направлениях. Прн изменении формы про-
межуточного звена может быть использо-
вана для блокирования поворотных звеньев
Пригодна для блокирования поворотного
звена (среднего на схеме) н двух поступа-
тельно переметающихся или поворотных
звеньев. Линин кратчайших расстояний
между осью среднего звена и осью каждого
крайнего звена должны пересекаться водной
точке оси среднего звена
Прмгохна для блокировзгня поступательно-
переыещающихся н поооротиых звеньев.
Оси звеньев должны помещаться и парал-
лельных плоскостях, линии кратчайших
расстояний между осями должны совпадать
Пригодна для блокирования поступательно
перемещающихся и поворотных звеньев.
Линия кратчайшего расстояния между
осями верхних (па схеме) звеньев и липни
кратчайшего расстояния между указанной
линией и осью нижнего звеня должны пе
ресекаться и зоне А
ЛИТЕРАТУРА И ИСТОЧНИКИ К ГЛАВАМ XIX И XX
1. Артоболевский И. И., Теория меха-
низмов и машин. Гостехиздат. 1910, 1951.
2. Артоболевский И. И., Курс теории
механизмов и машин, Гостехиздат, 1915.
3. Артоболевский И. И., Структура,
кинематика и кинетостатика многозвенных плоских
механизмов. Гостехиздат, 1939.
4. Артоболевский И. И., Механизмы
(пособие для инженеров, конструкторов и изобре-
тателей), изд. АН СССР, т. I, ll и 111, 1947—1961.
б. Артоболевский И. И., ьлохЗ. Ш.
34*
и Добро польский 13. В., Синтез мехаии <
моя, Гостехиздат, 1944.
6. Б а р а и о в Г. Г.. Кинематика н динамика
механизмов, Госэнергоизаат, ч. I, 1932; ч. II, 1934.
7. Бородаче» Н.А.. Обоснование мето-
дики расчета допусков и ошибок кинематических
цепей, изд. АН СССР, 194J.
в. Бруевич Н. Г„ Точность механизмов.
Гостехиздат, 1946.
9. Вяхирев С. В., Автоматы и полуавто
маты. Маштмз. 1939.
532
СВЕДЕНИЯ ,0 МЕХАНИЗМАХ РАЗЛИЧНЫХ ТИПОВ
10. Д о б ро в о л ь с * и й В. В.. Система не
ханизмов, Машгиз, 1943.
11. Добровольский В. В.. Теория меха
низмен. Машгиз. 1961.
12. Доброгурсяий С. О.. С о«о
лов Р. А. и Захарова Е. И.. Механизмы
(справочное руководство!. Машгиз, 1947.
13. Ж и т к о в А. А.. Методы и оборудование,
применяемые в США для балансирования ара так»
шихся деталей. .Американская техника и промыш-
ленность* М 9. 1947.
14. Зиновьев Вячеслав. Аналитические ме-
тоды расчета плоских механизмов, Гостехиздат.
1949.
13. Калашников Н. А.. Исследования
зубчатых передач, Машгиз, 1941.
16. К е т о в X. Ф. и К о л ч и н Н. И., Теория
механизмов и машин. Машгиз, 1939.
17. Кобринский Н Е., Кинематические и
динамические ошибки плоских механизмов, .Из-
вестия АН СССР, Отделение технических наук*.
М 3. 194-1. а также № 6. 1944 и № 2, 1946,
1&. К у л и н о в В. А. Определение моментов
инерции цилиндрических многоступенчатых дета-
лей по чертежу. .Исследования в области метал-
лорежущих станков*. Машгиз, 1952.
19. Л а п и д у с А. С.. Дачные по износу и ме-
тоду повышения износостойкости направляющих
металлорежущих станков. ЦЬТИ. 1950.
20. Л е в и г I. А., Кояффициент полезного гей
стпня быстроходных станков и способы его повы-
шения, ЦБТИ, 1950.
21. Малышев А. П., Кинематика мехвния-
мов, Гизлегпром. 1933.
22. П р о и н к о n А. С., Новые методы кине
магического проектирования кулачковых механиз
мои. .Вестник машиностроения- .4 5. I9S9.
23. Р е ш е т о в Л. Н.. Кулачковые механизмы,
Машгиз, 195-3.
24. Р у л е и к о Н. Ф., Планетарные передачи.
Машгиз. 194'.
25. СкворповаН А., Внутреннее зубчх
тос эвольвеитиос зацепление при разности чисел
зубьев колес, равной единице Труды ссмииара по
теории механизмов и машин, т. VII. вып. 25.
изд. АН СССР, 1949.
26. Труды семинара по теории машин и меха-
низмов за 1947—1952 гт„ изд. АН СССР.
27. 111 а у м я н Г. А., Основы теории проекти-
рования станков-автоматов и автоматических ли-
ний, Машгиз. |949.
28. Элементы механизмов. Оборокгиз. 1944.
29. Энциклопедический справочник .Машино-
строение*. т. 2. главы I—FV. Машгиз. 1948 и
30. Энциклопедический справочник .Уашиио-
строение*, т. 9. гл. II и XIII, Машгиз. 194».
ПРИЛОЖЕНИЕ9
МЕРЫ И ЕДИНИЦЫ
Приставка дав образованна кратных и дольных единиц измерении (по Г(Х*Т 7663-S5)
Кратность и доль- ное ть Приставки Сокращемяые обозначение Кратность и даль- ность Приставки Сокращенные обозначении
русскими буквами л а типе кн- ыи (гре- ческими) буквами русскими буквами латински мн (гре- ческими) буквами
10“ тера • • т т 10-> деци • • д d
10» гига • • г 0 10-2 сантн • . С С
10* мега • • м м 10-3 милли . . м ш
10» КИЛО о • к и 10-6 микро • • МК ►
io* 4 гекто . . л н IO-9 нами . . м п -
10' дека • • да da 10-12 ПИКО • • п р
I. МЕЖДУНАРОДНАЯ МЕТРИЧЕСКАЯ СИСТЕМА
I. Меры длины
Основная единица - метр
Название «.окрашенные обозначение 1'елнчииа 3 « 1 с. • 5 О'ношение к основной елмииие В старых русских мерах
Рус ское Латин- ское
Микромикрои ..«•••• Миллимикрон. ..... Микрон. . ...... Ангстрем ......... Миллиметр ........ Сантиметр Дециметр. Метр .......... (километр • . . Мириаметр . • . ... 1 М.М гм Ом • КМ «пр. И X «пш сш dm ш кт |MD 0.0 1 рц U.001 ц 0,000001 м^о.ОГП XX o.o:oaui мм 1'00 щ гхюа» ооорр OjOl м = 10 мм 0.1 м « 10 см - — 10 мм |03 см вп ию мм iwuouOp IOTOm; 1000С00 мм ю км — loom « 10—Ю 10-7 10—8 10—1 1 10 10* 10» 10* 10-12 10-» ю-6 10-1° 10-2 10-1 1 10* 10* 0ЛЭ37Э линии. О,46ЫЯ сотки -МЖв^“. = и,зэз;о хм. 2,2497? ерш. — — 3,93701 хм. 0,46,69 саж.- ™ 1.4кХ5О? арш. “ — 22, >97? врш. = » 3,281164 фт. — — 3937000 дм. 0,93.’383 врс. > « 468.0915 саж. 9,37383 врс.
• Литература и источники к приложению.
I. Эицнклоледический справочник .Машиностроение*, т. I, кп. 1-а, Машгиз, 1917,
X Краткий технический справочник ГГ| И. 1919.
534
ПРИЛОЖЕНИЕ
Проаолж. приложсапи
Название Сокращенные обозначения Величина В степени» см' Отношение к основной единице В старых русских мерах
Рус- ское Латин- ское
Квадратный миллиметр . . лл' 2. Me пип’ ры поверхности O.OoOOOl Jtf> 10—2 10—6 0,15500 кв. ли.
• сантиметр . . см' ст’ 0,0001 м' = 100 MM' 1 10—4 0,05061 кв. врш.— — 0,15600 кв. дм. 5,05123 кв. врш. —
. дециметр . . . дм' dm’ 0,01 m' — 100 cm'-* 10* 10—2
. метр .к» т1 — 10000 мм' 10000 cm' — 10< 1 = 15,500 кв. дм. 0.21967 кв. саж. —
. декаметр , яр) а а - 1 000000 MM' 100 M' 10е ю2 = 1,97704 кв. арш. 21,9672 кв. саж.
Квадратный гектометр (гектар) га ha 100a — 10000 M* ю8 кН 0.915299 лес.
Квадратный километр . . КМ1 km’ 1000000 M> 1010 кА 0,878687 кв. вре.
. мириаметр , . — — 100 CM' 1012 10е
Кубический миллиметр . . 3. чм' Меры тт* объема я емкое 0,000000001 jd- ти 10"# КЗ -9 0Д6102 куб. ли.
• сантиметр . . сяР ст* — 0,001 ex’ 6ДЮ001 м* 1 к -« 0,01139 куб. врш.
. дециметр . . дм* dm’ o.ooi ла — ю3 к —3 11,3864 куб. врш. — — 61,0237 куб. дм. 0,102958 куб. саж.—
. метр (стер). . м* т’ = lOOuOOT жж’-М 1000 л — 10 »л 1(16 1
Килолитр . кл kt 1000 л 106 103 —2,77987 куб. apul— — 35,3147 куб. фт.— — 61023,7 куб. дм. 2,033 бочки
Гекталитр . . гл hl 100 л 10’ 102 8,1305 ведра —
Декалитр . дкл dkl Юл 1п* 10 — 0,476 четверти — — .4,811 четверика 0,813 ведра —
Литр ........... Л 1 0.001 м> — 1000 елг1 10я 1 —0,381 четверика — — 3,0499 гарнца 0,081 ведра —
Децилитр " I dl 0.1 л — 100 см' 102 10—* —1,3000 вин.бут.— —1,8261 вод. бут. — — 0,3049 три. 0,813 чарки —
Сантилитр . . сл el 0,01 л — 10 см' 10* к -2 — 0,009 ведре
Миллилитр ....... мл ml 0,001 л - 1 см* 1 10“3
Микролитр — — 0.000001 л - 1 мм* 10—3 и
Микрограмм . 4 7 . Меры веса 0,000001 Г-0,001 мГ 10-в к -9 0,0000225 доли
Миллиграмм мГ mO 0,001 г - юоо т to—3 к -в 0,0225 доли
Сантиграмм сГ cO 0,01 Г - 10 мГ 0,1 г = ю сг 10-2 1С —5 0,225 доли 2.250 доли
Дециграмм ....... дГ dO 10-1 1Г —4
Грамм . г 0 10 дГ = \\ЯсГ — 1 10-» 0,1'7814 лота —
Декаграмм Лк Г dkO - 1000 мГ 10 г 10* к )-» —0,23443 эолот- вика — 22,50481 доли 2,3443 еолотинка
Гектограмм >Г hO 100 г 102 |0-> 23,4425 золотника
Килограмм кГ kO км» г I03 1 0,061048 пула -
Центнер q 100 к Г- юоооо г I06 10» — 2.441928 фунта — — 73,1417 лота 6,1048 пуда
Томна , т 1 (000 кГ - 10 К 10е to3 (1,0412 пуда
ПРИЛОЖЕНИЕ
535
II. СТАРАЯ РУССКАЯ СИСТЕМА МЕР
5. Меры длины
Основная единица — аршин
Название мер и единичные соотношения Сокращенное обозначение В метрических мерах
1 верста — 500 саженям ере. 1.С6в8Э км
1 сажень — 3 аршинам =7 футам саж. 2.13360 м
1 аршин о 1о вершкам = 28 дюймам арш. 0,7112 м = 71.120 гм
1 вершок = 1.75 дюйма BDUJ. 4,4450 см = 44.450 мм
фт. 0.3048 .« = 3>.4Э1> см
1 дюйм = 10 линиям дм. 2.540 см = 25.4 мм
I линия = 10 точкам ....... лн. 2,54 мм
1 точка тчк. 0.254 мм
1 сотая часть сажени («сотка») 2.134 см
6. Меры поверхности
1 кв. верста — 250 000 кв. саженям ...... кв. врс. — врс.’ 1.13806 КМ>
1 десятина » 2ФЮ кв. саженям .... дес. 1.09254 га — 10925,4 м'
] кв. сажень 9 кв. аршинам — 49 кв. футам кв. с. с. 4.55225 ж'
1 кв. аршин — 205 кв. вершкам кв. а. •- а.’ 0,506805 м'
] кв. вершок . кп. врш. — врш.1 19,758м см'
1 кв. фтт = 141 кв. дюймам кв. фт. —фт.’ 9.2963 дм‘ —6,0929 .«
КП. дм. ««дм.1 6.4516 см'
1 кв. линия KD. ЛН. -IM.1 6,4516 мм‘
7. Меры объема
1 куб. сажень = 27 куб. аршинам = 343 куб. футам = 789,60 велра = 46,266 четверти; вмешает 592.88 пуда воды' куб. с.; е? 9.71268 Ж*
1 куб. аршин=41 Об куб. вершкам =21952 куб. дюймам куб. а.; а.* 0.35973 ж*
1 куб. вершок куб. врш.; врш? 87.8244 см*
1 куб. фут=1728 куб. люймам=2,3020 ведра — =1,07912 четверика, вмещает ь9,14О фунта 28.3168 г»ж”
или 23,311 кг воды куб. фт.; фт?
1 куб. дюйм — 1600 куб. линиям . куб. дм.; дм? 16,3871 см'
1 куб. линия ли? 16,3871 мм"
' При наибольшей плотно сти (3,94* С).
8. Меры емкости (для жидкостей)
йоч. 4.920 гл
1 ведро — VX1 чаркам — 1" штофам — 20 пив- ным бутылкам — 16 внииым бутылкам — =750,<М дм*, вмещает 30,'1343 фунта воды . В. 1,230 йКЛ = 12,2994 л
1 штоф — 1 кружке — 10 чаркам ....... 1 чарка —0,01 всара —2 шкаликам ..... ШТ. 1,230 л
0,123 л
1 тынная или ИМОЧИДЯ бутылка — Чм ведра . в 0.7687 л
1 водочная или пивная бутылка — •/», ведра . •— 0.6150 л
1 шкалик — */1ш ведра - 0,0615 л
9. Меры емкости (для сыпучих г ел)
1 четверть — 8 четверикам ЧТ. 2.0991 гл
1 четверик =8 гарнцам — 1ISJ1. I о.и', вмешает 64.0731 фунта воды чх. 2,8239 дкл " 26, 2387 л
! 1 гариц • . , грн. 3,2798 л
10. Меры веса
1 берковеа — 10 пудам бер. 0,164 Л1 — 1,638 ц
п. >.016 т — И. 164 ч — 16.38!» КГ
1 фунт — 32 лотам . фн. 0,40961241 «Г—409,512/'
1 лот — 3 золотин кам Л. 12.797 Г
1 золотник = 96 долям в. ь.чг&г
1 доля — Чяи Фуига ал. 44.435 мГ
536
ПРИЛОЖЕНИЕ
111. АНГЛИЙСКАЯ СИСТЕМА МЕР
11. Меры длины
Основная единица — ярд
Название мер и единичные соотношения Английское название В метрических мерах
1 ярд — 3 футам — 36 дюймам ........ 1 фут — 12 дюймам — русскому футу .... 1 дюйм = русскому дюйму 1 англ, морская миля —61MU футам —1,7371 врс. 1 англ, морская сажень — 6 футам 1 кабельтов — 0,1 морской мили 1 непь — 100 авеньям — 22 ярдам — 66 футам statute mite yard toot (ft) inch (In) nautical tulle fathom cable's length chain 1.6093 «л 0.9144 .и 0. Э04В м 2,540.7 см 1,8532 км 1,8288 м 185,3 м 30.117м
12. Меры
поверхности
1 кв. англ, миля — 640 акрам . . . ♦ square mile 259 га = 2.58999 км
acre 0,404686 га
1 кв. ярд — 9 кв. футам square yard 0,8361 м'
1 кв. фут — 144 кв. дюймам . . . . square liiut 9.290 ОМ'
1 кв. дюйм square Inch 6.452 СМ'
• 13. Меры объема
1 регистр, тонна — 100 куб. футам . ... register ton 2,832 Н*
1 куб. ярд = 27 куб. футам . . . . cubic yard 0,754555 ж>
1 куб. фут = 1728 куб. дюймам . cubic toot 28.317
куб. дюйм
1
cubic Inch
16.387 CM'
14. Меры
емкости
1 квартер — 64 галлонам — 8 бушелям .... quarter 290.94 л
1 1 бушель — 8 галлонам галлон — 4 квартам ае 277.463 дм" = 0,3696 bushel 36.368 л
ведра — 7/19 бутылки Imperial gallon 4,546 .«
1 кварта v 2 пингам quart 1.1365 л
1 линта — Ода бутылки pint 0.56825 л
15. Меры веса
1 англ, тонна — 20 центнерам ton, long ton 1,0160470 m
1 hundred weight 50,802352 Kf
1 фунт —16. торг, унциям —7000 англ, гранам pound 0,4'1359
1 торг, унция •- 16 драхмяи ounce 28.3496Г
1 аптекарская унция — Ь алт. драхмам. . . . — 31,103 Г
1 dram 1,7/18 Г
1 апт. драима—3 скрупулам — 60 гранам . . 3,886 Г
1 англ, граи — торг, фк . grain 64.7989 мГ
IV. АМЕРИКАНСКАЯ СИСТЕМА МЕР'
16. Перевод американских мер в метрические
Название мер и единичные соотношения Америк а нс коя название В метрических мерях
1 амер, миля — 3 англ, милям ........ 1 тауншип — 86 кв. милям 1 (винный) галлон — 0,833 англ, галлона — — 4 квартам — 8 пиитам 1 СУДОЙ 18ЛЛ0И 1 баррель керосина — 42 галлонам 1 баррель пива — 31 галлону 1 малая теина — 2000 англ, фунтам ...... ‘ В США принята английская система с statute milt township gallon barrel short ton некоторыми изменениях 4,828 км (3,216 км' 8,787 л 4,4046 л 1,514 гл 1,173 гл 0,907 т ги, приводимыми здесь.
1 ТАБЛИЦЫ ДЛЯ ПЕРЕВОДА ОДНИХ МЕР В ДРУГИВ
17. Дюймы в миллиметры
(через Чи дюйма); 1 дюйм — 25,400 мм; 1 мм — 0,394 дюйма
Дюймы X Чм ‘к Ха ч. Чм Ч, ’Ь. •h Чм X "1м 1. “1м X “1м Дюймы
0 0.000 1.587 3.175 4,762 6,350 7,937 9.525 11,112 12.700 14,287 15.875 17,462 19.050 20.637 22,225 23.812 0
1 2S.4X 26.987 28.574 30.162 31,749 33.337 34.924 36.512 38.099 39.687 41.274 42,862 44,449 46,037 47,624 49,212 1
2 5O.8W 52.387 53.974 55.561 57,149 58.736 60,324 61.911 63,199 65,086 66,674 68.261 69.849 71,436 73.024 74,611 2
3 76,200 77,786 79,374 80,961 82.549 84.136 85,723 87.311 88.696 90.486 92,073 93,661 95.248 96,836 98.423 100.01 3
4 101.60 103.19 104,77 106,36 107.95 109.54 111.12 112,71 114,30 115,80 117,47 119,06 120,65 122,24 123,82 125,41 4
5 127.00 128.59 130.17 131,76 133.35 134.94 136,52 138,11 139.70 141,28 142,87 144,46 146,05 147.И 149,22 150,81 5
6 152,40 153.95 155.57 157,16 158.75 160,33 161.92 163,51 166,10 166,68 168.27 169.86 171,45 173,03 '74,62 176,21 6
1 177.80 179.38 180,97 182,56 184.1G 185.73 187,32 168,91 190.50 192,08 193,67 195,26 196,85 198,43 200,02 201,61 7
8 ззз.х 204.78 206.37 207.96 209.55 211,13 212,72 214,31 215.90 217,48 219.07 2Х.66 222,25 223,83 225.42 227,01 8
9 228.60 230.18 231.77 233.3G 234.95 236.53 235,12 2.ЧЭ.71 241.30 242,88 244.47 246,06 247.65 249,23 250.82 252,41 9
10 254.00 2S5..58 257.17 258.76 260.35 261.9.3 263.52 .‘65.11 266.70 268,28 269,87 271,46 273.00 274,63 276,22 277,81 10
11 279,40 280.98 282,57 284,16 285.74 287.33 288.92 290.51 292.09 293.66 295,27 '296,86 298.44 300,03 301,62 303,21 11 •
12 304.80 306.38 307.97 309,56 311.14 312,73 314,32 315,91 317,49 319,08 320,67 322,26 323,84 325,43 327,02 328,61 12
13 330.20 331.78 333.37 334.96 336.54 338.13 339.72 341.31 342,89 344,48 347.66 349,24 350.81 352,42 354,01 13
14 355.60 3S7.I8 358.77 360.36 361,9*1 363.53 365,12 366,71 368,29 368.88 371,47 373.06 374,64 376,23 .477.82 379.41 14
15 381,00 382.58 384,17 385.76 587,34 388,93 390,52 39-2,11 393,69 396,28 396,87 ЗЮ, 40 400,04 401,63 403.22 404.81 15
16 406,40 407.98 409.57 411,И 412,74 414.33 415,92 417.50 419,09 420,68 422,27 423,85 425,44 527,03 428.62 430.X 16
17 431.80 433.38 «М.97 436.55 438.14 4.39.73 441.32 442.90 444,49 446,08 447,67 449,25 450,84 452,43 454,02 455.60 17
18 457.30 458,78 460.37 461.95 463.54 465.13 466.72 468,30 •169,89 471,48 473.07 474,65 476,24 477,81 179,42 181,00 18
19 482.60 484,18 485.77 487.35 488,94 490.53 492,12 493.70 495.29 496,88 498,47 50O.U5 501,64 5«3,23 504.82 506,40 19
X 506.00 5Q9.58 511.17 512.75 514.34 515.93 517.52 519.10 520,159 522.23 523,87 525,45 527.01 528,63 530.22 531,80 X
21 533.40 534.98 536.57 538.15 539,74 541,33 542.92 544,50 546.10 547,68 549.27 550.85 552,44 554.03 556.61 557.Х 21
22 556.80 560.38 561.96 563.55 863.14 566.73 568.31 559.90 571.19 573,08 574,66 576.25 577,84 579.43 ,581.01 582.60 •п
23 584.20 585.78 587,36 588,95 390,54 592,13 593,71 595,30 596.89 598.48 600,06 601,65 603,24 604.83 606.4! 608.00 23
ПРИЛОЖЕНИЕ
63S ПРИЛОЖЕНИЕ
09 68 9» 8'6661 8'«951 0'1*861 8'8661 8'9961 8'1881 9'0681 8'9961 8'68X1 0'6861 9*1-961 O'Ht'Ot 8'4861 0'6961 9'9961 6'9861 9'0961 1'9061 £'8861 6'8961 9'££61 4'6851 11'4951 6'lKl 1'1851 2 9951 e'oai 9'6461 1'8961 4'8561 6'4451 9'6921 1*4551 £'9451 6'0951 £'•.251 4'8451 t'6861 6'£22l 5'061 9'2Hl 8 6551 9 t42l 5 9851 8'0651 0'0251 9'8861 5'6151 09 68 88
IV 9'4161 0'9161 8'8121 8'2121 9'1161 4'6061 1*8061 9'9061 6'80.11 C'tJOCI 4'1051 1'0061 9'8611 0'2611 8'9611 »'ran 48
9» 6'66П 9'0611 0'i.Bll 8'4811 8'9811 8'8811 4*6811 1'1811 9'6411 6'4211 £'9411 4'8411 ran 9'1411 0'0411 8'8911 98
9» 8*9911 8'9911 9'1'911 0'0911 8'0911 6'8811 C'49tl 4'9911 Г 8911 9'5911 6*0911 11'6811 4'4811 5*9811 9'8811 o'mi 98
88 8'1811 8'6£П е'йеп 9'9Ett o'sett 9 Sil 6'lEll E'OEXl 4'8511 ГШ1 9'9511 6'Kll £'6211 8'06U 6'6111 8 4111 88
е» 0'9111 8'8111 8'814 6'ttn 9'6011 1'8011 9'90tI 6'8011 e'eon 2'1011 Г ООП 9'8601 6'9601 8*9601 8'0601 6*6601 О
ст 9'0601 0'6810 8'1801 8'9901 6'8801 4'6801 1'1801 9'6401 6'4401 11'9401 4'8401 1'6401 9*1201 0'0401 8'8901 8'9901
I* 6'9901 9'1-901 0'6901 8'0901 8'8901 e'4901 4 9901 Г 8901 9'5901 6'0901 V 6101 4'4801 1*9801 9'88O| 0£801 8'ПО!
08 8'6601 E'BCOt 9'94.01 O'StOI 8'££01 6'tBOl E'OEOI 4'8601 t 4601 9'9501 6'C50l e'ssoi 4'0601 5*6101 9'4101 0'9101 08
6Е 8'8101 9'6101 6'И01 9'6001 0'8001 9'9001 6'8001 e'booi 4'1001 1'0001 69'866 £6'966 8£'966 94'£66 41'666 09’066 в'
не 00'686 18'686 684-96 eo'ier. 89'686 90'186 48'616 «8'446 OC'946 14'846 5l'>:46 re-146 86'696 98'896 44'996 06 £66 »:
4£ 09'696 10'6.96 88'096 1-8'896 96'496 99'9*96 40'896 88'696 «6'096 11)686 54'486 et'986 99'886 96’686 46'186 08'61*6 4£
96 06'866 19'оеб 60 '«6 88'CEO S8'l£6 96 ora 49'816 80'466 09'966 I6‘£56 6£'626 £4'066 91'616 99'416 46'916 08'816 9£
96 08'616 18'116 59'OTG €0'806 98'906 98'806 46'0)6 89'106 01'006 19'868 66'969 К '969 94'£69 91'664 29'068 00'688 SV
и: 09'688 18'988 88'888 ra'8.84 90'188 98'648 18'448 86'918 04'848 11'848 69'148 116'698 sv'we 94'998 41'598 оо res К
et 00'698 18'098 88'898 £5'488 99'998 90'898 48'698 88'098 DE'688 14'488 51'989 £9*818 £6'588 9£'l89 44'688 06'888 Ft
te 09‘9£8 Ю'9С6 88'888 CS'ICT 96'008 99'888 40 468 68'968 O6'£68 IC'658 64'058 81*618 99'418 96'918 4£'8l8 08'618 5£
и 05'118 19'609 00'908 88'908 98'808 96'roe 49'108 бп'оое 09 864 16'964 66'964 84 '£64 91'564 99'064 46'884 08'484 IE
ОС 084*94 16'881 59*684 80'184 98'614 98'444 96'944 69'844 01'1142 19'142 56'694 88'894 94'992 91'992 49" £9' 00'692 OF
66 П9'09£ 18'894 68'491 89'994 90'894 98'694 48'094 65'684 04'484 11'984 69'884 86'684 SV 184 94'6€4 4Г8-14 O9’9€4 65
86 00'966 t8'££4 68 I£4 86'0114 89'854 90'464 48'854 68 at <»‘«4 14'064 sretx 89'414 96'912 99'812 24'614 05'IU 86
а 09'606 to‘806 88'906 88'804 96'004 99'104 40'004 68'869 06'969 18'969 54'1*69 81'569 99'069 96*889 8£'299 08'999 45
к 06'189 19'689 €0'189 88'649 98'449 96'94» 89'819 60*819 09 149 16'699 01'899 84*999 91'999 99'£99 86'199 08'099 96
SC 08'899 18'199 €9'999 80'899 98'699 98'099 81'689 69'419 01'989 19'889 €6'.-89 8S189 92'6re 91'899 W9£9 (n'SFS SE
п О8'ега 18 US к'ore 89'869 90'469 98'989 88'859 66'569 04'0’9 11'619 ES'419 86'919 9£'8l9 94*619 81'159 09'6» 86
ня»<Г[Г •1. ”lr ’ll "In •1. "1. 4, "1, % •1, "1. 1, “Ii Ч RRVOqy
ПРИЛОЖЕНИЕ
539
IS. Доли дюйма в миллиметры
Доли люйма '1м 0,40 % 1.19 % 1.99 2.78 7ы 3.57 “fa 4.37 “fa 5.16 fa 5.95 **/•< 6,75 “fa
Доли аюОма fa Sfa “fa "fa -fa "fa “fa fa
ММ ог 9.13 9.92 10.72 11,51 12Д0 .13,10 13Д9 14,68 15.48
Доли аюйма ММ fa 16,27 17,07 '1Об п1„ 18,65 105 “fa 20,24 •7ч 2U® fa 21,83 fa 22,62 “fa 23.42
Доли аюйма “fa “fa ч„ 7- 7» 7м 7.. "fa “fa “fa
ММ 24.21 25,00 0.79 от 07 5.56 7.14 8.73 10,32 11,91
Доли дюйма "fa fa fa “fa fa fa “fa 7» 7ч
ММ 13.49 15.08 16,57 18.26 19,84 21,43 23/й 24,61 1.59 4. Д’
Доли аюйма •fa 7 ч “fa **<ч “/ч Ч. 7. 7. 7.
ММ Доли дюйма мм 7.94 1 25,40 11,11 Ч. 19.05 14.29 ‘h 12.70 17.46 7. 6.35 20.64 23,81 3.18 9.53 15,88 ПЗ
19. Миллиметры в дюймы
ММ Дюймы Дюймы Дюймы - Дюймы ММ Дюймы
0.01 0.0004 0,1 0,0034 1 0.0094 10 0.394 100 3,937
0.02 0.0008 0.2 0,1X179 2 0,0787 20 0,787 | 201 7,874
0,03 0.0012 ОД 0,0118 3 0.1181 30 1.181 300 11.811
0.04 0.0016 0.4 0.0158 4 0.1575 40 1,575 400 15.748
0.05 0,0020 0.5 0.0197 5 0,1969 50 1.959 500 19.685
о.об 0.0024 0.6 0.0236 6 0.2362 60 2,362 600 23.622
0.07 0.СП-28 0.7 0.0276 7 0,2756 70 2,756 700 27.559
0.08 0.0032 0.8 0.0315 8 0.3150 80 3,150 860 31,496
0,09 0.0035 0,9 0.0354 9 0,3543 3,543 920 35,433
20. Футы в метры
Футы м Футы Футы Футы ,м
1 0,3048 18 5,4864 35 10.668 15,850
• 2 0.6395 19 5,7911 36 10,973 53 16,154
3 0.9144 20 6.0950 37 11,278 54 16.459
4 1.2192 21 6,4107 38 11.582 55 16 764
5 1.5.'4О 22 6,7055 39 11.887 56 17,069
6 1,8288 23 7,0103 40 12,192 57 17,374
7 2.1336 24 7.3151 41 12.497 58 17,678
8 2,4384 25 7,6190 42 Г2.8О2 59 17,983
9 2.7432 26 7,9247 43 13,106 60 18,288
10 3.0480 27 8,2291 44 13.411 61 18,593
II 3.3528 28 8,5143 45 13.716 62 18.897
12 3,6.76 29 8.8391 46 14.021 63 19.202
13 3,9524 30 9.U4O 47 14.326 64 19.307
14 4.2672 31 9.4497 48 14,630 65 19,812
15 4,5720 32 9,7537 49 14.935 65 30,117
16 4.8768 33 10.0 8 60 15.240 67 20,421
17 5.181b 34 10,363 51 15,545 «8 20,726
540
ПРИЛОЖЕНИЕ
Продолжен™
Футы Футы Футы м Футы м
б» 21,031 77 23.46» 85 25,908 93 28.341
ТО 21,336 73 23.774 B5 26,213 94 28.751
71 21.641 79 24.079 87 26,517 95 28.956
72 21,94.5 ВО 24.381 88 26.822 9<3 29,261
73 22,250 81 24,659 89 27,127 97 29,1376
74 22.55® 82 24.SO3 90 27,432 98 29,870
75 22.8-Ю 83 25,298 91 27,737 99 3'1,175
76 23,165 М 25,603 92 28.042 180 30,480
21. Ярды в метры
Ярды м Ярды м Ярды М Ярды м
1 0,91438 11 10,06822 21 19.20206 I 31 28,3458'1
2 1,82877 12 10,9720» 22 20,11613 32 29.26027
3 2,74315 13 11,84698 23 21.0П1Н2 33 30,17415
4 3,65753 14 12.80137 24 21,91520 31 31,0-1904
6 4,59192 15 13,71576 25 22, №959 35 32,00342
6 5,48630 16 14,63014 26 23.77397 36 32,91780
7 6,40068 17 15.54452 27 24,64535 37 33.83219
8 7,31307 18 16,45890 28 25.60274 38 34.71657
9 8,22945 19 17,3732» 29 26.51712 39 35.66 96
10 9,14.183 20 18.267,7 30 27.43I5O 40 36.57534
22. Метры и Футы в ярды
м Футы Ярды м Футы Ярды Футы Ярлы
1 3,281 1,094 10 32.8118 10,936 100 328.0» 109,361
2 6.562 2.187 20 65,617 21.472 200 656,17 218.722
3 9,843 3,281 30 98,425 32.808 304. 328,1)83
4 13,123 4.37 4 40 131.234 43,8-14 Ф Ю 1312,31 437.441
5 16.104 5,468 50 161,042 54,081 51Ю 164-1,42 546,Ы»
6 19,685 6.562 Ш 196,850 68.617 бпп 1968,50 656,166
7 22,96. 7.655 7о 229,659 76.553 710 22'16,59 755,527
8 26.247 8,74» 80 262,467 87.489 «10 2624,67 874,88.8
9 29.628 9,842 90 29»Л76 98.425 ЭОН 1010 2952.73 3280,90 981,219 1093,61
23. Сводная таблица перевода линейных мер
1 мм раней 1 CM pilKII 1 м ряпеи 1 км ранен
мм •••••••.. А 10 10* 1СГ
см • « 10-1 1 10< 10>
м . 10-3 io-2 1 ТО1
К* . . . 10—ъ 1U—5 iu-a 1
ПРИЛОЖЕНИЕ
541
Продолжение
1 мм равен 1 см равен 1 м равен 1 км ране»
Вершков Аршин Саженей ....... Верст Точек ........ Дюймов ...... . Футов ........ Ярдов ........ 0,0224972 0,00140607 46870-Ю—8 9373.8.1O-10 3,937006 0,3937006 0.03937008 0,0032006 0,0010936 0,224972 0,0140607 0,0046870 93738-10—70 39,37008 3,937008 0,3937006 0,032806 0,010936 22,4972 1,40607 0,46870 93738-10-8 3937,006 393,7006 39,37006 3,2806 1,0936 22497,2 1406.07 468.696 0,93738 3937008 393700,8 39370,08 3280.84 1093,61
1 верш, ранен 1 арш. равей 1 саж. равна 1 верста равна 1 точка равна
мм см м км. ••«•••••» 44,450 4,44450 0,04443 4445-10—» 711.20 71,120 0.71120 7112-Ю-7 2133,60 213,360 2,13360 21336-10—7 I066M0 106680.0 1066.800 1.066800 0,2540 0,02540 254-Ю-в 254-Ю-9
Вершков. ..... Аршин........ Саженей . Верст Точек Линий Дюймов Футов ........ Ярдов 1 0,06250 0,020633 4167-1O-8 173 17,5 1,750 0,14583 0,0486 16 1 0,333333 6667.10—7 2800 280 28 2,33333 0.777778 48 Э 1 0,0020 S4:<J 840 84 7 2,33333 24000 1500 500 1 4200000 4211000 42000 3500 1166,6666 0,00671429 35714-Ю—8 119047-Ю-9 238-Ю-9 1 0.1 0,01 8333 10—7 2778-КГ"7
1 линия равна 1 дюйм равен 1 фут равен 1 ярд равен
мм . м • • • • 2,340 0,2540 0.00254 254-10-8 28,40 2,540 0,0254 254-10-7 304,600 30.4800 0,30480 3048-10“7 914,40 91.440 0.91440 9144-Ю-7
Вершков Аршин . ♦ . Саженей....... Верст ........ Точек Линий ........ Дюймов Футов ........ Ярдов ........ 0.0671429 0.00367)4 0,00119047 238-10-8 10 1 V.1 0.008333 0.002778 0,571429 0,035714 0,0119047 238-10—7 100 10 1 0.083333 0,02778 6,857136 0,428571 0,142857 2857*10—7 1200 120 12 1 0,33333 20,571429 1,285714 0,428571 8571-10—7 3600 360 36 3 1
М2
ПРИЛОЖЕНИЕ
24. Сводная таблица перевода квадратных н кубических мер
Квахратвых мер*-
Кв. саж. Кв. аршин Кв. верш. Кв. фут Кв. дюйм Кв. м Кв. см Кв. мм 4
Куб. саж. 1 9 2304 49 7056 4.55 4,55-10* 4.55-108 1 кв. саж. равна
Куб. арш. 27 1 256 5,44 784 0,506 5058 50,58-10» I кв. арш. равен
Куб. ерш. 11, 06-10* 4096 1 0,021 3,06 0,00196 19,76 1976 1 кв. верш, равен
Куб. фут. 343 12,7 0,0031 1 144 0,0929 929 929-10» 1 кв. фут. равен
Куб. хюАм. 59,27-10* 2,2.10* 5,36 1728 1 0,000645 6,45 64.5 1 кв. дюйм равен
Куб. м 9,7127 0,36 8,7В- КГ6 0,0283 0,0000164 1 10* 10» 1 кв. м равен
Куб. ем 9,7127-10* 36-10* 87,8 283-10» 15.4 1СЯ 1 10» 1 кв. см равен
Куб. лм 9,7127-10' 36107 8,78-10» 283-10» 164-10» 10» 10» 1 1 кв. мм равен
♦ 1 куб. саж. равна 1 ку4. a pin. ра* ем 1 куб. верш, равен 1 куб. фут равен 1 куб. дюйм равен 1 куб. м равен 1 куб. см равен 1 куб. мм равен
Кубических мер
25. Английские фунты в килограммы и обратно
КГ май английские фунты Английские фунты кГ КГ или английские фунты Английские фунты кГ 1 кГ или английские | фунты Английские фунты кГ
1 2,2046 0.4536 1 39,6832 8,1647 55 121,2542 24,9476
2 4,4092 0,9072 19 41,8878 8,6182 60 132,2773 27,2155
3 6.6139 1,3018 20 44,0924 9,0718 65 143ДХМ 29.4835
4 8.6185 1,8144 21 46,2970 9,5254 70 154,3236 31.7515
5 11,0231 2,2680 22 48,5017 9,9790 75 1653466 34.0104
6 13,2277 2,7216 23 50,7063 10,4326 80 176 лете 36,2874
7 15.4324 3,1751 24 52,9109 10,8862 90 198,4160 40.6233
8 17,6.370 3,6287 25 56.1155 11,3398 1О0 220.4622 45,3593
9 19,8416 4,0823 26 673202 11,78134 201 440.9245 90,7185
10 22.0462 4,5359 27 69,5248 12,2470 31» 661.3867 136,0777
11 24,2508 4,9695 28 61,7294 12,7046 40.3 881,8489 181,4370
12 26,4554 5,4431 29 63,9340 13,1542 500 1102,3115 226,7962
13 28.6601 5,8967 30 66.1387 13,17178 61» 1322.7734 272.1555
14 30,8647 6,3503 35 77,1617 15.8757 700 15-43,2356 317,5147
16 33.0693 6,8039 40 88.1849 18.1437 8OJ 1763.6978 362.8739
16 35,2739 7,2575 45 99,2079 20.4117 МО 1984,1601 4'в. 2332
17 37,4886 7,7111 50 110,2311 22,6796 1000 2204,6223 453,6924
26. Сводная таблица перевода весов
Килограмм Гро мм Пуд Фунт Лот Золотник Английский фунт
1 кГ ранен 1 1000 0,061 2.44 78 234 2,20
1 Г 0,001 1 0,000061 0,07244 0,078 0,234 0,0022
1 п. райей . ....... 1638 16380 1 40 1280 3840 36
1 ф. равен 0,4095 409,5 0,025 1 32 96 0.9
1 лот ранен 0,01280 12,80 0.0X778 0,0312 1 3 0,0282
1 зол. ранен 0,00427 4.27 0,00026 0,0104 0.333 1 0,0094
1 англ. ф. ровен..... 0,454 454 0,02769 1.1> 35,4 106,3 1
Л. Соотношения между различными единицами давления
Еанаица давления • Килограмм аа ква- дратный санти- метр или атмо- сфера техинче СХ1Ж В • . . . Бар ...... Льем Гектопьеха . . . Миллиметр ртутно- го столба . . . Метр яохяиого стол- ба Физическая атмо- сфера .... Английский фунт иа квадратный дюйм .... Тонна иа квадрат- ный дюйм . . Обозначений Tr'iiit'.c ск1я атмо- сфер! 1,0000 1.0917-10—6 1.019?-IO"2 1,01972 0,00136 0.10000 1,0332 0,07031 157,483 Бар 9,81-10® 1.0000 10 000 13 332 08 066 1.013-106 68 947 1544-10® Пьем 98.0665 0,0001 1,0000 100,00 0,13332 9.8066 101,325 6.8947 15444.3 Гектопьем 0.98067 l0—6 0,01000 1,00000 0,00133 O.O9BO7 1,01325 0,06895 154,463 MM рт. CT. 735,56 0,00075 7,5006 750,06 1,0000 73,556 760,00 51,716 11584.0 м вод. CT. 10,000 1.0197-10—s 0,10197 10,1972 0,0136 1,0000 10,332 0,70306 1574,85 физическая атмосфера 0,96784 0,987-10-® 0.009969 0,99692 0,00132 0,09678 1,0000 0,06805 152.420 Ii 14,223 14,5- >0—6 0,1450 14,ЯМ 0.01934 1.4223 14,696 1,0000 2240 д 1 м и I 6.3498 10-® 6,475-10-9 6.475-10-® 6,475-10-’ 8,6326-10—® 6,3496-10-* 6,561-10-3 4.464-10—* 1,0000
русские «Ле** ат 4 ал /ял •ил рт. ст. я вод. ст. втл фуНТ/КВ. ДЮЙМ iw/кв. дюйм междуна- родные kO(em* at » Pt tipi mm Ид m н,о atm Ibt/sq. m. tfiq. In.
ПРИЛОЖЕНИЕ
2Я. Соотиовеиш» между енергетическмми едввяиама
1 Единит. Абсолютный КМЛО ДЖОуЛЬ Интерната малькый килоджоуль Интерна- циональная килокало- рия Килокало- рия Нацио- нального Бюро Стандартов США Килокало- рия 20“ (ОСТ) Килокало- рия 15° Интерна- циональ- ный кило ватт-час Кило грамм о метр Сило-час
Абсолютный килоджоуль ..... 1 0.99361 0,23884 0,23900 0,23912 0,23890 2,772-10—4 101,972 3,7767-Ю-4
Интернациональный килоджоуль 1.00014 1 0,23889 O.2390S 0,23917 0,23895 2,778-10—4 101,991 3,7774-10—4
Интернациональная килокалория 4,18685 4.18605 1 1,00066 1,00116 1,00026 1.1628.10-3 426,94 1,5813-10—3
Килокалория Насиоиалыюео Бюро Стандартов США 4,18400 4.18330 0,9993'1 1 1,00050 <1.99959 1,1620-10“3 426,66 1,5802-Ю-2
Килокалория 20“ (ОСТ)...... 4.1*2 4.181*1 0,99881 0,99950 1 0.99909 1,1614-Ю-3 426,45 1,5794-Ю-3
Килокалория 15* ......... 4.18580 4.18500 0,99975 1,00041 1.00O9I 1 1,1626-10~3 426,83 1,6809-10“3
РЬггерштконадьный килоеатт-час 3600.69 3600.00 860,00 860,56 860,99 860,21 1 36767 1,3599
Кнлограммо-метр ......... 9.80665-10“3 9.8О473.10-3 2,3423-10“3 2.3438-Ю-3 2,3450-Ю-3 2,3428-10“3 2.7286-10—® 1 3,7037-10“®
Сило-час ............. 2647,80 2647.30 632,41 632,83 633,14 632.57 0,73636 270 000 1
Примечание. В качестве единицы измерения количества тепла и СССР принята 20-грыусМЯ большая калория (ккал), которая практиче-
ски (с точностью до 0X12*1,) равна количеству тепла, необходимому для нагревания 1 кГ воды от 1УЛ до 20,5“ С при нормальном атмосферном дав-
лении (OCT ВКС 62S9).
ПРИЛОЖЕНИЕ
ПРЕДМЕТНЫЙ
АЛФАВИТНЫЙ
УКАЗА ТЕЛЬ
35 Справочник г. I Зак. I4M
A
Абак Декарта 315
Абразивный износ механизмов 439
Абсолютная погрешность предельная 65
Абсциссы 238, 249
Адъюнкты 115
Алгебра векторная 226
Алгебраические уравнения 118
— Решение приближенное по методу
Лобачевского 129
Алгебраические функции 90
Алфавит греческий 5
---- латинский 5
Альтернирование тензора 236
Американские меры — Перевод в метри-
ческие 536
Амплитуда колебаний 98
Анализ векторный 230
---- гармонический 312
Аналитическая геометрия 238—257
---- в пространстве 249
---- на плоскости 238
Аналитическая статика 366
Аналитические функции—Вычеты 200
— Разложение в степенные ряды 197
Аналитическое выражение функций
приближенное 305—313
Английская система мер 536
Английские фунты — Перевод в кило-
граммы 542
Антилогарнфмирование 78
Аполлония теорема 243
Аппаратура измерительная 415
Аппликаты 249
Арифметическая прогрессия 80
Арифметические действия основные 63
Арифметические ряды 1-го порядка 80
----порядка выше 1-го 81
Арифмометры 340
Арккосинус 99
Арксинус 99
Арктангенс 99
Архимеда спираль 274, 275
Архимедовы винтовые поверхности 299
Асимптоты 261
---- гиперболы 245
Астроида 281
Аффикс 84
Аффинные ортогональные тензоры —
см. Тензоры
35»
Б
Балансировка деталей статическая 422
Балансировочные машины — Схемы 424
Бернулли теорема 329
--- уравнение 208
Бесселевы функции 58. 222. 223, 311
Бесселя уравнение 221
--- формула 303
Биквадратные уравнения 121
Бино.м Ньютона 74—76
Биномиальные ряды 152
Биномиальный закон распределения ве-
роятности 323
Биномиальный коэффициент — Вычисле-
ние 74
— Нахождение 75, 80
— Таблицы 40
Биномы дифференциальные — Интегри-
рование 161
Бинормали 284
Биссектрисы углов, образованных двумя
прямыми—Уравнения 242
Блокирующие механизмы — см. Меха-
низмы блокирующие
Бочки — Объем 111
Бэта-функция 178
В
Валлиса формула 136
Вариаторы планетарные 511
Вейерштрасса признак 177
Вектор-функцин линейные 236
Векторная алгебра 226
Векторно-векторное произведение 229
Векторное исчисление 226—234
Векторное поле 231—234
Векторные линии 231
Векторные потенциалы 234
Векторные проекции 227
Векторные уравнения 230
--- плоскости 251
Векторные функции 230
Векторный анализ 230
Векторы 226—см. также Векторная
алгебра
— Вихри 233
— Вычитание 227
— Годографы 230
ВЕКТОРЫ
- 548 -
гигроскопический эффект
— Дивергенция 232
— Интегралы линейные 233
— Проекция 227
— Произведения 228, 229
— Расхождение 232
— Сложение 227, 228
— Уравнения 230
— Циркуляция 233
Векторы Дарбу 292
--- коллинеарные 226
--- компланарные 227
—— кручения 284
--- скорости во вращательном движе
нии 229
---скорости вращения трехгранника
292
Величины бесконечно большие 135
--- бесконечно малые 135
--- обратные чисел 12
--- ограниченные 134
---постоянные—Таблицы 6
— случайные 322; — Ожидание мате-
матическое 326; — Отклонения 327;
— Распределение 323
Веревочные кривые 366
Веревочные многоугольники 364, 365
Вероятностные характеристики 326
Вероятность — Распределение — Табли
ца 322; —Теория 321—335
--- статистическая 324
Вероятные ошибки 331
Вершина кривой 268
Вещественные числа — Действия 62
Винтовое движение 377
Винтовые колеса 496
Винтовые линии 286. 289
Винтовые механизмы — см. Механизмы
винтовые
Винтовые пары — см. Пары винтовые
Винтовые поверхности 298. 299
Винты 286, 287
---механизмов винтовых с соосным
расположением пар 491
Вихри вектора 233
Вогнутость кривых 264
Возвратные уравнения третьей степени
120
--- четвертой степени 121
Волновые уравнения 225
Восьмизвеиные кривошипно-кулисные
механизмы — см. Механизмы криво
ишпно-кулисныс восьмизвенные
Вращение вокруг неподвижной оси 376
---твердых тел 396
--- трехгранника — Вектор скорости
292
Выкрашивание х'стллостное 439
Выпрямляемое™. абака Декарта —
Условие 315
Выпуклость кривых 264
Вычерчивание кривой 265
Вычеты аналитических функций 200
Вычисления — Оценка точности 66
----подходящих дробей 72
----приближенные 67
----с малыми числами 69
----с числами, мало отличающимися
от единицы 69
---- элементов фигур 102—114
Вычислительные машины 343, 347, 348
Вычитание на арифмометре 340
---- на вычислительных машинах 344.
347
Г
Гайки винтовых механизмов с соосным
расположением пар 491
Гамма-функция 178
— Таблицы 41
Гармонические функции 234
Гармонический анализ 312
Гармонический ряд 149
Гармонический синтез 313
Гаусса закон 323
---- формулы 183
Геликоиды 294, 298
Геодезическая кривизна поверхности 296
Геодезические линии на поверхности 296
Геометрическая прогрессия 80, 81
Геометрическая статика 352
Геометрические места — Уравнения 240
Геометрическое значение уравнения 239
Геометрия — Приложение интегрального
исчисления 189
---- аналитическая 238—257
---- аналитическая в пространстве 249
---- аналитическая па плоскости 238
---- дифференциальная 258—300
Гиперболические параболоиды 256. 257
Гиперболические спирали 262, 276
Гиперболические точки поверхности 296
Гнперболнческне уравнения 122
Гиперболические функции—см Функ
ции гиперболические
Гиперболические цилиндры —Уравне-
ния 256
Гиперболоиды — Уравнения 256
----однополостные 257
Г иперботы — Построение 248; — Урав
нення параметрические 246;—Эле
менты 244 , 245. 248
---- равнобочные 246
----сопряженные 245
Гипоидные колеса 496
Гипоциклоиды 281
Гипоциклоиды-рулетты 280
Гироскопический момент 399
Гироскопический эффект 399
ГИРОСКОПЫ
— 549 — ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Гироскопы 398
Гистограмма распределения 325
Годограф вектора 230
Головки зубьев эвольвеитных зацепле-
ний 493
Голоморфные функции 198
Гоммеля редукторы 508
Гониометрия 94
Градиенты скалярных функций 231
Градусная мера — Переаод в радиан-
ную 39
Графики бесселевых функций 222, 223
----движения точки 371
---- обратных тригонометрических
функций 99
---- полиномов Чебышева 224
----синусоидальных величин—По-
строение 97
---- тригонометрических функций 88—
91, 94, 99, 101; — Построение 97.
98
Графическое интегрирование 183, 211,
516
Графостатика 364
Греческий алфавит 5
Гульдена — Паппа теорема 364
Гуляева редукторы 507
Гюльдена правила 111
д
Давление на соприкасающихся поверх-
ностях удельное 442
Даламбера признак сходимости и рас-
ходимости рядов 150
------ принцип 387, 391
Даламбера-Эйлера условия 196
Дарбу вектор 292
Датчики 415
---- электрические 416
Движение — Устойчивость 392
---- винтовое 377
---- вращательное — Кинематика —
Формулы 376
---- машины — Характерные периоды
425
----твердых тел 379, 381
----твердых тел около неподвижной
точки 398; — Уравнения 401
----твердых тел плоско параллельное
377, 398
Движение точки — График 371
---- криволинейное 372, 374, 384
—— относительное 374 , 388
---- переменной массы 385
---- прямолинейное 369, 370, 384
Двойные интегралы 184
Двойные ряды 312
Двухкулисные механизмы — см. Меха-
низмы двухкулисные
Двухползуниые механизмы — см. Меха-
низмы двухползунные
Декарта абак 315
Декартовы координаты — см. Коорди-
наты прямоугольные
Деление на арифмометре 341
---- на вычислительных машинах 345.
347
---- ца логарифмической линейке 338
---- отрезка в данном отношении 238
----сокращенное 69
Делители наименьшие чисел 9
Делительные окружности 493
Детали — Балансировка статическая 422
---- механизмов — Износ 438
Диаграммы кинетической энергии меха-
низма — Построение 426
---- распределения мощности сил тре-
ния по поверхностям 441
---- удельного скольжения 442
Дивергенция вектора 232
---- потенциального ноля 234
Динамика 382
---- механизмов и машин 424
---- системы 388
---- тела переменной массы 399
---- твердых тел 396
---- точки 383, 386
Директрнссы гиперболы 243, 24)4
---- эллипсов 243
Дирихле теорема 306
Дискриминант 147
---- квадратного трехчлена 88
Дискриминантная кривая 268
Дифференциалы полные 114, 145
---- функций 138, 139, 145
Дифференциальная геометрия 258—300
Дифференциальное исчисление 134—153
Дифференциальные биномы — Интегри
рование 161
Дифференциальные зубчатые меха-
низмы— см. Механизмы зубчатые
дифференциальные
Дифференциальные уравнения 206—225
— Решения приближенные 211
— Системы 213
— Способ последовательных решений
211
Дифференциальные уравнения в полных
дифференциалах 208
---- в частных производных 224
---- вращения 396
---- высших порядков 213
---- криволинейного движения точки
384
—— линейные 215, 217
---- неоднородные 216
---- обыкновенные высших порядков
213
----однородные 207
ДИФФЕРЕНЦИАЛЬНЫЕ ФУНКЦИИ
550 — ИЗВЛЕЧЕНИЕ КВАДРАТНЫХ КОРНЕЯ
---- 1-го порядка 208;—Система 214
---- 1-го порядка обыкновенные 206
----приводящиеся к уравнениям с по-
стоянными коэффициентами 216
•--- прямолинейного движения точки
384
---- с разделенными переменными 207
Дифференциальные функции распреде-
ления верой!кости 322
Дифференцирование — Формулы 139
----графическое 143
---- графическое диаграмм кулачковых
механизмов 516
----- неявных функций 146
---- определенного интеграла ло пара-
метру 174
---- функций 139
----функций комплексного перемен-
ного 196
—— функций многих переменных 143
---- численное 304
Дроби 62
----десятичные 62;—Изменения от
перенесения запятой 64; — Обра-
щение в непрерывные 71
---- непрерывные 7.1
----непрерывные конечные — Прибли-
женные значения 73
---- непрерывные цепные 71
----обыкновенные — Действия 64
---- периодические 62; — Обращение в
простые 64
----подходящие — Вычисление 72
----простые 62; — Обращение в деся-
тичные 64
---- смешанные 62
Дробноленейные функции 90
Дуги — Длина 37, 39, 190, 259, 283
---- зацепления 493
----окружности — Длина в градусах —
Перевод в радианы 39; — Спря
мление 281
---- ппостранствениых кривых — Длина
283
Дюймы — Перевод в миллиметры 537,
539
Е
«е* — Основание натуральных логариф
мои 135
— Тябчины величин, связанных с «е» 7
Единицы — Системы 383
----давлении — Перевод одних в дру-
гие 543
---- механические 382
---- энергетические — Перевод одних в
другие 544
Ермолова признак сходимости рядов
150
Ж
<g> («ж») ускорение силы тяжести 372,
383 — Таблицы величин, связанных
с <g» 8
Жироскопы — см. Гироскопы
Жордана лемма 201
Жуковского теорема 421
---- функция 205
Жуковского-Грюэ правило 399
3
Задирание деталей механизмов 439
Закон Гаусса 323
---- Кулона 357
----Ньютона 1-й 383
---- Ньютона 2-й 383, 386
---- Ньютона 3-й 383
----биномиальный распределения ве-
роятности 323
---- больших чисел 328
•---всемирного тяготения 384
---- действия и противодействия 383
---- инерции 383
---- независимости действия сил 384
---- об ускорении и силе 383
---- распределения случайной вели-
чины 322
-— сохранения механической энергии
387
Законы арифметических действий 63
---- трения 434
Затылование зубьев фасонных фрез —
Применение логарифмической спи-
рали 276
Зацепления зубчатые 493; — Момен»
трения 437
---- цевочные 495
---- циклоидальные 494
---- эвольвентные 493
Зубчатые зацепления — см. Зацепления
зубчатые
Зубчатые механизмы — см. Механизмы
зубчатые
Зубчатые пары 495, 511, 513
Зубчатые передачи 495
---- конические 496
----переключаемые 501, 502
---- плоско-цилиндрические 496
Зубчатые храповые механизмы — см
Механизмы храповые зубчатые
Зубья авольвентные — Корригирован»*
494
И
Извлечение квадратных корней и*
арифмометре 341
---- ня логарифмической линейк* 877
---- сокращенное 69
ИЗВЛЕЧЕНИЕ КУБИЧЕСКИХ КОРНЕЯ — 551
КАСАГЕЛЬНЫВ
Извлечение кубических корней на лога-
рифмической линейке 337
Измерительная аппаратура 415
Износ — Распределение по поверхности
трения 440
---- абразивный 439
----деталей в механизмах 438. 443
---- коррозионный 439
Изогональная траектория 271
Изоклины 211
Изолированные точки кривой 263
Импульс силы 386
----ударный 402
Инварианты 247
Инверсоры 466
----Липкина 466
Интеграл Стильтьеса—Вычисление 192
— Фурье 308
Интегралы — Среднее значение — Тео-
рема 173
---- Эйлера 178
---- вероятностен 324
----двойные 184
---- кратные 184
---- криволинейные 186
----линейные вектора 233
---- неопределенные—Свойства 154; —
Связь с определенными 173; —
Таблицы 154. 165
---несобственные 174; — Главное зна-
чение 177; — Сходимость и рас-
ходимость — Признаки Коши
176
---- несобственные равномерно сходя-
щиеся 177
Интегралы определенные 172
— Вычисление 182
— Дифференцирование по параметру
174
— Интегрирование по параметру 174
— Интегрирование по частям 173
— Переменные — Замена 173
— Связь с неопределенными 173
— Таблицы 178
Интегралы от биномиальных диффе-
ренциалов 161
----от иррациональных функций —
Таблицы 168
----от нечетных функций 174
---- от рациональных функций — Та-
блицы 165
---- ог трансцендентных функций —
Таблицы 170
---- от четных функций 174
---- по комплексным переменным 196
---- по поверхности 187
---- расходящиеся 175
---- сходящиеся 174
---- тройные 185
---- эллиптические— Таблицы 59
Интегральное исчисление 154—193
— Приложение к геометрии и механике
189
Интегральные функции распределения
вероятности 322
Интегральный косинус 164
Интегральный логарифм 164
Интегральный признак сходимости ря-
дов 150
Интегральный синус 164
Интеграторы 343
Интеграфы 343
Интегрирование 155
— Метод Остроградского 159
— Применение 189—191
— Предел верхний 172
— Предел нижний 172
Интегрирование графическое 183. 211,516
----дифференциальных биномов 161
---- иррациональных функций 160
---- определенного интеграла по пара-
метру 174
----по частям определенного инте-
грала 173
---- рациональных функций 156
---- трансцендентных функций 161
---- численное 304
---- численное дифференциальных
уравнений 212
Интерполирование 303
---- квадратическое — Поправки 36
Интерполяционная поправка — Вычисле-
ние 32
Интерполяционная формула Лагранжа
304
Интерполяционные формулы — Остаточ-
ные члены 304
Интерполяция линейная — Пропорцио-
нальные части 35
Иррациональные функции—Интегриро-
вание 160
Иррациональные числа 63
Истирание деталей механизмов 438
Источники точечные 234
Исчисление дифференциальное 134—153
---- разностное 301—304
---- тензорное 234
Итераций метод 127'
К
Канонические уравнения поверхностей
2-го порядка 255
----прямой 253
Карно — Остроградского теорема 403
Касательные 259; — Длина 260; — коэф-
фициент угловой 260
---- к пространственной кривой 283
---- плоскости к поверхности 294; —
Уравнения 295
КАССИНИ ОВАЛ
- 552 —
КОСИНУСЫ
Кассини овал 265
Качение окружности по окружности 272
—— плоскости по плоскости 271
---- прямой по окружности 272
Квадрат разности 74
---- скалярный вектора 228
----суммы 74
Квадратическая погрешность средняя
305
Квадратическое интерполирование —
Поправки 36
Квадратическое отклонение среднее 305
Квадратные меры — Перевод одних в
другие 542
Квадратные уравнения 119
Квадратные функции 88
Квадраты наименьшие—Способ 330.
332
---- чисел 12
Килограммы — Перевод в английские
фунты 542
Кинематика 369
---- вращательного движения—Фор-
мулы 376
----кулачковых механизмов 515, 518
----плоских механизмов 413
---плоских шарнирных механизмов
466, 458
---- прямолинейного движения точки —
Формулы 370
---- твердых тел 375
Кинематические пары — Классификация
407;—Структура 407
----геометрически замкнутые 409
---- кулачкового типа 514
---- плоских механизмов — Давление —
Определение 421
----с промежуточными деформируе-
мыми телами 412
----с промежуточными телами качения
412
Кинематические схемы механизмов 413
Кинематический момент 389, 397
Кинетическая энергия — см. Энергия
кинетическая
Кинетостатика плоских механизмов 418,
456
---- точки 387
Клеро уравненне 209
Клинья регулировочные направляющих
410
---- сферические 111
Колебания маятников — Уравненне диф-
ференциальное 397
Колеса винтовые 496
----гипоидные 496
---- маховые—Момент инерции—On
ределение 428
Количество движения 386. 388, 402
Коллинеарные векторы 226
Кольцевой сектор — Площадь 107
Кольцо круговое — Площадь 106
Компланарные векторы 227
Комплексные переменные — Интегралы
196
— Функции 194—205
Комплексные ряды 194, 195
Комплексные числа 84; — Действия 62
----бесконечно малые 194
Конволютные винтовые поверхности 299
Конечные приращения — Формулы 141
----для функции нескольких перемен-
ных— Формулы 145
Конечные разности простейших функ-
ций 301
Конечные ряды числовые 80. 82
Конические поверхности 298
Конические сечения 249
Коноиды 294
Контакт изношенных пар 441
Конус трения 357, 434
Конусы — Уравнения 256, 298
---- круглые 109
---- усеченные ПО
----усеченные эллиптические 111
Конформные отображения 201
Конхоиды 273—276
Координаты — Начало — Перенос 250;—
Оси — Поворот 250; — Преобразова-
ние 239
---- вектора 228
---- косоугольные 238
---- обобщенные 368
---- полярные 239
---- прямоугольные (декартовы) 238,
249; — Преобразование 250
----точки пересечения прямых 242
----центра тяжести — Вычисление ин-
тегрированием 191
Копировальные устройства 470
Копры маятниковые 406
Копыта цилиндрические 109
Корни квадратные—Извлечение ва
арифмометре 341; — Извлечение на
логарифмической линейке 337
---- квадратные чисел 12; — Извлече-
ние сокращенное 69
-—- кубические — Извлечение на лога-
рифмической линейке 337
---- кубические чисел 12
----трансцендентных уравнений дей-
ствительные 122
---- чисел — Отделение 123; — Фор-
мулы 75
Коробки передач 499—501
---планетарные 510
Корригирование эвольвентных зубьев
494
Косинус интегральный 164
Косинусы — Логарифмы 48, 49
КОСОУГОЛЬНЫЕ КООРДИНАТЫ
—553—
ЛЕММА ЖОРДАНА
— Таблицы 44, 45
— Теорема 102. 114
Косоугольные координаты 238
Косоугольные треугольники — Решения
113
Котангенсы — Логарифмы 50, 51
— Таблицы 46, 47
Коши признак сходимости рядов 149,
150
----признак сходимости и расходимо-
сти несобственных интегралов 176
— теорема 197. 210
----формула 141
Коши — Адамара формула 195
Коэффициент Фурье обобщенный 305
----биномиальный — Вычисление 74; —
Нахождение 75. 80;—Таблицы 40
---- вариации 326
----восстановления 402
---- изменчивости 326
---- мгновенного трения 402
---- неравномерности врашеняя звена
приведения 427
----• перекрытия 493
---- полезного действия винтовой пары
490
---- полезного действия механизма —
Определение 429
---- потерь в механизмах 429
----трения 434; — Значения 436
---- трения для подвижных соединений
---- трения качения для катка на пло-
скости 437
----трения скольжения 357; — Значения
---угловой касательной 260
----устойчивости на опрокидывание
369
---- эпициклоиды угловой 280
Кратные интегралы 184
Кривизна линии 266
— поверхности 295
---- пространственной кривой 284
Криволинейные интегралы 186
Криволинейные шкалы 315
Кривошипно-коленные механизмы — см.
Механизмы кривошипно-коленные
Кривошипно-коромысловые шестизвен-
ные механизмы—см. Механизмы
плоские шарнирные шестизвенные
кривошипно-коромысловые
Кривошипно-кулисные механизмы — см.
Механизмы кривошипно-кулисные
Кривошипно-рычажные механизмы — см.
Механизмы кривошипно-рычажные
Кривошипно-шатунные механизмы — см.
Механизмы кривошипно-шатунные
Кривые 258 —см. также по их назва-
ниям, например: Дискриминантное
кривая. Кусочногладкие кривые;
Нецентральные кривые; Простран-
ственные кривые; Центральные кри-
вые: Циклоидальные кривые
— Вершины 268
— Выпуклость 264
— Вычерчивание 265
— Исследование 265
— Натуральное уравнение 268
— Построение 262
— Развертка 269
— Соприкосновение 266
— Точки особые 262. 263
— Траектории 271
— Эволюта 269
Кривые веревочные 366
--- второго порядка 242, 247
--- плоские 258
Кристоффеля — Шварца функция 205
Критерий Сильвестра 369
Круги — Периметр 106
— Площадь 12, 106
— Сегменты—Таблицы 37
— Элементы — Таблицы 37
Круговое кольцо — Площадь 106
Круговой сегмент — Площадь 107
Круговой сектор — Площадь 107
Круговые функции 91; — Таблицы 52
Кручение пространственной кривой 284
Куб разности 74
---суммы 74
Кубические меры — Перевод одних в
другие 542
Кубические уравнения 119
Кубы 108
--- чисел 12
Кулачково-коромысловые механизмы —
см. Механизмы кулачково-коромысло-
вые
Кулачково-ползунные механизмы —см
Механизмы кулачково-ползунные
Кулачковые механизмы —см. Меха
низмы кулачковые
Кулона закон 357
Кусочногладкие кривые 138
Л
Лагранжа уравнение 209, 391
---формула 141, 304
Лагранжа — Дирихле теорема 368
Лапласа оператор 234
---уравнение 196, 225, 234
--- функция — График 324
Лапласоаые преобразования — Таблица
219
Латинский алфавит 5
Лежандра функции 223
• Лейбница признак сходимости рядов
150
Лемма Жордана 201
ЛЕМНИСКАТЫ
— 554 —
МЕХАНИЗМЫ
Лемнискаты—Точки узловые 263
Линейки логарифмические — Правила
пользования 336
Линейная интерполяция—Пропорцио-
нальные части 35
Линейные меры — Перевод одних в
другие 540
Линейные системы — Решение 115
Линейные уравнения — Система 117, 128
----дифференциальные 215;—Система
217
Линейные функции 87
Линейчатые поверхности 298
Линин — Кривизна 266
— Образование при движении плоско-
сти по плоскости 271
— Семейство 268
Линин винтовые 286. 289
---- геодезические на поверхности 296
---- кривые плоские 258
----однородные — Центр тяжести 359
Липкина инверсоры 466
Липшица условие 210
Лобачевского метод приближенного ре-
шения алгебраических уравнений 129
Логарифм интегральный 164
Логарифмирование 78
Логарифмические линейки — Правила
пользования 336
Логарифмические номограммы 317
Логарифмические спирали — см. Спи-
рали логарифмические
Логарифмические уравнения 122
Логарифмические функции 91
Логарифмические шкалы 314
Логарифмический шаблон 314
Логарифмы 76
Логарифмы десятичные 77
---- постоянных величин — Таблицы б
---- тригонометрических функций 48
----факториалов — Таблицы 41
---- чисел 12
Логарифмы косинусов 48, 49
---- котангенсов 50, 51
---- натуральные 77
---- натуральные чисел — Таблица 42
---- синусов 48. 49
----тангенсов 50. 51
---- факториалов — Таблицы 41
Лорана ряд 198
Лучевые номограммы 316
Лучи — Уравнения полярные 242
---- винтов 287
Ляпунова теорема 329, 368
м
.Маклорена формула 142
Мальтийские механизмы—см. Меха-
низмы мальтийские
Мантисса логарифма 77
Маркова теорема 329
Масса тела — Вычисление интегрировав
нием 191
Массы вращающиеся — Уравновешива
ние 421
---- маховые — Расчет 427
---- уравновешивающие — Определение
графическое 423
Математические маятники 385
Математические обозначения 1—61
Математические приборы 336—348
Математическое ожидание случайной
величины 326
Матрица квадратная 115
Маховые колеса — Момент инерции —
Определение 428
Машины вычислительные 343, 347, 343
Маятники математические 385
---- физические — Колебания — Урав-
нение дифференциальное 397
Маятниковые копры 406
Медиана 327
Международная метрическая система —
см Метрическая система междуна-
родная
Мера градусная — Перевод в радиан
кую 39
Меры — Перевод одних в другие 537
---- веса — Перевод в другие 542
---- веса английские 536
---- веса международные 533, 534
----веса русские старые 535
---- длины английские 536
---- длины международные 533
----длины русские старые 535
---- емкости английские 536
----емкости международные 534
----емкости русские старые 535
---- квадратные — Перевод одних »
другие 542
----кубические — Перевод одних •
другие 542
----линейные — Перевод одних в дру-
гие 540
---- массы английские 536
---- массы международные 534
----массы русские старые 535
---- объема английские 536
----объема международные 534
----объема русские старые 535
---- поверхности английские 536
---- поверхности международные 534
---- поверхности русские старые 535
Метрическая система междупародн-к
533
Метры — Перевод в ярды 540
Механизмы — Детали — Износ 438
— Детали изнашивающиеся—У слоя»»
работы 440
МЕХАНИЗМЫ БЛОКИРУЮЩИЕ
555 _ МЕХАНИЗМЫ ПЛОСКИЕ ШАРНИРНЫЕ
— Динамика 424
— Классификация 407, 413
— К п д. 431
— Справочные данные 451—531
— Структура 407, 412
— Трение 433
Механизмы блокирующие 529—531
Механизмы винтовые с компенсацией
ошибок по шагу ходового винта и
его тепловых деформаций 492
----с несколькими степенями свободы
492
---- с соосным расположением кине-
матических пар 488; — Перемеще-
ние скоростей и касательных уско
рений — Построение плана 489
---- с соосным расположением пар —
Ошибка положения 491
---- с соосным расположением пар
двухзвенные 480
---- с соосным расположением пар
трехзвенные 489; — Типы 490
Механизмы двухкулисные 481
----двухползунные 482
Механизмы зубчатые 492
----дифференциальные 503, 508
---- для преобразования равномерного
вращательного движения — Схема
512
---- непереключаемые 498
---- неуправляемые 503; — Типы 504
---- переключаемые 498
---- планетарные 503
---- планетарные включения 508. 509
---- реверсивные—Типы 502
----с неподвижными осями колес 497
---- с подвижными осями колес 502
—— управляемые 508
---- храповые 527
Механизмы инверсоров 466
---- кривошипно-коленные 487
----кривошипно-коромысловые — Раз-
меры — Определение 460
Механизмы кривошипно-кулисные —
Ползуны — Скорость и ускорение —
Изменение 483; — Характеристика
484
---- восьмизвенные 484
----с вращающейся кулисой 480, 481
----с качающейся кулисой 480
----с поступательно движущейся ку-
лисой 481
---- шатунные шеетизвенные 484
---- шестизвенные 482
Механизмы кривошипно-рычажные 487
Механизмы кривошипно-шатунные
474: — Диаграмма 479; — П >аиы ско-
ростей и ускорений 477; — Разме-
ры — Определение 4бп
---- о прицепным шатуном 487
--- смешенные 477; — Анализ кинема-
тический 479; — Характеристика
478
--- центральные 474; — Характеристи-
ка 477
Механизмы кулачково-коромысловые
520, 524
Механизмы кулачково-ползунные 520.
523
Механизмы кулачковые 513
— Анализ кинематический 515
— Диаграммы—Графическое диффе-
ренцирование и интегрирование 516
— Кинематика 515
— К- п. Д 520, 522
— Проектирование 522
— Профилирование 518
— Скорость и ускорение—Опре деле
ине 520, 521
— Углы давления 520
— Углы передачи 520
Механизмы кулачковые плоские трех-
звенные 517; — Кинематика 518
---мальтийские 525;—Расчетные за-
висимости 526
---пантографов 467, 469
--- планетарные реверсивные 509, 510
Механизмы плоские — Анализ кинема-
тический 414
— Звенья — Силы инерции — Определе-
ние 418
— Исследование экспериментальное
414
— Кинематика 413
— Кинематические пары — Давление —
Определение 421
— Кинетостатика 418
— Ошибки 445
— Перемешения — Измерение 416
— Преобразование 449
— Проектирование 447
— Силы прнзеденные — Определенна
421
— Скорость — Измерение 418
— Ускорение — Измерение 418
Механизмы плоские кулачковые трех-
звенные 517; — Кинематика 518
--- с вращательными и поступатель-
ными парами 470. 482
---с поступательными парами —
Уравнения векторные для построе-
ния планов скоростей и ускорений
472
Механизмы плоские шарнирные 453
— Кинематика 456
— Кинетостатика -*56
— План скоригтей — Построение 4бв
— Ра «меры — Определение 459
Механизмы плоские iti-'риириыв анти
параллелограммов 465
МЕХАНИЗМЫ ПЛОСКИЕ ШАРНИРНЫЕ— 556 —
НОМОГРАММЫ
----двухкривошипиые — Передаточное
отношение — Изменение 464; —
Характеристика 464
---- многозвенные 465
---- направляющие 466
---- с остановами 466
Механизмы плоские шарнирные четы-
рехзвенные 457
— Кинематика 458
— План скоростей 458
— Типы 462
Механизмы плоские шарнирные шестн-
звенные — План сил — Построение
457; — Планы скоростей и ускоре
ннй 455
—— кривошипно-коромысловые 465
Механизмы ползунно-коленные 487
—— ползунно-кулисные 481
---- реверсивные планетарные 509, 510
---- роликовые храповые 528
---- рычажные с качающимся цилин-
дром 488
----с одними поступательными парами
451
----трехзвенные 451
Механизмы храповые 527; — Размеры
529
---- зубчатые 527
---- колодочные 529
---- роликовые 528
----с кулачками или эксцентриками
529'
---- фрикционные 528
----фрикционные пружинные 529
Механика — Приложение интегрального
исчисления 189
----теоретическая 352—406
Механические величины — Измерение
415
Механические единицы 382
Мещерского уравнение 386
Микрометры 489
Миллиметры — Перевод в дюймы 539
Миноры определителей 115
Мнимые эллипсоиды — Уравнения 255
Многозначные функции 99
Многоугольник сил 353
Многоугольники — Площадь 106
---- веревочные 364; — Применение 365
----правильные 1D4;—Элементы —
Таблица значений 105
----силовые 364
Мода 327
Модуль десятичных логарифмов 77
---- зацепления 493
Момент гироскопический 399
---- инерции 392;-—Определение инте-
грированием 191
----инерции маятника — Определены*
897
---- инерции механизма приведенный
426
---- инерции однородных тел 393
---- кинематический 389; — Уравнение
397
---- количества движения — Теорема
403
---- количества движения точки 386
----трения — Значение 436
---- трения в зубчатых зацеплениях
437
----трения в подшипниках 437
Моменты инерции единичные 419
---- пар 354
---- сил 354
Монжа обозначения производных функ-
ций многих переменных 144
Моногенные функции 196
Монотонные функции 137
Мощность 367
---- холостого хода механизмов 431
Муавра формула 86
Н
Наименьшие делители чисел 9
Направляющие для прямолинейного
движения 409
---- кругового движения 410
Натуральные логарифмы чисел—Та-
блица 42
Неоднородные дифференциальные урав-
нения 216
Неопределенности — Раскрытие 142
Неопределенные интегралы 154. 165, 173
Непрерывные дроби 71, 73
Непрерывные функции 136
Несобственные интегралы 174, 176, 177
Неубывающие функции 137
Неуправляемые зубчатые механизмы —
см Механизмы зубчатые неуправляе-
мые
Нецентральные кривые 247
Неявные функции — Дифференцирова-
ние 146
Ннкомеда конхоида 273
Ножки зубьев эвольвентных зацепле-
ний 493
Номограммы для определения скоро-
стей и ускорений в кулачковых ме-
ханизмах 521
---- г (зет) 319
---- из выравненных точек 318
----логарифмические 317
----лучевые 316
---- на параллельных шкалах 319
---- нулевого жанра 318
---- паспорта токарных станков 317,
319
НОМОГРАФИИ ПОРЯДОК УРАВНЕНИЯ— 557 —
ПАРАБОЛИЧЕСКИЕ СЕГМЕНТЫ
----с четырьмя переменными — Пи-
строение 319
----сетчатые 315, 316
----скорости резания 316, 317, 319
Номографический порядок уравнения
318
Номография 314—320
Нормали 259; — Длина 260, 267
---- к поверхности 294;— Уравнения
295
---- пространственной кривой 283
---- эвольвенты окружности — Длина
278
Ньютона бином 74—76
---- закон 1-й 383
------ закон 2-й 383, 386
---- закон 3-й 383
---- формулы 303, 304
Ньютона — Лейбница формула 173
О
Обобщенные координаты 368
Обобщенные силы 36S
Обозначения математические 1
---- Монжа производных функций мно
гих переменных 144
---- условные 1
Обратные величины чисел 12
Обратные функции 91, 99. 101, 196
Объем генеральной совокупности 328
---- однородный — Центр тяжести 359
----тела — вычисление 108; — Вычнс
ление интегрированием 190
----тела вращения 111
Обыкновенные уравнения дифференци-
альные 1-го порядка 206
Овал Кассини 265
Огибающая 268
Огива 326
Ограниченные величины 134
Однозначные функции — Особые точки
199
Однополостные гиперболоиды 257
Однородные уравнения дифференциаль-
ные 207
Ожидание математическое случайной
величины 326
Округление приближенных чисел 65
Окружности — Деление на п частей 105
— Длина 12
— Дуги — Длины в градусах — Пере-
вод в радианы 39
----Спрямление 281
— Качение по окружности 272
— Качение по прямой 272
— Уравнения 240. 242, 243
— Числовые зависимости 104
— Эвольвента 270, 272, 276—278
Окружности делительные 493
Окружность соприкасающаяся 266
---- трения 435
Оператор Лапласа 234
---- набла 231
Операционные исчисления 218
Определители 115
— Вычисление 116
— Свойства 116
Определенные интегралы — см Инте-
гралы определенные
Опрокидывание — Устойчивость 369
Ординаты 238, 249
----веревочных многоугольников 366
Орт бинормали 284
---- нормали пространственной кривой
284
Ортогональная траектория 271
Орты 250
---- главных нормалей — Производные
292
Оси координат — Поворот 250
Особые точки 199, 262, 263
Остаточные погрешности 331
Остроградского метод интегрирования
159
---- теорема 233
---- уравнение 403
---- формула 188
Остроградского — Г амильтона принцип
392
Отделение корней 123
Отклонение случайной величины 327
------ среднее квадратическое 305
Относительная погрешность предельная
65
Отображения конформные 201
Отрезки — Деление в данном отноше-
нии 238
---- полярные 260
Отрицательные числа — Действия 63
Оценка частости 330
Ошибка средняя квадратическая сред-
невзвешенного 332
Ошибки — Измерение 331, 332
---- вероятные 331
---- кажущиеся 331
----пантографа — Определение 469
---- плоских механизмов 445
---- положения винтовых механизмов
491
П
Пантографы 467; — Ошибки — Опреде-
ление 469
---- параллелограммные 468
Паппа — Гульдена теорема 364
Параболические сегменты — Плошало
107
ПАРАБОЛИЧЕСКИЕ ТОЧКИ ПОВЕРХН 558 —
ПОДНОРМАЛИ
Параболические точки поверхности 295
Параболические цилиндры — Уравнения
256
Параболоиды—Уравнения 256, 257
---- вращения 111
----гиперболические 256. 257
Параболы — Построение 246, 249
— Уравнения параметрические 247
— Элементы 246—249
Параллелепипед сил 353
Параллелепипеды прямоугольные 108
Параллелограмм сил 353
Параллелограммные пантографы 468
Параллелограммы — Площадь 106
Параллельность прямых — Услоаия 242
Параметризация 259
Параметрические уравнения — см.
Уравнения параметрические
Лары винтовые — К. п. д. 490
---- зубчатые 495, 511, 513
---- качательного движения 411
---- кинематические — см. Кинематиче-
ские пары
---- сил 355
---- шаровые 411
Паскаля треугольник 75 «
Передачи зубчатые — см. Зубчатые пе-
редачи
---- реечные — см. Реечные передачи
---- червячные — см. Червячные пере-
дачи
Переменные комплексные — см. Ком-
плексные переменные
Перемещение силы параллельное 356
Перемещения возможные — Принцип
368
Пересечение трех прямых — Условия
242
Перестановки 79, 115
Периметры плоских фигур — Вычисле-
ние 106—см. также названия фи-
гур с подрубрикой — Периметр, на-
пример: Круги — Периметр
Период синусоидальной функции 98
----функции 92
Периодические дроби 62, 64
Периодические функции 91
Перицнклонды 281
Перпендикулярность прямых — Условия
242
я («пи»)—Значение 63
— Таблицы величин, связанных с я 6
Пирамиды 108
Пифагора теорема 103
Планетарные вариаторы — см. Вариа-
торы планетарные
Планетарные зубчатые механизмы — см
Механизмы зубчатые планетарные
Планетарные коробки передач — ем.
Коробки передач планетарные
Планетарные редукторы — см. Редук-
торы планетарные
Планиметры 342
Планки регулировочные направляющих
410
Плоские механизмы—см. Механизмы
плоские
Плоские кривые 258
Плоскости — Движение по плоскости —
Образование линий 271:—Уравне
ния 251
--- нормальные к пространственной'
кривой 283
---параллельные—Уравнения 256
---пересекающиеся — Уравнения 256
---соприкасающиеся 284
---спрямляющие 284
Плотность вероятности 322
Площади фигур 106, 189, 190 — см.
также под названием фигур с под-
рубрикой — Площадь, например:
Круги — Площадь; Параболические-
сегменты — Площадь; Параллелограм-
мы — Площадь; Ромбы — Площадь;
Треугольники — Площадь
Пневматические прессы с качающимся'
цилиндром 488
Поверхности — Кривизна 295
— Линейный элемент 294
— Образование линиями 297
— Сечение 296
— Теория 293
— Точки — Классификация 296
— Уравнения 293
Поверхности винтовые 298, 299
--- вращения 298
---второго порядка — Вид — Опреде-
ление 255;—Теория 255; — Урав-
нения канонические 255
--- конические 298
--- кривые — Площадь — Вычисление
интегрированием 190
--- линейчатые 298
---- однородные—Центр тяжести 359-
------------------------------------ развертывающиеся 297
---тел—Вычисление 108
--- тел вращения III; — Площадь —
Вычисление интегрированием 190
--- уровня 231
--- центральные — Уравнение — Пре-
образование 256
---.цилиндрические 298
--- эвольвентные винтовые 299
Погрешности остаточные 331
--- приближенных чисел 65
Погрешность предельная абсолютная 63-
--- предельная относительная 65
--- средняя квадратическая 305
Подкасательные 260
Поднормали 260
ПОДСТАНОВКИ ЭНДЕРА
— 559 —
ПРЯМАЯ
Подстановки Эйлера 160
Подходящие дроби — Вычисление 72
Подшипники — Момент трения 437
Показательные уравнения 121
Показательные функции 91, 195, 302; —
Таблицы 52
Поле векторное 231—234
—— направлений 211
---- скалярное 230
---- соленоидальное 234
Ползунно-коленные механизмы — ем.
Механизмы ползунно-коленные
Ползунно-кулисные механизмы — см.
Механизмы ползунно-кулисные
Ползуны кривошипно-кулисных меха-
низмов — Скорость и ускорение —
Изменение 483
Полигоны распределения 325
Полиномы Чебышева 224
Полные дифференциалы 144, 145
Полодии 271
Положительные числа — Действия 63
Полюс однозначной функции 199
Полярные координаты 239
Полярные отрезки 260
Понтоны—Объем 109
Поправки для квадратического интер-
полирования 36
---- интерполяционные — Вычисление
32
Последовательность числовая — Предел
134
Постоянная Эйлера С 135
Постоянные величины—Таблицы 6
Потенциалы векторные 234
Потенциальная энергия 367
Потенцирование 78
Потери в механизмах 429
Поток векторного поля 232
Правила Гюльдена 111
Правило Жуковского-Грюэ 399
Предел функции 134
------ числовой последовательности 134
Предельная теорема 328
Предельные погрешности 65
Пределы—Теоремы 135
—— важнейшие 135
---- определенного интеграла 172
---- последовательности — Признаки
существования 135
Преобразование координат 239, 250
Преобразование уравнения параболоида
к каноническому виду 257
---- параболы 248
---- центральной поверхности к кано-
ническому виду 256
---- центральных линий к канониче
скому виду 248
Преобразования лапласовы — Таблица
219
Прессы пневматические с качающимся
цилиндром 488
Прецессия регулярная 399
Приближенные вычисления без точного
учета погрешностей 67
Приближенные числа — Округление 55
— Погрешности 65
Приборы математические 336—348
Призматоиды 108
Призмы 108
--- усеченные 108
Признак Вейсрштрасса 177
---Даламбера 150
---Ермакова 150
--- Коши 149, 150, 176
---Лейбница 150
--- сходимости рядов 149, 150
--- тензорный системы величин ац
236
Принцип Даламбера 387, 391
--- Остроградского — Гамильтона 392
--- Римана — Шварца 205
--- возможных перемещений 368
--- возможных перемещений для
удара 403
Приращения конечные — Формулы 141.
--- для функции нескольких перемеп
ных —Формула 145
Прогрессия арифметическая 80
—— геометрическая 80, 81
Проективные шкалы 314
Проектирование кулачковых механиз-
мов 522
--- плоских механизмов 447
Проекции 104
--- векторные 227
Произведение векторов 228, 229
Производные сложных функций 138. 145
--- функций 137
Пропорции 82
Пропорциональные части для линейной
интерполяции 35
Простейшие функции 301
Пространственные кривые 282
— Дуги —Длина 283
— Кривизна 284
— Кручение 284
— Нормали 283
— Расположение вблизи данной точки
292
— Уравнения 285
— Формулы 285, 288
Простые дроби 62
— Обращение в десятичные 64
Профилирование кулачковых механиз-
мов 518
Проценты 84
Прямая — Качение по окружности 272
— Пересечение с плоскостью 253
— Уравнения 240—242, 252, 863
ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ — S60 —
РЯДЫ
Прямоугольные координаты — см. Коор-
динаты прямоугольные
Прямоугольные параллелепипеды 108
Прямоугольные треугольники — Реше
ння 112
Прямые — Точки пересечения — Коор
дннаты 242
— Условия параллельности 242
— Условия перпендикулярности 242
Птолемея теорема 104
Пуассона теорема 329
---- уравнение 225
Пучок прямых — Уравнения 242
Р
Работа 366; — Вычисление графическое
367
---- иа конечном пути 367
---- силы тяжести '367
Равнобочные гиперболы 246
Равновесие—Устойчивость 368
----пар 356
---- сил, приложенных к твердому телу
353
---- систем сочлененных 356
----системы с трением 357
---- трех непараллельных сил в пло-
скости 354
Равномерные шкалы 314
Радиус кривизны 266
---- гиперболы 245
----логарифмической спирали 267. 276
---- параболы 246
---- поверхности 296
---- пространственной кривой 284
---- спирали Архимеда 275
----• циклоиды 267
Радиус-вектор точки 228
Радиусы кручения 284
Развертка кривой 269
Развертывающиеся поверхности 297
Разложение сил 353, 354
----силы инерции 387
Разложение функций — Случаи специ-
альные 307
----в бесконечные ряды 151
---- в ряды по бесселевым функциям
311
---- в ряды по полиномам Чебышева
311
----в ряды степенные 152
----в ряды Фурье 308
Размерности — Правило 382
Размещения 79
Разности конечные простейших функ-
ций 301
Разностное исчисление 301—304
Разность квадратов 74
— кубов 74
---- тензоров 235
Распределение — Гистограмма 325
— Полигон 325
— Широта 326
Распределение Стьюдента 328; — Та-
блица функции S(s) 334
—— вероятности — Дифференциальная
функция 322
----скоростей 378, 380
---- случайных величин нормальное —
График интегральной функции 324
---- статистическое 325
----ускорений .379, 380
Расстояние между точками 238
----от точки до прямой 241
Расходящиеся интегралы 175
Рациональные функции 87, 90. 156
Реакции опорные — Определение — При-
менение веревочного многоугольника
365
Ребро возврата 297
Реверсивные зубчатые механизмы — см.
Механизмы зубчатые реверсивные
Регулировочные клинья направляющих
410
Pcrv т;:ровояпые планки направляющих
410
Редукторы Гоммеля 508
---- Гуляева 507
---- планетарные 504; — К. п. д.—
Формулы 505; — Передаточные
отношения — Формулы 505, 506
Реечные передачи 497
Резольвенты 120
Ренкина способ спрямления дуги окруж-
ности 282
Решение треугольников 102, 112—114
---- уравнений 115—133
Рикката уравнение 208
Римана-Шварца принцип симметрии 205
Робертса — Чебышева теорема 461
Ролля теорема 141
Ромбы — Плошадь 106
Ротор вектора 233
Рулетты 271
— Уравнение 272
Рунге схема вычисления коэффициентов
313
Рунге — Кутта метод решения диффе-
ренциальных уравнений 212
Рычажные механизмы с качающимся
цилиндром — см. Механизмы рычаж-
ные с качающимся цилиндрам
Ряд Лорана 198
----Тэйлора 197, 198
Ряды — Применение в решении диффе-
ренциальных уравнений 211
---- арифметические 80, 81
---- биномиальные 152
С ПОСТОЯННАЯ ЭЙЛЕРА
- 551 -
СЛУЧАЙНЫЕ величины
---- гармонические 149
---- двойные 312
---- для сравнения 149
---- комплексные 194, 195
---- конечные числовые 80. 82
---- функциональные 151
---- Фурье обобщенные 305
----Фурье тригонометрические 306
----числовые — Признаки сходимости
149, 150; — Сходимость 149
С
С постоянная Эйлера 135
Самоприкосновения точки 263
Свертывание тензоров 236
Связи 352
Сегменты кругов — Площадь —Таблицы
37
----круговые — Площадь 107
----параболические — Площадь 107
----шаровые НО
Секторы кольцевые — Площадь 107
—— круговые — Площадь 107
----шаровые ПО
----эллиптические — Площадь 107
Семейство кривых — Дискриминантная
линия 269; — Огибающая 269
---- линий 268
----окружностей — Огибающая 269;
Уравнение 269
---- поверхностей огибающее 297
Сетки функциональные 315
Сетчатые номограммы 315, 316
Сечение поверхности 296
Сечения конические 249
Сила -инерции — Разложение 387
---- трения 357
----тяжести 367
Силовой многоугольник 364
Силовой план 364
Силовые линии векторного поля 231
Силы — Перемещение параллельное 356
— Разложение 353. 354
— Сложение 353, 364
— Уравновешивание 366
Силы инерции звеньев плоских меха-
низмов—Определение 418
---- непараллельные — Равновесие в
плоскости 354’
•---обобщенные 368
---- параллельные — Сложение 354
---- приведенные плоских механизмов
— Определение 421
---- приложенные к твердому телу —
Условия равновесия 358
---- уравновешивающие плоских меха-
низмов — Определение 421
Сильвестра критерий 369
33 Свряябчиик т. I 3«к. 1464
Симметрирование тензора 236
Симпсона формула 182
Синтез гармонический 313
---- механизмов 459, 460
Синус интегральный 164
Синусоидальные величины 97, 93
Синусоидальные функции—Период 98
Синусы — Логарифмы 48, 49
— Таблицы 44, Фэ
— Теорема 102, 114
Система координат сферическая 251
---- координат цилиндрическая 251
----линейная однородная с постоян-
ными коэффициентами 217
---- мер американская — Перевод в
метрическую 536
----- мер английская 536
---- мер метрическая международна»
533
---- мер старая русская 535
---- п дифференциальных уравнений
1-го порядка 214
---- сил — Приведение к заданному
центру 356
---- сил произвольная 356
Системы—Динамика 388
----дифференциальных уравнений 213
----дифференциальных уравнений ли-
нейных 217
---- единиц 383
---- линейных уравнений 117; — Реше-
ние приближенное 128
---- сил с трением 357
Скалярное поле 230
Скалярный квадрат вектора 228
Скаляры 226
Скалярные функции — Градиенты 23!
Скорость 370. 373, 376, 377, — Распре
деление 378, 380; — Сложение 375
---- звена приведения 427
---- механизмов — Определение 425
---- плоских механизмов — Измерение
418
---- резания — Номограммы логариф-
мические 316. 317, 319
Сложение векторов 227, 228
---- вероятностей — Теорема 321
---- двух параллельных сил 354
----на арифмометре 340
----пл вычислительных машинах 344.
347
---- пар 355
----сил 353, 364
---- скоростей 375
---- ускорений 375
Сложные функции — см Функции
сложные
Слой шаровой ПО
Случайные величины — см. Величины
случайные
случайные события
- 562 -
ТЕОРЕМА
Случайные события — см. События слу-
чайные
Смешанные дроби 62
Смятие 439
События случайные 321
Совокупность генеральная 328
Соединения (мат) 79
--- подвижные — Коэффициент трепня
435
--- скользящие подвижные 409
Соприкасающиеся окружности 266
Соприкосновение кривых 266
Сопряженные гиперболы 245
Сочетания 79
Специальные функции 221
Спноали Архимеда 274
— Поднормали 275
— Построение 274
— Применение в технике 275
— Радиус кривизны 275
Спирали' гиперболические 262, 276
---логарифмические 275; — Радиус
кривизны 267, 276; — Эволюта 270.
276
Спрямление дуги окружности 281
Среднее значение — Теорема 184
Среднее квадратическое отклонение 305
Средняя квадратическая погрешность
305
Старая русская система мер 535
Статика 352
--- аналитическая 366
--- геометрическая 352
Статистическая вероятность 324'
Статистическое распределение 325
Степени чисел — Формулы 74
Степенные функции 89
Степень перекрытия 493
Стильтьеса интеграл — Вычисление 192
Стирлинга формула 136, 303, 304
Стокса теорема 233
---формула 189
Стыодента распределение 328
— Таблиц., функции S (г) 334
Сумма кубов 74
Суммирование тензоров 235
Сферическая система координат 251
Сферические клинья — Поверхность 111
— Объем III
Сферические треугольники 114
Схема Рунге вычисления коэффицнен
тов 313
Сходимость рядов числовых 149, 150
Сходящиеся интегралы 174
т
Тангенсы — Логарифмы 50, 51
— Таблицы 46, 47
- Теорема 102
Тела 190; — Масса — Вычисление инте-
грированием 191
----вращения 11
•--- вращающиеся — Давление на опо-
ры 397; — Точка — Скорости и
ускорения 377
----вращающиеся твердые — Действие
удара 405
---- однородные — Момент инерции
393; — Центры тяжести 359
----переменной массы — Динамика 399
----твердые — Вращение 396; — Дви-
жение 379, 381, 398, 401;—Дина-
мика 396; — Кинематика 375
----твердые вращающиеся — Действие
удара 405
—— цилиндрические — Моменты инер-
ции единичные 419
Телеграфное уравнение 225
Телесные углы 104
Тензорное исчисление 234
Тензорный признак системы величин ан
236
Тензоры 234—236
Теорема Аполлония 243
—- Бернулли 329
---- Дирихле 306
----Жуковского 421
---- Карно — Остроградского 403
---- Коши 197, 210
---- Лагранжа — Дирихле 368
----Ляпунова 329, 368
---- Маркова 329
--- Остроградского 233
---- Паппа — Гульдена 364
---- Пифагора 103
---- Птоломея 104
----Пуассона 329
---- Робертса—Чебышева 461
----Ролля 141
----Стокса 233
---- Чебышева 328
---- Штурма 123
---- Эйлера 389
---- импульсов 389
---- кинетической энергии 387, 390, 401
----количества движения 386, 402
---- количества движения системы 388
----количества движения тел перемен-
ной массы 399
---- косинусов 102, 114
---- моментов количества движения
386, 389, 400, 403
----о вычетах 200
----о движении центра инерции 400,
403
---- о кинематическом моменте 390
---- о пределах 135
---- о среднем 184
---- о среднем значении интеграла 173
ТГ.ОРЕЛ5Ы
- 563 -
У1АР
---- потерн кинетической энергии 403
---- предельная 328
----синусов 102, 114
----сложения вероятностен 321
---- тангенсов 102
----умножения вероятностей 322
Теоремы динамики системы 388
---- динамики системы в применении
к удару 402
---- динамики точки 386
----дифференциального исчисления
141
Теоретическая механика 352—406
Теория вероятностей 321—335
---- кривых 2-го порядка 247
---- механизмов и машин 407—450
----ошибок 330
---- поверхностей 293
----поверхностей 2-го порядка 255
----- пределов — Основные понятия 134
---- точности механизмов 444
Тетраэдры — Обьем ПО
Точечные источники 234
Точка — Движение — Графики 371
— Движение криволинейное 372, 374,
384
— Движение относительное 374, 388
— Движение прямолинейное 369, 370,
384
— Динамика 383
— Закон движения 369
— Радиус и вектор 228
Точка возврата 262
---- прекращения кривой 264
---- разрыва 136
---- самоприкосновения кривой 263
Точки—Удар о поверхность 402
----гиперболы — Построение 245
---- кривой изолированные 263
---- лемнискаты узловые 263
----особые 262, 263
— особые однозначных функций 199
----перегиба кривых 264
---- переменной массы — Движение
385
---- пересечения прямых—Координа-
ты 242
----поверхности — Классификация 296
---- равноотстоящие узловые — Интер-
поляционные формулы 303
----трехкратные 263
---- угловые кривой 264
---- узловые 263
Точность механизмов — Теория 444
Top 111
- Поверхность—Вычисление 364
Траектория 372. 375
---- изогональная 271
— кривых 271
---- ортогональная 271
Трансцендентные уравнения 121
— Действительные корни 122
Трансцендентные функции — см. Функ-
ции трансцендентные
Трапеции — Площадь 106
— Формула 182
Трение в механизмах 433
---- верчения 433
---- жидкостное 435
----качение 357, 433
---- скольжения 357, 433, 434
Треугольник Паскаля 75
Треугольники—Площадь 106
— Решения 102, 112—114
— Углы — Тригонометрические функ-
ции 112
Треугольники косоугольные — Решения
113
-----прямоугольные — Решения 112
----сферические — Площадь 114; —
Решения 114
Трехгранники сопровождающие 284
Трехзвеиные механизмы — см. Меха-
низмы трехзвенные
Трехкратные точки кривой 263
Тригонометрические ряды Фурье 306
Тригонометрические уравнения 122
Тригонометрические функции — см.
Функции тригонометрические
Тригонометрия плоская—Формулы 94
Тронные интегралы 185
Труба 109
Тэйлора ряд 197, 198; — Применение в
решении дифференциальных уравне-
ний 211
---- формула 141, 145
У
Угловой коэффициент — см. Коэффи-
циент угловой
Угловые точки кривой 264
Углы — Деление — Применение спи-
рали Архимеда 275
----Эйлера 250
---- касательной с осями координат
261
---- нормали с осями координат 261
----треугольника — Тригонометриче-
ские функции — Зависимости 112
Угол давления 277, 520
---- между двумя прямыми 241
---- между плоскостями и прямыми
254
---- передачи 520
----телесный 104
---- трения 357
Уголки равнобокие—Центр тяжести —
Вычисление 364
Удар 402
36’
I
УЛАР ДВУХ ТЕЛ
- 564 —
ФОРМУЛА БЕССЕЛЯ
— Действие на вращающееся твердое
тело 405
— Центр 406
Удар двух тел 403
— Уравнения 404
Умножение вероятностей — Теорема
322
---- на арифмометре 340
---- на вычислительной машине 343,
347
---- на логарифмической линейке 338
----сокращенное 67
---- тензоров 236
Управляемые зубчатые механизмы—см.
Механизмы зубчатые управляемые
Уравнение Бернулли 208
---- Бесселя 221
•--- Клера 209
----Лагранжа 209, 391
----Лапласа 196, 225, 234
---- Мещерского 386
---- Остроградского 403
----Пуассона 225
---- Риккати 208
---- Эйлера 216, 398
---- телеграфное 225
Уравнения — Геометрическое значение
. 239
— Номографический порядок 318
— Решения 115—133
Уравнения алгебраические 118; — Ре-
шение приближенное по методу
Лобачевского 129
---- биквадратные 121
---- векторные для построения планов
скоростей и ускорений механизмов
472
---- возвратные 3-й степени 120
---- возвратные 4-й степени 121
---- волновые 225
•---геометрических мест 240
---- гиперболические 122
---- движения твердых тел 398
----движения твердых тел около не-
подвижной точки 401
— дифференциальные — см. Диффе-
ренциальные уравнения
---- квадратные 119
— кинематического момента 397
•--- кинетической энергии 397
—— колебаний маятника 397
—— кубические 119
•---линейные — Система 117, 128
----линейные нормальные 332
•---линейные условные 332
----логарифмические 122
—— математической физики 225
---- параболоида 256, 257
Уравнения параметрические гиперболы
246
---- окружности 243
---- параболы 247
---- прямой 241. 252
---- циклоиды 262
---- эллипса 241
Уравнения поверхности 293
---- показательные 121
---- полярные 242
---- пространственных кривых 285
----прямой 240—242, 252, 253
---- распространения тепла 225
---- семейства окружностей 269
---- теории потенциала 225
----трансцендентные 121; — Действи-
тельные корни 122
---- тригонометрические 122
---- у дара двух тел 404
---- функциональных шкал 314
---- центроиды 282
---- четвертой степени 120
---- эпициклоиды 272
Уравновешивание вращающихся масс
421
---- сил 366
Ускорение 370. 373, 375-^377; — Рас-
пределение 379, 380; — Сложение
375
------ звена приведения угловое 427
---- механизмов — Определение 425
---- механизмов плоских — Измерение
418
----силы тяжести — Таблицы величин
8
Условие Липшица 210
Условные обозначения I
Усталостное выкрашивание 439
Установки для измерения механических
величин 415
Устойчивость движения 392
---- на опрокидывание 369
---- равновесия 368
• Ф
Фазы синусоидальных величин 98
Факториалы целых чисел — Таблицы 41
---- чисел — Логарифмы — Таблицы 41
Факториальные функции 302
Фигуры — Элементы — Вычисление
102—114
---- однородные—Центр тяжести 360
---- плоские — Периметры — Вычисле-
ние 106; — Площадь — Вычисление
106, 189
Физические маятники — Колебания —
Уравнение дифференциальное 397
Формула Бесселя 303
— Валлиса 136
ФРЕНЕ ФОРМУЛА
- 565 -
ФУНКЦИИ ТРИГОНОМЕТРИЧЕСКИЕ
---- Гаусса 183
---- Коши 141
---- Коши — Адамара 196
---- Лагранжа 141, 304
—— Маклорена 142
---- Муавра 86
---- Ньютона 303, 304
---- Ньютона—Лейбница 173
—— Симпсона 182
---- Стирлинга 136, 303, 304
---- Стокса 189
— Тэйлора 141, 145
---- Фрейе 292
---- Чебышева 183
---- Эйлера 103
---- дифференцирования 139
---- интерполяционная — Остаточные
члены 304
- — конечных приращений 141
---- конечных приращений для функ-
ции нескольких переменных 145
---- приведения 92, 163
---- трапеций 182
Фрейе формула 292
Фрикционные храповые механизмы — см.
Механизмы храповые фрикционные
Функции — Графики 88—91, 94, 97—99.
101
— Дифференциалы 138
— Предел 134
— Приближенное аналитическое выра-
жение 305—313
— Производные 137
— Разложение 307
— Разложение в бесконечные ряды 151
— Разложение в ряд Фурье 308
— Разложение в ряды по полиномам
Чебышева 311
— Разложение в степенные ряды 152
— Экстремгльные значения — Опреде-
ление 147
Функции Бесселевы 58, 222, 223, 311
----Лежандра 223
---- алгебраические 90
---- аналитические — Вычеты 200; —
Разложение в степенные ряды 197
---- бесконечно большие 135
----бесконечно малые 135
---- векторные 230
---- гармонические 234
---- гиперболические 100; — Графики
101; — Таблицы 52
---- гиперболические комплексных пе-
ременных 196
---- гиперболические обратные 101
---- голоморфные 198
---- двух переменных — Формула Тэй-
лора 145
---- дифференциальные распределения
вероятности 322
---- дробнолинейные 90
---- заданные параметрически — Диф-
ференцирование 139
---- интегральные распределения ве-
роятности 322
---- иррациональные — Интегрирова
иие 160
---- квадратные 88
---- комплексного переменного 194—205
---- кратного аргумента 95
---- круговые 91; — Таблицы 52
---- линейные 87
---- логарифмические 91
——многих переменных — Дифферен
пирование 143
---- многозначные 196
---- монотонные 137
---- непрерывные 136
---- неубывающие 137
---- неявные — Дифференцирование
146
---- обратные 91, 99, 101, 196
---- ограниченные сверху (или снизу)
134
---- однозначные — Точки особые 199
---- периодические 91
---- показательные 91, 195, 302; —
Таблицы 52
---- половины аргумента 96
—— п^юстейшне— Конечные разности
---- распределения 193
---- распределения вероятности диффе-
ренциальные 322
----рациональные 87, 90; — Интегрн
рование 156
---- синусоидальные — Период 98
---- скалярные — Градиенты 231
Функции сложные—Дифференциал
полный 145
— Дифференциалы 139
— Дифференцирование — Цепное пра-
вило 139
— Производные 138
— Производные частные 145
Функции специальные 221
степенные 89
трансцендентные 90; — Интегри-
рование 161
Функции тригонометрические 91, 302
— Выражение через другие 96
— Значения — Таблицы 44
— Значения для некоторых аргументов
93
— Изменения по знаку и величине по
четвертям круга 93
— Логарифмы десятичные 48
Функции тригонометрические дополиц-
тельных углов — Зависимости 92
---- комплексных переменных 195
ФУНКЦИИ
- 566
(ЕТЫРЕХУГОЛЬНИКИ
----кратного аргумента 95
---- обратные 99
— одного аргумента — Соотношения
94
---- половины аргумента 95
----произведений углов — Преобразо-
вание в суммы 96
----суммы и разности углов 94
----суммы углов—Преобразование в
произведения 96
----углов треугольника — Зависимости
112
Функции факториальные 302
----целые рациональные 87
----эвольвентпые 277; — Графил 278
----элементарные 87—114
Функциональные ряды 151
Функциональные сетки 315
Функциональные шкалы — Уравнения
314
Функция Жуковского 205
---- Кристоффеля — Шварца
----Лапласа — График 324
1
1 з **
mtn 60
205 -
— Зиаче-
?_ 2 dt — Значе-
ния 61
---Ф(а)
---- эвольвентная ? = inv а — tg а — а —
Значения 57
Фунты английские — Перевод в кило-
граммы 542
Фурье интеграл 308
•---коэффициент обобщенный 305
—— ряд обобщенный 305
---- ряд тригонометрический 306
Футы — Перевод в метры 539
— Перевод в ярды 540
X
Характеристика логарифма 77
Характеристики вероятностные 326
Хорды — Длины — Таблицы 37
Храповые механизмы — см. Механизмы
храповые
ц
Цевочные зацепления — см. Зацепления
цевочные
Целые функции рациональные 87
Центр группирования 326
—— геодезической кривизны поверхно-
сти 296
----инерции — Движение — Теорема
400, 403
---- кривизны 266
•---линии 2-го порядка 247
---- параллельных сил 359
----тяжести 359; — Координаты —
Определение интегрированием 191
---- тяжести объемов 359
----тяжести плоской фигуры — Опре-
деление — Применение веревоч-
ного многоугольника 365
----тяжести фигур 360
---- удара для двух тел 406
Центральные кривые 247
— Уравнения — Преобразование 248
Центроиды 271
— Уравнения 272
Цепные дроби — см. Дроби непрерыв
ные
Циклоидальные зацепления — см. За-
цепления циклоидальные
Циклоидальные кривые 272, 278
Циклоиды 278. 279
— Радиус кривизны 267
— Уравнения параметрические 262
— Эволюта 270
Циклоиды-рулетты 278
Цилиндрическая система координат 251
Цилиндрические копыта 109
Цилиндрические поверхности 298
Цилиндры—Объем 109
— Поверхность 109
— Уравнения 256
Циркуляция вектора 233
Ч
Чаплыгина метод решения диффереи
циальных уравнений 212
Части пропорциональные для линейно4
интерполяции 35
Частость — Опенка 330
Частота 325
---- колебаний 98
Чебышева полиномы 224
----способ спрямления дуги окружно
сти 281
----теорема 328
---- формула 183
Червяк-зубчатая рейка 497
Червяк-червячная рейка 497
Червячные передачи 497
---- глобоидные 497
Четырехзвенные шарнирные механиз-
мы — см. Механизмы плоские шар-
нирные четы ре хзее иные
Четырехугольники 103
— Площадь 106
— Свойства 104
ЧИСЛА
- 567 -
ярды
Числа вещественные — Действия 62
---- иррациональные 63
---- комплексные 62, 84, 194
----отрицательные — Действия 63
---- положительные — Действия 63
---- приближенные 65
-- целые — Факториалы — Таблицы
41
Численное интегрирование дифферен-
циальных уравнений 212
Ш
Шаблон логарифмический 314
Шаг винта 286
---- зацепления 493
Шаровой слой НО
Шаровые пары 411
Шаровые сегменты ПО
Шаровые секторы ПО
Шары ПО
Шатунные кривые 461
Шестнзвенные кривошипно-кулисные
механизмы — см. Механизмы криво-
шипно-кулисные шестизвенные
Широта распределения 326
Шкалы криволинейные 315
—— логарифмические 314
—— проективные 314
---- равномерные 314
---- функциональные — Уравнения 314
Шкивы планетарные реверсивные 509
Штурма теорема 123
э
Эвольвента 270
. -- окружности 270, 272, 276, 278; —
Построение 277
Эвольвентные винтовые поверхности 299
Эвольвентиые зацепления 493
Эвольвентные функции — см. Функции
звольвентные
Эволюта гипоциклоиды 281
---- кривой 269
----логарифмической спирали 270, 276
—— циклоиды 270
Эйлера интегралы 178
---- подстановки 160
---- постоянная С 135
----способ решения дифференциаль-
ных уравнений 211
----теорема 389
---- углы 250
---- уравнение 216, 398
---- формула 103
Эквидистантные эвольвенты окружности
278
Экстремум 147, 148
Эксцентриситеты эллипсов 243
Электрические датчики 416
Элементарные функции 87—114
Эллипсоиды 111, 255
Эллипсы 107, 243, 244
Эллиптические интегралы — Таблицы 59
Эллиптические конусы усеченные —
Объем 111
Эллиптические параболоиды — Уравне-
ния 256
Эллиптические секторы—Площадь 107
Эллиптические точки поверхности 296
Эллиптические цилиндры — Уравнения
256
Энергетические единицы — Перевод
одних в другие 544
Энергия кинетическая 387
— Потеря — Теорема 403
— Теорема 387, 401
— Уравнения 397
Энергия кинетическая систем — Теоре-
ма 390
---- потенциальная 367
Эпициклоиды 279
— Коэффициент угловой 280
— Построение 280
Эпициклоиды-рулетты 279
Эффект гироскопический 399
Я
Ярды — Перевод в метры 540
Технический реавктор Т. Ф. Соколова
Переплет художника Л. Jt. Келвсиоео
Корр»xiop О. И. Семенова
Подписано к печати 17/XI-1955 г. Т-ОКЙ52.
Печ а Зв, Уч -им. лист. ЯвД Бум л. 18.
Тираж 50 001—851)00 на 13-А алгол)
Формат OOXW'» Заказ 1977
OiucHMiaiiu с матриц l-й типографии Машгим. Ленинград, ул. Моисеенко, 10
и )имографни 2* I Госстрой имата. г. Владимир