Механика зернистых сред и её применение в строительстве - Кандауров И.И.

Автор: Кандауров И.И.
Теги: подземное строительство земляные работы фундаменты строительство тоннелей строительство механика строительная механика статистическая механика стройиздат зернистые среды
Год: 1966
Похожие
Строительная механика сыпучих тел
Строительство промышленных и гражданских сооружений на слабых водонасыщенных грунтах
Сборник цен на изыскательские работы для капитального строительства
Справочник по строительству на вечномерзлых грунтах
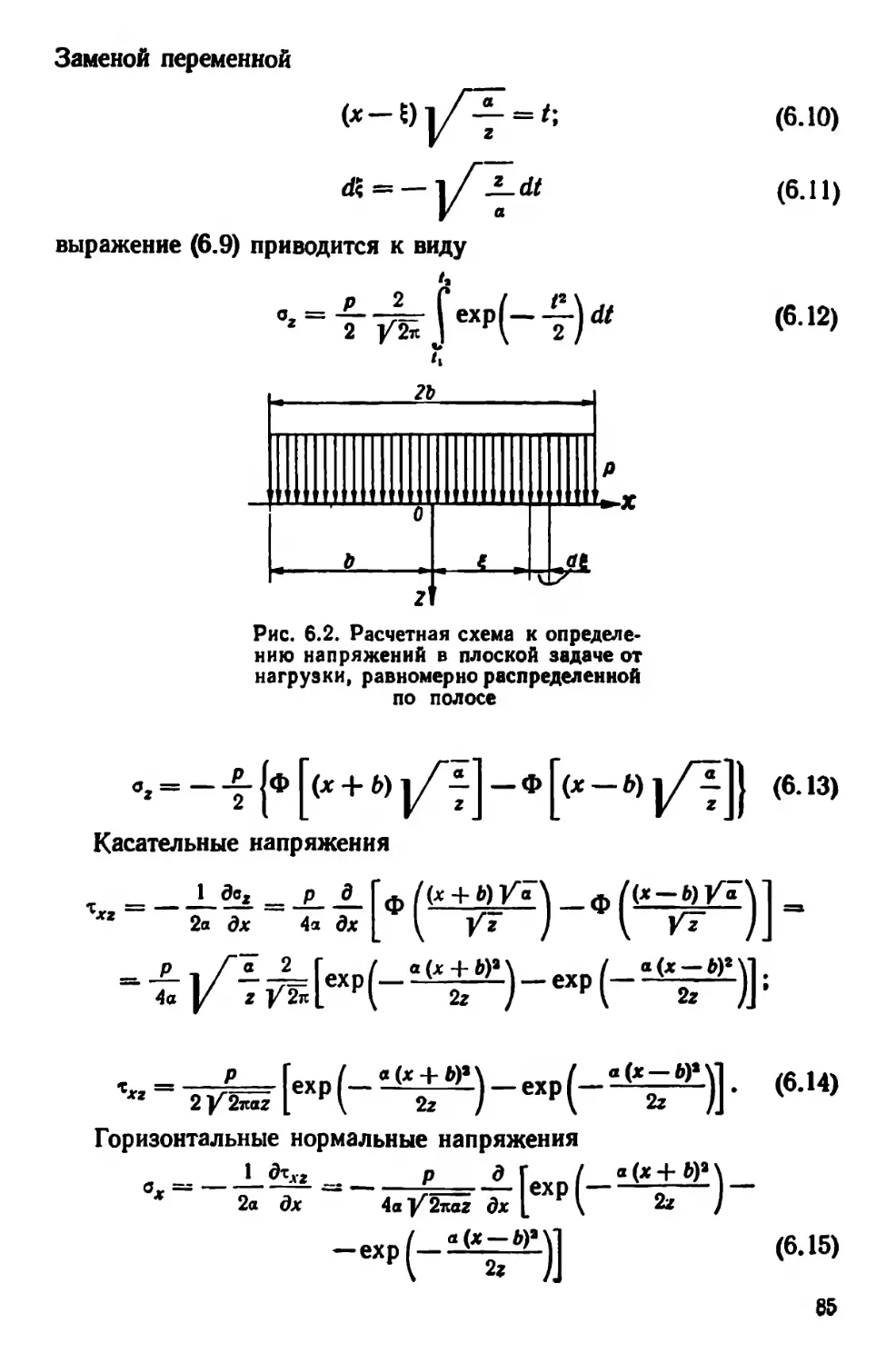
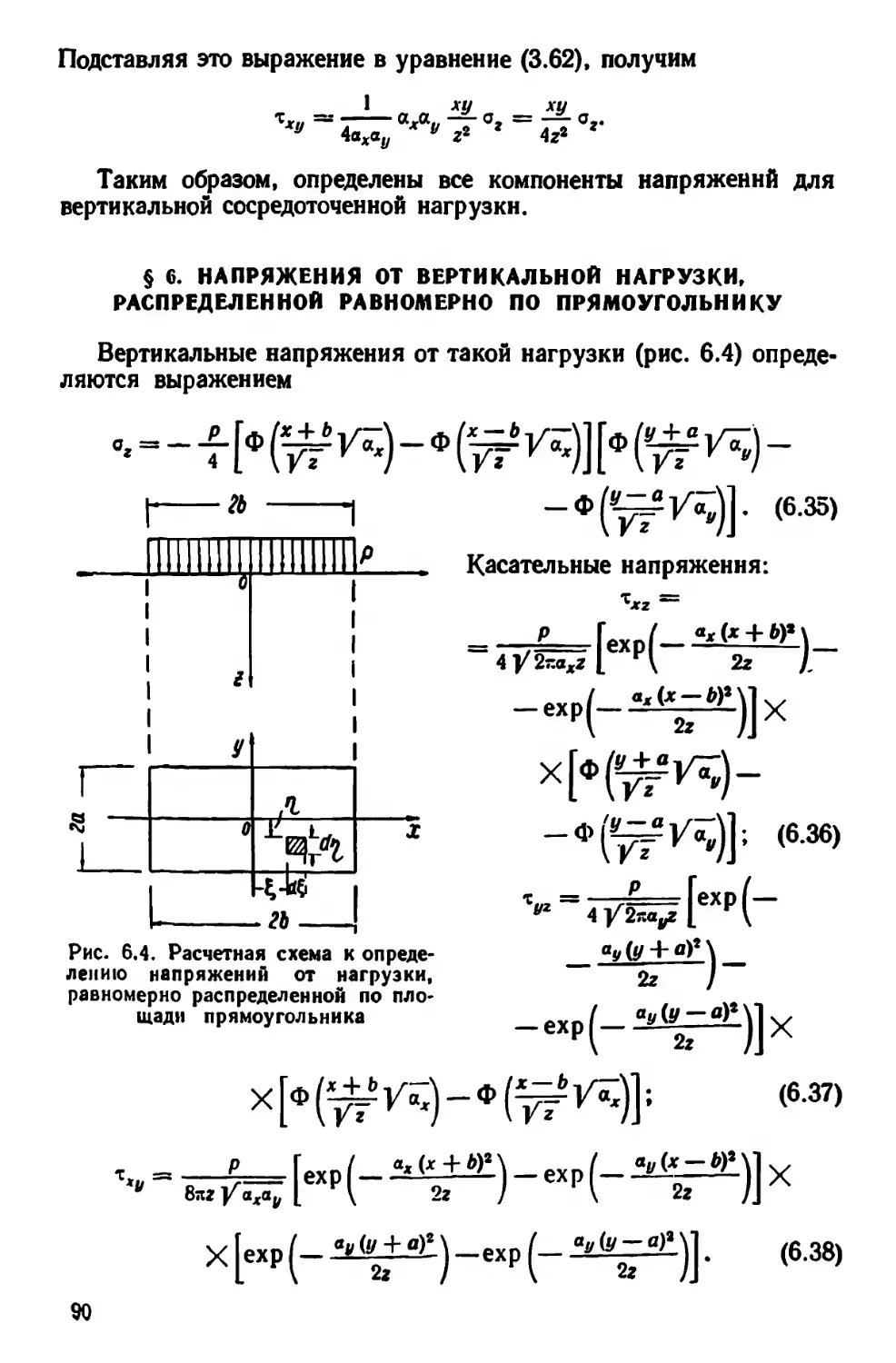
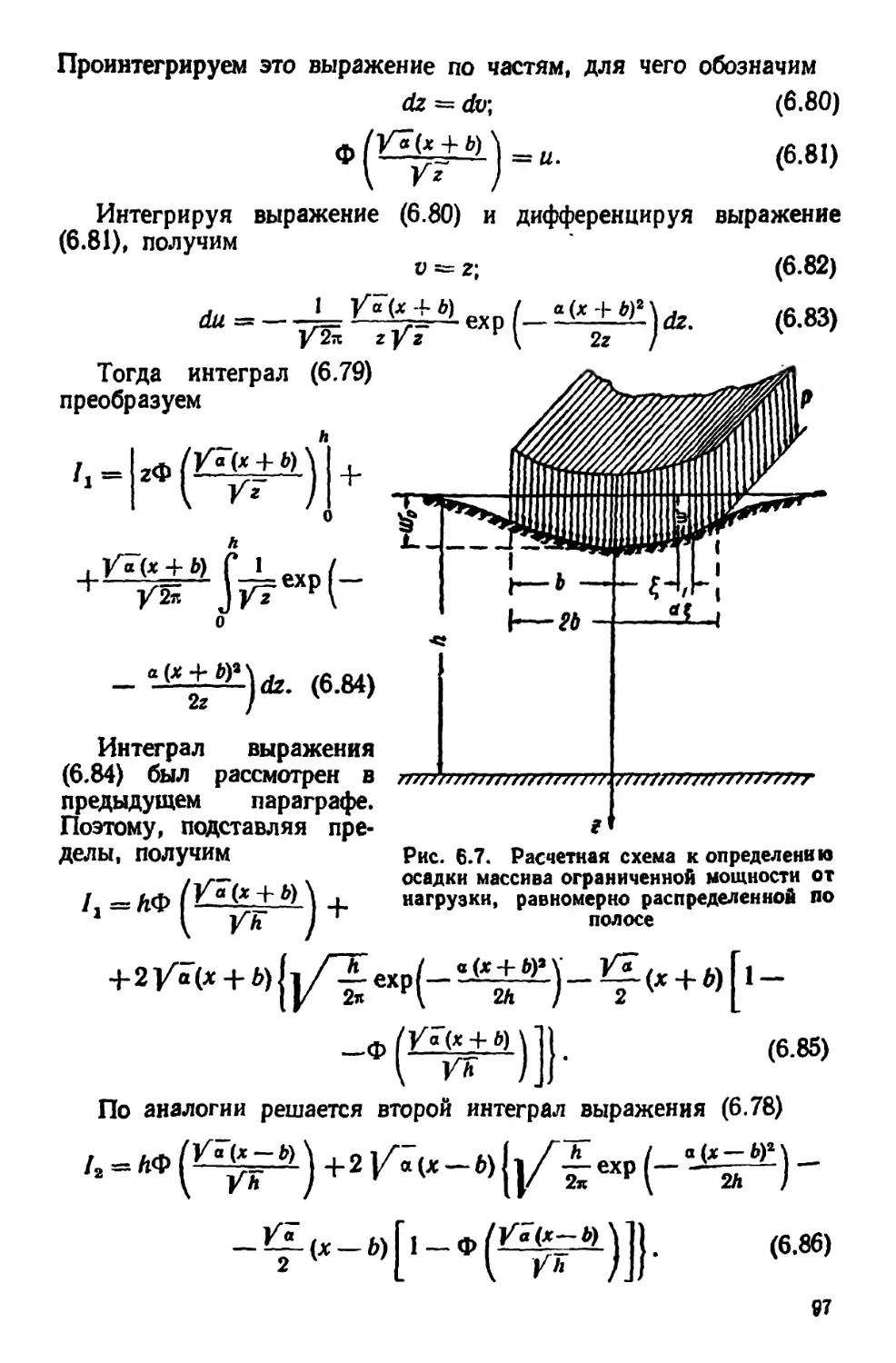
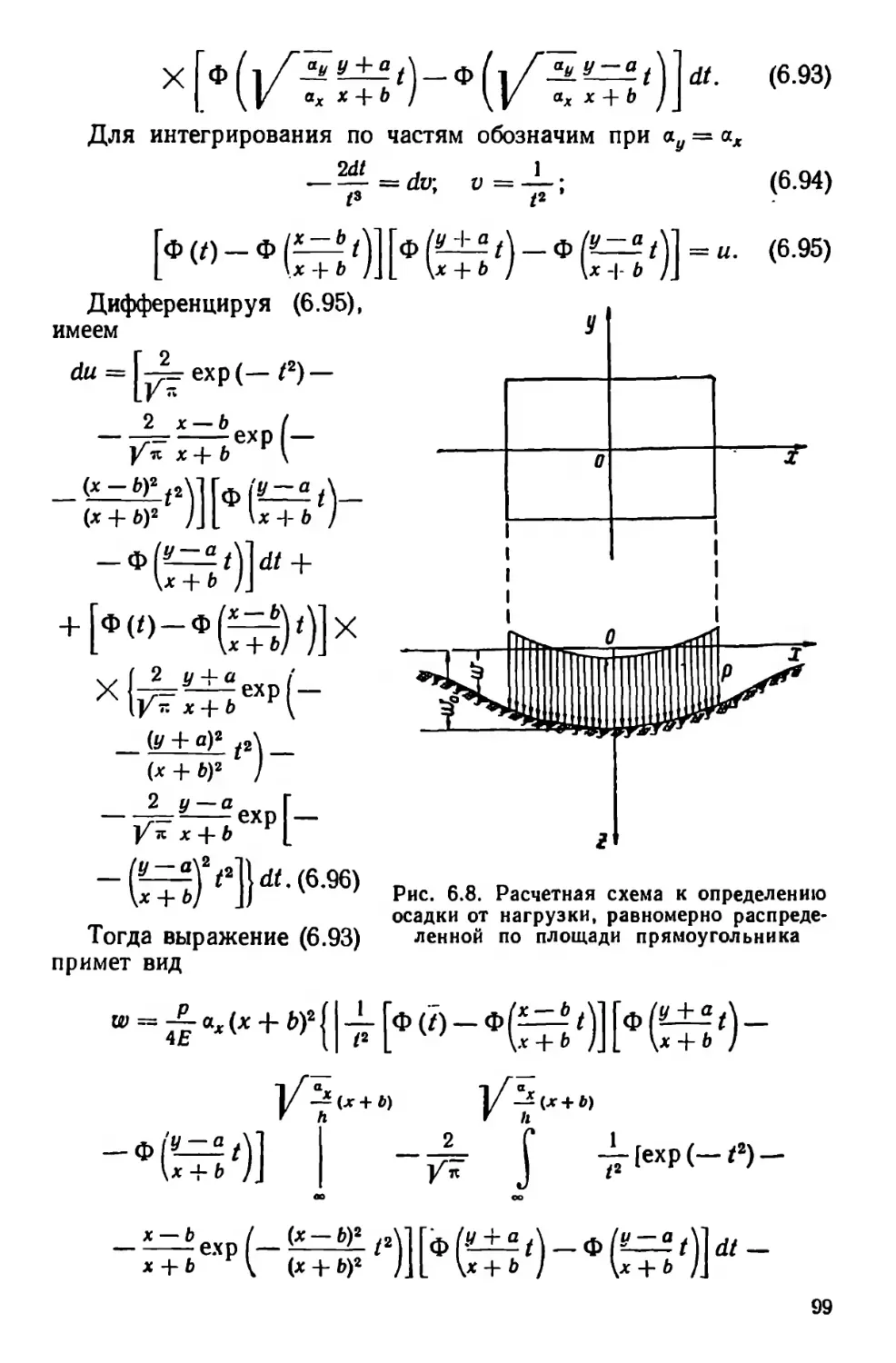
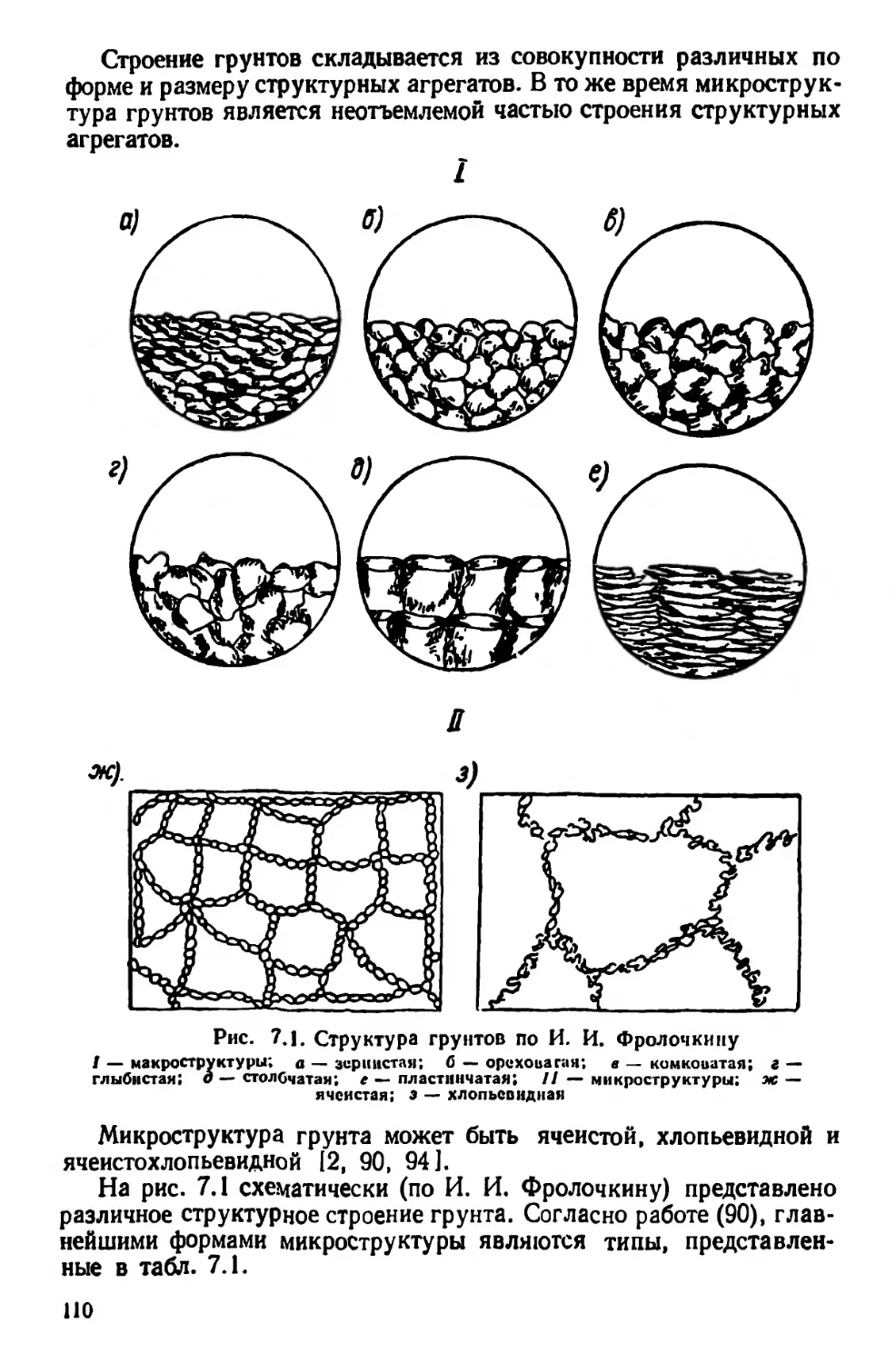
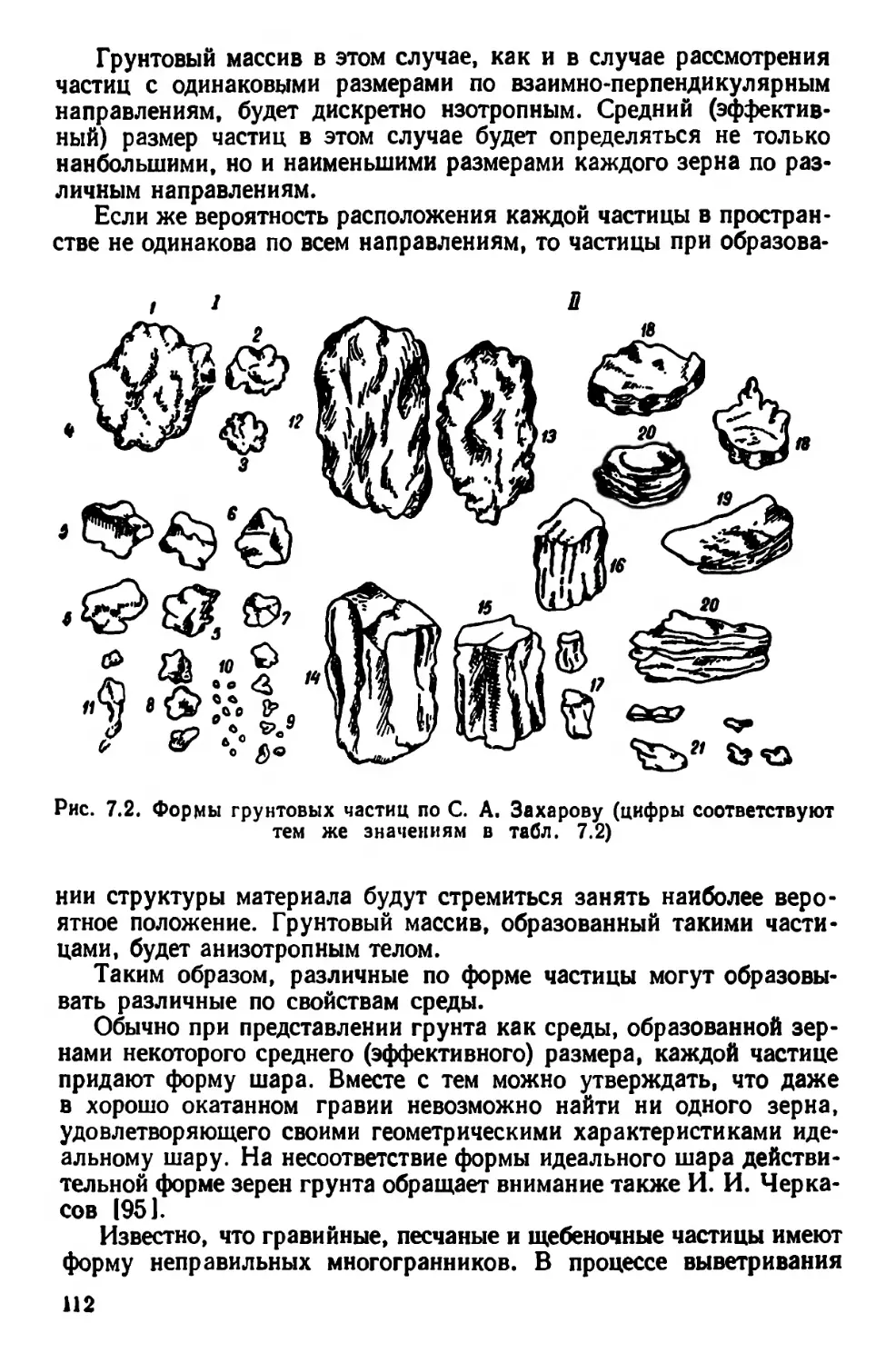
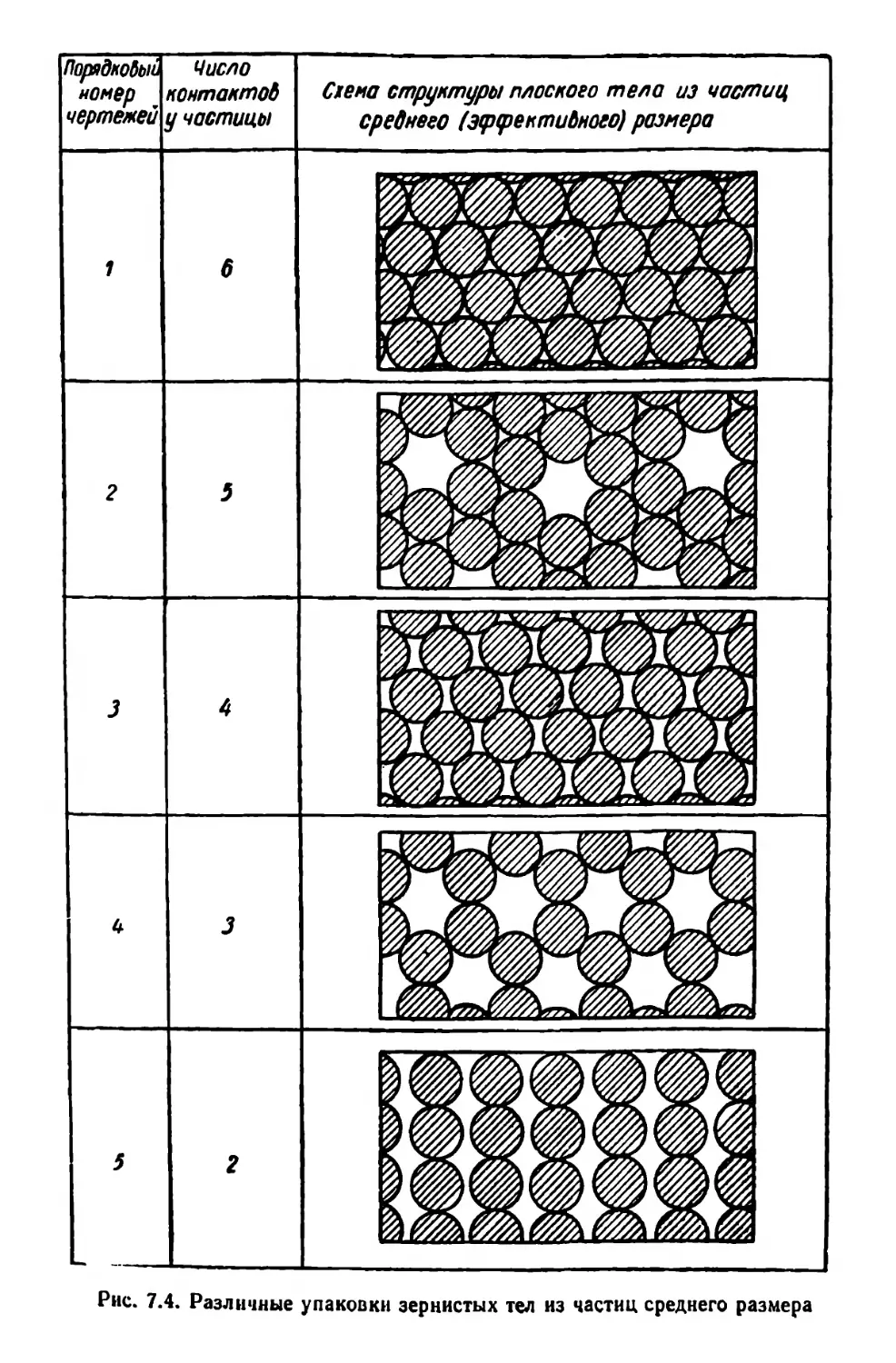
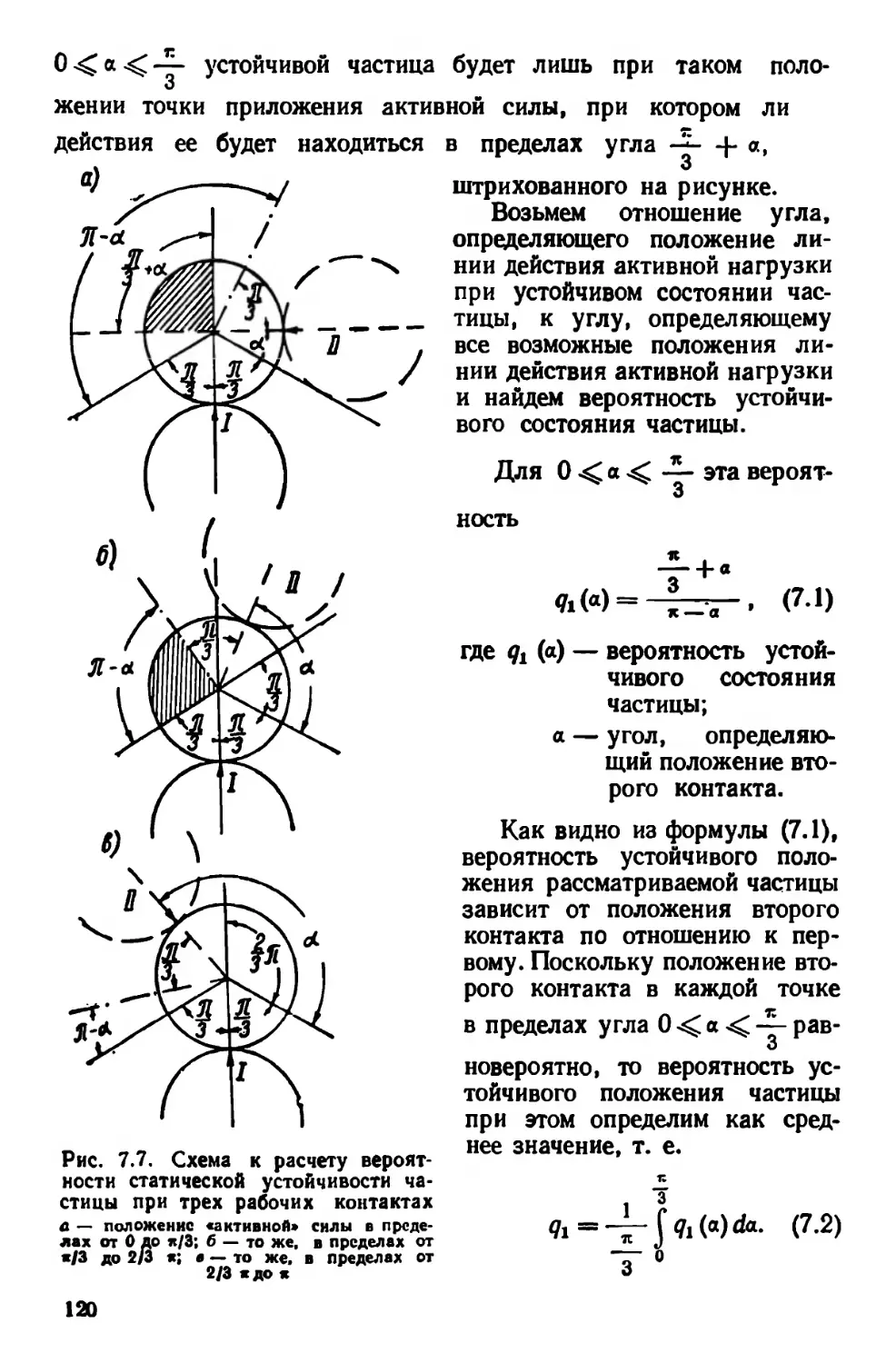
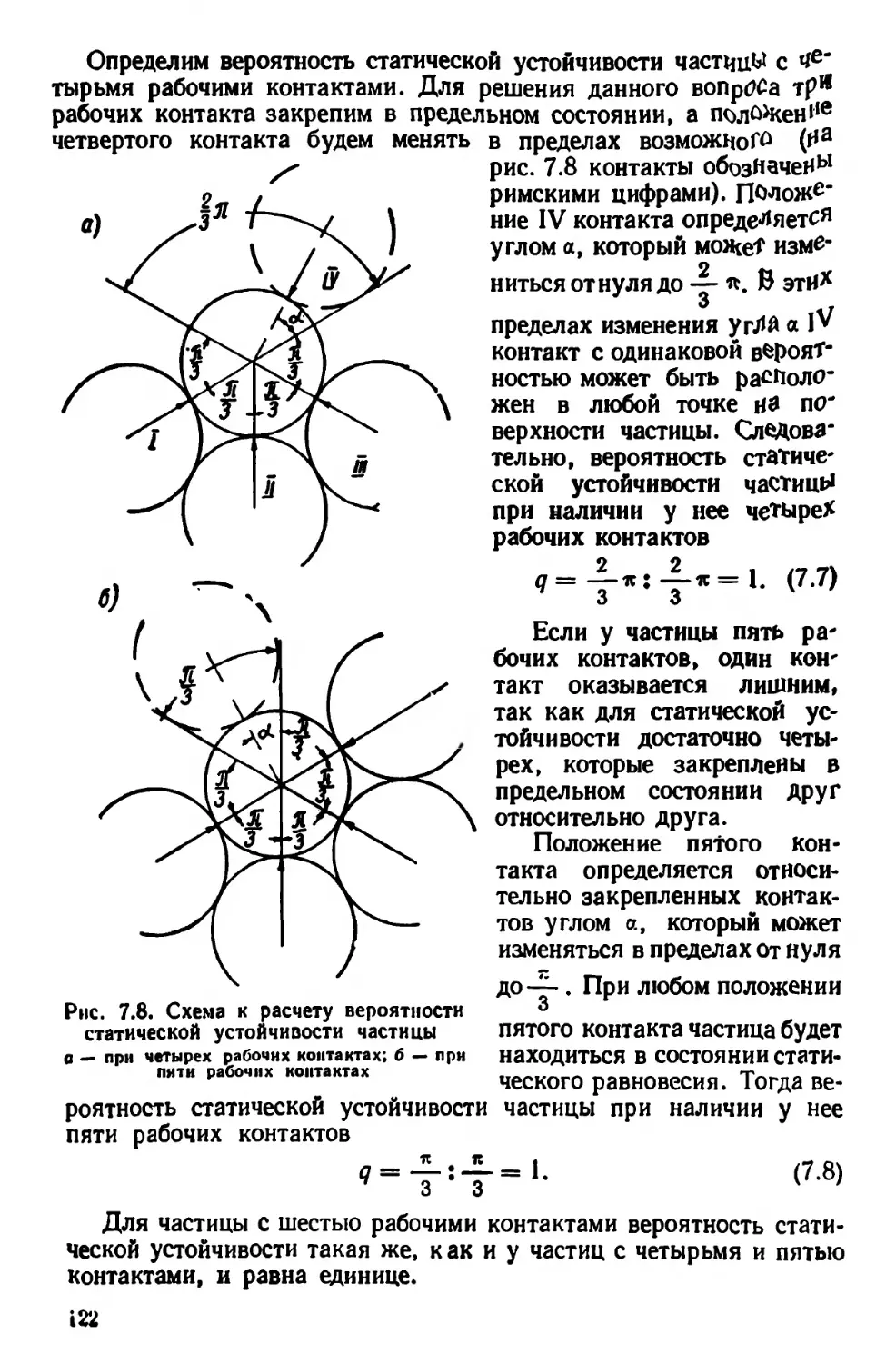
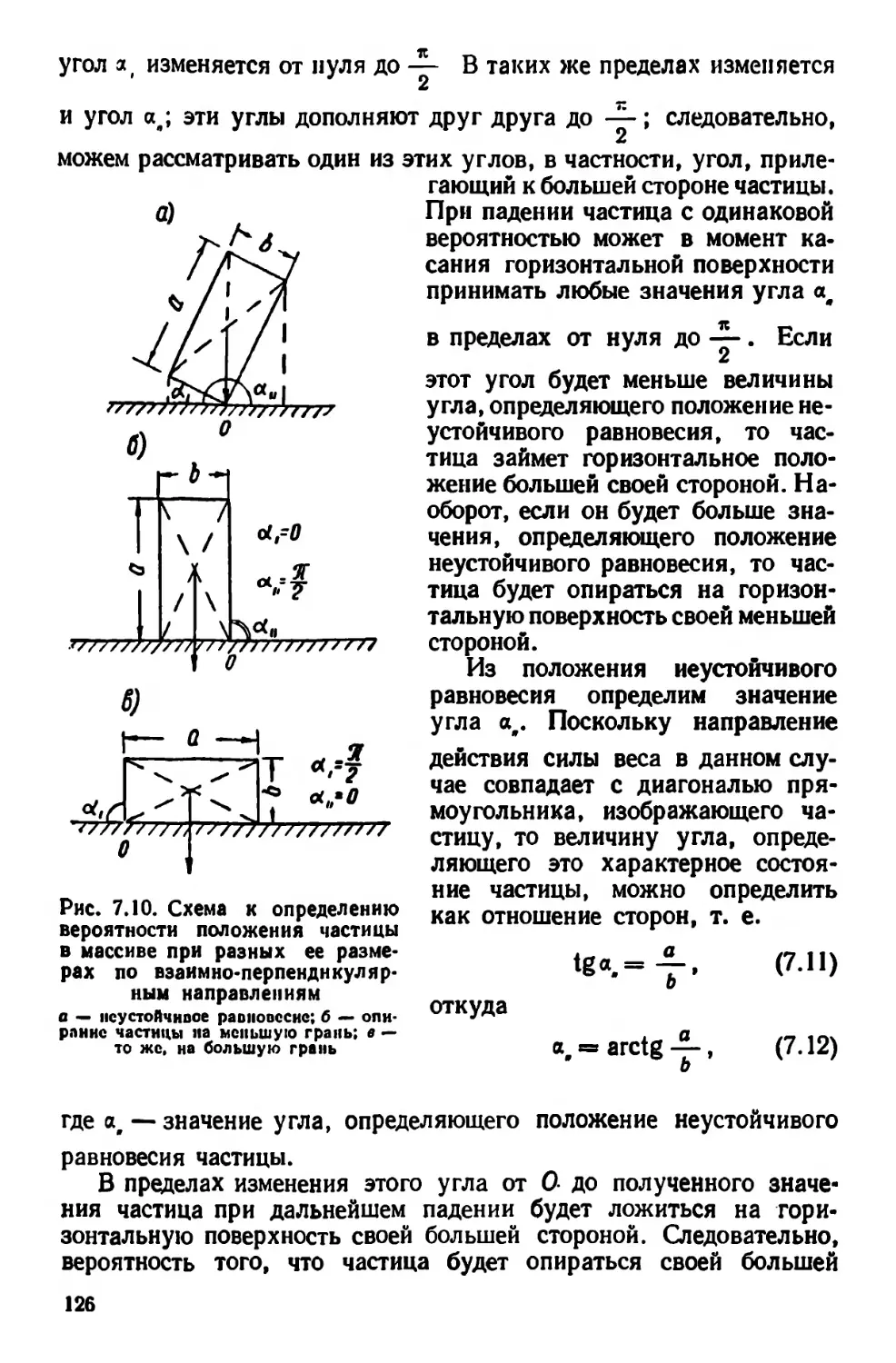
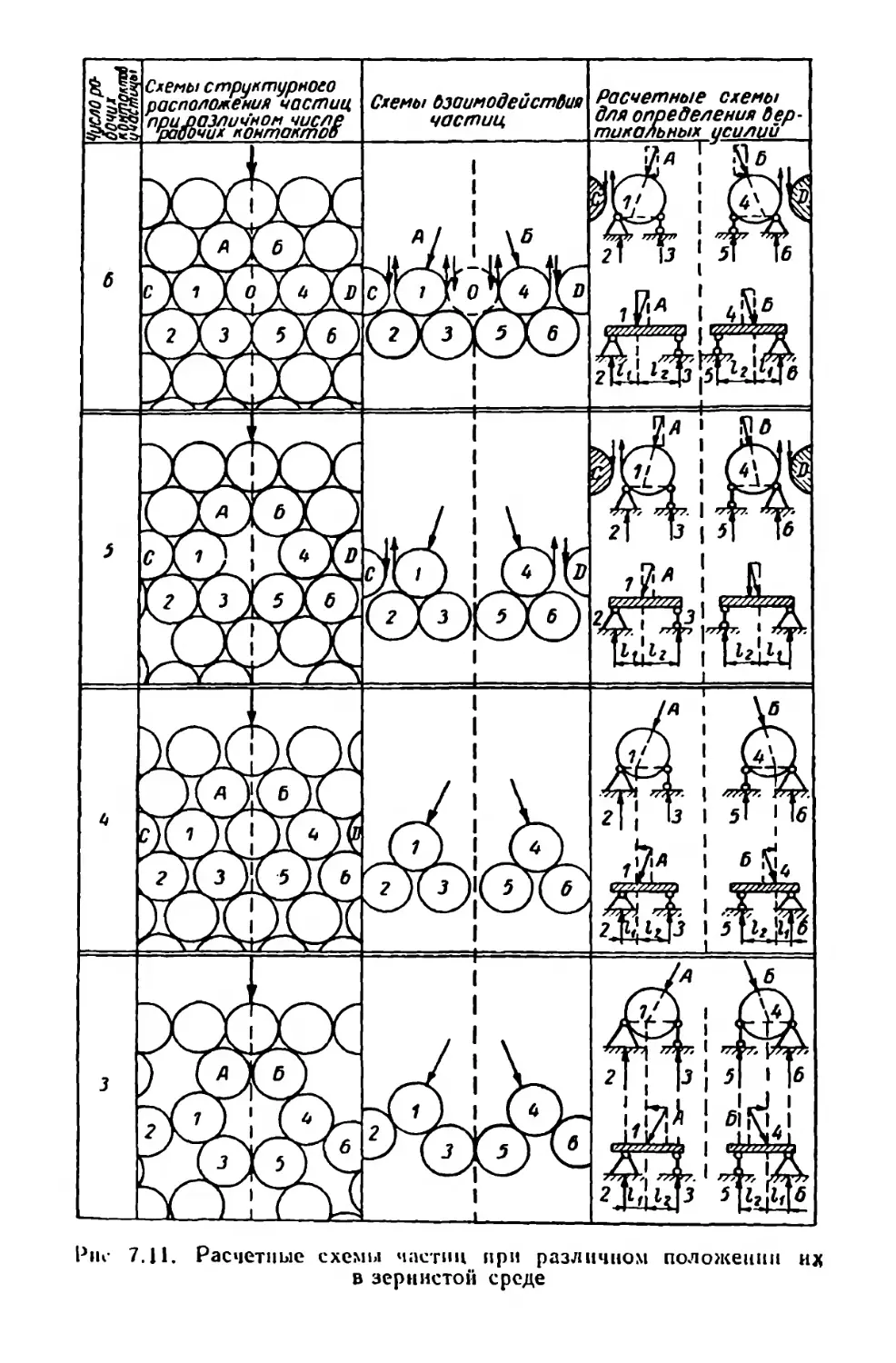
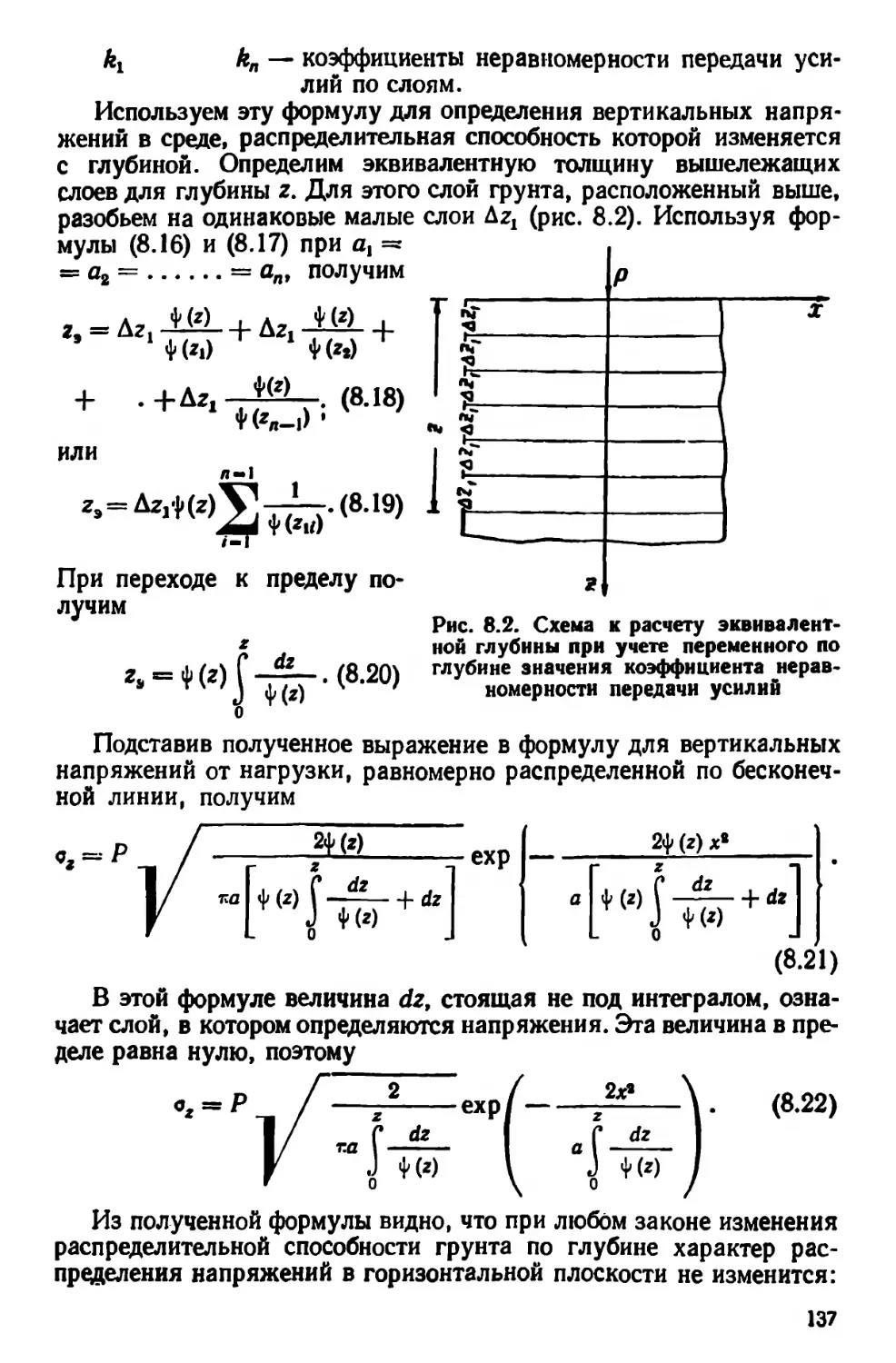
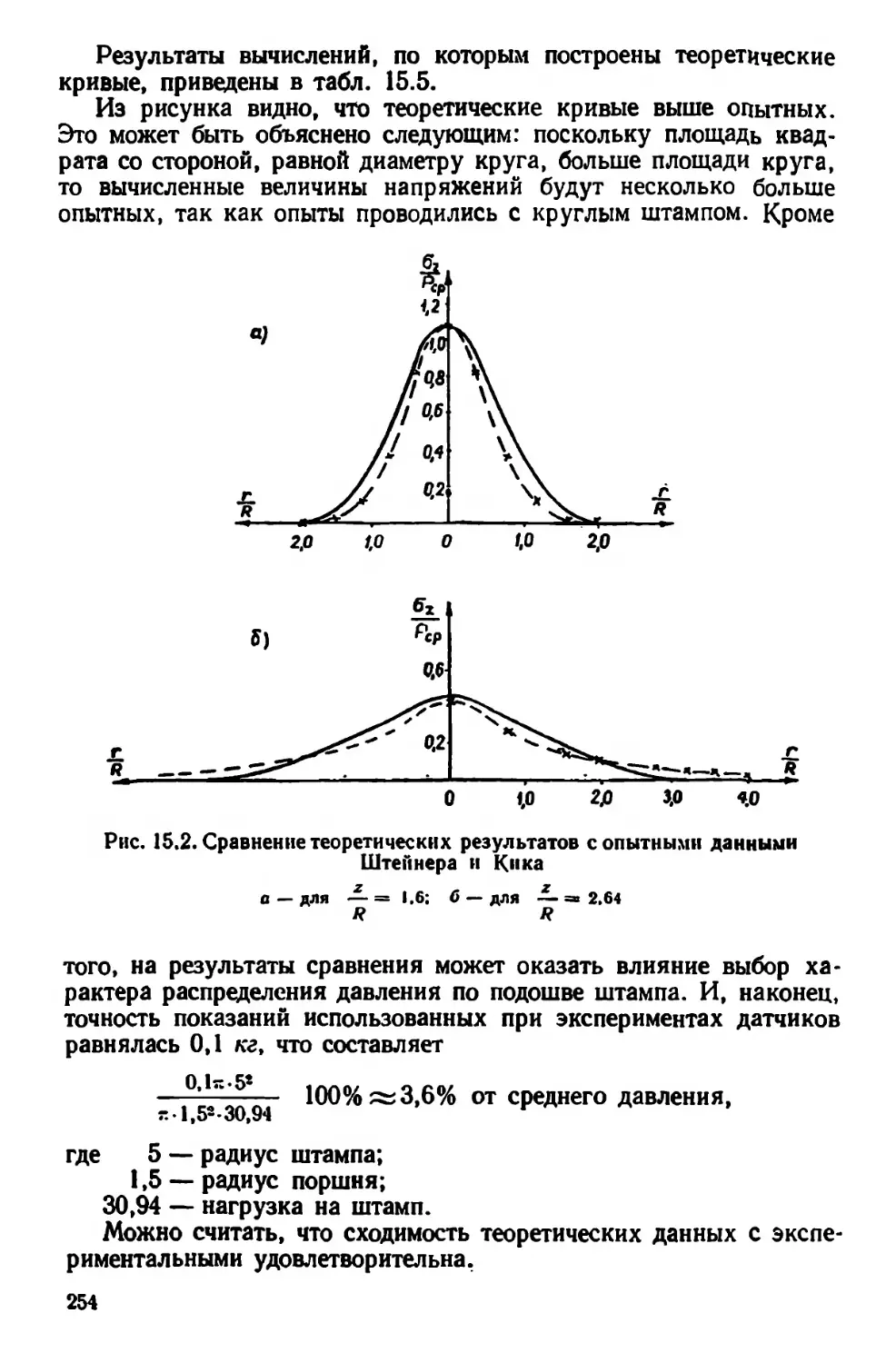
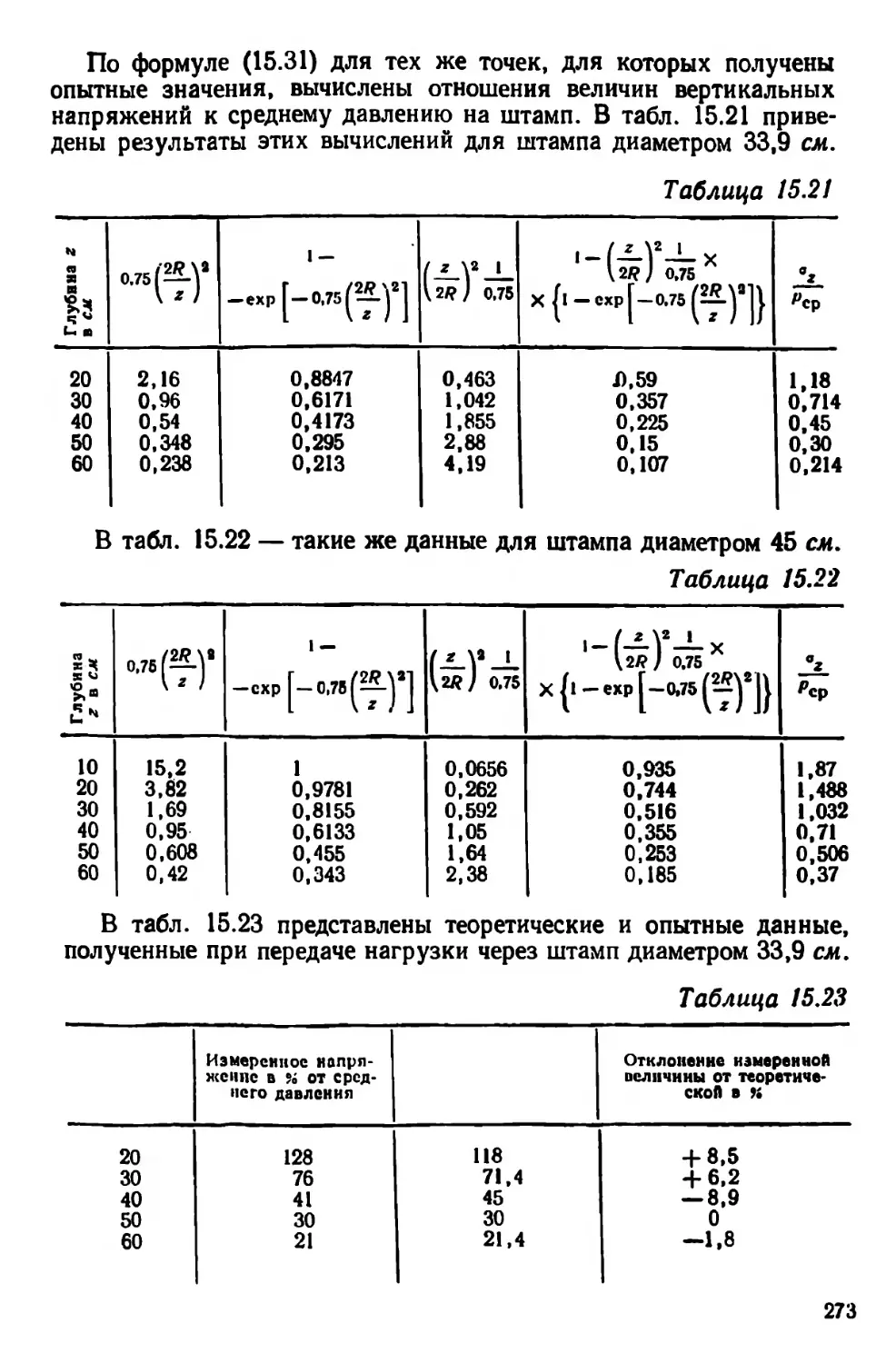
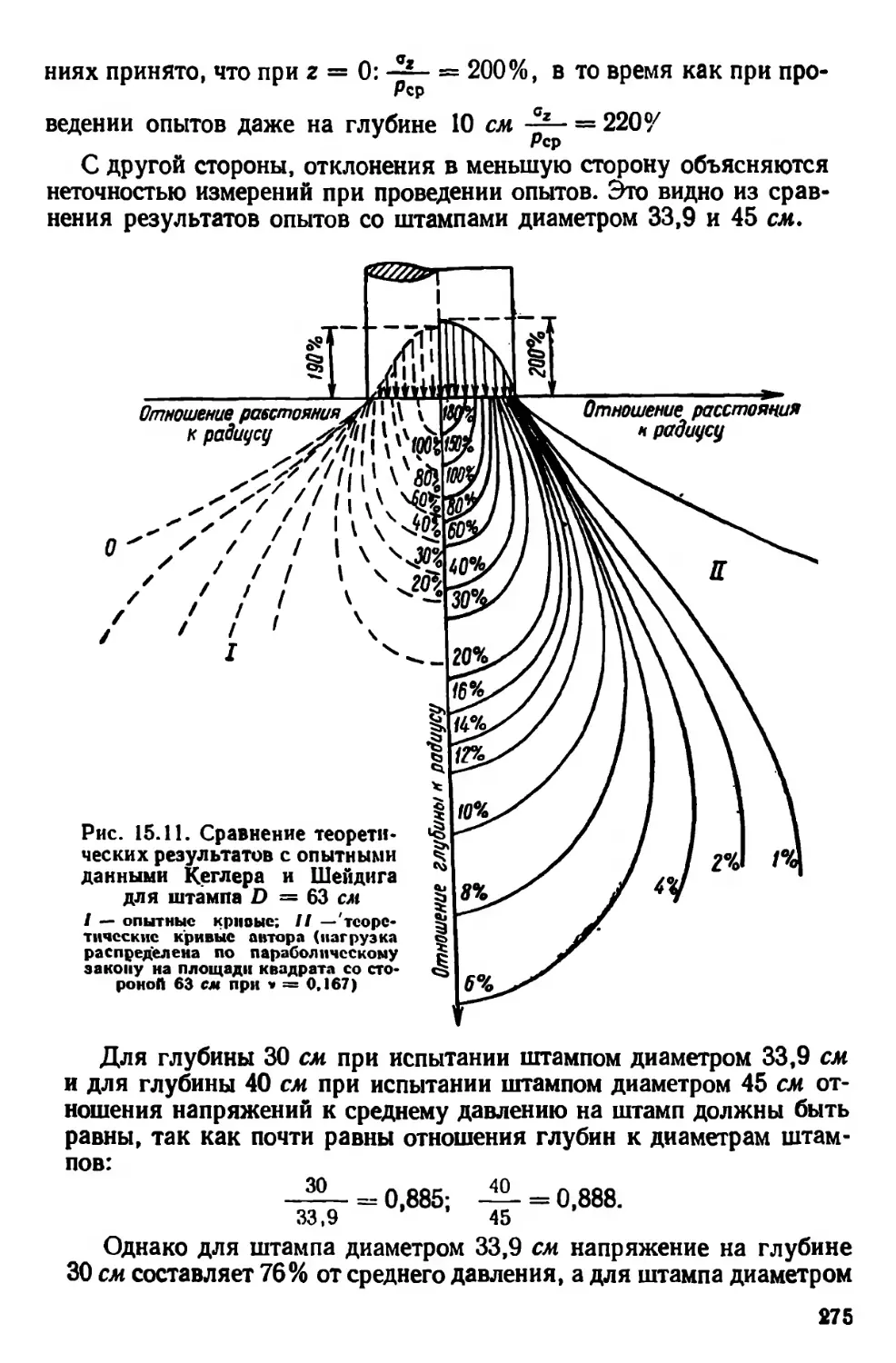
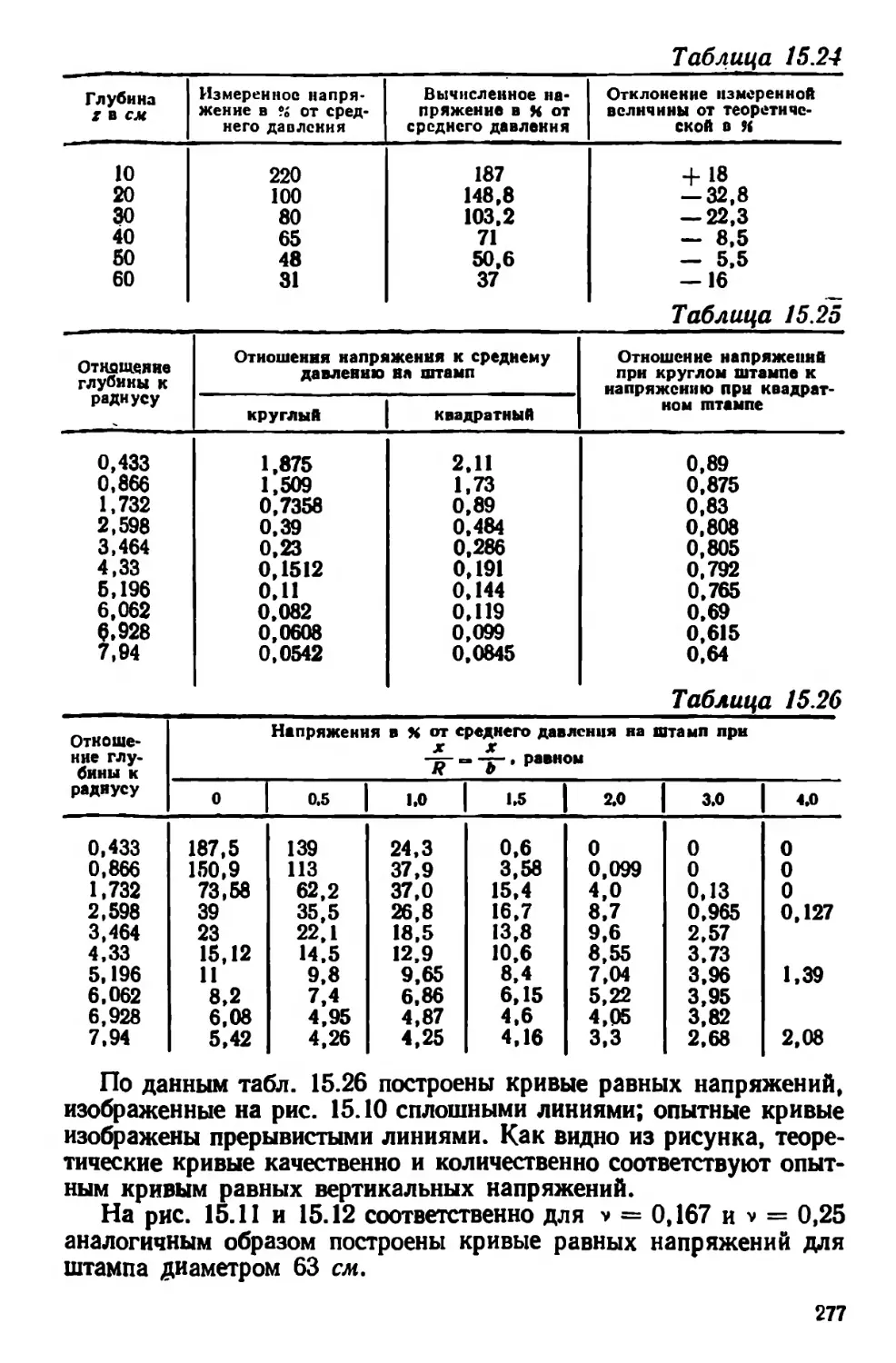
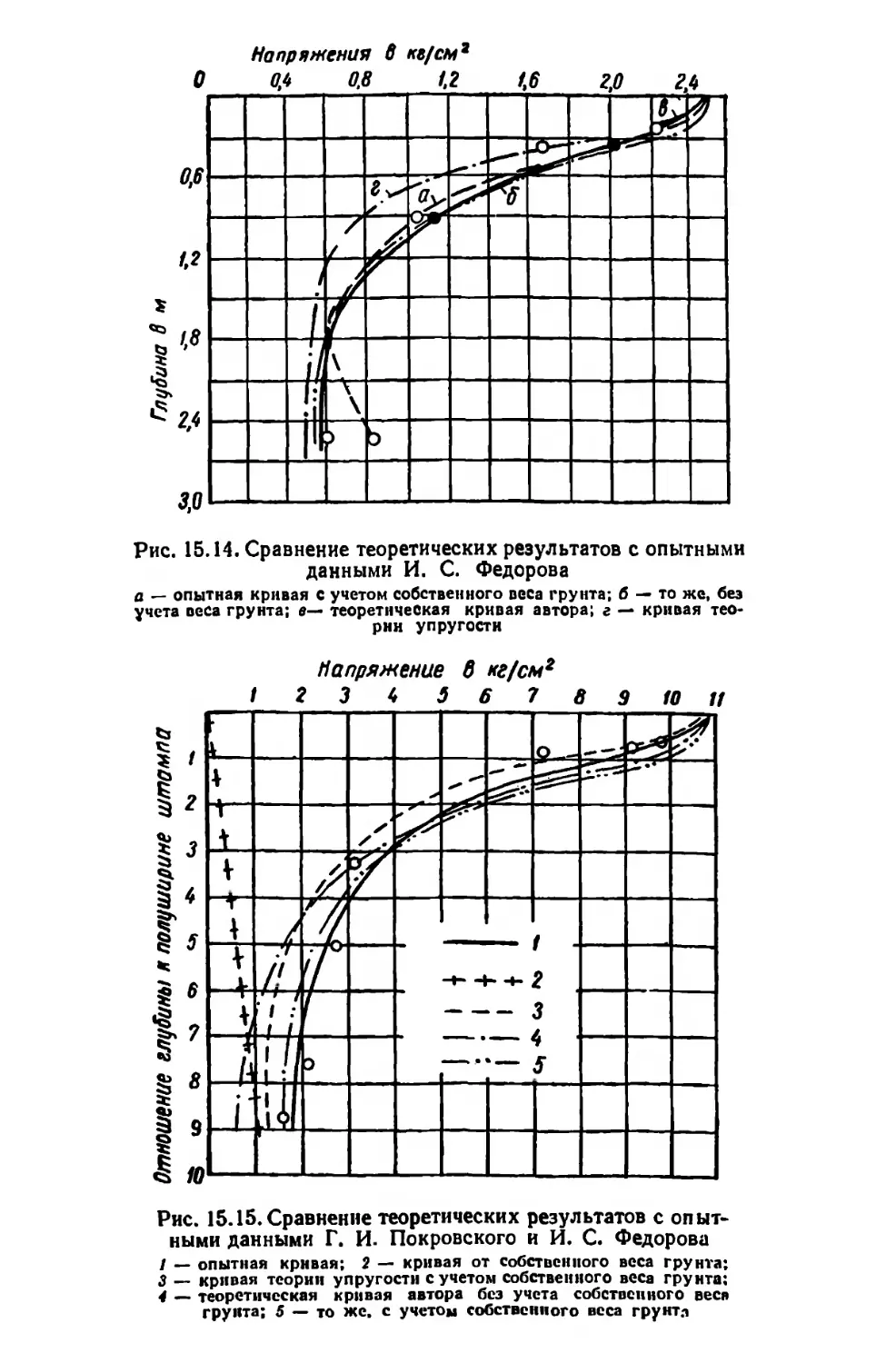
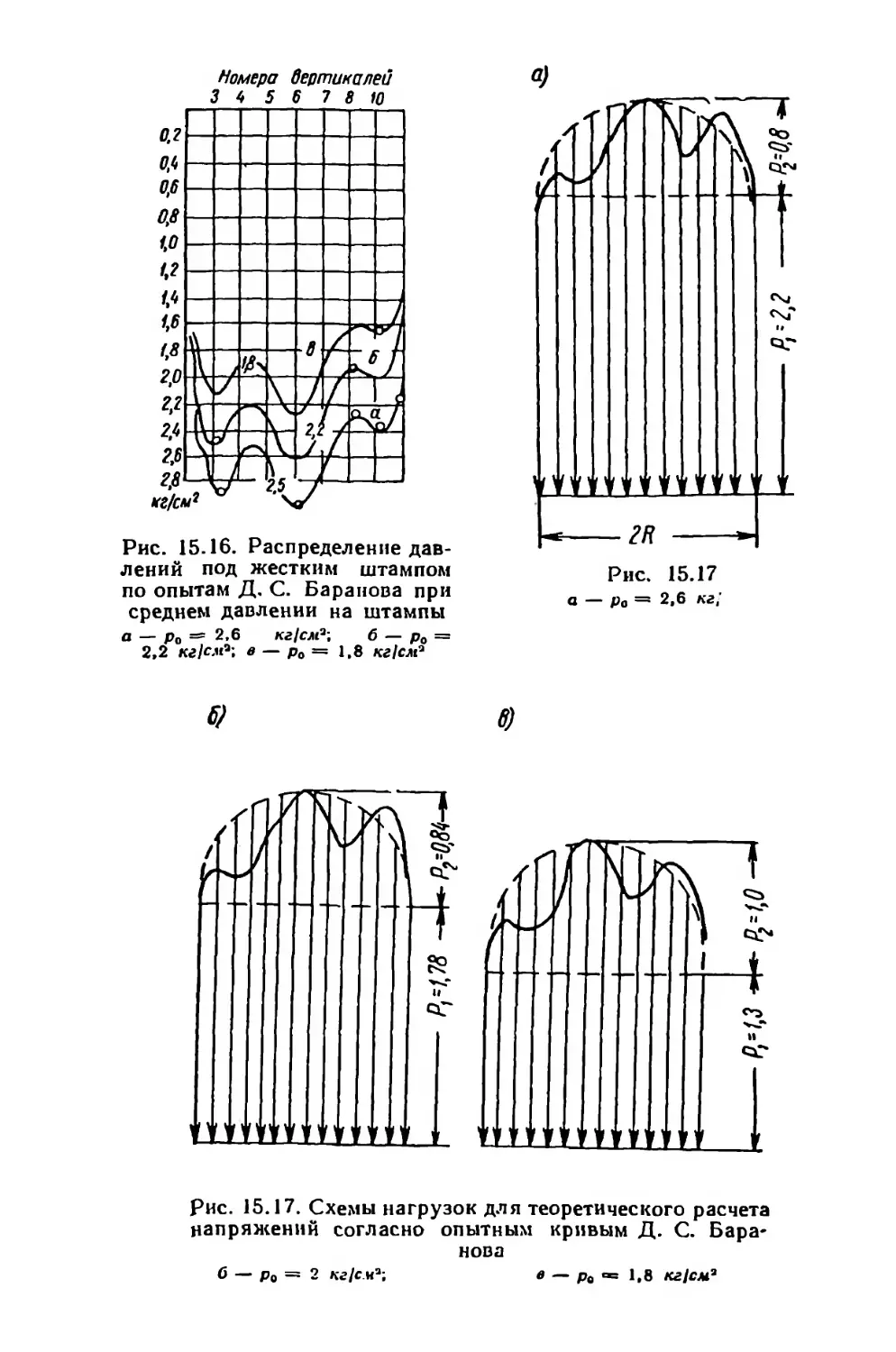
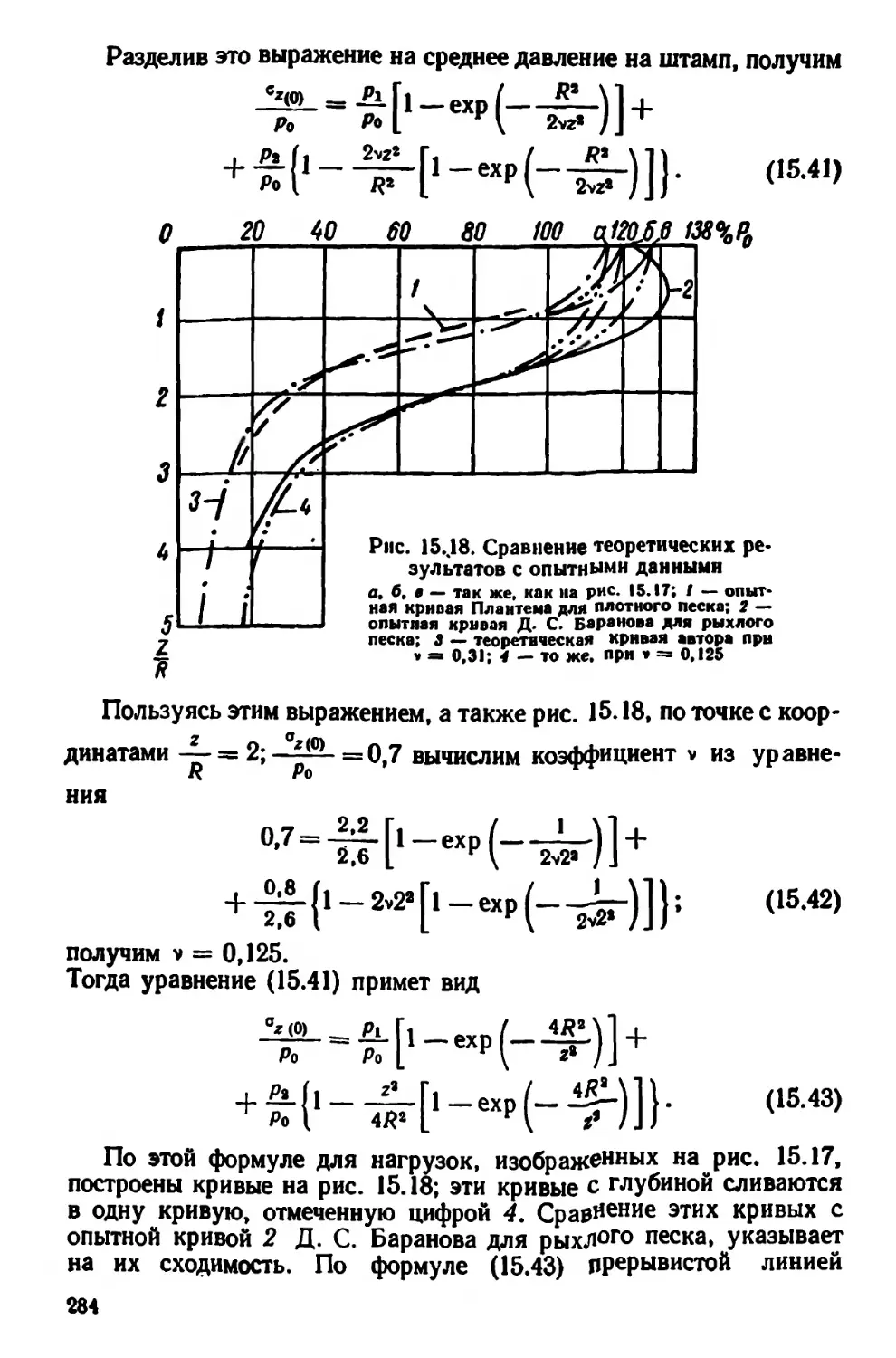
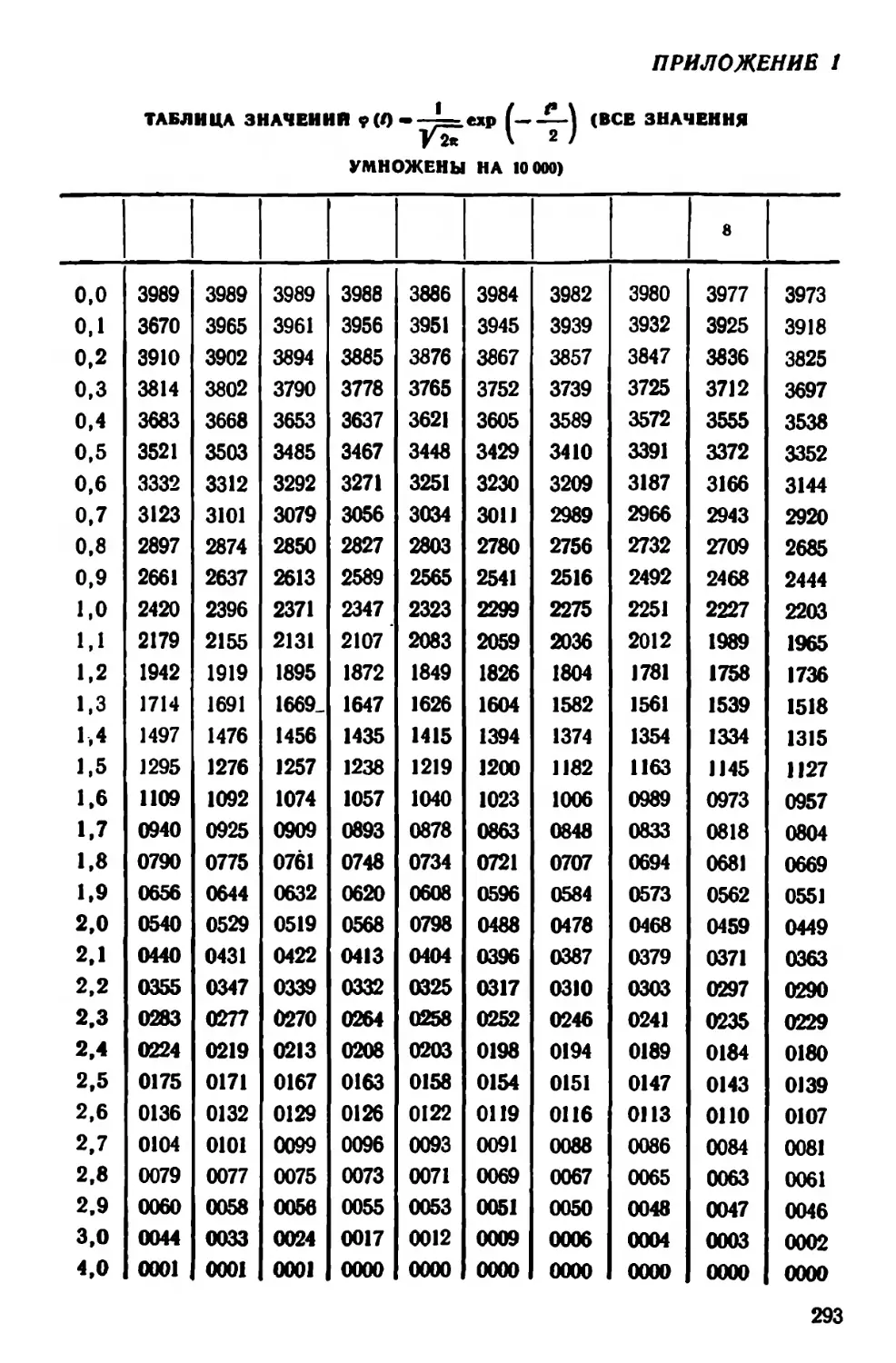
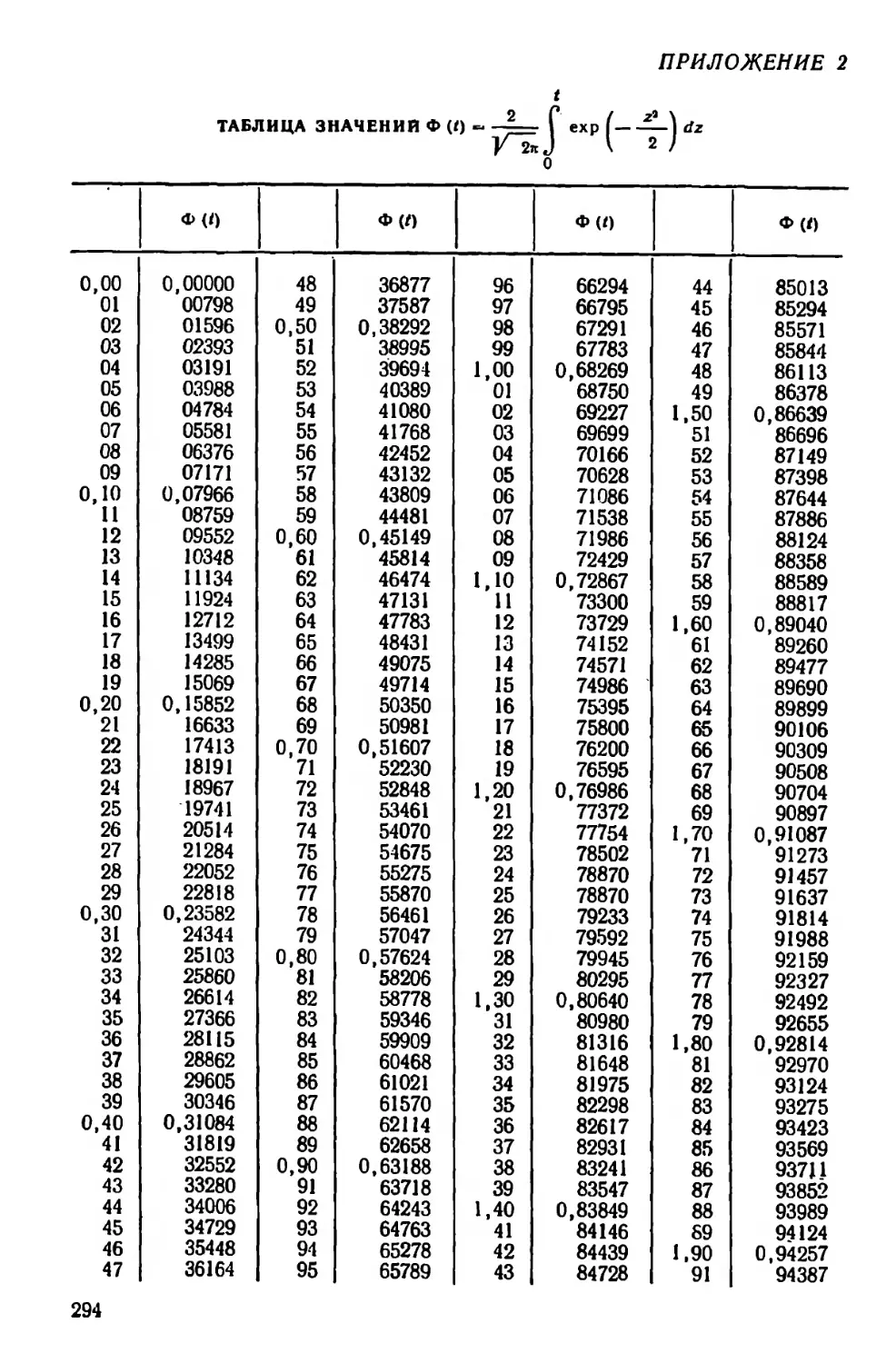
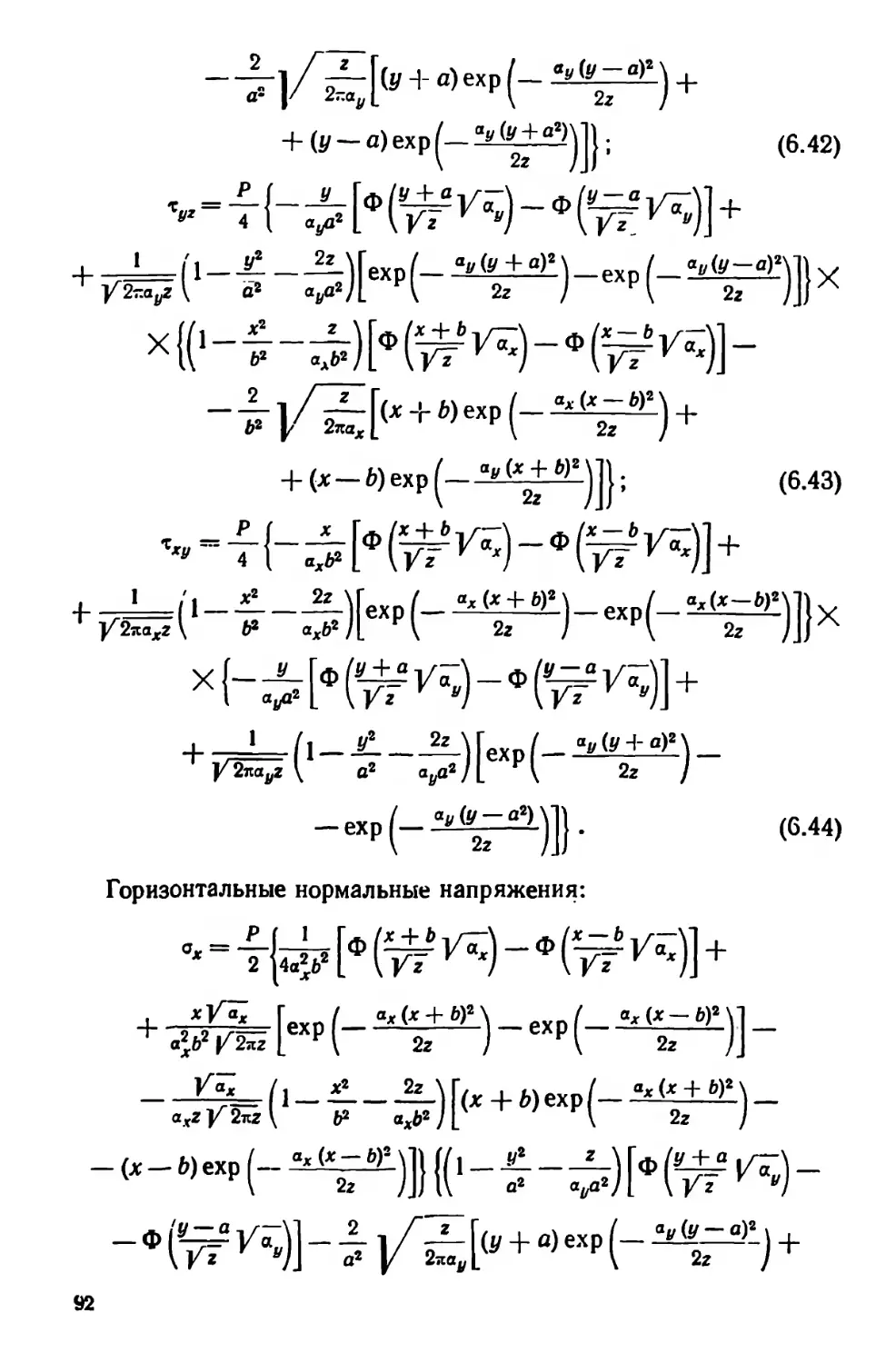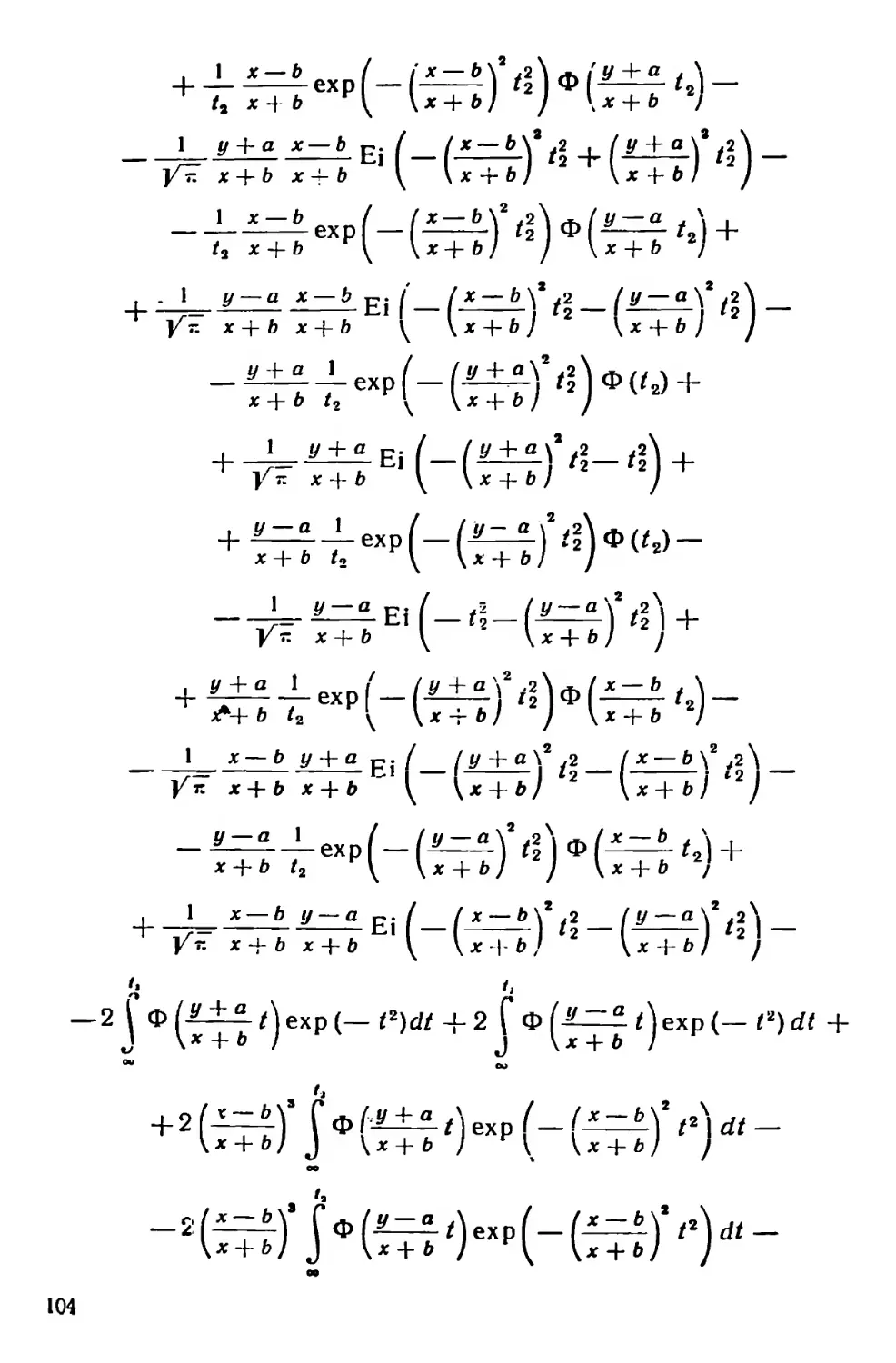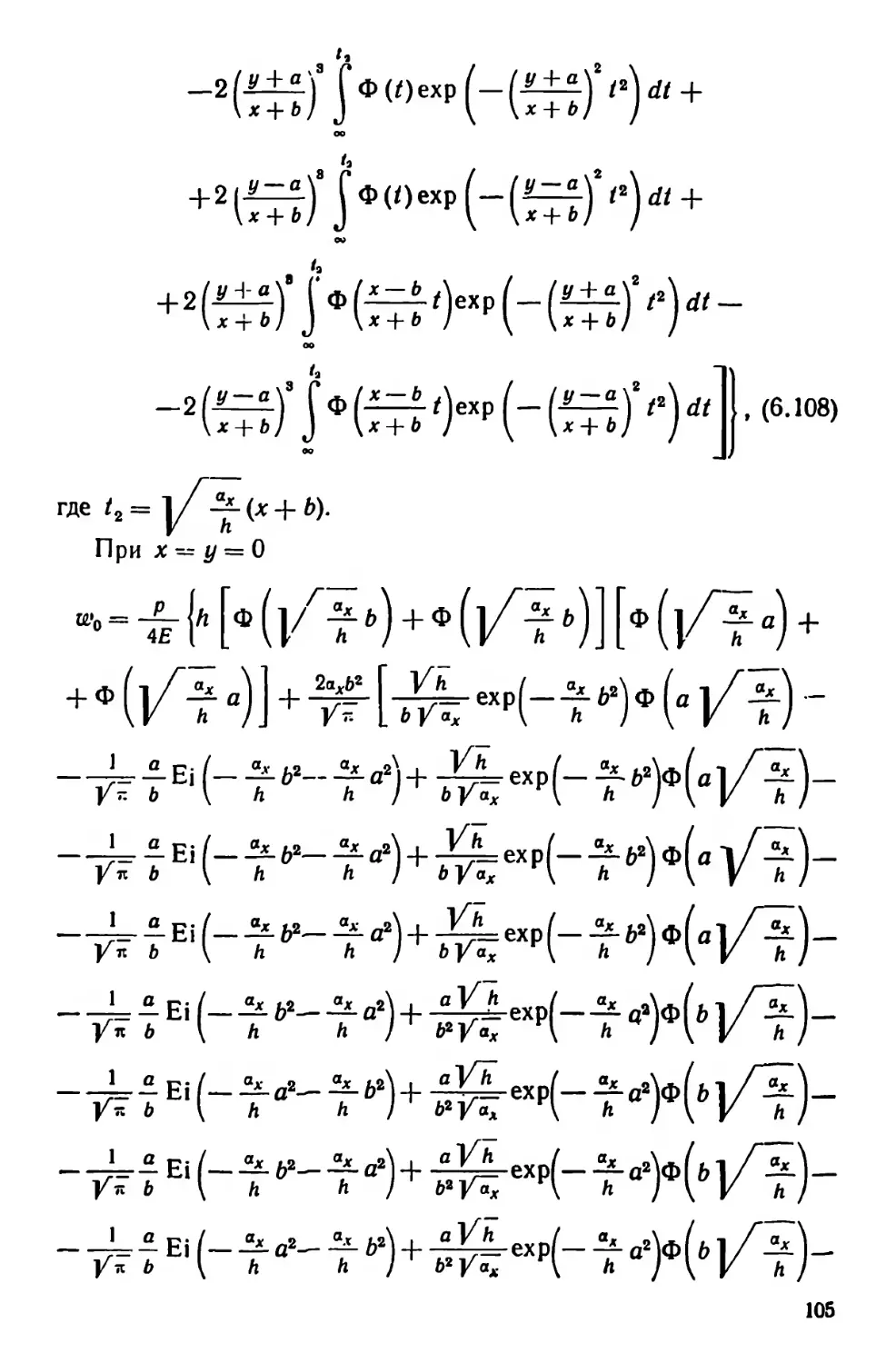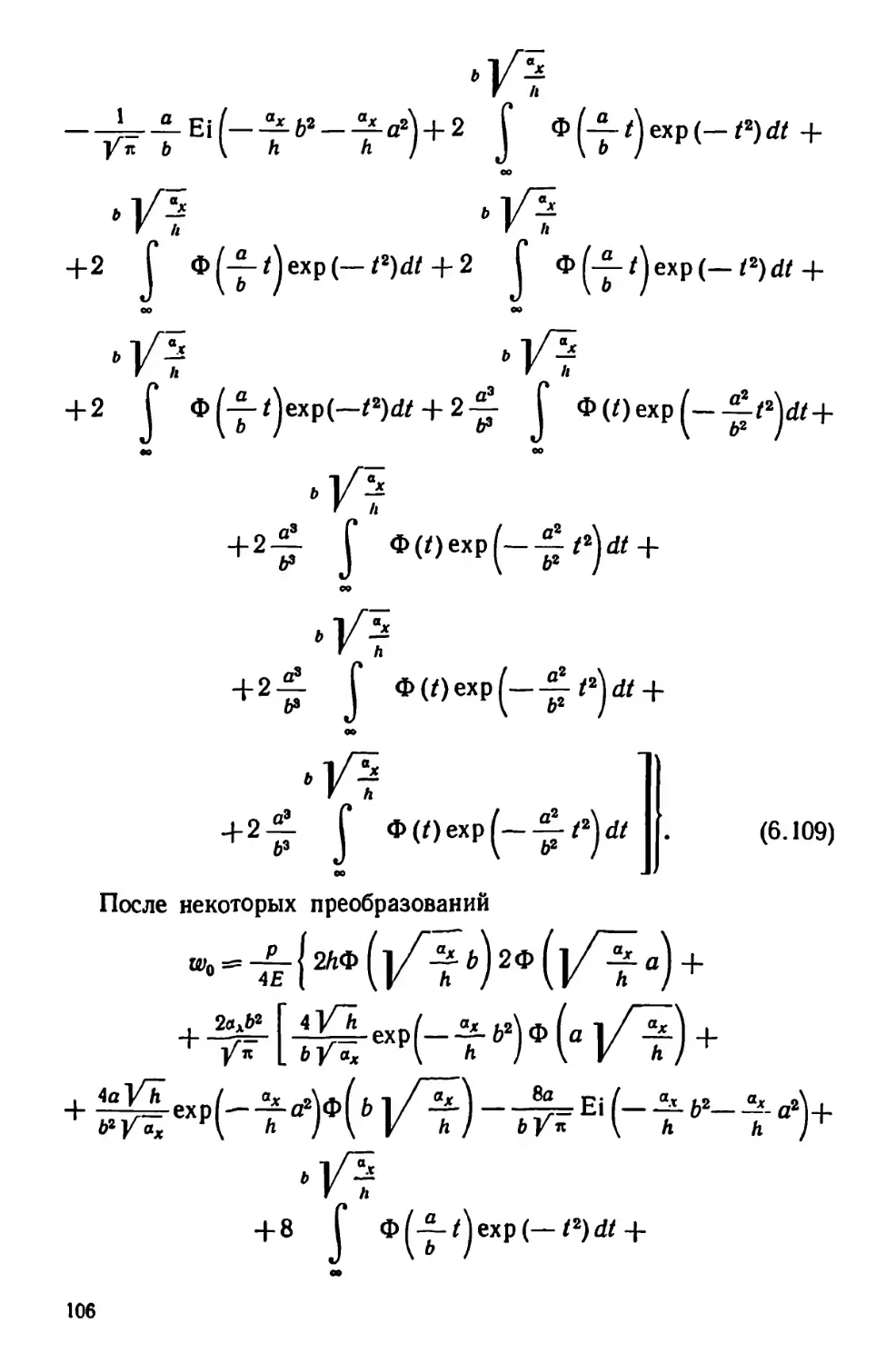Текст
                    й м е н а н и к a
зернистЬш сред
I и её применение
I в строительстве
И. И. КАНДАУРОВ
д-р техн, наук проф.
МЕХАНИКА
ЗЕРНИСТЫХ СРЕД
И ЕЕ ПРИМЕНЕНИЕ
В СТРОИТЕЛЬСТВЕ
ИЗДАТЕЛЬСТВО ЛИТЕРАТУРЫ ПО СТРОИТЕЛЬСТВУ
Ленинград 1966 Москва
УДК 624.131.51624. IfrtT?!
Научный редактор заслуж. деят. науки и техники РСФСР
д-р техн, наук проф. Н, К. Снитко
В книге излагаются полученные в последние годы резуль-
таты в статистической механике зернистых сред и дается их
практическое приложение к расчету напряженного состоя-
ния и деформаций сжатия зернистых грунтовых оснований.
При этом зернистая среда рассматривается как тело, состоя-
щее из совокупности твердых частиц разных размеров и
формы, к которой применимы законы теории вероятности и
математической статистики.
Книга рассчитана на инженеров-строителей, специали-
стов в области механики, строительной механики и других
областей знаний, где используются зернистые среды.
3-2-6
22-БЗ-10-65
ВВЕДЕНИЕ
§ 1. КРАТКИЙ ИСТОРИЧЕСКИЙ ОБЗОР
Под зернистой средой принято понимать тело, состоящее из от-
дельных соприкасающихся твердых зерен. Объем его складывается
из объема твердых зерен и пустот между ними, заполненных возду-
хом или жидкостью.
Зерна, расположенные на поверхности такого тела, могут легко
перемещаться по отношению к соседним зернам. Однако для перед-
вижения зерен, расположенных внутри тела, требуется свободное
пространство в окрестности зерна. Поэтому перемещение зерен
внутри массива может происходить, как правило, при разуплотне-
нии тела, т. е. при увеличении его объема.
Зернистые среды широко применяются в различных областях
техники.
Многие технологические процессы в химической промышленно-
сти связаны с применением гранулированных материалов и расче-
том скоростей перемещения твердого и жидкого (или газообразного)
реагентов в замкнутом объеме.
Задачи упорядочения и создания упаковок заданной плотности
возникают при производстве керамики, огнеупоров и абразивов,
в порошковой металлургии, в цементной промышленности, при про-
изводстве бетонов и асфальтобетонов.
Кристаллография и строение атомных ядер, экстремальные за-
дачи геометрии и нелинейного программирования также тесно свя-
заны с изучением упаковки зерен.
Вопросы проектирования и постройки силосных башен требуют
определения статического и динамического давления зернистых сред,
представляющих собой продукты сельскохозяйственного производ-
ства. Даже в такой области техники, как связь, важным является
изучение вибрации угольной зернистой массы в микрофонах.
Изучение зернистых сред представляет существенный инте-
рес для механики грунтов, горного дела и геологии при расчете
3
различных инженерных сооружений и анализе геологических
процессов.
Приведенный далеко не полный перечень областей применения
зернистых материалов свидетельствует об исключительной важно-
сти изучения механики зернистых сред.
Следует, однако, отметить, что зернистые среды изучены значи-
тельно меньше твердых тел и жидкостей, хотя и занимают между
ними промежуточное положение.
Г Дересевич [68 ] отмечает, что в течение по меньшей мере двух
с половиной веков вопросы механики зернистых сред привлекали
внимание многих выдающихся архитекторов, инженеров и физи-
ков, в том числе Кулона, Навье, Понселе, Ренкина, Буссинеска,
Сен-Вен ан а, Фламана, Винклера.
В 1956 г. Г. К. Клейн [40] писал, что необходимо исследовать
сыпучие тела в состоянии стационарного, т. е. устойчивого, или
упругого равновесия, а также в состоянии движения. В этом на-
правлении пока еще сделаны только первые шаги, но оба вопроса
имеют большое практическое значение. Сыпучие тела подчиняются
всем законам классической механики, и создание для них дискрет-
ной теории является уже сейчас своевременным.
Первые теоретические построения в механике грунтов базирова-
лись на представлении о грунте, как о теле, состоящем из шарооб-
разных частиц, не обладающих сцеплением.
Одной из первых в этом направлении была работа Купле, опуб-
ликованная в 1726 г. в Париже; в ней рассматривалось давление
грунта на подпорные стенки.
В 1773 г. известным французским физиком Кулоном была соз-
дана теория о давлении грунта на подпорные стенки, в'которой усо-
вершенствовалось решение Купле.
Теория Кулона базируется на возможности сдвига стенки и пре-
дельного равновесия призмы грунта, примыкающей к стенке. Тео-
рия Кулона развивалась многими исследователями и не утратила
своего значения до настоящего времени.
В 1798 г. Н. И. Фуссом при решении задачи об определении об-
разования колеи на грунтовых дорогах была высказана гипотеза
о прямой пропорциональности между нагрузкой на групт и его де-
формацией. При этом ученый полагал, что деформации грунта но-
сят остаточный характер и имеют место только под самой нагруз-
кой. Аналогичную гипотезу в 1867 г. выдвинул Винклер, который
деформации грунта считал упругими и для характеристики упру-
гих свойств основания ввел коэффициент пропорциональности ме-
жду нагрузкой и деформацией (коэффициент постели).
В 60-х годах прошлого столетия Г. Е. Паукером предложена
формула для определения глубины заложения фундамента. Основ-
ной предпосылкой построения этой формулы было условие устойчи-
вости призмы грунта против выпирания.
Развитие промышленности и особенно транспортного строитель-
4
ства во второй половине XIX столетия потребовало изучения грун-
тов и их внутренних механических свойств.
В 1879—1881 гг. Штейнером и Киком были проведены опыты по
изучению распределения давления в песчаных грунтах. Эти опыты
показали ошибочность представлений о распространении давления
грунта под постоянным углом и о равномерном распределении его
по горизонтали.
В 1889 г. русский ученый В. И. Курдюмов экспериментально
исследовал траектории движения частиц песка при вдавливании
в него модели фундамента. Проведенные исследования показали,
что траектории движения частиц грунта криволинейны и представ-
ление о плоских поверхностях скольжения в теоретических построе-
ниях является условным. Опыты В. И. Курдюмова на более высо-
ком уровне в 1952 г. повторил М. В. Малышев, у которого фотока-
мера, фиксировавшая траектории движения частиц, перемещалась
вместе со штампом.
Опыты В. И. Курдюмова, И. В. Яропольского и Н. П. Пузырев-
ского свидетельствуют о том, что формула Паукера не учитывает
ширины фундамента и приводит к неверным результатам.
Опыты Штейнера и Кика по распределению напряжений в пес-
чаных грунтах, а также В. И. Курдюмова и М. В. Малышева по
изучению траекторий движения частиц при предельном состоянии
подтверждают ошибочность многих первоначальных представлений
о механических свойствах грунтов и, в частности, зернистых сред.
В 1883 г. Буссинеск опубликовал решение о распределении на-
пряжений в идеальном упругом изотропном полупространстве от
приложенной к нему вертикальной сосредоточенной силы. Решение
Буссинеска давало криволинейную эпюру давления по горизонтали
и в этом качественно совпадало с опытными данными Штейнера и
Кика.
В 1909—1911 гг. Штрошнейдером были выполнены опыты по
изучению распределения давления в песке. В этих опытах также
отмечалась криволинейная эпюра давления по горизонтали, хотя
количественно она не совпадала с решением теории упругости.
В 1915 г. П. А. Миняев провел экспериментальное исследование,
результаты которого с качественной стороны позволили сделать
вывод о применимости формул теории упругости к связным и зер-
нистым грунтам при расчете напряженного состояния. Это явилось
стимулом для интенсивного приложения теории упругости к грун-
там. Почти за 50 лет много интересных результатов в этом вопросе
достигнуто Г. Э. Проктором, М. И. Горбуновым-Посадовым,
К. Е. Егоровым, Г. К. Клейном, Н. К. Снитко, В. Г. Короткиным,
Н. М. Герсевановым, П. А. Миняевым, Н. П. Пузыревским и др.
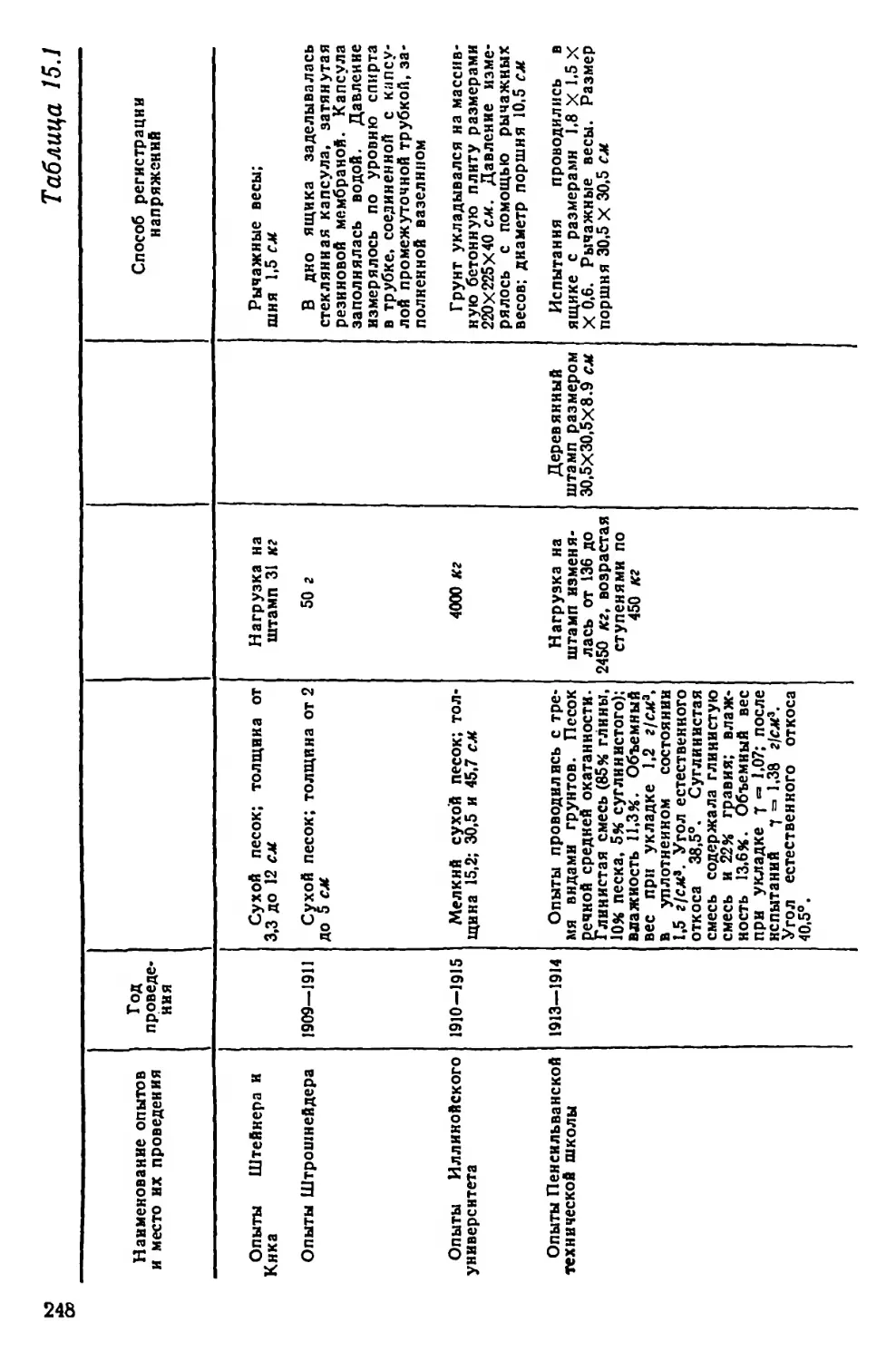
Опыты Иллинойского университета (1910—1915 гг.), Пенсиль-
ванской технической школы (1913—1914 Гт.), Американской ассо-
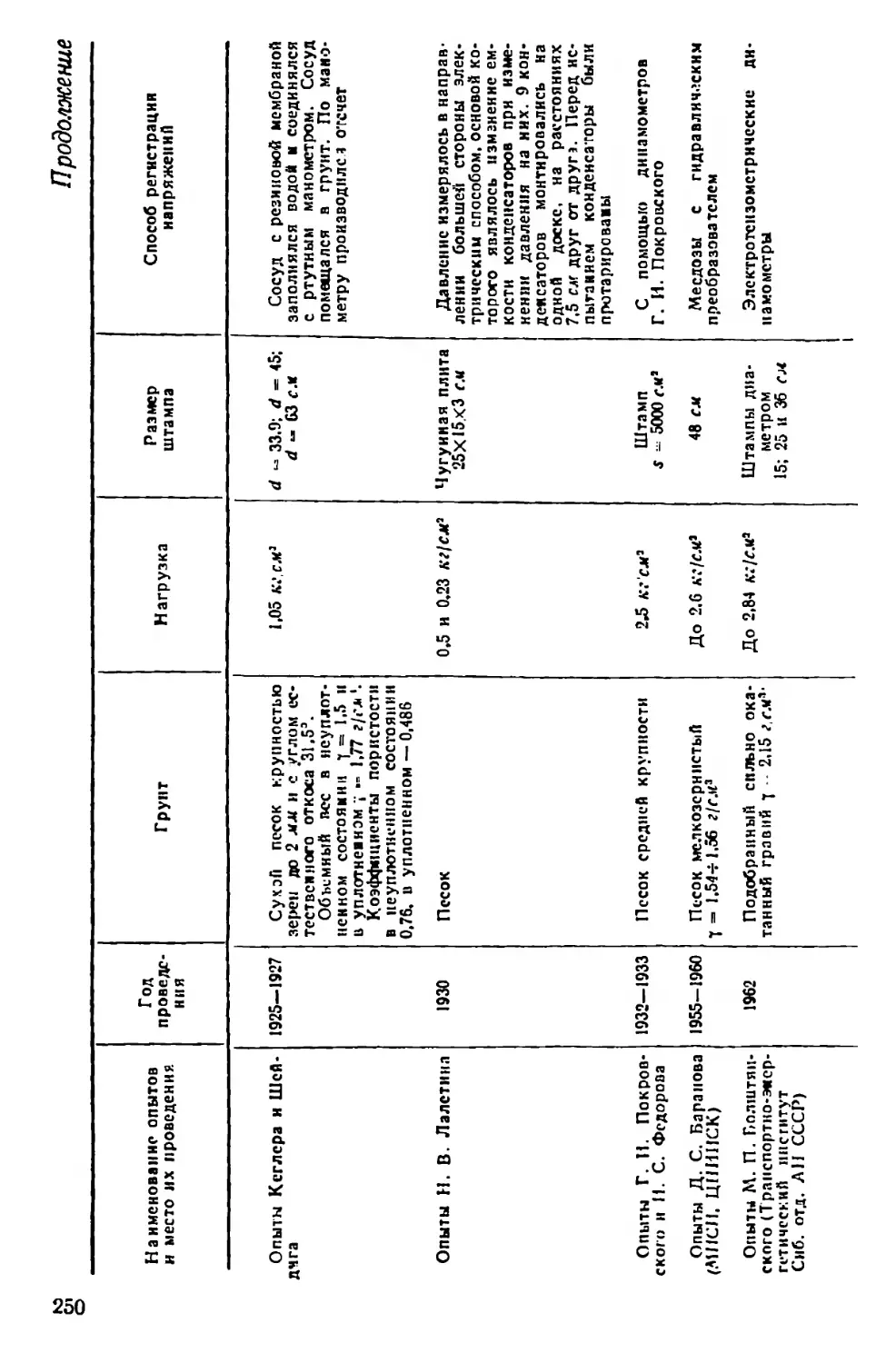
циации гражданских инженеров (1910 г.),Гольдбека (1917—1924 гг.),
Кеглера и Шейдига (1925—1927 гг.), Н. В. Лалетина (1930 г.),
5
И. С. Федорова и Р. И. Покровского (1932—1933 гг.), Плантема
(1952 г.), Д. С. Баранова (1955—1960 гг.), М. П. Болштянского
(1962 г.) свидетельствуют о том, что напряжения в песчаной среде
в 2—3 раза отличаются от вычисленных по формулам теории упру-
гости.
Это обстоятельство послужило в свое время причиной введения
в формулы теории упругости эмпирических коэффициентов, так на-
зываемых коэффициентов концентрации напряжений.
Первым на такую возможность сближения теоретических данных
с экспериментальными в 1929 г. обратил внимание Н. Ы. Иванов
[32 ]. В дальнейшем эта идея получила широкое развитие в работе
О. К. Фрелиха [91 ].
В 1954 г. Д. Тейлор [115] отмечал, что для осадочных песков
характерны более интенсивная концентрация напряжений непосред-
ственно под приложенной нагрузкой и меньшие напряжения по
периферии по сравнению с распределением напряжений по теории
упругости. Поэтому формулы Буссинеска и Верстергарда, основан-
ные на теории упругости, не пригодны для определения напряже-
ний, вызываемых в песках поверхностной нагрузкой. Модификации
этих формул для песков с применением коэффициента концентра-
ций напряжений весьма условны и являются чисто эмпирическими.
С именами К. Терцаги, Н. М. Герсеванова, В. А. Флорина,
В. Г. Булычева, Д. Е. Полыпина, Е. И. Медкова, С. А. Роза,
Б. Д. Васильева, Н. Н. Маслова и др. связывают изучение дефор-
мации грунта под нагрузкой как двух- и трехкомпонентных систем
(твердого скелета и пор, заполненных водой или водой и газом).
Разработка методов расчета скорости осадок сооружений на сжи-
маемых водонасыщенных грунтах составляет основу данного на-
правления.
Предметом изучения этого направления в механике грунтов яв-
ляются водонасыщенные глинистые грунты («грунтовые массы»)
без газа или с защемленным в порах газом.
Самостоятельное направление в механике грунтов занимает тео-
рия предельного равновесия грунтов. Существенный вклад в раз-
витие этого направления сделали В. Ренкин, Л. Прандтль, Г. Рейс-
нер, А. Како, В. И. Новоторцев, В. В. Соколовский, С. С. Го-
лушкевич, В. Г. Березанцев, Г. К. Клейн, А. А. Нечипорович,
Н. Н. Маслов, И. В. Федоров и др.
Для решения задачи об устойчивости оснований здесь исполь-
зуются уравнения равновесия, выведенные для сплошной среды,
а вместо уравнения неразрывности деформаций—уравнение, опре-
деляющее предельное состояние каждой точки массива.
Оригинальна работа Н. П. Пузыревского, опубликованная в
1929 г., в которой также применяются уравнения равновесия для
сплошной среды, а вместо уравнений неразрывности деформаций
используется условие, согласно которому касательное напряжение
в каждой точке является функцией полярного угла, определяющего
6
положение этой точки относительно начала координат. Интересны
в этих работах» с одной стороны» использование уравнений равно-
весия, полученных для сплошной среды, и» с другой стороны» за-
мена уравнений неразрывности деформаций новым условием. Та-
ким образом, сплошная среда наделяется здесь свойствами» отлич-
ными от свойств упругого сплошного тела.
Трудами В. А. Обручева, М. И. Сумгина, Н. А. Цытовича
и других в СССР созданы научные основы и практические методы
расчета оснований и проектирования фундаментов на вечномерзлых
грунтах.
Это направление в механике грунтов успешно развивается в ра-
ботах С. С. Вялова» X. П. Хакимова, М. Ф. Киселева» М. Н. Гольд-
штейна, Н. А. Пузакова, А. Е. Федосова, И. А. Золотаря и др. Ос-
новное внимание здесь уделяется изучению процессов оттаивания
и промерзания грунта и на этой основе расчету оснований и проекти-
рованию фундаментов.
Совершенно самостоятельной является область механики дорож-
ных и аэродромных покрытий. Особенностью этого направления
в механике грунтов является изучение слоистых систем в условиях
переменного водно-теплового режима и многократного воздействия
динамических нагрузок. Большой вклад в развитие этого направ-
ления сделали советские ученые А. К. Бируля, Н. Н. Иванов,
Г. И. Покровский, В. Ф. Бабков, А. М. Кривисский, Б. И. Коган,
Я. А. Калужский, Н. Я. Хархута, Р. М. Раппопорт и др.
В последние годы в связи со строительством крупных гидротех-
нических сооружений интенсивно развивается новое направление
в механике грунтов — изучение вопросов ползучести грунтов. Здесь
прежде всего необходимо отметить работы Н. X. Арутюняна,
В. А. Флорина, С. Р. Месчяна, Н. Н. Ермолаева и др.
Изучению тиксотропных свойств грунтов посвящен ряд работ
Б. М. Гуменского и М. В. Бунина.
С потребностями гидротехнического строительства связано
также изучение механических свойств скальных трещиноватых
оснований. Здесь следует отметить работы сотрудников ВНИИГ
им. Б. Е. Веденеева под руководством П. Д. Евдокимова, работы
ВНИИоснований и подземных сооружений и ВНИИВодгео.
В связи с разведкой нефти, изучением распространения сейсми-
ческих волн, расчетом сооружений на ударные и подвижные на-
грузки, вибропогружением свай, шпунтов и свай-оболочек при
создании фундаментов и опор мостов в последние годы интенсивно
развиваются вопросы динамики грунтов.
Большой вклад в развитие динамики грунтов сделали Г. И. Пок-
ровский, И. С. Федоров, С. А. Христианович, Е. И. Шемякин,
С. С. Григорян, Н. К. Снитко, Д. Д. Баркан, Р. А. Рахматулин,
О. А. Савинов, Г. А. Гениев и др.
Изучением динамических явлений в сыпучем теле, возникающих
при истечении его из отверстия (например, в силосах), занимается
7
С. Г. Тахтамышев. При изучении вопросов динамики моделью
грунта является сплошное тело.
Самостоятельное направление в изучении грунтов представляет
механика зернистых сред. Моделью зернистой среды здесь служит
тело, в котором отдельные зерна являются шарами или другими
выпуклыми телами, находящимися в соприкосновении в правиль-
ных порядках. При определении деформаций соприкасающиеся
тела в этой модели принимаются упругими и деформации их описы-
ваются с помощью контактной теории Герца (Миндлин, Дересевич
И др.).
В этом направлении значительные результаты достигнуты в раз-
витии контактной теории различных выпуклых геометрических
тел правильной формы.
Вместе с тем изучение самой зернистой среды, особенно под воз-
действием локальных нагрузок, при таком подходе связано с боль-
шими трудностями.
Наряду с развитием и изучением детерминированных моделей
не только в механике грунтов, но и вообще в строительной механике,
в настоящее время интенсивно начинают изучаться статистиче-
ские модели.
В 30-х годах статистические модели в сопротивлении материалов
были предложены Н. К. Снитко 1771, а в механике грунтов —
Г. И. Покровским [69].
В 1929 г. Г. И. Покровский на основе анализа эксперименталь-
ных опытов предложил эпюру давления в горизонтальной плоско-
сти описывать нормальной кривой Гаусса. На этой основе для вер-
тикальных напряжений в плоской задаче от сосредоточенной на-
грузки им получена следующая формула
где Р — давление на глубине Я;
Ро — наибольшее давление на единичной глубине;
х0 — координата наибольших давлений;
х — координата рассматриваемой точки;
с — некоторая постоянная, зависящая от рода грунтов.
Статистический подход к грунтам нашел продолжение в рабо-
тах Г. К. Клейна, М. Н. Троицкой, М. Н. Гольдштейна, Н. В. Ор-
натского, Р. А. Муллера, Ф. М. Шихиева, Б. С. Радовского,
И. Т. Сергеева, Ю. Литвинишина, Г И. Довженко и др. Он позво-
ляет лучше учитывать природу грунта и успешно решать задачи
статики и динамики зернистых сред.
Большое место в механике грунтов занимают так называемые
инженерные методы, основанные на различных допущениях, значи-
тельно упрощающих решение задачи.
8
§2. ПРЕДЛАГАВШИЕСЯ РАСЧЕТНЫЕ СХЕМЫ
И ПРИРОДА ЗЕРНИСТЫХ СРЕД
Грунт по природе своей является сложным физическим телом,
свойства которого зависят от большого количества факторов.
Каждая из расчетных моделей
грунта отражает то или иное его	|р
физическое состояние при работе	f
в различных природных условиях. I	I
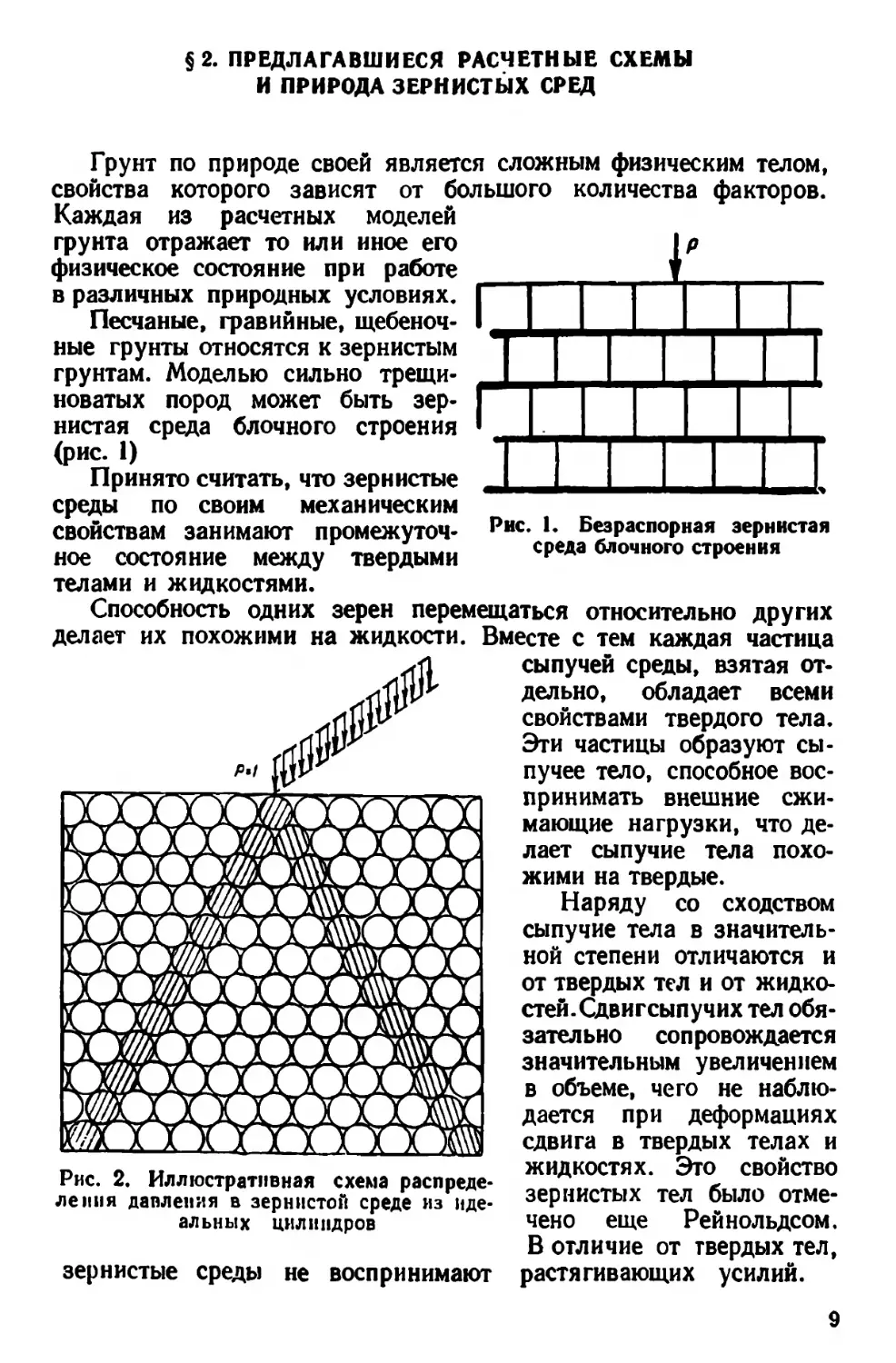
Песчаные, гравийные, щебеноч- I
ные грунты относятся к зернистым
грунтам. Моделью сильно трещи-	,
новатых пород может быть зер- |
нистая среда блочного строения ’	|	|	|	|	|	|
(рис. 1)	III I l li
Принято считать, что зернистые dl l 1111
среды по своим механическим
свойствам занимают промежуточ- Рис- Безраспорная зернистая
ное состояние между твердыми среда <5лочного строения
телами и жидкостями.
Способность одних зерен перемещаться относительно других
делает их похожими на жидкости. Вместе с тем каждая частица
Рис. 2. Иллюстративная схема распреде-
ле имя давления в зернистой среде из иде-
альных цилиндров
зернистые среды не воспринимают
сыпучей среды, взятая от-
дельно, обладает всеми
свойствами твердого тела.
Эти частицы образуют сы-
пучее тело, способное вос-
принимать внешние сжи-
мающие нагрузки, что де-
лает сыпучие тела похо-
жими на твердые.
Наряду со сходством
сыпучие тела в значитель-
ной степени отличаются и
от твердых тел и от жидко-
стей. Сдвигсыпучих тел обя-
зательно сопровождается
значительным увеличением
в объеме, чего не наблю-
дается при деформациях
сдвига в твердых телах и
жидкостях. Это свойство
зернистых тел было отме-
чено еще Рейнольдсом.
В отличие от твердых тел,
растягивающих усилий.
9
Отмеченные особенности природы зернистых сред указывают
на необходимость разработки для них своих расчетных схем.
Одной из первых моделей зернистых сред, учитывающей их ди-
скретную природу, была модель из одинаковых шаров плотной упа-
ковки для пространственной’задачи и одинаковых цилиндров плот-
ной упаковки для плоской задачи.
Рассмотрим с качественной стороны характер передачи усилий
в такой модели на примере
Рис. 3. Качественная картина
распределения давления в сре-
де из цилиндров одинакового
диаметра
а — схема опытной установки; б —
оптическая картина распределения
давлений
плоской задачи.
На рис. 2 изображена схема зер-
нистой среды из цилиндров одинако-
вых размеров. На поверхности среды
к одному из цилиндров приложена
вертикальная нагрузка. Если счи-
тать, что цилиндры абсолютно оди-
наковы и уложены симметрично от-
носительно нагрузки, то для жестких
цилиндров можно полагать, что внеш-
няя нагрузка воспринимается только
заштрихованными на рисунке части-
цами зернистой среды. Но вероятность
соблюдения всех указанных выше ус-
ловий практически равна нулю, и
действительная картина распределе-
ния усилий будет другой. Это поло-
жение подтверждается и эксперимен-
тальными данными [114].
На рис. 3 показана картина на-
пряженного состояния среды, образо-
ванной цилиндрами одинаковых диа-
метров; нарушение в силу статисти-
ческой природы явления указанных
выше условий ведет к искажению
предполагаемой детерминированной
картины распределения усилий в та-
кой среде. Вместе с тем из рисунка
видно, что усилия воспринимаются
цилиндрами, расположенными на ка-
кой-либо линии. В то же время боль-
шая часть цилиндров, образующих
среду, или вообще не воспринимает внешнюю нагрузку или вос-
принимает ее незначительно.
Совсем иная картина напряженного состояния, изображенная
на рис. 4, получается для среды, образованной случайным образом
из цилиндров разных диаметров. Сопоставляя рис. 4 и 3, нетрудно
усмотреть статистическую природу сил в зернистой среде, образо-
ванной различными по размеру частицами, по сравнению со средой
плотной упаковки из частиц одинакового размера. На рис. 5 можно
10
видеть аналогичную картину распределения давления в зернистой
среде из шаров разных диаметров.
Из сказанного ясно, что при составлении расчетной схемы сле-
дует осреднять не только размеры частиц зернистой среды, но и ус-
ловия передачи усилий через контакты. В некоторых литературных
источниках 197] ошибочно отождествляется распределение усилий
в среде цилиндров с распределением усилий в среде из блоков, хотя
это разные среды.
Первая среда является распорной; каждая ее частица ведет себя
внутри массива как клин, в силу чего при воздействии вертикаль-
ной нагрузки возникают горизонтальные составляющие усилия.
Вторая среда — безраспорная; распора в такой среде от верти-
кальных внешних сил в указанном выше смысле не возникает.
Рис. 4. Оптическая картина рас-
пределения давления в зернистой
среде из цилиндров разных диамет-
ров со случайным взаимным распо-
ложением
Рис. 5. Оптическая картина рас-
пределения давления в зернистой
среде из шаров разных диаметров
со случайным расположением каж-
дого шара в массиве
Отмеченное обстоятельство кажется простым и само собой ра-
зумеющимся. Вместе с тем во многих работах, даже изданных в по-
следние годы, распределение давления в среде из параллелепипе-
дов отождествляется с распределением давления в среде из цилинд-
ров.
Из сказанного вытекает что для каждой зернистой среды должна
быть своя расчетная схема, учитывающая структуру и вероятност-
ный характер распределения усилий и деформаций в ней.
Анализ различных структур грунтов, используемых в основа-
ниях инженерных сооружений, показывает, что для описания на-
пряжений и деформаций в них в допредельном состоянии можно
выделить три основные расчетные модели:
упругую модель, способную воспринимать растягивающие
усилия;
модель зернистой среды, не способную воспринимать растя-
гивающие усилия и создающую распор в среде при передаче внеш-
них нагрузок;
11
модель блочного строения или безраспорную среду.
Две последние модели относятся к зернистым средам и описы-
ваются в данной книге.
В настоящей работе изложены теоретические основы статисти-
ческой механики зернистых сред как дискретных сред. При этом
исследуется поведение зернистой среды, а не отдельных ее зерен.
Эти вопросы до сих пор недостаточно исследованы.
Книга написана в основном по материалам исследований автора
о распределении средних значений напряжений и деформаций как
в однородных, так и в многослойных зернистых средах, а также
исследований Р. А. Муллера о физических уравнениях зернистых
грунтовых сред и о приложении общих уравнений к расчету жест-
ких неподвижных подпорных стенок.
ЧАСТЬ ПЕРВАЯ
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ
БЕЗРАСПОРНЫХ ЗЕРНИСТЫХ
ОСНОВАНИЙ
Глава 1
СТРУКТУРНЫЕ ОСОБЕННОСТИ БЕЗРАСПОРНЫХ ЗЕРНИСТЫХ
ОСНОВАНИЙ
§ 1. РАЗМЕРЫ И ФОРМА БЛОКОВ БЕЗРАСПОРНЫХ ЗЕРНИСТЫХ
ОСНОВАНИЙ
Механические свойства зернистых сред определяются формой,
размерами и взаимным расположением частиц (зерен) в массиве.
Каждый из показателей может быть случайным или упорядоченным.
В упорядоченных системах, в свою очередь, различают ближний и
дальний порядок; при этом ближний порядок можно считать детер-
минированным, а дальний — случайным. Например, в целях соз-
дания упорядоченной зернистой среды можно выбрать форму и раз-
меры частиц в виде шаров или кубов или других строгих геометри-
ческих тел, установить размеры этих частиц и порядок их укладки.
Выполнение указанных условий и определяет ближний порядок
в зернистой среде.
Вместе с тем при изготовлении практически невозможно выдер-
жать точно заданную форму и размеры частиц и заданную укладку
зерен в теле среды. Иными словами, случайные факторы будут варьи-
ровать параметры среды и ее структуру относительно некоторого
заданного среднего состояния. Дальний порядок в указанном здесь
смысле будет обязательно случайным.
Все это относится также и к безраспорным зернистым средам.
Под безраспорными зернистыми средами понимаются такие, у ко-
торых не возникает распора (клинового эффекта) при распределе-
нии равномерной внешней нагрузки между частицами внутри мас-
сива.
13
Безраспорная зернистая среда может рассматриваться как ус-
редненная модель скальных трещиноватых оснований. Кроме того,
примерами таких сред могут быть кирпичные сухие кладки, бутовые
кладки и т. д.
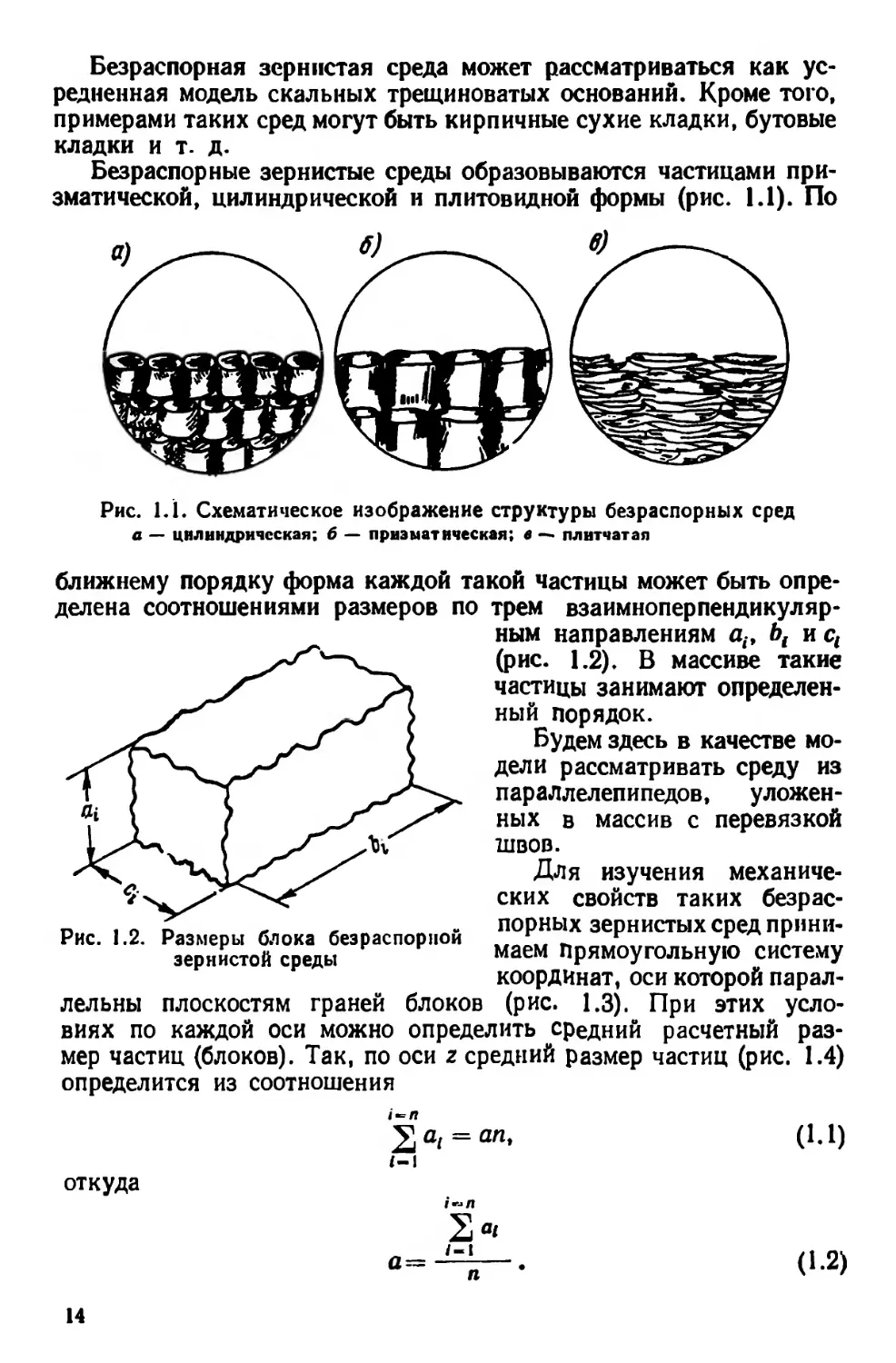
Безраспорные зернистые среды образовываются частицами при-
зматической, цилиндрической и плитовидной формы (рис. 1.1). По
Рис. 1.1. Схематическое изображение структуры безраспорных сред
а — цилиндрическая; 6 — призматическая; в — плитчатая
ближнему порядку форма каждой такой частицы может быть опре-
делена соотношениями размеров по трем взаимноперпендикуляр-
ным направлениям ait bt и с,
(рис. 1.2). В массиве такие
частицы занимают определен-
ный порядок.
Будем здесь в качестве мо-
дели рассматривать среду из
параллелепипедов, уложен-
ных в массив с перевязкой
швов.
Для изучения механиче-
ских свойств таких безрас-
Рис. 1.2. Размеры блока безраспорчой "орных зернистых сред прини-
зернистой среды	маем Прямоугольную систему
координат, оси которой парал-
лельны плоскостям граней блоков (рис. 1.3). При этих усло-
виях по каждой оси можно определить средний расчетный раз-
мер частиц (блоков). Так, по оси z средний размер частиц (рис. 1.4)
определится из соотношения
откуда
= ал»
/-1
2 о/
7-1
(1.1)
(1-2)
14
Аналогичным образом определяются средние размеры блоков
по осям х и у:
по оси х средний размер зерен
Рис. 1.3. Целесообразный вы-
бор направления осей коорди-
нат в безраспорной зернистой
среде
(1.3)
(1.4)
Рис. 1.4. К определению среднего раз-
мера блока по направлению оси z
Соотношения (1.2), (1.3) и (1.4) позволяют из частиц одинаковых
размеров построить модель зернистой безраспорной среды, эквива-
лентную изучаемой среде как по среднему числу частиц, приходя-
щихся на единицу длины, так и по числу промежутков между ча-
стицами (блоками).
Для зернистых безраспорных сред, у которых швы перевязаны
в направлении всех координатных осей, средние размеры блоков
необходимо сначала определять по сечениям, а затем находить для
них свое среднее значение. Для таких сред средний размер по оси 2
где
ni
(1.5)
(1.6)
а7 =
15
af — средний размер зерен по / й вертикали;
Мг — число вертикалей, по которым определяется средний раз-
мер зерен (блоков);
nj — число зерен по /*-й вертикали для интервала по оси z (о, 2).
При вычислении nz для всех вертикалей берется одинаковая
глубина.
Аналогичным образом определятся средние размеры вдоль осей
х и у\
вдоль оси х
вдоль оси у
(1.7)
(1.8)
(1.9)
(1.Ю)
Здесь /Ид.; Му — число сечений, по которым вычисляются средние
размеры соответственно вдоль осей х и у\
ntj\ Nj — число частиц в сечениях / соответственно вдоль
осей хну;
b{\ cf — средние размеры частиц (блоков) в /-ом сечении
соответственно вдоль осей х и у\
bt\ с{ — размеры частиц по направлениям осей х и у,
§ 2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ БЛОКОВ И РАСЧЕТНЫЕ СХЕМЫ
ДЛЯ НИХ
В § 1 было отмечено, что любая зернистая среда, даже детерми-
нированная по ближнему порядку, является статистической. В силу
имеющихся микронеровностей на поверхностях блоков напряжен-
ное состояние на контактах их носит статистический характер и
поэтому о напряжениях можно говорить лишь как об их математи-
ческом ожидании.
Рассмотрим теперь, какую расчетную схему можно принять для
частиц призматической, цилиндрической и плитовидной структуры.
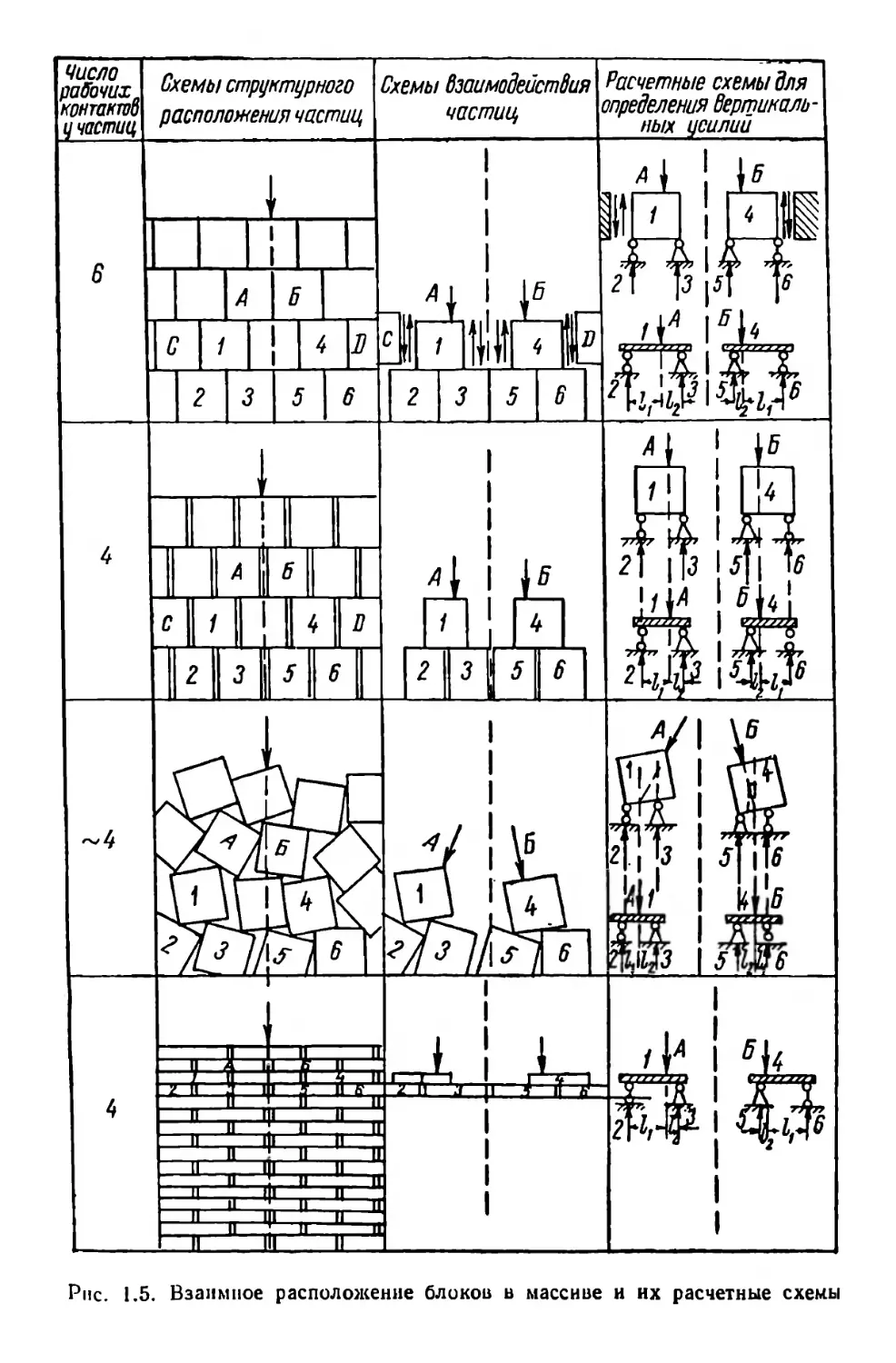
На рнс. 1.5 представлены различные случаи взаимного
16
Рис. 1.5. Взаимное расположение блоков в массиве и их расчетные схемы
расположения зерен и установлены их расчетные схемы. Из рисунка
видно, что для зерен призматической, цилиндрической и плитовид-
ной формы при рассмотрении характера распределения вертикаль-
ных напряжений (усилий) за расчетную схему в плоской задаче
может быть принят жесткий диск на двух опорах. Точка приложе-
ния равнодействующей силы носит здесь случайный характер.
Для пространственной задачи можно показать, что каждая ча-
стица имеет четыре опорных зерна. Расчетной схемой для простран-
ственной задачи, следовательно, будет жесткий диск на четырех
опорах.
Из сказанного следует, что для плоской задачи расчетная схема
каждой частицы при исследовании характера распределения верти-
кальных усилий (напряжений) в массиве может быть составлена
в виде жесткого диска на двух опорах при случайно выбранной
точке приложения силы от вышележащих частиц.
Для пространственной задачи наиболее вероятной расчетной
схемой будет схема жесткого диска на четырех опорах. Для каждой
частицы точка приложения активной силы здесь также выбирается
случайно. Можно сказать, что в целом для безраспорного основа-
ния передача усилия от частицы к частице в общем случае происхо-
дит неравномерно и случайным образом. При этом как неравномер-
ность, так и случайность эквивалентно могут быть оценены случай-
ным выбором для каждой частицы точки приложения активной
силы. Положением этой точки определяется неравномерность пере-
дачи активного усилия на опорные реакции.
Будем оценивать эту неравномерность коэффициентом неравно-
мерности передачи усилий, который представим как отношение
плеча, расположенного далее от линии действия внешней нагрузки,
к плечу, расположенному ближе к линии действия внешней
нагрузки. Согласно принятым на рис. 1.5 обозначениям выражение
для такого коэффициента запишем в виде
=4	(,и>
где kj — коэффициент неравномерности передачи (распределения)
усилий между частицами;
/1. /2 — расстояния от точки приложения активной силы
диску до опорных реакций.
Для различных частиц коэффициент неравномерности передачи
усилий различен. Он зависит от случайного выбора точки прило-
жения нагрузки, формы и размера зерен, их взаимного расположе-
ния, наличия и расположения микронеровностей на контактах,
ориентировки зерен и т. д.
Поскольку коэффициент неравномерности передачи усилий за-
висит от многих случайных факторов, то согласно предельной тео-
реме Ляпунова его распределение должно быть близким к нормаль-
ному.
18
На основе изложенного расчетную схему безраспорного зерни-
стого основания можно представить в виде опирающихся друг на
друга зерен среднего (эффективного) размера.
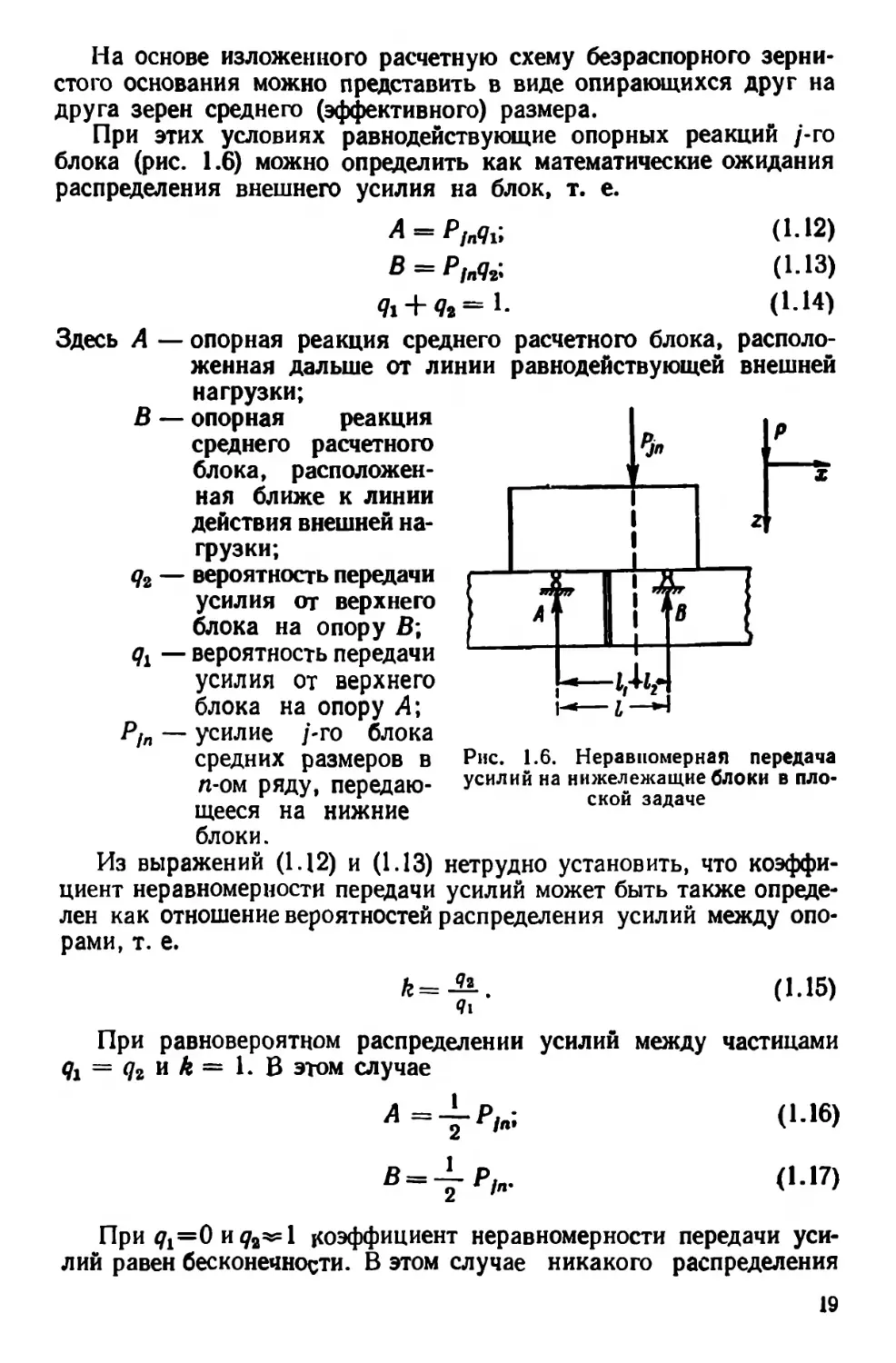
При этих условиях равнодействующие опорных реакций /-го
блока (рис. 1.6) можно определить как математические ожидания
распределения внешнего усилия на блок, т. е.
Л = Р/л91;	(1.12)
В = Р>М	(1.13)
?i + ?,= l.	(114)
Здесь А — опорная реакция среднего расчетного блока, располо-
женная дальше от линии равнодействующей внешней
нагрузки;
В — опорная реакция
среднего расчетного
блока, расположен-
ная ближе к линии
действия внешней на-
грузки;
q2 — вероятность передачи
усилия от верхнего
блока на опору В;
— вероятность передачи
усилия от верхнего
блока на опору Д;
Pfn — усилие /-го блока
средних размеров в
n-ом ряду, передаю-
щееся на нижние
блоки.
Рис. 1.6. Неравномерная передача
усилий на нижележащие блоки в пло-
ской задаче
Из выражений (1.12) и (1.13) нетрудно установить, что коэффи-
циент неравномерности передачи усилий может быть также опреде-
лен как отношение вероятностей распределения усилий между опо-
рами, т. е.
fe=-32-.	(1.15)
При равновероятном распределении усилий между частицами
q1 = q2 и k = 1. В этом случае
<|16)
В=4Р"-	О-17)
При ^=0 и 72«=1 коэффициент неравномерности передачи уси-
лий равен бесконечности. В этом случае никакого распределения
19
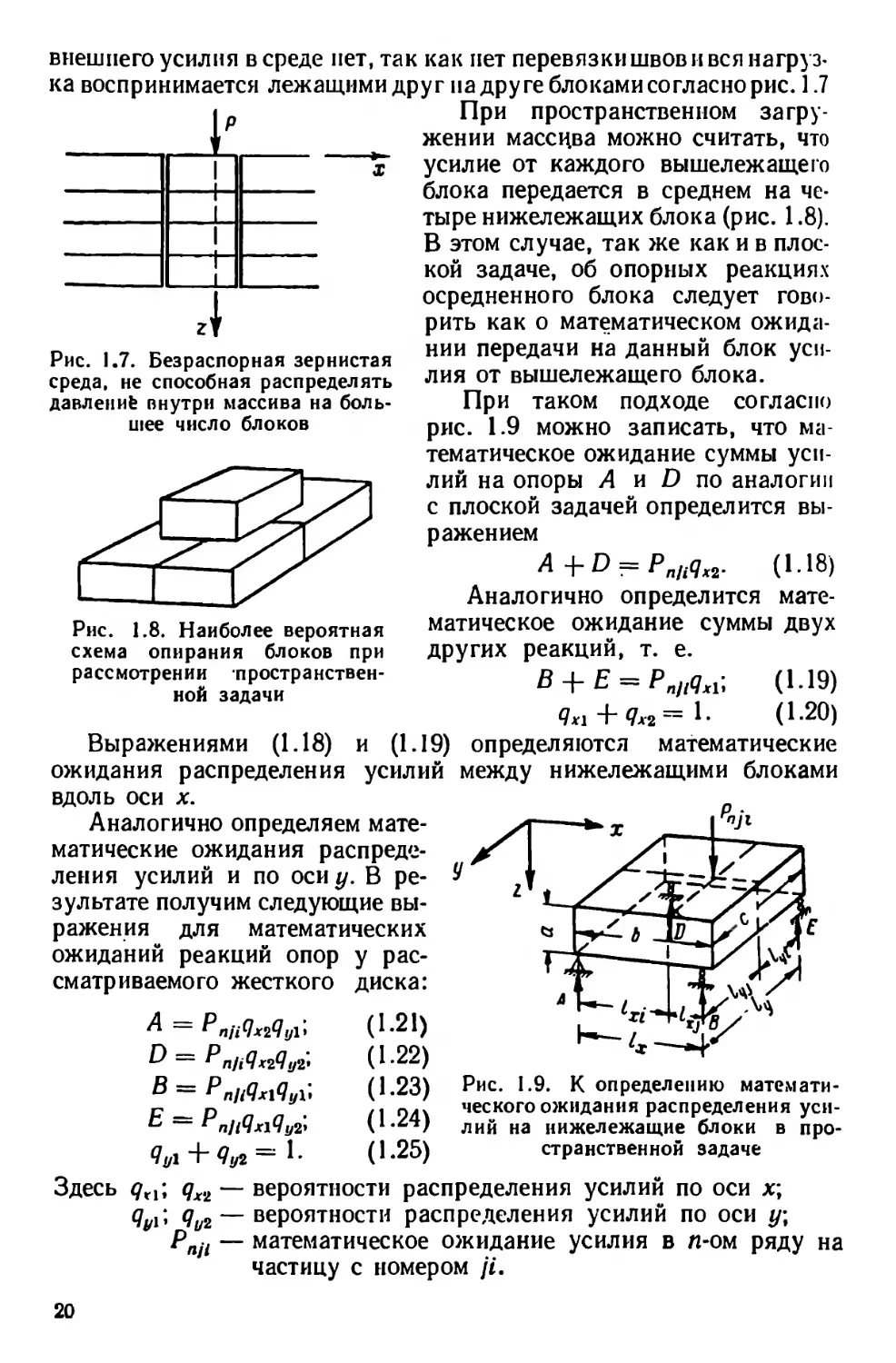
внешнего усилия вереде пет, так как нет перевязки швов и вся нагруз-
ка воспринимается лежащими друг на друге блоками согласно рис. 1.7
и
.1
Рис. 1.7. Безраспорная зернистая
среда, не способная распределять
давлений внутри массива на боль-
шее число блоков
Рис. 1.8. Наиболее вероятная
схема опирания блоков при
рассмотрении пространствен-
ной задачи
При пространственном за гру-
жении массива можно считать, что
усилие от каждого вышележащего
блока передается в среднем на че-
тыре нижележащих блока (рис. 1.8),
В этом случае, так же как и в плос-
кой задаче, об опорных реакциях
осредненного блока следует гово-
рить как о математическом ожида-
нии передачи на данный блок уси-
лия от вышележащего блока.
При таком подходе согласно
рис. 1.9 можно записать, что ма-
тематическое ожидание суммы уси-
лий на опоры А и D по аналогии
с плоской задачей определится вы-
ражением
Л -f- D = Pnfiqx2. (1.18)
Аналогично определится мате-
матическое ожидание суммы двух
других реакций, т. е.
В + Е = Р пцдх1\
ЯXI + Ях2 ~ 1 •
(1-19)
(1-20)
Выражениями (1.18) и (1.19) определяются математические
ожидания распределения усилий
вдоль оси х.
Аналогично определяем мате-
матические ожидания распреде-
ления усилий и по оси у. В ре-
зультате получим следующие вы-
ражения для математических
ожиданий реакций опор у рас-
сматриваемого жесткого диска:
= В niiqx2q	(1-21)
D = Pn/iqxzq^	(1-22)
B = Pnliqxlq^	(1-23)
в = PnitqXiq^	(i-24)
^i + ^2=l.	(1.25)
между нижележащими блоками
Рис. 1.9. К определению математи-
ческого ожидания распределения уси-
лий на нижележащие блоки в про-
странственной задаче
Здесь qxi-t qx2 — вероятности распределения усилий по оси х;
qyl\ Яу2 — вероятности распределения усилий по оси у\
Pnjl — математическое ожидание усилия в /1-ом ряду на
частицу с номером ji.
20
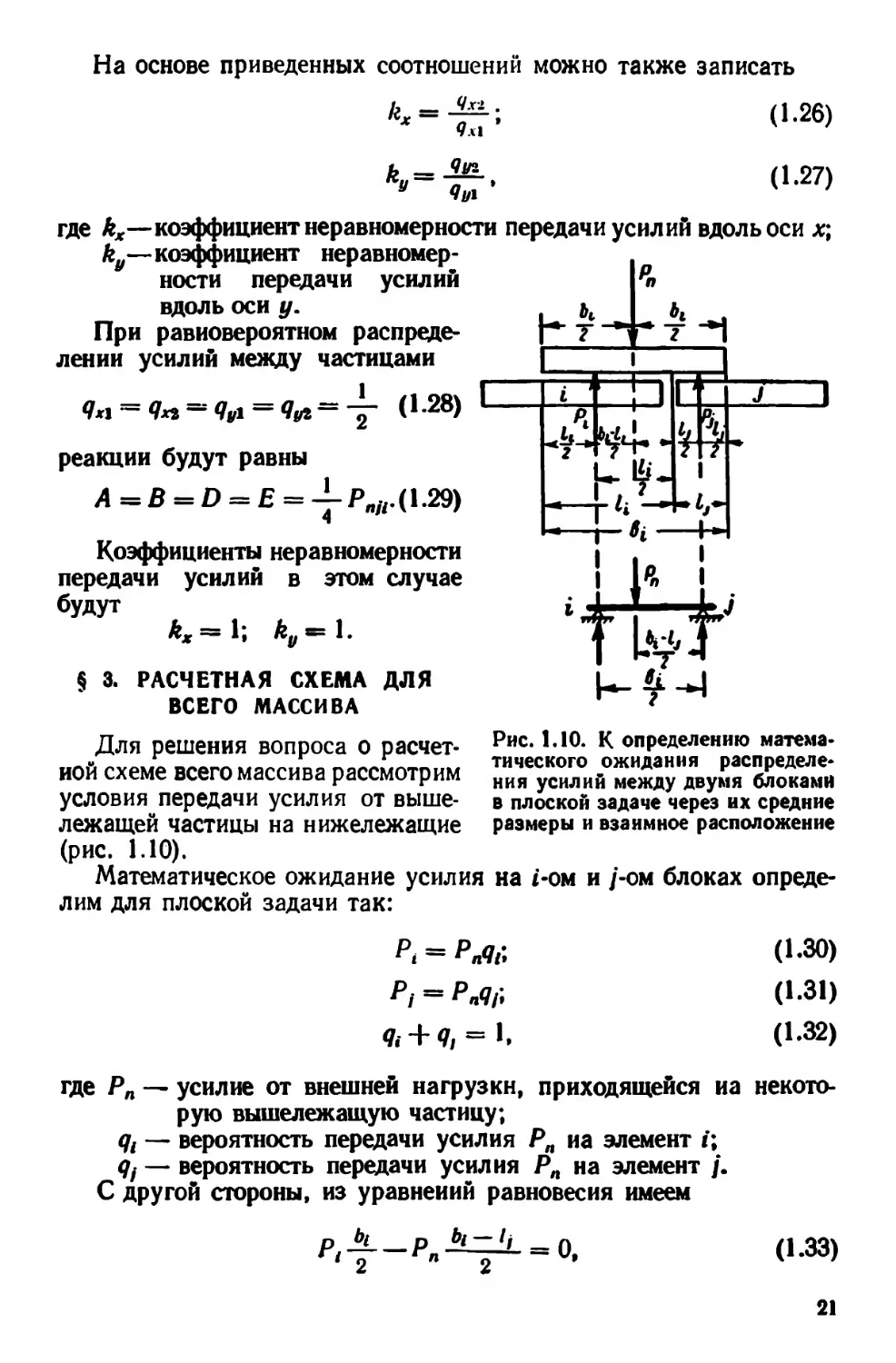
(1.27)
Рис. 1.10. К определению матема-
тического ожидания распределе-
ния усилий между двумя блоками
в плоской задаче через их средние
размеры и взаимное расположение
На основе приведенных соотношений можно также записать
=	(1.26)
где ^—коэффициент неравномерности передачи усилий вдоль оси х;
kg—коэффициент неравномер-
ности передачи усилий
вдоль оси у.
При равновероятном распреде-
лении усилий между частицами
Ях1 -	— Яу1 = Яуъ —	(1-28)
реакции будут равны
4=B = D = £ = -Lpn/,.(1.29)
Коэффициенты неравномерности
передачи усилий в этом случае
будут
£ж=1; ^-1.
§ 3.	РАСЧЕТНАЯ СХЕМА ДЛЯ
ВСЕГО МАССИВА
Для решения вопроса о расчет-
ной схеме всего массива рассмотрим
условия передачи усилия от выше-
лежащей частицы на нижележащие
(рис. 1.10).
Математическое ожидание усилия
лим для плоской задачи так:
на i-ом и /-ом блоках опреде-
Pi = Pn4l,
Qi + я, = 1.
(1.30)
(1.31)
(1.32)
где Рп — усилие от внешней нагрузки, приходящейся иа некото-
рую вышележащую частицу;
—	вероятность передачи усилия Рп иа элемент i;
—	вероятность передачи усилия Рп на элемент /.
С другой стороны, из уравнений равновесия имеем
р ______р h ~ 11 = л
<2 п 2	’
(1.33)
21
откуда
Р, = И]_1рл1.	(1.34)
\	°1 ]	bi
Если учесть, что //+// = и Pt + Р/ = Ря, то получим
Р/ = Рп-^-	О-35)
bl
Сравнивая выражения (1.30) и (1.31) с зависимостями (1.34)
и (1.35) находим
Рис. 1.11. Положение
частицы, не прини-
мающей участия в
распределении уси-
лий
Рис. 1.12. К определению вероятного значения коэф-
фициента неравномерности передачи усилий в плос-
кой задаче для всего массива по его структуре
В частном случае, когда qt = 1, qf = 0, из формул (1.30) и (1.31)
имеем Pt = Рп, a Р{ = 0, т. е. усилие от вышележащей частицы пол-
ностью передается на i частицу (рис. 1.11).
Полученные зависимости позволяют по структуре среды вычис-
лить интересующие нас вероятности qt и q2. Согласно рис. 1.12
можно подсчитать qt и qt для каждого блока; отрезки, относящиеся
к вычислению ql9 обозначены одним штрихом, а отрезки, по кото-
рым следует вычислять q/t— двумя штрихами. Согласно формулам
(1.36) и (1.37) длины этих отрезков необходимо поделить на длину
рассматриваемого элемента. Если рассмотреть N элементов, то сред-
нее значение вероятности концентрации усилий к линии действия
нагрузки вычислится по формулам:
’>4^"
(1.38)
(1.39)
22
Используя эти формулы, можно определить среднее для массива
значение коэффициента неравномерности передачи усилий
N
У 4i
k =	(140)
2^/
Так по реальной структуре можно построить эквивалентную ей
расчетную модель со средними размерами блоков и средними усло-
виями распределения усилий между частицами для плоской задачи.
Таким же образом можно вычислить коэффициенты неравно-
мерности передачи усилий и в пространственной задаче. Если рас-
смотренную плоскость принять за плоскость zoxt то на основании
формулы (1.40) можно записать
N
2 Ч1х
(1.41)
2 4jx
/=|
а для плоскости zoy
м
2
(1-42)
2^/v
здесь qtx\ qiy — вероятности концентрации усилий к линии дей-
ствия нагрузки соответственно вдоль осей х и у\
qfx\ qjy — вероятности рассеивания усилий соответственно
вдоль осей х и у.
сих пор речь шла об усилиях, приложенных к частицам. Та-
кой термин является непривычным для механики грунтов и меха-
ники зернистых сред. Вместе с тем от усилия на частицу можно пе-
рейти к среднему давлению на единицу площади, если разделить
усилие на площадь, занимаемую частицей. Если к тому же взять
эту величину с обратным знаком, то перейдем к термину «напряже-
ние». В зернистой среде внешняя вертикальная нагрузка вызывает
сжимающие напряжения. Если направить ось z вниз, то вертикаль-
ные напряжения будут со знаком минус. Знак остальных составляю-
щих напряжения, как будет видно из дальнейшего, однозначно оп-
ределяется знаком вертикального напряжения.
Размеры блоков и условия их опирания могут быть представлены
в виде единого показателя структуры безраспорной зернистой
среды:
23
для плоской задачи
4аЛ2 а =	; Ь2	(1-43)
для пространственной задачи ах = ——; *	62	(1.44)
4аАу	(1.45)
здесь а — коэффициент структуры безраспорной зернистой среды
в плоской задаче;
аж — коэффициент структуры безраспорной зернистой среды
вдоль оси х\
ау — коэффициент структуры безраспорной зернистой среды
вдоль оси у\
Ь, с, а — размеры блоков соответственно по направлениям осей
х, yt Z.
В приведенных формулах имеется один коэффициент, характе-
ризующий безраспорную зернистую среду в плоской задаче, и два—
анизотропную зернистую безраспорную среду в пространственной
задаче. Если среда изотропна по направлениям осей х и у, то ах =
= а у = а. В этом случае и в пространственной задаче среда харак-
теризуется одним коэффициентом структуры.
Глава 2
РАСПРЕДЕЛЕНИЕ ВЕРТИКАЛЬНЫХ НАПРЯЖЕНИЙ
В БЕЗРАСПОРНОМ ЗЕРНИСТОМ ОСНОВАНИИ В ПЛОСКОЙ
ЗАДАЧЕ
$ 1. РАВНОВЕРОЯТНАЯ ПЕРЕДАЧА УСИЛИЙ ОТ ВЫШЕЛЕЖАЩЕЙ
ЧАСТИЦЫ НА НИЖЕЛЕЖАЩИЕ
Пусть на поверхность зернистого безраспорного полупростран-
ства, изображенного на рис. 2.1, действует вертикальная нагрузка,
причем на каждую частицу поверхности приходится нагрузка, рав-
ная единице.
Назовем слой, на котором нагрузка в рассматриваемом сечении
передается на одну частицу, нулевым. Все остальные слои прону*
мер уем порядковыми числами сверху вниз.
24
Определим математическое ожидание вертикального усилия на
частицу, расположенную в любом слое. Усилия от каждой частицы,
расположенной в вышележащем слое, передаются на две частицы,
расположенные в нижнем слое.
Предположим, что размеры частицы одинаковы и усилия от
верхней частицы с одинаковой вероятностью распределяются на
две нижние частицы. На рис. 2.1 показаны вычисленные на основа-
нии этой предпосылки величины усилий, приходящихся на каж-
Рис. 2.1. Расчетная схема зернистой среды блочного строения в плоской за*
даче при равновероятной передаче усилия от вышележащей частицы на ни-
жележащие
дую частицу; при этом общий множитель j для каждого ряда
вынесен в крайний столбец.
Приведенная на этом рисунке система чисел по расположению
и по величинам представляет собой треугольник Паскаля,с помощью
которого, как известно, вычисляются биноминальные коэффициенты,
которые можно вычислить также путем разложения по формуле
бинома Ньютона следующего выражения
(14-1)" =CJ + C!, + C;+ -l-Cr'+CS, (2.1)
где Cnj С„;
С„ — сочетания.
25
Если умножить правую и левую части выражения (2.1) на ,
то получим величины усилий на частицы в n-ом ряду от единичной
нагрузки на поверхности
+ (т)”й + +(t)"c:-	(22)
Слагаемые в правой части зависимости (2.2) представляют собой
распределение вертикальных усилий в п-ом ряду рассматриваемого
сечения.
Например, для п = 4 имеем
или
В четвертом ряду соответственно расположены вертикальные
усилия на частицы, которые равны:
1 ,	4	6 .	4	1
16 ’	16 ’ 16 ’ 16 ’ 16
Таким образом, распределение вертикальных усилий на частицы
безраспорной среды в ряду подчиняется биноминальному закону.
В теории вероятностей доказывается, что кривая биноминаль-
ного распределения может быть аппроксимирована кривой нормаль-
ного распределения.
Для частицы т в слое п это будет
Начало координат кривой (2.3) в рассматриваемом сечении рас-
п
положено влево от точки приложения силы на величину —.
Перенесем начало координат кривой для всех слоев на линию
действия силы. Тогда для функции распределения усилий по ча-
стицам
р-= ]/-£ге*р(—гт’)-
(2.4)
26
где п — порядковый номер слоя, отсчитываемого от поверхности и
до границы слоя;
т — порядковый номер частицы в л-ом слое, отсчитываемой
вправо или влево от линии действия силы.
Зависимость (2.4) определяет величины вертикальных усилий
на блоки массива от единичной нагрузки на одну частицу на по-
верхности.
Для нагрузки, отличной от единицы и равной Р, математические
ожидания величин усилий на блоки при соблюдении принятых ра-
нее предпосылок будут пропорциональны величине нагрузки, т. е.
в этом случае величину ~Р можно рассматривать как скаляр единич-
ного вектора.
Таким образом, для нагрузки Р, приложенной к частице на по-
верхности, математическое ожидание распределения усилий между
частицами в массиве полупространства в рассматриваемом случае
подчиняется зависимости
<2-5>
где Р — нагрузка на одну частицу на поверхности по линии загру-
жения.
В случае равномерного загружения линии на поверхности с ин-
тенсивностью Р математическое ожидание усилия на частицу в мас-
сиве согласно зависимости (2.5) определится выражением
где с — размер частицы.
Перейдем теперь в этих зависимостях от номеров частиц к коор-
динатам. Согласно рис. 2.1 имеем
z = ап;	(2.7)
х = Ьт,	(2.8)
откуда
п=^-:	(2.9)
т=-у.	(2.10)
Подставляем в зависимость (2.6) вместо порядковых номеров
частиц их координаты по выражениям (2.9) и (2.10);

(2.U)
27
Разделим величину усилия на площадь, занимаемую частицей
в горизонтальной плоскости. В результате получим среднее значе-
ние вертикальных напряжений
(2.12)
где ог — вертикальное напряжение, отнесенное к изотропному телу;
Р2Х — вертикальное усилие на частицу (блок);
Ь, с — размеры частиц (блоков).
Подставляя в зависимость (2.12) выражение (2.11) для усилия
на частицу, получим для напряжений следующее выражение:
Из полученной зависимости видно, что максимальные значения
вертикальных напряжений будут при х = 0.
§ 2. НЕРАВНОВЕРОЯТНАЯ ПЕРЕДАЧА УСИЛИЙ ОТ ВЫШЕЛЕЖАЩЕЙ
ЧАСТИЦЫ НА НИЖЕЛЕЖАЩИЕ
В предыдущем параграфе рассматривалась задача, в которой
усилие, приходящееся на частицу, равновероятно распределяется
между двумя нижележащими частицами.
При этих условиях усилие на частицы, лежащие на оси z, т. е.
для т = 0, согласно зависимости (2.5) определяется выражением

(2.14)
При неравновероятном распределении усилий между частицами
выражение (2.14) примет, очевидно, другой вид, который будет
определяться соотношением приходящихся усилий на частицы. Та-
кое соотношение в предыдущей главе характеризовалось отноше-
нием опорных реакций А и В в расчетной схеме (рис. 1.6) и оцени-
валось коэффициентом неравномерности передачи усилий. При ра-
венстве плеч это отношение равно единице и характеризует случай,
рассмотренный в предыдущем параграфе, для которого усилия,
приходящиеся на частицы, расположенные на оси г, определяются
выражением (2.14). При другом соотношении усилия на частицы,
расположенные на оси z, возрастут пропорционально коэффициенту
неравномерности распределения усилий между частицами. В этом
случае будем иметь следующую зависимость:
Р„=РЙ1/	(2.15)
где k — коэффициент, определяемый выражением (1.11).
28
Зависимость (2.15) при равенстве плеч (коэффициент k = 1)
соответствует выражению (2.14).
Для определения характера распределения усилий между ча-
стицами в ряду т примем зависимость, аналогичную полученной
в предыдущем параграфе. По аналогии с выражением (2.6) получим
Р- = ^]/5ехр(-4^),	(2.16)
где х — некоторый коэффициент, который найдем из уравнения
равновесия.
В случае непрерывного равномерного загружения линии на по-
верхности нагрузкой, интенсивность которой Р, усилие на частицу
в массиве согласно зависимости (2.16) определится выражением
<2Л7)
где с—размер частицы.
Как и в предыдущем случае, порядковые номера частиц в выра-
жении (2.16) заменим через координаты; получим
Среднее значение напряжения, отнесенное ко всей площади, за-
нимаемой частицей, определится выражением
“--%— ёЛ <2|8>
Преобразуя это выражение, получим
12|9)
Определим теперь значение коэффициента х из условия равнове-
сия. Проектируем на ось г все силы, действующие на рассматривае-
мый массив по горизонтальному сечению:
откуда
х = АЛ
Подставляя значение х в выражение (2.16), получим следующую
зависимость для распределения вертикальных усилий между ча-
стицами:
Ршп - Pk ]/-^-ехр(-	•	(2.20)
29
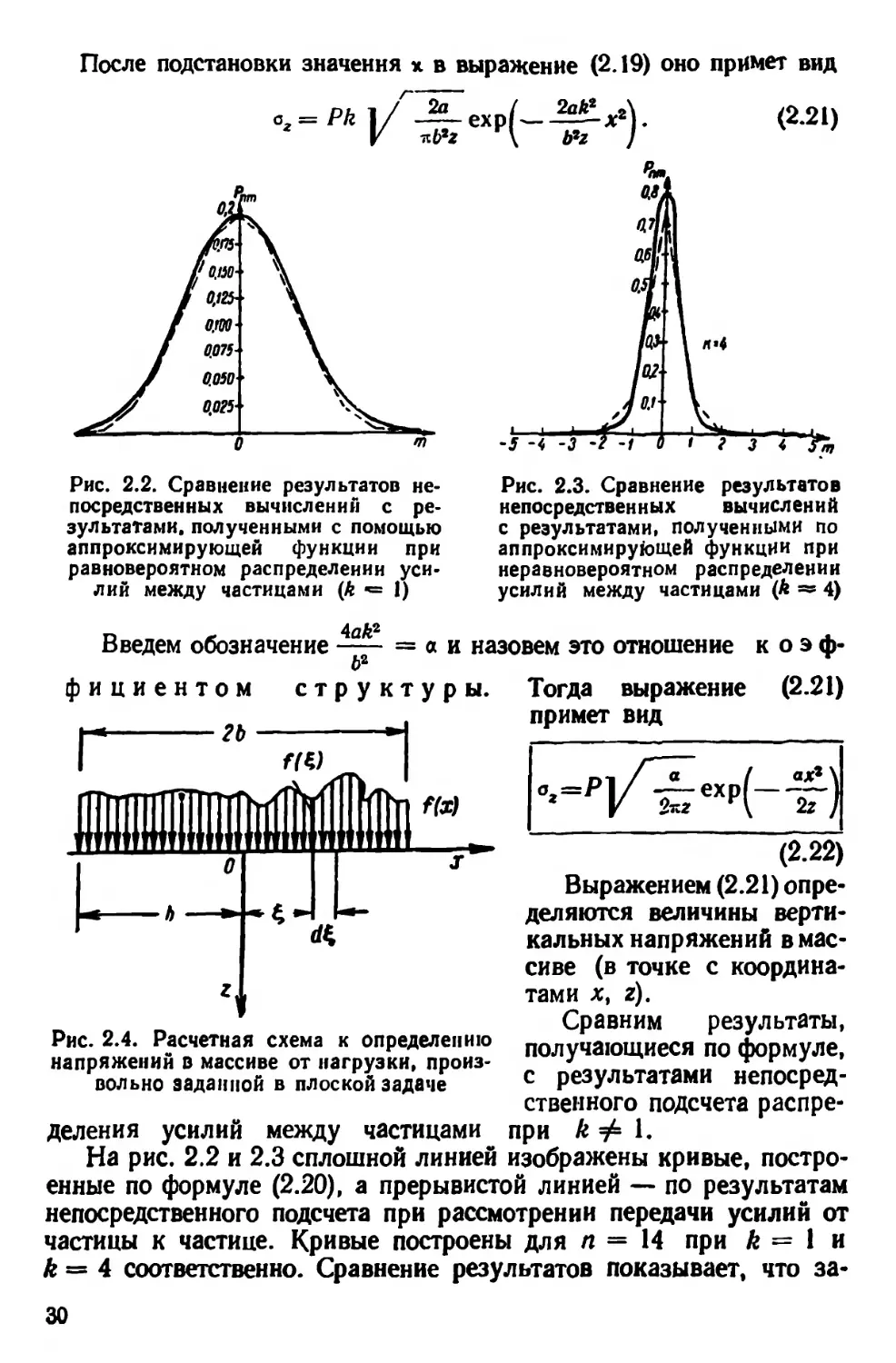
После подстановки значения х в выражение (2.19) оно примет вид
Рис. 2.2. Сравнение результатов не-
посредственных вычислений с ре-
зультатами. полученными с помощью
аппроксимирующей функции при
равновероятном распределении уси-
лий между частицами (k *= 1)
Рис. 2.3. Сравнение результатов
непосредственных вычислений
с результатами, полученными по
аппроксимирующей функции при
неравновероятном распределении
усилий между частицами (А ~ 4)
назовем это отношение
к о э ф-
d *	4аЛ2
Введем обозначение-------= а и
Ь2
Рис. 2.4. Расчетная схема к определению
напряжений в массиве от нагрузки, произ-
вольно заданной в плоской задаче
Тогда выражение (2.21)
примет вид
(2.22)
Выражением (2.21) опре-
деляются величины верти-
кальных напряжений в мас-
сиве (в точке с координа-
тами х, г).
Сравним результаты,
получающиеся по формуле,
с результатами непосред-
ственного подсчета распре-
деления усилий между частицами при k 1.
На рис. 2.2 и 2.3 сплошной линией изображены кривые, постро-
енные по формуле (2.20), а прерывистой линией — по результатам
непосредственного подсчета при рассмотрении передачи усилий от
частицы к частице. Кривые построены для п = 14 при k = 1 и
k = 4 соответственно. Сравнение результатов показывает, что за-
30
висимость (2.20) уже при п = 14 хорошо аппроксимирует сложную
зависимость распределения усилий между частицами в массиве.
На основе зависимости (2.22) вертикальные напряжения от про-
извольной полосовой нагрузки согласно рис. 2.4 определятся так:
/й ]7«>е»р[-	<2.23)
- ь
где f (0 — функция, описывающая характер нагрузки;
< — переменная интегрирования;
2Ь — ширина загруженной полосы.
§3. НАПРЯЖЕНИЯ ОТ НАГРУЗКИ, ОПИСЫВАЕМОЙ ПОКАЗАТЕЛЬНОЙ
ФУНКЦИЕЙ
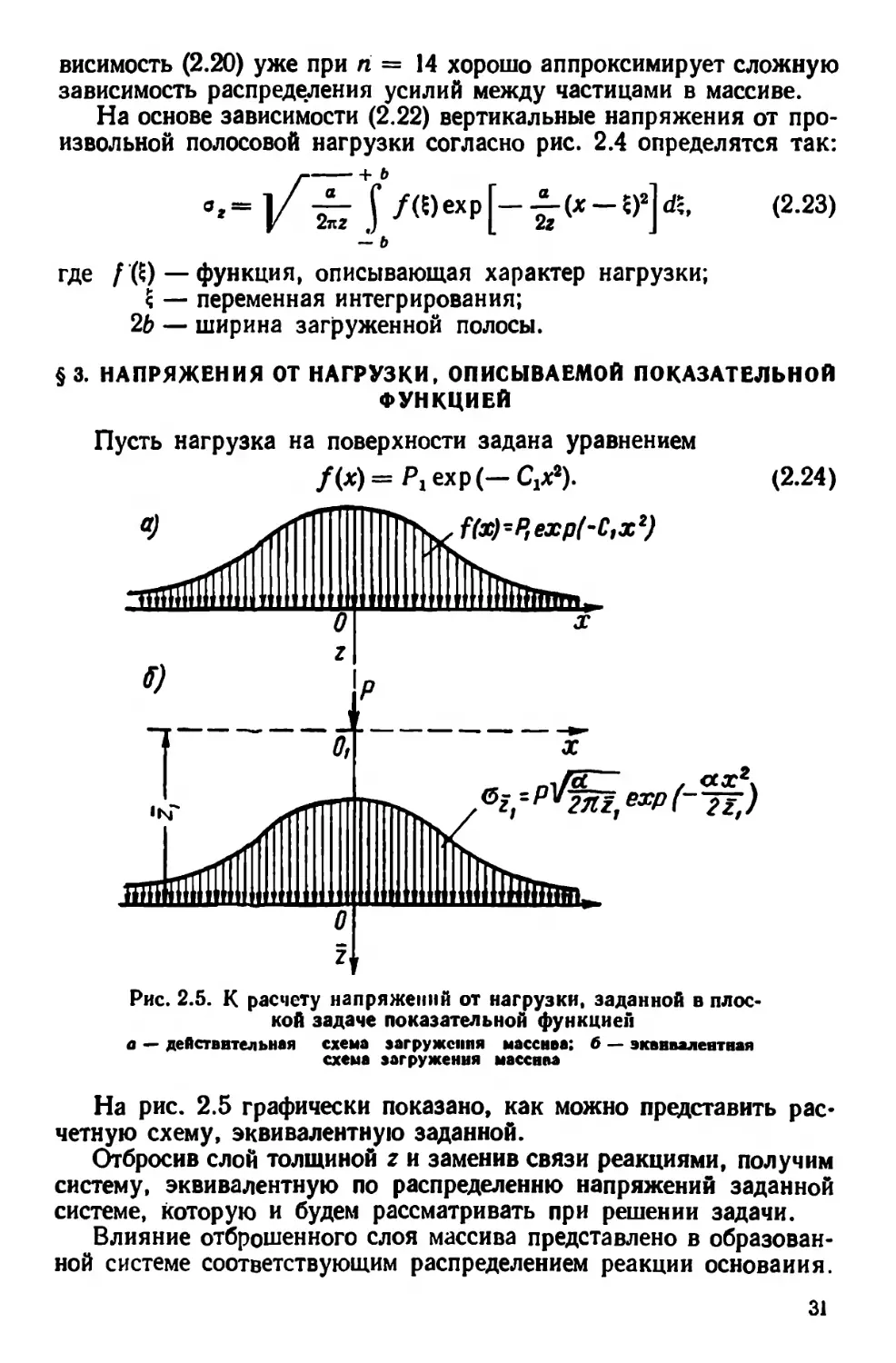
Пусть нагрузка на поверхности задана уравнением
/(х)= Р1ехр(—CjX2).	(2.24)
а) .............
ТПТЛШДШ........... ' ' ЖЛПТЙИпт
f(x)-Ptexp(-CiX2)
0

Рис. 2.5. К расчету напряжений от нагрузки, заданной в плос-
кой задаче показательной функцией
а - действительная схема эагружсппя массива: б — эквивалентная
схема эагруження массива
На рис. 2.5 графически показано, как можно представить рас-
четную схему, эквивалентную заданной.
Отбросив слой толщиной г и заменив связи реакциями, получим
систему, эквивалентную по распределению напряжений заданной
системе, которую и будем рассматривать при решении задачи.
Влияние отброшенного слоя массива представлено в образован-
ной системе соответствующим распределением реакции основания.
31
Начало координат в новой системе перенесем по оси г на поверх-
ность ее.
Образованная система имеет нагрузку, распределение которой
выражается уравнением
Сравнивая с (2.24), получим
(2.25)
(2.26)
На основе решения, полученного для линейной нагрузки на поверх-
ности, с учетом переноса координат для вертикальных напряжений
в любой точке массива имеем
а	/ ах2
—z----------exp I--------------
2it(zj + z) \	2^ + z]
(2.27)
где z — координата рассматриваемой точки в новой системе.
Подставляем в формулу (2 27) значение Zj и Р из выражения
(2.26)
Формулой (2.28) и определяется распределение вертикальных
напряжений в массиве от нагрузки, заданной уравнением (2.24).
§ 4. НАПРЯЖЕНИЯ В СЛОИСТОЙ СРЕДЕ ОТ ЛИНЕЙНОЙ
ВЕРТИКАЛЬНОЙ НАГРУЗКИ
Можно рассматривать передачу усилий от частицы к частице в
слоистой среде таким же способом, как это было сделано для случая
однородного массива.
Для верхнего слоя толщиной h (рис. 2.6) распределение средних
величин напряжений будет выражаться функцией распределения
тех же напряжений в однородном массиве, т. е.
(2И>
где Gj — коэффициент структуры среды верхнего слоя.
Рассмотрим распределение напряжений в нижнем слое. Соста-
вим новую расчетную систему (рис. 2.7) путем отбрасывания верх-
него слоя двухслойной системы и замены ее связей соответствую-
щими реакциями. Таким образом, от двухслойной системы перей-
32
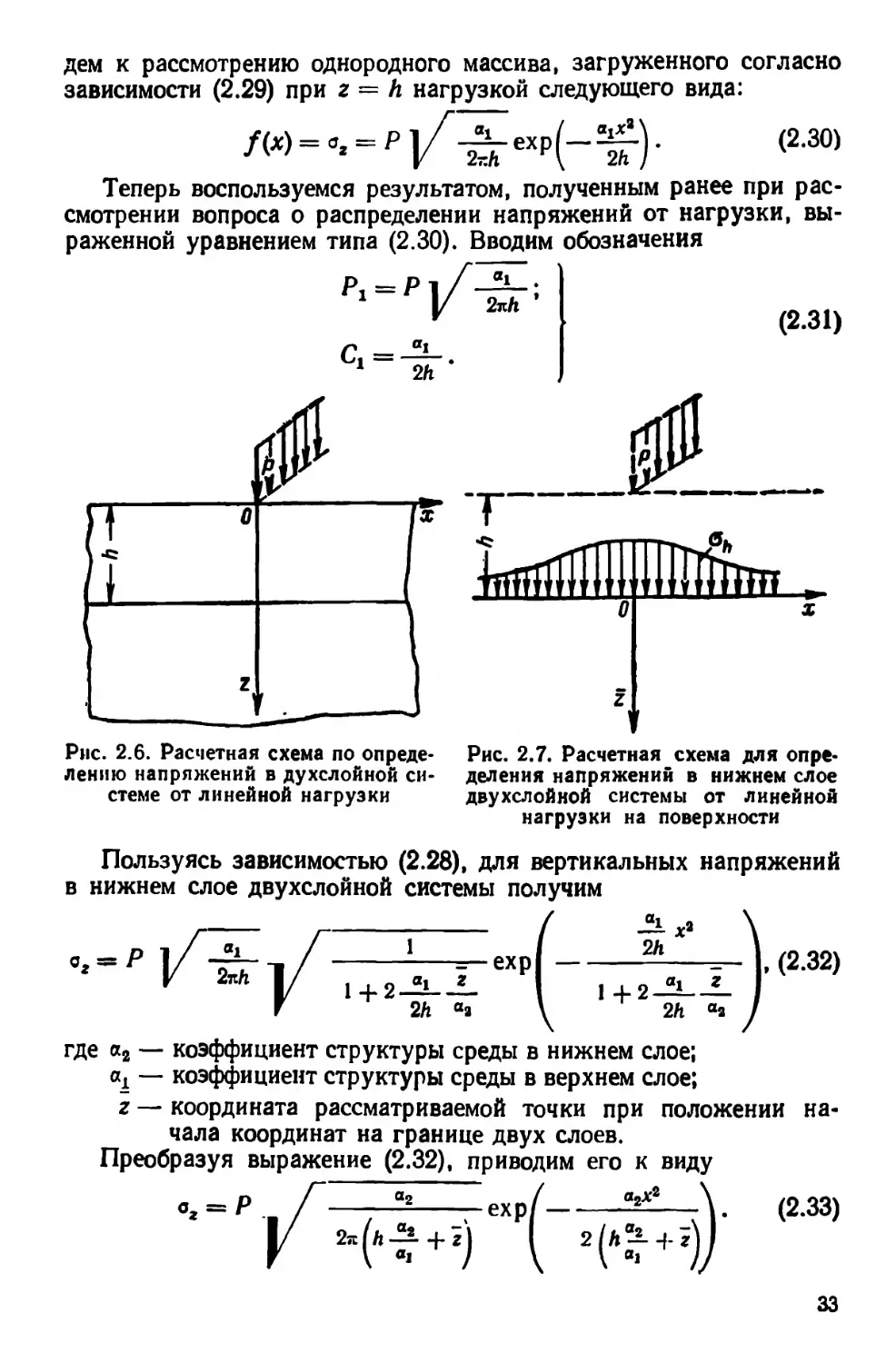
дем к рассмотрению однородного массива, загруженного согласно
зависимости (2.29) при z = h нагрузкой следующего вида:
Теперь воспользуемся результатом, полученным ранее при рас-
смотрении вопроса о распределении напряжений от нагрузки, вы-
раженной уравнением типа (2.30). Вводим обозначения
Рис. 2.6. Расчетная схема по опреде- Рис. 2.7. Расчетная схема для опре-
лению напряжений в духслойной си- деления напряжений в нижнем слое
стеме от линейной нагрузки двухслойной системы от линейной
нагрузки на поверхности
Пользуясь зависимостью (2.28), для вертикальных напряжений
в нижнем слое двухслойной системы получим
где а2 — коэффициент структуры среды в нижнем слое;
«1 — коэффициент структуры среды в верхнем слое;
z — координата рассматриваемой точки при положении на-
чала координат на границе двух слоев.
Преобразуя выражение (2.32), приводим его к виду
33
Сравним теперь это решение с выражением для напряжений в
однородном массиве со структурой нижнего слоя, которое имеет
вид

откуда
2 = Л^-+?.
в1
(2.35)
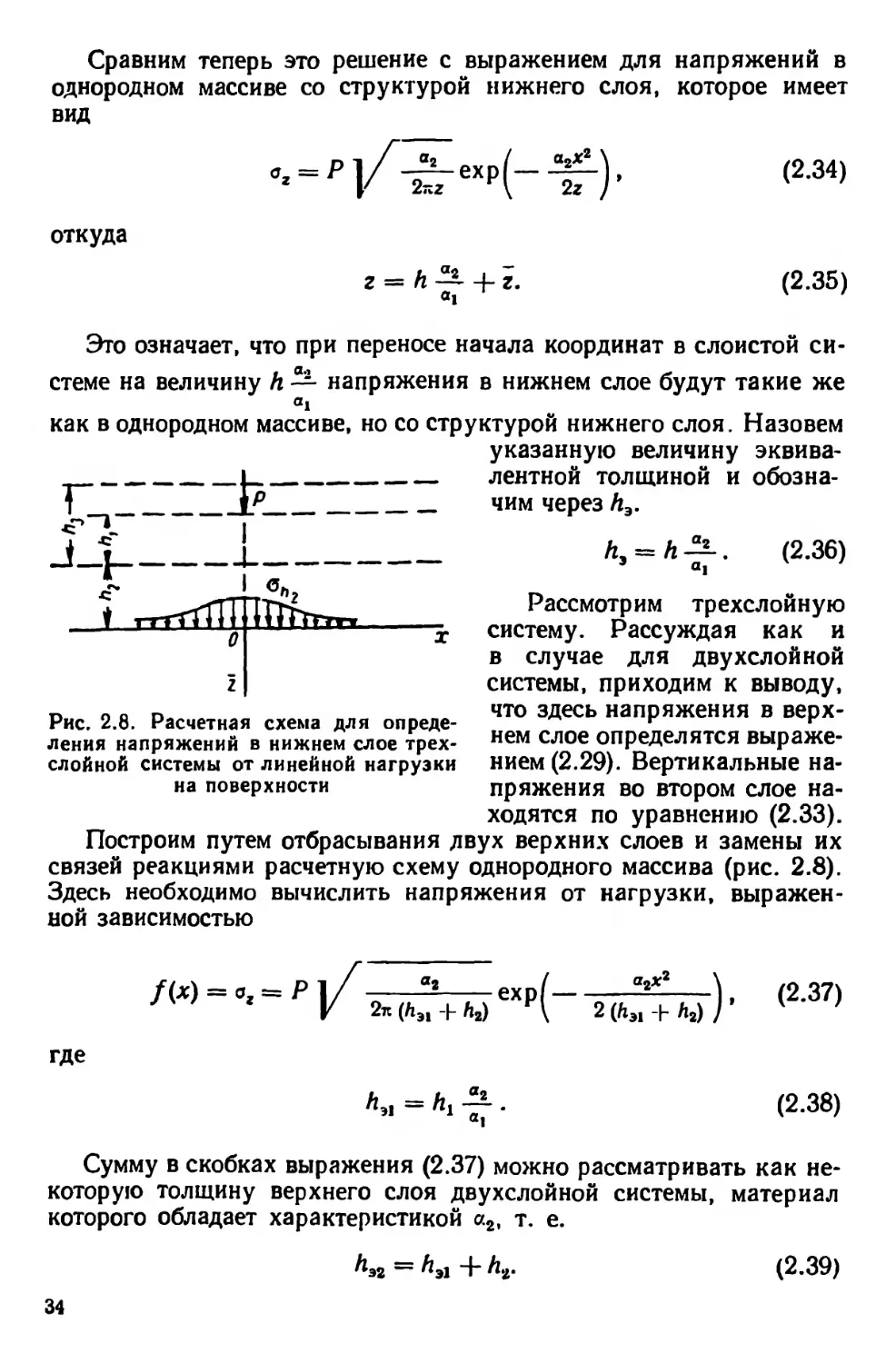
Рис. 2.8. Расчетная схема для опреде-
ления напряжений в нижнем слое трех-
слойной системы от линейной нагрузки
на поверхности
Это означает, что при переносе начала координат в слоистой си-
стеме на величину h — напряжения в нижнем слое будут такие же
как в однородном массиве, но со структурой нижнего слоя. Назовем
указанную величину эквива-
лентной толщиной и обозна-
чим через Лэ.
Лэ = h .	(2.36)
Рассмотрим трехслойную
систему. Рассуждая как и
в случае для двухслойной
системы, приходим к выводу,
что здесь напряжения в верх-
нем слое определятся выраже-
нием (2.29). Вертикальные на-
пряжения во втором слое на-
ходятся по уравнению (2.33).
Построим путем отбрасывания двух верхних слоев и замены их
связей реакциями расчетную схему однородного массива (рис. 2.8).
Здесь необходимо вычислить напряжения от нагрузки, выражен-
ной зависимостью
/(х) = о1==Р1/------------ехр(------------V (2.37)
7	И 2л(Лэ1-ЬЛ2) Ч 2(ЛЭ1-ЬМГ *	7
где

(2.38)
Сумму в скобках выражения (2.37) можно рассматривать как не-
которую толщину верхнего слоя двухслойной системы, материал
которого обладает характеристикой а2, т. е.
ЛЭ2 ЛЭ1 Л2.
(2.39)
34
В таком случае от трехслойной системы приходим к двухслой-
ной, для которой уже получено решение. Используя формулу (2.36),
для эквивалентного слоя трехслойной системы получим
ЛЭ = ЛМ^-.	(2.40)
Подставив в эту формулу вместо Лэ2 выражение (2.39), получим
ЛЭ = (Л91 + ЛМ)^-.	(2.41)
Подставим также в формулу (2.41) выражение (2.38); после под-
становки имеем
Л» »	(2.42)
«1	а2
На основе выражения (2.42) получим формулу для эквивалент-
ного слоя многослойной системы
*9 = AI-T- + Vr-+	(2.43)
э 1 «1	а2	" 1 ал_|
Формулой (2.43) определяется толщина эквивалентного слоя
для п—1 слоев, приведенных к n-ому нижнему слою. При опреде-
лении напряжений в промежуточных слоях уменьшается индекс п.
§5. НАПРЯЖЕНИЯ В СЛОИСТОЙ СРЕДЕ ОТ НАГРУЗКИ, ПРОИЗВОЛЬНО
ЗАДАННОЙ В ПЛОСКОЙ ЗАДАЧЕ
В предыдущем параграфе рассмотрен вопрос о распределении
напряжений в слоистой среде от линейной нагрузки. Естественно
возникает вопрос, имеет ли место установленная закономерность пе-
рехода от слоистой системы к однородной для произвольной верти-
кальной нагрузки в плоской задаче.
Для решения этого вопроса рассмотрим следующую задачу,
(рис. 2.9, а).
Положим, что нагрузка на поверхности представлена следующим
выражением:
А(Х) =	YУ(?)ехр[-Лг(х-с)2]^,	(2.44)
г л — b
где Ь, А — постоянные величины.
Для решения задачи о распределении напряжений от этой на-
грузки рассмотрим сначала задачу о распределении напряжений
в массиве от нагрузки
Р=/(х).	(2.45)
35
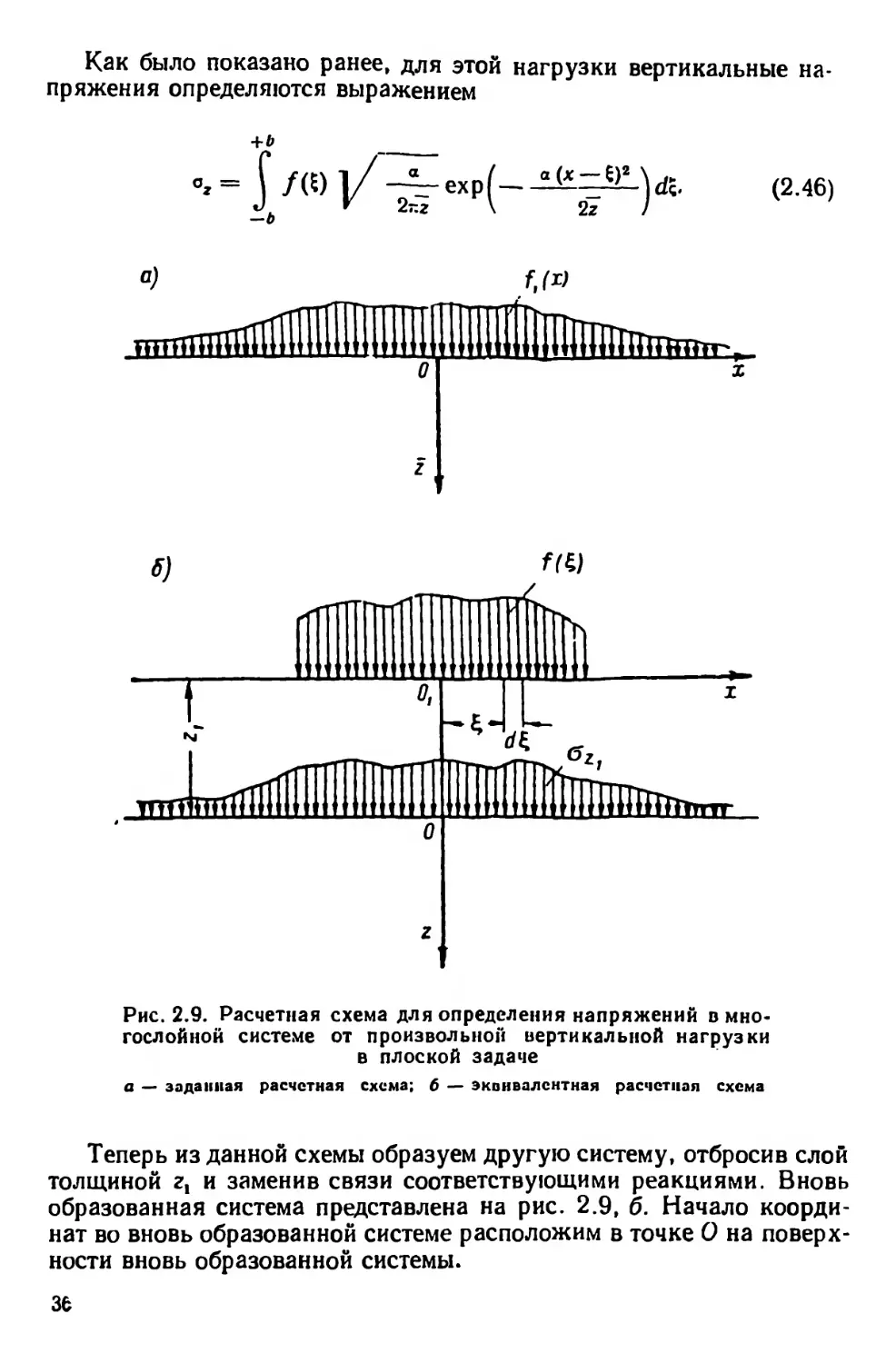
Как было показано ранее, для этой нагрузки вертикальные на-
пряжения определяются выражением
«(х-ё)2
27
(2.46)
б)	№
О
г
Рис. 2.9. Расчетная схема для определения напряжений в мно-
гослойной системе от произвольной вертикальной нагрузки
в плоской задаче
а — заданная расчетная схема; б — эквивалентная расчетная схема
Теперь из данной схемы образуем другую систему, отбросив слой
толщиной г, и заменив связи соответствующими реакциями. Вновь
образованная система представлена на рис. 2.9, б. Начало коорди-
нат во вновь образованной системе расположим в точке О на поверх-
ности вновь образованной системы.
36
Нагрузка на поверхности во вновь образованной системе опреде-
ляется на основе зависимости (2.46):
+ь
/(*’ г<)=% = f /«) |/^ехр(
-д
(2.47)
От этой нагрузки напряжения в массиве определяются как сумма
напряжений от элементарных сил
%- = J /10- г>)ех₽(--Л/*)
где vj — переменная интегрирования.
Координаты исходной системы связаны с координатами системы,
образованной выражением
г = г + zi-	(2.49)
Подставляя (2.49) в выражение (2.46), получим
" -р® у/	г'+’)-<2Ю)
—Л
Сравнивая выражения (2.48) и (2.50), имеем
А(*. *. + *)= J /,(>), г,)|/-£7ехр(~	<251>
в зависимости (2.47) можно рассматривать
как постоянную величину —^=-, т. е.
(2.52)
В этой зависимости величина а принимается соответствующей
рассматриваемой среде, и лишь величина зависит от параметра А.
>ешая выражение (2.52) относительно г1У получим
2Лг *
(2.53)
При образовании рассматриваемой системы толщина отбрасы-
ваемого слоя принималась произвольной. В частности, она может
37
быть равна величине, определяемой выражением (2.53). В этом слу-
чае выражение (2.47) будет тождественно выражению (2.44), т. е.
<2-54)
Подставляем вместо zx его значение из выражения (2.53) в зависи-
мость (2.51). Учитывая также (2.54), имеем
Л('-й7+г)- J	<2-55>
Из выражения (2.55) видно, что функции нагрузки и распреде-
ления напряжений выражаются одним уравнением с параметрами,
определяемыми вертикальной координатой рассматриваемой точки
и постоянными зернистой среды, т. е.
тк+г)'	<2Ж"
На основе приведенных решений рассмотрим вопрос о распреде-
лении напряжений в слоистой среде для произвольно заданной на-
грузки.
Пусть нагрузка на поверхности слоистой среды в пределах по-
лосы задана функцией (2.45). Распределение вертикальных напря-
жений в верхнем слое от такой нагрузки определится выражением
(2.46), согласно которому напряжения на границе между верхним
и вторым слоем (при z = hj
- f ]/йН[—Е>,1 «• ₽5”
Образуя новую расчетную схему путем отбрасывания верхнего
слоя и замены связей соответствующими реакциями, получим сог-
ласно зависимости (2.57) следующую функцию нагрузки
+ь
f ЯО|/^ехр[—(2.58)
-5
Функция нагрузки (2.58) удовлетворяет выражению (2.54). Сле-
довательно, распределение напряжений в верхнем слое новой рас-
четной схемы будет определяться согласно (2.55) и (2.56) той же
функцией (2.58), т. е.
e*"/(x>A-+zV	<2-59>
где «2 — коэффициент, характеризующий структуру второго слоя
системы.
за
Значение Аг определим, приравнивая правые части зависимости
(2.44) и (2.58):
+ ь	___
[	ехр Г—5Г(* -	=
— ь
+ ь
= [ /($)^ ехр [— Л?(ж— О2]	(2-60)
— ь
Из выражения (2.60) находим
Подставив значение Лд в формулу (2.59), получим
’, = /.(*. А.+	(2-62)
Обозначив в зависимости (2.62)
Ai-^ = A,i.	(2.63)
получим
Аэ1+г).	(2.64)
Перенесем начало координат по оси z на величину h91 вверх.
Тогда новая координата рассматриваемых точек массива будет свя-
зана со старой координатой зависимостью
z = A91 + z,	(?.65)
где z — новая координата.
Подставляя выражение (2.65) в зависимости (2.64), получим
°i=fi(x,z)-	(2.66)
Выражение (2.65) представляет функцию распределения напряже-
ний в однородном массиве. Таким образом, приходим к заключению,
что для определения величин напряжений во втором слое необхо-
димо верхний слой системы привести к эквивалентному по распре-
делению напряжений слою по формуле (2.63), а затем рассматривать
приведенные два слоя как однородную среду.
Аналогичным образом можно получить формулы для определе-
ния эквивалентных толщин вышележащих слоев любой многослой-
ной системы.
В результате приходим к выводу, что характер приведения сло-
истой системы к эквивалентной однородной среде по распределению
напряжений не зависит от вида заданной вертикальной нагрузки
на поверхности безраспорной слоистой системы.
39
Глава 3
РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В БЕЗРАСПОРНОМ
ЗЕРНИСТОМ ОСНОВАНИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
§ 1. РАВНОВЕРОЯТНАЯ ПЕРЕДАЧА УСИЛИЙ ОТ ВЫШЕЛЕЖАЩЕЙ
ЧАСТИЦЫ НА НИЖЕЛЕЖАЩИЕ ПРИ СОСРЕДОТОЧЕННОЙ НАГРУЗКЕ
Для выяснения связи между распределением усилий в плоской
и пространственной задачах рассмотрим частный случай равно-
вероятной передачи усилий от выше-
лежащей частицы на нижележащие. На
рис. 3.1 изображена расчетная схема
рассматриваемой задачи.
От единичной сосредоточенной
нагрузки, приложенной центрально
к частице, находящейся на поверх-
ности, распределение усилий по ча-
стицам в шести рядах сверху, вклю-
чая и нулевой ряд, представлено на
рис. 3.2. На шести представленных
Рис. 3.1. Расчетная схема опи- "Римерах можно установить законе-
рани я вышележащего блока на мерность в распределении усилии
нижележащие в пространствен- между частицами в слоях и выразить
ной задаче	это аналитической функцией.
Анализ показывает, что не только
для слоев, приведенных на рис. 3.2, но и для любого другого
слоя, распределение усилий между частицами подчиняется сле-
дующей функции:
(4"Г(1+1)Я (т)"(1+,)Л=(т)”(1+1)Я (i+,)Л> (31)
где п — номер рассматриваемого слоя.
Так, для п = 0 имеем
(4-)°(i+i)°(i+1)°=1.
Для слоя с номером п = 3 распределение усилий будет следую-
щим:
(у)3(‘ + 1)3(1 + I)3 =	(1 + 3 + 3 4-1) (1 +з + 3 + 1) =
= (т)Э (1+3 + 3+1. + 3+9 + 9 + 3 +
40
+ 3 + 9+9 + 3 + 1+3 + 3+1).
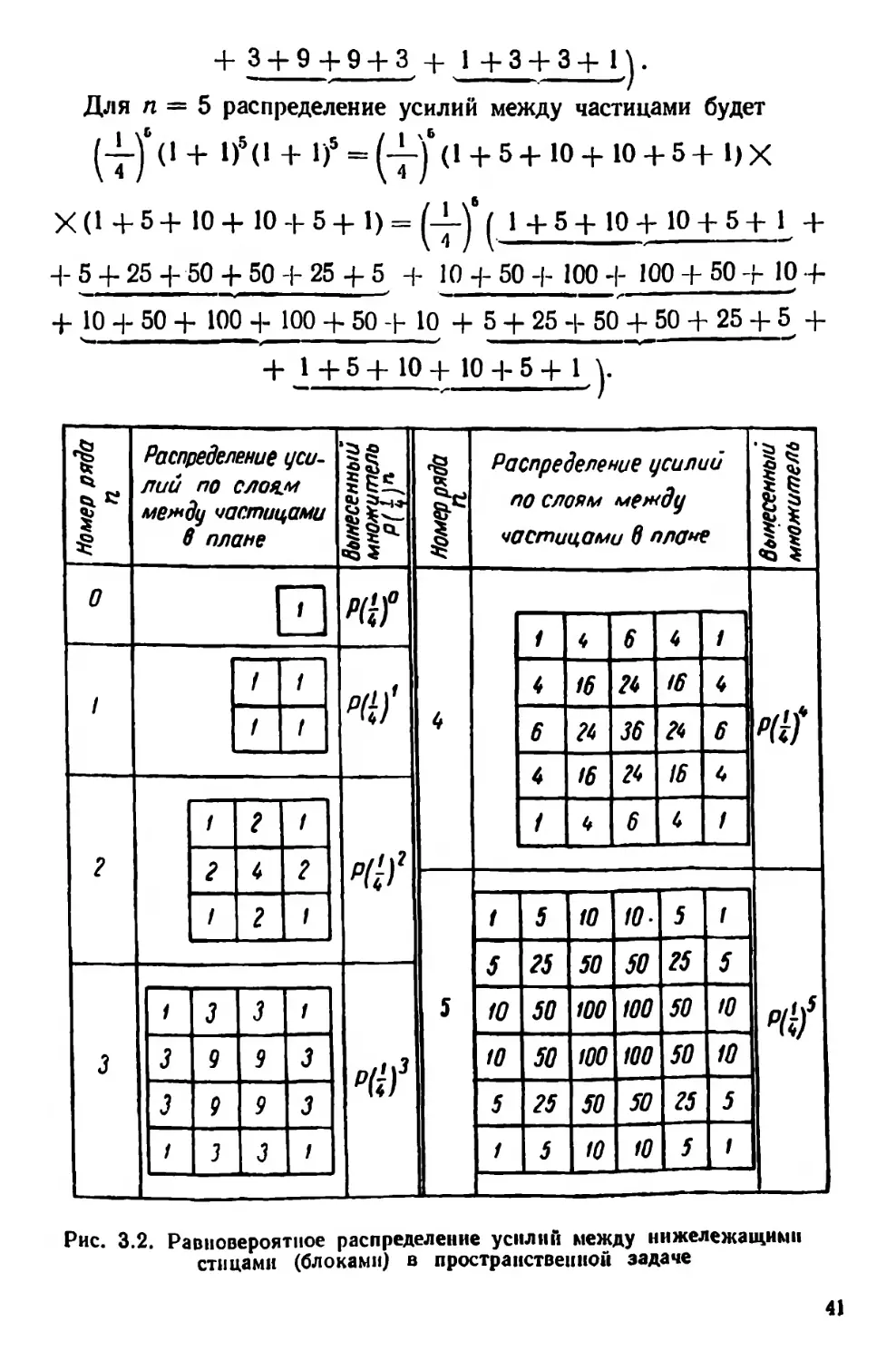
Для п = 5 распределение усилий между частицами будет
(т)1 <* + ‘)5(1 + 1)* = (4~У + 5 + 10 + 10 + 5 + 1) х
X (1 + 5 + 10 + 10 + 5 + 1) = (-J-)’ р + 5+ 10+ 10 + 5+ 1 +
4- 5 + 25 + 50 + 50 + 25 + 5 + 10 4- 50 4- 100 -|- 100 + 50 + 10 +
+ 10 + 50 + 100 + 100 + 50 + 10 + 5 + 25 4- 50 + 50 + 25 + 5 +
+ 1 + 5 + 10 + 10 + 5 + 1
Рис. 3.2. Равновероятное распределение усилий между нижележащими
стицами (блоками) в пространственной задаче
41
Приведенные примеры показывают, что распределение усилий
между частицами в рассматриваемой задаче подчинено выражению
(3.1), представляющему квадрат зависимости, определяющей рас-
пределение напряжений в плоской задаче.
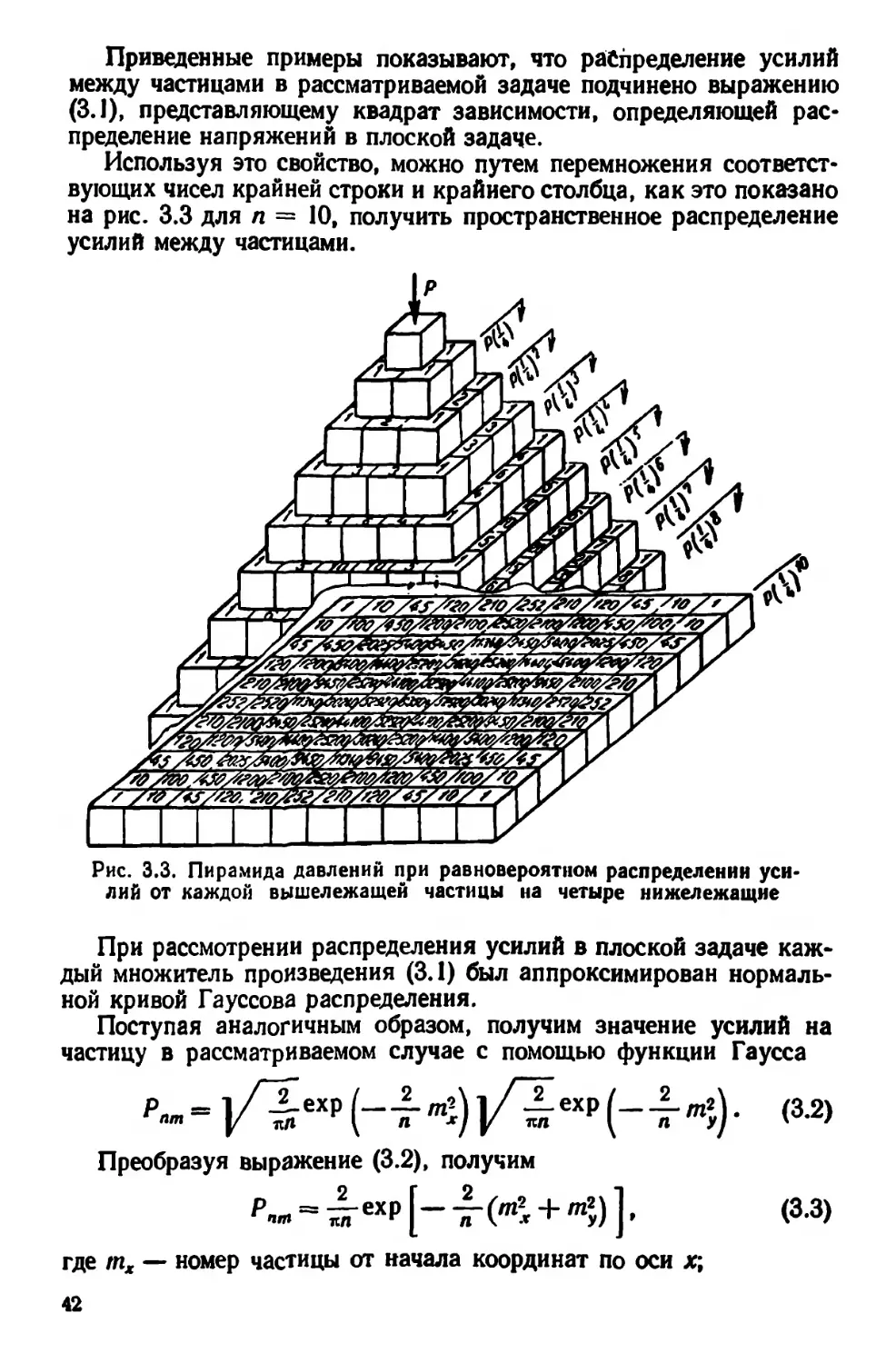
Используя это свойство, можно путем перемножения соответст-
вующих чисел крайней строки и крайнего столбца, как это показано
на рис. 3.3 для п = 10, получить пространственное распределение
усилий между частицами.
Рис. 3.3. Пирамида давлений при равновероятном распределении уси-
лий от каждой вышележащей частицы на четыре нижележащие
При рассмотрении распределения усилий в плоской задаче каж-
дый множитель произведения (3.1) был аппроксимирован нормаль-
ной кривой Гауссова распределения.
Поступая аналогичным образом, получим значение усилий на
частицу в рассматриваемом случае с помощью функции Гаусса
^m=]/iexp(-vml)|/^exp(—(3-2)
Преобразуя выражение (3.2), получим
+ ^)].	(3.3)
где тх — номер частицы от начала координат по оси х;
ту — номер частицы от начала координат по оси у\
п — номер слоя.
Как и в случае плоской задачи, связь между номерами частиц
и координатами осей устанавливается следующими зависимостями:
_ _ х . '
т*~ ~ь~’
(3.4)
п
Переходим в формуле (3.3) от номеров частиц к их координатам
и для вертикального усилия получаем следующую зависимость:
(3.5)
^ = ^ехр
Зависимостью (3.5) выражается распределение усилий между
частицами. Для определения средней величины напряжения разде-
лим усилие на площадь, занимаемую частицей. Тогда получим
(3.6)
2а
о =------ехр
itbcz
В случае сосредоточенной нагрузки Р выражение для напряже-
ний примет такой вид
2Ра
а. =-----ехр
г nbcz г
(3.7)
§ 2. НЕРАВНОВЕРОЯТНАЯ ПЕРЕДАЧА УСИЛИЙ ОТ ВЫШЕЛЕЖАЩИХ
ЧАСТИЦ НА НИЖЕЛЕЖАЩИЕ ПРИ СОСРЕДОТОЧЕННОЙ НАГРУЗКЕ
Средний размер зерна, приведенный в формуле (3.7), может при-
нимать любые значения. Выразим этот размер по оси г через размер
зерна другого материала зависимостью
а = ajA2,	(3.8)
где fli — размер зерен другого материала.
Подставляя выражение (3.8) в формулу (3.7), получим
аг = Л^-ехр [-	.	(3.9)
2 ncbz н L г U2 /J
Сравнивая формулу (3.9) с аналогичной формулой для верти-
кальных напряжений в плоской задаче, находим, что зависимость
(3.10) может рассматриваться для определения вертикальных на-
пряжений в зернистой безраспорной среде при неравновероят-
ном распределении усилий между частицами. Средний расчетный
43
размер зерен в этом случае равен abc, а коэффициент неравномерно-
сти передачи усилий — k. Введем обозначения
Назовем ах коэффициентом структуры среды вдоль оси х, а
— коэффициентом структуры среды вдоль оси у.
При введении указанных обозначений выражение (3.9) примет
вид
Oz = /> YYYsl exp *'£ + «Wj.	(3.12)
В случае произвольной вертикальной нагрузки вертикальные
напряжения
я, =	/(5, exp [-	+	dF, (3.13)
где F — площадь интегрирования;
7j — переменные интегрирования;
dF = di'd-q.
В заключение отметим, что здесь приведены зависимости для
вертикальных напряжений. Что касается горизонтальных и каса-
тельных напряжений, то они вычисляются по вертикальным напря-
жениям на основе физических уравнений и уравнений равновесия.
§ 3. НАПРЯЖЕНИЯ В СЛОИСТОМ ОСНОВАНИИ ОТ ПРОИЗВОЛЬНО
ЗАДАННОЙ НАГРУЗКИ НА ПОВЕРХНОСТИ
Для решения этой задачи докажем следующее утверждение.
Если нагрузка на поверхности может быть представлена функцией
= ^)ехр {- [Лх(х-О2 + А2(у-^)2]) dF, (3.14)
то распределение напряжений на глубине г определится выражением
где Лп ЛВ — постоянные параметры функции нагрузки;
44
F — площадь интегрирования;
— переменные интегрирования.
Для доказательства этого утверждения используем решение о
распределении напряжений в безраспорном массиве от нагрузки,
заданной уравнением
Р =	у).
Распределение напряжений от
нием
такой нагрузки выразится уравне-
<9
в) “г
а.

/ИМ
ТПтптт»

+ ^(4Г-(3.16)
Теперь верхний слой рас-
сматриваемого массива тол-
щиной z = гх отбросим и за-
меним связи реакциями. ______
В результате получим но- Т
вую расчетную схему: на-
грузка на поверхности опре-
делится из зависимости (3.16)
при г = Zj, т. е.
Л(*. !/) = «« =
= *?*“ Bi f /(I. ^exp I —
2kzi J	1
о
Рис. 3.4. Расчетная схема к определению
напряжений в многослойной системе
в пространственной задаче
а — заданная схема загружен ня; б — экви*
валентная схема эагруження

(3.17)
От снятия слоя толщиной z = и замены связей реакциями
напряжения в массиве не изменились и определяются выражением
(3.16). В новой, представленной на рис. 3.4 системе эти напряжения
для z > Zj можно рассматривать как вызванные нагрузкой по урав-
нению (3.17) и расположенной на поверхности вновь образованной
системы. Для новой системы начало координат перенесено по оси z
на zlt т. е.
г = г + г,	(3.18)
Где z — координата рассматриваемой точки во вновь образованной
системе.
4Б
Подставив (3.18) в формулу (3.16), получим выражение для на-
пряжений в новой системе координат

2z V (Zj + z) (Zj J- z)
ax(X-J)2
2^ + z)’
(3.19)
. —^)g
2(Zj + *)
Из сравнения (3.14) и (3.17) видно, что эти выражения будут тож-
дественны при соблюдении следующих условий:
_^В. = Я; 2«,	*	(3.20)
ах — Д • 2г, ’	*’	(3.21)
аУ _ л 2г,	2‘	(3.22)
Определим из этих условий параметры Bt и zt;
гч	2~Z1 гч
В. = - у== В =
V ахау
(3.23)
(3.24)
(3.25)
21	2Л, ’
7 — аУ
1	2Л2 ’
Из полученных формул видно, что для соблюдения тождества
между выражениями (3.14) и (3.17) необходимо величину zt при ах
определять по зависимости (3.24), а при ар — по зависимости (3.25).
Если руководствоваться этими соображениями и подставить значе-
ния Zj по формулам (3.24) и (3.25) в выражение (3.19), то получим
формулу для определения напряжений от нагрузки по выражению
(3.14), т. е.
в
o.
/«. ^)exp

dF.
(3.26)
(| + 2^г
\ av
Полученное выражение для напряжений от нагрузки по уравне-
нию (3.17) тождественно выражению (3.15).
4Ь
Рассмотрим далее распределение напряжений в слоистой среде
от произвольной нагрузки на поверхности.
Пусть нагрузка на поверхности среды распределена по площади
F и задана уравнением
Р=/(^).	(3.27)
Напряжения в верхнем слое системы от нагрузки, заданной
уравнением (3.27), получим в виде
о. = КрЕ [ /(?, п) ехр [- М* ~	Му - J)1] dF. (3.28)
Заменив связи реакциями и отбросив верхний слой, образуем
новую расчетную схему; нагрузка на поверхности будет равна ре*
акциям связей и определится из выражения (3.28) при z = ht:
/В. ,)exp [-	<3.»>
/71П] J	«lj	J
Таким образом» функцию напряжений во втором слое необхо-
димо искать от нагрузки на его поверхности, заданной уравнением
(3.29).
На основе доказанного выше, выражение для вертикальных на-
пряжений от такой нагрузки определится зависимостью
После некоторых преобразований формула примет вид
где г — координата рассматриваемой точки во вновь образованной
системе с началом координат на поверхности этой системы,
т. е. на границе между первым и вторым слоями»
47
Введем обозначения
h^ = h^-, *.„ = *•>,	(3.32)
У.	Г,
тогда
/(5. ^ехр
Г
[	2 (^1эх + г)
а =	г ”
2л + z) (Л»у + 2)
2 (Л1Э0 + 2) J
(3.33)
Для решения вопроса о распределении напряжений в третьем
слое образуем новую расчетную схему, отбросив в исходной системе
два верхних слоя и заменив связи реакциями. Начало координат
во вновь образованной системе расположим на ее поверхности. Ось
г направим по вертикальной оси исходной системы.
Выражение для нагрузки во вновь образованной системе полу-
чим из (3.33) при z =
Сд^ехрГ-^-^-
2n ]/(Л1Эх + Л2) (Л1э^ + Л2) J	L 2	+ Л«)
аУа(У->})а '
2 (Лир 4- Ла)
dF.
(3.34)
Поступая как и в предыдущем случае, получим следующую за-
висимость для напряжений от нагрузки по выражению (3.34):
------ С/(5.-^ехрГ-	-
2я]/(Л2эх + г)(Л29у+ z) I	[ 2(Лгэж + г)
где
_ ау,(У-^)а 1
2 (Л297 4- z) J
dF,
-V,	“.г,	“у, ау3
Из приведенных зависимостей видно, что в пространственной
задаче для анизотропной безраспорной среды необходимо вычис-
лить две эквивалентные толщины, связанные с осями координат
х и у. Аналогично эквивалентные толщины можно вычислить и
для многослойных систем. Так, для n-го слоя
Л<.-О»=А.:7Я+Лг^+'	+Vi^;
х»	(л—I)
48
*Чп h,y=^— +Л2— +	+*л
(л—I) эу	1	2	л—I аи
У»	Ь	у(п—|)
Подставляя эквивалентные толщины в общую формулу, получим
для напряжений в л-ом слое
тхпУп	у
2я (ft(n_|j 9Г + z)(ft(n_|j sy + Z)
а*я(*-Е)2 «уп<У~чР
2 0(Л—I) ЭЛ + г)	2 0(Л—I) эу + 2).
dF. (3.35)
Анализ полученных решений показывает, что для произвольно
заданной вертикальной нагрузки на поверхности среды вопрос о
распределении напряжений в пространственной задаче решается
путем введения независимых эквивалентных толщин по двум вза-
имно-перпендикулярным вертикальным плоскостям и вдоль осей
х и у. Если аХп = aUn = ап, но а<п =# Для всех слоев, то
^(л-1) эх ~ ^(л-1> эу ~ ^1 а"	+	+ Лл-1 ’
т. е. в частном случае получаем формулу для эквивалентного слоя,
как и в плоской задаче.
§4. БЕЗРАСПОРНЫЕ СРЕДЫ И УРАВНЕНИЯ РАВНОВЕСИЯ
Любой массив среды под действием внешних нагрузок постоянно
находится в статическом или динамическом равновесии. Выделим
некоторый объем среды из массива (рис. 3.5), и проанализируем,
какие силы на него действуют при условии, что среда обладает рас-
пределяющей способностью.
Размер выделенного объема по оси х равен Axt по оси г — Аг
и по оси у равен единице. Поскольку среда обладает распределяю-
щей способностью, то естественно предположить, что в среднем ин-
тенсивность вертикального давления по верхней грани объема
больше, чем по нижней. Кроме того, давление по нижней грани в
силу большого выравнивания его с глубиной более равномерно рас-
пределено, чем давление на верхней грани. Поэтому равнодейст-
вующая Рп по верхней грани приложена к рассматриваемому объему
среды с большим эксцентрицитетом, чем равнодействующая Рп по
нижней грани.
Поскольку равнодействующая по верхней грани отличается от
равнодействующей по нижней грани, для равновесия выделенного
объема необходимо к боковым граням приложить касательные силы
(напряжения).
49
В местах швов эти силы воспринимаются связующими блоками.
Если в среде швы не перевязаны, то такая среда не способна распре-
делять давление на большую площадь и в блоках такой среды не
возникают перерезывающие усилия. Для уравновешивания момента
сил, создаваемого вертикальными усилиями, необходимо к боковым
граням выделенного объема приложить горизонтальные усилия
также с эксцентрицитетом и разные по величине (опять же с учетом
распределяющей способности среды). Поскольку эти усилия также
различны по величине, то равновесие bi
оси х будет соблюдено при наличии по
(деленного ооъема вдоль
горизонтальным граням
объема касательных на-
пряжений (усилий).
Таким образом, рав-
новесие выделенного
объема безраспорной зер-
нистой среды возможно
лишь при наличии вер-
тикальных, горизонталь-
ных и касательных уси-
лий.
На рис. 3.6 изобра-
жен выделенный объем
под воздействием всех
составляющих напряже-
ния. При этом точки
приложения горизон-
тальных и вертикальных
равнодействующих сил
перенесены в центры гра-
ней выделенного объема
счет этого изменения ве-
напряжений по горизонтальным плоскостям
некоторого объема массива
при одновременном учете возможного за
личин касательных составляющих. Тогда вертикальная равнодей-
ствующая при усреднении напряжений по верхней грани
р“=(,’*+^л‘)л,;
по нижней грани
Горизонтальная равнодействующая по левой грани

по правой грани
Р ХП — ах^я-
50
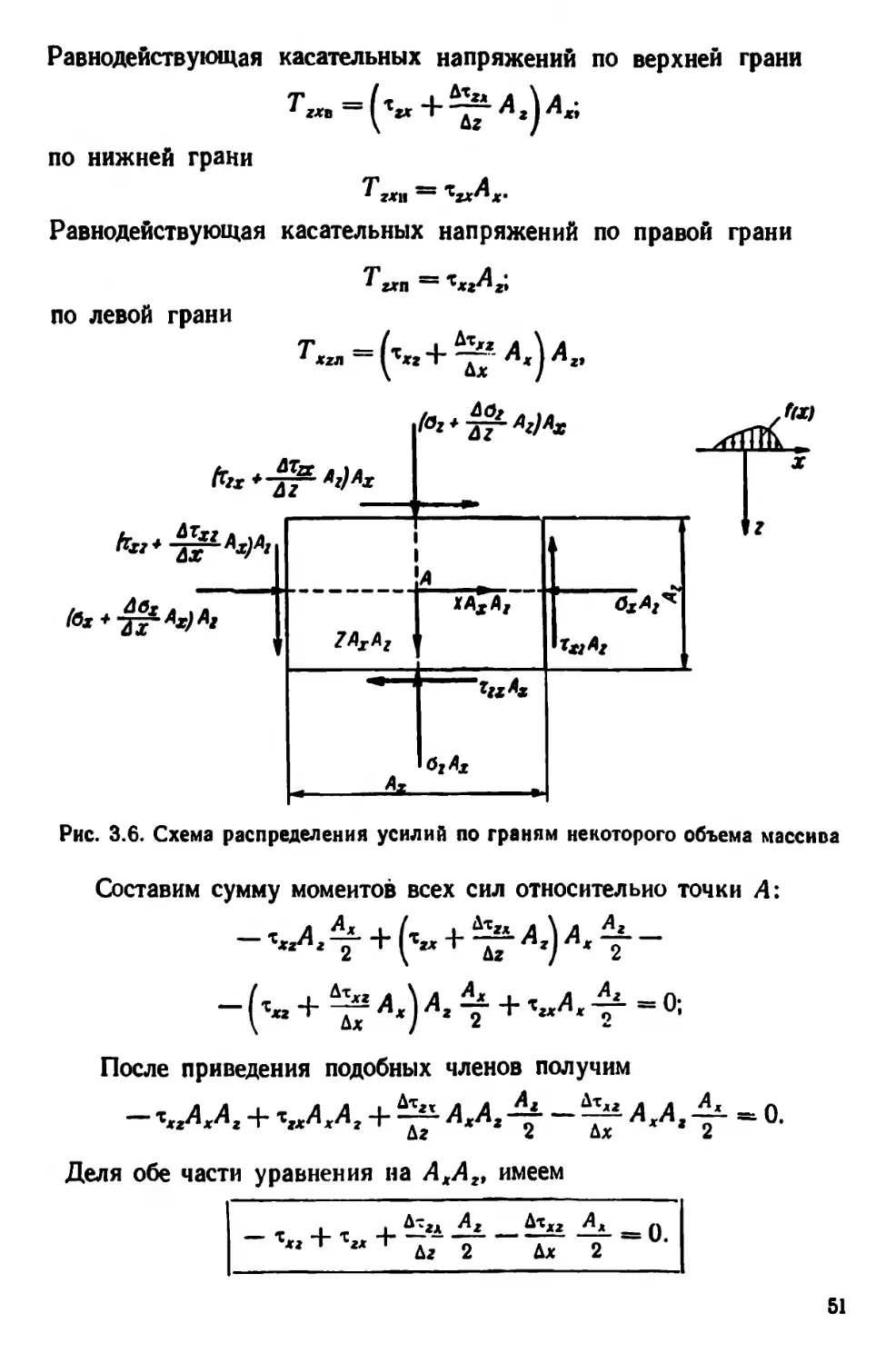
Равнодействующая касательных напряжений по верхней грани
по нижней грани
Равнодействующая касательных напряжений по правой грани
Т„п =
по левой грани
Рис. 3.6. Схема распределения усилий по граням некоторого объема массива
Составим сумму моментов всех сил относительно точки А:
После приведения подобных членов получим
-ЬгА,Аг + т„АжА, + АЖА, А - А,А, А ~ 0.
Деля обе части уравнения на АхАг, имеем
_ х + х хA- Л = о.
^-Ь'Чж-Г Д2 2 Дх 2
51
Далее» проектируя все силы на ось х, имеем
-	+ (°х + Л) Аг - х„А,+
+ (sx+ л,) Ал + ХА,Аг = 0.
После сокращения получаем
4.	4. х = 0.
Дх Дх
Аналогично получим уравнение равновесия» спроектировав все
силы на вертикальную ось:
hi. 1 *:« _l z = 0. Дг	Дх
Здесь X и Z — интенсивности объемных сил.
Нетрудно видеть» что получены уравнения в конечных разно*
стях, которые можно заменить уравнениями в частных производ*
ных, т. е.
। Az   d~-xz Ах  « .
дг 2	дх 2 ”U’
+	+ X = 0;
дх	дг
, &хг_ I 2 _ о
дг	дх
(3.36)
Полученные уравнения справедливы для любых размеров вьь
деленного объема среды» в том числе и для очень малого, как dz dx.
В сущности при такой постановке рассматривается некоторая
сплошная среда, эквивалентная по условиям равновесия зернистой
среде. Тогда из первого уравнения (3.36) получим
Аналогичным образом можно показать, что в среднем для зер*
нистой среды в пространственной задаче справедлива следующая
система уравнений равновесия:
+ *£» +	+ X = о-
дх ду дг
fyx I I &~Уг I у _ 0-
дх ду дг
+	= о-
дх ду дг
V —Vv:
62
Эти уравнения Навье используются для всех сплошных тел.
Здесь показано, что они (эти уравнения) в среднем справедливы и
для зернистых сред, способных распределять внешнюю нагрузку
на большую площадь.
§ б. ФИЗИЧЕСКИЕ УРАВНЕНИЯ ДЛЯ БЕЗРАСПОРНОЙ ЗЕРНИСТОЙ
СРЕДЫ
В рассматриваемой системе каждые две частицы (блока) связы-
ваются друг с другом через третий блок. Поскольку безраспорная
среда обладает распределяющей способностью, то вертикальные
Рис. 3.7. К определению напряжений между вертикальными уси-
лиями на соседние блоки и перерезывающими усилиями в связую-
щем блоке
усилия на соседние частицы будут различны и разность этих уси-
лий если не полностью, то частично будет восприниматься связываю-
щей их частицей. И чем больше эта разность, тем большее перере-
зывающее усилие воспринимается связующей частицей.
Таким образом, для физической характеристики данной среды
можно принять, что разность усилий на соседних частицах пропор-
циональна перерезывающему усилию, возникающему в связующей
частице. Такую гипотезу, хотя и в несколько иной трактовке,
применительно к зернистой среде впервые высказал Р. А. Мул-
лер [60 J.
Используя некоторые его положения, составим физическое урав-
нение для безраспорной зернистой среды. На рис. 3.7 изображена
53
расчетная схема, поясняющая суть изложенной гипотезы; перере-
зывающее усилие в связующей частице
Т . с, [ч— b(a. +	Ь VI = - С J?	— CJ>>, (3.37)
L \ Дх / J	д*
где Сж — коэффициент пропорциональности.
Разделив перерезывающее усилие в связующей частице на две
ее высоты (с учетом того, что это усилие приходится и на шов между
частицами), получим касательное напряжение по одной из граней
выраженное через частную производную от нормального на-
пряжения:
СХЬ* даг
2а дх *
(3.38)
В этом уравнении коэффициент пропорциональности также
пока неизвестен, как и коэффициент распределительной способно-
сти А. Если принять, что Сх =	, то
2а 2а ’
где а — коэффициент структуры среды.
С учетом этого соотношения для касательных напряжений по-
лучим
г
“ 2а дх *
(3.39)
Полученное выражение и будет физическим уравнением
для плоской задачи, характеризующим природу среды с точки зре-
ния ее главного механического свойства, т. е. способности распреде-
лять усилия.
В предположении, что Л = Z = 0, из выражений (3.36) по-
лучим
> + ^ = 0:	<зло>
д'г . дтхг р
дг дх
(3.41)
Дифференцируя физическое уравнение (3.39) по х и подставляя
его во второе из приведенных уравнений равновесия, получим
даг = I д%г
дг 2а дхг
(3.42)
54
Используя уравнение равновесия (3.40), имеем
аож =J_ дЧ .
дх 2а дхдг *
(3.43)
или
+ <3-44'
где Р (г) — произвольная функция интегрирования.
Значение произвольной функции Р (?) определим из следующих
условий: при z -> со при любом х величина ох -* 0 и -> 0, так
dz
как с глубиной для любой вертикали кривая для а2 асимптотически
приближается к оси z. Следовательно, Р (z) = 0, тогда
о = X = -L = _ _!_ Xi..	(3.45)
* 2а дг 4а» дхг 2а дх
Решение дифференциального уравнения (3.42) для вертикаль*
пых напряжений при следующих граничных условиях:
а2 = — Р при z = 0 в точке приложения нагрузки;
аг = 0 при z — 0 во всех остальных точках поверхности массива;
о2 -> 0 при X + СО
имеет вид
—₽]/£ехрни-
(3.46)
Если сравнить этот результат с тем, который был получен другим
путем, то нетрудно убедиться, что они тождественны. Дифференци-
руя выражение для аг по х, получим из (3.39)
<3 47>
Дифференцируя выражение для по z, получим значение <?х
от сосредоточенной вертикальной нагрузки
(3.49)
(3.50)
Поступая таким же образом, как и для плоской задачи, и учи-
тывая анизотропию, в структуре массива по осям х и у для касатель-
ных напряжений, получим
1 д<зг
________LX
**	2а, ду '
65
В соответствии с этим по направлениям осей х и у, как и в пло-
ской задаче, должны сохраняться соотношения между горизонталь-
ными и вертикальными напряжениями, т. е.
(3.51)
(3.52)
1
=----------;
1 д%г
°У 4а* W ’
где
„ — g • « — а
х 2СХР у 2С^
Сх; Су — коэффициенты пропорциональности;
a, bt с— размеры блоков (частиц);
ах; ау -т- коэффициенты структуры среды соответственно по
осям х и у.
Эти выражения представляют собой физические уравнения, от-
ражающие природу безраспорной зернистой среды с точки зрения
способности ее распределять внешнюю нагрузку.
Для решения пространственной задачи, кроме физических урав-
нений, необходимы уравнения равновесия.
Полагая объемные силы равными нулю, получим уравнения рав-
новесия:
д°г 1	। &ХХ2 __ п.	(3 53Ъ
дг	ду	дх	
1 ^ху । д*хг	Q. дх	ду	дг	(3.54)
дау I fry* । dxyz __ q ду	дх	дг	(3.55)
Дифференцируя физические уравнения (3.49) и (3.50) и подстав-
ляя их в первое уравнение равновесия, получим
4-	.	(3.56)
дг 2«ж дх* 2а„ ду*	'	'
Из второго и третьего уравнений с учетом зависимостей для ах
и Су находим
OhlL = ----	(3.57)
ду	ду*дх
Аналогично получаем
J*i..	(3.58)
дх 4ада^ дх*ду
56
Интегрируя (3.57) и (3.58), находим	
г); r 4ахау дудх	(3.59)
ъ-г~ * 4a.jfly дхду	(3.60)
Поскольку Хху = Xyxt то	
/(*. 2)=f(y, Z)=0.	(3.61)
В результате окончательно получаем	
1 д*аг	(3.62)
Хху-\х- 4в^ дхду •	
Глава 4
ДЕФОРМАЦИИ .БЕЗРАСПОРНОГО ЗЕРНИСТОГО ОСНОВАНИЯ
§ 1. ДЕФОРМАЦИИ СЖАТИЯ
Деформация безраспорного зернистого массива складывается
из деформации самих блоков и ослабленной (выветрившейся) толщи
материала в области контактов между ними. При неравномерной
нагрузке сжатие сопровождается поворотом блоков массива. Чем
больше неравномерность нагрузки на массив, тем больше повороты
блоков.
В силу того что отдельные блоки, образующие массив, опира-
ются друг на друга через микроконтакты, модуль упругости мате-
риала в областях контактов ниже модуля упругости материала са-
мих блоков. При изучении деформации безраспорного зернистого
основания можно считать, что каждый блок в отдельности является
элементом, упругие свойства которого определяются модулем уп-
ругости и коэффициентом Пуассона. Вместе с тем для массива в це-
лом нужно пользоваться обобщенным модулем упругости и не учи-
тывать коэффициента Пуассона, поскольку его боковые деформа-
ции в основном будут поглощаться имеющимися швами между
блоками, т. е. |л = 0.
Учитывая сказанное, при ах = ау = хху = хух = хгу = ху2 =
=	= 0, т. е. при неограниченной равномерно распреде-
ленной вертикальной нагрузке, можно считать, что деформация
67
сжатия блока происходит только в направлении оси г от напряже-
ния о2.
Согласно рис. 4.1 деформация сжатия блока
(4.1)
EfJfjCi Et<ibici
где Pt — усилие, приходящееся на i-й блок;
Еи— модуль упругости материала блока;
ЕК1 — модуль упругости материала в области контакта;
ai» ci — геометрические размеры блока;
Az, — толщина материала в области контактов.
Рис. 4.1.
Схема к расчету модуля сжатия безраспор-
ного зернистого основания
Такое раздельное рассмотрение деформации блока соответствует
имеющимся экспериментальным данным Б. Д. Зеленского (рис. 4.2).
Разделив обе части выражения (4.1) на alt а также приняв
ая —	, ПОЛУЧИМ
(4.2)
1 а. Еи ' а, ЕК1 “ к/ Е,
где Е, — обобщенный для блока модуль упругости;
ez — относительная деформация;
ем — относительная деформация монолита;
ew — относительная деформация материала в области контак-
тов.
58
Обобщенный модуль упругости блока
£мЕ„, y4-
Е,---------(4.3)
Ем +
Тогда обобщенный модуль упругости массива
1 N
1441
где N — число блоков массива, выбранных для определения модуля.
WIIT'I III
Blllllllll I III
Образец
1 Образец
* ” Образец
ЕЯ
ЕЕ
Тшп
Рис. 4.2. Опытные данные Б. Д. Зеленского по изучению де-
формации монолитов скальных пород
На основе выражения (4.2) относительную деформацию в сред-
нем по отношению к массиву можно определить так:
По аналогии	<4-5> <4-6> Ту-Т-	<47>
69
В зависимости от структуры (размеров блоков, областей контак-
тов, условий опирания) обобщенные модули по направлениям осей
х, yt г могут быть различными и в каждом конкретном слу-
чае должны вычисляться по формулам (4.3) и (4.4).
Кроме деформации сжатия, в безраспорных зернистых основа-
ниях имеет место поворот частиц.
В первом приближении можно принять, что повороты в массиве
в среднем пропорциональны касательным напряжениям, т. е.
1*2 ~	0*8)
lyz ~	(4.9)
Тг,=	<4-10)
здесь 6 — модуль сдвига поперечной упругости материала блоков.
§ 2. СВЯЗЬ СРЕДНИХ ВЕРТИКАЛЬНЫХ, ГОРИЗОНТАЛЬНЫХ
ПЕРЕМЕЩЕНИЙ И ПОВОРОТОВ В БЕЗРАСПОРНОЙ ЗЕРНИСТОЙ СРЕДЕ
Из зависимости (4.5) вертикальные перемещения
Для определения остальных перемещений воспользуемся полу-
ченными ранее соотношениями. Из зависимостей (4.5), (4.6) и (4.8)
находим
а, = £§;	(4.12)
ож=£ —;	(4.13)
дх
=	(4.14)
Кроме того, в уравнениях (3.39), (3.49) и (3.51) получены следую-
щие соотношения между горизонтальными, касательными и верти-
кальными напряжениями:
о = J_	(4.16)
4а2	2а дх	4	'
60
Дифференцируем уравнение (4.12) по х и подставляем его в вы-
ражение (4.15); подставляя также в это выражение зависимость
(4.14), получим
7„С=-——.	(4.17)
1X2	2а дхдг
Аналогично подставляя (4.13) и (4.15) в уравнение (4.16), по-
лучим
Е — — —	•
дх 4а2 дгдх2 *
после интегрирования по х имеем
« = -L^ + P(Z).
4а2 дхдг
При х -► оо перемещение « -> 0 и -—у—> 0, следовательно,
Р (z) = 0. Таким образом, горизонтальные перемещения связаны
с вертикальным соотношением
4а2 дхдг
с
При соотношении 6 —— (так как р = 0) уравнение (4.17) примет
вид
_____1_ &1О
“ дхдг ‘
По аналогии с плоской задачей для пространственной
w _ 1 d*w
4аз дгдх ’
1	д-w	1 d*w
и ~----------; "fX9 -------------;
4я2 дгду	ах дгдх
_____	1 д2ш е 	 1 д2и>
^уг ау дгду ’____________2ахау дхду ’
откуда
4ах	4ау v
у -	1 / 1		1	\
1ху 4 ду ау дх J'
Приведенные уравнения связывают средние перемещения и по-
вороты малых элементов эквивалентной сплошной среды. Эти урав-
нения аналогичны уравнениям неразрывности деформаций в теории
упругости, но отличаются от последних в связи с тем, что зернистая
61
среда в отличие от среды упругой не способна воспринимать растя-
гивающие усилия.
Нетрудно видеть, что приведенные соотношения справедливы
и для переменного по глубине модуля упругости.
§ 3. ДЕФОРМАЦИЯ СЛОЯ ОГРАНИЧЕННОЙ МОЩНОСТИ
ОТ ЛИНЕЙНОЙ НАГРУЗКИ
Безраспорные среды имеют ограниченную мощность. Обозна-
чив мощность через hlt получим деформацию массива от нагрузки,
распределенной по линии
(рис. 4.3):
Подставив в выражение
(4.18) вместо соответ-
ствующую зависимость для
напряжений, получим

Интегрируя, получим следующую зависимость для осадки мае*-.
сива
Из выражения (4.19) при х = 0 получим зависимость от верти-
кального перемещения (осадки) массива мощностью по линии
приложения нагрузки
§ 4. ДЕФОРМАЦИЯ ДВУХСЛОЙНОЙ СИСТЕМЫ ОТ НАГРУЗКИ,
РАСПРЕДЕЛЕННОЙ ПО ЛИНИИ
При решении вопросов о распределении напряжений в безрас-
порных средах было установлено, что слоистые системы могут при-
водиться к однородным эквивалентным средам.
62
Осадка слоистой системы по оси z складывается из суммы де-
формаций слоев. Так, для двухслойной системы, изображенной на
рис. 4.4, перемещение будет складываться из деформаций верхнего
слоя щ и нижнего слоя т. е.
w =	4- ш8.	(4.20)
Из зависимости (4.19) при а = ах и Е = Elt для деформации верх-
него слоя имеем
Cj I у £К	\ бП} / Z
‘-ф0й# <4-2|)
где Ej модуль упругости материала верхнего слоя.
Для определения деформации нижнего слоя воспользуемся фор-
мулой (4.18) при hY а и Е = Е9.
Подставляя в эту формулу выражение для напряжений во вто-
ром слое системы, получим
пу2==
Рис. 4.4. Расчетная схема к опреде-
лению осадки двухслойной системы
ограниченной мощности от линей-
ной нагрузки
л»
« I Г
2^(AM+z)
—U.
2 (Аэ1 + г) /
Интегрируем это выражение
^2 =

у2(л;
— Ф
(4.22)
В формуле (4.22) величина + А2 = ,гэ» тогда
Подставим теперь в зависимость (4.23) значение
-= Aj
63
После подстановки и преобразовании имеем
или
где
Подставим теперь выражения (4.21) и (4.24) в формулу (4.20); после
преобразований получим

Из соотношений (4.21) и (4.25) имеем
где — деформация от заданной нагрузки однородного массива
толщиной h3, состоящего из материала нижнего слоя;
о>1 — деформация от заданной нагрузки верхнего слоя.
§ Б. ДЕФОРМАЦИЯ МНОГОСЛОЙНОЙ СИСТЕМЫ ОТ НАГРУЗКИ,
ПРОИЗВОЛЬНО РАСПРЕДЕЛЕННОЙ ПО ПОЛОСЕ
Для решения вопроса о деформации многослойной системы
плоской задаче докажем следующее утверждение.
Если деформация слоя
1*з +Ь	_
w = т $ $ /(е) ]/~^ехр (“dUz' (4 26)
$4
а предел интегрирования h3 связан с некоторой величиной зависи-
мостью
=	(4.27)
то выражение (4.26) через зависимость (4.27) может быть представ-
лено в виде
w=т f j f/({) / £ехр (-
(4.28)
Произведем замену переменной интегрирования в выражении
(4.26) подстановкой
* =	(4.29)
где t — новая переменная интегрирования:
Л =	(4.30)
Пределы интегрирования по новой переменной получаем из выра-
жения
Z = z^-;	(4.31)
при г = 0	= 0;
при z —/z3 /а = Лэ-у-.	(4.32)
Подставив выражение (4.27) в формулу (4.32), получим
при z = Аэ /2 = h.
Произведя замену переменной, вместо (4.26) получим
>- f/(!) "р (“) *«•
Или меняя обозначение переменной интегрирования,
"-Ttn/ls)/5exp(-1Vz)“- ,433)
о -ь
Таким образом сформулированное выше положение доказано.
Определим теперь деформацию многослойной системы от произ-
вольно заданной нагрузки (рис. 4.5).
Общая деформация многослойной системы складывается из
суммы деформаций отдельных слоев, т. е.
w = щ + w2 Ч- оу3 4- оу4 +	4	(4.34)
где ttJj — деформация верхнего слоя в системе;
65
wa — деформация второго слоя в системе;
ш3 — деформация третьего слоя в системе;
— деформация четвертого слоя в системе;
шп — деформация л-го слоя в системе.
Рассмотрим отдельно каждое слагаемое выражения (4.34), зная,
что
1
w,= егР1'*’	(4,35)
где — деформация /-го слоя;
Рис. 4.5. Расчетная схема к определению осадки мно-
гослойной системы от произвольно заданной верти-
кальной нагрузки в плоской задаче
Et — модуль материала /-го слоя;
hi — толщина /-го слоя;
“ функция распределения напряжений в t-ом слое.
Напряжения в /-ом слое
% =0. (*„((_,) + г) =
+ь _________
= f /(0 \/ —1— --------=гехР (----di, (4.36)
V 2(Лп (I-1) + г) \	2(Ап (I—|) + г) )
где Ап (/_п — эквивалентная толщина всех вышележащих слоев,
приведенных по распределению напряжений к рас-
__ сматриваемому слою;
г координата по вертикальной оси рассматриваемой
66
точки при положении начала координат на границе
раздела верхних слоев и данного слоя.
Подставляя выражение (4.36) в зависимость (4.35), получим
л
ч=J °' (А"«-')+ г)	(4-37)
Для верхнего слоя системы деформация
1 Л»
=	(4.38)
где — толщина верхнего слоя;
z — координата, отсчитываемая от поверхности соответствую-
щего однородного массива.
Для второго слоя системы
wi = Tt +	(4.39)
где Е2 — модуль материала второго слоя;
h2 — толщина второго слоя;
ЛП(/-|) — приведенная эквивалентная толщина верхнего слоя по
_ распределению напряжений к материалу второго слоя;
z — координата по вертикальной оси, отсчитываемая вниз от
верхней границы второго слоя.
Произведя замену переменной интегрирования в выражении
(4.39) подстановкой
Лщ +2==z,	(4.40)
получим
или
1	1 ’Ч1
«О» = j М?)| ог (z)dz,	(4.41)
где Лэ2 — полная приведенная толщина двух верхних слоев по рас-
пределению напряжений к материалу второго слоя.
Согласно доказанному в данном параграфе положению второй
интеграл выражения (4.41)
АП1	Л1
j С2 (z) dz =	f a, (z) dz,	(4.42)
о	1 о
где
Лт = Л1^-.	(4.43)
67
После подстановки выражения (4.42) в зависимость (4.41) полу-
чим
АЭ2	Л1
«’2 = 7- ( °2(г)* — 7-77 f °г(«)(4.44)
о	1 о
Значение второго интеграла выражения (4.44) определим из
формулы (4.38)
л,
f «j (2) dz = Etwv	(4.45)
ь
Подставляем это значение интеграла в формулу (4.44):
ЛЭ2
= 7" f °2 (z) dz —	W1.	(4.46)
С9 J	Е2 “1
Заметим, что первый член выражения (4.46) представляет де-
формацию сжатия от заданной нагрузки однородного слоя толщи-
ной Аэг» состоящего из материала второго слоя. Учитывая это, по-
лучим
=	— тг®!.	И-47)
с2
где
1
Шэ2= ЁГ J ®»(z)d?.	(4.48)
О
Определим деформацию третьего слоя. Согласно формуле (4.37)
деформация этого слоя
л,
W, = 4“ J ’»(h«2 + z) *.	(4.49)
С3 о
где Е3 — модуль материала третьего слоя;
h^-— толщина третьего слоя;
г — координата рассматриваемой точки в третьем слое при
положении начала координат на границе раздела вто-
рого и третьего слоев;
^2=^32^-.
Выполняя те же операции, что и при определении деформации
второго слоя, преобразуем выражение (4.49)
Л эз
ш>= 4~ С °s(z)dz—4--^ f 3#(z)dz.	(4.50)
*-3 V	с3 u2 J
68
где
Аэз = Ап2 + А3 — Aj 4- А2-^- + As-
Определяя из выражения (4.48) значение второго интеграла вы-
ражения (4.50), получим
Лэз
f ot(z)<fe=w38EI	(4.51)
О
После подстановки выражения (4.51) в зависимость (4.50), получим
U'a = «'.s — ~Г	(4.52)
Сэ
где
I >
«>!»=— f <>3(2)<fe;	(4.53)
С3 g
F — F —
ГЭ2 — C2~ •
Рассмотрим теперь деформацию л-го слоя. Согласно зависимости
(4.37), деформация его
ля
= к J °" (л" <"->+ *) d~2'	(454)
где Еп — модуль материала п-го слоя (последнего);
Ля — толщина его;
А = А ап
% (Л-!)	(Я-1) а , •
Л—1
Производя в выражении (4.54) замену переменной интегриро-
вания подстановкой
АП<П-|( + * = *.
получим
I Л9П
wn = -=- f °n(z)d?;
£" л J
П (л-1)
или
. Ллл	.	лп (л—1)
»п=г- ( °n(z)dz — — С °n(z)<fe.
о	“п	о
где
^пл = Ая + Ап (я_1}.
69
Учитывая доказанное в данном параграфе положение, получим
. "пл	.	Аэ (я—1)
Wn = — Г °„(z)dz— — -~И- С o„(z)dz. (4.55)
Сд	Сл л—1 J
1 Лря	1 ^Иг1)
Обозначив — j ап (z) dz = wnn; -— J ая (z) dz = w9 (я_п;
F - *n = F
л-l %_| Мл-D’
получим	и>л = wnn — —	.	(4.56)
^л
Подставив эти выражения деформации слоев системы в фор-
мулу (4.34), получим
w = U)j + Wt —	Wt + tt»„ — ф-’ тл + w„—
^2	^3
-^w,+ +W -E-1SH=H.„	(4.57)
ЕЛ 93 1	1 ПЛ	9 (Л—1)	x 7
*	**n
Группируя члены в выражении (4.57), имеем
w = W""~ w-,,+ +(^-1)“’эз +
+(>-1ь+&-1)“4
Таким образом, в случае произвольной нагрузки деформация
слоистой системы может быть представлена через деформации от
заданной нагрузки эквивалентных однородных слоев из материалов,
образующих заданную систему.
При этом следует подчеркнуть, что толщины эквивалентных
однородных слоев не зависят от характера нагрузки, а определяются
лишь толщинами слоев конструкции, порядком расположения их
в системе и механическими характеристиками соответствующих
материалов.
§ 6. ДЕФОРМАЦИЯ МАССИВА ОТ ВЕРТИКАЛЬНОЙ СОСРЕДОТОЧЕННОЙ
НАГРУЗКИ
Подставив в формулу (4.18) выражение для напряжений от сос-
редоточенной нагрузки, получим
w = f ехр (_«***+dz.
2т.Е J г r 2z	)
о
70
Произведем замену переменной интегрирования подстановкой
ахх>Ч-Д|/У* =
2z
Тогда	_ «иа+«уУ*
2Л,
f WV)d(.
2гЕ _J t '
It) = РУд<аУ F I +
-----------------------)’
где Ei (t) — интегральная показательная функция.
§ 7. ДЕФОРМАЦИЯ СЖАТИЯ МНОГОСЛОЙНОЙ СИСТЕМЫ ОТ
ПРОИЗВОЛЬНО ЗАДАННОЙ НАГРУЗКИ (ПРОСТРАНСТВЕННАЯ
ЗАДАЧА)
Результаты, полученные в предыдущих параграфах, обобщим
для случая произвольно заданной нагрузки прн ах = ау = а.
Докажем следующее положение.
Деформация сжатия слоя
лэ
w=-Ь f <& С А/(?. о ехР (—(4-59)
£ I 1 Z71Z	\ £Л J
о о
где F — площадь распределения нагрузки;
ср; г — угол и радиус-вектор в цилиндрических координатах.
Предел интегрирования связан с некоторой величиной зависи-
мостью (4.27), поэтому выражение (4.59) может быть представлено
в виде
h
w = -1- — f dz f r)ex₽ (— -57)dF•	(46°)
t «1 J J 2kz	\ 2z /
о К
Произведя замену переменной интегрирования в выражении
(4.59) подстановкой (4,29), получим
w=-Н М	r) ехр (~	dF •
О
Меняя обозначения переменной интегрирования, имеем
/I
-НН>'1Н-£> <4<"’
О F
Таким образом сформулированное выше положение доказано.
П
Пользуясь выражением (4.34), рассмотрим деформацию сжатия
многослойной системы от произвольно заданной на поверхности
вертикальной нагрузки.
В общем виде формула для определения вертикальных напря-
жений в t-ом слое будет иметь вид
%=0.(Ап«-|> + г) =
= Lgl	(462)
J 2*("п (<-!)+ Z)	\ 2(Лп(/-1) + Z) /
где Лп (/_0 — эквивалентная толщина всех вышележащих слоев,
приведенных по распределению напряжений к рас-
сматриваемому слою;
z — координата рассматриваемой точки по вертикальной
оси при положении начала координат на границе
раздела данного слоя с вышележащими слоями.
Подставив выражение (4.62) в зависимость (4.35), получим фор-
мулу (4.37).
Поступая далее, как и для плоской задачи, деформацию сжатия
второго слоя определим выражением (4.47), третьего слоя — выра-
жением (4.52) и п-го слоя — (4.56).
В результате придем к выводу, что деформация слоистой системы
для пространственной задачи вычисляется, как и для плоской за-
дачи, по формуле (4.58).
Глава 5
УРАВНЕНИЯ ДИНАМИКИ ДЛЯ БЕЗРАСПОРНОЙ ЗЕРНИСТОЙ
СРЕДЫ
§ 1. СВЯЗЬ МЕЖДУ СОСТАВЛЯЮЩИМИ напряжений в плоской
ЗАДАЧЕ
При рассмотрении физических уравнений в статике отмечалось,
что каждые две частицы (блок) связываются друг с другом через
третий блок, в котором из-за разности вертикальных усилий на эти
блоки возникают касательные напряжения. Отмечалось также, что
разность усилий в соседних частицах пропорциональна перерезы-
вающему усилию в связующей частице.
Этими же свойствами будет обладать зернистая безраспорная
среда в динамике. Но в отличие от статики на величины усилий здесь
72
будут оказывать влияние инерционные силы» зависящие от переме-
щения частиц. Поэтому при решении вопроса о соотношении
составляющих напряжений в динамике необходимо рассматривать
силы, вызывающие перемещения частиц.
Согласно рис. 5.1 перемещение частицы в вертикальном направ-
лении осуществляется под воздействием вертикальных составляю-
щих напряжений и сил инерции
ab —
dz
* dl* \dz 1 dt*)

Рис. 5.1. К определению соотношений между динамическими верти-
кальными усилиями на соседние блоки и перерезывающим усилием
в связующем блоке
По аналогии усилие на соседнюю частицу составит
ab
(5.2)
Перерезывающее усилие в блоке, на который опираются два
данных блока, определится как разность между выражениями (5.1)
и (5.2):
где Cg — коэффициент пропорциональности, связывающий усилия
на блоки через производные от напряжений.
73
После преобразований выражение (5.3) примет вид
=—СйЬг — 1—— р—\.	(5.4)
dz g дх\дг 1 dt2 /	1	7
При статической нагрузке ~ = 0. В этом случае выражение
(5.4) после интегрирования по г примет вид
Ъ-----(5.5)
Но для статической нагрузки ранее было получено такое соот-
ношение между касательными и вертикальными напряжениями
Из выражений (5.5) и (5.6) находим» что
=	(5.7)
Подставляя это значение в выражение (5.4), получим
=_____(5.8)
dz 2adx\dz Г dt2 J	'	'
Уравнения равновесия для плоской задачи при равенстве нулю
объемных сил:
да2 , дтхг __ &W . дг + дх ~ ₽ дР '	(5.9)
дох , дтХ2 _ <Ри dx + dz	*	(5.10)
Из уравнения (5.9) находим	
&хг	(д*х	дЪ\ дх	\dz	*dl2J'	(5.11)
Дифференцируя выражение (5.8) по х, а (5.11) по z, имеем	
		1 дЧд,2 д^\ dzdx	2adx*\dz Vdt2)'	(5-12)
(5.13)
дхдг дг\дг 1 д1»)	'
Левые части выражений (5.12) и (5.13) равны. Приравниваем
правые части
«Дл Pdt») 2а дхг\дг РдР)	V ’
74
Обозначим
da2 d*w
— — р —
dz 1 ЭР
f-
(5.15)
Тогда выражение (5.14) примет вид
д/	1 ау
dz	2а dx*
(5.1С)
Решение уравнения
(5.16) при следующих
граничных условиях
f = — Р (t) при 2=0,
х = 0 в точке приложе-
ния нагрузки;
/ = 0 при 2=0,
т. е. во всех остальных
точках поверхности мас-
сива;
/ -> 0 при х -> ± со,
имеет вид
Рнс. 5.2. Зона вынужденных возмущений
в безраспорной зернистой среде от динамиче-
ской сосредоточенной нагрузки

(5.17)
Подставляем в это выражение значение f из (5.15):
_£>(/)./Л-ехр^- -£-хА.	(5.18)
dz v дР ' ' у 2« Ц & /	'	'
Учитываем также соотношение между вертикальными напряже-
ниями и перемещениями
dw 1 doz - d2w
1	_	— U 
дг Е 1 дг дгг
Подставляя эти значения в уравнение (5.18), получим
р d^w _
д? ""Ты*
(5.19)
(5-20)
Получено неоднородное уравнение гиперболического типа. Пра-
вая часть этого уравнения представлена в виде произведения двух
функций, одна из которых зависит только от /, а вторая от х и 2.
Уравнение (5.20) выражает вынужденные колебания безраспор-
ного основания. Правая часть этого уравнения показывает, что воз-
мущению подвергается лишь та часть массива, которая распределяет
статическую сосредоточенную нагрузку (рис. 5.2).
75
Если возмущающая нагрузка распределена по некоторой полосе
и может быть представлена в виде произведения двух функций»
одна из которых зависит только от /, а вторая от х9 т. е.
Р(х, =	(5.21)
то уравнение колебаний среды от такой нагрузки на основе выра-
жения (5.20) примет вид
—f	(5-22)
-ft
Если нагрузка расположена не в начале координат, то выраже-
ние (5.22) примет такой вид:
S-т 5<'> т |/Е р.гаехр(-=!^>, <,»,
где х0 — координата середины полосы, по которой распределена
нагрузка.
При подвижной нагрузке координата х0 является функцией
времени. В этом случае уравнение (5.23) будет
d2» р ______
д? Е Я2 “
---J Р8<Пехр(—(5.24)
-ft
Решение представленных здесь уравнений для того или иного
случая позволит определить динамические вертикальные перемеще-
ния массива, по которым можно определить горизонтальные пере-
мещения и повороты, а также составляющие напряжения в плоской
задаче.
Получим дифференциальное уравнение для горизонтальных пе-
ремещений, исходя из выражения (5.10).
Учитывая, что
ди	1	дох	р д2и
дх	Е	дх дх*
а также соотношение (5.8), получим
д-и р д*и I д	d*w\	tC псч
= (525)
76
Для сосредоточенной вертикальной динамической нагрузки под-
ставим в правую часть уравнения (5.25) соотношение (5.22) с ис-
пользованием выражения (4.5). Получим
р (/) Afi/Zexof_
дх2 Е di2 2аЕ дх [ |/ 2zz \ 2z /J
(5.26)
Это также неоднородное уравнение гиперболического типа. Ре-
шение его позволит определить горизонтальные перемещения. По
аналогии с уравнением (5.22) для нагрузки, распределенной по по-
лосе, имеем
д*и____р д2и
дх2	Е dt2
*1(0 1
2аЕ дх
(5.27)
& /
По аналогии с уравнением (5.24) для подвижной нагрузки будем
иметь
&и	р дги
дх2	Е dt2
М) д
2а£ дх
— *I* + *<O-T*l*\4g . (5.28)
§ 2. СВЯЗЬ МЕЖДУ КОМПОНЕНТАМИ НАПРЯЖЕНИЙ
В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ. УРАВНЕНИЯ ДИНАМИКИ
В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
По аналогии с формулой (5.8) и зависимостями в статике для ка-
сательных напряжений в пространственной задаче имеем
д<Хг _____1_ д /да2
dz	2ах дх \ dz	‘ dt2 / ’
дхуг __ 1_ д (даг  d*w \ .
дг 2а„ ду\дг Р дР/
дуХу ______1 d2 (даг ~ д^шх
дг	4axaff дхду \ dz ? dt2'
(5.29)
(5.30)
(5.31)
Уравнения равновесия для пространственной задачи при ра-
венстве нулю ободных сил:
=	(5.32)
дг ду дх dt2
77
д3х I I	.
дх ду	dz dt2 ’
. fcyx । дхУг _ д*и
ду * дх	дг	%/« *
(5.33)
(6.34)
(5.35)
(5.36)
(5.37)
Дифференцируем уравнение (5.29) по х, уравнение (5.30) по у,
и уравнение (5.32) по г:
d2xxz ___1_ д2 /дог_ dW ,
дхду	2ах дх3 \ дг	?dt2j
дгтУг ___1 g2	.
дудг	2atdy*(dz РдР/’
дг \dz Vdt2) дудг дхдг
Подставив выражения (5.35) и (5.36) в уравнение (5.37), получим
+ _L*L/*£_. (5.38)
дг\дг dt*) Иахд^\дг	vdt*)	2а, ду*\дг dt*) '
Используя выражение (5.15), получим
(5.39)
дг 2ах дх2 2лу ду2
Решение уравнения (5.39) при условиях:
/ = — Р (0 при z = 0, х == 0, у — 0, т. е. в точке приложения
сосредоточенной динамической нагрузки;
f = 0 при г — 0, х =£ 0, у 0, т. е. во всех остальных точках по-
верхности массива;
/->0 при Х->±оо, #-*±оо,
имеет вид
/= - Р (/) jg- exp (- g^g^) •	(540)
Переходя к прежним обозначениям, получим
<м'>
Подставляя выражение (5.19) в уравнение (5.41), получим
Л» р IPW Р(Г) Va^a, / gjr^+a^X .g
Т^--~Е-------------2a?-еХ₽\ & J' '&Л2)
Эго тоже неоднородное дифференциальное уравнение гиперболиче-
ского вида, характеризующее вынужденные динамические верти-
кальные перемещения.
78
Для динамической нагрузки, распределенной по площади, урав-
нение (5.42) примет вид
d2» р __________________________________
dz2 ~ Е dt* ~
=	J p2 (E; exp (----5* fr-JP + MS-l)8 j dF (5.43)
При действии подвижной нагрузки уравнение для перемещения
будет иметь вид:
d*w р d*w
dz2 е’ы*~~
=_ pi U)	Ср ($. 7])ехр (	dF
2ахЕ 2kz J 2	2 Н \	2z	/	*
(5.44)
где dF = dWij
Рассмотрим вопрос об определении касательных напряжений.
Учитывая, что
?Ь = Е —,	(5.45)
дг дгг	' '
Формулы (5.29), (5.30) и (5.31) примут вид
______________________р_#«Л	(5 46)
dt	2«х дх \dz«	Е дР/’	1	’
fry* __________________ р_^\.	(5 47)
дг	2аи ду \dz2 Е дР/’	1 '
д^__Е	а» /а2»____£_ачв\	,548.
дг 4a,flu дхду \dz2 Е дР)‘	' ' 1
д ld*w_______р д*ио>
ду \dz2	Е dt* ;

Интегрируя эти уравнения по z и учитывая, что при
Л	л	л д ld*w р d*itfx
х„->0, ^->0, tx^0,
---------L^\_4 0, получим
dy \dz* Е dt* )
‘ д (д*ш___р д*ш\ .
дх\дг2 Edt*)^
д {d*w___р d*w\ , #
дДдг»	Е dt*) *'
д* !д*ш___Р dgw\ .
дхдДдг2	Е dt*) Z’
(5.49)
(5.50)
(5.51)
2«х
Е
>" 2av
Е
**У 4ахау (
79
или
__ Е &1 / dw _________ р Г дгш &
4ахау дхду дг Е J dt2
(5.52)
(5.53)
(5.54)
Если учесть соотношение (5.19), то эти формулы можно предста-
вить в таком виде
Т"	2«ж 1	\	'И	— dz\-, дР )	(5.55)
	/да у	а с м	дР )	(5.56)
4аха^ \	' д2з2 дхду	г дхду J dt2 )		(5.57)
При — = 0 формулы (5.55), (5.56) и (5.57) идентичны соот-
dt2
ветствующим формулам для статической нагрузки.
Из уравнений (5.33) и (5.34) получим следующие зависимости
для горизонтальных перемещений
	д°х	д2и Рд12	__	дхху _	_ d*xz .	(5.58)
	дх		ду	дг	
	д<зу	дЪ Pdt2	__	дтХу _		(5.59)
	ду		дх	дг	
Учитывая, что		дох дх	_р<Ри. ~ дх»'		(5.60)
		д°у ду	рд»и. = £d?’		(5.61)
уравнения (5.58) и (5.59) примут вид
	_9_д^и __		1_	(I dxxz\ .		(5.62)
дх2	Tdi2''	Е	\ ду	дг /	
д^и _	р d2v __		1_	jd^xy		(5.63)
ду2	Е д12 “	Е	\ дх	дг /	
80
Дифференцируя выражения (5.52) и (5.53) по г, а выражение
(5.54) по х, затем по у и подставив их в уравнения (5.62) и (5.63),
получим
д2и р d2u  1 д [d^w р dau>\
дх2 'FdF “ 2^ d7\d? Е dt2)
__ 1 d3 / dw_______________р С dgw \
4аха|/ дхду2 у dz Е J дг2 }
д2и______р d2^ _ 1 d Zd*w____________р d4t>\
ду2	Е dt2 ~ Ъоу ду \dz2	Е dt2 J
__ 1 d3 / дю_______________p_ f d2»
4аха1/ дудх2 у dz E J dt2 j
(5.64)
(5.65)
Полученные формулы позволяют по вертикальным перемещениям
вычислить перемещения среды (по другим координатным осям),
а также и повороты
£
При G = — (так как р = 0) эти формулы примут вид;
1 d / дю__________р Г d*a>	\ а
dy у dz	Е J dt2	J '
__ 1 д2 / дю___________р С д*ю &
^ху 2ахвр дхду у dz	Е J dt2
(5.69)
(5.70)
(5.71)
81
Глава 6
ИСПОЛЬЗОВАНИЕ РЕШЕНИЙ ДЛЯ БЕЗРАСПОРНОЙ СРЕДЫ
ПРИ ОПРЕДЕЛЕНИИ НАПРЯЖЕНИЙ И ОСАДОК СКАЛЬНЫХ
ТРЕЩИНОВАТЫХ ОСНОВАНИЙ *
§ 1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ
В. А. Флориным отмечалось, что наряду с использованием схем
теории упругости необходимо создавать другие модели, эквива-
лентные по своим обобщенным
Рис. 6.1. Схема к расчету скального
трещиноватого основания
а — безраслорнос (блочное) зернистое ос-
нование; б —скальное трещиноватое ос*
новакие; а — упругое основание
свойствам реальной трещиноватой
скальной породе.
Здесь предлагается новый под-
ход в решении некоторых проблем-
ных задач для скальных трещино-
ватых оснований.
Для исследования напряжен-
ного состояния и деформаций скаль-
ного трещиноватого основания в
условиях, далеких от нарушения
прочности основания или сооруже-
ния, можно использовать следую-
щие методы:	____.
а)	применение теории упругости
к изучению напряженного состоя-
ния и деформаций скального моно-
лита без трещин;
б)	применение теории вероятно-
стей и математической статистики
к изучению напряженного состоя-
ния и осадок скального трещино-
ватого основания, состоящего из
разобщенных трещинами отдельных
блоков;
в)	комбинированное использова-
ние теории упругости и теории, по-
строенной для безраспорной среды,
для изучения скального трещинова-
того основания, занимающего про-
межуточное положение между мо-
нолитом и основанием блочного
строения (рнс. 6.1).
* Материал данной главы доложен на 2-м Всесоюзном съезде по теоре-
тической и прикладной механике 30 января 1964 г.
Если рассматривать скальное трещиноватое основание как про-
межуточное между упругим основанием и основанием блочного
строения, то значения напряжений и деформации в нем будут про-
межуточными между значениями, вычисленными для упругого ос-
нования и основания блочного строения. Например, для напряже-
ний и осадок
С2 упр СК бл»
№упр<^ск <“>бл;
упр	°Х СК	°* бл’»
°J/ynp	9у СК	°£/бЛ»
Snp ^ск хбл*
гДе °2ск» °хск» тск — напряжения в скальном трещиноватом
основании;
°2упр» °* упр» ^упр. тупР — напРяжения в упругом полупростран-
стве;
» °жбл» °^бл» хбл — напряжения в блочном массиве;
wynp — осадка упругого массива;
^ск — осадка скального трещиноватого осно-
вания;
w2 бл — осадка блочного основания.
Величины напряжений и осадок скального трещиноватого осно-
вания могут быть вычислены как математические ожидания, т. е.
ск = ЯупуРх упр “1“ Ябла2 бл»
°х ск в <7упр°х упр ”1" Яблах бл»
°^ск = Яупр9у упр' “Ь Яблаубл*
хск s Qynp^ynp “I" Яблхбл*
^ск = Qynp^ynp Ябл^бл»
Яупр + Ябл =
ГД® <7упр — вероятность приближения реального скального основа-
ния к упругому монолитному основанию;
Ябл “ вероятность приближения скального трещиноватого ос-
нования к основанию блочного строения.
Для вычисления напряжений и деформаций в упругом монолит-
ном основании используется теория упругости, а для вычисления
напряжений и деформаций в основании блочного строения — тео-
рия, построенная для безраспорной среды. Что касается вероятно-
стей приближения, то они должны определяться по характеру раз-
вития трещин в скальном трещиноватом основании на основе геоло-
гических обследований.
вз
§ 2. НАПРЯЖЕНИЯ ОТ ЛИНЕЙНОЙ ВЕРТИКАЛЬНОЙ НАГРУЗКИ
Для вертикальных напряжений от линейной нагрузки ранее
была получена формула
О, =
(6.1)
По вертикальному напряжению вычисляются горизонтальные и
касательные напряжения
J дзг
2а дх
Г ру^(-2х)а
[ /2лг 2г
_ I д*ъ .
4о‘ дх* 9
(6.2)
или

г Р( 2г ) — & °2*
I ____________1 д^„,
4а» дх* 2а дх ’
^xz _ J_o . X даг
дх 2z 2 ' 2г дх '
Из выражения (6.2)
&—2“'-
Тогда выражение (6.5) примет вид
= _L(Oz_ х2«„) = — L 0 \ = i .
дх 2z V z *2' 2z \ 2 г 2/ 2г г]
Подставив это выражение в формулу (6.4), получим
(6.3)
(6.4)
(6.5)
(6.6)
(6.7)
(6.8)
§ 3. НАПРЯЖЕНИЯ ОТ НАГРУЗКИ, РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ
ПО БЕСКОНЕЧНОЙ ПОЛОСЕ
Вертикальные напряжения (рис. 6.2) в безраспорном зернистом
основании от нагрузки, распределенной равномерно по полосе, оп-
ределяются выражением
+ й	__
— j₽ех₽ - °2]<к* (6,9)
Заменой переменной
выражение (6.9) приводится к виду
Рис. 6.2. Расчетная схема к определе-
нию напряжений в плоской задаче от
нагрузки, равномерно распределенной
по полосе
(6.10)
(6.11)
(6.12)
Горизонтальные нормальные напряжения
* 2а дх 4аУ2паг дх [	\ 2х )
-ехр Г- ^4^)1	(6.15)
65

(6.16)
$ 4. НАПРЯЖЕНИЯ ОТ ПОЛОСОВОЙ ПАРАБОЛИЧЕСКОЙ НАГРУЗКИ'
При нагрузке (рис. 6.3), заданной уравнением
<617>
вертикальные напряжения выражаются зависимостью
(6.18)
Подстановкой значений из (6.10) и (6.11)
преобразуем это выражение
Рис. 6.3. Расчетная
схема к определению
напряжений в плос-
кой задаче от нагруз-
ки, распределенной
на полосе по закону
параболы
Группируя правую часть и интегрируя ее, получим
г
86
лучим
о - р (i *г ИГфЛ'+Ц/^
2	2 I. 62 аб’-Ц УТ ) Д УТ j]
- £• /£[<-+•>"р (- ЧЯ+<—) Ч- 4F)]
(6.21)
Касательные напряжения
, =__L^=_____L_L(__p (i_2i__L\y
жг 2а дх '2а дх (	2 I, Ь‘ аЬг J
х[ф(уг/“)-ф(7Г^)]-^/Е[<' + 1'>х
(6.22)
’ - £ Н [ф (W Ч -ф (w|Z")]+('  F - й х
<6-a>
Группируя члены правой части, получим
а[ф(тгЧ-Ф(тгЧ1+
+ _е_ 11 _ л _ ап („р(_i<£±4i) -„к I- •JajLS.fl.
2^2r.az\ b2 aba/[ \ 2z /	2г /]
(6-24)
Из этого выражения с учетом (6.22) имеем
ЛЧф(^Ч-ф(тгЧ]+
+ТЙО- V	
(6.25)
Дифференцируем это выражение по х:
87
+®(1-£-2й(^“1'’(-"-аП-
 <(*.-<>) ех р (	(6.26)
&-£[ф(^)-ф(тг’/-)]+ X
*Н-^)-е«р(-^)] +
+тётМ-2.-йх
X [(X + Ь) ехр (-	- (X - b) exp (- ~^)] - (6.27)
Учитывая (6.27), для горизонтальных напряжений получим
- [ф (тт - ф (тг ^)]+X
х[“р(--^)-р«р(-^)]+
+ ^йг('-$-2i)x
X [(X + Ь) ехр (-	- (X - Ь) ехр (-	• (6.28)
Таким образом формулами (6.21), (6.24) и (6.28) определяется
напряженное состояние зернистого безраспорного основания от
параболической полосовой нагрузки.
$ Б. СОСРЕДОТОЧЕННАЯ ВЕРТИКАЛЬНАЯ НАГРУЗКА
Решение уравнения (3.56) для вертикальных напряжений при
граничных условиях;
при х « у = О вж = — Р
при |х|>0 ож = 0
|У|>О
88
При х-> ± оо
у -> + оо
о
имеет вид
О.
2z
(6.29)
Это решение совпадает с полученным ранее для тех же граничных
условий.
Дифференцируя это выражение по х, получим
д<зг
дх
«^+«^у--a^Oj (6ф30)
Подставляя (6.30) в выражение (3.49), получим
1 х
Ххг =---------------------------°z*
2 z г
Аналогично получаем значение
1 у
2 г °**
Дифференцируя выражение (6.30) по х, имеем
----------------------ex±0i_ax2L^.
дха-------------------2	2 дх
Подставляя сюда значение первой производной из (6.30), полу-
чим
1	х / х \	/ 9 х8 ах \
дх* ~ ~х z ~х г\ *х г °г) " (“* z8 z / **
Подставляем это значение производной в уравнение (3.51):
—	— о, —а.
\ 4 Z8	4ахг/	4axz \ г
Аналогичным образом получаем значение :
У \ 4 z*	4ayzJ	4a|fz\ z
Дифференцируем выражение (6.30) по у:
даа2	х да,	х / и '
-----а^~ ~ аи~
г ду	z \ v z t
дхду
— а.
(6.31)
(6.32)
(6.33)
(6.34)
ху -
=	-7- О,.
89
Подставляя это выражение в уравнение (3.62), получим
1 ху ху
—<39=— <39.
У 4а„в(, ж " г* ’	42« г
Таким образом, определены все компоненты напряжений для
вертикальной сосредоточенной нагрузки.
§ 6. НАПРЯЖЕНИЯ ОТ ВЕРТИКАЛЬНОЙ НАГРУЗКИ,
РАСПРЕДЕЛЕННОЙ РАВНОМЕРНО ПО ПРЯМОУГОЛЬНИКУ
Вертикальные напряжения от такой нагрузки (рис. 6.4) опреде-
ляются выражением

гь
	1Ш1Ш		1111111111» 	
	б г У	1	
j		/г	
J		0	и *	X 1
		k-w I -гь		
Рис. 6.4. Расчетная схема к опреде-
лению напряжений от нагрузки,
равномерно распределенной по пло-
щади прямоугольника
-ф(7Г/в*)]- (635)
Касательные напряжения:
=
= [ехр(- +
4)/2яажг[ *Д 2z /.
-exp(_^fc=iE.)]x
<636>
яу(у + в)*\
2г I
х[ф(уг1/“")-ф(тт^)];	,63!>
р
8пг У ахау

аД* —б)*\1
2г /]
X [ехр [— а(,(У2гГ-а)-) —ехр [
»у(у —°)*
(6.38)
90
Горизонтальные нормальные напряжения:
ох = —г Г(х 4- Ь) ехр (— — +	—
* 4Z /2каАа L '	\ Ъ J
- и - Ч .«р (-	][ф (ь±? ,4) - ф (Vr <в 39>
§ 7. НАПРЯЖЕНИЯ ОТ ПАРАБОЛИЧЕСКОЙ НАГРУЗКИ.
РАСПРЕДЕЛЕННОЙ ПО ПРЯМОУГОЛЬНОЙ ПЛОЩАДКЕ
Пусть нагрузка (рис. 6.5) выражается зависимостью
'(-•’’-'('-Ж'-й-
Вертикальные напряжения для такой нагрузки определяются за-
висимостью
Рис. 6.5. Расчетная
схема к определению
напряжений от на-
грузки, распределен-
ной на площади пря-
моугольника по за-
кону параболы
+ (а-у)ехр(-аИУ2+а^)][. (6.41)
Касательные напряжения:
91
Горизонтальные нормальные напряжения:
‘•=Я4ИФ(^Н(^)]+
-«- М- ^1№ - лф (W N -
-ф(тг^Ж /“Н-	+
92
+ (4r-a)exp[-^±^.)]];	(6.45)
+ (*-*>) ехр (- (<fe+-^-)]) •	(6.46)
Приведенными формулами определяется напряженное состояние
зернистого безраспорного основания от параболической нагрузки,
распределенной по площади прямоугольника.
§ 8. НАПРЯЖЕНИЯ ОТ НАГРУЗКИ, РАВНОМЕРНО
РАСПРЕДЕЛЕННОЙ ПО ПЛОЩАДИ КРУГА
Для решения этой задачи (рис. 6.6) лучше воспользоваться ци-
линдрическими координатами. Положим аж = а = а, т. е. рассмат-
риваем изотропную среду по направлениям осей х и у. Тогда урав-
нение (3.56) примет вид
=	+	(6.47)
дг 2а\дх*^ду*/	К 9
Соответствующим образом будут преобразованы зависимости
(3.49), (3.50), (3.51), (3.52) н (3.62)
1 да, е =— 2а дх ’’	(6.48)
1 да2 ,	(6.49)
= 1 . 4а2 дхду ’	(6.50)
93
= 1 .
°* ~ 4а« дх2 ’
1 д2зг
°у ~ 4а* ду2 ’
(6.51)
(6.52)
Приведенная система уравнений позволяет в цилиндрических
координатах получить следующую равносильную первой систему
ппппьр г	»г ! » '	дифференциальных уравнений: =	+	(6.53) д2 2а\дг2	г дг)	'	7 (6.54) ' 4«« аг»	'	’
Рис. 6.6. Расчетная	о, = —^;	(6.55) • 4ra« dr	V
схема к определению
напряжений от на*
грузки, равномерно
распределенной по
площади круга
" 2а дг *
т=т=о.
(6.56)
(6.57)
Следуя Б. С. Радовскому, проинтегрируем уравнение (6.53) для
аг при следующих условиях
»,i|; при°<'<*	(6.58)
1	(0 при г >R
Odr-*o^°°	(6-59)
о2->0	и — ->0 при г-> оо.	(6.60)
Используя преобразование Лапласа
F (г, s) = [ ог (г, z) ехр (— sz) dz,	(6.61)
b
уравнение (6.53) можно представить так:
—s) + -у —5> — 2sa [> (г, s) — -ф-j = 0.	(6.62)
Это модифицированное уравнение Бесселя. Его общее решение
имеет вид
F (г, s)-= А1„ ()/ 2^) + В К» (K&d?),	(6.63)
94
где /0(]/^2sar) и /C0(V2$«r) — функции Бесселя соответственно
первого и второго рода нулевого
порядка* от чисто мнимого аргу-
мента;
Л и В — постоянные интегрирования.
Определяя постоянные из условия (6.58), а также преобразован-
ных условий (6.59) и (6.60), получим Лапласово изображение искомой
функции (г, z):
при 0 < г < R
F (г, s) =	[1 - R	/„ (/2^г) Ki (/2мК)];	(6.64)
и при г > R
F(r,s) = -^-R ]/2^/tКо (]/2Йг),	(6.65)
где /t (V2saJ?) и /С, (yf2sar) — функции Бесселя соответственно
первого и второго рода первого порядка от чисто мнимого аргумента.
Используя формулу обращения Меллина, получим
7+/«
аг(г,г) = ~_ f — [1—₽]/r2®</0(]/2sar)K1(]/r2sa)?)]exp(sz)4fc.
’ Д. S	(6.66)
В результате интегрирования, выполненного Б. С. Радовским,
О,(Г, 2) = Р₽« J Ja(Vfyr) Ji (/2^?)	dp (6.67)
или
Ог(г, z) = pR J J0(r, х) Д(Ях)ехр^dx, (6.68)
о
где Jo (*» г), Л (Rx) — функции Бесселя первого рода соответственно
нулевого и первого порядка.
Используя выражения (6.56) и (6.68), получим для касательных
напряжений
Учитывая, что
получим
95
(6.Т2)
Выражениями (6.68), (6.69), (6.71) и (6.72) определяется напря-
женное состояние безраспорной зернистой среды от нагрузки, рав-
номерно распределенной по площади круга.
Для точек, находящихся на оси симметрии, т. е. при г = О,
эти выражения приводятся к виду
О.(0, г) = Рр-ехрJ;
e.(O,z)»«,(O,z) = -^exp(-^.
\,Д°. г)=«-
(6.73)
(6.74)
(6.75)
§ 9. ОСАДКА БЕЗРАСПОРНОГО МАССИВА ОТ НАГРУЗКИ. РАВНОМЕРНО
РАСПРЕДЕЛЕННОЙ ПО ПОЛОСЕ
Для нагрузки, распределенной по полосе шириной 2Ь (рис. 6.7),
осадка массива без учета влияния веса грунта
h +6	_
— 7 j* j /<6ге>
О — ъ
В случае нагрузки, равномерно распределенной по полосе, за-
висимость (6.76) принимает вид для точек с координатой х;
ю=±. С Г «г»
2£ JI \ V* /	\ V*
dz. (6.77)
Разобьем интеграл выражения (6.77) на сумму двух интегралов.
Тогда
й
(Уа^ + Ц
h
(6.78)
Рассмотрим первый интеграл*.
h
О
К У* /
(6.79)
96
Проинтегрируем это выражение по частям, для чего обозначим
dz = db;	(6.80)
(6.81)
Интегрируя выражение (6.80) и дифференцируя выражение
(6.81), получим
и =	(6.82)
du ----Л= ехр /_+	(6.83)
z/z Ч 2z /
делы, получим	Рис. 6.7. Расчетная схема к определению
( /•—	.	осадки массива ограниченной мощности от
г_а Iх + о) \ >	нагрузки, равномерно распределенной по
уh ) ~	полосе
+21^+и{р^„р(-^)-е
ф//а(х + й)\']1
У* )]Г
(6.85)
По аналогии решается второй интеграл выражения (6.78)
'• • « (ЯН+!	-«1/£ »’ (-	-
- <6Ri>
97
Подставляя значения вычисленных интегралов в выражение
(6.78), получим зависимость для деформаций массива
ю= рл Гф /Гм»+б)\ ф \ 1 .
2Е [ Д ГК ) Д ГК +
+г>а±а(1/^ехр(_-_£±»1)_
_bZ(x + i)[,-ф(^)]|-
Е>а=а(рЛхехр(^1!1)_
-^(х-6)[1-ф(^(х-Ь)]11.	(6.87)
§ 10. ОСАДКА БЕЗРАСПОРНОЙ СРЕДЫ ОТ НАГРУЗКИ, РАВНОМЕРНО
РАСПРЕДЕЛЕННОЙ ПО ПРЯМОУГОЛЬНОЙ ПЛОЩАДКЕ
Общее выражение для осадки (рис. 6.8) имеет вид:
Введем обозначения:
|/ ^.(х + 6) = /;	(6.89)
г = ^-<х±&1г.;	(6.90)
dz = —	л = _ 2». (< + *)» Л;	(6.91)
при 2 = 0 /х = со;
при z — h /г = |/Г-у(х + *).
Тогда имеем
(6.92)
» = --£- С	« + *)»Гф(п_фА]
4Е J <• L 17	V+*/J
98
(693,
Для интегрирования по частям обозначим при ау = ах
— —=dv,	t)=—;	(6.94)
/3	р	'
* w - ф : 'ШФ so - ф (s ')]-“ (б-95)
Дифференцируя (6.95),
имеем
du = [y=exp(— /2) —
2 х-6	/_
* +ь \
-SPri’S')-
-*(S')]d,+
+ [ф(,)_ф[£=4),)]х
_ (У + g)2 М __
(х + ЬУ )
-SS“PF
Тогда выражение (6.93)
примет вид
Рис. 6.8. Расчетная схема к определению
осадки от нагрузки, равномерно распреде-
ленной по площади прямоугольника
99
ф
(У + Д)2 уа\_-
(* + *2) /

После подстановки пределов осадка будет равна
ш=£|'!1ф(/?(*+б)) _ф(/^(х-б))]х
ХК1/ Т(г/ + а))"Ф(/T-(i/“0))]"
*|Z— (* + *)
(6.98)
После некоторых преобразований получим
w = ^{h [ф(]/?<х + Ь))_ф()/'Г(х-6))]Х
х[ф(]/^(*' + а))-'ф(]/ ‘Т(!'_в))]_
X
100
Рассмотрим интегралы, входящие в выражение (6.99).
Первый интеграл
(6.99)
f -iV “Р <-')* (Шi '->ф (Si ')+
+й SiEl Н1+(Si)’],5) -г jф (Si'>''1Ю]
Второй интеграл
J 7- “Р	ф (Si ')* 17 "Р ® ф (Si ')+
+rtSiBH'+(Si/]'O-2J*(Si')'’p<-'’,'“-
(6.101)
Третий интеграл
101
(6.102)
Четвертый интеграл
(6.103)
Пятый интеграл
-2ШУФ(',“''НН7)’'’]'"- <6|М>
Шестой интеграл

102
Седьмой интеграл
оо
Восьмой интеграл
Подставим теперь полученные значения интегралов в выра-
жение (6.99):
” -	+ч) -ф (/¥(х -s)) ]х
х[ф(/ -f <«+">)-ф(]/
103
- 2 j ф (Ш 0 ехр (- ™ + 2 J ф (ff? О ехр ("l2)dt +
104
-2(Й7ПФ<,,'хр
(-Ш’+
Ф(/)ехр
где /2 = рЛ^.(х + Ь).
При x — y — Q
“ т I* [ф (/т‘) + ф (1/т‘)] [ф (|/f “) +
+ф (/^ “)]+<	ехр(-т »)ф (»/^) '“
-тНа(-т^->’)+1Й'хр(-т^ф(»/^)-
-ТГ7Е|(-Тр’-Т“’) + ^“>'(-Т‘,)ф(«'/^)-
-ТГ7Е|(-Т4’-Т“х)+^“"(-Т^ф(«/^)-
-7? 7 Е| (“ Т f “*)+7 »# ]/¥ )-
-V=-7EI(-T“,-Ti')+^“K-f-Hil/|)-
-7Г7Е1(-т“--т"-)+^“|>(-т"’)ф(61/^)-
- 7Т 7 Е| (- f“-' Т "I +	«#
105
+ 2 —
b3
ь
4-2 —
&
(6.109)
После некоторых преобразований
106
или
a
+8v
tr
dt
(6.110)
J--5=^ exp
».-^И‘/тгН“/тг)_+
2
-5=Lexp(— ^-b2'
/г. L bVax Ч Л J
(-T “’)*(' /f)-J
-^Ь2—
h
b
+ 2
b
+ 2
При a = b получим
•w-’o =
^-f^lexp,
L »Yax
Л .
b I/ —
Г Л
!j + 4 J Ф(/)ехр(—t2)dt
Подставив значение интегралу J exp(— t2)^(t)dt
(6.111)
(6.112)
_EZx
в выражение (6.112), получим
ЬУ0 =
107
т»")+
(6.113)
_-2=е1(-^£^+Ф8(ь|/Г^^-1]). (6.114)
При Ъ -> со
w^-^-h.	(6.115)
По формуле (6.114) определяется осадка по оси квадратной пло-
щадки, равномерно загруженной нагрузкой интенсивностью р.
§ 11. ОСАДКА ПО ОСИ КРУГЛОЙ ПЛОЩАДИ. ЗАГРУЖЕННОЙ
РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ НАГРУЗКОЙ
Деформация массива по оси загруженной площадки
s»o = yj[1—ехр^—(6.116)
Интегрируя и подставляя пределы, получим
h
Решая интеграл зависимости (6.Ц7), получим
t»e = -V-£-йехр(—Ei/_(6.118)
Е Е ' 2ft )	2£ Ч 2ft )
“•-тр-'-К-Т
-2^Ei
2Е
(6.119)

ЧАСТЬ ВТОРАЯ
ЗЕРНИСТЫЕ ГРУНТОВЫЕ ОСНОВАНИЯ
(СЫПУЧИЕ ГРУНТЫ)
Глава 7
ДИСКРЕТНОСТЬ ГРУНТОВ
$ 1. ГРУНТЫ КАК ДИСКРЕТНЫЕ СИСТЕМЫ
Грунты по своему строению представляют весьма сложное фи-
зическое тело.
Каждый грунт состоит из комплекса твердых частиц, образую-
щих скелет, и заполнителя в виде находящихся в промежутках ме-
жду твердыми частицами воды и газов.
Отдельные твердые частицы, образующие грунтовый скелет,
соединены друг с другом весьма разнообразными связями, за-
висящими от размеров частиц, их формы, влажности грунта
И т. д.
Взаимное расположение и характер соединения элементарных
частиц друг с другом и заполнителя в виде находящихся в порах
грунта и газа образуют структуру грунта, которая является одним
из важнейших факторов, определяющих механические и физические
свойства грунта.
Структурные агрегаты отличаются друг от друга формой и раз-
мерами. По литературным данным, насчитывается до 30 форм струк-
турности грунта; с точки зрения механических свойств интерес
представляют геометрические формы структурных агрегатов. Клас-
сификация структурных агрегатов грунтов по их геометрической
форме предложена И. И. Фролочкиным [90). Согласно этой класси-
фикации структурное агрегаты делятся по размерам иа микроаг-
регаты и макроагрегаты. К микроагрегатам относятся такие, раз-
мер которых не виден невооруженным глазом.
109
Строение грунтов складывается из совокупности различных по
форме и размеру структурных агрегатов. В то же время микрострук-
тура грунтов является неотъемлемой частью строения структурных
агрегатов.
Рис. 7.1. Структура грунтов по И. И. Фролочкину
/ — макроструктуры; о — зернистая; б — орехоиагая; в — комковатая; г —
глыбистая; о — столбчатая; е — пластинчатая; 11 — микроструктуры; ж —
ячеистая; 9 — хлопьевидная
Микроструктура грунта может быть ячеистой, хлопьевидной и
ячеистохлопьевидной [2, 90, 94 ].
На рис. 7.1 схематически (по И. И. Фролочкину) представлено
различное структурное строение грунта. Согласно работе (90), глав-
нейшими формами микроструктуры являются типы, представлен-
ные в табл. 7.1.
110
Таблица 7.1
Класс		Вил			
1 11 III IV V VI	Кубовидная Призматическая Шаровидная Эллипсовидная Цилиндрическая Плитовидная	Крупная » Комкова* тая Зернистая Столбчатая Пластинча- тая	Средняя » Ореховатая Крупная » Плитчатая	Мелкая Глыбистая Средняя Чешуйча- тая	Пористая Мелкая
§ 2. РАЗМЕРЫ И ФОРМА ЗЕРЕН ГРУНТА
Как правило, грунты слагаются из частиц самых разнообраз-
ных размеров.
Для грунтов, встречающихся на строительстве, на основе много-
численных экспериментальных данных составлены рецепты опти-
мальных смесей. Соотношение различных размеров зерен в опти-
мальных смесях подобрано таким, при котором эти смеси под на-
грузкой в различных условиях эксплуатации оснований являются
наиболее устойчивыми. В нашем случае к зернистым относятся
среды, размер частиц которых превышает размер коллоидных ча-
стиц.
Для решения задачи о распределении напряжений в грунтовом
массиве важно правильно оценить влияние формы зерен.
Известно, например, что гравий в силу большой окатанности
зерен обладает по сравнению со щебнем той же крупности частиц
худшими механическими свойствами.
На рис. 7.2, где представлены типичные почвенные структурные
элементы по С. А. Захарову видно, что все частицы имеют форму не-
правильных многогранников и отличаются только размерами по
взаимно-перпендикулярным направлениям. Следовательно, если
для частиц с одинаковыми размерами зерен по взанмно-перпеиди-
кулярным направлениям при постоянной плотности грунта можно
считать, что число этих частиц на единицу длины во всех направ-
лениях грунтового массива будет приблизительно одинаковым, то
для частиц, у которых размеры по различным направлениям раз-
личны, число их на единицу длины в грунтовом массиве будет за-
висеть от ориентировки их относительно принятых осей координат.
Характеристика структурных образований приведена в табл. 7.2.
Если для частицы, имеющей различные размеры по взаимно-
перпендикулярным направлениям, любое положение в пространстве
равновероятно, то на единицу длины по любому направлению в грун-
товом массиве придется приблизительно одинаковое число зерен.
111
Грунтовый массив в этом случае, как и в случае рассмотрения
частиц с одинаковыми размерами по взаимно-перпендикулярным
направлениям, будет дискретно изотропным. Средний (эффектив-
ный) размер частиц в этом случае будет определяться не только
наибольшими, но и наименьшими размерами каждого зерна по раз-
личным направлениям.
Если же вероятность расположения каждой частицы в простран-
стве не одинакова по всем направлениям, то частицы при образова-
Рис. 7.2. Формы грунтовых частиц по С. А. Захарову (цифры соответствуют
тем же значениям в табл. 7.2)
нии структуры материала будут стремиться занять наиболее веро-
ятное положение. Грунтовый массив, образованный такими части-
цами, будет анизотропным телом.
Таким образом, различные по форме частицы могут образовы-
вать различные по свойствам среды.
Обычно при представлении грунта как среды, образованной зер-
нами некоторого среднего (эффективного) размера, каждой частице
придают форму шара. Вместе с тем можно утверждать, что даже
в хорошо окатанном гравии невозможно найти ни одного зерна,
удовлетворяющего своими геометрическими характеристиками иде-
альному шару. На несоответствие формы идеального шара действи-
тельной форме зерен грунта обращает внимание также И. И. Черка-
сов 195].
Известно, что гравийные, песчаные и щебеночные частицы имеют
форму неправильных многогранников. В процессе выветривания
112
Таблица 7.2
Форма структуры		Размеры попереч- ника в мм (для 1 и II типа)
I тип — кубовиднаи структура
Грани и ребра выражены плохо
Глыбистая — неправильная
форма и неровная поверхность
Комковатая — неправильная
форма, округлая и шерохова-
тая поверхность
Пылеватая
1	— Крупноглыбистая
2	— Мелкоглыбистая
3	— Крупнокомковатая
4	— Комковатая
5	— Мелкокомковатая
6	— Пылеватая
100
100—50
50—30
30—10
10—0,5
0,5
Грани и ребра выражены хорошо
Ореховатая — более или ме-	7 — Круп но ореховатая	10
нее правильная форма; поверх-	8 — Ореховатая	10—7
ность граней сравнительно ров- ная, ребра острые Зернистая — более или менее	9 — Мелкоореховатая	7—5
	10 — Крупнозернистая	5—3
правильная форма, иногда ок- руглая, с гранями то шерохо- ватыми и матовыми, то глад-	(гороховатая) 11 — Зернистая (крупинча- тая)	3—1
кими и блестящими	12 — Мелкозернистая (по- рош иста я)	1-0,5
II тип — призмовидная структура
Грани и ребра выражены плохо
Столбчатовидная — непра-	/3 — Кру пностолбчато вид-	50
вильная форма со слабовыра-	ная	
женными неровными гранями	14 — Столбчатовидная	50—30
и округлыми ребрами	15 — Тонкостолбчатовид- ная	30
Грани и ребра выражены хорошо
Столбчатая — правильная	16 — Крупностолбчатая	50
форма с довольно хорошо вы-	(тумбовидная)	
раженными гладкими боковы-	17 — Столбчатая	50-30
ми гранями,округлой головкой	18 — Тонкостолбчатая	30
и плоским основанием		
Призматическая — с плоски-	19— Крупнопризматиче-	50
ми поверхностями и острыми	ская	
ребрами	20 — Призматическая	50—30
	21 — Тонкопризматнческая	30-10
113
Рис. 7.3. Эквивалентность
окатанных и угловатых
форм грунтовых частиц
разрушению в первую очередь подвергаются острые ребра и углы,
и частицы приобретают окатанную форму.
Однако разнообразные условия выветривания материала не
способствуют образованию идеально шарообразных частиц. По-
следнее обстоятельство при рассмотрении передачи усилий от ча-
стицы к частице в целях большей общности позволяет для таких
частиц принять форму зерен в виде многогранников, поскольку
значительное отличие формы частиц от шарообразной создает ус-
ловия неравномерного распределения усилий от каждой вышележа-
щей частицы на частицы, расположенные ниже или дальше от точки
приложения нагрузки. Взамен частицы окатанной формы всегда
можно подобрать ее в виде многогранника, которая по характеру
передачи усилий будет эквивалентна
частице шарообразной или эллипсовид-
ной формы. Это может быть подтверж-
дено рис. 7.3, на котором штриховыми
линиями показана форма частиц в виде
многогранников, эквивалентных по ха-
рактеру передачи усилий частицам эл-
липсовидной формы.
При сланцеватом или плитчатом стро-
ении коренной породы гравийные час-
тицы имеют форму плиток, а песчаные—
форму листочков или чешуек. Пылева-
тые частицы имеют форму угловатых
зерен или пластинок. Для глинистых
частиц характерной формой зерен яв-
ляется пластинчатая. Для этих частиц еще менее подходит шаро-
образная форма. Вместе с тем при изучении вопроса о передаче
усилий форма многогранников с различными размерами граней как
форма эквивалентных зерен может быть приемлемой и для частиц
в виде плиток, чешуек, листочков и пластинок.
С другой стороны, при изучении вопроса о взаимном расположе-
нии зерен грунтовых частиц кубовидной, шаровидной, эллипсовид-
ной структур форму зерен среднего размера можно представить ша-
рообразной для пространственной задачи и круглой для плоской.
Следовательно, наиболее типичной формой зерен среднего (эф-
фективного) размера принимается форма многогранника. Шарооб-
разная форма частиц при этом рассматривается как предельный,
редчайший случай.
§ 3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ И ОРИЕНТИРОВКА ЗЕРЕН
Для решения вопроса о средних условия х передачи усилий (рас-
пределения напряжений) необходимо определить средние (наибо-
лее вероятные) условия взаимного расположения и ориентировки
зерен эффективного размера.
1Н
Непременным условием взаимодействия частиц в грунтовом
теле является наличие между ними точек контактов. При рассмот-
рении вопросов о взаимном расположении частиц будем различать
рабочие контакты и контакты касания (нерабочие контакты).
К рабочим контактам отнесем такие, в которых возникают ре-
активные силы, определяющие устойчивость частицы в простран-
стве. В противоположность этому, к контактам касания будем от-
носить такие, которые не принимают участия в передаче усилий
в грунтовом массиве.
Условимся, что нужно понимать под рабочим контактом с геомет-
рической точки зрения. В общем случае между каждой парой ча-
стиц может быть какое угодно число контактов, если за контакт
принимать некоторую изолированную площадь, на которой взаимо-
действуют частицы. Мы же в данном случае за контакт будем при-
нимать точечное соприкасание двух частиц, к которому приложена
реактивная сила, по величине и направлению представляющая
равнодействующую всех сил взаимодействия двух частиц. При та-
кой постановке вопроса каждая пара частиц может иметь только
один рабочий контакт. Связь эта может быть заменена сжимающей
нормальной силой и касательной к поверхности контакта силой
трения.
Нормальная и касательные реактивные силы в каждой точке
контакта являются составляющими одной силы взаимодействия
двух частиц, направленной в общем случае под углом к поверхно-
сти контакта.
Для решения вопроса о наиболее вероятном взаимном располо-
жении зерен среднего (эффективного) размера определим число
рабочих контактов у каждой частицы.
Рассмотрим характер взаимного расположения зерен кубовид-
ной, шарообразной и эллипсовидной структуры, придавая частицам
среднего (эффективного) размера круглую форму для плоской за-
дачи и шарообразную форму — для пространственной.
Обычно при решении этого вопроса определяют наиболее плот-
ную и рыхлую упаковку зерен исходя только из геометрических
соображений, не учитывая, однако, статическую устойчивость об-
разованного таким путем тела.
Попытку учесть это обстоятельство при рассмотрении рыхлой
структуры сыпучего тела сделали М. С. Бернштейн и А. Г. Иммер-
ман [14].
При рассмотрении наиболее плотного расположения частиц за-
дача сводится к отысканию наибольшего числа контактов у одной
частицы. Для плоскости эта задача эквивалентна известной геомет-
рической задаче: как положить на «большой» стол максимум оди-
наковых по размеру монет. Строгое математическое решение ее
дано в 1832 г. А. Туе [87 ]. Согласно этому решению, наибольшая
плотность заполнения плоскости будет при условии, если каждый
круг будет касаться шести расположенных рядом кругов. На
115
рис. 7.4 (первый ряд) изображена такая условная наиболее плот-
ная структура грунта. Очевидно, менее плотной по сравнению с рас-
смотренной является структура, у которой каждая частица будет
касаться не шести окружающих ее частиц, а пяти. Такая структура
изображена во втором ряду.
В третьем ряду изображена структура, у которой каждая ча-
стица касается четырех окружающих ее частиц. Эта структура
также образуется из наиболее плотной упаковки путем укладки
частиц с некоторым промежутком; число касаний у каждой частицы
не зависит от величины промежутка между частицами, если этот
промежуток не превышает величины частицы.
В четвертом ряду изображена структура, у которой каждая
частица имеет три контакта. Геометрически эта структура также
образуется из наиболее плотной упаковки путем изъятия из нее
частиц через одну.
В пятом ряду показана структура с двумя рабочими контактами
у каждой частицы. Контакты касания здесь показаны разрывами.
Из сравнения ее со структурой частиц с тремя контактами видно,
что последняя является более рыхлой и в то же время статически
более устойчивой.
Таким образом, для плоской задачи из круглых частиц одина-
кового размера можно создать структуры с шестью, пятью, четырьмя
тремя и двумя контактами у каждого зерна.
С точки зрения геометрического образования структура наибо-
лее плотной упаковки зерен с шестью точками касания у каждой
частицы является редчайшей. Если учесть силы трения между ча-
стицами, то даже для частиц круглой формы такую структуру можно
создать только специальной укладкой каждой частицы. В против-
ном случае она превратится в структуру с четырьмя точками ка-
сания у каждой частицы.
Структура с пятью точками касания с геометрической точки
зрения еще менее вероятна, чем структура плотной упаковки зерен,
так как при этом необходимо выполнить все условия плотной упа-
ковки и соблюсти к тому же свой строго определенный порядок
укладки зерен.
По сравнению со структурами плотной упаковки и с пятью кон-
тактами у каждой частицы структуру с четырьмя контактами частиц
получить значительно легче.
Число контактов у каждой частицы этой структуры не изменится
при изменении просвета между зернами в пределах 0 < А < а (где
А — величина просвета между частицами: а —размер зерна), тогда
как для структуры плотной упаковки промежуток между зернами
изменен быть не может, т. е. А = 0; не может быть изменен проме-
жуток между зернами и для структуры с пятью контактами.
С точки зрения сохранения структуры, системы зерен с пятью
и шестью контактами являются жесткими. Такие системы возможны
лишь при одном варианте укладки зерен. В то же время система
116
Рис. 7.4. Различные упаковки зернистых тел из частиц среднего размера
с четырьмя контактами позволяет путем изменения промежутка
между зернами создать бесчисленное множество вариантов, при
которых основное свойство системы (наличие четырех контактов
у каждой частицы) не изменится. Следовательно, с геометрической
точки зрения структура с четырьмя контактами зерен по сравнению
со структурой с шестью и пятью контактами более вероятна.
Структура с тремя контактами частиц не является жесткой в
смысле строгого соблюдения свободных расстояний между зернами.
Если для этой структуры каждую пару расположенных вертикально
друг над другом частиц рассматривать как одно зерно, то мы полу-
чим структуру из частиц удли-
ненной формы с четырьмя кон-
тактами у каждой частицы. На
основе этой аналогии можно сде-
лать вывод, что в данном случае
свободный просвет между час-
тицами может измениться в тех
же пределах, что и для структуры
с четырьмя контактами. Таким
образом, у этой структуры также
много вариантов взаимного рас-
положения зерен без измене-
ния числа контактов у частиц.
И, наконец, структура с двумя
рабочими контактами возможна
лишь при наличии у частиц
контактов касания с соседними
зернами. В противном случае ча-
стицы не заполняют плоскость и
Рис. 7.5. Схема к расчету вероятности
статической устойчивости частицы
при двух рабочих контактах
а — перемещение частицы по напраолению
равнодействующей: б — вращение частицы:
а — статическое равновесие частицы
не образуют структуры. Следовательно, для создания такой струк-
туры расположение зерен возможно единственным способом, что
делает ее с геометрической точки зрения маловероятной.
Рассмотрим вероятность каждой из этих структур с точки зрении
статической устойчивости.
Заменив связи реакциями, определим число рабочих конт-
актов, необходимое для равновесия частицы в случае плоской
задачи.
На рис. 7.5 изображена частица, имеющая два контакта, которые
заменены реактивными силами; в случае (а) частица будет переме^
щаться по направлению равнодействующей двух реактивных сил,
в случае (б) будет вращаться и лишь в случае (в), когда реактивные
силы на контактах равны но величине и направлены навстречу друг
другу по одной линии, частица будет находиться в статическом рав-
новесии.
Примем положение одного из контактов относительно частицы
неподвижным, а положение второго контакта будем менять по всей
поверхности частицы. Второй контакт может быть с одинаковой
118
' ,	2
вероятностью расположен в любой точке окружности на длине у ка.
Отсюда видно, что вероятность расположения контакта в точке О
весьма мала. Иными словами, структура из частиц с двумя
рабочими контактами в статическом отношении практически не
устойчива.
Рассмотрим статическое равновесие частицы с тремя рабочими
контактами, которые заменим сжимающими силами, направлен-
ными нормально к поверхности частицы. Для равновесия частицы
под воздействием этих сил необходимо, чтобы сумма моментов их
относительно какой-либо точки, а также сумма проекций всех сил
на оси координат равнялись нулю. Из рис. 7.6 видно, что линия
действия всех сил проходит через центр круга. Следовательно,
момент каждой из этих сил относительно
центра круга равен нулю. Принимая
далее частицу как жесткий диск, опи-
рающийся на две опоры и нагруженный
некоторой сосредоточенной нагрузкой,
две других реактивных силы будем опре-
делять как реакции опор жесткого диска.
В этом случае статическое равновесие
частицы возможно лишь при условии,
когда линия действия заданной нагрузки
проходит через центр круга и находится
в пределах угла, образованного линиями
действия опорных реакций. Следователь-
но, статическая устойчивость частицы
Рис. 7.6. Схема статического
равновесия частицы при
трех рабочих контактах
зависит только от взаимного положения
рабочих контактов. Этим обстоятельством мы и воспользуемся
в дальнейшем при решении вопроса о вероятности статической
устойчивости частицы с тремя рабочими контактами в плоской
задаче.
Один из контактов примем неподвижным относительно частицы.
Линию действия реактивной силы на втором контакте при предель-
ном положении второй частицы относительно первой (рис. 7.7) при-
мем за начало отсчета. Тогда положение второй частицы будем оп-
ределять уг?юм а, образованным линией начала отсчета и линией
действия реактивной силы. Третью и вторую частицы примем за
опоры рассматриваемой частицы. Реактивную силу контакта третьей
частицы будем считать заданной активной силой, положение ко-
торой с одинаковой вероятностью возможно в любой точке на по-
верхности данной частицы в пределах, допускаемых положением и
размерами двух первых частиц и размерами третьей. Линия дейст-
вия реактивной силы, принимаемой за активную, находится
в пределах Угла к—а при любом значении угла а. Однако устойчи-
вой частица будет не при любом положении точки приложения к
ней активно^ силы (третьего контакта). Из рис. 7.7 видно, что при
119
О < a устойчивой частица будет лишь при таком поло-
3
жении точки приложения активной силы, при котором ли
Рис. 7.7. Схема к расчету вероят-
ности статической устойчивости ча-
стицы при трех рабочих контактах
а — положение «активной» силы в преде-
лах от 0 до я/3; б — то же. в пределах от
*/3 до 2/3 а; в — то же. в пределах от
2/3 ж до ж
штрихованного на рисунке.
Возьмем отношение угла,
определяющего положение ли-
нии действия активной нагрузки
при устойчивом состоянии час-
тицы, к углу, определяющему
все возможные положения ли-
нии действия активной нагрузки
и найдем вероятность устойчи-
вого состояния частицы.
Для 0 а — эта вероят-
3
ность
т+в
(7-1)
где (а) — вероятность устой-
чивого состояния
частицы;
а — угол, определяю-
щий положение вто-
рого контакта.
Как видно из формулы (7.1),
вероятность устойчивого поло-
жения рассматриваемой частицы
зависит от положения второго
контакта по отношению к пер-
вому. Поскольку положение вто-
рого контакта в каждой точке
в пределах угла 0 а < — рав-
новероятно, то вероятность ус-
тойчивого положения частицы
при этом определим как сред-
нее значение, т. е.
. 3
<71 («)<*“• (7.2)
з 0
120
Подставляя в эту формулу значение вероятности из формулы
(7.1), получим
«	я	g
з	з	Т
= 41п—— 1 =4 0,41— 1 =0,64.
2
При положении второго контакта в пределах
к
"з
(7.3)
устойчивое положение частицы будет обеспечено при любом возмож-
ном положении точки приложения активной силы.
Для этого случая вероятность устойчивости частицы
1,
(7.4)
о
где q2 — вероятность устойчивости частицы при — < а < — я.
3	3
2
При положении второго контакта в пределах — я для
третьего контакта нет ни одной точки приложения активной силы,
соответствующей устойчивому положению частицы. Вероятность
устойчивого положения частицы для этого случая определится за-
висимостью
<7з =
(7.5)
2
где ft — вероятность устойчивости частицы при —
Таким образом, при различном положении второго контакта
у частицы будет различная вероятность статической устойчивости.
При определении вероятности устойчивости частицы мы условно
ограничивали для каждого из рассмотренных выше случаев поло-
жение второго контакта. В действительности второй контакт с оди-
наковой вероятностью может быть расположен в каждом из рассмот-
ренных пределов. Вероятность устойчивости частицы без ограниче-
ния области расположения второго контакта можно определить как
среднее арифметическое из значения вероятности устойчивости
частицы при частных случаях расположения второго контакта, т. е.
_ _ 91 + Яг 4 Яг _ 0.64 4~ 1 4~ 0 __ q 5-
1~	3	3
(7.6)
Следовательно, при трех рабочих контактах у частицы в 55 слу-
чаях из 100 можно ожидать статически устойчивого положения ее
и почти в 45 случаях — статически неустойчивого положения.
<7а =
121
Определим вероятность статической устойчивости частник с че-
тырьмя рабочими контактами. Для решения данного вопроса трй
рабочих контакта закрепим в предельном состоянии, а полненН®
четвертого контакта будем менять в пределах возможной (На
рис. 7.8 контакты обозначен151
римскими цифрами). Положе’
ние IV контакта определяется
углом а, который может измс-
Рнс. 7.8. Схема к расчету вероятности
статической устойчивости частицы
а — при четырех рабочих контактах; б — при
пяти рабочих контактах
нитьсяотнуля ДО It. В ЭТИ*
пределах изменения угМ a JV
контакт с одинаковой верояТ'
ностью может быть располо-
жен в любой точке ни по-
верхности частицы. Следова-
тельно, вероятность статиче-
ской устойчивости частицы
при наличии у нее четырех
рабочих контактов
9=V’:T’c=L (77)
Если у частицы пять ра-
бочих контактов, один кон-
такт оказывается лишним,
так как для статической ус-
тойчивости достаточно четы-
рех, которые закреплены в
предельном состоянии друг
относительно друга.
Положение пятого кон-
такта определяется относи-
тельно закрепленных контак-
тов углом а, который может
изменяться в пределах от нуля
до-4-. При любом положении
3
пятого контакта частица будет
находиться в состоянии стати-
ческого равновесия. Тогда ве-
роятность статической устойчивости частицы при наличии у нее
пяти рабочих контактов
9 = Т:-Г=1-	(7'8)
О Q
Для частицы с шестью рабочими контактами вероятность стати-
ческой устойчивости такая же, как и у частиц с четырьмя и пятью
контактами, и равна единице.
122
С целью сопоставления геометрических условий образования
различных структур со статической устойчивостью их под нагруз-
кой составим табл. 7.3.
Таблица 7.3
Число рабочих контактов у частицы	Вероятность образования из геометрических соображений		Наиболее вероятное число рабочих контактов у частицы
Шесть		1		
Пять	Qu < < Qu	1	—
Четыре	Qu	1	Четыре
Три	Qu ~ Qu	0,55	—
Два	Qu < < Qu	0	—
Вероятность образования той или другой структуры из геомет-
рических соображений сравнивается с вероятностью образования
структуры с четырьмя рабочими контактами у частицы; для плоской
задачи наибольшей вероятностью обладает структура, у которой
частицы имеют по четыре рабочих контакта. К этому выводу можно
также прийти, если за наиболее вероятное число контактов у частиц
принять среднее арифметическое из числа всех возможных струк-
турных образований, т. е.
N = 6 + 5 + 4 + 3 + 2 = *	у 9)
где N — среднее наиболее вероятное число рабочих контактов у
частицы.
При пространственном расположении частиц одинакового раз-
мера и шарообразной формы наиболее плотной упаковкой считается
гексагональная, при которой каждая частица касается двенадцати
других частиц. При этом, однако, взаимное расположение частиц,
окружающих данную частицу, может быть разнообразным, так как
эти двенадцать частиц укладываются относительно тринадцатой с не-
которым промежутком. Строго теоретического решения задача о
наиболее плотной пространственной упаковке шаров одинакового
размера пока не имеет [87, 95]. Поэтому по аналогии с плоской
задачей за наиболее плотную упаковку без строгого математиче-
ского обоснования принимают пока гексагональную упаковку (77 ].
Эта наиболее плотная упаковка частиц является редчайшей [33].
Самой рыхлой упаковкой частиц одинакового размера шарооб-
разной формы в пространственном расположении их будет такая,
у которой каждая частица имеет четыре рабочих контакта. Эта упа-
ковка с точки зрения статической устойчивости является маловеро-
ятной. Следовательно, число контактов у частицы в данном случае
может изменяться от четырех до двенадцати. Поскольку в плоской
задаче наиболее вероятным числом рабочих контактов у частицы
123
является среднее арифметическое из всех практически возможны*’
то можно считать, что в случае пространственного расположении
частиц наибольшей вероятностью обладает появление в структур6
частиц со средним числом контактов, т. е.
12+ 11 4- 10 4-94-8 + 74-64-5 + 4
где N — среднее наиболее вероятное число рабочих контактов У
частиц в случае их пространственного расположения.
Таким образом, для пространственной задачи наиболее типи4*
ным будет наличие у частиц восьми рабочих контактов. Это поД'
тверждается экспериментами [68 ].
На рис. 7.9 изображены различные варианты упаковки зерен-
При уплотнении материала число частиц с восемью и более рабочими
контактами возрастет, а при сдвигах (вследствие разуплотнения
материала) — уменьшается.
Рассмотрим ориентировку и взаимное положение зерен призма-
тической, цилиндрической и эллипсовидной структуры.
Для плоской задачи частицу этих структур можно представить
в виде прямоугольника. Тогда задача об ориентировке частиц в мае*
сиве сведется к определению вероятности того, какая из сторон
прямоугольника займет горизонтальное положение. При этом на
положение частиц помимо геометрического размера и положения
центра тяжести будут оказывать влияние и другие факторы: напри-
мер, взаимодействие частиц друг с другом, влияние инерционных
сил при высыпании, влияние скорости движения среды (воздуха
или воды), вязкость среды и т. д.
Однако в первом приближении можно принять, что определяю-
щими факторами будут их геометрические размеры и положение
центра тяжести каждой из них.
Если каждая частица состоит из одного материала (а это соот-
ветствует действительности в подавляющем большинстве случаев),
то вероятность ориентировки частицы кубовидной, цилиндрической
или плитовидной формы будет определяться относительными гео-
метрическими размерами частиц по взаимно перпендикулярным на-
правлениям.
На рис. 7.10 изображена частица при опирании на горизонталь-
ную плоскость углом, через который проходит линия действия силы
тяжести; в этом положении частица находится в неустойчивом рав-
новесии. Поэтому при решении задачи о вероятности опирания ча-
стицы на плоскость большей или меньшей стороной достаточно рас-
смотреть изменение положения частицы относительно одного из
ее углов.
Рассмотрим изменение углов а, и определяющих положение
частицы в момент касания ее горизонтальной поверхности. Если
поворачивать частицу вокруг точки О, то легко установить, что
124
Рис. 7.9. Схема различного взаимного расположения частиц среднего раз-
мера при образовании зернистого тела
угол af изменяется от пуля до В таких же пределах изменяется
и угол ав; эти углы дополняют друг друга до ; следовательно,
можем рассматривать один из этих углов, в частности, угол, приле-
гающий к большей стороне частицы.
При падении частица с одинаковой
вероятностью может в момент ка-
сания горизонтальной поверхности
принимать любые значения угла а.
Рис. 7.10. Схема к определению
вероятности положения частицы
в массиве при разных ее разме-
рах по взаимно-перпенднкуляр-
ным направлениям
а — неустойчивое равновесие; б — опи-
рание частицы на меньшую грань; в —
то же. на большую грань
в пределах от нуля до -у-. Если
этот угол будет меньше величины
угла, определяющего положение не-
устойчивого равновесия, то час-
тица займет горизонтальное поло-
жение большей своей стороной. На-
оборот, если он будет больше зна-
чения, определяющего положение
неустойчивого равновесия, то час-
тица будет опираться на горизон-
тальную поверхность своей меньшей
стороной.
Из положения неустойчивого
равновесия определим значение
угла а,. Поскольку направление
действия силы веса в данном слу-
чае совпадает с диагональю пря-
моугольника, изображающего ча-
стицу, то величину угла, опреде-
ляющего это характерное состоя-
ние частицы, можно определить
как отношение сторон, т. е.
tg« = v. (7.11)
О
откуда
e,= arctg —,	(7.12)
ь
где а, — значение угла, определяющего положение неустойчивого
равновесия частицы.
В пределах изменения этого угла от О до полученного значе-
ния частица при дальнейшем падении будет ложиться на гори-
зонтальную поверхность своей большей стороной. Следовательно,
вероятность того, что частица будет опираться своей большей
126
стороной на горизонтальную поверхность, определится выраже-
нием
<?e = ~ arctg.	(7.13)
*'	О
Вероятность же того, что частица будет опираться на горизон-
тальную поверхность меньшей стороной, определится зависимостью
?M = i-<fo = i-4arcte-r- <7Л4>
71 ь
Вероятность того, что частица меньшей стороной будет опи-
раться на горизонтальную поверхность, можно определить также
тождественным зависимости (7.14) выражением
<7м = 4агс‘е4	<715>
Проанализируем приведенные формулы. Из зависимости (7.13)
видно, что по мере относительного увеличения геометрических разме-
ров зерен вероятность укладки частицы большей стороной возрастает.
При —>оо или b -> 0 вероятность q6
1. Из этого следует, что
частицы в виде листочков будут с какой угодно большой вероятно-
стью стремиться занять горизонтальное положение. При этом ве-
роятность опирания частицы на малую сторону стремится к нулю.
Однако даже в этом случае при относительно малом размере сто-
роны Ь, поскольку она не равна нулю, вероятность опирания на
малую сторону частицы, как бы она ни была мала, не становится
равной нулю. Из этого вытекает, что даже при относительно малом
размере меньшей стороны частицы возможность опирания ее на эту
сторону не исключена.
Из сказанного вытекает, что при неодинаковых размерах зерен
по взаимно-перпендикулярным направлениям более вероятным бу-
дет такое расположение частиц, при котором их большая сторона
горизонтальна. Этот вывод для глинистых грунтов подтверждается
некоторыми теоретическими соображениями и экспериментальными
данными, полученными Г. И. Покровским [69, 72 J. При одновре-
менном падении большого числа частиц процесс образования струк-
туры будет значительно сложнее рассмотренного выше.
§ 4. РАСЧЕТНЫЕ СХЕМЫ ДЛЯ ЧАСТИЦ И ДЛЯ ВСЕГО МАССИВА
При решении вопроса о выборе расчетной схемы как для каждой
частицы, так и для всего массива, в силу огромного многообразия
взаимного положения зерен невозможно установить строгие коли-
чественные соотношения для каждого зерна в отдельности.
На основе анализа различных случаев взаимного расположе-
ния частиц покажем, что при решении вопроса о распределении
вертикальных напряжений в плоской задаче все частицы среднего
127
(эффективного) размера можно рассматривать как диски на двух
опорах.
На рис. 7.11 представлены расчетные схемы для зерен кубоВид-
ной, шарообразной и эллипсовидной формы при наличии у них ше-
сти, пяти, четырех и трех рабочих контактов. Наличие распора
сказывается в появлении горизонтальной составляющей, которая
создает момент и тем самым изменяет величину вертикальных Опор-
ных реакций. Однако влияние горизонтальной составляющей на
величину вертикальных реакций можно учесть путем переноса точки
приложения силы так, чтобы момент от горизонтальной составляю-
щей относительно опорных точек был равен нулю. При таком по-
ложении активной силы опорные реакции будут определяться ве-
личиной вертикальной составляющей и точкой приложения ее от-
носительно опор. Влияние силы трения данной частицы о соседние
также можно учесть переносом точки приложения нагрузки.
Рассмотрим структуру с шестью рабочими контактами у каждого
зерна. Для установления качественной стороны участия каждого
зерна в передаче усилий выбраны две частицы, одна из которых на-
ходится с правой, а другая 1 — с левой стороны от линии действия
внешней силы. На частицу 1 передается активное усилие от частицы
Л, расположенной ближе к точке приложения нагрузки. Частица 1
опирается на две частицы 2 и 3\ кроме того, она взаимодействует
с частицами С и О, С правой стороны от линии действия нагрузки
на частицу 4 передается активная сила от частицы Б. Частица 4
опирается на частицы 5 и 6 и соприкасается с частицами О и D.
Активные силы к частицам 1 и 4 приложены под углом к горизонту.
За счет трения рассматриваемые частицы вовлекают в распределе-
ние усилий соседние частицы. При этом роль в распределении Уси-
лий соседних частиц различна: если частицы С и D, расположенные
дальше от линии действия силы, лишь частично передают приходя-
щиеся на них за счет трения усилия на выбранные опорные зерна 2
и 6, то частица О полностью передает усилия на опорные
зерна 3 и 5.
Таким образом, при составлении расчетной схемы влияние тре-
ния с частицей О можно не учитывать. Заменив для каждой из рас-
сматриваемых частиц / и 4 опорные зерна опорами, получим диск,
расположенный на двух опорах. Переносом точки приложения ак-
тивной силы учитываем влияние горизонтальной составляющей ее
и силы трения о соседнюю частицу на вертикальные опорные реак-
ции. Расчетная схема для частицы с пятью рабочими контактами
будет отличаться от схемы с четырьмя контактами точкой приложе-
ния активной силы.
Расчетные схемы для частиц с четырьмя и тремя рабочими кон-
тактами от приведенных выше также будут отличаться лишь точкой
приложения активной силы.
Таким образом, для решения вопроса о распределении верти-
кальных усилий в грунтовом массиве, образованном из зерен
128
О 1Й	Схемы структурного расположения частиц поилазлич'ном числе рабочих контактов	Схемы Ьзаимодейстдия частиц,	Расчетные схемы для определения дер- спинальных исилци	
б	X X’jCjC г Х^а/а 2 с Y 1 X о Y 4 Хя (2 X3 JL5 X6 У Y Y । Y Y	Г i\j Гдд». 	Ci 1	 ( Г xlr*" f о» Ъ-у '—ft» 1	Ул ' &£,. i Л М ' it ]6 ! „Лс.. ЯгХТЙ, гИг-!??ррР<!^ 		—J— - 			
3	А А 1 X X Г АЛХ6А 2 vXjX5X62 ч JcAjJlJL		1	 1 0 JujCOCO 1 —1	5j/i ' 2\ Ь | А \1 i^/L!„„,R„ 2ХТф]ХЦ IhLuJ i Uuit 	i		1	1
4	Л )( 1 )(	)( 7Гл лГб X 7 JI! II Уг 2 УГз jjT 5 7ГЬ	1 1 1 1 \ / 1 \ । Л*\ ( 1 ) I ( 4 ) 2 Д 3 X 5 Д б I	/л । V/J LVj 1 GiJ Tri т; it 1 ЗЦгЩо	
3	X I 1 X X ) T^X6J vYjJ II)? У	\*Л о С 3 I 5 ) Ч- 1 ( 	Л	L	1 (		1	 I I / 1 \ /-Ч 1 -4 1 ) I ( 4 _> ( 3 X 5 ) К® О|О х~ I 	1		^/xi \б 7® 1 Ш 1 21 [ |j ) 5 1 |6 ! 6jj\j4!	
Рис 7.11. Расчетные схемы частиц при различном положении их
в зернистой среде
(структурных агрегатов) кубовидной, шарообразной и эллипсовидной
формы, за расчетную схему для каждой частицы а плоской задаче
может быть принят жесткий диск на двух опорах. Активная сила
к расчетному диску прикладывается при этом случайно.
Аналогично можно рассмотреть и пространственное взаимное
расположение частиц и установить для них расчетные схемы. При
этом для плотнейшей гексагональной упаковки при 12 рабочих
контактах н для упаковки при четырех контактах получим расчет-
ную схему для каждой частицы в виде жесткого диска, опирающе-
гося на три частицы.
Для наиболее вероятной упаковки при восьми рабочих контак-
тах у частицы (упаковка в виде тетраэдра) получим расчетную схему
в виде жесткого диска на четырех опорах. Распределение усилий
между опорами отдельного зерна будет носить при этом, как и в
плоской задаче, случайный характер.
В итоге можно отметить, что при исследовании характера рас-
пределения средних значений напряжений реальный зернистый
грунт может быть заменен зернистой средой, состоящей из частиц
среднего эффективного размера. Принцип осреднения может быть
использован в данном случае и в отношении условий передачи уси-
лий от частицы к частице. Так, для эквивалентной зернистой среды,
состоящей из частиц среднего размера, передача усилий от Каждой
частицы осуществляется в среднем на две частицы в плоской и на
четыре в пространственной задаче. При этих условиях, а также
при замене сил взаимодействия между двумя частицами равнодей-
ствующей, приложенной в точечном контакте, каждую частицу
можно рассматривать как элемент, имеющий две опоры в плоской
задаче и четыре — в пространственной задаче. Распределение уси-
лий между опорами в общем случае осуществляется неравномерно
и оценивается коэффициентом неравномерности передачи усилий kt
который определяется как отношение плеча, более удаленного от
линии действия внешней нагрузки /х, к плечу, ближе расположен-
ному к этой линии /2 (рис. 7.12), т. е.
£ =	(7.16)
Расчетная схема для всего зернистого грунтового основания мо-
жет быть представлена совокупностью элементарных схем, у кото-
рых частицы каждого более удаленного от точки приложения внеш-
ней нагрузки ряда являются опорами для частиц, расположенных
в предыдущем ряду. Такая расчетная схема позволит при исследо-
вании характера распределения напряжений производить анализ,
начиная от точки приложения нагрузки.
Зернистые грунтовые системы могут быть распорными и безрас-
порными. С точки зрения расчетной схемы безраспорные системы
характеризуются постоянным средним значением коэффициента
неравномерности передачи усилий для любой частицы, независимо
130
от удаления ее от точки приложения нагрузки. Распорные системы
имеют переменный коэффициент неравномерности передачи усилий,
который меняется от слоя к слою по мере удаления от точки прило-
жения нагрузки.
Схематично это можно представить так: выделим в массиве
группу частиц, расположенных слева от линии действия внешней
нагрузки (рис. 7.12, б); усилие от частицы А под углом к линии
действия нагрузки передается на частицу В. В свою очередь, частица
Рис. 7.12. Изменение расчетных схем зерен в массиве по
мере удаления их от точки приложения нагрузки по направле-
нию линии ее действия
а — к определению коэффициента k; б — изменение коэффициента к по
глубине
В приходящееся на нее усилие распределяет между частицами С
и D. При этом вертикальная составляющая усилия распределяется
между частицами С и D, а горизонтальная целиком воспринимается
частицей С, так как среда не воспринимает растягивающих усилий,
возникающих на контакте между частицами В и D. На контакте
между частицами В и С возникает не только меньшая по величине
сила, но и более наклонная к линии действия внешней нагрузки по
сравнению с усилием в контакте между частицами предыдущего
ряда (частицами Л и В). Изменение наклона усилия ведет к изме-
нению коэффициента неравномерности передачи усилий, причем
131
чем больше наклон, тем меньше коэффициент. Кром$ того, увеличе-
ние наклона усилия на контакте между частицами Д и В обуслов-
ливает увеличение горизонтальных составляющих н^ только в этом
контакте, но и во всех последующих, а также ведет к уменьшению
вертикальных составляющих напряжения.
Глава 8
вертикальные напряжения в однородном
ГРУНТОВОМ ОСНОВАНИИ В ПЛОСКОЙ ЗАДАЧЕ
$ 1. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДЛЯ БЕЗРАСПОРНОЙ СРЕДЫ
При решении вопроса о распределении напряжений в зернистом
грунтовом основании воспользуемся решениями о распределении
напряжений в безраспориом грунтовом основании для частного слу-
чая, когда размеры частиц по трем взаимно-перпендикулярным На-
правлениям равны, т. е. b = с = а.
Для вертикальных напряжений от сосредоточенной нагрузки
в плоской задаче
аг )'
(8-1)
Для произвольной полосовой нагрузки
<«=>
— ь
где а — размер частиц;
2d — ширина полосы, на которой распределена нагрузка;
f (х) — функция, выражающая характер распределения на-
грузки.
Для сосредоточенной вертикальной нагрузки в пространствен-
ной задаче
0,^ехр(-2А^).
(8.3)
132
Для произвольной вертикальной нагрузки в пространственной
задаче
<«<>
F
где F — площадь интегрирования;
dF=dbd^
Для слоистой безраспорной среды вертикальные напряжения
вычисляются по тем же формулам при замене вертикальной коорди-
наты на соответствующую эквивалентную, которая определяется
по формуле
=*» + *.	<8.5)
где Лэ — эквивалентная толщина всех вышележащих слоев;
z — координата рассматриваемой точки при положении начала
координат на верхней границе данного слоя.
Эквивалентная толщина вышележащих слоев
1 ап \ К )	2	\ л. /
где	Л2,	Ап1	—толщины слоев;
ait	a2t	ап	—размеры частиц по слоям;
kit	k2t	kn	—коэффициенты неравномерно-
сти передачи усилий по слоям.
Приведенные формулы как для плоской, так и для пространст-
венной задачи будут использованы при решении вопроса о распре-
делении напряжений в среде с переменным по глубине коэффици-
ентом неравномерности передачи усилий.
§ 2. О КОЭФФИЦИЕНТЕ НЕРАВНОМЕРНОСТИ ПЕРЕДАЧИ УСИЛИЙ
В первой части книги рассматривалась дискретная безраспорная
среда, свойства которой (с точки зрения распределения напряже-
ний) не менялись с глубиной или менялись скачкообразно от слоя
к слою.
Что касается зернистого грунта, то в нем за счет распора, взаим-
ного заклинивания и трения частицы в горизонтальных рядах
имеют связь с соседними частицами. Благодаря этому усилие, при-
ходящееся на каждую частицу, распределяется не на две нижележа-
щие частицы, как в плоской задаче (или на четыре в пространствен-
ной), а на большее число их.
Передача усилий на большее число частиц ведет к уменьшению
среднего значения коэффициента неравномерности передачи усилий
для каждого ряда по мере удаления от точки приложения нагрузки.
133
При рассмотрении вопроса о распределении усилий и напряже-
ний в безраспорной среде коэффициент неравномерности передачи
усилия k принимался постоянным для всех частиц. Постоянной
также принималась и ориентировка частиц. В распорной же среде
эти показатели будут меняться в широком диапазоне.
Значение коэффициента неравномерности передачи усилий для
одной частицы может колебаться в пределах от нуля до бесконеч-
ности, причем рассматриваемая частица не участвует в распределе-
нии усилий, а является как бы продолжением вышележащей частицы
в передаче усилий на частицу следующего слоя.
Поэтому при определении среднего значения k для всего массива
величины k = О' и Л = оо в расчет не принимаются. Однако при
этом изменяется соответствующий размер частиц.
Коэффициент неравномерности передачи усилий для каждой
частицы будет носить вероятностный характер. Величина этого
коэффициента в каждом конкретном случае будет определяться
размером, формой и взаимным положением частиц, плотностью ма-
териала, наличием и величиной сил трения между отдельными зер-
нами грунта, составляющими основной скелет структуры тела.
Кроме неравномерности распределения усилий между частицами
в ряду, рассматриваемый коэффициент характеризует собой угол,
под которым в безраспорной среде распределяется давление.
Положим для примера, что линия, определяющая угол, под ко-
торым распределяется давление в безраспорной среде, проходит
через точки с напряжениями, равными величине их для крайних
точек равновероятного распределения усилий между частицами.
При равновероятном распределении усилий между каждыми
двумя нижележащими частицами величина усилия на крайнюю
частицу в л-ом ряду от единичной нагрузки на частицу поверхности
При единичной нагрузке, но равномерно распределенной на по-
верхности по бесконечной прямой линии, эта формула примет вид
р"“ = в(т)"	(88)
где а — размер частицы.
Величину усилия, приходящуюся на частицу, разделим на пло-
щадь, занимаемую частицей, получим величину напряжения
,89>
Геометрическое место точек, для которых величина напряжения
равна значению, определяемому по (8.8) и будет границей распреде-
134
ления напряжений. Уравнение этих точек получим путем прирав-
нивания выражения (8.8) к полученной ранее зависимости для на-
пряжений при Р = 1, b = с = а, т. е.

(8.10)
где xit ?! — координаты точек, в которых напряжения равны
чине, определяемой выражением (8.8).
Заменив в уравнении (8.10) номер слоя через координату zn по-
лучим
1 / I \ а _ / 9Ь2	/	2k2X2. \
4-(т)	<«">
В общем виде это уравнение относительно коэффициента k не-
разрешимо; поэтому будем искать приближенное решение, для чего
преобразуем его к виду
(8J2)
Прологарифмируем его:
^.asJ_ln^_ + 2Lin2,	(8.13)
откуда
£ = -^1/ — + —1—In—;	(8.14)
*1 |/	2	4?!	«1	'	’
заменив под корнем отношение 2j- через номер слоя, получим
й = 1/211 + J-In	(8.15)
*1 р 2 4п itn
Из формулы видно, что коэффициент k пропорционален тангенсу
угла наклона прямой, ограничивающей зону распределения напря-
жений в безраспорном массиве (рис. 8.1).
Все сказанное выше относилось к безраспорной среде. Грунты
же в силу взаимного заклинивания частиц и распора распределяют
давление на большее число частиц, чем рассмотренная безраспор-
ная среда. Это ведет к изменению с глубиной среднего значения
коэффициента неравномерности передачи усилий в рядах. В силу
дискретности среды изменение это происходит от слоя к слою.
Следовательно, для грунтовой среды среднее значение коэффи-
циента неравномерности передачи усилий по рядам может быть
135
Рис. 8.1. Иллюстративная схема связи
коэффициента неравномерности пере-
дачи усилий с углом распространения
давления в безраспорной зернистой
среде
непрерывной функцией не координаты, а номера слоя. Поскольку
взаимное влияние частиц ведет к увеличению площади распределения
давления по мере удаления отточки приложения нагрузки, то можно
заключить, что средние значения коэффициентов неравномерности
передачи усилий по рядам уменьшаются от слоя к слою.
Из многочисленных экспериментальных данных [2; 8; 25; 69;
73; 84; 86; 88; 89; 107; 114] известно, что для грунтов зона распреде-
ления давления ограничивается не прямой, а кривой линией, тан-
генс угла наклона которой к горизонтальной оси уменьшается по
мере удаления от точки приложения нагрузки; для зернистых грун-
тов коэффициент неравномер-
ности передачи усилий умень-
шается по мере удаления рас-
сматриваемого ряда от точки
приложения нагрузки.
Коэффициент неравномер-
ной передачи усилий — по-
ложительная величина. По
этой величине (для упроще-
ния преобразований) будем
считать, что с изменением
номера слоя (или координаты
z) изменяется квадрат коэф-
фициента неравномерности пе-
редачи усилий.
Примем такую зависимость для переменного по глубине коэффи-
циента неравномерности передачи усилий
Аа = ф(г).	(8.16)
§ 3. ВЕРТИКАЛЬНЫЕ НАПРЯЖЕНИЯ В ЗЕРНИСТОМ ГРУНТОВОМ
ОСНОВАНИИ ОТ НАГРУЗКИ, РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ
ПО БЕСКОНЕЧНОЙ ЛИНИИ
Для решения вопроса о распределении напряжений в такой
среде используем полученное ранее решение о распределении на-
пряжений в многослойной безраспорной среде при == ct = at.
При рассмотрении распределения напряжений в многослойной
среде для произвольной нагрузки как в плоской, так и в пространст-
венной задачах было показано, что решение сводится к однородной
среде путем приведения всех вышележащих слоев к эквивалентному
слою, т. е.
где Aj	hn — толщины вышележащих слоев;
аа — средние (эквивалентные) размеры зерен по
слоям;
136
*1
k„ — коэффициенты неравномерности передачи уси-
лий по слоям.
Используем эту формулу для определения вертикальных напря-
жений в среде, распределительная способность которой изменяется
с глубиной. Определим эквивалентную толщину вышележащих
слоев для глубины z. Для этого слой грунта, расположенный выше,
разобьем на одинаковые малые слои Azj (рис. 8.2). Используя фор-
мулы (8.16) и (8.17) при at —
= а2 =.......= ап, получим
+
или
При переходе к пределу по-
лучим
Рис. 8.2. Схема к расчету эквивалент-
ной глубины при учете переменного по
глубине значения коэффициента нерав-
номерности передачи усилий
г’=+(г)т-(8-20)
Подставив полученное выражение в формулу для вертикальных
напряжений от нагрузки, равномерно распределенной по бесконеч-
ной линии, получим
2ф (г) х*_____
z	-1	’
И*) [-£- + *
(8.21)
В этой формуле величина dz, стоящая не под интегралом, озна-
чает слой, в котором определяются напряжения. Эта величина в пре-
деле равна нулю, поэтому
°, = Р
(8.22)
Из полученной формулы видно, что при любом законе изменения
распределительной способности грунта по глубине характер рас-
пределения напряжений в горизонтальной плоскости не изменится:
137
лишь кривые распределения напряжений в горизонтальной плоско-
сти переместятся с одной глубины на другую.
При выборе функции изменения коэффициента неравномерности
передачи усилий необходимо выполнить два условия:
1) ее значения по мере увеличения номера слоя должны умень-
шаться;
2) она должна приводить в частном случае к решению, соответ-
ствующему безраспорной среде.
Этим условиям удовлетворяет следующая функция
k2 =	,	(8.23)
где п — номер слоя, считая сверху;
Th — коэффициент пропорциональности, определяющий харак-
тер взаимной связи частиц друг с другом;
8 — некоторая постоянная.
Зная, что п = -у- и учитывая зависимость (8.16), получим

(8.24)
(8.25)
Подставляя выражение (8.25) в формулу (8.22), получим следую-
щую зависимость для вертикальных напряжений от нагрузки, рав-
номерно распределенной по бесконечной линии,
2Ч1(*+1)
1—4^14-5
2'.i0 -М)*2
(8.26)
При 8 = 0 выражение (8.26) преобразуется к виду, соответст-
вующему безраспорной среде.
При наличии распора и взаимного заклинивания усилие на ча-
стицы нижележащего слоя передается не только данной частицей,
но и соседними с ней. В этом случае частицы теряют свою индиви-
дуальность. Иными словами, при наличии связи между частицами
за счет трения или малого сцепления размер зерен не учитывается;
из формулы (8.26) видно, что это возможно при 3=1. Коэффициент
8 характеризует относительное число взаимосвязных частиц в го-
ризонтальных рядах. При 8 = 0 связь между частицами в горизон-
тальных рядах полностью отсутствует и среда обладает свойствами
безраспорной зернистой среды.
При о = 1 все или почти все частицы в горизонтальном ряду
связаны друг с другом за счет трения или малого сцепления. Если
138
связь осуществляется только за счет трения» то мы имеем дело с сы-
пучей грунтовой средой.
Полагая 8 = 1, на основании зависимости (8.26) получим выра-
жение для вертикальных напряжений в однородном грунтовом мас-
сиве от нагрузки, равномерно распределенной по бесконечной ли-
нии (плоская задача);
(8.27)
На основе этого выражения имеем зависимость для произволь-
ной полосовой нагрузки
______________________
=4 /4 J /<«ех₽ [- v (* - э2]	(8-28)
Глава 9
НАПРЯЖЕНИЯ В ОДНОРОДНОМ ЗЕРНИСТОМ ГРУНТОВОМ
ОСНОВАНИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
§ 1. НАПРЯЖЕНИЯ ОТ СОСРЕДОТОЧЕННОЙ НАГРУЗКИ
Как известно, распределение напряжений в безраспорной среде
от сосредоточенной нагрузки выражается зависимостью
«Хх2 + ауу2
2г
„	4Fa 4&а
где а, =---; а,. =----.
При b = с = а, ах = ау = для вертикальных
^ = ^ехр[.
учитывая, что х2 4- у2 = г2, получим
„ 2Л3	/	2Л2Г2
°’ = />-^ГехР(-57-
az
(9-1)
напряжений
(9.2)
(9.3)
139
Эта формула аналогична той, которая рассматривалась в пло-
ской задаче; используя эту зависимость, выразим характер распре-
деления напряжений от сосредоточенной нагрузки в среде с непре-
рывно меняющейся по глубине распределительной способностью
грунта:
(9.4)
При линейном изменении коэффициента распределительной спо-
собности грунта с глубиной подынтегральная функция, как было
показано при рассмотрении плоской задачи, имеет вид
Ф(г)=^-
(9-5)
где ifo — коэффициент распределительной способности грунта;
а — средний (эффективный) размер зерен.
После преобразований с учетом (9.5) выражение (9.4) примет
вид
ог = ^-ехр(-Л£-),	(9.6)
где г — координата точки в горизонтальной плоскости.
Эта зависимость определяет характер распределения верти-
кальных напряжений в грунтовой зернистой среде.
Обозначив 8^ = —, получим
e’=iex₽(-^-)-	<9-7)
Из выражения (9.7) нетрудно получить уравнения линий равных
напряжений, считая, что
const.	(9.8)
После некоторых преобразований и логарифмирования выра-
жения (9.6), получим
/•=+-^-1/^—1п-^- —, r= + zl/”2vln—--------—. (9.9)
Кривые пересекают ось г в точках, соответствующих уравнению
r = 0 = zJ|/41n1-b^,	(9.10)
140
откуда имеем первое уравнение
^ = 0.	(9.11)
Эта координата не зависит от величины напряжений, следовательно,
все кривые пучком сходятся в эту точку.
Второе уравнение
1п-4- = 0;	(9.12)
ИЛИ
—^- = 1,	(9.13)
откуда
Из выражения (9.14) видно, что с уменьшением величины напря-
жения увеличивается координата точки, в которой кривая данного
напряжения пересекает ось г.
§ 2. НАПРЯЖЕНИЯ ОТ ПРОИЗВОЛЬНО ЗАДАННОЙ НАГРУЗКИ
Для общего случая непрерывного изменения свойств среды по
глубине и произвольно заданной нагрузки
17 — переменная интегрирования;
г, а — координаты рассматриваемой точки;
<р — независимая переменная интегрирования.
Интегрируя по частям при переменной 17, получим
1
2п
/[«?,	“> «рЛехр
2F»(r, а, у)
(9.16)
-/(?. 0)-
141
Таким образом, для общего случая изменения распределитель-
ной способности грунта по глубине и произвольно заданной на-
грузки вертикальные напряжения в грунтовом массиве могут быть
определены по формулам (9.15) или (9.16). Если распределительная
способность грунта линейно связана с глубиной, выражение (9.15)
преобразуется к виду
у,	<р)
°, = j df ( /(?. »|)ехр	yfy
(9.17)
о •
при 8^ = — получим
Г (г, а.?)
J Ж’dexpf—(9-»8)
о о
Преобразуя таким же путем выражение (9.16), имеем
°.= —F(r, а, <р)]ехр[---------У) ]—/(?> °)~
Г(Л«,ф)
- f "И Л. |Л' *•
О
где F (г, а, ср) — уравнение контура площади, по которой распреде-
лена нагрузка, при начале координат на одной вертикали с рассмат-
риваемой точкой.
Если нагрузка равномерно распределена по некоторой площади,
то выражение (9.17) примет вид
. ।	F (г, 9, <р)
J ’>еХР(—<9-20>
О о
тогда выражение (9.19) будет таким
о.
р
2п
Сехр(-^-^Й-
О
(9.21)
— <Р1 •
Выше получено выражение для вертикальных напряжений от
произвольно заданной нагрузки в цилиндрических координатах.
В прямоугольных координатах это выражение будет таким:
+1, y-Ft (С)
=	J	(9.22)
—b У— /•,
гДе / (*, у) — функция, выражающая характер заданной нагрузки;
142
iq — переменные интегрирования по соответствующим
осям;
Л (*) — уравнение контура площадки, по которой распреде-
лена заданная нагрузка.
Если функцию нагрузки представить в виде произведений двух
функций, одна из которых будет зависеть только от х, а вторая —
от у, выражение (9.22) можно представить так:
—ь
X J A Oil) ехр [—
(9.23)
где
Л (*)•/•(?)-/(*» У)-
Для нагрузки, равномерно распределенной по некоторой пло-
щади, выражение (9.23) примет вид
+ ь
-ь
(х-Е)8
2>z2
(9.24)
где р — интенсивность равномерно распределенной нагрузки.
Для нагрузки, распределенной по прямоугольнику, зависимость
(9.23) можно представить как произведение выражений для рас-
пределения напряжений от двух полосовых нагрузок, т. е.
Для нагрузки, равномерно, распределенной,

2vz«
(9.26)
143
$ 3. УРАВНЕНИЯ РАВНОВЕСИЯ И ФИЗИЧЕСКИЕ УРАВНЕНИЯ
ДЛЯ ЗЕРНИСТОЙ ГРУНТОВОЙ СРЕДЫ
При рассмотрении безраспорной зернистой среды было показано,
что уравнения равновесия Навье применимы для зернистой среды,
если последняя способна распределять внешнее давление.
При составлении физических уравнений для зернистой грунто-
вой среды можно принять все положения, изложенные для безрас-
порной среды [60].
Для зернистой грунтовой среды разность вертикальных усилий
на соседних частицах пропорциональна сдвигающему усилию, воз-
никающему в связующей их частице.
При этой предпосылке для плоской задачи безраспорной зерни-
стой среды
CJP да-.
«г ________ - * . •
" 2а дх ’
при Ь = а
~	Сх
а да2
2 дГ'
Произведение Сх в этом выражении постоянно и связано с ко-
эффициентом распределительной способности k. Изменение по глу-
бине коэффициента распределительной способности для зернистой
среды равносильно увеличению размеров зерен, воспринимающих
внешнюю нагрузку. Поэтому в общем виде произведение Сх для
зернистой грунтовой среды следует принять зависящим от г. Тогда
следуя Р. А. Муллеру, в общем виде
хжг = —?(z)-^-.
дх
Поскольку коэффициент распределительной способности для
такой среды изменяется от слоя к слою, то
?(*) = >*,	(9.27)
где v — коэффициент пропорциональности.
Учитывая (9.27), физическое уравнение для зернистой среды
в плоской задаче примет вид
=	(9.28)
дх
Приведем уравнения равновесия для плоской задачи
4-2 = 0;	(9.29)
дг дх
-^- + -^-4-Х = 0.
дх дг
(9.30)
144
Дифференцируя выражение (9.28) по х и подставляя произвол*
ную в уравнение (9.29), получим (при Z = 0)
dzz
dz дх2
(9.31)
Дифференцируя
выражение (9.28) по z, получим
у	v2
дг	дх дхдг
(9.32)
Подставляя это значение производной в уравнение (9.30), имеем
при X = О
дсх	дзг	. e d2G2
—— = v —— -|- 'tz-----------— ;
дх	дх дхдг
(9.33)
интегрируя по х, получим
+ 'Z + Р (г).	(9.34)
дг
где р (г) — произвольная функция интегрирования.
Произвольную функцию р (z) определим при z ->оо, при любом
х и любой внешней нагрузке ах -* 0, о, -► 0 и -> 0. Дифферен-
дг
цируем по г зависимость (9.18);
? f7 (/»«. v)
=	| /(?. ч)ехр(—
<р Г (г, а, у)
f /(<?. Ч)ехр(—(9.35)
О о
Умножая на vz и определяя предел получаемого выражения при
г ->со, имеем
limvz = lim
z-» эо дг z-* «о
I
о
/(f. ?1)ехр(

2yz2
»0. (9.36)
2zvz4 J	J
о	о
Подставляя граничные условия в выражение (9.34), получим
Р(2)^0	(9.37)
Тогда
1
°ж = W, + *2—г-.
дг
(9.38)
145
Для определения физического смысла коэффициента v рассмот-
рим задачу для вертикальной равномерно распределенной нагрузки,
приложенной к зернистой полуплоскости. В этом случае для лю-
бого z величина вертикального напряжения о2 = р, т. е. интен-
сивности внешней нагрузки. Следовательно, = 0. Тогда
ах = vo2	(9.39)
Из этого соотношения видно, что v — коэффициент бокового
давления (распора).
Таким образом, в отличие от безраспорной среды в зернистой
грунтовой среде при равномерно распределенной нагрузке возни-
кает распор. Коэффициент бокового распора определяется лабора-
торным путем.
Из выражения (4.28) для заданной нагрузки тХ2 = 0, поскольку
=	= о
дх дх
Если учитывать вес среды, то в уравнениях равновесия необхо-
димо считать Z = 7. Тогда, следуя Р. А. Муллеру, получим такую
систему дифференциальных уравнений для определения напряжен-
ного состояния зернистой грунтовой среды:
= vz — т;	(9.40)
(9.41)
ОХ
Ox = vOj+v2-^- = ^ + ^-^-.	(9.42)
По аналогии для пространственной задачи получим следующие
физические уравнения:
„ до2 , VZ дх ’	(9.43)
\г= — у	ду	(9.44)
Уравнения равновесия для пространственной задачи:	
dJz । dbz j &xUz । 2, = О’ дх	дх	ду	(9.45)
! ^ХХУ 1	1 У = 0’	(9.46)
-	1	~— -j-	Т	— v> дх	ду	дх	
dzy । dx*v ।	у = 0 ду	дх	дх1	(9.47)
146
Дифференцируя (9.43) по х, а (9.44) по у и подставляя в уравне-
ние (9.45), после преобразований при Z = 0 получим
=	+	(9.48)
dz \ дх* ду* I	'	'
Дифференцируя по х уравнение (9.46), а по у уравнение (9.47)
и вычитая уравнение (9.47) из уравнения (9.46), получим
-----дЧу 4- — f—Х2____-Хуг 1—0	(9 491
дх* ду* dz t дх	ду ) U’
Используя зависимости (9.43) и (9.44), получим
дъх
дх*
^S- + ±Lz(^i.
ду* дг[ {ду*
д2зх	д*зу	д*зл	д*зг	. д*сх	д*зг	п
дх*	ду*	ду*	дх* дгду*	дгдх*
После некоторых преобразований
£ (’* -	- ',г Ь - -* -*-) •
Подставляя из выражения (9.48) производную от сг в зависимость
(9.50), получим

д*Ъ
дх*ду*
Су — '»с — v2Z2 d \ — y*z2 ,
Л 2 ду* ) дх*ду*
ИЛИ
. * г дх* ) ду* \ у * ду* }
В этом выражении величина сг зависит от х, у, г и определяется
из (9.48) при* заданных граничных условиях. Неизвестными здесь
являются ох и Су, которые также зависят от х, у, г. Следовательно,
правая и левая части этого уравнения являются функциями пере-
менных х, у, г. Обозначим их через F (х, у, z). Тогда получим два
дифференциальных уравнения
>95|>
I9-521
147
Одинаковые выражения в правых частях уравнений (9.51) и
(9.52) получаются в результате дифференцирования разных зависи-
мостей по х и по у. Поэтому
	°х — '"’г —	= 0,	(9.53)
откуда	°Х = м2 + *2«2 "TY •	(9.54) ОХ8
Аналогично	О и =	+ ^г2	•	(9-55)
Сопоставив уравнения (9.46), (9.54) и (9.43), получим
	= V =	(9-56)
Полученные зависимости позволяют путем дифференцирования
выражений для вертикальных напряжений определить все состав-
ляющие напряженного состояния зернистого грунтового массива.
§ 4. ОСЕСИММЕТРИЧНАЯ ПРОСТРАНСТВЕННАЯ ЗАДАЧА
В цилиндрических координатах уравнения равновесия для осе-
симметричной задачи имеют вид
^ + -^-(г-гг)+2 = 0;	(9.57)
02 ОГ
+	(9.58)
где Z; R — объемные силы.
В двух уравнениях имеется три неизвестных, что не позволяет
решить эти уравнения. Необходимо дополнительное физическое
уравнение. Им будет [60j соотношение между касательными и вер-
тикальными напряжениями
(9.59)
Подставляя это значение т2, в уравнение (9.57) при Z = О, после
некоторых преобразований получим
148
Поскольку нами рассматривается среда, не воспринимающая
растягивающих усилий, то для сосредоточенной вертикальной на-
грузки справедливо условие а0 = 0.
Учитывая это из второго уравнения равновесия при R = 0, по-
лучим соотношение между горизонтальными и касательными на-
пряжениями
4-(for) + r-^-=0-	(9-61)
or	oz
Можно доказать, что этому уравнению и выражению (9.59) удов-
летворяет соотношение
о, + **-$£-.	(9.62)
or*
Это равенство аналогично связи между ах и а2, а также и <зг
и справедливо для любой нагрузки. Далее из соотношения
°х + а, = °, + °0
определим общую зависимость для о0 при любой нагрузке.
Подставляя в это выражение значения ох, ау, <з„ получим
+ v’z* + VO, + *2га = V®, + **2*	+ «»•
ох*	оу*	or*
Из геометрических соотношений, используемых в теории
гости, известно, что при переходе от декартовых координат
линдрическим должно соблюдаться равенство
ау	ау	_ ау	1	д/
дх*	ду* дг*	г	дг	'
Если в уравнении (9.64) предположить, что
то получим
д*<зг . a2jz	д*аг . 1 даг
дх* ду*	дг* + г дг
(9.64)
УПРУ-
к ци-
(9.65)
(9.66)
(9.67)
Нетрудно видеть, что уравнения (9.65) и (9.67) тождественны,
если ог = /. Таким образом, для а0 может быть принята зависимость
(9.67). Для сосредоточенной вертикальной нагрузки это выражение
совпадает с ранее принятым, т. е. а0 = 0.
149
Глава 10
НАПРЯЖЕНИЯ В МНОГОСЛОЙНОЙ ЗЕРНИСТОЙ ГРУНТОВОЙ
СРЕДЕ
$ 1. ОБЩИЕ ПРЕДПОСЫЛКИ К РЕШЕНИЮ ЗАДАЧИ О НАПРЯЖЕННОМ
СОСТОЯНИИ СЛОИСТОГО ЗЕРНИСТОГО ОСНОВАНИЯ
При решении задачи о распределении напряжений в любой мно-
гослойной среде, в том числе и зернистой, существенными являются
условия на границах слоев. Принятыми на границах слоев усло-
виями в дальнейшем определяется само решение.
В литературе имеется много решений теории упругости для
тел, в которых на границе раздела плоско-параллельных слоев ка-
сательные напряжения принимаются равными нулю. Этим самым
по существу на границе раздела как бы вводится дополнительная
нагрузка, снимающая существующие касательные напряжения.
Принимаются и другие гипотезы, сущность которых также сводится
или к непосредственному приложению каких-либо сил на границе
или к приложению их через ограничение перемещений. Исходя из
сказанного, при решении задачи о распределении напряжений в зер-
нистой грунтовой среде положим, что вертикальные напряжения
в верхнем слое в силу передачи усилий от частицы к частице через
точки контактов распределяются, как в однородном массиве, а на
границе двух слоев определяются величиной, зависящей от тол-
щины слоя и распределяющей способности среды при заданной
внешней нагрузке, т. е.
v),	(10.1)
а горизонтальные нормальные и касательные напряжения для пло-
ской задачи определяются из соотношений
(10.2)
дх
О, =	—— 	(10.3)
дх*
Соответственно для пространственной задачи имеем
, =_>Л-Ц=*_;	(Ю.4)
дх
хуг----yh^a--,	(10.5)
“	ду
150
О- = VO . +	; х	z~h	дх*	(10.6)
а = va .4- У	z~h '	дуг	(Ю.7)
В то же время напряжения внутри слоя определяются соотноше-	
ниями для плоской задачи	
да, ’«=—«-г-; дх	(Ю.8)
ах = va v*z2 х	г	дх»	(10.9)
и для пространственной задачи	
„ ^z . « дх .	(10.10)
'в‘~	ду ’	(10.11)
ах = va -|- v*Zs	; 1	дх*	(10.12)
° у = *аг +	. и	ду*	(10.13)
Из приведенных зависимостей видно, что все составляющие
(Зх. су* txt* V) определяются через вертикальные напряжения. По-
этому для приближенного решения вопроса о напряженном состоя-
нии слоистой зернистой грунтовой среды достаточно рассмотреть
характер распределения вертикальных напряжений и по нему ре-
шить задачу об остальных составляющих напряжения. В дальней-
шем при рассмотрении только вертикальных напряжений будем
иметь в виду, что на границах слоев и в массиве имеются и другие
составляющие напряжения, связанные с вертикальными приведен-
ными соотношениями.
При этом относительная ошибка в определении горизонтальных
напряжений не превысит отношения коэффициентов распределитель-
ных способностей, а в определении касательных — корня из этого
отношения. Поэтому в дальнейшем будем касаться только верти-
кальных напряжений.
§ 2. НАПРЯЖЕНИЯ В СЛОИСТОЙ СРЕДЕ ОТ НАГРУЗКИ, РАВНОМЕРНО
РАСПРЕДЕЛЕННОЙ ПО БЕСКОНЕЧНОЙ ЛИНИИ
Как и для безраспорной среды, решение данной задачи начнем
с рассмотрения двухслойной системы.
Распределение вертикальных напряжений в верхнем слое можно
рассматривать как для однородного массива, поскольку передача
151
усилий от точки приложения нагрузки осуществляется через точки
контактов от частицы к частице. Исходя из этого, для распределе-
ния напряжений в верхнем слое можно считать, что
где Vj — коэффициент, характеризующий распределительную спо-
собность материала верхнего слоя.
Для решения вопроса о распределении напряжений в нижнем
слое отбросим верхний слой и связи заменим реакциями, которые
согласно зависимости (10.14) можно выразить как
где hr — толщина верхнего слоя.
Представим эту нагрузку как напряжения в однородном массиве,
сложенном из материала второго слоя. Для этого необходимо найти
эквивалентную замену параметрам верхнего слоя через параметры
нижнего слоя. Поскольку параметры материала остаются неизмен-
ными, то можно варьировать толщину слоя. Определим эквивалент-
ную толщину.
Из формул (10.14) и (10.15) имеем
(10.16)
где hA— эквивалентная толщина;
v2 — коэффициент распределительной способности среды вто-
рого слоя.
Эквивалентная толщина
(10.17)
При этих условия* выражение (10.15) преобразуется:
/ю=%.=^]/ЧЬехр(-^Н- (,0Л8)
Здесь h31 можно рассматривать как вертикальную координату
в однородном массиве, состоящем из материала второго слоя. Тогда
для точки с координатой z во втором слое
о = —------1/ —— ехр (--------------'i.	(10.19)
йэ, + г V	Ц 2v,(ft„ + 2)«J	'
Произведя подстановку (10.16) в зависимости (10.2) и (10.3),
получим
---V	для г = л,;	(10.20)
152
а* = v.%1 +	для 2 = Ai> (Ю.21)
x« =— У	для z = йа;
°- = V (V2°M + ^2Э1 Для 2 = h*
(10.22)
(10.23)
Из зависимостей (10.22) и (10.23) по аналогии с формулой (10.19)
для касательных и горизонтальных нормальных напряжений во
втором слое для точки с координатой z можно считать, что
-----МЛ,, + г) ;	(10.24)
F 'г	дх
о, =	[*2%, + г + V22(Лм 4- z)‘ ->,+* 1	(10.25)
v2 L 1	дл® J
Касательные напряжения, соответствующие вертикальным на-
пряжениям,
дЧ + Z
Ъ =- *2 (Лэ1 + г)---•	(Ю.26)
ОХ
т. е. полученные значения отличаются от тех, которые соответствуют
формуле (10.19), на множитель
Аналогично для горизонтальных напряжений
^=v2oh91+.4-v»(^14-z)2—±
(10.27)
Это выражение отличается от выражения (10.25) также множите-
лем —.
Рассмотрим далее трехслойную систему. Обозначим толщину
второго слоя через Л2. Согласно формуле (10.19) вертикальные на-
пряжения на границе второго и третьего слоев
+ ht г	Р \	2v4 (ЛЭ1 + /ц)2
(10.28)
По аналогии с предыдущим эквивалентная толщина через пара-
метр распределяющей способности третьего слоя определится из
выражения
(Лм+А»)|'Ч = Л»»Иъ
(10.29)
153
откуда
Тогда
°г-л1+/ц = Т~1/"-Л-ехр (------•	(Ю.З!)
«иг	I Zv3ft32 /
Горизонтальные и касательные напряжения, согласно зависимостей
(10.24) и (10.25), будут
т Ь".я +	<ю'32>
"0 33>
На основе зависимостей (10.31), (10.32) и (10.33) получим
следующие формулы для определения напряжений в третьем слое
°г Лм + г ]/ 2kv, еХр[ 2v3(ftM + г)’] ’	<1°*34)
’« = V [+ *1(йм + г)4	;	(10.35)
ъ =- /Z v, (лм+2)	.	(Ю.36)
Аналогично для многослойной среды эквивалентная толщина
вышележащих слоев
«.-»,/?+*/?+ +v.]AF- (“>•’’>
где	hn__x — толщины слоев;
ул — коэффициенты распределительной спо-
собности материалов слоев.
Затем, располагая начало координат на границе п—1 и п слоев,
по формулам (10.34), (10.35) и (10.36) определяем напряженное со-
стояние л-го слоя.
§ 3. НАПРЯЖЕНИЯ В МНОГОСЛОЙНОЙ СРЕДЕ ОТ НАГРУЗКИ,
ПРОИЗВОЛЬНО ЗАДАННОЙ В ПЛОСКОЙ ЗАДАЧЕ
Напряжения на границе между первым и вторым слоями опреде-
лим по формулам
- % -V /-5^1 /В”Р [-	<10-3”
154
’z = V*. + -'?ft?77':	(1039)
--"Л-Т1--	(10.40)
OX
Если в этих формулах сделать замену согласно соотноше-
нию (10.16), то напряжения на границе двух слоев будут выражены
через параметр коэффициента распределяющей способности нижнего
слоя, т. е.
___________________________
\ - ч - £ j (-) * (ЮЛ1>
°* =	для z = йэ1; (10.42)
(Ю.43)
Тогда напряжения во втором слое
X*. - 7^Рм-жИ*
—ь
(10.44)
(10.45)
(10.46)
=- V v (Аэ1+*) -’У*
Для г = h2t сделав в этих формулах подстановку из зависимости
(10.29), получим толщину эквивалентного слоя, определяемую фор-
мулой (10.30); таким же образом для многослойной системы получим
формулу для эквивалентного слоя, тождественную формуле (10.37).
§ 4. НАПРЯЖЕНИЯ В СЛОИСТОЙ СРЕДЕ ОТ СОСРЕДОТОЧЕННОЙ
ВЕРТИКАЛЬНОЙ НАГРУЗКИ
Как и для плоской задачи, получим составляющие давления на
границе двух верхних слоев системы:
р (	+	\
= 0*. = ^ехР
(10.47)
(10.48)
155
° ~ v.a. 4" ^Л? ——; У	1 "	1 1 Л/2 ’	(10.49)
т =_./Л хг	1 1 ал- ’	(10.50).
t — зй ±*1.. "2_	11 ду '	(10.51)
Тг,. =	 V.Al. 	— . 1 1 дхду	(10.52)
Сделав подстановку из выражения (10.16), получим	
Р	/ х2 + у2 \ .	(10.53)
&v^,CXP(	2,А )’	
= V	Для г = й,;	(10.54)
°« =	(”2Ч1 +	для г = Л*:	(10.55)
=—	для Z = йр Г V2	дх	(10.56)
\г =— 1/^7 '^31	ДЛЯ Z = Лр	(10.57)
- -1/з:,й - V V,	дхду •	(10.58)
Выражения (10.20), (10.21) и (10.23) позволяют, как и для пло-
ской задачи, получить следующие приближенные формулы для на-
пряженного состояния второго слоя:
ог =---------------ехр Г------+ -1;	(10.59)
2nv2(/>M + z)’ L 2МЛЭ1 + *)’]	'	'
Г	4-Z 1
°* = ^7	(ЛЭ1 + г)2 ——j ;	(10.60)
% = -%	+ МЛ* + г)2 —^-] ;	(10.61)
=— *г (A,i + г) —>	(Ю-62)
’2031 + г) —.	(10.63)
156
Полученные выражения аналогичны зависимостям для плоской
задачи; таким образом, и в пространственной задаче для сосредото-
ченной нагрузки эквивалентная толщина определяется по формуле
(10.29).
§6. НАПРЯЖЕНИЯ В СЛОИСТОЙ СРЕДЕ ОТ ПРОИЗВОЛЬНО ЗАДАННОЙ
НАГРУЗКИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
Пусть нагрузка на поверхности распределена по площади F
и выражена зависимостью
4 = f(x,y).	(10.64)
Как и в предыдущем случае, давление на второй слой опреде-
лится из формул:
- J[“ "~ам~а’] 1 '°'651
/=•
+	(»о.бб)
дЪ.
= + <10-67>
=— Vj/ij	для z = ht;	(10.68)
OX
c, =— Vjft]	для г = Л,;	(10.69)
ду
= 4ihi —— для 2 = ft,.	(10.70)
дхду
Используя выражение (10.17), получим
F
Формулы для горизонтальных и касательных напряжений бу-
дут аналогичны формулам (10.55), (10.56), (10.57) и (10.58), но ал
должно быть определено по формуле (10.71). Согласно этим форму-
лам и (10.71) напряженное состояние второго слоя приблизительно
можно определить из выражений:
О =----------!-----С/(ч. 7))ехр|—	(10.72)
А.1+‘	2^01,1 +г)’ J7 и1 2у4(Лэ1 + г)2 J '	'
°, =	i(Л„ + г)—:	(10.73)
157
°. = t	+ Z)S “V2-];	<l0-74)
=“ / V <лм + *) Ч —g‘‘+±-:	(Ю-75)
V /¥<Л»> + г)^-%^..;	(Ю.76)
r v2	ay
+	(10.77)
Таким образом, для эквивалентного слоя многослойной системы
получим зависимость, тождественную (10.29).
Глава 11
ПРИМЕНЕНИЕ ТЕОРИИ О НАПРЯЖЕННОМ СОСТОЯНИИ
К НЕКОТОРЫМ ЧАСТНЫМ СЛУЧАЯМ ЗАГРУЖЕНИЯ
ОСНОВАНИЯ
§ 1. НАПРЯЖЕНИЯ от ЛИНЕЙНОЙ ВЕРТИКАЛЬНОЙ НАГРУЗКИ
Вертикальные напряжения от нагрузки, изображенной на
рис. 11.1, /,
По вертикальному напряжению касательные напряжения
(112)
<"3>
Горизонтальные нормальные напряжения
°* = w»+	(11-4)
158
Рис. 11.1. Расчетные схемы плоского и пространственного
загружения грунтового массива
Вычислим вторую частную производную, учитывая, что первая
производная согласно выражениям (11.2) и (11.3) равна

(11.5)
159
Дифференцируя это выражение по х, имеем
д2?г_____0^____х d<s2
дх2 — vz2	vz2 дх ’
или, подставляя сюда выражение (11.5), получим
д2^ ________ аг ! х2
дх2 ~ \za v2z* °г*
Подставляя это выражение для второй производной в формулу
(11.4), имеем
X2 х2
Рх2 ( X2 \
§ 2. НАПРЯЖЕНИЯ ОТ НАГРУЗКИ. РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ
ПО БЕСКОНЕЧНОЙ ПОЛОСЕ
От нагрузки, распределенной по полосе (рис. 11.1, IV), верти-
кальные напряжения в каждой точке грунтового массива опреде-
лятся как от суммы нагрузок, распределенных по элементарным
площадкам, т. е.
+ь	_____
J("'6)
—и
При постоянной нагрузке
/(0 = Р-
Тогда выражение (11.6) примет вид
+&
••—р V~S- J “р [-	<* - в*]*
Для точек, находящихся на оси г, выражение для напряжении
получится из зависимости (11.7), если считать х = 0:
-(тй)-
160
Из выражения (11.7) легко установить, что для точек, находя-
щихся под полосой, при г -> 0 напряжение -> р, а для точек, на-
ходящихся вне пределов полосы загружения, при г -> 0 напряже-
ние -+ 0, т. е. решение удовлетворяет граничным условиям.
Касательные напряжения
да,
“	1/2 дх
f “
Горизонтальные напряжения определяются по формуле (11.4):
После дифференцирования и некоторых преобразований получим
+ тй ['* + ‘> (-	(-^)1 
§ 3. НАПРЯЖЕНИЯ ОТ НАГРУЗКИ, РАСПРЕДЕЛЕННОЙ НА ПОЛОСЕ
ПО ЗАКОНУ ПАРАБОЛЫ
Пусть распределение нагрузки по полосе (рис. 11.1, VI) опреде-
ляется уравнением
/W-p(i-i).
Тогда вертикальные напряжения в любой точке грунтового мас-
сива
Через табулированные функции этот интеграл может быть пре-
образован
J61
Для точек, находящихся на оси г, при х = 0 получим
,, = Р Г( 1 _	ф \ + ехр(- -М1.
° |д & J \*Kv/	\ 2vz /J
Выражением (11.8) в общем виде определяется характер распре-
деления напряжений от нагрузки в пределах полосы по закону па-
раболы.
Для вычисления касательных напряжений определим частную
производную по х:
± х2иФр + 6У —
+(-
1НФ(771)-Ф(77Г)]-
Тогда касательные напряжения
^[Ф(^)-Ф(Ш
Для определения горизонтальных нормальных напряжений про-
дифференцируем по х выражение (11.9):
L 2^ )	*4	2«=
Горизонтальные напряжения
• = ^С-^-7)[ФШ-Ф(7#)]-
§ 4. НАПРЯЖЕНИЯ ОТ ЛИНЕЙНОЙ ПОЛОСОВОЙ НАГРУЗКИ
Пусть согласно рис. 11.1, III нагрузка по полосе выражается
уравнением
/(x) = Q(x + «.
где Q — некоторая постоянная величина.
162
Вертикальные напряжения от такой нагрузки
z]/2v;c J	\	2'Z2 /
-ь
-“^[Ф(7#)-*(77Г)]-
Для определения касательных напряжений продифференцируем
по х это выражение:
тогда касательные напряжения
Для определения горизонтальных нормальных напряжений
продифференцируем по х выражение (11.10):
-----М«ф (—Цг^-М1 -	X
**	L F\ ъ* ) \	)
горизонтальные напряжения
ох = V9, + **2^+-$
Qzv/7

2
(х + Ь)2
2vz2
(х-6)»
2vza

26 (х —6)
163
или
Q v(b I X)
2
! b(b-x)
NZ2
(x + Ь)8
2vz«
2Qz't /v
V 2л
Хехр
(х~Ь)»\-|
2vza / ] *
$ 5. НАПРЯЖЕНИЯ ОТ ВЕРТИКАЛЬНОЙ ТРЕУГОЛЬНОЙ НАГРУЗКИ
Для решения данной задачи можно использовать результаты
предыдущего параграфа. Прежде всего вычислим напряжения от
линейной нагрузки, изображенной на рис. 11.1, //; напряжения
от такой нагрузки могут быть получены как разность напряжений
от равномерно распределенной и линейной нагрузок.
Вертикальные напряжения
-“₽(--(»•">
Горизонтальные нормальные напряжения
-=-^[фШ-ф(^)]+
+М2Фш-фт-ФМ1+
+^Я(2+^Н-^)-
"Ll2>
Касательные напряжения
("'3>
164
$ 6. НАПРЯЖЕНИЯ В ЗЕРНИСТОМ ГРУНТОВОМ ОСНОВАНИИ
ОТ ТРАПЕЦЕИДАЛЬНОЙ НАГРУЗКИ
Напряженное состояние зернистого грунтового основания от
трапецеидальной нагрузки можно определить как разность напря-
женных состояний от двух треугольных нагрузок с разными осно-
ваниями, ио одинаковыми наклонами граней, т. е. с одинаковыми
величинами Q. Пусть нижнее основание трапеции (рис. 11.1, V)
равно 26, а верхнее 2В. Тогда, пользуясь зависимостью (11.11),
для вертикальных напряжений получим
На основании зависимости (11.12) имеем значение горизонталь-
ных напряжений


- --5Й-) •“>’(
(ж— В)*
2vz2
(* + Д)а\1
165
Пользуясь формулой (11.13) для касательных напряжений, по.
лучим
§ 7. НАПРЯЖЕНИЯ ОТ НАГРУЗКИ. РАСПРЕДЕЛЕННОЙ В ПЛОСКОЙ
ЗАДАЧЕ ПО ЗАКОНУ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ
Пусть согласно рис. 11.1, VII нагрузка задана выражением
/(х) = Р1ехр(-С1х2),	(11.14)
где — постоянные параметры функции.
Вертикальные напряжения от этой нагрузки
°, -----(* ехр (— С15») ехр (— (*~{)* ) <й.
zV2r^ J	\ 2vz2 }
— OP
Решим этот интеграл
Ог------. Р1 ехр (----------——).	(11.15)
Kl+2vC,z’ Ц 1 + 2^»/	'
Из сравнения этого выражения с (11.14) можно установить, что
достаточно величину Рг разделить на выражение у 1 + 2C^z2, а
Ci на квадрат этого выражения, чтобы получить формулу для вер-
тикальных напряжений.
Касательные напряжения
vz[ 177+2^ 1 + г'с.г* х
Хехр(- тгй^-)]’
или
___________2Р1С1\хг	(_____х* \ _ 2CjVXZ
/(1 + 2^С1гг)» Р\ 1 + 2vCiZ* / ~ 1+2^ г'
Для определения горизонтальных напряжений возьмем вторую
производную по х от о,.
d8», ==_ 2Ct о ,	4С1*8 о
дхг 1 + 2Срг» °* + (I + 2CPZ8)» °г’
16S
Тогда
или
gg <ф
U+lbC.z»)*
ZC^z*
l + 2CPz» °J
4?z2
(1 4- Z^z*?	1 4- 2Cpz2
2Cpz8
где a2 определяется из выражения (11.15).
§ 8. НАПРЯЖЕНИЯ ОТ СОСРЕДОТОЧЕННОЙ ВЕРТИКАЛЬНОЙ
НАГРУЗКИ
Формула (9.7) выражает вертикальное напряжение от сосредото-
ченной силы. Это же выражение является решением уравнения
(9.60). Если в нем гг заменить л2 + у2, то оно примет вид
Р / л2 + у® \
°‘=-^ГеХР(--------2^-)-
В таком виде оно является решением уравнения (9.48). Исполь-
зуя соотношения (9.54) и (9.55), для горизонтальных напряжений
получим:
Из зависимостей (9.43), (9.44) и (9.56) вытекают следующие вы*
ражения для касательных напряжений:
_______* Р*	*2 + уа
хг	2 2	2™z® е Р \	2vz« ) ’
,_______У_а , Ру
ч ~ г» а‘~	2k-,z< еХр (	2w« / ‘
В цилиндрических координатах эти зависимости примут вид
а  ------------------— ехр (---—'j;
г 2?ivz2 r 2vz* )
г*	Рг* / г« \
^4-°‘=--Й5-ехр(-т5-);
О0 = 0; s» = °; St = °-
167
$ 9. НАПРЯЖЕНИЯ от нагрузки, описываемой показательной
функцией В ПРОСТРАНСТВЕННОЙ задаче
Пусть вертикальная нагрузка на поверхности массива выра-
жается зависимостью
/(г) = Р1ехр(-С1га),	(11.16)
где и Q — постоянные параметры.
Вертикальные напряжения от такой нагрузки
°»=— f f ехр I— С,(5s + 7|»)J X
— ©о —oo
Решив этот интеграл, получим
---------------£--------------ехр f_V
2___________________________________\	1+2>C1Z2 )
Сопоставление полученной формулы для вертикальных напря-
жений с выражением (11.16) показывает, что в рассматриваемом слу-
чае интегрирование сводится к делению параметров Рй и Ск на вы-
ражение (1 + SvCjZ2).
Другие составляющие напряжения:
д vz( Pl_______2C'r
dr \ 1 + 2»с^ 1 + 2^2»
x»"(—bflfer)-
___ 2Ctr<z
I + 2^2* 9 v
7. , 4Cpr«z«	2Cpz« \
G, v 11 4-	-----------------------1 o,
r \	(H- 2uC^ 1 + 2Cpz2 / 2
=	J- 4Ci'tr2zi \.
l+2Cpz« \ l + ^/CjZ* /’
i Л 1
2CP^
l+2vCtzt
или
2Cpza \ g
1 -h 2 ,ClZ* I 2	1 + 2>С1г« ’
168
Для напряжений на оси симметрии, т. е. при г = 0, формулы
принимают вид
ог ---------—------; т = 0;
/ * 2Ci'a2 \	vsz
о_ = ofl = v (1--------------] a =--------------.
r ®	\	1 + 2vCjz2 } г	1 + 2W
§ 10. НАПРЯЖЕНИЯ ОТ НАГРУЗКИ, РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ
по прямоугольнику
Для определения вертикальных напряжений в этом случае
(рис. 11.1, XI) воспользуемся формулой
Как видно из этой формулы, решение сводится к отысканию со-
ответствующих данных плоской задачи. Подобная плоская задача
была ранее рассмотрена. Поэтому выражение (11.17) принимает
вид
х[фШ-ф(трт)]' (1М8)
Формула (11.18) представляет в общем виде зависимость для
определения вертикальных напряжений в грунтовом массиве от на-
грузки, равномерно распределенной по площади прямоугольника
со сторонами 2b X 2а.
Горизонтальные нормальные напряжения:
169
[« + «>«Р(-	О/-»)ехр(-	] ] X
Касательные напряжения:
§ 11. НАПРЯЖЕНИЯ ОТ ПАРАБОЛИЧЕСКОЙ НАГРУЗКИ,
РАСПРЕДЕЛЕННОЙ ПО ПРЯМОУГОЛЬНИКУ
Пусть распределение нагрузки по площадке (рис. 11.1, XII)
выражено зависимостью
/(х, у) = р(1--£-) (1(11.19)
Здесь нагрузка представлена как произведение двух функции,
одна из которых зависит только от л, а вторая от у. Поэтому верти-
кальные напряжения также определяются как произведение двух
функций, т. е.
(*-6)а
2vz*
(у —*>)*
2vz«
(11.20)
Формула (11.20) представляет собой произведение двух анало-
гичных решений для вертикальных напряжений в плоской задаче
170
от параболической нагрузки, распределенной по полосе. Поэтому
Для параболической нагрузки, распределенной по квадрату,
формула (11.21) при b = а примет такой вид
(х + б)"
_____
Ь2 Ь2
I (у-ьр
^)11
(11.22)
Для точек, находящихся на вертикали, проходящей через угол
прямоугольной площадки, зависимость для напряжений получим
из этой же формулы, приняв х = Ь\ у = а:
171
Для точек, находящихся на оси загруженной площадки, зависи-
мость для напряжений получим из формулы (11.22), приняв
X = у = 0:
Для нагрузки, распределенной по прямоугольнику
Все полученные в данном параграфе формулы можно предста-
вить через среднее давление на площадку, если подставить значение
где рср — среднее давление на площадку.
Горизонтальные нормальные напряжения
<72
Касательные напряжения:
Так же, как и для вертикальных напряжений, из этих общих
формул можно получить частные значения.
§ 12. НАПРЯЖЕНИЯ В ЗЕРНИСТОЙ СРЕДЕ ПРИ НАГРУЗКЕ.
РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО ПЛОЩАДИ КРУГА
(РЕШЕНИЕ Б. С. РАДОВСКОГО)
Поставленная задача (рис. 11.1, X) представляет практический
интерес при расчете оснований сооружений с круглой подошвой.
Вертикальные нормальные напряжения в произвольной точке
173
М (г, z) полупространства могут быть определены путем интегри-
рования решения [43 ] для сосредоточенной силы по площади круга
R 2х
о2(г,	=	ехр[—-J^-(p24-r2 —2rpcos?)jpdpd<p, (11.23)
о о
где г, г — координаты рассматриваемой точки;
R — радиус круга, по площади которого равномерно распре-
делена нагрузка интенсивностью р;
v — коэффициент распределительной способности среды.
Для точек, расположенных под центром штампа (г == 0), интег-
рал (11.23) значительно упрощается
°г (0, г) = р [1 - ехр g-J ] •	(11.24)
Однако вследствие трудностей интегрирования выражения
(11.23) для произвольной точки массива отсутствует выражение для
определения напряжений.
Р. А. Муллер, исходя из математической аналогии между про-
цессом распределения вертикальных нормальных напряжений в
зернистой среде [63] и процессом блуждания броуновской частицы,
показал, что распределение вертикальных нормальных напряже-
ний выражается дифференциальным уравнением параболического
типа. Это уравнение при осесимметричной задаче в цилиндрических
координатах имеет вид
। 1
дг	\дг^ г дг )•
(11.25)
Чтобы получить выражение az (г, г) для произвольной точки
массива, проинтегрируем уравнение (11.25). Для приведения к ка-
ноническому виду дифференциальных уравнений параболического
Получим
(11.26)
типа заменим переменную по формуле и = —
= 1 1
ди \ дг2 г дг /
Уравнение (11.26) решается при следующих условиях, опреде-
ляемых внешней нагрузкой,
=/(')=Ипри 0$rD<R;	(1127)
I 0 при г > R\
а также при условиях
(11.28)
о2 -> 0 и —-> 0 при г -> со.
дг
Для решения уравнения (11.26) применяем преобразование
Лапласа
F{rt s) = Г o2(r,u) е Stt du.
(11.29)
174
Преобразованное уравнение (11.26) примет вид
+±.^^-а,-^Гг(г> S)-Z!ll=o
dr*	Г dr	V [ ' • ' S J
и представляет модифицированное уравнение Бесселя. Его общее
решение
F(r, s)-^ = AI0(y^r) + BKe(y±r),
где Z®( Vvr) и *•(	— соответственно функции Бесселя
' N к v ' первого и второго рода нуле-
вого порядка от чисто мнимого
аргумента;
А и В — постоянные величины.
Определяя постоянные из условия (11.27) и преобразованных ус-
ловий (11.28) и (11.29) с учетом некоторых соотношений, известных
из теории Бесселевых функций, получим Лапласово изображение
искомой функции а2 (г, z):
при
при г > R
F(r, s) = --?
где /j ( jZ-7- R— соответственно функции Бес-
'	4	' селя первого и второго рода
первого порядка от чисто мни-
мого аргумента.
Оригинал полученного изображения отсутствует в каталогах;
поэтому для обратного преобразования используем общую формулу
обращения Меллина
I ’ V”
°z(c = J exp(su)F(r, s)ds,
7-/»
имеем
"•‘'“’--sr'f	У?')»
Т-»
X ( )/ v ]exp(s«)d«.
175
В соответствии с правилами операционного исчисления заменяем
путь интегрирования в комплексной плоскости вдоль прямой, па-
раллельной мнимой оси. замкнутым контуром, имеющим разрез
вдоль всей отрицательной части вещественной оси. Тогда получим
“> -	4 /4(f	<•»>
ог(г, = Л(G x)Jj(R, х)ехр(— vux2)dx, (11.31)
о
где Jo (G х) и Ji(R, х) —функции Бесселя первого рода соответст-
венно нулевого и первого порядка.
При г = 0 имеем
Ог (О, и) = pR § Jl(Rx)wp(-'mx2)dx. (11.32)
О
Так как непосредственно вычислить последний интеграл затруд-
нительно, дифференцируя, получим
<Ь2 (0» ц)
du
= —pRvj	(R, x)exp(— уцх®)хМх.
0
(11.33)
Правая часть (11.33) содержит первый экспоненциальный инте-
грал Вебера, выражающийся через соответствующую экспоненци-
альную функцию. Подставив эту функцию в (11.33), получим после
интегрирования
оДО, U) = pp— ехр(— -£-)]•	(11.34)
Подставив в выражения (11.31) и (11.34) значение z из уравне-
ния и = ~, получим искомую формулу для определения верти-
кальных нормальных напряжений в произвольной точке массива
аг(г, Z) = pR^ J„(r, х) (R, x)exp(—dx, (11.35)
О
а для точек, принадлежащих оси симметрии,
в,(0, г)=р[1-ехр(--^)].
Последняя формула идентична с выражением (11.24).
По формуле (11.35) построены изолинии вертикальных нормаль-
ных напряжений (рис. 11.2, а). При вычислениях принималось
7 = Т •
176
Можно показать, что выражение для вертикальных нормаль-
ных напряжений, предложенное К. С. Теренецким, при г > R
с достаточно высокой точностью аппроксимирует решение (11.35)
при том же условии.
Используя полученное выражение, можно вывести формулы для
остальных компонентов напряжений.
Так, для касательных напряжений
\,г(г, г) = —
Рис. 11.2. Линии равных напряжений от равномерно распределен*
ной нагрузки по площади круга для 1/3
а — вертикальных пап ряжен и Л; б — касательных напряжений
Дифференцируя (11.30) и подставляя результат в (11.32), по-
лучим
|1,Ж>
причем для точек, лежащих на оси давления, \ г (0, г) = 0. По
формуле (11.36) построены изолинии касательных напряжений
(рис. 12.2, б).
Для произвольной точки массива аналогично
«’«(б	=
ог (г, z) = vo2
«• РI 2w«
)[«'•(-)-

т
Для точек, лежащих под центром штампа,
°о (0, г) = аг (0, г) = vaz (0, г) -	ехр (—
Таким образом, получены все компоненты напряженного состоя-
ния произвольной точки полупространства, состоящего из зерни-
стого материала.
§ 13. НАПРЯЖЕНИЯ ОТ НАГРУЗКИ, РАСПРЕДЕЛЕННОЙ ПО ПЛОЩАДИ
КРУГА ПО ЗАКОНУ ПАРАБОЛЫ (РЕШЕНИЕ Б. С РАДОВСКОГО)
Пусть характер распределения нагрузки
(рис. 11.1, IX) выражен уравнением
по кругу

Решая так же, как для равномерно распределенной нагрузки,
дифференциальное уравнение
dz \ дг* г дг /
при условиях, определяемых внешней нагрузкой,
"РиО<г<Л;
J 0 \	/ при г > к,
а также при условиях
Ч.</°°
о,-* 0 и — ->0 при г->со,
можно получить выражение для вертикальных нормальных напря-
жений в произвольной точке зернистого массива
Сг(г, Z) = 2P,J J0(r, x)A(P,x)exp(-^)4> <1L37)
где Jo (г, x) и J2 (R, x) — функции Бесселя первого рода соответст-
венно первого и второго порядка.
Определим напряжения в точках, лежащих на оси симметрии
(г = 0). Из формулы (11.37) имеем
vzM । dx
2 / к
са(0, z) = 2Pol
A (R. х)ехр
(11.38)
178
В формуле (11.38) произведем замену переменной
k = xR\ dk = Rdx,
получим
оДО,г) - 2Р„ J А(Л)ехр(-/А2)^-,	(11.39)
О
где
2R2
Продифференцируем выражение (11.39)
г)- = — 2Рвf (А) ехр (— tk*)kdk. (11.40)
dt	о
Из теории Бесселевых функций известно, что
/2(й)=4-л(л)-а(*). (идо
Подставляя (11.41) в выражение (11.40), получим
±£^. = _4Pof JI(fe)exp(-/F)<tt +
Ot	о
4-2Pof J0(Jfc)exp(-/F)faft.	(11.42)
О
Первый интеграл правой части уравнения (11.42) нами рассмот-
рен при выводе формулы для вертикальных напряжений от на-
грузки, равномерно распределенной по кругу,
j А(Л)ехр(-«*)<№= 1-ехр(-(11.43)
Второй интеграл представляет первый экспоненциальный ин-
теграл Вебера
j /.(ft)exp(-ik^kdk = 2.ехр (- 2-j.	(11.44)
Подставляя значения интегралов (11.43) и (11.44) в уравнение
(11.42), получим
= - 4Р0 + 4Р0ехр (- 2.) +	ехр(- 2.). (11.45)
179
Интегрируя уравнение (11.45)» получим
(0> г) = — 4tPo [ 1 — ехр -j-)] + С,
где С — постоянная интегрирования.
Из условия
«ДО, 2)|	+ Р0
'/-о
имеем
С = Р0.
Таким образом, вертикальные напряжения в точках, находя-
щихся на оси z,
Это совпадает с ранее полученным решением для вертикальных
напряжений по оси круга, загруженного параболической нагрузкой
[43 J.
Дифференцируя формулу (11.37), найдем выражение для каса-
тельного напряжения в произвольной точке массива
= — 2Р0'г J Jt(г, х) J2(R, х)ехр	dx.
О
Приводим выражения для определения других компонентов на-
пряжений
0o(Gz)= «2(г,
а, (г, г) =	(г, z) + 2P0v2z2
xdx—
— 4“ I Ji(r, *) x)exp(—
§ 14. ДАВЛЕНИЕ НА ПЛОЩАДКУ, РАСПОЛОЖЕННУЮ НА НЕКОТОРОЙ
ГЛУБИНЕ ОТ НАГРУЗКИ, РАСПРЕДЕЛЕННОЙ ПО КВАДРАТНОЙ
ПЛОЩАДКЕ
Определим суммарное давление на квадратную площадку, рас-
положенную на глубине z, от вертикальной нагрузки, равномерно
распределенной по такой же площадке на поверхности зернистого
основания. Данная схема соответствует опытам, проводившимся
Пенсильванским колледжем.
160
Рассмотрим случай, когда площадка на глубине смещена по оси
х и не смещена по оси у по отношению к загруженной площадке на
поверхности.
Вертикальные напряжения от нагрузки, равномерно распреде-
ленной по площади квадрата
о,= Р_|ф /'Л±*\_ф/^\1Гф/£+»\_ф/£хП1.
4 I J I z v III I ?У7 I I zpS )J
(11.46)
Для того чтобы определить давление на некоторую площадку на
глубине z, необходимо проинтегрировать выражение (11.46) по этой
площадке, т. е.
х+ь +ь
«[[ф^-фМ]х
4 J J L \г/	\ гУ'1 / J
jt—Ь —Ь
х f ф - ф (1 *J.	(П.47)
[ \zysj \ 2 У V ]J
После интегрирования имеем
Рх= {(, + 2Ь)Ф + (х-26)Ф	-
_ 2хФ ( « ) + 4В [ехр (-	ехр (- ^1) -
\ z У v /	У v [	\ 2vz2 /	\ 2vza /
_ 2ехр (_ jqll U Ф ( » )	[1 - ехр (- —)1|.
\ 2\za/JJ I \z/v ) У? L \
(11.48)
Определим отношение давления на площадку на глубине г к дав-
лению на штамп, равному
Ра = 4Ь*р,	(11.49)
где р — интенсивность нагрузки;
b — половина ширины штампа.
Делим выражение (11.48) на (11.49). Получим
-Н--Ш '"'вд
181
Для горизонтальной площадки, расположенной на глубине г
строго под загруженной площадкой, выражение (11.50) примет вид
(при х = 0)
Определим величину давления на квадратную площадку на глу-
бине z при распределении нагрузки на поверхности по площади
квадрата на основании параболического закона. Вертикальные на-
пряжения в этом случае
(11.52)
где рср — среднее давление на штамп.
Для определения давления на площадку проинтегрируем выра*
жение (11.52), получим
182
После интегрирования получим следующую формулу для дав-
ления на площадку:
Разделим выражение (11.53), определяющее давление на пло-
щадку, на величину нагрузки на штамп:
Ра=№рср.
После деления получим формулу, определяющую отношение
давления на площадку к нагрузке на штамп, т. е.
2х .
b U2 +
[72L4-2Y +
зь ут |д b	I

183
^[(тг-'Н-£)-Я- <"S4>
При положении площадки под штампом» т. е. если х = 0, фор-
мула (11.54) преобразуется к виду
§ 16. ВЕРТИКАЛЬНЫЕ НАПРЯЖЕНИЯ ПО ОСИ КРУГА,
ЗАГРУЖЕННОГО КОНУСООБРАЗНОЙ НАГРУЗКОЙ
Характер распределения нагрузки по кругу (рис. 11.1, VIII)
выражается уравнением
Для решения вопроса о распределении вертикальных напряже-
ний по оси круга, как и в случае параболической нагрузки, вос-
пользуемся формулой
/[<?; F(r, а, <р)] ехр | — -v)j —/(?, 0) —

(11.55)
Параметры и функции этого выражения для рассматриваемого
случая имеют следующие значения

F (г, а, <р) = R-,
/(f. *)=/(К) = 0;
/(?. 0) = /(0) = Р;
= 2Р;
д/(у. ’i)р _______ч\  _____Р_
<4 \ Я /	Я
184
После подстановки этих значений формула (11.55) примет вид
После интегрирования и подстановки пределов получим
= р[1—-1Л2»к ф(_*_YI.
L 2R r 1 г Л
§ 16. НАПРЯЖЕНИЯ ОТ ГОРИЗОНТАЛЬНЫХ НАГРУЗОК
Рассмотрим распределение напряжений от сосредоточенной
силы. Приведем решение, полученное Р. А. Муллером [621. По-
скольку внешняя нагрузка направлена здесь вдоль оси л, то в урав-
нениях, составленных для вертикальных напряжений, поменяем
местами переменные х и г. В результате для напряжения ах в пло-
ской задаче получим уравнение
дх дг2
(11.56)
Для сосредоточенной горизонтальной силы это уравнение ре-
шается при следующих граничных условиях:
прих->0)
при г -> со ох -> 0;
при г < 0 ах = 0;
при z = 0	= 0.
Решение уравнения (11.56) при указанных граничных условиях
Вертикальные и касательные напряжения в этом случае
Z2
Z
Ххг — Xzx- х ах*
Для сосредоточенной нагрузки горизонтальные напряжения
ах = + —— ехр (—	I Хгх = ~ ах\
2тх2 \ 2vxa /	*
185
У
~ Уг	Уг
у- °*;	V“ Х2 в*-
Для плоской равномерно распределенной горизонтальной на*
грузки (рис. 11.3)
Z1
Рис. 11.3. Схема к расчету напряжений
от горизонтальной равномерно распре-
деленной полосовой нагрузки
где	т — интенсивность горизонтальной на-
грузки;
— Ei (— у) ss I ехР(~ 0, __ интеГральная показательная функ-
J * ция.
У
Для произвольной горизонтальной нагрузки в плоской задаче
решение для <зг можно получить путем интегрирования выражения
ал — Г —т=Х^==- ехр Г— -—г*	1
J 2лу (х — 6)2 L 2 v (х 8) J
—ь
o,= ^ + vW^;	(11.57)
186
Для пространственной задачи при направлении усилий вдоль оси х
= ± f г‘> ехр (- 2--+ to!) dK
* -j 2r.v(x-6)2 4	2v(x-e)2 /
Остальные компоненты напряжения определяются путем диффе-
ренцирования формул, аналогичных (11.57) и (11.58).
§ 17. НАПРЯЖЕННОЕ СОСТОЯНИЕ ЗЕРНИСТОГО ГРУНТОВОГО
МАССИВА У НЕПОДВИЖНОЙ ПОДПОРНОЙ СТЕНКИ i
Напряженное состояние для зернистой среды при принятой си-
стеме координат (рис. 11.4) может быть получено из следующих
уравнений (для плоской задачи,
принимая напряжения сжатия по-
ложительными):
О*-60)
Рис. 11.4. Схема загру жени я мас-
сива произвольной нагрузкой
у неподвижной подпорной стенки
+	(11.61)
где 7 — объемный вес грунта.
Уравнение (11.59) должно быть
решено при определенных на-
чальных и граничных условиях; начальным условием является на-
грузка на поверхности массива грунта
Ч-о = р(х)‘	(lL62)
Рассмотрим граничные условия для уравнения (11.59). Для не-
ограниченного массива, когда вертикальная сила в среде может
распространяться безгранично, граничным условием является
требование о том, чтобы в бесконечно удаленной точке производ-
ная напряжения стремилась к бесконечно малой величине, т. е.
— —> 0 при	со.	(11.63)
дх
Граничное условие у стенки должно соответствовать тому, что
вертикальная сила не может распространяться безгранично. Вер-
тикальное напряжение у стенки не передается полностью на ни-
жележащие слои грунта, а частично воспринимается самой стенкой
за счет сил трения и сцепления с грунтом из-за шероховатости
• § 17 написан Р. А. Муллером.
187
подпорной стенки. Если стенка абсолютно гладкая, то вертикаль-
ная сила полностью передается на нижележащие слои, касательные
напряжения между стенкой и грунтом равны нулю, т. е.
-^-=0прих = 0.	(11.64)
дх
Если стенка абсолютно шероховатая, то вертикальная сила вос-
принимается полностью ею и не передается на нижележащие слои,
т. е.
о2 = 0 при х=0.	(11.65)
Если стенка обладает конечной шероховатостью, то условия
(11.64) и (11.65) выполняются лишь частично. Тогда
+ Daz = 0 при х = 0.	(11.66)
Коэффициент D характеризует шероховатость стенки и имеет
размерность, обратную линейной. Если D = 0, коэффициент шеро-
ховатости стенки равен нулю, получим условие (11.64).
Если коэффициент шероховатости безгранично увеличивается,
D -> со, получим условие (11.65).
Отметим, что граничное условие (11.66) для уравнения (11.59)
является распространенным. В теории теплопроводности оно выра-
жает тот факт, что теплообмен между поверхностью тела и окружаю-
щей средой происходит по закону конвективного теплообмена т. е.
пропорционально разности температур тела и среды.
В теории блуждающих частиц и теории диффузии условие (11.66)
выражает тот факт, что на границе ряд частиц поглощается экраном,
а ряд частиц отражается и т. д.
Таким образом, для определения напряженного состояния
грунта необходимо решить уравнение (11.59) при начальном усло-
вии (11.62), граничных условиях (11.63) и (11.66), а также восполь-
зоваться выражениями (11.60) и (11.61).
Как известно, решение неоднородного уравнения (11.59) можно
представить как сумму решения неоднородного уравнения (11.59)
при нулевых начальных условиях и решения однородного уравне-
ния (11.59) при начальных условиях (11.62), т. е. как сумму напря-
женных состояний грунта от собственного веса и от поверхностных
нагрузок.
Рассмотрим эти задачи раздельно. Определим напряженное со-
стояние от собственного веса грунта. Нам необходимо решить урав-
нение (11.59) при граничных условиях (11.63) и (11.66) и началь-
ном условии
а2=0 при 2 = 0.	(11.67)
В теории теплопроводности готового решения этой задачи нет.
Задача осложняется тем, что коэффициент в уравнении (11.59) за-
188
висит от координаты z. Схема решения такова. Общее решение не-
однородного уравнения можно представить как сумму частного ре-
шения (11.68) и общего решения однородного уравнения при на-
чальном условии (11.67), краевых условиях (11.64) и (11.66), а также
дополнительном граничном условии, вызванном частным решением
(11.58)
«й = тг;	(11.68)
°xi = пг.
Задача сводится к решению уравнения
при начальном условии ог(х, 0) = 0
и краевых условиях -~-(0, 2) +	— а2(0, z)]=0;	(11.70)
<j2 = (со, г) = 0.
Иными словами, задача сводится к решению уравнения тепло-
проводности (11.69), когда температура среды есть функция времени.
Разность результатов решений уравнений (11.68) и (11.69) будет
общим решением уравнения (11.59). Уравнение (11.69) при условиях
(11.70) непосредственно не решается. После подстановки
4=т	(11-71)
уравнение (11.69) сводится к каноническому виду
=	(11.72)
а условие (11.70) к виду сг (х, 0) = 0;
^-(0, Z) + D к/й-оДО, г)1 =0;	(11.73)
OX	L	J
а,(со, т) =0.
Уравнение (11.70) при условиях (11.72) имеет известное в теории
теплопроводности решение
- /h V* [erfc гй _ ехр (vD4+Ох)егГс(^й+D
где
erfc = f ехр(— №)dx.	(11.74)
Функция erf с х —табулированная функция (erfcO = 1).
189
После проведения необходимых выкладок получим выражение
для вертикальных напряжений
<з2 = fz — -рехр
,/jLAerfc-A-
У 2v D ]/2>z
— exp (v 4- Dx\ erfc (—~=—Dz 1 Г—.
\ 2	)	\V2^z у 2 J
При D = 0
„	„	°z = V
При D = co
—^г) + 1*1/ -^-erfc-^.
2vz8/ у/ 2v l/2vz
(И.75)
(И.76)
(11.77)
Для решения (11.76) необходимо раскрыть неопределенность
в первой части выражения (11.75).
При х-^оо	(11.78)
Прн х = 0
°z = 7
, / к 1 Г1	/ D*z*\ r / D У*у \
1 / ----1 — exp v ——-1 erfc —z I
У 2у D	\ 2 J \]/2	/
(11.79)
Таким образом, вертикальные напряжения в массиве распреде*
ляются следующим образом. Вертикальное давление грунта у стенки
определяется по формуле (11.79); при z-> со
(11.80)
Коэффициент шероховатости D определяет наибольшую вели-
чину вертикального давления у стенки по формуле (11.80).
Дифференцируя выражение (11.75) по х, получим по формуле
(11.60) касательные напряжения в массиве
Выражение для ххг принимает вид
при D = 0	= 0;
при х -► со тХ2 -> 0;
при х= 0
-> /^7 Г / Г (dV2v \ «
= 12 у т l^exp (v —) erfc	г j -1
190
Дифференцируя выражение (11.81) по х, получим по формуле
(11.61) горизонтальные напряжения в массиве
= VO2 — fvj/v Z2D
, Г к / D2za . ~ \ е
]/ Техр\ ~ + Dx)erfc
Выражение для ах примет вид
при D = 0 сх = v?z;
X
V<2v z
при СО
при х= О
°* = п*;
Решение для напряженного состояния грунта удобнее предста-
вить в безразмерных координатах.
Введем следующие обозначения
КН ’
г =пИ\
х=тН.
Здесь Я —высота подпорной стенки.
Получим следующие выражения

I т!\ .
п — п ехр [——- + Т/и
r \ 2vn8/
erfc
(11.82)
f ля 1
+
m
J/r2v л
191
Соответственно напряжения в грунте у подпорной стенки при т = О

п9
К9
Рис. 11.5. Распределение
горизонтального давления
грунта на подпорную стен-
ку от собственного веса
грунта в зависимости от
коэффициента шероховато-
сти при коэффициенте бо-
кового распора грунта v =
= 0,7
Напряжения в грунте вдали от под-
порной стенки стремятся к следующим
величинам
° г = tz;
= 0;
= П*-
На рис. 11.5 показано распределение
горизонтального давления на стенку —
по формуле (11.83) при v = 0,7 и раз-
личных величинах К или коэффициента
шероховатости по формуле (11.82).
Определение напряженного состояния
грунта от поверхностных нагрузок
при засыпке
Пусть на засыпке действует сосредо-
точенная линейная нагрузка (рис. 11.6).
Необходимо решить однородное уравне-
ние
—- = vZ ——
дг дх9
(11.84)
при краевых условиях (11.63) и (11.65) и начальном условии
Р при х = xlt z = 0;
о2 = 0 при х/хь z = 0.
Эта задача теории теплопроводности сводится к определению
влияния мгновенного источника тепла на полуограниченное тело
при граничном условии третьего рода.
Приведем конечные результаты в безразмерных координатах.
Обозначим
*1 = гН\
Oj = JU —Гф' (тТГ] | Ф'(т±г}' -
1 рЧ 2пН \	/	\ рЧ п /
192
(т + г
К
Рис. 11.6. Схема приложения
линейной сосредоточенной на-
грузки на засыпку у подпор-
ной стенки
|А2.ф"^.-И
Н К \ У^п)‘
Для гладкой подпорной стенки
при D = О
2
Ф'
v л
V п
т — г
vn
т
т
V Л
Горизонтальное давление на гладкую подпорную стенку
(11.85)
Суммарное горизонтальное давление на стенку
Рассмотрим действие равномерно распределенной нагрузки
(рис. 11.7). Необходимо решить уравнение (11.84) при краевых ус-
ловиях (11.63) и (11.65), а также начальном условии
аг = q при z = 0.
193
Путем подстановки (П.71) решается задача охлаждения П0ЛУ‘
ограниченного тела при заданной начальной температуре и гра-
ничном условии третьего рода.
Решение будет иметь следующий вид
т„ = —Ф'
Рис. 11.7. Схема приложения равно*
мерно распределенной нагрузки на за*
сыпку у подпорной стенки
Выражения для а2, txz и <зх при увеличении координаты х стре-
мятся к следующим величинам
0 пр/ Л->ОО.
ож-> vg
Для гладкой подпорной стенки (при оэ) выражения для
напряжений примут вид
°z=q\
194
Рассмотрим далее действие сосредоточенной силы (рис. 11.8).
В данном случае необходимо решить систему уравнений для про-
странственной задачи [60]
dz \ дх» ду* J’
дх*
о = vo -4-	•
У V0^VZ ду^
• = v2-2 d2O;
2 дхду
Система уравнений должна быть
решена при краевых условиях
(11.64) и (11.65) и начальном
условии
= Р при х = гН\ у = г = 0;
о2 = 0 при z = 0;
х ф гН, либо у 0.
Рис. 11.8. Схема приложения со-
средоточенной силы на засыпку
у подпорной стенки
Приведем окончательное решение для компонент напряжен-
ного состояния, вводя дополнительное обозначение
У=/Я;
с = Л_!_ ф' /JL] Гф' (а-'}+ф (п + C.YI _
г Н2 4n2v \ vn2 / I \ Vе» п /	\ п /J
+— 1 Ф' /—1 Гф"' / m~f + ф'" (т
г~Г Н2 4п2 \vn2H \V »n)
195
+——ф' (—। p У
И2 2К*	\уп*)	\ yVn / Я« 2Кп \wi2 /	\ /Гл) ’
Для частного случая гладкой подпорной стенки горизонтальное
давление
Р 1 Г* /	/« + г’\
ах =--------ехр г----1—1.
Я« ™ л< F \ 2wt» )
Суммарная горизонтальная сила, действующая на стенку,
Рассмотрим действие рав-
номерно распределенной по-
лосовой нагрузки q шириной
ЬН на расстоянии гН от под-
порной стенки (рис. 11.9).
Приведем решение для
гладкой подпорной стенки
Рис. 11.9. Схема приложения равно-
мерно распределенной полосовой на-
грузки на засыпку у подпорной стенки
°х= vaz + q-~-
4
Горизонтальное давление у подпорной стенки

Аналогично можно определить напряженное состояние грунта
от других более сложных нагрузок на поверхности засыпки у под-
порной стенки.
196
Сравнение полученного решения с известными решениями
и экспериментальными данными
В литературе известны решения задачи об определении напря-
женного состояния грунта, ограниченного подпорной стенкой, на
основе теории упругости лишь для гладкой подпорной стенки.
Для частного случая гладкой подпорной стенки Каротер-
сом предложен так называемый метод изображений [94]. В этом слу-
чае горизонтальное давление на неподвижную гладкую подпорную
стенку будет равно удвоенному давлению от действия местной
нагрузки, определенному для неограниченного массива при отсутст-
вии подпорной стенки. Такое решение совпадает с эксперименталь-
ными данными. Как следует из теории теплопроводности, условие
(11.64), для гладкой подпорной стенки сводится также к методу изоб-
ражений, который находит таким образом в настоящей работе допол-
нительное обоснование и подтверждение.
Следовательно, предложенный Фрелихом и Головенчицом спо-
соб расчета горизонтального давления приводит к заниженным в
два раза результатам.
В Советском Союзе экспериментальное определение горизонталь-
ного давления на неподвижную подпорную стенку при наличии за-
грузки за стенкой проводилось Дуброва [24], Лубеновым и др.
Для иллюстрации на рис. 11.10 приведено сравнение горизонталь-
ного давления грунта на подпорную стенку от действия линейной
распределенной нагрузки при различных коэффициентах бокового
распора грунта и по теории упругости (по методу Каротерса). Как
видно из рис. 11.10, решения, полученные по статистической тео-
рии, более совпадают с экспериментальными данными, чем решения
на основе теории упругости.
Таким образом, можно сделать вывод о том, что статистическая
модель зернистого грунта может быть с большим основанием ис-
пользована для определения напряженного состояния зернистой
среды, ограниченной подпорными стенками и нагруженной поверх-
ностными нагрузками.
Глава 12
ДЕФОРМАЦИИ ЗЕРНИСТОГО ГРУНТОВОГО ОСНОВАНИЯ
§ 1.	О ПРИРОДЕ ДЕФОРМИРУЕМОСТИ ГРУНТОВ
В работе Н. В. Орнатского [67] отмечаются следующие физи-
ческие причины сжимаемости грунтов:
1.	Деформации адсорбционных пленок в местах опирания грун-
товых частиц друг на друга.
197
Рис. 11.10. Распределение горизонтального давления грунта на подпорную стенку от действия линейной
распределенной нагрузки Р = 20 кг
а — при нагрузке, приложенной иа расстоянии х, = 0,27 Я; б — то же, при х, = 0,54 Я; в — то же, при х, = 0,81 Я; г —
то же, при Xi = 1,08 Я; 1 — по опытам Г. А. Дуброва; 2 — по статистической (дискретной) теории при т = 0,4; 3 — по ста-
тистической (дискретной) теории при v = 0,5; 4 — по теории упругости
2.	Упругие и остаточные деформации грунтовых зерен.
3.	Взаимные перемещения грунтовых зерен.
4.	Деформации защемленного газа при изменениях давления.
5.	Выходы пузырьков газа в атмосферу при прорывах защем-
ляющих водяных пленок.
Каждая из этих причин проявляется в большей или меньшей
степени в зависимости от свойств грунта и условий его загружения.
При деформации сжатия все эти причины будут сказываться на
уменьшении пористости материала. Чем меньше пористость мате-
риала, тем больше площадь контактов между частицами и меньше
сжимаемость грунта. Это положение подтверждается многочислен-
ными испытаниями грунтов. Характер полученных в этих условиях
кривых зависимости деформации от нагрузки показывает, что по
мере увеличения нагрузки, уменьшается пористость материала и
возрастает его сопротивляемость деформированию. Из этого выте-
кает, что сжимаемость материала внешней нагрузкой (даже состоя-
щего из совершенно одинаковых зерен) на различных уровнях по
глубине будет различной в связи с предварительным уплотнением
слоев весом грунта, расположенного выше.
Это известное положение играет существенную роль при реше-
нии вопроса о деформации сжатия, особенно в тех случаях, когда
толща сжимаемого слоя является значительной.
При малой толще сжимаемого слоя, когда напряжения от собст-
венного веса малы, сопротивляемость материала деформированию
для всей толщи может быть принята одинаковой.
Кроме деформаций сжатия, в грунтовом массиве могут иметь
место сдвиги и выпирания.
В отличие от деформаций сжатия, развивающихся во всей толще
массива, сдвиги и выпирания происходят в основном в областях
приложения нагрузки.
Осадку грунтового массива можно определить как сумму осадок
от деформации сжатия и деформации сдвигов, т. е.
w = t»c4-tt>n,	(12.1)
где w — осадка поверхности массива;
&уп — осадка поверхности массива от сдвигов (перемещений);
и»с — осадка поверхности массива от деформации сжатия.
Поскольку в данной работе вопросы предельного состояния не
рассматриваются, не будем рассматривать вопрос и о деформации
сдвигов. Причем деформацию сжатия будем определять как дефор-
мацию зерен без изменения структуры среды. В общем случае за-
висимость между нагрузкой и деформацией грунтов является нели-
нейной, однако вопрос о характере этой зависимости остается пока
нерешенным.
В инженерной практике при расчете осадок оснований широкое
применение находит гипотеза линейно-деформируемого тела [17,
27, 88].
199
Известны также решения указанной задачи на основе методов
теории вероятностей. Здесь М. Н. Троицкой 1831, Г К. Клейном
[40] на основе идеи Г. И. Покровского [69] для описания процессов
деформации сжатия получены теоретические решения, подтверж-
дающиеся экспериментальными данными.
Для расчета деформируемости грунта, расположенного на глу-
бине, воспользуемся зависимостью, полученной М. Н. Троицкой
на основе идеи проф. Г. И. По-
кровского при условии отсут-
ствия бокового сдвига или
выпирания (рис. 11.1, а):
Х = —In Рс + р , (12.2)
L Ре 1	’
где X — относительная дефор-
мация грунта под
нагрузкой р;
L; рс — постоянные, опреде-
ляемые по данным
компрессионной кри-
вой.
Дифференцируя выраже-
ние (12.2), получим
Л= J------(12.3)
Рс + Р
откуда тангенс угла на-
клона касательной к оси де-
формаций
-^-=L(pc + p). (12.4)
ал
Применительно к грунту,
расположенному на глубине,
величина нагрузки опреде-
ляется весом вышележащих
слоев
Р = 7*.	(12.5)
Рис. 12.1. Схема к определению дефор-
мации сжатия грунта
а—к определению переменного модуля дефор-
мации; б — к определению относительной де-
формации элементарного объема грунта
где t — объемный вес грунта;
z — глубина расположения рассматриваемого слоя грунтового
массива.
Подставляя выражение (12.5) в формулу (12.4), получим зави-
симость сопротивляемости грунта внешней нагрузке от глубины
расположения рассматриваемого слоя в грунтовом массиве
£=-^- = £(рс + тг).
а А.
(12.6)
200
Рассмотрим теперь вертикальную деформацию некоторого эле-
ментарного объема грунта (рис. 12.1, б), находящегося на глубине z.
Относительная деформация такого объема грунта
	-^- = -2г- = —.	(12.7) дг	dp	Е (г)	' 4Х
Подставляя значение для тангенса угла наклона по выражению
(12.6) в зависимость (12.7), получим
	-^ =	2»	.	(12.8) dz	L(pc + 7Z)
Из выражения (12.8) для вертикальной деформации рассматри-
ваемого элемента грунта получим зависимость
	dw=		.	(12.9) НРс + п)	1
На основе зависимости (12.9) вертикальная деформация всего
грунтового массива определится как сумма деформаций малых эле-
ментов	w = f	— = C -^—dz.	(12.10) J L(pc + 7z) J E(z)	'	' о	о
При (12.10)	рассмотрении небольших толщин (Л) массива выражение примет вид 1 Л	Л w=——$<,jd2 = — [a2dz.	(12.11) Lpc 0	to
В общем случае для переменного модуля деформации связь между
напряжениями и перемещениями по другим осям можно выразить
как	— = —2^-	(12.12) дх	£ (г)	v	'
По аналогии с безраспорной зернистой средой для средних зна-
чений поворота элементарного объема грунта получим соотношения
7» = -^-^;	(12.14)
Ъ* = д	(12.15)
’.--йг-	<|2|6>
где G (г) — среднее значение модуля поперечного сдвига материала.
201
§ 2.	СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЯМИ
Формулой (12.10) в общем случае определяют вертикальное сме-
щение от вертикальной нагрузки. Для отыскания остальных состав-
ляющих перемещения через вертикальное воспользуемся соотноше-
ниями между компонентами напряжения и перемещения и физиче-
скими уравнениями.
Рассмотрим сначала плоскую задачу. Касательные напряжения
с вертикальными связаны следующим образом
дъг —vz— дх	(12.17)
Учитывая, что а2=	, а из выражения дг	(12.14)	=
= С(^)ТГжг» на основе зависимости (12.17) получим	
G(Z)t„ = -«£(z)^- дгдх	(12.18)
или 	vzAW		2vz-^-. 1X2	в(г) дгдх	дгдх	(12.19)
Учитывая далее, что	
С = V3-|-V2Z2	, *	2	дх2	(12.20)
а из выражения (12.12)	
	(12.21)
получим Е (г) -у- = vE (г)	+ Л'Е (г) дх	дг	дгдх2	(12.22)
fa	уац) I *гг» дх	дг	дгдх2	(12.23)
Для сплошной равномерно распределенной вертикальной на-
грузки
ди	дш
— = v
дх	дг
(12.24)
По аналогии с плоской задачей для пространственной имеем сле-
дующие соотношения:
*L = V +	(12.25)
дх	дг	дгдх2
+**_**_;	(12.26)
ду	дг	дгду*	'
202
Т« = —
ozdx
о №
7-=-2vz1^:
Txu — — 2>2z2 ———.
ix"	dzdxdy
(12.27)
(12.28)
(12.29)
Из представленных соотношений нетрудно установить их взаим-
ную связь. Эти уравнения аналогичны уравнениям неразрывности
деформаций в теории упругости, но отличаются от них, так как от-
ражают среду не сплошную, а состоящую из зерен. Уравнения вы-
ведены для переменного модуля сжимаемости материала по глубине
и модуля сдвига.
§ 3. ОСАДКА ОДНОРОДНОГО ГРУНТОВОГО ОСНОВАНИЯ ОТ НАГРУЗКИ,
РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО БЕСКОНЕЧНОЙ ЛИНИИ
При принятии постоянного по глубине значения модуля дефор-
мации грунта осадка слоя'ограниченной мощности вычисляется по
формуле
1 л
w = — f a/fz,	(12.30)
Е о
где Е — модуль сжатия грунта.
Для рассматриваемого случая загружения вертикальные напря-
жения
=4 V 2<* ехр (-		(,2-31)
После подстановки выражения (12.31) в формулу (12.30) получим
(12.32)
Для решения интеграла произведем замену переменной интег-
рирования подстановкой
= t,	(12.33)
2vz2
Тогда
_________________________________
w = —j	(12.34)
203
Интеграл выражения (12.34) является интегральной показатель-
ной функцией. Поэтому
w =-----~ / 2^ Ei	— "I,	(12.35)
2Е У	2\Л2 )'	4	'
где Ei —2^2) — интегральная показательная функция.
§ 4. ОСАДКА ОДНОРОДНОГО ГРУНТОВОГО МАССИВА ОГРАНИЧЕННОЙ
МОЩНОСТИ ОТ НАГРУЗКИ, РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО
БЕСКОНЕЧНОЙ ПОЛОСЕ
При постоянном по глубине модуле деформации грунта , осадка
массива определяется по формуле (12.11).
Распределение вертикальных напряжений для рассматриваемого
случая выражается зависимостью
•-Т[Ф(7РГ)-Ф(7РГ)]-	('2.36)
Подставив выражение (12.37) в формулу (12.11), получим
— ^-[1Ф(-7^-)л-/ф(-7РТ-)л1- "237>
L0	О	J
После интегрирования и некоторых преобразований получим
следующее выражение для осадки грунтового основания ограни-
ченной мощности:
»-^(‘[фШ-ф(ттЯ]-
- К2- [<« + ») В' (-	-(«-») В (-!^-)]). (12.38)
Для точек, находящихся на вертикальной плоскости, проходя-
щей через ось симметрии загруженной полосы, при х = 0 выраже-
ние (12.38) преобразуется к виду
<,239>
При равномерном загружении всего полупространства (6 -> со)
Пшф(-4=Й= 1;
\ну„)
lim&Eif--—) = 0	(12.40)
\	2>/i2 /	'	’
и выражения (12.39)» (12.40) примут вид
204
§ б. ОСАДКА ОДНОРОДНОГО ГРУНТОВОГО МАССИВА ОГРАНИЧЕННОЙ
МОЩНОСТИ ОТ ПАРАБОЛИЧЕСКОЙ НАГРУЗКИ. РАСПРЕДЕЛЕННОЙ
ПО БЕСКОНЕЧНОЙ ПОЛОСЕ
Вертикальные напряжения в рассматриваемом случае
После подстановки в выражение (12.11) значения для вертикаль-
ных напряжений из формулы (12.41) для осадки получим такую за-
висимость:
После интегрирования и некоторых преобразований это выраже-
ние примет вид
+ +	(12.43)
205
Для точек, находящихся на оси загруженной полосы, при х = О
осадка на основе выражения (12.43) выразится зависимостью
§ 6. ОСАДКА ОДНОРОДНОГО ГРУНТОВОГО МАССИВА ОГРАНИЧЕННОЙ
МОЩНОСТИ ОТ НАГРУЗКИ, РАСПРЕДЕЛЕННОЙ НА БЕСКОНЕЧНОЙ
ПОЛОСЕ по линейному закону и по закону треугольника
Вертикальные напряжения от нагрузки, распределенной по ли-
нейному закону f (х) = Qx на полосе шириной b
"2Л4)
После подстановки зависимости (12.44) в выражение (12.11),
получим
+4^Ь[ех₽(-^-)-ех₽(-(12Л5)
о
После интегрирования
а, = JL Гф /	_ ф+
2Е I I U/» / I л/Т /J
. Л«]/2^ г / х2 \	/ (х — 6)2 \7 ,
+-гтИехрг i^-)-exp(—4Н]+
+ 6(x-6)K^Ei(—
При х = 0 этим выражением определится осадка в начале коор-
динат
*=1-т^-р - «₽(--&-)]	* (- тй •
206
Определим осадку грунтового массива от нагрузки, распреде-
ленной в пределах полосы шириной 2Ь по закону треугольника.
Вертикальные напряжения для этого случая
ЧНН^)-мШ+('-‘ИтЙ] +
Подставим это выражение для вертикальных напряжений в фор-
мулу (12.11). Тогда для осадки грунтового массива от треугольной
нагрузки получим
+(,_4)ф(^)]й+^р[.хр(_^)_
<‘2“>
После интегрирования и некоторых преобразований
§ 7. ОСАДКА ОДНОРОДНОГО ГРУНТОВОГО МАССИВА ОГРАНИЧЕННОЙ
МОЩНОСТИ ОТ НАГРУЗКИ, ЗАДАННОЙ ПО ЗАКОНУ ТРАПЕЦИИ
Для решения этой задачи воспользуемся уже полученным зна-
чением осадки грунтового основания от нагрузки, заданной по за-
кону треугольника. Осадку от нагрузки, заданной по трапеции,
определим как разность осадок от двух треугольных нагрузок.
Тогда
’ - % [<-+* (трг)+“ - « ф	-
207
a—£-[(« +»ф(-^-) + <*-<
-<- + в>ф(т7г)-<—в|ф(^7г)] +
Приведенными ‘формулами определяется осадка грунтового мае*
сива ограниченной мощности от нагрузки, заданной по закону тра*
пеции.
§ 8.	ОСАДКА ОДНОРОДНОГО МАССИВА ОГРАНИЧЕННОЙ МОЩНОСТИ
ОТ СОСРЕДОТОЧЕННОЙ НАГРУЗКИ
Распределение вертикальных напряжений от сосредоточенной
нагрузки в однородном грунтовом массиве выражается зависимо*
стью
(12-47)
где Р — сосредоточенная вертикальная нагрузка на поверхности
массива.
После подстановки выражения (12.47) в (12.11), получим для
осадки массива ограниченной мощности
w = —— f — ехр (---dz.
2s-Е J z«	2vz2 )
о
После интегрирования
Для полупространства (при h -> со) это выражение примет вид
w = —1Л2itv
2Er Y
§ 9.	ОСАДКА ОДНОРОДНОГО ГРУНТОВОГО МАССИВА ОГРАНИЧЕННОЙ
МОЩНОСТИ ОТ СОСРЕДОТОЧЕННОЙ НАГРУЗКИ ПРИ ПЕРЕМЕННОМ
ЗНАЧЕНИИ МОДУЛЯ ДЕФОРМАЦИИ ПО ГЛУБИНЕ
При изменении модуля деформации грунта с глубиной по зависи-
мости (12.6) осадка грунтового массива от сосредоточенной нагрузки
h
w = С-------------?-----ехр (----) dz. (12.48)
J z2 (pc + 72)	2vz2 /
о
208
При рс -> О
л
w=^£rf^exp(~й-)л>	(12Л9)
о
После интегрирования
“’=^гехр(-^-)-	(12-б0)
Из выражения (12.50) видно, что по мере удаления от точки прило-
жения нагрузки затухание осадки происходит весьма интенсивно.
Для грунтового полупространства, т. е. при h -> со,

Из этого выражения видно, что осадка поверхности грунтового
полупространства по мере удаления от точки приложения нагрузки
убывает обратно пропорционально квадрату расстояния до рас-
сматриваемой точки. Эго подтверждается решением, полученным
Г. К. Клейном [40].
§ 10.	МАКСИМАЛЬНАЯ ОСАДКА ОДНОРОДНОГО ГРУНТОВОГО
МАССИВА ОГРАНИЧЕННОЙ МОЩНОСТИ ОТ НАГРУЗКИ, РАВНОМЕРНО
РАСПРЕДЕЛЕННОЙ ПО КРУГЛОЙ ПЛОЩАДКЕ
Вертикальные напряжения по оси загруженной площадки для
рассматриваемого случая
в1 = р[1-ехр(-^-)1,	(12.51)
где р — интенсивность нагрузки на единицу площади;
R — радиус круга загруженной площадки;
v — коэффициент распределительной способности материала.
Осадка массива по оси загруженной площадки при принятии
постоянного значения модуля деформации (сжатия) грунта по глу-
бине и при распределении вертикальных напряжений по формуле
(12.51) определится выражением
После интегрирования
f (4[1 - ехр (- ^)] +	[1 -Ф (^)][ .<12.52)
Выражением (12.52) определяется максимальная осадка слоя
ограниченной мощности от нагрузки, равномерно распределенной
по круглой площадке.
209
Определим максимальную осадку грунтового полупространства
от рассматриваемой нагрузки.
Максимальная осадка однородного полупространства опреде-
лится как предел выражения (12.52) при h -► со; для решения
этого вопроса определим предел выражения
1 —ехр/——
у = Нт---------1—.	(12.53)
Л-* ОО	1
Пользуясь правилом Лопиталя, находим
У =	__RLexp(__RLA	₽»еХр(— -lim..-*’	1 2v - - = lim	L_^d = 0. (12.54) 	1	ЧП h*
Учитывая выражения (12.53) и (12.54), получим предел зависи-
мости (12.52)
(12.55)
Е у 2у
где р — интенсивность нагрузки.
Формулу (12.55) можно выразить через площадь загруженной
площадки	_
а»0=-Й^,	(12.56)
Еу2у
где F — площадь загруженного круга.
Заметим, что формула (12.56) по структуре аналогична зависи-
мости, полученной Н. Н. Ивановым экспериментально для разных
штампов.
§ 11. МАКСИМАЛЬНАЯ ОСАДКА ОДНОРОДНОГО ГРУНТОВОГО МАССИВА
ОГРАНИЧЕННОЙ МОЩНОСТИ ОТ НАГРУЗКИ, РАСПРЕДЕЛЕННОЙ
НА КРУГЛОЙ ПЛОЩАДКЕ ПО ПАРАБОЛЕ
Рассмотрим случай, когда нагрузка распределена по площади
круга и выражена уравнением
/(г) = 2р(1—£-),	(12.57)
где р — среднее удельное давление на загруженной площадке;
г — текущая координата;
R — радиус загруженного круга.
Распределение вертикальных напряжений по оси загруженной
согласно уравнению (12.57) площадки выражается зависимостью
210
Тогда максимальная осадка грунтового массива ограниченной
мощности
С0О =
2г2м Г. /
-^-[1-ехр(
После интегрирования
/?8 VI
2уЛ« /]
2h’v Г. / Я8 \1 ,
^г[1-ехр(“^-)] +

(12.59)
По формуле (12.59) определяется максимальная осадка однородного
грунтового массива ограниченной мощности от параболической на-
грузки распределенной по площади круга.
Максимальная осадка грунтового полупространства от нагрузки,
выраженной уравнением (12.57), определится как предел выраже-
ния (12.59) при h -> со.
Предел первого слагаемого выражения (12.59) при h -► со, как
-было показано в предыдущем параграфе» равен нулю. Вычислим
предел второго слагаемого, для чего, применяя несколько раз пра-
вило Лопиталя, рассмотрим предел выражения
№	Л«
h
= 0.
Таким образом, второй член выражения (12.59) при h -> со
в пределе равен нулю.
Следовательно, максимальная осадка однородного грунтового
полупространства, как предел выражения (12.57) при h -► об
4pR У*. _____ Уе
ЪЕ У^ ЗЕ У 2* ’
(12.60)
где Г — площадь загруженной круглой площадки.
Формула (12.60) также по структуре имеет вид формулы, полу-
ченной Н. Н. Ивановым экспериментально для различных форм
площадок загружения.
211
§ 12. ОСАДКА ОДНОРОДНОГО ГРУНТОВОГО ПОЛУПРОСТРАНСТВА ОТ
НАГРУЗКИ, РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО ПРЯМОУГОЛЬНИКУ
При равномерной загрузке площади прямоугольника размером
2а X 2Ь распределение вертикальных напряжений в грунтовом
массиве выражается уравнением
Представим это выражение в развернутой форме в виде произве-
дения интегралов вероятности
— Ф
При постоянном по глубине значении модуля деформации и при
распределении вертикальных напряжений по зависимости (12.62)
осадка однородного грунтового массива ограниченной мощности
ГЛ	h
_0
h
у—
zV
о
h
[фр
(12.64)
0 0
Нетрудно заметить, что все интегралы выражения (12.63) имеют вид
h
'-J ‘ 
и
Поэтому для решения интегралов выражения (12.63) достаточно
рассмотреть интеграл (12.64). Решение этого интеграла:
л
dz = ЛФ|
dt.
w
о
h

212
При Л -> со это выражение преобразуется к виду

(12.65)
(12.66)
(12.67)
Подставив решения интегралов (12.66) и (12.67) в выражение
(12.65), получим

+ г|„(Л+1/‘+(Л)-]].
(12.68)
Воспользуемся соотношением (12.68) для решения задачи об
осадке однородного грунтового полупространства от нагрузки,
равномерно распределенной по прямоугольнику. Полагая в выра-
жении (12.63) h -> со, получим
* Решение интегралов правой части выражения (12.65) приведено в книге
И. М. Рыжика и И. С. Градштейна «Таблицы интегралов, сумм, рядов и про*
иэведений», 1951 г., стр. 253.
313
На основе решения (12.68) выражение (12.69) представим в виде
_ VLГ_Л=Г in(JL±£. +1/	+
2 |_ /v \ х — b V	\ х — Ь ) )
После некоторых преобразований получим
(x+6)lnJL+£+l^+^i^±^
у — а 4- у (х + Ь)2 + (У °)8


+
+(у + a)In * + b + Vte4-o)a4-«±X +
х — »+k (» + а)» +(« — »)*
+ (x—ь) in	+
У + a + V (x+ *)«+(!/4 »)*
+ (y - a) In
* + 6+ Vi!/-o)* + (x + ft)* J
(12.70)
214
По центру загруженной площадки (при х = у = 0) осадка
wt =	(Мп a + /f+-ga + a In	_
8y vE __e + y b2 + fl2	—	+
bin -a + ]/t, + o8 -aIn+
a + V & + a2	b + У a2 + b2.
или
W0 =
(bin i±y*+°L loin » + /°*+** fun)
4У^Е	—а + У> + в»	-6+У a2**2 ]
Интересно отметить, что по структуре формула (12.71) анало-
гична соответствующей формуле теории упругости. Для сравнения
приводим формулу теории упругости в принятых обозначениях
50 = [bln	+gln	+	,
«Е [	V»» + a»-a	Уб» + а»—bj
где E = ^Ut;
1 —p
p — коэффициент Пуассона;
Яупр — модуль упругости.
Осадка точки, расположенной в вершине угла загруженного
прямоугольника, определится на основе выражения (12.70) при
х = Ь\ у = а\
Wba= .	(bln	+ аln HVZ+E) .
ba 4/vE \	Ь	о /
Осадка точки, расположенной в середине большой стороны пря-
моугольника, определится на основе выражения (12.70) при х = 0;
у = — а, т. е.
W°a 4 У~Е
b	, У4а2 + 624-6
= = ----+а In ту =— ---
y4a2-^b2 — b
Формула теории упругости для осадки этой же точки поверхно-
сти имеет вид
Sb=^(bln-
ь кЕ I у
где Е = -^~.
1—	и2
. (12.72)
+ aln +
V 4а2 + b2 - b
ь
. (12.73)
215
Таким образом, формулы имеют одинаковую структуру и от-
личаются лишь множителем перед скобками, который в (12.72) за-
висит от коэффициента распределительной способности грунта. Вы-
бором этого коэффициента можно с помощью излагаемой в данной
работе теории получить результаты, совпадающие с данными теории
упругости. Однако для различной структуры грунтов эти коэф-
фициенты будут различными.
Глава 13
ДЕФОРМАЦИЯ СЖАТИЯ МНОГОСЛОЙНЫХ ЗЕРНИСТЫХ
- ГРУНТОВЫХ СИСТЕМ
§ 1.	ДЕФОРМАЦИЯ СЖАТИЯ СЛОИСТОЙ СИСТЕМЫ ОТ НАГРУЗКИ.
РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО БЕСКОНЕЧНОЙ ЛИНИИ
(ПЛОСКАЯ ЗАДАЧА)
При определении осадки будем исходить из того же условия на
границе раздела двух слоев, которое принималось при рассмотре-
нии распределения напряжений в многослойных системах. Опреде-
лим вертикальные деформации сжатия, которые дают возможность
вычислить перемещения и по другим осям.
Вертикальная деформация сжатия многослойной системы скла-
дывается из деформации отдельных слоев ее, т. е.
w =	4- w2 + tt>3 +	+ wnt
(13.1)
где w — деформация сжатия всей системы;
— деформация сжатия верхнего слоя;
w2 — деформация сжатия второго сверху слоя;
wn — деформация сжатия слоев от 3-го до л-го в порядке
нумерации сверху вниз.
Определим слагаемые выражения (13.1). Деформацию сжатия
верхнего слоя найдем как осадку от рассматриваемой нагрузки слоя
ограниченной мощности, т. е.
(13.2)
где Р — интенсивность нагрузки, распределенной по линии;
— модуль сжатия материала верхнего слоя;
216
vj — коэффициент распределительной способности материала
верхнего слоя;
— толщина верхнего слоя.
Деформацию сжатия второго сверху слоя определим как дефор-
мацию массива ограниченной мощности от нагрузки, т. е.
/(*) = % = т 1/тгехр (-тУ •	(,3-3)
Так же, как и при рассмотрении напряженного состояния слои-
стой системы, введем обозначения
2v,Af С*'
(13.4)
(13.5)
При этом выражение (13.3) примет вид показательной функции,
для которой деформация сжатия слоя ограниченной мощности

. (13.6)
Подставив в это выражение параметры второго слоя и значения
и из (13.4) и (13.5), получим
После некоторых преобразований
где £а — модуль сжатия материала второго слоя;
йа — толщина второго слоя;
va — коэффициент распределительной способности материала
второго слоя.
Формула (13.8) определяет деформацию сжатия второго слоя.
217
Определим деформацию сжатия третьего слоя. Вертикальные на-
пряжения на границе второго слоя с третьим выражаются зависи-
мостью
(13.9)
Как и в предыдущем случае, обозначим
(13.10)
Кроме того, в выражение (13.6) подставим параметры третьего
слоя, т. е.
* = *.;	(13.12)
Е = £,;	<13.13)
Л=Л„	(13.14)
а вместо Pj и С, — выражения (13.10) и (13.11). Тогда получим
(13.15)
216
После некоторых преобразований
По формуле (13.16) определяется деформация сжатия третьего
слоя. По аналогии с выражениями (13.8) и (13.16) можно определить
деформацию сжатия /-го слоя
Определим деформацию сжатия последнего слоя многослойной
системы. На основе полученных зависимостей имеем
(13.18)
где Еп — модуль сжатия л-го слоя;
— показатель распределительной способности n-го слоя;
hn — сжимаемый слой однородного массива ограниченной мот*
ности из материала л-го слоя.
219
Подставив выражения (13.2), (13.8), (13.16) и (13.18) в зависи-
мость (13.1), получим
220
Из выражения (13.20) видно, что общая деформация слоев равна
сумме деформаций сжатия соответствующих однородных слоев огра-
ниченной мощности от заданной нагрузки.
Выражение (13.20) можно представить так
(13.21)
где о>91 — деформация сжатия однородного слоя мощностью Лх
от заданной нагрузки Р; слой толщиной Ах образован
из материала верхнего слоя системы;
—	деформация сжатия однородного слоя мощностью
Лх ]/^- + от заданной нагрузки Р; однородны’
слой мощностью Ах	образован из материала
второго слоя системы;
—	деформация сжатия однородного слоя мощностью
1/ — + 1/ — + h9 от заданной нагрузки Р;
»	^3	» v3	___ _________
однородный слой толщиной Лх 1/ — + 1/	+ ha
образован из материала третьего слоя системы;
—	деформация сжатия однородного слоя мощностью
Л||/Г-Л_ + Л2|/’^-+ +Лл_,отзадаииой
нагрузки Р; однородный массив дайной толщины
образован из материала (п—1)-го слоя системы;
—	деформация сжатия однородного массива толщиной
Лх jA— + Л2	и образованного из
материала n-го слоя (последнего слоя системы).
221
Таким образом, деформация сжатия многослойной системы от
заданной нагрузки может быть определена как сумма значений де-
формаций соответствующих эквивалентных однородных массивов
от той же нагрузки, умноженных на коэффициенты, зависящие от
отношения модулей сжатия и распределительной способности гра-
ничных слоев системы.
$ 2. ДЕФОРМАЦИЯ СЖАТИЯ МНОГОСЛОЙНОЙ СИСТЕМЫ НАГРУЗКОЙ,
ПРОИЗВОЛЬНО ЗАДАННОЙ В ПЛОСКОЙ ЗАДАЧЕ
Пусть распределение нагрузки в плоской задаче в пределах по-
лосы
р = /(х).	(13.22)
Распределение вертикальных напряжений в однородном массиве
от такой нагрузки подчинено зависимости
'-7 J /«>'»₽[-	,13 И)
—ъ
где 2Ь — ширина полосы загружения;
— коэффициент распределительной способности материала.
Определим осадку многослойной системы по формуле (13.1).
Деформация сжатия верхнего слоя многослойной системы при
распределении в нем напряжений согласно выражению (13.23) оп-
ределяется зависимостью
г—— — hi	+b
- - Т V тк f 7 J /(i> “Р (~	"3-м>
о	— ь
где W] — деформация сжатия однородного массива мощностью hlt
состоящего из материала верхнего слоя системы;
Ei — модуль сжатия материала верхнего слоя;
Aj — толщина верхнего слоя системы.
Определим деформацию сжатия второго слоя многослойной си-
стемы. Распределение вертикальных напряжений во втором слое
от произвольно заданной нагрузки выражается зависимостью
+ь
X Г/(0ехр/-------- (*~Д- -Ade,
J (	+ j
(13.25)
222
где va — коэффициент распределительной способности материала
второго слоя.
Деформация сжатия второго слоя
Произведя замену переменной интегрирования подстановкой
Ах/^ + г = Л	(13.26)
Г »2
получим
____________+»
’>—sr/ir	J	<13 27)
‘./з -
Выражение (13.27) представим в виде разности двух интегралов
2v/> )
Заменив во втором интеграле одну из переменных интегрирова-
ния подстановкой
< =	(13.28)
получим
___+»
^ = 4-1/f
у XltVg J	• J	\
о	—Ь
W1 I
223
(,зи>
О —6
Второй интеграл через выражение (13.24) может быть представ-
лен как
h. +Л	_____
J V J	ехр (—= в,,£* У =
“ W91^1
(13.30)
Первый интеграл выражения (13.29) представляет собой дефор-
мацию однородного массива ограниченной мощности ht + Лг>
образованного из материала второго слоя многослойной системы.
Обозначим эту осадку
tt>ea =
(13.31)
Учитывая соотношения (13.30) и (13.31), выражение (13.29) пред-
ставим в следующем виде
I / Vf
^ = ^2-^17; J/v
(13.32)
Выражение (13.32) определяет деформацию сжатия второго слоя
в системе.
Рассмотрим деформацию сжатия третьего слоя системы. Распре-
деление вертикальных напряжений в третьем слое многослойной
системы выражается зависимостью
°Л| +л*+*
/({)ехр
--------—-----------(13.33)
^’(л* V1F+a‘ У'*+г))
224
Деформация сжатия третьего слоя многослойной системы при
распределении напряжений в нем по зависимости (13.33) определится
выражением
где Е3 — модуль сжатия материала третьего слоя;
v9 — коэффициент распределительной способности материала
третьего слоя;
Л8 — толщина третьего слоя.
Произведя в этом выражении замену переменной интегрирова-
ния подстановкой
Л1 + Л2 + Z~t,
(13.34)
получим
или
(X —Э*
dldt.
225
Произведем замену переменной интегрирования t под вторым
интегралом подстановкой
/ =	(13.35)
тогда
____+»
-4?/^ j	<13-зб>
О	—ь
Первый член выражения (13.36) представляет собой деформацию
от заданной нагрузки однородного массива ограниченной мощности
образованного из материала третьего слоя
системы. Обозначим эту деформацию
1	1 /	1 Ч/
и
*‘р<п’ + *’ 1/Г< + А’ +»
х f Tj/(Oexp(_Ji£?')dWZ- {13-37)
О	— ь
Второй интеграл выражения (13.36) может быть определен на
основе зависимости (13.31)
+» ' _______________________________
|	Y J /(0 ехр (-	V 2kvs . (13.38)
Учитывая соотношения (13.37) и (13.38), выражение (13.36),
получим
Wi=W3S-w,t-^y^.	(13.39)
Выражение (13.39) определяет деформацию сжатия третьего слоя
в системе. Сравнивая (13.39) с (13.32) видим, что эти выражения
226
имеют одинаковую структуру и отличаются только индексами, опре-
деляющими принадлежность тех или иных параметров различным
слоям. По аналогии можно получить зависимость для описания
деформации сжатия любого слоя в системе. Так, для /-го слоя
^7—1 _ Г '‘j—1
(13.40)
где шэ/ — деформация сжатия от заданной нагрузки
'2l + As/21 +
массива мощностью
разованного из материала /-го слоя;
— деформация сжатия от заданной нагрузки
массива мощностью Я]
однородного
+ Л/, об-
однородного
+	+Л/-Р
образованного из материала (/—1)-го слоя:
Е{ — модуль сжатия материала /-го слоя;
Е, । — модуль сжатия материала (/—1)-го слоя.
На основе приведенных зависимостей деформация сжатия по-
следнего слоя системы
w=w,—w,.„	(13.41)
п эп э(л—I) Enf^n	'	*
где w9n — деформация сжатия однородного массива ограниченной
мощности hx + Л*+	+ hn от заданной
нагрузки;
— деформация сжатия однородного массива ограниченной
мощности h{ р/~+ h2 р/*+	+ h л_р об-
разованного из материала (п—1) слоя системы;
Еп — модуль сжатия материала последнего слоя системы;
— модуль сжатия материала предпоследнего слоя си-
Подставив выражения (13.24), (13’32), (13.39), (13.40) и (13.41)
в зависимость (13.1), получим
® = ^»,+ -Is-1/-^ + тКУ-?- +
т *2	£3 г
ИЛИ


227
+ Юээ(,-^-/-^)+	+
+ «-э(я_.,(1—(13.42)
Формула (13.42) и определяет деформацию сжатия многослойной
системы от произвольно заданной нагрузки в плоской задаче. Из
этой формулы видно, что при любой нагрузке деформация много-
слойной системы может быть определена через соответствующие
деформации от той же нагрузки эквивалентных однородных масси-
вов ограниченной мощности, образованных последовательно из ма-
териалов слоев системы. Полученная формула аналогична формуле
для случая нагрузки, равномерно распределенной по бесконечной
ЛИНИН.
$ 3. ДЕФОРМАЦИЯ СЖАТИЯ СЛОИСТОЙ СИСТЕМЫ
ОТ СОСРЕДОТОЧЕННОЙ НАГРУЗКИ (ПРОСТРАНСТВЕННАЯ ЗАДАЧА)
Осадка многослойного зернистого грунтового основания в рас-
сматриваемом случае также складывается из деформаций сжатия
отдельных слоев его и определяется по формуле (13.1).
Таким образом, для вычисления осадки слоистой системы необ-
ходимо определить деформацию сжатия каждого слоя.
Деформацию сжатия верхнего слоя можно рассматривать как
деформацию от заданной нагрузки слоя ограниченной мощности,
т. е.

где Р — сосредоточенная нагрузка;
hx — толщина верхнего слоя системы;
-wsl — деформация сжатия однородного слоя ограниченной мощ-
ности;
— модуль деформации материала верхнего слоя;
vj — коэффициент распределительной способности материала
верхнего слоя;
г — координата точки, в которой определяется осадка.
Определим осадку второго слоя системы. Вертикальные напря-
жения во втором сверху слое многослойной системы от сосредото-
ченной вертикальной нагрузки на поверхности
(13.44)
где v2 — коэффициент распределительной способности материала
второго слоя.
228
При распределении вертикальных напряжений во втором слое
по зависимости (13.44) деформация сжатия его
» Р„- ( "7--7=----ГГехР (-----7--7=----ГГ
Произведя в этом выражении замену переменной интегрирования
подстановкой
I'M"1 /£ + *)
получим
f -р(-т)^ (13.45)
г
л. W
После интегрирования выражения (13.45) и подстановки преде-
лов получим 
8 2Е4г И 2^8 I \ftiFv!/
- Ф (----------!=------\1	(13.46)
\ J/ +л^ yj
Прибавляя и вычитая единицу в квадратных скобках, предста-
вим это выражение в таком виде
2Е’Г г™,	Гъ(л, ]/-!+»,) )
(|3”>
Первый член выражения (13.47) представляет собой деформацию
сжатия от сосредоточенной нагрузки Р однородного грунтового мас-
сива мощностью Лд + Л2, образованного из материала вто-
рого слоя системы. Обозначим эту осадку
229
Выражение в квадратных скобках второго члена зависимости
(13.47) определим через осадку однородного массива нз формулы
(13.43)
(13,49)
Учитывая соотношения (13.48), (13.49) и выражения (13.47) для
деформации сжатия второго слоя системы, получим
W2 = W3Z —	(13.50)
Таким же путем можно получить формулу для определения де-
формации сжатия любого слоя системы. Так, для третьего слоя
деформация сжатия
т3=ш^—lA^,	(13.51)
где Е3 — модуль деформации материала третьего слоя;
пуэ3 — деформация сжатия от нагрузки Р однородного массива
ограниченной мощности hx 1/ — + h21/ — + Л3, обра-
»	* Уз
зованного из материала третьего слоя.
Для последнего слоя системы деформация сжатия
l/Ar- -	(13.62)
где доэл — деформация сжатия от сосредоточенной нагрузки Р
однородного массива ограниченной мощности
hi + Ла |Л-^- +	+ hnt образованного из
материала последнего (нижнего) слоя;
^(л-п—деформация сжатия от сосредоточенной нагрузки
однородного массива___________ограниченной мощности
Ail/S"+/'sp<vr+A’l/^zr+ +
+ hn_[t образованного из материала (п— 1)-го слоя;
En~t — модуль сжатия материала (л—1)-го слоя;
Еп — модуль сжатия материала последнего слоя.
Подставив выражения (13.43), (13.50), (13.51) и (13.52) в фор-
мулу (13.1), получим
с2 r	Ьэ 3
230
Группируя члены этого равенства, получим
Сравнивая полученное выражение с решениями для деформации
сжатия многослойных систем в плоской задаче, находим, что эти
зависимости аналогичны.
§ 4. ДЕФОРМАЦИЯ СЖАТИЯ МНОГОСЛОЙНОГО ЗЕРНИСТОГО
ГРУНТОВОГО ОСНОВАНИЯ ОТ ПРОИЗВОЛЬНО ЗАДАННОЙ
ВЕРТИКАЛЬНОЙ НАГРУЗКИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
Деформация сжатия многослойного грунтового основания от
произвольно заданной нагрузки в пространственной задаче склады-
вается из деформации сжатия слоев, составляющих основание, и
определяется выражением (13.1); вычислим эти составляющие.
Распределение вертикальных напряжений в верхнем слое си-
стемы от произвольно заданной нагрузки выражается зависимостью
113531
F
где f (г\ <р) — функция, выражающая нагрузку;
F — площадь, по которой распределена нагрузка;
Vj — коэффициент распределительной способности мате-
риала верхнего слоя;
г, <р; г — координаты.
При распределении вертикальных напряжений по зависимости
(13.53) деформация сжатия верхнего слоя составит
л.
=dkH]f(T'т)ехр(-^)№ (13-54)
где — осадка от заданной нагрузки однородного массива мощ-
ностью Alt образованного из материала верхнего слоя
системы;
— модуль деформации материала верхнего слоя.
Определим деформацию сжатия второго слоя в системе при про-
извольно заданной нагрузке на поверхности слоистого основания.
Для рассматриваемого случая загружения распределение вер-
тикальных напряжений во втором слое системы при начале
231
координат на границе первого и второго слоев выразится уравнением
(13.55)
При распределении напряжений во втором слое по зависимости
(13.55)	деформация сжатия этого слоя
=
X ехр (---------7=-----TrXdFdz,
(13.56)
где v2 — коэффициент распределительной способности материала
второго слоя;
Еа ~ модуль деформации материала второго слоя;
Л8 — толщина второго слоя.
Произведя замену переменной интегрирования г в выражении
(13.56)	подстановкой (13.26), получим
Ю2=5-2^ J Т)еХР("’Й5')‘,ЛИ
“'«=^7 У Н/(г’’)ехр("2^)Л?Л~
О	F
J -И/(г-	<1357'
О	F
Первый член выражения (13.57) представляет собой осадку от
заданной нагрузки однородного массива мощностью A, j/^2L -|_
232
состоящего из материала второго слоя. Обозначим эту осадку через
л. +Л,
«и = tV f i [/(»•. <Р) ехр (- dFdt. (13.58)
Второй интеграл выражения (13.57) преобразуем, произведя в
нем замену переменной интегрирования t подстановкой (13.28);
получим
л, jAj-
f ^jf(r,.)exp^-^dFdt^
О	F
- к	^)‘,rav <|зм)
0 F
Интеграл в первой части выражения (13.59) определим из фор-
мулы (13.54)
j -^г J/(г> т) ехР (—	= 2«и»ы£л«
OF	11
Подставив это значение интеграла в выражение (13.59), получим
j ’ у j f(r' ехр (“ dFdt =	(13-60)
Учитывая принятое обозначение (13.58), а также выражения
(13.60) и (13.57), получим деформацию сжатия второго слоя системы
(13.61)
2
Определим деформацию сжатия третьего слоя системы. Распре-
деление вертикальных напряжений в третьем слое многослойной
системы от произвольно заданной вертикальной нагрузки выра-
жается зависимостью
°л.+л.+ж —	/	/—	г—	\* С ф) X
Х«хр/----------,.—	----я-Vf. <1362>
233
Деформация сжатия третьего слоя системы при распределении
вертикальных напряжений в нем по выражению (13.62)
»» = 9 *F С -----7= !—7=----п- f /('. ?) X
X ехр f-------dFdz. (13.63)
к цА1]/^+А,у^+г);
Произведя в этом выражении замену переменной интегрирова-
ния z подстановкой (13.34), получим
Л, +Й, +Ла
_ Я/(г>
Представив этот интеграл в виде разности двух интегралов, по-
лучим
V ^+Ал
w’=iir J Я/(г’?)exp("^-)d™“
о	F
О	F
где v3 — показатель распределительной способности материала
третьего слоя системы;
Е3 — модуль деформации материала третьего слоя системы;
Л3 — толщина третьего слоя системы.
Первое слагаемое зависимости (13.64) представляет собой выра-
жение для деформации сжатия от заданной нагрузки однородного
массива мощностью ht 1/	4- й2 у — 4- Л3, состоящего из мате-
r va	Г v>
риала третьего слоя.
Обозначим это выражение через
]/	+1ъ	--- +ла
f 4-f/(6T)X
о	/•
Хехр(—-tlAdFdt.	(13.65)
234
Под вторым интегралом выражения (13.64) произведем замену
переменной интегрирования подстановкой (13.35). После замены
переменной второй интеграл выражения (13.64) примет вид
А*/^+А>/^
J -И/(г> ?)exp(-^)d™ =
О	F
-/1 J	’)'«р(-^г)<« («“)
О	F
Интеграл в правой части выражения (13.66) определим из выра-
жения (13.58)
J	V)“p(—=	(13.67)
О 4 F
На основе этого соотношения и зависимости (13.66) второй ин-
теграл выражения (13.64) может быть представлен как
Л1]/г2Г+Л, j/s:
= ws2E2 У v2vs-	(13.68)
Принимая во внимание обозначение (13.65), соотношение (13.67)
и выражение (13.64), получим
“>3 = «>33 — w*2	]/-— •	(13.69)
£3 r v3
Эта формула определяет деформацию сжатия третьего слоя в си-
стеме; она по структуре аналогична формуле (13.61). В силу этого
для определения деформации сжатия последнего слоя в системе
имеем такую зависимость
W =™ -и>,1я ..	]/r^=L-(13.70)
Л 9П	Э (Л—I)	1/	'	*
где и>эя — деформация сжатия от заданной нагрузки однород-
ного массива мощностью А, 1/ — + Л21/ —	+
1	"*п г vn
+ Лл, состоящего из материала последнего слоя;
шэ<л-п — осадка от заданной нагрузки однородного массива
235
мощностью hi р/ + Лг|/ 4-	. + Ля_1
состоящего из материала (п—1)-го слоя системы;
£л_, — модуль сжатия материала (п—1)-го слоя системы;
Еп — модуль сжатия материала л-го слоя системы.
Подставим выражения (13.54), (13.61), (13.69) и (13.70) в формулу
(13.1); получим
Ш= ШЭ1	У+ 0Уэа	I/-7- +
с2	2	£3 г ’8
Д- W — W .^я~1 1 / _л~~1
эи ^(H-D Еп у уп •
Группируя члены этого равенства, получим
По формуле (13.71) определяется деформация сжатия многослойной
системы от произвольно заданной нагрузки в пространственной за-
даче; она аналогична формуле, полученной для деформации сжатия
многослойной системы в плоской задаче. Вместе с тем следует под-
черкнуть, что входящие в эти формулы величины шэ2 w9n
различны, так как определяются для разных нагрузок.
Г лава 14
УРАВНЕНИЯ ДИНАМИКИ ДЛЯ ЗЕРНИСТОЙ ГРУНТОВОЙ
СРЕДЫ ПРИ УПРУГИХ ДЕФОРМАЦИЯХ ЗЕРЕН
§ 1. СВЯЗЬ МЕЖДУ СОСТАВЛЯЮЩИМИ НАПРЯЖЕНИЙ И УРАВНЕНИЯ
ДИНАМИКИ В ПЛОСКОЙ ЗАДАЧЕ
Согласно рис. 14.1, перемещение частицы грунта в вертикальном
направлении происходит под воздействием вертикальных состав-
ляющих напряжений и сил инерции, которые можно выразить так:
(14.1)
*	\дг v dl* )
236
Усилия на соседнюю в ряду частицу по аналогии с зависимостью
(14.1) и через приращение напряжений по оси х выразится так:
L\ dz г д(г дх \dz и д/2 У]’	'	’
где b — средний размер зерен.
Разность между этими величинами вызывает скалывающие уси-
лия в частицах, на которые опираются рассматриваемые зерна.
Эта разность связана определенной зависимостью с касательными
напряжениями. Определим ее как некоторую функцию от каса-
тельных напряжений
Рис. 14.1. Схема к определению связи между динамическими
усилиями на соседние в ряду зерна и перерезывающим уси-
лием в связующей частице
/<’->—<1,Л)
Разделив обе части равенства на д8, получим
—/(’„)=—Ч—-р—(14-5>
& J ' п' дх \ дг v dt* I
При статической нагрузке = 0, тогда
dt*
237
С другой стороны, при статической нагрузке касательные напря-
жения с вертикальными связаны следующим соотношением
(14.7)
Разделив обе части выражения (14.7) на vz, получим
Txz   dgz
VZ	дх
(14.8)
Продифференцируем это уравнение по z
-2_рнЛ=—(14.9)
дг \ vz ) дхдг
Правые части выражений (14.6) и (14.9) одинаковы, следо-
вательно,
Теперь выражение (14.5) примет вид
-*-р*4-----L/(14.11)
дг ) дх \ дг ? dt2 )	1	'
Приведем уравнения равновесия при равенстве нулю объемных
сил
+	(14.12)
дг	дх	dt2
^.+ ±Н. = рА,	(14.13)
дх	дг	dt2
Разделив уравнение (14.12) на vz, получим
_Lp«\ =----(14.14)
дх \ w /	* \ дг v dt* J	'	’
Дифференцируем выражения (14.11) по х и (14.14) по z
(14.15)
дгдх J дх*\дг r dt* )	'
(14.16)
дхдг { *г J дг [ « \ дг **« /]
Левые части выражений (14.15) и (14.16) равны, следовательно,
(14.17)
дг [	\ дг r dt2 /J дх2 \ дг r dt2 /	'
Умножив и разделив правую часть этого уравнения на vz, полу-
чим
д Г 1 / дзг _________ d2u> \ I , d2 Г 1 / дз2
дг [	( дг Р dt* ~	« \ дг
Р-§4]. силе»
238
Обэзначив выражение в квадратных скобках
получим
1 / дзг	д2ш \
--- ----£	р 	J
'Z \ дг----------dt2 J
дг дх*
(14.19)
(14.20)
Решение уравнения (14.20) при следующих граничных условиях
f = — Р (i) при г = 0, х = 0, т. е. в точке приложения сосредото-
ченной нагрузки;
f = 0 при z = 0, х 0,
т. е. во всех остальных
точках поверхности мас-
сива;
f -> 0 при х -> ± оо
имеет вид
--£-)• I142"
Подставив в выраже-
ние (14.21) значение f из
Рис. 14.2. Схема, показывающая область
вынужденных возмущений среды при со-
средоточенной динамической нагрузке
(14.19), получим
(14.22)
дз, д*ш
—-----р------
дг	г д/2
VZ	/	X*	\
г-—ехр (--------).
Vfctvz2	\	2w2	/
или
---р (О
(14.23)
Учитывая, что
о2 = £^1и^=Е^,	(14.24)
1 dz дг дг*	'	'
имеем
d*w_______р dl*w _________ Р (/)
дг* Е dt2 ~ Е
/V /	х2
— ехр I--—
2к	2>z«
(14.25)
Уравнение (14.25) является неоднородным уравнением гипербо-
лического типа; оно выражает вынужденные колебания грунтового
массива от вертикальной сосредоточенной динамической силы. Пра-
вая часть этого уравнения при принятых граничных условиях по-
казывает, что вынужденному возмущению подвергается лишь та
часть массива, которая распределяет внешнее давление от статиче-
ской вертикальной силы (рнс. 14.2).
239
Если возмущающая нагрузка распределена по полосе шириной
2Ь и может быть представлена в виде произведения двух функций,
одна из которых зависит только от tt а вторая только от х, т. е.
Р(х, 0 =	(14.26)
то уравнение колебаний грунтовой среды от такой нагрузки опре-
делится так:
, +ъ
д2^____Р_ _ Pi (0 - Г С р /п у
dz2 Е dt2 Е У 2т. J 21
-Ь
X expf-J^-U,	(14.27)
\	Z'/2X	1
При подвижной нагрузке вертикальные колебания основания
определятся уравнением
d2ay р д2® _ Pi (О 1/~ f р /t\v
г~ У тг J Рг(6)Х
X ехр f—	•	(14.28)
Рассмотрим поперечные колебания грунтового массива. Для
этого уравнение (14.12) продифференцируем по z, а (14.13) по х
д2тхг _____ д	/	дэг__ д*и>	\ #
dxdz	dz	\	dz	dt*	/
dhxz ___ d	(	dix __ d*u	\
dxdz	dx	\	dx	dt2	J ’
(14.29)
(14.30)
Поскольку левые части уравнений (14.29) и (14.30) равны, то
приравниваем и правые части, т. е.
*23.	(14.31)
dx \ dx r dt2 I dz \ dz r dl2 /
Дифференцируя no z выражение (14.23), имеем
Подставляя это выражение в уравнение (14.31), получим
Интегрируя по х, имеем
dox d^u
dx r dt2
=-₽(of41/'-iexP(-^-)^ + />"(2: 0. (14.34)
240
где Рп (z, t) — произвольная функция интегрирования.
При х -> оо -> 0,	-> О,
н	дх dt*
Поскольку
Следовательно Р„ (г, 0 = 0.
Тогда выражение (14.34) примет вид
dx ->0.
^L_p^_=_p(z)
дх v dt* v '
(14.35)
(14.36)
д*и____р д*и
дх* T~di*
Для нагрузки, распределенной по полосе, поперечные колебания
выразятся зависимостью
д*и р д*и____
~дХ* ~е1Й*-
+ь
---^=г- f Р2 (5) Г С (х — ЕГехр (—(14.38)
Z3£)/2r.-, J LJ	\ 2vz« J J
—b
Для подвижной нагрузки уравнение колебаний выразится так:
% —F > =------^7^- Г Х
дх* Е dt* z*Ey2r^ J
x|k—л» (О — Ч*ехр
1-—dx) <К.
2vz‘ / I
(14.39)
Касательные напряжения, а следовательно, и повороты при ко*
лебаниях, определим из уравнения (14.12)
&хг =__ / дах __ д*ш 1
дх \ dz Р dt*~t
(14.40)
Из выражения (14.23) подставим в правую часть возмущающую
функцию для сосредоточенной вертикальной силы
-^. = Р(/)1/’ _^_ехр(——(14.41)
дх ' '	2-	2vz« /	'
241
Интегрируем это выражение по х
= Р(0JехР (—^~)dx + Pn^’	(14-42)
х-*0;	fexp(---^-)d*->-0.
Следовательно, Рп (z, 0 = 0;
тогда	___
= Р (О	f ехр(- -^г)dx-	( М.43)
Для нагрузки, распределенной по полосе,
= Pi V) f р* (?) Г f ехр (—	(*4-44)
I	I I	\	М wif	/	[
—ъ
Для распределенной и подвижной нагрузок
Ъ = РЛП J PtG) [ j ехр (- 1Х~^~еР)л] dt (14.45)
—ъ
где х0 (0 — координата положения нагрузки как функция времени.
§ 2. СВЯЗЬ МЕЖДУ КОМПОНЕНТАМИ НАПРЯЖЕНИЯ
В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ. УРАВНЕНИЯ ДИНАМИКИ
В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
По аналогии с формулой (14.11) и соотношениями между напря-
жениями для статической нагрузки получим следующие зависимо-
сти между касательными и вертикальными напряжениями в дина-
мике:
д j	f тлг	, 		д I	'д:г	— Р-	d2w \, -	It
дг 1	. vz 1	1 дх 1	( dz		dt2 )
д 1	1	1		ds2		d^w \
				— р-	
дг ’		।	ду 1	i дг		dt2 )
д .	( хху	\	д^		— р	д^ \
дг ’	>2z2	1 дхду	\ дг		dt2 j
(14.46)
(14.47)
(14.48)
Уравнения равновесия для пространственной задачи при ра-
венстве объемных сил нулю;
д<зг . дтгУ . дтхг d,2w .
дг ду дх Р dt2 ’
дчх	.	дчху	 дгхг	= д2и	.
дх	’ ду	дг	Р dt2 ’
дзу		д^уХ дъуХ	__дЧ*
ду дх	дг	' dt2
(14.49)
(14.50)
(14.51)
242
Разделив обе части уравнения (14.49) на vz, получим
д I ~zy \ । д /	\ _____ । /
ду \ уг J дх \ 'а )	\ дг
Продифференцируем выражение (14.52) по z:
&
дудг
д
дхдг
1 / да,	\1
— I—5------Р---II •
уг \ дг	г	dt2	/J
(14.52)
(14.53)
Продифференцируем уравнения (14.46) по х и (14.47) по у и сло-
жим их:
д2
дхдг
Э2 / ггу \ ______ д2 / дзг ___ d^w \
дудг \ ^ ) дх2 \ дг Р dt2 )
д2 / дзг ___ д*ш \
дуг \ дг ₽ дР ) '
(14.54)
Левые части уравнений (14.53) и (14.54) одинаковы, следовательно
д I / дзг __________ d^w \1_______ д2 / дзх d2w \
Р dt2	Р dt2 )
, д2 / дзх d'-w \
ду2 \ дг r dt2 /
(14.55)
Разделив и умножив правую часть этого уравнения на vz, получим
Воспользовавшись обозначением (14.19), имеем
(14.57)
Решение уравнения (14.57) при граничных условиях
f = — Р (/), при z = 0, х = 0, у = 0, т. е. в точке приложения
сосредоточенной динамической нагрузки;
f = 0, при z = 0, х 0, у 0, т. е. во всех остальных точках
поверхности массива;
/->0 при х-*±со; у-*±оо
имеет вид
или, подставив из (14.19) значение f, получим
_!_ (*£- _ р	(/)-!— ехр	(14.59)
\ дг 1 dt2 ) V 7 2*уг2 н \ 2уг2 )	'
243
Умножая на vz, имеем
дог d*W	I / Х3 + у3 \ Z1 . спч
17~р^---------Р(°-£7ехр(-------w )•	(,460)
Сопоставив соотношения (14.24) и (14.62), получим
г-%-------Р(/)-±-ехр (-* + £).	(14.61)
dz3	Е dt3	к 7 2nEz r \	№ J '	7
Для процесса колебаний в пространственной задаче получено
также неоднородное уравнение гиперболического типа, которое
выражает вынужденные колебания массива. При этом правая часть
уравнения (14.61) соответствует области, в которой грунт при ди-
намике приходит в возмущение.
Если представить нагрузку как произведение функции, завися-
щей только от времени, и функции, зависящей от переменных х
и у, т. е.
РЮ-РДОРИ*.	(14.62)
уравнение колебаний для нагрузки, распределенной по некоторой
площади, будет иметь вид
р
"dz*
—	ч)ехр(-
/
(»-^+(У-ч)1	(14.63)
где F — площадь, по которой распределена нагрузка.
Уравнение колебаний грунтового основания от подвижной на-
грузки имеет вид
р dty _ р 1
dz3 Е dt3	J 2nEz
X f P,(I; 4)exp(-(хгх.(0-1)» + (у-».(0-^\dF (1<64)
F
Из выражений (14.46), (14.47), (14.48) и (14.60) находим зависи-
мости для касательных напряжений
ИЛИ
2г». =— (’_£_[_/’(/) —— ехр (—	1 dz 4-
« J дх L 2м Е\ 2м» Л
+ Ря(*.Х,у).	(И.66)
При z->«; ^-0; ([4"[“Р(0^'еХР(~2Й^)]</г'>0-
244
Следовательно, Рк (/, х, у) 0 и выражение (14.66) принимает
вид
Аналогично
— С JL Гр (?) ехр (— -*+ауа) 1 dz.
2л J дх L \	2vZ /-1
— f JL ГР(/)ехр(—	1 dz.
2л J ду	\	2vz“ / J
На основе выражений (14.48) и (14.60), имеем
Интегрируя по z, получим
+ РЛ*> у).
(14.67)
(14.68)
(14.69)
(14.70)
При £->со
следовательно Рк (/, х, у) = 0. Тогда
-2L
дхду
Х*У
\*z Г
7Г J
P(t)exp
(14.71)
Для решения задачи о поперечных колебаниях воспользуемся
уравнениями равновесия (14.50) и (14.51). Из уравнения (14.50)
имеем
дзх____ д2и __ дтху _________дххг
дх Р dt* ду dz
(14.72)
Дифференцируем по у выражение (14.71), по z (14.67) и подста-
вив в уравнение (14.72), имеем
д<зх  д*и __	\*z Г д*
дх	?~dt* STJ дхду*
Р (ОехР
dz —
у___д_
2л дх
Р(/)ехр( —
х* +у*
2vz2
(14.73)
Аналогичным образом преобразуем уравнение (14.51):
д<зу _ d*v __ y*z С д*
~ду Р’дР” 27J дудх*
Р (1)ехр
Учитывая, что
дах ___е д*и
дх дх*
Р(/)ехр
(14.74)
(14.75)
245
дау __ дги
ду ду-
(14.76)
уравнения (14.73) и (14.74) относительно переменных и и и примут
вид
д2и р д2и ______ у
а?	2г£
М «£['<')«₽(”
Р (0е*Р
(14.77)
d2v р дги
ду2 ~~F~d^
VZ
X2 -Г У2
» '
|2
1 й/L’ '' * \ 2v22
Для нагрузки, распределенной по площади F, эти уравнения
преобразуются к виду
№ р №_____________(О L, f Р г- УЧ v
----------------2т.Е Г . !(” ')Х
(14.78)
дх2 Е dt2
&
дхду2
(*~е)2-н
2vz*
2 а2
dF ;	(14.79)
дЪ р д2и _____________	(/)
ду2 dt2 2т.Е
------ехр —
дх2ду г \
Вводя переменные во времени координаты положения нагрузки,
получим уравнения колебаний от подвижной нагрузки
д2и_____р д2и _
дх2	Е dt2 2кЕ
j Ра(«; v)x
F
1Х-М')-6Р+[У-Уи(*)-
дхду2
2vz2	/ J
(Q—-EJa~1~	*	(14 81)
2vz«
д
246
a*»	р _________’Pi(0 (,-лСр
ду*	Е dt* 2-Е I * J *
ехр
[X - Х„ (О - С1- + [У - Уо (0 - чР
2-,г2
dz dF +
+ f Р2(«; ч) — ехр (—1Х Ло(О ;F + Iy	, (14.82)
I	dj/ \	2\z2	j • j
где dF = d\df[.
Глава 15
СРАВНЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ С ОПЫТНЫМИ
ДАННЫМИ И ТЕОРИЕЙ УПРУГОСТИ
§ 1. ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ. ИСПОЛЬЗУЕМЫЕ ДЛЯ
ПРОВЕРКИ ТЕОРЕТИЧЕСКИХ РЕЗУЛЬТАТОВ
Для проверки теоретических результатов используем экспери-
ментальные данные, полученные различными исследователями [8,
12, 57, 73, 84, 107]. Основные сведения об этих экспериментах при-
ведены в табл. 15.1.
§ 2. СРАВНЕНИЕ ТЕОРЕТИЧЕСКИХ ДАННЫХ С ОПЫТНЫМИ ДАННЫМИ
ИЛЛИНОЙСКОГО УНИВЕРСИТЕТА
При проведении опытов в Иллинойском университете, помимо
изучения распределения напряжений, одновременно велись наблю-
дения за движением частиц; грунт под штампом при испытании на-
ходился в предельном состоянии. Это обстоятельство вызывало пе-
рераспределение напряжений по подошве штампа. Однако характер
распределения давления по подошве штампа неизвестен. Поэтому
для построения теоретических кривых поступим так. Положим, что
в предельном состоянии распределение напряжений по подошве
штампа имеет колоколообразную эпюру и выражается уравнением
2\z/ta
(15.1)
где Ря — давление по подошве штампа;
Р — заданная нагрузка в кг;
247
кэ
So
Наименование опытов и место их проведения	Год проведе* ния	
Опыты Штейнера и Кнка Опыты Штрошнейдера	1909—1911	Сухой песок; толщина от 3,3 до 12 см Сухой песок; толщина от 2 до 5 см
Опыты Иллинойского университета	1910-1915	Мелкий сухой песок; тол- щина 15,2; 30,5 и 45,7 см
Опыты Пенсильванской
технической школы
1913—1914
Опыты проводились с тре*
мя видами грунтов. Песок
речной средней окатанности.
Глинистая смесь (85м глины,
10М песка, 5% суглинистого):
влажность 11,3%. Объемный
вес при укладке 1,2 г{см\
в уплотненном состоянии
1,5 г[см*. Угол естественного
откоса 38,5°. Суглинистая
смесь содержала глинистую
смесь и 22% гравия; влаж«
ность 13,6%. Объемный вес
при укладке у = 1,07; после
испытаний у = 1,38 г/сж3.
Угол естественного откоса
40,5°.
Таблица 15.1
		Способ регистрации напряжений
Нагрузка на штамп 31 кг		Рычажные весы; шня 1,5 см
50 г		В дно ящика заделывалась стеклянная капсула, затянутая резиновой мембраной. Капсула заполнялась водой. Давление измерялось по уровню спирта в трубке, соединенной с капсу- лой промежуточной трубкой, за- полненной вазелином
4000 кг		Грунт укладывался на массив- ную бетонную плиту размерами 220X225X 40 см. Давление изме- рялось с помощью рычажных весов; диаметр поршня 10,5 см
Нагрузка на штамп изменя- лась от 136 до 2450 кг, возрастая ступенями по 450 кг	Деревянный штамп размером 30,5X30,5X 8.9 см	Испытания проводились в ящике с размерами 1,8 X 1,5 X X 0,6. Рычажные весы. Размер поршня 30,5 X 30,5 см
1917—1924	Песок сы состава	ЮЩРГО
	Размер фракции в мм	Содержание в %
	6-2,5	
	2,5-1,2	
	1,2-0,8	
	0,8—0,6	
	0,6—0,5	
	0,5—0,3	
	0,3-0,2	
	0,2-0,1	
Опыты Американской
ассоциации гражданских
инженеров
Песок
Щебень
Гравий (от 6 до 38 мм)
Среднее давление
на подошву
штампа колеба-
лось от 0,4 до
2,5 кг/см*. При
d = 34,3 см
Р «= 2270 кг. При
d = 20.3 см
Р = 1800 кг
Р - 5650 и
Р - 3400 кг
Металлические
штампы
d = 20,3 и
d = 34,3 см
Герметически закупоренная
коробка диаметром 14 см. сое-
диненная с баллоном сжатого
воздуха.
При прогибе латунной мем-
браны на 2,0025 мм замыкалась
электрическая цепь, размыка-
ние которой осуществлялось
сжатым воздухом, по давлению
которого измерялась величина
напряжений
Шпалы
15X 25X 224 см
Пружинный динамометр за-
кладывался в грунт. Показания
снимались по мессурам, соеди-
ненным с пружинным динамо-
метром
КЗ
ё
Наименование опытов и место их проведения	Год проведе- ния	Грунт
Опыты Ксглсра и Шей* дчга	1925-1927	Сухой песок крупностью зерен до 2 мм и с углом ес- тественного откоса 31,5Э. Объемный вес в неуплот- ненном состоянии f — 1,5 и в уплотненном у = 1,77 ?/<’.* Коэффициенты пористости в неуплотненном состоянии 0,76, в уплотненном — 0,486
Опыты Н. В. Лалстнна	1930	Песок
Опыты Г. 11. Покров- ского и 11. С. Федорова	1932-1933	Песок средней крупности
Опыты Д. С. Баранова (.МИСИ. ЦПНИСК)	1955-1960	Песок мелкозернистый 7 = 1.54-7 1,56 г [с. и3
Опыты М. П. Болштяп- ского (Транспортно-э«ср- гетнческиЙ институт Снб. отд. АН СССР)	1962	Подобранный сильно ока- танный гравий т - 2,15 г,смл‘
Продолжение
Нагрузка	Размер штампа	Способ регистрации напряжений
1,05 кг,см3	d ~ 33.9; d = 45; d - 63 см	Сосуд с резиновой мембраной заполнялся водой и соединялся с ртутным манометром. Сосуд помещался в грунт. По мано- метру производился отсчет
0,5 и 0,23 кг/см*
2.5 кг см3
До 2.6 кг/см3
До 2,84 кг/см3
Чугунная плита
25X15X3 см
Штамп
s - 5000 см3
48 см
Штампы дна*
метром
15; 25 и 36 см
Давление измерялось в направ-
лении большей стороны элек-
трическим способом, основой ко-
торого являлось нзмэненне ем-
кости конденсаторов при изме-
нении давления на них. 9 кон-
денсаторов монтировались на
одной доске, на расстояниях
7,5 см друг от другэ. Перед ис-
пытанием конденсаторы были
протарированы
С помощью динамометров
Г. И. Покровского
Месдозы с гидравлическим
преобразоватслем
Электротснзометрические ди-
намометры
v — коэффициент распределительной способности грунта (ко-
эффициент бокового давления);
Л — некоторая постоянная.
Если нагрузка задана уравнением (15.1), то распределение на-
пряжений выразится зависимостью
о =------------ехр Г------------1.	(15.2)
2ут. (Л2 -1- z2) F [ 2v (Л2 + z2) J
Поскольку нагрузка при проведении экспериментов передава-
лась на штамп, то представим ее через среднее давление на штамп
P = P0*R2,	(15.3)
где р0 — среднее давление на штамп в кг!см2\
R — радиус штампа в см.
После подстановки выражения (15.3) в (15.2), получим
с = ——ехр Г---------------------1.	(15.4)
4	2>(*2 + z2)	2v(*2 + z2) J
Разделив правую и левую части выражения (15.4) на среднее
давление на штамп, получим
— --------—-----ехр [--------—----1,	(15.5)
Ро 2у(Л2 + гЭ L 2у(Л24-22)]
откуда при г = 0 получим выражение для вертикальных напряже-
ний по оси действующей нагрузки
%,
Ро 2у (/i2 + z2)
(15.6)
Выражением (15.6) воспользуемся для определения величины А.
Из опытов для глубины 15 см имеем = 3, а для глубины 30 см
= 1; на основании выражения (15.6) имеем
300 =-----—-----;
2-.(Л‘+ 15*)
(15.7)
И	
100 =	(15.8)
2>(Л2 + 302) ’	
Разделив выражение (15.7) на (15.8), получим	
3 = Л2 + зо2 Л2 + 152 *	(15.9)
откуда	
10,5 см.	(15.10)
251
На основе выражений (15.-5), (15.6), (15.7), (15.8) и (15.10) полу-
чим уравнения для построения кривых распределения напряжений
на глубине 15 и 30 см:
®zej5£3L==300exp [_
100
50
О
Ро
2v(10,5»+15>)J
г3
2ч337
°Z - 30 см
Ро
100 ехр (•
2vl012 )
(15.12)
В полученных формулах
остается определить коэффи-
циент V. Для этого прирав-
няем одну из ординат экспе-
риментальной кривой к выра-
жению (15.11) или (15.12).
Целесообразно выбирать орди-
нату ближе к оси действия на-
грузки, т. к. при этом относи-
тельная ошибка будет меньше.
Возьмем ординату, расположенную в 10 см от оси нагрузки для
глубины 15 см. Эта ордината равна 116, тогда
116 = 300 ехр
откуда	v»0,15.	(15.14)
Следовательно, выражения (15.11) и (15.12) можно представить так
Таблица 15.2
40 30 20 Ю № 20 J5“4cm
Расстояния 6 сн от оси штампа
§
Рис. 15.1. Сравнение теоретических ре-
зультатов с опытными данными Илли-
нойского университета
а — для z = 16 см; б — для 2 = 30 гм
•);	(15.11)
(15.13)
		= 30
	Значси	ше р0
5	236	92,31
10	116	73
20	6,7	28,65
30	0,048	5,84
= 100 ехр (-
(15.15)
—V
303 )
(15.16)
Вычисленные по формулам
(15.15) и (15.16) величины .для
разных значений аг приведены
в табл. 15.2.
По данным табл. 15.2 на рис. 15.1 прерывистой линией нанесены
теоретические кривые. Как видно из рисунка, теоретические кривые
252
достаточно хорошо согласуются с экспериментальными. Для глу-
бины 15 см наибольшие расхождения имеются лишь для малых на-
пряжений. Причиной этого могут быть: произвольность выбора
характера распределения давления по подошве штампа при построе-
нии теоретических кривых, а также большие относительные погреш-
ности экспериментальных данных при измерении относительно ма-
лых величин.
§ 3. СРАВНЕННБ ТЕОРЕТИЧЕСКИХ РЕЗУЛЬТАТОВ С ОПЫТНЫМИ
ДАННЫМИ ШТЕЙНЕРА И КИКА
Для сравнения используем данные, приведенные В. Ф. Бабко-
вым [841 в табл. 15.3.
Таблица 15.3
I № серин I	Давление иа штамп в кг	Толщина слоя в см	Осадка штампа в см	Давление на поршень в кг на расстоянии от осн штампа в см										
				0			в	8	10	12	14	16	18	20
1 2	30,97 30,97	8 13,2	1.5 2,0	3,0 1,2	2,3	1,0 0,7	0,4 0,3	0,1 0,4	0,0 0,3	0,2	0,2	0,1	0,1	0,1
Учитывая, что радиус штампа, через который передавалась на-
грузка, равнялся 5 см, а радиус поршня 1,5 см, составим ту же таб-
лицу в относительных величинах (табл. 15.4).
Таблица 15.4

§•
£
1
2
0,394
0,394
1,6
2,64
Напряжение в % от среднего давления на штамп
на расстоянии в долях от радиуса штампа
0	0.4
108	82
43,2 -
По данным табл. 15.4 на рис. 15.2 прерывистыми линиями по-
строены кривые, а сплошными линиями показаны теоретические
кривые для нагрузки, распределенной по параболе на площади
квадрата при v = 0,14.
Параболический характер распределения нагрузки принят по-
тому, что штамп при испытаниях погружался в песок, а это вело
к перераспределению напряжений по его подошве. В таких случаях,
как показывают экспериментальные работы [57, 73, 84, 107), эпюра
давления по подошве принимает параболический вид.
253
Результаты вычислений, по которым построены теоретические
кривые, приведены в табл. 15.5.
Из рисунка видно, что теоретические кривые выше опытных.
Это может быть объяснено следующим: поскольку площадь квад-
рата со стороной, равной диаметру круга, больше площади круга,
то вычисленные величины напряжений будут несколько больше
опытных, так как опыты проводились с круглым штампом. Кроме
Рис. 15.2. Сравнение теоретических результатов с опытными данными
Штейнера и Кика
а — для — = 1.6; б — для — = 2,64
того, на результаты сравнения может оказать влияние выбор ха-
рактера распределения давления по подошве штампа. И, наконец,
точность показаний использованных при экспериментах датчиков
равнялась 0,1 кг, что составляет
——--------- 100%	3,6% от среднего давления,
г.-1,52-30,94
где 5 — радиус штампа;
1,5 — радиус поршня;
30,94 — нагрузка на штамп.
Можно считать, что сходимость теоретических данных с экспе-
риментальными удовлетворительна.
254
Таблица 15.5
§ 4. СРАВНЕНИЕ ТЕОРЕТИЧЕСКИХ РЕЗУЛЬТАТОВ С ОПЫТНЫМИ
ДАННЫМИ ШТРОШНЕЙДЕРА
На рис. 15.3 представлены опытные кривые Штрошнейдера, при-
веденные В. Ф. Бабковым [84]. Масштаб изображения этих кривых
ьоъ
Рис. 15.3. Сравнение теоретических результатов с опытными данными
Штрошнейдера
настолько мал, что теоретические кривые сливаются с опытными.
Для большей наглядности кривые изображены прерывистыми ли-
ниями в увеличенном масштабе. Сплошными линиями изображены
теоретические кривые, построенные для нагрузки, распределенной
на площади квадрата по параболическому закону при v = 0,17.
Поскольку испытания проводились с круглым, а не с квадратным
штампом, то теоретические результаты должны быть несколько
больше опытных.
Теоретические значения напряжений в процентах от среднего
давления на штамп, по которым произведено построение кривых,
приведены в табл. 15.6.
255
Таблица 15.6
Для точек, расположенных по глубине на оси штампа, имеются
количественные значения измеренных Штрошнейдером напряже-
ний, с которыми сравним теоретические результаты. В табл. 15.7
приведены опытные данные Штрошнейдера.
Таблица 15.7
		Глубина в см	Измеренное напряжение в г/сж’
50	0,75	2	10,8
50	0,75	3	5,0
50	0,75	4	2,8
Определим теоретические значения для нагрузки, распределен-
ной на площади круга по закону параболы, поскольку испытания
проводились с песком и при опытах наблюдалось выдавливание
песка в стороны. При этом происходило перераспределение давле-
ния под штампом.
Для вертикальных напряжений имеем
Коэффициент v вычислим по одному из значений измеренных на-
пряжений, а по двум другим проверим справедливость теоретиче-
ской формулы. Для вычисления коэффициента * используем опыт-
ное значение напряжений для глубины 2 см. Тогда получим
откуда v 0,167.
*256
При этом значении v приведенная выше формула примет вид
Вычисленные по формуле (15.18) результаты, опытные данные
Штрошнейдера, а также теоретические результаты О. К. Фрелиха
представлены в табл. 15.8
Таблица 15.8
Глубина о см	Измеренное Штрошней- дером напря- жение	Вычислен- ные О. К. Фре- лихом	Вычисленные автором	Разница в % теоретических результатов по отношению к опытным данным	
	в г]см*			О. К. Фрелиха	автора
2	10,8	11,93	10,62	+10.3	—1,7
3	5,0	5,3	4,96	+ 6	—0,6
4	2,8	2,97	2,81	+ 6	—0,4
Из сравнения теоретических результатов с опытными данными
Штрошнейдера видно, что теоретические кривые с качественной сто-
роны вполне соответствуют опытным. Расхождения же в количест-
венном отношении объясняются, с одной стороны, различием формы
штампа, применявшегося при опытах (круглый) и использованного
для подсчета теоретических напряжений (квадратный) и, с другой
стороны, точностью графических построений при увеличении мас-
штаба изображения опытных кривых.
Сравнение теоретических напряжений по оси загруженного
круглого штампа с опытными напряжениями, указывает на хоро-
шее совпадение теоретических и опытных данных.
§ 5. СРАВНЕНИЕ ТЕОРЕТИЧЕСКИХ РЕЗУЛЬТАТОВ С ОПЫТНЫМИ
ДАННЫМИ ПЕНСИЛЬВАНСКОГО КОЛЛЕДЖА
Измерительная площадка при проведении опытов в Пенсильван-
ском колледже имела размеры 30,5 X 30,5 см и равнялась площадке
через которую осуществлялась передача нагрузки на грунт. Таким
образом, измерялось, не действительное напряжение в точке, а сред-
нее напряжение на площадку, которое для точек, расположенных
ближе к линии действия нагрузки, будет меньше действительных
напряжений. Это обстоятельство не позволяло непосредственно
производить сопоставление напряжений в каждой точке.
Необходимо подчеркнуть, что многими исследователями опытные
данные Пенсильванского колледжа неправильно сравнивались
с решениями теории упругости. Неточность заключалась в том, что
257
средние давления на площадку больших размеров в опытах отож-
дествлялись с напряжением в точке по оси штампа. При Этом по-
лучались напряжения даже меньше тех, которые дает теория
упругости. Чтобы не повторить эту ошибку, воспользуемся реше-
нием для давления на площадку на глубине от нагрузки, рас-
пределенной по прямоугольной площадке на поверхности. При
этом рассмотрим два случая давления на прямоугольную пло-
щадку: от нагрузки, равномерно распределенной на площади
прямоугольника, и распределенной на прямоугольной площадке
по закону параболы.
Для нагрузки, равномерно распределенной по площади прямо-
угольника, давление на площадку, расположенную на некоторой
глубине непосредственно под штампом, определяется по формуле
Для нагрузки, распределенной на площади прямоугольника по
закону параболы, формула для давления на площадку под штампом
на глубине z имеет вид
(15.20)
Вычисленные по формулам (15.19) и (15.20) отношения дав-
ления на площадку к давлению на штамп представлены в табл.
15.9 и 15.10
Таблица 15.9
Z b при V ~ 0,125	А. пр» ра				•V 	. равном b			
	0	0.5	1.0		2.0	2.5	3.0	4.0
1.0	0,7375	0,6338	0,4295	0,2201	0,0606	0,0051	0,00027	0,000037
1.5	0,6218	0.5524	0,3917	0,2162	0,0836	0,0193	0,0056	0,00043
2,0	0,5164	0,4678	0,3502	0,2136	0,1009	0,0359	0,0089	0.0024
2,5	0,4225	0,39	0,2886	0,2033	0,1128	0,0510	0,0367	0,0112
3,0	0,3465	0,2897	0,2621	0,1900	0,1174	0,0631	0,0384	0,0040
4,0	0,2350	0,2249	0,1951	0,1551	0,1131	0,0741	0,0495	0,0109
5,0	0,1671	0,1646	0,1462	0.1239	0,1066	0,0741	0,0510	0,0437
6,0	0,1236	0,1212	0,1115	0,09869	0,0836	0,0657	0,0523	0,0263
258
Расстояния от оси штампа
Рис. 15.4. Сравнение теоретических результатов с опытными данными Пен-
сильванского колледжа для песчаных грунтов (цифры на кривых обозначают
глубину, на которой измерялось давление)
а - 1-ая серия опытов; б — 2-ая серия опытов: / — опытные данные; 2 — теоретические
данные
Расстояния от оси штампа в см
Рис. 15.5. Сравнение теоретических результатов с опыт-
ными данными Пенсильванского колледжа для глинистых
и суглинистых грунтов (цифры на кривых обозначают глу-
бину, на которой измерялось давление)
а — для суглинистых грунтов; б — для глинистых грунтов
Отношение глубины к половине ширины штампа Отношение глубины к половине ширины штампа
О)
I
2
3
4
5
6
7
8
9
б)
1
2
3
4
5
6
7
8
9
Давление на площадку на глубине
в % от давления на штамп
э a S S а &
Рис. 15.6. Сравнение теоретических ре-
зультатов с опытными данными Пен-
сильванского колледжа для давлений
по оси загруженного штампа
а опытные данные I-ой серил; б — опытные
данные 2-ой серии; I; 2 — теоретические кри-
вые при различ пых v; 3 — опытные кривые;
п 77 оп^т,’ая1. кривая при нагрузке ниже
и, ю KejcM ; 5 — то же. при нагрузке от 1,46
до 2,92 кг]см*
Давление на площадку на глубине
в Ь/о От давления на штамп
О £>	<53	Q	<=э	СЭ	S3	£
Ту?	у	*>.	%	7	?
Таблица 15.10
-i— при v.
b
равном
—— при ------, равном
Л, *
0.3	0.125
1.5	2.0	2.5	3,0
0,67	1,0
1.0	1,5
1,34 2,0
1,67 2,5
2,0	3,0
2,68 4,0
3,35 5,0
4.0	6,0
0,8533
0,7203
0,5866
0,4619
0,3777
0,2505
0,1740
0,1237
0,7345
0,6328
0,5564
0,4238
0,2321
0,1194
0,4619
0,4236
0.3760
0,3740
0,2798
0,2028
0,1554
0,1149
0.1853
0,2037
0,2732
0,2044
0,1937
0,1628
0,1296
0,1060
0,03585	0,0037	0,00012
0,0648	0,0127	0,0045
0,0839	0,0294	0,0069
0,1038	0,0463	0,0270
0,1172	0,0567	0,0300
0,1117	0,0767	0,0393
—	0,0724	0,0533
0,863	0,0794	0,0437
0,0000
0,00024
0,0017
0.0028
0,0036
0,0256
0,0266
По данным табл. 15.9 на рис. 15.4 и 15.5 прерывистой линией
построены теоретические кривые для песчаных грунтов при v =
= 0,125, а для глинистых и суглинистых грунтов при v = 0,3.
На рис. 15.6 построены опытные и теоретические кривые для по-
ложения измерительной площадки на разной глубине под штампом.
Кривая для малых удельных давлений на штамп построена в пред-
положении, что эпюра давлений под штампом может быть прибли-
зительно выражена функцией

(15.21)
которая представляет разность двух эпюр: равномерно распределен-
ной нагрузки и нагрузки, распределенной по параболе. Следова-
тельно, для определения давления от такой нагрузки можно вос-
пользоваться данными табл. 15.9 и 15.10.
Обозначим через коэффициент табл. 15.9, а через коэффи-
циент табл. 15.10. Тогда давление на площадку от равномерно рас-
пределенной нагрузки
Рх(р) = 462Ра1;
а давление от нагрузки, распределенной по параболе
(15.22)
^п(р) = «грср468 = 46«-^-а,.	(15.23)
где рср — среднее удельное давление на штамп (р<т =	•
Давление на площадку от нагрузки, представленной выражением
(15.21), определится как разность формул (15.22) и (15.23), т. е.
₽<n 1/(х, {/)! = 462Р	.	(15.24)
262
Среднее давление на штамп от нагрузки, выраженной зависи-
мостью (15.21),
₽, “ Р - Р„ - Р -	- Р (1 -	- 0.5S5P, (IS.2S)
откуда давление на штамп
4-ft + 0
dx f f(x, £/)^ = 462 O,555P.
-6
(15.26)
Разделив выражение (15.24) на (15.26), получим отношение дав-
ления на площадку на глубине к давлению на штамп
Рхп[/(х. У)1	gl 2,25 _ 2,25ц-«g
V +?	0,555	1,25
j dx j /(x, y)dy
—b	—b
(15.27)
Вычисленные по формуле (15.27) отношения для x ® 0 представ-
лены в табл. 15.11.
Таблица 15.11
ь	Отношение давления на площадку к давлению на штамп при . равном							
	1	1.5	2.0	2.5	3.0	4.0	5.0	6.0
0	0,645	0,543	0,472	0,394	0,325	0,224	0,163	0,1228
Из сравнения видно, что теоретические данные (кривые) под-
тверждаются экспериментальными данными для песчаных, глини-
стых и суглинистых грунтов. Из сравнения теоретической и опытной
кривых для малых удельных нагрузок на штамп видно, что у краев
штампа наблюдается значительно большая концентрация напряже-
ний, чем выраженная зависимостью (15.21)
§ 6. СРАВНЕНИЕ ТЕОРЕТИЧЕСКИХ РЕЗУЛЬТАТОВ
С ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ ГОЛЬДБЕКА
Для сравнения с теоретическими результатами используем опыт-
ные данные Гольдбека для вертикальных напряжений по оси загру-
женного штампа, полученные в результате проведения двух серий
испытаний.
Данные первой серии испытаний Гольдбека представлены
табл. 15.12.
263
Таблица 15.12
Глубина в см	Диаметр штампа в см	Нагрузка в кг	Среднее давление на штамп в кг/см1*	Измеренное напряжение В KifCM*	Отношение измеренного напряжения к среднему давлению на штамп
30.5	34,3	815	0,885	0,7	0,79
30.5	34,3	1359	1,475	1,12	0.76	о 3|25
30.5	34,3	1812	1,97	1.6	0,81
30,5	34,3	2265	2,46	2,19	0,89
61.0	34,3	815	0,885	0,18	0,204	)
61,0	34,3	1359	1,475	0,39	0.264	1 0.2423
61,0	34,3	1812	1,97	0,51	0.259 J
91,4	34,3	815	0,885	0,08	0,0905 )
91.4	34,3	1359	1,475	0,13	0,088	1 0,09527
91.4	34,3	1812	1,97	0,21	0,107 J
121,9	34,3	815	0,885	0,04	0,0452	1
121,9	34,3	1359	1,475	0,06	0,0407	1 0,0473
121.9	34,3	1812	1,97	0,11	0,056	)
152,4	34,3	815	0,885	0,02	0,0226 )
152,4	34,3	1359	1,475	0,04	0,0271	1 0,02607
152,4	34,3	1812	1,97	0,056	0,0285 J
В табл. 15.13
Гольдбека,
представлены данные второй серии испытаний
Таблица 15.13
Глубина в см	Диаметр штампа в см	Нагрузка в кг	Среднее давление на штамп в кг!с.^	Иэмеренное напряжение в кг/сл?	Отношение измеренного напряжения к среднему давлению на штамп	
15,2	20,3	135,9	0,42	0,49	1.17	
15,2	20,3	271,8	0,84	0,84	1.0	
15,2	20,3	407,7	1,26	1,18	0,94	0,924
15,2	20,3	543,0	1,68	1.6	0.955	
15,2	20,3	1087,0	3,36	1,86	0,554	
30,5	20,3	135,9	0,42	0,16	0,381	1	
30,5	20,3	271,8	0,84	0,42	0,5	1	0.448
30,5	20,3	407,7	1,26	0,58	0,46	1	
30,5	20,3	543,0	1,68	0,76	0,452 J	
61,0	20,3	135,9	0,42	0,04	0,0952	
61,0	20,3	271,8	0,84	0,07	0,0832	
61,0	20,3	407,7	1,26	0,09	0,0715	0,0779
61,0	20,3	543,0	1,68	0,15	0,0892	
61,0	20,3	1087,0	3,36	0,17	0,0506	
91.4	20,3	407,7	1,26	0,04	0,0318 1	1
91,4	20,3	543,0	1,68	0,06	0,0357	0,0361
91,4	20,3	634,0	1,96	0,08	0.0408 )	1
264
Определим теоретически величины напряжений. Поскольку ис-
пытания производились с песчаным грунтом, для которого под жест-
ким штампом наблюдалась колоколообразная эпюра давлений, то
для вычисления напряжений используем формулу для нагрузки,
распределенной на площади круга по параболе
так как D = 2R,
то
i =	(|5.Я>
Подставляя в эту формулу среднее значение отношения напряже-
ния к давлению на штамп для глубины г = 30,5 см, получим
0,8125 = 2|l-±^.[l-exp(------’«Uli
I	34,32 L F \ 8v30.54 ) J J
откуда v 0,137, a 8v = 1,1.
Подставив это значение коэффициента в (15.29), получим следую-
щую расчетную формулу
£-2('-4ЙН'-'”(-тЙ]Ь
Вычисления, выполненные по формуле (15.30), приведены
табл. 15.14.
Таблица 15.14
Глубина z в см	г 34.3		(vR		.	(	343»\	₽ср
30,5	0,8892	0,8689	1,15	0,3166	0,6834	0,8124
61,0	1,7784	3,4756	0,2877	0,7498	0,2502	0,261
91,4	2,6647	7,803	0,12813	0,8798	0,1202	0,1242
121,9	3,554	13,8802	0,07204	0,9305	0,0695	0,071
152,4	4,4431	21,6936	0,0461	0,9550	0,0450	0,0476
Для оценки второй серии испытаний примем то же значение ко-
эффициента V,
Подставив в формулу (15.29) значения D » 20,3 см и v = 0,137,
определим теоретически значения вертикальных напряжений для
сравнения с опытными данными второй серии испытаний (табл. 15.15).
265
Таблица 15.15
Глубина г в см	2 20,3		(v)t.	-та	—та	Рср
15,2	0,7488	0,6161	0,6231	0,1973	0,8027	1,011
30,5	1,4976	2,4644	0,4058	0,6666	0,3334	0,3568
61,0	2,9952	9,8576	0,10144	0,9035	0,0965	0,0974
01.4	4,4928	22,1796	0,045865	0,95595	0,04405	0,046
Сравним теоретические значения отношений напряжений к сред-
нему давлению с опытными данными; результаты представим в
табл. 15.16.
Таблица 15.16
Опытные данные 1-й серии	Теоретиче- ские данные	?• отклоне- ния опытных данных от теоретических	Опытные данные 2-й серии	Теоретиче- ские данные	?• отклоне- ния опытных данных от теоретических
0,79	0,8124	-3	1.17	1,011	+ 15,5
0,76	0,8124	—7	1.0	1,011	— 1
0,81	0,8124	-0,5	0,94	1,011	— 7,0
0,89	0,8124	+9,5	0,955	1,011	— 5.5
0,204	0,261	-22	0,554	1,011	—45
0,264	0,261	+ 1	0,381	0.3568	+ 6,5
0,259	0,261	- 1	0,5	0,3568	+40
0,0905	0,1242	-28	0,46	0,3568	+28,5
0,088	0,1242	—30	0,452	0,3568	+26.5
0,107	0,1242	—14	0,0952	0,0974	— 2
0,0452	0,071	-37	0,0832	0,0974	— 14,5
0,0407	0,071	-43	0,0715	0,0974	—26,5
0,056	0,071	—21	0,0892	0,0974	- 8,5
0,0226	0,0476	—52,5	0,0506	0,0974	—48
0,0271	0,0476	—43	0,0318	0,046	—31
0,0285	0,0476	—30	0,0352 0,0408	0,046 0,046	—23,5 -11,5
Из сравнения видно, что наибольшие отклонения опытных дан-
ных от теоретических имеют место при малых значениях напряже-
ний. Эго обстоятельство может указывать на систематическую ошиб-
ку в измерениях, которая при значительных напряжениях мало ска-
зывается на результатах сравнения, а при малых напряжениях ее
влияние может оказаться решающим. Судя по данным первой се-
рии опытов, систематическая ошибка в измерении напряжений со-
ставила около 2% от среднего давления на штамп. Во второй серии
опытов явно завышенными являются результаты испытаний для
глубины 30,5 см. Если данные для этой глубины не принимать во
266
внимание» а также не принимать во внимание сильно отличающиеся
результаты для глубин 15,2 см (цифру 0,554) и 61,0 см (цифру0,0506),
то можно полагать, что систематическая ошибка в измерении напря-
жений во второй серии опытов составляла примерно 1,0%.
Если считать, что на осредненных опытных данных сказывались
указанные систематические ошибки, то для средних значений по-
лучим результаты, представленные в табл. 15.17.
Таблица 15.17
Среднее значе-
ние опытных
данных 1-й се*
рнн
К отклоне-
ния опытных
данных от тео-
ретических
Среднее зна-
чение опыт-
ных данных
2-й серии
% отклоне-
ния опытных
данных от
теоретических
0,8125	0,8325	0,8124	0	4-2,5	1,016	1,026	1,011
0,2423	0,2623	0,261	—8	4-0.5			
0,095	0,115	0,1242	-23,7	4-7,7	0,0848	0,0948	0,0974
0,047	0,067	0,071	- 3,4	—5,5	0,036	0,046	0,046
0,026	0,046	0,0476	-45,4	-3,5			
4-0,5 4-1.6
—13	—2,7
—22 О
При сравнении теоретических результатов с экспериментальными
данными Гольдбека вычисления велись по формуле, полученной
для нагрузки, распределенной по площади круга по параболиче-
скому закону.
Для нагрузки, равномерно распределенной по площади круга,
теоретические значения отношений величин напряжений к среднему
давлению на штамп приведены в предпоследних столбцах табл. 15.14
и 15.15; эти данные изображены графически на рис. 15.7: там же
построены теоретические кривые для нагрузки, распределенной по
площади круга равномерно и по параболе. Кроме того, для сравне-
ния изображена кривая теории упругости для нагрузки, равно-
мерно распределенной по площади круга, и кривая по формуле
(15.29) для v = 0,125.
Из приведенного рисунка видно, что теоретические кривые ав-
тора достаточно хорошо согласуются с экспериментальными данными
Гольдбека. Близко к опытным данным лежит и кривая, построенная
для v = 0,125.
Однако кривая, построенная для v = 0,137, лучше согласуется
с опытными данными.
На рис. 15.8 представлены теоретические результаты распреде-
ления напряжений на глубине 137 см и опытные данные Гольдбека
для разных диаметров штампов при одинаковой удельной нагрузке
267
Рис. 15.7. Сравнение теоретических результатов с опытными данными Гольдбека для вертикальных напряжений по
оси загруженного штампа
а — нагрузка, рапномерно распределенная по кругу; б; в — нагрузка, распределенная по кругу 'и параболе; 1 — кривая теории
упругости; 2 — кривая автора при v = 0,137; 3 — то же; 4 — то же, при * = 0,125; 5 — опытные данные Гольдбека (l-ая серия); 6 —
то же, 2-ая серия
на штамп. Теоретические кривые построены для нагрузки, распре-
деленной на подошве штампа по параболическому закону.
Значения напряжений по оси определялись по формуле (16.29)
для круглого штампа. Остальные значения напряжений вычисля-
Рис. 15.8. Сравнение теоретических результатов с опытными данными
Гольдбека при удельном давлении на штамп 2,43 kzIch? и разных пло-
щадях штампов для глубины 137 см
I — опытные данные; 2 — теоретические данные
лись по формуле для квадратного штампа по соответствующей ве-
личине напряжения на оси. Величины напряжений вычислены для
* = 0,137.
Из сравнения видно, что теоретические результаты почти
совпадают с экспериментальными данными.
269
В табл. 15.18 приведены результаты вычислений по формуле
(15.29) отношений напряжений на оси к среднему давлению на
штамп.
Таблица 15.13
Площадь штампа в см-	Диаметр штампа D в см	О’	о» Ыа’			4Я- -(-£)]	
7750	99	2,1	0,476	0,6212	0,3788	0,795	0,41
3800	69,6	4,24	0,236	0,7897	0,2103	0,892	0,216
1840	48,4	8,8	0,114	0,8927	0,1073	0,945	0,11
950	34,8	17,2	0,0581	0,9435	0,0565	0,971	0,058
345	21,0	46,7	0,0214	0,9788	0,0212	0,9885	0,023
§ 7. СРАВНЕНИЕ ТЕОРЕТИЧЕСКИХ РЕЗУЛЬТАТОВ С ОПЫТНЫМИ
ДАННЫМИ КОМИССИИ ПО НАПРЯЖЕНИЯМ В ЖЕЛЕЗНОДОРОЖНОМ
ПУТИ АМЕРИКАНСКОЙ АССОЦИАЦИИ ГРАЖДАНСКИХ ИНЖЕНЕРОВ
На рис. 15.9 представлены кривые распределения давления в пес-
чаном грунте на глубине 45 см при передаче нагрузки через шпалу.
Опытные кривые изображены сплошными линиями, причем верх-
няя кривая соответствует сечению под шпалой в месте приложения
нагрузки. Поскольку нагрузка передавалась на штамп в двух ме-
стах, то таких сечений два. Нижняя кривая соответствует среднему
сечению шпалы, свободному от нагрузки. Кривые этн получились
различными в силу изгиба шпалы при испытаниях и перераспределе-
ния за этот счет напряжений по подошве шпалы. Поскольку не из-
вестен аналитический характер перераспределения напряжений
под шпалой, то необходимо определить средние значения их и срав-
нить с ними теоретические результаты. Кривая с крестиками изоб-
ражает распределение средних значений напряжений. Теоретиче-
ская кривая распределения напряжений изображена прерывистой
линией. Построена она по формуле для нагрузки, распределенной
на полосе по параболе при v = 0,125.
В табл. 15.19 приведены результаты вычислений для глубины
45 см при передаче нагрузки через шпалу шириной 20 см.
Таблица 15.19
ь	Отношение напряжения к среднему давлению на шпалу при -г-. равном О						
	0	1	2	3	4	5	6
10 ~ ,,й	0,482	0,408	0,237	0,0825	0.0255	0,0043	0,0006
270
a)
|	70
Расстояния от оси шпалы в см
SO 40 30 20 10 0 10 20 30 40 30
Расстояния от оси шпалы В см
Рис. 15.9. Сравнение теоретических результатов с опытными
данными Комиссии по напряжениям в железнодорожном по-
лотне в песчаном грунте на глубине 45 см
а — под одной шпалой; б — под тремя шпалами / — кривая под нагруз-
кой; 2 — кривая в середине шпалы; 3 — кривая средних значений; 4 —
теоретическая кривая; 5 — опытные кривые средних значений Напряже-
ний от нагрузки на 1 шпалу; «5 — теоретические напряжения от нагрузки
на 1 шпалу; 7 — опытные кривые напряжений от нагрузки на 3 шпалы;
3 — теоретические кривые напряжений от нагрузки на 3 шпалы
По этим результатам построена теоретическая кривая для на-
грузки, передающейся через одну шпалу; на основе этих данных
в табл. 15.20 приведены величины напряжений на той же глубине
от нагрузки, приложенной к трем шпалам, расположенным друг
от друга на расстоянии 50 см.
Таблица 15.20
	Отношение напряжения к среднему давлению на шпалу при 4—. равном О						
	0	1	2	3	4	5	6
От центральной шпалы	0,482	0,408	0,237	0,0825	0,0255	0,0043	0,0006
От левой шпалы	0,0043	0,0006	—	—	—	—	—
От правой шпалы	0,0043	0,0255	0,0855	0,0237	0,408	0,482	0,408
Суммарная нагруз- ка	0,4906	0,4341	0,3195	0,3195	0,4335	0,4863	0,4086
На рис. 15.9, б представлено сравнение теоретических и экспе-
риментальных данных, откуда видно, что расхождений почти нет.
§ 8. СРАВНЕНИЕ ТЕОРЕТИЧЕСКИХ РЕЗУЛЬТАТОВ С ОПЫТНЫМИ
ДАННЫМИ КЕГЛЕРА И ШЕЙД И ГА
Анализ экспериментальных данных Кеглера и Шейдига показы-
вает, что при испытаниях эпюра распределения давления по подошве
штампа имеет параболический вид. Поэтому для вычисления тео-
ретических величин вертикальных напряжений на оси штампа вос-
пользуемся формулой (15.29).
Коэффициент v определим по какому-либо опытному значению
напряжений. Так, при испытании штампом с диаметром 2R =
= 33,9 см отношение величины напряжения к среднему давлению
на штамп составляет 0,3.
Подставив эти данные в формулу, получим
откуда v = -L; 8v = -L; _1_ — 0,75. Тогда
о	3 8v

272
По формуле (15.31) для тех же точек, для которых получены
опытные значения, вычислены отношения величин вертикальных
напряжений к среднему давлению на штамп. В табл. 15.21 приве-
дены результаты этих вычислений для штампа диаметром 33,9 см.
Таблица 15.21
Глубина z в см	о,5(^У			-(-Г— \2R) 0,75 X (1 — ехр 0.75 (	X	4
20	2,16	0,8847	0,463	Л,59		1,18
30	0,96	0,6171	1,042	0,357		0,714
40	0,54	0,4173	1,855	0,225		0,45
50	0,348	0,295	2,88	0,15		0,30
60	0,238	0,213	4,19	0,107		0,214
В табл. 15.22 — такие же данные для штампа диаметром 45 см.
Таблица 15.22
Глубина г в см	-(т)‘	1 — _схр[_0.7»(^у]	(-Y- \2R) 0.75	-Й)и«	^ср
10	15,2	1	0,0656	0,935	1,87
20	3,82	0,9781	0,262	0,744	1,488
30	1,69	0,8155	0,592	0,516	1,032
40	0,95	0,6133	1,05	0,355	0,71
50	0,608	0,455	1,64	0,253	0,506
60	0,42	0,343	2,38	0,185	0,37
В табл. 15.23 представлены теоретические и опытные данные,
полученные при передаче нагрузки через штамп диаметром 33,9 см.
Таблица 15.23
	Измеренное напря- жение в % от сред- него давления		Отклонение намеренной величины от теоретиче- ской в %
20	128	118	+ 8,5
30	76	71,4	+ 6,2
40	41	45	— 8,9
50	30	30	0
60	21	21,4	
273
Аналогичные данные приведены в табл. 15.24 для штампа диа-
метром 45 см.
Из приведенного сравнения видно, что теоретические результаты
достаточно хорошо согласуются с экспериментальным для штампа
Рис. 15.10. Сравнение теоретических результатов с опытными данными Кег-
лера и Шейдига для штампа D = 33,9 см
диаметром 33,9 см и несколько хуже — для штампа диаметром
45 см.
Это объясняется тем, что, с одной стороны, распределение дав-
ления по подошве штампа при испытаниях отличалось от принятого
при теоретических вычислениях. Так, при теоретических построе-
274
ниях принято, что при z = 0:	= 200%, в то время как при про-
Рср
ведении опытов даже на глубине 10 см = 220%
С другой стороны, отклонения в меньшую сторону объясняются
неточностью измерений при проведении опытов. Это видно из срав-
нения результатов опытов со штампами диаметром 33,9 и 45 см.
Отношение расстояния
н радиусу
8%
6%
Рис. 15.11. Сравнение теоретн-
ческих результатов с опытными
данными Кеглера и Шейдига
для штампа D = 63 см
/ — опытные кривые; II — 'теоре-
тические кривые автора (нагрузка
распределена по параболическому
закону на площади квадрата со сто-
роной 63 см при * = 0.167)
60
40
Отношение равстояния
к радиусу

1 \ КЭД,

Для глубины 30 см при испытании штампом диаметром 33,9 см
и для глубины 40 см при испытании штампом диаметром 45 см от-
ношения напряжений к среднему давлению на штамп должны быть
равны, так как почти равны отношения глубин к диаметрам штам-
пов:
= 0,885; — = 0,888.
33.9	45
Однако для штампа диаметром 33,9 см напряжение на глубине
30 см составляет 76% от среднего давления, а для штампа диаметром
275
45 см напряжение на глубине 40 см, по данным экспериментов,—
лишь 65%. Из этого сравнения видно, что измеренные напряжения
при испытаниях со штампом диаметром 45 см ниже действительных
примерно на 10—15%.
Сравним опытные кривые линий равных напряжений с теорети-
ческими. Для построения теоретических кривых линий равных
напряжений воспользуемся решением, полученным для нагрузки,
распределенной по параболическому закону на площади квадрата.

Отношение расстояния
нрадиусу
ие расстояния
радиусу
Рис. 15.12. Сравнение теорети-
ческих результатов с опытными
данными Кеглера и Шейдига для
штампа и = 63 см
I — опытные данные; II — теоретичес-
кие кривые автора (нагрузка распре-
делена по параболическому закону на
площади квадрата со стороноП 63 см
при v ® 0,25)
При этом в целях сближения теоретических условий загружения
с опытными величины напряжений для квадратного штампа пере-
считаем на круглый.
Путем сопоставления величин вертикальных напряжений по
оси загруженного круглого и квадратного штампов получим коэф-
фициент, которым и воспользуемся для вычисления приближенных
значений вертикальных напряжений для нагрузки, распределенной
по параболическому закону на площади круга.
В табл. 15.25 приведены данные для случая загружения одина-
ковой удельной нагрузкой круглого и квадратного штампов.
Пользуясь коэффициентами табл. 15.25 пересчитаем НаПРяЖения,
вычисленные для квадратного штампа. В результате Для круглого
штампа при -j— = 0,75 получим приближенные значения Напря-
жений, приведенные в табл. 15.26.
276
Таблица 15.24
Глубина Z в см	Измеренное напря- жение в % от сред- него давления	Вычисленное на- пряжение в X от среднего давления	Отклонение измеренной величины от теоретиче- ской в И
10	220	187	+ 18
20	100	148,8	— 32,8
30	80	103,2	— 22,3
40	65	71	— 8,5
60	48	50,6	— 5,5
60	31	37	— 16
Таблица 15.25
Отношение глубины к радиусу	Отношения напряжения к среднему давлению на штамп		Отношение напряжений при круглом штампе к напряжению при квадрат- ном штампе
	круглый	|	квадратный	
0,433	1,875	2,11	0,89
0,866	1,509	1,73	0,875
1,732	0,7358	0,89	0,83
2,598	0,39	0,484	0,808
3,464	0,23	0,286	0,805
4,33	0,1512	0,191	0,792
5,196	0,11	0,144	0,765
6,062	0,082	0,119	0,69
6.928	0,0608	0,099	0,615
7,94	0,0542	0,0845	0,64
Таблица 15.26
Отноше- ние глу- бины к радиусу	Напряжения в % от среднего давления на штамп при -J-, равном						
	0	0.5	|	1Л 1	1.5	2,0	3.0	4.0
0,433	187,5	139	24,3	0,6	0	0	0
0,866	150,9	113	37,9	3,58	0,099	0	0
1,732	73,58	62,2	37,0	15,4	4,0	0,13	0
2,598	39	35,5	26,8	16,7	8,7	0,965	0,127
3,464	23	22,1	18,5	13,8	9,6	2,57	
4,33	15,12	14,5	12,9	10,6	8,55	3,73	
5,196	11	9,8	9,65	8,4	7,04	3,96	1,39
6,062	8,2	7,4	6,86	6,15	5,22	3,95	
6,928	6,08	4,95	4,87	4,6	4,05	3,82	
7,94	5,42	4,26	4,25	4,16	3,3	2,68	2,08
По данным табл. 15.26 построены кривые равных напряжений,
изображенные на рис. 15.10 сплошными линиями; опытные кривые
изображены прерывистыми линиями. Как видно из рисунка, теоре-
тические кривые качественно и количественно соответствуют опыт-
ным кривым равных вертикальных напряжений.
На рис. 15.11 и 15.12 соответственно для v = 0,167 и v = 0,25
аналогичным образом построены кривые равных напряжений для
штампа диаметром 63 см.
277
Если считать, что при построении теоретических кривых трудно
было точно учесть характер распределения давления по подошве
штампа, то на основе приведенного сравнения можно сделать вывод
о подтверждении теоретических результатов опытными данными Ке-
глера и Шейдига.
§ 9. СРАВНЕНИЕ ТЕОРЕТИЧЕСКИХ РЕЗУЛЬТАТОВ С ОПЫТНЫМИ
ДАННЫМИ Н. В. ЛАЛЕТИНА
Для сравнения теоретических данных с экспериментальными
[57,84] опытные кривые Н. В. Лалетина изобразим в относительных
100
сг S
Ч 50
$ §
1Г5
зр гр <р о op 1р гр зр "
Отношение расстояния к половине
ширйны штампа
Рис. 15.13. Сравнение теоретических
результатов с опытными данными
Н. В. Лалетина
а — для 9 см', б — для г = 13 ом
координатах, на которые за-
тем нанесем теоретические
кривые.
При построении теоретиче-
ских кривых мы встречаемся
с большими трудностями, по-
скольку неизвестен характер
распределения давления по по-
дошве прямоугольного штампа
с соотношением сторон 5 3
при измерении напряжений
в плоскости большей стороны.
Поэтому сравнение будем про-
изводить по степени убывания
теоретических и опытных зна-
чений напряжений по мере
удаления рассматриваемых
точек от оси штампа; будем
считать, что теоретические
значения напряжений по оси
штампа равны опытным. На-
пряжения для остальных то-
чек вычислим по формуле, по-
лученной для параболической
нагрузки, распределенной по
площади прямоугольника, и
пропорционально уменьшим
или увеличим их в соответ-
ствии с соотношением теоре-
тического и принятого напря-
жений для точки на оси
штампа.
Вычисленные таким обра-
зом величины относительных напряжений приведены в табл. 15.27.
По этим данным кривые на рис. 15.13 нанесены сплошными ли-
ниями.
278
Таблица 15.27
Отношения напряжений к среднему давлению на штамп при
равном
9 см
12 см
0	0,25	0,5	1.0	1.5	2.0	3.0
0,852 0,2148	0,797 0,2089	0,634 0,1950	0,135 0,1468	0,01 0,0918	0,0002 0,0478	0 0,0053
Из этого сравнения видно, что при одинаковых значениях напря-
жений по оси штампа опытные и теоретические величины напряже-
ний в горизонтальной плоскости одинаково качественно убывают
по мере удаления от оси штампа.
§ 10. СРАВНЕНИЕ ТЕОРЕТИЧЕСКИХ РЕЗУЛЬТАТОВ С ОПЫТНЫМИ
ДАННЫМИ Г. И. ПОКРОВСКОГО И И. С. ФЕДОРОВА
В табл. 15.28 приводятся экспериментальные данные, получен-
ные И. С. Федоровым [73; 891.
Таблица 15.2,8
Глубина о м	Среднее значение вертикальных напряжений в кг!см*	Среднеквадратнческая ошибка в ?•
0	2,48	0,24
0,42	2,09	0,053
0,94	1,14	0,058
1,74	0,64	0,06
2,55	0,6	0,035
Приведенные в табл. 15.28 значения вертикальных напряжений
получены с учетом влияния собственного веса грунта, объемный вес
которого 1,7 г!см?. Поэтому при определении теоретических значе-
ний напряжений необходимо учитывать влияние собственного веса
грунта.
Если учесть, что среднее давление на штамп при испытаниях со-
ставляло 2,5 кг!см\ то на основе данных табл. 15.28 можно для тео-
ретических вычислений принять равномерное распределение давле-
ния по подошве штампа (давление на поверхности под центром
штампа, равное 2,48 кг/см2, близко к равномерному).
В этом случае для вычисления вертикальных напряжений по
оси квадратного штампа воспользуемся формулой
115321
где р — удельное давление; в рассматриваемом случае р =
= 2,5 кг!см-\
Ъ — половина ширины штампа.
279
Коэффициент v определим по напряжению в какой-либо точке,
например для глубины 94 см:
5000	[	\ 94/v /J
где 5000 — площадь квадратного штампа.
Решая это уравнение, получим v = 0,18.
Вычисленные по формуле (15.32) значения напряжений при
м = 0,18 приведены в табл. 15.29.
Таблица 15.29
	Напряжения опытные в кг/см*	Напряжения от внешней нагрузки в кг1слР	Напряжение от собствен- ного веса грунта в кг[см*	Суммарные напряжения в кг [см*	Разность в %
0	2,48	2,5	0	2,5	—0,5
42	2,09	2,24	0,0714	2,31	-9,5
94	1.14	0,98	0,16	1.14	0
174	0,64	0,342	0,296	0,638	0
255	0,6	0,167	0,433	0,6	0
На рис. 15.14 приведено графическое сравнение теоретических
результатов с экспериментальными данными И. С. Федорова.
На рис. 15.15 приведено сравнение теоретических результатов
с экспериментальными данными, полученными Г. И. Покровским и
И. С. Федоровым (73, 89, 84] для удельной нагрузки на квадратны*
штамп, равной 10,75 кг!см*.
Из сравнения видно, что теоретические результаты почти сов-
падают с экспериментальными данными Г. П. Покровского и
И. С. Федорова.
§ 11. СРАВНЕНИЕ ТЕОРЕТИЧЕСКИХ РЕЗУЛЬТАТОВ С ОПЫТНЫМИ
ДАННЫМИ Д. а БАРАНОВА И ПЛАНТЕМА
В последние годы (1949—1960 гг.) Плантема и Д. С. Барановым
12 ] с помощью самой современной аппаратуры проведены опыты по
измерению напряжений в рыхлых и плотных песчаных грунтах;
Интересно отметить, что эти работы в основном подтверждают
результаты, полученные ранее другими исследователями с менее
совершенной аппаратурой. По-видимому, имевшие место система-
тические ошибки исключались при обработке опытов по равенству
объемной эпюры внешней нагрузке.
В 1955—57 гг. Д. С. Барановым под руководством Н. А. Цыто-
вича [2] проведены интересные опыты по одновременному опреде-
лению контактных давлений по подошве штампа и измерению вер-
тикальных напряжений внутри песчаного массива; это прзволяет
280
a — опытная кривая с учетом собственного веса грунта; б — то же, без
учета веса грунта; е— теоретическая кривая автора; г — кривая тео-
рии упругости
Напряжение в кг{см2
ными данными Г. И. Покровского и И. С. Федорова
1 — опытная кривая; 2 — кривая от собственного веса грунта;
3 — кривая теории упругости с учетом собственного веса грунта:
4 — теоретическая кривая автора без учета собственного веса
грунта; 5 — то же. с учетом собственного веса грунта
определить теоретически напряжения внутри массива и сравнить
их с опытными. Д. С. Барановым получена сложная картина давле-
ний по подошве штампа, изображенная на рис. 15.16 кривыми, со-
ответствующими трем ступеням нагрузки. Цифры на кривых пока-
зывают среднее давление на штамп.
Из анализа опытных данных, полученных Д. С. Барановым,
видно, что давление по подошве штампа близко к равномерному
с небольшой параболичностью к центру. Поэтому эпюру по подошве
представим состоящей из двух эпюр: равномерной и параболиче-
ской (рис. 15.17). Аналитически эпюра будет выражаться зависи-
мостью
/(')=*+р2(1--£
\ к*
(15.33)
где рг — интенсивность равномерно распределенного давления;
R — радиус круга, по которому распределена нагрузка;
г — координата круга, на границе которого определяется
давление;
р2 — наибольшая ордината параболического давления.
Пользуясь экспериментальными данными, определим параметры
аналитической зависимости; для кривой а (рис. 15.16)
Р1 + Р2 = 3,0; р0 = Р1 +-у-= 2,6,	(15.34)
откуда
Pi = 2,2; р2 = 0,8.	(15.35)
Для кривой, изображенной на рис. 15.16, б,
Pi + Р» = 2.62; р. +	= 2,2,	(15.36)
откуда
Pi =1,78; р2 = 0,84.	(15.37)
Для кривой, изображенной на рис. 15.16, в,
Pi + Р» = 2.3; р, +	= 1,8;	(15.38)
откуда
Pi=l,3; р2=1,0.	(15.39)
Полученные величины отмечены на рис. 15.17 для всех трех ступе-
ней нагрузки.
Вертикальные напряжения по оси штампа от сложной нагрузки
, (0) - р, [1—ехр(— -£-)] +
&-)])•
(15.40)
282
Номера вертикалей
3 4 5 6 7 8 Ю
Рис. 15.16. Распределение дав-
лений под жестким штампом
по опытам Д. С. Баранова при
среднем давлении на штампы
а — Ро == 2.6	кг/см* -,	6 — р0 =
2,2 кг/с«а; в — р0 = 1.8 кг 1см*
Рис. 15.17
а — р0 = 2,6 кг,'
б/	6)
рис. 15.17. Схемы нагрузок для теоретического расчета
напряжений согласно опытным кривым Д. С. Бара-
нова
б — р0 = 2 кг{см*;
в — Ра 1,8 кг{см'
Разделив это выражение на среднее давление на штамп, получим
Пользуясь этим выражением, а также рис. 15.18, по точке с коор-
динатами -i-=e 2;-^- =0,7 вычислим коэффициент v из уравне-
J\ Ро
НИЯ
0.7-g.[l_exp(-^r)] +
+1т(1-2’2’[|-“р(-тк)]);	"5'42>
получим v = 0,125.
Тогда уравнение (15.41) примет вид
('5Л3’
По этой формуле для нагрузок, изображенных на рис. 15.17,
построены кривые на рис. 15.18; эти кривые с глубиной сливаются
в одну кривую, отмеченную цифрой 4. Сравнение этих кривых с
опытной кривой 2 Д. С. Баранова для рыхЛ0Г0 песка, указывает
на их сходимость. По формуле (15.43) прерывистой линией
284
с точкой построены кривые
при v = 0,31; сравнение их
с опытной кривой /, получен-
ной Плантема для плотного
песка, говорит о совпадении
теоретических и практических
данных.
§ 12. СРАВНЕНИЕ
ТЕОРЕТИЧЕСКИХ РЕЗУЛЬТА-
ТОВ С ОПЫТНЫМИ
ДАННЫМИ
М. П. БОЛШТЯНСКОГО
М. П. Болштянский 111]
проводил опыты с целью изу-
чения распределяющей спо-
собности гравия как дорожно-
строительного материала. На-
пряжения измерялись в су-
глинистом грунте, находя-
щемся под слоем гравия раз-
личной толщины.
На рис. 15.19 и 15.20
приводится выполненное
М. П. Болштянским сравне-
ние опытных и теоретических
данных.
На рис. 15.19 представ-
лены напряжения по оси дей-
ствия нагрузки в долях от
среднего давления под штам-
пом; на вертикали нанесены
точками показания трех ди-
намометров.
М. 11. Болштянский отме-
чает, что опытные данные
вполне соответствуют кривой
распределения напряжений по
дискретной теории при v, =
= 0,34 и v0 = 0,33. В то же
время напряжения, опреде-
ленные по теории упругости
как для двухслойного осно-
вания при-|п- = 0,1, в 2—3
раза меньше измеренных.
Рис. 15.19. Сопоставление эксперимен-
тальных и теоретических данных
1 — кривая по теории упругости при Ео: Е,—
«= 0,1; // — кривая по статистической (дис-
кретной) теории при v, = 0,34; ». ® 0,33; I —
гравий; 2 — суглинок
Рис. 15.20. Сопоставление опытных дан-
ных М. П. Болштянского с кривой
статистической (дискретной) теории при
/ — показания верхнего динамометра; 2 —
показания среднего динамометра; J — по-
казания нижнего динамометра
285
На рис. 15.20 приведены показания динамометров, расположен-
ных на большей глубине; по опытным точкам относительно кривой,
построенной на основании статистической (дискретной) теории,
также видно, что теоретические результаты почти соответствуют
опытным данным.
§ 13. СРАВНЕНИЕ ТЕОРЕТИЧЕСКИХ РЕЗУЛЬТАТОВ С ОПЫТНЫМИ
ДАННЫМИ РАЗЛИЧНЫХ ИССЛЕДОВАТЕЛЕЙ
Воспользуемся графиком, построенным В. Ф. Бабковым [84];
на этом графике, кроме экспериментальных, имеются теоретические
кривые, построенные по формулам теории упругости и теории Фре-
лиха для нагрузки, распределенной по площади круга равномерно
и по параболическому закону.
В соответствии с этим теоретические кривые по разработанной
автором теории также построены для нагрузки, распределенной по
площади круга равномерно и по параболическому закону для v ==
= 0,125. В табл. 15.30 приведены результаты вычислений.
Таблица 15.30
Отношение глубины к радиусу	Напряжения ц % от среднего давления при нагрузке	
	равномерной	параболической
0	100	200
1	98	151
-2	63.2	73,6
3	35,9	39
4	22	23
5	14,8	15,1
6	10,5	11
7	7,8	8,2
По данным табл. 15.30 на графике (рис. 15.21) нанесены теоре-
тические кривые (V — для нагрузки, равномерно распределенной
по площади круга; VI — для нагрузки, распределенной на площади
круга по параболическому закону).
Кривая / построена по формуле теории упругости для нагрузки,
равномерно распределенной по площади круга. Кривая // построена
также по формуле теории упругости, но для нагрузки, распределен-
ной на площади круга по параболическому закону.
Кривая III построена по формуле Фрелиха для нагрузки, рас-
пределенной равномерно по площади круга при коэффициенте кон-
центрации напряжений = 6. Кривая IV также построена по фор-
муле Фрелиха при = 6, но для нагрузки распределенной на пло-
щади круга по параболическому закону.
Из сравнения видно, что теоретические кривые автора более со-
ответствуют экспериментальным данным, чем кривые теории упру-
гости и теории Фрелиха.
286
$ 14. СРАВНЕНИЕ ВЕРТИКАЛЬНЫХ НАПРЯЖЕНИЙ
от ВЕРТИКАЛЬНОЙ сосредоточенной нагрузки с данными
ТЕОРИИ УПРУГОСТИ
По теории упругости вертикальные напряжения от сосредоточен-
ной нагрузки в пространственной задаче
(15.44)
По теории дискретного распределения напряжений вертикаль-
ные напряжения от той же нагрузки
(15л5)
Преобразуем эти выражения
где Р — сосредоточенная нагрузка;
z; г — цилиндрические координаты;
v — коэффициент, характеризующий взаимную связь частиц.
Правые части выражений (15.46) и (15.47) являются функциями
отношения координат рассматриваемой точки; если выделить ка-
кую-либо горизонтальную плоскость и анализировать только пра-
вые части этих выражений, то можно установить характер измене-
ния напряжений и угол, под которым распределяется основная
часть внешнего давления (рис. 15.22).
Для решения этой задачи составлена табл. 15.31 по формулам
(15.46) и (15.47)
Таблица 15.31
г 2	z’ при ».		равном		У УПР р
	0.125	0.167	0,25	0.33	
0	1,2724	0,9541	0,6362	0,4775	0,4775
0,1	1,2228	0,9259	0,6236	0,4702	0,4657
0,2	1,0847	0,8462	0,5873	0,4497	0,4029
0,3	0,8877	0,7284	0,5314	0,4178	0,3849
0,4	0,6708	0,5904	0,4620	0,3756	0,3294
0,5	0,4681	0,4507	0,3558	0,3298	0,2733
1.0	0,0233	0,0475	0,0861	0,1065	0,0844
1.5	0,0001	0,0011	0,0071	0,0164	0,0251
2,0	0,0000	0,0000	0,0001	0,0012	0,0085
2,5	0	0	0,0000	0,0000	0,0034
2,59	0	0	О	0,0000	0,0029
4,91	0	0	0	0	0,0001
287
Напряжение в	от среднего давления на штамп
20	40	00	00 /00	120	f40 160	180 200
§
У Е7
▼ 8
▲ 9
J

Рис. 15.21. Сравнение теоретиче-
ских результатов с опытными дан-
ными различных исследователей
для напряжений по оси загру-
женной площадки
/ — по Штейнеру и Кику; 2 — по
ШтрошнеЙдеру; 3 — по Ксглеру и
Шеидигу (1-я серия); 4 — то же (2-я
серия); 5 — по Гольдбеку (1-я серия);
6 — то же (2-я серия); 7 — по План-
тема (рыхлый песок); 8 — по данным
Иллинойского университета; 9 — по
И. С. Федорову (ВИОС); /, //—кривые
теории упругости; ///, IV — кривые
Фрелиха; V. VI — кривые автора;
VII — опытная кривая Д С. Баранова
(рыхлый песок); VIII — опытная кри-
вая Плантема (плотный песок)
Рис. 15.22. К сопоставлению
ординат вертикальных на-
пряжений по статистической
теории и теории упругости
под двумя сосредоточенными
нагрузками и их равнодей-
ствующей
/ — ио дискретной (статистиче-
ской) теории; 2 — по теории
упругости
Последнее значение величины v = 0,33 выбрано с таким расче-
том, чтобы при г = 0 по формуле (15.47) получить такие же значе-
ния напряжений по линии действия силы, как и по формуле (15.46).
Правая часть обоих формул в этом случае равна 0,4775.
Из сопоставления двух крайних столбцов табл. 15.31 видно,
что формула (15.47) по сравнению с формулой (15.46) дает большую
концентрацию напряжений к линии действия силы. Так, при
— > 1,5 величины, вычисленные по формуле (15.47), больше ве-
личин, вычисленных по формуле (15.46), а при -у- > 1,5 — наобо-
рот. При > 2 величины, вычисленные по формуле (15.47), по
сравнению с данными последнего столбца настолько малы, что их
практически можно приравнять к нулю. Таким образом, давление
в грунте распределяется под некоторым углом к линии действия
нагрузки.
Из анализа данных табл. 15.31 вытекает, что при уменьшении
коэффициента v (что соответствует уменьшению связности частиц
грунта)' происходит еще большая концентрация напряжений к ли-
нии действия нагрузки по сравнению с результатами, полученными
по теории упругости.
Произведем теперь сравнение напряжений для плоской задачи.
В теории упругости вертикальные напряжения от сосредоточен-
ной нагрузки
По теории дискретного распределения напряжений вертикаль-
ные напряжения
в’—г1/Чг«р(—Йг-)-	(1549)
После преобразований получим
*упр - __
(15.50)
(15.51)
По данным формул (15.50) и (15.51) построена табл. 15.32.
Из анализа этой таблицы видно, что выводы для пространствен-
ной и плоской задач аналогичны. Кроме того, при равенстве напря-
жений по линии действия нагрузки в пространственной задаче
289
Таблица 15.32
у-	z при у. равном				°z -р-< "О теории упру- гости
	0.125	0,167	0.25	0.33	
0,0	1,128	0,9768	0,7976	0,691	0,636
0,1	1,084	0,9479	0,7818	0,6304	0,624
0,2	0.9616	0,8663	0,7363	0,6508	0,588
0,3	0,787	0,7457	0,6663	0,6046	0,536
0,4	0,5947	0,6044	0,5792	0,5436	0,473
0,5	0,415	0,4614	0,4837	0,4773	0,406
1.0	0,0207	0,0486	0,1079	0,1541	0,159
1.5	0,0001	0,0011	0,0089	0,0237	0,0601
2,0	0,00001	0,00002	0,0002	0,0017	0,0254
2,5	0	0	0,00003	0,00006	0,0121
2,59	0	0	0	0,00003	0,0107
4,91	0	0	0	0	0,001
величины напряжений в плоской задаче, вычисленные по формуле
(15.49), больше величин, вычисленных по формуле (15.48). Это
говорит о том, что введением коэффициента концентрации напря-
жений в формулы теории упругости не может быть решен вопрос
о распределении напряжений в зернистой среде, так как для раз-
личных нагрузок этот коэффициент будет различным.
Для подтверждения сказанного рассмотрим следующую задачу.
Положим, что действительное распределение вертикальных напря-
жений в зернистой среде от сосредоточенной нагрузки выражается
уравнением (15.45). С другой стороны, по формуле Фрелиха
а — —/	* V
°2“ 2«г» lyz’+T5/ •
где vj — коэффициент концентрации напряжений.
Приравнивая эти выражения при г = 0, получим
р _ цР
2kz2v 2№ *
откуда
(15.53)
Положим, далее что (рис. 15.22) к массиву приложены две со-
средоточенные силы Р, расположенные на небольшом расстоянии
друг от друга.
Определим величину напряжения по линии приложения равно-
действующей по формуле (15.45)
Ог =	ехр (- -Д-) .	(15.54)
г	н \ 2vz2 /	'
где fj — удаление силы Р от точки приложения равнодействующей.
290
с другой стороны, по формуле (15.52)
откуда
(15.55)
Приравнивая выражения (15.54) и (15.55), получим
(15.56)
Сравнивая (15.53) и (15.56), видим, что коэффициент концентра-
ции напряжений не является параметром среды, так как зависит
от характера приложения нагрузки; это обстоятельство неодно-
кратно отмечалось экспериментаторами.
Из рис. 15.22 видно, что при одинаковых ординатах напряжений
под двумя сосредоточенными нагрузками вычисленные по разным
формулам величины напряжений под равнодействующей уже отли-
чаются друг от друга.
ЗАКЛЮЧЕНИЕ
«Единство природы обнаруживается в „поразительной
аналогичност11**;дифференииальных уравнений, относящихся
к разным областям явлений».
(В. И. Ленин» Соч., 5 изд., т. 18, стр. 306)
Изучение допредельного напряженного состояния и деформа-
ций зернистых безраспорных и зернистых грунтовых (распорных)
сред показало, что для них могут быть построены эквивалентные
модели сплошных тел, обладающих трением, но не способных вос-
принимать растягивающие усилия.
Для таких моделей применимы дифференциальные уравнения
равновесия Навье, но не пригодны уравнения совместности, исполь-
зуемые в теории упругости. Для зернистых сред (а, следовательно,
и для их эквивалентных моделей) следует применять свои физиче-
ские уравнения, учитывающие их дискретную природу.
Сопоставление уравнений теорий упругости и пластичности
свидетельствует о том, что они отличаются только физическими
уравнениями. Для упругой среды таким физическим уравнением
является уравнение совместности; для пластичной среды уравнение
предельного состояния в каждой точке тела.
291
Все сказанное позволяет сделать более широкое обобщение: для
любых сплошных и зернистых тел, обладающих трением, применимы
дифференциальные уравнения равновесия Навье. По этому свой-
ству зернистые среды в допредельном состоянии в среднем похожи
на тела сплошные.
С другой стороны, отличие упругих тел от пластичных и сплош-
ных от зернистых отражается в их особых физических уравнениях.
Приведенные в работе решения показывают, что напряжения
и деформации в дискретной среде зависят прежде всего от ее струк-
туры. Сравнение зернистых сред с континуальными свидетельст-
вует о коренном различии их. В теории упругости свойства сплош-
ных сред определяются модулем упругости и коэффициентом Пуас-
сона. Других параметров для учета особенностей строения среды
теория упругости не имеет. Не учитывает теория упругости и ста-
тистическую природу зернистых сред. Иными словами, распреде-
ление напряжений и деформаций в зернистых средах относится к
другому виду физических явлений, связанных с дискретной и ста-
тистической природой строения изучаемого физического тела.
Явления теплопроводности и диффузии, коагуляции, турбулент-
ного течения жидкости, переноса взвешенных частиц в потоке газа
и жидкости, броуновского движения, течения жидкости в пористых
средах аналогичны рассматриваемому явлению. Изучение механи-
ческих свойств зернистых сред показывает применимость к ним по-
истине универсального уравнения Смолуховского-Колмогорова.
В механике зернистых сред, как и в теории диффузии, игнори-
руется индивидуальность каждой отдельно взятой частицы и учи-
тывается лишь то их общее, что влияет на механические свойства
среды в целом. Решение задачи относительно средних значений по-
зволяет от конечных размеров зерен переходить к бесконечно
малым элементам и пользоваться не конечно-разностными, а диф-
ференциальными уравнениями; распределение напряжений и де-
формаций в зернистых средах аналогично фильтрации жидкости
в пористой среде. Поры в такой среде так же дискретны, как и зерна
в зернистой среде. Вместе с тем движение жидкости в пористой среде
выражается дифференциальными уравнениями для распределения
напряжений в зернистых средах. Зерна, опираясь друг на друга
в точках контактов, создают сложный лабиринт материальной ос-
новы, воспринимающей и распределяющей внешнюю нагрузку.
Скелет из зерен является здесь полным аналогом пор в пористой
среде.
В любом из указанных выше явлений можно найти аналогию
с распределением давления в, зернистых средах.
Принято считать, что уравнения математической физики пара-
болического типа выражают неравновесные процессы. В данной
работе показано, что эти уравнения выражают не только процессы,
но и состояния равновесия, если время в них заменить соответст-
вующей координатой пространства.
292
ПРИЛОЖЕНИЕ 1
ТАБЛИЦА ЗНАЧЕНИЯ ? Ю ехр \ (ВСЕ ЗНАЧЕНИЯ
V* \ 2 )
УМНОЖЕНЫ НА 10 000)
									8	
0,0	3989	3989	3989	3988	3886	3984	3982	3980	3977	3973
0,1	3670	3965	3961	3956	3951	3945	3939	3932	3925	3918
0,2	3910	3902	3894	3885	3876	3867	3857	3847	3836	3825
0,3	3814	3802	3790	3778	3765	3752	3739	3725	3712	3697
0,4	3683	3668	3653	3637	3621	3605	3589	3572	3555	3538
0,5	3521	3503	3485	3467	3448	3429	3410	3391	3372	3352
0,6	3332	3312	3292	3271	3251	3230	3209	3187	3166	3144
0,7	3123	3101	3079	3056	3034	ЗОН	2989	2966	2943	2920
0,8	2897	2874	2850	2827	2803	2780	2756	2732	2709	2685
0,9	2661	2637	2613	2589	2565	2541	2516	2492	2468	2444
1.0	2420	2396	2371	2347	2323	2299	2275	2251	2227	2203
1,1	2179	2155	2131	2107	2083	2059	2036	2012	1989	1965
1,2	1942	1919	1895	1872	1849	1826	1804	1781	1758	1736
1,3	1714	1691	1669_	1647	1626	1604	1582	1561	1539	1518
1,4	1497	1476	1456	1435	1415	1394	1374	1354	1334	1315
1,5	1295	1276	1257	1238	1219	1200	1182	1163	1145	1127
1.6	1109	1092	1074	1057	1040	1023	1006	0989	0973	0957
1,7	0940	0925	0909	0893	0878	0863	0848	0833	0818	0804
1,8	0790	0775	0761	0748	0734	0721	0707	0694	0681	0669
1,9	0656	0644	0632	0620	0608	0596	0584	0573	0562	0551
2,0	0540	0529	0519	0568	0798	0488	0478	0468	0459	0449
2,1	0440	0431	0422	0413	0404	0396	0387	0379	0371	0363
2,2	0355	0347	0339	0332	0325	0317	0310	0303	0297	0290
2.3	0283	0277	0270	0264	0258	0252	0246	0241	0235	0229
2,4	0224	0219	0213	0208	0203	0198	0194	0189	0184	0180
2,5	0175	0171	0167	0163	0158	0154	0151	0147	0143	0139
2,6	0136	0132	0129	0126	0122	0119	0116	0113	ОНО	0107
2,7	0104	0101	0099	0096	0093	0091	0088	0086	0084	0081
2,8	0079	0077	0075	0073	0071	0069	0067	0065	0063	0061
2.9	0060	0058	0056	0055	0053	0051	0050	0048	0047	0046
3,0	0044	0033	0024	0017	0012	0009	0006	0004	0003	0002
4,0	0001	0001	0001	0000	0000	0000	0000	0000	0000	0000
293
ПРИЛОЖЕНИЕ 2
t
ТАБЛИЦА ЗНАЧЕНИЙ Ф (0 -— ( ехр (— —) dz
XTj I 2)
	Ф(П		Ф(П	Ф(О			Ф(/)
0,00	0,00000	48	36877	96	66294	44	85013
01	00798	49	37587	97	66795	45	85294
02	01596	0,50	0,38292	98	67291	46	85571
03	02393	51	38995	99	67783	47	85844
04	03191	52	39694	1,00	0,68269	48	86113
05	03988	53	40389	01	68750	49	86378
06	04784	54	41080	02	69227	1,50	0,86639
07	05581	55	41768	03	69699	51	86696
08	06376	56	42452	04	70166	52	87149
09	07171	57	43132	05	70628	53	87398
0,10	0,07966	58	43809	06	71086	54	87644
И	08759	59	44481	07	71538	55	87886
12	09552	0,60	0,45149	08	71986	56	88124
13	10348	61	45814	09	72429	57	88358
14	11134	62	46474	1,10	0,72867	58	88589
15	11924	63	47131	И	73300	59	88817
16	12712	64	47783	12	73729	1,60	0,89040
17	13499	65	48431	13	74152	61	89260
18	14285	66	49075	14	74571	62	89477
19	15069	67	49714	15	74986	63	89690
0,20	0,15852	68	50350	16	75395	64	89899
21	16633	69	50981	17	75800	65	90106
22	17413	0,70	0,51607	18	76200	66	90309
23	18191	71	52230	19	76595	67	90508
24	18967	72	52848	1,20	0,76986	68	90704
25	19741	73	53461	21	77372	69	90897
26	20514	74	54070	22	77754	1,70	0,91087
27	21284	75	54675	23	78502	71	91273
28	22052	76	55275	24	78870	72	91457
29	22818	77	55870	25	78870	73	91637
0,30	0,23582	78	56461	26	79233	74	91814
31	24344	79	57047	27	79592	75	91988
32	25103	0,80	0,57624	28	79945	76	92159
33	25860	81	58206	29	80295	77	92327
34	26614	82	58778	1,30	0,80640	78	92492
35	27366	83	59346	31	80980	79	92655
36	28115	84	59909	32	81316	1,80	0,92814
37	28862	85	60468	33	81648	81	92970
38	29605	86	61021	34	81975	82	93124
39	30346	87	61570	35	82298	83	93275
0,40	0,31084	88	62114	36	82617	84	93423
41	31819	89	62658	37	82931	85	93569
42	32552	0,90	0,63188	38	83241	86	93711
43	33280	91	63718	39	83547	87	93852
44	34006	92	64243	1,40	0,83849	88	93989
45	34729	93	64763	41	84146	89	94124
46	35448	94	65278	42	84439	1,90	0,94257
47	36164	95	65789	43	84728	91	94387
294
Продолжение
	Ф(О		Ф(/)		Ф (/)	Ф(0	
92	94514	44	98531	96	99692	48	99950
93	94639	45	98571	97	99702	49	99952
94	94762	46	98611	98	99712	3,50	0,99953
95	94882	47	98649	99	99721	51	99955
96	95000	48	98686	3,00	0,99730	52	99957
97	95116	49	98723	01	99739	53	99958
98	95230	2,50	0,98758	02	99747	54	99960
99	95341	51	98793	03	99755	55	99961
2,00	0,95450	52	98826	04	99763	56	99963
01	95557	53	98859	05	99771	57	99964
02	95662	54	98891	06	99779	58	99966
03	95764	55	98923	07	99786	59	99967
04	95865	56	98953	08	99793	3,60	0,99968
05	95964	57	98983	09	99800	61	99969
06	96060	58	99012	3,10	0,99806	62	99971
07	96155	59	99040	11	99813	63	99972
08	96247	2,60	0,99068	12	99819	64	99973
09	96338	61	99095	13	99825	65	99974
2,10	0,96427	62	99121	14	99831	66	99975
11	96514	63	99146	15	99837	67	99976
12	96599	64	99171	16	99842	68	99977
13	96683	65	99195	17	99848	69	99978
14	96765	66	99219	18	99853	3,70	0,99978
15	96844	67	99241	19	99858	71	99979
16	96.923	68	99263	3,20	0,99863	72	99980
17	96999	69	99285	21	99867	73	99981
18	97074	2,70	0,99307	22	99872	74	99982
19	97148	*71	99327	23	99876	75	99982
2,20	0,97219	72	99347	24	99880	76	99983
21	97289	73	99367	25	99885	77	99984
22	97358	74	99386	26	99889	78	99984
23	97425	75	99404	27	99892	79	99985
24	97491	76	99422	28	99896	3,80	0,99986
25	97555	77	99439	29	99900	81	99986
26	97618	78	99456	3,30	0,99903	82	99987
27	97679	79	99473	31	99907	83	99987
28	97739	2,80	0,99489	32	99910	84	99988
29	97798	81	99505	33	99913	85	99988
2,30	0,97855	82	99520	34	99916	86	99989
31	97911	83	99532	35	99919	87	99989
32	97966	84	99549	36	99922	88	99990
33	98019	85	99563	37	99925	89	99990
34	98072	86	99576	38	99928	3,90	0,99990
35	98123	87	99590	39	99930	91	99991
36	98172	88	99602	3,40	0,99933	92	99991
37	98221	89	99615	41	99935	93	99992
38	98269	2 90	0,99627	42	99937	94	99992
39	98315	Q1	99639	43	99940	95	99992
2,40	0,98360	У1 Q9	99650	44	99942	96	99992
41	98405	У2 ПО	99661	45	99944	97	99993
42	98448	Уо Од	99772	46	99946	98	99993
43	98490	УЧ 95	99682	47	99948	99	99993
295
ПРИЛОЖЕНИЕ 3
ТАБЛИЦА ЗНАЧЕНИЙ ИНТЕГРАЛЬНОЙ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ
	- EI (- 0		- EI (- 0		- Ei (- 0
0,0001	8,633225	0,080	2,026941	1,20	0,1584084
0,0005	7,024187	0,085	1,971116	1,25	0,1464134
0,0010	6,331539	0,090	1,918745	1,30	0,1354510
0,0015	5,926574	0,095	1,869453	1,35	0,1254168
0,0020	5,639391	0,10	1,822924	1,40	0,1162193
0,0025	5,416747	о.п	1,737107	1,45	0,1077774
0,0030	5,234925	0,12	1,659542	1,50	0,1000196
0,0035	5,081274	0,13	1,588899	1,60	0,0863083
0,0040	4,948241	0,14	1,524146	1,70	0,0746546
0,0045	4,830957	0,15	1,464462	1,80	0,0677131
0,0050	4,726095	0,16	1,409187	1,90	0,0562044
0,0055	4,631284	0,17	1,357781	2,00	0,0489005
0,0060	4,544771	0,18	1,309796	2,50	0,0249149
0,0065	4,465227	0,19	1,264853	3,00	0,0130484
0,0070	4,391617	0,20	1,222651	3,50	0,0069701
0,0075	4,323123	0,25	1,044283	4,00	0,0037794
0,0080	4,259082	0,30	0,9056767	4,50	0,0020734
0,0085	4,198955	0,35	0,7942154	5,00	0,0011483
0,0090	4,142295	0,40	0,7023801	5,50	0,0006409
0,0095	4,088725	0,45	0,6253813	6,00	0,0003601
0,0100	4,037930	0,50	0,5597736	6,50	0,0002034
0,0150	3,637433	0,55	0,5033641	7,00	0,0001155
0,0200	3,354708	0,60	0,4543795	7,50	0,0000658
0,0250	3,136508	0,65	0,4115170	8,00	0,0000377
0,0300	2,959119	0,70	0,3737688	8,50	0,0000216
0,0350	2,809888	0,75	0,3403408	9,00	0,0000124
0,0400	2,681264	0,80	0,3105966	9,50	0,0000072
0,0450	2,568376	0,85	0,2840193	10,00	0,0000042
0,0500	2,467898	0,90	0,2601839	11,00	0,0000014
0,0550	2,377459	0,95	0,2387375	12,00	0,0000005
0,0600	2,295307	1,00	0,2193839	13,00	0,0000002
0,0650	2,220111	1,05	0,2018728	14,00	0,0000001
0,0700	2,150838	1,10	0,1859909	—	—
0,0750	2,086668	1,15	0,1715554	—	—
296
ПРИЛОЖЕНИЕ 4
ЗНАЧЕНИЯ ВЕРТИКАЛЬНЫХ НАПРЯЖЕНИИ ОТ НАГРУЗКИ.
РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО ПОЛОСЕ ПРИ — - 0-?
ь
Отноше- ние 2zV 2v	Отношение напряжений к интенсивности нагрузки на поверхности О-	х -^=- при	 равном						
	Р			b			
b	0	0.1	0,2	0,3	0,4	0,5	|	0.6
0.1	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1.0000
0.2	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1.0000
0.3	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	0.9S99
0.4	1,0000	1,0000	1,0000	1,0000	1,0000	0,9998	0,9976
0.5	1.0000	1.0000	1,0000	1,0000	0,9996	0,9976	0,9882
0,6	1,0000	1,0000	0,9999	0,9996	0,9976	0,9908	0,9704
0.7	1.0000	0.9998	0,9994	0,9976	0,9924	0,9783	0,9470
0.8	0.9996	0.9992	0,9976	0,9934	0,9830	0.9614	0.9214
0.9	0,9983	0.9974	0,9940	0,9861	0,9704	0,9420	0,8965
1.0	0,9953	0,9936	0,9878	0,9760	0,9551	0,9213	0,8710
1.1	0.9898	0,9873	0,9792	0,9636	0,9384	0.9008	0,8480
1.2	0,9816	0,9783	0.9679	0,9500	0,9202	0.8804	0,8268.
1.3	0.9704	0.9666	0,9546	0,9338	0.9029	0.8610	0.8076
1.4	0,9566	0,9524	0,9393	0,9171	0,8849	0.8426	0.7899
1.5	0.9405	0,9362	0.9216	0,8994	0,8668	0.8246	0,7733
1.6	0,9230	0.9182	0,9044	0,8812	0.8490	0.8076	0,7578
1.7	0,9039	0,9892	0,8854	0,8625	0.8308	0,7908	0,7431
1.8	0,8841	0,7894	0.8658	0,8438	0.8132	0.7745	0,7290
1.9	0,8633	0.8591	0,8412	0,8249	0.7955	0,7588	0,7154
2.0	0.8428	0,8386	0,8261	0,8052	0,7780	0,7432	0,7022
2.1	0,8228	0,8180	0,8062	0.7872	0.7608	0,7282	0.6894
2,2	0.8014	0.7978	0.7866	0,7686	0.7437	0.7130	0.6766
2.3	0.7809	0.7778	0,7674	0,7500	0,7272	0,6982	0.6640
2.4	0.7612	0.7578	0,7536	0,7326	0,7106	0,6819	0,6515
2.5	0,7423	0,7389	0.7300	0.7152	0,6948	0,6694	0.6396
2.6	0,7234	0,7204	0,7119	0,6982	0,6793	0.6554	0,6272
2.7	0,7054	0.7025	0.6946	0,6816	0,6641	0.6418	0,6155
2.8	0.6875	0.6850	0,6777	0.6656	0.6492	0.6283	0.6038
2.9	0.6704	0,6684	0,6623	0.6503	0,6313	0.6155	0,5924
3.0	0.6538	0.6520	0,6454	0.6353	0.6209	0.6026	0,5820
3.1	0.6382	0.6362	0,6306	0.6208	0.6070	0.5902	0,5703
3.2	0.6234	0.6212	0.6129	0,6066	0,5939	0.5784	0.6598
3.3	0.6086	0,6068	0,6017	0.5931	0,5814	0.5664	0,5490
3.4	0.5946	0.5930	0.5817	0.5799	0,5691	0,5553	0,5388
3.5	0.5809	0.5794	0.5748	0.5674	0,5572	0,5442	0.5286
3.6	0.5681	0.5636	0,5624	0.5552	0,5455	0,5325	0.5188
3.7	0.5552	0.5541	0,5501	0.5436	0,5346	0.5230	0.5095
3.8	0.5431	0.5413	0.5374	0.5323	0,5235	0,5130	0.5004
3.9	0.5315	0.5307	0.5269	0,5214	0.5132	0.5034	0.4911
4.0	0.5202	0.5193	0.5161	0,5106	0,5025	0,4938	0.4824
4.1	0.5098	0.5088	0,5054	0,5006	0.4936	0.4846	0.4739
4.2	0.4990	0,4984	0.4955	0.4904	0,4840	0,4757	0.4653
4.3	0.4895	0.4885	0,4841	0.4810	0,4750	0.4670	0,4573
4,4	0.4798	0.4789	0.4760	0.4721	0.4662	0.4584	0.4494
4,5	0.4706	0.4695	0.4671	0,4631	0,4571	0,4504	0.4439
4.6	0.4614	0.4603	0.4589	0.4542	0,4494	0.4422	0,4396
4.7	0.4528	0,4522	0,4496	0.4460	0.4410	0,4350	0,4274
4.8	0.4441	0.4434	0.4414	0.4380	0,4336	0.4278	0.4204
4.9	0.4361	0.4354	0,4335	0.4303	0,4258	0.4204	0.4134
5,0	0,4279	0.4276	0,4258	0,4228	0,4185	0.4134	0.4066
5.5	0.3928	0.3926	0.3908	0,3888	0,3852	0.3810	0.3764
6.0	0,3623	0,3617	0,3612	0,3594	0,3556	0,3535	0.3474
6.5	0,3364	0,3363	0.3352	0,3331	0,3316	0,3294	0,3258
7.0	0.3138	0,3136	0,3128	0,3116	0.3099	0.3078	0.3052
7.5	0.2938	0,2936	0,2934	0,2920	0.2906	0,2892	0,2870
8.0	0.2767	0,2761	0,2756	0,2748	0,2737	0,2718	0.2695
8.5	0,2608	0,2603	0,2599	0,2592	0.2582	0,2570	0,2559
9.0	0.2464	0,2463	0,2460	0,2458	0,2450	0,2435	0,2426
10,0	0,2228	0,2227	0,2220	0,2220	0,2214	0,2202	0,2198
• Приложения 4—12 составлены Г. И. Довженко.
297
ПРИЛОЖЕНИЕ 5
ЗНАЧЕНИЯ ВЕРТИКАЛЬНЫХ НАПРЯЖЕНИИ ОТ НАГРУЗКИ.
РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО ПОЛОСЕ ПРИ — = 0.7 4- 1.2
ь
Отноше- ние 2г У~2у b	Отношение напряжения к интенсивности нагрузки на поверхности °г	х 	 при	> равном Р	ь					
	0.7	0.8	0,9	1,0	1.1	1.2
	1.0000	1.0000	0,9976	0,5000	0.0024	0
	1.0000	0.9976	0,9214	0.5000	0.0786	0,0024
	0.9976	0.9704	0,8272	0,5000	0,1729	0,0297
	0.9830	0.9214	0.7602	0,5000	0.2398	0,0786
	0.9552	0.8710	0,7143	0,5000	0,2857	0,1290
	0.9214	0.8272	0,6812	0,5000	0.3188	0,1728
	0.8872	0.7900	0.6569	0.5000	0.3431	0.2100
	0.8556	0.7602	0,6384	0.5000	0.3616	0.2398
	0.8272	0.7350	0.6232	0,5000	0.3768	0.2650
	0.8020	0.7143	0,6137	0.5000	0.3863	0,2857
	0.7796	0.6964	0.6014	0,5000	0,3986	0,3036
	0.7602	0.6811	0.5933	0.5000	0,4067	0.3198
	0.7430	0.6682	0.5862	0.5000	0.4138	0.3318
	0.7274	0.6568	0.5800	0,5000	0.4200	0,3431
	0.7132	0.6466	0,5744	0,4999	0.4254	0,3530
	0.7006	0.6372	0.5694	0.4998	0,4300	0.3620
	0.6888	0.6286	0.5651	0.4996	0.4388	0,3698
	0.6774	0.6204	0,5610	0,4992	0.4372	0,3770
	0.6668	0.6140	0.5564	0,4986	0,4403	0.3818
	0.6561	0.6060	0,5524	0,4976	0,4424	0.3876
	0.6459	0,5984	0,5490	0,4964	0,4440	0.3924
	0.6358	0,5910	0.5440	0,4949	0,4452	0.3962
	0.6256	0.5844	0,5392	0,4930	0,4465	0.3994
	0.6157	0.5764	0,5344	0.4908	0.4468	0,4020
	0.6054	0.5686	0.5292	0.4882	0.4462	0.4042
	0.5959	0.5612	0,5240	0,4852	0,4454	0.4054
	0.5858	0.5531	0.5178	0,4819	0.4442	0.4067
	0.5760	0.5455	0.5128	0,4783-	0,4428	0.4068
	0.5662	0.5376	0,5071	0,4744	0,4406	0,4080
	0,5570	0.5297	0.5008	0,4704	0.4387	0.1064
	0.5475	0.5219	0,4948	0,4662	0,4360	0.4054
	0.5381	0.5141	0,4884	0,4615	0.4334	0,4034
	0.5329	0.5065	0.4825	0,4568	0.4298	0,4024
	0.5201	0.4987	0,4760	0.4522	0.4266	0,4005
	0.5108	0.4915	0.4699	0,4470	0.4228	0.3990
	0.5026	0.4837	0.4638	0.4419	0.4194	0,3956
	0.4936	0.4714	0.4570	0,4369	0,4160	0,3979
	0.4852	0,4691	0,4509	0.4318	0.4114	0,3901
	0.4774	0,4618	0.4446	0,4264	0,4074	0,3871
	0.4693	0,4545	0,4386	0.4214	0,4030	0.3841
	0.4616	0.4477	0.4326	0,4165	0,3988	0,3806
	0.4540	0,4410	0,4264	0,4110	0,3947	0,3770
	0.4463	0,4344	0.4206	0.4059	0.3900	0.3735
	0.4393	0,4274	0,4144	0,4008	0.3860	0,3704
	0.4318	0,4211	0,4088	0,3956	0,3815	0,3665
	0,4250	0,4148	0,4029	0.3906	0.3774	0.3628
	0.4182	0,4084	0.3974	0,3857	0.3730	0.3595
	0.4121	0,4026	0.3922	0,3806	0.3684	0,3556
	0.4054	0.3964	0,3868	0,3758	0,3642	0,3522
	0.3994	0.3906	0,3811	0,3710	0,3601	0.34&2
	0.3702	0.3638	0.3560	0.3480	0,3396	0,3299
	0.3445	0.3392	0.3336	0,3272	0.3202	0,3127
	0.3217	0.3178	0.3134	0,3078	0,3016	0,2960
	0.3021	0.2987	0,2947	0,2904	0,2858	0,2807
	0.2842	0.2814	0.2784	0.2746	0.2707	0.2668
	0.2683	0.2659	0,2632	0.2602	0,2570	0.2534
	0.2542	0.2521	0.2490	0,2473	0,2451	0.2412
	0.2403	0.2391	0,2371	0,2350	0,2330	0,2301
	0.2186	0.2173	0,2155	0.2113	0,2126	0,2103
298
ПРИЛОЖЕНИЕ 6
ЗНАЧЕНИЯ ВЕРТИКАЛЬНЫХ НАПРЯЖЕНИЙ ОТ НАГРУЗКИ.
РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО ПОЛОСЕ ПРИ — « 1.3 -т- 4.0
ь
Отноше- ние 2z 2v b	Отношение напряжения к интенсивности нагрузки на поверхности ’z	А- —— при 	, равном Р	ь					
	1.3	1.4	1.5	2.0	3.0	4.0
0.1	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000
0.2	0,0000	0,0000	0.0000	0,0000	0,0000	0,0000
0,3	0,0024	0,0000	0,0000	0,0000	0.0000	0,0000
0.4	0,0170	0,0024	0,0002	0,0000	0,0000	0,0000
0,5	0,0448	0.0118	0,0024	0,0000	0,0000	0,0000
0,6	0,0786	0,0296	0,0097	0,0000	0,0000	0,0000
0,7	0,1128	0,0530	0,0217	0,0000	0,0000	0,0000
0.8	0,1444	0,0786	0,0386	0,0002	0,0000	0,0000
0.9	0,1728	0,1044	0,0580	0,0008	0,0000	0,0000
1.0	0,1980	0,1290	0,0787	0,0022	0,0000	0,0000
1,1	0,2204	0,1520	0,0992	0,0051	0,0000	0,0000
1.2	0,2398	0,1731	0,1194	0,0092	0,0000	0,0000
1.3	0,2568	0.1922	0,1385	0,0148	0,0000	0,0000
1,4	0,2722	0,2095	0,1562	0,0217	0,0000	0,0000
1,5	0,2860	0,2254	0,1731	0,0298	0,0001	0,0000
1,6	0,2980	0.2398	0,1884	0,3085	0,0002	0,0000
1,7	0,3092	0,2530	0,2030	0,0480	0,0004	0,0000
1,8	0,3176	0,2649	0,2162	0,0580	0,0008	0,0000
1,9	0,3272	0,2757	0,2284	0,0684	0,0014	0,0000
2,0	0,3352	0,2856	0,2396	0,0786	0,0024	0,0000
2.1	0,3421	0,2944	0,2498	0,0888	0,0030	0,0000
2,2	0,3482	0,3026	0,2594	0,0992	0,0051	0,0000
2.3	0,3537	0,3098	0,2682	0,1094	0,0070	0,0001
2,4	0,3583	0,3165	0,2778	0,1192	0,0092	0,0002
2,5	0,3628	0,3220	0,2834	0,1285	0,0118	0,0004
2,6	0,3657	0,3273	0,2900	0,1378	0,0148	0,0006
2,7	0,3678	0,3320	0.2958	0,1464	0,0181	0,0008
2,8	0,3709	0,3354	0,3010	0,1550	0,0217	0,0012
2,9	0,3727	0,3386	0,3054	0,1631	0,0255	0,0017
3,0	0,3766	0,3413	0,3096	0,1708	0,0396	0,0024
3,1	0,3741	0,3433	0,3130	0,1778	0,0336	0,0031
3,2	0,3745	0,3447	0,3157	0,1843	0,0383	0,0040
3,3	0,3742	0,3460	0,3182	0,1906	0,0430	0,0051
3,4	0,3734	0,3466	0,3200	0,1964	0,0474	0,0063
3,5	0,3729	0,3471	0,3214	0,2019	0,0524	0,0076
3,6	0,3713	0,3472	0,3224	0,2067	0,0572	0,0092
3,7	0,3701	0,3466	0,3232	0,2115	0,0620	0,0108
•3,8	0,3684	0,3458	0,3236	0,2156	0,0668	0,0127
3,9	0,3659	0,3450	0,3234	0.2194	0,0717	0,0146
4,0	0,3641	0,3438	0,3232	0,2230	0,0763	0,0168
4,1	0,3618	0,3424	0,3228	0,2259	0,0806	0,0189
4,2	0,3593	0.3410	0,3224	0,2288	0,0854	0,0213
4,3	0,3568	0,3389	0,3210	0,2310	0,0898	0,0238
4,4	0,3538	0,3372	0,3200'	0,2332	0,0941	0,0263
4,5	0.3514	0,3350	0,31’87	0,2350	0,0985	0,0288
299
Продолжение приложения 6
Отноше- ние 2у Ь	Отношение напряжения к интенсивноегн нагрузки на поверхности °2	* —— при 	 , равном Р	ь					
	1.3	1.4	1.5	2.0	3.0	4.0
4,6	0,3484	0,3328	0,3172	0,2368	0,1024	0,0314
4,7	0,3454	0,3304	0,3154	0,2380	0,1062	0,6332
4,8	0,3420	0,3281	0,3136	0,2394	0,1102	0,0369
4,9	0,3392	0,3256	0,3120	0,2402	0,1138	0,0398
5,0	0,3358	0,3234	0,3100	0,2412	0,1172	0,0425
5,5	0,3204	0,3098	0,2994	0,2422	0,1321	0,0563
6,0	0,3048	0,2960	0,2873	0,2402	0,1432	0,0634
6,5	0,2902	0,2842	0,2754	0,2358	0,1513	0,0812
7,0	0,2754	0,2696	0,2637	0,2304	0,1565	0,0910
7,5	0,2620	0,2572	0,2522	0,2240	0,1596	0,0994
8,0	0,2497	0,2466	0,2418	0,2173	0.1614	0,1058
8,5	0,2380	0,2346	0,2314	0,2104	0,1611	0,1111
9,0	0,2277	0,2244	0,2216	0,2040	0,1606	0,1148
10,0	0,2086	0,2064	0,2042	0,1906	0,1566	0.1293
ПРИЛОЖЕНИЕ 7
ЗНАЧЕНИЯ ГОРИЗОНТАЛЬНЫХ НАПРЯЖЕНИЙ ОТ РАВНОМЕРНО
РАСПРЕДЕЛЕННОЙ ПОЛОСОВОЙ НАГРУЗКИ ПРИ — =0+0.6
ь
Отноше- ние 8zv b	Отношение горизонтального напряженн ах на поверхности 		 при Р				я к интенсивности нагрузки Х- , равном b		
	0	0.1	0.2	0.3	0.4	0.5	0.6
0,1	0,1250	0,1250	0,1250	0,1250	0,1250	0,1250	0,1250
0,2	0,1250	0,1250	0,1250	0.1250	0,1250	0,1250	0,1250
0,3	0,1250	0,1250	0,1250	0,1250	0,1250	0,1250	0,1250
0,4	0,1250	0,1250	0,1250	0,1250	0,1250	0,1248	0,1222
0,5	0,1250	0,1250	0,1250	0,1250	0,1244	0,1221	0,1147
0,6	0,1250	0,1250	0,1248	0,1242	0,1222	0,1165	0,1055
0,7	0,1249	0J247	0,1240	0,1221	0,1176	0,1092	0,0964 0,0892 0.0847 0.0791 0,0756 0,0731 0.0708 0,0687
0,8 0,9 1,0 1.1 1.2 1,3	0,1242 0,1226 0,1192 0,1143 0,1080 0,1010	0,1238 0,1218 0,1180 0,1129 0,1067 0,0997	0,1216 0,1189 0,1143 0,1087 0,1025 0,0959	0,1184 0,1131 0,1079 0.Ю38 0,0963 0,0902	0,1117 0,1054 0,0994 0,0937 0.0885 0,0837 0,0790 0,0782 0 0702	0,1017 0,0951 0,0888 0,0845 0,0810 0,0767 0 0737	
1,4	0,0935	0,0923	0,0891	0,084b 0,0789 0,0733 0,0679 0,0629 0,0581 (J.U534		0,0706	0,0668
1,5	0,0859	0,0849	0,0823			0^0672	0,0646
1,6	0,0784	0,0777	0,0759		0 0660	о’0639	0.0625
1,7	0,0715	0,0709	0,0698		0.0617	0,0607	0,0600
1,8	0.0649	0,0646	0,0639		0 0577	0,0574	0,0575
1,9 2,0	0,0588 0,0535	0,0588 0,0536	0,0573 0,0553		О’0538	0,0543	0,0550
300
ПРИЛОЖЕНИЕ 8
ЗНАЧЕНИЯ ГОРИЗОНТАЛЬНЫХ НАПРЯЖЕНИЙ
ОТ РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПОЛОСОВОЙ НАГРУЗКИ ПРИ
-i- - 0,7 4- 1,2
b
Отношение 8z у b	Отношение горизонтального напряжения к интенсивности нагрузки					
	9Х на поверхности —* пр Р			и	• равном b		
	0,7	0,8	0.9	1.0	1.1	1.2
0.1	0,1250	0.1260	0,1217	0^0625	0,0033	0.0000
0.2	0J250	0,1222	0.0892	0.0625	0,0358	0,0028
0,3	6’1220	0,1053	0,0734	0.0625	0,0516	0.0197
6.4	0,1119	0'0892	0.0675	0.0625	0,0575	0.0358
0.Б	6'0994	0,0791	0,0653	0,0625	0.0597	0.0459
0.6	6.0892	0,0732	0.0642	0,0625	0.0608	0,0518
0.7	6.0819	0.0697	0.0635	0,0625	0.0615	0.0541
0.8	6.0769	0.0675	0.0633	0,0625	0.0617 _	0.0575
0,9	6.0733	0.0661	0.0630	0.0625	0.0620	0,0589
1.0	6,0707	0.0653	0.0631	0.0625	0.0619	0.0597
1.1	6'0689	0,0645	0,0628	0.0625	0.0622	0.0605
1,2	0,0674	0,0640	0.0628	0,0625	0.0622	0.0608
1.3	0'0664	0.0637	0.0626	0,0625	0.0624	0»0в13
1.4	0.0653	0,0633	0.0625	0.0624	0.0624	0,0615
1,5	6^0642	0.0627	0.0622	0.0624	0,0624	0.0616
1.6	0,0630	0.0617	0,0620	0.0621	0,0623	0,0616
1.7	0.0615	0,0612	0,0812	0.0618	0,0620	0.0617
1.8	0'0599	0.0602	0,0606	0.0613	0,0616	0.0615
1.9	0,0581	0.0589	0,0597	0.0606	0,0612	0.0614
2,0	0.0560	0,0573	0,0584	0.0596	0.0605	0.0606
ПРИЛОЖЕНИЕ 9
ЗНАЧЕНИЯ ГОРИЗОНТАЛЬНЫХ НАПРЯЖЕНИЙ
ОТ РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПОЛОСОВОЙ НАГРУЗКИ ПРИ
 «= 1,3 4" 4.0
ь
Отношение 8х у		Отношение горизонтального напряжения к интенсивности нагрузки					
		ах на поверхности	пр Р			и —*— . равном Ь		
Ъ							
		1,3	1.4	1.5	2.0	3.0	4.0
0.1		0.0000	0.0000	0,0000	0.0000	0,0000	0,0000
0.2		0.0000	о.оооо	0.0000	0.0000	0,0000	0,0000
0.3		0.0030	0,0000	0,0000	0.0000	0,0000	0.0000
0.4		0.0137	0.0028	0.0002	0.0000	0.0000	0.0000
0.5		0.0256	0,0103	0,0029	0.0000	0.0000	0.0000
(	),6	0,0358	0.0195	0,0085	0.0000	0.0000	0.0000
(	),7	0,0431	0.0286	0,0158	0.0000	0.0000	0.0000
(	1.8	0,0481	0,0358	0,0224	0.0004	0.0000	0.0000
0,9		0,0517	0.0403	0.0299	0.0012	0.0000	0.0000
	.0	0.0543	0.0459	0,0357	0.0029	0.0000	0.0000
1.1		0,0561	0.0493	0,0404	0.0053	0.0000	0.0000
1.2		0.0575	0.0518	0.0436	0.0065	0,0000	0,0000
	.3	0.0584	0.0537	0.0474	0.0120	0.0000	0.0000
1Л 1.5		0.0591	0,0553	0.0498	0.0153	0.0001	0.0000
		0.0599	0.0565	0.0517	0.0196	0.0002	0.0000
1,6		0.0601	0,0574	0.0534	0.0233	0.0005	0.0000
1.7		0,0605	0.0581	.0,0574	0.0268	0.0009	0.0000
1.8		0,0605	0.0587	0.0657	0.0300	0.0017	0.0000
1	I.» 1.0	0,0606 0.0605	0.0591 0.0592	0.0565 0.0571	0.0331 0.0357	0.0026 0.0089	0.0000 0.0000
301
ПРИЛОЖЕНИЕ 10
ЗНАЧЕНИЯ КАСАТЕЛЬНЫХ НАПРЯЖЕНИИ ОТ НАГРУЗКИ.
РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО ПОЛОСЕ ПРИ
х „
----— О -Г 0,6
ь
Отношение	Отношение напряжения к интенсивности нагрузки на поверхности ^ZX	X 	—	при	, равном						
	Р . Р			ь			
Ь	0	0,1	0.2	0,3	0.4	0,5	0,6
0.1	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000
0.2	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000
0,3	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0001
0.4	0,0000	0,0000	0,0000	0,0000	0,0000	0,0003	0,0026
0.5	0,0000	0,0000	0,0000	0,0000	0,0005	0,0026	0,0109
0.6	0,0000	0,0000	0,0001	0,0006	0,0026	0,0088	0,0238
0,7	0,0000	0,0002	0,0008	0,0026	0,0075	0,0183	0,0382
0.8	0,0000	0,0008	0,0025	0,0066	0,0149	0,0296	0,0519
0.9	0,0000	0,0023	0,0057	0,0125	0,0238	0,0410	0,0640
1,0	0,0000	0,0044	0,0105	0,0197	0.0334	0,0519	0,0744
1,1	0,0000	0,0071	0,0158	0,0274	0,0427	0,0616	0,0831
1,2	0,0000	0,0100	0,0212	0,0349	0,0513	0,0702	0,0903
1,3	0.0000	0,0127	0,0264	0,0416	0,0588	0,0774	0,0962
1,4	0,0000	0,0151	0,0308	0,0474	0,0651	0,0833	0,1010
1,5	0,0000	0,0170	0,0343	0,0520	0,0701	0,0879	0,1046
1,6	0,0000	0,0185	0,0370	0,0556	0,0738	0,0913	0,1073
1,7	0,0000	0,0196	0,0389	0,0580	0,0764	0,0935	0,1090
1,8	0,0000	0,0202	0,0402	0,0595	0,0779	0,0948	0,1098
1,9	0,0000	0,0205	0,0401	0,0603	0,0786	0,0953	0,1098
2,0	0,0000	0,0207	0,0410	0,0604	0,0786	0,0950	0,1093
2,1	0,0000	0,020б	0,0408	0,0600	0,0780	0,0940	0,1081
2,2	0,0000	0,0203	0,0403	0,0592	0,0769	0,0927	0,1066
2,3	0,0000	0,0200	0,0394	0,0578	0,0754	0,0910	0,1046
2,4	0,0000	0,0194	0,0385	0,0566	0,0736	0,0892	0,1024
2,5	0,0000	0,0189	0,0376	0,0553	0,0718	0,0868	0,0999
2,6	0,0000	0,0183	0,0364	0,0536	0,0697	0,0844	0,1008
2,7	0,0000	0,0178	0,0356	0,0519	0,0675	0,0819	0,0946
2.8	0,0000	0,0172	0,0348	0,0503	0,0655	0,0787	0,0918
2,9	0,0000	0,0166	0,0329	0,0485	0,0633	0,0768	0,0889
3,0	0,0000	0.016Г	0,0317	0,0470	0,0612	0,0743	0,0861
3,1	0,0000	0,0154	0,0306	0,0452	0,0590	0,0718	0,0834
3,2	0,0000	0,0149	0,0284	0,0436	0,0570	0,0694	0,0806
з.з	0,0000	0,0144	0,0283	0,0420	0,0549	0,0670	0,0779
3,4	0,0000	0,0137	0,0273	0,0404	0.0530	0,0646	0,0753
3,5	0.0000	0,0133	0,0264	0,0389	0,0510	0,0623	0,0727
3,6	0,0000	0,0129	0,0253	0,0375	0,0492	0,0597	0,0701
3.7	0,0000	0,0120	0,0243	0,0362	0.0474	0,0581	0,0678
3,8	0,0000	0,0116	0,0236	0,0349	0,0457	0,0559	0,0655
3,9	0,0000	0,0114	0.0226	0,0336	0,0440	0,0540	0,0632
4,0	0,0000	0,0110	0,0217	0,0323	0,0425	0,0520	0,0611
4,1	0,0000	0,0106	0,0210	0,0312	0,0410	0,0503	0.0591
4,2	0,0000	0,0102	0,0202	0,0301	0,0396	0,0485	0,0571
302
Продолжение приложения 10
Отношение 2z b	Отношение напряжения к интенсивности нагрузки на поверхности						
	XXZ	TZX	X				равном		
	Р	Р			-при	 b			
	0	0,1	0.2	0,3	0,4	0.5	0,6
4,3	0,0000 0,0000	0,0098	0,0198	0,0290	0,0381	0,0470	0,0552
4 4		0,0094	0,0188	0,0280	0,0368	0,0454	0,0533
4,5	0,0000	0,0091	0,0179	0,0270	0,0356	0,0438	0,0516
4,6	0^0000	0,0087	0,0176	0,0261	0,0341	0,0425	0,0499
4,7	0 0000	0,0085	0,0169	0,0252	0,0332	0,0410	0,0483
4,8	0,0000	0,0082	0,0163	0,0244	0,0322	0,0396	0,0467
4,9	0,0000	0,0080	0,0157	0,0235	0,0310	0,0383	0,0-152
5,0	0,0000	0,0077	0,0153	0,0228	0,0301	0,0372	0,0-138
5,5	0 0000	0,0065	0,0130	0,0194	0,0256	0,0317	0,0375
6,0	0,0000	0,0057	0,0112	0,0167	0,0222	0,0273	0,0319
6,5	0 0000	0,0048	0,0097	0,0145	0,0192	0,0238	0,0282
7,0	0,0000	0,0042	0,0084	0,0126	0.0168	0,0208	0,0247
7.5	0 0'000	0,0037	0.0075	0,0111	0,0148	0,0181	0,0219
8,0	0,0000	0,0033	0,0066	0,0099	0,0131	0,0163	0,0195
8,5	0,0000	0,0030	0,0059	0,0088	0,0117	0,0146	0,0174
9,0	0 0000	0,0027	0,0053	0,0079	0,0105	0,0131	0,0156
0,0	0,0000	0,0022	0,0043	0,0065	0,0086 п	0,0107 РИЛОЖ	0,0129 ЕНИЕ 11
ЗНАЧЕНИЯ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ ОТ НАГРУЗКИ,
РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО ПОЛОСЕ ПРИ
- 5— = 0,7 4- 1,2
b
Отношение 2z^~ 2*	Отношение	напряжения к \vz Р	интенсивности нагрузки па поверхности			
			'гл 	при — Р	V —, равном b		
b	0.7	0.8	0,9	1.0	1.1	1.2
0,1	0,0000	0,0000	0.0026	0,1410	0,0026	0,0000
0,2	0,0000	0,0026	0,0519	0,1410	0,0519	0,0026
0,3	0,0026	0,0238	0,0904	0,1410	0.0904	0,0238
0,4	0,0149	0,0519	0,1099	0,1410	0,1099	0,0519
0,5	0,0334	0,0744	0,1202	0,1410	0,1202	0,0744
0,6	0,0519	0,0904	0,1262	0,1410	0,1262	0,0904
0,7	0,0677	0,1018	0,1300	0,1410	0,1300	0,1018
0,8	0,0803	0,1099	0,1325	0,1410	0,1325	0,1099
0,9	0,0903	0,1158	0,1342	0,1410	0,1312	0,1158
1,0	0,0985	0,1202	0,1355	0,1410	0,1355	0,1202
1,1	0,1048	0,1236	0,1365	0,1410	0,1365	0,1286
1,2	0,1098	0,1262	0,1372	0,1410	0,1372	0,1262
1,3	0,1138	0,1282	0,1377	0,1410	0,1377	0,1283
1,4	0,1170	0,1298	0,1381	0,1410	0,1382	0,1300
1,5	0,1193	0,1310	0,1383	0,1409	0,1385	0,1313
303
Продолжение приложения //
Отношение
2г 1^2»
b
Отношение напряжения к интенсивности нагрузки на поверхности
Xxz	х2х	х
----«------- при----, равном
Р	Р	Ь
1,6 1,7 1,8	0,1210 0,1220 0,1222	0,1313 0,1319 0,1317	0,1384 0,1381 0,1377	0,1407 .0,1405 0,1400	0,1387 0,1388 0,1387	0,1324 0,1333 0,1339
1,9	0,1219	0,1310	0,1369	0,1398	0,1384	0,1342
2,0	0,1211	0,1300	0,1358	0,1385	0,1380	0,1344
2,1	0,1197	0,1286	0,1345	0,1373	0,1372	0,1343
2,2	0,1180	0,1261	0,1328	0,1358	0,1362	0,1399
2,3	0,1159	0,1253	0,1368	0,1342	0,1353	0,1333
2,4	0,1135	0,1223	0,1286	0,1323	0,1339	0,1324
2,5	0,1109	0,1197	0,1261	0,1301	0,1317	0,1311
2,6	0,1082	0,1170	0,1236	0,1278	0,1298	0,1297
2,7	0,1054	0,1142	0,1203	0,1253	0,1277	0,1281
2,8	0,1024	0,1112	0,1180	0,1227	0,1255	0,1262
2,9	0,0995	0,1082	0,1151	0,1200	0,1231	0,1252
3,0	0,0965	0,1051	0,1120	0,1172	0,1206	0,1221
3,1	0,0935	0,1021	0,1091	0,1143	0,1179	0,1198
3,2	0,0905	0,0991	0,1060	0,1115	0,1153	0,1170
3,3	0,0898	0,0961	0,1031	0,1085	0,1126	0,1151
3,4	0,0848	0,0931	0,1001	0,1057	0,1099	0,1126
3,5	0,0821	0,0903	0,0979	0,1028	0,1072	0,1101
3,6	0,0794	0,0874	0,0944	0,1000	0,1044	0,1076
3,7	0,0767	0,0847	0,0915	0,0972	0,1016	0,1050
3,8	0,0742	0,0820	0,0888	0,0945	0,0991	0,1026
3,9	0,0718	0,0795	0,0861	0,0917	0,0964	0,1001
4,0	0,0694	0,0769	0,0835	0,0891	0,0939	0,0976
4,1	0,0671	0,0745	0,0810	0,0868	0,0914	0,0951
4,2	0,0649	0,0721	0,0786	0,0841	0,0888	0,0927
4,3	0,0629	0,0699	0,0762	0,0817	0,0864	0,0903
4,4	0,0609	0,0677	0,0738	0,0793	0,0840	0,0879
4,5	0,0589	0,0655	0,0712	0,0770	0,0817	0,0856
4,6	0,0571	0,0635	0,0695	0,0748	0,0795	0,0834
4,7	0,0553	0,0616	0,0674-	0,0727	0,0773	0,0813
4,8	0,0536	0,0597	0,0654	0,0705	0,0752	0,0791
4,9	0,0519	0,0579	0,0635	0,0689	0,0730	0,0770
5,0	0,0503	0,0561	0,0617	0,0666	0,0712	0,0750
5,5	0,0432	0,0484	0,0534	0,0579	0,0621	0,0658
6,0	0,0374	0,0420	0,0465	0,0506	0,0545	0,0580
6,5	0,0327	0.0367	0,0407	0,0444	0,0478	0,0512
7,0	0,0287	0,0323	0,0359	0,0392	0,0425	0,0455
7,5	0,0254	0,0287	0,0318	0,0349	0,0379	0,0406
8,0	0,0226	0,0255	0,0284	0,0311	0,0339	0,0364
8,5	0,0174	0,0203	0,0255	0,0280	0,0305	0,0327
9,0	0,0182	0,0206	0,0203	0,0252	0,0275	0,0297
10,0	0,0150	0,0169	0,0189	0,0209	0,0228	0,0246
304
ПРИЛОЖЕНИЕ 12
ЗНАЧЕНИЯ КАСАТЕЛЬНЫХ НАПРЯЖЕНИИ ОТ НАГРУЗКИ,
РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО ПОЛОСЕ ПРИ
b
1.3 ч- 4.0
	Отношение напряжения к		интенсивности нагрузки на поверхности			
Отношение		TAZ	X			
2z		Р		при	, равном Р	b			
b						
	1.3	1.4	1.5	2,0	3.0	4,0
0.1	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000
0.2	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000
0.3	0,0026	0,0001	0,0000	0,0000	0,0000	0,0000
0.4	0,0149	0.0026	0,0003	0,0000	0,0000	0,0000
0.5	0,0334	0,0109	0,0026	0,0000	0,0000	0,0000
0.6	0,0519	0.0238	0,0088	0.0000	0,0000	0,0000
0,7	0,0677	0.0382	0,0183	0.0000	0,0000	0,0000
0.8	0.0803	0,0519	0,0296	0.0003	0,0000	0,0000
0.9	0.0903	0,0640	0,0410	0.0010	0,0000	0,0000
1.0	0.0985	0,0744	0,0519	0.0026	0,0000	0,0000
1.1	0.1048	0.0831	0.0616	0.0052	0,0000	0,0000
1.2	0.1098	0.0903	0,0702	0.0088	0,0000	0,0000
1.3	0.1140	0,0966	0.0781	0.0132	0,0000	0,0000
1,4	0.1174	0,1018	0.0847	0.0182	0,0000	0,0000
1,5	0.1202	0.1061	0,0904	0.0237	0,0001	0.0000
1,6	0.1225	0,1098	0,0954	0.0294	0,0003	0,0000
1.7	0.1244	0.1130	0,0997	0,0352	0,0005	0,0000
1.8	0.1260	0,1157	0,1035	0,0410	0,0014	0,0000
1,9	0.1272	0.1179	0,1068	0.0466	0,0016	0,0000
2.0	0.1282	0.1197	0,1096	0.0519	0,0026	0,0000
2.1	0.1288	0,1212	0,1119	0.0569	0,0037	0,0000
2,2	0.1298	0,1224	0,1139	0.0615	0,0052	0,0001
2,3	0.1291	0,1232	0,1155	0,0660	0,0069	0,0001
2.4	0,1289	0,1236	0,1168	0,0701	0,0088	0,0003
2.5	0,1284	0,1237	0,1176	0,0739	0,0109	0,0004
2.6	0.1276	0,1236	0,1181	0,0774	0.0132	0,0007
2.7	0.1265	0,1236	0,1184	0.0804	0,0157	0,0010
2,8	0.1252	0,1225	0,1183	0,0633	0,0183	0,0014
2.9	0.1237	0.1216	0,1180	0,0857	0,0210	0,0019
3.0	0.1220	0,1205	0,1163	0.0879	0.0237	0,0026
3.1	0.1202	0,1191	0,1155	0.0897	0,0265	0.0033
3.2	0.1183	0,1176	0.1145	0,0913	0,0293	0.0042
3,3	0.1162	0.1150	0,1134	0,0925	0.0321	0,0052
3,4	0.1141	0.1142	0,1131	0.0935	0,0348	0,0062
3,5	0.1119	0.1112	0,1117	0.0943	0.0374	0,0074
3.6	0.1096	0.1092	0,1101	0.0948	0,0400	0.0087
3,7	0.1073	0,1073	0,1084	0.0952	0,0425	0,0101
3,8	0.1050	0,1063	0,1066	0,0953	0,0449	0,0115
3,9	0,1027	0.1042	0,1048	0,0952	0,0472	0,0130
4,0	0.1003	0.1021	0,1029	0,0950	0,0493	0,0146
4,1	0,0980	0.1000	0,1010	0,0946	0,0512	0,0162
4.2	0.0957	0,0978	0,0991	0.0941	0,0532	0,0179
4,3	0.0934	0,0956	0,0971	0,0934	0,0550	0,0195
4,4	0.0911	0,0936	0,0952	0.0928	0,0565	0,0211
4,5	0.0890	0,0914	0,0932	0,0919	0,0581	0.0228
4,6	0.0868	0,0894	0,0913	0,0910	0,0593	0,0245
4,7	0,0846	0,0873	0,0893	0,0900	0,0605	0,0261
4,8	0,0825	0,0853	0.0874	0,0890	0,0617	0,0278
4,9	0,0809	0,0833	0,0855	0,0880	0.0626	0,0293
5,0	0,0785	0,0814	0,0836	0.0868	0.0635	0.0308
5,5	0,0698	0.0722	0,0748	0.0807	0.0661	0,0377
6,0	0,0613	0,0641	0,0667	0,0713	0,0666	0,0431
6,5	0.0544	0,0571	0,0597	0.0681	0,0656	0,0470
7,0	0.0484	0,0511	0,0535	0,0627	0.0636	0,0493
7,5	0.0433	0,0458	0,0481	0,0570	0,0609	0,0506
8,0	0.0389	0,0412	0,0434	0,0521	0,0580	0,0508
8,5	0,0351	0,0373	0,0393	0,0477	0,0548	0.0504
9,0	0.0318	0,0338	0,0358	0,0438	0,0518	0,0494
10,0	0.0264	0,0281	0,0298	0.0372	0,0457	0,0461
305
ПРИЛОЖЕНИЕ 13
ВЕРТИКАЛЬНЫЕ НАПРЯЖЕНИЯ ОТ НАГРУЗКИ.
распределенной на полосе по параболе
Отношение —— при у, ь				Отношение напряжения к максимальной ординате ннтен-							
				СИвнести давления				°z „	 X		- . равном	
	равном						Рмах	1.5рСр	ь		
0,33	0.25	0.167	0,125		0,25	0.5			2.0	3,0	4,0
0,308	0,352	0,433	0,5	0,9688	0,9063	0.1791	0,1254	0,0003	0	0	0
0.615	0,71	0.866	1.0	0,8762	0,8173	0,65303	0,2196	0.0208	0.0005	0	0
1.23	1.41	1.732	2.0	0,6283	0,6034	0,5304	0,3154	0,1313	0.0339	0,0011	0
1.84	2,12	2.598	3.0	0.4634	0,4508	0.4208	0.3169	0,1982	0,1032	0.0114	0.0016
2.46	2.82	3,464	4,0	0,3564	0,3550	0,3427	0,2868	0,2134	0,1493	0.0400	0.012
3.08	3,54	4,330	5.0	0,2853	0,2732	0,2624	0.2518	0,2058	0,1668	0,0729	0,022
3.68	4.25	5,196	6.0	0,2506	0,2418	0,2364	0.2237	0,1954	0,1633	0.0921	0,0323
4.3	4,95	6.062	7,0	0.2299	0.2010	0,2068	0,1919	0.1723	0,1464	0,0979	
4,91	5.66	6,928	8,0	0,2094	0,1920	0.1877	0,1775	0.1708	0,1389	0,1312	
5.51	6,36	7,94	9.0	0.1939	0.1828	0.1730	0,1628	0,1524	0,1182	0.0958	0,0749
ПРИЛОЖЕНИЕ н
ВЕРТИКАЛЬНЫЕ НАПРЯЖЕНИЯ ОТ НАГРУЗКИ,
РАСПРЕДЕЛЕННОЙ по ПОЛОСЕ
ПО ЗАКОНУ РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА
Отношение
2z р'ду
b
Отношение напряжения к среднему давлению на поверхности —
гср
X
при----------------------------. равном
0,01	1,9944	1,0	0,0028	0	0
0,05	1,9718	1,0	0,0141	0	0
0,1	1,9436	1,0	0,0282	0	0
0,2	1,8872	1,0	0,0564	0	0
0,3	1,8308	1,0	0,0846	0	0
0,4	1,7744	1,0	0,0028	0	0
0,5	1,7180	0,9997	0,1410	0,0003	0
0,6	1,6614	0,0087	0,1693	0,0014	0,0001
0,7	1,6051	0,9960	0,1974	0,0040	0,0003
0,8	1,5486	0,9909	0,2257	0,0091	0,0004
0.9	1,4926	0,9840	0,2535	0,0160	0,0005
1.0	1.4370	0,9754	0,2810	0,0245	0,0006
1.2	1.3284	0,9492	0,3331	0,0508	0,0027
1,4	1,2261	0,9195	0,3791	0,0802	0,0077
1,6	1,3336	0,8852	0,4151	0,1135	0,0181
1,8	1.0485	0,8466	0,4441	0,1496	0,0312
2,0	0,9697	0.8079	0,4672	0,1837	0,0469
306
zoe
ПРИЛОЖЕНИЕ 16
ВЕРТИКАЛЬНЫЕ НАПРЯЖЕНИЯ ПО ОСИ ЗАГРУЖЕННОГО КРУГА
конусообразной нагрузкой
Отношение —-— при R				Отношение напряжения к среднему давлению на штамп —— Рср
0.33	0.25	0,167	0,125	
0,0308	0,0352	0,0433	0,05	2,9334
0,308	0,352	0,433	0,5	2,3349
0,368	0,425	0,52	0,6	2,2020
0,43	0,495	0,606	0,7	2,0691
0,491	0,566	0,692	0,8	1,9362
0,551	0,636	0,79	0,9	1,8051
0,615	0,71	0,865	1.0	1,6746
0,92	1,06	1,3	1.5	1,1250
1,23	1.41	1,73	2.6	0,7620
1,54	1.77	2,16	2,5	0,5346
1,84	2,12	2,6	3,0	0,3957
2,15	2,47	3,03	3,5	0,3174
2,46	2,82	3,46	4,0	0,2547
3,08	3,54	4,33	5,0	0,1770
3,68	4,25	5,2	6,0	0,1243
4,3	4,95	6,06	7,0	0,1062
4,91	5,66	6,92	8,0	0,0885
5,51	6,36	7,9	9,0	0,0761
6,15	7,09	8,65	10,0	0,0672
6,75	7,78	9,51	11,0	0,0619
7,35	8,5	10,4	12,0	0,0569
8,00	9,2	11,27	13,0	0,0312
8,59	9,9	12,1	14,0	0,0266
9.2	10,60	13,0	15,0	0,0223
9,8	11,03	13,85	16,0	0,0185
10,4	12,0	14,7	17,0	0,0160
11,02	12,7	15,6	18,0	0,0145
11.64	13,42	16,45	19,0	0,0126
12,26	14,15	17,3	20,0	0,011
308
ПРИЛОЖЕНИЕ 17
МАКСИМАЛЬНАЯ ОРДИНАТА ДЕФОРМАЦИИ СЖАТИЯ ш0 СЛОЯ
ОГРАНИЧЕННОЙ МОЩНОСТИ Л НАГРУЗКОЙ.
РАСПРЕДЕЛЕННОЙ ПО ПЛОЩАДИ КРУГА
Отношение толщины сжимаемого слоя к радиусу загруженной площадки				2wcf У 2v PR для нагрузки, рав* номерно распреде- ленной	РсрЯ для параболической нагрузки
	при R		V, равном			
0.125	0,167	0.25	0.33		
0,05	0,0433	0,0352	0,0308	0,05	0,05
0,5	0,433	0,352	0,308	0,5	0,4896
0,6	0,52	0,452	0,368	0,6	0,5820
0,7	0,606	0,495	0,43	0,7	0,6714
0,8	0,692	0,566	0,491	0,7998	0,7577
0,9	0,79	0,636	0,551	0,8992	0,8393
1,0	0,865	0,71	0,615	0,9987	0,9173
1,5	1,3	1,06	0,92	1,4579	1,2386
2,0	1,73	1,41	1,23	1,8264	1,4628
2,5	2,16	1,77	1,54	2,0981	1,6166
3,0	2,6	2,12	1,84	2,2992	1,7317
3,5	3,03	2,47	2,15	2,4862	1,8196
4,0	3,46	2,82	2,46	2,6002	1,8865
5,0	4,33	3,54	3,08	2,7796	1,9781
6,0	5,2	4,25	3,68	2,8883	2,0489
7,0	6,06	4,95	4,3	2,9815	2,1217
8,0	6,92	5,66	4,91	3,0407	2,2088
9,0	7,9	6,36	5,51	3,1213	2,1139
10,0	8,65	7,09	6,15	3,1553	2,1675
11,0	9,51	7,78	6,75	3,1708	2,1943
12,0	10,4	8,5	7,35	3,1878	2,2376
13,0	11,27	9,2	8,0	3,2129	2,2847
14,0	12,1	9,9	8,59	3,2603	2,3089
15,0	13,0	10,6	9,2 '	3,2788	2,3209
16,0	13,85	11,03	9,8	3,2868	2,3328
17,0	14,7	12,0	1Q.4	3,3044	2,3426
18,0	15,6	12,7	11,02	3,3224	2,3438
19,0	16,45	13,42	11,64	3,3404	2,3448
20,0	17,3	14,15	12,26	3,3504	2,3487
“ 1	1 “	1 - 1	1 "	3,5449	1	2,3633
309
ЛИТЕРАТУРА
1. Бабков В. Ф., Гербурт-Гейбович А. В. Основы грунто-
ведения и механики грунтов. Автотрансиздат, 1956.
Баранов Д. С. Измерительные приборы, методика и некоторые
результаты исследования распределения давлений в песчаном грунте. Гос-
стройиздат, 1959.
3.	Б и ру ля А, Д. Об упругих и пластичных деформациях щебеноч-
ных покрытий. Труды ХАДИ, сб. 6, 1939.
4.	Березанцев В. Г, Расчет прочности оснований сооружений.
Госстрой издат, 1960.
5.	Б ар тле т т М. С. Введение в теорию случайных процессов.
ИЛ, 1958.
6.	Безухов Н. И. Теория упругости и пластичности. Госстройиздат
1953.
7.	Баркан Д. Д. Динамика оснований и фундаментов. Стройвоен-
мор издат, 1948.
8.	Бунин М. В. О критериях качества смесей. Изв. высш. уч. завед.
Строительство и архитектура, № 10. Новосибирск, 1958.
9.	Болотин В. В. Статистические методы в строительной механике.
Госстройиздат, 1961.
10.	Берг А. И. Кибернетику на службу коммунизму. Изд. АН СССР,
1963.
11.	Б о л ш т я некий М. П. Экспериментальное исследование на-
пряжений в неоднородном грунте. Автореферат диссертации. Новосибирск,
1962.
12.	Б р и л л ю 9 н Л. Наука и теория информации. Госфизматнздат,
1960.
13.	Б е р н ш т е_й н М. С., И м ме р м а н А. Г. О статических свой-
ствах несвязного сыпучего тела в предельном равновесии. Массивные и стерж-
невые конструкции. Госстройиздат, 1952.
14.	Булычев В. Г. Теория газонасыщенных грунтов. Стройвоен-
мориздат, 1948.
15.	Васильев Б. Д. Основания и фундаменты. Госстройиздат, 1955.
16.	Горбунов -Посадов М. И, Расчет конструкций на упругом
основании. Госстройиздат, 1953.
17.	Голушкевич С. С. Плоская задача теории предельного равно-
весия сыпучей среды. Гостехиздат, 1948.
18.	Г ерсеванов Н. М. Динамика грунтовой массы. ОНТИ, 1938.
19.	Г р и г о р я н С. С. Современные задачи динамики грунтов. Сб.
Аннотации 2-го Всесоюзного съезда по теоретической и прикладной механике.
Изд. АН СССР, 1964.
310
20.	Гольдштейн М. Н. О путях развития механики грунтов.—
Ж. «Основания, фундаменты и механика грунтов», 1960, Ns 1.
21.	Гнеденко Б. В., Колмогоров А. Н. Предельные распре*
деления для сумм независимых и случайных величин. Гостехтеориздат, 1949.
22.	Гениев Г А. Некоторые вопросы динамики сжимаемых пластич-
ных сред в условиях двухмерных движений. Всесоюзный съезд по теорети-
ческой и прикладной механике. Изд. АН СССР. 1960.
23.	Д о л м а m о в Б. И. Определение допускаемого давления на грунт
по условию критически напряженного состояния. Научные труды ЛИСИ,
вып. 2, 1951.
24.	Д у б р о в а Г. А. Взаимодействие грунта и сооружений. Изд. «Реч-
ной транспорт», 1963.
25.	Д р а н и ш н и к о в П. И. Деформация грунтов под клиновидными
штампами. Новое в строительной технике. Киев, Изд. Акад, архит. УССР,
1953.
26.	Довженко Г. И. Распределение напряжений в зернистом грун-
товом основании. Сб. К? 4 ВАТТ, 1963.
27.	Е г о р о в К. Е. Методы расчета конечных осадок фундаментов. Сб.
трудов науч.-исслед. ин-та оснований и фундаментов «Физика и механика
грунтов». Машстройиздат, 1949.
28.	Е в д о к и м о в П. Д. Прочность оснований и устойчивость гидро-
технических сооружений на мягких грунтах. Госэнергоиздат, 1956.
29.	3 е л е н с к и й Б. Д. Основные направления исследований дефор-
маций скальных пород как оснований бетонных плотин. Проблемы инженер-
ной геологии в строительстве. Материалы совещания по инженерно-геологи-
ческим исследованиям скальных оснований гидротехнических сооружений.
АС и А СССР. Госстрой издат. 1961.
30.	3 е н к о в Р. Л. Механика насы ных грузов. Машгиз, 1952.
31.	Зеленин А. Н. Основы физической теории резания грунтов экс-
кавационными машинами. Резание грунтов. Сб. статей АН СССР, 1951.
32.	И в а н о в Н. Н. Взаимодействие колеса и дороги. Сб. ЛИИПС
№ 100, 1929.
33.	Китайгородский А. И. Порядок и беспорядок в мире ато-
мов. Гостехтеориздат, 1956.
34.	Курдюмов В. И. К вопросу о сопротивлении естественных ос-
нований. 1891.
35.	К р и в и с с к и й А. М. Конструирование и расчет нежестких до-
рожных одежд по местному предельному равновесию. Диссертация. Авто*
трансиздат, 1963.
36.	Коган Б. И. Напряжения и деформации многослойных покрытий.
Труды ХАДИ, вып. 14, 1953.
37.	Келдыш В. М., Гольденблат И. И. Некоторые вопросы
метода предельного состояния. Материалы к теории расчета по предельному
состоянию, вып. 11. Стройиздат, 1949.
38.	К р у т о в В. И. К вопросу о расчете оснований, сложенных на-
сыпными грунтами. Научно-технический бюллетень «Основания и фунда-
менты», Ns 20, 1957.
39.	Кузнецов В. И. Упругое основание. Госстройиздат, 1952.
40.	К л е й н Г. К. Строительная механика сыпучих тел. Госстройнз-
дат, 1956.
41.	Колмогоров А. Н. Статистическая теория колебаний с непре-
рывным спектром. Юбилейный сборник АН СССР, т. 1, 1947.
42.	К а н д а у р о в И. И. Основные предпосылки дискретной теории
распределения напряжений и деформаций сжатия в грунтовых средах. Ин-
формационный бюллетень ВАТТ, Ns 17, 1958.
43.	К а н д а у р о в И. И. Теория дискретного распределения напря-
жений и деформаций сжатия в однородных и многослойных грунтовых осно
ваниях военно-траиспортных и других сооружений. Изд. ВАТТ, 1959.
311
44.	Кандауров И. И. Теория дискретного распределения верти-
кальных напряжений и деформаций сжатия в однородных и слоистых грунто-
вых основаниях. Всесоюзный съезд по теоретической и прикладной механике.
Аннотация докладов. Изд. АН СССР, 1960.
45.	Кандауров И. И. К теории распределения напряжений в зер-
нистых грунтовых основаниях.— Ж* «Основания, фундаменты и механика
грунтов», 1960, Хе 4.
46.	К а н д а у р о в И. И. О распределении напряжений в зернистых
(грунтовых) основаниях. Известия АН Арм. ССР, т. 13, Хе 6, 1960.
47.	Кандауров И. И. О распределении напряжений в однородной
безраспорной зернистой среде. Известия ВНИИГ, т. 73, 1963.
48.	Кандауров И. И. Распределение напряжений в многослойных
безраспорных средах. Известия ВНИИГ, т. 74, 1964.
49.	Кандауров И. И. Напряжения и деформации в скальных тре-
щиноватых основаниях. Всесоюзный съезд по теоретической и прикладной
механике. Тезисы докладов. Изд. АН СССР, 1964.
50.	Кандауров И. И. Об использовании дискретной теории для
исследования напряжений по подошве жестких сооружений на мягких грун-
тах. Труды координационных совещаний по гидротехнике, вып. III. Гос-
энергоиздат, 1962.
51.	Литвинишин Е. Перемещения сыпучих сред как стохастиче-
ский процесс. Бюллетень Польской академии наук, т. 3, вып. 4, 1955.
52.	Литвинишин Е. Дифференциальные уравнения сдвижений
горных пород. Бюллетень Польской академии наук, отд. 4, 1, 1953.
53.	Литвинишин Е. Теоретическое обоснование сдвижения гор-
ных пород как стохастического процесса и его экспериментальная проверка.
Доклад на Европейском конгрессе по сдвижению горных пород. Лиде, 1957.
54.	Литвинишин Е., Б о д ж ио н и	С молярский А.
Новые исследования массива на основе уравнений стохастических процессов.
Доклад на Международном конгрессе по горному давлению, Париж, 1960.
55.	Л у бе нов Р. В., Яковлев П. И. Исследование давления
грунта с равномерно распределенной нагрузкой на неподвижную стену. На-
учные труды, Гидротехника, вып. II. «Морской транспорт», 1962.
58.	Лыков А. В. Теория теплопроводности. Гостехтеориздат, 1952.
57.	Л а л е т и н Н. В. Электрический способ измерения давлений,
исследования грунтов. Сводка лабораторных работ. Изд. ВИА, 1929/1930.
58.	Маслов И. Н. Прикладная механика грунтов. Автотрансиздат,
1963.
59.	М у л л е р Р. А. О статистической теории сдвижения горных по-
род и деформации земной поверхности, вызванных горными работами. Во-
просы проектирования и защиты зданий и сооружений от влияния горных
выработок. Центрогипрошахт. Сб. статей. 1961.
60.	М у л л е р Р. А. О напряженном состоянии зернистой грунтовой
среды. Вопросы проектирования и защиты зданий и сооружений на основа-
ниях, деформируемых горными выработками. Центрогипрошахт. Сб. статей,
1962.
61.	М у л л ер Р. А. О деформативном состоянии зернистой грунто-
вой среды. Труды Всесоюзного научно-исследовательского маркшейдерского
института, сб. L, 1963.
62.	М у л л е р Р. А. К статистической теории распределения напряже-
ний в зернистом грунтовом основании.— Ж. «Основания, фундаменты и ме-
ханика грунтов», 1962, Xs 4.
53.	Малышев М. В. Теоретические и экспериментальные исследо-
вания несущей способности песчаного основания. Изд. ВОДГЕО, 1953.
64.	М а л м е й с т е р А. К. Упругость и неу пру гость бетона. Изд.
АН Латв. ССР, 1957.
65.	Н о в о т о р ц е в В. И. Опыт применения теории пластичности
к задачам об определении несущей способности оснований сооружений. Изве-
стия НИИТ, т. 22, 1938.
312
66.	Ничипорович А. А., X р ус талев Н. Я* Устойчивость
водоподпорных бетонных сооружений на нескальных грунтах. Госстройиздат,
1957.
67.	О р н а т с к и й Н. В. Механика грунтов. Изд. МГУ, 1962.
68.	Проблемы механики. Сб. статей под ред. X. Драйдена и Т. Кармана,
вып. III., ИЛ, 1961.
69.	П о к р о в с к и й Г. И. Исследования по физике грунтов. ОНТИ,
70.	Пановко Я. Страхов Г. И., Богданов В. И. Статиче-
ское давление засыпки на днище и стенки силоса. —Ж- «Строительная
механика и расчет сооружений», 1965, № 4.
71.	Покровский Г. И., Булычев В. Г. О деформации сжатия
грунтов. Сб. ВНОС № 2 «Основания и фундаменты», 1934.
72.	Покровский Г. И., Ф е д о р о в И. С. Труды ВИС. Сб. № 6,
1935.
73.	П о к р о в с к и й Г. И., Некрасов А. А. Статистическая тео-
рия грунтов. Вестник ВИА. Сб. VI, 1934.
74.	П о л ь ш и н Д. Е., Токарь Р. А. Приближенный графический
метод расчета сооружений на устойчивость. Сб. НИИоснований и фундамен-
тов, № 18, 1962.
75.	Роза С. А. Механика грунтов. Госстройиздат, 1963.
76.	С е р г е е в И. Т. К теории распределения напряжений в грунто-
вых основаниях. Строительство сооружений на лёссовых породах. Вып. II.
Изд. Воронежского университета, 1963.
77.	С н и m к о Н. д. Теория прочности металлов с учетом виутрикри-
сталлической структуры. Изд. ВТА, 1946.
78.	Снитко Н. К. Строительная механика грунтов. Изд. ВТА, 1947.
79.	С н и т к о Н, К. Статическое и динамическое давление грунтов и
расчет подпорных стенок. Госстройиздат, 1963.
80.	С о б о л е в С. Л. Уравнения математической физики. Гостехтеор-
издат, 1954.
81.	С о к о л о в с к и й В, В. Статика сыпучей среды. Изд. АН СССР,
1942.
82.	С а в и н о в О. А. Фундаменты под машины. Госстройиздат, 1955.
83.	Труды координационных совещаний по гидротехнике. Под ред.
П. Д. Евдокимова. Вып. III. Госэнергоиздат, 1962.
84.	Труды ДорНИИ, вып. I. Исследование методов расчета толщины
дорожных покрытий. Дориздат, 1938.
85.	Т е р е н е ц к и й К. С. Дорожная одежда как распределяющая
среда. Труды САДИ, № 9, 1948.
86.	Т и м о ш е н к о С. П, Теория упругости. ОНТИ, 1934.
87.	Тот Л. Ф. Расположение на плоскости, на сфере и в пространстве.
ИЛ, 1958.
88.	Ф л о р и н В. А. Основы механики грунтов. Госстройиздат, ч. I,
1959; ч. И, 1061.
89.	Ф е д о р о в И. С. Исследование распределения напряжений в
грунте и осадок фундаментов при помощи моделей.— Ж. техн, физ., т. 5,
вып. 6, 1935.
90.	Фролочкин И. И. Структура грунтов как фактор их деформа-
ции. Резание грунтов. Сб. статей АН СССР, 1951.
91.	Ф р е л и х О. К. Распределение давления в грунте. ОНТИ, 1938.
92.	X а к и м о в X. Р. Расчет осадки сооружений на естественном ос-
новании и определение активной зоны грунта. ОНТИ, 1936.
93.	X ристианович С. А., Ш е м я к и н Е. И, О динамической
сжимаемости прочных горных пород и металлов.— Ж- «Прикладная механика
и теоретическая физика», № 3, 9—15, 1964.
94.	Ц ы т о в и ч Н. А. Механика грунтов. 'Госстройиздат, 1963.
95.	Черкасов И. И. Механические свойства грунтовых оснований.
Автотрансиздат, 1958.
313
96.	Ill и x ue в Ф. M. Применение статистических методов к изучению
грунтов. Изв. АН АзССР, 1960.
97.	Ярополъский И. В. Основания и фундаменты. Госстрой издат,
1954.
98.	Т a k a h a s h i and Sato J. On the Theory of Elastic Waves
in Granular Substance. Bull. Earthquake Res. Institute. Japan, Vol., 27, 1949,
Vol. 28, 1950.
99.	M i n d I i n R. D. Compliance of Elastic Bodies in Contact. Journal
of Applied Mechanics, Vol. 16, 1949.
100.	M i n d I i n R. D. Mechanics of Granular Media. Proc. 2-nd U. S.
Nat. Congr. Appl. Meeh. Ann Arbor. Mich. 1954, New York, 1955.
101.	H ar a G. Theorie der akustischen Schallausbreitung in gekornten
Substanzen und expert men telle Untersuchung an Konlepulver. Elektrische
Nachrichtentechnik, Vol. 12, 1935.
102.	LidaK. Velocity of Elastic Waves in a Granular Substance. Bull.
Earthquake Res. Institute. Japan, Vol. 17, 1939.
103.	Starkey B. J., Lock С. M. Short Range Propagation of Meeh a-
ical Disturbances in the Ground, J. Appl. Phys., 1954, 25, N 6.
104.	V ar I a n R. N. Asupra unei probleme teoretice relative la calculue
sistemelor rutiere nerigide. Rev. transp, 1957, 4, N 8.
105.	Spangler M. G.t M i c k I e Jack L. Lateral Pressures on
Retaining Walls due to Backfill Surface Loads. Highway Res. Board Bull.,
1956, N 141.
106.	Lorenz Hans. Uber die Berechnung des Erddruckes infolge
iner Linienlast. Bautechnik (Berlin), 1954, 31, N 10.
107.	К о g I er. Die Ermessung der Spannungen im Grund. Bautechnick,
1930, 42, N 4.
108.	Henry R. Reynolds and Protopapadanis P. Practical Problems
In Soil Mechanics. London, 1948.
109.	Hveem F. N. Pavement Deflections and Fatigue Failures. High*
way Res. Board Bull., 1955, N 114.
110.	Coss и P. Una verifies sperimentale delle pressioni in condizioni
statiche entro i sill per material! incoeranti. Cemento, 1958, N 1, 55.
111.	D rap G. Essai sur les affaissements de surface et les mouvements
interieurs d’un milieu soumis au dehouillement. Rev. ind. mindrale, 1957,
39, N 2.
112.	В о uss i nes q Application des potentials. Raris, 1885.
113.	T e r z a gh i К., P e c k R. B. Soil Mechanics in Engineering Prac-
tice, 1948.
114.	D a n t и P. et S a n t i n i C. San tint. Progrds recents de la
photoeiasticimetrie. Construction, 1961, v. XVI, Nil.
115.	Taylor D. Fundamentals of Soil Mechanics. New York—London,
1954.
ОГЛАВЛЕН И Е
Стр.
Введение	.	3
§ 1.	Краткий исторический обзор	3
§ 2.	Предлагавшиеся расчетные схемы и природа зернистых сред 9
Часть первая
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ БЕЗ РАСПОРНЫХ ЗЕРНИСТЫХ ОСНОВАНИЯ
Глава /. Структурные особенности безраспорных зернистых оснований 13
§ 1.	Размеры и форма блоков безраспорных зернистых оснований 13
§ 2.	Взаимное расположение блоков и расчетные схемы для них 16
§ 3.	Расчетная схема для всего массива	21
Глава 2. Распределение вертикальных напряжений в безраспорной зер-
нистом основании в плоской задаче	24
§ 1.	Равновероятная передача усилий от вышележащей частицы
на нижележащие .	.	.	.	.	24
§ 2.	Неравновероятная йередача усилий от вышележащей частицы
на нижележащие .	.	...	28
§ 3.	Напряжения от нагрузки, описываемой показательной функ-
цией	...	.	.	.	.	31
§ 4.	Напряжения в слоистой среде от линейной вертикальной на-
грузки	...	32
§ 5.	Напряжения в слоистой среде от нагрузки, произвольно за-
данной в плоской задаче	35
Глава 3. Распределение напряжений в безраспорном зернистом основании
в пространственной задаче ...	. .	40
§ 1.	Равновероятная передача усилий от вышележащей частицы на
нижележащие при сосредоточенной нагрузке	.	40
§ 2.	Неравновероятная передача усилий от вышележащих частиц
на нижележащие при сосредоточенной нагрузке .	.	. 43
§ 3.	Напряжения в слоистом основании от произвольно заданной
нагрузки на поверхности .	44
§ 4.	Безраспорные среды и уравнения равновесия . .	49
§ 5.	Физические уравнения для безраспорной зернистой среды 53
Глава 4, Деформации безраспорного зернистого основания	57
§ 1.	Деформации сжатия .	.	....	.	... 57
§ 2.	Связь средних вертикальных, горизонтальных перемещений
и поворотов в безраспорной зернистой среде	60
315
§ 3.	Деформация слоя ограниченной мощности от линейной на*
грузки	.	62
§ 4.	Деформация двухслойной системы от нагрузки, распределен-
ной по линии	.	.	62
§ 5.	Деформация многослойной системы от нагрузки, произвольно
распределенной по полосе	64
§ 6.	Деформация массива от вертикальной сосредоточ
грузки	....	.	70
§ 7.	Деформация сжатия многослойной системы от произвольно
заданной нагрузки (пространственная задача)	71
Глава 5. Уравнения динамики для безраспорной зернистой среды 72
6 1. Связь между составляющими напряжений в плЬской задаче. 72
§ 2. Связь между компонентами напряжений в пространственной
задаче. Уравнения динамики в пространственной задаче 77
Глава 6. Использование решений для безраспорной среды при определе-
нии напряжений и осадок скальных трещиноватых оснований 82
§ 1.	Общая постановка задачи	82
§ 2.	Напряжения от линейной вертикальной нагрузки . .	84
§ 3.	Напряжения от нагрузки, равномерно распределенной по
бесконечной полосе	84
§ 4.	Напряжения от полосовой параболической нагрузки	86
§ 5.	Сосредоточенная вертикальная нагрузка	.	88
§ 6.	Напряжения от вертикальной нагрузки, распределенной рав-
номерно по прямоугольнику .	... 90
§ 7.	Напряжения от параболической нагрузки, распределенной
по прямоугольной площадке	.	91
§ 8.	Напряжения от нагрузки, равномерно распределенной по
площади круга ...	93
§ 9.	Осадка безраспорного массива от нагрузки, равномерно рас-
пределенной по полосе	96
§ 10.	Осадка безраспорной среды от нагрузки, равномерно распре-
деленной по прямоугольной площадке .	. 98
§ 11.	Осадка по оси круглой площади, загруженной равномерно
распределенной нагрузкой	108
Часть вторая
ЗЕРНИСТЫЕ ГРУНТОВЫЕ ОСНОВАНИЯ (СЫПУЧИЕ ГРУНТЫ)
Г лава 7. Дискретность грунтов	109
§ 1.	Грунты как дискретные системы	109
§ 2.	Размеры и форма зерен грунта.......................... 111
§ 3.	Взаимное расположение и ориентировка зерен .	114
§ 4.	Расчетные схемы для частиц и для всего массива	127
Г лава 8. Вертикальные напряжения в однородном грунтовом основании
в плоской задаче ...	132
§ 1.	Некоторые частные случаи для безраспорной среды	132
§ 2.	О коэффициенте неравномерности передачи усилий . . 133
§ 3.	Вертикальные напряжения в зернистом грунтовом основании
от нагрузки, равномерно распределенной по бесконечной ли-
нии	136
Глава 9. Напряжения в однородном зернистом грунтовом основании в
пространственной	задаче	139
§ 1.	Напряжения от	сосредоточенной	нагрузки	139
§ 2.	Напряжения от	произвольно	заданной	нагрузки	141
316
§ 3.	Уравнения равновесия и физические уравнения для зернистой
грунтовой среды	144
§ 4.	Осесимметричная пространственная задача	148
Г лава 10. Напряжения в многослойной зернистой грунтовой среде 150
§ 1.	Общие предпосылки к решению задачи о напряженном состоя-
нии слоистого зернистого основания	150
§ 2.	Напряжения в слоистой среде от нагрузки, равномерно рас-
пределенной по бесконечной линии	151
§ 3.	Напряжения в многослойной среде от нагрузки, произвольно
заданной в плоской задаче ....	. .	154
§ 4.	Напряжения в слоистой среде от сосредоточенной вертикаль-
ной нагрузки ...	.155
§ 5.	Напряжения в слоистой среде от произвольно заданной на-
грузки в пространственной задаче	157
Глава 11. Применение теории о напряженном состоянии к некоторы
стным случаям загружения основания .	158
§ 1.	Напряжения от линейной вертикальной нагрузки .	158
§ 2.	Напряжения от нагрузки, равномерно распределенной по
бесконечной полосе................................. .	160
§ 3.	Напряжения от нагрузки, распределенной по полосе по за-
кону параболы.................	...	.	161
§ 4.	Напряжения от линейной полосовой нагрузки . .	162
§ 5.	Напряжения от вертикальной треугольной нагрузки . .	164
§ 6.	Напряжения в зернистом грунтовом основании от трапецеи-
дальной нагрузки .	..................... 165
§ 7.	Напряжения от нагрузки, распределенной в плоской задаче
по закону показательной функции........................... 166
§ 8.	Напряжения от сосредоточенной вертикальной нагрузки .	167
§ 9.	Напряжения от нагрузки, описываемой показательной функ-
цией в пространственной задаче	. .	. .	.168
§ 10.	Напряжения от нагрузки, равномерно распределенной по
прямоугольнику. .	....	.	. . 169
§ 11.	Напряжения от параболической нагрузки, распределенной
по прямоугольнику ....................... .	170
§ 12.	Напряжения в зернистой среде при нагрузке, равномерно
распределенной по площади круга (решение Б. С. Ра дон-
ского) . .	................. ............ 173
§ 13.	Напряжения от нагрузки, распределенной по площади круга
по закону параболы (решение Б. С. Радовского) ....	178
§ 14.	Давление на площадку, расположенную на некоторой глу-
бине от нагрузки, распределенной по квадратной площадке 180
§ 15.	Вертикальные напряжения по оси круга, загруженного
конусообразной нагрузкой .	184
§ 16.	Напряжения от горизонтальных нагрузок	185
$ 17.	Напряженное состояние зернистого грунтового массива у
неподвижной подпорной стенки	187
Глава 12. Деформации зернистого грунтового основания	197
§ 1.	О природе деформируемости грунтов	197
§ 2.	Связь между перемещениями	.	202
§ 3.	Осадка однородного грунтового основания от нагрузки, рав-
номерно распределенной по бесконечной линии	203
§ 4.	Осадка однородного грунтового массива ограниченной мощ-
ности от нагрузки, равномерно распределенной по бесконеч-
ной полосе	...	204
§ 5.	Осадка однородного грунтового массива ограниченной мощ-
ности от параболической нагрузки, распределенной по бес-
конечной полосе	205
317
§ 6.	Осадка однородного грунтового массива ограниченной мощ-
ности от нагрузки, распределенной на бесконечной полосе по
линейному закону и по закону треугольника .	206
§ 7.	Осадка однородного грунтового массива ограниченной мощ-
ности от нагрузки, заданной по закону трапеции	207
§ 8.	Осадка однородного массива ограниченной мощности от сос-
редоточенной нагрузки	.	.	208
§ 9.	Осадка однородного грунтового массива ограниченной мощ-
ности от сосредоточенной нагрузки при переменном значении
модуля деформации по глубине	208
§ 10.	Максимальная осадка однородного грунтового массива огра-
ниченной мощности от нагрузки, равномерно распределенной
по круглой площадке	209
§11.	Максимальная осадка однородного грунтового массива огра-
ниченной мощности от нагрузки, распределенной на круглой
площадке по параболе	210
§ 12.	Осадка однородного грунтового полупространства от на-
грузки, равномерно распределенной по прямоугольнику 212
Глава 13. Деформация сжатия многослойных зернистых грунтовых систем 216
§ 1. Деформация сжатия слоистой системы от нагрузки, равно-
мерно распределенной по бесконечной линии (плоская задача) 216
§ 2. Деформация сжатия многослойной системы нагрузкой, про-
извольно заданной в плоской задаче .	....	222
§ 3.	Деформация сжатия слоистой системы от сосредоточенной на-
грузки (пространственная задача) ...	.	228
§ 4.	Деформация сжатия многослойного зернистого грунтового ос-
нования от произвольно заданной вертикальной нагрузки в
пространственной задаче	231
Глава 14. Уравнения динамики для зернистой грунтовой среды при уп-
ругих деформациях зерен	236
§ 1.	Связь между составляющими напряжений и уравнения дина-
мики в плоской задаче .	.	. .	..............236
§ 2.	Связь между компонентами напряжений в пространственной
задаче. Уравнения динамики в пространственной задаче 242
Г лава 15. Сравнение полученных результатов с опытными данными и тео-
рией упругости	.	247
§ 1.	Экспериментальные данные, используемые для проверки тео-
ретических результатов	. .	247
§ 2.	Сравнение теоретических данных с опытными данными Илли-
нойского университета .	...	247
§ 3.	Сравнение теоретических результатов с опытными данными
Штейнера и Кика	z . .	.	. 253
§ 4.	Сравнение теоретических результатов с опытными данными
Штрошнейдера ...	. .	255
§ 5.	Сравнение теоретических результатов с опытными данными
Пенсильванского колледжа .	. .	.... 257
§ 6.	Сравнение теоретических результатов с экспериментальными
данными Гольдбека ...	.	.	.	263
§ 7.	Сравнение теоретических результатов с опытными данными
Комиссии по напряжениям в железнодорожном пути Амери-
канской ассоциации гражданских инженеров ...................270
§ 8.	Сравнение теоретических результатов с опытными данными
Кеглера и Шейдига	.... 272
§ 9.	Сравнение теоретических результатов с опытными данными
Н. В. Лалетина	278
§ 10. Сравнение теоретических результатов с опытными ными
Г. И. Покровского и И. С. Федорова	279
318
§ 11.	Сравнение теоретических результатов с опытны и данными
Д. С. Баранова и Плантема	. 280
§ 12.	Сравнение теоретических результатов с опытными данными
М. П. Болштянского	.	. . 285
§ 13.	Сравнение теоретических результатов с опытными данными
различных исследователей ....	...	286
§ 14.	Сравнение вертикальных напряжений от вертикальной сосре*
доточенной нагрузки с данными теории упругости	287
Заключение	291
Приложения	293
Литература	310
Иван Иванович Кандауров
МЕХАНИКА ЗЕРНИСТЫХ СРЕД И ЕЕ
ПРИМЕНЕНИЕ В СТРОИТЕЛЬСТВЕ
Бланк для заказов 1965 г. № 10/22
Стройиздат Ленинградское отделение
Ленинград, пл. Островского, 6
Редактор издательства
Технически!) редактор С. Л. Шапиро
Корректоры: С. Л. Ч ареков, Р. М. Юзефович
Переплет художника А. П. Рыбакова
Сдано в набор 27/Х 1965 г.	Подписано к печати 9/11 1966 г.
М 13574. Формат бумаги 60х90*/м. Бум. л. 10 № 2 Камского бумкомбината, печ. л. 20.
Учетно-издат. л. 19,32	Тираж 5000 экэ.	Изд. № 901 Л
Заказ 2406 Цена в переплете 1 руб. 07 коп.
Ленинградская типография № 4 Главполнграфпрома Комитета по печати при
Совете Министров СССР. Социалистическая. 14.