ПИТЕР
С. Н. Старков
ЧЕБНОЕ
ПОСОБИЕ
Справочник
по математическим формулам
и графикам функций
для студентов
РМУЛ - 12
УЧЕБНОЕ
И
ПОСОБИЕ
С. Н. Старков
Справочник
по математическим формулам
и графикам функций
для студентов
С^ППТЕР’
Москва * Санкт-Петербург • Нижний Новгород * Воронеж
Ростов-на-Дону * Екатеринбург • Самара * Новосибирск
Киев * Харьков * Минск
2009
ББК 22.19я22
УДК 519.6(03)
С77
Старков С. Н.
С77 Справочник по математическим формулам и графикам функций
для студентов. — СПб.: Питер, 2009. — 235 с.: ил. — (Серия
«Учебное пособие»).
ISBN 978-5-91180-830-3
Первая часть данного справочника содержит более 1200 формул элементар-
ной и высшей математики, расположенных в 34 разделах. Во вторую часть вошло
более 1200 рисунков, представляющих собой графики функций и их преобразования
(элементарные и неэлементарные), а также изображения кривых на плоскости.
Издание предназначено для студентов и преподавателей высших учебных за-
ведений технического и естественнонаучного профиля; большая часть справоч-
ника может быть полезна учащимся и преподавателям средних учебных заведений.
ББК 22.19я22
УДК 519.6(03)
Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы
то ни было форме без письменного разрешения владельцев авторских прав.
ISBN 978-5-91180-830-3
© ООО «Питер Пресс», 2009
Содержание
Некоторые обозначения...........................13
Часть 1. Формулы................................15
1.	Формулы сокращенного
умножения и другие тождества...................17
2.	Формулы разложения многочленов на множители.. 18
Разложения на множители некоторых многочленов 2-й, 3-й и 4-й степе-
ни • Схема Горнера деления многочлена на двучлен • Теорема о подбо-
ре корней многочлена с целочисленными коэффициентами • Разложе-
ние многочлена и-й степени на простейшие множители
3.	Действия с дробями..........................  20
4.	Средние величины. Пропорции. Проценты.........21
5.	Модуль (абсолютная величина)..................22
6.	Степени и корни. Логарифмы....................27
Степени с натуральным, целым и рациональным показателем. Арифме-
тический корень • Свойства арифметических корней • Свойства степени
с действительным показателем • Свойства логарифмов
7.	Прогрессии.....................................    25
Арифметическая прогрессия • Геометрическая прогрессия
8.	Решение уравнений................................  36
Рациональные уравнения • Уравнения, содержащие знак модуля • Ир-
рациональные уравнения • Показательные уравнения • Логарифмичес-
кие уравнения • Тригонометрические уравнения
9.	Решение неравенств..................................  28
Рациональные неравенства • Неравенства, содержащие знак модуля
• Иррациональные неравенства • Показательные неравенства • Лога-
рифмические неравенства • Тригонометрические неравенства
б
Содержание
10.	Тригонометрические формулы.........................31
Основные тождества • Свойства четности и нечетности • Формулы сло-
жения • Формулы кратных углов • Формулы половинных углов • Фор-
мулы преобразования суммы в произведение • Формулы преобразования
произведения в сумму • Выражение функций через тангенс половинного
угла • Формулы приведения • Обратные тригонометрические функции
• Дополнительные тождества • Связь радианной и градусной меры угла
• Таблица значений тригонометрических функций
11.	Типовые способы замены переменной..............36
12.	Формулы геометрии..............................37
Треугольники • Вычисление площади треугольника • Теорема Пифагора
• Теорема синусов • Теорема косинусов • Четырехугольники • Вычисле-
ние площади четырехугольника • Окружность и круг • Вычисление объ-
емов и площадей поверхности
13.	Векторы.............................................39
Прямоугольные и полярные координаты точки на плоскости • Пря-
моугольные и цилиндрические координаты точки в пространстве
• Прямоугольные и сферические координаты точки в пространстве
• Проекция вектора на ось • Проекции вектора на оси прямоугольной
системы координат OXYZ • Задание вектора в координатной форме
• Расстояние между двумя точками • Модуль (длина) вектора • На-
правляющие косинусы вектора • Единичный вектор • Нулевой вектор
• Вектор, противоположный вектору • Равенство векторов • Сложение
и вычитание векторов • Умножение вектора на число • Орт ненулевого
вектора • Признак коллинеарности двух ненулевых векторов • Линей-
ная комбинация векторов • Линейная независимость системы ненулевых
векторов • Линейная зависимость системы векторов • Связь коллинеар-
ности и линейной зависимости двух векторов • Связь компланарности
и линейной зависимости трех векторов • Разложение вектора по базису
в пространстве • Разложение вектора по трем некомпланарным векто-
рам • Разложение вектора по базису прямоугольной системы координат
OXYZ • Преобразование координат в пространстве • Преобразование ко-
ординат на плоскости при параллельном переносе и повороте осей • Вы-
числение скалярного произведения в координатной форме • Угол меж-
ду векторами • Условие перпендикулярности двух ненулевых векторов
• Вычисление векторного произведения в координатной форме • Усло-
вие коллинеарности двух векторов • Вычисление смешанного произве-
дения в координатной форме • Условие компланарности трех векторов
Содержание
7
14.	Прямая на плоскости................................46
Уравнение прямой, проходящей через заданную точку перпендику-
лярно заданному вектору • Общее уравнение прямой • Неполные
уравнения прямой • Нормальное уравнение прямой • Уравнение пря-
мой в полярных кординатах • Уравнение прямой с угловым коэффици-
ентом • Уравнение прямой «в отрезках» • Параметрическое уравнение
прямой, проходящей через заданную точку параллельно заданному век-
тору • Каноническое уравнение прямой, проходящей через заданную
точку параллельно заданному вектору • Уравнение прямой, проходя-
щей через две заданные точки • Угол между двумя прямыми • Рассто-
яние от точки до прямой • Расстояние от начала координат до прямой
• Условие пересечения двух прямых и координаты точки пересечения
• Условие совпадения двух прямых • Условие принадлежности трех
заданных точек одной прямой
15.	Плоскость и прямая в пространстве..................50
Уравнение плоскости, проходящей через заданную точку перпендикуляр-
но заданному вектору • Общее уравнение плоскости • Неполные уравне-
ния плоскости • Нормальное уравнение плоскости • Уравнение плоскос-
ти «в отрезках» • Уравнение плоскости, проходящей через три различные
точки, не лежащие на одной прямой • Расстояние от точки до плоскости
• Угол между двумя плоскостями • Параметрическое уравнение прямой
в пространстве, проходящей через заданную точку параллельно заданному
вектору • Каноническое уравнение прямой в пространстве • Уравнение
прямой в пространстве, проходящей через две различные точки • Угол
между прямой и плоскостью • Задание прямой в пространстве как линии
пересечения двух непараллельных плоскостей
16.	Уравнения некоторых кривых на плоскости............53
Эллипс • Окружность • Гипербола • Парабола • Архимедова спираль
• Астроида • Декартов лист • Улитка Паскаля • Кардиоида • Конхоида
Никомеда • Лемниската Бернулли • Локон Аньези • Циклоида • Эпи-
циклоиды • Эпитрохоиды • Розы • Гипоциклоиды • Гипотрохоиды
17.	Канонические уравнения поверхностей 2-го порядка...57
Эллипсоид • Однополостной гиперболоид • Двухполостной гипербо-
лоид • Конус второго порядка • Эллиптический параболоид • Гипер-
болический параболоид • Эллиптический цилиндр • Гиперболический
цилиндр • Параболический цилиндр • Пара пересекающихся плоскос-
тей • Пара параллельных плоскостей
8 Содержание
18.	Определители.......................................58
Определитель первого порядка • Определитель второго порядка • Опре-
делитель третьего порядка • Определитель и-го порядка • Алгебраичес-
кое дополнение • Свойства определителей • Решение системы п линей-
ных алгебраических уравнений с п неизвестными по формулам Крамера
19.	Матрицы............................................61
Прямоугольные матрицы размера тхп • Равенство матриц • Нулевая
матрица • Противоположная матрица • Сложение матриц одинакового
размера • Умножение матрицы на число • Умножение матриц согласо-
ванного размера • Свойства единичной матрицы • Обратная матрица
• Вычисление обратной матрицы методом присоединенной матрицы
• Решение системы п линейных алгебраических уравнений с п неиз-
вестными методом обратной матрицы • Ранг матрицы • Теорема Кро-
некера-Капелл и о совместности систем т линейных уравнений с п не-
известными
20.	Пределы и непрерывность............................65
Свойства сходящихся последовательностей • Сходимость монотонной
и ограниченной последовательности • Критерий Коши сходимости пос-
ледовательности • Свойства функций, имеющих предел (правила вы-
числения пределов) • Односторонние пределы функции • Условие су-
ществования предела функции • Пределы функции «на бесконечности»
• Бесконечные пределы • Замечательные пределы • Бесконечно малые
и бесконечно большие функции • Таблица эквивалентных бесконечно
малых • Точки разрыва • Свойства функций, непрерывных на отрезке
21.	Производная и дифференциал.........................70
Конечные и бесконечные производные • Односторонние производные
• Условие существования производной функции • Существование произ-
водной и непрерывность • Производные основных элементарных функций
(таблица производных) • Производные гиперболических функций • Пра-
вила дифференцирования • Производная сложной функции • Производ-
ная обратной функции • Производная функции, заданной параметрически
• Производная функции, заданной неявно • Производная показательно-
степенной функции • Производные высших порядков • Формулы Тей-
лора и Маклорена • Теорема Ферма. Необходимое условие экстремума
функции • Теорема Ролля • Теорема Лагранжа • Теорема Коши • Прави-
ло Лопиталя для раскрытия неопределенностей • Уравнение касательной
к графику функции • Уравнение нормали к графику функции • Прибли-
Содержание
9
женные вычисления с помощью дифференциала • Дифференциалы вы-
сших порядков • Выражение производных через дифференциалы
22.	Неопределенный интеграл...........................77
Первообразная • Неопределенный интеграл • Свойства неопределенно-
го интеграла • Таблица интегралов • Метод интегрирования с помощью
замены переменной • Метод интегрирования по частям • Интегрирова-
ние рациональных дробей • Интегрирование простейших рациональных
дробей • Интегралы от некоторых рациональных дробей • Интегралы от
некоторых иррациональных функций • Интегралы от некоторых показа-
тельных и логарифмических функций • Интегралы от некоторых триго-
нометрических функций
23.	Определенный интеграл.............................85
Связь определенного и неопределенного интеграла • Формула Ньюто-
на-Лейбница • Свойства определенного интеграла • Оценки значения
определенного интеграла • Метод интегрирования с помощью замены
переменной • Метод интегрирования по частям • Вычисление площадей,
длин дуг и объемов с помощью определенного интеграла
24.	Несобственные интегралы...........................88
Несобственные интегралы 1-го рода • Несобственные интегралы 2-го рода
• Гамма-функция • Значения некоторых несобственных интегралов
25.	Частные производные
и дифференциалы функций нескольких переменных.... 91
Частная производная функции • Производная функции по направле-
нию • Частные производные высшего порядка • Полная производная
сложной функции • Частные производные сложной функции • Част-
ные дифференциалы • Полный дифференциал • Дифференциалы и-го
порядка • Формула Тейлора • Необходимые условия экстремума фун-
кции • Достаточные условия экстремума функции • Уравнение каса-
тельной плоскости и нормали к поверхности
26.	Кратные интегралы.................................94
Вычисление двойного интеграла через повторные • Свойства двой-
ного интеграла • Вычисление двойного интеграла в полярных корди-
натах • Вычисление площадей и объемов с помощью двойного инте-
грала • Вычисление тройного интеграла через повторные • Свойства
тройного интеграла • Вычисление тройного интеграла в цилиндри-
ческих и сферических кординатах • Вычисление объемов с помощью
тройного интеграла
10 Содержание
27.	Криволинейные и поверхностные интегралы.........96
Вычисление криволинейных интегралов 1-го рода • Вычисление криво-
линейных интегралов 2-го рода • Формула Грина • Вычисление поверх-
ностных интегралов 1-го рода • Вычисление поверхностных интегралов
2-го рода • Формула Стокса • Формула Гаусса-Остроградского
28.	Дифференциальные операции векторного анализа....98
Оператор Гамильтона • Градиент функции • Производная функции по
направлению • Дивергенция вектор-функции • Ротор вектор-функции
• Оператор Лапласа. Дифференциальные операции 2-го порядка
29.	Числовые и степенные ряды.......................99
Сходящиеся и расходящиеся числовые ряды • Свойства сходящихся число-
вых рядов • Необходимое условие сходимости числового ряда • Достаточ-
ное условие расходимости числового ряда • Знакопостоянные числовые
ряды. Достаточные признаки сходимости и расходимости • Знакопере-
менные и знакочередующиеся числовые ряды. Абсолютная и условная
сходимость • Сложение и умножение степенных рядов • Дифференци-
рование и интегрирование степенных рядов • Разложения функций в сте-
пенные ряды • Значения сумм некоторых числовых рядов
30.	Тригонометрические ряды Фурье...................105
31.	Элементы теории
обыкновенных дифференциальных уравнений..........106
Дифференциальное уравнение с разделенными переменными • Диффе-
ренциальное уравнение с разделяющимися переменными • Дифферен-
циальное уравнение, однородное относительно аргумента и функции
• Линейное дифференциальное уравнение 1-го порядка • Уравнение
Бернулли • Уравнение в полных дифференциалах • Линейное одно-
родное дифференциальное уравнение 2-го порядка с постоянными ко-
эффициентами • Линейное однородное дифференциальное уравнение
и-го порядка с постоянными коэффициентами
32.	Комплексные числа..............................111
Степени числа i • Алгебраическая форма комплексного числа о Равенс-
тво комплексных чисел • Комплексно сопряженное число • Модуль ком-
плексного числа • Аргумент комплексного числа • Множество значений
аргумента • Действия над комплексными числами в алгебраической фор-
ме • Свойства действий над комплексными числами • Тригонометричес-
кая форма комплексного числа • Действия над комплексными числами
в тригонометрической форме • Показательная форма комплексного числа
Содержание 11
• Действия над комплексными числами в показательной форме • Рас-
стояние между точками • Уравнение прямой • Уравнение окружности
• Разложение многочлена на линейные множители • Основная теорема
алгебры
33.	Элементы теории
функций комплексной переменной......................  116
Основные функции комплексной переменной • Гиперболические функ-
ции • Производная функции комплексной переменной • Вычисление
интегралов • Формула Ньютона-Лейбница • Теорема Коши • Инте-
гральная формула Коши • Ряды Тейлора • Ряды Лорана • Особые точ-
ки • Классификация изолированных особых точек • Вычеты. Основная
теорема о вычетах
34.	Элементы теории вероятностей......................120
Число сочетаний без повторений из п элементов по k • Число размеще-
ний без повторений из п элементов по k • Число перестановок без пов-
торений из п элементов по п • Число размещений с повторениями из
п элементов по k • Формула Стирлинга • Свойства операций сложения
и умножения событий • Правило сложения вероятностей • Условная
вероятность. Независимые события • Правило умножения вероятнос-
тей • Формула полной вероятности • Формула Байеса. Пересчет ве-
роятностей гипотез • Повторение испытаний с двумя исходами. Фор-
мула Бернулли • Функция распределения случайной величины • Ряд
распределения дискретной случайной величины • Плотность распреде-
ления непрерывной случайной величины • Математическое ожидание
и дисперсия дискретной случайной величины с п значениями • Математи-
ческое ожидание и дисперсия непрерывной случайной величины • Сред-
нее квадратическое отклонение • Биномиальное распределение • Распре-
деление Пуассона • Равномерное распределение • Нормальное распреде-
ление • Неравенство Чебышева
Часть 2. Графики функций.........................127
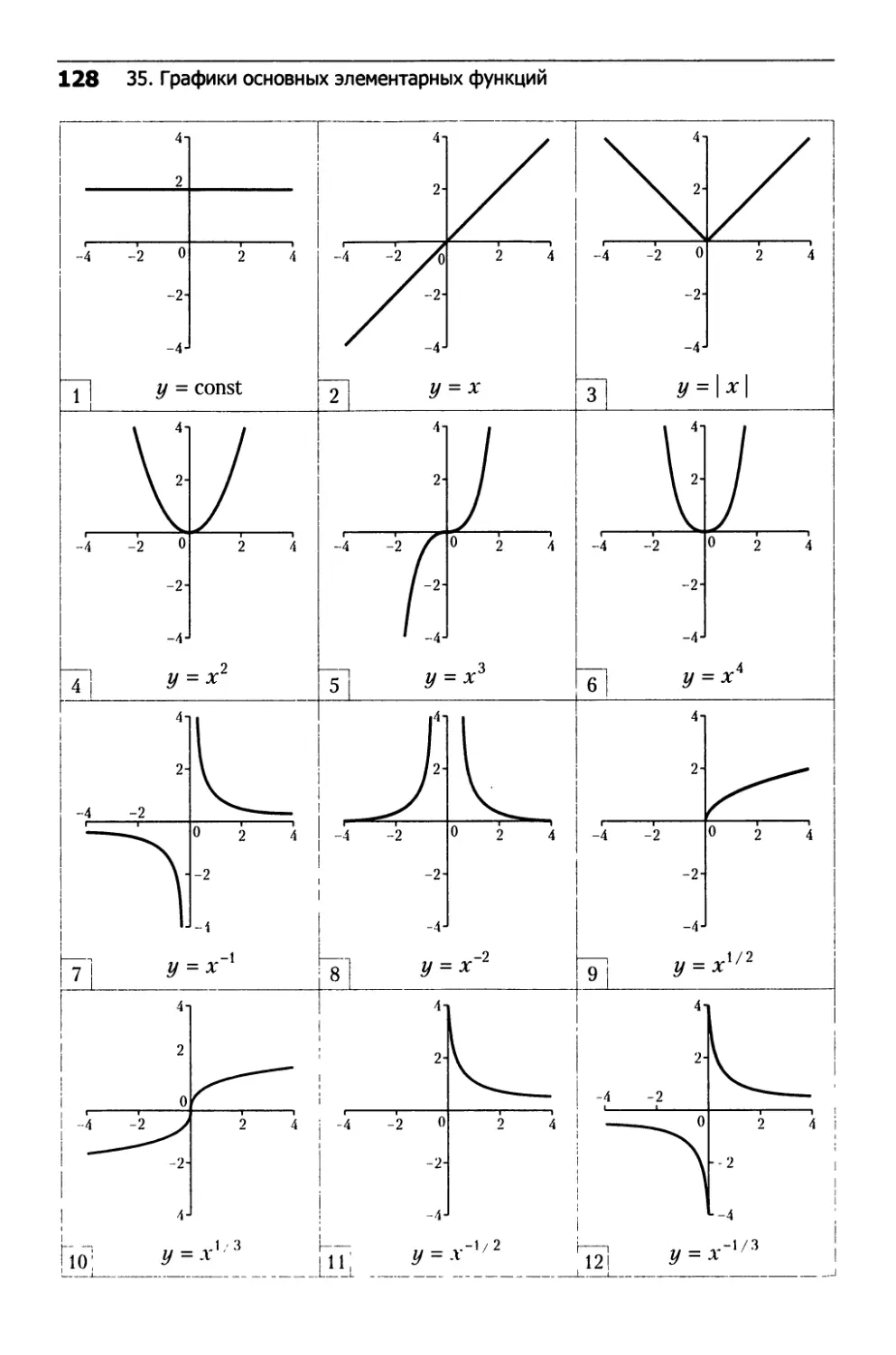
35.	Графики основных элементарных функций........128
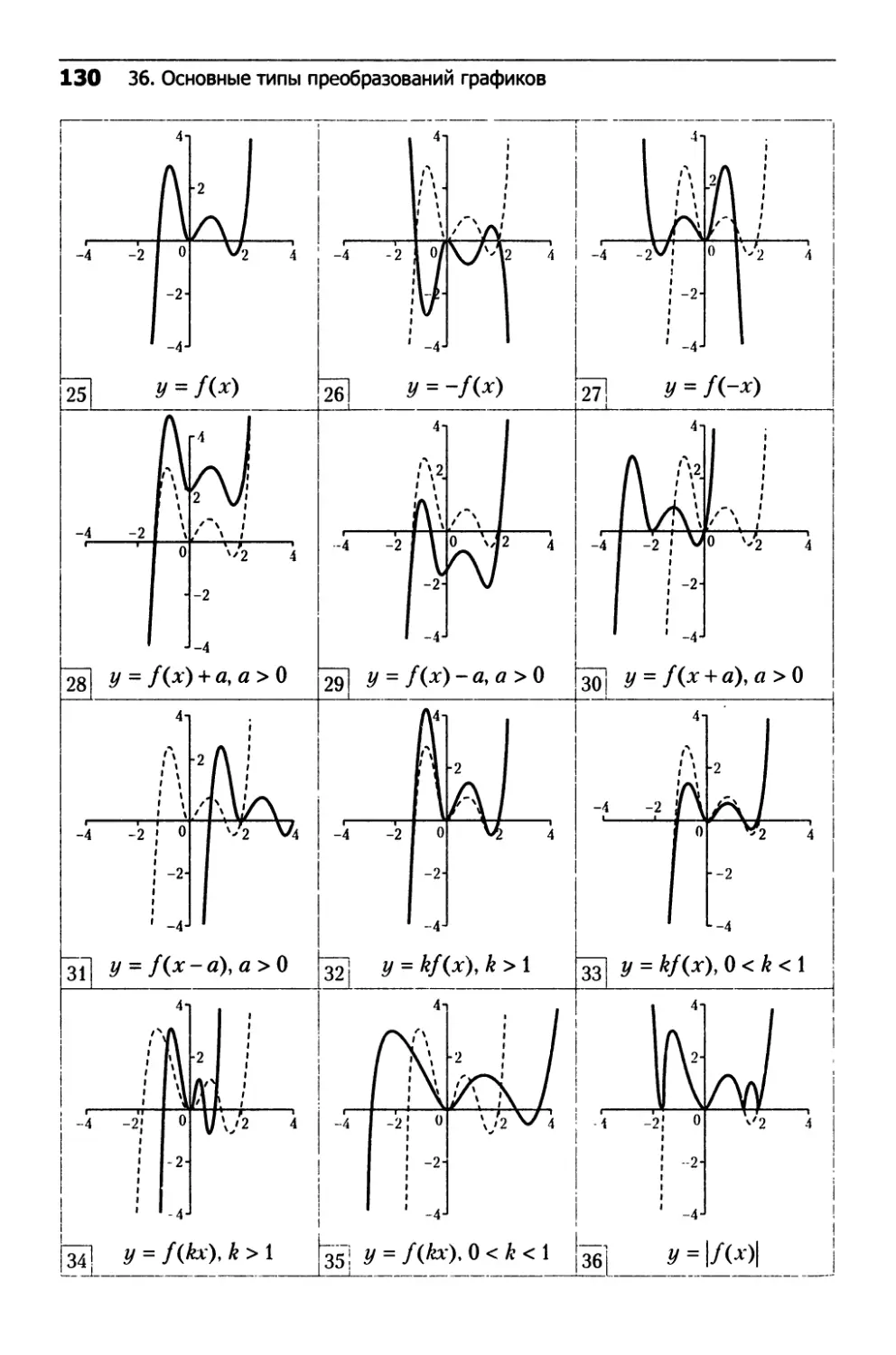
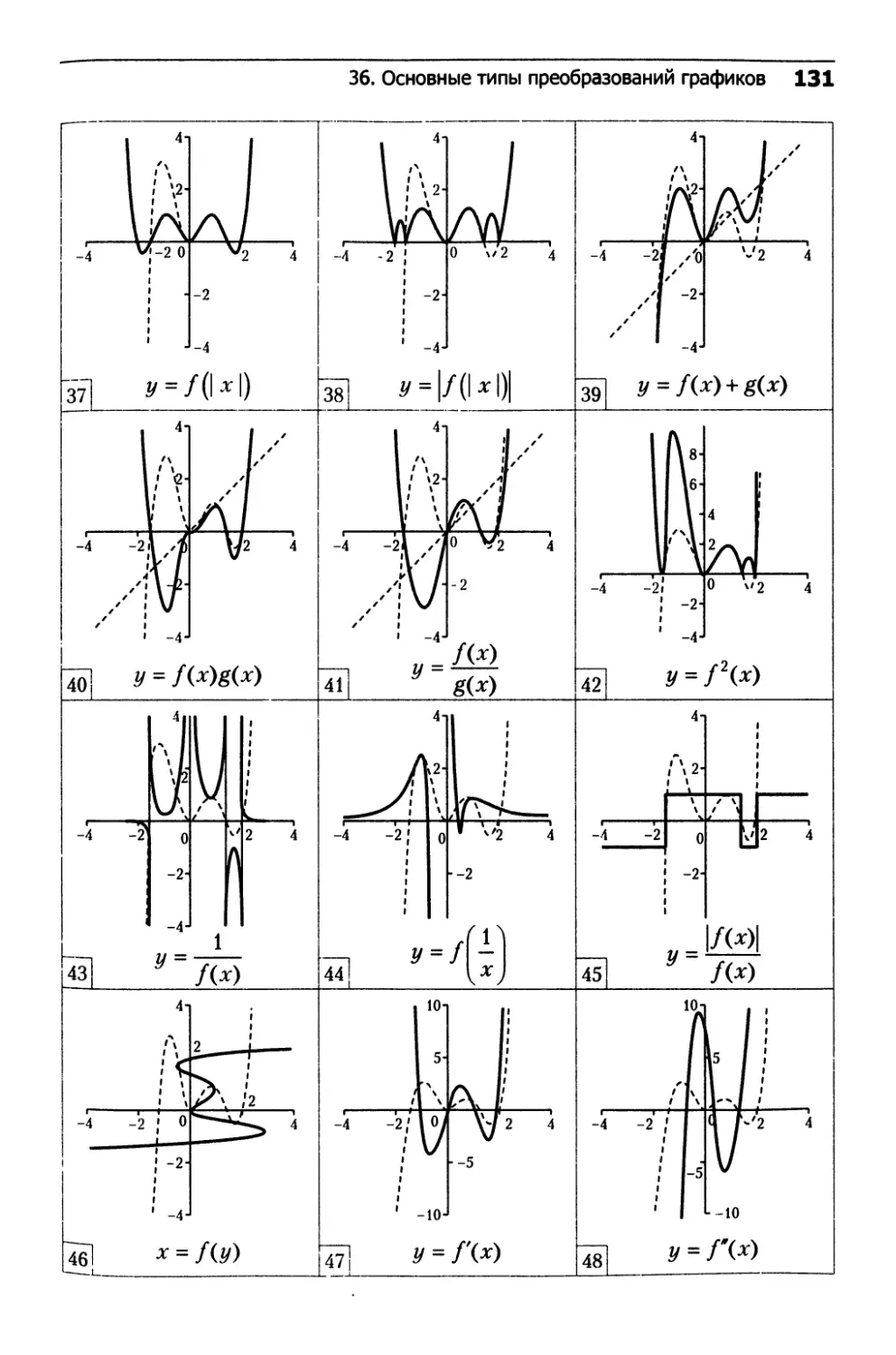
36.	Основные типы преобразований графиков.......130
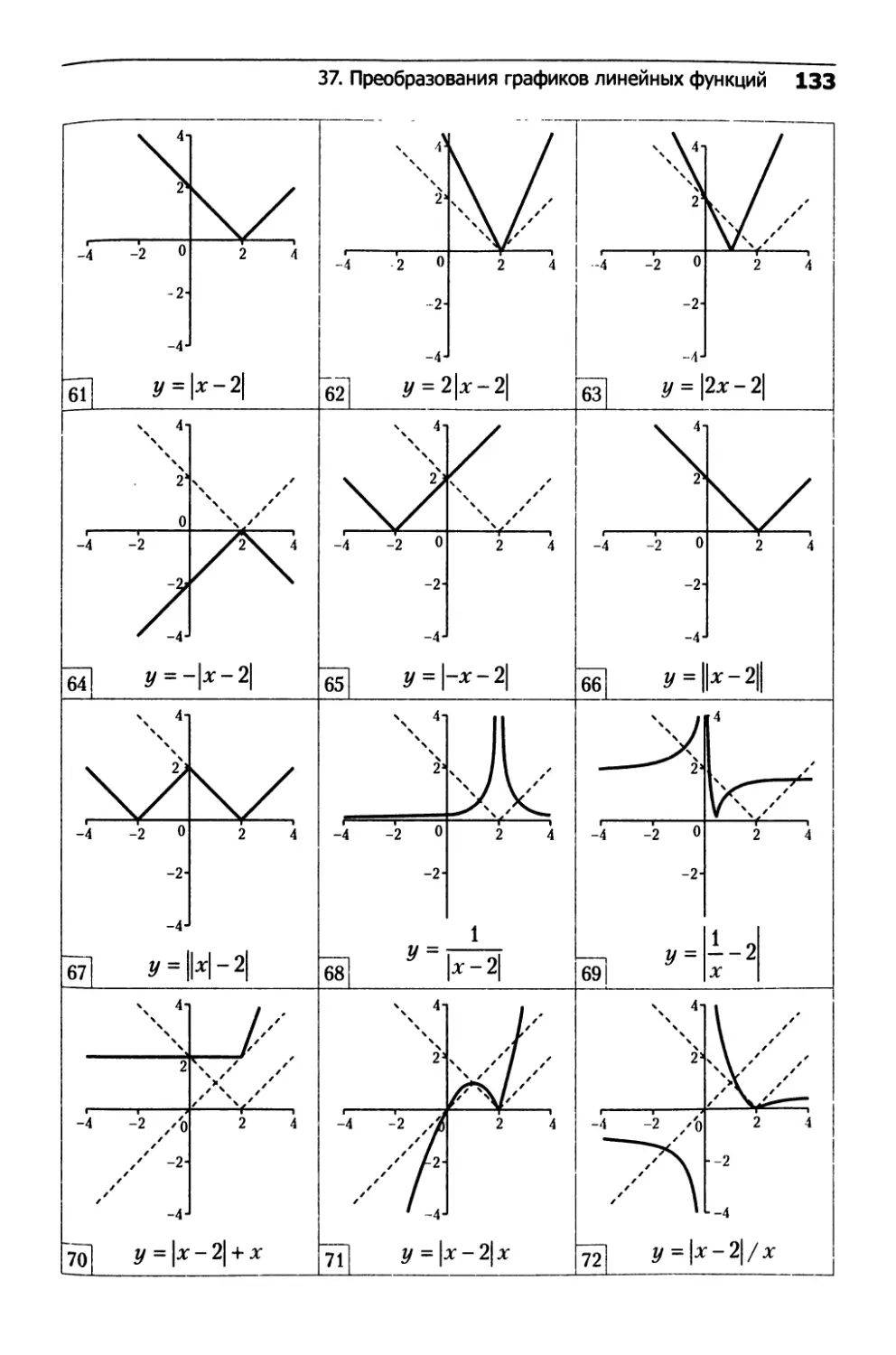
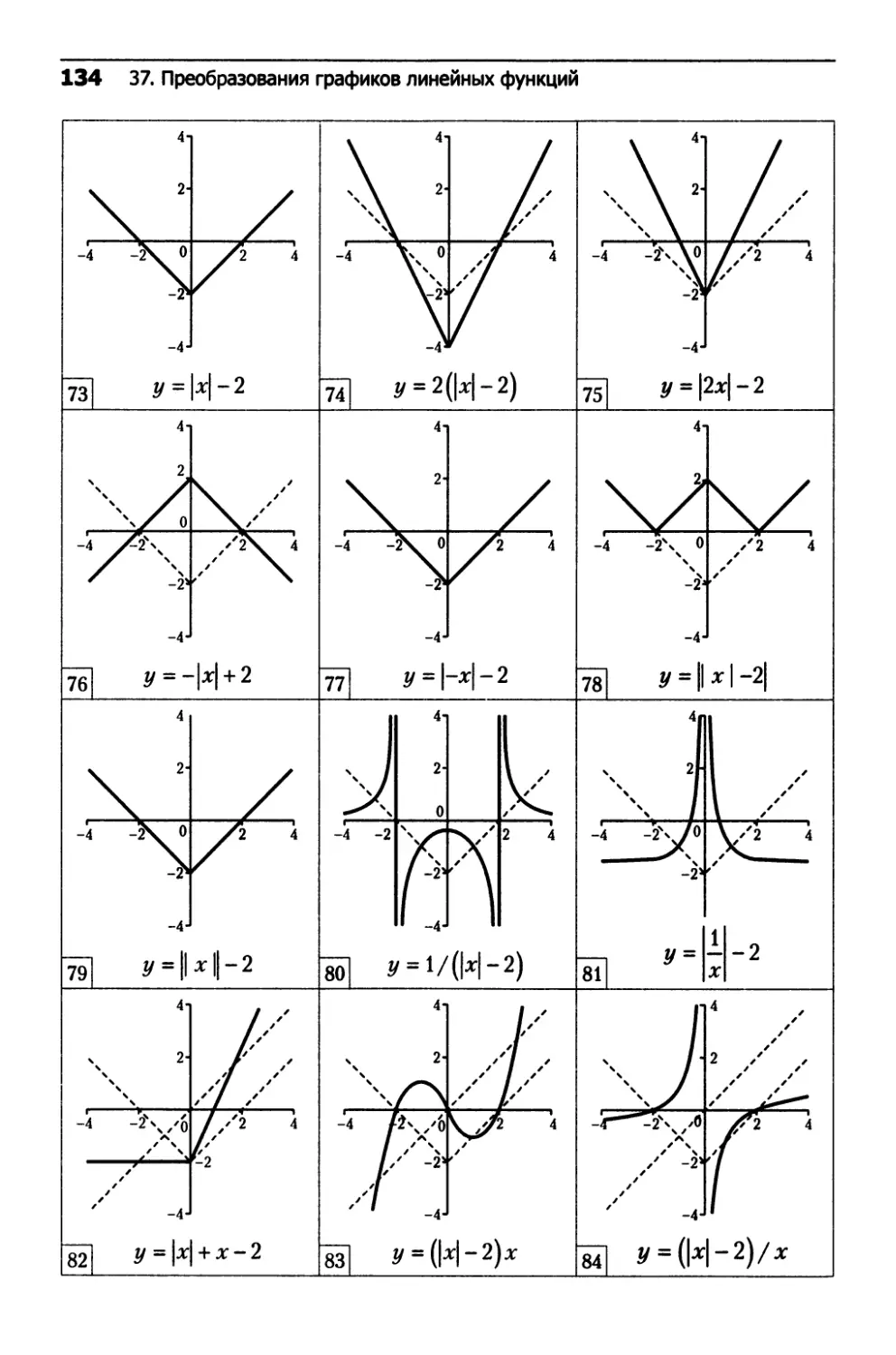
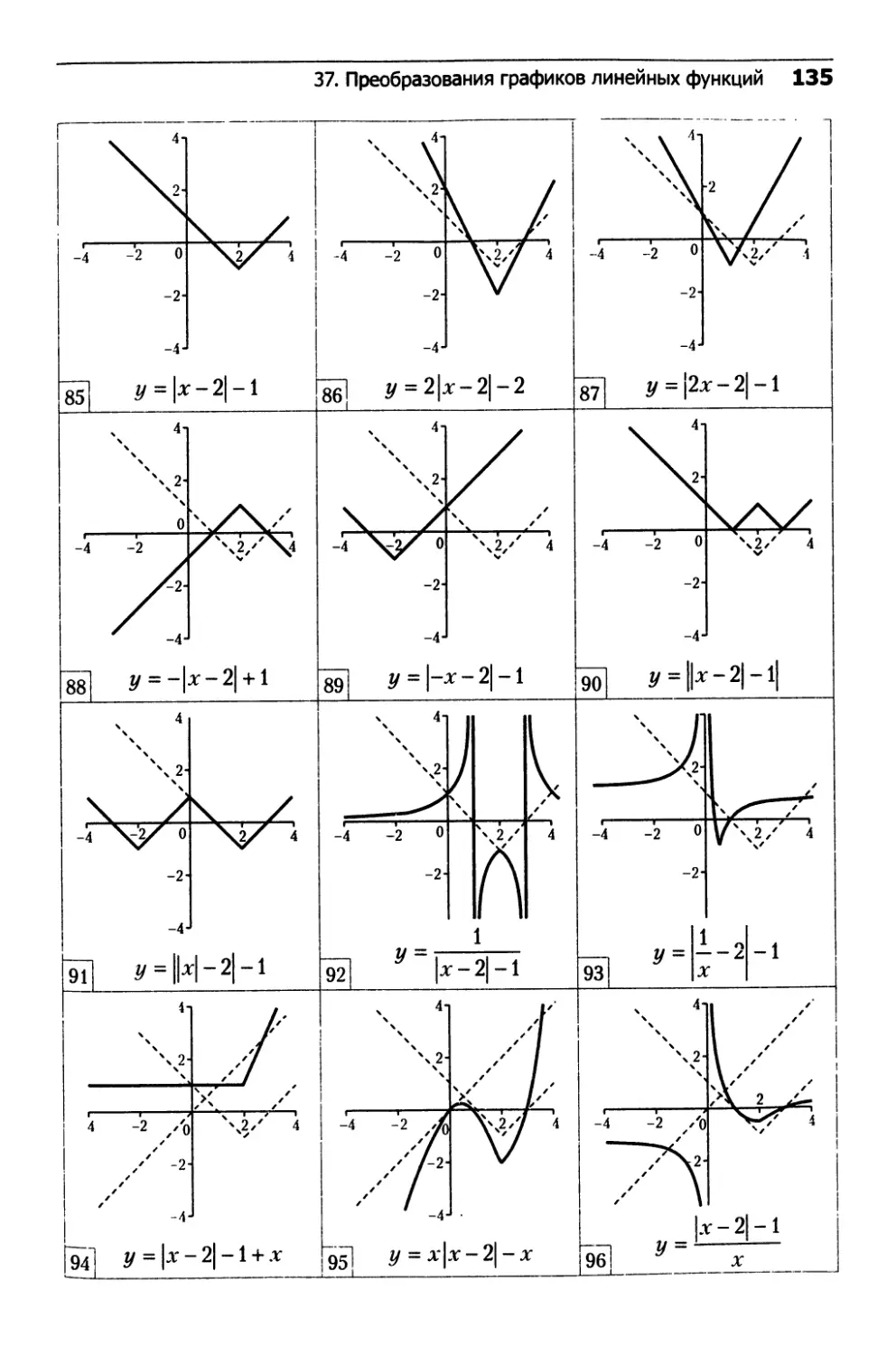
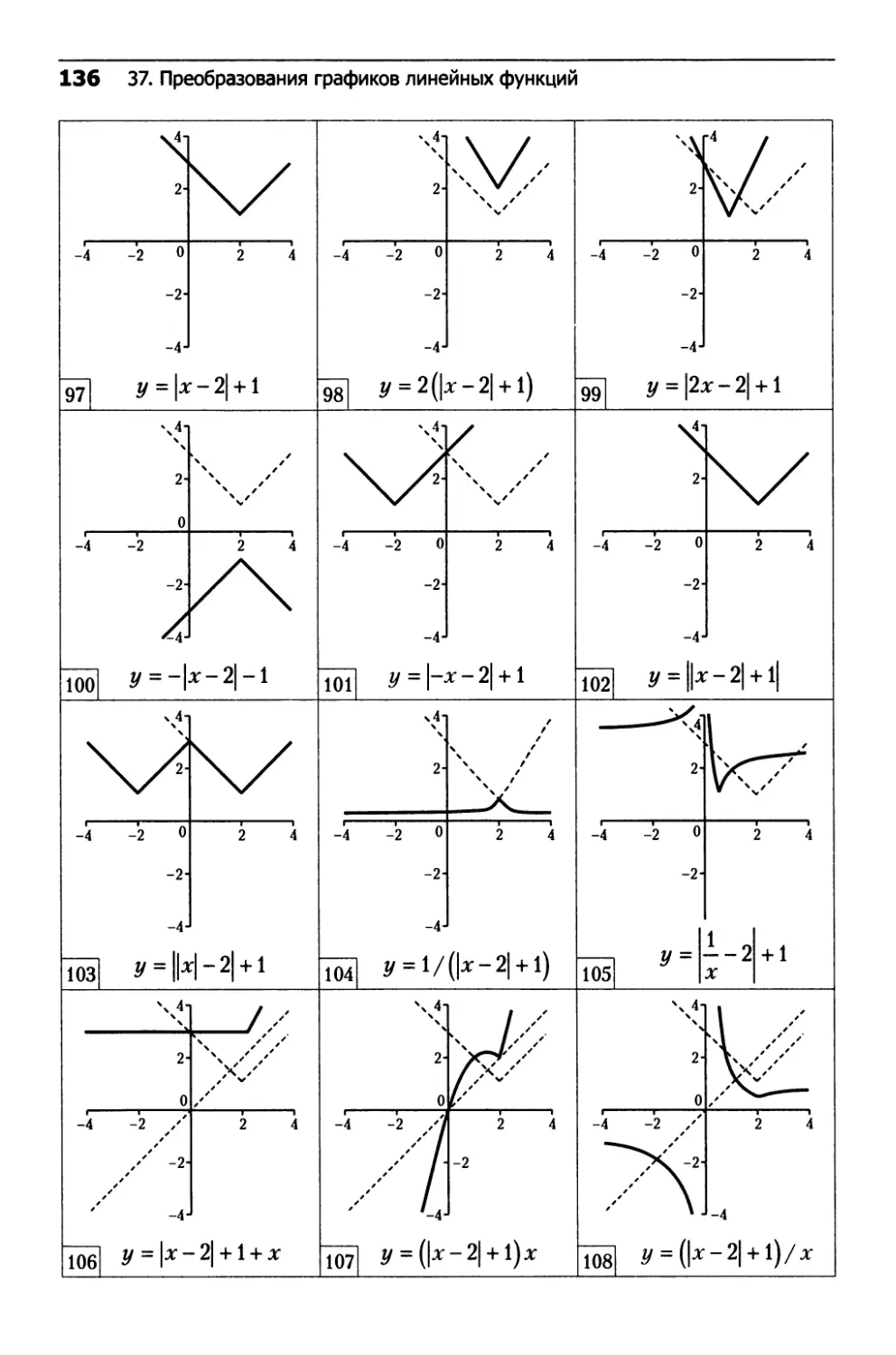
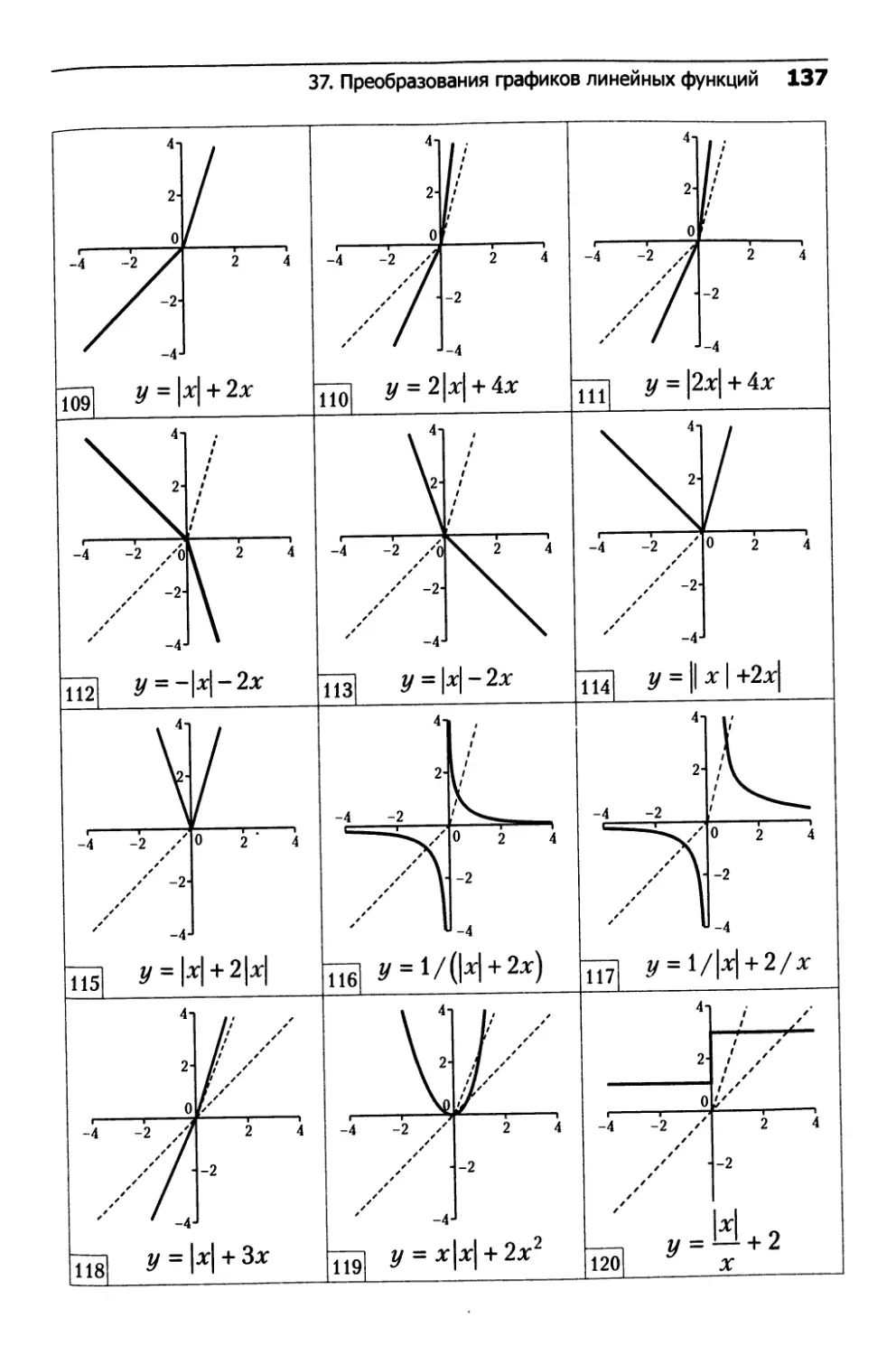
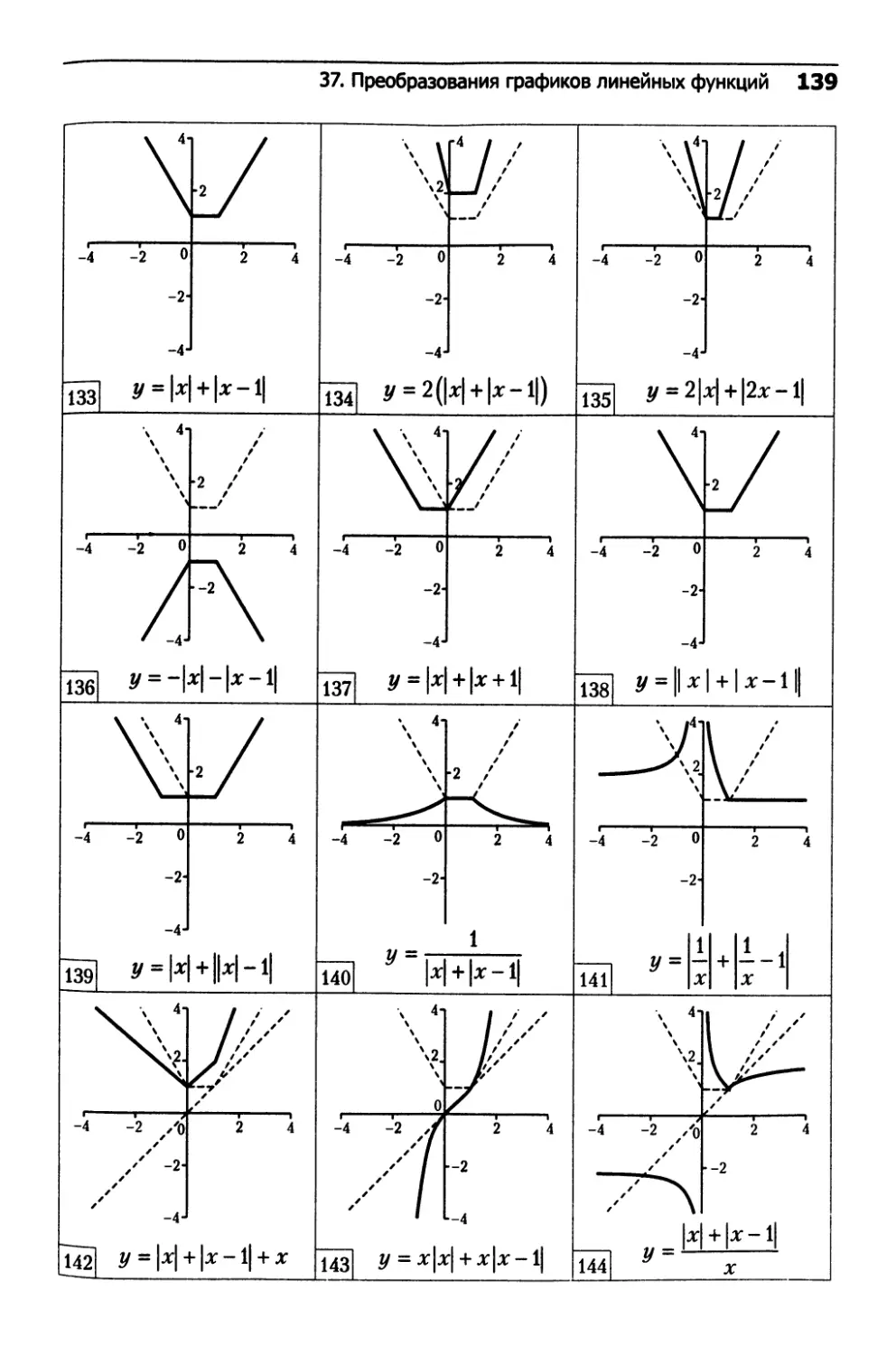
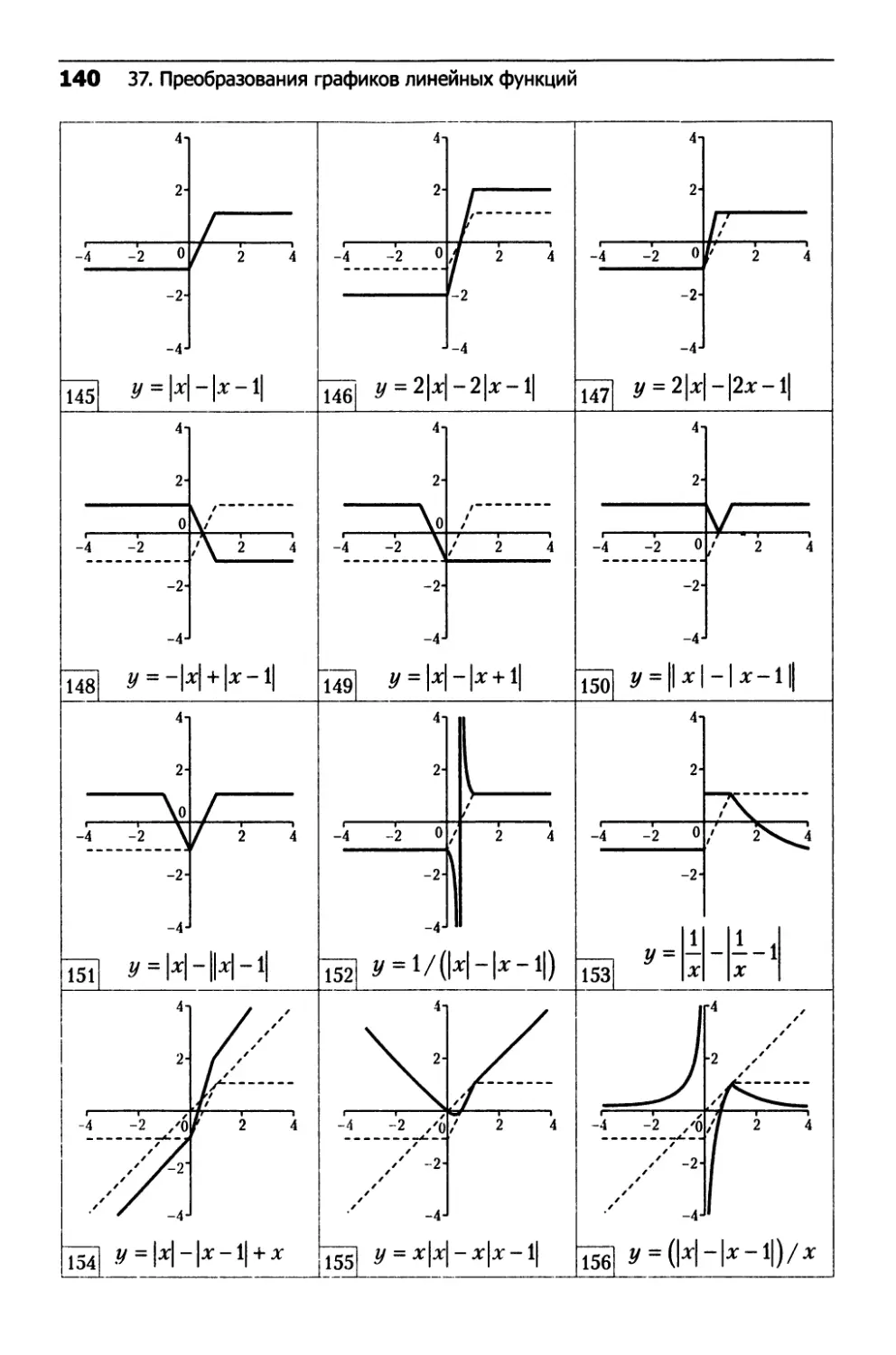
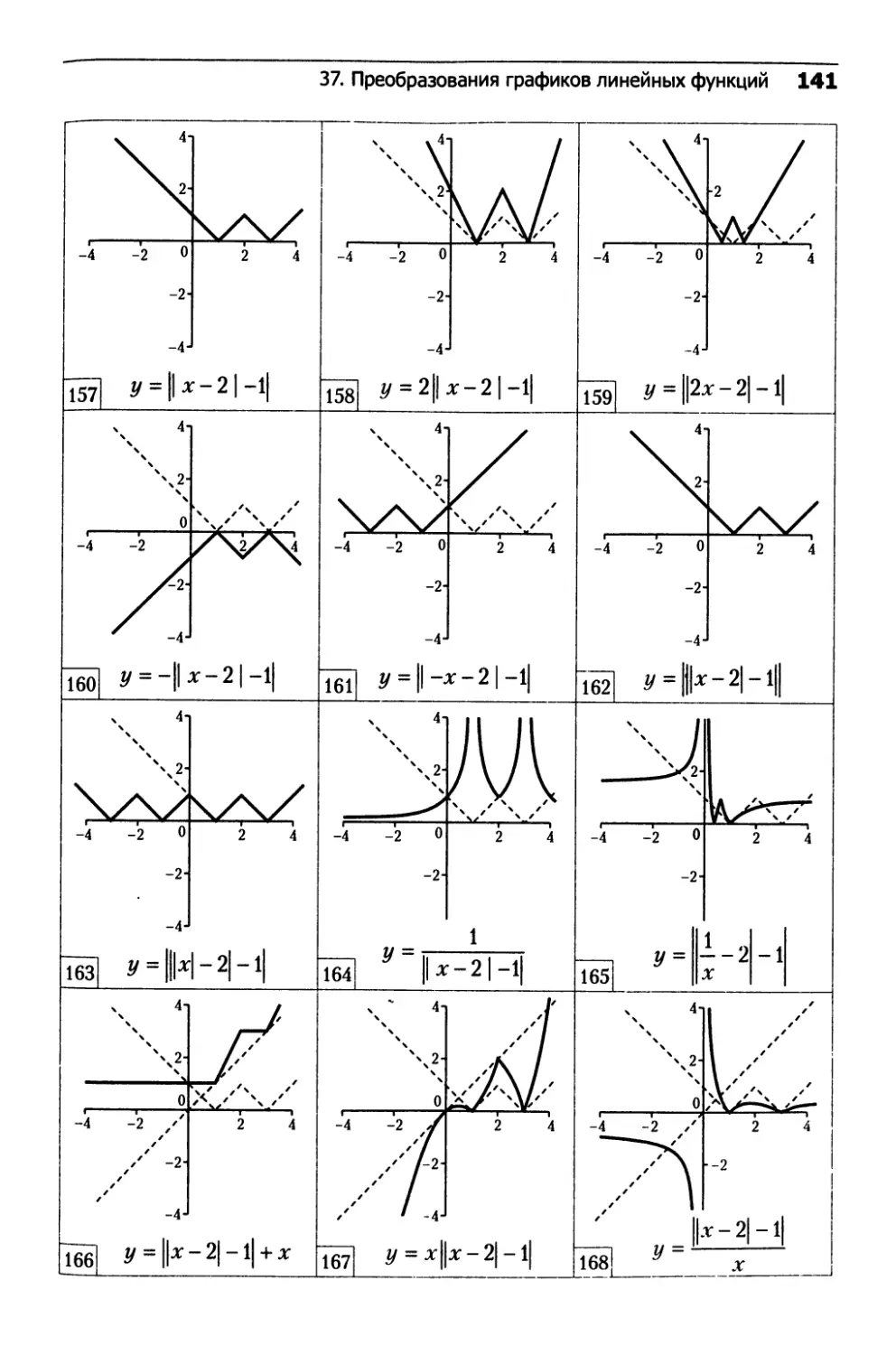
37.	Преобразования графиков линейных функций.....132
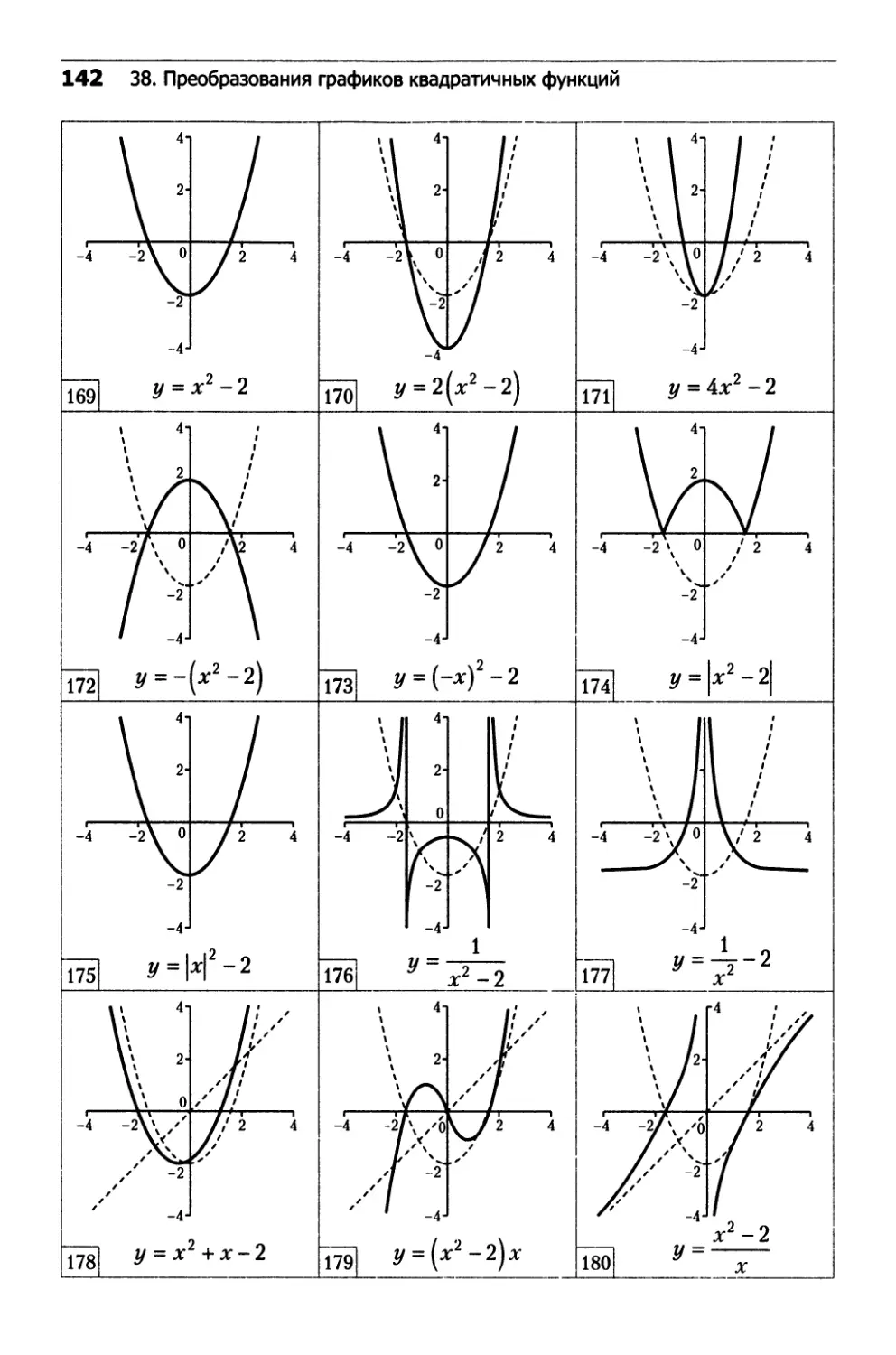
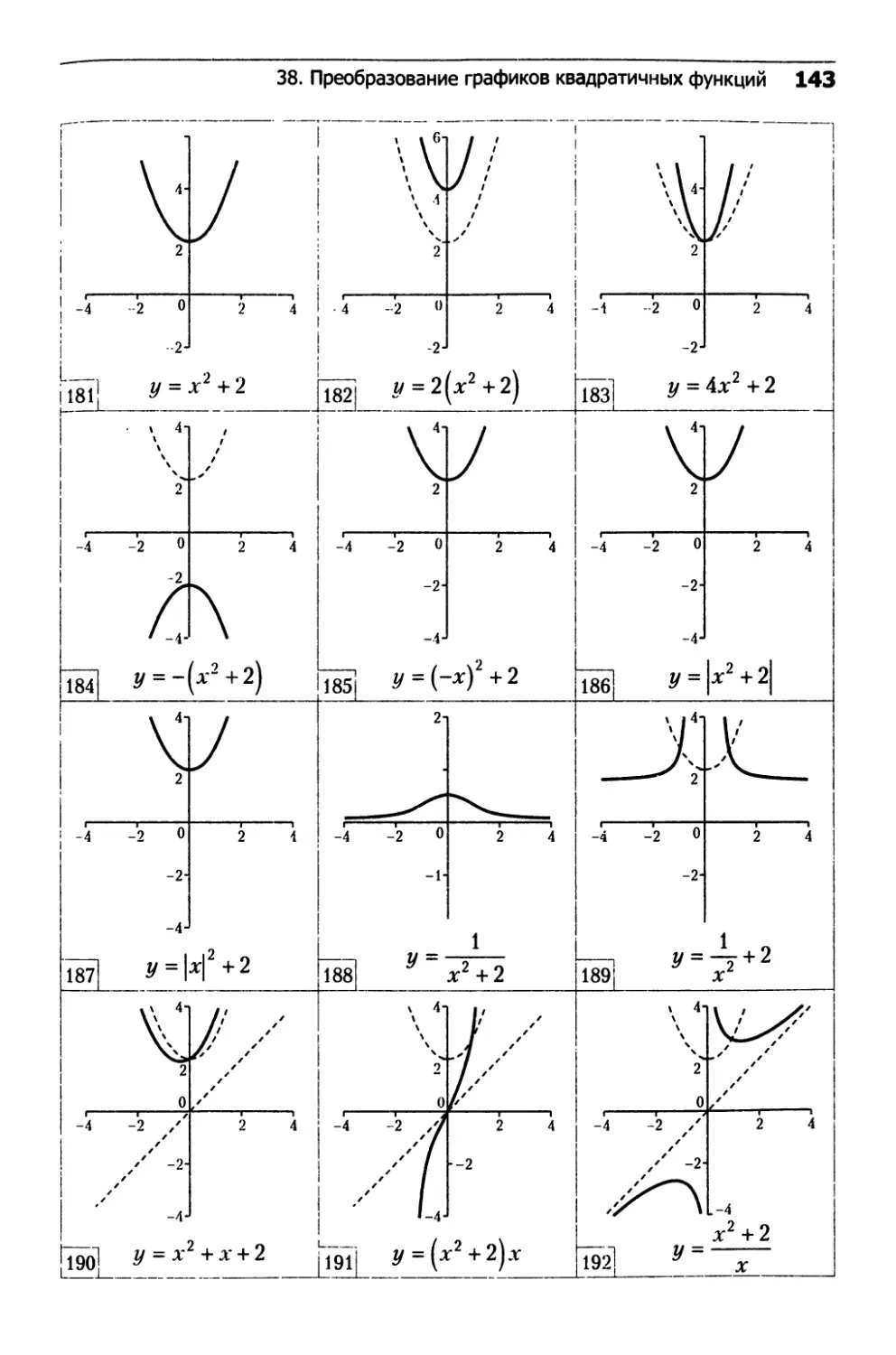
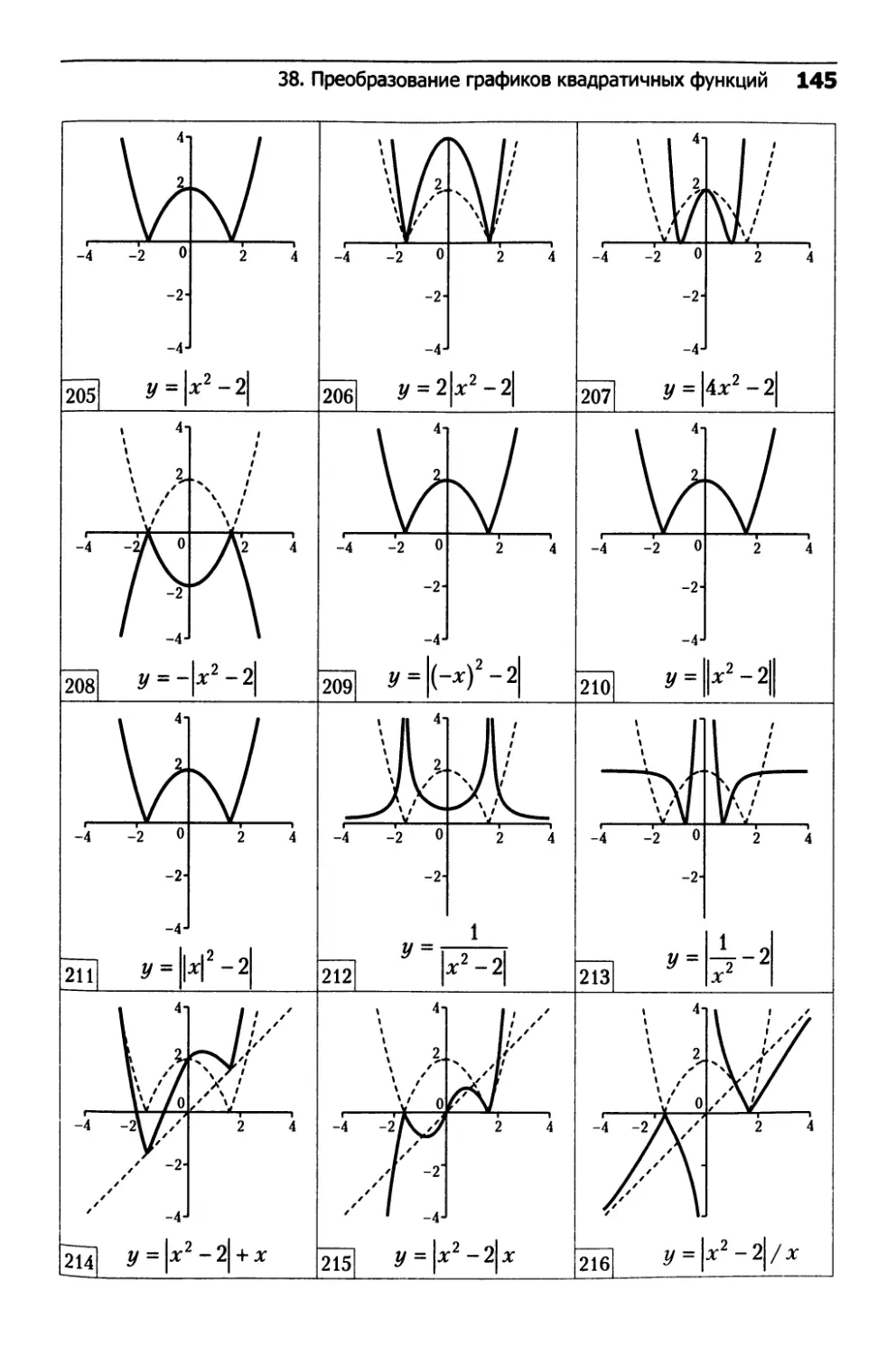
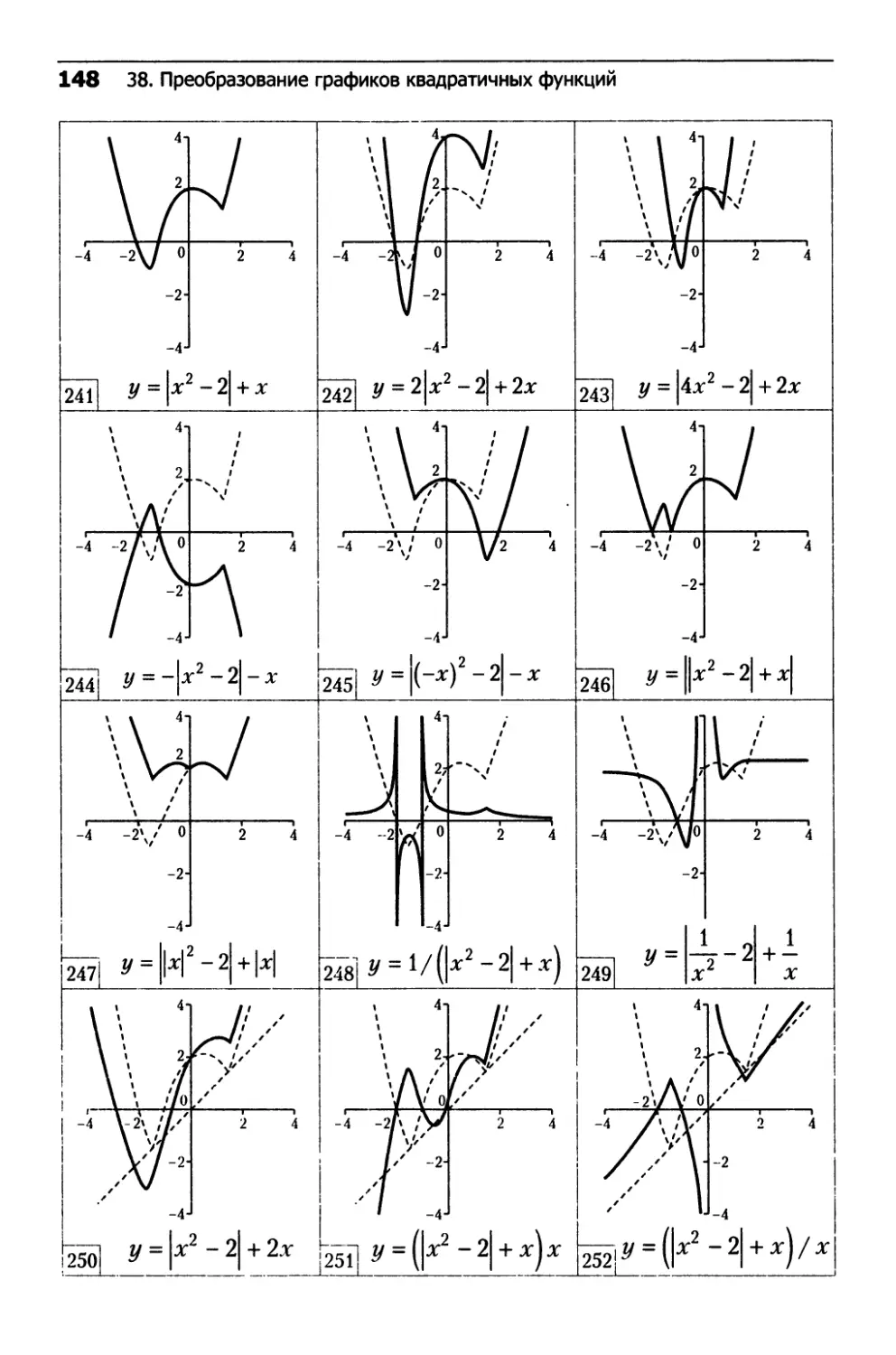
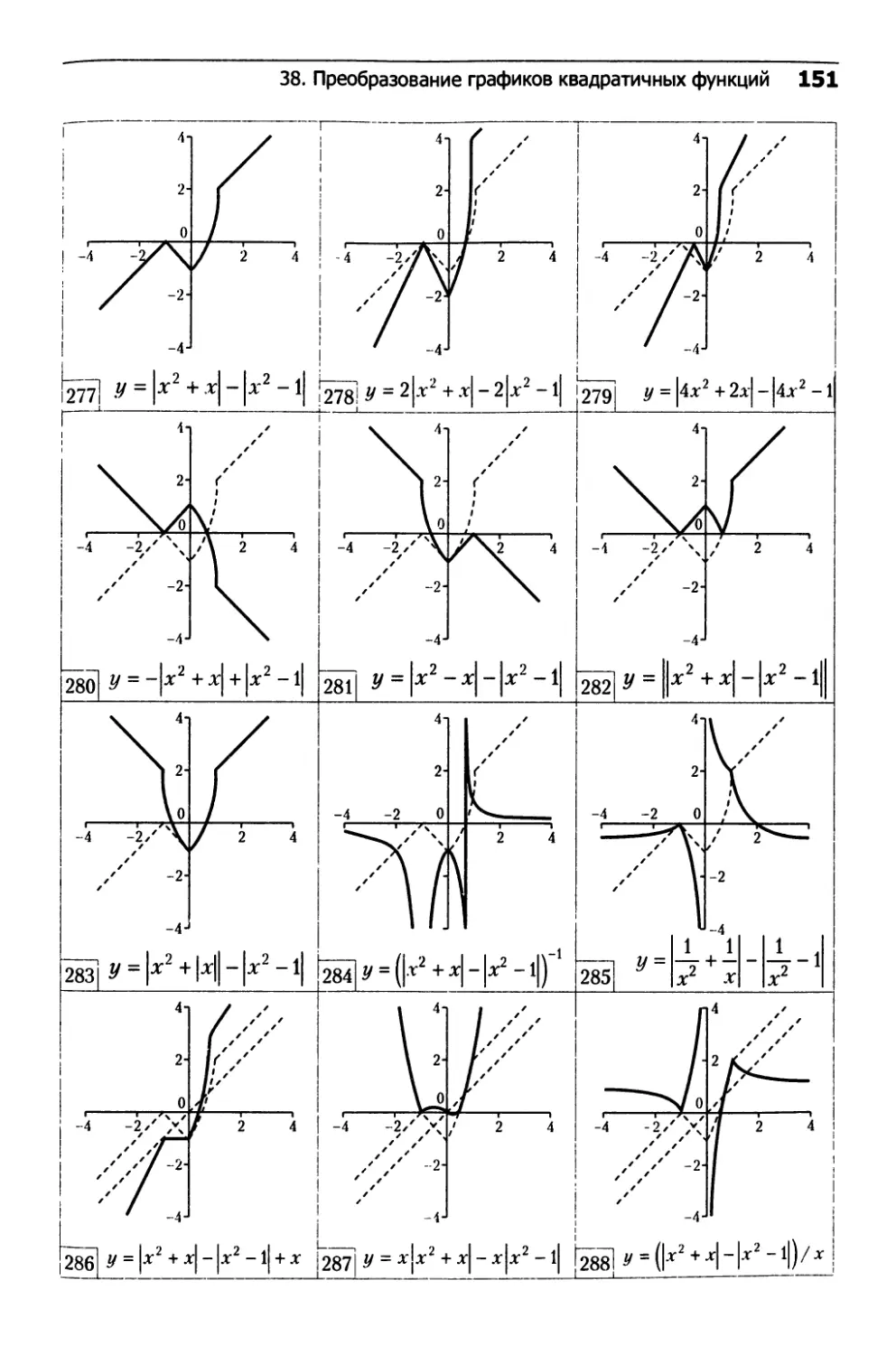
38.	Преобразование графиков квадратичных функций.142
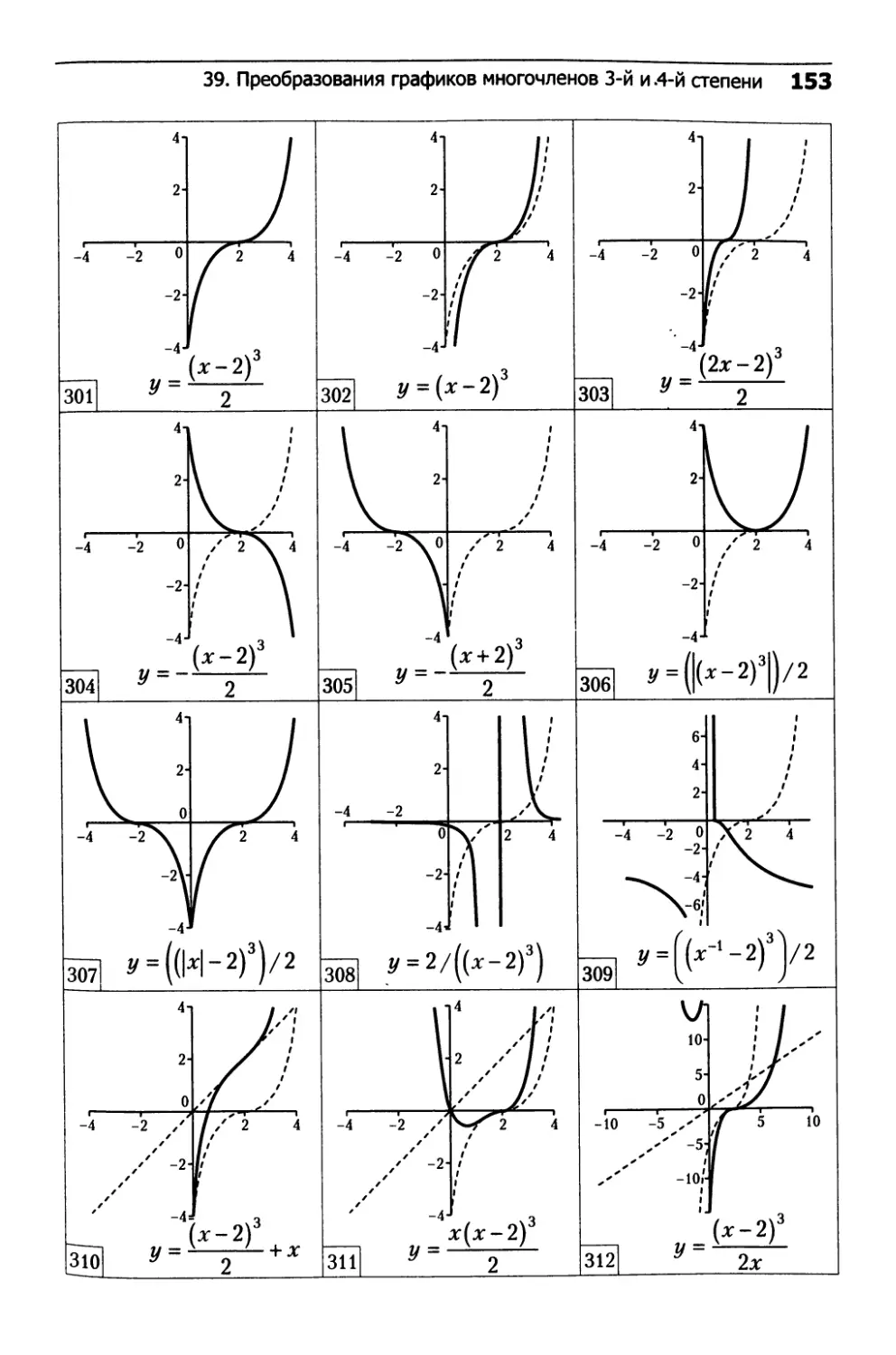
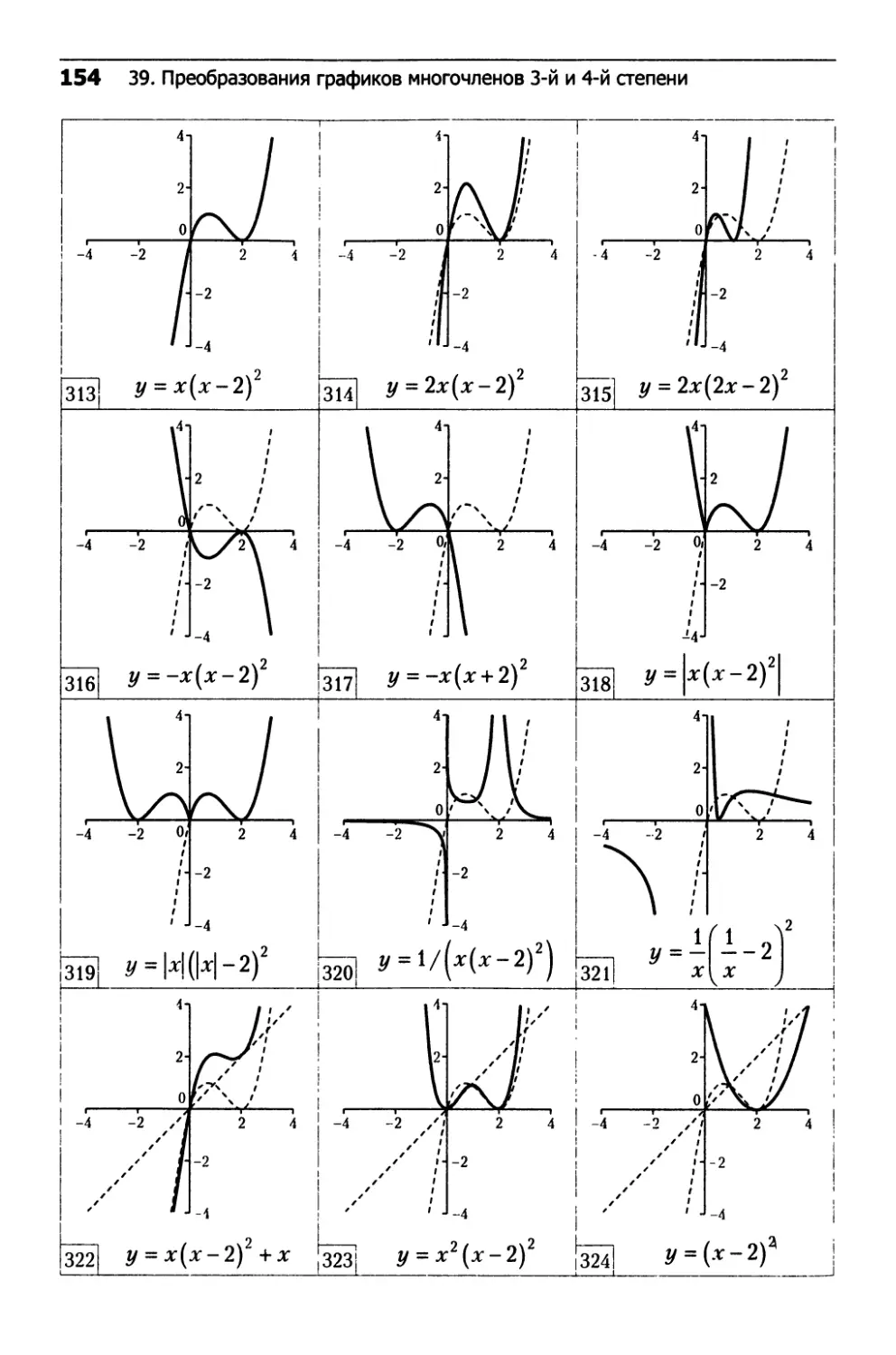
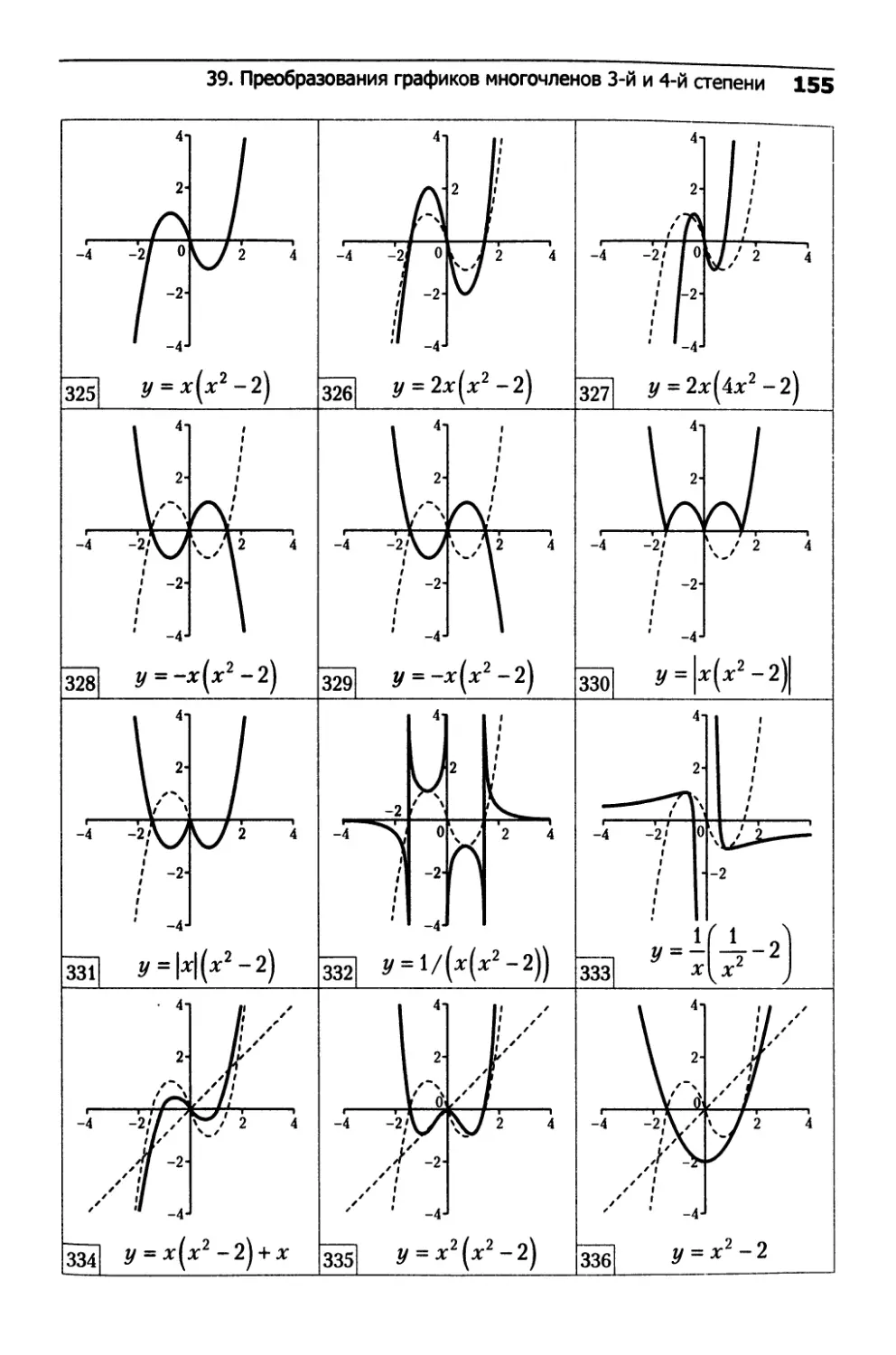
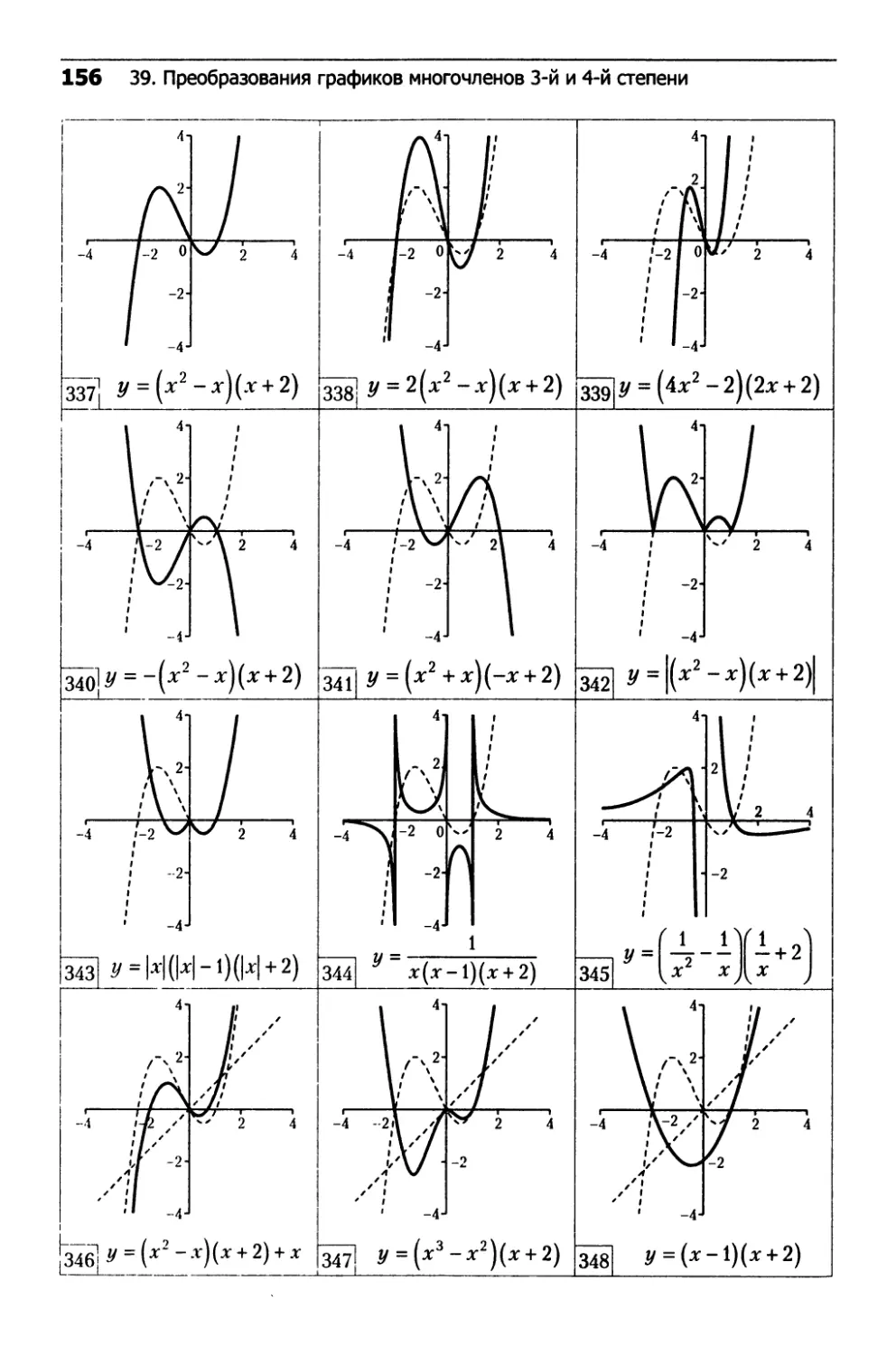
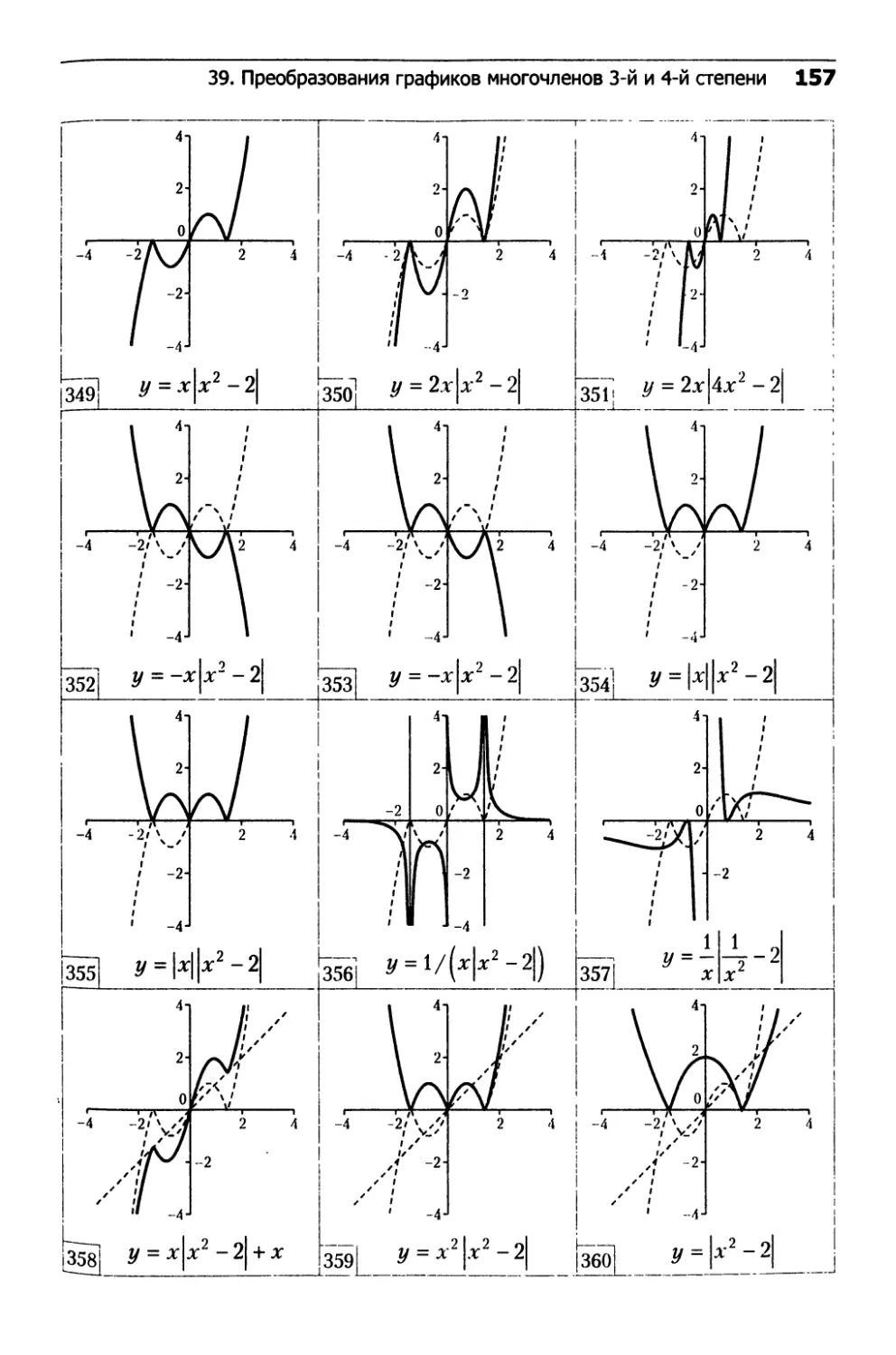
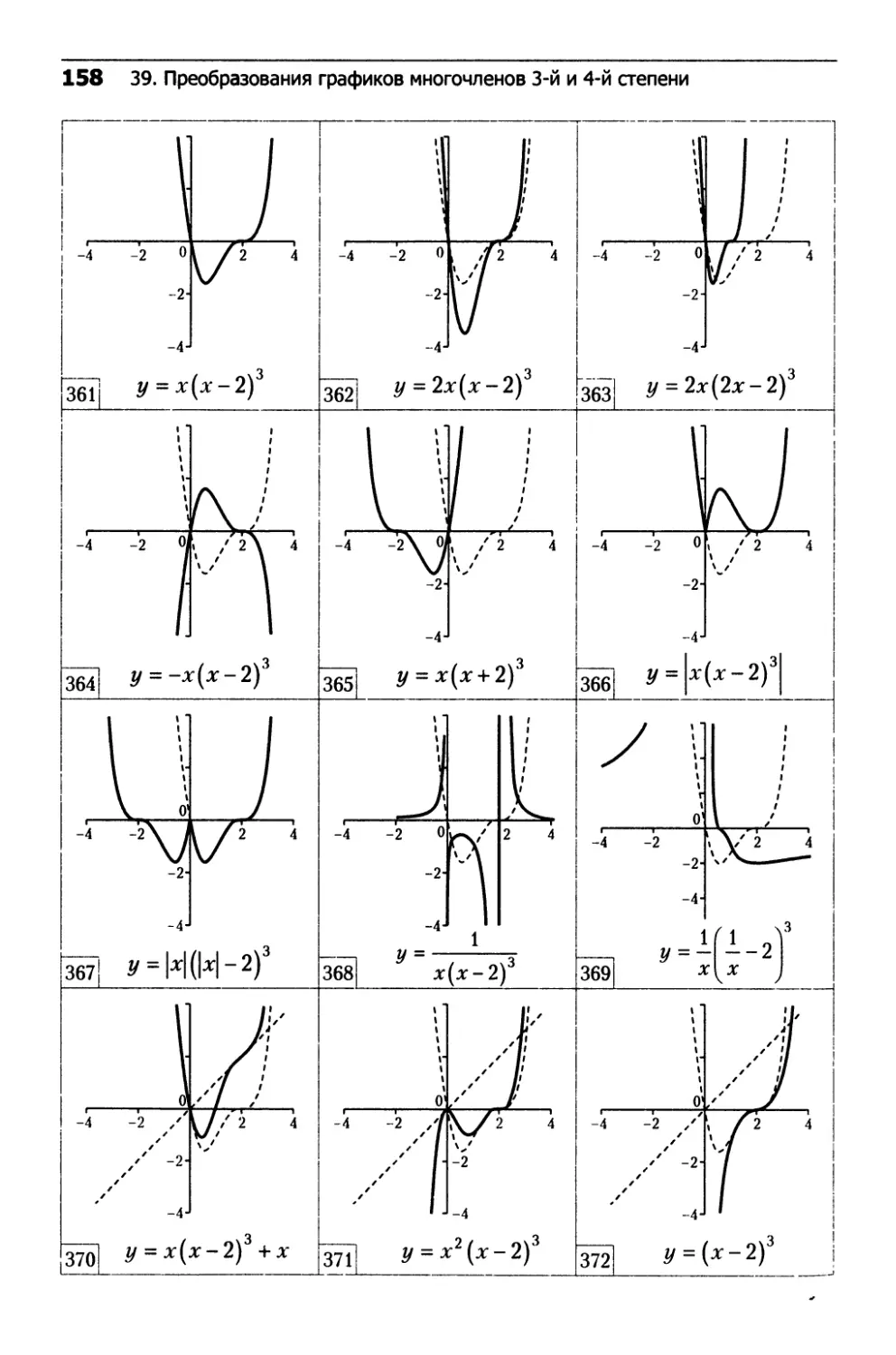
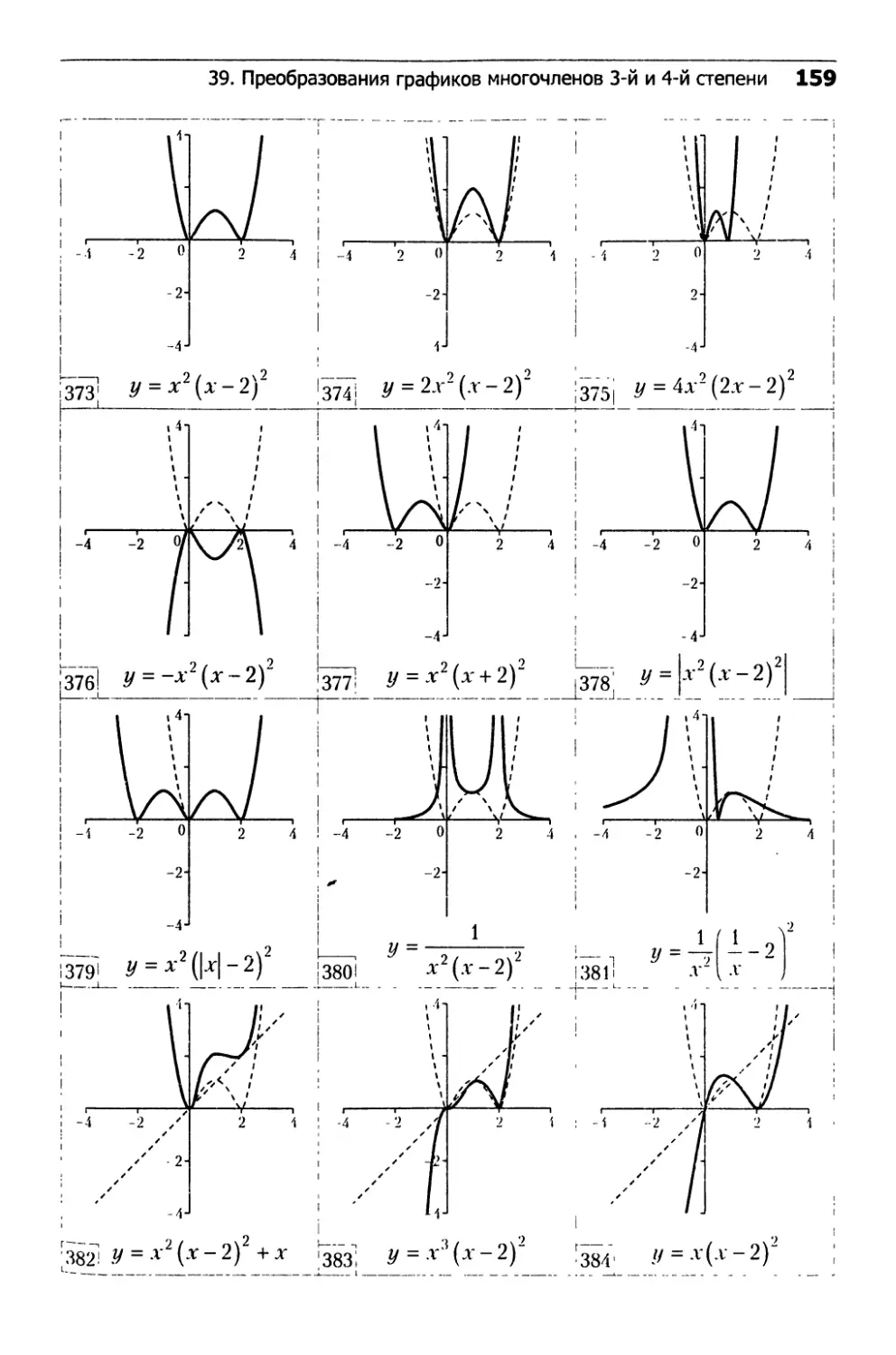
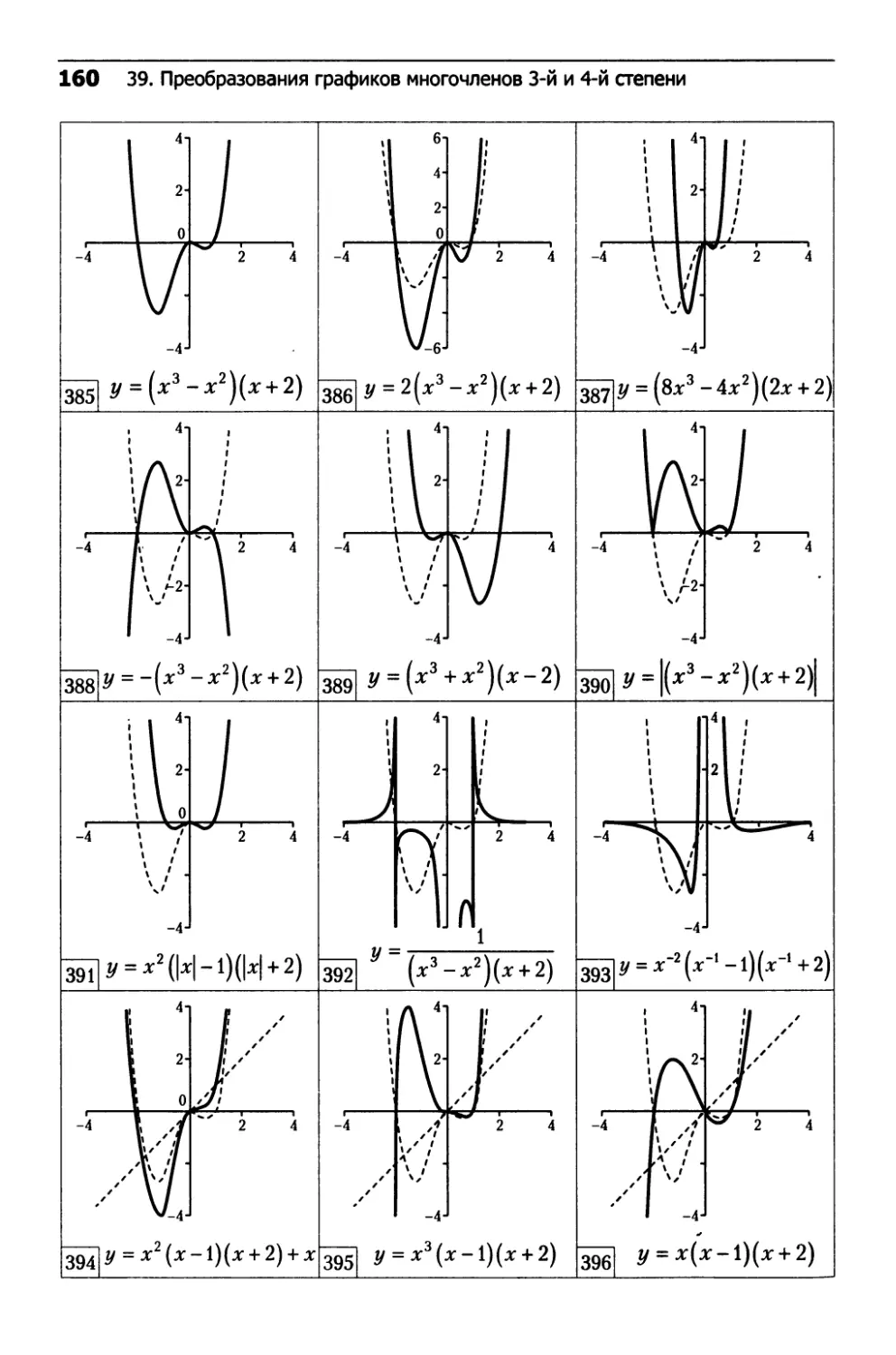
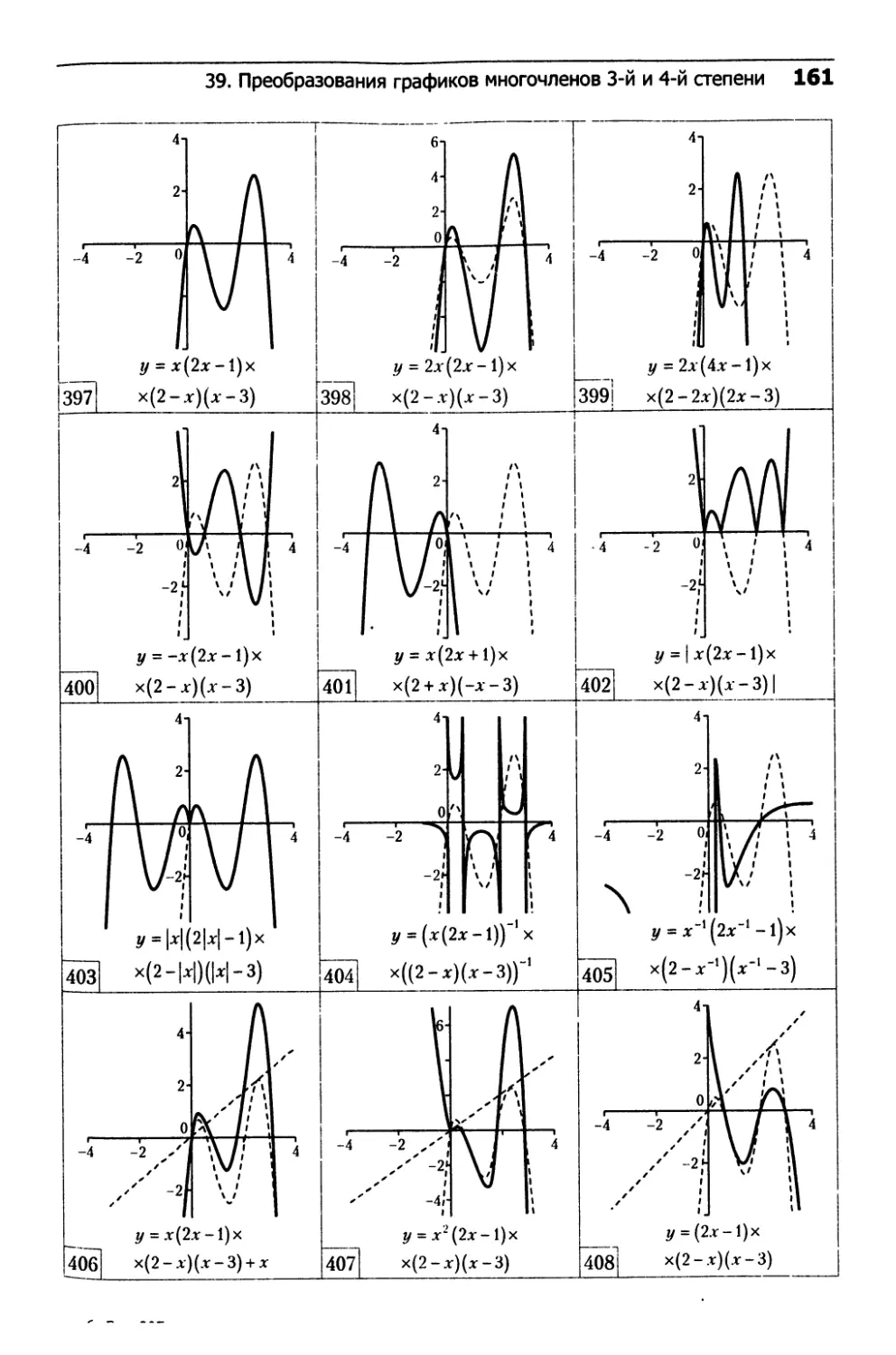
39.	Преобразования графиков
многочленов 3-й и 4-й степени...................152
12 Содержание
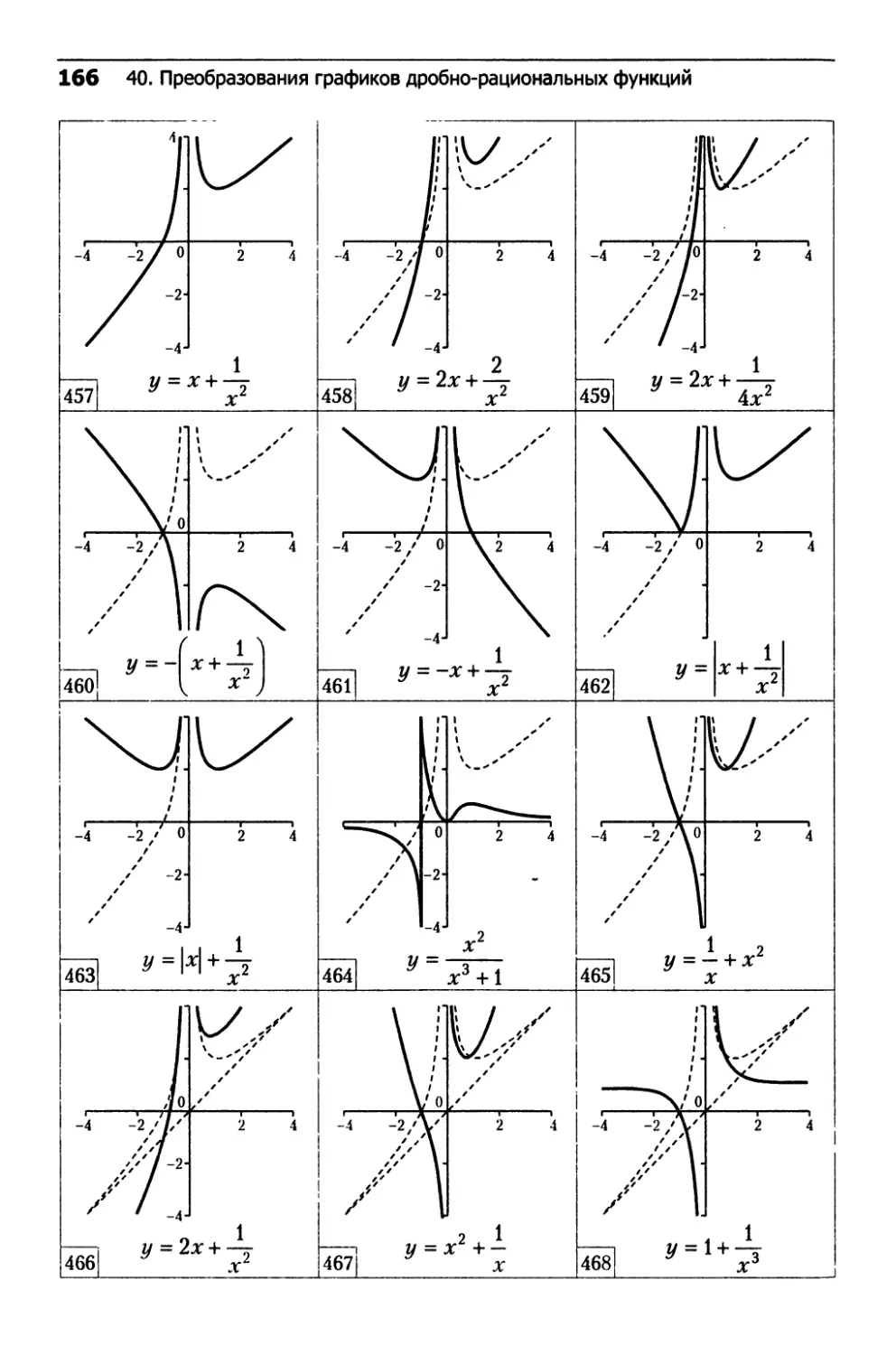
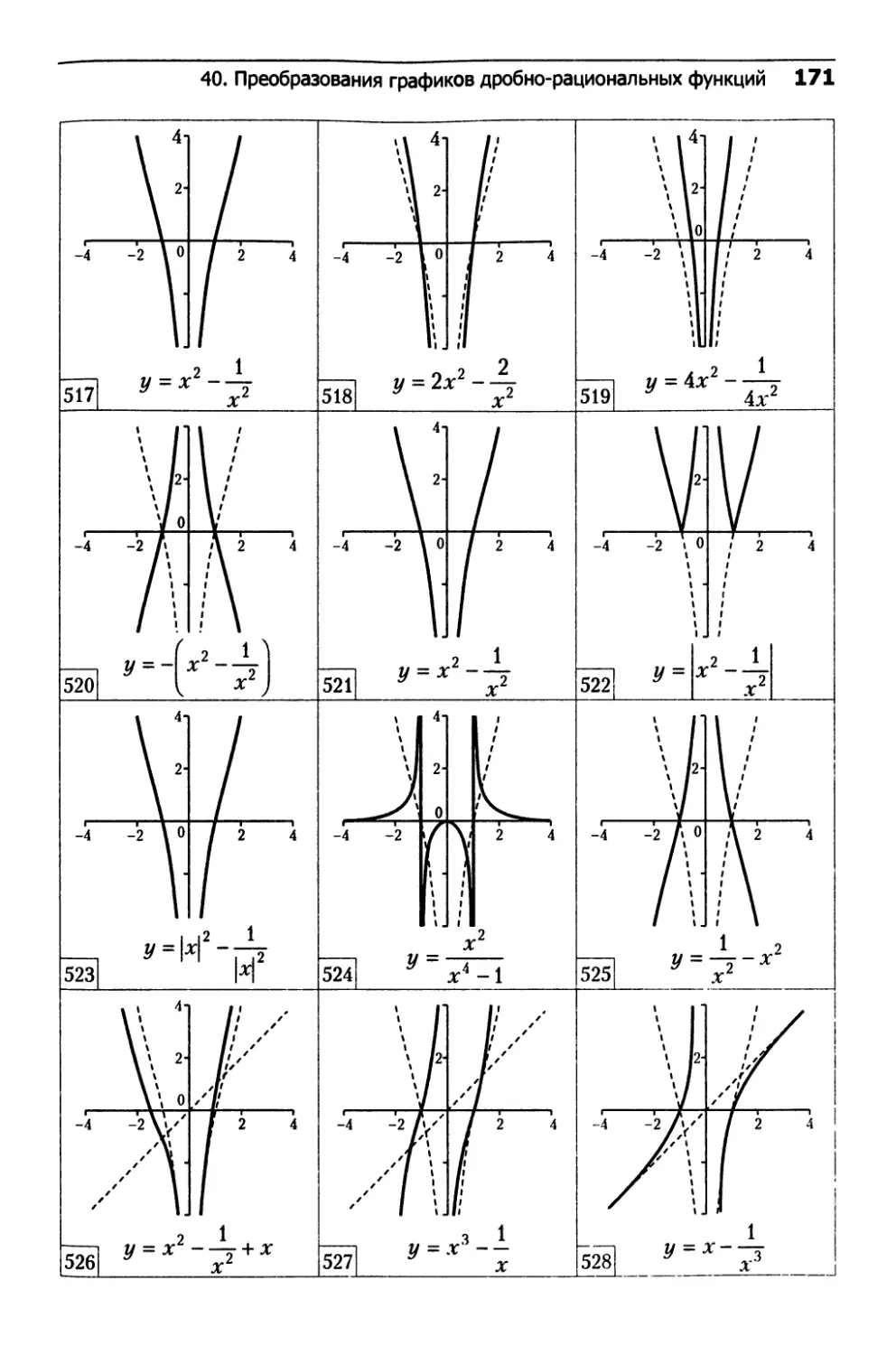
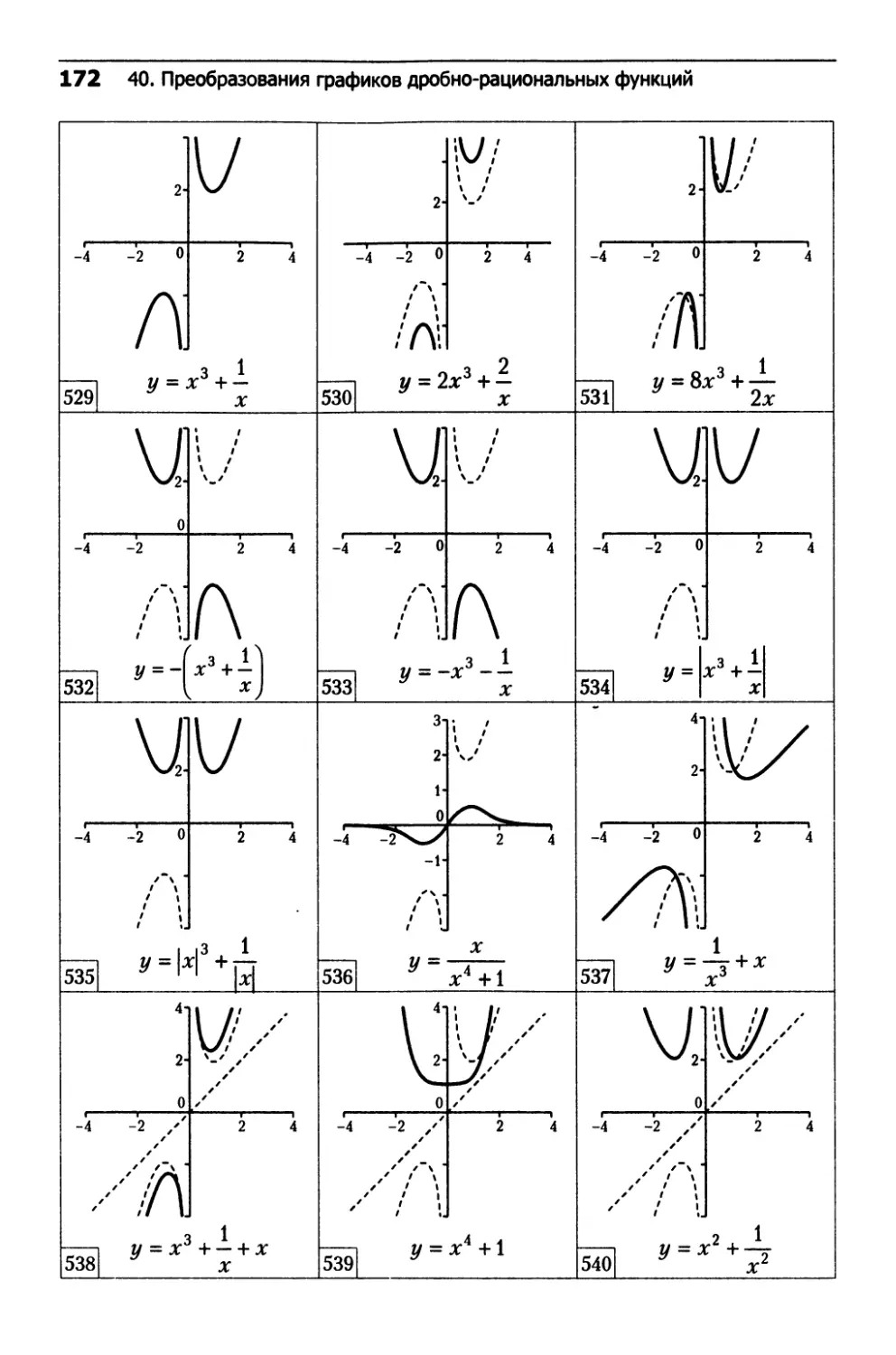
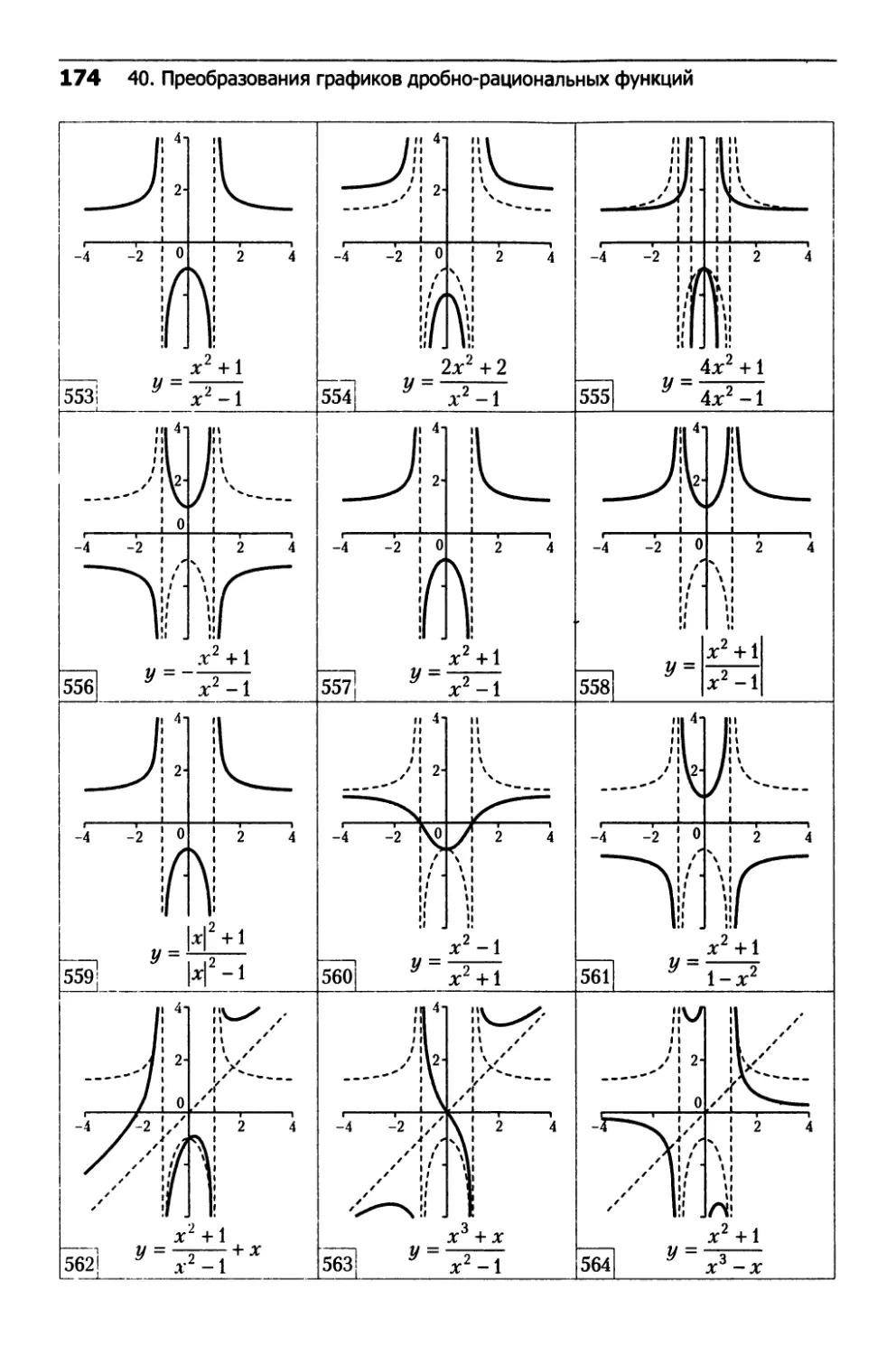
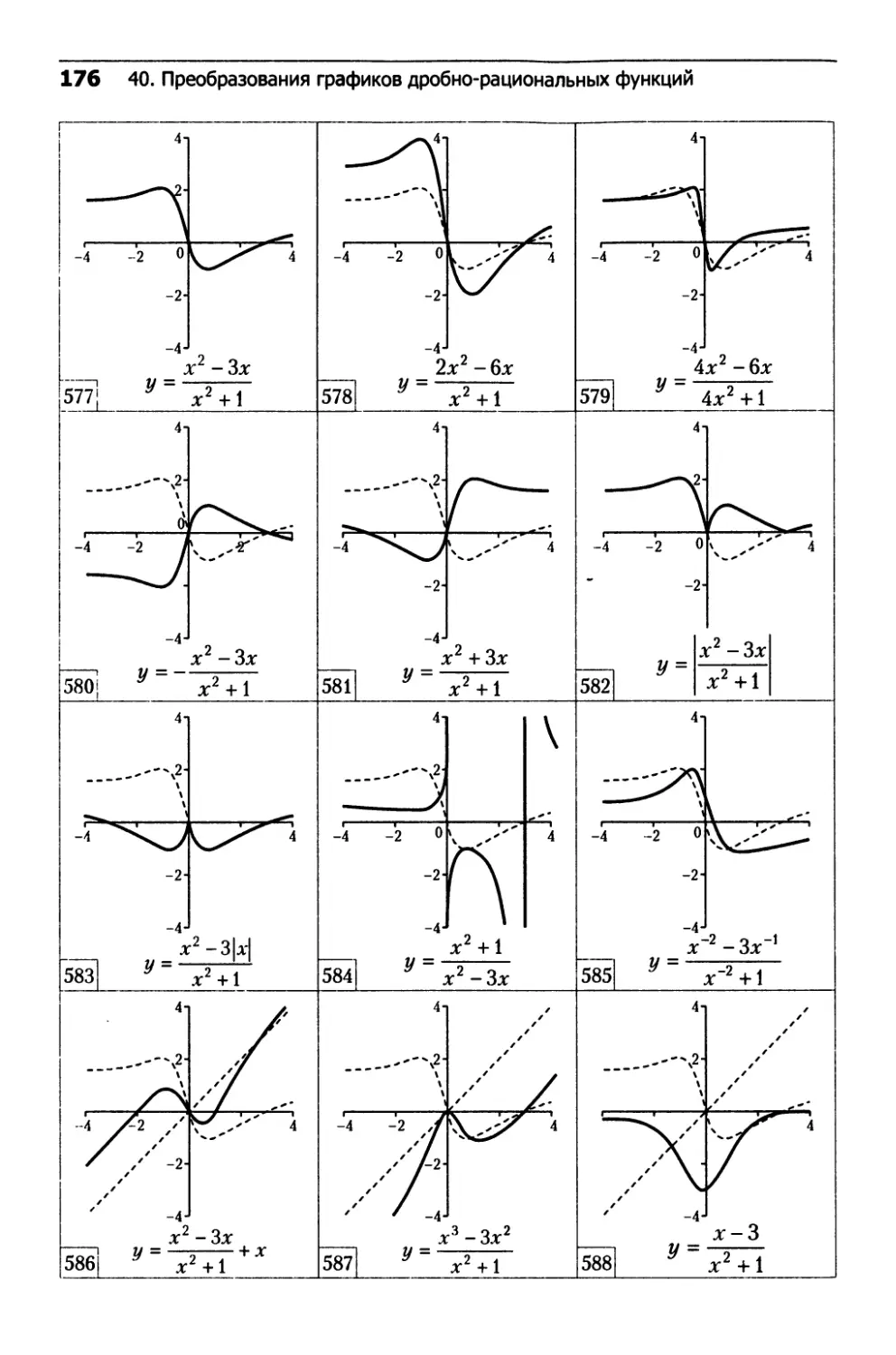
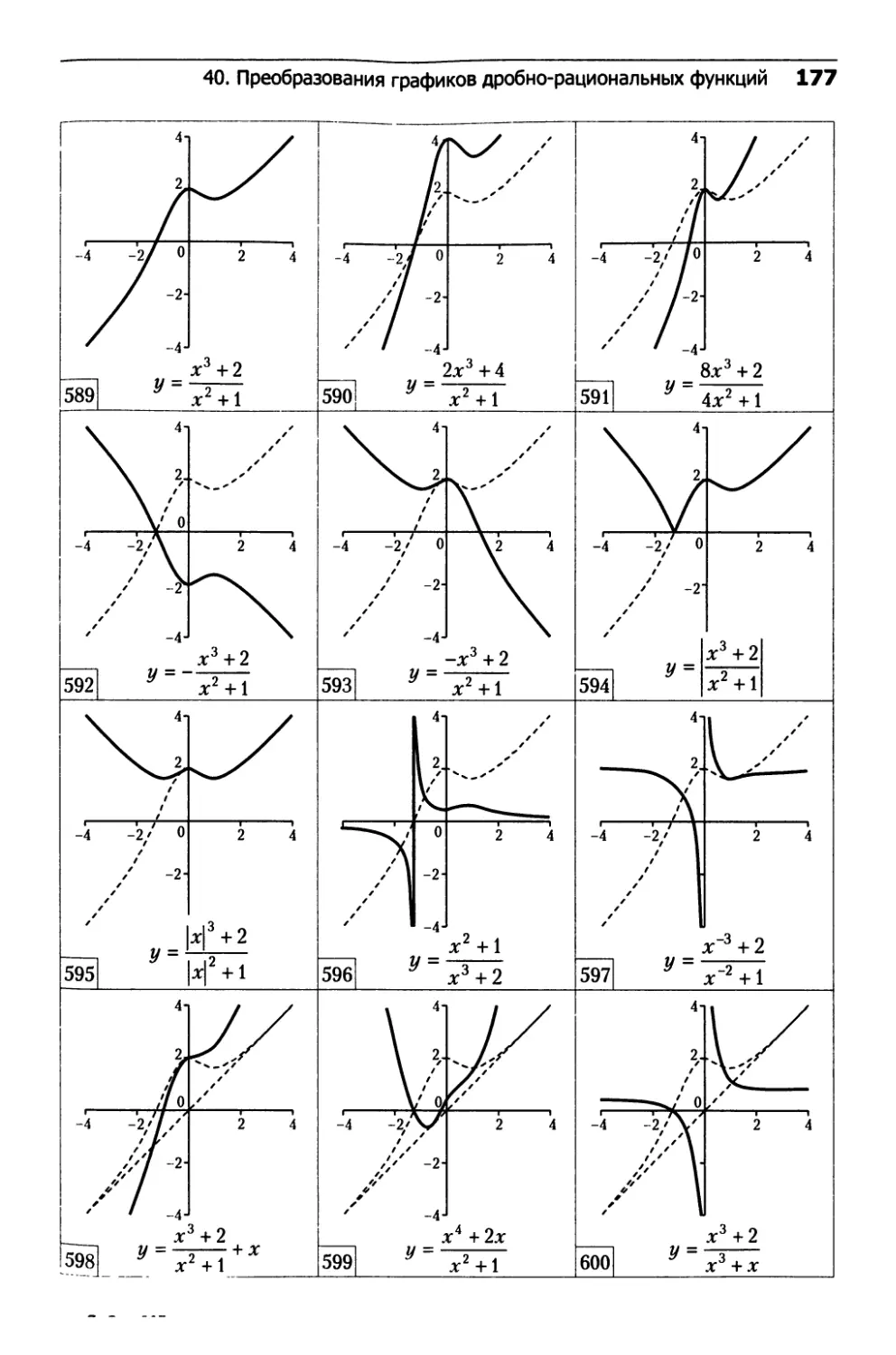
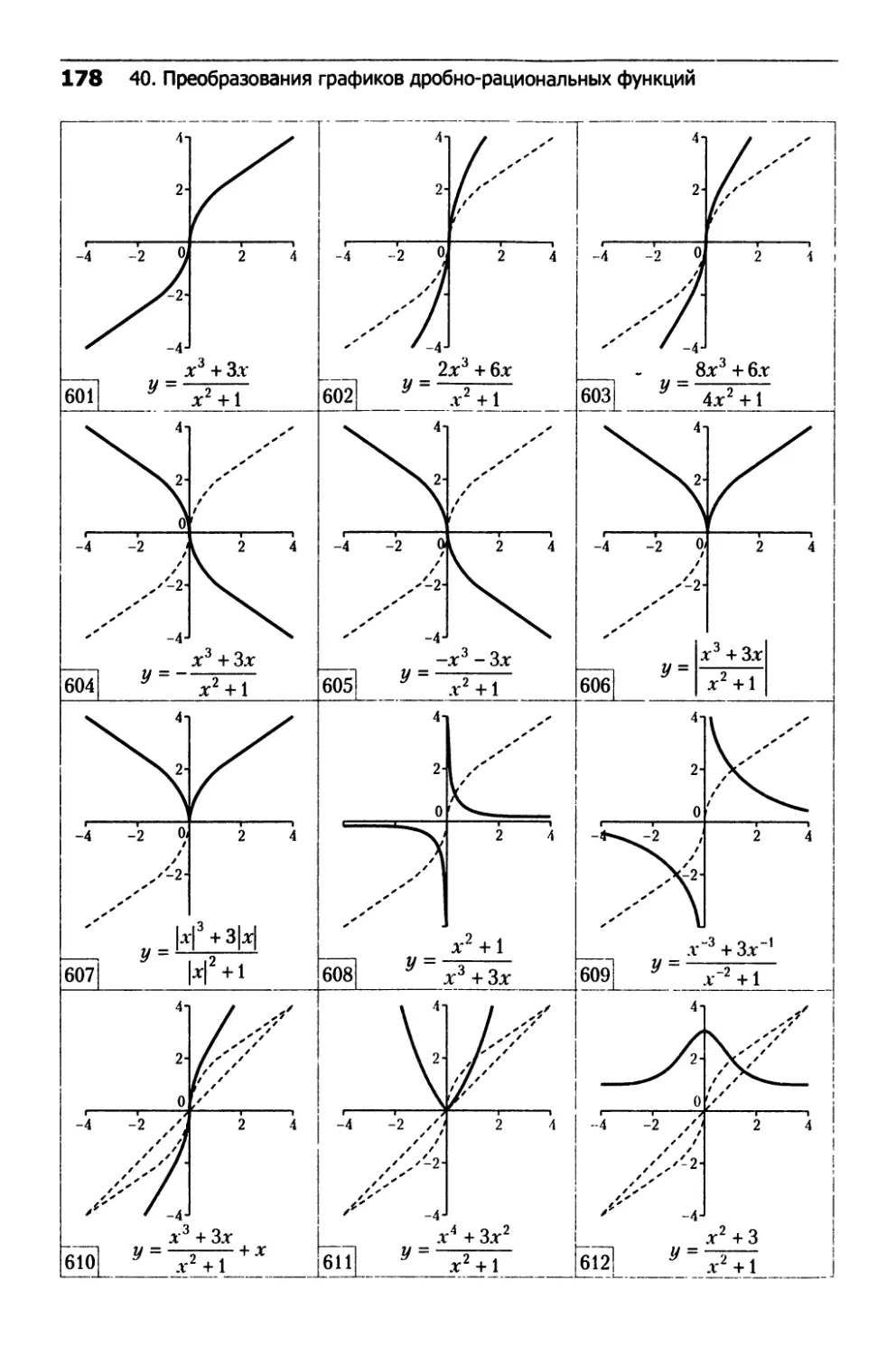
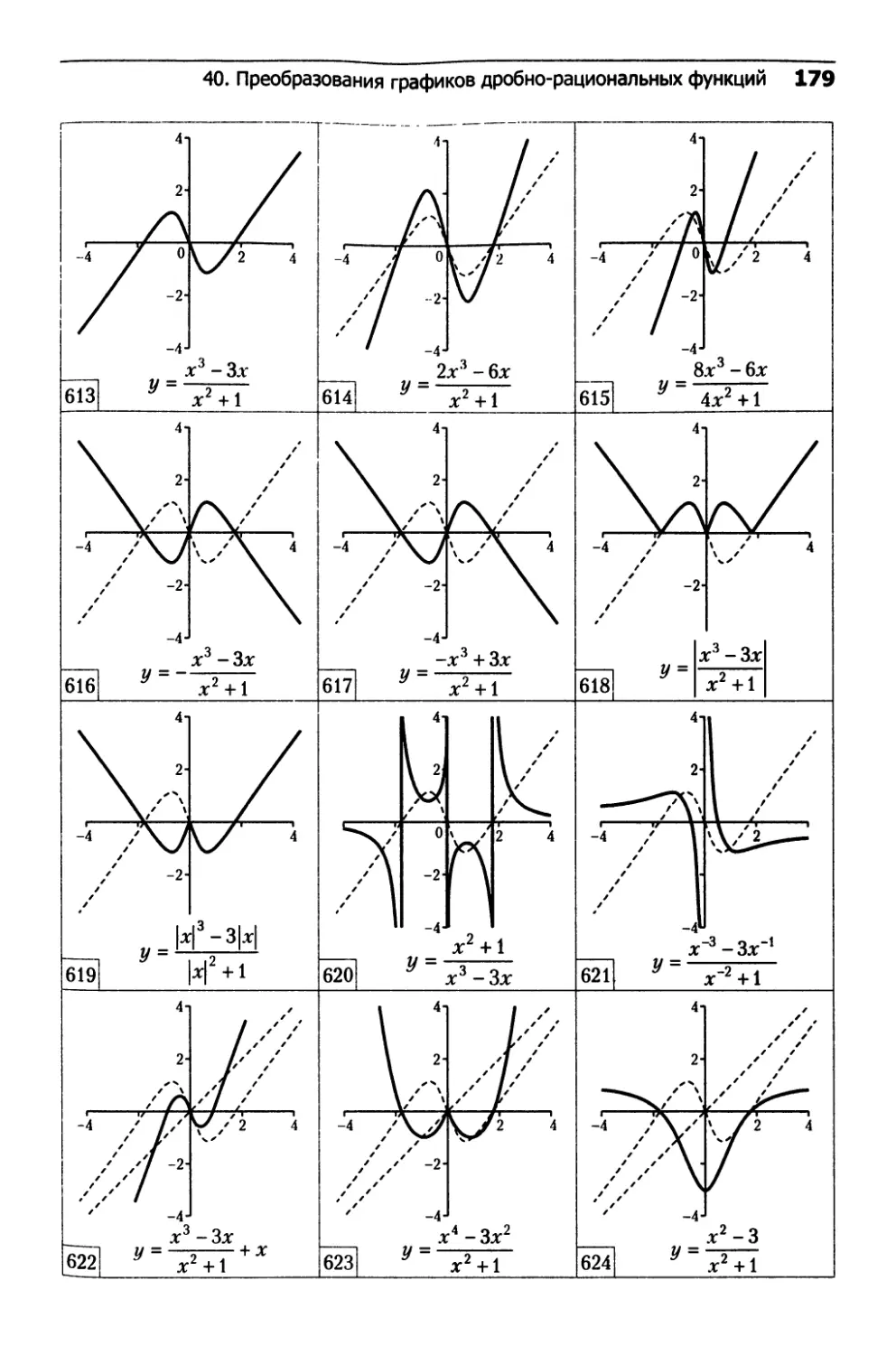
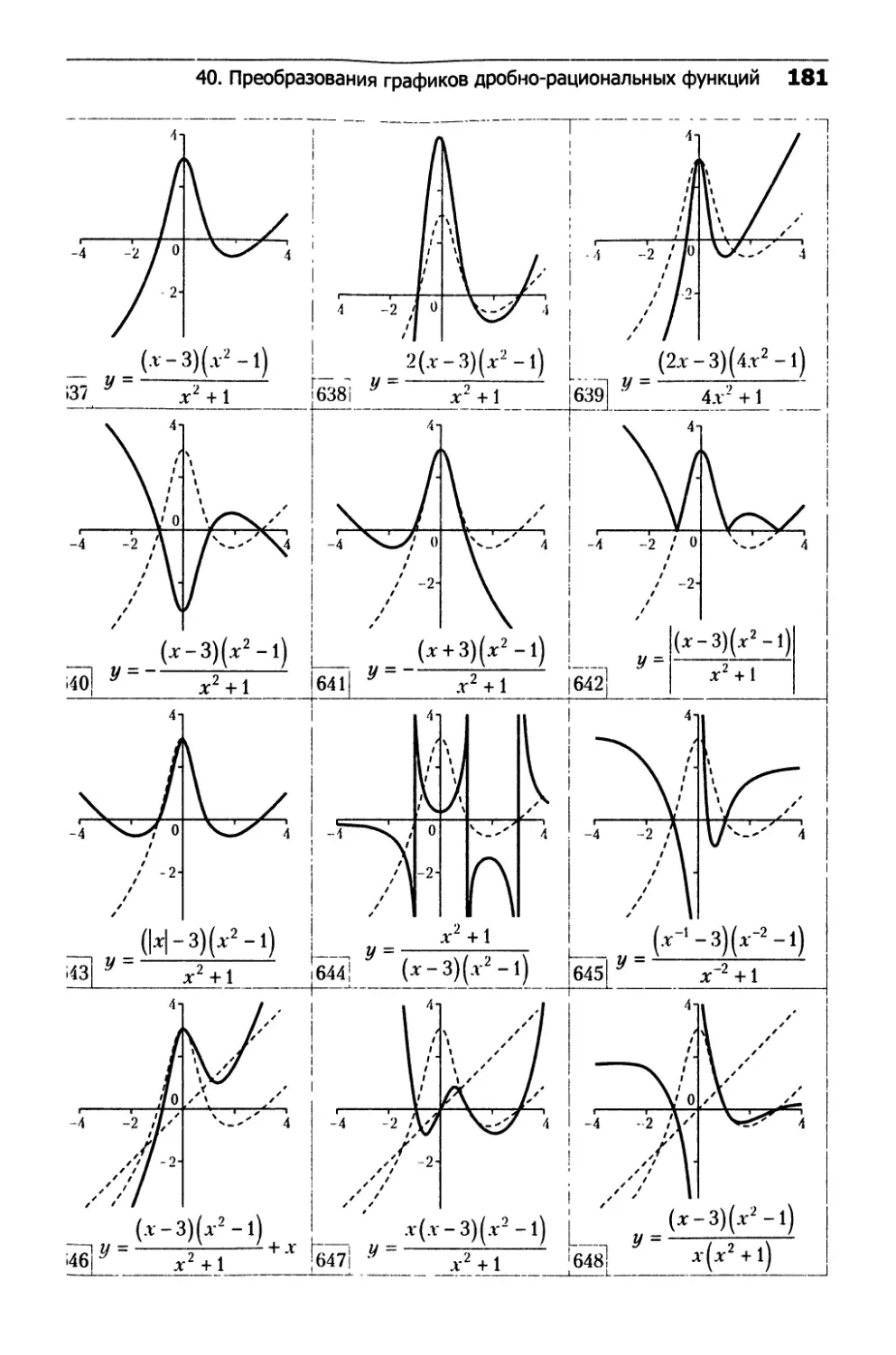
40.	Преобразования графиков
дробно-рациональных функций.......................162
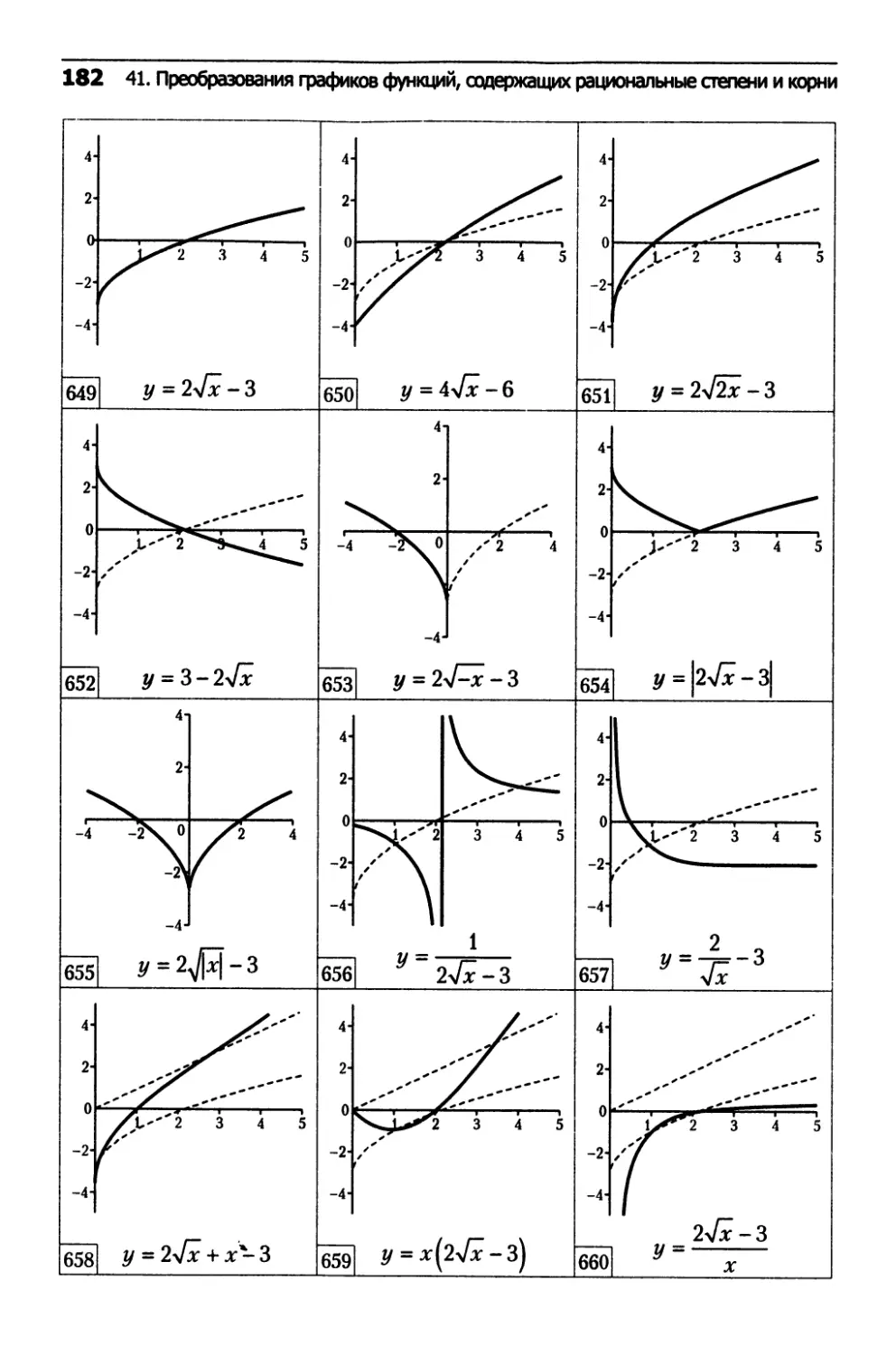
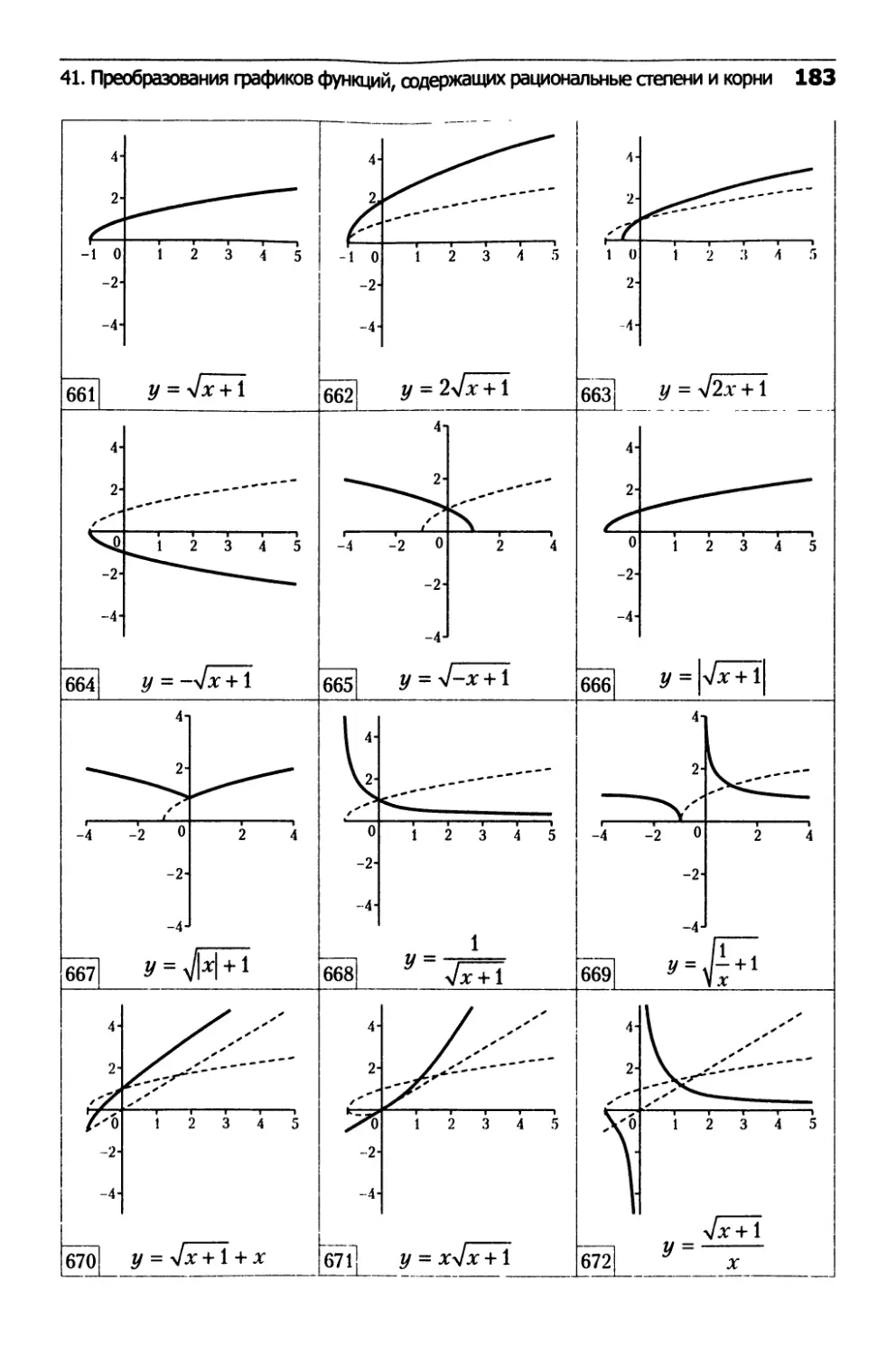
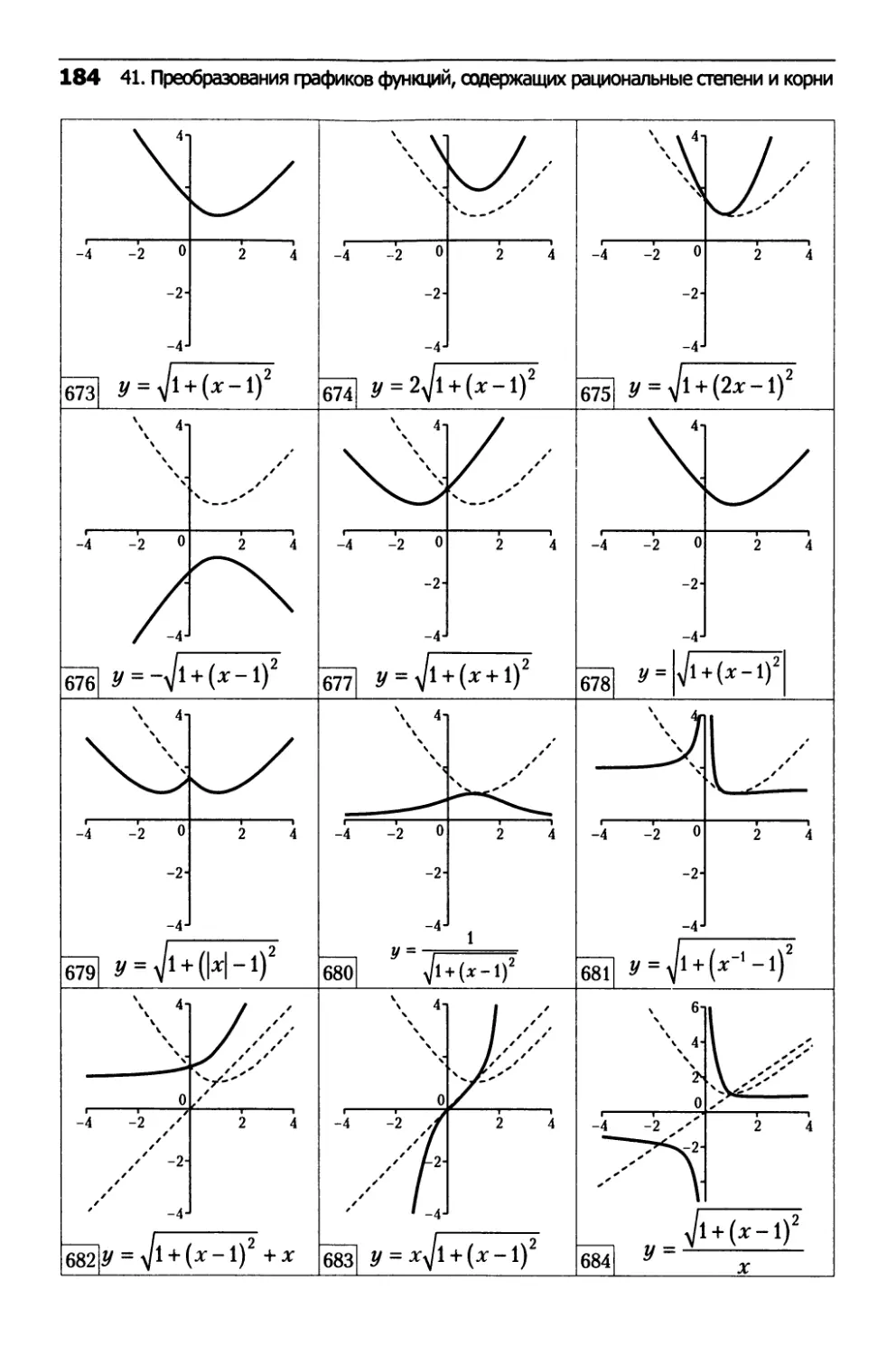
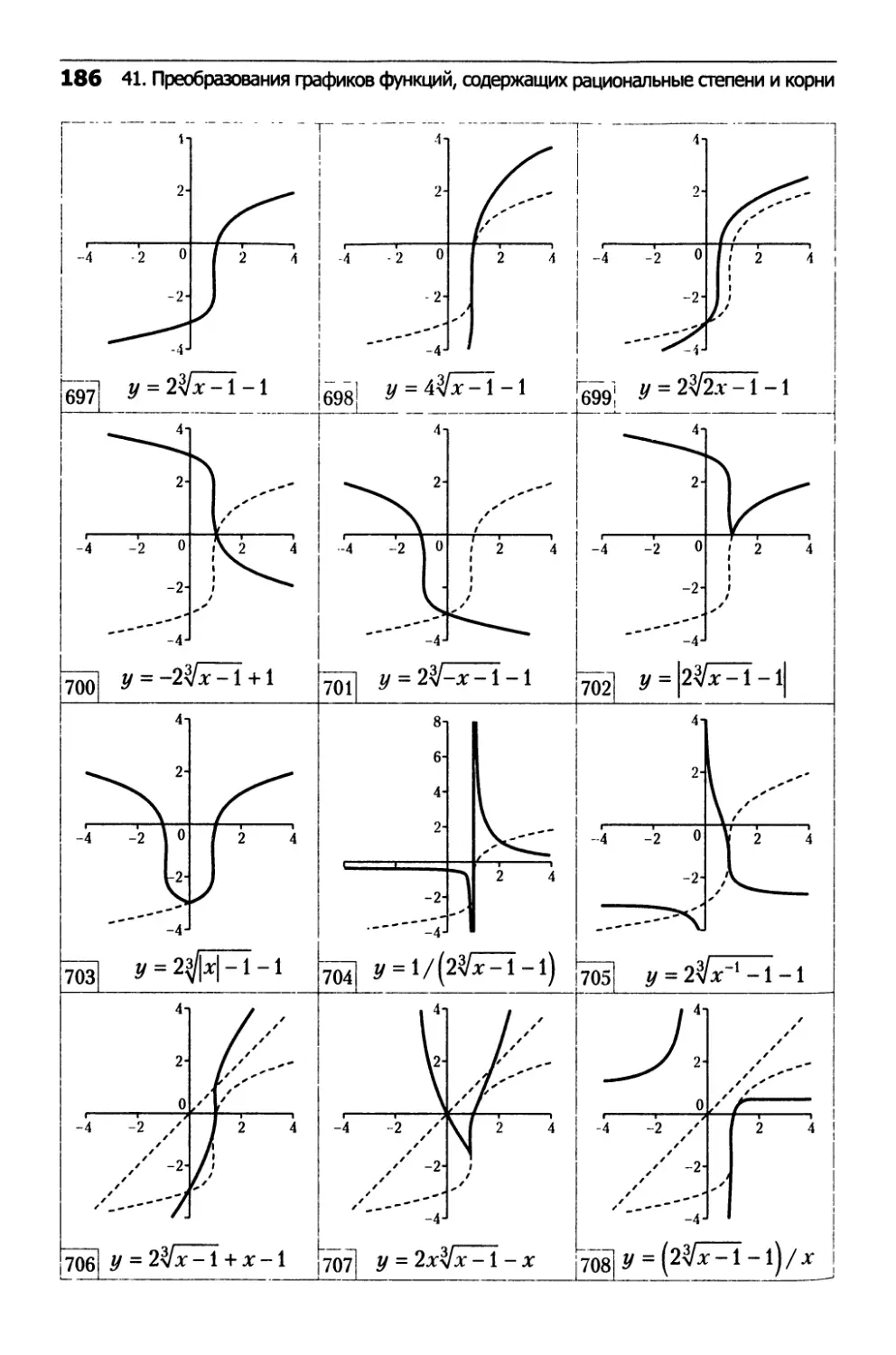
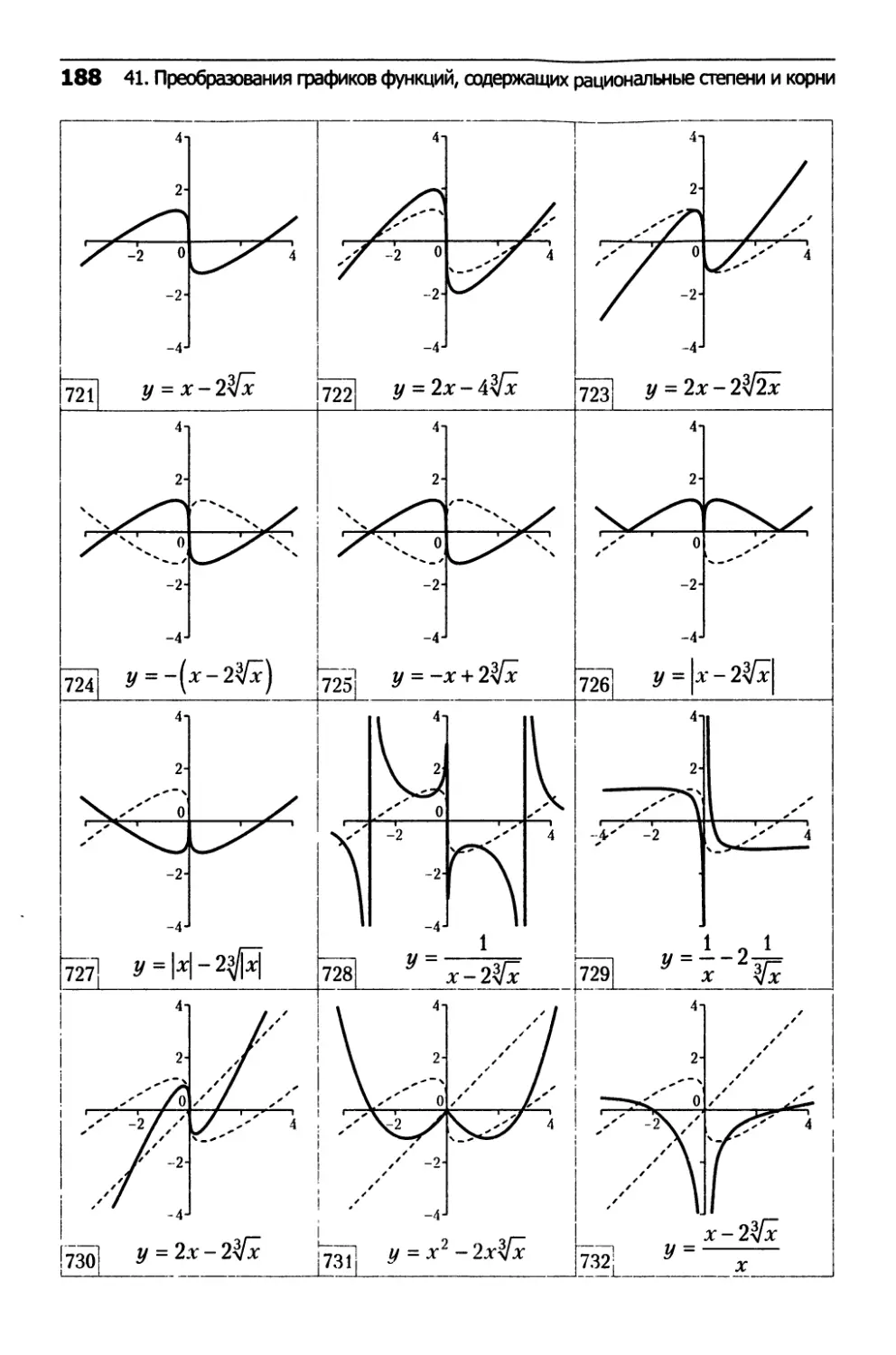
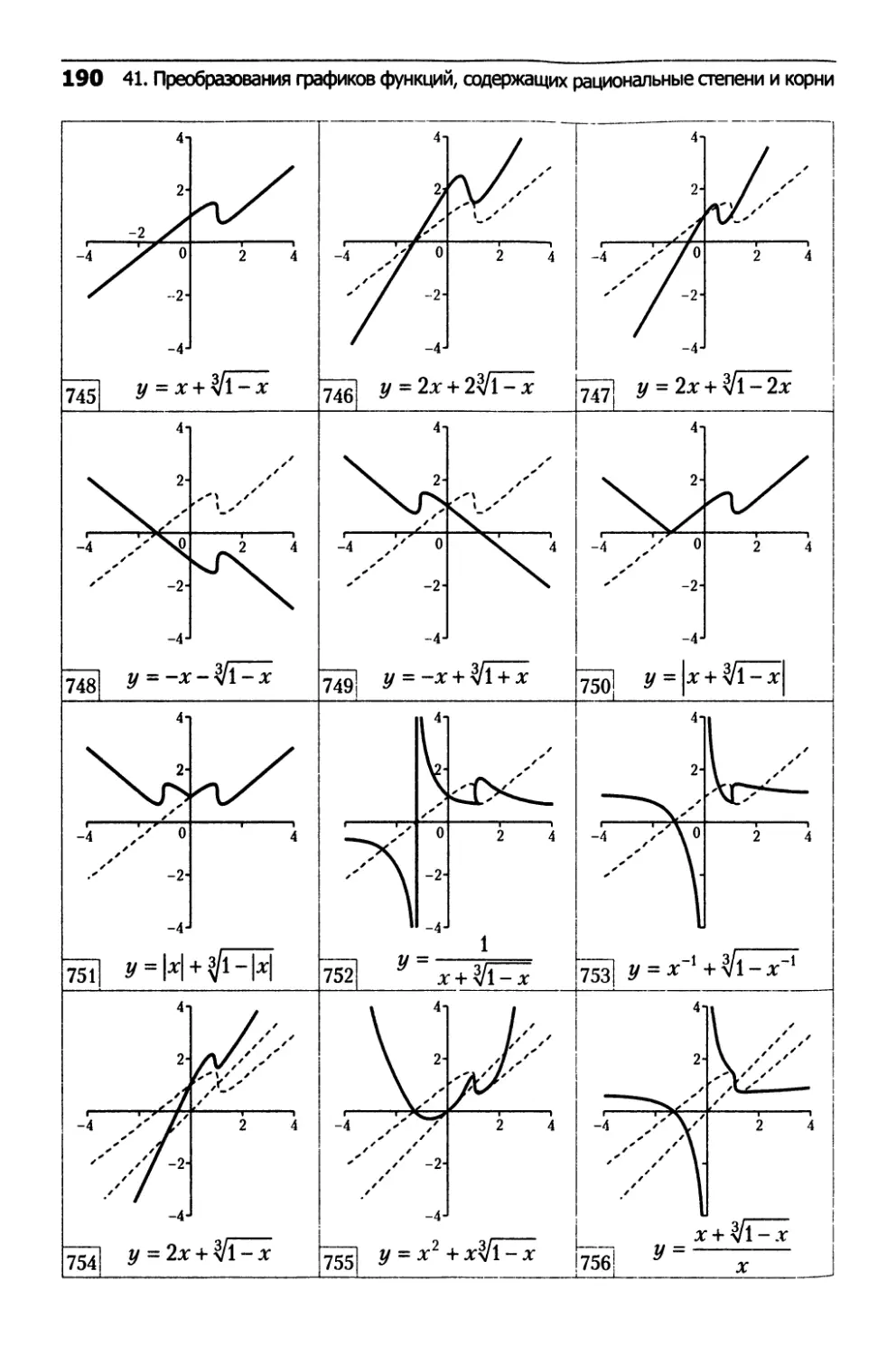
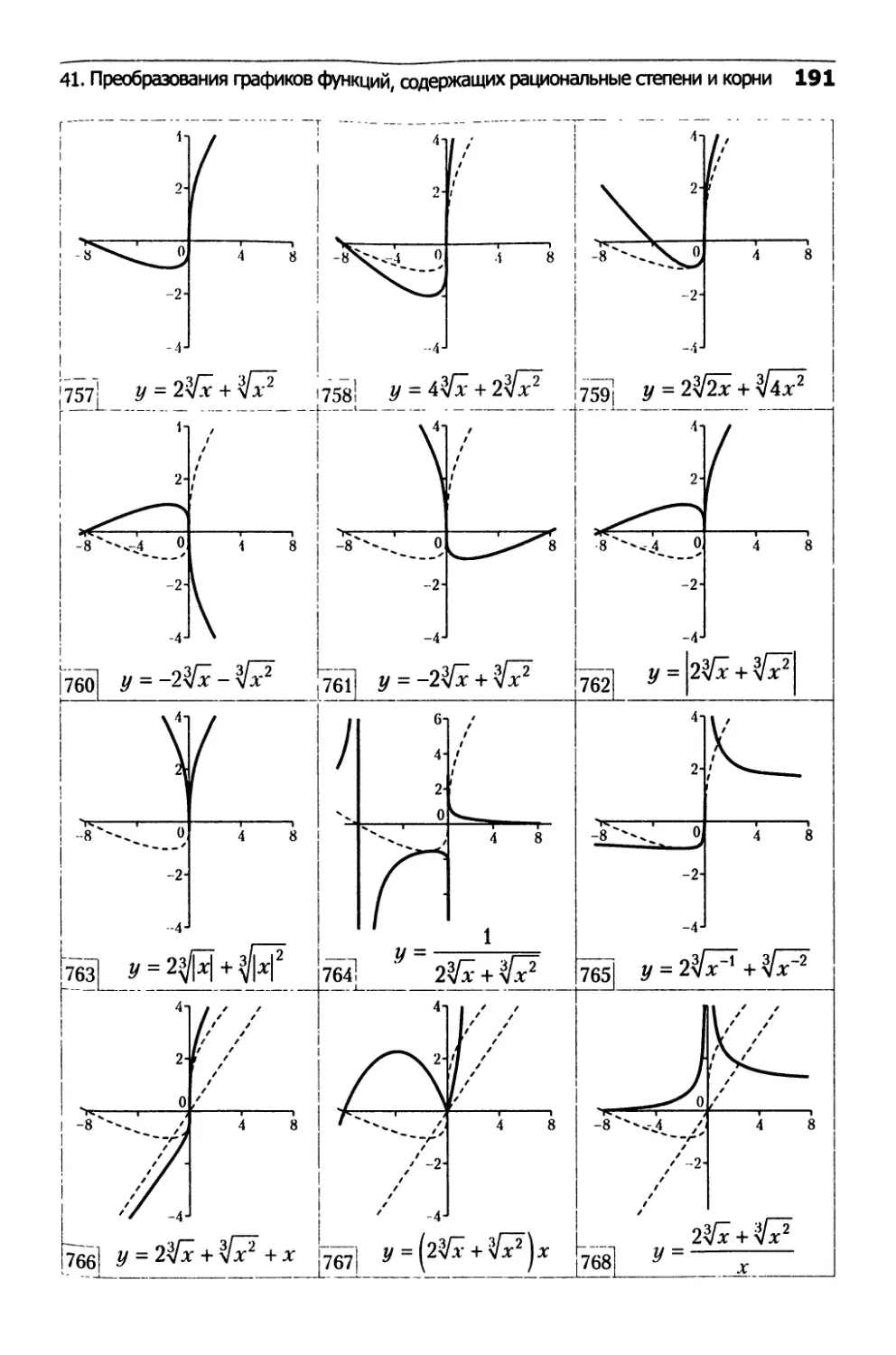
41.	Преобразования
графиков функций,
содержащих рациональные степени и корни...........182
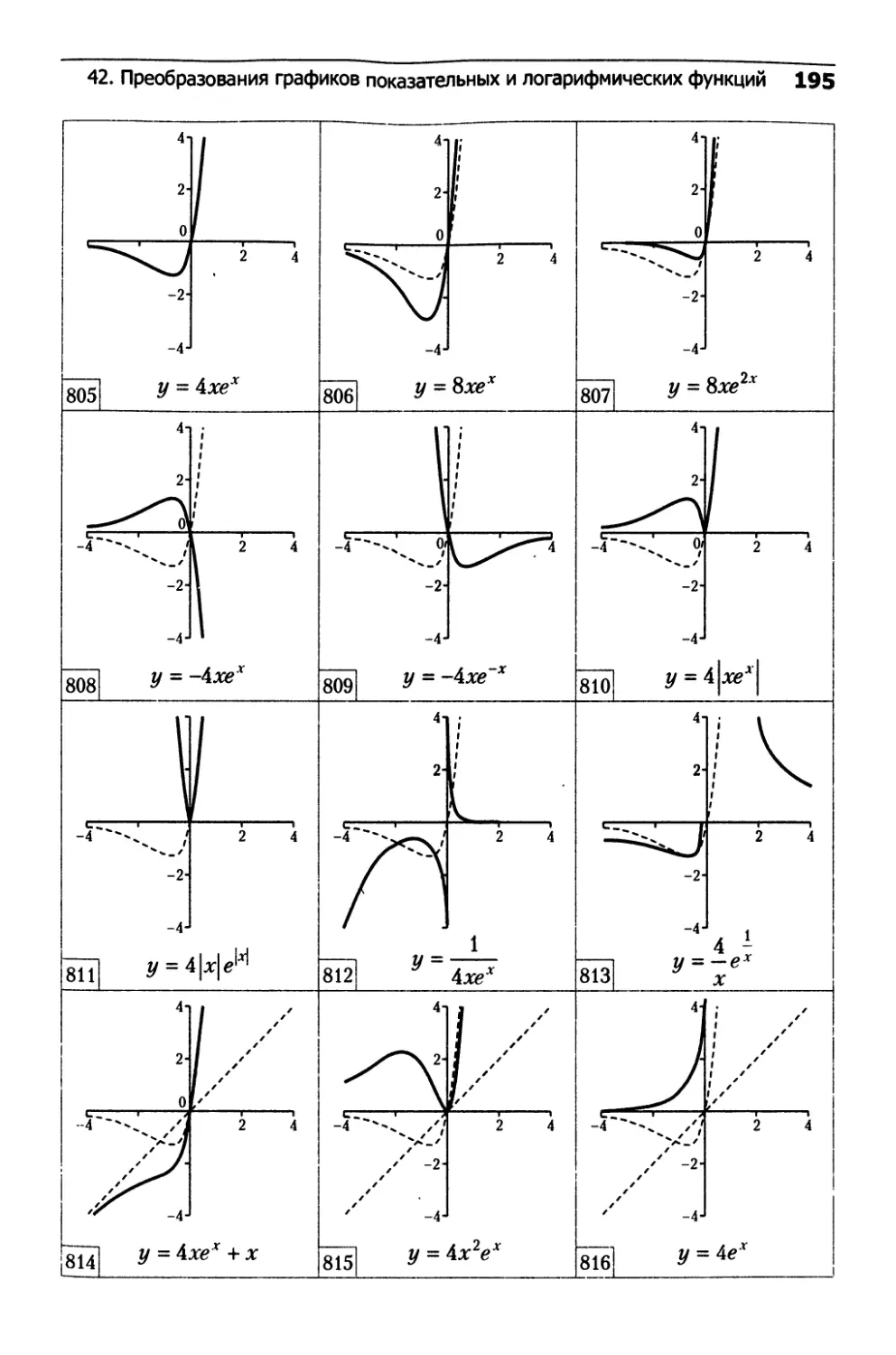
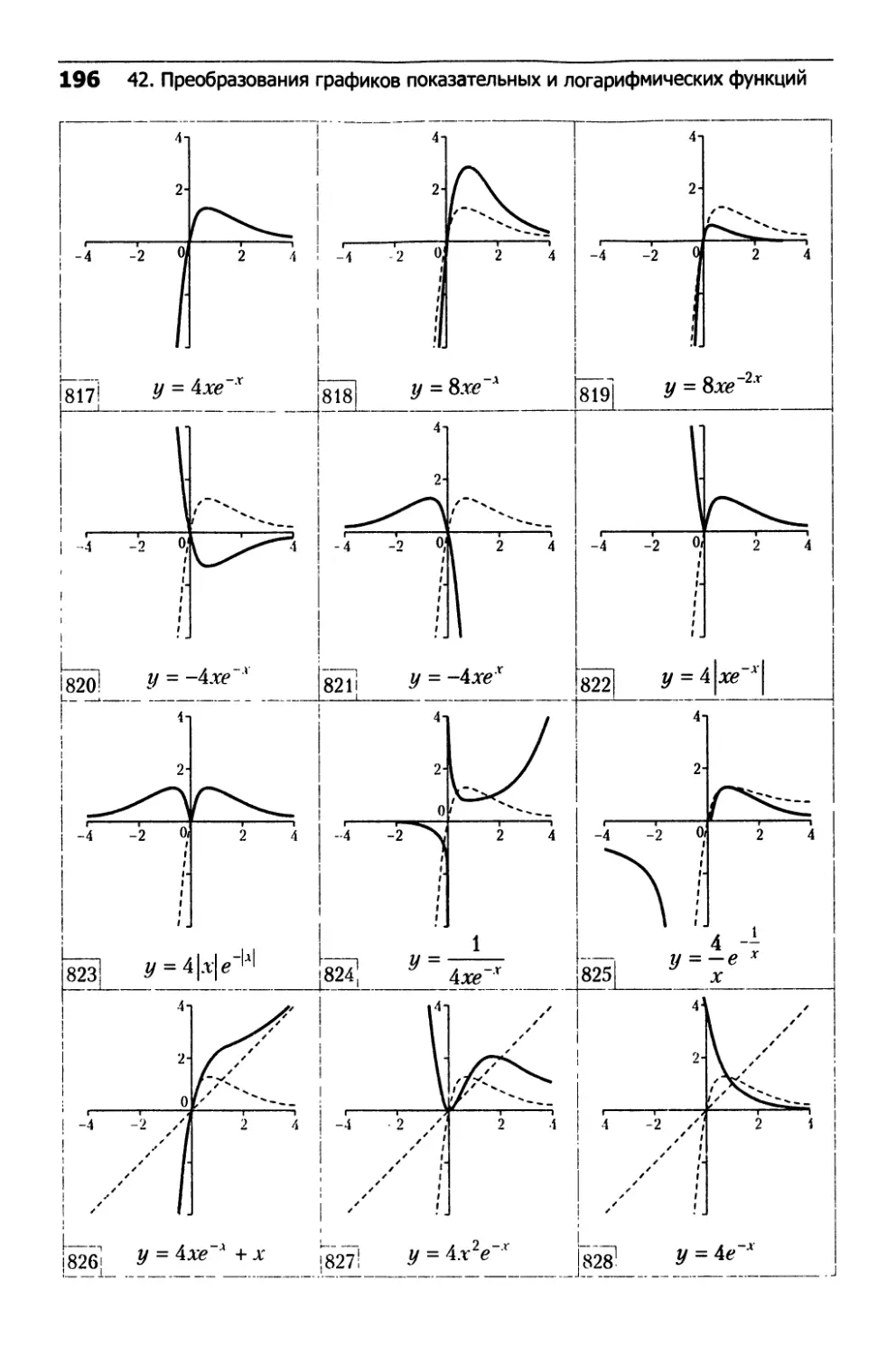
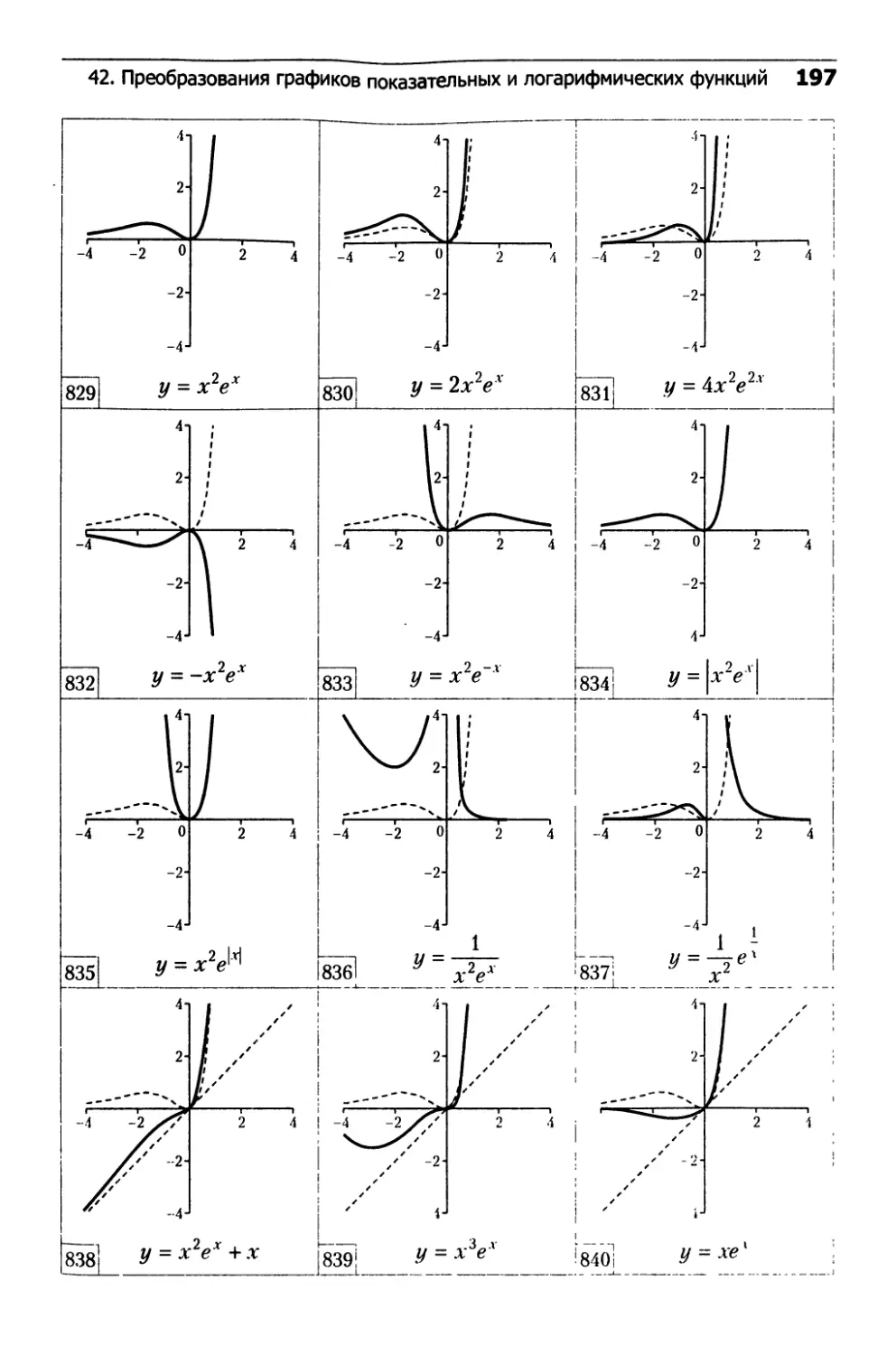
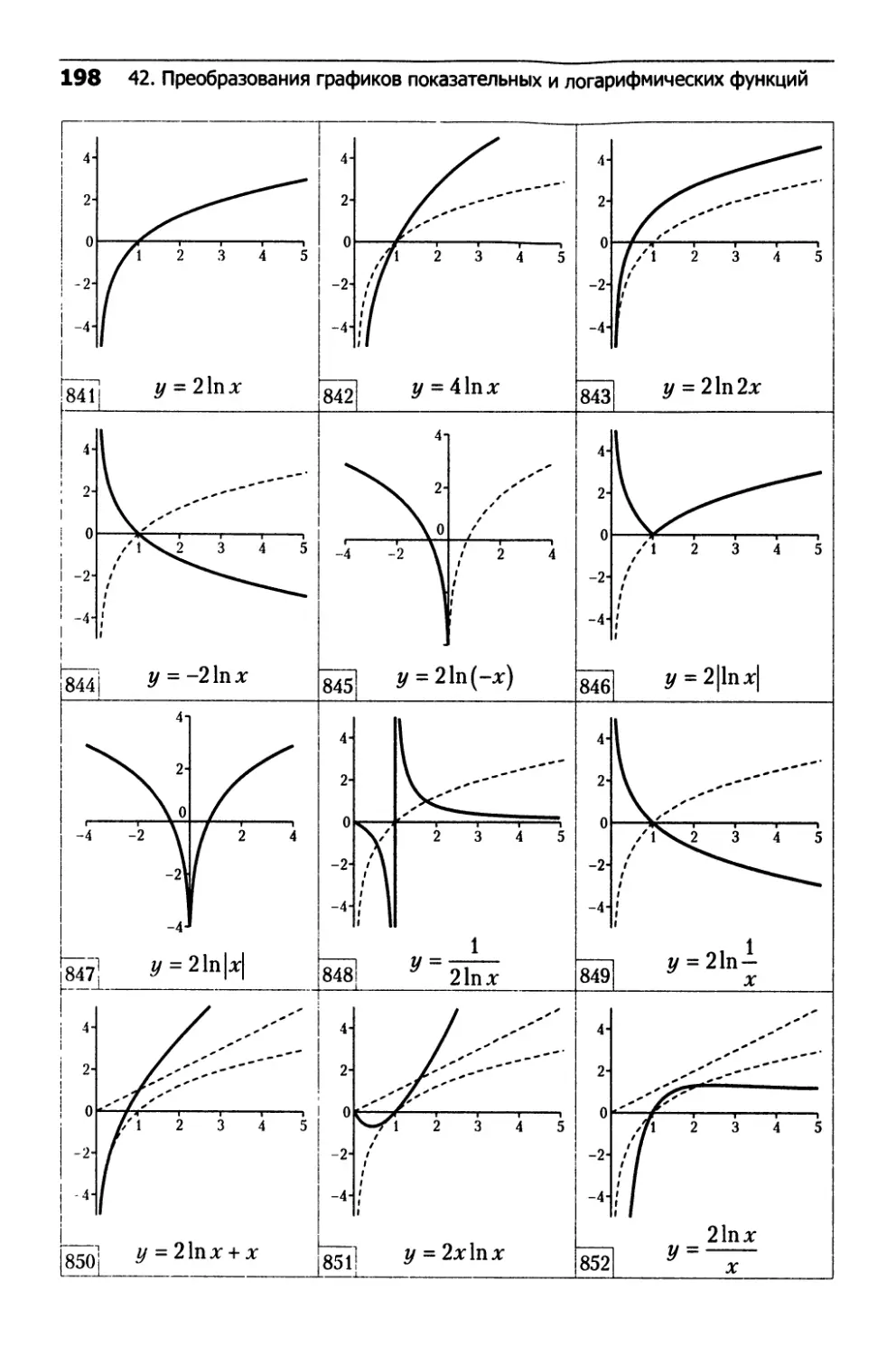
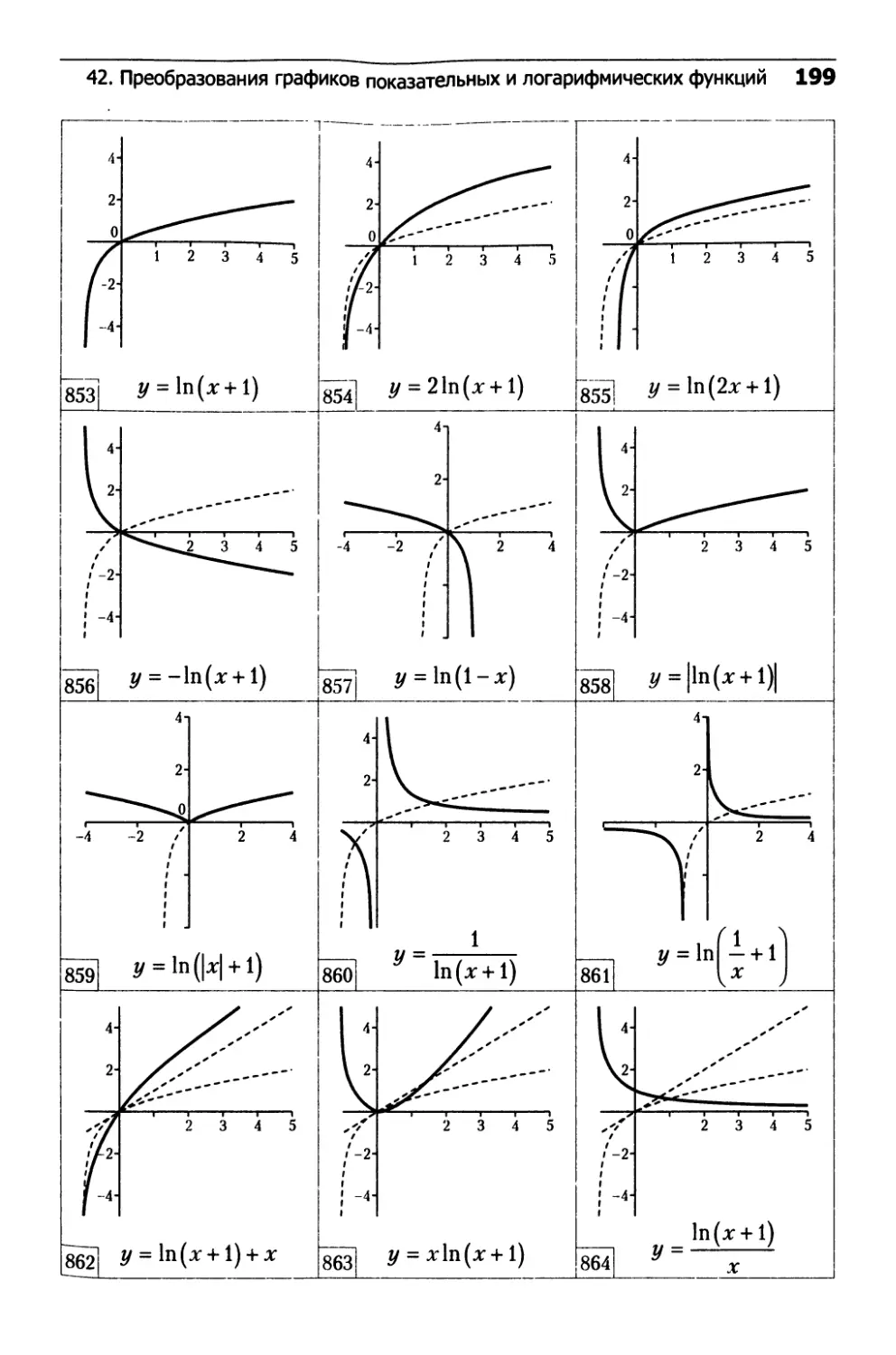
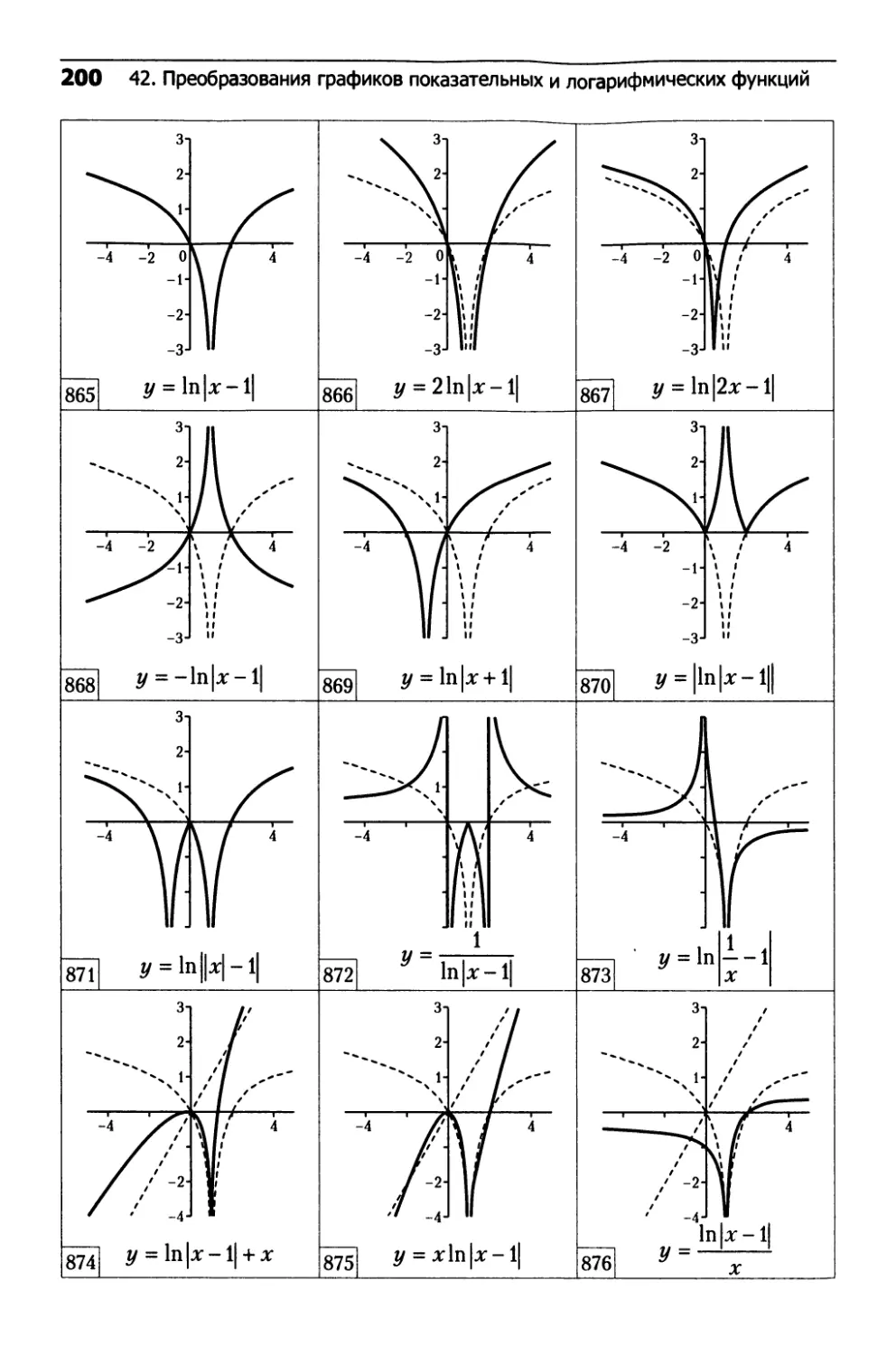
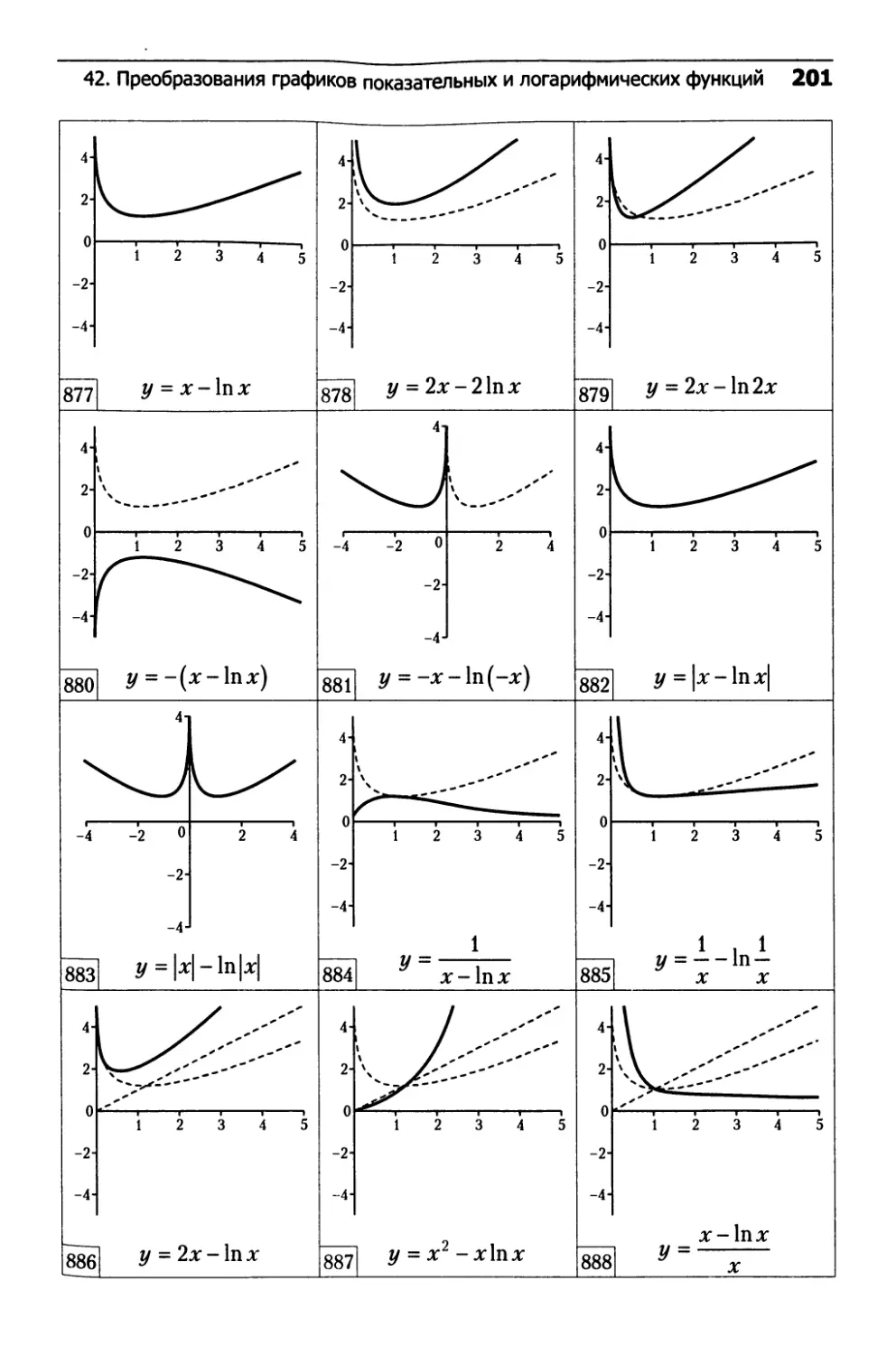
42.	Преобразования графиков
показательных и логарифмических функций...........192
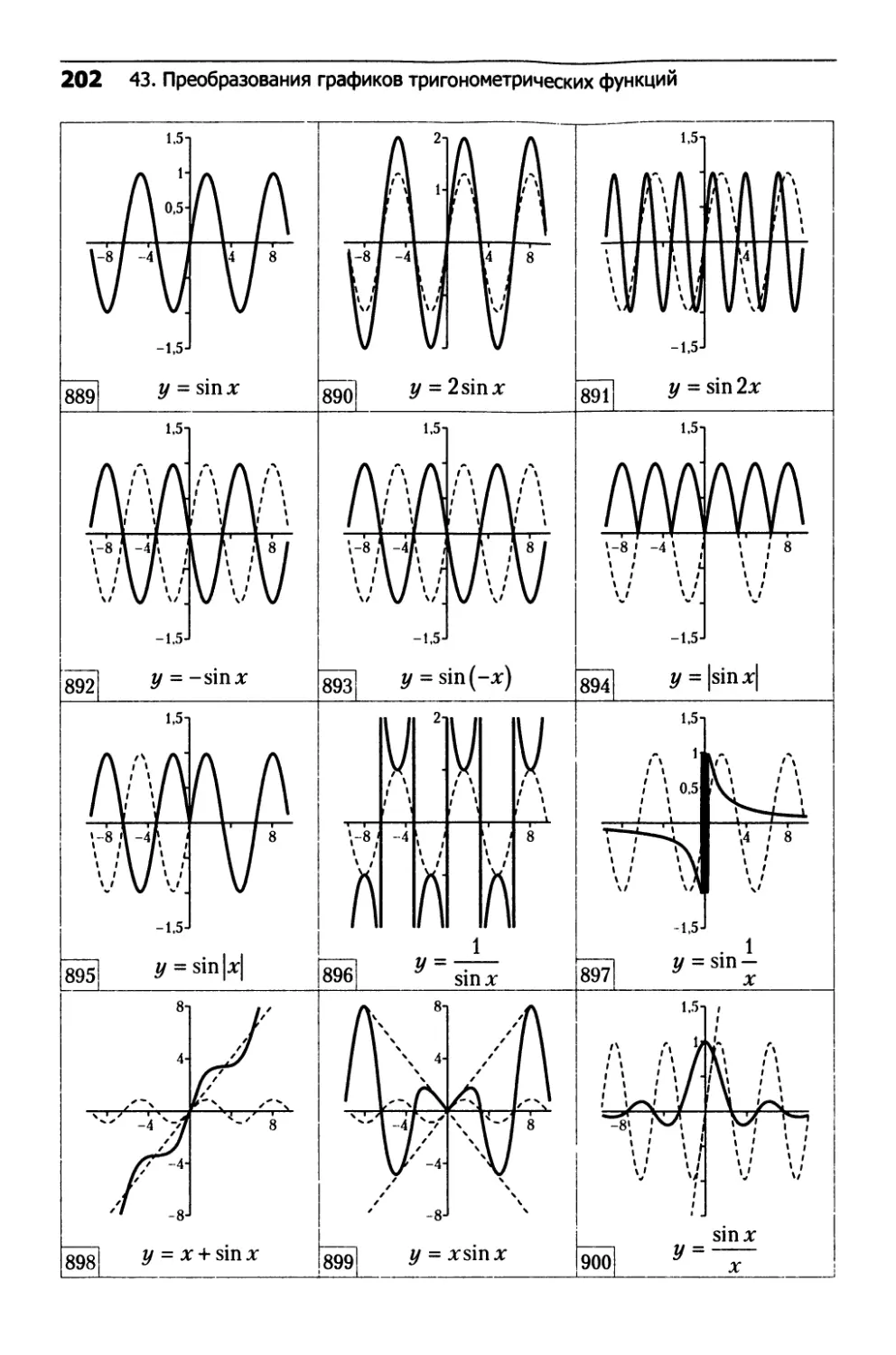
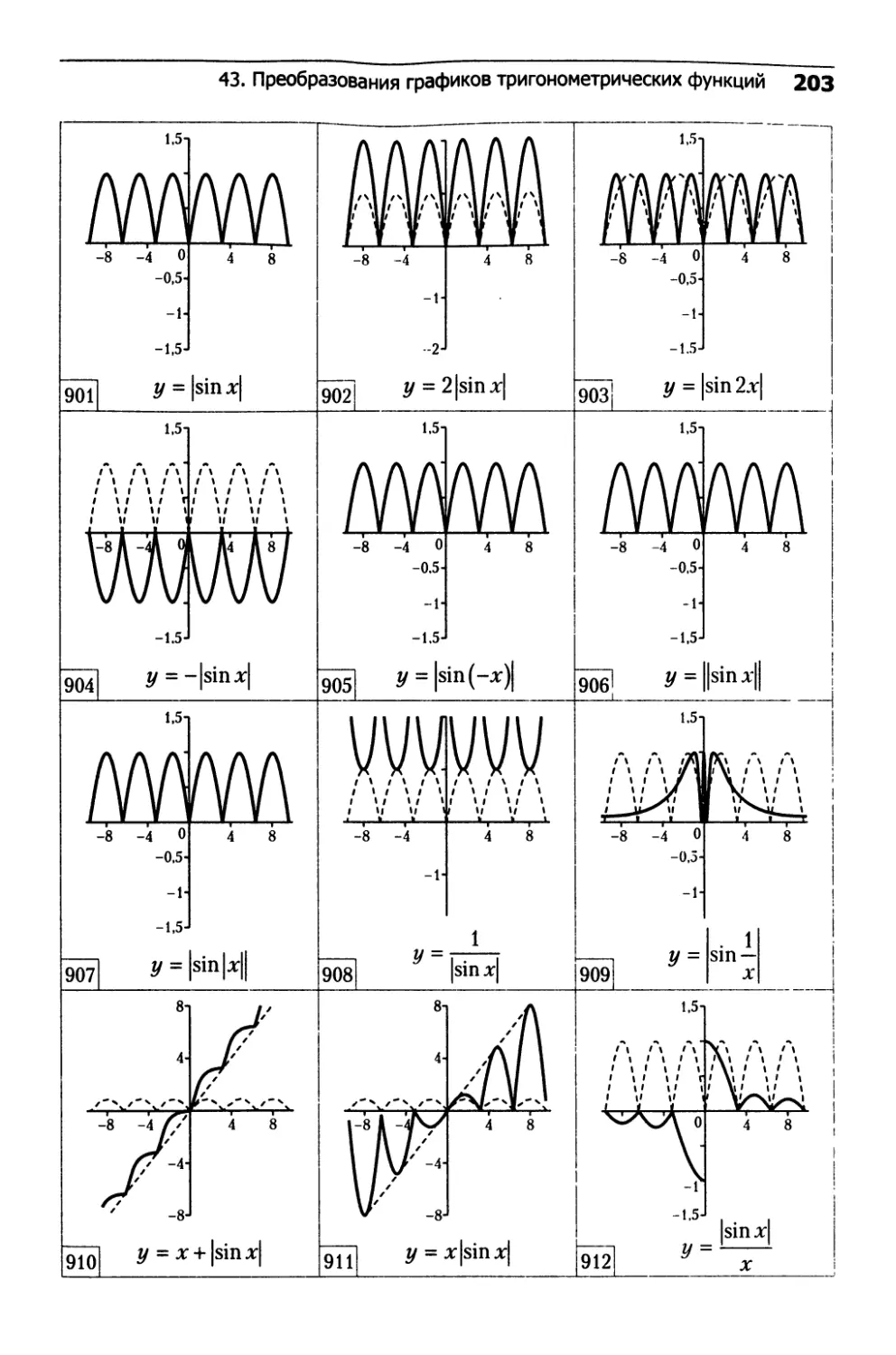
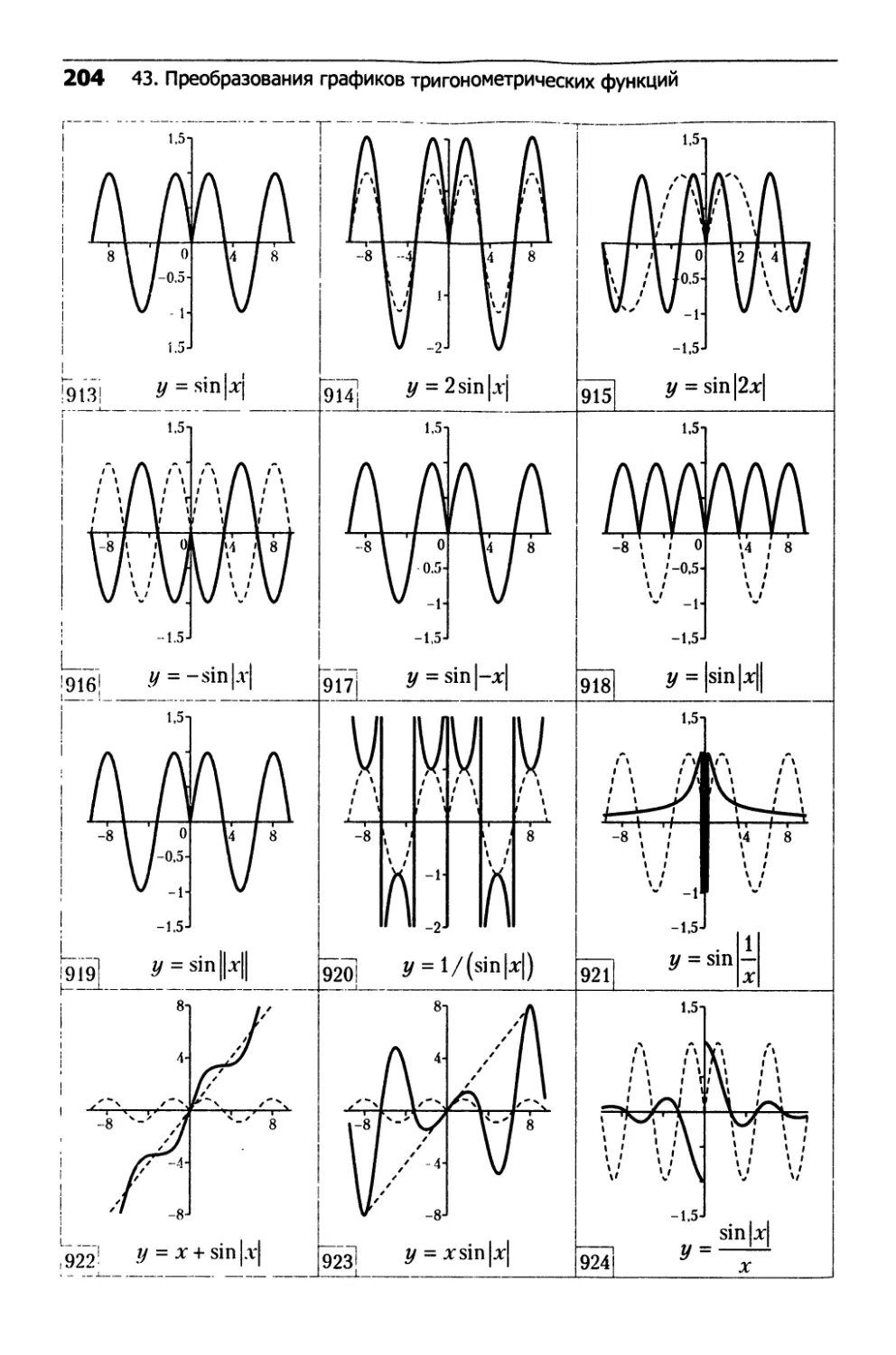
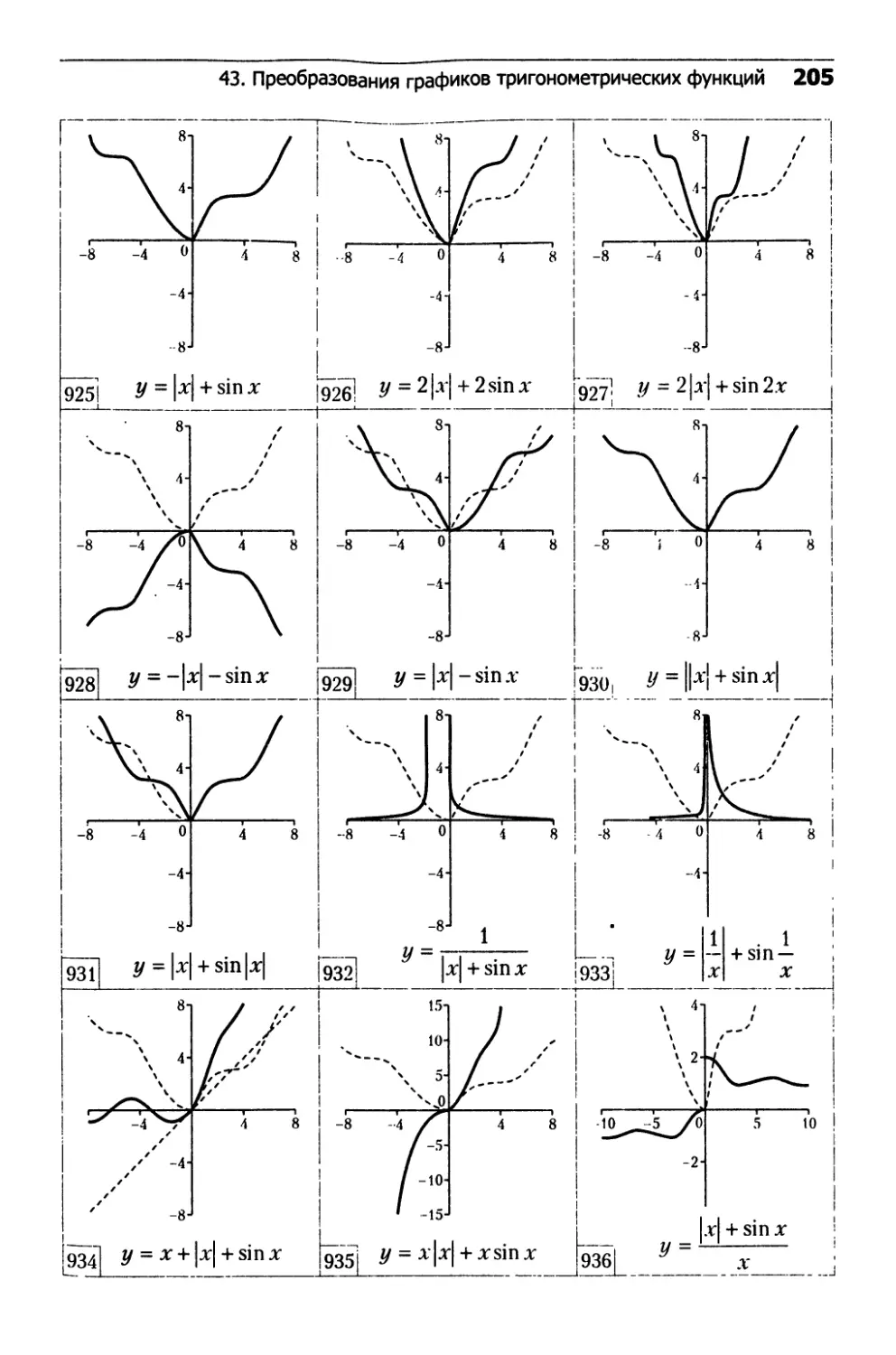
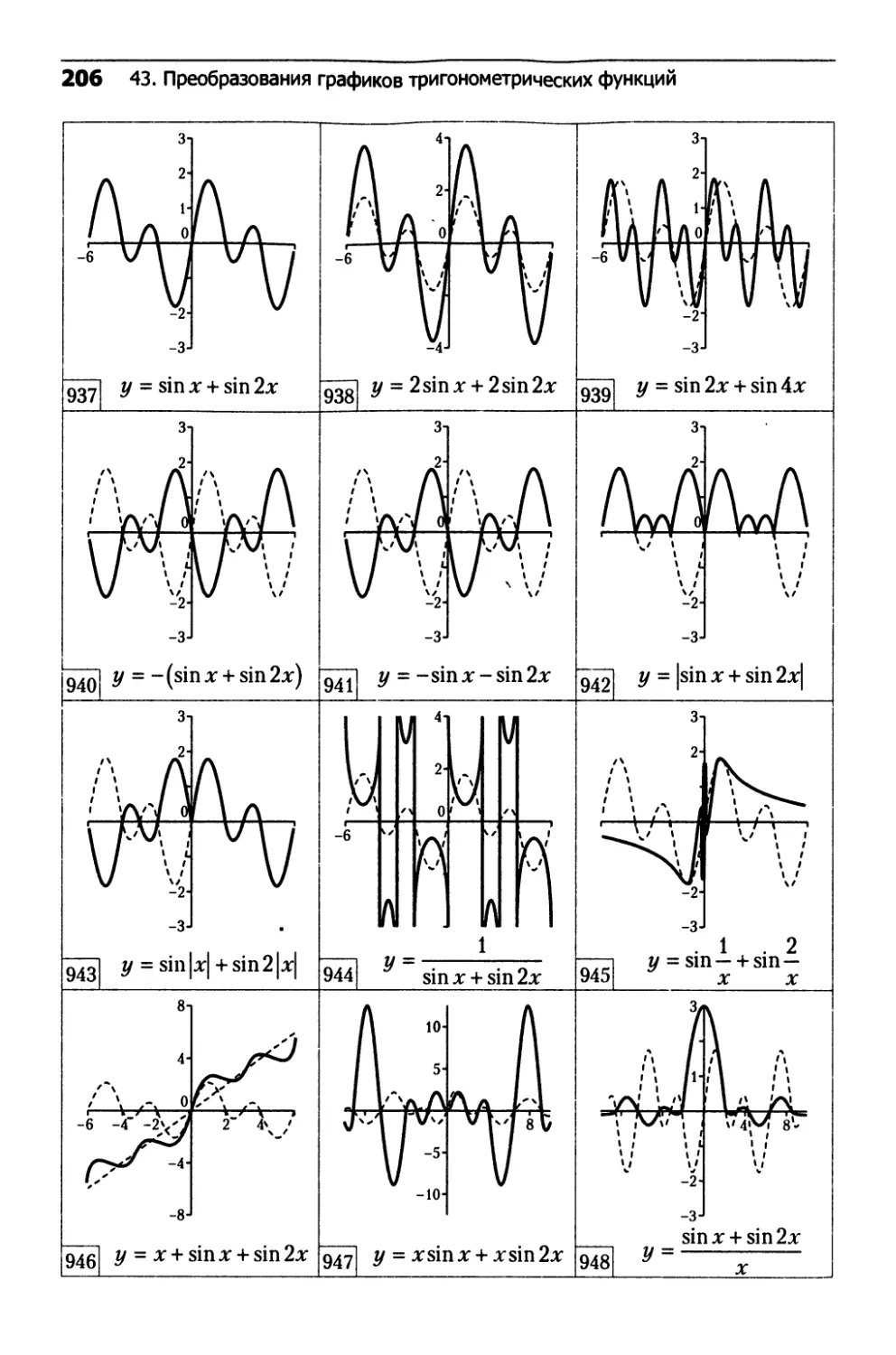
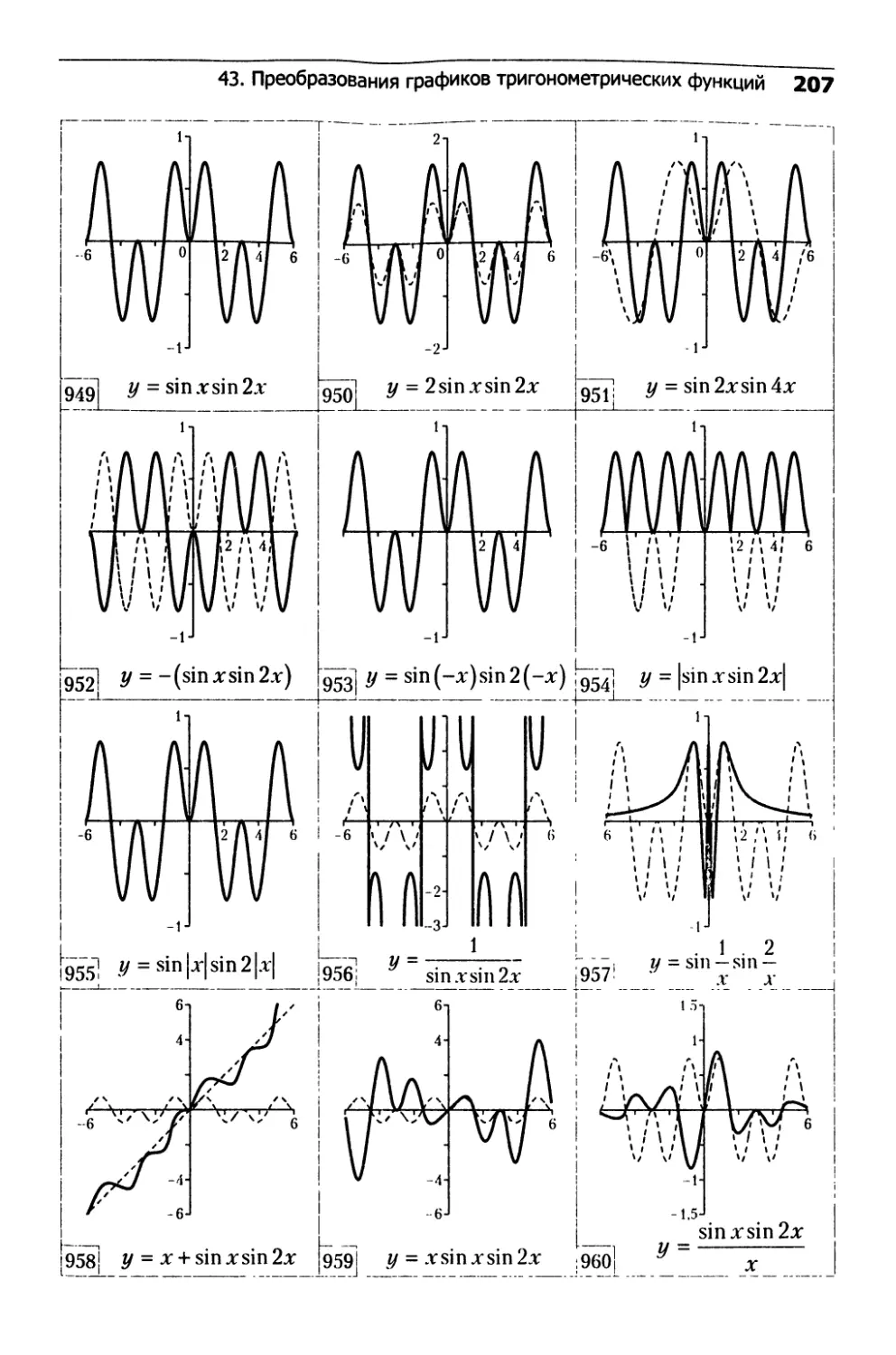
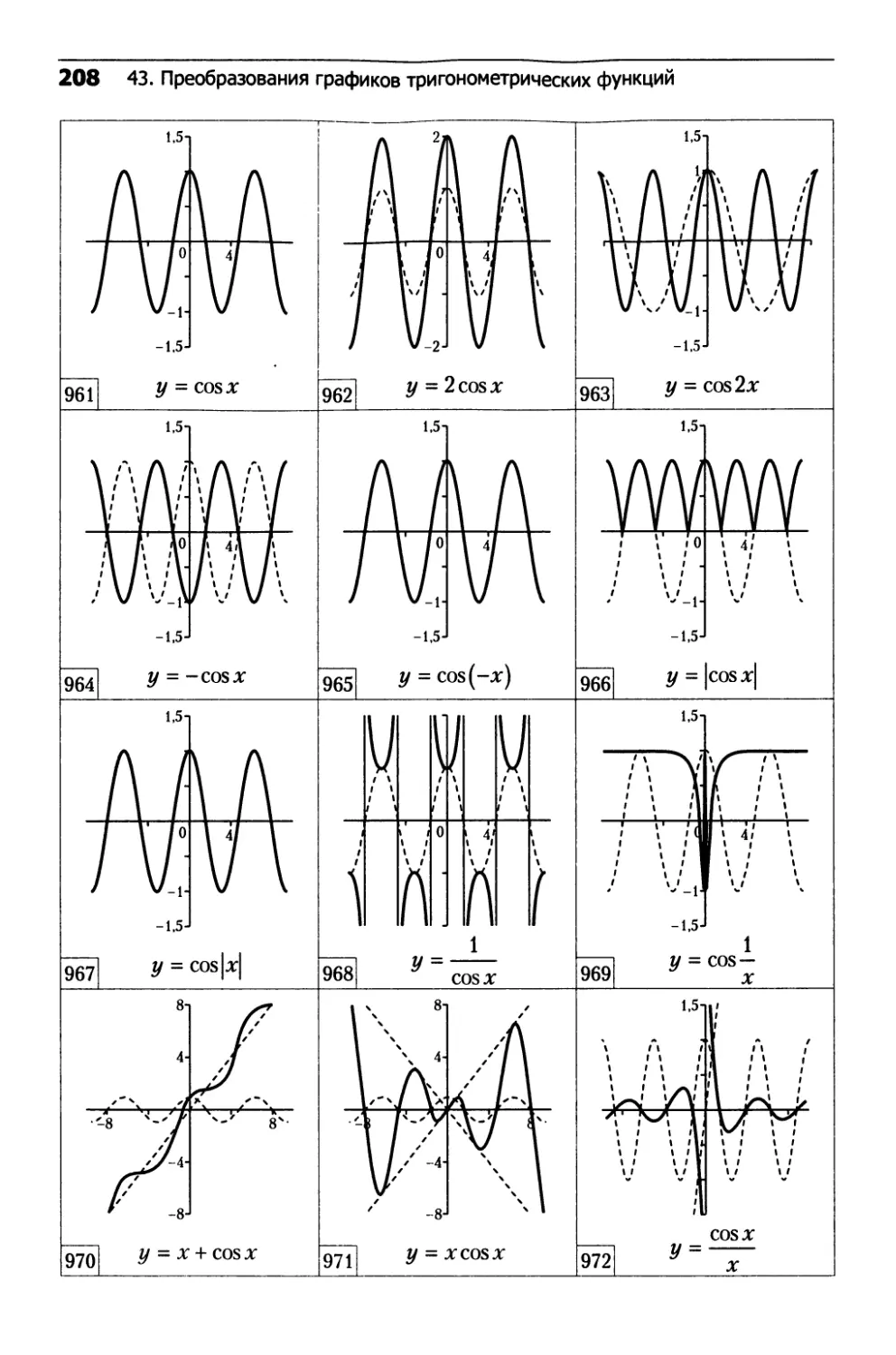
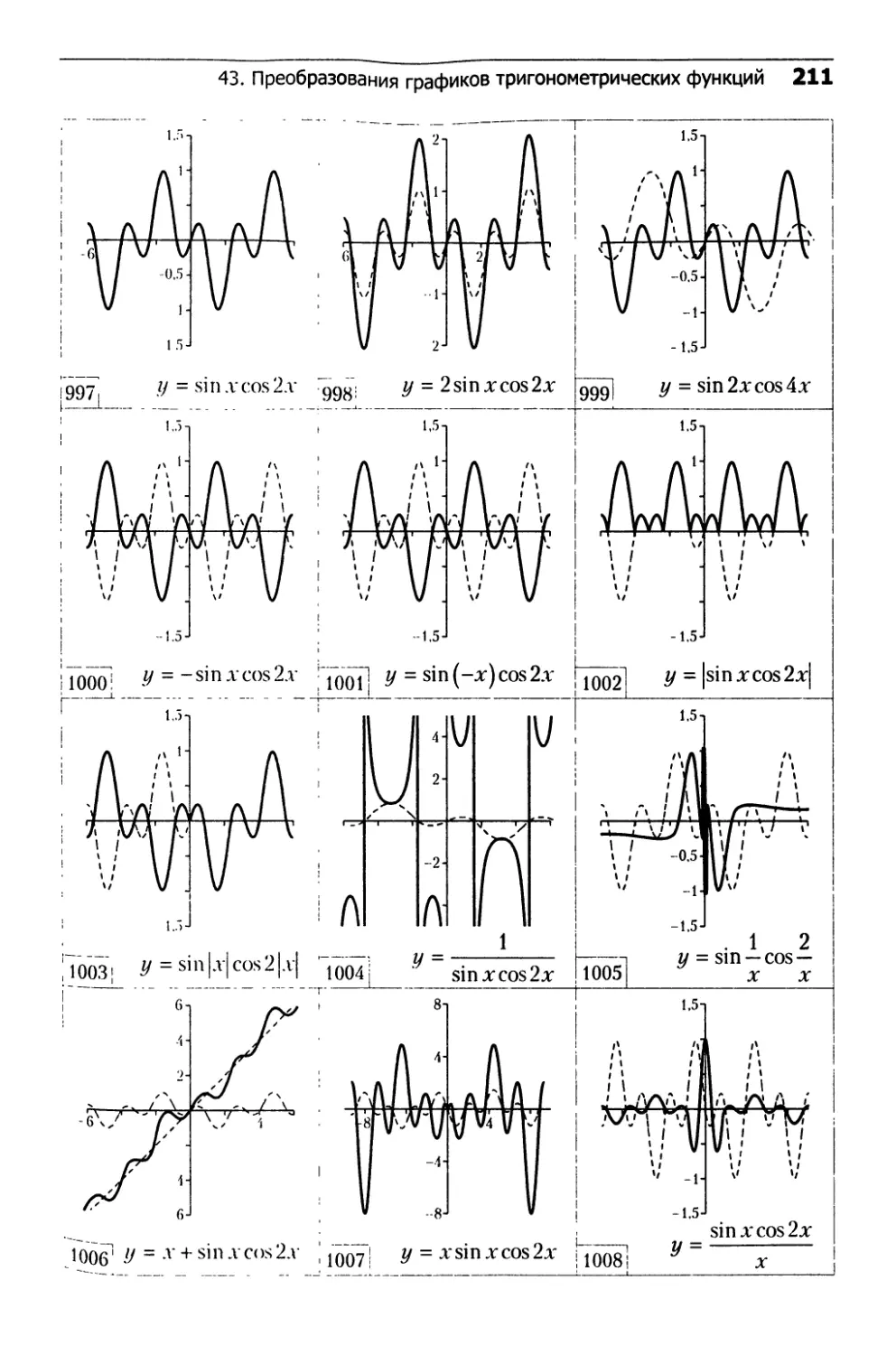
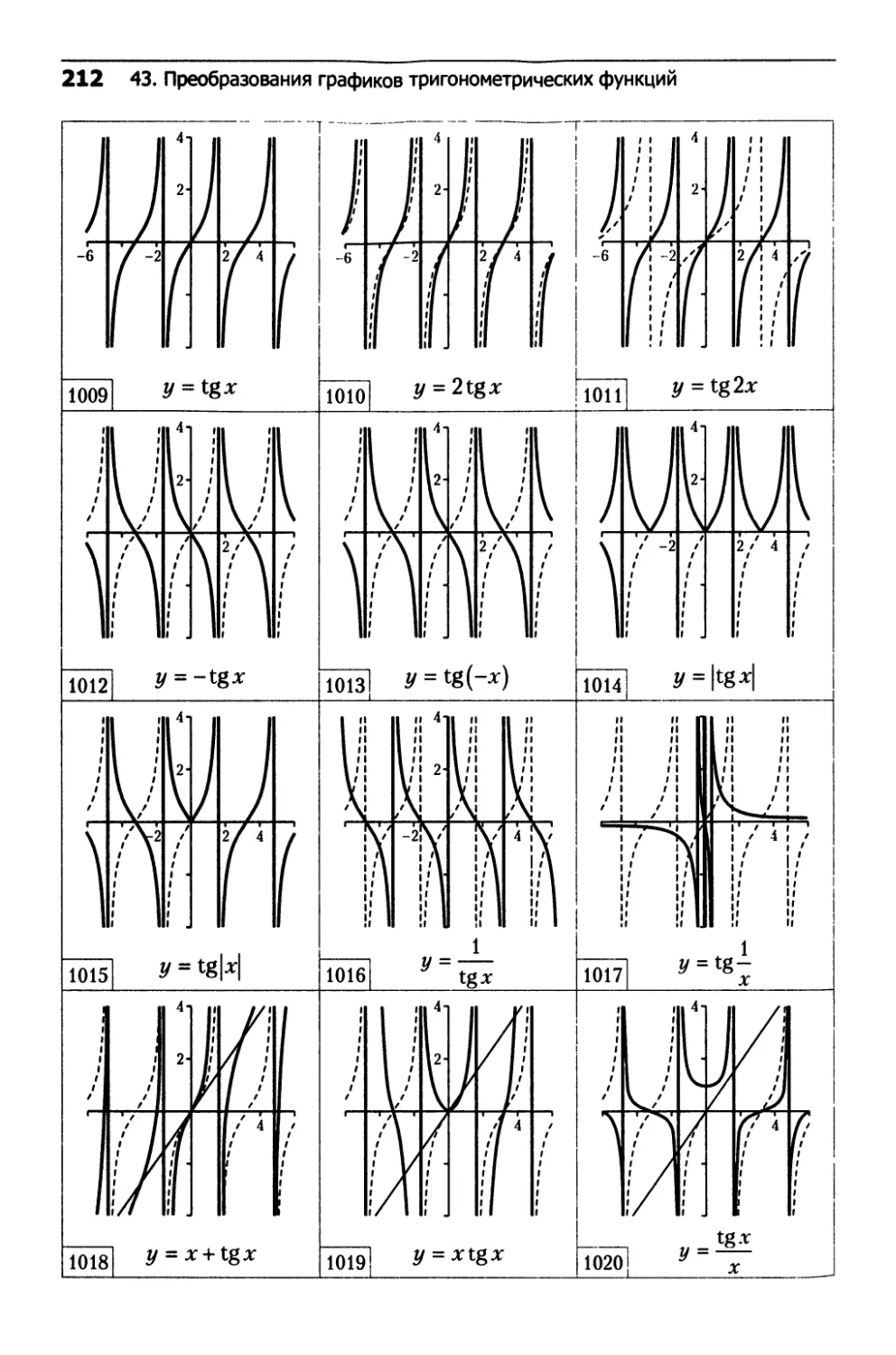
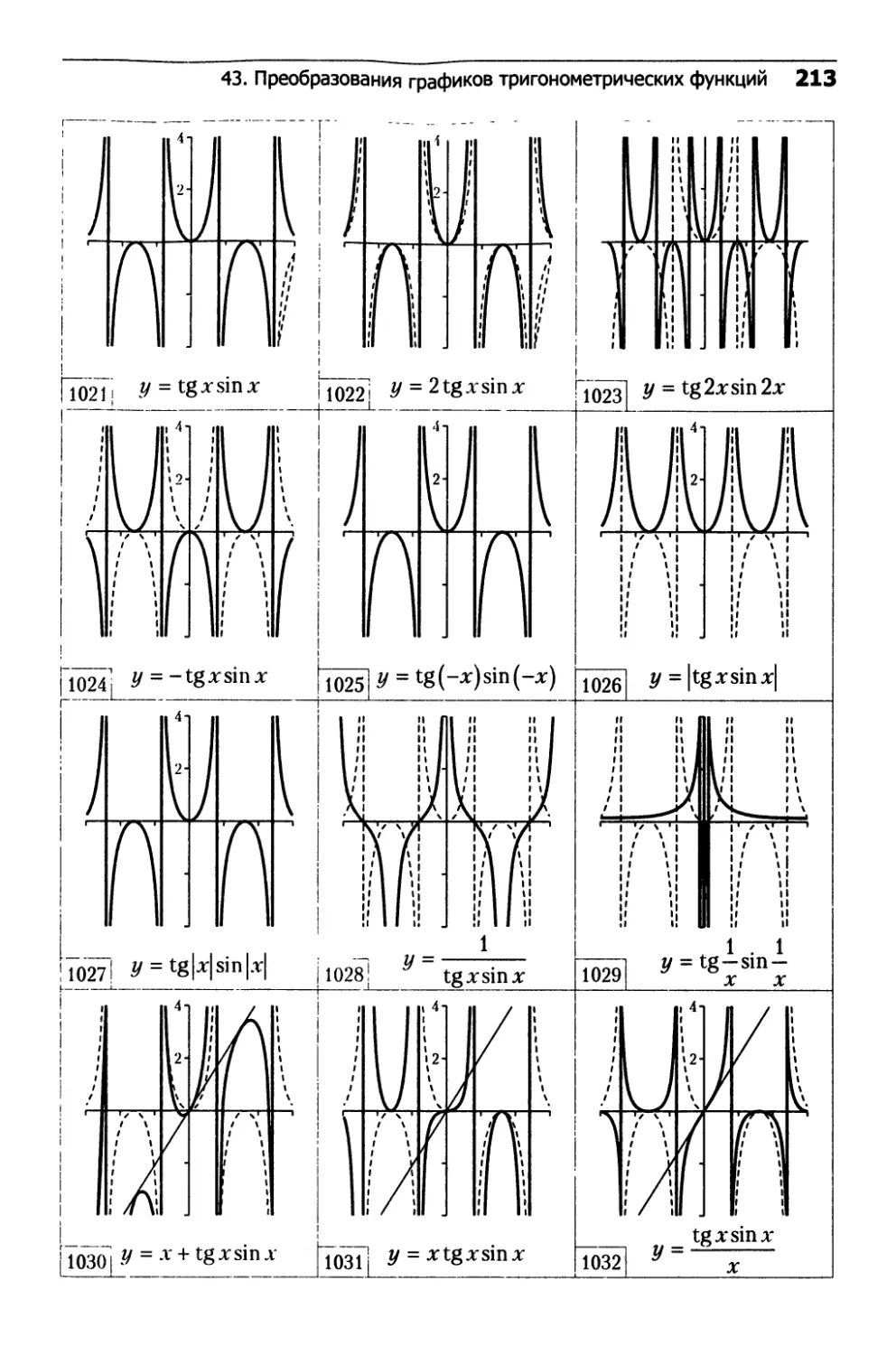
43.	Преобразования графиков
тригонометрических функций........................202
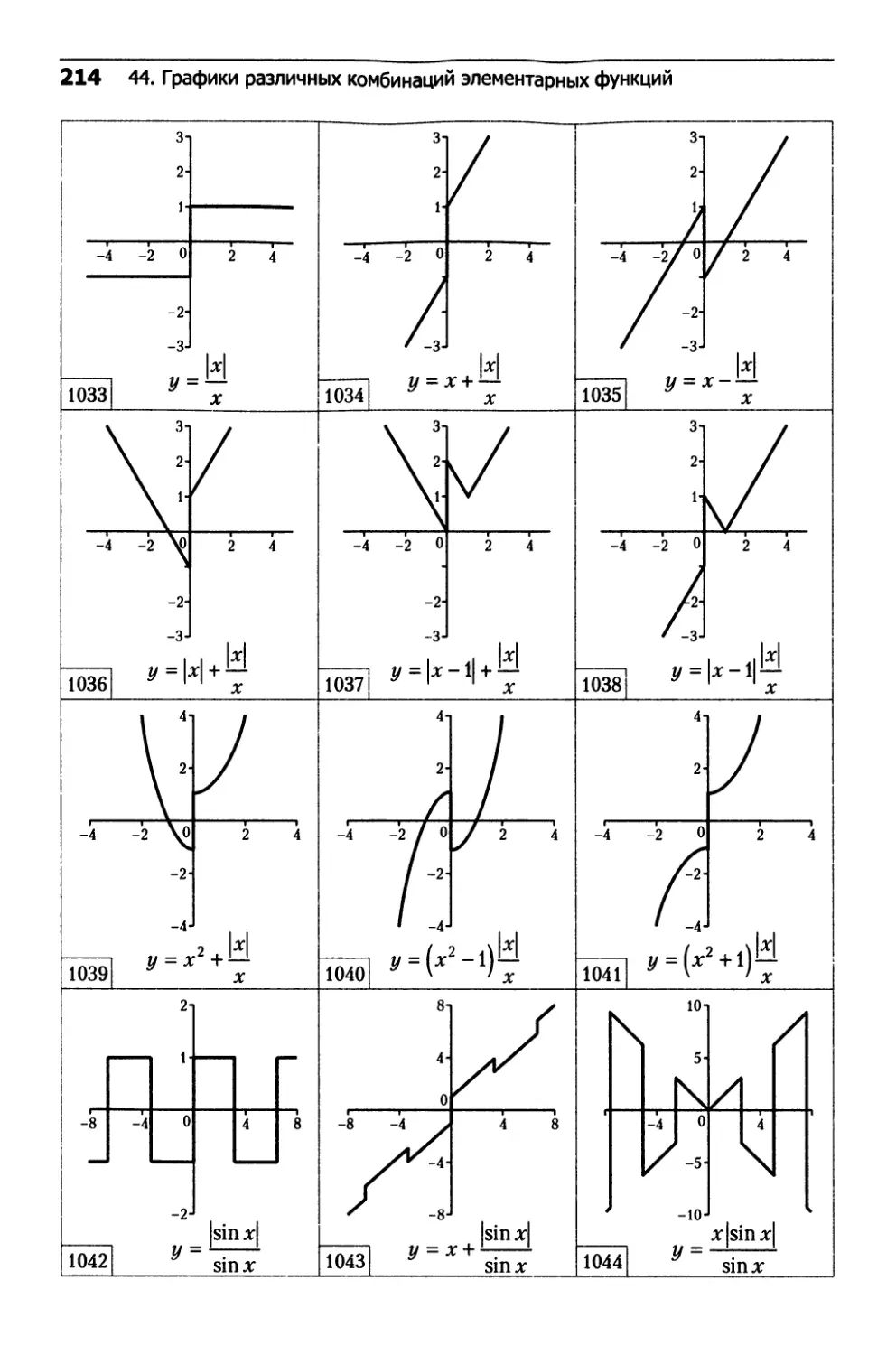
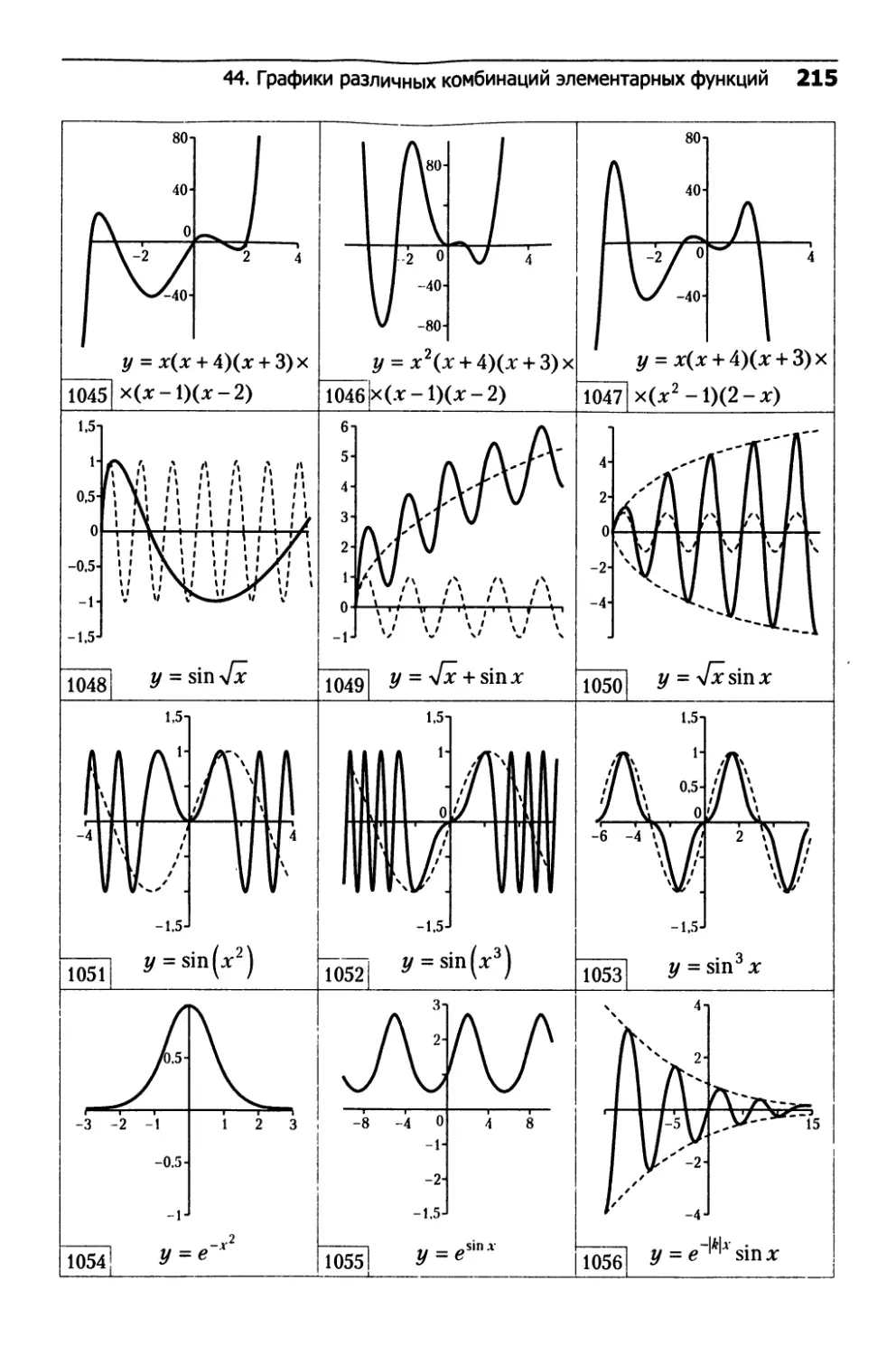
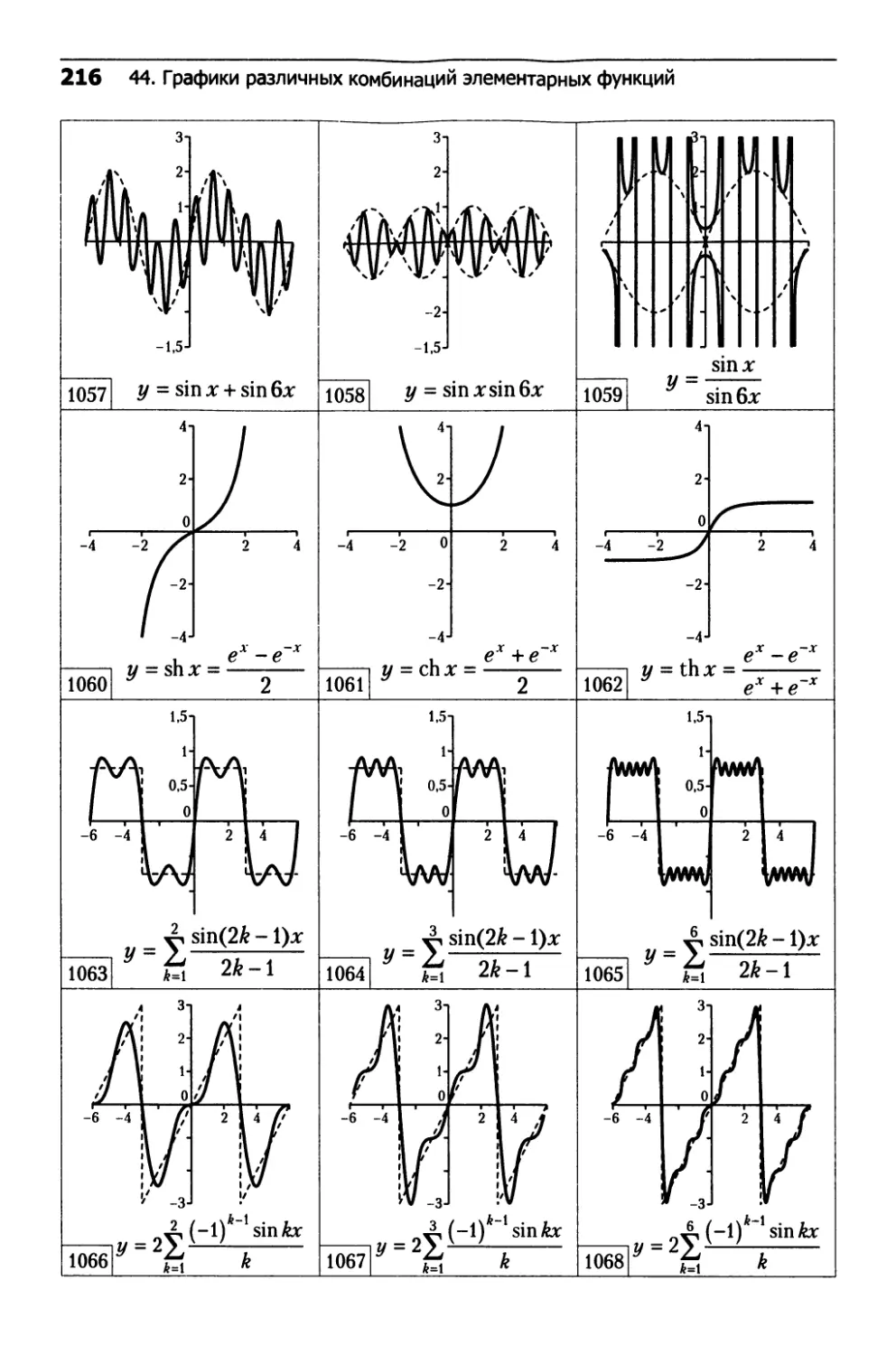
44.	Графики различных комбинаций
элементарных функций..............................214
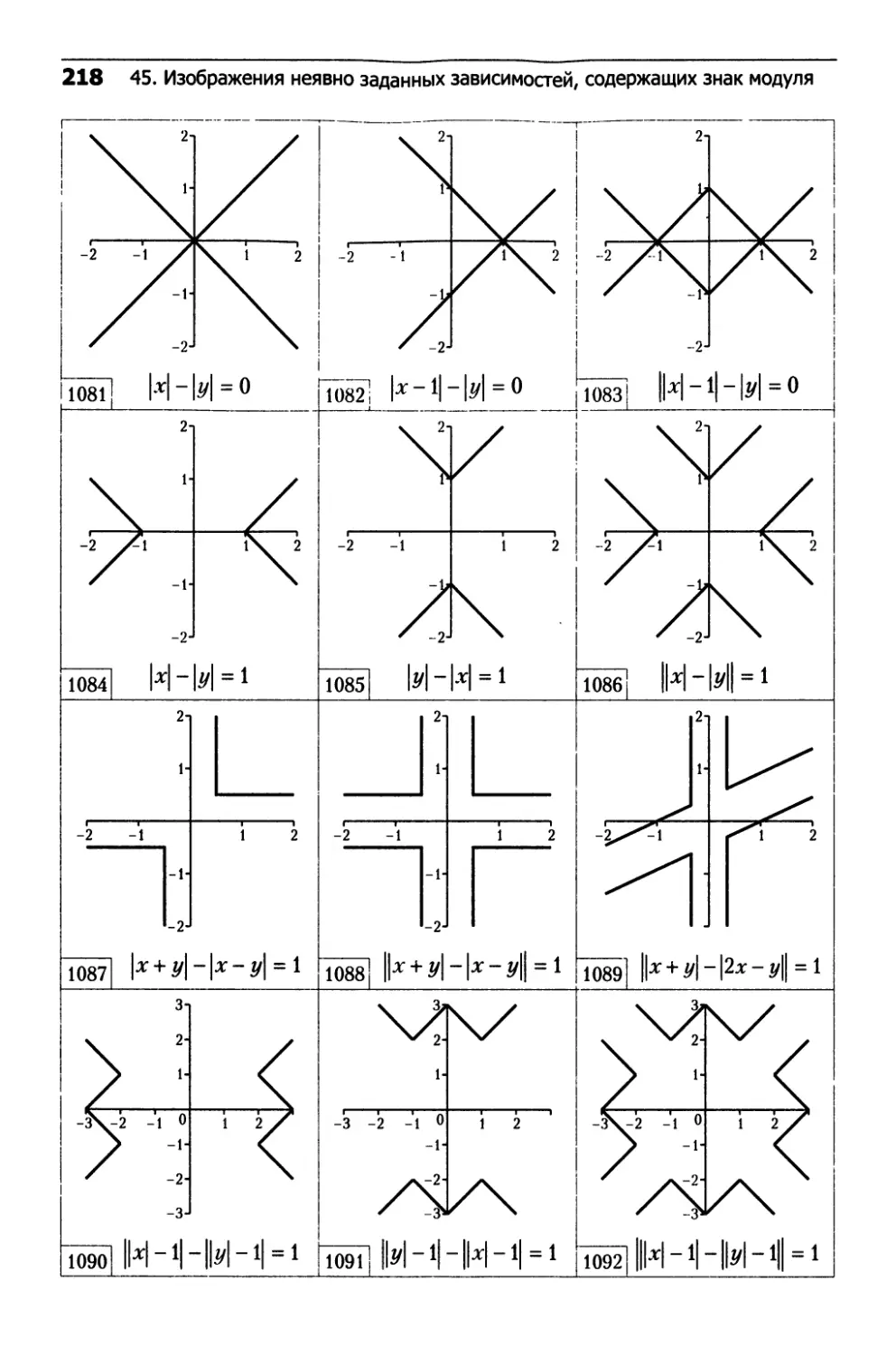
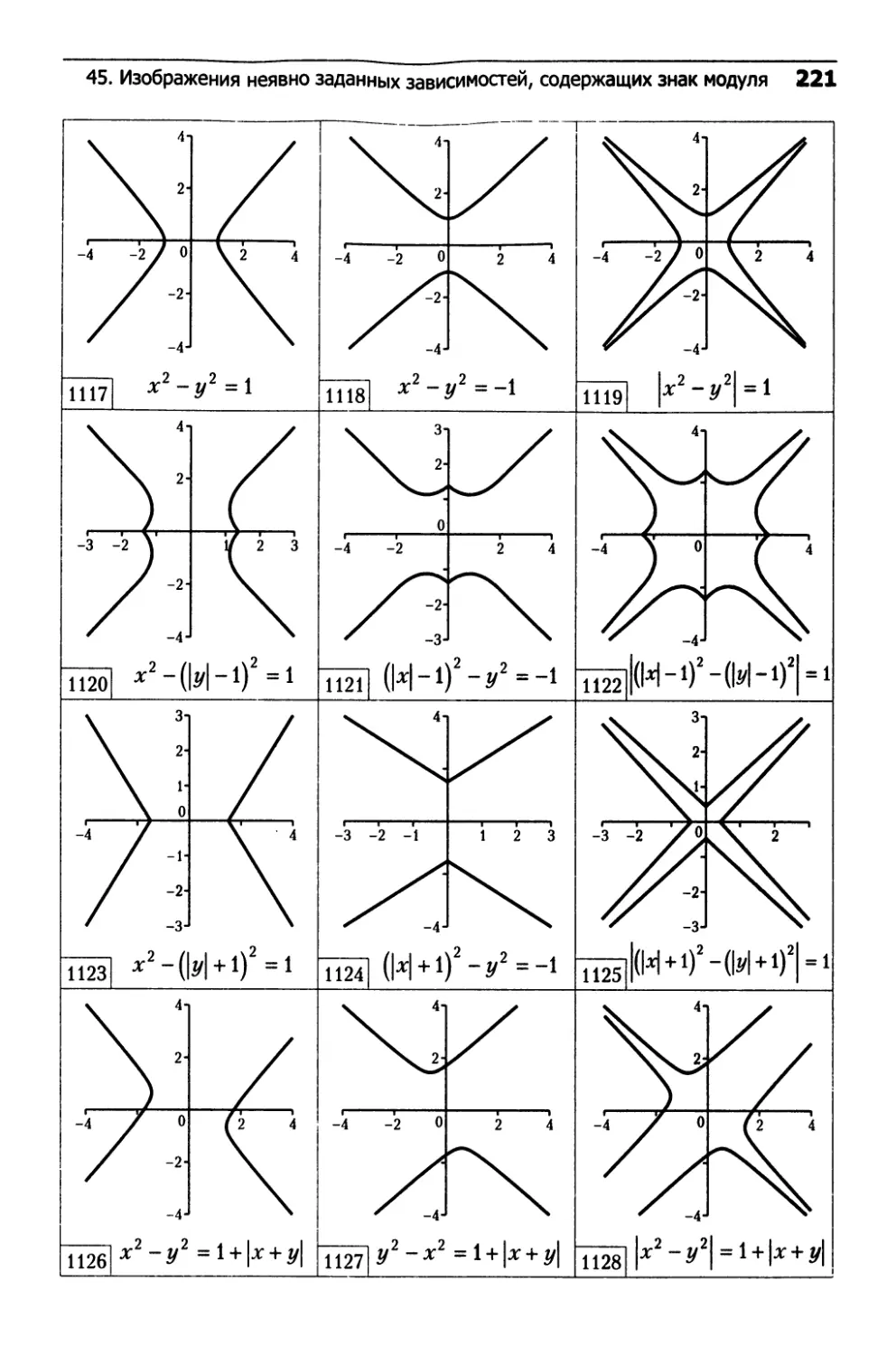
45.	Изображения неявно заданных зависимостей,
содержащих знак модуля............................217
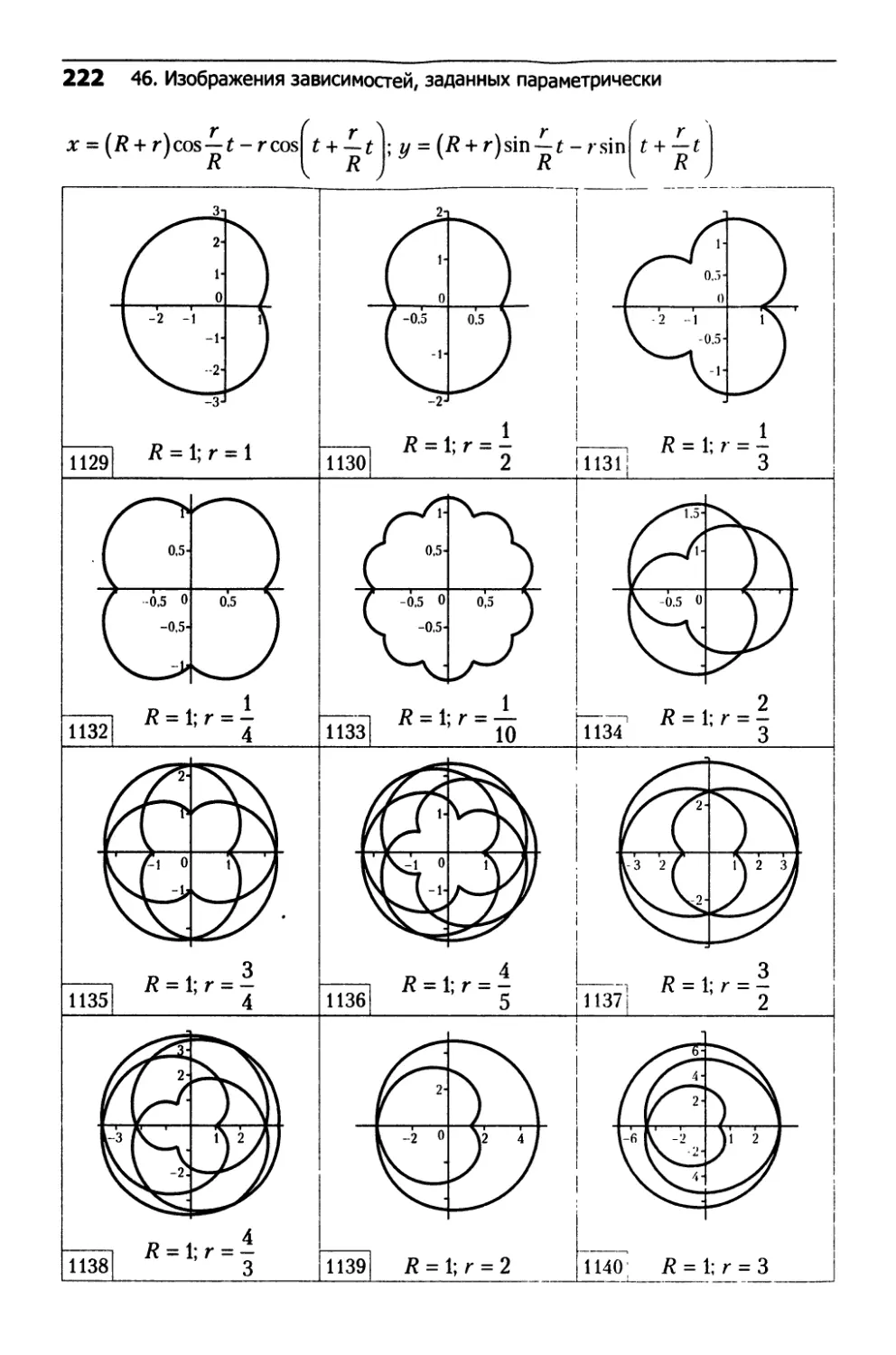
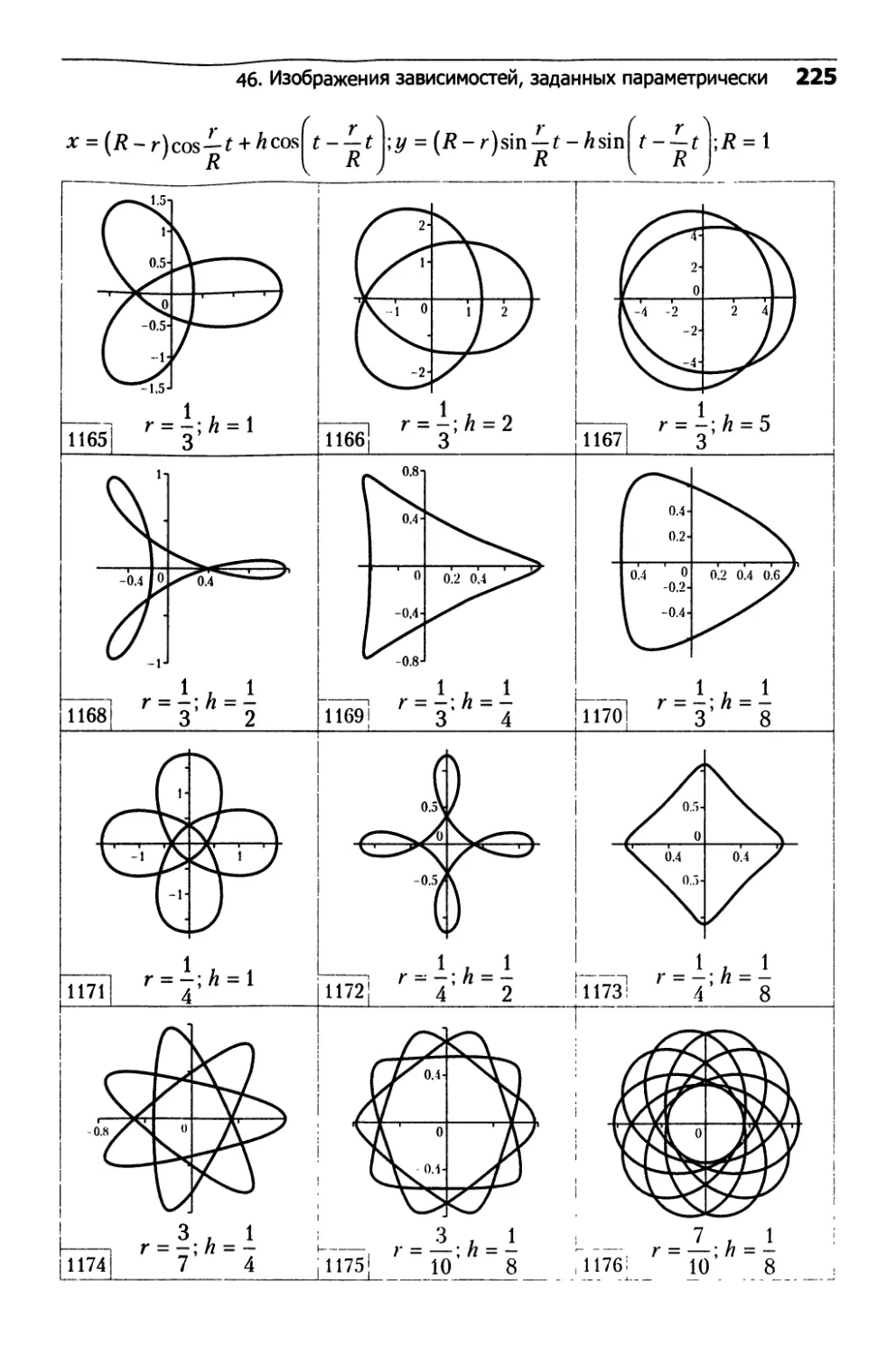
46.	Изображения зависимостей,
заданных параметрически...........................222
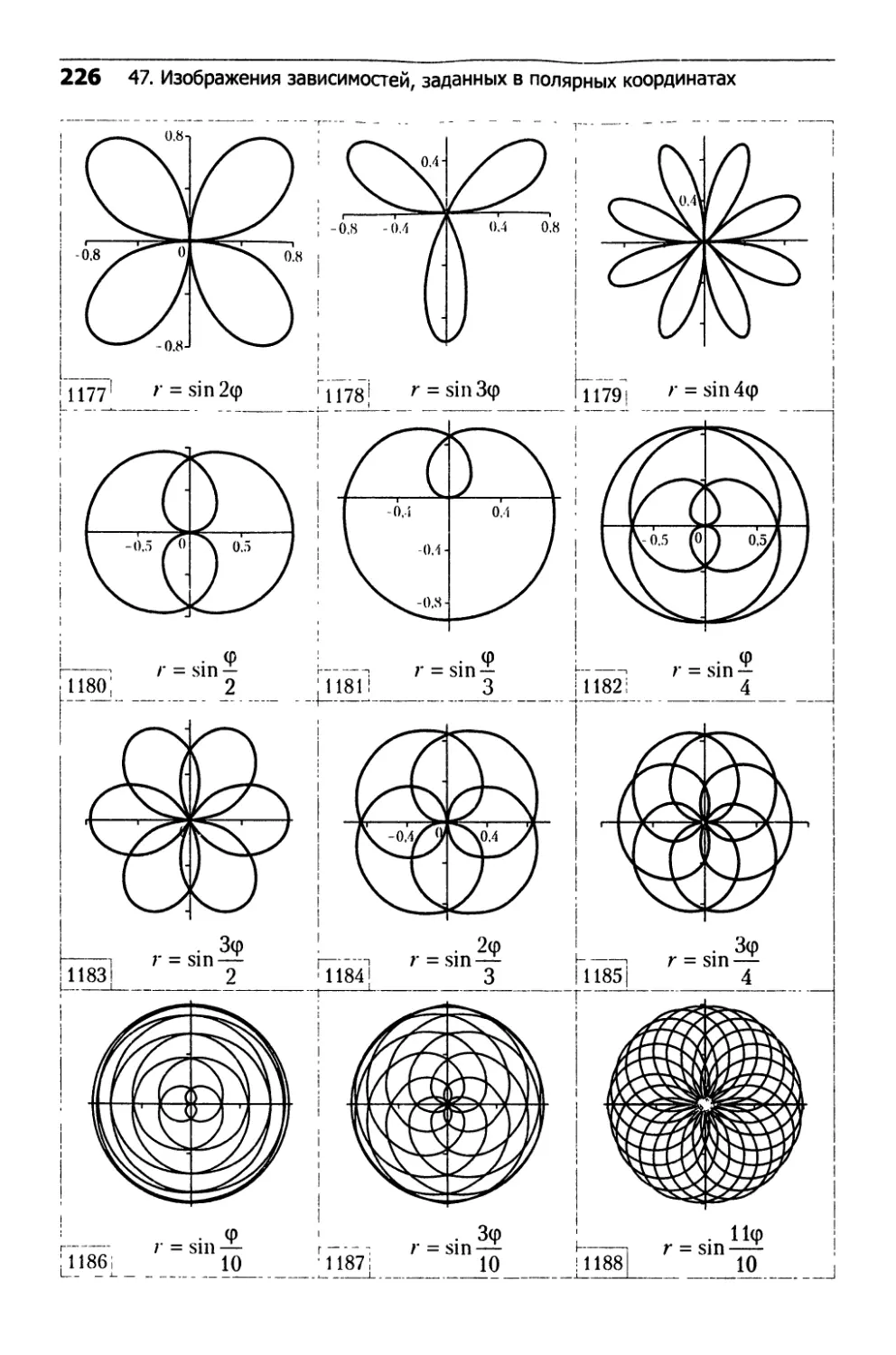
47.	Изображения зависимостей,
заданных в полярных координатах...................226
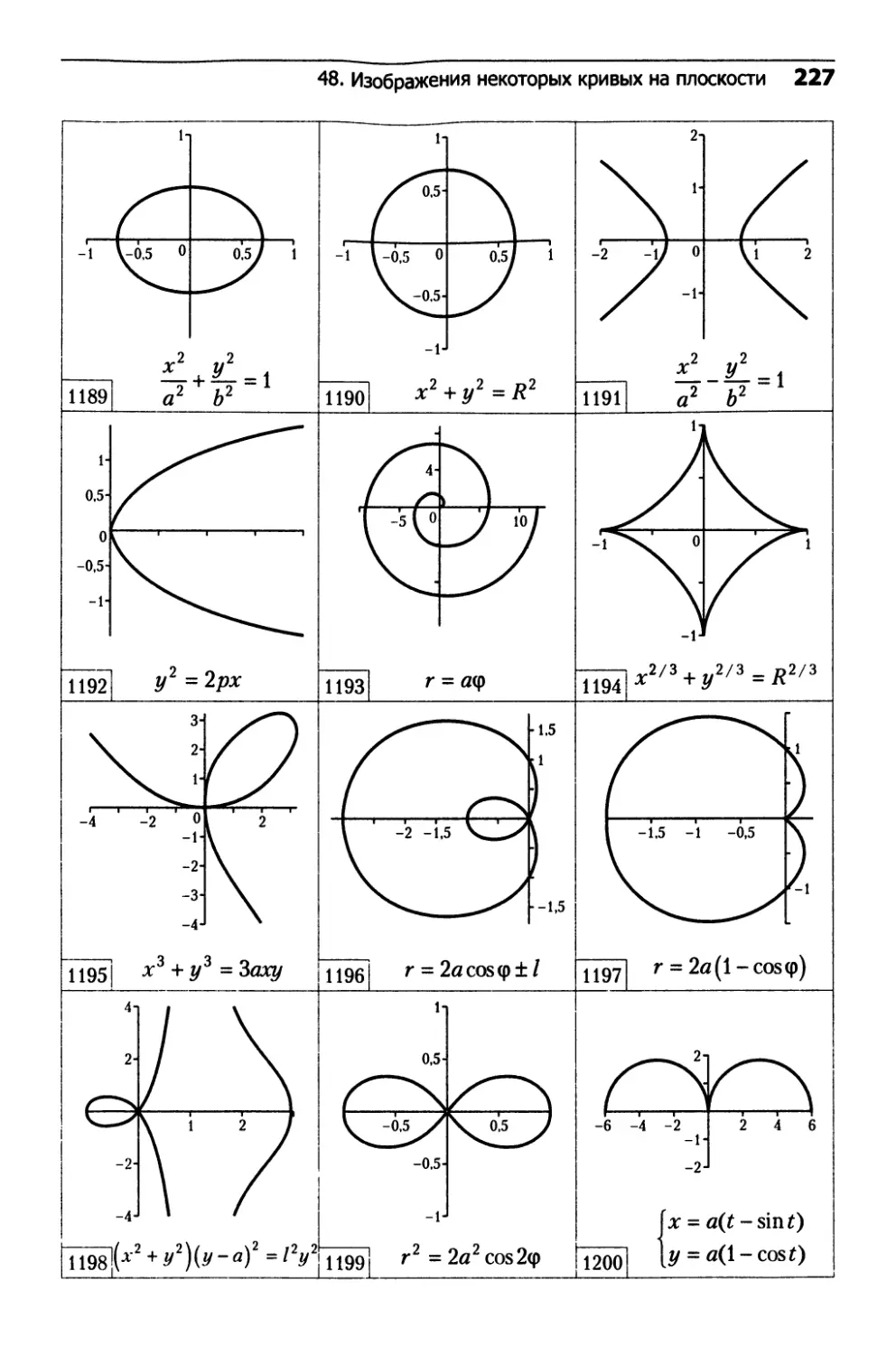
48.	Изображения некоторых кривых на плоскости.....227
49.	Изображения поверхностей 2-го порядка.........228
Литература........................................229
Алфавитный указатель основных формул..............231
Некоторые обозначения
□	N — множество натуральных чисел
□	Z — множество целых чисел
□	Q — множество рациональных чисел
□	К — множество действительных чисел
□	С — множество комплексных чисел
□	0 — пустое множество
□	хе К — х принадлежит множеству К
□	х ? R - х не принадлежит множеству К
□	А и В — объединение множеств А и В
□	Ап В — пересечение множеств А и В
□	а = Ь — а равно b
□	а*Ь — а не равно b
□	а>Ь; а>Ь — а больше Ь\ а больше или равно b
□	а <Ь\ а<Ь — а меньше 6; а меньше или равно b
□	а = Ь — а тождественно равно b
□	а~Ь — а приближенно равно b
□	(а; Ь) — интервал (открытый промежуток), а < х < b
□	[а;Ь); (а,Ь] — полуинтервалы, а<х<Ь, а<х<Ь
□	[а; 6] — отрезок (замкнутый промежуток), а<х<Ь
□	(а;+°°); (а;+°°); (-°°;6); (-°°;6] — числовые лучи,
а<х<+«>; а<х<+«>; -«><х<6; -«><х<6
□	(-оо;+оо) — числовая прямая, -©о < х < -к»
□	£7(х0) — окрестность точки х0, то есть любой интервал (а; 6), такой,
что х0 е (а; Ь)
□	U (х0) — проколотая окрестность точки х0, то есть любой интервал
(а;6), такой, что х0 6 х * х0
14 Некоторые обозначения
□	Vx — любое значение х; для любого значения х
□	Зс — существует значение с
□	А => В — из А следует В (если выполнено Л, то выполнено В\ А — до-
статочное условие для В, В — необходимое условие для Л)
□	Л <=> В — из Л следует В и одновременно из В следует Л (Л — необхо-
димое и достаточное условие для В; Л и В равносильны)
□	/1 = £1	/2 = #2 “ уравнения равносильны (эквивалентны)
□ /1 > S\ **	> 82 “ неравенства равносильны (эквивалентны)
□	7i = gi. /2= &	/1 > gi 	— система уравнении; неравенств 7г > g2
□	7 =gi. ./2=^2’.	ft > gi — совокупность уравнении; неравенств f2>g2
□	г(х;г/); r(x;z/;z) — радиус-вектор ОМ точки М(х;г/) на пло-
скости; точки М(х; у\ z) в пространстве
□	det А — детерминант (определитель) матрицы А
Часть 1. Формулы

1.	Формулы сокращенного
умножения и другие тождества (п е N)
(1.1)	a2 -b2 = (а - 6)(а + 6) — разность квадратов
(1.2)	(а - b)2 =а2 - 2аЬ + Ь2 — квадрат разности
(1.3)	(а + b)2 = а2 + 2аЬ + Ь2 — квадрат суммы
(1.4)	а2 + Ь2 = (а + Z>)2 - 2аЬ
(1.5)	(а + 6 + с)2 =а2 +b2 +с2 +2(ab + bc + ca)
(1.6)	а3 - Ь3 = (а - b)(a2 + ab + Ь2) — разность кубов
(1.7)	а3 + Ь3 = (a + b)(a2 -ab + b2} — сумма кубов
(1.8)	(а - Ь)3 = а3 - За2Ь + ЗаЬ2 -Ь3 — куб разности
(1.9)	(а + Ь)3 = а3 + За2Ь + ЗаЬ2 +Ь3 — куб суммы
(1.10)	a3 + b3 =(a + b)3 -3ab(a + b)
(1.11)	a4 -й4 = (а -b)(a + b)(a2 + 62)
(1.12)	а4 -64 = (а-Ь){а3 +a2b + ab2 +Ь3^
(1.13)	(а - й)4 = а4 - 4а36 + 6а262 - 4а63 + 64
(1.14)	(а + Z>)4 = а4 + 4а3й + 6а262 + 4а/>3 + 64
(1.15)	а4 +Z>4 =(а + 6)4 -4(a + b)2ab + 2a2b2
(1.16)	а4 + Z»4 = {а2 - >/2а6 + Ь2)^а2 + ЛаЬ + Ь2)
(1.17)	а4 +a2b2 +bA =(а2 -ab + b2^{a2 +ab + b2}
(1.18)	а5 -Ь5 =(а-2>)(а4 +a3b + a2b2 +ab3 +Z»4)
18 Часть 1. Формулы
(1.19)	а5 + Ь5 = (а + Ь) (а4 - a3b + a2b2 - ab3 + Z>4)
(1.20)	ап -Ь" = (а-Ь)(ап^ +ап-2Ь + ап-3Ь2 +... + abn'2 + 6""1)
(1.21)	а2" -Ь2” = (а + b)(a2n~' -a2n~2b + ... + ab2n~2-д2"-1)
(1.22)	a2n+i +b2"+l =(а + Ь)(а2п -а2п~'Ь + ...-ab2n'x +Ь2п)
(1.23)	Формула бинома Ньютона: (я + Ь)п = j? Cknan~kbk =
k=0
п п „-1,	...-(п-k + 1) k k
= а + -а b +... + —----------i--------- а b +... + b
1	1-2 ... k
2.	Формулы разложения
многочленов на множители
□ Разложения на множители некоторых многочленов 2-й, 3-й и 4-й
степени
(2.1)	х2 + 2ах + а2 = (х + а)2
(2.2)	х2 - (а + b)x + ab = (x- а)(х - Ь)
(2.3)	х3 ± Зах2 + За2х ± а3 = (х ± а)3
(2.4)	х3 ± а3 = (х± а)(х2 + ах + а2)
(2.5)	х3 + (а + р)х2 + (ар + q)x + aq = (x + a) (х2 + px + qy
р2 -iq< 0
(2.6)	х3 - (а + 2b)x2 + (2ab + b2}x - ab2 = (х - а)(х - Ь)2
(2.7)	х3 - (а + b + с)х2 + (ab + bc + са)х - abc = (х - а)(х - Ь)(х - с)
(2.8)	х3 + х - а3 - а = (х - а) (х2 + ах + а2 +1)
(2.9)	х3 + х2 + х - а3 - а2 - а = (х - а)[х2 + (а + 1)х + а2 + а +1]
(2.10)	х4 - а4 = (х - а)(х + а)(х2 +я2)
(2.11)	х4 - (а2 +62)х2 +а2Ь2 = (х - а)(х + а)(х - Ь)(х + Ь)
(2.12)	х4 +(а2 +62)х2 +а2Ь2 =(х2 +а2)(х2 +Ь2}
2.	Формулы разложения многочленов на множители 19
(2.13)	х4 + а2х2 +а4 ^х2 -ах + а2Цх2 + ax + a2j
(2.14)	х4 +а4 zzfx2 ->/2ах + а2^х2 + Лах + а2}
(2.15)	х4 + 2х3 + Зх2 + 2х +1 = (х2 + х +1)2
□ Схема Горнера деления многочлена на двучлен
р (х)	R
(2.16)	—— = Q_ <(х) +--------деление с остатком;
х-с	х-с
Рп(х) = адх” + ^х"-1 + а2х"~2 +... + ап_}х + а„;
Qn-t(x) =	+ bi*"2 + ЬгХп~3 +... + bn_2x + b„_t;
А) = ®0’ = + сА» = в2 + сЬ^...; t>n_f = on_j + cbn_2,
R = an+ cbn_i, Pn(x) = (x - с)0„_1 (x) + R, R = Pn (c)
(теорема Безу)
P (x)
(2.17)	P„(c) = 0 <=>  ”  = Qn-i(.x) ~ деление без остатка;
P„(x) = (x-c)Q„_1(x)
□ Теорема о подборе корней многочлена с целочисленными коэффи-
циентами
(2.18)	Если многочлен
Рп(х) = х" + OjX"'1 + fyx"-2 +... + a„_tx + a„;aieZWk имеет це-
лые корни, то они находятся среди делителей свободного члена ап
□ Разложение многочлена n-й степени на простейшие множители
(2.19) Случай п различных действительных корней:
Р„(х) = °ох" + «1*"-1 + вгх"-2 + - + ап-\х + ап~
= a(i(x-xx){x-x2)..\x-xn')
(2.20)	Случай I действительных корней кратности kt:
Р„(х) = Oqx" + Ojx"-1 + с^х"'2 +... + a„_tx + an =
= «0 (x - Xj )*... (x - xz (x2 + PjX + qx p ... (x2 + psx + qs p ;
p2 -^,<0 Vi
20 Часть 1. Формулы
3.	Действия с дробями
4 \ I	Л ’ d i С * Ь 1 1 л
(3.1)	— ± — =---;	— сложение и вычитание
4 ’ b d bd
(3.2)	^±£ = ^£; 6*0
b b ь
/	/\ Cl С d * С « j Л
(3.4)	= -—т; о, а * 0 — умножение
b	d	bd
/ с\ Г'Ч	С	d	«	J	Л
(3.5)	—: — = -—; о, с, а * 0 — деление
Ъ	d	be
а
(3.6)^-	= ^-; b,c,d*O
£ be
d
у rj Cl * C d	f	л
(3.7)	-— = -; о, c * 0 — сокращение
be b
(3.8)	— • с = c • — =	0 — умножение дроби на число и числа на
b b b
дробь
(3-9)?=Л=‘?; ь*°
b -b ь
(3.10)	у: с =	; 6, с Ф 0 — деление дроби на число
Ъ be
а
(3.11)^	= -^-; 6, с*0
с be
(3.12)	с: v = —“; ci, b Ф 0 — деление числа на дробь
b а
(3.13)-	= — ; а, Ьф О
а а
b
4. Средние величины. Пропорции. Проценты 21
(3.14)—	= —; а,
а а
b
4.	Средние величины.
Пропорции. Проценты
□ Средние величины
(4.1)	Среднее арифметическое п чисел: та =	+	+	+ - + ап
п
(4.2)	Среднее геометрическое п чисел: mg =	-а2-а3-... • ап
п
(4.3)	Среднее гармоническое п чисел: mh = —-------р
01^2^3	ап
(4.4)	Неравенство для средних величин: если ai > 0 Vi, то
> mh
□ Пропорции
а с
(4.5)	— = — <=> ad = be — основное свойство пропорции
b d
а с	a b	b d	cd
(4-6> Т =	=	=	= Т
b d	cd	ас	а b
Нахождение неизвестных членов пропорции:
z/ _ч х	с	Ьс
,, а	с	ad
(4.8) - = — <=> х = —;
х d	с
,, а	х
b d	b
а с	Ьс
(4.10) т = —<=>х = —
b х	а
22 Часть 1. Формулы
Производные пропорции:
с a±b c + d
,,	а	с	a±b	c + d
(412> Т =	----=-----
b	d	а	с
b	d	a-b	c-d
, , , а с а а + с с
(4.U) -=	=
b a b b+d d
□ Проценты
(4.15)	= 0,01а - 1 % от числа а
100
(4-16)	• х = 0,Olar - х % от числа а
100
(4.17)	у =	<=> х = —- а составляет х % от b
b 100 Ь
5.	Модуль (абсолютная величина)
. . [а, если а > 0
(5.1)	I л I = 5_ если < о — определение модуля числа
1 г/ м f/(х)» если f(x) 0
(5.2)l/	(x)| = f' '	J\’ п
[-f(x), если /(х) < 0
(5.3)	|а|>0
(5-4) | а |= 0 <=> а = 0
(5.5)	| а |> а
(5.6)	| а |> -а
(5.7)	|-a |=| а |
(5.8)	|a + Z>|<|a| + |Z>| (модуль суммы не больше суммы модулей)
(5.9)	| а + b | = | а | +1 b | <=> а • b > 0
6. Степени и корни. Логарифмы 23
(5.10)	| а - b | > | а | -1 b | (модуль разности не меньше разности модулей)
(5.11) | а21=| а |2= а2
(5.16)	|а| + |6|=0<=>а = 6 = 0<=>
а = 0
6 = 0
6.	Степени и корни.
Логарифмы (и, k е N; а, 6, с, х, у е К)
□ Степени с натуральным, целым и рациональным показателем. Ариф-
метический корень
(6.1)	ап =аа...а (п множителей, п > 1)
(6.2)	ах = а
(6.3)	а0 = 1; а * 0
(6.4)	ап =-L;a*0
(6.5)	ах =-;а*0
а
(6.6)	л/а = b <=> bn = а-, b >0 — арифметический корень
(6.7)	З/б = 0
(6.8)	ak/n = >[а^; a>0;keZ — степень с рациональным показателем
(6.9)	ах/п =
(6.10)	2^ =\а\
24 Часть 1. Формулы
(6.11)	4а2 =\а\
(6.12)	2л+^ =а > о
(6.13)	2п+4^ = а
(6.14)	4а2 = а
□ Свойства арифметических корней (а, b > 0; с > 0)
(6.15)	^6 = ^-^
<6Л6’К
(6.17)	(Ч[а)к = х/?
(6.18)	=кУа
(6.19)	>[а =
□ Свойства степени с действительным показателем
(а, b > 0)
(6.20)	ахау = ах+у
(6.21)	^-~ = ах~у
ау
(6.22)	(ab}x =ахЬх
/ \Х X
(6.23)	v = —
W ъх
(6.24)	(ах)У =аху
□ Свойства логарифмов (а, b > 0; а, Ь *1; х, у > 0)
(6.25)	а108»* =х — основное логарифмическое тождество
(6.26)	loga а = 1
(6.27)	logal = 0
(6.28)	loga (ху) = loga х + loga у
7. Прогрессии 25
(6.29)	loga - = loga x - loga у
J
(6.30)	logap (x“) = • loga x-, p * 0
(6.31)lo	gax = ^
log* о
(6.32)	loga/> = —!—
log* a
(6.33)	alog‘c = clog‘a; a, b, c > 0; b *1
(6.34)	log10x=lgx; logexslnx; e=2,71828
7.	Прогрессии
□ Арифметическая профессия (ne N)
(7Л) an+1 =an+d
(7.2)a„	=a1+(n-l)rf
(7.3)a„	= a"-^a^;n>2
(7.4)	Sn = a{ + a2 +... + an =
(7.5)5,Д2,,1+(”~1)<1"
(7.6)l	+ 2 + 3 + ... + „ = ^
.	.0 q q q	q Л^(и + 1)
(7.7)	(l + 2 + 3 + ... + n) =13 +23 +33 + ... + п3 = - v4 ’
(7.8) l + 3 + 5 + ... + (2n-l) = n2
(7.9)	2 + 4 + 6 + ...+ 2n = n(n + l)
□ Геометрическая профессия (n 6 N; bx Ф 0; q * 0)
(7.10)	fen+1 = V<7
(7.11)	Ьп=Ьх дп-'
26 Часть 1. Формулы
(7.12)	6n2=Vi bn^n>2
(7.13)	Sn = А, + +... + bn = -1-q * 1
1-9
(7.14)5„	=^;9 = 1
(7.15)5=	limS„=A_;|9|<l
h-»°°	1 - q
8.	Решение уравнений
□ Рациональные уравнения
(8.1)	ах + Ь = 0, а*0<=> х = ~—
а
(8.2)	ах + Ь = 0, а = 0,6 = 0 <=> хе К
(8.3)	ax + b = 0, а = 0, д*О<=>0
(8.4)	ах2 +bx + c = 0,a*0,D = b2- 4ас > 0 <=> Xj 2 = ————
' 2а
(8.5)	ах2 + Ьх + с = 0, а * 0, D = Ь2 - 4ас = 0 <=> х = ——
2а
(8.6)	ах2 +bx + c = 0,a*0,D = b2- 4ас < 0 <=> 0
□ Уравнения, содержащие знак модуля
(8.7)	| х | = а, а > 0 <=> xt = а, х2 = -а
(8.8)	| х | = а, а = 0 <=> х = О
(8.9)	| х| = а, а <0 <=> 0
g(x) > 0
(8.10)	| /(х) |= g(x) <=> • Г/(х) = g(x)
|_/(х) = -g(x)
□ Иррациональные уравнения
(8.11) 4х = а,а>0^ х = а2
(8.12) 4х = а, а<О<=>0
8. Решение уравнений 27
(8.13)	х/х = а <=> х = а3
(8.14)77w=g(x)«
g(x) > О
/(x) = g2(x)
□ Показательные уравнения
(8.15)	ах = Z>, а>0, а#1,2>>0<=>х = loge b
(8.16)	ах = Ь, а > 0, а Ф1, b < 0 <=> 0
(8.17)	а/(х) =	а,Ь>0, а,Ь*1&
<=> /(х) logc а = g(x) logc b, с > 0, с * 1
□ Логарифмические уравнения
(8.18)	loga x = b, а>0, а * 1 <=> х = а6
[ f( > О
(8.19)	loga /(х) = loga g(x), а > О, а * 1 <=>
[/(А/ ~ ё\Х)
□ Тригонометрические уравнения
(8.20)	sin х = а, | а |< 1 <=> х = (-1)” arcsin а + пп, п 6 Z
(8.21)	sinx = 0 <=> х = пп, пе Z
Л
(8.22)	sinx = -1 <=> х = - — + 2т, пе%
(8.23)	sinx = l<=>x = ^ + 2т, п е Z ]
(8.24)	sin х = а, | а |> 1 <=> 0
(8.25)	cosx = а, | а |< 1 <=> х = iarccosa + 2пп, пе Z
(8.26)	cosx = 0 <=> х = + пп, пе Z
(8.27)	cosx = -1 <=> х = п + 2пп, пе Z
(8.28)	cos х = 1 <=> х = 2пп, п е Z
(8.29)	cos х = а, | а |> 1 <=> 0
(8.30)	tg х = а <=> х = arctg а + пп, п е Z
(8.31)	tgx = 0 <=> х = пп, пе Z
28 Часть 1. Формулы
(8.32)	tgx = -1 <=> х = ~ + пп, пе%
(8.33)	tgx = 1 <=> х = — + пп, neZ
к
(8.34)	ctg х = а <=> х = arcctg а + пп, п е Z
Л
(8.35)	ctgx = 0 <=> х = — + пп, л 6 Z
Зя
(8.36)	ctg х = -1 <=> х = — + пп, п 6 Z
4
(8.37)	ctgx = 1 <=> х = — + пп, пе Z
4
9. Решение неравенств
(9.1)	/(х)>О«Г^>®
|_/(х) = О
(9.2)	/(х)<О«Г^<^
|_/(х) = О
□ Рациональные неравенства
(9.3)	ах + Ь>0, а > 0 <=> х > —
а
(9.4)	ох + 6 > 0, а < О <=> х < -—
а
у
(9.5)	ах + 6 < О, л > 0 <=> х < —
а
(9.6)	ах + 6 < О,а<0<=>х>--
а
Гх< Xi
(9.7)	а(х- х«)(х- х2) > О, а > 0, х< < х2 <=>
|_х > х2
(9.8)	а(х - xt)(x - х2) < О, а > О, xt < х2 <=> xt < х < х2
(9.9)	а(х-х<)2 >О, а>0<=> Х
9. Решение неравенств 29
(9.10)	а(х - Xj)2 < 0, а > 0 <=> 0
(9.11)	ах2 + bx + c>0,a>0,D = b2- 4ас < 0 <=> х 6 R
(9.12)	ах2 +bx + c<O,a>O,D = b2- iac < 0 <=> 0
□ Неравенства, содержащие знак модуля
(9.13) \ х\< а, а > 0 -а < х < а
(9.14) |х|<а,а<О<=>0
х<-а
х>а
(9.15) |х|>а, а>0<=>
(9.16) |х|>а,a<0<=>xe R
(9.17) | /(х) |< g(x) <=> -g(x) < /(х) < g(x) <=>

□ Иррациональные неравенства
(9.19) 4х >а, а > 0 <=> х > а2
(9.20) Vx >а, а < 0 <=> х > О
(9.21) 4х <а, а>0<=>0<х<а2
(9.22) 4х < а, а < 0 <=> 0
(9.23) Чх > а <=> х > а3
(9.24) Их < а <=> х < а3
(9.25) Jf(xj<g(x)^
(9.26) VTU)>g(x)«
/(х)>0
g(x) > О
,f(x)<g2(x)
’ |g(x) > О
1/(х) > g2(x)
|g(x)<0
Д/(х)>0
/(х) < g(x)
/(х) > -g(x)
30 Часть 1. Формулы
□ Показательные неравенства
(9.27)	ах >Ь, 0 < а < 1, Z? > 0 <=> х< loga b
(9.28)	ах >Ь, 0<а<1, Z><0<=> xeR
(9.29)	ах >b, а>1, 6 > 0 <=> х >logab
(9.30)	ax>b, a>i, хе R
(9.31)	ах < Ь, 0<а<1, b >0 <=> х> loga b
(9.32)	ах <Ь, 0 < а < 1, 6 < 0 <=> 0
(9.33)	ах <Ь, а>1, b>0& х< loga b
(9.34)	ах < b, а > 1, b < 0 <=> 0
□ Логарифмические неравенства
(9.35) logax>b, 0<а<1<=>0<х<а6
(9.36) logax>b, а>1<=> х>аь
(9.37) logax<b, 0 < а < 1 <=>х>аь
(9.38) lqgax<b, а>1<=>0<х<а6
	/(х) > 0
(9.39) loga /(х) > loga g(x), 0 < а < 1 <=>	g(x) > 0 /(х) < g(x)
(9.40) loga /(х) > loga g(x), а > 1 <=>
/(х) > О
g(x) > О
/(х) > g(x)
□ Тригонометрические неравенства ( п е Z )
(9.41)	sinx<а, |а| < 1 <=> -л-arcsina + 2тг <х<arcsina + 2пп
(9.42)	sin х < а, а < -1 <=> 0
(9.43)	sinx<l<=>x*^ + 2пп
(9.44)	sinx < а, а > 1 <=> хе К
(9.45)	sin х > а, |а| < 1 <=> arcsin а + 2лп < х < л - arcsin а + 2лп
10. Тригонометрические формулы 31
л
(9.46)	sin х > -1 <=> х * - — + 2лп
(9.47)	sinх > а, а <-!<=> хе IR
(9.48)	sin х > а, а > 1 <=> 0
(9.49)	cos х < а, |а| < 1 <=> arccos а + 2пп < х < 2л - arccos а + 2ли
(9.50)	cosx < а, а < -1 <=> 0
(9.51)	cosx < 1 <=> х Ф 2пп
(9.52)	cosx < а, а>1<=>хеК
(9.53)	cos х > а, |а| < 1 <=> - arccos а + 2лп < х < arccos а + 2лп
(9.54)	cos х > -1 <=> х * л + 2лп
(9.55)	cos х > а, а < -1 <=> х е К
(9.56)	cos х > а, а > 1 <=> 0
Л
(9.57)	tgx < а <=>-— + лп < х <arctga + пп
Л
(9.58) tgх>а <=> arctgа + пп<х< — + пп
(9.59)	ctgx < а <=> arcctga + пп < х < л + пп
(9.60)	ctgх>а<=>лп<х<arcctgа + пп
10. Тригонометрические формулы
При использовании формул, содержащих тангенсы и котангенсы, не-
обходимо учитывать вид областей определения левой и правой частей
формулы
□ Основные тождества
(10.1) sin2 а + cos2 а = 1 — основное тригонометрическое тождество
(10.2) tga =
sin а
cos а
(10.3) ctga = —=
tga
cos а
sin a
32 Часть 1. Формулы
(10.4)	l + tg2a =—5—
cos a
(10.5)	1 + ctg2 a = —
sin a
□ Свойства четности и нечетности
(10.6)	sin(-a) = -sina
(10.7)	cos(-a) = cos a
(10.8)	tg(-a) = -tga
(10.9)	ctg(-a) = - ctg a
□ Формулы сложения
(10.10)	sin(a ± p) = sin a cos p ± cos a sin p
(10.11)	cos(a±p) = cos a cos рт sin a sin P
(10.12)	tg(a±P)= tg“±tgP
iTtgatgP
□ Формулы кратных углов
(10.13)	sin 2a = 2 sin a cos a
(10.14)	cos2a = cos2 a - sin2 a = 2cos2 a -1
(10.15)	tg2a = 2tg“ .
1 - tg2 a
(10.16)	sin3a = 3sina-4sin3a
(10.17)	cos 3a = 4 cos3 a - 3 cos a
(10.18)	tg3a=3tga~tg3“
1-	3tg2 a
□ Формулы половинных углов
(10.19)	2sin2|
= 1 - cos a — формула понижения степени
(10.20) 2 cos2
Ct ]	.
— = 1 + cos a — формула понижения степени
10. Тригонометрические формулы 33
fa) sina 1-cosa
(10.21)	tg - =--------= —------
I 2 I 1 + cosa sin a
□ Формулы преобразования суммы в произведение
(10.22)	sin a ± sin Р = 2 sin a± cos	-
(10.23)	cos a + cos P = 2 cos —* cos	--
(10.24)	cos a - cos p = -2 sin a* sin -
(10.25)	tgattgp= sin(a±P>
cosacosp
□ Формулы преобразования произведения в сумму
(10.26)	sin a sin Р = [cos(a - Р) - cos(a + р)]
(10.27)	cosacosp = ^[cos(a-Р) + cos(a + Р)]
(10.28)	sin a cos р = [sin(a - p) + sin(a + p)]
□ Выражение функций через тангенс половинного угла
(10.29) sina =
1 + tg2|?
1-tg2 -
6 2
(10.30)	cos a =---->—
4 . 21 Ct
1+ g 2
(10.31)	tga =-----
1-tg2[?
34 Часть 1. Формулы
□ Формулы приведения
(jr
(10.32)	sin ^-а =cosa
(10.33)	sin(n±a) = +sina
(Зл )
(10.34)	sin — ± а = - cos а
(10.35)	sin(2n ± а) = ± sin а
f л	)
(10.36)	cos — ±а =Tsina
к 2	,
(10.37)	cos(n ± а) = - cos а
(Зп	\
(10.38)	cos —±а =±sina
к	,
(10.39)	cos(2n ± а) = cos а
Гл
(10.40)	tg —±а =+ctga
(2 J
(10.41)	tg(n±a) = ±tga
(Зл А
(10.42)	tg ^±а = + ctga
(10.43)	tg(2n ± а) = ± tg а
а Обратные тригонометрические функции
(10.44)	- < arcsin а < , sin(arcsin а) = а, | а | < 1
Л Л
(10.45)	arcsin(sinх) = х, - — <х< —
(10.46)	0 < arccos а < л, cos(arccosa) = а, | а |< 1
(10.47)	arccos(cos х) = х, 0 < х < л
(10.48)	- с arctg а < , tg(arctgа) = а
(10.49)	arctg(tgx) = х, - с л <
(10.50)	0 < arcctg а < л, ctg(arcctg а) = а
10. Тригонометрические формулы
35
(10.51)	arcctg(ctgi) = х, 0 < х < л
(10.52)	arcsin а + arcsin(-a) = 0, | а | < 1
(10.53)	arccosa + arccos(-a) = л, | а | < 1
(10.54)	arctga + arctg(-a) = 0
(10.51э)	arcctga + arcctg(-a) = л
(10.56)	arcsin a + arccos a = —,
|a|<l
71
(10.57)	arctg a + arcctg a = —
□ Дополнительные тождества
(10.58)	sin2 a - sin2 0 = sin(a + 0) sin(a - 0)
(10.59)	cos2 a - cos2 0 = sin(a + 0)sin(0 - a)
(10.60)	cos2 a - sin2 0 = cos(a + 0) cos(a - 0)
(10.61)	sina±cosa =
4
(10.62)	(sin a ± cos a)2 =l±sin2a
(10.63)	(sin a + cos a)2 + (sin a - cos a)2 = 2
(10.64)	(sin a + cos a)2-(sin a-cos a)2 =2 sin 2a
(10.65)	sin3 a ± cos3 a = (sin a ± cosa)(l + sin a cos a)
(10.66)	(sina±cosa)3 =(sina±cosa)(l±sin2a)
(10.67)	cos4 a - sin4 a = cos 2a
(10.68)	sin4 a + cos4 a = 1 - 2sin2 acos2 a
□ Связь радианной и градусной меры угла
(10.69)	360° = 2л радиана ® 6,2832 радиана
2л
(10.70)	1° =--радиана «0,0175 радиана
360
(10.71)	1 радиан =	« 57,2958°
2л
36 Часть 1. Формулы
□ Таблица значений тригонометрических функций (10.72)
О а 0°	а	sina, 0	'	0	cos а 1 •	tga 0	ctga
30°	п	’	1 —	1	— 6	'	2	& 2	3	ч/З
45°	t=i I	V2 2	1	1
60°	ts I со	2	>/з	ч/З 3
90°	- 1 1 2	1	0	—	0
180°	л '	0	-4	0	—
270°	зл : 2 i -1	0	—	0
360°	2л *	0	1	0	-
11.	Типовые способы
замены переменной
(11.1)	х + р = у=> х2 + 2рх + р2 =(х + р)2 = у2
(11.2)	х + р = у => х2 + 2px + q = y2 + q-p2
f b V с
---	4- —
2а I а
Ь	э
(11.3)	х + — =	+fcr + c =
2а
Ь}2
2а
2 Ь2 - 4ас
= а
= а у
(11.4)	\[х = у;х>0=> х = у&,4х = у\ >[х = у2
(11.5)	х + — = у, х * 0 => х2 + -Д- = у2 - 2; х3 + -Д = у3 - Зг/
х	х2 / хл
(11.6)	х + у = и, ху = v => х2 + у2 = и2 - 2v; х3 + у3 = и3 - 3uv
12. Формулы геометрии 37
(11.7)	х + у + z = и, ху + yz + zx = v, xyz = w=>
=> х1 2 + у2 + z2 = и2 - 2v, х3 + у3 + z3 = w3 - 3wt> + 3®
(11.8)	sinx = t=>sin2x = t2, cos2x = l-i2
, t2 1	1
(11.9)	tgx = £;cosx*0=>sin x =---------7. cos x =-r
1 + r	1 + r
(11.10)	cos2x = t=>sin2x = ~~> cos2 x = —
t2-l
(11.11)	sinx±cosx = г => sinx• cosx = ±—-—
« X x «	• 2f	1-Z2
(11.12)	tg — = t; cos — * 0 => sin x =--; cos x =-7-
2’2	1 + t2 1 + t2
12.	Формулы геометрии
□ Треугольники (a, b,c — стороны; a, P, у — углы, противолежащие
сторонам a; b; с ; h — высота, проведенная к основанию a\R — радиус
описанной окружности г — радиус вписанной окружности)
(12.1)	Сумма внутренних углов треугольника: a + р + у = 180°
(12.2)	Соотношение между сторонами (неравенство треугольника):
а + Ь>с; Ь + оа; с + а> b
(12.3)	Периметр и полупериметр: Р = а + Ь + с; р = а+^ + с
□ Вычисление площади треугольника
(12.4)	S = ^ah = ^absiny
(12.5)	S = ^ = p.r
(12.6)	5 = у]р(р - d)(p - b)(p - с) — формула Герона
(12.7)	Площадь равностороннего треугольника со стороной a: S =-
4
1
(12.8) Площадь прямоугольного треугольника с катетами a, b: S = —ab
38 Часть 1. Формулы
□ Теорема Пифагора
(12.9)	В прямоугольном треугольнике квадрат гипотенузы равен сум-
2	2	12
ме квадратов катетов: с =а +Ь
□ Теорема синусов
(12.10)	Стороны треугольника пропорциональны синусам противо-
а b с
лежащих углов:----=-----=-----
sin a sin Р sin у
□ Теорема косинусов
(12.11)	Квадрат стороны треугольника равен сумме квадратов двух
других сторон без удвоенного произведения этих сторон на
косинус угла между ними: с2 = а2 + b2 - 2a6cosy
□ Четырехугольники (dv d2 — диагонали; а, Р, у, 8 — углы ф — угол
между диагоналями; h — высота, проведенная к основанию а\ R — ра-
диус описанной окружности; г — радиус вписанной окружности).
(12.12)	Сумма внутренних углов выпуклого четырехугольника:
а + Р + у + 8 = 360°
□ Вычисление площади четырехугольника
(12.13)	Площадь выпуклого четырехугольника: S = ^d{d2 зтф
(12.14)	Площадь параллелограмма (а и Ь — стороны; а — угол между
строками): S = ah- absina
(12.15)	Площадь ромба {а — сторона; а — угол между строками):
S = ah = a2 sin а = - d<d2
2 1 2
(12.16)	Площадь прямоугольника со сторонами а и b*. S = ab
(12.17)	Площадь квадрата со стороной a: S = а2
а । ь
(12.18)	Площадь трапеции с основаниями а и b: S = —-— h
□ Окружность и круг (7? — радиус окружности, круга)
(12.19)	Длина окружности: L = 2nR
(12.20)	Длина дуги окружности с центральным углом а0 (в градусах)
ot°
или Р (в радианах): L = nR- = R • Р
13. Векторы 39
(12.21)	Площадь круга: 5 = nR2
(12.22)	Площадь сектора круга с центральным углом а (в градусах)
или Р (в радианах): S = nR2 • Т?2Р
□ Вычисление объемов и площадей поверхности (5осн — площадь ос-
нования, Н — высота):
(12.23)	Объем призмы: V = $жнН
(12.24)	Объем кругового цилиндра (R — радиус основания):
V = 5Ж„Н = TtR2H
(12.25)	Площадь боковой поверхности кругового цилиндра (R — ра-
диус основания): S6()K = 2tiRH
(12.26)	Объем кругового конуса (R — радиус основания):
V = -SH = -itR2H
3	3
(12.27)	Площадь боковой поверхности кругового конуса (L — образую-
щая конуса): 5бок = nRL
(12.28)	Объем пирамиды: V = — 5^ Н
3
4 Q
(12.29)	Объем шара радиуса R: V = — nR
3
(12.30)	Площадь поверхности сферы радиуса R: S = 4л/?“
13.	Векторы
Основные понятия и линейные операции
□ Прямоугольные и полярные координаты точки на плоскости
{х = Г COS ф
; 0 < г < +°о; 0 < ф < 2л или -л < ф < л
у = Г5Шф
(13.2)	г = yjx2 + у2
(13.3)
X
COS ф = —
г
у
81Пф = —
г
40 Часть 1. Формулы
□	Прямоугольные и цилиндрические координаты точки в пространстве
(13.4)
X = ГСОБф
z/ = rsin(p; 0 < г <-н»; 0 < ф < 2л; - °° < z <+°°
z = 2
□	Прямоугольные и сферические координаты точки в простран-
стве
(13.5)
(13.6)
х = rcos9sin0
у = rsin9sin0; 0 < г < +©о; 0 < ф < 2л; 0 < 0 < л (а)
z = TCOS0
х = rcoscpcosO
у = г sin (pcosO; 0 < г < +°о; 0 < <р < 2л; - — < 0 < — (б)
z = rsin0
□	Проекция вектора АВ с началом в точке А и концом в точке В на
ось и
(13.7)	ПриАВ = |лв| cos <р; |ав| — длина вектора; <р — угол между на-
правлением оси и вектором, 0 < <р < л
□ Проекции вектора АВ на оси прямоугольной системы координат
OXYZ
(13.8)	A(xt;y1;zi); B(x2;y2;z2);
ПрохАВ = х2 - Хр ПртАВ = у2- ух\ПртАВ = z2 - zx
□ Задание вектора в координатной форме
(13.9)	АВ = {х2 -xf,у2 -yx\z2 -ztj
□ Расстояние между двумя точками
(13.10)	I АВ 1= 7(^2-^1)2+(1/2-1/1)2+(22-21)2
□ Модуль (длина) вектора а = {х; у, z}
(13.11)	| а |= yjx2 + у2 + z2; | а |> О
13. Векторы 41
□ Направляющие косинусы вектора а = {х; у; z}
(13.12)	cosa = cosp = cosy = -4-
|a|	|a|	|a|
(13.13)	cos2 a + cos2 P + cos2 у = 1
□ Единичный вектор e
(13.14)	| ё|=1
□ Нулевой вектор О
(13.15)	б = {0; 0; 0}; | б | = 0; направление не определено
□ Вектор, противоположный вектору а = {х; у, г]
(13.16)	-a = {-x;-z/;-z}; | -а |=| а |
□ Равенство векторов a = {x1;yi;z1} и b = {х2;у2;z2}
Xj = х2
(13.17)	a = 6 <=>  г/j = г/2
Л = z2
□ Сложение и вычитание векторов а = {хр г/pZj} и b = {x2;y2;z2}
(13.18)	a + b = {x1 + x2;yt + y2;zt + z2]
(13.19)	а - b = а + (-б) = {xt - х2,ух -y2,Z\ - z2]
(13.20)	а + b = b + а (коммутативность сложения)
(13.21)	(a + *) + c = a + (b + cj (ассоциативность сложения)
□ Умножение вектора на число
(13.22)	аа = аа = {ах; аг/; az}
(13.23)	| аа |=| а | • | а |
(13.24)	а(ра) = (ар) а (ассоциативность числовых сомножителей)
(13.25)	а(а + й) = аа + ab (дистрибутивность числового сомножителя
относительно суммы вектров)
(13.26)	(а + Р)л = аа + Ра (дистрибутивность векторного сомножи-
теля относительно суммы чисел)
42 Часть 1. Формулы
□ Орт ненулевого вектора
(13 27) <7° = — = —' — • —
й ИЮ
= {cos a; cos Р; cos у}; а * О
(13.28) а0 =1;
а = |а| • (2°
□	Признак коллинеарности двух ненулевых векторов
(13.29 ) «||6<=>« = Х6 <=> — = — = —; нулевой вектор считается кол-
л2 у2 z2
линеарным любому вектору
□	Линейная комбинация векторов
(13.30)	Ь = \ах 4-Х2я2 +... + ^пап
□ Линейная независимость системы ненулевых векторов
(13.31)	Векторы а{, а2,...,ап называются линейно независимыми,
если их линейная комбинация равна нулю только при условии
равенства нулю всех коэффициентов:
Xj щ + А,? я2 +... + Xw ап = 0 => X । = Х9 = ... = Х/? = 0
□ Линейная зависимость системы векторов
(13.32)	Векторы ах, а2,...,ап называются линейно зависимыми, если
существуют числа Xvk2,....Xn, хотя бы одно из которых не
равно нулю, и выполняется равенство
4- Х2Л2 4-... 4- Хп(1п = 0
□ Связь коллинеарности и линейной зависимости двух векторов
(13.33)	а||6<=> а и Ь линейно зависимы
□ Связь компланарности и линейной зависимости трех векторов
(13.34)	а; Ъ\ с компланарны <=> а\ Ь; с линейно зависимы
□ Разложение вектора по базису в пространстве
(13.35)	Базис (вр е2; е3)—упорядоченная совокупность трех линей-
но независимых векторов. Любой вектор можно представить
в виде а = Х16?1 -ьХ2е2 4- Х3е3; Х1,Х2,Х3 называются координа-
тами вектора в базисе
13. Векторы 43
□	Разложение вектора по трем некомпланарным векторам
(13.36) d = \а + X2fe + Х3с <=>
dx —	+ X2Z>r +
dy ~ \ау + ^2^у + ^3Су А.рЛ2;Л3
dz =	+ X2bz 4- Х3с2
□	Разложение вектора по базису прямоугольной системы коорди-
нат OXYZ
(13.37 ) Базис {г\ j\ — упорядоченная совокупность трех попарно
перпендикулярных единичных векторов. Любой вектор мож-
но представить в виде а = ах i 4- ау j 4- az k = хг 4- у j 4- zk
□	Преобразование координат в пространстве
(13.38 ) Если г = xi 4- yj 4- zk в системе координат OXYZ,
г = х^ + у^ + z{k{ в системе координат OiXiYiZi
ООх=х01 + у0] + 201,
ii = а11г + а12у + а13&
Л =а21г’ + а22? + а23^
Гх = а311 + а32) + а33£
ТО
х = х0 + anxt 4- а21г/! 4- a3iz{
# = #0 + а12*1 + <W1 + <W1
2 = 20+а13х1+а23г/1+а33г1
□	Преобразование координат на плоскости при параллельном пере-
носе и повороте осей
(13.39)	Если г = xi + уj в системе координат OXY, г = xp’j 4- y{j{
в системе координат OxXJi\, ОО{ = xQi 4- yQ j,
ц = coscp • г + sincp • j	[x	= x0	4-x1coscp-z/1sincp
.	_	_ ,	TO	s
jx = -sincp- i 4- coscp • j	[У	= Уп	+ xi sincp4-г/, coscp
Скалярное произведение двух векторов
(13.40)	а • b = | а | • | b | coscp; ср — угол между векторами
(13.41)	а • b = | а | ПраЬ = | b | Прьа
(13.42)	ПраЬ = | b | coscp; Прьа = | а | coscp
44 Часть 1. Формулы
(13.43)	a b-b a (коммутативность)
(13.44)	[aaj • b = а[а • bj (ассоциативность скалярного произведения
относительно числового множителя)
(13.45)	(a + b)-c = a-c + b-c (дистрибутивность скалярного произве-
дения относительно суммы вектров)
(13.46)	а а=|а| |а|=|д|2>0(скалярныйквадрат)
(13.47)	а-0 = 0 Ь = 0
(13.48)	а е = | а | coscp = Преа\ |е| = 1
□ Вычисление скалярного произведения в координатной форме
(13.49)	а • b = х{х2 + у (у г + zfa
□ Угол между векторами
(13.50)	скф = Ji =	.....
I а I ' I I <]х2 + у2 + 2,2 yjx2 + у 2 + 2г2
□ Условие перпендикулярности двух ненулевых векторов
(13.51)	a Lb <=$ ab = 0 х{х2 + уху2 +	= 0; нулевой вектор счи-
тается перпендикулярным любому вектору
(13.52)	Таблица скалярного умножения базисных векторов прямо-
угольной декартовой системы координат:
i • i = 1; i • j = 0; i k = 0
j • i = 0; j • j = 1; j • k = 0
k • i = 0; k • j = 0; k k = 1
Векторное произведение двух векторов
(13.53)	Вектор с называется векторным произведением двух век-
торов, c = axb,если: | с | = | а | • | b | sincp; ска. скЬ\ а;Ь;с
образуют правую тройку.
(13.54)	а х b = -Ь х а (антикоммутативность)
13. Векторы 45
(13.55)	(оса) х b = a(axft) (ассоциативность векторного произведе-
ния относительно числового множителя)
(13.56)	(a + b}xc = axc + bxc (дистрибутивность векторного произ-
ведения относительно суммы вектров)
(13.57)	аха = 0
(13.58)	ах0 = 0ха = 0
□ Вычисление векторного произведения в координатной форме
i
(13.59)	c=axft= хх
х2
3 k
Ух *1
У2 Ч
= (У\г2 - г/2г1) * + (х221 - Х122 ) 3 + (Х1 #2 - *2*6 ) *
(13.60)	Таблица векторного умножения базисных векторов прямо-
угольной декартовой системы координат:
i х i = б; i х j = k; ixk = -j
jxi = -k; jxj = O; jxk = i
kxi = j; kxj = -i; k x k = 6
□ Условие коллинеарности двух векторов
« j
(13.61)	а|| b <=> ахЬ = Ъ <=> ух
*2 У2
(13.62)	Вычисление площади параллелограмма, построенного на двух
векторах: S = la х b\
Смешанное произведение трех векторов
(13.63)	abc = a-(bxcj
(13.64)	abc = bca = cab = -bac = -cba = -acb
46 Часть 1. Формулы
□ Вычисление смешанного произведения в координатной форме
(13.65) abc =
*1
х2
х3
У\ 21
У2 22
Уз 2з
= *1#22з + У\г2хз + 21л2Уз - гхУ2хЗ - У\х2г3 - х\г2Уз
(13.66) Смешанное произведение трех базисных векторов прямо-
угольной декартовой системы координат: i j k = 1
□ Условие компланарности трех векторов
(13.67) а; Ь; с компланарны <=> abc = 0 <=>
Xi
х2
х3
У\ 21
У2 22
Уз 2з
= 0
(13.68) Вычисление объема параллелепипеда, построенного на трех
векторах: V = абс
14.	Прямая на плоскости
□ Уравнение прямой, проходящей через заданную точку М0(х0; г/0)
перпендикулярно заданному вектору
(14.1)	(г - г0) • п = 0 — векторная форма, й = {Л;В} * 0
(14.2)	г-й + С = 0
(14.3)	А(х - х0) + В(у - Уо) = О — координатная форма
□ Общее уравнение прямой
(14.4)	Ах + Ву + С = 0; Л2+В2*0
□ Неполные уравнения прямой
(14.5)	Л = 0, В*0=> By+ С = 0 — уравнение прямой, параллельной
оси ОХ
(14.6)	у = 0 — уравнение прямой, совпадающей с осью ОХ
(14.7)	В = 0; А * 0 => Ах + С = 0 — уравнение прямой, параллельной
оси OY
14. Прямая на плоскости 47
(14.8)	х = 0 — уравнение прямой, совпадающей с осью OY
(14.9)С	= 0=>Ах +By = 0 — уравнение прямой, проходящей через
начало координат
□ Нормальное уравнение прямой
(14.10)	г • п° - р = 0 - векторная форма
(14.11)	xcosa + z/sina- р = 0 — координатная форма
□ Уравнение прямой в полярных кординатах
(14.12)	г = —-
cos((p-a)
□ Уравнение прямой с угловым коэффициентом
(14.13)	у-уц = k(x-xQ); k = ——xt * х0
xt -х0
(14.14)	у = kx + b, k = ——х^О;
k - tg ф — тангенс угла между осью ОХ и прямой;
Мо (х0; г/0); (xi’У\) ~ точки, принадлежащие прямой
□ Уравнение прямой «в отрезках»
(14.15)	—+ —= 1;
а b
□ Параметрическое уравнение прямой, проходящей через задан-
ную точку М0(х0;г/0) параллельно заданному вектору
5 = {si;52} * 0
(14.16)	г = г0 + s-t; -оо<^<4-©о— векторная форма
х = х0 + $<£
; - ©о < t < +оо — координатная форма;
У = Уо +
= 0 => х = х0 (уравнение прямой, параллельной оси ОУ);
s2 = 0 => у = у0 (уравнение прямой, параллельной оси ОХ)
(14.17)
48 Часть 1. Формулы
□ Каноническое уравнение прямой, проходящей через заданную точ-
ку Л/0(х0; 2/0) параллельно заданному вектору $ = {st; $2} * О
(14.18)	=	(S1=O^x = xo; х2=О^г/ = г/о)
S2
□ Уравнение прямой, проходящей через две заданные точки Mt (xt; у{)
и М2(х2;г/2)
(14.19)
х2 - Xj у2 - У1
(14.20)	z/ = ^tx+^2~^
х2 - Xj
х2 - Xj
(14.21)
1
Х1
У\
1
х2
У2
1
х
У
= 0
□ Угол между двумя прямыми
(14.22)	Z( : г • пг + Q = 0; Z2: г • п2 + С2 = 0 => coscp =
____________________	I «1 I • I «2 I
(14.23)	Zj ||	<=> «11| п2 <=> ДВ2 - Л2В( = 0 — условие параллельности
(14.24)	Z1±Z2<=>n1-n2=0<=> ДА + А А = 0 — условие перпенди-
кулярности
(14.25)	Zj : г = rt + Sj • t; L2:r = r2+s2t=^ coscp =
_ _	ki I • I s21
(14.26)	Lx || Z2 <=> 5i II $2 — условие параллельности
(14.27)	Zj ± Z-2 <=> $i • s2 = 0 — условие перпендикулярности
-k,
(14.28)	Zt : z/ = ^1x + 61; :y = k2x + b2=>tg(p = ^-^-
1 4- /^«2
(14.29)	Zj || L2 <=>	= ^2 — условие параллельности
(14.30)	Z1±Z2<=>^2=-^-----условие перпендикулярности
14. Прямая на плоскости 49
□ Расстояние от точки	(х{; ух) до прямой
(14.31)	rf = lAci+^i+Cl
(14.32)	d=\xt cosa + у{ sina - р |
□ Расстояние от начала координат до прямой
(14.33)	d = .
(14.34)	d=\-p\
□ Условие пересечения двух прямых и координаты точки пересе-
чения
(14.35)	Ц : Atx + Вху + Ct = 0;	+ С2 = 0.
А
в2
ф 0, то прямые пересекаются в одной точке
	A Q		С1 д
с координатами х =	В2 С2	-.«/ = 	G Л
	д		д
□ Условие совпадения двух прямых
(14.36)	L{ : А{х + В{у + Ct = 0; L2 : А2х + В2у + С2 = 0.
п А A
Если — = — = — , то уравнения определяют одну и ту же прямую.
□ Условие принадлежности трех заданных точек
A(xt; У\ )> Я(х2 ’ У 2 )’ Q*3» Уз ) ОДНОЙ прямой L
(14.37) А, В, Сё L <=> *2 ~X1 =
	х3	-х2	У:	5 ~У2
	1	1	1	
(14.38) ДВ.Се £<=>	Xj	х2	*3	= 0
	У1	У2	Уз	
50 Часть 1. Формулы
15. Плоскость и прямая
в пространстве
Плоскость в пространстве
□ Уравнение плоскости, проходящей через заданную точку
Л/о (л0; г/0; z0) перпендикулярно заданному вектору
(15.1)	(г - r0 j • п = 0 — векторная форма, п = {Л; В; С} * б
(15.2)	r-w + D = 0
(15.3)	А(х- х0) + В {у - г/0) + С (z - z0) = 0 — координатная форма
□ Общее уравнение плоскости
(15.4)	Ax + By + Cz + D = Q\ Л2+В2+С2*0
□ Неполные уравнения плоскости
(15.5)	Л = 0 => By + Cz + D = 0 — уравнение плоскости, параллельной
оси ОХ
(15.6)	B = 0=>Ar + Cz + Z) = 0— уравнение плоскости, параллельной
оси OY
(15.7)	C = 0=>Ax +By+ D = 0 — уравнение плоскости, параллель-
ной оси OZ
(15.8)Л	= В = 0=>Сг + £) = 0— уравнение плоскости, параллельной
плоскости OXY
(15.9)	z = 0 — уравнение плоскости, совпадающей с плоскостью
OXY
(15.10)	В = С = 0=>Аг + £ = 0 — уравнение плоскости, параллель-
ной плоскости OYZ
(15.11)	х = 0— уравнение плоскости, совпадающей с плоскостью
OYZ
(15.12)	A = C = 0=>By + D = 0 — уравнение плоскости, параллель-
ной плоскости OXZ
15. Плоскость и прямая в пространстве 51
(15.13)	у = 0 — уравнение плоскости, совпадающей с плоскостью
OXZ
(15.14)	£) = 0=>Аг + Вг/ + Сг = 0— уравнение плоскости, проходя-
щей через начало координат
□ Нормальное уравнение плоскости
(15.15)	г • п° - р = 0 — векторная форма
(15.16)	х cos а + у cos Р + z cos у ~ р = 0 — координатная форма
□ Уравнение плоскости «в отрезках»
(15.17)-	+ — + - = 1; а,6,с*0
а о с
□	Уравнение плоскости, проходящей через три различные точки
Af, (хр г/р г,), М2 (х2; у2; z2), М3 (х3; г/3; z3), не лежащие на одной
прямой
(15.18)
X-Xj
х2 -х,
Х3-Х(
У ~У\
У2-У1
Уз~У1
z~zt
z2~zl
z3~zi
= 0
□	Расстояние от точки Л/, (хр г/р ) до плоскости
(15.19)	P-.Ax + By + Cz + D = 0=>d = ^AXi.+ Byi+CZi+D^
у1а2+В2+С2
(15.20)	d =| Xj cosa + ух cos0 + zt cosy - p |
□ Угол между двумя плоскостями
(15.21)	Pt; : г • щ + Dj = 0 => cos(p =
I ”1 I • I «2 I
__ ___ ABC
(15.22)	Pt || P2 <=> «j || n2 <=> — = — = — — условие параллельности
Л2 Вг C2
(15.23)	P, ± P2 <=> Hj • n2 = 0 <=> AtA2 + BlB2 + C(C2 = 0 — условие пер-
пендикулярности
52 Часть 1. Формулы
Прямая в пространстве
□ Параметрическое уравнение прямой в пространстве, проходящей
через заданную точку Мо (х0; yQ; z0 ) параллельно заданному векто-
РУ 5 = {$р$2;$3}*0
(15.24)	r = r0+s t — векторная форма; -<»<£<+<»
х = х0 + stt
у = y0+s2t — координатная форма; -*»<?<+«>
г = z0 + s3t
(15.25)
□	Каноническое уравнение прямой в пространстве
(15.2б)^. = ^^ = ^;
51 s2 S3
($J = о => х = х0; s2 = 0 => у = г/0; 53 = 0 => z = z0)
□	Уравнение прямой в пространстве, проходящей через две раз-
личные точки М{ (хр г/р г,), М2 (х2; у2; z2)
х~хх _ У~У\ _ г~г1
x2-xt у2-ух z2-zx
□	Угол между прямой L и плоскостью Р
(15.28)	L:r = r0+s-t; Р: г • n + D = 0 => sin<p = ... r[
HtI
(15.29)	Z||P<=>s±n<=>n-s = 0 — условие параллельности прямой
и плоскости
(15.30)	Z J- Р <=> 51| Z? <=> 5 х Z? = 0 —- условие перпендикулярности пря-
мой и плоскости
□ Задание прямой в пространстве как линии пересечения двух непарал-
лельных плоскостей
А{х + В{у + C<z + D{=§ — — _
; хп7 Ф 0
Л2х + В2у + C2z + D2=0
(15.31)
16. Уравнения некоторых кривых на плоскости 53
16. Уравнения некоторых
кривых на плоскости
Уравнения кривых 2-го порядка
□ Эллипс (см. ч. 2, рис. 1189):
2	2
X If
(16.1)	— + -^- = 1 — каноническое уравнение эллипса
а Ь
/	^2
(16.2)	е = v1—- — эксцентриситет эллипса
V а
х = a cos t
(16.3)	<	; 0 < t < 2л — уравнение эллипса в параметрической
[у = osin£
форме
Р
(16.4)	г =---------уравнение эллипса в полярных координатах
l-ecos(p
□ Окружность (R — радиус окружности):
(16.5)	х2 + у2 = R2 — уравнение окружности с центром в начале ко-
ординат (см. ч. 2, рис. 1105)
(16.6)	(х - х0)2 + {у - г/0)2 = R2 — уравнение окружности с центром
вточке (х0;г/0) (см. ч. 2,рис. 1111)
(16.7)	у = yQ ± y]R2 - (х - х0)2 — уравнения верхней (4-) и нижней (-)
полуокружности центром в точке (х0; yQ)
(16.8)	(х-х0)2 4- (у-Уъ)2 =0 — вырожденная окружность (точка
(Wo))
(16.9)	е = 0 — эксцентриситет окружности
(16.10)
X ““ 1^, cos t
; 0 < t < 2л — уравнение окружности с центром
у = /? sin £
в начале координат в параметрической форме
54 Часть 1. Формулы
(16.11)
х = х0 + R cos t
; 0 < t < 2л — уравнение окружности с цент-
у — у0 4- 7?sint
ром в точке (х0;г/0) в параметрической форме
(16.12)	r = R— уравнение окружности с центром в начале кординат
в полярных координатах
(16.13)	г = 27? sin <р —уравнение окружности с центром в в точке (0; R)
в полярных координатах
(16.14)	г = 27?cos<p —уравнение окружности с центром в в точке (7?;0)
в полярных координатах
□ Гипербола (см. ч. 2, рис. 1191):
х^ и2
(16.15)	—у - \ = 1 — каноническое уравнение гиперболы
а Ь
(16.16)	е = J1 + —у — эксцентриситет гиперболы
V а1
(16.17)	г =---------уравнение одной ветви гиперболы в поляр-
l-ecos<p
ных координатах
х^ и2
(16.18)	—у - ^у = 0 — две пересекающиеся прямые (см. ч. 2, рис. 1081)
а Ь2
□ Парабола (см. ч. 2, рис. 1192):
(16.19)	у2 =2рх — каноническое уравнение параболы
(16.20)	г = —------уравнение параболы в полярных координатах
l-cos<p
Уравнения некоторых замечательных кривых
□ Архимедова спираль (см. ч. 2, рис. 1193)
(16.21)	г = а(р
□ Астроида (см. ч. 2, рис. 1194)
(16.22) х273 + г/2/3 = Т?2/3
16. Уравнения некоторых кривых на плоскости 55
(16.23)
х = R cos3 —
4
. з t
у = 7? sin -
4
□ Декартов лист (см. ч. 2, рис. 1195)
(16.24) х3 + у3 = Залу
(16.25) 
3at
1 + t3
3at2
1 + f3
(16.26) г =
a sin (p cos (p
Sin Ф + COS ф
□ Улитка Паскаля (см. ч. 2, рис. 1196)
(16.27) (х2 + у2 - 2ахj = I2 (х2 + у2)
х = a cos2 t +1 cos t
(lo.zo)
[y = flsin£cos£ + /sin£
(16.29)	г = 2асо8ф±/
□ Кардиоида (см. ч. 2, рис. 1197)
(16.30)	(х2 + у2 -2ох) = 4а2 (х2 + у2)
х = 2а cos t - a cos 2t
у = 2flsin£-flsin2£
(16.32)	г = 2л(1-со8ф)
□ Конхоида Никомеда (см. ч. 2, рис. 1198)
(16.33)	(х2 + у2) (у - а)2 = 12у2
(16.34)	г = -^-±1
8Шф
(16.31)
□ Лемниската Бернулли (см. ч. 2, рис. 1199)
(16.35) г2 = 2a2cos2<p
56 Часть 1. Формулы
□ Локон Аньези (см. ч. 2, рис. 188)
з
(16.36) у = ^-2
х + а
□ Циклоида (см. ч. 2, рис. 1200)
х = a(t - sin t)
у = а(1 - cost)
(16.37)
□ Эпициклоиды (см. ч. 2, рис. 1129-1140)
(16.38)
X = (R + г) cos — t - г cos t + — t
V 7	R	[ R
т	(r
у = (7? + r)sin — t - rsin £4—£
R	I R
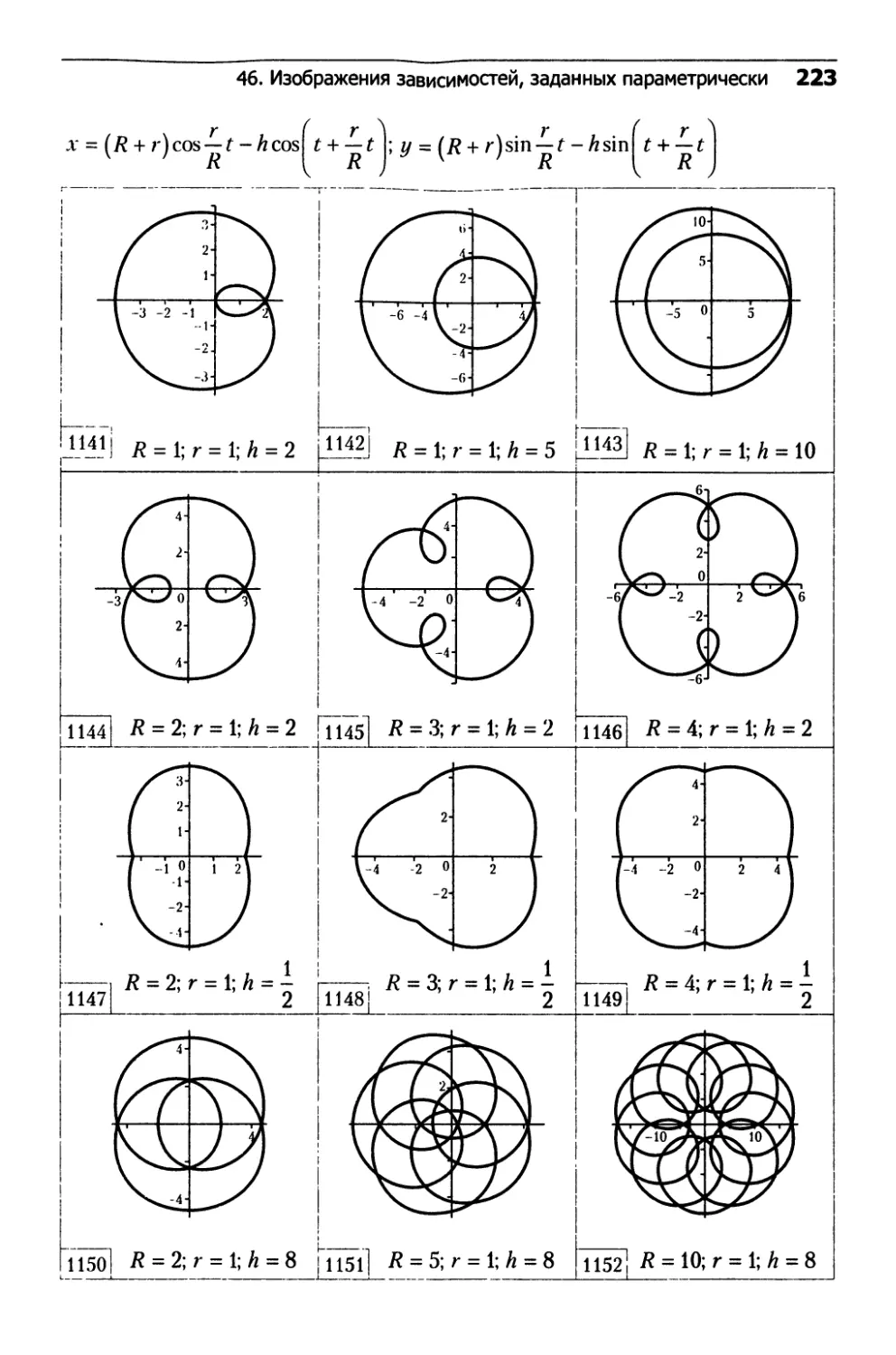
О Эпитрохоиды (см. ч. 2, рис. 1141-1152)
(16.39)
x = (/?4-r)cos —£-/zcos Г4- —
V 7 R ( R
T	(	T
у = (7? + r)sin — t - Asin t-\—t
R	I	R
□ Розы (см. ч. 2, рис. 1177-1188)
(16.40)
x = (R + r)cos—t - A cos t + — t
V ’ R l Я J
у = (7? + r)sin —t - Asin t + —tl
R	R j
= R + r
(16.41) r = asinA(p
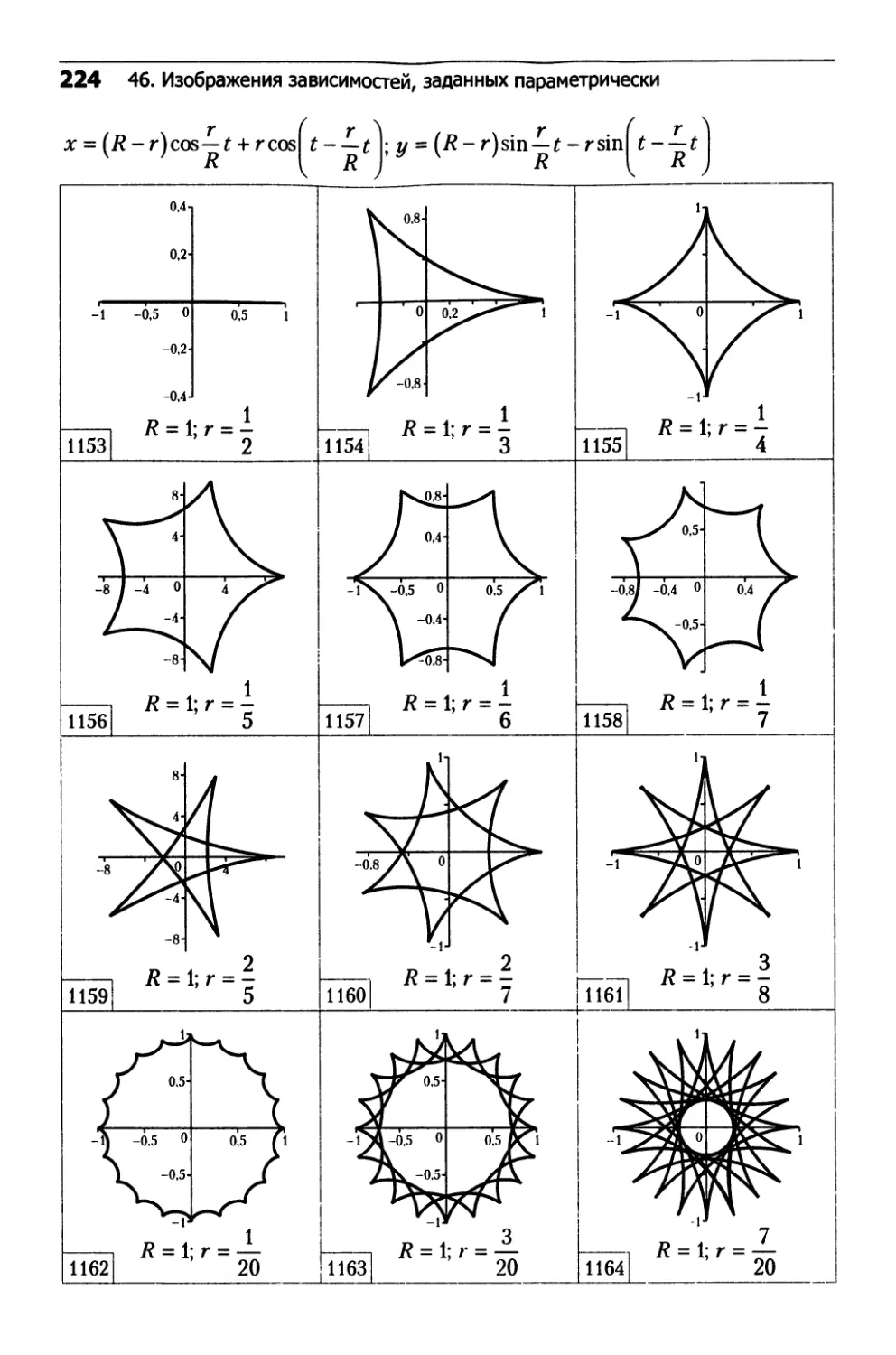
□ Гипоциклоиды (см. ч. 2, рис. 1153-1164)
(16.42)
x = (R-r)cos—t + rcos t- — t
v ’ R	[ R
у = (R - r)sin — t - rsin t- — t
R	^7?
17. Канонические уравнения поверхностей 2—го порядка 57
□ Гипотрохоиды (см. ч. 2, рис. 1165-1176)
(16.43) •	Г	( г А x = (R-r)cos — t + hcos t 1 ’	R	[	R	) r	(	r	\ y = (R-r)sin — t-hsin t	1 R	\	R
17.	Канонические уравнения
поверхностей 2-го порядка
□	Эллипсоид
(17.1)	^- + ^- + 4 = 1 (см. ч. 2, рис. 1201)
а b с
(17.2)	х2 + у2 + z2 = R2 — сфера (см. ч. 2, рис. 1202)
□ Однополостной гиперболоид
2	2	2
(17.3)	\ \ = 1 (см. ч. 2, рис. 1203)
а b с
□ Двухполостной гиперболоид
2	2	2
(17.4)	= -1 (см. ч. 2, рис. 1204)
а b с
□ Конус второго порядка
(17.5)	^- + ^--4 = 0 (см. ч. 2, рис. 1205)
а2 Ь2 с2
□ Эллиптический параболоид
(17.6)	z =	(см. ч. 2, рис. 1206)
а 1г
□ Гиперболический параболоид
(17.7)	z =	- 4 (см. ч. 2, рис. 1207) ,
а b
58 Часть 1. Формулы
□ Эллиптический цилиндр
(17.8)	= 1 (см. ч. 2, рис. 1208)
а2 Ь2
□ Гиперболический цилиндр
(17.9)	= 1 (см. ч. 2, рис. 1209)
а b
а Параболический цилиндр
(17.10)	у2 = 2рх (см. ч. 2, рис. 1210)
□ Пара пересекающихся плоскостей
х2 z2
(17.11)	^-±- = 0 (см. ч. 2, рис. 1211)
а2 с~
□ Пара параллельных плоскостей
х2
(17.12)	= 1 (см. ч. 2, рис. 1212)
а2
18.	Определители
А — квадратная матрица размера п х п
□ Определитель первого порядка
(18.1) Д = | А | = detA = det(a11) = «11
□ Определитель второго порядка
(18.2) Д=|А| =detA =
«и
«21
а\2
а22
«21
~ «И ’«22 “ «12 '
□ Определитель третьего порядка
	«п	«12	«13	
(18.3) Д = | А| =detA =	«21	«22	«23	=
	«31	«32	«33	
18. Определители 59
= «1Г
«22
«32
«23	„	«21
“«12 ’
й33	«31
«23 . „	«21 «22
„ +0‘з-	„
«33	«31 «32
- «И • «22 ' «33 + «12 ’ «23 ’ «31 + «13 ' «21 ' «32 ~
- «и • «2з • «32 “ «12 • «21 ’ «33 ~ «13 ' «22 * «31
□ Определитель n-го порядка
(18.4) Разложение по первой строке:
«п
A = detA=a21
«12	—	«1л
«22	-	«2л
«л2	•"	«пл
=Е°1А=Е<-1),+Уа1Ли
;=1 ;=1
«»1
(18.5) Разложение по i-й строке; i = 1,2,..., п:
	«и	«12	•	• «1»
Д = det А =	«21	«22 •	• «2»
	«л1	«л2	•	«лл
п	п
7=1	7=1
(18.6)	Определитель треугольной матрицы:
«И 0	«12 «22	«в «23	•••	«1л - «2л	-«н -а22-а33 •.	,,Qnn
0	0	...	о «„„		
□ Алгебраическое дополнение Ау элемента atJ
(18.7)	Д, =(-1)'+7 М?; i = l,2,...,n; j = 1,2,.... п;
Mjj — минор элемента atJ — определитель п -1 прорядка,
получаемый из исходного вычеркиванием i -й строки и j -го
столбца
□ Свойства определителей
(18.8)	Определитель транспонированной матрицы равен определите-
лю исходной матрицы, | Аг |=| А |
60 Часть 1. Формулы
(18.9)	Если все элементы какой-либо строки (столбца) определителя
равны нулю, то А = О
(18.10)	Если определитель имеет две одинаковые строки (столбца),
то А = О
(18.11)	Если элементы какой-либо строки (столбца) определителя про-
порциональны элементам другой строки (столбца), то А = О
(18.12)	Если все элементы какой-либо строки (с голбца) определи-
теля имеют общий множитель, то его можно вынести за знак
определителя.
(18.13)	Если в определителе переставить какие-либо две строки (столб-
ца), то величина определителя поменяет знак: At = -А
(18.14)	Если к какой-либо строке (столбцу) определителя прибавить
другую строку (столбец), умноженную на одно и то же число,
то величина определителя не изменится: At = А
□ Решение системы п линейных алгебраических уравнений с п неиз-
вестными по формулам Крамера
(18.15)	Матричная запись системы линейных уравнений:
012	-
«22	...	^2
ап2 —
^пп	ап\
19. Матрицы 61
(18.16)	Если АХ = В; А = det А * 0, то система имеет, и притом
единственное, решение X =
f Аг
д
^2
д
(формулы Крамера)
*л
д
(18.17)	Если система однородная, то есть АХ = 0, и Д = det А * 0, то

19. Матрицы
□ Прямоугольные матрицы размера тхп
(19-1)
«11
«21
«12	-	«1л
«22	- «2л
;	— элемент г-й строки и у’-го
столбца
&т2	••• ^тп ?
(19.2) Матрица-строка: А1хл = (о,, а12 ... а1я)
(19.3) Матрица-столбец: А^ =
«11
«21
«mt
62 Часть 1. Формулы
(19.4) Транспонированная матрица:					а21 а22	... ат^ - ат2
Аг = R = тхп **пхт	^12	- л21 а22 ...	г с с o' o' :	Т	CN J34 о4 :		
	кати1 ат2 -	®тп ;		^Хп	а2п	••• ^mn ?
		а11 1	а,2			
(19.5) Квадратная матрица: Алх„ =		а21	1	я22		а2п	
		*	яп2		апп )пхп	
		<а11	а12	Л13		«1/
(19.6) Треугольная матрица: Алхл =		0	а22	а23 -		а2п
		0	0		0	Qnn
						пп Jnxn
		Ч I	3 (	) ...	(Г	
(19.7) Единичная матрица: Е = Е„ =		°	1 с	> ...	0	
		0 1	3 ..	. 0	1 )пхп	
□ Равенство матриц
(19.8)	Amxz2 — Втех/2 <=> а у — by у i — 1,2, ,..уШу j — 1,2,..., и
□ Нулевая матрица
(19.9)	Amxn = 0mxn ау =0; i = 1,2,..., m; j = 1,2,n
□ Противоположная матрица
(19.10)	B^ — —Awxw <=> by — —fly, i — 1,2, ...,ти, j — 1,2,..., и
□ Сложение матриц одинакового размера
(19.11)	Стхп — А^^ + Вшхл <=> Су — а,у + by у i — 1,2,...,/и, j — 1,2,..., и
(19.12)	А + В = В + А (коммутативность сложения)
(19.13)	А + (В + С) = (А + В) + С (ассоциативность сложения)
19. Матрицы 63
□ Умножение матрицы на число
(19.14)	С = аА = Аа <=>	= аа^; i = 1,2,/тг; j = 1,2,...,и
(19.15)	а (РА) = (аР) А (ассоциативность умножения на число)
(19.16)	а(А + В) = аА + аВ (дистрибутивность умножения на число
относительно сложения матриц)
(19.17)	(а + Р) А = аА + РА (дистрибутивность умножения числа на
матрицу относительно сложения чисел)
□ Умножение матриц согласованного размера
(19.18)	Стх1 — Атхп • Bwx/ <=> Су —	• bkj —
k=i
= ai\b\j + ai2b2j + - + Ginbnj; * = !> 2,m; j = 1,2,..., /
(19.19)	A(B + C) = AB + AC (дистрибутивность умножения)
(19.20)	(В 4-С) A = BA 4-CA (дистрибутивность умножения)
(19.21)	A(BC) = (AB)C (ассоциативностьумножения)
(19.22)	ВА Ф АВ (некоммутативность умножения в общем случае)
□ Свойства единичной матрицы
(19.23)	AWXWEW = E„AWXW = Awxw
(19.24)	А^Е„=А^
(19.25)	E„AWX/W = Апхт
□ Обратная матрица
(19.26)	А-1 называется обратной к А = Апхп,
если А • А-1 = А-1 А = Е
□ Вычисление обратной матрицы методом присоединенной матрицы
(19.27) А'1 = Д^;А'
%
Л12
Ап
Л21 ... д/
Аг ••• Аг
Ап ••• Ап.
Д = det А * 0;
Av — присоединенная матрица; Ду — алгебраическое допол-
нение элемента i = 1,2,...,j = 1,2,..., и
64 Часть 1. Формулы
□ Решение системы п линейных алгебраических уравнений с п неиз-
вестными методом обратной матрицы
(19.28)	АХ = В; det А * 0 « X = А ’В;
□ Ранг матрицы
(19.29)	Минором матрицы Awxrz порядка k называется определитель
квадратной матрицы, содержащей элементы, стоящие на пере-
сечении произвольных k строк и k столбцов матрицы. Рангом
ra??g(A) матрицы Awxz? называется число, равное наибольше-
му порядку отличных от нуля миноров матрицы.
(19.30)	0 < rang(А) < min{?w, п}, где min{?w,n} — наименьшее из чисел
т и п
(19.31)	rawg(A) = 0 <=>	= 0 V/, j
□ Теорема Кронекера-Капелли о совместности систем т линейных
уравнений с п неизвестными
(19.32)	АХ = В имеет решениям rang (А) = rang (А | В) = г;
(19.33)	Если г = п , то решение единственно, если г < и, то решений
бесконечно много
(19.34)	Если система однородная, то есть АХ = 0, то: она совместна
и имеет по крайней мере одно нулевое решение X = 0; при
г = п она имеет единственное нулевое решение X = 0
20. Пределы и непрерывность 65
20. Пределы и непрерывность
Предел числовой последовательности
(20.1)	Число а называется пределом (конечным пределом) последо-
вательности {xn} = x1,x2,x3,...,x„,..., lim хп = а,
п—*оо
если Ve > 0 3N = N (е): \/п > N => \хп - а\ < е
(20.2)	Последовательность {а„} называется бесконечно малой, если
lim а„ = 0, то есть если Ve > 0 ЗУ : Vn > У => |а J < е
И-»°°
(20.3)	Последовательность {х„} называется бесконечно большой,
lim	хп	= °°, если VE > 0	ЗУ :	Чп > N => \хп I > Е
(20.4)	lim	хп	= -н» , если	\/Е > О	ЗУ :	\/z? >	N => хп> Е
(20.5)	lim	хп	= -о®, если	VE > О	ЭЛТ:	\/п >	N => хп < -Е
(20.6)	lim	х„	= а <=> х„ =	а + а„;	lim а„	= О
п—>°°	п—>°°
(20.7)
lim а„ = 0; а„ * 0 Vn <=> lim
J
а,
□ Свойства сходящихся последовательностей
(20.8)	lim (хп ±yn}= lim хп ± lim уп (предел суммы и разности)
(20.9)	lim (хпуп) = lim хп • lim уп (предел произведения)
п—»оо
(20.10)	lim (схп) = с • lim хп; с — постоянная
П—И->оо
(	\	lim хп
(20.11)	lim — =	; уп 0 Vn; lim уп * 0 (предел дроби)
»-Н Уп J	hm Уп	п^°°
X 7	w-»oo
(20.12)	Предельный переход в неравенстве:
lim хп = lim уп =а\ xn<zn< уп Yn => lim zn = а
П—>оо	П—^оо	П—>оо
□ Сходимость монотонной и ограниченной последовательности
(20.13)	Если последовательность {хп} не убывает (хп ^xn+i Чп)
и ограничена сверху ( ЗЛ/ : хп < М Yn ), то она сходится,
и lim хп = а < М
66 Часть 1. Формулы
(20.14)	Если последовательность {х„} не возрастает (хп > х//+1 \/п )
и ограничена снизу (Зт : х„ >т\/п),то она сходится,
и lim хп = а>т
П-^оо
□ Критерий Коши сходимости последовательности
(20.15)	lim хп = а <=>
<=> (\/е > 0 ЗУ = У (е): Чт > N, \/п > N => \хт - х„| < е)
Предел функции
(20.16)	Число а называется пределом (конечным пределом) функции
f (х) в точке х(), lim f (х) = я, если f (х) определена в неко-
А-».Г0
торой окрестности J7(x0) или U (х0) и если
Ve > 0 38 = 8(e) > 0: Ух, 0 <| х — х0 |< 8 ==> |/(х) - а\ < е
(20.17)	lim f(x) = a<=$ f(x) = a + a(x), lima(x) = 0
Л-^.Г0	X—>Xq
□ Свойства функций, имеющих предел (правила вычисления пре-
делов)
(20.18)	lim (/(x)±g(x)) = lim /(х)± lim g(x) (предел суммы
X—>Х0	>4)	Х-»Х0
и разности)
(20.19)	lim (/(x)g(x))= lim /( х)- lim g(x) (предел произведе-
х-»х0	х'—>х0	х—>х0
ния)
(20.20)	lim (cf (х)) = с lim f (х); с — постоянная
X—>Ху	х->х0
fix} А*)
(20.21)	lim Z_L_2 = ±_; lim g(A-)^0 (предел дроби)
^og(x) hmg(x) -r-*x0
х-»х0
□ Односторонние пределы функции
(20.22)	Число а называется пределом функции в точке х0 слева,
lim (х) н /(х0 - 0) = а, если
Ve>0 38 = 8(е) > 0: Vx, х0 -8<х<х0 => |/(х)-а| < е
20. Пределы и непрерывность 67
(20.23)	Число а называется пределом функции в точке х0 справа,
lim f (х) = / (х0 + 0) = л, если
х—►Xq +0
Ve > 0 38 = 5(e) > 0: Vx, х0 < х < х0 + 8 => |/(х) - а\ < е
□ Условие существования предела функции
(20.24)	lim /(х) = а<=> lim /(х) = lim /(х) = а
х—>Xq	х—>хо-О	х—>х0+0
□ Пределы функции -«на бесконечности»
(20.25)	lim f (х) = e « Ve > 0 3D > 0: Vx, |х|> D => |/(х)-а| <е
X—>оо
(20.26)	lim f(x) = а <=> Ve > 0 3D> 0: Vx, x< -D=> |/(x)-a| < e
x—>-«»
(20.27)	lim f (x) = a <=> Ve > 0 3D > 0: Vx, x > D => |/(x) - a\ < e
□ Бесконечные пределы
(20.28)	Предел функции называется бесконечным, lim f (х) = °°,
х-»х0
если V£ > 038 > 0: Vx,0 <| х - х0 |< 8 => |/(х)|>Е
(20.29)	lim f (х) = +<», если
х-»х0
V£ > 0 35 > 0: Vx, 0 <| х-х0 |< 8 => j\x)>E
(20.30)	lim f (х) = -о», если
х->х0
V£ > 0 38>0: Vx, 0<| х-х0 |<8 => /(х) < -£
□ Замечательные пределы
(20.31)	lim^^ = l — первый замечательный предел
х->0 х
(	1Y (	1 f
(20.32)	lim 1 + — = е; lim 1 + — = е — второй замечательный
X J	П J
предел; е = 2,71828
(20.33)	lim (1 + х)х =е
(20.34)	lim
х->0 X
68 Часть 1. Формулы
(20.35)	UmHl±21 = l
х—>0	X
(20.36)	lim —— = Ino
х—>0 X
ех -1
(20.37)	lim----- = 1
х-»0 х
(20.38)	lim ~1 = а
>0 X
(20.39)	lim^^—^ = -
х—»о	х 2
□ Бесконечно малые и бесконечно большие функции
(20.40)	Если lim а(х) = 0, то а (х) называется бесконечно малой
х->х0
при х —> х0
(20.41)	Если lim f (х) = °° ( lim f (х) =	, lim f (х) = +«> ),то f (х)
Х-»Х0	Х^Х(}	х->х0
называется бесконечно большой при х —> х0
(20.42)	а(х) — бесконечно малая и а(х) 0 при х * х0
1 *
<=> —т—г — бесконечно большая
а(х)
(20.43)	Если lim а(х)= lim Р(х) = 0и lim ^у^ = 1,тоа(х)иР(х)
г—»хо	Х—ЬХц	Х—ЬХц р(х)
называются эквивалентными бесконечно малыми при х —»х0,
а(х)~р(х)
□ Таблица эквивалентных бесконечно малых при х -» 0
(20.44)	х + х2 ~ х
(20.45)	х + у[х ~ 4х
(20.46)	х + 4х + х2 - \[х
(20.47)	(1 + х)" -1 - пх
(20.48)	(1 + х)2 -1-2х
20. Пределы и непрерывность 69
(20.49)	(1 + х)3 -1 - Зх
(20.50)	<УГ+х-1~-
п
(20.51)	>Я+х-1-^
(20.52)	ax-l~xlna
(20.53)	е™ -1 - ах
(20.54)	ех -1 - х
(20.55)	loga (1 + х) - xloga е
(20.56)	1п(1 + х) - х
(20.57)	sin ах - ах
(20.58)	sin х - х
(20.59)	sin" х - х"
х3
(20.60)	х - sin х - —
(20.61)	arcsin х - х
г3
(20.62)	l-cosx~y
(20.63)	tgx~x
х3
(20.64)	tgx-x- —
3
x3
(20.65)	tg x - sin x ~ —
Непрерывность функции и точки разрыва
(20.66)	Функция f (х) называется непрерывной в точке х0, если: /(х)
определена в точке х0, 3 lim /(х ), lim/(х) = /(х0)
.г->.г0	.г-»х0
(20.67)	Функция /(х) называется непрерывной в точке х0 слева
(справа),если lim /(х) = /(х0) lim /(х) = /(х0)
х—>.г0 -0	х-+ х0 +0	\
(20.68)	Критерий непрерывности. Функция f (х) непрерывна в точке
х0<=> lim /(х) = /(х0)= lim /(х)
х-».го-0	х-».г0+0
70 Часть 1. Формулы
□ Точки разрыва
Если в точке х0 не выполняется хотя бы одно из условий непрерыв-
ности, то х0 называется точкой разрыва.
(20.69) х0 — точка разрыва 1-го рода, если
3 lim /(х); 3 lim /(х); lim /(х)* lim /(х)
х—>хо-О	х—>хо+О	х—>хо-О	х-»хо+О
(разрыв называется скачком) или если
3 lim /(х),но А(х0)^ lim f (х) или f (х) не определена
г->л0	‘	х-»х0
в х0 (разрыв называется устранимым)
(20.70) х0 — точка разрыва 2-го рода, если хотя бы один из пределов
lim /(х); lim /(х) бесконечен или не существует.
х—>х0 -0	х—>х0
□ Свойства функций, непрерывных на отрезке
Если функция f (х) непрерывна в каждой точке отрезка [«; h], то:
(20.71) f (х) ограничена на этом отрезке, то есть
ЭМ > 0: |/(х)| < М Vx е [а; Ь]
(20.72)	f (х) достигает минимального и максимального значения на от-
резке, то есть За,Pg [я;: f (а) = min/(х); f (Р) = max/(х)
(теорема Вейерштрасса);
(20.73)	при условии f (я) • f (6) <0 Зсе (я; 6): / (с) = О
21.	Производная и дифференциал
Производная функции
(21.1)	Если функция у = /(х) определена в некоторой окрестно-
сти точки х0, то производной функции в точке х0 называют
предел г/'. (х0) =/'(х0) = lim	=
Дх—>0 Дх
= Hm /(х0+Дх)-/(х0) = Hm /(х)-/(х0)
Дх—>0	Дх	.v->-r0 X - Х()
21. Производная и дифференциал 71
Если предел конечен, то говорят, что в точке л0 функция имеет про-
изводную (конечную производную)
□ Бесконечные производные
(21.2)	Если lim — бесконечен (равен - ©о ), то говорят, что
Д.г-»0 Дх
в точке х0 функция имеет бесконечную производную
□ Односторонние производные
(21.3)	(х0) = /'(х0 “ 0) = ^m0 ^ Y° "	_ левая произ-
водная
(21.4)	/+'(х0) = /'(х0 + 0) =	— правая про-
изводная
□ Условие существования производной функции
(21.5)	/'(х0) = А <=> (х0) = Д' (х0) = А
□ Существование производной и непрерывность
(21.6)	Если существует конечная производная /'(х0),то /(х) в точке
х0 непрерывна
□ Производные основных элементарных функций (таблица произ-
водных)
(21.7)	с'= 0, с —постоянная
(21.8)	х' = 1
(21.9)	(ха) =оха‘1, acR
Ci Y	i
(21.11)	— = ~
lх )	х
(21.12)	(ax>j =ах\па
72 Часть 1. Формулы
(21.13)	(г)' = ех
(21.14)	(logax)'=-^-
хшя
(21.15)	(1пх)' =|
(21.16)	(sinx) = cosx
(21.17)	(cosx) =-sinx
(21.18)	(tgx)'=-4-
COS X
(21.19)	(ctgx)' =----
sin x
(21.20)	(arcsin x) =	*
Vl-x2
(21.21)	(arccosx) =—. *
Vl-x2
(21.22)	(arctgxV =——y
1 + x
(21.23)	(arcctgx) =--y
1 + x2
□ Производные гиперболических функций
,	ex - е-х
(21.24)	(sh x) = ch x; sh x = —-—
,	ex + e-x
(21.25)	(chx) =shx;chx = —-—;
(21.26)	(thx) =—;thx = ^
ch2 x chx
(21.27)	(cthx)' =-^—;cthx = |^
21. Производная и дифференциал 73
□ Правила дифференцирования ( и 
(21.28)	(ш) =си, с —постоянная
(21.29)	(и ± г>) = и ± v
(21.30)	[uv] =uv + uv
(21.31)	(/2(х))' =2/(х)/'(х)
и
V
(21.32)
(21.33)
1
uv-uv „
---2--. V*0
V
(21.34)	(uvw) = uvw + uvw + uvw'
□ Производная сложной функции Л(х) = /(g(x))
(21.35)	h'(x) = (/(g(x))) = fg (g) • g'r (x);	,
□ Производная обратной функции
(21.36) Если у = /(х); х =	(г/), то
1 , 1
/И’ ХУ “
□ Производная функции, заданной параметрически
(21.37)	Если х = х(£), у = г/(^), а < t < b, тоу'х =
xt
□ Производная функции, заданной неявно
(21.38)	Если функция г/(х), а < х < b, задана в виде F(x,z/) = 0,to
у'х (х) находят из уравнения F'x (х, у (х)) = О
□ Производная показательно-степенной функции ( w(x) > 0 )
= uv Inw • v + vuv 1 • и
74 Часть 1. Формулы
(21.40) (,?j=(ufj
(правило для запоминания)
«=C()DSt
r=const
(21.41)	(хЛ)' =х' (1 + In а )
□ Производные высших порядков
(21.42)	г/'(х) — производная 1-го порядка (первая производная);
У* - (у') <у" = (У*) > •••» УМ =	) (вторая, третья,..., «эн-
ная» производная, пе N); у^ (.г) = j/(x)
(21.43)	(си ± а)(н) = си(п) ± vw; с — постоянная
(21.44)	(uv)(re> = ^Ски(к\;("~к>;Ск = --- П' (формула Лейбница)
k=o	k\(n-ky.
(21.45)	(uv) =(u'v + uv') = u”v + 2u'v +uv"
(21.47)	(xa)( * = a(a-l)(a-2)• • • (a- и + l)x“ ";ae R
(21.48)	= 0; me N; n > m
(21.49)	[айхп +alxn~1 + ... + an^ * =n!a0
(21.50)	(ar)( > =(lna)"av
(21.51)	=anex;ae R
(21.52)	(ev)(n> =ex
(21.53)	(M«
xn
(21.54)	(sinx)(n) =sin(x + —
I 2 >
(21.55)	(cosx)(n) =cosfx + ^~l
21. Производная и дифференциал 75
□ Формулы Тейлора и Маклорена
w f(k) (х )
(21.56)	/(*) = Х-Г“\х”ло) +^?(х) ~ формула Тейлора;
k=o
Z ч /(л+1) (х0 + 0(х- х0))	„+1
R-w=~—(kiji—~(л' ’ х° > ; 0 =6 ‘1
" /(i) (о)
(21.57)	/(х) =	—т~'хк + Rn (х) ~ формула Маклорена;
k=o
I «Л I / v X j W tr J.
"v 7 (и + 1)!
□ Теорема Ферма. Необходимое условие экстремума функции
(21.58)	Если функция у = f (х) дифференцируема в точке х = с
и принимает в этой точке максимальное или минимальное
значение, то /'(с) = 0
□ Теорема Ролля
(21.59)	Если функция у = /(х) непрерывна на [я;Ь], дифференциру-
ема на (а; Ь) и f(a) = f(b), то Зсе(я;6): /'(с) = 0
□ Теорема Лагранжа
(21.60)	Если функция у = f (х) непрерывна на [я; Ь], дифференциру-
ема на (а,Ь), то 3cg (я; 6): /(&)- f (^) = /
□ Теорема Коши
(21.61)	Если функции f (х) и g(x) непрерывны на [а;Ь],
дифференцируемы на (а;Ь) и g'(x) 0, то
3cg (a;b):
/(b)-/W f(c)
g(l>}-g(a)	g'(c)
□ Правило Лопиталя для раскрытия неопределенностей
(21.62)	Если lim /(х)= lim g(x) = 0,функции/(х) и g(x) диффе-
х-*.го	.Г—>.V(j
ренцируемы в окрестности U(х0), g(x) 0, g'(x) Ф 0 в этой
76 Часть 1. Формулы
. /'(*) , /(*)
окрестности и 3 lim '	, то 3 пт —-j— и выполнено ра-
г-»х0 g (х)	x->*og(x)
.. fM .. ГМ
венство lim —^—7 = lim —77—7.
^og(x) J4-rog(x)
Аналогичное правило применяется при
lim /( х) = lim g(x) = «j
X—>Xq	X—>Xq
□ Уравнение касательной к графику функции
(21.63)	у-у0 = /'(х0)(х-х0)
□ Уравнение нормали к графику функции
(21.64)	(?/-t/o)/'(xo) + (-r"-ro) = o
Дифференциал функции
(21.65)	Ау = f (х + Ar)- f (х) — приращение функции
(21.66)	Если Аг/ = А&х + а (Ах) Ах, где А — число, lim а (Ах) = 0, то
функцию называют дифференцируемой в точке
(21.67)	/'(х) существует и конечна <=> /(х) дифференцируема
(21.68)	dy = /'(х)Ах = f'(x)dx — дифференциал функции
(21.69)	dx = Ах
(21.70)	б/(ам) = а ч/м
(21.71)	d(u ± а) = du ± dv
(21.72)	d (га») = udv + vdu
(21.73)	d(“\=vdu~udv. r#0
I V
(21.74)	Инвариантность формы дифференциала первого порядка: если
у = f (и); и = <р(х), то dy = y'xdx = y'uu'xdx = y'udu
□ Приближенные вычисления с помощью дифференциала
(21.75)	/(х0 + Дх) = /(х0) + /'(х0)Дх
22. Неопределенный интеграл 77
□ Дифференциалы высших порядков
(21.76)	dxy = dy = f'(x}dx
(21.77)	d2y = d(dy) = f’(x)(dx}2 = f'(x)dx\ dx2 = {dx)2
(21.78)	dny = d(dn~xy] = /")(x)(&)” = /(n) (x)dxn-, dxn e (dx)n
□ Выражение производных через дифференциалы
(21.79)/	= J; / = ^f;...;^=^
dx dx	dx
22.	Неопределенный интеграл
□ Первообразная
(22.1)	F(x) называется первообразной для f(x) на заданном проме-
жутке, если 3F'(x) и F'(x) = f(x)
□ Неопределенный интеграл
(22.2)	|/ (х) dx = F (х) + С; С — произвольная постоянная
□ Свойства неопределенного интеграла
(22.3)	(f/(x)dr)'=/(x)
(22.4)	</| f (х) dx = f (x) dx
(22.5)Jr	(x)«!r = F(x) + C
(22.6)	pF(x) = F(x) + C
(22.7)	Jx/(x)<& = Ajf(x)dx; Л*0
(22.8)	J (/ (x) ± g (x)) dx = | f (x) dx ±j g (x) dx
□ Таблица интегралов
(22.9)	jOdx=C
(22.10)	jldx = fdx = x + C
78 Часть 1. Формулы
(22.11)	j(ax + b)dx = ^x2 +bx + C
(22.12)	j(aox" +alxn~i +... + an^dx =	x"+1 + —
П'
——т-dx = arctgx + C
1 + xr
1 j 1	. X „
—z---7dx = -arctg— + C
x+a2 a a
1 <Zx = ^-ln
x2-a2 2a
х-а
J_dx = arcsin x + C
-x2
1	X
===== dx = arcsin — + C
2	_ -r2	a
1
(22.25)	|sinxdx = - cos х + С
(22.26)	|cos xdx = sin x + C
22. Неопределенный интеграл 79
(22.27)	f—l_dr = tgx + C
J COS X
(22.28)	f —4— dx = - ctg x + C
J sin“ x
(22.29)	| sh xdx = ch x + C
(22.30)	| ch xdx = sh x + C
(22.31)	f—~dx = -cthx + C
J sh2 x
(22.32)	Г-Ц— dx = thx + C
J ch x
□ Метод интегрирования с помощью замены переменной
(22.33)	Метод подведения под знак дифференциала:
]7(ф(х))ф'(х)</г = ]7(ф(х))</ф(х) = J/(iz)t/w|
<22.34)	.,.,w
(22.35)	J/НеЦ
□ Метод интегрирования по частям
(22.36)	J и (х) v' (х) dx = и (х) v (х) - J v (х) и (х) dx
(22.37)	J udv = uv - j vdu
□ Интегрирование рациональных дробей
(22 38) f 1W+1	т>п-,1<п -,
Л, (*); CU Л,-Л-гО: я, (х)
многочлены. [ 1 (
JQ„W
сводится к сумме интегралов от простейших рациональных
дробей методом неопределенных коэффициентов
80 Часть 1. Формулы
□ Интегрирование простейших рациональных дробей
г А
(22.39)	Простейшая дробь 1-го типа: |-dx = Л1п|х-а|+С
J х-а
(22.40)	Простейшая дробь 2-го типа:
f—— dx = ~—---------------------J-
J / \n	yj _ 1 /	\W-1
пе N; п > 2
(22.41)	Простейшая дробь 3-го типа:
в_Ар
г Ах + В j г At , г 2 л
J —-------dx = I ---2dt + J~-- 2 dt ’
J x2 + px + q	J г + СГ J t +a
42
>0
2
р2 - iq < 0; t = х + а2 = q -
(22.42)	Простейшая дробь 4-го типа:
г Ах + В j л г tdt (п
--------------dx =А\---------+ В -
J / О	\П	J / 9
dt
и g N; и > 2; р2 - 4^ < 0; f = х + р а2 = <7 - I |
\2
(22.43)	J tdt
J ✓ 9	9 \ fi
----------------- + C; n > 2
2(п-1)(г2 +a2j
(22.44)	J-----
J / 9	9\П
n-1
+Я1-
a
dt o
--------r! n - 2
9 \W-1
1
1
□ Интегралы от некоторых рациональных дробей
(22.45) f—!— dr = iln|ar + 6| + C
(22.46) f—4-ln|ox +Al+ C
J ax + b a a1
22. Неопределенный интеграл 81
(22.47) f^4«Zr = -x + J ex + d	c	be-ad c2	ln|cx + d\ + C
(a48)j(z+4U)=	—Ц-ь a - b	x + b r.	, 	+C;a^b x + a
(22-49)/(х+Х+б)='	—(a In |x + a| - b In |x + Z>|) + C; a * b	
(22.50)	dr =hn J xz +az 2	|x2 + a2	|+c
x2	,	X	_
------ ax-x-a- arctg — + C
2 + a2	a
(—---------= г-1 — In
2ax2+bx + c y/b2-iac
b2 - 4ac > 0
2ax + b- 4b2 -4ac
2ax + b + 4 b2 -4ac
dx
2	2ax + b _ ,2	. Л
—------------ r .... arctg . ...-	+ C; b - 4ac < 0
ax + bx + c yj4дс -fa2	5/4ac - b2
dx	2	> 2 . л
—		=-----------+ C; b - 4ac = 0
ax2 +bx + c 2ax + b
xdx	1 .	I	2 > I	b t	dx	„
—	-------=—In ar +bx + c	—5--------+ C
ax2 +bx + c	2a	1	1	2aJ ax	+bx + c
1	,	1 . (x + a)2	1 2x-a „
------X- dx = —7 In -----'—Z + -V7= arctg —r~ + C
x3+a3 6a x-ax + a2, a2\/3 a\l3
r x ,	1, x2-ax + a2 1	2x-a „ (22.57)		?dx = — In	г—+ r arctg г +C Jx3+a3	6a (x + a)2 aV3	aV3 (22.58) [ Л--ч<£г = -1п|х3 + а3| + С J x3 + a	3 1	1

82 Часть 1. Формулы
□ Интегралы от некоторых иррациональных функций
(22.65)	14ах + bdx = у- у](ах + b)3 + С
(22.66)	Jxdax + bdx =	\j(ax + b)3 + С
(22.67)	l-T----dx = -dax + b + C
} 4^+Ь а
(22.68)	f— dx =	dax + b + С
J dax + b За2
(22.69)	J Vx2 + a2dx = л/х2 + а2 + — In х + Vx2 + а2 + С
(22.70)	J xylx2 + a2dx = ± ^х2 + а2) +С
(22.71)	f \la2 - x2dx = — Va2 - х2 + — arcsin — + С
i	2	2 а
(22.72)	/ x4a2-x2dx = -|^(а2-х2)3 + С
22. Неопределенный интеграл 83
□ Интегралы от некоторых показательных и логарифмических функций
(22.73)	[ e^dx = 1	+ С
J	а
(22.74)	Jxexdx = ех (х -1) + С
(22.75)	J xnexdx = хпех - nj xn~lexdx + С
(22.76)	J ех sin xdx = ех (sin х - cos х) + С
(22.77)	Jех cosxdx = ^ех (sinx + cosx) + С
(22.78)	|lnx<£r = x(lnx-l) + C
(22.79)	jin2 xdx = xln2 x-2xlnx + 2x + C
(22.80)	J In" xdx = xln”x - n[ In”-1 xdx + C,n* -1
(22.81)	jxlnxdx = x2
fl	1)
-Inx— + C
2	4
(22.82) fx" lnxdx = xn+i
Inx 1
□ Интегралы от некоторых тригонометрических функций
(22.83)	J sin2 xdx =	1 sin 2х + С
(22.84)	J sin3 xdx = ± cos3 х - cos х + С
(22.85)	[ sin” xdx = - 1лг— + — [ sin"’2 xdx + С
J	п	п J
(22.86)	j-L-dx = -^--: 1
J sm х	2 sin x 2
+ —Intg — +C
2	°2
2
<2287)1-у;Л = - ’
cosx n-2 t 1	,	„
----------5— +------ -------5— dx + C
n -1 sin" 1 x n -1J sin” 2 x
84 Часть 1. Формулы
(22.88)	J cos2 xdx =	+ 4 sin 2x + C
(22.89)	J cos3 xdx = sin x - 4 sin3 x + C
(22.90)	J cos" xdx = cos".1——
J	n
+ -—- f cos" 2 xdx + С
п J
(22.91)	[-4—^ = sl?*~
J cos x 2 cos x
lx n » _
tg - + - + c
2 4 I
+ -ln
2
(22.92)	f—L-dx = —-----------
J cos" x n -1 cos" 1.
n—2r 1	,	„
---- ----75—	+ C
n -1 J cos” 2 X
t	, sin(m + n)x sin(?n-n)x „ ,	,
(22.93)	Г sin mx sin nxdx =-?--;--------------- + €>,тгг n1
3	2(m + n) 2(m-n)
e	, cos(n? + n)x cos(m-n)x ,	,
(22.94)	sin mx cos nxdx =------£--------7----7— + C; m n
3	2{m + n) 2(m-n)
t	, sin(m + n)x sin(m-n)x •	,	,
(22.95)	cos mx cos nxdx = —7---7— + —7-------- + C;m * n
v 3	2(m + n) 2(m-n)
r dx	1	 ftsinx-acosx + Va2 +b2
I 	~	— I -----1П	ф f	+
J flsinx + bcosx y]a2+b2 asinx + ocosx
(22.97)	jtgxdr = -ln|cosx| + C
(22.98)	j ctg xdx = In |sin x| + C
(22.99)	J arcsin xdx = x arcsin x + >/l - x2 + C
(22.100)	Jarccosx^/r = xarccosx- Vl-X2 +c
(22.101)	JarctgxJr = xarctgx - In 71 + x2 +C
(22.102)	Jarcctgxdlr = xarcctgx + Invl + x2 + C
23. Определенный интеграл 85
23. Определенный интеграл
□ Связь определенного и неопределенного интеграла
(23.1)	Если /(х) непрерывна на отрезке [а; Ь], то функция
X
j f (£) dt — одна из первообразных для f (х), то есть
а
= /(х); хе[а;/>]
(23.2)	\f(x)dx = \f(t)dt + C; xe[a;i]; С — произвольная посто-
fl
янная
□ Формула Ньютона-Лейбница
ъ
(23.3)	J f (х) dx = F (х)|’ = F (b) - F (a)
fl
□ Свойства определенного интеграла
b	b
(23.4)	$ldx = $dx = b-a
a	a
(23.5)	j/(x)<& = 0
fl
fl	b
(23.6)	J f (x)dx = -J f(x)dx
b	a
b	c	b
(23.7)	j f (x)dx = j/(x)dx +1/(x)dx (аддитивность)
fl	fl	c
b	b
(23.8)	j Af (x) dx = Aj f (x) dx\ A — постоянная
a	a
b	b	b
(23.9)	J(/ (x) ± g (x)) dx = J f (x)dx ± Jg (x) dx
a	a	a
86 Часть 1. Формулы
(23.10)	Если /(х) — четная, то J f(x)dx = 2 |/(х)<7х
-а	0
а
(23.11)	Если /(х) — нечетная, то j j\x)dx = Q
-а
□ Оценки значения определенного интеграла (а < Ь)
ь
(23.12)	f(x) > 0; а < х < b => ^f(x)dx > 0
а
b
(23.13)	/(х) < g(x); а < х < b => jf(x)dx <
а
ь
J g(x)dx
а
а
а
(23.15)	in< f(x)<M\a<x<b=$
а
(23.16)	Если f (х) непрерывна на отрезке [я; Ь], то
ь
3cg (a;b): j f(x)dx = f(c)(b - а) (теорема о среднем)
а
□ Метод интегрирования с помощью замены переменной
Ь	Ф(/>)
(23.17)	|/(ф(х))ф'(х)^ = j f(u)du
а	Ф(<?)
Ф(Р)	Р
(23.18)	J /(x)rfr = f/(<p(i))<p'(O^
Ф(а)	а
□ Метод интегрирования по частям
b	ь
(23.19)	j u(x)v(x)dx = и(.г)г(х)|а - J v(x)u(x)dx
а	а
b	b
(23.20)	j udv = iw |д - j* vdu
23. Определенный интеграл 87
□ Вычисление площадей, длин дуг и объемов с помощью определен-
ного интеграла
(23.21)	Вычисление площади криволинейной трапеции, ограничен-
ной графиком непрерывной функции /(х), /(х) > 0; а < х < Ь,
ь
и прямыми х = а;х = Ь;у = 0: S = j f{x)dx
а
(23.22)	Вычисление площади криволинейной трапеции, ограни-
ченной графиком функции, заданной в параметрической
₽
форме х = <р(0;у = у(£);а < £ < р: S = J\|/(£)ф'(£)<#
а
(23.23)	Вычисление площади криволинейного сектора, ограничен-
ного графиком непрерывной функции г = г(ф) и лучами
ф = а; ф = Р; 0 < а < Р < 2л (в полярных координатах):
1 р
а
(23.24)	Вычисление длины дуги кривой, заданной непрерывной функ-
цией /(х), имеющей непрерывную производную, а < х < b:
ь _________
L = j 71 + f'2{x)dx
а
(23.25)	Вычисление длины дуги кривой, заданной функцией
в параметрической форме х = <p(t); у = ф(0; а < t < Р:
₽ .------------
L = J V(P2(f) +
а
(23.26)	Вычисление длины дуги кривой, заданной функцией
г = г(ф), имеющей непрерывную производную в области
₽ 1-----------
определения а < ф < Р: L = J 7г(ф) + г/2(ф)«/ф
а
(23.27)	Вычисление объема тела вращения, образованного криволи-
нейной трапецией, ограниченной графиком непрерывной неот-
рицательной функции /(х); а < х < Ь и прямыми х = ст, х = b
ь
при вращении вокруг оси ОХ : V = л| f\x)dx
88 Часть 1. Формулы
(23.28)	Вычисление объема тела через площадь поперечного сечения
ь
S(x), перпендикулярного оси ОХ : V = j S(x)dx
а
(23.29)	Вычисление площади поверхности тела вращения,
образованного графиком непрерывной, имеющей непре-
рывную производную, неотрицательной функции /(х)
при вращении вокруг оси ОХ в области определения
ь ____________
a<x<b: S = 2л|*f(x)y/i + f\x)dx
а
(23.30)	Вычисление площади поверхности тела вращения,
образованного графиком функции, заданной в пара-
метрической форме х = ф(£); у = у(£); у(£) > 0; а < t < Р :
₽ .--------------
s = 2л|* ж(Оуф'2(О + ж'2(0^
а
(23.31)	Вычисление площади поверхности тела вращения,
образованного графиком непрерывной, имеющей
непрерывную производную, функции г = г(ф) в облас-
ти определения а < ф < Р, при вращении вокруг оси ОХ:
ь	____________
S = 2тг| г(ф)зт(ф)^2(ф) + r'2((p)d(p
а
24. Несобственные интегралы
□ Несобственные интегралы 1-го рода
(24.1)	Если /(х) непрерывна при а < х < -к», то несобственным ин-
тегралом по бесконечному промежутку называют
-к»	В
f f{x)dx= lim \f(x)dx = lim F(B)-F(a)
J	J	B^+oo
a	a
(24.2)	Если /(x) непрерывна при -о© < x < b, то
b	b
J f(x)dx= lim J f(x)dx = F(b) - lim F(A)
-oo	A
24. Несобственные интегралы 89
(24.3)	| f(x)dx= J j\x)dx + J j\x)dx,Vc, ceR
-oo	-oo	c
T i
(24.4)	— dx. При a > 1 интеграл существует (сходится), при a < 1
Jt xa
интеграл расходится
(24.5)	Признак сходимости и расходимости несобственных инте-
гралов 1-го рода (признак сравнения): если 0 < f(x) < g(x) при
а < х < +оо, то из сходимости j g(x)dx следует сходимость j f {x)dx,
а	а
из расходимости j j\x)dx следует расходимость j g(x)dx
а	а
□ Несобственные интегралы 2-го рода
(24.6)	Если /(х) непрерывна при а < х < b, lim f(x) = oo, то не-
x^b-Q
собственным интегралом от разрывной функции называют
b	b-s
j f (x)dx = lim j f (x)dx
a	a
(24.7)	Если f(x) непрерывна при a<x<b,
b	b
lim f(x) = oo , TO J f(x)dx = lim J f (x)dx
a	я+S
(24.8)	Если f (x) непрерывна при a<x<b, кроме точки
b	c	b
x = с; lim /(x) = °o, to J f(x)dx = J f(x)dx + J f(x)dx
X^C	a	a	c
г 1
(24.9)	—dx. При 0 < a < 1 интеграл существует (сходится), при
J
о л
a > 1 интеграл расходится
(24.10)	Признак сходимости и расходимости несобственных ин-
тегралов 2-го рода (признак сравнения): если 0 < /(х) < g(x)
90 Часть 1. Формулы
при а < х < b, lim f(x) = lim g(x) = то из сходимос™
x-^b-Q	x—>b-Q
h	b
jg(x)dx следует сходимость ^f(x)dx, из расходимости
a	a
b	b
^f(x}dx следует расходимость jg(x)dx
a	a
□ Гамма-функция
(24.11)	Г(х) = J e^t^dt — сходится при x>0
о
(24.12)	Г(х)>0;Г(х + 1) = хГ(х) при х>0
(24.13)	Г| | = у/п; Г(1) = 1; Г(п +1) = и!; пе N
□ Значения некоторых несобственных интегралов
г 1
(24.14)	\-—=dx = 2
Jo Vx
(24.15)	f 1 dx = —
14^7 *
(24.16)	f-V<& = l
i *
+~ .
(24.17)	f——dx = it
jLl + X
(24.18)	[ e dx =	>
/ r\ / 4п\ г sin ox j it
(24.19)		dx = -;a>0
ox
(24.20)	f e"ar sin nxdx =  — -у; a > 0
n	a1 + тс
25. Частные производные и дифференциалы функций нескольких переменных 91
25.	Частные производные
и дифференциалы функций
нескольких переменных
□ Частная производная функции и = f {x^x2,^xtl) по переменной
xk в точке (х1,х2,....х?/)
(251)	=
ах/, *
= lim	+ Ц,тНу--У»)-/(Л1^2--'^-Л)
М>->0	\xk
□ Производная функции и = f (xt, х2,..., хп) по направлению
/(cosa; cos₽; cosy)
Э/ dj	df а df
(25.2)	— cos а + — cos Р + — cos у
dl dx	dy dz
□	Частные производные функции и = f (х\,х2,...,хп) высшего по-
рядка
Э2/
и т. д.
<254>дашя
ох} Эл/ J ЭХ| ол ,
д2/
Эл\Эх2
д3/ .
Эл12Эх2
И т. д.
Э
Э"/
-----7—;... ит. д.
□	Полная производная сложной функции
(25.6) и = f(xvx2,...,xn), х, = <р, (t);
df_ =	+	+ , Э/ d(p„
dt дх} dt Эх2 dt дхп dt
92 Часть 1. Формулы
(25.7)	и = f(t,x2,.г„),х,	;
df _ df Э/ </<p2 ! Э/ </<p„
dt dt dx2 dt dxn dt
□ Частные производные сложной функции
(25.8)	и = /(х1.х2,...,х„),х1 =<р, (^,Г2.tm);
=У Эф£ + У Эф^+ +У Э<р^. k =
dtk ЭХ] dt^ Эх2	дхп dt&
□ Частные дифференциалы функции и = f (х,, х2,..., хп)
(25.9)</	= ^-dxt\ i = l,2,...,n
дх-
□ Полный дифференциал функции и = f (xvx2,...,xn)
(25.10)	df = ^-dx'i + ^-dx2 + ... + ^-dxn
dX]	0X2
□ Дифференциалы и-го порядка функции и = f(x,y)
(25.11)	df = ^-dx + ^-dy
дх ду
(25.12)	d2f = ^-4-(dx)2 +2^-£-dxdy + ^Х(Ф)2
Эх2	дхду ду2
(25.13)d3	f =	+ 3^-(dxf dy +
дх	дх dy
dxdy	dy
(25.14)	dnf =	• (Л)" + n-^-(dx)n-1 dy +...
dx	dx dy
„(„-о (n-^i)_2\/_(Л)-‘+... +	 (</,,)'
k\ dxn-kdykK ’ V	dyn
25. Частные производные и дифференциалы функций нескольких переменных 93
□ Формула Тейлора для функции и = /(х, у)
(25.15)	bf = f (х + Дх, у + Дг/)- f (х, у) =
_df(x,y) d2f(x,y)
= I1 +	2!
dn^f (x + 0Дх, у + 0Ду)
Rn —---------------------;
n	(п + 1)!
+ R"
O<0<1
□ Необходимые условия экстремума функции и = / (х, у)
(25.16)	Если в точке (х0,г/0) функция и = f(x,y) имеет макси-
мум или минимум и существуют частные производные
Э/(хо,г/о).Э/(хО)г/о)	д/(х0,г/0) _ Э/(х0,г/0)
,	, то---------—	~	— v. 1 ОЧКИ.
дх ду	дх	ду
в которых все частные производные 1-го порядка равны
нулю, называются стационарными
□ Достаточные условия экстремума функции и = / (х, у)
(25.17)	Если в окрестности стационарной точки (х0, г/0) существуютне-
прерывные частные производные функции w = f(x,y) первого
и второго порядка, то:
—	при условии В2 - AC <Q; A>Q в точке (х0, z/0) функция
имеет минимум;
—	при условии В2 - АС < 0; А < 0 в точке (х0, г/0) функция
имеет максимум;
—	при условии В2 - АС > 0 в точке (х0,yQ) экстремума нет.
Здесь А =
d2f(x0,y0) в = д2/(х0,у0) с = Э2/(х0,у0)
Эх2 ’ дхду ’ Ъу2
□ Уравнение касательной плоскости и нормали к поверхности
z = /(x,z/) в точке (x0;z/0;z0)
(25.18)	Э/(д°;Д'о)(х-х0) +	- Л) -(* - г») - °
ОХ	оу
(2519) Х~Х° = У~Уо = г~г°
7 д/(х0-,У0)	df(x0;y0)	-1
Эх	ду
94 Часть 1. Формулы
26. Кратные интегралы
□	Вычисление двойного интеграла через повторные
ь
(26.1) §f(x,y)dxdy = |
D	а
'Уг(х)	b Уг(х)
| f(x,y)dy dx = ^dx | f(x,y)dy,
j/M	J ° J'iW
a<x<b
У1 (x)<y< y2 (x)
d
(26.2) || f (x, y) dxdy = J
D	c
A d хг{у)
| f(x,y}dx dy = $dy | f(x,y)dx;
^i(v)	J c XM
c<y <d
Xl (y)^x< X2 (y)
□	Свойства двойного интеграла
(26.3)	||f (x,y)dxdy = || f(x,y)dxdy + || f(x,y)dxdy (аддитивность);
D	Di	D2
D = D{ u D2 ; D{ и D2 не имеют общих внутренних точек
(26.4)	|| Af (х, у) dxdy = Л|| f ( х, у) dxdy; А — постоянная
D	D
(26.5)	||(/(х, у) ± g (х, у)) dxdy = ^f(x,y) dxdy +1| g (х, у) dxdy
D	D	D
(26.6)	f (x, y) < g(x, y)	|| f (x, y) dxdy < ||g(x, y) dxdy
D	D
(26.7)	|| f (x, y) dxdy < |||/ (x, г/)| dxdy
D
D
□ Вычисление двойного интеграла в полярных кординатах (см. (13.1))
(26.8)	||f (х, у) dxdy = ||/ (rcos<p,rsin(p)rt/nrf<p =
D	D,
0	Г2(ф)
= |j(p I /(rcos(p,rsin(p)r</r
а Г|(ф)
26. Кратные интегралы 95
□ Вычисление площадей и объемов с помощью двойного интеграла
(26.9)	Вычисление площади фигуры, ограниченной границей облас-
ти D : S = || dxdy
D
(26.10)	Вычисление объема цилиндрической фигуры, ограничен-
ной областью D и графиком функции z = /(х, у) > 0 :
V = f (x,y)dxdy
D
□	Вычисление тройного интеграла через повторные
ftJ»2Mj Z^X.y)
J f (x,y,z)dz dy dx =
(26.11) JJJ f (х, у, z)dxdydz = j
v
ft Уг(х) гг(х'У)
= $dx J dy J f(x,y,z)dz\ V:
a y,(x) zt(x,y)
a<x<b
У\ {x)<>y<y2(*)
z1(x;z/)<z<z2(x;i/)
□	Свойства тройного интеграла
(26.12)	$ f(x, у, z) dxdydz =
v
JJJf (x’ z) dxdydz + JJJ/ (x, y, z) dxdydz (аддитивность);
Ц	v2
V = V{ u V2; Vt и V2 не имеют общих внутренних точек
(26.13)	Af(x, у, z) dxdydz = >1JJJf (x,y,z)dxdydz
v	v
(26.14)	JJJ(/ (x, y, z) ± g (x, y, z)) dxdydz =
V
= JJJ f (x, y, z) dxdydz ± JJJg (x, y, z) dxdydz
V	V
(26.15)	f (x, 2/, z) < g(x, 2/, z) =>
=> JJJ f (x,y, z)dxdydz < JJJg(x, y, z)dxdydz
V	V
96 Часть 1. Формулы
(26.16)	JJJ f(x,y, z) dxdydz < JJJ|/ (x, у, z)| dxdydz
v
v
□ Вычисление тройного интеграла в цилиндрических и сферических
кординатах (см. (13.4)-(13.6))
(26.17)	f (x,y,z}dxdydz = JJJ f (r cos <p, r sin <p, z) rdrdqdz
V	V,
(26.18)	JJJ f (x,y,z) dxdydz =
v
= JJJ f (r sin 0 cos <p, r sin 0 sin ф, r cos 0) r2 sin QdrdydQ
(26.19)	JJJ/(x,y,z)dxdydz =
v
= JJJ/ (r cos 0cos <P>r cos 6s'n Ф>r s'n 9) r2 cos QdrdtydQ
4
О Вычисление объемов с помощью тройного интеграла
(26.20)	V = JJJdxdydz
v
27.	Криволинейные
и поверхностные интегралы
□ Вычисление криволинейных интегралов 1-го рода
(27.1)f/	(x,z/(z)J/ =
L
= \f{x(t),y(t),z(t))^x\t))2 л-(у\1))2 +{z'{t))2dt
(27.2)	J/(x,г/)J/ = j/(x(?),z/(f))^(x'(?))2 + (/(?))2dt
L
(27.3)	J/(x,z/)J/ = J/(x,z/(x))^l + (/(x))2dx
L	a
27. Криволинейные и поверхностные интегралы 97
□ Вычисление криволинейных интегралов 2-го рода
(27.4)	^P(x\y\z)dx+ Q(jx\y\z}dy + R(jx,y\z]dz =
L
Г2
= ^Px'(t) + Qy'(t) + Rz'(t')')dt-, P = P(x(t);z/(i);z(r));
'l
Q = Q(x(t);z/(t);z(t)); R = P(x(t);z/(r);z(f))
(27.5)	]P(x;y)dx + Q(x;y)dy =
L
= {(P(x(f);y(f))x'(f) + Q(x(«);j((r))/(f))<*
b
(27.6)	J P (x; y) dx + Q (x; y) dy = J (P (x; у (x)) + Q (x; у (x)) /(x)) dx
L	a
□ Формула Грина
(27.7)	jjf W = | Pdx + Qdy
d v °x oy J L
□ Вычисление поверхностных интегралов 1-го рода
(27.8)	flf(x,y,z)dS = jj/(x,y,z(x,
S	D
dz
\2
dxdy
. Эх
□ Вычисление поверхностных интегралов 2-го рода
(27.9)	jj Pdydz + Qdzdx + Rdxdy = jj (P cos a + Q cos P + R cos y) dS;
5	5
n = (cos a; cos P; cos y)
□ Формула Стокса
(27.10)	j Р (х; у\z) dx + Q(х; у\z) dy + R (x; y\z) dz =
L
ЭЯ_Э£>
dy dz
cos а +
'dP_ dR
dz dx
a dQ dP\ be
----cos6+ —cosy dS
Эх I Эх dy
J	\.	J )
98 Часть 1. Формулы
(27.11)	ф a- dr = jjn rota dS
L	S
□ Формула Гаусса-Остроградского
(27.12)	JJ Pdydz + Qdzdx + Rdxdy = JJJ
(27.13)	<JJ>a • ndS = JJJdiva dV
S	V
28. Дифференциальные
операции векторного анализа
□	Оператор Гамильтона
□	Градиент функции
(28.2)	grad/ = V/ = 7^ + }^ + ^
дх ду dz
□ Производная функции по направлению
(28.3)	^y = 7-V/ = ^-cosa + ^-cosP + ^-cosy
dl	дх ду dz
□ Дивергенция вектор-функции а(х, у, z) = {ar; ау; az}
—	- да	да..	Эа
(28.4)	diva = V • а = —- + —- + —-
дх	ду	dz
□ Ротор вектор-функции а(х, у, z) = |ах; ау; а2}
(28.5) rota = V х а =
i j k
AAA
дх dy dz
ах	az
29. Числовые и степенные ряды 99
□ Оператор Лапласа. Дифференциальные операции 2-го порядка
^2	^2	^2
(28.6)	V • V = V2 = А = —- + —- + —- — оператор Лапласа
Эх2 Эг/2 Эг2
дх ду dz
(28.8)	div (grad /) = V • V/ = Д/
(28.9)	grad (diva) = V (v • a)
(28.10)	rot (grad/) = Vx(V/) = 6
(28.11)	div(rota) = V-(Vxa) = 0
(28.12)	rot (rota) = Vx(Vxa)
29.	Числовые и степенные ряды
Числовые ряды
(29.1)	Выражение вида ^1ап=ах+а2+- + ап+... называется числовым
рядом	я=1
□ Сходящиеся и расходящиеся числовые ряды
п
(29.2)	Sn = ^ak = 4- а2 4-... 4- ап — частичная сумма ряда.
*=1
Если 3 lim Sn = S, то ряд называется сходящимся, а S — сум-
п—>°°
мой ряда. Если lim Sn бесконечен или не существует, то ряд
п—>°°
называется расходящимся
□ Свойства сходящихся числовых рядов
оо	оо
(29.3)	Если ап сходится, то ап сходится
я=1	n=l+k
оо	оо
(29.4)	Если ^ап = S, то сап = cS;c — постоянная
л=1	п=1
100 Часть 1. Формулы
оо	оо	оо
(29.5)	Если ^ап =	^b„ = S2, то ^(ап ± Ьп) = ± 52
//=1	и=1	п=1
□ Необходимое условие сходимости числового ряда
(29.6)	Если У ап сходится, то lim ап = О
«=1
□ Достаточное условие расходимости числового ряда
оо
(29.7)	Если не выполнено условие lim ап = 0, то У ап расходится
Л—>°°	,
П=1
□ Знакопостоянные числовые ряды. Достаточные признаки сходи-
мости и расходимости
(29.8)	Первый признак сравнения: если 0 < ап < bn Vne N, то: из
оо	оо
сходимости ^Ьп следует сходимость из расходимости
п=1	п=1
^ап следует расходимость ^Ьп
п-\	п=1
(29.9)	Второй (предельный) признак сравнения:
если ап > 0; Ьк > О Vn, k 6 N; lim — = /; 0 </<<», то У а„
п^°°Ьп	£ "
оо	И	П=1
и ^Ьп или оба сходятся или оба расходятся
п=1
(29.10)	Признак Даламбера: если ап > 0 Wg N; lim = /, то при
и-»°° ап
оо
I <1 ряд ап сходится, при I > 1 ряд расходится
п=1
(29.11)	Радикальный признак Коши: если ап > 0 \/z? 6 N; lim = /,
я—>«>
оо
то при I < 1 ряд ап сходится, при I > 1 ряд расходится
п-\
(29.12)	Интегральный признак Коши: если /(х) — неотрицательная
невозрастающая непрерывная функция при х > 1, то ряд
ОО
X ~ /(0 + /(2) + ••• и интеграл j f(x)dx сходятся или
п=\	1
расходятся одновременно
29. Числовые и степенные ряды 101
00 1
(29.13)	Ряд £4- при а < 1 расходится, при а > 1 сходится
z=l
°° 1	11
(29.14)	Ряд — = 1 + - + - + ... расходится
п=\п	2 3
(29.15)	Ряд jr~^- = l + - + - + ... сходится
и=1 Л 49
□ Знакопеременные и знакочередующиеся числовые ряды. Абсолют-
ная и условная сходимость
оо
(29.16)	Если ряд ап | = | ах | +1 а2 | +...+1 ап | +... сходится, то ряд
п=\
оо
= ах + а2 +... 4- ап 4-... также сходится и называется абсо-
п—\
лютно сходящимся. Исследование ряда на абсолютную сходи-
мость производится с помощью признаков сходимости знако-
постоянных рядов
оо	оо
(29.17)	Если ряд ^ап сходится, а ряд ап | расходится, то ряд
И=1	И=1
оо
ап называется условно (не абсолютно) сходящимся
п=1
(29.18)	Признак сходимости знакочередующегося ряда (признак
Лейбница): если Ьп > 0 Vn; bn > bn+x Vn; lim bn = 0, то
>сю
оо
(-l)w-1few сходится (тип сходимости исследуется допол-
п=Л
нительно)
°°	1	1
(29.19)	Ряд	-—-— = 1 —	4- —...	сходится	условно
и=1	п 2	3
°°	j	|
(29.20)	Ряд	У -—— = 1 —	4- —...	сходится	абсолютно
п2	4	9
(29.21)	Оценка суммы сходящегося знакочередующегося ряда: если
оо	п
Ё(-1)"Ч = 5; £	= S„, то |5„ - 5| < />„+1
И=1	k=\
102 Часть 1. Формулы
Степенные ряды
(29.22)	Ха„(л-х0)" =
и=0
= Oq + ах (х - х0) + а2 (х - х0) +... + ап (х - х0)"+...
(29.23) Если lim
ап
= с > 0, то У ап (х - х0)” сходится в интервале
>1=0
|х-х0| < R; R =
1 = Нш _£к_
с an+i
называется радиусом сходимости.
Сходимость при х = х0 ± R исследуется дополнительно. Если
R = +«>, то интервал сходимости (-<»; + «>)
Если lim = с > 0, то R = - = lim -Д=
V I п |	>	_	/II
С	п
□ Сложение и умножение степенных рядов (|х - х0| < /?; R — наимень-
ший из радиусов сходимости заданных рядов)
(29.25)	^а„(х-х0)” ± ^6„(х-х0)" = ^(а„ ±6„)(х-х0)”
и=0	и=0	п-0
(29.26)	£а„(х-х0)” £/>„(х-х0)" = £с„(х-х0)";
и=0	п=0	и=0
ся=а06п+аД_1+... + аД
□ Дифференцирование и интегрирование степенных рядов
(29.27)	5(х) = £ая(х-х0)я; |х-х0|</?=>
п=0
ОО	1
=> S'(x) = пап (х- xQ; |х - х0| < R
п-\
(29.28)	5(х) = ^ап(х-х0)”; |х-х0|<7?=>
п=0
X	оо /	\П+1
^]s(x)dx=^an[X~Xo) ; |х-х0|<R
О	и=0	И +1
29. Числовые и степенные ряды 103
□ Разложения функций в степенные ряды
о» /•(”) (х \
(29.29)	f (х) = £---(х - х0)" — ряд Тейлора
п=о п-
(29.30)	f (х) =	———-х" — ряд Маклорена
п=о
х"
п!
(29.31)	(1 + х)“ =1 + Х
Л=1
a(a-ii 9	.	.
= 1 + ах + —-------х +...; agN; х <1
2!
(29.32)
(29.33)
(29.34)
—= У х" =1 + х + х2+...; |х|<1
1 “ х л=0
—— =	(-1)"х" = 1 - х + х2 -...; | х |< 1
1 + х „-о
——г = У (- 1)”х2" = 1 - х2 + х4 -...; | х |< 1
1 + х2 ~0
I--- х х2 1 • 3 • х3
(29.35)	717^ = 1 + ^-^- + ^^.-...; |х|<1
X» д» * Ч Zi * ч * и
°° ТП	Yn
(29.36)	ех = У — = 1 + х + — + ... + — + ...; -°о<х
2! п!
(29.37)	ln(l + x) = ^(-l)"-1 — =
п=1	п
X2 X3	, <\П-\ ХП	.	. .
= х-----+----- + (-1)	— + ...; -1<х<1
2	3 v ’ п
~	х2"-'
(29.38)	sin х = У ------— =
ix (2п-1)!
х3 х5
= X-----+------... +	----г---
3!	5!	(2п-1)!
104 Часть 1. Формулы
- (-1)"х2"
(29.39) cosx = £ v >	=
»to (2я)!
. х*	х4	(-1)"х2л
2!	4!	(2п)!
/ОА ,лч .	X3 2х5	17х7
(29.40) tgx = x +— +--------+------...;
v 7 6	3	15	315
...	.	1-х3 1-3-х5 1-3-5-х7
(29.41) arcsin х = х +---+-----+-----------
2'3	2-4-5	2-4-6-7
JT
(29.42) arccosx = —
(	1-х3 1-3-х5 1-3-5-х7
X +-----4-------4-----------
2-3	2-4-5	2-4-6-7
3	5	7
(29.43)	arctgx = х- — + — - — +...; | х|< 1
3	5	7
_ (	^3	„5	7
(29.44)	arcctgх~~^~ х~~з” + ”5-7”
□ Значения сумм некоторых числовых рядов
(29.45)	1 + | + | + | + ... = 2
(29.46)	— + —+ —+ ... = -
v 7 10 100 1000 10000	9
1111
(29.47)	— + — + — + — + ... = 1
1-2 2-3 3-4 4-5
(29.48)	- + — + — + — +	-
1-3 3-5 5-7 7-9	2
(29.49)	2 + - + - + — + ... = е
2 6 24
(29.50)	1-| + |-| + ... = 1п2
(29.51)	1-- + |-- + ... = -
v 7	3 5 7	4
30. Тригонометрические ряды Фурье 105
111
(29.52)	i + -L + -L+-L+... = 2L
22 З2 42	6
(29.53)	1- — + — - — 4-... = sin 1
v 3! 5! 7!
30.	Тригонометрические
ряды Фурье
(30.1)	Если 2/— периодическая функция /(х) и производная f'(x)
на отрезке [-/; I] непрерывны или имеют конечное число точек
разрыва 1-го рода, то f (х) раскладывается в ряд Фурье:
г/ \ «о	kltx ,	. km} 1 f Г/ \J
f(x)= 9	^cos——+ ^sin—— ; aQ = -J f(x)dx;
2	z	1 J -i
i
ak = 11 /(x)cos^^dbr; ke N; bk = 1| f [x)sin^^dx; ke N
I [	I	I I	I
Сумма ряда равна значению /(х) в каждой точке непрерывности
и значению^ limo/(x) + lim Q/(x)j в точках разрыва х(
(30.2)Ес	ли/(х) четная, то/(х) = —+ j^a^cos^s а0 = у f f (х)dx;
,	2 ы ‘ 'о
а* = VJ/(x)cos^Zr,ke N
1 о	1
(30.3)	Если /(х) нечетная, то
/(х) =	bk =у |7(x)sin^oM6 N
Л=1	1	Z о	z
(30.4)	Если I = п, то
/(х) = — + У (аА cosAx+ Z>£ sin Ах); а0 = — | f(x)dx;
2 k=i	п-л
106 Часть 1. Формулы
1 л	। п
ak = — j /(x)cosfctrfr; ke N; bk = — j f (x)sinkxdx; ke N
-Л	-Л
□ Разложения некоторых функций в ряд Фурье
. f—1; —л<х<0
(30.5)	Если/(х) = ]
[+1; 0 < х < л
4 sin(2£-l)x
то / х) = -£—^7—г2-
лЬ1 2£-1
(30.6)	Если /(х) = х; -л<х<л,то /(х) = 2^Г (-1)*+1 s*n^x
k=i	k
(30.7)	Если /(х) = |х|; -л<х<л,то / (х) = - - - У COSffi + У.Х
2 п л=о (2k +1)
31.	Элементы теории обыкновенных
дифференциальных уравнений
Дифференциальные уравнения 1-го порядка
(31.1)	F(x,у,у) = 0 — общий вид
(31.2)	М(x,y)dx + N (x,y)dy = 0 — дифференциальная форма
(31.3)	у' = /(х,г/) — уравнение, разрешенное относительно произ-
водной
(31.4)	Задача Коши (задача с начальным условием):
y' = f(x,y)
У(^о) = Уо
□ Дифференциальное уравнение с разделенными переменными
(31.5)	f(x)dx + g(y)dy = 0. j f(x)dx + j g(y)dy = С — общий инте-
грал
□ Дифференциальное уравнение с разделяющимися переменными
(31.6) /1(x)g1(z/)6& + f2(x)g2(y)dy = 0; /2(^1 (у) °;
31. Элементы теории обыкновенных дифференциальных уравнений 107
у — dx + [ dy — С — общий интеграл
/2(*) J gi(y)
(31.7)	у' = f(x)g(y); g(y) * 0. |	= J f(x)dx + С - общий инте-
грал	ё\У)
□ Дифференциальное уравнение, однородное относительно аргумен-
та и функции
(31.8)	М(х, y)dx + ЛГ(х, y)dy = 0;
M(tx,ty) = tnM(x, y)\ N(tx,ty) = tnN(x,y); Vt, t > 0.
Решается методом замены переменно
z(x) = —; у = zx; dy = zdx 4- xdz и сведением к уравнению
х
с разделяющимися переменными
М(1, z)dx 4- ЛГ(1, z)(xdz 4- zdx) = 0
(31.9)	у' = f(x,y)\ f(tx,ty) = f(x,y)\ V£, £ > 0.
z(x) = —\y = zx\y' = z + xz'; z + xz = /(l,z(x))
(31.10) / = /f^
; z(x) = — \y = zx,y =z + xz\ z + xz = f(z)
X
О Линейное дифференциальное уравнение 1-го порядка
(31.11)	у'(х) + р(х)у(х) = 0 — однородное линейное
уравнение. у(х) = Се $pWdx — общее решение
(31.12)	у'(х) 4- р(х)у(х) = q(x) — неоднородное линейное уравнение.
у(х) = e~$pMdx Г С 4- j q(x) J	dx} — общее решение
□ Уравнение Бернулли
(31.13)	у'(х) 4- р(х)у(х) = yaq(x)-, а Ф 0; а Ф 1. Решается методом за-
мены переменной z(x) = г/1-<х и сведением к линейному урав-
нению z'(x) 4- (1 - a)p(x)z(x) = (1 - a)<?(x)
108 Часть 1. Формулы
□ Уравнение в полных дифференциалах
(31.14)	М(х, y)dx + N(x,y)dy = 0;	.
ду дх
(х>у)	X	у
j М(х,y)dx + N(x,y)dy = j M(x,yQ)dx + j N(x,y)dy = C —
(*о^о)	*b	Уо
общий интеграл
Дифференциальные уравнения и-го порядка
□ Линейное однородное дифференциальное уравнение 2-го порядка
с постоянными коэффициентами
(31.15)	у\х) + ру'(х) + qy(x) = О
(31.16)	Характеристическое уравнение: k2 + pk + q = 0; ;	— корни
характеристического уравнения
(31.17)	Случай различных действительных корней k2 :
у = Схе^х + C2eklх — общее решение
(31.18)	Случай кратного действительного корня k = = k2:
у = Cxekx + С2хе^ — общее решение
(31.19)	Случай пары комплексных сопряженных корней kx 2 = а ± Р?:
у = ecn (Ct cos Рх + С2 sin Рх) — общее решение
□ Линейное однородное дифференциальное уравнение и-го порядка
с постоянными коэффициентами
(31.20)	yw (х) + pjz/"'0 (х) +... + р„у (х) = О
(31.21)	Характеристическое уравнение:
kn 4- pxkrl~{ 4-... 4- рп = 0; ^,^2,..^kn — корни характеристиче-
ского уравнения
(31.22)	Общее решение: у = С{у{ (х) 4- С2у2 (х) 4-... 4- Спуп (х),
где У1 (х); у2 (х); ...;уп (х) —совокупностьлинейно независи-
мых частных решений, соответствующих корням характерис-
тического уравнения. Сг — произвольные постоянные
31. Элементы теории обыкновенных дифференциальных уравнений 109
Правило нахождения частных решений:
(31.23)	Если k — простой действительный корень, то получаем одно
частное решение у =
(31.24)	Если k — действительный корень кратности г, то получаем г
частных решений у = у = хе^у = xr~xekx
(31.25)	Если 2 = а ± Р? — пара простых комплексных сопряженных
корней, то получаем два частных решения
у = е™ cosРх; у = е™ sin Рх
(31.26)	Если 2 - а ± Рг — паРа комплексных сопряженных корней
кратности г, то получаем 2г частных решений
у = 6™ cosPx; у = хе™ cosPx;...;у = xr~xe™ cosPx;
у = е™ sin Рх; у = хе™ sin Рх;...; у = xr'[e™ sin Рх
Решения некоторых
дифференциальных уравнений
□ Уравнения с разделяющимися переменными
(31.27)	У' = У	у = Сех
(31.28)	У = у2	1 у = -	= 0 х + С
(31.29)	II 1 н	у2 - х2 = С
(31.30)	II 1 1 н	х2 + у2 = С
(31.31)	^1 н II	у = Сх
(31.32)	^1 н 1 II	II н 1
(31.33)	, 2у у = — X	у = Сх2
110 Часть 1. Формулы
(31.34)	, У2 у =4 X	X У~ 1-Сх
(31.35)	у' = ех*у	ех +е~у =С
□ Однородные уравнения
(31.36)	II + 1 ц	у2 = х2(21п|х| + С)
(31.37)	, х-у У = Х + У	х2 -2ху-у2 = С
(31.38)	х2у - у1 - ху = 0	— = -\nCx~ у = 0 У
(31.39)	[х? +у2]у' = 2ху	У2 — х2 = Су, у = 0
(31.40)	(х2 + y2)dx + xydy = 0	2у2 + х2 = Д- X
(31.41)	ху -у-хеу/х	у = -xln(lnCx)
□ Линейные уравнения 1-го порядка и уравнения Бернулли
(31.42)	у' + ху + х = 0	у = Се ,2 -1
(31.43)	у + у = ех	у = -ех + Се~х 2
(31.44)	У~У = ех	у = ех(х + С)
(31.45)	у' - у = sin х	•<	1 у = Сех - - (sin х + cos х)
(31.46)	, У У ~ — xsmx X	у = x(C-cosx)
(31.47)	о II CN + ^>1 н 1	2х
(31.48)	у+2у = у2е?	у\ех +Се2х) = 1; у = 0
32. Комплексные числа 111
□ Уравнения в полных дифференциалах
(31.49)	2xydx 4- (x2 -y2^dy = 0	3x2y - y3 =C
(31.50)	(z/2 -x^y-y + x2 =0	x3 - 3xy + y3 =C
(31.51)	jra/'cosiy + sinz/ = 0	xsin у = C
□ Линейные уравнения 2-го порядка
(31.52)	y" - У = 0	у = Схех + С2е~х
(31.53)	/ + ^ = 0	у = Q cos х + С2 sin х
(31.54)	/ - 4/ + 5y = 0	у - е2х (Cf cos х + С2 sin х)
(31.55)	у” - у + x2 = 0	у = Схех + Схе~х + х2 + 2
(31.56)	у" + у = ex	у = i ех 4- Сх cos х 4- С2 sin х
(31.57)	у + у = sin х	г/ = Q cos х 4- С2 sin х - — cos х
32. Комплексные числа
□ Степени числа i ( л, т 6 Z )
(32.1)	i2 =-1 — основное свойство числа i
(32.2)	z° =z4 =z8 =... = iin =1
(32.3)	z1 = i5 = z9 =... = z4n+1 = i
(32.4)	i2 = z6 = z10 =... = z4"+2 = -1
(32.5)	z3 = z7 = z11 =... = z4n+3 = -z
(32.6)	z° = Г4 = Г8 =... = Г4" = iim = 1
(32.7)	Г1 = z'5 = z'9 =... = z'(4n+,) = z4”1'1 = -z
(32.8)	z“2 = z'6 = Г10 =... = r(4”+2) = z4'"-2 = -1
112 Часть 1. Формулы
(32.9)	Г3 = Г7 = Г11 =... = Г(4и+3) = iim~3 = i
(32.10)	i2n =(-1)"
(32.11)	i2n+i = (-!)”/
(32.12)	iin+m = im
□ Алгебраическая форма комплексного числа (х; у 6 R)
(32.13)	z = x+iy; х = Re z — действительная часть числа; у = Im z —
мнимая часть числа
□ Равенство комплексных чисел
(32.14)	zt = z2 <=> х{ + iyt =х2+ iy2 <=> xt = х2; yt = у2
(32.15)	а = 0<=>х + й/ = 0<=>х = 0;г/ = 0
□ Комплексно сопряженное число
(32.16)	z = х- iy
(32.17)	z = z<=>ze R
□ Модуль комплексного числа
(32.18)	r=\z\ = Jx2+ у2; | z |>0
(32.19)	| z |=| z |
□ Аргумент комплексного числа <р = arg z (главное значение аргумента)
(32.20)
cos (р = |^|
И
У
sin<p = -5
И
=> <р; 0 < <р < 2л (или -л < ф < л)
(32.21)	argz =2n-argz (или argz =-argz)
□ Множество значений аргумента
(32.22)	Arg z = ф + 2л£, k 6 Z
32. Комплексные числа 113
□ Действия над комплексными числами в алгебраической форме
(32.23)	Сложение и вычитание:
Zi+Z2= (х, + iy{) + (х2 + й/2) = (Xj + х2) + i(y{ + у2)
(32.24)	z + z =2х;х = ^-
(32.25)	Zj -z2 = (Xj - х2) + i(y{ -у2)
(32.26)	z - z = 2yi; у =	-
Zl
(32.27)	Умножение:
Zj • z2 = (Xj + zz/t) • (x2 + iy2) = XjX2 - y{y2 + z(x^2 + X2Z/t)
(32.28)	z-z = r2
(32.29)	z2 = x2 - y2 + 2xyi
(32.30)	z3 = x3 - 3xy2 + z(3x2z/ - z/3)
(32.31)	Деление:	= iA =	+,. У^-х^
z2 x2 + iy2 I Z2 I2 x2 + y2 X 2 + y\
(32.32)1	= 4 = -^--/.
z Г X + у X + у
(32.33)	1 = 4 = ^—
Z Г X + у X + у
□ Свойства действий над комплексными числами
(32.34)	zx + z2 = z2 + z{ (коммутативность сложения)
(32.35)	(zt 4- z2) 4- z3 = Zj 4- (z2 4- z3) (ассоциативность сложения)
(32.36)	zxz2 = z2zt (коммутативность умножения)
(32.37)	(ZjZ2)z3 = Zj(z2z3)(ассоциативность умножения)
(32.38)	Zj(z2 4- z3) = zxz2 4- ZjZ3 (дистрибутивность умножения отно-
сительно сложения)
114 Часть 1. Формулы
□ Тригонометрическая форма комплексного числа
(32.39)	z - r(cos(p + i sin ф)
□ Действия над комплексными числами в тригонометрической
форме
(32.40)	z, • z2 = • r2 (C0S(<Pi + Ф2) +* sin(9t + ф2))
(32.41)	— = — • (cos(9t - ф2 ) + i sin(9t - ф2 ))
z2 r2
(32.42)	Возведение в степень:
zn = rn (cos иф 4- i sin иф); п е N — формула Муавра
(32.43)	Извлечение корня:
пГ пг( ф4-2л& . . ф4-2л^
yJZ = у/г\ cos ---4-1 sin ---- = wk;
V п	п )
neN;k = 0,1, 2,...л-1
(32.44) VI =
2itk . . 2nk}
----4- l sin
= wk\ k = 0,1, 2,
...,n -1
(32.45)	Vi = ±1
(32.46)	= wk; wt = 1;
„/—г (	л(2& + 1) . . л(2^ + 1)^	л _
(32.47)	W-l = cos— --------- +1 sin — ----- = wk; k = 0,1, 2,...,n -1
V n	n )
(32.48)	V-l = +i
ЗГ7	.	1 . >/3	1 . у/з
(32.49)	<l-l=wk; Wl=-i-w2=- + i — ; w3=--i —
□ Показательная форма комплексного числа
(32.50) z = reiv
32. Комплексные числа 115
(32.51)	Формулы Эйлера:
..	+	. е,ф-е-1ф
г = coscp + zsincp ;cos(p =-----; sin ф =---—----
(32.52)	e? = i; em = -1; e*‘ = -i; e2m = 1
□ Действия над комплексными числами в показательной форме
(32.53)	21 • г2 = г1г/(ф|+ф2)
(32.54)	- = — -е^ф|-ф2^
z2 г2
(32.55)	г” =
. ф+2л£
(32.56)	• е~"~; 6 = 0,1,2..........п-1
□ Расстояние между точками zt = xt + iy{ и z2 = х2 + iy2
(32.57)	d = \z2-zt\
□ Уравнение прямой, проходящей через точку z0 = х0 + iy0 и образу-
ющей угол а с осью ОХ
(32.58)	z = z0 + te'“; 16 К
□ Уравнение окружности с центром в точке z0 = х0 + iy0
(32.59)	z = z0 +Reit-, 0<£<2л
□ Разложение многочлена на линейные множители
(32.60)	P„(z) = Oqz” + a,z"-1 + a2zn~2 +... + an_{z + a„ =
= a^z - zt)(z - z2)...(z - zny, a,’ zj € c n 1
□ Основная теорема алгебры
(32.61)	Любое уравнение и-й степени с комплексными коэффициен-
тами P„(z) = Oqz” 4- Ojz"’1 + chz^2 +... 4- an_xz 4- ar =0, n > 1
, имеет n комплексных корней, если каждый корень считать
столько раз, какова его кратность
116 Часть 1. Формулы
33. Элементы теории функций
комплексной переменной
(33.1) z = x + iy; w = f(z) = u(x,y) + iv(x,y); x,z/eR; z,z^eC;
м(х, у) = Re f(z) — действительная часть функции;
^(х, г/) = Im f(z) — мнимая часть функции
□ Основные функции комплексной переменной
(33.2) w = az + b
if П .
—I z + - I — функция Жуковского
z^ = z”; wgN
w = zn = tfz = х/
(33.3) w =
(33.4)
(33.5)
Ф + 2л& . . ф + 2я^
------+ г sin-	 = wk;
п-----п )
яеУ;Ь0,1,2,...,п-1
(33.6)	w = ez = ex*iy = ex(cos у + isin y)
(33.7)	w = Ln z = In z + 2nki; kel- многозначная функция;
In z = In | z | +i arg z — главное значение логарифма
(33.8)	w = za =eaLnz; aeC
(33.9)	w = az = e2Ln"; aeC
(33.10)	^ = sinz= -2.-
+ в”*2
(33.11)	a> = cosz= 2
(33.12)	® = tgz = ^-
cosz
/ О О 1 O \	4-^e COS Z
(33.13)	^ = ctgz =----
sinz
33. Элементы теории функций комплексной переменной 117
□ Гиперболические функции
в2 — в”2
(33.14)	w = sh z =----
(33.15)	w = chz = —-—
(33.16)	® = thz = —
chz
(33.17)	® = cthz = ^
shz
□ Производная функции комплексной переменной
(33.18)	Производной однозначной функции /(z) в точке z называ-
ется предел f\z) = lim — г +	. функция, имеющая
Az->0	Az
в каждой точке области непрерывную производную, называ-
ется аналитической в этой области
(33.19)	Условия Коши-Римана: для того чтобы функция
/(z) = и(х, у) + iv(x,y) была аналитической в области, не-
обходимо и достаточно, чтобы в этой области существовали
непрерывные частные производные функций w(x, г/); v(x, у)
ди ди ди	ди
и выполнялись условия: — = —; — =-----
дх ду ду	дх
(33.20)	Вычисление производной аналитической функции:
ч ди	.ди	ди	.ди	ди	.ди	dv	.dv
f (z) = — + i — =---i — =-----1 — = — +i —
dx	dx	dy	dy	dx dy	dy dx
□ Вычисление интегралов
(33.21)	Если /(z) = u(x, у) + iv(x,y), то
j /(z) dz = j w(x, y)dx- v(x, y) dy + ij v(x, y)dx + u(x, y) dy
l	i	i
(33.22)	Если /: z(£) = x(t) + iy(t); <t < £2, to
r2
J/(z)tZz = J/(z(0)z'(O<*
I «1
118 Часть 1. Формулы
□ Формула Ньютона-Лейбница
(33.23)	Если /(z) аналитическая в односвязной области, zvz2 —
точки внутри области, F'(z) = /(z), то
f/(z)Jz = F(z2)-F(z1)
□ Теорема Коши
(33.24)	Если /(z) аналитическаяводносвязнойобласти, у —замкну-
тый контур в этой области, то <£ /(z)dz = О
У
□ Интегральная формула Коши
(33.25)	Если /(z)аналитическая водносвязной области, Zq — точка
внутри области, у — замкнутый контур в этой области, охва-
тывающий точку z0, то /(z0) = —d dz
2ni J z - zft
Y u
(33.26)
Y (Z~Zo)
□ Ряды Тейлора
(33.27)	Если f(z) — аналитическая в круге |z - z0| < R, то ее можно
однозначно разложить в этом
ос
круге в ряд Тейлора f(z) ~^cn(z- Zq^\
п-0
c„=— (zq ) =	—r dz\ p < R
(33.28)	T^-=
*	и=0
(33.29)	e2 = У —; zeC
(33.30)	ln(l + z) = У	|z| < 1
“ (-1)лг2п+1
(33.31)	sinz = У --------r-; Z6 C
Й (2n + l)l
33. Элементы теории функций комплексной переменной 119
(33.32)	cosz=£4^-—; zeC
п=0 (2”)!
(33.33)	tgz = z + |-z3 Л? + ...; |z|<5
ОI Э!	Z
□ Ряды Лорана
(33.34)	/(z) = J с„ (г - Zo )" = £ сп (z - z() )п + § сп (г - z0 )"
п=-,к	п--<х)	n=Q
-1
сп (z - z0 )w — главная часть ряда;
Л--ОО
с„ (z - z0 )” — правильная часть ряда
и=о
(33.35)	Если /(z) — аналитическая в кольце
г < |z - z0| < R\ 0 < г < R < оо , то ее можно однозначно разло-
жить в этом кольце в ряд Лорана
/<2) = Е с„(г-г0)";с„=-^ J ; /-(г^+-г < р < 7?
□ Особые точки
(33.36)	Если /(z) — аналитическая в круге 0 < |z - z0| < R, а в точке
z0 не является аналитической, то точка z0 называется изоли-
рованной особой точкой
□ Классификация изолированных особых точек
(33.37)	Если z0 — особая точка и f(z) = ^cn(z~ z0 )”; 0 < |z - z0| < R,
n=0
to Zq называется устранимой особой точкой
(33.38)	Если z0 — особая точка и
/(*) = Ё Cn{z-^ + ЁСП(2“го)”;C-m *0;0< |z-z0|< 7?,
п--т	n=Q
то z0 называется полюсом порядка т
(33.39)	Если z0 — особая точка и f (z) =	сп (z - z0 )w; 0 < |z - z0| < R,
п=-ж
то z0 называется существенно особой точкой
120 Часть 1. Формулы
□ Вычеты. Основная теорема о вычетах
(33.40)	Вычетом аналитической функции /(z) в точке z0 называется
коэффициент с_! в разложении /(z) в ряд Лорана
Res/(z) = с_( =J -Д^-^;0<р<7?
г=г»	2пг |г-4Р (г - z<>)
(33.41)	Если f(z) аналитична в ограниченной односвязной области D
за исключением конечного числа изолированных особых точек
Zp z2;...; zn,y — замкнутый контур, лежащий в D и охватыва-
ть
ющийвсеточки	, то jf(z)dz = 2ni^Res f(z)
у	k=\ z=Zk
34. Элементы теории вероятностей
Формулы комбинаторики
(сочетания, размещения, перестановки)
□ Число сочетаний без повторений из п элементов по k
(34'1)с"’ё(^;"'=1'2'3'-'* 0!-1
(34.2) с; = С’ = 1
(34.3) с,‘ =с„"-‘
<34.4)С,‘:1’=С,‘+С“
□ Число размещений без повторений из п элементов по k
(34.5)	= п(п - 1)(п - 2)-... • (и - k +1) = -г-^—
( 7? К I!
(34.6)4=	С„Ч
□ Число перестановок без повторений из п элементов по п
(34.7)	Рп = п(п-1)(п -2)-...! = «!
(34.8)	Р„= 4"
34. Элементы теории вероятностей 121
□ Число размещений с повторениями из п элементов по k
(34.9)	Ап = пк
□ Формула Стирлинга
(34.10)	При п -> оо п\ » yllitn f—1
)
Классическая формула вычисления вероятности
(34.11)	Если множество всех возможных исходов случайного экспери-
мента состоит из п равновозможных и взаимно исключающих
исходов — элементарных событий, то вероятность события А
равна Р(Л)= —,где тА — число исходов, благоприятству-
п
ющих событию А,п — число всех возможных исходов
Алгебра событий
(34.12)	Достоверным событием называется событие, которое насту-
пает всегда; обозначается символом Q
(34.13)	Невозможным событием называется событие, которое не про-
исходит никогда; обозначается символом 0
(34.14)	Суммой событий А + В называется событие С, состоящее
в выполнении хотя бы одного из событий А или В (или Л,
или В, или обоих вместе)
(34.15)	Произведением А В событий называется событие С, состоя-
щее в совместном выполнении обоих событий А и В
(34.16)	Противоположным к А событием называется событие А,
состоящее в невыполнении события А
(34.17)	События А и В называются несовместными, если А • В = 0
□ Свойства операций сложения и умножения событий
(34.18)	А + В = В +А, А В = В А (коммутативность)
(34.19)	(Л + В) + С = А 4- (В + С); (А • В)- С = А • (В + С) (ассоциатив-
ность)
(34.20)	Л (В 4- С) = АВ 4- АС (дистрибутивность)
122 Часть 1. Формулы
(34.21)	А +А = А , А +А = С1; A + Q = £l ; А + 0 = А
(34.22)	А-А = А; А-А = 0; A-Q = А; А-0 = 0
Алгебра вероятностей
(34.23)	Р(0)=О
(34.24)	Р(Я)=1
(34.25)	0<Р(А)<1
(34.26)	Если из события А следует событие В, то Р(А) < Р(В)
□ Правило сложения вероятностей
(34.27)	Р(А + В)=Р(А)+Р(В)-Р(АВ)
(34.28)	Р(А + В + С)=Р(А)+Р(В)+Р(С)~
-Р(АВ)-Р(ВС)-Р(АС)+Р(АВС)
(34.29)	Если события А и В несовместны, то
Р(А + В)=Р(А)+Р(В)
(34.30)	Р(А) + Р(А) = 1
□ Условная вероятность. Независимые события
(34.31)	Условной вероятностью события В при усло-
вии выполнения события А называется выражение
Р(В|А)=
Р(АВ)
Р(А)*0
(34.32)	События А и В называются независимыми, если
Р(В\ А)=Р(В)
□ Правило умножения вероятностей
(34.33)	Р(А В)=Р(А) Р(В\А)
(34.34)	Р(А • В • С) = Р (А)Р(В | А)- Р(С | (А • В))
34. Элементы теории вероятностей 123
(34.35)	Если события А и В независимы, то
Р(ЛВ)=Р(Л)Р(В)
□ Формула полной вероятности
(34.36)	Если события Н^Н2,..:.)Нп образуют полную группу, то есть
= Я И Н, • Hj = 0; Ij,TO Р(А)= ^Р^Н^Р^А । Hk ):
k=\	k=\
события Н{;Н2;...;Нп называютя гипотезами: P(Hk) назы-
ваются априорными вероятностями гипотез
□ Формула Байеса. Пересчет вероятностей гипотез
(34.37)	P(Hk\A)= nPSrik)P(A'Hk^ ; k = 1,2.п; Р(НК | Л) назы-
£р(н*)р(л|я*)
k=l
ваются апостериорными вероятностями гипотез
□ Повторение испытаний с двумя исходами. Формула Бернулли
(34.38)	Если производится п независимых опытов, в каждом из ко-
торых может произойти событие А («успех») с вероятно-
стью р или событие А («неудача») с вероятностью q = 1 - р.
то вероятность выполнения события А ровно т раз равна
Рп (т) = С™pmqn~m; q = 1 - р; т = 0,1,2,..., п
(34.39)	Ря(0)=^;Р„(п)=р”
Случайные величины
□ Функция распределения F (х) случайной величины X
(34.40)	F (х) = Р {X < х}; х е К
(34.41)	Если х2 > Xt, то F(x2)> F(х()
(34.42)	F(-oo)= 0; F(+oo)= 1
(34.43)	F (х) непрерывна слева
(34.44)	P{a<X<b}=F(b)-F(a)
124 Часть 1. Формулы
□ Ряд распределения дискретной случайной величины
(34.45)	Pk = р {* = xk }; k = 1,2.п,£ pk = 1;
k=\
X	X j	х2		хп	
р	Pl	Р2		Рп	
□ Плотность распределения непрерывной случайной величины
(34.46)/(х) = Г(х)
ь
(ЗА AT) Р{а<Х <b} = \f(x)dx
а
(34.48)	f(x) = P{-oo<X<x}= j f(x)dx
(34.49)	/(х)>0
(34.50)	J f(x)dx = \
□ Математическое ожидание и дисперсия дискретной случайной ве-
личины с п значениями
п
(34.51)	М(Х) = £рЛ
(34.52)	Л(Х) = М(Х -М(Х))2 = %Pk (xk -М(Х))2
k=i
9 П
(34.53)	D (X) = M (x2) - (M (X)) =2 Pk4 ~
^Pkxk
□ Математическое ожидание и дисперсия непрерывной случайной ве-
личины
(34.54)	М(Х) = { xf(x)dx
(34.55)	£>(Х) = Л/(Х-М(Х))2 = J (х-М(Х))2 f(x)dx
, о»	С оо	Л2
(34.56)£>	(Х)=Л/(Х2)-(Л/(Х))2 = J х2/(х)Л- J xf(x)dx
7
34. Элементы теории вероятностей 125
□ Среднее квадратическое отклонение
(34.57)	о = ylD(X)
□ Биномиальное распределение
(34.58)	Дискретная случайная величина X имеет биномиаль-
ное распределение, если ее возможные значения равны
0,1,2,...,п, а вероятности равны рт = Р{Х = т} = C'"pmqn~m ;
О < р <i; q = 1- р;т = 0,1,2,...,и
(34.59)	М (X) = пр-, D(X) = npq
□ Распределение Пуассона
(34.60)	Дискретная случайная величина X имеет распределение Пу-
ассона, если ее возможные значения равны 0,1,2,..., т....а ве-
ТП
_______________ _ Г* (хг _	& -а _ . Л____ Л 4 г*
(34.61)	M(X) = a;D(X) = a
□ Равномерное распределение
(34.62)	Непрерывная случайная величина X имеет равномерное рас-
пределение в интервале (а;Ь), если плотность распределения
Г/ \	1	’ Л I V I
равна f(x) = b-a
0,	х&(а-,Ь)
(34.63)	М(Х) = ^;О(Х) = ^Ь
0, х< а
(34.64)	F(x) = 
1, х> b
(34.65)	Р{а<Х<р}=£——;а<а<0<2>
Ь-а
126 Часть 1. Формулы
□ Нормальное распределение
(34.66)	Непрерывная случайная величина X имеет нормальное
распределение, если плотность распределения равна
. (т~а)2
/(*) = —
сту2л
(34.67)	М(Х) = а;О(Х) = ст2
х (х-а)2	.	.
(34.68)	F(x) = —^= f e~^dx = 4>\	1 + -
ст>/2л	у 0 J 2
(34.69)	Ф (х) = -== f е 2 dt — функция Лапласа, интеграл
вероятностей
(34.70)	Ф (0) = 0; Ф (-х) = -Ф (х); Ф (+~) = |; ф (-«) = -|
(34.71)	Р{а<Х<р}=фП^1-Фр^1
V о J \ G J
(34.72)	Р{ |Х - а\ < I} = 2Ф^ j
(34.73)	Р{ |Х - а| < ka } = 2Ф (k)
(34.74)	Р{|Х-а|<а} = 2Ф(1) = 0,682
(34.75)	Р{|Х-а|<2ст} =2Ф(2) = 0,954
(34.76)	Р{ |Х - а\ < За } = 2Ф (3) = 0,997 — «правило трех сигм»
□ Неравенство Чебышева
Для любой случайной величины X с математическим ожиданием тх
и дисперсией Dx и любого числа а > 0:
(34.77)	Р{ |Х -тх | > а}<
(34.78)	Р{\Х-тх\<а}>1-^-
Часть 2. Графики функций
128 35. Графики основных элементарных функций
35. Графики основных элементарных функций 129
130 36. Основные типы преобразований графиков
36. Основные типы преобразований графиков 131
132 37. Преобразования графиков линейных функций
37. Преобразования графиков линейных функций 133
134 37. Преобразования графиков линейных функций
37. Преобразования графиков линейных функций 135
136 37. Преобразования графиков линейных функций
37. Преобразования графиков линейных функций 137
138 37. Преобразования графиков линейных функций
37. Преобразования графиков линейных функций 139
140 37. Преобразования графиков линейных функций
4-1 2-		4-1 2-	1		41 2-	
			//			У 	,
-4	-2	0	/	2	4	-4	-2	0	,/	2	4	-4	-2	0	'	2	4
				о.	
-4- 145] У=\х	-|лг-1|	Цб] У = 2|х1	-4 -2|х-1|	— L -4- Нт] У ~ 2|х1	|-|2х-1|
4-1 2-		4-1 2-		4- 2-	
0	. t -	\о			
-4	-2	/\ 2	4	-4	-2	/	2	4	-4	-2	0	/24
-2- -4* Не] у =_1-	г| + |х -1|	-2- -4- 149| ^ = И	-l*+1l	-2- -4- 150] НИ	
4-1 2-		41 2-		41 2-	
'	, \о	/	,		/		
	/ i <	-4	-2	0	/24	-4	-2	0	
-2- -4- 151] У = И		-2- -4- 151] * = 1/(1		-2- 1 153|	х	-1-1 X
4-1 2-	//'	41 2‘	✓ у		Г4 -2 z//Z
U1	। JuJ \\  ! >1	\\ ! - 1	к 1	ЧХоч	f	2	4 -|х-1| + X	-4	-2 / "2‘ -4- 155] У = Х\А	/	2	4 - х\х -1|	-4	-2 У -2- -4- Иб] У = (И	-|х-1|)/х
37. Преобразования графиков линейных функций 141
142 38. Преобразования графиков квадратичных функций
38. Преобразование графиков квадратичных функций 143
144 38. Преобразование графиков квадратичных функций
38. Преобразование графиков квадратичных функций 145
146 38. Преобразование графиков квадратичных функций
38. Преобразование графиков квадратичных функций 147
148 38. Преобразование графиков квадратичных функций
38. Преобразование графиков квадратичных функций 149
150 38. Преобразование графиков квадратичных функций
38. Преобразование графиков квадратичных функций 151
152 39. Преобразование графиков многочленов 3-й и 4-й степени
39. Преобразования графиков многочленов 3-й и .4-й степени 153

39. Преобразования графиков многочленов 3-й и 4-й степени 155

39. Преобразования графиков многочленов 3-й и 4-й степени 157

39. Преобразования графиков многочленов 3-й и 4-й степени 159

39. Преобразования графиков многочленов 3-й и 4-й степени 161
162 40. Преобразования графиков дробно-рациональных функций
40. Преобразования графиков дробно-рациональных функций 163
164 40. Преобразования графиков дробно-рациональных функций
40. Преобразования графиков дробно-рациональных функций 165
166 40. Преобразования графиков дробно-рациональных функций
40. Преобразования графиков дробно-рациональных функций 167
168 40. Преобразования графиков дробно-рациональных функций
40. Преобразования графиков дробно-рациональных функций 169
170 40. Преобразования графиков дробно-рациональных функций
		\V;J V • v 1 \ 1 '-'2-	V/ » t » / V /	w
-4	-2	0	2	4	-4	-2 0	2	4	-4	-2	0	2	4
-2-		-2-		-2-
		-4-		
-4-1				-4-1
	• У =	2	1 + —9		1 У = 2:	2	2 V +—7	. 2	1 	1 у = 4x +	z-
505|	*	x2	506	*	x2	507] У	4r2
\	1 \	1 ч-'2-	\ / \_z	V		
-4	-2	0	2	4	-4	-2	0	2	4	-4	-2	0	2	4
Л	Л	-2-		-2-
—। 508	2	1 X + — X )	—i	У - x 509|	2	1 + — X	2	1 	1	у =	+ -7 510|	X2
ч		\ г \ / i-	V / V /	
-4	-2	0	2	4	-2	-1	0	i 2	-4	-2	0	2	4
-2-		-1- -2-		-2-
у = |х 511|	|2	1 1 + 7~p	-3- 5Й] У~	X2 x4 + 1	"4 1	2 y = T2+x
V	V / »	/ z	\ •	Ц/	
1 	0		0		0 ,zZ
i -4	-2 Z-Z	2	4	1 -4	-2 /	2	4	-4	-2 У	2	4
/Z -2- : Z	-4-		/h		
i-—। у = x2 '514! *	1 + —y + X x	V/71 У = • э15|	3	1 rJ + — X	y=x+^
40. Преобразования графиков дробно-рациональных функций 171
172 40. Преобразования графиков дробно-рациональных функций
40. Преобразования графиков дробно-рациональных функций 173
174 40. Преобразования графиков дробно-рациональных функций
40. Преобразования графиков дробно-рациональных функций 175
176 40. Преобразования графиков дробно-рациональных функций
4-1					41 д		
-4	-2	0 -2' -4-	4	-4	-2	0 -2- -4-			-4	-2	0lZ^>'	4		
					-2- -4-		
_ х2 - Зх '577! У~ х2+1		_ 2х2 - 6т 5781 У~ х2 +1			_ 4х2 -6х 57э] У~ 4х2 + 1		
41 	--'\2-		4-1 				4- 	*~ч2-	L		
-4	-2 У -4-	х2 -Зх	-4 -2- -4- J	Ч ' 4 г2 + Зх		-4	-2	0 -2- j	с2 - Зх	''	4
580; У х2 +1		581] У x2+i			—।	У ~ 582	х2 +1	
41 \		4-1 -'""Ч		\	41		
-4 -2- -4- Л	4 :2-ЗЫ	-4	-2	0	К х2 4-1	4	-4	-2	0 -2- -4J _ - Х	A ^-Зх4	
583	У х2 + 1		584| У х2-3х			585| у х-2+1		
41 	-\2-	//	41 	.--'ч2- V			4- 	-^2- V		
-4 Z2 / /	/ -2- '	-4- _ х2	4 - Зх	“4	~2 /1 / /-2- /Z	' -4- _ X	3-З.г2	4	/ ''	-4- 	>	и =	х-3	
586|	* х2 +1		587|	* х2 + 1			588|	’ х2 +1		
40. Преобразования графиков дробно-рациональных функций 177
178 40. Преобразования графиков дробно-рациональных функций
40. Преобразования графиков дробно-рациональных функций 179
180 40. Преобразования графиков дробно-рациональных функций
40. Преобразования графиков дробно-рациональных функций 181
182 41. Преобразования графиков функций, содержащих рациональные степени и корни
41. Преобразования графиков функций, содержащих рациональные степени и корни 183
184 41. Преобразования графиков функций, содержащих рациональные степени и корни
41. Преобразования графиков функций, содержащих рациональные степени и корни 185
186 41. Преобразования графиков функций, содержащих рациональные степени и корни
41. Преобразования графиков функций, содержащих рациональные степени и корни 187
188 41. Преобразования графиков функций, содержащих рациональные степени и корни
41. Преобразования графиков функций, содержащих рациональные степени и корни 189
190 41. Преобразования графиков функций, содержащих рациональные степени и корни
41. Преобразования графиков функций, содержащих рациональные степени и корни 191
192 42. Преобразования графиков показательных и логарифмических функций
42. Преобразования графиков показательных и логарифмических функций 193
194 42. Преобразования графиков показательных и логарифмических функций
42. Преобразования графиков показательных и логарифмических функций 195
196 42. Преобразования графиков показательных и логарифмических функций
42. Преобразования графиков показательных и логарифмических функций 197
198 42. Преобразования графиков показательных и логарифмических функций
42. Преобразования графиков показательных и логарифмических функций 199
200 42. Преобразования графиков показательных и логарифмических функций
42. Преобразования графиков показательных и логарифмических функций 201
202 43. Преобразования графиков тригонометрических функций
43. Преобразования графиков тригонометрических функций 203
204 43. Преобразования графиков тригонометрических функций
Гэьз! ^ = sinW
у = 2sin|.r|
1,5-1
1,5-
;	-1.5J	-1,5-*
Ы ^ = ~sinlXl ___________________917| y = sinH
1,5-
43. Преобразования графиков тригонометрических функций 205
206 43. Преобразования графиков тригонометрических функций
43. Преобразования графиков тригонометрических функций 207
958| У = x + sinxsin2r |959] У = xsinxsin2x .960]
208 43. Преобразования графиков тригонометрических функций
962]
у = 2cosx
965]
у = X + COS X
1.5-1
-1,5J
у = cos(-x)
у = XCOSX
43. Преобразования графиков тригонометрических функций 209
210 43. Преобразования графиков тригонометрических функций
3]	г -- ь 	3.
9851 у = sinx + cos2x g86j у = 2sini; + 2cos2x гд87 у = sin2x + cos4x
з]	:	з-|	।	3-
994j у = x + sin x + cos2x ,995"; у = xsin x + xcos2x ^9^
sin x + cos 2 л
У =------------
X
43. Преобразования графиков тригонометрических функций 211
у = si П Л' COS 2х gg^ у = 2 sin X COS 2х gggl У = sin 2х cos 4 а*
997
i 1000: У = -sinxcos2x
‘1003- у = sin|A-|cos2|.v|
1004 j
у = sin —cos —
x x
Юоб1 У ~ л*+ s’n л cos 2л*
sin х cos 2 х
।	_ sinxcos2x
10071 У = -Tsin.rcos2x	У~ x I
212 43. Преобразования графиков тригонометрических функций
1009|	» =	юю| У = 2^х	1011| У =
1012] У =	10131 У = 1§(-х)	1014] У = М
43. Преобразования графиков тригонометрических функций 213
10301 у = х + хsinv |7озТ| у = ^tgxsinx
_	_ tgxsinx
10321 У~ х
214 44. Графики различных комбинаций элементарных функций
44. Графики различных комбинаций элементарных функций 215
216 44. Графики различных комбинаций элементарных функций
з->
— 1,5-*
10571 У- sin х + sin
1,5-1

з-
2-
-2-
-1,5-
10581	# = sinxsin6x
10611
-4J
у = ch x =
ex x
2
1.5-1
45. Изображения неявно заданных зависимостей, содержащих знак модуля 217
218 45. Изображения неявно заданных зависимостей, содержащих знак модуля
45. Изображения неявно заданных зависимостей, содержащих знак модуля 219
220 45. Изображения неявно заданных зависимостей, содержащих знак модуля
45. Изображения неявно заданных зависимостей, содержащих знак модуля 221
222 46. Изображения зависимостей, заданных параметрически
46. Изображения зависимостей, заданных параметрически 223
sin — t - Asinl t + — t
R	R
= (/? + r)cos — t -/zcos t + — t ; у = (R 4- r)
I R J '
1143l 7? = 1; r = 1; Л = 10
114б| R = 4; r = 1; h = 2
115p] Д = 2; r = 1; h = 8	= 5; r = 1; h = 8
ЙЙ] Д- 10;г = 1;Л = 8
224 46. Изображения зависимостей, заданных параметрически
46. Изображения зависимостей, заданных параметрически 225
226 47. Изображения зависимостей, заданных в полярных координатах
48. Изображения некоторых кривых на плоскости 227
228 49. Изображения поверхностей 2-го порядка
Литература
1.	Бронштейн И, Н., Семендяев К. А. Справочник по математике. Для
инженеров и учащихся вузов. М.: Наука, 1964.
2.	Бугров Я. С. Высшая математика. В 3 т.: учеб для вузов/ Я. С. Буг-
ров, С. М. Никольский; под ред. В. А. Садовничего. Т. 2: Дифферен-
циальное и интегральное исчисление. М.: Дрофа, 2005.
3.	Бугров Я. С., Никольский С. М. Высшая математика. Дифференци-
альные уравнения. Кратные интегралы. Ряды. Функции комплекс-
ного переменного. М.: Наука. Главная редакция физико-математи-
ческой литературы, 1981.
4.	Вентцель Е. С., Овчаров Л. А. Теория вероятностей. М.: Наука. Главная
редакция физико-математической литературы, 1973.
5.	Вирченко Н. А., Ляшко И. И., Швецов К. И, Графики функций: Справоч-
ник. Киев: Наукова думка, 1979.
6.	Воднев В. Т. Математический словарь высшей школы: Общая часть/
В. Т. Воднев, А. Ф. Наумович, Н. Ф. Наумович; Под редакцией
Ю. С. Богданова. М.: Изд-во МПИ, 1988.
7.	Выгодский М. Я. Справочник по высшей математике. М.: ACT: Аст-
рель, 2006.
8.	Выгодский М. Я. Справочник по элементарной математике. М.: Аст-
рель, 2003.
9.	Двайт Г. Б. Таблицы интегралов и другие математические фор-
мулы. М.: Наука. Главная редакция физико-математической ли-
тературы, 1978.
10.	Ильин В. А., Позняк Э. Г. Аналитическая геометрия. М.: Наука. Главная
редакция физико-математической литературы, 1981.
1	{.Кожухов И. Б., Прокофьев А. А. Математика. Школьникам и абиту-
риентам. М.: Махаон, 2005.
12.	Камке Э. Справочник по обыкновенным дифференциальным урав-
нениям. М.: Наука. Главная редакция физико-математической ли-
тературы, 1976.
230 Литература
13.	Корн Г., Корн Т. Справочник по математике для научных работни-
ков и инженеров. М.: Наука. Главная редакция физико-математиче-
ской литературы, 1974.
14.	Кудрявцев Л. Д. Краткий курс математического анализа: Учебник
для вузов. М.: Наука. Главная редакция физико-математической лите-
ратуры, 1989.
15.	Рыбасенко В. Д., Рыбасенко И, Д. Элементарные функции: Форму-
лы, таблицы, графики. М.: Наука. Главная редакция физико-математи-
ческой литературы, 1987.
16.	Савелов А. А. Плоские кривые. Систематика, свойства, примене-
ния. (Справочное руководство). М.: Государственное издатель-
ство физико-математической литературы, 1960.
17.	Смирнов В. И. Курс высшей математики, т. 1, т. 2. М.: Наука. Главная
редакция физико-математической литературы, 1974.
18.	Старков С. Н. Математические формулы и графики функций. СПб:
Питер, 2006.
1$. Цикунов А. Е. Сборник математических формул. СПб: Питер,
2006.
20. Цыпкин А. Г., Цыпкин Г. Г. Математические формулы. Алгебра.
Геометрия. Математический анализ. М.: Наука. Главная редак-
ция физико-математической литературы, 1985.
21. Шипачев В. С. Высшая математика. Учеб, для вузов/В. С. Шипачев.
М.: Высшая школа, 2002.
Алфавитный указатель
основных формул
А
Абсолютная величина (5.1) - (5.16)
Абсолютная
и условная сходимость (29.16)
Алгебра вероятностей (34.23) - (34.35)
Алгебра событий (34.12) - (34.22)
Аргумент комплексного числа - (32.20)
Арифметическая прогрессия (7.1) - (7.9)
Арифметический корень (6.6),
(6.15)-(6.19)
Б
Биномиальное
распределение (34.58) - (34.59)
в
Векторное произведение (13.53) - (13.62)
Векторы (13.1) - (13.68)
Вычеты (33.40)
Вычисление объемов
и площадей поверхности (12.23) - (12.30)
г
Гамма-функция (24.11) - (24.13)
Геометрическая прогрессия (7.10) - (7.15)
Гиперболические функции
(21.24) - (21.27), (33.14) - (33.17)
Градиент (28.2)
д
Двойной интеграл (26.1) - (26.10)
Действия с дробями (3.1) - (3.14)
Дивергенция (28.4)
Дисперсия (34.52) - (34.53),
(34.55) - (34.56)
Дифференциал (21.65) - (21.79),
(25.9)-(25.14)
Дифференциальные уравнения
1-го порядка (31.1) - (31.14)
Длина вектора (13.11)
Е
Единичный вектор (13.14)
Единичная матрица (19.7),
(19.23)-(19.25)
3
Замечательные пределы (20.31) - (20.39)
к
Комплексные числа (32.1) - (32.61)
Криволинейные интегралы (27.1) - (27.7)
Кривые на плоскости (16.1) - (16.43)
л
Линейная комбинация векторов (13.30)
Линейная независимость
системы векторов (13.31)
Линейное дифференциальное
уравнение 2-го порядка (31.15) - (31.19)
Линейное дифференциальное
уравнение n-го порядка (31.20) - (31.26)
Логарифмы (6.25) - (6.34)
232 Алфавитный указатель основных формул
м
Математическое ожидание (34.51), (34.54)
Матрицы (19.1) - (19.34)
Модуль (5.1) - (5.16)
Модуль вектора (13.11)
Модуль комплексного числа (32.18)
н
Направляющие косинусы вектора (13.12)
Неопределенный
интеграл (22.1) - (22.102)
Непрерывность функции (20.66) - (20.73)
Неравенство Чебышева (34.77) - (34.78)
Несобственные интегралы (24.1) - (24.10)
Нормальное
распределение (34.66) - (34.76)
о
Обратные тригонометрические
функции (10.44) - (10.57)
Окружность и круг (12.19) - (12.22),
(32.59), (16.5)-(16.14)
Оператор Гамильтона (28.1)
Оператор Лапласа (28.6) - (28.7)
Определители (18.1) - (18.17)
Определенный интеграл (23.1) - (23.31)
Орт вектора (13.27)
Основное тригонометрическое
тождество (10.1)
Основные функции
комплексной переменной (33.2) - (33.17)
Особые точки (33.36) - (33.39)
п
Перестановки (34.7) - (34.8)
Плоскость (15.1) - (15.23)
Плотность
распределения (34.46) - (34.50)
Поверхности 2-го порядка (17.1)-(17.12)
Поверхностные интегралы (27.8) - (27.9)
Полярные координаты (13.1) - (13.3)
Правило Лопиталя (21.62)
Правило сложения
вероятностей (34.27) - (34.30)
Правило трех сигм (34.76)
Правило умножения
вероятностей (34.33) - (34.35)
Предел числовой
последовательности (20.1) - (20.15)
Предел функции (20.16) - (20.65)
Преобразование
координат (13.38) - (13.39)
Признак коллинеарности
двух векторов (13.29)
Производная (21.1) - (21.55)
Производная по направлению (28.3)
Пропорции (4.5) - (4.14)
Проценты (4.15) - (4.17)
Прямая в пространстве (15.24) - (15.31)
Прямая на плоскости (14.1) - (14.38),
(32.58)
р
Равномерное
распределение (34.62) - (34.65)
Разложение вектора по базису (13.35)
Разложение многочлена
на множители (2.19) - (2.20)
Размещения (34.5) - (34.6), (34.9)
Распределение Пуассона (34.60) - (34.61)
Расстояние между точками (13.10), (32.57)
Расстояние от точки
до плоскости (15.19) - (15.20)
Расстояние от точки
до прямой (14.31) - (14.32)
Решение неравенств (9.1) - (9.60)
Решение уравнений (8.1) - (8.37)
Ротор (28.5)
Алфавитный указатель основных формул 233
Ряд Лорана (33.34) Ряд Тейлора (29.29) - (29.44), (33.27) - (33.33)	Типовые способы замены переменной (11.1)-(11.12) Точки разрыва (20.69) - (20.70)
с	Треугольники (12.1)-(12.11) Тригонометрические
Связь радианной и градусной меры угла (10.69) - (10.71) Скалярное произведение (13.40) - (13.52) Сложение и вычитание векторов (13.18) - (13.21) Смешанное произведение векторов (13.63) - (13.68) Сочетания (34.1) - (34.4) Среднее арифметическое (4.1) Среднее гармоническое (4.3) Среднее геометрическое (4.2) Степени (6.1) - (6.24) Степенные ряды (29.22) - (29.44) Сферические координаты (13.5) - (13.6) Схема Горнера (2.16) - (2.17)	ряды Фурье (30.1) - (30.7) Т ригонометрические формулы (10.1) - (10.72) Тройной интеграл (26.11) - (26.20) У Умножение вектора на число (13.22) - (13.26) Условие коллинеарности двух векторов (13.61) Условие компланарности трех векторов (13.67) Условие перпендикулярности двух векторов (13.51) Условия Коши-Римана (33.19) Условная вероятность (34.31)
т	ф
Таблица значений тригонометрических функций (10.72) Таблица интегралов (22.9) - (22.32) Таблица производных (21.7) - (21.23) Таблица эквивалентных бесконечно малых (20.44) - (20.65) Теорема косинусов (12.11) Теорема Кронекера - Капелли (19.32) - (19.34) Теорема Коши (21.61), (33.24) Теорема Лагранжа (21.60) Теорема о подборе корней многочлена (2.18) Теорема Пифагора (12.9) Теорема Ролля (21.59) Теорема синусов (12.10) Теорема Ферма (21.58)	Формула Байеса (34.37) Формула Бернулли (34.38) - (34.39) Формула бинома Ньютона (1.23) Формула Гаусса-Остроградского (27.12) Формула Грина (27.7) Формула Маклорена (21.57) Формула Муавра (32.42) Формула Ньютона-Лейбница (23.3), (33.23) Формула полной вероятности (34.36) Формула Стирлинга (34.10) Формула Стокса (27.10) Формула Тейлора (21.56) Формулы Крамера (18.16) - (18.17) Формулы комбинаторики (34.1) - (34.9) Формулы Эйлера (32.51) Функция распределения (34.40) - (34.44)
234 Алфавитный указатель основных формул
ц
Цилиндрические координаты (13.4)
ч
Частные производные (25.1) - (25.19)
Четырехугольники (12.12) - (12.18)
Числовые ряды (29.1) - (29.21),
(29.45) - (29.53)
Старков Сергей Николаевич
Справочник по математическим формулам
и графикам функций для студентов
Заведующий редакцией
Руководитель проекта
Ведущий редактор
Технический редактор
Литературный редактор
Корректоры
Верстка
А. Сандрыкин
А. Юрченко
Ю. Сергиенко
С. Романов
А. Пасечник
Н. Солнцева
С. Романов
Подписано в печать 31.10.08. Формат 60x90/16. Усл. п. л. 15. Доп. тираж 3000. Заказ
ООО «Питер Пресс», 198206, Санкт-Петербург, Петергофское шоссе, д. 73, лит. А29.
Налоговая льгота — общероссийский классификатор продукции ОК 005-93,
том 2; 95 3005 — литература учебная.
Отпечатано в ОАО «Техническая книга».
190005, Санкт-Петербург, Измайловский пр., д. 29.