Медицинская статистика. Медицинское информационное агентство - Герасимов А.Н.

Введение. Типовая схема статистического анализа клинических данных
1.1.2. Смена групп наблюдения и возрастные изменения
1.2. Доказательная медицина и дизайн исследования
1.3. Статистическая обработка как вид математической обработки
Глава 2. Планирование эксперимента и ввод данных
2.2.2. Подготовка к работе с пакетом статистических программ и работа с файлами сданными
Глава 3. Анализ частот и оптимизация рисков
3.2. Частоты, риски и относительные риски
4.2. Современный подход. Аксиоматика Колмогорова
4.3. Вычисление вероятностей. Условные, априорные и апостериорные вероятности
4.5. Закон больших чисел. Расчет необходимого объема наблюдений
4.6. Функция распределения числовой случайной величины. Непрерывные и дискретные случайные величины. Распределения Бернулли, биномиальное, Пуассона, нормальное, «хи-квадрат», Стьюдента и Фишера
Глава 5. Отбор и поиск данных. Элементы математической логики
Глава 6. Элементы математической статистики
6.2. Ошибки первого и второго рода. Выбор доверительной вероятности
6.3. Сравнение частоты и вероятности. Доверительные вероятности
6.3.2. Расчет доверительных границ к медиане и другим процентилям
6.4.1. Вариант ручного счета — сравнение собственных результатов с литературными данными, сопоставление данных разных источников друг с другом, проверка на однородность
6.4.2. Сравнение наборов частот при помощи критерия х2- Условия применимости критерия х2
6.4.3. Расчет частоты совместного распределения и определение достоверности различий при помощи критерия х2
6.4.4. Определение достоверности различий распределений в подгруппах при помощи критерия х2 и критерия Колмогорова—Смирнова
7.2. Лирическое отступление о статистической терминологии и трудностях перевода
7.3. Расчет параметров в статистических пакетах
7.4. Проверка гипотезы на принадлежность наблюдаемой случайной величины классу случайных величин
Глава 8. Содержательный анализ среднего арифметического
8.2. Среднее арифметическое и нелинейность ущерба
8.3. Выскакивающие варианты и среднее арифметическое
8.4. Классификация переменных «scale», «ordinal» и «nominal»
9.2. Оценка моментов. Катастрофа неробастности старших моментов
9.4. Построение оценок при помощи метода наибольшего правдоподобия
Глава 10. Интервальные оценки параметров. Определение достоверности различий
10.2. Определение достоверности различия дисперсии
10.3. Определение достоверности различия средних. Критерий Стьюдента
10.4. Расчет достоверности различия средних арифметических с помощью пакетов статистических программ
10.5. Расчет доверительных границ к математическому ожиданию
11.2. Расчет коэффициента корреляции и анализ взаимосвязи двух переменных
11.3. Сопоставление расчета коэффициента корреляции с другими методами анализа взаимосвязи двух переменных
11.4 Расчет доверительных границ коэффициента корреляции и достоверности различий коэффициентов корреляции
Глава 12. Проверка корректности предположения о применимости центральной предельной теоремы и непараметрические методы
12.2. Отбрасывание выскакивающей варианты
Часть 3. Прогнозирование и некоторые дополнительные методы
13.2. Прогнозирование и деление переменных на классы scale и nominal
13.3. Прогнозирование ожидаемого значения и задача о наилучшем приближении
13.4. Линейный прогноз по одному коэффициенту корреляции. Уточнение коэффициента корреляции для того случая, когда переменная задана со случайной ошибкой
13.6. Анализ согласованности тестов. Приложение к психологии и педагогике
13.8. Применение корреляционного анализа к динамическим рядам
13.8.4 Применимость методов статистического анализа для анализа динамических рядов
Глава 14. Повышение точности прогнозирования и анализ его ценности
14.2. Многофакторное нелинейное прогнозирование как потенциально мощный практически неприменимый метод. Информационная модель, неявно используемая в многофакторном линейном прогнозе
14.3. Проверка качества прогноза. Авторешаемость и скользящий экзамен
14.4. Анализ практической ценности прогноза. ROC-кривые и оптимальный выбор соотношений чувствительность/эффективность и надежность/достоверность
16.2. Определение факторов риска для выживаемости при помощи регрессии Кокса
Глава 17. Кластерный анализ и задачи классификации
Глава 18. Морфометрия и статистический анализ изображений
18.2. Анализ распределения ориентации объектов на плоскости
18.3. Изучение трехмерных объектов по их срезам
Приложение 3. Использование электронной таблицы Excel для проведения типовых статистических расчетов
Автор: Герасимов А.Н.
Теги: медицинские науки здравоохранение медицина
ISBN: 5-89481-456-1
Год: 2007
Похожие
Статистика в медицине и биологии. Том 1. Теоретическая статистика
Учебное пособие по медицинской статистике
Применение непараметрических критериев статистики в медико-биологических исследованиях
Статистика в медицине и биологии. Том 2. Прикладная статистика здоровья
Текст
                    АН. Герасимов
МЕДИЦИНСКАЯ
СТАТИСТИКА
УЧЕБНОЕ ПОСОБИЕ
Рекомендовано Учебно-методическим объединением по медицинскому
и фармацевтическому образованию вузов России в качестве
учебного пособия для студентов медицинских вузов.
к Л.
♦£*
Медицинское информационное агента но
Москиа
2007

61
5
Г37
Герасимов А.Н.
Г37 Медицинская статистика: Учебное пособие. — М.: ООО «Ме-
дицинское информационное агентство», 2007. — 480 с. : ил.
ISBN 5-89481-456-1
В книге, подготовленной заведующим кафедрой медицинской
информатики и статистики ММА им. ИМ. Сеченова, речь идет
о статистической обработке медицинских данных с помощью па-
кетов статистических программ, то есть о теории вероятностей и
математической статистике для медиков. Излагаются не только
математические результаты и технические приемы обработки дан-
ных, но и некоторые вопросы планирования статистических ис-
следований и интерпретации полученных результатов. Структура
и последовательность изложения материала резко отличается от
обычной для учебников по теории вероятностей и математической
статистике. В них, в соответствии с внутренней логикой, внача-
ле излагается теория вероятностей, затем на основе изложенного
аппарата — математическая статистика, а в конце обсуждаются
вопросы практического применения, в частности использования
программного обеспечения. А в этой книге последовательность
изложения материала соответствует последовательности действий
при статистической обработке данных, поэтому книгу нужно ос-
ваивать параллельно с обработкой фактических данных. Книга
состоит из двух параллельно излагаемых частей. При описании
того, как нужно вводить данные и использовать конкретные мето-
ды обработки данных, дается точное описание, как пользоваться
программой и какие команды нужно выполнять. При описании же
того, как нужно понимать полученные результаты, даются необхо-
димые элементы теории.
УДК Ы
ЬЬК 5
ISBN 5-8948I-456-I © Герасимом ЛИ , 2007
<П> Оформление. ООО «Медицинское
информационное агентство», 200/

Статистика знает псе.
Ильф и Петров,
«Двенадцать стульев»

ПРЕДИСЛОВИЕ
О названии этой книги
Термин «медицинская статистика» может пониматься по-
разному, вплоть до правил ведения отчетной документации
в медицинских учреждениях. В данном случае речь идет о
статистической обработке медицинских данных с помощью
пакетов статистических программ, то есть о теории вероят-
ностей и математической статистике для медиков.
На сторонних специалистов, не знакомых со специфи-
кой вопроса, термин «медицинская статистика» часто про-
изводит такое же неоднозначное впечатление, как «женская
ботаника» или «грузинская арифметика». Однако необхо-
димость выделения медицинской статистики как отдельной
учебной дисциплины обусловлена целым рядом объектив-
ных и субъективных факторов, среди которых следующие.
♦ специфические стандарты в дизайне исследовали
наличие ограничений юридического, экономичеекс
го и этического характера;
♦ большая сложность изучаемых явлений, наличие << '
водок» и сбивающих факторов и, как следствие, ■с ■
нозначность интерпретации полученных резулЫ'
♦ наиболее часто решаемые задачи не полностью
надают с такоными n других предметных облает

Предисловие^
5
♦ при анализе клинических данных имеются стандарт-
ные требования к объему и характеру анализируемых
данных, связанные с трудоемкостью их сбора, что на-
кладывает однотипные ограничения на выбор мето-
дов исследования;
♦ имеются некоторые отличия в «моде» на выбор методов
исследования и формы представления результатов;
♦ в современной математической статистике и теории
вероятностей есть методы анализа, специально разра-
ботанные под медико-биологические приложения;
♦ уровень базовой математической подготовки боль-
шинства современных врачей и студентов-медиков
нельзя назвать недостаточно высоким. Он ужасен.
Зачем эта книга
Необходимо учебное пособие по сложному со всех точек
зрения статистическому анализу клинических медицинских
данных для людей, не имеющих базовой математической
подготовки в объеме, считающемся абсолютно необходи-
мым для всех других естественно-научных дисциплин.
Статистический анализ всегда представлял для меди-
ков существенную проблему, однако за последние годы он
превратился в задачу почти неразрешимую. Повсемест-
ное внедрение персональных компьютеров сняло большую
часть технических проблем при статистической обработке
данных, но, как следствие, значительно расширило спектр
практически применимых методов статистического анализа
и резко подняло уровень требований к качеству статистиче-
ской обработки. В результате врач обычно не может не толь-
ко самостоятельно, но и при помощи технически образован-
ных родственников провести надлежащий статистический
анализ, так как он не в состоянии сформулировать, что ему
нужно от статистического анализа, и понять, что означают
полученные результаты.
Большинство известных мне аспирантов, докторантов
и соискателей из числа врачей к моменту начала статистиче-
ского анализа диссертационных результатов приходили

Медицинская t
"ист,,.
' crnamuc
к выводу, что они идиоты. Однако массовый характер «
ния приводит к мысли, что в основе затруднений лежа/
столько субъективные, сколько объективные причины ' 1
В определенной степени медикам не повезло в том in
по времени совпало два процесса, освоение количественны
методов исследования, естественное для любой естествен-
но-научной дисциплины, достигшей определенной степени
зрелости, и широкое внедрение персональных компьютеров
В итоге внедрение количественных методов анализа в меди-
цину пошло чрезвычайно быстрыми темпами, что привело
к разрыву между содержанием медицинского образования и
теми требованиями, которые встают перед врачами, особен-
но занимающимися научной работой. Речь здесь не сводится
только к незнанию определенных математических терминов
и приемов. Значительные проблемы возникают также при
планировании эксперимента и интерпретации его результа-
тов из-за некритичного подхода к используемым результа-
там и неумения проводить формальные логические рассуж-
дения, доказывая следствия из принятых постулатов.
Поэтому в данной книге излагаются не только матема-
тические результаты и технические приемы обработки дан-
ных, но и некоторые вопросы планирования статистических
исследований и содержательной интерпретации полученных
результатов, до чего математики обычно не снисходят.
Почему эта книга
Несколько лет назад, когда мне пришлось готовить КУРС
для аспирантов Московской медицинской академии имен"
ИМ. Сеченова по статистической обработке диссертацией^
ных результатов, я столкнулся с тем, что мне практиче1>
нечего посоветовать в качестве учебных пособий М"0^.
численные современные пособия по прикладной матема ^
ческой статистике были практически недоступны, та.к ^
авторам этих книг не приходило в голову, что серьез"10" ^ ',
тистической обработкой данных могут заниматься »яШ1'-
знающие, чтотакое интеграл Имеющиеся же отеча-и" ||а
книги по статистике дли меликои были ориентирован-

Предисловие
7
технологию ручного счета и поэтому практического интере-
са уже не представляли. В них приводятся формулы для рас-
четов (в том числе и приближенные), достоверность разли-
чий определяется с помощью таблиц критических значений,
а набор методов анализа крайне невелик.
Более того, изучение этих пособий скорее могло принес-
ти вред, чем пользу, так как для обеспечения «доходчивости»
и простоты жертвовалось точностью и строгостью.
Ряд имеющихся современных переводных книг по при-
кладной статистике в меньшей степени страдает этими не-
достатками, но, все-таки, явно недостаточен как по объему
излагаемых методов, так и по глубине изложения. Чтение
этих книг полезно, но недостаточно.
Необходимость более строгого и глубокого анализа на-
копленных фактических данных в медицине — не только
личная точка зрения автора. В последние годы она становит-
ся распространенной и в среде медиков, что, правда, иногда
принимает достаточно экзотические формы, такие, как «до-
казательная медицина».
Еще одна причина, затрудняющая использование меди-
ками специальной литературы по теории вероятностей и ма-
тематической статистике, — чрезмерная «сухость» и абстрак-
тность изложения. Современные врачи — люди конкретные,
поэтому в настоящей книге помимо общих положений при-
водится много примеров, в том числе бытового характера.
Для кого эта книга
Первоначальные заготовки предназначались для аспиран-
тов-медиков и врачей, занимающихся научной деятельно-
стью. Однако скорость развития медицины столь велика, что
уже сейчас значительная часть излагаемого материала может
и должна использоваться во время преподавания студентам-
медикам.
Из-за универсализма статистических методов книга
представляет интерес и для лиц, занимающихся статистиче-
ской обработкой в иной предметной области, а также осваи-
вающих пакеты статистических программ SPSS и Statislica.

8
статистика
Однако книга не является руководством по этим пакетам
статистических программ, и в ней описываются только те
возможности и режимы работы, которые нужны для описы-
ваемых статистических расчетов.
Современные программы, работающие в среде Windows,
обычно сделаны таким образом, что одно и то же действие
можно выполнить большим количеством разных спосо-
бов. Мой многолетний опыт преподавания информатики
говорит, что мужчин это обычно восхищает, а женщин раз-
дражает. Поэтому в данной книге для каждой манипуля-
ции приведено описание только одного способа его выпол-
нения.
Как пользоваться этой книгой
Правило Джексона:
При обучении студентов-медиков
первостепенное значение должно
уделяться тому, чтобы они все вре-
мя бодрствовали.
Артур Блох
«Законы Мерфи для медиков»
Принятая здесь структура и последовательность изложения
материала отличается от обычной для учебников по теории
вероятностей и математической статистике. В них в соот-
ветствии с внутренней логикой математической теории вна-
чале излагается теория вероятностей, затем на основе изло-
женного аппарата — математическая статистика, а в конце,
если доходят руки, обсуждаются вопросы практического
применения, в частности использования программного
обеспечения.
В этой книге последовательность изложения материала
соответствует последовательности действий при статисти-
ческой обработке данных, поэтому данную книгу нужно ос-
ваивать ПАРАЛЛЕЛЬНО с обработкой фактических данных.
При этом книга не построена по принципу набора рецеп-
тов. Для выполнения описываемых действий нужно знать не

Предисловие
9
только то, что написано в этом разделе, но и то, что излага-
лось ранее.
Фактически книга состоит из двух параллельно излагае-
мых частей. При описании того, как нужно вводить данные
и использовать конкретные методы обработки данных, дает-
ся точное описание, как пользоваться программой и какие
команды нужно выполнять. При описании же того, как нуж-
но понимать полученные результаты, даются необходимые
части теории. Эти фрагменты значительно более абстракт-
ны. Обсуждение некоторых вопросов, непосредственно не
использующихся в статистическом анализе, но полезных для
более глубокого понимания изложенного материала, оформ-
лено в виде лирических отступлений.
В качестве пакетов статистических программ использу-
ются два: SPSS и Statistica, как наиболее принятые в совре-
менной практике биомедицинских исследований.
К сожалению, для обработки данных использования толь-
ко возможностей пакетов статистических программ обычно
не хватает. В частности, статистические пакеты практически
не дают возможности сравнивать собственные результаты с
литературными. Поэтому некоторые статистические расче-
ты приходится проводить самостоятельно. В данной книге
излагается, как делать это при помощи электронной табли-
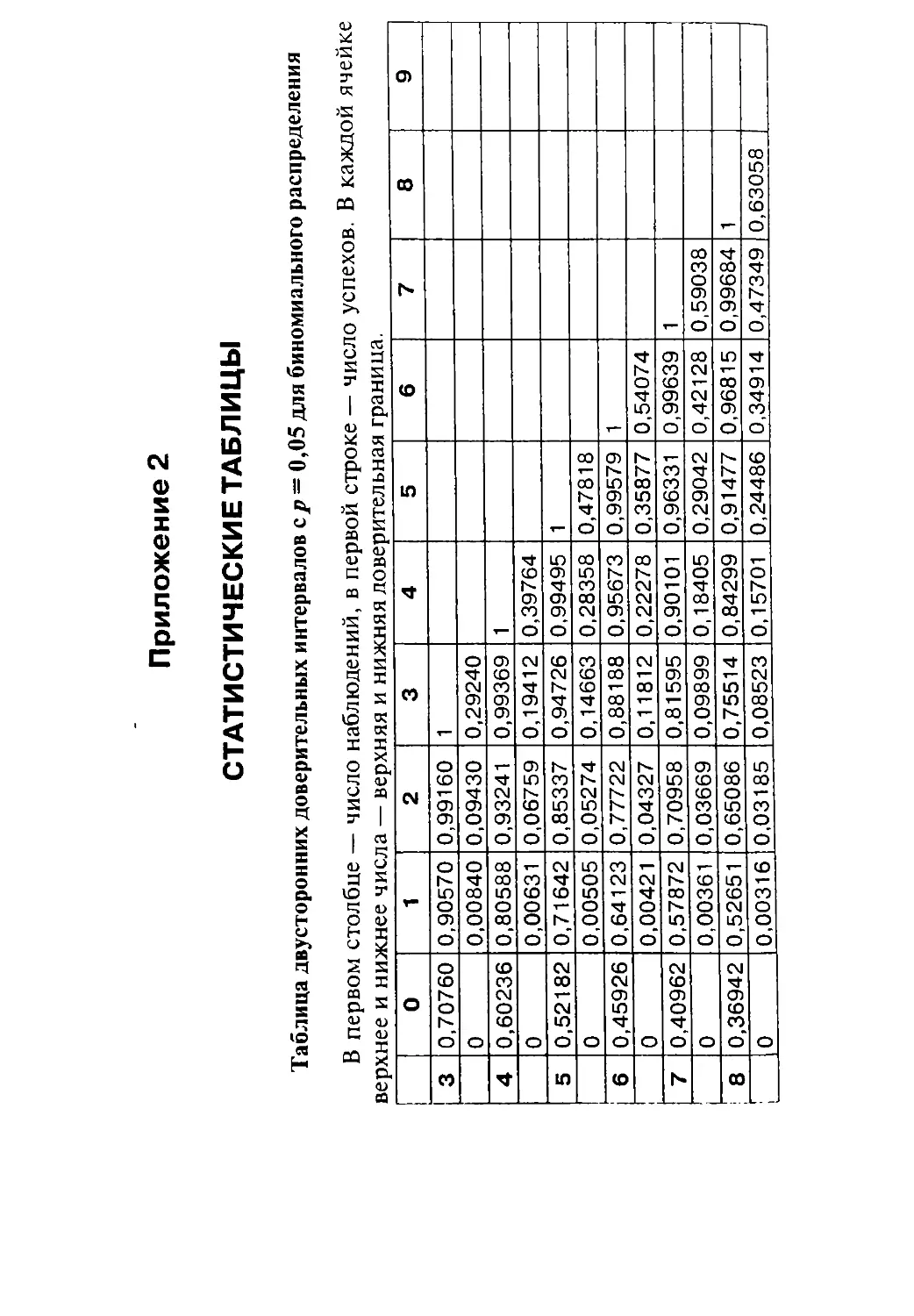
цы Excel, но для упрощения работы в конце книги приводят-
ся некоторые статистические таблицы.
Для тех, кто не читают книги от начала до конца, а про-
листывают их в поисках нужного фрагмента, в начале каждо-
го раздела кратко излагается его содержание.
Перед изложением содержания приведена типовая схе-
ма статистической обработки клинических медицинских
данных.

ВВЕДЕНИЕ
Типовая1 схема статистического анализа
клинических данных
№
3.1
Описание шага
Где описана
техника
расчетов
3
Определение целей и .за-
дач анализа, сбор ;ынных
Кодировка и ввод данных
Исследование каждой пе
ременной по отдельности
Для дискретных пере-
менных — расчет частот,
построение столбиковых
или круговых диаграмм
2 2
Где изложена
необходимая
теория
4
" 1, 2 1,4,5
3.1
3.2
Для непрерывных пере-
менных — расчет па-
раметров, построение
частотной гистограммы,
анализ распределения на
симметричность
и компактность
7.3
3 2, 4
7.1,8
1 В некоторых статьях используются выражения типа «была
ведена обычная статистическая обработка», которых нужно из а
так как специалистов они повергают в ярость. В качестве пр (И
боле:)
попробуйте написать в статье, что больные обычными - е не-
были подвергнуты стандартному лечению. Каждое статистичес аТЬ|
следование индивидуально, и полученные в ходе анализа рез^еТОдов
обязательно вызывают необходимость выбора тех или иных
дальнейшего анализа.

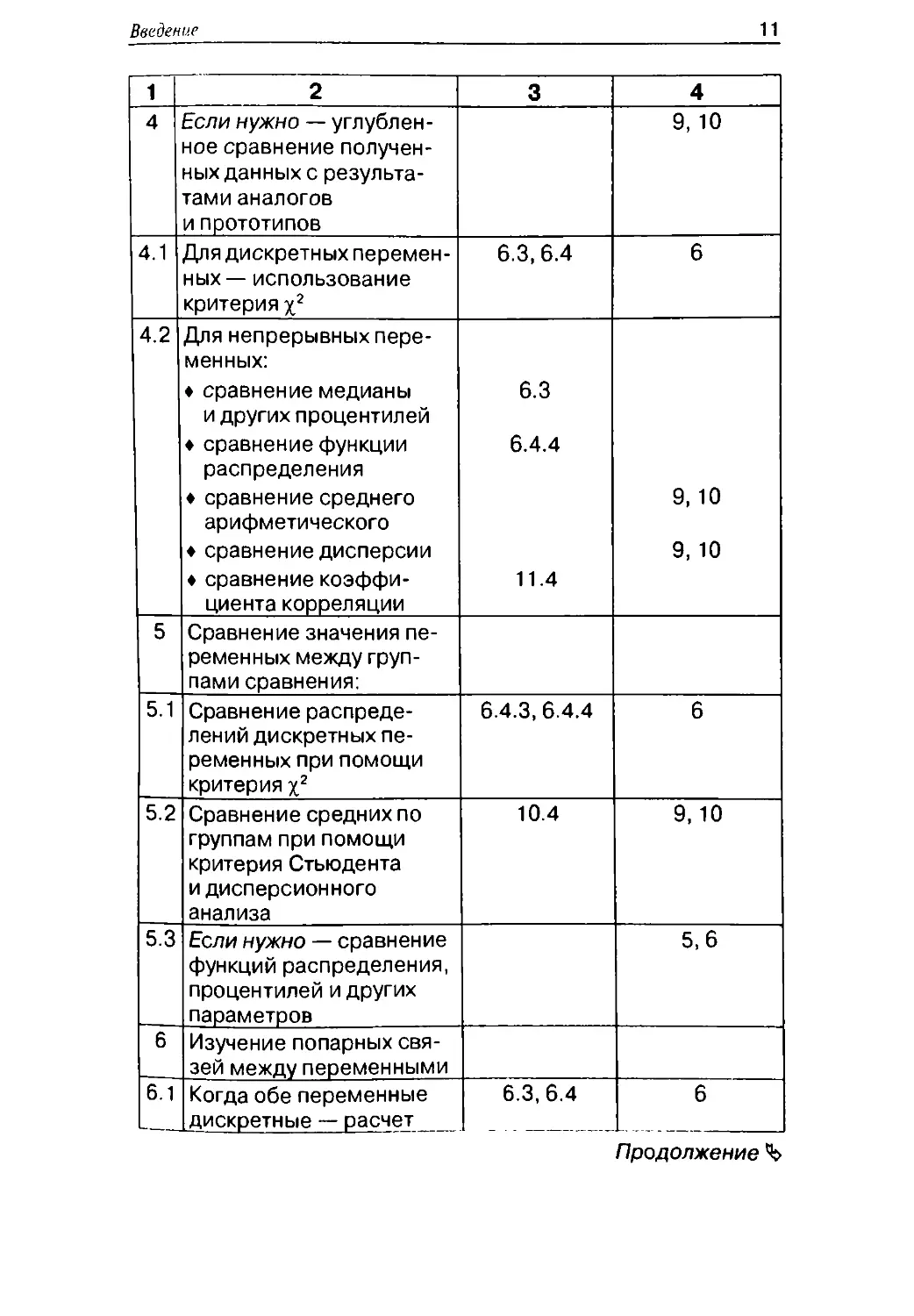
Введение
11
1
4
4.1
4.2
5
5.1
5.2
5.3
6
6.1
2
Если нужно — углублен-
ное сравнение получен-
ных данных с результа-
тами аналогов
и прототипов
Для дискретных перемен-
ных — использование
критерия х2
Для непрерывных пере-
менных:
♦ сравнение медианы
и других процентилей
♦ сравнение функции
распределения
♦ сравнение среднего
арифметического
♦ сравнение дисперсии
♦ сравнение коэффи-
циента корреляции
Сравнение значения пе-
ременных между груп-
пами сравнения:
Сравнение распреде-
лений дискретных пе-
ременных при помощи
критерия х2
Сравнение средних по
группам при помощи
критерия Стьюдента
и дисперсионного
анализа
Если нужно — сравнение
функций распределения,
процентилей и других
параметров
Изучение попарных свя-
зей между переменными
Когда обе переменные
дискретные — расчет
3
6.3,6.4
6.3
6.4.4
11.4
6.4.3,6.4.4
10.4
6.3,6.4
4
9,10
6
9,10
9,10
6
9,10
5,6
6
ПродолжениеЬ

12 ^^!1£^1£тат^
Продолжен
1
6.2
6.3
7
8
2
частот совместного
распределения, опре-
деление достоверности
различий при помощи
критерия х2
Когда одна переменная
дискретная, а вторая
непрерывная — расчет
средних арифметических
по подгруппам и опре-
деление достоверности
различий при помощи
критерия Стьюдента и
дисперсионного анализа,
расчет других условных
параметров
Когда обе переменные
непрерывные — расчет
коэффициента корреля-
ции, построение и анализ
диаграммы совместного
распределения
Если используются
данные в динамике:
определение достовер-
ности изменений,анализ
снижения тяжести пато-
логического состояния
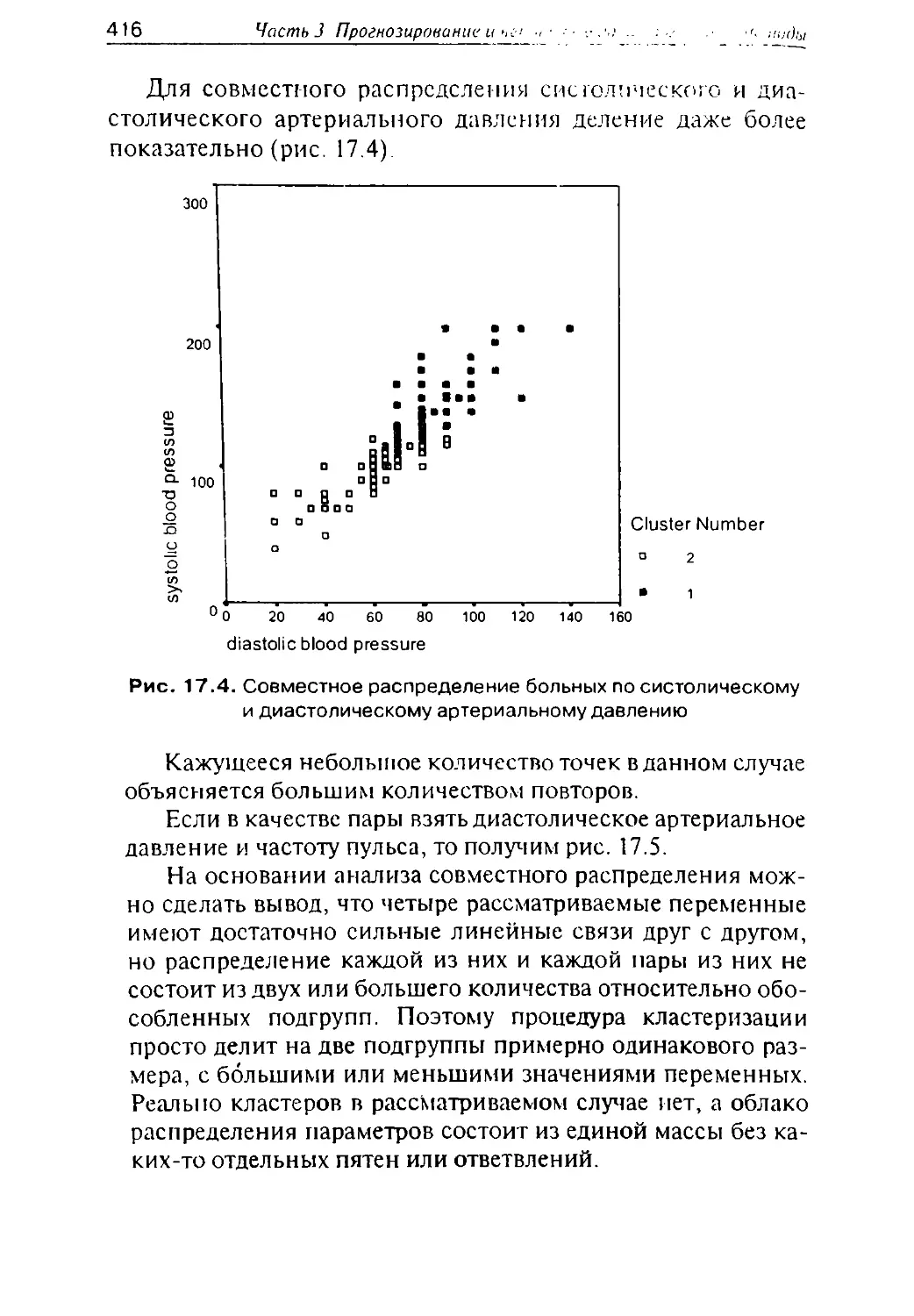
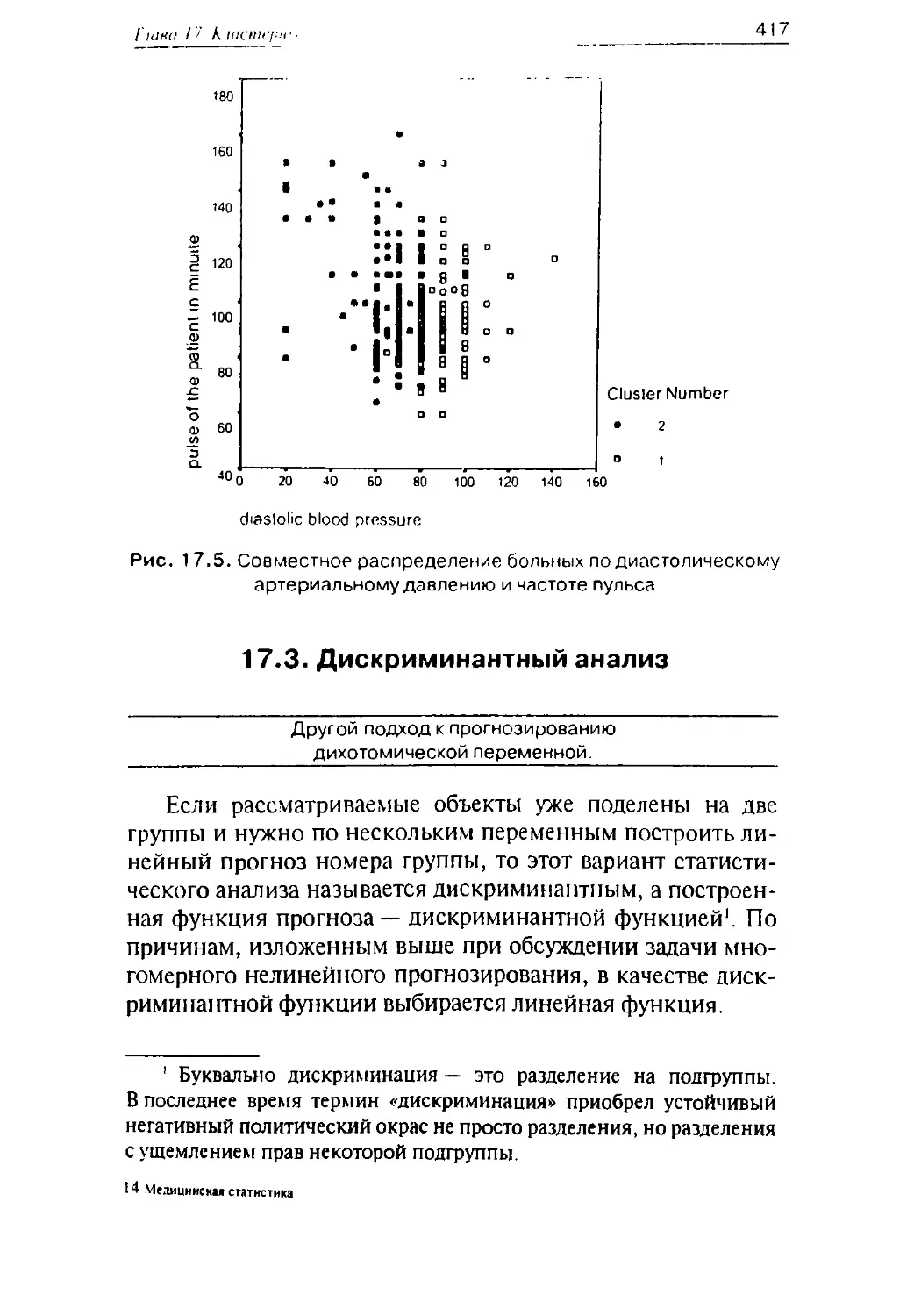
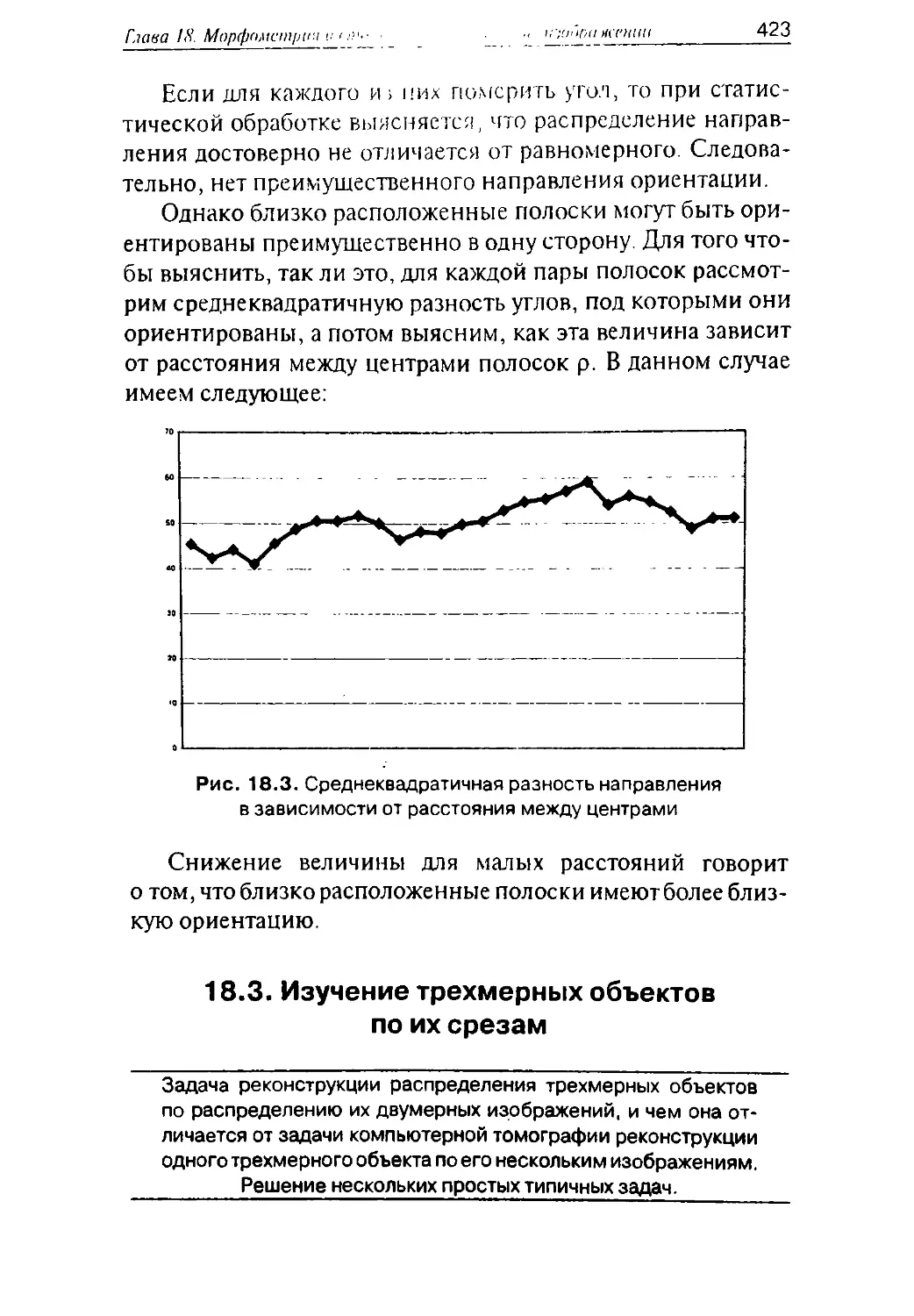
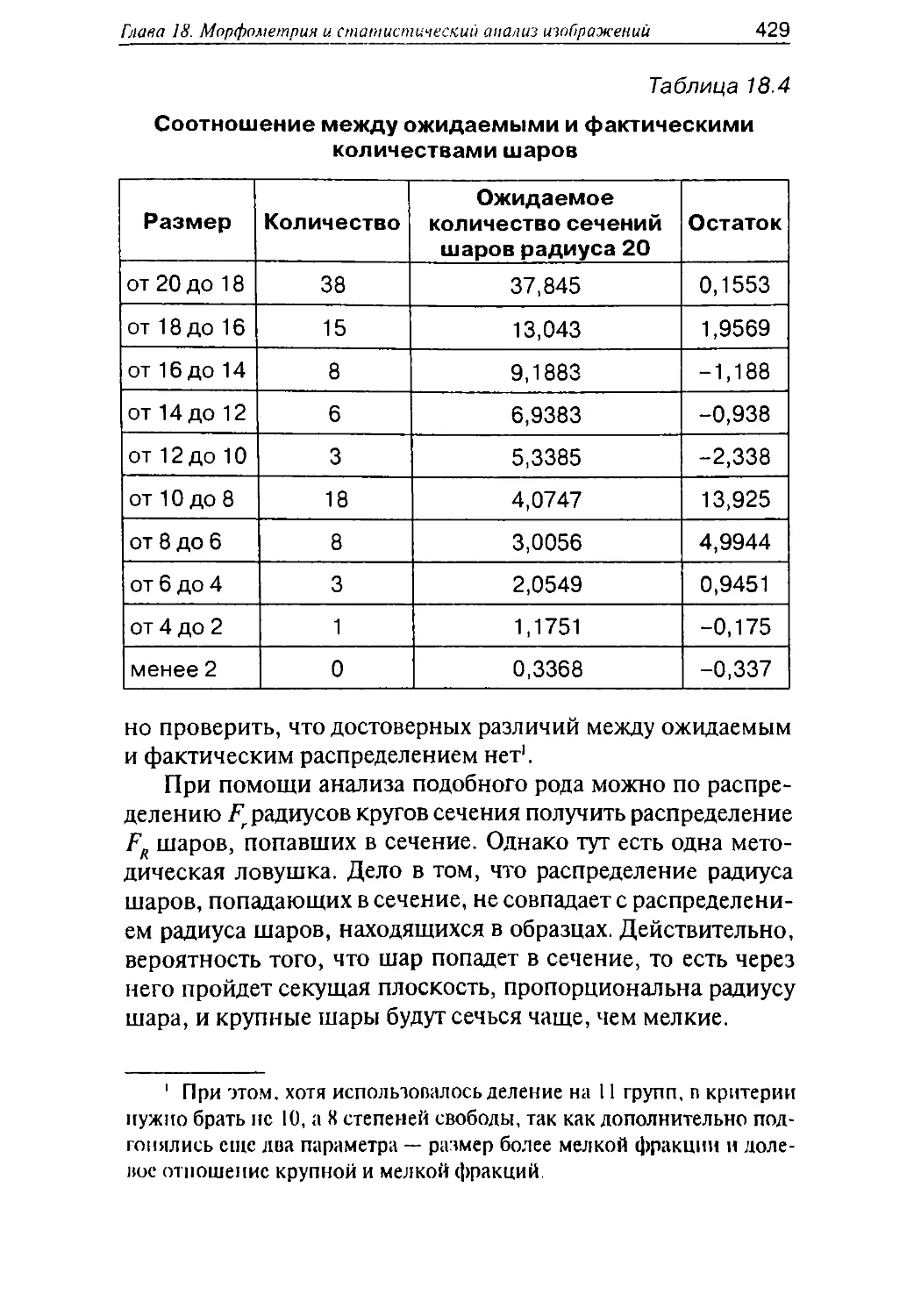
при помощи методов
корреляционной адапто-
метрии
Если нужно — прогнози-
рование значения одной
переменной по несколь-
ким другим. Использо-
вание условных средних
и линейной регрессии,
анализ клинической цен-
ности прогноза, постро-
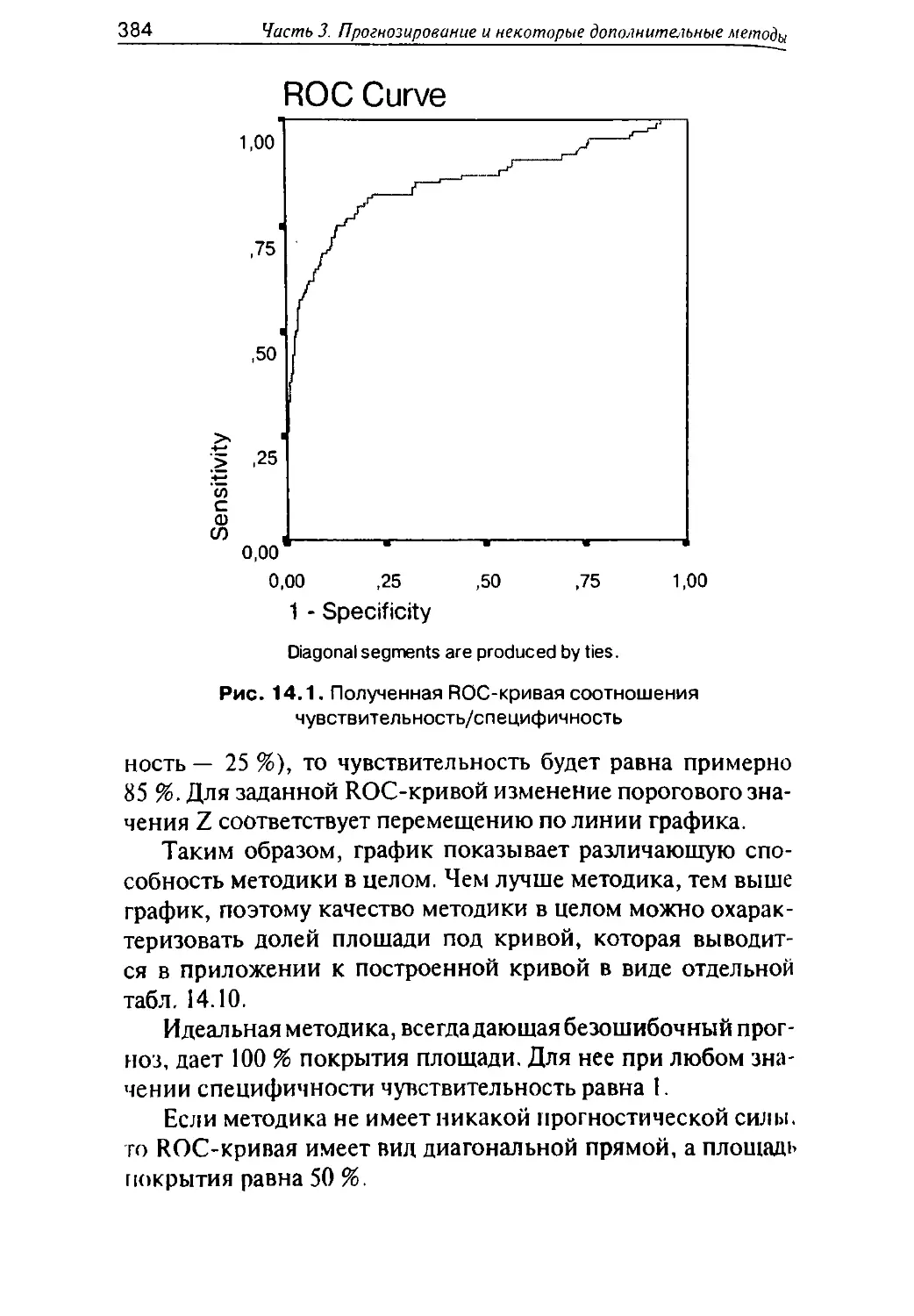
ение и анализ ROC-кри-
3
10.4
11.2
Приложе-
ние № 1,ва-
риант № 15
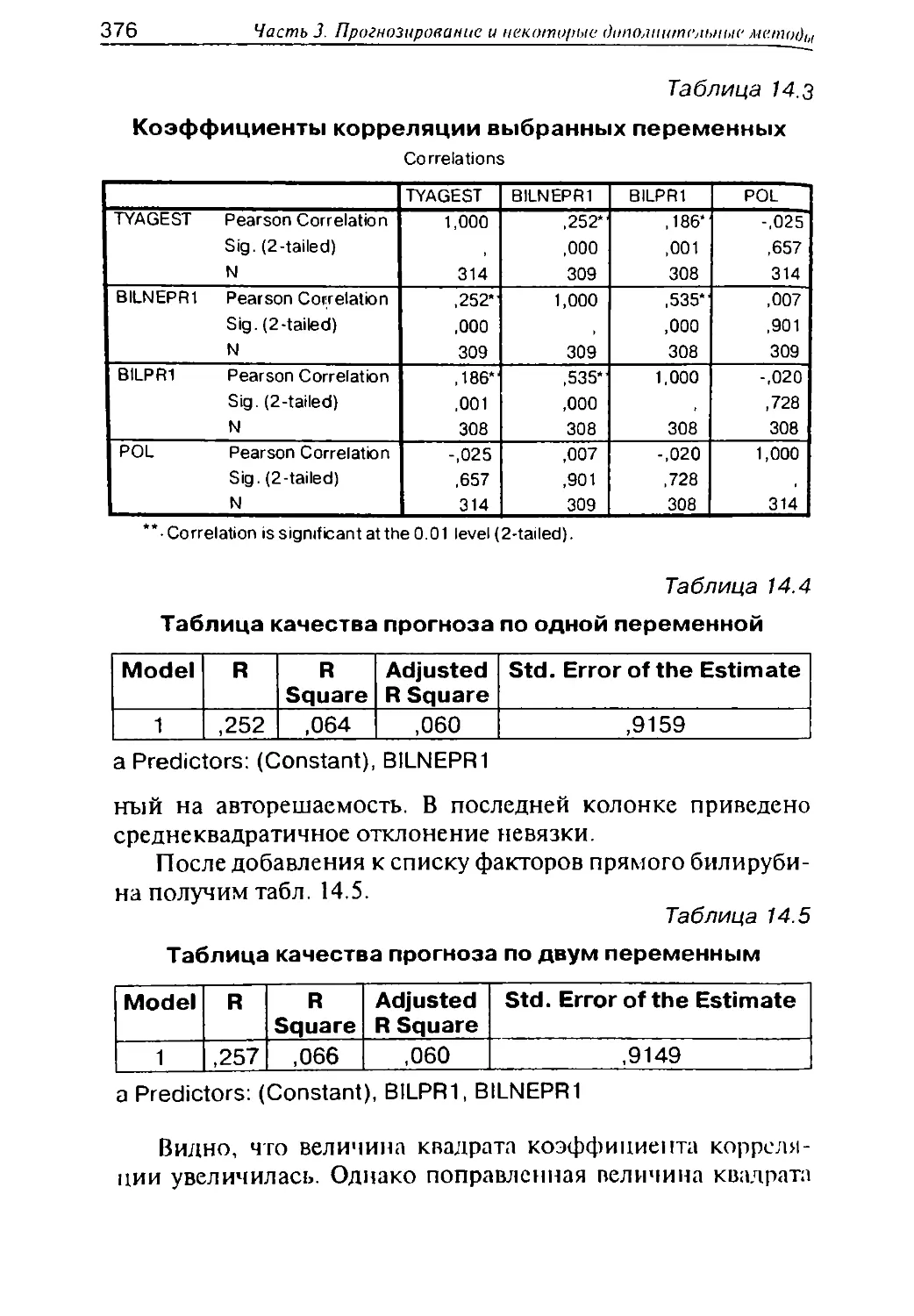
13.7, 14.4,
14.5
4~~~~~~1
9, 10
11
15
13, 14

Введение
13
1
9
10
11
12
2
вых, анализ соотношения
чувствительность/эф-
фективность
Если используются дан-
ные типа анкет: анализ
ответов на вопросы на
согласованность, оп-
ределение надежности
тестов
Если используются дан-
ные типа продолжитель-
ности до наступления
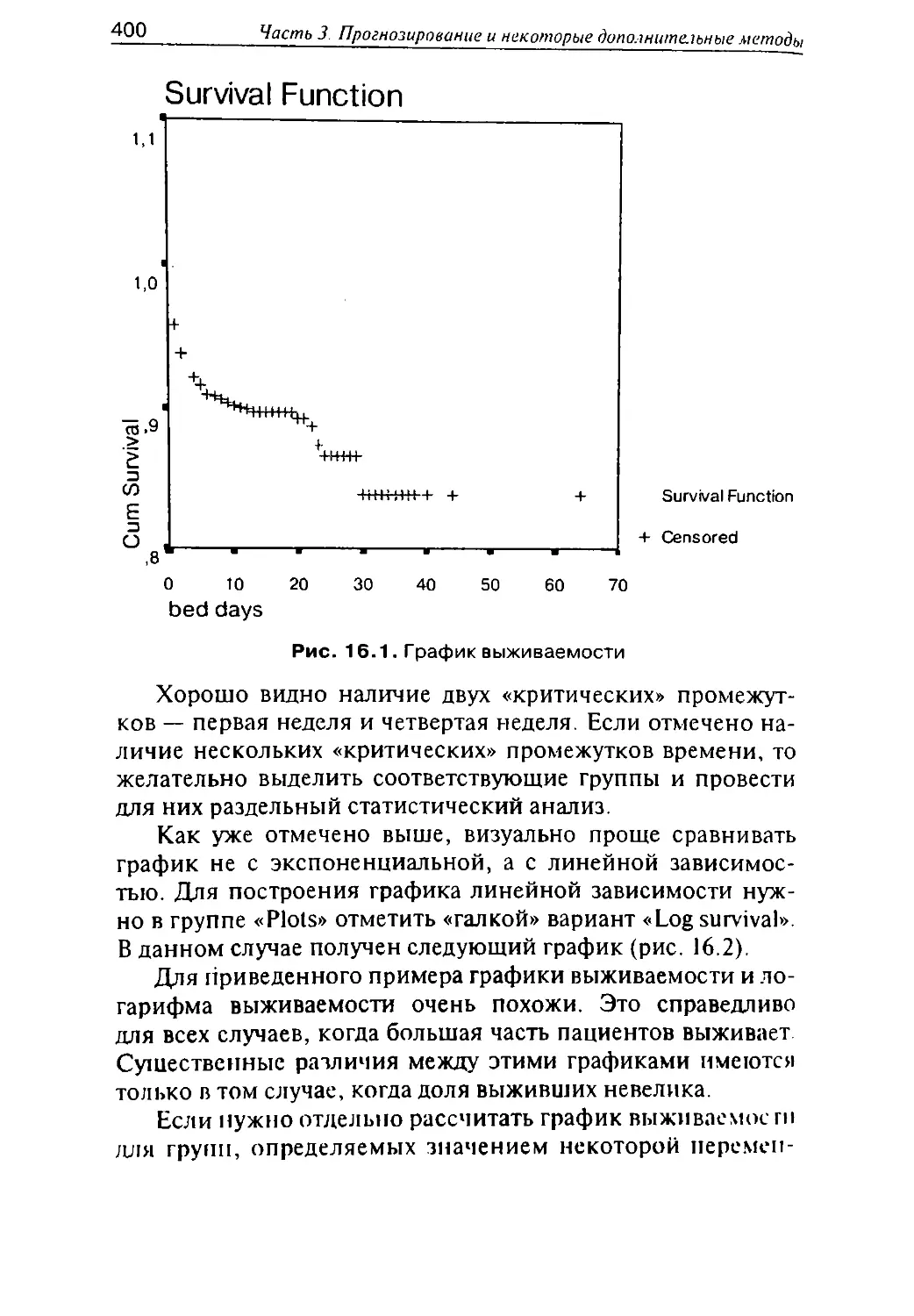
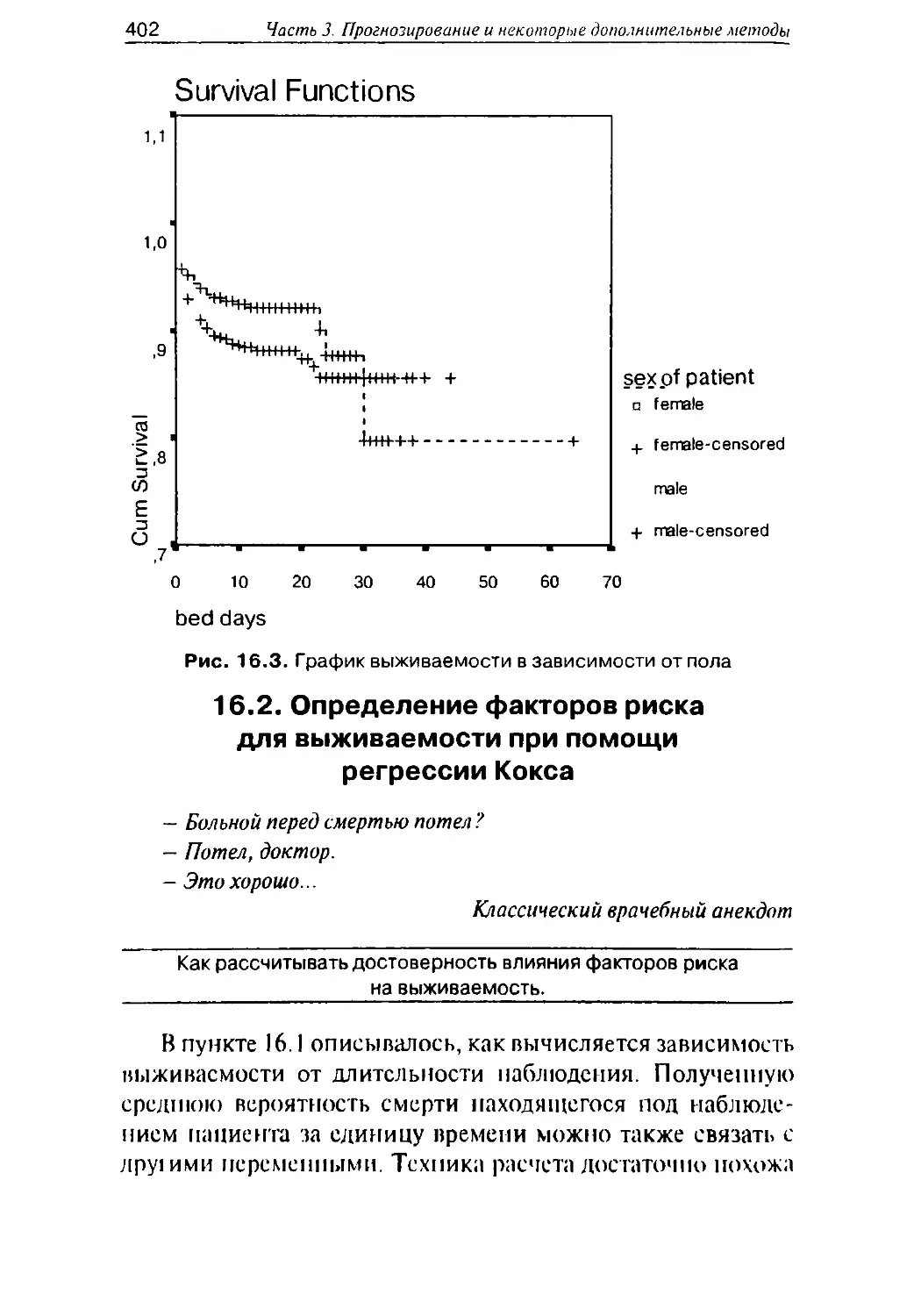
события: анализ выжи-
ваемости по Каплан-
Майер, нахождение фак-
торов риска при помощи
регрессии Кокса
Если нужно — классифи-
кация объектов,кластер-
ный анализ
Содержательная интер-
претация полученных
статистических резуль-
татов, сопоставление с
поставленными целями и
задачами исследования.
В случае существенных
расхождений1 — возврат
к пункту 1 и призовая
игра
3
13.6
16.1,16.2
17.1,17.2
4
16
17
1
Вспомогательные операции: Установка фильтров (раздел 5.1).
' Опытные научные рукоподители стараются так сформулировать
иели и задачи, чтобы при любом результате нельзя было сказать, что
работа окончилась неудачей. Особенно популярны формулнронки
типа «Исслсдоиать особенности течения заболевания ...у больных...».

ЧАСТЬ 1
АНАЛИЗ BFPOflTHOCTI И

Глава 1
НАЗНАЧЕНИЕ И ВОЗМОЖНОСТИ
СТАТИСТИЧЕСКОГО АНАЛИЗА
Есть ложь, есть наглая ложь и есть
статистика.
Бисмарк
Чтобы заниматься статистикой,
одной математики мало. Надо еше
и совесть иметь.
Неофициальный сайт студентов ме-
ханико-математического факуль-
тета МГУ им. MB. Ломоносова, раз-
дел «Высказывания преподавателей»
1.1. Статистические связи
и причинно-следственные связи
Врач — пациенту:
— Вам нужно не напрягаться, побольше отдыхать, в общем, лю
бить себя. ^
—Доктор, но ведь еще вчера Вы мне говорили, что мне нужно соо
людать диету и бегать по утрам?
— Ах, батенька. Вы просто не подозреваете, как быстро прогре<-
сирует медицинская паука.
Известный медицинский анекооп

Глава 1 Назначение и возможности статистического анализа
17
Интерпретация статистических закономерностей (как причинно-
следственных) неоднозначна. Возникающие при этом сложности,
примеры ошибок.
Каждый, кто хоть немного имел дело с медициной, знает,
как она «замусорена» неправильными результатами. Многие
эффективные методы лечения через некоторое время оказы-
ваются неэффективными, а ранее известные факторы риска
из таковых исключаются.
Одна (о других мы поговорим ниже) из причин этого —
в чрезмерной легкости в интерпретации медиками получен-
ных статистических закономерностей как причинно-следст-
венных.
При помощи статистической обработки данных мы мо-
жем найти только очень слабый — статистический — тип
связи между явлениями, по принципу, что когда одно, тогда
обычно и другое. Интерпретировать полученные статисти-
ческие связи как причинно-следственные нужно с предель-
ной осторожностью, так как каждая полученная статисти-
чески закономерность может быть объяснена целым рядом
разных способов.
1.1.1. Сцепленные факторы
и репрезентативные выборки
Доклад на биомедицинском конгрессе о влиянии сильных магнитных
полей на организм. Докладчик: «Было получено, что при увеличении
напряженности магнитного поля в 100раз подопытную крысу сплю-
щивает в лепешку». В зале овация. Вопрос из зала: «А как Вы увеличи-
вали напряженность магнитного поля ?» Докладчик: «Очень просто —
сдвигали полюса магнита».
Известный анекдот
Первая проблема при интерпретации статистических
связей как причинно-следственных состоит в том, что мы
можем найти статистическую связь с одним фактором, а ис-
тинной причиной является совсем другой фактор, с ним свя-
занный, но в исследовании не учтенный.

18
Часть I. Акали) вуронтн,,,
Рассмотрим несколько примером, перный и» которых
пародия на научное исследование из известного сборники
«Физики шутят», а псе другие — реальные примеры меди
цинских исследований или их аналоги.
Проверим гипотезу о том, что употребление в пищу све-
жих огурцов вредно для здоровья. Для этого возьмем группу
лиц, в течение длительного времени подвергавшуюся воз-
действию гипотетической вредности, то есть в течение 70 лет
и более употреблявших в пищу свежие огурцы. При обследо-
вании этой группы выясняем, что большая часть этих людей
уже умерла, а те, кто еще живы, плохо себя чувствуют. Из
этого делаем вывод, что употребление свежих огурцов вред-
но для здоровья.
Надеюсь, что читатель уже понял, где его обманывают.
В данном случае исследовалась заболеваемость и смерт-
ность в опытной группе, которая по условиям эксперимента
состояла из лиц старше 70 лет, а сравнивалась она не с за-
болеваемостью и смертностью в аналогичной возрастной
группе, а со среднепопуляционными данными. Сравнивать
опытную группу нужно не с ними, а с данными для конт-
рольной группы с таким же возрастным составом. К сожале-
нию, сравнение опытной группы с популяцией в целом без
выяснения сопоставимости возрастного состава — нередкая
вещь даже в современных исследованиях.
Однако для проведения корректного сравнения недо-
статочно формирования контрольной группы такого же
возрастного состава, как и опытная. Так, если проверять на
канцерогенность губную помаду, сравнивая заболеваемость
раком между опытной группой лиц, использующих губную
помаду, и контрольной группой лиц с таким же возрастным
распределением, но не использующих губную помаду, то мы
получим, что губная помада — сильный канцероген, вызы-
вающий рак шейки матки.
В данном случае можно догадаться, что причина полу-
ченных различий не в канцерогенности губной помады,
а втом, что в современном обществе мужчины значительно
реже пользуются губной помадой и не болеют раком шейки
матки из-за ее отсутствия. Если бы мы меньше знали о гуо-

Глава I Иозначеные и. возможности статистического анализа ^9
ной помаде, то полученное различие вполне могло бы быть
интерпретировано как действительно свидетельствующее
о канцерогенности.
Поэтому контрольная группа должна соответствовать
опытной не только по возрастному распределению, но и по
всем другим параметрам, включая половое, профессиональ-
ное, территориальное распределение и т.д.
Правильно сформированные сравниваемые группы, от-
личающиеся по исследуемому фактору и идентичные по всем
остальным, часто называют репрезентативной выборкой.
ВЫВОД: репрезентативных выборок не существует.
Действительно, совершенно невозможно сформировать
группы, которые по одному фактору различались бы, а по
всем другим — нет. Выделение по какому-то одному факто-
ру обязательно влечет и различия по другим факторам, с ним
сцепленным, причем именно они могут быть причиной раз-
личий.
Например, в 1970-х годах в СССР было проведено ис-
следование о связи артериальной гипертонии и курения.
В результате было получено, что у курящих женщин среднее
давление выше, чем у некурящих, тогда как у мужчин связь
обратная: у курящих мужчин давление в среднем ниже, чем у
некурящих. Причиной полученного различия была сильная
связь возраста с артериальным давлением (с возрастом сред-
нее артериальное давление повышается), а также разная воз-
растная структура курящих у мужчин и женщин. У женщин
курили в основном старшие возраста, те, кто начали курить
в войну, а у мужчин больше курила молодежь.
В 1980-х годах мне довелось обрабатывать данные о забо-
леваемости жителей города Шевченко кишечными инфекци-
ями. Сам город Шевченко — очень своеобразное место. Он
стоит на берегу Каспийского моря, окружен полупустыней и
застроен типовыми пятиэтажными домами. Из-за закрытого
статуса он имел сильную ведомственную медсанчасть, кото-
рая собирала данные не о заболеваемости в целом, а о каж-
дом случае заболевания по отдельности. При статистическом
анализе данных я дал команду рассчитывать коэффициенты
корреляции всего со всем (с тем, чтобы на дурацкие корреля-

20 _______I_L£_^wi«o^
ции просто не обращать внимания) и получил достоверную
положительную связь между заболеваемостью дизентерией
Флекснера и номером квартиры.
При попытке осмыслить данную связь удалось догадать-
ся, что номер квартиры «сцеплен» с этажом. После перехода
от номера квартиры к номеру этажа было получено, что на
первом и пятом этажах заболеваемость различалась раза в
три. Причина этого была вполне понятна: в городе не очень
хорошо работал водопровод, из-за слабого напора вода на
верхние этажи поступала не всегда, и жители верхних этажей
в условиях жаркого климата запасали питьевую воду впрок.
Еще один собственный пример. Один из аспирантов за-
нимался фармакоэпидемиологией, то есть исследовал забо-
леваемость для того, чтобы выявить потребность населения
в лекарственных средствах. При анализе заболеваемости са-
харным диабетом в России было выявлено, что разные реги-
оны имеют достоверно различающиеся уровни заболеваемо-
сти (точнее, превалентности, так как речь идет не о впервые
выявленных случаях заболеваемости, а о доле лиц, у кото-
рых имеется данное неизлечимое хроническое заболевание).
Различия между регионами составляли примерно 10 %.
Помимо данных о заболеваемости сахарным диабетом
имелся набор показателей, характеризующих уровень соци-
ально-экономического развития региона. При их сопоставле-
нии с заболеваемостью была получена сильная положительная
достоверная связь с количеством личных легковых автомашин
надушу населения. Действительно, выхлопные газы легковых
автомобилей — сильный загрязняющий фактор.
Если бы мы меньше знали о патогенезе сахарного диабета
и его факторах риска, то на этом анализ можно было бы за-
вершить. Однако данная связь современным представлениям
не соответствует, но может быть легко объяснена «наводкой»
от истинного фактора. Так, в современной России есть регио-
ны преимущественно городские и с заметной долей сельско-
го населения, более богатые и более бедные. В преимущест-
венно городских регионах выше средние доходы и больше
личных автомобилей, однако структура питании в болы«еИ
степени провоцирует заболевания сахарным диабетом.

Глава I. Назначение и возможности статистического анализа
21
Поэтому объяснить имеющиеся различия в соответствии
с принятыми воззрениями нетрудно. Труднее и интереснее
выяснить, действительно ли структура питания является
фактором, влияющим на вероятность развития диабета.
Полученные различия можно объяснить и другим обра-
зом. Во-первых, в современной России в сельских регионах
средняя продолжительность жизни меньше, чем в городах,
из-за чего при прочих равных условиях доля лиц с сахарным
диабетом в городах должна быть выше. Во-вторых, из-за
лучшей обеспеченности медицинским обслуживанием диаг-
ноз «сахарный диабет» в городе будет поставлен раньше, что
должно приводить к различиям в зарегистрированной доле
больных с сахарным диабетом. Численная прикидка показы-
вает, что этих двух факторов вполне достаточно, чтобы объ-
яснить имеющиеся 10% различия.
Другой пример. Пусть я исследую, какие факторы влия-
ют на выживаемость женщин с раком молочной железы. Для
более аккуратного анализа выживаемости женщин, умерших
от причин, не связанных с раком, будем отбрасывать, а вы-
живаемость, как обычно в онкологии, будем считать по доле
больных, которые после постановки диагноза в течение 5 лет
были живы.
Тогда наличие сахарного диабета утяжеляет состояние
больного и, следовательно, должно уменьшать выжива-
емость. Если же провести статистическое сравнение вы-
живаемости женщин с сахарным диабетом и без него, то у
женщин с сахарным диабетом выживаемость, скорее всего,
будет выше.
Причин этого, по крайней мере, две. Во-первых, средний
возраст больных сахарным диабетом больше, чем у лиц без
сахарного диабета. А в более пожилом возрасте рак молоч-
ной железы протекает медленнее и более благоприятно, чем
в молодом.
Во-вторых, так как речь идет о лицах, которым до момен-
та выявления рака молочной железы был поставлен диагноз
«сахарный диабет», то вероятность выявления сахарного
Диабета зависит также и от уровня медицинского обслужива-
ния в районе проживания, а также от активности сотрудни-

22
Часть I. Анализ вероятностей
чества больной с системой здравоохранения. Если у больной
вовремя выявлен сахарный диабет, то и вероятность раннего
обнаружения рака молочной железы у нее тоже выше, а при
выявленных вовремя случаях рака выживаемость выше.
1.1.2. Смена групп наблюдения
и возрастные изменения
Есть неопровержимые статистические доказательства того, что
на самом деле детей приносят аисты. Темпы падения численности
аистов и рождаемости в Европе полностью совпадают
Анекдот из Интернета
Особенно тяжело интерпретировать закономерности,
связанные с возрастом, длительностью заболевания и т. д.,
так как, во-первых, состав анализируемых групп может со
временем меняться, а во-вторых, можно спутать закономер-
ности, связанные с возрастом, с закономерностями, связан-
ными с изменениями условий.
Пусть я исследую выживаемость лиц, получивших про-
никающие ранения абдоминальной области. При анализе
причин смерти я выясняю, что в большинстве случаев пост-
радавшим делают операцию сразу после прибытия в боль-
ницу и что среди умерших велика доля лиц, которые умер-
ли на операционном столе. Поэтому мне совершенно ясна
причина высокой летальности — в чрезмерной поспешности
хирургов, которые сразу переходят к оперативному вмеша-
тельству без надлежащей подготовки. Для проверки своей
гипотезы я издаю приказ, согласно которому такие боль-
ные должны не сразу отправляться на операционный стол,
а предварительно в течение двух недель получать курс об-
щеукрепляющей терапии (витамины, психологическая раз-
грузка, беседы о здоровом образе жизни). Нет сомнений, что
после введения такой прогрессивной схемы летальность на
операционном столе значительно снизится. Действительно,
тем, кто пережил двухнедельный цикл предоперационной
подготовки, операция уже пс страшна.
Несмотря на кажущуюся абсурдность предлагаемых ме-
роприятий, нет сомнений в том, что внедрение во врачеб-

Глава I. Назначение и возможности статистического анализа
23
ную практику мероприятий, снижающих одну из форм ле-
тальности, но повышающих общую летальность, — обычная
практика. Дело в том, что не все виды летальности и других
неблагоприятных последствий от лечения могут быть оцене-
ны с одинаковой точностью. Врач наблюдает больного лишь
в течение некоторого времени после лечения, поэтому до-
статочно точно знает об осложнениях сразу после лечения и
значительно хуже — об осложнениях отдаленного периода.
Поэтому он скорее всего выберет тот метод лечения, кото-
рый уменьшает потери на этапе лечения и сразу после него,
пусть даже за счет значительного увеличения частоты от-
даленных последствий. На это его будет толкать не только
«искаженный» профессиональный опыт, но и современная
организация здравоохранения, при которой за послеопера-
ционные осложнения он юридически и экономически отве-
чает значительно больше, чем за отдаленные последствия.'
Связь доступности наблюдения объекта после воздейст-
вия с результатами этого воздействия неизбежно искажает
личный опыт. Так, все мы неоднократно слышали пропаган-
ду лично опробованных способов исцеления. Однако любое
основанное на личном опыте представление об эффективности
проведенного лечения всегда позитивно, так как в случае нега-
тивного опыта его некому бы было пропагандировать.
Следующий пример. Для изучения возрастных измене-
ний в организме я обследовал состояние здоровья у боль-
шого количества граждан России разного возраста. В час-
тности, был получен (гипотетический) график динамики
количества зубов в зависимости от возраста (динамика пер-
вых дней — в увеличенном виде на врезке), представленный
ниже (рис. 1.1).
На графике видна достаточно сложная динамика количе-
ства зубов. Прямая интерпретация подобного графика — не-
однократные смены зубов (по крайней мере 3 смены — у мла-
1 Еще один пример из той же группы. Хорошо известно, что и бли-
жайшие дни после выдачи зарплаты смертность возрастает. Однако из
JToro не следует, что если вообще перестать платить зарплату, то смерт-
ность снизится.

Рис. 1.1. Динамика среднего количества зубов
в зависимости от возраста
денцев, детей и пожилых лиц около 70), и единственное, что
удерживает меня от такой интерпретации — твердое знание,
что у людей зубы меняются только один раз (вторая смена
отдельных зубов — редчайший случай, который не может из-
менить полученную картину).
Наблюдаемая динамика в первые дни жизни связана
с тем, что при некоторых врожденных аномалиях рождают-
ся дети с зубами, однако они обычно нежизнеспособны, что
и вызывает падение среднего количества зубов в первые дни
жизни почти до нуля. Немонотонное изменение количества
зубов у детей — действительно следствие замены молочных
зубов на коренные, однако увеличение среднего количества
зубов у 70-летних — следствие изменения рассматриваемого
контингента. Из-за разной длительности жизни у мужчин
женщин происходит изменение полового состава на преиму
щественно женский, а у пожилых женщин того же возрас
среднее количество зубов может быть больше, чем У МУ*4!1 т
Следовательно, популяционная динамика показателей
возраста может отличаться от динамики у каждого отделы
гт_ ._-. -....„ПИКИ И1
го члена популяции. Для изучения возрастной динамики
пои
тор-
которого признака лучше проводить неоднократные "ii (
ные обследования одних и тех же лиц. Однако такой п° кС'_
не только требует организации сложного многолетнего
перимента, но и в ряде случаев просто невозможен

/ Назначение и возможности статистического анализа
25
Другая проблема состоит в том, что зависимости, кото-
рые мы считаем возрастными, могут быть связаны с измене-
ниями условий жизни.
Я несколько раз был на летнем отдыхе на море в Кали-
нинградской области. Среди большого количества отдыхаю-
щих там иностранцев очень легко было выделить группы по-
жилых немцев, которые в детстве жили в этих местах и после
войны были репатриированы. Скажу прямо, что такого коли-
чества сильно кривоногих людей я не видел нигде и никогда.
Причина этого в том, что детство этих людей пришлось на
времена воюющей Германии, когда с качеством еды было
очень плохо, и у многих из них в детстве был тяжелый рахит.
Поэтому если изучать кривоногость как медицинскую про-
блему на основании жителей Германии, то можно прийти к
выводу, что кривоногость — заболевание, которое в первой
половине жизни почти не встречается, но часто развивается
в возрасте около 70 лет.
Еще один реальный пример. Современная тактика борь-
бы с потерями от рака молочной железы основана на раннем
выявлении. Эффективность ее подтверждена, в том числе,
и статистикой, так как после перехода на эту тактику сред-
няя продолжительность жизни женщин с выявленным ра-
ком увеличивалась.
Но средняя продолжительность жизни женщин после
выявления рака увеличится и в том случае, если при раннем
выявлении рака никакого лечения не назначать и, вообще,
никому об этом не говорить. Поэтому при оценке расчетного
увеличения продолжительности жизни за счет раннего вы-
явления нужно вычитать длительность промежутка времени
°т раннего выявления до ожидаемого планового выявления,
из-за чего эффективность тактики раннего выявления будет
меньше.
Необходимость достаточно точной оценки результатив-
°сти мероприятий связана с тем, что в арсенале современ-
но здравоохранения есть много в принципе полезных, но
С|"' чатратиых методов диагностики и лечения Реали.ю-
'Нее их »а разумные депыи невозможно, поэтому вопрос
1 "^ о том, использовать или нет данный метод, а о том,

какой из имеющегося набора методов выбрать для использо-
вания за счет лучшего соотношения «эффект/стоимость».
1.1.3. Причина или следствие
.. и правда ли ветер дует оттого, что
деревья трясутся...
О. Генри «Вождь краснокожих»
Вторая причина сложности интерпретации статистиче-
ских закономерностей как причинно-следственных в том,
что очень легко перепутать причину и следствие.
Например, если исследовать заболеваемость и смертность
лиц, которые принимают выписанный им врачами нитро-
глицерин, то выявится, что заболеваемость и смертность от
болезней сердечно-сосудистой системы в этой группе значи-
тельно больше, чем в группе сравнения с таким же половым,
возрастным, профессиональным составом и т. д.
Однако в данном случае болезни не являются следствием
принятых лекарств. Наоборот, именно из-за того, что у жите-
лей было больное сердце, они и принимали нитроглицерин.
Очередной пример реально проведенной работы. В од-
ном из центров санэпиднадзора проводили работу по выяв-
лению факторов путей передачи для дизентерии Зонне при-
менительно к местным условиям.
Как известно, дизентерия Зонне — инфекционное забо-
левание с фекально-оральным механизмом передачи, для
взрослых наиболее активным считается алиментарный путь
передачи (для детей активен также и контактно-бытовой),
причем традиционно наиболее подозрительными продукта-
ми считаются молоко и молочнокислые продукты.
Работники местного центра решили выяснить, не инфи-
цируются ли жители также от овощей и фруктов, которые
покупают на местном рынке. Для этого они в течение года
покупали на рынке продукты и брали с них смывы. У них
действительно получилось, что в то время, когда заболевае-
r,Cfiv„ ШШС срелмсй- количество смывов, содержат»*
нозбудители дизентерии Зонне, также было выше среднего
""«" о они сделали вывод, что значительная доля пифии»'

Глава I. Назначение и возможности статистического анализа
27
рованных заразилась именно от овощей и фруктов, куплен-
ных на рынке.
К сожалению, полученные данные ничего не опровер-
гают и не подтверждают. Действительно, если значитель-
ная часть населения инфицировалась от этих продуктов, то
повышение инфицированности продуктов должно вызвать
повышение заболеваемости. С другой стороны, даже если
от этих продуктов вообще никто не заражается, то повы-
шение заболеваемости дизентерией Зонне все равно при-
водит к увеличению вывода ее возбудителей во внешнюю
среду.
Более информативно было бы сравнение сроков наступ-
ления подъема заболеваемости и подъема инфицированно-
сти продуктов, однако из-за сложности рассматриваемой
связи, на которую, в частности, влияет меняющийся уровень
коллективного иммунного статуса, однозначно трактовать
полученные результаты было бы сложно.
Приведу еще один пример. В одной из зарубежных (авст-
ралийских) статей по организации здравоохранения был
приведен результат о выживаемости больных разной степе-
ни тяжести в зависимости от того, нарушают ли они боль-
ничный режим. При этом было получено, что в группе тя-
желых больных нарушающие режим выживают лучше, чем
не нарушающие. Авторы статьи интерпретировали это так:
некоторые нарушения режима, хотя и вредны здоровью, но
повышают настроение больного и т.д.
Может быть, конечно, что это все и так. Однако мне ка-
жется, что иной тяжелый больной, который вот-вот умрет,
может, и хотел бы нарушить режим, да вот возможности для
этого у него уже нет. Используемое же деление на легких,
средних и тяжелых больных для рассматриваемой задачи
слишком грубое. Поэтому в данном случае, скорее всего, пе-
репутали причину и следствие.
Таким образом, выяснить, что является причиной, а что
следствием, на основании Только статистических наблюде-
ний нельзя. Более того, может быть ситуация, когда одно-
временно наблюдаемые явления вообще не находятся в не-
посредственной причинно-следственной связи.

Пример. На основании исследования внутригодов "
намики заболеваемости дизентерией Зонне в Могь-d^ Ди~
е- с «и^КВе я ВЫ-
ЯСНИЛ, что москвичи больше болеют в то время, когда ч
носят черные очки. Ще
Задание на дом. Выясните, являются ли черные очки п
чиной дизентерии или ее следствием.
Резюме
Одновременно встречаемые явления могут быть незави-
симыми следствиями одной причины. Статистические
исследования способны выявить лишь очень слабый тип
связи — статистические связи между явлениями, то есть за-
кономерности типа «когда одно, тогда обычно и другое». Для
выявления причинно-следственных связей нужны другие
методы, основанные на оценке результатов воздействия на
изучаемое явление.
1.2. Доказательная медицина
и дизайн исследования
В больнице проводится клиническое испытание методом двойно-
го слепого эксперимента. Больной приходит к врачу и спрашивает
«А почему мне поменяли лекарство?» Врач (очень осторожно).
— А почему Вы вообще думаете, что Вам поменяли лекарство.
— Ну как же, раньше таблетки, которые мне давали, вун
плавали, а теперь тонут. „
Анекдот с одного из медицинских сайт
Одна из стандартных причин, приводящих к ложным стат
ческим закономерностям, — ошибки в дизайне исслеД2__——-—"
Одной из реакций медицинского сообщества н ра-
нившиеся проблемы стало появление так называемо
зателыюй медицины. яиииН'
Противоречивость имеющихся в современных м HflTitf
ских научных публикациях результатов затрудняетПра1|Ы л„-
иа их основе решений. Поэтому были сформулиро^^цЫ
зумги о том, что п публикации должны быть внятно

Глава 1 Назначение и возможности статистического анализа
29
дизайн исследования, исходные материалы и методы их ста-
тистической обработки, и сформированы организационные
структуры, которые занимаются сопоставлением разных ре-
зультатов, опубликованных по одной теме, и созданием на их
основе критических обзоров и практических рекомендаций.
Такие структуры могут иметь различную форму организа-
ции: либо государственную (или с фиксированным штатом
чиновников с врачебным образованием, или экспертные со-
веты с финансированием через гранты на разработку опре-
деленной тематики; иногда они подчиняются Министерству
здравоохранения или его аналогу, иногда — напрямую пре-
зиденту), либо общественную (например, Кохрайновское
сообщество).
В рамках доказательной медицины совершенно спра-
ведливо обращается внимание на необходимость надлежа-
щего дизайна эксперимента. Действительно, невнимание
к этапу планирования приводит к неадекватным резуль-
татам.
Приведу только один собственный пример. Одна из ас-
пиранток делала работу по исследованию эффективности
лечения гипертонической болезни. В имеющемся у нее на-
боре больных использовалось два разных препарата. При
статистической обработке результатов было получено, что
второй препарат заметно и достоверно эффективнее первого:
при практически одинаковых средних величинах артериаль-
ного давления до начала лечения первый препарат снижал в
среднем давление меньше, чем второй. К счастью, аспирант-
ка оказалась грамотной и вместо того, чтобы написать вывод
о большей эффективности второго препарата, начала удив-
ляться, с чего бы два близких препарата имели столь заметно
Различающуюся эффективность. Поэтому было продолжено
Дальнейшее сравнение групп, и в результате было выявлено,
1|то больные, получавшие первый препарат, имели значи-
тельно больший средний возраст, чем получавшие второй
"Репарат. После этого уже я предпринял попытку начать
■Смущаться на ту тему, что если препараты давали по назна-
чению (например, один имел некоторые противопоказания
Или просто был дороже, чем другой, и не нее больные могли

30 Часть,А^В1У2тн01
'очей
его купить), то об этом нужно предупреждать, и анализ буДет
проведен с учетом этого фактора. Однако аспирантка объ
яснила, что препараты давались всем лечившимся, а смена
препарата была обусловлена тем, что весной давали одИн
летом он кончился, а осенью достали другой, и происходило
это все в 1998 году. После этого все стало ясно: летом в стра-
не произошел дефолт и в больницу попало много молодых
мужчин с первым приступом артериальной гипертензии.
Понятно, что лечение молодых первичных больных эффек-
тивнее, чем пожилых хроников.
При дальнейшем анализе были отдельно проведены срав-
нения результативности лечения в каждой возрастной груп-
пе и получено, что эффективность препаратов идентична.
В рамках доказательной медицины в качестве стандарта
предлагается так называемый двойной слепой эксперимент,
когда в одной больнице сравнивается эффективность двух пре-
паратов, выбор препарата производится случайным образом
и ни больной, ни врач не знает, кому какой препарат дают.
Такой дизайн исследования действительно позволяет
избежать многих «наводок» от третьих факторов, однако от
всех проблем избавиться таким образом невозможно.
Во-первых, при помощи такого рода исследования мож-
но лишь сравнивать эффективность двух методов лечения в
тех условиях, когда неизвестно, какой из методов лечения
лучше. Если же речь идет о получении оценки сравнитель-
ной эффективности методов лечения тогда, когда мы знаем,
что один из них лучше, но не знаем — насколько, то двойной
слепой эксперимент приводит к увеличению медицинских
потерь.
Во-вторых, достаточно часто приходится оценивать эф
фективность метода лечения, который назначается по по*
заниям и, следовательно, не может (не должен) пр°вер*
ся методом двойного слепого эксперимента. В этом слу
нужно использовать другие подходы. п0/Г
■ ак, я помогал доктору Катаеву провести анализ _
чепиых данных по изучению эффективности эндос^'
ско.о лечения хирургических больных с язвой *елУд*»
■юмощи фибрииопого клея. В случае кровоточащей язвь

Глава J. Назксмение и возможности статистического анализа
31
лудка обычно применяется операция по ушиванию язвы, но
среди больных встречаются такие, у которых вероятность не
пережить такую операцию достаточно велика. В этом случае
через эндоскоп язву заклеивали клеем на основе фибрина
человека. В агрессивном содержимом желудка фибриновая
пленка держалась около 6 часов, поэтому через 6 часов через
эндоскоп язву осматривали и, если она не зарубцевалась, за-
клеивание повторяли.
Если сравнить летальность больных, которым приме-
нялся этот метод лечения, с летальностью других больных
с язвой желудка в хирургическом отделении, то летальность
в первой группе будет больше. Однако это не является до-
казательством неэффективности этого метода лечения, так
как он применялся для самых тяжелых больных. Для оцен-
ки истинной эффективности метода лечения применялся
прогноз вероятности летального исхода у больного с язвой
желудка по данным анамнеза и эндоскопического обследо-
вания. В результате было получено, что у больных с исполь-
зованием фибрииового клея летальность была ниже, чем у
больных с такой же степенью тяжести, но не получавших
этого лечения.

32
Часть 1. Анализ вероятного,
Другое, более общее ограничение к использованию nnejl
лагаемого дизайна как панацеи от ошибок интерпретации
в том, что применимо оно лишь к сравнению эффективности
двух методов лечения, что является достаточно узкой зада-
чей. Чаще встречаются задачи оценки благоприятных или
неблагоприятных факторов, влияющих на эффективность
назначенного лечения, такие, например, как наличие опре-
деленных сопутствующих заболеваний.
Кроме того, исследование не обязательно проводится
й клинике, а может быть популяционным. В этом случае так-
же не удается избежать «наводок» со стороны третьих факто-
ров при помощи ослепления выбора испытуемых.
1.3. Статистическая обработка
как вид математической обработки
Популярна притча о семи слепцах, встретивших слона и спорящих
друг с другом, так как у них сложилось разное впечатление в зави-
симости от того, какую часть слона они ощупали. Но даже если бы
слепцы ощупали слона целиком, все равно полного впечатления о нем
они бы не составили. Единственное различие — они бы друг с другом
не спорили.
Статистический анализ данных—лишьчастный и очень специа-
льный способ математического анализа. Его сильная сторо-
на—в возможности анализа малоизученных явлений, слабая
сторона — в малом объеме получаемой информации.
В современной медицине статистические методы иссле-
дования используются достаточно широко, а термин «мате-
матическая обработка» часто считается синонимом «статис
тическая обработка».
Это неправильно. Статистическая обработка— лишь
частный и очень специальный вид математической обработ
ки. Его широкое использование в современной медицине
связано с тем, что сейчас количественные методы описан""
состояния исследуемых объектов используются уже очеш-
широко, но вот законы их функционирования на колнче^
венном уровне обычно не известны.

ачение и возможности статистического анализа
33
"Оторванность» статистически
х методом ооработкн or
и""м, и мелос™-!*.»!. Так как ирн ч"*1""

34
Част/, I /,....,,.. - , •■ :л?ц
зе используются универсальные подходы, то их можно ис^
пользовать для анализа и малоизученных закономерностей.
С другой стороны, то, что специфика изучаемого явления в
полной мере не используется, уменьшает объем и качество
полученной при анализе информации.
Рассмотрим, например, эпидемиологию инфекционных
болезней, имеющую хорошо развитую (по меркам боль-
шинства других медицинских дисциплин) теорию. При опи-
сании законов эпидемического процесса используются та-
кие термины, как активность механизма передачи, сезонные
и круглогодичные факторы, коллективный иммунный статус
и т. д. При анализе же фактических данных речь в основном
сводится к статистической обработке показателей заболева-
емости, то есть проявлений эпидемического процесса, а не
самого эпидемического процесса.
В тех случаях, когда изучаемое явление исследовано до-
статочно глубоко, статистические методы отходят на второй
план, а основным методом математического анализа служат
имитационные математические модели. Например, в фарма-
кокинетике для описания динамики концентрации вещества
в организме используются однокамерные и многокамерные
модели.
Пусть Л — концентрация некоторого вещества (напри-
мер, лекарства) в системном кровотоке, V— скорость повы-
шения концентрации из-за притока из внешнего источника,
а X — скорость падения концентрации вещества из-за его
вывода или нейтрализации. Тогда динамика концентрации
описывается дифференциальным уравнением
Обычно принимают, что скорость падения концентра
пин а не записи г от времени и концентрации Тогда на ге\
промежутках промени, па которых вещее гпо из внешнего
исючника не поступает, конценфапия падает жепонепци-
.ип.по Кои на промежутке времени oi /до i ♦ \/потесню не
nnummii, 10 Ad ♦ \г) ли) <• ' v

гцаве ^означение и возможности статистического анализа 35
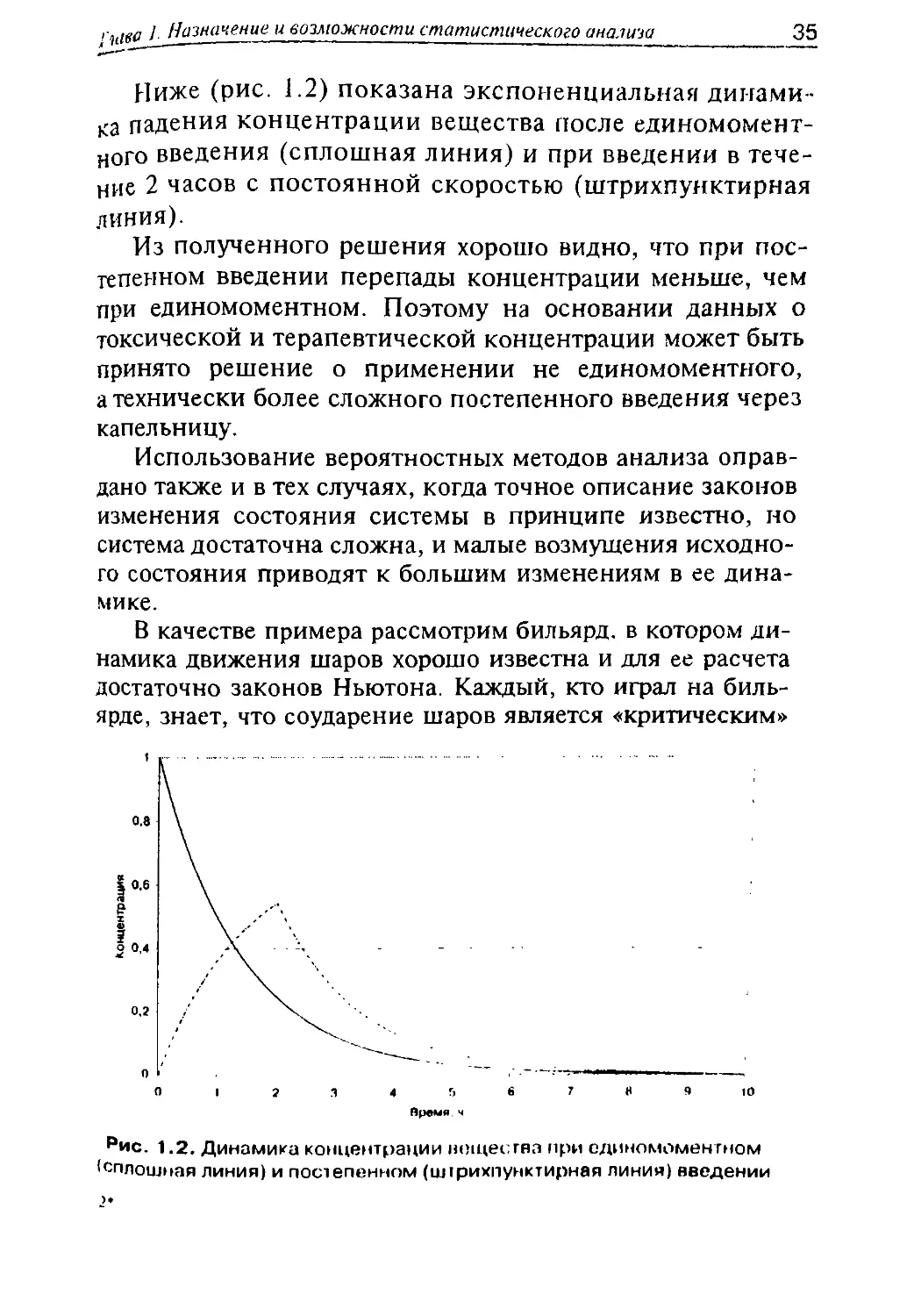
Ниже (рис. 1.2) показана экспоненциальная динами-
ка падения концентрации вещества после единомомент-
ного введения (сплошная линия) и при введении в тече-
ние 2 часов с постоянной скоростью (штрихпунктирная
линия).
Из полученного решения хорошо видно, что при пос-
тепенном введении перепады концентрации меньше, чем
при единомоментном. Поэтому на основании данных о
токсической и терапевтической концентрации может быть
принято решение о применении не единомоментного,
а технически более сложного постепенного введения через
капельницу.
Использование вероятностных методов анализа оправ-
дано также и в тех случаях, когда точное описание законов
изменения состояния системы в принципе известно, но
система достаточна сложна, и малые возмущения исходно-
го состояния приводят к большим изменениям в ее дина-
мике.
В качестве примера рассмотрим бильярд, в котором ди-
намика движения шаров хорошо известна и для ее расчета
достаточно законов Ньютона. Каждый, кто играл на биль-
ярде, знает, что соударение шаров является «критическим»
Првмя. ч
рис. 1.2. Динамика концентрации нощесгвп при единомоментном
(сплошная линия) и постепенном (илрихпунктирная линия) введении

36
Часть I. Анализ верантносшеи
событием, после которого ошибки в приданном игроком на-
правлении движения шара резко возрастают. Поэтому заби-
вать шар в лузу без соударений шаров запрещено правилами
(это слишком просто), а забить шар после нескольких соуда-
рений значительно сложнее, чем после одного.
Чем больше соударений с другими шарами претерпевает
шар, тем больше возрастают отклонения его траектории от
расчетной, вызванные ошибками в направлении исходного
удара и внешними воздействиями. Расчеты показывают, что
к 40 соударениям то, об какой борт ударится исходный шар,
зависит от столь малых возмущений, как гравитационное
притяжение единичного электрона, летающего по орбите
Плутона. Поэтому хотя изучаемая система и является детер-
минированной (не имеющей элементов случайности), но
при большом количестве соударений изучать ее приходится
как стохастическую (случайную).
Каждый, кто занимался интригами, хорошо знает, что
рассчитать результат достаточно сложной интриги совер-
шенно невозможно, и после нескольких взаимодействий
между ее участниками действие начинает разворачиваться
совсем не так, как ожидалось.
Таким образом, широкое использование статистических
методов анализа соответствует современному уровню меди-
цинской науки и свидетельствует об определенном (проме-
жуточном) уровне ее зрелости. Однако этот уровень достиг-
нут недавно и не без труда.
Еше в 50-х годах XX столетая ведущие специалисты в об-
ласти медицины публиковали в центральной советской прес-
се программные статьи о принципиальной неприменимости
статистических методов анализа к клинической практике,
!ак как каждый пациент абсолютно индивидуален Сам я не
однократно становился свидетелем жарких дискуссии о том
что такое .клиническое мышление» Однако если в 80-е голы
у шнпческос мышление противопоставляй! естестеппо-па
учпому. ю сейчас к шнпческос мышление обычно пошнно
impvioi как лоношяюшее ее гес ничто научное и вк поча
книге и (соя iiieiiiii|iiriciMie навыки, основанные \и\ обще
НИИ С II.IH1H НЮМ

рпава I Назначение и возможности статистического анализа 37
1.4. Случайные и контролируемые условия
Хочешь точно знать свое ближай-
шее будущее — ударь по лицу по-
лицейского.
Станислав Ежи Лец
Любое статистическое исследование апеллирует, пусть даже
и мысленно, к повторяемости эксперимента. При разном вир-
туальном повторении наблюдаемой ситуации степень вариа-
бельности наблюдаемых данных различна. Поэтому статисти-
ческие закономерности, достоверные при одном виртуальном
воспроизведении ситуации, могут быть недостоверными при
другом виртуальном воспроизведении.
Часто встречается утверждение, что статистический
анализ необходим только для выборочных исследований,
и необходимость в определении статистических погрешно-
стей связана только с тем, что исследование проводится не
сплошное, и нужно распространить полученные выбороч-
ные результаты на всю генеральную совокупность.
Я считаю, что это совершенно неверно. Пусть, например,
я провел сплошное исследование и выяснил, что средний
рост всех 11-летних мальчиков, живущих в Москве, состав-
ляет 145,237 см, тогда как средний рост 11-летних мальчиков
в Санкт-Петербурге — лишь 145,228 см. Ну и что? Могу ли я
на основании этого утверждать, что данные различия неслу-
чайны, что и при тех же условиях средний рост мальчиков
в Москве действительно был бы выше? Понятно, что и при
абсолютно тех же условиях средний рост мальчиков от года
к году повторялся бы не в точности.
Для того чтобы понять, действительно ли данное разли-
чие существенно, нужно рассмотреть виртуальную Москву и
виртуальный Санкт-Петербург, а полученные сплошные ре-
зультаты обследования Москвы и Санкт-Петербурга— как
выборочные исследования из виртуальной Москвы и вирту-
адьного Санкт-Петербурга.
Сложная методическая проблема состоит в том, что если
мы (пусть и мысленно) повторяем эксперимент, мы должны
к°икрстизироиать, что именно означает «в таких же условиях».

38
Часть 1. Анализ вероятностей
Предположим, что мы в токсикологическом экспери-
менте над крысами определяем дозу LDj0, то есть такую дозу,
при которой погибает половина крыс. Тогда если бы все
крысы были идентичны и находились в одинаковом состо-
янии и одинаковых условиях, то определить LD50 было бы в
принципе невозможно, так как при одних дозах все крысы
бы погибали, а при других — выживали. Поэтому различие
в реакции однозначно говорит о различиях в изучаемых объ-
ектах и/или условиях.
При повторении (пусть и мысленном) эксперимента ус-
ловия его проведения делят на контролируемые и неконтро-
лируемые. Контролируемые воспроизводят от эксперимента
к эксперименту, а неконтролируемые — нет, и именно их
наличие и приводит к случайности результата. Например,
при лечении больного его схема лечения контролируется,
а его индивидуальные особенности — нет.
В зависимости от схемы проведения эксперимента деле-
ние на контролируемые и неконтролируемые условия может
быть различным. Так, при эксперименте в нескольких кли-
никах условия содержания больного, профессиональные ка-
чества лечащих врачей и другие условия также будут разли-
чаться, из-за чего вариабельность результатов лечения будет
больше, чем для одного врача в одной больнице.
Если мы определяем статистическую достоверность по-
лученных различий, то мы всегда при этом апеллируем к
некоторой схеме воспроизведения эксперимента. При из-
менении схемы меняется и статистическая вариабельность
полученных результатов. Поэтому различия, статистически
достоверные для одной схемы мысленного воспроизведения
эксперимента, при другой схеме будут недостоверными.
Приведу пример одной реальной работы. В одном из
больших пионерских лагерей на берегу Черного моря был
отмечен высокий уровень заболеваемости ОРЗ, в том числе
и с большим удельным весом скарлатины. При эпидемиоло-
гическом исследовании, проведенном В.В. Жуковым, было
выяснено, что:
1 Заезд детей на начало смены происходит единовре-
менно.

Jza~±~~~~''~~-;-'--~~^
2. В лагере отдыхают дети из разных частей СССР и
следовательно, отличающиеся по носимым возбуди-
телям и иммунитету к ним.
3 У детей, живущих в больших благоустроенных корпу-
сах (но с большими палатами и общими столовыми),
за время смены наблюдался как рост заболеваемости
ОРЗ, так и увеличение доли тяжелых форм, тогда как
у детей, живущих в брезентовых палатках армейского
образца, роста заболеваемости не наблюдалось.
4. Микробиологическое исследование выделенных изо-
лятов стрептококка показало, что за время смены их
патогенность возрастает.
После этапа наблюдения и анализа, длившегося два года,
было решено проводить бицеллинопрофилактику в очагах
ОРЗ. В результате этого на третий год заболеваемость скар-
латиной снизилась в несколько раз.
При статистической обработке результатов (техника ко-
торой будет изложена ниже) было получено, что в предпо-
ложении об одинаковой вероятности заболеть скарлатиной
полученные различия высокодостоверны. Следовательно,
мы получили статистическое подтверждение того, что вве-
денные противоэпидемические мероприятия эффективны.
С другой стороны, мы знаем, что заболеваемость скар-
латиной изменяется из года в год. С учетом этого вероят-
ность того, что при полной неэффективности вводимых
мероприятий год проведения мероприятий попадет на год
минимальной заболеваемости из трех изученных, равна '/3.
Следовательно, при данной постановке задачи полученные
различия недостоверны, а для получения достоверных раз-
личий нужно продолжать эксперимент в течение длительно-
го срока, случайно выбирая, в какой год будет проводиться
Гншеллинопрофилактика в очаге, а в какой нет.

Глава 2
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
И ВВОД ДАННЫХ
Только по окончании исследова-
ния понимаешь, с чего его нужно
было начинать.
Избитая истина
2.1. Этапы статистического исследования
Этапы любого большого проекта:
1. Шумиха.
2. Неразбериха.
3. Поиски виноватых.
4. Наказание невиновных.
5. Награждение непричастных.
Из юмора программистов
Обычная последовательность статистической обработки дан-
ных и ее недостатки, или почему плохо вначале собрать все
данные, а потом их обработать
Обычно выделяют следующие этапы исследования
1) определение целей и задач исследования,
2) определение объектов исследования, сбор данных;
3) статистическая обработка результатов (включая ин-
терпретацию полученных результатов).

г ава 2. Планирование эксперимента и ввод данных 41_
На этапе статистической обработки данных обычно вы-
деляют следующие подэтапы:
1) кодировка и ввод данных в компьютер;
2) анализ каждого из параметров по отдельности (на-
пример: было обследовано столько больных, из них
мужчин столько, женщин столько, распределение по
возрастам.., летальность такая, что достоверно ниже,
чем приведенная в литературе для другой схемы лече-
ния (такая-то величина), и т. д.;
3) анализ взаимосвязи параметров (например, леталь-
ность у мужчин и женщин достоверно не отличается,
но существенно и достоверно зависит от возраста...).
Достаточно часто также требуется научиться прогнози-
ровать одни параметры на основании других.
Обычно этапы исследования реализуют именно в этом
порядке. Однако подобная схема может быть неудачной.
Действительно, только на завершающем этапе выясняет-
ся, были ли достигнуты цели и задачи исследования. Кроме
того, вначале определяется объем исследования, а лишь в са-
мом конце выясняется, был ли он достаточен для выявления
искомых закономерностей.
Таким образом, проводимая работа может привести
к неудаче, и исследователь узнает об этом лишь по ее завер-
шению. Другая крайность — проводится огромное дорого-
стоящее исследование, а после обработки его результатов
выясняется, что искомый результат можно было достичь на
группе в 40 больных, причем исследуемые значения можно
было определять не точно (сложно и дорого), а приблизи-
тельно, то есть быстро и просто.
Плохо и то, что если в процессе работы выясняются ин-
тересные закономерности, то их нельзя развить, перейдя
к Развернутому описанию интересных параметров.
Поэтому более разумной представляется схема исследова-
НИя, при которой сбор данных и их статистическая обработка
Роизводятся параллельно, и по мере увеличения объема дан-
ых статистическая обработка повторяется несколько раз.
Одна из возможных схем проведения эксперимента —
■Деление этапа пилотажного исследования, на котором на

42
Часть 1. Анализ вероятностей
небольшом объеме данных, собранных по упрощенной схеме
(например, не строгие количественные значения, а быстро
определяемые полукачественные), проводят статистическую
обработку, единственная цель которой — определить опти-
мальные набор параметров и объем выборки для дальнейше-
го исследования.
2.2. Кодирование и ввод данных
Цифры не управляют миром, но
показывают, как мир управляется.
Гёте
Ввод данных в пакетах статистических программ
2.2.1. Общие замечания
Это чрезвычайно важный этап исследования, от качества
проведения которого в значительной степени зависит ус-
пешность всей работы целиком, и допущенные на этом эта-
пе недочеты устранить в дальнейшем сложно.

Г ава 2. Планирование эксперимента и ввод данных 43
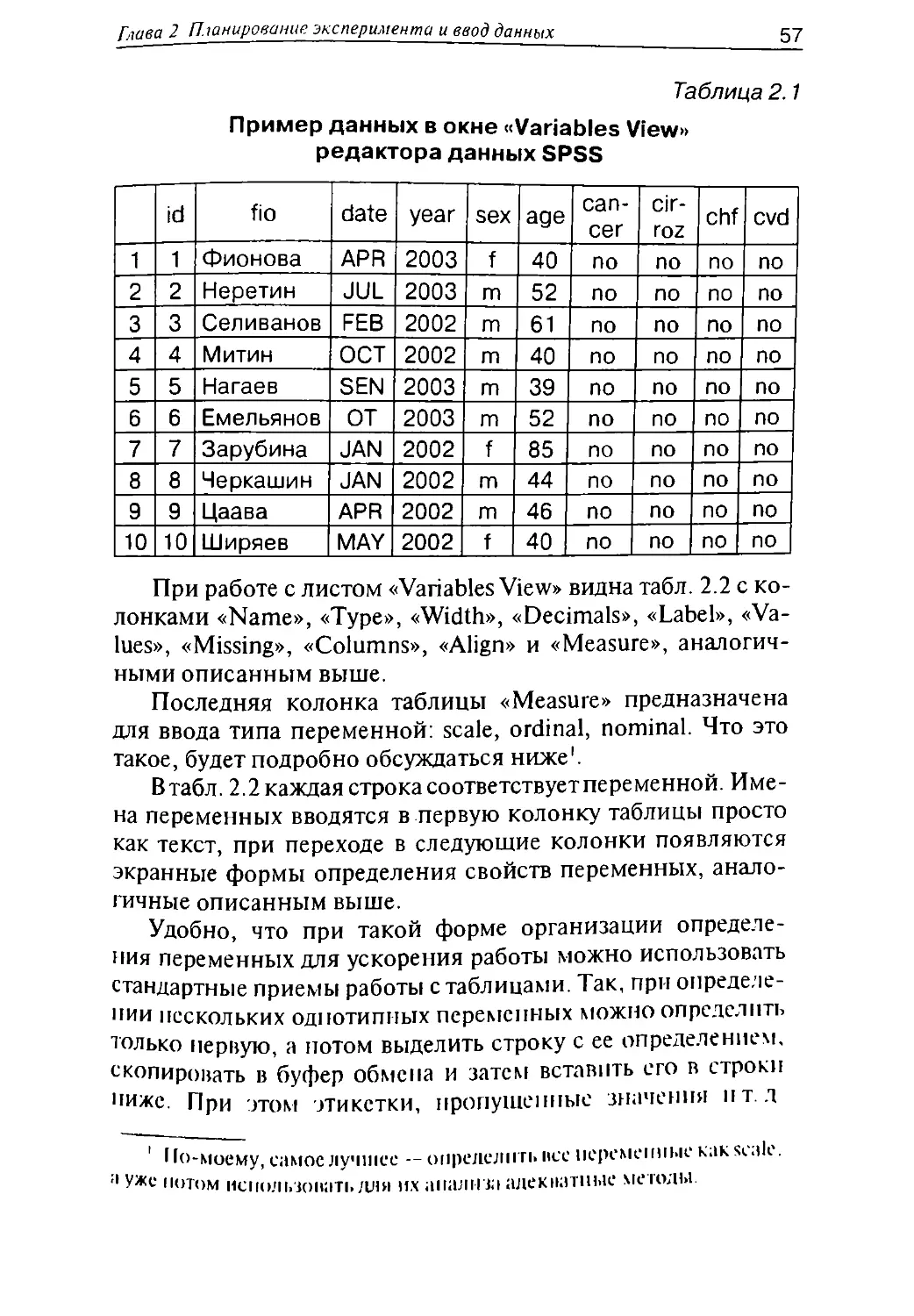
Для ввода данных они должны быть оформлены в виде
таблицы, причем желательно, чтобы таблица была одна. Тех-
ника работы со статистическими программами такова, что в
них значительно проще выделить часть данных и временно
работать с ними, чем сопоставлять данные, полученные из
разных таблиц.
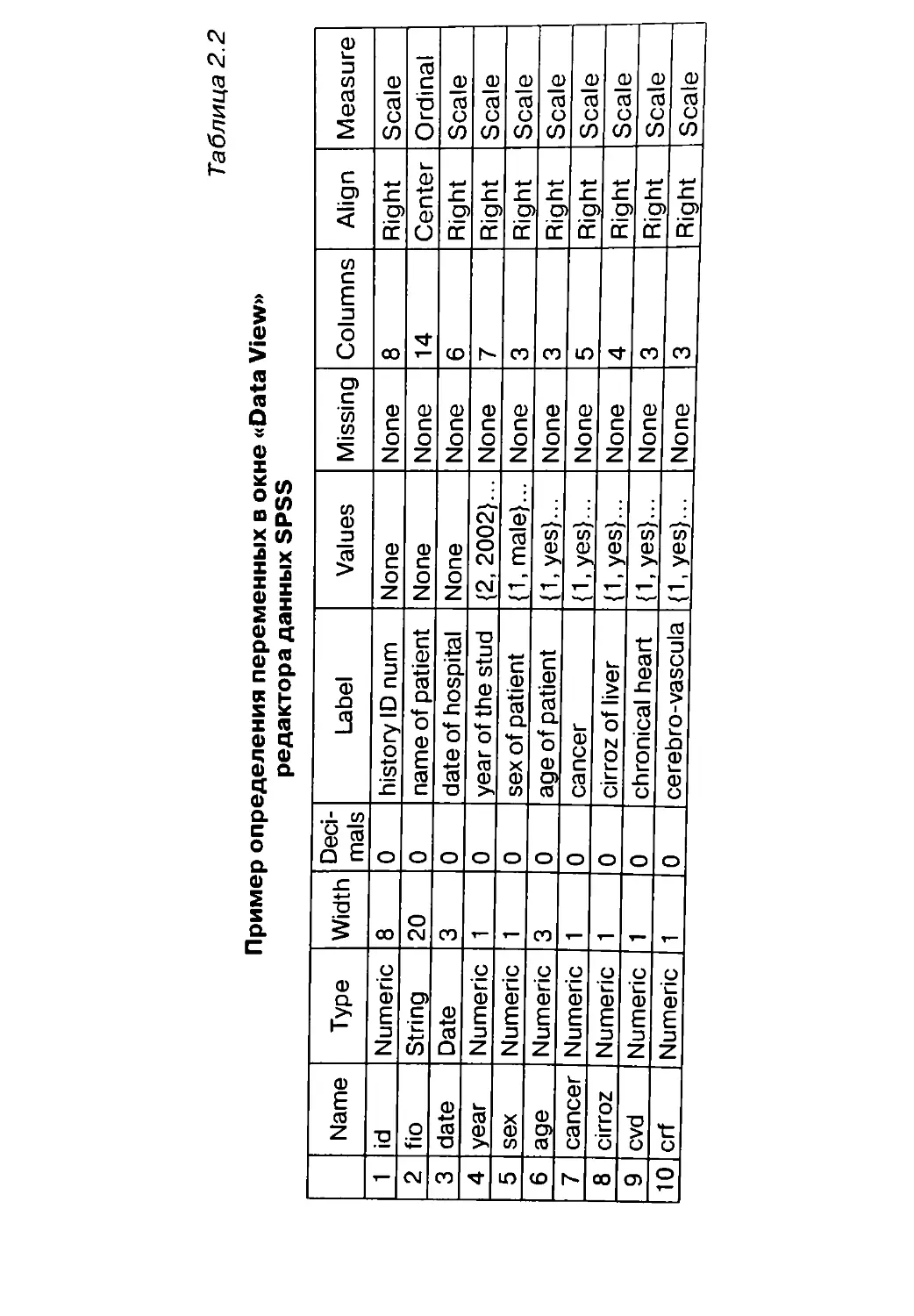
Колонки таблицы называются переменными (variables),
а строки — случаями (cases).
При этом крайне желательно придерживаться следую-
щих правил.
1. Первая переменная должна быть номером по порядку.
Дело в том, что при анализе данных (особенно при поиске
ошибок) удобно сортировать таблицу по значениям пере-
менных. Тогда для того, чтобы восстановить привычный ис-
ходный порядок, будет достаточно отсортировать исходные
данные по значению этой переменной.
2. Вся информация об исследуемых объектах должна
быть закодирована в виде значений переменных. Например,
если имеются две группы больных, то должна быть введена
переменная «номер группы», в которой единица будет соот-
ветствовать первой группе, а двойка — второй.
Многие врачи, привыкшие работать с электронной таб-
лицей Excel, стараются разнести больных из разных групп
по разным частям таблицы, выделить их цветом, отделить их
Друг от друга пустыми строками и так далее. Здесь все это не
нужно: порядок ввода случаев при статобработке не учитыва-
ется, пустые строки также не учитываются (хотя и мешают).
3. Для числовых переменных нужно вводить именно само
число, а не его округленное значение или групповую при-
надлежность. Например, следует вводить измеренную тем-
ПератУРУ тела, а не вариант «нормальная», «субфебрильная»
Или «Фебрильная». Ввод огрубленного значения вызывает
Потерю части информации, а новую переменную, в которой
УДет групповая принадлежность, будет легко вычислить уже
РеДствами самого статпакета.
4 Для переменных с числовым значением нужно вводить
енно число. Если при подсчете количества лейкоцитов в
Ле 3Рения в данных написано «от 3 до 5», то нужно волевым

44
Часть 1 Анализ вероятностей
образом решить, какое именно число соответствует этой за-
писи (например, 4). Если имеется запись «все поле зрения»,
то волевым образом нужно решить, какое число будет вво-
диться в этом случае (например, 100).
5. Обычной является такая ситуация, когда не все данные
определены у всех испытуемых. В этом случае можно просто
пропустить соответствующее значение, оставив пустое место.
Однако иногда данные могут отсутствовать по разным
причинами, и при анализе нужно учитывать причину отсутст-
вия значения. Например, при вводе значения переменной
«Менархе» данные могут отсутствовать, в частности, по сле-
дующим причинам:
1. Пациент — мужчина, ему не положено1.
2. Пациент — девочка, у которой менструации еще не
начались.
3. Известно, что менструации были, но возраст их на-
чала неизвестен. Например, пациент — пожилая жен-
щина, которая помнит, что «это» было, но забыла,
когда, а других источников информации нет.
4. Неизвестен ни факт начала менструаций, ни их воз-
раст. Например, в условиях примера пункта 3: дама не
помнит, когда это было и было ли вообще. Другой ва-
риант: пациент — девочка 13 лет, находящаяся после
аварии в коматозном состоянии, другие родственни-
ки погибли, из-за полученных при аварии поврежде-
ний матку пришлось ампутировать.
5. Менструаций не было по причине хронической бере-
менности.
В этом случае причины отсутствия информации можно
кодировать разными невозможными значениями, напри-
мер-1, ..., -5, а при определении переменной задать, что
отрицательные значения следует считать пропущенными.
6. Если были проведены повторные обследования, то
для их результатов нужно завести отдельные переменные.
Например, «СОЭ1»— для скорости оседания эритроцитов
' Необходимое нсвете соиремеиныч iionaiiiiii уточнение пациент —
мужчина или был им ранее

момент госпитализации, «СОЭ2» — для повторного ана-
лиза через неделю после госпитализации, «СОЭЗ» — для ре-
зультата перед выпиской.
7. В каждой переменной для каждого пациента должно
быть только одно значение (или ничего, если оно не опре-
делено).
Это самое сложное для практического выполнения тре-
бование, так как врачи очень любят определять колонки,
в которых вводится не одно, а несколько значений через за-
пятую.
Так если у больного не один, а несколько диагнозов сра-
зу, то нужно задать несколько переменных, например: «Диаг-
ноз!», «Диагноз2» и «ДиагнозЗ». Часто лучше для каждого
актуального диагноза выделить отдельную переменную, в ко-
торую будет вводится информация о том, есть он или нет.
Если при постановке диагноза указывается его выражен-
ность, то лучше вводить не наличие, а степень выраженности.
Например, не наличие ожирения, а его стадию.
При определении набора переменных общее требова-
ние — каждая переменная должна соответствовать одной
смысловой единице описания, и для каждого случая все пе-
ременные должны иметь одно и только одно значение. По-
этому набор переменных, используемых для кодирования
Данных, может не полностью совпадать с используемым для
ручного описания больных. Например, для больных с пере-
ломами вместо одной переменной «Диагноз» можно исполь-
зовать следующий набор:
1) локализация (например, левая нога);
2) форма (например, осколочный);
3) есть ли смещение;
4) открытый или закрытый.
Другой пример. Если вводится переменная «цвет волос»,
значение «лысый» не является значением этой перемен-
., ' так как могут быть лысые брюнеты и лысые блондины.
5Начеыы,1
Иол «лысый» соответствует переменной «количество
иКо 'Я ■Чостат°чч« полного описания естественного цвета
ичсства волос на голове придется использовать четыре

46
Часть 1. Анализ вероятностей
переменные: «исходный цвет волос», «форма облысения»,
«степень выраженности облысения» и «выраженность
седины».
8. Все переменные, по которым будет проводится стати-
стическая обработка, желательно определять как числовые,
и вводить не текст, а число, например не вариант текстового
диагноза, а номер диагноза. При этом даты можно оставлять
в формате дат, так как с ними тоже можно производить вы-
числения. Обычно единственная актуальная текстовая пере-
менная — фамилия больного.
9. Нельзя слишком дробить возможные значения пере-
менной, пытаясь максимально точно описать особенности
пациентов, так как в этом случае все встречаемые значения
будут редкими и проводить их статистический анализ будет
невозможно.
Если какое-то возможное значение встречается в еди-
ничных случаях, то детализацию значений переменной нуж-
но обобщить, объединив этот вариант значения с близкими
к нему.
Также не имеет смысл выделять отдельные переменные
под значения, которые будут редко встречаться. Например,
возможно, имеет смысл при описании сопутствующих забо-
леваний выделить переменную «Нарушения эндокринной
системы», а не пытаться точно описать каждую форму.
10. Степень детализации набора переменных и из значе-
ний зависит от содержания исследования. Например, если
исследуются больные с пневмонией, то, возможно, имеет
смысл наличия любого онкологического заболевания с не-
легочной локализацией объединить в одно сопутствующее
заболевание. Если же речь идет о больных с рецидивами
рака после проведенного лечения рака молочной железы, то
в этом случае описание локализации и формы рака должно
быть полным.
11. Желательно, чтобы (в тех случаях, когда это возмож-
но) при нумерации нарастание некоторого содержательно-
го значении соответствовало нарастанию кодирующего его
номера Например, при описании тяжести боныюго лучше
пользоваться следующей нумерацией: I — легкая; 2 — сред

няя; 3 - тяжелая; чем нумерацией: ] - легкая; 2 - тяжелая;
3 - средняя.
2.2.2. Подготовка к работе с пакетом
статистических программ и работа
с файлами сданными
Человеку свойственно ошибаться,
но окончательно все запутать мо-
жет только компьютер.
Законы Паркинсона применительно
к вычислительной технике
В данной книге будут рассматриваться два пакета статисти-
ческих программ: SPSS как основной и Statistica как альтер-
нативный.
Разные версии SPSS очень близки друг к другу, поэто-
му в данной книге моменты, зависящие от версии, будут
явно обсуждаться. Различий между версиями Statistica зна-
чительно больше, и в этой книге описывается работа в вер-
сии 6.0.
На настоящий момент эти две программы — наиболее
часто использующиеся в биомедицинских исследованиях.
Их отличает как высокий уровень реализации статистичес-
ких методов расчета, так и достаточное удобство в практи-
ческом использовании. Так, они работают в среде Windows,
понимают наиболее популярные форматы данных и резуль-
таты своих расчетов оформляют в виде стандартных доку-
ментов, откуда таблицы и графики могут быть скопированы
в Другие программы при помощи обычной процедуры рабо-
ты с буфером обмена.
У этих программ есть два стандартных окна — окно ре-
актора данных и окно протокола результатов статистнче-
иих расчетов (открывается после выполнения статистиче-
ских расчетов или чтения файла с сохраненным протоколом,
чг -,a,'St'ca ,,тих°|«>" может быть несколько). Переключение
,е*"У ними окнами осуществляется стандартными приема-
Ми Windows.
ф,)Рма opiainuaiiiiH окоп в иич программах несколько
' ^чается. И SPSS огкрынаюгея исшисичме окна, между

48
Часть 1. Анализ вероятностей
которыми можно переключаться как между независимыми
программами. В Statistica открывается одно большое окно,
в котором располагается одно или несколько подчиненных
окон.
Обе программы можно рассматривать как «открытые
программные продукты» в том смысле, что помимо мето-
дов статистического анализа, реализованных в виде команд
и встроенных в устанавливаемые версии, можно выполнять
и программы, написанные на внутреннем языке програм-
мирования. В SPSS это специфичный для этого пакета про-
грамм язык, для Statistica — версия языка «Visual Basic for
Application». Так как умение программировать в ближайшие
годы вряд ли будет широко распространенным явлением в
среде медиков, даже активно занимающихся научной рабо-
той, то вариант использования пакетов программ с самосто-
ятельным дописыванием программных модулей в этой книге
далее обсуждаться не будет.
Если для анализа данных Вам желателен метод, не
реализованный в имеющихся версиях статистических
программ, то можно не писать нужную программу само-
стоятельно, а поискать ее в интернете или в «бонусных»
дополнениях на дисках с дистрибутивами статистических
программ.
В отличие от этих коммерческих продуктов, имеется бес-
платный пакет Epilnfo, дистрибутив которого можно полу-
чить по адресу www.cdc.gov. В целом он менее удобен, хотя
некоторые функции в нем реализованы удачно. В частности,
в нем имеются специальные модули для ввода и анализа эпи-
демиологической информации в полевых условиях, ориен-
тированные на расследование вспышек инфекционной за-
болеваемости.
Имеется также достаточно много разнообразных неболь-
ших программ, работающих в DOS-моде, в том числе прила-
гаемых на лискетах к книгам по прикладной статистике При
часто высоком уровне реализации статистических методов
очень неудобно то, что результаты расчетов они показывают
на жранс или, и лучшем случае, сохраняют текстовом фай-
ле, откуда данные приходится переписывать

Глава 2. Планирование эксперимента и ввод данных
49
Имеющиеся в настоящий момент версии SPSS работают
с одним и тем же форматом файлов с данными и практически
идентичны по возможностям. Поэтому при выборе версии
следует ориентироваться только на то, работает ли данная
версия с имеющейся версией Windows. Так, под Windows XP
работают версии начиная с версии 10. В отличие от SPSS,
версии Statistica имеют заметные различия и сохраняют дан-
ные в файлах разных форматов.
В обеих программах используются отдельные файлы для
данных и файлы для результатов статистических расчетов.
В SPSS файлы с данными имеют расширение .sav, а файлы
с результатами расчетов — расширение .spo. Альтернатив-
ным форматом данных для SPSS являются файлы с расши-
рением .рог. В отличие от исходных файлов с расширением
sav, файлы с расширением .рог понимаются и программой
Statistica, поэтому при помощи этого формата можно легко
осуществлять обмен данными между SPSS и Statistica.
В программе Statistica данные хранятся в файлах с расши-
рением .sta, файлы с графикой имеют расширение .stg, а ре-
зультаты расчетов — в файлах с расширением .stw.
При выборе версий категорически не рекомендуется уста-
навливать локализованные (переведенные на русский язык)
варианты. Во-первых, локализованные версии часто работают
менее устойчиво, чем исходные. Во-вторых, качество перевода
обычно ужасно. Например, в одной из версий опция «S.E. mean»
(standard error of mean, или стандартная ошибка среднего ариф-
метического) была переведена как «мера Ю.В.». В некоторых
случаях перевод не просто бессмысленный, а провоцирующий
неправильное понимание. Так, команда «select cases» (выбрать
случаи) переведена как «переключить регистры».
При этом переведенные и ненерепеденные на русский
язык версии программ реально работают с русским языком
примерно одинаково плохо, так как перевод ограничивает-
ся заменой команд в меню с английских на русские, а рабо-
тают программы с русскими текстами при помощи средств
Windows, таких как- встроенные шрифты.
Для того чтобы редактор данных и SPSS поддерживал
Работу с русскими шрифтами, нужно выполнить команду

50
Часть I. Анализ вероятностей
«View/Fonts»1, выбрать в качестве используемого шрифта
русифицированный (например, Axial) и выбрать кодировку
«кириллическая». Там же можно поменять и размеры отоб-
ражаемых шрифтов и т. п. К сожалению, при настройке
отображения файла с результатами расчетов этого сделать
не удается. При изменении настроек можно поменять один
шрифт на другой, но нельзя выбрать другую кодировку. По-
этому тексты на русском языке будут отображаться ^руси-
фицированным шрифтом, то есть прочесть их нельзя.
Однако в большинстве случаев эту недоработку разработ-
чиков программы удается легко обойти. Если Вы выделяете
таблицу с результатами расчетов и копируете ее в буфер об-
мена, то при вставке таблицы в документы программ Word
и Excel шрифт обычно2 меняется на русский. Если такая ав-
томатическая замена не происходит, то имеет смысл вооб-
ще отказаться от ввода имен переменных и этикеток на рус-
ском языке. Автоматическая русификация надписей также
не всегда происходит в графиках, и их приходится править.
Впрочем, в данном случае это обычно излишне, так как в
любом случае качество получаемых в SPSS графиков недо-
статочно. Если они используются как рабочие материалы, то
эти недоработки несущественны, а при подготовке графи-
ков к публикации или презентации их все равно приходится
обычно перестраивать в Excel.
В Statistica работа со шрифтами аналогично работе в Excel.
Шрифт определяется не для всей таблицы с данными или
результатами расчетов, а для выделенного набора ячеек при
помощи команды «Format/Cells».
1 Здесь и далее запись команд через косую черту означает необхо-
димость их последовательного выполнения. В данном случае нужно
щелкнуть левой кнопкой мыши на команде «View» и в развернувшем-
ся меню щелкнуть на команде «Fonts».
2 Опыт показал, что будет или нет происходить такая автомати-
ческая замена, зависит от того, какая версия Windows установлена на
компьютере. Если первоначально была установлена русифицирован-
ная версия, то такая замена происходит, если стоит англоязычная вер-
сия или русифицированная версия установлена поверх англоязычной,
то нет.

Глава 2 Планирование эксперимента и ввод данных
51
Структура данных в таблице SPSS очень близка к таковой
втаблицах реляционных баз данных (например, dBase, Access
и т. д.), то есть каждая переменная должна иметь свое имя и
тип. Основные типы — текстовый, числовой и даты, причем
смешение данных в переменной одного типа не допускается.
При этом в таблице SPSS при определении свойств перемен-
ной имеются некоторые добавления. Так, у переменной кро-
ме имени может быть этикетка, то есть произвольная текс-
товая надпись, расшифровывающая ее смысл. Аналогичные
этикетки могут быть и у значений. Кроме этого, может быть
определен набор дополнительных отсутствующих значений
(см. раздел 2.2.1). Поэтому если данные уже введены в ка-
кую-то распространенную базу данных, то можно открыть
этот файл в SPSS, а затем, если нужно, доопределить этикет-
ки и пропущенные значения и командой «File/Save as» со-
хранить в виде таблицы с данными.
Несколько тяжелее экспортировать данные, если они
уже введены в таблице Excel. Перед экспортом они долж-
ны быть приведены в вид, максимально подобный данным
в базе данных, то есть скомпонованы в виде одной таблицы
на одном листе. Каждая колонка должна строго соответст-
вовать одной переменной. При этом первую строку нужно
отвести под ввод имен переменных (объединения ячеек и
подзаголовков недопустимы), а остальные — под данные.
Пустые строки должны быть удалены. Также недопустимо
использование каких-либо комментариев или посторон-
, них записей, так как если в столбце хотя бы в одной ячейке
стоит не число, а текст, то вся колонка будет воспринята
как текстовая. Так как версии SPSS понимают только до-
статочно старые форматы Excel, то желательно сохранить
файл в формате Excel 4. Для этого, работая с файлом в уста-
. новленной версии Excel, нужно выполнить команду «File/
Save as», поменять имя файла и, если нужно, директорию,
а потом в строке выбора типа файла щелкнуть на кнопке с
треугольником и из появившегося списка выбрать вариант
файла Excel 4 (с расширением xls) В этом типе файла мо-
жет быть сохранен только один текущий лист, поэтому к
появляющемуся предупреждению о возможной потере

52
Часть I. Анализ вероятностей
данных нужно относиться спокойно. Далее нужно закрыть
Excel, запустить SPSS, выполнить команду «File/Open»,
поменять, если нужно, директорию, в списке типов фай-
лов щелкнуть на кнопке с треугольником и из появивше-
гося списка выбрать вариант файла Excel с расширением
.xls. После этого выбрать нужный файл щелчком по его
имени в окне выбора файла, щелкнуть на кнопке «Open»
и на появившейся диалоговой форме с вопросом, откуда
брать данные, поставить щелчком «галочку» на квадратике
с подписью «Read variable names» и нажать кнопку «ОК».
В открывшемся окне будет представлен отчет об успеш-
ности конвертации данных.
Если введенное в Excel название колонки соответствует
представлениям SPSS о допустимых именах переменных,
то оно будет сохранено в виде имени, если нет — то в виде
этикетки. Более подробное описание того, какие имена
SPSS считает допустимыми, приведено в следующем раз-
деле.
При такой конвертации некоторые переменные могут
определиться неправильно. В этом случае можно переопре-
делить неправильно распознанные свойства переменных,
например указать, что данная переменная не текстовая,
а числовая.
В программе Statistica требования к именам аналогичны,
но поддерживается только два основных типа переменных —
текстовый и числовой, причем у числового есть три подти-
па: Double — для переменных, которые могут иметь нецелые
значения, Integer— для целых чисел и Byte — для коротких
целых. Даты считаются не форматом хранения чисел, а фор-
матом их показа, при этом даты считаются как число дней,
прошедших с начала летоисчисления. Так, число 4,75 при
показе в виде даты становится 6 часами вечера 3 января ну-
левого года.
Помимо типови этикеток, которые в Statistica, коки в SPSS,
определятся на уровне переменных, можно аналогично Excel
задать параметры отображения содержимого отдельных па-
борон ячеек. Для этого нужно выделить мышью требуемый
набор ячеек и выполнить команду «Formal/Cells».

Глава 2 Планирование эксперимента и ввод данных
53
2.2.3. Ввод данных в статпакете
В этом разделе рассмотрим случай, когда данные не экспор-
тируются из заранее подготовленного файла, а вводятся не-
посредственно.
В SPSS перед вводом данных нужно определить пере-
менные.
В верхней части окна, открытого редактором данных SPSS,
ниже строки с именем открытого файла, расположены строка
с текстовыми командами и панель с кнопками выполнения
некоторых команд и переключения режимов (рис. 2.1).
В младших версиях для определения новой переменной
нужно, находясь в окне редактора данных (а не в окне работы
с протоколом результата), поставить курсор в самую левую
пустую колонку и выполнить команду «Data/Define variable».
После этого появится экранная форма с полем для ввода
имени переменной и четырьмя дополнительными кнопка-
ми: «Type», «Columns Format», «Labels» и «Missing Values».
Стоящее по умолчанию имя новой переменной «VarOOOl»
лучше поменять на что-нибудь более осмысленное. Име-
на разных переменных не должны совпадать, они должны
быть не более чем из 10 символов и состоять из букв, цифр
и некоторых специальных знаков. Например, знак подчер-
кивания использовать можно, а пробел и точку — нет. Кро-
ме того, первым символом обязательно должна быть бук-
ва, а большие и маленькие буквы считаются одинаковыми.
SPSS при работе с именами переменных имеет одну ошибку,
которая характерна для программных продуктов, разраба-
тываемых группой разработчиков, — требования к именам
переменных неодинаковы у разных программных модулей,
входящих в состав пакета. Например, в результате экспорта
Данных можно создать переменную с именем, содержащим
) ПНЕВМО-1 .SAV - SPSS Data Editor
Fie Ed» View date Transform Analyze Graphs UtUet Window Help
gjaiaj5| _2J_J fcjaj м| £l£l fl-i-lnif^^l
Рис. 2.1. Строка с текстовыми командами и панель
с кнопками редактора данных SPSS

54
Часть 1. Анализ вероятностей
точку, однако некоторые методы анализа такую переменную
«не видят». Поэтому требования к простоте имен желательно
строго выполнять.
После ввода.имени переменной нужно нажать на кнопку
«Туре» и определить тип и формат переменной. Актуальные
типы: Numeric (числовой), Date (даты) и String (тексты), на
остальные можно не обращать внимания.
При выборе типа Numeric нужно также задать его отоб-
ражаемый формат, для чего определить числовые парамет-
ры «Decimal places» (количество числовых знаков после за-
пятой) и «Width» (общее количество отображаемых знаков).
Например, для определения возраста пациента определяем
тип как Numeric 3.0 (то есть количество знаков после запя-
той равно нулю, так как число традиционно вводится как
целое, а общее количество знаков — 3, так как могут быть
пациенты старше 100 лет). Если вводится вес в килограммах
с точностью до 100 граммов, то формат отображения будет
Numeric 5.1, так как нужен один знак после запятой, три зна-
ка на отображение веса тех, кто тяжелее 100 кг, и еще один
знак под запятую. Если вводятся показатели близорукости
или дальнозоркости (например, для левого глаза) в диопт-
риях, то формат будет Numeric 5.1, так как при измерении с
точностью до '/2 диоптрии нужен один знак после запятой,
два знака перед запятой нужно для задания значения в 10 ди-
оптрий и больше (100 и больше быть не может), а еще один
числовой знак нужен для хранения знака, так как эта вели-
чина может быть и отрицательной.
При этом задается именно формат отображения, а не
хранения значения. Так, если вы определите вес как целое
число, то при вводе нецелого значения в таблице редактора
данных будет показываться округленное до целого значение,
но хранится и обрабатываться будет именно исходное точ-
ное значение. Если переопределить переменную, добавив ей
отображаемых знаков после запятой, то исходное введенное
нецелое значение покажется вновь. Потеря точности введен-
ных данных из-за округления будет происходить лишь в том
случае, если данные сохраняются в файле в «неродном» фор-
мате (например, Excel) или копируются через буфер обмена.

Глава 2. Планирование эксперимента и ввод данных
55
По умолчанию числовые переменные определяются как
Numeric 8.2, что в большинстве случаев достаточно, и можно
не определять формат переменной более точно.
При выборе типа Date нужно выбрать вариант формата
из предлагаемого списка (краткий формат или развернутый,
американский или европейский тип записи).
При выборе типа String нужно задать максимальную дли-
ну текста в символах.
По окончании выбора типа переменной нужно нажать на
кнопку «Continue». Аналогичным образом кнопка «Continue»
и во всех других случаях вызывает возврат на один шаг назад
в предыдущую форму.
Для задания этикеток нужно нажать на кнопку «Labels».
В верхнее поле с заголовком «Variable Label» можно ввес-
ти произвольный текст, расшифровывающий смысл пере-
менной. Например, для переменной с именем ADS задать
этикетку «Систолическое артериальное давление». Если
нужно задать этикетку на значение переменной, то в поле с
заголовком «Value» надо ввести числовое значение, а в поле
«Value Label» — текст этикетки значения. После этого нуж-
но нажать на кнопку «Add», которая станет доступной толь-
ко после ввода значения и этикетки. Например, при вводе
пола (который должен быть определен как числовое поле,
см. раздел 2.2.1) можно на число 1 «повесить» этикетку «ж»,
а на число 0 — этикетку «м».
В протоколе статистических расчетов будут отображать-
ся именно этикетки, а не имена переменных и их числовые
значения.
Нажав на кнопку «Columns Format», можно переопреде-
лить режим показа содержимого колонки, выбрав режим вы-
равнивания (влево, вправо или посередине) и отображаемую
ширину колонки в символах. Впрочем, поменять отобража-
емую ширину колонки удобнее другим приемом, аналогич-
ным характерному для работы с Excel. Для этого нужно при
работе с данными поместить курсор мыши на уровень сгро-
ки с названиями колонок на границу кнопок с названиями
временных и при нажатой левой кнопке мыши «оттащить»
'Раницу в сторону, задав нужную ширину.

56
Часть 1. Анализ вероятностей
Нажав на кнопку «Missing Values» при определении пере-
менной, можно задать дополнительные пропущенные зна-
чения. По умолчанию дополнительных пропущенных значе-
ний нет. Если выбрать вариант «Discrete missing values», то
активизируется несколько окошек, в которые можно ввести
одно или несколько дополнительных пропущенных значе-
ний. При выборе «Range of missing values» задается интервал,
в котором лежат пропущенные значения. Для этого активи-
зируются два окна, в которых нужно задать самое маленькое
и самое большое значение из интервала пропущенных зна-
чений.
В последнем предлагаемом режиме можно определить
сумму двух первых вариантов, то есть интервал пропущен-
ных значений и еще одно дополнительное значение.
Так можно определять переменные последовательно,
одну за другой. Если нужно вставить переменную в середи-
ну таблицы, то необходимо поставить курсор в ту колонку,
перед которой будет добавлена новая, и выполнить команду
«Data/Insert Variable». В результате будет вставлена колонка
с дурацким названием типа «VarOOOl». Дальше нужно поста-
вить курсор в нее и командой «Data/Define Variable» опреде-
лить имя и параметры переменной.
В старших версиях SPSS окно редактора данных — не
одна большая таблицы, а два наложенных друг на друга лис-
та. Организация переходов между ними очень похожа на
Excel: в левом нижнем углу имеется два ярлыка с этикетками
«Data View» и «Variables View» (рис. 2.2).
При работе с листом «Data View» данные оформлены
и виде табл. 2.1, в которой колонки соответствуют перемен-
ным, а строки — случаям.
В этом режиме можно вводить данные и проводить статис-
тические расчеты, по нельзя определять новые переменные
< | ► |\РдЫ View X Variable View /
Рис. 2.2. Ярлыки и левом нижнем yi лу окна редакюра
данных SPSS

Глава 2 Планирование эксперимента и ввод данных
57
Таблица 2.1
Пример данных в окне «Variables View»
редактора данных SPSS
1
2
3
4
5
6
7
8
9
10
id
1
2
3
4
5
6
7
8
9
10
fio
Фионова
Неретин
Селиванов
Митин
Нагаев
Емельянов
Зарубина
Черкашин
Цаава
Ширяев
date
APR
JUL
FEB
OCT
SEN
ОТ
JAN
JAN
APR
MAY
year
2003
2003
2002
2002
2003
2003
2002
2002
2002
2002
sex
f
m
m
m
m
m
f
m
m
f
age
40
52
61
40
39
52
85
44
46
40
can-
cer
no
no
no
no
no
no
no
no
no
no
cir-
roz
no
no
no
no
no
no
no
no
no
no
chf
no
no
no
no
no
no
no
no
no
no |
cvd
no
no
no
no
no
no
no
no
no
no I
При работе с листом «Variables View» видна табл. 2.2 с ко-
лонками «Name», «Type», «Width», «Decimals», «Label», «Va-
lues», «Missing», «Columns», «Align» и «Measure», аналогич-
ными описанным выше.
Последняя колонка таблицы «Measure» предназначена
для ввода типа переменной: scale, ordinal, nominal. Что это
такое, будет подробно обсуждаться ниже1.
Втабл. 2.2 каждая строка соответствует переменной. Име-
на переменных вводятся в первую колонку таблицы просто
как текст, при переходе в следующие колонки появляются
экранные формы определения свойств переменных, анало-
гичные описанным выше.
Удобно, что при такой форме организации определе-
ния переменных для ускорения работы можно использовать
стандартные приемы работы с таблицами. Так, при определе-
нии нескольких однотипных переменных можно определить
только первую, а потом выделить строку с ее определением,
скопировать в буфер обмена и затем вставить его в строки
"иже. При этом этикетки, пропущенные значения и т. д.
' I lo-моему, самое лучшее — определить псе переменные как
:> Уже потом испольюнап. дли их аиалша адекнатиые методы

Таблица 2.2
Пример определения переменных в окне «Data View»
редактора данных SPSS
1
2
3
4
5
6
7
8
9
10
Name
id
fio
date
year
sex
age
cancer
cirroz
cvd
erf
Type
Numeric
String
Date
Numeric
Numeric
Numeric
Numeric
Numeric
Numeric
Numeric
Width
8
20
3
1
1
3
1
1
1
1
Deci-
mals
0
0
0
0
0
0
0
0
0
0
Label
history ID num
name of patient
date of hospital
year of the stud
sex of patient
age of patient
cancer
cirroz of liver
chronical heart
cerebro-vascula
Values
None
None
None
{2,2002}...
{1, male}...
{1, yes}...
{1,yes}...
{1,yes}...
{1,yes}...
{1,yes}...
Missing
None
None
None
None
None
None
None
None
None
None
Columns
8
14
6
7
3
3
5
4
3
3
Align
Right
Center
Right
Right
Right
Right
Right
Right
Right
I Right
Measure
Scale
Ordinal
Scale
Scale
Scale
Scale
Scale
Scale
Scale
Scale

Глава 2. Планирование эксперимента и ввод данных 59
будут скопированы, и все, что нужно, — поправить имена
переменных.
Если нужно вставить новую переменную в середину
списка, то для этого достаточно щелкнуть на нужной строке
правой кнопкой мыши и в появившемся контекстном меню
выбрать строку «Insert Variables».
В программе Statistica при создании нового файла с дан-
' ными сразу предлагается определить не только количество
I переменных, их имена и типы, но и количество случаев. При
дальнейшей работе можно увеличить выбранные размеры
j таблицы. Для вставки новых столбцов и строк проще всего
) не пользоваться командами из командного меню, а вызывать
!; контекстное меню. При щелчке правой кнопки мыши по се-
рым кнопкам с номерами и именами переменных, располо-
женным над таблицей с данными, вызывается контекстное
меню с командой «Add variables», а при щелчке по серым
кнопкам с номерами строк левее таблицы с данными — кон-
< текстное меню с командой «Add cases».
После определения набора переменных данные в ячейки
таблицы вводятся так же, как и в электронной таблице. Для
ввода значения нужно перейти в нужную ячейку (нужный
случай и нужная переменная), что можно сделать щелчком
левой кнопки мыши по ячейке или перемещая точку ввода
j по таблице кнопками перемещения курсора. Если таблица
1 достаточно велика и целиком не отображается, то для сме-
! ны отображаемой части таблицы можно пользоваться вер-
i тикальной и горизонтальной линейками прокрутки правее
j и ниже таблицы с данными.
Для быстрого перехода в самую первую колонку доста-
точно нажать на клавишу «Ноте», а в самую последнюю —
клавишу «End».
; После ввода данных в ячейку нужно нажать клавишу
\ «Enter» или клавишу перемещения курсора, например кла-
| вишу«->».
! В SPSS при вводе данных таблица автоматически рас-
ширяется вниз. В Statistica размеры определенной таблицы
I Фиксированы, и для ее расширения вниз нужно выполнить
| команду добавления строк, как это описано выше.

60
Часть 1. Анализ вероятностей
В SPSS существует два разных режима показа введенных
числовых данных. В одном из них в таблице видны введен-
ные числовые значения, в другом — этикетки значений (если
они определены). Переход между этими режимами осущест-
вляется нажатием на кнопку с изображением бирки, распо-
ложенной на панели элементов (вторая справа).
В старших версиях SPSS, если работа идет в режиме по-
каза этикеток, то при щелчке мышью в ячейке для ввода дан-
ных появляется список возможных вариантов, из которых
можно выбрать нужный.
В Statistica эти режимы реализованы аналогичным обра-
зом, причем даже рисунок бирки на кнопке очень похож.
2.2.4. Вычислимые переменные
При статистической обработке данных часто нужно работать
с переменными, значение которых можно вычислить на ос-
новании других переменных. Например, если имеется систо-
лическое идиастолическое артериальное давление, то можно
вычислить пульсовую разность. Не нужно непосредственно
вводить вычисленные вручную или другой программой чис-
ловые значения для пульсового давления, проще определить
новую переменную вместе с ее начальными значениями.
В SPSS это можно сделать при помощи команды «Trans-
form/Compute» (в младших версиях она недоступна при
работе с окном протокола результатов расчетов, и предва-
рительно нужно перейти в окно редактора данных). После
ее выполнения появится форма выражений конструктора
(рис. 2.3). В верхнем левом углу формы в поле с заголовком
«Target variable» нужно ввести имя переменной. Если это
новое имя, то в результате будет добавлена новая колонка,
а если переменная с таким именем уже существует, то в про-
цессе вычисления ее значения будут заменены на новые.
При вычислении существующей переменной SPSS выдает
предупреждение о потере старых значений и просит для под-
тверждения нажать на кнопку «ОК»
То, что новая вычисленная переменная добавляется
к таблице справа, не всегда удобно. Для того чтобы вычис-
ленная переменная была рядом, нужно вначале поставить

Глава 2. Планирование эксперимента и ввод данных
61
ф bilateral pneumonia,, | Oft | Paste | Head | Cancel | Help
■-—гз\ плои- тагаров :—лгтт—ztroz—тп гт*—по—ггго—h ,
Рис. 2.3. Форма вычисления значения переменной
курсор в нужное место таблицы и командой «Data/Insert
Variable» вставить новую колонку, потом командой «Data/
Define Variable» задать ей нужное значение и уже потом вы-
полнять команду «Transform/Compute».
Например, для того чтобы по переменным sistad и diastad
с величиной систолического и диастолического давления
вычислить ADPULS с величиной пульсовой разницы, нужно
в поле «Target Variable» ввести ADPULS, а в большое поле с
заголовком «Numeric Expression» — формулу для ее вычис-
ления, в данном случае sistad-diastad. Начинать формулу со
знака «=» не нужно.
Проще и надежнее не вводить формулу как текст, а сфор-
мировать ее при помощи конструктора выражений. В данном
случае нужно найти переменную sistad в списке переменных,
имеющемся в левой нижней части формы, щелкнуть по ней
левой кнопкой мыши и щелчком по кнопке с изображением
треугольника острием вправо «сбросить»1 имя переменной
буксировкой имени переменной из окна и окно пользоваться
ьзя — этот способ работы в SPSS не поддерживается

62
Часть 1. Анализ вероятностей
в окно «Numeric Expression». После этого нужно ввести знак
«минус», что можно сделать либо с клавиатуры, либо щел-
чком мышью на кнопке со знаком минуса, потом в списке
переменных найти переменную diastad, «сбросить» ее в поле
ввода формул щелчком по кнопке с треугольником и нажать
на кнопку «ОК». При этом в списке переменных показыва-
ется этикетка имени, а «сбрасывается» имя.
Так определяется только начальное значение перемен-
ной. Если Вы добавите новые случаи или поменяете значе-
ние переменной sistad или diastad в уже введенных данных,
то переменная ADPULS пересчитываться автоматически не
будет. Для ее повторного вычисления придется повторять
процедуру с самого начала.
Введенная в окно «Numeric Expression» формула являет-
ся текстом, и ее можно корректировать и править обычным
образом. Для повторного использования формулу лучше
выделить («покрасить» движением мыши с нажатой левой
клавишей) и скопировать в буфер обмена, после чего пере-
ключиться в любой текстовый редактор и вставить ее из бу-
фера обмена. Тогда для повторного вычисления достаточно
открыть текстовым редактором сохраненный текст с заго-
товками формул, выделить нужную мышью и скопировать ее
в буфер обмена, потом переключиться в SPSS и вставить из
буфера обмена. Особенно удобна такая техника в том случае,
когда приходится использовать большое количество одно-
типных формул.
Если количество переменных велико, поиск нужной пе-
ременной в списке может занять много места. Для упрощении
этой операции можно щелкнуть по имени любой переменной
в общем списке переменных, а потом начать нажимать на
клавиатуре на клавишу с первой буквой имени. В этом режи-
ме выделенное имя переменной будет перемещаться между
именами, начинающимися с лой буквы В рассмотренном
примере для поиска имени sislad нужно один или несколько
раз нажать ил клавишу с буквой «s». К сожалению, -нот трюк
работает только с латинскими буквами
Помимо арифметических операций при вычислении но-
ной переменной можно пользоваться обширным списком

Глава 2. Планирование эксперимента и ввод данных
63
встроенных функций, список которых находится в нижнем
правом углу формы вычисления значения переменной. На-
пример, если в течение первых суток после госпитализации
у больного дважды мерили температуру (переменные Т1 и
Т2), то для нахождения максимальной переменной в поле
«Target Variable» введем имя ТМАХ (нужно, чтобы оно не
использовалось другими переменными), потом в списке
в правом нижнем углу формы найдем функцию МАХ, вы-
делим ее щелчком, а потом щелчком на кнопке с треуголь-
ником острием вверх скопируем ее имя в окно «Numeric
Expression». Потом в списке переменных слева найдем и
выделим щелчком переменную Т1, скопируем ее слева на-
право щелчком по кнопке острием вправо и получим вы-
ражение МАХ(Т1,). После этого нужно переместить курсор
в позицию после запятой, но до закрывающей скобки, вы-
брать слева переменную Т2 и переместить ее слева направо
кнопкой с треугольником острием вправо, получив искомое
выражение МАХ(Т1 ,Т2).
При статистической обработке данных часто нужно
округлять данные. Для этого можно воспользоваться фун-
кцией отбрасывания дробной части TRUNC. Например,
если имеется переменная VES с весом больных с точно-
стью до 100 г, то для определения новой переменной со
значением с точностью до килограмма можно воспользо-
ваться выражением TRUNC(VES). Заметим, что эта опера-
ция отбрасывает дробную часть, а не округляет значение.
Например, при преобразовании веса в 82,8 мы получим 82.
Для того чтобы округлять значение, то есть приближать
его к наиболее близкому целому, нужно ввести выражение
TRUNQVES+0.5).
Часто нужно огрублять значения с точностью не до еди-
ницы, а до другого круглого значения. Если нужно вычис-
лить возрастную группу с шагом в 10 лет, то можно восполь-
зоваться выражением
TRUNC(VOZRAST/10)*10. В этом
случае значению 10 будут соответствовать испытуемые в
"трасте от 10 до 19 лет, значению 20 - п возрасте от 20 до
2,) и г д Если, к примеру, нужно огрубить переменную V до
,,л,|<>й сотой, то это сделает выражение TRl)NC(V*U)0)/100

64
Часть I. Анализ вероятностей
В некоторых случаях нужно вычислять группы с пере-
менным шагом. В этом случае можно воспользоваться неак-
куратностью большинства современных программ, которые
позволяют смешивать логические и арифметические выра-
жения и при этом неверные логические выражения счита-
ют нулем, а верные — единицей. Например, пусть выделя-
ются возрастные группы так, что первая группа — больные
моложе 18 лет, вторая — от 18 до 50, третья — от 51 до 80 и
четвертая — от 81. В этом случае номер группы может быть
вычислен выражением 1+(VOZRAST>18)+(VOZRAST>50)+
+(VOZRAST>80). Идея таких выражений в том, что за каж-
дое превышение граничного между группами значения нуж-
но добавлять единицу.
Выделение групп может быть и более сложным, с исполь-
зованием значений других переменных. Пусть, например,
у меня помимо переменной VES с весом в килограммах есть
переменная POL, равная единице для мужчин и нулю для
женщин. Пусть первая группа — те, кто весит не более 50 кг
для женщин и 58 кг для мужчин, третья — те, кто тяжелее
90 кг для женщин и 105 кг для мужчин, а вторая — промежу-
точные значения. Тогда номер группы может быть вычислен
при помощи выражения 1+(POL=0)*((VES>50)+(VES>90))+
+(POL=1)*((VES>58)+(VES>105)).
Как было сказано выше, при вводе данных желательно
разделять информацию по переменным. Однако при ана-
лизе данных часто нужно сравнивать больных по группам,
формирующимся по значению не одной, а нескольких пере-
менных. Например, если для больных вирусными гепатита-
ми имеется переменная «ВидВируса» с вариантами 1 = ВГА
(вирусный гепатит А), 2 = ВГБ, 3 = ВГС, 4 = ВГД и 5 = ВГЕ и
переменная «Тяжесть» с вариантами 1 = легкая, 2 = средней
тяжести и 3 = тяжелая, то для определения новой перемен-
ной, задающей одновременно вид вируса и его тяжесть, мож-
но воспользоваться выражением 10*ВидВируса+Тяжесть
Например, значение 21 будет соответствовать ВГБ средней
тяжести, а 13 — тяжелому ВГА.
Мри работе в Statislica дли вычислении значении новой
переменной нужно при добавлении се в поле для впода эти-

Глава 2. Планирование эксперимента и ввод данных 65
кетки имени или формулы ввести формулу для ее вычисле-
ния, начинающуюся со знака «=». При записи формулы ссы-
латься на значения имеющихся переменных можно двумя
способами. Можно или аналогично описанному выше сти-
лю SPSS писать имя переменных, или ссылаться на номер
колонки по порядку, для чего писать выражение вида V№.
Например, если sistad и diastad введены в третью и четвер-
тую колонку таблицы, то можно писать выражение =sistad-
—diastad или =V3—V4. Для вызова списка встроенных функ-
ций нужно нажать кнопку «Functions».
В отличие от SPSS, в Statistica формулы не только начи-
наются со знака «=», но и постоянно хранятся. Для повтор-
ного вычисления значения переменной по введенной ранее
формуле нужно выполнить команду «Data/Recalculate».
2.2.5. Поиск грубых ошибок
В процессе ввода возможны ошибки, в том числе и грубые,
когда вводятся невозможные очень большие или очень ма-
ленькие значения.
Наличие грубых ошибок можно быстро обнаружить, рас-
считав таблицу с максимальными и минимальными значе-
ниями переменных, однако эта таблица не содержит инфор-
мации о том, в каких строках исходной таблицы содержатся
эти значения.
Для быстрого поиска самых больших и маленьких значе-
ний переменной можно упорядочить таблицу по значению
этой переменной. Для этого в обоих статпакетах нужно вы-
полнить команду «Data/Sort Cases», выбрать нужную пере-
менную из списка и выбрать режим сортировки (по возрас-
танию или убыванию). После выполнения команды самые
маленькие и большие значения будут в верхних и нижних
строках таблицы, где их легко обнаружить.
После исправления ошибок может быть желательно
восстановление исходного порядка строк. Для этого нуж-
но упорядочить таблицу по значению первой переменной
(вариант упорядочения — по возрастанию), которая в со-
ответствии с п. 2.2.1 должна быть номером случая по по-
рядку.
3 МедИцн„сюи „„К1ИЫ

Глава 3
АНАЛИЗ ЧАСТОТ
И ОПТИМИЗАЦИЯ РИСКОВ
Есть вещи столь серьезные, что по
их поводу можно только шутить.
Гейзенберг
3.1. Расчет частот
Доктор — пациенту: «Батенька, day Вас тяжелая болезнь, от кото-
рой умирают 9 из 10, но Вы не беспокойтесь — как раз 9 моих преды-
дущих пациентов с этим диагнозом умерли»
Старый анекдот
Определение частоты, ее расчет в пакетах
статистических программ.
Определение. Если при N наблюдениях событие наблю-
далось в п случаях, то частота события равна n/N.
Расчет частоты значений переменной — простая базовая
оиераиия статистического анализа. В SPSS для лого нужно
выполнить команду «Analyze/Descriptive Siatistics/Frequen-
cies», выбрать щелчком левой кнопки мыши пленом списке
переменных имя нужной неременной, нажатием па кнопку с
треугольником острием вправо переместить переменную in
левого списка в правый и нажать кнопку «ОК» И ре lyjii.raie

Глава 3. Анализ частот и оптимизация рисков
67
будет открыто второе окно с протоколом выполненных рас-
четов, в котором появится таблица с заголовком «Report».
Например, при анализе больных язвой желудка по полу
были получены следующие результаты (табл. 3.1).
Таблица 3.1
Пример таблицы с расчетом частот
Valid
Total
1
2
Total
Frequency
477
105
582
582
Percent
81,96
18,04
100
100
Valid
Percent
81,96
18,04
100
Cumulative
Percent
81,96
100
Здесь во втором столбце таблицы представлены возмож-
ные значения: единицами кодировались мужчины, а двойка-
ми — женщины. В третьем столбце приведено число людей,
так что было 477 мужчин, 105 женщин, а всего — 582 паци-
ента. Следует обратить внимание на двукратный подсчет
общего количества: в предпоследней строке приводится ко-
личество пациентов, у которых пол был определен, а в ниж-
ней — общее количество случаев. Здесь они совпадают, так
как пол всех пациентов был задан.
Четвертый и пятый столбец — частоты встречаемости
данного значения в процентах. При этом в четвертом столб-
це — частота встречаемости по отношению ко всем случаям,
а в пятом — по отношению к тем случаям, в которых пере-
менная была определена (что в нашем случае совпадает).
Шестой столбец — частота нарастающим итогом, то есть
частота встречаемости данного и меньших значений. В рас-
сматриваемом случае этот столбец не нужен, но при иссле-
довании переменных, имеющих большое количество разных
значений, он может быть полезен. Например, при исследо-
вании возраста в этом столбце будет приведена частота па-
циентов с данным и меньшим возрастом
В программе Statistica для расчета частот можно выпол-
нить команду «Statistics», в развернувшемся меню выбрать
з»

68
Часть I /и:a 'iuj ■■■■■■■
команду «Basic statistic/Tables». В появившемся списке вы-
брать «Frequency tables» и нажать кнопку «ОК». Далее нажать
кнопку «Variables:» и выбрать нужную переменную из спис-
ка, после чего нажать на кнопку «Summary: Frequency tables»,
и в результате появится аналогичная таблица.
Частоты встречаемости часто представляют в виде частот-
ных диаграмм и гистограмм. В SPSS для построения диа-
граммы частот нужно выполнить команду «Graphs/Bar», и на
появившейся форме нажать на кнопку «Define». Далее в по-
явившейся форме выбрать нужную переменную и нажатием
на кнопку1 с треугольником в нижней половине формы пе-
реместить ее в поле с заголовком «Category axis»2. В верхней
части формы имеется группа из пяти радиокнопок3. Верхние
четыре варианта позволяют выбрать, что показывать на гисто-
1 При повторном построении частотной диаграммы нужное поле
будет занято именем той переменной, которую Вы анализировали ра-
нее. Для построения новой диаграммы нужно вначале «освободить
место», для чего щелкнуть левой кнопкой мыши на занятом поле.
В результате расположенная рядом кнопка с треугольником поменяет
вид — треугольник будет указывать не направо, а налево. Нажав на эту
кнопку, Вы «сбросите» выбранную переменную в общий список. Эта
техника справедлива и для всех остальных статистических расчетов.
1 В верхней части формы имеется другое поле для выбора пере-
менной, но в описываемом режиме оно неактивно.
3 Для выбора одного варианта из предлагаемого набора в программах
под WINDOWS традиционно используются так называемые радиокноп-
ки. Каждая из них — кружок с поясняющим текстом справа. Выбранный
вариант отмечается жирной черной точкой в середине. Выбор варианта
производится щелчком по кругу или (иногда) поясняющему тексту. При
выборе нового варианта выбранный ранее вариант отключается
В ряде случаев желательно иметь несколько независимо работа-
ющих групп радиокнопок. В этом случае они помещаются не на фор-
му, а на расположенную на форме панель, имеющую вид прямоуголь-
ника произвольных размеров Границы панели обычно выделяются
линией, в правом верхнем углу панели может быть ее название Распо-
ложенные на разных панелях и формах радиокнопки переключаются
независимо
Для меня как человека, п дни своей юности активно пользован
iiiemoi радиолой Гигопла. название «радиокнопки» представляется
исимочигслыю удачным

f.iuea J •■';.- ^,'£- частот и оптимизация рисков
69
грамме: частоты или количества, а также частоты (количе-
ства) данного значения или нарастающим итогом. Пятый
вариант, который позволяет построить диаграмму средних
значений по подгруппам, будет обсуждаться ниже.
Например, при анализе возраста больных язвенной бо-
лезнью получается следующее (рис. 3.1).
Несмотря на большое (582 пациента) количество больных
диаграмма получается не очень ровная, что явно связано со
слишком большим количеством вариантов значения пере-
менной. Кроме того, частотная диаграмма может «обманы-
вать», пропуская при построении ни разу не встретившиеся
значения. Так, для больных около 90 лет некоторые значения
возраста ни разу не встречались, и диаграмма их не показала.
Поэтому для переменных, принимающих слишком мно-
го значений, целесообразнее строить не диаграмму, а гисто-
грамму (команда «Graphs/Histogram», далее выбрать нужную
переменную). Гистограмма отличается от диаграммы тем,
что при ее построении близкие значения объединяются в
одно. SPSS сам выбирает оптимальный шаг гистограммиро-
вания и значение, с которого начинается выделение групп.
Вмешаться в этот процесс простыми средствами нельзя, по-
ш
шы
* -о -с * # + +
*£<j><?<J,#»'l'##'V4^'<V#**
Рис. 3.1. Частотная диаграмма возраста больных
язвенной болезнью

70
Часть 1. Анализ вероятностей
этому если гистограмма Вас не устраивает, то проще (и лучше)
создать новую переменную с округленными значениями, как
это описано в п. 2.2.4, и построить частотную диаграмму.
Например, если при анализе возраста больных язвой
строить частотную диаграмму только для женщин, то полу-
ченная диаграмма не слишком красива (см. рис. 3.2).
Если при помощи выражения TRUNC(VOZRAST/10)*10
создать новую переменную, содержащую округленные до
10 лет значения, и определить для числовых значений этой
переменной соответствующие этикетки значений, то полу-
ченная диаграмма примет следующий вид (рис. 3.3).
Построенные в SPSS графики обычно можно рассматри-
вать только как промежуточные рабочие материалы. Для под-
готовки рисунков для статей или презентаций можно рассчи-
тать таблицу частот исходной или округленной переменной,
как это описано выше, потом скопировать ее в Excel и там
построить диаграмму. Если же качество полученных в SPSS
графиков достаточно, то для их «доводки» нужно дважды
щелкнуть левой кнопкой мыши по графику в отчете о выпол-
нении статистических расчетов. В результате откроется новое
(третье) окно — редактора графиков (рис. 3.4), которое поз-
волит, например, поменять цвета, толщину и стиль линий.
5 , Г] Г| Г| 1
4.5
4
3.5
з п п п гт гт m
2,5
1.5
0.5
о II iii.li.. ч и in inn in н in in н in in п in in 11 in mi и in ii им и и
t 8 8 R R 8 Я S ; J * 8 Я J J 8 8 8 г J С 8 8 8 t 8
Рис. З.2. Частотная диаграмма возраста женщин,
больных язвенной болезнью

20
IS
10
s
до !0 21-10 31-40 41-50 SI-60 (1-70 71-10 1140 (окне
90
Рис. 3.3. Частотная гистограмма возраста женщин,
больных язвенной болезнью
Для этого нужно щелчком левой кнопки выделить ту
часть графика, которую нужно преобразовать. Потом щелч-
ком по кнопке на панели выбрать преобразуемое свойство и
выбрать нужный вариант. Например, на приведенном при-
мере выбранная часть— столбики диаграммы, а нажатая
кнопка с изображением прямоугольника с косой штрихов-
кой (вторая слева) — изменение способа штриховки.
В Statistica для построения частотной диаграммы нужно
выполнить команду «Graphs/Histograms», потом выбрать за-
кладку «Quick», нажать на кнопку «Variables», выбрать нуж-
ную переменную, а также поменять, если нужно, количество
классов гистограммирования (по умолчанию — 10).
Кроме расчета частот значения одной переменной часто
нужно определить частоты совместного распределения двух
переменных. Один способ расчета уже рассмотрен: можно,
как это описано в п. 2.2.4, из двух разных переменных сде-
лать одну, а потом получить для нее частоты. Однако лучше
это сделать непосредственно.
В SPSS для этого нужно выполнить команду «Analyze/
descriptive Statislic/Crosstabs». В появившейся форме пуж-

72
Часть I Анализ вероятностей
ъатжтьш
moo,
JS.C Х1Л JT.S 37.9 38.4 1».8 ЭМ 39.»
ЗМ 37,4 37.7 38.2 З1.в 39.» 3».в 41.»
temperature <rf me patient
Рис. 3.4. Окно редактирования графиков
но выбрать из списка две переменные, одна из которых бу-
дет соответствовать строкам формирующейся таблицы, а
вторая — столбцам (поля «Columns» и «Rows»). Например,
при выборе поля Pol как строки и поля Kogaokr (цвет кожи
больного в момент поступления) как столбца будет получена
табл. 3.2.
Таблица 3.2
Пример таблицы с анализом совместного
распределения двух переменных
POL * KOGAOKR Crosstabulation
POL
Total
1
2
KOGAOKR
1
128
23
151
2
332
71
403
3
6
4
10
Total
466
98
564
Здесь у переменной Pol значение «I» соответствует мужчи-
нам, а «2» — женщинам. У переменной Kogaokr значение «I»

Глава 3. Анализ частот и оптимизация рисков
73
соответствует розовому цвету кожных покровов, «2» — блед-
ному и «3» — бледному с синевой. Так, например, видно, что
поступило 128 «розовых» мужчин и 4 «синих» женщины.
В указанном режиме программа рассчитывает количест-
во встретившихся вариантов. Для того чтобы получить кроме
количества еще и частоту, нужно после выполнения коман-
ды «Analyze/Descriptive Statistic/Crosstabs» нажать кнопку
«Cells» и в группе «Percentages» отметить1 нужный вариант
расчета частот. Возможны три варианта — «Row» для расчета
частот в каждой строке по отдельности, «Column» для расче-
та в каждом столбце по отдельности и «Total» для расчета час-
тоты каждого варианта пары значений по отношению к обще-
му набору наблюдений. Например, при определении расчета
частоты количества «синих» женщин при варианте расчета
«Rows» их количество будет делиться на общее количество
женщин, частота будет равна 4/98 » 4,1 %. В этом режиме таб-
лица расчета частот примет следующий вид (табл. 3.3).
Таблица 3.3
Пример таблицы с расчетом частот совместного
распределения двух переменных
POL* KOGAOKR Crosstabulation
POL
Total
1
2
Count
% within POL
Count
% within POL
Count
% within POL
KOGAOKR
1
128
27,5 %
23
23,5 %
151
26,8 %
2
332
71,2%
71
72,4 %
403
71,5%
3
6
1,3 %
4
4,1 %
10
1,8%
Total
466
100,0%
98
100,0%
564
100,0%
' Для выбора произвольного набора возможных вариантов в прог-
раммах под WINDOWS традиционно используются так называемые
checkbox'bi. Каждый из них — квадрат с поясняющим текстом спра-
ва. Если вариант выбран, то в квадрате появляется крестик или «га-
лочка». Включение/отключение добавления варианта производится
Щелчком по квадрату или (иногда) тексту. В отличие от радиокнопок,
checkbox'bi переключаются независимо друг от друга.

74
Часть I. Анализ вероятностей
При варианте «Column» деление будет производиться на об-
щее количество «синих» больных, и частота будет равна 4/10 =
=40 %. В этом случае таблица примет следующий вид (табл. 3.4).
Таблица 3.4
Пример таблицы с другим вариантом расчета частот
POL * KOGAOKR Crosstabulation
POL
Total
1
2
Count
% within
KOGAOKR
Count
% within
KOGAOKR
Count
% within
KOGAOKR
KOGAOKR
1
128
84,8 %
23
15,2%
151
100,0%
2
332
82,4 %
71
17,6%
403
100,0%
3
6
60,0 %
4
40,0 %
10
100,0%
Total
466
82,6 %
98
17,4%
564
100,0%
При варианте «Total» деление будет производиться на
общее количество больных, у которых обе переменные были
определены, и частота составит 4/564 » 1,8 %.
В Statistica для построения таблицы совместного распре-
деления можно выполнить команду «Statistics/Basic Statistics
and Tables/Tables and banners/Specify tables (select variables)».
В результате появится форма, в которой можно выбрать до
шести переменных. Далее нужно выбрать одну переменную
в первом поле и одну — во втором и нажать кнопку «ОК.» два
раза. Если после этого нажать на кнопку «Summary», то будет
получена таблица с количеством встретившихся вариантов.
Для расчета частот нужно перейти на закладку «Options» и в
группе «Compute tables» отметить нужные варианты расчета
частот (опции «Percentage of total count», «Percentage of row
counts» и «Percentage of column counts»).
В SPSS при построении таблицы частот совместного рас-
пределения берутся вес возможные значения переменных,
вне зависимости от их величины В Statistica дробные значе-
ния округляются до целых.

(fl[1ea 3. Анализ частот и оптимизация рисков
75
Чаше всего описанный анализ частот применяется к пе-
ременным, имеющим целые значения. При анализе пере-
менных с нецелыми значениями в зависимости от характера
решаемой задачи иногда удобен подход SPSS, а иногда —
Statistica. В любом случае добиться нужного эффекта можно
при помощи описанной выше техники определения новых
переменных с вычислением их значения.
Для графической иллюстрации частотного распреде-
ления двух переменных в SPSS можно выполнить коман-
ду «Graphs/Bar». Помимо исходного варианта диаграммы
«Simple» имеются также варианты «Clustered» и «Stacked».
Нужный вариант нужно выбрать щелчком по картинке в ле-
вой части формы, а уже потом нажать на кнопку «Define».
В появившейся форме в нижней части имеется уже не
одно, а два поля для выбора переменных. В поле «Category
axis», как и ранее, выбирается переменная, для которой рас-
считываются частоты. Второе поле используется для выбора
переменной, по значениям которой исходная выборка де-
лится на группы.
В варианте «Clustered» строится не одна, а несколько
частотных диаграмм (рис. 3.5):
В варианте «Stacked» столбцы частотной диаграммы де-
лятся на части, соответствующие разным группам. Так,
в данной диаграмме женщины «сели» мужчинам на «голову»
(рис. 3.6).
Обе диаграммы хорошо показывают тот факт, что с уве-
личением возраста доля женщин увеличивается.
В Statistica один из вариантов построения диаграммы сов-
местного распределения — команда «Graphs/3D Sequential
Graphs/Bivariate Histograms», далее надо нажать на кнопку
«Variables» и выбрать две нужные переменные.
3.2. Частоты, риски и относительные риски
Пупкина в метро все время прищемляло дверями. Вначале он терпел,
п потом перестал верить в теорию вероятностей.
Одна иj старых «Литературных газет»,
раздел «Стенгазета клуба «12 стульев»

76
Часть 1. Анализ вероятностей
до 20 30-39 30-59 70-79 90-99
20-29 40-« 60-49 80-89
ВОЗРАСТ
Рис. 3.5. Частотная диаграмма возрастной группы больных
язвенной болезнью, кластеризованная1 по полу
30.39 3039 70-79 90-99
40.» «0.69 10.»
ВОЗРАСТ
Рис. 3.6. Частотная диаграмма возрастной группы больных
язвенной болезнью, стеккеризованная по полу
1 Нормального русского перевода у калек с английского «клас-
теризованная» и «стеккеризованная» нет. Буквальный перевод слов
«кластер» и «стек» — «созвездие» и «магазин» (не тот, в котором про-
дукты продают, а тот, который есть у автомата Калашникова). Однако
термины «созвезданутая диаграмма» и «обмагазиненная диаграмма»
выглядят еще хуже.

гыва 3. Анализ частот и оптимизация рисков
77
Содержательный анализ частот, чувствительность
и специфичность.
Используемые разными авторами термины «частота», «ве-
роятность», «шансы» и «риск» очень близки друг к другу. В сов-
ременной терминологии «вероятность» соответствует истин-
ной частоте наступления некоторого события, а «частота» — ее
оценке по имеющемуся набору наблюдений, содержащей из-
за этого некоторую статистическую погрешность. Подробно
различие между этими понятиями будет разбираться ниже.
Термин «шансы» активно использовался на начальном
этапе развития теории вероятностей, когда в основном ра-
ботали с вероятностями, равными доле. Например, понятие
«один шанс из тысячи» соответствует вероятности в 0,001.
Понятие «риск» фактически идентично понятию «вероят-
ность», но часто используется для описания отношения веро-
ятностей. Относительный риск определяется как отношение
вероятностей для двух подгрупп — группы риска и группы
сравнения. Он показывает, во сколько раз принадлежность
к группе риска повышает вероятность наступления события.
Атрибутивный риск определяется как относительный риск
минус единица. Он показывает, какова добавка вероятности
по сравнению с исходной. Например, если в группе курящих
заболеваемость раком легких в 2,5 раза больше, чем в сопо-
ставимой группе некурящих, то относительный риск равен
250 %, а атрибутивный риск равен 150 %.
Частый вариант сопоставления относительных рисков ■—
анализ соотношения между предположением о наличии
болезни и ее истинным наличием. Результаты эксперимен-
тальной проверки можно представить в виде табл. 3.5.
Таблица 3.5
Расчет чувствительности и эффективности
Болезнь:
Нет
Есть
Всего
Предположение о наличии болезни:
Нет
А
С
А+С
Есть
В
D
B+D
Всего
А + В
C + D
A+B+C+D

.■-..с.;-..::з вероятностей
В табл. 3.5 используются следующие обозначения:
А — количество истинных отрицательных диагнозов;
В — количество ложноположительных диагнозов;
С — количество ложноотрицательных диагнозов;
D — количество истинных положительных диагнозов.
В этом случае доля правильных диагнозов будет равна
(А + D)/(A + В + С + D), а доля неправильных диагнозов —
(В + С)/(А + В + С + D).
Ошибки диагностики могут быть как за счет ложнопо-
ложительных, так и за счет ложноотрицательных диагнозов.
Так как ущерб от ложноположительных и ложноотрицатель-
ных диагнозов может быть различен, то для более точного
описания качества диагностики используют понятия «чувст-
вительность» и «специфичность».
Чувствительность определяют как D/(C + D), то есть
доля больных, у которых был поставлен диагноз о наличии
болезни.
Специфичность определяют как А/(А + В), то есть долю
здоровых, у которых предполагалось отсутствие болезни.
Данные термины описывают качество диагностики
с точки зрения врача, то есть насколько полно они выявля-
ют наличие болезни и насколько часто они ставят наличие
болезни у тех, у кого ее нет. С точки зрения пациента более
интересны другие соотношения.
Частота заболевания равна (В + D)/(A + В + С + D).
Частота наличия заболевания при положительном диа-
гнозе равна D/(B + D).
Частота наличия заболевания при отрицательном диа-
гнозе равна С/(А + С).
Отношение шансов при положительном и отрицатель-
ном диагнозе равно (D/(B + D))/(C/(A + С)).
Если рассматривать лиц, у которых имеется предположе-
ние о наличии болезни, как группу риска, а лиц, у которых
имеется предположение об отсутствии болезни, — как груп-
пу сравнения, то это отношение шансов есть относительный
риск
Эти понятия будут многократно новгорпо обсуждать-
ся и дальнейшем, во-первых, при пналтс условных вероит-

■■'тка i- Анализ частот и оптимизация рисков 79
лостей, а во-вторых — при анализе качества прогнозирова-
ния и ROC-кривых.
Рассмотрим пример. Пусть в рамках программы выявле-
ния рака молочной железы у женщин старшей возрастной
группы в результате маммографии были получены следу-
ющие результаты (табл. 3.6).
Таблица 3.6
Пример расчета чувствительности и эффективности
Болезнь:
Нет
Есть
Всего
Предположение о наличии болезни:
Нет
1257
2
1259
Есть
118
24
142
Всего
1375
26
1401
Тогда с точки зрения врача чувствительность составит
24/(2+24) * 92,3 %, а специфичность - 1257/(1257+118) * 91,4 %,
и кажется, что метод достаточно «сбалансирован» — чувст-
вительность и специфичность близки друг к другу.
При анализе с точки зрения пациента частота заболева-
ния равна 26/1401 » 1,9 %, вероятность заболевания при от-
рицательном диагнозе — 2/1259» 0,16 %, а вероятность за-
болевания при положительном диагнозе — 24/142 » 16,9 %.
Отношение шансов при положительном и отрицательном
диагнозе (относительный риск) равно (24/142)/(2/ L259) »
* 106,4, то есть метод действительно имеет хорошие различа-
ющие возможности. С другой стороны, явным недостатком
метода является слишком большое количество ложнополо-
жительных диагнозов, так как при положительном первич-
ном диагнозе вероятность наличия рака лишь 16,9 %.
Поэтому если бы на основании только этого одного ис-
следования принималось решение об оперативном лечении,
то из 6 оперированных женщин у 5 рака бы не было, и от
практического использования такой схемы диагностики
и лечения преда было бы больше, чем пользы.
В рассматриваемом случае при наличии положительного
первичного диагноза проводятся повторные исследования.

80
Чоо-.ч ■ Ai,n;;ifj вероятностей
и выбранное соотношение ложноположитсльных и ложно-
отрицательных диагнозов достаточно разумно.
Достаточно часто для постановки диагноза используется
не один тест, а два или более, причем второй и следующие
применяются в том случае, когда первый дал положитель-
ный результат. В этом случае при создании первого теста
разумно определить его таким образом, чтобы количество
ложноположительных результатов было больше, чем ложно-
отрицательных.
Вопросы оптимального выбора вероятностной стратегии
будут обсуждаться в следующем разделе.
3.3. Управление рисками и поиск наилучшего
решения. Игры с противоположными
интересами (задача о двух пивных)
Что наша жизнь? Игра!
А. С. Пушкин «Пиковая дама»
Анализ частот и выигрышей для поиска наилучшей стратегии.
В тех случаях, когда на вероятность исходов можно воз-
действовать, желательно делать это оптимальным образом,
чтобы в рамках имеющихся возможностей максимально
уменьшить вероятность неблагоприятного исхода или увели-
чить вероятность благоприятного исхода. Пусть, например,
для некоторой болезни известно, что инвестиции каждого
мегабакса в ее выявление увеличивают вероятность обна-
ружения на 8 %, а инвестиции в лечение — вероятность вы-
здоровления на 10 %. Тогда если инвестировать п мегабаксов
в диагностику и т — в лечение, то количество вылеченных
больных увеличится в (1 + 0,08 • п) х (1 + 0,1 • т).
Пусть суммарно на инвестиции выделено 10 мегабаксов.
Тогда если в диагностику инвестируется п мегабаксов, то в
лечение— (10 - п), и увеличение количества вылеченных
больных равно (1 + 0,08-я) х (1 + 0,1 -(10 - и)), что после
раскрытия скобок и приведения подобных дает -0,008 • п- -
-0,06-л + 2.

/,„>№ .'' Анаш-j частот и оптимизация рисков
81
Задачи такого рода часто сводятся к поиску максимума
„ли минимума полинома от аргумента, принадлежащего не-
которому отрезку. Найти их можно на основании следующе-
го результата. N
Теорема. Если Q(x) = J^ak xk- полином N-Й степени от
аргумента х, который принадлежит отрезку [х х . ], то макси-
мальные и минимальные значения полинома "c^xfмогут быть
при х, равном xmin, xmax, а также, тех величинах х, для которых
Q'(x) = |>* k хк-^0.
Следовательно, максимальное значение может быть
в крайних точках л=0, «=10, а также при том л, при котором
-0,008 • 2 • п - 0,06 = 0, то есть при л = 3,75. Теперь для по-
иска наилучшего решения нужно проверить три возможных
варианта. При минимальном значении (все идет на лечение)
« = 0 получаем (1 + 0,08-л) х (1 +0,1-(Ю-л)) = (1 + 0) х
х (1 + 1) = 2. При максимальном значении л = 10 (все идет
на диагностику) получаем (1 + 0,08-л) х (1 + 0,1 -(10 - л)) =
= (1 + 0,8) х (1 + 0) = 1,8. И при третьем возможном варианте
(1+ 0,08-3,75) х (1+0,1-(10-3,75)) = (1+0,3) х (1+0,625) =
= 2,1125. В результате получаем, что лучшее решение — вы-
делить 3,75 мегабакса на диагностику и 6,25 — на лечение.
Значительно более сложен поиск оптимального реше-
ния в случае, когда стратегия выбора определяется не одним
действующим лицом, а несколькими, причем их интересы
не совпадают. Часть математики, посвященная анализу та-
ких задач, называется теорией игр.
Частным случаем игр являются так называемые игры
с противоположными интересами, при которых выигрыш
одной стороны является проигрышем другой.
В качестве понятного бытового примера пусть игроками
являются муж, получивший зарплату и стремящийся ее про-
пить, и жена, стремящаяся у него эти деньги отобрать.
После работы муж может пойти в одну из двух пивных.
На основании многолетнего опыта известно, что если жена
Яадает, в какую пивную пойдет муж, то oi ia без труда отбирает

82 Часть ! Лии :и.-; вероятностей
у него деньги, но если не угадает, то до появления жены
в первой пивной муж успевает пропить тысячу рублей, а во
второй — 500 рублей. Задача мужа — максимизировать коли-
чество пропитых денег, задача жены — минимизировать эту
сумму1.
В соответствии с выбором мужем и женой пивных коли-
чество пропитых денег будет определяться табл. 3.7.
Таблица 3.7
Выигрыши игроков при разных исходах
Выбор мужа
пивная 1
пивная 2
Выбор жены
пивная 1
0
500
пивная 2
1000
0
Если муж будет осознанно выбирать пивную, то знающая
его привычки жена пойдет туда же и пропить не удастся ни-
чего. С другой стороны, если жена заранее решит, в какой
пивной караулить мужа, то знающий ее привычки муж пой-
дет в другую пивную. Поэтому для обеих сторон лучше не ре-
шать заранее, а выбирать пивную случайно.
Пусть муж выбирает первую пивную с вероятностью Р ,
а жена — с вероятностью Рж. Тогда (подробное изложение
используемой техники вычисления вероятностей смотри
в следующих разделах) вероятность выбора второй пивной
для мужа составит 1— Рм, а для жены — (1 — Р ). Сумма в
1000 рублей может быть пропита в том случае, если муж пой-
дет в первую пивную, а жена — во вторую. Вероятность этого
события равна />м х (1 - Рж). Сумма в 500 рублей может быть
пропита в том случае, если муж пойдет во вторую пивную,
а жена — в первую, вероятность этого события составит Р. х
1 Лица, которым ис нравятся действующие объекты и i мужа, жены
и двух пивных, могут рассматривать задачу об олигархе, налоговой инс-
пекции и двух оффшорных компаниях

[лава 3 Анализ частот и оптимизация рисков 03
В результате среднее количество пропитых денег соста-
вит 1000 х Рмх (1 - рж) + 500 х Ржх (1 - PJ = ЮОО х Р,+ 500 х
х Рх~ 150° х Л,х рж в зависимости от того, с какой частотой
Pv муж выбирает пивные, у жены оптимальный выбор часто-
ты Рж будет, вообще говоря, разный, и наоборот. В этом слу-
чае стандартным решением будет так называемая минимакс-
ная стратегия, то есть такая, при которой каждый из игроков
рассчитывает оптимальную величину исходя из предполо-
жения о самой неблагоприятной для него стратегии против-
ника. В этом случае если первый игрок придерживается ми-
нимаксной стратегии, а второй от нее отходит, то выигрыш
первого игрока увеличивается, а второго — уменьшается.
Итак, пусть при фиксированной частоте Ржмуж ищет для
себя оптимальную стратегию, то есть находит максимум по-
линома Q(P ) = (1000 - 1500 х Р ) х Р + 500 х Р .
^-ч м' ч ж' м ж
В соответствии с приведенной в начале раздела теоремой
максимум может быть при минимальной и максимальной
величине Ри, то есть при Ры = 0 и Ры = I, а также при том зна-
чении Рм, при котором Q\PJ = (1000 - 1500 х PJ = 0. Однако
для рассматриваемого случая Q'(^M) может быть равен нулю
только при Рж = 2/3, поэтому при всех других значениях Рж
«подозрительными» на наличие максимума могут быть толь-
ко значения Рм = 0 и Ры - 1.
При Рм= 0 (выбор второй пивной) среднее количество про-
питых денег Q(PJ = 500 х Рж, а при Ри= 1 (выбор первой пив-
ной) Q(P ) = 1000 х (1 - PJ. Поэтому при выбранном Рж нужно
выбирать максимум из 500 х Рж и 1000 х (1 - PJ. Как легко
видно, при Рж < 2/3 больше первое выражение, то есть мужу
лучше ходить*в первую пивную, а при Рж > 2/3 больше второе
выражение, то есть мужу лучше ходить во вторую пивную.
Выигрыш мужа — максимум из выражений 500 х Рл
и 1000 х(1 - PJ (см. рис. 3.7).
Цель жены— уменьшить выигрыш мужа. Из графика
(рис 3.7) видно, что самый маленький средний выигрыш
мужа - в том случае, если жена выбирает первую пивную с
вероятностью 2/3. Следовательно, наилучшая (минимакс-
ная) стратегия жены - в лпух случаях из трех караулить мужа
У первой пивной.

84
Часть 1 Липли.
■:;cijOHr?iHocfiieii
Средний выигрыш мужа при его оптимальной стратегии
1000
900
800
700
воо
S00
400
300
200
100
-Рж'|
0,1
0.2
0,4
ОЛ
Рис. 3.7. Зависимость среднего выигрыша мужа при оптимальной
стратегии от стратегии жены
Повторив аналогичным образом анализ с переменой иг-
роков, получаем, что для мужа наилучшая стратегия — также
посещать первую пивную в 2 случаях из 3.
Если оба игрока придерживаются этой стратегии, то
среднее количество пропитых денег равно 333 и 1/3 рубля.
Если один из игроков отходит от минимаксной стратегии, то
его выигрыш уменьшается.
3.4. Игры с непротивоположными интересами
(задачи о двух аспирантах
и о трех разбойниках)
Честность — замечательная вещь,
когда все вокруг честные, а ты
один — жулик.
Марк Твен
Продолжение анализа поиска оптимальной стратегии
для случая, когда возможна организация коалиций.
В разобранном выше случае, когда игроков два и они
играют друг против друга, выигрыш одного есть проигрыш

f.wea J. Анализ частот и оптимизация рисков
85
другого. Поэтому игроки не могут образовывать коалицию
и договариваться о выборе стратегии, которая устраивала бы
всех. Для игр с непротивоположными интересами оптималь-
ное поведение игроков может быть другим.
Пусть три ординатора кафедры эпидемиологии (додип-
ломного уровня) после окончания обучения решили остать-
ся в аспирантуре. Они могут подавать документы на одну из
двух кафедр эпидемиологии — додипломного и постдиплом-
ного уровня. На каждой из них есть по одному месту; пара-
метры претендентов на получение места в случае конкурса
практически одинаковы. Известно, что третий аспирант уже
подал документы на додипломный уровень. Какова опти-
мальная стратегия для первого и второго аспиранта?
Если оба они подадут документы на додипломный уровень,
то в результате будет три претендента на одно место и вероят-
ность поступления в аспирантуру составит '/3. Если оба пода-
дут на постдипломный уровень, то будет конкурс в два претен-
дента на место и вероятность поступления составит '/2.

86
Часть I. Анализ вера: тностей
Если они будут случайным образом выбирать, на какую
кафедру подать документы, и будут выбирать додипломную
кафедру с вероятностью р, тогда для первого претендента
возможны следующие случаи:
1. Первый и второй подали на додипломную кафедру.
Вероятность события р\ конкурс— 3 человека на
одно место.
2. Первый подал на додипломную кафедру, второй — на
постдипломную. Вероятность события р{\ — р), кон-
курс — 2 человека на место.
3. Первый подал на постдипломную кафедру, второй —
на додипломную. Вероятность события (1 — р)р, кон-
курса нет.
4. Первый и второй подали на постдипломную кафедру,
вероятность события (1 -р)2, конкурс — 1 человек на
2 места.
В результате вероятность поступления
<Кр)=^р2+^р-0-р)+(1-рУр+^(1-р)\
После раскрытия скобок и приведения подобных полу-
2 11
чаем Q(p) = ~±p2+lp+±. Так как вероятностьр находится в
пределах от нуля до единицы, то в соответствии с изложен-
ной в предыдущем разделе техникой поиска максимума по-
линомов вычисляем, что Q(0) = 1/2 и Q{\) = 1/3. Далее для
поиска других возможных значений, «подозрительных» на
максимум, вычисляем Q'(p) = --p+L. Этот полином равен
нулю при р = 3/8. Подставляя его в Q(p), находим, что в этом
случае вероятность поступления равна 0,59375. Следователь-
но, при случайном независимом выборе шансы на поступ-
ление выше, подавать документы на додипломную кафедру
нужно с вероятностью 3/8, и в этом случае вероятность по-
ступления будет 0,59375.
Однако наилучшей стратегией в данной ситуации будет дру-
гая. Можно встретиться с вторым претендентом и договорить-
ся подавать документы на разные кафедры, а потом случайным
образом разыграть, кто на какую кафедру подает документы

i'uitto J- Анализ частот и оптимизация рисков 87
В этой ситуации с вероятностью '/2 претендент подает до-
кументы на додипломную кафедру в условиях конкурса 1 че-
ловек на два места и с вероятностью '/2 на постдилломную ка-
федруприотсутствииконкурса. Вероятностьпервогособьгтия
равна '/2, и вероятность поступления в этом случае — также
'/ вероятность второго события — '/2, а поступление гаран-
тировано. В результате вероятность поступления '/2 х '/, +
+ '/2 = 0,75, что существенно лучше, чем полученное выше
решение при независимом поведении игроков.
Однако у стратегии согласованных действий есть свои
тонкие места. Пусть в рассматриваемой ситуации у подав-
шего заранее документы шансы не такие же, как у первого
и второго игрока, а немного выше (вероятность его поступ-
ления в случае конкурсного отбора немного выше, чем у
рассматриваемых претендентов). Тогда у того претендента,
которому выпало подавать документы на додипломную ка-
федру и шансы которого немного ниже '/2 появляется ис-
кушение нарушить договоренность и подать документы на
постдипломную кафедру, повысив свои шансу до '/2 В этом
случае оба претендента подают документы на постдиплом-
ную кафедру и их шансы на поступление падают до '/,.
В результате получили, что при согласованной стратегии,
которую игроки нарушают для улучшения своих шансов,
вероятность поступления меньше, чем у полученной выше
стратегии оптимальных несогласованных действий.
Еще больше усложняется ситуация в случае, когда взаимо-
действующих игроков несколько, а также учитываются нели-
нейности выигрыша. Один из возможный вариантов— попу-
лярная в занимательной математике задача о трех разбойниках.
Ситуационная задача.1 Пусть трем разбойникам нужно
поделить награбленное Как им разделить добычу с vmctom
ioio, что они не домеряют друг другу и жульничают'*
Стандартное решение таково Пустьони мыбср\ г первою,
второго и третьего разбойника Тогда первый полечи i юбычу
"а три части, второй ныберст и) грех предложенных uneii
' Решение ситуационных шлам популярна»! и юнременныч ме
чицинских ну »ах форма обучении профессиональной лея re чынч i it

88
Часть I Анапа:: иероятностей
одну себе, третий разбойник выберет одну долю из двух ос-
тавшихся, а первый разбойник заберет оставшуюся долю.
Соль предложенного решения в том, что при таком ре-
шении первый разбойник должен поделить добычу на рав-
ные доли, так как в результате он получит самую маленькую
долю. Однако при серьезном рассмотрении это решение так-
же оказывается неудовлетворительным.
Во-первых, добыча может оказаться не делимой на рав-
ные части. Вспомним, например, сказку о коте в сапогах,
которая начинается с деления на троих братьев наследст-
ва — мельницы, осла и кота. Подвариант — когда ценность
отдельных предметов не равна ценности их суммы. Напри-
мер, если среди награбленного есть сейф и ключ от него, то
желательно, чтобы оба предмета оказались у одного.
Во-вторых, разбойники находятся в неравных условиях,
а в условиях взаимной подозрительности и жульничества вы-
бор из них первого, второго и третьего — задача неразрешимая.
Даже в условиях хорошей делимости добычи из-за неизбежных
ошибок деления первый разбойник получит меньше других.
В-третьих, разбойники могут образовывать коалиции.
Например, первый и второй разбойник могут образовать за-
говор против третьего. Первый выделяет одну большую долю
и две маленькие, второй выбирает большую долю, третий и
первый получают по маленькой, но потом первый и второй
разбойник заново делят свои доли.
Кроме того, даже при отсутствии коалиций разбойни-
ки могут подозревать, что другие объединились против них
в коалицию1.
1 История, которую я, будучи студентом мехмата МГУ, слышал
от преподавателя математики из Ижевска, находящегося в команди-
ровке: «Еду я как-то на трамвае и обсуждаю с несколькими своими
студентами задачу о трех разбойниках в частном случае однородной
непрерывно делимой добычи, а именно о разделе бутылки водки на
троих. На остановке у медучилища входит седовласый профессор в
окружении стайки щебечущих девушек, садится, начинает прислу-
шиваться, а потом громогласным шепотом подзывает девиц: «Идите
сюда, послушайте. Типичный случай шизофрении. Нормальные люди
могут поделить бутылку на троих, а ОНИ — нет!».

fiuea 1 Анализ частот и оптимизация рисков
89
Задача выработки согласованной стратегии усложняется
при увеличении количества разбойников, так как при доста-
точно большом количестве плохо согласующихся друг с дру-
гом хозяйствующих субъектов, преследующих свою выгоду,
они начинают действовать фактически независимо друг от
друга.
Обычно в математических моделях экономики (включая
как производственный сектор, так и игру на бирже, порт-
фельные инвестиции и т. д.) предполагается, что отдельные
разбойники действуют независимо, преследуя свою выгоду.
Мои коллеги, занимающиеся этой областью математики,
жаловались, что в России в связи с увеличивающейся моно-
полизацией такие модели работают все хуже и хуже.

Глава 4
ЭЛЕМЕНТЫ
ТЕОРИИ ВЕРОЯТНОСТЕЙ
На следующем листе был приказ об отдаче
под суд сотрудника Группы Научной охраны
X. Тойти в соответствии с Директивой «О при-
внесении порядка» «за злостное потакание за-
кону больших чисел, выразившееся в посколь-
знутии на льду с сопутствующим повреждением
голеностопного сустава, каковая преступная
прикосновенность к случайности (пробабилит-
ность) имела место 11 марта с. г.». Сотрудника
X. Тойти предлагалось впредь во всех докумен-
тах именовать пробабилитиком X. Тойти...
Аркадий и Борис Стругацкие
«Улитка на склоне»
4.1. Исторический экскурс.
Случай равновероятных шансов
и логические ловушки
Изучение неправильных мыслей вредно
Конфуций
Случай исходов с равновероятными шансами
Неоднозначности определения понятия «равновероятный».

nana '<■ Элементы теории вероятностей 91
С помощью статистических программ рассчитать частоту
того или значения — дело быстрое и простое. К сожалению,
обычной является ситуация, когда известна одна частота,
а найти нужно совсем другую.
Изучением свойств частот и выяснением, как по одним
частотам определить другие частоты, занимается теория ве-
роятностей.
Возникла она в самом начале XVIII века с решения одной
задачи, которую маркиз de 1'Hospital предложил для решения
Бернулли1.
Ситуационная задача. Пусть два одинаково искусных иг-
рока играют (и при этом не жульничают!) в кости до 10 по-
бед. Пусть при счете 9 : 8 им пришлось прервать игру. Как им
разделить деньги, стоящие на кону?
Разумеется, деление поровну не подойдет, так как пер-
вый игрок ближе к победе, чем второй. Часто предлагаемое
решение: 9/17 отдать первому игроку и 8/17 — второму, так
как они сыграли 17 партий, из которых в 9 победил первый
и в 8 — второй.
Однако такое решение не подходит. Действительно,
пусть игроки играют до 20 побед и счет 19 : 18 в пользу пер-
вого. Тогда ситуация в точности такая же, как и раньше, то
есть первому до победы не хватает одной победы, а второ-
му — две, но долевое соотношение выигранных и проигран-
ных партий уже иное.
Заметим, что для определения выигравшего достаточно
сыграть еше две партии, что дает 4 различных исхода:
1) обе партии выигрывает первый игрок;
2) первую партию выигрывает первый игрок, вторую —
второй;
3) первую партию выигрывает второй игрок, вторую —
первый;
4) обе партии выигрывает второй игрок.
В первых трех случаях выигрывает первый игрок, а в чет-
вертом — второй. Так как игроки одинаково искусны, то ве-
роятность каждого из четырех исходов одинакова. Следова-
Хорошо известному также работами по фи шке газон

92
Часть 1 Анализ вероятностей
тельно, шансы игроков на выигрыш соотносятся как 3 к 1,
и первому игроку1 следует отдать 74 ставки, а второму — 74.
Рассмотрим еще один пример. Будем для простоты счи-
тать, что вероятности рождения мальчиков и девочек оди-
наковы и на вероятность рождения ребенка данного пола не
влияет то, какого пола были предыдущие дети (и то, и дру-
гое — не совсем точно). Какова доля семей с детьми одного
пола среди трехдетных семей?
Перечислим все возможные варианты: МММ (все маль-
чики), ММД (два старших ребенка — мальчики, младший —
девочка), МДМ, МДД, ДММ, ДМД, ДДМ, ДДД. Таким
образом, имеется 8 вариантов, по заданным условиям они
равновероятны и два из них соответствуют однополым де-
тям. Итого имеем вероятность в 2/g = '/4.
Частая модификация задачи с несколькими равноверо-
ятными исходами — когда сообщается дополнительная ин-
формация о том, что некоторые исходы невозможны. Пусть,
например, у моего соседа двое детей и я знаю, что по край-
ней мере один из этих детей — мальчик. Какова вероятность
того, что второй ребенок тоже мальчик?
Аналогично рассмотренному выше примеру возможно
4 равновероятных варианта: ММ, МД, ДМ и ДД. В связи с
полученной дополнительной информацией вариант ДД (оба
ребенка — девочки) невозможен. Следовательно, остаются
три возможных варианта ММ, МД и ДМ. В результате по-
лучаем, что вероятность того, что второй ребенок мальчик,
равна '/,-
Если же сообщается информация не просто о том, что
один из детей мальчик, а что старший — мальчик, то остает-
ся два возможных варианта: ММ и МД. В этом случае веро-
ятность того, что второй ребенок мальчик, равна '/
Поэтому при анализе такого рода ситуаций информацию
о том, что именно известно, нужно формулировать очень
1 К этому моменту медики, имеющие хорошую базовую подго-
товку по биологии, обычно вспоминают Менделя с горохом. Дейст-
вительно, расчет частот встречаемости разных вариантов сочетаний
генов - хорошая и традиционная модель для теории вероятностей

Гд а 4. Элементы теории вероятностей УЗ
аккуратно, малозаметные уточнения приводят к изменению
результата.
В рассматриваемом случае набора равновероятных ис-
ходов вероятностная задача сводится к комбинаторной. Для
определения вероятности успешного исхода нужно опреде-
лить общее количество возможных исходов N и количество
успешных исходов п. Тогда вероятность успешного исхода
будет равна n/N.
Так, при игре в кости обычно бросаются два кубика,
а выпавшие на них очки суммируются. На каждом кубике —
шесть граней, поэтому общее количество вариантов при
бросании одного кубика равно 6, а двух — 36 (при каждом
варианте значения первого кубика есть 6 вариантов у второ-
го кубика, итого количество вариантов 6 х 6 = 36).
Суммарное количество очков на двух кубиках может быть
от 2 до 12. Сумма в 2 может быть только в том случае, если
на обоих кубиках выпали единицы. Следовательно, вероят-
ность выпадения двойки равна '/36.
Сумма в 3 может быть уже получена двумя разными спо-
собами — и как единица на первом кубике и двойка на вто-
ром, и как двойка на первом кубике и единица на втором.
Поэтому вероятность выпадения суммы в 3 очка равна 2/36 ~
Сумма в 4 может быть набрана уже тремя вариантами:
1 + 3, 2 + 2иЗ + 1. Поэтому вероятность выпадения 4 очков
равна У36 = У12.
При дальнейшем увеличении суммы количество возмож-
ных комбинаций увеличивается вплоть до суммы 7, которая
может быть набрана 6 способами. Поэтому сумма в 7 очков
выпадает с вероятностью 6/36 = '/6. При дальнейшем увели-
чении суммы количество комбинаций уменьшается вплоть
До суммы 12, которая может быть набрана только как 6 + 6
'л выпадаете вероятностью '/36.
При игре в рулетку имеется 37 возможных вариантов вы-
павшего значения — от 0 (зеро) до 36. Если игрок ставит на
°лно число, то его выигрыш в 36 раз больше поставленного
"а кон (к поставленному добавляют эту величину, увеличен-
ную в 35 раз). При постановке на комбинацию из нескольких

94
Часть 1. Анализ вероятности;
вариантов выигрыш пропорционально снижается. Поэтому
при случайном равновероятном выпадении выигрышных
номеров при любой стратегии игрок в среднем получает36/
от поставленной на кон ставки. "
Выгодно играть в рулетку только в том случае, когда вы-
падающие номера выигрышей не являются равновероят-
ными или независимыми. Так, например, у Джека Лондона
в его рассказах красочно описана история игры на кривой
рулетке. Другой в принципе возможный вариант — угадыва-
ние возможного выпавшего номера по тому, у какого номера
рулетки крупье выпускает шарик, в том случае, если крупье
бросает шарик слишком стереотипно1.
Однако в некоторых других азартных играх ситуация не
столь однозначная. Так, в казино помимо рулетки широко
распространена карточная игра «Блэк Джек». В нее игрок
также играет с крупье, сама игра похожа на игру в очко, но
правила игры у игрока и крупье не совсем симметричны.
В ХТХ и начале XX века эта широко распространенная
игра приносила владельцам казино стабильный доход, при-
мерно такой же, как и игра в рулетку. Однако в середине
XX века на основании изложенных понятий теории веро-
ятности был проведен математический анализ этой игры и
была найдена оптимальная стратегия игрока, при которой
его средний выигрыш практически равен среднему проиг-
рышу. Более того, при дальнейшем анализе было получе-
но, что если игрок знает, какие карты вышли в предыдущих
раскладах, то он может так модифицировать свою стратегию
игры, что в среднем окажется в выигрыше.
Реально помнить все вышедшие карты и варианты моди-
фикации стратегии очень сложно, поэтому были также при-
думаны упрощенные варианты подсчета использованных
карт, позволяющие игроку в среднем выигрывать больше,
чем проигрывать.
В связи с этим в казино были значительно ужесточены
правила игры в «Блэк Джек» Сами правила игры были моли-
1 Владельцы кашпо хорошо чнают о таких но »можиостя\ и успеш
но с ними борются

фицированы в невыгодную для игроков сторону. Для услож-
нения слежения за вышедшими картами введено использо-
вание наборов из большого количества колод. Кроме того,
казино следит за тем, чтобы игроки не проносили в игровые
залы вычислительную технику, средства связи и так далее,
а также наблюдают за процессом игры с тем, чтобы выявить
«счетчиков» — тех, кто считает вышедшие карты и вообще
слишком хорошо играет. Были внесены также и соответству-
ющие дополнения в законы, регулирующие работу казино,
в соответствии с которыми казино имеют право не допускать
в игровые залы любых лиц без объяснения причин. Все это
отражено, например, в популярном кинофильме «Человек
дождя».
Сами задачи расчета количества комбинаций могут быть
весьма сложными (например, для получения вероятности
схождения пасьянса нужно рассчитать количество возмож-
ных раскладов карт, при которых этот пасьянс сходится), но
вероятностная подоплека решаемой задачи проста.
Суммировать вероятности вариантов можно и в том слу-
чае, если их вероятности неодинаковы. Например, если при
обследовании выяснено, что у 2 % населения ->- инсулино-
зависимый диабет и у 1 % — инсулинонезависимый диабет,
то всего диабет у2% + 1% = 3%.
Итак, если известны вероятности всех исходов, то для
определения вероятности выигрыша нужно просуммировать
вероятности всех выигрышных исходов. Если вероятности
исходов известны, то это можно сделать; а вот что делать
в том случае, когда они неизвестны?
Выше разбирались ситуации, когда имеется /^возможных
исходов и при этом известно, что вероятности их одинаковы.
Тогда вероятность каждого исхода равна 1/N.
Однако возможны и ситуации, когда неизвестно, одинако-
вы или нет вероятности разных исходов, но при этом нет ни-
каких возможностей выяснить, какой из них более вероятен,
а какой - менее. Тогда кажется абсолютно естественным из
соображений симметрии считать их равновероятными.
Однако этотестественный выбор быстро приводит к проти-
воречиям Дело в том, что информация об отсутствии различии

96 Чисть 1 Анализ вероятностей
и информация об отсутствии возможности выявить разли-
чия — все-таки разные вещи.
Самая лучшая известная мне иллюстрация этих разли-
чий — логическая задача о старом пирате из старого журнала
«Квант»1.
Задача. Поймали как-то старого пирата. Во время суда
судья сказал:
— Мерзавец! Ты заслуживаешь ста казней, но у меня есть
только одна, поэтому я приговариваю тебя к повешению, а в
качестве дополнительного наказания — тебя повесят в один
из дней на следующей неделе, причем до тех пор, пока за то-
бой не придут на рассвете, ты не будешь знать, в какой имен-
но день тебя повесят. Да будет так!
— Очень хорошо, ваша честь, — сказал пират, который
служил у Флинта канониром и поэтому был в курсе тогдаш-
них воззрений на теорию вероятностей. — Приговор выне-
сен и не может быть изменен, но Вам придется меня отпус-
тить, потому что приговор невозможно исполнить.
— Это почему же?
— Дело в том, что последний день, когда меня можно по-
весить, — воскресенье на следующей неделе. Однако если
до воскресенья меня еще не повесят, то в воскресенье рано
утром я буду знать, что меня повесят именно сегодня. Сле-
довательно, в воскресенье меня повесить не могут. Но тогда
отпадает и суббота, та как рано утром в субботу я буду знать,
что меня должны повесить в субботу или воскресенье, но
воскресенье отпадает, следовательно, меня должны повесить
сегодня. Поэтому в субботу меня повесить также нельзя. Пе-
ребирая все дни недели, получаем, что и в них меня тоже по-
весить нельзя. Следовательно, приговор неисполним!
— Посмотрим! — сказал судья, который был специали-
стом по логике.
В результате пирата повесили в четверг, причем до тех
пор, пока за ним не пришли, он не знал, в какой день его
повесят.
1 Журнал занимательной математики и физики для старшеклас-
сников.

I'uwu 4. Элементы теории вероятностей
97
Поэтому вопрос о том, какими свойствами должны обла-
дать вероятности наблюдаемых событий, достаточно тонок.
При описании эксперимента, условий отбора образцов
и так далее часто говорят о случайном независимом равно-
мерном отборе. Равномерность означает, что вероятность
выбора разных вариантов одинакова. Однако этого недоста-
точно: выбор, равномерный с одной точки зрения, может
быть не равномерным с другой точки зрения.
Например, пусть мы наблюдаем через световой микро-
скоп с круглым полем зрения тонкий прямой сосуд и хотим
определить, с какой вероятностью видимая часть сосуда
принимает ту или иную длину. В этом случае рассматривае-
мая задача — о сечении круга случайной прямой.
Задача. Пусть имеется круг единичного радиуса, кото-
рый пересечен случайной прямой. Какова вероятность того,
что длина хорды, то есть части прямой, находящейся внутри
круга', больше >/з ?
Решение № 1. Проведем радиус, перпендикулярный хор-
де. Пусть h — расстояние от центра круга до пересечения
хорды с радиусом (рис. 4.1).
Рис. 4.1. Расстояние от центра круга до центра хорды
На этом и двух следующих рисунках круг и вписанный
в него равносторонний треугольник со стороной 7з изобра-
жены точечными линиями, а секущая прямая — толстой
1 Величина может быть пыбраиа прои шольно, но. так как V3 -
Длина стороны вписанного и окружность равностороннего треуголь-
ника, то искомая вероятность ищется проще нсего
^ Медицинская с гвтистика

98 Часть 1. Анализ вероятностей
черной линией. На этом рисунке перпендикулярный секу-
щей радиус изображен тонкой черной линией.
Тогда если h < '/2, то длина хорды больше 75, а если Л > '/
то длина хорды меньше 7з . Так как h — в пределах от 0 до ] и
равномерно распределена, то искомая вероятность равна '/
Решение № 2. Рассмотрим длину дуги между точками пе-
ресечения прямой и линии. Пусть а — угол, под которым эта
дуга видна из центра (рис. 4.2).
Рис. 4.2. Угол, под которым видна хорда
Дуга, отсеченная хордой, выделена сплошной линией.
Угол а может быть от 0 до 180°. Сторона равносторон-
него треугольника видна под углом 120°, а если хорда видна
под меньшим углом, то она короче. Следовательно, веро-
ятность того, что случайная хорда будет короче 7з , равна
120/180 = 2/3. В результате получили, что вероятность того,
что хорда длиннее S , равна 1/3.
Решение № 3. Рассмотрим положение точки О в середине
хорды (рис. 4.3).
Рис. 4.3. Положение середины хорды

■ Л Элементы теории вероятностей 99
/,,'rti^J*• .11—1 — ■—-—■—■ -■■—■. - ■ . ...-. ■ ■— . ■ ■■—
Серым цветом закрашен круг радиуса '/г
Если точка середины хорды лежит внутри закрашенно-
го круга, то длина хорды больше 7з , а если вне, то мень-
ше. Однако площадь закрашенного круга составляет '/4 от
■здошади всего круга, а точка середины хорды располагается
случайно. Следовательно, вероятность того, что длина хор-
ды больше %/з , равна 1/4.
В результате имеется 3 разных решения, основанных на
предположениях о равномерности распределения разных ве-
личин:
1) расстояния от хорды до центра;
2) угла, под которым видна хорда;
3) положения точки середины хорды.
Какая из них окажется ближе к истине, зависит от того,
каким именно образом прямая бросается на круг.
Для экспериментальной проверки нарисуем во дворе
круг и будем кидать в него камешки. Если считать, что ка-
мень, попавший в крут, дает середину хорды, то правильным
решением будет решение № 3.
При другом способе проверки будем, находясь в середине
круга, закручивать метлу и отмечать точку, на которую будет
указывать ручка от метлы после остановки. Если выбранные
таким образом две точки соединить отрезком, то правиль-
ным решением будет решение № 2.
Если взять ручку от метлы и закатывать ее в круг (так что
Направление ручки перпендикулярно направлению броска).
то 'травильным решение будет № 1.
Следовательно, простого указания на случайность выбо-
Ра образца недостаточно, нужно достаточно точно описы-
!,ать, каким образом он получается.
Например, если в приведенном выше примере световой
1ИкРоскопии сосуда выбирать срез вне зависимости от на-
' 1'<ия там сосуда, то для срезов, на которых есть сосуды, ие-
^'ятность того, что видимая длина сосуда будет больше 7з
Радиуса круглого поля зрения, равна '/,. Однако в рсачь-
. ■ ' ^'следовании не все срезы будут браться в исследование
г 'МО|'Утотбрасы»ап>см сосуды с видимой тчфчмолименно
' ,{этом случае «длинные» сосуды будуч огбраковываться

100
Часть i. Анализ вероятностей
чаще, чем короткие. С другой стороны, очень короткие со-
суды, проходящие вдоль границы поля зрения, могут отбра-
ковываться из-за того, что для них внутренняя часть сосуда
частично находится внутри поля зрения, а частично — вне,
и трудно определить длину отрезка сосуда.
Поэтому для корректного измерения распределения
размеров изображения объекта нужна точно заданная
формальная процедура, по которой определяется, какой
объект берется в работу, а какой отбраковывается. В этом
случае можно вычислить поправки на «краевые» эффек-
ты и т. д.
4.2. Современный подход.
Аксиоматика Колмогорова
— А если вы убьете невинного?
— Мы не можем убить невинного.
Это исключено.
— Почему исключено?
— Потому что, согласно опреде-
лению и неписанным законам,
каждый, кого ликвидировал пред-
ставитель власти, является потен-
циальным преступником.
Р. Шекли «Билет на
планету Транай»
Современное определение базовых понятий
теории вероятностей.
В течение двухсот с лишним лет с момента возникно-
вения теория вероятностей была достаточно «мутной» дис-
циплиной, основанной на скользких предположениях о том.
какими свойствами обладает вероятность. Основой теории
вероятностей и математической статистики была имении
математическая статистика. Сама дисциплина была полу-
экспериментальной и считалась частью физики
Основными терминами древней теории вероятностен
и математической статистики были: варианта (встретив-

Глава 4- Элементы теории вероятностей
101
шееся в наблюдениях значение), выборочная совокупность
(набор реально наблюдавшихся значений при конечном ко-
личестве наблюдений), генеральная совокупность (предел
выборочной совокупности при неограниченном увеличе-
нии объема наблюдений), а также определяющиеся по этим
наборам выборочные и генеральные частоты, средние и так
далее.
Проблему необходимого уточнения базовых понятий
решил в 1930-х годах А.Н. Колмогоров. После этого теория
вероятностей и математическая статистика стала частью ма-
тематики, причем базисом является именно теория вероят-
ности, а статистика — ее надстройка.
Современная теория вероятностей использует с легкой
руки Колмогорова аксиоматический подход, в рамках ко-
торого с самого начала задается язык теории вероятностей
и свойства вероятности, которыми можно пользоваться.
Базовое определение. Случайная величина (синоним —
распределение) задается тремя объектами: множеством эле-
ментарных событий, множеством событий и вероятностью
событий.
Те значения, которые может принимать случайная вели-
чина, называются элементарными событиями. Например,
для случайной величины «Возраст больного в годах» элемен-
тарным событием будет число 48. Все, что требуется от мно-
жества элементарных событий, — это чтобы оно было непус-
тым, то есть содержало хотя бы один элемент.
В принципе элементарными событиями могут быть
весьма сложные объекты. Например, если мы исследуем
термометры, то каждый термометр описывается уже не
числом, а числовой функцией— зависимостью показа-
ния термометра от истинной температуры. Если речь идет
о случайных процессах, например о динамике заболевае-
мости, то элементарным событием является функция от
времени.
При анализе рентгенограмм элементарным событием
будс| рентгенограмма весьма сюжиый обьекг Работать с
изображениями значшелыю сложнее, чем с числами, к маем-
иости потому, что для изображсипн можно по-разному

102
Часть I Анализ вероятностей
определять, какие изображения близки друг к другу, а ка-
кие — нет1.
Мы в дальнейшем в основном будем рассматривать бо-
лее простой случай переменных, принимающих числовые
значения (или, в крайнем случае, когда значением случай-
ной величины является несколько числовых значений). На-
пример, «артериальное давление» состоит из упорядоченной
пары чисел, первое из которых больше2 второго.
Наборы3 элементарных событий называются событиями.
В частности, любое элементарное событие является событием.
1 Можно определить близкие рентгенограммы как рентгенограм-
мы, у которых яркости точек близки друг к другу. Однако в этом слу-
чае одинаковые рентгенограммы, но полученные при разном среднем
уровне яркости, будут сильно различаться. Можно требовать близости
не яркости отдельных точек, а яркости точек по сравнению со средней
яркостью. Тогда рентгенограммы с разной яркостью будут близки, но
будут различаться рентгенограммы с разной контрастностью. Кроме
того, при таком поточечном сравнении разными будут считаться оди-
наковые рентгенограммы, полученные со сдвигом.
Большая сложность формализации того, что является одинако-
вым изображением, а что разным, особенно хорошо видна на примере
создания систем автоматического распознавания изображений. Не-
смотря на огромные усилия, автоматические системы по-прежнему
хуже справляются с задачей, чем человек.
2 Строго говоря, больше или равно, причем равенство выполняет-
ся только для нулевых значений.
3 Вопрос о том, все ли наборы элементарных событий можно счи-
тать событиями, весьма нетривиален. Если Вы будете смотреть книги
по теории вероятностей и математической статистики для специали-
стов, имеющих приличную математическую подготовку, то Вы найде-
те там о-алгебры, интегралы Лебега (обычного интеграла Римана тут
недостаточно) и прочие малоприятные веши. Дело в том, что даже для
числовых случайных величин все возможные множества элементар-
ных событий брать в качестве событий нельзя, так как с некоторым»
такими событиями начинаются проблемы Однако во второй полови
не XX века математикам удалось выяснить, что с любым событием
для построения которого можно чадать конечный конструктивный
алгоритм, проблем быть не может. Поэтому Вы можете не обращать
никакого внимания на эти тонкости любой рассматриваемый Вами
конкретный набор элементарных событий есть событие Итого, при

Глава 4- Элементы теории вероятностей
103
Событие может состоять и из нескольких элементарных
событий. Например, для указанной случайной величины
«Возраст больного в годах» одно из событий — «пациент-
несовершеннолетний», то есть ему менее 18 лет. Если набор
возможных элементарных событий бесконечен, то и в со-
бытиях также может быть бесконечное число элементарных
событий.
Для числовых и других не слишком сложных случайных
величин любой конкретно заданный набор элементарных
событий есть событие.
Приведем теперь несколько примеров.
1. Бросание симметричной игральной кости.
Всего имеется 6 элементарных событий: «очко», «2 очка»,
...«6 очков». Событие — любой набор из элементарных со-
бытий, например «чет» — сумма элементарных событий
«2 очка», «4 очка» и «6 очков».
Вероятность любого элементарного события равна 1/6,
вероятность события — количеству входящих в него элемен-
тарных событий, деленному на 6.
Набор элементарных событий может быть и беско-
нечным.
2. Будем бросать симметричную монету до тех пор, пока
не выпадет решка. Элементарные события: «решка выпала
на л-й раз», где п- 1,2, 3,.... Вероятность этого элементар-
ного события — 1/(2").
Другой аналогичный пример — скольких пациентов при-
мет врач до тех пор, пока один из них не напишет на него
жалобу.
чин для необходимости работать с достаточно сложной техникой две.
Первая — то, что элементарные события в общем случае могут быть не
числами, а весьма сложными объектами. Вторая — в том, что в совре-
менной математике под множествами понимают любые наборы объек-
тов, даже существующие в очень слабом смысле Так, множество всех
алгоритмов, то есть конечных однозначных наборов инструкций, хоти
и бесконечно, но счетно, то есть его можно пересчитать Множество
же всех числовых множеств несчетно, то есть намного больше Следо-
вательно, для почти всех множеств чисел нет никакого способа у нить,
m каких чисел они состоят

'04 Часть 1. Анализ вероятностей
3. Равномерное распределение на отрезке [0,1].
Здесь элементарные события — числа, не меньшие нуля
и не большие единицы. События: множества (с оговорками,
приводимыми в примечании) из чисел. Если событие А со-
стоит только из чисел отрезка [0,1], то вероятность события
А равна длине множества А. В частности, если 0 < а < Ь < 1,
то P([a,b\) = b-a.
4. При определении рН раствора может получиться число
в пределах от 0 до 14. Между любыми двумя значениями рН
возможно промежуточное значение (для чего достаточно два
раствора смешать вместе).
В общем виде требуемые свойства вероятностей таковы:
1. Вероятность Р(А) того, что произойдет событие
А, — число, которое не может быть меньше 0 или
больше 1.
2. Вероятность того, что произойдет хоть что-нибудь,
равна 1.
3. Если Av Av... — набор событий, любая пара кото-
рых не имеет общих элементарных событий (то
есть любые два события из этого набора не могут
произойти одновременно), то Р(А{ или А2 или...) =
= Р(Л,) + Р(А2) +...
Основная прелесть аксиоматики Колмогорова состоит
в том, что на этом она заканчивается. Как видно, постули-
руемые свойства вероятности очень просты и интуитивно
приемлемы, а все тонкие моменты о возможных свойствах
выборочных частот остаются вне «поля зрения».
Рассмотрим простой пример. Пусть 60 % больных ОРЗ бо-
леют вирусными заболеваниями, 10 % — стрептококкозами
и 30 % — иными бактериальными инфекциями. Определим
долюбольныхбактериальнымиинфекциями Таккакбольной
бактериальной инфекцией может болеть либо стрептокок-
ком, либо нестрептококковой инфекцией (но не тем и иным
одновреме!пю), то получаем искомую вероятность как 10 °с +
4 30% =40%.
К решении) ной >адлчп можно также подойти с другом
с тропы Гак как Поиыюй более i либо вирусной инфекцией,
либо бактериальной (по не одновременно обоими), то их

Глава 4. Элементы теории вероятностей
105
суммарная вероятность равна 100 %. Итого доля бактериаль-
ных инфекций равна 100 % - 60 % = 40 %.
При сопоставлении старого подхода к определению ве-
роятностей, основанного на выборочных частотах, и подхо-
да Колмогорова, видно, что в старом подходе вероятность
определялась только для вариант, то есть элементарных со-
бытий, а при современном — для событий, то есть не только
элементарных событий, но и их наборов.
Если случайная величина принимает конечное количест-
во возможных значений, то усложнение конструкции за счет
введения вероятности событий избыточно, так как получить
вероятность события можно просто просуммировав вероят-
ности входящих в него элементарных событий. Если же слу-
чайная величина может принимать бесконечное количество
разных значений, то знания вероятности элементарных со-
бытий может быть недостаточно.
Пусть мы меряем рН некоторых биологических проб.
Тогда при достаточно точном определении рН значения
разных проб не будут в точности повторяться. В генераль-
ной совокупности ни одно значение не будет повторяться
больше одного раза, и, следовательно, генеральная частота
любой варианты равна нулю.
При определении вероятности событий будет опреде-
ляться не только вероятность отдельных значений, но и
вероятность того, что рН попадает в тот или иной проме-
жуток.
Безусловная оправданность перехода на современную
аксиоматическую теорию вероятностей и математическую
статистику основана на том, что на ее основе работать про-
ще, чем в предыдущей системе понятий. Поэтому математи-
ки перешли на нее быстро и дружно.
К сожалению, 70 лет оказались недостаточно большим
сроком, чтобы эти новации дошли до всех специалистов
в иных областях знания.

106
Часть I Анализ вероятностей
4.3. Вычисление вероятностей.
Условные, априорные и апостериорные
вероятности
Проект дополнения в уголовный кодекс:
За хищения в особо крупных размерах — расстрел (условно), за
проезд в трамвае без билета — реабилитация (посмертно).
Современный анекдот
Как по одним частотам вычислить другие.
Как было упомянуто в начале раздела 4, часто при помо-
щи пакета статистических программ мы получаем частоты
одних событий, а нам нужны частоты других событий. В этом
разделе будет излагаться техника вычисления вероятностей.
В базовых свойствах вероятности постулируется, что ве-
роятность того, что произойдет хоть что-нибудь, равна 1.
Кроме того, для любого события А события «А» и «не Л» — не
пересекаются, следовательно, вероятность их суммы равна
сумме вероятностей. Тогда Р(А + не А) = Р(А) + Р(не А) = 1.
В результате получили следующую теорему.
Теорема 1. Дне А) = 1 - Р(А)
Например, если 68 % аспирантов оканчивает аспиранту-
ру, представив диссертацию для защиты, то 32 % оканчива-
ют аспирантуру без представления диссертации для защиты.
Из заданного аксиоматически свойства суммирования
вероятностей непересекающихся событий можно сделать
вывод и для пересекающихся событий.
Теорема 2. Р(А или В) = Р(А) + Р(В) - Р(Аи В).
Пример. Пусть после проведения некоторой операции
осложнения (любые) наблюдаются у 14% оперированных,
причем у 9 % наблюдается спаечная болезнь, а у 8 % - иные
формы осложнений. Тогда и спайки, и другие формы ослож-
нений будут наблюдаться у9% + 8%-14% = 3% больных
Достаточно часто в добавление к известной вероятности
события имеется также некоторая дополнительная инфор-
мация, которая меняет эту вероятность Например, леталь-
ность больных, поступинших и больницу с острой кроио-

Глава 4. Элементы теории вероятностей
107
точащей язвой желудка, составляет около 10 %. Однако если
больному больше 80 лет, то эта летальность — 30 %.
Для описания таких ситуаций были введены так называ-
емые условные вероятности. Они обозначаются как Р{Л/В)
и читаются «вероятность события Л при условии события 5».
Например, если в имеющемся массиве данных было
500 больных и их них 50 умерли, то частота летальных случаев
определяется как — = 10 %. Если же из 500 больных 100 были
старше 80 лет и из них 30 умерли, то летальность среди лиц
старше 80 определяется как — = 30 %. Кроме того, условные
вероятности можно определить не только из прямого опре-
деления частоты, но и из комбинаций других вероятностей.
В этом случае для вычисления условной вероятности ис-
пользуется формула
Р(А/В) = Р{АНВ).
Р(В)
Например, пусть среди больных, поступивших в больни-
цу с острой кровоточащей язвой желудка, 20 % — больные
старше 80, причем среди всех больных доля умерших боль-
ных старше 80 лет — 6 % (напомним, что доля всех умерших
больных составляет 10 %). В этом случае
„,-, „. „„, ДУмер и старше 80) 6% ,..,
Р(У мер/Старше 80)= — - = = 30% .
V V/ v ' Р(старше80) 20%
При использовании условных вероятностей часто поль-
зуются терминами априорной (буквально — до опыта) и
апостериорной (буквально— после опыта) вероятности
Действительно, если мы не знаем возраста больного, то ве-
роятность (априорная) его смерти мы оцениваем в 10 9с, но
если узнали и выяснили, что ему больше 80, то вероятность
(апостериорная) летального исхода оценивается уже и 30 %
Для иллюстрации описанной выше техники работы с ве-
роятностями также определим вероятность летального исхо-
да у больных не старше 80 лет В условиях рассматриваемого
примера было скашно, ч го с rapine 80 iei 20 "^ нацией юн.

108
Часть 1. Анализ вероятностей
следовательно, не старше 80 лет — 80 %. Далее, общая леталь-
ность— 10%, причем 6% всех пациентов— люди старше
80 лет с летальным исходом. Таким образом, люди не старше
80 лет с летальным исходом составляют 10% -6% =4%.
Итого:
d/a/ /и опч /'(Умер и не старше 80) 4 % , _
Р(Умер/Не старше 80) = — - - = = 5 %
Р(Не старше 80) 80%
Ничего не зная о пациенте, мы оцениваем вероятность
летального исхода в 10 %. Если мы выясняем, не старше ли
он 80 лет, то в зависимости от результата мы оцениваем ве-
роятность летального исхода в 30 % или 5 %. Узнав о пациен-
те еще что-нибудь, мы сможем еще уточнить вероятность его
летального исхода и т. д.
Приведенную выше формулу для определения условной
вероятности легко понять. Действительно, умножим обе
части на Р(В) и получим
НА/В) х Р(В) = Р(АиВ).
Фактически левая и правая часть формулы — разные
способы регистрации одного и того же события «А и В». Если
для регистрации этого события мы сразу выясняем, не слу-
чилось ли и событие А, и событие В, то это схема регистра-
ции, соответствующая правой части равенства. Если же мы
вначале выясняем, не произошло ли событие В, а уже только
в этом случае выясняем, не произошло ли и событие А то это
схема левой части равенства.
Пользуясь условными вероятностями, можно по одним
вероятностям вычислять другие, например менять местами
событие и условие.
Рассмотрим эту технику на примере анализа связи риска
заболевания ревматизмом (ревматической лихорадкой) и од-
ного из антигенов, являющихся для него фактором риска
1астота заболевания ревматизмом - около I % Обозна-
чим наличие ревматизма как R<, тогда Л Я*) = 0 oV
v 95Н4ибсГ,,,ГГСМа бУДвМ °Г) °ШаМ:,1Ь Как ^-'Его находя,
У 95 Л больных ревматизмом „ у ь % лиц, рспмап, ,мом w

Глава 4. Элементы теории вероятностей
109
болеющих. В наших обозначениях это: условные вероятно-
сти Р{А+/РС) = 0,95 и P(A+/R-) = 0,06.
На основании этих трех вероятностей будем последова-
тельно определять другие вероятности.
Прежде всего если заболеваемость ревматизмом Д/Г) =
= 0,01, то вероятность не заболеть P(Rr) = 1 - P(R") = 0,99.
Из формулы для условной вероятности Р(А+ и JT) =
= P(A+/F) х Р(1Г) = 0,95 х 0,01 = 0,0095, или 0,95 % популя-
ции одновременно и болеют ревматизмом, и имеют антиген.
Аналогично Р(А+ и В~) = Р{А+/Вг) х P(R~) = 0,06 х 0,99 =
= 0,0594, или 5,94 % популяции носят антиген, но ревматиз-
мом не болеют.
Так как все имеющие антиген или болеют ревматизмом,
или им не болеют (но не одновременно и то, и другое), то
сумма двух последних вероятностей дает частоту носитель-
ства антигена в популяции в целом:
Р(А+) = Р(А+ и IT) + Р(А+ и R-) = 0,0095 + 0,0594 = 0,0689.
Соответственно доля людей, не имеющих антиген, равна
Р(А-) = \-Р(А+) = 0,9311.
Так как заболеваемость ревматизмом равна 1 %, а доля
лиц, имеющих антиген и болеющих ревматизмом, равна
0,95 %, то доля лиц, болеющих ревматизмом и не имеющих
антигена, Р(А~ и /Г) = P{F) - Р(А+ и /Г) = 0,01 - 0,0095 =
= 0,0005.
Теперь будем двигаться в обратную сторону, переходя
от вероятностей событий и их комбинаций к условным ве-
роятностям. По исходной формуле условной вероятности
Ш/О^"^'^—» 0,1379 , или примерно 13,8%
Р(А*) 0,0689
лиц, носящих антиген, заболеют ревматизмом. Так как забо-
леваемость популяции в целом лишь 1 %, то факт выявления
антигена повышает вероятность заболевания ревматизмом
примерно в 14 раз.
d/d'/a-v W »А) °'0005
Аналогичным образом /,(R/A)=———— = ——- =
Р(А) 0,9311
- 0,000054, то есть тот факт, что при проверке антигена не
обнаружено, снижает нероятпость заболевания ревматизмом
примерной 19 раз.

110
Часть 1. Анализ вероятностен
При проведенном анализе частот заболевания ревматизмом
и носительства антигена мы решали задачу «по действиям», как
школьники младших классов на уроке арифметики. Если свер-
нуть все промежуточные вычисления в одну формулу, то это
будет так называемая формула полной вероятности Байеса.
Технически подобные вычисления несложны, однако
при их проведении легко «заиграться».
Рассмотрим еще одну задачу, относящуюся к этому классу.
Пусть известно, что в неком городе 40 % вспышек ОРЗ в дет-
ских дошкольных учреждениях — стрептококковой природы
и 60 % — иной природы. При этом при любых стрептококко-
зах 10 % заболевших имеют ангину, тогда как при любых дру-
гих возбудителях доля больных с ангиной составляет 3 %.
Какова вероятность возникновения ангины?
К событию «ангина» относятся два исхода: ангина при
стрептококкозе и ангина при других ОРЗ. Вероятность пер-
вого исхода равна 0,4 х 0,1 = 0,04; вероятность второго исхо-
да — 0,6 х 0,003 = 0,018. Итого вероятность возникновения
ангины равна 0,058, или ангина встречается в 5,8 % случаев.
Определим далее долю стрептококкозных ангин среди
всех ангин в рассматриваемой задаче. Вероятность стрепто-
коккозной ангины 0,04; суммарная вероятность анги-
ны 0,058; следовательно, доля стрептококкозной ангины
0,04/0,058 = 20/29, и в 20 случаях из 29 ангина — стрептокок-
козного происхождения.
Рассмотрим теперь следующее развитие нашей задачи
Пусть в дошкольном учреждении развивается вспышка, вы-
званная некоторым (одним) возбудителем, и у первого до-
школьника развилась ангина. Какова вероятность того, что
у второго дошкольника из той же вспышки также разовьется
ангина?
Итак, если у первого дошкольника ангина, то, как уста-
новлено выше, с вероятностью 20/29 вспышка — стрепто-
коккошая и с вероятностью 9/29— не стрептококкозная
При cTpcinoKOKKoic вероятность ангины 0.1, и других случа-
ях 0,03 Итого вероятное п. наступления ангины у шорою
лошколытка раина 0,1 (20/29) l 0,03 > (*)/29) - 2,27/29, что
примерно равно 0,078

Глава 4. Элементы теории вероятностей
111
Кажется, что задача решена, однако это не так: послед-
ний вывод неправилен.
Здесь мы используем следующую схему анализа: у нас
имеется исходная (априорная) вероятность наступления того
или иного события. Далее мы проводим некоторые испыта-
ния, которые говорят, что произошедший исход относится
уже не ко всему набору, а к некоторой их совокупности. По
этой совокупности пересчитываются (апостериорные) ве-
роятности наступления возможных исходов, на основании
чего имеется возможность расчета вероятности наступления
любого интересующего нас события.
Однако обычно этой априорной вероятности нет. Так,
например, в рассматриваемой задаче предполагалось, что у
любого стрептококкоза вероятность ангины 0,1, а у нестреп-
тококкоза — 0,03. Но это, естественно, не так: у стреп-
тококкозов имеются штаммы различной вирулентности,
нестрептококкозы же — вообще набор микробов и вирусов
с совершенно разными характеристиками.
4.4. Независимые события
Классификация болезней по С.Г. Паку и НА. Мухину1:
1. Инфекционные болезни, для которых вызывающий их возбуди-
тель известен.
2. Инфекционные болезни, для которых вызывающий их возбуди-
тель пока неизвестен.
3. Болезни от таблеток.
Определение независимых событий.
Вычисление вероятности цепочки событий.
Достаточно часто наблюдаемое событие является после-
довательностью нескольких составных частей.
1 Сергей Григорьевич Пак— член-корр РАМН, профессор, Jan.
кафедрой инфекционных болсшей ММЛ им ИМ Сеченова
' Николай Алексеевич Мухин академик РАМН, профессор, ми
кафедрой терапии проф болсшей ММА им ИМ Сеченова, главный
врач клиники проф болечнеп

112
Часть I. Анализ вероятностей
Определение. События А и В независимы, если вероят-
ность того, что они произойдут одновременно, равна произ-
ведениям их вероятностей, то есть Р(А и В) = Р(А) х Р(В).
Определение. Две случайные величины называются неза-
висимыми, если любое событие первой случайной величины
не зависит от любого события второй случайной величины.
Обратите внимание на то, что это — определение неза-
висимых событий, а не доказанная теорема о свойствах не-
зависимых событий. Вопрос о том, что можно считать неза-
висимыми событиями, а что нет, — очень сложен. Поэтому
математики вновь воспользовались аксиоматическим под-
ходом и использовали свойство объекта в качестве его опре-
деления.
С другой стороны, введенное определение независимо-
сти событий хорошо согласуется с интуитивным представ-
лением о независимости. На основании этого определения
и введенного в предшествующем пункте понятия условной
вероятности легко получить следующий результат.
Теорема. Если А и В— события с ненулевой вероятно-
стью, то они независимы тогда и только тогда, когда Р(А) =
= f\A/B).
Следовательно, для независимых событий условные
и безусловные вероятности совпадают. События независи-
мы тогда и только тогда, когда информация о том, произош-
ло ли одно из них, не меняет вероятность того, что произой-
дет другое событие.
Например, определим вероятность того, что в семье
с двумя детьми оба рожденных ребенка — мальчики. Тогда
(в ранее высказанных предположениях) вероятность рожде-
ния мальчика (для каждого из двух детей) равна 0,59, а так
как эти события независимы, то вероятность искомого со-
бытия равна 0,5 х х 0,5 = 0,25.
Другой пример.
Ситуационная задача. Пусть для оборудования операци-
онной нам нужно закупить аппарат для обеспечения искус
слюнного дыхания. Мы можем воспользоваться двумя мо-
делями. Первая — дорогая импортная модель, которая стоит
К) 000$, но зато дает один отката 100 тысяч операций. Кроме

fAafta 4. Элементы теории вероятностей 113
этого нам предлагают дешевую отечественную модель, которая
стоит всего 1000$, но отказывает на каждой сотой операции.
Будем ли мы поддерживать отечественного производителя?
Покупать аппарат второго типа, несмотря на его деше-
визну, мы не должны: фатальный отказ оборудования на
каждой сотой операции недопустим. Покупать аппарат пер-
вого типа — заметно дороже. Однако есть и лучший выход.
Можно купить четыре аппарата второго типа и подклю-
чить их одновременно, так что при отказе одного из них па-
циент будет снабжаться воздухом от других. Вероятность не-
зависимого отказа одновременно четырех аппаратов равна
0,01 х 0,01 х 0,01 х 0,01 =0,00000001. Таким образом, закупка
четырех аппаратов второго типа не только в два с полови-
ной раза дешевле закупки аппарата первого типа, но и на-
дежнее — в этом случае вероятность отказа составляет лишь
одну стомиллионную.
Еще один пример такого рода.
Ситуационная задача. Вы собираетесь лететь на самолете
чартерным рейсом. При ближайшем осмотре самолета Вы
приходите в ужас оттого, что его моторы работают с явны-
ми перебоями, но стюардесса Вас утешает, так как, действи-
тельно, каждый из моторов примерно на одном рейсе из ста
отказывает, но самолет четырехмоторный, а если что, он и на
трех моторах долетит. Полетим или откажемся?
Для принятия обоснованного решения вычислим неко-
торые вероятности.
Для каждого двигателя вероятность того, что он откажет,
равна 0,01, следовательно, вероятность того, что он не отка-
жет, равна 0,99. Поэтому вероятность того, что не откажет ни
один из двигателей, равна 0,99 х 0,99 х 0,99 х 0,99 = 0,96059601.
Соответственно, вероятность того, что откажет хоть один из
Двигателей, равна 1 - 0,96059601 = 0,03940399
Далее, вероятность того, что первый из двигателей от-
кажет, а остальные — нет, равна 0,01 х 0,99 х 0,99 х 0,99 ~
= 0,00970299. Такова же вероятность того, что второй отка-
жет, а остальные— пет, и так далее Таким обраюм, перо
ятность того, что один из четырех двигателей откажет, а ос
тальные - нет, равна 4 х 0,0097029ч = 0.03Ш 1%

114
Часть I Анализ вероятностей
Искомая вероятность того, что у него откажет не более
одного двигателя, равна сумме вероятностей того, что не
откажет ни один из двигателей, и того, что откажет один
из четырех двигателей, то есть 0,96059601 + 0,03881196 =
= 0,99940797. Соответственно, вероятность того, что откажет
более одного двигателя, равна 1 - 0,99940797 = 0,00059203,
или примерно 6 таких отказов на 10 тысяч полетов.
Решение о том, нужно ли отказываться от поездки при ве-
роятности гибели в дороге 0,0006, следует принимать уже на
основании оценки ценности поездки. В принципе, при сред-
ней продолжительности жизни в 70 лет (или около 25 тысяч
дней) вероятность смерти за день около 0,00004, или всего в 15
раз меньше. Поэтому если вы более чем на две недели летите в
абсолютно безопасное место (или летите на отдых и лечение, в
результате которого ожидаемое увеличение продолжительнос-
ти жизни больше чем на две недели), то эта поездка оправдана.
В начале этой книги я упоминал, что слабым местом
современных медиков часто является их невысокая мате-
матическая подготовка. Однако у медиков есть и свои силь-
ные стороны, одна из которых — развитое чувство здравого
смысла. Поэтому при занятии с группой к этому моменту
слушатели обычно начинают понимать, что их где-то обма-
нывают, хотя и не могут понять, где именно.
Основное «тонкое место» подобных расчетов — требо-
вание к независимости событий. Действительно, то, что
одновременно произойдет несколько редких независимых
событий, маловероятно. Однако у них может быть некото-
рая общая компонента, и даже если доля этой компоненты
в общей частоте отказов каждого конкретного агрегата мала,
ее вклад может коренным образом поменяться при опреде-
лении частоты массовых отказов.
В рассмотренном примере с самолетом есть причины
отказа моторов (плохие метеоусловия, некачественное го-
рючее и т. д.), действующие одновременно, поэтому веро-
ятность массового отказа будет выше, чем было получено
в расчетах.
Вернемся к рассмотренному выше примеру с отечествен-
ным аппаратом искусственного дыхания. Такие причины

1'лава 4. Элементы теории вероятностей
115
отказов, как случайные механические поломки и т. д., дейст-
вительно, достаточно независимы, и в этом случае дублиро-
вание повышает надежность системы в целом. Если же часть
их отказов происходит из-за того, что их система электропи-
тания не снабжена соответствующими фильтрами и броски
напряжения в сети выводят их из строя, то при соответству-
ющем броске они одновременно будут выходить из строя,
и увеличение количества аппаратов надежность не повыша-
ет. Если механические поломки происходят из-за того, что
аппараты быстро изнашиваются в процессе эксплуатации,
то после нескольких сот операций аппараты начнут массово
выходить из строя.
К сожалению, дать однозначные рекомендации типа
«из-за возможной зависимости причин, вызывающих от-
каз, один импортный аппарат будет работать надежнее, чем
четыре отечественных» мы также не можем. Дело в том, что
реально проверить надежность аппарата на 10 тысячах опе-
рациях невозможно, и приводимые величины наработки на
отказ также являются чисто расчетными, причем считают-
ся они именно по той схеме, которую мы здесь критикуем.
В отказоустойчивых аппаратах обычно имеется дублирова-
ние, и расчетная величина надежности определяется произ-
ведением вероятностей.
Хорошим иллюстративным примером несоответствия рас-
четной и фактической надежности является авария на Черно-
быльской АЭС. Там для предотвращения разрушения реактора
имелось несколько независимых систем обеспечения безопас-
ности. Каждая из них была достаточно надежна (хотя в них и
бывали отказы), но из-за их независимости и большого коли-
чества вероятность одновременного отказа всех систем была
астрономической. К сожалению, при оценке безопасное™
разработчики не учли такого маловероятного, но общею для
всех систем защиты, фактора, как то, что украинское Мини-
стерство энергетики пришлет на АЭС обязательную програм-
му проведения испытаний (просто скопированную с программ
проверки тепловых электростанций), н ходе которых псе сие
темы защиты должны быть отключены вручную, и оператора,
который действительное KUI чту программу выполнять

116
Часть I. Анализ вероятностей
При расчете вероятности набора событий очень часто ис-
пользуется предположение об их независимости. Например,
при определении эффективности метода лечения исполь-
зуется предположение о том, что результат лечения одного
пациента не зависит от результата лечения другого. Однако
в том, насколько это предположение справедливо, нужно
тщательно разбираться.
Например, если мы анализируем частоты летального
исхода у хирургических больных, то кажется естественным
считать это независимыми событиями. Однако если часть
больных умирает после операции от внутрибольничных ин-
фекций, то факт смерти одного из них от инфекционных ос-
ложнений повышает вероятность смерти других от инфек-
ционных осложнений.
Даже если речь идет только о летальности на операцион-
ном столе, то и в этом случае данные события не являются
независимыми. Так, если хирургические больные появля-
ются в результате тяжелых катастроф, стихийных бедствий
и т. д., то их летальность выше как вследствие более тяжело-
го состояния, так и из-за невозможности значительно увели-
чить объем медицинской помощи без ущерба качеству. Поэ-
тому тот факт, что случайно взятый больной умер, повышает
вероятность того, что он — жертва стихийного бедствия,
следовательно, это повышает вероятность того, что и дру-
гие — тоже жертвы стихийного бедствия и, следовательно,
у них вероятность летального исхода выше.
Понятно, что для всех инфекционных заболеваний факт
появления одного больного увеличивает вероятность появ-
ления других больных. Однако вопрос о том, какие заболе-
вания инфекционные, а какие нет, весьма сложен.
Во время выступления на одном из ученых советов меди
ко-профилактического факультета ММА им. ИМ Сечено
на, посвященного работе кафедры инфекционных болезней,
Сергей Григорьевич Пак отмечал, что круг болезней, отно-
сящихся к инфекционной патологии, все время возрастает
Так, вплоть до середины XX века гепатиты лечили гепато-
логи, потом было выявлено наличие вирусных гепатитов,
и большая часть гепатиток перешла в ведение инфекннони-

Глава 4. Элементы теории вероятностей
117
стов. Более новый пример — роль Helicobacter pillory в раз-
вития язвы желудка. При этом считается, что к настоящему
моменту описано лишь 20 % вирусов человека. Далее Сергей
Григорьевич выдвинул тезис о том, что все болезни человека
на самом деле имеют инфекционную основу, просто не для
всех них роль микроорганизмов в патогенезе выявлена. По-
сле этого слово взял академик Николай Алексеевич Мухин и
сказал, что полностью согласиться с Сергеем Григорьевичем
он не может, так как есть еще один класс болезней — от таб-
леток.
В большинстве разделов в качестве эпиграфа использу-
ются шутливые высказывания. Эпиграф этого раздела абсо-
лютно серьезен1.
Необоснованное использование предположения о неза-
висимости в действительности зависимых событий приводит
к неправильному расчету вероятностей. Особенно велико это
расхождение при определении вероятности встречаемости
большого набора одинаковых событий. В предположении о
независимости эти вероятности должны быть очень малы-
ми, тогда как в действительности это может быть не так.
Например, за то время, пока я иду от метро до работы,
я встречаю около 100 прохожих. Вероятность того, что встре-
ченный будет мужского пола, равна примерно '/, (на самом
деле даже немного меньше, так как в этих местах женщины
встречаются несколько чаше). Поэтому вероятность того,
что тридцать подряд идущих людей окажутся мужского пола,
порядка ОД)30, а следовательно, вероятность того, что среди
встреченных мною по дороге людей будет набор в 30 мужчин
подряд, - около 100 х 0Д)31\ что примерно равно КГ Сле-
довательно, даже если ходить на работу каждый лень, вклю-
чая выходные и праздники, то упомянутое событие буче г
происходить примерно раз в 30 тысяч лег
Реально оно происходит значительно чаше - примерно
pa \ в месяц я встречаю солдат, илуших строем п расположен-
ную рядом баню
' Пол 1-е го-ню рлчумпопуж-кит-.т.ик.и.нт.и-и пронок.чиюи
по чаостренной формутропке

118
Часть I. Анализ вероятностей
4.5. Закон больших чисел.
Расчет необходимого объема наблюдений
Лозунгу них был такой: «Познание бесконечности требует бесконеч-
ного времени». С этим я не спорил, но они делали из этого неожидан-
ный вывод: «А потому работай не работай — все едино».
Аркадий и Борис Стругацкие
«Понедельник начинается в субботу»
Как статистические погрешности вычисления частоты
зависят от объема наблюдений.
Выше использовались два разных понятия: частота и ве-
роятность. Частота определяется как доля успешных испы-
таний в имеющемся наборе наблюдений, а вероятность —
как истинное свойство события, которое проявляется через
частоту. Однако для практического использования хорошо
было бы знать, насколько частота может отличаться от веро-
ятности.
Ответ на этот вопрос дает первый краеугольный камень
классической теории вероятностей, называемый законом
больших чисел.
Теорема (закон больших чисел). По мере увеличения объ-
ема наблюдений частота стремится к вероятности.
С философской точки зрения тот факт, что когда-нибудь
мы все узнаем достаточно точно, не может не обнадеживать.
Однако для практического использования нужен другой ре-
зультат: насколько могут различаться частоты и вероятности
при данном объеме наблюдений.
Ответ на этот вопрос дает так называемый усиленный
закон больших чисел. Пусть Р{А) - вероятность события А
a PN(A) - его частота, определенная по ^наблюдениям.
Теорема (усиленный закон больших чисел). IР{А)-Р (А)\
порядка ^!И[£^))
7/v
На двух следующих рисунках прицелен пример .имене
ния выборочной частоты п чависимостн от объема выборки
Vice при постепенно увеличивающемся оиьсме выборки

Глава 4. Элементы теории вероятностей
119
определялась выборочная частота события, вероятность ко-
торого равна 0,3. На рис. 4.4 представлен участок с объемом
выборки от 1 до 100, на рис. 4.5 — от 1 до 1000.
1 11 21 31 41 51 61 71 81 Э'
Рис. 4.4. Зависимость частоты от объема выборки (Р= 0,3)
0,6 п
0,5
0,2
I 101 201 '"11 1И1 ''«I 1-Л Yf" I"'
Рис. 4.5. Зависимости ч.чстош от оСп.емл ны6п|»и (Р ОЗ)

120
Часть 1. Анализ вероятностей
При этом усиленный закон больших чисел — достаточно
пессимистичный результат. Он говорит о том, что по мере
увеличения объема наблюдений точность определения ча-
стоты нарастает достаточно медленно, пропорционально
квадратному корню из количества наблюдений. Для того
чтобы повысить точность в 10 раз, нужно объем наблюдений
увеличить в 100 раз.
Поэтому современная медицина, как и большинство дру-
гих опирающихся на эмпирический опыт наук, — наука пре-
имущественно первого знака после запятой. Для того чтобы
получить частоту с точностью до одной десятой, нужны сотни
наблюдений, для точности в два знака — в десятки тысяч. Так
как общее количество всех людей, живущих или живших ког-
да-нибудь, около 10 миллиардов, то есть 10"\ то этого объема
наблюдений недостаточно для получения каких-то частот
с точно известными пятью десятичными знаками.
На основании усиленного закона больших чисел можно
определить, какой объем наблюдений нужен для получения
необходимой точности.
Пример. Пусть, например, на основании совершенство-
вания техники проведения операций ожидаемый эффект от
снижения летальности — 10 % от исходного уровня. Выясним,
удастся ли статистически доказать эффект. В качестве модели
возьмем всю Москву, длительность проведения эксперимента
определим в год, а в качестве операции возьмем самую часто
проводимую — операцию по удалению аппендицита.
Пусть половина операций проводится по старой схеме,
а половина — по новой. В год в Москве проводится порядка
80 тысяч операций по удалению аппендицита, летальность
этой операции около 1 %.
Если половина операций (то есть 40 тысяч) проводит-
ся но старой схеме, то из усиленного закона больших чиссл
получаем, что статистическая погрешность определения
.//VI) (I -/VI»
вероятности легального исхода составит V.
./0,1)1 (I 0,(11)
v 0,0497% При проветеппп 40 п.юп oiupi
/40000

ций по новой схеме ожидаемая погрешность 1 .JLI^LUI-
Jn
£009 (1-0,009)
Шш ==0'0472%- Но ожидаемый эффект от
снижения летальности должен составить 10% от исход-
ной летальности, то есть 0,1 %, причем для подтверждения
этого нам нужно будет сравнивать две частоты, определяе-
мые со статистическими погрешностями порядка 0,05%.
В результате получаем, что ожидаемый эффект близок
к статистической погрешности, и доказать его мы не сможем.
И ведь это мы взяли всю Москву на целый год в качестве
виртуального полигона, в качестве операции выбрали самую
частую — удаление аппендицита, а в качестве ожидаемого эф-
фекта запланировали целых 10 % от исходной летальности!
Для того чтобы снизить статистическую погрешность, ска-
жем, в 4 раза, нужно брать в 16 раз больше наблюдений. В дан-
ном случае для получения достоверных различий в качестве
полигона нужно брать на год уже не Москву, а всю Россию
4.6. Функция распределения числовой
случайной величины. Непрерывные
и дискретные случайные величины.
Распределения Бернулли, биномиальное,
Пуассона, нормальное, «хи-квадрат»,
Стъюдента и Фишера
Нет никакого смысла добиваться
точности, если вы не понимаете
того, о чем говорите
Фон Нейман
Некоторые часто встречающиес^сг^ча^ныс ?шпичины
Как уже было отмечено, дня шаиия закона расиредеде
ния случайной величины нужно определим, не тотько перо
ятносги 01 дельных значений, по и ич напоров

122
Часть I. Анализ вероятностей
Однако для однозначного задания распределения чис-
ловой случайной величины £, достаточно знать вероятности
событий £, <х, где х — произвольное число. Эти значения ве-
роятностей называются функцией распределения и обозна-
чается как F^x), так что по определению F (х) = Р(Ь\ < х).
Например, если рассматриваемая случайная величина
Е, — пол больного, 60 % больных — мужчины и мужчины ко-
дируются единицами, а женщины — двойками, то
F^ (х) = 0, если х < 1
- F^ (х) = 0,6, если 1 < х < 2
F^ (х) = 1, если х>2
Зная функцию распределения FAx), мы знаем и вероят-
ность попадания случайной величины £, на любой промежу-
ток отх, до х2, которая равна (F(x2) — F(xx)).
В современной англоязычной литературе функцию рас-
пределения часто называют CDF (cumulative density function).
Зная вероятности попадания в любой интервал, мы мо-
жем сконструировать и любое другое интересующее нас со-
бытие.
В ряде рассмотренных примеров случайная величина
могла принимать всего одно из нескольких возможных зна-
чений. Обобщением таких случайных величин являются
дискретные случайные величины, которые могут принимать
только одно значение из некоторого (конечного или беско-
нечного) набора Хг Х2,.... Их можно задать набором вероят-
ностей /*,= Р(£, = X), Р2= Р(£, = Х7).... Примером дискретной
случайной величины с бесконечным количеством значений
может служить приведенный в качестве примера № 2 случай
с подбрасыванием монеты до выпадения первой «решки». Ей
также можно придать «околомедицинский» вид. Пусть веро-
ятность того, что подсаженная женщине оплодотворенная
яйцеклетка приживется, равна '/,. Тогда данная случайная
величина — количество операций, которое нужно сделать до
достижения успеха.
Другим, противоположным классом числовых случайных
величин являются непрерывные случайные величины, у ко

[щва 4. Элементы теории вероятностей
123
торых существует плотность распределения' pt,(x), то есть
такая числовая функция, что для любого промежутка I*,, х2]
вероятность того, что случайная величина примет значение
из этого промежутка, равна длине промежутка, умноженно-
го на значение плотности распределения в некоторой внут-
ренней точке промежутка. Например, для приведенного в
примере № 3 равномерного распределения на отрезке [О, I ]
плотность распределения равна единице для точек внутри
этого отрезка и нулю — для точек вне отрезка.
В современной англоязычной литературе плотность рас-
пределения часто называют PDF (point density function).
Непрерывную природу имеют такие переменные, как рН
раствора, вес и рост пациента и т. д. Заметим, что значения
их обычно представляются как дискретная величина, напри-
мер рост измеряется с точностью до сантиметра и т. д., но это
связано не с содержательным смыслом величины, а с техни-
кой ее измерения и погрешностями округления.
Таким образом, дискретные и непрерывные случайные
величины представляют из себя две противоположности.
У непрерывных случайных величин вероятность выпадения
любого конкретного значения равна нулю, поэтому при ис-
следовании никакие два измерения разных объектов не дают
одинаковых значений (если повышать точность измерений,
то любую пару объектов можно различить). В частности, лю-
бая случайная величина не может быть одновременно и не-
прерывной, и дискретной.
Обычно исследуемые числовые случайные величины яв-
ляются либо непрерывными, либо дискретными. Тем не ме-
нее это, строго говоря, необязательно: могут быть числовые
случайные величины, не являющиеся ни непрерывными, ни
дискретными. Однако любую числовую случайную величи-
ну можно представить как сумму независимых непрерывной
и дискретной случайных величин
При исследовании частот встречаемости значений лис
кретных и непрерывных случайных величин целесообразны
1 Плотное и. распределения определяет! как проипччшля or
функции распределения. Продолжение фрты героическая нопьп
ка «на пальцах» объясни in мьи и потния ••нротг-одмия»

124
Часть 1. Анализ вероятностей
разные приемы. Например, если исследуется пол пациентов,
то это дискретная случайная величина, которая принимает
два значения, и для ее анализа достаточно определить доли
мужчин и женщин. Техника вычисления частот встречае-
мости значений была описана выше, в разделе 3.1.
Приведем несколько примеров часто встречающихся
дискретных случайных величин.
1. Распределение Бернулли
Случайная величина, которая с вероятностью р равна
единице и с вероятностью q — 1 — р равна нулю.
Ее математическое ожидание (или среднее арифметиче-
ское, к вопросу о соотношении этих понятий мы вернемся
позже) равно р, а дисперсия1 равна р х q = рх (I — р).
Распределение Бернулли естественно возникает при рас-
смотрении случайных событий, которые произойдут (едини-
ца) или не произойдут (ноль). Например — летальный исход
приданном заболевании.
Распределение Бернулли однопараметрическое, т. е. точ-
ное распределение конкретной случайной величины зада-
ется одним параметром р (равным математическому ожида-
нию, или среднему).
2. Биномиальное распределение
Пусть 4р ^2'••' ^>n~ независимые случайные величины,
распределенные по Бернулли с одним и тем же р. Пусть слу-
чайная величина ч =£,+ ... + t,N. Тогда г) распределена бино-
миально с параметрами (р, N).
Ее математическое ожидание равно р х N. Вероятность
того, что г) = л, где п — 1, 2,..., N, равна
Р[п) = [С„/Щр"х(1-рУ"
где С* — количество сочетаний из N по п, называемое также
биномиальным коэффициентом, a/V!=lx2x3x...x/V~
факториал.
1 Квадратный кореш, ич дисперсии насыпается среднекналра-
тичпмм отклонением и служит мерой разброса случайной иелпмнны
Смысл и способы измерения математического ожидании ансперсип
и других параметром будет подробно обсуждаться и нижеследующих
ра шелах

[лава 4. Элементы теории вероятностей
125
Для практического расчета частот биномиального рас-
пределения пользоваться этой формулой не обязательно, так
как в электронных таблицах есть встроенные функции расче-
та этих показателей. Например, в электронной таблице Excel
имеется функция БИНОМРАСЩл; М; р; «интегральный»),
где показатель «интегральный» показывает, следует ли счи-
тать частоты (для этого следует в качестве значения этого
показателя подставить 0) или частоты нарастающим итогом
(в этом случае следует подставить 1).
Так, для биномиального распределения с показателями
Р{п) = БИНОМРАСЩя; N;pfi).
Пример биномиального распределения: количество ле-
тальных случаев и из ^больных при условии, что летальный
исход каждого больного равновероятен и летальные исходы
разных больных независимы.
Например, пусть у нас есть 10 больных с ожидаемой ле-
тальностью 10 %, тогда вероятность того, что умрут 2 боль-
ных из 10, определяется как БИНОМРАСП(2;10;0,1;0) =
= 0,1937. Если же мы хотим определить вероятность того,
что умрут не более 2 больных, то в этом случае вычисляем
БИНОМРАСЩ2; 10;0,1 ;0) = 0,9298.
Другой пример — биномиальное распределение (0,2; 3)
(распределение количества умерших из 3 больных с леталь-
ностью 20 %).
Среднее ожидаемое количество умерших здесь — 0,6, ко-
торое получается из-за того, что с вероятностью 38,4 % уми-
рает один больной, 9,6 % —два и 0,8 % — три (см. гистограм-
му частот на рис. 4.6).
Биномиальные случайные величины — двухпараметри-
ческое семейство.
У биномиальной случайной величины математическое
ожидание равно р х /V и дисперсия — рх(1-р)\ N.
Еслидве не зависимые случайная величины распределены
биномиальное показателями (/.i./V,) и (/),/У,)соогве1ственм(),то
их сумма распределена биномиально с показателями (/>,,V +
+ /V,). (Если/;у них рашичпы. m сумма не биномиальная
случайная величина )

126
Часть I. Анализ вероятностей
0,6 т-
0,5 "
о.з
0,2
0,1
о I 1 1 '■ 1
0 12 3
Рис. 4.6. Гистограмма частот биномиального
распределения с параметрами (0,2;3)
Биномиально распределенные с параметрами (p,N) слу-
чайные величины могут принимать целые значения в преде-
лах от 0 до N, причем частота встречаемости каждого значе-
ния в этих пределах больше нуля, хотя может и быть очень
мала.
Если математическое ожидание (еще раз напомню, что
это — формализация понятия среднего арифметического)
биномиально распределенной случайной величины мень-
ше '/2, то частоты значений монотонно убывают, и наиболее
вероятное значение — 0, менее вероятное — 1, еще менее ве-
роятно — 2 и так далее.
Если математическое ожидание — в пределах от '/ до 1,
то наиболее часто встречаемым значением может быть или
О, или 1, но и в этом случае начиная с 1 все дальнейшие зна-
чения становятся вся более маловероятными. Например,
для биномиального распределения с параметрами (0,2;3) ма-
тематическое ожидание равно 0,2 х 3 = 0,6, то есть как раз
находится в пределах между '/., и 1. На рис. 4.6 приведена
гистограмма его частот.
Если математическое ожидание больше единицы и мень-
ше /V- !, то гистограмма частот относительно симметрична
с максимумом около математического ожидании, причем

I.uiea 4. Элементы теории вероятностей
127
чем больше (на большее количество единиц) математичес-
кое ожидание отстоит от 0 и N, тем оно симметричнее. При-
меры приведены на рис. 4.7 и 4.8. Видно, что гистограмма на
рис. 4.8 значительно более симметрична.
0,3
0,25-
0,2
015
o,t
0,05
О
|
1 i
Рис. 4.7. Гистограмма частот биномиального
распределения с параметрами (0,2;8)
U.
Рис. 4.8. Гискмрамма часки биномиаммимо
распрйдоменин с параметрами (О ?.:Ю)

128
Часть I Анализ вероятностен
Если же параметры биномиального распределения та-
ковы, что его математическое ожидание близко к N, то его
гистограмма частот такова, как в первых разобранных слу-
чаях, но в «перевернутом» виде. Например, если мы рас-
сматриваем распределение количества умерших больных и
летальность больше 50 %, то вместо нее можно рассмотреть
распределение количества выживших больных, и в этом слу-
чае выживаемость будет менее 50 %.
Поэтому, например, из приведенного выше можно ут-
верждать, что если математическое ожидание биномиальной
величины больше N— '/2, то для этого распределения чем
больше значение, тем больше его частота, и т. д.
3. Распределение Пуассона
Это распределение получается из биномиального в том
случае, когда р очень мало, а N очень велико, т.е. случайная
величина является суммой большого количества маловеро-
ятных событий. Это однопараметрическая случайная вели-
чина, задаваемая своим математическим ожиданием А,. Для
нее имеем следующее распределение вероятности.
Р(п) = [\п I п\]хе-\
В отличие от биномиального распределения, для распре-
деления Пуассона не обязательно, чтобы вероятности на-
ступления события были одинаковы, достаточно, чтобы они
были малы.
Приведем примеры гистограммы частот для пуассоновой
случайной величины. В приведенных ниже примерах гисто-
граммы частот «обрезаны», так как для больших значений ча-
стоты не равны нулю, хотя и очень малы (см. рис. 4.9—4.11).
У пуассоновой случайной величины дисперсия равна ма-
тематическому ожиданию.
Для реальных ситуаций (когда/? хотя и мало, но конечно)
величина отклонения Р(п) от пуассоновской порядка пли
меньше р2.
Сумма двух независимых пуассоновых случайных вели-
чин с математическими ожиданиями Я, и Х2 есть пуассонова
случайная величина с математическим ожиданием Xt + Я,
По Пуассону с хорошей точностью распределена абсо-
лютная заболеваемость (по, естественно, не интенсивная.

[лава 4. Элементы теории вероятностей
129
0,45
0,4
0,35
0,3
0,25
0,2
0,15
0,1
0,05
П
■
j
i
i
!
I
I
I
I
Рис. 4.9. Гистограмма частот распределения Пуассона
со средним 0,7
0,25
0,2
0,15
01
0,05
Т
■""".1 м
И 9 Ю
Рис. 4.10. Гиглшрпммачпгло! рагнреди'^нич Пу.кгон.!
ГО Г.р1'ДНИМ 3

130
Часть I. Ана/i
■ ис-ронтностеи
0,08 г
0,07
0,06
0,05
0,04
0,03
0,02
0,01
0
гГ
г
г
г
г-
.,,.— . ^-rff- .—
~-|
-
~
-1
-|
tfh^
Рис. 4.11. Гистограмма частот распределения Пуассона
со средним 30
так как пуассоновы распределения не выдерживают умно-
жения на число).
Приведем пример расчета. Пусть в среднем за сутки
в больницу привозят двух больных с инфарктом. Определим,
насколько вероятно поступление относительно большого
количества больных. Например, пусть под возможных боль-
ных с инфарктом зарезервировано 5 коек. Насколько веро-
ятно, что их не хватит?
Будем проводить расчеты в предположении, что все случаи
инфарктов — независимы и что вероятность возникновения
инфаркта не меняется день ото дня. В этом случае количество
больных с инфарктом распределено по Пуассону. В соответ-
ствии с приведенным выше примером вероятность того, что
будет не более 5 пациентов, получаем как ПУАССОН(5;2;1) *
« 0,9834 (заметим, что в данном случае используется поло-
жительное значение показателя «интегральный», так как нас
интересуют частоты нарастающим итогом), или в 1,63 % пяти
выделенных коек будет не хватать
Если критически подойти к полученным результатам, то
ясно, что основной недостаток проведенных расчетов щи-

Пава 4. Элементы теории вероятностей 131
можно, необоснованные предположения о независимости
случаев инфаркта, на основании которых и делался вывод
о том, что количество больных распределено по Пуассону.
Хорошо известно, что количество госпитализированных с
инфарктом больных существенно колеблется день ото дня,
так как на заболеваемость инфарктом существенно влияют
природные (погода и др.) и социальные (праздники, выдача
зарплаты, игры сборной по футболу и др.) факторы.
Все три вышеприведенных примера случайных вели-
чин — дискретные. Дадим теперь несколько примеров не-
прерывных случайных величин.
4. Равномерное распределение на отрезке [а, Ь]
Имеет плотность распределения р(х) — \/(Ь - а), если х
принадлежит отрезку [а,Ь\, и р(х) - О в противном случае.
Его математическое ожидание равно (Ь + а)/2, а дисперсия
равна (1/6) х (Ь - а)2. Это двухпараметрическое семейство,
которое разными авторами задается или концами отрезка,
или величинами математического ожидания и дисперсии.
5. Нормальное распределение
Двухпараметрическое семейство, задается математиче-
ским ожиданием т и дисперсией D. Имеет плотность рас-
1 С1-"1)'
пределения /К*) = . е 20 .
V2n£»
Несмотря на жутковатую плотность распределения, нор-
мальные случайные величины часто используются в статис-
тике. Для изучения причин этого будет выделен целый па-
раграф.
Сумма двух независимых нормальных случайных вели-
чин с параметрами (m,,/),) и {m2,D2) есть нормальная случай-
ная величина с параметрами {m^+mvDl+D2).
Упомянем еще о нескольких случайных величинах, полу-
чающихся на основании нормальной и часто встречающихся
в статистических расчетах.
6. Распределение %2п («хи-квадрат» с п степенями свободы)
Однопараметрическое семейство с целочисленным па-
раметром п. Пусть ^,, £,,,..., ^п— независимые нормальные
случайные величины с математическими ожиданиями, рав-

132
Часть I. Анализ вероятностей
ными нулю, и дисперсиями, равными единице. Тогда слу-
чайная величина %гп = £ + ^2+ ... + \ распределена как х2„
(«хи-квадрат» с п степенями свободы).
7. Распределение Стьюдента
Пусть £, — нормальная случайная величина с нулевым ма-
тематическим ожиданием и единичной дисперсией, a t| рас-
пределена как %2п и они независимы. Тогда случайная вели-
чина Т = Z— имеет распределение Стьюдента (или Г-рас-
п
пределение) с п степенями свободы.
8. Распределение Фишера—Снедекора
Если f, и т| — независимые распределенные по %2„ с п и m
степенями свободы соответственно случайные величины, то
V
случайная величина F = -^j имеет ^-распределение с (п,т)
степенями свободы. ут
Большинство указанных случайных величин часто ис-
пользуются в статистике из-за того, что при выполнении не-
которых условий (типа бесконечно большой выборки и не-
зависимости случайных величин) конструируемые из оценок
параметров случайные величины имеют соответствующее
распределение. Так, оценка дисперсии нормальной случай-
ной величины распределена как «хи-квадрат», отношение
двух аналогичных оценок — как F-распределение и т. д. По-
нятно, что ни одно из реальных распределений в точности не
соответствует этим предельным случаям хотя бы уже потому,
что нет независимых случайных величин, равно как нет аб-
солютно чистых химических веществ, репрезентативных вы-
борок и философского камня. Поэтому в тех случаях, когда
можно оценить величины погрешности реальных распреде-
лений по сравнению с идеальными, то можно пользоваться
полученными результатами с соответствующими поправка-
ми, если же ли отклонения оценить не удается, го кос ран
по приходится пользоваться идеализированными результа-
тами, гак как ничего ipyi ого пег

Глава 5
ОТБОР И ПОИСК ДАННЫХ.
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ
ЛОГИКИ
Непосредственно для проведения статистической обработки
данных нужен только раздел 5.1. Необходимость дальнейше-
го изложения элементов математической логики обусловле-
но двумя обстоятельствами:
1. Значительная часть современной научной литерату-
ры используется не в виде источников на бумажных
носителях, а в виде электронных копий, поиск кото-
рых осуществляется в интернете или локальных базах
данных при помощи запросов Для эффективного
поиска нужных источников приходится пользовать-
ся достаточно сложными запросами, которые нельзя
правильно сформулировать без знания некоторых
элементов математической логики.
2 Современные врачи, как практические работники,
так и научные работники, плохо владеют навыками
формальной логики, что не только приводит к ошиб-
кам в рассуждениях, но и не даст возможное!и дока-
зать безошибочность даже верных рассуждений.

134
Часть I Анализ вероятностей
5.1. Отбор случаев при работе
со статистическими программами
Использование фильтров для отбора части наблюдений при
проведении расчетов в пакетах статистических программ.
При обработке данных обычной является ситуация, ког-
да нужно определить частоту или величину каких-то пара-
метров не у всех наблюдаемых, а только у некоторых, напри-
мер, рассчитать частотную гистограмму распределения по
возрасту только у женщин.
В случае частот это можно сделать при помощи изложен-
ной выше техники расчета условной вероятности, но проше
сделать это непосредственно.
В SPSS для этого используется аппарат так называемых
фильтров. Для их использования нужно выполнить команду
«Date/Select Cases» (в младших версиях доступна только из
окна работы с данными). В появившейся далее форме вы-
брать вариант «If condition is satisfied» и нажать на кнопку с
надписью «IF» (надпись активизируется только после выбо-
ра варианта).
В результате появится форма задания условия отбора,
очень похожая на окно задания выражений при создании
вычислимых переменных.
Например, если нужно отобрать только испытуемых
женского пола, что закодировано значением «2» переменной
«sex», то условие отбора будет sex = 2. Как и при вычислении
значения переменной, можно ввести необходимое выраже-
ние как текст, но надежнее сконструировать его, выбирая
имена переменных, встроенных функций и отношений из
имеющегося списка.
Если при выборе испытуемых нужно, чтобы одновре-
менно выполнялось несколько условий, то их следует соеди-
нить знаком «&». Например, для поиска женщин моложе 40
лет можно пользоваться условием (sex=2)&(VOZRAST<40)
Если нужно выполнение одного из условий, то их соединя-
ют знаком «|». Например, если имеется несколько групп
испытуемых, что кодируется переменной GRUPPA, то для
пыбора испытуемых первой и третьей группы можно поль-

Гмеа 5. Отбор и поиск данных. Элементы математической логики 135
зоваться выражением (GRUPPA=l) | (GRUPPA=3). При за-
дании условия отбора знаки «&» и «|» можно не искать на
клавиатуре, а вводить нажатием на кнопку с изображением
этого символа на форме. Более подробно создание сложных
условий отбора будет обсуждаться в следующих разделах.
После задания условия отбора нужно последовательно
нажать на кнопки «Continue» и «ОК». В результате в окне
данных номера строк случаев, не соответствующих условию
отбора, будут зачеркнуты. При дальнейшем проведении ста-
тистических расчетов будут использоваться данные только
тех случаев, которые соответствуют текущему фильтру (ус-
ловию отбора).
Для снятия фильтра нужно выполнить команду «Date/Select
Cases», выбрать вариант «All cases» и нажать на кнопку «ОК».
При работе с формой выбора в нижней части имеется
переключатель «Unselected cases are» с вариантами «Filtered»
и «Deleted». По умолчанию стоит вариант «Filtered», то есть
невыбранные случаи временно исключаются из статисти-
ческой обработки. Если выбрать вариант «Deleted», то не-
выбранные случаи будут удалены из файла1.
В Statistica есть два разных способа отбора части данных
для проведения статистической обработки.
При первом способе для выбора данных нужно выпол-
нить команду «Data/Subset-Random Sampling». В появив-
шейся форме нажать на кнопку «Variables» и выбрать список
нужных переменных, после чего нажать на кнопку «Cases» и
отобрать нужные случаи. В появившейся форме нужно ука-
зать, какие случаи будут включены (все при выборе вариан-
та «All cases» или некоторые при выборе варианта «Specific,
selected by»), а потом можно задать, какие случаи будут ис-
ключены из отобранного набора. Для задания включаемых
или исключаемых наборов есть два разных способа В полях
«Expression» можно ввести условие отбора аналогично гому,
как это делается в SPSS, а в полях «or case number» можно
задать набор нужных номеров случаев. В результате выбран
' Если Вы любите щелкать мышью по чю пи попали и смотреть.
что и) этого выйдет, то иначал»- сохраните копию файла с данными

136
Часть I. Анализ вероятностей
ные переменные и данные будут скопированы в новый на-
бор данных, с которым можно проводить независимую ста-
тистическую обработку.
При втором способе при выборе метода анализа нуж-
но нажать кнопку «Select Cases», отметить вариант «Enable
Selection Condition» и задать условие отбора аналогично опи-
санному выше. При проведении дальнейшей статистической
обработки данных установленный таким образом фильтр
также будет действовать, о чем можно догадаться на осно-
вании того, что при выборе методов анализа кнопка «Select
Cases» будет находиться в нажатом состоянии. Для снятия
фильтра нужно нажать на эту кнопку и отменить выбор ва-
рианта «Enable Selection Condition».
5.2. Вычисление истинности
высказываний
Все люди смертны. Сократ — человек
Следовательно, Сократ смертен.
Все кошки смертны. Сократ— смертен.
Следовательно, Сократ — кошка.
Известные примеры верного
и неверного силлогизма
Элементы формальной логики: как по истинности составных
частей логического высказывания вычислить истинность всего
высказывания.
Определение. Высказыванием будем называть любое ут-
верждение, которое может быть истинным и ложным.
Определение. Эквивалентными высказываниями будем
называть два высказывания, которые всегда одновременно
истинны или ложны.
Используя логические операции, можно из нескольких
исходных высказываний делать новое, точно так же как при
помощи арифметических операций vio>kho из нескольких
чисел получать новое число
С использованием методов математической логики мож-
но вычислять, истинно ли данное высказывание, точно так

f,t,nfta 5. Отбор и поиск данных. Элементы математической логики 137
же как при помощи арифметики можно вычислить величину
числового выражения1.
В поисковых системах и в пакетах статистических про-
грамм обычно используются три логические операции: НЕ,
И и ИЛИ.
Логическая операция НЕ в программах чаще всего обоз-
начается как NOT. Например, NOT(VOZRAST<40) эквива-
лентно тому, что возраст равен 40 или больше. В математи-
ке отрицание высказывания А обычно обозначается как А,
иногда как --А. Вычисление А очень просто — оно ложно,
если А истинно, и истинно, если А ложно.
Легко вычислить, что НЕ(НЕ А) эквив&чентно А. Дейст-
вительно, если А истинно, то (НЕ А) ложно, следовательно,
НЕ(НЕ А) истинно. Если же А ложно, то (НЕ А) истинно,
следовательно, НЕ(НЕ А) ложно. В результате получили, что
при всех возможных вариантах А и НЕ(НЕ А) одновременно
истинно или ложно, следовательно, эти высказывания экви-
валентны.
Особых проблем с использованием этой операции нет,
хотя всегда, когда речь идет о формализации утверждений,
сформулированных на естественных языках, имеются смыс-
ловые нюансы и неизбежные огрубления. Так, в русском
языке частица «не» иногда означает отрицание, а иногда —
Бог знает что, в том числе вежливую формулировку3. Поэто-
му в русском языке второе отрицание иногда снимает первое
отрицание, а иногда его таинственным образом усиливает.
Интересно заметить, что не во всех языках второе отрица-
ние усиливает первое, например в английском языке такого
1 На самом деле очень точная аналогия, так как логические опе-
рации можно рассматривать как арифметические и наоборот, если в
качестве поля чисел выбрать набор только из двух элементов, напри-
мер из нуля и единицы, и считать, что единица плюс единица равна
единице
2 Например, если на вопрос «Не выходите ли Вы на следующей
Остановке'» Вы получили ответ «Да», то что ко означав! что от
петивший будет выходить или нет'' Наиболее правильная ингерпре
тация такою ответа что пассажир ныделывается и нарывается на
гРУбость

138
Часть I Анализ вероятностей
нет. Поэтому при переводе с русского на английский или
наоборот некоторые выражения приходится переводить как
их формальное отрицание. Например, фраза «Я ничего не
знаю» переводится как «I now nothing», то есть «Я знаю ниче-
го». Сказать по-английски «Я ничего не знаю» в буквальном
переводе было бы нескромно, так как с точки зрения фор-
мальной логики «Я ничего не знаю» означает «Нет ничего,
чего бы я не знал», то есть «Я знаю все».
Логическая операция И в программах обозначается или
как AND, или знаком «&». В математической логике для обоз-
начения этой операции используются символы «&» или «л».
Высказывание (А И В) истинно тогда и только тогда, когда
истинно и А, и В. Легко проверить, что (А И В) эквивалентно
(В И А), атакже что ((А И В) И С) эквивалентно (А И (В И С)),
то есть если требуется выполнение нескольких обязательных
условий, то все равно, в каком порядке их выдвигать.
При формализации утверждений на естественном язы-
ке, использующих связку «и», сложность связана с тем, что
эта связка используется для двух совершенно разных фун-
кций — для связывания логических условий и в качестве
краткого эквивалента связки «а также» при перечислении.
Так, когда в правилах поступления в вуз записано, что за-
числяются лица, набравшие проходной балл и получившие
положительные оценки на всех экзаменах, то здесь связка
понимается как логическая операция — требуется выполне-
ние и того, и другого условия. Если же в правилах поступле-
ния написано, что документы принимаются от выпускников
средних школ и медицинских училищ, то здесь «и» понима-
ется как знак перечисления, а того, чтобы абитуриент окон-
чил и школу, и медучилище, не требуется.
Как хорошо известно, если какое-нибудь устройство мож-
но собрать неправильно, то найдется человек, который это
сделает. Поэтому желательно стараться пользоваться форму-
лировками, не допускающими неоднозначного понимания1.
1 В любом случае перевод высказываний с естественного языка
на язык формальной логики их огрубляет, приводит к потере нюан-
сов. Так, с точки зрения формальной логики (А и В) и (В и А) лепи

Глава 5. Отбор и поиск данных Элементы математической логики 139
Логическая операция ИЛИ в программах обозначается
или как OR, или знаком «|». В математической логике для
обозначения этой операции используется символ v, хотя в
инженерных приложениях обозначение в виде вертикальной
черты также встречается достаточно часто.
С корректностью бытового использования связки «или»
дело обстоит очень плохо. Во-первых, имеется две разные
связки «или» — исключающая и не исключающая. В исклю-
чающем варианте А или В истинно, когда истинно или А,
или В, но не оба варианта одновременно. В не исключающем
варианте А или В истинно, когда истинно или А, или В, или
и А, и В.
В математической логике операция ИЛИ использует-
ся как не исключающая, то есть для истинности А ИЛИ В
достаточно, чтобы был истинен хотя бы один из операндов.
Аналогично связке «И» (А ИЛИ В) эквивалентно (В ИЛИ А),
а ((А ИЛИ В) ИЛИ С) эквивалентно (А ИЛИ (В ИЛИ С)).
Рассмотрим табл. 5.1 — таблицу истинности результатов
логических операций.
Таблица 5.1
Таблица истинности результатов
логических операций
А
1
Истина
Истина
Ложь
Ложь
В
2
Истина
Ложь
Истина
Ложь
НЕА
3
Ложь
Ложь
Истина
Истина
АИВ
4
Истина
Ложь
Ложь
Ложь
А ИЛИ В
5
Истина
Истина
Истина
Ложь
Здесь в первой и второй колонках стоят все возможные
комбинации исходных высказываний, а в колонках с третьей
валентны. Однако в естественной речи фразы «Маша вышла замуж
и родила» и «Маша родила и вышла замуж» вряд ли будут считаться
эквивалентными, хотя, строго говоря, в обоих сообщается только то,
что произошли эти два приятных события, а не в каком порядке они
произошли и что было причиной, а что — следствием

140
Часть /. Анализ вероятностей
по пятой — результаты применения к ним логических опе-
раций.
В бытовом использовании исключающий и не исключа-
ющий вариант не разделяются, и о том, какой именно вари-
ант имел в виду автор, можно только догадываться.
Основная проблема с бытовым использованием логичес-
ких связок даже не в том, что не отделяются эти два варианта
связки, а в том, что люди вообще не в ладах с логическим
мышлением и постоянно путают связки «И» и «ИЛИ». На-
сколько мне известно, у некоторых народов Крайнего Севе-
ра эти связки в языке вообще не отделяются и обозначаются
одним словом. Если кому-то кажется, что мы сильно от них
ушли в вопросах логики, то это не так.
Поэтому когда я в трамвае вижу рядом с сиденьем выпол-
ненную по трафарету надпись «Места пассажиров с детьми,
престарелых, беременных и инвалидов», то я как специа-
лист по математической логике сразу понимаю, для кого эти
места — для престарелых беременных инвалидов с детьми.
С точки зрения логики нужно было использовать не связку
«и», а связку «или».
Некоторым может показаться, что использование слож-
ных запросов с логическими связками нужно только в каких-
то сложных случаях. Однако это не так, и для эффективного
поиска и отбора нужно использовать достаточно сложные
условия.
Например, пусть мне нужно из имеющегося списка боль-
ных найти пенсионеров по возрасту (у них другие условия
оплаты медицинского обслуживания). Вспоминаем, что по
нынешнему законодательству России пенсионерами по воз-
расту являются мужчины старше 60 лет и женщины старше
55 лет, и сразу замечаем языковую неточность — мы гово-
рим, что возраст должен быть больше некоторой ветчи-
ны, тогда как реально— больше или равно. Записывая ус
ловие отбора на языке запросов, получаем (POI = *м» AND
VOZRAST>=60) AND(POI =<-ж» AND VOZRAST 55). Oi
иако при выполнении этого запроса никто не будег найден
потму что это •-• не запрос на поиск пенсионеров но uoi-
pauy, а запрос на поиск пожилых гермафролиюн Дли вы

Глава 5. Отбор и поиск данных Элементы математической логики 141
полнения запроса требуется, чтобы пол был одновременно
и мужской и женский. Поэтому, хотя на естественном языке
мы говорим «мужчины и женщины», при поиске нам нуж-
но формулировать это как «мужчины или женщины». Пра-
вильный вариант запроса на поиск пенсионеров по возрасту
будет (POL=«m» AND VOZRAST>=60) OR (РОЬ=«ж» AND
VOZRAST>=55).
Приведу еще несколько примеров эквивалентных выска-
зываний:
1. НЕ (А И В) эквивалентно (НЕ А) ИЛИ (НЕ В).
2. НЕ (А ИЛИ В) эквивалентно (НЕ А) И (НЕ В).
3. (А ИЛИ В) И С эквивалентно (А И С) ИЛИ (ВИС).
4. (А И В) ИЛИ С эквивалентно (А ИЛИ С) И (В ИЛИ С).
Примеры 1 и 2 показывают, что при внесении НЕ внутрь
скобок связки И и ИЛИ переходят друг в друга.
Формулы 3 и 4 соответствуют алгебраическому тождес-
тву (А + В)хС = АхС + ВхС. Однако можно заметить,
что логические операции более симметричные, чем алгебра-
ические, так как тождество (А х В) + С = (А + С) х (В + С)
в алгебре не выполняется.
Для проверки эквивалентности двух высказываний мож-
но вычислить их истинности при всех возможных вариантах
входящих в них компонент. Если результаты будут всегда сов-
падать, то эти высказывания эквивалентны. Эти вычисления
удобно проводить в виде таблиц вычисления истинности.
В качестве примера проведем проверку примера № 1 (табл. 5.2).
Таблица 5.2
Пример таблицы вычисления истинности высказывания
А
1
Истина
Истина
Ложь
: Можь
в
2
Истина
Ложь
Истина
Ложь
АиВ
3
Истина
Ложь
Ложь
Ложь
НЕ
(АИВ)
4
Ложь
Истина
Истина
Истина
НЕ А
5
Ложь
Ложь
Истина
Истина
НЕ В
6
Ложь
Истина
Ложь
Истина
(НЕ А)
ИЛИ
(НЕ В)
7
Ложь
Истина
Истина
Истин,

142
i... I Ai:,.;.пи вероятностей
В первых двух колонках таблицы стоят все возможные
комбинации истинности исходных высказываний. На ос-
новании приведенной выше таблицы истинности вычис-
ляем колонку № 3. После этого на основании определения
операции НЕ заполняем колонку № 4, меняя истину и ложь
местами. В результате в колонке № 4 — истинность первого
высказывания.
На основании определения операции НЕ заполняем
колонку № 5, меняя в содержимом колонки № 1 истину и
ложь местами. Аналогично по колонке № 2 заполняем ко-
лонку № 6. После этого по значениям колонок № 5 и № 6
с использованием таблицы истинности операции ИЛИ за-
полняем колонку № 7. Теперь для завершения проверки
достаточно убедиться, что содержимое колонок № 4 и № 7
совпадает.
Вычисление истинности высказываний совершенно не
обязательно делать вручную — логические функции НЕ, И
и ИЛИ входят в список встроенных функций в ЕхсеГе.
При поиске текстовых значений во многих поисковых
системах можно также использовать операторы Like, озна-
чающий приблизительное равенство, и Near, означающий,
что одно искомое слово должно быть недалеко от другого.
Точная реализация этих операторов в разных поисковых
системах неодинакова.
5.3. Теории и подтверждающие примеры
Ни один эксперимент не гопорит теории
«Да». Он может сказать только или «Нет»,
или «Может быть».
Альберт Эйнштейн
Что такое теория с точки зрения математической погики"
почему ее нельзя доказать, но можно опровор! ну>ь.
В поисковых системах обычно используюкя m и.ко ло-
гические операции НЕ, И и ИЛИ Друпю ютческис опе-
рации не исполыуклея, в частости потому, что н к ккч пче

f.inea 5. Отбор и поиск данных. Элементы математической логики 143
ской логике' их можно выразить через комбинации НЕ, И
и ИЛИ2.
Однако большинство научных результатов выражается
в форме «Если..., то ...», поэтому отдельно изучим операцию
логического следствия.
В математической логике эта операция чаще всего изоб-
ражается знаком «=>», реже «о» или «->». В выражении А=>В
высказывание А называют посылкой, а В — следствием.
Истинность этой операции задается табл. (5.3).
Таблица 5.3
Таблица истинности
логического следствия
А
Истина
Истина
Ложь
Ложь
В
Истина
Ложь
Истина
Ложь
А=>В
Истина
Ложь
Истина
Истина
При первом взгляде таблица истинности вызывает непри-
ятие. Действительно, то, что из истины следует истина, верно,
а то, что из истины следует ложь, неверно. Но почет верно
то, что изо лжи следует истина и что изо лжи следует ложь?
В качестве примера приведем безусловно верное выска-
зывание «если прошел дождь, то трава — мокрая». Это вы-
сказывание верно, несмотря на то, что может быть ситуация,
когда дождя не было и трава сухая (изо лжи следует ложь)
или когда дождя не было, но трава мокрая (изо лжи следует
истина), например, из-за того, что ее полили из шланга
Легко проверить, что выражение А ^> В эквивалентно
выражению НЕ В => НЕ А. Например, утверждение «если
' В которой любое высказывание может быть только либо истин
ным, либо ложным
' Строго говоря, и и 1 спя'юк «И* и «ИЛИ» можно оставить только
одну, так как другая чсреч нее выражается Однако и чгом случае jkbii
налетное выражение окачивается очень длинным и мачоионигным

144
Часть I Анализ вероятностей
прошел дождь, то трава — мокрая» эквивалентно утвержде-
нию «если трава сухая, то дождя не было».
В утверждении А => В посылку А часто называют необ-
ходимым условием, а следствие В — достаточным условием.
Действительно, на основании таблицы истинности можно
понять, что если В истинно, то А => В истинно вне зависимос-
ти от значения А, то есть истинности В достаточно. Если же
А => В верно, то для истинности В необходимо, чтобы А тоже
была истинна. Поэтому А называют необходимым условием.
Заметим, что если истинно и А => В, и В => А, то высказы-
вания А и В эквивалентны, то есть одновременно истинны
или ложны.
В соответствии с-изложенной выше техникой можно про-
верить, что ((А => В)И(В => С)) => (А => С) — тождественно
верное утверждение, то есть если В есть следствие А, а С есть
следствие В, то С есть следствие А.
Еще два примера всегда истинных утверждения:
1. (АИВ)^А.
2. А => (А ИЛИ В).
Легко также проверить, что А => В эквивалентно (НЕ А)
ИЛИ В.
Таким образом, формальная (или математическая) логика
исследует только вопрос, как по истинности одних высказы-
ваний вычислить истинность высказываний, совершенно не
интересуясь вопросом, в каких логических, то есть причин-
но-следственных, отношениях состоят посылки и следствия1.
Поэтому следующие утверждения являются истинными:
1. Если фамилия этого врача— Иванов, то фамилия
этого врача Иванов.
2. По пятницам дважды два равно четырех».
3. Если дважды два равно пяти, то дважды два равно
семи.
При помощи логических операций можно из одних ут-
верждений делать другие. Однако для этого нужно какие-то
' Точно так же, как в арифметике мы знаем, что 1 + 1=2 пне зави-
симости, о чем идет речь — яблоках, крысах или студентах и согласны
ли они,чтобы их складывали.

[лава 5. Отбор и поиск данных. Элементы математической логики 145
исходные утверждения иметь. Для точной формализации
этого процесса в математической логике определяется, что
такое теория.
Определение. Теория состоит из языка, аксиом, теорем
и правил вывода.
Язык теории — список использующихся в ней терминов
и понятий.
Аксиомы — список принятых на веру положений. Они
состоят из двух частей — аксиомы логики, в простом слу-
чае — аксиомы классического исчисления высказываний,
и аксиомы собственно теории. В качестве аксиом логики
можно взять список всех тождественно истинных логиче-
ских высказываний типа (А И В) => А.
Теоремы — список высказываний, который определяется
двумя следующими шагами:
1. Любая аксиома есть теорема.
2. Результат применения правил вывода к теоремам есть
теорема.
Правила вывода — в случае классического исчисления
высказываний правило единственно и формулируется сле-
дующим образом: если А и А => В — теоремы, то В — тоже
теорема.
Приведенная конструкция проста, однозначна и изящна,
но очень абстрактна. Для того чтобы было понятнее, о чем
идет дело, приведу некоторые примеры.
Прогресс в науке не ограничивается просто добавлени-
ем новых фактов. В результате крупных прорывов меняется
сама область исследования, что связано с изменением сис-
темы используемой терминологии. Так. в рамках классиче-
ской механики речь шла о положении и скорости тел, п рам-
ках термодинамики — об описании вероятности нахождения
механической системы в том или ином состоянии, в рамках
квантовой механики состояние системы описывается Ч'-функ-
пией, а с точки зрения общей теории относительности речь
идет об искривлении структуры пространства-времени
Еще не так давно при описании боношн врачи укачына
ми, имеется ли преобладание черной желчи и не находи mi in
Hoiibnoii ii<vi. властью стихии иотдуха I? настоящий момент

146
Часть I. Анализ вероипнюс,ц,.
при одной и той же болезни специалисты, работающие по
разным специальностям и в рамках разных теорий, говоря i
кто — о необходимости вывода шлаков из организма1, кто -
о последствиях Эдипова комплекса, кто — о необходимости
вести здоровый образ жизни2.
Задающие «ядро» теории аксиомы должны быть обобще-
нием имеющихся экспериментальных данных и других те-
оретических результатов, например: «Приобретенные при-
знаки не наследуются».
Из сформулированных аксиом теории при помощи логи-
ческих операций можно получить другие положения, то есть
теоремы. Например, в рамках арифметики можно доказать
теорему (а = b + с) => (Ь = а — с). Из правила вывода получа-
ем, что если а = b + с есть теорема, то и b = а — с есть теорема.
Поэтому, если к законам арифметики в качестве аксиомы
добавить постулат «Коммунизм есть советская власть плюс
электрификация всей страны», то в качестве теоремы полу-
чим, что «Советская власть есть коммунизм минус электри-
фикация всей страны».
Если верны аксиомы теории, то верны и все теоремы.
Следовательно, если мы получаем, что фактическим данным
не соответствует хотя бы одно логическое следствие из при-
нятой теории, то теория неверна.
Иногда удобнее проверять не сами аксиомы теории, а ло-
гические следствия из них. Например, я выдвигаю теорию,
что все работающие в ректорате секретарши — рыжие. Так
как А => В эквивалентно (НЕ В) => (НЕ А), то можно про-
верять либо утверждение СЕКРЕТАРША => РЫЖАЯ, либо
НЕ РЫЖАЯ => НЕ СЕКРЕТАРША. Для проверки первого
утверждения мне нужно обойти ректорат и выяснить, рыжие
ли там секретарши. Для проверки второго утверждения мож-
но встать утром на проходной и у всех не рыжих женщин вы-
яснить, не секретарши ли они.
1 Иногда, слушая медицинскую рекламу, чувствуешь себя не че-
ловеком, а какой-то домной.
г Здоровый обра) жижи- то, что врачи предписывают другим,
но сами не соблюдают

Глава 5. Отбор и поиск данных. Элементы математической логики 147
Так как сформулированные положения теории должны
выполняться всегда, то любой, даже единичный, факт не-
выполнения положения теории ее отвергает, а любое, даже
большое, количество экспериментальных подтверждений не
является доказательством ее истинности.
Проиллюстрирую этот пример. Предположим, я выдви-
нул теорию «Ночью все кошки серы». Для ее эксперимен-
тального подтверждения я могу ловить по ночам кошек и
выяснять, что они действительно серые, но мне это делать
лень. Тогда я могу переформулировать свое положение в эк-
вивалентной форме «Ночью все не серое — не кошки». Для
ее подтверждения мне достаточно ночью пойти в свой каби-
нет, найти все не серые предметы (например, надетую на мне
зеленую пижаму) и убедиться в том, что это — не кошки.
Изложенная в этом разделе казуистика мало применима
к современной клинической медицине просто потому, что
она еще практически не в состоянии сформулировать насто-
ящие научные теории. Ее современный уровень — обобще-
ния типа «у большинства больных...», к которым логические
преобразования неприменимы и для которых отдельные рас-
хождения неизбежны. Однако для настоящей теории даже
редкие расхождения — крах. Представьте себе, какой была
бы, например, химия, если бы было известно, что иногда мо-
лекулы не состоят из атомов.

Глава 6
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ
СТАТИСТИКИ
6.1. Статистические гипотезы
и доверительная вероятность
Доверяй, но проверяй.
Козьма Прутков
Определение понятий «статистическая гипотеза»
и «доверительная вероятность».
Так как любые эмпирически известные' нам закономер-
ности могут быть случайными совпадениями и нет ничего,
что бы мы знали об окружающей нас действительности со
100-процентной надежностью, то для работы с ними нужно
отработать технику использования потенциально неверных
заключений.
Обычно после формулирования этого тезиса во время за-
нятий слуигатели начинают возражать, что есть абсолютно
известные факты, например, что все люди умрут.
Это совершенно необязательно. Может быть, что люди
на самом деле — крылатые летающие трехногие бессмертные
морально совершенные создания, а те двуногие смертные
А нее известные нам закономерности — эмпирические

fraea 6. Элементы математической статистики 149
моральные уроды, которых мы массово наблюдаем, — ред-
кие мутации, которые бывают один раз на миллион. Просто
вот так случайно получилось, что все 10 миллиардов людей,
которые жили или живут на Земле, — мутанты.
Более изощренный пример. Известно, что сигналы от
рецепторов до головного мозга доходят посредством элект-
рических импульсов. Кроме этого, нас окружают электро-
магнитные поля как искусственного, так и естественного
происхождения. Все, кто хоть немного изучали квантовую
механику, знают, что у любого, даже слабого и однородного,
электромагнитного поля возможны (хотя и маловероятны)
большие флюктуации, при которых может генерироваться
поле любой мощности и конфигурации. Следовательно, все
электрические сигналы, которые доводят до мозга информа-
цию, могут быть искажены случайными наводками от вне-
шних электромагнитных источников.
Итак, предположим, что во время лекции по философии
по вопросам теории познания вы играете в карты со своим
соседом и через некоторое время замечаете, что каждый раз,
когда он сдает карты, то достает себе туза. После 20 партий
это начинает настораживать.
Если вы играете стандартной колодой из 36 карт, то
(так как тузов 4) вероятность случайно достать туза равна
4/36 = 1/9. Вероятность того, что это событие повторит-
ся случайно 20 раз, равна (1/9)20*10-". Следовательно, для
того чтобы такая серия выпала случайно, нужно сыграть
порядка 1019 партий. Если затрачивать на партию всего по
одной минуте и не отвлекаться на еду, сон, отдых и т. д., то
на это уйдет более 20 тысяч миллиардов лет. Если учесть,
что наша Вселенная существует1 всего несколько миллиар-
дов лет, то это более чем длительный срок. Поэтому, хотя
чисто теоретически возможно, что серия из 20 гузоп вы-
пала случайно, но общественность вас не осудит, если вы
в это не поверите.
Итак, общая схема проверки статистической гипотезы
следующая.
' По современным физическим представлениям

150
Часть I. Анализ вероятностей
Шаг 1. Принимается на веру некоторая статистическая ги-
потеза.
Эта гипотеза часто называется нулевой гипотезой. При-
меры статистических гипотез:
♦ вероятность события равна некоторой величине1;
♦ события независимы;
♦ случайная величина принадлежит некоторому классу
случайных величин;
♦ случайные величины независимы;
♦ случайные величины одинаково распределены;
♦ параметр случайной величины находится в пределах
некоторого отрезка;
♦ параметры двух случайных величин равны2.
Шаг 2. Определяется вероятность того, что произойдут та-
кие события, какие реально произошли.
В рассмотренном примере с картами явно вычислялась
вероятность набора наблюдаемых событий. При проверке
других гипотез часто приходится использовать другой под-
ход — конструировать некоторую новую величину, и опре-
делять, как она должна быть распределена в предположе-
нии об истинности статистической гипотезы. Например,
если мы проверяем гипотезу о том, что две наблюдаемые
случайные величины распределены нормально с одина-
ковыми дисперсиями, то в предположении об истинности
этой гипотезы отношение оценок дисперсий этих случай-
ных величин по набору наблюдаемых значений должно
1 Тут есть некоторая кажущаяся неточность формулировки. Пусть,
например, по литературным данным частота осложнения у аналогич-
ных больных равна 12 %. Понятно, что вероятность осложнения на
любом другом контингенте не будет в точности равна 12 %, а будет
хоть немного больше или меньше, и при достаточном увеличении объ-
ема наблюдений это можно будет выявить Поэтому и проверять эту
гипотезу вроде не нужно — и так понятно, что она будет неверна Од-
нако в реальности нас интересует другое: больше вероятность 0,12 или
меньше Если мы можем достоверно отличить вероятность ог 0,12, то
мы можем сказать, где частота больше — у нас или по литературным
данным
1 См. предыдущую сноску

f.iaea 6 Элементы Mui::c:;,: ;■-.- ,.:_„. -; -.татистики 151
быть распределено как распределение Фишера—Снеде-
Кора. Поэтому можно определить вероятность того, что в
предположении об истинности статистической гипотезы
отношение дисперсий будет таким, как получилось, или
большим.
Шаг 3. Если полученная вероятность оказывается слишком
малой, то статистическая гипотеза отвергается.
Если полученные значения слишком маловероятны, то
статистическая гипотеза отвергается.
6.2. Ошибки первого и второго рода.
Выбор доверительной вероятности
— А что Вам нужно получить в процессе статистической обра-
ботки ?
— Мне нужно, чтобы «пэ» было меньше пяти сотых.
Из реального диалога автора с одним из докторантов
Доверительную вероятность нужно выбирать на основании
того, к какому ущербу приводят ошибки при проверке
статистической гипотезы.
В предыдущем разделе использовался термин «малове-
роятные события». Для его уточнения введем определение.
Определение. Доверительная вероятность — величина,
принятая как разделяющая вероятные и маловероятные со-
бытия.
Доверительная вероятность традиционно обозначается
как «/>», то есть маленькой латинской буквой «то».
В качестве доверительной вероятности обычно выбира-
ют круглые числа: 0,05, 0,01, 0,001 и так далее.
Строго говоря, использование круглых чисел доверитель-
ной вероятности — наследие старой техники ручного про-
ведения статистических расчетов. При ней обычно рассчи-
тывается некоторая величина, которая показывает степень
отличия фактических наблюдений от ожидаемых, а потом
нужно перевести эту величину в вероятность
Так как в большинстве случаев сделать это при помо-
щи простых формул нельзя, то использовались таблицы

152
Часть 1. Анализ вероятностей
с критическими значениями. Например, пусть для критерия
«хи-квадрат» с двумя степенями свободы была получена вели-
чина 11,7. При ручной технике расчета можно взять таблицу
критических значений «хи-квадрат» распределения и выяс-
нить, что при двух степенях свободы при р = 0,001 критичес-
кое значение равно 13,815, при/> = 0,01 критическое значение
равно 9,21, а при р = 0,05 критическое значение равно 5,99.
Следовательно, величина в 11,7 меньше критического значе-
ния для р = 0,01 и больше, — для р = 0,001, и различия досто-
верны с р < 0,01, но не достоверны с р = 0,001.
В настоящее время это не нужно, так как современные
статистические пакеты программ не только рассчитывают
величину различия, но и точную величину соответствующей
доверительной вероятности. Если же критерий «хи-квадрат»
или другие популярные статистические тесты рассчитыва-
ются не в пакетах статистических программ, а, например,
в электронной таблице Excel, то с ее же помощью можно оп-
ределить и величину доверительной вероятности, так как в
Excel имеется ряд встроенных функций, позволяющих полу-
чить величину доверительной вероятности. Так, для крите-
рия «хи-квадрат» имеется встроенная функция ХИ2РАСП от
двух аргументов, первый их которых — величина различия,
а второй — число степеней свободы. В рассматриваемом
случае ХИ2РАСП(А6;2) = 0,00288, то есть различие досто-
верно с р = 0,00288. Огрублять полученную таким образом
доверительную вероятность до р < 0,01 не нужно.
Таким образом, доверительная вероятность — не вероят-
ность некоторого события, а вопрос доверия. Из жизненного
опыта мы знаем, что пагубны и чрезмерная легковерность,
и чрезмерная подозрительность.
При проверке статистической гипотезы возможны ошиб-
ки двух родов. Ошибка первого рода — принять на веру не-
правильную статистическую гипотезу, то есть чрезмерная
легковерность. Ошибка второго рода — не согласиться с пра-
вильной гипотезой, то есть чрезмерная подозрительность.
Вероятность ошибки первого рода, то есть принятия
ложпоположитсльной гипотезы, среди потока ложных гипо-
тез равна доверительной вероятности Вероятность ошибки

Глава 6. Элементы математической статистики
153
второго рода, то есть отказа от правильной гипотезы, только
на основании доверительной вероятности рассчитать нельзя,
нужно знать, какие именно гипотезы поступают на проверку.
Уменьшение доверительной вероятности, то есть ужесточе-
ние критериев проверки, уменьшает вероятность ошибок пер-
вого рода, но увеличивает вероятность ошибок второго рода.
Поэтому никакого единого оптимального выбора доверитель-
ной вероятности нет и быть не может. Выбирать ее нужно на ос-
новании величины ущерба от ошибок первого и второго рода.
Для современной медицины характерно стереотипное
использование доверительной вероятности в 0,05, а также
абсолютизирование понятия «достоверные различия».
В технических дисциплинах обычно выбирают значи-
тельно более жесткие условия проверок статистических ги-
потез и работают с доверительными вероятностями от 0,001
и меньше. Так почему же врачи столь легковерны?
Обычно приводят два объяснения, почему в медицине
работают с менее жесткими критериями:
1) в технике изделия одинаковые, а в медицине все люди
разные;
2) сложно набрать достаточно испытуемых.
Первый аргумент вообще не выдерживает никакого серь-
езного анализа. Как обсуждалось выше, чем больше разно-
образие между исследуемыми объектами, тем проще пользо-
ваться статистическими методами.

154
Часть I AhujUU (■;'.-,-•".■ v.-. ', -../,_,,.
Второй аргумент тоже не столь безупречен. На основа-
нии изложенной ниже в разделе о центральной предельной
теореме техники легко получить, что для перехода отр = 0,05
к р = 0,001 объем наблюдений нужно увеличить примерно
в 2,5 раза.
В случаях, когда ущерб от ошибок первого и второго рода
сопоставим, выбор/? = 0,05 действительно разумен. Так, при
постановке диагноза ошибка первого рода — поставить не-
правильный диагноз, ошибка второго рода — отказаться от
предполагаемого правильного диагноза и оставить пациента
без диагноза. Ущерб от обеих ошибок близок1, и выбор «мяг-
кого» критерия правомочен.
Если же речь идет о проверке готовности самолета к рейсу,
то ошибка первого рода — выпустить в рейс самолет, который
разобьется, а ошибка второго рода — не выпустить в рейс са-
молет, который благополучно долетит. Здесь ущерб от ошиб-
ки первого рода много больше, чем от ошибки второго рода,
и нужны значительно более жесткие критерии проверки.
Если бы инженеры, так же как и врачи, работали с дове-
рительной вероятность в 0,05, то они бы строили самолеты,
которые разбиваются в каждом двадцатом рейсе, и мосты,
которые бы разваливались при прохождении каждого двад-
цатого поезда.
В некоторых случаях выбор/> = 0,05 не просто обоснован,
а даже слишком жесток. Так, если в больнице, возможно, на-
чинается увеличение заболеваемости внутрибольничными
инфекциями, то проведение противоэпидемических мероп-
риятий обосновано и при доверительной вероятности повы-
шения заболеваемости порядка 0,1.
Однако механическое перенесение «мягких» стандартов
клинической медицины на теоретическую медицину совер-
шенно неправильно, так как вреда от неправильной публи-
кации значительно больше, чем пользы от правильной.
Это усугубляется следующими двумя обстоятельствами:
1. Современная практика публикации статей в науч-
ных медицинских журналах: печатать статьи с по-
' Примеры ситуаций, когда это не так, читателю предлагается до
думать самостоятельно.

Глава 6. Элементы матслн ■■■■;. v^:^ стиптстики
155
ложительными результатами и не печатать с отри-
цательными. Поэтому если 20 независимых групп
исследователей занимается проверкой эффективно-
сти предложенного метода лечения, который на самом
деле неэффективен, и одна из них получит ложнопо-
ложительный результат, а остальные установят, что
метод неэффективен, то в результате будет опублико-
вана одна статья — о статистически подтвержденной
эффективности метода.
2. Использование современных вычислительных средств
дало возможность проводить сравнения с большим
количеством переменных, из-за чего ложноположи-
тельные результаты из возможных стали неизбежны-
ми. Так, в средней кандидатской диссертации боль-
ные охарактеризованы по паре сотен параметров.
Поэтому если проводится сравнение достоверности
ср = 0,05 различия нескольких групп, то ожидается
Юложноположительных различий; если же сравни-
вать все параметры друг с другом, то общее количе-
ство пар становится около 20 тысяч и, следовательно,
ожидаемое количество ложнодостоверпых связей —
порядка тысячи. При современном стиле изложения,
при котором описываются только достоверные раз-

156
Часть ■. Анализ вероятностей
личия, а обо всех проводимых сравнениях, не давших
достоверных различий, даже не упоминается, этих
ложноположительных связей с лихвой хватит для на-
писания диссертации.
В результате современная медицина замусорена ложно-
положительными результатами.
В каждой отдельной работе ложноположительные связи
неизбежны. Выявить их можно потом в результате работы
по сопоставлению и обобщению результатов, полученных
разными группами исследователей. В современной практи-
ке работ по доказательной медицине это называется мета-
анализом1, такие результаты регулярно публикуются, в част-
ности, Кохрайновским сообществом. Примеры такого ана-
лиза будут приведены ниже. Однако для того, чтобы резуль-
1 Не слишком точный термин, лучше бы подошел кроссанализ.
В математике, в которой эти вопросы были изучены раньше и на более
высоком уровне, приставка «мета» означает более серьезную проце-
дуру — не объединение данных одного уроння, а повышение уровня
абстракции. Например, если «аппендицит» — пример диагноза, то
«гипердиагностика» — пример метадиапюза

Элементы математической статистики
таты исследования можно было использовать для дальней-
шего анализа и обобщения, они должны быть описаны до-
статочно полным образом.
Резюме
1. Выбор доверительной вероятности нужно делать на
основании сопоставления ущерба от ложноположи-
тельных и ложноотрицательных выводов.
2. В любой конкретной работе наличие ложноположи-
тельных и ложноотрицательных результатов неизбеж-
но. Поэтому практические и теоретические выводы
нужно делать на основании сопоставления результа-
тов разных исследований, а сами результаты исследо-
вания должны быть описаны достаточно подробно,
так, чтобы такое обобщение было возможно.
6.3. Сравнение частоты и вероятности.
Доверительные вероятности
Из руководства Шингмена по медицинскому жаргону:
НА ОСНОВАНИИ МОЕГО ОПЫТА - однажды;
В СЛУЧАЕ, НАБЛЮДАВШЕМСЯ ПОСЛЕ АНАЛОГИЧНОГО -
дважды;
В ЦЕЛОМ РЯДЕ СЛУЧАЕВ - трижды
Артур Блох «Законы Мерфи для медиков»
6.3.1. Расчет доверительных границ
к частоте встречаемости
Расчет достоверности различия частоты и вероятности
с помощью электронной таблицы Excel, определение
доверительных границ к частоте.
Рассмотрим пример. Пусть по литературным данным
частота осложнений у некоторой категории больных рав-
на 12 %, а в исследуемой группе из 40 больных осложнения
Пыли только у 2, то есть у 2/40 = 5 %. Выясним, является ли
>то различие достоверным.

158
ArsuAWj вероятностей
В электронной таблице Excel при помощи функции
БИНОМРАСП можно рассчитать вероятность данного зна-
чения или данных и меньших значений. Эта функция имеет
четыре аргумента. Первых из них — число успехов, то есть
в данном случае количество больных с осложнениями. Вто-
рой аргумент — число испытаний, то есть в данном случае
количество больных. Третий аргумент — вероятность успе-
ха, то есть в данном случае частота осложнений по лите-
ратурным данным. Четвертый аргумент называется «интег-
ральная» и показывает, нужно ли рассчитать вероятность
того, что будет в точности столько успехов или столько или
меньше успехов. Если нужно определить вероятность этого
количества успехов, то в качестве значения аргумента мож-
но ввести ноль, а если данного или меньшего значения — то
единицу.
В данном случае вероятность того, что при ожидаемой
частоте осложнений 12 % из 40 больных число осложне-
ний будет 2 или меньше есть БИНОМРАСП(2;40;0,12;1),
что равно 0,126. Так как это достаточно большая величина,
в частности большая, чем 0,05, то даже при р = 0,05 досто-
верных различий между наблюдаемой частотой и вероят-
ностью нет.
Пусть теперь в группе из 40 человек было 10 осложне-
ний. Тогда вероятность того, что при вероятности 0,12 из
40 человек будет 9 или меньше осложнений есть БИНОМ-
РАСП(9;40;0,12;1), что равно 0,9825. Следовательно, вероят-
ность того,чтобудетЮилибольшебольных,равна 1—0,9825 =
= 0,0125. В результате получаем, что различия между ожида-
емой вероятностью 0,12 и наблюдаемой частотой достовер-
ны с р = 0,0125.
Подобным образом можно не только определять досто-
верность различия наблюдаемой частоты и ожидаемой веро-
ятности, но и получить, в каких пределах при заданной до-
верительной вероятности могут находиться вероятности, не
отличающиеся достоверно от наблюдаемой частоты.
Пусть из 40 больных у 10 наблюдались осложнения, то
есть частота осложнений была равна 25 %. Возьмем в качест-
ве доверительной вероятности р = 0,05. Вероятность того,

Глава 6. Элементы математической статистики
159
что при вероятности х из 40 больных осложнения будут у 10
или менее, равна БИНОМРАСП(10;40;л:;]). Подбором па-
раметрах находим, что БИНОМРАСП(10;40;0,387;1) * 0,05.
Следовательно, с доверительной вероятностью р = 0,05 веро-
ятность осложнений меньше 0,387.
Для получения оценки вероятности осложнений с другой
стороны нужно найти, при какой величине х вероятность
того, что из 40 больных осложнения будут у 10 или более,
равна 0,05. Но если вероятность того, что будет 10 или бо-
лее осложнений равна 0,05, то вероятность того, что будет
9 или менее осложнений, равна 0,95. Следовательно, нужно
найти такое х, что БИНОМРАСП(9;40;х; 1) = 0,95. Подбором
находим, что БИНОМРАСП(9;40;0,14237;!) «0,95. Следова-
тельно, с доверительной вероятностью р = 0,05 вероятность
осложнений больше 0,142.
Определение. Полученные оценки возможной вероят-
ности называются односторонними доверительными интер-
валами.
В результате получено, что с р — 0,05 вероятность ослож-
нений меньше 38,7 % и с р = 0,05 вероятность осложнений
больше 14,2 %. Так как вероятность не может быть одновре-
менно больше 38,7 % и меньше 14,2 %, то получение веро-
ятностей, больших и меньших ожидаемых, — несовместные
события. Следовательно, вероятность того, что вероятность
осложнения будет больше 38,7 % или меньше 14,2 %, равна
0,05 + 0,05 = 0,1. Следовательно, с доверительной вероят-
ностью р = 0,1 вероятность осложнений должна находиться
в интервале от 14,2 до 38,7 %.
Определение. Полученная оценка возможной вероят-
ности называются двусторонним доверительным интер-
валом.
Таким образом, из двух односторонних оценок с дове-
рительной вероятностью р можно получить двусторонний
Доверительный интервал с доверительной вероятностью 2р.
Поэтому если нужно получить двусторонний доверитель-
ный интервал с доверительной вероятностью 0,05, то од-
носторонние доверительные интервалы нужно подбирать с
Доверительной вероятностью 0,025. В нашем случае для р =

160
\7.\л---, /. Ann шз вероятностей
= 0,05 двусторонний доверительный интервал будет от 12,7 %
до41,2%.
Таблица двусторонних доверительных интервалов с р =
= 0,05 для биномиального распределения приведена в при-
ложении № 2 под номером 1.
Следует обратить внимание на то, что наблюдаемая ча-
стота в 2,5 % не находится посередине доверительного интер-
вала, поэтому записать его в виде М± т невозможно. Форма
представления М ± т стала стереотипной из-за того, что в
наиболее часто использующемся случае — оценке среднего
арифметического при помощи критерия Стьюдента — дове-
рительные границы симметричны.
Как видно, для определения доверительных границ к на-
блюдаемой частоте нужно либо потратить некоторое время
на подбор параметров, либо воспользоваться статистиче-
скими таблицами. В электронной таблице Excel в явном
виде расчет доверительных границ к частоте не затабулиро-
ван. Имеется похожая функция КРИТБИНОМ, но она дела-
ет обратную операцию — определяет при заданном р, какой
самой большой или самой маленькой может быть частота1,
тогда как нам нужно вычислить, какой может быть вероят-
ность при заданной частоте.
Полученные оценки справедливы только в том случае,
когда рассматриваемая случайная величина распределена
биномиально, то есть отдельные случаи независимы и рав-
новероятны. Как уже упоминалось выше, проверка исходов
на независимость — дело тонкое2. Вторая возможная причи-
на небиномиальности распределения — неодинаковость ве-
роятности исходов для разных случаев
1 Точнее, она определяет максимальное колнчестно наблюдаемых
случаев, а для получений частоты нужно результат поделить на колн-
честно наблюдений.
' Полому и настоящее мремя чаше нсполыусгся не для указания
того, какие причины могут принесен к неточности ре ту дыаеоп статис-
тической обработки собс шейного исследонаиня. сколько для критики
результатом исслсдонапмИ других anropon

Глава 6 Элементы .'■;.;..
:•.': мистики
161
Пусть мы рассматриваем количество осложнений среди
больных, поступающих в палату по скорой помощи. Если
в палату больные направляются в порядке поступления, то
с определенными оговорками' можно считать их исходы
равновероятными. Если при поступлении более тяжелые
больные направляются преимущественно в палату к более
опытному врачу, то распределение количества осложнений
в палате биномиально, просто в разных палатах — разные
распределения. Если же палата формируется так, чтобы в
ней половина больных была тяжелой, а половина — лег-
ких, с тем чтобы легкие больные ухаживали за тяжелыми,
то количество осложнений уже не будет распределено бино-
миально.
Если вероятность наступления регистрируемого события
для каждого испытуемого мала, а количество испытуемых
велико, то количество событий распределено по Пуассону.
Расчет доверительных границ для распределения Пуассона
аналогичен, распределение Пуассона затабулировано в Excel
встроенной функцией ПУАССОН. Проверка на примени-
мость распределения Пуассона мягче, чем биномиального
распределения, так как требуется только независимость и
маловероятность отдельных событий, а не равенство их ве-
роятностей.
Есть, правда, некоторый дополнительный элемент не-
точности, так как распределение Пуассона — не сумма боль-
шого количества маловероятных независимых событий,
а сумма бесконечно большого количества независимых бес-
конечно маловероятных событий. Однако, если вероятность
рассматриваемых независимых событий меньше q, то истин-
ное распределение будет отличаться от распределения Пуас-
сона меньше или порядка д2.
1 Даже в этом случае возможны тонкости. Например, если могут
поступить больные, пострадавшие в результате массовой аварии или
стихийного бедствия, то они обычно более тяжелые Следовательно,
если поступает тяжелый больной, то вероятность того, что следующий
больной — тоже тяжелый, увеличивается.
6 Медицинская стистика

162
Часть J А чал из вероятностей
Рассмотрим, например, распределение количества моск-
вичей, у которых за некоторый день' были переломы. Если
исключить больных с привычными переломами, то для ос-
тавшихся вероятность перелома за сутки мала, например,
меньше 0,01. Следовательно, рассчитанные в предположе-
нии о пуассоновости вероятности будут отличаться от ис-
тинных менее или порядка 0,0001.
Таблица двусторонних доверительных интервалов для
распределения Пуассона приведена в приложении № 2 под
номером 2.
При помощи такого рода расчетов можно также выяснить,
действительно ли при массовом сравнении были получены
достоверные различия. Пусть, например, при сравнении двух
групп по 42 параметрам было получено 5 достоверных раз-
личий с р = 0,05. Количество ложноположительных разли-
чий при отсутствии истинных различий будет распределено
биномиально с количеством наблюдений 42 и вероятностью
успеха 0,05. Рассчитав БИНОМРАСП(4;42;0,05;1) * 0,9427,
получаем, что 5 или более ложноположительных различий
можно получить с вероятностью 1 - 0,9427 = 0,0573. Сле-
довательно, статистическая гипотеза о том, что полученные
различия ложноположительны, не может быть отвергнута с
р = 0,05, и, возможно, все полученные различия — ложнопо-
ложительные.
6.3.2. Расчет доверительных границ к медиане
и другим процентилям
Страшная мысль Стивена: 50 % хи-
рургов — ниже среднего уровня.
Артур Блох
«Законы Мерфи для медиков»
Расчет достоверности различий частоты и вероятности,
определение доверительных границ к процентилям.
1 В разные дни — разные распределения Пуассона, отличающие-
ся ожидаемым количеством переломои. Например, и гололед перело-
мом больше Есть также авральное для транматологоп 1 января, когда
пьяные россияне массово катаются с ледяных горок

Глава 6. Элементы математической статистики
163
Если исследуемая числовая случайная величина £, прини-
мает много возможных значений, то попытка исследования
ее распределения путем нахождения частоты каждого конк-
ретного значения малопродуктивна. В этом случае лучше ис-
следовать частоту не данного значения, а данного или мень-
шего значения. На языке раздела 4.6 это означает, что нужно
исследовать функцию распределения.
Один из возможных способов описания функции рас-
пределения числовой случайной величины — задание ее
процентилей.
Определение. Если £, — непрерывная числовая случайная
величина, то процентилем1 вероятности р называется такая
величина Х(р), что Р(£,<Х(р)) = р.
Здесь р — вероятность, которая должна быть больше нуля
и меньше единицы.
Например, 10%-й процентиль— такая величина, что в
10 % наблюдений мы получаем величины, меньшие процен-
тиля, а в 90 % наблюдений — большие.
Приведенное определение, строго говоря, подходит толь-
ко для непрерывных случайных величин, у которых функ-
ция распределения непрерывна. Если функция определения
имеет разрывы, как это бывает, в частности, у дискретных
случайных величин, то искомое значение может попасть в
разрыв функции распределения, и для заданного р может
не существовать такого X, что Р(Ъ<Х) = р. В этом случае оп-
ределим Х(р) как самое маленькое из таких значений х, что
1\£><х)>р.
При работе с пакетом статистических программ оценка
процентиля не требует каких-то сложных манипуляций. Для
этого можно2, как описано в разделе 3.1, рассчитать табли-
цу частот встречаемости, а потом по колонке «Cumulative
Percent» найти нужную величину. Например, пусть мы нс-
' Примечание для лип, имеющих ба юное математическое обра ю-
,а"ие: если F— функция распределения, то F ' проценгнль
Другой, более прямой способ получения неличин процентилей
л'Дет описан ниже, в разделе, посняшенном расчету параметров

164
Часть I. Анализ вероятностей
Таблица 6.1
Таблица распределения больных по возрасту
Age of
patient
Valid
i
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Frequency
3
2
4
6
3
5
4
1
2
2
4
3
1
3
2
2
5
1
3
Percent
0,753769
0,502513
1,005025
1,507538
0,753769
1,256281
1,005025
0,251256
0,502513
0,502513
1,005025
0,753769
0,251256
0,753769
0,502513
0,502513
1,256281
0,251256
0,753769
Valid
Percent
0,753769
0,502513
1,005025
1,507538
0,753769
1,256281
1,005025
0,251256
0,502513
0,502513
1,005025
0,753769
0,251256
0,753769
0,502513
0,502513
1,256281
0,251256
0,753769
Cumulative
Percent
0,7537688
1,2562814
2,2613065
3,7688442
4,5226131
5,7788945
6,7839196
7,0351759
7,5376884
8,040201
9,0452261
9,798995
10,050251
10,80402
11,306533
11,809045
13,065327
13,316583
14,070352
i
———
i
1
i
|. .
56
57
i 58
59
60
'"~6l"~
62
""o'JT
~6~4~
10
9
4
2
4
6
7
"' "з
9
2,512563
2,261307
1,005025
0,502513
1,005025
1,507538
1,758794
0,753769
2,261307
2,512563
2,261307
1,005025
0,502513
1,005025
1,507538
1,758794
0,753769
2,261307
44,221106
46,482412
47,487437
47,98995
48,994975
50,502513
52,261307
53,015075
55,276382

Глава 6 Элементы м«пъ\*1!::Ш'.и кои статистики 165
65
66
Frequency
8
8
Percent
2,01005
2,01005
Valid
Percent
2,01005
2,01005,
Cumulative
Percent
57,286432
59,296482
93
95
Total
1
1
398
0,251256
0,251256
100
0,251256
0,251256
100
99,748744
100
следуем распределение больных по возрасту и получили таб-
лицу, фрагменты которой приведены в табл. 6.1.
В соответствии с приведенным выше определением
10%-м процентилем возраста будет 27 лет, а 50%-м процен-
тилем — 61 год.
Определение. 50%-й процентиль называется медианой.
Таким образом, медиана — величина, делящая выборку
на две части одинакового размера.
Определение. Квартилями называются 25%-й, 50%-й и
75%-й процентили.
Следовательно, медиана — частный случай квартиля.
В соответствии с определением медианы она может трак-
товаться как характерное значение. Обычно как характерное
значение трактуется среднее арифметическое, однако по
целому ряду причин, которые будут подробно разбираться
ниже, в случае некомпактного и сильно асимметричного
распределения среднее арифметическое — плохой кандидат
на звание характерного значения. В этих случаях медиана
дает боле'е точное представления об «обычной» величине
изучаемой переменной.
Вообще говоря, и в том случае, когда распределение ком-
пактно или относительно симметрично, медиана может за-
менить среднее арифметическое, так как в этом случае эти
два параметра близки. Поэтому для описания характерного
значения медиана предпочтительнее среднего арифметиче-
ского. Однако у среднего арифметического есть некоторые
дополнительные полезные свойства, которых нету медианы.
В частности, среднее арифметическое суммы двух случайных
величин равно сумме их средних арифметических, тогда как

166
4w пч. Анализ вероятностей
для медианы таких формул не существует — даже для случая
независимых случайных величин медиана суммы зависит не
только от медиан своих слагаемых, но и от формы их распре-
деления. Поэтому в современной практике медиана актив-
но используется только для сильно варьирующих и сильно
асимметричных распределений, например содержания йода
в организме.
Изучим теперь задачу об определении доверительных
границ к процентилю.
Пусть Р — вероятность, для которой определяются до-
верительные границы для процентиля. Пусть xt,...xN— име-
ющийся набор из N наблюдений, a XX,...XN— тот же набор
наблюдений, но переупорядоченный в порядке возрастания
значения. Предположим, что процентиль равен X. Пусть
4 — количество наблюдений, в которых полученное значе-
ние было меньше X. Тогда по определению процентиля слу-
чайная величина £ распределена биномиально с числом наб-
людений Nvt вероятностью Р.
Продолжим рассмотрение приведенного выше примера.
Пусть у нас имеется 398 наблюдений. Возьмем доверитель-
ную вероятность р = 0,05 и вычислим для нее двусторонние
доверительные границы для медианы.
Для определения нижней доверительной границы нам
нужно найти такое п, что вероятность того, что биномиаль-
ное распределение с 398 наблюдениями и вероятностью 0,5
(напоминаю, что это — вероятность того, что случайная ве-
личина меньше медианы) принимает значение п или мень-
ше с вероятностью 0,025 (напоминаю, что для определения
двусторонних доверительных границ с вероятностью р нуж-
но найти односторонние доверительные вероятности с ве-
роятностью р/2). При расчете в Excel это удобно делать при
помоши встроенной функции КРИТБИНОМ В данном
случае определяем КРИТБИНОМ(398;0,5,0,025) и получа-
ем значение 179 Следовательно, вероятность того, что при
398 наблюдениях случайной величины будет 179 или менее
успехом, не меньше 0,025. а вероятность того, что успехов
Пуле г 178 или меньше, меньше 0,025 Следоваге п,но, с дове-
рительной вероятностью/» = 0,025 статистическая гпштма

Глава 6 Элементы .i/cw.-y.-.o-w;^,^:^и_ статистики 167
о том, что медиана меньше или равна Хт, должна быть от-
вергнута.
При определении доверительных границ по приведенной
таблице удобнее работать не с номером упорядоченного ряда
наблюдений, а с его частотой нарастающим итогом. Поделив
]78 на общее количество наблюдений 398, получаем 44,7 %.
Далее находим, что в приведенной выше табл. 6.1 возраст
в 56 лет соответствует частоте 44,2%, а возраст в 57 лет —
46,5 %. Следовательно, с доверительной вероятностью 0,025
медиана возраста больше или равна 57 годам.
Для нахождения оценки сверху в Excel находим, что
КРИТБИНОМ(398;0,5;0,975) = 219. Следовательно, с дове-
рительной вероятностью р = 0,025 статистическая гипотеза о
том, что медиана больше или равна Хт, должна быть отверг-
нута. Так как 220/398 = 55,276382 %, то находим, что верхняя
доверительная граница медианы — 64 года.
В результате получили, что с доверительной вероятно-
стью р = 0,05 медиана возраста находится в пределах от 57
до 64 лет.
При определении верхней границы медианы в данном
случае пришлось прибегнуть к маленькой хитрости. Дело в
том, что SPSS, в котором рассчитывалась таблица частот, оп-
ределяет их с большой точностью, но показывает получив-
шиеся проценты с точностью до одного знака после запятой.
Поэтому по исходной таблице нельзя было определить, чему
была равна верхняя граница — 64 или 65 годам. Для этого
таблицу частот пришлось через буфер обмена скопировать в
Excel и уже там повысить количество отображаемых знаков.
Аналогичным образом при расчете доверительных гра-
ниц к 10%-му процентилю получаем КРИТБИНОМ(398;
0,1 ;0,025) = 28, и далее 27/398 = 6,9 %, что соответствует 21 го-
ду, а КРИТБИНОМ(398;0,1;0,975) = 52, и далее 53/398 =
= 13,3%, что соответствует 32 годам. Следовательно, 10%-й
ироцентиль возраста с р = 0,05 находится в пределах от 21 до
32 лет.
В завершение раздела еще раз напомню, что, для того
чтобы не проводить самостоятельно такие расчеты, можно
воспользоваться таблицей, приведенной в конце книги.

168
Чисть /. Анализ вероятностей
6.4. Сравнение набора частот
с набором вероятностей и наборов
частот с набором частот.
Критерий х2 («хи-квадрат»)
При объяснении этого критерия врачам
самое сложное — убедить их в существо-
вании греческой буквы «хи».
Собственное наблюдение
6.4.1. Вариант ручного счета — сравнение
собственных результатов с литературными
данными, сопоставление данных разных
источников друг с другом, проверка
на однородность
Расчет достоверности одновременных различий нескольких
частот и вероятностей, графическое представление
доверительных границ к частоте в модном виде.
В рассмотренном в предыдущем пункте случае определя-
лась достоверность отличия частоты от вероятности. Часто
нужно сравнивать не одну частоту с одной вероятностью,
а набор частот с набором вероятностей или несколько на-
боров частот друг с другом. Сделать это можно при помощи
критерия х2
Пусть изучаемая величина может принимать не два,
а п разных значений, ожидаемая вероятность k-то значения
равна рк, а из N наблюдений k-t значение встретилось N(k)
раз. Для определения достоверности отличия набора частот
N(k)/Noi вероятностейрк проведем следующие расчеты.
Шаг 1. Для каждого к определим ожидаемое количество
Nu(k) наблюдений, в котором встретилось к-е значение, по
формуле М0(к) = jVx pk (ожидаемое количество не обязатель-
но целое!);
Шаг 2. Для каждого к определим существенность Д раз-
ности ожидаемого и фактического количества наблюдении
к-ro значения по формуле Ak={N(k) - Nu(k))2/N0{k).

Глава 6. Элементы математической статистики
169
Шаг 3. Просуммируем существенности разности Д = Д, +
+ ...+ V
Шаг4. Определяем вероятность^того, что случайная ве-
личина, распределенная как %2 с N — 1 степенью свободы1,
принимает значения, равные или большие Д. Искомую веро-
ятность можно вычислить в электронной таблице Excel при
помощи встроенной функции ХИ2РАСП от двух аргумен-
тов, первый из которых равен Д, а второй равен N—\.
В предположении о достаточности объема наблюдений2
и о том, что различия частот от вероятностей обусловлены
только случайными факторами, случайная величина Д рас-
пределена как х2 с N— 1 степенью свободы. Следовательно,
полученная вероятность р — доверительная вероятность ста-
тистической гипотезы о том, что различия частот от вероят-
ностей случайны.
Для того чтобы обосновать приведенную схему, проведем
вычисления ожидаемой величины значений Ак разности и Д
разности, для чего придется пользоваться техникой расчетов
моментов, которая будет объясняться ниже3.
В предположении о независимости исходов и случайно-
сти различий между вероятностями и частотами для каждого
к случайная величина N(k) распределена биномиально с ко-
личеством наблюдения N и вероятностью успешного исхода
рк, следовательно (см. раздел с определением биномиальной
величины), имеет математическое ожидание N х рки дис-
персию Nxpkx(l—pk). Поэтому случайная величина N(k) —
- N0(k), равная N(k) — Nx pk, имеет нулевое математическое
ожидание и дисперсию, равную N х рк х (1 - рк). Так как ма-
тематическое ожидание квадрата случайной величины равно
сумме квадрата ее математического ожидания и дисперсии
' Одна степень свободы пропадает из-за того, что сумма частот
равна единице. Более точные выкладки см. ниже.
2 См. обсуждение в конце раздела.
' Если уж книга призывает к критическому восприятию име-
ющейся литературы и необходимости обосновывать выводы, то и
собственные указания нужно, по возможности, подтверждать дока-
зательствами Лица, читающие книгу первый раз, могут пропустить
часть с выкладками и перейти к примеру

170
Часть i. Анализ вероятностей
(см. соответствующие разделы ниже), то математическое
ожидание случайной величины (Щк) - Щк))1 равно Nx ркх
х (1 - рк), а математическое ожидание Ак = (N(k) - N0(k))2/
Ng(k) равно Nxpkx(\ -pk)/(Nxpk), то есть равно 1 - рк.
В результате получили, что ожидаемое среднее значение
каждой Акравно 1 -рк, а ожидаемое значение их суммы А = А, +
+ ...+ Д„есть(1-/>,)+...+ ( 1 -PN) = \ +•■•+ 1 -0>,+-+/>л)
= дг_ (р +...+ pN) = #- 1. Вопрос о том, насколько форма
полученного распределения близка к х2-распределению, бу-
дет обсуждаться ниже, в разделе о центральной предельной
теореме.
Пусть, например, в некоторой рассматриваемой группе из
лиц трудоспособного возраста наблюдалось 154 случая смерти
от разных причин. Сравним ее со структурой смертности жи-
телей трудоспособного возраста г. Москвы за 1993—1998 годы.
В приведенной ниже табл. 6.2 в первой колонке — назва-
ния причины смерти, во второй — количество случаев в изу-
чаемой группе, в третьей — набор частот в процентах, которые
берутся как ожидаемые вероятности. В соответствии с приве-
денным выше алгоритмом расчета для определения величин
в четвертой колонке (ожидаемого количества смертей) нуж-
но общее количество смертей (154) умножить на содержимое
третьей колонки, то есть ожидаемую долю, и разделить на 100,
так как доля приведена не в долях единицы, а, как это обыч-
но делается в медицине, в процентах. Ожидаемая величина А,
приведенная в пятой колонке, равна единице минус ожидае-
мой доле, деленной на сто. И наконец, шестая колонка рассчи-
тывается по формуле, приведенной в начале раздела в шаге 2
алгоритма расчета. Строка «ВСЕГО» получается суммирова-
нием числовых значений для отдельных причин смерти.
Полученная величина различий составляет 19,288. Так как
причины смерти разбиты на 6 подгрупп, то количество степе-
ней свободы равно 5. Вычислив в Excel ХИ2РАСП( 19,288,5).
получаем 0,0017. Следовательно, с доверительной вероят-
ностью/? = 0,0017 структура смертности в исследуемой груп-
пе отличается от структуры в Москве за 1993-1998 годы
Прицеленная схема ручного счета хороша тем, что поз-
воляет также провести содержательный пиал из и выяснить,

Глава 6. Элементымиг^ся'.ппачесхйи статистики 171
Таблица 6.2
Сравнение частот и ожидаемых вероятностей
Причины
смерти
1
Травмы и
несчастные
случаи
Болезни
сердца и
сосудов
Злокачест-
венные ново-
образования
Болезни ор-
ганов дыха-
ния
Болезни ор-
ганов пище-
варения
Другие при-
чины
ВСЕГО
Факт,
колич.
2
47
38
19
17
8
25
154
Ожидаемая
доля, %
3
33,88
31,03
13,49
4,69
5,62
11,29
100
N0
4
52,175
47,786
20,775
7,2226
8,6548
17,387
154
Ожид.
д
5
0,6612
0,6897
0,8651
0,9531
0,9438
0,8871
5
Факт.
Д
6
0,5133
2,0041
0,1516
13,236
0,0495
3,3338
19,288
за счет каких вариантов получены основные отличия. Так,
в данном случае основное различие в смертности получено
за счет смертей от болезней органов дыхания, которые в рас-
сматриваемом случае более часты, чем ожидалось.
Если исключить эту группу из рассмотрения, то в резуль-
тате получим табл. 6.3.
В данном случае при пяти сравниваемых подгруппах
ХИ2РАСП(6,3875;4) = 0,172, то есть различия недосто-
верны.
Для иллюстрации хорошо приводить графики частот с до-
верительными границами. Для того чтобы построить нужный
график в Excel, немного переделаем исходную табл. 6.2.
Для этого вставляем третью колонку с долей смертель-
ных исходов п процентах, рассчитывая ее делением ко-

172
Часть 1. Анализ вероятностей
Таблица 6.3
Сравнение частот и ожидаемых вероятностей
после исключения одной из причин смерти
Причины
смерти
1
Травмы и
несчастные
случаи
Болезни серд-
ца и сосудов
Злокачествен-
ные новооб-
разования
Болезни орга-
нов пищева-
рения
Другие при-
чины
ВСЕГО
Факт,
колич.
2
47
38
19
8
25
137
Ожидаемая
доля, %
3
33,88
31,03
13,49
5,62
11,29
95,31
N0
4
46,416
42,511
18,481
7,6994
15,467
130,57
Ожид.
А
5
0,6612
0,6897
0,8651
0,9438
0,8871
4,0469
Факт.
А
6
0,0074
0,4787
0,0146
0,0117
5,8751
6,3875
личества смертей в данной группе на общее количество
смертей (то есть 154). Пятую и шестую колонку рассчиты-
ваем так, как это было описано в пункте 6.3. В данном слу-
чае определяем двусторонние доверительные интервалы
для вероятности с р = 0,05, то есть для количества смер-
тей п находим максимальную вероятность Р , такую что
БИНОМРАСП(п;154;Ртах;1) «0,025 и минимальную вероят-
ность Z^, такую, что БИНОМРАСП(п-1;154;Рт.п;1) «0,975,
и заполняем полученными величинами колонки номер 5 и 6,
умножая на сто, чтобы получить значение в процентах. Для
получения «плюсовой» погрешности отнимаем от содержи-
мого пятой колонки содержимое третьей колонки. Для по-
лучения «минусовой» погрешности вычитаем из третьей ко-
лонки шестую (см. табл. 6.4).
Далее в Excel строим гистограмму частот и вероятностей
с доверительными границами. Техника построения подроб-
но изложена и конце книги, и приложении № 3.

Главе 6. Элементы математической статистики
173
Таблица 6.4
Доверительные границы к частоте
Причины
смерти (
1
I Травмы
и не-
счастные
случаи
Болезни
сердца и
сосудов
I Злока-
чест-
венные
новооб-
разова-
ния
Болезни
органов
дыхания
Болезни
органов
пищева-
рения
Другие
причины
ВСЕГО
Кол.
факт.
2
47
38
19
17
8
25
154
Доля
факт.,
%
3
30,52
24,68
12,34
11,04
5,19
16,23
Доля по
Москве,
%
4
33,88
31,03
13,49
4,69
5,62
11,29
100 | 100
Вероят-
ность, %
Мах
5
38,44
32,26
18,6
17,09
9,98
23,02
Min
6
23,36
18,09
7,59
6,56
2,27
10,79
Погреш- I
ность, %
+
7
7,92
7,58
6,25
6,06
4,78
6,79
-
8
7,16
6,58
4,74
4,48
2,93
5,44
По гистограмме (рис. 6.1) хорошо видно, что достовер-
ные (с р = 0,05 и двусторонними доверительными интервала-
ми) различия между частотой и вероятностью — только для
смертей от болезней органов дыхания, а во всех остальных
случаях величина второго столбика находится в пределах
между «рогами» статистической погрешности.
Строго говоря, определяемая критерием х1 достоверность
различия набора частот и вероятностей и наличие в сравни-
ваемых наборах достоверно различающейся пары частоты

174
Часть 1. Анализ вероятностей
Экстенсивные пикаэа!ели смертносшжителей трудоспособного населения
45,00
«,00
35.00
30 00
25,00
го.оо
15.00
ю.оо-1
Ь 00 |
0,00 L
ЙиЬьШ
D Доля факт.
D Доля по Москве
/ /
Рис. 6.1. Гистограмма фактических и ожидаемых долей
и вероятности — вещи разные. Может быть, что ни одна час-
тота не отличается от вероятности достоверно, но большинс-
тво различий близко к значимым, поэтому по совокупности
набор частот отличается от набора вероятностей.
Может быть и обратная ситуация, когда в наборе одна
пара различается, а все остальные — нет, а по совокупности
различие недостоверно. В этом случае различие в паре мож-
но считать ложнодостоверным.
Очень похожая техника расчетов используется в том слу-
чае, если имеется ряд частот, а проверяемая статистическая
гипотеза — то, что эти частоты достоверно не различаются.
В этом случае объединяем все исследования и рассчитываем
общую частоту, а потом для каждого исследования опреде-
ляем существенность расхождения.
Пусть у нас имеется 8 разных больниц, в которых для опреде-
ленного типа больных фиксировались осложнения (табл. 6.5).
В приведенной таблице в первой колонке — номер боль-
ницы по порядку, во второй — количество больных, в треть-
ей — количество больных с осложнениями. Просуммировав
общее количество больных и больных с осложнениями, на-
ходим, что общая частота осложнений равна 192/805 * 0,2385.
Умножив эту частоту па количество больных в этой больни-
це, находим ожидаемое количество осложнений. Величину

Таблица 6.5
Сравнение частот с совокупной частотой
№ п/п
1
1
2
3
4
5
6
7
8
ВСЕГО
Больных
2
244
75
93
70
100
100
84
39
805
Осложнений
3
48
15
22
24
28
22
25
8
192
No
4
58,196
17,888
22,181
16,696
23,851
23,851
20,035
9,3019
192
А
5
1,7864
0,4663
0,0015
3,1957
0,7218
0,1436
1,2305
0,1822
7,728
А находим, как и ранее, по формуле шага 2. Ожидаемую
величину Д для каждой больницы рассчитывать в данном
случае не нужно, так как в проверяемой статистической ги-
потезе вероятности осложнений в разных больницах равны,
и, следовательно, при условии истинности статистической
гипотезы ожидаемая величина равна 1 - 0,2385 = 0,7715.
В данном случае суммарная величина А = 7,728. Анало-
гично описанному выше находим, что для 7 степеней свобо-
ды эта величина х2-распределения соответствует вероятности
в 0,36, то есть различия недостоверны. Поэтому результаты
разных бо льниц можно объединить и считать, что частота
осложнений — 23,85 %.
Для иллюстрации проводимого анализа на однородность
часто рисуют графики частоты с доверительными граница-
ми, причем в рамках доказательной медицины модно делать
это в виде не вертикальных столбиков, а горизонтальных
графиков, а у линий, отображающих доверительные гра-
ницы, почему-то не принято рисовать окончание «рогов»
(в Excel для их удаления нужно выделить «рога» щелчком,
вызвать правой кнопкой контекстное меню и войти в пункт
"Формат полос погрешностей/Вид»). В остальном подго-
товка таблицы и построение графика аналогично приведен-
ному выше.

176
Часть I./\:-ic.^:. >;Л7>;:о;. ,сяэд
В данном случае график выглядит следующим образом
(рис. 6.2).
На полученном графике толстой вертикальной линией
изображена частота осложнений в целом, ромбами — часто-
та осложнений в данной больнице.
Так как проверка на различие частот не дала достовер-
ных различий, то данные разных исследований можно объ-
единить. В таких случаях часто показывают процесс объеди-
нения и уточнения результатов. Для этого при объединении
будем под первым номером брать результат первого исследо-
вания, под вторым — результат объединения первого и вто-
рого исследования, под третьим — результат объединения
первых трех исследований. В этом случае аналогичный гра-
фик будет иметь следующий вид (рис. 6.3).
Получающиеся графики в виде «елочек» показывают, как
при последовательном объединении результатов, сопровож-
дающемся увеличением общего объема наблюдений, умень-
шается статистическая погрешность полученной частоты.
После всех объединений частота осложнений оказывается
23,85 %, а ее доверительные границы с р = 0,05 — от 20,95
до 26,95 %.
Еще раз напомню, что при расчете доверительных границ
используется два предположения — о том, что частота иссле-
дуемого события в разных исследований одинакова, и о том,
Сравнительный анализ частоты осложнений е 8 больницах
Рис. 6.2. Диаграмма частот осложнений в разных больницах,
построенная в стиле доказательной медицины

[лава 6. Элементы математической статистики
177
Частота осложнений по результатам последовательного объединения
8 исследований
Ф"
♦
♦"
♦-
Ф~
-♦
♦
0 °-05 °.i O.tS ОД 05S 03 0,36 0.« 0.« 05
Рис. 6.3. Диаграмма частот осложнений нарастающим итогом
что в каждом исследовании события независимы, так как-
только в этом случае суммарное количество событий во всех
исследованиях распределено биномиально.
Мы выше осуществляли проверку частот осложнений
в разных больницах на достоверность различий и выяснили
при помощи критерия у}, что достоверных различий между
больницами нет. Если обнаружены достоверные различия,
то это еще не означает, что риск осложнения в разных боль-
ницах достоверно различается. Причиной различий может
быть и зависимость отдельных случаев осложнения друг от
друга.
Если бы достоверные различия были выявлены, то подоб-
ное объединение делать было бы нельзя. Однако из того, что
мы в процессе проверки не обнаружили наличия достоверных
различий между частотами, еще не следует, что их на самом
деле нет. Поэтому вывод о полученной оценке частоты следу-
ет делать в очень осторожной форме: «Если различий между
частотами осложнений в разных больницах нет или они мало-
существенны, то с доверительной вероятностью р = 0,05 ча-
стота осложнений находится в пределах от 21 до 27 %».
Если достоверные различия обнаружены, то в этом слу-
чае единичным испытанием приходится считать уже не от-
дельного больного, а отдельную больницу, то есть мы имеем
дело не с 805 наблюдениями, а всего с 8.

178
Часть I Анализ вероятностей
В этом случае для оценки средней по больнице частоты
осложнений используются следующие два подхода:
1. Рассчитываем среднее арифметическое и средне-
квадратичное отклонение частоты осложнений по
больнице, что в данном случае составляет 24,74 и
5,37 %. Далее при помощи критерия Стьюдента (бу-
дет подробно обсуждаться ниже) определяем, что
прир = 0,05 и 8 наблюдениях / = 2,36, откуда 5,37 % х
х 2,36 = 12,69 %. В результате получаем, что средняя
по больнице вероятность осложнения с доверитель-
ной вероятностью р = 0,05 находится в интервале
24,74 ±12,69%.
2. В соответствии с изложенным в п. 6.3.2 можно оп-
ределить доверительные границы к медиане частоты
осложнений по больницам. Однако при определении
двусторонних доверительных интервалов с довери-
тельной вероятностью р = 0,05 выясняется, что 8 на-
блюдений для этого недостаточно. Если перейти к бо-
лее мягкому критерию односторонних доверительных
интервалов ср = 0,05, то получаем, что оценкой медиа-
ны по 8 наблюдениям будут самое большое и самое
маленькое значение. Следовательно, с доверительной
вероятностью р = 0,05 медиана частоты осложнений
больше 19,67 % и с доверительной вероятностью р =
= 0,05 медиана частоты осложнений меньше 34,29 %.
Как хорошо видно, при таких вариантах расчета стати-
стическая погрешность определения частоты осложнений
значительно больше. Второй недостаток этих вариантов
расчета — то, что рассчитывается не средняя для больного
вероятность осложнения, а средняя или медиана данных по
больнице. Если вероятность осложнения зависит от коли-
чества больных в больнице, то среднее по больным и среднее
по больнице различается.
Кроме того, при варианте № I используется предположе-
ние о нормальности распределения средней частоты ослож-
нений но больнице, что может по соответствовать действи-
тельности и также приводить к грубым ошибкам (подробное
обсуждение будет ниже).

Глава 6. Элементы математической статистики
179
6.4.2. Сравнение наборов частот при помощи
критерия х2- Условия применимости критерия %2
Второе следствие из первого закона Чисхолма:
Всякий раз, когда кое-что вроде начинает получаться, оказыва-
ется, что вы чего-то недосмотрели.
Артур Блох «Законы Мерфи для медиков»
«Ручная» проверка достоверности связи двух дискретных
случайных величин,
В разделе 6.4.1 было изложено использование крите-
рия х2 ДЛЯ определения достоверности различий частот и
вероятности. Очень похожая технология используется и
при «ручном» определении достоверности различий набора
частот.
Пусть, например, при анализе структуры заболеваемости
детей кишечными инфекциями были выявлены следующие
данные (табл. 6.6).
Таблица 6.6
Сравнение наборов частот
Возбудитель
Шигеллы
Сальмонеллы
Др. бактери-
альные ин-
фекции
Возбудитель
не выявлен
Всего
Контингент
н/о дошк.
9
24
17
34
84
орг. дошк.
12
26
14
42
94
школьники
23
11
29
94
157
Всего
44
61
60
170
335
Здесь используется достаточно стандартное деление на
неорганизованных дошкольников, то есть детей дошкольно-
го возраста, не посещающих детские учреждения, организо-
ванных дошкольников, то есть детей этою возраста, посеща-
ющих детские учреждения, и детей школьного возраста

180
. > . лностеи
Аналогично предыдущему разделу рассчитаем ожидае-
мое количество случаев. Например, обшая доля шигелл по
всем контингентам составила 44/335, а количество случаев
заболевания среди неорганизованных дошкольников — 84,
следовательно, ожидаемое количество шигеллезов — 84 х
х (44/335). В общем, для получения значения в каждой ячей-
ке таблицы ожидаемого количества случаев заболевания по
контингентам нужно перемножить величины, стоящие в той
же строке и столбце в графах «Всего», и разделить получен-
ное число на общее количество случаев заболевания. В ре-
зультате получим табл. 6.7:
Таблица 6.7
Ожидаемое количество случаев заболевания
Возбудитель
Шигеллы
Сальмонеллы
Др. бакте-
риальные
инфекции
Возбудитель
не выявлен
Всего
Контингент
н/о дошк.
11,03
15,30
15,04
42,63
84
орг. дошк.
12,35
17,12
16,84
47,70
94
школьники
20,62
28,59
28,12
79,67
157
Всего
44
61
60
170
335
Далее для каждой ячейки «внутренней части» делим
квадрат разности фактического и ожидаемого числа случаев
заболеваний на ожидаемое число случаев заболеваний. Для
граф «Всего» такое преобразование не делаем, а по-преж-
нему суммируем числа и строках или столбцах.
Существенность различий между фактическими и ожи-
даемым чмелом случаев заболевания приведена в табл. 6.8.
В результате получаем величину различия в 26,81. Для оп-
ределения достоверности различий вновь используем встро-
енную функцию расчета х'-расмределеиии, причем в данном
нариантс число пенсией свободы п определяется как произ-

; математической статистики "t3 Ч
Таблица 6.8
Существенность различий фактического и ожидаемого
числа случаев заболевания
Возбудитель
Шигеллы
Сальмонеллы
Др. бактери-
альные ин-
фекции
Возбудитель не
выявлен
Всего
Контингент
н/о дошк.
0,37
4,95
0,25
1,75
7,33
орг. дошк.
0,01
4,61
0,48
0,68
5,78
школьники
0,27
10,82
0,03
2,58
13,70
Всего
0,66
20,38
0,76
5,00
26,81
ведение количества вариантов значения одной переменной
минус единица на количество вариантов значения другой
переменной минус единица. В данном случае имеется четы-
ре варианта групп для возбудителя и три — для контингента.
Следовательно, количество степеней свободы равно (4 - 1) *
х (3 - 1) = 6. Так как ХИ2РАСП(26,81;6) * 0,00016, то с дове-
рительной вероятностью р « 0,00016 получаем, что различия
в частотах заболеваемости между разными контингентами
достоверны.
При анализе последней таблицы хорошо видно, что ос-
новные различия образовались за счет сальмонеллезов. При
сопоставлении таблицы фактических и ожидаемых коли-
честв получаем, что причина различий — в меньшей доле за-
болеваемости сальмонеллезами школьников, чем дошколь-
ников.
При использовании критерия %2 в этом и предыдущем
разделе рассчитывались некоторые величины и утвержда-
лось, что они распределены как х^-распределение, где п —
число степеней свободы.
Это не совсем точно. Даже при истинности нулевой ги-
потезы полученная случайная величина распределена не как
'^-распределение, а несколько иначе. Все, что утверждается

182
'• "rucmtu
относительно полученного распределении - .;;■, 47 о при уве-
личении количества наблюдений полученное распределение
будет стремиться к х2-распределению.
На практике можно пользоваться критерием %2 для срав-
нения наборов частот при выполнении следующих двух ус-
ловий:
1. Общее количество наблюдений — не менее 50.
2. Количество наблюдений1 каждого варианта значе-
ния — не менее 7 (в крайнем случае — не меньше 5).
В рассмотренном в этом разделе примере общее коли-
чество наблюдений— 335, а минимальное количество на-
блюдений — шигеллезы у неорганизованных дошкольни-
ков — равно 9. Следовательно, критерий х2 в данном случае
применим.
При сравнении набора частот с набором вероятностей
нужно выполнение следующих трех условий:
1. Общее количество наблюдений — не менее 50.
2. Для каждого варианта значения количество успеш-
ных наблюдений не менее 7 (в крайнем случае — не
меньше 5).
3. Для каждого варианта значения количество неуспеш-
ных наблюдений не менее 7 (в крайнем случае — не
меньше 5).
В примере предыдущего раздела суммарное количество
наблюдений было равно 805. Минимальное количество слу-
чаев наблюдения осложнений было в больнице № 8 и было
равно 8. Минимальное количество больных без осложнений
также было в этой больнице и было равно 31. Следовательно,
применение критерия х2в этом случае также возможно.
Если критерий х2 применяется для слишком малых объ-
емов наблюдений, то полученные достоверности различий
оказываются завышенными, то есть неправомочное приме-
нение критерия может дать достоверные различия там, где
их на самом деле нет.
' Проверка применимости будет выдерживаться точнее, если
брать не фактические количества, а ожидаемые количества, которые
рассчитывались при определении достоверности различий В данном
случае — 11,03

Глава 6. Элементы математической статистики
183
Кроме того, приведенные выше ограничения касаются оп-
ределения наличия не слишком высокой достоверности раз-
личий типа канонической р = 0,05. В приведенном выше при-
мере достоверность различий была оценена в 0,00016, то есть
высокодостоверно. Для надежного получения таких высоких
достоверностей приведенных требований к объемам наблю-
дений недостаточно, нужны более жесткие требования.
Второй недостаток использования критерия %2 в описан-
ном варианте состоит в том, что он говорит о наличии каких-
то достоверных различий, но обычно не дает возможности
определить, какие именно частоты достоверно различаются,
а какие — нет.
Оба имеющихся недостатка можно решить при помощи
одной и той же операции — переходу к анализу таблиц 2 на 2, в
которых имеется только два варианта значений переменной по
строкам и столбцам. Дело в том, что для таблиц 2 на 2 есть так
называемое точное решение Фишера — уточненный способ
расчета разности частот, при котором полученная величина
распределена как у} вне зависимости от объема наблюдений.
Для приведенного примера анализа структуры заболева-
емости легко получить (сравнивая организованных и неор-
ганизованных дошкольников), что достоверных различий
между ними по структуре заболеваемости нет. Кроме того,
если в исходной таблице выбросить шигеллезы, то достовер-
ных различий также не будет. Следовательно, имеет смысл
укрупнить деление по контингентами, сравнивая дошколь-
ников со школьниками, и деление по возбудителям, срав-
нивая шигеллезы с другими объединенными группами забо-
леваний. Для получившейся таблицы 2 на 2 точное решение
Фишера дает р = 0,00000026. При этом за счет укрупнения
групп достоверность полученных различий даже возросла.
Приведенные выше формальные требования к примени-
мости критерия х2 также показывают, в каких случаях он хо-
рошо работает, а в каких — нет. Если исследуется связь между
Двумя переменными, каждая из которых имеет лишь неболь-
шое количество возможных значений, то критерий х: — все,
что нужно. Если переменные принимают достаточно много
Разных значений, то возможных пар значений оказывается

184
Часть I Анализ нероятностец
слишком много, и в результате наблюдений требуется чрез-
мерно много. Второй недостаток критерия х2 — в том, что он
разные значения переменных считает разными в одинаковой
степени. Например, если мы будем искать связь между воз-
растом (в годах) больных и полом, то при примерно 50 раз-
ных вариантах значения возраста у нас будет около ста раз-
ных возможных подгрупп. Так как есть более и менее частые
варианты значений, то для формальной применимости кри-
терия нужны многие тысячи наблюдений. Кроме того, этот
критерий не учитывает, что значения переменной «Возраст»
с близкими числовыми значениями ближе друг к другу, чем с
сильно различающимися. Поэтому общих тенденций, слабо
выраженных в каждой возрастной группе, этот критерий не
выявит.
6.4.3. Расчет частоты совместного распределения
и определение достоверности различий
при помощи критерия %2
Проверка гипотезы о независимости двух дискретных
переменных с помощью пакета статистических программ.
Техника расчета таблицы совместного распределения
была описана выше, в разделе 3.1.
При работе с SPSS для применения критерия %2 нужно
после выполнения команды «Analyze/Descriptive Statistic/
Crosstabs» и выбора переменных щелкнуть на кнопке
«Statistics» и щелчком левой кнопки мыши по надписи
«Chisquare» поставить «галочку» в квадратике и отметить
применение критерия, после чего нажать кнопки «Continue»
и «ОК». В результате кроме таблицы совместного распределе-
ния будет выдана таблица результатов применения критерия.
Например, при исследовании связи у больных вирусными ге-
патитами между видом возбудителя и фактом употребления
наркотиков была получена следующая связь (табл. 6.9).
Достоверность различий показывает (табл. 6.10).
Формальные минимальные условия применимости кри-
терия х2 выполнены, так как общее количество наблюде-

Г.шва 6 Элементы математической статистики 185
Таблица 6.9
Таблица числа исходов при совместном
распределении
HEPATITE * NARC Crosstabulation
Count
HEPATITE
Total
VGA
VGB
VGC
VGD
NARC
-
100
72
36
5
213
+
15
13
57
12
97
Total
115
85
93
17
310
Таблица 6. W
Таблица применения критерия «хи-квадрат»
Chi-Square Tests
Pearson Chi-Square
Likelihood Ratio
Linear-by-Linear
Association
N of Valid Cases
Value
79,068
78,750
65,193
310
df
3
3
1
Asymp. Sig.
(2-sided)
,000
,000
,000
ний— 310, а минимальное значение— 5. Однако, так как
требования выполняются по минимуму, а различия высоко-
достоверны, то в реальности различия могуг быгь достовер-
ны, но не с такой высокой степенью различия, как р < 0.001
Кроме того, не очень ясно, какие именно виды гепатита
различаются, а какие — нет.
Поэтому начнем устанавливать фильтры, как это опи-
сано в разделе 5.1. При выборе только первой и четверкой
групп получаем усеченную табл. 6.11
Для нее таблица применения критерии х; имеет уже сле-
дующий вид (табл. 6.12).
Так как это — таблица 2 на 2, то дня пес имсетсп точное
решение Фишера. Поэтому появляется строка «Fisher's Пх.и-t

186
Часть I. Анализ вероятностей
Таблица 6.11
Таблица числа исходов для двух выбранных
вариантов гепатита
HEPATITE * NARC Crosstabulation
Count
HEPATITE
Total
VGA
VGD
NARC
—
100
5
105
+
15
12
27
Total
115
17
132
Таблица 6.12
Применение критерия «хи-квадрат» к таблице 2 на 2
Chi-Square Tests
Pearson Chi-
Square
Continuity
Correction
Likelihood Ratio
Fisher's Exact
Test
Unear-by-Linear
Association
N of Valid Cases
Value
30,142
26,710
24,097
29,914
132
df
1
1
1
1
Asymp.
Sig.
(2-sided)
,000
,000
,000
,000
Exact
Sig.
(2-sided)
,000
Exact
Sig.
(1-sided)
,000
Test», а помимо столбца «Asympt. Sig.» (приближенная досто-
верность различий) появляются столбцы «Exact Sig.» (точная
достоверность различий). Следовательно, доля лиц, отрица-
ющих употребление наркотиков, среди больных вирусны-
ми гепатитами А и Z) действительно достоверно различается
с/?< 0,001.
Меняя фильтр, продолжаем расчет достоверности разли-
чий, и сравниваем таким образом все пары гепатитов.
В Statistica для построения таблицы совместного распре-
деления можно выполнить команду «Statistics/Basic Statistics

Тлею 6 Элементы математической статистики
187
and Tables/Tables and banners/Specify tables(select variables)».
После выбора на появившейся форме двух переменных и
нажатия кнопки «ОК» два раза появится форма, в которой
нужно щелкнуть по закладке «Options», после чего щелчком
поставить «галочку» в строке с заголовком «Pirson & M-L chi
square». Для таблиц 2 на 2 нужно также поставить «галочку»
в строке «Fisher exact, Yates, McNear (2 x 2)». Для просмотра
результатов применения теста нужно щелкнуть по закладке
«Advanced» и нажать кнопку «Detailed two-way tables».
Если таблица совместного распределения уже имеется, то
определить достоверность различий по критерию %2 проще все-
го с помощью программы statcalc.exe, входящей в состав сво-
бодно распространяемого пакета Epilnfo 5.0 (см. раздел 2.1).
Она хороша тем, что для таблиц 2 на 2 не только считает дове-
рительную вероятность в точном решении Фишера, но и оп-
ределяет доверительные границы для относительных рисков.
6.4.4. Определение достоверности различий
распределений в подгруппах при помощи
критерия х2 и критерия
Колмогорова—Смирнова
Как определить, являются ли два набора значений
наблюдениями одной случайной величины или нет.
Пусть на приведенном выше материале больных вирус-
ными гепатитами мы хотим выяснить, одинаковое ли рас-
пределение по возрасту у лиц, признающих и отрицающих
употребление наркотиков.
Как было сказано выше, прямой анализ связи возраста
пациентов с какой-то другой переменной при помощи кри-
терия х2 малопродуктивен из-за слишком большого коли-
чества образующихся групп сравнения. Однако мы можем
«огрубить» значение переменной, воспользовавшись опи-
санной выше техникой округления переменных.
Техника расчета таблицы совместного распределения
была описана выше, в разделе 2.2.3. Так, вычислим новую
переменную VOZI0, у которой значение 10 будет соответс-

188
Часть 1 Анализ вероятностей
твовать возрасту пациентов от 10 до 19 лет, значение 20 — от
20 до 29 и так далее. В этом случае при анализе их связи по-
лучим следующие табл. 6.13 и 6.14.
Таблица 6.13
Таблица совместного распределения
с округленной переменной
VOZ10 * NARC Crosstabulation
Count
VOZ10
Total
10,00
20,00
30,00
40,00
50,00
NARC
-
49
104
40
15
5
213
+
31
55
9
1
96
Total
80
159
49
16
5
309
Таблица 6.14
Результаты применения критерия «хи-квадрат»
Chi-Square Tests
Pearson Chi-Square
Likelihood Ratio
Linear-by-Linear
Association
N of Valid Cases
Value
13,672
16,830
12,237
309
df
4
4
1
Asymp. Sig.
(2-sided)
,008
,002
,000
Формально критерий у} в данном случае неприменим,
так как количество отрицающих употребление наркотиков
в группе от 40 до 49 — 1 человек, а в группе от 50 и старше
таких не было. Однако хорошо видно, что после укрупнения
групп или установки фильтров с переходом к анализу таблиц
2 па 2 различия будут высокодостоверными.
Проиллюстрировать связь можно при помощи описанных
н разделе 3.1 диаграмм совместного распределения (рис 6.4)

Глава 6. Элементы математической статистики
189
NARC
Mssing 1000 ?0.СО 30.00 40.00 50.00
VOZ10
Рис. 6.4. Количество признающих употребление наркотиков
в разных возрастных группах
Однако при описанном варианте использования критерия
X2, во-первых, есть некоторый элемент волюнтаризма в про-
извольности выделения групп, в пределах которых происхо-
дит объединение значений непрерывной переменной. Кроме
того, при округлении значения переменной теряется часть
информации. Во-вторых, критерий х2 не использует ту ин-
формацию, что близкие значения округленной переменной
более близки и с содержательной точки зрения, чем далекие.
Поэтому с задачей анализа достоверности различий рас-
пределений в двух сравниваемых группах значительно лучше
справляется критерий Колмогорова—Смирнова.
Для расчетов в SPSS нужно выполнить команду «Analyze/
Nonparametric tests/Two independent-Samples Tests». В появив-
шейся форме щелчком левой кнопкой мыши по квадратику с
подписью «Kolmogorov-Smirnov Z» отметить применение тес-
та, потом из списка переменных выбрать в поле «Test Variable
List:» переменную, у которой исследуется распределение
(вданном случае— возраст), а в поле «Grouping Variable:» —
переменную, по значениям которой выделяются подгруп-
пы. Далее нужно щелкнуть на кнопке «Define Groups...» и в
двух числовых окошках задать числовые значения второй
переменной, соответствующие двум сравниваемым группам

(п данном случае отрицание употребления наркотиков коди-
ровалось нулем, а признание - единицей). После нажатия
кнопок «Continue» и «ОК» появляется табл. 6.15.
Таблица 6.15
Результат применения критерия
Колмогорова-Смирнова
Test Statistics
Most Extreme Differences
Kolmogorov-Smirnov Z
Asymp. Sig. (2-tailed)
Absolute
Positive
Negative
VOZRAST
,196
,036
-,196
1,598
,012
Таким образом, различия распределения по возрасту до-
стоверны с р = 0,012.
Тест Колмогорова—Смирнова — также асимптотический,
о чем говорит соответствующая надпись. Практические усло-
вия его применимости — размеры групп от 50. Так как в рас-
сматриваемом случае 96 человек признавали употребление
наркотиков и 213 — отрицали, то тест вполне применим. В слу-
чае выборок меньшего размера обычно пользуются критерием
Манна—Уитни, который обладает меньшей различающей спо-
собностью, но применим и для наблюдений малого объема (и
также имеется в списке доступных методов анализа команды
«Analyze/Nonparametric tests/Two independent-Samples Tests»).
В отличие от критерия Стьюдента и других аналогичных
тестов, достоверность полученных результатов не зависит от
формы распределения исследуемой переменной, поэтому
никаких дополнительных оговорок или проверок на приме-
нимость теста делать не нужно.
В Statistica для применения теста Колмогорова—Смирно-
ва нужно выполнить команду «Statistics/Nonparametrics», вы-
брать вариант «Comparing two independent samples (groups)»,
нажать кнопку «OK», нажав на кнопку «Variables», выбрать
переменные, и потом нажать на кнопку «Kolmogorov-Smirnov
two-samples lest».

ЧАСТЬ 2
АНАЛИЗ ПАРАМЕТРОВ

Глава 7
ПАРАМЕТРЫ СЛУЧАЙНЫХ
ВЕЛИЧИН
Среднестатистическому американцу 32 года. Его рост — 167сан-
тиметров, вес - 68 килограммов, он на 53 % женщина, на 11 % негр
и всегда чуть-чуть беременный.
Старая* статистическая шутка
7.1. Что такое параметр
При осмотре пострадавшей на левой полужопице было обнару-
жено два синяка размером с пятикопеечную монету1 и один раз-
мером с двухкопеечную монету, на правой полужопице — два
синяка размером с трехкопеечную монету. Итого: побоев на
18 копеек.
Из реального протокола о «снятии побоев»3
Определение понятия «параметр», наиболее часто использу-
емые параметры. Задание параметров случайной величины
как способ задания распределения, альтернативный заданию
частот.
' Из тех времен, когда слово «негр» не считалось политически не-
корректным
2 Описание размера повреждений на основе размера монет
стандартная практика судебно-медицинских экспертов.
1 Цитируется по памяти.

Глава 7. Параметры случайных величин
193
Как уже неоднократно обсуждалось выше, для перемен-
ных, которые принимают много разных значений, описы-
вать распределение через расчет частот отдельных значений
неудобно. В этом случае есть другой подход к описанию рас-
пределения, основанный не па задании частот, а на задании
параметров.
Определение. Параметром случайной величины называ-
ется любая числовая функция от функции распределения
случайной величины.
Таким образом, параметр — число, описывающее те или
иные особенности распределения. Для того чтобы составить
достаточно полное описание распределения, нужен не один,
а несколько разных параметров.
Ниже приведены примеры параметров числовых случай-
ных величин.
Максимум — максимальное возможное значение случай-
ной величины £. Для дискретных случайных величин с ко-
нечным набором возможных значений максимум — самое
большое из элементарных событий с ненулевой вероятнос-
тью. В общем виде — минимум1 из таких х, что Р{^<х) = 1.
Если случайная величина может принимать сколь угодно
большие значения, то не определен (бесконечно велик).
Минимум — минимальное возможное значение случай-
ной величины £. Для дискретных случайных величин с ко-
нечным набором возможных значений минимум — самое
маленькое из элементарных событий с ненулевой вероят-
ностью. В общем виде — минимум из таких х, что Р(&х) * 1.
Если случайная величина может принимать сколь угодно
малые значения, то не определен (бесконечно мал).
Размах — разность между максимумом и минимумом.
Мода — самое часто встречаемое значение. Для дискрет-
ных случайных величин определяется как элементарное со-
бытие с самой большой вероятностью.
Для непрерывных случайных величин это определение
не подходит, так как для них вероятность каждого конкрет-
ного значения равна нулю. В этом случае моду определяют
1 Точная нижняя грань.
7 Мслииинскм (пагистика

194
!сп-,'1ь г. /шализ параметров
как такое значение, в котором плотность распределения
максимальна.
Часто понятие1 «мода» расширяют, требуя, чтобы ве-
роятность или плотность вероятности имела не максимум,
а лишь локальный максимум, то есть была более вероятна
не для всех значений, а только для достаточно близких зна-
чений. При таком определении мода может быть не одна.
В этом случае говорят о многомодальном характере распре-
деления.
Например, если исследовать распределение роста взрос-
лых жителей, то будет наблюдаться два локальных максиму-
ма: один в районе 165 см, второй — в районе 175 см. Бимо-
дальность распределения вызывается тем, что у женщин и
мужчин распределения одномодальные, но с существенно
различающимися модами.
Медиана и другие процентили — см. раздел 6.3.2.
Математическое ожидание — формализация понятия
«среднее арифметическое». Математическое ожидание слу-
чайной величины £, обозначается как М(^). Это самый важ-
ный со всех точек зрения параметр, его обсуждению будет
посвящено несколько разделов. Многие другие параметры
определяются на его основе.
Момент я-го порядка МД). Определяется как М(^л), то
есть среднее арифметическое от л-й степени случайной
величины. Первый момент равен математическому ожи-
данию.
Центральный момент я-го порядка Л/Д). Определяется
как М{{Ъ, — М(£))п). Для его вычисления нужно вычесть из
случайной величины ее среднее арифметическое, а потом
рассчитать n-й момент. Следовательно, второй центральный
момент — средний квадрат отклонений от среднего, третий
центральный момент — средний куб отклонения от среднего
и так далее. Первый центральный момент равен нулю, вто-
рой имеет отдельное название — дисперсия Д£).
' Строго говоря, в этом случае мода уже не будет параметром, так
как параметр — функция, принимающая одно числовое значение, а не
несколько.

/>...
.; ;':i"<->ix. величин
195
Дисперсия £>(£,) — второй центральный момент. Так как
дисперсия — квадратичная величина, то и измеряется она в
квадратных единицах. Например, дисперсия роста измеряет-
ся в квадратных сантиметрах, возраста — в квадратных годах, а
артериального давления — в каких-то совершенно диких еди-
ницах: квадратных миллиметрах квадратного ртутного столба.
В качестве меры разброса обычно используется квадратный
корень из дисперсии — среднеквадратичное отклонение а(£).
Среднеквадратичное отклонение о-(£) определяется как
о(^) = у[Щ). Измеряется в тех же единицах, что и исходная
случайная величина.
Для сравнения степени вариабельности разных перемен-
ных удобно использовать коэффициент вариации.
Коэффициент вариации определяется как о(£)/М(£). Этот
показатель — безразмерная величина, обычно его переводят в
проценты. При помощи его можно сравнивать степень вари-
абельности разных величин. Например, у студентов средний
рост около 170 см, а среднеквадратичное отклонение роста —
около 7 см, следовательно, коэффициент вариации роста
7/170 « 4,1 %. Средний вес студентов около 70 кг, а средне-
квадратичное отклонение — около 7 кг, следовательно, коэф-
фициент вариации — 10 %. Таким образом, вес — примерно в
2,5 раза более вариабельный показатель, чем рост.
Коэффициент вариации получают путем «обезразмерива-
ния» среднеквадратичного отклонения. Примерно аналогич-
ным путем получают коэффициенты асимметрии и эксцент-
риситета.
Коэффициент асимметрии определяется на основе третье-
го центрального момента. Равен нулю для симметрично рас-
пределенных случайных величин, положителен, если правый
«хвост» частотной гистограммы длиннее левого, и отрицате-
лен, если левых «хвост» длиннее правого.
Коэффициент эксцентриситета1 определяется на основе чет-
вертого центрального момента. Показывает степень нском-
1 Редкий пример очень удачного обозначения статистического
термина. Эксцентрично ведущая себя случайная величина •-• та, у ко
торой изредка бывает неожиданно большие или маленькие значении
7*

196
'-.'.■■'■/ни параметров
пактности распределения. Равен нулю для нормально распре-
деленных случайных величин, отрицателен, если случайная
величина распределена более компактно, чем нормальная, и
положителен, если случайная величина распределена менее
компактно. Большая величина коэффициента эксцентриси-
тета указывает на наличие «выскакивающих вариант».
Значения среднего арифметического, среднеквадратич-
ного отклонения, коэффициентов асимметрии и эксцентри-
ситета позволяют составить общее представление о характере
распределения переменной. Например, у больных вирусны-
ми гепатитами средний возраст был 25,1 года, среднеквадра-
тичное отклонений 8,1 года, коэффициент асимметрии 1,3 и
коэффициент эксцентриситета 1,5. Следовательно, распре-
деление больных по возрасту должно быть заметно асиммет-
рично вправо и относительно некомпактно. Реальная гис-
тограмма частотного распределения приведено на рис. 7.1.
ГГ31
■
■
*■
■
к
г*
?
ш
f
**
ч*
t
f
*
•г
<t
1
41
j_\. . \ 1
1 .J**K«V*"uJ
^1 r—
lb.o 20.0 Z50 30,0 35,0 40,0 45,0 50,0 55.0
17,5 22,5 27,5 32.5 37,5 42,5 47,5 52.5
VOZRAST
Рис. 7.1. Гистограмма распределения больных
вирусными гепатитами по возрасту
не похожие на обычно принимаемые значения. Хорошей иллюстра-
цией непредсказуемого поведения таких величин являются цирковые
клоун ы -эксцентри ки.

Глава 7. Параметры случайных величин
197
Для прямого билирубина среднее арифметическое со-
ставляло 20, среднеквадратичное отклонение 28,5, коэффи-
циент асимметрии 4 и коэффициент эксцентриситета 23,8.
Следовательно, данный параметр должен сильно варьи-
ровать (среднеквадратичное отклонение больше среднего
арифметического), а его распределение должно быть сильно
асимметрично вправо и быть существенно некомпактно, что
и подтверждается гистограммой фактических значений на
рис.7.2.
Sid. Dev - 28.55
Meal - 20,0
N - 288,00
BILPR2
Рис. 7.2. Гистограмма распределения больных вирусными
гепатитами по величине прямого билирубина
Среди перечисленных параметров на звание характерного
значения претендуют по крайней мере три: математическое
ожидание, мода и медиана. Если случайная величина рас-
пределена относительно симметрично и компактно, то эти
Фи параметра близки друг к другу. Для некомпактных асим-
метричных распределений эти три параметра могут сильно
Различаться, и вопрос о том, какой из них можно иеполь-
:и>вать для задания «типичного» значения, требует серьезно-
го изучения. Так, например, для рассмотренного примера

198
Часть 2. Анализ параметров
с прямым билирубином среднее арифметическое составило
20,04, но при этом значения, меньшие 20,02, наблюдались
у 65,3 % больных.
У некомпактных асимметричных распределений помимо
неоднозначности содержательной интерпретации результа-
тов имеются значительные технические сложности с прове-
дением статистических расчетов и анализом их результатов.
Все это будет подробно обсуждаться ниже.
Правило. При работе с некомпактными асимметричны-
ми распределениями нужно держать ухо востро.
В процессе анализа с исходными наблюдаемыми ве-
личинами часто приходится проводить некоторые мани-
пуляции. Это часто приводит к изменению как функции
распределения, так и параметров. Например, пусть у боль-
ных артериальной гипертензией в течение нескольких дней
осуществляется мониторирование артериального давления
при помощи носимого датчика. Тогда, например, мы можем
ввести такой показатель, как максимальное диастоличес-
кое давление за текущие сутки. Понятно, что максималь-
ное давление за сутки распределено не так, как давление,
и среднее арифметическое из максимального за сутки диа-
столического давления больше1, чем среднее диастоличес-
кое давление.
Наиболее частая операция, с которой нам далее придется
иметь дело — взятие среднего арифметического из несколь-
ких наблюдений. Это актуально не только в том случае, когда
у одного больного берется несколько измерений в динамике,
но и в том случае, когда от анализа распределения по боль-
ным мы переходим к распределению по группам больных,
например как в пункте 6.4.1, когда от анализа частоты ос-
ложнений у больного переходили к анализу средней частоты
осложнений по разным больницам.
1 Уточнение для педантов: больше или равна, но равна только для
тех, у которых за время мониторирования величина диастолическо-
го давления была постоянной. Наиболее вероятные объяснения этого
феномена: или монитор был сломан, или пациент мертв.

Параметры случайных величин
199
7.2. Лирическое отступление
о статистической терминологии
и трудностях перевода
Когда я слышу слово «дискурс»,
я хватаюсь за свой симулякр.
В. Пелевин «Шлем ужаса»
Что означают английские и русские
названия статистических терминов.
Математика выгодно отличается от большинства других
научных дисциплин строгостью и однозначностью термино-
логии. К сожалению, к статистике это относится в меньшей
степени. Причин для этого, по крайней мере, три:
1. Как уже упоминалось ранее, в старые времена в сис-
теме базовых понятий теории вероятностей и мате-
матической статистики царил хаос до тех пор, пока
в 30-х годах XX века Колмогоров не навел порядок.
Прогресс был столь очевиден, что профессиональные
математики перестроились сразу. К сожалению, про-
шедших с тех времен 70 лет оказалось недостаточно,
чтобы дошло до всех, поэтому и в некоторых издаю-
щихся сейчас книгах используются такие термины,
как «генеральная совокупность», «выборочная сред-
няя», «генеральная средняя» и т. д.
2. Основная терминология теории вероятностей и ма-
тематической статистики формировалась в первой
половине XX века и ранее, а до Второй мировой
войны языком науки был немецкий. Поэтому мно-
гие современные термины русскоязычной статис-
тики — переводы их аналогов с немецкого, точные,
но тяжеловесные1. Особенно тяжело выговаривается
1
Есть апокриф о том, что когда п 20-е голы советские математики
по заказу правительства писали массовые учебники по дифференци-
альному и интегральному исчислению, то редакторы для экономии
бумаги и типографской краски внесли предложение писать слово
«дифференцирование» и т. и. через одну букву «ф». После контрпре-

200
Часть 2. Анализ параметров
«среднеквадратичное отклонение». Тут даже у про-
фессионалов нет единообразия. Так, в высшей сте-
пени достойной современной энциклопедии по те-
ории вероятностей и математической статистики,
включенной в список рекомендуемой литературы,
в статьях, написанных разными авторами, встре-
чаются все четыре варианта написания этого тер-
мина: «среднеквадратичное отклонение», «среднее
квадратичное отклонение», «среднеквадратичес-
кое отклонение» и «среднее квадратическое откло-
нение».
3. В англоязычной традиции сложилась своя терми-
нология, а статистические пакеты написаны в ос-
новном на английском1 языке, поэтому букваль-
ный перевод терминологии провоцирует ошибки.
Например, «среднеквадратичное отклонение» на-
зывается «standard deviation», но использование
термина «стандартное отклонение» пока считается
ошибочным.
Естественно, при русификации статистических пакетов
такие мелочи во внимание не берутся, поэтому это еще одна
причина, по которой лучше пользоваться нелокализованны-
ми версиями.
Так как начиная со второй половины XX века язык
науки — английский, то имеется тенденция к сближению
англоязычной и русскоязычной терминологии. Многие
«свежие» статистические термины в русском языке —
кальки с их английских вариантов, например, «робаст-
ность».
Для удобства читателя приводится таблица переводов
и толкований статистических терминов (табл. 7.1).
лложения со стороны математиков для получения значительно боль-
шей экономии писать слово «коммунизм» через одну букву «м» —
предложение было снято.
1 Точнее, американском. Например, цвет обозначается словом
«color», а не «colour» Впрочем, еще Марк Твен заметил «У нас с анг-
личанами много общего, за исключением языка».

Глава 7. Параметры случайных величин
201
Таблица 7.1
Перевод терминов с комментариями
Краткое
английское
название
Sig
Std
SE mean
L.__
Полное
английское
название
Frequency
Percent
Cumulative
Percent
Probability
Signification
Mean
Standard
Deviation
Standard
Error of
Mean
Range
Русское
название
Частота в
процентах
Частота на-
растающим
итогом в
процентах
Вероятность
Доверитель-
ная вероят-
ность
Математи-
ческое ожи-
дание
Среднеквад-
ратичное
отклонение
Среднеквад-
ратичное
отклонение
среднего по
группе
Размах
Стандартное
обозначение
и смысл
Количество на-
блюдений
Доля наблюдений
данного значения
Доля наблюдений
данного и мень-
ших значения
Формализация
понятия частоты
р. Вероятность
получения ложно-
положительного
результата
М. Формализация
понятия среднего
арифметического.
Для обозначения
среднего арифме-
тического из на-
бора наблюдений
{xj используется
обозначение х
о. Мера характер-
ного разброса
о(х). Имеет смысл
статистической
погрешности вы-
числения сред-
него арифметиче-
ского
Разность между
максимальным
Продолжение Ь

202 '•■ '■ ■■ ■ <-,ii'..nr, параметров
Окончание табл. 7.1
Краткое
английское
название
Var
ANOVA
Sum
df
Полное
английское
название
Variance
Skewness
Kurtosis
Median
Mode
Analysis of
Variance
Summa
Русское
название
Дисперсия
Коэффици-
ент асиммет-
рии
Коэффици-
ент эксцент-
риситета
Медиана
Мода
Дисперсион-
ный анализ
Сумма
Число степе-
ней свободы
Стандартное
обозначение
и смысл
и минимальным
значением
D, а2. Квадрат
среднеквадратич-
ного отклонения
Мера асимметрии
распределения
Мера некомпакт-
ности распреде-
ления
Me. Значения боль-
шие и меньшие
медианы должны
встречаться в 50 %
наблюдений
Самое часто встре-
чаемое значение
Определение
достоверности
различия между
средними по не-
скольким под-
группам на осно-
вании сравнения
различий внутри и
между группами
Эффективное
количество на-
блюдений
(с учетом того, что
некоторые наблю-
дения могут быть
«потеряны» из-за
необходимости
проведения под-
гонки параметров)

Г.и?а .'. Параметры случайных величин
203
7.3. Расчет параметров
в статистических пакетах
Если одной женщине для того, чтобы выносить ребенка, нужно 9 ме-
сяцев, то за сколько времени выносят одного ребенка 9женщин?
Арифметическая задачка
Расчет параметров с помощью пакетов
статистических программ,
В SPSS имеется два разных варианта расчета, отличаю-
щихся набором доступных параметров.
1. Команда «Analyze/Descriptive Statistics/Descriptives»,
выбрать нужные переменные (щелкнув по их имени в левом
списке доступных переменных и нажав на кнопку с треуголь-
ником острием направо), нажать кнопку «Options...» и на по-
явившейся форме отметить нужные параметры.
Более подробно: на появившейся форме имеется два типа
элементов управления: квадратики (checkbox'bi) и кружочки
(радиокнопки). Щелчком по нужной круглой радиокнопке
можно выбрать один из доступных вариантов упорядочения
переменных (можно рассчитывать параметры не для одной
переменной, а сразу для нескольких). Вариант «Variable list»
означает вывод переменных в порядке их выбора, вариант
«Alphabetic» — упорядочивание по имени, варианты «Ascending
means» и «Descending means» —упорядочивание в порядке воз-
растания или убывания среднего арифметического.
В верхней части формы имеется список доступных пара-
метров, их перевод смотри в табл. 7.1. Параметры, отмечен-
ные «галочкой», рассчитываются. Ставить и снимать галоч-
ки можно щелчком по квадратику.
Если не менять набор рассчитываемых параметров, то дли
использующегося и качестве примера распределения боль-
ных вирусными гепатитами по возрасту получим табл. 7.2.
Содержимое колонки с заголовком «N» говорит, что все-
го в исследовании было 312 больших, у которых был опреде-
лен возраст.
Гели мы выберем псе возможные параметры, то помучим
очень широкую шблипу, которая не будет и тезап. в лист и с

204
;■'■.."/■::■* 2 Анализ параметров
Таблица 7.2
Таблица значений параметров
(краткий набор)
Descriptive Statistics
VOZRAST
Valid N (listwise)
N
312
312
Mini-
mum
15,00
Maxi-
mum
55,00
Mean
25,1282
Std.
Deviation
8,1119
которой неудобно работать. В этом случае лучше «повернуть ее
на бок», поменяв местами строки и столбцы. В математике та-
кое преобразование таблиц называется транспонированием.
Для этого можно щелкнуть получившуюся таблицу пра-
вой клавишей мыши и выбрать команду «Сору». Потом пе-
реключиться в Excel, вставить таблицу из буфера обмена и
тут же, не снимая выделения, опять скопировать ее в буфер
обмена. Потом переключиться на чистый лист, выполнить
команду «Правка/Специальная вставка», и в появившейся
форме отметить вариант «транспонировать». После этого
полученную таблицу уже можно вставлять в документ Word.
В данном случае мы получим табл. 7.3.
Таблица 7.3
Таблица значений параметров
(более полный набор)
Descriptive
Statistics
N
Range
Minimum
Maximum
Sum
Mean
Std.
Deviation
Statistic
Statistic
Statistic
Statistic
Statistic
Statistic
Std.
Error
Statistic
VOZRAST
312
40
15
55
7840
25,128
0,4592
8,1119
Valid N
(listwise)
312

Глава 7. Параметры случайных бы.<чип
205
Descriptive
Statistics
Variance
Skewness
Kurtosis
Statistic
Statistic
Std.
Error
Statistic
Std.
Error
VOZRAST
65,803
1,3383
0,138
1,5399
0,2752
Valid N
(listwise)
2. Если после выполнения «Analyze/Descriptive Statistics/
Frequencies», которая ранее описывалась для получения
таблиц частот, нажать на кнопку «Statistics...», то появляет-
ся форма, имеющая более широкий выбор параметров, чем
описанная в пункте 1. В ней имеется возможность выбора
моды и медианы, а также квартилей и любых других про-
центилей. Для добавления расчета процентилей имеется
группа «Percentile Values». В ней имеется три дополнитель-
ные возможности: добавление расчета квартилей, добавле-
ние расчета процентилей при делении набора наблюдений
на несколько равных по численности групп (по умолча-
нию — 10) и добавление расчета конкретных процентилей.
В последнем случае нужно щелкнуть по квадратику с назва-
нием «Percentile(s):», в активизировавшееся после этого поле
правее надписи ввести число и нажать кнопку «Add».
На появившейся форме не нужно отмечать опцию «Values
are group midpoint».
Если при расчете параметров распределения больных по
возрасту отметить все параметры, а также добавить расчет
квартилей, 10%-х, 90%-х процентилей, то в результате будет
получена табл 7.4.
Кроме таблицы со значениями параметров будет рассчи-
тана и таблица частот.
Если отметить опцию «Values are group midpoint*», то па-
тетический пакет будет считать, что данные получены ок.
румсиием, и мри расчете медианы и других прицеп гилей
будет пытаться восстановим, исходное распределение, ка-
ким оно было до округления II результате будет получено не

206
Часть 2. Анализ параметров
Таблица 7.4
Таблица значений параметров
(полный набор)
Statistics
VOZRAST
N
Mean
Std. Error of Mean
Median
Mode
Std. Deviation
Variance
Skewness
Std. Error of Skewness
Kurtosis
Std. Error of Kurtosis
Range
Minimum
Maximum
Sum
Percentiles
Valid
Missing
10
25
50
75
90
312
2
25,1282
,4592
23,0000
20,00
8,1119
65,8034
1,338
,138
1,540
,275
40,00
15,00
55,00
7840,00
17,0000
19,0000
23,0000
29,0000
37,0000
фактическое (в данном случае целое) значение, а его вроде
бы более точная оценка. Реально возрастание точности ма-
лосущественно, но результаты расчетов труднее объяснять.
В Statistica для расчетов параметров можно выполнить
команду «Statistics/Basic Statistics and Tables/Descriptive
Siatisiics», нажать кнопку «OK», далее нажать кнопку «Va-
riables» и выбрать нужную переменную или их набор. После
иыбора переменных (одна переменная выбирается щелчком
ivj ее имени, добавление — щелчком при нажатой клави-
ше ♦Ctrl») нажать кнопку «ОК», далее перейти на закладку

Глава,' I'u,'■■:.-..-, .1 ■<>:. . :;4ri:i:i,ix вг.шчии 207
«Advanced» (щелчком по этикетке закладки), выбрать нуж-
ные параметры и нажать кнопку «Summary».
7.4. Проверка гипотезы на принадлежность
наблюдаемой случайной величины
классу случайных величин
Сразу несколько моих коллег, работавших в поздние советские вре-
мена в так называемых ящиках (закрытых учреждениях, в том числе
НИИ), рассказывали, что именно у них директор института в чине
генерала издал приказ, что на территории института все распреде-
ления считаются нормальными
Собственные воспоминания
Как проверить статистическую гипотезу о том, что
наблюдаемая случайная величина нормальна,
распределена по Пуассону или принадлежит
какому-то другому классу, заданному
с точностью до значения нескольких
параметров.
Коэффициенты асимметрии и эксцентриситета часто рас-
считывают для проверки нормальности исследуемого распреде-
ления, так как из того, что они достоверно отличаются от нуля,
следует, что исследуемая случайная величина ненормальна.
Во всех приведенных выше примерах полученные оцен-
ки коэффициентов асимметрии и эксцентриситета были по
крайней мере в несколько раз больше статистической пог-
решности их вычисления. Поэтому все случайные величины
были ненормальными.
Другой подход к проверке на нормальность — сравнение
полученной функции распределения с функцией распределе-
ния нормально распределенной случайной величины, напри-
мер, при помощи критериев х2 или Колмогорова—Смирнова.
Эти два разных по «идеологии» подхода часто использу-
ются при проверке статистической гипотезы о принадлеж-
ности наблюдаемой случайной величины к некоторому
классу случайных величин (не обязательно нормальным),
задаваемым с точностью до нескольких параметров. Напри-

208
Част» 2
мер, пусть мы исследуем распределение количества ,мкь, гос-
питализированных в больницу по скорой помощи, и хотим
выяснить, распределено ли оно по Пуассону.
Пусть у нас за 200 дней исследования получены следу-
ющие данные (таблю 7.5).
Таблица 7.5
Фактическое число госпитализированных
Количество больных, госпитализи-
рованных за день
Сколько дней было с таким коли-
чеством госпитализированных
больных
0
78
1
44
2
28
3
26
4
20
5
4
При проведении расчетов (см. следующие разделы) по-
лучаем, что среднее арифметическое числа госпитализиро-
ванных за день было равно 1,39, а дисперсия равна 2,13. При
расчете доверительных границ выясняем, что на основании
критерия Стьюдента с доверительной вероятностью р = 0,05
среднее число госпитализированных равно 1,39 ± 0,2, а на
основании критерия Фишера—Снедекора — что с р = 0,05
дисперсия находится в интервале от 1,73 до 2,57. На основа-
нии этого можно сделать вывод о том, что с р - 0,05 среднее
арифметическое меньше дисперсии. А так как для распре-
деления Пуассона математическое ожидание равно диспер-
сии, то наблюдаемая случайная величина не распределена
по Пуассону.
Другой подход — рассчитать различия между наблюда-
емыми и ожидаемыми частотами, например, при помощи
критерия х2. В этом случае проверяемая гипотеза — не то,
что наблюдаемая случайная величина распределена задан-
ным образом, а то, что она — из класса случайных величин,
поэтому вначале определим, какая распределенная по Пуас-
сону случайная величина — самая близкая к ней.
Так как при задании распределенной по Пуассону слу-
чайной величины единственный свободный параметр — ма-
тематическое ожидание, то в качестве первого шага рассчи-
■i;icm среднее количество больных за день и получим 1,39.

Глава 7. Пар(,.\ыт;;и :\,i jj-„•;-,.;,- ее.vjmuh 209
Далее рассчитаем частоту значений для распределения Пу-
ассона с математическим ожиданием 1,39. Из-за того, что
для этой случайной величины частоты значений, равных 5 и
больше, около 1 %, то есть при 200 наблюдениях ожидаемое
количество становится слишком малым, то приходится объ-
единять величины количество госпитализированных боль-
ных за день со значением «4» и более в одну группу. Далее
аналогично пункту 6.4.1 составим табл. 7.6.
Таблица 7.6
Сравнение фактического распределения с Пуассоном
Случаев
госпитализации
за день
1
0
1
2
3
4 и более
ВСЕГО
Факт,
колич.
2
78
44
28
26
24
200
Ожи-
даемая
доля, %
3
24,91
34,62
24,06
11,15
5,26
100
N0
4
49,82
69,24
48,12
22,3
10,52
200
Ожид.
А
5
0,7509
0,6538
0,7594
0,777
0,9474
4
Факт.
Д
6
15,95
9,2
8,42
0,61
17,27
51,45
Сопоставляя пятую и шестую колонку, выясняем, что
различие между ожидаемым и фактическим распределением
существенно для всех вариантов, за исключением 3 случаев
госпитализации за день.
Далее аналогично пункту 6 4.1 рассчитываем, насколь-
ко для ^-распределения вероятно принять значения в 51.45
или более. При этом берем х2-распределсние не с 4 степе-
нями свободы (на единицу меньше, чем количество групп),
а с 3 степенями свободы, так как перед проверкой мы подби-
рали тестовое распределение Пуассона с таким же математи-
ческим ожиданием, как наблюдаемое среднее.
IIрани.ю. Пели при помощи геста х' проверяется гипоте-
за о том, что наблюдаемый набор значений \хк) шачепня
случайной величины, заданной с точностью до п парамет-
ров, несли ожидаемые значения параметров подбираются

210
Часть 2 Анализ параметров
по тому же набору значений {хк), то при расчете достовер-
ности различий число степеней свободы х2-распределения
нужно уменьшить на п.
В данном случае получаем, что доверительная вероят-
ность равна 3,9 х 10"", то есть очень мала. В рассматрива-
емом случае тест х1 намного лучше отверг гипотезу о пуас-
соновости наблюдаемого распределения, чем сравнение
математического ожидания и дисперсии, однако в других
случаях результат может быть иной.
С содержательной точки зрения то, что наблюдаемое рас-
пределение — не пуассоново, достаточно интересно. Это оз-
начает, что либо среднее ожидаемое количество случаев гос-
питализации не постоянно, а меняется ото дня ко дню, либо
случаи госпитализации не являются независимыми и встре-
чаются групповые случаи.

Глава 8
СОДЕРЖАТЕЛЬНЫЙ АНАЛИЗ
СРЕДНЕГО АРИФМЕТИЧЕСКОГО
Средняя температура по палате может выть 36,6' и в том случае,
когда большая часть больных бьется к лихорадке, а несколько уже ос-
тывают.
Стиран i татистическая шутка
8.1. Расчет среднего арифметического
и математического ожидания. Линейные
свойства математического ожидания,
дисперсии и среднеквадратичного
ожидания
Пифагоровы штаны по вес сторо-
ны равны
Неизвестный автор
Определение математического ожидания и моментов,
их линейные свойства.
Если при N наблюдениях случайной величины были
получены величины *,,...,хл„ то среднее арифметическое х
можно получить как х = (xt+...+xN)/N. Другой, иногла более
Удобный способ расчета среднего арифметического — через
частоты. Если из /V наблюдений встречалось п разных зпа-

212
Часть 2. Анализ параметров
чений ЛГ,,...,Хп с частотами />,,...,/*,, то х = JTj x р{ +...+ ля х />я.
Например, если 20 % студентов сдает анатомию на пятерку,
40 % - на четверку, 30 % - на тройку и 10 % - на двойку, то
среднее арифметическое отоценки на экзамене равно 5 х 0,2 +
+ 4 х 0,4 + 3 х 0,3 + 2 х 0,1 = 1 + 1,6 + 0,9 + 0,2 = 3,7.
Аналогичным образом определяется и математическое
ожидание случайной величины, которая может принимать
конечное количество возможных значений Х(,...,Хп: М(%) =
= Хх х р +...+ Хх р с единственным изменением, что здесь
{рк} — не частоты, а вероятности. Так как при увеличении
объема наблюдений частота стремится к вероятности, то при
увеличении объема наблюдений среднее арифметическое
стремится к математическому ожиданию.
Если рассматриваемая числовая случайная величина
принимает бесконечно много разных значений, то техно-
логию вычисления математического ожидания нужно не-
сколько уточнить. В этом случае рассматривают следующую
конструкцию: приближают исходную случайную величину
дискретной случайной величиной с конечным числом зна-
чений и вычисляют математическое ожидание этой диск-
ретной случайной величины. После этого берут более точ-
ное приближение новой дискретной величиной и так далее.
Предел математического ожидания дискретных случайных
величин с конечным числом значений, все более точно при-
ближающих исходную случайную величину, и называют ма-
тематическим ожиданием этой случайной величины.
Для корректности приведенного определения нужно,
чтобы предел математических ожиданий существовал и не
зависел от выбора конкретной реализации приближающих
последовательностей. Это, к сожалению, бывает не всегда,
поэтому бывают случайные величины, для которых матема-
тическое ожидание определить нельзя.
Для того чтобы математическое ожидание существова-
ло, достаточно, чтобы рассматриваемая случайная величина
была ограничена, то есть имела конечные максимум и мини-
мум. Так как все практически встречаемые переменные ог-
раничены, то «практические специалисты» обычно не обра
тают на этот момент достаточного внимания, считая то, чго

Глава 8. Содержательный анализ среднего арифметического
213
случайная величина может не иметь среднего арифметиче-
ского, математической заморочкой. И совершенно напрас-
но, так как формальные проблемы типа расходимости пре-
делов никогда не существуют сами по себе и порождают либо
содержательные проблемы при интерпретации, либо техни-
ческие проблемы при вычислении. С обеими проблемами
мы познакомимся ниже, в разделах, посвященных выскаки-
вающим вариантам и центральной предельной теореме.
Даже в случае отсутствия технических проблем при вычи-
слении среднего арифметического могут быть содержатель-
ные проблемы, связанные с неоднозначностью трактовки.
Пример. В адрес администрации г. Москвы поступила кол-
лективная жалоба жителей «спального» района на перегружен-
ность по утрам автобусов, идущих в сторону центра. При из-
учении обоснованности жалобы было выяснено следующее:
1. Плановая загрузка автобусов — 60 пассажиров.
2. В утренние часы по рабочим дням средняя загрузка
рейсов, идущих в сторону центра, — 90 пассажиров.
3. В то же время средняя загрузка рейсов, идущих от
центра, — 10 пассажиров.
Так как половина рейсов — в сторону центра, полови-
на — от него, то средняя загрузка автобусов — 90 х 0,5 + 10 х
х 0,5 = 50, что составляет 5/6 от плановой загрузки.
Выводы комиссии по проверке: в связи со средней загру-
женностью автобусов только на 5/6 — снять 1/6 автобусов с
маршрута и направить на коммерческие перевозки по марш-
руту Москва—Амстердам.
С другой стороны, из 100 пассажиров 90 едут в переполнен-
ном автобусе к центру, а 10 — от центра. Поэтому с точки зре-
ния пассажиров средняя загруженность автобусов равна 90 х
х 0,9 + 10 х 0,1 = 82, и автобусы действительно перегружены1.
' Данный расчет проводился в предположении, что во всех авто-
бусах, идущих в центр, — по 90 пассажиров, а в автобусах, идущих от
центра. — по 10 пассажиров. Реально наполненность автобусов варь-
ирует, причем чем бол ыие в нем пассажиров, тем больше вероятность
попасть именно в него. Поэтому средняя цифра с точки прения пасса
жира будет не 82 человека, а еще больше.

214
'ha mh 2 Лнапп параметр/т
Алогичным обра юм с ючки зрении врачей, работающих
в большинстве поликлиник, их мссю рабогы — спокойное и
удобное для посетителей, большую часть времени попасть на
прием к врачу несложно, и лишь изредка, во время эпидемий
ОРЗ,гам —сумасшедшийдом Сточки чрепия пациента, как
ни попадешь в поликлинику — там сумасшедший лом.
Рассмотрим сше один пример. Пусть в некотором районе
20 % семей бездетны, 40 %имеютодного ребенка, 30 % —двух
детей и 10 % — трех детей. Тогда среднее количество детей в
семье равно 0 х 0,2 + 1 х 0,4 + 2 х 0,3 + 3 х 0,1 = 1,3. С другой
стороны, если случайно выбирать ребенка, то вероятность
его выбора будет не такой же, как вероятность выбора семьи,
а пропорционально изменится в соответствии с количеством
детей в семье. Из бездетных семей ребенок выбран быть не
может, вероятность того, что он из однодетной семьи, про-
порциональна 0,4, вероятность того, что он из двухдетной
семьи, пропорциональна 2 х 0,3 = 0,6, вероятность того,
что он их трехдетной семьи, пропорциональна 3 х 0,1 = 0,3.
Итого сумма 0,4 + 0,6 + 0,3 - 1,3. Следовательно, если слу-
чайно выбирать детей, то вероятность выбора из однодетной
семьи равна 0,4/1,3, вероятность выбора из двухдетной се-
мьи равна 0,6/1,3 и вероятность выбора из трехдетной семьи
равна 0,3/1,3. Следовательно, с точки зрения детей среднее
количество детей в семье равно I х 0,4/1,3 + 2 х 0,6/1,3 + 3 х
х 0,3/1,3 = 2,5/1,3* 1,923.
Большое удобство работы с математическим ожиданием
и средним арифметическим — в их хорошей согласованнос-
ти с линейными операциями. Это позволяет вычислить ма-
тематическое ожидание линейной комбинации по матема-
тическим ожиданиям их составных частей.
Пусть с — любая константа, at, их\ — любые случайные
величины. Тогда выполняются следующие равенства:
1. М(с) = с.
2. М(сх^) = гхЩ).
3. М(с + п) = М{%) + М(х\).
Смысл первого равенства очень прост: если что-то всегда
принимает некоторое значение, то и среднее тоже равно ему
же Это свойство можно обобщить: если случайная величи-

I'.iaea H. Содержа/т' и.ныи ,uui in ;, рпШ.'.-ч ирш/щгпшчс^о.п 215
на принимает значении и интервале от л до Л', то и среднее
значение лежит в этом интервале Смысл второю равенства
также абсолютно прозрачен
Важно, что третье равенство выполняется всегда, вне за-
висимости оттого, зависят друг от друга случайные величины
£, и п или нет. Например, если средний арифметический вес
больного до обеда был равен 80 кг и средний вес съеденного
обеда— I кг, то средний вес больного после обеда — 81 кг,
вне зависимости оттого, все ли ели одинаково или что более
толстые больные выпросили у тощих соседей себе часть пор-
ции. Есть достаточно много похожих равенств для других
параметров, которые выполняются только для независимых
случайных величин.
Из этих свойств следует, что математическое ожидание
любой линейной комбинации случайных величин равно ли-
нейной комбинации математических ожиданий случайных
величин.
Например, пусть среднее арифметическое возраста боль-
ных мужского пола — 40 лет, женского — 50 лет и 60 % боль-
ных — женщины. Тогда средний возраст больных равен 40 х
х 0,4+ 50x0,6 = 46.
Линейность математического ожидания справедлива
не только для сумм, но и для произведений случайных ве-
личин.
4. Если £, и г| — независимые случайные величины, то
Щхт1) = Щ)хЛ/(т1).
Например, если барахлящий автоматический прибор для
измерения артериального давления в среднем завышает сис-
толическое артериальное давление на 10 % и величина, во
сколько раз завышается давление, случайна и не зависит от
истинной величины систолического давления, то истинное
среднее систолическое артериальное давление равно 90 % от
полученного в результате измерения.
Как было определено в п. 7.1, на основании математиче-
ского ожидания можно определить моменты, то есть матема-
тические ожидания степеней случайной величины. Первый
момент совпадает с математическим ожиданием. Для второ-
го момента справедливы следующие равенства:

216
Часть 2 Лип.пи ппримсщ/шп
5. М2(с) = с2.
7. Если £, и 11 — независимые случайные величины, то
Для старших моментов формулы аналогичны.
Для дисперсии, то есть второго центрального момента,
справедливы следующие свойства:
8. 0(с)=().
9. D(cxt,) = c1x ад.
10 Если i и п — независимые случайные величины, то
/)^ + n) = Z)^) + Z)(n).
Если прочесть последнее равенство, то получается, что
средний квадрат отклонения суммы двух независимых слу-
чайных величин равен сумме их квадратов отклонения.
Формулировка подозрительно похожа на теорему Пифагора,
согласно которой сумма квадратов катетов равна квадрату
гипотенузы.
Действительно, независимые случайные величины ведут
себя подобно перпендикулярным отрезкам. Очень удобно,
что при анализе случайных величин можно пользоваться
геометрическими аналогиями.
Последнее равенство можно обобщить:
М.Щ + л) = ОД + Дч) + 2/^,л) х о(4) х о-(л), где
/<%,!!)— коэффициент корреляции случайных вели-
чин £, и г\, который будет подробно изучаться ниже.
В школьной геометрии аналог этого равенства называется
теоремой косинусов и читается как «квадрат длины противо-
лежащей стороны треугольника равен сумме квадратов длин
прилежащих сторон плюс произведение длин прилежащих
сторон, умноженное на косинус угла между ними». Следова-
тельно, аналог косинуса утла — коэффициент корреляции.
Так как среднеквадратичное отклонение есть квадратный
корень из дисперсии, то из линейных свойств дисперсии
сразу получаем свойства среднеквадратичного отклонения
12. а(с) = 0.
13. а(сх 4) =1 d ха(£).
14. Если £, и г) — независимые случайные величины, то

Глава 8. Содержательный анализ среднего арифметического
217
Свойство 13 говорит, что из среднеквадратичного от-
клонения выносится не константа, а ее модуль. Например,
а(-Ч) = <*£)■
Из свойств 13 и 14 следует, что среднеквадратичное от-
клонение линейной комбинации случайных величин вычис-
ляется не так, как математическое ожидание. В частности,
если Е, и г| — независимые одинаково распределенные слу-
чайные величины, то математическое ожидание их разно-
сти равно нулю, а среднеквадратичное отклонение их раз-
ности — в -Л раз больше среднеквадратичного отклонения
каждой из исходных случайных величин. Другой пример
«неодинаковости» поведения математического ожидания и
центральных моментов — математическое ожидание разно-
сти двух независимых случайных величин равно разности их
математических ожиданий, а дисперсия разности равна сум-
ме их дисперсий.
В разделе 7.1 было определено два набора параметров —
моменты и центральные моменты. Между ними есть соотно-
шения, позволяющие по одним вычислять другие. Наиболее
известно и актуально для практического анализа соотноше-
ние вторых моментов:
15. М&) = МЧК) + Щ).
Имеются аналогичные, но более сложные соотношения
и для старших моментов.
Например, если математическое ожидание случайной ве-
личины равно 10 и среднеквадратичное отклонение равно 5,
то математическое ожидание квадрата случайной величины
равно 10 х 10 + 5 х 5 = 100 + 25 = 125.
Приведенное соотношение позволяет вычислить мате-
матическое ожидание и среднеквадратичное отклонение
результатов объединения нескольких экспериментов, ана-
логично тому, как выше определяли частоты и их довери-
тельные границы после объединения нескольких экспери-
ментов.
Пусть в первом исследовании на 80 больных в резуль-
тате лечения диастолическое давление снизилось в сред-
нем на 20 мм рт. ст. при среднеквадратичном отклонении
15 мм рт. ст., а во втором исследовании на 20 больных сред-

218
Част/, 2 Ана in i na/>ii ч>'и ; ■>.,
нее снижение составило 25 мм рт. ст. при срсдпеквадранг i
ном отклонении 20 мм рт. ст.
Так как достоверных различий между результатами этих
исследований не обнаружено (как это делать, будет изложе-
но ниже), то эти два исследования можно объединить.
Так как после объединения 80 % результатов относятся
к первому исследованию и 20%— ко второму, то среднее
снижение давления в объединенном исследовании будет
равно 20x0,8+ 25x0,2= 16 + 5 = 21.
В первом исследовании средний квадрат снижения был
равен 20 х 20 + 15 х 15 = 400 + 225 = 625. Во втором исследова-
нии средний квадрат снижения был равен 25 х 25 + 20 х 20 =
= 625 + 400 = 1025. Следовательно, в объединенном исследо-
вании средний квадрат снижения давления равен 625 х 0,8 +
+ 1025 х 0,2 = 500 + 205 = 705. Так как из соотношения № 14
дисперсия равна разности математического ожидания квад-
рата и квадрата математического ожидания, то в объединен-
ном исследовании дисперсия равна 705 -21x21= 705 - 441 =
= 264. Следовательно, среднеквадратичное отклонение
в объединенном эксперименте равно ,/264 = 16,25.
Наличие линейных свойств математического ожидания
очень удобно для анализа. Поэтому хотя с некоторых точек
зрения среднее арифметическое хуже описывает характерное
значение, чем медиана или мода, обычно стараются работать
со средним арифметическим и на анализ медианы переходят
только в очень асимметричных и некомпактных распределе-
ниях. Дело в том, что для моды и медианы аналогов свойств
1 -3 нет. Даже для независимых случайных величин медиана
их суммы совершенно не обязательно совпадает с суммой
медиан.
Также становится понятно, почему в качестве меры раз-
броса выбрано именно среднеквадратичное отклонение,
которое вычисляется, скажем честно, достаточно затейли-
вым образом: вначале вычисляется средний квадрат откло-
нения от среднего, а потом из него — квадратный корень.
Значительно более естественной мерой кажется, например,
среднее отклонение — среднее арифметическое из модуля
отклонения от среднего. Однако для среднего отклонения,

[пава <У. Содержательный анализ среднего арифметического
219
как и других мер отклонения, отличных от среднеквадратич-
ного, аналогов соотношений 11 —13 нет.
Одна из частых операций, проводимых в ходе статисти-
ческой обработки, — расчет среднего арифметического из
нескольких наблюдений. Пусть у нас ^|,...,£,я— независи-
мые случайные величины, распределенные так же, как^ (это
мы формализуем, чтоозначает несколько независимых на-
блюдений). Положим ^п= (£( +...+ Ъ>п)/п. Сразу замечу, что
распределение £,п — не такое, как у исходной £.
Тогда справедливо следующее:
16. A/(U = ^(U.
18. о(!;л)=о(0/^.
Соотношение № 18 дает объяснение усиленному закону
больших чисел — почему при увеличении объема наблю-
дений статистическая ошибка определения частоты падает
пропорционально единице, деленной на квадратный корень
количества наблюдений.
8.2. Среднее арифметическое
и нелинейность ущерба
— Скажите, Шура, честно, сколько вам нужно денег для счастья ? —
спросил Остап. — Только подсчитайте все.
— Сто рублей, — ответил Балаганов...
И. Ильф, Е. Петров
«Золотой теленок»
Часто числовой показатель и эффект от него связан
нелинейно. Для уменьшения разрыва между средней
величиной и средним эффектом можно ввести
функцию ущерба.
Одна из проблем при содержательном анализе состоит
втом, что обычно нам нужно знать не среднее арифметиче-
ское от некоторой величины, а средний ущерб, связанный
с этой величиной, причем сама величина и ущерб связаны
нелинейно.

220 Часть 2. Анализ параметров
Для того чтобы смысл проводимого анализа был более
понятен, утрируем ситуацию.
Ситуационная задача. Пусть в силу внешних обстоя-
тельств вам нужно выбрать одно из двух: или один раз вы-
прыгнуть из окна с десятого этажа, или десять раз с первого.
Что вы выберете?
Надеюсь, что большинство выберут второе, хотя суммар-
ное количество этажей в обоих случаях одинаково. Почему
второй выбор удачнее?
Дело в том, что ущерб от прыжка с десятого этажа не
в 10 раз, а в значительно большее количество раз больше,
чем ущерб от прыжка с первого этажа.
Рассмотрим другой вариант.
Ситуационная задача. Пусть в силу внешних обстоя-
тельств вам нужно выбрать одно из двух: или с вероятностью
'/, выпрыгнуть из окна с двадцатого этажа, или один раз с де-
сятого. Что вы выберете?
Здесь предпочтительнее выбор первого варианта, хотя
математическое ожидание количества этажей в обоих случа-
ях равно 10. В данном случае ущерб от прыжка с двадцатого
этажа примерно равен ущербу от прыжка с 10 этажа, а в пер-
вом случае событие осуществляется с вероятностью '/ .
Следовательно, если рассматривать зависимость ущерба
от прыжка от высоты прыжка, то вначале ущерб будет расти
быстрее, чем линейно, а потом — медленнее, чем линейно.
Для достаточно больших величин рост ущерба прекратится.
Рассмотрим более приятную задачу.
Ситуационная задача. Пусть в силу внешних обстоятельств
вам нужно выбрать одно из двух: или вам дают миллиард
долларов, или с вероятностью 1/100 дают сто один миллиард
долларов. Что вы выберете?
Хотя во втором случае математическое ожидание от вы-
игрыша больше, но большинство все-таки выберет первый
вариант. Дело в том, что кайф от ста одного миллиарда долла-
ров хотя и больше, чем от одного миллиарда, но не в сто раз.
На анализе соотношения «прибыль/польза» основаны
некоторые идеи инвестиционной деятельности. Инвести-
ции отличаются друг от друга как средней прибыльностью,

Глава 8. Содержательный анализ среднего арифметического
221
так и рискованностью. Понятно, что при одинаковой рис-
кованности более выгодны инвестиции с большей прибыль-
ностью.
Так как функция кайфа от денег растет медленнее, чем
линейно, то при одинаковой средней прибыльности средний
кайф больше от тех вложений, которые имеют меньшую рис-
кованность. Поэтому из инвестиций с одинаковой ожидае-
мой прибыльностью нужно выбирать менее рискованные.
Наиболее сложный вопрос— об оптимальном соотно-
шении прибыльности и рискованности, то есть — какое уве-
личение прибыльности должно компенсировать увеличение
рискованности. Ответ на этот вопрос для разных инвесторов
различен, так как оптимальный выбор зависит от индивиду-
альной функции кайфа, которая у разных игроков различна.
Если насыщение удовлетворения наступает на относительно
малых выигрышах, то оптимальная стратегия — небольшие
гарантированные прибыли. Если насыщение наступает мед-
ленно и функция кайфа примерно линейна, то предпочтите-
лен выбор очень выгодных, пусть и рискованных вложений.
В качестве примера литературного персонажа с высоким
порогом насыщения можно привести Остапа Бендера — он
хотел выиграть очень много и в результате проиграл все.
Вопрос о нелинейности ущерба и характере этой нели-
нейности часто встает перед врачом при выборе варианта
лечения. Пусть, например, имеется заболевание одного из
двух парных органов и есть два варианта лечения: или уда-
лить больной и оставить здоровый орган, или попытаться
вылечить здоровый орган с риском в результате потерять
оба. В этом случае выбор оптимальной стратегии зависит
не только от вероятности успеха двух вариантов лечения, но
и от соотношения ущерба.
Например, пусть имеется тяжелое инфекционное гной-
ное поражение одного глаза и можно или удалить его и ос-
тавить второй глаз незатронутым, или попытаться вылечить
больной глаз с риском потерять второй. Тогда при первом
варианте лечения у больного остается один глаз; при вто-
ром варианте лечения если вероятность успешного лечения
равна р, то среднее количество глаз после лечения равно 2р.

222
Часть 2- Анализ параметров
Если вероятность успеха р больше '/2> то кажется, что второй
вариант лучше. В действительности если р больше '/2, но су-
щественно меньше 1, то выбирать следует первый вариант
лечения, так как ущерб от потери одного глаза при наличии
здорового не в два, а в значительно большее количество раз
меньше ущерба от потери обоих глаз.
В некоторых случаях потеря одного из двух парных органов
имеет многократно меньший ущерб, чем потеря обоих орга-
нов. Наверно, самый точный пример— тестикулы. В случае
яичников или почек соотношение уже не столь явно, так как
потеря одного из органов снижает качество жизни и ее ожида-
емую продолжительность. Если же речь идет о головном мозге,
то туп уже все равно — удалять одно полушарие или оба.
Для того чтобы иметь возможность проводить точный
анализ рассматриваемых понятий, введем некоторые опре-
деления.
Определение. Функцией ущерба U(x) можно назвать лю-
бую непрерывную строго монотонно возрастающую функ-
цию, то есть такую, что если х < у, то U(x) < U(y), и если х и у
близки, то U(x) и U(y) тоже близки.
В качестве функции ущерба можно брать также и строго
монотонно убывающую функцию. Все, что нужно — непре-
рывность и сохранение направления изменения значений
функции на всем интервале определения.
Определение. Средним по функции ущерба U от случай-
ной величины \ назовем U-\M(U(Q).
Например, если на рентгенограмме легкого обнаружено два
округлых образования диаметром 1 и 2 см, то среднее арифме-
тическое из их диаметров — 1,5 см. Если же мы интересуемся
не линейным размером образования, а его объемом, то, так
как объем пропорционален кубу линейного размера, можно
взять U(x) = х\ В этом случае средний ущерб будет равен (1 +
+ 2ч)/2 = 4,5, а среднее по ущербу — ^5 -1,651. Следователь-
но, средний по объему диаметр образования — 1,651 см.
Приведем наиболее популярные из такого рода средних
Среднее квадратичное определяется как среднее по функ-
ции ущерба U(x) ~ х2. Среднее квадратичное из набора *,,... ,.т,
рассчитывается как л/х,2 +... + х*.

Глава S Содержательный анализ среднего арифметического
223
Среднее геометрическое определяется как среднее по фун-
кции ущерба U(x) — ln(x). Среднее геометрическое из набора
х,,...,х(можно также рассчитать как ^х,х...ххя .
Например, в биохимии или иммунологии среднее ариф-
метическое из исходных величин малопоказательно из-за
того, что у некоторой части исследуемых встречаются очень
высокие величины, много большие, чем у других, из-за чего
среднее арифметическое определяется не столько основной
массой испытуемых, сколько лицами с самыми большими
показателями. В этом случае работают не с исходными кон-
центрациями, а с их логарифмами (или «разведениями»), то
есть фактически со средним геометрическим.
Среднее гармоническое определяется как среднее по фун-
кции ущерба U(x) = \/x. Среднее квадратичное из набора
х,,...,хп можно также рассчитать как l/O/x, +...+ 1/хи).
Для расчета среднего по ущербу в статистическом пакете
нужно определить новую вычисляемую переменную, равную
ущербу (как это делать, обсуждалось выше), потом рассчитать
среднее арифметическое от этой переменной и уже самостоя-
тельно рассчитать от нее обратную к функции ущерба.
В качестве примера различия между исходным показа-
телем и ущербом от него приведем таблицу смертности и
«потерянных полноценных лет жизни», определяемых как
число лет, не дожитых до 65.
Причины смертности в США с учетом не дожитых пол-
ноценных лет жизни (до 65) из расчета на 100 000 населе-
ния (цит. по учебнику «Эпидемиология» В.Д. Белякова
и Р.Х. Яфаева) приведены в табл. 8.1.
Причина резких различий между величинами смертно-
сти и ущерба от смерти от разных причин в том, что умершие
от разных причин имеют разное распределение по возрасту.
При этом приводимая таблица — благополучная страна в
благополучное время. Если взять таблицы смертности для
современной России, то у нас структура смертности, харак-
терная для воюющей страны: 14 % мальчиков не доживают
до 28 лет, умирая в основном от немедицинских (убийства,
самоубийства, травмы, отравления, утонули и т. д.) при-
чин. Поэтому, хотя доля случаев смерти от немедицинских

Таблица 8. /
Смертность и число недожитых лет
в зависимости от причины
Причина смерти
Все причины
Непреднамеренные увечья
Злокачественные опухоли
Сердечные заболевания
Убийства, самоубийства
Врожденные отклонения
Недоношенность
Синдром неожиданной
смерти младенцев
Склероз головного мозга
Хронические болезни пе-
чени и цирроз
Пневмония и грипп
Хронические болезни
легких
Диабет
Потерянных
полноценных
лет жизни
число
11761 000
2 308 000
1 803 000
1 563 000
1 247 000
684 000
470 000
314 000
266 000
233 000
163 000
123 000
119 000
ранг
1
2
3
4
5
6
7
8
9
10
11
12
Смертных
случаев на
100 000
населения
число
866,7
40,1
191,6
324,4
20,6
5,6
3,5
2,4
65,3
11,3
25
29,8
15,6
ранг
4
2
1
7
10
11
12
3
9
6
5
8
причин в современной России около 1/3, на них приходится
около 2/3 ущерба, определяемого как сокращение продол-
жительности жизни по сравнению с ожидаемой.
8.3. Выскакивающие
варианты и среднее
арифметическое
Удачно проведенным считается эксперимент, в котором для согласо-
вания с теорией нужно выкинуть менее половины наблюдений.
Законы Мерфи

Глава 8. Содержательный анализ среднего арифметического
225
Для некоторых случайных величин их среднее арифметическое
определяется основной массой «обычных» значений, а для
некоторых— редкими, но очень большими или маленькими
значениями. Во втором случае при анализе среднего ариф-
метического имеются как технические, так и содержательные
проблемы.
В зависимости от характера распределения случайной
величины ее среднее арифметическое может определяться
как основной массой «обычных» наблюдений, так и редко
встречающимися, но очень большими или очень малыми ве-
личинами.
Например, если брать потери в дорожно-транспортных
происшествиях, то, хотя на слуху и крупные авиационные'
и другие катастрофы, большая часть погибших — жертвы
небольших автомобильных ДТП. Если же взять потери от
аварий на атомных электростанциях, то один Чернобыль дал
больше, чем все остальное.
Аномально большие или малые значения, непохожие на
основную долю значений случайной величины, называют
выскакивающими вариантами.
С переменными, у которых среднее арифметическое оп-
ределяется выскакивающими вариантами2, работать очень
тяжело как с содержательной, так и с технической точки зре-
ния. Из-за того что среднее арифметическое мало похоже на
основную массу наблюдений, для их описания мало одного
среднего арифметического, среднеквадратичного отклоне-
ния и т.д., нужны еще процентили. Также для относитель-
но точного определения среднего арифметического нужно
очень большое количество наблюдений, так как нужно не
чтобы просто всех наблюдений было много, а чтобы было
много наблюдений с выскакивающими вариантами.
1 При изучении книги рекордов Гиннеса я с удивлением узнал,
что и сейчас количество людей, погибающих в авиационных катастро-
фах, меньше, чем количество людей, которых насмерть залягал осел
И при этом многие боятся летать на самолете, но никто не боится еч-
дить на осле.
2 С точки зрения статистики «чтоб у вас все повыскакивало» —
ирашное профессиональное проклятие
п Ме/миишская сгашсшка

226
Часть 2. Анализ параметров
Так, уже десятки лет на АЭС работают тысячи реакторов.
Несмотря на это, ущерб от атомных электростанций мы зна-
ем с точностью до порядка, так как, может, нам не повезло,
что была катастрофа типа Чернобыля, а может — наоборот
повезло, что такая катастрофа была только одна.
Технические проблемы с расчетом среднего арифмети-
ческого связаны с тем, что не у всех числовых случайных
величин определено математическое ожидание. Для некото-
рых показателей определить среднее арифметическое просто
невозможно. Проявляется это в том, что при увеличении ко-
личества наблюдений среднее арифметическое не стремится
к некотому пределу, а неограниченно растет, или падает, или
совершает случайные скачки.
Как уже было сказано ранее, наличие выскакивающих
вариант можно оценить по величине коэффициента эксцент-
риситета.
Обычно самое лучшее, что можно сделать с выскакива-
ющими вариантами, — выбросить их из исследования. Чаще
всего это обусловлено не столько техническими, сколько со-
держательными мотивами. Пусть, например, мы наблюдаем
лечащихся в стационаре больных с заболеваниями печени и
для оценки эффективности лечения определяем изменение
уровня билирубина. Тогда если из 100 больных один за время
лечения заболеет вирусным гепатитом, то он даст столь боль-
шое повышение уровня билирубина, что «забьет» положитель-
ный эффект лечения всех остальных больных. В этом случае
данного больного нужно выбросить из группы исследуемых.
Чаще всего аномально большие или малые показатели
бывают именно у больных с другой патологией, «затесав-
шихся» в массив, поэтому отбрасывание их правильно со
всех точек зрения. Единственное, что нужно сделать честно-
му исследователю для того, чтобы его данные потом можно
было использовать для сопоставления и обобщения, — ука-
зать при описании исследуемого материала, что эта процеду-
ра была выполнена.
В некоторых случаях отбрасывание выскакивающих вари
ант некорректно. В этом случае можно сделать следующее:

Глава 8. Содержательный анализ среднего арифметического
227
1. Перейти от переменной к чему-то типа ущерба от пе-
ременной, причем подобрать функцию ущерба так,
чтобы полученная в результате переменная была рас-
пределена более прилично. Например, в иммуноло-
гии обычно работают не с количествами, а с их лога-
рифмами.
2. Перейти от исходной переменной к ее рангу, на-
пример самому маленькому значению приписать
значение 1, следующему — 2 и так далее. Такая про-
цедура называется ранжированием и будет подроб-
но обсуждаться ниже. Положительный результат
ранжирования — то, что после него любая случай-
ная величина распределена равномерно, а следова-
тельно, очень компактно. Недостатком ее является
то, что полученные средние менее информативны.
Например, информация о том, что средний возраст
254 больных женщин на 7,5 лет больше, чем у 174
больных мужчин, абсолютно понятна. Сообщение
же о том, что средний ранг возраста женщин на 35,4
больше среднего ранга возраста мужчин, значи-
тельно менее ценно. Для того чтобы извлечь из него
информацию о реальной величине этой разницы,
нужно иметь описание распределения больных по
возрасту.
На самом деле переход к рангу — замаскированный пере-
ход от средних арифметических к процснтилям.
Часто при ранжировании приписывают такие числа, что-
бы полученная случайная величина была максимально по-
хожа на нормально распределенную. С технической точки
Фения это еще удобнее, но интерпретировать полученные
различия еще тяжелее
3 Перейти от средних арифметических и друшх момен-
тов к процснтилям.
4 Работать с исходными данными стандартным обра-
юм, но при >том помнить, что псе результаты, рас
считанные па основании достоверности различий,
\ioryi оказания неверными

228
Часть 2. Анализ параметров
8.4. Классификация переменных «scale»,
«ordinal» и «nominal»
Подчитано, что петербуржцы, про-
живающие на солнцепеке, выиг-
рывают 20 процентов здоровья.
Козьма Прутков
Среднее арифметическое можно корректно определять
только для тех переменных, для которых можно не только
точно сказать, какое значение больше, а какое меньше,
но и насколько велика эта разница. ^^
С формальной точки зрения с любой числовой случайной
переменной можно проводить любые арифметические ме-
роприятия, в частности рассчитывать для нее среднее ариф-
метическое. Однако исследуемые переменные на самом деле
не всегда или не совсем являются числовыми, иногда они
только кодируются числами. Это различие между содержа-
тельной величиной и кодирующим ее числом уже обсужда-
лось выше в разделе 8.2.
Для того чтобы вычисление среднего арифметического
(а также других параметров) имело точный содержательный
смысл, нужно, чтобы при сравнении любых двух значений,
которые может принимать исследуемая случайная величина,
можно было корректно определить их разность. Переменные
такого типа называются «scale». В русском варианте иногда
используют буквальный перевод — «шкалируемые», иногда
более точный по смыслу — «измеряемые».
Если для значений переменной можно корректно ска-
зать, какое из них больше, а какое меньше, но нельзя сказать
на сколько, то такие переменные относят к классу «ordinal».
Русские переводы — «порядковые», «ранжируемые», «орди-
нальные» Типичный пример переменной такого класса —тя-
жесть больного в градации «легкий»/«средний»/«тяжелый»
Можно корректно сказать, что вариант «тяжелый» хуже
«среднего», а он -- хуже «легкого», но нельзя сказать, во
сколько раз разница между «тяжелым» и «средним» больше
или меньше, чем разница между «средним» и «легким».

Глава 8. Содержательный анани среднего арифметического
229
Если же для переменной нельзя корректно сказать, ка-
кое значение больше, а какое меньше, то такие перемен-
ные относят к классу «nominal», или «номинальные», или
«неупорядочиваемые», или «неранжируемые». Типичный
пример такой переменной — группа крови. Нельзя сказать,
что вторая группа крови — промежуточная между первой
и третьей.
Деление на эти три класса достаточно неформально,
так как зависит от характера проводимого анализа. Напри-
мер, если анализируется прямой экономический ущерб,
то переменная «длительность нахождения на больничном
листе» — измеряемая, так как прямой ущерб оценивается
именно по сумме потерянных рабочих дней и выплат по
больничному листу. Если же речь идет о социальных поте-
рях или полном экономическом ущербе, то эта переменная
уже порядковая, так как здесь один бюллетень на четыре
недели не равноценен четырем бюллетеням по одной не-
деле из-за того, что в первом случае вероятность инвали-
дизации больше.
Если имеется несколько разных образцов цвета (напри-
мер, светофильтров), то, если речь идет о мощности свето-
вого потока, данную величину можно считать измеряемой.
Если речь идет о цвете (для монохромных цветов — по рас-
положению в радуге), то можно сказать, что зеленый идет за
желтым, а синий — за зеленым, но нельзя сказать, где разни-
ца больше, то есть переменная — порядковая. Если же речь
идет о выборе предпочтений цветов в тесте Лютера, то пере-
менная — номинальная.
При работе с переменными типа цвета волос или цвета
глаз в разных областях используют разные градации Так, из-
вестно, что среди ярко выраженных блондинов аллергиков
больше, поэтому в аллергологии чем темнее цвет волос, тем
лучше. В акушерстве считается, что рыжие «кровят» больше.
В психиатрии серо-стальной цвет глаз — признак повышен-
ной вероятности заболевания эпилепсией
Корректно определение параметров только для и (меряс
mux переменных Для порядковых переменных ироцепгнли
мода и медиана — коррекшые параметры, а математическое

230
Часть 2. Анализ параметров
ожидание, среднеквадратичное отклонение и т. д. — не сов-
сем. Впрочем, при работе с такими переменными вычис-
лять среднее арифметическое и т. п. не только можно, но и
нужно. Существенных ошибок здесь нет, показатель типа
«средний балл» вполне корректен, нужно только не ограни-
чиваться расчетом средних, а анализировать еще и частоты.
Для номинальных переменных расчет параметров — полный
бред1. В качестве эксперимента попробуйте выписать теле-
фонные номера своих знакомых и дозвониться им всем сразу
по среднеарифметическому номеру.
Вся изложенная выше теория среднего по ущербу может
рассматриваться как то, как из порядковой переменной сде-
лать измеряемую. Однако этот подход применим только в
том случае, если ущерб монотонно зависит от исходного зна-
чения переменной. Если функция ущерба немонотонна, то
по чисто техническим причинам нельзя определить среднее
по ущербу, так как в этом случае функция, обратная к функ-
ции ущерба, не будет взаимно однозначной.
Например, если рассматриваются больные с эндокрин-
ными заболеваниями, то маркером тяжелой формы забо-
левания может быть как избыточный, так и недостаточный
вес. В этом случае сравнивать средний вес больных разных
групп некорректно, лучше работать с такой переменной,
как «модуль отклонения веса от нормы». Возможно, же-
лательна и дальнейшая работа по уточнению переопреде-
ления значения переменной, так как, во-первых, четверо
больных с превышением нормы на 10 килограммов — это
не совсем то, что трое больных с нормальным весом и
один — с превышением на 40 килограммов, а во-вторых,
превышение веса на 40 килограммов — плохой прогности-
ческий признак, но недобор до нормы 40 килограммов —
уже катастрофа.
Измеряемые переменные могут быть как непрерыв-
ными, так и дискретными. Порядковые переменные чаще
дискретные, но могут быть и непрерывными. Используе-
мые в статистической обработке номинальные переменные
И одна ич частых студенческих ошибок

Глава 8. Содержательный анализ среднего арифметического 231
обязательно должны быть дискретными, потому что невоз-
можно анализировать непрерывную номинальную пере-
менную'.
Переменные, которые принимают только два разных
значения, называют дихотомическими. К этому классу пере-
менных относятся все варианты ответов на вопрос типа «да
или нет». Типичный представитель дихотомической пере-
менной — пол испытуемого. С дихотомическими перемен-
ными можно работать и как с переменными типа scale, и как
с переменными типа ordinal, и как с переменными типа
nominal, в зависимости от того, какой метод анализа удоб-
нее. При этом разные методы анализа дают в точности оди-
наковые результаты (см. раздел 11.3). Так, например, если
значения переменной кодируются нулями и единицами, то
утверждение, что среднее арифметическое равно 0,2, экви-
валентно тому, что единиц 20 %.
1 Это должна быть переменная, у которой псе значения несравни-
мы и которая никогда не попторяется Такие пелмчины, безусловно,
существуют, например личность человека, но статистическому апали -
чу они не поддаются

Глава 9
ТОЧЕЧНЫЕ ОЦЕНКИ
ПАРАМЕТРОВ
Математическая обработка похо-
жа на мясорубку. Из плохого мяса,
как ни старайся, хороших котлет
не сделаешь.
Г. Вейль
Определение. Точечной оценкой параметра назовем способ
определения ожидаемого значения параметра случайной ве-
личины по набору ее наблюдений.

Глава 9 ..' >Г-':г\}!^^' ':''г--'"
9,1, О ш^ай Аенме понятия оценки.
Качество оценки
Абсолютно точное время показы-
вают только стоящие часы, да и то
только два раза в сутки.
Льюис Кэрролл
Как по наблюдаемым значениям прогнозировать значение
параметра, и насколько точен этот прогноз.
Пусть имеется 7 наблюдений х(,...,х7 некоторой случай-
ной величины ^ и мне хочется указать ожидаемую величину
ее математического ожидания. Тогда у меня есть несколько
предложений по ее оценке:
1. (х,+...+ х7)/7.
2. (х, + х3)/2.
3. 4.
4. х,.
5. 2х3-х4.
6. (х-х2)2/2.
7. (Мах + Min)/2.
8. Me.
Здесь в варианте № 7 Мах и Min — максимальное и мини-
мальное значение из наблюдаемого наборах,,...,х7, а в вариан-
те № 8 Me — стандартная оценка медианы, то есть четвертое,
по величине значение из наблюдаемого ряда набора х,,..., х7.
Наиболее употребительной является оценка типа № 1 —
среднее арифметическое среди всех наблюдений. Однако из
того, что что-то является наиболее часто используемым, еще
не следует, что это лучший выбор.
Основная прелесть оценки типа № 3 в том, что для нее
вообще не нужны какие-то фактические данные1. Неплоха
также и оценка типа № 4 — один раз померил, и хватит.
Основное возражение против оценки типа № 3 в том, что
она наверняка даст ошибочное значение. Но и стандартная
' В современной литературе ж> называют «метод использования
экспертных оценок».

234
Чоспи, 2 '!</(.' ш: пира метров
оценка типа № 1 тоже наверняка даст неточное значение ма-
тематического ожидания, а какое-то другое число
Для того чтобы выяснить, какой способ оценки парамет-
ров лучше, придется ввести ряд формальных определений
Определение. Оценочной функцией f. параметра X от п
аргументов назовем любую функцию от п аргументов, при-
нимающую числовые значения
В этой книге говорится почти исключительно о число-
вых случайных величинах, поэтому и далее речь будет идти
о числовых функциях от числовых аргументов.
Перечисленные выше восемь способов угадывания ма-
тематического ожидания соответствуют восьми разным оце-
ночным функциям от 7 аргументов.
Определение. Оценкой параметра случайной величины
£, при помощи оценочной функции /х параметра X от п ар-
гументов назовем случайную величину, определяемую как
^(^,,..., £л), где 4,,• ••, \п — независимые случайные величины,
распределенные так же, как \.
Например, среднее арифметическое от возраста больных
по группе из 7 человек — оценка математического ожидания
возраста больных при помощи оценочной функции типа № 1.
Таким образом, оценка — новая случайная величина,
распределение которой зависит как от распределения ис-
ходной случайной величины, так и оттого, какая оценочная
функция была выбрана.
Теперь можно перейти к выяснению, какая оценка и в ка-
ком смысле лучше.
Определение. Оценка параметра случайной величины £,
при помощи оценочной функции fx параметра X от п аргу-
ментов называется несмещенной, если Л/(/^,,..., £, )) = X.
Таким образом, несмещенная оценка — такая, которая в
среднем дает правильное значение.
Понятно, что «хорошая» оценка должна быть несмещен-
ной. В разделе 8.1 указывалось, что математическое ожида-
ние среднего арифметического из нескольких наблюдений
равно математическому ожиданию исходной величины.
Следовательно, оценочные функции №№ 1, 2 и 4 порожда-
ют несмещенные оценки.

Глава 9. Точечные оценки параметров
Однако оценка типа № 5 тоже несмещенная. Действитель-
но, на основании линейных свойств математического ожида-
ния М(2^3- £4) = M(2Q + Д/(Ч4) = 2Щ3) - Л/(У = 2Л/(£) "
Иногда имеется дополнительная информация о возмож-
ном виде наблюдаемой случайной величины. Эту информа-
цию можно и нужно использовать, и в этом случае можно
пользоваться не только несмещенными оценками, а оценка-
ми, несмещенными для таких случайных величин.
Определение. Оценка параметра случайной величины £,
при помощи оценочной функции fx параметра X от п аргу-
ментов называется несмещенной на множестве случайных
величин *F, если для любых Е, из ЧУ M(fx(^v..., Z,n)) - X.
Например, если случайная величина распределена сим-
метрично, то ее математическое ожидание совпадает с медиа-
ной. В этом случае оценка типа № 8, то есть стандартная
оценка медианы, является и несмещенной оценкой матема-
тического ожидания.
В случае симметричного распределения несмещенной
оценкой будет и оценка типа № 7 — полусумма максималь-
ного и минимального значения.
Более того, для случайных величин, распределенных по
Пуассону, оценка типа 6 — тоже несмещенная. Действи-
тельно1, так как i,{ и Ъ,2 — одинаково распределенные случай-
ные величины, то они имеют одинаковые математические
ожидания, следовательно, М(£,-Ь,2) = 0. Это независимые
случайные величины, и Д^,-^2) = /)(£,) + Д-£2) = D(^,) +
+ (-\)гЩ2) = Щх) + 0£2) = 2Щ). Так как математиче-
ское ожидание квадрата случайной величины равно сум-
ме квадрата ее математического ожидания и дисперсии, то
Л/((^,-42)2) = 2Щ,). Следовательно, оценка типа № 6 дает не-
смещенную оценку дисперсии, которая для случайных вели-
чин, распределенных по Пуассону, совпадает с математиче-
ским ожиданием.
Иногда добиться несмещенности оценки не удается, и ис-
пользуется ее несколько более слабый предельный вариант.
' Далее используются свойства, приведенные в разделе 8.1.

236
Часть 2. Анализ параметров
Определение. Оценка параметра случайной величины £, при
помощи оценочной функции^ параметра X от п аргументов на-
зывается состоятельной, если при п -> со Л/(/^(4,,..., £я)) -> X.
Таким образом, состоятельные оценки — оценки, сме-
щенность которых стремится к нулю при увеличении объема
наблюдений.
Если у нас имеется несколько несмещенных оценок, то
есть оценок, дающих в целом правильное значение парамет-
ра, но с некоторыми статистическими погрешностями, то
лучше будет та оценка, у которой статистические погреш-
ности меньше.
Определение. Одна несмещенная оценка параметра X по
и наблюдениям называется эффективнее другой несмещен-
ной оценки параметра X по п наблюдениям, если для любой
случайной величины Е, ее дисперсия меньше.
Определение. Одна несмещенная оценка параметра X по п
наблюдениям называется эффективнее другой несмещенной
оценки параметра X, по п наблюдениям на множестве *Р, если
для любой случайной величины £, из Ч? ее дисперсия меньше.
Несмещенность и эффективность оценок часто трактуют
в терминах наличия систематической и случайной ошибки. Если
речь идет только о задаче оценки одного параметра в одной
серии наблюдений, то систематическая и случайная ошибка
одной величины одинаково неприятны. Например, если вы в
кого-то стреляете, то все равно, отчего вы промахиваетесь —
оттого, что у винтовки сбит прицел, или оттого, что у вас дро-
жат руки. Однако в целом регулярная ошибка хуже случайной
тем, что при увеличении объема наблюдений случайная ошиб-
ка уменьшается, а регулярная — нет. Например, если есть воз-
можность стрелять в цель достаточно долго, то даже при дрожа-
щих руках когда-нибудь цель будет поражена, а вот при точной
стрельбе из кривой винтовки в цель не попасть никогда.
Сравним теперь эффективность несмещенных оценок
математического ожидания типа №№ I, 2, 4 и 7. Как было
показано в разделе 8.1, дисперсия среднего арифметиче-
ского из п наблюдений в п раз меньше дисперсии одного
наблюдения. Поэтому дисперсия оценки (§,+...+ §7)/7 рав-
на D(t,)/7, дисперсия оценки (£, + £ )/2 равна Щ>)/2, а дис-

Глава 9. Точечные оценки параметров
237
Персия оценки £,,, естественно, равна Die,). Вычислим теперь
дисперсию оценки типа № 5.
В этом случае £>(2^3- £4) = Щ%3) + ДЧ<) = 22Щ3) +
+ (-1)2Щ4) = 4Д£3) + D(Q = 5Z>(4) Следовательно, этот
способ оценки математического ожидания даже значитель-
но хуже, чем типа № 4 (оценки по одному наблюдению).
Доказана теорема, что для нормально распределенных
случайных величин оценка типа № 1 (через среднее арифме-
тическое) — самая эффективная среди всех. Поэтому в паке-
тах статистических программ и т. п. оценка математического
ожидания через среднее арифметическое среди всего набора
наблюдений используется не только как вариант по умолча-
нию, а просто как единственно возможная.
Однако если симметрично распределенная случайная
величина распределена компактнее, чем нормальная1, то
оценка типа № 7 (полусумма максимума и минимума) — не-
смещенная оценка, которая имеет меньшую дисперсию, чем
стандартная оценка через среднее арифметическое. Если же
симметрично распределенная случайная величина распре-
делена менее компактно, чем нормальная (что для фактиче-
ских данных встречается чаще всего), то стандартная оценка
медианы — несмещенная оценка математического ожида-
ния, которая имеет меньшую дисперсию, чем стандартная
оценка через среднее арифметическое.
Достаточно часто наблюдаемую случайную величину
можно интерпретировать как «зашумленную» редко встре-
чающимися грубыми ошибками. Например, пусть для изме-
рения уровня кислотности биологических образцов в виде
растворов с включениями взвесей и фрагментов использует-
ся автоматический цифровой рН-метр, который, если пла-
вающий в растворе фрагмент замыкает электроды датчика,
выдает значение в 9999,99. Тогда если датчик замыкает при-
мерно на каждом сотом образце, то среднее арифметическое
рН раствора будет больше 100. В этом случае среднее ариф-
метическое от показаний рН-метра будет характеристикой
не кислотности образцов, а их гомогенности.
Например, рашюмерио распределена

238
Часть 2 Анализ параметров
Для описания устойчивости оценки к таким ошибкам ис-
пользуют следующую характеристику.
Определение. Робастностыо оценки называется ее устой-
чивость к сильным возмущениям малой доли наблюдений.
Как легко видеть, стандартная оценка математического
ожидания через среднее арифметическое неробастна.
Резюме
По умолчанию для оценки математического ожидания
используется среднее арифметическое.
Достоинства этой оценки:
1. Несмещенность.
2. Предельная эффективность при работе с нормальны-
ми случайными величинами.
3. Возможность использования при работе с перемен-
ными, для которых отсутствует дополнительная ин-
формация о возможном виде их распределения.
Недостатки этой оценки:
1. При работе с некоторыми специальными классами
случайных величин есть более эффективные оценки.
2. Оценка неробастна, поэтому при работе со средним
арифметическим нужно также анализировать распре-
деление на наличие выскакивающих вариант.
В некоторых случаях, когда имеется достаточно подроб-
ная информация о возможном характере распределения изу-
чаемой случайной величины, более эффективными оценка-
ми математического ожидания может оказаться не среднее
арифметическое, а другие оценки.
9.2. Оценка моментов. Катастрофа
неробастности старших моментов
Почему использование набора моментов для описания
распределения случайной величины оказывается
малопродуктивным.
Хотя все моменты и центральные моменты определяются
на основании математического ожидания степени случай-

Глава 9 Точенные оценки параметров 239
ной величины, при их оценке через среднее арифметическое
обнаруживаются дополнительные подводные камни.
Рассмотрим пример. Пусть при проведении мониториро-
вания артериального давления у 100 пациентов среднее сни-
жение артериального давления в период сна по сравнению с
периодом бодрствования составило в среднем 20 мм рт. ст. с
разбросом от 0 до 40 и среднеквадратичным отклонением в
10. Тогда дисперсия снижения давления составит 100, третий
центральный момент по модулю будет порядка 1000 или ме-
нее, а четвертый центральный момент — порядка 10 000.
Если оценивать статистические погрешности опреде-
ления этих величин, то есть то, насколько результаты в од-
ной группе отличаются от результатов в другой группе (эта
техника будет подробно разбираться ниже), то для матема-
тического ожидания погрешность будет порядка 1 мм, для
дисперсии — порядка 10, для третьего центрального момен-
та — порядка 100 и для четвертого центрального момента —
порядка 1000.
Пусть у нас один пациент из наблюдаемого массива пе-
ред сном примет снижающий давление препарат, из-за чего
его давление упадет не на 20, а на 50 мм рт. ст. Это приведет
к тому, что у одного пациента из 100 давление снижается на
30 мм больше расчетного, откуда снижение среднего ариф-
метического давления для группы из 100 больных составит
0,3 мм. Для дисперсии повышение квадрата отклонения со-
ставит 900, что даст увеличение дисперсии примерно на 9.
Для третьего центрального момента изменение составит около
270, а для четвертного центрального момента — около 8000.
Для математического ожидания смещение на 0,3 в не-
сколько раз меньше статистической погрешности, поэтому
не слишком существенно. Для дисперсии увеличение на 9 —
порядка статистической погрешности, поэтому заметно по-
нижает точность расчета. Для третьего центрального момен-
та смещение на 270 в несколько раз больше статистической
погрешности, а для четвертого момента смещение не только
значительно больше статистической погрешности, но и при-
мерно равно исходному значению четвертого центрального
Момента.

240
Чч, >пь 2 Лии Hi ■ r.i.
Итак, для набора из КЮ пациентов при одном ns\k;v
нии, которое в несколько раз больше обычного (и koiojhk
и выскакивающей вариантой считать нельзя) искажение
математического ожидания практически незаметно, дне
Персии — невелико по сравнению с исходной величиной, но
сопоставимо со статистической ошибкой, для третьего цент-
рального момента — в несколько раз больше статистической
погрешности, а для четвертого нет рального момента — уве
личиваетего вдвое Про пятые и более старшие центральные
моменты и говорить не приходится — там искажения окон
чательно «забьют» исходную величину
И ведь рассматривается пример с редкими и достаточно
небольшими искажениями!
Следовательно, при увеличении порядка определяемо-
го момента степень неробастности его стандартной оценки
через среднее арифметическое возрастает. Если неробаст-
ность оценки математического ожидания существенна толь-
ко для «плохих», сильно некомпактных распределений, то
неробастность оценки дисперсии существенна уже практи-
чески всегда. Неробастность же оценок старших моментов
практически не дает возможности их определить по реальным
данным. Поэтому на практике четвертый центральный мо-
мент выборочного распределения рассчитывается не столько
для того, чтобы оценить величину четвертого центрального
момента исследуемой величины, сколько для оценки неком-
пактности наблюдаемых значений. Оценки же моментов на-
чиная с пятого и выше практически не используются.
Причина понижения робастности при увеличении по-
рядка момента в том, что числовая случайная величина Ъ,"
обычно распределена менее компактно, чем £, причем чем
больше п, тем более выражена эта некомпактность.
В качестве примера возьмем распределение Пуассона со
средним X = 1 как пример очень компактно распределенной
случайной величины. Для того чтобы лучше была видна ве-
роятность малых событий, построим гистограмму в лога-
рифмическом масштабе (рис. 9.1).
Для распределения Пуассона со средним 1 частота встре-
чаемости десяти составляет лишь около 10~7, то есть десяти-

Глава 9. Точечные оценки параметров
241
ТТ
и
mm
и
5 6
9 10
тг
Рис. 9.1. Частотная гистограмма распределения Пуассона
со средним, равным единице (левые столбики),
и пятой степени от него (правые столбики)
кратное превышение среднего значения наблюдается лишь
примерно в одном случае на 10 миллионов наблюдений. Для
пятой степени от этой случайной величины значение «10»
встречается чаше, чем один раз на 100 наблюдений.
Многократно различаются не только вероятности боль-
ших отклонений, но и скорость убывания вероятности по
мере увеличения отклонения. Так, для исходного распреде-
ления Пуассона вероятность события «10» в 10 раз менее ве-
роятна, чем события «9». Для пятой степени распределения
Пуассона это соотношение примерно равно двум.
Для «обычных», не столь компактных распределений
различие в распределении исходной случайной величины
и ее степеней еще более грубое.
Указанные эффекты не дают возможности в полной
мере использовать естественный для современной матема-
тики аппарат приближения при помощи полиномов и т. п.
Действительно, для того чтобы у двух числовых случайных
величин совпадали вероятности событий, необходимо и до-
статочно, чтобы были равны все их моменты1. Поэтому для
полного задания распределения числовой случайной вели-
1 В том случае, если случайные величины распределены таким об-
разом, что все их моменты определены.

242
Часть 2. Ана.ип параметров
чины достаточно задать величины ее моментов1. Однако из-
за описанных выше эффектов прямое использование такого
подхода для статистического анализа данных оказывается
малопродуктивным.
9.3. Оценка дисперсии
Большая часть грандиозных глу-
постей — попытки скрыть мелкие
промахи.
Как оценивать дисперсию и об одной старой ошибке,
последствия которой не изжиты до сих пор.
Хотя формально все моменты и центральные моменты
определяются на основании математического ожидания, их
оценка имеет дополнительные технические сложности.
В соответствии с определением дисперсия — математи-
ческое ожидание квадрата отклонения случайной величины
от своего математического ожидания. Поэтому если извест-
но, что случайная величина имеет математическое ожидание
т, то ее стандартная оценка по наблюдениям хх,...,хи имеет
вид:
5=((х,-/я)2+...+ (х"-/и)2)//1. (1)
В соответствии с несмещенностью стандартной оценки
математического ожидания через среднее арифметическое,
это несмещенная оценка дисперсии.
Задача определения дисперсии у случайной величины
с известным математическим ожиданием достаточно специ-
фична. В качестве примера можно привести обработку кар-
1 Примечание для математиков. Вероятность события — интеграл
по функции распределения от индикаторной функции, то есть функ-
ции, равной единице на элементарных событиях, принадлежащих
событию, и нулю в противоположном случае Следовательно, вероят-
ность события — частный случай линейного функционала — интег-
рала но функции распределения. Однако интеграл от Xя по функции
распределения Ь\х) — л-й момент, а множество полиномов плотно.

Глава 9. Точенные оценки параметров
243
диограмм, энцефалограмм и др., в которых средняя величина
отведения аппаратно фиксирована. Значительно чаще у слу-
чайной величины неизвестны и математическое ожидание,
и дисперсия. В этом случае совершенно естественно в оцен-
ку (1) вместо известного математического ожидания подста-
вить его стандартную несмещенную оценку х—(х{ +...+х)/п.
В этом случае из оценки (1) имеем следующую оценку:
S=((xt- х)2+...+(хп-хУ)/п. (2)
Наверное, именно кажущейся естественностью постро-
ения этой оценки можно объяснить тот факт, что только в
XXвеке заметили, что эта оценка— смещенная. Причина
смещенности в том, что по одному и тому же набору наблю-
дений оцениваются и среднее арифметическое, и отклоне-
ние от него, и эти величины не являются независимыми.
Причем не только доказать, что оценка (2) смещена, но и
получить необходимую поправку очень просто, что мы сей-
час и сделаем.
Заметим, что если прибавить к наблюдаемой случайной
величине константу, то величина оценки S не изменится.
Следовательно, без ограничения общности можно считать,
что математическое ожидание наблюдаемой случайной ве-
личины Ъ, равно нулю.
Вычислим математическое ожидание оценки S. Так как
математическое ожидание суммы случайных величин равно
сумме их математических ожиданий вне зависимости от их
независимости, то M(S) = -(M((t>l -if)2 +... + Л/((^„ -if)2)-
п
Так как^— среднее арифметическое, то (^-jf)2 =(£,-
-(§, +...+4„)/л)2 =1 —^, —£,7 -...—£„ . Заметим, чтоесл и /*/,
{ п п п )
то 't,. и ^ — независимые случайные величины с нулевым
математическим ожиданием, поэтому математическое ожи-
дание их произведения равно произведению их математиче-
ских ожиданий, то есть нулю. Поэтому при раскрытии ско-
бок и взятии математического ожидания остается только
математическое ожидание от квадратов, и

244
Часть 2 ,\h;i,:u
л/((^,чУ)=л/
/7-1,
4, И'
, + м
^-i \л
Ч„
откуда
*&-ej> vK> т "fe>-+ тГ(С)
Так как все £. — случайные величины с нулевым матема-
тическим ожиданием, то математическое ожидание их квад-
рата равно их дисперсии, а так как они распределены так же,
как и с,, то дисперсии Е,. Следовательно,
Так как членов с коэффициентом — \/п2 в сумме п— 1, то
Л'(М)>(^1^
-]
(п-\)2
- («-.)Dft)~ „2
*<&)+
Мы вычислили математическое ожидание (£, -£ ). Всего
в сумме таких членов п, следовательно,
и '
и математическое ожидание оценки (2) равно ^-D(^). Сле-
п
довательно, для того чтобы получить несмещенную оценку
дисперсии, нужно в выражении (2) делить не на п, а на п - 1,
то есть использовать оценку
^((х,-х)2+...+(хп-х)2)/(/7- 1). (3)
После этого математика кончается и начинается поли-
тика.
Так как эта ошибка была обнаружена достаточно поз-
дно, то уже был проведен анализ большого количества
фактических данных по ошибочной методике. При анали-

Глава 9 Точечные оценки nupj :i:-г,;,., ■,.,
245
зс существенности регулярной ошибки с использованием
смещенной ошибки дисперсии получается, что она много
меньше случайной ошибки при количестве наблюдений
от 30 и больше, поэтому для уже проведенных исследо-
ваний с достаточно большим количеством наблюдений
поднимать исходные данные и проводить расчеты заново
не нужно. Поэтому для того, чтобы как-то выкрутиться из
щекотливой ситуации, были даны следующие рекоменда-
ции: для исследований с объемом менее 30 наблюдений
нужно при расчете дисперсии делить на п - 1, а при на-
блюдениях с большим объемом наблюдений можно и на
я, причем даже лучше на л, чем на п — 1, потому что так
легче.
При более внимательном анализе рекомендация не
выдерживает никакой критики. Во-первых, даже если
регулярная ошибка и меньше случайной, то зачем ее до-
бавлять? Во-вторых, сама рекомендация при обработке
больших объемов наблюдения делить на и, потому что это
обычно круглое число и на него делить легче, — просто
смехотворна, так как исходный объем работы при сумми-
ровании всех наблюдений, вычитании полученного сред-
него арифметического из имеющихся наблюдений, возве-
дении разности в квадрат и их суммировании несравненно
больше, чем одно деление. В эпоху компьютеров и кальку-
ляторов на что делить — на п или п — 1 — уже совсем все
равно.
Наверно, именно из-за абсурдности рекомендации во
многих современных руководствах по-прежнему предпи-
сывается при ручном расчете дисперсии для наборов ме-
нее 30 делить на п - I, а для наборов в 30 и более — на
п Ьолее того, даже во многих современных программах
есть два варианта расчета дисперсии — правильного и с
регулярной ошибкой. При этом правильный вариант мо-
жет называться «выборочный», ошибочный — «генераль-
ный»
Иногда по названию нельзя понять, о чем идет речь Тог
да нужно рассчитать оба и использовать тог, который боль-
ше на 1//;-ю.

246
Часть 2. Анапы i параметра/;
9.4. Построение оценок при помощи метода
наибольшего правдоподобия
Пранда часто выглядит неправдо-
подобно, и только ложь всегда вну-
шает доверие.
Цитата по памяти*
Как конструировать оценки параметров. Данный раздел
требует наличия базовых знаний по математическому
анализу.
В разделе 9.1 приводились примеры оценочных функций
и обсуждалось, какие оценки и в каком смысле хороши или
плохи. Здесь изучим вопрос, как сконструировать оценку
параметра. Наиболее используемый для этого метод называ-
ется методом наибольшего правдоподобия (likelihood).
Пусть у нас имеется дискретная величина ^, заданная
с точностью до параметра X, то есть для любого элементар-
ного события х его вероятность Р(Ъ,=х) есть функция от А..
Пусть при /^наблюдениях случайной величины Ъ, были полу-
чены значенияx,,...,xv. Положим L= P(^ = х,) x...x Р(^ = хЛ,),
то есть L — вероятность того, что будет получен именно тот
набор наблюдаемых значений, который и был в действитель-
ности. Так как L вычислялась как произведение вероятно-
стей, зависящих от X, то L — функция от А.. В качестве оцен-
ки параметра X по набору наблюдений х,,..., xN возьмем то
значение X, при котором L максимально.
Следовательно, при оценке по методу наибольшего прав-
доподобия берется то значение параметра, при котором на-
блюдаемый набор значений наиболее вероятен.
При нахождении максимума функции L(X) обычно легче
находить не максимум самой функции L, а максимум ее ло-
гарифма \п(ЦХ)). Так как логарифм — монотонно возраста-
' Так как цитировать по памяти, не приводя источника, — очень
плохой стиль, то в качестве моральной поддержки привожу высказы-
вание Сзади: «Подобно пустому сосуду наполнился я чужой мудро-
стью, но, по глупости своей, забыл, что и от кого узнал».

Глава 9. Точечные оценки параметров
247
ющая функция, то максимум L и максимум ln(L) достигается
при одних и тех же значениях параметра А..
Пример. Пусть £, — случайная величина, распределенная
по Пуассону с неизвестным математическим ожиданием А..
Тогда в соответствии с определением распределения Пуассо-
на вероятность того, что она примет целое значение х, равна
Xх
—е'х- Если в результате наблюдений был получен набор
х!
значений х,,..., xN, то
цХ) = ~е-хх...х^е-х =Г''""« ——' -e~XN
Перейдя от функции правдоподобия L к ее логарифму,
имеем
1п(ДА))=1п(Ах'+ +х") + 1п( ! ) + \п(е-ш) =
х,!х...хл:Л,!
= (х,+... + *„) -ln(A.) + ln(——! -)-ХЛГ
Л| IX ... X Луу .
Для нахождения максимума продифференцируем по-
лученное выражение по А., в результате чего получим
—— 1п(ДА))=(х, +... + xN)/X-N, откуда максимум при
ак
—\n(L(\))=(x,+... + x„)/X-N = 0,umi(xl+... + x„)/N=X.
dX
В результате получили стандартную оценку математичес-
кого ожидания через среднее арифметическое.
Наблюдаемая случайная величина не обязательно долж-
на быть известна с точностью до одного неизвестного па-
раметра. Таких параметров может быть несколько, в этом
случае ищется максимум L как функции от нескольких пе-
ременных.
Аналогичным образом можно пользоваться методом на-
ибольшего правдоподобия и при анализе непрерывных слу-
чайных величин. В этом случае для построения функции
правдоподобия L нужно брать произведения не вероятно-

248
Часть 2. Анализ параметров
стей наблюдаемых элементарных событий, а произведения
плотностей вероятности.
Пример. Пусть наблюдаемая случайная величина £, рас-
пределена разномерно на неизвестном отрезке [а,Ь]. В силу
определения равномерно распределенной на отрезке случай-
ной величины плотность вероятности р(х) = \/(Ь — а), если х
принадлежит отрезку \а,Ь], и нулю в противном случае. Сле-
довательно, для данного набора наблюдений хр..., xN функ-
ция L равна \/{b - a)N, если все х,,..., ^принадлежат отрез-
ку [а,Ь], и нулю в противном случае. Если взять два разных
отрезка, к каждому из которых принадлежат все наблюде-
ния х,,..., -Хд, то функция правдоподобия L = \/(b — a)Nбудет
больше для отрезка меньшей длины. Следовательно, макси-
мальное значение функции наибольшего правдоподобия до-
стигается на отрезке минимальной длины, содержащем все
наблюдения х,,..., х^ Но это — отрезок от минимального до
максимального значения из набора х,,..., х^ Следовательно,
оценкой параметра а служит минимальное из наблюдаемых
значений, а оценкой параметра Ь — максимальное из наблю-
даемых значений.
Качество полученных при помощи метода наибольшего
правдоподобия оценок достаточно высокое. Они состоятель-
ны и достаточно эффективны, хотя и не всегда несмещены.
Например, при построении оценки дисперсии нормально
распределенной случайной величины метод даст «древнюю»
смещенную оценку с делением на N, а не N— 1.
Резюме
Пакеты статистических программ определяют оценки
только наиболее часто используемых параметров и при
этом не пользуются никакой дополнительной информа-
цией о возможном виде распределения исследуемой слу-
чайной величины. Если такая дополнительная информа-
ция имеется, то может быть сконструирована специальная
оценка параметра, более точная, чем стандартная универ-
сальная.
Стандартная оценка математического ожидания несме-
шенная, по в то же время неробастна. Неробастность стан-

Глава 9. Точечные оценки параметров 249
дартных оценок старших моментов столь велика, что прак-
тически ими нельзя пользоваться.
До сих пор достаточно часто используется смещенная
оценка дисперсии. Пользоваться ею не нужно ни при каких
условиях.

Глава 10
ИНТЕРВАЛЬНЫЕ ОЦЕНКИ ПАРАМЕТРОВ.
ОПРЕДЕЛЕНИЕ ДОСТОВЕРНОСТИ
РАЗЛИЧИЙ
Лекция по математике в военном вузе. Преподаватель:
— Чему равно число п ?
— Примерно 3,14159.
— Неправильно, курсант Иванов. Записывайте: в соответствии
с приказом генштаба л равно 3,1. В случае особой необходимости мо-
жет достигать 4—5, в военное время — до 7.
Студенческий анекдот
В главе 9 исследовался вопрос о том, какое наилучшее зна-
чение параметра можно получить на основании имеющихся
наблюдений. В этой главе будет выясняться, насколько ве-
роятны расхождения между ожидаемыми и истинными зна-
чениями параметров.
В соответствии с главой 9, если используется несмещен-
ная оценка, то математическое ожидание оценки равно ис-
комому параметру. Однако оценка, даже несмещенная, —
случайная величина, которая может принимать значения, не
совпадающие со своим математическим ожиданием.
Для того чтобы рассчитать вероятность того или иного
отклонения оценки от ее математического ожидания, нуж-
но знать, как оценка распределена. Однако распределение
опенки зависит как от используемой оценочной функции,
так и от распределения наблюдаемой случайной величины.

Глави 10. Интервальные оценки параметров
251
Тут мы попадаем в своего рода замкнутый круг. Дело не
столько в технических сложностях, хотя и вычисление рас-
пределения оценки при известных оценочных функциях и
распределении случайной величины может быть весьма не-
тривиально, сколько в том, что для расчета распределения
оценки нужно знать распределение исходной случайной ве-
личины, а если оно известно, то зачем у нее по наблюдаемым
данным оценивать параметры?
В разделе 6.3.2 было показано, как рассчитать довери-
тельные границы к медиане и другим процентилям. Однако
процентили — специфический случай параметров, так как
он фактически не использует функцию распределения слу-
чайной величины, а работает с ее рангами.
Другой возможный подход к исследованию распределе-
ния оценки — получить для нее не точные, а приближенные
распределения. При этом, так как основная оценка мате-
матического ожидания — среднее арифметическое, а боль-
шинство оценок других параметров (кроме процентилей)
основано на математическом ожидании, то центральный
вопрос для изучения распределения оценок — как распре-
делено среднее арифметическое из набора независимых на-
блюдений случайной величины.
10.1. Центральная предельная теорема
Если физику дают задачу исследовать устойчивость стула на четы-
рех ножках, он исследует устойчивость стула на четырех ножках.
Если математику дают задачу исследовать устойчивость стула на
четырех ножках, он вначале исследует устойчивость стула на одной
ножке, потом — на двух ножках, а потом переходит к случаю стула
с бесконечным количеством ножек.
Из сборника «Физики шутят»
В каких случаях можно считать, что среднее арифметическое
распределено нормально Самый технически тяжелый момент
всей данной книги.
Центральная предельная теорема и закон больших
чисел —дна кита, па которых стоит теория вероятностей.

252
Часть 2 Аналиъ пирометров
Часто центральную предельную теорему (ЦПТ) форму-
лируют в следующей форме:
Вульгарная формулировка ЦПТ. Среднее арифметическое
из 30 или более наблюдений распределено практически нор-
мально.
Эта формулировка, присутствующая в большинстве учеб-
ников по прикладной статистике, неверна.
Для того чтобы дать правильную формулировку ЦПТ,
вначале введем формальное определение меры отклонения
случайной величины от нормальных случайных величин.
Определение. Пусть £, — числовая случайная величина
с математическим ожиданием М и дисперсией D. Возьмем
П — нормально распределенную случайную величину с ма-
тематическим ожиданием М и дисперсией D. Пусть 8(х) =
= \F(x) — F (х)\, где F(x), как обычно, функция распределе-
ния, то есть вероятность того, что случайная величина мень-
ше или равна х. В качестве меры ненормальности Д(£) возь-
мем максимум1 из функции 5(х).
Правильная формулировка ЦПТ. Пусть £, — числовая слу-
чайная величина с математическим ожиданием Л/и диспер-
сией D, Ъ,к — независимые случайные величины, распреде-
ленные_так же, как £, и %п — среднее арифметическое из п % ,
то есть £и= (£, +...+ £,п)/п. Тогдапри п -»°оД(£п) -> 0.
У средних арифметических ^п помимо приближения фун-
кции распределения к нормальному уменьшается и вариа-
тивность. Действительно, из линейных свойств математиче-
ского ожидания и дисперсии следует, что Л/(£я) = М, a Z)(£, ) =
= D/n. Прямым следствием этого является усиленный закон
больших чисел, согласно которому статистическая погреш-
ность определения частоты падает пропорционально корню
из числа наблюдений.
В формулировке этой теоремы важно каждое условие,
и невыполнение любого из них может приводить к тому, что
предел не сходится к нормальному. В качестве иллюстрации
приведем ряд контрпримеров.
' Примечание дли лиц с математическим образованием точную
нсрхннио грань, гак как рассматринаемаи функция 8(дг). вообще гопо
ря, может быть рафынпой

Глава 10. Интервальные, оценки. ... ,; ;.ч-.я{Ю<-:
253
В качестве первого требования случайная величина долж-
на иметь конечное математическое ожидание М и диспер-
сию D. Проблема здесь не только в том, что для случайных
величин с бесконечными математическим ожиданием или
дисперсией и у среднего из нескольких наблюдений соот-
ветствующий параметр также будет бесконечным, и нельзя
выбрать «похожее» нормальное распределение, так как у них
эти параметры должны быть конечны.
Основная сложность в том, что у случайных величины
с бесконечными математическим ожиданием или диспер-
сий последовательность выборочных средних арифметиче-
ских не сходится, а бесконечно флюктуирует, часто порож-
дая все более дикие распределения. В качестве иллюстрации
расходящегося процесса рассмотрим игру в орлянку, при-
чем правила такие: в случае выигрыша ставка не удваива-
ется, а учетверяется, но ставить на кон нужно всегда только
все деньги. Тогда, с одной стороны, играть выгодно, так как
после каждой игры математическое ожидание суммы выиг-
рыша удваивается. С другой стороны, когда-нибудь вы обя-
зательно все проиграете. В результате в пределе имеем бес-
конечно богатого человека, у которого с вероятностью 1 нет
ни копейки.
Второе требование теоремы — что суммировать нужно
одинаково распределенные случайные величины. Действи-
тельно, если мы рассматриваем количество больных диа-
бетом в Москве и 120 близлежащих селах, то, несмотря на
большой объем наблюдений в 121 субъекте, на самом деле
это будут данные по Москве с небольшими добавками.
Есть усиления ЦПТ, в которых доказывается нормаль-
ность среднего и в случае независимых неодинаково распре-
деленных случайных величин. Одинаковость распределения
можно заменить на более мягкое требование соразмерно-
сти, чтобы при увеличении количества членов суммы от-
носительный вклад каждой случайной величины стремился
к нулю.
Следующее требование — независимость наблюдений.
Как обсуждалось выше при определении этого понятия, не-
смотря на кажущуюся прозрачность требования обосновать

254
Часть 2. Анализ параметров
его правомочность очень сложно. Например, количество за-
болевших для антропонозных инфекций во многих случаях
нельзя считать нормально распределенным, так как инфи-
цирование одного повышает вероятность инфицирования
других. В качестве формального контрпримера рассмотрим
случай, когда все \к равны (не одинаково распределены,
а именно равны, то есть принимают одинаковые значения).
Тогда Ъ,п = \, и никакой сходимости к нормальному распреде-
лению при увеличении объема наблюдений не наблюдается.
Далее, в формулировке теоремы указывается сходимость
для каждой исходной случайной величины, но не указана
скорость сходимости и нет никаких оценок типа «если ко-
личество наблюдений больше того-то, то...». Этих общих
оценок скорости сходимости для всех случайных величин
просто не существует, для каждой она своя. Более того, для
любого количества наблюдений п можно придумать случай-
ную величину, которая после п суммирований сама с собой
еще будет далека от нормальной.
В качестве примера возьмем миллиард наблюдений. Рас-
смотрим распределение Бернулли с р, равным одной милли-
ардной. Тогда сумма миллиарда таких случайных величин
будет распределена с очень хорошей точностью как распре-
деление Пуассона с математическим ожиданием, равным
единице, а, как было показано выше, эта случайная величи-
на имеет форму распределения, очень далекую от нормаль-
ного1.
Разумеется, сходимость к нормальному распределению
будет и для этого случая. Если увеличить количество сумми-
рований до ста миллиардов, то в результате будет распреде-
ление Пуассона со средним в сто, которое уже достаточно
близко к нормальному.
Хотя общих оценок скорости сходимости к нормально-
му распределению нет, есть оценки скорости сходимости
ь зависимости от коэффициента эксцентриситета. Если у
случайной величины коэффициент эксцентриситета около
Полес Оли 1кий к медицине пример — тболеиаемость жителей
Москвы ОРЭ ja одну миллиардную долю секунды.

Глава 10. Интервальные оценки u<:paMfinr<:";
255
нескольких единиц или меньше, то при работе с доверитель-
ной вероятностью р = 0,05 стандартного требования к коли-
честву наблюдений в 30 или больше действительно достаточ-
но. Медленно сходятся к нормальному случайные величины
с большими коэффициентами эксцентриситета. Поэтому
наличие выскакивающих вариант не только затрудняет со-
держательный анализ среднего арифметического, но и по-
рождает технические сложности, понижая точность оценки
математического ожидания.
Последняя тонкость в формулировке ЦПТ связана имен-
но с самим определением величины отклонения распреде-
ления от нормального. В качестве меры была принята раз-
ность вероятностей. Поэтому если обе вероятности малы,
но многократно отличаются друг от друга, то с точки зрения
выбранной меры они будут отличаться мало.
Рассмотрим в качестве примера распределение Пуассона
с математическим ожиданием, равным 1. При «прямом» рас-
чете вероятности того, что эта случайная величина больше
или равна 8, получаем малую вероятность примерно в Ю-5.
Если же эту случайную величину приближать нормальным
распределением с таким же математическим ожиданием
и дисперсией, то есть равными единице, то событие «быть
равным или больше 8» есть событие «отклониться от мате-
матического ожидания в одну сторону больше, чем на 7 сред-
неквадратичных отклонений», что для нормального распре-
деления получаем вероятность 1,3 х 10~12. С одной стороны,
обе вероятности малы, поэтому приближение имеет ошибку
около одной стотысячной. С другой стороны, фактическая
вероятность примерно в десять миллионов раз больше, чем
полученная на основании приближения нормальной слу-
чайной величиной.
При этом распределение Пуассона - компактная слу-
чайная величина, имеющая маловероятные большие от-
клонения. В общем случае справедлива теорема Чебышева
о том, что отклонение от математического ожидания боль-
ше, чем на п среднеквадратичных отклонений имеет вероят-
ность меньше \/п\ поэтому для менее компактных случай-
ных величин с единичными математическим ожиданием

256
Чисть 2- Анализ параметров
и дисперсией вероятность принять значение в 8 или больше
менее 1/49.
При использовании предположения о нормальности
распределения среднего арифметического наиболее грубые
расхождения происходят именно в области маловероятных
больших уклонений. Полученные в предположении о нор-
мальности распределения среднего арифметического оцен-
ки вероятности больших расхождений безумно малы, тогда
как они просто малы.
При этом ВСЕ оценки достоверности различия матема-
тического ожидания и других основанных на нем параметров
рассчитываются пакетами статистических программ в пред-
положении о нормальности распределения выборочного среднего
арифметического. Проверка обоснованности этих предполо-
жений и оценка величины полученных ошибок возлагается
на пользователя1.
Резюме
Вопрос о том, можно ли пользоваться предположением
о нормальности распределения выборочного среднего, до-
статочно сложен и требует отдельной проверки. Основная
ошибка, к которой приводит необоснованное использова-
ние предположения о нормальности — многократное (на-
пример, на порядок порядков) завышение достоверности
различий. Все оценки достоверности различий математи-
ческого ожидания и т. д. в пакетах статистических программ
делаются в предположении о нормальности распределения.
Проверка корректности этого предположения — обязатель-
ная часть статистического анализа, которая возлагается на
исследователя.
1 Самые тяжелые вопросы, которые задают на защите диссерта-
ций па -шанис кандидата медицинских наук:
- Л !ачем, собственно. Вы пес jto исследонали?
Ну и что >то дает для клинической практики''
— Л нормальны ли паши распределении''
Задают их достаточно редко, так как они считаются слишком
«терскими», но готовить на них отпет нужно

Глава 10. Интервальные оценки пани .:л-.г,о...,
257
10.2. Определение достоверности
различия дисперсии
Как определять достоверность различия оценок дисперсии.
Пакеты статистических программ хорошо рассчитывают
достоверность различий выборочных средних арифметиче-
ских, но обычно не определяют достоверность различия
выборочных дисперсий. Поэтому даже при анализе факти-
ческих данных с помощью статистических пакетов досто-
верность различия придется рассчитывать самостоятельно.
Рассмотрим следующую последовательность задач.
1. Определение достоверности отличия выборочной
дисперсии от ожидаемого значения.
2. Определение доверительных границ к выборочной
дисперсии.
3. Определение достоверности различия двух выбороч-
ных дисперсий.
Пример 1. Пусть по имеющимся литературным данным,
полученным по большому объему наблюдений1, среднеквад-
ратичное отклонение возраста больных острым холецисти-
том равно 15, а полученное по 45 наблюдениям значение
равно 19,2. Определим, может ли такое различие быть слу-
чайным.
При стандартной оценке дисперсии S = ((*, ~х)2+...
...(х —х)2)/(п — 1) рассчитывается сумма квадратов откло-
нения от среднего арифметического. Если предположить,
что наблюдаемая случайная величина распределена нор-
мально с дисперсией D и математическим ожиданием М, то
(х — М)2 — квадрат нормально распределенной случайной
величины с математическим ожиданием, равным нулю,
1 Это должно означать, что количество наблюдений в «литератур-
ных» данных во много раз больше, чем в собственных, поэтому ста-
тистическая погрешность литературных данных много меньше и ею
можно пренебречь. На практике такие формулировки обычно означа-
ют, что или в литературном источнике данные описаны недостаточно
подробно, чтобы можно было рассчитать их статистическую достовер-
ность, или автор не знает, как это делать.
9 Медицинская сшисгикл

258
Часть 2. Анализ параметров
и дисперсией, равной D, то есть имеет вид D х ^, где £, рас-
пределена как х2-распределение с одной степенью свобо-
ды, а сумма (х, - М)1 +...(хн- М)2 распределена как Z)x^, где
Ь\ — х2-распределение с п степенями свободы. По причинам,
изложенным в разделе 9.3, в оценке дисперсии нужно не
только делить на п — 1, но и «пропадает» одна степень свобо-
ды, поэтому оценка 5" распределена как (D/(n - 1)) х £„_,, где
4„_i ~ х2-РасгФеДеление с п — 1 степенями свободы.
В данном случае ожидаемая дисперсия D — 152 = 225,
а полученное значение составило 19,22 = 368,64. Следо-
вательно, (225/44) х ^ = 368,64, откуда ^ « 72,09. Далее с
помощью электронной таблицы Excel рассчитываем веро-
ятность того, что распределенная как х24 случайная вели-
чина принимает значение в 72,09 или более, что можно сде-
лать с помощью встроенной функции ХИ2РАСП. Так как
ХИ2РАСП(72,09;44) * 0,00048, то заключаем, что с односто-
ронней доверительной вероятностью р = 0,00048 различия
в дисперсии достоверны.
Пример 2. В условиях примера № 1 определим довери-
тельные границы для полученной оценки дисперсии.
В электронной таблице Excel имеется встроенная фун-
кция ХИ20БР, рассчитывающая для данной вероятности р
такое значение х, что вероятность того, что х2-распределе-
ние примет данное или большее значение, равна р. Полу-
чаем, чтоХИ2ОБР(0,025;44) = 64,2, а ХИ2ОБР(0,975;44) =
= 27,57. Следовательно, с вероятностью 0,95 х2-распре-
деление с 44 степенями свободы находится в пределах от
27,57 от 64,2. Так как фактическая оценка дисперсии воз-
раста составила 368,64, то ее доверительные границы с р =
= 0,05 - от 368,64 х 27,57/44 до 368,64 х 64,2/44, или от 231
до 537,9, а доверительные границы к среднеквадратично-
му отклонению (нужно извлечь квадратный корень) — от
15,2 до 23,2.
То, что доверительные границы к среднеквадратичному
отклонению получились практически симметричными, —
следствие достаточно большого количества наблюдений
Для меньшего количества наблюдений выражена асиммет-
ричность оценки.

[ливи 10. Интервальные оценки параметров
259
Пример 3. Пусть в условиях примера № 1 также известно,
что приведенная в литературе величина среднеквадратично-
го отклонения рассчитана по 100 наблюдениям. Определим
достоверность различия двух выборочных дисперсий.
Две полученные величины среднеквадратичного от-
клонения — 19,2 и 15, то есть отношение дисперсий равно
(19,2/15)2= 1,6384.
Так как стандартная оценка дисперсии нормальной
случайной величины распределена как %2Jn, где п — число
степеней свободы, то есть на единицу меньше количества
наблюдений, то отношение двух оценок из нормально рас-
пределенных случайных величин с одинаковой дисперсией
имеет распределение Фишера—Снедекора (см. раздел 4.6),
в данном случае — с 44 и 99 степенями свободы. Для рас-
чета функции распределения такой случайной величи-
ны в Excel имеется встроенная функция FPACn, а так как
FPACn(l,6384;44;99) « 0,022, то с доверительной вероятно-
стью р = 0,022 среднеквадратичное отклонение достоверно
больше, чем приводимое в литературном источнике.
Содержательный анализ различия дисперсий в сравнива-
емых группах обычно тяжелее, чем анализ различия средних
арифметических. Например, если при тех же средних зна-
чениях дисперсия артериального давления в первой группе
больше, чем во второй, то это может свидетельствовать как
о большей разнородности первой группы, так и о том, что
характерный для нее патологический процесс может приво-
дить не к смешению среднего показателя, а к его большей
нестабильности. Чаще всего такой анализ нужен для того,
чтобы показать, что, несмотря на отсутствие различий в
средних величинах, сравниваемые группы неодинаковы, на-
пример чтобы объяснить причину возникновения различий
между собственными и литературными данными.
Например, пусть мы сравниваем частоту тяжелых ослож-
нений при остром холецистите в военном госпитале и город-
ской больнице и выясняем, что в госпитале она существен-
но выше. При анализе возрастного состава выясняем, что
средний возраст больных в госпитале примерно совпадает со
средним возрастом больных в городской больнице, так как
У»

260
Часть 2. Анализ параметров
в нем лечатся как молодые военнослужащие, так и ветераны
Великой Отечественной войны. Однако сравнение диспер-
сий даст достоверное различие и позволит дать объяснение
различию частоты осложнений.
При сравнении распределения двух групп по возрасту пра-
вильнее было бы не ограничиваться сравнением их средних
арифметических и дисперсий, а провести полное сравнение
распределения, например, при помощи критерия Колмого-
рова—Смирнова, как это описано выше. Но для этого нужно
иметь полные данные по возрастному распределению, кото-
рые вряд ли будут представлены в статье. Однако в статьях
обычно приводят данные о средних величинах показателей
и их среднеквадратичных отклонениях (или других показа-
телях, которые позволяют вычислить среднеквадратичное
отклонение).
При определении достоверности различий дисперсии ис-
пользовалось предположение о нормальности наблюдаемой
случайной величины, так как только в этом случае оценки
дисперсий и их отношения есть х2-распределение и распре-
деление Фишера—Снедекора. Понятно, что реально наблю-
даемые случайные величины не будут нормальными. Поэто-
му для применимости используемой техники нужно, чтобы
распределение оценки практически не зависело от формы
распределения исходной случайной величины, то есть цент-
ральная предельная теорема выполнялась с достаточной точ-
ностью. Используемые в примерах объемы наблюдений в 45
и 100 позволяют считать полученные достоверности разли-
чия дисперсий достаточно точными в том случае, если рас-
пределение возраста больных достаточно «приличное». При
этом при оценке применимости ЦПТ при оценке дисперсии
требования к форме распределения более жесткие, чем при
проверке достоверности различия средних арифметических,
так как, как указано в разделе 9.2, возведение в квадрат «пор-
тит» форму распределения.
Вопросы проверки применимости предположений, на
которых основаны расчеты достоверности различий диспер-
сий и других моментов, будут подробно обсуждаться в гла-
ве 12.

Глава JO. Интервальные оценки пары;-?.•■
261
10.3. Определение достоверности различия
средних. Критерий Стьюдента
От того, что какая-то глупость обще-
принята, она не перестает быть глу-
постью.
Артур Блох
«Законы Мерфи для медиков»
Как определять достоверность различия оценок
средних арифметических.
Ручной расчет достоверности различий выборочных
средних чаще всего нужен в том случае, когда приходится
сравнивать собственные данные с литературными. Однако
мы разберем возможные варианты сравнения более подроб-
но, включая те случаи, которые хорошо рассчитываются в
пакетах статистических программ, чтобы продемонстриро-
вать имеющиеся «подводные камни».
Рассмотрим следующую последовательность примеров:
1. Сравнение выборочного среднего с точно заданным
значением в случае известной дисперсии.
2. Сравнение выборочного среднего с точно заданным
значением в случае неизвестной дисперсии.
3. Сравнение двух выборочных средних в случае извест-
ной дисперсии.
4. Сравнение двух выборочных средних в случае, если
известно, что дисперсия в группах равна.
5. Сравнение двух выборочных средних в группах оди-
накового размера.
6. Определение достоверности изменения среднего
в динамике.
7. Сравнение двух выборочных средних в группах раз-
ного размера.
Пример 1. Пусть по литературным данным, основанным
на большом количестве наблюдений', средняя арифметиче-
ская температура больных, поступающих с острым холе-
' См. примечание к предыдущему разделу.

262
Часть 2 Ана/ius параметров
циститом, составляет 38,2°С при среднеквадратичном от-
клонении 0,65°. Пусть у нас было 47 больных со средней
температурой 38,5ГС. Определим достоверность различий.
Для этого рассчитаем t = (x-M)/o(x), где х — среднее ариф-
метическое из наблюдаемых значений, М— ожидаемое зна-
чение, а о"(Зс) — ожидаемое среднеквадратичное отклонение
среднего арифметического из наблюдений.
В качестве первого шага нужно рассчитать коэффициент
эксцентриситета для распределения больных по температу-
ре. Пусть он невелик, что при объеме наблюдений в 47 дает
возможность пользоваться предположением о примерной
нормальности распределения среднего арифметического.
Этот шаг необходим для всех приводимых ниже вариантов,
далее приводить его мы не будем.
Если бы распределение исследуемых больных имело
математическое ожидание 38,2 и среднеквадратичное от-
клонение а = 0,65, то среднее арифметическоех из 47 на-
блюдений имело бы математическое ожидание М{х) в 38,2
и среднеквадратичное отклонение c(Зc) = 0,65/^/47 =0,095.
Наблюдаемое среднее арифметическое составило 38,51, что
на 38,51 — 38,2 = 0,31 больше ожидаемого. Поделим разность
между полученным и ожидаемым средним арифметическим
на среднеквадратичное отклонение среднего арифметиче-
ского и получим величину / = 0,31/0,095 = 3,27. Эта величи-
на традиционно обозначается буквой /. В том случае, когда
выполняется нулевая гипотеза о том, что наблюдаемая слу-
чайная величина имеет М = 38,2 и среднеквадратичное от-
клонение с = 0,65, сконструированная таким образом новая
случайная величина t имеет нулевое математическое ожида-
ние и единичную дисперсию. Для расчета вероятности таких
уклонений нормально распределенной случайной величины
воспользуемся электронной таблицей Excel. Имеющаяся
в ней встроенная функция НОРМСТРАСП вычисляет ве-
роятность того, что нормально распределенная случайная
величина с нулевым математическим ожиданием и еди-
ничной дисперсией меньше указанного значения. Так как
НОРМСТРАСП(3,27) * 0,99946, то вероятность принять
значение в 3,27 или больше примерно равна 1 — 0,99946 =

Глава 10. Интервальные оценки параметров
263
= 0,00054. Следовательно, нулевая гипотеза о том, что наблюда-
емая случайная величина имеет математическое ожидание 38,2
и среднеквадратичное отклонение 0,65 должно быть отвергнуто
с односторонней доверительной вероятностью р = 0,00054 или
двусторонней доверительной вероятностью р = 0,00108.
Говорить в данном случае о достоверности различия сред-
них арифметических не совсем корректно, так как достовер-
ные различия могут быть получены как за счет превышения
среднего по сравнению с ожидаемым, так и за счет повышения
среднеквадратичного отклонения наблюдаемой величины.
Приведенный пример относился к случаю, когда в нуле-
вой гипотезе были представлены ожидаемые величины и ма-
тематического ожидания, и дисперсии наблюдаемой случай-
ной величины. Чаще встречается другой случай, когда нужно
сравнить с ожидаемым значением выборочное среднее из
наблюдаемой случайной величины, выборочное среднее ко-
торой также неизвестно. В этом случае опять сконструируем
случайную величину t=(x-M)/s(x), где s(x) —оценка ожи-
даемого среднеквадратичного отклонения. Так как стандар-
тная оценка среднеквадратичного отклонения распределена
как %\, деленная на к, то в предположении об истинности ну-
левой гипотезы случайная величина Г распределена по Стью-
денту с к, степенями свободы, где к — на единицу меньше
количества наблюдений. Критерий Стьюдента часто также
называют критерием Т.
Пример 2. Пусть у нас было 47 больных со средней тем-
пературой 38,5 ГС и среднеквадратичным отклонением
0,65°. Сравним полученное среднее с литературным средним
в38,2°С.
Аналогично примеру № 1 рассчитаем показатель /= 3,27.
В электронной таблице Excel для расчета нужной вероятнос-
ти имеется встроенная функция СТЬЮДРАСП от трех ар-
гументов, первых из которых — величина /, второй — число
степеней свободы, то есть для стандартной оценки диспер-
сии на единицу меньше количества наблюдений, а третий
называется «хвосты», имеет возможные значения 1 или 2 и
показывает, какую доверительную вероятность рассчитыва-
ют — одностороннюю или двустороннюю.

264
'liunih ..' I',,/ in , ihs/iitui m:
В нашем случае СТЬЮДРАСП(3.27,46 2) ^ 0,00204, то
есть полученное выборочное среднее лосговсрио отличасгся
от тестового значения с двусторонней доверительной веро-
ятностью р = 0,00204
Полученная в этом примере доверительная вероятность
примерно в два раза больше, чем в примере № 1 Причина
уменьшения достоверности различий в том, что в условиях
примера № 2 дополнительная статистическая погрешность
может быть связана не только с определением среднего
арифметического, но и с определением среднеквадратично-
го отклонения.
Пример 3. Пусть у нас было две группы недельных крыс
из 48 и 35 особей соответственно, причем особей второй
группы исследовали в состоянии искусственного стрес-
са, вызванного обездвиживанием и длительной щекоткой1.
Пусть для некоторого гормонального показателя среднее в
первой группе было равно 4,27, а во второй — 4,08, причем
среднеквадратичная погрешность теста, по оценке фирмы-
изготовителя, была равна 0,5
Так как различия в показателях между разными крысами
близки к ошибке самого способа измерения, то можно поп-
робовать этими различиями пренебречь и в качестве первого
шага проверить предположение о том, что оба полученных
средних — результат наблюдения случайных величин с сов-
падающим средним и со среднеквадратичным отклонением,
равным 0,5
Пусть {хк} — набор значений в первой группе из п наблю-
дений, а {ук} — набор значений во второй группе из m наблю-
дений, а Зс и у — средние арифметические соответственно в
первой и второй группе. Рассмотрим случайную величину £, =
= х — у. Тогда, так какх и у— средние арифметические
из случайной величины с одним математическим ожи-
данием, то их математические ожидания совпадают и,
следовательно, математическое ожидание 4 равно нулю.
1 Это не шутка, а организация экспериментального исследования
в одной реальной диссертационной работе. Сам бы я до такого не до-
думался.

10. Интервальные оценки параметров
265
На основании линейных свойств моментов имеем, что
6(x-y) = ^o2(x)+o1(y) = ^a2/n+o!/m=asl\/n + \/m, где о —
среднеквадратичное отклонение одного наблюдения. Так
как* и у — средние из достаточно большого количества на-
блюдений, то (после соответствующей проверки) их можно
считатьраспределеннымипримернопормалыю,атаккаксум-
ма и разность двух независимых нормально распределенных
случайных величин распределена нормально, то и Ъ, = х — у
можно также считать нормально распределенной.
В результате получили, что при условии истинности ну-
левой гипотезы разность средних распределена нормально с
нулевым математическим ожиданием и среднеквадратичным
отклонением, равным 0,5^/1/48 + 1/35 = 0,11. Так как наблюда-
емая разность средних оказалась равной 4,27 — 4,08 = 0,19, то
f* 0,19/0,11« 1,71. Следовательно, получили, что сконструи-
рованная нами случайная величина /, которая при истинности
нулевой гипотезы должна быть распределена нормально с ну-
левым математическим ожиданием и единичной дисперсией,
приняла значение 1,71. Далее при помоши имеющейся в Excel
встроенной функции вычисляем НОРМСТРАСП(1,71) и
* 0,956, откуда при односторонней доверительной вероят-
ности р - 0,044 среднее в первой группе достоверно больше
среднего во второй группе.
При взятии двусторонних доверительных границ получа-
ем р = 0,088, то есть даже с минимальным стандартным р =
= 0,044 различия недостоверны. На самом деле различия вряд
ли окажутся достоверными и при рассмотрении односторон-
них границ, так как достоверность различий рассчитывалась
в предположении о том, что разница истинных показателей
между крысами много меньше погрешности метода и ею
можно пренебречь. Если это предположение неверно, то
достоверность различий окажется меньше (см. следующий
пример).
Пример 4. Пусть у нас было две группы недельных крыс
из 48 и 35 особей, для некоторого показателя среднее в пер-
вой группе было равно 4,27 при среднеквадратичном откло-
нении 0,52, а во второй — 4,08 при среднеквадратичном от-
клонении 0,58. В качестве нулевой гипотезы предположим,

286 V«ifw» ». ■tun in i /.и/юучтрол
что математические ожидания и среднсквадра гичные откло-
нения в обеих группах совпадают
Для начала нужно получить согласованную оценку дис-
персии в предположении об истинности нулевой гипотезы.
В первой группе оценка дисперсии равна 0,523 s 0,2704, а во
второй - 0,58' * 0,3364. Если бы размеры групп были оди-
наковы, то в качестве согласованной оценки дисперсии по
двум рядам наблюдений нужно было бы брать их полусумму,
но так как первая группа больше, то ее нужно брать с боль-
шим весом.
При оценке дисперсии рассчитывается среднее из на-
боров квадратов отклонения от среднего арифметического.
При этом, как исследовалось в разделе 9.3, при стандартной
оценке дисперсии один член суммы «пропадает» за счет за-
висимости между набором отклонений от среднего ариф-
метического и средним арифметическим, вычисляемым по
там же наблюдениям. Поэтому при объединении наборов из
птт наблюдений их оценки дисперсии нужно объединять
с весами и —. Для нашего случая имеем объ-
я+Л1-2 л+м-2
единенную оценку дисперсии
откуда согласованная оценка среднеквадратичного отклоне-
ния ^0,2986-0,546- Далее аналогично примеру № 3 средне-
квадратичное отклонение разности двух средних арифмети-
ческих равно 9{S-f)~o^\Jn^\]m-0,546^1/48+1/35-0,121,
и/»(4,27-4,08)/0,121«1,56.
В данном варианте расчета разность средних делится не
на заданную изначально величину среднеквадратичного от-
клонения, а на ее оценку, полученную по набору наблюде-
ний, следовательно, полученная величина распределена не
нормально, а по Стьюденту. В этом случае для расчета досто-
верности различий нужно также задать количествогтепеней
свободы. Так как оценка дисперсии была получена объеди-
нением двух оценок с количеством степеней свободы 47 и 35,
то общее количество степеней свободы равно 47 + 35 = 82.

Глава 10. Интервальные оценки параметров
267
Так как СТЬЮДРАСП(1,56;82;2) * 0,12, то различия не-
достоверны.
Следует также обратить внимание, что полученная дву-
сторонняя доверительная вероятность несколько больше,
чем полученная в примере № 3 величина р - 0,088, так как в
этом расчете учитывалось, что различие между крысами свя-
зано не только с инструментальной погрешностью измере-
ния и было немного больше его.
При интерпретации полученных различий в схеме расче-
та примера № 4 нельзя говорить о достоверности различий
средних арифметических в сравниваемых группах, так Как в
нулевой гипотезе утверждалось более сильное предположе-
ние — о том, что в сравниваемых группах совпадали й сред-
ние арифметические, и дисперсии. Поэтому при получении
достоверных различий вывод более общий — что различают-
ся или средние арифметические, или дисперсии.
Если требуется определить достоверность различий сред-
них арифметических по группам безотносительно равенства
или различия дисперсий, то схема расчета немного другая.
Пример 5. Пусть При клинической проверке эффектив-
ности двух препаратов для лечения больных с артериальной
гипердензйей в группе из 40 Мюльных, принимавших первый
препарат, вреднее унижение артериального систолического
давления составило 35 мм рт. ст, при среднеквадратичном
отклонении; 15, я во: второй группе из 40 больных— 26 при
среднеквадратичном отклонении 18. Определим достовер-
ность различия среднего снижения а двух группах.
Пусть {#*}— результаты наблюдений,в первой груп-
пе, &{ук}— во второй группе, ах му~ их средние
арифметические. Рассмотрим новую случайную вели-
чину Ьк = хк- ук. Тогда o(6)*>/o---(*HeVb. «■■* соответ-
ствии с линейными свойствами среднего арифметиче-
ского и среднеквадратичного отклонения 8 =«.# -у и
cr(S") = Jh 2(x)+0^OOV« , где «— количество наблюдений в
каждой из групп. В нашем случае 6 = 35 - 26 « 9, а а(&)~
^^/p^TIFy^» 3,7. Следовательно, t» 9/3,7 « 2,43. Так как
рассматривалась случайная величина — среднее арифмети-

268
Часть 2 Анализ параметров
ческое из 40 пар разностей показателей в первой и второй
группе, то оценка дисперсии разности показателей имела
39 степеней свободы. Следовательно, полученная величина
/при условии истинности нулевой гипотезы должна быть
распределена по Стьюденту с 39 степенями свободы, а так
как СТЬЮДРАСП(2,43;39;2) « 0,02, то различия среднего
арифметического в двух группах достоверны с р — 0,02.
Часто нужно определить не достоверность различия
среднего арифметического в двух группах, а достоверность
изменения некоторой величины у испытуемых в динамике.
Пример 6. Пусть при недельном цикле снижения веса
у 25 женщин их средний вес в понедельник утром был равен
87,5 кг при среднеквадратичном отклонении 8,5 кг, а в пят-
ницу вечером — 86 кг при том же среднеквадратичном от-
клонении. Оценим достоверность изменений.
Аналогично примеру № 5 среднеквадратичное отклоне-
ние разности средних будет равно а(5) = J(8,52 +8,52 )/25 = 2,4.
Так как разность средних равна 87,5 — 86 = 1,5, то /и 1,5/2,4 «
« 0,62, что дает недостоверные различия.
Причина недостоверности полученных различий — не
в том, что изменения в весе действительно недостоверны,
а в том, что расчетбыл проведен неправильно. В условиях при-
мера № 5 предполагалось, что результаты измерений в первой
и второй группе независимы друг от друга, поэтому дисперсия
разности показателей в первой и второй группе равна сумме
дисперсий показателей в первой и второй группе.
В данном случае это, конечно, совершенно неверно. По-
нятно, что те, у кого в начале цикла вес больше, и в конце
цикла в среднем будут иметь вес больше, поэтому рассчиты-
вать среднеквадратичное отклонение величины снижения
веса на основании среднеквадратичных отклонений в груп-
пах в начале и конце исследования нельзя
В данном случае требуется провести дополнительное
«прямое» исследование —для каждого испытуемого рассчи-
тать величину снижения веса, а потом в условиях примера
№ 2 сравнить полученное среднее с нулем.
Чаще всего нужно в условиях примера № 5 сравнивать
средние величины в группах безотносительно дополнитель-

Глава 10. Интервальные оценки параметр-/?
269
ных предположений о равенстве дисперсий, но только груп-
пы имеют разную численность.
Пример 7. Пусть при клинической проверке эффектив-
ности двух препаратов для лечения больных с артериальной
гипертензией в группе из 50 больных, принимавших первый
препарат, среднее снижение артериального систолического
давления составило 35 мм рт. ст. при среднеквадратичном
отклонении 15, а во второй группе из 30 больных — 26 при
среднеквадратичном отклонении 18. Определим достовер-
ность различия среднего снижения в двух группах.
Пусть {хк} — результатынаблюдений в первой группе,
а {ук} — во второй группе, а х и у — их средние арифметиче^
ские.Рассмотримслучайнуювеличину£= х- у.Тогда,таккак х
и у — средние арифметические из случайной величины с од-
ним математическим ожиданием, то их математические ожи-
дания совпадают и, следовател ьно, математическое ожидание
^ равно нулю. При определении ее среднеквадратичного отк-
лонения имеем о(х -у) = Jo2(x)+o7(y) = Ja(xf / п+о{у? / т,
что в рассматриваемом случае дает о (Зс - у) = ,/152/50 + 262/30 =
=5,2, откуда /«(15 — 26)/5,2« 1,73. После этого для определе-
ния достоверности различия нужно ответить только на один
технический вопрос: какое количество степеней свободы для
распределения Стьюдента нужно брать в этом случае?
Этот, казалось бы, мелкий технический вопрос в наибо-
лее часто используемой схеме применения критерия Стью-
дента вскрывает имеющиеся серьезные проблемы. Если сам
критерий Стьюдента — точно сформулированный матема-
тический результат, то его практическое применение полно
какой-то нездоровой мистики, включая название критерия.
Начать с того, что автором критерия Стьюдента был не
человек по фамилии Стьюдент, а известный английский
статистик Госсет. Просто в то время он работал на пивова-
ренную компанию Гиннеса, по условиям контракта не имел
права публиковать результаты в открытой печати и подписал
свою статью псевдонимом «Student». Поэтому, строго го-
воря, в соответствии с правилами русского языка критерий
Стьюдента нужно называть критерием студента.

270
Част/, 2 Ami на параметров
Наиболее часто используемая схема применения крите-
рия Стьюдента — пример № 7, то есть сравнение выбороч-
ных средних по рядам наблюдений разной длины. Но в этом
случае критерий Стьюдента неприменим, так как сконструи-
рованная там стандартным образом случайная величина / не
распределена по Стьюденту. Исследование распределения t
в этом случае — одна из центральных и нерешенных задач
современной математической статистики.
С практической точки зрения эту техническую проблему
обычно можно обойти. Для этого достаточно при определе-
нии достоверности различий рассчитать две вероятности —
одну с количеством степеней свободы, на единицу меньше
количества наблюдений в первой группе, а вторую — на еди-
ницу меньше количества наблюдений во второй группе. Ис-
тинная вероятность будет где-то между ними.
Если размеры групп достаточно велики (несколько десят-
ков или более), то полученные вероятности уже практически
не зависят от количества степеней свободы, и при увеличе-
нии количества степеней свободы распределение Стьюдента
стремится к нормальному. Поэтому при сравнении среднего
арифметического из достаточно больших групп эта техни-
ческая сложность малосущественна.
Однако основная и общая проблема применения крите-
рия Стьюдента не в том, что в схеме примера № 7 непонятно,
какое количество степеней свободы нужно брать, а в том, что
во всех случаях общим требованием является нормальность
изучаемого распределения. Если количество наблюдений в
группах достаточно велико, то полученное распределение
t на основании центральной предельной теоремы не зави-
сит от вида исходного распределения, но в этом случае и не
нужно пользоваться критерием Стьюдента, так как t будет
распределено практически нормально. Действительно, слу-
чайная величина t конструируется как r=(x-y)/s(x-J), где
six-у) — оценка среднеквадратичного отклонения разности
средних арифметических. В соответствии с разделом 10.2,
при увеличении количества наблюдений коэффициент ва-
риации оценки среднеквадратичного отклонения стремит-
ся к пулю и знаменатель в отношении становится все ближе

Глава 10. Интервальные оценки пог/амапп.л-
271
к ненулевой константе. Поэтому форму распределения от-
ношения (x-y)/s(x-y) для больших групп определяет толь-
ко числитель, распределение которого в соответствии с ЦПТ
стремится к нормальному.
Следовательно, критерий Стьюдента нужен только для
сравнения средних по малым выборкам из заведомо нормаль-
но распределенной случайной величины. Такая задача может
встретиться, например, если мы сравниваем средний возраст
больных по нескольким городам. Однако в большинстве слу-
чаев анализируемая случайная величина не обязательно рас-
пределена нормально (даже если это и так, то по малому объему
наблюдений мы доказать не можем). Поэтому для малых вы-
борок критерий Стьюдента обычно неприменим, а для боль-
ших — не нужен, так как для этого случая достаточно ЦПТ.
Резюме
1. Критерий Стьюдента— самый часто используемый
в современных медико-биологических исследовани-
ях статистический критерий.
2. Наиболее часто критерий Стьюдента используется для
определения достоверности различия средних ариф-
метических, полученных по выборкам разной длины.
3. В этой наиболее часто используемой схеме примене-
ния критерия Стьюдента им пользоваться нельзя.
4. В большинстве случаев, когда критерием Стьюдента
пользоваться можно, он не нужен.
5. Никакого Стьюдента никогда не существовало.
10.4. Расчет достоверности различия
средних арифметических с помощью
пакетов статистических программ
Как определять достоверность различия средних
арифметических по подгруппам с помощью
пакетов статистических программ.
Пакеты статистических программ определяют досто-
верность различий средних арифметических по подгруппам
в предположении о том, что в каждой подгруппе анализируе-

272
Часть 2. Анализ параметров
мый показатель распределен нормально, его математическое
ожидание в разных подгруппах одинаково, но дисперсии в
подгруппах могут различаться. Если желательно определить
достоверность различий в иных исходных предположениях,
то придется прибегнуть к варианту ручного счета, описанно-
го в разделе 10.3.
В SPSS для определения достоверности отличия среднего
арифметического от ожидаемого значения1 нужно выполнить
команду «Analyze/Compare Means/One-Sample T Test», выбрать
(перебросив из левого списка в правый) нужную переменную и
задать в окошке «Test Value» величину, с которой сравнивается
среднее арифметическое, после чего нажать на клавишу «ОК».
Например, при сравнении среднего возраста больных пневмони-
ей с ожидаемым значением в 50 лет появляются табл. 10.1 и 10.2.
Таблица. 10.1
Параметры возраста пациентов
One-Sample Statistics
age of patient
N
1032
Mean
54,53
Std. Deviation
18,57
Std. Error Mean
,58
Таблица. 10.2
Сравнение среднего возраста пациентов с 50 годами
One-Sample Test
age of
patient
Test Va-
lue = 50
t
7,844
df
1031
Sig.
(2-tailed)
,000
Mean Dif-
ference
4,53
95%
Confidence
Interval of the
Difference
Lower
3,40
Upper
5,67
1 Это значение предполагается известным абсолютно точно. Рас-
считав достоверность отличия от значении, i;uiaiiiioro си тестнон ста-
тистической погрешностью, непосредственно в пакете статистических
программ нельзя Как это сделать вручную, описано н разделе 10.3.

Глава 10. Интервальные оценки параметров
273
Таблица 10.1 показывает, что всего было 1032 больных,
у которых был известен возраст, среднее арифметическое
возраста было равно 54,53, среднеквадратичное отклонение
было равно 18,57 и среднеквадратичное отклонение средне-
го по группе возраста составило 0,58, то есть средний возраст
больных мы знаем с точностью около I года.
Таблица 10.2 показывает результат сравнения получен-
ного среднего арифметического с ожидаемым значением в
50 лет. «Mean Difference» (разность между средними) пока-
зывает, что фактическое значение оказалось больше ожидае-
мого на 4,53. Далее для применения критерия Стьюдента рас-
считывается величина t, то есть во сколько раз эта разность
больше среднеквадратичного отклонения среднего, что в
данном случае дало 7,844. Так как используется стандартная
оценка дисперсии, то количество степеней свободы (df) на
единицу меньше количества наблюдений. При помощи кри-
терия Стьюдента определяется двусторонняя доверительная
вероятность совпадения «Sig. (2-tailed)», которая оказывает-
ся меньше 0,001 (в таблице приведено только значение 0,000,
так как большее количество знаков не умещается). Поэтому
можно сказать, что различия достоверны с р < 0,001. Для того
чтобы получить более точную величину достоверности раз-
личия, можно скопировать эту таблицу в Excel и посмотреть
там величину полученного числа, что даст р = 1,1 х Ю-14.
Для проверки применимости критерия Стьюдента рас-
считаем параметры распределения больных по возрасту,
в котором к стандартному минимальному набору добавим
коэффициент эксцентриситета.
В результате (табл. 10.3) получаем, что коэффициент экс-
центриситета отрицательный, то есть случайная величина
распределена еще компактнее, чем нормальная, а так как ко-
личество наблюдений в 1032 весьма велико, то условия цент-
ральной предельной теоремы выполняются с очень хорошей
точностью (с запасом) Однако и в этих условиях писать о
достоверности различия р в десять тысяч раз меньше одной
миллиардной было бы непростительной наглостью
Последние дне колонки табл. 10 2 показывают величину
доверительного интервала для разности между фактическим

274
Часть 2. Анализ параметров
Таблица. 10.3
Расширенный набор параметров возраста пациентов
Descriptive Statistics
age of
patient
Valid N
I (listwise)
N
Statis-
tic
1032
1032
Mini-
mum
Statis-
tic
15
Maxi-
mum
Statis-
tic
95
Mean
Statis-
tic
54,53
Std.
Deviation
Statistic
18,57
Kurtosis
Statistic
-.733
Std.
Error
,152
и ожидаемым значением при р = 0,05. Из них следует, что
разность ожидается в пределах от 3,4 до 5,67, или, что то же
самое, что доверительные границы среднего возраста с р =
= 0,05 — от 53,4 до 55,67 лет.
В Statistica для выполнения такого расчета нужно выпол-
нить команду «Statistics/Basic Statistics and Tables/t-test, single
sample», нажать кнопку «OK», в окне на уровне заголовка
«Test all means against:» задать ожидаемое значение средне-
го арифметического, нажать на кнопку «Variables:», выбрать
нужную переменную и нажать последовательно кнопки
«ОК» и «Summary».
Для определения достоверности различия средних в под-
группах статистические пакеты обычно используют не не-
посредственно критерий Стьюдента, а некоторую вариа-
цию метода, называемую дисперсионным анализом (часто
называют AN OVA). В этом случае рассчитываются средние
квадраты разности значений внутри и между группами. Если
средний квадрат разности значений для случаев, относящих-
ся к разным группам, больше, чем средний квадрат разности
случаев из одной группы, то это свидетельствует о различии
средних по подгруппам.
Для иллюстрации приведу пример. Предположим, мне
пришла в голову нетривиальная мысль о том, что по длине
стоны женские ноги отличаются от мужских. Статистиче-
скую проверку >гой гипотезы можно осуществить следу-
ющими способами-

Глава 10. Интервальные оценки параметров
275
1. Рассчитать средние и среднеквадратические отклоне-
ния длины стопы мужчин и женщин, найти достовер-
ность различия.
2. Попытаться выяснить, на что (по длине стопы) боль-
ше похожи женские ноги — на ноги других женщин
или мужчин. Если средняя длина размеров стоп у
мужчин и женщин одинакова, то переход от обшей
выборки к подгруппам из лиц одного пола не умень-
шит дисперсию.
Определение достоверности различий дисперсий прово-
дится при помощи методов, описанных в разделе 10.2. При
использовании дисперсионного анализа, как и критерия
Стьюдента, предполагается нормальность исследуемого рас-
пределения, поэтому реально им можно пользоваться только
в тех случаях, когда для каждой подгруппы объем наблюдений
достаточно велик для того, чтобы было можно считать, что
центральная предельная теорема справедлива. При сравнении
двух подгрупп критерий Стьюдента и дисперсионный анализ
дают идентичные результаты, однако дисперсионный анализ
без проблем обобщается на число групп, большее двух
В SPSS для определения достоверности различия средне-
го по группам нужно выполнить команду «Analyze/Compare
Means/Means», после чего имя переменной, для которой бу-
дет рассчитываться среднее арифметическое, перебросить в
окно «Dependent List», а переменную с номером группы —
в окно «Independent List» (такая переменная должна быть)1
После этого нужно нажать кнопку «Options», поставить щел-
чком мыши «галку» рядом с опцией «Anova table and eta»
(иначе достоверность различий рассчитываться не будет),
а также, если нужно, изменить набор рассчитываемых и под-
1 Частая ошибка начинающих пользователей — перспутывание
какую из двух переменных куда перебрасывать В нижнем окне *не и
нисичых переменных» неегда должна стоять дискретная переменная.
имеющая небольшое количество значений Обычно ло переметим
класса «nominal»' В верхнем окне « ивмеимых переменных» - пере-
менная типа «scale», на крайний случай класса «oulmab4 \ уж кю от
кого на самом леле зависит лечо другое к статистической oopadoive
отношения не имеющее

276
Часть 2. Анализ параметров
группах параметров. В левом списке представлены те пара-
метры, которые могут быть рассчитаны, но не рассчитывают-
ся, в правом — те, которые рассчитываются. По умолчанию
для каждой группы рассчитывается среднее арифметическое,
количество наблюдений и среднеквадратичное отклонение.
Добавим в этот список расчет среднеквадратичного откло-
нения среднего по группе (Std. Error of Mean), для чего выде-
лим эту строку щелчком левой кнопки мыши в левом списке
и щелчком по кнопке с изображением треугольника между
этими списками перенесем его в правый список. Для выпол-
нения расчета нужно нажать кнопки «Continue» и «ОК».
В результате будет выдано три таблицы. В первой пред-
ставлена информация о том, у какой части случаев опреде-
лены исследуемые переменные. Вторая таблица содержит
значения параметров (по подгруппам и в целом), третья —
результат применения дисперсионного анализа.
Например, при сравнении среднего возраста мужчин
и женщин, больных пневмонией, получаем табл. 10.4 и 10.5.
Таблица 10.4
Средний возраст мужчин и женщин
Report
age of patient
sex of patient
male
female
Total
Mean
52,29
58,11
54,53
N
634
398
1032
Std. Deviation
17,61
19,51
18,57
Std. Error of Mean
,70
,98
,58
Так, получено, что средний возраст мужчин примерно на
6 лет меньше, чем женщин. При определении достоверности
различий (табл. 10.5) рассчитывается отношение «F» квадратов
разностей между и внутри групп. Последняя колонка показыва-
ет достоверность различий. В результате получаем, то различия
достовср! ил с р < 0,001, а так как (как было проверь ю выше) рас-
пределение больших по возрасту компактно и группы велики, то
н полученную оценку достоверности различия можно верить.
В тех случаях, когда сравниваемых групп больше двух,
информация о наличии достоверных различий не уточняет,

Глава 10. Интервальные оценки параметров
277
Таблица. 10.5
Проверка достоверности различий среднего
возраста мужчин и женщин при помощи
дисперсионного анализа
ANOVA Table
age of pati-
ent * sex of
patient
Between
Groups
Within
Groups
Total
(Combined)
Sum of
Squares
8283,009
347315,735
355598,744
df
1
1030
1031
Mean
Square
8283,009
337,200
F
24,564
Sig.
,000
какие именно подгруппы различаются, а какие — нет. Поэ-
тому нужно при помощи установки фильтра оставить толь-
ко две подгруппы и провести их сравнение, потом поменять
фильтр, оставив другие две подгруппы, и т. д.
В Statistica для сравнения средних по подгруппам нуж-
но выполнить последовательность команд «Statistics/Basic
Statistics and Tables/t-test, independent, by groups» и нажать
кнопку «OK». Далее нажать кнопку «Variables» и аналогич-
ным образом выбрать зависимую и независимую (здесь она
называется «группирующая») переменные. После нажатия
на кнопку «ОК» происходит возврат на предыдущую фор-
му, причем в окнах «Code for Group 1:» и «Code for Group 2»
стоят два разных значения независимой переменной. Про-
грамма Statistica сразу предлагает перейти на попарный ана-
лиз средних по подгруппам. Если групп несколько, то дан-
ный расчет нужно повторить несколько раз, меняя значения
и этих окнах. Для вывода таблицы с результатами расчетов
нужно нажать кнопку «Summary».

278
Часть 2 Анализ параметров
Часто нужно определять достоверность не различия не-
которого показателя между группами, а его изменения в
динамике. В обоих статистических пакетах есть методы,
позволяющие сделать это непосредственно. Однако лучше
создать новую переменную со значениями, равными раз-
ности этих показателей (как это быстро сделать, описано в
разделе 2.2.4), и сравнить ее среднее арифметическое с ну-
лем. Такой подход позволит также исследовать корректность
расчета доверительной вероятности при помощи анализа на
выскакивающие варианты, а также, что часто очень важно,
выяснить, какие факторы влияют на величину изменения
показателя.
10.5. Расчет доверительных границ
к математическому ожиданию
Данные представлены в виде М ± т.
Стандартная фраза во многих медицинских работах
Разные варианты представления результатов в виде М±т,
как их понимать и как по одним вариантам
восстанавливать другие.
Приведенная в качестве эпиграфа фраза ужасна не сама
по себе, а тем, что обычно не приводится никаких уточнений
по поводу того, какое Ми т. Если в качестве Мчаще всего
приводится среднее арифметическое, тотв разных работах
означает разные величины.
В качестве примера еще раз приведем таблицу анализа
среднего возраста больных пневмонией (табл. Ю.6).
Таблица 10.6
Параметры возраста
One-Sample Statistics
age of patient
N
1032
Mean
54,53
Std. Deviation
18,57
Std. Error Mean
,58
В качестве претендентов на звание т могут выступать
следующие величины:

[лава Ю- Интервальные оценки параметров
279
1) а(£) = 18,57, где Z,— возраст больных. В этом случае
m описывает характерный разброс,
2) /хо(4) = 1,96x18,57 = 36,4. Здесь коэффициент f подби-
рается таким образом, чтобы 95 % наблюдений (при
условии, что наблюдаемая случайная величина рас-
пределена нормально) попадали в промежуток М±т,
то есть в 54,53 ± 36,4 года, или в данном случае от 18
до 91 года; в этом случае т задает интервал, в который
попадает большая часть наблюдений;
3) а(О = 0,58, где£— средний по группе возраст боль-
ных; в этом случае т задает статистическую погреш-
ность определения среднего;
4) >xc(£f) = 1,96x0,58 = 1,14. Здесь m определяет ширину
доверительного интервала для среднего арифметиче-
ского, так что с доверительной вероятностью р = 0,05
математическое ожидание возраста больных находит-
ся в интервале 54,53 ± 1,14, то есть от 53,39 до 55,67.
Величина коэффициента t рассчитывается на основа-
нии критерия Стьюдента и зависит от двух параметров — от
доверительной вероятности р и количества степеней свобо-
ды п, которое в случае стандартной схемы оценки дисперсии
на единицу меньше количества наблюдений. При заданной
доверительной вероятности при увеличении числа степеней
свободу величина /уменьшается, но не до нуля, а до конеч-
ного предела..При р = 0,05 предельное значение / пример-
но равно 1,96, прир = 0,01 оно примерно равно 2,576, а при
р - 0,001 оно примерно равно 3,29. В Excel рассчитать коэф-
фициент можно при помощи функции СТЬЮДРАСПОБР.
Например, для рассматриваемого случая
СТЬЮДРАСПОБР(0,05;1031) = 1,962267.
Все четыре варианта представления результатов как М±т
встречаются в литературе, и каждое из них имеет свои сильные
стороны. Первый вариант хорошо описывает характерный
разброс, второй— промежуток, в который попадает боль-
шинство значений, третий— статистическую погрешность
среднего арифметического, четвертый — интервал значений,
к которому должно принадлежать математическое ожидание.

280
Часть 2 Ани. пп параметров
Кроме того, варианты представления 2 и 4 рассчитывают-
ся при каком-то конкретном выборе доверительной вероят-
ности и объеме наблюдений. В приведенных примерах было
выбранор= 0,05, но выбор можетбыть и иным. В этом случае
величина /будет другой и представления 2 и 4 изменят вид.
Один вариант представления легко пересчитать в другой.
Так как варианты 2 и 4 отличаются от вариантов 1 и 3 со-
ответственно умножением на консганту Л то для перевода
из 1 в 2 и из 3 в 4 нужно т умножить на t, а для перевода из 2
в I или 4 в 3 нужно на /разделить. Так как среднеквадратич-
ное от среднего по группе в корень из размера группы мень-
ше среднеквадратичного одного наблюдения, то для перепо-
да из 1 в 3 и из 2 в 4 нужно разделить т на -J~N, а для перевода
из 3 в 1 или из 4 в 2 — умножить т на -Jr7, где IV— количество
наблюдений.
Резюме
Существует несколько разных вариантов представления
результатов в виде М ± т, поэтому в материалах и методах
должно быть точно описано, какой именно вариант выбран.

Глава 11
КОРРЕЛЯЦИОННЫЙ
АНАЛИЗ
С содержательной точки зрения рассматриваемые перемен-
ные можно разделить на типы nominal, ordinal и scale. Для
описания переменных типа nominal нужно рассчитать часто-
ты встречаемости отдельных значений, а рассчитывать зна-
чение среднего арифметического и других параметров для
них совершенно бессмысленно. При описании переменных
типа scale в первую очередь обращают внимание на их сред-
нее арифметическое, а потом — на то, как случайная вели-
чина от нее отклоняется. Для переменных промежуточного
типа ordinal можно использовать оба метода описания, но
некоторые специальные методы анализа будут обсуждаться
ниже при описании непараметических методов.
Соответственно при анализе связи двух переменных есть
3 разных варианта и три основных метода анализа:
1. Если обе переменные типа nominal, то нужно рас-
считать таблицу частот совместного распределения и
проверить ее при помощи критерия х2 Никаких дру-
гих вариантов анализа нет.
2. Если одна переменная типа nominal, а вторая — типа
scale., то нужно по значениям переменной типа
nominal «разрезать» выборку на подгруппы и сравнить
распределение переменной типа scale » подгруппах.

28?
В к.гич тис nepftoi t>iii.ir.ii>(ii.i'iiiii iipi' ном. .iniu ;un .-(мы
С НЮ.1ГН1Л И 111 .UlLllCpi HOI I HOI «i .111.1 111 l.l oil pi- 1С I Я Km
ДОСТОВСрНОСГ!. р.ЩИ'ШЧ ipclHIIV .ipili|i\!, lll'liч lll\ IK'
iio.lipyiin.iM Желательно ним ik <>: p.iinninuiu я
сравнить также .ipyme парампры например .mi
Персию, л Uk*.c oiipc.le inn. до» ют-риск п. рлмичин
функции раснроле лепим например при помощи
критерия Колчоюрова- (мирном.»
Если обе переменные класса scale го есть в первую
очередь описываются своим средним, ю в качестве
первого шага аналита естественно выяснить как и»
чененне среднего одной переменной влияет на ичме
пенис среднею лрутои переменной )тл втанчюсвил.
описывается к*»xJ><|»huhcmг»»м корреляции
11.1. Определение коэффициента
корреляции
Что такое коэффициент корреляции и как ом соотносится
с созмес'иым распределением двух числовых переменных
В раиелс 7 1 было приведено определение моментов
н центральных моментов для одной переменной Его легко
распространить и ил совместное распределение двух пере-
менных
Определение. Смешанным моментом порядка (л.А.) слу-
чайных величин \ и ц назовем математическое ожидание
произведения »и/» и и А-й степеней. \/як(1.г\) = /Vffc," • rj')
Определение. Сметанным центральным моментом по-
рядка (п.к) случайных величин \ и п, назовем \ink{Z,,r\) -
= 'V ,(4„.П,.)- где $„ = с - M(i) и Пр= п- М(ц)
По сопоставлению моментов и смешанных моментов
случайных величин можно выяснить характер их связи
В частности, если случайные величины £, и ц независимы, то
<Ч, Д.п) - мд) х .щч) и ияд.л) = мя(4) * йДп)-
Так как первый це1гтральный момент любой случайной
величины равен нулю, то для независимых случайных вели-

Глава П. Корреляционный анализ
283
чин смешанный центральный момент порядка (1,1) должен
быть равен нулю.
Для зависимых случайных величин величина и,, зави-
сит не только от тесноты связи этих переменных, но и от их
дисперсии, так как даже для почти постоянных случайных
величин даже при их сильной связи величина ц,, будет мала.
Поэтому для описания тесноты связи желательно этот сме-
шанный момент «отнормировать».
Определение. Коэффициентом корреляции Ь, и г\ назовем
•**>~£гт?
о($) о(л)
Коэффициент корреляции показывает силу и направле-
ние линейной связи. Несложно доказать', что коэффициент
корреляции находится в пределах от —1 до +1, причем ра-
венства — 1 или +1 он достигает только в том случае, если £,
и т) линейно зависимы, то есть для некоторых констант aw b
выполняется равенство Е, = а + Ь -г\. В этом случае коэффи-
циент корреляции равен +1, если константа b положительна,
и равен — 1, если она отрицательна.
Знак коэффициента корреляции показывает общее на-
правление линейной связи. Он положителен, если увеличе-
ние значения одной переменной в целом соответствует уве-
личению значения другой переменной, и отрицателен, если
увеличение значения одной переменной в целом соответст-
вует уменьшению значения другой переменной. Для неза-
висимых случайных величин он равен нулю, но обратное
неверно — если случайные величины зависимы, но характер
связи не линеен, то коэффициент корреляции может быть
равен нулю.
Модуль2 коэффициента корреляции описывает силу ли-
нейной связи — чем он больше, тем связь сильнее.
Если к случайной величине прибавить константу, то ко-
эффициент корреляции с ней не изменится. Если случайную
1 Это является прямым следствием неравенства Коши—Швар
иа—Буняковского.
3 Точнее, не сам модуль коэффициента корреляции, а квадрат ко-
эффициента корреляции (см. обсуждение в следующих разделах).

284 Часть 2. Анализ параметров
величину умножить на положительную константу, то коэф-
фициент корреляции с ней не изменится, если на отрица-
тельную — то поменяет знак.
Так как коэффициент корреляции анализирует только
линейную составляющую связи, то он делает это хорошо,
выявляя даже достаточно слабые связи. Но, так как откло-
нения от линейной связи он не выявляет, в дополнение к
расчету коэффициента корреляции нужно проводить визу-
альный характер связи переменных.
Для непрерывных переменных это можно делать при по-
мощи построения точечного рисунка совместного распре-
деления, на котором каждая точка — некоторый случай, его
Л'-координата — величина первой переменной, а F-коорди-
ната — величина второй переменной.
Например, если две рассматриваемые случайные величи-
ны независимы (и, следовательно, имеют нулевой коэффи-
циент корреляции) и распределены примерно нормально, то
точечный рисунок совместного распределения имеет при-
мерно следующий вид (рис. 11.1).
о ♦♦
Рис. 11.1. Пример совместного распределения двух
независимых случайных величин
Для случая положительно коррелирующих (с коэффици-
ентом корреляции около +0,7) случайных величин пример
распределения изображен на рис. 11.2.
О Л*
в».
«#
«о
о- 8
<
о о

Глава I J. Коррыяционный анализ
285
о
о
i *
1 V»
! о
о
о
о
«0
♦
о 8
о *
«1
о оо %"* ««о»
о" i>"o
» о
о
о
о «oV
!о*»%»
* 0
♦ «„
>о* *
0
о *
о «
0 °
о ♦
о
о о
о
0
0
о»
0
Рис. 11.2. Пример совместного распределения двух положительно
коррелированных случайных величин
Для случайных величин с коэффициентом корреляции
около —0,7 пример распределения изображен на рис. 11.3.
о о
? *> о
*о оо % ° * «► о
Рис. 11.3. Пример совместного распределения двух отрицательно
коррелированных случайных величин
Нулевой или небольшой коэффициент корреляции мо-
жет быть также в случае сильной, но немонотонной связи
(рис. П.4).
Подобный характер связи бывает в тех случаях, когда
неблагоприятными значениями являются как большие, так
и малые показатели.

286
Часть 2 Ани :из параметров
Го
«о
ч,
о о
оо о
Рис. 11.4. Пример совместного распределения двух зависимых
случайных величин, имеющих нулевой коэффициент корреляции
Частым и интересным отклонением от общей примерно
линейной зависимости является «пятнистость», при которой
исследуемые объекты делятся на несколько подгрупп, в каж-
дой из которых свои распределения переменных и характер
связи между ними. Например, при исследовании взаимосвя-
зи роста и веса испытуемых результат может быть примерно
следующим (рис. 11.5).
t
_ -
--
—
%&$с
<Г"*~
О :
j
Рис. 11.5. Пример совместного распределения роста и веса
Дня хорошо видных «пятна» соответствуют делению на
мужчин и женщин. Если же и качестве испытуемых рассмат-

Глава II. Корреляционный una.in;
287
риваются больные с тромбозами нижних конечностей, то
картина взаимосвязи может быть следующая (рис. 11.6).
О 20 40 60 ВО ЮО >20
Вес «г
Рис. 11.6. Пример совместного распределения роста и веса больных
с тромбозами нижних конечностей
Появившаяся третья группа с малыми показателями
роста и веса — больные с ампутированными нижними ко-
нечностями.
Для того чтобы точечный график хорошо показывал ха-
рактер совместного распределения, нужно, чтобы точки,
показывающие значения разных случаев, не накладывались
друг на друга. Поэтому если хотя бы одна из анализируемых
при помощи расчета коэффициента корреляции переменных
принимает немного разных значений, то точечный график
совместного распределения становится малопоказателен.
В этом случае можно анализировать частоты или средние
в подгруппах (см. следующий раздел).
Как и для всех моментов, основанных на математичес-
ком ожидании, оценка коэффициента корреляции основана
на расчете среднего арифметического и поэтому неробастна.
Поэтому если анализируемые переменные имеют выскаки-
вающие варианты, то проводимый в пакетах статистических
программ расчет достоверности различии коэффициентов
корреляции может быть неверным. Кроме того, если обе
переменные имеют выскакивающие варианты, то высокое

288
Часть 2 Анализ параметров
значение коэффициента корреляции может быть получено
не за счет общей тенденции, характерной для большинства
наблюдений, а за счет связанности аномально больших или
малых значений.
Резюме
Коэффициент корреляции определяет только общую
линейную компоненту связи двух переменных. Для анализа
общего характера связи переменных нужно также анализи-
ровать их совместное распределение.
11.2. Расчет коэффициента корреляции
и анализ взаимосвязи двух
переменных
Чем дальше в лес,
тем больше дров.
Русская народная
пословица
Расчет коэффициента корреляции и проверка связи
на линейность.
В SPSS для расчета коэффициентов корреляции между
двумя или несколькими переменным нужно выполнить ко-
манду «Analyze/Correlate/Bivariate», выбрать нужные пере-
менные и нажать кнопку «ОК». Выбор переменных осущест-
вляется обычным образом — на форме имеется два списка
переменных: правый содержит выбранные переменные
(в начале работы он пуст), а левый — остальные переменные.
Для переноса переменной из одного списка в другой нужно
щелкнуть по имени переменной левой кнопкой мыши и на-
жать кнопку, расположенную между этими списками.
В соответствии с пунктом П.1 коэффициенты корреля-
ции можно рассчитывать для переменных типа scale и ordinal
и нельзя для переменных типа nominal.
Например, при анализе фактических данных больных
пневмониями получим табл. 11.1.

\'\ава II Корреляционный aiKjjW. 289
Таблица 11.1
Таблица коэффициентов корреляции
Соте la lions
^е» о' iwlicnt Pearson Corrc'alion
S.g (2-laited)
N
age ol patient Pearson Con elation
Sig (2-la lied |
N
puteo ol the patent In Pearson Correlation
minuite Sio (2-laitad)
temperature of die patient Pearson Correialion
Slg (2-tailed)
N
systolic blood pressure Pearson Correlation
Slg.(2-talfed)
diastolic blood pressure Pearson Conelation
Sig. (2-tailed)
N
УМЕР Pearson Correlation
Slg (2 -tailed)
N
1.000
ЮЭ2
.153*
,000
1032
.080*
,010
1032
-,06S*
.035
1032
.042
.178
1032
.000
995
1032
,056
.073
103 1
. IS3-
,000
1032
1,000
1032
-.074"
,018
1032
•.304'
,000
1032
.161'
,000
1032
,099'
.001
1032
,112'
.000
1031
pulse of
lite patient
-.oecr
,010
1032
-.074'
018
1032
1,000
1032
.310'
.000
1032
-,2S4-
.000
1032
•.229-
.000
1032
.285'
,000
1031
temperature
-.065'
,035
1032
-.304-
,000
1032
.310"
.000
1032
1.000
1032
-.112-
,000
1032
-.097"
,002
1032
,024
,451
t03l
systolic blood
,042
.178
1032
.161"
.000
1032
.254"
,000
1032
■.11?
,000
1032
1,000
1032
,881'
.000
1032
■.340-
.000
1031
diastolic
blood
,000
.995
1032
.099'
,001
1032
-.229*
,000
1032
-.097*
.002
1032
.881"
.000
1032
1,000
1032
-.399-
.000
1031
-.056
,073
1031
,112'
,000
1031
,285'
,000
1031
.024
,451
1031
-.340-
.000
Ю31
,399-
.000
1031
1,000
1031
" Correlation is significant at theO 01 level (2-tailed).
' Correlation is significant attheO 05 level {2-tailed).
Для того чтобы найти коэффициент корреляции двух пе-
ременных, нужно выбрать строку и столбец с именами этих
переменных и взять ячейку таблицы на их пересечении. По-
лученная таблица симметрична, так как коэффициент кор-
реляции случайных величин £ и г\ совпадает с коэффици-
ентом корреляции случайных величин г\ и ^. На диагонали
таблицы стоят единичные коэффициенты корреляции, так
как коэффициент корреляции с самим собой — положитель-
ный и самый сильный.
В каждой ячейке таблицы стоят три числа. Верхнее — по-
лученная оценка коэффициента корреляции. Для удобства
достоверно отличающиеся от нуля коэффициенты корреля-
ции отмечены звездочками. Второе число — достоверность
отличия коэффициента корреляции от нуля, третье — коли-
чество наблюдений, по которым рассчитывался коэффици-
ент корреляции.
Например, в колонке «sex of patient» в строке «age of
patient» стоит число +0,153, которое говорит о положитель-
ной корреляционной связи. Так как при вводе данных о поле
пациента мужчины кодировались единицами, а женщи-
10 Медицинская с гатиешка

290
Час»:'., .;' Анализ параметров
ны — двойками, то положительная связь говорит о том, что
средний возраст женщин (у которых значение переменной
«Пол» больше) больше, чем мужчин. Второе число в таблице
говорит о том, что коэффициент корреляции достоверно от-
личается от нуля с р < 0,001.
Удобство работы в пакетах статистических программ
с коэффициентом корреляции — в том, что есть возмож-
ность быстро получить большое количество коэффициентов
корреляции между всеми выбранным переменными. Так,
сразу видно, что в качестве факторов риска смерти больно-
го можно рассматривать пожилой возраст, высокую часто-
ту сердечных сокращений и низкое артериальное давление,
тогда как пол и, возможно, температура на вероятность смер-
ти достоверно не влияют. Недостатков этого анализа два: во-
первых, при нелинейности связи коэффициент корреляции
может не показать всю взаимосвязь, а во-вторых, при работе
с дискретными переменными проще интерпретировать не
сам коэффициент корреляции, а средние арифметические
или частоты по подгруппам. Поэтому ограничиваться расче-
том коэффициента корреляции не нужно, следует проводить
дополнительный анализ. Так как корреляционному анализу
можно подвергать дискретные переменные типа ordinal и не-
прерывные типа scale, то возможно три варианта.
Вариант 1. Обе переменные типа ordinal.
Здесь нужно рассчитывать частоты совместного распре-
деления и определять достоверность различия при помощи
теста х2-
Подвариант 1. Обе переменные принимают только два
значения (дихотомические).
Например, при анализе связи смертности и пола было
получено отсутствие достоверных связей с р = 0,073. При
расчете совместного распределения получаем табл. 11.2.
Тест х2дает табл. 11.3.
Таким образом, у мужчин доля умерших — 11,8 % про-
тив 8,3 % у женщин. Результат определения достоверности
различий совпадает: р = 0,073. Так как объем наблюдений
достаточно велик как и целом, так и для каждого варианта
совместного распределения, то полученная при помощи ре-

Глава II. Корреляционный аналп
291
Таблица 11.2
Таблица связи пола пациента и вероятности его смерти
sex of patient * УМЕР Crosstabulation
sex of
patient
Total
male
female
Count
% within sex
of patient
Count
% within sex
of patient
Count
% within sex of
patient
УМЕР
,00
559
88,2 %
364
91,7%
923
89,5 %
1,00
75
11,8 %
33
8,3 %
108
10,5%
Total
634
100,0%
397
100,0%
1031
100,0%
Таблица 11.3
Достоверность связи пола пациента
и вероятности его смерти
Chi-Square Tests
Pearson Chi-
Square
Continuity
Correction
Likelihood Ratio
Fisher's Exact Test
Linear-by-Linear
Association
N of Valid Cases
Value
3,221
2,856
3,311
3,217
1031
df
1
1
1
1
Asymp.
Sig.
(2-
sided)
,073
,091
,069
,073
Exact
Sig.
(2-
sided)
,076
Exact
Sig.
(1-
sided)
,044
шения Фишера точная оценка достоверности различия до-
статочно близка: р = 0,076.
При переходе от двусторонних к односторонним оцен-
кам доверительная вероятность падает (для некоторых ва-
ю*

'/... 'ir \'t,i ill ■ /;i;/>i/wi »i/ii„
риаитоп проверяемых спннспнсскпх niiioiei и hviiiocih
вдвое, juih некоторых примерно u ma paia), по ному по
лученное раиичис и смертности ока п.жастся достоверным
с односторонней доверии- п.пои нсрояшос п.ю р 0.044
Нрсчхлыаи- при работе с переменными ihii.i •■ и или пси
для поиска достоверных свя ieii u клчечтве первом» nun.i луч-
ше всего рассчитан, между мсеми ними ко чффнпист корре
линии. }атсм .гчя lex пар, винорых получилась/юствернаи
свя и,, рассчитать частоты совместною распрелеления и при
помощи точного решения Фишера найти точную достовер-
ностъ свя иг При этом для малых объемом наблюдения не-
которые связи, которые при корреляционном анализе кача-
лись достоверными, могут оказаться ислосгоисрными Если
коэффициент корреляции межлу двум дихотомическими пе-
ременными окачался не отличающимся достоверно от нуля,
то достоверных свячей нет
Подвариант 2. Одна или обе переменные принимают не-
сколько значений.
Например, рассмотрим свя »ь межлу смертью пациента
и количеством лейкоцитов в его крови, причем при кодиров-
ке количества лейкоцитов они были поделены на 4 группы
♦ меньше 4», «от 4 до 9», «от 9 до 25» и «больше 25».
При расчете коэффициента корреляции получаем табл. 11 4
Таблица 11.4
Корреляционная связь исхода
и количества лейкоцитов
Correlations
УМЕР Pearson Correlation
Sig. (2-tailed)
N
white blood cell count Pearson Correlation
Sig. (2-tailed)
N
1,000
1031
,062*
,048
1031
white blood
,062*
,048
1031
1,000
1032
* Correlation is significant at the 0.05 level (2-tailed).

I .j*j li Л".-/"!' isw.iOHi-.Ki, ..•!,.' с ,
293
To сеть связь слабая, по лостовсрная за счет большого
объема наблюдении. Поэтому при поиске прогностических
факторов летального исхода на основании одного коэффи-
циента корреляции кажется, что обращать особое внимание
на количество лейкоцитов не нужно.
При расчете частот летального исхода по подгруппам по-
лучаем табл. 11.5.
Таблица 11.5
Совместное распределение исхода
и количества лейкоцитов
white blood cell count * УМЕР Crosstabulation
1
; white
| blood cell
jcount
j
i
I
Total
<4
4-9
9-25
>25
Count
% within white blood
cell count
Count
% within white blood
cell count
Count
% within white blood
cell count
Count
% within white blood
cell count
Count
% within white blood
cell count
УМЕР
,00
30
52,6 %
302
98,1%
554
93,6%
37
50,0 %
923
89,5 %
1,00
27
47,4 %
6
1,9%
38
6,4 %
37
50,0 %
108
10,5 %
Total
57
100,0%
308
100,0%
592
100,0%
74
100,0%
Ш31
100,0%
Отдаст нам иысокодосюнсрную сняи. (габл I !.(>).
Для того чм)бы выяснить, между какими группами до-
екжерные различия ecu., а между какими пег, можно 1акже
рассчитан, средние значения переменной «Умер» it рлшмх
группах (табл II 7)

294
Часть 2. Анализ параметров
Таблица 11.6
Достоверность связи исхода и количества лейкоцитов
Chi-Square Tests
Pearson Chi-Square
Likelihood Ratio
Linear-by-Linear Association
N of Valid Cases
Value
240,268
168,813
3,915
1031
df
3
3
1
Asymp. Sig.
(2-sided)
,000
,000
,048
Таблица 11.7
Вероятность смерти в зависимости
от количества лейкоцитов
Report
УМЕР
white blood
cell count
<4
4-9
9-25
>25
Total
Mean
,4737
1.948E-02
6.419E-02
,5000
,1048
N
57
308
592
74
1031
Std.
Deviation
,5037
,1384
,2453
,5034
,3064
Std. Error
of Mean
6.672E-02
7.888E-03
1.008E-02
5.852E-02
9.542E-03
В табл. 11.7, как и во многих других, представления чисел
типа 1.948Е-02 означают 1,948 • Ю-02. На основании ее вид-
но, что в первой и четвертой группах достоверных различий
в смертности нет, а все остальные группы различаются до-
стоверно. В группе «от 4 до 9» смертность около 2 %, в группе
«от 9 до 25» смертность около 6,5 %, а в группе очень мало-
го или большого количества лейкоцитов смертность около
50 %. Получили, количество лейкоцитов — сильный про-
гностический фактор летального исхода, который не дал
высокого коэффициента корреляции только из-за нелиней-
ности связей.
Следовательно, при анализе связи между переменными,
имеющими больше 2 значений, в отличие от подварианта I
полагаться на расчет коэффициента корреляции нельзя: мо-

Глава П. Корреляционный аналиг
295
гут быть отбракованы пары переменных, имеющие сильную
нелинейную связь.
Вариант 2. Одна переменная типа ordinal, вторая — типа
scale.
Например, коэффициент корреляции между возрастом
больных и фактом их смерти равен 0,153. Положительная
достоверная корреляция означает, что с возрастом вероят-
ность смерти в целом возрастает.
Более показательной эта связь будет в том случае, если
сравнить средние по подгруппам, что в данном случае дает
табл. 11.8.
Таблица 11.8
Средний возраст умерших и выживших пациентов
Report
age of patient
УМЕР
,00
1,00
Total
Mean
53,83
60,63
54,54
N
923
108
1031
Std. Deviation
18,84
14,98
18,58
Std. Error
of Mean
,62
1,44
,58
В такой форме представления статистической связи ее
проще интерпретировать.
Однако если связь между переменными нелинейная, то
коэффициент корреляции может ее не выявить или выявить
не целиком.
Для получения достоверности различия между распреде-
лением переменной типа scale в подгруппах, задаваемых зна-
чениями переменной типа ordinal, можно воспользоваться
критерием Колмогорова—Смирнова (см. выше) или, в слу-
чае недостаточного объема наблюдений, критерием Ман-
на—Уитни.
Для выявления нелинейности связи можно объединить
близкие значения переменной типа scale в одну группу, как
это описано в пункте 2.2.4, и рассчитать частоты перемен-
ной типа nominal в этих подгруппах. Если переменная типа
nominal дихотомическая (принимает два разных значения),

296
Часть 2 Анализ параметров
то технически проще анализировать не частоты, а средние
значения.
Например, в рассмотренном примере вычислим новую
переменную «ВозрЮ» округлением возраста пациентов до 10
в меньшую сторону (так, значение 10 означает возраст от 10
до 19, 20 — от 20 до 29 и т. д.) и рассчитаем таблицу со сред-
ними значениями переменной «Умер» (табл. 11.9).
Таблица 11.9
Доля умерших в зависимости от возраста
Report
УМЕР
ВОЗРЮ
10,00
20,00
30,00
40,00
50,00
60,00
70,00
80,00
90,00
Total
Mean
,0000
1.299Е-02
3,488Е-02
,1270
,1340
,1024
,1154
,2115
,1538
,1048
N
46
77
86
189
194
166
208
52
13
1031
Std.
Deviation
,0000
,1140
,1846
,3338
,3416
,3041
,3203
,4124
,3755
,3064
Std. Error
of Mean
,0000
1.299E-02
1.990E-02
2.428E-02
2.452E-02
2.360E-02
2,221 E-02
5.719E-02
,1042
9.542E-03
Для того чтобы быстро построить график средних по под-
группам с доверительными границами, можно выполнить
команду «Graphs/Error Bar», выбрать щелчком мыши вариант
«Simple», нажать на кнопку «Define», переменную «ВозрЮ»
выбрать как «Category Axis», а переменную «Умер» — как
«Variable».
Из полученного графика (рис. 11.7) хорошо видно, что
возрастание вероятности летального исхода от возраста не
линейно, а со «скачком» в районе 40 лет.
Складывается впечатление, что внутри групп (до 40 лет)
и (40 лет и старше) корреляционной связи между возрастом
больного и вероятностью его смерти нет.

Глава II. Корреляционный анализ
297
N=46 77 86 189 194 166 208 52 13
10,00 20,00 30,00 40,00 50,00 60,00 70,00 80,00 90,00
Рис. 11.7. Частота летального исхода по возрастным группам
Выясним, так ли это. Установим фильтр «Возраст < 40»
и рассчитаем коэффициент корреляции (табл. 11.10).
Таблица 11.10
Корреляционная связь исхода и возраста
у больных до 40 лет
Correlations
year of the study
УМЕР
Pearson Correlation
Sig. (2-tailed)
N
Pearson Correlation
Sig. (2-tailed)
N
year of
the study
1,000
,
209
,060
,388
209
УМЕР
,060
,388
209
1,000
t
209

298
'Itniiih .} Лни.пп параметров
В этой liompyimc сияя, недостоверна. Установим теперь
фильтр «Возраст >= 40» и еще раз рассчитаем коэффициент
корреляции (табл. 11.11).
Таблица 11.11
Корреляционная связь исхода и возраста
у больных старше 40 лет
Correlations
year of the study
УМЕР
Pearson Correlation
Sig. (2-tailed)
N
Pearson Correlation
Sig. (2-tailed)
N
year of
the study
1,000
»
823
,012
,736
822
УМЕР
,012
,736
822
1,000
1
822
В этой подгруппе коэффициент корреляции также не-
достоверный. Поэтому при анализе связи между смертью и
возрастом пациента можно огрубить возраст до групп «до 40»
и «40 и больше» (табл. 11.12).
Таблица 11.12
Смертность больных
до 40 лет и старше
Report
УМЕР
ВОЗРАСТ 40 лет
или больше
нет
да
Total
Mean
1.914Е-02
,1265
,1048
N
209
822
1031
Std.
Deviation
,1373
,3326
,3064
Std. Error
of Mean
9.500E-03
1.160E-02
9.542E-03
Так как выявленная связь нелинейна, но монотонна, то
переход к «огрубленной» переменной упрощает интерпре-
тацию зависимости, но не повышает существенно величи-
ну корреляционной связи и ценность этой переменной как
фактора прогноза летального исхода.

Глава II Корреляционный анализ
299
Рассмотрим теперь связь между летальным исходом и тем-
пературой больного в момент госпитализации. Коэффици-
ент корреляции не выявляет наличие связи (табл. 11.13).
Таблица 11.13
Корреляционная связь исхода и температуры
при поступлении
Correlations
УМЕР
temperature of
the patient
Pearson Correlation
Sig. (2-tailed)
N
Pearson Correlation
Sig. (2-tailed)
N
УМЕР
1,000
t
1031
,024
,451
1031
temperature
of the patient
,024
,451
1031
1,000
i
1032
Для анализа характера связи огрубим величину темпера-
туры пациента, отбросив дробную часть величины, и анало-
гично рассмотренному выше получим табл. 11.14.
Таблица 11.14
Частота летальных исходов в зависимости
от температуры больного при госпитализации
Report
УМЕР
ТЕМПОКР
36,00
37,00
38,00
39,00
40,00
41,00
Total
Mean
1,0000
,1221
7.143Е-02
4.955Е-02
,2464
,5000
,1048
N
5
172
490
222
138
4
1031
Std. Deviation
,0000
,3283
,2578
,2175
,4325
,5774
,3064
Std. Error
of Mean
,0000
2.504E-02
1.165E-02
1.460E-02
3,681 E-02
,2887
9.542E-03

300
Часть 2. Анализ параметров
В данном случае хорошо видно, что связь сильная, но не-
линейная. Наиболее высока летальность у больных с очень
маленькой (менее 37°) или большой (4 Г и более) температу-
рой, а наименьшая — в группе от 39° до 40°. Для линеаризации
связи рассчитаем новую переменную ABSDEVT — модуль
отклонения температуры от 39°. Для нее имеем табл. 11.15.
Таблица 11.15
Корреляционная связь исхода и модуля отклонения
температуры от 39°
Correlations
УМЕР
ABSDEVT
Pearson Correlation
Sig. (2-tailed)
N
Pearson Correlation
Sig. (2-tailed)
N
УМЕР
1,000
t
1031
,201
,000**
1031
ABSDEVT
,201
,000**
1031
1,000
f
1032
** Correlation is significant at the 0.01 level (2-tailed)
To есть для этой переменной имеем высокодостоверную
положительную корреляционную связь.
В том случае, когда анализируемая переменная типа
ordinal имеет не два, а большее количество разных значе-
ний, то нужно при помощи фильтра выделять часть объема
наблюдений, содержащих только два разных значения пере-
менной типа ordinal, и проводить анализ. При этом если вы-
является, что для каких-то двух или более разных значений
переменной типа ordinal распределение переменной типа
scale достоверно не различаются, то эти значения перемен-
ной типа ordinal нужно объединять.
В качестве примера рассмотрим анализ связи между систо-
лическим артериальным давлением больных и количеством их
лейкоцитов, которое изначально определялось как одно из 4
возможных значений: менее 4, от 4 до 9, от 9 до 25 и более 25.
Расчет коэффициента корреляции дает формально до-
стоверную, но слабую и не очень достоверную связь, которая

I hi ни II Кп/>[ччн1(ш>ннни ,; i
301
была гшин icna го ii.ko i.icu-i .miточно on h.iiioio ko.iii'ic
ctiui n;if) полонии (iaf> i 11 Id)
Тпбпица 1116
Корреляционная свяль количества лейкоцитов
и систолического давления
Correlations
i white blood cell count
; systolic blood
pressure
u
white
blood
cell
count
systolic
blood
pressure
f
Pearsor^Correlation I 1,000] -,068
Sk] (2-tailed)
N
1032
Pearson Correlation i -.068
Sijji (2-tailed.
N
.030*
1032
.030'
1032 j
1,000 |
—-j
"i032~'1
* Correlation is significant at the 0 05 level (2-tailed)
Выделение при помощи фильтров подгрупп позволяет
получить значительно более сильные коэффициенты кор-
реляции Так, если рассчитывать коэффициент корреляции
только для первой и второй группы количества лейкоци-
тов, то коэффициент корреляции с давлением будет рапным
+0.3cS6 и отличаться от нуля с р < 0.001.
Если рассчитать среднее давление у пациентов с разным
количеством лейкоцитов, то получим табл. 11.17.
Однако из того, что в первой и четвертой группах сред-
ние величины систолического давления достоверно не раз-
личаются, еще не следует, что в них функция распределения
систолического артериального давления не отличается до-
стоверно.
Для проверки этой гипотезы выполняем команду
«Analize/Nonparametric Tests/2 Independent Samples», отме-
чаем применение теста Колмогорова—Смирнова, поставив
«галку» в нижней части формы рядом с этой опцией, выби-
раем переменную с систолическим артериальным давлением

302
Часть 2 Ana нп парпметроя
Таблица 11.17
Среднее систолическое давление
в зависимости от количества лейкоцитов
Report
systolic blood pressure
white blood cell count
<4
4-9
9-25
>25
Total
Mean
107,54
128,93
123,52
109,39
123,25
N
57
309
592
74
1032
Std.
Deviation
22,93
17,68
19,48
25,41
20,55
Std. Error
of Mean
3,04
1,01
,80
2,95
,64
в окно «Test Variable List», а переменную с группой количе-
ства лейкоцитов — в поле «Grouping Variable». Далее нужно
нажать на кнопку «Define Groups» и в появившейся форме с
двумя полями задать числовые значения, кодирующие при-
надлежность к сравниваемым группам (в нашем случае это
1 и 4). В результате получаем табл. 11.18.
Таблица 11.18
Определение достоверности различия распределения
по систолическому артериальному давлению в группах
очень малого и очень большого количества лейкоцитов
Test Statistics
Most Extreme Differences
Kolmogorov-Smirnov Z
Asymp. Sig. (2-tailed)
Absolute
Positive
Negative
systolic blood pressure
,088
,052
-,088
,499
,965
a Grouping Variable: white blood cell count
Из табл. П. 18 следует, что в первой и четвертой группах
распределение по давлению достоверно не различается, сле-
довательно, при анализе взаимосвязи переменных эти две
группы можно (и нужно) объединить, для чего создадим

Глава 11 Корреляционный анализ
303
новую переменную «1объед». Во всех остальных вариантах
сравнения различия окажутся достоверными уже просто из-
за достоверности различия средних арифметических, поэто-
му объединить какие-то другие подгруппы нельзя.
Для анализа нелинейности связи новой переменной
с систолическим артериальным давлением огрубим систо-
лическое артериальное давление с шагом в 20 мм рт. ст. и
создадим новую переменную ADS20. Так как переменная с
объединенным значением групповой принадлежности ко-
личества лейкоцитов имеет 3 значения, то проведем 3 по-
парных сравнения, по очереди отбрасывая первую, вторую
и третью группу.
Для первого сравнения поставим фильтр 1объед = 1 и рас-
считаем переменной «1объед» средние по подгруппам значе-
ний переменной ADS20 (табл. 11.19).
Таблица 11.19
Связь систолического артериального давления
и среднего количества лейкоцитов в группах кроме
очень большого и малого количества лейкоцитов
Report
white blood cell count
ADS20
40,00
60,00
80,00
100,00
120,00
140,00
160,00
180,00
200,00
Total
Mean
3,00
3,00
2,89
2,69
2,67
2,59
2.56
2,63
2,50
2,66
N
2
2
27
257
363
193
45
8
4
901
Std. Deviation
,00
,00
,32
,46
,47
,49
.50
,52
.58
,47
Std. Error of Mean
,00
,00
6.16E-02
2.89E-02
2.48E-02
3.56E-02
7.49E-02
,18
.29
1.58E-02
В результате получаем, что при отбрасывании больных
с очень большим или малым количеством лейкоцитов связь
между систолическим артериальным давлением и количеством

304
Част*, 2 Ana на параметров
лейкоцитов монотонная отрицательная — с увеличением
давления количество лейкоцитов в среднем уменьшается.
Если при помощи фильтра отбросить больных со второй
группой лейкоцитов, то получим табл. 11.20.
Таблица 11.20
Связь систолического артериального давления
и среднего количества лейкоцитов в группах,
кроме второй группы количества лейкоцитов
Report
white blood cell count
ADS20
40,00
60,00
80,00
100,00
120,00
140,00
160,00
180,00
200,00
Total
Mean
2,33
1,33
1,98
2,58
2,78
2,78
2,79
2,67
3,00
2,64
N
3
12
49
224
272
127
28
6
2
723
Std. Deviation
1,15
,78
1,01
,82
,63
,63
,63
,82
,00
,77
Std. Error of Mean
,67
,22
,14
5.45E-02
3,81 E-02
5.58E-02
,12
,33
,00
2.87E-02
Здесь связь монотонная положительная. Если отфильт-
ровать третью группу, то получим табл. 11.21.
Таблица 11.21
Связь систолического артериального давления
и среднего количества лейкоцитов в группах,
кроме третьей группы количества лейкоцитов
Report
white blood cell count
ADS20
40,00 i
60,00
80,00
joo,qo_
Mean
1,00
1,00
1,11
1,63
N
1
10
28
127
Std. Deviation
I
,00
,31
,48
Std. Error of Mean
t
,00
5.95E-02
4.30E-02 _

Глава 11. Корреляционный анилт
305
ADS20
120,00
140,00
160,00
180,00
200,00
Total
Mean
1,80
1,85
1,87
1,75
2,00
1,70
N
151
94
23
4
2
440
Std. Deviation
,40
,36
,34
,50
Std. Error of Mean
3.26E-02
3.69E-02
7.18E-02
,25
,00 ,00
,46 2.18E-02
Следовательно, рассматриваемая связь немонотонна по
количеству лейкоцитов и монотонна по артериальному дав-
лению во всех вариантах сравнения, поэтому переменная
с систолическим артериальным давлением не нуждается
в перегруппировке для «линеаризации» связи.
Вариант 3. Обе переменные типа scale.
Например, в приведенной выше таблице коэффициент
корреляции между систолическим и диастолическим арте-
риальным давлением равен 0,881, то есть существует очень
сильная положительная связь. Для анализа отличия связи от
линейной выполним команду «Graphs/Scatter...», выберем
вариант «Simple» и нажмем кнопку «Define». Далее имя од-
ной из рассматриваемых переменных переместим в поле «X
axis», а другое — в поле «Y axis». В качестве примера по оси
Xвозьмем систолическое, а по оси Y— диастолическое дав-
ление.
Часто для анализа совместного распределения удобно,
что в SPSS точки совместного распределения можно выде-
лить разным цветом в зависимости от значения третьей пе-
ременной, например умер ли данный больной. Для этого
выберем имя переменной «УМЕР» в поле «Set Market by»,
нажмем кнопку «OK» и в результате получим рис. 11.9.
Кажущееся количество больных меньше фактического,
так как из-за округления артериального давления при из-
мерении многие пары значений в точности повторяются и
точки «накладываются» друг на друга. Хороню видно, что
характер связи действительно линейный. Большая часть то-
чек, соответствующих летальному исходу, сгруппирована в
нижнем левом углу, что показывает, что низкое давление яв-
ляется сильным неблагоприятным признаком.

306
Часть 2. Анализ параметров
140
1
120
1
100
1
80
0
3
ел i
$60
\ш.
о.
■а
840
п
о
—
220
to
to
0
a
■ ■
"
• •
щ
0
systolic blood
□
D □
d □ а а а
D О О D
CHD D E D D ■ D
о
апепш a a n
Cdcd
• aoa ■
•
i
■ - '
YMEP
° 1,00
о ,00
100 200 300
pressure
Рис. 11.9. Совместное распределение величин систолического
и диастолического давления, выделенного цветом
в зависимости от исхода
В программе Statistica для расчета коэффициента кор-
реляции между переменными нужно выполнить команду
«Statistics/Basic Statistics and Tables/Correlation matrices» и на-
жать кнопку «ОК». Потом нажать кнопку «One variable list» и
выбрать нужные переменные. Так как для этого метода нуж-
но выбрать не одну, а несколько переменных, то добавление
переменных к списку выбранных производится стандартны-
ми для Windows операциями. Щелчок левой кнопкой мыши
на имени переменной выбирает ее, щелчок на имени другой
переменной не добавляет ее в список выбранных перемен-
ных, а меняет выбранную ранее переменную на указанную.
Для добавления переменной нужно щелкнуть на фоне при-
жатой клавиши «Ctrl». Для добавления группы последова-
тельно идущих имен переменных можно щелкнуть в послед-
нюю из них на фоне прижатой клавиши «Shift».

// Корреляционный анализ
307
После определения набора переменных нужно щелк-
нуть по закладке «Quick» и щелкнуть по кнопке «Summary:
Correlation matrix». В результате будет получена таблица с
коэффициентами корреляции. Для того чтобы кроме коэф-
фициентов корреляции выдавались также достоверности от-
личия их от нуля и объем наблюдений, нужно щелкнуть по
закладке «Options» и поменять вариант «Display simple matrix
(highlight p's)» на вариант «Display r, p-levels and N's». При
выборе варианта «Display detailed table and results» выдается
большая подробная таблица с дополнительными данными,
смысл которых будет обсуждаться позже.
Если на закладке «Quick» щелкнуть по кнопке «Scatterplot
matrix for selected variables», то будут получены точечные гра-
фики совместного распределения.
11.3. Сопоставление расчета коэффициента
корреляции с другими методами анализа
взаимосвязи двух переменных
В чем разница между анализом коэффициента корреляции
и другими методами анализа связи двух переменных.
Как было показано в предыдущем разделе, при анализе
взаимосвязи двух переменных можно пользоваться большим
количеством методов анализа, и одни из них дополняют дру-
гие. В этом разделе опишем, в каких случаях они идентичны,
а в каких — нет, и в чем разница.
1. Обе переменные дихотомические.
В этом случае расчет коэффициентов корреляции вы-
явит все достоверно связанные переменные, а достоверность
отличия коэффициента корреляции от нуля дает такой же
результат, как применение теста х2- Однако и в этом случае
желательно рассчитывать таблицу частот совместного рас-
пределения, так как, во-первых, полученную таблицу частот в
подгруппах проще интерпретировать, чем коэффициент кор-
реляции, а во-вторых, критерий %г в решении Фишера даст
точное, а не приближенное значение достоверности связи.

308
Часть 2. Анализ параметров
2. Одна переменная дихотомическая, вторая — типа ordi-
nal с несколькими значениями.
В случае немонотонной связи переменных коэффициент
корреляции может не выявить наличие связи или описать ее
как слишком слабую. Поэтому в любом случае нужно рас-
считывать таблицу частот совместного распределения и при-
менять тест х2.
Если переменная ordinal принимает много разных значе-
ний, то надо использовать вариант анализа № 3.
3. Одна переменная дихотомическая, вторая — типа scale.
Достоверность отличия коэффициента корреляции от
нуля совпадает с достоверностью различий средних у пере-
менной типа scale в подгруппах, задаваемых значениями ди-
хотомической переменной. Однако желательно рассчитать
средние по подгруппам, так как эти результаты проще ин-
терпретировать.
Если коэффициент корреляции не отличается от нуля до-
стоверно, то надо проверить наличие достоверных различий в
распределении переменной типа scale по подгруппам, задава-
емым значениями дихотомической переменной, при помоши
теста Колмогорова—Смирнова или иных непараметрических
методов. Если достоверные различия не обнаружены, то мож-
но считать переменные независимыми и анализ прекратить.
Если коэффициент корреляции или непараметрические
тесты указали на наличие достоверной связи, необходимо
продолжить анализ характера связи на монотонность и линей-
ность. Для этого, если переменная типа scale принимает мно-
го разных значений, надо «округлить» ее, а потом рассчитать
среднее значение от дихотомической переменной по подгруп-
пам, задаваемым значениями переменной с округленными
значениями, и проверить ее на монотонность и линейность.
4. Обе переменные типа ordinal с несколькими значе-
ниями.
Если у переменных значений немного, то в добавление
к коэффициенту корреляции надо рассчитать таблицу ча-
стот совместного распределения и применить тест у}. Если у
одной или обоих переменных достаточно много разных зна-
чений, то можно воспользоваться вариантами № 5 и № 6.

I 1(1ви 11. КоррС'ЛЯЦиоННЬШ W-ПЦТ.
309
5. Одна переменная типа ordinal, другая — типа scale.
Помимо расчета коэффициента корреляции нужно вы-
яснить, насколько взаимосвязь переменных линейна (вне
зависимости от того, достоверно отличается коэффициент
корреляции от нуля или нет).
В качестве первого шага надо рассчитать среднее значение
переменной типа scale в подгруппах, задаваемых значениями
переменной типа ordinal. Если среднее зависит от значения
переменной типа ordinal немонотонно или существенно не-
линейного коэффициент корреляции плохо описывает связь
переменных, в реальности связь значительно сильнее.
Даже в том случае, когда связь между значением перемен-
ной типа ordinal и средним арифметическим от переменной
типа scale примерно линейна, нужно продолжить проверку
линейности зависимости. Для этого нужно вычислить новую
переменную типа scale с округленным значением, а также
для каждого значения переменной типа ordinal — новую ди-
хотомическую переменную: равна переменная типа ordinal
этому значению или нет. Далее аналогично варианту № 3
надо проверить на линейность связи.
6. Обе переменные типа scale.
Помимо расчета коэффициента корреляции нужно по-
строить точечный график совместного распределения и про-
верить его на линейность. В случае нелинейности связи надо
по возможности переопределить переменные так, чтобы
связь была более линейной.
11.4. Расчет доверительных границ
коэффициента корреляции и достоверности
различий коэффициентов корреляции
Как рассчитать доверительные границы к оценке
коэффициента корреляции (в статпакете такие
возможности не представлены).
Пакеты статистических программ определяют достовер-
ность отличия полученной оценки коэффициента корреля-
ции от нуля, но не рассчитывают достоверность отличия его

310
Часть 2. Анилт параметров
от других тестовых значений или достоверность различий двух
полученных оценок коэффициентов корреляции. Поэтому
эту часть анализа придется производить самостоятельно.
Пусть £, и л — нормально распределенная пара числовых
случайных величин, имеющая коэффициент корреляции
0?(£,,Г|), а г— стандартная опенка их коэффициента корре-
ляции, полученная по W наблюдениям. Тогда есть теорема о
том, что для функции Дх) = 0,5 х ln(( I + х)/( I - х)) величина
J(r) распределена нормально с математическим ожидани-
ем, равным/(W), и дисперсией, равной \/(N - 2). Это дает
возможность свести задачу определения достоверности раз-
личий в оценках коэффициента корреляции к уже хорошо
отработанной задаче определения достоверности различий
среднего арифметического от нормально распределенной
случайной величины.
Функция fix) называется преобразование Фишера. Она,
а также обратная к ней функция затабулированы в Excel под
именами ФИШЕР и ФИШЕРОБР.
Пример 1. Пусть полученная по 45 наблюдениям оценка
коэффициента корреляции равна 0,62, тогда как по литера-
турным данным корреляция должна быть равной 0,38. Опре-
делим достоверность различия.
Прежде всего, с помощью Excel берем преобразование
Фишера от обоих коэффициентов корреляции: ФИШЕР
(0,62) » 0,725 и ФИШЕР(0,38) * 0,4. Разность фактического
и ожидаемого значения 0,725 - 0,4 = 0,325. В предположении
об отсутствии достоверных различий эта разность должна быть
распределенанормальноснулевымматематическиможидани-
ем и дисперсией, равной 1/(45 - 2) «0,0232. Среднеквадратич-
ное отклонение разности должно быть равным ]/,— = 0 1525.
/>/43
Следовательно, отношение фактической разности к ожида-
емому среднеквадратичному отклонению t = 0,325/0,1525 *
* 2,13. Так как НОРМСРАСП(2,13) * 0,9834, то вероятность
того, что нормально распределенная случайная величина
примет значение, большее 2,13, равна 1 - 0,9834 = 0,0166.
Следовательно, полученная оценка коэффициента корреля-
ции отличается от ожидаемого значения 0,38 с односторон-

; ■„■«,; // к,<п ■■:■<" ■ и ' '
III'И ЛОВСpil 10 ll.llill! I., j" '-I . IUK II.Hi /1 П.0|Ы> И 111 ДИУСТОрОП
licit доверию п.нои ворочшоо u.h> /> 0.0 42
Пример 2. live п. по iviciiii.Di пи 4^ ii.io.iK> юниям опенка
коэффициент корро мшип рлвнл 0.(0 Опрело шм ее доне
рительные i рлннцы е /> (i.ltS
Aii.iToiirnio приво ichhomn выше <1>И III N'(0.(>2i ~ (I.72S
I/, (I ls?s
сосрсднсквлдрлтчным oik доменном рлинхгм У U\
Гак как НОРЧС TOblNO.O'M - 1.%. m нормально распре
деленная случайная величина с верой i нос п.к» 0.V5 не «икло
няегся от своего математического ожидания больше, чем на
1.% своего среднеквадратичного отклонения (Следователь-
но, с доверительной вероятностью р - 0.05 величина Г(!Й)
лежит в интервале 0.725 t 1.% • 0,1 >2>. то есть от 0.426 до
1.024 Так как ФИНН P(0.42f.) * ().4(iv л ФИПП.Р< 1.024) =
г 0.771. то с р = 0.05 ко мрфиниснг коррс линии в интерва-
ле от 0.403 до 0.771
Получаемые при этом доверите тьные границы для коэф-
фициента корреляции не совсем симметричны, так как сим-
метрично распределен не сам выборочный ко крфнпиент
корреляции, а преобразование Фишера от него А преобра-
зование Фишера хотя и монотонно, но нелинейно
Пример 3. Пусть полученная по 45 наблюдениям опенка
коэффициента корреляции равна 0.б>2. а полученная по дру-
гой группе из 82 наблюдений оценка коэффициента корре-
ляции равна 0.25 Определим достоверность различия
Аналогично примеру № I ФИШЕР(0.62) = 0.725 и
ФИШЕР(0.25) = 0.255 Разность фактического и ожидаемого
значения 0,725 - 0.255 = 0,47
Дисперсия преобразования Фишера от первой оценки
равна 1/43, а дисперсия преобразования Фишера от второй
оценки равна 1/80 Так как они независимы, то дисперсия
их разности должна быть равна сумме дисперсий, или 1/43 +
+ 1/80 = 0,0,69. откуда среднеквадратичное отклонение разно-
сти равно 0,192. В результате имеем / = 0,47/0,192 * 2,44, а так
как НОРМСРАСП(2,44) = 0,992756, то достоверность разли-
чий равна 2 ж (1 - 0,992756) = 0,0145. Следовательно, коэффи-
циенты корреляции различаются достоверно с р = 0,0145.

312
Часть 2. Анализ параметров
К сожалению, аналогично сравнению средних арифмети-
ческих при помощи критерия Стъюдента и дисперсионного
анализа, а также сравнению дисперсий при помощи крите-
рия Фишера—Снедекора приведенные расчеты достоверно-
сти различий оценок коэффициента корреляции верны толь-
ко для нормально распределенных случайных величин. Так
как для фактических данных это заведомо неверно, то дан-
ная схема расчета применима только тогда, когда получен-
ные результаты уже практически не зависят от нормальности
изучаемых распределений, то есть когда объем наблюдений
достаточно велик, чтобы в соответствии с центральной пре-
дельной теоремой оценка коэффициента корреляции была
распределена практически нормально.

Глава 12
ПРОВЕРКА КО